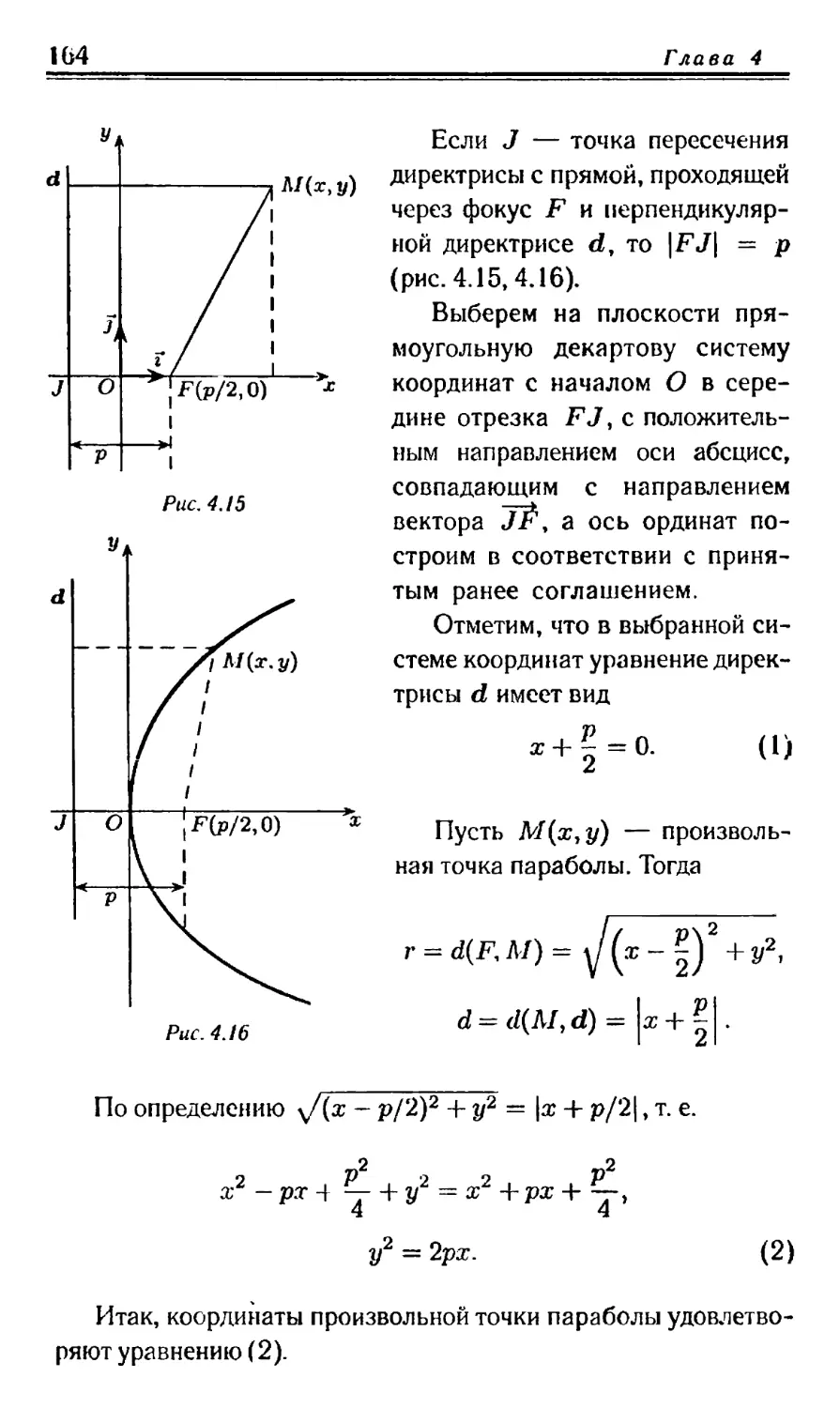
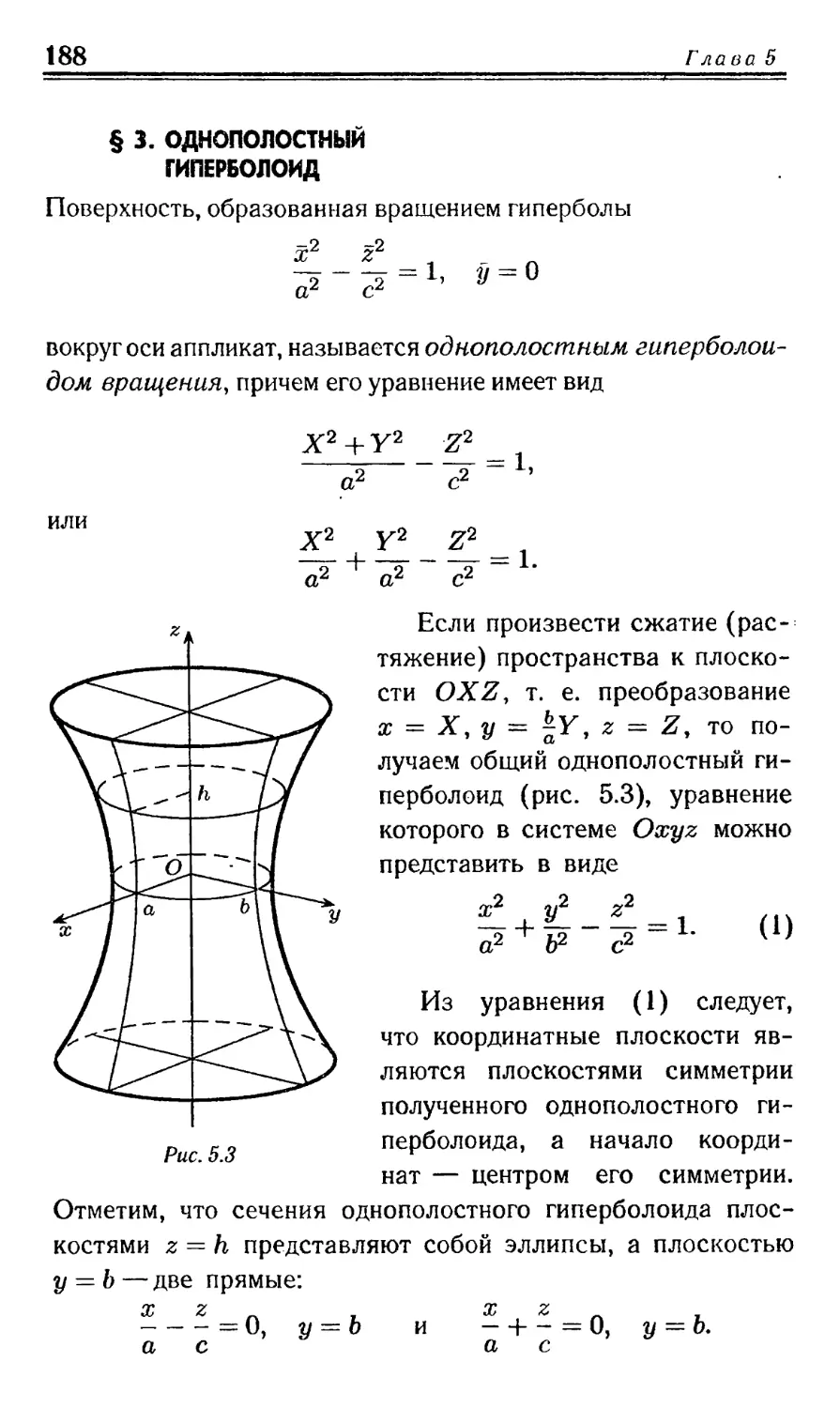
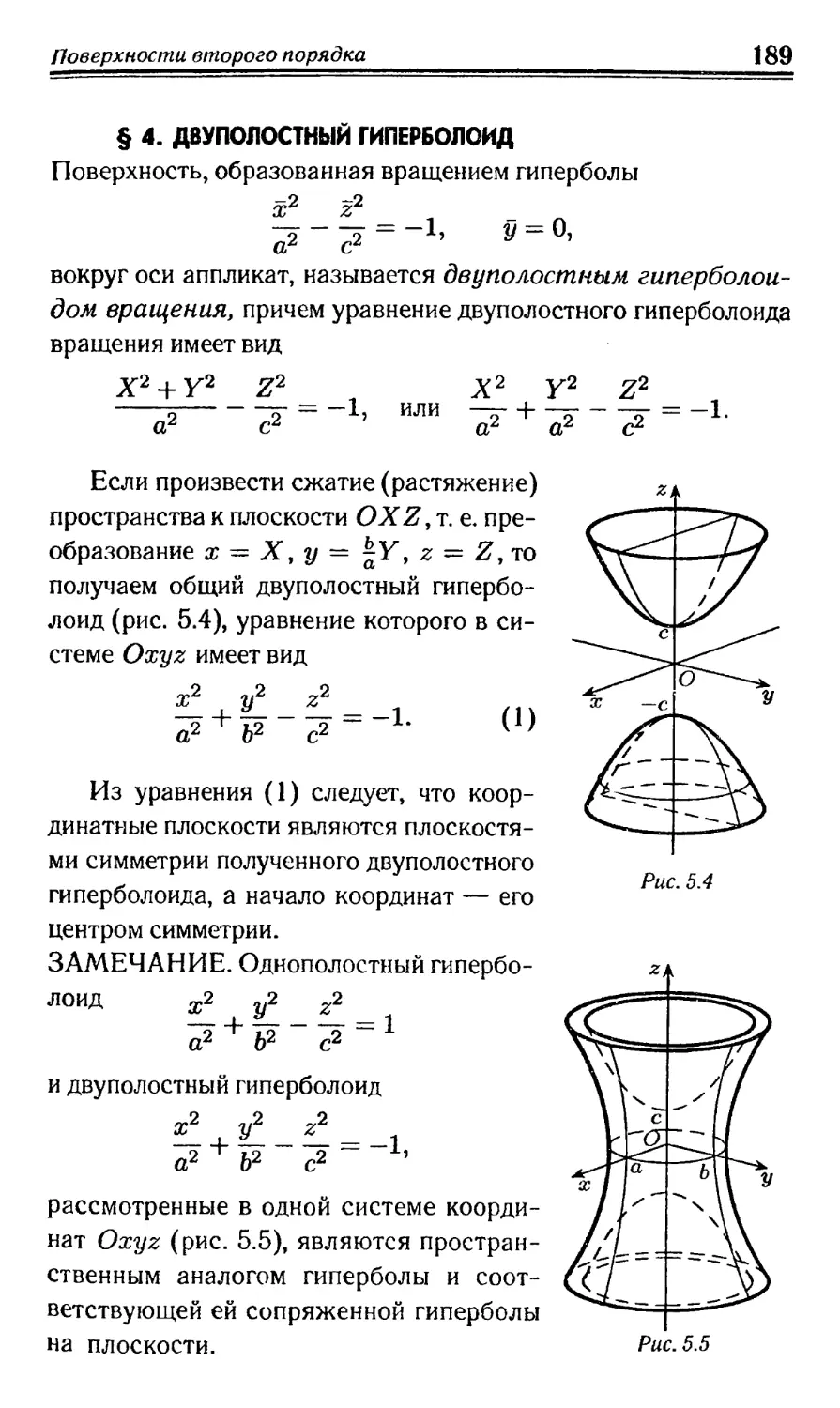
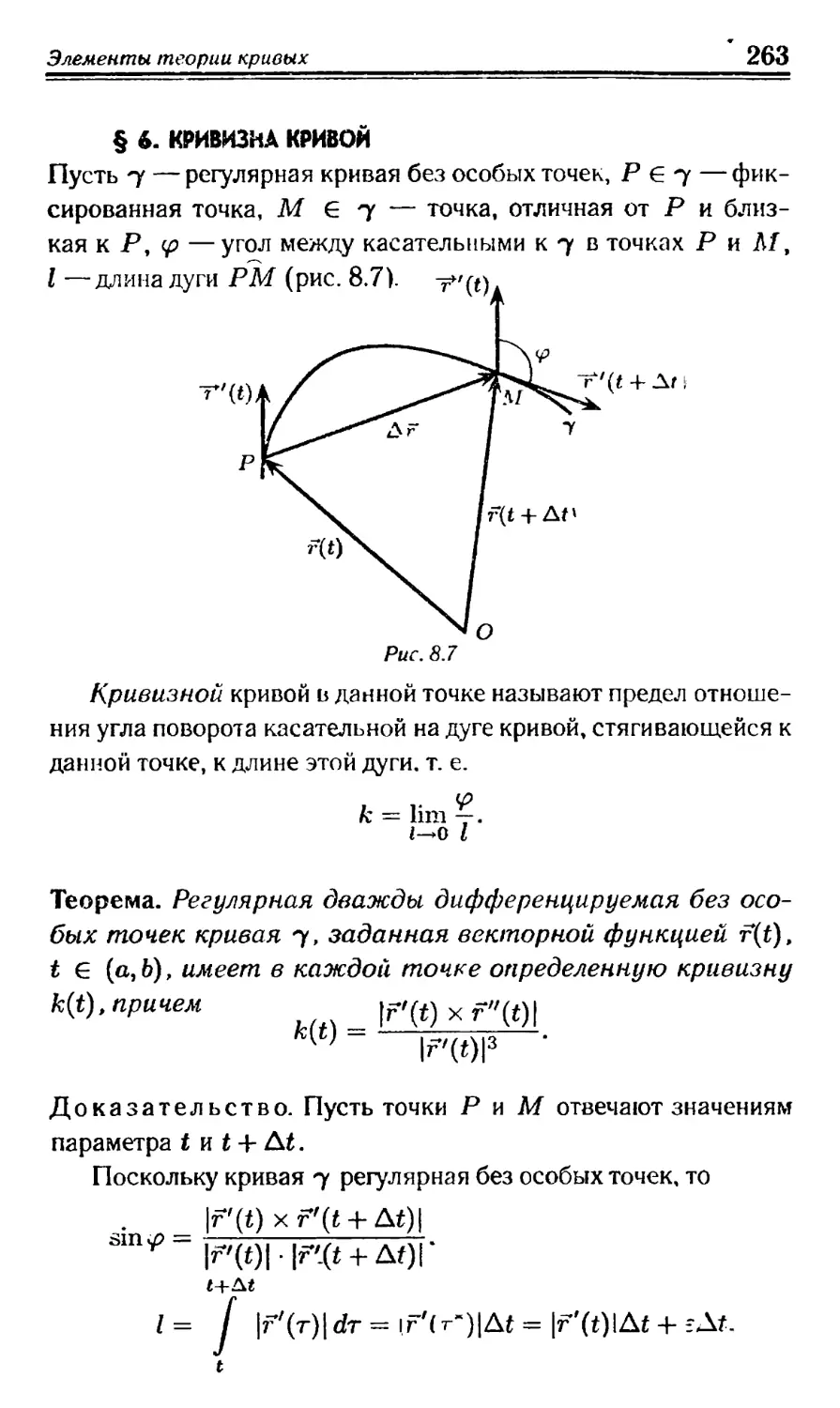
Text
В. Ф. КУЗЮТИН, Η. А. ЗЕНКЕВИЧ, В. В. ЕРЕМЕЕВ
ГЕОМЕТРИЯ
УЧЕБНИК ДЛЯ ВУЗОВ
Под редакцией
Н. А. ЗЕНКЕВИЧА
h
лань
•Санкт-Петербург· 2003 «Москва«Краснодар·
ББК22.151
К 89
Кузютин В· Фм Зенкевич KL Α., Еремеев В· В.
К 89 Геометрия: Учебник для вузов. — СПб.: Издательство
«Лань», 2003. — 416 с, ил. —(Учебники для вузов.
Специальная литература).
iSBN 5-8114-0480-8
Основу учебного пособия составляет материал курса лекций,
читавшегося авторами на протяжении ряда лет в рамках основного курса
«Геометрия» на факультете прикладной математики — процессов
управления Санкт-Петербургского государственного университета.
Учебное пособие состоит из трех частей: аналитическая,
дифференциальная и многомерная геометрия, каждая из которых разбита на
главы и параграфы. В конце каждой главы приводятся задачи с решениями
и набор упражнений для самостоятельной работы.
Рекомендуется в качестве учебного пособия для студентов
математических, экономико-математических и технических специальностей
университетов.
ББК22.151
Рецензенты:
π φ. м. п., проф. Η. А. МАТВЕЕВ, к. φ. м. н., проф. Μ. Φ. РОМАНОВ
Оформление
С Л ШАПИРО, А. Ю.ЛАПШИН
Генеральный директор А. Л. Кноп
Директор издательства О. В. Смирнова
Главный редактор /О. А. Сандулов
Художественный редактор С. J1. Шапиро
Редактор А. В. Андреев
Подготовка иллюстраций JI. В. Буракова
Верстка в Ш^Х А. С. Сигов, М. Ю. Сторожев
Выпускающие О. В. Шилкова, Н. К. Белякова
ЛР№ 065466 от 21.10.97
Гигиенический сертификат
78.01.07.953.Π.00Ι665.03.02 от 18.03.2002, выдан ЦГСЭН в СПб
Охраняется законом РФ
об авторском праве. (с) Издательство «Лань», 2003
Воспроизведение всей книги (?) В Φ Кузютин
или любой ее части Η А Чр u
запрещается без письменного ;?' if ρ КС опло
разрешения издателя. "· В. сремеев, Ζυυό
«Любые попытки нарушения закона @ Издательство «Лань»,
будут преследоваться художественное
в судебном порядке. оформление, 2003
ОГЛАВЛЕНИЕ
Предисловие научного редактора я
Ч асть 1
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Глава I. Системы координат 12
§ 1. Векторы 12
§ 2. Линейные операции над векторами 15
§3. Линеал 18
§ 4. Линейная зависимость и независимость 20
§ 5. Геометрический смысл линейной зависимости и
независимости векторов на плоскости и в трехмерном пространстве . . 22
§ 6. Базис линеала .... 25
§ 7. Размерность линеала ... 29
§ 8. Изоморфизм линеалов . 30
§9. Аффинные пространства . . 33
§ 10. Аффинные системы координат 35
§11. Декартовы прямоугольные системы координат па прямой,
плоскости и в трехмерном пространстве 37
§ 12. Геометрический смысл декартовых координат на прямой 40
§ 13. Геометрический смысл декартовых координат на плоскости . 42
§ 14. Геометрический смысл декартовых координат в трехмерном
пространстве 45
§ 15. Деление вектора в заданном отношении 46
§ 16. Полярно система координат на плоскости 48
§ 17. Обобщенные полярнче координаты на плоскости 50
§ ! 8. Цилиндрическче координаты в трехмерном пространстве . 51
§ 19. Сферические координаты в трехмерном пространстве ... 52
§ 20. Скалярное произведение векторов 54
§ 21. Евклидовы, нормированные и метрические пространства . . 58
§ 22. Векторное произведение векторов 61
§23. Смешанное произведение трех векторов 68
§ ?4. Двойное векторное произведение 72
Глава 2. Преобразование координат 80
§ 1. Преобразование координат на декартовой оси 80
§2. Преобразование декартовых прямоугольных координат на
плоскости, ... 80
§ 3. Преобразование декартовых прямоугольных координат в
трехмерном пространстве 85
§ 4 Преобразование координат в трехмерном пространстве с
помощью углов Эйлера . 88
§ 5. Преобразование координат в многомерном линеале 91
§ 6. Преобразование аффинных координат 95
Глава 3. Линии и поверхности первого порядка 102
§ I. Уравнения линий и поверхностей 102
§ 2. Алгебраические линии и поверхности 109
§ 3, Векторное и общее уравнение плоскости в трехмерном
пространстве (прямой на плоскости) 112
§4. Уравнение «в отрезках» плоскости в трехмерном
пространстве (прямой на плоскости) 115
§5. Параметрические уравнения плоскости . ... 116
§ 6. Уравнение с угловым коэффициентом прямой на плоскости . 117
§ 7. Взаимное расположение плоскостей в пространстве (прямых
на плоскости) 119
§ 8. Геометрический смысл неравенств первой степени 122
§ 9. Нормированное уравнение плоскости (прямой на плоскости) 124
§ 10. Пучки плоскостей (прямых на плоскости) . , 127
§ 11. Связки плоскостей 130
§ 12. Гиперплоскость 130
§ 13. Векторное параметрическое, параметрические и общие
векторные уравнения прямой в пространстве 131
§ 1 \. Угол между прямыми и их взаимное расположение в
трехмерном пространстве 134
§ 15. Угол между прямой и плоскостью. Взаимное расположение
прямых и плоскостей в трехмерном пространстве 135
§ 16. Связка прямых в трехмерном пространстве . 136
Глава 4. Линии второго порядка 144
§ 1. Эллипс 144
/./. Каноническое уравнение (144) 1.2. Исследование
формы (146) 1.3. Параметрические уравнения (148)
IА. Эксцентриситет^^) 1.5. Фокальные радиусы (149)
1.6. Директрисы (149) /,7. Уравнение в полярных
координатах (151) 1.8. Построение эллипса (151)
§2. Гипербола 152
2,1. Каноническое уравнение (152) 2.2. Исследование
формы (155) 2.3. Параметрические уравнения (158)
2.4. Эксцентриситет (159) 2.5. Фокальные радиусы (159)
2.6. Директрисы (160) 21. Уравнение гиперболы в
полярных координатах (161) 2.8. Построение гиперболы по
точкам (162)
5
§3. Парабола ... . . 163
«?.Л Каноническое уравнение (lb3) 3.2. Исследование
формы (165) 3.3. Уравнение парабош в полярных
координатах (167) 3.4. Построение парабоъы по точ-
кам {167)
§ 4. Преобразование коэффициентов общего уравнения линии
второго порядка при пара/иельном переносе системы ко
ординат . . 168
§ 5. Упрощение общего уравнения линии второго порядка при
параллельном переносе системы координат 169
§ 6, Преобразование коэффициентов общего уравнения линии
второго порядка при повороте системы координа г 170
§ 7. Упрощение общего уравнения линии второго порядка при
повороте системы координат 172
§8. Приведение к каноническому виду общего уравнения линии
второго порядка 173
Глава 5. Поверхности второго порядка . 185
§ I. Урав1 еиия поверхностей вращения .185
§ 2. Эллипсоид . . . - 186
§ 3. Одноиолостный гиперболоид .... 188
§ 4. Двуполостный гиперболоид 189
§ 5. Эллиптический параболоид . . 190
§6. Гиперболический параболоид ... 190
§ 7. Цилиндрические поверхности 192
§8. Цилиндры второго порядка . . 193
§ 9. Конические поверхности 193
§ 10. Конические поверхности второго порядка 194
§ 11. Прямолинейные образующие о злополостного гиперболоида 196
§ 12. Прямолинейные образующие гиперболического параболоида 198
§ 13. Преобразование коэффициентов общего уравнения
поверхности второго порядка при параллельном переносе системы
координат 198
§ 14. Упрощение общего уравнения поверхности второго порядка
при параллельном переносе системы координат 200
§ 15, Преобразование коэффициентов общего уравнения
поверхности второго порядка при повороте системы координат 201
§ 16. Упрощение общего уравнения поверхности второго порядка
при повороте системы координат 202
§ 17. Приведение к каноническому виду общего уравнения
поверхности вт >ροι о порядка .... . . 201
§ 18. Классификация пииерхнос гей второго поря ;ка . 208
§ 19. Гиперповерхности второго порядка . . . . ... 211
Глава 6. Исследование линий и поверхностей второго порядка,
заданных уравнениями общего вида, с помощью
инвариантов ... 214
§ 1. Преобразование квадратичной формы к новым переменным 214
§ 2. Инварианты общею уравнения линии второго порядка
относительно преобразования координат ... ...... 215
§ 3. Инварианты общего уравнения поверхности второго порядка
относительно преобразования координат 220
§4. Исследование общего уравнения линии второго порядка с
помощью инвариантов .... 227
§ 5. Исследование обшего уравнения поверхности второго
порядка с помощью инвариантов ... ... 229
\_i Q р Τ h /
ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
Глава 7. Элементы векторного анализа . ... 238
§ 1. Векторная функция. Предел. Непрерывность ... 238
§ 2. Производная вектооной функции. Формула Тейлора 240
§3 Неопределенный и определенный интеграл от векторной
функиии ... 247
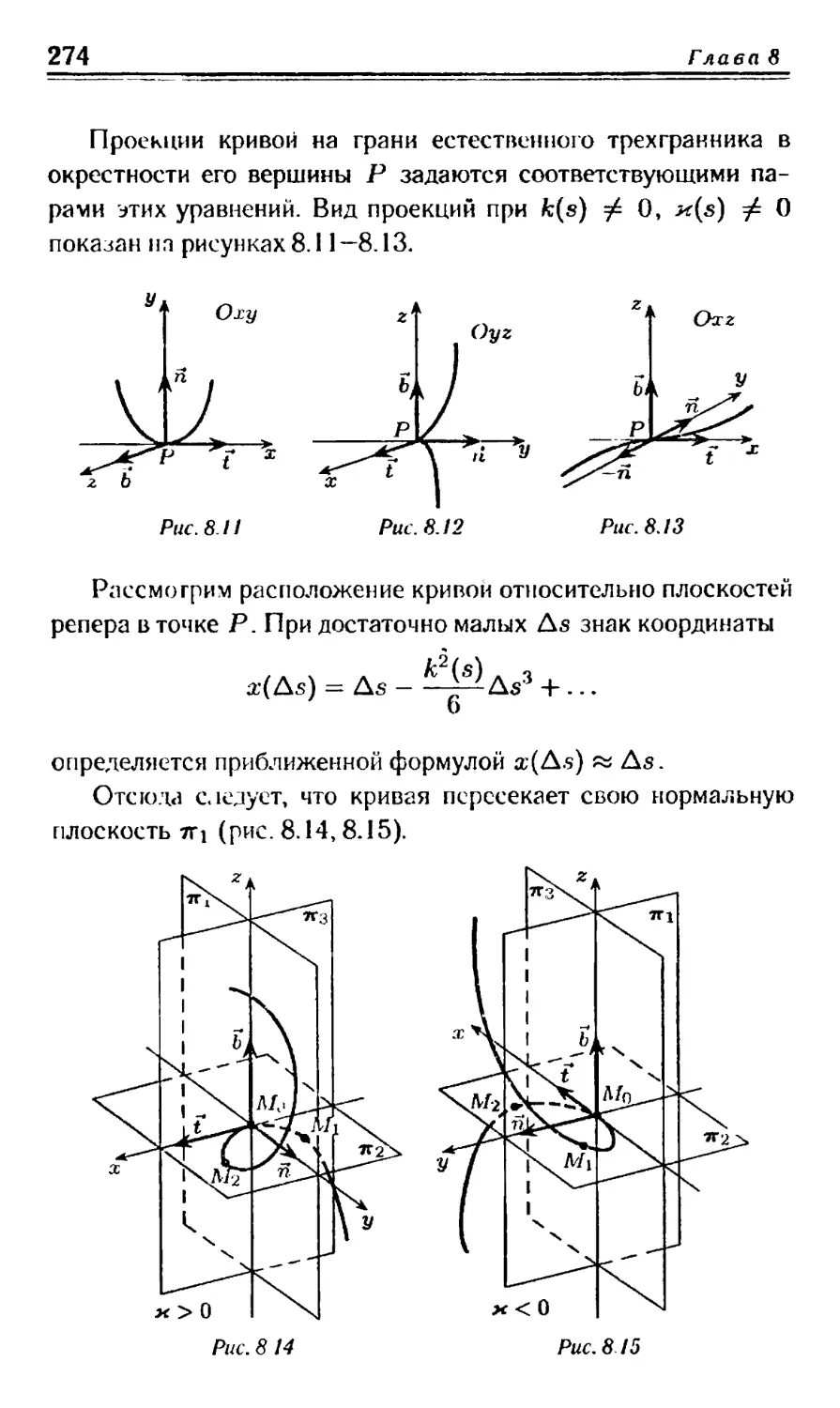
Глава 8. Элементы теории кривых . . 251
§ 1. Понятие ьривой ... 251
§ 2. Касательная к кривой. Нормальная плоскость кривой . . 253
§ 3. Соприкасающаяся плоскость кривой. Спрямляющая
плоскость кривой. Нормаль. Главная нормаль Бинормаль . 255
§4. Длина дуги кривой ... 258
§ 5. Ее гестг ли ι я параметризация ... 260
§ 6. Криви гна кривой 263
§7. Кручение кривой . 265
§ 8. Формулы Френе ... 269
§ 9. Взаимное расположение кривой и граней естественного трех-
граниика . . . ... 272
§ 10. Натуральные уравнения кривой . . 276
§11. Неявное уравнение кривой на плоскости 278
§ 12. Огибающая однопараметрического семейства плоских
кривых 279
§ 13. Эволюта плоской кривой . 281
§ 14. Эвольвента плоской кривой . ... 282
7
Глава 9. Элементы теории поверхностей 293
§ I. Понятие поверхности ... 293
§ 2. Касательная прямая к поверхности. Касательная плоскость
и нормаль к поверхности . 300
§ 3. Первая квадратичная форма . ... 306
§4. Длина дуги кривой на поверхности 306
§ 5. Угол между кривыми на поверхности 307
§ 6. Площадь поверхности , . 308
§ 7. Вторая квадратичная форма поверхности 310
§ 8. Кривизна кривой, лежащей на поверхности .311
§9. Главные кривизны . . . 313
§ 10. Поверхности вращения 315
§ 11. Линейчатые поверхности . . . 316
Ч а ст ьЗ
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
Г л а в а 10. Геометрическая структура систем линейных уравнений 324
§ 1. Векторное пространство Rn 324
§2. Системы линейных уравнений . . . 329
§ 3. Многомерные плоскости 332
§ 4. Взаимное расположение многомерных плоскостей . 336
§ 5. Уравнения геометрических объектов в евклидовом
пространстве 340
§ 6. Топология евклидова пространства 312
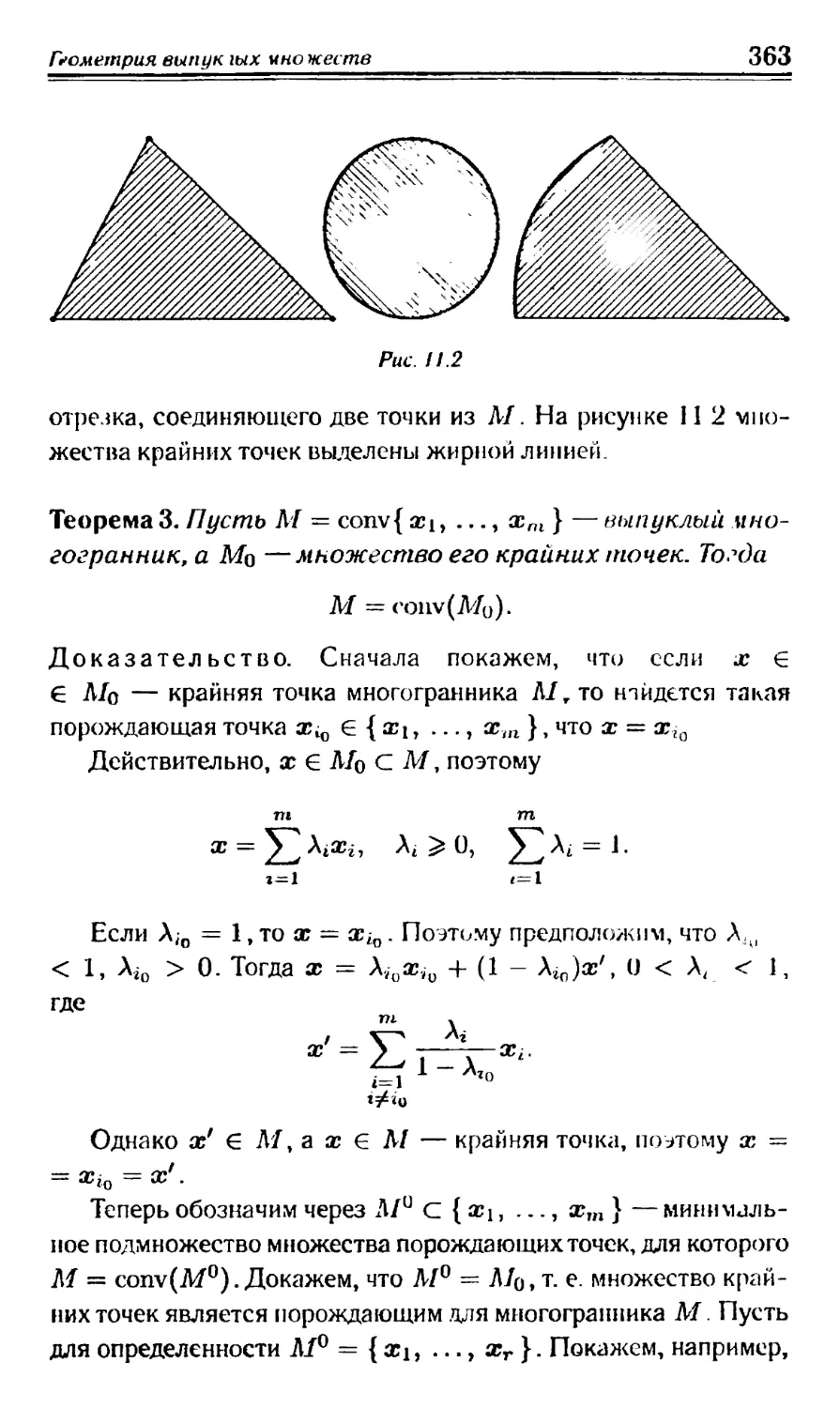
Глава П. Геометрия выпуклых множеств . ... 358
§ 1. Выпуклые множества 358
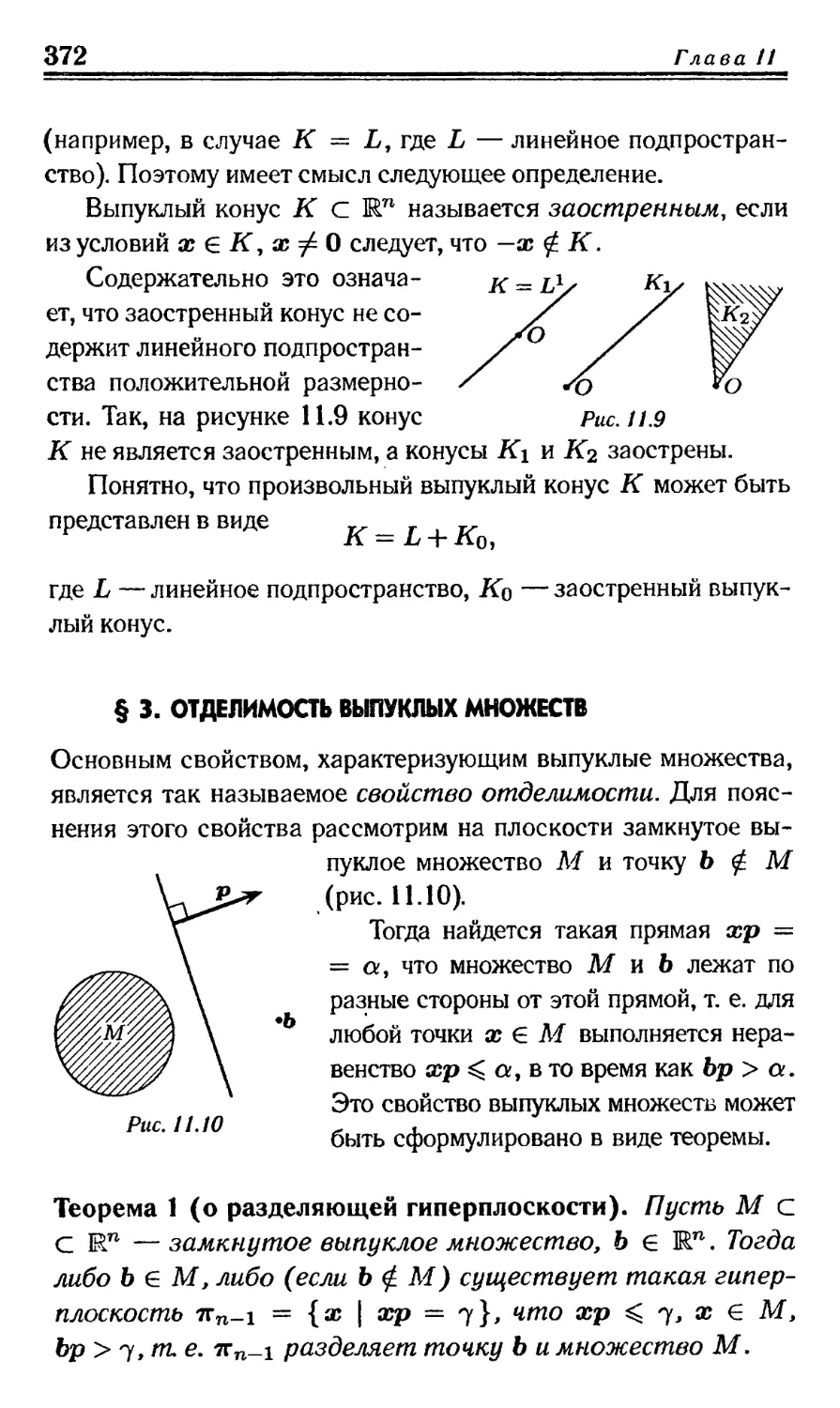
§ 2. Выпуклые конусы . 366
§3. Отделимость выпуклых множеств . 372
§ 4. Конечные конусы 377
§ 5. Выпуклые цилиндры . 384
Глава 12, Геометрическая структура систем линейных неравенств 389
§ 1. Выпуклое многогранное множество ... . 389
§ 2. Грани многогранного множества . 393
§ 3. Параметрическое уравнение многогранного множества . 398
§4. Геометрия задачи линейного программирования 403
4.J. Формулировка задачи линейного
программирования (403) 4,2. Геометрическая интерпретация решения
а////(405)
Предметный указатель . 411
Литература 416
ПРЕДИСЛОВИЕ НАУЧНОГО РЕДАКТОРА
Современная геометрия занимает особое место в
математике благодаря наглядности многих образов, с которыми она имеет
дело, В то же время эта наглядность сегодня успешно
подвергается формализации и далеко идущему абстрагированию, что
обусловило успехи, достигнутые современной геометрией и ее
приложениями.
Такое двойственное место геометрической науки в
современной математике предопределило ее особую роль, поскольку
зачастую именно в геометрических идеях и образах заложены
выдающиеся идеи основных математических открытий. Многие
геометрические понятия рождались из конкретных задач меха-
пики, физики, а также из необходимости решения
математических задач в экономике.
С другой стороны, если посмотреть на предметы, которые
в той или иной степени изучаются в связи с геометрией на
разных стадиях обучения, то можно увидеть такие названия:
«Планиметрия», «Стереометрия», «Аналитическая геометрия»,
<ч Проективная геометрия», «Дифференциальная геометрия»,
«Неевклидова геометрия» и т. п., не говоря уже о названиях,
связанных с топологией. Проблема заключается не в изучении
различных разделов геометрической науки, а зачастую в
различных аксиоматических подходах в таких разделах, что вызывает
значительные затруднения у обучающихся·
Эта проблема давно известна в кругу педагогов,
занимающихся обучением геометрии. Начиная примерно с «Эрлангенской
программы» Ф. Клейна, стало ясно, что в основе многих
геометрических теорий скрывается одна-единственная
дисциплина — линейная алгебра. Такое понимание послужило толчком
к включению во многие учебные планы дисциплины «Линейная
алгебра и геометрия» (это касается специальности «Прикладная
9
математика», а также многих технических и экономических
специальностей). Несмотря на очевидную рациональность
указанного подхода, здесь имеется другой недостаток, когда
собственно геометрические идеи и структуры ставятся в зависимость от
идеи и структуры изложения курса линейной алгебры или
математического анализа. Как следствие, геометрические методы
имеют вспомогательный (зачастую иллюстративный) характер.
Главная цель настоящей книги — рассказать на доступном
и достаточно наглядном языке о некоторых классических и
современных достижениях геометрии, связанных как с
внутренними математическими задачами, так и с приложениями, и
подготовить читателя к освоению других разделов математической
программы-
Авторы при написании данного учебного курса «Геометрия»
придерживались традиций Ленинградской — Петербургской
математических школ по обучению прикладной математике,
когда изучение алгебры, геометрии и математического анализа
ведется в рамках различных учебных курсов, при этом гармонично
дополняя и развивая друг друга.
Учебное пособие написано на основе курса лекций по
«Геометрии», подготовленного, успешно прочитанного и читаемого
авторами студентам I курса факультета прикладной
математики — процессов управления Санкт-Петербургского
государственного университета на протяжении 30 лет. Следует отметить,
что на факультете с тридцатилетней историей впервые курс
«Геометрии» был прочитан профессором Л. А. Петросяиом. Тогда в
рамках названного курса помимо традиционно геометрических
разделов были прочитаны геометрические основы выпуклого
анализа и тем самым сложилась настоящая структура курса,
отличительной чертой которого является его прикладная
направленность. Это предопределяется в первую очередь
требованиями учебного плана к конструктивности и аппаратности
излагаемого материала, а также специализацией студентов на ранних
стадиях обучения в областях механики, процессов управления
и методов прикладной математики.
Дальнейший положительный опыт чтения авторами
различных разделов курса «Геометрия» в рамках курсов
«Математика», «Основы математического анализа и линейной алгебры»,
«Математика в экономике ν для технических, экономических
10
■и экономико-математических специальностей университетов
Санкт-Петербурга и дал моральные основания авторам
опубликовать данное учебное пособие для широкого круга студентов.
Предлагаемое пособие состоит из трех частей и в основ-
дам покрывает традиционный университетский курс геометрии:
аналитическая, дифференциальная и многомерная геометрии·
В первой части на основе аксиоматического подхода
излагаются векторная алгебра, различные системы и
преобразования координат в векторных и точечных пространствах реальных
размерностей. Изучаются алгебраические линии и поверхности
-первого и второго порядков.
Во второй части исследованы проблемы анализа векторных
функций, заданных параметрическими уравнениями,
рассмотрены основные положения теории кривых и поверхностей.
Третья часть логически завершает классические темы
аналитической и дифференциальной геометрии, распространяя
основные понятия на многомерный случай· Систематически изложена
геометрия выпуклых множеств, специально исследованы
линейные геометрические объекты в многомерном пространстве.
В заключение приведен список литературы, который ни в
коем случае не претендует на полноту и отражает лишь симпатии
авторов.
Пособие может быть использовано как геометрическая
основа для математических курсов механики, математической
экономики, теории оптимизации, исследования операций,
дифференциальных уравнений, оптимального управления. Материалы
отдельных глав и разделов могут быть использованы в курсах
«Высшей математики».
Мы рекомендуем данное учебное пособие для студентов
математических, экономико-математических и технических
специальностей университетов, хотя первые главы вполне доступны
и школьникам старших классов.
Авторы пособия выражают искреннюю признательность
рецензентам за ценные замечания и пожелания, которые
улучшили текст рукописи. Авторы также будут признательны всем
читателям, которые выскажут свое мнение о книге.
Н.А.ЗЕНКЕВИЧ
Часть первая
АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ
I Предмет аналитической геометрии заключается в исследовании
l геометрических объектов с помощью аналитических методов,
в основе которых лежит так называемый метод координат.
Сущность этого метода заключается в том, что различным
геометрическим объектам сопоставляются некоторым
стандартным способом уравнения или системы уравнений, а изучение
свойств геометрических объектов сводится к изучению свойспв
уравнений.
Создание координатного метооа бы го подготовлено еще
трудами древнегреческих математиков: Хпомония (III век
до н. э.)> Гиппарха (160-125 гг. до н. э., уроженец г. Никеи),
Птоломея (II век, правитель Египта, уроженец г. Пелузия).
Систематическое развитие координатный метод получил в
работах французского математика Пьера Ферма (1601-1650)
и особенно в работе «Dicours de la methode pour bien conduire sa
raison» (1637) французского математика Рене Декарта (1596-
1650). Декарт начал применять знания по алгебре к решению
геометрических задач на основе принципа координат. Условно
1637 г. считают годом рождения аналитической геометрии.
Введение системы координат было толчком к открытию
дифференциального исчисления.
Систематическое изучение пространственных шний и
поверхностей на основе координатного метода было осуществлено
впервые Л. Эйлером (1707—1783).
Метод координат является мощным аппаратом,
позволяющим привлекать дгя исследования геометрических объектов
методы математического анализа и алгебры. Аналитическая
геометрия объединила геометрию с алгеброй и анализом, чпю
плодотворно сказалось на развитии названных разделов математики.
Глава 1
СИСТЕМЫ КООРДИНАТ
§ 1. ВЕКТОРЫ
При построении математической (в том числе и геометрической)
теории необходимо постулировать основные понятия и
аксиомы, определяющие суть данной теории. В евклидовой геометрии
такими основными понятиями являются точка, прямая,
плоскость. Постулируются и необходимые аксиомы, например,
широко известная аксиома о параллельности прямых. Вообще в
традиционной геометрии Евклида 15 аксиом.
Для аналитической геометрии одно из основных понятий —
это понятие вектора. Именно использование векторов позволяет
перейти от чисто геометрического к алгебраическому
исследованию свойств геометрических объектов.
Обычно под вектором (геометрическим вектором)
понимается направленный отрезок. Отрезок — это часть прямой, значит,
вектор в определенном смысле вторичное понятие по
отношению к прямой и точке· Придерживаясь аналитического подхода
к анализу геометрических объектов, мы склоняемся к тому, что
вектор наряду с точкой является основным понятием
аналитической геометрии. На этой основе мы будем строить
аксиоматику евклидовой геометрии. Однако сначала приведем
геометрическую концепцию векторов и операций над ними, которые по
необходимости будем использовать в дальнейшем.
Вектором (геометрическим вектором) называют
отрезок, для которого указано, какая из его граничных точек
является начальной и какая — конечной.
Системы координат
13
Начальную точку называют началом, или точкой
приложения вектора, а конечную — концом вектора.
Под направлением вектора понимают направление от его
начала к концу Направление отмечается стрелкой, помещаемой
у конца вектора (рис. 1.1).
Длина, или модуль вектора, есть
длина соответствующего отрезка,
определяющего данный вектор.
Обычно вектор обозначают двумя бук- Рис {f
вами, над которыми ставится стрелка,
обращенная острием вправо, причем первая буква обозначает
начало вектора, а вторая — конец· Так, например, вектор с
началом А и концом В обозначают символом . Иногда
вектор обозначают одной буквой со стрелкой, помещенной сверху
этой буквы, например, а (рис. 1.1). Длину вектора обозначают
соответственно как \АВ\, \а\ и т. д.
Отметим, что вектор может быть определен полностью одним
из следующих способов: 1) заданием начала и конца; 2) заданием
начала (конца) вектора, его направления и длины.
Вектор называют нулевым, если его начало и конец
совпадают. Нулевой вектор обозначают обычно символом 0. Нулевой
вектор не имеет определенного направления (направление
произвольно), и его длина равна нулю: |б| =0.
Вектор называют единичным, если его
длина равна единице в принятой системе из- | 1
мерения(рис. 1.2).
Векторы называются компланарными, -
если они расположены в одной плоскости ^
или в параллельных плоскостях. Рис-,2
Векторы коллинеарны, если они лежат либо на одной
прямой, либо на параллельных прямых (рис. 1.3). Нулевой вектор
считают коллинеарным любому вектору.
Коллинеарные векторы одинаково направлены (сонаправ-
лены), если у векторов, имеющих общее начало и длины,
равные длинам исходных векторов, и расположенных на прямой,
параллельной прямым, на которых находятся исходные векторы,
14
Глава I
концы расположены по одну сторону от общего начала
(векторы а, сиб, рис. 1.3). В противном случае коллинеарные
векторы противоположно направлены (например, α и d, рис. 1.3).
Направления неколлинеарных векторов не подлежат сравнению.
Ортом произвольного ненулевого
вектора называют единичный вектор,
коллинеарный исходному и имеющий то
же направление, что и исходный вектор.
Векторы равны, если они коллине-
арны, имеют одинаковую длину и
одинаковое направление (векторы α и с, рис. 1.3). Для равных
векторов а и с используют обозначение α = с.
Векторы противоположны, если они коллинеарны, имеют
одинаковую длину, но направления их противоположны (век-
торы b и d, рис. 1.3). Для противоположных векторов bud
используют обозначение 5 = — d.
Если два вектора равны, то каждый из них может быть
получен параллельным переносом другого.
Ясно, что если α = 6, то и 5 = а (симметричность). Кроме
того, если а = 6, b = с, то а = с (транзитивность).
Заметим, что равенство векторов определено с точностью до
их положения в пространстве. Иными словами, мы не различаем
двух равных векторов, имеющих разные точки приложения.
Под углом между векторами понимают наименьший угол
между ними, когда векторы приведены к общему началу.
В аналитической геометрии обычно рассматриваются
свободные векторы, т. е. векторы, точки приложения которых
произвольны. Приведенное понятие равенства векторов определено для
системы свободных векторов Свободные векторы всегда можно
перенести так, чтобы их точки приложения совпали. При этом
направления векторов и их длины сохраняются. Этим свойством
пользуются при определении линейных операций над векторами.
В физике и механике, кроме свободных векторов,
рассматривают скользящие и связанные векторы. Скользящие
векторы в обязательном порядке расположены на одной прямой, а
связанные векторы имеют общее начало.
Системы координат
15
§ 2. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
Говорят, что векторы следуют друг за другом, если начало
каждого из них, начиная со второго, совпадаете концом
предыдущего вектора (рис. 1.4).
Суммой векторов, следующих друг за другом,
называется вектор, начало которого совпадает с началом первого вектора,
а конец— с концом последнего вектора (рис. 1.5):
Суммой произвольно расположенных векторов
называется сумма векторов, следующих друг за другом, построенных,
начиная с некоторой точки О, и равных соответственно данным
векторам (рис. 1.6).
•Ч Ю: ίάϊ
Рис, 1.4 Рис. 1.5 Рис. L6
Из данного определения непосредственно следуют
известные правила треугольника или параллелограмма для сложения
неколли неарных векторов.
Подчеркнем, что сумма произвольно расположенных
векторов не зависит от того, как выбрана начальная точка О при
построении векторов, следующих друг за другом.
Свойства суммы векторов:
1°. a + b = b + a (коммутативность);
2°. (а + 5) + с — а + (Ь+ с) (ассоциативность);
3°. а + 0 = а (особая роль нулевого вектора);
4°. а + (—а) = б (свойство противоположного вектора).
Указанные свойства непосредственно вытекают из
определения суммы векторов.
Разностью векторов α и b называют такой вектор άΛ
который в сумме с вектором В дает вектор а, т. е. d+b = а (р^с. 1.7).
Разность векторов d обозначается d = a — b.
16
Глава I
Ясно, что а — Ъ = а + (—Ь).
Последнее равенство позволяет
построение разности двух векторов α — В
заменить построением суммы вектора а
и вектора —6, противоположного
вектору 5. Указанное правило удобно
применять при построении алгебраической
суммы нескольких векторов.
Произведением, вектора а на вещественное число а
называется вектор ρ = cm, определяемый следующим образом:
вектор ρ коллинеарен вектору а, имеет направление вектора а,
если а > О, и направление, противоположное вектору а,
если а < 0, при этом |р| = \а\ · \а\.
Ясно, что если а = 0 или а = 0, то вектор ρ = аа = 0.
Заметим также, что если е — это орт вектора а ф 0, то а = |а|ё\
откуда е = щЗ.
Теорема. Если ненулевые векторы а и Ь коллинеарны, то
любой из них представим через другой, т. е. найдется
такое число α ^ О, что вектор Ь = аа.
Доказательство. Рассмотрим векторы Ъ и с ~ аа, где а —
= |5|/|а|, если а и Ь сонаправлены, и а — — \Ь\/\а\ в противном
случае. Векторы бис коллинеарны, ибо вектор с коллинеарен
—» —·
вектору а, а вектор а коллинеарен вектору Ь. Модули векторов Ь
и с равны, так как
lei - g · Щ = Й-
Векторы Ъ и с одинаково направлены по построению а. Поэтому
Ь = с.
Свойства произведения вектора на число:
1°. Χ(μα) = (Χμ)α (ассоциативность);
2°. (λ + μ)α = λα + μα (дистрибутивность относительно
суммы чисел);
3°. Х(а + 6) = Χα + Xb (дистрибутивность относительно
суммы векторов);
4°. 1 · а = а (свойство единицы).
Системы координат
17
Доказательство. Будем предполагать, что λ Φ О, μ ^ 0
и \а\ Φ О, ибо если λ = 0, или μ = О, или \а\ = 0, то указанные
равенства очевидны.
Свойство /°. Пусть ρΊ = Α(μα), а и = (λμ)α. Ясно, что ρΊ
и и коллинеарны. Кроме того, |ρΊ| = |λ| · |μ| · |α|, |й| = |λ| χ
χ |μ| · \α\, τ. e. |ρΊ| = |p2| · Если λ и μ одного знака, то векторы р\
и р2 имеют то же направление, что и вектор а, если же λ и μ
разных знаков, то оба вектора имеют направление,
противоположное вектору а. Итак, векторы pi и р2 коллинеарны, одинаково
направлены и имеют одинаковые модули, т. е. λ(μα) = (λμ)α.
Свойство 2°. Пусть с! = (λ + μ)α, С2 = λα + μα. Ясно,
что с\ и С2 — коллинеарны· Предположим, что λ и μ имеют
одинаковый знак. Тогда
Ι^Ι = |Α + μ||3| = (|λ| + ΜΜ
Ιδ| = |Α3| + Μ = (|λ| + |μ|Μ
т.е. |ci| = |с2|.
Кроме того, с! и с% имеют одинаковое направление,
совпадающее с направлением вектора а, если λ>0 и μ>0, или
направление, противоположное вектору а, если λ < 0 и μ < 0. Отсюда
заключаем, что, если числа λ и μ одного знака, то с\ = С2.
Предположим, что λ и μ имеют разные знаки, и для
определенности пусть λ > 0, μ < 0 и |λ| < |μ|. Тогда
\ο1\ = \(Χ + μ)α\ = {\μ\^\Χ\)\αΙ
\с2\ = \Χα + μα\ = \μα\ - \Ха\ = (|μ| - |λ|)|α|,
откуда |ci| = |сг|.
Кроме того, векторы с\ и &2 имеют направления,
противоположные вектору а, т. е. векторы с± и С2 сонаправлены. Отсюда
заключаем, что с\ = С2.
Свойство 3°. Если векторы а и Ь коллинеарны, то согласно
теореме вектор Ъ представим в виде Ъ = αα, где а = \Ь\/\а\ или
а = — \Ь\/\а\. Тогда с учетом уже доказанных свойств имеем
(λ(1 + α))α = λ((1 + а)а) = Х(а + аа) = λ(α + 5),
(λ(1 + а))а = (1 + а)(Ха) = Ха + Χαα = Λα + Xb.
18
Глава ί
Отсюда X(a + b) = λα + \b.
Пусть а и b — неколлинеарные векторы (рис. 1,8, 1.9).
Построим θΆ = а и АЁ = Ь. Тогда = а + Ь. Далее строим
оЬ = λα и Об = Х(а + Ь) (λ > 0, рис. 1.8; λ < 0, рис. 1.9).
Рис. 1Я Рис. L9
Треугольники ОАВ и OCD подобны, а тогда CD и АВ
параллельны, причем ^ = ^ = |А|. Следовательно, CD =
= |λ|ΑΒ, а поэтому Cl5 = \АЁ = ЛЬ. Поскольку ОЙ = об +
+ CD, то Х(а + Ь) = λα + ЛЬ.
Свойство 4°. Следует из определения операций умножения
вектора на число.
Рассмотренные операции — сложение векторов и
умножение вектора на вещественное число — называются линейными
операциями над векторами. Изученные свойства дают
право производить операции в векторной алгебре над векторами по
тем же правилам, по которым производятся операции в обычной
алгебре над вещественными числами.
§ 3. ЛИНЕАЛ
Оказывается, что линейные операции над элементами можно
ввести и в множествах другой природы, постулируя необходимые
свойства в форме аксиом. Такой подход представляется
перспективным в том плане, что исследование ряда геометрических
объектов сводится к векторной алгебре.
Линейным пространством, или линеалом, называют
множество L = {ж, у, Z) ..., 5, р, ... } элементов произвольной
природы, называемых векторами, для которого:
1) задано правило, по которому любым двум элементам
х,у € L сопоставляется элемент s 6 L> называемый их суммой
и обозначаемый s = χ + у;
Системы координат
19
2) задано правило, по которому каждому элементу χ £ L
и любому вещественному числу λ G Μ сопоставляется элемент
ρ е L, называемый произведением ж на λ и обозначаемый
ρ = Аж;
3) заданные правила при любых ж, уу ζ е L и любых
вещественных числах λ, μ 6 Ш подчинены аксиомам:
1°. х + у = у + х.
2°. {x + y) + z = x + (y + z).
3°. Существует нулевой вектор OgL, такой что χ + О = ж.
4°. Для каждого ж е L существует ж' e L, что ж + ж' = О.
5°. λ(μχ) = (Χμ)χ.
6°. (λ + μ)χ = Аж + /у,ж.
>. А(ж + г/) = Аж + А2/.
8°. 1-ж = ж.
Следует отметить, что в приведенном определении не
накладывается никаких ограничений на природу элементов
множества L и конкретное задание правил операций суммы (ж, у) —►
-* ж + у и умножения на число (А, ж) —> Аж.
Существует много различных линеалов. Для задания
конкретного линеала надо задать множество L и операции
сложения и умножения на число. Если в качестве векторов
рассматривать направленные отрезки и традиционные линейные операции,
то можно построить следующие линеалы: линеал V1 —
множество всех свободных векторов на прямой; линеал V2 —
множество всех свободных векторов на плоскости; линеал V3 —
множество всех свободных векторов в трехмерном пространстве;
простейший линеал θ = {0}, состоящий из одного нулевого
элемента О.
Другим примером является линеал Шп = {а = (аьа2,
• · · ? ^п)} — множество упорядоченных наборов η
вещественных чисел, где η — произвольное число, причем линейные
операции вводятся так:
о 4-6= (αΪ7α2} ..., αη) + (6ι,62, -·-, Ьп) =
λα = λ(αι, α2, ..., αη) = (λαι, Αα2, . -., λαη).
20
Глава I
Линеал Rn = {α = (а^аг* ..., ап)} иногда называют
координатным пространством.
Отметим, что все линеалы, за исключением простейшего
линеала Θ, имеют бесконечное количество элементов. Поскольку
элементы произвольных линеалов обычно называются
векторами (из линейного пространства), то сами линеалы —
векторными пространствами, что напоминает всякий раз о
необходимости обращения к сложившимся геометрическим
представлениям, вытекающим из рассмотрения линейных
векторных пространств V1, V2, V3 , изучаемых в курсе аналитической
геометрии.
В дальнейшем, во избежание недоразумений, где это
необходимо, векторы пространств V1, V2, V3 будем называть
геометрическими векторами и выделять стрелкой: a, AJu и т. д.
§ 4. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ
И НЕЗАВИСИМОСТЬ
Пусть L — произвольный линеал, щ е L, г = 1, . .., п, — его
элементы (векторы).
Элемент (вектор) ρ = Х^=1агаьгде аь i = If··» n> —
произвольные вещественные числа, называется линейной
комбинацией элементов (векторов) αϊ, а^, .. ·, ап. В этом
случае говорят, что элемент (вектор) ρ разложен по элементам
(векторам) αχ, <ΐ2,..., αη.
Элементы (векторы) αϊ, α2, -.-, αη называются
линейно зависимыми, если существуют такие вещественные числа
λι, Α2,.. ., λη, среди которых хотя бы одно отлично от нуля, что
Σ/=ιλίαί = °·
Элементы αϊ, α2, ..., αη называются линейно
независимыми, если равенство Σ7=ι ^*α* = О возможно лишь в случае,
когда вещественные числа λι, λ2, ..., λη одновременно равны
нулю.
Отметим, что всякий ненулевой элемент αϊ можно
рассматривать как линейно независимую систему, ибо равенство
λαι = О возможно лишь при условии λ = 0.
Системы координат
21
Теорема 1. Необходимым и достаточным условием
линейной зависимости а\, α<ι, ..., ап является возможность
разлоэюения по крайней мере одного из этих элементов по
остальным.
Доказательство. Необходимость. Пусть элементы αχ,
α2, .--, απ линейно зависимы, что означает Υ^^ι\ατ = О,
причем хотя бы одно из чисел λι,λ·2, ..., λη отлично от нуля,
например, λ* ^0.
Тогда
λ* , , ν^ ^k
г-1
Υ] Так + а*+ Σ ~Гак = Οι
к=1 λ* fc=t+i λί
т. е. элемент щ может быть разложен по элементам αχ,α2,
..., Ог_ χ, &г+1 ι · · · * О-п ·
Достаточность. Пусть элемент а^ разложен по
элементам αι,<Ζ2,..., aj-i,aj+i,..., απ>т. е.
j — l n
Тогда .^
2J λ^α/c - a31 + 22 λ*α* = °>
что означает линейную зависимость элементов αχ, α2,... , αη,
ибо Aj = -1^0,
Теорема 2. £сли хотя бы один из элементов αχ, а2,..., ап
нулевой, то эти элементы линейно зависимы.
Доказательство Пусть о, = О,тогда
5^0-ок + 1-а,+ 53 0·α* = 0, Ajf = 1 ^ 0,
что и означает линейную зависимость указанных элементов.
Теорема 3. Если среди η элементов какие-либо η — 1
элементов линейно зависимы, то и все η элементов линейно
зависимы.
22
Глава I
Доказательство. Пусть для определенности элементы а\9
«2* ---τ αη-ι линейно зависимы, т. е. существуют числа λι,
λ2,. - -, λη_ι, причем хотя бы одно из них отлично от нуля, такие
что Σ™=ι \iG>i = О, а элемент ап произвольный. Указанное
равенство сохранится, если добавить к обеим его частям элемент
О · ап = 0. Тогда Σί=ι λ* α* + 0 · αη = О, причем хотя бы
одно из чисел λχ, Х2, ..., λπ_ι отлично от нуля, что и означает
линейную зависимость элементов а\, а-2»· · ·» ап -
Подчеркнем, что утверждение теоремы о линейной
зависимости сохраняет силу, если среди указанных η элементов
предварительно установлена линейная зависимость не η — 1 элемента,
а любого другого, меньшего π — 1, числа элементов.
Следствие. Если система элементов линейно независима, то
и любое непустое подмножество этой системы также линейно
независимо.
§ 5. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ЛИНЕЙНОЙ ЗАВИСИМОСТИ И НЕЗАВИСИМОСТИ
ВЕКТОРОВ НА ПЛОСКОСТИ
И В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Вернемся к исследованию линейных пространств
геометрических векторов.
Теорема 1. Необходимым и достаточным условием
линейной зависимости двух векторов линейного векторного
пространства V2 является их коллинеарность.
Доказательство. Необходимость. Пусть векторы а и В
линейно зависимы, т. е. Х\а + А26 = 0, причем хотя бы одно
из чисел λι, λ2 отлично от О. Пусть для определенности λ2 Φ
Φ О- Тогда ^а + b = б и b = —j^a, т. е. векторы а и b
коллинеарны.
Достаточность. Пусть векторы α и b коллинеарны.
Будем считать, что среди них нет нулевого вектора, ибо в
противном случае в силу теоремы 2 § 4 эти векторы будут линейно
зависимы.
Системы координат
23
Если векторы а и В ненулевые и коллинеарные, то вектор 5,
как отмечалось ранее, представим в виде В = λα. Тогда Ха +
+(— 6) = б, что и означает линейную зависимость векторов а и В.
Следствие 1. Если векторы а и В неколлинеарны, то они
линейно независимы.
Следствие 2. Среди двух нсколлинеарных векторов не может
быть нулевого вектора.
Доказательство· Действительно, в противном случае данные
векторы были бы линейно зависимыми в силу теоремы 2 § 4.
Теорема 2. Необходимым, и достаточным условием
линейной зависимости трех векторов в линейном
пространстве V3 является их компланарность.
Доказательство, Необходимость. Пусть векторы а, В, с
линейно зависимы, т. е. существуют вещественные числа α, β,
7, такие что аа + βΒ + ηο = б, причем хотя бы одно из них не
равно нулю. Пусть η φ 0. Тогда
<*- βψ - яг
-α+ -Ь + с = 0,
7 7
или
с — а о.
7 7
Векторы — -α, —&Β коллинеарны соответственно
векторам α и 6, и их сумма, т. е. вектор с, будет лежать в плоскости
векторов а и 5. Следовательно, векторы а, Ь, с компланарны.
Достаточность. Пусть векторы а, В, с компланарны.
Будем считать, что среди них нет ни одной пары коллинеарных
(и тем самым ни одного нулевого вектора), ибо в противном
случае в силу теорем 2,3 § 4 три данных
вектора будут линейно зависимыми.
Приведем векторы а, Ь, с к общему
началу О (рис. 1.10). Проведем через точ- О ёГ
ку С прямую Са, параллельную векто- Рис. U0
ру α и пересекающую прямую Ob в точке В. Далее,
параллельно вектору Ь спроектируем точку С на прямую Оа. Векторы
и 6, а также ОА и α коллинеарны. Тогда, в силу теоремы § 2,
24
Глава 1
θΑ = аа, Ue = рЪ. Однако с = θΑ + ОЁ = аа + рЪ,
откуда аа + РЬ + (—1)с = 0, что и означает линейную зависимость
векторов а, В, с.
Следствие К Если векторы а, 5, с некомпланарны, то они
линейно независимы в V3.
Следствие 2. Среди трех некомпланарных векторов не может
быть двух коллинеарных.
Доказательство. Действительно, в противном случае
указанные векторы очевидно были бы линейно зависимы.
Следствие 3. Каковы бы ни были два неколлинеарных
вектора α, 5 на плоскости, всякий другой вектор с, компланарный с а
и 5, может быть разложен по векторам α и 5 в виде с = αα + /56.
Теорема 3. Любые четыре вектора линейного
пространства Vs линейно зависимы.
Доказательство. Пусть а, Ь, с, d — произвольные векторы
в пространстве. Будем считать, что среди этих векторов никакие
три не являются компланарными, ибо в противном случае в силу
теоремы 3 § 4 данные четыре вектора будут заведомо линейно
зависимы.
Приведем все векторы к общему началу О (рис. 1.11)
и проведем через конец вектора d плоскости,
параллельные плоскостям, в которых лежат пары векторов с и 5, α
и с,α и Ь соответственно.
Обозначим через А, В, С
соответственно точки пересечения указанных
плоскостей с прямыми Оа, 06, Ос.
Векторы θΑ и а, ОЁ и 6, ОО и с
коллинеарны. Поэтому Оа = аа> ОВ =
= рь, СЮ = 7с\ Однако d = θΑ +
+ ОЁ + Об, откуда аа + рЬ + ηο +
+ {-l)d = 0, что и означает линейную
зависимость векторов а, 6, с, d.
Следствие. Каковы бы ни были три некомпланарных вектора а,
Ь, с пространства У3, любой вектор d пространства V3 может
-» -* -♦
быть разложен по векторам а, 6, с в виде d = аа + РЪ + ^с.
Системы координат
25
Итак, подводя итоги, можно сделать следующие выводы:
• всякие два вектора на прямой линейно зависимы;
• всякие три вектора на плоскости линейно зависимы;
• всякие четыре и более вектора в трехмерном
пространстве Vs линейно зависимы;
• всякий ненулевой вектор а представляет собой
линейно независимую систему, причем любой другой ненулевой
вектор 6, коллинеарный α, может быть представлен через
вектор а в виде 6 = аа;
• всякие два неколлинеарных вектора а, В на плоскости
линейно независимы, причем любой третий вектор с,
компланарный а и 6, может быть разложен по векторам а
и Ь в виде с = аа + 0Ь\
• всякие три некомпланарных вектора а, б, с
трехмерного пространства линейно независимы, причем любой
четвертый вектор d пространства V3 может быть разложен
по векторам а, 6, с в виде d = аа + fib + ус.
§ 6. БАЗИС ЛИНЕАЛА
Упорядоченный набор линейно независимых элементов
(векторов) €ι, €2, -.., ете линеала L называется базисом линеала,
если для каждого элемента (вектора) χ € L найдутся такие
вещественные числа Xi, г = 1,., ·, п, что
χ
Ση
г=1
Последнее равенство называют разложением элемента
(вектора) χ по базису в\, е2,..., еп.
На основании полученных в предыдущем параграфе
результатов можем утверждать следующее:
β в векторном пространстве V1 произвольный ненулевой
вектор может быть взят в качестве базисного;
9 в векторном пространстве V2 упорядоченная пара
неколлинеарных векторов образует базис;
• в векторном пространстве V3 упорядоченная тройка
некомпланарных векторов образует базис.
26
Глава I
В пространстве Rn векторы (элементы) и\ = (1,0, ..., 0),
и2 = (0,1,0, ..., 0), ..., ип = (0,0, ..·, 0,1) являются
линейно независимыми, так как равенство нулевому элементу
их линейной комбинации Σ™=1 ctiUi = 0 возможно лишь при
условии, когда сц, = 0, г = 1,..., п.
Согласно определению линейных операций в Шп любой
вектор χ е Жп, χ = {хи χ2, ·- · 5 Хп)* линейно выражается через
векторы их, и2, -. ■, ип\ χ = 5ZS=i ж*^г-
Таким образом, векторы tti, и2ч ...» г*п образуют базис
пространства Шп.
Отметим, что в определении базиса порядок элементов
существенен, поскольку, переставляя элементы базиса, мы получаем
снова базис, но другой.
Числа х\, Χ2,..., хп ■ фигурирующие в разложении
элемента χ линеала L по заданному базису е\, е2,..., еп,
называются координатами вектора χ относительно рассматриваемого
базиса.
Теорема 1. Всякий элемент линеала L может быть
единственным образом разложен по базису е\, е2,..., еп> тем
самым его координаты относительно заданного базиса
определяются однозначно.
Доказательство. Допустим, что для некоторого элемента χ
наряду с разложением χ — Σ*=ι xLe>i существует еще и
другое разложение ж = $2lLi2/«c*· Почленно вычитая последнее
равенство из предыдущего, получаем
η
Базисные элементы ei, е2,.. -, еп линейно независимы,
поэтому для всех г = 1,..., η имеем Xi = yi·
Теорема 2. При сложении элементов линеала L их
координаты складываются, а при умножении элемента на
вещественное число все его координаты умножаются
на это число.
Системы координат
27
Доказательство. Пусть элементы βι, β2, ...» еге образуют
базис в L, χ и у — произвольные элементы из L, А —
произвольное вещественное число из = х + у,р = Хх.
Разложим ж, у, в,ρ по базису:
η η η η
г=1 г=1 г~1 г=1
Используя аксиомы 1°—8° линеала L, получаем
η η η
S = X + y = Y^ Χ& + Σ Угег = X](^i + 2/*)еЬ
г=1 г=1 г=1
, V v П
4=1 ' г=1
В силу единственности разложения по базису имеем s< —
= %г +Vi* Pi = λΧ^ 1 = 1,2, ..., П.
Теорема 3. Если каждый из п + 1 элементов у0, у\,..., уа
линеала L представим в виде линейной кочбинации η
линейно независимых элементов х\, х2,... > хп того же
линеала, т. е. п
УЗ =Σλυ-Χ;, Jf = 0,..-,П, (1)
то элементы у{}, у\,..., уп линейно зависимы.
Доказательство. Доказательство проведем методом
математической индукции по η.
Если η = 11 то уо = λχοχι, у\ = ХцХ\, причем оба числа
λ ίο и Ац отличны от нуля, ибо в противном случае элементы у0
и 2/1 линейно зависимы (один из элементов нулевой).
Умножим з/о на Ац, а τ/ι — на Аю и вычтем почленно. Тогда
λπϊ/ο — λιο2/ι = О. Последнее равенство при условии Аю φ О,
Ац Φ 0 означает линейную зависимость элементов уо> у\.
Предположим, что теорема справедлива для η элементов.
Докажем ее справедливость для η + 1 элемента.
По индукционному предположению имеем, что если каждый
из η элементов j/0, у χ,..., yn-i линеала L представим в виде
линейной комбинации η — 1 линейно независимых элементов
28
Глава I
Χι у Х2 >. · · · Xn-i того же линеала L, т. е. yj = Σ^1 λϋχζ > J =
= 0t .♦., η — 1, то элементы s/o, S/ii ··■» 2/η-ι линейно зависимы.
Не уменьшая общности, будем предполагать, что в равен-
ствах(1) Аю φ О, ибо если Ai0 = 0 для всех г = 1, 2,..., η,το
утверждение теоремы следует из индукционного предположения.
Введем в рассмотрение вспомогательные элементы Zj при
3 = 1, 2,..., п\
ζ3 = Уз ~ Т^-УО = Σ XiJXi ~ Τ1 Σ Xi°Xi =
λιο fri Mo Й
Каждый из η указанных вспомогательных элементов Zj
является линейной комбинацией η — 1 линейно независимых
элементов х2,..., жп. По индукционному предположению
элементы Zj линейно зависимы, т. е. существуют числа μι, μ2, >.., μη»
не равные нулю одновременно, такие что Σ^=ι /Ai^j = О, т^ е.
ς> (* - ё*) ■ °-
Отсюда следует соотношение
Σ^^ + ("Σ^)τ)ι'ό==0,
что означает линейную зависимость элементов уо, 2/ι, ..., Уп>
так как хотя бы одно из чисел μι, /i2, ..., Μη отлично от нуля.
Следствие, Любые п +1 элементов в пространстве W1 линейно
зависимы.
Доказательство. Любой из векторов
Xl = (,^ΐ) #2> · · · ϊ ^п/'
Ж2 == (#1 > · · · > ^п/^ * " * J ^n+1 == V^l ? · ■ * ι *^п /
пространства Еп можно разложить по базису этого
пространства ui = (1,0, ..., 0), tt2 = (0,1,0, ..., 0), ..., ип —
= (0,0,-.-,0,1) в виде Xj = Σ"=1χ{ν,ί, j = l n + 1. А
тогда по теореме 3 элементы χχ, x2,...yxn+i линейно зависимы.
Системы координат
29
§ 7. РАЗМЕРНОСТЬ ЛИНЕАЛА
Линеал L называют конечномерным (n-мерным), если в нем
имеется линейно независимая система, состоящая из η
элементов, а всякая система, содержащая более η элементов, является
линейно зависимой.
Число η называют размерностью линеала L и обозначают
символом dim(L) = п.
Таким образом, размерность пространства — это
наибольшее число его линейно независимых элементов.
Если линеал L является η-мерным, то его обычно
обозначают символом U1 ·
Ясно, что dimiV1) = 1, dim(V2) = 2, dim(V3) = 3.
В силу следствия к теореме 3 § 6 dim(IRn) = π.
Линеал θ, содержащий единственный элемент (нулевой),
является нульмерным.
Линеал L называется бесконечномерным, если для
любого натурального числа N в нем найдется линейно независимая
система, состоящая из N элементов.
Примером бесконечномерного линеала является линейное
пространство непрерывных на заданном отрезке функций.
Теорема. Для того чтобы линеал L был n-мерным,
необходимо и достаточно, чтобы в нем существовал базис,
состоящий из η элементов.
Доказательство. Необходимость. Если линеал
является η-мерным, то в нем есть линейно независимая система eif
β2, - -., en, состоящая из п элементов. Добавив к этой системе
произвольный элемент χ е L, получаем линейно зависимую
систему ei, €2,..., еп, х, причем элемент χ линейно выражается
через элементы е\, €2, -.., еп. Тогда элементы е\, €2,..., е„
образуют базис линеала L.
Достаточность. Если линеал L имеет базис βχ, β2,. ·., en,
то любой из η + 1 произвольных элементов г/о5 2/1 ,·'.., Уп из L
представим в виде линейной комбинации базисных элементов,
а тогда в силу теоремы 3 § 6 рассматриваемая система из п-Ы
30
Глава I
элемента уо, у γ, ..., уп линейно зависима. Это означает, что
линеал L является η-мерным. Таким образом, размерность
линеала L равна числу элементов, составляющих его базис.
Мы убедились, что в линеалах Р(п=1,2,3)и1п имеют
место следующие утверждения.
Утверждение 1. Любая система элементов этих линеалов,
состоящая более чем из η элементов, линейно зависима.
Утверждение 2. В названных линеалах существуют линейно
независимые системы элементов, состоящие из η элементов.
Эти утверждения не вытекают из аксиом 1°—8°
произвольного линеала. В связи с этим при аксиоматическом построении
геометрии надлежит либо эти утверждения принять за
аксиомы, либо сформулировать новую аксиому, с помощью которой
можно их доказать.
9° {аксиома размерности). Линейное пространство L
конечномерно и его размерность равна п.
Отметим, что при выполнении этой аксиомы из
сформулированных ранее аксиом 1°—8° линеала очевидно вытекают
приведенные выше утверждения 1,2.
Таким образом, в η-мерном линеале Ln всякий базис
состоит из η упорядоченных линейно независимых элементов, причем
любой элемент линеала Ln единственным образом представим в
виде линейной комбинации базисных элементов.
§ 8. ИЗОМОРФИЗМ ЛИНЕАЛОВ
Рассмотрим векторные пространства одной размерности и
покажем, что они тождественны относительно линейных
операций.
Соответствие между элементами двух линеалов L и U
называется взаимно однозначным, если каждому элементу из L
отвечает единственный элемент из I/, причем каждый элемент
из V отвечает одному лишь элементу из L.
Два линеала L и V называются изоморфными
(обозначение: L « L'), если между элементами этих линеалов
можно установить такое взаимно однозначное соответствие
Системы координат
31
φ: χ е L —> φ(χ) G V, что у?(Аж) = А^(ж), </?(# + #) =
= φ{χ) + <р(у), где х, у € L, λ — любое вещественное
число.
При этом данное взаимно однозначное соответствие часто
называют линейным изоморфизмом.
Теорема !. Все линеалы одной и той же размерности
изоморфны.
Доказательство. Пусть линеалы L и Ζ/ являются
n-мерными. Выберем в L некоторый базис βι, €2,.. -, еп, а в V —
базис е\, е'2, . -., е'п. Сопоставим элементу χ = Σι=ι xiei G ^
элемент ψ (χ) G £/:
(TO ν 71
t=l ' г=1
имеющий те же координаты, что и элемент ж, но в базисе
Установленное соответствие ^ является взаимно
однозначным вследствие теоремы о единственности разложения
элемента по базису. Свойства изоморфизма выполняются в силу
теорем о координатах суммы векторов и координатах произведения
вектора на вещественное число:
/ П ч ТО
Ψ(Χ + У) = Φ Ι Σ&τ + Vi)e'i ) = $^(Яг + У'1№ =
η η
= Y^xie'i + ^|/<e{ = ψ(χ) + ip(y),
г=1 г=1
f ТО ν П TO
ψ(αχ) = ф\^2(аХг)еЛ = ^{ахг)е[ = а^хсе[ = αψ(χ).
Μ=1 ' г=1 г=1
ЗАМЕЧАНИЕ. Рассмотренный в теореме 1 изоморфизм
называют координатным изоморфизмом. Подчеркнем, что
координатный изоморфизм зависит от выбора базисов в L и Ζ/.
Следствие. Каждое η-мерное линейное пространство Ln
изоморфно координатному пространству Rn.
32
Глава I
Отметим, что при координатном изоморфизме
произвольного линеала Ln и координатного линеала W1 любому элементу
χ € Ln y представленному с помощью некоторого базиса βχ,
^2, ·.-, е?г из Ln в виде χ = Σ™=1#?β2, сопоставляется
упорядоченный набор чисел (х\уХ2^ · -, #n) G 1^п>
компоненты которого суть координаты элемента χ G Ln относительно
фиксированного базиса.
Теорема 2. Изоморфные линеалы имеют одну и ту же
размерность.
Доказательство. Пусть η-мерный линеал Ln изоморфен
линеалу V при линейном изоморфизме.
Убедимся, что нулевому элементу 0 € Ln при линейном
изоморфизме φ соответствует нулевой элемент <^(Q) G V.
Действительно, для любого элемента χ G Ln по
аксиоме 3° линейного пространства имеем равенство х + 0 = ж, и
потому φ(χ + 0) = φ(χ) - В силу линейного изоморфизма φ(χ +
+ 0) = φ(χ) + φ(0). Сравнивая последние равенства, получаем
φ(χ)+φ(0) = φ{&), откуда в силу той же аксиомы 3° заключаем,
что <^(0) есть нулевой элемент в V.
Пусть е\, ег,..·, еп — произвольный базис в Ln, и φ{&\)ι
..., <^(еп) — образы названных элементов в V при линейном
изоморфизме φ. Составим в L' линейную комбинацию
η
£>¥>(*) = *(0). О)
г=1
В силу свойств линейного изоморфизма <^ и взаимно
однозначного соответствия нулевых элементов линеалов Ln и U
имеем соотношение ΣΓ=ι α^β* = 0. Откуда, вследствие
линейной независимости элементов е\,..., еп, получаем о^ = 0, г =
= 1, 2,..., η. Но тогда из равенства (1) следует, что элементы
φ(βί), г = 1 f 2,..., η, из Ζ/ линейно независимы.
Таким образом, размерность L' не менее п. Она же не может
быть и более п, ибо в противном случае при обратном взаимно
однозначном соответствии φ"1: V —> Ln получили бы в Ln
более чем η линейно независимых элементов.
Системы координат
33
Следствие 1. Конечномерные линеалы разных размерностей
неизоморфны.
Следствие 2. Бесконечномерный линеал не может быть
изоморфен никакому конечномерному линеалу.
Итак, существенной характеристикой конечномерного
линеала является его размерность. Линеалы, имеющие
одинаковую размерность, изоморфны. Свойства линеалов,
выраженные в терминах алгебраических операций сложения
и умножения на вещественное число, у изоморфных линеалов
одинаковые.
С алгебраической точки зрения изоморфные линеалы
тождественны. На этом факте основывается, в сущности, и
метод координат, на котором базируется аналитическая
геометрия.
По следствию из теоремы 1 все η-мерные линеалы
изоморфны координатному линеалу Шп.
Таким образом, в теории η-мерных линеалов, не теряя
общности, можно ограничиться изучением линеала Εη,
поскольку очевидно, что с помощью обратного изоморфизма
φ~ι: Rn —> Ln полученные в Шп утверждения,
сформулированные в терминах основных операций сложения и умножения на
вещественное число, переносятся на исходный линеал Ln.
§ 9. АФФИННЫЕ ПРОСТРАНСТВА
Наряду с линеалами рассматриваются аффинные пространства,
элементы которых, называемые точками, определенным
образом связаны с векторами — элементами линеалов.
Аксиоматизируя построение вектора по двум точкам, можно определить
аффинное пространство.
Аффинное пространство — это множество £ элементов
произвольной природы, называемых точками, для которых:
1) задан некоторый, ассоциированный с £, линеал L;
2) задано соответствие, сопоставляющее любым двум
точкам А, В <Ξ £ некоторый элемент АВ 6 L с началом в А
и концом в В;
34
Глава I
3) выполняются следующие две аксиомы:
10°. Для произвольной точки Лб£ и любого элемента и € L
существует единственная точка В € £, такая что АВ = it.
И". Для произвольных трех точек Л, В, С имеет место
равенство
Если в последней аксиоме положить А = В = С\ то
получаем АЛ = О, а если С = Л, то имеем ЖД = —А/5, что
соответствует известным ранее фактам.
Обратим внимание на то, что согласно определению
аффинное пространство некорректно рассматривать без
ассоциированного с ним линеала L.
Будем полагать, что размерность аффинного пространства £
совпадает с размерностью ассоциированного с £ линеала L,
и будем обозначать ее символом dim(£).
Если dim(£) = η, то аффинное пространство
называют η-мерным и обозначают символом £п.
В аффинной геометрии, изучающей объекты аффинных
пространств, имеются два основных понятия — вектор и
точка, и три основных отношения: отношение между тремя
векторами а,6,с:с = а + 6; отношение между двумя векторами а,
Ъ и вещественным числом а: 6 = аа; отношение между двумя
точками Ау В и вектором и: Аи = гх. Причем названные
отношения удовлетьоряют всем сформулированным одиннадцати
аксиомам.
Приведем пример аффинного пространства.
Рассмотрим реальное точечное
трехмерное пространство V3. Фиксируем
некоторую точку О и будем
рассматривать всевозможные радиус-векторы
с началом в точке О (рис. 1.12). Под
Рис. 1.12 точками аффинного пространства £3,
с которым ассоциирован линеал V3, будем понимать концы
соответствующих радиус-векторов, причем двум точкам А и В
сопоставляется вектор АВ = ?в — г а € V3.
Заметим, что при такой формализации мы отождествляем
точку А с радиус-вектором гд -
Сиапемы координат
35
Для интересующегося читателя покажем формально, что
любое линейное пространство можно рассматривать и как
аффинное, ассоциированное с самим собой.
Действительно, пусть L — линейное пространство.
Рассмотрим аффинное пространство с элементами из L, где
аффинное отношение устанавливается следующим образом: ао =
= 6 — а, где ао — это вектор с началом в α и концом в Ь.
Непосредственно проверяется, что аксиомы 10° и 11° выполнены.
В дальнейшем условимся рассматривать аффинные
пространства с фиксированной точкой, тогда мы будем иметь и
точки, и векторы.
В аналитической геометрии мы будем изучать в основном
реальные аффинные пространства (точки на прямой, на
плоскости, в трехмерном пространстве), с которыми
ассоциированы линеалы V1, V2, V3 и которые называются
соответственно — прямая, плоскость, трехмерное пространсгво (или, ради
сокращения, просто пространство).
§ t0. АФФИННЫЕ СИСТЕМЫ КООРДИНАТ
Аффинная система координат Ое^-.-вп в аффинном
пространстве £п есть совокупность, состоящая из
произвольной точки О, называемой началом координат, и базиса βχ, β2,
..., еп из ассоциированного с £п линеала Ln.
Подчеркнем, что аффинная система координат задается
двумя разнородными объектами — точкой О из аффинного
пространства и базисом в\, β2, ..., еп из ассоциированного с
аффинным пространством линеала.
Пусть А — произвольная точка аффинного
пространства £п. Вместе с началом координат О точка А определяет
радиус-вектор ОА е Ln, координаты которого определяются
из разложения по базису ei, в2, .. -, еп: ОА = х\е\ + #2^2 +
г* · · · "ι ·Εη&η ·
Аффинными координатами произвольной точки А € &п
называют координаты соответствующего элемента
(радиус-вектора) Ln и обозначают символом A(xi,x2j ..., xn)-
36
Глава 1
Ясно, что координаты точки А однозначно
определяются ввиду единственности разложения элемента по заданному
базису.
Произвольный вектор Atf € Ln можно представить как
разность соответствующих радиус-векторов:
АЁ = гв -гА- (1)
Если вектор АЁ задан координатами своего начала
А(х\, Х27 -.., хп) и конца Б(з/ъ 2/2) ··-, Уп) относительно
базиса ei, e2, ..., еп, то его координаты относительно того
же базиса определяются из соотношения (1) как коэффициенты
разложения по названному базису в виде
АЁ = (у\- xi)ei + (у2 - я2)е2 + . -. + (уп - Хп)еп,
и обычно используют обозначение
АЁ(У\ - Х\, 2/2 ~ Ζ2, · - , Уп - Хп)-
Прямой в аффинном пространстве £п, задаваемой точкой
Aq е £п и отличным от нулевого вектором и € Ln9
называется множество всех точек Ρ G £n f для которых AqP = tu,
t € (—оо, +оо).
При рассмотрении аффинных систем координат в
реальных пространствах: в трехмерном пространстве, на
плоскости и на прямой, базисные векторы соответствующих
линеалов V3, V2, V1 приводятся в общее начало (рис. 1.13—1.15).
ei
О
Рис. 1.13 Рис. 1.14 Рис. 1.15
Прямые в рассматриваемых пространствах, определяемые
началом координат О и соответствующими базисными
векторами, называются осями координат (Оё\, Оёг, Оё$ на рис. 1.13;
Oei, Oe2 на рис. 1.14; Оег на рис. 1.15).
Системы координат
37
В трехмерном аффинном пространстве рассматривают
также координатные плоскости, определяемые соответствующими
парами координатных осей (Oeie2, Oeieb, Ое^е^ на рис, 1.13).
Заметим, что задание системы координат дает определенную
ориентацию в пространстве. В связи с этим введем следующие
определения.
Тройка базисных векторов e\, ёг, ёз называется правой
(левой), если по этим векторам после приведения их к общему
началу можно направить соответственно большой, несогнутый
указательный и средний пальцы правой (левой) руки (рис. 1.13).
Пара базисных векторов ei, e2 называется правой (левой),
если кратчайший поворот от первого базисного вектора ко
второму происходит против (по) часовой стрелки.
Система координат правая (левая), если ее базис
правый (левый). В дальнейшем ради определенности будем
рассматривать только правые системы координат.
§ 11. ДЕКАРТОВЫ ПРЯМОУГОЛЬНЫЕ
СИСТЕМЫ КООРДИНАТ НА ПРЯМОЙ, ПЛОСКОСТИ
И В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Особое место среди аффинных систем координат занимает
декартова прямоугольная система координат как наиболее
часто используемая на практике.
Базис называется ортонормированным, если базисные
векторы единичные и попарно перпендикулярные.
Аффинная система координат с ортонормированным
базисом называется декартовой прямоугольной системой
координат.
Иногда рассматривают декартовы косоугольные системы
координат, у которых базисные векторы единичные, но
пересекаются под произвольными углами.
В дальнейшем декартову прямоугольную систему координат
будем обозначать ДПСК- Аффинные координаты вектора (точки)
в ДПСК называются декартовыми прямоугольными
координатами вектора (точки) в данной ДПСК-
38
Глава ί
к
-V-
Χ
У
1
о"
Ό
Рис. 1.16
У
χ
Рис. 1.17
О
χ
Рис. 1J 8
Рассмотрим ДПСК в трехмерном про- ζ
странстве, на плоскости и на прямой. Так, 11
на рисунке 1.16 изображена ДПСК в
трехмерном пространстве: OTjk, г ± fy г ± к,
j -L к, |г1 = 1, \j\ = 1, \к\ = 1;
координатные оси: ОТ— ось абсцисс, О J— ось
ординат, Ок — ось аппликат; координатные
плоскости: OtJy ОТ к, Ojk. На рисунке 1.17
показана ДПСК на плоскости: Огу,
координатные оси: Ог— ось абсцисс, Oj— ось
ординат, а на рисунке 1.18 — ДПСК на
прямой: здесь одна координатная ось— ось
абсцисс Ог.
В соответствии с вышеизложенным
прямую, на которой выбрана начальная
точка, называемая началом координат, и
указан единичный вектор, приведенный в
начало, называемый направляющим вектором,
называют декартовой осью координат (рис. 1.16, 1.17,1.18).
Декартовы координаты произвольного вектора α
относительно заданного базиса суть коэффициенты его разложения по
данному базису. Поэтому при η — 3: а = хг + УЗ + zk, или
а(х, у, ζ); при η = 2: а = хг + yj, или а(х, у); при η = 1:
α = хТ, или а(х).
Таким образом, вектор при заданной системе координат в
трехмерном пространстве есгь упорядоченная тройка
вещественных чисел, на плоскости — упорядоченная пара
вещественных чисел, на прямой — число.
Декартовы координаты произвольной точки
относительно заданной системы координат суть декартовы
координаты соответствующего радиус-вектора этой точки
относительно той же системы координат (рис. 1.19—1.21). В
пространстве при η = 3 имеем гм = ОМ = хмг + УмЗ + ζμ&7
М(хм7 ум^ z\t)\ на плоскости при η = 2 имеем т^ = ON =
= ΧΝΪ+yNj, Ν(;τ^,2/;ν); на прямой при га = 1: tq = OQ = xqT,
Q(xq)-
Системы коорЗиншп
39
11КТ '
у г*
о
tnS
N
Хдг X
Рис. U 9
Рис, 1,20
Рис, 1.21
Рис, 1,22
В трехмерном пространстве координаты точки относительно
первого» второго и третьего базисных векторов г, j, k называют
соответственно абсциссой, ординатой и аппликатой
Подчеркнем, что координаты точки указываются строго в
установленном порядке: абсцисса, ордината и затем аппликата.
На плоскости точка имеет
абсциссу и ординату, на прямой — только
абсциссу.
Произвольный вектор в
рассматриваемых пространствах Vх, V2, V3
определяется как разность соответствующих
радиус-векторов АВ = г в - rAf и его
декартовы координаты находятся из
следующих соотношений (рис. 1.22):
АЁ = г в - гА = (хБг + УвЗ + zDk) - (хАг + УаЗ + zAk) =
= {хв - χα)Ϊ+ {ув - Уа)з + (zb - zA)k.
Тогда при
η = 3: χτϊΖ =хв- χα, Ум =Ув -УА, *а&= zb- zA,
aS(xb - χα, Ув - УА, ζΒ - ζΑ)\
/г = 2: xj% =хв ~ хА> УТЬ = Ув - УАу
АЁ(хв -хА, ув-Уа);
η = 1: χχ& = xD -ха>
АЁ(хб-ха)-
Таким образом, координаты произвольного вектора, заданного
координатами своего начала и конца, определяются как
разности соответствующих координат конца и начала этого вектора.
40
Глава 1
§ 12. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ДЕКАРТОВЫХ КООРДИНАТ НА ПРЯМОЙ
Алгебраической мерой вектора декартовой оси называют
относительное число, абсолютное значение которого есть
отношение длины этого вектора к единице измерения длин, причем
знак « + » берется, если этот вектор и направляющий
вектор оси являются сонаправленными, и « — », когда указанные
векторы имеют противоположные направления.
Алгебраическую меру вектора IS обозначают символом АВ. Очевидно,
что \АЁ\ = \АВ\.
Теорема» Всякий вектор АЁ на оси может быть предсщав-
лен в виде АЁ = АВг, где г — направляющий вектор оси,
АВ — алгебраическая мера вектора АЁ.
Доказательство. Пусть АВ — произвольный вектор
декартовой оси. Тогда векторы АВ и ρ = АВГ равны, поскольку \р\ =
= \АВ\\г\ = \АЁ\9 векторы Atf и ρ коллинеарны и сонаправле-
ньк Действительно, если АВ > 0, то по определению
алгебраической меры векторы АЁ и г имеют одинаковое направление,
но ρ и Г также имеют одинаковое направление. Следовательно,
в данном случае АВ = р. Если АВ < 0, то ρ имеет
направление, противоположное вектору Г, но и вектор АВ имеет
также направление, противоположное вектору Г, а тогда векторы ρ
иАЁ сонаправлены, поэтому опять
Следствие К Координата произвольного вектора на декартовой
оси равна его алгебраической мере, а координата произвольной
точки на оси равна алгебраической мере соответствующего ей
радиус-вектора.
Можно показать, что между точками декартовой оси и
множеством вещественных чисел существует взаимно однозначное
соответствие, поэтому декартова ось ОТ есть геометрическая
интерпретация множества вещественных чисел.
Лемма Шаля. При любом расположении точек А, В, С на
оси алгебраические меры векторов АЙ, ВО, АО связаны
соотношением АВ + ВС = АС.
Системы координат
41
Доказательство, Будем предполагать, что все три точки А,
В, С — различные, ибо если две из них совпадают, приведенное
равенство сводится к очевидному тождеству. Рассмотрим четыре
случая.
1) АЁ, ВО и ось Ог имеют одно и то же направление
(рис. 1.23). Тогда имеем равенства ~КЁ = |А£?|, ВС = |Ш?|
.Далее, ЛС =\I8\ = \а8\ + \Шб\ = -^
= АВ + ВС.
2) А^ивЗ имеют
противоположные направления,
причем \АЁ\ > \Шб\ (точка С
расположена между А и В)
(рис. 1.24). Тогда BU =-\Шв\,
АВ = \АВ\. Следовательно,
Ж =\Ж\ = {\АЁ\-\ВО\) =
= \АЁ\ + (-\вб\) = ~АВ + ВС.
3) АЁ и Вб имеют проти-
воположные направления, при- <
чем \АЙ\ < \ВС\ (точка С вне ? а6 4Й
о
о
—*
"F
?>
ш JP
~А& Вб
А ^В "С
Рис. 1.23
АЁ
Ж1 вб
А V В
Рис. 1.24
—з^·
"^
,< ■ >ί
отрезка АВ) (рис. 1.25). Тогда О С А в
~АВ = |ЛЗ|, ВС = -|βδ| и р«с. /.25
ЛС = -\лб\ = -(|Ж?| - |ЛЗ|) =
= \К&\ + (-\вб\) = AD + ВС.
4) ]Йив5 имеют
одинаковое направление, но проти- Ж?
воположное направлению оси ^ _,, _^
(рис. L26). Тогда АВ = -|АЁ|, Q г> с< в< А »
ве=-\вд\* Puc.L26
АС = -|ЛЗ| = — (|аЗ| + |БЙ|) =
= (-pS|) + Н#б|) = АВ + ВС.
Лемма доказана.
Следствие 2· Координата произвольного вектора декартовой
оси равна разности координат его конца и начала.
42
Глава /.
Доказательство. В самом деле, по лемме Шаля, ОА+АВ =
= О В , т. е. ж л + АВ = Χβ, откуда χχέ = АВ = хв — ха-
Расстояние между двумя произвольными точками
декартовой оси А(ха) и В(хв) находится по формуле d(A>B) =
= \хв - хд\, так как d(A, В) = \АЁ\ = \АВ\ = \хв - ха\ .
§ 13. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ДЕКАРТОВЫХ КООРДИНАТ НА ПЛОСКОСТИ
Проекцией произвольной точки плоскости на некоторую ось
параллельно другой оси называется точка пересечения с
данной осью прямой, проходящей через заданную точку и
параллельной другой оси.
Спроектируем начало А и конец В
произвольного вектора АЁ плоскости
3 на декартовы оси координат Ог, Oj
параллельно другой оси
соответственно (рис. 1.27).
^ Геометрической проекцией
вектора АЁ на ось Ог называют вектор,
имеющий началом проекцию Ах
начала А данного вектора на эту ось, а концом — проекцию Вх
конца В данного вектора на эту ось (рис, 1.27). В дальнейшем будем
использовать обозначение
Projk A3 = АХВХ}
Рго?0?Аё = А^у.
Алгебраической проекцией вектора на ось называется
алгебраическая мера геометрической проекции данного вектора
на эту ось. Алгебраическая проекция обозначается так:
Ргсу^лЗ = А^Щ.
Теорема 1. Декартовы прямоугольные координаты
вектора на плоскости равны алгебраическим проекциям
вектора на оси координат
Системы координат 43
Доказательство. На основании определения суммы
векторов и теоремы § 12 имеем (рис. 1.27):
АЁ = Аб + Ш$ = аЖ + Аув1 = {АхВх)г + ДДДГ=
= (РгоЙгЯЗК + (PmiaOJAe)j.
Таким образом, координаты вектора на плоскости
представляют собой упорядоченную пару чисел, первое из которых есть
алгебраическая проекция данного вектора на ось абсцисс, а
второе— алгебраическая проекция данного вектора на ось ординат.
Можно утверждать, что вектор на плоскости, определяемый с
точностью до точки приложения, есть упорядоченная пара чисел.
Отметим, что для однозначного построения вектора на
плоскости, определяемого упорядоченной парой чисел, достаточно,
например, указать координаты его начала или конца.
Можно доказать, что между точками плоскости и
всевозможными парами вещественных яисел существует взаимно
однозначное соответствие.
Координатные оси Ог, Of разбивают плоскость на четыре
квадранта, в каждом из которых для всех точек каждая из
координат сохраняет постоянный знак.
Теорема 2. Алгебраическая проекция суммы векторов на
некоторую ось равна сумме алгебраических проекций на
ту же ось слагаемых векторов. Алгебраическая
проекция на некоторую ось произведения вектора на
вещественное число равна произведению данного
вещественного числа на алгебраическую проекцию на ту же ось
данного вектора:
Projf (ci + c2) = Proj? С! + Projf с2>
Projf ac\ = a Projf ci.
Доказательство. Выберем систему координат так, чтобы
начало ее совпадало с началом на оси I, а ось I совпала с осью ОГ.
Теперь нетрудно видеть, что утверждение этой теоремы вытекает
из теорем о координатах суммы векторов и произведения вектора
на вещественное число.
44
Глава I
Углом наклона вектора к оси называют угол, на который
следует повернуть направляющий вектор оси до совмещения его
с ортом заданного вектора, приведенным в начало координат на
оси (рис. 1.28, L29).
к
О г
В'
Рис. /.29
Теорема 3. Алгебраическая проекция вектора на ось
равна произведению его длины на косинус угла наклона
этого вектора к данной оси, т. е. Projf АЁ =\АЁ\ cos а, где
а — угол наклона вектора АВ к оси I.
Доказательство. Пусть угол а —острый (рис. 1.28). В этом
случае Projf Ad имеет направление, совпадающее с
направлением оси /, и
Projf АЁ = Projf АЁ = АПВ7 = |Ζί?| - | АЙ| cos α.
Допустим, что угол а —тупой (рис. 1.29). В данном случае
вектор Projf AB имеет направление, противоположное
направлению оси I и
Projf АЁ = Projf АЁ = ЖВ7 = -|Ζί?| =
= -(|А^| соб(к — а)) = \АЁ\ cos а.
Когда а = π/2, то А! В1 = б, cos(7r/2) = Ои указанная
формула верна.
Если а —угол наклона вектора к оси абсцисс Οι, то
хв - χΑ = Proj£rAJ§ = АХВХ = \АЁ\ cos а.
Отсюда имеем формулу для нахождения угла наклона а
вектора АЙ к оси Οι:
Системы координат
45
§ 14. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ДЕКАРТОВЫХ КООРДИНАТ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Проекцией некоторой точки пространства на данную ось
параллельно данной плоскости называется точка
пересечения с заданной осью плоскости, проходящей через
рассматриваемую точку и параллельной
данной плоскости (рис· 1.30).
Спроектируем вектор
трехмерного пространства на оси
Ог9 Of, Ok соответственно
параллельно координатным
плоскостям Ojk, Oik, ΟΪ?9 т. е.
Zk
\вг
А
Л
и
и
τ /
λ Αζ
\о
г
А
/
ι
У*
\
%L-
l/
/
ZS7
5u
ρ5
в'
Рис. 1.30
получим векторы АХВХ% АуВуу
ΑΖΒΖ (рис. 1.30). Указанные
векторы суть геометрические
проекции заданного вектора Ао на соответствующие
координатные оси параллельно соответствующим координатным
плоскостям:
Proj£? АЁ = аЖ> Рю^АЁ = AyBy,
Теорема. Декартовы прямоугольные координаты вектора
в трехмерном пространстве равны алгебраическим
проекциям данного вектора на оси координат.
Доказательство. На основании определения суммы
векторов и теоремы § 12 имеем:
АЁ = АЁ + DE = Zz? + AZB\ = АХВХ + АуВу + AZBZ =
= (ΙΛΚ+ (АЛ) з + (ДА)* =
= (Рго^Л^гЧ (Рго^Л% + (Prof^ АЁ)к.
Таким образом, координаты вектора в трехмерном
пространстве представляют собой упорядоченную тройку чисел,
первое из которых есть алгебраическая проекция данного вектора
46
Глава I
на ось абсцисс, второе — алгебраическая проекция данного
вектора на ось ординат, и третье — алгебраическая проекция
указанного вектора на ось аппликат.
Можно утверждать, что вектор в трехмерном пространстве,
определяемый с точностью до его точки приложения, есть
упорядоченная тройка чисел.
Для однозначного построения вектора в пространстве,
определяемого тройкой чисел, достаточно, например, указать
координаты его начала или конца.
Таким образом, мы лишний раз убедились, что между
точками трехмерного пространства и всевозможными
упорядоченными тройками вещественных чисел существует взаимно
однозначное соответствие.
Координатные плоскости разбивают пространство на восемь
октантов, в каждом из которых для всех точек каждая из
координат сохраняет постоянный знак.
§ 15. ДЕЛЕНИЕ ВЕКТОРА
В ЗАДАННОМ ОТНОШЕНИИ
Будем говорить, что точка М, не совпадающая с точкой В,
делит вектор АВ в отношении λ ^ —1, если
Пусть га, г в —
радиус-векторы начала А и конца В
вектора А§. Найдем радиус-вектор гм ?в
точки М, делящей вектор AJj в
отношении λ (рис. 1.31). В силу (1) О
гм -тА = \{тв - гм) и
г м =
га + Агв
1 + А
η
Отсюда, если
ΧΑ+λΧΒ
Рис. 1.31
О)
(2)
3: хм =
1 + λ
Ум
УА + ^УВ
1 + λ
ζμ =
ΖΑ+λΖΒ_
1-ЬА
Системы координат
47
χΑ + λχΒ Ул+Ьув
п = 2: 1м = -гр-, № = ____;
гсл + Ажв
n=l: *« = -i^X-
Отметим, что если Μ лежит внутри отрезка АВ, то λ > О,
а когда Μ расположена вне отрезка АВ, то λ < 0. Ясно, что
А = 0, если Μ совпадает с А, и λ имеет сколь угодно большую
абсолютную величину, если Μ достаточно близка к В. Наконец,
λ не существует, если Μ совпадает с В.
Убедимся, что если точка Μ делит вектор в отношении
λ, то
А=^. ,3)
MB х '
В самом деле, если точка Μ расположена внутри вектора
, то векторы АЙ и MU одинаково направлены, их
алгебраические меры имеют одинаковый знак. Следовательно, λ > 0
и потому из соотношения \АЙ\ = |Л||мЗ| имеем
\АЙ\ _ AM
\мЁ\ Шв '
Если точка Μ расположена вне вектора Atf, to
векторы AM и MB противоположно направлены, а их
алгебраические меры имеют противоположные знаки. Следовательно,
λ < 0 и поэтому из соотношения \АЙ\ = \λ\\Μή\ следует
μ| = β- и а=™
\мЁ\ мв"
Принимая во внимание, что AM = Atf + Βλ£, и
воспользовавшись леммой Шаля, получаем
AM АВ + ВМ АВ , ч
λ = -= = — — = + (-1).
MB MB MB v ;
Если точка М удаляется в бесконечность на оси в том или
ином направлении,%то АВ/МВ стремится к 0, так как числитель
этой дроби постоянен, а знаменатель по абсолютной величине
неограниченно возрастает. Следовательно, 1ιπΐΜ->±οολ = — 1.
48
Глава ί
Отметим, что ни при каком положении точки Μ на оси
величина λ не равна —1. В самом деле, λ отрицательно, если Μ
вне вектора Ad, но в этом случае никогда вектор AM не равен
вектору
ЗАМЕЧАНИЕ. Пусть точка М, не совпадающая с точкой В,
делит вектор ~Аи в отношении λ φ — 1 в аффинном
пространстве £п,где Α(αι, α2>..., αη), B(bi,b2, ..., bn). Тогда
координаты точки M(xijX2> . ■·, хп) вычисляются также
по формуле (2):
_ at + Xbj .
Xl — , Ζ — 1, Ζ, . . . , 7Ί,
поскольку формула (2) не зависит ни от размерности
пространства, ни от его природы, ни от системы координат.
§ 16. ПОЛЯРНАЯ
СИСТЕМА КООРДИНАТ
НА ПЛОСКОСТИ
Для определения положения точки на плоскости, кроме
рассмотренных декартовых и аффинных систем координат, часто
применяют и неаффинные системы, например, полярную систему
координат.
Полярной системой координат на плоскости
называется система, определяющими элементами которой являются:
1) точка О — полюс; 2) луч Ор,
исходящий из полюса, — полярная ось\
3) единица измерения длин на
полярной оси; 4) единица измерения углов;
5) положительное направление
отсчета углов (рис. 1.32). Обычно углы из- Рис- L32
меряют в радианах и под положительным направлением их
отсчета понимают направление, противоположное вращению часовой
стрелки.
Полярным радиусом ρ точки Μ называется расстояние
от этой точки Μ до полюса О: ρ = d(0,M), 0 < р < +οο.
Системы координат
49
Полярным углом φ некоторой точки М, отличной от
полюса, называется угол между полярной осью О ρ и лучом ОМ:
φ = Ζ(Ορ,ОМ), 0 < φ < 2тг.
Упорядоченная пара чисел (ρ, φ), взятых в указанном
порядке, называется полярными координатами точки Μ на
плоскости, при этом используется обозначение Μ(ρ, φ).
Отметим, что полярный радиус полюса равен 0, а полярный
угол полюса не определен.
При указанных ограничениях: 0 < ρ < +оо, 0 ^ ψ < 2π,
между точками плоскости, отличными от полюса, и
упорядоченными парами (ρ, φ) существует взаимно однозначное
соответствие.
В некоторых случаях полярный угол рассматривают в
следующих пределах: —π < φ < π. Иногда вообще
отказываются от рассмотрения ограничений на полярный угол и его
измеряют с точностью до ±2πη, где η — натуральное число.
Пусть полярные и декартовы
координаты связаны следующим
образом: начало декартовой
системы координат совпадает с
полюсом О, базисный вектор Г
совпадает с масштабным вектором е
полярной оси Ор,ось Оj
направлена так, чтобы система координат
была правой (рис. 1.33).
Тогда координаты полярные (ρ, φ) и декартовы (#, у) одной
и той же точки Μ плоскости связаны соотношениями
Μ(Ριφ)
Μ (χ,у)
Рис. L33
х = р cos φ,
у = ρ sm φ
(i)
ρ = у/х2 +y2, cos φ =
χ
smy> =
У
(2)
у/X2 + У2 ' \/х2 + У2
Отмстим, что формулы (1) получаются в силу определения
косинуса и синуса, а формулы (2) — путем простых
преобразований соотношений (1)
50
Глава I
§ 17. ОБОБЩЕННЫЕ ПОЛЯРНЫЕ КООРДИНАТЫ
НА ПЛОСКОСТИ
При решении задач приходится рассматривать точки, лежащие
на одной прямой, проходящей через полюс, и расположенные по
разные стороны от полюса (рис. 1.34). Α(-ρΑ,φ + π\ΜΆ(ρΑ,φ)
В этом случае удобно считать, что
все точки данной прямой имеют
одно и то же значение полярного угла,
например, φ — Ζ(Ορ,ΟΑ) или φ9 =
= Δ{Ορ, OB) = φ + π.
φ + π
Β(ρΒ,<ρ + π)
В{-рв, ψ)
Рис. 1.34
Условимся, что если в качестве полярного угла берут угол φ%
то для точек луча О А (рис. 1.34) полярные радиусы будут
положительными, а для точек луча ОБ — отрицательными. В
частности имеем А{рАЛ φ) и Б(—рв, φ) - Если же в качестве полярного
угла берут угол φ9 = φ + π, то для точек луча ОБ полярные
радиусы считают положительными, а для точек луча О А —
отрицательными, в частности имеем А(—ρ α , φ + тг), В(рв, φ + π).
Полярные координаты, в которых допускаются
отрицательные значения для полярного радиуса, называются
обобщенными полярными координатами. При этом, если для точки Μ
полярный радиус отрицателен, то полярный угол отсчитывает-
ся от полярной оси до луча, имеющего направление,
противоположное лучу ОМ.
Для любой точки Μ плоскости
(рис. 1.35) можно рассматривать как
обычные полярные координаты (ρ,φ),
так и обобщенные (р',у?')> причем
связь между этими координатами
определяется формулами
Μ(ρ7φ)
^(pV) = M(-plV?f7r)
Ψ
Рис. 1.35
Ρ =-Α
φ = φ + π.
Отметим, что и в случае обобщенных полярных координат
формулы (1) § 16 остаются в силе:
χ = ρ cos φ = (—ρ') cos(y/ — π) = //cos./?',
у = ρβιηφ = {-ρ') sin(y/ — π) = p'sinc^'.
Системы координат
51
§ 18. ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Для определения положения точки в трехмерном пространстве
кроме декартовых и аффинных систем координат используют
еще цилиндрические координаты.
Определим цилиндрическую систему координат. Для
этого в фиксированной плоскости 7г определяют
полярную систему координат с полюсом О и полярной осью
Ору а через точку О проводится ось Ok с началом в
точке Оу направляющим вектором к и перпендикулярная
плоскости 7г (рис. 1.36).
Пусть Μ — любая точка
пространства, N — ее
ортогональная проекция на
плоскость π, (ρ,φ) — полярные
координаты точки N на
плоскости 7Г, ρ € [0,+оо), φ е
€ [0,2π), Μζ — проекция
точки Μ на ось Ок параллельно
плоскости π, причем ΟΜζ = Рис. 1.36
= ζ, — оо < ζ < -Кю.
Упорядоченная тройка чисел (ρ,φ,ζ), взятая именно
в таком порядке, называется цилиндрическими
координатами точки М, при этом используется обозначение
Μ(ρ,φ,ζ).
Между точками трехмерного пространства, отличными от
точек оси Ok, и упорядоченными тройками чисел (ρ,φ,ζ), где
ρ € (0,4-оо), φ е [0,2π), ζ € (—оо,+оо), цилиндрическая
система координат устанавливает взаимно однозначное
соответствие·
Пусть цилиндрические и декартовы системы координат
связаны следующим образом: они имеют общее начало в
точке О, общую ось Ok с базисным вектором к,
базисный вектор г совпадает с масштабным вектором е
полярной оси, ось О J выбрана так, чтобы базисные векторы Г, J, к
образовывали правую тройку.
52
Глава I
Тогда цилиндрические координаты (ρ, φ> ζ) и декартовы
(ж, j/, ζ) одной и той же точки Μ трехмерного пространства
связаны соотношениями
χ = ρ cos <£>, у — Ρ sin <£>, г = ζ.
Отметим, что наименование «цилиндрические координаты»
связано с тем, что поверхность ρ = const является цилиндром
с образующими, параллельными оси Ок.
§ 19. СФЕРИЧЕСКИЕ КООРДИНАТЫ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Помимо уже известных систем координат для определения
положения точки в трехмерном пространстве используют
сферические координаты.
Определим сферическую систему координат. Для этого
на некоторой плоскости π фиксируется точка О — полюс
и через нее проводятся луч От в плоскости η с
началом в точке О и ось Ok с направляющим вектором /с,
перпендикулярным плоскости π (рис. 1.37).
Пусть Μ — некоторая
точка пространства и N — ее
ортогональная проекция на
плоскость π; ρ —сферический pa·*
диус, т. е. ρ — d(OyM); ρ €
€ [0,+оо)- Угол φΎ на
который следует повернуть против
часовой стрелки, если
смотреть со стороны
положительного направления вектора А\
луч От до совмещения его с лучом ONy называется
долготой, φ = Z(Om, ON), φ Ε [0,2π). Угол θ между лучом
ОМ и его проекцией ON, называется широтой, причем
θ = Ζ{ΟΝ, ОМ), θ е [-π/2, π/2].
Упорядоченная тройка чисел (р, (ру 0), взятая именно в
таком порядке, называется сферическими координатами
точки М, при этом используется обозначение Μ(ρ, φ% θ).
Рис. 1.37
Системы координат
53
Между всевозможными точками трехмерного
пространства, отличными от полюса, и упорядоченными тройками
чисел (ρ, φ, 0), где ρ е (0,+оо), φ <Ξ [0,2π)> θ е [-π/2,π/2],
сферические координаты устанавливают взаимно однозначное
соответствие.
Подчеркнем, что для полюса сферический радиус ρ = О,
а углы φ и θ —любые.
Пусть сферические и декартовы системы координат связаны
следующим образом: они имеют общее начало О, общую ось
Ok, ось О? направлена по лучу 0га, ось О J выбрана так, чтобы
тройка векторов г, fy к была правой.
Тогда сферические и декартовы координаты одной и той
же точки Μ трехмерного пространства связаны
соотношениями
χ = ρ cos θ cos φ,
у = pcos#sin<£,
ζ = psinfl.
Отметим, что наименование «сферические координаты»
связано с тем, что поверхность ρ = const является сферой с
центром в начале координат.
Иногда в качестве широты θ рассматривают угол между
осью Ок и лучом ОМ, θ = Z(Ok,OM), 0 ^ θ ^ π. В этом
случае связь между сферическими и декартовыми координатами
одной и той же точки выражается соотношениями
χ — psin0cos<£>,
у = psinflsiny?,
ζ = pcos0.
При заданной системе координат в трехмерном пространстве
положение точки определяется тремя координатами, на
плоскости — двумя координатами, на прямой — одной координатой.
Этот факт в механике интерпретируют следующим образом: в
трехмерном пространстве точка имеет три степени свободы, на
плоскости — две степени свободы, на прямой — одну степень
свободы.
54
Глава ί
§ 20. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Углом между векторами а и Ь называется угол, не
превосходящий 7г, между векторами а' и 5', равными о и В
соответственно и имеющими общее начало (рис. 1.38).
Если ненулевые векторы коллине-
арны и одинаково направлены, то угол
между ними полагают равным 0; если
ненулевые векторы коллинеарны и
противоположно направлены, то угол
между ними считают равным π. Рис. 1.38
Скалярным произведением а · b двух векторов а и b
называется произведение их модулей на косинус угла между ними, т. е.
—# —*
a-b=\a\- \b\ cos φ. (1)
Если а = б или 5 = б, то α · b = 0.
Ясно, что аа— \а\2, т. е. \а\ = у/а- а, причем а · а > 0, если
а — ненулевой вектор.
Два ненулевых вектора называются ортогональными, если
их скалярное произведение равно нулю.
Обозначим через а и Ь соответственно оси, определяемые
векторами аиб. Тогда по теореме об алгебраической проекции
вектора на заданную ось имеем
—♦ ~*
ProJa & = Η C0S Ψ у ProJb G = 1^1 cos Ψ·
В силу определения скалярного произведения получаем
а-6=|а|Рго£Ь, а ■ Ъ = |*| Projg 3. (2)
Понятие скалярного произведения векторов впервые
появилось в механике. Если вектор α изображает силу, точка
приложения которой перемещается из начала в конец вектора 5,
то работа А указанной силы определяется равенством А = \а\ χ
x|6[cos<p.
ЗАМЕЧАНИЕ. Наряду с введенным обозначением будем
использовать, когда это удобно, другую форму записи скалярного
произведения: (а, 6).
Системы координат 55
g- - ' — - ,
Свойства скалярного произведения:
1°. a-b = ba (коммутативность);
2° λ(α · b) = (λα) · В (ассоциативность относительно
числового множителя);
3°. (а + 5) · с = α ■ с + 6 ■ с (дистрибутивность относительно
суммы векторов);
4°. α · а > О, если а — ненулевой вектор; α · α = 0, если
α — нулевой вектор.
Доказательство. Первое свойство непосредственно
вытекает из определения скалярного произведения. Второе свойство
справедливо в силу соотношений (2) и теоремы об
алгебраической проекции произведения вектора на вещественное число.
Действительно, имеем
(λα) Ь = \Ъ\ Projg(Ao) = А|Ь| Proj£ а = \(а-Ъ).
Третье свойство следует из соотношений (2) и теоремы об
алгебраической проекции суммы векторов, так как
(а + Ъ) - с = с · (а + Ь) = |с| Рго£(а + Ь) =
= |cI(I>roJS a + Proj£ 6) = а ■ с + Ь · с.
Наконец, четвертое свойство вытекает непосредственно из
определения.
Теорема 1. Скалярное произведение двух векторов а и Ь,
заданных в произвольной аффинной системе координат
Οβι&2β3 своими координатами α(χι,τ/ι,ζι) и Ь{х2,У2,%2)>
находится по формуле
a-b = xix2(ei - ei) + (хху2 + X2Vi)(ei -e2) +
+ У\У2{€2 · е2) + (xiz2 + £2*i)(ei · е3) +
+ (2/1*2 + 2/2*i)(e2 · е3) + ziz2(e3 · е3). (3)
Доказательство. Формула (3) получается с помощью
простых вычислений, если воспользоваться
представлениями заданных векторов через базис a = x\t\ + y\C2 +
+ *1^з> b = Х2в\ + ?/2^2 + *2^3э и свойствами скалярного
произведения.
56
Глава I
Величины gtj = е* - ^-, г = 1, 2, 3; j = 1, 2, 3,
называются метрическими коэффициентами системы
координат Ое&ёз* Для вычисления скалярного произведения двух
векторов в аффинной системе координат необходимо знать
координаты этих векторов и метрические коэффициенты системы
координат.
Следствие 1. Модуль произвольного вектора a(xuyuz\) в
произвольной аффинной системе координат вычисляется по
формуле
\а\ = Va-a =
= Vsfpi^ (4)
Следствие 2. Угол φ между двумя векторами a(xi,yuzi)
и £(χ2ι2/2, ζ?) в аффинной системе координат Оёхё^ёз
находится по формуле -* г
φ = arccos =г, (5)
|α|·|6|
где для вычисления выражения под знаком арккосинуса следует
воспользоваться формулами (3) и (4).
Следствие 3· Для ДПСК справедливы формулы:
(6)
n = 3: a = x\i + y\J+z\ki Ь = Х2?+ 2/г/+ ъК
а · 6 = χιχ2 + 2/12/2 + ζι*2,
|α| = λ/x\ + y\ + z\, <p = Z(o, K),
х\Х2+У\У2+г\ Z2 (7)
V? = arccos . . „ ==;
V* ι + 2/i + *i ' Vж2 +У2+4
n = 2: a = χιΓ+ 2/iJ, 6 = ж2г*+ 2/2 j*, α · b = #i#2 + 2/12/2, (8)
|o| = V4 + 2/?, ^ = Z(a,6),
^1^2 + 2/12/2 (9)
V = arccos —/ 2 . 2;
λΛι + 2/i * V*2 + 2/2
—» —·
η = 1: α = χιΓ, b = #2*» л · ft = а^жг»
|o| = ja;i|, y> = Z(a, 6), ν3 = arccos
X\X2 (10)
ΝιΙΝΓ
Системы координат
57
Поскольку расстояние между двумя точками А(ха,Уа^а)
и В(хв>ув>гв) в трехмерном пространстве равно модулю
вектора AS(xb — %а, У в - У л у *в — ζ а) »то в силу соотношения (7)
в случае декартовой прямоугольной системы координат
получаем следующую формулу для нахождения расстояния между
названными точками:
d(A, В) = у/{хБ - хА)2 + (Ув ~Уа)2 + {zb - zA)2. (11)
Аналогично расстояние между двумя точками А(ха,Уа)
и В(хв,Ув) на плоскости находится по формуле
d(А В) = у/(хв~ха)2 + (ув-Уа)2, (12)
а расстояние между двумя точками А(ха) и В(хв) на прямой
соответственно по формуле
d(A,B) = \xB-xA\. (13)
Теорема 2. Необходимым и достаточным условием
ортогональности двух ненулевых векторов в трехмерном
пространстве а{х\) ух, ζχ) и Ъ(х2, 2/2ι ζ2), заданных в ДПСК
своими координатами, является равенство
xiX2 + yiy2 + ziz2 = 0. (14)
Доказательство. Утверждение непосредственно следует из
определения скалярного произведения и выражения (6).
Теорема 3. Декартовы прямоугольные координаты
вектора а{х\, 2/1, z\) равны скалярным произведениям этого
вектора на соответствующие базисные векторы:
—*
xi = aiy У\=а-Ъ z\=a-L· (15)
Доказательство. Пусть Г,£к —ортонормированныйбазис.
Тогда а = χχΐ + y\j + z\k, причем
-*
а · г = х\г- г + yij- г + z\k · г = Х\\
—ф
а ■ j = χιϊ- j + yij- j + zik· J= yi;
a> к = #ιΓ* к + yij- к + z\k · A: = z\.
58
Глава I
Рассмотрим в ДПСК Otjk вектор ОЙ.
приведенный в общее начало с ортом е
(рис. 1.39).
Косинусы углов а, /?, 7» которые
составляет орт е с базисными векторами
Г, J, fc, называются направляющими
косинусами вектора ОЙ.
Теорема 4. Направляющие косинусы вектора суть
координаты орта данного вектора.
Доказательство. Пусть е — орт вектора Ом, е = ехг +
+ eyf+ ezk. Тогда в силу теоремы 3 и определения скалярного
произведения имеем
ех = е-г = \e\\i\cosa =-cosa,
ву = е*3 = |e||Jl cos/3 = cos/3,
ez = e· k = |el|fc|cos7 = cos 7,
что и требовалось доказать.
Следствие. Для направляющих косинусов справедливо
соотношение cos2 a + cos2 β + cos2 7 = 1.
Пусть e*(cosa,cos/3,cos7) — единичный вектор, / — ось.
определяемая вектором в, и(х,?у,г) — произвольный вектор.
Тогда а ё = |е| Proj" а, Proj" а = χ cos a + у cos β + ζ cos ^.
§ 21. ЕВКЛИДОВЫ НОРМИРОВАННЫЕ
И МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
Линейное η-мерное пространство называется евклидовым
векторным η-мерным пространством, если в нем задана
функция, сопоставляющая двум любым элементам а и Ь этого
пространства вещественное число, называемое скалярным
произведением и обозначаемое а-Ъ, причем выполняются аксиомы:
12°. ab = ba\
13°. Х(а - Ь) = (λα) · Ь для любого AgR;
14°. (а + Ь) · с = а ■ с + 6 · с;
15е. а · а > О, если α φ 0; a · a = 0, если a = 0.
Рис. 1.39
Системы координат
59
Раздел математики, изучающий евклидовы пространства,
называется евклидовой геометрией. Евклидова геометрия
имеет два основных понятия (точка и вектор), четыре основных
отношения, удовлетворяющих сформулированным пятнадцати
аксиомам (ср. понятие аффинной геометрии в § 9).
Рассмотренные ранее линейные векторные пространства V1,
V2 7 V3 со скалярным произведением, определяемым по
формуле (1) § 20, представляют собой евклидовы векторные
пространства размерностей, соответственно, 1,2,3.
Векторное пространство Шп будет евклидовым η-мерным
пространством, если ввести в нем скалярное произведение для
его любых двух элементов α(αι,α<2, .. -, ап) и Ь(ри #2? · ·, Λι)
по формуле а · Ь = Υ^=ι афг.
Элементы векторного пространства α и 6 называются
ортогональными, если а · Ь = 0. Заметим, что в пространствах V2
и V3 понятия перпендикулярности и ортогональности совпадают.
Теорема I. Для любых двух элементов а и b произвольного
евклидова пространства верно неравенство
(а.Ь)2^(а-а)(Ь.Ь), (I)
называемое неравенством Коиш—Буняковского.
Доказательство. На основании аксиомы 15° имеем
неравенство (λα — Ъ) · (λα — Ъ) ^ 0, которое можно представить в
ВИД6 λ2(α ■ α) - 2λ(α · Ь) + (Ь ■ 6) £ 0.
Так как а · α > 0, то необходимым и достаточным условием
неотрицательности квадратного трехчлена является
неположительность его дискриминанта, т. е. (а ■ Ь)2 - (а - а) (6 ■ Ь) < 0.
Теорема доказана.
Из неравенства (1) следует, что -1 ^ J^^) ^ j Кроме
того, в любом евклидовом векторном пространстве имеем
\а\ = у/α а,
/( аЬ аЬ
а если φ = Δ\α, Ъ), то cos φ = г—:——τ, φ = arccos
\α\ · |6|' - — \α\ · \b\'
60
Глава ί
и в любом евклидовом точечном пространстве (т. е.
аффинном пространстве, в котором ассоциированный линеал
является евклидовым векторным пространством) можно находить
расстояние между точками:
<*(Д в) = \а£\ = VaS-aE.
Линейное η-мерное пространство L называется
нормированным, если имеется правило, посредством которого всякому
элементу χ е L ставится в соответствие вещественное число,
называемое нормой указанного элемента и обозначаемое
символом ||χ||, причем это правило подчинено аксиомам:
1'. ||ж|| ^ 0, если χ φ 0; ||ж|| = 0, если χ = 0;
2'. ||λα|| = |λ| · ||я|| для любого χ е L и произвольного
вещественного числа λ;
3'. ||ж + 2/|| ^ ||ж|| + H2/II для любых х,у eL.
Теорема 2. Всякое евклидово пространство можно
рассматривать как нормированное, если норму в нем опредвг-
лить равенством м .. /
IfII = уж-ж. (2)
Доказательство. Справедливость для нормы (2) первых
двух аксиом вытекает из соответствующих аксиом для
скалярного произведения. Убедимся в справедливости аксиомы 3' для
нормы (2). При этом будем опираться на неравенство Коши-
Буняковского, переписанное в виде
\х · 2/| ^ \/хх · у/у- 2/·
Тогда
\\х + у\\ = у/{х + у) · (ж + у) = yj(x ■ χ) + 2{х · у) + {у · у) ^
^ у(х - ж) + 2у/х-х у/у-у + {у-у) =
= ^{у/^^Л-у/у^)2 = ||*|| + Ml-
Сосредоточив внимание на линейных операциях в
множестве, мы пришли к понятию линейного (векторного) пространства,
а потом аффинного (точечного) пространства. Введя скалярное
Системы координат
61
произведение в ассоциированном векторном пространстве, мы
пришли к евклидову точечному пространству. Обратим теперь
внимание на одно лишь свойство точечного множества — на
наличие расстояния в нем. Это приводит нас к понятию
метрического пространства.
Множество называется метрическим пространством,
если каждой паре его элементов ее, у сопоставляется по некоторому
правилу неотрицательное вещественное число р(х,у),
называемое расстоянием, причем это правило подчинено аксиомам:
1". р(х, у) > О, если хфу\ р(х7 у) = 0, если χ = у\
2". p{x,y) = p{y,x)\
3"· р(х, У) ^ р(«, ζ) + ρ(ζ, у).
Отметим, что нормированное пространство можно
превратить в метрическое, если положить р(ж, у) = \\х — у\\ ·
Линейное метрическое пространство легко превратить в
нормированное, если положить ||ж|| = р(ж,0).
§ 22. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Наряду со скалярным произведением в векторной алгебре в
векторных пространствах V геометрических векторов определено
векторное произведение.
Векторным произведением вектора а на вектор Ь
называется вектор с, обозначаемый символом с = о χ Ь и
определяемый следующим образом:
1) модуль вектора с равен произведению модулей векторов а
и & на синус угла между ними, т. е. \с\ = \а\ · |6| sin φ, φ = Ζ(α, b);
2) вектор с ортогонален
каждому из векторов а и &;
3) вектор с направлен так,
что упорядоченная тройка
векторов а, Ь, с является правой
/ t лг\\ Рис· 140
(рис· 1.40).
Ясно, что если хотя бы один из векторов нулевой или если
векторы а и Ь коллинеарны, то их векторное произведение есть
0 (нулевой вектор).
62
Глава I
ЗАМЕЧАНИЕ. Наряду с введенным обозначением будем
использовать, когда это удобно, другую форму записи векторного
произведения: [а,Ь].
Понятие векторного произведения впервые появилось в
механике. Если вектор 6 представляет приложенную в некоторой
точке N силу, а вектор а направлен из некоторой точки О в
точку 7V, то вектор ах b является моментом силы Ь относительно
точки О.
Лемма. Векторное произведение двух неколли неарных
векторов а и е, один из которых а — произвольный
вектор, а другой е — единичный вектор, есть вектор О А",
построенный следующим образом:
1) векторы Sue приведены к общему началу О;
2) вектор ОА = а спроектирован на плоскость π,
перпендикулярную к вектору е и проходящую через О, при
этом получен вектор ОА';
3) вектор ΟΑή получается поворотом вектора О А! в
данной плоскости на угол π/2 так, чтобы упорядоченная
тройка ОА', е, О А" была правой.
Доказательство. Рассмотрим векторы ОА" и с = а х е.
Пусть ψ — угол между векторами а и ё\ а — угол между
вектором а и его проекцией на плоскость 7Г. Нетрудно видеть, что
вектор е лежит в той же плоскости, что и векторы а и О А'
(рис. 1.41, 1.42). Тогда векторы си ОА" ортогональны
плоскости, определяемой векторами е, α, Ο Α', и, следовательно, они
коллинеарны. Кроме того,
\с\ = |a[|e|sinv? = |a|sinv?,
Рис. 1.41
Рис. ί.42
Системы координат
63
VA<\ = \ОЛ\ - Ncos. = < 7}™W "*>· °< ** **
1 ' i| cos (φ - π/2), π/2 <φ<π7
поэтому \ОА"\ — |α| sin <^> = |с|. По построению тройка векторов
ОЛ\ е, OA')f — правая.
Далее, в силу того, что О ^ а < π/2, тройка векторов а,
е, О А" будет правой. Но по построению векторного прои
введения тройка а, еу с также правая, поэтому си О А" одинаково
направлены. Отсюда О Л" = а х е.
Свойства векторного произведения:
1°. а х 5 = —(6 χ а) (антикоммутативность);
2°. Λ(α χ Β) = (λα) χ 6 (ассоциативность относительно
числового множителя);
3°. (а+Ь)хс = ахс+5х с (дистрибутивность относительно
суммы векторов);
4°. ах а = 0 для любого вектора а.
Доказательство. Свойство /°. Будем считать, что векторы
α и 6 неколлинеарны, иначе свойство 1° очевидно.
Рассмотрим векторы c = axbnd = bxaa обозначим через φ
угол между а и Е. Ясно, что |с| = \а χ b\ = \a\\b\smip, \d\ =
= |a||6|sin<p,T. е. |с| = |d|. Векторы си d коллинеарны, так как
они перпендикулярны плоскости, определяе- kg
мой векторами α и 5. Далее, согласно
определению векторного произведения, упорядочен-
пые тройки векторов а, 6, с и 6, a, d правые, а
это влечет противоположную направленность
векторов end (рис. 1.43). Поэтому векторы с
и d противоположны, т. е. α χ δ = —(6 χ а). Рис. 1.43
Свойство 2°. Будем считать, что векторы α и & неколлине-
арные и λ т^ 0. Рассмотрим векторы с = λ(α χ б), d= (λα) χ 5
и обозначим через φ угол между α и 5, а через ψ — угол между
λα и Ь.
Ясно, что φ — ψ, если λ > 0, и ψ = π - φ, если
λ < 0 (рис. 1.44, 1.45). Векторы end коллинеарны, так
как они перпендикулярны плоскости, определяемой
векторами а и Ь. Модули указанных векторов равны, поскольку
64
Глава I
ах Ь
axb^
Χα
Ρα
c*d
Рис. 1.45
\c[ = \d\ = |Λ||α||5| sin <p. Далее, если λ > 0, то а и λα
одинаково направлены, а значит, и векторы α χ 5 и (λα) χ 6 одинаково
направлены. Если λ < 0, то α и λα противоположно
направлены, но в обоих случаях векторы λ(α χ В) и (λα) χ 5 одинаково
направлены. Поэтому с = d.
Свойство 3°. Будем считать, что ни один из векторов а, Ь
и с не является нулевым, иначе приведенное свойство очевидно.
Докажем сначала справедливость равенства (а + 6)хе = ах
χ е + б χ ёГ, где е— единичный вектор. Будем предполагать, что
векторы а, б, ё*некомпланарны.
Приведем векторы е, а, а + Ь к общему началу О и
спроектируем векторы α, α + б, б на плоскость 7г, ортогональную
вектору е и проходящую через точку О. При этом получим
соответственно векторы ОА', ОВ\ А'ВГ (рис. 1.46). Построим,
как указано в лемме, векторы ОА"' 0&\А'В". По
определению суммы векторов ОВ" = ОА" + А"£". Но в силу леммы
О? = α χ е, А"ВЛ = б χ е, Ш? = (а + б) χ е, поэтому
(а+ 5) χ ё* = ах е + б χ е.
Ясно, что если ё\ а, 6 компланарны, то доказательство и
соответствующий чертеж несколько упрощаются.
Ρν с. 1А6
Системы координат
65
Пусть е—орт вектора с. Тогда с = Хе, поэтому
(а+ 6) хс=(й + 6) χ (Ае) =
= А((а + 6)хе) = А(ахе + 6хе) =
= λ(α х е) + Х(Ь χ е) = а х (Аё) + 6 χ (Аё) =
—*
= а х с + бхс.
Свойство 4°. Справедливость указанного соотношения
непосредственно вытекает из определения векторного
произведения.
Заметим, что равенства
λ(α х Ь) = α χ (λ&),
αχ (Ь + с) =axb + axc
легко получить из второго и третьего свойства, используя
свойство антикоммутативности. Действительно,
α χ (\Ь) = -(А6) χ о = -\{Ь χ о) = λ(α χ 6),
αχ (6 + с) = -(6 +с) ха = -(6 χ о + сх а) =
= ах& + йхс.
Доказанные свойства позволяют при векторном
перемножении векторных многочленов выполнять действия почленно
и производить объединение числовых множителей. При этом
нужно тщательно следить за порядком векторных множителей.
Теорема I. Векторное произведение векторов a(xi,yi,zi)
и Ь(х2,У2,22), заданных своими декартовыми
прямоугольными координатами, находится по формуле
—
2/ι *ι
2/2 22
г +
Ζί Χι
Ζ2 Χ2
-* ι
.7 +
х\ 2/1
Х2 2/21
(1)
г J k
;? w Γ Ι I \У1 *1|-», ΙΛ1 *1| -*. |·*Ί 5/11 г·
α χ 6= Ian 2/ι «il = I U + l I 7+I \k =
\X2 2/2 Z2
= (2/1*2 ~ y2Zi)t+ (zxx2 - z2xi)f+ (xiy2 - #22/ι)&·
Доказательство. Пусть г, J, fc —ортонормировамныйбазис
декартовой прямоугольной системы координат. Тогда
а = Χιϊ+ yij + ζφ, b — χ2ΐ+ у2?+ z2k.
66
Глава i
Ясно, что в правой ДПСК
Гх г'— 0, JxT— — /с, кхг = %
гх?=к, /х/=б, kxj^-г,
Г χ А: = —£ fx к = гу к χ к = 0.
В силу свойств векторного произведения
axb= {Xit + yij + zik) χ {Х2?+У2?+ *2к) =
= а^жгОГх г*) + ^i2/2(?x Л + £ιζ2<Τχ fc)+
+ У1Х2ЦХ г) + yiy2(jx j) + yiz2(jx k)+
+ zix-2(k хг) + ziy2(k x/)+ z\z2{k χ к) =
—*
= (У1*2 _ 2/2^1 )Г+ (^1^2 - Ζ2Χΐ)Ι+ {Х\У2 ~ Х2У\)к.
ЗАМЕЧАНИЕ. Аналогично тому, как это сделано в теореме 1,
можно получить формулу векторного произведения в аффинных
координатах. Действительно, пусть а{х\,у\,ζχ) и b(x2>y2,z2)
заданы своими координатами относительно произвольного
базиса ё*ье2,е3. Тогда
axb= (хгёг + уге2 + zic3) х {х2ё\ + у2е2 + г2е3) =
= (yiz2 - y2z\){e2 х ёз) + {ζ\χ2 - z2xi)f^3 x ei)+
+ (^i2/2 -x2yi)(ei X e2),
что символически может быть записано так:
а х Ь =
е2 х ез е3 х ei ei x e2
a?i ?/i -ει
^2 2/2 *2
(2)
Таким образом, векторное произведение в аффинной
системе координат вычисляется по формуле (2), аналогичной
формуле (1), но в базисе ё^ х ёз > ^з х ё\, ei x ё*2 (см. задачу 9 в конце
главы). При этом следует подчеркнуть, что формула (1) верна,
если исходная ДПСК— правая система координат.
Теорема 2. Необходимым и достаточным условием
коллинеарности двух ненулевых векторов а и b является равен-
ство а х Ъ = 0.
Системы координат
67
Доказательство. Необходимость. Пусть а и Ь коллинеар-
ны. Тогда угол ψ между ними равен 0, если они одинаково
направлены, и равен π, если они противоположно направлены, но
в любом случае \а χ 5| = Ja||5| sin</? = 0.
Достаточность. Пусть α χ Ъ = 0, т. е. \а χ b\ = 0. Но
\а χ Ь\ = |a||i;|sin<£> = 0, откуда sin</? = 0, следовательно,
φ = тг/с, к е Ζ, т. е. векторы α и 5 коллинеарны.
Теорема 3. Модуль векторного произведения двух неколли-
неарных векторов а и b равняется площади S
параллелограмма, построенного на этих векторах после приведения
их к общему началу, т. е.
\а χ 6| = S.
(3)
Доказательство. Известно, что площадь
параллелограмма равна произведению длин его смежных сторон на
синус угла между ними (рис. 1.47): ^ в
Sobda = \0А\\Ш\пп1р9 где ^ JC ^D
φ — угол между векторами ^^^/^ °^^^т^^у^
θ1 и Ш. Отсюда ja χ Ь| - «^ а А
= \а\ |5| sin φ = Sobda· Puc'L47
Следствие 1. Векторное произведение векторов а и Ъ можно
выразить формулой axb = Sey где ь — орт векторного
произведения а х 6, S — площадь параллелограмма, построенного
на приведенных к общему началу векторах а и Ь.
Следствие 2. Площадь параллелограмма, построенного на двух
неколлинеарных векторах a(xi,yi7zi) и Ъ(х2,У2,%2)> заданных
своими прямоугольными декартовыми координатами и
приведенных к общему началу, определяется по формуле
S =
\
\У\ *\
2/2 Z2
2
+
Xl Ζ\
Χ2 Ζ2
2
+
£l 2/1
^2 ?/2
Доказательство. Указанное равенство вытекает из
соотношений (3), (1) и формулы для определения модуля
вектора.
68
Глава I
ЗАМЕЧАНИЕ. Поворотом или
псевдовекторным произведением вектора а, лежащего на
плоскости, называют вектор [а], получающийся
поворотом вектора а на угол π/2 по часовой стрелке
(рис. 1.48).
Отметим, что псевдовекторное произведение обладает
следующими свойствами:
1°. [a + b] = [a] + [bl
2°. [λα] = λ[α];
3°. [α] = б тогда лишь, когда α = 0.
Выведем формулу псевдовекторного произведения вектора
α в координатах. Пусть вектор а в правой ДПСК Оху имеет
координаты (х, у). Тогда
[а] = [хг + yj] = х[г] + y[j] = уг- xj =
г J
χ у
§ 23. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ
ТРЕХ ВЕКТОРОВ
Смешанным произведением трех векторов а, 6, с называется
ЧИСЛО ,_ - ^ _ Л - ,.ч
(а, 6, с) = (а х 6) ■ с.
Из определения ясно, что смешанное произведение равно
нулю, если хотя бы один из данных векторов нулевой, или если
любые два из них коллинеарны.
Пусть, к примеру, векторы бис коллинеарны. Тогда 5 = Ас,
а поэтому (а, 5, с) = (ах Ас) · с — λ(α χ с) · с, но (а х с) 1 с.
Следовательно, (α χ с) - с = 0.
Теорема 1. Смешанное произведение трех векторов
a(si,j/b3i), Ь(^2,2/2,^2). с(а;3,уз^з), заданных своими
декартовыми прямоугольными координатами, находится по
формуле
\&i 2/1 *ι|
(а, Ь:с) =
%2 2/2
!*з Уз
*2
^3
(2)
Системы координат
69
Доказательство. В силу известного из курса алгебры
свойства определителя, теоремы 1 § 22 и теоремы 1 § 20 имеем
xi 2/1
Х2 2/2
хз Уз
ζι
Ζ2
Ζ3
= я3
2/1 ζι
г/2 ζ2
-г/з
XI Ζι
%2 Ζ2
+ Ζ3
xi 2/11
X2 2/21
= (axb) -с = (a,6,e).
Теорема 2. Необходимым и достаточным условием
компланарности трех векторов а, В, с является равенство нулю
их смешанного произведения (а, 6, с) = О,
До ка за те л ьств о. Необходимость. Если векторы ауВус
компланарны, то вектор axb ортогонален плоскости
векторов а и 6, а следовательно, и вектору е, а тогда
(ах6)-с = 0.
Достаточность. Пусть (а, 6, с) = 0. Будем считать, что
среди данных векторов нет нулевого и никакие два из них не
являются коллинеарными, ибо иначе сразу можно утверждать,
что векторы а, В, с компланарны. Пусть S = \а χ Ь\ч е—орт
вектора ах В.
Тогда
{a,b,c) = (axb) c = Se- c= S\e\\c\ cosZ(e*,с) = 0,
откуда £{е,с) = π/2 и с лежит в плоскости векторов а, В. т. е.
векторы а, 6, с компланарны.
Теорема 3. Смешанное произведение (а, Ву с) трех
некомпланарных векторов равно объему V параллелепипеда,
построенного на векторах-сомножителях, взятому со
знаком «+», если тройка правая, и со знаком « — », если эта
тройка левая, т.е. .. ^ г _,
\{аХс)\ = К
Доказательство. Пусть S— площадь параллелограмма,
построенного на векторах, равных векторам а и В
соответственно и исходящих из общей точки. Допустим, что е — орт
вектора а х 6, а h — высота параллелепипеда, построенного
70
Глава I
Рис. 1.49 Рис. 1.50
на векторах, равных векторам а, В, с и исходящих из
общей точки, при условии, что основанием служит параллело-
1рамм, построенный на векторах, равных а и Ь соответственно
(рис. 1.49,1.50).
Ясно, что а х Ь = Бел е- с = |e|Proj*c = Proj|c. Отметим,
что Proj|c = +Λ, если тройка векторов а, 6, с является правой,
и Proj^c = —hy если левой.
Тогда
(й,Ь,с>(ахЬ).с = 5е · с = 5(±Л) - ±V,
причем берем « + », если тройка (а, 6, с) правая, и « — », если эта
тройка левая.
Следствие. Верно равенство
(а х Ь) ■ с = α ■ (6 х с). (3)
Доказательство. В самом деле, в силу коммутативности
скалярного произведения а · (Ь χ с) = (5 χ с) · ат и нам достаточно
показать, что (α χ 6) · с = (Ь χ с) ■ а. Последнее равенство
очевидно, ибо абсолютная величина каждого из чисел равна объему
параллелепипеда, построенного на векторах а, 5, с, исходящих
из общей точки, и, кроме того, эти числа имеют одинаковые
знаки, так как тройки векторов а, 6, с и 6, с, а имеют одинаковую
ориентацию.
ЗАМЕЧАНИЕ 1. Отметим, что приведенные свойства
смешанного произведения векторов позволяют вычислять его в
произвольном базисе.
Действительно, пусть векторы α(#ι,2/ι,*ι), Ь(х2,У2^2)^
с(хз,2/з,^з) заданы в произвольном базисе ё\% $2, ёз- Тогда,
воспользовавшись формулой (2) § 22 и тождеством (3), имеем
Системы, координат
7ί
(a,b,c) = (α χ b) с =
= {{У\-1 ~ z№)(?2 x e3) + (?ι3Γ2 - а?1«2)(ё*з х e*i)+
+ (жιί/2 - ^2ϊ/ι)(<4 x e2)) · (a-j^i + Узе2 + ~ус3) =
= oc3(yiz2 - y2Zi)(eu€2,e3) + y3(zxx2 - Z2Xi)(cue2)c2)-{
+ z5{xiy2 -Х2У\)(е1у€2,ё3).
Тогда, в силу известных из алгебры свойств определителя,
получаем
(а,Ь,с) =
Х\ У\ Z\
Х2 У2 Z2
^3 УЗ Z3
(ё\,е2,ез).
(4)
Заметим, что формула (2) справедлива лишь в случае правой
исходной ДПСК-
ЗАМЕЧАНИЕ 2. Из теоремы 3 следует, что (а, 5, с) > О
((а, 6,с) < 0), когда тройка векторов а, В, с — правая
(левая). Поэтому правую (левую) тройку векторов еще называют
положительно (отрицательно) ориентированной.
На плоскости можно ввести аналог операции смешанного
произведения.
Смешанным произведением векторов α и б в плоскости
(псевдоскалярным произведением) называют скалярное
произведение вектора α на поворот вектора 5, при этом используют
обозначение (а, [В]).
Введенная операция обладает следующими свойствами:
1°. (г,й) = -(Ма1);
2°. (а, [В]) =0 лишь тогда, когда векторы а и В коллинеарны;
3°. (а, [6]) > 0 ((а, [В]) < 0) лишь тогда, когда векторы а и
В образуют правую (левую) пару. Поэтому правую (левую) пару
векторов плоскости называют положительно
(отрицательно) ориентированной.
Вычислим псевдоскалярное произведение векторов а и В в
координатах. Пусть α и В имеют в некоторой правой ДПСК
координаты (хъЗ/ι), (^2?ί/2) соответственно. Тогда
(a, [b]) = (xit + yij} у2г- x2f) = х\Уг - %2У\ =
Я?1 J/1
Х2 У2
(5)
72
Гласа I
В произвольном базисе ё\, е2 псевдоскалярное
произведение векторов а{хиУ\) и 6(2:2,2/2) вычисляется по формулам
(а, [&]) = (a:ie*i + у\е2, [z2ei + 2/2е2]) =
= (#iei +s/ie2,a^[ei] + У2Ш) =
= г/1Ж2(е2> [ei]) + яш(е1, [е2]) = (жц/г - s2J/i)(ei, [e2])·
Поэтому
(а, [6]) =
«ι Ш
Х2 2/2
(ехЛЗг])·
(6)
Заметим, что при доказательстве формулы (6) мы
воспользовались свойством (ei, [е2]) = — (ebi [<?ι])·
§ 24. ДВОЙНОЕ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
Двойным векторным произведением трех векторов а, 5, с
называется вектор а х (bx с).
Теорема· Двойное векторное произведение равно среднему
вектору произведения, умноженному на скалярное
произведение двух остальных, минус другой вектор внутреннего
произведения, умноженный на скалярное произведение двух
остальных: _
ах(Ьхс) = Ь(а*с) — с (а · 6).
Доказательство. Введем ортонормирован-
ный базис Г, J, k у взяв вектор Гколлинеарным
вектору а, а вектор /расположив
ортогонально Г в плоскости векторов а и Ь (рис. 1.51),
Ясно, что
а = χ\ΐ + 0J+ 0&,
—> —#
Ь = гс2? + У23 + 0Λ,
с = хзг + УзЗ + z-zk.
Тогда
(1)
Рис. 1.51
b X с —
ΐ Τ к
Х2 2/2 О
#3 2/3 *з
= 2/223г*- ^2^з/+ (#22/3 - а?з1&)*'
Системы координат
73
ах (bx с) =
г 3 к
χι О О
2/2^3 -#2^3 Х2УЗ -ЯЗ?/2|
= -^ι(^22/3 - х-зу-2)з~ X\X2Z?,k.
Далее, а · с~ xix^, a-b = χιΧ2,
b(a · с) — c(a ■ b) =
= ххх3(х2г + У2З + Щ - xix2{xtf + УзЗ + ZA =
= -(^1^22/3 - Х1ХзУ2)з~ xiX2Z3k = ax (bx c).
Следствие. Верна формула
—* —* -♦
(ax b) x c = b(a · c) — a(6 - c).
Доказательство. В силу антикоммутативности векторного
произведения, формулы (1), коммутативности скалярного
произведения, имеем
(а х Ь) χ с = —с χ (α χ b) =
= -а(с-6) + 6(с-а) =
—* —·
= b(a · с) — a(b- с).
ЗАДАЧИ И УПРАЖНЕНИЯ
\. Доказать, что каково бы ни было конечное множество
точек А\, А^, ..., Ап (но, прямой, на плоскости или
в трехмерном пространстве), существует, и притом
только одна, такая точка Μ3 что
Ήλχ + ША2 +... + ШЛп = а
Решение. Обозначим через г* радиус-вектор точки Aiy
г == 1, 2, ..., п, и пусть г — радиус-вектор точки М. Тогда
MAi = ?i - г, г = 1,2,..., п. Суммируя по г последние
равенства, получаем
η η
^МАг = ^{Гг-Г)=б.
г=1
г=1
74
Глава I
Откуда nf= Σ2=ιЪ, следовательно, f = ~
ΣΓ=ι^.Существование и единственность точки М следуют из
единственности решения приведенного уравнения.
2. В плоскости треугольника ЛВС найти такую
точку, чтобы сумма векторов, идущих из этой точки к
вершинам треугольника,, была равна б.
Решение. Пусть Μ— искомая точка. Из решения
предыдущей задачи точка Μ существует и единственна, при
этом ее радиус-вектор г равен r= \{fy 4- гЬ + гз), где
ίΊ,^ 1^з — радиус-векторы вершин А, Ву С соответственно.
11айдсм точку Μ. По условию МА =
- -(Ш + Мб). Тогда из правила
параллелограмма сложения векторов и
определения равенства векторов
получаем, что точка Μ должна лежать на
медиане Δ ABC, проведенной к стороне рис. 1.52
ВС (рис. 1.52).
Аналогично из равенств мЗ = -(мЛ + мб)ч Мб =
= - (мА + MS) следует, что точка Μ должна лежать на
медианах, проведенных к сторонам АС и АВ, т. е. точка Μ —
точка пересечения медиан.
ЗАМЕЧАНИЕ. Следует отметить, что при решении
сформулированных задач мы попутно установили известную теорему
о том, что медианы треугольника пересекаются в одной точке,
при этом радиус-вектор точки пересечения медиан вычисляется
через радиус-векторы вершин ААВС по приведенной формуле.
З.Даны два ненулевых вектора а и В. Представить
вектор Ь в виде суммы двух векторов χ и у так, чтобы
вектор χ был коллинеарен вектору а, а вектор у
ортогонален вектору а.
Решение. По условию задачи а^Ои вектор χ коллинеарен
вектору а. Поэтому χ = λα, где λ — некоторое вещественное
число. Поскольку у = Ь — χ и у ортогонален вектору а, то
0 = у- а = (6 — х) -а = а-Ь — А(а-а).
Откуда λ = (α · b)/(a ■ а). Поэтому χ — |^|α, у = Ь— gfja.
Системы координат
75
4. Даны два неколли неарных вектора а а б. Найти
вектор х, компланарный векторам а и b и
удовлетворяющий системе уравнений α · χ = I, b- x = 0.
Решение. Поскольку х компланарен векторам α и 5, а
векторы α и б неколлинсарны, то они образуют базис плоскости, а
поэтому χ = аа + /Зб. Для нахождения координат вектора χ в
базисе а, 6 подставим его представление в систему уравнений.
Получим
"α(α·α)Η-0(α·0) = 1,
α(α-6)+/3(6-6) = 0.
Отсюда
Ь-6
а
(α·α)(ί>*&)-(α&)2
Таким образом,
о? =
β
а
(a-a){b-b)-{a-b)2
{b-b)a-(a-b)b
(a-a){b-b)-{a-b)2
Задание. Доказать, что в условиях сформулированной
задачи (а · а)(б ■ б) - (а · б)2 ^ 0.
5· Даны два ненулевых вектора a ub. Найти вектор г, >ш-
ляющийся ортогональной проекцией вектора б «а /2p<z~
мую, направление которой определяется вектором а.
Решение. По условию задачи вектор α φ
Φ 0, а б — ^ортогонален α (рис. 1.53).
Поскольку с коллинеарен вектору а ф б, то
с = λα. Из условия ортогональности
—♦ -♦ —*
0=(Ь — с)-а=(Ь — Аа) - а = а- Ь — Х(а ■ а).
Отсюда λ = (α ■ b)/(a-a)y и поэтому с = J§a.
6. Даны два ненулевых вектора а и п. Найти вектор Ь,
являющийся ортогональной проекцией вектора а на
плоскость, перпендикулярную вектору п.
Решение. По условию задачи η Φ б,
вектор а — Ь коллинеарен вектору η и вектор б
ортогонален вектору η (рис. 1.54). Поэтому
а-б = Ап,гдеА = |^.Тогдаб = а-§|й.
Рис. 154
76
Глава I
7. Найти необходимые и достаточные условия, при
которых операция векторного произведения ассоциативна,
т. е. выполняется равенство (axb) χ с = ах (В χ с).
Ρ е ш е н и е. По свойствам двойного векторного произведения
(ахЬ)хс = Ь(а-с)-а(Ь>с),
ах(Ьхс) = 6(а-с)-с(а>&).
Поэтому должно быть выполнено равенство
а(Ь-с) = с{а-Ъ).
Отсюда с необходимостью следует, что либо α и с
коллинеарны, либо Ь ■ с = 0, α · Ь = 0.
Проверим, будут ли полученные условия достаточными.
Второе условие таковым очевидно является. Покажем
достаточность первого из них.
Пусть векторы α и с коллинеарны. Если хотя бы один из
векторов равен б, то ответ очевиден. Предположим, что а ф 0.
Тогда с = λα. Вычислим
а(Ь ■ с) = а(Ь ■ λα) = Xa(b · α), с{а · b) = λα(α ■ Ь)>
Откуда a(b · с) = с(а · 6). Значит, искомые условия таковы:
а) α и с коллинеарны; б) 5- с = 0 и а - Ь = 0.
8. Доказать тождества:
a)(axb)-(cx<5= r^ r J·
о ■ с о · α
—# -♦ —*_*—# -^ _#. _* _* _»
б) (axb)x(cxd) = с{ауЬ,а)—(1(а^ЬуС) = b(a,c,d)—a(6,c,d).
в)(ахЬ,Ьхс,сха) = (а, 5, с)2.
г) <ί(α, 5, с) = а(Ь, с, d) + 5(c, a, d) + с(а, 6, d).
а Ь с
ι —* ι
\ау by с-у\
д)(а,Ь,с)(хху) =
e)(a,b,c){x,y,z) =
χ · а ж · 6 ж ■ с
у-а у-Ь у*'С
г · а г · о ζ · с
Системы координат 77
Решение.
а) По свойствам смешанного и двойного векторного
произведений
(ох Ъ) -(ex d) = (a,b,(cx d)) = ((ex d),a,6) =
—* —# —* —# —*
= ((с χ d) χ α) · Ь= (d(c· о) — c(d- a)) · b =
= (b-d){a-c)-(b'c){a-d).
б) По формулам разложения двойного векторного
произведения, с одной стороны,
{α χ Ъ) χ (с χ d) = с((а χ b) · ίί) - d{(a xb)c) =
—* —* —♦ —*
= c(a, b,d) — d(a} 6, c),
а с другой стороны,
—* ~# —* —* —# —*
(axi)x(cxd) = b(a - (c χ d)) — a(b · (c χ d)) =
= b(a, c} d) — a(6, c, d).
в) Используя свойство смешанного и двойного
векторного произведения, а также второе из доказанных тождеств,
получаем
(ах b,bx с,сх а) = ((ax b) χ (bx с)) · (ex a) =
= (b(a> 6, c) — c(a, 6,6)) · (c χ a) =
= (a,6,c)(6- (ex a)) = (a,6,c)2.
г) Указание. Воспользоваться тождеством б).
д) Воспользуемся тождествами а) и г), полагая d = χ χ у.
Тогда
(χ χ у)(α,Ь,с) = а(Ь,с,(хху)) + Ь(с,α, (χ χ у)) +
+ с(а,&,(* χ £)) = Й((£х с) · (f x j/)) +
+ b((c χ α)-(χ χ у)) + г({а xb)-(xx у)) =
1 -♦ —ψ
\b ■ χ &· у
—# ^* -* -*
\с- χ су
+ b
—· —* —# —»
с- а: с - у
а-х а-у
+ с
а - χ а- у\
—# —♦
Ь- χ Ь-у\
что является разложением искомого определителя третьего
порядка по первой строке.
е) Указание. Воспользоваться тождеством д).
78
Глава I
9. Дан базис elf e2, е$. Доказать, что векторы
$2 х е3, е3 х еь ё\ х е2
также образуют базис. Какую ориентацию будет иметь
базис из с/екторных произведений?
Решение. Из тождества 8в) и некомпланарности ёьёЬэёз
имеем
(е2 х е3,ёз х ei,ei χ е2) =
= (ei х ё2,С2 хе3,е3 х ё\) = (еье2,е3)2 > 0.
Поэтому векторы е2 х ёз, ё*з χ ^ι, ё\ х ^2 также образуют
базис, при этом обязательно правый (положительно
ориентированный).
10. Даны три некомпланарных вектора a, b и с. Найти
вектор х, удовлетворяющий системе уравнений
а-х = ау b^x — β^ с-я? = 7-
Указание. Разложить вектор χ в базисе 5 χ с,с χ α, а х 6.
~ _ а(Ь хс)+ /?(с х а) + у(а χ 5)
Ответ: а: = — ^—' -.
(а,6,€)
11. Найти необходимое и достаточное условие того, чтобы
уравнение α χ χ = Ь, где а Ф 0, имело решение, и
получить общее решение этого уравнения.
Решение. Пусть χ — решение уравнения. Тогда с
необходимостью имеем а · b = 0. Проверим достаточность этого условия.
Для этого попробуем искать решение уравнения в виде щ =
= Х(а х 6). Подставим его в исходное уравнение. Тогда λ(α χ
χ (α χ 6)) = 6, следовательно, λ(α(α · 6) — Ε(α · α)) = 6. Отсюда
—λ6(α · α) = 6 и, окончательно, λ = —1/(α · α).
Таким образом, при условии α ■ 6 = 0 вектор #о = —(α χ
χ δ)/(α · α) является частным решением уравнения, а, значит,
условие является необходимым и достаточным.
Найдем общее решение уравнения. Пусть χ — произвольное
решение уравнения. Тогда α χ χ = b и а х xq = b. Откуда
—φ
α χ {χ - xq) = 0, т. е. векторы χ - xq и α — коллинеарны.
Системы координат
79
Поскольку а φ б, то найдется такое число а, что χ - xq = cm.
Таким образом, решение указанного уравнения существует тогда
и только тогда, когда а - b = 0, а его общим решением является
вектор χ = -(αχ Ь)/{а · а) + аа.
12· Найти вектор χ из системы уравнений а± · χ = α, α2 ^
χ χ = b, где U\ · α2 Φ· 0, α2 ■ b = 0.
Ρ е ш е ни е. Домножим обе части второго из уравнений вскторно
на вектор а\. Тогда αχ χ (α2 χ χ) = α\ χ 6. Поэтому
α2(αι · x) — χ(3ι - ο>2) = ο,ι χ 6»
где αϊ ■ ж = о;. Отсюда получаем вектор if:
αα2 — αϊ χ 6
a; — — .
α\ ■ α2
Глава 2
ПРЕОБРАЗОВАНИЕ КООРДИНАТ
§ 1. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
НА ДЕКАРТОВОЙ ОСИ
Пусть на прямой введены две оси координат с одним и тем же
направляющим вектором, причем начало Οχ новой оси 0\г имеет
на старой оси Ог координату α (рис. 2.1).
Рассмотрим произвольную точку М, имеющую
координату χ относительно старой оси Ог и координату х'
относительно новой оси ΟιΓ. Установим связь г^^г^ Щх)
между координатами точки Μ в ста- О ^θ{{ά) Mix')
рой и новой системах координат. На Рис. 2Л
основании леммы Шаля ΟΟι+ΟχΜ = ОМ> откуда χ = α + χ'.
Указанное преобразование координат на оси называется
переносом начала координат.
Общее преобразование координат на оси связано с
переходом к новому началу О и к новой единице измерения длин.
В этом случае связь между координатами некоторой точки в
старой и новой системах координат определяется линейным
соотношением χ = ах' + β, где а ф 0.
§ 2. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ
КООРДИНАТ НА ПЛОСКОСТИ
Будем рассматривать на плоскости две произвольные декартовы
прямоугольные системы координат: первая — ОГ/,
определяемая началом О и базисом г, J, и вторая — О' ΐ*ψ, определяемая
началом О' и базисом г1, f (рис. 2.2, 2.3).
Преобразование координат
81
Рис, 2.2
Рис. 23
Пусть начало второй системы О1 имеет координаты (а, 6)
относительно первой системы координат, т. е. Ο'(α,ό), а
произвольная точка Μ плоскости имеет координаты (х,у)
относительно первой системы и (х',г/) относительно второй
системы, новые базисные векторы г\ j' представляются следующим
образом через старый базис Г, jf:
-♦/
z+t
I =OLul + OCi23y 3 =<*2\1 + Οί223,
(1)
где otij — направляющие косинусы векторов г", f
относительно г,э, т. е. ац = cos/.(i}T'), αΐ2 = cosZ^T7), «21 =
= COS Ζ(ϊ*, J ') , α22 = COS Ζ(£ f) .
Матрица /Л Л ч
А=(*п а12\
\<*21 «22/
называется матрицей перехода от базиса г*, J к базису г*',/'.
/7 я прр
ОЙ = Об' + СГМ = аг + bf+ х'г' + y'j\
хг + у2- аг + bj + ж;(ацГ+ ai2J) + у'{a2it + a22J) =
= (a + χ'аи + у'ос2\)г + (6 + ж'ахг + y'a22)j,
и в силу единственности разложения вектора по базису получаем
формулы преобразования координат:
χ = а + х'ап + у'а2ъ У = Ь + х'аю + y'ot22. (2)
Матрицу
А' =
, _ /an агЛ
\<*12 »22/
называют матрицей преобразования координат. Она
является транспонированной к матрице Л, причем первый столбец ее
82
Глава 2
содержит координаты вектора Ϊ* относительно базиса Г, j,
второй столбец— координаты вектора f относительно базиса Г, j.
Отметим, что dct А* ф О, ибо векторы Г' и f образуют
базис.
Из равенств (2) следует, что каковы бы ни были две
прямоугольные декартовы системы координат на плоскости,
координаты любой точки относительно первой системы являются
линейными функциями координат той же точки относительно
второй системы.
Данное утверждение останется в силе и для двух общих
декартовых систем координат на плоскости.
В дальнейшем будем различать два случая в
зависимости от того, являются ли рассматриваемые системы
координат системами одной или противоположных ориентации
(рис. 2.2, 2.3).
В обоих случаях обозначим через φ угол между векторами Г'
и Г, т. е. ψ — Ζ(Γ,Γ').
Допустим, что системы Oiju ОТ'J*' одной и той же правой
ориентации (рис. 2.2).
В этом случае ψ = Ζ(Γ,Γ') = Z(J5if'), а потому первая
система координат может быть совмещена со второй посредством
параллельного переноса вдоль вектора Ои* и последующего
поворота вокруг О' на угол φ.
Далее,
ап = cos/(Г,?') = cosy?,
c*i2 = cos Z(J, г9) = cos(7r/2 - φ) = sin φ,
a2\ = cos Ζ (г" J') = cos(<^ + π/2) = — sin φ,
α22 = cosZ(J, J') = cosy>.
Отсюда формулы преобразования координат на плоскости и
матрица преобразования имеют вид
χ = а + χ cos φ —у1 sin φ,
ι ι \ )
у = b + X sin φ + y cos <p,
д,= /со5„ -sin„\ dctj4< = 1.
\siny> cosy? /
Преобразование координат
83
Разрешая уравнения (3) относительно х' и у\ получаем
формулы обратных преобразований:
х1 = (х — a) cosy? + (у — Ь) sin ψΛ
yf — — (χ — a) sin φ + (у — b) cos ψ.
Допустим теперь, что системы Otf и О'г' j' имеют
противоположные ориентации, причем система Oij — правая, а
О'г'/'— левая (рис. 2.3).
Тогда ψ = Z.(t,i,)f Z(£J') = π — φ, а потому первую
систему координат невозможно совместить со второй
посредством параллельного переноса и поворота. В этом случае
требуется после параллельного переноса еще изменить направление
оси ординат на противоположное, т. с. осуществить зеркальное
отражение этой оси.
Имеем
Qn = cosZ(r,r') = cos ν?,
ο?ΐ2 = cos Z(jf, ?') = cos(7r/2 — φ) = sin φ>
a2\ = cosZ(?, jf') = cos(7r/2 — φ) = sin у?,
α22 = cos Ζ (J, J') = cos(tt — ν?) = - cos^p.
Поэтому из (2) в случае систем с разной ориентацией
формулы преобразования координат и матрица
преобразования имеют вид
χ = а + х9 cos φ + y* sin φ,
у = b + xf sin φ — у' cos <p,
Α·=(™ψ sinM, d*it'--l.
\smy> —cos φ J
Разрешая (4) относительно х9 и у*, получим формулы
обратных преобразований в рассматриваемом случае:
х' — (х — a) cos φ + (у — b) sin <p,
ί/ = (χ — α) sin φ— (у — b) cos y>.
ЗАМЕЧАНИЕ. В дальнейшем условимся рассматривать
лишь правые системы координат и переходы от одной правой
системы к другой правой системе, если нет особых оговорок.
84
Глава 2
Напомним, что квадратную матрицу А порядка η называют
ортогональной у если
aka,j = <
10, з Φ К
где а*- — к-и столбец матрицы А и ак · o>j —скалярное
произведение в Еп.
Ясно, что матрица А! преобразования координат
ортогональная, так как векторы %i\j' образуют ортонормированный
базис (см. (2), (3), (4) соответственно).
Вследствие этого факта преобразование, определяемое
формулами (3), называется ортогональным. Оно
распадается на сумму двух преобразований, одно из которых есть
параллельный перенос системы координат, а другое— поворот
относительно начала О' на угол φ. Полагая в (3) φ = 0,
имеем формулы преобразования координат при параллельном
переносе вдоль вектора 00'\
χ = а + х\
причем
А =
Полагая в (3) а = Ь = 0, получим формулы преобразования
координат при повороте системы вокруг начала О на угол ψ
против часовой стрелки:
χ = х1 cos φ— у' sin φ9
у = χ9 sin φ + у1 cos ψ.
Такое преобразование называется однородным
ортогональным преобразованием.
Любая ортогональная матрица второго порядка с
определителем, равным 1 (—1), задает преобразование одной
прямоугольной системы координат на плоскости в другую
прямоугольную с тем же началом и той же (противоположной)
ориентацией·
«·
Преобразование координат
85
§ 3. ПРЕОБРАЗОВАНИЕ
ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Пусть в трехмерном пространстве рассматриваются две
произвольные декартовы прямоугольные системы координат:
первая — Oijk, определяемая
началом О и базисом Г, j j fc, и
вторая — Ο'ΐ' j' fc\ определяемая
началом Of и базисом ?', jf', k'.
Установим формулы, по которым
преобразуются координаты
произвольной точки Μ пространства при
переходе от одной системы
координат к другой (рис. 2.4).
Пусть начало О' второй системы имеет координаты (а, 6, с)
относительно Oijk, т. е. 0'{α^,ο). Новые базисные векторы
представляются через базис г*, j> к:
г9 = аиг + «i2jf+ «13&,
f = «21?+ «22J* + «2з£, (1)
£' = «3ΐ?+ «32J* + «зз&·
Рис. 2А
Матрица
«11 «12 «13
В — I «21 «22 «23
^«31 «32 «ЗЗу
является матрицей перехода от базиса г, j, к к базису Г', jf', &'.
Допустим, что произвольная точка Μ плоскости имеет
координаты {x7y>z) относительно первой системы и (x',y',z')
относительно второй системы.
Далее,
ОМ = ОО' + О'М,
#г*+ yj + zk = αΐ+ 6f + ск +
+ х'(апг + oci2j + disk) + 2/'(of2i«*4- Q22/+ <*2з£) +
+ г'{аз\г + a32J*+ <*зз£) = (α + х'ац + t/'a2i + 2'α3ΐΚ+
+ (b + x'ai2 + ί/'θ!22 + zfa32)T+ (с + ж'ахз + 2/'<*23 4- 2'а3з)£,
86
Глава 2
и в силу теоремы о единственности разложения вектора по
базису получаем формулы преобразования координат.
χ = а + x'aii + у'&2\ + z'asi,
у = Ъ + x'cl\2 + 2/022 + ζ'α32ι (2)
ζ = с + #'αΐ3 + у'&23 + ζ'α33·
Матрицу
ran c*2i «3i
В' = I C*12 <*22 ^32
<οΐ3 а2з оззу
также называют матрицей преобразования координат. Она
является транспонированной к матрице В, причем первый
столбец ее содержит координаты вектора %\ второй — координаты
вектора J', и третий — координаты вектора к' относительно
базиса Г, /, к, и, кроме того, detB' φ О, ибо векторы ?', J', &'
образуют (ортонормированный) базис.
Коэффициенты afcs (к = 1, 2, 3, 5 = 1, 2, 3) вформуле(1)
суть направляющие косинусы новых базисных векторов 7', J',
&' относительно базиса Г, jf, fc:
an =cosZ(r,7'), Q12 = cosZ(J,r'), ai3 = cosZ(fc,?'),
a2\ = cos Ζ (ζ J')> a22 = cosZ(£,f'), a23 = cosZ(fc,J'),
a3i = cosZ(^fc'), a32 = cosZ^fc')* азз = cosZ(fc,fc').
Из формул (2) следует, что каковы бы ни были две
прямоугольные.системы координат в пространстве, координаты любой
точки относительно первой системы являются линейными
функциями координат той же точки относительно второй системы.
Ясно, что это утверждение сохраняет силу и для двух
общих декартовых систем координат в пространстве. При этом
в силу аналитического и геометрического смысла смешанного
произведения базисных векторов г\ j ', fc', имеем
detB' = {i'J',k') = +l,
если векторы образуют правую тройку, и
detB' = (t'J\k') = -l
в случае левой тройки.
Преобразование координат 87
Отметим, что матрица В* также ортогональная, поскольку
»11 +«12+^13 = 11
2
2
°!ΐ + а22 + °1з = !>
^31+^32+^33 = ^ ,3)
®>\\&2\ + Oi\2Ci22 + θΊ3<*23 = О,
Οί\\Οίζΐ + «12^32 + #13^33 = О,
«21^31 + <^22^32 + ^23^33 = 0.
Вследствие этого, преобразование координат в трехмерном
пространстве, определяемое формулами (2), называют
ортогональным, а если осуществляется только поворот системы
координат (а = b = с = 0), то — однородным ортогональным
преобразованием.
Любая ортогональная матрица третьего порядка с
определителем, равным 1 (—1), задает преобразование одной
прямоугольной системы координат в пространстве в
другую прямоугольную систему с тем же началом и той же
(противоположной) ориентацией.
Если
В =
то базис при преобразовании координат не меняется, и формулы
преобразования имеют вид
χ = а + χ',
ζ = с + ζ'.
Такое преобразование является параллельным переносом.
В заключение отметим, что рассуждения, используемые при
выводе формул преобразования координат на плоскости и в
пространстве аналогичны за исключением особенностей,
связанных с размерностью пространств. Это позволяет провести
необходимые обобщения на пространства произвольной
размерности (см. § 5).
88
Глава 2
§ 4. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
С ПОМОЩЬЮ УГЛОВ ЭЙЛЕРА
Преобразование декартовой прямоугольной системы
координат Ozj*k в другую декартову прямоугольную систему 0%'J9kf
с тем же началом определяется формулами (2) § 3 при
условии а — Ь = с = 0, причем между девятью
коэффициентами этого преобразования имеется шесть связей, определяемых
соотношениями (3) § 3.
Поэтому преобразование одной прямоугольной системы
координат в пространстве в другую с тем же началом зависит лишь
от трех независимых параметров,
Л· Эйлер (1707—1783) доказал, что преобразование одной
прямоугольной системы координат в пространстве в
другую прямоугольную систему координат той же ориентации
и с тем же началом можно осуществить тремя преобра^
зованиями, каждое из которых является поворотом вокруг
осей координат одной из данных систем и вспомогательных
прямоугольных систем координат.
Для определенности будем
считать, что системы Oijfk и Ог'з'к1
правые. Рассмотрим три угла фл
θ, φ, полностью характеризующие
расположение второй системы
относительно первой (рис. 2.5).
Для точного определения этих
углов введем в рассмотрение ось Ой,
определяемую линией пересечения
плоскостей Огз и Ог 'j ', началом О
и единичным вектором и, направление которого выбирается
таким, что тройка векторов к> к\и — правая.
Обозначим через ф = /.(г,й) угол между векторами г ичг,
отсчитываемый в плоскости Огз в направлении
кратчайшего поворота от Г к J, т. е. в случае правой системы координат
против часовой стрелки, если смотреть со стороны вектора fe,
0<^<2тг;
Рис. 2.5
Преобразование координат 89
θ = Z(fc, k') —угол между векторами к и &',
отсчитываемый в плоскости этих векторов против часовой стрелки, если
смотреть со стороны вектора й, 0 < θ < π;
ψ = Z(t?,?') — угол между векторами й и г*',
отсчитываемый в плоскости Ог'з1 в направлении кратчайшего
поворота от г9 к /', т. е. в случае правой системы координат
против часовой стрелки, если смотреть со стороны вектора fc',
О ^ φ < 2π.
Указанные углы называются углами Эйлера, и каждый из
них имеет свое название: ф —угол прецессии, θ —угол
нутации, φ — угол собственного вращения.
Теперь преобразование системы Oijk в систему Oz'j'k'
можно представить в виде последовательного выполнения трех
поворотов. Первый из них — поворот системы Oij к на угол ф
вокруг оси Ofc, переводящий эту систему в систему Ox\y\Z\b
для которой Ох\ совпадаете Ой, Οζγ — с Ок. Второй —
поворот системы Ox\y\Z\ на угол θ вокруг оси Ох\ (Ой),
переводящий эту систему в систему Ох2У2*2 » для которой Ох2 совпадает
с Ой. И, наконец, третий из них — поворот системы Ох2У2*2
на угол φ вокруг оси Ок\ переводящий эту систему Ох2У2%2 в
Ог'з'к*.
В силу формул (3) § 2 этой главы для первого поворота
справедливы формулы
χ = χι cos ф — ул sin ф,
у = #isin^ + 2/icos^, (1)
ζ — ζ\.
Для второго поворота имеем формулы
х\ = #2,
Уг = 2/2 cos θ - Z2 sin 0, (2)
2ι = 2/2 sin θ + ζ2 cos 0,
и для третьего поворота, соответственно, имеем
Х2 = х1 cos φ — у1 sin ψ,
У2 = х9 sin φ Л-у1 cos φ, (3)
z2 = ζ'.
90
Глава 2
Откуда
х = ж'(cos φ cos ψ — sin φ sin ф соз θ) —
— у'(sin φ cos ф + cos φ sin -0 cos 0) + zf sin 0 sin ф>
у = a;'(cos <p sin ^ + sin <p cos ^ cos 0) — (4)
— 2/'(sin<£>sin^ — cos <p cos ^ cos 0) — г'sin 0 cos ^>
ζ = χ1 sin </? sin 0 + у' cos </? sin 0 + ζ* cos 0.
Заметим, что ни направления осей координат, ни величина
углов Эйлера не зависят от того, где выбрано начало первой и
второй систем координат, а потому общее преобразование
координат в пространстве можно рассматривать как суперпозицию
параллельного переноса и трех поворотов в соответствующих
координатных плоскостях.
Общее преобразование при условии, что обе системы правые,
имеет вид , ^ , , п f / /ч
χ = а + Fi(^f 0, φ, χ , у , ζ ),
у = 6 + F2(^>, 0, φ} χ\ г/, г'),
г = с + F3(^>, 0, φ, xf, y\ ζ'),
где функции Fi, F2, F3 определяются правыми частями
формул (4).
ЗАМЕЧАНИЕ 1. Переход от одной ДПСК Otjk к другой
ДПСК Ot'J'k'у имеющей то же начало и ту же ориентацию,
может быть осуществлен тремя поворотами, соответственно на
углы Φ,θ,φ вокруг трех осей Оку Ой, Ок\ которые определены
исходной системой Oifk и углами ф, 0, φ.
Для системы Ot'j'k' углы Эйлера являются
независимыми параметрами, причем эти параметры могут
принимать произвольные значения в пределах 0 ^ ф < 2π,
0 < 0 <7г,0 < φ<2π и каждому набору ф> 0, φ отвечает
вполне определенная система координат Ог'э 'к*.
Предположим, что с твердым телом, имеющим
закрепленную точку О, жестко связана система координат Ог'^'к*.
Тогда различные возможные положения тела взаимно однозначно
соответствуют различным положениям этой системы координат,
а значит, вполне определяются углами Эйлера системы Ог'з'к*
относительно неподвижной системы Oifk.
Преобразование координат
91
Таким образом, все возможные положения твердого тела с
одной закрепленной точкой О вполне определяются тремя
независимыми параметрами — углами Эйлера. В механике этот факт
выражают так: тело с одной закрепленной точкой имеет три
степени свободы.
Если допустить свободное перемещение твердого тела в
пространстве, то к трем независимым параметрам (углам Эйлера)
присоединяются еще три — координаты точки нового начала О' t
в которую перемещается точка О. В этом случае говорят, что
твердое тело, свободно перемещающееся в пространстве,
имеет шесть степеней свободы, т. е. его положение определяется
шестью независимыми параметрами.
ЗАМЕЧАНИЕ 2. Корабль можно рассматривать как твердое
тело, находящееся во взаимодействии с жидкостью. При
изучении движения корабля рассмотрим две системы координат:
такую неподвижную систему Οξηζ, что поверхность воды
совпадает с плоскостью Οξη, и систему координат Gxyz,
жестко связанную с кораблем, где <7(ξο> ϊ?ο> Со) — центр тяжести
корабля.
Тогда, с учетом сказанного в замечании 1, положение
корабля в системе Οξηζ единственным образом определяется шестью
величинами: координатами центра тяжести (£(ь*?сьСо) и
углами Эйлера, которые в этом случае соответственно
называются: ψ —угол рысканья, θ —угол крена, φ —угол дифферента.
§ 5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
В МНОГОМЕРНОМ ЛИНЕАЛЕ
Пусть еь в2, - ·. у еп и е[,е'2у ..., е'п —два произвольных
базиса η-мерного линеала Ln. Разложим элементы е\, е!2 %..., е'п
по базису eJt ег,..., еп:
е\ = απβι + αΐ2β2 + ... + aineni
е'2 = OL2iBi + OL22C2 + - - - + Ос2п^п, , .
en = αη1^ΐ + Οίπ2^2 + . - . + Ofnnen.
92
Глава 2
Матрицу
Л =
«11 «12
«21 «22
(2)
\рсп\ аП2 ...
называют матрицей преобразования базиса, или
матрицей перехода от первого базиса βι, β2, ..., еп ко второму
е[, е'2 е'п, причем элементы г -и строчки этой матрицы суть
координаты базисного элемента е\ относительно базиса eif
Подчеркнем, что det Α φ О, ибо векторы (элементы)
с1 » е2»
е^ линейно независимы.
Нетрудно видеть, что обратный переход от базиса е\ , е'2,... t
е^ к базису βι? β2,..., еп осуществляется с помощью
матрицы А""1, т. е. обратной к матрице А. В самом деле,
преобразование (1) формально можно записать в матричном
виде
е' = Ае, (3)
где
е' =
е'2
\</
е =
е2
В силу того, что detA φ 0, матрица А имеет обратную
матрицу А"1, т. е. такую, что А"1 А = Е\ из курса алгебры
известно,что
А21
det A det А
Ш^
inl_
detA
ι-i -
(4)
iln
А2£
< det Л det А
det A/
где Aifc — алгебраическое дополнение элемента aik
определителя матрицы А. Тогда, умножая равенство (3) на матрицу A~L
слева, получаем
А~1е' = А~1Ае, е = А~1е\
(5)
Преобразование координат
93
Aue\+A2ie'2 + '·
Cl detA
Ayle\ + A22e'2 + · ·
Cz~ detA
_ Alne\ + A2ne'2 + -
• + Anle'n
>
• + An2e'n
>
■ ■ + А е!
(6)
Пусть χ — произвольный вектор (элемент) из Ln, причем
χ = χχθχ + х2е2 + h Xn^ny (7)
X = ίΓχβχ + #2e2 + ' ' " + %nen· (8)
Подставив в (8) вместо ж выражение (7) и вместо элементов
βχ, е'2у ..., е^ их выражения в соответствии с формулами (1),
получим:
х\е\ + x2e2-i Ухп^п = ^i(anei + #12^2 + ^αιηΒη)+
+ χ'η(αηιΒι + αη2^2 Η h «ηπ^η)- (9)
Из (9) в силу единственности разложения по базису
вытекают формулы перехода от координат (х'ц ..., х'п)
относительно базиса е[, е2у ..., е'п к координатам (яχ, ..., #п)
относительно базиса βχ, β2, -. -, en:
#x = αχι^χ + α2ι^2 + · ■ · + #м1#п>
^2 = #12#χ + α22^2 + - · · + αη2%η, ..^
#η = Οί\ηΧι + Of2n^2 + · ■ « + ΟίηηΧη,
Матрица преобразования координат А! является
транспонированной к матрице А\
(ац #21 ■·· <*ni\
#12 #22 ... θίη2
Α' =
\ct\n 0ί2η ..· αηη/
(11)
причем элементы j-ro столбца этой матрицы суть координаты
базисного элемента е^ относительно базиса βχ, е2,..., еп.
94
Глава 2
Подставив в (7) вместо χ выражение (8) и вместо элементов
βι, β2ν -.., еп их выражения в соответствии с формулами (6),
получим
J ~l
I 9
ziei + ...+xnen =
xi{Ane[ + A2ie'2 + ... +
detA
+
, *2(Ai2ei+Л22е'2 + ... + Л,2е/п)
_| __ _ 1_ _ _ _ _|_
+
detA
^n\Aine^ + Л.2пв2 + «■«·+- AnnBn)
detA
(12)
Из равенства (12) в силу единственности разложения по
базису вытекает формула перехода от координат (xux2l ..., хп)
относительно базиса βχ, β2,.. -» е„ к координатам (х^ х'2, ..., х'п)
относительно базиса е[ , е2,..., е'п:
АПХг + Αγ2Ϊ2 + ■ ■ - + ΛιηΧη
detA
/ A<z\X\ + Аъ2%2 + · · . + ^2n^n
«i =
а:2 —
detA
(13)
*n =
Λα^ι + Лп2х2 + ... + А
пп%п
detA
Соответствующая Matрица преобразования координат
JLn_\
4- Л \
И-1) =
\
Ли-
detA
detA
AtlL·
Ml
detA
A22
detA
An1
detA
A2n
detA
det A det A
detA
является матрицей, транспонированной к обратной
матрице А"1.
Итак, если А — матрица перехода от базиса βι,
β2, ..., еп к базису е'^е^,.. .,е^, το матрица перехода
от координат произвольного элемента относительно базиса
βι,β2,...,βη к координатам того же элемента относительно
базиса е[у е'2,..., е'п есть матрица, транспонированная к
обратной матрице.
Преобразование координат
95
§ 6. ПРЕОБРАЗОВАНИЕ
АФФИННЫХ КООРДИНАТ
Аффинные координаты являются обобщением понятия
декартовых координат. Поэтому формулы преобразования декартовых
координат могут быть получены как частный случай формул
преобразования аффинной системы координат. В данном параграфе
мы исследуем в основном случай преобразования аффинных
координат в пространстве. Однако читатель уже настолько
подготовлен, что может просто получить формулы преобразования
координат на плоскости и прямой самостоятельно (см. задачи 1,2).
Рассмотрим две аффинные системы координат Ое^с^ и
О'ё^ёоёз в пространстве (рис. 2.6).
Пусть Μ —произвольная
точка пространства. Обозначим
через (xyy,z) координаты точки Μ в
системе координат Оё^ёз; через
(х'.у'.г') — координаты этой же Рис. 2.6
точки в системе координат О'с'^е^ (#о,2/о>2о) — коораинаты
точки О* в системе координат Оё\ё2е^.
Имеет место равенство
Ш = о6' + сум. (1)
Однако —-> _
ОМ = Χ€ι + уе2 + ze3,
Οθ[ = хцёу + у0е2 + zoe3,
Разложим базисные векторы е[, е92, е$ по базису ё\, е2, е*з -
Получаем формулы
е[ =аце! + «12^2 + «1зёз,
е2 = «2i ё\ + α22β2 + a2seSj (2)
63 = «31^1 + α32^2 + азз^з-
Матрица преобразования базиса имеет вид
(an ai2 «13'
а2\ а22 «23
«31 «32 «33,
96
Глава 2
Непосредственно проверяется формула
(ё1>ё*2>ёз) = detA3(ei,e2,e3). (3)
Из формулы (3) получаем, что det A3 φ О, поскольку векторы
в1,е2,ез и ^Ϊϊ^2>^3 — базисы, а поэтому линейно независимы.
Кроме того, если det Аз > 0, то обе системы координат имеют
одинаковую ориентацию, а если det A3 < 0 — противоположную.
Подставляем разложения для векторов
в равенство (1), при этом векторы ё*{, ё2, ёз заменяем по
формулам (2). Тогда
(х - х0 - αχγχ' - Q2i2/' - osi^ei +
+ {У ~ 2/о - oti2x' - а22у' - ct32z')e2 +
+ (ζ - zq - alsxf - а2зу' - аззг'Кз = б.
Векторы €ι, ё*2, ё*з линейно независимы. Поэтому
коэффициенты линейной комбинации равны нулю. Следовательно,
χ = х0 + ощх' + а2\у' + asiz',
у = Уо + Oii2x' + ос22у' + αΖ2ζ\ (4)
ζ = zq + deux' + а23у' + азз*'
— формулы преобразования координат при переходе от
системы координат 0'ё\е'2ё'ъ к системе координат Оё\ё2ёз.
Поскольку det Л3 Φ О, то формулы (4) можно однозначно
разрешить относительно а/, у', ζ':
χ' = х'0 + а'пх + а'21у + a'31z,
У' = Уо + ос12х + а22у + α32ζ, (5)
ζ' = ζ0 + α'13ζ + a23y + a'S3z
— формулы преобразования координат при переходе от системы
координат Оёуё2ёз к системе координат O'e^e^ (обратное
преобразование), где ^ , ^ , _, , _,
ei = апег + а12е2 + а13е3,
е2 = а21ег + а22е2 + а23е3,
^3 = «31^1 + а32^2 + α33^3
— формулы преобразования базиса, (xq.Vq, ζ$) — координаты
точки О в системе координат О'е^е^.
Преобразование координат
97
Пусть А3 = 2?з> где Е3 — единичная матрица третьего
порядка (базисы не меняются). В этом частном случае
формулы (2) и (4) примут соответственно вид е± = е[, е2 = е2, ёз =
= eg, и ж = гго + х\ у = З/о + 2/'. г = го + г' — формулы
преобразования координат при параллельном переносе начала
системы координат.
ЗАМЕЧАНИЕ I. Из формул (2), (4) и (5) видно, что
произвольное преобразование координат состоит из параллельного
переноса начала системы координат и преобразования базиса
(поворота базисных векторов, изменения длин базисных векторов н
углов между ними).
ЗАМЕЧАНИЕ 2. Предположим, что базис е{, е^, е%
получается из базиса еь е^, ез с помощью непрерывного
преобразования относительно параметра t на промежутке [0, 1]. Это
означает, что
e[(t) = αιι(ί)βϊ + α12(ί)β2 + <*13(0*3,
^(О = a2i(t)ei + a22(t)e2 + a23{t)e3}
*з(*) = α3ΐ(ί)^ι + a32(t)e2 + a33{t)e3,
где aij(t) — непрерывные на [0, 1] функции, при этом е[(0) =
= ei , ^(0) = е2у g*(0) - е3, е{(1) = е{, ё*(1) = eg, ё$(1) = ё£.
Рассмотрим матрицу
/ftll(t) «12(0 <*1з(*)\
Л*(0 = («21(0 «22(0 «23(*)1
\α3ι(ί) α32(ί) азз(*)/
и ее определитель det Аз(£), который также является
непрерывной функцией на отрезке [0, 1].
Введем в рассмотрение вспомогательную функцию
φ{1) = (βί(ί),βϊ(ί),^(ί)) = det A3(t)(eue2,e3).
Функция (to(t) также непрерывна на [0, 1], при этом φ(0) =
= (еье21бз) и φ(1) = (е^е^ё^).
Поэтому если базисы ё\, е2, е3 и е[, е^, е3 имеют
одинаковую ориентацию, то существует непрерывное преобразование,
такое что <p(t) > 0, t e [0, 1], т. е. det A3(t) > 0.
98
Глава 2
Если же базисы противоположной ориентации, например,
(еье21ез) > 0, а {%&%) < 0, то φ(0) > 0, а φ(1) < 0.
Тогда по известной из математического анализа теореме Коши
существует такая точка ίο € (0, 1), что <p(to) = О, а поэтому
dcti43(to) = 0,т-е. (e{(io),^(i0)3^(i0)) =0.
Таким образом, при непрерывном преобразовании одного
базиса в базис противоположной ориентации обязательно
необходимо пройти положение линейной зависимости векторов.
Пусть системы координат ОехёЬёз и О'ё^е^ являются
декартовыми прямоугольными системами координат. Тогда формулы
преобразования базиса имеют вид (2), а преобразования
координат — (4) (обратного — (5)). В этом случае можно уточнить
геометрический смысл коэффициентов. В формулах (2) as\, α321
а3з — это направляющие косинусы вектора e's в системе
координат Oei^es. В этом случае detAs = ±1, причем « + »
берем в случае, если обе системы координат имеют одинаковую
ориентацию, и « — », если противоположную.
ЗАМЕЧАНИЕ 3. Исходя из замечания 2, получаем, что
одну ДПСК можно получить из другой с помощью
непрерывного преобразования (параллельный перенос и поворот), если они
имеют одинаковую ориентацию. Если же ориентация
противоположная, то требуется разрывное преобразование
(параллельный перенос, поворот и зеркальное отражение одной из осей).
ЗАДАЧИ И УПРАЖНЕНИЯ
1с Доказать, что формулы преобразования аффинных
координат на плоскости имеют вид
χ = а + х'ац + j/a^i,
у = 6 + х!ах2 + у'&22>
где ζ
Аг=Гп а>2
4^21 #22
— матрица преобразования базиса (какого в какой?).
Какой вид будут иметь формулы обратного
преобразования и каков смысл коэффициентов обратного
преобразования?
Преобразование координат
99
Получить формулы преобразования декартовых
координат как частный случай преобразования аффинных
координат
2. Доказать формулу (3) § 6.
3· Доказать, что в случае преобразования аффинных
координат на плоскости формула (3) $ 6 примет вид
(eii[^l)=deti42(eil[e2l)1
где (ё"ь[ё2]) —псевдоскалярное произведение.
Что можно сказать относительно det Ач?
Какие выводы можно сделать относительно
непрерывного преобразования базисов на плоскости (одной или
противоположной ориентации)?
4. Доказать, что формулы преобразования аффинных
координат на прямой имеют вид
χ = xq + ol\\x'
и пояснить смысл параметров.
Что можно сказать о непрерывном преобразовании
базисов?
Уточнить смысл параметров в случае преобразования
декартовых координат на прямой.
5. Найти формулы перехода от аффинной системы
координат Оху, у которой \ё\\ = |ё*2| = 1, /(ё\,е2) = ω,
к такой прямоугольной системе координат Ох'у*,
положительными направлениями осей которой
являются биссектрисы первого и второго координатных углов
аффинной системы, а длина базисных векторов также
равна 1. Будут ли системы координат иметь
одинаковую ориентацию?
Решение. Формулы
преобразования координат имеют вид
х1 = хац +2/<*2ь
у' = ха{2 +2/с*22,
{;
_ Λ*ιι θί2Λ
\ai2 «22/ '
Рис. 2.7
00
Глава 2
где {cctJ} — коэффициенты разложения базиса ei, e^ по базису
с[% Со,т. е. е] = аце[ + а^е^, ё-г = сс2\ё[ + «22^2- Вычислим
коэффициенты oci3?, г = 1, 2; j = 1, 2. Как видно из рисунка 2.7,
αη = cos (ω/2), αΐ2 = - sin (ω/2),
c*2i = cos (ω/2), c*22 = sin (ω/2),
det A = 2 sin (ω/2) cos (ω/2) = sin ω > 0, 0 < ω < π.
Получаем, что χ' = (χ + у)cos (ω/2), у* = (у — χ) sin (ω/2).
Системы имеют одинаковую ориентацию.
6· Написать формулы преобразования прямоугольных
координат на плоскости, если начало новой системы
располагается в точке 0'(—3, -2), угол от оси Ох до оси
О'х' равен -arccos(-4/5) и указанные системы
координат имеют противоположную ориентацию.
Ρ е ш е н и е. Из условия задачи следует, что система координат
О'х'у1 получается из Оху параллельным переносом, поворотом
системы координат и зеркальным
отражением оси Оу. Рассмотрим
систему координат Ох"у",
получающуюся параллельным переносом О'х'у' в
точку О (рис. 2.8). Тогда, если ввести
обозначение φ = — arccos (-4/5), то Рис. 2.8
г' = — cos (π - <р)г — sin (π - φ)ϊ,
J' = — sin (π — φ)ΐ+ cos (π — (p)j,
или
w 4^ 3W w 3^ 4^
Поэтому формулы преобразования координат имеют вид
я; = -3 - (4/5)*' - (3/5)г/, У = -2 - (3/5)*' + (4/5)|Л
7. Прямоугольная система координат 0'х"у" получена
из системы координат Оху параллельным переносом в
точку О'(хо, уо) и поворотом на угол φ против часовой
стрелки. Найти координаты нового центра и базисных
векторов в исходной системе координат Оху.
Ответ: Ο'(ζο,ί/ο)> **" = (cos¥>>sinΦ). Τ = (-sin<p,cos<p).
Преобразование координат
101
& Прямоугольная система координат 0"х"у" получена
из системы координат Оху поворотом на угол φ
против часовой стрелки (Ох'у*) и параллельным переносом
центра в точку Ο"(χο>ί/ο)· Найти координаты
центра О" и базисных векторов ΐ", f в исходной системе
координат Оху.
Решение. После поворота системы координат на угол φ
формулы преобразования примут вид χ — :r'cos<p - j/'sin<p, у =
= a;'sin<£ + 2/cosv?-
Таким образом, г" = (cos^, sin v?), f = (—sin^cos^).
После параллельного переноса х' = хо + х" , у' = т/о + у".
°ЗТ0МУ χ = (хь + я") cos <р-{уо+ у") sin φ,
2/ = (#о + χ") sin φ + (yo + у") cos <ρ.
Откуда формулы преобразования координат при переходе от
Опх"у" к Оху примут вид
χ = хо cos φ — yo sin φ + χ" cos <p — у" sin <£,
j/ = xo sin φ + yo cos φ + χ" sin ψ + у" cos φ9
Таким образом, 0"(xq cos (p-yosintp, xo sin ^ + 2/o cos φ) t Γ" =■
= (cos <p, sin <p), f = (— sin y>, cos y?).
9. Начало системы координат находится в вершине
ромба, сторона которого равна 2, а оси совпадают со сто-
ронами, причем угол между ними равен 2π/3. Найти
формулы преобразования при переходе к прямоугольной
системе координат, начало которой располагается в
точке пересечения диагоналей, а оси совпадают с
указанными диагоналями (меньшая диагональ лежит на
оси абсцисс).
Ответ: χ = 1 + sr' - (>/3/3)?Л у = 1 + х' + (λ/5/3)ϊΛ
Глава 3
ЛИНИИ И ПОВЕРХНОСТИ
ПЕРВОГО ПОРЯДКА
§ 1. УРАВНЕНИЯ ЛИНИЙ И ПОВЕРХНОСТЕЙ
Важнейшим в аналитической геометрии является вопрос об
аналитическом представлении линий на плоскости, а также линий
и поверхностей в пространстве при помощи уравнений,
связывающих координаты точек названных объектов.
Местоположение произвольной точки относительно
фиксированной однозначно определяется ее радиус-вектором или
ее координатами, если система координат задана. Поэтому
существуют различные виды уравнений линий и поверхностей в
зависимости от того, в каком пространстве и в какой системе
координат они рассматриваются. По возможности мы будем
одновременно рассматривать поверхности, линии на
плоскости и линии в пространстве, показывая тем самым аналогии и
различия в понятиях и определениях.
Векторным уравнением поверхности S (линии L на
плоскости) называется уравнение вида
F(r) = 0 (1)
или
F(fi = б, (2)
где г — радиус-вектор, рассматриваемый в пространстве У3
{У2),г F — совокупность операций над радиус-вектором, если
радиус-вектор г любой точки Μ (г), лежащей на поверхности S
(на линии L), удовлетворяет уравнению (I) или (2), а любое
решение г уравнения (1) или (2) является радиус-вектором
некоторой точки М(г)у лежащей на поверхности S (на линии L).
Линии и поверхности первого порядка
103
Векторное уравнение не зависит от системы координат.
Однако в пространствах разной размерности одно и то же
уравнение может описывать различные геометрические объекты.
Например, векторное уравнение
{r-a)-{r-a) = R2 (3)
определяет в трехмерном пространстве V3 сферу с центром в
точке А(а) и радиусом R (рис. 3.1); в двухмерном пространстве
V2 — окружность с центром в точке А(а) и радиусом R (рис. 3.2);
на прямой V1 —две точки Μχ(α+ Л^Я) и М2(а— щЛ).
Рис.3 Λ Рис. 3.2
Уравнением поверхности S (линии L на плоскости)
относительно заданной декартовой системы координат
называется уравнение
F(x> У у ζ) = 0 (соответственно, F(x, у) = 0), (4)
если координаты (х, у, ζ) (или (ху у)) любой точки этой
поверхности S (линии L) удовлетворяют этому уравнению, а любые
числа {x,y>z) (или (ж, у)), удовлетворяющие уравнению (4),
являются координатами точки данной поверхности S (линии L).
В частности, уравнение (4) может иметь вид
у = /(ж, ζ) (соответственно» у = f(x)).
В ДПСК в трехмерном пространстве Oxyz уравнение (3)
имеет вид Л Л Л
(*-а)2 + (у-/?)2 + (г-7)2 = Я2, (5)
где Α(α,β,Ί) — центр сферы с радиусом Я, М(х, у,ζ) —
произвольная точка этой сферы.
104
Глава 3
В ДПСК на плоскости Оху уравнение (3) имеет вид
(х - а)2 + (у - β)2 = Я2, (6)
где А(а, β) — центр окружности с радиусом Я, М(х, у) —
произвольная точка этой окружности.
В ДПСК на прямой Ох уравнение (3) определяет точки
Μχ (а + R) и М2(а — R), где а — координата точки А.
В то же самое время уравнение (6) в трехмерном
пространстве описывает круговую цилиндрическую поверхность.
Уравнением поверхности S относительно
цилиндрических координат (плоской линии L относительно
полярных координат) называется уравнение
F(p, φ, ζ) = 0 (соответственно, F(p, φ) = 0), (7)
если цилиндрические координаты (ρ,φ,ζ) (полярные
координаты (ρ, φ)) любой точки данной поверхности S (данной линии L)
удовлетворяют уравнению (7), а с другой стороны, любые
числа (ρ,φ,ζ) (соответственно, (ρ,φ)), удовлетворяющие
уравнению (7), представляют собой цилиндрические (полярные)
координаты точки, лежащей на данной поверхности S (на данной
линии L).
В частности, уравнение (7) может иметь вид
ρ = /(φ>ζ) (соответственно, ρ = ρ{φ))- (8)
ПРИМЕРЫ
1) Уравнение спирали Архимеда.
Пусть задана некоторая полярная система координат с
полюсом О и полярной осью О ρ. Составим
уравнение линии, описываемой точкой
ψ Μ (ρ, φ), которая движется равномерно со
_ скоростью и по лучу Ох, выходящему из
р полюса О при условии, что луч Ох
вращается в плоскости с постоянной угловой
Рис. 3.3 скоростью ω вокруг точки О (рис. 3.3).
Линии и поверхности первого порядка 105
Предположим, что в начальный момент точка Μ совпадает с
точкой О и луч Ох совпадает с осью О/э. За время t точка Μ
пройдет по Ох путь ρ = ut,a луч Ох повернется на угол φ =
= ωΐ. Отсюда ρ = ηφ(ω или ρ = αφΛ где а = и/ω = const.
Таким образом,
1 ρ-αφ = 0 (9)
— уравнение рассматриваемой линии в полярной системе
координат.
Мы видим, что неременная точка М{р,<р)у исходя из
полюса О, движется вокруг полюса в положительном направлении,
одновременно удаляясь от него, т. е. точка Μ описывает
некоторую спираль. Кривая, определяемая уравнением (9), называется
спиралью Архимеда.
2) Уравнение прямой в полярных координатах.
Пусть ОР есть перпендикуляр, опущенный из начала
полярной системы координат на прямую d, η — орт вектора UP,
е—единичный вектор на полярной оси Ор, θ = /.(е,п), ρ =
= \θΡ\ (рис. 3.4). Произвольная точка Μ(ρ,φ) принадлежит
прямой линии d лишь тогда, когда
Рго£я ОЙ = р.
Отсюда получаем
φζοζ(φ-θ)=ρ (10)
— уравнение прямой d в полярной системе координат.
3) Уравнение окружности (кругового цилиндра) в
полярных координатах (относительно цилиндрических
координат).
Напишем в полярной системе координат уравнение
окружности с центром в точке О'(ро> φο) и радиусом г (рис. 3.5),
\Μ(β,φ)
Рис. ЗА
Рис. 3.5
106
Глава 3
Произвольная точка Μ(ρ1φ) принадлежит названной
окружности лишь тогда, когда |0'М|2 = г2. Отсюда получаем
уравнение заданной окружности в полярной системе координат:
р2 + pi - 2рр0 cos (φ - φ0) = г2. (11)
Последнее уравнение в трехмерном пространстве
относительно цилиндрической системы координат Ορφζ определяет
круговой цилиндр (рис. 3.6) с прямолинейными образующими,
параллельными оси Ок, радиусом г и осью симметрии р = р0, φ=φο.
Уравнением поверхности S
относительно сферических
координат называется
уравнение вида
Рис, 3.6
Ffo <М) = 0, (12)
если координаты (ρ,φ,θ)
любой точки, лежащей на данной
поверхности S, удовлетворяют
этому уравнению, и, с другой
стороны, любые числа (Ρ)ψ,θ) , ρ € [0, +оо), φ е [0,2π),
θ е [—π/2,π/2], удовлетворяющие уравнению (12), являются
координатами точки, лежащей на данной поверхности S.
В частности, уравнение (12) может иметь вид
P = /i(M) (V = /2(A0) или θ = Μρ,φ)). (13)
Например, в сферических координатах уравнение сферы
с радиусом г > 0 и центром в начале координат имеет вид
ρ = г.
Параметрическими уравнениями поверхности S
относительно декартовой системы координат называется
совокупность уравнений вида
x = x(u,v), y = y{u,v), z = z(u,v), (14)
где функции х(иу ν), y{u> ν), г(щ ν) имеют одну и ту же плоскую
область определения Ω, если для любой точки М(я, у, ζ)
поверхности S найдутся такие (и, ν) € Ω, что χ = х{иу ν), у = у(щ ν) f
Линии и поверхности первого порядка
Ш7
ζ = z(u, υ), и, с другой стороны, для любой пары чисел (u>v) e Ω
соответствующая точка M{x{U)V).y(u,v))Z(u,v)) принадлежит
данной поверхности.
Числа {u^v) называются криволинейными или
внутренними координатами точки на поверхности S.
Аналогичным образом определяются параметрыческие
уравнения поверхности относительно цилиндрических и
сферических координат.
Например, параметрические уравнения сферы с радиусом
г > О и центром в начале координат относительно декартовой
системы координат можно представить в виде
х = г cos θ cos φ, у = rcosflsin^, 2 —r sin 0, (15)
где параметры φ и θ суть долгота и широта точек сферы,
причем область изменения этих параметров Ω определяется
неравенствами 0 <; φ < 2π, —π/2 ^ θ ^ π/2.
Параметрическими уравнениями линии L относительно
заданной ДПСК Oxyz называется совокупность уравнений вида
x = x(t), y = y{t), z = z(t), (16)
где функции x{t), y{t), z(t) имеют одну и ту же область
определения Ω, если для любой точки M(x,y,z) линии L найдется
такое значение t е Ω, что χ = x(t), у = у(1), ζ = z(t), и, с
другой стороны, для любого значения t из области определения Ω
соответствующая точка M{x{t),y(t),z{t)) принадлежит данной
линии L.
Аналогично определяются параметрические уравнения
линии на плоскости относительно заданной ДПСК Оху.
В качестве примера
составим параметрические уравнения f | **\Μ(χ^)
окружности, лежащей в
плоскости Оху с радиусом г > 0 и
центром в начале координат (рис. 3,7).
Пусть М(х,у) — произвольная
точка окружности, е — орт ОЙ,
t = Z(T,e), причем t е [0,2π). Рис. 3.7
108
Глава 3
По определению тригонометрических функций cosi = χ /г,
sin t = у J r. Отсюда получаем параметрические уравнения
данной окружности относительно системы координат Оху:
x = rcost, y = rsint, 0 ^ ί < 27Г. (17)
Заметим, что параметрические уравнения спирали
Архимеда (9) относительно полярной системы координат имеют вид
p — uty <p = u>t, t € [0, -foo). (18)
Уравнение линии в пространстве можно представить в
виде системы двух уравнений, задающих поверхности,
пересекающиеся по этой линии. Ясно, что заданная линия в пространстве
таким способом определяется неоднозначно, ибо вместо этих
поверхностей можно взять любую другую пару поверхностей,
пересекающихся по той же линии.
Допустим, что поверхности S\ и S2 пересекаются по
линии L и определяются соответственно векторными уравнениями
F(f) = 0 и G(r) = 0. Тогда векторное уравнение линии L в
трехмерном пространстве определяется системой уравнений
\G(f) = 0. {Щ
Уравнение линии L в трехмерном пространстве в ДПСК
Oxyz определяется системой уравнений вида
F(x)y,z) = 0, (20)
G(x,y,z) = 0,
{
где F{x,y,z) = 0, G(x>y,z) = 0 суть уравнения поверхностей
Si и 52 в заданной ДПСК, пересекающихся по линии Ь, т. е.
L = Si П S2.
Например, окружность, задаваемая в плоскости Оху
уравнением х2 + у2 = г2, может быть определена в трехмерном
пространстве в виде пересечения двух поверхностей:
ι
х2 + У2 = г2,
2 = 0,
Линии и поверхности первого порядка
109
либо в параметрической форме:
χ = г cos ί, у = г sin £, г = 0, t G [0,2тт).
Для нахождения точек пересечения поверхностей, а также
поверхностей и линий, нужно рассматривать совместно
уравнения, определяющие указанные геометрические объекты.
Поверхность (линия) своим уравнением определяется
однозначно. Одна и та же поверхность (линия) может задаваться
различными уравнениями. Вид уравнения поверхности (линии)
зависит как от самой поверхности (линии), так и от выбора
системы координат. Чтобы получить уравнение поверхности (линии)
относительно новой системы координат, достаточно в
имеющемся уравнении вместо рассматриваемых в данном уравнении
координат подставить их выражения через новые координаты.
§ 2. АЛГЕБРАИЧЕСКИЕ ЛИНИИ
И ПОВЕРХНОСТИ
Напомним, что алгебраический полином η-го порядка двух
переменных есть сумма конечного числа слагаемых вида Cikx%yk, где
г, к — целые неотрицательные числа, г + к < гг, а С^ —
постоянные, причем хоть одно Сгк в случае г + к = η не равно нулю.
Уравнение вида F(x,y) = 0 называется алгебраическим
уравнением η-го порядка относительно двух переменных,
если выражение F{x^y) суть алгебраический полином гг-го
порядка относительно хну.
Теорема 1. Если плоская линия в некоторой ДИСК
задана алгебраическим уравнением порядка п, то данная
линия и в любой другой ДПСК определяется алгебраическим
уравнением того же порядка.
Доказательство. Пусть линия L в некоторой декартовой
прямоугольной системе координат на плоскости определяется
уравнением
Y^dkxV = 0, i + k^n,
i7k
по
Глава 3
где г, к — целые неотрицательные числа, Сц^ — постоянные,
причем хотя бы для одной пары гик, составляющих в сумме тг,
соответствующая постоянная dk отлична от нуля.
Воспользовавшись формулами преобразования координат
при переходе от системы Оху к любой новой прямоугольной
системе О'х'у': . t . /
J x = а + х ctn+y 6*21,
у = Ь + х'а12 + у'(У22>
получаем уравнение линии L относительно системы 0'х'т£\
Y^Cih(a + χ* αιλ + у'а21)\Ь + x'a12 + у'(*22)к = 0.
Отсюда ясно, что уравнение линии L в системе О'х'у*
представляет собой алгебраическое уравнение порядка не выше, чем
η. Следовательно, порядок алгебраического уравнения,
определяющего линию L, не может повыситься при переходе к
новой системе координат О'х'у'\ Ясно, что порядок
указанного уравнения не может и понизиться, ибо в противном случае,
при обратном переходе от системы О'х'у9 к системе Оху он
должен был бы повыситься, но последнее, как мы доказали,
невозможно.
Доказанная теорема устанавливает, что алгебраический
характер уравнения линии L и его порядок представляют
собой свойства, порождаемые самой плоской линией. Эти
свойства не связаны с выбором декартовой прямоугольной системы
коордиьат.
Напомним, что алгебраический полином η-го порядка
трех переменных есть сумма конечного числа слагаемых вида
CijkXiy:izk, г, j, к — целые неотрицательные числа, г + j +
-f к < η, Cijk — постоянные, причем хотя бы одно Сць в случае
г+3+к = пне равно нулю.
Уравнение вида
F{x,y,z)=0
называется алгебраическим уравнением η-го порядка
относительно трех переменных, если выражение F(x,y,z) суть
алгебраический полином η-го порядка относительно х> у и ζ.
Линии и поверхности первого порядка
ш
Теорема 2* Если поверхность в некоторой ЦП С К задана
алгебраическим уравнением порядка п, то данная
поверхность и в любой другой декартовой прямоугольной
системе координат определяется алгебраическим уравнением
того же порядка.
Доказательство этой теоремы аналогично доказательству
теоремы 1 и опирается на тот факт, что каковы бы ни были
произвольные декартовы прямоугольные системы координат,
координаты (x,y,z) любой точки пространства относительно
системы Oxyz являются линейными функциями координат (х'.у'^г')
той же точки относительно системы O'x'tfz' .
Вследствие справедливости доказанных теорем
корректными будут следующие определения.
Поверхность (плоская линия) называется алгебраической
порядка п, если в некоторой системе декартовых
прямоугольных координат она определяется алгебраическим уравнением
η-го порядка. Всякую неалгебраическую поверхность (плоскую
линию) будем называть трансцендентной.
Пространственную линию называют алгебраической, если
она может быть определена как пересечение двух
алгебраических поверхностей.
Мы будем изучать плоские алгебраические линии первого и
второго порядка, определяемые алгебраическими уравнениями
соответственно первого порядка, общий вид которых
Ах + By + С = О,
где Л и Б не равны нулю одновременно, и второго порядка,
общий вид которых
Ах2 + Вху + Су2 +Вх + Еу + Г = Оу
где Л, Б, С не равны нулю одновременно.
В курсе аналитической геометрии изучают алгебраические
поверхности первого и второго порядка, определяемые
алгебраическими уравнениями, соответственно, первого порядка, общий
вид которых
Ах + By + С ζ + D = О,
112
Глава 3
где числа А, В, С не равны нулю одновременно, и
алгебраическими уравнениями второго порядка, общий вид которых
Ax2 + By2 + Cz2 + Dxy+Exz + Myz+Kx+Ly+Fz+Q = 0,
где коэффициенты А, В>СУ D, Ε, Μ не равны нулю
одновременно.
§ 3. ВЕКТОРНОЕ И ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
(ПРЯМОЙ НА ПЛОСКОСТИ)
Нормальным вектором η плоскости π (прямой ρ на
плоскости) называется любой ненулевой вектор, ортогональный
данной плоскости π (прямой р)(рис. 3.8).
Рис. 3.8
Теорема. Всякая плоскость π в трехмерном пространстве
(прямая ρ на плоскости) с нормальным вектором п, про*·
ходящая через точку Мо(го), задается векторным
уравнением
г-п + £> = 0, (1)
где D = -fb ■ п.
Доказательство. Пусть произвольная точка Μ (г) G 7г
(М(г) ер).Тогда
{?— го) -п = О,
т-п — го · η = О,
f.n + JD = Of
где D = —fb · п, т. е. радиус-вектор произвольной точки
плоскости π (прямой ρ) удовлетворяет уравнению (1).
Линии и поверхности первого порядка
113
Теперь пусть радиус-вектор некоторой точки М(г)
удовлетворяет уравнению (1). Покажем, что эта точка M(r) e π
(M(f)ep).
Радиус-вектор г0 есть решение уравнения (1), то есть
г0 * η + D = 0.
Вычитая почленно это тождество из уравнения (1),
получим эквивалентное уравнение (г — fft) * η = 0. Последнее
означает, что для любого вектора г, удовлетворяющего
уравнению (1), вектор г — fo ортогонален вектору η, а поэтому лежит в
плоскости π (на прямой р), и, следовательно, точка Μ (г) е π
(M(f)tp).
Таким образом, уравнение (1) является уравнением
рассматриваемой плоскости π в трехмерном пространстве (прямой ρ на
плоскости).
Следствие. Всякая плоскость π в трехмерном пространстве
(прямая ρ на плоскости) с нормальным вектором п(А,В,С)
(га(А, В)), проходящая через точку M(x0i y0, z0) (М(х0у у0)) в
фиксированной ДПСК Oxyz (Оху), определяется
алгебраическим уравнением первой степени
Ах + By + С ζ + D = 0 (Ах + By + D = 0). (2)
Доказательство. В самом деле, пусть M{x,yyz) (М(х,у))—
произвольная точка плоскости π (прямой р),
рассматриваемой в заданной ДПСК. Тогда в силу определения скалярного
произведения из векторного соотношения (г — го)-п = 0 имеем
(х - х0)А + (у - 2/o)J5 + (ζ - z0)C = 0
((x-zo)A + (y-tjo)B = 0).
Отсюда получаем
Ах + By + Cz + D = 0 ( Аж + By + D = 0),
где D = -Axq - Byo - Cz0 (D = -Ax0 - By0 )·
Уравнение (2) является уравнением первой степени, так как
коэффициенты А, ВУС (А, Б) не обращаются в нуль
одновременно, ибо вектор η ненулевой.
114
Глава 3
Уравнение (2) называют общим уравнением плоскости
в трехмерном пространстве (прямой на плоскости) в
Щ\СКОхуг{ОхуУ
Заметим, что если п(Д В, С) (п(Д В))— нормальный
вектор, a M(xoyyo,zo) (М(#о,2/о))— координаты точки на
плоскости π (прямой ρ на плоскости) в аффинной системе
координат Оёг&ёз (Oeie2), то уравнение плоскости 7г (прямой ρ на
плоскости) примет вид
A'x + B'y + C'z + D' = 0
(А'х + В? у + D'= 0),
где
А1 = Аё12 + Вё1-ё2 + Сё1>ёг,
В' = Аег · е2 + Ве22 + Се2 · е3,
С'^М-ез + Б^-ез + Сез2,
D* = -х0(Ае? + Вег * 62 + Cei - е3) -
-уо(Аех · е2 + Вё2 + Се2 · е3) -
-^oi-Aei · е3 + Ве2 ■ е3 + Се32)
{А' = Ае? + Вёх · е2,
В/ = М-ё2 + Ве22>
D1 = -хо(Аёг2 + Bei · е2) - ifo(4ei · е2 + Бе22)).
В силу теорем предыдущего параграфа можно утверждать, что
в любой аффинной системе координат произвольная плоскость
(прямая на плоскости) определяется алгебраическим уравнением
первой степени.
Таким образом, алгебраические поверхности (алгебраические
линии) первого порядка суть плоскости (прямые на плоскости)·
Пусть три различные точки N\ (x\ ,у\ ,ζ%),
N2(x2,y2,z2), ЛГзОяз>Уз,*з) из Ж3 не лежат
на одной прямой (рис. 3.9).
Установим общее уравнение плоскости,
проходящей через указанные три точки, не
лежащие на одной прямой. Отметим, что
> >
векторы ΝχΝ2 и ΝχΝ% не коллинеарны.
>Ν2
Линии и поверхности первого порядка
115
Произвольная точка N(x, у, ζ) пространства лежит в
плоскости, определяемой векторами ΝχΝ2 и ΝχΝ3, тогда и только
тогда, когда векторы Ν±Ν, Ν\Ν2, ΝχΝ^ компланарны, т. е.
когда смешанное произведение этих векторов равно нулю. Отсюда
общее уравнение указанной плоскости имеет вид
х-χι у - 2/1 ζ-ζι
Х2 -Х\ У1- У\ Z2 - Ζι
#3 - Х\ Уз - У\ ζ3 - ζι
= 0.
§ 4. УРАВНЕНИЕ «В ОТРЕЗКАХ» ПЛОСКОСТИ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
(ПРЯМОЙ НА ПЛОСКОСТИ)
Общее уравнение плоскости (прямой на плоскости) называется
полным, если все его коэффициенты Л, В, С (Л, В)отличны
от нуля. Если хотя бы один из названных коэффициентов равен
нулю, то уравнение называется неполным.
Полное уравнение
Ax + By + Cz + D = 0 (Ax + By + D = G)
можно переписать в виде (D Φ 0)
Х , У , Ζ ! ί Х , У
+ —^ + ^7^ = 1
\-D/A*-D/B Ll·
-Ό ΙΑ -Ό J В -Ό jC \-D/A ' -DJB
или
ί + ϊ + ί-ι (- + | = ι). (ί)
a b с \α ο Ι
Уравнение (1) называют уравнением плоскости [прямой
на плоскости) «в отрезках».
Числа а, 6, с (числа а, 6) имеют простой геометрический
смысл — они равны алгебраическим мерам соответствующих
векторов:
а = ОА\ Ъ = ОВ', с = ОС (а = ОА\ Ь = ОВ')у
I
где А\В*, С" —точки пересечения данной плоскости (прямой)
с соответствующими осями координат (рис. 3.10).
ίΐ6
Глава 3
Рис.3 JO
В самом деле, прямая на плоскости χ/a+y/b = 1 пересекает
ось абсцисс (у = 0) в точке А'{а^ 0) и ось ординат (χ = 0) — в
точкеБ'(0,Ь).
Плоскость х/а + у/Ь + ζ/с = 1 пересекает ось абсцисс (у —
= 0, ζ = 0) в точке Α'(α,Ο,Ο), ось ординат (ее = 0, ζ = 0) в
точке В'(0,6,0), ось аппликат(х = 0, у = 0) в точке С;(0,0,^)·
Уравнение плоскости (прямой на плоскости) «в отрезках»
удобно использовать при построении плоскости (прямой).
§ 5. ПАРАМЕТРИЧЕСКИЕ
УРАВНЕНИЯ ПЛОСКОСТИ
Пусть даны 7г — некоторая плоскость в трехмерном
пространстве, точка Mo(fb) G π и два неколлинеарных
вектора а^Ь, компланарных плоскости
π (рис. 3.11).
Произвольная точка М{т)
принадлежит плоскости тг тогда и
только тогда, когда
r = ro + ua + vb,
(1)
Рис. 3.11
где и, ν — произвольные параметры, —ос < и < +ос, —оо <
< ν < +оо.
Уравнение (1) называют векторным параметрическим
уравнением плоскости. Выясним геометрический смысл
параметров и, v. Для этого введем в плоскости π аффинную си-
стему координат М$аЪ с центром в точке Mq и базисом а, Ь.
Линии и поверхности первого порядка
117
Тогда вектор MqM является радиус-вектором точки Μ в
системе координат Moab и параметры и, ν будут аффинными
координатами точки Μ в системе координат Moab. В связи с этим
параметры и, ν называют плоскостными или внутренними
координатами точки Μ (рис. 3.11).
В качестве нормального вектора рассматриваемой плоскости
можно взять вектор η = α χ 6. Тогда уравнение плоскости π
можно записать в виде
(f-f0).(oxb) = 0
или
(f-fb,a,6) = 0. (2)
Пусть в некоторой фиксированной ДПСК трехмерного
пространства рассматриваемые векторы имеют координаты г(х, у, ζ),
*4)(soiifo,3o)f β(αι,α2,α3), Ь(А,А2,#з)· Тогда
параметрические уравнения данной плоскости относительно указанной ДПСК
имеют вид χ = Χο + α1η + β1ν,
У = Уо + ос2и + β2ν, (3)
ζ = ζ0 + а$и + β$υ.
Общее уравнение плоскости в указанной ДПСК
определяется равенством
\x-xo у-уо ζ-ζ0\
Oil &2 «3
βΐ β2 β
3
= 0. (4)
§ 6. УРАВНЕНИЕ
С УГЛОВЫМ КОЭФФИЦИЕНТОМ ПРЯМОЙ
НА ПЛОСКОСТИ
Уравнением с угловым коэффициентом прямой на
плоскости называют уравнение прямой, приведенное к виду
y = Kx + D. (1)
Выясним смысл коэффициентов К и D в уравнении (1).
Прямая ρ пересекает ось ординат Oj( χ = 0) в точке N(0, D).
118
Глава 3
«i
t
-ρ*
3
о
к nw
\N
L0
<г
Iе*
,-"ρ
is
Рис.З./2
Отсюда D есть алгебраическая мера вектора отсекаемого
этой прямой на оси ордлнат: D = ON (рис. 3.12).
Углом наклона прямой ρ к оси абсцисс называют
наименьший положительный угол а, на который следует повернуть ось
абсцисс Ог вокруг точки J пересечения этой прямой с данной
осью, чтобы ось совпала с прямой р.
Если прямая параллельна оси абсцисс, то ее угол наклона
считают равным нулю. Ясно, что 0 ^ а < π.
Пусть θ = ^(Г, е), где е — орт нормального вектора η
рассматриваемой прямой.
Тогда а = θ — π/2, если α — острый угол, α = θ 4- π/2, если
α — тупой угол, но в обоих случаях tg α = — ctg θ.
У прямой у = К χ + D, общее уравнение которой
Кх - у + D = О,
нормальный вектор га(К, -1) и его орт
J к
л/i + K2
)
Но у единичного вектора е координаты равны направляющим
косинусам, т. е. e(cos/3X,cosру)у причем βχ = Θ, ру = θ - π/2,
если α — острый угол; βχ = 0, βν = тг/2 - 0, если а —тупой
угол, но в обоих случаях cos Д. = cos 0, cos/9^ = sin θ и
COS0 ='■■', S1I10 =
А тогда
т.е. К = tga.
λ/Τ+ΊΡ'
tga = — ctg0 =
COS0
Линии и поверхности первого порядка
119
Таким образом, коэффициент К в уравнении (1) есть тангенс
угла наклона прямой к оси абсцисс и его называют угловым
коэффициентом прямой на плоскости.
Подчеркнем, что угловой коэффициент прямой,
параллельной оси абсцисс, равен нулю, а угловой коэффициент прямой,
ортогональной оси абсцисс, не существует.
§ 7. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
В ПРОСТРАНСТВЕ
(ПРЯМЫХ НА ПЛОСКОСТИ)
Под углом φ между плоскостями πι, Ж2 (прямыми на
плоскости р\, Ρ2) понимают угол между их нормальными
векторами.
Пусть плоскости πι, π2 (прямые ρι,Ρ2) заданы
уравнениями
πχ: г ·ηι + D\ = 0, (1)
π2: τ · п2 + D2 = 0 (2)
или
πι: Агх+Biy+Ciz+Di =0 (рг: Αχχ+Βιν+Όχ =0), (3)
π2: A2x+B2y+C2z+D2 =0 (ρ2: A2x+B2y+D2 =0). (4)
Тогда угол φ между этими плоскостями (прямыми на
плоскости) находится по формулам
Й1-П2 /сч
φ = arccos (5)
|ηι|· |ГС2|
ИЛИ АИа + БА + С^ /ft,
φ = arccos . , ^ . , Λ (6)
/ ЛьАд + ВА \
[ у? = arccos —=====—, . . ι ·
Возможны следующие случаи взаимного расположения
названных плоскостей (прямых на плоскости).
120
Глава 3
1) Плоскости 7Γι, 7Γ2 (прямые на плоскости pi, р2)
перпендикулярны (πι ± 7Г2 (pi Χ Ρ2 )) При УСЛОВИИ
пх · п2 = 0, (7)
или
>Μ2+Βι£2 + CiC2 = 0 (yM2 + BiB2 = 0). (8)
2) Плоскости 7τι, π2 (прямые на плоскости pi, рг)
параллельны (πι || 7г2 (pi || Р2)) при условии ηι = Лпг, т. е.
щ Хп2=0,
или
А
А2
2 i?2 Сг \^2 ^2/
(9)
(10)
3) Плоскости πχ, 7Г2 (прямые на плоскости Ρι, Ρ2)
пересекаются при условии τΤχ Φ Хп2, т. е.
П1 X П2 ^ б,
(11)
или
Ι-Βι Сг
\В2 С2
+
ill Сг
А2 С2
+
Аг Βλ
А2 В2
°> й*1)<12)
4) Плоскости πι, π2 (прямые р\, р2) совпадают, когда они
параллельны и существует общее решение системы (1), (2) или
системы (3), (4), т. е. при условии, когда й\ = Хп2 и существует
общее решение гЬ системы (1), (2) или, что то же самое,
Ai = Bi=Ci
А2 В2 С2
и существует решение (xo,yo,zo) системы (3), (4) (^
и существует решение (хо, уа) системы (3), (4)).
в2
Теорема. Два векторных уравнения (1) и (2) определяют
одну и ту же плоскость (прямую на плоскости) тогда и
только тогда, когда
ηι = Лп2, D\ = λ£>2·
(13)
Линии и поверхности первого порядка 121
Доказательство. Необходимость. Если уравнения (1),(2)
определяют одну и ту же плоскость (прямую на
плоскости), то п\ = Хп2 и существует общее решение системы
уравнений (1), (2), т. е. верны тождества гЬ · п\ + Όχ = О,
fon2 + D2 = 0. Из первого тождества получаем A(f0-n2) +
+ Όχ = О, а тогда, сравнивая со вторым тождеством, имеем
DX = \D2.
Достаточность теоремы очевидна, ибо при условиях (13)
уравнения (I) и (2) эквивалентны.
Следствие. Необходимым и достаточным условием того, что два
уравнения (3) и (4) определяют одну и ту же плоскость
(прямую на плоскости), является пропорциональность
коэффициентов этих уравнений:
В2 С2 D2 \A2 В2 D2)' { '
А2
Пусть прямые р\ур2 на плоскости заданы
соответственно уравнениями с угловыми коэффициентами y = kix + bi,
у = к2х + Ь2у а αϊ, α2 — их углы наклона к оси абсцисс
(рис. 3.13).
Рис. 3.13
Углом наклона второй прямой р2 к первой pi будем
называть угол φ7 по абсолютной величине меньший 7г, на
который следует повернуть прямую р\ вокруг точки J
пересечения прямых pi, р2 до совмещения с прямой р2, причем углу φ
припишем знак « + » или « — » в зависимости от того, будет ли
указанный поворот совершаться против часовой стрелки или по
часовой стрелке.
122
Глава <?
Ясно, что φ = аг — αϊ, следовательно,
tga2-tgQ;i
tg^ = tg(a2 -αι) =
l + tgaitgGs
T-e" f fa-fci
Условие параллельности указанных прямых
fei = к2 (15)
вытекает из того, что в этом случае tgv? = 0.
Условие ортогональности этих прямых
^^ + 1 = 0, (16)
или
kl = ~ Л?
вытекает из того, что в этом случае φ = π/2 , tg φ не существует,
и знаменатель в выражении для tg φ обращается в 0.
§ 8. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
НЕРАВЕНСТВ ПЕРВОЙ СТЕПЕНИ
Как уже известно, векторное уравнение rn + D = UB
трехмерном пространстве определяет плоскость и имеет вид Ах + By +
+ С ζ + D = 0, а на плоскости оно определяет прямую и имеет
BwAx + By + D = 0.
Теорема 1. Пусть плоскость π (прямая на плоскости р)
задана векторным уравнением г · η + D = 0. Тогда для всех
точек Μ (г), лежащих по одну сторону от этой
плоскости π (прямой р), выполняется неравенство r-n+D>0,
а для всех точек Μ(τ^β лежащих по другую сторону
от плоскости π (прямой р), выполняется неравенство
f-n + D<0.
Доказательство. Пусть Mi(ri), M2(f2) —произвольные
точки, лежащие по разные стороны от плоскости π (прямой р).
Тогда существует внутренняя точка М(г) вектора М\М2,
Линии и поверхности первого порядка
123
Рис. 3.14
лежащая на ллоскости тг (прямой р), которая делит вектор
М\М.2 в некотором отношении λ > О (рис. 3.14), где
ЩЙ = ХШШ, f-fi=A(f2-f), (1 + Х)г = гг + Хг2,
т.е. r = (r1 + Af2)/(l + A).
Поскольку Μ {г) е 7г (M(f) 6 ρ), то г удовлетворяет
уравнению плоскости (прямой), т. е.
П + Af2 _
Отсюда
следовательно,
_ fi · η + D
Г2 * П + D
Однако λ > 0, поэтому величины г ι fi+D и f^-n+D имеют
разные знаки. Теорема доказана.
Пусть плоскость 7г (прямая на плоскости ρ) задана
уравнением f · η + D = 0. Множество точек
7г+ = {Μ{η I r n + D > 0} (ρ+ = {M(r) I f - η 4- D > 0})
называют положительным полупространством
(положительной полуплоскостью), а множество точек
тг- = {M(r) |r-nH-D<0} (p~ = {M(r) |r-n + JO<0})
называют отрицательным полупространством
(отрицательной полуплоскостью).
Теорему 1 можно переформулировать следующим образом:
плоскость 7г (прямая на плоскости р), заданная векторным
124
Глава 3
уравнением r-n+D = 0, делит все пространство (всю плоскость)
на два полупространства (на две
полуплоскости)—положительное и отрицательное (положительную и отрицательную).
Теорема 2. Пусть плоскость π (прямая на плоскости р)
задана векторным уравнением г · η + D = 0. Тогда,
если начало ее нормального вектора отложить от
некоторой точки плоскости π (прямой р), то конец
вектора η будет лежать в положительном полупространстве
(в положительной полуплоскости) (рис. 3.15).
Рис. 3.15
Доказательство. Радиус-вектор конца вектора η с началом
в произвольной точке М(г) плоскости 7г (прямой ρ) есть вектор
г + п. Подставляя этот радиус-вектор в левую часть уравнения
плоскости (прямой), имеем
(г + η) · η + # = г · η + D + η · η = η · η > О,
что и требовалось доказать.
§ 9. НОРМИРОВАННОЕ УРАВНЕНИЕ ПЛОСКОСТИ
(ПРЯМОЙ НА ПЛОСКОСТИ)
Теорема 1. Расстояние от произвольной точки N(r\)
трехмерного пространства (плоскости) до фиксированной
плоскости π (прямой ρ на плоскости), заданной векторным
уравнением Г-.Й + О = 0, (1)
определяется по формуле
d(N,n) (d(AT,p)) =
In · η + D\
щ
(2)
Линии и поверхности первого порядка
125
Доказательство. Пусть Мо(гЬ) — произвольная точка
плоскости π (прямой ρ), Ν* — ортогональная проекция
произвольной точки трехмерного пространства (плоскости) N(f\) на
плоскость π (на прямую р), N'e— ось, определяющаяся
начальной точкой N' и ортом е вектора η (рис. 3.16).
Щгг)
Щп)
е Мо(го)
Рис. 3.16
Тогда расстояние от точки N(ri) до плоскости тг (до
прямой р) находится следующим образом:
ά{Ν,π) id(N,p)) = \Рго&,ёЩЙ\ = '"'^ =
\(ri-r0)-n\ \fi-n-fo-n\
\п\
η
Отсюда, приняв во внимание, что г0 · η + D = 0, получаем
формулу (2).
Нормированным векторным уравнением плоскости
(прямой на плоскости) называют векторное уравнение
вида (1) с единичным нормальным вектором и отрицательным
свободным членом.
Если обе части уравнения (1) умножить на нормирующий
множитель dbl/|n|, причем знак этого множителя взять
противоположным знаку свободного члена Z), то получаем нормированное
векторное уравнение заданной плоскости (прямой на плоскости):
f.n'-p' = 0, (3)
где
п' = п/\п\ sign(—D),
p, = D/|n|signD>0.
126
Глава 3
Здесь η' — единичный орт, коллинеарный вектору п,
р7 — расстояние от начала координат О до
рассматриваемой плоскости π (прямой ρ на плоскости), что следует из
формулы (2).
Отклонением δ произвольной точки N от плоскости тг
(от прямой р)у заданной уравнением (3), называют
алгебраическую меру Ν'Ν вектора Ν'Ν на оси Ν'η, где TV' —
ортогональная проекция точки N на рассматриваемую плоскость π
(на прямую р)(рис. 3.16):
δ = WN. (4)
Отметим, что
\δ\=ά(Ν,ιτ) (d(N,p))
— расстояние от точки N до плоскости π (до прямой р),
причем δ = d(Ny π) (d(N, ρ)), если N лежит по ту же сторону от
плоскости π (от прямой р), куда направлен нормальный
вектор п', или, что то же самое, если точка N и начало
координат О лежат по разные стороны от плоскости π (прямой р);
δ = -ά(Ν,π) (-d(N,p)), если N лежит по ту сторону, куда
направлен вектор — п', противоположный нормальному вектору
п', или, что то же самое, если точки N и О лежат с одной
стороны от плоскости π (от прямой р); и, наконец, δ = 0, если Ν € π
(Ν ер).
Теорема 2. Отклонение произвольной точки N(fi)
трехмерного пространства (плоскости) от плоскости π (от
прямой ρ на плоскости), заданной нормированным
уравнением (3), определяется по формуле
δ = f\ -η* —ρ'. (5)
Доказательство. Пусть Мо(гЬ) — произвольная точка
плоскости π (прямой р)(рис. 3.16). Тогда
δ = WN = Projfr^, Mo^ = η' - ЩЙ =
*Ί — го) · η = ri · η — го - η =η·η — ρ .
Теорема доказана.
Линии и поверхности первого порядка
ΥΠ
Нормированное уравнение плоскости π трехмерного
пространства относительно фиксированной ДПСК Oxyz имеет вид
χ cos а + у cos β 4- ζ cos7 — Ρ* — 0, (6)
где f(x,y,z), n'(cosa,cos/?,cos7), а величины cos α, cos/3,
cos 7 — направляющие косинусы нормального вектора η'.
Нормированное уравнение прямой ρ на плоскости
относительно фиксированной ДПСК Оху имеет вид
хсоъв + ys\n0 - р' = О, (7)
где θ = ^{г,п') —угол между базисным вектором оси абсцисс
ОТ и нормальным вектором прямой п\ причем
п'{соъв)Соъ{к/2 — 0)), или n'(cos0,sin0).
Отклонение δ произвольной точки ЛГ(я*,2/*,2*)
пространства от плоскости 7г, заданной уравнением (6), находится по
формуле
δ = ж* cos α + у* cos β + г* cos 7 — ρ'- (8)
Отклонение δ произвольной точки N(x*,y*) плоскости от
прямой р, заданной уравнением (7) в этой плоскости, находится
по формуле
δ = χ* cos θ + у* sin θ - ρ*. (9)
ЗАМЕЧАНИЕ. По знаку отклонения δ можно определить, в
положительном или отрицательном полупространстве (в положи-
тельной или отрицательной полуплоскости) находится
рассматриваемая точка.
§ 10. ПУЧКИ ПЛОСКОСТЕЙ
(ПРЯМЫХ НА ПЛОСКОСТИ)
Пучком плоскостей с центром в ρ (пучком прямых на
плоскости с центром в точке Р) называется множество всех
плоскостей (прямых на плоскости), проходящих через одну и ту
же прямую ρ (точку Р).
128
Глава 3
Теорема. Уравнение пучка плоскостей с центром в ρ
(уравнение пучка прямых с центром в точке Р), определенным
как пересечение двух различных плоскостей (двух
различных прямых на плоскости) этого пучка:
р(Р):
[f-iii+Di = 0,
имеет вид
(I)
(2)
a(f · щ + Di) + β(? · n2 + D2) = 0,
где а и β — произвольные вещественные числа, не
равные 0 одновременно.
Доказател ьство(для пучка плоскостей)· При произвольных
α и β уравнение (2) определяет плоскость, проходящую через
прямую (1), так как
а(г · щ + Di) + β{τ · η2 + D2) =
= f · (anι + /3n2) + αΌχ + /Ш2 = 0,
а вектор αηχ+βη,2 ^ б и, кроме того, для любой точки Μ(fo) € ρ
справедливо тождество
a(r0 · Й! + Di) + 0(ro ■ n2 + D2) = 0.
Покажем обратное, т. е. что уравнение любой плоскости,
проходящей через прямую (I), можно представить в виде (2).
Плоскости πι и π2, определяемые уравнениями (1),
пересекаются, а потому их нормальные векторы п\, п2 не параллельны
и лежат в некоторой плоскости π, перпендикулярной прямой (1)
(рис. 3.17).
Рис. 3.17
Линии и поверхности первого порядка
129
Пусть 7Гз — произвольная плоскость рассматриваемого
пучка, проходящая через прямую (1), причем ее уравнение имеет вид
f\n3 + D3=0. (3)
Убедимся, что уравнение плоскости π3 можно представить в
виде (2).
Нормальный вектор плоскости 7г3 лежит в плоскости я\ а
потому существуют α и β такие, что η3 = ατίχ +βη2, поскольку
векторы ηι и п2 линейно независимы.
Пусть Μ (го) — произвольная точка на прямой (1). Тогда ее
радиус-вектор должен также удовлетворять уравнению (3), т. е.
fo · ηι + Dy = О,
Го ■ П2 + D2 = О,
го · (ani + βη2) + D3 = 0,
следовательно,
а(г0 · й{) + β{?ο ■ п2) + D3 = 0.
Но тогда с учетом первых двух тождеств получаем
Όζ = αϋ1 + βΌ2.
Итак, нашлись такие числа α и /?, что уравнения
произвольной плоскости 7г3 пучка представлены в виде (2). Теорема
доказана.
ЗАМЕЧАНИЕ. Если центр пучка ρ (Ρ) задан в ДПСК в
трехмерном пространстве (на плоскости) системой уравнений
А2х + В2у + C2z + D2 = 0,
(р. ГАцг + ВЦ/+ Dx = 0, \
то уравнение соответствующего пучка плоскостей с центром в ρ
(прямых на плоскости с центром в Р) имеет вид
а{Агх + Вху + Cxz + Dx) 4-β{Α2χ + В2у + C2z + Д>) = 0
(α(Αχχ + Вху + Di) + /3(Λ2ζ + В2г/ + D2) = 0).
130
Глава 3
§11. СВЯЗКИ ПЛОСКОСТЕЙ
Связкой плоскостей в К3 с центром в точке Q называется
множество всех плоскостей, проходящих через данную точку Q.
Теорема. Уравнение связки плоскостей с центром в точке
Q{xq, Уо·>ζο) имеет вид
А(х - х0) + В(у - у0) + C(z - *о) = 0, (1)
где А, В, С — произвольные вещественные числа, не
равные нулю одновременно.
Доказательство. В самом деле, всякая плоскость,
определяемая уравнением (1), проходит через точку Q(xq, у$, ^о) ·
Кроме того, любая плоскость связки, проходящая через
Q(xQ,yo,zo)y однозначно определяется заданием ее
нормального вектора п(Д В,С), а потому определяется уравнением (1).
§ 12. ГИПЕРПЛОСКОСТЬ
Гиперплоскостью в η-мерном аффинном пространстве
называют геометрическое место точек Μ (г) (М(х\,Х2, · - -, хп))»
радиус-векторы г (координаты (ζχ,α^,.-. ^хп)) которых
удовлетворяют векторному(линейному)уравнению
г -п + D = 0 (αχχι +а2Х2 + ·-■ + апхп + D = 0), (1)
где п(аь ^2? ■ · · ι Gn) — нормальный вектор гиперплоскости, Z),
flbfi2,"-ifin — вещественные числа.
Если D = 0, то уравнение (1) определяет гиперплоскость,
проходящую через начало координат О(0?..., 0).
Геометрическое место таких точек Μ (я? ι, £2? - ·«> я?п)»что
X'i — \J* ι* — J-j . · » у /С X, го ~i Xj · · . ^ /cj
#fc ^ 0, Xfc G (-oo, +oo)
(х^ = 0, ^£ (~°o> +oo), г = 1, ..., fc — 1, fc + 1, .. -, n)
называют k-\\ координатной осью (fc-й координатной
плоскостью) в заданной системе координат Ох\Хъ ...хп.
Линии и поверхности первого порядка
131
Теорема 1. Две гиперплоскости
г- щ + Dr = О, г ■ п2 + D2 = 0 (2)
параллельны, если коллинеарны их нормальные векторы
nL(ai,. ..,an) # П2(6ь ... ,bn)t rn e.
τίχ = Χή2
a^ _ θ2 _ On
Теорема 2· Необходимым и достаточным условием того,
чтобы две гиперплоскости, определяемые уравнениями (2)
совпадали, является выполнение соотношений
щ = λη27 Di = \D2,
те.
αχ _ θ2 _ _ αη _ Όγ
b\ b2 bn D2'
Доказательство этих теорем совершенно аналогично
доказательству соответствующих теорем, сформулированных для
плоскостей в трехмерном пространстве.
§ 13. ВЕКТОРНОЕ ПАРАМЕТРИЧЕСКОЕ,
ПАРАМЕТРИЧЕСКИЕ И ОБЩИЕ
ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ
Направляющим вектором d прямой ρ в пространстве R3,
называется любой ненулевой вектор, коллинеарный данной
прямой (рис. 3.18).
Произвольная точка M(f) e R3
принадлежит прямой р, проходящей
через точку Mo(fo) с направляющим век-
тором dy тогда и только тогда, когда
векторы d и MqM коллинеарны, т. е.
—*
г — го = td, а потому Рас. 3.18
r = ro+td, te(-oo, +00). (I)
132 Глава 3
Уравнение (1) называют векторным параметрическим
уравнением прямой ρ в пространстве R3,
В трехмерном пространстве Ш3 уравнение (1) можно
записать в виде ,_ ^х г -
{?-r0)xd = 0. (2)
Пусть относительно ДПСК Oxyz в пространстве R3 r(x,y,z),
Π)0&ο*!/ο>2ο) — радиус-векторы точек Μ, Μ0; ά{α,,β,η) —
направляющий вектор прямой р. Тогда из уравнения (1) получаем
параметрические уравнения рассматриваемой прямой ρ в IR3:
χ = xo+ta, у = yo+ίβ, ζ = zo+ty, t e (-οο,+οο). (3)
Если считать, что параметр t есть время, то уравнения (1), (3)
определяют закон движения материальной точки по прямой ρ
с постоянной скоростью d. Из уравнений (3) нетрудно
получить канонические уравнения прямой ρ в системе
координат Oxyz:
х-хр _ У-Уо _ z- Zq
а " β ~ 7 ' К '
Подчеркнем, что обращение в нуль одного из знаменателей
в уравнении (4) влечет обращение в нуль и соответствующего
числителя. Если, например, β = 0, то по крайней мере одно
из чисел 7 или а отлично от нуля, так как вектор d ненулевой.
Поэтому если /? = 0,ноа^0,тов соответствии с соглашением
о пропорциях (х — х0) · 0 = (у — yo)oi, следовательно, у = уо-
Прямую ρ пространства R3, являющуюся пересечением
двух различных непараллельных плоскостей
f-fii + Di=Q и г · П2 4- D2 = О,
можно определить системой этих двух уравнений
Г'Пх + D\ = О,
г ■ т?2 + Дг = 0.
(5)
Уравнения (5) называют общими векторными
уравнениями прямой в пространстве IR3.
В случае двухмерного пространства IR2 в системе
координат Оху имеем r(x,y), fo(ff(hito) — радиус-векторы точек Μ
Линии и поверхности первого порядка
133
и Мо; d(a, β) — направляющий вектор прямой ρ в R2. Поэтому
получаем
x = xQ + ta, y = yo + tp, te(-oo,+oo) (6)
— параметрические уравнения прямой ρ в R2;
х - Д?о _ У-Уо (7,
а ~ β ( )
— каноническое уравнение прямой в R2.
Нетрудно заметить, что каноническое уравнение прямой на
плоскости можно привести к виду
βχ-ay-l· (ауо - βχο) = 0 (8)
или, если, например, а Ф О, то
а а
Таким образом, прямая ρ с направляющим вектором d(ot, β),
заданная каноническим уравнением (7), также может быть
определена общим уравнением (8) с нормальным вектором
η(β, —а) или уравнением с угловым коэффициентом (9), причем
ее угловой коэффициент к = β/α.
Отметим, что для прямой на плоскости, определяемой общим
уравнением ах + by + с = 0 с нормальным вектором п(а, Ь), в
качестве направляющего вектора можно взять d(b> —a).
В случае η-мерного пространства Rn в системе координат
Ох\х2 · · · %п имеем: τ{χ\,χ2, - - -, хп) > гЬОбнь #20, · · ·> Хпо) —
радиус-векторы точек М, Mo, d(ai9a2j - ·.,otn) —
направляющий вектор прямой рв!п,
%2 =Х20+tOt2,
)
Хп = ХпО + t&n, t € (—ОО, +Οθ)
— параметрические уравнения прямой ρ в Rn,
Xi — Хю Х2 — £20 χη - ХпО /1И
= = .. ■ = ν 11 >
α ι α2 ап
— канонические уравнения прямой ρ в Rn.
134
Глава 3
§ 14. УГОЛ МЕЖДУ ПРЯМЫМИ
И ИХ ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Углом между прямыми р\ и рг называют угол, образуемый их
направляющими векторами.
Пусть прямые р\ и р2 заданы векторными
параметрическими уравнениями
Р\ ·■ г = η -f dxt, p2: r = r2+ d2t, t € (-оо, +ос),
либо параметрическими уравнениями относительно
фиксированной ДПСК
Р\: x = xi + ant, y = yi+Pit, г = 21+71*;
Р2'. X = X2 + <*2t, y = y2+02t, Z = Z2 + 72t, t € (—ΟΟ,+Οο),
—* —*
где di(ai,/Si,7i), ^2(θ2,/?2,72) —направляющие векторы.
Угол между прямыми pi и рг определяется соотношениями
-φ -+
φ = arccos —^
или
<£> = arcras
<*1<*2+01/3-2+7172
v4 + #+7?VaI + $ + 7?
Возможны следующие случаи взаимного расположения
прямых в пространстве К3:
1) Прямые pi и р2 лежат в одной плоскости, когда
—» —+
(v2-ri,di,d2) = 0,т. е.
Х2 -Xl V2- Vl Z2 - ZL
ot\ β\ 7».
OL2 fc 72
= 0;
—* -*
2) Прямые pi и рг скрещиваются, когда (fa—fi,di,d2)^0t
т. е.
^2 - я?1 2/2 - 2/1 ζ2 - ζ\
αϊ Α 7ι
а2 β2 72
^0;
Линии и поверхности первого порядка
135
3) Прямые перпендикулярны между собой (pi Lp2 \ когда
-* —*■
d\ · 02 = 0, т. е. αια·2 + βνβι + 7ΐ72 = 0;
4) Прямые параллельны (pi || рг) и не совпадают, когда
di х d2 = б или, что то же самое, ^ = ^ = ^, и (fi - f2) χ
χ J! ^ б; 2^2
5) Прямые ρχ и рг совпадают, когда d\ χ d2 = б, (η. — гг) х
χ ίΓι = б;
6) Прямые pi и р2 пересекаются, когда (n-r^dbik) =0,
но di xd2^0.
§ IS. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ
И ПЛОСКОСТЕЙ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Пусть θ = Z(d>n) —угол, образуемый направляющим
вектором d прямой ρ и нормалью тг плоскости π (рис. 3.19).
Рис. 3.19
Углом между прямой и плоскостью называют угол между
этой прямой и ее ортогональной проекцией на данную плоскость.
Пусть в пространстве прямая ρ и плоскость 7г заданы
уравнениями
р: r = ?o + dty тг : г -п + D = 0
или
ρ : χ = хо + at, у = у0 + βίΎ ζ = г0 + 7*ι * G (—«>» +оо);
7Г : Ля + By + С ζ + D = 0,
где d(a,/?,7) — направляющий вектор прямой и п(Л,В}С) —
нормальный вектор плоскости.
136
Глава 3
Угол φ между прямой ρ и плоскостью π определяется
соотношениями
7Г
φ = — — θ у если θ — острый угол;
7Г
φ = θ — — , если θ — тупой угол,
причем
или
dn
θ = arccos -тц—,
\d\\n\
aA + PB + <yC
О = arccos
у/а2 + β2 + 72 · VA2 + В2 + С2'
Возможны следующие случаи взаимною расположения
прямой ρ и плоскости π:
1) Прямая и плоскость параллельны (р|| π), когда d-n = О,
т. е. аЛ + /Ш+тС = 0;
2) Прямая и плоскость перпендикулярны (ρ ± π), когда
<Гхй = б,т.е.З[ = § = £;
3) Прямая ρ пересекает плоскость π, когда d - η Φ 0;
4) Прямая ρ лежит в плоскости 7г, когда й-п = 0и
r0*n+D=0tT. е. аЛ+/?Б+7С=0 и Ах0 + Вг/о+Сг0+1)=0.
§ 16. СВЯЗКА ПРЯМЫХ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Связкой прямых в пространстве с центром в точке N
называется множество всех прямых, проходящих через точку N.
Теорема· Каноническое (векторное) уравнение связки
прямых в пространстве с центром N(tfo> irtb ^o) (-N(ro))
имеет вид
α β
((r-r0)xd = 0, ά{α&η)\ (1)
где α, β. η — произвольные вещественные числа, не
равные нулю одновременно.
Линии и поверхности первого порядка
137
Доказательство. С одной стороны, всякая прямая,
определяемая уравнениями (1), проходит через точку N(xo,yo,z0).
Кроме того, любая прямая связки, проходящая через N(xo,yo,zo),
однозначно определяется заданием помимо точки N ее
направляющего вектора ά(α,β^)Ύ а потому она описывается
каноническим уравнением, совпадающим с уравнением (1).
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Прямая I и плоскость π заданы соответственно
уравнениями _ _ _ ^ г -
г = го + £а, г = ri + гео + vc.
Найти точку пересечения прямой и плоскости.
Решение. Запишем общее векторное уравнение плоскости π.
Поскольку Ь и с*неколлинеарны, то в качестве нормального
вектора η плоскости 7Г можно взять вектор η = 5 χ с. Тогда общее
уравнение плоскости π примет вид (г — fi, 5, с) = 0.
Пусть Μ (г) = ίΠπ — искомая точка. Тогда параметр £,
соответствующий вектору г в уравнении прямой, находится из
условия
{r0 + ta-ri,b,c) = 0,
или
(а, 6, c)t = (ri - f0, &, с). (1)
Если (а,5,с) = 0 и (ri — ?о,Ъ,с) Ф> 0, то решение
уравнения (1) не существует (прямая I параллельна 7г).
Если {а,Ьус) = 0 и (г\ — го,£,с) = 0, то уравнение (1)
выполняется для любого t (прямая I лежит в плоскости π).
Наконец, если (а,Ь, с) ^ 0, то точка Μ единственна, при этом
* ^ » (п-гоХс)^
τ = г0 Η ^ а.
(Й А с)
2· Прямая I и плоскость 7Г заданы соответственно
уравнениями
r = fo + ta> r-n + D = Q.
Написать уравнение ортогональной проекции V
прямой I на плоскость π.
138
Глава 3
Решение. Если I ортогональна π, т. е. векторы а и η кол-
линеарны, то V вырождается в точку Μ (г) = ίΠπ, причем
ее радиус-вектор, как следует из решения предыдущей задачи,
равен _ _
го · η + D _
г - г0 —-—а.
а · η
В противном случае V = π'ΓΊπ
для такой плоскости π', что I С
С тг' и π 1 тг' (рис. 3.20).
Уравнение плоскости π' имеет вид
(f-f(h α> η) =0,
поэтому прямая ί; = π' Π π
задается системой уравнений
ir-n + D = Q>,
\(г-гоУа,п) = 0
Рас. 3.20
3. Стороны двугранного угла заданы плоскостями
πι: г*· ni + £>ι = 0, π2: г · й2 + D2 = 0.
Написать уравнения биссекторных плоскостей
двугранного угла.
Решение. Биссекторная плоскость π двугранного угла есть
геометрическое место точек Μ (г), для которых
или (см. § 9)
\f ·ηι + Di| |f ·η2 +Дг|
ы
n2
Освобождаясь от знака модуля в последнем равенстве,
получаем уравнение двух биссекторных плоскостей для смежных
двугранных углов
Г · П\ + D\ _ Г · П2 + 1>2
ИЛИ
\Ы Μ/
Линии и поверхности первого порядка
139
4. Найти расстояние от точки
A(fo) до прямой I: f = fi+ta
в пространстве.
Решение. Пусть N — основание
перпендикуляра, опущенного из точки
А на прямую I, a f\ — радиус-вектор
точки B(f\) на прямой I (рис. 3.21).
Тогда расстояние d(A, I) от точки А
до прямой I равно
d(AJ) = \АЙ\ = \Ш\ sin Z.{a,WA)
5. Найти ортогональную проекцию А'(г') точки A('rO)
на прямую I: f=fi+ ta.
Решение. Ортогональная проекция точки А на прямую I рав-
на А! = Ι ΓΙ π, где плоскость π перпендикулярна I и Л е π.
Поскольку уравнение плоскости
7г: (г — го) α = О,
то (см. решение задачи 1)
-, _ (n>-n)-aw
г =тч + — а.
а- а
6. Написать уравнение общего перпендикуляра I к двум
непараллельным прямым
h: f=f\ +a\t,
l2: f= T2 -Vwity
αι x «2 Φ 0.
Решение. Общий перпендикуляр I есть прямая,
перпендикулярная прямым ίι, 12 и пересекающая их. Поскольку
αι χ α2 ^ б,
то в качестве направляющего вектора прямой £ возьмем вектор
а = αϊ χ θ2· Тогда 2 = πι Π π2, где плоскости πι, 7Г2 таковы,
ха| l(ro-fi) χα|
ϊ||α|
α
140
Глава 3
Рис. 3.22
что Ιγ С πι, ί2 С π2, Ϊ С πι, Ϊ С 7г2 (рис. 3.22). Поэтому
уравнения плоскостей имеют вид
πι : {τ — η,αϊ,αϊ χ α2) = 0,
π2 : (f - f2, α2, αϊ χ α2) = 0,
откуда получаем уравнение искомой прямой:
I . f(r-fbabai xa2) = 0,
' \(r-F2?a2,ai x a2) = 0.
7. Найти необходимые и достаточные условия того, что
три плоскости πι, π2, π3-'
πχ: Γ· ηι +Di = 0,
7v2:fn2 + D2=0} (2)
π3". f -Яз + Д* = 0
пересекаются в одной точке, и найти точку
пересечения этих плоскостей.
Решение. Для того чтобы πι, π2, π3 пересекались в одной
точке, необходимо и достаточно, чтобы плоскости πι и π2
пересекались, и их линия пересечения I = πι П π2 пересекала
плоскость π3 в единственной точке. Условие пересечения
плоскостей πι и π2, как известно, имеет вид а = щ χ η2 φ 0,
при этом вектор а является направляющим вектором прямой Ϊ.
Условие пересечения прямой I и π3 имеет вид а · пз φ 0 или,
окончательно,
(п1,п2,Яз) т^О. (3)
Линии и поверхности первого порядка
141
Пусть теперь выполнено условие (3). Найдем точку Μ (г)
пересечения плоскостей (2). Для этого заметим, что при
выполнении условия(3) векторы й\ хп2, п2 хпз, «з хй\ некомпланарны
(см. задачу 9 главы 1).
Действительно,
{йу χ п2, п2 х п3, п3 х щ) =
= ((ηι χ п2) х (п2 х п3),пз х щ) —
= (η2(ηι,η2,η3) - пз(г?ьп2,Я2),пз х «Ί) =
= (ni,n2,n3)2^0.
Разложим вектор г по базису ηι χ й2, п2 х пз, η3 χ ηι:
г = сх(щ χ п2) + β(η,2 х пз) + 7(^3 х ^ι)·
Тогда система уравнений (2) примет вид
Р(п1,п2уп3) + Di = О,
7(ηι,η2,η3) + ί>2 = 0,
α(ηι,η2,η3) + Dz = 0.
Откуда
А» Л £>ι As
(Й1,Й2,Йз)' (П1,П2,П3)' (Wi,n2,n3)'
и точка Μ пересечения плоскостей (2) имеет радиус-вектор
_ ^ £>! (η2 χ п3) + Αζ (пз х "ι) + £>э(Й1 х Я2)
(пьп2,пз;
8. Найти точку А"(г"), симметричную точке А(г0)
относительно прямой I: r = Fi + at.
Указание. Воспользоваться решением задачи 5.
итвет: г =2г\—го + 2 —— а.
а-а
9. Написать уравнение перпендикуляра V, опущенного из
точки A(fo) на прямую I: r = fi+at.
Ответ: Г: <" J ^ J
Цг - г0, γι - го, α) = 0.
142
Глава 3
10* Вычислить расстояние dili.h) между двумя прямыми
Ιι : г = т\ + dytt 1<ι : г = т^ + atf для случаев:
а) αϊ χα2 φ б (прямые скрещиваются или пересекаются);
б) αϊ χ а2 = 0 (прямые параллельны).
г\ \ мш ι \ 1(^2 -П, аи а2)\
Ответ:а)^ь<2)= ^ χ g. , ;
6)^,1,) = I(ft-,?>XU|.
ΚΙ
11. Найти точку B(fi), симметричную точке A(tq)
относительно плоскости π: г-η + D = 0.
Ответ: ri = го — 2—-—-—п.
η ■ η
12. Векторы θΆ = α, θί = Ъ, Об = с компланарны,
причем а и Ь неколлинеарны. Найти вектор ОЙ = ?м
где Μ — точка пересечения прямых ОС и АВ.
^ (а, Ь - а, а х 6) _
Ответ: г = λ—^ ^-с.
(с}Ь — α,α χ Ь)
ХЗ.Даны четыре вектора оА = а,ОЁ = Ь,об = с903 =
= d, причем а, Ь, с некомпланарны и прямая OD
пересекает плоскость ABC в некоторой точке Μ. Найти
Ответ: г = —=rz =: ^——а.
(d, b,c) + (d, с, а) + (d, α, b)
14. Доказать, что
а) уравнение всякой прямой в пространстве с направляю-
щим вектором а может быть записано в виде τ χ α — b,
где а ■ 5 = 0;
б) уравнение rxa = b при условии а ф 0, а · Ъ = 0 огсре-
деляет прямую с направляющим вектором а, проходящую
через точку с радиус-вектором г$ = (ах Ь)/{а · а).
15· Найти необходимые и достаточные условия, при
которых три плоскости 7tfc : г- пь + Dk = 0, к = 1, 2, 3,
принадлежат одному пучку плоскостей.
Ответ: (пип2,п3) = 0, Ζ>ι(η2 хп3)+02(п3 χπι) + Ζ)3(ηι χ
х я2) = б и по крайней мере один из векторов п2 х пз ♦ из х ί?ι,
ήχ χ П2 отличен от б (см. задачу 7).
Линии и поверхности первого порядка 143
16. Найти необходимое и достаточное условие, при
котором четыре плоскости я^: r-nk + D^ = О, к = 1,2,3, 1,
образуют тетраэдр.
Указание. Воспользоваться решением задачи 7.
Ответ: (ηι,η2,π3) φ О, (/?ι,η4,η3) ^ 0, (п2,пз,Я4) ^
^ 0, (^,^,η!) ^ О·, -Z>i(n2,r?3,n4) + #2(^1, %й4) -
- />з(пьЯ2,п4) + ί>4(ηι,η2,η3) ^ 0.
17. Пусть центр Ρ связки плоскостей задан системой
* -*
Р: <
f-ni+Di =0,
Г*-7?2 +£>2 = 0, (ηι,η2,η3) т^О-
г'-пз + .Оз = 0,
Доказать, что уравнение связки плоскостей с центром
в Ρ имеет вид г- (ащ + βηι + 7^3) + αι^ι + β&2 + 7^з = 0,
где α, β, η — вещественные параметры уравнения связки.
Глава 4
ЛИНИИ ВТОРОГО ПОРЯДКА
§ 1. эллипс
1.1. Каноническое уравнение
Эллипсом называется геометрическое место точек, для каждой из
которых сумма расстояний до двух фиксированных точек Fi и F2
плоскости, называемых фокусами, есть постоянная величина 2а,
причем она больше, чем расстояние 2с между фокусами:
2а > 2с.
(1)
Выберем декартову
прямоугольную систему координат
Оху так, что её начало О —
середина отрезка F\F2, а ось абс-
Рис41 цисс находится на прямой,
проходящей через Fi и F2, и имеет направление вектора OF2
(рис. 4.1). Пусть М(х,у) — произвольная точка эллипса. Тогда
JFi(-CiO) О
F2(c,0)
по определению +d(F2,M) = 2α
(2)
или
уДх - (-с))2 + у2 + \/(ж - с)2 + ΐ/2 = 2а,
\/(я + с)2 + ί/2 + \/(ж - с)2 + у2 = 2а,
\/(ж + с)2 + у2 = 2а - V(x-c)2 +у2,
(ж + с)2 + г/2 = 4а2 - 4aV(x - с)2 + у2 + (х - с)2 + у2,
х2 + Чхс + с2 = 4а2 - 4aV(x - с)2 + у2 + х2 - 2хс + с2,
4а\/(ж - с)2 4- г/2 = 4а2 - 4жс, а\/(ж - с)2 + у2 - а2 - же,
(а2-с2)я2 + «У =aV-c2).
Линии второго порядка
145
Отсюда, положив ,222 /iU
fr = a -<r, (3)
получаем Ь2х2 + а2у2 = а2Ь2, и, окончательно, уравнение
которому удовлетворяют координаты произвольной
точки М(х,г/) эллипса.
Убедимся, что любая точка М(ж, ?/) плоскости, координаты
которой удовлетворяют (4), лежит на рассматриваемом эллипсе.
Действительно,
d(FuM) = ч/(з:-(-с))2+^ =
=^+c)2+62(i-S)
= у ж2 + 2гсс + с2 + б2 - ^Ц-
о+ —
/a2 — b2 „ 7 ΓΙ ~
= J 2—ж + 2жс + b + с =
и аналогично d(F2, Μ) = |о - ~|. Далее,
d(Fl,M) = a+—, (5)
a
Л/У»
d{F2lM) = a-—t (6)
a
так как из соотношения (4) \х\ ^ at а из неравенства (1)
О < с < а. Тогда d{FuM) + d(F2lM) = 2a, а это означает, что
точка М(ж, ?/) лежит на данном эллипсе.
Итак, уравнение (4) является уравнением эллипса, причем
его называют каноническим уравнением эллипса.
Подчеркнем, что в полученном уравнении (4), определяющем
рассматриваемый эллипс с фокусами на оси абсцисс, а > 6, что
непосредственно следует из равенства (3).
146
Глава 4
Фокусы эллипса, определяемого уравнением (4) при условии
b > α, располагаются на оси ординат.
Если в уравнении (4) Ь = а, то оно имеет вид х2 + у2 = а2,
т. е. является уравнением окружности радиуса а с центром в
начале координат. В этом случае фокусы Fi и F2 совпадают, ибо
с = 0 в силу равенства (3). Поэтому окружность можно
рассматривать как частный случай эллипса. В дальнейшем, если нет
специальной оговорки, будем считать, что уравнение (4)
определяет эллипс с фокусами на оси абсцисс, т. е. в этом уравнении
а> Ь.
1.2. Исследование формы
Поскольку уравнение (4) содержит χ и у в четной степени, то,
если точка М(х, у) лежит на эллипсе, тогда и точки М'{х^ —у)
и М"{—х,у), симметричные с точкой Μ относительно осей Ох
и Оу, лежат на том же эллипсе. Кроме того, точка М'"(—х, —у),
симметричная точке М(х,у) относительно начала координат,
также лежит на эллипсе (рис. 4.2).
χ = —а
М"{
А''
М'"(-
,
-ж, у)
в» -У)
у1
ΐ
в
о \
В'
Μ(χ>ι
у
АГ'(ж,
χ = а
/) у = ъ
\а **
-у)
у = -Ъ
Рис. 4.2
Поэтому для эллипса, заданного уравнением (4), осями
симметрии являются оси координат, а центром
симметрии— начало координат.
Линии второго порядка
147
Эллипс расположен внутри прямоугольника, сторонами
которого являются отрезки прямых χ = ау χ = —а, у =
= Ьу у = -by так как из соотношения (4) имеем \х\ ^ а,
\у\ ^ Ь (рис, 4.2). Вершинами эллипса будем называть
точки пересечения его с осями координат. Эллипс (4)
имеет четыре вершины: Л(а,0), Б(0,Ь), Л'(-а,0), J3'(0, -6)
(рис. 4.2).
У эллипса, определяемого уравнением (4), в котором а > Ьу
будем называть большой полуосью отрезок О А или О А', а
малой полуосью — отрезок ОВ или ОВ', большой осью —
отрезок АА'У малой осью — отрезок ВВ1'. Отметим, что фокусы
эллипса расположены на большой оси.
Из соотношения (4) имеем у = ±^Va2 — x2у причем в
первой четверти ^
у = -у/а2 — χ2, Οζχζα. (7)
Функция
а
f:xe[0}a]->-y/a2-x2
является убывающей. Значения ее убывают от 6 до 0 при
возрастании χ от 0 до а. График функции / представляет
собой часть эллипса, расположенную в первой четверти. Для
построения полного эллипса следует воспользоваться
отмеченными свойствами симметрии этой кривой.
Любая прямая пересекает эллипс не более чем в двух
точках, ибо точки пересечения всевозможных прямых с эллипсом
находятся из решения системы
X 77
+ то" = 1, y = kx + d
или системы
о2 Ь2
х2 у2
-о + То = !> χ = α·
αζ Ъг
Таким образом, эллипс, определяемый уравнением (4), есть
замкнутая выпуклая линия, имеющая центр симметрии в точке О
и две взаимно перпендикулярные оси симметрии, совпадающие с
осями координат.
148
Глава 4
1.3. Параметрические
уравнения
Эллипс можно получить с помощью равномерного сжатия
окружности
х'* + у* = а2 (8)
к одной из координатных осей. Произведем, например,
равномерное сжатие плоскости к оси абсцисс, т. е. преобразование,
при котором точка (х\ у9) переходит в точку (ж, у), где
М)
{
X = X
α χ
.У = (ЪШ, (9)
причем Ь < а (рис. 4.3). Тогда
окружность (8) преобразуется в
линию, определяемую уравнени-
2 2
ем 2р + |у = 1, т. е. в эллипс
с фокусами на оси абсцисс, ибо
здесь а> Ь.
Пусть М(Х)У) —
произвольная точка эллипса (4),
N{x'->y') — точка на окружности (8), соответствующая
точке Μ при преобразовании (9), t = Ζ(Γ,Ом), 0 ^ t < 2π.
Тогда χ9 = α cost и у9 = asini, и в силу (9)
Рис. 4.3
χ = acost, y = bsmt7 О < t < 2π.
(10)
Уравнения (10) называют параметрическими
уравнениями эллипса(4). Параметр t называют эксцентрическим
углом точки Μ на эллипсе. Отметим, что для нахождения
угла t произвольной точки Μ эллипса следует
сначала построить окружность на большой оси эллипса как на
диаметре, затем через точку Μ провести прямую,
параллельную оси ординат до пересечения в точке N с построенной
окружностью, причем точки Μ и N должны лежать по
одну и ту же сторону от большой оси эллипса. Тогда
Линии второго порядка
149
1.4. Эксцентриситет
Эксцентриситет ε эллипса есть отношение половины
расстояния между фокусами к длине большой полуоси:
с
е = -.
а
(11)
Ясно, что для эллипса ε < 1, ибо а > с в силу (1). Далее, с
учетом соотношения (3), ε2 = ξρ = а ~2Ь = 1 — (J) , откуда
-iR^· l·^·
(12)
т. е. эксцентриситет ε определяется отношением длин полуосей
fc/α, и отношение длин полуосей Ь/а определяется
эксцентриситетом ε.
Эксцентриситет характеризует форму эллипса, а именно
степень его «вытянутости»: чем больше эксцентриситет ε, тем
более эллипс вытянут вдоль оси абсцисс.
В частности, для окружности ε = О, ибо с = 0. Таким
образом, для эллипса
0<ε< 1.
(13)
1.5. Фокальные радиусы
Отрезки, соединяющие
любую точку эллипса с его
фокусами, называются
фокальными радиусами
эллипса: г ι = FiM\ Г2 = F2M
(рис. 4.4). В силу (5), (6),
'П) η = α + εχ,
Т2 — а — ex.
Рис. 4.4
1.6. Директрисы
Две прямые, перпендикулярные прямой, проходящей через
фокусы эллипса, и расположенные симметрично по отношению
к центру эллипса на расстоянии α/ε от него, где а — длина
150
Глава 4
большой полуоси, ε — эксцентриситет эллипса, называются
директрисами эллипса (рис. 4,4).
Уравнения директрис эллипса, определяемого
уравнением (4), где а > 6, имеют вид
di: χ = —α/ε, аъ : χ = α/ε. (14)
В силу соотношения (13) α/ε > α, —α/ε < —α, τ. е.
директрисы эллипса отстоят от его центра дальше, чем
соответствующие вершины, а значит, они расположены вне эллипса.
Фокус и директрису, расположенные по одну сторону от
малой оси эллипса, будем называть соответствующими друг другу,
а расстояние между ними — фокальным параметром.
Теорема. Отношение расстояния г произвольной точки
эллипса до каждого из фокусов к расстоянию d той же
точки до соответствующей фокусу директрисы есть
величина постоянная, равная эксцентриситету эллипса.
Доказательство. Ради определенности рассмотрим фокус
F2(c,0) и соответствующую ему директрису d<i с уравнением
χ = α/ε. Пусть δ — отклонение произвольной точки
эллипса от директрисы <22- Уравнение директрисы аг\ χ - α/ε =
= 0 имеет нормированный вид, ибо ее нормальный вектор п(1>0)
единичный и свободный член отрицательный. А тогда
г _ Г2 _ α — εχ _ α — εχ _
Доказанное свойство эллипса можно положить в основу его
определения.
Эллипсом называют геометрическое место точек, для
каждой из которых отношение расстояния г до некоторой
фиксированной точки, называемой фокусом, к расстоянию d
этой же точки до некоторой фиксированной прямой,
называемой директрисой, есть величина постоянная и меньшая
единицы: r/d = ε < 1.
ЗАМЕЧАНИЕ. Для эллипса, определяемого уравнением (4),
где b > α, уравнение директрис имеют вид у = Ь/ε, у = —Ь/ε.
Линии второго порядка
151
1-7. Уравнение в полярных координатах
Пусть I — эллипс с фокусами F\ и i^, с директрисами d\ и
d2, с эксцентриситетом ε. Обозначим через J\, J2 точки
пересечения прямой F1F2 с директрисами di и <22. Предположим,
что ρ — фокальный параметр, равный расстоянию от фокуса до
соответствующей
директрисы, a Fie" — декартова ось,
определяемая прямой F1F2,
началом i*\ и базисным
вектором е, совпадающим с
ортом вектора J\F\. Введем
полярную систему координат с
полюсом Fi и полярной осью Рис-45
i*ip, совпадающей с положительной полуосью оси Fie(рис. 4.5).
Если Μ(ρ> ψ) — произвольная точка на эллипсе и М' — ее
проекция на ось Fie", то в силу доказанной теоремы и леммы
Шаля
_ г _ djM.Fi) _ ρ _
€~ d~ d{M,d{) ~ |J^j "
ΛΜ' J1F1 + FiM' ρ + pcosy>
Откуда ρ = ρε + ρε cos φ, поэтому уравнение эллипса в
полярной системе координат имеет вид
ρε
Р =
1 — ε cos φ'
(15)
1.8. Построение эллипса
Требуется построить эллипс, определяемый уравнением
χ
+
б2
= 1,
где а>Ъ.
Первый метод. Проведем окружности с\ и сг с центром в
начале координат и с радиусами соответственно а и b (рис. 4.6).
Пусть луч OS пересекает окружности с\ и сг соответственно
152
Глава 4
М{х,у)
в точках Ρ и Q. Допустим, что Рх — проекция точки Ρ на
ось абсцисс, Qy — проекция Q на ось ординат, t = Ζ(Γ, О?),
О < t < 2π; М(х,у) — точка пересечения прямой,
проходящей через Ρ и параллельной Оу, с прямой, проходящей
через Q и параллельной Ох.
Ясно, что χ = ОРх =
= acost, у — OQy — bsint.
В силу соотношения (10),
точка М(х,у) лежит на
эллипсе. Аналогично можно
построить ряд других точек эллипса,
а затем, используя найденные
точки, построить полностью его
график.
Второй метод. Сначала
строим вершины Α(α,0), Α'(-α,Ο), 23(0,6), В'(0,-6).
Затем находим фокусы Fi и F2 как точки пересечения
окружности с радиусом α с центром в точке В с осью абсцисс.
Точку М(х,у) определим как пересечение окружности радиуса η
с центром в точке Fi и окружности с радиусом г2 = 2а — Т\
с центром в F2, где т\ — произвольное положительное число,
заключенное между 0 и 2а.
Ясно, что М(х,у) лежит на эллипсе (4), ибо d{M,F\) +
+d(M7F2) = ri + 2a-ri = 2a. Используя ряд точек,
построенных указанным способом, можно построить полностью график
эллипса (4).
Рис. 4.6
§ 2. ГИПЕРБОЛА
2.1. Каноническое уравнение
Гиперболой называется геометрическое место точек, для
каждой из которых абсолютная величина разности расстояний до
двух фиксированных точек Fi и F2 плоскости, называемых
фокусами^ есть постоянная величина 2а, причем эта
величина меньше, чем расстояние 2с между фокусами: 2а < 2с, и она
отлична от нуля, т. е. 0 < a < с.
Линии второго порядка
153
Выберем ДПСК с началом в точке О в середине отрезка
F1F2, причем ось абсцисс определим прямой, проходящей
через точки F\ и F2 с направлением вектора F\F2, а ось ординат
строим так, как условились ранее.
Пусть М(х, у) — произвольная точка гиперболы. Тогда
|d(FbM)-d(F2,M)| = 2a,
d{Fu M)-d{F2,M) = ±2a,
^(ж + с)2 + j/2 - у/(х - с)2 + 2/2 = ±2о,
у/{х + с)2 + у2 = ±2а + у/(х - с)2 +"^,
х2 + 2жс + с2 + у2 = 4а2 ± Аау/{х - с)2 + у2 +
+ я2 -гже + ^ + у2,
±4а>/(я - с)2 4-1/2 = 4жс - 4а2,
±ау/(х — с)2 + 2/2 = хс — а2,
а2(х2 - 2хс + с2 + у2) = ж2с2 - 2a2sc + a4,
х2(а2-с2) + аУ = а2(а2-с2),
х\с2-а2)-а2у2 = а2{с2-а2).
Отсюда, положив Ь2 = с? — а2, получаем \?х2 — а2у2 = α2δ2.
Поэтому уравнение, которому удовлетворяют координаты любой
точки гиперболы, имеет вид _2 ,,2
Убедимся, что любая точка М(х,у), координаты которой
удовлетворяют уравнению (1), лежит на данной гиперболе.
В самом деле, ,
d{FuM) = у/{х + с)2 + у2 = «/(х + с)2 + 62 (^ - Л -
= Jx2 + 2хс + с2 + —%- -Ь2 =
а2
= ^х2 + 2хс + <? + ^—р^-(?+а2 =
I с χ I / ся?\
= ^/χ2 + 2^+-^--χ2 + α2 = ^(α + -) =
и, аналогично, d(F27 Μ) = |α — &\.
сх\
а-\ ,
a I
154
Глава 4
Из (I) имеем ξ? > 1, или |rr| ^ а. Если χ ^ а, то учитывая,
что а <с, получим
d{FuM) = a+—y d{F2yM) = -a+—,
а а
Если χ ^ —α, то
d(FbM) = - — - α, d(F2,M) = а - —.
а а
(2)
(3)
В обоих случаях |d(Fi, M) — tf(F2, М)| = 2at a
следовательно, точка М(ху у) лежит на гиперболе. А тогда уравнение (1)
является уравнением гиперболы, причем его называют
каноническим уравнением гиперболы.
ЗАМЕЧАНИЕ. Абсолютная величина разности расстояний от
произвольной точки Μ плоскости до двух фиксированных
точек Fi и F2 той же плоскости при условии, что точки Fi, F2
и Μ не лежат на одной прямой, меньше расстояния между
точками Fi и F2, ибо разность двух сторон треугольника меньше
третьей стороны.
Геометрическое место точек j< —2с >[ м
плоскости, для которых абсо- S Fx F2 H
лютная величина разности рас- Рис. 47
стояний до двух фиксированных точек F\ и F2 есть величина
постоянная, равная расстоянию между точками F\ и F2 (2a =
= 2с, т. е. а = с), есть совокупность лучей F2# и FiS прямой,
на которой лежат точки Fx и F2 (рис. 47).
Геометрическое место точек
плоскости, для которых
абсолютная величина разности до
двух фиксированных точек Fi
и F2 есть величина постоянная,
Рис.4.8 равная нулю (а = 0),
представляет собой прямую, перпендикулярную F\F2 и проходящую
через середину отрезка FiF2 (рис. 4.8).
Последние два случая (а = си а = 0) исключены
ограничением, приведенным в определении: а < с и а ф 0.
Линии второго порядка
155
2.2. Исследование формы
Координаты произвольной точки М(хуу) гиперболы
фигурируют в ее уравнении (1) в четных степенях. В связи с этим
вместе с точкой М{х, у) данной гиперболе принадлежат
точки М'{х, —у), М"(—х,у), Мт{-х^—у), что означает:
гипербола (1) имеет две оси симметрии, совпадающие с осями
координат, и центр симметрии, совпадающий с началом координат
Рис. 4.9
Вершинами гиперболы называются точки пересечения ее с
осями симметрии. Гипербола (1) имеет две вершины: А'(—α,Ο)
и А{а, 0).
Рассмотрим точки В(0, Ь) и £'(0, — Ь), лежащие на оси
ординат и точки С(—а, 6), D(a, b), K(ay —b), L(—ay —b).
Прямоугольник CDKL называется основным
прямоугольником гиперболы (1).
У гиперболы (1) будем называть действительной осью
отрезок АА', мнимой осью отрезок ВВ*, действительной
полуосью — отрезок О А* или ОА, мнимой полуосью — отрезок
ОВ' или ОВ. Отметим, что фокусы гиперболы (1) расположены
на действительной оси.
Из уравнения (1) имеем:
y2 = b2(i-1)' у2-^2-"2)- (4)
156
Глава 4
Следовательно, в первой четверти
у = -ух2 — α2, χ ^ α. (5)
а
Из уравнения (4) вытекает, что в полосе \х\ < а точек
гиперболы (1) не имеется.
Функция
д: χ G [а; +оо) —> - ух2 — а2
а
является возрастающей, ибо ее производная у1 = fb*_ 2 при
χ Ε (α, +оо) положительна, причем функция д возрастает от О
до +оо при возрастании ж от α до -f оо.
График функции д представляет собой часть графика
гиперболы, расположенную в первой четверти.
Расстояние d от произвольной точки гиперболы Μ (ж, у),
лежащей на части гиперболы, определяемой уравнением (5), до
прямой у = (Ь/а)х, определяемой диагональю LD основного
прямоугольника, находится по формуле:
, __ \Уа — Μ _ \Ь\/х2 — о? — Ьх\ _ b
Си —
X
_ _ ._ \Jx2 — α2
Va2 + Ь2 с с'
а26 а2Ь
с|ж + у/х2 — а2| с (ж + v's2 ^ о2)
Ясно, что Нтж_,+оо d = 0.
Напомним, что прямую j/ = кх + с называют наклонной
асимптотой некоторой кривой, если при χ —> +оо (х -> —оо)
выполняется условие _. / / ч f \
lim (шж) — for — с) = 0.
ж—+оо V^v / )
(ж—►—оо)
В силу последнего, можно утверждать, что прямая у =
= (Ь/а)х является для части гиперболы, определяемой
уравнением (5), асимптотой.
Из сравнения уравнения (5) и уравнения асимптоты видно,
что все точки рассматриваемой части гиперболы находятся с
одной стороны от асимптоты и ближе к оси абсцисс, чем
соответствующие точки данной прямой.
Линии второго порядка
157
Используя свойства симметрии гиперболы (1), на
основе графика ее части, построенной в первой четверти, можно
построить полный ее график (рис. 4.9).
Гипербола (1) имеет две ветви, пересекающие ось абсцисс и
расположенные в двух областях, одна из которых ограничена
отрезком DK и продолжением лучей OD и ОК, а другая
симметрична указанной области относительно оси ординат.
Асимптоты гиперболы (1) определяются диагоналями ее основного
прямоугольника и их уравнения имеют вид
У= -ffi У = —х- (6)
а а
Гиперболу, у которой полуоси равны, называют
равносторонней, и ее уравнение имеет вид х2 — у2 = а2.
Уравнения асимптот равносторонней гиперболы таковы: у =
= х> У = —я· Основной прямоугольник равносторонней
гиперболы есть квадрат, и, вследствие этого, ее асимптоты
перпендикулярны друг другу.
Две гиперболы, которые определяются уравнениями
ί!_ι>! = 1 _ξ! + ^! = 1 (7)
о2 δ2 ' а2 Ъ2 ' К}
в одной и той же системе координат при одних и тех же значениях
полуосей о и 6, называются сопряженными друг с другом. Эти
гиперболы имеют общие асимптоты (рис. 4.10).
Рис. 4.10
158
Глава 4
2.3. Параметрические уравнения
Уравнение (1) можно переписать в виде
(МИН)-1-
Ясно,что§ + £ /О, f-f 5*6.
Положим| + 1=«.!-{ = 1.
Тогда
-00 < t < +00, ί ^ Ο
С другой стороны, при любом £ φ О точка с координатами (8)
лежит на гиперболе (I), в чем убеждаемся при подстановке
выражений (8) в уравнение (1).
Уравнения (8) называются параметрическими
уравнениями гиперболы (1).
Пусть точка М(х, у) лежит на правой ветви гиперболы (1 )f
для которой χ ^ α. Тогда § (t + |·) ^ α, а потому ^-gti ^ 1,
т.е. t >0.
Обратно, если t > О, то χ ^ α и точка M(x,j/) лежит на
правой ветви.
Аналогично, при t < 0 получаем левую ветвь гиперболы
(рис. 4.11).
а·
(8)
Яыс.
■.4J/
Линии второго порядка
159
2.4. Эксцентриситет
Эксцентриситетом ε гиперболы называют отношение
половины расстояния между фокусами к длине действительной полу-
оси: / /т
ε = с/а. (9)
Для гиперболы ε > 1, ибо 0 < а < с. Кроме того, ε2 =
= с2/а2 = (а2 + Ь2)/а2 = 1 + Ь2/а2.
Откуда ε = y/i + b2/a2, а следовательно, b/a = ν'ε2 - 1.
Таким образом, эксцентриситет определяется отношением 6/а,
5 отношение Ь/а определяется эксцентриситетом.
Эксцентриситет гиперболы характеризует форму ее
основного прямоугольника, а именно, величину угла между
асимптотами, т. е. форму самой гиперболы. Заметим, что у
равносторонней гиперболы ε = \/2.
2.5. Фокальные радиусы
Отрезки, соединяющие произвольную точку гиперболы с ее
фокусами, называют фокальными радиусами (рис. 4.12).
В силу предыдущих соотношений при χ ^ а для правой ветви
гиперболы
г\ = а + εχ, r2 = —a + ex. (10)
При χ ^ — α для левой ветви гиперболы
η = — а — εχ, Г2 = α — ex. (11)
Рис. 4.12
160
Глава 4
2.6с Директрисы
Две прямые, перпендикулярные прямой, проходящей через
фокусы гиперболы, и расположенные симметрично по отношению к
центру гиперболы на расстоянии α/ε от него (где а —длина
действительной полуоси, ε — эксцентриситет гиперболы) называют
директрисами данной гиперболы (рис. 4Л 2).
Уравнения директрис d\ и с^ гиперболы (1) имеют вид
χ = —, χ = —. (12)
ε ε
Директрисы гиперболы (1) расположены в полосе \х\ < а,
ибо для точек директрис \х\ = | ± α/ε\ < а, так как для
гиперболы ε > 1 ♦
Фокус и директриса гиперболы, расположенные по одну
сторону от мнимой оси гиперболы, называют соответствующими
друг другу.
Теоремао Отношение расстояния г от произвольной
точки гиперболы до каждого из фокусов к расстоянию d той
же точки до соответствующей фокусу директрисы есть
величина постоянная и равная эксцентриситету:
г
Доказательство. Для определенности рассмотрим правый
фокус F2(c,0) и правую директрису cfe, определяемую
уравнением χ — α/ε = 0. Пусть δ — отклонение произвольной
точки М(хуу) гиперболы от директрисы d2. Уравнение названной
директрисы χ — α/ε = О — нормированное, ибо ее нормальный
вектор п(1,0) —единичный.
Если М(#, у) лежит на правой ветви гиперболы, то
г Г2 —α + εχ__—α + εχ__
Если М(х, у) лежит на левой ветви гиперболы, то
г г 2 α — εχ α — εχ
d -<5 -а? + §
~χε-\-α
= ε.
Линии второго порядка
161
Доказанное свойство гиперболы можно положить в основу
ее определения.
Гиперболой называется геометрическое место точек, для
каждой из которых отношение расстояния г до некоторой
фиксированной точки, называемой фокусом, к расстоянию d той
же точки до некоторой фиксированной прямой, называемой
директрисой, есть постоянная величина, большая единицы, т. е.
rid = ε > 1.
2 2
ЗАМЕЧАНИЕ. Для гиперболы — %ς + %2 = 1 уравнения
директрис имеют вид у = Ь/ε и у = —Ь/е.
2.7. Уравнение гиперболы
в полярных координатах
Пусть h и fo — ветви гиперболы с эксцентриситетом ε, с
фокусами F\, F2 и соответствующими им директрисами d\, d2.
Допустим, что J\, J2 — точки пересечения прямой F\F2 с
директрисами d\, d2 соответственно, ρ — фокальный параметр,
равный расстоянию от фокуса до соответствующей ему
директрисы, F2e—декартова ось, определяемая прямой, проходящей
через точки F\ и F2, с началом в точке F2 и с направляющим
вектором, совпадающим с ортом вектора J2F2, F2p — полярная
система координат, определяемая полюсом F2 и полярной осью
F2p, совпадающей с положительной полуосью декартовой оси
Рис. 4.13
162
Глава 4
Если Μ(ρ,φ)—произвольная точка правой ветви 12
и А/' — се проекция на ось F2e, то, используя доказанную
теорему и лемму Шаля, имеем
г ^d(M,F2) = ρ ρ
* <W<fc) |j£jj?| J2M'
Ρ
J2F2 + F2M' Ρ + Ρ cos ν?
Отсюда p = pe-\- ρε cos ν?, а следовательно
ρε
/5 =
1 — ε cos </?
— уравнение правой ветви 12 в полярной системе координат
Если Ν(ρ,φ) — произвольная точка левой ветви Ιγ
и Ν' — ее проекция на ось, то в силу последней теоремы
d(N,F2) ρ ρ
ε =
d(N,d2) jjTjv»! -J2N'
Ρ
- (<№ + F2N') -P-P cos φ
Отсюда p= —ρε cos φ — ρε, а потому
p. ~Ρε
1 +£COS<£
— уравнение левой ветви 1\ в полярной системе координат.
2.8. Построение гиперболы
по точкам
Построим гиперболу, определяемую уравнением (1).
Сначала начертим основной прямоугольник LCDK,
используя числа а и 6, а затем начертим асимптоты гиперболы
(рис. 4.14).
Отметим, что на рисунке 4.14 АВ = у/а2 + Ь2. Но а2 + Ь2 =
= с2, а потому УШ = с Тогда точки пересечения
окружности с центром в точке О и с радиусом АВ определяют фокусы
гиперболы Fi и F2
Линии второго порядка
163
Рис. 4Λ4
Пусть Γι —некоторое число и Г2 = 2α + Γχ. Точки
пересечения окружностей с центрами в фокусах и радиусами т\
и Г2 лежат на гиперболе. Меняя число п, мы будем
получать разные точки гиперболы, а по ним можно строить
искомый график.
§ 3. ПАРАБОЛА
3.1. Каноническое уравнение
Напомним, что для эллипса и гиперболы отношения
расстояния г от произвольной точки до некоторой фиксированной
точки, называемой фокусом, к расстоянию d от той же точки
до некоторой фиксированной прямой, называемой
директрисой, есть величина постоянная, равная e = r/d, причем для
эллипса 0 < ε < 1, а для гиперболы ε > 1. Осталось
рассмотреть случай, когда ε = 1.
Параболой называют геометрическое место точек, для
каждой из которых расстояние г до некоторой
фиксированной точки плоскости F, называемой фокусом,
равно расстоянию d до некоторой фиксированной прямой d,
называемой директрисой.
В соответствии с предыдущим иногда говорят, что у
параболы эксцентриситет ε = 1.
Расстояние ρ от фокуса параболы до се директрисы
называется фокальным параметром параболы.
104
Глава 4
Рис. 4ЛЬ
Если J — точка пересечения
М(х у) Директрисы с прямой, проходящей
через фокус F и
перпендикулярной директрисе dy то \FJ\ = ρ
(рис. 4.15,4Л6).
Выберем на плоскости
прямоугольную декартову систему
координат с началом О в
середине отрезка FJ, с
положительным направлением оси абсцисс,
совпадающим с направлением
вектора JF, а ось ординат
построим в соответствии с
принятым ранее соглашением.
Отметим, что в выбранной
системе координат уравнение
директрисы d имеет вид
* + |-0.
(1)
х Пусть М(х,у) —
произвольная точка параболы. Тогда
г = d{F, M)
v/Ry
+ 2/2,
Рис. 4.16
d = d{M,d) = \х + %\
По определению \J{x - ρ/2)2 + у2 = \χ + ρ/2|, т. е.
2 2
9 Ρ 9 9 Ρ
ж -ρ.τ-1 ^- + у = a; + pa; + —,
4 4
j/2 = 2ρχ.
(2)
Итак, координаты произвольной точки параболы
удовлетворяют уравнению (2).
Линии второго порядка
165
Убедимся, что любая точка Л/(х,у), координаты которой
удовлетворяют уравнению (2), лежит на данной параболе.
В самом деле, из (2) следует, что у точек, координаты
которых удовлетворяют (2), абсциссы положительны, т. с.
χ > 0. Тогда
г = d(FtM) = \/(*-f)2 + 2/2 =
= ,Jx*-px+^+2px = \J(x + l)2 = x+ f,
d = d{M,d) =
x + V-
X+2
откуда г = rf, и, следовательно, точка M(x,y) лежит на
данной параболе. Таким образом, уравнение (2) является
уравнением параболы, причем его называют каноническим уравнением
параболы.
ЗАМЕЧАНИЕ. Можно сформулировать следующее общее
определение эллипса, отличного от окружности, параболы
и гиперболы.
Геометрическое место точек плоскости, для каждой из
которых отношение расстояния г до фиксированной
точки F, называемой фокусом, к расстоянию d до
фиксированной прямой d, называемой директрисой, есть
постоянная величина ε = r/d, представляет собой либо эллипс,
если 0 < ε < 1, либо параболу, если ε = 1, либо
гиперболу, если ε> 1. Число ε называют эксцентриситетом
соответствующего геометрического места точек.
3.2. Исследование формы
Так как уравнение (2) содержит ординату в квадрате, то,
если точка М(х,2/) лежит на параболе, тогда и точка М(х, — у)
также лежит на параболе. Поэтому ось абсцисс является осью
симметрии для параболы (2).
Вершиной параболы называется точка пересечения ее с
осью симметрии. Вершина параболы (2) в указанной системе
координат совпадает с началом координат.
166
Глава 4
Из уравнения (2)
следует, что у точек,
лежащих на параболе, абсциссы
неотрицательные, и,
следовательно» вся парабола (2)
расположена в правой
полуплоскости.
В первой четверти график
параболы совпадает с
графиком функции
Рис, 4.17
f:xe [0;+оо) -> т/2рх.
2 =2ру
Ясно, что в
промежутке (0,+оо) функция /
возрастающая, ибо в этом
промежутке ее производная для
любого χ положительна,
причем при возрастании ж от О
до +оо значение функции
возрастает от 0 до +оо.
Построив график
функции / и воспользовавшись
свойством симметрии
параболы, можно полностью
построить график параболы (2)
(рис. 4.16).
Используя
соответствующие преобразования
системы координат, можно установить, что нижеследующие
уравнения определяют также параболы (рис. 4.17,4,18):
.2
= -2ру
Pile. 4J8
у" = -2рх, ρ > 0;
χ2 = 2ру, ρ > 0;
х2 = —2ру, ρ > 0.
(3)
(4)
(5)
Причем параболы (2) и (3) симметричны относительно оси
ординат, а параболы (4) и (5) — относительно оси абсцисс.
Линии второго порядка
167
М(х,у)
3.3. Уравнение параболы в полярных координатах
Пусть I — парабола с фокусом F и директрисой d. Допустим,
что J — точка пересечения директрисы с прямой, проходящей
через фокус и перпендикулярной <2, ρ = \JF\ — фокальный
параметр параболы, Fe —
декартова ось с началом в точке F
и направляющим вектором,
являющимся ортом вектора XF,
Fp — полярная система
координат с полюсом в точке F и
полярной осью Fp,
совпадающей с положительной полуосью
декартовой оси Fe (рис. 4.19). Рис. 4Λ9
Если М(р, φ) — произвольная точка на параболе и М' —
ее проекция на ось Fef то, по определению, d(M, F) = d(M, d) ,
Т' е' ρ = |JA?| = 7М7 = IF + WM7 = р + pcos<p.
Отсюда ρ = ρ + ρ cos φ, а следовательно,
p=—^—
1 — cos φ
— уравнение параболы в полярных координатах.
3.4. Построение параболы по точкам
Из уравнения (2) находим величину параметра ру выбираем
произвольно положение фокуса F и на расстоянии ρ от F
проводим директрису d, а затем прямую, проходящую через F\
перпендикулярную директрисе
и пересекающую ее в точке J
(рис. 4.20).
Далее строим
прямоугольную декартову систему
координат Оху с началом в середине
отрезка JF, причем ось абсцисс
определяем прямой, проходящей
через точки J и F, с
направляющим вектором, совпадающим
Рис. 4.20
ΐοδ
Глава 4
с направлением вектора ТР. а ось ординат проводим так, чтобы
Оху была правой.
Проведем прямую I с той же стороны по отношению к
директрисе d, где находится начало координат, причем так, чтобы
прямая I была параллельна директрисе d и находилась от нее
на расстоянии d > р/2. Начертив окружность с центром в F и
радиусом dy получаем в пересечении этой окружности с прямой
I две точки рассматриваемой параболы.
Изменяя величину d, можно указанным способом
построить ряд точек данной параболы, а затем, используя полученные
точки, построить искомый график параболы·
§ 4. ПРЕОБРАЗОВАНИЕ КОЭФФИЦИЕНТОВ
ОБЩЕГО УРАВНЕНИЯ
ЛИНИИ ВТОРОГО ПОРЯДКА
ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИСТЕМЫ КООРДИНАТ
Эллипс, парабола» гипербола, определяемые соответствующими
каноническими уравнениями в рассмотренных декартовых
прямоугольных системах координат, представляют собой
алгебраические линии второго порядка. Возникает вопрос о том,
какие еще существуют на плоскости алгебраические линии второго
порядка.
В силу теоремы 1 § 2 главы 3 алгебраическая линия второго
порядка Z, и определяемая общим уравнением второго порядка
ацх2 + 2а12ал/ + а22У2 + 2а^х + 2а2з2/ + <*зз = О, (i)
где а\\, а\2, а-22 не равны нулю одновременно, не изменяет свой
порядок, если от данной ДПСК перейти к другой ДПСК.
Условимся группу слагаемых ацх2 + 2а\2ху + о>22У2
-левой части уравнения (1) называть группой старших членов,
а группу слагаемых 2αΐ3# + 2а^зУ + ^зз —линейной частью
уравнения (1).
Поставим целью выбрать такую ДПСК, в которой
уравнение (J) линии I примет наиболее простой, так называемый
канонический вид, позволяющий установить геометрические
характеристики этой линии.
Линии второго порядка
169
Рассмотрим систему координат О'х'у'', получаемую
параллельным переносом системы Оху вдоль вектора ОО'. Ранее
были установлены соответствующие формулы преобразования
координат
χ = х' + х0у у = у' + 2/о,
где (х,у) — координаты произвольной точки в системе Оху,
{х',у') — координаты той же точки в системе О'х'у',
(#о>2/о) —координаты начала О' в системе Оху.
Уравнение(1) линии I в системе О'х'у' имеет вид
аи{х'2 + 2х'хо + х1) +
+ 2а12(х'у' + х'уо + хоу' + х0Уо) + а22(у'2 + 2у'у0 + у%) +
+ 2αι3(χ' + xq) + 2а2з{у' + Уо) + «зз = О,
ana/2 + 2а12х'у' + а22у'2 + 2«'13s' + 2«232/' + «зз = 0, (2)
где / /ъ\
«13 = вцЯо + «122/0 + «13, (о)
«23 = «12^0 + «222/0 + «23- (4)
Выражение для а33 представимо в виде
«33 = («11^0 + «122/0 + «13)Л'0 +
+ («12#0 + «222/0 + «2з)2/0 + βΐ3#0 + α23ΪΛ) + «33- (5)
Отсюда в силу (3), (4)
а33 = (G13 + α13)^0 + («23 + а2з)У0 + «33- (6)
Подчеркнем, что при параллельном переносе системы
координат коэффициенты группы старших членов не изменяются.
§ 5. УПРОЩЕНИЕ ОБЩЕГО УРАВНЕНИЯ
ЛИНИИ ВТОРОГО ПОРЯДКА
ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИСТЕМЫ КООРДИНАТ
Попытаемся выбрать начало О'(хо,уо) системы координат
О'х'у' так, чтобы коэффициенты а'13 и а23 уравнения (2) § 4
равнялись нулю. Из соотношений (3), (4) § 4 имеем:
{«ЦЖО+«122/0+«13 = О, ,j.
«12#0 + «222/0 + «23 = 0.
170
Глава 4
Последняя система имеет единственное решение, если
Δ =
CLu Q>12
& 12 <*22
= «11^22 - 0?2 Φ 0- (2)
Итак, если выполнено условие (2), то в системе координат
О'х'у9, у которой начало О1 имеет координаты (жо> Уо) *
найденные из (1), упомянутое уравнение (2) § 4 имеет вид
avlx'2 + 2al2x'y' + a22yf2 + а33 = 0, (3)
причем в силу соотношения (6) § 4
азз = αΐ3^ο + α23ϊ/ο + аз3' ^
Отметим, что, если точка М(х\уг) лежит на линии Z,
т. е. ее координаты {х'>у') удовлетворяют уравнению (3),то
М'(—#', -у') таюке расположена на линии I, ибо ее координаты
(—зг\ -у') удовлетворяют тому же уравнению (3).
Таким образом, если условие (2) выполнено, то существует
точка О'(хо,уо) такая, что точки линии I располагаются
симметрично относительно нее, т. е. эта точка является центром
симметрии линии Почку О'(яо>г/о) называют центром линии,
а саму линию — центральной.
Подчеркнем, что линия I, определяемая общим уравнением,
является центральной, если
|лц αι2|
Δ =
Ф0.
|U12 α22|
Изученные эллипс и гипербола, определяемые своими
каноническими уравнениями, являются центральными линиями.
§ 6. ПРЕОБРАЗОВАНИЕ КОЭФФИЦИЕНТОВ
ОБЩЕГО УРАВНЕНИЯ ЛИНИИ ВТОРОГО ПОРЯДКА
ПРИ ПОВОРОТЕ СИСТЕМЫ КООРДИНАТ
Рассмотрим систему координат Оху, получаемую поворотом
системы Оху вокруг начала на положительный угол ψ.
Ранее были установлены соответствующие формулы
преобразования координат χ — χ Cos φ - у sin φ,
у = χ sin φ + у cos φ>
Линии второго порядка
171
где (х, у) — координаты произвольной точки в системе Оху,
(£> у) — координаты той же точки в системе Оху.
Общее ураннение линии I в системе Оху имеет вид
αϊ ι (χ2 cos2 φ — 2xy cos φ sin φ + у2 sin2 ψ) +
+ 2ai2(x2 cos φ sin φ + xy cos2 φ —
— xy sin2 φ — у2 sin φ cos φ) -f
+ ^22 (s2 si**2 ^ + 2xy ^ φ cos φ + у2 c<>«2 y?) +
-f 2αΐ3(ί cos v? - £ sin <p) + 2а2з(я sin v? + ?/ cos φ) + α3Λ = (λ
йц52 + 2ai2xy + Й22^2 + 2αι3ί + 2а2з£ + азз = О, (2)
где
ац = ancos2<^-h2ai2COsv?sin<^ +a22sin2<^, (3)
о о
άΐ2 = — ац cos<^sin^ + <Zi2COs ^ —ai2sin φ +
+ a22 sin φ cos ψ = αχ2 cos 2φ —— sin 2φ, (4)
Й22 = an sm v? — 2aj2 sin φ easy? + агг cos </?, (5)
«13 = ai3 cos ν? + θ23 sin φ, (β)
«23 = —«13 sin φ + а2з cos φ, (7)
азз = озз- (8)
Подчеркнем, что при повороте системы коораинат
свободный член общего уравнения не меняется
ЗАМЕЧАНИЕ. Вспоминая, что
1 4- cos 2φ — 2 cos2 у»,
1 — cos 2φ = 2 sin y>,
2 sin ^ cos <£ = sin 2y?,
из (3), (4), (5) будем иметь
2ац = ац(1 -hcos2^) + 2&i2 sin 2y? + а2г(1 - cos2<^).
2δΐ2 = 2ai2cos2y?- (ац -a22)sin2y?,
2Й22 = вц(1 - cos 2φ) - 2ai2sin2<£ -fa22(l -fcos2v?),
172
Глава 4
ИЛИ
2йц = (ац + агг) + ((ац - агг) cos2</> + 2αχ2 sin2<p),
2αΐ2 = —(ац - α22) «in 2<р -f 2αι2 cos 2y>,
2а22 = (ац + а22) - ((ац - а22) cos2</> + 2ai2 sin 2φ).
А тогда
4αηα22 - Аа\2 = (ац + а22)2 - (ац - а2г)2 cos2 2φ -
— 4αι2(αχι — а22) cos2y?sin2v? —
— 4а22 sin2 2φ - 4α*2 cos2 2<ρ +
+ 4ai2(an — α22) cos2<^sin2<^ — (ац — α22)2 sin2 2<^ =
= (ац + α22)2 ~ (ац - α22)2 - 4α22 = 4аца22 - 4а?2.
Следовательно,
йц<*22 - ά22 = ац022 ~ α12. (9)
§ 7. УПРОЩЕНИЕ ОБЩЕГО УРАВНЕНИЯ
ЛИНИИ ВТОРОГО ПОРЯДКА
ПРИ ПОВОРОТЕ СИСТЕМЫ КООРДИНАТ
Если в исходном общем уравнении линии I коэффициент
αΐ2 т^ 0, то за счет выбора угла φ можно добиться того, чтобы в
уравнении (2) § 6 той же линии в системе Оху коэффициент άχ2
был равен нулю. Для этого следует потребовать в силу (4) § 6 ,
чтобы ац - а22 . 0 Λ
αχ2 cos 2φ sin 2φ = 0.
Последнее однородное тригонометрическое уравнение
сводится к уравнению
, п О.Ц - а22 А , п ац - а22
al2ctg2(p = 0, ctg2y> = —— ,
решение которого есть
φ = -arcctg-^- — + -га, η = 0,±1,±2,... (1)
2 2αΐ2 2
Из соотношения (1) нетрудно найти искомый
положительный угол.
Линии второго порядка
173
§ 8. ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ
ОБЩЕГО УРАВНЕНИЯ
ЛИНИИ ВТОРОГО ПОРЯДКА
/ случай. Если
* _ |αιι αΐ2
αϊ 2 θ22
/о,
то линия I является центральной и ее уравнение в системе
координат О'х'у', полученной параллельным переносом системы
Оху вдоль вектора ОО', где О'(жсь2/о) — центр данной линии,
имеет вид
апх'2 + 2ai2x'y + а22у'2 + <*зз = °>
причем
«зз = αΐ3*ο + β232/ο + <*зз- (I)
В случае, когда а\2 = 0, то в названной системе координат
0*х'у' уравнение линии I уже имеет канонический вид
а11х'2+а22у'2+а'ы=Ъ. (2)
В случае, когда а\2 ^ 0, следует рассмотреть систему
координат О'ху, получаемую поворотом системы О'х'у'
вокруг начала О' на положительный угол φ, определяемый в
силу соотношения (1)§7. Тогда в системе О'ху уравнение
линии I имеет канонический вид
ацх2 + а22У2 + а'зз = °> (3)
где йп, 022, находятся по формулам (3), (5) § 6, а а'33 — по
формуле (1).
В силу соотношения (9) § 6,
Δ =
ац а\2
0<\2 0.22
2 ~ - -2 *-
= ^11^22 — CL\2 = аП^22 — ^12 = ^11^22,
т. е. Δ = ац022· Так как определитель Δ ф 0, то ац / О,
Й22 7^0.
Если а!33 τ1 0, то уравнение (3) представимо в виде
~2 ~2
1 ■ * -1. (4)
5ц θ22
174
Глава 4
Пусть Δ > 0, т. е- аца22 > 0- Это означает, что
коэффициенты an и ά22 имеют один и тот же знак. Не уменьшая
общности, будем считать, что эти коэффициенты положительны, ибо в
противном случае уравнение (3) можно умножить на — 1.
Тогда, если — а33 > О, то уравнение (3) определяет эллипс;
если а'33 — О» Т0 уравнение (3) определяет точку О'(0,0)
(«вырожденный» эллипс); если —033 < 0, то уравнение(3) не
определяет никакой фигуры («мнимый» эллипс).
Пусть Δ < 0, τ, е. йцЙ22 < 0. Следовательно, йц и Й22
имеют противоположные знаки. Не ограничивая общности,
будем считать, что йц > 0, U22 < 0.
Тогда, если — а33 > 0, то уравнение (3) определяет гиперболу
с фокусами на оси абсцисс системы О'ху. Если — а33 < 0, то
уравнение (3) определяет гиперболу с фокусами на оси ординат
системы О'ху. Если а!33 = 0,то из (3) получим уравнение
{\/&ηΧ + \/-й22У) ' (y/άϊΐΧ ~ \/-Й22 υ) = 0,
которое определяет пару прямых, пересекающихся в начале
координат системы О'ху («вырожденная» гипербола):
\fiiuX + >J-Q>22 У = 0, у/йиХ - \/~Й22 У — 0-
2 случай. Если
Δ =
л
αηα22-αΐ2 = °> (5)
^11 G12
|αΐ2 α22|
то линия I не обладает единственным центром. При этом когда
в уравнении (1) § 4 коэффициент а\2 = 0, то в силу
соотношения (5) л ибо ап = 0, либо агг = 0,т. е. если для определенности
считать, что ац — 0, то уравнение линии I таково:
<*222/2 + 2а>\зх + 2а2зУ + озз = 0. (6)
Если же в уравнении (1) § 4 а\2 ^ 0, то следует
рассмотреть систему Оху, получаемую поворотом системы Оху вокруг
начала О на угол <р, определяемый в силу соотношений (1) § 7.
Тогда в системе Оху коэффициент уравнения 2 § 6 αΐ2 = 0,
и, кроме того, на основании предыдущего можно утверждать,
что либо йц = 0, либо Й22 = 0. Не ограничивая общности,
Линии второго порядка
175
будем считать ац = 0, вследствие чего уравнение линии I в
системе Оху будет иметь вид
0222/2 + 2йцх + 2«232/ + «зз = 0, 171
где а,22» «13 > ^23 находятся по формулам (5)— (7) § 6.
Уравнение (7) преобразуем к виду
а22\У + ^-) + 2U13J - ?^ + аз* = U. (8)
\ «22/ «22
ПОЛОЖИМ х' = X, у' = У + 02з/022, Т. Μ. Χ = χ',
У = 2/*-а2з/в22·
В системе координат Ο'χ'ψ, получаемой параллельным
переносом системы Оху вдоль вектора ОО7, где О'(0, -«23/022),
уравнение линии Ϊ имеет вид
а22УП + 2ai3x' + ci = 0, (9)
причем ^2
сг = «зз-^· (Ю)
^22
Если оказалось, что άΐ3 = 0, то в системе О'х'у* уравнение
линии I имеет канонический вид
й^/Чс, =0. (11)
Если же й[з φ 0, то из уравнения (9) получаем
Й222/'2 + 2а13(#' + Ci/2di3) = 0.
Положим ж" = х9 + Ci/2ci3, у" = 2/', т. е. а:' = ж" -
— С1/2Й13, у' = у"- В системе координат 0"х"уп, получаемой
параллельным переносом системы О'х'у' вдоль вектора С'О" у
где 0"(—ci/2ai3,O), уравнение линии Ζ имеет канонический вид
G222//J+2a13a:/,-0. (12)
Итак, когда Δ = | £{£ «221 = 0> то уравнение линии I может
быть приведено либо к виду (11), либо к виду (12).
Пусть Δ = 0 и йи = 0, тогда из уравнения (11) имеем
о>22Уа = —с\* причем для определенности полагаем ао2 > О,
176
Глава 4
в противном случае последнее уравнение можно умножить на
—1. Если с\ < 0» то уравнение (11) определяет в системе OVj/
две прямые, у' = \J-c\ja22 и у1 — — yj—cxjam,
параллельные оси абсцисс; если ci = 0, то можно считать, что
уравнение (11) определяет пару совпадающих прямых; если с\ > О, то
уравнение (11) не определяет никакой линии, или, как говорят,
определяет «мнимую параболу».
Пусть Δ = 0 и αΐ3 φ 0, тогда из уравнения (12)
получаем уравнение ?/'2 = — Щ^х" * которое определяет в системе
О19х91 у" параболу.
Итак, если Δ > 0, то уравнение (1) § 4 определяет либо
эллипс, либо точку («вырожденный» эллипс), либо «мнимый»
эллипс; если Δ =- 0 — либо параболу, либо две параллельные
прямые, либо две совпадающие прямые, либо «мнимую»
параболу; если Δ < 0 — либо гиперболу, либо две пересекающиеся
прямые («вырожденную» гиперболу).
В связи с изложенным, уравнение (1) § 4 называют
эллиптическим, если Δ > 0; гиперболическим, если Δ < 0;
параболическим, если Δ = 0.
Вычислив коэффициенты соответствующего уравнения (3),
(11) или (12), можно найти каноническое уравнение линии Ζ,
заданной общим уравнением (1)§ 4, и установить ее
геометрические характеристики. Более того, изложенные методы
приведения общего уравнения (1)§4 линии I к каноническому
виду, позволяют построить соответствующую систему координат, в
которой уравнение линии I имеет канонический вид. В
дальнейшем будет показано, как установить канонический вид уравнения
линии I, используя лишь коэффициенты общего уравнения (1).
ЗАДАЧИ И УПРАЖНЕНИЯ
1· Написать уравнение эллипса, оси которого
параллельны осям координат, касающегося осей Ох и Оу
соответственно в точках А(5,0) и В(0,3).
Решение. Так как оси эллипса параллельны осям координат,
а точки А и В являются точками касания эллипса с осями Ох
Линии второго порядка
177
и Оу> то его центр располагается в точке С(5,3). Поэтому
уравнение эллипса:
(*-5)2 | (У-3)2=1
а*
Ь2
Поскольку точки А и В лежат на эллипсе, то их координаты
удовлетворяют его уравнению. Поэтому, подставляя поочередно
координаты в выписанное уравнение, имеем
1-х
5-1
а2
Следовательно, а = 5, 6 = 3, поэтому искомое уравнение
(*~5)2 . (у-З)2 «
25 ^ 9 ~~ х'
2. Эллипс и гипербола имеют общие фокальные хорды,
пи е. хорды, проходящие через фокусы и
перпендикулярные к фокальной оси. Выразить эксцентриситет
гиперболы εΓ через эксцентриситет эллипса ε3.
Решение- Вычислим величину
фокального радиуса точки Μ
пересечения эллипса и гиперболы (рис. 4.21).
Для эллипса имеем г<^ъ = аэ —
—еэх = аэ—еэсэ, а фокальный радиус
гиперболы равен ггг = —ат + еГх =
= —аГ + егсг.
Так как фокусы гиперболы и эллипса совпадают, то сг = сэ =
= с и Г2э = Г2г· Поэтому аэ — еэс = — ат + £гс, аэ/с — еэ =
= —аг/с + εΓ. Отсюда 1/ε3 — ε3 = — 1/εΓ + εΓ· Следовательно,
εΓ = 1/еэ.
3. Вершина параболы находится β точке С(2,6), а ее
ось параллельна оси Оу. Зная, что на оси Ох
парабола высекает хорду АВ, длина которой равна
в, написать уравнение параболы.
Решение. Ось параболы параллельна оси Оу, поэтому
очевидно, что точка (2,0) делит отрезок АВ пополам. Следовательно,
точки А и В имеют координаты соответственно (—1,0) и (5,0).
Вершина параболы находится в точке С(2,6), поэтому уравнение
Рис. 4.2/
178
Глава 4
параболы можно записать в виде (х — 2)2 = 2р(у — 6). Так как
точка В принадлежит параболе, то, подставляя ее координаты в
уравнение параболы, находим:
ρ =*=-?, (ж-2)2 = -|(2/-6).
4. Определить тип линии, написать ее каноническое
уравнение и найти каноническую систему координат:
Ьх2 + 4ху + 8у2 - 32я - 56у + 80 = 0.
Решение. Выпишем коэффициенты указанного уравнения:
an = 5, а\2 = 2, а^ = 8,
αΐ3 = —16, G23 = —28, азз = 80.
Так как определитель Δ = | Si^ ад I = [ill ^ 0, то линия
центральная. Найдем центр симметрии — точку (#ο>3Λ))· Ее
координаты должны удовлетворять системе линейных уравнений:
{5хо + 2уо = 16,
2хо + 8г/о = 28,
решением которой являются х$ = 2, г/о = 3· Осуществим
параллельный перенос системы координат в точку О1 (2,3) по
формулам χ = х' + 2,2/ = г/ + 3. Тогда получаем уравнение
5х'2 + 4х'г/' + 8j/2 - 36 = 0.
Повернем систему координат 0'х*у* на угол φ> где φ найдем
из условия
Тогда по известным формулам из тригонометрии имеем
cos2</? = 3/5, sin 2^ = —4/5,
cos φ = 2/y/b) sin φ = —1/\/5.
В результате поворота получаем каноническую систему
координат О'ху, в которой уравнение линии имеет вид
ЙцЖ2 + 022Т/2 + ^33 = 0,
Линии второго порядка ^^^^^ 179
an = an cos ^ + 2αΐ2 cos y? sin φ +
о 4 4 1
+ α22 sin"5 <ρ = 5·--2·-+8--=4,
5 5 5
α22 = an sin2 </? — 2αΐ2 sin<pcos<p +
о 14 4
+ a22cos2<p = 5·- + 2·- + 8·- = 9,
5 5 5
йзз = —36.
Следовательно, 4х2+9у2 -36 = 0, т. е.
получаем, что линия — эллипс с
каноническим уравнением ^- + \ = 1 (рис. 4.22).
Базисными векторами канонической
системы координат являются векторы
ei = (cos φ^ sin φ), e2 = (— sin ^, cos φ)
или
y* /У
3\
о
e2j\
-S2?a
/ 1
2
-^
"ac
Рыл 4.22
5. Определить тип линии, написать ее каноническое
уравнение и найти каноническую систему координат:
х2 - Аху + Ау2 + Ах - Зг/ - 7 = 0.
Решение. Выпишем коэффициенты указанного уравнения:
а\\ = 1, «12 — -2, а22 = 4,
^13 = 2, агз = -3/2, а3з = -7.
Так как определитель Δ = | _\ ~~2\ = 0, то линия
нецентральная (параболического типа). Повернем исходную систему
координат на такой угол <р9 что ctg2φ = Q^~^22 = |. Тогда
1
3 . 0 4 2
cos2<p=-, sin2<p=-, cos^>=—^=,
5 5 γ/5
sin ν? =
ι/5'
Получаем новую систему координат Оху , в которой
исходное уравнение имеет вид
ζ ζ2 . ^ ~~2
ац5г + Й22У + 2αι3ί + 2а2зУ + йзз = 0,
180
Глава 4
где
<2ц =
0,22 =
013 =
023 =
-ί
η 4 „
-2·- + 4·
0
1 _
5 ~
,1 л 4 л 4
= 1..+2._ + 4.в =
= ai3Cosv? + a23sinv? =
= -«13
sin φ + d23
COS</7
0,
5,
:2-
=
2
7ъ
-2-
3
2*
1
7ь~
1
3
2 '
=
2
71
ν/5
2 '
-ν/5,
«33 = «33-
Таким образом, имеем уравнение Ъу2 4- y/bx — 2\/5?/ — 7 = 0.
Для дальнейшего упрощения полученного уравнения
выделим полный квадрат по переменной у:
.(,-£)\*(.-£)-a
Осуществим параллельный
перенос системы координат Оху
по формулам χ = χ —
у = у — у/Ъ/Ъ. Получаем
уравнение параболы Ъу2 + у/5х =
= 0, или у2 = -2 ■ ^х в
канонической системе координат
О'ху, базисные векторы
которой равны соответственно ё\ =
(рис. 4.23).
Установим зависимость между исходной и канонической
системами координат. Сначала осуществили поворот системы
координат. Поэтому 2 1
χ = χ cos φ — у sin φ = —j^x
' v5
1
Рис. 4.23
лг
2 .
у = a: sin <£> + ?/cos <p = —pxH—^=y.
v/5 у5
Линии второго порядка
181
Затем провели параллельный перенос. Поэтому формулы
преобразования координат имеют вид
Поскольку для точки О': χ = О, у = О, то 0'(3,2) в системе
координат Оху.
6. Исследовать зависимость типа линии второго порядка
от параметра a G (—оо, +оо):
х2 - 2у + а(у2 - 2х) = 0.
Решение. Перепишем указанное уравнение в виде
х2 + ау2 — 2аж — 2у = 0.
Определитель Δ = | J £ | = а. Если а = 0, то линия
нецентральная и совпадает с параболой х2 = 2j/. Если α ^ 0, то
линия центральная, а исходное уравнение приводится к виду
(х2 - 2аж + а2) + а ( у2 j/ + -^ ) - а2 - 1/а = 0,
\ а от/
(ж - а)2 + а(у - 1/а)2 - (1 + а3)/а = 0.
Центр симметрии указанной линии находится в точке (а, 1/а).
Очевидно, что при а < —1 выполнено неравенство (1 +
+α3)/α > 0. Поэтому для указанных значений параметра имеем
гиперболу с действительной осью, параллельной оси Ох. Если
α = —1, то уравнение принимает вид (х +1)2 — (у +1)2 = 0.
Таким образом, имеем две пересекающиеся прямые χ + у + 2 = 0,
х - у = о. В случае —1 < α < 0 имеем (1 + α3)/α < 0, а
следовательно, уравнение определяет гиперболу с действительной
осью, параллельной оси Оу. Наконец, при а > 0 выполнено
неравенство (1 + α3)/α > 0. Поэтому при указанных значениях
параметра уравнение задает эллипс·
182
Глава 4
7. Написать уравнение равносторонней гиперболы,
одна из вершин которой находится в точке (3,3),
действительная ось параллельна оси Ох, при
условии, что ось Оу данная гипербола пересекает в
точках, расстояние между которыми равно 18.
Ответ: х2 - у2 - ЗОх + 6у + 72 = 0.
8· Найти фокус и директрису параболы у2+8х+4у—4 = 0.
Ответ: F(-l, -2), χ - 3 = 0.
9· Гипербола χ2 — у2/9 — 1 имеет с эллипсом общие фокусы.
Найти уравнение этого эллипса, если известно, что он
проходит через точку Л(\/5,6).
Ответ: Й + Й = 1-
10. Определить эксцентриситет эллипса, если расстояние
между фокусами есть: а) среднее арифметическое длин
осей; б) среднее геометрическое длин осей.
Ответ: а) ε = 4/5; б) ε = л/(л/5-1)/2.
11. Дан эллипс j$ + \ = 1. Написать уравнение
равносторонней гиперболы, имеющей с этим эллипсом общие
фокальные хорды.
Ответ: х2 -у2 = 4.
12. Вычислить длину фокальной хорды, перпендикулярной
оси симметрии параболы у2 = 2рх.
Ответ: 2р.
13. Определить тип линии второго порядка, написать
ее каноническое уравнение и найти каноническую
систему координат:
а) Зж2 - 2ху + Зу2 - 2х - 10у - 13 = 0;
б) 2х2 - 12ху - 7у2 - 24х + 22у + 67 = 0;
в) 9х2 - 24ху + 16у2 - ЬОх + 50у + 51 = 0;
г) 8х2 + 12ху + 17у2 + 4х- 22у + 18 = 0;
д) Ъх2 - 12ху - Юх + 12у 4- 5 = 0;
е) х2 + 4ху + 4у2 - 6х - \2у + 8 = 0;
ж) 5ж2 - Uxy + Ьу2 + 6х - 18у - 15 = 0;
з) х2 - ху + у2 + χ + у + 1 = 0;
и) х2 - 4ху + 4у2 - 4х + 8у + 4 = 0;
к) 9ж2 + 12ху + 4у2 - 36ж - 24у + 40 = 0.
Линии второго порядка
183
Ответ:
а)эллипс =л „ρ
^ + 'τ-1. 0'(1,2),
б) гипербола ^2 9-.2
^--| = -ι, ο'(3,-ΐ),
в)парабола
»2 = f, ο'(ι,-ι),
ei
(!·!)· *■(-!·!)'
г) «мнимый» эллипс
+ j/2 + l = 0, O'C-l.l),
X _2
1/4
д) две пересекающиеся прямые
ei —
τ-?=°· °'(1·0)'
_3 2_\
е) две параллельные прямые
2 1 _,/3 6\
- _ fJI i\ .Jj_ η
ж) гипербола ^_^2/б=1) 0'(-2,-1),
184
Глава 4
з) «вырожденный» эллипс
г2 + ^=о, (У {-1,-1),
и) пара совпадающих прямых
;";· 0'8·"δ; 2
к) «мнимая» парабола
~2
ж^ = -4/13,
О' (™ ™)
* ~ WIT νΐδ)' *2~\ чДз'лЛз)5
14. Определить тип линии второго порядка в зависимости
от величины параметра а е (-ос, +оо);
а) х2 + 2аху + у2 — а = 0;
б) а(х2 + у2) -2ху + 2х + 2у + а = 0.
Ответ:
а) при а < — 1 — гипербола с действительной осью на оси
абсцисс; при а = — 1 —«мнимая» парабола; при — 1 < а < 0 —
«мнимый» эллипс; при а = 0 — вырожденный эллипс; 0 < а <
< 1 —эллипс; а — 1 —пара параллельных прямых ж + у = ±1;
а > 1 — гипербола с действительной осью на оси ординат;
б) при а < — 1 — «мнимый» эллипс; при а = —1 — пара
совпавших прямых χ + у - 1 = 0; при — 1 < а < 1 —гипербола
с действительной осью на оси абсцисс; при а = 1 — парабола;
при 1 < а < 2 — эллипс; при а = 2 — «вырожденный» эллипс;
α > 2 — «мнимый» эллипс.
Глава 5
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
§ 1. УРАВНЕНИЯ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
Поверхностью вращения называют поверхность,
образованную вращением в пространстве плоской кривой вокруг прямой,
расположенной в ее плоскости, называемой осью вращения.
Сечения поверхности плоскостями, проходящими через ось
вращения, называют меридианами, а линии пересечения
плоскостями, перпендикулярными оси вращения, называют
параллелями.
Отметим, что меридианы суть плоские кривые, конгруэнтные
кривой, вращением которой образована поверхность, а
параллели — окружности с центрами на оси вращения и расположенные
в параллельных плоскостях.
Пусть поверхность S\ образована вращением линии 1\,
расположенной в плоскости Оху и определяемой уравнением
Fi(S,y) = 0, 2 = 0, (1)
вокруг оси ординат.
Плоскость π, проходящая
через произвольную точку
пространства Μ(Χ1Υ,Ζ) перпендикулярно
оси ординат (рис. 5.1), пересекает
эту ось в точке J(0, У, 0), причем
d{J,M) = y/X2 + Z2. (2)
Произвольная точка Μ(Χ,Υ, Ζ) ζ χ
пространства Ж3 принадлежит Рис. 5.1
186
Глава 5
поверхности S\ лишь тогда, когда названная плоскость π
пересекает линию Ιχ в точке Р(я,г/,0) плоскости OiJ и d(J,P) =
= d(J,M),T.e. |J| = V^T^> S = K (3)
Отсюда, поскольку координаты точки Ρ удовлетворяют
уравнению (1), уравнение поверхности Si имеет вид
Fl(±y/X* + Z29Y)=0. (4)
В уравнении (4) берется знак « + », если точка Ρ лежит в
полуплоскости Оху, где χ > 0, и « — » в противном случае.
Аналогичным образом можно убедиться в справедливости следующих
утверждений.
Уравнение поверхности 52, образованной вращением
линии 12, расположенной в плоскости Οχζ и определяемой урав-
нением г /- -\ л - гл /к\
F2{x,z) = 0y y = 0, (5)
вокруг оси аппликат, имеет вид
F2(±\/X2 + r2, Z) = 0. (6)
Уравнение поверхности 5з, образованной вращением линии
i3, расположенной в плоскости Οχζ и определяемой уравнением
F3(xyz)=0, » = 0f (7)
вокруг оси абсцисс, имеет вид
fs{x,±Vy2 + z2) = q. (8)
§ 2. ЭЛЛИПСОИД
Поверхность, образованная вращением эллипса
X V
^ + 12=Х> г==0
сг Ъг
вокруг оси ординат, называется эллипсоидом вращения, а его
уравнение имеет вид
X2 + Z2 l·^
о2 + б2 " '
Поверхности второго порядка
187
χ, у, ρ
1 1 = 1.
а2 Ь2 а2
Если произвести сжатие
(растяжение) к плоскости Оху,
т. е. преобразование χ = X,
у = У, ζ = ξΖ, то
получаем трехосный эллипсоид
(рис. 5.2), уравнение которого
в системе Oxyz имеет вид
х2 у2 ζ2
Рис. 5.2
а*
Ь2
(1)
Из уравнения (I) видно:
1) координатные плоскости являются плоскостями
симметрии полученного эллипсоида;
2) начало координат является центром симметрии
эллипсоида;
3) эллипсоид представляет собой ограниченную
поверхность, заключенную в параллелепипеде \х\ < а, \у\ ^ 6,
И ^ с.
Числа а > О, Ь > 0, с > 0, фигурирующие в уравнении
эллипсоида и равные соответственно алгебраическим мерам
векторов оА,оЁ,об, отсекаемых эллипсоидом на
положительных полуосях Ox, Оу, Oz, называются полуосями
эллипсоида.
Поскольку эллипсоид ограничен, то линия пересечения его с
любой плоскостью является ограниченной линией. Среди
кривых второго порядка таковой является лишь эллипс, который
и будет указанной линией пересечения эллипсоида с
плоскостью.
Если все три полуоси равны: а = b = с, то эллипсоид
представляет собой сферу. Нетрудно видеть, что любой эллипсоид
можно получить из сферы равномерным сжатием относительно
двух перпендикулярных плоскостей.
188
Глава 5
§ 3. ОДНОПОЛОСТНЫЙ
ГИПЕРБОЛОИД
Поверхность, образованная вращением гиперболы
х2 ζ2 Λ
az cz
вокруг оси аппликат, называется однополостным
гиперболоидом вращения, причем его уравнение имеет вид
Х2+У5
а<
О Х5
ИЛИ
Xs
а<
'9 9
Если произвести сжатие
(растяжение) пространства к
плоскости OXZ, т. е. преобразование
χ = X, у = |F, я = Z, то
получаем общий однополостный
гиперболоид (рис. 5.3), уравнение
которого в системе Oxyz можно
представить в виде
х2 у2 ζ2
г» I . о О Х·
а?
V
(1)
Из уравнения (1) следует,
что координатные плоскости
являются плоскостями симметрии
полученного однополостного
гиперболоида, а начало
координат — центром его симметрии.
Отметим, что сечения однополостного гиперболоида
плоскостями ζ — h представляют собой эллипсы, а плоскостью
у = b—две прямые:
Рис. 5.3
*-^=0, у = Ь
а с
и
я z
- + - = О,
а с
У
Поверхности второго порядка
189
§ 4. ДВУПОЛОСТНЫЙ ГИПЕРБОЛОИД
Поверхность, образованная вращением гиперболы
х2
ζ2
or с1
вокруг оси аппликат, называется двуполостным
гиперболоидом вращения, причем уравнение двуполостного гиперболоида
вращения имеет вид
Ζ2
,2
Χ2 + Υ2 _Ζ^_
или
<Г
Χ2 Υ2
-7Г +
= -1.
а*
а£
Если произвести сжатие (растяжение)
пространства к плоскости ΟΧΖ, т. е.
преобразование χ — X, у = |У, г = Ζ, то
получаем общий двуполостный
гиперболоид (рис. 5.4), уравнение которого в
системе Oxyz имеет вид
х2
аг
У1
Ь2
(1)
Из уравнения (1) следует, что
координатные плоскости являются
плоскостями симметрии полученного двуполостного
гиперболоида, а начало координат — его
центром симметрии.
ЗАМЕЧАНИЕ. Однополостный
гиперболоид χ2 у2 2
_ + — - — = 1
Of
b2
и двуполостный гиперболоид
2 2 2
ЯГ 2Г z _ л
рассмотренные в одной системе
координат Oxyz (рис. 5.5), являются
пространственным аналогом гиперболы и
соответствующей ей сопряженной гиперболы
на плоскости.
Рис. 5 А
Рис. 5.5
190
Глава 5
§ 5. ЭЛЛИПТИЧЕСКИЙ ПАРАБОЛОИД
Поверхность, образованная вращением параболы
-Л
χ
ζ =
-ϊ> 2/ = °»
а*
вокруг оси аппликат, называется эллиптическим,
параболоидом, вращения, при этом его уравнение имеет вид
Κ + Κ = ζ.
а'
а'
(1)
Если произвести сжатие (растяжение)
пространства к плоскости ΟΧΖ, т. е.
преобразование χ = X, у = ~У, ζ = Ζ,
то получаем общий эллиптический
параболоид (рис. 5.6), уравнение которого в
системе Oxyz можно представить в виде
о2 Ь2 ~ *"
(2)
Рис. 5.6
Из уравнения (2) следует, что
плоскости Oxz и Oyz являются плоскостями симметрии
эллиптического параболоида, а ось Oz — его осью симметрии. Точку, в
которой ось симметрии пересекает эллиптический параболоид,
называют его вершиной. Эллиптический параболоид (2) имеет
вершину в начале координат.
Линии пересечения эллиптического параболоида
плоскостями ζ = /ι, h > 0, представляют собой эллипсы, а плоскостями
χ = h\ и у = /?2 — параболы.
§ 6. ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД
Гиперболическим параболоидом называют поверхность,
уравнение которой в системе Oxyz имеет вид
χ
У1
Ъ2
(1)
Поверхности второго порядка
191
Отметим, что линия пересечения гиперболического
параболоида (1) с плоскостью χ = hi есть парабола ζ — -φ = — *£,
х = hoy которая получается параллельным переносом параболы
ζ = — ^, χ = О, когда ее вершина перемещается в точку с
координатами (/i2>0, ^$), скользя при этом по параболе ζ = ~μ,
» = 0.
Таким образом,
гиперболический параболоид (1) образуется при
параллельном перемещении
параболы ζ = —yt* x = О, когда ее
вершина движется вдоль параболы
ζ = £?, у = 0 (рис. 5.7); Нетрудно
видеть, что гиперболический
параболоид (1) может быть также
образован параллельным переносом параболы ζ = ^ > у = 0, когда
ее вершина движется вдоль параболы ζ = — ]£, χ = 0.
Из уравнения (1) следует, что плоскости Οχζ и Oyz
являются плоскостями симметрии гиперболического параболоида, ось
Oz — его ось симметрии. Точку, в которой ось симметрии
пересекает гиперболический параболоид, называют его вершиной.
ЛШК7
Рис. 5.8
Сечения гиперболического
параболоида (1) плоскостями πι: ζ = hi,
hi > 0, и π2: ζ = h2y h2 < 0,
представляют собой гиперболы (рис. 5.8),
плоскостью ζ = 0 —две прямые у =
= Ьх/а, ζ = 0 и у = -Ьх/ау ζ = 0
(рис. 5.9), а плоскостями χ = h$ и
У = /i4 —параболы (рис. 5.10).
Рис. 5.10
192
Глава 5
§ 7. ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ
Цилиндрической поверхностью с образующей, параллельной
оси Ozy называют такую поверхность, что вместе со всякой
точкой этой поверхности ей принадлежат все точки прямой,
проходящей через данную точку параллельно оси Oz.
Всякую прямую, целиком лежащую на цилиндрической
поверхности, называют ее образующей, а линию пересечения этой
поверхности с произвольной плоскостью, не проходящей через
образующую, называют ее направляющей.
Ясно, что цилиндрическая поверхность с образующей,
параллельной оси аппликат, может быть образована движением
прямой, которая скользит по направляющей, оставаясь
параллельной оси Oz.
Теорема. Всякое уравнение вида
F(x,y) = 0, (l)
не содержащее переменной ζ, определяет в пространстве
цилиндрическую поверхность с образующей, параллельной
оси Oz.
Доказательство. Если произвольная точка Мо(£о,2/о,2о)
лежит на поверхности, определенной равенством (1), то
справедливо равенство F(xo,yo) = 0.
Для всякой точки М(:г, г/, ζ), лежащей на прямой,
параллельной оси Oz и проходящей через Мо(#о, г/о, ζο),
справедливо χ = xq, у = г/о» а ее аппликата ζ принимает произвольное
значение. А тогда координаты точки Μ удовлетворяют
уравнению (1), и, следовательно, она лежит на поверхности с
уравнением (1). Отсюда приходим к выводу, что эта поверхность является
цилиндрической с образующими, параллельными оси Oz.
ЗАМЕЧАНИЕ 1. Отметим, что в качестве направляющей линии
цилиндрической поверхности (1) можно взять линию F(x,y) —
= 0,z = 0, лежащую в плоскости Оху.
ЗАМЕЧАНИЕ 2. Уравнения F{x,z) = 0, F(y,z) = 0
определяют соответственно цилиндрические поверхности с
образующими, параллельными осям Оу и Ох.
Поверхности второго порядка
193
§ 8. ЦИЛИНДРЫ
ВТОРОГО ПОРЯДКА
Различаются три типа цилиндрических
поверхностей второго порядка с
образующей, параллельной оси аппликат:
эллиптический цилиндр (рис. 5.11)
χ2 ν2
а*
Ъ2
Рис.5.И
гиперболический цилиндр (рис. 5.12)
X'
а*
У1
Ь2
7ϊ-ί? = 1.
Рис. 5.12
параболический
цилиндр (рис. 5.13)
у2 = 2рх.
У названных
цилиндрических
поверхностей направляющими линиями в
плоскости Оху являются соответственно эллипс,
гипербола, парабола, а образующими —
прямые линии, параллельные оси Οζ и
скользящие по указанным направляющим.
Рис. 5.13
§ 9. КОНИЧЕСКИЕ ПОВЕРХНОСТИ
Конической поверхностью с вершиной в начале координат
называют такую поверхность, что вместе со всякой
точкой этой поверхности, отличной от начала координат, ей
принадлежат все точки прямой, проходящей через данную
точку и начало координат.
Всякую прямую, целиком лежащую на конической
поверхности, называют ее образующей, а линию пересечения этой
поверхности с произвольной плоскостью, не содержащей
образующую и вершину, называют ее направляющей.
194
Глава 5
Ясно, что коническая поверхность может быть образована
движением образующей, которая скользит по направляющей и
проходит через начало координат.
Напомним, что функция F(x,y,z)y определенная для
любых значений аргумента, называется однородной функцией
степени π, есчи для любого вещественного числа t справедливо
равенство
F{tx,ty,tz) = tnF(x,y,z).
Теорема. Всякое уравнение
F(x,y,z) = 0, (1)
в котором F(x,y,z) есть однородная функция степени п,
определяет коническую поверхность.
Доказательство. Если произвольная точка Λ/ο(^Οϊ2/Οι^ο)
лежит на поверхности, определяемой уравнением (1), то верно
равенство F(x0,yQ,zo) = 0. Пусть M(x,y,z) — произвольная
точка на прямой, проходящей через начало координат 0(0,0,0)
и точку Μο(:γο, у0, г0).
Ясно, что векторы Ото и ОМ коллинеарны, причем
|ΟΛ?ο| φ 0, а тогда существует такое вещественное число t, что
ОМ = t · OMq , т. е. χ = tzo, у = tyo, ζ = tzQ.
В силу того, что функция F(x,y,z) является однородной,
имеем F(x,y,z) = F(tXQ,ty0,tzo) = tnF{x0,yo,z0) = 0.
Последнее означает, что M(x,yyz) лежит на
поверхности (1). А тогда уравнение (1) определяет коническую
поверхность с вершиной в начале координат.
§ 10. КОНИЧЕСКИЕ ПОВЕРХНОСТИ
ВТОРОГО ПОРЯДКА
В силу теоремы из § 9 уравнение
аг Ьг сг
определяет коническую поверхность второго порядка.
Поверхности второго порядка
195
Из уравнения (1) следует, что
начало координат, оси координат и
координатные плоскости являются
соответственно центром симметрии, осями
симметрии и плоскостями симметрии
рассматриваемого конуса. Для
конуса (1) вершиной является начало
координат (рис. 5.14).
Сечение конуса (1) плоскостью
ζ = h представляет собой эллипс
а2 Ь2 с2'
ζ = /ι,
Рис, 5.14
ИЛИ
£ + £-!
s* дг
ζ = /ι,
(2)
где s = aft/c, ρ = bh/c, который можно рассматривать как
направляющую линию конуса {1). А тогда конус (1) может быть
образован при движении прямой, проходящей через начало
координат и скользящей по направляющей (2) (рис, 5Л4).
Отметим, что конус
2^2
х У" *
а2 Ь2 с2
(3)
связан с однополостным гиперболоидом
о "ι »ο η *■
О"
Ь2
(4)
и двуполостным гиперболоидом
tf2 #2
α2 + 62
(5)
следующим образом: всякая плоскость, проходящая через
ось Ог, пересекает гиперболоиды по гиперболам, а ко-
«ус — по двум образующим, которые являются асимптотами
этих гипербол (рис. 5Л5).
196
Глава 5
Рис. 5.15
В част ности, плоскость у = 0
пересекает гиперболоиды (4), (5) по гиперболам
•г „2 ~ '
а
χ
-"^ = -1,
а конус(3)
по прямым
2 Л
Z*
2-*=°'
т. е. ζ = ^х и ζ = — ~ж, которые
являются асимптотами этих гипербол· В
связи с этим конус (3) называют
асимптотическим для гиперболоидов (4) и (5)
(рис. 5.15).
§ 11. ПРЯМОЛИНЕЙНЫЕ ОБРАЗУЮЩИЕ
ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА
Помимо цилиндров и конусов поверхностями второго
порядка, которые содержат прямолинейные образующие, являются
однополостный гиперболоид и гиперболический параболоид.
Рассмотрим однополостный гиперболоид, определяемый
уравнением
Τ? ΐΡ 7λ
(1)
ξ! j- ί - — = ι
α2 + b2 с2 '
которое представимо в виде
(f-:)(i+f)-0-5)(1+S)- <2>
Всякая прямая р\, определяемая как линия пересечения
плоскостей
Ξ _ £ - Α (ι - 2Ϊ * + *-λ(ι + ν\
a с V1 ь)' a + c-XV+b)'
(3)
при любом отличном от нуля значении λ целиком лежит на
гиперболоиде (1), ибо координаты всякой точки, удовлетворяющие
уравнениям (3), одновременно удовлетворяют уравнению (1),
которое получается почленным перемножением уравнений (3).
Поверхности второго порядка
197
Аналогично можно убедиться, что всякая прямая р'х>
определяемая как линия пересечения плоскостей
Ξ _ £ = А Л + »Л * + ί = 1(ι-!ί)
ас V 6/ а с λ V 6/
(4)
при любом отличном от нуля значении λ лежит на
рассматриваемом гиперболоиде.
Можно показать, что прямые ρχ и рх
различны.
Итак, однополостный гиперболоид (1)
покрыт двумя различными семействами
прямых (рис. 5.16).
Нетрудно видеть, что через каждую
точку гиперболоида (1) проходит
некоторая прямая семейства р\ и некоторая
прямая семейства рх.
Убедимся в этом, например, для
случая семейства р\, ибо доказательство для
случая семейства р'х совершенно аналогично·
В самом деле, пусть точка N{x\yy\^z\) лежит на
гиперболе. 5. /0
лоиде (1), т. е.
α2 +
й
б2
с2
(5)
Подберем такое значение λι, отличное от нуля, чтобы числа
#1,2/1, ζι удовлетворяли первому из уравнений (3) при λ = λι,
*_£к=А1Л_£). (б)
ас V Ъ /
Тогда при λ = λι числа х\, у\, ζχ удовлетворяют и второму
уравнению (3), ибо в противном случае, если
а с λι V b /
'J)
то после перемножения равенств (6) и (7) получаем
а
,2
62'
т. с. ^-^ + |^7^1, что противоречит равенству (5).
198
Глава 5
§ 12. ПРЯМОЛИНЕЙНЫЕ ОБРАЗУЮЩИЕ
ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА
Аналогично рассуждая, можно
показать, что гиперболический
параболоид, определяемый равенством
*> 2
х У /1ч
г = *-&· (1)
Puc s 17 которое представимо в виде
-(:-|)(М). <2>
покрыт двумя семействами прямых д\ и д'х, которые
соответственно задаются уравнениями
—(Н)· Ч(Н)· <3>
где А — произвольное, отличное от нуля число (рис. 5.17).
§ 13. ПРЕОБРАЗОВАНИЕ КОЭФФИЦИЕНТОВ
ОБЩЕГО УРАВНЕНИЯ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ
СИСТЕМЫ КООРДИНАТ
Эллипсоиды, гиперболоиды, параболоиды, цилиндры, конусы,
изученные ранее, представляют собой алгебраические
поверхности второго порядка. Возникает вопрос о том, какие еще
существуют алгебраические поверхности второго порядка.
В силу известной теоремы алгебраическая поверхность
второго порядка 5, определяемая общим уравнением второго порядка
€1цх2 + а22у2 + озз^2 + 2a>ioxy + 2а2зуг + 2a\$xz +
+ 2ay/ix 4- 2а24У + 2аз4^ + «и — 0, (1)
где ац, а22, <?зз, Gi2, С23* а*3 не Равны нулю одновременно,
рассматриваемая как геометрический объект, не изменится, если
от данной ДПСК перейти к другой ДПСК.
Поверхности второго порядке
199
Условимся группу слагаемых
ацх2 + а22У2 + йзз*2 + 2αΐ2^2/ + 2a2^yz + 2α13χζ
левой части уравнения (1) называть группой старших членов.
а группу Л , Л о .
2ан^ + 2α242/ + 2α34^ + ^44
—линейной частью уравнения (1)
Зададимся целью отыскать такую ДПСК, в которой
уравнение (I) поверхности S примет наиболее простой, так
называемый канонический вид, позволяющий установить
геометрические характеристики этой поверхности
Рассмотрим систему координат O'x'y'z' % получаемую
параллельным переносом системы Oxyz вдоль вектора ОО*'. Ранее
были установлены соответствующие формулы преобразования
координат: , , , . ^
х = х +х0у у = у +Уо> ζ = ζ+ζ0} [2\
где (х,у,ζ) — координаты точки в системе координат Oxyz,
{х\у\ zf) — координаты той же точки в системе O'x'y'z'.
Уравнение (I) поверхности S в системе O'x'y'z' примет вид
ац{х'2 + 2х'гг0 + *о) + <*22(г//2 + 2у'у0 + у%) +
+ азз(*/2 + 2z'zQ + zl) + 2ai2{x'y' + х'уо + у'хо + хоуо) +
+ 2a23{y'z' + y'zo + z'y0 + 2/oZo) +
+ 2αι$(χ'ζ' + x'zq + z'xo + xoz0) +
+ 2аы(х' + Xq) + 2a2A(y' + yo) + 2aM{z' + ζΌ) + α44 = О,
-3,
или, вводя соответствующие обозначения, получаем
апх'2 + а22у'2 + азз*'2 + 2а12х'у + 2а23у'ζ' +
+ 2αχζχζ + 2а'ых' + 2а'2Ау' + 2α'3Δζ' + а'ы = О,
где
а14 = α11^0 + G122/0 + Gl3^0 + Gl4> < 4 ί
<4ΐ -^«12^0 + G22i/0 + ^23^0 + G24, (^*
^34 = «13^0 + Я232/0 + ^33^0 +^34) ■ 61»
«44 = αιιχο + α222/ο + G33^o + 2а^хоУо + 2a23yoz-o +
+ 2<2ΐ33?ο2ΰ + 2auXo + 2«242/ο + 2аз4^о + &44·
(i I
200
Глава 5
Выражение для αΛί представимо в виде
а'44 — (ацХо + а,12Уо + αΐ32ο + «14)^0 +
+ (ai2Xo + а22Уо + «гз^о + 024)2/0 +
+ (αΐ3·το + «2з2/о + «зз*о + «34)*о +
+ 014^0 + «2i2/0 + «34^0 + «44·
Откуда в силу (4), (5), (6)
«П = («14 "+ «1ΐ)^0 + («24 + й24)У0 + («34 + «34)<*0 + θ44· (8)
При параллельном переносе системы координат
коэффициенты группы старших членов не изменяются.
§ 14. УПРОЩЕНИЕ ОБЩЕГО УРАВНЕНИЯ
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ
СИСТЕМЫ КООРДИНАТ
Попытаемся выбрать начало О'(хо»уо,^о) системы коорди-
iidT O'x'y'z' так, чтобы коэффициенты а'14, а24, а34
уравнения (3) § 13 равнялись нулю, т. е.
( ацх0 + «122/0 + «к 2о + «м = О,
< αΐ2^ο + «222/0 + агз^о + «24 =-"0, (1)
1«ΐ3·το + о.2зУо + «зз^о + аз4 = 0.
Последняя система имеет единственное решение, если
δ =
«И «12 «13
«12 «22 «23
Οΐ3 023 «33
Φ 0. (2)
Ит<ж, если выполнено условие (2), то в системе координат
O'x'y'z', у которой начало О1 имеет координаты {xq^o,zo)9
найденные из системы (1), уравнение рассматриваемой поверх
ности имеет вид
α π а'2 + а22у'2 + α-^ζ'2 + 2аг2х'у'+
-г 2a23y'z' + 2αι3χ'ζ' + а'44 = О, (3)
Поверхности второго порядка
20!
где
^44 = G14^0 + ^242/0 + а34^0 + <244- (4)
Отметим, что если точка M{xf,y\z') лежит на
поверхности S% т. е. ее координаты {x\y\zt) удовлетворяют
уравнению (3), то точка Л/'(—я', —у'у —zf) также расположена на
поверхности S, ибо ее координаты удовлетворяют тому же
уравнению (3).
Таким образом, если условие (2) выполнено, то существует
точка Ο'(χο>2/ο>2ο) такая, что точки поверхности S
располагаются симметрично относительно нее, т. е. она является центром
симметрии поверхности.
В связи с этим точку Ο'(#ο>2/ο>2ο) называют центром
поверхности S, а саму поверхность — центральной.
Подчеркнем, что поверхность S, определяемая
уравнением ( 1 ) § 13 является центральной, если выполнено условие (2).
§ 15. ПРЕОБРАЗОВАНИЕ КОЭФФИЦИЕНТОВ
ОБЩЕГО УРАВНЕНИЯ
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ПРИ ПОВОРОТЕ СИСТЕМЫ КООРДИНАТ
Рассмотрим систему координат Оху1Л получаемую поворотом
системы Oxyz вокруг начала координат. Пусть в исходной
системе координат поверхность S определяется уравнением
ацх2 + а22у2 + CL33Z2 + 2<i\2xy + 2a23yz + 2агзхг +
+ 2о,!4Х + 2а2Лу + 2a$\z + а44 = 0. (1)
Ранее были установлены соответствующие формулы
преобразования координат ~ ~ ~
у = ха2\ + у&22 + 5а2з, (2)
ζ = яа31 + 2/с*з2 + 5а3з,
где (х,у,ζ) —координаты произвольной точки в системе Oxyz;
(χ,у,ζ) —ее же координаты в системе Oxyz; (ο^,ο^,α^) —
координаты (направляющие косинусы) 5-го орта (s = 1, 2, 3)
системы Oxyz относительно системы координат Oxyz.
202
Глава 5
Уравнение (1) поверхности S в системе Oxyz примет вид
ипх2 + Й222/2 + a^z2 +
+ 2^122У + 2a>23yz + 2a\$xz +
+ 2άι4ί + 2024У + 2α 34^ + <*44 = 0· <3)
Нетрудно убедиться, что при повороте системы координат
коэффициенты группы старших членов уравнения (3)
выражаются через ctij и коэффициенты группы старших членов
уравнения (L); коэффициенты линейной части й14, а>24. йз4
выражаются через &ij и коэффициенты αι^, α24 > «341 свободный член «44
не изменяется.
Ясно, что если в исходном уравнении (I) аи = 0, а24 = 0,
«34 = 0, то и в уравнении (3) будем иметь άχ4 = 0, Й24 = 0,
й;54 =0.
§ 16. УПРОЩЕНИЕ ОБЩЕГО УРАВНЕНИЯ
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ПРИ ПОВОРОТЕ СИСТЕМЫ КООРДИНАТ
Теорема. Существует система координат Ох"у"ζ"',
получаемая поворотом исходной системы, в которой
коэффициенты при х" у" ,у" ζ'\χ" ζ" общего уравнения
поверхности второго порядка S равны нулю.
Доказательство. Пусть σ — сфера, определяемая в Oxyz
уравнением х2 + у2 + ζ2 = 1. Рассмотрим функцию
/: М(х,ууг) в σ -> ацх2 + а22У2 + азз*2 +
+ 2ai2xy + 2a2$yz + 2ai3xz. (1)
Функция / задана и непрерывна на замкнутом ограниченном
множестве σ. В курсе математического анализа
устанавливается, что непрерывная функция, заданная на замкнутом
ограниченном множестве, достигает на зтом множестве своего
минимального и максимального значения.
На основании этого можно утверждать, что функция /
достигает своего максимального значения в своей области задания.
Поверхности второго порядка
203
Пусть G — та точка сферы σ, в которой значение функции /
является максимальным.
Введем новую систему координат OJcyz, сохранив начало 0,
направив новую ось Oz по прямой OG и выбрав в качестве
положительного направления на ней направление вектора OG,
расположив обычным образом оси Ох и Оу в плоскости,
перпендикулярной оси Oz. Ясно, что система Oxyz получается
поворотом системы Oxyz на некоторый угол вокруг начала О,
причем точка G в системе Oxyz имеет координаты (0,0,1).
Используя формулы (2) предыдущего параграфа, в системе
координат Oxyz функцию / можно определить так:
/: М(х, у, ζ) е σ -> апх2 + а22у2 + йзз*2+
+ 2ai2xy + 2а2зР + 2αι3ί5? (2)
причем сфера σ определяется уравнением х2 + у2 + ζ2 = 1.
Согласно выбору системы Oxyz максимальное значение
функции / достигается при χ = 0, у = 0, ζ = 1. Если в
функции / положим χ = 0, ζ = 1, то получим функцию /ι одного
переменного у:
fi'.ye [-1,1] -> а22У2 + 2а2з2/ + &«, (3)
которая достигает максимума при у = 0, и вследствие этого по
теореме Ферма
#1
dy
= 2а22У + 2а2з!у=о = 2йи = 0,
у=0
откуда а2з = 0.
Если в выражении (2) функции / положить у = 0, 5 = 1, то
получим функцию f-2 одной переменной х:
/2: х е [-1,1] -» апх2 + 2άί3χ + α33, (4)
которая достигает максимума при χ = 0, и вследствие этого по
теорече Ферма
#2 1
-— = 2йцж + 2αΐ3|ί=ο = 2αι3 = 0, откуда αι3 = 0.
йХ \х=0
204
Глава 5
Χ
У
ζ
=
=
=
χ"
χ"
ζ*'
cos φ — у"
sin φ + у"
sin φ,
cos v?,
Если теперь ввести систему координат Ох"у"ζ"',
получаемую поворотом системы Oxyz вокруг оси Oz на положительный
угол φ, измеряемый против часовой стрелки в плоскости Оху,
то координаты преобразуются по формулам
(5)
Как и при рассмотрении линий второго порядка,
соответствующим выбором угла φ можно добиться того, чтобы
коэффициент а"2 при х"у" равнялся нулю, т. е. а"2 = 0.
В силу полученных результатов можно утверждать, что в
системе Ох"у"ζ" уравнение поверхности S имеет вид
апх +а22у +α33ζ +
+ 2а'{Ах" + 2а'^у" + 2α%4ζ" + α44 = 0.
Теорема доказана.
Отметим, что совокупность рассмотренных преобразований
(двух поворотов) системы Oxyz называют иногда
стандартным преобразованием заданной системы координат.
§ 17. ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ
ОБЩЕГО УРАВНЕНИЯ
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
/ случай. Если
|ац а\2 а\з
δ = |αΐ2 G22 G23
Gl3 G23 ОЗЗ
*о,
то поверхность S является центральной. Ее уравнение в системе
координат O'x'y'z', полученной параллельным переносом
системы Oxyz вдоль вектора ОО*, где О'(хо> 2/о> zq) — центр этой
поверхности, имеет вид
апх'2 + а22У*2 -Ι- «зз-'2 +
+ 2al2x'y' + 2a2*y'z + 2avsx ζ1 + а'ы = 0, (1)
Поверхности второго порядка
205
причем
«44 = «и#о + «242/0 + «34^0 + а44, (2)
где хо, τ/ο, ζο находят из системы (1) § 14.
Если αΐ2 φ 0, «23 φ 0, αΐ3 φ 0, то нужно выполнить
стандартное преобразование системы O'x'y'z', т. е. рассмотреть
систему координат 0'x"y"z", получаемую двумя
специальными поворотами системы O'x'y'z' вокруг начала 0\ в которой
уравнение поверхности S будет иметь канонический вид
«цЯ + α222/ + «зз* + α44 = °- w)
В дальнейшем будет показано, что в случае δ ф0 ни один из
коэффициентов а!{х, α"2, «зз не Равен нулю.
2 случай. Если
δ =
an «12 «13
«12 «22 «23
«13 «23 «33
= 0, (4)
то поверхность S не обладает единственным центром.
Как установлено ранее, после стандартного
преобразования системы координат Oxyz, а именно, в системе
координат Ox"y"zh\ получаемой двумя специальными поворотами
системы Oxyz, уравнение поверхности S имеет вид
а^а/'Ч«2^'2+4^ (5)
В дальнейшем будет показано, что в случае δ = 0 один или
два коэффициента группы старших членов в уравнении (5) равны
нулю.
Уравнение (5) с помощью параллельных переносов и
специальных поворотов соответствующих систем координат можно
привести к одному из следующих видов:
«33 = 0. «34 = 0, «11 *2 + «222/2 + <>44 = 0, (6)
«зз = 0, «34 Φ 0, а'{хх2 + оЬй2 + 2α?4Ι = 0, (7)
«зз = 0, oj2 = 0f «24 = 0, α'3'4 = 0, а'^х2 + a44 = 0, (8)
«зз = 0, αί>'2 = 0, α%Αφ0, «J4^0, а»1р+с§ = 0. (9)
206
Глава 5
В самом деле, после ряда преобразований нетрудно получить
приведенные результаты.
I) Если «зз — 0, «34 = 0,то уравнение (5) можно
преобразовать следующим образом:
Л11 \ * + ~ I + а22 I 2/ + — 1 + а« = Οι
\ Gll/ V а22/
"2 п2
ГЛе β44 = «14 - zfr - -#-.
II 22
Положим
„ft „П
„" ι аН - // , α24
//
χ +-jt=x, у + -ητ = V* ζ" = zy т. е.
aU β22 „
ft - "Ί4 // — ^24 //
а11 а22
В системе координат Oxyzy получаемой из системы Ox19yflz"
параллельным переносом вдоль вектора с началом в точке О и
_ // //
концом в точке θ(—^тА, -^S0)» УРавнсние (5) примет вид (6).
2) Если а"3 = 0, а"л Φ 0, то уравнение (5) допускает
следующее преобразование:
η"2
f- + 24'4z" + а44 = 0,
а22
»»(*"+ί)+ * (*"+ί)+ 2°- (*"+4)=°·
_//2 "2
гдес = а44-^--^-.
Положим
ап а22 2а34
" = а14 Лу/ - а24 _//
В системе координат Oxyz, получаемой из системы Oxfiynz"
параллечьным переносом вдоль вектора с началом в точке О
и концом в точке 0\-^,-^,-i£jr), уравнение (5) примет
вид (7).
fJoeepxHO-.mu второго порядка
207
3) Если α"3 = 0, й22 = 0, то уравнение (5) имеет вид
а'1хх"2 + 2а'{Ах" + 2αί>'42/" + 2α'^ζ" + а44 = 0.
Последнее уравнение можно переписать так:
2
+ 2а'^у" + 2α'^ζ" + ан = О,
°"'(*"+ί!
α"2
ГДе 044 = ^44 — ~№
Положим
αϊι
* = ^ + ^И, У = ^ * = *"> т.е.
В системе координат Oxyz, полученной из системы Ох"у"ζ"
параллельным переносом вдоль вектора с началом в точке О и
концом в точке О(-^,0, θ), уравнение (5) приводится к виду
с![хх2 + 2а"Ау + 2а'з'4£ + а44 = 0. (10)
Если азз = 0, af22 = 0, а^ = 0, а^ = 0, то уравнение (10)
примет вид (8).
4) Пусть теперь αί[3 = 0, о!{2 = 0, α£4 φ 07 α£4 φ 0.
Рассмотрим систему 0&§27 получаемую из системы 0#у£
с помощью поворота вокруг оси Ох на угол </?, измеряемый
против часовой стрелки в плоскости Oyzy при этом формулы
преобразования имеют вид
х = £, у = |rcosv? — £sin<p, 5 = ysinv? + zcos</?.
В системе Оху! уравнение (10) имеет вид
αί'ι*2 + 2^24 (^ cos V7 ~~ * ^ У7) +
+ 2а"4(£ sm^ + l cos γ?) + а44 = 0,
т. е.
аи ^2 + ^(2«24 cos V* + 2аз4 s*n У7) +
-Ь 1(2^34 cos Ψ — 2а24 sin <p) 4- G44 = 0.
208
Глава 5
Выберем угол φ так, чтобы коэффициент при ζ равнялся
нулю, т. е. 034 cos φ — а^ sin φ = 0. Тогда
// // л ^24
«34ctg^ - <*24 = 0, Ctg<£ = —,
α34
у> = arcctg -^г + πη, η (Ξ Ζ.
α34
При найденном значении угла у? в системе Olyf
уравнение (10) имеет вид „ ~о -
a^ar 4- суЧ-а44 = 0.
Последнее
Положим
ж = ж,
χ = х7
уравнение перепишем в виде
// -2 , (- х ^44 λ η
auaT + cly-\ 1 =0.
\ с /
ζ ~ , 044 ζ =
У = У+ , ζ = ζ,
с
~ г G44 ~ г
у = у , ζ = ζ.
С
т. е.
В системе координат, получаемой параллельным переносом
из системы Oxyz вдоль вектора с началом в точке О и концом в
точке О (0, — ^, 0), уравнение (5) имеет вид (9).
Вычислив коэффициенты в уравнениях (3), (6) — (9),
нетрудно установить вид поверхности, определяемой уравнением (1).
§ 18. КЛАССИФИКАЦИЯ
ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
Как только что установлено, общее уравнение поверхности
второго порядка S
опх2 + а22У2 + <*зз22 + 2а\2ху + 2a^yz + 2aisxz +
+ 2аых + 2α24ϊ/ + 2а34^ + &44 = 0 (1)
может быть приведено к одному из следующих видов:
если δ Φ 0, то
αηχ +a22y +α33ζ + α44 = 0> \ζ)
Поверхности второго порядка
209
если δ = 0, то, соответственно,
апж +а22у + α33ζ +
+ 2a'/4:r" + 2aJ4y" + 2а'3'4г" + а44 = 0, (3)
в частности,
οί[λχ2 + а'22у2 + а44 = 0, если а'3'3 = 0, а34 = 0; (4)
о!{хШ2 + а22у2 + 2a'34f = 0, если а'33 = 0, а"4 / 0; (5)
α'ΙγΧ2 + ά44 = 0, если а33 = 0, а22 = 0, (6)
«24 = 0> аз4 = 0;
с![хх2 + су = 0, если а3'3 = 0, а"2 = 0, (7)
aj4 / 0, а34 ^ 0.
Установим, какие поверхности определяет уравнение (1) в
каждом из названных случаев.
/ случай. Если δ Φ 0, то, как уже отмечалось, в этом
случае ни один из коэффициентов а"х, а22, а33 уравнения (2) не
равняется нулю.
Пусть α44 ψ 0 и все коэффициенты a'd, а^, а33 одного
знака.
Если знак коэффициента а44 противоположен знаку
коэффициентов α'γι, α22, а33, то уравнение (1) определяет эллипсоид.
Если знак коэффициента а44 совпадает со знаком
коэффициентов а"х, а22, а33, то уравнение (2), а следовательно, и
уравнение (1), не определяет никакой поверхности, или, как говорят,
определяет «мнимый» эллипсоид.
Пусть α44 Φ 0 и из четырех коэффициентов а"х, а22, а33,
«44 лва одного знака, а два других — противоположного.
Тогда уравнение (2), а следовательно, и уравнение (1), определяет
однополостный гиперболоид.
Пусть α44 Φ 0 и знак одного из первых трех коэффициентов
αϊΐι α22> азз> α44 противоположен знаку остальных
коэффициентов. В этом случае уравнение (1) определяет двуполостный
гиперболоид.
210
Глава 5
Пусть 6*44 = 0. Если коэффициенты разных знаков, то
уравнение (1) определяет конус второго порядка, а если
коэффициенты а"х, а'22, G-зз одного знака, то уравнение (1) определяет
точку, или, как говорят, «мнимый» конус.
2 случай. Если δ = 0, то в этом случае один или два
коэффициента группы старших членов обращаются в нуль, как
отмечалось в предыдущем параграфе.
Если азз = 0, ^34 = 0, δ44 φ 0, а коэффициенты a"lf
О22 имеют знак, противоположный знаку 644, то уравнение (4),
а потому и уравнение (1), определяет эллиптический цилиндр
второго порядка с образующими, параллельными оси аппликат.
Если же коэффициенты о!(х, а22 имеют разные знаки, то вне
зависимости от знака 644 уравнение (4) описывает
гиперболический цилиндр второго порядка с образующей, параллельной оси
аппликат.
Если a'/j, a"2, 644 имеют одинаковые знаки, то
уравнение (4), а следовательно, и уравнение (1 \ не определяет никакой
поверхности, или, какюворят, определяет «мнимый» цилиндр.
Если «зз = 0, О34 = 0, 544 = 0 и знаки у
коэффициентов α"λ, а'22 разные, уравнение (1) определяет пару
пересекающихся плоскостей, а если указанные знаки совпадают, то
уравнение (1) не определяет никакой поверхности, или, как
говорят, определяет пару «мнимых» пересекающихся плоскостей
(ось О ζ).
Если а"3 = 0, Оз4 ?έ 0, то в случае, когда а"1г а'^
имеют одинаковый знак, уравнение (5) (уравнение (1)) определяет
эллиптический параболоид, а если противоположные —
гиперболический параболоид.
Если а"3 = 0, αί>2 = 0, а^ = 0, а^4 — 0, то при условии
Й44 φ 0 и противоположности знаков коэффициентов g'/j , Й44
уравнение (6), а значит и уравнение (1), определяет пару
параллельных плоскостей. А при условии Й44 т^Ои когда знаки у а!{х,
Й44 одинаковые, уравнение (1) не определяет никакой
поверхности, или, как говорят, определяет пару «мнимых» параллельных
плоскостей. В случае Й44 = 0 уравнение (6), а следовательно, и
уравнение (1) описывает пару «совпадающих» плоскостей.
Поверхности второго порядка
211
Если Лзз = О» а22 = О» а24 ^ О· G34 Φ О· то уравнение (7),
а потому и уравнение (1), определяет параболический цилиндр
второго порядка с образующими, параллельными оси аппликат.
Итак, уравнения (2), (4) — (7) определяют:
(2) — либо эллипсоид, либо гиперболоид, либо конус;
(4) — либо цилиндр (эллиптический или гиперболический),
либо пару пересекающихся плоскостей;
(5) — параболоид (эллиптический или гиперболический);
(6) — пару плоскостей (параллельных, «мнимых» или
«совпадающих»);
(7) — параболический цилиндр.
§ 19. ГИПЕРПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Гиперповерхностью S второго порядка в η-мерном
вещественном пространстве Еп называют геометрическое место
точек χ = (^ι,α^,.-.,Εη), удовлетворяющих уравнению вида
η η
Σ aikXiXk +2^bfcZfc + c = 0, (1)
где ££fc=1 €LikXiXk — квадратичная форма, a Σϊ=ι Ькхк
—линейная форма переменных χι, ^2» ■··, ^ni с — вещественное
число.
Исследование гиперповерхностей второго порядка проводят
с помощью метода, сходного с методом, примененным при
изучении алгебраических линий π поверхностей второго порядка в
трехмерном пространстве.
ЗАДАЧИ И УПРАЖНЕНИЯ
1· Написать уравнение эллипсоида с противоположными
вершинами в точках (0,0,6) и (О,0, -2), зная, что
плоскость Оху пересекает его по окружности с радиусом
равным 3.
Решение. Нетрудно видеть, что обе вершины лежат
«а оси Οζ. Следовательно, центр симметрии эллипсоида
212
Глава 5
находится в точке (0,0,^^) = (0,0,2), а значит, его уравнение
можно записать в виде
*2 , У2 , (*-2)2 ...
ft2 -1" ^ С2
Так как плоскость Оху пересекает эллипсоид по
окружности, то очевидно, что а = Ь. Точка (0,0,6) лежит на
эллипсоиде, поэтому (4/с)2 = 1, или с2 = 16. Запишем уравнение
эллипсоида в виде
х2 + У2 ι (z-2)2 2 л 2 2/ (z-2)2\
-^- = 1-ЧёГ"' или * +у =аЧ1" ιβ )·
При ζ = 0 имеем окружность радиуса 3. Следовательно,
За2/4 = 9, а2 = 12. Поэтому окончательно получаем уравнение
а2 , У2 , (*~2)*
12 12 16
2. Написать уравнение эллиптического параболоида, зная,
что плоскости χ = а, у = Ь пересекают его по
параболам с вершинами (а,0,с) и (0,6, с), плоскость Оху
касается параболоида в его вершине, а плоскости Oxz% Oyz
являются его плоскостями симметрии.
Решение. Заметим, что поскольку Оху касается вершины
параболоида, a Oxz и Oyz — плоскости симметрии, то вершина
параболоида находится в точке (0,0,0). Поэтому его уравне-
2 2
ние можно записать в виде γ + *- = 2ζ. При χ = а
имеем параболу с вершиной в точке (а,0,с). Поэтому а2/р = 2с,
или ρ = а2/(2с). При у = Ь имеем параболу с вершиной в
точке (0,6,с), т. е. b2/q = 2с, следовательно, q = b2/(2c).
Окончательно, о 9
χ у
— + — = 2z
2с 2с
3· Написать уравнение двуполостного гиперболоида,
плоскости симметрии которого совпадают с
координатными плоскостями, проходящего через точку Л(0,0,3),
если известно, что плоскости Oxz и Oyz пересекают
Поверхности второго порядка
213
указанную поверхность по гиперболам, асимптоты
которых составляют с осью Oz углы, равные
соответственно | и ^.
Ответ: 9х2 + у2 - Зг2 = -27.
4. Написать уравнение гиперболического параболоида,
плоскости симметрии которого совпадают с плоско-
стями Οχ ζ и Oyz, если известно, что он проходит
через гиперболу ξ? — fc = 1, ζ = с, а координатная
плоскость Оху пересекает его по паре прямых.
Ответ: g_g_s=o.
5. Составить уравнение эллипсоида, плоскости
симметрии которого совпадают с координатными
плоскостями, если он проходит через точку (1,1,3) и окружность
х2 + У2 + ζ2 = 9, ζ = χ.
Ответ: Ъх2 + 4у2 + Зг2 =36.
6. Найти прямолинейные образующие однополостного
2 2 2
гиперболоида ^- + \ — j§ = 1, проходящие через точку
4(2,6,8).
Ответ: χ = 2, у = 6 +St, ζ = 8 + 4ί; χ = 2 + 8t, у = 6 + 9t,
2 = 8 + 20ί.
Глава 6
ИССЛЕДОВАНИЕ ЛИНИЙ И ПОВЕРХНОСТЕЙ
ВТОРОГО ПОРЯДКА,
ЗАДАННЫХ УРАВНЕНИЯМИ ОБЩЕГО ВИДА,
С ПОМОЩЬЮ ИНВАРИАНТОВ
§ 1. ПРЕОБРАЗОВАНИЕ КВАДРАТИЧНОЙ ФОРМЫ
К НОВЫМ ПЕРЕМЕННЫМ
Квадратичной формой переменных χ ι, Χ2, · - - > #п называют
однородный многочлен второй степени относительно этих
переменных.
Всякая квадратичная форма допускает запись в следующем
симметричном виде:
η
Ф(яъЯ2|..-,ял) = 5Ζ aijXiXj, (I)
где aLj = aji, или, в вид&матричного равенства,
(2)
где
А =
/он
021
• θ2η
\Onl
аг =
χ =
Q-nn/
\Xl, 3?2> · · · > %n)·
(3)
(«*»— знак транспонирования). При этом вектор χ
называется вектором переменных, матрица А — матрицей квадратичной
формы, а определитель det.4 — определителем квадратичной
формы.
Подчеркнем, что прежде чем определить матрицу
квадратичной формы, нужно записать эту форму в симметрическом виде.
Исследование линий и поверхностей с помощью инвариантов 215
Сделаем замену переменных в квадратичной форме (1) по
формулам χι = αηχ[ + αΐ22, + ... + ain<t
хп = ап\х[ + аП2Х92 Η
"Г OlnnXnf
которые можно переписать в виде матричного равенства
X г== 0/2D |
*=( Ч,ж ι г =
\xj \x'J '
/an
«21
\αηι
d\2 ■ ■ . ainy
<*22 · - · &2п
&п2 - · · CLrm/
(5)
(6)
С —матрица преобразования.
Теорема. Если в квадратичной форме
с матрицей А перейти к новым переменным х[,х^ ... >х'п
по формулам χ = CxJ с матрицей преобразования С, то
получим квадратичную форму
Ф(*;,4> ■■■,<) = *'*С*АСх'
с матрицей А' = С* АС и det Af = det .A(detC)2.
Доказательство. Из выражения (5) в силу известной
теоремы высшей алгебры имеем * ,* _,+
χ = χ С . (7)
В силу соотношений (2), (7), (5)
Ф(хи -··> а?п) = а?*Ат = х'*С*АСх' = Φ^,^ό,... ,я4),
причем матрица Л' й определитель det Л' рассматриваемой
квадратичной формы относительно переменных я^, :г'2, ... х'п
определяются соотношениями
А' = С* AC, det Л' = det j4(det С)2. (8)
216
Глава 6
% 2. ИНВАРИАНТЫ ОБЩЕГО УРАВНЕНИЯ
ЛИНИИ ВТОРОГО ПОРЯДКА
ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ КООРДИНАТ
Пусть в некоторой ДПСК Оху линия второго порядка I
определяется общим уравнением
ацх2 + 2а\2ху + а22У2 + 2а\3х + 2а23у + а33 = 0. (1)
Уравнение линии I в любой ДПСК получается из (1), если в
него вместо χ и у подставить их выражения согласно формулам
преобразования при переходе от системы Оху к системе О'х'у':
χ = х0 + х'ац + у'оси, У = Уо + #'«21 + #'«22,
гдеО'(а;о,г/о),
«11 ОС12
«21 «22
.2. _
= ±1,
«11 + «21 = !> «12 + «22 = !» «11«12 + «21 «22 = 0,
J2 _
«11 + «12 = *» «21 + «22 = 1) «11«21 + «12«22 = 0.
Уравнение линии I в системе О'х'у1 имеет вид
а^х12 + 2а'12х'у' + а'22у'2 + 2а'13х' + 2а232/' + а33 = 0.
(2)
(3)
(4)
(5)
Выражение /(ац, αι2, α22, ахз, а2з> азз) > не являющееся
константой, называют инвариантом уравнения линии I
относительно преобразования координат, если, каковы бы ни были
ДПСК Оху и О'х'у',
/(ац, αΐ2, α22, αχ3, агз, азз) = /(а'п > а'12, а22> α'ΐ3> а2з> азз)·
Теорема 1. Инварианты общего уравнения линии I
второго порядка относительно преобразования координат
суть
J(A) =
ац — λ αχ2
Ι αΐ2 Й22 "" λ
ί
J3 =
Λ = ац + α22, J2 =
ац αΐ2 ахз
αΐ2 α22 агз
αΐ3 агз а3з
•
ац αΐ2
αΐ2 α22
, (6)
(7)
Исследование линий и поверхностей с помощью инвариантов 217
Доказательство. Для начала заметим, что при
параллельном переносе системы координат коэффициенты группы
старших членов не меняются, а потому величины (6) не зависят от
выбора #о и уо в соотношениях (2), поэтому являются
инвариантами относительно параллельного переноса.
Докажем, что J(X), Ji, J2 — инварианты однородного
ортогонального преобразования (поворота системы координат). Для
этого наряду с переходом по формулам (2) от системы Оху к
новой системе координат рассмотрим преобразование
квадратичной формы относительно переменных х\, х2
αηΧι + 2αϊ2χιΧ2 + 0*22X2 ~ Ηχϊ + xl) (8)
к новым переменным х[, х2 по формулам:
XI = ацх[ + Qi2^2> χ2 = <Χ2ΐΧ[ + «22^2» (9)
где dij (г, j = 1,2) — те же, что и в соотношении (1), ay (i, j =
= 1,2)—те же, что и в выражении (2).
При этом слагаемое λ(ζ2 + х2) преобразуется в X(xf + х%)
в силу условий ортогональности (4) для коэффициентов а^ в
соотношениях (9), а сама квадратичная форма относительно х[,
х2 имеет вид
а[гх? -f 2а'12х'гх2 + α22χξ - Х(х? + х2), (10)
где a[j (i,j = 1,2) — те же, что и в выражении (5).
В силу формулы (3) определитель преобразования (9) равен
±], а тогда можно утверждать, что определители форм (8) и (10)
равны, т. е. для любого λ определитель
\ац - X а\2
J'(A) =
α'ιι - λ «12
α12 °22 — ^
0>\2 Q-22 — λ
= J(X)
является инвариантом уравнения линии I. Поскольку, в свою
очередь,
J(A) = λ2 - (an + α22)λ + (оца22 - α\2) = λ2 - Λ λ + J2,
то для любого λ справедливо λ2 — λJ\ + J2 = A2 - XJ[ + J2,
а следовательно, для различных систем координат Оху и OxV
218
Глава 6
выполняются равенства J\ = J[, 3<ι = J^ т. е. Jy, Jo
являются инвариантами уравнения линии I относительно однородного
ортогонального преобразования координат.
Теперь рассмотрим квадратичную форму
аих\ + а22%2 + азз^з + 2ai2xiX2 + 2а2з#2#з + 2αΐ3#ι£3 00
и ее определитель
3 =
Oil Gl2 Gl3
<Н2 ^22 ^23
<*13 ^23 ^33
Заметим, что если χ\ — χ, χ2 = у, хз = 1» то квадратичная
форма (11) совпадает с левой частью уравнения (1).
Перейдем в этой форме к новым переменным по формулам:
^1 = Oti\x[ + αΐ2#2 + #0^3ι
х2 = d2ix\ + α22^2 + 2/о^з» О2)
xs = 0 · х[ + 0 ■ х2 + 1 · #з>
где а*? (г, j = 1,2) — те же, что и в соотношении (2),
причем если х'3 = 1, то указанное преобразование тождественно
преобразованию (2). Тогда
= ±1.
Следовательно, определители исходной квадратичной формы (11)
и преобразованной равны, т. е. определитель J3 является
инвариантом уравнения линии I.
Итак, инвариантами уравнения (1) линии I при
преобразовании координат являются определители J[X), J\ t J2, J$.
Qll «12 XO
«21 «22 2/0
0 0 1
=
#11 Oii2
«21 «22
Теорема 2. Величина
J2 =
flu
Gl3
Ol3
ОЗЗ
4-
022
023
^23
«33
является инвариантом уравнения линии I относительно
однородного ортогонального преобразования (поворота
системы координат).
Исследование линий и поверхностей с помощью инвариантов 219
Доказательство. Действительно, при преобразовании
х = χ'αχ ι + у'аи, у = х9а2\ + г/'а22,
где otij (i,j = 1,2) удовлетворяют (4), коэффициенты
уравнения (5) а[3 = αΐ3^ιι + а2з#21> «23 = αΐ3^ΐ2 + ^23^22-
Поэтому с учетом того, что а33 = α33ι J\ — инвариант, и в силу (4)
получаем
& =
а'п а'13
а13 а33
+
а22 G23
а23 а33
«ззWi + а'22) - (а?з + 4з) =
= ЛззЛ - («11 + «?2)а13 - 2(ац021 +012^22)^13^23-
- (»2l + С*22)а23 = аЗЗ<Л - (β?3 + а2з) = J2i
т. е. J2 — инвариант относительно однородного ортогонального
преобразования.
Теорема 3. Если инвариант J2 = J3 = 0, mo J2
является инвариантом и относительно параллельного переноса
системы координат.
Доказательство. Если в уравнении (1) αι2 ψ О, то, как
известно, всегда существует однородное ортогональное
преобразование (поворот системы координат), при котором в
уравнении (5) а'12 = 0. При этом в силу соотношения Jo = 0 либо
а\г = 0, либо а'22 = 0. Ради определенности допустим, что
а(22 = 0. Тогда уравнение линии I принимает вид
а'пх'2 + 2а'13х' + 2а'23г/' + а33 = 0.
Заметим, что по условию теоремы
Js =
Отсюда следует а23 = 0, поэтому в данном случае
уравнение линии I имеет вид
Κι
0
кз
0
0
«23
«13
«23
озз
= -о'цОзз = 0
а!пх'2 + 2а\3х' + о3з = 0.
220
Глава 6
От системы Ох'у' перейдем к системе Оху по формулам
х' = xq + х, у' = уо + Уу где хо и уо — произвольно заданные
числа. Тогда _ _2 ~_ _
оцг + 2а,1зх + азз = 0,
где бц = а'ц, 613 = а'цХо + а!з· йзз = о!пх^ + 2013X0 + озз,
поэтому
J2 =
Оц αΐ3
δ 13 озз
= йп(й'ца:о + 2αί3χο + Лзз) -
/2 2 г\ ι ι /2 τ
— О.цХ0 — ^йцй^Хо — UJ3 — »/2r
что и требовалось доказать.
§ 3. ИНВАРИАНТЫ ОБЩЕГО УРАВНЕНИЯ
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
ОТНОСИТЕЛЬНО
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
Пусть в некоторой ДПСК Оху ζ поверхность S второго порядка
определяется общим уравнением:
ацх2 + а22У2 + азз*2 + 2а12ху + 2а2зуг + 2сцзхг +
+ 2αί4χ + 2а24У + 2α^ζ + α44 = 0. (1)
Уравнение поверхности S в любой другой ДПСК
получается из уравнения (1), если в него вместо х, у, ζ подставить их
выражения согласно формулам преобразования при переходе от
системы Oxyz к системе O'x'y'z1
χ = хо + х'аи + 3/0:12 + ζ'оси,
У = Уо + s'<*2i + у'с*22 + ζ'α23, (2)
ζ = zq + х'аз1 + у'осз2 + я'^зз,
где O'(xo,yo,zo), а матрица преобразования является
ортогональной и ее определитель
Оц 012 «13
0*21 0>22 С*23
"31 «32 «33
= ±1.
(3)
Исследование линий и поверхностей с помощью инвариантов 221
Уравнение поверхности S в системе O'x'y'z' имеет вид
а'пх'2 + о'22$/2 + а'33г'2 + 2а'12х'у' + 2а'23у''ζ' + 2α'13χ'ζ'+
+ 2а'их' + 2а'24у' + 2α'Μζ' + а44 = 0. (4)
Выражение <^(°1Ь °22, озз, «12» · · · > аз<ь οάλ) , не являющееся
константой, называют инвариантом уравнения поверхности
S относительно преобразования координат, если, каковы бы ни
были ДПСК Oxyz и O'x'y'z', справедливо равенство
φ{α\\, й22, · · · ι аз4,044) = V>(aii» а22, · · ·, аз4> а44)· (5)
Теорема 1. Инварианты общего уравнения
поверхности второго порядка относительно преобразования
координат суть:
|ац-А αΐ2 αί3
J(X) = \ αϊ 2 агг - λ агз
I Qi3 θ23 азз — λ|
Λ = α-η +а22 + азз,
J2 =
Jz =
«И ^12
^12 ^22
+
G22 ^23
G23 »33
Gil Gi2 ^13
kl2 »22 G23
1^13 ^23
G3
3
+
an αι3
a13 U33
j
J4 =
ац ai2 ai3 an
Gl2 ^22 ^23 ^24
Gl3 ^23 «33 ^34
ttl4 U24 a34 ^44
Доказательство. Как известно, при параллельном
переносе системы координат коэффициенты группы старших
членов не изменяются, а потому, очевидно, J(A), Jlf J2, J3
являются инвариантами относительно параллельного
переноса системы координат. Докажем, что указанные
величины— инварианты относительно однородного ортогонального
преобразования (поворота системы координат).
222
Глава 6
Для этого наряду с переходом по формулам (2) к новой
системе координат O'x'y'z' рассмотрим преобразование
квадратичной формы относительно переменных х\, х2, хз
аих\ + а22х\ + азз^з + 2αΐ2^ι^2 +
+ 2α23^2^3 + 2αΐ3#ι£3 - Кх\ + xl + хз) (6)
к новым переменным х\,х'2, х'% по формулам
χι = апх[ 4- αΐ2^2 + «13^з>
^2 = «21^1 + Of22^2 + «23^3» (7^
^3 = «31^1 + а32^2 + а33#3>
где aVj (i,j — 1,2,3)— те же, что и в выражении (Ι),ο:^
( г, j = 1,2,3) — те же, что в соотношении (2).
Слагаемое Х{х\-\-х\+х%) преобразуется в Xix'i+x'i+x'i) в
силу условия ортогональности матрицы преобразования по
формулам (7), а сама квадратичная форма относительно x[,xf2ixf3
имеет вид
^11·^1 ■ ^22*^2 "^~ ^33^3 * ^^12*^1 "^2 ■ ^^23^2^3 ■
+ 2a^4-M^i2 + 42+42)> (8)
где a^ (iyj — 1,2,3) — те же, что ив выражении (4).
В силу соотношения (3) определитель преобразования (7)
равен ±1, а тогда можно утверждать, что определители
квадратичных форм (6) и (8) равны, J'(A) = J(A) для любого λ, а
следовательно, определитель J(A) является инвариантом
уравнения поверхности S.
С другой стороны, определитель J(A) есть многочлен
j(A) = -A3 + A2Ji-AJ2 + J3
относительно А. В связи с тем, что для различных систем
координат Oxyz и OVj/V при любых А справедливо равенство
-А3 + Л А2 - J2A + J3 = -λ3 + J(A2 - J^A + Jj,
то Ji = J{, J2 = J2» J3 = J3. T- e- определители Ji, J2,
J3 — инварианты уравнения поверхности S относительно
преобразования координат.
Исследование линий и поверхностей с помощью инвариантов 223
Рассмотрим квадратичную форму
О О 9 9
αγχΧγ + (122*2 + α33^3 + ^44^4 + 2a\2*l^2 + 2(1\$ΧγΧ$ *
+ 2α23^2^3 + 2ΰ24^2^4 + 2034^3^4 . (9)
определитель которой совпадает с J^, а при х\ = х, х2 = у,
х3 = ζ у х\ = 1 ока равна левой части уравнения поверхности (1).
Перейдем в этой форме к новым переменным по формулам
преобразования „ Л # , Л # , Л / , „ /
r r Xl = «ll^i + «12^2 + «13#3 + ^0^4>
^2 = «21 #1 + «22#2 + «23^3 + 2/0^4,
з>з = «3ix'i + 0:32X2 + «зз^з + ^0^4»
s4 = 0 · xi + 0 - #2 f 0 · X3 + 1 ■ х'Л,
где ctij {i,j = 1,2,3) — те же, что и в выражении (2) Но
справедливо соотношение
(Ю)
an G12 «13 хо
«21 «22 «23 2/0
«31 «32 «33 zq
0 0 0 1
«11 «12 «13
«21 «22 «23
«31 «32 «33
= ±1.
В силу последнего равенства определители исходной
формы (9) и преобразованной равны, т. е. J4 является инвариантом
уравнения поверхности S.
Итак, инвариантами уравнения (1) поверхности S
относительно преобразования координат являются определители */(А),
J 11 J2 у Jo , J A ·
Теорема 2. Величины
J* =
J2 =
an ai2
an
Oi2 G22 a24
Я14 a24 <M4
an ai4
a\4 044
+
a
a
+
22
24
an
ахз ai4
Л13 G33 ^34
«14 034 a 14
Q>24
CL44
4
азз о
a34 a
+
341
44 J
G22 #23 β24
#23 a33 ^34
a24 Q<M G44
являются инвариантами относительно однородного
ортогонального преобразования (поворота системы
координат).
224
Глава 6
Доказательство. Расе мотрим вспомогательное ура внение
апх2 + а22У2 + азз*2 + 2av2xy + 2а2зУ* -f 2а\зхг +
+ 2аых + 2а2лУ + 2α34* + «44 - λ(χ2 + у2 + ζ2) = 0. (11)
После однородного ортогонального преобразования,
выполненного по формулам (2) при xq = г/о = *о = 0, получаем
уравнение
а'ца;'2 + 0221/2 + <*зз*/2 + 2а'12х'у' + 2α'2:$'ζ' + 2α\3χ'ζ' +
+ 2а;4хЧ2а/24^Ч2а,34гЧа^-А(а:/2 + 2/,2 + ^2) = 0. (12)
Для уравнений (11) и (12) справедливо J^ = J41 т. е.
«11 "" λ αΐ2 «13 «14
012 «22 — λ α23 «24
β 13 «23 «33 - λ аз4
β 14 «24 «34 «44
α
14
α24
αιι "" λ α12 α13
α12 α22 ~~ ^ α23
α13 α2β α33 ~~ λ «34
• # » ,
α44
α
14
α
24
α
34
Последнее соотношение справедливо для любых значений λ,
а поэтому, используя известное свойство определителей
ац+6ц «12+&12 -·■ CLin+bin
«21 0.22 · ■ · «2п
«,,ι
«7l2
Oil
α2ι
«12
«22
«In
«2n
+
bll &12
«21 «22
bin
«2n
|«nl «η2 ... «ηη| l«nl «η2 ··■ «nnl
сравниваем коэффициенты при λ и λ2 в левой и правой частях с
учетом равенства а44 = «44» получаем
h =
an «12 «14
012 «22 α24
ftl4 O04 «44
+
an αΐ3
«13 ОЗЗ
«14 «34
αΐ4
аз4
θ44
-ι-
«22 «23 «24
«23 «33 «34
«24 «34 «44
α11 α12 α14
«12 α22 ^24
α14 α24 α44
+
α
α'ι3 α'
11 αΐ3 "14
«13 α33 α34
34 α44
«14 Ο9
+
«22 α23 α24
Λ/ Λ/ Λ/
«23 α33 α34
α24 «34 α44
— ^з>
Исследование линий и поверхностей с помощью инвариантов 225
j2 =
\ац аи
α и ^44
+
=
022 Я 24
«24 &44 J
1 / г
|G14 α44
+
+
^33 «34
^34 «441
\а22 а21
L/ §
|α24 α44
=
+
G33 α31
α34 α44
Ji.
Таким образом, J$ и Л — инварианты уравнения (1)
относительно однородного ортогонального преобразования.
ЗАМЕЧАНИЕ. В общем случае указанные величины не
являются инвариантами относительно параллельного переноса
системы координат, а потому называются полуинвариантами
уравнения поверхности.
Теорема 3· Если в результате однородного
ортогонального преобразования (поворота системы координат)
уравнение (1) можно привести к виду
а\хх'2 + о!22у'2 + 2а\2ху* + 2о!ых' + 2а'ыу + а'44 =0, (13)
то J$ — инвариант и относительно параллельного
переноса системы координат.
Доказательство. Для начала заметим, что для
уравнения (13) справедливо соотношение J3 = J4 = 0, а
полуинвариант
\ап а12 а14
Js =
а12 а22 а24
а
14
$24 ^44
Осуществим параллельный перенос системы координат по
формулам х' = χ + хо, у* = у + уо, ζ' = ζ. Тогда получаем
уравнение
а'пх2 + а!22у2 + ^ofl2xy + 2ацх + 2а2ьу + 644 = О,
где
α и = а'ц^о + α'ΐ22/ο + α'ΐ4>
«24 = d\ 2^0 + »222/0 + <*24*
Й44 = (614 + а'ы)х0 + (α24 + «24)2/0 + «'u-
226
Глава 6
Вычислим полуинвариант
./з =
«11 «12 «14
а12 а22 «24
«14 «24 «44
«и «12 «и^о + а'^о + й'м
«12 «22 «12^0 +«22^/0 +«24
«14 «24 «44
а
11
12
12
/
22
«14
«24
«Ίΐ^Ο^α'^ϊ/Ο+αΉ «12*0 + «22?/0 + «24 «ί4^0+«24?/0 + «44
«11 «12 «14
«12 «22 «24
«14 «24 «44
что и требовалось доказать.
Теорема 4· Если в результате однородного
ортогонального преобразования (поворота системы координат)
уравнение (1) можно привести к виду
а'пх'2 + 2а\Ах + а'44 = 0,
(14)
то Ji — инвариант и относительно параллельного
переноса системы координат.
Доказательство. Заметим, что для уравнения (14)
справедливы соотношения J2 = Js — -h = Л = 0.
В уравнении (14) сделаем замену переменных по формулам
а/ = χ + хо, у9 = у, ζ' = ζ, получаем уравнение
«ίΐ^2 + 2άΐ4^ + ^44 = 0,
где ой = о'ц Jo + «и 1 «44 = «Ί 1^0 + 2а'14а:о + «44 · Тогда
J2 =
«11 «14
«14 «14
а
11
а'цЖо + β'ΐ4
а'пхо + а'14 а'цжд + 2^'14#ο + «44
а
11
а
14
«П^О + «14 «14х0 + «44
«И «14
«14 «44
= J2.
Таким образом, 3<χ является инвариантом относительно
параллельного переноса системы координат.
Исследование линий и поверхностей с по мощью инвариантов 227
§ 4. ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ
ЛИНИИ ВТОРОГО ПОРЯДКА
С ПОМОЩЬЮ ИНВАРИАНТОВ
Рассмотрим линию второго порядка J, определяемую в ДПСК
общим уравнением
ацх2 + а22У2 + 2αΐ2Χ2/ + 2αι3α: + 2а2зУ + «зз = 0 (1)
и вычислим ее инварианты Ji, J2 , J3, J (X) = λ2 — Ji A + J2 -
Как известно, в системе координат, получаемой поворотом
исходной системы на специально выбранный угол, уравнение (1)
примет вид 2 , п..2
ахг + Ру' + ax + by + d = 0,
(2)
где коэффициенты а и β можно найти с помощью
инварианта J(A):
J(A) =
«и - λ αι2
Ol2 O22 — λ
α-λ Ο
Ο /?-λ
= (α-Χ)(β-Χ).
Отсюда видно, что α, β — корни уравнения ,/(λ) = 0, т. е.
уравнения
λ2 - A Ji + J2 = 0.
(3)
Если при этом J2 Φ О, то корни уравнения (3) отличны от
нуля. В этом случае линия I — центральная, и, как было показано,
ее уравнение в соответствующей системе координат имеет вид
ах2 + Ру2 + μ = О, причем величину μ можно найти, используя
определитель J3:
■7з =
«11 «12 «13
«12 «22 «23
«13 «23 «33
=
a 0 0
0 0 0
0 0//
= a/fyi = J2/i, μ
J2
Таким образом, если J2 φ 0, то уравнение линии I в
соответствующей системе координат примет вид
Х\х2 + Х2У2 + -г = О,
J2
где Αι, Аг —корни уравнения (3).
228
Глава 6
Если J2 = 0, то один из корней уравнения (3) равен нулю.
Ради определенности допустим, что а = О, тогда β = J\.
Ранее было показано, что при J<i = О в соответствующей
системе координат уравнение (1) принимает либо вид
(4)
либо
/V + 2»х = О,
Py2-rq = 0.
Для уравнения (4)
(5)
h =
10
0
\и
0
β
0
ν\
0
о
= -ν2β=-ν23λ,
следовательно,
ν
/ *
Таким образом, в случае, когда J2 = 0, J3 Φ 0, уравнение (1)
после соответствующего преобразования координат примет вид
^+ 2»^J = 0.
Для уравнения (5)
J3 =
■о
Ρ
о
0
в
0
01
0
я\
= 0,
а так как инвариант Зъ = 0, то инвариантом является J2.
Для уравнения (5)
\β о|
J2 =
0 ς
= Λ<7,
следовательно, q = J2/J1.
Итак, если 3ι — 0, J3 = 0, то уравнение (1) в
соответствующей системе координат имеет вид
2 . «fe
«Л
Исследование линий и поверхностей с помощью инвариантов 229
§ 5. ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДНА
С ПОМОЩЬЮ ИНВАРИАНТОВ
Рассмотрим поверхность второго порядка S, определяемую в
некоторой ДИСК общим уравнением
ацх2 4- α22ί/2 + азз*2 + 2ai2xy + 2a23yz + 2al3xz-l·
+ 2αΐ4Χ+ 2α24?/ + 2ο3ι^ + α44 = О (I)
и подсчитаем инварианты Ji, J2, J3, «/4 и
J(A) = -A3 + A2J1-AJ2 + J3.
В системе координат, получаемой из исходной в результате
ортогонального преобразования, уравнение (1) примет вид
ах2 + 0у2 + -yz2 + ах + by + cz + d = 0, (2)
где коэффициенты α, β, ■у можно найти, используя инвариант
J(A):
Ια-λ О О
J(A)= 0 β-Χ Ο
| 0 0 7-λ|
= (α-λ)(/?-λ)(7-λ).
Отсюда видно, что α, β и 7 — корни уравнения ./(А) = О,
т. е. уравнения
-λ3 + λ2Λ - AJ2 + J3 = 0.
(3)
Если инвариант J$ φ 0, то корни уравнения (3) отличны от
нуля. В этом случае поверхность S — центральная и в
соответствующей системе координат ее уравнение имеет вид
ах2 + ру2 + 7*2 + μ = О,
причем μ можно найти при помощи инварианта 3±\
J4 =
α 0 0 0
0/300
0 0 7 0
О 0 0 μ
= αβη/μ = Ημ
230
Глава 6
Отсюда μ = J4/J3 у а поэтому уравнение поверхности S при
Js φ О в соответствующей системе координат имеет вид
(4>
где λι, λ2, Аз — корни уравнения (3).
Если J3 = О, З2 φ 0, то один из корней уравнения (3) равен
нулю. Ради определенности будем считать 7 = 0.
Ранее было показано, что в этом случае в соответствующей
системе координат уравнение (1) имеет вид либо
ах2 + ру2 + 2ρζ = θ,
либо
ах2 + ру2 + г = 0,
Если имеет место уравнение (5), то
Ια 0 О О
0/300
J4~ 0 0 0 ρ
|0 0 ρ О
следовательно,
(5)
<6>
α(-ρ2β) = -ρ2.Ι2 φ 0.
Таким образом, когда выполняются соотношения J2 ^ О,
J3 = о, J* φ 0, уравнение (1) после соответствующего
преобразования примет вид
λ1χ2 + λ2</2+2^-^ = 0,
где λι, Л2 — отличные от нуля корни уравнения (3).
Когда имеет место уравнение (6), инвариант
Ja =
а О О О
0/000
0 0 0 0
О 0 0 г
= 0.
Исследование линий и поверхностей с помощью инвариантов 231
Поскольку инвариант J% также равен нулю, то уравнение (1)
в данном случае имеет еще один инвариант J3, который для
уравнения (6) можно представить в виде
■73 =
α 0 0
0/3 0
0 0 г
+
МО
0 0 0
0 0 г
+
α 0 0
0 0 0
0 0 г
= αβτ — 3<ιτ.
Итак, если 3% =0, За = 0, J2 φ 0, то в соответствующей
системе координат уравнение (1) имеет вид
Xix2 + Х2У2 + Φ
о,
где λι, λ2 — отличные от нуля корни уравнения (3).
Допустим теперь, что Зъ = 0, 3% = 0. Тогда уравнение (3)
имеет два нулевых корня, а уравнение (1) после
соответствующего преобразования координат приводится либо к виду
ах + 2qy = 0,
(?)
либо к виду
αχ2 + ρ = 0. (8)
Очевидно, что как для уравнения (7), так и для уравнения (8)
инвариант J4 = 0, а следовательно, величина 3% является
инвариантом. Но для уравнения (7) J3 = -q2Ji, причем 3\ = α,
поэтому уравнение (1) в случае 32 = 0, 3$ = 0, З4 = 0, З3 φ 0
после соответствующего преобразования имеет вид
А1Яг2 + 2А/-^» = 0,
где λι — ненулевой корень уравнения (3).
Если имеет место уравнение (8), то выполнены равенства
J2 = о, Зз = 0, 3± = 0, с/з = 0. Но тогда величина Зъ
является инвариантом уравнения (I). При этом для (8) З2 = Jip,
где 3\ = а. Следовательно, в данном случае в соответствующей
системе координат уравнение (1) имеет вид λχχ2 + J2/J1 = 0,
где λι —ненулевой корень уравнения (3).
232
Глава 6
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Определить тип поверхности второго порядка и
написать ее каноническое уравнение:
а) 7х2 + 6у2 + bz2 - Аху - Ayz - 6х - 24у + 18z + 30 = 0.
Решение. Выпишем коэффициенты уравнения: ац =7, а22 =
= 6» «зз = 5, а\2 = -2, а2з = -2, αΐ3 = 0, αΐ4 = -3,
024 = —12, аз4 = 9, й44 = 30. Так как инвариант
7 -2 01
Л =
Оц Οΐ2
О12 «22
Ol3 «23
«13
«23
«33
==
= -2 6 -2
0 -2
= 162 ^ 0,
то поверхность является центральной, и ее уравнение в
канонической системе координат имеет вид
=2
^2
За
λιχ + λ2Γ + А3Г + — = 0,
«/з
где
J4 =
«11
«12
«13
αΐ4
αΐ2
«22
«23
«24
αΐ3
β23
азз
аз4
«14
U24
«34
«44
7
-2
0
-3
-2
6
-2
-12
0
-2
5
9
-3
-12
9
30
= -972.
а λι, λ2, Аз — корни уравнения J(A) = —λ3 + J\X2 — J2A
+ J3 = 0, причем
J\ = an + «22 + «33 = 18,
J2 =
a22
«23
«23 «33
=
6
-2
+
-2
5
an
«12
ai2 «22
+
7
-2
+
-2
6
an
ai3
ai3 «33
+
7 01
0 5|
= 99.
Следовательно, имеем уравнение -Л3 + 18λ2 - 99А + 162 =
= 0. Его корни Αι = 3, Л2 = 6, λ3 = 9. Поэтому окончательно
уравнение поверхности
Зх2 + 6г/2 + 9ζ2 = б,
или
-2 -2
ат _2 я
Т + ^ +27з
= 1.
Это уравнение определяет эллипсоид.
Исследование линий и поверхностей с помощью инвариантов 233
б) 7x2+7y2 + 16z2-lQxy-8yz-8xz-l6x-16y-8z+72 = О
Решение. Вычислим инварианты;
30,
1 7
|-5
1 7
-5
-4
-5
7
+
-5 -4
7 -4
-4
16
7 -4
-4 16
+
= 0,
7 -4
1-4 16
Ji =
J3 =
следовательно, поверхность нецентральная
Далее, инвариант
17-5-4 -8
-5 7 -4 -8
-4 -4 16 -4
-8 -8 -4 72
= 216,
J4 =
= -24 · 362 φ Ο,
a J(A) = -λ3 + 30λ2 - 216λ = 0, и его корни λι = 0, λ2 = 12,
Аз = 18.
Тогда уравнение поверхности можно представить в виде
>~2
>.-.2
\2хг + 18jT + 2ρζ = 0, где р =
1±
</2
Г362 · 24
216
= 12.
Окончательно, имеем поверхность
2х2 + З^2 + 4f = 0 —эллиптический параболоид.
в) 2х2 + 5у2 + 2z2 - 2ху + 2yz - 4xz + 2х - 10у - 1z -1 = 0.
Решение. Вычислим инварианты
12-1-2
-1 5 1
-2 1 2-1
1-5-1 -1
2 -1 -2
-1 5 1
-2 12
= 0, J4 =
Л =
J2=|_
J(A) = -λ3 + 9λ2 - 18Α = 0,
λι = 3, λ2 = 6, Аз = 0.
-5
= 0.
2
|-1
-1
5
+
2
-2
-2
2
+
5 1
1 2|
= 18 φ 0, Ji = 9,
234
Глава 6
Так как J3 = J4 = 0, то вычисляя полуинвариант
Js =
2 -1
-1 5
1 -5
+
2
2
1
-2
2
-1
1
-1
-1
+
5 1 -5
12-1
-5 -1 -1
получаем уравнение поверхности в виде
~2
Зх£ + бзг -6 = 0, или
х2
^2
+ Г = 1,
-108,
которое определяет эллиптический цилиндр.
Последнее уравнение можно получить иначе. Изменяя на
величину ε коэффициент ац, получаем
Л
Jie
2 + ε
-1
-2
2+ε
-1
-2
1
-1
5
1
-1
5
1
-5
-2
1
2
=
-2 1
1 -5
2 -1
-1
-1
ε
0 0
-1 5 1
-2 12
= 9ε,
ε 0 0
0 0 0
-2 1 2
1
-5 -1
01
-6
-1
-ι
= -54ε.
Так как J3 = J a — 0, J2 φ 0, 3^ε Φ 0, то уравнение
поверхности б канонической системе координат можно записать
ВШШе 3*2 + 6*2 + г = 0,
где г = Ιΐΐϊΐε_»ο j^ = —6. Поэтому опять имеем то же уравнение,
г) 4х2 + у2 + L·2 - Аху + Ayz - Sxz - 2Ъх + 2у + 16г+45 = 0.
Решение. Вычислим инварианты:
Ji=9,
Jz
4
-2
-4
-2
1
2
-4
2
4
=
1 2
2 4
: +
4
-4
= 0, J4 =
-4
4
+
4 -2
-2 1
= (
4 -2 -4 -14
-2121
-4248
-14
t
1 8
45
= 0.
Далее, J(X) = —λ3 + 9λ2 = 0, и корни этого уравнения λι = 9,
λ2 = 0,λ3 = 0.
Исследование линий и поверхностей с по нощью инвариантов 235
Полуинвариант
■/з =
4
-2
-14
-2
1
1
-14
1
45
+
4
-4
14
-4 11
4 8
Я 45
· +
1 2 11
2 4 8
1 8 45
= -324
поэтому в канонической системе коордикат уравнение
поверхности имеет вид
9 /324 7 4
^ + 2\/ -д-1/ = Q> ИЛИ * + о S = Q·
Это — параболический цилиндр.
2. Определить тип линии второго порядка е зависимости
от величины параметра а е (—ос, +ос)■:
αχ2 - 2ху + 2у* - 2х -г 2у - 1 = 0.
Решение. Вычислим инварианты указанной кривой: J{ = а +
+ 2,J2 = 2α-1, J3 = 1-3α, J(A) - λ2 -<ДА + J2. Отсюда
следует, что при а Ф 1/2 линия является центральной, а се
уравнение в канонической системе координат имеет вид
AiS2 + X2f + (1 - 3α)/(2α - 1) = 0.
Если α > 1/2, το λι > 0, λ2 > 0, так как Λιλ2 = Ji > U и
λι + λ2 = «Λ > 0, следовательно, при α > 1/2 получаем эллипс.
Если 1/3 < а < 1/2, то λχλ2 < 0, поэтому получаем
гиперболу.
При α = 1/3 инвариант Jz = 0. Поскольку по-прежнему
Ai>2 < 0, то получаем две пересекающиеся прямые.
Если а < 1/3, то в силу соотношения λιΑ2 < 0 вновь
получаем гиперболу.
При а = 1/2 — парабола, так как J2 = 0, J3 = -1/2*
Ji = 5/2, а поэтому получаем
5 2 п /Ь2
2S +2V2T5S = °·
или у +
Sv^
ί = 0.
236
Глава 6
3. Определить тип поверхности второго порядка и
написать ее уравнение в канонической системе координат:
а) Зх2 + Зу2 + 3z2 - 2yz + 6х - 1 = 0.
Ответ: За;'2 + 2у'2 + Az'2 —4 = 0 — эллипсоид;
б) х2 + Ay2 + 9z2 + Аху + Ylyz + 6xz - 1 = 0.
Ответ: две параллельные плоскости 14г/2 = 1;
в) х2 - Ау2 + Az2 + Axz - 8у -4 = 0.
Ответ: две пересекающиеся плоскости Ьх12 — Ау92 = 0;
г) 2х2-Ay2-7z2-16xy-2Qyz-Axz+12x+6y-12z-18 = 0.
Ответ: 2zf = 2х12 — у12 —гиперболический параболоид;
д) 10х2 + Ау2 - bz2 - 32ху + Axz - 28yz + 3 = 0.
Ответ: 6х'2 - 9у'2 = 1 — гиперболический цилиндр;
е) Аху + Axz + Ayz + 8у + Az — 1 = 0.
Ответ: χ12 + у'2 — 2zf2 =0 — конус второго порядка;
ж) Ах2 + Ау2 + ζ2 - 8ху + Axz - Ayz + 6x- 12y -4 = 0.
Ответ: 2хг = Зу'2 —параболический цилиндр.
4. Определить тип линии второго порядка в зависимости
от величины параметра а е (—оо,+оо);
а) х2 + Ааху + Ау2 = 1;
Ответ: при а < — 1 — гипербола; при а = — 1 —две
параллельные прямые; при — 1 < а < 1 — эллипс; при а = 1 —две
параллельные прямые; при а > 1 —гипербола;
б) 2ах2 - Ааху + 2у2 + 2а - 1 = 0;
Ответ: при а < 0 — гипербола; при а = 0 — пара
параллельных прямых; при 0 < а < 1/2 — эллипс; при а = 1/2 —
вырожденный эллипс; при 1/2 < а < 1 — «мнимый» эллипс; при
а = 1 — «мнимая» парабола; при а > 1 — гипербола;
в) х2 — Аху + Аау2 — 2х + 2у — 1=0.
Ответ: при α < 7/8 — гипербола; при а = 7/8 — две
пересекающиеся прямые; при 7/8 < а < 1 — гипербола; при
а = 1 —парабола; при а > 1 —эллипс.
Часть вторая
ЭЛЕМЕНТЫ
ДИФФЕРЕНЦИАЛЬНОЙ
ГЕОМЕТРИИ
В предыдущей части нас интересовали проблемы,
связанные с уравнениями геометрического объекта, а также
двойственная задача: как по уравнению определить сам
геометрический объект. В литературе эти задачи
иногда называют прямой и обратной задачей
аналитической геометрии.
Теперь нас будут интересовать локальные свойства
геометрического объекта, т. е. поведение кривой или
поверхности в окрестности некоторой точки. Сама
постановка проблемы указывает на тесную взаимосвязь
данного раздела с математический анализом функции
многих переменных. По ходу изложения будет также
видна связь приводимых результатов с проблемами
механики и теории дифференциальных уравнений.
Наш опыт преподавания дифференциальной
геометрии показал, что для понимания материала необходимо
тщательно изучить теории плоских и
пространственных кривых, а также поверхностей в реальном
трехмерном пространстве. В некоторых случаях, когда это не
требует специальных обобщений, мы будем приводить
естественные многомерные аналоги для пространств
более высокой размерности.
Глава 7
ЭЛЕМЕНТЫ
ВЕКТОРНОГО АНАЛИЗА
§ 1. ВЕКТОРНАЯ ФУНКЦИЯ.
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ
Соответствие г, при котором каждой точке χ множества Ω
евклидова пространства Жш сопоставляется вектор т{х)
множества Q евклидова пространства Rp, называется векторной
функцией векторного аргумента:
χ е Ω - {(хи ..., хт)} с Шт -> r{x) eQ =
= {(n,...,rp)}cRp.
При этом множество Ω называют областью задания
векторной функции, а множество Q — множеством значений
этой функции.
Если Ω = {χ} — множество точек на прямой, то имеем
векторную функцию одного скалярного аргумента г(х).
Если Ω = {(#1, ..., Хт)} С Шт — множество точек
евклидова пространства, то имеем векторную функцию нескольких
скалярных аргументов г(х\у ..., хт).
Пусть (гь ..., гр) — координаты вектора г(х) € Q С Шр.
Ясно, что задание векторной функции г(х) равносильно
заданию скалярных функций г\{х\^ ..., хш)у Г2(жь...,#т), ··■»
Если начала указанных векторов совместить с началом
соответствующей декартовой системы координат, то точечное
множество концов рассматриваемых радиус-векторов будем
называть годографом векторной функции. В случае ρ = 3
годограф векторной функции одного скалярного аргумента есть,
Элементы секторного анализа
239
вообще говоря, кривая, а годограф векторной функции двух
переменных — поверхность.
Постоянный вектор го называют пределом векторной
функции г(х) при χ —> xq и обозначают \\тх^а:ог(х) = го, если
Ππίχ^ο \г(х) — г0| = 0 (здесь | ■ | берется в Rp).
Отметим, что
\r(x)\ = Vr2l+rl + -" + 41
а условие х{хих2,. -.,хт) —* ж0(хю,^2о>- · -,£то) означает,
что
\х-х0\ ->0
(здесь [ · | берется в Шт), что влечет
Я1 -» #10, #2 -» ^20т · ■ ·> %т —> ^т0-
Для вектор-функции имеют место теоремы о пределах,
аналогичные теоремам о пределах для скалярных функций.
Теорема 1. Если
lim г (χ) = Го, lim q(x) = <?о> 1ни μ(#) = μο>
lim (г(ж) ± д(ж)) = r0 ± go, lim /л(ж)г(ж) = jU(jr0,
α—»хо аг—>жо
lim г (ж) · д(ж) = го · go, Ит г (ж) χ q(x) — vq χ g().
Доказательство приведенных утверждений нг отличается от
доказательства аналогичных теорем для скалярных функций.
Например, докажем последнее утверждение. Ясно, что
| (г(ж) - г0) х (q(x) - qr0) + (r(x) - r0) x go -
- ((?(«) — «ο) χ*ό| = | (r{x) - r0) x д(ж) -
- (r(x) - r0) x go + (*·(«) - r0) x go -
-д(ж)хг0-г0хд0| =
= \r(x) χ q(x) - r0 χ д(ж) + r0 χ д(ж) - r0 x go [ ■
Отсюда
Иж)хд(ж)-г0хд0|<
^ |г(ж)-г0|·|д(ж)-д0| + |г(ж)-r0|·|до| + |д(ж)-д0| Ы-
240
Глава 7
Из условия теоремы следует, что правая часть неравенства
стремится к нулю, когда χ —* xq. Следовательно,
lim г (χ) χ q(x) = Го х до-
Векторная функция г (ж), заданная в точке xq и в некоторой
се окрестности, непрерывна в xq , если
lim г(ж) = г(а?о).
Теорема 2. £суш векторные функции r(x), q(x) и скалярная
функция μ(χ) непрерывны в точке xq, то в этой точке
непрерывны также векторные функции
r{x)±q(x)y μ{χ)ν(χ)ί
r(x) - q(x), r(x) χ q{x).
Указанные утверждения являются непосредственным
следствием свойств предела.
§ 2. ПРОИЗВОДНАЯ
ВЕКТОРНОЙ ФУНКЦИИ.
ФОРМУЛА ТЕЙЛОРА
В дальнейшем нас будут интересовать в основном векторные
функции скалярного аргумента со значениями в реальных
пространствах, т. е. случаи, когда га = 1 и ρ < 3.
Обозначим векторную функцию скалярного аргумента через
г = f(i), t е Τ С Μ, подчеркивая тем самым
принадлежность значения некоторому реальному векторному пространству
V* (глава 1,§3).
Мы будем проводить изложение в основном для
пространства V3, хотя все основные понятия естественно переносятся и
на случаи V1 и V2.
Производной векторной функции по ее скалярному
аргументу называют предел отношения приращения функции
Элементы векторного анализа 241
к соответствующему приращению аргумента, когда приращение
аргумента стремится к нулю:
т= т.ш g«±Mz3i>.
v 7 di Δ*—о At
Функция дифференцируема в точке ί, если в этой точке
существует ее производная.
ЗАМЕЧАНИЕ. Если переменную t рассматривать как время,
то векторная функция r(t) представляет собой закон движения
материальной точки по годографу этой функции, а производная
r'(t) равна скорости движения точки по годографу.
Если f(t) G V3 и векторы ё\, е2, ё*з составляют базис в V3,
то
f(t) = x{t)eY + y(t)e2 + z(t)c3
и
τ '(ί) = af(t)ei + y'{t)e2 + z'(t)e3.
Понятно, что во всех случаях производной векторной
функции в точке будет вектор.
Теорема 1. Если f(t)t q(t)f fi(t), λ(ί) —дифференцируемые в
точке t функции, то в этой же точке дифференцируемы:
mm,
f(t)-q(t),
r(t) x <?(*),
причем
l) (fw±flt))' = f4t)±r(t);
2) (A(t)f(t))' = X'(t)f(t) + X{ty(t);
3) (m · mY=rf(t) ■ m+f(t) . q'ity,
4) (f(t) χ g(i))' = r'(t) χ flt) + f(t) x Г(*);
5) (г~(*ШШ))' =
= (f'(*). m, m)+(*m m#o)+(m> т,рЩ.
242
Глава 7
Доказательство. Эти правила дифференцирования
векторных функций получаются тем же путем, как и соответствующие
формулы дифференцирования скалярных функций.
В самом деле,
«0±«>)'-^Ш±М-
Δ£-*0 Δί
Δί-0 Δί Δί->0 Δί W V Wf
{Α(<№))' = lim А<У» - Ш» (^AA)(f+Af)-Af^
4 V У W/ Δί—0 Δί Δί-*0 Δί
ΔΛ(γ+Δγ) , ,. ΑΔγ ,
= lim τ- V hm —— = Ar+Ar ,
Δί-»0 Δί Δί-»0 Δί
(f(().f(t))'=Hm^M) =
V W 1W/ Δί-0 Δί
(f + Δτ) · (q+Aq) - f· q
= hm — =
Δί->0 Δί
ι· ^-{g+Aq} , Δ^-r ., „,., .,
= hm ^ -+ hm —г—= r -q+rq ,
Δί-»0 Δί Δί-*0 Δί
Έ. (f+Ar)x(g+A^)-fxQ
= lira τ-- =
Δί-*0 Δί
r Arx(q+Aq) fxAq ^ ^ ^
= lim -^ — + hm — = r xq+rxq\
Δί^ο Δί δ*->ο Δί
— (г χ q)f ·ρ+ (г χ q) ·ρ' = (f' x g+7rx <f') -p+
Если векторная функция г* = r(s), a s = s(i), f(s) и
s(t)t—дифференцируемые функции, то
df df ds
dt ds dt
Производная векторной функции r'(t) называется второй
производной функции f(t) и обозначается f"(i). Аналогичным
образом определяются производные более высоких порядков:
f<*>(i) = (f^-'Hi))'.
Элементы векторного анализа
243
Функция, имеющая непрерывные производные до к -го
порядка включительно на некотором отрезке, называется к раз
дифференцируемой на этом отрезке.
Теорема 2. Если f(t) — векторная функция, к раз
дифференцируемая в t, то имеет место формула Тейлора:
At2
f{t + At) = f{t) + At f'(t) + -y-?"{t) + ... +
+ ^- (f(fc) (t) + e(t, At)), где VrniQ φ, At) = 0.
Доказательство. В случае, если векторы ё\, ёг, е3
составляют базис, имеем
f(t) = x{t)e\ + y(t)e2 4- z(t)e3.
Для скалярных функций χ = x(t), у = y(t), ζ — z(t), к раз
дифференцируемых на отрезке [ί, t + At], имеет место формула
Тейлора:
Δί2
x{t + At) - x(t) + Atxf{t) + -y-x"(t) + · · · +
+ ^(*W«+ei), J5o^=0.
Δί2
y(i + Δί) = y(t) + At y\t) + -^-y"(t) + '■· +
2!
+ i^V)(*)+^2), limE8=0,
Δί2
z(i + Δί) = z{t) + Δί ζ'{t) + -^-*"(ί) + · · · +
(Δ0*
+ ^(г«№ + £з), lime, = 0.
Умножая эти равенства соответственно на е\, e*2i ёз и
складывая, получаем искомую формулу Тейлора.
Теорема 3· Производная векторной функции,
сохраняющей постоянный модуль и изменяющей направление,
перпендикулярна самой функции.
244
Глава 7
Доказательство. Если вектор f(t)y изменяя направление,
сохраняет свою длину, то г ■ т= |f|2 = const. Поэтому (г· г)9 —
= 0, т. е. г9 - г + τ « τ9 = О, 2(Γ· г9) = 0, откуда следует, что
г f JL г .
Теорема 4. Производная векторной функции,
сохраняющей направление и изменяющей свой модуль, коллинеарна
самой функции.
Доказательство. Пусть вектор f(t) изменяет модуль и
сохраняет направление, определяемое вектором е, т. е. r(t) =
= \r(t)\e. Тогда
df(t)
= ^№)ie>(s№)i)-ra|rW=
л
\\т) {)-
что и означает коллинеарность f9(t) и r(t).
Теорема 5. Переменный вектор из V3, параллельный
заданной плоскости, компланарен своей первой и второй
производной.
Доказательство. Если вектор f(t), изменяясь, остается
параллельным плоскости с нормальным вектором п, то f(t)-n = 0.
Поэтому «г . п & , „
Отсюда следует, что векторы r(t),r9(t),r9/(t) компланар-
НЫ'Т·6· (r(t),r'(t),r"(t))=0.
Пусть задана декартова прямоугольная система координат
Oijk.
Векторной круговой функцией β(φ) называют векторную
функцию, которая каждому углу φ £ [О,2π] сопоставляет
единичный вектор ε(φ) плоскости Ог?, составляющий с ортом г
угол φ9 отсчитываемый от г против часовой стрелки, если
рассматривать указанный вектор с конца вектора /с.
Элементы векторного анализа
245
Заметим, что годографом векторной круговой функции е(ф)
является окружность единичного радиуса.
Наряду с β{ψ) определим другую векторную круговую
функцию
9(ψ) = ε\φ + ~) * Ψ е [0,2тг].
Очевидно, что векторы е(<£>), д{ф)у к составляют правый
ортонормированный базис вУ3,и потому
β\φ) = 1, $2(φ) = 1, Ρ = 1,
—» -*
ex g = k, gx к = е, к χ e = д.
Векторные круговые функции представимы в виде
ё\ф) = Tcos φ + J*sin φ, 9{ψ) = —«*sin φ + Jcos <£>,
причем ,_ ,_
«е ^ . dg
Понятие производной векторной функции скалярного
аргумента естественным образом переносится на пространства
произвольной размерности. Так, если имеется векторная функция
x = x(t),t €ТсМ,где
x(t) = (xi{t),x2{t),...fxp(tj) eRp,
то ее производная
x\t) = (a?i(t),4(t),... ,4(*))ι * е Τ с R.
Рассмотрим теперь векторную функцию векторного
аргумента Г = Г(Х),ГД£Х= {Χΐ,Χ2,·-.,Χτη)> Г = (гЬ Г2, . . - , Тр) .
Частной производной векторной функции в точке ж0 ="
= (χι, χ®, -.. > ^) по переменной χι называется предел
отношения приращения функции по переменной χι к соответствующему
246
Глава 7
приращению аргумента, когда приращение аргумента стремится
к нулю, т. е.
дг
(χ°) = τΧι(χ°) =
dXi
_ ,. r\%lf'">xi—\ixi +AXj,Xi+i,- · · iXrn) ~Г\Хι,... ,Xi ,...,Xm)
&Xi->o Axi
Из ланного определения следует, что
Как уже было отмечено ранее, годографом векторной
функции двух скалярных аргументов г = f(u,v) Ε V3, (u>v) G D,
D С l2, является, вообще говоря, поверхность. Остановимся
подробнее на рассмотрении именно таких функций.
Сначала заметим, что если βι,^, ёз — базис в
пространстве V3, то справедливо равенство
г(щ ν) = х(и} v)ev + у(щ v)e2 + z{u, v)c3.
Тогда согласно определению частной производной
дг _ dx(u,v) ^ dy(u,v) _ dz(u,v) _
тг- = ru = — tx + -^— е2 + —τζ е3,
ии an ait ии
дг _ дх(а, г) _ ду(и, ν) _ dz(u, v) _
-ΖΓ=Τυ = - βχ Η 62 Η г €3-
αν ου αν αν
Векторная функция г = r(u,v) 6 V3, (it,г;) 6 D, называется
дифференцируемой β точке (щ ν), если ее полное приращение
в этой точке для любых Аи, Αν можно представить в виде
Аг = г {и + Аи. ν + Αν) — r(u> v) =
= ru(v, v)Au + гу(щ ν) Αν + е{и7 ν, Δ?/, Αν),
где векторная функция ε* удовлетворяет условию:
e{u,v7Au,Av) я
hm —, =- = 0.
Δα—о, у/Дгл2 + Αν2
Δ*/->0
Элементы векторного анализа
247
Главная линейная часть приращения ти{щ v)Au+rv(u1 ν) Αν
называется дифференциалом векторной функции г = f(uyv) и
обозначается dr.
Положим Аи = du, Av = dv. Тогда выражение для
дифференциала примет вид df= rudu + rvdv.
Очевидно, что любая частная производная векторной
функции опять является векторной функцией тех же аргументов.
Поэтому можно, в свою очередь, рассмотреть ее частные
производные: β д2т{щу) _ ( .
д _. , d2r(u,v) ^
—тч^г/) = dv2 = rw(w,i;).
Полученные производные Пш(и,г;), ги^(г^,г;), r^v(u,i;)
называются частными производными второго порядка.
Аналогично определяются и частные производные более
высоких порядков.
Поскольку дифференциал векторной функции также
является векторной функцией, то можно определить дифференциал
второго порядка:
d2r = d(dr) =
= d(fu du + fv dv) = fuu du2 + 2ruv du dv 4- fvv dv2.
§ 3. НЕОПРЕДЕЛЕННЫЙ
И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ОТ ВЕКТОРНОЙ ФУНКЦИИ
Неопределенный интегралом от непрерывной векторной
функции f(£), f е Г, называют семейство векторных функций g{t)
{первообразных) для которых выполнено:
Неопределенный интеграл обозначают fr(i) dty t е Г.
248
Глава 7
Определенным интегралом Ja f(i) dt от непрерывной
векторной функции f(t) на отрезке [а, Ь] называют вектор,
определяемый равенством &
j r(t) dt = g(b) - д{а),
а
где g{t) —первообразная вектор-функция.
Пусть векторная функция f(t) задана на отрезке [а, Ь] и
f(t) G Vs, причем t\, ё?2, ёз составляют базис в V3. Тогда
f(i) = x(t)ei + 2/(i)e2 + г(03ь
j f(t) dt = ex j x{t) dt + e2 j y(t) dt + e3 f z{t) dt,
b b b b
j r\t) dt = ex j x(t) dt + e2 j y(t) dt + e3 f z(t) dt.
a a a a
Отметим, что основные свойства интегралов для скалярных
функций сохраняются и для интегралов от векторных функций.
Сформулируем эти свойства в виде теоремы, которую приведем
без доказательства.
Теорема- Если r(t) — непрерывная на [α,ί>] функция,
а < d < Ь, С — постоянная величина, q— постоянный
вектор, то
b d b x
ί f{t) dt= ί r(t) dt+ ί f(t) dt, £- ir(t)dt = f(x),
a a d α
b b b b
ί Cf{t) dt = C ί f(t) dty f q · r(t) dt = qf f(t) dt,
a a a a
b b
f(qxr(t))dt = qx ff(t)dt.
В заключение также еще раз отметим, что в отличие от
скалярного случая неопределенный интеграл от векторной функции
Элементы векторного анализа
249
является семейством векторных функций, а определенный
интеграл — вектором.
Понятие интеграла от векторной функции естественно
переносится на случай произвольной размерности:
J x(t)dt: = ( / xi(t)dt, / x2{t)dt,..., xp(t)dt) ,
b , b b Ь \
I x(t) dt=[ Ι χι (t) dt, I x2{t) dt,..., I xp(t) dt J,
a ^a a a '
если x(t) = (xi{t),X2(t),... ,Xp(t)).
ЗАДАЧИ И УПРАЖНЕНИЯ
ί. Доказать, что f(t) — с, где с — постоянный вектор,
тогда и только тогда, когда для любого t e (fo^i)
выполнено условие \r'(t)\ = 0.
Решение. Если f(t) = (z(t),y(t),z(t)),TO
|f'| = yjx,2+y'2+z'2.
Следовательно, если для любого t е (£ο>*ι) |^'(01 = 0> то
х1 = у' = χ1 = 0. Тогда x(t) = 7i, y(t) = 72, z{t) = 73, где
7i — постоянные числа, для любого t G (ίο^ι) · Таким образом,
f(t) = с, где с = (7ь72,7з)-
2. Доказать, что если r(t) удовлетворяет уравнению
г" = ff χ с, где с — постоянный вектор, то
(r\r'\r^ = -(r'-c)(r'xc)2.
Решение. Заметим, что г"' = (г ")' = (г' хс)' = г " χ с\ Тогда
смешанное произведение
(^Λγ,,,) = (γ/,γ,,^// хс>
= г'. (г" χ (г" χ с)) = г9 · (Г"(г". с) - сг"2),
но г" ■ с - (г',с,с) = 0. Поэтому {r',r",rm) = ~(f' · сг"2) =
250
Глава 7
3. Доказать, что годографом векторной функции
f(t) = acosi + б skit, α χ 5 Φ 0, является эллипс.
Решение. Пусть а = аё\, 5 = ββ2, где ei и ёг — орты
векторов а и b соответственно. Так как α χ Ь Φ 0, то эти
векторы неколлинеарны, а потому ё\ и ёг образуют базис. Выберем
систему координат Ое^. Тогда заданная векторная функция
f(t) = (acost)ei + (j9sint)e2. Следовательно, точки
годографа имеют координаты χ = acosi, у = flsint и удовлетворяют
уравнению эллипса ж2 2
μ — = 1
a2 + /?2
4. Выразить через ff и с величину {г1 χ г")2, если
известно, что векторная функция f(t) удовлетворяет
уравнению г" = г' χ с, где с — постоянный вектор.
Ответ: f/2(r' x с)2.
5. Доказать, что годографом векторной функции г (£) =
= αί2 + Ы + с, где aybyc — постоянные векторы, причем
α χ Β φ б, является парабола.
6. Доказать, что если а и Ъ — неколлинеарные
постоянные векторы, то годографом векторной функции
r{t) = acht + bsht является гипербола.
7.Доказать, что
/ ψε(φ) άφ = ε(φ) - φ§(φ) + с,
где ε(φ) —векторная круговая функция, 9{φ)=ε(φ+%).
Главе 8
ЭЛЕМЕНТЫ ТЕОРИИ КРИВЫХ
§ 1. ПОНЯТИЕ КРИВОЙ
Перейдем к исследованию кривой, заданной уравнением
(параметрическим или неявным). Для этого сначала попытаемся
определить само понятие кривой, сознательно избегая при этом
возникающие технические сложности.
Отображением f некоторого множества Ω
метрического пространства πι в метрическое пространство 7Г2
называют соответствие, при котором каждой точке X
множества Ω С πι сопоставляется некоторая точка f(X)
пространства π2·
Точку f(X) называют образом точки X, множество /(Ω)
всех точек f(X), составленное из образов всех точек множества
Ω, называют образом множества Ω.
Отображение / называют одно-однозначным, если
образы несовпадающих точек различны.
Отображение /множества Ω с щ в пространство тх2
называют непрерывным, если для любой точки X е Ω и
любого ε > 0 существует δ > О такое, что как только pi(X<> Υ) <
< δ, так сразу p2(f(X), f(Y)) < ε, где ρι(-) и ρ2(·) — метрики
пространств πι и π2 соответственно.
При обратном к отображению / отображении f^1
множества /(Ω) точке f(X) G /(Ω) сопоставляется точка X.
Отображение / множества Ω в пространство называют
топологическим, если оно одно-однозначно, непрерывно и
обратное отображение f~l непрерывно.
252
Глава 8
При этом говорят, что множество Ω и его образ /(Ω)
топологически эквивалентны или гомеоморфны.
Элементарной кривой называют множество точек
пространства, являющееся образом отрезка при топологическом
отображении его в пространство.
Точки, соответствующие конечным точкам отрезка,
называют конечными точками элементарной кривой. Две
элементарные кривые называются примыкающими, если одна или обе
пары их конечных точек совпадают между собой.
Кривой линией называют множество точек пространства,
которое состоит из конечного или счетного множества
элементарных кривых, примыкающих друг к другу.
Пусть 7 —элементарная кривая, являющаяся образом
промежутка а < t < Ъ при топологическом отображении / его
в пространство Е3, x(t), y(t)y z(i) — координаты точки на
кривой 7, соответствующей значению t € (α, b).
Систему равенств χ = x(t), у = y{t), ζ = z(t), t G (α, 6),
называют уравнениями кривой 7 в параметрической
форме или параметризацией кривой 7- При этом говорят,
что кривая 7 параметризована при помощи названных
уравнений.
Считая x(t), y(t), z(t) координатами радиус-вектора f(t)
соответствующей точки кривой 7, мы получим векторную
функцию r(t), t 6 (а,Ь), годографом которой является данная
кривая. Этот способ задания кривой с помощью векторной функции
скалярного аргумента равнозначен параметрическому способу
задания кривой.
Допустим, что кривая 7 задается векторной функцией f(t),
t e (α, b). Заменим параметр t параметром и с помощью
соотношения t = д{и)у и е (α,/З), где д — строго
возрастающая и непрерывная функция· Тогда получаем новую
параметризацию кривой 7» а именно, г = г(д(и))у и G (α,/З).
Таким образом, одну и ту же кривую можно задать различными
параметризациями.
Кривую 7 называют регулярной без особых точек,
если эта кривая допускает параметризацию с помощью такой
Элементы теории кривых
253
векторной функции г = f(<), t € (a,b), которая к раз
дифференцируема (к — целое число, к ^ 1) и |г'(£)| φ О,
t е (а, Ъ).
В случае fc = 1 регулярную кривую называют гладкой.
Соответственно в пространстве ШР параметризация χ =
= x(t), t G (α,6), где x(t) = (si(t),x2(<)> ···, ^p(O) ПРИ
соответствующих предположениях также задает некоторую
кривую *у.
§ 2. КАСАТЕЛЬНАЯ К КРИВОЙ.
НОРМАЛЬНАЯ
ПЛОСКОСТЬ КРИВОЙ
Пусть 7 — некоторая кривая, Ρ — фиксированная
точка и Μ—подвижная точка на кривой у, РМ— хорда
кривой (рис. 8.1).
Прямая РМ стремится к
прямой РТ при Μ —» Ρ,
если угол φ между этими прямыми
стремится к нулю, когда Μ —> jy \?{t + &t)
-*Р.
Касательной к кривой 7 в
точке Ρ называют прямую РТ, Q/
к которой стремится хорда РМ,
когда Μ -> Р. Рис. 8J
Теорема· Гладкая кривая у (без особых точек) имеет в
каждой точке единственную касательную, причем
касательная в точке Р, отвечающей параметру t3 имеет
направляющий вектор r'(i).
Доказательство. Если точка Μ отвечает параметру t +
+ Δί и определяется радиус-вектором r(t + At)9 то
вектор ΔΓ = f(t + Δί) - f(t) определяет направляющий вектор
хорды РМ.
Пусть направляющий вектор прямой РТ определяется
вектором r'(i). Убедимся, что прямая РТ является касательной к
кривой 7- В самом деле, если Μ —> Ρ, то Δί —> 0. Поскольку
254 Глава 8
■ ...II .... - f
вектор Af(t)/At коллинеарен направляющему вектору Аг
хорды РМ и ,. _,, ,
lim Ar At = r'(t),
то угол между прямыми РМ и РТ стремится к нулю, когда
Μ —+ Ρ, т. е. РТ есть касательная к кривой 7-
Теорема доказана, ибо у гладкой кривой 7 (без особых точек)
в каждой точке существует f'(t), причем \f'(t)\ φ 0.
Пусть ρ — радиус-вектор произвольной точки Q на
касательной РТ к кривой 7 в точке Ρ (рис. 8.1). Вектор Ρζ5 = ρ —
— f(t) коллинеарен вектору f\t) в силу доказанной теоремы,
поэтому
μ- f(t) = ur'(t).
Отсюда получаем уравнение касательной к кривой 7 B
точке Ρ в векторной форме:
p(u)=r(t)+uf'(t),
где и е (-оо, -foo) — параметр, определяющий положение
точки на касательной, t G (α, b) — параметр, определяющий точку
Ρ на кривой 7 ■
Нормальной плоскостью кривой в точке Ρ называют
плоскость, проходящую через точку Ρ перпендикулярно касательной
в этой точке.
Согласно определению векторное уравнение нормальной
плоскости π в точке P(f(t)) имеет вид:
(Д-fW) ■**(*) = о,
где ρ — радиус-вектор произвольной точки плоскости 7г.
Понятно, что понятия касательной к кривой и нормальной
плоскости (гиперплоскости) в заданной точке переносятся и на
случай произвольной размерности. Так, если кривая 7 задана
параметризацией χ = ж(£), x(t) = (#ι(*),#2(ί)> -··,#?(*))> τ0
уравнение касательной к кривой и нормальной плоскости в точке
P(x(t)) соответственно имеют вид:
у(и) = x(t) + ux'{t), и € (—оо, +оо).
(y-x(t))-x'(t)=0.
Элементы теории кривых
255
§ 3. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ КРИВОЙ.
СПРЯМЛЯЮЩАЯ ПЛОСКОСТЬ КРИВОЙ.
НОРМАЛЬ.
ГЛАВНАЯ НОРМАЛЬ.
БИНОРМАЛЬ
Пусть 7 — некоторая кривая, Ρ е 7 — фиксированная точка,
Μ G 7 — подвижная точка, РТ — касательная к кривой в
точке Ρ, ΡΤΜ — плоскость, проведенная через касательную
РТ и точку Μ (рис. 8.2).
Плоскость РТМ стремится к
плоскости π при Μ -^ Ру
если угол между этими плоскостями
стремится к нулю, когда Μ —► Р.
Плоскость 7Г, к которой
стремится плоскость РТМ, когда Μ —►
—» Ρ, называют соприкасающейся
плоскостью кривой 7 в точке Р, Рис. 8.2
Теорема. Регулярная, без особых точек, дважды
дифференцируемая кривая 7> заданная векторной функцией
f(t), t e (a,b), имеет единственную соприкасающуюся
плоскость в каждой точке Р, отвечающей
параметру t, в которой векторы r'(t), г"(£) неколлинеарны.
В этой точке Ρ нормальный вектор η
соприкасающейся плоскости определяется векторным произведением
r'(t)xr"(t).
Доказательство- Если точка Μ отвечает параметру t + At
и определяется радиус-вектором f(t + At), то вектор Аг =
= r(t + At) - f(i) лежит в плоскости РТМ.
Пусть π — плоскость с нормальным вектором ft = ff(t) χ
χ r"{t), проходящая через касательную РТ к кривой 7 в точ~
ке Р. Убедимся, что плоскость π является соприкасающейся
плоскостью кривой 7 в точке Р.
Из формулы Тейлора
Ат = г'At + \r"At2 + \eAt2, lim ε = б.
2 2 Δ*—ο
256
Глава 8
Тогда после умножения всех членов последнего соотношения
на скалярную величину 2/At2 и векторного умножения слева на
г' имеем
9 2
(г' хАт) = —(?' χ г7) + (Г χ г") + (Г χ ε)-
Δί2ν ' At
Приняв во внимание, что в качестве нормального вектора
плоскости РТМ можно взять вектор га = ~^{тг χ Ат)у и
что г' χ г' = б, г' χ г" = га, имеем из последнего равенства
гп = η + (г' χ έ).
Если Μ —► Ρ, то Δί —> 0 и угол между плоскостями РТМ
и 7Г стремится к нулю, так как стремится к нулю угол между их
нормальными векторами тип, поскольку Нтдг^о гп = п, ибо
lim if' χ ε) = б.
Таким образом, плоскость 7г — соприкасающаяся плоскость
кривой 7 в точке Р, причем, так как векторы г'(£) и r*"(i)
неколлинеарны, она единственна, ибо единственным образом
определяется в точке Ρ ее нормальный вектор.
Пусть ρ— радиус-вектор
произвольной переменной точки Q,
лежащей в соприкасающейся
плоскости кривой 7 в точке Р.
Тогда векторы
г'(*)> г"(*), p$=p-m
лежат в соприкасающейся
плоскости кривой 7 (рис. 8.3), и поскольку векторы r'(t) и г"(£)
неколлинеарны, то _ ^/J4 - ^„
/9 - г(£) = Ur +VT .
Отсюда получаем уравнение соприкасающейся плоскости
кривой 7 в точке Ρ в виде
р(и, v) = f(t) + ur'(t) + vr"{t),
и е (—oo, +oo), ν G (—oo, +эо)>
где и, ν — аргументы векторной функции ρ, t —
фиксированный параметр, соответствующий точке Р.
Элементы теории кривых
257
Если учесть, что векторы p — r{t), r'(t), r"(t) компланарны,
то получаем векторное уравнение соприкасающейся плоскости
кривой 7 в точке Ρ в другом виде:
Если рассматривать параметр t как время, то f"(t) есть
вектор ускорения при движении точки по кривой 7 в соответствии с
законом r = r{t).
Итак, при любом способе движения по кривой вектор
ускорения в данной точке расположен в
соприкасающейся плоскости кривой в этой точке. В связи с этим
соприкасающуюся плоскость иногда называют плоскостью
ускорения.
Пусть 7 — некоторая кривая, Ρ е 7 — фиксированная
точка, АВ —касательная, πι —нормальная плоскость, 7г2
—соприкасающаяся плоскость (рис. 8.4).
Прямую, проходящую через произвольную точку кривой Ρ
перпендикулярно касательной к кривой в этой точке, называют
нормалью кривой в указанной точке (CD, MN).
Нормаль, лежащую в соприкасающейся плоскости кривой,
называют главной нормалью кривой (CD).
Нормаль, перпендикулярную соприкасающейся плоскости
кривой, называют бинормалью кривой (MN).
Плоскость, определяемую касательной к кривой и
бинормалью в той же точке, называют спрямляющей
плоскостью (7Гз).
Рис. 8 А
258
Глава 8
§ Л. ДЛИНА ДУГИ КРИВОЙ
Пусть 7 = АВ —дуга кривой, являющаяся образом замкнутого
отрезка [а,Ь] при топологическом отображении. Разобьем дугу
АВ нгл η частичных дуг точками: А = Aq, Αι, ..., Ап = В и
впишем в нее ломаную с вершинами в этих точках, причем
каждое звено ломаной будет хордой
соответствующей частичной дуги
(рис. 8.5).
Длиной дуги кривой
называют предел периметра ломаной
линии, вписанной в данную дугу, если
число звеньев этой ломаной линии
неограниченно возрастает, а длина
каждого звена стремится к нулю.
Теорема. Если j — дуга загадкой кривой и г = f(t), t e
G [α, b]9 — ее гладкая параметризация, то ее длина s(*y)
определяется по формуле
ь
*(7)=УУ(«)И.
а
Доказательство. Пусть т\ = г(и) —радиус-векторы
точек А1У причем длина хорды Ai-iAi, г = 1,2, ..., г?,
определяется длиной соответствующего вектора
\Α~Ϊ%\ = \Δ?Α = \Ъ - f\-i\.
Тогда периметр вписанной ломаной sn = Σ^=1 |Δγ^| .
Предположим, что Ati = it — ti-i > 0 для любого г —
= 1,2, ..., η 9 т. е. номера точек возрастают вместе с
возрастанием параметра. Следовательно,
Элементы теории кривых
259
Но так как
lim
Δη
то
Afft)
Δί,-
= |r,(*i)|+ei,
= |r'(fi)|,
lim ε* = 0.
Тогда с учетом последнего соотношения периметр ломаной
п ι л -
- = Σ
i=l
Δίί
Когда η —* +оо, а Δ^ —> 0, первое слагаемое при переходе
к пределу обратится в определенный интеграл, т. е.
η b
Δί*-*0 *=1 ^
Докажем теперь, что в нашем случае предел второго
слагаемого равен нулю. Действительно, пусть ε = max \si\. Тогда
г=1
Y^SiAul ^e^Ati =s(b-a).
i=l
Ho Si —> 0 при Δ<* —> 0, следовательно, ε —> 0, когда
Δί;—>0,т. е. η
lim Υ^ε,Δίΐ = 0.
Δίΐ-^0 г=1
А тогда для нахождения длины s(*y) дуги 7 = ЛВ имеем
ь
e(7) = nUm *n= f\?'{t)\dt,
что и требовалось доказать.
Если гладкая кривая задана уравнениями в К3
J? = tf(0i i/ = iK*)> г = ^(*)> ie[a,6],
260
Глава 8
то ее длина
ь
s
= ί yjxf2{t) + y'2{t) + z'*{t)dt.
Если гладкая кривая задана уравнениями в R3
У = У{х), ζ = ζ(χ), χ в [α, 6],
то ее длина
ь
s= ί ^/l+y'2{x)+z'2(x)dx.
Заметим, что совершенно аналогично можно вычислить
длину дуги кривой в пространстве произвольной размерности Rp.
Так, например, если χ = x{t), x(t) = (χι(ί), Χ2(ί)> ··■» #ρ(0)»
t e [α, b], — гладкая кривая, то ее длина s равна
ь ь
8= f\x'{t)\dt = ί y/xf{t) + X?{t) + ...+ X,2{t) dt.
§ 5. ЕСТЕСТВЕННАЯ ПАРАМЕТРИЗАЦИЯ
Пусть 7 — гладкая кривая без особых точек, г = r(t), t G
G (α,6), — параметризация кривой 7» ^(^(*о)) — начальная
точка, отвечающая параметру ίο (рис. 8.6).
Μ Длина дуги кривой 7»имеющей начало
в J и конец в точке М, соответствующей
ν параметру ί, определяется формулой
t
s(t) = J\r'(T)\dT.
to
Рис.8.6 Функция s = s(t), t e (a,b),
является однозначной, дифференцируемой и монотонно возрастающей,
поскольку и»
- = |r'(t)| > 0
Элементы теории кривых
261
при t G (α, 6). Поэтому существует обратная функция t =
= t{s) , также являющаяся однозначной, дифференцируемой и
монотонно возрастающей функцией. Следовательно, между
точками кривой 7 и значениями длины дуги, отсчитываемой от
начальной точки J, существует взаимно однозначное и
непрерывное соответствие. Отметим, что точкам кривой, расположенным
по разные стороны от начальной точки J, соответствуют
значения параметра s разных знаков· Так, например, при t < £0
значение s(t) < О, при t > to значение s(t) > 0.
Поскольку между точками кривой 7 и значениями длины
дуги s существует взаимно однозначное и непрерывное
соответствие, то длину дуги s можно принять за новый параметр,
который будем называть натуральным параметром, а сама
параметризация г = r(s)> s G (а,/?), называется естественной
параметризацией.
Подчеркнем, что значение натурального параметра для
некоторой точки кривой равно по абсолютной величине длине дуги
кривой между точкой, принятой за начальную, и данной точкой,
причем знак натурального параметра выбирается в зависимости
от выбора направления движения по кривой, условно принятого
за положительное.
Теорема. Естественная параметризация r = f(s)
регулярной кривой без особых точек является регулярной, причем
|f'(s)| = l.
Доказательство. Пусть f(t), t Ε (α,b), — некоторая
параметризация регулярной кривой 7 без особых точек и для
произвольной точки M(r(t)) G 7 в окрестности
начальной точки J(f(to)) G 7 Длина соответствующей дуги JM
определяется формулой
t
s(t) = J\f'(T)\dr.
Поскольку
5r = \f'(t)\ = у/гЩ > 0, t€(a,6).
262
Глава 8
a f(t) является к раз дифференцируемой по t, то у
функции ό(ί) существует обратная, также к раз дифференцируемая
функция l(s).
Отсюда следует, что естественная параметризация
f(s) = f(t(s))
является регулярной и без особых точек, причем
df{s) df dt df { ds\ df 1
\dt)
ds dt ds dt \dtj dt |r'(i)|'
поэтому \ff(s)\ = 1.
Таким образом, первая производная радиус-вектора точки
кривой по натуральному параметру есть единичный вектор,
направленный по касательной. Теорема доказана.
ЗАМЕЧАНИЕ 1. Отметим, что из формулы
As= J \?{τ)\άτ
S
в силу произвольности s и As следует \f'(s)\ = 1 в любой точке
кривой.
ЗАМЕЧАНИЕ 2. Верно и обратное: если производная радиус-
вектора точки кривой по некоторому параметру по абсолютной
величине в любой точке кривой равна единице, то этот параметр
натуральный. В самом деле, в этом случае
t t
= Ι \τ\τ)\άτ= ί dr^t
ЗАМЕЧАНИЕ 3. Если f(s), s ε (ο,β), — естественная
параметризация кривой 7· т0 1^'(6>)1 = 1» а поэтому вектор
r"{s) ± f'(s)y т. е. направлен по нормали кривой. Более
того, поскольку r"(s) лежит в соприкасающейся плоскости
кривой 7» то r"{s) направлен по главной нормали данной
кривой.
Элементы теории кривых
263
§ 6. КРИВИЗНА КРИВОЙ
Пусть 7 —регулярная кривая без особых точек, Ρ е 7
—фиксированная точка, Μ € 7 — точка, отличная от Ρ и
близкая к Ρ, φ —угол между касательными к 7 β точках Ρ и М,
I —длина дуги РМ (рис. 87). т>'(0;
'(t + Лг i
Рис. 87
Кривизной кривой в данной точке называют предел
отношения угла поворота касательной на дуге кривой, стягивающейся к
данной точке, к длине этой дуги, т. е.
k = lim —.
Теорема. Регулярная дважды дифференцируемая без
особых точек кривая у, заданная векторной функцией r(t),
t G (а,Ь), имеет в каждой точке определенную кривизну
k(t), причем
вд =
F(t)xf{t)\
\r'(t)\3 '
Доказательство. Пусть точки Ρ и Μ отвечают значениялт
параметра ί и t + At.
Поскольку кривая 7 регулярная без особых точек, то
. _ \f'(t)xr'(t + At)\
sm^~HOI -|r'_(i + Af)r
i+Δί
/= ί |7^(r)|dr=ir'(r-)|Ai=|r'(i)IAi + -:Ai-
264
Глава 8
где с > 0 при Δ£ —» 0. При преобразовании выражения для
длины I мы воспользовались формулой среднего значения для
интеграла и непрерывностью функции r'(t) на интервале
[Μ + Δί].
Приняв во внимание формулу Тейлора
f'(t + At) = r'(t) + f "(*)Δί + ^Δ*. lim ε = 0,
с Δί-*ϋ
имссм . |P(i)xf"(*)l+*A
|Γ'(ί)|2 + μ
причем
Jim δ = 0, lim w = 0.
Δί->0 Δί—0
Воспользовавшись известным замечательным пределом,
окончательно получаем
fc(i) = lim γ = lim —--*- · -^— = lim -—-*- ■ lim ^ -
(|г'(«)хг"(*)1 + *)д« |r'xf"|
= lim
ff/|3
δ*-ο (|f'(ΟΙ2 + Αθ(Ι^(*)|Δί + εΔί) \f
ЗАМЕЧАНИЕ 1. Если в качестве параметра на кривой выбрана
длина дуги, т. е. кривая задана естественной параметризацией
f = ffa), se (а,Ь),
то \f '(s)\ = 1, s e (α, b), и вектор г "(s) JL r '(s) ,sG(a,6).
Отсюда следует, что кривизна кривой, заданной
естественной параметризацией, определяется формулой
k(s) = \r»(s)U se{a,b).
ЗАМЕЧАНИЕ 2. По определению кривизна кривой
неотрицательна. Однако во многих случаях для плоских кривых
целесообразно кривизне отнести знак в зависимости от направления
вращения вектора г '(£).
ЗАМЕЧАНИЕ 3. Если кривая задана параметрическими
уравнениями в Е3
χ = x(t), у = y(t), z = z(t), t G (a, 6),
Элементы теории кривых
265
ТО
k2(t) = (
V
у'
~ ft
У
ζ'
Ζ
2
+
X9
V,"
X
ζ'
ζ
2
+
Χ*
nit
χ
y'\
у 1
Если плоская кривая задана параметрическими уравнениями
x = x(t), y = y(t), te{a,b),
то
k2(t)
J~Ji\2
(x'y" - y'x")
(^/2 + 2//2)3
Если плоская кривая задана уравнением у = у{х)у
χ G (а, Ь), то
к2(х) =
У
7/2
(1 + 2/'2)3"
ЗАМЕЧАНИЕ 4. Кривая, имеющая всюду кривизну, равную
нулю, является либо прямой, либо открытым отрезком прямой.
Доказательство. В самом деле, в этом случае k(s) =
= |r*"(s)| = 0, а потому r"(s) = 0. Следовательно, f(s) = as+by
где α, 6 — постоянные векторы.
p(t 4- At)
§ 7. КРУЧЕНИЕ КРИВОЙ
Пусть 7 — регулярная кривая без особых точек, Ρ е
€7 — фиксированная точка, Μ е 7 — точка, отличная от
Ρ и близкая к ней, φ — угол между нормальными
векторами β(ί) и β(ί + At) соприкасающихся плоскостей кривой 7
в точках Ρ и М, I —длина дуги
РМ(рис. 8.8).
Напомним, что нормальный
вектор соприкасающейся
плоскости кривой лежит на бинормали
этой кривой в рассматриваемой
точке.
Абсолютным кручением \>с\
кривой в данной точке называют
предел отношения угла поворота
r(t + At)
266
Глава 8
бинормали на дуге кривой, стягивающейся к данной точке, к
длине этой дуги: φ
|х| = lim —.
1 ι->ο I
Теорема. Регулярная трижды дифференцируемая кривая 7
без особых точек, заданная векторной функцией f(t), t G
G (α, Ь), имеет в каждой точке, где кривизна отлична от
нуля, определенное абсолютное кручение, причем
|(ЛгЛг"')1
1 '" |f'xf"|2 '
Доказательство. Пусть точки Ρ и Μ отвечают
соответственно значениям параметра t и t + At. Если кривизна кривой
7 в точке Ρ отлична от нуля, то она отлична от нуля и в точках,
близких к Р, в частности, в точке М.
В точках, где кривизна отлична от нуля, векторы f'(t) и
r"(t) неколлинеарны, а поэтому в указанных точках существуют
определенные соприкасающиеся плоскости. Нормальные
векторы этих плоскостей в точках Ρ и Μ кривой 7 определяются
соответственно векторами
P(t) = f(t) х г "(t) = {f x f")P
0(t + At) = r'(t + At) χ f"(t + At) = (f' χ f")M.
Тогда по формуле Тейлора имеем
(г' х f")M = (г* х г")Р + {f х f")'PAt + αΔέ,
lim α = 0,
следовательно,
(r xr )M =
= (f' x f")P + (f " χ f")PAt + (f' χ f'")ρΔί + αΔί,
т. с.
(f' χ r")M = (r' x f")p + (r' x r'")PAt + αΔί. {1)
Эчеченпш теории кривых
267
—· —*
Далее, если ψ —угол между векторами fj(t) и d{t ' ΔΜ. то
|(^хг")рх(г'х?")а/|
sin v =
|(Р χ г")/>|-|<г' χ г")
л Л
Используя распределительное свойство векторного проил-
ведення и формулу а χ (6 χ г) = 6(α · г) - с(а - έ), получаем
(г' χ f ")р х (f х г")л/ = (г' χ г")р χ
х ((г7 х г")р + (г' х /r,//)pAi + &Δί) -
- (f' χ f")p χ (γ' χ τ'")ρΔί + (f' x f")ρ χ αΔί =
= f'(Λ r", r'")ΡΔΐ - f'"({r' x f")f')ρΔί Η- «Δί =
= Γ^Γ//,Γ//,)ρΔΑ + ΛΔ/,
где
lim -tf = 0.
Принимая во внимание, что
I = If'(ί)ΙΔί + ε At, lim ε = О,
14/1 Δί—Ο
имеем
J>r| = lim у = lim ——- · —-— = lim ——7 · lim
6\At
χ
i—о / z—o sin 0 / ν ->f> sin ψ i—о /
δ!™ο VIΡ χ f"\P(\f' χ f"|P + |f χ f'"\PAt + ίϊΔ/)
X (\f\pAt + tAt)J = .
= Нр1(г',гЛг'")1р = \(Г',Г",?'")\Р
\r' x f'lplf'lp \f' χ r"|p *
Теорема доказана.
ЗАМЕЧАНИЕ 1. Если кривая задана естественной
параметризацией f = f{s), s € (о, 6), то |f(.s)| = 1 и 7r'(s) ± г"(β),
s G (α, b), причем ее кривизна
k(8) = \f(8)U 5 6(С,Ь)..
268
Глава 8
В этом случае
| И*), гл*), г "'(*))!
|Х| ~ A,-2(s)
Кручением κ кривой 7 B точках, в которых определено
абсолютное кручение, называют величину
(f.(r'(№'[t),rm{t))
"К) \f'(t) χ r"(t)\2 '
ЗАМЕЧАНИЕ 2. Кручение кривой 7» заданной естественной
параметризацией, определяется формулой
Таким образом, кручение кривой может быть как
положительным, так и отрицательным.
ЗАМЕЧАНИЕ 3. Кручение плоской кривой равно нулю, так как
вектор бинормали в этом случае совпадает с нормальным
вектором плоскости, в которой лежит кривая, и остается неизменным
во всех точках кривой.
Верно и обратное: если кручение во всех точках кривой равно
нулю, то эта кривая плоская. В этом случае вектор бинормали
сохраняет постоянное направление, причем во всех точках он
ортогонален вектору касательной, т. е.
ζ df
поэтому
|(A-f> = o.
Отсюда
β[) · f= С, С = const,
т. с. радиус-вектор любой точки кривой удовлетворяет
уравнению плоскости, в которой расположена кривая.
Элементы теории кривых
269
§ 8. ФОРМУЛЫ ФРЕНЕ
В каждой точке регулярной кривой 7> вообще говоря, можно
определить три прямые, проходящие через эту точку:
касательную АВУ главную нормаль CD, бинормаль MN, и три
плоскости: нормальную πι, соприкасающуюся π2 и спрямляющую π3
(рис. 8.9).
ль
Рис. 8.9
Пусть кривая 7 задана естественной параметризацией f =
= r(s), s € (a,b). Тогда вектор t = f'(s) является
единичным направляющим вектором касательной к кривой 7· Вектор
r"(s) ортогонален вектору Г и лежит в соприкасающейся
плоскости, а потому выберем единичный вектор η главной
нормали коллинеарным вектору r"(s), а именно, η есть орт
вектора r"(s). В качестве единичного вектора бинормали возьмем
вектор Ь = Гх п.
Таким образом, определенные единичные векторы Г, n, b
образуют правую тройку, называемую репером Френе, причем
(^п,&) = 1.
Три полупрямые, исходящие из произвольной точки Ρ
кривой и имеющие направление векторов Г, п, 5,
являются ребрами трехгранного угла, называемого естественным
трехгранником.
Векторы естественного трехгранника t> n, b меняются при
движении точки по кривой и являются функциями длины дуги.
270
Глава 8
Вычислим их производные по натуральному параметру и найдем
разложение этих производных по векторам Г,п,Ь.
Пусть кривая *у задана произвольной параметризацией
f=r\t)y te (α,6).
Отметим, что вдоль всей локально рассматриваемой кривой
Г-Г=1, η·η = 1, b - fc = 1, (1)
f-n = 0, Γ·6 = 0, η· 6 = 0- (2)
Поскольку векторы t,n,b единичные, то t' ± f, n' J_ n,
bf _L 6, а потому
Р = *н + г/Ь, (3)
η' = μί+χ6, (4)
6' = λί+ ση. (5)
Для наглядности соотношения (3)—(5) можно представить в
виде таблицы:
г
π'
Ь'
*
0
μ
А
η
fc
0
σ
b
ν
χ
0
Из соотношений (2) имеем
Ρ-η + Γ·η' = 0, Ρ·6 + Γ·ϊ' = 0, η'·6 + η·6' = 0. (6)
Умножая равенство (3) скалярно на η и равенство (4) на
F, а затем складывая почленно, получаем, воспользовавшись
соотношениями (6),
к-τι · η + uft · η 4- μ( · f+ >А * Г= 0,
откуда А: + /ι = 0, т. е. μ = — А*.
Аналогичным образом получаем λ = -νψ σ — —χ.
Формулы (3)-(5) принимают вид
-Ну . -*
£ = кп + vb}
и' = -fcf+^6, (7)
6' = —uf— jrfi,
Элементы теории кривых
271
или в виде таблицы:
Ρ
η'
b'
—#
t
0
-k
~v
η
k
0
— УС
·*
h
V
X
0
Если кривая задана естественной параметризацией г = r(.s)t
s е (о,β), то f'(s) = t, Ρ = r"(s)% причем векторы r'(s)
и r"(s) лежат в соприкасающейся плоскости и f/f(s) ± r'(s).
В связи с этим Ρ ± 6, а потому в формулах (7) ν = 0.
Из соотношений (7) для естественной параметризации
кривой получаем формулы
Ρ = k(s)n,
η' = -k(s)t + x(s)b,
b — ->r(s)n,
или в виде таблицы:
t'
η'
b'
-φ
t
0
-fc
0
η
k
0
—yt
b
0
*И
0
Эти формулы называют формулами Френе, по имени
французского математика Жана Фредерика Френе (1816—
1900), опубликовавшего их в 1852 г. Независимо, почти в
то же самое время, эти формулы были получены другим
французским геометром Жозефом Альфредом Серре (181
ΟΙ 885).
Выясним геометрический смысл величин k(s) и >c{s),
входящих в формулы Френе.
Из формул Френе \Р\ = |A;(s)n| = k(s), поскольку η есть
орт вектора r"(s) и потому k(s) > 0.
С другой стороны, \Р\ = \r"(s)\ = fc(s),i7ie k(s) —кривизна
кривой 7 в заданной точке.
Таким образом, величина k(s) в формулах Френе есть
кривизна кривой в рассматриваемой точке.
272
Глава 8
Далее, из формул Френе имеем
ds
d?r -.
— = t' = k(s)n,
—з = (fe(s)-n)' = k'n + kn' = jfc'n + *(s)(-fc(s)f+x(s)b),
(f',r"'/") = (f'xf")-r'" =
= (fx fc(*)*0 ■ (k'(s)n-k2(s)t + k(s)K(s)fy =
= fe2(s)>tr(s),
откУда r~>/ *=>" ^'"\
_ (r ,r ,r )
MS; " fc2(s) ·
С другой стороны, кручение кривой, заданной естественной
параметризацией, определяется формулой
Таким образом, величина >c{s) в формулах Френе есть
кручение кривой в рассматриваемой точке.
ЗАМЕЧАНИЕ. Формулы Френе иногда называют
деривационными.
§ 9. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
КРИВОЙ
И ГРАНЕЙ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА
При исследовании свойств кривой в окрестности произвольной
точки Ρ оказывается удобным выбрать декартову
прямоугольную систему координат Ptnb, приняв точку Ρ за начало, а έ,
η, b — за базисные векторы.
Построенную таким образом систему координат называют
каноническим подвижным репером кривой.
Элементы теории кривых
273
Пусть в точке P{s) кривой 7 построен канонический репер
(рис. 8.10). Будем давать естественному параметру как
положительные, так и отрицательные приращения As, причем в точке
Ρ будет As = 0.
Тогда получаем на кривой
точки М, близкие к Р, причем их
радиус-векторы Af(As)f имеющие
начало в точке Р, будут показывать
расположение кривой относительно
плоскостей построенного репера.
По формуле Тейлора
f(s + As)
Рис. 8 JO
As
Asn
Af(As) = r'(s)As + r"{s)-^- + · ■ · + fr(») + e(s,As)) -^
lim eis, As) = 0.
Воспользовавшись формулами Френе, имеем в заданной
точке ?>(s)=t,
?"(s) = (f-'(s))' = t' = *(s)n,
f'"(s) = (fc(s)n)' = fc'(s)n + k(s)(-k(s)t + *r(s)6),....
Таким образом,
Af(As) = (As
k(s)
+
fc'(s)
(^ + ^ + ...)«+(ttf(')AJ
As* +
..-)&,
причем выражения, заключенные в скобках, суть координаты
радиус-вектора Af(As) точки Μ кривой, а следовательно, и
самой точки относительно системы координат Ptnb:
x(As) = As
*2(*)л„3
As6 + .
y(As) = ^As* + ^-As* + ...,
(1)
(2)
(3)
274
Глава в
Проекции кривой на грани естественною трехгранника в
окрестности его вершины Ρ задаются соответствующими
парами этих уравнений. Вид проекций при k(s) φ О, yc{s) φ О
показан ил рисунках 8.11—8.13.
Рис. 8. II
Рис. 8.12
Puc.8J3
Рассмотрим расположение кривой относительно плоскостей
репера в точке Р. При достаточно малых As знак координаты
x(As) = As -
*2(*)л„э
6
As* + ...
определяется приближенной формулой x(As) & As,
Отсюда следует, что кривая пересекает свою нормальную
плоскость πι (рис. 8.14,8.15).
х>0
ч
Μ
i
I
^n~-^4
KM»
ι \—
I
| N.
N.
| N.
<
:0
L"i
-K-i
Рис. 8 14
Рис.815
Элементы теории кривых
275
При достаточно малых As знак координаты
y(As) = -±r&s2 + -^As3 + ..
ζ ο
определяется приближенной формулой
Поскольку кривизна fc(s) > 0, то знак координаты y(As) не
меняется при перемене знака As.
Таким образом, y(As) ^ 0, и, следовательно, все близкие
точки кривой расположены с одной и той же стороны от
спрямляющей плоскости 7Гз кривой, причем вектор η ориентирован в
ту сторону от спрямляющей плоскости, где находятся ее близкие
точки.
При достаточно малых As знак координаты
/а ч k(s)*£(s) А з
z(As) = v ' v 'As6 + ...
6
определяется приближенной формулой
/ а ч k(s)x(s) Л з
z(As) к ч ' v 'As0.
Поскольку k(s), x(s) остаются фиксированными в
точке Р, приходим к выводу, что изменение знака z(As)
происходит только при изменении знака As. Таким
образом, кривая переходит с одной стороны соприкасающейся
плоскости пх<1 на другую.
Выясним геометрический смысл знака кручения яг. С этой
целью рассмотрим поведение части кривой относительно
канонического репера, построенного в одной из внутренних точек
этой части.
Возьмем три точки на кривой: точка Mq = Ρ — начало
репера, причем для нее As = 0. Точка Мг (As) расположена
до начала репера и для нее As < О· Точка M2(As) расположена
после репера и для нее As > 0 (рис. 8Л4,8.15).
276
Глава 8
При и > 0 имеем ζ(Μι) < О, z(MQ) = О, г(М2) > О.
Таким образом, в этом случае при возрастании Δ.* кривая
пересекает соприкасающуюся плоскость 7Г2 в направлении вектора
В («снизу вверх»)(рис. 8.14).
При к < О имеем z{M{) > О, z(M0) = 0, z(M2) < О.
Отсюда приходим к выводу, что в данном случае кривая
пересекает соприкасающуюся плоскость π2 в направлении, обратном
направлению вектора b («сверху вниз»)(рис. 8.15).
Получаем, что если я > О, то точка Μ переходит по
кривой с одной стороны соприкасающейся плоскости на другую в
положительном направлении бинормали, а если к < 0, то в
отрицательном направлении.
Таким образом, знак кручения показывает, как
«закручивается» кривая относительно канонического репера — по часовой
стрелке (ж > 0) или против нее ( χ < 0). Отметим, что это
различие хорошо известно в природе и технике. Например, у
стеблей батата ус > О, а у стеблей хмеля к < 0. В технике
различие правой и левой нарезки винтов также связано со знаком
кручения.
Подчеркнем, что деривационные формулы Френе дают
возможность продолжить процесс отыскания членов в
разложениях (1)—(3) до бесконечности, что приводит к представлению
названных разложений в виде сходящихся рядов. В этом случае
говорят, что кривая является аналитической и ее можно задать
аналитической вектор-функцией.
§ 10. НАТУРАЛЬНЫЕ УРАВНЕНИЯ КРИВОЙ
Заметим, что коэффициенты разложения вектор-функции Af(As)
в ряд по степеням As выражаются только через кривизну и
кручение кривой. Это дает основание полагать, что кривизна
и кручение определяют кривую. Действительно, любая гладкая
кривая без особых точек, кривизна которой в любой ее точке
не равна нулю, связана с тремя функциями: длиной дуги θ(ί),
причем s'(t) > 0, кривизной k(t) > 0 и кручением >*(*)>
которые всегда могут быть вычислены по известной параметризации
Элементы теории кривых
277
кривой г = f(t). При перемещении кривой в пространстве ни
одна из указанных величин не изменяется, что
непосредственно следует из их определения, т. е. они являются инвариантами
кривой. Если кривая задана естественной параметризацией г =
= f(s), то кривизна и кручение будут являться функциями длины
дуги:
k = k(s), *с = k(s).
Система этих двух соотношений называется натуральными
уравнениями кривой.
Натуральные уравнения полностью определяют форму
кривой, ибо связывают инварианты, которые не меняются при
преобразовании координат (при изменении положения указанной
кривой в пространстве относительно системы координат).
Теорема 1. Пусть две гладкие кривые 71 и 72 без особых
точек, заданные своими параметризациями f=fi(s)uf =
= r2{s) соответственно, имеют одинаковую длину. Если в
соответствующих точках ki(s) = k2{s), h\(s) = *c2{s), то
Ίι и 72 отличаются лишь положением в пространстве.
Доказательство. Пусть 5 = 0. Переместим 72 так> чтобы
ее начальная точка А2(г2(0)) совпала с начальной точкой
Άι(π(0)) кривой 7ι· Вращением кривой 72 добьемся того,
чтобы совпали соответствующие орты канонического
подвижного репера. Этого всегда можно добиться, ибо обе тройки
являются правыми, а орты взаимно ортогональными. Тогда при s = 0
«1(0) = f2(0), ηχ(0) - n2(0), bi(0) = U(0).
Рассмотрим вспомогательную функцию
а(з) = ti(s) ■ t2(s) + πι(5) ■ n2(s) + bi(s) · b2(s).
Тогда с учетом формул Френе
t[ · t2 + h · t2 + ή[ · n2 + Hi · n2 + b[ -b2+bib2 =
= /citfi · t2 + Γι ■ k2n2 -f (—fcib + Kih) ■ n2 +
+ ni ■ (-k2t2 + н2Ь2) + (-^1^1) ■ 62 + Ь\ ■ (-я2п2).
ασ
Is
278
Глава 8
Поскольку ki{s) = £2(3) > xi(s) = ^2(5), то af(s) = 0«
Следовательно, a(s) = const. Заметим, что σ(0) = 3, а
потому для любого 5 справедливо равенство a(s) = 3. Отсюда, в
частности, следует, что ti(s) · £2(5) = I, поэтому t\(s) = £2(5),
f[(s) = f^s). Так как г\(0) = г2(0), то fi(e) = f^(s), что и
требовалось доказать.
Теорема 2· Пусть k(s) и и{в) —любые дифференцируемые
функции, причем k(s) > 0. Тогда существует
единственная, с точностью до положения в пространстве, кривая,
для которой k(s) и k(s) являются соответственно
кривизной и кручениея.
Доказательство основывается на теореме существования и
единственности решения системы обыкновенных
дифференциальных уравнений.
Таким образом, система уравнений к = k(s)y χ = *<{s),
где 5 — длина дуги, k(s) и >c(s) — соответственно кривизна и
кручение кривой, определяет полностью, вплоть до положения в
пространстве, соответствующую кривую.
§ 11. НЕЯВНОЕ УРАВНЕНИЕ КРИВОЙ НА ПЛОСКОСТИ
Допустим, что плоская кривая *γ задана своей параметризацией
χ = χ(ί), у = y(t), t е (α, β)9 χ'2 + у* φ 0.
Если из этих уравнений исключить параметр £, то получим
неявное уравнение плоской кривой *у:
F{x,y)=0. (1)
Ясно, что указанные функции x(t) и y(t) будут обращать в
тождество уравнение (1), т. е.
F(s(f)>2/(i))=0.
Продифференцируем это тождество по ί, тогда
Fxx' + Fyy' = 0,
(2)
Элементы теории кривых
279
где Fx = §~, Fy — |^ — частные производные по χ и у
соответственно.
Особой точкой плоской кривой называется такая точка
(^о,2/о)> что Fx(x0,y0) = Fy(x0,yo) = 0.
В дальнейшем будем считать, что кривая 7 не имеет
особых точек. Заметим также, что соотношение (2) определяет
отношение координат направляющего вектора касательной r'(t).
Действительно, если, например, Fx φ 0, то из (2) следует
Fxy
Тогда с учетом уравнения касательной в произвольной точке
X - x(t) Y- y(t) Х-х _Y-y
*'(*) ~ </'(*) ' -V*FV/FX- у' '
Fx(X-x)+Fy(X-y)=0, (3)
где (Χ, Υ) —произвольная точка на касательной, (я, у)
—точка на кривой 7. в которой проведена касательная. Таким
образом, соотношение (3) определяет касательную прямую к плоской
кривой 7» заданной неявным уравнением (1).
Нормалью плоской кривой называют прямую,
перпендикулярную касательной и проходящую через точку касания.
Непосредственно из условия (2) и данного определения следует, что
направляющий вектор нормали ή = (Fx,Fy), а потому ее
уравнение имеет вид Χ — χ Υ — у
**Х i*y
§ 12. ОГИБАЮЩАЯ
ОДНОПАРАМЕТРИЧЕСКОГО СЕМЕЙСТВА
ПЛОСКИХ КРИВЫХ
Рассмотрим уравнение _, „ /|Ч
^ F(xjyiC)=0> (i)
где F — непрерывная, дифференцируемая функция трех
аргументов. Будем считать, что для любого фиксированного
значения параметра С уравнение (1) задает некоторую плоскую
кривую. Поэтому при всевозможных значениях С получаем
семейство плоских кривых.
280
Глава 8
Огибающей однопараметрического семейства
плоских кривых называется кривая, которая каждой своей
точкой касается некоторой кривой указанного семейства, а
каждым своим куском касается бесконечного числа кривых
семейства (1). Точка прикосновения огибающей к кривой
семейства называется характеристической точкой кривой
семейства.
Ясно, что в характеристической точке кривая семейства и
огибающая должны иметь общую касательную.
Допустим, что семейство (1) имеет огибающую. Любая точка
огибающей по определению имеет общую точку с кривой
семейства, а сама эта кривая, в свою очередь, определяется
значением параметра С. Поэтому, если χ = <р(С)у у = ф(С) —
параметрические уравнения огибающей, то выполнено тождество
F(<^(C), ^(C), С) = 0. Продифференцировав последнее
соотношение по параметру С, получаем
δ^άφ д£аф flF^j, ί2ν
дх dC + dydC дС У '
Пусть уравнения кривой семейства имеют вид χ = х(£), у =
= y(t). Так как в характеристической точке у огибающей и этой
кривой общая касательная, то справедливы соотношения
άφ _ dx dip _ dy
dC = dt' dC~ ~dt*
Подставляя их в равенство (2), получаем
/d£dx d£dy\ d£_Q
\дх dt + Oy dt) + дС ~ '
Выражение, стоящее в скобках, в силу соотношения (2)
предыдущего параграфа равно нулю. Следовательно, координаты
характеристической точки удовлетворяют уравнению Fc = 0.
Таким образом, если огибающая существует, то ее точки
удовлетворяют системе уравнений
F(x,y,C)=Q, Fc(x,y,C) = Q. (3)
Элементы теории кривых 281
Исключив из системы (3) параметр С, либо выразив χ и у
через С, получаем уравнение дискриминантной кривой
данного семейства. Если огибающая существует, то она обязана
входить в состав дискриминантной кривой, которая в общем
случае может иметь несколько ветвей.
Выясним необходимые условия, при которых кривая χ =
= φ(0), у = *Ф{С), уравнения которой получаются из
системы (3), является огибающей. Для этого
продифференцируем по С очевидное тождество F(<p(C)> ф(С), С) ξ 0. Так как
Fc = 0,то
dFdv £Fd£ ,4)
dxdC dydC У '
Но из этого соотношения пропорциональность координат
направляющих векторов касательной и огибающей следует лишь
тогда, когда Fj + Fy Φ 0, ибо в противном случае условию (4)
будут удовлетворять любые координаты. Таким образом, если
однопараметрическое семейство допускает огибающую, то она
является ветвью дискриминантной кривой, в каждой точке
которой не равны нулю одновременно частные производные Fx и Fy.
В противном случае, если Fx = Fy = 0, то соответствующая
ветвь определяет множество особых точек.
§ 13. ЭВОЛЮТА ПЛОСКОЙ КРИВОЙ
Эволютой плоской кривой называется огибающая ее нормалей.
Пусть регулярная кривая 7 без особых точек задана
естественной параметризацией f = r(s)y s € (ос,β). Как
известно, уравнение нормали в произвольной
точке имеет вид (рис. 8.16)
(R-.r(s))-r'{s) = 0. (1)
Поэтому нормали данной кривой
образуют однопараметрическое
семейство прямых, где s — параметр.
Продифференцируем соотношение (1) по
параметру s. Тогда с учетом равенства Рис. 8.16
7
282
Глава 8
\r*(s)\ = 1 получаем систему для определения огибающей
указанного семейства:
(R - г) · τ' = О, {R - τ) ■ г" = 1, (2)
но r'(s) = f(s), r"{s) = k(s)n(s). Поэтому из соотношения (1)
следует, что (R — г) ± L С другой стороны, Г ортогонален
вектору п, следовательно, π коллинеарен вектору R - r(s). Тогда
для некоторого λ справедливо равенство
R-f(s) = Xn(s). (3)
Найдем соответствующее значение λ. Для этого
заметим, что (R - f(s)) · (k(s)n(s)) = 1, а тогда с
учетом (3) имеем Xk(s)(n-n) = 1, откуда окончательно получаем
А = 1/ад=Р(*).
Величина p(s), обратная кривизне кривой, называется
радиусом кривизны.
Таким образом, радиус-вектор R произвольной точки
эволюты плоской кривой вычисляется по формуле
R = f(s) + p(s)n(s),
а сама эта точка называется центром кривизны. Поэтому
эволюта есть геометрическое место центров кривизны плоской
кривой (рис. 8.16/
ЗАМЕЧАНИЕ I. Расстояние между соответствующими
точками эволюты и данной кривой равно радиусу кривизны, так как
это расстояние ρ = JjR — f(s)\ = \p(s)ft(s)\ = p(s).
ЗАМЕЧАНИЕ 2. Точки эволюты лежат на нормали кривой со
стороны ее вогнутости, так как p(s) > О,
§ 14. ЭВОЛЬВЕНТА ПЛОСКОЙ КРИВОЙ
Ортогональной траекторией однопараметрического
семейства линий называется кривая, пересекающая каждую линию
семейства под прямым углом.
Эвольвентой кривой 7 называется ортогональная
траектория ее касательных.
Элементы теории кривых
283
Пусть 7 — регулярная кривая без особых точек, а г =
= r(s), s е {а,0)у — ее естественная параметризация. Так как
по определению эвольвента пересекает касательные к кривой 7,
то любая ее точка должна удовлетворять уравнению касательной
R = r{s) + \t{s), (!)
где t(s) — орт касательной, a R — радиус-вектор точки
эвольвенты. Для каждого s значение А свое и численно равно
расстоянию от кривой до эвольвенты. Найдем указанное λ = X(s). Для
этого продифференцируем R(s), получаем
dR
ds
f'(s) + ~t(s) + λ(β)Γ(β) = (l + ^\ Γ + A/m. (2)
—*
Заметим, что R (s) — направляющий вектор касательной к
эвольвенте, а значит, он ортогонален вектору t(s). Если обе
части соотношения (2) скалярно умножить на вектор t(s)y то
получаем 1 + X'(s) = 0. Откуда имеем X(s) = —s + c, где с —
произвольная постоянная. Таким образом, уравнение эвольвенты
принимает вид β , w7 v
R = r(s) + (s + c)t(s).
В уравнении эвольвенты присутствует произвольная
постоянная. Это означает, что у кривой 7 существует бесконечное
число эвольвент. Возьмем две из них, например, при с = с\
а при с = С2, соответственно,
RV)=r>(s) + (-s + C2)t(s).
Тогда расстояние между соответствующими точками
эвольвент постоянно, ибо расстояние ρ = \R^ — R^\ = \{c\—C2)t\ —
= |ci -c2|.
ЗАМЕЧАНИЕ 1. Кривая 7 no отношению к своей эволюте
является эвольвентой.
ЗАМЕЧАНИЕ 2. Пусть точке Мо на кривой 7 отвечает
значение s — so, а точке М, соответственно, s = s\, причем si > so.
Возьмем произвольно с = ci. Тогда если М2 и Μχ — точки
284
Глава 8
Рис. 8.17
на эвольвенте, отвечающие точкам Mq
и Μ соответственно (рис. 8.17), то
|M0M2| = |A(so)|=so-ci;
\MM1\ = \X(81)\=s1-cl.
Поскольку длина дуги ММо равна
51 - S0 , ТО
|ΜΜχ| = si -ci =
= (si -so) + (so -ci) =
= MMq + \M0M2\·
Отсюда следует простой способ построения эвольвенты.
Рассмотрим гибкую нерастяжимую нить, наклеенную на
кривую 7· Если натягивать нить и одновременно отделять ее от 7
так, чтобы нить была направлена по касательной, то ее
свободный конец опишет эвольвенту.
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Между двумя параллельными прямыми проведена
окружность с радиусом R, касающаяся этих прямых в точках
А и В. Из точки А выпущен луч, пересекающий
окружность в точке С и вторую прямую в точке М. На
луче АС отложен отрезок
АК, причем
\АК\ = \СМ\.
Составить уравнение
траектории точки К при ера-
щении луча АС вокруг
точки А (циссоида Диоклеса).
Решение. Выберем систему
координат Аху, в которой ось
Ах направлена по диаметру
АВ (рис. 8Л8). Обозначим
Рис. 8.18
Элементы теории кривых
285
угол МАВ через φ. Так как Ζ АС В = π/2, то ZMBC = φ
Тогда
\MB\ = \AB\tg<p = 2Rtg<p,
|МС| = \МВ\ sin φ = 2fltgy?sinv?.
По условию задачи \АК\ = |МС|, а значит, при ν? € (0, π/2)
ж = \AK\cosip = 2.Rtgv?sinv?cosv? = 2#sin2v? = χ{φ),
у = IАЙГ) sin φ = 2R tg φ sin ν? sin <^? =
= 2iZtgy?sin2 φ = у (φ).
Заметим, что если положить t = ctg^?, то получаем другую
параметризацию этой же ветви циссоиды
2# 2Я Л ,Л
Ж=^П;. y=^i' *€(0,+oo).
Если из полученных уравнений исключить t, то найдем
неявное уравнение циссоиды:
а3=2/2(2Я-:г).
2. Луч ОС вращается вокруг точки О с постоянной
угловой скоростью ω. Точка Μ движется по лучу ОС
со скоростью, пропорциональной пройденному пути
\ОМ\. Составить уравнение траектории точки Μ
(логарифмическая спираль).
Решение. По условию задачи скорость пропорциональна
пройденному пути, т. е. ν = г' = Ar\t), где λ —
коэффициент пропорциональности. Следовательно, если г(0) = ffc,
то f(t) = ?oeXt. Но угол φ, на который повернулся луч,
равен ωί. Поэтому окончательно имеем f(t) — roek<p > где к — Χ/ω,
φ = ωί.
3. Окружность с радиусом R катится без скольжения по
прямой. Составить уравнение траектории точки Μ,
лежащей на окружности (циклоида).
Решение. Введем систему координат Охуу в которой ось Ох
совпадает с указанной в условии задачи прямой (рис. 8.19).
286
Глава 8
О Ε В х
Рис. 8.19
Пусть и начальный момент точка Μ находилась в начале
координат, АВ _L Οχ, ΔΜΑΒ = ty \АВ\ = \АМ\ = R.
Тогда
х = \ОЕ\ = \ОВ\ - \ЕВ\ = МВ- \ЕВ\ =
= Rt — Rsint = x(t),
у = \МЕ\ = \АВ\ - \AF\ = R- Rcost = y{t).
Окончательно, параметрические уравнения циклоиды:
χ = R(t — sin t),
у = jR(1 — cosi).
4. Круговой цилиндр χ2 + у2 = Я2 вращается вокруг
собственной оси с постоянной угловой скоростью ω. По
образующей цилиндра движется точка Μ с
постоянной скоростью v. Составить параметрические
уравнения траектории точки Μ (винтовая линия)·
Решение. Допустим, что в начальный момент времени точка
Μ совпадала с точкой A(R70,0) (рис. 8.20). Если в качестве
параметра выбрать время t, то угол φ — ω£, ζ = \ΜΝ\ — vt,
χ = Rcosip, у = Rsinuj. Следовательно, параметрические
уравнения винтовой линии χ = Rcosy?, у = Rshup, z = ky>,
где к = ν/ω.
Б. Луч ОС, исходящий из начала прямоугольной
системы координат Oxyz и составляющий угол θ € (0, π/2)
с осью Οζ9 равномерно вращается вокруг нее с
постоянной угловой скоростью ω. Точка Μ движется по
лучу ОС с постоянной скоростью v. Написать
параметрические уравнения траектории точки Μ (коническая
винтовая линия).
Элементы теории кривых
287
Решение. Заметим, что \ОМ\ = vt, где t — время (рис. 8.21).
Пусть N — ортогональная проекция точки Μ на плоскость
Оху. Тогда \ON\ = |OMjsin0, φ = Λί. Поэтому
χ = |OiV|cos<p, у = \ΟΝ\ζη\φ, ζ = |ОД/|сок0,
или, с учетом ранее полученных соотношений, параметрические
уравнения конической винтовой линии имеют вид
χ = г?£ sin # cos art,
у = irt sin 0 sin art,
ζ = vtcosO.
zk
Рис. 8.20
6* Сфера с радиусом R пересекается с поверхностью
кругового цилиндра х2 +y2 — Rx — 0. Написать
параметрические уравнения кривой пересечения ("кривая Вивиани).
Решение. Точки кривой Вивиани удовлетворяют сие теме
уравнений х2 + у2 + z2 = R2, х2 + у2 — Rx = 0. Но последнее
соотношение можно представить в виде (х - Я/2)2 + у2 = R2/4.
Поэтому можно положить χ — if = тг cosi, у = тг sini. Тогда,
подставив выражения для χ и у в уравнение сферы, получаем
2 е>2
ζ = R —
(R R X
{2 + 2C°St)
—- snr t =
4
R2 R2
= ~z 7Г cos t
2 2
tf2sin2|
288
Глава 8
Следовательно, параметрические уравнения кривой Вивиани:
R, ч R . t
χ = — (1 + cost), у = —sini, z = ±Rsm—.
Zt L·* Ζ*
7. Найти дискриминантную кривую однопараметриче-
ского семейства полукубических парабол
F(x, у, с) = (у + с)2 - (х + с)3 = 0.
Решение. Найдем производную по параметру с:
ас
= 2(г/ + с)-3(ж + с)2=0.
{
Таким образом, для определения дискриминантной кривой
имеем систему уравнений
(у + с)2 -(х + с)3 = 0,
-с=§0г + с)2.
Используя второе соотношение, получаем
9(х + с)4 - 4(х + с)3 = 0.
Поэтому либо х+с = 0, а значит, у+с = 0,либо х+с = 4/9,
а тогда у + с = 8/27. Таким образом, искомая дискриминант-
ная кривая имеет две ветви: у=хиу=х— 4/27. При этом,
так как во всех точках первой
ветви Fx = Fy = 0, то
кривая у = χ не является
огибающей (это множество
особых точек). В свою очерэдь, во
всех точках второй ветви
справедливы соотношения Fx =
= -16/27, Fy = 16/27, а
поэтому прямая у = χ - 4/27
является огибающей
семейства полукубических парабол
(рис. 8.22).
Рис. 8.22
Элементы теории кривых
289
8. Найти эволюту эллипса, заданногомараметрическими
уравнениями χ = a cost, у = bsint.
Решение. Запишем уравнение нормали в произвольной точке
эллипса
—a sin t(X — a cos t) + b cos t(Y — b sin t) — 0.
Следовательно,
(-asint)X + (bcost)Y = -(b2 - a2) sin2i.
Таким образом, нормали эллипса образуют семейство
F(X,F,i) = 0, Так как Fx = -asini, Fy = bcost, то для
любого t справедливо соотношение F^ + Fy ^ 0. Поэтому дис-
криминантная кривая совпадает с огибающей нормалей —
эволютой. После дифференцирования по параметру t получаем
систему для определения эволюты
{
—(asint)X + (bcost)l^ = (б2 — a2) sin i cos ί,
-(acosi)X - (bsini)F = (б2 - a2)(cos21 - sin21).
Ее решением являются функции
Х =
а*
Ь2
а
cos ί,
Υ =
b2
or
sin31.
Параметрические уравнения вида X = lcos3t, Υ = Ζ sin3 ί
определяют кривую, которая называется астроидой. Поэтому
эволюта эллипса является
астроидой, вытянутой вдоль малой оси
эллипса (рис. 8.23).
9, Для кривой у2 = х, х2 =
= ζ написать уравнение
соприкасающейся плоскости,
проходящей через точку
(-1,0,-3),
Решение. Сначала найдем
параметрические уравнения кривой. Рис. 8.23
290
Глава 8
Для этого положим .τ = ί2. Тогда у = ί, ζ = t4. Уравнение
соприкасающейся плоскости в произвольной точке
2т
2
y-t
1
О
z-t4
т2
о,
т. с. 6t2x—8t3y~ζ+3ί4 = 0. Соприкасающаяся плоскость
должна проходить через заданную точку, а поэтому координаты точки
удовлетворяют уравнению искомой плоскости. Следовательно,
имеем -6£2 + 3 + 3ί4 = 0, откуда (ί2 - I)2 = 0, т. е. t = ±1.
Таким образом, при ί = 1 получаем плоскость 6х - 8т/ — ζ + 3 = 0,
а при t = —1 плоскость 6я + 8у — ζ + 3 = 0.
10- Доказать, что кривизна и кручение винтовой линии
f(t) = (αcost, asini, hi) связаны соотношением hk = ax\
При каком значении h кручение максимально?
Решение. Так как
(Г ,Г ,7' ) =
—asini a cost h
l—a cos ί —asini 0
asini —aoosi 0
|?/xf/f = a2(a2 + fc2),
= /га ,
то кручение
Λα2
χ =
а2 (а2 + /ι2) α2 + h2
- /(Λ).
Вычислим производную указанной функции:
ί
dh
a
~h2
a2 + h2
В силу очевидных неравенств /'(a — 0) > 0. /'(a + 0) <
< 0 получаем, что при h = а функция /(/ι) достигает
своего максимума. С другой стороны, так как |г*'| = \/а2 + h2, то
кривизна , α
k =
α2 + Λ2'
следовательно, hk = αχ
Элементы теории кривых 29!
11. Составить параметрические уравнения траектории
конца туго натянутой нерастяжимой нити,
сматываемой с неподвижной круглой катушки с
диаметром 2R.
О τ в ет: χ = R(t sin t + cos i)y у = R{sin t -t cos t).
12. Отрезок АВ длины l скользит своими концами по осям
прямоугольной системы координат Оху. Из точки О
опущен перпендикуляр ОМ к отрезку АВ. Найти
уравнение траектории точки Μ (четырсхлспестковая роза).
Ответ: χ = J sin t cos21, у = /sin2tcosf, или (χ2 + у2)3 =
= l2x2'y2.
13. Составить уравнение кривой -γ — множества точек
касания прямых, проведенных из начала координат к
окружности с радиусом, R, центр которой
перемещается по оси абсцисс (кгнша).
Ответ: у2(у2 + х2) = R2x2.
14. Найти пары точек, в которых касательные к
циклоиде χ = R(t — sin£)f у = Я(1 — cost) взаично
перпендикулярны.
Ответ: t\ — £2 = (2k + 1)π, где k —любое целое число.
15. Найти огибающую семейства прямых, образующих с
координатными осями треугольники площадью 2h2 =
= const.
Ответ: гипербола ху = h2.
16. Найти огибающую однопараметрического семейства
прямых χ cos С + ysmC — р = 0.
Ответ: окружность х2 + у2 = р2.
17. Найти эволюту параболы у2 = 2рх.
Ответ: χ = ρ + 3ί2/(2ρ), у = t3/p2.
18. Отрезок длины I скользит своими концами по осям
прямоугольной системы координат. Найти огибающую
семейства прямых, содержащих этот отрезок.
Ответ: астроида х2^ + у2/3 = I2/3.
19. Найти касательную к кривой f(t) = (3f - ί3, St2,2t + t3),
параллельную плоскости Gx + 2y + 2z — 1 =0.
Otrpt· £±£ — a-12 _ z-14 x±2 _ y^Z _ z±4
UIBC1, -3 " 4 ~ 5 » 0 ~~ -1 ~ I ·
232
Глава 8
20. Найти угол, образованный осью Oz и нормальной
плоскостью к кривой χ — a{t — sini), у = α(1 — cost), ζ =
=■ 4asin(i/2) в точке t = \.
Ответ: ~.
21· Найти главную нормаль кривой χ = cost, у = sini,
ζ — t, t € [0, |j параллельную плоскости x-y+3z—l = 0.
Ответ: х- j/ = о, я = ^.
22. Через точку М(0,2,2) провести спрямляющую
плоскость для кривой χ = £2, у = 1 +1, z = 2f.
Ответ: re = 0, 5х - 4у - 8г + 24 = 0.
23· Найти длину дуги кривой За2χ = у3, 2yz = а2,
отсекаемую плоскостями χ = α/3, χ = 9α.
Ответ: 9α.
24. Найти длину дуги кривой χ = a(t — sini), у = α(1—cosi),
xr = 4α cos(£/2), ie [0,2π].
Ответ: 8>/2α.
25. Доказать, что кривая r(t) = (I + 2£ + ί2,2 - 5t + ί2,1 +
+ ί2) — плоская, и найти уравнение плоскости, в
которой лежит эта кривая.
Ответ: 5х + 2у - lz - 2 = 0.
26. Дана гиперболическая винтовая линия *ух: χ = achi, ΐ/ =
= ashi, ζ = at. Доказать, что кривая 72! х = ci> У =
= \/2clni, ^ = ct~l при соответствующем выборе
параметра с является той же гиперболической винтовой
линией.
Глазе 9
ЭЛЕМЕНТЫ
ТЕОРИИ ПОВЕРХНОСТЕЙ
§ 1. ПОНЯТИЕ ПОВЕРХНОСТИ
Перейдем к исследованию свойств поверхностей. Как и раньше,
нас будут интересовать в первую очередь поверхности в
трехмерном пространстве. Однако начнем изложение с обсуждения
понятия самой поверхности.
Элементарной поверхностью называют множество точек
пространства, являющееся топологическим отображением круга
и ограничивающей его окружности.
При этом точки, являющиеся топологическим отображением
точек окружности, называются граничными точками.
Отметим, что граничные точки образуют замкнутую кривую,
называемую границей элементарной поверхности.
Говорят, что две элементарные поверхности склеены, если
они находятся в таком взаимном расположении, при
котором части их границ или обе границы целиком совпадают
между собой.
Подчеркнем, что в результате склеивания элементарных
поверхностей может снова получиться элементарная поверхность,
но может получиться и такое множество точек, которое не
является элементарной поверхностью.
Поверхностью называют множество точек пространства,
которое может быть склеено из конечного или счетного
множества элементарных поверхностей.
Отметим, что полная поверхность шара может быть
склеена из двух его полушарий, каждое из этих полушарий является
294
Глава 9
элементарной поверхностью. Плоскость может быть склеена из
счетного числа прямоугольников.
Пусть поверхность S является топологическим
отображением плоской области D в трехмерное пространство Ж3, и точке
Pq с координатами (и, ν) в системе O'uv соответствует на
поверхности S точка Ρ с координатами (х>у}ζ) в системе Ог$к
(рис. 9.1).
Рис. 9 Л
Таким образом, координаты точек поверхности S являются
функциями координат точек плоской области D
χ = х(щу), у = y{u,v), ζ = z(u,v), (u,v) € D. (])
Уравнения (1) определяют положение в пространстве концов
радиус-векторов с началом в точке О
r = r{x{u,v)iy{u,v),z(u,v)), (щь) £ D, 12)
причем годограф вектор-функции двух скалярных аргументов
f= f(u,v),(u,v) € Dy совпадает с поверхностью 5.
Уравнения (1) называют параметрическими уравнениями
поверхности, уравнение (2) — векторным уравнением
поверхности, при этом говорят, что поверхность
параметризована, а величины и, ν являются криволинейными
координатами ее точек.
В силу непрерывности отображения всякой линии в
области D соответствует некоторая линия на поверхности S.
Элементы теории поверхностей
295
Координатными линиями данной параметризации
называют линии на поверхности, соответствующие прямым и = const и
ν = const.
В силу однозначности соответствия через каждую точку
параметризованной поверхности проходит одна и только одна
линия семейства и — const и оцна и только одна линия семейства
ν = const. В этом случае говорят, что эти оба семейства вместе
образуют правильную координатную сеть.
Поскольку отображение взаимно однозначное, то
уравнения (I) могут быть разрешены относительно ич vf а координаты
точек поверхности связаны соотношением
F(x,y,z)=0, (3)
которое называют неявным уравнением поверхности.
Если поверхность является отображением некоторой
области плоскости 0%з в трехмерное пространство с
фиксированной ДПСК Ozfk, причем соответствующие точки Р0 и
Ρ лежат на прямой, параллельной оси Ок, то ее уравнение
представляется в виде
* = f(*,v)· (4)
В этом случае абсцисса и ордината точки поверхности
играют роль криволинейных координат, а координатные линии
являются линиями пересечения поверхности плоскостями,
параллельными координатным плоскостям Of к и Огк.
Поверхность называют регулярной, если у каждой точки
этой поверхности есть окрестность, допускающая регулярную
параметризацию, т. е. параметризацию вида
r = f(uyv) = r(x(u,v),y(u1v)Jz(u,v))) iii, v) € D,
где функции
χ = x(uyv), у = у(и,у), z = z(uyv). iu,v) E Dy
к раз непрерывно дифференцируемы в области D
При к = 1 поверхность называют гладкой.
296
Гласа 9
Точку регулярной поверхности называют обыкновенной
(неособой), если существует такая регулярная параметризация
некоторой ее окрестности» что в этой точке ранг матрицы
А
(dv ду dz
Ои ди ди
дх §л fa
dv dv dv
)
равен двум. В противном случае точку называют особой.
Введем обозначения
дг(и, ν)
ди
г,, =
дг(и, ν)
ге- ^ (д^ ду_ dz\ _ (дх ду dz\
Ги\ди'ди'ди)' Τυ\δυ'0υ'9υ)·
Позднее будет показано, что векторы ги и fv суть
направляющие векторы касательных к координатным линиям на
поверхности в рассматриваемой точке.
Так как строки матрицы А состоят из координат векторов
faj rVy и ранг матрицы А для обыкновенной точки равен двум,
то указанные векторы fu, fv являются для обыкновенной точки
линейно независимыми, и, следовательно, fuxfv Φ 0.
Приведем некоторые примеры параметризованных
поверхностей.
1) Пусть в плоскости π фиксирована точка 0' и два некол-
линеарных вектора оиб, приведенные в общее начало О',
причем координаты произвольной точки Μ € π в системе O'ab суть
и, v. Тогда получаем векторное уравнение с криволинейными
координатами U, V ПЛОСКОСТИ 7Г В
В|«е r = r0 + ua + vb,
-ос < и < +эс, (5)
—оо < ν < +оо,
где τ — радиус-вектор
произвольной точки плоскости π,
fo — радиус-вектор точки О'
(рис. 9.2).
М(щу)
Рис. 92
Элементы теории поверхностей
297
В этом случае координатные линии суть прямые,
параллельные прямым, определяемым направляющими векторами а и 6.
2) Пусть в плоскости 7г задана полярная система координат
с полюсом в точке О', с направляющим единичным вектором
полярной оси ё\, и Л/ — произвольная точка плоскости 7г с
полярными координатами (ρ,φ).
Тогда, считая указанные (ρ, φ) криволинейными
координатами, уравнение плоскости π можно представить в виде
ΚΑ ψ) = ^о + pcosc^ei + psin </?е2,
<о>
0 < ρ < +оо, 0 < у? < 27г,
где г — радиус-вектор произвольной точки Μ плоскости π,
fo — радиус-вектор точки О', ё*2 — единичный вектор,
лежащий в плоскости π и ортогональны вектору в\.
Уравнение (6) можно переписать в виде
τ(ρ,φ) = τη+ρέ(φ), (7|
где β(φ) — круговая функция.
Координатные линии на рассмотренной плоскости π при
указанной параметризации суть окружности (р = const, ρ > 0)
и лучи, исходящие из точки О' (φ — const).
Точку О1 называют особой
точкой указанной координатной
сети (рис. 9.3).
3) Зафиксируем диаметр АВ
сферической поверхности
радиуса а. Окружности,
полученные при пересечении
поверхности сферы плоскостями,
содержащими диаметр АВ, будем называть меридианами.
Пусть долгота φ — угол между плоскостью меридиана,
принятого за начальный (φ = 0), и плоскостью данного
меридиана, причем 0 < φ < 2π.
Окружности, полученные при пересечении сферической
поверхности плоскостями, ортогональными диаметру АВ, будем
называть параллелями.
298
Глава 9
Параллель, отвечающую плоскости, про ходя щей через центр
сферы, называют экватором.
Широта φ — угловая мера дуги меридиана, заключенно-
то между плоскостью данной параллели и плоскостью экватора,
взятая со знаком « + » или « —» в зависимости от того, в
какой — верхней или нижней от экватора — части сферической
поверхности находится параллель (рис. 9.4).
Предположим для простоты, что центр сферы находится в
начале О декартовой прямоугольной системы координат OZjk,
нача!ьный меридиан (<р = 0) находится в плоскости ОТк,
долгота φ отсчитывается в положительном направлении от ΐ к jf,
причем 0 < φ < 2π, экваториальная плоскость совмещена с
плоскостью OfjT, широта ф > 0 для точек с положительными
аппликатами и ф < 0 — в противном случае.
Отметим, что (рис. 9.5) Рис- 9.5
?=ο$ = οϊάι+ Mj% = оЙх + ойу + щ]$ =
= (a cos ф cos φ)ΐ + (a cos ф sin φ)$ + (α sin ф)к.
Тогда векторное уравнение сферической поверхности
радиуса α и с криволинейными координатами φ и ф имеет вид
τ(ψι Ψ) = о ((^cos φ + J sin φ) cos ф + k sin ψ),
π π (8)
Элементычпеории ηоверхностей
299
где ν(φ,ψ) — радиус-вектор произвольной точки А/
сферической поверхности, или
r(ip,%b) ^a((T((p)cos0 + fcsin,0),
тг π (9ι
(К^<2тг, -- ^φ<~,
где β{φ) — круговая вектор-функция. Координатные .пинии
сферической поверхности суть меридианы и параллели
(рис. 9.4,9.5).
В заключение параграфа отметим, что понятие поверхности
естественно обобщается на случай пространства произвольной
размерности. Так, параметризация
(10)
где
fai,^,...,^*) eU С ПС, к <р,
вообще говоря, задает поверхность Sk размерности А; в
пространстве W. В случае к = ρ - 1 имеем парамегризацию
поверхности Sp-iy или гиперповерхности. Понятно, что любая
поверхность в трехмерном пространстве является
гиперповерхностью.
Аналогичным образом вводятся понятия регулярном
поверхности, обыкновенной и особой точек поверхности.
Неявным уравнением гиперповерхности S в Шр будет
уравнение вида
F(x) = F(zux2>...>xP) = 0· (П)
Обыкновенной точкой гиперповерхности S, заданной
уравнением (II), называется точка ж0 = (х?7 х%, — Хр), в которой
частные производные dF(x°)/dxi ,г = 1,2,...,р,
одновременно не равны нулю, т. е. вектор '
\ ОХ\ ОХ2 ΟΧ ρ J
называемый градиентом функции F в точке ж°% не равен О.
300
•Глава 9
§ 2. КАСАТЕЛЬНАЯ ПРЯМАЯ К ПОВЕРХНОСТИ.
КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
И НОРМАЛЬ К ПОВЕРХНОСТИ
Пусть на поверхности S, заданной
векторным уравнением
f=f[u,v)f (ηΊν)Εϋ} (Ι)
лежит кривая I, параметризованная
при помощи параметра t (рис. 9.6).
В этом случае каждому параметру
t £ (α, β) соответствует точка кривой
P(u,v), лежащая на поверхности S, которой, в свою очередь,
соответствуют определенные значения криволинейных
координат (и, ν). Таким образом, криволинейные координаты точек
кривой I, принадлежащей поверхности 5, являются функциями
параметра t
Рис. 9£
и
= u(t), v = v(t), te(a,P).
(2)
Уравнения (2) называют внутренними уравнениями
кривой на поверхности.
Если внутренние уравнения (2) кривой заданы, то ее
параметрическое уравнение в векторной форме имеет вид
г = г(гх(*), *;(*)), te(a,p).
(3)
Прямую называют касательной прямой к поверхности
о заданной точке, если она касается в этой точке некоторой
кривой, лежащей на этой поверхности.
Направляющий вектор касательной прямой к поверхности
определяется касательным вектором соответствующей кривой:
df dfdu dfdv
<ft = du~dt+dv'dt}
и, если
df
r„ =
df
dv'
то
df ^ du ^ dv
= rW77 + rv
dt
dt
dt'
Элементы теории поверхностей
301
а поэтому
dr = f^du + fvdv. i 41
Векторы fu и fv называются координатными
векторами той точки поверхности, криволинейные координаты которой
используются при их вычислении.
Теорема. Координатные векторы в точпе поверхности
суть направляющие векторы прямых, касательных к
координатным линиям в указанной точке.
Доказательство. Пусть, например, внутренние
параметрические уравнения одной из координатных линий (рис. 9.71 суть
и = const, ν — £, £е (—00,00).
ν =г const
Рис. 9J
Тогда направляющий вектор касательной прямой в данной
точке к соответствующей координатной линии определяется
соотношением
dr or du or dv
dt du dt dv dt
Аналогичный результат получаем и для другой координатной
линии. Теорема доказана.
Подчеркнем, что из формулы (4) следует, что направляющий
вектор всякой касательной прямой к поверхности в данной точке
dr = rudu+fvdv является линейной комбинацией координатных
векторов, соответствующих рассматриваемой точке, и его
направление (duy dv) определяется отношением дифференциалов
криволинейных координат du и dv в этой точке.
Поскольку все направляющие векторы касательных
прямых к поверхности в данной точке выражаются линейно через
302
Глава 9
координатные векторы в этой точке, то все они компланарны.
А тогда все касательные прямые к поверхности в данной точке
лежат в одной плоскости.
Плоскость, имеющая общую точку с поверхностью и
содержащая все касательные прямые к поверхности в
рассматриваемом точке, называется касательной плоскостью к
поверхности в рассматриваемой точке.
Ясно, что касательная плоскость к поверхности содержит
координатные векторы ги и fv, и ее нормальный вектор η
определяется соотношением n = fuxfv.
Если ρ — радиу'с-вектор произвольной точки Μ
касательной плоскости π к поверхности в точке, соответствующей
радиус-вектору f(uyv)y то векторы ρ— г, ги и fv компланарны,
и уравнение /-# ^^ ^ч _ /г.
(р-г,ги,гу)=0 (5)
является уравнением касательной плоскости π.
Прямую, ортогональную касательной плоскости к
поверхности в данной точке и проходящую через эту точку, называют
нормалью к поверхности в указанной точке.
Очевидно, что вектор n(u^v) = (ru χ fv)/\ru χ rv\ является
единичным вектором нормали к поверхности в заданной точке.
Ясно, что в некоторой окрестности каждой точки гладкой
поверхности существует непрерывное векторное поле нормалей.
Однако есть поверхности, на которых не существует в целом
непрерывного векторного поля нормалей. Примером такой
поверхности является лист Мебиуса, получаемый из
прямоугольника ABCD путем склеивания сторон АВ и CD таким
образом, что при этом точка А совпадает с С, а точка В — с D
(рис. 9.8).
в
А
С
D
Рис. 9.8
Элементы теории поверхностей
303
Поверхности, на которых существует в целом непрерывное
векторное поле нормалей, называют двусторонними.
Поверхности, иа которых не существует в целом непрерывное векторное
поле, называют односторонними.
Предположим теперь, что регулярная без особых точек
поверхность S задана неявным уравнением F(x>y,z) = 0. Если
на ней задана некоторая кривая 1, имеющая параметрические
уравнения χ = x(t)% у = y(t), z = z(t)y то должно быть
выполнено тождество F(x(t),y(t)7z(t)) = 0. Продифференцируем
последнее соотношение по t, получаем
dF^d^ + dFd^ + dFdz{t)=0
дх dt ду dt dz dt
Как известно, вектор t = (£'(£):ί/'(0>2'(0) является
направляющим вектором касательной к кривой I. Но все эти
векторы лежат в касательной плоскости поверхности S,
построенной в соответствующей точке. Поэтому η ± Г, т. е. η t =
= 0. Но тогда нормальный вектор поверхности Я, как следует из
соотношения (6), коллинеарен вектору
gradF
/UF OF 0F\
\дх9 ду' dz)
Таким образом, уравнение касательной плоскости,
проходящей через точку М{х$, г/о, zq) , имеет вид
Fx(x - хо) + Fy(y -yo)+Fz(z-zu) = 0,
где Fx = ^, Fy = ~^, Fz = ^j вычисляются в точке Λ/, а
каноническое уравнение нормали записывают в виде
х-хр = у-уо = ζ- zq
В особых точках поверхности, как известно, \п\ = \ги χ гъ \ =
= 0. Следовательно, Fx = Fy = Fz = 0. Эго означает, что
касательные к различным кривым на по!зерхности, проходящие
через особую точку поверхности, уже не лежат в одной плоскости,
а образуют, вообще говоря, некоторый конус второго порядка с
вершиной в указанной точке.
304
Глава 9
Действительно, так как Fx = Fy = Fz — 0, то справедливо
тождество Fxx'+Fyy' + Fz z' = 0, дифференцируя которое по t.
получаем
d2F
дх2
\dt)
n d2F dx dy d2F
дхду dt dt dy2
ey
+
jPFdxdz nd2F dydz d2F(dz\
dx dz dt dt ' дг/ с?г dt dt ' с?г2 \dt J
SFcPx c?Fd^/ &F^£
+ dx dt2 + 0y dt2 + dz dt2
= 0. (7)
Если точка P(x,y,z) лежит на касательной к линии на
поверхности, то ее координаты удовлетворяют уравнению
Х-ХО У - 2/0 Ζ - Zq
χ'
Следовательно,
У
χ
Х(х - я0), 2/' = A(j/ - j/o)» ζ9 = А(г - г0),
где λ — коэффициент пропорциональности. Подставляя эти
соотношения в уравнение (7) и сокращая на λ2, получаем
§J-(I - *°)2+2ϋ(ι -1о)(г' -ш)+w{v"№)2+
+2έ£(*-*ο)(2-*°)+
δ2/^ С?2/*1
+ 2ττ-Έτ(ν ~ Vo)(z -ζ0) + -^-Ύ{ζ- г0)2 = 0.
dydz
dz2
Полученному уравнению удовлетворяют все точки любой
касательной в точке Μ. Поскольку найденное соотношение, если
d2F
a2F
d2F d2F
дхду
d2F
дх ду дат dz
d7F d2F
~5у*~
d2F
dydz
d2F
'dz2'
3*0,
| dx dz dy dz
определяет конус второго порядка с вершиной в точке М, то и
особая точка называется конической (рис. 9.9).
Элементы теории поверхностей
305
Рис. 9.9
Если указанный инвариант равен нулю, то
полученное уравнение может определять,
например, пару плоскостей, что соответствует
самопересечению поверхности (рис. 9.10).
В заключение
параграфа приведем
уравнение касательной
гиперплоскости и нормали к
гиперповерхности, заданной
неявным уравнением, в неособой точке.
Рис. 9.10 Пусть уравнение гиперповерхности S
задано неявно:
F(x0) = F(xu X2, - - -,xv) = 0,
и точка Xq = (^ι,^2,·--,я?р) € S является обыкновенной
(неособой), т. е. gv&dF(xo) Φ Ο.
Рассмотрим произвольную регулярную кривую I, заданную
параметризацией χ = x(t), лежащую на поверхности S и
проходящую через точку xq . Последнее означает, что хо = ж(^о)
при некотором ίο € Г.
Поскольку указанная кривая лежит на поверхности, то
имеем тождество F(a;i(t),a:2(i)i - - - ,^ρ(ί)) = 0, ί G Г.
Дифференцируя его при t = to, получаем
gradF(iCo) '^'(to) =
dFjxp) dF(x0)
= -diTXl{to) + · ■ ·+ -д^Гх"м = α
Откуда следует, что градиент функции F в точке xq
ортогонален касательной к произвольной кривой на
гиперповерхности, проходящей через хо, т. е. ортогонален касательной
гиперплоскости. Поэтому уравнения касательной гиперплоскости и
нормали гиперповерхности соответственно имеют вид:
(х - х0) · grad F(x0) = 0,
χ = xq + ugradF(a;o) =0, и е {—oo, +oo).
306
Глава 9
§ 3. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА
Пусть S — регулярная поверхность без особых точек, г =
= г (и, υ), (и, υ) е Dn — ее векторное уравнение. п(и, ν) —
единичный вектор нормали поверхности в заданной точке.
При изучении поверхностей важную роль играют
квадратичные формы, связанные с поверхностью:
I = dr2} II=~drdn.
Первая квадратичная форма поверхности I = df2
является квадратичной формой дифференциалов du и dv:
I = df2 = (fudu + fvdv)2 = r2da2 + 2(fu rv)dudv + r2dv2.
Первая квадратичная форма является положительно
определенной, ибо она обращается в нуль только при du = dv = 0, а
для остальных значений du и dv она положительна.
В самом деле, пусть df2 = 0, тогда ru du + fv dv = б, и если
при этом du и dv не равны нулю одновременно, то векторы ги
и fv коллинеарны, т. е. fuxfv = б, что противоречит условию
отсутствия особых точек на поверхности.
Если воспользоваться обозначениями
E = r2, F = fu-rv, G = f2s
то первая квадратичная форма записывается в виде
I = Edu2 + 2Fdudv + Gdv2.
Рассмотрим некоторые вопросы теории поверхностей,
связанные с первой квадратичной формой.
§ 4. ДЛИНА ДУГИ КРИВОЙ НА ПОВЕРХНОСТИ
Пусть I —дуга регулярной кривой на поверхности S,
определяемой внутренними уравнениями
и = u(t), ν = v(t), t € [ίο, 111,
причем u(t) и v(t) —дифференцируемые функции с
непрерывными производными.
Э.геченты теории поверхностей
307
Длина s дуги I, определяемой векторной функцией г =
= r(u(i),v(t)) = f(t), t £ [<ο»*ι]. находится по формуле
и
s= f\f'{t)\dt.
Поскольку
\r'(t)\dt = \r'(u(t),v{t))\dt = \df(u,v)l
то из последней формулы имеем
8= f\r'{t)\dt= j\df{u,v)\= Iy/dF*= fy/ϊ. (1)
«о
I
Если ввести явно переменную интегрирования £, то
to
Таким образом, для вычисления длин дуг кривых на
поверхности достаточно знать первую квадратичную форму, а точнее, ее
коэффициенты Еу Ff G. Используя внутренние уравнения
кривой, следует выразить и и ν через t в квадратичной форме /,
найти *§* и ^, подставить полученные результаты в
подынтегральное выражение, а затем вычислить полученный
определенный интеграл.
§ 5. УГОЛ МЕЖДУ КРИВЫМИ НА ПОВЕРХНОСТИ
Углом между двумя пересекаю-
щимися кривыми 1\ и fa, лежащими
на поверхности, называют угол между
направляющими векторами
касательных к этим кривым в точке
пересечения (рис. 9.11).
Касательные векторы кривых Ιχ
и 12 будем различать, используя разные
Рис.9 J1
308
Глава 9
обозначения для дифференциалов криволинейных координат,
соответствующих измерениям последних вдоль изучаемых
кривых (рис. 9.1 1):
dr = fudu + fv αν, δτ = ru 6u + rv δν.
Тогда dr-δτ
cos θ =
Однако
\άτ\\δτ\
\df\2 = Edu2 + 2Fdudv + Gdv2,
\δτ\2 = Εδη2 + 2Γδυ,δν + Gov2,
df ■ δν = fr2 dud и + ru · fv{dv£v + άνδν) + f2 άνδν,
поэтому
Εάηδη + F(dudv + άνδν) + Gdvov
cos<? = м —.
VEdu2+2Fdudv + Gdo2 · y/Εδυ2 + 2Εδιιδν + G6v2
Подчеркнем, что на данной поверхности в заданной точке
угол между двумя кривыми зависит от отношения
дифференциалов криволинейных координат, взятых вдоль кривых в точке их
пересечения.
Угол θ между координатными линиями в данной точке
называют координатным углом.
Поскольку для координатных линий имеем du = 0, dv Φ 0 и
*"Ό.«" = 0.™ cose = F/VEG.
Отсюда, например, следует, что для того чтобы координат-
ные линии пересекались под прямым углом и образовывали так
называемую ортогональную координатную сеть, необходимо и
достаточно, чтобы F = 0.
§ 6. ПЛОЩАДЬ ПОВЕРХНОСТИ
Пусть требуется вычислить площадь области Ω на некоторой
поверхности, причем область Ω определяется параметризацией
г = г(щу), (и, v) e D (рис. 9.12).
Разобьем область Ω на частичные области Ω ι, Ω2, - -., Ωη -
Во внутренней точке каждой частичной области Ω^ построим
Элементы теории поверхностей
309
касательную плоскость π и на нее спроецируем
соответствующую частичную область.
Пусть Δ5χ — площадь плоской области, получившейся
после проецирования Ω*. Составим сумму
η
i=l
Площадью области Ω на поверхности называют предел S
суммы Sn при неограниченном возрастании числа частичных
областей и при стягивании каждой частичной области к точке:
S = lim Sn.
η—>оо
Выберем границы частичных областей так, чтобы они
совпали с координатными линиями. Рассмотрим одну из
частичных областей Ωτ, предположив, что ограничивающие ее
кривые пересекаются в точках Pi(u^\v^), P2(uw + Au^\v^),
P3(u(i) + AuW,t/W + Δν&), Ρ4(««,t/W + Δν<*>).
Спроецировав эту частичную область на касательную
плоскость π в точке Pi{u^\v^)9 получаем криволинейный
четырехугольник Р1Р2Р3Р4.
Отметим, что в силу формулы Тейлора
р[р2 = f(«W + Δ«(<>,«W) - г(и^Мг)) =
АР! = f(J*>,!;<*> + Δν<*>) - f(«wf v(t)) =
= ΓνΔι/(ι) + ε*2Δ?/*\
причем
lim έι = 0, lim ε2 = 0.
310
Глаоа 9
Пренебрегая малыми более высокого порядка малости, мы
можем принять проекции векторов Р\Рг и Р\Р* на касательную
плоскость равными векторам гиАи^ и fvAv^.
И снова, отбросив малые более высокого порядка, заменим
площадь ASi плоской проекции ΡχΡ^Ρ^Ρ^ площадью
параллелограмма, построенного на векторах гиАи^ и τγΔι/(^ как на
сторонах.
Получаем ASi = \ru(u^\v^) x rv(u^,v^)\Au^Av{i\
η
S = lim Sn = lim V \fu χ fv\Au^Av{i\
Таким образом, площадь области Ω заданной поверхности
выражается двойным интегралом
S= ff\ruxrv\dudv. (1)
D
В силу тождества Лагранжа
\ги х rv\2 = r?fj - (^ . ^)2 = EG-F2 (2)
имеем
S = // JEG-F2dudc.
= ffVzc--
D
Можно показать, что интеграл (1) не зависит от выбора
параметризации.
§ 7. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ
Пусть S — регулярная поверхность без особых точек, г =
= г(гцг>), (η,ν) е D, — ее регулярная параметризация,
п(и, ν) — единичный вектор нормали поверхности в точке Р(гх, г>).
Второй квадратичной формой поверхности называется
выражение
II = — df- dn>
и поскольку
df =rudu + fv άν} dn = nu du + nv dv>
Элементы теории поверхностей
311
то
II = —dr · dn = (—fu ■ nu) du2 +
+ {-?u -nv -fv · nu) dudv + (-fi, · iiv) dv2. (1)
Если ввести обозначения
L= -ru-nU} 2Л/ = -τηην-τν-ηη, Ν = -fvnvy (2)
то
// - /, du2 + 2M du dv + N dv2. (3)
Поскольку df-n = Ο,το d(dr-n) = 0, и d2rn + dr-dn = 0.
Откуда —dF- da = ά2τ·ή.
А тогда
II = d2rn. (4)
Следовательно,
// = (тчш · ?г) dix2 + 2(fttu ■ ή) du dv + (rrr · r?) d*;2. (5)
Из формул (5) и (3) имеем
L = fuu -n, Μ = fuv · π, Ν = fvv - η, (6)
где
?Т(гх, ν) = —
г« х г«
7'u X 7'-y
|f„ x r„j y/EG-F2'
Поэтому окончательно получаем
VEG^F2
y/EG - F2
y/EG-F2'
§ 8. КРИВИЗНА КРИВОЙ. ЛЕЖАЩЕЙ НА ПОВЕРХНОСТИ
Пусть на регулярной поверхности
S\ заданной векторной функцией
f = ?г(и,г>), (иуь) G £>, с
единичным вектором нормали η в
точке P(u,v)% лежит регулярная
кривая f, проходящая через P(u>v) и
имеющая в этой точке направление
(du,dv)(pnc.9.!3).
312
Глава 9
Если в качестве параметра на кривой I выбрана длина
дуги s, то кривая I задается уравнением
? = r(s) = r(u(s),v(s)), s е (α, β),
и вектор f"(s) направлен по главной нормали η ι кривой I в
точке Р, примем его модуль равен кривизне А: кривой I в точке Р.
По правилу дифференцирования сложной функции имеем
r'(e) = rX+rX, m
-*// /\ -* /2.0-* //»-· /2.-*//.-*// * '
г (s) = ruuuf + 2ruvusvs + rvvv/ + ruus + rvvs -
Если φ — угол между векторами пищ, то, приняв во
внимание, что η JL fUj ή JL rV9 имеем после умножения
соотношения (1) скалярно на вектор η
fa так как ds2 = df2 = J, то
__ Ldu2 +2Mdudv + Ndv2 _ /J
kC0S(p ~ Edu2 + 2Fdudv + Gdv2 ~ Г ( }
Правая часть выражения (2) зависит только от отношения
du/dv, т. е. от направления кривой I в точке Р. В связи с
этим для всех кривых I на поверхности S, проходящих через
точку Ρ в заданном направлении (du:dv)y выражение к cos φ
равно некоторой постоянной fcn, т. е,
ксоыр = кп. (3)
Последнее соотношение выражает смысл теоремы Менье
(1754-1799).
Нормальным сечением поверхности S в точке Ρ
называется линия пересечения с плоскостью, проходящей через нормаль
поверхности в этой точке.
Если кривая представляет собой нормальное сечение
поверхности S в направлении (ащ dv), то φ = 0 и к — кп.
Таким образом, величина ка — кривизна нормального
сечения поверхности в направлении (du,dv); она называется
Элементы теории поверхностей
313
нормальной кривизной поверхности S в данной точке Ρ и в
данном направлении (du,dv).
Отметим, что величина кп есть проекция вектора кривизны
τ "(s) кривой I на единичный вектор нормали поверхности S в
точке Р, и ее называют также нормальной кривизной линии /.
§ 9. ГЛАВНЫЕ КРИВИЗНЫ
Как уже отмечалось, нормальная кривизна в заданной точке
Ρ регулярной поверхности S зависит от выбора направления
(cfu, dv) на поверхности и равна
Л _ Ldu2 + 2Mdudv + Ndv2
"~ I Edu2 + 2Fdudv + Gdv2'
Направление на поверхности называется главным, если
нормальная кривизна в этом направлении достигает
экстремального значения.
Пусть (ξ, η) — произвольное направление в точке Ρ G S.
Тогда
If + iiito + Nf
kfl~ E? + 2FtV + GV* -kM>> (,)
где коэффициенты L, Μ, Ν, Е, F, G не зависят от переменных
ξ и η. Если положить ξ = cost, η = sinί, то при t G [0,2π]
определятся всевозможные направления· Но тогда
_ Lcos2t + 2М costsint + N sm21 _ f
n~~ Ecos2t+ 2F costsint+ G sin21 ~ ^'
Так как первая квадратичная форма / является
положительно определенной, то k(t) — непрерывная функция, а
следовательно, достигает на интервале [0,2π] наибольшего и
наименьшего значения. Поэтому в каждой точке регулярной поверхности
существуют по крайней мере два главных направления.
Значение нормальной кривизны в главном направлении в
точке Ρ называется главной кривизной.
314
I лава 9
Соотношение (1) определяет тождество
(L - kE)f + 2(М - kF)£V + (Ν - kG)V2 - 0.
Продифференцируем это тождество сначала по ξ, а затем
его же по г/. В главном направлении производные нормальной
кривизны к^ = 0, №η = 0. Откуда получаем два соотношения
(L - кЕ)£ + (Μ - kF)V = 0,
(Μ - fcF)£ + (iV - kG)V = 0. l
Полученные уравнения можно рассматривать как систему
однородных линейных алгебраических уравнений
относительно ξ и г?. Она имеет ненулевое решение, ибо в каждой
точке поверхности существуют по крайней мере два главных
направления. Следовательно, определитель матрицы этой системы
должен быть равен нулю. Поэтому
= (L-kE)(N-kG)-(M-kFy =
2 _
L-kE M-fcF|
M-kF N-kG\
= (EG-F2)k2-{EN-2MF+LG)k + {NL-M2) = Q. (3)
Так как в каждой точке поверхности два главных
направления, то уравнение (3) имеет два вещественных корня /ci и &2,
совпадающих с главными кривизнами. При этом либо к\ = hi,
либо fci Φ k<i.
Если к\фк2> то этим корням отвечают два главных
направления (£ι,7/ι) и (^2)^2), которые можно найти из системы
(L - кгΕ)ξί + (Μ - ktF)n = 0,
(Μ - hF)^ + {N- kiG)rh = 0, % = 1,2.
{!
Пусть к\ = k2 = к. Так как система (2) всегда имеет по
крайней мере два линейно независимых решения, то в данном
случае L_kE = 0^ Λί - JfcF = 0, Ν - kG = 0,
поэтому L = kE, Μ = kF, N = kG, а значит,
kn = — — к = const,
Эгементы теории поверхностей
315
т. е. нормальная кривизна поверхности в данной точке
постоянна (не зависит от направления). В данной ситуации любое
направление является главным.
Допустим, что ki и ki — главные кривизны регулярной
поверхности в данной точке.
Средней кривизной Η поверхности в данной точке
называется полусумма ее главных кривизн
Гауссовой кривизной К поверхности называется
произведение ее главных кривизн К = fcifo -
Заметим, что главные кривизны — корни квадратного
уравнения (3), а потому
К
LN-M2
EG - F2
Н =
EN-2FM + GL
2(EG-F2)
§ 10. ПОВЕРХНОСТИ ВРАЩЕНИЯ
Пусть поверхность S образована вращением плоской кривой I
вокруг оси Ок. Плоскость π, проходящая через I и ось Ок,
пересекает плоскость Qffno прямой ОР;, причем <р = Ζ(ι7β(φ)),
где β(φ) — единичный вектор
с началом в О на прямой ОР\
0 ^ φ < 2тг.
В подвижной плоскости π
будем рассматривать систему
координат Oe(ip)k с осями Οη
и Οζ (рис. 9Л4).
Пусть η = η(ί), С = С(*)> * £ (<*!$)» — параметрические
уравнения линии / в указанной подвижной системе координат.
Векторное уравнение поверхности S имеет вид
г = ffe>, t) = η(ί)β(φ) + ζ(ί)£, 0 ^ φ < 2тг, t G (α, /3),
Рис. 9.14
316
Глава 9
где г(φ} t) — радиус-вектор произвольной точки Ρ(φ> t) на
поверхности S.
Подчеркнем, что координатные линии на поверхности S суть
параллели (t = const) и меридианы (φ = const).
Вычислим первую квадратичную форму поверхности
вращения, приняв во внимание, что
—jp- = 9(ψ) > 9(ψ)= ~^sin φ + jcos φ}
df= η(ί)ο{φ) άφ + (i/(t)efo>) + C(t)k) dt}
а поэтому j = (djf = η2άψ2 + (j/2 + ς/2) Λ,ι
т. е. Е = η2, F = 0, G = η,2+ζ'2.
Поскольку в последнем выражении отсутствует
произведение дифференциалов (F = 0), то координатная сеть, состоящая
из меридианов и параллелей, ортогональна.
§ II. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
Линейчатой поверхностью называют поверхность,
описанную движением прямой, называемой образующей,
пересекающей при движении некоторую кривую I, называемую
направляющей поверхности (рис. 9.15).
Пусть уравнение направляющей
кривой I имеет вид ρ = р(и), и е
£ (&>Р)у а единичный вектор
образующей d в точке,
соответствующей значению параметра и, есть
μ{μ).
Уравнение линейчатой
поверхности S, образованной движением образующей d,
пересекающей направляющую I, имеет вид
i\u,v) = р(и) + νμ(υ)τ и G (α,β), ν G (-oo, +oo),
где r(u,v) —радиус-вектор произвольной точки P(u,v) на
поверхности S.
Элементы теории поверхностей
317
Поскольку fu—p,iL + νμ*ητ rv = μ(ιι),τσнормальный вектор
линейчатой поверхности имеет вид
П = ги хти = р^х μ + υ{μΙ χ μ).
Первая квадратичная форма произвольной линейчатой
поверхности с учетом состояний "μ*2 = 1, μ^ ■ μ = 0 имеет вид
/ = (df )2 = ({р'и + μ» du + μ(η) dv)2 =
= (pL2 + 2pL ' vLv + Й2^2)du* + 2μ · р'и du dv + dv2.
Линейчатая поверхность называется развертывающейся
поверхностью, если ее касательная плоскость остается
неизменной вдоль прямолинейной образующей, в противном случае
линейчатую поверхность называют косой поверхностью.
Рассмотрим три примера,
исчерпывающие класс развертывающихся
линейчатых поверхностей.
Коническая поверхность с
вершиной в точке М(ро) и направляющей
Ρ — Ρ(ν) имеет уравнение r(u,v) =
= Ро + νμ(ν), где μ{υ) — единичный - ро
вектор, коллинеарный ρ — μο, и тем Puc.9J6
самым является линейчатой поверхностью* Направление
нормального вектора, вычисленного в произвольной точке
образующей, остается неизменным, так как n(u,v) = (μ^ χ μ)ν
(рис. 9.16). Таким образом, коническая поверхность есть
развертывающаяся поверхность, и ее первая квадратичная форма
имеет вид _ , ,_2 -/2 2 ι 2 » 2
J = (dr У = μύ V du2 + dvJ\
Цилиндрическая поверхность с направляющей ρ — р(и)
и образующей с постоянным единичным направляющим
вектором μ, имеет уравнение p(u,v) = р(и) + νμ, и для нее
нормальный вектор n(u,v) = р'и χ μ остается неизменным вдоль
образующей, т. е. всякая цилиндрическая поверхность является
развертывающейся, а ее первая квадратичная форма
/ = p'u2du2 + 2(Й · μ) du dv + dv2.
318
Глава 9
Поверхность, образованная касательными к некоторой
кривой ρ = р(и), также является развертывающейся поверхностью.
Действительно, для указанной поверхности направляющий
вектор образующей μ[η) = й, а поэтому нормальный вектор
касательной плоскости в произвольной точке образующей совпадает
с вектором (р"и χ р^)ь и не меняет своего направления.
Следовательно, поверхность касательных является
развертывающейся, а ее первая квадратичная форма имеет вид
I = (Й + vftu)2 du2 + 2(Й2 + vplu - Й) dudv + р[2 dv2.
ЗАДАЧИ И УПРАЖНЕНИЯ
{.Плоская кривая χ — fi(v), z = f2(v),лежащая в плоско-
ста Οχ ζ и не пересекающая ось Οζ, вращается вокруг
указанной оси. Найти параметрические уравнения по-
лученной поверхности вращения.
Решение. Зафиксируем произвольно ν = ν\> Тогда точка с
координатами (Λ(^ι),Ο, /2(^1)) при вращении плоской кривой
опишет окружность с радиусом f\{v\). Параметрические
уравнения указанной окружности имеют вид χ = fi{vi)cosu, у =
= fi(vi)sinu, z = /2(^1). В силу произвольности vi
искомыми уравнениями поверхности будут являться соотношения χ =
= fi(v)cosu9 у = fi(v)sinu, ζ = f2(v).
2. Написать уравнение цилиндрической поверхности с
направляющей ρ = р(и) и образующими, параллельными
постоянному вектору а.
Решение. Очевидно, что для любого фиксированного и
получим точку на направляющей с радиус-вектором р(и) , а поскольку
образующая цилиндрической поверхности есть прямая, то
вектор-функция т{щ ν) — р(и) + να задает произвольную точку на
указанной цилиндрической поверхности.
3. Задана точка М(ро) и кривая I : ρ = р(и).
Написать параметрические уравнения конуса с вершиной в
точке Μ и направляющей I.
Решение. Для любого фиксированного и имеем радиус-
вектор р(и) точки, лежащей на кривой Ζ, а следовательно,
Элементы теории поверхностей
319
направляющий вектор образующей конической поверхности
совпадает с вектором р(и) — рЬ· Тогда параметрические
уравнения конической поверхности г {и, v) = ро + v{p{u) — ро) -
4. Составить уравнение линейчатой поверхности,
образующие которой перпендикулярны вектору η и
пересекают прямую f=a + ubu кривую ρ — ρ(ν).
Решение. Очевидно, что направляющий вектор образующей
т = а + иЪ - ρ(ν). Но по условию m ■ η = 0. Поэтому
μ(ν) -η — а - η
откуда т = a+b(p(v)-n—a-n)/(b-n) — p(v). Поэтому уравнение
искомой линейчатой поверхности
-/х ч -/ ч ч (^ rp{v)^n — an _, Л
?(λ,ν) = ρ(ν) + \ (а + Ьнк } ^ ρ(ν)).
\ о-п /
5. Найти параметрическое уравнение поверхности,
образованной касательными к данной кривой ρ = р(и)
(торса). Является ли торс линейчатой поверхностью?
Решение. Направляющие векторы касательных,
определяющих указанную поверхность, равны р'(и). Поэтому
параметрическое уравнение торса f{u^v) = р(и) + vp'(u).
Непосредственно из определения следует, что торс является линейчатой
поверхностью.
6. К поверхности xyz+8 = 0 провести касательную
плоскость, параллельную плоскости 2х + 2у + 2z — 5 = 0.
Решение. Уравнение касательной плоскости в произвольной
точке (хо, 2Ль ^о) данной поверхности имеет вид
2Л)2оО - so) + яо*о(г/ - ϊ/ο) + А)2/оО - *о) = 0.
Так как плоскости параллельны, то их нормальные векторы
коллинеарны, т. е. y$zo __ x^zo __ Уо%о
~2~ = ~2~ = ~1Г"
Следовательно, хо = г/о = zq- Но хоУо^о +8 = 0, поэтому
х0 = у0 = zq = -2. Таким образом, искомое уравнение имеет
вид х + у + ζ + 6 = 0.
320
Глава 9
7. Найти длину дуги кривой, заданной уравнением ν =
= ηη, на поверхности с первой квадратичной формой
I = du2 + ψ{ύ\ν)2dv2 между точками Mi(ui,vi) и
M2(u2,v2).
Решение. Так как dv = η du, το
I = ds2 = du2 + Λ (sM2(72 du2),
7
а следовательно, ds2 = (1 + sh2 u) du2. Поэтому
TX2 U2
S
U2 U2
= I y/l + (shu)2 du = I en и du = shu2 — shui.
8. Найти площадь четырехугольника, лежащего на
поверхности с первой квадратичной формой I = du2 +
+ {и2 + a2)dv2> ограниченного линиями и = 0, и = а,
ν = 0, ν = 6.
Решение. Площадь указанной поверхности
а Ь
S= ffy/EG-F2dudv= f f\/u2 + a2dvdu =
D 0 0
= 6 / y/tf+a*du = b |«^±? + ^in|w + y/tf^tf\\
0 ^ '
= ^(V2+ln(v^+l)).
9. Найти угол между линиями αν + βυ. = 0, ην + ηη = 0,
где αη — βη^Ο,πα поверхности с первой квадратичной
формой I = du2 + dv2.
Решение. Ясно, что adv + βάη = 0, ηδν +ηδη = 0.
Следовательно, dv = (—β/a) du, δν = {—η/η) би. Тогда
cosy? =
du δη + (-g du) (-ДДц) _ αΊ + βΐ}
du6u
4^ξφ^$ V^TWs/ψΤ^
где φ —угол между указанными линиями в точке их пересечения.
Э гементы теории поверхностей
321
10о Вычислить нормальную кривизну поверхности ζ = §- +
+ γ- в точке Р(0,0) в направлении dy : dx — 7.
Решение. Непосредственной проверкой убеждаемся, что / =
= dx2 +dy2, a // = (l/p) dx2 + (1/g) dy2. Поэтому нормальная
кривизна /w \2
_ \άχ2 + \dV2 _ p + j(d£j _ 4 + P72
d^ + dy* ι^Λ*«Λ2 Ρ<2(1+72)'
1 +
11. Окружность (χ — a)2 + у2 = β2, ζ = О, где а > R,
вращается вокруг оси Оу* Найти параметрические
уравнения поверхности вращения (тора).
Ответ: χ = (а + Я cos u) cos г>, у = Rsinu, ζ = (α +
+ R cos и) sin ν.
12o Направляющая цилиндрической поверхности задается
уравнениями χ = f\{v), у = /г(^)* г = 0, α ее
образующие параллельны оси Οζ. Найти параметрические
уравнения цилиндра.
Ответ: х = fi(v)y y = f2{v), z = u.
13о Написать неявное уравнение конуса с вершиной в
точке (1,1,1) и направляющей χ = acosu, у = bsinu, ζ — 0.
Ответ: b2(x - ζ)2 +a2(y - ζ)2 = a2b2{z -Ι)2.
Но Найти неявное уравнение цилиндрической поверхности
с направляющей ρ = (cos щ sin и, 0) и прямолинейными
образующими, параллельными вектору а = (1,-3,2),
Ответ: (2х - ζ)2 + (2у + Зг)2 = 4.
15о Составить уравнение линейчатой поверхности,
образованной прямыми, параллельными плоскости Оху и
пересекающими кривую χ = и, у = и2, ζ = и3 и ось Οζ.
Ответ: χ = uvy у = vu2, ζ = u3.
16. Принадлежат ли точки А(3,5, -4) и J5(l,3,2)
поверхности т{щ ν) = (и + ν, и — ν} uv) ?
Ответ: точка А принадлежит; точка В не принадлежит.
П.Дана параметризация f(u,v) = (-q^-, ^qp^r, TF+Z*)
некоторой поверхности. Показать, что уравнения χ =
= ucosv, у = ^sint>, z = и2 определяют эту же
поверхность.
322
1лава 9
18. Составить уравнения касательной плоскости и
нормали к тору £ = (\/2 + cos г/) cost;, у — sin г/, ζ = (\/2 +
+ cos и) sin г; β точке Μ (и = \; ν = |) .
Ответ: χ + >/2*/ + ~ ~ 4 = 0.
19. Через точки Л(0,1,0) и Б(1,0,0) провести плоскость,
касательную к поверхности г (и, ι) = (и, v, а2 + о2).
Ответ: ζ = 0, 2х г 2у - ζ - 2 = 0.
20. Построить касательную плоскость к поверхности у =
= χ2 + ζ2, перпендикулярную вектору а = (2,1, ~ 1).
О г нет: 8я + 4,у - 4^ + 5 = 0.
21. Через точку М(1,2,1) провести плоскость,
касательную к поверхности х2 + у2 — ζ2 = 0.
Ответ: χ - ζ = 0, Зх - 4?/ + bz = 0.
22. Написать уравнения прямых, проходящих через точку
Л/(1,1,2) и перпендикулярных поверхности х2 ~l· у2 +
+ 2z2 = 10.
Ответ: х + 2 = // + 2 = 2-1;х-1=у-1 = (г-2)/4.
23. Дана поверхность ζ = аху. Найти угол между
координатными Линиями X = Xq, у = 7/0·
Ответ: cosu> = , a2*cf
24. Найти периметр ρ и внутренние углы α, β, η
криволинейного треугольника, ограниченного линиями и ^ αν,
и = —αν, υ = 1, лежащего на поверхности с первой
квадратичной формой I = du2 + (и2 + a2) dv2.
Ответ: ρ = а(л/3 + 2 + 1п(л/3 + 2))\ а = |, 0 = 7 =
= arccos(l/\/3).
25. Найти нормальную кривизну гиперболического
параболоида ζ = χ2 -у2 в точке М(х = 0- у = 0) β направлении
dy : dx — β : €Υ.
Ответ: fcn = *£#.
26. //а поверхности f{vyv) — (и2 + с2, и2 - v2,uv) дана
точка Μ (и = 1,ί> = 1). Вычислить кривизну нормального
сечения в точке 1\1, проходящего через касательную к
линии ν = а2.
°твет:^·
Часть третья
ЭЛЕМЕНТЫ
ВЫПУКЛОГО
АНАЛИЗА
В данном разделе мы ограничимся исследованием
класса выпуклых геометрических объектов. Это
объясняется в первую очередь прикладной
стороной указанного класса моделей: именно
выпуклые фигуры лежат в основе теории оптимизации
(линейной и нелинейной), а также теории
оптимальных процессов управления. Представленный
теоретический материал позволяет получить
исчерпывающее представление о многомерных
плоскостях, многогранниках, конусах и
цилиндрах, покрывающих класс линейных
геометрических объектов, которые описываются
системами линейных уравнений и неравенств
(многогранные множества). В конце раздела показано,
как элементарное применение теории приводит
к геометрическому решению задачи линейного
программирования.
Все доказанные теоремы сопровождаются
соответствующими геометрическими
интерпретациями, что позволяет использовать
данный материал в качестве введения в выпуклый
анализ.
Глава 10
ГЕОМЕТРИЧЕСКАЯ СТРУКТУРА
СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
§ 1. ВЕКТОРНОЕ ПРОСТРАНСТВО W1
Начнем изложение с необходимых сведений из теории
векторных пространств. Данный материал является
непосредственным развитием главы 1 применительно к векторному
пространству Rn.
Напомним, что под вектором α е Rn мы понимаем
упорядоченную систему η вещественных чисел, т. е. α = (αϊ, ..., αη).
В дальнейшем векторы (элементы Rn) будем обозначать
латинскими строчными буквами, а скаляры — греческими. Так, если
Ь е Шп, то Ь = (ри ..., βη), где ft е К, г = 1, 2,..., п.
Предполагается, что в Шп введены линейные операции
(сложения и умножения на вещественное число) по правилам
α+ 6= (αι,...,αη) + {βι,...,βη) =
λα = λ(αι,...,αη) = (λαι,·..,ΑαΛ).
Тогда пространство Rn с введенными операциями
представляет собой линейное (векторное) пространство, или линеал
(глава 1,§3).
Множество L С R71 называется линейным
подпространством, если для любых а, Ь 6 L и любого вещественного λ
выполняется a + b€LyXa€L.
Любое линейное подпространство является линеалом.
Размерностью линейного подпространства L с Rn
(обозначается dim(L)) называется максимальное число линейно
Геометрическая структура систем линейных уравнений 325
независимых векторов подпространства, а базисом —
максимальная упорядоченная система линейно независимых векторов
из L.
Пространство Rn является линейным подпространством,
при этом dim(En) = п. Другими словами, Rn —
подпространство максимальной размерности.
Заметим, что ранее мы определяли базис линеала как
упорядоченную систему линейно независимых векторов, если любой
вектор линеала можно представить в виде их линейной
комбинации (глава 1, § 6). Введенное выше определение эквивалентно
данному в силу справедливости следующей теоремы.
Теорема 1 (о базисах)· Для того чтобы линейно
независимая система векторов е\,..., er € L образовывала базис
линейного подпространства L, необходимо и
достаточно, чтобы любой вектор у е L был представлен в виде
линейной комбинации этих векторов, nt е. у = ΣΓ-^ι **'е* ■
Доказательство. Достаточность. Предположим, что
любой вектор у € L можно представить в виде у = Σ*=1 Кег
Тогда L. не содержит никакого большего набора независимых
векторов, так как любое множество, состоящее более чем из τ
векторов, должно быть зависимо (по теореме 1 § 4 главы 1).
Таким образом, dim(L) = ги векторы е^;, г = 1,..., г, составляют
базис.
Необходимость. Пусть ei,..Mer образуют базис
подпространства L. Тогда diin(L) = г и векторы ei,...,cny e L
линейно зависимы, так что Σ!=ι ^ei+Xy = О, где А Φ 0 (в
противном случае векторы е\,..., еГ были бы линейно зависимы)
Таким образом, получаем у = — χΣΓ=ι^*β*' что и дает
требуемую линейную комбинацию.
Введем в пространстве Шп теоретико-множественные
операции.
Пусть А,В С Ш" — некоторые множества, А е Ш. Тогда в
Шп можно ввести следующие операции над множествами:
АГ\В = {с\сеА,с€В} — пересечение:
AUB = {с\се А или се В} — объединение:
326
Глава iO
Л + В = { с I с = α + 6, ае A be В} — сумма Aw В
(если для каж шго с € Л + В представление с = а 4- Ь
единственно, то говорят о прямой сумме множеств и пишут Л 3jl?).
ΧΑ = {с | с = Аа, а е Л } — умножение на
вещественное число.
Е-сли ЛсЕп, Бс Rm, то >;ожно ввести операцию
декартового произведения множеств
Ах В = {{а.Ъ)\ае А, ЬеВ],
где ЛхВсГхГ- Rn+rn, а (а, Ь) — пара векторов.
Для любого множества А с Rn можно построить
линейную оболочку множества, обозначаемую Lin (Л) и
представляющую собой множество всевозможных линейных комбинаций
векторов из Л, т. е.
Lin(i4)
<α α — \jAfca2, a e Л >.
^ ι * ^
Линейная оболочка любого множества является линейным
подпространством (см. упр. 4 данной главы).
1 !<шомним, что ранее в пространстве W1 было введено
скалярное произведение двух векторов α = (αϊ,... ,au) и Ь =
— (βι>- · · у %) πο правилу п
ab = У^а2^.
2 = 1
Нетрудно убедиться, что введенное указанным образов
скалярное произведение удовлетворяет необходимым аксиомам,
поэтому пространство Rn со скалярным произведением является
евклидовым и в дальнейшем будет также обозначаться R71.
Для любого множества В с Rn можно ввести операцию,
сопряжения: , . ^ Λ _.
1 В* ^ {х\ху^Оу уеВ},
где множество В* называется сопряженным к В.
Пусть Л = {ctij} —матрица порядка mxn.B дальнейшем
будс м применять следующие обозначения:
а* = (α4ι> atrl) еШп — г-я строка матрицы Л,
а3 = (aijj ..., amj) G Rm — j-й столбец матрицы Л.
Геометрическая структура систем линейных уравнении 327
Ясно, что матрица А может быть задана своими
строками или столбцами, т. е. А = [аьа2, ---, ат] или А
= [а1, а2 у . ·., ап].
Максимальное число τ9 (г9/) линейно независимых строк
(столбцов) матрицы А называют стро*и иным (столбцовым)
рангом матрицы А.
Соответственно максимальная система {αι.α2ι . ··, а*}
({а1, ·.., аг }) линейно независимых строк (столбцов)
матрицы А называется строчечным (столбцовым) базисом
матрицы А.
Другими словами, система векторов {αχ.α2, ..., α,'}
( { α1,..., ar }) образует базис линейного подпространства
Lin{ а\, а,2У ..., ar/ } (Lin{ a1, ..., ar }). Понятно, что числа
г' = dim(Lin{aif ... > ат }), г" = dim(Lin{al. ..., α71 })
являются соответственно строчечным и столбцовым рангами
матрицы А. Из алгебры также хорошо известен результат,
который мы приведем без доказательства.
Теорема 2 (о ранге матрицы). Для любой матрицы А
I II
Г = Г .
Общее значение г строчечного и столбцового рашов
называется рангом матрицы и обозначается
г = гапк(Л) = та — г' = г".
Следствие. Пусть αϊ,..., ar — произвольные числа, а векторы
аь ..., огеЕп линейно независимы. Тогда система линейных
уравнений
а,гУ = а,·. г = 1, ..., гу
всегда имеет решение.
Доказательство. Пусть А = {αϊ, . , аГ\ — матрица, у
которой векторы oi,...,ar являются строками. По теореме о
ранге матрицы г' = г" = г. Пусть а1, ..., аг —столбцовый
базис матрицы А.
328
Глава 10
Рассмотрим вектор а = (αι, ...7 ar) е Ег. Векторы
а* .., а' образуют базис Rr , поэтому по теореме о базисах
г
а тогда вектор з/ = (ηι? - -., ^г?0, ..., 0) € Rn и дает искомое
решение.
С помощью операции скалярного произведения можно
ввести операции умножения матрицы на вектор. Действительно,
пусть А = {ocij} — матрица порядка τη χ η, χ = (ξι, ..., £m) G
€Rm,s/ = fab --, г?п)еКп.Тогда
(771 771 ν
m m
г=1 г=1
Ау=(<цу,..., amy) = ΙΣ Ъ<*ц, ■.., Σ Ъа™) )
η
Используя различные формы записи произведения матрицы
на вектор, получаем различные (эквивалентные) формы записи
систем линейных уравнений. Действительно, система η линейных
уравнений с m неизвестными &, &» ·■ -t Cm» матрицей
коэффициентов А = {aij} порядка πι χ η и вектором свободных
членов системы 6 = (βι,.. - ,/?п) может быть записана в одном из
эквивалентных видов:
χ А = 6;
i—1
• 1
хаР =/3j, j = 1, ...,η;
τ»
У^&<4? = ftj> j = l,...,n.
t=l
(1)
(2)
(3)
(4)
Геометрическая структура систем линейных уравнений 329
Аналогично, если система т линейных уравнений имеет η
неизвестных η\, ryi» ■ · * Лп, ту же матрицу коэффициентов А
и вектор с = (7ь72>--->7ш) свободных членов системы, то
она может быть записана в одном из следующих эквивалентных
Ау = с; (5)
η
5^7fraJ=c; (6)
Ог?/ = 7г> i = l,...,m; (7)
η
Σ)%<4ΐ=7ι> i=l,...,m. (8)
В дальнейшем будем пользоваться одним из этих видов
системы уравнений без специальных ссылок.
Перед тем как переходить к рассмотрению материала
следующего параграфа, советуем рассмотреть упражнения 1—4
этой главы.
§ 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
В данном параграфе мы выведем основные свойства множества
решений системы линейных уравнений, которые определяют его
алгебраическую структуру.
Теорема 1 (об однородной системе линейных уравнений).
Рассмотрим систему линейных уравнений
χ А = О, (I)
где А —матрица порядка тхп. Если гапк(Л) = г, томно-
жество L = {χ \ χ А = 0} —линейное подпространство,
причем dim(L) =rn — r.
Доказательство. Пусть х\, Х2 € L и λ — вещественное
число. По свойствам произведения матрицы на вектор имеем:
(χι + Х2)А = х\А + хоА = О, (Хх\)А = Х(х} А) = О,
поэтому L —линейное подпространство.
330
/ лава 10
Покажем, что dim(L) = τη — г. Пусть а\% .,., ат —
строчечный базис матрицы Л. Тогда
г
°* = 5^^ife0lt к = r + l,...,m.
Рассмотрим векторы Ь/с = (-μι*, ..., —/*rfc> 0,... ,1.0— ,0) G
G Rm, где 1 находится на fc-ом месте, fc = r + l,...,m.
Эти векторы независимы (легко проверить от противного), Ь^ е
е L, fc = r + 1,...,m (по построению). Покажем, что любой
вектор χ = (ξχ,..., ξϊη) G L можно представить к виде линейной
комбинации векторов {Ь^}, fc = r + l,...t77?.
Действительно, рассмотрим вектор
m
Вектор ж' = (£[>--,ξ'7η) является линейной комбинацией
решений системы (1), поэтому xf e L. По построению ξ[ =
=. о, i: = г + 1, ..., т. Тогда из (1) Σί=ιίίαΐ = О* н0 по
предположению αχ,..., аг линейно независимы. Поэтому ξ^ =
= 0,? = 1,...,г. Таким образом, ж' = Ои
777
Тогда по теореме о базисах m — г векторов br+i, ..., bm
образуют базис L, причем dim(L) — τη — г.
Следствие. Пусть L с Rm —линейное подпространство. Тогда
dim(L) + dim(L*) = m.
ЗАМЕЧАНИЕ. Доказательство теоремы конструктивно,
поскольку позволяет построить базис пространства решений
системы (1)(см. упр. 5).
Рассмотрим неоднородную систему линейных уравнений
хА = Ь.
(2)
Геометрическая структура систем гинейных уравнений 33 1
Пусть X = {х \ хА = Ь} — множество решений сие re
мы (2), a xq е X — се частное решение. Из линейной алгебры
известно, чти
X = {χο} + L = {х\х = х0 + у. j/€L}, (31
где L — множество решений соответствующей однородной
системы (1). Множество X, представленное в виде (3), иногда
называют сдвигом L на вектор ж0.
Докажем теорему о разрешимости системы линейных
уравнений, которая нам будет нужна в дальнейшем.
Теорема 2 (о разрешимости системы линейных уравнений).
Справедлива одна из следующих альтернатив: либо имеет
решение система линейных уравнений
хЛ = Ъ, (1)
либо ичеет решение система
Ау = Оу Ьу-1. (Г>)
Доказательство. Системы (4), (5) одновременно иметь
решение не могут. Действительно, предположим противное. Пусть
χ — решение системы (4), а у—системы(5). Подставим χ \\(\)
и умножим получившееся тождество на вектор у. Тогла
О = х(Ау) = Ьу ^ I.
Противоречие и доказывает невозможность одновременного
существования решения систем (4) и (5).
Пусть (4) не имеет решения. Предположим, что векторы
αϊ, ..., аг образуют строчечный базис матрицы А. Тогда
векторы αχ,,.., αΓ, 6 линейно независимы, поскольку в противном
случае существует решение χ системы (4). Поэтому для любых
чисел с*ь ..., аг, α по следствию к теореме о ранге матрицы
система уравнений
{щу = а„ г= 1, ..,r, ^
\by = a
332
Глава 10
имеет решение. Положим аг = 0, г = 1,..., г; а = 1 и заметим,
что
г
ак = 2jAifcflbi, fc = г + 1,...,:
г=1
т.
Тогда, подставляя решение у системы (6) в (5), получаем
<*>iy = 0, i = 1, ..., г,
г
<ЗД = 5Z λ**(α*2/) = °' fc = Г + 1, . . . , Ш,
г=1
Рассмотрим геометрическую интерпретацию теоремы. Пусть
L = Lin{ai, ..., am}. Тот факт, что система (4) имеет
решение означает, что Ь е L.B противном случае Ь ф. L.
Тогда по теореме 2 существует
вектор У у для которого α^τ/ = 0, г =
= 1, ..., ш.т.е. j/ e I*, при
этом by = 1. Таким образом, из
теоремы 2 следует, что либо Ь е
G I/, либо найдется у £ L*, для
которого by = 1 > 0, т. е. угол
между векторами b и у острый
(рис. 10.1).
В целях проверки усвоения пройденного материала
разберите решения упражнений 5— 10 этой главы.
Рис. 10 J
§ 3. МНОГОМЕРНЫЕ
ПЛОСКОСТИ
В данном параграфе мы введем понятие многомерной
плоскости, которое обобщает традиционные понятия плоскости и
прямой. Оказывается, что совместная система линейных
уравнений является неявным уравнением такой плоскости, а
линейное подпространство — многомерной плоскостью, проходящей
через начало координат.
Геометрическая структура систем линейных уравнении 333
Пусть 9Ят — аффинное пространство, которому
соответствует линейное пространство Шт (dim(iHm) = dim(Mm) = τη)
и IS С Шт — линейное подпространство (dim(Lr) = г).
Подмножество πΓ С 9tm
аффинного пространства называется
г-мерной плоскостью в
направлении подпространства U С Шт>
проходящей через точку С G πΓ>
если для любой точки В е пг
вектор cS eLr.
Из определения следует, что
dim(7rr) = dim(Lr) = г. Данное
определение естественно
обобщает понятие плоскости на
многомерный случай (рис· 10.2).
Рассмотрим некоторые частные случаи.
Пусть г = т. Тогда 7rm = iHm, т. е. плоскость совпадает со
всем пространством.
При г = т — 1 имеем гиперплоскость.
Случай г = 1 отвечает прямой в пространстве д\ш.
Если г = 0, то имеем точку С
Выведем параметрическое уравнение многомерной
плоскости 7ГГ. Пусть ж — радиус-вектор произвольной точки В е πΓ,
а?о — точки С, a gi,..., qr £ U — базис подпространства LT.
Тогда для того, чтобы точка В е яу, необходимо и достаточно,
чтобы вектор = ж - жо G £г, а тогда из теоремы о базисах
Рис. 10.2
ИЛИ
ж
- а?о = /]Т№>
i=I
ж
= a?o + J]nft, VTb г = 1,...,г,
(1)
i=l
где τι, ..., ττ — параметры уравнения. Уравнение (1)
называется параметрическим (явным) уравнением многомерной
плоскости 7ту.
334
Глава W
Говорят, что точки Со, Ci, ..., Сг находятся в общем
положении, если не существует (г — 1) -мерной плоскости,
содержащей все точки. Понятно, что точки Со, Ci, ..., Cr G SHm
находятся в общем положении тогда и только тогда, когда
векторы СоСь - · ■, СоСг е U линейно независимы. В этом
случае существует единственная плоскость 7гг, содержащая Со,
С\,..., Ст и имеющая уравнение
г
Рассмотрим теперь неоднородную систему линейных
урапиениВ χΑ = ь (3)
где А — (т χ ?г)-матрица, гапк(Л) = г. Тогда множество X
всех решений системы может быть представлено в виде
X = {хо} + Lm"r, (4)
где Lm~~r = {ж | хА = 0} — линейное подпространство
решений соответствующей однородной системы. Из (4) имеем,
что любое решение χ е X может быть представлено в виде
πι—г
X = Х0 + Σ Ti4U (5)
где жо — частное решение системы (3), a qy,..., qm-r —базис
линейного подпространства Lm~r.
Сравнивая (1) и (5), получаем, что неоднородная система (3)
есть неявное уравнение многомерной плоскости nm-r,
проходящей в направлении подпространства Lm~T = {χ \ χ А = 0}
через точку C(xq).
Заметим, что попутно мы показали, как по неявному
уравнению плоскости построить параметрическое уравнение. Для
этого необходимо найти частное решение х$ системы (3) и базис
подпространства Lm~~r.
ЗАМЕЧАНИЕ. В дальнейшем в качестве аффинного
пространства 9Ят будем рассматривать пространство К771, т. е. случай,
когда *Rm = W4 Напомним, что аффинное соответствие в этом
Геояетоическая структура с папе ч линейных уравнений 335
случае устанавливается так: ао = Ъ — а; а, 6 е Rm.
Содержательно это означает, что мы отождествляем точку
аффинного пространства с ее радиус-вектором. Это вполне оправтцшо,
когда положение геометрических объектов рассматривается
относительно фиксированной точки. В дальнейшем в зависимости
от смысла вектор а е Шт будем называть как вектором, так и
точкой.
Рассмотрим уравнения плоскостей в пространстве Шт.
Многомерная плоскость 7гг может быть задана двумя способами:
7ГГ = 1 χ \χ = xQ +^Τϊφ > = {Χ Ι хА = Ь}, (6)
^ I i=] ^
где А — (т χ η) -матрица, гапк(Л) = т — г.
Если xQ e Lr ъ где U — направляющее подпространство,
то 7ГГ = LT, и уравнение линейного подпространства (г-мерной
плоскости, проходящей через точку О(0) пространства) примет
вид , I г .
I/ = lx \x = Y^Tiqu \/τέϊ i = l,...,rL (7)
^ I *=i '
в частности, уравнение пространства Rm таково:
R'
m
(8)
где qfi, ..., qm e Km —линейно независимые векторы. Так,
прямая πι имеет уравнение
πι = { ж | χ = х0 + rq7 те (-оо, +оо) }, (9)
а линейное подпространство
L1 = {х | ж = тд, те (-оо,+оо)}. (10)
Уравнение гиперплоскости rrm-\ (Lm~l) удобно записать в
неявном виде
*Vn-i = {ж | ха^ а}, (II)
а
Lm~1 = {x\xa = 0}. (12)
336
Глава 10
§ 4. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
МНОГОМЕРНЫХ ПЛОСКОСТЕЙ
Пусть плоскости 7гг и π*; проходят в направлении линейных
подпространств U и Lk и через точки М(жо) и Ν{χ{)
соответственно. Пусть параметрическое уравнение этих плоскостей
имеет вид г
7гг: χ = хо + y^Tjbj,
" («)
7Tfc'. 05 = 05ι +^5jCj, /С > Г.
Будем также рассматривать случаи, когда плоскости заданы
неявными уравнениями
7ΐγ: хА = Ь или xai=Pj, j = l,...,n,
7г^: ж£? = с
или
жЬг'=7*>
X^«**jO^ Αν ^^ 7 »
(2)
Говорят, что плоскости пг и π^ параллельны, если Lr С
С ίΛ\ Данное определение является естественным
обобщением понятия параллельности плоскостей на многомерный случай
(рис. 10.3).
Рис. 10.3
Найдем условия, при которых плоскости, заданные
уравнениями (1), параллельны. Для этого рассмотрим матрицу, у
которой базисные векторы {Ьг}, i = 1> · · · ι f\ и {cj}, j = 1, ..., k9
направляющих подпространств U и Lk являются столбцами
(строками):
[bb...,br,cb...,Cfc].
Если
rMik[bL,..,,br,cit...,Cfc] = fc, (3)
то плоскости 7ГГ и 7ГА:, заданные уравнениями (1), параллельны.
Геометрическая структура систем линейных уравнений 337
Пусть теперь плоскости 7ГГ и 7г^ заданы уравнениями (2),
гапк(Л) = т — г, гапк(Б) = т — к.
Рассмотрим линейные подпространства
V = Lin{a\ ..., αη}, L^=Un{bl3 ..., 6s}.
Нетрудно заметить, что V = (Lr)* и V1 = (Lfc)*, где в
данном случае U = {х \ ха^ = О, j = 1,... , η} и Lfc =
= {ж | хЪ? = 0, j = l,...,s}. Поскольку из включения
(Lr)* 3 (L*)* следует включение Lk D ΙΛ,το получаем, что
необходимым и достаточным условием параллельности
плоскостей 7ГГ и π&, заданных уравнениями (2), является условие
rank[A, В\ — т — г. (4)
Говорят, что плоскости тгг и πίς пересекаются, если
Понятно, что
сформулированные определения
не являются
взаимоисключающими. Так, плоскости Рис. 10.4
могут быть параллельны и иметь общую точку (рис. 10.4).
Найдем условия пересечения плоскостей.
Для того чтобы две плоскости 7г& и 7гг, заданные
уравнениями (1), пересекались, необходимо и достаточно, чтобы система
линейных уравнений
г к
я?1 - ж0 = 5Z Tibi ~ Σ δ& (5)
имела решение. Но по известной теореме алгебры система (5)
имеет решение тогда и только тогда, когда
rank[bi, ■··! Ьг,сь ..., ck,xi - х0] =
= rank[bi, ..., ftr, сь · ■ ·, с*Ь (6)
что и дает требуемое условие.
338
Глава 10 *
Если плоскости 7ГГ и 7Tfc заданы уравнениями (2), то анало
гичные рассуждения приводят к условию
\А В
гапк[Л, В] ~ rank
(7)
Допустим, что π^Ππ/e /0и обозначим πρ = πΓΠπ^. Тогда
7гр — это р-мерная плоскость в направлении подпространства
U Π Lk, проходящая через точку ж' е тггП^, при этом из
алгебры известно, что
ρ = dim(Lr П Lk) = r + k- dim(Lr + Lk). (8)
Таким образом, две плоскости пересекаются в единственной
точке, если выполнено условие (6) (или (7)) и
LrC\Lk = {0} (или Lr + Lk = Lr®Lk). (9)
Говорят, что плоскости 7гг и 7г* скрещиваются, если они
не параллельны и не пересекаются.
Непосредственно из определения получаем условия, когда
плоскости 7гг и 7Tfc, заданные соотношениями (1), скрещива-
ются: rankfbj,..., br? cj,..., ск) φ к,
гапк[Ьь ..., br, сь. ·., ск] φ (10)
Φ rank[bl5... ,br.,cb... ,с/с,Ж1 - scq].
Если же уравнения плоскостей заданы в виде (2), то условия
скрещивания плоскостей имеют вид
J Λ В\
гапк[Л, В\фт — г, гапк[Д В] ^ rank
Ь с
(11)
Понятно, что плоскости не любых размерностей могут
скрещиваться в пространстве Шш. Так, в R2 прямые не MOiyr
скрещиваться, точно также не могут скрещиваться двумерные
плоскости, прямая и плоскость в R3.
Получим соотношения на размерности, при которых
плоскости 7гг и 7Г& скрещиваться не могут. Так если
dim(Lr + Lk) = m,
Геометрическая структура систем линейных уравнений 339
то соотношение (10) не выполнено, однако всегда справедливо
соотношение dim(Lr + Lk) = τ + k - dim(Lr Π Lk). Поэтому
при выполнении условия
г + k - dim(Lr П Lk) ^ m (12)
плоскости 7гг и 7Tfc скрещиваться не могут. В частности,
гиперплоскость не может скрещиваться ни с одной плоскостью
положительной размерности, поскольку
(т - 1) + к - aim{Lm'1 Π Lk) ^ m - 1 + к - (к - 1) = т.
Сформулируем алгоритм для проверки взаимного
расположения плоскостей 7ГГ и 7Г^, заданных уравнениями (1).
1) Сформировать матрицу [bi, ..., br, с\, ..., с*].
2) Вычислить rank[6i, ..., bryCi, ..., Cfc,sci — 5Co], а
попутно найти и rank[bi, -.., br, ci, ..., c^].
3) Если выполнено условие (3), но не выполнено (6), то πΓ
и 7Γ£ собственно параллельны (параллельны, но не
пересекаются). Если выполнены условия (3) и (6), то πΓ с 7Г^. В
частности, если г = к, то 7ГГ = π^. Если же условия (3) и (6) не
выполняются (т. е. выполнено (10)), то πΓ и π* скрещиваются.
Теперь покажем, как построить плоскость, содержащую две
данные плоскости пг и π^, заданные уравнениями (1). Сначала
заметим, что 7гг с Мт,7Г/с С Ет, а пространство Rm само
является плоскостью. Поэтому корректно сформулировать данную
задачу так: по плоскостям πΓ и 7г* построить такую плоскость
7ГР минимальной размерности р, что πρ Э πΓ и πρ э π*.
Рассмотрим плоскость πρ, проходящую через точку М(хо)
в направлении подпространства LP = Lin{bi, ..., br> Ci,
.,., c^, «ι — жо}· Покажем, что πρ D πΓ и πρ D π^.
Действительно, по построению плоскости πρ имеем, что Lr С LP
и Lk С LP, поэтому плоскость πρ параллельна плоскостям πΓ
и *rjt (ρ ^ г, ρ ^ fc). Далее, ж0 € 7гр и я?о € 7ГГ, поэтому
7ГР П 7ГГ ^ 0. Следовательно, πΓ С 7гр. С другой стороны,
заметим, что х\ — хо е LP, поэтому выполнено xq + {х\ —
— xq) = χχ е 7гр. Но Κι е тг* по условию. Следовательно,
*р Π π* ^ 0, а тогда π* С πρ.
340
Глава 10
Пусть теперь 7г5 — произвольная плоскость такая, что π3 э
D тгг и 7гя э π*. Покажем, что тогда π3 D πρ.
Действительно, если L5 — направляющее подпространство плоскости
7TS и ж' — радиус-вектор точки, через которую проходит π3,
τυ Lr С L\ χ' - χ0 e L\ Lk с L3, a/ - αϊ G Ls.
Поэтому Lr + Lk с Ls, a?i - жо G £5 и, следовательно, ί^ =
= Lin{6i, ..., brjci, ..., c^,ici -a?o} С Ls. Понятно, что
7TS П 7Γρ φ 0, а тогда πρ С π6.
Таким образом, мы построили плоскость πρ минимальной
размерности, содержащую плоскости πΓ и π*.
Заметим, что задача построения плоскости πρ обобщает
на многомерный случай такие задачи аналитической
геометрии в пространстве, как построение плоскости, проходящей
через точку и прямую; плоскости, проходящей через две
пересекающиеся (параллельные) прямые. Эта задача в случае двух
скрещивающихся прямых, пересекающихся прямой и
плоскости, собственно параллельных прямой и плоскости сводится к
написанию уравнения трехмерного пространства.
§ 5. УРАВНЕНИЯ
ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
На вещественной прямой с помощью отношения «больше»,
«меньше» и «равно» можно сравнить два любых числа.
Подобным образом можно поступить и в линейном пространстве Мп.
Пусть χ = (ξι, ..., ξη) е Шп. Будем говорить, что вектор χ
строго положительный (χ > О), если ξ* > 0, г = 1, ..., η.
Будем говорить, что вектор χ положительный (χ ^ О),
если ξζ ^ 0, г = 1, ..., п, и существует г'о: ξ2·0 > 0.
Будем говорить, что вектор χ неотрицательный (χ ^ О),
если ξί ^ 0, г = 1,..., п.
С помощью отношений >, ^, ^ можно сравнивать в
пространстве Шп векторы.
Пусть даны два вектора χ = (ξ1} ..., ξη), у = (т?ь ■ · ·, Vn) ■
Тогда х > у (строго больше), если χ — у > 0У χ ^ у (больше),
если χ -у > О,и х^у (не меньше), если χ - у ^ О.
Геометрическая структура систем линейных уравнений 341
Обозначим буквой F одно из этих отношений: F е
£ {>,^> = }· Поскольку с помощью F можно сравнивать не
все, а только некоторые векторы в Кп, то F называется
отношением частичного порядка в Еп.
Приведем без доказательства свойства отношений порядка
(сами доказательства свойств тривиальны):
1) Если xFy и yFz, то xFz.
2) Если xFy и А > 0, то (Xx)F(Xy). В случае λ < 0 имеем
(Xy)F(Xx).
3) Если x\Fyi и sc2F2/2,to (χι +x2)F(yi +2/2).
4) Если α ^ О и χ > у, то ха > уа. Если а > О и χ ^ у,
то жа ^ г/а.
Рассмотрим пространство Шп и приведем уравнения
геометрических объектов, которые нам потребуются в дальнейшем.
7Γι(#ο5 о) = { ж | ж = хо + λα, λ ^ 0 } — луч, исходящий
из точки xq в направлении вектора а;
(а) = 7Γι(0,α) = {χ \ χ = λα, λ ^ 0} — полупрямая в
направлении вектора а;
[а, Ь\ = { ж | ж = λα + (1 - А)Ь, λ 6 [0,1] } — отрезок,
соединяющий а и 6;
π~_χ = {ж | жа ζ а} — отрицательное
полупространство с граничной гиперплоскостью 7Γη_ι = {ж | жа = а}
(если обратное неравенство, то положительное полупространство
πί-ι )-
(α)* = {ж|жа^0} — частный случай отрицательного
полупространства π^_χ, когда πη_χ = {ж|жа = 0} = L71""1;
Е£+ = { ж | ж ^ О } — неотрицательный ортант;
Ш! = { ж ( ж ^ О } — неположительный ортант;
5(ж,а) = {у | |j/ — ж| < а } — открытый шар радиуса а с
центром в ж;
5(ж, а) = { г/ | |j/ — ж| < а } — замкнутый шар радиуса а с
центром в ж;
Ρ = {X = (ξι, ..., ξη) I Of ^ £ < <Ч+, * = 1.
..., η } — параллелепипед;
F = { χ | жфж ^ а2 }, где Q — симметричная,
положительно определённая матрица, — η -мерный эллипсоид.
342
Глава 10
ЗАМЕЧАНИЕ. В пространстве Шп можно ввести и отношение
полного порядка, с помощью которого можно сравнивать любые
векторы.
Будем говорить, что χ >- О (лексикографически
положителен), если первая отличная от 0 компонента & > 0.
Тогда χ >~ уу если χ - у >- О. Аналогично, χ У О
(лексикографически неотрицателен), если χ >- О или ж = О.
Понятно, что для отношений порядка >-, >:
справедливы все свойства, которые справедливы и для отношения
частичного порядка F.
§ 6. ТОПОЛОГИЯ
ЕВКЛИДОВА ПРОСТРАНСТВА
В заключение главы рассмотрим основные топологические
понятия в Rn, связанные с понятием открытого и замкнутого
множеств. В первую очередь здесь важен понятийный аппарат,
поэтому доказательства утверждений при первом чтении можно
пропустить.
Известно, что в пространстве Ш0, можно ввести метрику или
расстояние между двумя точками жиг/:
р(х,у) = \\χ - у\\ = \χ-ν\ = л/(®-»)(»-у)· U)
Тогда пространство Еп с метрикой ρ становится метрическим,
поскольку (1) удовлетворяет аксиомам метрики.
Любое подмножество X С Шп с метрикой ρ
называется метрическим подпространством. Метрическое
пространство Кп с метрикой ρ будем обозначать (Μη,ρ), а
подпространство X с метрикой ρ — (Χ, ρ).
Множество Μ С Rn называется открытым, если для
всякого ж е Μ существует ε > 0, для которого 5(аз,ε) С Λ/.
Говорят, что точка χ е Μ является внутренней точкой
множества Λ/, если существует ε > 0, для которого 5(α?,ε) С
С М. Множество int(M) всех внутренних точек называется
внутренностью множества М.
Геометрическая структура систем линейных уравнении 343
Таким образом, из этих определений получаем, что
int(M) — всегда открытое множество, а множество Μ является
открытым тогда и только тогда, когда
Л/= int(M) = {x\xeM, 3e>0:S(x,e)cM}.
Множество G С Шп называется замкнутым, если G =
= ЕП\М, где Μ — открыто, а Шп\М = {х eRn \ χ £ М}
называется дополнением Μ до Rn.
Множество U С Шп называется окрестностью ж, если
существует S(x,e) С ГУ, ε > 0.
Открытый шар S(x^a) является открытым множеством,
поскольку для у е S(x,a) : р(х,у) < α и S(y>a - p(x,y)) Я
С S(x>α). Действительно, пусть г е S(y,a — р{х,у)) . Тогда
р(ж, ζ) < р(ж, у) + р(у, ζ) < α, т. е. ζ е 5(ж, а).
Внешностью множества Μ с Шп (обозначается ext(M))
называется внутренность его дополнения, т. е. ext(M) =
= int(En\M).
Содержательно внешность Μ является множеством всех
точек Шп , каждая из которых есть центр по крайней мере одною
шара радиуса ε > 0, не пересекающегося с М.
Понятно, что int(M) Π ext(M) = 0.
Множество дМ С Μ точек, не принадлежащих ни
внутренности int(M), ни внешности ext(M) множества Μ\ называется
границей М,т. е.
дМ = {х\хеМ, х<£ int(Af), χ £ ext(M) },
а точки χ е дМ называются граничными точками
множества М.
Поскольку Шп\дМ = int(M) U cxt(M) открыто, то дМ
замкнуто.
Теорема Х.Для того чтобы точка χ е Μ принадлежала
дМ (была граничной), необходимо и достаточно, чтобы
любая окрестность U{x) точки χ содержала
одновременно как точки из М, так и из Rn\M.
344
Глава 10
Доказательство. Пусть χ G Μ и любая окрестность U(x)
точки χ пересекается одновременно с Μ и Rn\M. Тогда χ φ
£ int(M) и χ £ ext(M), поэтому χ G дМ. Обратно, пусть
χ G дМ и U{x) — произвольная окрестность точки ж.
Пересечение U{x) Π Μ ψ 0, так как в противном случае U(x) 6
6 ЕП\М и χ е ext(M). Точно так же видно, что окрестность
U(x) пересекается с МП\М, ибо в противном случае U(x) с Μ
иже int(M). Теорема доказана.
Понятно, что int(M), ext(M), дМ попарно не пересекаются
иГ = int(M) U дМ U ext(M).
Задание открытых множеств в Шп определяет топологию
на Шп. В этом случае Шп называют топологическим
пространством.
Множество МсГ называется ограниченным, если
существует шар S(x, a) Э М, а < +оо.
Так, например, отрезок, шар, эллипсоид,
параллелепипед— ограниченные множества. Луч, плоскость,
полупространства, ортанты — неограниченные множества.
Определим последовательность {ж*} = {ж1г..,ж^...}
как отображение N—*Rn, где N — множество натуральных
чисел. Будем говорить, что χ — предел последовательности
{xi}, или χ = limi-^ooХг> если lim^oo/>(#ь#) — 0.
Равносильное определение: для любого ε > 0 существует такое
натуральное число N£t что для всех г > N£ выполняется
Xi € 5(ж,е).
Точка χ G Шп — предельная для М, если для любого
δ > 0 : (S(x,S)\{x}) ПМ^0.
Замыканием Μ для множества Μ назовем множество,
получившееся из Μ присоединением к нему всех предельных точек
множества М.
Теорема 2. Пусть Μ с Шп, α Μ — замыкание М. Тогда
Μ — замкнутое множество.
Доказательство. Для доказательства замкнутости
необходимо показать, что множество G = ЕП\М открытое.
Предположим противное, т. е. существует точка χ G G, которая
Геометрическая структура систем линейных уравнений 345
не является внутренней. Это означает, что для любой
окрестности U точки χ выполнено соотношение U <£G.
Возьмем последовательность шаров {S(x> εη)}^=1, где еп =·
= ε/η, ε > 0. По предположению S{x,en) <£ G для всех п,
поэтому 5(ж,еп) Π Μ Φ 0 для всех п. Возьмем в каждом
шаре S{x,en) предельную точку хп € Μ, η G N. Однако
жп е S(xye)y где S(x>e) —открытое множество. Поэтому для
каждого хп существует окрестность U(xn) С S(x}en). Но по
определению предельной точки в U(xn) найдется точка хп €
ем.
Таким образом, мы можем построить последовательность
точек {tfnl^Lj, Хп € S(x,en), хп е М, £п = ε/η, ε > 0, которая
сходится к χ. Следовательно, χ — предельная точка множества
М. Противоречие и доказывает утверждение.
Теорема 3· Μ = Μ тогда и только тогда, когда Μ —
замкнутое множество.
Доказательство. Для любого Μ С Шп выполнено: Л/ с Л/.
Покажем, что если Μ — замкнутое множество, то Μ э Μ.
Действительно, если Μ —замкнуто, то G = Шп\М —открыто.
В этом случае для любой точки χ е G найдется ε > 0, такое,
что S(x, ε) сС,т.е. S(x,e) Π Μ = 0, поэтому G не содержит
предельных точек множества М. Таким образом, Μ С М, т. е.,
если Μ —замкнутое множество, то Μ = Μ.
Если же Μ не является замкнутым множеством, то Μ Φ Μ,
поскольку Μ замкнуто.
Следствие. Замыкание Μ является наименьшим замкнутым
множеством, содержащим Μ.
Доказательство. Пусть F э Μ и F — замкнуто. Тогда F =
= F D М, при этом согласно теореме 2 Μ замкнуто и следствие
доказано.
Замкнутое и ограниченное множество в Шп будем называть
компактным (или компактом).
Вообще, множество Μ в метрическом пространстве
(Х,р) называется компактным, если из любой
последовательности {хпУп^г с Μ можно выбрать сходящуюся
346
Глава 10
подпоследовательность с пределом из А/, т. е. V{xn}%Li С
С Μ 3{хПк} : Hindoo хПк = ж € Μ.
Свойство компактности в Шп эквивалентно замкнутости и
ограниченности множества. Образ компактного множества при
непрерывном отображении двух метрических пространств
является компактным множеством. Напомним, что на языке
последовательностей функция ψ : Шп —> Е1 называется
непрерывной в ж, если из того, что Нпц-юс хг = х следует, что
\ϊτηί^00ψ(χί) = φ(χ).
ЗАДАЧИ И УПРАЖНЕНИЯ
1.Доказать, что если Li, ^2 С Еп —линейные
подпространства, а X — вещественное число, то L\ + L2,
XLi, L\ (Ί L2 также являются линейными
подпространствами.
2. Пусть Li, L2 С Rn —линейные подпространства.
Будут ли линеалами: a) L\ χ L2; б) L\\JL2?
Ответ: а)будет, если в W1 χ W1 введены следующие линейные
операции: для любых пар (а, Ь), (с, d) е W1 x W1, любого λ €
G Ш справедлив^ соотношения (а, 6) + (с, d) = (а + с, b + d),
λ(α, Ь) — (λα, Xb); б) в общем случае нет.
З.Доказать, что если L е Ш71 — линейное
подпространство, то L* = {х \ ху = О, у е L} и является
линеалом.
Указание. Воспользоваться определением сопряженного
множества и тем, что из у € L следует (—у) е L.
4. Пусть А С Жп. Доказать, что Lin(A) — наименьшее
(по включению) линейное подпространство,
содержащее множество А.
Решение. Сначала заметим, что если а,Ь € 1лп(Л) и λ е R,
то а + Ь G Lin(A) и λα е Lin(A), т. е. L\n(A) —линеал в Шп.
По построению имеем Lin(A) э А. Теперь возьмем
произвольный линеал L э Л. Тогда L = Lin(L) Э 1лп(Л) 3 А.
5. Пусть L с 1Кт — линеал и а1, а2,..., ar e L — базис L.
Найти базис L*.
Геометрическая структура систем линейных уравнений 347
Решение. Построим матрицу А = [а1, а2, ..., аг). Ясно, что
rank(A) — г. Согласно задаче 3 линеал L* = {х \ ха1 =
= 0, г = 1, ..., г}, т. е. L* = {ж [ хА = О}. Тогда
по теореме 1 § 2 базисными векторами линеала L* являются
Ьк = (-μι*, ...,-ДгьО,...,0, 1 ,Ο,.-.,ϋ),
А; = Г + 1,... ,?7l,
где μι* —коэффициенты разложения fc-й строки матрицы А по
ее строчечному базису αϊ, аг, ■ , <χΓϊ τ· е· afc = Σ1=ιμ«Λαί»
А: = г + 1,..., m.
6. Линейные подпространства U и Lk заданы базисами
а\,.. ·, аг и Ь\ ,..., bk соответственно. Найти базисы
подпространств U + Lk и U Π Lk.
Решение. По определению U + Lk = Lin{ щ9 ..., аг, 6ι,
..., 6fc },a поэтому dim(Lr + Lfc) = rank[ab .... ar,&i,... ,6^],
а базис суммы линейных подпространств— это столбцовый
базис матрицы [αϊ, ..., аГ1 Ьь ..., 6*].
Пусть векторы αϊ, ..., ar, bi, ..., bs составляют базис
подпространства Lr + Lk. Разложим по этому базису векторы
Г S
bj ^Y^aijai+^P.jbi, j = s + 1, ..., к,
и рассмотрим векторы
г
г=1 г=:1
о = Y2aiJa* = ъз ~~ Σ&Ά> j = θ +1, -.-, fc.
По построению Cj G Lr и с, G Lk y т. е. c,- G LrflLfc,
j = s + 1, ,.., fc.
Из основного тождества линейной алгебры имеем
dim(Lr + Lk) = dim U + dim Lk - dim(/7 Π Lfc),
или в нашем случае dim(Lr П Lk) = к — в, т. е. размерность
пересечения равна числу векторов {с^}.
348
Глава 10
Осталось показать, что векторы {с,}, j = s + 1...., /г,
линейно независимы. Действительно, рассмотрим линейную
комбинацию векторов к ь s
3=9+1 j=s+l ^ i=l '
Если хотя бы один из коэффициентов λ^ φ О, то
соответствующий вектор bj представим в виде линейной комбинации
оставшихся векторов {Ьг}» г = 1, ..., fc, i ^ j, что
противоречит тому, что bi,...5bfc образуют базис. Поэтому Xj — О,
j = s + 1, ..., fc, и векторы {с^}, j = в + l,...,fc, линейно
независимы.
7. Доказать, что Lr+Lk = Lr@Lk тогда и только тогда,
когда rank[ai, . - -, аг, t>i, .. ., Ъ^\ = τ + к, где а\,..., аг
ubi,...M Ьк — базисы U и Lk соответственно.
8. Доказать, что для любого линейного
подпространства L справедливо соотношение L** = L (теорема
двойственности для линейных подпространств).
Решение. По определению сопряженного подпространства
справедливо L С L**. Покажем обратное включение.
Пусть αϊ, ..., От € L —базис подпространства.
Предположим противное, т. е. 5 G L**, но b φ L. Это означает, что
система линейных уравнений Σ[=ι&αι = b не имеет решений.
Тогда по теореме 2 § 2 имеет решение система щу = О, г =
= 1, .., г, by = 1. Первая группа равенств означает, что у €
е L* y a последнее, что b g L**. Противоречие и доказывает
утверждение.
9. Пусть Li, L2 С Rn —линейные подпространства,
причем L\ С ί/2 · Доказать, что L\ D L\ ·
10. L\, L2 С Mn —линейные подпространства. Доказать
тождества:
a)(Li+Jk)* = £iriLS;
6)(LinL2r-LI+L3.
Решение.
а) Пусть ?/ 6 (£ι +Ь2)*. ТогДа 2/(ж1 + ж2) = 0, ж ι G Lit
ж2е!/2· Полагая последовательно #2 - 0 и х\ = 0, получаем,
что уху = 0, χι € Li\ ух2 = 0, #2 е 1/2,т, е. у е LJ ΠΖ^.
Гео метрическая структура систем линейных уравнений 349
Обратно, если у е L\ П L\, то ух\ = О, ух2 = 0. Поэтому
у{х\ + xz) = yxi +ух2 = 0, х\ G L\, ж2 £ ί/2. Следовательно,
2/G (Li+Z,2)*.
6) L\, L2 — линейные подпространства. Из предыдущего
тождества, а также теоремы двойственности (задача 8) следует
(Ц + L*2y = Lf П L£* = Li Π L2.
Тогда (Li nl2)m = {L\ + Ц)** = L\+L*2.
11. Плоскость 7гг задана уравнением х = xq + Σ^ιΤΐφ.
Написать неявное уравнение плоскости 7ΐγ.
Решение. Пусть L = Lin{ ςι, ·.., qr } — направляющее
подпространство плоскости 7гг, Тогда L* = {у \ yqt = 0, г =
= 1,..., τ }. Допустим, что а\, ..., <zm_r — базис L*.
Следовательно, L = Ι/** = { χ | жаг = 0, г = 1, ..,, т — г }. Таким
образом, осталось найти правую часть аг,г = 1,...,т — г,
системы уравнений. Подставляя жо в систему, находим а* = жоа*»
г = 1,..., m — г.
Ответ: (ж — xo)a,i = 0,г = 1,...,т~г.
12. Доказать, что если πΓ и π к — многомерные
плоскости в Шт, то 7ΐγ П π/t и 7гг + π^ также являются
многомерными плоскостями, и написать уравнения этих
плоскостей.
Решение. Если πΓΠπ^ φ 0,το пересечение 7ГгП7Гь очевидно
является плоскостью. Пусть ж* е πγ П π* ^ 0. Тогда для
того чтобы χ е 7гг Π π/t, необходимо и достаточно, чтобы χ —
-ж* GLrnLfc, где U, Lfc — направляющие подпространства
плоскостей πν и π^, т. е. 7ггП^ — плоскость, проходящая
через точку ж* в направлении подпространства U n Lk.
Предположим теперь, что
г
rcr = lx\x = XQ + 5^пЬА >,
^ I t=l '
< Ж Ж = Ж ι + \^ SjCj ?.
7Tfc - < Ж
350
Глава 10
Тогда
!
к ч
т. е. 7гг + 7Г* — плоскость, проходящая через точку xq + χχ в
направлении линейного подпространства
L = Lin{bi, ..., Ъг,си ..., с/, } = Lr — L ".
Если плоскости заданы неявными уравнениями
7гг: xAi=b{y ivk- xA<2 = ΐ>2*
то уравнение плоскости 7гг П π^:
хА2 = Ь2-
{:
Для написания параметрических уравнений необходимо
найти точку ж* и базисы подпространств 1/ + Lk t Lr n Lk.
В итоге получаем:
{
7ГГ П 7Tfc = < Ж
!
Ж = X
г=1 '
г s ч
Ж = Ж0 + 2Ci +
где {Ьь ..., 6r»ci, ..., cs}, {аь . -., a/c_s} —базисы
подпространств Lr + Lk, Ι/ Π Lk соответственно.
13· Пусть π к и тгг — плоскости в пространстве Ж™, а
πι —плоскость их пересечения. Доказать, что
а) если скрещивающиеся плоскости 7Γ& и π. лежат в
плоскости π3, то
О (fc + г - 0 + 1;
(1)
б) если в Ет имеются скрещивающиеся плоскости π*, и
7гг положительных размерностей, то к <ζ т — 2 и
г < т - 2-
Геометрическая структура систем линейных уравнений 351
14. Пусть в Ш7п плоскости π^ и тгг таковы, что
к + г - I ^ ш, где I = dim(7Tfc П я>). (2)
Доказать, что πκ и πΓ пересекаются.
Решение. Если к или г равно т, то утверждение очевидно.
Пусть к < т и г < т. Если яу и π^ параллельны, то / =
= min{A;,r}, что противоречит (2). Если πΓ и π^ скрещивают-
ея, то выполняется (1) при s = га, что также противоречит (2),
Поэтому плоскости 7Г£ и 7ΐγ пересекаются.
15. Найти базис суммы и базис пересечения двух
подпространств L\, L2 С Ш4, если L\ определяется своим
базисом а\ = (1,1,0,1), а>2 = (2,0,1,0), a L2 —системой
линейных уравнений ξι —2ξ2+ξ^~2^4 = 0, ξι—2ξ2_^4 = 0.
Решение. Базисными векторами подпространства L2
являются линейно независимые решения данной системы линейных
уравнений. Поскольку ранг матрицы указанной системы
равен 2, то в четырехмерном пространстве, очевидно, существуют
только два таких вектора. Таковыми, например, являются
векторы bi = (1,0,1,1), 62 = (0,1,-2,-2). При этом, так как
rank [αϊ, 02,61,62] = 3, а векторы αι,α2,6ι —линейно
независимы, то они составляют базис L\ + £2- Построим базис
пересечения данных подпространств. Для этого найдем
разложение вектора &2 по базису суммы. С этой целью решим систему
линейных алгебраических уравнений
αϊ + 2α2 + βι = 0,
αϊ = 1,
α2+/?ι = -2,
αϊ + βι = -2,
откуда находим αϊ = 1, α2 = 1, βι = -3, т. е. 62 = αϊ +
! θ2 — 3&ι. Поэтому вектор с = Οι + o2 = 3&i + 62 является
базисным вектором пересечения подпространств Li и L2 -
16. Найти базис суммы и базис пересечения двух
подпространств Li и L2, заданных своими базисами; L\: 01 =
= (1Д,0,0), 02 - (0,1,1,0), 03 = (0,0,1,1), L2: &i =
= (1,0,2,0), 62 = (0,1,2,2), 63 = (2,1,2,1).
352
Глава 10
О τ в е т: базисом суммы являются векторы αχ, а2, «з» &ι.а
базисом пересечения — векторы сх = (1,3,8,6), с2 = (4,3,2,3).
17. Показать, что Lx + L2 = Lx® L2 = ЖА и представить
вектор ζ = (—2,0,3,-1) в виде суммы векторов, один
из которых принадлежит L\ с базисом αχ = (2,1,2,0),
а2 = (1,2,2,1), а другой— L2 с базисом Ъх = (-1,1,2,1),
Ь2 = (1,1,1,2).
Решение. Непосредственной проверкой убеждаемся, что
векторы αι,α2,6ι,ί>2 —линейно независимы, а потому L\ + L2 =
= L\@ L2 = Ε4. Найдем разложение вектора ζ по указанным
векторам. С этой целью запишем систему линейных уравнений:
(2α1+α2-β1+β2 = -2,
\αχ + 2α2+βχ+β2=0,
J 2αι + 2α2 + 2βχ + β2 = 3,
(α2+βί+2β2 = -1.
Ее решением являются числа: αϊ = 1, α2 = — 1, βχ = 2,
β2 = — 1. При этом вектор χ = αχαχ + θί2α2 = (1, —1,0, —1) £
£ Ιχ, а вектор у = Α^ + /?2Ь2 = (-3,1,3,0) £ L2.
18о Подпространство L\ имеет базис αχ = (1,1,1,1), а2 =
= (0,1,1,1), α подпространство L2 задано системой
уравнений: 2ξχ + 3ξ2 - ξ3 + U = 0, ξι + ξ2 ~ ^£з + & =
= 0, £2 + £з* = 0. Доказать, что L\ + L2 = Li θ L2,
w представить вектор ζ = (0,5,1,-1) в виде суммы
z = x + y, где χ £ Llp у £ L2.
Ответ: χ = (2,3,3,3), у = (-2,2,-2,-4).
19· Найти общее уравнение линейного
подпространства L, если известен его базис: αχ = (3,2,1,0),
α2 = (1,-1,2,2),α3 = (2,2,2,1).
Ответ: ξχ + 3ξ2 - 9ξ3 + 10ξ4 = 0.
20. Показать, что точки А(—1,1,0,1,5), В(2, -1,3,4,0),
(7(1,2,7,6,3) находятся в общем положении.
Написать параметрическое и общее уравнение плоскости,
проходящей через указанные точки.
Решение. Имеем: АЁ(3, -2,3,3, -5) и Ж?(2,1,7,5, -2).
Поскольку построенные векторы линейно независимы, то точки А,
Геометрическая структура систем линейных уравнений 353
Ву С находятся в общем положении. Тогда параметрическое
уравнение искомой плоскости χ = xq + Т\АВ + т2АС, где rL
и т2 — произвольные вещественные числа, или ξι = -1 + 3ri +
+ 2τ2,ξ2 = 1-2η+Τ2,ξ3 = Зг!+7г2, ξ4 = 1 + 3η + 5τ2,
ξ5 = 5 — 5τι — 2г2. Для того чтобы получить общее уравнение
плоскости, можно, например, исключить параметры т\ и г2 из
этих пяти соотношений. Для этого из первых двух уравнений
находим 1, 1,
П = ^(ξι - 2b + 3), r2 = -(26 + 36 - 1),
а затем подставим в оставшиеся соотношения. В результате
получим систему линейных уравнений: 17ξι + 15ξ2 — 7ξ3 + 2 = О,
13ξι + 9ξ2 - 7ξ4 + 11 = 0, 9ξι - 4ξ2 + 7ξ5 - 22 = 0.
21. Найти параметрическое уравнение плоскости в Ε5,
если известно ее общее уравнение: ξι - 4ξ2 + 2ξ3 — & + £s +
+ 3 = 0, ξι + 2ξ2 - ξ3 + 2ξ4 - ξ5 - 3 = 0.
Решение. Точка Л(1,1,0,0,0) лежит в данной плоскости, так
как ее координаты удовлетворяют системе уравнений,
задающих плоскость. Линейно независимые решения соответствующей
однородной системы составляют базис направляющего
подпространства. В нашем случае он состоит из трех векторов: αϊ =
- (-1,-1,-1,1,0), α2 = (1,1,0,0,3), α3 = (0,1,2,0,0).
Поэтому параметрическое уравнение данной плоскости примет вид:
& = 1 -η +?2, 6 = 1 -τι +т2 + тз, £з = -т\ +2т3, £4 = п,
6> = 3т2.
22. Написать общее и параметрическое уравнение
плоскости, проходящей через точку Л(0,3,0,2) в
направлении подпространства L3 с базисом а± = (1,1,1,1),
а2 = (0,2,0,1), а3 = (1,0,2,3).
Ответ: ξλ = гг + т3, ξ2 = S + η + 2г2, ξ3 = тг + 2τ3,
ξ4 = 2+ri+r2+3r3; общее уравнение 4^ι-ξ2-5ξ3+2ξ4-1 = 0.
23· Даны три плоскости:
*ί: ei-6+£4-l=0, ξ2 - 2ξ3 - 2С4 + 1 = 0,
тг2: 6 = 1, £2 = 1 + 4τ, Сз = 2 + г, ξ4 = 1 + г,
α π3 проходит через точку 0(0,0,0,0) β
направлении подпространства с базисом с\ — (0,1,0,1), с2 =
= (1,6.2,1). Установить их взаимное расположение.
354
Глава 10
Решение. Направляющее подпространство LL плоскости тг\л
проходящей через точку Л(2Т 1.1,0), определяется системой
линейных однородных алгебраических уравнений ξι — £з + £4 = 0,
£? - 2ξ3 — 2ξ4 — 0, а следовательно, имеет ба^ис, состоящий
\\:\ двух векторов αϊ = (—1,2,0.1), а2 = (1,2,1,0). Плоскость
7Г-2 является прямой, проходящей через точку В\ 1,15 2,1) с
направляющим вектором Ь = (0,4,1,1). Поэтому вектор АВ =
= ( 1,0,1,1). Так как
nmkfcii, а2,Ь] = rank
rank [α ι, α·ζ, AU] — rank
-1
1
0
-1
1
-1
2
2
-4
2
2
О
0
1
1
0
1
1
г
0
1(
г
0
1
= 2
3,
то плоскости 7п и π2 параллельны.
Поскольку iank[ai,a2,ci,C2] = raiik[ai,a2,Ci,C2,OA] =
= 3,то плоскости πι и 7Г3 пересекаются. Наконец,
rank[ci,C2,6] ■= rank
rank [ci, C2, Ь, О/э] = rank
0
1
0
Ό
1
о
1
1
6
1
1
ί)
4
1
0
2
1
0
2
1
2
1
1
1
1
1
1
1
= 3,
= 4,
а потому плоскости 7Г2 и π3 скрещлваются.
24. В R4 dtf «ы dee плоскости π ι : ξι - ξ2 -:- 2£з — 6 — 2 = 0,
2ξι + 6 - 3ξ3 + ί4 - 6 =- 0 ы π2 : ξι + ξ2 + 6 + ξ4 - 7 = 0.
Установить их взаимное расположение.
Ответ: плоскости π\ и π 2 пересекаются.
25- Найти плоскость минимальной размерности, которой
принадлежат одновременно прямая ξι = Ι +τ, ξ-2 = 2т,
£з = —т. & ^ -Зт ι/ плоскость 7Г : 2ξι + ξ2 + 4£з — 4 = 0,
36+6-8 = 0.
Решение. Данная прямая имеет направляющий вектор а =
= (1,2,-1,-3) и проходит через точку А(жо), #о = (1,0,0,0).
Геометрическая с труктура систем линейных уравнений 355
Решив соответствующую систему линейных уравнений,
нетрудно найти, что плоскость проходит через точку В(2? 0,0,2), а
направляющее подпространство имеет базис, состоящий из двух
векторов by — (1,-2.0,-3), Ь2 = (0,-4,1,0). Поскольку
rank[6i,62?tt] — 2, гапк[Ььб2,а,Л/У] = 3, то прямая и
плоскость параллельны. Л тогда параметрическое уравнение
искомой плоскости имеет вид:
χ = xq + ribi + т2Ь2 + т3АВ}
т.е. ξι = 1+Τ!+Τ3,ξ2 = -2г1-4г2|£з = ^·& = -3η+2τ3.
Для того, чтобы построить общее уравнение данной
плоскости, можно найти нетривиальное решение однородной системы
линейных уравнений, матрица которой составлена из координат
базисных векторов направляющего подпространства:
ξι - 2£2 - 3ξ4 = 0.
ξι+2ξ4 = 0.
Выписанной системе удовлетворяет точка (4,5,20, —2).
Следовательно, направляющее подпространство плоскости 7Г имеет
общее уравнение 4ξι +5£2+20£з~2£4 = 0, а тогда в силу
принадлежности точки А плоскости, общее уравнение π записывается
в виде 4ξι + 5ξ2 + 2G& - 2£4 = 4.
26. Даны плоскость ξι + ξ2 + 1 = 0* £з — £ι — 1 = 0 и прямая
ξι = 1 + τ, ξ2 = 2 + 4т, & = 3 + Зт, £4 - 5 + 5т. //а-
писать уравнение плоскости минимальной
размерности, проходящей через данную плоскость параллельно
указанной прямой.
Решение. Для начала найдем базис направляющего
подпространства данной плоскости. С этой целью найдем
нетривиальные линейно независимые решения соответствующей
однородной системы ξι + ξ2 = 0, £з — £ι = 0; получаем
векторы αχ = (0,0,1,1), а2 = (1,-1,0,0). С другой
стороны, очевидно, что плоскость проходит через точку j4(—1,0,1,0).
В свою очередь, направляющий вектор прямой Ъ имеет
координаты (1,4,3,5). Так как rank[ai,a2,b] = 3, то указанные
356
Глава 10
векторы линейно независимы, а потому будут служить базисом
направляющего подпространства искомой плоскости. А тогда,
решив систему линейных уравнений
Ui + 4ζ2 + 3ξ3 + 5^4 = О,
получаем вектор с = (2,2,5, —5), координаты которого служат,
как известно, коэффициентами общего уравнения упомянутого
подпространства. С учетом того, что точка А должна лежать в
искомой плоскости, окончательно получаем ее общее уравнение:
2ξι+2ξ2 + 5ξ3-5ξ4-3 = 0.
27. Установить взаимное расположение плоскостей πι и
7г2 в Е5 и написать уравнение плоскости, проходящей
через обе указанные плоскости, если πι : ξι + £г +
+ & = 1, 2ξχ + & - & = 1. 2ξ2 + 2ξ3 - ξ* - 26 =
= 4, a π2 проходит через точку В(0, —1, —1, —2,0) в
направлении подпространства с базисом Ь\ = (1,1,1,0,0),
Ь2 = (0,1 ,1,1,0).
Ответ: пересекаются; 5ξι + 3ξ2 - 8ξ3 + 5ξ4 + 15ξδ + 5 = 0.
28. Через пряную πι : ξι = 1 + τ, ξ2 = 2, ξ3 = 1 + 2τ,
ξ4 = г, провести плоскость минимальной размерности
параллельную плоскости π2 : ξι + ξ3 + ξ4 = 1 > ξι *~ & +
+ 2ξ4 = 2.
Ответ: ξι - 4ξ2 - 3ξ3 + 5ξ4 +10 = 0.
29. Доказать, что функция φ{χ) = ах непрерывна в любой
точке χ е Кп.
Решение. Пусть {хг}°1г — последовательность точек из Rn,
сходящаяся к х. Тогда р(х^х) - ► 0. Однако
юо
Р(Хг,х) =
η
λ,Σ(6-ω2>$-^ΐι i = i,...,n.
где ξ], ξ^, ji = 1, ..., η, — компоненты векторов Xi к χ
соответственно. Отсюда следует, что Цт*_юс^· = £j»
j = 1,.... п. Теперь заметим, что φ(χ) = ах = Σ^=ια;?£.ί·
Гео метрическая структура систем линейных уравнении 357
Откуда
η η η
SO. Доказать, что параллелепипед
Ρ = {χ Ι χ = (ζι,.-.,ξη). aj ^ Cj ^ ^ j = Ι,.,.,η}
является компактом.
Решение. Заметим, что Ρ — ограниченное множество.
Покажем, что Ρ — замкнутое множество. Рассмотрим
произвольную последовательность {xi}<*Ll С Р, сходящуюся к точке
χ = (ξι, ..., ξη). Покажем, что тогда χ е Р. Посколь-
КУ аз ^ ζ) ^ Pjf 3 = 1» ■·■» п* ПРИ любом ^ то в
каждой последовательности {Cj}^, j = 1, ..., η,
существует сходящаяся подпоследовательность. Выберем единую
сходящуюся подпоследовательность для всех j = 1, ..., п. Пусть
это будет последовательность {х1к}™=1 С {жг}^1? где жч. =
= (£ifc,. -. i£nfc)- Последовательность {а^}^ сходится к ж
(как подпоследовательность сходящейся последовательности),
при этом она сходится к χ покомпонентно (по построению).
Учитывая, что ctj ^ ξ** *ξ pj, j = 1, .,., η, и переходя к
пределу в неравенствах, получаем, что otj ζ ξ^ ^ Pj , jϊ = 1, ..., η,
что и требовалось доказать.
Глава И
ГЕОМЕТРИЯ
ВЫПУКЛЫХ МНОЖЕСТВ
§ 1. ВЫПУКЛЫЕ МНОЖЕСТВА
Целью данного параграфа является введение такого понятия как
выпуклые многогранники. Однако начнем изложение с
основного понятия данного раздела — выпуклого множества.
Множество Μ С Шп называется выпуклым, если для любых
X], х2 G Μ и А € [0,1] выполняется условие Χχι + (1 — Χ)χ·ζ £
6 Л/.
Содержательно определение означает, что если Μ выпукло,
то вместе с любыми двумя точками х\уХ2 € Μ оно должно
содержать и все точки отрезка, соединяющего х\ ИЖ2-
Например, многомерная плоскость и все геометрические
объекты § 5 главы 10 являются выпуклыми множествами.
Попятно, что открытый шар S(x, а) — выпуклое множество.
Однако множество S(x,a)\{x} невыпукло.
Назовем χ = Y^ILi ХгХ%, λ* ^ 0, г = 1, ..., m, Σ2=ι ^г =
= 1, выпуклой линейной комбинацией точек жц .. ·, хт ■
Выпуклой оболочкой conv(M) множества Μ назовем
множество всевозможных выпуклых линейных комбинаций
точек из М, т. е.
conv(M)= I х \x = ^XiTi,Xi > 0> У^г = l>Xj € МУг >. (1)
^ I г г *
Данное определение предполагает, что для
построения conv(M) необходимо рассмотреть всевозможные
выпуклые линейные комбинации разных наборов точек из Μ. Однако
Геометрия выпуклых множеств
359
оказывается, что для построения conv(M) достаточно брать
выпуклые линейные комбинации вида
га т
Y2 -Μ*! λ* > О, ]Р Xi = 1, χ, е Л/,
причем т ^ η + 1. Этот факт составляет содержание
известной георемы Каратеодори (1907 г.), которую мы приведем без
доказательства.
Теорема 1. Если Μ С Шп, то каждая точка из
выпуклой оболочки conv(M) есть выпуклая линейная
комбинация η + 1 или меньшего числа точек из М.
Понятие выпуклой оболочки имеет принципиальное значение
в силу справедливости следующего утверждения.
Георема 2. Множество Μ с Шп выпукло тогда и только
тогда, когда Μ = conv(M).
Доказательство, Сначала покажем, что conv(M)
—выпуклое множество. Пусть
г i
χ" = γ^β^';, β3>ο, ]Γ& = ι, а';ем,
3 3
— две точки из conv(M). Тогда
\х' + (1 - Х)х" =
* j
Поскольку а\ е М, а" € М, λα* > 0, (1 - λ)/^ > 0 и
Σ(λα0+5>-λ)/% =
= А£а* + (1-А)]Г>:=А + (1-А) = 1.
360
Глава //
то \х' + (1 — \)х" € conv(A/)f и множество conv(M)
выпукло. Для завершения доказательства осталось показать, что если
χ ι. ..., хт € Μ, где Л/ — выпуклое множество, то
т т
х = ]Г К*1 е Л/, λ^ 0, 5^ Ai = 1. (2)
Доказательство этого факта будем вести по индукции по
числу т.
Гели т = 2, то (2) выполняется в силу выпуклости
множества Л/. Поэтому предположим, что (2) выполняется для к
точек, где к < j<a, и покажем, что оно справедливо для т.
Рассмотрим
га т
X == У ΛιΧι1 Λϊ ^ Uj У Λΐ ^= 1.
г=1 г=1
Предположим, что существует коэффициент 0 < А^ < 1
(в противном случае либо χ = Xi G Μ, либо ж € Μ по
индукционному предположению). Введем в рассмотрение вектор
*' = Σ ГГжь 0 < Am < 1. (3)
Заметим, что j^j^ > 0, ΣΞα* T^fc = l- Поэтому по
индукционному предположению χ* G Μ, но ж = Атжт +
-+- (1 - Ат)ж', и в силу выпуклости Μ имеем χ G Μ. Теорема
доказана.
Следствие. Множество conv(A/) — наименьшее (по
включению) выпуклое множество, содержащее М.
Доказательство. Пусть Μ С Шп. Тогда по теореме 2
conv(AZ) — выпуклое множество. По определению conv(M) D
D Μ. Если Μ — выпуклое множество, то conv(M) = Μ.
Возьмем произвольное выпуклое множество Ρ D Μ. Тогда
Ρ = conv(P) D conv(M) D M, что и требовалось доказать.
Ил теоремы следует, что можно сформулировать
эквивалентное определение выпуклого множества.
Множество Μ выпукло, если оно содержит все выпуклые
линейные комбинации своих точек.
Геонаяприя выпуклых множеств
361
Приведем механическую интерпретацию понятия
выпуклости. Пусть МсЕп. Рассмотрим систему материальных точек
х\,..., Xk € Μ с массами т\,... f m^ соответственно. Тогда
к
. л ГП\ Л l· TTlk
— центр тяжести этой системы материальных точек. Поэтому
Μ с Шп выпукло, если центр тяжести любой системы
материальных точек из Μ принадлежит множеству Л/.
Лемма. Если Μ, Μχ, М2 — выпуклые множества, то
выпуклыми являются и множества:
1) М1пМ2;
2) Μι+Λ/2;
3) AM.
Доказательство. Рассмотрим вектор χ = Хх\ + (1 — А)ж2,
λ G [0,1], где χι, Χ2 € Μι П М2. Тогда в силу выпуклости М\
и М2 вектор χ е Μι и χ 6 М2, т. е. ж G Μι Π М2 и, тем самым,
множество Μι П М2 выпукло.
Пусть теперь cci, ж2 6 Мг + М2. Тогда х\ = £c'i + ж",
ж2 = ж2 + ж2 , где αΊ, ж2 е М2, а?'/, х'{ е М2. Откуда
χ = (Ая?; + (1 - λ)*ί>) + (Аж7/ + (1 - А)ж'2'),
где первое слагаемое— вектор из Μι, а второе— из М2 в силу
выпуклости Μι и М2. Поэтому χ € Μι + М2, а следовательно,
множество Μι + М2 является выпуклым.
Допустим, х\, ж2 6 AM. Тогда ж = Α(αχΊ) + А(1 — а)ж2.
где х[> ж2 е М. В силу выпуклости множества Μ имеем α#Ί +
+ (1 — а)ж2 € Μ, α G [0,1], а тогда χ е AM, что и требовалось
доказать.
Определим размерность выпуклого множества Л/ с К".
Пусть π э Μ — плоскость в Rn. Тогда размерностью
выпуклого множества Μ с W1 будем называть минимальную
из размерностей таких плоскостей 7г, что π D Μ. При этом
dim(M) = (ϋηι(π).
362
Глава //
Рис. ИЛ
Так, размерность отрезка равна 1, размерность треугольника
равна 2, размерность тетраэдра — 3 (рис. 11.1).
Пусть 7ГГ D Μ — плоскость минимальной размерности,
содержащая выпуклое множество Μ. Известно, что πΓ может
иметь одно из следующих уравнений:
7ГГ = < X \ X = Хо + Yj ^iQi \ = { х Ι χΑ = Ь}-
Поэтому dim(M) = dim(7rr) = dim(Lr) = η — гапк(Л) = τ\
где LT — направляющее подпространство для 7гг.
Пусть { #1, ..., хш } с Еп — конечная система точек.
Тогда Μ — conv{ жь ..., ж™ } называется выпуклым
многогранником, порожденным точками { Х\^ . · - , Жт }, а точки
хг, г = 1, ..., т, — порождающими точками для
многогранника Μ.
Примером выпуклого многогранника служит
параллелепипед Ρ.
Из рисунка 11.1 видно, что не все порождающие точки будут
вершинами выпуклого μηογοι ранника.
Пусть Jl/ cln — выпуклое множество. Точка ж € Μ
называется крайней точкой (или вершиной) множества
А/, если из того, что χ = Хх\ + (1 - А)ж2, 0 < λ < 1У
х\,Х2 € Мч следует
X — Х\ = Х2-
Содержательно определение означает, что крайняя точка
выпуклого множества не может быть внутренней точкой пи одного
Геометрия выпук гых иножесте
363
Рис. 11.2
отрезка, соединяющего две точки из Л/. На рисунке 11 2
множества крайних точек выделены жирной линией.
Теорема 3. Пусть Μ = conv{ жь ..., хт } — выпуклый
многогранник, а Мо —множество его крайних точек. Tosda
Μ =<Ό1ΐν(Μο).
Доказательство. Сначала покажем, что если χ е
G Л/о — крайняя точка многогранника Л/гто нтйдется такая
порождающая точка XiO е { х\у *. ., хш }, что χ = хго
Действительно, χ е Л/о С М, поэтому
т
т
X
= Σ А*жь К ^ о, ]Г Λί = ι.
г=1
*=1
Если А,0 = 1, то χ = ж*0. Поэтому предположим, что AJ;1
< 1, Aio > 0. Тогда ж = X^xh + (1 - Агс)ж', 0 < А<_ <г 1,
где
г/г.
*'=ΣΓ
А,
Χι-
%*0
Однако χ9 6 Mt а ж е Л/ — крайняя точка, поэтому ж =
•Его — ^ ·
Теперь обозначим через Д/° С {ж ι, ..., хт } — мини\иль-
ное подмножество множества порождающих точек, для которого
Μ = conv(M°). Докажем, что М° = Λ/ο, т. е. множество
крайних точек является порождающим для многогранника Μ. Пусть
для определенности М° = { }. Покажем, например,
364
Глава II
что хг е М° — крайняя точка многогранника М. Для этого
представим хг в виде
хг = Аж; + (1 - \)χ", χ1 е м7 χ" е л/, о < λ < ι,
Ж — / ^\&г, & — У ^ \ xii
г=1 г=1
г г
^ г=1 г=1
Тогда
г г г
Жг = 5^(Αλ' + (1 - X)\")Xi = ]^//·»«£ι /'г ^0, ^Мг = 1.
11усть μ7. < 1, следовательно,
r-l
жг — > а^,
Mr
= ΣΓ£!
г=1
что противоречит тому, что М° = {жь ..., жг } —
минимальное подмножество порождающих точек. Поэтому μτ = 1,
μ* = 0, г = 1, ..., г — 1. Но
μι = аа; + (ι - а)л? = о,
0<А<1, А^О, А'/^0, ι = 1, ...,γ-1,
откуда следует, что \[ = А" = 0, г = 1, ..., г — 1. Поэтому
AJ. = А" = 1, т. е. хт = х* = хп, что и доказывает тот факт, что
хг — крайняя точка Μ.
Доказанная теорема позволяет написать параметрическое
уравнение выпуклого многогранника
М—lx ж = ^А2жг Аг ^ 0, г = 1>...,г, У^К = 1 f,
где ж2 —крайние точки многогранника М.
Для выпуклых множеств справедлив более общий результат,
который мы приведем без доказательства.
Теорема 4„ Пусть МсЕп — выпуклый компакт, a Mq с
С Μ — мио жество его крайних точек. Тогда Μ = conv(Mo) -
Геометрия выпуклых множеств
365
В частности, этот результат справедлив для эллипсоида F
и замкнутого шара S(x^a)· Понятно, что коайними точками в
этом случае будут граничные точки.
Выясним топологические свойства выпуклого многогранника.
Теорема 5, Выпуклый многогранник является компактным
множеством в Шп.
Доказательство. Пусть Μ = conv{a?i, ..., xr}
—выпуклый многогранник. Покажем, что Μ — ограниченное
множество. Для этого возьмем произвольную точку χ е Μ такую,
что
/] КХг, К 5* 0, ^ Xi = 1.
г
X
i=l 2=1
Тогда
\х\ ^ 7 ^г|жг| ^ У^ Xi max \xi\ = max \xi\ — α < +оо.
~i .л г=1,...,г г=1,...,г
г=1 г=1
Таким образом, Μ С 5(0, а) и ограниченность доказана.
Покажем теперь, что Μ — замкнутое множество. Для этого
достаточно показать, что если
lim xk =x, {а?*}Г\ СМ,
тоже М.
Поскольку хк € М, то
г
Χ = У^^гкХгу
2=1
Г
/ ^ ^гЛ = 1» -АгАг ^ О? 2 = 1, . . . , Г, «=1,2,....
Каждая числовая последовательность {λ^}^, г = 1,
..., г, ограничена, поэтому из нее можно выбрать
сходящуюся подпоследовательность. Поскольку последовательностей
{Xik}j ί = 1,-.., ^, конечное число, то можно выбрать такую
подпоследовательность номеров к\, &2. ■ ■ · > что все
последовательности Xiki, J = 1, 2, , сходятся.
366
Глава П
Пусть Нт^^оо Ajjtj- = λ^ ^ 0. Понятно, что Αι -f A2 +
+ -·■ + Ar = 1. Тогда последовательность ΣΓ=ι Kkj&i* 3 —
= 1,2, ..., сходится и при этом
г г
ж = lim y^A/fc ж, = У^ А^а?г £ М.
j—*оо ^—' z—'
Теорема доказана и, тем самым, теорема 5 действительно
является частным случаем теоремы 4.
§ 2. ВЫПУКЛЫЕ КОНУСЫ
Перейдем теперь к изучению важнейшего подкласса выпуклых
множеств, а именно, выпуклых конусов.
Множество ΚΧύ с Мл называется конусом с вершиной в
#о Ξ Κχο, когда оно обладает свойством: если χ G ΚΧϋ, то и
все точки луча Xq + Х(х — xq) для любого А ^ 0 принадлежат
множеству КХо.
К примеру, конусами являются: луч πι(ίτ0,α); многомерная
плоскость 7гг; π^-ι (^η-ι) — полупространство; ортант R+
(К* ).
Следует заметить, что согласно определению, конус КХо
является множеством неограниченным, а вершина xq не
обязательно является крайней точкой для КХо (она даже может не
быть граничной точкой).
Важным частным случаем конуса, как мы увидим в
дальнейшем, является конус с вершиной в нуле. Далее, когда речь
будет идти о таких множествах, будем говорить просто конус (не
указывая вершину) и обозначать К.
Одной из важнейших особенностей эгого класса является то,
что конус КХо с вершиной в xq всегда может быть представлен
как сдвиг конуса К на вектор х0, т. е. КХо = {хо} + К, где
К={у\у = Х(х- х0)> А > 0, χ е КХо }.
Конусами являются: (а) — полупрямая, U — линейное
подпространство, (а)* —полупространство, ортант Έ!\ {Wl\
пространство En.
Геом.гприя выпуклых множеств
367
Конус КХо с рершиной и хо называется выпуклым кони
сом, если КТл —выпуклое множество.
В случае, когда конус имеет вершину в О, можно дать н
другое, эквивалентное первому (см, ниже теорему I), определен ^
выпуклости конуса.
Конус А называется выпуклым, если для чюбых х{у
Х2 € К ВЫПОЛНеНО уСЛОВИС Χγ +Χ2 6 А'
Таким образом, выпуклый конус К С
Cln — это множество, замкнутое
относительно операций сложения и умножения
на неотрицательное число, т. е. является
обобщением понятия линеала.
На рисунке 11.3 показан пример
выпуклого конуса К\ и невыпуклого К2. рис tt $
Теорема 1. Для конуса К (с вершиной в О) оба опреде.и ни я
выпуклого конуса эквивалентны.
Доказательство. Пусть К с Rn —выпуклый конус (в
смысле первого определения). Тогда для любых х\% χι 6 ΑΓ. λ е
G [0,1], все точки χ = \χχ + (1 — Х)Х2 € ΑΓ. Положим А =■ 1/2.
В этом случае χ = 2ΐί£2. £ А\ но AT — конус, поэтому χΛ +
+ Х2 = 2 (Ж|^Ж2) Е/(,а тогда К — выпуклый конус согласно
второму определению.
Покажем теперь, что из второго определения следует перзое.
Пусть К С Ш71 — выпуклый конус. Тогда для любых χ^ , х2 ^
G К их сумма Ж1+Ж2 € К. Кроме того, Ххг е Ку (1-А)ж2 е К
для любого λ € [0,1], так как К — конус, но тогда \х\ + (1 -
- Х)х2 G К в силу выпуклости конуса К, что и требовалось
доказать.
Выпуклыми конусами являются: (а) — полупрямая,
(а)* — полупространство, U — линейное подпространство.
Покажем, что множества
К1 = {х\хА^О], К2={у\у=хА, ж^О},
АГ3- {х \хА = 0, х^О]
— выпуклые конусы.
368
Глава //
Так, если χ € К1, то (Хх)А £ 0, λ ^ 0, т. е. КА — конус.
Вместе с тем, из ас ι, х2 £ .jFiT1 следует, что (ж χ + ж2)А = Х\А +
+ ж2 А ^ О, т. е. asi + х2 е if1 -
Таким образом, множество решений однородной системы
линейных неравенств является выпуклым конусом.
Аналогично проверяется, что К2 и К3 —выпуклые конусы.
Остановимся более подробно на операции сопряжения
множества К* = {у | ух < 0, χ € К}. Содержательно К*
состоит из таких векторов, которые образуют неострые углы с
каждым из векторов конуса К. В качестве примера, пусть L С
С М71 — линейное подпространство, L* — сопряженное
подпространство, К* — сопряженный конус к L. Покажем, что
L* = К*, т. е. сопряженный конус совпадает с сопряженным
подпространством (см. также задачу 3 главы 10).
Действительно, для j/gL* имеем ух = О, χ G L, т. е. у е
е К*. Если же у е К*> то ух < 0, χ G L, но L —линейное
подпространство, поэтому (—х) 6 L, а тогда (—х)у ^ 0, или
ху ^ 0. Следовательно, уж = 0 и у G L*, что и требовалось
доказать.
В качестве следующего примера покажем, что (а)* =
= {ж | жа ^ 0} — сопряженный конус к (а) = {χ \ χ =
= λα. λ ^ 0 }.
Действительно,
К* = {у\ух<0, хе{а)} =
= {у\ у(Аа) < 0, λ > 0} = {у | г/а < 0} = (а)*.
В дальнейшем мы покажем, что (а)** = (а).
Теорема 2 (алгебра выпуклых конусов). Если К, К\,
К<2 — выпуклые конусы, то К\ + 1<2, К\ П К2, К* —
выпуклые конусы и, кроме того,
1) К * — зал* кнутое множество.
2) (/ч+Л*.)* = Л7ПК2*.
3) iq + io2c{i<inK2y.
4) К** D/С.
5) Если Κι с /ν2. то К2 С /Cf.
Геометрия выпуклых множеств
369
Рис. НА
Доказательство. Согласно лемме § 1 получаем, что Κχ +К2 ,
Κι П К2 — выпуклые множества (рис. 11.4). Покажем, что и К*
также выпукло. Действительно, если ж = Χχι + (1 — Χ)χ2ι λ 6
е [О,1], χι , Х2 е К*, то для произвольного у £ К справедливо
ху = \х\у + (1 - Х)х2У ^ 0, т. е. χ е К* (рис. 11.4).
Остается показать, что Κι + К2, Κχ Π К%, /С* являются
конусами, что делается проверкой определения. Покажем,
например, что Κι + К2 — конус. Для этого возьмем χ е К\ + К2
и рассмотрим Хх = Ажх + Аж2, λ > О, Ж1 G Κι, х2 € 1<2-
Поскольку Κι и К2 — конусы, то Хх € Κχ + К2, X > О,
поэтому Κι + К2 —конус.
5) Если χ е К2 ,то жу ^ 0, 2/ G К*2 - Но Κχ С К2, поэтому
&У ^ 0, 2/ £ Κι, и ж е Щ, что и требовалось доказать.
1) Покажем, что К* —замкнутое множество.
Действительно, пусть у е К. Рассмотрим сходящуюся последовательность
{#fc}£lx С К*, ж = limbecxk. Тогда ж*2/ ^ 0, ft = 1, 2,....
и, переходя к пределу при к —> оо и вспоминая, что <£>1(ж) =
= τ/ж — непрерывная функция, получаем ух ^ 0, т. е. χ € /С*,
что и требовалось доказать.
2) Пусть у G (Κι + К2У ■ Тогда уж ^ 0, χ е Кг + К2, или
y(xi -}- Ж2) ^ 0, х\ е Κχ9 χ2 G К2. Полагая последовательно
χι = О и ж2 = 0, получаем х2у ^ 0, жХ2/ ^ 0, Xi G Κι, ж2 G
G К2, т. е. у G К£ П К2 . Покажем обратное включение. Пусть
у е К* П К2 . Тогда уж1 ^ 0, г/ж2 ^ О, Ж1 G Κχ, ж2 G А"2,
а поэтому 2/(жх 4- ж2) ^Оиг/е (Κχ + К2)*, так что свойство 2
доказано.
3) Если у е Щ + Щ, то г/ = ^ + г/2, yi £ Kf г/2 - Щ,
при этом ?/1Ж1 ^ 0, χι е Κι, и г/2#2 ^ 0, ж2 ^ К2. Поэтому
370
Глава it
Рис. 11.5
Рас. П.б
ух = (г/ι 4- 2/2)^ = 2/ι# + У2& < 0, χ € К\ П /С2 и свойство 3
доказано.
4) Если ж € К у то жг/ < 0, у 6 А*, поэтому χ е К** и
свойство доказано.
Заметим, что в множестве выпуклых конусов свойства 3 и 4
не могут быть улучшены, о чем говорят следующие примеры.
Пусть К = {х\х = (£ь£2), ξι > 0, ξ2 > 0} U {(0,0)}.
Тогда /Г* ^ЛГ (рис. П.5).
Теперь рассмотрим
К{ = {х\х={£г&), ξι<0, ί2>0}υ{(0,0)},
К2 = {х\х=(Ъ&), ξι>0, ξ2>0}υ{(0,0)}.
Гогда К{ + IQ φ (Κλ Г» К2У (рис. 11.6).
Определим коническую оболочку множества. Сначала
заметим, ч го если х\, ..., жт € Rn, το вектор
т
Ж
— } Аг£&г7 А ^ и? Ζ — 1}. . . ^ ?Т??
г=1
называется неотрицательной линейной комбинацией
векторов α?ι,..., хт.
Пусть Л/ С Мп. Тогда конической оболочкой множества
Μ (обозначается со(М)) называется множество всевозможных
неотрицательных линейных комбинаций векторов из il/, т. е.
со(М) = < χ \х = Υ2 λίΧί, λ, > 0, xL € Μ >
Геометрия выпуклых множеств
371
Рис, it J
Можно показать, что при построении со(М) достаточно
ограничиться линейными комбинациями из не более чем η■ + 1
векторов из Μ (ср. с теоремой Каратеодори § I).
Лемма. со(М) — наименьший выпуклый конус,
содержащий множество Μ.
Указание. Для доказательства утверждения сначала следует
показать, что со(М) — выпуклый конус. Далее доказать, что
К = со(К) 'тогда и только тогда, когда К — выпуклый
конус· Теперь пусть К D Μ — выпуклый конус. Тогда К =
= со(К) Dco(M)DM.
Примеры конических оболочек некоторых
множеств:
1) М = [жьж2](рис. 117);
2) Μ = {χ I \x - а\ < а} = 5(α,α)
(рис. 11.8). Если О € £(а, а), то со(М) = Е2.
3) К = {х | χ = Хщ и G V, V =
= conv{5Ci, - ·., хг }} = co(V) — коническая
оболочка многогранника V.
ЗАМЕЧАНИЕ. Из леммы следует, что К = со(К) лишь в
случае, когда К — выпуклый конус. Поэтому можно дать
эквивалентное определение выпуклого конуса.
К С W1 называется выпуклым конусом, если К содержит
все неотрицательные линейные комбинации векторов из К.
В заключение еще раз заметим, что вершина выпуклого
конуса К необязательно является крайней точкой выпуклого
множества К. Более того, она может являться внутренней точкой К
372
Глава it
(например, в случае К = L, где L — линейное
подпространство). Поэтому имеет смысл следующее определение.
Выпуклый конус К С R71 называется заостренным, если
из условий χ € Ку χ ^0 следует, что —χ ^ К.
Содержательно это означа- к = L1
ет, что заостренный конус не
содержит линейного
подпространства положительной
размерности· Так, на рисунке 11.9 конус
К не является заостренным, а конусы Κι и Къ заострены.
Понятно, что произвольный выпуклый конус К может быть
представлен в виде
К = L + Ао,
где L — линейное подпространство, jFCq — заостренный
выпуклый конус.
§ 3. ОТДЕЛИМОСТЬ ВЫПУКЛЫХ МНОЖЕСТВ
Основным свойством, характеризующим выпуклые множества,
является так называемое свойство отделимости. Для
пояснения этого свойства рассмотрим на плоскости замкнутое
выпуклое множество Μ и точку Ь £ Μ
(рис. НЛО).
Тогда найдется такая прямая хр =
= с*, что множество Μ и 6 лежат по
разные стороны от этой прямой, т. е. для
любой точки χ € Μ выполняется
неравенство хр < о?, в то время как Ьр > а.
Это свойство выпуклых множеств может
быть сформулировано в виде теоремы·
♦ь
Рис. 11.10
Теорема 1 (о разделяющей гиперплоскости). Пусть Μ с
СВП — замкнутое выпуклое множество, Ь G W1. Тогда
либо Ь G М, либо (если Ъ £ М) существует такая
гиперплоскость 7Γη_ι = {х | хр = 7Ь что ХР ^ 7^ х € ^>
Ьр> ^,те. 7Γη_ι разделяет точку b и множество М.
Гео четрия выпуклых множеств
373
Доказательство. Определим для любой точки жеМ
функцию расстояния φ{χ) = \х — Ь\. Эта функция непрерывна на
замкнутом множестве Μ. Если Μ —ограниченное множество,
то по теореме Вейерштрасса функция ψ{χ) достигает минимума
в одной из точек М.
Если выпуклое множество Μ
неограниченно, то рассмотрим замкнутый шар S(byct)
такой, что S(bya)nM = Mf Φ 0 (рис. 11.11).
Поскольку S(b}a) — выпуклое и замкнутое
множество, то М' = S(6,a)flM —
выпукло, замкнуто и ограничено. Поэтому
функция φ(χ) на М' достигает минимума. Рис. //.//
Пусть
min φ(χ) = min \x - b\ = \а - b\ = φ{α).
асбМ' хЕМ*
Рассмотрим гиперплоскость 7Γη_ι = {у \ у(Ь — а) = 7}·
Пусть 7Γη_ι проходит через точку а. Тогда 7Γη_ι = {у \ у{Ь —
— а) = а(Ь — а) }.
Ясно, что точка b $ πη-\ - Пусть b лежит в положительном
полупространстве относительно 7Γη_ι, т. е. 6(6—а) > а(Ь — а).
Покажем, что ни одна точка с € М' не принадлежит этому
полупространству. Предположим противное: пусть существует
с € М', для которой с(Ь — а) > а(Ь — а). Поскольку с, а €
е М' и М' — выпукло, то λα + (1 - А)с £ М\ А € [0,1]. По
построению минимум ψ{χ) = \х — Ь\ на М' достигается в точке
а € М', поэтому минимум φ(χ) на отрезке [а, с] достигается
в точке а, т. е. при А = 1. Если показать, что min^^c] φ(χ)
достигается при 0 < А < 1, то теорема будет доказана. Для этого
рассмотрим
с)А + (Ь-с)2.
2(а-с)2>0.
^2(А) = (Аа + (1-А)с-Ь)2 =
= (а-с)2А2-2(а-е)(Ь
Имеем
#2(А)
dX
О,
откуда λ = (а - с)(6 - с)/(а - с)2, ^^
374
Глава tl
Таким образом, min^6[0lij^2(^) достигается в точке,
соответствующей Х0 = (а- с)(Ь - с)/(а - с)2. Однако
аЬ — а2 < (Ъ- а)су
поэтому
(а- с)(Ъ-с) <{а- с)2.
Следовательно, минимум функции ψ(λ) достигается при А <
< 1. Пусть λ = λ0. Если 0 ^ λ0 < 1, то λ0α + (1 - А0)с е М',
что противоречит тому, что минимум φ{χ) на М9 достигается в
точке а. Если λ0 < 0, то Х^а + (1 — А0)с ^ М'. Однако
функция ψ2(λ) является выпуклой и принимает минимальное значение
при Ао < 0. Тогда ^2(1) > 02(О), т. е. φ(α) > <р{с)9 что опять
противоречит тому, что φ(χ) достигает минимума в точке а.
Таким образом, точка с не может лежать по одну сторону от
гиперплоскости, что и точка Ь. Теорема доказана.
Гиперплоскость 7Γη_ι = {χ \ χρ = 7} называется опорной
к множеству Μ в точке а е М, если для всякого χ € Μ
выполняются соотношения χρ < 7 и ар = 7-
Таким образом, теорема 1 утверждает, что выпуклое
замкнутое множество Μ можно отделить от любой точки Ъ $. Μ с
помощью опорной гиперплоскости.
Если неравенства в условиях теоремы выполняются как
строгие, т. е. хр < η, χ € Μ\ bp > 7» то говорят о
строгом разделении точки и множества. Заметим, что теорема 1
верна и в формулировке строгой отделимости, для доказательства
достаточно гиперплоскость провести через точку (а + Ь)/2.
Докажем теперь теорему отделимости в следующей
альтернативной формулировке.
Теорема 2 (о неотрицательных решениях систем линейных
уравнений). Справедлива одна из следующих
альтернатив: либо система я /1Ч
χ А = Ь (1)
имеет неотрицательное решение, либо имеет решение
система неравенств
Atj ^ О, by < 0. (2)
Геометрия выпуклых множеств
375
Рассмотрим геометрическую
интерпретацию теоремы. Пусть
множество К = {у \ у = χ А,
χ ^ 0 }. Множество К —
выпуклый конус, и оно замкнуто. Теорема
утверждает, что либо точка Ь € К\
либо, если 6 φ К, то найдется
вектор у, который составляет нетупой угол с каждым из векторов
конуса К и тупой угол с вектором Ь. Таким образом, выпуклый
конус К и точка b лежат по разные стороны гиперплоскости
тгп_1 = {ζ | zy = 0} (рис. 11Л2). Таким образом, теорема 2
является теоремой отделимости для выпуклого конуса К.
Доказательство. От противного несложно показать, что
альтернативы (1) и (2) одновременно выполняться не могут.
Предположим, что система хА = b вообще не имеет
решения. Тогда по теореме 2 § 2 главы 10 имеет решение система
Ау = О, by = -1, поэтому теорема в этом случае доказана.
Теперь предположим, что система (1)
т
г=1
имеет решение, но не имеет неотрицательного. Покажем, что
система (2) имеет решение. Доказательство будем вести индукцией
по числу га строк матрицы А.
Пусть т = 1. Тогда ξχα,ι = b имеет отрицательное решение
ξι < 0. Рассмотрим у = —Ь; а\у = — b2/Ci ^ 0, уЪ = —б2 < 0,
т. е. база индукции доказана. Пусть утверждение справедливо
для т — 1. Докажем для га.
Пусть система уравнений
771—1
Σ &** = Ь (3)
г=1
не имеет неотрицательного решения. Тогда по индукционному
предположению существует решение у' системы
о>гУ* ^ 0, г = 1, ..., га — 1; by9 < 0.
(4)
376
Глава /I
Если ашу' > 0, то теорема доказана. Поэтому пусть
о>тУ* < 0. Рассмотрим вспомогательную систему
т— 1
Σ iiCLi = Б, (5)
2=1
где щ = {ату')а,г - (щу')ат, Б = (ату')Ь - {Ьу')ат.
Покажем, что (5) не имеет неотрицательного решения.
Предположим обратное, т. е. ж = (ξι,...,ξηι) ^ 0 —
неотрицательное решение системы (5). Подставим его в (5) и полученное
тождество умножим на 1/(ату'). Тогда
т—1
ату'
.J Fit X
~, Σ Ь({агпУ')щ - {aiy')am) =
—f({amy')b-(byf)am),
ί=1
«m2/
отсюда
т—1 ., / т—1
У2 &«* + 7 ( V - Χ, &(αιί/) )лт = 6.
ΐ=1 0т2/ V г=1 '
Обозначим , / m-i
7=^(ν-Σ«^))
Так как 7 ^ 0, то система (1) имеет неотрицательное
решение, что противоречит предположению. Поэтому (5) не имеет
неотрицательного решения и по индукционному предположению
существует у — решение системы
'а*2/>0, i = l,...,m-l, _.
Ъу<0. К '
{
Построим вектор у = {ашу')у—{ату)у$'. Непосредственной
проверкой убеждаемся, что
о>гУ = щу ^ 0, г = 1,. -., га - 1;
Ьу = Ьу< 0, ат2/ = 0,
т. е. г/ — решение системы (2), а тем самым теорема полностью
доказана.
Геометрия выпуклых множеств
377
Заметим, что опорная гиперплоскость к выпуклому конусу
К проходит через точку О, т. е. вершину конуса. Этот факт не
является случайным в силу справедливости следующей теоремы.
Теорема 3. Всякая гиперплоскость, опорная к выпуклому
конусу К, проходит через точку О (вершину конуса).
Доказательство. Пусть гиперплоскость 7Γη_ι = {χ \ хр =
= 7 } является опорной к конусу К в точке а е К, т. е. для всех
χ € К справедливы соотношения хр < 7> αΡ = 7 Рассмотрим
точку αα, а > 0. По определению конуса аа € К, поэтому
а(ар) ^ч, а^£ 0. Поскольку р(аа) = а{ар) = αη, то ση < 7
для любого α ^ 0. Отсюда {а — \)η < 0. При а = 0 получаем,
что 7 ^ 0, а при а = 2 получаем, что 7^0. Таким образом,
7 == 0, а уравнение опорной гиперплоскости имеет вид хр = 0,
а значит, точка О принадлежит этой гиперплоскости.
В заключение приведем теорему о разделяющей
гиперплоскости для незамкнутых выпуклых множеств.
Теорема 4. Пусть Μ с Шп — выпуклое
множество (необязательно
замкнутое) и пусть Ъ ^ int(M). Тогда
существует такая гиперплоскость 7Γη_ι =
= {χ | хр = 7}' что Ьр = η и хр < η
для любого χ € М.
На рисунке 11.13 приведен пример
отделения круга от всех точек R+.
§ 4. КОНЕЧНЫЕ КОНУСЫ
Данный параграф посвящен конечным конусам. Конечный конус
для выпуклых конусов имеет такое же значение, как выпуклый
многогранник для выпуклых множеств.
Пусть αχ, ..., ат е Шп. Тогда выпуклый конус К =
= co{ai, ..., am} называется конечным конусом,
порожденным векторами αϊ, ..., am, а сами векторы называются
порождающими для конечного конуса К.
378
Глава II
Выпишем различные уравнения конечного конуса:
К =со{аь... ,ат} =
{I m ι
I г=1 '
τη т
г=1 г=1
где (а) = {г/ | у = Аа, λ > 0}, А = [аь .-·, ат] — (т х
χ η) -матрица.
Таким образом, конечный конус есть сумма конечного числа
полупрямых (отсюда и название). В дальнейшем будем
пользоваться одной из указанных эквивалентных форм записи.
Теорема 1 (двойственность для конечных конусов). Если
К — конечный конус, то К** = К.
Доказательство. Для любого выпуклого (в том числе
конечного) конуса справедливо К** D К. Покажем, что для конечного
конуса справедливо и обратное включение. Действительно, пусть
К = со{аь - - ·, Cbr}. Предположим противное, т. е. Ь € К**, но
Ь £ К. Тогда система Σ£=1 ξ%α% — & не имеет неотрицательного
решения. В этом случае по теореме 2 § 3 имеет решение система
щу ^ 0, г = 1, ..., г; &у > 0.
Тогда уа ^0У а е К, поскольку
4=ι ' i=i
ξί^Ο, г = 1,..., г,
т. е. г/ 6 X*. Однако в этом случае Ь £ К**, так как by > 0.
Противоречие и доказывает теорему.
ЗАМЕЧАНИЕ. Теорема двойственности справедлива и в
более общей формулировке, а именно, если выпуклый конус К
является замкнутым множеством, то i£** = К.
Следствие 1. Если К — конечный конус, то К — замкнутое
множество.
Геометрия выпуклых множеств
379
Следствие 2. Пусть К = {χ \ χ А ^ О}. Тогда К* =
= {z\z = Ay, y^O].
Доказательство. Пусть С = {ζ \ ζ = Ау^ у > 0}. Для
того, чтобы К = С*, необходимо и достаточно, чтобы χζ ^ О,
χ € К, ζ € С. Для этого необходимо и достаточно, чтобы
ж(Лу) < 0, ж G К9 у ^ 0. Но это эквивалентно хЛ ^ О,
χ е К, что верно по построению К. Поэтому А"* = С** = С.
В качестве примера конечного конуса можно взять линейное
подпространство L С Rn. Действительно, если αι,...,αΓ 6
eL—базис!/, то г г
г=1 i=l
Ортант R+ —конечный конус, поскольку R+ = Σ^ιί^Ο»
где гц = (0,..., 071,0,..., 0) € Rn, а 1 находится на г -ом
месте, г = 1,...,п.
Докажем теперь, что множество решений произвольной
однородной системы линейных неравенств является конечным
конусом. Для доказательства необходим вспомогательный результат.
Лемма 1. Множество неотрицательных решений системы
уравнений ^ = Q (|)
является конечным конусом. ,///^^ п к+
Результат леммы геометрически
понятен, поэтому мы приведем его без
доказательства.
Следствие. Пусть L —линейное
подпространство. Тогда L П R™ — конечный
конус (рис. 11.14).
Доказательство. Рассмотрим L* и пусть а1, ..., а5 €
€ L* — базис L*. Рассмотрим К = {у \ уа* = 0; г = 1 ,
,.м5; у ^ 0 }. По лемме К — конечный конус. Покажем, что
К = L П Rip. Пусть у е К, тогда уа* = О, г = 1, ..., s, т. е.
у е L** = L. С другой стороны, у G R+ . Поэтому у е Lf) R™.
Обратно, если у е LDR!p,то уа1 = 0, г = 1,..., s, α* € L*,
?/ > 0. Таким образом, у € К н следствие доказано.
380
Глава It
Заметим также, что конечный конус L П R+ заострен.
Перейдем к формулировке и доказательству основного
результата данного параграфа.
Теорема 2. Рассмотрим однородную систему линейных
неравенств
хА<0
(2)
и множество решений К = {χ \ χ А ^ 0} этой системы.
Тогда К — конечный конус.
Геометрически данный результат прозрачен.
Действительно, η η
K={x\xA^Q} = f\{x\xaj ^0}= f}(aj)*
представляет собой пересечение полупространств,
которое является конечным конусом (рис. 11./5).
Доказательство. Рассмотрим линейное
подпространство
£ = {у I у = хА}
и пересечение L П R+. По следствию к
лемме 1 L П R™ — конечный конус, поэтому
Рис, ИЛЬ
£ П Щ = £(!*)-
г=1
Возьмем векторы Х{, для которых у* = — &ιΑΛ г = 1,... ,г,
и рассмотрим конус г
*:' = 5>,·).
г=1
Далее обозначим L = {ж | жЛ = 0} —линейное
подпространство решений однородной системы линейных уравнений; L
—конечный конус, поэтому я
Построим конечный конус
г=1 7 = 1
(3)
Геометрия выпуклых множеств
381
Покажем, что К = К. Действительно, допустим, что χ € К.
Тогда -у = -хА ^ 0, т. е. -у е L П R+. Поэтому
г
-у = X^Aij/i, Χι ^ 0, г = 1,...,г,
г=1
ИЛИ
г
—Ж Уж ^ у λΐ\ tC^Ajj
г=1
откуда после переноса в левую часть имеем (х — ΣΓ=ι X%Xi)A —
= 0. Это означает, что вектор χ — Х^=1 Х%Хг € Ly \ ^ 0. Но
тогда
иже^.т.е. мы доказали, что К с К.
Покажем обратное включение. Пусть справедливо
соотношение (4). Тогда, домножая его справа на матрицу Л, получаем
г q r
хА = Σ Xi(xiA) + Υ^μ^Α) = - Σ χ№ = °>
поскольку з/г € R+, λ ^ 0, г = 1, -.., г. Теорема доказана.
ЗАМЕЧАНИЕ 1. Нетрудно показать, что конус К' заострен,
поэтому теорема означает, что конечный конус решений К
однородной системы линейных неравенств есть сумма заостренного
конуса К9 и линейного подпространства L = { χ \ хА = 0 }.
ЗАМЕЧАНИЕ 2. Важность доказанной теоремы 2
заключается в том, что она указывает, что однородная система линейных
неравенств — это неявное уравнение конечного конуса.
Действительно, пусть К = co{ai, ..., am}. Рассмотрим
К* = {У I Уа% < 0, г = 1,...,т}. К* —это конечный
конус. Пусть К* = со{Ьь...,Ь5}. Теперь рассмотрим jRT** =
= { ζ | zbj ^ 0, j = 1,..., s}, но К** = К, поэтому искомый
конус К = {ζ | ^bj ^ 0, j = 1,..·,θ}, и уравнение ζΒ й
й 0, В = [bi,..., bs] — неявное уравнение конечного конуса К.
Приведем теперь теорему, которая подытоживает
алгебраические свойства конечных конусов.
382
Глава ί!
Теорема3 (алгебра конечных конусов). Если К, К\, К2 —
конечные конусы, то К*, Κι + К2, К^ Π К2 — конечные
конусы и
1) К — замкнутое множество;
2) К** = К;
3) (Κι+Κ2)*=ΚΪΓ\ΚΖ;
4) Щ + Щ = (К1Г\К2)*.
Доказательство. Пусть К = со{аь · ■ · ^т}- Сопряженное
к нему множество К* = {у \ ущ <0, t = l,...,m} является
конечным конусом по теореме 2.
Для суммы конечных конусов доказательство
очевидно. Свойство 3 справедливо для любого выпуклого конуса,
свойства 2 и 1 — содержание и следствие теоремы двойственности.
Поскольку К\ и К2 —конечные конусы, то К* + К2 —
конечный конус. По свойству 2 и свойству 3:
(К1 + ΚΙ)* = К{* П К? = Κι П К2.
Слева конус конечный, поэтому и справа конечный конус.
В силу теоремы двойственности
(Κι η к2у = (κι + iqy* = κι + щ,
а значит, справедливо свойство 4.
Вектор χ φ О, χ € К называется крайним для выпуклого
конуса К, если из того, что χ = (х\ + х2)/2, χι, х2 € К,
следует, что χι = \х> х2 = μχ для некоторых λ ^ 0, μ ^ 0.
Содержательный смысл
определения понятен. Так, на рисунке 11.16
крайними являются векторы αϊ и а2.
Хотелось бы, конечно, получить
для конечных конусов описание, по-
^ добное теореме 3 § 1 и утверждать,
что конечный конус является
конической оболочкой своих векторов. Однако это неверно. Так,
существуют конечные конусы, у которых нет крайних векторов
(например, линейное подпространство). Вместе с тем имеет место
следующий результат.
Гео нетрия выпуклых множеств
383
Теорема 4. Конечный заостренный конус К является
конической оболочкой конечного множества своих крайних
векторов (суммой своих крайних полупрямых).
Таким образом, мы получаем параметрическое уравнение
конечного конуса К:
{I г s
χ \х = ^2 ^ίχί + 5J Нхр
А/^ 0. г =!,...,г, Vpj, j = l,...,sL
где χι — крайние векторы заостренного конуса Kq, a x'j —
базисные векторы подпространства L, Kq + L = К.
Главным отличием понятий крайней точки выпуклого
множества и крайнего вектора выпуклого конуса является то, что
вектор О может являться крайней точкой конуса и не может
быть крайним вектором. В то же время очевидно, что точка О
является крайней для заостренного конуса К. В самом деле,
пусть О = (ж' + ж")/2, где ж', ж" Ε К. Отсюда χ' = -ж", что
противоречит определению заостренного конуса.
Векторы αχ, ..., аш называются положительно
независимыми, если уравнение т
]П&а* = 0 (5)
не имеет положительных решений.
Если векторы {а*)™^ положительно независимы, то конус
К = со{аь ..., ат} заострен. Действительно, пусть у =
= ΣΧι &аг, & > 0, и у е К. Пусть у φ О, тогда -у <£ К,
так как в противном случае (5) имеет положительное решение.
Докажем обратное утверждение.
Лемма 2о Пусть а\, ..., аш — ненулевые векторы. Если
конус К = со{аь ..., ат} заострен, то векторы αϊ,..., аш
положительно независимы, т. е. из условий Σ™:ΐ ^*а* = *)'
Χι ^ 0, следует, что Αι = Аг = ■ · · = Am = 0.
Доказательство. Доказательство проведем индукцией по
га. При т = 1 утверждение очевидно, поскольку αλ φ О. Пусть
384
Глава II
оно верно для fc ^ m - 1 и предположим, что Σ™=λ Ка*г = О,
Л^ > 0, г — 1,. ·. ,т. Тогда λχαι = ~Ύ^2^α^· Поскольку
Y^L2^гаг £ К, λ\α\ е If, το согласно определению
заостренного конуса \\сь\ — 0 = Σ™=2 λ%α>%. Тогда λι = 0 и
по предположению λ2 = Аз = ■ · · = Ат = 0.
Теперь перейдем к доказательству теоремы 4. Пусть К =
= co{ai, ..., ат}. Среди векторов αϊ, ..., ат вычеркнем
тот, который можно представить в виде неотрицательной
линейной комбинации остальных, а затем повторим эту операцию
среди оставшихся векторов и т. д. Тогда придем к набору
векторов, например αϊ, ..., ar (r ^ га), обладающему
следующим свойством: К = co{ai, ..., аг} и никакой из векторов
Ог, i = 1, ..м г, не является неотрицательной комбинацией
остальных.
Покажем, что все векторы этого множества являются
крайними. Допустим, что αϊ — не крайний. Тогда а\ = £Г=1^аь
где \г^0. Отсюда (1 - λι)αχ = $ZJ_2 λ*α* ·
Если λχ > 1, то (1 — λι)αι G Κ, (λι — 1)αι € К, т. е. αχ =
= О; если λι = 1, το Y^i=2 λ^α* = О, чего быть не может в силу
леммы и поскольку среди а^ нет равных; в случае λι < 1 имеем
αχ = j3X" Σ^=2 ^ja>j t т. е. αϊ является неотрицательной
линейной комбинацией векторов α2, ..., аг, что также невозможно.
Теорема доказана.
§ 5. ВЫПУКЛЫЕ ЦИЛИНДРЫ
Множество Са С W1 называется цилиндром с направлением
α φ О, если вместе с каждой точкой χ G Са оно содержит точки
вида χ + та, τ G (—сю, +оо).
Содержательно данное определение означает, что вместе с
каждой точкой χ цилиндр Са содержит и всю прямую
{у \ у — Χ + TQ, Те (-ΟΟ,+ΟΟ)}.
Замкнутое выпуклое множество, обладающее свойством
цилиндра, называется выпуклым цилиндром.
Геометрия выпуклых множеств
385
Понятно, что плоскость 7гг (в
частности, πι), подпространство U (в частности,
W1) являются выпуклыми цилиндрами. Так,
для плоскости 7гг направление α
необходимо взять из направляющего подпространства
Рис. 11.17 и (рис. 11.17).
Понятно, что dim(Ca) ^ 1 (Са ψ 0), поскольку выпуклый
цилиндр Са содержит по крайней мере одну прямую.
Естественным образом можно ввести понятие
цилиндрической оболочки множества.
Цилиндрической оболочкой Са(М) множества Μ с Шп
с направлением а ф О называется наименьший выпуклый
цилиндр, содержащий М.
Так, цилиндрической оболоч - ^^ :—^тгь
кой точки является прямая, ци- рис ц !8
линдрической оболочкой прямой (с направлением,
непараллельным прямой) является двумерная плоскость (рис. 11.18).
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Доказать, что замыкание выпуклого множества
выпукло.
Доказательство. Пусть Μ — выпуклое множество и Μ —
его замыкание. Пусть х,у € Μ и w = (1 — Х)х + Ху, X G [0Л].
Для χ и у найдутся также последовательности {а?г-}э {yt} с
С М, что Итг ^оо хг = х, limj-^oo уг = у. Ввиду непрерывности
Wi = (I - X)Xi + Xyi > W = (1 - Х)Х + Ху.
woo
Но {wi} С М, поэтому w е М,
2. Пусть Μ = conv{asi, ..., хш} — выпуклый
многогранник. Построить плоскость πΓ минимальной
размерности, которая содержит множество Μ.
Решение. Рассмотрим векторы хг; — Х\, г = 2,..., т , и
матрицу [ж2 — Х\, ■.., Хт —х\] · Тогда г = dim(7rr) — гапк[ж2 — #ι *
..., хт — х{\, а плоскость -πγ определяется точкой х\ и
направляющим подпространством V = Lin{a?2 — #ι.. ., хт - х\}·
S86
I лава II
Проиллюстрируем по «ученное решение на числовом ириме-
ое Пусть Л/ = conv{a?i, а?2, #3,^4}, где
χι = (1,-1,2.-1),
ij = (1,1,1,1),
х2 = (2,1,-3,1),
хл = (2,0,3,0).
Тогда
rank
/ 1 0 1\
2 2 1
-5 -1 1
V 2 2 1/
= rank
/1 0 1\
0 2-1
0-16
\() 2 -1/
= 3.
Это означает, что точки xit х2, хз. #4 находятся в общем
положении (§ 3 главы 10), поэтому через них можно провести
единственную плоскость размерности 3. Итак, dim(M) = 3.
Плоскость π минимальной размерности имеет уравнение
ξ2 = -1-f 2ri+2r2+r3,
ξ4 = -1+2τι+2τ2 + τ3.
ξι = 1+τι+т3,
ξ3 = 2 - 5τι - r2 + гз,
З.Дано множество
Κ{χυ) = { χ I ж = (1 - А)ж0 + λι*} Λ > 0, « 6 V },
<?(te V — выпуклый многогранник. Показать, что
множество K(xq) выпукло.
Решение. Рассмотрим точки х\х'' £ K(xq), т. е.
х' = (1 - λ>ο + AV, ж" = (1 - λ'>0 + A'V,
λ'^0, λ">0, u',u"eV.
Покажем, что точки χ — μχ' -\-{\ — μ)χ" € -К"(зсо), μ € [0,1].
Действительно,
ж = μ#' + (1 -μ)»" =
= (1 - λ')μχ0 + λ'/ш' - (1 - λ")(1 - μ)χο + λ"(1 - μ)η" =
= (ΐ-(Λ"-λ"μ + λ'μ))#υ +
^λ -Α μ+Α μ) (λ„_λ„ λ, « + λ„_λ> + λ,/* J ·
Гсо четрия выпуклых мно wrens
387
Число А" - Χ" μ + Χ'μ = Χ'μ + λ"(1 - μ) > 0, при этом
λ'μ + λ"(1-μ)
Χ" - Χ"μ + Χ'μ Χ'·'- Χ"μ + Χ'μ
11усть 7 = Χ" — Χ" β + X'f · Тогда
ж = (1 - 0«ο+7 (^' + (ΐ ^ ^) ~")
где гЛ и" € V. Поэтому г* = ^fuf + (l - Κ^)ή>" G К, a тогда
ж = (1 - 7)^о + 7™ € ^(*ο)ι
и выпуклость /£(жо) доказана.
4. Доказать, что K{xq) = { ж | ж = (1 - X)xq + Хи, А >
> О, *г € V }, где V — выпуклый многогранник,
является выпуклым конусом с вершиной в жо-
Доказательство. Из предыдущей задачи следует, что
множество K(xq) выпукло. Поэтому достаточно доказать, что
К(хо) —конус с вершиной в ж0.
Действительно, пусть χ е K(xq) и μ ^ 0. Рассмотрим точки
у = х0 + μ(χ - х0) = хо + μ (О ~ А)ж0 + Хи - ж0) =
= Жо + λμ(ιι — ж0) = (1 — Χμ)&ο + А/ш, Χμ ^ 0,
т. е. у <Ξ /Г(жо) и, следовательно,. K(xq) — выпуклый конус с
вершиной в х0.
Б.Для конуса К = {ж | жЛх ^ О, жЛ2 = 0} написать
уравнение сопряженного конуса.
Решение. Конус К — конечный, при этом К = Κι Л К-2, где
jFsTi = {ж | хА\ ^ 0}, jRT2 = {& \ &М = 0} —конечные
конусы. Тогда по теореме 3 К* = (Κι Г) А'г)* = /<7 + Щ-
С другой стороны,
771 П\
Кх = {χ\χΑλ ^0}= f]{x\xa^)j ^Q}= Г)(а(Ш)*,
7С2 = {χ Ι χΑ2 = 0} = f]{я: | ха™> = 0} = f) I^\
odS
Глава II
{2)ί7
где (α)* —полупространство, Lm x —линейное
подпространство размерности т — 1. Поэтому
^-Σ(β(1)0**=Σ(β(1^)={*|*=Σ^α(1)<» Л^°}>
# г=1 г=1 ^ I г=1 '
i=l i=l ^ I j=l J
Таким образом, окончательно
{Ι τΐι n2
x \χ=Σχία{1)ί+Σν3α
λζ^Ο, t = l,...,ni, V/ij, j = 1,..m^2[·
6. Доказать, что если выпуклый конус К замкнут, то
К**=К.
Решение. Поскольку для любого выпуклого конуса имеет
место включение К С К**, то для доказательства утверждения
достаточно показать обратное включение, т. е· К** С К.
Предположим обратное, т. е. а е К**, но а £ К. К
замкнутому конусу К и точке а ф К можно применить теорему о
разделяющей гиперплоскости (теорема 1 § 3) с учетом теоремы 3 § 3
о том, что всякая гиперплоскость, опорная к конусу, проходит
через О. Пусть ρ — нормальный вектор гиперплоскости,
разделяющей множество К и точку а. Тогда хр ^ О для всякой
точки χ е К и ра > 0. Отсюда вытекает, что ρ € К* и
поэтому а ^ К**, поскольку скалярное произведение векторов аир
больше нуля. Это противоречие доказывает, что А*** С К.
7.Доказать, что выпуклый цилиндр не имеет крайних
точек.
8. Показать, что если С\ и С2 — выпуклые цилиндры с
направлением а, то С1+С2 и С\ ПС2 также являются
выпуклыми цилиндрами с направлением а.
9. Пусть Μ с Шп — выпуклое множество.
а) пусть Μ открыто их 6 А/. Доказать, что если
χ е Ή, то χ € дМ, т. е. χ — граничная точка М.
б) доказать, что внутренность int(M) выпукла.
Глава 12
ГЕОМЕТРИЧЕСКАЯ СТРУКТУРА
СИСТЕМ ЛИНЕЙНЫХ НЕРАВЕНСТВ
§ 1. ВЫПУКЛОЕ МНОГОГРАННОЕ МНОЖЕСТВО
Исследуем геометрический смысл множества решений системы
линейных неравенств. Это с необходимостью приведет к понятию
многогранного множества, которое, как увидим в дальнейшем,
включает все вышерассмотренные геометрические объекты.
Рассмотрим систему линейных неравенств
xAub<&xaj ^Pjy j = 1,...,η<*Σ&α* =6> ί1)
где А — (тхп) -матрица.
Множество Μ = {χ \ χ А й Ь} называется многогранным
множеством, заданным системой ограничений (1). Система
ограничений (1) — неявное уравнение Μ.
Может оказаться, что множество Μ пусто. Таково, например,
множество, задаваемое ограничениями ξι < 1, —ξ! < -3 в
пространстве R1. В связи с этим оговорим заранее, что все
утверждения этой главы относительно многогранного множества Μ
относятся к тому случаю, когда оно не является пустым.
Лемма· Многогранное множество Μ, заданное
системой (1), является множеством выпуклым и замкнутым.
Доказательство. Если arlf X2 G Μ, λ е [0,1],то
(λχ! + (1-Α)χ2)Α =
= Χ(χιΑ) + (1 - λ)(χ2Α) ^ АЫ- (1 - Х)Ь = Ь,
т. е. Χχι + (1 - А)ж2 G Μ.
390
Глава 12
Покажем теперь, что Μ — замкнутое множество. Пусть ж =
= lim^oo Χχ , Хг € Л/. Тогда жгс^ ^ 0j, г = 1, 2, ... ; j = 1.
..., π. Поскольку функция у>(ж) = жа непрерывна (задача 29
главы 10), то, переходя к пределу по г —> оо, получаем жа·* ^ /9j.
j = 1,..., η, т. е. χ е Μ.
Возникает естественный вопрос о структуре множества Μ.
Теорема 1. Пусть Μ — сопу{жь .., ,хш}, Хг € W1, г =
= 1, ..., т, — выпуклый многогранник. Тогда Μ
является множеством решений некоторой системы линейных
неравенств.
Доказательство. Обозначим xt = (ж^1) € Rn+1, г = 1,
..., т, и Μ = сопу{жь.. . ,жт}- Рассмотрим К = Σϋι(*«)·
Тогда
Множество К* — конечный конус. Пусть о? = (с^,—/3j),
j = 1, ..., Ι, — порождающие векторы для конуса К , т. е.
~К* = Σ1!.=1(aJ"). Покажем, что Μ — множество решений
системы ха3 ^"/%, j = 1, ..., Ζ.
Действительно, пусть ж б М, тогда ж = (ж,1)бМ,жбК
и ха? ^ 0, j = 1, ..., Ζ,τ. е. жа^ < /^-, j =Л, ...^J. Пусть
χ — решение системы. Тогда χ = (ж, 1) € К = К, откуда
χ е Λί и ж е Μ, что и требовалось доказать.
Многогранное множество Μ, заданное (1), является
выпуклым, поэтому справедливо понятие размерности. Оказывается,
что для него можно конструктивно найти размерность.
Пусть Μ — многогранное множество, заданное (1).
Ограничение иод номером j называется жестким, если xaj = Pj для
любой точки ж € Μ, т. е. оно выполняется как равенство для
всех точек ж € М.
Понятно, что любое ограничение в виде равенства в (1)
является жестким ограничением для Μ. Однако и некоторые
неравенства в (1) могут быть жесткими ограничениями. Например, у
системы ξι - ξ2 ^ 0, -ξι + & ^ 0 оба ограничения жесткие.
Геометрическая структура систем линейных неравенств 391
Теорема 2. Пусть Μ С Шт — многогранное множество,
заданное системой ограничений {1), σ — ранг подсистемы
жестких ограничений системы (I). Тогда
ρ = dim(M) = m — σ.
Доказательство. Пусть 1\ и h —совокупности номеров
жестких и нежестких ограничений множества Μ соответственно.
Тогда
χα3=β^ jeli, х еМ, (2)
поэтому Μ С itm-ai где 7rm_a — плоскость, которая
имеет уравнение (2). Откуда ρ ^ т — σ, где σ — ранг матрицы
системы (2) (системы жестких ограничений).
Теперь рассмотрим систему линейных однородных уравнений
xaj=Q, j'e/ь (З)
Поскольку ранг системы (3) равен σ, то найдутся πι — σ
линейно независимых решений sclf ..., Xm-σ системы (3)
(теорема 1 § 2 главы 10). Кроме того, для любого j e h найдется
вектор yj, удовлетворяющий системе (1), для которого
yjaj <βά.
Полагая q
где q — число нежестких ограничений множества Μ, имеем
yo*j<Pj, ie/2. (4)
Б силу выпуклости множества Μ вектор уо е Μ, Из
неравенств (4) вытекает, что при любом j = 1,..., m — σ к
достаточно малом ε > 0 справедливо соотношение уо + sxj е М.
Допустим теперь, что множество Μ С 7г, где плоскость π
имеет уравнение k _ _
XX} — <Afcу К "==- Ly · · » t '·
Поскольку уо е Μ и ί/ϋ + ε#ΐ € Μ, то
ж;6* = -({bk, y0 + еавО - (Ь*,у0)) = -(** - λΛ) = 0.
392
Глаоа 12
Итак, система однородных уравнений
хЬк = О, к = 1,--.,?,
имеет τη — σ линейно независимых решений Xi. Следовательно,
среди векторов Ьк, А: = 1, ..., J, имеется не более чем σ
линейно независимых, т. е. βΐηι(π) > т — σ. Откуда ρ ^ т — σ.
Сравнивая последнее неравенство с полученным выше
неравенством ρ ^ т — σ, заключаем, что ρ = т — σ и теорема
доказана.
В § 4 главы 11 показано, что множество решений однородной
системы является конечным конусом.
Многогранное множество, Μ, заданное системой (1),
называется многогранным конусом с вершиной в ж0, если
Л/ — конус с вершиной в xq .
Теорема 3. Для того чтобы множество Μ, заданное
системой ограничений (1), было многогранным конусом с
вершиной в хо, необходимо и достаточно, чтобы
Μ = { χ | χα? ^ xqQ?, j = 1, .. -, η },
т. е. xaJ ^ xoaj, j = lt ..., n, — неявное уравнение
многогранного конуса с вершиной в xq.
Доказательство. Необходимость. Пусть Μ, заданное
системой ограничений (1), является многогранным конусом с
вершиной в xq. Допустим, что существует точка χ G Μ, для
которой xaj > хоа* для некоторого j, т. е. (ж — &oW > 0.
Поскольку Μ — конус с вершиной в жо, то xq + Х(х — хо) €
6 Μ для всех λ ^ 0. Однако (х — xq)o? > 0, xoaj < Pj,
поэтому (хо + А(ж - x0),aj) > /% при достаточно больших
А > 0. Следовательно, для указанных λ точки (хо + \{х -
- жо), aJ") £ Μ, что противоречит тому, что Μ — конус. Данное
противоречие и доказывает, что для многогранного конуса Л/
справедливо xaj < x$ai, j = 1,..., п.
Достаточность. Пусть
Μ = { χ | χα3 ^ а?оаЛ j = 1,..., η }
Геометрическая структура систем линейных нсравенапи 393
и пусть χ G Л/. Рассмотрим точки хо 4- Х(х — х0), λ ^ 0. Тогда
(хо + Х(х — xo)idj) = χοο?+λ(χ — xq)clj =
= ХхоР+(1-X)xqclj ^Xxoaj+(l-X)x0aj =ж0а7, j = Ι,...,/i,
следовательно, xq + Х(х — хо) G Л/ для любого λ ^ 0t т. е
Μ — конус с вершиной в а?о·
ЗАМЕЧАНИЕ. Из теоремы следует, что многогранное
множество Μ является многогранным конусом с вершиной в О тогда
и только тогда, когда система ограничений, задающая Л/, —
однородная система линейных неравенств, т. е.
хА^О (5)
— неявное уравнение многогранного конуса с вершиной в О
(конечного конуса; см. замечание 2 § 4 главы 11).
§ 2. ГРАНИ МНОГОГРАННОГО МНОЖЕСТВА
Пусть Μ — многогранное множество, заданное системой
ограничений . i: .
хА < Ъ&ха? ^pj, j = l,...,n, (I)
где А — (m χ η)-матрица.
Множество Гр с Л/ называется ρ-мерной гранью
многогранного множества Л/, заданного системой ограничений (1),
если
1) Гр — выпуклое множество размерности р;
2) из представления χ = Χχι + (1 - λ)#2> жбГр;жьж26
G Л/, 0 < λ < 1, следует, что a?i, х2 G Гр.
Содержательно второе условие означает, что точка χ € Гр
может быть внутренней для отрезка из М, соединяющего лишь
две точки грани Гр.
Пусть Μ — выпуклый многогранник,
например, тетраэдр (рис. 12.1). Видно, что
он имеет четыре 0-мерных, шесть
одномерных, четыре двумерные, одну трехмерную
грань. Полезно отметить, что согласно
определению понятие 0-мерной грани дословно Рис-,2-1
394
Глава 12
повторяет определение крайней точки (вершины) выпуклого
множества, т. е. для многогранного множества эти понятия
совпадают. Одномерные грани называют ребрами.
Множество Μ является ρ-мерной гранью, где ρ = т — а,
σ — ранг системы жестких ограничений системы (1), при этом
само множество Μ = Гтах — максимальная грань Μ (грань
максимальной размерности).
Данное определение грани принято называть
геометрическим, поскольку оно отражает геометрические свойства грани.
Приведем еще одно (алгебраическое) определение грани.
Множество Τ ρ с Μ называется ρ-мерной гранью
многогранного множества М, заданного системой ограничений (1),
если: I) Гр — выпуклое множество, dim(rp) = р\ 2) система
ограничений Гр получается из (1) заменой ряда неравенств на
равенства.
Теорема 1. Пусть Μ — многогранное множество,
заданное системой (1). Тогда указанные определения грани Г
эквивалентны.
Доказательство. Пусть Г с Μ —грань множества Μ
согласно первому определению. Тогда для χ е Г будет выполнено
Очевидно, что 1\ С /, где 1\ — множество жестких
ограничений системы (1). Пусть Г; — многогранное множество,
заданное системой ограничений (2), которая получается из (1) заменой
ряда неравенств на равенства. Покажем, что Г = Г'. Понятно,
что Г с Г' (по построению), поэтому необходимо доказать лишь
обратное включение.
По построению системы (2) для каждого j φ Ι найдется
точка х30 6 Г, такая, что scja* < β$. Тогда точка Хо = ]С7£/а^'жси
О < olj < 1, j £ I, Σ^ι Щ1 = 1, принадлежит Γ (Γ — выпуклое
множество). Кроме того,
(x0aj=pj, jely ί3.
Геометрическая структура систем линейных неравенств 395
Пусть х € Г'. Рассмотрим точку х' = х0 + е(х0 — х)ч
ε > 0. Понятно, что х9 G Г' при достаточно малом ε > 0. Итак,
a? G Г' с М, ж' G Г' С М, ж0 G Г, причем
1 , ε
1 + ε 1+ε
В этом случае из первого определения грани следует, что х.
xf £ Г. Таким образом, точка ж € Г' принадлежит Г, т. е.
Г' с Г. Так как Г с Г7 (см. выше), то получаем Г = Г'.
Пусть теперь Г с Μ — грань многогранного множества Μ
согласно второму определению, система ограничений которого
И)
имеет вид Газа^ = ft, j e I,
Пусть χ е Г представимо в виде
х = Да/ + (1 - А)ж", х', х" е М, 0 < λ < 1.
Заметим, что
ж'а7 ^ ft, a/V < ft, j = 1, ..., η, (δ)
Подставим χ в левую часть системы ограничений (1):
xaj = X(x'aJ) + (1 - \){x"aj) = ft, j e J,
откуда
x'a* = i(ft-(l-A)(«"o»-)) ^ i(ft-(l-A)ft) =ft, j el,
{
т.е. \αία?=βά, jely
\x'a^pj} j$I,
следовательно, ж'еГ. Аналогично показывается, что xff £ Г,
т. е. Г — грань многогранного множества Μ согласно первому
определению, и теорема доказана.
Следствие· Пусть х$ — 0-мерная грань (крайняя точка)
многогранного множества М, заданного системой (1). Тогда ж0
—решение системы
хо, г = Pjv, г = 1,,.. , m, ,gv
ι
жа' ^ ft, j ^ д,
396
Глава 12
,α
Згп
линейно независимые столбцы матри-
где ап,
цы А.
Вместе с максимальной гранью (самим множеством М)
имеет смысл говорить о грани rmin минимальной
размерности (минимальной грани). Понятно, что если rank(A) = г, то
rank(rmin) = т — г. Поэтому непосредственно из теоремы 1
получаем следующее утверждение.
Теорема 2. Для того чтобы множество М, заданное си-
стс мой (1), имело крайние точки, необходимо и
достаточно, чтобы гапк(Л) = m (dim(rmin) = 0).
Случай, когда гапк(Л) = т, будем называть регулярным.
Обратимся κ рассмотрению многогранного конуса с
вершиной в xq , заданного системой ограничений (1). По теореме 3 § 1
в эгом случае система ограничений может быть записана в виде
хо?^ xqo?j j = 1, ..., η <& хА ^ XqA = b. (7)
Вершина xq g Ka0 и удовлетворяет системе
хА = b = XqA, (8)
асо
которая совместна. Если гапк(Л) = г, то
множество решений системы (8) имеет размерность
πι — г. По определению грани система (8) задает
уравнение грани, причем грани минимальной
размерности. У многогранного конуса она
единственна (все неравенства переведены в равенства), при
Рис 12 2 этом в качестве вершины хо многогранного
конуса К можно взять любую точку грани rmin.
Так, на рисунке 12.2 К является двугранным углом. В качестве
вершины конуса К можно взять любую точку xq на ребре Γηΐι„.
В частности, в регулярном случае (гапк(Л) = т) имеем
единственную вершину х0 конуса Ку которая называется еще
острием конуса.
Теорема 3· Конус К = {х\ χ А ^ 0} заострен тогда и
только тогда, когда rank(A) = m.
Геометрическая структура систем линейных неравенств 397
Данный результат может быть получен и прямой
проверкой определения заостренного конуса, сформулированного в § 2
главы 11.
ЗАМЕЧАНИЕ. Полезно отметить, что понятия вершины
многогранного конуса и вершины (крайней точки) многогранного
множества не совпадают. Так, многогранный конус вообще может
не иметь крайних точек (гапк(Л) < т), в то время как конус
имеет вершину (рис. 12.2). Такое терминологическое
несоответствие сложилось исторически в ходе независимого исследования
конусов и выпуклых множеств.
Теорема 4 (характеристика крайних решений). Решение χ
системы неравенств
является крайним вектором в том и только том случае,
если множество столбцов ο,ΐ, для которых ха* = 0 имеет
ранг т — 1.
Доказательство. Пусть / с {1, .-., п} — множество ин-
дексов, таких, что Схаз = Qy j € Iy
Предположим сначала, что {aj}, j е J, имеет ранг т - 1.
Тогда вектор χ является крайним, поскольку из χ = а?' + χ",
χ'α? ^ 0, x"aP ^ 0, j = 1,..., n, следует
(χ'α*' = -х"а.з> 0, jel, (x"a* = -x'a,i ^0,
j€/,
откуда ж'а·7 = 0, χ"ο? = 0, j € I. Но из теоремы 1 § 2 главы 10
размерность множества решений системы (1) равна 1, поэтому
χ' = \ху хи = μχ^ при ЭТОМ
x'aj = Xxaj ^ 0, хпа? = μχο? < 0, j $ J,
откуда λ > 0, μ > 0.
Теперь предположим, что χ является крайним решением
системы (9) и пусть / — множество индексов j, для которых xaj =
= 0. Если χ φ О, то это множество векторов {aJ}, j G /,
398
Глава 12
имеет ранг меньший, чем т. Если его ранг меньше, чем т — 1,
то по теореме 1 § 2 главы 10 мы можем найти второе решение
χ системы уравнений ха3 = О, j € I, которое не зависит
о г х. Выберем теперь ε Φ U настолько малым, что х' = \(х +
+ εχ) и хи = \{х — ех) удовлетворяют неравенствам ха? < 0,
j $ I · Тогда х1 и ж" удовлетворяют (9) и линейно независимы.
Однако χ = х* + х", поэтому χ не является крайним вектором.
Противоречие и доказывает теорему.
ЗАМЕЧАНИЕ. Важность доказанных теорем состоит в том,
что они дают конструктивные средства для вычисления,
вообще говоря, всех решений системы однородных неравенств,
если гапк(Л) — т (регулярный случай). Действительно,
согласно теореме 3 в этом случае конус К = {χ \ χ А ^ О} за-
острей. Тогда по соответствующей теореме § 4 главы 11 конус
К представим в виде суммы крайних полупрямых, т. е. для него
справедливо соотношение:
= JjAibj, Xi ^ 0, г = 1,...,г >,
где bi — крайние векторы конуса К,
а теорема 4 дает способ нахождения
крайних векторов. Так, для
трехгранного конуса картина имеет вид, как на
рисунке 12.3.
§ 3. ПАРАМЕТРИЧЕСКОЕ УРАВНЕНИЕ
МНОГОГРАННОГО МНОЖЕСТВА
Основная цель данного параграфа — выяснить структуру и
получить параметрическое уравнение многогранного множества.
Пусть Μ — многогранное множество, заданное системой
ограничений
т
χ А < Ь & ха? ^ β,·, jг = 1, ..., η <Ф ^2&а* - Ь (^
Тогда имеет место следующая теорема о представлении,
которую приведем без доказательства.
Iсо четричгасая структура систем линейных неравенств 399
Теорема 1 (регулярный случай). Если гапк(Л) = т, то
Μ = Μ' + Κ, где Mf = conv{sci,... ,жг} — выпуклый
многогранник, К = {х | жЛ ^0} —конечный заостренный
конус, xif г = 1,..., г, — крайние точки множества Μ.
Данная теорема устанавливает структуру многогранного
множества в регулярном случае. Имеет место аналогия между
структурой множества решений систем линейных уравнений и
строением многогранного множества. ξ3ψ
Напомним, что плоскость π =
= {ж | χ А = Ь} есть сдвиг
линейного подпространства L =
= {х | хЛ = 0} иа вектор xq,
т. е. 7г = {жо}+1/, где ж0 —любая
точка из π (рис. 12.4). Рис. 12.4
В качестве иллюстрации к
утверждению теоремы рассмотрим рисунок 12.5.
Множество Μ представляет
наклонный треугольный цилиндр в М3,
ограниченный плоскостью ABC.
Многогранник М' в данном случае cctl
треугольник, порожденный крайними точками
А, Ву С. Конус К представлял4
собой луч, исходящий из начала координат,
параллельный образующей пилнплоа.
Следствие. В условиях теоремы любой вектор χ е Μ прс: :та-
вим в виде
Г S Г
■4 = 1 j=l г=1
\i > 0, г = 1,..., г; jij > 0, j; = 1,. ., ΰ, (2)
где Жг е Λ/, г = 1, ..., г, — крайние точки многогранного
множества il/, a bj, j; = 1, ..., s, ■— крайние векторы заостренного
конуса if = { χ | ж Л й О }.
Уравнение (2) есть параметрическое уравнение чного-
гранного множества в регулярном случае.
400
Глава 12
Перейдем к рассмотрению общего случая. Пусть Μ
—многогранное множество, заданное системой ограничений (I):
m
χ Α 5Ξ b <=> ^2 &аг = b*
г=1
и пусть гапк(Л) = г < т. Фиксируем строчечный базис
матрицы А. Пусть это будут векторы αχ,..., аг. Для остальных строк
имеем: г
dj = ]Р<5г,аь j = r + 1,..., m. (3)
2 = 1
Подставляя (3) в (1), получаем эквивалентную (I) систему
m
г=1 ^ j=r+l
Теперь рассмотрим многогранное множество М° f
определяемой системой ограничений
Σ(& + Σ u*&W ^ь>
t=i\ j-r+i / (4)
^ =0, j =r + lf..-,m,
и линейное подпространство Lm~r t определяемое однородной
системой линейных уравнений
&+ Σ №=0' * = 1,-·.^· (5)
j=r+l
Заметим, что ранг матрицы системы (4) равен ш, т. е. для
многогранного множества М° имеет место регулярный случай,
а ранг матрицы системы (5) равен г, т. е. dim(Lm~r) = т — т
(см. теорему 1 § 2 главы 10). Тогда имеет место следующая
теорема о представлении.
Теорема 2 (общий случай). Пусть Μ —многогранное
множество, заданное системой ограничений (1), гапк(Л) =
= τ < m. Тогда Μ = М° + Lm~r, где М°
—многогранное множество, заданное системой (4), Lm~r — линейное
подпространство, заданное системой (5).
Геометрическая структура систем линейных неравенств 401
Перед доказательством
проиллюстрируем утверждение теоремы для
общего случая (рис. 12.6).
Здесь Μ — цилиндр,
неограниченный в обе стороны (М° — множество,
ограниченное треугольником ABC).
Крайних точек у Μ нет, однако
достаточно очевидно, что Μ можно
представить в виде суммы треугольника ABC
и подпространства L. Оказывается, что
эта картина типична для общего случая
множества Μ. PuCt t26
Доказательство. Пусть χ G M° + Lm~r. Покажем, что
χ е Μ. Поскольку χ G М° + Lm~r, то χ = χ* + ж", где
χ* е м\ х" е l™-\ χ = (&,...,ω, xf = (β,·..,ω.
χ"
:(£iV--,0· Тогда
1 V ?=r+l '
г=
=Σ(«+ Σ ^)°.+Σ(ί"+ Σ «?μ·«*<*
поскольку первая сумма справа не превосходит Ь, а вторая
равна нулю. Таким образом, жбМи, тем самым, M°+Lm~r с Μ.
Докажем обратное включение. Пусть χ е М. Рассмотрим
вектор as' = (ξ£,..., ξ^) > построенный следующим образом:
ΎΠ
£ = & + Σ iAr
.Ci = 0i j = r + l,...,m.
1,
,rt
По построению ж' G M°. Теперь рассмотрим χ" = χ — х\
*" = (#,...,&). Тогда
6' = _ Σ) &%
i=r+i
2 1>· . . f Τ,
m.
402
Глава 12
Подставим компоненты векторы х" в левую часть (5). Тогда
т mm
&+ Σ 3%· = - Σ 6^j+ Σ ^=ο, t=i,....r,
т. е. x" является решением системы (5), или х" £ Lm~r\
Теорема доказана.
Следствие 1. В условиях теоремы 2
M = Mi + K° + Lm-r, (6)
где Мр — выпуклый многогранник, порожденный крайними
точками многогранного множества М°, а К0 — конечный
конус, порожденный крайними векторами неограниченных ребер
множества М°, Lm~r —линейное подпространство,
определяемое системой (5).
Следствие 2. В условиях теоремы 2 любой вектор χ е Л/
представим в виде
г s т~г
г
^Πλ* = 1, Аг>0, /Xj^O, г =■!,.·.,r, j = l,...,s, (7)
где {xi} — крайние точки множества Л/°, {bj} — крайние
векторы неограниченных ребер М°, {с^} — базисные векторы
линейного подпространства Lni~r.
Уравнение (7) есть параметрическое уравнение
многогранного множества в общем (нерегулярном) случае.
Следствие 3, В условиях теоремы 2 многогранное множество
Ы можно представить в виде
Μ = Μ? + К,
где К = { χ | хЛ ^ О } — конечный конус, a il/f — выпуклый
многогранник, порожденный крайними точками многогранного
множества А/0.
Заметим, что К = К° 4- Lm~T, где К° —заостренный
конус, a Lm~~r — линейное подпространство, определяемые
соотношениями (4), (5). В заключение параграфа отметим, что
Геометрическая структура систем линейных неравенств 403
многогранное множество Μ в нерегулярном случае
является выпуклым цилиндром, где в качестве направления а φ О
образующих можно взять любой вектор а Φ О, а е L7n~r
(ср. рисунок 12.6).
Действительно, по теореме 2 в нерегулярном случае
M = M°+Lm-r,
где Lm~r —линейное подпространство. Пусть а е Lm"r, а ф
Φ О и ж е М. Рассмотрим точки вида ж + га,г6 (—оо, + оо).
Поскольку χ е Μ, то ж = жо + ж', где жо G М°, ж' G Lm~r.
Тогда ж + га = Жо + (ж7 + та) = ж0 + ж", где ж" = ж' + га.
Однако ж' е Lm"r, α Ε Lm~r, поэтому ж" е Lm~~r, а тогда ж +
+ та € М° + Lm~r = Μ, т. е. Μ — цилиндр с направлением а.
С другой стороны, многогранное множество Μ — всегда
выпуклое множество, поэтому Μ — выпуклый цилиндр с
направлением α Φ О, где в качестве а можно взять любой ненулевой вектор
из подпространства Lm""r (см. § 2 главы 11).
§ 4. ГЕОМЕТРИЯ ЗАДАЧИ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
4.1. Формулировка задачи
линейного программирования
Под задачей линейного программирования (ЗЛ П) понимают
задачу нахождения наибольшего или наименьшего значения
линейной функции многих переменных при линейных ограничениях
типа равенств и неравенств.
ПРИМЕР 1 (Задача планирования жилищного
строительства).
Имеется т проектов домов, в которых имеются
квартиры η типов. Известны следующие величины: ац —
количество квартир типа j в доме проекта г; 7г — стоимость дома
проекта i; Pj — потребности в квартирах типа j в
плановый период. Требуется выбрать наиболее экономичный план
строительства.
404
Глава 12
Обозначим через χ = (£ι, . ♦., £m) план строительства,
где ξι — количество домов проекта г в плане х. Тогда
условия задачи накладывают на план χ следующие ограничения:
т
Σξί<*ί3> ft, j = l,...,n; (1)
*=ι
Ci>0, i = lr..,m. (2)
При этом требуется минимизировать суммарные затраты
на строительство
та
5^ii7i-^min· (3)
Таким образом, мы получим задачу нахождения минимума
функции (3) при ограничениях (1), (2). Это и есть ЗЛП.
В достаточно общей формулировке в матричном виде задачу
линейного программирования можно сформулировать так:
Ι φ(χ) = сх —> min,
\ хА ^ Ь, (4)
ж>0,
где А- {огад}, Ь = (/?ь ·■·, /?п),с= (7ι>···»7™)-
Множество Μ = {χ \ χ А ^ Ь, χ ^ О} называется .иио-
жеством допустимых решений задачи (4), а ж е Μ
—допустимым решением.
Точка х* е М, для которой сх* < са:, ж 6 М,
называется оптимальным решением^ а величина еж* — значением
ЗЛП (4).
Заметим, что множество Μ является многогранным, а сама
задача (4) означает нахождение наименьшего значения функции
φ(χ) = сх на множестве Μ.
Если Μ является выпуклым многогранником, то по
теореме Вейерштрасса оптимальное решение х* е Μ всегда
существует. В противном случае требуется дополнительное
исследование.
Геометрическая структура систем линейных неравенств 405
4.2. Геометрическая интерпретация решения ЗЛП
Пусть задана ЗЛП (4) и Μ — множество ее допустимых
решений. Предположим, что xq G Μ — некоторое допустимое
решение. Проведем через точку xq гиперплоскость
тг° = {χ | (х — хо)с = 0}
с нормальным вектором с. Если существует χχ е М, которая
принадлежит (тг°)", то φ(χι) < <р(жо)·
Действительно, если х± е (тг°)~, то (х\ - ж0)с < 0 или
сх\ < cxq , при этом, если гиперплоскость 7г° не является
опорной к множеству М, то найдется χι е М, для которой это
неравенство строгое.
Проведем теперь гиперплоскость π1 с нормальным
вектором с через точку χχ: π1 = { χ \ (χ — х\)с = 0 } и будем искать
точку х2 е Μ, Χ2 € (π1)- и т. д.
Такой процесс параллельного перемещения
гиперплоскости в направлении вектора —с может быть продолжен до
тех пор, пока гиперплоскость не займет опорное положение
к множеству Μ (если опорной гиперплоскости в
направлении —с не существует, то ЗЛП (4) не имеет оптимального
решения).
Пусть π* = {х | хс = 7 } — опорная гиперплоскость и
X* = Μ Г) π* — множество точек пересечения ее с множеством
М. Покажем, что х* G X* —оптимальное решение ЗЛП (4).
Действительно, поскольку х* е X*, то х* G М. Но ж* G
G π*, откуда ж*с = 7» жс ^ 7* ж е ^f * т- е* ψ(χ*) = сж* ^
еж = v>(cc), χ G Μ, что и требовалось доказать.
Итак, множество оптимальных решений ЗЛП (4) есть X*.
В частности, если Μ — многогранный конус с вершиной в xq и
решение существует, то жо € X*.
ПРИМЕР 2. Пусть множество допустимых решений
ЗЛП (4) Μ С Шт имеет вид, представленный на
рисунках 12.7-12.10. Если вектор с направлен как на
рисунке 12.7, то оптимального решения нет. В
случае, изображенном на рисунке 12.8 и рисунке 12.9,
406 Глава 12
Рис. 12.7 Рис. 12.8
Рис. 12.9 Рис. 12.10
оптимальное решение, соответственно, Xq и х%. Если
же решение ЗЛП существует и вектор с ортогонален
грани, скажем, Г{, как на рисунке 12.10, то X* = Г\.
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Найти грани многогранного множества М,
определяемого системой ограничений
ξι +ξ2 Ζ 0, -ξι+6 < 0, ξ2 > -2, -ft + 2ξ2 < 2. (1)
Решение. Заметим, что у множества Μ с Μ2 нет жестких
ограничений, поэтому dim(M) = 2-0 = 2 и максимальная
грань Μ двумерна. Ранг матрицы системы ограничений равен 2,
поэтому dim(rmin) = 2 — 2 = 0, следовательно, у множества Μ
есть крайние точки, а поэтому имеет место регулярный случай.
У множества Μ не более четырех ребер, поэтому количество
вершин не более четырех.
Геометрическая структура систем линейных неравенств 407
Найдем вершины множества Μ:
Xl<
6+6 = 0,
6+6 = 0,
6 > -2,
Ι -ξι + 26 < 2,
Χ2-
6+6 = 0,
6 = "2,
-6+6<ο,
-6+26<2,
«3Λ
-6+6 = 0,
-6+26 = 2,
6+6 >0,
6 > -2.
(2)
Решением систем (2) соответственно являются х\ = (0,0),
ж2 = (2,-2),ж3 = (2,2).
Ребра многогранного множества Μ задаются уравнениями:
Г}:
Г?:
6+6=0,
-6+6<о,
6 > -2,
-ξι + 26 < 2,
6+6>0,
-6+6<0,
6 = "2,
-ξι + 26 < 2,
Γί
2.
Γί:
6+6>ο,
-6 + 6 = ο,
6 > "2,
,-6+2ξ2<2,
6«+6>ο,
-6+6<ο,
6 > -2,
-6+26 = 2-
Приведенные уравнения — это неявные уравнения ребер
множества М. Найдем параметрические уравнения ребер. Для
этого заметим, что χι, ж2 € Г}, х\, а?з € Г?, х2 € Tf, гез € Г},
т. е. Г}, Г? — отрезки, a rf. Г| — лучи. Найдем
направляющие векторы этих лучей. Для этого достаточно взять
ненулевые векторы, удовлетворяющие соответствующим однородным
системам: ( ξι+ξ2>0, Г 6+6>0,
-6+6<0, . . 1-6+6 < 0,
6 = 0, 2 ] б>о,
1-6 + 26 < 0, 1-6+26 = 0,
Ьц<
(3)
Отсюда bi = (1,0), 62 = (2,1) —направляющие векторы
ребер Γι и Г* соответственно. Тогда параметрические уравнения
ll<^ ~ 1ΐ6 = 2λ, λ € [0,11;
= 2 + 2λ,
λ>0; "1'1ξ2 = 2 + λ, λ>0.
= 2λ,
-2λ, λ €[0,1];
,з. /6=2 + λ,
Γί
408
Глава 12
2. Написать параметрическое уравнение множества М,
заданного системой (1).
Решение. Согласно решению задачи I имеет место регулярный
случай. Поэтому Μ = Μ1 + К, где М1 = сопу{ж1,Ж2,ж3},
К = со{6ьЬ2}; хьЖ2,жз — крайние точки множества Μ
(см. (2)), 6Ь &2 — крайние векторы неограниченных ребер
множества Μ (см. (3)). Поэтому параметрическое уравнение
множества Μ имеет вид
tti = 2X2+2Xa+fa+2fo, λ! + λ2 + λ3 = l,At ^0, λ2 ^0,
l& = -2λ2 +2Аз + Α, /?ι ^ 0, fa Ζ 0, λ3 Ζ 0.
(4)
Построим множество Μ графически. Многогранник Μ1
представляет собой треугольник, а конус К порожден крайними
векторами Ьх и 62 (рис. 12.11). К каждой точке х' G М1
прибавим конус К. Тогда Μ = Σβ'^Λί^ί35'} + К), и мы получим
множество Л/, изображенное на рисунке 12.12.
rf
bi Г?
Pwc. /2.12
3. Написать параметрическое уравнение множества Μ,
определяемого системой ограничений
-£ι-ξ2-2ξ3<0,
-ξι+6<0,
-& - & < 0»
1-6+26 + 6^2.
(5)
Решение. Данная система (5) не имеет жестких ограничений,
поэтому dim(M) = 3 — 0 = 3. Ранг матрицы системы равен 2,
поэтому dim(rmin) = 3 — 2 = 1 и имеет место нерегулярный
случай.
Геометрическая структура систем линейных неравенств 409
Рассмотрим столбцы матрицы системы ограничений:
а1 = (-1,-1,0,-1),
а2 = (-1,1,-1,2),
а3 = (-2,0,-1,1).
Понятно, что а1 и а2 линейно независимы, причем а3 =
= а1 + а2. В нерегулярном случае Л/ = Mq + L, где А/0 —
многогранное множество, определяемое системой ограничений
(6+бХ + (6 + 6)а2<*>,
А = 0,
е
ИЛИ
-(6+6)-(6+6Хо,
~(6+6) + (6 + 6Х0,
-(6+6X2,
-(6+6)+ 2(6+6X2,
6 = 0.
Таким образом, Mq — многогранное множество,
определяемое системой ограничений
-6-6<0,
-6+6<0,
-6 < 2, i6.i
-6 + 2ξ2 < 2,
. 6=0-
ί
Заметим, что система ограничений (6) имеет тот же вид,
что и система (1). Поэтому М0 = Mq + Ко, где Λ/q =
= сопу{жьх2,яз}, К0 = со{6ь62}, х\ = (070,0), х2 =
= (2,-2,0), х3 = (2,2,0), Ъг = (1,0,0), Ь2 = (2,1,0).
Линейное подпространство L определяется системой
{
6+6 = о, т
6 + 6 = 0
и является прямой. Направляющий вектор с этой прямой имеет
вид с = (-1,-1,1). Поэтому Μ = Mj 4- К0 + L, где Л/<| -
= conv{a?i,iC2,iC3}, К0 = co{i>i,62}, L = Lin{c}.
410
Глава 12
Тогда параметрическое уравнение многогранного
множества Μ имеет вид
ί£ι=2λ2+2λ3+/?ι+2Α,-7ι,
и2 = -2А2 + 2Аз + 02-7ъ
| λι + λ2 + λ3 = 1,
А;^0, г = 1,2,3,
\β\ > 0, 02 > 0, 71 € (-оо, +оо).
Изобразим множество Μ
графически. Для этого запишем
множество Μ в виде
М= £({*} + !,).
Тогда ясно, что Μ будет
цилиндрическим множеством как
на рисунке 12.13 (ср. рис. 12.6).
4. Доказать, что
многогранное множество Μ =
= {χ Ι χ А й b} —выпуклый многогранник, в том и
только том случае, когда Μ ограничено.
Решение, Μ = М<} + К0 + L'= М{) + К, где М0Х —
выпуклый многогранник, а К — конечный конус. Поэтому Μ не
может быть выпуклым многогранником, если содержит хотя бы
один вектор χ Φ О, так как в этом случае К содержит всю
полупрямую (х).
Тгким образом, для того чтобы Μ было выпуклым
многогранником, необходимо и достаточно, чтобы К = {О}, но это и
означает, что Μ ограничено.
Попутно мы решили следующую задачу.
Б. Доказать, что множество Μ = {χ \ χ Α ^ Ъ}
является выпуклым многогранником тогда и только тогда,
когда система χ Α ^ О не имеет ненулевых решений.
Указание. К — { χ \ χ А й О }.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсцисса 39
Аксиома размерности 30
Алгебра выпуклых конусов 368
Алгебра конечных конусов 382
Аппликата 39
Астроида 289
Б
Базис линеала 25
— линейного полпространства 325
— матрицы столбцовый 327
строчечный 327
— ортонормированный 37
Бинормаль 257
В
Вектор 12, 18
—, алгебраическая мера 40
— геометрический 12, 20
— единичный 13
— координатный 30/
— крайний 382
— лексикографически
неотрицательный 342
положительный 342
—. модуль 13
—, направление 13
— направляющий 38, 131
— неотрицательный 340
— нормальный 112
— нулевой 13
— положительный 340
— строго положительный 340
— , точка приложения 13
Векторная функция 238
векторного аргумента 238
1 дифференциал 247
дифференцируемая в точке 241,
246
, интеграл неопределенный 247
, — определенный 247
круговая 244
, множество значений 238
, непрерывность в точке 240
, область задания 238
, первообразная 247
, предел 239
, производная 240
скалярного аргумента 238
, частная производная 245,247
Векторы
— коллинеарные 13
— компланарные 13
—, левая пара (тройка)37
—, линейная комбинация 20
—, выпуклая 358
—, неотрицательная 370
—линейно зависимые 20
независимые 20
— одинаково напраапенные 13
— ортогональные 54
— положительно независимые 383
— порождающие для конечного
конуса 377
— . правая пара (тройка)37
— противоположно исправленные 14
— противоположные 14
— равные 14
—, разность 15
— сонанравленние 13
—, сумма 15
Выпуклая линейная комбинация 358
Выпуклый многогранник 362
Геометрия аффинная 34
— евклидова 59
Гипербола 152
, асимптоты 156
вершины 155
действительная ось 155
, — полуось 155
директрисы 160
, мнимая ось 155
, — пилуось 155
основной прямоугольник 155
— равносторонняя 157
412
Предметный указатель
— сопряженная /57
—, уравнение в полярных
координатах /6/
— t — каноническое 154
—, — параметрическое 158
—, фокальные радиусы 159
—, фокальный параметр /61
—, фокусы 152
—, эксцентриситет J 59
Гиперболоид вращения /88,189
—двуполостный 189
— однополостный 188
, прямолинейные образующие
196
Гиперплоскость /30
— опорная 374
— разделяющая 372,377
Гиперповерхность 21 I, 299
Годограф 238
Гомеоморфизм 252
1радиент 299
■ д
Длина вектора 13
—дуги кривой 258
Долгота Ь2, 297
ДПСК—см. Система координат
декартова прямоугольная
3
Задача линейного программирования
403
И
Изоморфизм 30
— координатный»?/
—линеалов 30
—линейный 31
Инвариант 216
—линии второго порядка 216
— поверхности второго порядка 221
К
Каппа 291
Касательная 253,300
Квадратичная форма 214
Компакт 345
Конус 195, 366
—асимптотический 196
— .вершина 366
— второго порядка 194
— выпуклый 367,371
— заостренный 372
— конечный 377
— мнимый 2/0
— многогранный с вершиной в точке
392
—, острие 9Θ6
— с вершиной в нуле 366
Координаты аффинные 35
— вектора 26
— внутренние 107,117
—декартовы прямоугольные 37
— криволинейные 107\ 294
— плоскостные 117
— полярные 49
обобщенные 50
— сферические 52
— цилиндрические 51
Косинусы направляющие 58
Коэффициент угловой 119
Коэффициенты метрические 56
Кривая 252
— Вивиани 287
— гладка я 253
—дискриминантная 281
— ? касательная прямая 253
—, кривизна 263
—, кручение 268
—, — абсолютное 265
—линия 252
— , нормаль 257\ 279
—, особая точка 279
— регулярная 252
— f уравнение неявное 278
— f уравнения внутренние 300
—, — натуральные 277
—, — параметрические 252
— элементарная 252
примыкающая 252
Кривизна 263
Кручение 265
Л
Лексикографический порядок 342
Лемма Шаля 40
Линеал (линейное пространство) 18
—бесконечномерный 29
— конечномерный 29
— нульмерный 29
Линия 102
— алгебраическая ///
— винтовая 286
гиперболическая 292
коническая 286
— второго порядка / / /
— координатная 294
—трансцендентная ///
—,уравнение 103
—, — в полярных координатах /04
— t — векторное 108
—, — параметрическое 107
— центральная 170
Μ
Матрица ортогональная 84
— перехода 81,85,92
Предметный указатель
413
— преобразования базиса 92
координат 81,86
Меридиан 185, 297
Многогранное множество 389
, грани 393
, ребра 394
регулярное 396
, уравнение неявное 389
, уравнения параметрические
399
Множества топологически
эквивалентные 252
Множество
—, внешность 343
—, внутренность 342
—, внутренняя точка 342
—, выпуклая оболочка 358
— выпуклое 358
, вершина 362
, крайняя точка 362
—, граница 343
—, граничные точки 343
— допустимых решений 404
— замкнутое 343
—, замыкание 344
— компактное 345
— t коническая оболочка 370
—, линейная оболочка 326
— ограниченное 344
— открытое 342
—, предельная точка 344
— сопряженное 326
—, умножение на число 326
— .цилиндрическая оболочка 385
Η
Неравенство Коши-Буняковского 59
Нормаль 257,302
— главна я 257
о
Образ множества 251
— точки 251
Объединение множеств 325
Огибающая 280
Ограничение жесткое 390
Окрестность 343
Ордината 39
Ориентация 37
— пары векторов 37
— системы координат 37
— тройки векторов 37
Орт 14
Ортант неотрицательный 341
— неположительный 341
Ось вращения 185
— координат декартова 38
— полярная 48
Отклонение точки от плоскости 126
от прямой 126
Отношение частичного порядка в Rn
341
Отображение 251
— непрерывное 251
— одно-однозначное 251
— топологическое 251
Π
Парабола 163
—, вершина 165
—, директриса 163
—,уравнение в полярных
координатах 167
—, — каноническое 165
—, фокальный параметр 163
—, фокус 163
—, эксцентриситет 163
Параболоид гиперболический 190
, вершина 191
, прямолинейные образующие
198
— эллиптический 190
, вершина 190
Параллель 185, 297
Параметр натуральный 261
Параметризация 252
— естественная 261
Перенос начала координат 80
Пересечение множеств 325
Плоскости параллельные 336
— пересекающиеся 337
— скрещивающиеся 338
Плоскость
— f касательная к поверхности 302
— многомерная 333
уравнение параметрическое
333
— нормальная 254
— спрямляющая 257
— t уравнение векторное
параметрическое 116
—, — «в отрезках»/15
—, — неполное /15
—,— нормированное 125
—, — общее 114
—, — полное 115
—ускорения 257
Площадь области 309
— поверхности 308
Поверхность 293
—алгебраическая ///
— вращения 185
—, вторая квадратичная форма 310
— второго порядка / / /
— t главное направление 313
— гладкая 295
414
Предметный указатель
— двусторонняя 303
— коническая 193
— ~ , направляющая 193
— — , образующая 193
> вершина 193
— косая 317
— , кривизна гауссова 315
—, — главная 3/3
—, — нормальная 313
—, — средняя 315
— линейчатая 316
—, нормаль 302
—, нормальное сечение 312
—, обыкновенная точка 296
— односторонняя 303
—, особая точка 296
—, первая квадратичная форма 306
— развертывающаяся 317
— регулярная 295
— трансцендентная ///
—, уравнение 103
—, — в сферических координатах 106
—, — в цилиндрических координатах
104
—, — векторное 102, 294
—, — неявное 295
—, — параметрическое 106» 107, 294
— центральная 201
— цилиндрическая 192
1 направляющая 192
, образующая 192
— элементарная 293
, граница 293
, граничные точки 293
склеенная 293
Подпространство линейное 324
— метрическое 342
Полуинварианты 225
Полуплоскость отрицательная 123
— положительная 123
Полупространство отрицательное 123
— положительное 123
Полюс 48
Преобразование координат
ортогональное 84,87
однородное 84,87
стандартное 204
Проекция вектора на ось 42
алгебраическая 42
геометрическая 42
—точки 42
Произведение векторов векторное 61
двойное векторное 72
псевдоскалярное 71
скалярное 54
смешанное 68
— множеств декартово 326
— псевдовекторно^ (поворот) 68
Пространство аффинное 33
— векторное 20
— евклидовj 58
— координатное 20
— линейное — см. Линеал
— метрическое 61
— нормированное 60
— топологическое 314
Прямая 36
— касательная к кривой 253
к поверхности 300
уравнение «в отрезках»//5
— векторное параметрическое
132
— каноническое 132
— неполное//5
— нормированное 125
— общее 114, 132
— полное 115
— с угловым коэффициентом 117
Пучок плоскостей 127
— прямых на плоскости 127
Радиус кривизны 282
— полярный 48
— сферический 52
Разложение по базису 25
Размерность выпуклого множества
361
—линеала 29
—линейного подпространства 324
Ранг матрицы столбцовый 327
строчечный 327
Репер канонический подвижный 272
— Френе 269
Решение допустимое 404
— оптимальное 404
Свойство отделимости 372
Связка плоскостей 130
— прямых в пространстве 136
Сдвиг подпространства на вектор 331
Сеть координатная правильная 295
Система координат аффинная 35
декартова прямоугольная 37
левая 37
полярная 48
правая 37
сферическая 52
цилиндрическая 51
Спираль Архимеда 104
— логарифмическая 285
Сумма множеств 326
— прямая 326
Пред четный указатель
415
Теорема Каратеодорн 359
— Мсньс«Ш
Тор 321
Торс 319
Точка внутренняя 342
— коническая особая 304
— крайняя 362
— неособая 296
— обыкновенная 299
— особая 279, 296
— порождающая 362
— предельная 344
— характеристическая 280
Траектория ортогональная 282
Трехгранник естественный 269
у
Углы Эйлера 89
Угол дифферента 91
— координатный 308
— крена 91
— между векторами 54
пересекающимися кривыми 307
плоскостями 119
прямой и плоскостью 135
прямыми 134
— наклона вектора к оси 44
— нут j ции 59
— полярный 49
— прецессии 89
— рысклньиР/
— собственного вращения 89
Уравнение второго порядка
гиперболическое 176
—, группа старших членов 168,
199
т линейная часть /68ч 199
параболическое 176
эллиптическое 176
Φ
Формула Тейлора 243
Формулы деривационные 272
— Фр^нс 271
ц
Центр кривизны 282
— линии второго порядка 170
— поверхности второю порядка 201
Циклоида 285
Цилиндр 38-/
— второго порядка 193
— выпуклый 384
— гиперболический 193
— мнимый 2/0
— параболический 193
— эллиптический 193
Циссоида Диоклеса 284
Четырехлепестковая роза 291
ш
Широта 52, 298
Эвольвента 282
Эволюта 281
Экплтор 298
Эллипс 144
—, большая ось 147
—, — полуось 147
—, вершины 147
—чдиректрисы 150
— f малая ось 117
— t — полуось 147
—, уравнение в полярных
координатах 151
— t — каноническое 145
, - параметрическое 148
— , фокальные радиусы 149
—, фокальный параметр 150
— , фокусы 144
—, эксцентриситет 149
—, эксцентрически угс ι Ν
Эллипсоид 187
— вращения 186
— мнимый 209
—, полуоси 187
ЛИТЕРАТУРА
1. Александров А. Д., Нецвстаев Н. /О. Геометрия. М.: Наука, 1990.
2. Александров П. С. Курс аналитической геометрии и линейной алгебры
М.: Наука, 1979.
3. Ашманов С. А. Линейное программирование. М.: Наука, 1981.
4. Бахвалов С. В., Моденов П. С, Пархоменко А. С. Сборник задач по
аналитической геометрии. М.: Наука, 1964.
5. Беклемишев Д. В. Курс аналитической геометрии \\ линейной алгебры.
М.: Наука J 985.
6. Беклемишева Л. A.t Петрович А. Ю., Чубарое И. А. Сборник задач по
аналитической геометрии и линейной алгебре. М.: Наука, 1987.
7. ГейлД. Теория линейных экономических моделей. М.: ИЛ, 1963.
8. Ефимов п. В., Розендорн Э. Г. Линейная алгебра и многомерная
геометрия. М.: Наука, 1970.
9. Зенкевич Η. Α., Кузютин В. Ф. Элементы выпуклого анализа.
СПб.: Изд-во СПбГУ, 1993.
10. Ильин В. Α., ПознякЭ. Л Аналитическая геометрия. М.: Наука, 1981.
11. Кузютин В. Ф. Элементы векторного анализа, теории кривых и
поверхностей. СПб.: Изд-во СПбГУ, 1993.
12. Кузютин Д. β., Культина М. В., Вишнякова Е. В, Алгебра векторов и
матриц. Элементы аналитической геометрии. СПб.: Изд-во ΙΒΙ, 2001.
13. Норден А. П, Краткий курс дифференциальной геометрии. М.: Физматгиз,
1958.
14. Погорелое А. В. Дифференциальная геометрия. М.: Наука, 1974.
15. Позняк Э. Г.. Шикин Е. В. Дифференциальная геометрия. М.: Изд-во
МГУ, 1990.
16. Постников М. М. Аналитическая геометрия. М.: Наука, 1979.
17. Постников Μ. Μ. Линейная алгебра и дифференциальная геометрия.
М.: Наука, 1979.
18. Рокафеллар Р. Выпуклый анализ. М.: Наука, 1973.
19. Чарин В. С. Линейные преобразования и выпуклые множества.
Киев: Изд-во КГУ, 1978.
Вячеслав Федотович КУЗЮТИН, Николай Анатольевич ЗЕНКЕВИЧ,
Владимир Валерьевич ЕРЕМЕЕВ
ГЕОМЕТРИЯ
ИЗДАТЕЛЬСТВО «ЛАНЬ»
lan@lpbl.spb.ru, www.lanpbl.spb.ru
193012, Санкт-Петербург, пр Обуховской обороны, 277.
Издательство: тел./факс: (812) 262-24-95, 262-11 -78
pbl@1pbl.spb.ru. print@lpbl.spb.ru
Торговый отдел: 193029, Санкт-Петербург, ул. Крупской, 13.
факс: (812) 567-54-93, тел.: 567-85-78, 567-14-45. 567-85 82, 567-85-91
trade@]iitipbl.spb.ru
Филиал в Москве:
109263, Москва, 7-я ул. Текстильщиков, 5,
тел.: (095) 919-96-00, 787-59-47, 787-59-48
lannisk@gpress.ru
Филиал в Краснодаре:
350072, Краснодар, ул. ЖлоГч ι. l/l, тел.: (8612) 74-10-35.
Слано в набор 19.07.00, Подписано в печать 03 ΠΛ03. Буvara типографская Формат 81 X 108/32.
Гарнитура Литературная. Печать офсетная \с л ι 21,84. Уч.-изд. л 25,80. Тираж 5000 экз.
Заказ №1862
Отпечатано с готовых диа позитиве и ιιΦΙ ΜΙ владимирская книжная типография
600000. ι Владимир, ОмиГр:.екий up., л 7
Качество печати соответствует качеству представленных диапозитивов
I
ψ
■ ■ ■ ·