Сборник задач по физике с решениями и ответами: Механика: Для абитуриентов и учащихся 9 — 11 классов / Под ped. А.Н. Долгова. М.: МИФИ, 2000. — 132 с.
Авторы: А.Н. Долгов, B.IL Протасов, Б.Н. Соболев
В настоящий сборник включены задачи по механике, предлагавшиеся за последние годы на вступительных письменных экзаменах в МИФИ, в лицеи при МИФИ, а также на олимпиадах им. И.В. Курчатова и И.В. Савельева. Для основной части задач приведены решения, для задач с однотипным решением даны только ответы.
Сборник предназначен для поступающих в МИФИ и физико-математические лицеи при МИФИ, а также может быть использован студентами младших курсов и слушателями всех форм подготовительного обучения.
Рекомендован редсоветом МИФИ в качестве учебного пособия
ПРЕДИСЛОВИЕ
Предлагаемый читателю сборник задач по механике является первой частью учебного пособия по физике, которые предназначены для повторения основных разделов физики, изучаемых в средней школе, и для самостоятельной подготовки к вступительному экзамену в вуз.
Ограниченность объема издания, с одной стороны, и нецелесообразность дублирования школьных учебников, с другой, не позволили поместить подробный теоретический материал. Однако авторы стремились к каждому разделу дать краткое, но вместе с тем последовательное изложение основных положений теории, опираясь на которые абитуриент сможет научиться отвечать на вопросы, связанные с объяснением явлений окружающего мира, и решать типовые задачи.
При работе с пособием следует иметь в виду, что оно содержит, в основном, экзаменационные задачи. Решение их достаточно для успешной подготовки к вступительным экзаменам в МИФИ. Однако для слабо подготовленных учащихся скорее всего понадобится привлечение более легких задач, другого дидактического материала и, возможно, помощь и объяснение преподавателя.
Задачи повышенной сложности отмечены звездочкой
3
1. КИНЕМАТИКА
Кинематика — раздел механики, изучающий движение без рассмотрения причин, вызывающих движение.
Приведем основные определения физических величин и понятий. использующиеся в ньютоновской механике.
Механическое движение — изменение с течением времени положения тела в пространстве относительно других тел.
Тело отсчета —- тело, относительно которого рассматриваются положения других тел в пространстве.
Система отсчета — система координат, связанная с телом отсчета, и выбранный метод отсчета времени, т.е. часы.
Материальная точка — тело, размерами и формой которого можно пренебречь в условиях данной задачи.
(Абсолютно) твердое тело — тело, расстояние между любыми двумя точками которого остается постоянным при его движении. Понятия материальной точки и абсолютно твердого тела позволяют исключить из рассмотрения деформацию тела при его движении.
Поступательное движение — движение, при котором отрезок прямой, соединяющий любые две точки твердого тела, перемещается параллельно самому себе. При поступательном движении все точки тела движутся с одинаковыми скоростями и ускорениями.
Вращательное движение — движение, при котором все точки твердого тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Эти окружности лежат в плоскостях, перпендикулярных оси вращения.
Радиус-вектор г — вектор, проведенный из начала системы координат в интересующую нас точку пространства. Положение материальной точки в^пространстве может быть задано ее радиус-вектором.
Траектория —- линия, описываемая движущейся материальной гонкой в пространстве.
4
Путь — длина участка траектории от начального до конечного положения материальной точки.
Перемещение (приращение радиуса вектора) — вектор AF , соединяющий начальную и конечную точки участка траектории, пройденного за промежуток времени Az.
Скорость — физическая величина, характеризующая как быстроту движения, так и его направление в данный момент времени.
Средняя скорость < у > определяется как
_ Аг
< v >= — .
AZ
(11)
Средняя скорость прохождения пути < vy > (средняя путевая скорость) равна отношению пути A.S', пройденному телом за промежуток времени Л/, к этому промежутку времени:
(Мгновенная) скорость
v =
1-
1Ш1 — =
Д/->0 Az
dr dt
(1.3)
является векторной величиной, равной первой производной по времени от радиус-вектора движущейся точки. Мгновенная скорость у направлена по касательной к траектории (см. рисунок), средняя скорость < v xs > направлена вдоль секущей АВ. Если Az -» 0. то в пределе точки А иВ
сольются в одну точку Л и секущая превратится в касательную. (Мгновенная) путевая скорость
AS vy = lim —- = Д/->0 Az
dS dl
(1.4)
равна первой производной пути по времени и равна по величине мгновенной скорости.
5
Ускорение — физическая величина, характеризующая быстроту изменения скорости по модулю и направлению.
Мгновенное ускорение — векторная величина, определяемая первой производной скорости по времени:
Av dv d (dr A
a= hm — = — = — — .	(1.5)
A/—>0 А/ dt dt \ dt)
Знания математики в рамках школьной программы позволяют указать рациональную форму записи уравнений движения, удобную при решении задач.
Движение с постоянной скоростью v = const (не путать с равномерным движением v - |v| - const). Проинтегрируем левую и правую части равенства (1.3) в пределах от t0 до t, где tq, t — время. соответствующее началу и произвольному моменту движения. Получим
г dr ,	_ г
I — dt = v \dl
J dt	J
г(1	fo
или r(t)-r(to) = v-(t -t0).
Обозначим r(r0) s r(), тогда
r(t) = rQ + v-(t-t0).	(1.6)
При /о =0 уравнение движения с постоянной скоростью принимает вид
r(r) = r0+v-Z.	(1.7)
Движение с постоянным ускорением а = const. Проинтегрируем левую и правую части равенства (1.5) в пределах от t0 до t. Действуя аналогично предыдущему случаю получим
[ —dt = a[dt.
6
Отсюда
v(t)-v(f0) = a (f-to).
Обозначим v({q ) s Vg, т.е.
v(O = vg +a-(t-t0),
(1 8)
и проинтегрируем обе части равенства (1.8) в тех же пределах.
‘ dr	1	1
\~J~dt = vo\dt + a^(t -t0)dt.
z0	l0	l0
Интегрирование даст
_(t-tn) f-’‘0=vg-(/-tg)+a------	<1.9)
При tg = 0 получим систему уравнений движения с постоянным
ускорением:
v(Z) = vg + at;
-	- at2
r(t) = r0 +Vg? + —.
(1.10)
При решении некоторых кинематических задач на прямолинейное движение иногда оказывается полезным геометрический смысл понятий модулей скорости, перемещения и пути, проходимого материальной точкой, а именно:
изменение модуля скорости тела за промежуток времени Д/ = = ?2 ~ 1\ равно площади под графиком зависимости ускорения а(1) в этом промежутке; если не изменяется направление движения:
перемещение тела за промежуток времени Д/ равно площади под графиком зависимости v(t) в этом промежутке, где v — про-
екция вектора v на ось вдоль направления движения:
путь, пройденный телом за промежуток времени Д/. равен площади под графиками зависимости jy(t)| в этом промежутке.
7
Вектор ускорения материальной точки или выделенной точки твердого тела (в этом случае его называют полным ускорением) удобно разложить на два взаимно перпендикулярных компонента.
Тангенциальное ускорение ах характеризует изменение модуля скорости и направлено по касательной к траектории ах = ах  т, где ах — проекция вектора ускорения а на направление скорости, т — единичный вектор (|т| = 1), направление которого совпадает с
, ДМ ^|v|
направлением скорости v. ах = lim ---=----- (производная мо-
Дг->0 A? dt
дуля скорости по времени).
Нормальное ускорение ап характеризует изменение скорости по направлению и перпендикулярно вектору скорости ап=ап п , где п — единичный вектор, перпендикулярный вектору скорости, ап — модуль нормального ускорения.
На рисунке представлен пример разложения полного ускорения на две составляющие а = ах +ап. Случай А — скорость тела возрастает. случай Б — скорость тела убывает.
Любой, достаточно малый участок плавной (без изломов) траектории. можно аппроксимировать (приближенно представить) дугой окружности. При малой длине рассматриваемого участка траектории величина скорости на нем остается практически постоянной и движение тела представляет собой равномерное движение по окружности, т е. тело движется с центростремительным ускорением, направленным к центру окружности и равным по величине v2
йц (. = —, где R — радиус окружности, v — скорость тела на дан-
ном участке траектории.
8
Рассмотрим малый участок траектории между точками Му и М2, и выделим точку М в середине этого участка. Проведем через точки Му. М2 и М окружность. Центром этой окружности является точка С, лежащая на пересечении перпендикуляров к касательным, проведенным через точки Му и М2 - При приближении точек Му и М2 к точке М точка С будет стремиться к некоторому предельному положению, которое называется центром кривизны траектории в точке М. а предельное значение радиуса окружности, которая была использована для аппроксимации траектории — радиусом кривизны траектории в точке М. Соответственно величина нормально-
V2
го ускорения в точке М оказывается равной а„ =-----, где v —
Якр
мгновенная скорость тела и Акр — радиус кривизны в точке М (Якр = СМ\
В некоторых задачах движение тел одновременно рассматривается по отношению к различным системам отсчета. Если скорости много меньше скорости света в вакууме, то справедлив закон сложения скоростей:
vH = vll+v0.	(1П)
Скорость движения материальной точки по отношению к системе отсчета, принимаемой за неподвижную v(1. равна векторной сумме скоростей движения точки в подвижной системе vlf и скорости движения подвижной системы относительно неподвижной vg .
При решении ряда задач удобно пользоваться принципом взаимной независимости движений.
В применении к твердому телу этот принцип позволяет рассматривать движение любой точки твердого тела как сумму двух простейших движений: поступательного, и вращательного. В част
9
ности. скорость произвольной точки твердого тела vT можно представить как
' Т = VBp VnOCT -
где vnoCT — скорость поступательного движения, vBp — линейная скорость точки, обусловленная его вращением.
Часто удобно рассматривать движение тел относительно оси. проходящей через точки, для которых v1[0CT = 0. Эту ось называют мгновенной осью вращения. В этом случае движение тела можно рассматривать как чисто вращательное.
Пусть выбранная точка М твердого
7И	тела, совершающего вращательное дви-
/	жение. движется по окружности радиу-
—► сом К Проведем фиксированную в про-\	/	странстве ось ОА в плоскости окружно-
сти через ее центр О. выбранный в каче-
стве начала координат, и радиус-вектор г = ОМ . Положение точки М на окружности определяется значением угла ср (измеренного в радианах) между осью ОА и радиус-вектором г . По определению центральный угол, равный одному радиану, стягивает дугу длинной. равной радиусу окружности, т.е. cp = .S’//?.
Угловая скорость (вращения) определяется как
.. Аср с1(£> со = lim —— = — Az->0 А/ clt
Угловая скорость всех точек твердого тела, совершающего вращательное движение, одинакова, таким образом угловая скорость характеризует движение твердого тела в целом. Величина скорости (в этом случае ее принято называть линейной скоростью), с которой выбранная точка М тела движется по окружности, связана с \ гловой скоростью соотношением:
v = со - R.
10
а ее центростремительное ускорение можно выразить как
а.. „ =&~  R .
Ц- ь
ЗАДАЧИ
1.К	Самолет летит горизонтально со скоростью v = 470 м/с. Человек услышал звук от самолета через t = 21 с после того, как самолет пролетел над ним. На какой высоте летит самолет? Скорость звука с = 330 м/с.
1.2?	Сверхзвуковой «самолет» летит со скоростью v = 1000 м/с на высоте Н = 4 км над поверхностью Венеры. Звук от «самолета» дошел до космонавтов, находящихся на поверхности планеты, через t = 3 с после того, как он пролетел над их головами. Какова скорость звука в атмосфере Венеры?
1.3.	‘Тело, двигаясь прямолинейно под углом ai =60° к оси ОХ в плоскости XOY, прошло отрезок пути А'| = 40 м. Затем, двигаясь прямолинейно под углом а2 =120° к той же оси, прошло 52 = 80 м. Полное время движения t = 4 с. Определить модуль средней скорости |< v >| и средний модуль ckopocthJ< v >| тела.
1.4.	На одной из двух параллельных взлетно-посадочных полос самолет, двигаясь со скоростью V] под углом а к линии горизонта, совершает посадку, а на второй — другой самолет взлетает со скоростью v 2 под углом р к линии горизонта. Какова (по модулю) скорость второго самолета относительно первого?
1.5.	Для тел, движущихся прямолинейно вдоль оси ОХ, установить соотношение их скоростей в момент времени г0, если в момент времени t = 0 тела покоились. Проекция вектора ускорения на ось ОХ — ах, изменяется со временем так. как показано на рисунках а, б, в и г.
11
1.6.	Тело движется вдоль оси ОХ. В момент времени t = Ос проекция вектора скорости на ось г — vqa' = -3 м/с. Проекция вектора ускорения на ось зависит от времени следующим образом: в интервале 0с</<4с ах = +1,5 м/с2. в интервале 4с</<6с ах= -1.0м/с2 и 6с</<8с ах = -0.5 м/с* . Какой путь пройдет тело к моменту времени t = 8 с? Построить один под другим графики зависимостей от времени / проекции скорости vx(t), координаты х(/), а также пути S(t), проходимого телом [ х(0) = 0 ].
1.7.	Тело движется вдоль оси ОХ. В момент времени t = Ос проекция вектора скорости на ось = +5.0 м/с. Проекция вектора ускорения на ось зависит от времени следующим образом: в интервале Ос</<3с ах = -1,0 м/с2. в интервале Зс</<6с йа. =-2.0 м/с2 и 6 с </<10с ах - +0.5 м/с2 . Какой путь пройдет тело к моменту времени t = 10 с?
12
1.8.	Как определить начальную скорость пули, выпущенной из игрушечного пистолета, располагая только секундомером9
1.9.	Тело уронили с высоты Н = 100 м без начальной скорости. Какова его средняя скорость за время полета?
1.10.	Тело падает с высоты Н = 100 м без начальной скорости. За какое время тело проходит вторую половину пути.
1.11.	Аэростат поднимается с постоянной скоростью v() = 2 м/с. На высоте /7 = 100 м с него сбрасывают без начальной скорости относительно аэростата груз. Сколько времени будет падать груз?
1.12.	Аэростат опускается с постоянной скоростью vq =2 м/с.
На высоте Н = 300 м с него сбрасывают без начальной скорости относительно аэростата груз. Сколько времени будет падать груз'?
1.13.	С поверхности Земли вертикально вверх бросают два мяча. Наибольшая высота подъема одного из них оказалась в 3 раза больше, чем другого. Во сколько раз отличается у них продолжительность полета? Сопротивление воздуха мало.
у 1.14* Камень брошен в вакууме вертикально вверх с поверхности планеты. С какой начальной скоростью его надо бросать, чтобы подъем на высоту /7 = 20 м занял 1 = 3 с? Ускорение свободного падения на планете g = 8 м/с2 .
1.15?	В момент, когда трамвай имеет скорость v0 = 10 м/с. включают тормоза, и трамвай начинает двигаться равнозамедленно. При каком ускорении он пройдет за / = 2 с путь 5 = 8 м?
1.16.	Маленький шарик скользит без трения один раз по желобу АВС, а другой раз — ADC. AD и ВС — вертикальны, углы АВС и ADC закруглены. Скорость шарика в точке А равна нулю. Изобразить графически для обоих случаев зависимость скорости шарика от времени, если АВ = ВС = CD = AD.
1.17.	Шарик скользит без трения один раз по желобу АВС. а другой раз — ADC. АВ и CD — вертикальны, углы АВС и ADC закруг
13
лены. Начальная скорость шарика в точке А одна и та же и достаточна для достижения точки С. Изобразить графически зависимость скорости шарика от времени, если АВ = ВС = CD = AD. Рассмотреть три варианта относительно расположения точек А, В, С, D. приведенных на рисунках а, б и в.
")	о)	в)
1.18.	Тело брошено с поверхности Земли с начальной скоростью v0 под углом а к линии горизонта. Пренебрегая сопротивлением воздуха определить: а) длительность полета; б) дальность полета; в) максимальную высоту подъема над поверхностью Земли.
1.19.	Из двух труб, расположенных на Земле, с одинаковой скоростью бьют струи воды под углами а = 30° и р = 60° к горизонту. Найти отношение дальностей падения воды на Землю. Сопротивление воздуха мало.
1.20.	Из двух труб, расположенных на Земле, с одинаковой скоростью бьют струи воды под углами а = 60° и р = 45° к горизонту. Найти отношение наибольших высот подъема струй воды, вытекающих из труб. Сопротивление воздуха мало.
1.21.	С поверхности Земли бросили два мяча под углами а = 30° и Р = 45° к линии горизонта. Дальность полета мячей оказалась одинаковой. Найти отношение начальных скоростей, с которыми бросали мячи. Сопротивление воздуха мало.
1.227Т	ело бросают вдоль плоского склона (вверх) со скоростью Vy под углом р к склону. Угол наклона склона к линии горизонта — а, причем а + р < тт / 2. На каком расстоянии от точки бросания тело упадет на склон? Сопротивлением воздуха пренебречь.
14
1.237	Мяч бросают под углом а <я/2 к горизонт}' со скоростью Vq с вершины горы, склон которой составляет угол 0 < л / 2 с линией горизонта. На каком расстоянии / от точки бросания мяч упадет на склон? Сопротивлением воздуха пренебречь.
1.247	Мяч бросают со дна прямоугольной ямы со скоростью Vq =20 м/с под углом а =60° к линии горизонта. Глубина ямы /у = 10 м, расстояние от точки бросания до стенки ямы / = 10 м. ускорение свободного падения можно принять g = 10 м/с2 . Вылетит ли мяч из ямы?
1.25.	Мяч бросают под углом а к го-	„X а
ризонту с одного края ямы на другой,	_____
который ниже на h. Ширина ямы — 1. С	л	J h
какой минимальной начальной скоро-	|	'ииш
стью vc) надо бросить мяч, чтобы пере-	р-------
бросить яму? Сопротивлением воздуха	ПТТПТПТ,
пренебречь.
1.2б7Т	очечное тело свободно падает на наклонную плоскость с некоторой высоты в точку А. С помощью горизонтальной полуплоскости ВС для него устроена «ловушка». При падении с какой высоты тело попадет в «ловушку» (проскочит между точками В и /?)? Все столкновения, испытываемые телом — абсолютно упругие.
Рассмотрите два варианта задачи: 1) расстояние между полуплоскостью ВС и наклонной плоскостью BD = I м. А1) = 4 м, угол наклона плоскости к линии горизонта а = 45°: 2) расстояние между полуплоскостью ВС и наклонной плоскостью BD = 2 м, AD = 12 м, угол наклона плоскости к линии горизонта а = 45° .
1.27ГТ	очечное тело бросили с поверхности Земли под углом а к горизонту с начальной скоростью v(J. Пренебрегая сопротивлением воздуха, определить нормальное и тангенциальное ускорения в начальной точке траектории и в наивысшей точке подъема. Определить радиус кривизны в этих точках.
15
R/2
1.28* На горизонтальной поверхности. лежащей на глубине R / 2 ниже уровня Земли, покоится полусфера радиуса R. С какой минимальной скоростью v0, под каким углом а и с какого расстояния S надо бросить с
поверхности Земли камушек, чтобы он перелетел через полусферу, коснувшись ее в верхней точке?
1.29.*Воздушный шар радиуса R покоится на высоте 2R над поверхностью Земли. С какой минимальной начальной скоростью vg, под каким углом а и с какого расстояния S надо бросить с горизонтальной поверхности Земли камень, чтобы он перелетел через шар, коснувшись его в верхней точке?
1.30	? Через какой интервал времени происходят две последовательные встречи минутной и секундной стрелок часов? На какой угол при этом успевает повернуться минутная стрелка?
1.31	* Пропеллер самолета радиусом R -1,5 м вращается с частотой п - 2,0 • 103 оборотов в минуту. Какова скорость точки на конце пропеллера при посадке самолета, если посадочная скорость самолета относительно Земли v -161 км/ч ?
1.32	? Две	параллельные
ДВИЖУТСЯ СО СКОРОСТЯМИ V] а) в одном направлении; б) в воположных направлениях, рейками зажат диск радиуса R. Проскальзывание между диском и рейками отсутствует. Какова угловая скорость вращения диска и скорость его центра?
V// 
рейки и V2: проти-МежДу
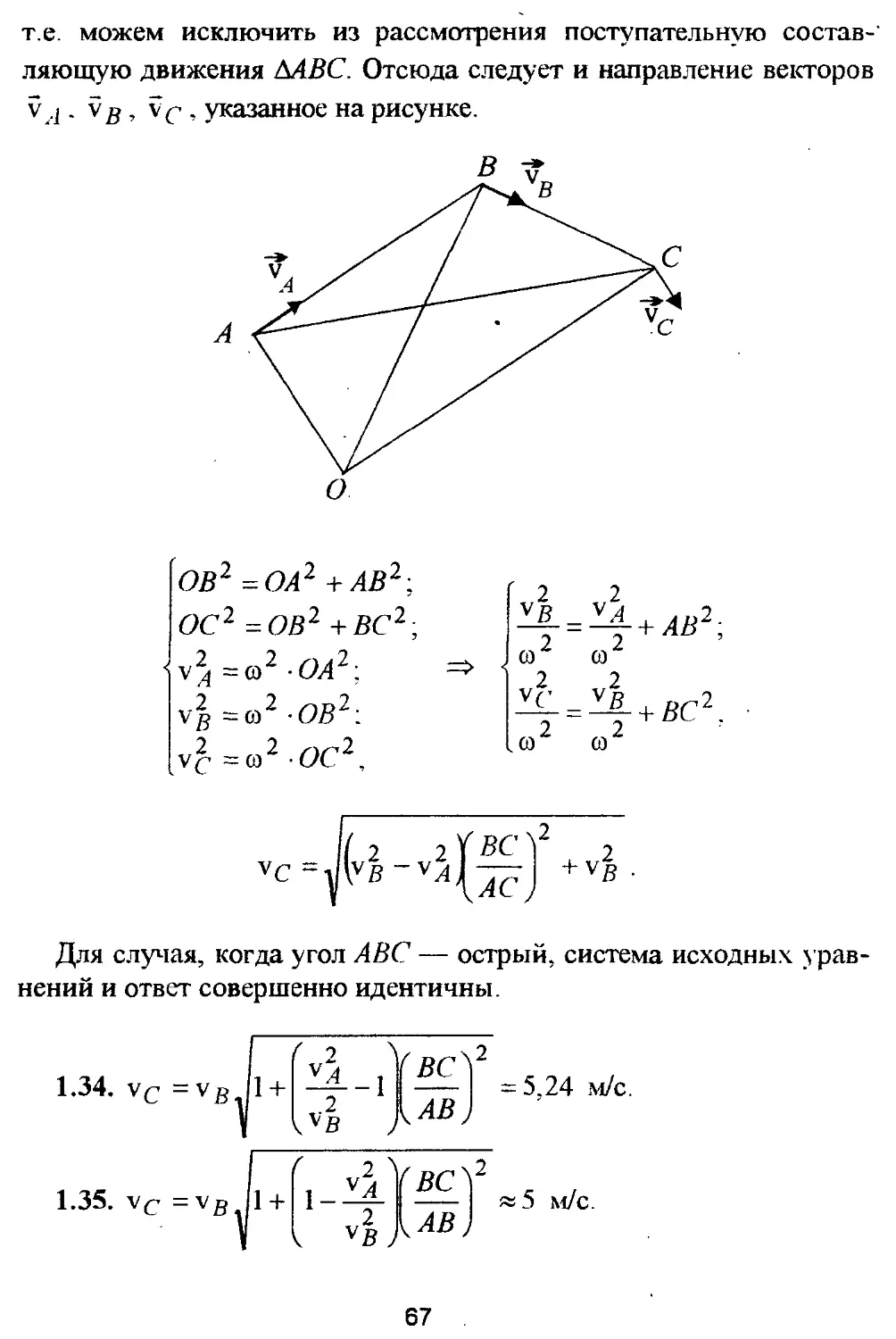
1.33?Треугольник АВС движется в некоторой плоскости таким образом, что скорость вершины А направлена вдоль стороны АВ, а скорость вершины В — вдоль стороны ВС. Считая заданными дли-
16
ны сторон АВ и ВС, а также скорости указанных точек и vg, определить скорость точки С.
1.34.	*Стержень АС движется в пространстве таким образом, что в данный момент времени скорость точки А направлена под углом к АС и v 4 = 6,0 м/с, а скорость точки В стержня направлена вдоль стержня и V g =5.0 м/с. ЛВ = 10,5 м; ВС = 5,0 м. Определить скорость точки С. Точка В лежит между точками А и С.
1.35.	Треугольник ЛВС движется в пространстве таким образом, что в данный момент времени скорость точки А направлена вдоль стороны АВ и v 4 = 3,0 м/с: а скорость точки В направлена вдоль
стороны ВС и vg=4.0 м/с. Угол АВС— острый, АВ = 2.6 м: ВС = 3,0 м. Определить скорость точки С.
1.36.	Стержень АС движется в пространстве таким образом, что в данный момент времени скорость точки А направлена вдоль АС и v 4 = 3,0 м/с; а скорость точки В, лежащей между точками А и С, направлена под некоторым углом к АС и vg = 4.0 м/с. АВ = 2.6 м; ВС = 1,4 м. Определить скорость точки С.
1.37.	Колесо радиуса R катится по горизон-тальной поверхности без проскальзывания та-ким образом, что его ось О движется с посто- ( 'ia* \ янным ускорением «у. Начальная скорость —1— колеса равна нулю. Определить скорость и ус- \ j / корение точек колеса А, В, С и D через время t	i
после начала движения.	'
17
2.	ДИНАМИКА
Динамика — раздел физики, в котором изучаются как причины, по которым тела движутся тем или иным образом, так и следствия, к которым приводят эти причины.
Изменения в движении тел являются результатом их взаимодействий с другими телами. В ньютоновской механике эти взаимодействия описывают на языке сил, действующих между телами.
Основу динамики составляют три закона Ньютона. Первый за~ кон выделяет системы отсчета, в которых уравнения динамики имеют наиболее простой вид. Эти системы отсчета называют инерциальными. Под ними понимают такие системы отсчета, относительно которых материальные точки, не подверженные воздействию других тел, движутся равномерно и прямолинейно, или, как говорят, по инерции. Второй закон Ньютона устанавливает связь между кинематической характеристикой движения — ускорением а и динамическими характеристиками взаимодействия, т е. силами взаимодействия. Он имеет вид
ma = F,	(2.1)
т — масса (инертная) тела.
Когда на тело действуют несколько сил, то под F понимают результирующую (равнодействующую) всех сил. Каждая из этих сил Fj сообщает телу ускорение а,, как будто других сил нет. Это положение называют принципом независимости действия сил. В соответствии с ним силы и ускорения можно разложить на составляющие, использование которых часто упрощает решение задач. Второй закон Ньютона в более общей формулировке имеет вид
=	(2.2)
dt
18
т.е. скорость изменения импульса материальной точки равна действующей на него силе. Еесли сила F — постоянна, то можно записать, что изменение импульса тела под действием силы F в течении интервала времени At:
= р - ро = F • At.	(2.3)
где F  At называют импульсом силы.
Третий закон Ньютона связывает между собой силы, с которыми тела действуют друг на друга. Он подразумевает, что если какие-либо два тела взаимодействуют друг с другом, то силы, возникающие между ними:
приложены к разным телам;
равны по величине:
противоположны по направлению:
действуют вдоль одной прямой:
имеют одну и ту же природу.
Ключевая роль третьего закона Ньютона объясняется возможностью установить все силы, которые влияют на движение рассматриваемого тела.
Выражения для сил, входящих в уравнения динамики (2.1) или (2.2), берутся из других разделов физики, где изучается их природа.
Движение твердого тела зависит не только от величины действующих сил, но и от точки их приложения.
Применение второго и третьего законов Ньютона к системе взаимодействующих тел позволяет сформулировать закон движения центра масс системы в очень простом виде: центр масс системы тел движется так, как двигалась бы материальная точка с массой, равной сумме масс всех тел, входящих в систему, под действием силы, равной векторной сумме всех внешних сил, действующих на тела рассматриваемой системы (называемой равнодействующей силой). Отсюда следует, что под действием только внутренних сил центр масс не может приобрести ускорение.
Решение динамических задач начинается с анализа всех сил, действующих на интересующее нас тело, т е. с установления с какими иными телами и каким образом оно взаимодействует (с одним и тем же телом может существовать несколько видов взаимодействия).
19
Основное уравнение динамики -— второй закон Ньютона — векторное уравнение. Для удобства решения его превращают в систему алгебраических уравнений, проецируя уравнение (или уравнения. записанные для каждого из интересующих нас тел) второго закона Ньютона на специально выбранные направления (оси).
Во многих задачах приходится рассматривать трение тел друг о друга. При наличии трения силу R, с которой одно тело действует на другое, удобно рассмотреть как сумму двух сил: силы N, направленной перпендикулярно (по нормали) к поверхности контакта (сила реакции опоры), и силы трения FTp, направленной по касательной к поверхности. При скольжении тел относительно друг друга модули этих составляющих силы R связаны между собой (приближенным) законом Кулона— Амонтона, установленным экспериментально: Атр = цек • N. где цск — коэффициент трения (скольжения), зависящий от рода соприкасающихся тел. Сила FTp направлена в этом случае противоположно вектору скорости (направлению движения). В случае, когда взаимодействующие тела неподвижны относительно друг друга, выполняется соотношение: /*’гр < цек  N. и направление силы FTp определяется из условия неподвижности тел. Если тело круглой формы (шар, цилиндр) катится по поверхности, то возникает третья разновидность силы трения —- трение качения (первые две называют силами трения скольжения и покоя). При этом выполняется соотношение: А’тр = Цкач ' и, обычно цкач « цск.
ЗАДАЧИ
2.1.	В каких точках приложена сила, которая заставляет автомобиль двигаться по шоссе?
2.2.	Почему поезд движется, если масса локомотива (и, соответственно. сила нормального давления его на полотно дороги) во много раз меньше массы состава? Почему, трогаясь с места, машинист локомотива первоначально дает вагонам тяжело груженого состава толчок?
2.3.	Объясните, почему человек может бежать по тонкому льду, на котором не может стоять, не проваливаясь?
20
2.4.	Имеется деревянный прямоугольный параллелепипед, у которого одно ребро значительно превышает два других. Как с помощью одной только линейки определить коэффициент трения бруска о поверхность пола в комнате?
2.5.	Даны: деревянная доска, брусок и транспортир. Как определить коэффициент трения бруска о поверхность доски с помощью только этих предметов?,
2.6.	Трогаясь со станции, поезд некоторое время движется практически равноускоренно. Как определить его ускорение в этот период с помощью нити, 100-граммовой гирьки и масштабной линейки?
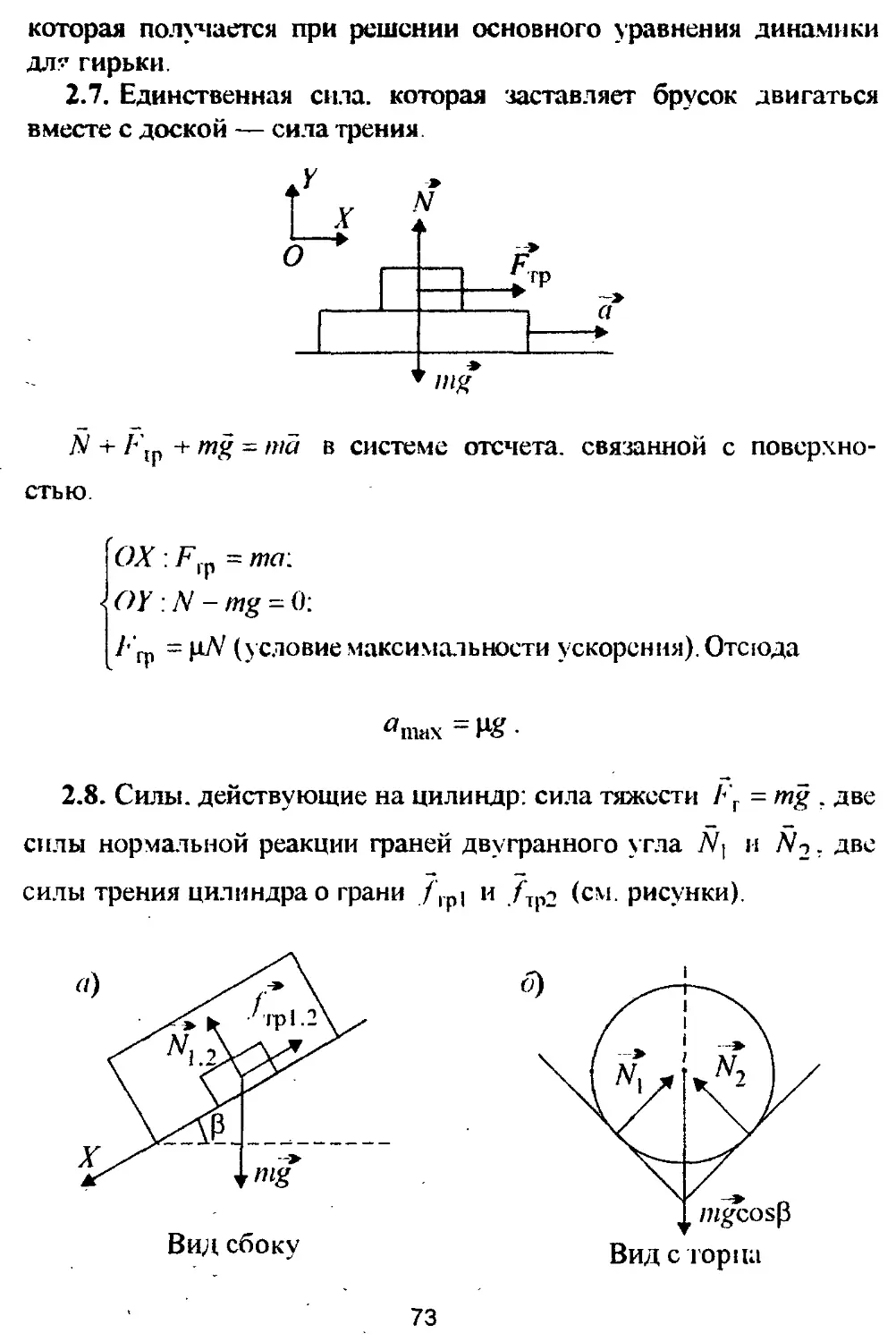
2.7.	На доске, движущейся по горизонтальной поверхности с ускорением, находится брусок. При каком максимальном ускорении доски «щах брусок не будет соскальзывать с нее? Коэффициент трения скольжения ц задан.
2.8?	Определите ускорение цилиндра, скользящего по желобу, имеющему вид двугранного угла с раствором а = 90° . Ребро двугранного угла наклонено к горизонту под углом р = 60°. Плоскости двугранного угла образуют одинаковые углы с горизонтом. Коэффициент трения между цилиндром и поверхностью желоба ц = 0.7.
2.9.	Небольшой брусок пускают вверх по наклонной плоскости, составляющей угол а = 60° с горизонтом. Коэффициент трения ц = 0,8 . Определите отношение времени подъема бруска вверх /| ко времени его соскальзывания до первоначальной точки.
\/ 2.10?Брусок массы т = ] кг равномерно втаскивают за нить вверх по наклонной плоскости, составляющей угол а = 30° с горизонтом. Коэффициент трения ц = 0,8. Найдите угол р. который должна составлять нить с наклонной плоскостью, чтобы натяжение нити было наименьшим. Чему оно равно?
2.11?	На наклонной плоскости находится брусок, к которому приложена направленная вверх вдоль наклонной плоскости сила F = kmg, где к ~ 1,5 и mg — сила тяжести. Коэффициент трения Ц = 0,8 . При каком угле наклона плоскости ускорение бруска будет минимальным и каково оно?
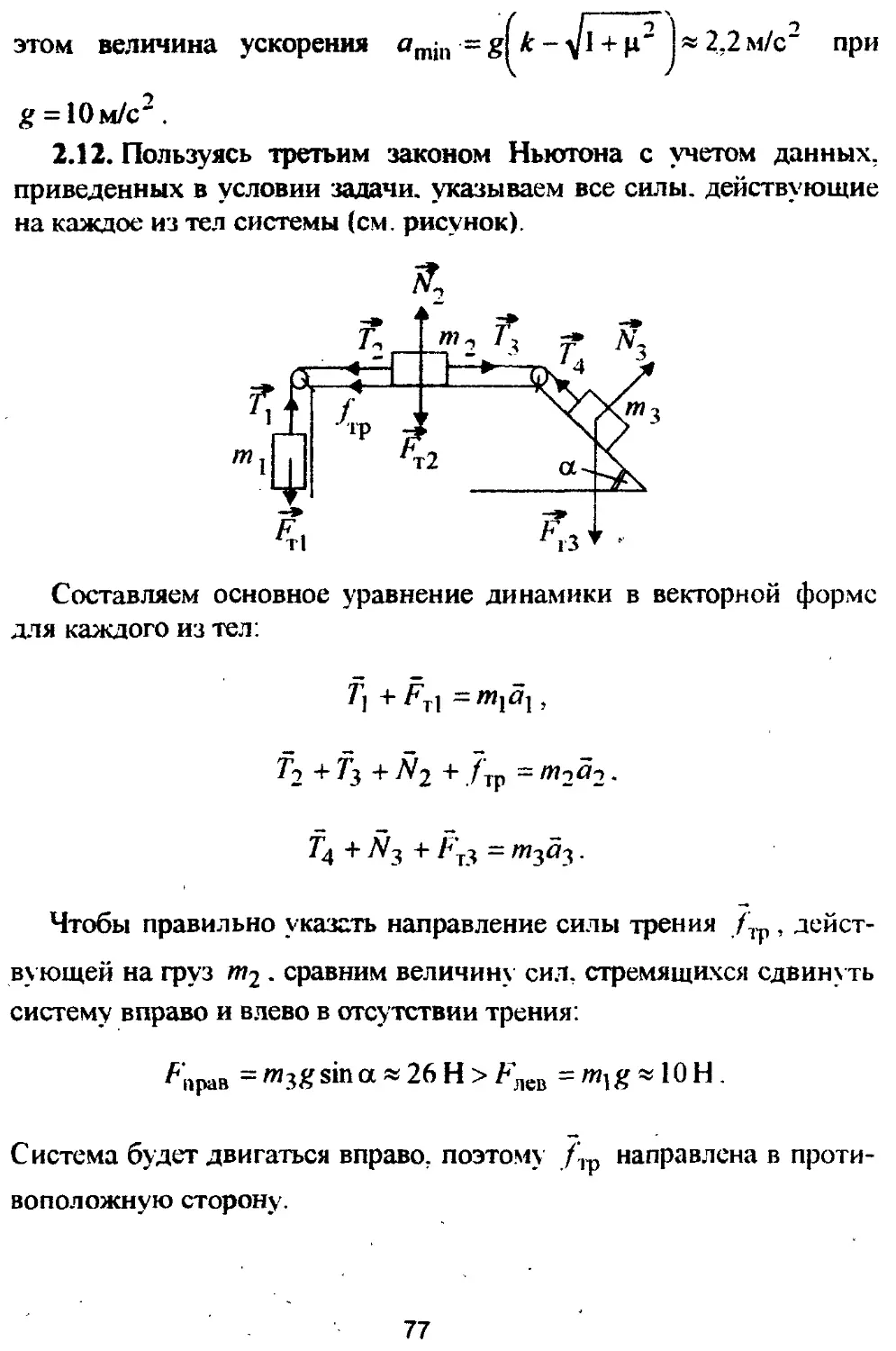
2.12.	Для системы тел. связанных невесомыми и нерастяжимыми нитями, определить установившееся натяжение нити между телами т2 и /Из при условии, что начальная скорость тел была рав
21
на нулю. Массы тел т\ =1 кг; m2 = 2 кг; т3 = 3 кг; угол наклона плоскости, на которой находится тело т$, к линии горизонта а = 60°; коэффициент трения между телом т2 и соответствующей горизонтальной поверхностью ц = 0,2; тела /П] и т3 действие силы трения не испытывают, в блоках трение отсутствует.
2.13.	Для системы тел. связанных невесомыми и нерастяжимыми нитями, на наклонной плоскости определить натяжение нити между телами т2 и т3. которое установится, если тела отпустить без начальной скорости. Массы тел = 1 кг; =2 кг; w3 = 3 кг: угол наклона плоскости к линии горизонта а = 30° ; коэффициент трения между телом т3 и плоскостью р. = 0,3 ; другие тела не испытывают действия силы трения.
2.14.	Для системы тел, связанных невесомыми и нерастяжимыми нитями, определить установившееся натяжение нити между телами п?] и т2 при условии, что начальная скорость тел равна нулю.. Массы тел п-ц =1 кг; т2 = 2 кг; т3 = 3 кг; угол наклона плоскостей к линии горизонта а = 45°; коэффициент трения между телом W] и наклонной плоскостью ц = 0,3; тела т2 и т3 действия силы трения не испытывают, в блоке трение отсутствует.
22
т7
«з
2.15.	Для системы тел. связанной невесомыми и нерастяжимыми нитями, определить установившееся натяжение нити между телами /и2 и W3 при условии, что начальная скорость тел была равна нулю. Массы тел п-ц = 1 кг; т2 = 2 кг; =3 кг; угол наклона плоскости, на которой находятся тела пц и т2. к линии горизонта а = 30°; коэффициент трения между телом и соответствующей горизонтальной поверхностью ц = 0,2; тела и /т?2 действия силы трения не испытывают, в блоке трение отсутствует.


J 2.16. Определить ускорение, с которым движется брусок, помещенный на горизонтальную поверхность, под действием приложенных к нему сил F] ~ 20 Н и /-2=10Н, а = 45° и р = 30°. Ко
эффициент трения бруска о плоскость ц = 0,2; масса бруска: а) т-2 кг; б) /я = 10 кг; в) т- \ кг. Ускорение свободного падения g -10 м/с2 .
2.17.	*Определить ускорения, с которыми движутся шар и клин. Массы клина т и шара М, угол между гранями клина а заданы. Движение тел ограничено вертикальной и горизонтальной поверхностями. Трение отсутствует. Рассмотреть два-случая относительного расположения шара и клина, показанных на рисунках а и б.
23
2.18	? Определить ускорения, с которыми движутся два одинаковых цилиндра и призма. Массы призмы т и каждого из цилиндров М. угол между гранями призмы а заданы. Ось симметрии призмы —. вертикальна. Движение тел ограничено горизонтальной поверхностью. Трение отсутствует.
2.19	? Определить ускорения, с которыми движутся клинья и цилиндр. Массы цилиндра т и каждого из клиньев М, угол при оснований клина а заданы. Движение тел ограничено горизонтальной поверхностью. Трение отсутствует.
2.20	?Стержень, закрепленный таким образом, что он может перемещаться только в вертикальном направлении, нижним концом опирается на гладкий клин, лежащий на горизонтальной плоскости. Масса стержня — т, масса кли-
на — М. угол при основании клина — а. Трение отсутствует. С ка-
ким ускорением движется клин?
;	2.21? Шарик радиуса R, двигающийся
поступательно со скоростью v и одновременно вращающийся вокруг горизонтальной оси (см. рисунок), перпендикулярной плоскости рисунка, с угловой скоростью й. такой, что aR » v, испытывает соударение с плоской поверхно-
стью. Деформации шарика при ударе — упругие. Угол падения —
а. Коэффициент трения — р. После удара шарик продолжает вра-
24
щаться в прежнем направлении с мало изменившейся угловой скоростью. Определить угол отражения р. Время соударения мало.
Рассмотреть два случая вращения шарика: а) против часовой стрелки; б) по часовой стрелке.
2.22?	Шарик. движущийся со ско-	’
ростью v0, испытывает соударение с	i
«бегущей» горизонтальной плоской \ а' о дорожкой Скорость дорожки 0 хук/// > V»VO • Деформации шарика при	2»
ударе— упругие. Коэффициент тре-	>
ния — ц. Угол падения — а. При отскоке скорость шарика меньше v. Определить угол отражения р. Время соударения мало.
Рассмотреть два случая относительного движения шарика и дорожки: а) шарик «догоняет» дорожку; б) шарик движется навстречу дорожке.
у/ 2.23. В некоторый момент времени тело начинает скользить вверх по наклонной плоскости со скоростью vq. Угол наклона плоскости к линии горизонта — а, коэффициент трения — ц. Какой путь пройдет тело за время от начала движения. Плоскость — протяженная.
2.24.	Тело массой т, находящееся на высоте Н над поверхностью Земли, подбрасывают вертикально вверх со скоростью vq . Какой путь пройдет тело за время t после начала движения, если сила сопротивления воздуха постоянна и равна F, а тело — неупругое? Плотность тела много больше плотности воздуха.
2.25.	В некоторый момент времени несжимаемому телу, находящемуся глубоко под поверхностью воды и далеко от. дна водоема, сообщили скорость V(j в направлении вертикально вниз. Плотность воды— р0; плотность тела— р. Какой путь пройдет тело за время t от начала движения, если трением о жидкость можно пренебречь?
2.26.	Тело уронили с некоторой высоты в воду без начальной скорости, при этом была измерена глубина его погружения за 1 с после его вхождения в воду. Установлено, что если начальную высоту уменьшить в к = 4,5 раза, то глубина погружения уменьшится в I = 1,9 раз. Утонет ли тело в воде? Сопротивлением (трением) воздуха и воды пренебречь.
25
2.27*	Тело уронили с некоторой высоты в воду без начальной скорости, при этом была измерена глубина его погружения за 1 с после вхождения в воду Установлено, что если начальную высоту увеличить в к = 8,3 раза, то глубина погружения увеличится в / = 3.5 раза. Утонет ли тело в воде? Сопротивлением (трением) воздуха и воды пренебречь.
2.28.	Телу массой т, находящемуся на горизонтальной поверхности, сообщают скорость vg вдоль поверхности и прикладывают к нему две постоянные силы F] = mg!2 под углами
Р < а < 90° к горизонту'. Какой путь
пройдет тело за время Z() после начала движения, если коэффициент трения — ц9
2.29.	Искусственный спутник Земли летит с выключенными двигателями по круговой орбите вокруг Земли. Почему тела в нем невесомы?
2.30.	При каком периоде вращения Земли вокруг своей оси тела на экваторе были бы невесомы? Радиус Земли К.л = 6,37 • 106 м.
2.31.	Первый в мире космонавт Ю.А. Гагарин на корабле-спутнике «Восток-1» двигался вокруг Земли по круговой орбите на высоте Н = 251 км над поверхностью Земли. Радиус Земли R., = 6.37 -106 м. Определить период обращения его вокруг Земли.
2.32.	Подлетев к незнакомой планете, космический корабль перешел на круговуто орбиту. Могут ли космонавты оценить среднюю плотность вещества планеты, пользуясь для этой цели только часами?
2.33.	Спутник запущен в плоскости экватора по круговой орбите так. что все время находится над одной и той же точкой экватора. Определить радиус орбиты спутника. Радиус Земли Rt = = 6,37 -I06 м.
2.34.	Спутник запущен в плоскости экватора по круговой орбите так. что все время находится над одной и той же точкой экватора. Определить орбитальную скорость спутника. Радиус Земли А3 = = 6.37 106 м.
26
3.	ЗАКОНЫ СОХРАНЕНИЯ ИМПУЛЬСА И ЭНЕРГИИ
В раде случаев решение динамических задач облегчается использованием законов сохранения импульса и энергии. Особенно эффективным является использование этих законов в тех случаях, когда действующие силы непостоянны и непосредственное решение уравнений динамики с помощью элементарной математики невозможно.
Закон сохранения импульса формулируется для так называемых замкнутых систем взаимодействующих тел, под которыми понимаются такие системы, в которых на тела действуют только внутренние силы, т е. тела системы взаимодействуют только друг с другом.
Суть закона сохранения импульса: суммарный импульс замкнутой системы тел остается величиной постоянной при любых процессах. происходящих в системе, т.е. если F) = б, то
р, = const.
i
В некоторых случаях закон сохранения импульса можно применять и к незамкнутым системам. Эти случаи следующие.
1)	внешние силы действуют на систему, но их равнодейству ю-щая равна нулю;
2)	если сумма проекций всех внешних сил, приложенных к системе тел, на некоторое направление (например, ось ОХ) равна нулю. то сумма проекций импульсов тел системы на это направление сохраняется, т.е. pix = const;
i
3)	продолжительность взаимодействия очень мала, а внешняя сила ограничена по величине (такая ситуация возможна, например,
27
при столкновении тел, когда внешней силой является сила тяжести).
При поступательном движении тела механическая работа постоянной силы F равна произведению модуля силы на перемещение центра масс ДА и на косинус угла между векторами силы и перемещения.
А - FAS cos а.
Если при перемещении тела модуль силы изменяется, то работа силы ^численно равна площади под графиком зависимости модуля силы от перемещения.
Механическая энергия характеризует способность тела совершать механическую работу. Полная механическая энергия складывается из кинетической Ек и потенциальной энергии Еп:
Е -Е + Е
^мех т 
Кинетическая энергия — энергия движущегося тела:
„ wv2
£к ------.
к 2
Потенциальной энергией обладают системы тел, взаимодействующие за счет консервативных сил, т.е. сил, работа которых зависит только от начального и конечного положений взаимодействующих тел. но не от формы их траектории.
Закон сохранения энергии утверждает, что энергия не исчезает и нс возникает, а лишь переходит из одной формы в другую.
Приращение механической энергии системы Д^мех равно сумме работ внешних сил Лвнеш и неконсервативных внутренних сил Л11К (к неконсервативным силам относятся, например, сила трения или сила сопротивления среды):
Д^мех = ^внеш + ^нк •
28
Для замкнутых систем Лвнеш = 0. поэтому изменение механической энергии может происходить только за счет неконсервативных внутренних сил.
При отсутствии внешних и неконсервативных сил механическая энергия системы не изменяется:
^мех =	~ const •
ЗАДАЧИ
3.1.	Ящик весом Р, имеющий форму куба с длиной ребра п. перемещают равномерно по горизонтальной поверхности. Найти отношение работ: при. перемещении ящика волоком и кантованием (путем опрокидывания через ребро). Коэффициент трения при движении ящика волоком ц.
3.2.	Камень массой т = 1 кг брошен вертикально вверх. Какую кинетическую энергию ему надо сообщить при бросании, чтобы на высоту Я = 30 м он поднялся за время / = 6 с? Сопротивлением воздуха пренебречь, g = 10 м/с2 .
3.3.	Из длинной полоски резины жесткости к сделали рогатку. Найдите кинетическую энергию «снаряда», выпущенного из этой рогатки, если резину растянули с силой F и отпустили.
3.4.	Тело соскальзывает с гладкой горки высотой Н и затем движется горизонтально по шероховатой поверхности (коэффициент трения ц). Какое расстояние по горизонтальному участку пути пройдет тело до остановки?
3.5.	Автомобиль с работающим двигателем въезжает на обледенелую гору, поверхность которой образует угол а с горизонтом. Какой высоты гору может преодолеть автомобиль, если его начальная скорость у подножия V, а коэффициент трения колес о лед Н-
3.6.	Совершает ли работу сила тяготения, действующая на спутник. при движении спутника по круговой орбите? По эллиптической орбите?
29
3.7.	Может ли искусственный спутник с выключенными двигателями летать вокруг Земли по орбите, плоскость которой не проходит через центр Земли?
3.8.	Как изменяются кинетическая, потенциальная и полная механическая энергия спутника при движении по эллиптической орбите с выключенными двигателями? Сопротивлением движению
пренебречь.
।	\/ 3.9. В точке А горизонтального диска,
О • 4 къл-ОВъ рвРащающегося ВОКРУГ вертикальной оси, V/П ! 1ГГ77ТТ 77/7/Awf^lnPHKPenjieHa пружина. на другом конце которой прикреплен груз В массы
т = 20 г Жесткость пружины к = 1 Н/м.
расстояние ОА = 5 см. длина пружины в недеформированном состоянии /0 = 10 см. Какова будет потенциальная энергия пружины
при вращении диска с угловой скоростью w = 100 рад/с?
3.10.	Два мальчика на катке хотят сравнить, кто из них больше по массе и во сколько раз. Как им выполнить свое намерение с помощью одной лишь рулетки?
3.11.	Лодка стоит неподвижно в стоячей воде. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние h сдвинется лодка относительно берега, если масса человека — т. масса лодки — М. длина лодки — £? Сопротивлением воды пренебречь.
3.12.	На железнодорожной платформе, движущейся по инерции со скоростью v. укреплено орудие. Ствол орудия направлен в сторон} движения платформы и приподнят над горизонтом. Орудие производит выстрел, после чего скорость платформы уменьшается в 3 раза. Найти скорость vCH снаряда относительно Земли. Масса
снаряда — т. масса платформы с орудием — А/.
3.13.	Скользившее по горизонтальной поверхности со скоростью v() тело массой т испытывает абсолютно упругий удар, столкнуъшись с телом массы М. На какую величину h сожмется пружина, к которой прикреплено второе тело, если
жесткость пружины равна к, а коэффициент трения о горизонталь-
ную поверхность равен ц?
30
V 3.14? Гиря массой т падает на чашку пружинных весов с высоты Н и испытывает абсолютно упругий удар. На какую величину А сожмется пружина весов после удара, если масса чашки равна М. а коэффициент жесткости пружины равен Л?


М
3.15.	Тело массы т. летевшее вертикально вверх со скоростью v() испытало абсолютно упругое столкновение с телом массы М. подвешенным на пружинке, жесткость которой равна к. На какую величину h сожмется пружинка?
3.16.	На какую глубину А2 в жидкость плотности р() погрузится упавшее с высоты h\ над ее поверхностью тело плотностью р Сопротивлением воздуха и жидкости пренебречь.
3.17.	На какую высоту А2 наД поверхностью жидкости, плотность которой равна ру. подскочит тело плотности р, которое было погружено на глубину А] ? Сопротивлением воздуха и жидкости пренебречь.
3.18?	Небольшое тело начинает соскальзывать с вершины полусферы радиуса R - 20 см, неподвижно лежащей на горизонтальной поверхности. На какой высоте Н от опоры тело оторвется от поверхности полусферы? Трением пренебречь.
3.195	Небольшое тело соскальзывает вниз по наклонному скату, переходящему в цилиндрическую поверхность радиуса R = 20 см. Какова должна быть наименьшая высота Н ската, чтобы тело, по
31
пав через отверстие внутрь цилиндрической поверхности, сделало «мертвую петлю», не отрываясь от стенок? Трением пренебречь.
3.20.	С помощью копра массой т, падающего с высоты Н, забивают сваю массой М. Какова средняя сила сопротивления грунта, если при одном ударе свая погружается на /? Удар считать абсолютно неупругим.
т	3.21. Молот, падая с высоты Н. нано-

сит удар по свае. На какую глубину h погрузится свая в грунт после удара, если масса молота — т. масса сваи — М, средняя сила сопротивления грунта — F. а удар молота по свае можно считать абсолютно упругим?
3.22.	Два шарика массами ту и т2 подвешены на длинных нитях так, что они соприкасаются и их центры масс находятся на одной высоте. Шарик массой ту отводят в сторону на натянутой нити. поднимая его на высоту Н, и отпускают. На какую высоту поднимутся шарики после абсолютно неупругого центрального удара?
3.23.	Сидящий в неподвижной лодке человек бросает в горизонтальном направлении камень массой ту со скоростью v0 относительно лодки. Масса человека с лодкой w2 Какую работу совершил человек при бросании камня, если лодка может свободно перемещаться? Сопротивлением воды пренебречь.
3.24.	Пуля массой ту, летящая горизонтально, попадает в середину деревянного шара массой /и2, подвешенного на длинной нити и застревает в нем. При этом шар поднимается на высоту Н. Какова была начальная скорость пули?
3.25?Ш	ар, скользивший по гладкой горизонтальной поверхности со скоростью vj = 20 м/с. испытывает лобовое соударение с покоившимся шаром, имеющим те же геометрические размеры, и приобретает скорость иу =8 м/с. В каких пределах может изменяться доля первоначальной кинетической энергии системы, которая перейдет во внутреннюю энергию?
32
4. СТАТИКА
Статика изучает равновесие тел. В инерциальной системе отсчета твердое тело находится в равновесии, если выполняются два условия:
векторная сумма всех действующих на тело сил равна нулю.
(4.1)
i
алгебраическая сумма моментов всех сил, действующих на тело, относительно произвольной оси равна нулю:
(42) i
Момент силы М равен произведению модуля силы |f| на ее плечо. Плечо силы — кратчайшее расстояние h от оси вращения до линии действия силы (см. рисунок).
В рамках школьного курса физики задачи статики рассматриваются для систем, в которых все действующие силы лежат в одной плоскости; в этой ситуации ось для расчета моментов сил необходимо ориентировать перпендикулярно плоскости их действия. Выбор оси производится исключительно из соображений удобства решения задачи: уравнение моментов будет тем проще, чем больше сил будут иметь равные нулю моменты. В уравнение моменты входят как алгебраические величины: моменты сил, стремящихся повернуть тело по часовой стрелке, берутся с одним знаком, например минус, против часовой стрелки с противоположным — со зна-
33
ком плюс. При составлении уравнения моментов необходимо точно определить место приложения каждой силы.	*
Центр масс — такая точка твердого тела или системы тел, которая движется так же, как и материальная точка массой, равной массе всей системы в целом т = £	, на которую действует та же
i
результирующая сила, что и на тело (систему тел):

(4.3)
vu м — скорость центра масс; vz — скорость отдельных тел системы (материальных точек).
Положение центра масс твердого тела или системы тел (материальных точек массой от,-) можно найти по формулам:

i
(4.4)
У т,У.
Л’ц.м = ~’
2л»
i
YmiZi
ZU. м =	•
i
Уравнение (4.4) легко получается при дифференцировании по времени выражений (4.3).
Центр тяжести —точка приложения равнодействующей веех сил тяжести, действующих на частицы этого тела при любом его положении в пространстве. Если линейные размеры тела малы по сравнению с радиусом Земли, то центр масс совпадает с центров
34
тяжести. Сумма моментов всех элементарных сил тяжести относительно любой оси, проходящей через центр тяжести, равна нулю.
При выполнении условия равновесия (4.1) равно нулю ускорение центра масс тела. При выполнении условия равновесия (4.2) отсутствует угловое ускорение вращения. Поэтому, если в начальный момент времени тело покоилось, то оно будет оставаться в покое и дальше.
ЗАДАЧИ
4.1.	У какой из двух веревок, изображенных на рисунке, центр тяжести расположен выше. Веревка на рисунке а висит свободно, а на рисунке б удерживается в натянутом состоянии внешней силой F. Веревки имеют одинаковую длину, а точки их крепления расположены на одном уровне.
«)
6}
4.2.	Муравей решил утащить к муравейнику соломинку. Как ему следует поступить; если сила, с которой он может тянуть соломинку, несколько меньше максимальной силы трения покоя.
4.3.	Однородная доска массой т в горизонтальном положении покоится на двух точечных опорах. С какой силой доска давит на каждую из опор, если одна из них удалена от края доски на четверть, а другая — на треть длины доски?
4.4.	Кирпич лежит на наклонной плоскости, прилегая к ней всем основанием. Какая половина кирпича — верхняя или нижняя — оказывает большее давление на наклонную плоскость?
7777777777777777
4.5.	Между двумя одинаковыми ящиками, стоящими на полу,
вставили палку, немного не доходящую до пола. К верхнему концу
35
A
В
палки приложена горизонтальная сила F Какой из ящиков сдвинется раньше при постепенном увеличении силы F? Трение суще-*' ственно.
4.6.	Для подготовки к работе в условиях невесомости одетые в скафандры космонавты тренируются в воде. При этом сила тяжести. действующая на них, уравновешивается выталкивающей силой. В чем отличие такой невесомости от настоящей?
4.7.	Рычаг изогнут так, что его стороны АВ = ВС = CD и образуют прямые углы. Ось рычага— в точке В. Сила F приложена перпендикулярно АВ в точке А. Определить минимальное значение силы, которую нужно приложить к плечу BCD, чтобы рычаг находился в равновесии. Массой рычага пренебречь.
4.8.	Лестницу прислонили к гладкой стенке. При какой минимальной величине угла а между лестницей и полом лестница еще не будет падать, если коэффициент трения между лестницей и полом равен ц?
4.9.	Рыболов решил определить, какую нагрузку выдерживает леска, располагая для этой цели гирей массы 1 кг и линейкой. Как должен быть поставлен соответствующий опыт?
4.10.	В вашем распоряжении имеется однородная деревянная рейка, линейка, лист фанеры и гладкий металлический лист. Как с помощью только этих предметов определить коэффициент трения дерево о дерево?
4.11.	Картина массой т, которую можно считать однородным телом, подвешена к стене на нити, как показано на рисунке. Угол между плоскостью картины и нитью — прямой. С какой силой картина действует на стену? Куда направлена эта сила?
4.12.	Однородный стержень массой т удерживается неподвижно под углом а к горизонту с помощью подставки в виде призмы 'и
36
перпендикулярной к нему стены. Трение между стержнем и подставкой отсутствует. С какой силой стержень действует на стену? Куда направлена эта сила?
4.13.	Однородный стержень массой т удерживается неподвижно в горизонтальном положении с помощью подставки в виде призмы и нити, как показано на рисунке. С какой силой стержень действует на подставку? Куда направлена эта сила?
4.14.	* Лестница опирается на вертикальную стену и пол. При каких значениях угла между лестницей и полом она может стоять, если коэффициенты трения лестницы о пол и о стену равны Ц| и
ц2 соответственно.
4.15.	*Катушку, находящуюся на горизонтальной поверхности, тянут за четыре намотанные на нее нити. Силы прикладываются под углами к линии горизонта aj=45o. a2=30°. 0,3=60°. 04 = 45°, величины сил относятся, как : F2 : F3 : F4 = 1:2:3:2 . Отношение радиуса обода катушки и радиуса цилиндра, на который намотаны нити, R! г = 2. Проскальзывание отсутствует. В какую сторону покатится катушка?
37
4.16.	Центр тяжести пустого цилиндрического стакана выше дна стакана. В стакан наливают воду. Докажите, что положение центра тяжести стакана с водой будет самым низким в том случае, когда он совпадает с уровнем воды в стакане.
4.17?	В гладкой сферической чаше лежит невесомый стержень с точечными массами ту = 0,5 кг и т^ = 0,4 кг. Длина стержня равна А>/3 , где R — радиус сферы. Определить, под каким углом к линии горизонта расположен стержень.
4.18?	При каком отношении М/т масс призмы Л/ и цилиндров т цилиндры будут раскатываться по горизонтальной поверхности при условии, что между призмой и цилиндрами нет проскальзывания. Коэффициент трения между цилиндрами и поверхностью ц = 0,4; угол между боковой гранью
призмы и вертикальной осью симметрии а = 45°. При каких значениях коэффициента трения между призмой и цилиндром возможно осуществление вышеописанной ситуации?
,	4.19?При каком Отношении М /т
Ж масс призмы М и цилиндров т цилиндры будут скользить по горизонтальной поверхности и не будут катиться? Рассмотреть два варианта начальных условий: а) угол между боковой, гранью призмы и вертикальной осью симмет----------------------- рии а - 30°, коэффициенты трения между призмой и цилиндрами щ =0,4, между цилиндрами и поверхностью Ц2 = 0.2 ; б) а = 45°.	= 0,3 , Ц2 ~ № 
4.20? На катушку, находящуюся на горизонтальной поверхности, намотана нитка, за которую тянут с силой F, Радиус цилиндра, на который намотана нитка — г. радиус обода катушки — А, масса катушки — т, коэффициент трения-скольжения между катушкой и 38
полом — р. С какой минимальной силой --------------»
Fmin надо тянуть за нитку, чтобы катушка /	\ F
вращалась, но не катилась? Расчет Fmjn ( .
провести при следующих численных значе- \	—
ниях параметров:
а)	р = 0,85, г = 4 см, R - 7 см, т = 2 кг;
б)	р = 0,5. г = 7.5 см, R = 10 см. т = 2 кг;
в)	р = 0,85, г = 8.5 см, R = 10 см, т = 2 кг;
г)	р = 0,7. г = 9,5 см, R = 10,5 см. т = 2 кг.
39
5.	МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Колебательным движением или колебаниями называют движения. которые характеризуются повторяемостью во времени.
Колебания называют периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени, называемыми периодом колебаний Т.
Простейший тип периодических колебаний — гармонические (синусоидальные)колебания
x = y4sin((o/ + (po),	-	(5.1)
где А— амплитуда колебаний, <о/+<р0— фаза колебаний, 2л ,
со = — = 2лу — циклическая или круговая частота, v — частота
колебаний. <р() — начальная фаза колебаний.
Первая и вторая производные гармонически изменяющиеся величины х также следуют гармоническому закону, причем
х + <о2х = 0.	(5.2)
Это есть дифференциальное уравнение гармонических колебаний.
Для определения характеристик колебаний можно пользоваться формулой для полной механической энергии W системы, в которой кинетическую и потенциальную энергию следует представить как некоторую функцию отклонения системы от положения равновесия. Под отклонением х понимают «обобщенную» координату. Это может быть декартова координата, угол отклонения и т.д. Выражение для энергии системы будет иметь вид
W = Ах2 + В(х)2,	(5.3)
40
где А и В — константы, определяемые параметрами системы. Первое слагаемое в (5.3) представляет собой потенциальную энергию системы, а второе — ее кинетическую энергию.
В отсутствии неконсервативных сил полная энергия сохраняется, поэтому
Отсюда следует, что
 А п
х + — х = 0, В
т.е. получается уравнение гармонических колебаний. Частота
(5-4)
ЗАДАЧИ
5.1.	В какой автомашине трясет меньше— пустой или нагруженной? Почему?
5.2.	На старых разъезженных грунтовых дорогах автомобиль может сильно раскачиваться. Почему это происходит?
5.3.	Разработайте метод определения объема комнаты с помощью длинной и тонкой нити, часов и гирьки.
5.4.	Математический маятник раскачивается около положения равновесия. Как меняется в зависимости от угла отклонения от положения равновесия потенциальная, кинетическая и полная энергия? Постройте графики этих зависимостей.
5.5.	Изменится ли период колебаний маятника от того, что его поместили в воду? Маятник обладает идеально обтекаемой формой и его трением о воду можно пренебречь.
5.6?	К телу массы М. находящемуся на т
гладкой горизонтальной поверхности,	I у
прикреплен стержень и пружина, длина 
41
 т
которой равна в недеформированном состоянии. По стержню свободно (без трения) перемещается муфта массы т, также прикрепленная к пружине. Пружин)' сжали таким образом, что ее длина стала равна /. и затем отпустили. Какова амплитуда колебаний тела М относительно горизонтапьной поверхности, если первоначально тела покоились? Стержень и пружина невесомы.
5.7	.*В стакан, масса которого Л7 и внутренний диаметр /. поместили маленькую шайбу массой т. которая без трения скользит по внутренней поверхности стакана. ПерЬоначально тела по-
коились. шайба находилась на высоте h от дна стакана. Какова амплитуда колебаний стакана относительно гладкой горизонтальной поверхности, на которой он находится?
5.8	?Призма. масса которой равна М. находится на гладкой горизонтальной поверхности. К вершине призмы прикреплена невесомая горизонтальная ось. вокруг которой вращается невесомый стержень длины /. на конце стержня за
креплен маленький шарик массой т. Какова амплитуда колебаний призмы относительно горизонтальной поверхности.
5.9	?Определите период малых свободных колебаний маятника, состоящего из двух взаимно перпендикулярных, невесомых, жестко скрепленных стержней длиной I = 1 ми трех маленьких шариков А. В и С массой т~\ кг каждый, вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости чертежа. Трение отсутствует, g = 10 м/с2 .
Различные варианты соединения стержней и их крепления относительно точки О показаны на рисунках а, б, в и г, где:
a)	OD-.DB , AD = DC -
б)	AO=OD, BD = DC,
в)	АО = ОВ;
г)	АВ = ВС.
42
S'. М
5.10	* Цилиндрический сосуд с площадью основания S разделен массивным поршнем массой М. который может свободно перемещаться в горизонтальном направлении, на две части объемом V каждая. В каждой половине сосуда содер
жится v молей идеального газа при постоянной температуре Т. Поршень соединен невесомой пружиной жесткостью к с основанием сосуда. Каков период малых колебаний поршня?
5.11	? Замкнутый цилиндрический сосуд с площадью основания 5 разделен массивным поршнем массой Л/, который может свободно перемещаться в горизонтальном направлении. В одной части со
суда содержится V| молей идеального газа, в другой— v2 молей при постоянной температуре Т. Каков период малых колебаний поршня?
5.12	* Замкнутый цилиндрический сосуд с площадью основания Л’ и объемом V разделен массивным поршнем массой Л/, который может свободно перемещаться в горизонтальном направлении. В левой и правой частях сосуда содержится по v MO-
S’. М
v.T,		v.r2
43
V, Г
/Л • v. Т
лей идеального газа и поддерживаются постоянные температуры 7] и Т2 соответственно. Теплообмен отсутствует. Каков период малых колебаний поршня?
5.13	? Замкнутый цилиндрический сосуд с площадью основания S' разделен на две части массивным поршнем, который может без трения перемещаться в вертикальном направлении. В каждой из частей сосуда содержится v молей идеального газа при постоянной температуре Т. давление в верхней части равно р]. в нижней — у>2 Каков период малых колебаний поршня9
44
6. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ
Этот раздел физики включает в себя подразделы «Гидростатика» и «Аэростатика», а также «Гидродинамика» и «Аэродинамика».
Воздействие отдельных частей жидкости или газа друг на друга характеризуют скалярной физической величиной, называемой давлением.
Основной закон статики жидкостей и газов — закон Паскаля, согласно которому давление, производимое внешними силами в каком-либо месте среды (жидкости или газа), передается по всем направлениям без изменения. Проявлением этого закона служит закон сообщающихся сосудов, в соответствии с которым однородная жидкость в сообщающихся сосудах устанавливается на одном уровне.
Если несжимаемая жидкость находится в поле тяжести, то на глубине Н ее гидростатическое давление
Р = PgH,
где р — плотность жидкости, g— ускорение свободного падения. При выводе этого соотношения полагается, что в точках жидкости, отстоящих друг от друга на расстоянии Н поле тяжести можно считать однородным. Неоднородность давления в жидкости на разных уровнях приводит к тому, что на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная по величине весу вытесненной этим телом жидкости. Эту силу называют силой Архимеда.
При описании движущейся жидкости вводят понятие линий тока, под которыми понимают такие линии, касательные к которым в любой точке совпадают с направлением вектора скорости жидко
45
сти v в этих точках. Если вектор скорости v в каждой точке жидкости не зависит от времени, то картина линий тока не будет меняться во времени, а движение жидкости в этом случае называют стационарным. При стационарном движении несжимаемой жидкости справедливо уравнение неразрывности:
V'jiS] = V2*$2 ?
где 5] и 6'2 — площади поперечных сечений потока жидкости, перпендикулярных направлению скорости, а V] и vj — скорости течения жидкости в этих сечениях.
Уравнение неразрывности при стационарном движении жидкости означает постоянство расхода ее в единицу времени.
Жидкость называют идеальной, если при движении жидкости можно пренебречь ее вязкостью, т.е. силами трения между слоями жидкости. Для идеальной жидкости математическим выражением закона сохранения механической энергии является уравнение Бернулли:
pv2
р + pgH +	= const.
В данной формуле Н — высота некоторой точки линии тока, р и у — давление и скорость жидкости в этой точке соответственно. Высота Н любой точки отсчитывается от одного уровня, условно принятого за нулевой.
ЗАДАЧИ
6.1.	Почему не устраивают газонапорные башни по аналогии с водонапорными?
6.2.	Каково соотношение (больше, меньше, равно) между весом налитой в сосуд жидкости и силой давления на дно 5 сосуда? Сосуды выполнены из цилиндрических и конических поверхностей
46
(штрихпунктирной линией обозначена ось симметрии соответствующей поверхности).
S


6.3.	Сосуд без дна, стенки которого образованы двумя цилиндрическими и одной плоской поверхностями, имеющий размеры, показанные на рисунке, стоит на столе. Края сосуда плотно прилегают к поверхности стола. Вес сосуда равен G. В сосуд, наливают жидкость. После того, как уровень жидкости дос
47
. 2Г< , 77777////////
тигнет верхнего края сосуда, сосуд приподнимается. Определите плотность налитой жидкости.
6.4? В боковую стенку широкого стакана, из которого пил виски ковбой Jhon, случайно попала пуля, выпущенная из кольта ковбоем S^n’oM. Найдите величину реактивной силы, которая будет стремиться сдвинуть с места стакан, находившийся в этот момент на стойке бара. Площадь поперечного сечения дырки от пули 5 мала, а высота уровня напитка над отверстием и его плотность равны соответственно Н и р. Пуля осталась внутри стакана.
6.5.	Из неплотно прикрытого водопроводного крана струйкой вытекает вода. Как с помощью только линейки определить скорость истечения воды из крана?
6.6.	В каком направлении надо сообщить вращение футбольному мячу при подаче углового удара с линии ворот, чтобы мяч мог попасть в ворота при отсутствии ветра?
6.7.	Два корабля идут параллельными курсами на близком расстоянии друг от друга. Почему при одинаковом направлении движения корабли сближаются?
6.8.	Почему большие оконные стекла при сильном ветре выдавливаются наружу?
6.9.	Постоянный ветер дует над океаном, где образовались небольшие гребни и впадины волн. Каким образом ветер может увеличить высоту^ гребней и глубину впадины?
\j 6.10. Пробирку длиной L = 1 м заполнили атмосферным воздухом под давлением Р() =105 Па, закрыли легким подвижным поршнем и погрузили в сосуд с жидкостью на глу'бину Н = 40 м. Какая часть длины пробирки а = х / L будет заполнена га
зом? Температура постоянна, давление насыщенных паров — мало, Ртах =1,26 г/см3 (глицерин), £ = 10м/с2 .
48
РЕШЕНИЯ И ОТВЕТЫ
1. Кинематика
1.1. Так как у>с, то фронт звуковой волны представляет собой коническую поверхность с вершиной в том месте, где в данный момент находится самолет. Скорость звука с характеризует скорость распространения фронта волны и направлена она всегда по нормали к фронту вол
ны (см. рисунок). За время t, когда человек услышит звук самолет
пройдет расстояние Nt, а фронт волны от точки, расположенной
над человеком, пройдет расстояние ct. Из подобия прямоугольных
треугольников	ОС В	и ОАВ:	— = —=====	или
h —
Ct
-9900 м.
49
. J-S'f + 5? - 2S,S2 cos(1 80° - a2 + a,) l< v >| =1------------------------------------------------
= 10^7 м/с,
< v >=	+ ^2 = 30 м/с.
Z	X
1.4.	Воспользуемся законом сложе-	\
ния скоростей (1.11). В качестве не- a--------- у" _
подвижной системы координат возь-мем систему отсчета, связанную с Землей, а в качестве движущейся — систему координат, связанную с первым самолетом. Тогда vH = v2, <u = <21- <()=<!- или v2=v1+v2].
где v2] — скорость второго самолета относительно первого (см. рисунок). Применив теорему косинусов, получим
|<21| = уу? +v2 -2vjv2 cos(a + P).
1.5.	Скорость, набранная телом к моменту времени 10, определяется площадью под графиком зависимости ускорения ах от времени Поэтому получим
\ 1 < v2 < v-s (для рисунков а и б);
V} < V] < v2 (для рисунка в);
v2 < v3 < V1 (л™ рисунка г).
1.6.	Уравнения зависимостей vx(0, x(t) и S(t) в заданных временных интервалах имеют следующий вид.
При 0с<?<4с
vx(/) = -3 + 1,5г, vx(2) = 0, vx(4) = 3 м/с;
x(t) = -3/ + 0,7512, х(0) = 0 м, х(2) = -3 м, х(4) = 0 м.
50
При t = 2 с скорость меняет направление на противоположное, поэтому получаем
при 0 с < / < 2 с
S(t) = |x(t) - х(0)| = |- 3t + 0,75г21, 5(2) = 3 м;
51
при 2с<7<4с
S(t) = 5(2) + |х(7) - x(2)| = 3 +1- 3t + 0,7572 + з|, 5(4) = 6 m;
при 4c<7<6c
vx(t) = 3-(t-4r) = l-t, vx(4) = 3 м/с, vx(6) = l м/с, x(t) = 3(t - 4) - 0,5(7 - 4)2, x(4) = 0, x(6) = 4 m,	,
5(7) = 5(4) + |x(0 -x(4)| = 6 + |з(7 -4) - 0,5(7 - 4)2|, 5(6) = 10 m;
m.
при 6с<7<8с
vx(7) = l-O,5(7-6), vx(6) = l м/с, vx(8) = 0,
х(7) = х(6) + vx(6)(7 - 6) - аох ~ У = 4 + (t - 6) - 0,25(7 - 6)2,
х(6) = 4 м, х(8) = 5 м,
5(0 = 5(6) + |х(7)-х(6)| = 10 +|(7 - 6)-0,25(7-6)2|, 5(8) = 11
Графики соответствующих зависимостей vx(7), х(7) и 5(7) казаны на рисунках. Самое простое решение получается при числении площади под графиком зависимости скорости
1	„ „ 3 + 1	1-2 ,,
_-------2 +----= 11 м.
2	2	2
ПО-
ВЫ-
OT
времени: 5(8) = — • (-3) -2 + • 3 • 2 +
Ответ: 5(8) = 11 м.
1.7. 5 = 27,5 м.
1.8. Необходимо выстрелить из пистолета вертикально вверх и измерить время полета пули t. В пренебрежении сопротивлением воздуха скорость можно найти из уравнений движения пули вверх и вниз, в которых путь, пройденный пулей, полагается одинако-
гг	g t
вым. Тогда vq =	.
1.9. По определению средней скорости <v>= —, hi — время Ы
и	/gW	.
полета, но Н = g ——, отсюда < v >=	= 22,4 м/с.
52
1.11.	Уравнение движения груза:
При падении на Землю y(t) = 0, те. 5t2 - It - IDO = 0 . Физическое решение этого уравнения: t = 4,7 с.
1.12.	Время падения груза t = 4,3 с.
1.13.	Ось у направим вертикально вверх. Отсчет координат будем производить от поверхности Земли. Так как проекция начальной скорости на ось у положительна, а проекция ускорения отрицательна, уравнения движения каждого из тел будут иметь вид
y(z) = v0/-^-,
а скорость тел будет меняться по закону: v(?) = v0 - gt.
В точке наибольшего подъема v(Z) = 0, отсюда время подъема
У о „
/под до наивысшей точки ?под = —. Подставляя это время в урав
нение движения, найдем, что начальная скорость и высота подъема Н связаны соотношением:
v0=^2Hg ,
поэтому /под =	• •
Время подъема тел и время их свободного падения на Землю равны, поэтому общая продолжительность полета /П()Л равна удвоенному времени подъема, т е.
53
Продолжительность полета двух тел, высота подъема которых
различается в 3 раза, будет отличаться в п ~
раз.
1.14.	v() = 2Н +^- = 18.7 м/с. и 21
1	2v0? ~ 25	2
1.15.	а------------= 6м/с .
t2
1.16.	Графики зависимостей скоростей шара от времени I как при движении по желобу АВС. так и при движении по желобу ADC представляют собой два переходящих один в другой линейных участка. Особенности этих зависимостей следующие (см. рисунок):
площади под графиками этих зависимостей равны (следствие того факта, что пути, проходимые шаром по желобам АВС и ADC равны);
время движения шара по желобу A DC меньше времени его
движения	по желобу ЛВС:	<г2;
конечные скорости движения по обеим желобам равны: v(/|) = v(t2).
Докажем последнее утверждение.
По участку АВ шар движется с ускорением а = g sin а , а — угол наклона участка к горизонту. При этом зависимость скорости шара от времени v(/) = gsin а • t, а уравнение движения шара име-
^2
ет вид x(z) = gsin а • — (ось х направлена вдоль желоба). Скорость
шара в точке В получается из этих уравнений, если путь, пройденный шаром х(?), положить равным длине желоба /. Тогда скорость шара в точке В
54
v g = y/2gl sin a .
Аналогичные уравнения, описывающие движение шара по участку ВС, имеют вид
v(t) = vB+gt = -Jlglsma + gt
и
2 x(t) = ^2gl sin a • t +	.
Полагая путь шара на участке ВС равным длине желоба, т е. х(/) = /. находим время движения его по участку ВС
J2gl sin а + 2ga - ^2g/sina g
И скорость шара в точке С. nc = ^2glsm.a. + 2gl .
Аналогичные уравнения описывают движение шара по желобу ADC.
На участке АР:
v(t) = gt;
gt2
Х(0= 2 '
Скорость в точке D vd =-figi 
На участке DC:
v(?) = V£) + g sin a • t = yfogl + g sin a • t, i--------------	t^
x(t) = y]2gl -t + gsina- —.
Скорость в точке С при прохождении желоба ADC:
у с' = yj2glsma + 2gl,
55
т.е. Ус' = V(;’. что и требовалось доказать. (Для доказательства этого равенства проще воспользоваться законом сохранения механической энергии, который утверждает, что в поле консервативных сил, каковыми являются силы тяготения, кинетическая энерги^ приобретаемая телом, не зависит от формы пути, а зависит только от его начального и конечного положений.)	)
Еще одной особенностью приведенных зависимостей является параллельность линейных участков AD и ВС, а также DC и АВ, обусловленная равенством ускорений шара на соответствующих участках желобов.
1.17.
См. решение задачи 1.16.
1.18.	Введем систему координат: начало координат совпадает с точкой «старта», ось OY направлена вертикально, ось ОХ — горизонтально (вдоль поверхности Земли), вектор v() и координатные оси лежат в одной плоскости. Запишем в виде уравнения условие падения тела на поверхность Земли: в момент падения y(t) = 0. Тело движется с постоянным ускорением а = g , где g — ускорение свободного падения. Спроектируем уравнение движения
r(t) = r0 + v0 -Г + п —
56
на ось ОУ, получим y(r) = v0 • sin ot -г - g —, далее решаем систему:
у = 0;
t2 => y = vosma-t-g — ,
=> gt2 - 2v0 sin a • I = 0, =>
=> t(gt - 2Vo sin a) = 0.
Имеется два решения: i] =0 соответствует моменту «старта», 2vn sin a
to =-------- соответствует моменту падения и равно длительно-
g
сти полета.
Чтобы определить дальность полета спроектируем уравнение 2
движения r(/) = r0 + v0 •/•— на ось ОХ, получим x(t) = v0 cos a • t. подставим в полученное уравнение время, соответствующее моменту падения
2vq • sin a • cos a Vo -sin2a Xmax =	~	
g	g
Далее запишем в виде уравнения условие прохождения телом верхней точки траектории: вектор скорости тела в этот момент направлен горизонтально, т.е. vy = 0. Спроектируем уравнение движения v(?) = v() + а • t на ось OY. Получим v t, (t) = v0 • sin a - g • t. Далее решаем систему:
vy =v0 sina-g-L
57
vq • sin a
=> время подъема до верхней точки траектории I =-— под-
g
2-2	*
,.	vi-sm'a *
ставляем в уравнение дшцу(О, получим угаах =-----.
2« Г
1.19.	хтах(а = ЗО°)/хтаХ(Р = 60°) = 1.
1.20.	утах(а = 60°)/утах(р = 45°) = 3/2.
1.21.
v()(a - 30°)/v()(P = 45°) =
№
1.22. Значительно облегчить процедуру решения может удачный
выбор системы координат. Воспользуемся системой координат.
изображенной на рисунке.
В момент падения тела на склон у(0 = 0, нас же интересует хтах тела, поэтому проектируем уравнение движения
на оси ОХ и OY и решаем систему:
у = 0;
< у = v0 sinp • t -
Х = V() COSp-/ -
2 g • cos a • t
2
'J g • sin a • t
2vosinp
/| — 0 — момент «старта». t-> =---------момент падения,
gcosa
_ 2vjj sin p • cos(a + P) л max —	т ’ •
gcos'a
58
1.23. Уравнения движения мяча:
2
x(t) = v() cos(a + P)f + g sin p  —.
/2
y(t) = v0 sm(a +P)r -gcosp —
Ось X направлена вдоль склона, ось У перпендикулярна линии горизонта.
2vn
Решая эти уравнения, найдем I =-----—. В правильности от-
gcos“P
вета убеждаемся, подставив сюда р - 0. Получим результат, который и следовало ожидать при решении задачи о теле, брошенном под углом к горизонту (см. задачу 1,18).
1.24. Очевидно, что выполнение условия Vmax >h не гарантирует вылет мяча из ямы. Необходимым условием является у > h при х = / Решаем систему.
x = Z;	-
/	g/“
• х = vo cos a  f. => t =------, => у-I- tga---2—-— .
{2 vocosa	2vq cos2 a
у = vq sin a • t - g —,
59
При подстановке численных значений параметров нетрудно убедиться, что условие y>h выполняется, т.е. мяч из ямы выле-
V. гит	’
1.25. Уравнения движения мяча:
x(t) - v0 cos a t,
y(t) = v0 sma-t-y.
Начало системы координат в точке бросания, ось X направлена вдоль линии горизонта в сторону бросания мяча, ось Y перпендикулярна к оси X и направлена вверх. Минимальная скорость мяча 'Dinin может быть найдена из условия, чтобы траектория мяча в некоторый момент времени прошла через точку с координатами х = /. у - -h.
Решая получающуюся систему уравнений, находим
v  =—l— I g  °lTun cos а у 2(1 tga + h)
В правильности ответа можно убедиться, подставив сюда, например, h = 0 и получив тот же результат, который следует ожидать при решении задачи о теле, брошенном под углом к горизонту.
1.26. Обозначим высоту, с которой падает тело h. Скорость тела в момент удара о наклонную плоскость равна v = ^2gh . Так как удары абсолютно упругие, скорость тела после удара не изменится, а угол его вылета по отношению к наклонной плоскости будет равен (я/2 - а).
Выберем систему координат, совместив начало координат с точкой падения тела на наклонную плоскость, а оси координат направим так, как показано на рисунке.
Тело будет двигаться вдоль оси X с ускорением а д- = g sin а и начальной скоростью =vsina, а вдоль оси У с ускорением
60
ay = -g cosa и начальной скоростью v^y = v cosa . Уравнения движения вдоль осей Хи У:
t2	. t2
y-v cosa -t-g cosa-----; x - v sina • t + g sina • —.
При высотах падения тела Л, меньших некоторой Лтах. тело будет всегда попадать в «ловушку». Эту высоту можно найти, определив наибольшее удаление тела от наклонной плоскости утак и сравнив его с расстоянием Н от точки В до плоскости — Н = BD . Чтобы узнать утах, определим промежуток времени между двумя последовательными ударами тела о плоскость. Полагая у = 0. найдем время первых двух касаний тела с плоскостью /| = 0 и 2v t~> = —. а также промежуток времени между ними g	.	'
*	2v	'	.
At = /э - Г] - —. Этот Промежуток неизменен между любыми по-g
следовательными соударениями тела с плоскостью, так как при абсолютно упругих столкновениях уравнения движения тела неизменны.
Дальше всего тело удалится от наклонной плоскости в момент Д/ v
времени 1 = — = — и это удаление составит:
2 g
61
v2
Лпах - —cosa=ncosa.
2S
H
Если ymax <H. т.е. А<Лтах =----«1,41 м, то тело в любом
cos a
случае будет захвачено ловушкой.
Н
----, т.е. утах = Я, то координаты точки мак-cos a
симального удаления тела от наклонной плоскости при первом отскоке (хтах , утах) находятся вне ловушки (см. рисунок), так как
Если h = hmiiX =
3v2
xmax = x2<z2 = vo= 0) = ——sina =3Asm a =
= ЗЯ tga </ ==ЛЛ.
(по условию задачи Я = 1 м, a = 45°, AD-4 м). Поэтому у тела есть шанс захватиться «ловушкой» при первом отскоке и при /? > /гп1ах Максимально возможная высота падения тела в этом случае может быть найдена из условия прохождения траектории тела через точку В горизонтальной полуплоскости, т.е. координаты точки касания должны быть В(1,Н):
Я = vcosa • t - еcosa —;
2
,	.	. t2
/ = vsina  / + psina —.
2
Решая эти уравнения относительно t и приравнивая их друг другу, после несложных преобразований найдем
62
2
8 sin a(— - tga [H
Таким образом, в первом случае (Н -1 м, I = 4 м) тело попадет в «ловушку», если высота падения будет меньше Л,р, т.е. h <	«1,5 м. Во втором случае тело попадет в «ловушку» при
падении с высоты h < 3,5 м.
1.27. Полное ускорение, с которым движется тело, во всех точках траектории одинаково и равняется ускорению свободного падения g . В начальной точке траектории (см. рисунок):
ах = -g • sin a , ап = g • cos a,
2	2
n v0 . v0
Лкр ~	~
f a„	g- cos a
В наивысшей точке подъема тело движется горизонтально со скоростью v - Vq cos a . В этой точке ускорение тела равно g и направлено оно вертикально вниз. Следовательно,
=0, ап =g,
2	2	2
v- v0 -cos a n__—-----—-----------
Из приведенного расчета видно, что в верхней точке траектории тела, брошенного под углом к горизонту, радиус кривизны наименьший.
1.28. Касание будет единственным только в том случае, когда верхняя точка полусферы и верхняя точка траектории камня совпадет, т.е. вертикаль, проходящая через эту общую точку, будет осью 63	'
симметрии и для полусферы, и для параболы, которая является траекторией камня.
Проектируем уравнения движения камня на координатные оси и полунаем:
равномерное движение вдоль оси ОХ (см. рисунок) с постоянной скоростью v у ~^ох - vo 'Cosа. описываемое уравнением х = \ ox1 ~ vo cosa'1 
равнопеременное движение вдоль оси OY. описываемое уравне-gt2
нием у = v0 sin a • t - 2—, co скоростью, меняющейся по закону
Vj = v() sin a - gl.
В наивысшей точке подъема камня vy - 0. следовательно, вре-vq sin a
мя подъема камня до этой точки /под =------, а высота этой точ-
g
2  2
„ Vo sin a ки над Землей у ---------.
2g
Если точкой касания является верхняя точка полусферы, то
y = R/2. Тогда v0=^—. С другой стороны, в верхней точке sin a
траектории камня нормальное ускорение камня ап равно ускорению свободного падения
2	2	2
v v() cos. а о ^=8‘8°
В выражении для ап в качестве радиуса кривизны траектории камня взят радиус полусферы, так как только в этом Случае касание 64
будет единственным при минимально возможной начальной скорости камня (см. решение задачи 1.27).
Из полученных соотношений следует, что угол бросания, при котором скорость камня будет минимальна, равен amin =45° . Соответствующая минимальная скорость v™"1 = -j2gR , а минимальное расстояние .Vmin, с которого надо бросить камень, чтобы он перелетел через полусферу
Lmin У
= v О cosamin ' ^под =	s*n amin ' cosamin ~	•
g
1.29. Угол бросания, при котором скорость камня будет мини-t 2	„		2^2 г
мальна. определяется условием: tg a = a5 или sma = ——. Соот-
3
гт ветствующая минимальная скорость камня v0 =-----'----=	.
sin a Минимальное расстояние, с которого следует бросать камень. У = SRctga min = 2-^2R .
Указание. См. решение предыдущей задачи.
1.30. Угловая скорость секундной стрелки ®с = (2л/60) рад/с. минутной ым = (2л/3600) рад/с . Если t— указанный интервал времени, а время t. то
[“м ' = <р;
|о)с • / = ср + 2л.
Отсюда находим
/ =----—---= 61 с, ср - 2 л ——-= 0,106 рад ~ 6. Г .
о с — о м	со с — 0) м
1.31.	Угловая скорость вращения пропеллера
до = 2л • п - 2.09 К)2 рад/с.
65
скорость поступательного движения v = 44,7 м/с . Воспользуемся принципом взаимной независимости движений. Скорость указанной точки пропеллера относительно Земли й ~ vnoCT + vBp , причем ' пост 4-^вр и I' пост| ~ v  |vBp| —
Отсюда получаем и =	+ v2 =317м/с .
1.32.	Отсутствие проскальзывания означает, что скорости точек А к В диска, в которых диск касается реек, совпадают со скоростями реек. Пусть для определенности V] > V2 • Скорость точек А и В можно представить в виде векторной суммы скоростей поступательного движения центра диска О и скорости вращательного движения вокруг оси, проходящей через центр диска (перпендикулярно плоскости чертежа):
+ vbPJ г
=^О + Увр.В-
причем vBp /( =~vBp £ . Запишем эти уравнения в проекциях на ось X. Для случая а):
( V] = vq + со • /?;	vl~v2	Vj+vj
у	=> СО =-------- V п =----
[у? =v<j -& R	2R	2
Для слу чая б) аналогичным образом получаем
V1+V9	V1 — V 9
СО = —--— ,У() = ~----
2R	2
1.33.	Рассмотрим вначале случай, когда угол АВС— тупой. Проведем ОА1АВ и ОВ1ВС. Построением нашли неподвижную точку О. относительно которой треугольник ЛАВС совершает в данный момент вращательное движение (через точку О перпендикулярно плоскости чертежа проходит «мгновенная ось вращения»).
66
т е. можем исключить из рассмотрения поступательную составляющую движения ЛАВС. Отсюда следует и направление векторов v j . v в, v f , указанное на рисунке.
OB2 =ОА2 + АВ2;
ОС2 = ОВ2 +ВС2, < v2 =со2 -ОА2:
v2B = со2 -ОВ2: v2 = со2 ОС2,
Г 2	2
2	2
со со
2	2
^^ + вс
2	2
I со со
1/~2	2 Y ВС '22
VC “л \VB ~ VA 1 -777 +VB  V	\, J
Для случая, когда угол АВС — острый, система исходных уравнений и ответ совершенно идентичны.
1.34. vc =vB
VA
2
f>C\2
—	- 5.24 м/с.
AB J
1.35. Vf = vB 11 +
l vjpBj
5 м/с.
2
2
67
1.36.
( 2
Vfi 2
AB
«5 м/с.
VC ~VA, Д+
1.37. Воспользуемся законом взаимной независимости движений твердого тела и представим движение колеса как сумму двух движений — вращательного и поступательного, а именно: каждая
точка колеса описывает окружность вокруг оси колеса и вместе с ним участвует в прямолинейном движении, т е. v = vBp + vnocT , где
' пост = vo ~а0 * р вр| одинаков для точек А, В, С и D, так как они равноудалены от оси вращения (оси колеса О). Направление вектора vBp для каждой точки совпадает с направлением касательной к окружности, по которой движется точка, совершая вращательное движение, или, что то же, ортогонально радиусу, проведенному от оси вращения в рассматриваемую точку. Из условия непроскальзывания следует =0 => |vBp| - c/qI, используя рисунок. находим |v| = |vd | = V2 • qqI , |vc | = 2а0/.
Ускорение точек тела, совершающего сложное движение, представим аналогичным образом а - авр + апост , где апост = а0, кроме того, авр = а„ + аг, где ои и о. — нормальное и тангенциальное ускорения соответственно при движении по окружности. Для каждой из точек А. В. С и D.
68
atA
Ы= VBP|2 !R = alt2 !R,
axB
%
---►
В
Используя чертеж, находим
Ы =
2 2 «о£
R
+
/ 2 2 V apt
R
2 \2
1 + ^-
R
а0 -
2 2 «0^
69
2.	Динамика
2.1.	Причиной начала движения автомобиля служит сила трения FTp. которая возникает при вращении колес, приложена к ободу колес со стороны дорожного покрытия в соответствии с третьим законом Ньютона в точке их касания с поверхностью шоссе и направлена по движению автомобиля.
2.2.	Проследим, как начинается движение поезда в двух вариантах сцепления локомотива и вагонов:
а)	сцепление локомотива с составом и вагонов между собой — «жесткое», т.е. поезд представляет собой абсолютно твердое тело;
б)	сцепление локомотива с составом и вагонов между собой — «мягкое», т.е. между ними существуют упругие связи.
Вариант а). «Движущая сила» локомотива — это горизонтальная составляющая силы взаимодействия локомотива с рельсами, т е. сила трения покоя, если отсутствует проскальзывание колес локомотива, или сила трения скольжения, если есть проскальзывание. Сила, препятствующая движению поезда. — сила трения качения. действующая на локомотив и вагоны состава. Таким образом. условие возможности движения поезда (по горизонтальной поверхности) запишется:
М-с ' Мд > Цк  (Мд + Nc),
где цс и цк — коэффициенты трения скольжения и качения; Nn и — силы нормального давления на рельсы локомотива и состава соответственно. Иначе,
цс -т>р.к (т+М),
где т и М— массы локомотива и состава. Так как при взаимодействии колес поезда с рельсами выполняется условие цс » цк , то движение поезда становится возможным при условии т«М .
Вариант б). При наличии упругих
/\ллллд..[—~~-~i ¥	связей появляется возможность начать
ТПТТГП77777ТПш7ТТП7 движение поезда при менее жестких ус-
ловиях. Рассмотрим модельную ситуа
70
цию — состав состоит из одного вагона, а локомотив и состав связаны пружиной, которая первоначально находится в недефор.миро-ванном состоянии. Трогаясь с места локомотив начинает растягивать пружину и приобретает одновременно кинетическую энергию. Предположим, в некоторый момент времени сила упругости пружины скомпенсировала «движущую сил}» локомотива с учетом приложенной к нему силы трения качения, но оказалась меньше силы трения качения, приложенной к составу, т.е. оказалась недостаточно велика, чтобы заставить состав двигаться. Однако движение локомотива по инерции приводит к тому, что его приобретенная к этому моменту времени кинетическая энергия будет преобразовываться в потенциальную энергию пружины (вплоть до полной остановки локомотива), а сила упругости будет возрастать. Движение поезда в этой ситуации может начаться даже при условии:
цс • т < цк • (т + М).
Как видим, второй вариант является предпочтительным с точки зрения затраты усилий на приведение поезда в движение. Именно поэтому машинист, трогая с места тяжело груженый состав, дает вагонам толчок.
2.3.	Допустим, что стоящий на тонком льду человек может провалиться. если масса его т. т.е. сила давления на лед Р = mg . Когда человек бежит по льду, результат его действия на лед зависит нс от величины этой силы, а от величины импульса этой силы, который представляет собой произведение Р на промежуток времени действия этой силы на лед Д/. В соответствии со вторым законом Ньютона РД/ = телДу. именно импульс силы является естественной мерой воздействия, необходимого для изменения движения тела, на которое оказывается воздействие (в данном случае на лед), те,, — масса того участка льда, с которым соприкасается нога человека Поскольку время соприкосновения ног человека со льдом Д/ нс велико, лед не успевает приобрести заметного количества движения тел v и человек может бежать по льду, не проваливаясь.
2.4.	Измерив длину ребер параллелепипеда, поставим его на пол так. чтобы его длинное ребро было перпендикулярно полу. Выровняв плоскость линейки параллельно полу на небольшой высоте Н
71
от него, будем толкать линейкой параллелепипед в горизонтальном направлении с такой силой, чтобы брус скользил по полу. Из второго закона Ньютона следует, что предельное значение внешней силы F, заставляющей брус скользить, равно силе трения скольжения F = Flp(. = p.mg . т — масса параллелепипеда.
Постепенно увеличивая высоту линейки над полом //. найдем такое ее положение Нтах, при котором брус будет опрокидываться. а нс скользить. Опрокидывание бруса, т.е. его вращение относительно оси 00' (см. рисунок), произойдет в том случае, если сумма моментов всех действующих на него сил относительно этой оси
бе дет больше нуля, т.е. > 0 или FH - mg — > 0. Подставляя
сюда значение F = [img. Н =Нтих. находим ц = —-—, а —
2Н тах сторона основания параллелепипеда.
2.5.	Положив брусок на доску и, приподнимая доску за один конец. нужно определить наклон доски, при котором брусок начнет соскальзывать с нее. С помощью транспортира измеряется этот е гол наклона доски к горизонте а(). Коэффициент трения бруска о дерево ц находится из условия Ft? < pTV, N— сила реакции опоры. Это условие даст ц = tga().
2.6.	Необходимо нить с привязанной к ней гирькой подвесить за свободный конец к потолку и измерить длину нити /. а также отклонение гирьки от вертикали Аг . Тогда ускорение поезда можно найти по формуле:
g&x
а = -	.
F - Дг2
72
которая получается при решении основного уравнения динамики ДЛ" гирьки.
2.7.	Единственная сила, которая заставляет брусок двигаться вместе с доской — сила трения
N + Ftp + mg - та в системе отсчета, связанной с поверхно
стью.
ОХ : Fi p = та.
< OY :N - mg- 0:
/•’Гр - цА' (условие максимальности ускорения). Отсюда
"max = №
2.8.	Силы, действующие на цилиндр: сила тяжести /<г = mg . две силы нормальной реакции граней двугранного угла 7V] и jV2 г двс силы трения цилиндра о грани /|р| и /тр2 (см. рисунки).
73
Так как цилиндр обладает осевой симметрией и плоскости двугранного угла симметричны относительно вертикали
|/тр11 ~ |/тр21 ~/тр •
По закон) Кулона — Амонтона = ц/V .
Основной закон динамики для цилиндра имеет вид
та = mg + N{+N2 + 7iPl + ZP2 •
Так как цилиндр неподвижен в плоскости сечения, перпендикулярного ребру двугранного угла. то. проектируя это уравнение на ось. перпендикулярную ребру, получим (см. рисунок б)
27Vsin—1 = /ngcosp.
В проекции на ребро (ось ОХ) уравнение динамики для цилиндра запишется, как тах = mg sin р - 2/Vp. . Подставляя сюда N, находим ускорение цилиндра
( . о gcosp	.2
ах = g sm р - ---— I * 3.71 м/с .
sin а / 2 )
2.9.	Обозначим а\ — ускорение, с которым брусок поднимается вверх. с/2 — ускорение, с которым он опускается вниз.
74
Скорость бруска при подъеме меняется по закону v(/) = = v() - a^t. поэтому время подъема находится из условия v(/j) = 0. т.е. = v0 /aj. При этом путь /, пройденный бруском за это время.
.	Я]/?	1	7 r-r	-
равен / =vq/] —у- = ~a\h  При спуске брусок начинает движение без начальной скорости, поэтому спуск его до первоначальной ,	1	2
точки, как следует из уравнения его движения, равен 1 =
Отсюда
. Величина ускорений для движения бруска
вверх и вниз легко находится из второго закона Ньютона. Проектируя уравнение второго закона на ось X (см. рисунок), находим: при движении вверх я, = g(sina + pcosa). при движении вниз
. .	/1 /sina-pcosa _
а1 ~ &(Sin a ” И cos a). В итоге — = --------= 0,61.
/2 ysina + pcosa
2.10.	Систему’ координат выберем так, как показано на рисунке.
Основное уравнение динамики: та = mg + Т + N +	. В про-
екциях на оси координат (движение равномерное, а = 0):
ОХ: 0 = 7’ cos р - /ф - mg sin a .
OY: 0 = N + T sinp- mg cos a. Кроме того,	= \iN .
Отсюда
_ sina + ucosa
Г =------------mg .
cosp + gsinp
75
Положим ц = ctgy.
Поделим и домножим числитель и знаменатель этого выражения на ф + ц“ . Тогда
(sin а + цcos а)
7 - mg	.
у 1 + ц" sin(y + Р)
Натяжение нити Т будет наименьшим, если sin(y + Р) примет наибольшее значение, т.е.
Рпип ~ 2 или
smPmm =-;=Ё=г39".
V1 + H
При этом 7’min	3 н
2.11.	На брусок действуют четыре силы: сила тяжести /<\ - mg , сила реакции опоры N. сила трения и внешняя сила F. Проектируя основное уравнение динамики для бруска на направления его движения, найдем
а - g[k ~ (sin а + poos а)].
Преобразуем это выражение, положив
ц = ctgP: sinp = -? -; cos Р =	—..
№
Тогда и = g[A - гр" cos(a - p)j. Ускорение бруска будет ми-нимальным. если cos(a - Р) = 1. т.е. a =P = arcctgp = 51,3°. При
76
этом величина ускорения amul = g^£ - у I + р2 J ® 2,2 м/с2 при g = 10 м/с2.
2.12.	Пользуясь третьим законом Ньютона с учетом данных, приведенных в условии задачи, указываем все силы, действующие на каждое из тел системы (см. рисунок).
Составляем основное уравнение динамики в векторной форме для каждого из тел:
71 + = «!«!,
?2 + Г3 + ,/тр ~ ^2а2 •
Тд +	+ F .
Чтобы правильно указать направление силы трения /1р , действующей на груз w?2 • сравним величину сил, стремящихся сдвинуть систему вправо и влево в отсутствии трения:
^'прав = w3gsina « 26 Н > Ллев = m}g «10 Н
Система будет двигаться вправо, поэтому /|р направлена в противоположную сторону.
77
Систему уравнений динамики необходимо дополнить законом Кулона — Амонтона:
/тр =М^2
и соотношениями между силами натяжения нитей, следующими из третьего закона Ньютона:
= Т,
!Л!=|Лгг"-
|п =Кг|
(Блоки изменяют направления действия сил натяжения.)
Принимая во внимание нерастяжимость нити. те. |<Л| | = |£72| - |о3| = а, проектируем уравнения динамики на направление движения и направление, перпендикулярное ему.
7 -m}g-m}a, N2 =m2S\ Tq-T- /1р = m2a\ m3g sin a - Го = m^a.
Решая эту систему относительно Го, находим
т _/изя[т](1+sina) + m2(p + sina)] / () —------------------------~ 1 7.0 П
+ Ш2 + ™3
Как и следовало ожидать, сила натяжения 7g (как, впрочем, и ускорение системы а) обратно пропорциональна суммарной массе всей системы, которая является мерой инертности системы.
, ., т №g(m\ + w2) cos a
L, I J. / ^3 —--------—----—	/ rl .
W| +ГП2 +^3
, 1Л7	+ w3)l2s‘na + pcosa] _
L. 14. / [ -) =---------------------— 1 э. J Г1 .
W] + и?2 +• m3
78
2.15. Г,, = ^('”1*'”2Хзш° + Ц)£105н
mi + m2 +
2.16. Из условия задачи следует, что начальная скорость бруска v() = 0 . Возможные состояния тела: тело скользит по поверхности (влево или вправо), тело покоится, тело отрывается от поверхности и движется прямолинейно под углом к горизонту. Проверим возможность реализации каждого из сценариев во всех рассматриваемых случаях. Для этого зададим систему координат (см. рисунок) и найдем результирующую силу Fpe3. действующую вдоль оси OY:
Fpe3 = -mg + Fi sin a + F> sin p .
Для случаев а) и б) F^ < 0. следовательно, тело не отрывается от поверхности. Для случая в) Fpe3 « 5.5 Н > 0. поэтому тело отрывается от поверхности.
Для случаев а) и б) рассмотрим результат действия сил вдоль горизонтальной оси. Пусть сила трения F’1р направлена по оси ОХ. те. ускорение а направлено против оси ОХ. Уравнения динамики в проекциях на оси ОХ и OY и уравнение закона Кулона — Амон-тона запишутся следующим образом:
ОХ: F\p + F\ cos а - F2 cos p = max; • OY : A + F\ sin а + F2 sin p - mg = 0;
Flp=pA. .
Л	p(mg - Pi sm a - F2 sm P) + /ч cos a - F2 cos p
Отсюда ar =—------.----------------=---------
m
79
Подстановка численных значений параметров дает:
а) ах ь 2.7м/с3.
о) ах * 2.2 м/с",
т.е. получили результат, противоречащий сделанному предположению (ах <0). Пусть теперь сила трения Fip направлена против оси ОХ. т.е. ускорение а направлено по оси ОХ (ах > 0). Соответствующая система уравнений, описывающих движение тела:
OX -Frp + Л] cos а - F; cos р = тах', - ОУ :N + F} sin а + sin р - wg = 0;
л	u(-/wg + F, sin а + F> sin р) + b\ cos а - IX cos р
Откуда а х =---------!!--------------------------=----.
Дзя случаев:
а)	ах * 2.9 м/с2 >0 — результат не противоречит сделанному предположению:
б)	ах ~ -1.1 м/с2 <0 — результат противоречит сделанному предположению.
Таким образом, в случае а) тело будет двигаться в направлении оси ОХ с ускорением ах » 2,9 м/с2, а в случае б) тело не может скользит ни вдоль оси ОХ, ни против нее, следовательно, оно покоится. В случае в) система уравнений в проекциях на оси ОХ и ОУ выглядит следующим образом;
ОХ : Л | cos а - F2 cos р = тах:
ОУ : F\ sin а + F2 sin р - mg = та v.
Следовательно, оторвавшись от поверхности, тело будет двигаться / 2	9	7
прямолинейно с ускорением а = Jax + а~ « 10,5 м/с” под углом
av
ср = arctg —— * 60° к линии горизонта.
ах
80
2.17. Случай a).
Силы,, действующие на клин и шар, показаны на рисунке. Основное уравнение динамики для шара и клина соответственно есть:
Мам = Mg + N2 +&\. -
тап, = mg+ N{
По третьему закону Ньютона: N{ =-N^ (|2V]' =|М|= ) Так как движение тел ограничено вертикальными и горизонтальными поверхностями. то спроектируем уравнение движения для шара на горизонтальную направление, а уравнение движения для клина на вертикальное направление:
Мам = TV cos а; тат = mg - Nsina.
Опускание клина на высоту h приводит к перемещению шара в горизонтальном направлении на расстояние /, причем h - Zctga.
2 at1 2
Так как h = —, а 1 = —-—, то ат = a^ctga. Используя эту связь между ускорениями, решаем полученную систему уравнений:
tga
ам
=g
, М >
I + —tg'a т
1 + —tg“a т
Случай б).
_ . S tg«
tg a + — т
81

tg2a
8 2 M tg a + —
m
№2a
2.18. ciyj
gtga
2M
----Htg"a
m
am
2 2M ' tga +--
m
2.19.
S tga
L'Xl	2M-
tg'a+-----
m
am
gtg2a
t 2	2Л/
tg a +---
m
2.20.
« = £
tga
M
— + tg"a m
2.21.	Случай а): шарик вращается против часовой стрелки.
В промежуток времени т, в течение которого шарик соприкасается с поверхностью, на него со стороны поверхности действуют две силы: N— сила реакции поверхности, направленная по нормали к ней; Л’1р — сила трения, направленная вдоль поверхности в сторону, противоположную оси ОХ, и обусловленная проскальзыванием шарика при его вращении против часовой стрелки в силу условия соЛ»v. В соответствии со вторым законом Ньютона действие каждой из этих сил изменяет соответствующие компоненты импульса шарика:
&РУ = Ру ~Ру=№,
&Рх = Рх ~Рх= ^грт =	
Оси координат ОХ и OY выбраны так, как показано на рисунке. Здесь р\, и ру — конечная (после удара) и начальная (до удара) составляющие импульса шарика по оси У; р* и р" — соответст-
82
вующие составляющие импульса по оси ОХ. Знак минус в правой части второго уравнения учитывает тот факт, что сила трения обусловлена проскальзыванием шарика при его вращении и направлена в сторону, противоположную направлению рх.
Так как при ударе о поверхность деформации шарика упругие, то после столкновения составляющая импульса шарика по оси OY Ру = Ру= wvcosot. т.е. не изменяет своей величины, но изменяет направление на противоположное. Поэтому полное изменение величины составляющей импульса шарика по оси OY при ударе равно
&Py - Imvcosa = Nt .
Составляющие импульса шарика по оси ОХ до и после соударения
Рх ~ РуЦ$ т
рх - rovsina.
Часть Импульса рх определяется составляющей импульса по оси OY: Ру = rovcosa и углом отражения р. Окончательно для Дрх находим
Лрх = wvcosa • tgP - rovsina = -уМ.
Поделив правые и левые части равенств, для Лрх и Лру найдем
tgP - tga = -2ц.
83
Для случая б):
tgP = tga + 2ц.
В этом случае сила трения	обусловлена проскальзы-
ванием шарика при его вращении по часовой стрелке и направлена по оси X.
2.22.	a) tgP = tga + 2р, б) tgP = tga - 2ц.
2.23.	Так как плоскость — протяженная, то это означает, что тело не покидает наклонную плоскость. Опишем кратко особенности движения тела. При движении вверх оно вначале будет замедляться и спустя некоторое время Л, остановится. Дальнейшее поведение тела зависит от угла наклона плоскости к горизонту а. Если а достаточно мал. то тело останется в покое. Если а равен или больше некоторого а тах. то тело будет соскальзывать с наклонной плоскости равноускоренно.
В зависимости от того, какие случаи реализуются, рассмотрим различные варианты движения.
I вариант:	Тело движется замедленно (ускорение на-
правлено против скорости). Величину ускорения найдем, решив соответствующую задачу динамики для тела, движущегося вверх по наклонной плоскости
<7] = g(sin a + geos a).
Время подъема до высшей точки определим из условия равенства нулю скорости тела в этой точке:
VQ
5 g(sina +pcosa)
Из уравнения движения находим, что при t < тело пройдет путь
р .	2
5 = Vyt-~(sma + pcosa)/ .
84
II вариант: t >t3. Тело соскальзывает с наклонной плоскости Ускорение тела
а2 =g(sina -pcosa).
n	n	sinfa - P) Z
Положив здесь ц = tgp. представим a2 в виде a2 - g~7=	'
 	 .Vw7 •
Таким образом, соскальзывание будет возможным, если sin(a - Р) > 0. т.е. при a > amin = arctgp.
При a < amm тело будет покоится.
В этом случае путь, пройденный телом S3. можно найти, подставив t = t3 в формулу для пути при t < . Тогда
J 2g(sina + pcosa)
Если a > amu), то путь, пройденный телом, будет равен
S — S3 + ci2
2
7
Vn /	£	7
---------у--------+ — (sin a — ц cos a )(с — ) .
2g(sina + pcosa) 2
2.24.	Время подъема тела т =---— Путь, пройденный телом.
mg + F
, R
при подъеме до высшей точки п =-------. Время падения тела
2(mg + F)
(2т(Н + h)
на Землю Д/ =-------— .
V mg-F
о J? + F / т у
Если t < т , то 5 = V()/-----1 .
85
, Я ~ F!т.	,2
Если т </ < т + А/. то Л = h + -—2-(/ - т) .
2
Если / > т + А/. то S -2h + Н .
2.25.	Если ро < р, то тело будет безостановочно погружаться с (Ро I
1-----. За время t оно погрузится на глубину
Р J
2	1 Р )
Если ро > р. то тело вначале будет погружаться, а затем всплы-r,	Vl)
вать Время погружения в этом случае равно т = —------г-.
к р J
Если t < т , глубина погружения составит
gt2(
5 =	^--1 .
2 I Р
Если I > т, то путь, пройденный телом от начала движения,
2.Q. _
2g
I Р
g РО
+ £ Рр._1(/_т)2
2к Р
2.26.	При падении тела с высоты Н скорость его перед вхождением в воду будет равна v () - y]2gH . Если плотность тела р больше плотности воды ро, то глубину его погружения Н\ за время I можно посчитать по формуле:
Z7-V,.^2fl Р(>1
~voz + — 1---
2 к Р J
86
Если же р < pg, то глубина погружения Н2 за время t
2 к Р J
(см. решение задачи 2.25). Вторая формула относится только к слу-
Vn
чаю t < т = —--------, где т — время погружения, соответствую-
к р )
щее остановке тела в воде.
При уменьшении начальной высоты в к раз скорость тела перед .	f2^
входом в воду будет равна vq^ = J, а глубина погружения за
V к
время А/ = 1 с — в случае р > Ро:
Я11- +
I t 2l pj
в случае р < Ро:

£ £0--1 2l р
-Г	, Я1 Н2
Так как по условию задачи / =-= ——, то для случая р > ро
Н U Н 2к
получаем
1=-==—)—Ц,
V к М р) а для случая р < р0
/=-=------Le—2.
V к * 1р )
87
Оба выражения для / дают
(/-I)
При / = 1.9 и к = 4.5
(/-1)
>0.
Следовательно, р() < р. т.е. исходные данные соответствуют случаю. когда тело при падении в воду утонет.
2.27.	= 1 _	. При к = 8,3 ; I = 3,5
Р v S ч 1 J
Р^>1 р
т е. р() > р . Следовательно, тело будет плавать в воде.
Указание. См. решение предыдущей задачи.
2.28.	Так как Fj sin а + F2 sin Р с mg , то тело будет скользить вдоль поверхности, не отрываясь от нее. При этом так как р <а, т.е. /72 cos Р > -^1 cos а = то вначале тело будет тормозиться, а затем или остановится, или, сменив направление движения на противоположное, будет разгоняться.
У скорение при торможении
g
П] - — {(cosP - cos а) + |Д2 - (sin а + sin Р)]},
а при разгоне
g
а2 = — {(cos р - cos а) - ц[2 - (sin а + sin Р)]}.
88
Время, когда произойдет изменение направления движения на v0 противоположное, т =—.
2 <71/
Если t < т. то Л = v0/--— .
7 V() При t ~т тело пройдет путь 5 =----.
2а\
Если ц[2 - (sin а + sin 0)] > cos 0 - cos а, то движение тела на этом закончится, так при этом соотношении между углами а и 0 выполняется условие: < [iN.
Если ц[2 - (sin а + sin 0)] < cos 0 - cos а. то, изменив направление движения на противоположное, тело продолжит движение с ускорением а2 и за время t пройдет путь
s = J_ + 22.(,_,)2
laj 2
2.29.	Спутник и все тела внутри него находятся в состоянии свободного падения в поле тяготения нашей планеты. Единственная внешняя сила, приложенная к спутнику и находящимся в нем телам, — сила притяжения Земли (или сила тяжести, если высота орбиты
над поверхностью Земли Н <<R3, где — радиус Земли), которая сообщает им одно и тоже направленное к центру Земли ускорение, равное по величине
ЧЛЛЛЛЛЛ/
“N Я
ф ,,,,ГТ1...........
/7/7/7X7777///
X nig nig
a = G------
(Я3+Я)2
= g.
где G — гравитационная постоянная, М3 — масса Земли.
Если рассмотреть тела внутри спутника, неподвижные относительно него и находящиеся на вертикальном подвесе или на глад-89
кой горизонтальной опоре, то окажется, что в соответствии со вторым законом Ньютона сила взаимодействия этих предметов с подвесом или опорой оказывается равной нулю (отсутствует).
В проекциях на ось X уравнение второго закона Ньютона для этих тел в системе отсчета, связанной с Землей, выглядит следующим образом:
wg - N = та.
N = 0
Отсутствие этих сил и означает пребывание системы, т.е. тел внутри спутника, в состоянии невесомости.
2.30.	7' =	® 1.4 ч.
2.31.	Основной -закон динамики для вращательного движения:
та 2 (R3 + Н) = G тМз .
(Я3 +Н)2
тМ з	о	7 gR3
но mg = G —. т.е. GM3 = g7?3 . Отсюда со" =--------. или
*3	‘	(Я3+77)3
7,_271_271(А3+Я) Ir3+/J ч со R3 у g
2.32.	Да, смогут. Измерив период обращения Т космического корабля вокруг планеты, космонавты могут оценить среднюю плотность вещества планеты по формуле:
Л7П	3 М„ Зтс
р = —— —-----и-«-----.
V	4л r3	T2G
которая получается при решении основного уравнения динамики для вращательного движения. В этой формуле Л1([ — масса плане
90
ты. R — ее радиус. G — гравитационная постоянная. V — объем планеты. Предполагается, что высота орбиты много меньше радиуса планеты.
2.33.	«Зависание» спутника над одной и той же точкой экватора Земли означает, что угловая скорость вращения Земли вокруг своей оси и угловая скорость обращения спутника вокруг Земли совпадают, т е. период обращения спутника вокруг Земли Т = 24 ч. Сле-
/	2
довательно. Н = 3—Ц--------R3 № 35,8  106 м (см. задачу 2.31).
V 4п2
2.34.	v = со(А3 + Н) = — 3^ = з1^	« з,07. ю3 м/с
Т \ 4тг2 V Т
(см. задачу 2.33).
91
3.	Законы сохранения импульса и энергии
3.1.	Работа при перемещении ящика волоком Ав на расстояние а равна Ав = цРа .
При кантовании ящика меняется положение его центра тяжести относительно Земли. Минимальная работа Ак, которую нужно совершить для однократного кантования ящика, т.е. перемещение его на то же самое расстояние а, равна разности потенциальных энергий ящика, когда он опирается на ребро, а его центр тяжести находится на вертикали, проходящей через это ребро, т.е. на диагонали сечения(см.рисунок)
W? =Р-41 п 2
и потенциальной энергии ящика, опирающегося на грань
=Р~,
п 2
т.е. Лк = fKnp - fKnr (>/2 -1). Следовательно,	—.
3.2.	7'=^^- = —(— + —У =612,5 Дж.
2	2 1/	2 J
3.3.	Если сила натяжения рогатки F то каждая резинка рогатки растягивается с силой F / 2. При этом удлинение каждой из рези-
та V
нок составляет х = —. Кинетическая энергия «снаряда», выпу-2/г
92
щенного из рогатки, равна удвоенной работе по растяжению каждой из резинок рогатки Н. т.е.
3.4.	S = —. Кинетическая энергия Е = mgH, приобретаемая те-М-
лом при спуске с горки высотой Н за счет изменения его потенциальной энергии в поле силы тяжести, расходуется на совершение работы против силы трения , тормозящей движение тела
А = Fjp • 5 = pmgS .
3.5.	При подъеме на высоту Н потенциальная энергия автомобиля возрастает на величину
U2 —U\ = &U = mgH.
Кинетическая энергия автомобиля убывает, ее приращение
2	2
Е2-Ех =ЛЕ = 0- — = -—.
1	2	2
Сила трения, приложенная к автомобилю со стороны склона, совершает работу
А - \xN • S = pmg cos а • —-.
sin а
93
Выражение закона сохранения энергии (в обобщенном виде) запишется следующим образом:
А// + А£ — А => Н <---------
2g(l-pctga)
— Нтах. 
3.6.	При движении спутника по круговой орбите работа силы тяготения равна нулю, так как в любой точке траектории направление действующей силы перпендикулярно перемещению спутника.
При движении спутника по эллиптической орбите работа силы тяготения отлична от нуля на отдельно взятых участках траектории.
3.7.	Нет. Сила притяжения спутника к Земле будет иметь составляющую. не лежащую в плоскости орбиты.
3.8.	При удалении спутника от планеты по эллиптической орбите кинетическая энергия спутника убывает, а потенциальная энергия возрастает. При этом полная механическая энергия остается неизменной. При приближении спутника к планете по эллиптической орбите изменения кинетической и потенциальной энергии меняют знак по отношению к тому случаю, когда спутник удаляется от планеты.
3.9.	Сила F(J), необходимая для
k / F (/)	удержания шара на диске, линейно рас-
/	тет с увеличением длины пружины /:
________ F(0 = Wi/ц.е = та 2Vo + /) -
--------------►	/0 = ОА . Тангенс угла наклона этой зависимости к\ = та2 - 20 Н/м.
В то же время сила упругости пружины Fy (Z), которая удерживает шар, растет с увеличением длины пружины значительно медленнее: Fy. (/) = к(1 - Iq ). Тангенс утла наклона этой зависимости как функции / равен жесткости пружины, т е. к = 0,1 Н/м. Поэтому при данных условиях задачи пружина будет растягиваться неограниченно, что нереально. Следовательно, потенциальную энергию
94
пружины при вращении диска с угловой скоростью со = 100 рад/с определить нельзя.
3.10.	Мальчикам нужно оттолкнуться друг от друга и потом с помощью рулетки измерить расстояния 5] и • которые каждый из них проедет до полной остановки. Из закона сохранения импульса следует, что массы мальчиков будут обратно пропорциональны их начальным скоростям.
W] v2
т2 V]
Начальные скорости мальчиков в свою очередь связаны с их удалением 5 отточки отталкивания соотношением:
2
5 = —
2а
В направлении движения на каждого из мальчиков действует единственная сила — сила трения скольжения. Поэтому из второго закона Ньютона: та = yvng, следует, что ускорения мальчиков бу-
_	т-t -J $2
дут одинаковыми. Следовательно. —- = --.
т2
3.11.	Предположим, что человек движется с постоянной скоростью v. Сумма внешних сил, приложенных к системе «лодка — человек» (сила тяжести, сила Архимеда), равна нулю. Можем воспользоваться законом сохранения импульса. Рассмотрим импульс системы до начала движения и в процессе движения в проекциях на ось, направленную вдоль направления движения человека, в системе отсчета, связанной с берегом, и составим уравнение:
0 = w(v - v л) - Mv л
_	mv
где ул — скорость лодки относительно берега. vn =---. сле-
т +М
довательно, время движения человека и, соответственно, лодки,
L .	mL ,.	„ .
t~— => п = \л1=-------. Из последней формулы следует, что
v	т +М
95
центр тяжести всей системы остается неподвижным. Это обстоятельство остается справедливым и при сколь угодно малых перемещениях человека относительно лодки, а следовательно, полученный результат справедлив при любом способе перемещения человека относительно лодки, а не только при равномерном движении.
3.12.	Так как в горизонтальном направлении на платформу внешние силы не действуют, то полное количество движения в этом направлении остается неизменным, т.е.
(w+M)vCH
, , v
- т\,.„cosa +Л7 — =>
си	3
=> veH
v т + —М
у з mcosa
3.13.	Изменение состояния сталкивающихся тел описывается законами сохранения импульса и энергии:
гтц =Mn + mw, у	у	у
mN о _Mn	ти
~2~~ 2 + 2 ’
где v и и — проекции векторов скорости тел массой т и М сразу после столкновения на ось, направленную вертикально вниз.
Решение этой системы дает v = —--
т
v	Mv2
Кинетическая энергия —-—, полученная при столкновении телом, прикрепленным к пружине, расходуется на совершение работы против силы трения \imgh и на работу по сжатию пружины
г-	ЛА'2 TJ I ^2 г,
——. Следовательно, —-— = ydign +	. Решая это уравнение
относительно h, находим
96
3.14.	Скорость v , приобретаемую гирей при падении ее с высоты Н, можно найти из закона сохранения механической энергии (гиря и Земля — замкнутая система):
При абсолютно упругом ударе импульс и механическая энергия системы не меняются, тогда как сами импульсы и энергии гири и чаши весов меняются за счет локальных внутренних упругих сил. Внешние силы (силы тяжести) при локальном взаимодействии не меняют импульсы и энергии гири и чашки, поэтому в момент удара гирю и чашку можно считать замкнутой системой.
Законы сохранения импульса и механической энергии при абсолютно упругом ударе гири о чашку весов имеют соответственно вид
mv = MV + mw,
2
wv Л/Г2 mu
-----—--------------I--------
2	2	2
где и — проекция скорости гири, а Г — скорости чашки весов сразу после удара на ось, направленную вертикально вниз.
Решая систему уравнений, получаем
1+"
97
Величину сжатия пружины весов h найдем из закона сохранения полной механической энергии системы «чашка весов — Земля» (эта система замкнута):
, MV2 kh2
теп -1---— ——
2	2
В этом уравнении mgh — изменение потенциальной энергии , МУ2 чашки весов при опускании ее на высоту п, ——------- начальная
' kh2 кинетическая энергия чашки весов. —-----потенциальная энер-
гия. запасаемая пружиной весов при ее сжатии. Решая получившееся квадратное уравнение относительно h. находим
, mg(. Г. ЪкНМ h = -z- 1+ 11 +----
к V V g(m+M)2 ,
3.15.	/?=.— 11 +
к [11 g(m+M)2
Указание. См. решение задачи 3.14.
3.16.	При погружении в жидкость тело совершает работу против силы Архимеда. Примем за начало отсчета потенциальной энергии глубину, на которую погрузится тело. Тогда закон сохранения энергии для системы «тело — Земля» имеет вид
mg{hx + h2) = FAh2.
Подставляя сюда т = рУ и FA =P(jPg (V— объем тела), нахо-
дим /?9 = ---Л] .
Ро-Р
3.17.	h = ^^-h}. Р
Указание. См. решение задачи 3.16.
98
3.18.	На соскальзывающее с полусферы тело действуют две силы: сила тяжести mg и сила реакции опоры N. В момент отрыва от поверхности N обращается в нуль. В этот момент уравнение движения в проекциях на ось OY имеет вид
а — угол между радиусом-вектором точки отрыва, задающим ось OY. и вертикалью.
Величина скорости в момент отрыва находится из закона сохранения механической энергии (Земля и тело — замкнутая система):
Совместное решение этих уравнений дает Н = — R.
3.19.	На тело действуют две силы: сила тяжести = mg и сила реакции опоры N. В любой точке «мертвой петли» первая сила неизменная как по величине, так и по направлению, вторая же изменяется от одной точки к другой как по величине, так и по направлению. При этом наименьшее значение сила реакции опоры принимает в верхней точке петли. Поэтому отрыв возможен именно в этой точке, когда N = 0. Скорость тела в момент отрыва vq может быть найдена из второго закона Ньютона для вращательного движения (в проекции на ось, направленную вертикально вниз):
в котором для верхней точки следует положить N = 0. Итак,

99
Наименьшую высоту ската Н. при которой тело сделает «мертвую петлю», можно найти из закона сохранения полной механической энергии (тело и Земля — замкнутая система), в котором в качестве конечного состояния берется состояние, соответствующее положению тела в момент его отрыва от цилиндрической поверхности:
2
mgH = mg • 2R +	•
Отсюда Н =2.5 R
3.20.	При свободном падении копра его и Землю можно рассматривать как замкнутую систему, в которой взаимодействие частей системы обусловлено только внутренними силами — силами тяготения. Поэтому скорость копра перед его ударом о сваю v можно найти из закона сохранения энергии:
mv~
где — кинетическая энергия копра в момент удара о сваю, mgH — изменение его потенциальной энергии в поле сил тяжести. Отсюда
v = y/2gH .
В момент удара копра о сваю систему «копер + свая» также можно считать замкнутой, так как обмен импульсами и энергиями между частями системы в процессе соударения обусловлен преимущественно внутренними (упругими) силами. Благодаря малости времени удара величина этих сил весьма значительна и импульсы их во много раз больше импульсов всех внешних сил (сил тяготения). Именно поэтому систему «копер + свая» можно считать замкнутой, т.е. для нее будут выполняться закон сохранения импульса.
100
Для неупругого столкновения копра о сваю закон сохранения импульса в проекции на ось сваи имеет вид
ту = (т + М)и ,
где и — скорость копра и сваи после удара. Отсюда
т+М т+М
После неупругого удара копра о сваю они продолжают совместное движение и свая погружается на глубину / в грунт. Закон сохранения энергии для системы «копер + свая -г Земля» запишется, как
(т+М)и2 ----------h(m + M)gl - Fl .
Здесь первое слагаемое в левой части — кинетическая энергия копра и сваи, второе слагаемое — изменение их потенциальной энергии при погружении на глубину I, F — средняя сила сопротивления грунта. FI работа силы сопротивления грунт i.
Подставляя сюда и. находим
F = g(m+M)
, Н т2
1 +----------7
1 (М + т)2
3.21.	Скорость молота перед падением на сваю v = ^2gH . Ско-2v г- г
рость сваи после удара о нее молота и = —-. 1 лубина погруже-
+1
т
^mgH
ния сваи h -----------------. В случае абсолютно упругого
iY
(F - wg) — +1 \w J
удара в процессе столкновения выполняются законы сохранения энергии и импульса!
101
3.22.	h-H---
(m}+m2)2
3.23.	/I - -№1.
2(wq + m2)
3.24.	v = J2^|l + ^|. V ml )
3.25.	Обозначим »i] и m2 — массы соответственно шара «снаряда» и шара «мишени», и2 — скорость шара «мишени» после соударения. г) — доля первоначальной кинетической энергии системы. которая может перейти во внутреннюю энергию. По определе-ДЖ
нию г) = —;-— . где &WK = Т,- Тf — разность кинетических энер-Л
гий начального 1} и конечного Tj- состояний системы. По усло-,2
вию задачи 7', = W|X1- Чтобы найти и. посчитаем, какие значения 2	'
сможет принимать кинетическая энергия конечного состояния системы. При соударении в процессе деформации шаров возникают мгновенные (ударные) силы, величина которых весьма значительна. За время, равное продолжительности удара, которое очень мало. импульсы внутренних сил во много раз больше импульсов всех внешних сил (в данном случае сил тяжести), приложенных к системе. Поэтому в процессе соударения можно пренебречь влиянием всех внешних сил и считать, что система соударяющихся шаров является замкнутой, т.е. в ней выполняется закон сохранения количества движения. Закон сохранения количества движения при соударении шаров имеет вид: »i]Vi = m\U\ + m2u2. При лобовом, соударении скорость Vi шара до удара и скорости обоих шаров после удара iq и и2 направлены вдоль одной прямой — оси ОХ, проходящей через их центры масс.
Деформация шаров в процессе соударения влияет на их относительную скорость. Если до соударения относительная скорость ша-
102
ров была равна v0TH = vj - v2 - vj (до соударения второй шар покоился), то после него она равна w0TH = w2 - Щ и может принять любое значение в диапазоне 0<wOTH <v0TH. При определении иотн принято во внимание, что w2 может быть направлена только в направлении v j.
Обозначим ™- = ——— = к . тогда 0 < к < 1. При к = 1 удар v отв	v 1
абсолютно упругий, так как относительная скорость шаров в процессе соударения не изменилась. При к = 0 удар абсолютно неупругий; после соударения оба шара движутся вместе с одинаковой скоростью «1 = «2.
Из определения к получаем w2 =W] +£v]. Подставляя w2 в закон сохранения импульса, находим
(тг - km2 )vj	wij (1 + k)v^
U ] ~. W 9 =-----------------------
......	“ W] +АИ2
ту + аи2
Изменение кинетической энергии рения равно
системы в результате соуда-
ДЖК
2	2	2
_ W]V1	АИ1«1 w2zr2 _
”	2
mlm2 2„ ,2 ------—-------Vj (1 -k 2(»i] + m2)
Пользуясь кинетической энергию
этим соотношением, найдем долю энергии, которая может перейти
первоначальной во внутреннюю
ДЖ Ш'у n=-^- =—“ Ti т\
+ т~>
Коэффициент в г|, зависящий от связь между и। и V]:
масс частиц выразим, используя
2
2
m2
mj + m2
1
V] J(l+fc)
103
Окончательно r| = I 1 - — 1(1 - к).
I V1)
Таким образом, при максимально возможном к = 1 г) = 0, при
к = 0 г, = 1--- . Следовательно, г, заключено в диапазоне
I V1J
«1
V]
При заданных в условии задачи скоростях шаров 0 < г) < 0,6 .
104
4.	Статика
4,1.	Чтобы натянуть свободно висящую веревку внешняя сила должна совершить некоторую положительную работу АЛ по изменению формы веревки против сил тяжести. Поэтому закон сохранения энергии при таком изменении имеет вид
W =W +А. V Jtl
где JVC и — потенциальные энергии свободной и натянутой
веревок соответственно.
Так как потенциальная энергия веревок пропорциональна расстоянию от их центра тяжести до поверхности Земли, т е. W ~ h. то отсюда следует, что hc >hH . где hc и /гн — высоты над Землей
центров тяжести свободной и натянутой веревок соответственно. Следовательно, центр тяжести свободно висящей веревки выше.
чем у натянутой.
4.2.	Муравей должен толкать соломинку в направлении муравейника поочередно приподнимая ее за концы и поворачивая на некоторый угол (см. рисунок).
4.3.	Рассмотрим условие равновесия доски (см. рисунок). На нее действуют силы реакции опор 7V) и > и сила тяжести mg, приложенная посредине доски (так как доска однородная, именно здесь находится центр тяжести). Длину доски обозначим I. Составим уравнение моментов относительно оси, проходящей через точку А, в которой доска касается левой опоры, перпендикулярно плос
кости чертежа:
I 1 I М \1 1 On mg---------- No I-------= 0.
(2 4) I 4 3
105
з
Отсюда N2= — mg. Аналогично для оси, проходящей через точку В:
К! (. I l\ I г\ п „2 ~3~4 ~Л2~3 J0, Nj = 5mg-
В соответствии с третьим законом Ньютона силы, с которыми доска давит на каждую из опор А и В. равны по величине силам N] и /V-. соответственно.
2	3
Ответ: R 4 =	= — mg, Rg = N2 = ~7mg 
4.4.	Нижняя половина кирпича оказывает большее давление на наклонную плоскость. Сила давления нижней половины
г 1	(	h .
FH = — mg\ cos а + —sm а
2	1	а
сила давления верхней половины
к I	(	b .
rB = — mg cos а----sin а
2	1	а
а — длина кирпича, h — высота кирпича, а — угол наклона плос
кости.
Указание. Условие равновесия для моментов сил (4.2) удобно
записать относительно центра тяжести кирпича.
4.5.	Сила F/. действующая со стороны палки на, левый (по отношению к направлению F) ящик, приложена в нижней точке ящика, а сила F2- действующая на правый ящик' приложена в верхней точке. По третьему закону Ньютона со стороны ящиков на палку будут действовать силы F\ и F2 (см. рисунок), равные по величине и противоположные по направлению силаь^ F{ и
106
F2 соответственно: F\ = -F{; F2 = -F2 . Величину сил F\ и F-> найдем из условия равновесия:
OX: F + Ft -F2 -0.
Отсюда F2 = F] + F, т.е. F2 > F]. Следовательно, F2 > F{ . По
этому при увеличении силы F раньше сдвинется правый ящик.
4.6,	При моделировании невесомости в бассейне на космонавтов действует сила сопротивления среды, которая будет препятствовать движению по инерции. Кроме того, внутренние органы космонавтов в бассейне не будут находиться в состоянии невесомости и будут функционировать иначе, чем в условиях невесомости.
4.7.	Минимальное значение силы будет в том случае, когда ее
плечо наибольшее. Поэтому Fmjn = -7=.
. V2
4.8.	Силы, действующие на лестницу. указаны на рисунке. Лестницу будем считать однородным телом, длину ее обозначим /. Условие равновесия (4.1) запишем, проектируя силы на ось OY. а уравнение моментов (4.2) запишем относительно оси, проходящей через точку Л, в которой лестница касается стены:
7Vi - mg - 0;
N^l cos а - F^p/sin а - mg cos а = 0.
Лестница не будет падать, если FTp < цУ( .
Решая приведенные уравнения и неравенство, получим
1 “>amin = arctg—.
2ц
4.9.	Между двумя опорами, находящимися на одном уровне, например между двумя гвоздями в стене, груз подвешивается на лес-
107
а ке так, чтобы один конец лески был закреплен на одной опоре, а второй конец мог свободно перемещаться по JL	,, другой (см. рисунок). При этом груз
up	должен свободно скользить по леске.
-»	За свободный конец леска выбирается
до тех пор, пока она не порвется.
Измеряется расстояние между опорами а и длина лески Z между опорами, при которой произошел ее разрыв. Силу натяжения нити Т. при которой произошел разрыв, и. следовательно, максимальную нагрузку лески можно найти из условия равновесия груза, подвешенного между опорами, по формуле:
mgl
Самостоятельно дайте объяснение другому варианту опыта, показанному’ на следующем рисунке.
4.10.	На горизонтально расположенный лист фанеры установить перпендикулярно к нему металлический лист. Деревянную рейку поставить под большим углом к листу фанеры так, чтобы другим концом она опиралась на металлический лист. Плавно уменьшать угол наклона рейки по отношению к листу фанеры, измеряя при этом высоту точки касания рейки с металлическим листом Н и расстояние между точками касания рейки и металли-
ческого листа с листом фанеры I (см. рисунок). Предельные значения Н nl, при которых рейка еще не скользит, определяют коэффициент трения	ч
/
ц = --
2Н
108
Эта формула получается при рассмотрении условий равновесия рейки, которые в данном случае имеют вид
/тр<№в-
NB~mg = Q:
№ + Н2 mg—------cosamin +
+ ApV^2 + #2 sin“min ~+H2 cosamin = О
(см, решение задачи 4,8).
При записи условий равновесия сделано допущение, что коэффициент трения (и, соответственно, сила трения) рейки о металлический лист пренебрежимо мал,
4.11.	Силы, действующие на картину и удерживающие ее на стене, показаны на рисунке. Картину считаем однородным телом, длину рамки в плоскости рисунка обозначим I.
Условие равновесия (4.1) запишем, проектируя силы на оси координат:
OX: W-7’sina = 0;
OY: Лтр + Т cos a - mg = 0 .
Уравнение моментов относительно оси, проходящей через точку А:
mg-^cosa -Tl = 0.
mg
Отсюда Т = cos a . Подставляя Т в уравнения для проекции
х/ mg сил. находим N =--cos a sin а и
2
109
i-p = тё ~ T cos & = mg 1 -
cos2 a ~~2
Сила, с которой стена действует на картин)' в точке А, является равнодействующей сил N и FTp . Величина этой силы равна
« = Jf2 + N2 =	71 + 3sin2a .
V ‘Р	2
По отношению к стене направление силы R определяется углом р. для которого
N	cos a sm a
tgP = — = —-^тр	1 + sin a
или
_	| cos a sin a A
P = arctg|------— .
V 1 + sin2 a )
В соответствии с третьим законом Ньютона картина действует на стену с силой, равной по модулю силе R и противоположной ей по направлению.
Заметим, что направление силы R должно проходить через точку пересечения линий, вдоль которых действуют силы Т и mg, так как сумма моментов всех сил относительно этой точки должна быть равна нулю.
„	_. mg - 2	\ cos a sin а
Ответ: R - —— у 1 +osin a.p = arctg---------— .
2	у 1 + sin а ,
4.12.	/*’ =-----. р =---а. р— угол между линией действия
2 cos а 2
силы на подставку и осью стержня.
, , „ ,, mg Г „	2 о (ctea^	\
4.13.	Л =	у 1 + э sm a , р = arctgl — I, р -— угол между
осью стержня и линией действия силы.
110
1 — Ц1Цт
4.14.	a>amin = arctg ——L-— (см. решение задачи 4.8).
2И1
4.15.	Величины моментов сил относительно мгновенной оси вращения, проходящей через точку касания катушки с поверхностью. можно записать в виде
cos a., +1 г .
/ = 1.2.3. 4. Л’г берется в относительных единицах, а, — угол силы F, по отношению к линии горизонта. Выражение р, =[ — cos а, +1 |г представляет собой плечо силы Ft. Оно нахо-у г	)
дится с помощью простейших геометрических построений (см. рисунки а и б).
Знак «минус» здесь получается для сил. направленных от поверхности. а знак «плюс» — для сил. направленных к поверхности.
Складываем полученные моменты сил и находим знак суммарного вращающего момента
к R
rd — cos aj
V г
М =
Л R Л (R
1 + r2 —cosa2 +1 - r3 — C0SCI3 +1 -
J V	\ r	J
-/4 — cos a. 4 - 1
= +0,9.
M > 0, следовательно, катушка покатится вправо. '
111
4.16.	При наполнении стакана водой уровень воды и соответственно ее центр тяжести повышаются относительно дна стакана, вследствие чего центр тяжести стакана с водой понижается относительно центра тяжести пустого стакана хс (имеется в виду стакан, у которого толщина стенок и дна сравнимы). При некото-тяжести ром количестве воды в стакане ее уровень совпадет с положением центра тяжести стакана с водой. Докажем, что это хв положение центра тяжести стакана с водой
наинизшее. Примем его за начало отсчета оси ОХ, которую направим вдоль оси симметрии стакана (см. рисунок).
Тогда в соответствии с определением (4.3) положение центра тяжести стакана с водой хц т должно удовлетворять условию:
хс/яс -рИхв = 0,
т.е. хц т = 0, где тс — масса стакана, р — плотность воды, V — ее объем. Найдем теперь, как изменится положение центра тяжести стакана с водой, если уровень воды в стакане изменится по сравнению с рассмотренным уровнем на величину Дх в ту или иную ситуацию. В этом случае новое положение центра тяжести
хс/яс -р(И±Дх5)
Хц Г =
+WB
(V ,	_ „
(хс-рИхв) ±рДх! --5хв I + р-^—
тй + /яв
Л’ — площадь дна стакана.
При записи этого выражения учтено, что изменение уровня во-.
ды на Дх меняет положение центра тяжести воды на —, а также тот факт, что увеличение (уменьшение) объема воды приближает
112
(удаляет) центр тяжести воды к началу координат. В последнем выражении для Хц т слагаемые, содержащиеся в круглых скобках, равны нулю: первое — так как оно является результатом условленного ранее выбора начала координат, а второе— в силу того, что — = 5хв.
2
Как видим. Хц т > 0, что и доказывает сделанное выше утвер
ждение.
.	т}-т2 Я2	,
4.17.	sm а =------— —------------—. / — длина стержня.
2(т}+т2)^у	(т}+т2у
Указание. Стержень будет занимать равновесное положение в чаше тогда, когда центр тяжести системы точечных масс будет находиться на вертикали, проведенной через центр сферической ча
ши.
4.18.	Вследствие симметрии системы относительно вертикальной плоскости, проходящей через вершину призмы параллельно оси цилиндра, нет смысла рассматривать всю систему в целом. Достаточно ограничиться одним цилиндром и той половиной призмы, с которой он взаимодействует (см. рисунок).
На рисунке и TVj — силы трения и нормального давления, дейст
вующие на цилиндр со стороны клина, соответственно. Аналогичные силы, действующие со стороны цилиндра на клин, обозначены, как /','р и N{. По третьему закону Ньютона:
7тр=-7тр-М=-^'-
Л Гр и N2 — силы, действующие со стороны поверхности на цилиндр.
Систему координат выберем так, как показано на рисунке.
113
Условие раскатывания цилиндров означает, что момент сил. вращающих цилиндр против часовой стрелки, относительно оси цилиндра должен быть больше или равен моменту сил. вращающих его по часовой стрелке, т е.
/тр — гр •
При выводе этого условия принято во внимание, что плечи каждой из сил f и F)p одинаковы и равны радиусу цилиндра. Моменты других, действующих на цилиндр сил. равны нулю, так как их направление проходит через ось цилиндра.
Условие отсутствия проскальзывания между призмой и цилиндрами означает, что
для цилиндра: У, + mg 4- У2 4- /у +	= 0,
Mg	7' с
для клина: —— + У । + /™ = 0.
2	1
Проектируя эти уравнения на выбранные оси и принимая во внимание, что
|/тр | ~ |/тр | ~ i
и
|у1| = |у1'| = уь
получим систему уравнений:
У] cos а - / sin а - /у = 0:
< - У] sin а - mg 4- У2 -./ cos а = 0;
Л/i?
------+ У| sin а + / cos а - 0.
I 2
Сложив второе и третье уравнение системы, найдем
У2
( М\
I w + у Н 
114
При раскатывании призмы и цилиндров Flp = pNi Используя эту связь, исключим из первого и второго уравнений системы AS
N\ (cosa - psina) - /(sin a + pcosa) - pmg = 0 .
Домножив это уравнение на sin a, а третье уравнение системы на (cos a - psin а) и вычитая из одного из этих уравнений другое, получим
Му
f -——(cosa - psin a) - pmgsin a.
Воспользуемся условием раскатывания:
M ,	ч
g — (cos a - psin a) - pm sin a
f M\
>pg| m + ~ .
V £ J
Отсюда
M 2p(l+sina) m cos a - p(l + sin a)
Подстановка численных значений дает —>55. Данная ситуа-т
ция может осуществиться лишь в том случае, если призма в месте ее соприкосновения с цилиндром не проскальзывает по цилиндру, т.е. если силой, вращающей цилиндр вокруг его оси, является сила трения покоя. Это условие можно записать, как
,/тр —	>
где ро — коэффициент трения скольжения между призмой и цилиндром. С другой стороны, как отмечалось,
./тр—М^2-
г	N2
Следовательно, эта ситуация осуществляется, если ро > р-.
115
Отношение 7V2 / Щ можно определить из первого уравнения вышеприведенной системы, если положить в нем /гр = FTp =pV2 
N2 cos a	cos а
Тогда = ~7,------:---7 и Но :-------• Для а = 45° ц0 > 0,41.
/V ]	р.(1 + sm а) 1 + sm а
4 19	- 2(sina + Ц] cosa)
 и? / Ui
' mm _J_ - Sm a - Ц] cos a
M-2
a)
% 1.46:6)1 — 1	«3.1.
\ m ) v ' min
4.20. Вращение катушки без ее у “	качения по поверхности возможно в
том случае, если катушка проскаль-fF	зывает, т.е. сила трения FTp Дейст-
/ /'Т'Х М/-	вующая на катушку, принимает
I ( Г “/“Г у---------► максимально возможное значение,
\ nia ‘L,- /	равное силе трения скольжения
—-------------- /Lp = F^ =pN, N — сила реакции
^ip	опоры (см. рисунок). Связь между
величинами сил Елр и N найдем из условия равновесия сил. действующих на катушку F + Frp + N + mg = 0 . Это уравнение следует дополнить также условием, которое обеспечивает вращение катушки. Оно подразумевает. что вращающий момент силы F относительно оси катушки должен быть, по крайней мере, не меньше вращающего момента силы трения, т.е.
F • г > F^,  Я.
Проектируя условие равновесия сил на оси выбранной системы координат и объединяя полученные уравнения с условиями, выражающими скольжение и вращение катушки, сведем задачу к необходимости решения следующей системы уравнений и неравенств:
116
OX : Л’ cos a - F^ = 0:
OY: Fsin a - mg + N = 0;
Fr^F^R.
В этих уравнениях a — угол между’ направлением действия силы F и поверхностью. Область углов а. при которых возможно вращение, ограничена значениями a>a = arccos~ Это ограничение получается при совместном решении неравенства и первого уравнения системы.
Модуль силы F(a), которая может обеспечить выполнение условий задачи, является функцией угла а. Зависимость F(a) получается при совместном решении первых трех уравнений системы:
F(a) =------------
cos а + ц sm a
Минимальное значение Fniin достигается при тех углах, при которых знаменатель этого выражения максимален. Решая задачу на экстремум функции / (a) = cosa + psin a , или преобразуя /(а) к виду /'(а) = -^1 + ц2 cos(a - 0), где tg0 = р . заключаем, что максимум функции /(а) на промежутке 0<а<л72 приходится назначение а|Пах =0 = arctgp. При этом же значении а1Пах модуль силы F(a) принимает минимальное значение.
Вид зависимостей /(а) и F(a) на промежутке 0<а<тг/2 качественно показан на рисунках.
На графике F(a) отложены также два возможных значения уг-
ла а - а] и а2. соответствующие двум различным значениям ми-*
нимальнои силы. В первом случае, т.е. когда а] <а1Пах. вращение
117
катушки, но не ее качение возможно при минимальной силе
' mm ” г ,u-max ' i---— 
*
В другом случае, когда а 2 > а тах , минимальное значение силы
*	г
достигается при угле а = а2 = arccos —. т.е.
*	pwg
^mni — (а 2 ) —	I-----;— 
r/R + ^l~(r/R)-
Численный расчет дает
*	4	*
a)	am.,v =arctg0.85 = 40.4°i a =arccos — -55°; атяу <а :
' 111x1л	-	-у	IJldA
F =----------...........» И 4 Н
1 тт	/---------— п*
r/R + iijl-tr/R)2
б)	«max = 26.6°; а* =41.4°; атах <а‘; Fmin «9;3 Н;
Б) а„„ =40,4"; а* =31,8"; ат„ >«'; f„n =-Я=«13 Н;
г)	атах  а = 25,2 , ctmax >а .	~ 11,5 Н. ч
118
5.	Механические колебания
5.1.	В нагруженной. Масса нагруженной машины больше, вследствие этого частота колебаний машины (см. (5.3) и (5.4)), те. ее тряска, будет меньше для нагруженной машины по сравнению с пустой.
5.2.	Разъезженные дороги обладают определенной периодичностью в расположении ухабов, которая зависит как от скорости прошедших по дороге автомобилей, их массы, так и от собственной частоты колебаний рессор. При езде по таким дорогам ухабы в свою очередь играют роль вынуждающей силы, которая заставляет рессоры автомобиля колебаться в такт их расположению. Раскачивание становится особенно заметным, когда собственная частота рессор автомобиля совпадет с частотой расположения ухабов на
у
дороге v » —. v — скорость автомобиля. А/ — среднее расстоя-Д/
ние между гребнями ухабов
5.3.	К одному концу нити некоторой длины / привязать гирьку и. подняв нить с гирькой за другой ее конец, привести груз в движение в вертикальной плоскости под действием силы тяжести. Измерить время Д/. за которое будет совершено п полных колебаний получившегося маятника. Период маятника будет равен Т = —. В п
свою очередь, Т = 2п — , g—ускорение свободного падения. От-118
сюда длина нити маятника может быть найдена, как
4я2и2
Далее с помощью этой нити можно измерить длину, ширину и высоту комнаты и вычислить ее объем. Дробные доли длины можно получать посредством складывания нити вдвое, вчетверо и т.д.
119
5.4.	Примем за начало отсчета потенциальной энергии математического маятника уровень, соответствующий его наинизшему положению (см. рисунок). Тогда при угле отклонения а потенциальная энергия маятника будет равна
РИП (а) - mgh = wg/(l - cos а).
Кинетическая энергия маятника зависит, как от его угла отклонения от положения равновесия, так и от начального угла отклонения а(). Чтобы найти эту' зависимость, воспользуемся законом сохранения энергии, записав выражение для полной механической энергии при двух положениях маятника: одно соответствует углу а, а другое — максимальному углу отклонения ад . Тогда

или
mgl(l - cos <х()) = mgl(\ - cos а) + И'к (а).
Отсюда I¥K(a) = mgl(cosa -cosa0). Графики зависимостей кинетической. потенциальной и полной энергии от угла а показаны на
5.5.	Изменится. Кинетическая энергия маятника, погруженного в воду /Гк . как функция угла отклонения а, имеет вид
120
2	2,2	,2 / . \2
1ТГ ту то I ml da] к 2	2	2 V dt )
Потенциальная энергия погруженного в воду маятника (Тпп меньше потенциальной энергии непогруженного на величину работы А. которая совершает выталкивающая сила.
Жпп = С -^ = wg/(I-cosa)-pBFg/(l-cosa),
где /(1-cosa) — изменение высоты маятника в поле сил тяготения и выталкивающей силы. К— объем маятника. рв — плотность воды.
гг	а а	„	Vgl 2
При малых углах sin — « —. поэтому /ТГ1 «(р - рв) -у-a . р — плотность материала маятника. В соответствии с (5.3) и (5.4) период колебаний маятника можно найти, как отношение соответствующих коэффициентов при обобщенных координатах:
Т = 2п
ф_£»
I р;
5.6.	Направим ось ОХ вдоль гори-
зонтальной поверхности (см. рису- У А ДАд
нок) и пусть начало координат совпа- 1 ™ v V V и| *и 
дает с положением центра тяжести
тела массой М. Тогда в соответствии с определением (4.4) в случае сжатой пружины центр тяжести системы будет находиться в точке с координатой
„сж _ цт“М + /я’
пне	।
а в случае распрямленной пружины в точке х£т =------. По-
М + т
скольку в процессе колебаний грузов суммарный импульс системы в направлении оси ОХ остается неизменным (внешние силы — си-121
лы тяжести — перпендикулярны оси ОХ), положение центра тяжести системы относительно горизонтальной поверхности не изменяется Это означает, что относительно горизонтальной поверхности груз М будет колебаться с амплитудой, равной разности ХцЖ и
Ypac т е А - храс - хсж -
М + т
5.7.	А =.—.-Jllh-h2 .
М + т
т +М
5.9.	Рассмотрим случай а).
Пусть угол отклонения маятника от вертикали в произвольный ,	/	\	с/Ф
момент времени t мал и равен <р (см. рисунок). 1огда со = — есть dt угловая, a v = со/? — линейная скорость в этот же момецт времени любой точки маятника, отстоящей от оси вращения на расстояние R. Для шариков, закрепленных на концах стержней.
RA=RC=J2^ RB =d,
122
Кинетическая энергия всего маятника в целом в момент времени t равна сумме кинетических энергий, составляющих его шаров.
Г Ч 2	2	2,2	,2( ^ф
^кин — 2 V Л +	+ VC та 1 ~ т [
Так как маятник находится в однородном поле сил тяжести, то его потенциальная энергия определяется положением его центра тяжести. При заданном расположении шаров центр тяжести маятника находится на вертикальном стержне на расстоянии 7/6 от 7 I 2
точки пересечения стержней и на расстоянии —ь —= —7 от точки 2 6 3
подвеса маятника. Поэтому потенциальная энергия маятника, отсчитываемая от самого нижнего положения центра тяжести, будет равна
Епот = 3mgh ,
Z || 2 )	2
где Зт — масса маятника, /? = —/-, —7 -х — высота подъ-
3	]{3 J
ема центра тяжести (см. рисунок). При малых углах ip
Х«?/ф,
поэтому
£пот =3wg|7 1-^1-ф2
Так как трение отсутствует, то полная механическая энергия маят
ника
^полн — ^кин + Епот ~	, I + mglq>
\dt )
dE
co временем не изменяется, т.е. —^2^2- = 0 . Дифференцируя dt
О'
£'полн п0 времени, получаем ср" + — <р = 0. Это уравнение совпада
123
ет с уравнением гармонических колебаний (5.3), для которого час-
2 J?
тота колебаний со = —. Отсюда Т = 2 л.
2 с.
Рассмотрим еше один вариант решения. Известен период коле-
баний математического маятника Т = 2л — , где /м
длина
подвеса математического маятника.
Подберем длину подвеса такой, чтобы период колебаний математического маятника и предложенной системы совпали (при равенстве масс).
Проведем мысленный эксперимент: отклоним оба маятника на один и тот же угол а от вертикали и отпустим без толчка. Если в дальнейшем при произвольном угле отклонения р от положения равновесия угловые скорости маятников совпадают, то можно утверждать. что и периоды их колебаний совпадают, так как они. колеблются синхронно. Воспользуемся законом сохранения механической энергии для математического маятника
(1_ cos а) = 3mglM (1 - cos Р) +
3mw2l^
2
и для предложенной системы
V 2	V 2
mgl(l - cos а) + mg —/[1 _ cos(a + 45°)]+ mg—/[1 - cos(a - 45°)]=
л/2	V2
= mgl{\. - cos P) + mg — /[1 - cos(p + 45°)] + mg-^- /[1 - cos(p - 45°)]
m&^l^ ! э ты 2	+ ~2
2
124
Проведем соответствующие преобразования приведенных выражений и получим систему уравнений:
2g(cos0-cosa) = o»2 -ZM;
2g(cos 0 - cos а)-а2 • /

б)
7’ = 2 л — — а 2.4 с. ]2g
в)
Т = 2л, --*2.15 с.
Vg
г) Г = 2л — *3.14 с. V g
5.10.	Пусть поршень сместится вправо относительно равновесного положения на х. Тогда давление газа в левой (рх) и правой (р2) частях сосуда можно найти из уравнений состояния газа в этих частях:
px(V + xS) = vRT,
p2(V-xS) = vRT.
Силы, с которыми газ будет действовать на поршень, соответственно равны: слева— Fx= pxS, справа— F2 ~ Р2$  Справа на поршень будет действовать также и упругая сила Fyn = кх.
Основное уравнение динамики для поршня имеет вид
ma = pxS - p2S - кх.
Подставляя сюда р\ и р2 из уравнений состояний газа и делая несложные преобразования, получаем
та = -х
2vRTS2
V2
125
При выводе этого соотношения ввиду малости колебаний поршня полагалось, что У" - (xS)“ « V . Так как а - х, то
IvRTS2 +кУ2
х ч--------------х = 0 .
тУ2
В соответствии с (5.2) и (5.4) это есть уравнение гармонических колебаний, период которых
тУ2
“ \2vRTS2 + кУ2
I 2
I тУ vjv2
S2RT(yx + v2)3
' mV2l\T2 vRS2(T} -72)(7] +72)2 '
[vRT'(P2 ~ Pl)
gs(p[ + pl)
126
6.	Механика жидкостей и газов
6.1.	Природа давления, оказываемого на окружающие тела жидкостями и газами, различна. Для жидкостей существенны межмолекулярные взаимодействия, вследствие чего они имеют определенный объем и. заполняя сосуды, могут тем самым производить в поле тяготения гидростатическое давление. Величина его пропорциональна высоте столба жидкости, равной глубине погружения. На использовании давления столба жидкости и основана работа водонапорных башень.
Газы не производят заметного гидростатического давления, если только речь не идет о столбе газа высотой в километры, так как молекулы газов движутся независимо друг от друга, заполняя весь представляемый им объем. Давление, которое производят газы на стенки сосудов, обусловлено столкновениями молекул газа со стенками сосудов. Величина давления будет одинаковой по всему объему сосуда.
6.2.	Вес жидкости — это сила, определяемая как Р = mg. где т — масса жидкости, g — ускорение свободного падения. Так как т = рГ . то Р = pgK , р — плотность жидкости, V— ее объем.
Сила давления жидкости на дно сосуда Рд равна произведению гидростатического давления Ргст = pgh на площадь дна сосуда 5. т.е.
Рд = pghS.
где h — глубина погружения дна сосуда относительно поверхности налитой в нем жидкости.
Из формул для Р и /д следует, что соотношение между ними зависит от того, как относятся между собой объем налитой в сосуд жидкости V и объем прямого цилиндра с площадью основания 5 и образующей h.
Из приведенных рисунков видно, что для сосудов а), з) и л) V = hS и поэтому 7д = Р . Для сосудов б), в), и), м), п) V <hS и. следовательно. Р <РЛ. Для сосудов г), д). е), ж), к), п), о) и р) V > hS и Р > Рд .
127
6.3.	Сила, которая поднимает сосуд вверх, есть сила давления жидкости, приложенная к плоской кольцеобразной поверхности. Силы давления жидкости, приложенные к другим поверхностям сосуда, взаимно скомпенсированы.
Из условия равновесия сил. действующих на кольцеобразную поверхность, находим
G = Sp = it(R2 - г2 )pgH ,
где .S' — площадь кольца, р — давление, оказываемое жидкостью на
G
кольцеобразную поверхность. Отсюда р =------------.
K(R2-r2)gH
6.4.	Воспользуемся уравнениями непрерывности и Бернулли, записанными для двух сечений жидкости и У
.2	'	2
Р + Р£Я] +^~ = P + pgH2 +~--
В обеих частях уравнения Бернулли Р = Pq — атмосферное давление. Я| и Н2 будем отчитывать от дна стакана. Тогда //] - Н2 = Н По условию задачи Sj » 5. В этом случае из уравнения непрерывности следует, что v»vj. Поэтому слагаемым
2	2
PV1	PV
—— по сравнению с —— можно пренебречь. Таким образом, ско-
рость истечения жидкости из отверстия v - yjlgH (формул^ Торичелли, 1641 г.).
Масса жидкости, вытекающей в единиц)' времени из стакана, p5v, а импульс, уносимый струей жидкости в единицу времени, равен
ДР / Д/ = pSv • v = IpgHS.
128
Это и есть реактивная сила F = IpgHS, стремящаяся сдвинуть
стакан с места.
6.5.	С помощью линейки нужно измерить диаметры сечения струи в двух находящихся на некотором расстоянии друг от друга местах — и d^. и расстояние между этими сечениями Н (см. рисунок). Считаем струю непрерывной стационарно текущей идеальной жидкостью, которая имеет форму тела вращения с постепенно убывающим сечением. Уравнение Бернулли для выбранных сечений запишется, как
где иу и w2 — скорости истечения воды в сечениях 1 и 2 соответственно. Расход во
ды в непрерывной струе постоянен, т.е. количество жидкости, проходящей через любое сечение струи в единицу времени, неизменно. поэтому для сечений 1 и 2
= $2и2 >
где У} и У2 — соответствующие площади сечений. Решая полученную систему уравнений относительно и у. находим
ul =
IgH 2gH
$1
6.6.	Чтобы мяч при подаче углового удара с линии ворот мог в них попасть при отсутствии ветра, ему надо сообщить вращение в сторону ворот (см. рисунок).
129
В соответствии с законом Бернулли давление в движущейся жидкости или газе оказывается меньше в тех точках, где модуль скорости движения больше. В данном случае модуль скорости воздуха относительно мяча больше со стороны ворот, так как он является суммой модулей скоростей поступательного движения слоев воздуха относительно мяча vn и движения, добавляемого этим слоям вращающимся мячом, vBp, т.е.
VOTH ~ vn vep 
С противоположной стороны мяча модуль скорости движения относительно мяча меньше, так как он равен разности модулей этих скоростей, т.е.
voth = vn ~ vBp 
Поэтому давление воздуха возле мяча со стороны ворот будет меньше, чем с противоположной стороны. В результате на мяч будет действовать сила, перпендикулярная направлению его движения. Следствием этого воздействия будет криволинейное движение мяча в сторону ворот.
6.7.	При движении корабль увлекают за / \	/\ собой ближайшие к ним слои воды. Модуль
//	)л скорости течения этих слоев между корабля-
7 J	х ми. следующими попутным курсом на близ-
ком расстоянии, в два раза выше модуля их скорости с противоположных бортов (см. рисунок). Поэтому в соответствии с законом Бернулли давление воды со стороны внешних бортов будет выше, чем со стороны внутренних, т.е. на корабли будет действовать сила, стремящаяся их сблизить.
6.8.	В соответствии с законом Бернулли давление в движущейся жидкости или газе оказывается меньше там, где модуль скорости движущейся среды больше. В комнате воздух практически покоит
130
ся. а за окном движется. Чем сильнее ветер, тем меньше давление воздуха за окном, тем больше оконные стекла выдавливаются наружу.
6.9.	Высота гребней и глубина впадин волн может увеличится, если усилится ветер. При этом относительное изменение модуля скорости над гребнем волны самое большое, а над впадиной оно меньше. В соответствии с уравнением Бернулли над гребнем волны
,	PV \ с
гидродинамическое давление (слагаемое ) упадет больше, чем над впадиной, что и приведет к большему увеличению гидростатического давления в гребне (слагаемое pg//) и. следовательно, к увеличению высоты волн.
6.10.	Газ в пробирке сжимался изотермически, поэтому его давление удовлетворяет уравнению:
Prx = PoL, или
Это давление уравновешивается давлением столба жидкости над поршнем: рст = р0 + pg(H -х) = р0 + pg/,1 — - а I. Приравнивая эти давления и решая полученное квадратное уравнение относительно а, находим
Ро + ZCk ( Ро + я _ _Ро_ ^pgL 2L) yV2pgZ, 2L J pgL '
Из двух возможных значений а оставляем то, которое удовлетворяет условию: 0 < а < 1. Итак,
I/	\2
И_й>_+"_] -ае.ол
jpgL 2LJ yUpgi 2£J pgL
131
СОДЕРЖАНИЕ
Предисловие...........................................3
Задачи Решения и отвегы
I . Кинематика............................4	11	49
2.	Динамика............................. 18	20	70
3	Законы сохранения импульса и энергии.27	29	92
4.	Статика.............................. 33	35	105
5	Механические колебания................40	41	119
6.	Механика жидкостей и газов............45	46	127