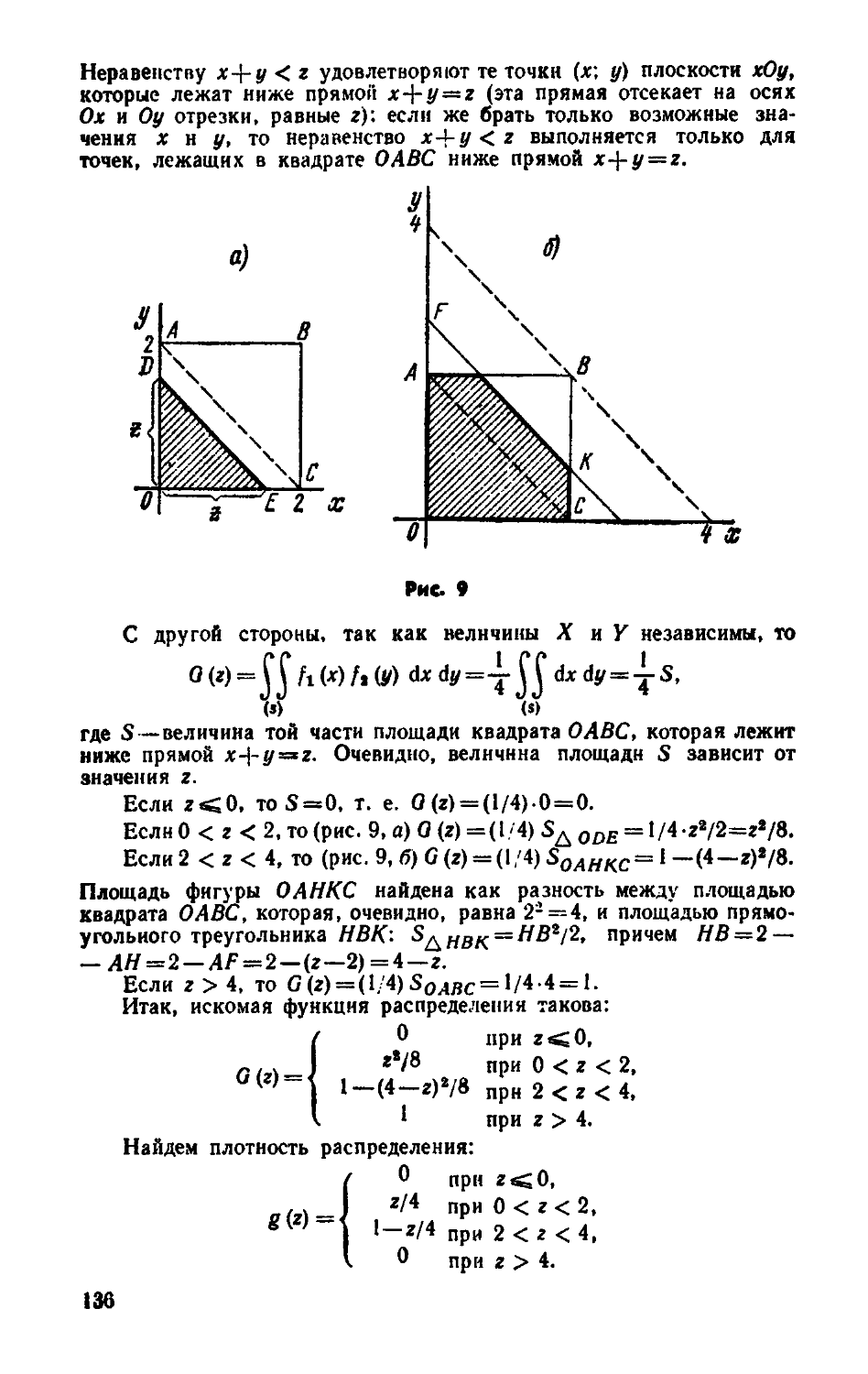
Text
В. Е. ГМУРМАН
РУКОВОДСТВО
К РЕШЕНИЮ ЗАДАЧ
ПО ТЕОРИИ
ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ
СТАТИСТИКЕ
ИЗДАНИЕ ТРЕТЬЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством
высшего и среднего
специального образования
СССР
в качестве учебного пособия
для студентов
высших техническим
учебных заведений
Москва «Высшая школа» 1979
ББК22. 171
Г11
УДК 519.2 @76)
Рецензент
докт. техн. наук, проф. Судаков Р. С.
Гмурман В. Е.
Г11 Руководство к решению задач по теории
вероятностей и математической статистике:
Учеб. пособие для студентов втузов.—3-е изд.,
перераб. и доп.—М.: Высш. школа, 1979.—
400 с, ил.
В пер.: 75 к.
В пособии приведены необходимые теоретические сведения и
формулы, даны решения типовых задач, помещены задачи для
самостоятельного решения, сопровождающиеся ответами и указа-
указаниями. Большое внимание уделено методам статистической обра-
обработки экспериментальных даииых. Настоящее издание дополнено
следующими новыми разделами: ранговая корреляция, моделиро-
моделирование случайных величии, случайные функции.
Предназначается для студентов втузов, может быть полезно
лицам, применяющим вероятностные и статистические методы при
решении практических задач.
„ 20203-135 м 17ПММПП0 5178
Г 001@1)—79 32~79 1702060000 ББК 22.171
Владимир Ефимович Гмурман
РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО ТЕОРИИ
ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Редактор Ж. И. Яковлева. Переплет художника В. И. Казаковой.
Художественный редактор В. И. Пономаренко. Технический ре-
редактор Н. В. Яшукова. Корректор Г. И. Кострикова.
ИВ М« 1642
Изд. № ФМ-631. Сдано в набор 26.09.78. Подп. в печать
03.01.79. Формат 84x108/32. Бум. тип. Wi 2. Гарнитура лите-
литературная. Печать высокая. Объем 21 усл. печ. л. 21,24 уч.-изд. л.
Тираж 130 000 экз. Зак. №3177. Цена 75 коп.
Издательство «Высшая школа», Москва, К-51, Неглииная ул.,
д. 29/14
Ордена Октибрьской Революции и Ордена Трудового
Красного Знамени Первая Образцовая типография имеив
А. А. Жданова Союзполиграфпрома при Государственном коми-
комитете СССР по делам издательств, полиграфии в киижиой торговли,
Москва, М-54, Валовая, 28.
© Издательство «Высшая школа», 1975
© Издательство «Высшая школа», 1979, с изменениями
ОГЛАВЛЕНИЕ
Предисловие 7
Часть первая
Случайные события
Глава первая. Определение вероятности 8
§ 1. Классическое и статистическое определения вероят-
вероятности 8
§ 2. Геометрические вероятности 12
Глава вторая. Основные теоремы 18
§ 1. Теоремы сложения и умножения вероятностей ... 18
§ 2. Вероятность появления хотя бы одного события ... 29
§ 3. Формула полной вероятности 31
§ 4. Формула Бейеса 32
Глава третья. Повторение испытаний 37
§ 1. Формула Бернулли . . > . 37
§ 2. Локальная и интегральная теоремы Лапласа .... 39
§ 3. Отклонение относительной частоты от постоянной ве-
вероятности в независимых испытаниях 43
§ 4. Наивероятнейшее число появлений события в незави-
независимых испытаниях 46
§ 5. Производящая функция 50
Часть вторая
Случайные величины
Глава четвертая. Дискретные случайные величины ...... 62
§ 1. Закон распределения вероятностей дискретной случай-
случайной величины. Законы биномиальный и Пуассона . . 62
§ 2. Простейший поток событий 60
§ 3. Числовые характеристики дискретных случайных ве-
величин 63
§ 4. Теоретические моменты 79
Глава пятая. Закон больших чисел Р2
§ 1. Неравенство Чебышева 82
§ 2. Теорема Чебышева 85
3
Глава шестая. Функции и плотности распределения вероятнос-
вероятностей случайных величин 87
§ 1. Функция распределения вероятностей случайной ве-
величины 87
§ 2. Плотность распределения вероятностей непрерывной
случайной величины 91
§ 3. Числовые характеристики непрерывных случайных
величин 94
§ 4. Равномерное распределение 106
§ 5. Нормальное распределение 109
§ 6. Показательное распределение и его числогые харак-
характеристики 114
§ 7. Функция надежности 119
Глава седьмая. Распределение функции одного и двух случай-
случайных аргументов " . . 121
S 1. Функция одного случайного аргумента 121
§ 2. Функция двух случайных аргументов 132
Глава восьмая. Системы двух случайных величин 137
§ I. Закон распределения двумерной случайной величины 137
§ 2. Условные законы распределения вероятностей состав-
составляющих дискретной двумерной случайной величины 142
§ 3. Отыскание плотностей и условных законов распре-
распределения составляющих непрерывкой двумерной слу-
случайной величины 144
§ 4. Числовые характеристики непрерывной системы двух
случайных величин 146
Часть третья
Элементы математической статистики
Глава девятая. Выборочный метод 151
§ 1. Статистическое распределение выборки 151
§ 2. Эмпирическая функция распределения 152
§ 3. Полигон и гистограмма 152
Глава десятая. Статистические оценки параметров распределе-
распределения 157
§ 1. Точечные оценки 157
§ 2. Метод моментов 163
§ 3. Метод наибольшего правдоподобия 169
§ 4. Интервальные опенки 174
Глава одиннадцатая. Методы расчета сводных характеристик
выборки 181
§ 1. Метод произведений вычисления выборочных средней
и дисперсии 181
§ 2. Метод сумм вычисления выборочных средней и дис-
дисперсии 184
§ 3. Асимметрия и эксцесс эмпирического распределения 186
Глава двенадцатая. Элементы теории корреляции 190
§ 1. Линейная корреляция 190
4
§ 2. Криволинейная корреляция 196
§ 3. Ранговая корреляция 201
Глава тринадцатая. Статистическая проверка статистических
гипотез 206
§ I. Основные сведения 206
§ 2. Сравнение двух дисперсий нормальных генеральных
совокупностей 207
§ 3. Сравнение исправленной выборочной дисперсии с ги-
гипотетической генеральной дисперсией нормальной со-
совокупности 210
§ 4. Сравнение двух средних генеральных совокупностей,
дисперсии которых известны (большие независимые
выборки) 213
§ 5. Сравнение двух средних нормальных генеральных
совокупностей!! дисперсии которых неизвестны и оди-
одинаковы (малые независимые выборки) 215
§ 6. Сравнение выборочной средней с гипотетической ге-
генеральной средней нормальной совокупности .... 218
§ 7. Сравнение двух средних нормальных генеральных со-
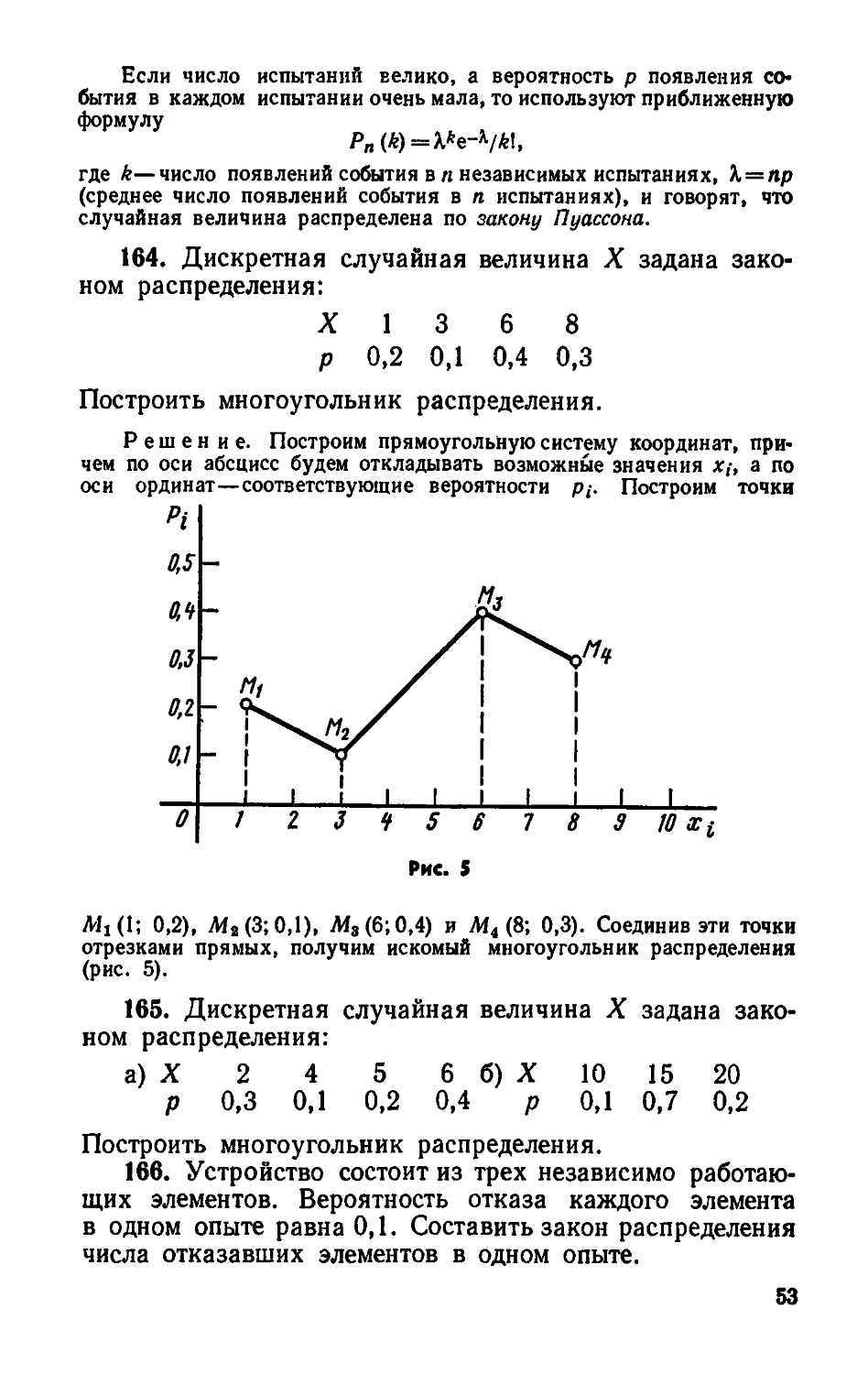
совокупностей с неизвестными дисперсиями (зависи-
(зависимые выборки) 226
§ 8. Сравнение наблюдаемой относительной частоты с ги-
гипотетической вероятностью появления события . . . 229
§ 9. Сравнение нескольких дисперсий нормальных гене-
генеральных совокупностей по выборкам различного
объема. Критерий Бартлетта 231
§ 10. Сравнение нескольких дисперсий нормальных гене-
генеральных совокупностей по выборкам одинакового
объема. Критерий Кочрена 234
§ 11. Сравнение двух вероятностей биномиальных распре-
распределений 237
§ 12. Проверка гипотезы о значимости выборочного коэф-
коэффициента корреляции 239
§ 13. Проверка гипотезы о значимости выборочного коэф-
коэффициента ранговой корреляции Спирмена 244
§ 14. Проверка гипотезы о значимости выборочного коэф-
коэффициента ранговой корреляции Кендалла 246
§ 15. Проверка гипотезы об однородности двух выборок
по критерию Вилкоксона 247
§ 16. Проверка гипотезы о нормальном распределении
генеральной совокупности по критерию Пирсона . . 251
§ 17. Графическая проверка гипотезы о нормальном рас-
распределении генеральной совокупности. Метод спрям-
спрямленных диаграмм 253
§ 18. Проверка гипотезы о показательном распределении
генеральной совокупности 268
§ 19. Проверка гипотезы о распределении генеральной
совокупности по биномиальному закону 272
§ 20. Проверка гипотезы о равномерном распределении
генеральной совокупности 275
§ 21. Проверка гипотезы о распределении генеральной со-
совокупности по закону Пуассона 279
Глава четырнадцатая. Однофакториый дисперсионный анализ 283
6
§ 1. Одинаковое число испытаний на всех уровнях . . . 283
§ 2. Неодинаковое число испытаний на различных уровнях 289
Часть четвертая
Моделирование случайных величин
Глава пятнадцатая. Моделирование (разыгрывание) случайных
величин методом Монте-Карло 294
§ 1. Разыгрывание дискретной случайной величины . . . 294
§ 2. Разыгрывание полной группы событий 295
§ 3. Разыгрывание непрерывной случайной величины. . . 297
§ 4. Приближенное разыгрывание нормальной случайной
величины 302
§ 5. Разыгрывание двумерной случайной величины.... 303
§ 6. Оценка надежности простейших систем методом Мон-
Монте-Карло 307
§ 7. Расчет систем массового обслуживания с отказами
методом Монте-Карло 311
§ 8. Вычисление интегралов методом Монте-Карло .... 317
Часть пятая
Случайные функции
Глава шестнадцатая. Корреляционная теория случайных
функций 330
§ 1. Основные понятия. Характеристики случайных функ-
функций 330
§ 2. Характеристики суммы случайных функций .... 837
§ 3. Характеристики производной от случайной функции 339
§ 4. Характеристики интеграла от случайной функции . . 342
Глава семнадцатая. Стационарные случайные функции .... 347
§ 1. Характеристики стационарной случайной функции 347
§ 2. Стационарно связанные случайные функции 351
§ 3. Корреляционная функция производной от стационар-
стационарной случайной функции 352
§ 4. Корреляционная функция интеграла от стационарной
случайной функции 355
§ 5. Взаимная корреляционная функция дифференцируе-
дифференцируемой стационарной случайной функции и ее производ-
производных 357
§ 6. Спектральная плотность стационарной случайной
функции 360
§ 7. Преобразование стационарной случайной функции
стационарной линейной динамической системой . . . 369
Ответы 373
Приложения 387
ПРЕДИСЛОВИЕ
В настоящем издании помещено более 900 задач, содержание
которых соответствует новой программе для инженерно-технических
в инженерно-экономических специальностей высших учебных заве-
заведений.
В начале каждого параграфа приведены необходимые теорети-
теоретические сведения и формулы; затем даны решения типовых задач и
задачи для самостоятельного решения. Ко всем задачам имеются
ответы, а к части задач — указания.
Автор стремился составить задачи так, чтобы они были доступны
в по возможности не требовали большой затраты времени на вычис-
вычисления. Задачи расположены в порядке постепенного возрастания
трудности их решения. Задачи повышенной трудности отмечены
звездочкой. Последовательность изложения и терминология соответ-
соответствуют пятому изданию книги автора «Теория вероятностей и мате-
математическая статистика».
В связи с включением новых разделов (методы моментов и макси-
максимального правдоподобия, ранговая корреляция, метод Монте-Карло
и его применение к расчету систем массового обслуживания и вы-
вычислению интегралов, случайные функции и др.) добавлено более
300 задач и частично изменена нумерация задач.
Книга предназначена для студентов высших технических учеб-
учебных заведений и для лиц, применяющих вероятностные и статисти-
статистические методы для решения задач практики.
Автор просит читателей присылать свои замечания и предло-
предложения в адрес издательства «Высшая школа».
Огромный труд по сплошной проверке решений задач выполнили
Данилов Г. В. (Ухта) и Солоницын Л. В. (Ухта). Частично прове-
проверили ответы Купчикова Л. М. (Нижний Тагил) и Смирнов И. В.
(Москва). Ценные советы прислали Алиев Г. А. (Баку), Данилов Г. В.,
Кудрявцев В. А. (Ленинград). Подготовить рукопись к печати по-
помогла Пекарь П. Г. Всем названным выше лицам приношу искрен-
искреннюю благодарность.
Особую признательностъ выражаю проф. Судакову Р. С. за ряд
полезных замечаний, способствовавших улучшению книги.
Автор
Часть первая
СЛУЧАЙНЫЕ СОБЫТИЯ
Глава первая
ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
§ 1. Классическое и статистическое
определение вероятности
При классическом определении вероятность события определяет-
определяется равенством
Р(А) = т/п,
где т — число элементарных исходов испытания, благоприятствующих
появлению события А; л—общее число возможных элементарных
исходов испытания. Предполагается, что элементарные исходы обра-
образуют полную группу и равнсвозможны.
Относительная частота события А определяется равенством
где т—число испытаний, в которых событие А наступило; п—общее
число произведенных испытаний.
При статистическом определении в качестве вероятности события
принимают его относительную частоту.
1. Брошены две игральные кости. Найти вероятность того, что
сумма очков на выпавших гранях — четная, причем на грани хотя
бы одной из костей появится шестерка.
Решение. На выпавшей грани «первой» игральной кости мо-
может появиться одно очко, два очка, .... шесть очков. Аналогич-
Аналогичные шесть элементарных исходов возможны при бросании «второй»
кости. Каждый из исходов бросания «первой» кости может сочетать-
сочетаться с каждым из неходов бросания «второй». Таким образом, обшее
число возможных элементарных исходов испытания равно 6-6 = 36.
Эти исходы образуют полную группу и в силу симметрии костей
равловоэможны.
Благоприятствующими интересующему нас событию (хотя бы на од-
одной грани появится шестерка, сумма выпавших очков—четная) явля-
являются следующие пять исходов (первым записано число очков, выпав-
выпавших на «первой» кости, вторым—число очков, выпавших на «второй»
кости; далее найдена сумма очков):
1) 6, 2; 6+2 = 8, 2) 6. 4; 6 + 4=10, 3) 6, 6; 6 |6-12, 4J,6;
2 + 6 = 8, 5) 4, 6; 4 + 6 --10.
Искомая вероятность равна отношению числа исходов, благопри-
благоприятствующих событию, к числу всех возможных элементарных исхо-
исходов: Р 5/36.
2. При перевозке ящика, в котором содержались 21 стандартная
н 10 нестандартных деталей, утеряна одна деталь, причем неизвестно
какая. Наудачу извлеченная (после перевозки) из ящика деталь
оказалась стандартной. Найти вероятиссть того, что была утеряна:
а) стандартная деталь; б) нестандартная деталь.
8
Решение, а) Извлеченная стандартная деталь, очевидно, не
могла быть утеряна; могла быть потеряна любая из остальных 30
детглеЗ B1 + 10—1=30), причем среди них было 20 стандартных
B1—I = 20). Вероятность того, что была потеряна стандартная де-
деталь, Р— 20/30 = 2/3.
б) Среди 30 деталей, каждая из которых могла быть утеряна, бы-
было 10 нестандартных. Вероятность того, что потеряна нестандартная
деталь, Р = 10/30= 1/3.
3. Задумано двузначное число. Найти вероятность
того, что задуманным числом окажется: а) случайно на-
названное двузначное число; б) случайно названное двузнач-
двузначное число, цифры которого различны.
4. Указать ошибку «решения» задачи: брошены две
игральные кости; найти вероятность того, что сумма вы-
выпавших очков равна 3 (событие А).
«Решение». Возможны два исхода испытания: сумма выпавших
очков равна 3, сумма выпавших очков не равна 3. Событию А благо-
благоприятствует один исход; общее число неходов равно двум. Следова-
Следовательно, искомая вероятность Р(Л)=1/2.
Ошибка этого «решения» состоит в том, что рассматриваемые ис-
исходы не являются равновозможными.
Правильное решение. Общее число равновозможных исхо-
исходов равно 6-6=36 (каждое число очков, выпавших на одной кости,
может сочетаться со всеми числами очков, выпавших на другой кости).
Среди этих исходов благоприятствуют событию А только два исхода
(в скобках указаны числа выпавших очков): (Г, 2) н B; 1). Следо-
Следовательно, искомая вероятность Р(Л) = 2/36=1/18.
5. Брошены две игральные кости. Найти вероятности
следующих событий: а) сумма выпавших очков равна семи;
б) сумма выпавших очков равна восьми, а разность —
четырем; в) сумма выпавших очков равна восьми, если
известно, что их разность равна четырем; г) сумма выпав-
выпавших очков равна пяти, а произведение—четырем.
в. Куб, все грани которого окрашены, распилен на
тысячу кубиков одинакового размера, которые затем тща-
тщательно перемешаны. Найти вероятность того, что на)да-
чу извлеченный кубик имеет окрашенных граней: а) одну;
б) две; в) три.
7. Монета брошена два раза. Найти вероятность того,
что хотя бы один раз появится «герб».
8. В коробке шесть одинаковых, занумерованных ку-
кубиков. Наудачу по одному извлекают все кубики. Найти
вероятность того, что номера извлеченных кубиков по-
появятся в возрастающем порядке,
9. Найти вероятность того, что при бросании трех
игральных костей шестерка выпадет на одной (безраз-
лично какой) кости, если на гранях двух других костей
выпадут числа очков, не совпадающие между собой (и
не равные шести).
Решение. Общее число элементарных исходов испытания рав-
равно числу сочетаний из шести элементов по три, т. е. С«.
Число исходов, благоприятствующих появлению шестерки на
одной грани и различного числа очков (не равного шести) на гранях
двух других костей, равно числу сочетаний из пяти элементов по
два, т. е. с\.
Искомая вероятность равна отношению числа исходов, благо-
благоприятствующих интересующему нас событию, к общему числу воз-
возможных элементарных исходов: P=C|/Cj = l/2.
10. В пачке 20 перфокарт, помеченных номерами 101,
102, ... , 120 и произвольно расположенных. Перфора-
торщица наудачу извлекает две карты. Найти вероят-
вероятность того, что извлечены перфокарты с номерами 101
и 120.
11. В ящике 10 одинаковых деталей, помеченных но-
номерами 1, 2, .... 10. Наудачу извлечены шесть дета-
деталей. Найти вероятность того, что среди извлеченных дета-
деталей окажутся: а) деталь № 1; б) детали № 1 и № 2.
Решение, а) Общее число возможных элементарных исходов
испытания равно числу способов, которыми можно извлечь шесть де-
деталей из десяти, т. е. С*о.
Найдем число исходов, благоприятствующих интересующему нас
событию: среди отобранных шести деталей есть деталь № 1 н, сле-
следовательно, остальные пять деталей имеют другие номера. Число
таких исходов, очевидно, равно числу способов, которыми можно
отобрать пять деталей из оставшихся девяти, т.е. С%.
Искомая вероятность равна отношению числа исходов, благопри-
благоприятствующих рассматриваемому событию, к общему числу возможных
элементарных исходов: Р=Св/С"о = с?/С|о=О,6.
б) Число исходов, благоприятствующих интересующему нас со-
событию (среди отобранных деталей есть детали № I и № 2, следо-
следовательно, четыре детали имеют другие номера), равно числу способов,
которыми можно извлечь четыре детали из оставшихся восьми, т. е. С\.
Искомая вероятность Р=С%/С\0— 1/3.
12. В ящике имеется 15 деталей, среди которых 10
окрашенных. Сборщик наудачу извлекает три детали. Най-
Найти вероятность того, что извлеченные детали окажутся
окрашенными.
13. В конверте среди 100 фотокарточек находится
одна разыскиваемая. Из конверта наудачу извлечены 10
карточек. Найти вероятность того, что среди них окажет-
окажется нужная.
Ю
14. В ящике 100 деталей, из них 10 бракованных. На-
Наудачу извлечены четыре детали. Найти вероятность того,
что среди извлеченных деталей: а) нет бракованных; б)
нет годных.
15. Устройство состоит из пяти элементов, из которых
два изношены. При включении устройства включаются
случайным образом два элемента. Найти вероятность того,
что включенными окажутся неизношенные элементы.
16. Набирая номер телефона, абонент забыл последние
три цифры и, помня лишь, что эти цифры различны,
набрал их наудачу. Найти вероятность того, что набра-
набраны нужные цифры
17. В партии из N деталей имеется п стандартных. На-
Наудачу отобраны т деталей. Найти вероятность того, что
среди отобранных деталей ровно k стандартных.
Решение. Общее число возможных элементарных исходов ис-
испытания равно числу способов, которыми можно извлечь т деталей
из Л' деталей, т. е. Cjy—числу сочетаний из Л' элементов по т.
Подсчитаем число исходов, благоприятствующих интересующему
нас событию (среди т деталей ровно к стандартных): к стандартных
деталей можно взять из п стандартных, деталей С* способами; при
этом остальные т—к деталей должны быть нестандартными; взять
же т—к нестандартных деталей из N—я нестандартных деталей
можно С^~* способами. Следовательно, число благоприятствующих
исходов равно CknC^Zkn-
Искомая вероятность равна отношению числа неходов, благо-
благоприятствующих событию, к числу всех элементарных исходов:
18. В цехе работают шесть мужчин и четыре жен-
женщины. По табельным номерам наудачу отобраны семь че-
человек. Найти вероятность того, что среди отобранных
лиц окажутся три женщины.
19. На складе имеется 15 кинескопов, причем 10 из
них изготовлены Львовским заводом. Найти вероятность
того, что среди пяти взятых наудачу кинескопов ока-
окажутся три кинескопа Львовского завода.
20. В группе 12 студентов, среди которых 8 отлич-
отличников. По списку наудачу отобраны 9 студентов. Найти
вероятность того, что среди отобранных студентов пять
отличников.
21. В коробке пять одинаковых изделий, причем три
из них окрашены. Наудачу извлечены два изделия.
Найти вероятность того, что среди двух извлеченных
11
изделий окажутся: а) одно окрашенное изделие; б) два
окрашенных изделия; в) хотя бы одно окрашенное
изделие.
22. В «секретном» замке на общей оси четыре диска,
каждый из которых разделен на пять секторов, на ко-
которых написаны различные цифры. Замок открывается
только в том случае, если диски установлены так, что
цифры на них составляют определенное четырехзначное
число. Найти вероятность того, что при произвольной
установке дисков замок будет открыт.
23. Отдел технического контроля обнаружил пять
бракованных книг в партии из случайно отобранных 100
книг. Найти относительную частоту появления брако-
бракованных книг.
Решение. Относительная частота события А (появление бра-
бракованных книг) равна отношению числа испытаний, о которых по-
появилось событие А, к общему числу произведенных испытаний:
W(A) = 5/100 = 0,05.
24. По цели произведено 20 выстрелов, причем заре-
зарегистрировано 18 попаданий. Найти относительную час-
частоту попаданий в цель.
25. При испытании партии приборов относительная
частота годных приборов оказалась равной 0,9. Найти
число годных приборов, если всего было проверено 200
приборов.
§ 2. Геометрические вероятности
Пусть отрезок / составляет часть отрезка L. На отрезок L на-
наудачу поставлена точка. Если предположить, что вероятность попа-
попадания точки на отрезок / пропорциональна длине этого отрезка и
не зависит от его расположения относительно отрезка /., то веро-
вероятность попадания точки на отрезок / определяется равенством
Р = Длина //Длина L.
Пусть плоская фигура g составляет часть плоской фигуры G.
На фигуру G наудачу брошена точка. Если предположить, что ве-
вероятность попадания брошенной точки на фигуру g пропорциональна
площади этой фигуры и не зависит ии от ее расположения относи-
относительно G, ни от формы g, то вероятность попадания точки в фигуру g
определяется равенством
Р — Площадь g, Площадь G.
Аналогично определяется вероятность попадания точки в про-
пространственную фигуру v, которая составляет часть фигуры V:
Р = Объем f/Объем V.
12
26. На отрезке L длины 20 см помещен меньший от-
отрезок / длины 10 см. Найти вероятность того, что точка,
наудачу поставленная на больший отрезок, попадет
также и на меньший отрезок. Предполагается, что веро-
вероятность попадания точки на отрезок пропорциональна
длине отрезка и не зависит от его расположения.
27. На отрезок О А длины L числовой оси Ох наудачу
поставлена точка В{х). Найти вероятность того, что
меньший из отрезков ОВ и ВА имеет длину, большую,
чем L/3. Предполагается, что вероятность попадания
точки на отрезок пропорциональна длине отрезка и не
зависит от его расположения на числовой оси.
28. В круг радиуса R помещен меньший круг
радиуса г. Найти вероятность того, что точка, наудачу
брошенная в большой круг, попадет также и в малый
круг. Предполагается, что вероятность попадания точки
в круг пропорциональна площади круга и не зависит
от его расположения.
29. Плоскость разграфлена параллельными прямыми,
находящимися друг от друга на расстоянии 2а. На
плоскость наудачу брошена монета радиуса г < а. Найти
вероятность того, что монета не пересечет ни одной из
прямых.
30. На плоскость с нанесенной сеткой квадратов со
стороной а наудачу брошена монета радиуса г<а/2.
Найти вероятность того, что монета не пересечет ни одной
из сторон квадрата. Предполагается, что вероятность по-
попадания точки в плоскую фигуру пропорциональна пло-
площади фигуры и не зависит от ее расположения.
31. На плоскость, разграфленную параллельными пря-
прямыми, отстоящими друг от друга на расстоянии 6 см, на-
наудачу брошен круг радиуса 1 см. Найти вероятность
того, что круг не пересечет ни одной из прямых. Предпо-
Предполагается, что вероятность попадания точки на отрезок
пропорциональна длине отрезка и не зависит от его
расположения.
32. На плоскости начерчены две концентрические
окружности, радиусы которых 5 и 10 см соответственно.
Найти вероятность того, что точка, брошенная наудачу
в большой круг, попадет также и в кольцо, образованное
построенными окружностями. Предполагается, что веро-
вероятность попадания точки в плоскую фигуру пропорцио-
пропорциональна площади этой фигуры и не зависит от ее распо-
расположения.
13
33. Внутрь круга радиуса R наудачу брошена точка.
Найтн вероятность того, что точка окажется внутри впи-
вписанного в круг: а) квадрата; б) правильного треуголь-
треугольника. Предполагается, что вероятность попадания точки
в часть круга пропорциональна площади этой части и
не зависит от ее расположения относительно круга.
34. Быстро вращающийся диск разделен на четное
число равных секторов, попеременно окрашенных в белый
и черный цвет. По диску произведен выстрел. Найти ве-
вероятность того, что пуля попадет в один из белых сек-
секторов. Предполагается, что вероятность попадания пули
в плоскую фигуру пропорциональна площади этой фи-
фигуры.
35. На отрезке ОА длины L числовой оси Ох наудачу
поставлены две точки: В(х) и С (у), причем у^х. (Коор-
(Координата точки С для удобства
дальнейшего изложения обо-
обозначена через у). Найти ве-
вероятность того, что длина
отрезка ВС меньше длины
отрезка ОВ (рис. 1, а). Пред-
Предполагается, что вероятность
попадания точки на отрезок
пропорциональна длине это-
этого отрезка и не зависит от
его расположения на число-
числовой оси.
Решение. Координаты то-
точек В и С должны удовлетворять
неравенствам 0<*<Z.,(Xf/«?L,
у^х. Введем в рассмотрение
прямоугольную систему коорди-
координат хОу. В этой системе указанным
неравенствам удовлетворяют координаты любой точки, принадле-
принадлежащей прямоугольному треугольнику ОКМ (рнс. 1, б). Таким образом,
этот треугольник можно рассматривать как фигуру <?, координаты
точек которой представляют соответственно все возможные значения
координат точек В и С.
Длина отрезка ВС должна быть меньше длины отрезка ОВ, т. е.
должно иметь место неравенство у—х < х, или у < 2х. Последнее
неравенство выполняется для координат тех точек фигуры G (прямо-
(прямоугольного треугольника ОКМ), которые лежат ниже прямой у=2х
(прямая ON). Как видно из рнс. 1, б, все эти точки принадлежат
заштрихованному треугольнику ONM. Таким образом, этот треуголь-
треугольник можно рассматривать как фигуру g, координаты точек которой
являются благоприятствующими интересующему нас событию (длина
отрезка ВС меньше длины отрезка ОВ).
Н
Рис. 1
Искомая вероятность
Р = Пл. g/Пл. С = Пл. ONM/Пл. ОКМ =1/2.
36. На отрезке ОА длины L числовой оси Ох наудачу
поставлены две точки В(х) н С(у). Найти вероятность
того, что длина отрезка ВС меньше расстояния от точки О
до ближайшей к ней точке. Предполагается, что веро-
вероятность попадания точки на отрезок пропорциональна
длине отрезка и не зависит от его расположения на чис-
числовой оси.
37. На отрезке О А длины L числовой оси Ох наудачу
поставлены две точки: В(х) и С (у), причем у^х. Найти
вероятность того, что длина отрезка ВС окажется меньше,
чем L/2. Предполагается, что вероятность попадания
точки на отрезок пропорциональна длине отрезка и не
зависит от его расположения на числовой оси.
38. На отрезке ОА длины L числовой оси Ох наудачу
поставлены две точки: В(х) и С (у). Найти вероятность
того, что длина отрезка ВС окажется меньше, чем L/2.
Предполагается, что вероятность попадания точки на
отрезок пропорциональна длине отрезка и не зависит от
его расположения на числовой оси.
39. Задача Бюффона (французский естествоиспыта-
естествоиспытатель XVIII в.). Плоскость разграфлена параллельными
прямыми, отстоящими друг от друга на расстоянии 2а.
На плоскость наудачу бросают иглу длины 21 (/ < а).
Найти вероятность того, что игла пересечет какую-ни-
какую-нибудь прямую.
a) Q
X
Решение. Введем следующие обозначения: х—расстояние от
середины иглы до ближайшей параллели; <р—угол, составленный
иглой с этой параллелью (рис. 2, а).
Положение иглы полностью определяется заданием определенных
значений х и <р, причем х принимает значения от 0 до а; возможные
15
значения <р изменяются oi 0 до п. Другими словами, середина иглы
может попасть в любую из точек прямоугольника со сторонами а
и я (рис. 2,6). Таким образом, угог прямоугольник можно рас-
рассматривать как фигуру G, точки которой представляют собой все
возможные положения середины иглы. Очевидно, площадь фигуры О
равна да.
Найдем теперь фигуру g, каждая точка которой благоприятствует
интересующему нас событию, т. е каждая точка этой фигуры может
служить серединой иглы, которая пересекает ближайшую к ней
параллель. Как видно из рис. 2, а, игла пересечет ближайшую к ней
параллель при условии *</sin«r, т. е. если середина иглы попадет
в любую из точек фигуры, заштрихованной на рис. 2,6.
Таким образом, заштрихованную фигуру можно рассматривать
как фигуру g. Найдем площадь этой фигуры:
ч я
Пл. g= \ ts\n<fd<f = — /cos<p I =21.
о I»
Искомая вероятность того, что игла пересечет прямую
Р = Пл. g/Пл. 0=2//(ла).
40. На отрезке ОА длины L числовой оси Ох наудачу
поставлены две точки: В(х) и С {у). Найти вероятность
того, что из трех получив-
/Г
н п
6)
В(х) С(у) А х
Рис. 3
все
р у
шихся отрезков можно по-
построить треугольник.
Решение. Для iwо что-
чтобы из трех отрезков можно бы-
было построить треугольник, каж-
каждый из отрезков должен быть
меньше суммы двух других.
Сумма всех грех отрезков равна
L, поэтому каждый из отрезков
должен быть меньше L/2.
Введем в рассмотрение пря-
прямоугольную систему координат
хОу. Координаты любых двух
точек В и С должны удовлетво-
удовлетворять двойным неравенствам:
0<*<L, 0<y<L. Этим
неравенствам удовлетворяют ко-
координаты любой точки М (дг, у),
принадлежащей квадрату OI.DL
(рис. 3, а). Таким образом, этот
квадрат можно рассматривать
как фигуру G, координаты точек
возможные значения координат точек
которой представляют
В и С.
1. Пусть точка С расположена правее точки В (рис. 3,6). Как
указано выше, длины отрезков ОВ,ВС,СА должны быть меньше Z./2,
т. е. должны иметь место неравенства х < Z./2, у—х < Z./2, L—у <
< L/2, или, что то же,
х < L/2, у < х-|-L/2, у > L/2. (*)
16
2. Пусть точка С расположена левее точки В (рис. 3, в). В этом
случае должны нметь место неравенства у < L/2, х—у < Z./2, L —
— х< L/7, илн, что то же,
у < L/2, у > х—Ш, х > L/2. (««)
Как видно ил рис. 3. а, неравенства (•) выполняются для коор-
координат точек треугольника EFH, а неравенства (•*) — для точек
треугольника КНМ. Таким образом, заштрихованные треугольники
можно рассматривать как фигуру g. координаты точек которой
благоприятствуют интересующему нас событию (из трех отрезков
можно построить треугольник).
Искомая вероятность
Р = Пл. g/Пл. G= (Пл. Д EFH+ Пл. Д КНМ)/Пл. UOLDL= 1/4.
41. В сигнализатор поступают сигналы от двух уст-
устройств, причем поступление каждого из сигналов равно-
возможмо в любой момент промежутка времени длитель-
длительностью Т. Моменты поступления сигналов независимы
один or другого. Сигнализа-
Сигнализатор срабатывает, если разность
между моментами поступления
сигналоп меньше / (/ < Г). Най-
Найти вероятность того, чго сиг-
сигнализатор срабатывает за вре-
время Т, если каждое из уст-
устройств пошлет но одному сиг-
сигналу.
Решение. Обозначим момен-
моменты поступления сигналов первого
и второго устройств соответствен- рне, 4
но через х и у. В силу условия
задачи должны выполняться двойные неравенства: 0<дг<Т,
0<i/<7\
Введем в рассмотрение прямоугольную систему координат хОу.
В этой системе двойным неравенствам (гдовлетворяют координаты
любой точки, принадлежащей квадрату ОТ AT (рис. 4). Таким обра-
образом, этот квадрат можно рассматривать как фигуру G, координаты
точек которой представляют все возможные значения моментов по-
поступления сигналов.
Сигнализатор срабатывает, если разность между моментами
поступления сигналов меньше /, т. е. если у—х < / при у > х н
х—у < I прн х > у, или, что то же,
у<х + 1 при у>х, (*)
y>x—t при у<х. (««)
Неравенство (*) выполняется для координат тех точек фигуры G,
которые лежат выше прямой у = х и ниже прямой у—х-\-1; нера-
неравенство (**) имеет место для точек, расположенных ниже прямой
у — х и выше прямой y = x—t.
Как видно из рис. 4, все точки, координаты которых удовлет-
удовлетворяют неравенствам (•) и (**) принадлежат заштрихованному
17
шестиугольнику. Таким образом, этот шестиугольник можно рас-
рассматривать как фигуру g, координаты точек которой являются бла-
благоприятствующими срабатыванию сигнализатора моментами времени
х и у.
Искомая вероятность
—2 (T—i)*/2_t BT—t)
42. Задача о встрече. Два студента условились встре-
встретиться в определенном месте между 12 и 13 часами дня.
Пришедший первым ждет второго в течение 1/4 часа,
после чего уходит. Найти вероятность того, что встреча
состоится, если каждый студент наудачу выбирает момент
своего прихода (в промежутке от 12 до 13 часов).
43*. Найти вероятность того, что из трех наудачу
взятых отрезков длиной не более L можно построить
треугольник. Предполагается, что вероятность попадания
точки в пространственную фигуру пропорциональна
объему фигуры и не зависит от ее расположения.
Указание. Ввести в рассмотрение пространственную систему
координат.
44. Наудачу взяты два положительных числа х и у,
каждое из которых не превышает двух. Найти вероят-
вероятность того, что произведение ху будет не больше единицы,
а частное у/х не больше двух.
45. Наудачу взяты два положительных числа хну,
каждое из которых не превышает единицы. Найти веро-
вероятность того, что сумма х + у не превышает единицы,
а произведение ху не меньше 0,09.
Глава вторая
ОСНОВНЫЕ ТЕОРЕМЫ
§ 1. Теоремы сложения и умножения вероятностей
Теорема сложения вероятностей несовместных событий. Вероят-
Вероятность появления одного из двух несовместных событий, безразлично
какого, равна сумме вероятностей этих событий:
Следствие. Вероятность появления одного из нескольких по-
попарно несовместных событий, безразлично какого, равна сумме веро-
вероятностей этих событий:
18
Теорема сложения вероятностей совместных событий. Вероят-
Вероятность появления хотя бы одного из двух совместных событий равна
сумме вероятностей этих событий без вероятности их совместного
появления:
Р (А + В) = Р (А) + Р (В)-Р (АВ).
Теорема может быть обобщена на любое конечное число сов-
совместных событий. Например, для трех совместных событий
+ +) () + () +
+ Р(С)~Р (АВ)—Р (АС)—Р (ВС) + Р (ABC).
Теорема умножения вероятностей. Вероятность совместного по-
появления двух событий равна произведению вероятности одного из
них на условную вероятность другого, вычисленную в предположении,
что первое событие уже наступило:
Р(АВ) = Р(А)РА(В).
В частности, для независимых событий
Р(АВ) = Р(А)Р(В),
т. е. вероятность совместного появления двух независимых событий
равна произведению вероятностей этих событий.
Следствие. Вероятность совместного появления нескольких
событий равна произведению вероятности одного из них на условные
вероятности всех остальных, причем вероятность каждого последую-
последующего события вычисляют в предложении, что все предыдущие собы-
события уже наступили:
... Ап) = Р (At)P А,Ш-Р A,A*(Ab) ••• Р АгА,... А^^Ап),
где Pa,Ai... An-i Мп)—вероятность события Ап, вычисленная в пред-
предположении, что события Alt A2, .... Ап-г наступили.
В частности, вероятность совместного появления нескольких
событий, независимых в совокупности, равна произведению вероят-
вероятностей этих событий:
P(A1At... Ап) = Р(Аг)-РШ ...Р (Ап).
46. На стеллаже библиотеки в случайном порядке
расставлено 15 учебников, причем пять из них в пере-
переплете. Библиотекарь берет наудачу три учебника. Найти
вероятность того, что хотя бы один из взятых учебников
окажется в переплете (событие А).
Решение. Первый способ. Требование—хотя бы один
из трех взятых учебников в переплете—будет осуществлено, если
произойдет любое из следующих трех несовместных событий: В—один
учебник в переплете, С—два учебника в переплете, D—три учеб-
учебника в переплете.
Интересующее нас событие А можно представить в виде суммы
событий: A = B + C + D. По теореме сложения,
P(A) = P(B)+P(C) + P(D). (•)
19
Найдем вероятности событий В, С и D (см. решение задачи 17.
гл. I. f 1):
Р (B) = Cic!o/Ci8 = 45/91, P (С) = С!С1Ш'С?5=2О.'91,
Подставив эти вероятности в равенство (*), окончательно по-
получим
р (А) = 45/91 + 20/9! +2/91 = 67/91.
Второй способ. События А (хотя бы один из взятых трех
учебников имеет переплет) и А (ни один из взятых учебников не
имеет переплета) —противоположные, поэтому Р(А)~-Р(А)~ I
(сумма вероятностей двух противоположных событий раина единице).
Отсюда Р(А) = \—Р (А).
Вероятность появления события А (ни один из взятых учебников
не имеет переплета)
Р (Л) = С?о/С?5 = 24/91.
Искомая вероятность
р (А) = 1 —Р (А) = 1 —24/91 = 67/91.
47. В ящике 10 деталей, из которых четыре окрашены.
Сборщик наудачу взял три детали. Найти вероятность
того, что хотя бы одна из взятых деталей окрашена.
48. Доказать, что если событие А влечет за собой
событие В, то Р(В)^Р(А).
Решение. Событшг В можно представить в виде суммы несои-
местных событий А и А В: _
В=А\АВ.
По теореме сложения вероятностей несовместных событий по-
получим _ _
Р (В) = Р (А + АВ) = Р (А) + Р (АВ).
Так как P(AB)Ss>0, то Р(В)^Р(А).
49. Вероятности появления каждого из двух незави-
независимых событий Л, и Аг соответственно равны pY и р3.
Найти вероятность появления только одного из этих
событий.
Решение. Введем обозначения событий: В\ — появилось только
событие А\\ В%— появилось только событие Аг. _
Появление события Вх равносильно появлению события AxAt
(появилось первое событие и не появилось второе), т. е. Вх —AxAi.
Появление события Bt равносильно появлению события AtA2 (по-
(появилось второе событие и не появилось первое), т. е. #2=<4i-42.
Таким образом, чтобы найти вероятность появления только
одного из событий А\ и А2, достаточно найтн вероятность пояиления
одного, безразлично какого, из событий Bt и Bt. События BL и В3
20
несовместны, поэтому применима теорема сложения:
Остается найти вероятности каждого из событий Вх и В2. События
Ах и Аг ^независимы, следовательно, независимы события Ах и А%,
а также Ал и At, поэтому применима теорема умножения:
Подставив эти вероятности в соотношение (¦), найдем искомую
вероятность появления только одного из событий А{ и Aj.
P(Bl---Bi)---piqt-\-q,pt.
50. Для сигнализации об аварии установлены два
независимо работающих сигнализатора. Вероятность того,
что при аварии сигнализатор сработает, равна 0,95 для
первого сигнализатора и 0,9 для второго. Найти веро-
вероятность того, что при аварии сработает только один
сигнализатор.
51. Два стрелка стреляют по мишени. Вероятность
попадания в мишень при одном выстреле для первого
стрелка равна 0,7, а для второго—0,8. Найти вероят-
вероятность того, что при одном залпе в мишень попадает
только один из стрелков.
52. Вероятность одного попадания в цель при одном
залпе из двух орудий равна 0,38. Найти вероятность
поражения цели при одном выстреле первым из орудий,
если известно, что для второго орудия эта вероятность
равна 0,8.
53. Отдел технического контроля проверяет изделия
на стандартность. Вероятность того, что изделие стан-
стандартно, равна 0,9. Найти вероятность того, что из двух
проверенных изделий только одно стандартное.
54. Вероятность того, что при одном измерении неко-
некоторой физической величины будет допущена ошибка,
превышающая заданную точность, равна 0,4. Произведены
три независимых измерения. Найти вероятность того,
что только в одном из них допущенная ошибка превысит
заданную точность.
55. Из партии изделий товаровед отбирает изделия
высшего сорта. Вероятность того, что наудачу взятое
изделие окажется высшего сорта, равна 0,8. Найти веро-
вероятность того, что из трех проверенных изделий только
два изделия высшего сорта.
21
56. Устройство состоит из трех элементов, работающих
независимо. Вероятности безотказной работы (за время /)
первого, второго и третьего элементов соответственно
равны 0,6; 0,7; 0,8. Найти вероятности того, что за
время t безотказно будут работать: а) только один эле-
элемент; б) только два элемента; в) все три элемента.
57. Вероятности того, что нужная сборщику деталь
находится в первом, втором, третьем, четвертом ящике,
соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероят-
вероятности того, что деталь содержится: а) не более чем в трех
ящиках; б) не менее чем в двух ящиках.
58. Брошены три игральные кости. Найти вероятности
следующих событий: а) на каждой из выпавших граней
появится пять очков; б) на всех выпавших гранях по-
появится одинаковое число очков.
59. Брошены три игральные кости. Найти вероятности
следующих событий: а) на двух выпавших гранях поя-
появится одно очко, а на третьей грани—другое число очков;
б) на двух выпавших гранях появится одинаковое число
очков, а на третьей грани—другое число очков; в) на
всех выпавших гранях появится разное число очков.
60. Сколько надо бросить игральных костей, чтобы
с вероятностью, меньшей 0,3, можно было ожидать, что
ни на одной из выпавших граней не появится шесть
очков?
Решение. Введем обозначения событий: А—нн на одной из
выпавших граней не появится 6 очков; А,-—на выпавшей грани <-й
кости (( = 1,2, ..., п) не появится 6 очков.
Интересующее нас событие А состоит в совмещении событий
Аи А2, .... А„, т. е. A~AiAt ... Ап.
Вероятность того, что на любой выпавшей грани появится число
очков, не равное шести, равна Р(А/) — 5/6.
События А; независимы в совокупности, поэтому применима
теорема умножения:
По условию, E/6)" < 0,3. Следовательно, п log E/6) < log 0,3.
Отсюда, учитывая, что log E/6) < 0, найдем: п > 6,6. Таким образом,
искомое число игральных костей л За 7.
61. Вероятность попадания в мишень стрелком при
одном выстреле равна 0,8. Сколько выстрелов должен
произвести стрелок, чтобы с вероятностью, меньшей 0,4,
можно было ожидать, что не будет ни одного промаха?
62. В круг радиуса R вписан правильный треугольник.
Внутрь круга наудачу брошены четыре точки. Найти
22
вероятности следующих событий: а) все четыре точки
попадут внутрь треугольника; б) одна точка попадет
внутрь треугольника и по одной точке попадет на каж-
каждый «малый» сегмент. Предполагается, что вероятность
попадания точки в фигуру пропорциональна площади
фигуры и не зависит от ее расположения.
63. Отрезок разделен на три равные части. На этот
отрезок наудачу брошены три точки. Найти вероятность
того, что на каждую из трех частей отрезка попадает
по одной точке. Предполагается, что вероятность попада-
попадания точки на отрезок пропорциональна длине отрезка
и не зависит от его расположения.
64. В читальном зале имеется шесть учебников по
теории вероятностей, из которых три в переплете. Библио-
Библиотекарь наудачу взял два учебника. Найти вероятность
того, что оба учебника окажутся в переплете.
Решение. Введем обозначения событий: А—первый взятый
учебник имеет переплет, В—второй учебник имеет переплет. Веро-
Вероятность того, что первый учебник имеет переплет, Р (А) = 3/6= 1/2.
Вероятность того, что второй учебник имеет переплет, при усло-
условии, что первый взятый учебник был в переплете, т. е. условная
вероятность события В, такова: Рд(В) — 2,5.
Искомая вероятность того, что оба учебника имеют переплет, по
теореме умножения вероятностей событий равна
Р (АВ) = Р (А) РА (В) = 1/2-2/5=0,2.
65. Среди 100 лотерейных билетов есть 5 выигрыш-
выигрышных. Найти вероятность того, что 2 наудачу выбранные
билета окажутся выигрышными.
66. В цехе работают семь мужчин и три женщины.
По табельным номерам наудачу отобраны три человека.
Найти вероятность того, что все отобранные лица ока-
окажутся мужчинами.
Решение. Введем обозначения событий: А—первым отобран
мужчина; В—вторым отобран мужчина, С—третьим отобран муж-
мужчина. Вероятность того, что первым будет отобран мужчина,
Р (Л) = 7/10.
Вероятность того, что вторым отобран мужчина, при условии,
что первым уже был отобран мужчина, т. е. условная вероятность
события В следующая: Рд (В) = 6/9 = 2,3.
Вероятность того, что третьим будет отобран мужчина, при усло-
условии, что уже отобраны двое мужчин, т. е. условная вероятность
события С такова: РАЯ(С) = 5,8.
Искомая вероятность того, что все три отобранных лица ока-
окажутся мужчинами,
Р(АВС) = Р (А)РА(В)РАВ (С) = 7/10-2/3-5/8 = 7/24.
23
67. В ящике 10 деталей, среди которых шесть окра-
окрашенных. Сборщик наудачу извлекает четыре детали.
Найти вероятность того, что все извлеченные детали
окажутся окрашенными.
68. В урне имеется пять шаров с номерами от 1 до 5.
Наудачу по одному извлекают три шара без возвращения.
Найти вероятности следующих событий: а) последова-
последовательно появятся шары с номерами 1, 4, 5; б) извлеченные
шары будут иметь номера 1, 4, 5 независимо от того,
в какой последовательности они появились.
69. Студент знает 20 из 25 вопросов программы. Найти
вероятность того, что студент знает предложенные ему
экзаменатором три вопроса.
70. В мешочке содержится 10 одинаковых кубиков
с номерами от 1 до 10. Наудачу извлекают по одному
три кубика. Найти вероятность того, что последовательно
появятся кубики с номерами 1, 2, 3, если кубики из-
извлекаются: а) без возвращения; б) с возвращением (из-
(извлеченный кубик возвращается в мешочек).
71. По данным переписи населения A891 г.) Англии
и Уэльса установлено: темноглазые отцы и темноглазые
сыновья (А В) составили 5% обследованных лиц, темно-
темноглазые отцы и светлоглазые сыновья (АВ) — 7,9%, свет-
светлоглазые отцы и темноглазые сыновья (АВ)-— 8,9%, свет-
светлоглазые отцы и светлоглазые сыновья (АВ)—78,2%.
Найти связь между цветом глаз отца и сына.
_Решение. JTo услопию, Я (АВ) =0,05; Р (.АВ) =0,079;
Р(АВ) =0,089; Р (АВ) = 0,782.
Найдем условную вероятность того, что сын темноглазый, если
отец темноглазый:
р (н\ Р{АВ) Р(ЛД> Q-05 mo
Рл{В) —РТЛТ-Р(АВ)* -Я (^-0,05-t-0.079-°'39-
Найдем условную вероятность того, что сын светлоглазый, если
отец темноглазый:
РА (В) = 1 — ЯА (В) = 1 —0,39 =г.0,61.
Найдем условную вероятность того, что сын темноглазый, если
отец светлоглазый:
р (В) Р{1В)- Р(А~В) °>Ш 0 102
* W Я (А) ~Р (АВ) 4 Р (АёГ°№+ 0782-О>1^-
Найдем условную вероятность того, что сын светлоглазый, если
отец светлоглазый: _
Ят (В) -1 -Я- (В) --. I -0,102-0,898.
24
72. Найти вероятность Р (А) по данным вероятностям:
Р (ЛЯ) = 0,72, Р (.45) = 0,18.
Решение. Событие А можно представить в виде суммы сле-
следующих доух несовместных событий: А — АВ ¦- АВ. По теореме сло-
сложения вероятностей несовместных событий получим
Р(А) = Р(АВ~ АВ)-=Р(АВ) г Р(АВ) = 0,72 + 0,18 = 0,9.
73. Найти вероятность Р(АВ) по данным вероятнос-
вероятностям: Р(А) = а, Р(В)^-Ь, Р(А+В) = с.
Решение. Используя тождество Р (А)~-Р (АВ) \-Р (АЪ),
найдем
Р(АВ)^Р(А)-Р(АВ)=-а-Р(АВ). (*)
Из равенства Я (А ;- В) — Р (А) ¦¦¦ Р {В) —Р (АВ) выразим Р (АВ):
Р(АВ)=Р(А) + Р(В)-Р(А\ В), а ; Ь—с. (**)
Подставив (**) в (*), получим
Р (АВ) ~-а—(а-\-Ь—О=с—Ь.
74. Найти вероятность Р(АВ) по данным вероят-
вероятностям:
Решение. Используя тождество Я (В) = Р (АЪ) + Я (АВ).
найдем Я (АВ):
Р (АВ)=-Р (В)—Р (АВ) - (I — Ь)-Р (АВ).
Подставив в последнее равенство Р(АВ) = с—Ь (см. задачу 73),
получим
Р (АН) ----1 -Ь— (с-Ь) = 1 — с.
75. Наступление события А В необходимо влечет на-
наступление события С. Доказать, что Р(А) + Р(В) —
Р(С)<1
()<
Решение. По условию, наступление события АВ влечет
наступление события С, поэтому (см. задачу 48)
Используя тождества
Р(А) = Р(АВ)-\ Р(АВ), Р(В) = Р(АВ)-\ Р(АВ),
Р (АВ) f Я (АВ)-\-Р (Ifi) = 1 — Р (АВ~)
и учитывая неравенство (*), получим
Р(А) + Р (В)-Р (С)<,[Р (AB)J-P (АВ)\\ [Р (АВ)-\-Р(АВ)]~
—Я (ЛВ) =-- Р (АВ) г Я (АЪ)-\-Р (Лй)= ! — Р (АВ) < 1.
25
Замечание. Рекомендуем читателю самостоятельно убедиться,
что и в частном случае, когда С = АВ, справедливо неравенство
Р(А)+Р(В)-Р(АВ)<,\.
76. Доказать, что
Предполагается, что Р (А) > 0.
Решение. В силу замечания к задаче 75 справедливо нера-
неравенство
Воспользуемся тождествами
Р(АВ)=Р(А)-РА(В), Я(б) = 1-Я(б). (**)
Подставив (**) в (*), получим
или _
Р(А).РА(В)^Р(А)-Р(В).
Разделив обе части неравенства на положительное число Я (А),
окончательно имеем
77. Наступление события ABC необходимо влечет
наступление события D. Доказать, что
) — P(D)<2.
Решение. По условию, наступление события ABC необхо-
необходимо влечет наступление события D, следовательно (см. задачу 48),
Р (D)^P (ABC). Таким образом, если будет доказано неравенство
Р(А)-тР(В)-\Р(С)-Р(АВС)<к2, (*)
то будет справедливо и неравенство, указанное в условии задачи.
Докажем неравенство (*). Воспользуемся тождествами:
Я (А)-=Р (АВС)-.-Р (АВС)---Р (АВС)-\-Р (ABC),
) = Р (ABC)-
Р(АВС)+-Р (ABQ-
Р (ABC,-, P (ABC) \
Р (ABC),
-Р (ABC).
Г)
Из трех событий А, В, С можно составить следующую полную
группу «сложных событий», состоящих из появлений и непоявлений
рассматриваемых трех событий:
ABC—появились все три события,
~АВС, ABC, ABC—появились два события, а третье не появи-
появилось,
ABC, ABC, ABC—появилось одно событие, а два других не
появились,
ABC—не появились все три события.
26
Сумма вероятностей событий, образующих полную группу, равна
единице, поэтому
Р (АВС) + Р(АВС)+Р (АВС)+Р (АВС) +
+ Р (ABQ + P (АВС)+Р (АВС)+Р (АВС)= I.
Отсюда
Р (АВС) + Р (АВС) + Р (АЪС)±Р (АВС) =
= 1—[Я (ifiC)-f Р (АВС)+Р (АВС) + Р (ABC)]. (***)
Подставив (**) в (*) и используя (***), после упрощений получим
Я (А) + Р (В) + Р (С)—Р (АВС) =
=2—[2Я (АВС)-\-Р (АВС)+Р (АВС~) + Р (ABC)].
Учитывая, что каждое слагаемое в квадратной скобке неотри-
неотрицательно, окончательно получим
Р (А)+Р {В) + Р (С)-Р (Z>)<2.
78. Вывести теорему сложения вероятностей для трех
совместных событий:
— Р (АВ) — Р{АС)—Р (ВС) + Р(АВС).
Предполагается, что для двух совместных событий тео-
теорема сложения уже доказана:
Решение. Сведем сумму трех событий к сумме двух событий:
А + В+С = (А + В)-\-С.
Воспользуемся теоремой сложения вероятностей двух событий:
(С)-Р
= Р (А + В) + Р (С)-Р
Применим теорему сложения вероятностей двух совместных со-
событий дважды (для событий А и В, а также для событий АС и ВС):
Р (A J-S+C) = P (А)-1-Я (S)-P (АВ)+Р (О-
-{Р (АС)-гР (ВС) - Р [(АС) (ВС)]).
Учитывая, что Р [(AC) (BC)]=P (ABC), окончательно получим
Р (А + В+С) = Р (А) + Р (В)+Р (О-
— Р(АВ)—Р (АС)—Р (ВС)+Р (ABC).
79*. Даны три попарно независимых события А, В, С,
которые, однако, все три вместе произойти не могут.
Предполагая, что все они имеют одну и ту же вероят-
вероятность р, найти наибольшее возможное значение р.
_Реше_ние. Первый способ. По условию Р (ABC) = Ot
Р(А) = Р(В) = Р(С)=1-р, Р(АВ)=Р(А)Р(В) =
27
Найдем вероятности каждого из следующих событий, образую-
образующих полную группу:
АЪС, ВЖ, CAB, ABC, АСВ, ВСА, ABC, ~АВС.
Для того чтобы найти вероятность события ABC, представим
событие АВ в виде суммы двух несовместных событий: АВ = ABC -i-
-f ABC. По теореме сложения,
Р (АВ) = Р (АВС):\-Р (АВС~).
Отсюда
Аналогично найдем _ _
Р(АСВ) = Р(ВСА)=рг.
Для того чтобы найти вероятность события ABC, представим
событие АВ в виде суммы двух несовместных событий: АВ=АЪС-\-АЪс.
По теореме сложения, _ _
Р (АВ) = Р (ABQ-YP (АЪС).
Отсюда
() —Р
Аналогично найдем
Р (В~АС)=Р
Найдем вероятность события ABC: для этого достаточно вы-
вычесть из единицы сумму вероятностей остальных событий, образую-
образующих полную группу:
Я (ЛЙГ) = 1-[3<р-2ргН-Зр*] = 3р*-3р+1.
Учитывая, что любая вероятность заключена между нулем и
единицей, потребуем, чтобы все найденные вероятности удовлетво-
удовлетворяли этому условию:
] 0<р-2р*<1, (*)
{ 0<Зрг-Зр+1<1.
Решив каждое из неравенств системы, найдем соответственно:
0<р<1, 0<р<1/2, 0<р<1.
Таким образом, наибольшее возможное значение р, которое
удовлетворяет всем трем неравенствам системы (*), равно 1/2.
Второй способ. Введем обозначение Р (А-\-В-\-С) = к.
Пользуясь теоремой сложения для трех совместных событий и учи-
учитывая, что Р(А) = Р{В) = Р(С) = р, Р(АВ) = Р{АС) = Р(ВС) = р*,
Р(АВС) = 0, получим
* = Я (А) + Р (ВL-Р (С)—Р (АВ) — Р (АС) —
— Я (ВС) ^-Р (АВС) = Зр—Зр2.
Решив это уравнение относительно р, получим
р = A ± У I — 4*/3)/2.
Если р = A— у I — 4*/3)/2, то р достигает максимального зна-
значения р=1/2 (при * = 3/4).
28
Если p = (l-L У\—4Аг/3)/2, то, на первый взгляд, р^ 1/2.
Покажем, что допущение р > 1/2 приводит к противоречию. Дейст-
Действительно, р > 1/2 при условии, что 1— 4А/3 > 0, или, так как
А = 3р—Зр-, прн условии, что ра —р+1/4 > 0. Отсюда
р= 1/2 ± |/"j/4— '/4 = 1/2.
Итак, наибольшее возможное значение р= 1/2.
§ 2. Вероятность появления хотя бы одного события
Пусть события Аи Аг А„ независимы в совокупности,
причем P(Ai) = pt, Я(/4») = р , Р(А„)-=р„, пусть в результате
испытания могут наступить гее события, либо часть из них, либо
HI! ОДНО ИЗ НИХ.
Вероятность наступления события А, состоящего в появлении
хотя бы одного из событий А\, Аг, •••, А„, независимых в совокуп-
совокупности, равна разности между единицей и произведением вероятно-
вероятностей противоположных событий Аи Аг, ..., Ап:
В частности, если все я событий имеют одинаковую вероят-
вероятность, равную р, то вероятность появления хотя бы одного из этих
событий
Р (Л> I .. qn-
80. В электрическую цепь последовательно включены
три элемента, работающие независимо один от другого.
Вероятности отказов первого, второго и третьего эле-
элементов соответственно равны: /7, =0,1; />, = 0,15; р3 = 0,2.
Найти вероятность того, что тока в цепи не будет.
Решение. Элементы включены последовательно, поэтому тока
в цепи не будет (событие А), если откажет хотя бы один из элементов.
Искомая вероятность
l-(l -0,1) A -0,15) A-0,2) = 0,388.
81. Устройство содержит два независимо работающих
элемента. Вероятности отказа элементов соответственно
равны 0,05 и 0,08. Найти вероятности отказа устрой-
устройства, если для этого достаточно, чтобы отказал хотя бы
один элемент.
82. Для разрушения моста достаточно попадания одной
авиационной бомбы. Найти вероятность того, что мост
будет разрушен, если на него сбросить четыре бомбы,
вероятности попадания которых соответственно равны:
0,3; 0,4; 0,6; 0,7.
83. Три исследователя, независимо один от другого,
производят измерения некоторой физической величины.
29
Вероятность того, что первый исследователь допустит
ошибку при считывании показаний прибора, равна 0,1.
Для второго и третьего исследователей эта вероятность
соответственно равна 0,15 и 0,2. Найти вероятность того,
что при однократном измерении хотя бы один из иссле-
исследователей допустит ощибку.
84. Вероятность успешного выполнения упражнения
для каждого из двух спортсменов равна 0,5. Спортсмены
выполняют упражнение по очереди, причем каждый делает
по две попытки. Выполнивший упражнение первым полу-
получает приз. Найти вероятность получения приза спорт-
спортсменами.
Решение. Для вручения приза достаточно, чтобы хотя бы
одна из четырех попыток была успешной. Вероятность успешной
попытки р = 0,5, а неуспешной q=\—0,5 = 0,5. Искомая вероятность
Р = 1 _ q*= 1 —0,5*=0,9375.
85. Вероятность попадания в мишень каждым из двух
стрелков равна 0,3. Стрелки стреляют по очереди, причем
каждый должен сделать по два выстрела. Попавший
в мишень первым получает приз. Найти вероятность того,
что стрелки получат приз.
86. Вероятность хотя бы одного попадания стрелком
в мишень при трех выстрелах равна 0,875. Найти вероят-
вероятность попадания при одном выстреле.
Решение. Вероятность попадания в мишень хотя бы при
одном из трех выстрелов (событие А) равна
Р(Л)=1-<Д
где q — вероятность промаха.
По условию, Я (Л) = 0,875. Следовательно,
0,875=1—9», или <?» = 1—0,875 = 0,125.
Отсюда q= ^/0,125=0,5.
Искомая вероятность
р=1— 9=1—0,5 = 0,5.
87. Вероятность хотя бы одного попадания в цель
при четырех выстрелах равна 0,9984. Найти вероятность
попадания в цель при одном выстреле.
88. Многократно измеряют некоторую физическую
величину. Вероятность того, что при считывании показа-
показаний прибора допущена ошибка, равна р. Найти наимень-
наименьшее число измерений, которое необходимо произвести,
чтобы с вероятностью Р > а можно было ожидать, что
хотя бы один результат измерений окажется неверным.
30
§ 3. Формула полной вероятности
Вероятность события А, которое может наступить лишь при
появлении одного из несовместных событий (гипотез) Blt Вг,..., Вп,
образующих полную группу, равна сумме произведений вероятно-
вероятностей каждой из гипотез на соответствующую условную вероятность
события А:
Р(А) = Р (Вд-Рв, (А) + Р (Вг)-Рв,(А)+--- + Р(В„)Рвп(А), (•)
где Р (Вг)+Р (Вг) + ... +Р (В„) = 1.
Равенство (*) называют формулой полной вероятности.
89. В урну, содержащую два шара, опущен белый
шар, после чего из нее наудачу извлечен один шар.
Найти вероятность того, что извлеченный шар окажется
белым, если равновозможны все возможные предположе-
предположения о первоначальном составе шаров (по цвету).
Решение. Обозначим через А событие—извлечен белый шар.
Возможны следующие предположения (гипотезы) о первоначальном
составе шаров: В\—белых шаров нет, Вг—один белый шар, В3 —
два белых шара.
Поскольку всего имеется три гипотезы, причем по условию они
равновероятны, и сумма вероятностей гипотез равна единице (так
как они образуют полную группу событий), то вероятность каждой
из гипотез равна 1/3, т. е. Р (В{)=Р F2) = Я (Вя) = 1/3.
Условная вероятность того, что будет извлечен белый шар, при
условии, что первоначально в урие не было белых шаров, Яд, (A) = 1/3.
Условная вероятность того, что будет извлечен белый шар,
при условии, что первоначально в урне был одни белый шар,
p(A)m
)m
словная вероятность того, что будет извлечен белый шар, при
условии, что первоначально в урне было два белых шара
РвЛЛ) = 3/3=1.
Искомую вероятность того, что будет извлечен белый шар,
находим по формуле полной вероятности:
Р (А)=Р (S,)-PBl (A) + P (Вг)-РВ,(А) +
90. В урну, содержащую п шаров, опущен белый
шар, после чего наудачу извлечен один ш?р. Найти
вероятность того, что извлеченный шар окажется белым,
если равновозможны все возможные предположения о пер-
первоначальном составе шаров (по цвету).
91. В вычислительной лаборатории имеются шесть
клавишных автоматов и четыре полуавтомата. Вероят-
Вероятность того, что за время выполнения некоторого расчета
автомат не выйдет из строя, равна 0,95; для полуавто-
полуавтомата эта вероятность равна 0,8. Студент производит рас-
расчет на наудачу выбранной машине. Найти вероятность
31
того, что до окончания расчета машина не выйдет из
строя.
92. В пирамиде пять винтовок, три из которых снаб-
снабжены оптическим прицелом. Вероятность того, что стре-
стрелок поразит мишень при выстреле из винтовки с опти-
оптическим прицелом, равна 0,95; для винтовки без оптиче-
оптического прицела эта вероятность равна 0,7. Найти вероятность
того, что мишень будет поражена, если стрелок произве-
произведет один выстрел из наудачу взятой винтовки.
93. В ящике содержится 12 деталей, изготовленных
на заводе № I, 20 деталей —на заводе № 2 и 18 дета-
деталей— на заводе № 3. Вероятность того, что деталь, изго-
изготовленная на заводе № 1, отличного качества, равна 0,9;
для деталей, изготовленных на заводах N° 2 и № 3, эти
вероятности соответственно равны 0.6 и 0,9. Найти
вероятность того, что извлеченная наудачу деталь ока-
окажется отличного качества.
94. В первой урне содержится 10 шаров, из них 8
белых; во второй урне 20 шаров, из них 4 белых. Из
каждой урны наудачу извлекли по одному шару, а затем
из этих двух шаров наудччу взят один шар. Найти
вероятность того, что взят белый шар.
95. В каждой из трех урн содержится 6 черных и 4
белых шара. Из первой урны наудачу извлечен один
шар и переложен во вторую урну, после чего из вто-
второй урны наудачу извлечен один шар и переложен
в третью урну. Найти вероятность того, что шар, наудачу
извлеченный из третьей урны, окажется белым.
96. Вероятности того, что во время работы цифровой
электронной машины произойдет сбой в арифметическом
устройстве, в оперативной памяти, в остальных устрой-
устройствах, относятся как 3:2:5. Вероятности обнаружения
сбоя в арифметическом устройстве, в оперативной памяти
и в остальных устройствах соответственно равны 0,8; 0,9;
0,9. Найти вероятность того, что возникший в машине
сбой будет обнаружен.
§ 4. Формула Бейеса
Пусть событие А может наступить лишь при условии появле-
появления одного из несовместных событий (гипотез) Bt, fi2, ..., В„, кото-
которые образуют полную группу событий, Если событие А уже про-
произошло, то вероятности гипотез могут быть переоценены по фор-
формулам Бейеса
_?™^„_,,, „,
32
где
Р(А) = Р(В1)Рв>(А)+Р(Вг)РВ1(А)+...+Р(Вп)РВп(А).
97. Два автомата производят одинаковые детали,
которые поступают на общий конвейер. Производитель-
Производительность первого автомата вдвое больше производитель-
производительности второго. Первый автомат производит в среднем
60% деталей отличного качества, а второй—84%. На-
Наудачу взятая с конвейера деталь оказалась отличного
качества. Найти вероятность того, что эта деталь про-
произведена первым автоматом.
Решение. Обозначим через А событие—деталь отличного
качества. Можно сделать два предположения (гипотезы): Bj—деталь
произведена первым автоматом, причем (поскольку первый автомат
производит вдвое больше деталей, чем второй) Я (Si) =2/3; В2 —
деталь произведена вторым автоматом, причем Я(Й2) = 1/3.
Условная вероятность того, что деталь будет отличного каче-
качества, если она произведена первым автоматом, PBt(A)=0,6.
Условная вероятность того, что деталь будет отличного каче-
качества, если она произведена вторым автоматом, Яд, (Л) =0,84.
Вероятность того, что наудачу взятая деталь окажется отлич-
отличного качества, по формуле полной вероятности равна
Р(А) = Р (Bt) PBl (A) +P (й2) РвгМ) = 2/3 0,6+1 /3-0,84 = 0,68.
Искомая вероятность того, что взятая отличная деталь произ-
произведена первым автоматом, по формуле Бейеса равна
Р (Я1 Р(Вг)Р„АА) 2/3-0,6 10
98. В пирамиде 10 винтовок, из которых 4 снабжены
оптическим прицелом. Вероятность того, что стрелок
поразит мишень при выстреле из винтовки с оптическим
прицелом, равна 0,95; для винтовки без оптического
прицела эта вероятность равна 0,8. Стрелок поразил
мишень из наудачу взятой винтовки. Что вероятнее:
стрелок стрелял из винтовки с оптическим прицелом
или без него?
99. Число грузовых автомашин, проезжающих по
шоссе, на котором стоит бензоколонка, относится к числу
легковых машин, проезжающих по тому же шоссе как
3:2. Вероятность того, что будет заправляться грузовая
машина, равна 0,1; для легковой машины эта вероят-
вероятность равна 0,2. К бензоколонке подъехала для заправки
машина. Найти вероятность того, что это грузовая машина.
100. Две перфораторщицы набили на разных перфора-
перфораторах по одинаковому комплекту перфокарт. Вероятность
2 Гмурман в. Е. 33
того, что первая перфораторщнца допустит ошибку, рав-
равна 0,05; для второй перфораторщицы эта вероятность
равна 0,1- При сверке перфокарт была обнаружена
ошибка. Найти вероятность того, что ошиблась первая
перфораторщица. (Предполагается, что оба перфоратора
были исправны.)
101. В специализированную больницу поступают
в среднем 50% больных с заболеванием К, 30%—с за-
заболеванием L, 20%—с заболеванием М- Вероятность
полного излечения болезни К равна 0,7; для болезней L
и М эти вероятности соответственно равны 0,8 и 0,9.
Больной, поступивший в больницу, был выписан здоро-
здоровым. Найти вероятность того, что этот больной страдал
заболеванием К.
102. Изделие проверяется на стандартность одним из
двух товароведов. Вероятность того, что изделие попадет
к первому товароведу, равна 0,55, а ко второму—0,45.
Вероятность того, что стандартное изделие будет признано
стандартным первым товароведом, равна 0,9, а вторым —
0,98. Стандартное изделие при проверке было признано
стандартным. Найти вероятность того, что это изделие
проверил второй товаровед.
103. Событие А может появиться при условии появ-
появления лишь одного из несовместных событий (гипотез)
Bv В2, ...,Вп, образующих полную группу событий.
После появления события А были переоценены вероят-
вероятности гипотез, т. е. были найдены условные вероятности
РА (В/) (( = 1,2 п). Доказать, что
104. Событие А может появиться при условии появ-
появления одного из несовместных событий (гипотез) Вг, В2,
5,, образующих полную группу событий. После появле-
появления события А были переоценены вероятности гипотез,
т. е. были найдены условные вероятности этих гипотез,
причем оказалось, что Py4(fl1) = 0,6 и РА E2) = 0,3. Чему
равна условная вероятность РА (В3) гипотезы В3?
105. Имеются три партии деталей по 20 деталей
в каждой. Число стандартных деталей в первой, второй
и третьей партиях соответственно равно 20, 15, 10. Из
наудачу выбранной партии наудачу извлечена деталь,
оказавшаяся стандартной. Деталь возвращают в партию
и вторично из той же партии наудачу извлекают деталь,
34
которая также оказывается стандартной. Найти вероят-
вероятность того, что детали были извлечены из третьей партии.
Решение. Обозначим через А событие—в каждом из двух
испытаний (с возвращением) была извлечена стандартная деталь.
Можно сделать три предположения (гипотезы): fij—детали извле-
извлекались из первой партии; fi8—детали извлекались из второй партии;
В3—детали извлекались из третьей партии.
Детали извлекались из наудачу взятой партии, поэтому вероят-
вероятности гипотез одинаковы:
Р (ВО = Р (В2) = Р (й3) = 1 /3.
Найдем условную вероятность Яв, (А), т. е. вероятность того,
что из первой партии будут последовательно извлечены две стандарт-
стандартные детали. Это событие достоиерно, так как в первой партии все
детали стандартны, поэтому
РвЛА)=\.
Найдем условную вероятность Рв,(А), т. е. вероятность того,
что из второй партии будут последовательно извлечены (с возвра-
возвращением) две стандартные детали:
Рв, (А) = 15/2015/20 = 9/16.
Найдем условную вероятность РВг (А), т. е. вероятность того,
что из третьей партии будут последовательно извлечены (с возвра-
возвращением) две стандартные детали:
ЯВ8(Л) = Ю/2010/20=1/4.
Искомая вероятность того, что обе извлеченные стандартные
детали взяты из третьей партии, по формуле Бейеса равна
РА(В3)
(В,) Рв, (А)
=4/29
= lll
1/3-1 + 1/3-9/16+1/31/4
106. Батарея из трех орудий произвела залп, причем
два снаряда попали в цель. Найти вероятность того, что
первое орудие дало попадание, если вероятности попада-
попадания в цель первым, вторым и третьим орудиями соот-
соответственно равны /?! = 0,4, /?2 = 0,3, /?з = 0,5.
Решение. Обозначим через А событие—два орудия попали
в цель. Сделаем два предположения (гипотезы): Вх—первое орудие
попало в цель; В\—первое орудие не лопало в цель.
По условию, Р(В;1) = 0,4; следовательно (событие fi8 противопо-
противоположно событию Si),
Я (Й2) = 1—0,4 = 0,6.
Найдем условную вероятность Рв, (А), т. е. вероятность того,
что в цель попало два снаряда, причем один из них послан первым
орудием и, следовательно, второй — либо вторым орудием (при этом
третье орудие дало промах), либо третьим (при этом второе орудие
дало промах). Эти два события несовместны, поэтому применима
2* 35
теорема сложения:
рВ1(Л) = р
Найдем условную вероятность Яд, (Л), т. е. вероятность того,
что в цель попало два снаряда, причем первое орудие дало промах.
Другими словами, найдем вероятность того, что второе и третье ору-
орудия попали в цель. Эти два события независимы, поэтому приме-
применима теорема умножения:
ЯвЛЛ) = Р2-Рз = 0,3-0,5 = 0,15.
Искомая вероятность того, что первое орудие дало попадание,
по формуле Бейеса равна
Р(В,)РВ,(А)
= 0,40,5/@,4-0,5 + 0,60,15) = 20/29.
107. Три стрелка произвели залп, причем две пули
поразили мишень. Найти вероятность того, что третий
стрелок поразил мишень, если вероятности попадания
в мишень первым, вторым и третьим стрелками соответ-
соответственно равны 0,6, 0,5 и 0,4.
108. Два из трех независимо работающих элементов
вычислительного устройства отказали. Найти вероят-
вероятность того, что отказали первый и второй элементы, если
вероятности отказа первого, второго и третьего элемен-
элементов соответственно равны 0,2; 0,4 и 0,3.
Решение. Обозначим через А событие—отказали два эле-
элемента. Можно сделать следующие предположения (гипотезы):
fit—отказали первый и второй элементы, а третий элемент
исправен, причем (поскольку элементы работают независимо, приме-
применима теорема умножения)
Р(й1) = р1р8?3 = 0,2.0,4.0,7 = 0,056;
Вг—отказали первый и третий элементы, а второй элемент
исправен, причем
P(S2) = Pi•Рз-7а = 0.20,3 0,6 = 0,036;
fi3—отказали второй и третий элементы, а первый—исправен,
причем
fi4—отказал только один элемент; Вь—отказали все три эле-
элемента; Bt—ни один из элементов не отказал.
Вероятности последних трех гипотез не вычислены, так как при
этих гипотезах событие А (отказали два элемента) невозможно и зна-
значит условные вероятности Яд4(/4), Яд, (Л) и Рв,(А) равны нулю,
следовательно, равны нулю и произведения Р (Вц)-РВ,(А), Я(б5)х
хЯя,(Л) н P(Bt)-PB(А) [см. ниже соотношение (*)] при любых
значениях вероятностей гипотез Bt, Въ и Вв.
Поскольку при гипотезах Si, Bit B3 событие А достоверно, то
соответствующие условные вероятности равны единице:
36
По формуле полной вероятности, вероятность того, что отказали
два элемента,
вЛ) + (ъ)Вь() + (в)в>()
0,056-1+0,036 •4-0,096-1= 0,188. (*)
По формуле Бейеса, искомая вероятность того, что отказали
первый и второй элементы,
^iA) 0,056
°3
109*. Две из четырех независимо работающих ламп
прибора отказали. Найти вероятность того, что отказали
первая и вторая лампы, если вероятности отказа пер-
первой, второй, третьей и четвертой ламп соответственно
равны: /?г = 0,1, />2 = 0,2, /7, = 0,3 и /?4 = 0,4.
Глава третья
ПОВТОРЕНИЕ ИСПЫТАНИЙ
§ 1. Формула Бернулли
Если производятся испытания, при которых вероятность появ-
появления события А в каждом испытании не зависит от исходов других
испытаний, то такие испытания называют независимыми относитель-
относительно события А. В § 1—4 этой главы рассматриваются независимые
испытания, в каждом из которых вероятность появления события
одинакова.
Формула Бериулли. Вероятность того, что в п независимых
испытаниях, в каждом из которых вероятность появления события
равна р@ < р < 1), событие наступит ровно k раз (безразлично,
в какой последовательности), равна
или
Pn(k)= п|
k\(n-k)\P q '
где q=\—p.
Вероятность того, что в п испытаниях событие наступит: а) ме-
менее k раз; б) более k раз; в) не менее * раз; г) не более k раз, —
находят соответственно по формулам:
ПО. Два равносильных шахматиста играют в шах-
шахматы. Что вероятнее: выиграть две партии из четырех
37
или три партии из шести (ничьи во внимание не прини-
принимаются)?
Решение. Играют равносильные шахматисты, поэтому веро-
вероятность выигрыша р= 1/2; следовательно, вероятность проигрыша q
также равна 1/2. Так как во всех партиях вероятность выигрыша
постоянна и безразлично, в какой последовательности будут выиг-
выиграны партии, то применима формула Бернулли.
Найдем вероятность того, что две партии из четырех будут
выиграны:
Найдем вероятность того, что будут выиграны три партии из
шести:
P6C)=C?pV=6-5-4/(l-2-3)-A/2K.A/2K=5/16.
Так как Я4 B) > Яв C), то вероятнее выиграть две партии из
четырех, чем три из шести.
111. Два равносильных противника играют в шахматы.
Что вероятнее: а) выиграть одну партию из двух или две
партии из четырех? б) выиграть не менее двух партий
из четырех или не менее трех партий из пяти? Ничьи
во внимание не принимаются.
112. Монету бросают пять раз. Найти вероятность
того, что «герб» выпадет: а) менее двух раз; б) не менее
двух раз.
ИЗ. а) Найти вероятность того, что событие А по-
появится не менее трех раз в четырех независимых испы-
испытаниях, если вероятность появления события А в одном
испытании равна 0,4;
б) событие В появится в случае, если событие А на-
наступит не менее четырех раз. Найти вероятность наступ-
наступления события В, если будет произведено пять независи-
независимых испытаний, в каждом из которых вероятность
появления события А равна 0,8.
114. Устройство состоит из трех независимо работаю-
работающих основных элементов. Устройство отказывает, если
откажет хотя бы один элемент. Вероятность отказа каж-
каждого элемента за время t равна 0,1. Найти вероятность
безотказной работы устройства за время t, если: а) рабо-
работают только основные элементы; б) включен один резерв-
резервный элемент; в) включены два резервных элемента.
Предполагается, что резервные элементы работают в
том же режиме, что и основные, вероятность отказа
каждого резервного элемента также равна 0,1 и устрой-
устройство отказывает, если работает менее трех элементов.
38
115. В семье пять детей. Найти вероятность того,
что среди этих детей: а) два мальчика; б) не более двух
мальчиков; в) более двух мальчиков; г) не менее двух
и не более трех мальчиков. Вероятность рождения маль-
мальчика принять равной 0,51.
116. Отрезок АВ разделен точкой С в отношении 2:1.
На этот отрезок наудачу брошены четыре точки. Найти
вероятность того, что две из них окажутся левее точки
С и две—правее. Предполагается, что вероятность попа-
попадания точки на отрезок пропорциональна длине отрезка
и не зависит от его расположения.
117. На отрезок АВ длины а наудачу брошено пять
точек. Найти вероятность того, что две точки будут
находиться от точки А на расстоянии, меньшем х, а
три—на расстоянии, большем х. Предполагается, что
вероятность попадания точки на отрезок пропорцио-
пропорциональна длине отрезка и не зависит от его расположения.
118. Отрезок разделен на четыре равные части. На
отрезок наудачу брошено восемь точек. Найти вероят-
вероятность того, что на каждую из четырех частей отрезка
попадет по две точки. Предполагается, что вероятность
попадания точки на отрезок пропорциональна длине от-
отрезка и не зависит от его расположения.
§ 2. Локальная и интегральная теоремы Лапласа
Локальная теорема Лапласа. Вероятность того, что в п неза-
независимых испытаниях, в каждом из которых вероятность появления
события равна р@ < р < 1), событие наступит ровно k раз (без-
(безразлично, в какой последовательности), приближенно равна (тем
точнее, чем больше п)
Здесь
,-*2/2 „_ k—np
Таблица функции ф(х) для положительных значений х приве-
приведена в приложении 1; для отрицательных значений х пользуются
этой же таблицей [функция ф(*) четная, следовательно, ф(—*) =
= ф (*))•
Интегральная теорема Лапласа. Вероятность того, что в п
независимых испытаниях, в каждом из которых вероятность появле-
появления события равна р @ < р < I), событие наступит не менее к±
раз и не более k2 раз, приближенно равна
39
Здесь
— функция Лапласа,
х'=(k1—np)lVnpq, x" = (ki—np)/V~npq~.
Таблица функции Лапласа для положительных значений
<х<5) приведена в приложении 2; для значений х>5 полагают
ф(х) = 0,5. Для отрицательных значений х используют эту же таб-
таблицу., учитывая, что функция Лапласа нечетная [Ф (—х) = — Ф (*)].
119. Найти вероятность того, что событие А насту-
наступит ровно 70 раз в 243 испытаниях, если вероятность
появления этого события в каждом испытании равна 0,25.
Решение. По условию, n=243; fc = 70; р =0,25; <?=0,75.
Так как л=243—достаточно большое число, воспользуемся локаль-
локальной теоремой Лапласа:
Pn(k)= J_ ф(лО,
У npq
где х = ik—np)l Vnpq.
Найдем значение х;
70—243-0,25 9,25 , „_
— -=1,о7«
rnpq У 243 -0,25 -0,75 6,75
По таблице приложения 1 найдем qs A,37) =0,1561. Искомая
вероятность
Рш G0) = 1/6,75 -0,1561 =0,0231.
120. Найти вероятность того, что событие А наступит
1400 раз в 2400 испытаниях, если вероятность появле-
появления этого события в каждом испытании равна 0,6.
Решение. Так как п велико, воспользуемся локальной теоре-
теоремой Лапласа:
Р„(к)= ' ф(*).
\ЩР
Вычислим х:
х_р—пр_ 1400—24000,6 _ 40
Vnpq ~ У 2400 -0,6 0,4 "~ 24 ~
Функция ф(^)=—^=е~лг*/'2—четная, поэтому ф(—1,67)=ф( 1,67).
По таблице приложения 1 найдем ф( 1,67) = 0,0989.
Искомая вероятность
Я24оо A400) = 1/24-0,0989=0,0041.
121. Вероятность поражения мишени при одном выст-
выстреле равна 0,8. Найти вероятность того, что при 100
выстрелах мишень будет поражена ровно 75 раз.
40
122. Вероятность рождения мальчика равна 0,51.
Найти вероятность того, что среди 100 новорожденных
окажется 50 мальчиков.
123. Монета брошена 2N раз (N велико!). Найти веро-
вероятность того, что «герб» выпадет ровно N раз.
124. Монета брошена 2N раз. Найти вероятность того,
что «герб» выпадет на 2т раз больше, чем надпись.
125. Вероятность появления события в каждом из 100
независимых испытаний постоянна и равна р = 0,8. Найти
вероятность того, что событие появится: а) не менее 75 раз
и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.
Решение. Воспользуемся интегральной теоремой Лапласа:
Я„(*1> *2) = Ф(*")-Ф(*').
где Ф(дс)—функция Лапласа,
x' = (kl—np)lV'npq, х" = {к2—пр)/У~прТ.
а) По условию, и = 100; р=0,8; <7=О,2; *i=75; *2=90. Вычи-
Вычислим х' и х":
х, h—np^ 75-100-0,8 = _j 25.
Vnpq У 100 0,8-0,2 ' '
хГ= k2-np= 90-100-0,8 дйК
Vnpq К1" 100.0,8-0,2
Учитывая, что функция Лапласа нечетна, т. е. Ф(—х) — —Ф(х),
получим
РюоG5; 90) = ФB,5)-Ф(-1,25) = ФB,5) + ФA,25).
По таблице приложения 2 найдем:
Ф B,5) =0,4938; Ф A,25) =0,3944.
Искомая вероятность
ЯюоG5; 90) =0,4938+0,3944 = 0,8882.
б) Требование, чтобы событие появилось не менее 75 раз, озна-
означает, что число появлений события может быть равно 75 либо 76
либо 100. Таким образом, в рассматриваемом случае следует при-
принять kt=75, *2=100. Тогда
д, k1-np_ 75-100-0,8 _ , 25.
Vnpq У 1000,80,2
^^kj—np_ 100—1000,8 ^5
~ Vnpq ~~ ^100-0,80,2 ~
По таблице приложения 2 найдем Ф A,25) =0,3944; ФE)=0,5.
Искомая вероятность
Р100G5; 100)=ФE)-Ф(-1,25)=ФE)+ФA,25) =
= 0,5+0,3944=0,8944.
в) События—«Л появилось не менее 75 раз» и «Л появилось
не более 74 раз» противоположны, поэтому сумма вероятностей этих
41
событий равна единице. Следовательно, искомая вероятность
РшФ: 74) = 1-РюоG5; 100) = 1-0,8944=0,1056.
126. Вероятность появления события в каждом из 2100
независимых испытаний равна 0,7. Найти вероятность
того, что событие появится: а) не менее 1470 и не более
1500 раз; б) не менее 1470 раз; в) не более 1469 раз.
127. Вероятность появления события в каждом из 21
независимых испытаний равна 0,7. Найти вероятность
того, что событие появится в большинстве испытаний.
128. Монета брошена 2N раз (N велико!). Найти веро-
вероятность того, что число выпадений «герба» будет заклю-
заключено между числами N—V~2N/2 и N + V2N/2.
129. Вероятность появления события в каждом из
независимых испытаний равна 0,8. Сколько нужно про-
произвести испытаний, чтобы с вероятностью 0,9 можно было
ожидать, что событие появится не менее 75 раз?
Решение. По условию, р=0,8; q = 0,2; ^=75; k2 = n;
Р„ = G5, и) =0,9.
Воспользуемся интегральной теоремой Лапласа:
или
V »ря 1
Подставляя данные задачи, получим
L Уи-0,8-0,2 J [ /n-0,8-0,2 J
Очевидно, число испытаний и > 75, поэтому У~п/2 > ^75/2 ~
~ 4,33. Поскольку функция Лапласа — возрастающая и ФD)~0,5,
то можно положить Ф(У~п/2)=0,5. Следовательно,
Таким образом,
По таблице приложения 2 найдем Ф( 1,28) = 0,4. Отсюда и из
соотношения (*), учитывая, что функция Лапласа нечетная, получим
G5—0,8и)/@,4 У"п) = —1,28.
Решив это уравнение, как квадратное относительно У~п, полу-
получим Уп=10. Следовательно, искомое число испытаний «=100.
130. Вероятность появления положительного резуль-
результата в каждом из п опытов равна 0,9. Сколько нужно
42
произвести опытов, чтобы с вероятностью 0,98 можно
было ожидать, что не менее 150 опытов дадут положи-
положительный результат?
§ 3. Отклонение относительной частоты
от постоянной вероятности в независимых испытаниях
Оценка отклонения относительной частоты от постоянной веро-
вероятности. Вероятность того, что в п независимых испытаниях, в каж-
каждом из которых вероятность появления события равна р @ < р < 1),
абсолютная величина отклонения относительной частоты появления
события от вероятности появления события не превысит положи-
положительного числа е, приближенно равна удвоенной функции Лапласа
при х = е Ynlpq:
131. Вероятность появления события в каждом из 625
независимых испытаний равна 0,8. Найти вероятность
того, что относительная частота появления события откло-
отклонится от его вероятности по абсолютной величине не
более чем на 0,04.
Решение. По условию, я = 625; р = 0,8; <7 = О,2; 8=0,04.
Требуется найти вероятность Р(| т/625—0,81< 0,04). Воспользу-
Воспользуемся формулой
(It-
Имеем
) =2Ф ( 0,04 1/ "'" ) =2Ф
По таблице приложения 2 найдем Ф B,5) =0,4938. Следовательно,
2ФB,5) =2-0,4938 = 0,9876. Итак, искомая вероятность приближенно
равна 0,9876.
132. Вероятность появления события в каждом из 900
независимых испытаний равна 0,5. Найти вероятность
того, что относительная частота появления события откло-
отклонится от его вероятности по абсолютной величине не бо-
более чем на 0,02.
133. Вероятность появления события в каждом из
10 000 независимых испытаний равна 0,75. Найти веро-
вероятность того, что относительная частота появления собы-
события отклонится от его вероятности по абсолютной вели-
величине не более чем на 0,01.
134. Французский ученый Бюффон (XVIII в.) бросил
монету 4040 раз, причем «герб» появился 2048 раз.
43
Найти вероятность того, что при повторении опыта Бюф-
Бюффона относительная частота появления «герба» откло-
отклонится от вероятности появления «герба» по абсолютной
величине не более чем в опыте Бюффона.
135. Вероятность появления события в каждом из
независимых испытаний равна 0,5. Найти число испыта-
испытаний п, при котором с вероятностью 0,7698 можно ожи-
ожидать, что относительная частота появления события
отклонится от его вероятности по абсолютной величине
не более чем на 0,02.
Решение. По условию, р = 0,5; <7 = О,5; е=0,02;
Р (| т/и—0,51 <0,02) = 0,7698.
Воспользуемся формулой
Р(\т/п-р
В силу условия
или Ф@,04 УТ) =0,3849.
По таблице приложения 2 найдеи Ф A,2) = 0,3849. Следова-
Следовательно, _ _
0,04 /и = 1,2, или /и=30.
Таким образом, искомое число испытаний я =900.
136. Сколько раз нужно бросить игральную кость,
чтобы вероятность неравенства
| т/п—1/61< 0,01
была не меньше чем вероятность противоположного не-
неравенства, где т—число появлений одного очка в п
бросаниях игральной кости?
Решение. Воспользуемся формулой
По условию, р=1/6, <7 = 5/6, е = 0,01. Вероятность осуществления
неравенства, противоположного заданному, т.е. неравенства \tnjn—
—1/61 > 0,01, равна
Согласно условию должно ийеть место неравенство
2ф(е ]/—j^!-5
или
4ф(е )/-^- )Ssl-
44
Отсюда
По таблице приложения2 найдем Ф@,67) =0,2486; Ф@,68) = 0,2517.
Выполнив линейную интерполяцию, получим Ф @,6745) =0,25.
Учитывая соотношение (*) и принимая во внимание, что функ-
функция Ф (*)— возрастающая, имеем
—S* 0,6745, или 0,01 л/ , я =0,6745.
pq V 1/6-5/6
Отсюда искомое число бросаний монеты гаЗг632.
137. Вероятность появления события в каждом из не-
независимых испытаний равна 0,2. Найти наименьшее число
испытаний п, при котором с вероятностью 0,99 можно
ожидать, что относительная частота появлений события
отклонится от его вероятности по абсолютной величине
не более чем на 0,04.
138. В урне содержатся белые и черные шары в отно-
отношении 4:1. После извлечения шара регистрируется его
цвет и шар возвращается в урну. Чему равно наимень-
наименьшее число извлечений п, при котором с вероятностью 0,95
можно ожидать, что абсолютная величина отклонения
относительной частоты появления белого шара от его
вероятности будет не более чем 0,01?
139. Вероятность появления события в каждом из 400
независимых испытаний равна 0,8. Найти такое положи-
положительное число е, чтобы с вероятностью 0,99 абсолютная
величина отклонения относительной частоты появления
события от его вероятности 0,8 не превысила е.
Решение. По условию, и = 400, р = 0,8, <? = 0,2. Следова-
Следовательно,
2Ф (е /400/@,8 -0,2) ) = 0,99 или Ф E0е) = 0,495.
По таблице приложения 2 найдем Ф B,57) = 0,495, значит 50е=
= 2,57. Отсюда искомое число е=0,05.
140. Вероятность появления события в каждом из
900 независимых испытаний равна 0,5. Найти такое по-
положительное число е, чтобы с вероятностью 0,77 абсо-
абсолютная величина отклонения относительной частоты по-
появления события от его вероятности 0,5 не превысила е.
141. Вероятность появления события в каждом из
10000 независимых испытаний равна 0,75. Найти такое
положительное число е, чтобы с вероятностью 0,98 аб-
45
солютная величина отклонения относительной частоты
появления события от его вероятности 0,75 не превысила е.
142. Отдел технического контроля проверяет на стан-
стандартность 900 деталей. Вероятность того, что деталь
стандартна, равна 0,9. Найти с вероятностью 0,95 гра-
границы, в которых будет заключено число т стандартных
деталей среди проверенных.
Решение. По условию, п = 900, р = 0,9, </ = 0,1. Следовательно,
2Ф(е]/ 900/@,9 0,1)) = 0,95, или Ф AQ0e) = 0,475.
По таблице приложения 2 найдем Ф( 1,96) = 0,475, значит
100е= 1,96. Отсюда е « 0,02.
Таким образом, с вероятностью 0,95 отклонение относительной
частоты числа стандартных деталей от вероятности 0,9 удовлетворяет
неравенству
| т/900—0,9 К 0,02, или 0,88 < т/900 < 0,92.
Отсюда искомое число m стандартных деталей среди 900 прове-
проверенных с вероятностью 0,95 заключено в следующих границах:
792<т<828.
143. Отдел технического контроля проверяет 475 из-
изделий на брак. Вероятность того, что изделие бракован-
бракованное, равна 0,05. Найти с вероятностью 0,95 границы,
в которых будет заключено число т бракованных изде-
изделий среди проверенных.
144. Игральную кость бросают 80 раз. Найти с веро-
вероятностью 0,99 границы, в которых будет заключено число т
выпадений шестерки.
§ 4. Наивероятнейшее число появлений события
в независимых испытаниях
Число ?0 (наступления события в независимых испытаниях,
в каждом из которых вероятность появления события равна р) на-
зывают наивероятнейшим, если вероятность того, что событие насту-
наступит в этих испытаниях k0 раз, превышает (или, по крайней мере, не
меньше) вероятности остальных возможных исходов испытаний.
Наивероятнейшее число k0 определяют из двойного неравенства
пр —<7<*0< *Р + Р,
причем:
а) если число пр—q—дробное, то существует одно наивероят-
наивероятнейшее чи^ло k0;
б) если число пр—q—целое, то существует два наивероятней-
ших числа, а именно: #ф и ko+l;
в) если число пр—целое, то наивероятнейшее число ko = np.
145. Испытывается каждый из 15 элементов некото-
некоторого устройства. Вероятность того, что элемент выдержит
46
испытание, равна 0,9. Найти наивероятнейшее число
элементов, которые выдержат испытание.
Решение. По условию, п= 15, р = 0,9, q=0,\. Найдем наи-
наивероятнейшее число k0 из двойного неравенства
пр—<7<#0 < пр + р.
Подставив данные задачи, получим
15-0,9—0,1 <*0< 15-0,9+0,9, или 13,5<*0< 14,4.
Так как k0—целое число и поскольку между числами 13,4 и
14,4 заключено одно целое число, а именно 14, то искомое наиве-
наивероятнейшее число Лго= 14.
146. Отдел технического контроля проверяет партию
из 10 деталей. Вероятность того, что деталь стандартна,
равна 0,75. Найти наивероятнейшее число деталей, кото-
которые будут признаны стандартными.
147. Товаровед осматривает 24 образца товаров.
Вероятность того, что каждый из образцов будет признан
годным к продаже, равна 0,6. Найти наивероятнейшее
число образцов, которые товаровед признает годными
к продаже.
Решение. По условию, и = 24;р = 0,6; q = 0,4. Найдем наи-
наивероятнейшее число годных к продаже образцов товаров из двойного
неравенства пр— <?< *0 < 'Ф + Р- Подставляя данные задачи, получим
24-0,6— 0,4<?0< 24-0,6+0,6, или 14<*0<15.
Так как пр—q = H—целое число, то наивероятнейших чисел
два: #о=14 и *0 + 1=15.
148. Найти наивероятнейшее число правильно наби-
набитых перфораторщицей перфокарт среди 19 перфокарт, если
вероятность того, что перфокарта набита неверно,
равна 0,1.
149. Два равносильных противника играют в шах-
шахматы. Найти наивероятнейшее число выигрышей для
любого шахматиста, если будет сыграно 2N результатив-
результативных (без ничьих) партий.
Решение. Известно, что если произведение числа испытаний п
на вероятность р появления события в одном испытании есть целое
число, то наивероятнейшее число
ka = np.
В рассматриваемой задаче число испытаний я равно числу сы-
сыгранных партий 2N; вероятность появления события равна вероят-
вероятности выигрыша в одной партии, т. е. р = 1/2 (по условию против-
противники равносильны).
Поскольку произведение np=2N-l/2 = N—целое число, то иско-
искомое наивероятнейшее число kt выигранных партий равно N,
47
150. Два стрелка стреляют по мишени. Вероятность
промаха при одном выстреле для первого стрелка равна
0,2, а для второго—0,4. Найти наивероятнейшее число
залпов, при которых не будет ни одного попадания в ми-
мишень, если стрелки произведут 25 залпов.
Решение. Промахи стрелков есть независимые события, по-
поэтому применима теорема умножения вероятностей независимых со-
событий. Вероятность того, что оба стрелка при одном залпе промахнутся,
р = 0,2-0,4 = 0,08.
Поскольку произведение ир = 25-0,08 = 2—целое число, то наи-
наивероятнейшее число залпов, прн которых не будет ни одного попадания,
ko = np = 2.
151. Два стрелка одновременно стреляют по мишени.
Вероятность попадания в мишень при одном выстреле
для первого стрелка равна 0,8, а для второго—0,6. Найти
наивероятнейшее число залпов, при которых оба стрелка
попадут в мишень, если будет произведено 15 залпов.
152. Сколько надо произвести независимых испытаний
с вероятностью появления события в каждом испытании,
равной 0,4, чтобы наивероятнейшее число появлений со-
события в этих испытаниях было равно 25?
Решение. По условию, *О = 25; р = 0,4; q = 0,6. Восполь-
Воспользуемся двойным неравенством
np—q<k0 < пр + р.
Подставляя данные задачи, получим систему неравенств для
определения неизвестного числа:
0,4я—0,6<25, 0,4и + 0,4>25.
Из первого неравенства системы найдем и< 25,6/0,4 = 64.
Из второго неравенства системы имеем п > 24,6/0,4 = 61,5.
Итак, искомое число испытаний должно удовлетворять двой-
двойному неравенству 62<я<64.
153. Вероятность появления события в каждом из
независимых испытаний равна 0,3. Найти число испы-
испытаний п, при котором наивероятнейшее число появлений
события в этих испытаниях будет равно 30.
154. Вероятность появления события в каждом из
независимых испытаний равна 0,7. Найти число испыта-
испытаний п, при котором наивероятнейшее число появлений
события равно 20.
155. Чему равна вероятность р наступления события
в каждом из 49 независимых испытаний, если наивероят-
наивероятнейшее число наступлений события в этих испытаниях
равно 30?
48
Решение. По условию, п = 49, *0 = 30. Воспользуемся двой-
двойным неравенством пр—q<k0 < пр + р. Подставляя данные задачи,
получим систему неравенств для определения неизвестной вероятно-
вероятности р:
49р + р > 30, 49р-A-р) <30.
Из первого неравенства системы найдем р > 0,6. Из второго не-
неравенства системы найдем р<0,62.
Итак, искомая вероятность должна удовлетворять двойному не-
неравенству 0,6 < р < 0,62.
156. Чему равна вероятность р наступления события
в каждом из 39 независимых испытаний, если наивероят-
нейшее число наступлений события в этих испытаниях
равно 25?
157. Батарея произвела шесть выстрелов по объекту.
Вероятность попадания в объект при одном выстреле
равна 0,3. Найти: а) наивероятнейшее число попаданий;
б) вероятность наивероятнеишего числа попаданий; в) ве-
вероятность того, что объект будет разрушен, если для
этого достаточно хотя бы двух попаданий.
Решение. По условию, я = 6; р = 0,3; ? = 0,7. а) Найдем
наивероятнейшее число попаданий по формуле
np—q<k0 < пр + р.
Подставив данные задачи, получим
6-0,3—0,7<?0 < 6-0,3 + 0,3 или 1,1<*о<2,1.
Отсюда *„ = 2.
б) Найдем вероятность наивероятнеишего числа попаданий по
формуле Бернулли
Р, B) = С2вр V = ^| 0,3* - 0,7* = 0,324.
в) Найдем вероятность того, что объект будет разрушен. По
условию, для этого достаточно, чтобы было или 2, или 3, или 4, или
5, или 6 попаданий. Эти события несовместны, поэтому вероятность
разрушения объекта равна сумме вероятностей этих событий:
Р = Р„ B) + Р, C) + Рв D) + Р„ E) + Рв F)-
Однако проще сначала найти вероятность Q противоположного со-
события (ни одного попадания или одно попадание):
Q = рв @) + Р„A) = ?• + CW =0,7» + 6-0,3-0,7» = 0,42.
Искомая вероятность того, что объект будет разрушен,
P = l—Q = l—0,42 = 0,58.
158. Прибор состоит из пяти независимо работающих
элементов. Вероятность отказа элемента в момент вклю-
включения прибора равна 0,2. Найти: а) наивероятнейшее
49
число отказавших элементов; б) вероятность наивероят-
нейшего числа отказавших элементов; в) вероятность от-
отказа прибора, если для этого достаточно, чтобы отказали
хотя бы четыре элемента.
§ 5. Производящая функция
В предыдущих параграфах этой главы рассматривались испыта-
испытания с одинаковыми вероятностями появления события; рассмот-
рассмотрим испытания, в которых вероятности появления события раз-
различны.
Пусть производится п независимых испытаний, причем в первом
испытании вероятность появления события А равна Рь во втором —
р2, ..., в л-м испытании — рп; вероятности непоявления события А
соответственно равны qlt q2, ...,qn; Pn(k)— вероятность появления
события Ann испытаниях ровно к раз.
Производящей функцией вероятностей Р„ (k) называют функцию,
определяемую равенством
фп (г) = (/V + <h) (ргг + q2)... (рпг -f <?„)•
Вероятность Р„ (k) того, что в и независимых испытаниях, в пер-
первом из которых вероятность появления события А равна plt во вто-
втором Pi и т. д., событие Л появится ровно k раз, равна коэффициенту
при г* в разложении производящей функции по степеням г. На-
Например, если и =2, то
фг (г) = (Piz+<h) (ргг + q2) = р,р2г2 + (piq2 + p2qi) г + ?1?2.
Здесь коэффициент рхрг при г2 равен вероятности Ра B) того,
что событие А появится ровно два раза в двух испытаниях; коэф-
коэффициент Piqz^-ptqi при г1 равен вероятности Ра(•) того, что собы-
собыА фф ° бй
ф Piqz^ptqi р р р а() ,
тие А появится ровно один раз; коэффициент при z°, т. е. свободный
и Р2 @) того, что событие А не
член <h?2 Равен вероятности Р2 @) того, что событие А не появится
ни одного раза.
Заметим, что если в различных испытаниях появляются раз-
различные события (в первом испытании событие Аъ во втором —
событие А2 и т. д.), то изменяется лишь истолкование коэффициен-
коэффициентов при различных степенях г. Например, в приведенном выше раз-
разложении коэффициент piPi определяет вероятность появления двух
событий Ai и А2-
159. Устройство состоит из трех независимо работаю-
работающих элементов. Вероятности безотказной работы элемен-
элементов (за время t) соответственно равны: р1 = 0,7; рг = 0,8;
р3 = 0,9. Найти вероятности того, что за время t будут
работать безотказно: а) все элементы; б) два элемента;
в) один элемент; г) ни один из элементов.
Решение. Вероятности безотказной работы элементов соот-
соответственно равны: р! = 0,7; р2 = 0,8; Рз —0,9, поэтому вероятности
того, что элементы откажут, ^t=0,3; <72 = 0,2; qs = 0,l.
50
Составим производящую функцию:
<Рз (г) = (Pi2 + ft) (р2г + <7
= @,72+0,3) @,8г + 0,2) @,9г+0,1) =
=0,504г3 + 0,398га + 0,092г + 0,006.
а) Вероятность того, что три элемента будут работать безотказно,
равна коэффициенту при г3: Р3C) =0,504.
б) Вероятность того, что два элемента будут работать безотказ-
безотказно, равна коэффициенту при г2: Р3 B) = 0,398.
в) Вероятность того, что один элемент будет работать безотказно,
равна коэффициенту при г1: Р3A) = 0,092.
г) Вероятность того, что ни один из элементов не будет работать
безотказно, равна свободному члену: Р3@) = 0,006.
Контроль: 0,504+0,398+0,092 +0,006= 1.
160. Из двух орудий произведен залп по цели. Ве-
Вероятность попадания в цель для первого орудия равна
0,8, для второго—0,9. Найти вероятности следующих
событий: а) два попадания в цель; б) одно попадание;
в) ни одного попадания; г) не менее одного попадания.
161. Из трех орудий произведен залп по цели. Ве-
Вероятность попадания в цель для первого орудия равна
0,8, для второго—0,85, для третьего—0,9. Найти вероят-
вероятности следующих событий: а) три попадания в цель;
б) два попадания; в) одно попадание; г) ни одного по-
попадания; д) хотя бы одно попадание.
162. Четыре элемента вычислительного устройства рабо-
работают независимо. Вероятность отказа первого элемента
за время / равна 0,2, второго—0,25, третьего—0,3, чет-
четвертого—0,4. Найти вероятность того, что за время /
откажут: а) 4 элемента; б) 3 элемента; в) 2 элемента;
г) 1 элемент; д) ни один элемент; е) не более двух эле-
элементов.
163. Две батареи по 3 орудия каждая производят
залп по цели. Цель будет поражена, если каждая из
батарей даст не менее двух попаданий. Вероятности по-
попадания в цель орудиями первой батареи равны 0,4; 0,5;
0,6, второй—0,5; 0,6; 0,7. Найти вероятность поражения
цели при одном залпе из двух батарей.
Часть вторая
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Глава четвертая
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
§ 1. Закон распределения вероятностей
дискретной случайной величины.
Законы биномиальный и Пуассона
Дискретной называют случайную величину, возможные значения
которой есть отдельные изолированные числа (т. е. между двумя
соседними возможными значениями нет созможных значений), кото-
которые эта величина принимает с определенными вероятностями. Дру-
Другими словами, возможные значения дискретной случайной величины
можно перенумеровать. Число возможных значений дискретной слу-
случайной величины может быть конечным или бесконечным (в послед-
последнем случае множество всех возможных значений называют счетным).
Законом распределения дискретной случайной величины называют
перечень ее возможных значений и соответствующих им вероятностей.
Закон распределения дискретной случайной величины X может быть
задан в виде таблицы, первая строка которой содержит возможные
значения дс/, а вторая—вероятности р,-:
X Xi *2 . . • Хп
р pi p2 ... р„
п
где 2р, = 1.
t=l
Если множество возможных значений X бесконечно (счетно), то
ряд Pi + Pa+... сходится и его сумма равна единице.
Закон распределения дискретной случайной величины X может
быть также задан аналитически (в виде формулы)
или с помощью функции распределения (см. гл. VI, § 1).
Закон распределения дискретной случайной величины можно
изобразить графически, для чего в прямоугольной системе координат
строят точки Mi fa; pt), Мг (х2; рг), ..., М„(хп; р„) (дс,—возможные
значения X, pi—соответствующие вероятности) и соединяют их от-
отрезками прямых. Полученную фигуру называют многоугольником
распределения.
Биномиальным называют закон распределения дискретной слу-
случайной величины X—числа появлений события в я независимых
испытаниях, в каждом из которых вероятность появления события
равна р; вероятность возможного значения X = k (числа k появлений
события) вычисляют по формуле Бернулли:
/»„<*)-<&*«»-*.
52
Если число испытаний велико, а вероятность р появления со-
бытия в каждом испытании очень мала, то используют приближенную
формулу
/>„(*)-Х*е-*/*1.
где k—число появлений события в я независимых испытаниях, Х = пр
(среднее число появлений события в и испытаниях), и говорят, что
случайная величина распределена по закону Пуассона.
164. Дискретная случайная величина X задана зако-
законом распределения:
X 1 3 6 8
р 0,2 0,1 0,4 0,3
Построить многоугольник распределения.
Решение. Построим прямоугольную систему координат, при-
причем по оси абсцисс будем откладывать возможные значения х,; а по
оси ординат—соответствующие вероятности р,\ Построим точки
0,5
0,4
0,3
0,2
0,1
I
0 lZ3t56 7 83WXi
Рис. 5
Mi(l; 0,2), Af2C;0,l), AfsF;0,4) и Af4 (8; 0,3). Соединив эти точки
отрезками прямых, получим искомый многоугольник распределения
(рис. 5).
165. Дискретная случайная величина X задана зако-
законом распределения:
а) X 2 4 5 6 б) X 10 15 20
р 0,3 0,1 0,2 0,4 р 0,1 0,7 0,2
Построить многоугольник распределения.
166. Устройство состоит из трех независимо работаю-
работающих элементов. Вероятность отказа каждого элемента
в одном опыте равна 0,1. Составить закон распределения
числа отказавших элементов в одном опыте.
53
Решение. Дискретная случайная величина X (число отказав-
отказавших элементов в одном опыте) имзет следующие возможные значе-
значения: *i = 0 (ии один из элементов устройства не отказал), х2 = 1
(отказал один элемент), х3 = 2 (отказали два элемента) и *4 = 3 (от-
(отказали три элемента).
Отказы элементов независимы один от другого, вероятности от-
отказа каждого элемента равны между собой, поэтому применима фор-
формула Бернулли. Учитывая, что, по условию, и = 3, р = 0,1 (следо-
(следовательно, q — \— 0,1 =0,9), получим:
Р,@) = <73 = 0,93 = 0,729; P3(l) = CW = 3-0,l .0,9* = 0,243;
Р3B)=Сзр2(? = 30,1г0,9 = 0,027; Р3C)=р3 = 0,13 = 0,001.
Контроль: 0,729 + 0,243 + 0,027+0,001 =1.
Напишем искомый биномиальный закон распределения X:
X 0 1 2 3
р 0,729 0,243 0,027 0,001
167. В партии 10% нестандартных деталей. Наудачу
отобраны четыре детали. Написать биномиальный закон
распределения дискретной случайной величины X—числа
нестандартных деталей среди четырех отобранных и по-
построить многоугольник полученного распределения.
168. Написать биномиальный закон распределения
дискретной случайной величины X—числа появлений
«герба» при двух бросаниях монеты.
169. Две игральные кости одновременно бросают два
раза. Написать биномиальный закон распределения ди-
дискретной случайной величины X—числа выпадений чет-
четного числа очков на двух игральных костях.
170. В партии из 10 деталей имеется 8 стандартных.
Наудачу отобраны две детали. Составить закон распре-
распределения числа стандартных деталей среди отобранных *>.
Решение. Случайная величина X—число стандартных деталей
среди отобранных деталей — имеет следующие возможные значения:
*1 = 0; *з = 1; xs = 2. Найдем вероятности возможных значений X по
формуле (см. задачу 17, гл. 1, § 1)
(N—число деталей в партии, я— число стандартных деталей в пар-
партии, т—число отобранных деталей, к—число стандартных деталей
*> Рассматриваемый закон называют гипергеометрическим. См.:
урман В. Е. Тес
М:, 1977, гл. VI, § 8.
54
Гмурман В. Е. Теория вероятностей и математическая статистика.
- 1977,
среди отобранных), находим:
Р(Х
Р(Х
= 0)
= 2)
Составим искомый закон
X
р
Св'Сг
Clo
С\-&
Си
1
10-9/A -2)
8-2 16
'~45"~45:
8-7/A-2)
45
распределения:
0
1/45 :
1 2
16/45 28/45
1
45'
28
=45-
Контроль: 1/45+16/45+28/45 = 1.
171. В партии из шести деталей имеется четыре стан-
стандартных. Наудачу отобраны три детали. Составить закон
распределения дискретной случайной величины X—числа
стандартных деталей среди отобранных.
172. После ответа студента на вопросы экзаменацион-
экзаменационного билета экзаменатор задает студенту дополнительные
вопросы. Преподаватель прекращает задавать дополни-
дополнительные вопросы, как только студент обнаруживает не-
незнание заданного вопроса. Вероятность того, что студент
ответит на любой заданный дополнительный вопрос,
равна 0,9. Требуется: а) составить закон распределения
случайной дискретной величины X—числа дополнитель-
дополнительных вопросов, которые задаст преподаватель студенту;
б) найти наивероятнейшее число /?„ заданных студенту
дополнительных вопросов.
Решение, а) Дискретная случайная величина X—число за-
заданных дополнительных вопросов—имеет следующие возможные зна-
значения: *i=l, *2=2, xa = 3 xk=k, ... Найдем вероятности этих
возможных значений.
Величина X примет возможное значение xt=\ (экзаменатор
задаст только один вопрос), если студент не ответит на первый воп-
вопрос. Вероятность этого возможного значения равна 1—0,9 = 0,1.
Таким образом, Р(Х = 1) = 0,1.
Величина X примет возможное значение хг = 2 (экзаменатор за-
задаст только два вопроса), если студент ответит на первый вопрос
(вероятность этого события равна 0,9) и не ответит на второй (вероят-
(вероятность этого события равна 0,1). Таким образом, Р (Х=2)=0,9 -0,1 =0,09.
Аналогично найдем
Р(Х = 3) = 0,9*-0,1 =0,081, ...,Р(Х = *) = 0,9*-1-0,1, ...
Напишем искомый закон распределения:
XI 2 3 ... k
р 0,1 0,09 0,081 ... 0,9*-*-0,1 ...
55
б) Наивероятнейшее число k0 заданных вопросов (наивероятней-
шее возможное значение X), т. е. число заданных преподавателем
вопросов, которое имеет наибольшую вероятность, как следует из
закона распределения, рапно единице.
173. Вероятность того, что стрелок попадет в мишень
при одном выстреле, равна 0,8. Стрелку выдаются патроны
до тех пор, пока он не промахнется. Требуется: а) соста-
составить закон распределения дискретной случайной величины
X—числа патронов, выданных стрелку; б) найти наиве-
наивероятнейшее число выданных стрелку патронов.
174. Из двух орудий поочередно ведется стрельба по
цели до первого попадания одним из орудий. Вероятность
попадания в цель первым орудием равна 0,3, вторым — 0,7.
Начинает стрельбу первое орудие. Составить законы рас-
распределения дискретных случайных величин X и Y—числа
израсходованных снарядов соответственно первым и вто-
вторым орудием.
Решение. Пусть события Л/ и В/ — попадание в цель соот-
соответственно первым и вторым орудием при i-м выстреле; А/ и 5,-—
промахи.
Найдем закон распределения случайной величины X—числа
израсходованных первым орудием снарядов. Первое орудие израсхо-
израсходует один снаряд (Х—\), если оно попадет в цель при первом
выстреле, или оно промахнется, а второе орудие при первом выстреле
попадет в цель:
Первое орудие израсходует два снаряда, если оба орудия при
первом выстреле промахнутся, а при втором выстреле первое ору-
орудие попадет в цель, или если оно промахнется, а второе орудие при
втором выстреле попадет в цель:
р2 = р (X = 2) = Р (AjB1Ai + A1~BrfiB2) =
= 0,7.0,3-0,3 + 0,7.0,3.0,7-0,7 = 0,21 @,3 + 0,49) = 0,79.0,21.
Аналогично получим
Р(Х = *) = 0,790,21*-1.
Искомый закон распределения дискретной случайной величины
X— числа снарядов, израсходованных первым орудием:
X 1 2 3 k
р 0,79 0,79-0,21 0.79-0.212 ... 0,79-0,21*-1 ..,
Контроль: 2р,- = 0,79/A-0,21) = 0,79/0,79=1.
Найдем закон распределения дискретной случайной величины
Y—числа снарядов, израсходованных вторым орудием.
Если первое орудие при первом выстреле попадет в цель, то
стрельба из второго орудия не будет произведена:
56
Второе орудие израсходует лишь один снаряд, если при первом
выстреле оно попадет в цель, или если оно промахнется, а первое
орудие попадет в цель при втором выстреле:
p2 = P(K=l) = P(^iBH-liSi'42) = 0,7-0>7 + 0,7.0,3.0,3 = 0,553.
Вероятность того, что второе орудие израсходует два снаряда,
Рз=Р (К = 2) = Р (Iifl,J2B,4¦А1'В1А2'ВгАз).
Выполнив выкладки, найдем р3 = 0,553-0,21.
Аналогично получим
P(K = A) = 0,5530,21*-1.
Искомый закон распределения дискретной случайной величины
Y — числа снарядов, израсходованных вторым орудием:
Y 0 1 2 ... *
р 0,3 0,553 0,553-0,21 ... 0,553.0,21а-1 ...
Контроль: 2Р/ = 0,3+ @,553/1 —0,21) = 0,3 + @,553/0,79) =
= 0,3+0,7=1.
175. Два бомбардировщика поочередно сбрасывают
бомбы на цель до первого попадания. Вероятность попа-
попадания в цель первым бомбардировщиком равна 0,7, вто-
вторым—0,8. Вначале сбрасывает бомбы первый бомбарди-
бомбардировщик. Составить первые четыре члена закона распре-
распределения дискретной случайной величины X—числа сбро-
сброшенных бомб обоими бомбардировщиками (т. е. ограни-
ограничиться возможными значениями X, равными 1, 2, 3 и 4).
176. Учебник издан тиражом 100000 экземпляров.
Вероятность того, что учебник сброшюрован неправильно,
равна 0,0001. Найти вероятность того, что тираж содер-
содержит ровно пять бракованных книг.
Решение. По условию, п— 100000, р — 0,0001, 6 = 5. Собы-
События, состоящие в том, что книги сброшюрованы неправильно, неза-
независимы, число п велико, а вероятность р мала, поэтому восполь-
воспользуемся распределением Пуассона
Р„(*)=ААГ*/*.
Найдем л:
Х = пр= 100000-0,0001 = 10.
Искомая вероятность
РюооооE) = Ю5-е-1в/5=108-0,000045/120 = 0,0375
177. Устройство состоит из 1000 элементов, работаю-
работающих независимо один от другого. Вероятность отказа
любого элемента в течение времени Т равна 0,002. Найти
вероятность того, что за время Т откажут ровно три
элемента.
Указание. Принять е~2 = 0,13534.
57
178. Станок-автомат штампует детали. Вероятность
того, что изготовленная деталь окажется бракованной,
равна 0,01. Найти вероятность того, что среди 200 дета-
деталей окажется ровно четыре бракованных.
179. Завод отправил на базу 500 изделий. Вероят-
Вероятность повреждения изделия в пути равна 0,002. Найти
вероятности того, что в пути будет повреждено изделий:
а) ровно три; б) менее трех; в) более трех; г) хотя бы
одно.
Решение. Число и=500 велико, вероятность р=0,002 мала
И рассматриваемые события (повреждение изделий) независимы, по-
поэтому имеет место формула Пуассона
Pn(*)=A*-e-Ay*!.
а) Найдем к:
Я=ир=500-0,002 = 1.
Найдем вероятность того, что будет повреждено ровно 3 (k = 3)
изделия:
Рюо C) =e-V3! =0,36788/6=0,0613.
б) Найдем вероятность того, что будет повреждено менее трех
изделий:
= E/2) е-1 = E/2)- 0,36788=0,9197.
в) Найдем вероятность Р того, что будет повреждено более трех
изделий. События «повреждено более трех изделий» и «повреждено
не более трех изделий» (обозначим вероятность этого события че-
через Q)—противоположны, поэтому P + Q = l. Отсюда
Используя результаты, полученные выше, имеем
Р = 1 — [0,9197+0,0613] =0,019.
г) Найдем вероятность Рг того, что будет повреждено хотя бы
одно изделие. События «повреждено хотя бы одно изделие» и
«ни одно из изделий не повреждено» (обозначим вероятность этого
события через Qi) — противоположные, следовательно, Pi + Qi = l.
Отсюда искомая вероятность того, что будет повреждено хотя бы
одно изделие, равна
P1 = l_Qi=l-PB(l0@) = l-e-l= 1-0,36788=0,632.
180. Магазин получил 1000 бутылок минеральной
воды. Вероятность того, что при перевозке бутылка ока-
окажется разбитой, равна 0,003. Найти вероятности того,
что магазин получит разбитых бутылок: а) ровно две;
б) менее двух; в) более двух; г) хотя бы одну.
Указание. Принять е-»=0,04979.
58
181. а) Устройство состоит из большого числа неза-
независимо работающих элементов с одинаковой (очень малой)
вероятностью отказа каждого элемента за время Т. Найти
среднее число отказавших за время Т элементов, если
вероятность того, что за это время откажет хотя бы
один элемент, равна 0,98.
Решение. Из условия задачи следует (поскольку число эле-
элементов велико, элементы работают независимо и вероятность отказа
каждого элемента мала), что число отказов распределено по закону
Пуассона, причем требуется найти параметр Я (среднее число отка-
отказов).
Вероятность того, что откажет хотя бы один элемент, по усло-
условию равна 0,98, следовательно (см. задачу 179, п. г), 1—е"Л=0,98.
Отсюда
е~* = 1—0,98=0,02.
По таблице функции е~* находим X =3,9. Итак, за время Т работы
устройства откажет примерно четыре элемента.
б) Найти среднее число А, бракованных изделий в партии изде-
изделий, если вероятность того, что в этой партии содержится хотя бы
одно бракованное изделие, равна 0,95. Предполагается, что число
бракованных изделий в рассматриваемой партии распределено по
закону Пуассона.
Указание. Принять е~3 =0,05.
182. Доказать, что сумма вероятностей числа появле-
появлений события в независимых испытаниях, вычисленных
по закону Пуассона, равна единице. Предполагается, что
испытания производятся бесчисленное количество раз.
Решение. В силу закона Пуассона
Используем разложение функции е* в ряд Маклорена:
Известно, что этот ряд сходится при любом значении х, поэтому,
положив х=к, получим
2
Найдем искомую сумму вероятностей 2 Рп (*)> учитывая, что е
не зависит от k и, следовательно, может быть вынесено за знак
суммы:
2 рп&)= 2Х*е-я/*! = е-Я 2Д1
k=0 ft=0 k=0
59
Замечание. Утверждение задачи следует немедленно из
того, что сумма вероятностей событий, образующих полную группу,
равна единице. Приведенное доказательство преследует учебные цели.
183. Вероятность выигрыша по одному лотерейному
билету р = 0,01. Сколько нужно купить билетов, чтобы
выиграть хотя бы по одному из них с вероятностью Р,
не меньшей, чем 0,95?
Решение. Вероятность выигрыша мала, а число билетов,
которое нужно купить, очевидно, велико, поэтому случайное число
выигрышных билетов имеет приближенно распределение Пуассона.
Ясно, что события «ни один из купленных билетов не является
выигрышным» и «хотя бы один билет—выигрышный» — противопо-
противоположные. Поэтому сумма вероятностей этих событий равна единице:
Рп @) + Р = 1, или Р = 1 -Р„@). (*)
Положив k = 0 в формуле Пуассона Рп (?) = Л*е~ /k\, получим
Следовательно, соотношение (*) примет вид
Р = 1— е~\
По условию, PSsO,95, или 1— e~*SsO,95. Отсюда
е"* < 0,05. (**)
По таблице функции е~* находим e~s=0,05. Учитывая, что
функция е~*—убывающая, заключаем, что неравенство (•*) выпол-
выполняется при X;=s3, или при яр:&3. Следовательно, п^3/р =
= 3/0,01 =300. Итак, надо купить не менее 300 билетов, чтобы выиг-
выиграть хотя бы по одному из них.
§ 2. Простейший поток событий
Потоком событий называют последовательность событий, которые
наступают в случайные моменты времени.
Простейшим (пуассоновским) называют поток событий, который
обладает следующими тремя свойствами: стационарностью, «отсутст-
«отсутствием последействия» и ординарностью.
Свойство стационарности состоит в том, что вероятность появле-
появления k событий в любом промежутке времени зависит только от
числа & и от длительности t промежутка времени и не зависит
от начала его отсчета. Другими словами, вероятность появления k
событий за промежуток времени длительностью t есть функция, за-
зависящая только от ? и /.
Свойство «отсутствия последействия» состоит в том, что вероят-
вероятность появления k событий в любом промежутке времени не зависит
от того, появлялись или не появлялись события в моменты времени,
предшествующие началу рассматриваемого промежутка. Другими
словами, предыстория потока не влияет на вероятности появле-
появления событий в ближайшем будущем.
Свойство ординарности состоит в том, что появление двух или
более событий за малый промежуток времени практически невоз-
60
можно. Другими словами, вероятность появления более одного со-
события за малый промежуток времени пренебрежимо мала по срав-
сравнению с вероятностью появления только одного события.
Интенсивностью потока X называют среднее число событий,
которые появляются в единицу времени.
Если постоянная интенсивность потока X известна, то вероят-
вероятность появления k событий простейшего потока за время t опреде-
определяется формулой Пуассона
Замечание. Поток, обладающий свойством стационарности,
называют стационарным; в противном случае—нестационарным.
184. Показать, что формулу Пуассона, определяющую
вероятность появления k событий за время длитель-
длительностью t
(
Т\—' * '
можно рассматривать как математическую модель про-
простейшего потока событий; другими словами, показать,
что формула Пуассона отражает все свойства простей-
простейшего потока.
Решение. Из формулы (*) видно, что вероятность появления
k событий за время длительностью /, при заданной интенсивности X,
является функцией только А и Л что отражает свойство стационар-
стационарности простейшего потока.
Формула (*) не использует информации о появлении событий
до начала рассматриваемого промежутка времени, что отражает
свойство отсутствия последействия.
Покажем, что рассматриваемая формула отражает свойство орди-
ординарности. Положив А=0 и Л=1, найдем вероятность непоявле-
непоявления событий и вероятность появления одного события:
Следовательно, вероятность появления более одного события
Используя разложение функции e~w в ряд Маклорена, после эле-
элементарных преобразований получим
Сравнивая Р< A) a Pt(k> 1), заключаем, что при малых значе-
значениях / вероятность появления более одного события пренебрежимо
мала по сравнению с вероятностью наступления одного события,
что отражает свойство ординарности.
Итак, формула Пуассона отражает все три свойства простейшего
потока, поэтому ее можно рассматривать как математическую модель
этого потока.
61
185. Среднее число заказов такси, поступающих на
диспетчерский пункт в одну минуту, равно трем. Найти
вероятность того, что за 2 мин поступит: а) четыре
вызова; б) менее четырех вызовов; в) не менее четырех
вызовов.
Решение. По условию, Х=3, / = 2, А=4. Воспользуемся
формулой Пуассона
1
а) Искомая вероятность того, что за две 2 мин поступит четыре
вызова
б) Событие «поступило менее четырех вызовов» произойдет, если
наступит одно из следующих несовместных событий: 1) поступило
три вызова; 2) поступило два вызова; 3) поступил один вызов;
4) не поступило ни одного вызова. Эти события несовместны, по-
поэтому применима теорема сложения вероятностей несовместных со-
событий:
Pt (k < 4) =Рг C)+Рг B) + Pt A) + Pt @) =
63-e~e (fie~* 6-е-*
=5-^-+^2j-+5-yI-+ е-« =е-» C6 +18 + 6 +1)-
=0,0025-61 =0,1525.
в) События «поступило менее четырех еызовов» и «поступило
не менее четырех вызовов» противоположны, поэтому искомая вероят-
вероятность того, что за 2 мин поступит не менее четырех вызовов,
Р (*3s 4) = 1 — Р (к < 4) = 1 —0,1525 = 0,8475.
186. Среднее число вызовов, поступающих на АТС
в одну минуту, равно двум. Найти вероятность того,
что за 4 мин поступит: а) три вызова; б) менее трех
вызовов; в) не менее трех вызовов. Поток вызовов пред-
предполагается простейшим.
187. Доказать, что для простейшего потока событий
Указание. Использовать теорему о сумме вероятностей про-
противоположных событий:
При отыскании искомого предела применить правило Лопиталя,
62
§ 3. Числовые характеристики дискретных случайных
величии
Характеристикой среднего значения случайной величины слу-
служит математическое ожидание.
Математическим ожиданием дискретной случайной величины
называют сумму произведений всех ее возможных значений на их
вероятности:
М (X) = x1p1 + x2pz+,.. +х„р„.
Если дискретная случайная величина принимает счетное множество
возможных значений, то
причем математическое ожидание существует, если ряд в правой
части равенства сходится абсолютно.
Математическое ожидание обладает следующими свойствами.
Свойство 1. Математическое ожидание постоянной величины
равно самой постоянной:
М{С) = С.
Свойство 2. Постоянный множитель можно выносить за
знак математического ожидания:
М(СХ) = СМ(Х).
Свойство 3. Математическое ожидание произведения взаимно
независимых случайных величин равно произведению математических
ожиданий сомножителей:
М (*Л ... Х„) = М (Хг)-М (Х2) ...М (Х„).
Свойство 4. Математическое ожидание суммы случайных
величин равно сумме математических ожиданий слагаемых:
Математическое ожидание биномиального распределения равно
произведению числа испытаний на вероятность появления события
в одном испытании:
Характеристиками рассеяния возможных значений случайной
величины вокруг математического ожидания служат, в частности,
дисперсия и среднее квадратическое отклонение.
Дисперсией случайной величины X называют математическое
ожидание квадрата отклонения случайной величины от ее матема-
математического ожидания:
Дисперсию удобно вычислять по формуле
D(X)=M(X*)-[M(X)]*.
Дисперсия обладает следующими свойствами.
Свойство 1. Дисперсия постоянной равна нулю:
D(C) = 0.
63
Свойство 2. Постоянный множитель можно выносить за знак
дисперсии, предварительно возведя его в квадрат:
Свойство 3. Дисперсия суммы независимых случайных вели-
величин равна сумме дисперсий слагаемых:
Дисперсия биномиального распределения равна произведению
числа испытаний на вероятности появления и непоявления события
в одном испытании:
D(X) = npq.
Средним квадратическим отклонением случайной величины на-
называют квадратный корень из дисперсии:
о(Х)=\ГЩХ).
188. Найти математическое ожидание дискретной слу-
случайной величины X, заданной законом распределения:
а) X —4 6 10 б) X 0,21 0,54 0,61
р 0,2 0,30,5 ' р 0,1 0,5 0,4 "
Решение, а) Математическое ожидание равно сумме произ-
произведений всех возможных значений X на их вероятности:
Л! (Х) = -4-0,2-!-6-0,3+10-0,5 = 6.
189. Найти математическое ожидание случайной вели-
величины Z, если известны математические ожидания X и Y:
a) Z = X + 2Y, Af(X) = 5, M(Y) = 3; б) Z = 3X+4Y,
Af(X) = 2, M(Y) = 6.
Решение, а) Используя свойства математического ожидания
(математическое ожидание суммы равно сумме математических ожи-
ожиданий слагаемых; постоянный множитель можно вынести за знак
математического ожидания), получим
М (Z) = М (X + 2К) = М (X) + М BY) = М (X)+2М (К) =
=5+2-3=11.
190. Используя свойства метематического ожидания,
доказать, что: а) М (X — Y) = M(X)—M(Y); б) матема-
математическое ожидание отклонения X—М(Х) равно нулю.
191. Дискретная случайная величина X принимает
три возможных значения: хх = 4 с вероятностью рг = 0,5;
х2 = 6 с вероятностью р2 = 0,3 и х, с вероятностью р3.
Найти х3 и р3, зная, что М(Х) = 8.
192. Дан перечень возможных значений дискретной
случайной величины X: xt =—1, х2 = 0, дг8 = 1, а также
известны математические ожидания этой величины и ее
квадрата: Af(X) = 0,l, Af(X2) = 0,9. Найти вероятности
64
Pv P»< Pa> соответствующие возможным значениям xlt
xa, xs.
Решение. Пользуясь тем, что сумма вероятностей всех воз-
возможных значений X равна единице, а также принимая во внима-
внимание, что М (Л) =0,1, М (Х2)=0,9, составим следующую систему
трех линейных уравнений относительно неизвестных вероятностей:
)+8 + P
(-lJPi+08p2+l2-p3 = 0,9.
Решив эту систему, найдем искомые вероятности: pj=0,4,
рг=0,1, р8=0,5.
193. Дан перечень возможных значений дискретной
случайной величины X: х, = 1, х2 = 2, xs — 3, а также
известны математические ожидания этой величины и ее
квадрата: М(Х) = 2,3, М(Хг) = 5,9. Найти вероятности,
соответствующие возможным значениям X.
194. В партии из 10 деталей содержится три нестан-
нестандартных. Наудачу отобраны две детали. Найти матема-
математическое ожидание дискретной случайной величины X —
числа нестандартных деталей среди двух отобранных.
Указание. Воспользоваться решением задачи 17, гл. 1, § 1.
195. а) Доказать, что математическое ожидание числа
появлений события А в одном испытании равно вероят-
вероятности р появления события А.
Указание. Дискретная случайная величина X—число появ-
появлений события в одном испытании—имеет только два возможных
значения: *i = l (событие А наступило) и хг = 0 (событие А не
наступило).
б) Доказать, что математическое ожидание дискрет-
дискретной случайной величины X—числа появлений события А
в п независимых испытаниях, в каждом из которых ве-
вероятность появления события равна р—равно произве-
произведению числа испытаний на вероятность появления собы-
события в одном испытании, т. е. доказать, что математи-
математическое ожидание биномиального распределения М(Х)=пр.
196. Найти математическое ожидание дискретной слу-
случайной величины X—числа таких бросаний пяти играль-
игральных костей, в каждом из которых на двух костях по-
появится по одному очку, если общее число бросаний
равно двадцати.
Решение. Воспользуемся формулой
М(Х)=пР,
3 Гыурыан В. Е. 65
где п—общее число испытаний (бросаний пяти костей); X—число
появлений интересующего нас события (на двух костях из пяти
появится по одному очку) е п испытаниях; Р—вероятность появления
рассматриваемого события в одном испытании.
По условию, п=20. Остается найти Р—вероятность того, что
на гранях двух из пяти костей появится по одному очку. Эту
вероятность вычислим по формуле Бернулли, учитывая, что вероят-
вероятность появления одного очка на грани одной кости р = 1/6 и, сле-
следовательно, вероятность непоявления q = l—1/6=5/6:
lY EY 5'453 5*
Искомое математическое ожидание
М(Х)=пР =20 — 2-3.
197. Устройство состоит из п элементов. Вероятность
отказа любого элемента за время опыта равна р. Найти
математическое ожидание числа таких опытов, в каждом
из которых откажет ровно т элементов, если всего про-
произведено N опытов. Предполагается, что опыты незави-
независимы один от другого.
Решение. Обозначим через X число опытов, в которых отка-
откажет ровно т элементов. Так как опыты независимы и вероятности
интересующего нас события (в одном опыте откажет ровно т эле-
элементов) в этих опытах одинаковы, то применима формула
где N—общее число опытов; Р—вероятность того, что в одном
опыте откажет ровно т элементов.
Найдем вероятность Р по формуле Бернулли:
Подставив (**) в (*), получим искомое математическое ожидание:
198. Бросают п игральных костей. Найти математи-
математическое ожидание числа таких бросаний, в каждом из
которых выпадет ровно т шестерок, если общее число
бросаний равно #.
199. Бросают п игральных костей. Найти математи-
математическое ожидание суммы числа очков, которые выпадут
на всех гранях.
Решение. Обозначим через X сумму числа очков, которые
выпадут на всех гранях, через Х( (t=\, 2, ..., я) —число выпавших
очков на грани 1-й кости. Тогда, очевидно,
Следовательно,
66
Очевидно, псе величины X; имеют одинаковое распределение,
а следовательно одинаковые числовые характеристики и, в частнос-
частности, одинаковые математические ожидания, т. е. М (Х,) = М (Хй) =
= ...=М(Х„).
В силу (*) получим
М(Х) = пМ(Х1). (*•)
Таким образом, достаточно вычислить математическое ожидание
величины Хи т. е. математическое ожидание числа очков, которые
могут выпасть на первой кости. Для этого напишем закон распре-
распределения Xi.
Xt 1 2 3 4 5 6
р 1/6 1/6 1/6 1/6 1/6 1/6
Найдем
М (Х,)=1.1/6+2-1/6 + 3-1/6+4.1/6 + 5-1/6 + 6.1/6 = 7/2. (**•)
Подставив (***) в (**), окончательно получим
М(Х) = G/2)п.
200. Отдел технического контроля проверяет изделия
на стандартность. Вероятность того, что изделие стан-
стандартно, равна 0,9. В каждой партии содержится пять
изделий. Найти математическое ожидание дискретной
случайной величины X—числа партий, в каждой из
которых окажется ровно четыре стандартных изделия,—
если проверке подлежит 50 партий.
201. Доказать: 1) М (Y) = aM {X) + b, если Y = aX+b;
2) M(Y)= 2,atM(X;) + b, если К=2(а/
202. События Аи Аг, ..., А„несовместны и образуют
полную группу; вероятности появления этих событий соот-
соответственно равны pv p2, ..., р„. Если в итоге испытания
появляется событие At (t = 1, 2, ..., п), то дискретная
случайная величина X принимает возможное значение х{,
равное вероятности р( появления события А(. Доказать,
что математическое ожидание случайной величины X имеет
наименьшее значение, если вероятности всех событий
одинаковы.
Решение. Возможные значения величины X по условию
равны вероятности р/ событий Ас, вероятность возможного значе-
значения pi, очевидно, также равна р,-. Таким образом, X имеет следую-
следующее распределение:
X pi p2 ... рп
Р Р\ Рг ••• Рп
Найдем математическое ожидание X:
6/
Рассматриваемые события образуют полную группу, поэтому Р\-\-рг-\-
+ ...+р„ = 1.
Из дифференциального исчисления известно, что если сумма
независимых переменных постоянна, то сумма квадратов этих пере-
переменных имеет наименьшее значение в случае равенства переменных.
Применительно к рассматриваемой задаче это означает: сумма (*),
т. е. математическое ожидание М (X), имеет наименьшее значение,
если вероятности всех событий, образующих полную группу, равны
между собой, что и требовалось доказать.
203. Доказать, что математическое ожидание диск-
дискретной случайной величины заключено между наимень-
наименьшим и наибольшим ее возможными значениями.
Решение. Пусть X—дискретная случайная величина, задан-
заданная законом распределения:
X Xi хг...хп
Р Pi Pf-Pn
Обозначим наименьшее и наибольшее возможные значения X соот-
соответственно через т и М. Тогда
...+ Мр„
= M(Pl+pt+...+pn) = M.
Итак,
Аналогично легко вывести, что
М(Х)^т. (**)
Объединяя (*) и (**), окончательно получим
т<М (Х)<,М.
204. Дискретная случайная величина X принимает k
положительных значений xlt дг3, ..., хк с вероятностями,
равными соответственно ри р2, ..., рк. Предполагая, что
возможные значения записаны в возрастающем порядке,
доказать, что
Решение. Принимая во внимание, что
68
получим
?!
Pkn~«>\Xk) ^ ^ Pk n-
*
?l
lm (
Так как по условию возможные значения X записаны в возрас-
возрастающем порядке, т. е. х(< хк (i—\, 2 k—l), то
Следовательно,
Я^.оо /И (Л")
205. Доказать, что если случайные величины Xlt X2,
..., Х„ независимы, положительны и одинаково распре-
распределены, то
,, Г Xt 11
Решение. Введем в рассмотрение случайные величины
Заметим, что знаменатели этих дробей не могут быть равными нулю,
поскольку величины X,- (I = 1, 2, ..., п) положительны.
По условию, величины А",- одинаково распределены, поэтому и
величины Y i также одинаково распределены и, следовательно, имеют
одинаковые числовые характеристики, в частности, одинаковые ма-
математические ожидания:
М (Уг) = М (Yt) =...=M (Yn). (••)
Легко видеть, что Yi+Y,+ ...+К„=1, следовательно,
М (Кг + К2+ • • • + Yn)=M A) = 1.
Математическое ожидание суммы равно сумме математических ожи-
ожиданий слагаемых, поэтому
В силу (••) имеем лЛ1 O'i) = 1 - Отсюда М (К1) =
Учитывая (*), окончательно получим
69
206. Доказать, что если случайные величины Xlt Xs,
Ха, Xt, Хъ независимы, положительны и одинаково рас-
распределены, то
А x+x+x I 3
x1+xi+xa+xi+x6
Указание. Представить дробь, стоящую под знаком матема-
математического ожидания, в виде суммы трех дробей и воспользоваться
решением задачи 205.
207. Найти математическое ожидание дискретной слу-
случайной величины X, распределенной по закону Пуассона:
X 0 1 2 ... k ...
е b?L
Решение. По определению математического ожидания для
случая, когда число возможных значений X есть счетное множество,
4=0
Учитывая, что при А=0 первый член суммы равен нулю, при-
примем в качестве наименьшего значения k единицу:
Положив k—l=m, получим
т=0
V^* х
Принимая во внимание, что У."т\~ ' окончательно имеем
т=0
М{Х)=%.е-Ь.еЬ=Х.
Итак,
М(Х) = %,
т. е. математическое ожидание распределения Пуассона равно пара-
параметру этого распределения %.
208. Случайные величины X и Y независимы. Найти
дисперсию случайной величины Z = 3X + 2Y, если из-
известно, что ?>(Х) = 5, D(Y) = 6.
Решение. Так как величины X и Y независимы, то незави-
независимы также и величины ЗА" и 2Y. Используя свойства дисперсии
(дисперсия суммы независимых случайных величин равна сумме
дисперсий слагаемых; постоянный множитель можно вынести за знак
дисперсии, возведя его в квадрат), получим
D (Z) = D {ZX+2Y) = D CX)+?> BY) = 9D (X) + W (К)=9• 5+4.6=69.
70
209. Случайные величины X и Y независимы. Найти
дисперсию случайной величины Z = 2X + 3Y, если из-
известно, что ?>(Х) = 4, ?>(И) = 5.
210. Найти дисперсию и среднее квадратическое от-
отклонение дискретной случайной величины X, заданной
законом распределения:
X —5 2 3 4
р 0,4 0,3 0,1 0,2
Решение. Дисперсию можно вычислить исходя из ее опреде-
определения, однако мы воспользуемся формулой
которая быстрее ведет к цели.
Найдем математическое ожидание X:
М(Х) = —5- 0,4+2-0,3+3.0,1 +4- 0,2 = — 0,3.
Напишем закон распределения X2:
X2 25 4 9 16
р 0,4 0,3 0,1 0,2
Найдем математическое ожидание X2:
М (Х2) = 25.0,4 + 4.0,3+9-0,1 + 16-0,2= 15,3.
Найдем искомую дисперсию:
D (X) = М (X2) — [М (X)]2 = 15,3—(-0.3J = 15,21.
Найдем искомое среднее квадратическое отклонение:
а (X) = \ПЩ) = V^l5l2T= 3,9.
211. Найти дисперсию и среднее квадратическое от-
отклонение дискретной случайной величины X, заданной
законом распределения:
а) X 4,3 5,1 10,6 б) X 131 140 160 180.
р 0,2 0,3 0,5' р 0,05 0,10 0,25 0,60
212. Дискретная случайная величина X имеет только
два возможных значения jcx и хг, причем равновероят-
равновероятных. Доказать, что дисперсия величины X равна квад-
квадрату полуразности возможных значений:
Решение. Найдем математическое ожидание X, учитывая,
что вероятности возможных значений хх и х2 равны между собой и,
следовательно, каждая из них равна 1/2:
Найдем математическое ожидание X2:
(*2 + ^)/2-
7!
Найдем дисперсию X:
213. Найти дисперсию дискретной случайной вели-
величины X—числа появлений события А в пяти независи-
независимых испытаниях, если вероятность появления событий А
в каждом испытании равна 0,2.
Решение. Дисперсия числа появлений события в независимых
испытаниях (с одинаковой вероятностью появления события в каж-
каждом испытании) равна произведению числа испытаний на вероятнос-
вероятности появления и непоявления события:
D(X) = npq.
По условию, я = 5; р = 0,2; q = 1—0,2 = 0,8.
Искомая дисперсия
D(X) = npq = 5-0,2- 0,8 = 0,8.
214. Найти дисперсию дискретной случайной величи-
величины X—числа отказов элемента некоторого устройства в
десяти независимых опытах, если вероятность отказа
элемента в каждом опыте равна 0,9.
215. Найти дисперсию дискретной случайной вели-
величины X—числа появлений события А в двух независи-
независимых испытаниях, если вероятности появления события в
этих испытаниях одинаковы и известно, что М (X) = 1,2.
Решение. Первый способ. Возможные значения величи-
величины X таковы: *1 = 0 (событие не появилось), xt=l (событие по-
появилось один раз) и Хз=2 (событие появилось два раза).
Найдем вероятности возможных значений по формуле Бернулли:
/М0) = <72; Pt(l)=Clpq=2pq; Р8B) = Р2-
Напишем закон распределения X:
возможные значения 0 1 2
вероятности q2 2pq рг
Найдем М(Х):
В силу условия М(Х) = \,2, т. е. 2р=1,2. Отсюда р = 0,6 и, сле-
следовательно, 9 = 1—0,6 = 0,4.
Искомая дисперсия
D(X) = npq = 2-0,6.0,4 = 0,48.
Второй способ. Воспользуемся формулой М (X) = пр.
По условию, М(Х)=\,2; л=2. Следовательно, 1,2=2р. Отсюда
р = 0,6 и, значит, <7=0,4.
Найдем искомую дисперсию:
D(X) = npq = 2-0,6.0,4 = 0,48.
Разумеется, второй способ быстрее ведет к цели.
72
216. Найти дисперсию дискретной случайной величи-
величины X—числа появлений события А в двух независи-
независимых испытаниях, если вероятности появления события в
этих испытаниях одинаковы и известно, что М (Х)=0,9.
217. Производятся независимые испытания с одина-
одинаковой вероятностью появления события А в каждом
испытании. Найти вероятность появления события А, если
дисперсия числа появлений события в трех независимых
испытаниях равна 0,63.
218. Дискретная случайная величина X имеет только
два возможных значения: xt и х2, причем х2 > хх. Веро-
Вероятность того, что X примет значение xlt равна 0,6.
Найти закон распределения величины X, если матема-
математическое ожидание и дисперсия известны: М(Х)=\,А;
D(X) = 0,24.
Решение. Сумма вероятностей всех возможных значений
дискретной случайной величины равна единице, поэтому вероятность
того, что X примет значение *2, равна 1—0,6 = 0,4.
Напишем закон распределения X:
X xi х2
Р 0,6 0,4 (*)
Для отыскания Х\ и х3 надо составить два уравнения, связываю-
связывающие эти числа. С этой целью выразим известные математическое
ожидание и дисперсию через *i и *2.
Найдем М (X):
М(Х) = 0,6*1 + 0,4*2.
По условию, М (X) = 1,4, следовательно,
0,6*!+0,4дг8 = 1,4. (*•)
Одно уравнение, связывающее *i и *2, получено. Для того чтобы
получить второе уравнение, выразим известную дисперсию через xt
и хг.
Напишем закон распределения Лг:
Найдем
Найдем
L
М (Хг):
t
дисперсию:
)(Х) = М(Х
х' х\ *!
р 0,6 0,4
Ц(Х*) = 0,6*!+0,4*1.
*)—[М (Х)]2 = 0,6*?+0,4*1—!,42.
Подставляя D(X) = 0,24, после элементарных преобразований
получим
0,6*? + 0,4*1 = 2,2. (•**)
73
Объединяя (**) и (***), имеем систему уравнений
Г 0,6*1 + 0,4*2= 1А
\ 0,6*1+0,4*1 = 2,2.
Решив эту систему, найдем два решения:
*х=1; *2 = 2 и *i=l,8; *2 = 0,8.
По условию *2 > *i, поэтому задаче удовлетворяет лишь первое
решение:
*, = 1; *2=2. (****)
Подставив (****) в (*), получим искомый закон распределения:
X 1 2
р 0,6 0,4
219. Дискретная случайная величина X имеет толь-
только два возможных значения: xt и х2, причем хх < х2.
Вероятность того, что X примет значение хи равна 0,2.
Найти закон распределения X, зная математическое
ожидание М (X) = 2,6 и среднее квадратическое откло-
отклонение <т(Х) = 0,8.
220. Дискретная случайная величина X имеет только
три возможных значения: jcx = 1, ха и х3, причем jc, <
<х2<л,. Вероятности того, что X примет значения xt
и х2 соответственно равны 0,3 и 0,2. Найти закон рас-
распределения величины X, зная ее математическое ожида-
ожидание М(Х) = 2,2 и дисперсию D(X) = 0,76.
221. Брошены п игральных костей. Найти дисперсию
суммы числа очков, которые могут появиться на всех
выпавших гранях.
Решение. Обозначим через X дискретную случайную вели-
величину—сумму числа очков, которые выпадут на всех гранях, через
Xi (/=1, 2, ..., п) — число очков, выпавших на грани t-й кости.
Тогда
X
Очевидно, все величины X/ имеют одинаковое распределение,
следовательно, одинаковые числовые характеристики и, в частности,
одинаковые дисперсии, т. е.
Так как рассматриваемые случайные величины независимы, то
дисперсия их суммы равна сумме дисперсий слагаемых:
В силу (*) получим
D(X)=nD(X1). (**)
Таким образом, достаточно вычислить дисперсию случайной ве-
величины Xi, т. е. дисперсию чнсла очков, которые могут выпасть на
74
«первой» кости. Сделаем это. Напишем закон распределения Xti
Xt I 2 3 4 5 6
р 1/6 1/6 1/6 1/6 1/6 1/6
Найдем М (Xj):
м (Xl)=14+2 • -6-+3 • I+4 • i+5 • т+6' т=т-
Напишем закон распределения Х\:
Х| 1 4 9 16 25 36
р 1/6 1/6 1/6 1/6 1/6 1/6
Найдем М {Х\) и D (Х{):
М (Л&-1 -1+4 4+9 • Т+16 ' Т+25 • -+36 • Т-Т'
Найдем искомую дисперсию, для чего подставим (***) в (**):
) C5/12)n.
222*. Вероятность наступления события в каждом
испытании равна р @<р< 1). Испытания производятся
до тех пор, пока событие не наступит. Найти: а) мате-
математическое ожидание дискретной случайной величины
X—числа испытаний, которые надо произвести до появ-
появления события; б) дисперсию величины X.
Решение, а) Составим закон распределения величины X —
числа испытаний, которые надо произвести, пока событие не наступит:
X 1 2 3 ... *
р р qp q*p ... qb^p ... (•)
Здесь <7=1—р—вероятность непоявления рассматриваемого собы-
события.
Найдем М (X):
Итак, М(Х) = \/р.
Пояснение. Покажем, что 1 +2q+3q2+ ...+kqk~l-\- ...=
=1/A—qJ. Так как 0 < q < 1, то степенной ряд (относительно q)
s=i+<?+<?8+...+<?*+•..=i/(i-<?)
можно почленно дифференцировать и сумма производных членов
ряда равна производной от суммы ряда, т. е.
S' = l+2,7+3?* + ..•+*<7*-1+... = 1/A-<72). Г)
б) Будем искать дисперсию величины X по формуле
D(X) = M(X*)-[M(X))K
Учитывая, что М(Х) = \/р, получим
75
Остается найти М (Хг). Напишем закон распределения X2, исполь-
используя распределение (*):
X* 1» 2а 3* ... Л2 ...
Р р qp q*p ... q^P ...
Найдем М(Хг):
М (Х2) = 1
Итак,
М(Х*) = B-р)/р*. ("*•)
Найдем искомую дисперсию, для чего подставим (****) в (***):
D(X) = B-p)/p*-
Пояснение. Покажем, что
Действительно,
+...) = <7/A-<7)« [см.
Дифференцируя обе части равенства по q, получим
223. Производятся многократные испытания некото-
некоторого элемента на надежность до тех пор, пока элемент
не откажет. Найти: а) математическое ожидание дискрет-
дискретной случайной величины X—числа опытов, которые надо
произвести; б) дисперсию X. Вероятность отказа эле-
элемента в каждом опыте равна 0,1.
Указание. Воспользоваться результатами задачи 222.
224. Доказать неравенство М [X—(*,+xk)/2]2 > D (X),
где х{ и xk—любые два возможных значения случайной
величины X.
Решение. 1) Допустим, что (Xi+xk)/2 = M(X). Тогда
2) Допустим, что (xi+xk)/2 Ф М(Х). Докажем, что в этом случае
76
Преобразуем левую часть неравенства, используя свойства ма-
математического ожидания:
Вычитая и прибавляя [М (X)]* в правой части равенства, получим
Объединяя (*) и (**), окончательно имеем
225. Доказать, что если случайная величина X имеет
наименьшее и наибольшее возможные значения, соответ-
соответственно равные а и Ь, то дисперсия этой случайной ве-
величины не превышает квадрата полуразности между
этими значениями:
D(X)<Z\(b-a)/2}*.
Решение. Воспользуемся неравенством (см. задачу 224)
Докажем теперь, что
М [Х-(
(Отсюда и нз (*) следует справедливость доказываемого неравенства.)
С этой целью преобразуем математическое ожидание:
М ЦЬ — о)/2]2 = Л![Х—(а + Ь)/2+(Ь—Х)]г =
= М[Х—(а-\ Ь)/2]* + М[(Ь-Х) (Х-а)].
Второе слагаемое правой части равенства неотрицательно (это
следует из того, что b—наибольшее и о—наименьшее возможные
значения), поэтому первое слагаемое не превышает всей суммы:
М [Х-(о+6)/2]2< М 1(Ь-а)/2]«-.
Учитывая, что математическое ожидание постоянной величины
равно самой постоянной, окончательно получим
М [Х-(
226. Доказать, что если X и Y—независимые случай-
случайные величины, то
D (XY) = D(X)-D (Y) + пЮ (X) + тЮ (Y),
где т = М(Х) и n = M(Y).
Решение. По формуле для вычисления дисперсии
D (XY) = М [(XY)*] -[М (XY)]K
Учитывая, что X и К—независимые величины и, следовательно,
X3 и Y2 также независимы и что математическое ожидание произве-
произведения независимых случайных величин равно произведеиию их мате-
77
матических ожиданий, получим
D (XY) = М [Л2 -К2] - [М (X) ¦ М (К)]2 =
= M(X2)M(V2)-mV. О
По определению дисперсии,
D(X) = M(X2)—m2,
Отсюда
Подставив (•*) в (*), после упрощений окончательно имеем
D (XY) = D(X)D (Y) + n2D (X) 4- m*D (К).
227. Найти дисперсию дискретной случайной вели-
величины X, распределенной по закону Пуассона:
X 0 1 2 ... k
Р е-* te
Решение. Воспользуемся формулой
D(X) = M(X2)-[M(X)]*.
Так как М (Х) = % (см. задачу 207), то
Напишем распределение случайной величины Л2, учитывая, что
вероятность того, что X* примет значение А2, равна вероятности
того, что X примет значение k (это следует из того, что возможные
значения X неотрицательны):
Хг О2 1* 2» ... к*
Найдем математическое ожидание Xh
М (Х*)= ^ '*А
А!
Учитывая, что при *=0 первый член суммы равен нулю, получим
Положив k—l=m, имеем
г »
Lm = o m=0
78
Принимая во внимание, что
]Г т ^ =Я, (см. задачу 207),
т= 0
J^e"*
05
2j m!
т=0 т=0
имеем
AJ (X2) = X (Я, -f-1) = Xs+Я,. (**)
Подставим (**) в (*):
Итак, дисперсия распределения Пуассона равна параметру А,.
§ 4. Теоретические моменты
Начальным моментом порядка k случайной величины X называют
математическое ожидание величины Xk:
В частности, начальный момент первого порядка равен матема-
математическому ожиданию:
Центральным моментом порядка k случайной величины X на-
называют математическое ожидание величины [X—М(Х)]Ь:
В частности, центральный момент первого порядка равен нулю:
[Н = М[Х—М(Х)]=0;
центральный момент второго порядка равен дисперсии:
ца = М [X—М (Х)]а = D (X).
Центральные моменты целесообразно вычислять, используя фор-
формулы, выражающие центральные моменты через начальные:
Ha = v»— vi,
N=V3— 3vxvi+2vi,
H4 = V4—4vxV8+6viV2—3v*.
228. Дискретная случайная величина X задана зако-
законом распределения:
л 1 3
р 0,4 0,6
Найти начальные моменты первого, второго и третьего
порядков.
Решение. Найдем начальный момент первого порядка:
79
Напишем закон распределения величины Хг:
X2 1 9
р 0,4 0,6-
Найдем начальный момент второго порядка:
\г=М (Х*)=1 0,4+90,6 = 5,8.
Напишем закон распределения величины А:
X3 I 27
р 0,4 0,6
Найдем начальный момент третьего порядка:
vs = М (Ха) =1-0,4+ 27 0,6 = 16,6.
229. Дискретная случайная величина X задана зако-
законом распределения:
X 2 3 5
р 0,1 0,4 0,5
Найти начальные моменты первого, второго и третьего
порядков.
230. Дискретная случайная величина X задана зако-
законом распределения:
X 1 2 4
р 0,1 0,3 0,6
Найти центральные моменты первого, второго, третьего
и четвертого порядков.
Решение. Центральный момент первого порядка равен нулю:
W=0.
Для вычисления центральных моментов удобно воспользоваться
формулами, выражающими центральные моменты через начальные,
поэтому предварительно найдем начальные моменты:
\x = M(X) =1-0,1+ 2-0,3+ 4-0,6=3,1;
vs = Af(X2)= 1-0,1+ 4-0,3+ 16-0,6=10,9;
¦va=M(X*)= 1-0,1+ 8-0,3+ 64-0,6=40,9;
v4=M(.X*)=l 0,1 + 160,3+256 0,6= 158,5.
Найдем центральные моменты:
H8 = Vl-v!=10,9-3,l» = l,29;
Hs = v3—3viVs!+2v!=40,9—3-3,1 -10,9+2-3,13=—0,888;
Ш = v4—4vsvi + &v2v i— 3v* =
= 158,5—4-40,9-3,1+6-10,9-3,lli—3-3,l4=2,7777.
231. Дискретная случайная величина X задана зако-
законом распределения
X 3 5
р 0,2 0,8
80
Найти центральные моменты первого, второго, третьего
и четвертого порядков.
Указание. Найти предварительно начальные моменты и выра-
выразить через них центральные моменты.
232. Доказать, что центральный момент второго по-
порядка (дисперсия) ца = М[Х—М(Х)]г меньше обычного
момента второго порядка \х, = М[Х—С]2 при любом СФ
ФМ(Х).
Решение. Для простоты записи введем обозначение М(Х)=т.
Прибавим и вычтем т под знаком математического ожидания:
цг = М [X—С]2 = /И [(X—т) + (т-С))* =
= /И [(X—отJ+2(от — С)(Х—т)+(т~С)*].
Математическое ожидание суммы равно сумме математических
ожиданий слагаемых, поэтому
цг = /И [X — от]2 + /И [2(от—С)(Х-т)] + М [от—С]2.
Вынося постоянную величину 2 (от—С) за знак математического ожи-
ожидания и учитывая, что математическое ожидание постоянной (от—СK
равно самой постоянной и что по определению М [X—/п|2=ц2,
получим
-С)./И [Х-от]+(от-СJ.
Принимая во внимание, что математическое ожидание отклонения
X—от равно нулю, имеем
Отсюда
ц2=Цз—(т — С)а.
Из этого равенства заключаем, что центральный момент второго
порядка меньше обычного момента второго порядка при любом С Ф т.
233. Доказать, что центральный момент третьего по-
порядка связан с начальными моментами равенством
Решение. По определению центрального момента,
Используя свойства математического ожидания и учитывая, что
М (X) есть постоянная величина, получим
= М(Х<>)—ЗМ(Х)-М(Х*)+ЗМ3(Х)—М3(Х)
= М(Х*)—ЗМ(Х)-М(Х*)+2М3(Х). (*)
По определению начального момента,
vx = М (X), v8 = М (X2), v3 = М (X3). (••)
Подставив (**) в (*), окончательно получим
81
234. Доказать, что центральный момент четвертого
порядка связан с начальными моментами равенством
ц4 = v4—4vs vt + 6v?v2—3v{.
235. Пусть X = X1 + XS, где Xt и Хг — независимые
случайные величины, имеющие центральные моменты
третьего порядка, соответственно равные ц\ и ц|. Дока-
Доказать, что Из = М'з + f*!» гДе И*—центральный момент треть-
третьего порядка величины X.
Решение. Введем для простоты записи следующие обозначе-
обозначения математических ожиданий: М(Х{)=а1, /И(Х2)=а2. Тогда
М (X) = M(Xt + Хг) = М (XJ+М (Хг)
По определению центральный момент третьего порядка,
Используя свойства математического ожидания (математическое
ожидание суммы равно сумме математических ожиданий слагаемых,
математическое ожидание произведения независимых величин равно
произведению математических ожиданий сомножителей), получим
Цз = М l(X1-ai?+3(X1-a1)*{X2-ai) +
(X1-a1)-(Xt-ai)* + (Xi-ai)*] =
l-al)* + M[3(Xl-a1)*]-M[Xt-a2] +
Учитывая, что математическое ожидание отклонения (разности
между случайной величиной и ее математическим ожиданием) равно
нулю, т. е. М[ХЛ — ах]=0 и M [Xs—a2]=0, окончательно имеем
Глава пятая
ЗАКОН БОЛЬШИХ ЧИСЕЛ
§ 1. Неравенство Чебышева
Неравенство Чебышева. Вероятность того, что отклонение
случайной величины X от ее математического ожидания по абсолют-
абсолютной величине меньше положительного числа г, не меньше чем 1 —D(X)/e2:
Р (| Х — М (X) | < e)Ss I —D(Х)/г*.
236. Используя неравенство Чебышева, оценить веро-
вероятность того, что случайная величина X отклонится от
своего математического ожидания менее чем на три сред-
средних квадратических отклонения.
82
237. Доказать неравенство Чебышева в форме
Р (| X—М (X) | > е) < D (Х)/е*.
Указание. Воспользоваться тем, что события | X— М (X) | < 8
\Х — М(Х)\^г—противоположные.
238. Используя неравенство Чебышева в форме, при-
приведенной в задаче 237, оценить вероятность того, что
случайная величина X отклонится от своего математи-
математического ожидания не меньше чем на два средних квад-
ратических отклонения.
239. Используя неравенство Чебышева, оценить веро-
вероятность того, что \Х — М(Х)\<0,2, если D(X)= 0,004.
240. Дано: Р{\Х — М(Х)\< е)>0,9 и D(X) = 0,009.
Используя неравенство Чебышева, оценить е снизу.
241. Устройство состоит из 10 независимо-работающих
элементов. Вероятность отказа каждого элемента за
время Т равна 0,05. С помощью неравенства Чебышева
оценить вероятность того, что абсолютная величина раз-
разности между числом отказавших элементов и средним
числом (математическим ожиданием) отказов за время Т
окажется: а) меньше двух; б) не меньше двух.
Решение, а) Обозначим через X дискретную случайную вели-
величину— число отказавших элементов за время Т. Тогда
() р , ,
D (X) = npq = 10 0,05 0,95 =0,475.
Воспользуемся неравенством Чебышева:
Подставив сюда М(Х)=0,5; D(X) =0,475, 8 = 2, получим
Р(\Х— 0,51 < 2) 3s 1—0,475/4=0,88.
б) События \Х—0,51 < 2 и \Х—0,5 |Ss 2 протипоположны, поэ-
поэтому сумма их вероятностей равна единице. Следовательно,
—0,5|Ss 2X1—0,88=0,12.
242. В осветительную сеть параллельно включено 20
ламп. Вероятность того, что за время Т лампа будет
включена, равна 0,8. Пользуясь неравенством Чебышева,
оценить вероятность того, что абсолютная величина раз-
разности между числом включенных ламп и средним числом
(математическим ожиданием) включенных ламп за время Т
окажется: а) меньше трех; б) не меньше трех.
243. Вероятность появления события А в каждом
испытании равна 1/2. Используя неравенство Чебышева,
83
оценить вероятность того, что число X появлений собы-
события А заключено в пределах от 40 до 60, если будет
произведено 100 независимых испытаний.
Решение. Найдем математическое ожидание и дисперсию дис-
дискретной случайной величины X— числа появлений события А в 100
независимых испытаниях:
M(X) = np = 100-l/2=50; D(X) = npq = 1001/2-1/2=25.
Найдем максимальную разность между заданным числом появле-
появлений события и математическим ожиданием М(Х)=50:
8 = 60—50 = 10.
Воспользуемся неравенством Чебышева в форме
Р (| Х — М (X) |<е)&1 -D{X)ltK
Подставляя /И(Х)=50, D(X)=25t e = 10, получим
Р(\Х—501 < 10)?il—25/102=0,75.
244. Вероятность появления события в каждом испы-
испытании равна 1/4. Используя неравенство Чебышева, оце-
оценить вероятность того, что число X появлений события
заключено в пределах от 150 до 250, если будет произ-
произведено 800 испытаний.
245. Дискретная случайная величина X задана зако-
законом распределения
X 0,3 0,6
р 0,2 0,8
Используя неравенство Чебышева, оценить вероятность
того, что \Х — М(Х)\<0,2.
Решение. Найдем математическое ожидание и дисперсию ве-
величины X:
= @,3*-0.2Н-0.62 0,8)—0,54" =0,0144.
Воспользуемся неравенством Чебышева в форме
Р (| Х — М (X) | < e)Ss I —D (Х)/е*.
Подставляя М(Х)=0,54, D(X) =0,0144, е=0,2, окончательно
получим
Р (| X— 0,541 < 0,2) Зэ 1 —0,0144/0,04 =0,64.
246. Дискретная случайная величина X задана зако-
законом распределения
X 0,1 0,4 0,6
р 0,2 0,3 0,5
Используя неравенство Чебышева, оценить вероятность
того, что \Х — М(Х)\< V
84
§ 2. Теорема Чебышева
Теорема Чебышева. Если последовательность попарно независимых
случайных величин Xi, Xt Хп, ... имеет конечные математические
ожидания и дисперсии этих величин равномерно ограничены (не
превышают постоянного числа С), то среднее арифметическое слу-
случайных величин сходится по вероятности к среднему арифметиче-
арифметическому их математических ожиданий, т. е. если е — любое положи-
положительное число, то
Я Я
У X
lim Р [ — У Xt — — V М
<8 =1.
В частности, среднее арифметическое последовательности попарно
независимых величин, дисперсии которых равномерно ограничены и
которые имеют одно и то же математическое ожидание а, сходится
по вероятности к математическому ожиданию а, т. е. если 8—любое
положительное число, то
. а <в) = 1.
1=1 J
247. Последовательность независимых случайных ве-
величин Xlt Xit ..., Хп, ... задана законом распределения
Хп — па О па
р 1/Bп2) 1 — 1 /я» 1/Bл2)
Применима ли к заданной последовательности теорема
Чебышева?
Решение. Для того чтобы к последовательности случайных
величин была применима теорема Чебышева, достаточно, чтобы эти
величины были попарно независимы, имели конечные математиче-
математические ожидания и равномерно ограниченные дисперсии.
Поскольку случайные величины независимы, то они подавно
попарно независимы, т. е. первое требование теоремы Чебышева
выполняется.
Проверим, выполняется ли требование конечности математиче-
математических ожиданий:
М(Хп) = — лаA/2л2)+0A — 1/л2) + лаA/2л2)=0.
Таким образом, каждая случайная величина имеет конечное (равное
нулю) математическое ожидание, т. е. второе требование теоремы
выполняется.
Проверим, выполняется ли требование равномериой ограничен-
ограниченности дисперсий. Напишем закон распределения Х%:
Xl л2а2 0 л*а»
р 1/Bл2) 1-1/л2
85
или, сложив вероятности одинаковых возможных значений,
л:„2 nv> о
р 1/л2 1—1/л*
Найдем математическое ожидание М
М(Хп) = п2а2-1/п*=а*.
Найдем дисперсию D(Xn), учитывая, что
Таким образом, дисперсии заданных случайных величин равно-
равномерно ограничены числом а*, т. е. третье требование выполняется.
Итак, поскольку все требования выполняются, к рассматривае-
рассматриваемой последовательности случайных величин теорема Чебышева
применима.
248. Последовательность независимых случайных ве-
величин Xv Xt, .... Хп, ... задана законом распределения
Хп а -а
р я/Bи + 1) (я + 1)/Bя+1)
Применима ли к заданной последовательности теорема
Чебышева?
249. Последовательность независимых случайных вели-
величин Хх, Х2, ..., Хп, ... задана законом распределения
Хп п + 1 —п
р я/Bя + 1) (я + 1)/Bя + 1)
а) Убедиться, что требование теоремы Чебышева о
равномерной ограниченности дисперсий не выполняется;
б) можно ли отсюда заключить, что к рассматриваемой
последовательности теорема Чебышева неприменима?
250*. Последовательность независимых случайных вели-
величин Хх, Х2, ..., Хп, ... задана законом распределения
Хп —па 0 па
р 1/2" 1 —1/2" 1/2»
Применима ли к заданной последовательности теорема
Чебышева?
Решение. Поскольку случайные величины Хп независимы,
то они подавно и попарно независимы, т. е. первое требование тео-
теоремы Чебышева выполняется.
Легко найти, что М(Хп)=0, т. е. требование конечности мате-
математических ожиданий выполняется.
Остается проверить выполнимость требования равномерной огра-
ограниченности дисперсий. По формуле
учитывая, что М(Хп)=0, найдем (выкладки предоставляется вы-
выполнить читателю)
Временно предположим, что я изменяется непрерывно (чтобы
подчеркнуть это допущение, обозначим я через х), и исследуем на
экстремум функцию <р (х) = х2/2х~1.
Приравняв первую производную этой функции нулю, найдем
критические точки ^=0 и *2 = 2/1п2.
Отбросим первую точку как не представляющую интереса (я не
принимает значения, равного нулю); легко видеть, что в точке
*2 = 2/1п2 функция <р(х) имеет максимум. Учитывая, что 2/1п2^= 2,9
и что я— целое положительное число, вычислим дисперсию D(Xn)=
л2
= 2^-гха2 для ближайших к числу 2,9 (слева и справа) целых чисел,
т. е. для я=2 и л = 3.
При я=2 дисперсия D (Х2) = 2а?, при я = 3 дисперсия D(X3)=
=(9/4) а2. Очевидно,
(9/4) а2 > 2а2.
Таким образом, наибольшая возможная дисперсия равна (9/4) а2,
т. е. дисперсии случайных величии Хп равномерно ограничены
числом (9/4) а2.
Итак, все требования теоремы Чебышева выполняются, следо-
следовательно, к рассматриваемой последовательности эта теорема при-
применима.
251. Последовательность независимых случайных вели-
величин Xit Xt, ...,Xn, ... задана законом распределения
хп -Уз о Уз
р 1/3 1/3 1/3
Применима ли к заданной последовательности теорема
Чебышева?
Замечание. Поскольку случайные величины Xt одинаково
распределены и независимы, то читатель, знакомый с теоремой Хин-
чина, может ограничиться вычислением лишь математического ожи-
ожидания и убедиться, что оно конечно.
Глава шестая
ФУНКЦИИ И ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН
§ 1. Функция распределения вероятностей
случайной величины
Функцией распределения называют функцию F (х), определяющую
для каждого значения х вероятность того, что случайная величина X
примет значение, меньшее х, т. е.
F(x) = P(X<x).
Часто вместо термина «функция распределения» используют
термин «интегральная функция распределения».
Функция распределения обладает следующими свойствами:
87
Свойство 1. Значения функции распределения принадлежат
отрежу [0; 1]:
0<F(at)<1.
Свойство 2. Функция распределения есть неубывающая
функция:
F(x2)^F(x1), если хг > хх.
Следствие 1. Вероятность того, что случайная величина X
примет значение, заключенное в интервале (а, Ь), равна приращению
функции распределения на этом интервале:
Р(а< X <b) = F(b)—F(a).
Следствие 2. Вероятность того, что непрерывная случайная
величина X примет одно определенное значение, например хи равна
нулю:
Р (* = *,) =0.
Свойство 3. Если все возможные значения случайной вели-
величины X принадлежат интервалу (а, Ь), то
F(x) — 0 при х<а; F(x) = l при
Следствие. Справедливы следующие предельные соотношения:
lim F(x)=0, Urn F(x) = \.
X-+ - 00 X -* CO
Свойство 4. Функция распределения непрерывна слева:
lira F(x) = F(x0).
t
252. Случайная величина X задана функцией распре-
распределения
!0 при х^С—1,
C/4)х + 3/4 при — 1<x<1/3,
1 при х > 1/3.
Найти вероятность того, что в результате испытания
величина X примет значение, заключенное в интервале
@, 1/3).
Решение. Вероятность того, что X примет значение, заклю-
заключенное в интервале (а, Ь), равна прнращенню функции распределения
на этом интервале: Р (а < X < b)=F(b)—F(а). Положив а=0,
6=1/3, получим
Р@<Х< \/3)=F(\/3)-F(Q) =
= [C/4) * + 3/4],=1/8-[C/4) *+3/4]х=0= 1/4.
253. Случайная величина X задана на всей оси Ох
функцией распределения F(x) = l/2 + (arctgx)/n. Найти
вероятность того, что в результате испытания величина X
примет значение, заключенное в интервале @, 1).
88
254. Случайная величина X задана функцией распре-
распределения
(О при х<—2,
l/2 + (l/n)arcsin(x/2) при — 2<х<2,
1 при х>2.
Найти вероятность того, что в результате испытания ве-
величина X примет значение, заключенное в интервале
(-1. О-
255. Функция распределения непрерывной случайной
величины X (времени безотказной работы некоторого
устройства) равна F(x) = l—е-*/т (х^О). Найти вероят-
вероятность безотказной работы устройства за время х^Т.
256. Случайная величина X задана функцией распре-
распределения
{О при х<2,
0,5* при 2<х<4,
1 при х>4.
Найти вероятность того, что в результате испытания X
примет значение: а) меньшее 0,2; б) меньшее трех; в) не
меньшее трех; г) не меньшее пяти.
Решение, а) Так как при х<2 функция F(x)=0, то
F@, 2) = 0, т. е. Р (X < 0, 2)=0;
б) P(X<3) = .FC) = l0,5*—1]*=3=1,5—1=0,5;
в) события Х^Зи Л<3 противоположны, поэтому Р (Х^3)+
+ Р(Х<3) = 1. Отсюда, учитывая, что Р (X <3) = 0,5 [см. п. б)],
получим Р(^^3) = 1-0,5=0,5;
г) сумма вероятностей противоположных событий равна единице,
поэтому Р (X Ss 5) -f P (X < 5) = 1. Отсюда, используя условие,
в силу которого при х > 4 функция F (х) = 1, получим Р (X Ss 5) =
= 1— Р(Х<5) = 1— f E) = 1 —1=0.
257. Случайная величина X задана функцией распре-
распределения
@ при х^.0,
х* при 0<х<1,
1 при х>1.
Найти вероятность того, что в результате четырех неза-
независимых испытаний величина X ровно три раза примет
значение, принадлежащее интервалу @,25, 0,75).
258. Случайная величина X задана на всей оси Ох
функцией распределения F(x) = 1/2 + A/л) arctg(jc/2).
Найти возможное значение xv удовлетворяющее условию:
89
с вероятностью 1/4 случайная величина X в результате
испытания примет значение, большее xt.
Решение. События X<Xi и X > Xi— противоположные,
Р (X ) Р (X ^ 1С Р (X )
поэтому Р (X < хг) + Р (X > х^) = 1. Следовательно, Р (X < лч) =
=1— Р(Х >хг) = 1 —1/4 = 3/4. Так как Р (Х = ^)=0, то
Р (Х<*!) = Р (Х = ^) + Р (X < *i)=P (X < xt) = 3/4.
По определению функции распределения,
Р (X < Xi) = /7(Jfi) = l/2 + (l^)arctg(^i/2).
Следовательно,
l/2 + (l/n)arctg(^1/2) = C/4), или arctg (Xj/2) = я/4.
Отсюда *i/2=l, или ^ = 2.
259. Случайная величина X задана на всей оси Ох
функцией распределения F (х) = (\/2)-\-(\/л) arctg(A:/2).
Найти возможное значение хх, удовлетворяющее условию:
с вероятностью 1/6 случайная величина X в результате
испытания примет значение,
большее xt.
260.Дискретная случай-
случайная величина X задана зако-
законом распределения
X 2 4 7
р 0,5 0,2 0,3
Найти функцию распределе-
распределения F {х) и начертить ее гра-
0,1
0,5
"Н 7^ х Фик-
0
Рис 6 Решение. 1. Если *<2,
то F(x)=0. Действительно, зна-
значений, меньших числа 2, величина X не принимает. Следовательно,
при *<2 функция F (х) = Р (X < х) = 0.
2. Если 2 < Ж 4, то ^(^ = 0,5. Действительно, X может при-
принять значение 2 с вероятностью 0,5.
3. Если 4<*<7, то F(x) = 0,7. Действительно, X может
принять значение 2 с вероятностью 0,5 и значение 4 с вероят-
вероятностью 0,2; следовательно, одно из этих значений, безразлично
какое, X может принять (по теореме сложения вероятностей несов-
несовместных событий) с вероятностью 0,5+0,2 = 0,7.
4. Если х > 7, то F (х) — 1. Действительно, событие Х^7 досто-
достоверно и вероятность его равна единице.
Итак, искомая функция распределения имеет вид
0 при *<2,
Plr\-j °'5 ПРИ 2<*<4-
f (х>-\ 0,7 при 4<х<7,
1 при х > 7.
График этой функции приведен на рис. 6.
90
261. Дискретная случайная величина задана законом
распределения
X 3 4 7 10
р 0,2 0,1 0,4 0,3
Найти функцию распределения и построить ее график.
§ 2. Плотность распределения вероятностей
непрерывной случайной величины
Плотностью распределения вероятностей непрерывной случай-
случайной величины называют первую производную от функции распреде-
распределения: f(x) = F' (х).
Часто вместо термина «плотность распределения» используют
термины «плотность вероятностей» и «дифференциальная функция».
Вероятность того, что непрерывная случайная величина X при-
примет значение, принадлежащее интервалу (а, Ь), определяется ра-
равенством ь
Я(а<Х< *) = $/(*)dx.
а
Зная плотность распределения, можно иайти функцию распреде-
X
ления F (x)= \ f(x)dx.
— 00
Плотность распределения обладает следующими свойствами:
Свойство 1. Плотность распределения неотрицательна, т. е.
/WO
Свойство 2. Несобственный интеграл от плотности раепре-
00
деления в пределах от —оо до оо равен единице: \ f(x)dx=l.
— 00
В частности, если все возможные значения случайной величины
ъ
принадлежат интервалу (а, Ь), то X / (х) d*=l.
а
262. Дана функция распределения непрерывной слу-
случайной величины X
' 0 при х^О,
sin а; при 0<а;<я/2,
1 при х > я/2.
Найти плотность распределения f(x).
Решение. Плотность распределения равна первой производной
от функции распределения:
( 0 при х < О,
f(x)=F' (*) = j cosx при 0<*<я/2,
V 0 при х > я/2.
Заметим, что при х=0 производная F' (х) не существует.
91
0
sin
1
2x
при
при
при
X
0
X
<
>
0,
х ^ я/4,
я/4.
263. Дана функция распределения непрерывной слу-
случайной величины X:
F(x) =
Найти плотность распределения f(x).
264. Непрерывная случайная величина X задана
плотностью распределения /(х) = C/2) sin Зл; в интервале
(О, я/3); вне этого интервала / (х) = 0. Найти вероятность
того, что X примет значение, принадлежащее интервалу
(я/6, я/4).
ь
Решение. Воспользуемся формулой Р (а < X < Ь) = \ / (х) Ах.
а
По условию, а = п/6, 6 = я/4, / (*) = C/2) sin 3*. Следовательно,
искомая вероятность
Я/4
Р (я/6 < X < я/4) = C/2) \ sin 3* dx= V"~2/4
я/6
(выкладки предоставляется выполнить читателю).
265. Непрерывная случайная величина X в интервале
@, со) задана плотностью распределения / (л;)=осе-оиг(а>0);
вне этого интервала /(х) = 0. Найти вероятность того,
что X примет значение, принадлежащее интервалу A, 2).
266. Плотность распределения непрерывной случайной
величины X в интервале (—я/2, я/2) равна f(x) =
= B/я) cos8 x; вне этого интервала /(х) = 0. Найти веро-
вероятность того, что в трех независимых испытаниях X
примет ровно два раза значение, заключенное в интер-
интервале @, я/4).
267. Задана плотность распределения непрерывной
случайной величины X:
@ при х<0,
cos а; при 0< х<я/2,
0 при х>я/2.
Найти функцию распределения F(x).
Решение. Используем формулу
92
Если х<0, то /(*)=0, следовательно,
О
F(x)= [ 0d*=0.
Если 0 < х < я/2, то
О
F{X)~X $
Если х > я/2, то
О я/2 х
F(x)= \ 0d*+ \ cos*d* + \ Od* = sin*
Я/2
= 1.
-оо О я/2 О
Итак, искомая функция распределения
(О при *<0,
sin* при 0 < *<я/2,
1 при х > я/2.
268. Задана плотность распределения непрерывной
случайной величины X:
(О при х^.0,
sin а; при 0< а;<я/2,
О при х>п/2.
Найти функцию распределения F(x).
269. Задана плотность распределения непрерывной
случайной величины X:
(О при х^.1,
х—1/2 при 1 <х<2,
О при х > 2.
Найти функцию распределения F(x).
270. Задана плотность распределения непрерывной
случайной величины X:
{О при х < я/6,
3 sin За; при я/6<л:<я/3,
О при х > я/3.
Найти функцию распределения F(x).
271. Плотность распределения непрерывной случайной
величины X задана на всей оси Ох равенством /(*) —
= 4С/(е* + е~*). Найти постоянный параметр С.
Решение. Плотность распределения / (*) должна удовлетво-
00
рять условию \ /(*)d.K=l. Потребуем, чтобы это условие выпол-
— 00
93
нялось для заданной функции:
со
4С f < d* ж_1
-0D
Отсюда
Найдем сначала неопределенный интеграл
exdx
Затем вычислим несобственный интеграл:
оо О Ь
С dx . С dx . р
J е* + е~А" о-»-х J е*+е~*"*"{,_,.„, J
-оо о О
о
= lim arctge* + lira arctge* =
= lim [arctgl—arctge0] + lira [arctge6—arctg 1]=я/2.
Таким образом,
00
dx я
2". (**)
Подставив (**) в (*), окончательно получим С = 1/2л.
272. Плотность распределения непрерывной случайной
величины X задана на всей оси Ох равенством /(а) =
=2С/A+х2). Найти постоянный параметр С.
273. Плотность распределения непрерывной случайной
величины X в интервале @, я/2) равна f (x) = С sin 2x;
вне этого интервала /(*) = 0. Найти постоянный пара-
параметр С.
274. Плотность распределения непрерывной случай-
случайной величины X задана в интервале @, 1) равенством
f (х) = С • arctg х; вне этого интервала /(х) = 0. Найти
постоянный параметр С.
§ 3. Числовые характеристики
непрерывных случайных величин
Математическое ожидание непрерывной случайной величины X,
возможные значения которой принадлежат всей оси Ох, определяется
равенством
J xf(x)dx,
— СО
94
где f(x)—плотность распределения случайной величины X. Предпо-
Предполагается, что интеграл сходится абсолютно.
В частности, если все возможные значения принадлежат интер-
интервалу (а, Ь), то
ъ
Все свойства математического ожидания, указанные выше для
дискретных случайных величин (см. гл. IV, § 3), сохраняются и для
непрерывных величин.
Если Y=<p(X)—функция случайного аргумента X, возможные
значения которого принадлежат всей оси Ох, то
Л1[Ф(Л:)]= J
В частности, если возможные значения X принадлежат интер-
интервалу (а, Ь), то
ь
Если математическое ожидание М (X) существует и кривая рас-
распределения симметрична относительно прямой х=С, то М(Х)—С.
Модой Ма (X) непрерывной случайной величины X называют
то ее возможное значение, которому соответствует локальный макси-
максимум плотности распределения. В частности, если распределение
имеет два одинаковых максимума, то его называют бимодальным.
Медианой Ме (X) непрерывной случайной величины X называют
то ее возможное значение, которое определяется равенством
Р [X < Ме (X)] =/> [X > Ме (X)).
Геометрически медиану можно истолковать как точку, в которой
ордината / (х) делит пополам площадь, ограниченную кривой рас-
распределения.
Дисперсия непрерывной случайной величины X, возможные зна-
значения которой принадлежат всей оси Ох, определяется равенством
00
D(X)= J [x-M(X))*f(x)dx,
— 00
или равносильным равенством
*•/(*) d*-[AI(A)]«.
В частности, если все возможные значения X принадлежат ин-
интервалу (а, Ь), то
ъ
или
a
Все свойства дисперсии, указанные выше для дискретных слу-
случайных величин (см. гл. IV, § 3), сохраняются и для непрерывных
величин.
Среднее квадратическое отклонение непрерывной случайной ве-
величины определяется так же, как и для дискретной величины:
о(Х)=УЩХ).
Если Y = <p(X) — функция случайного аргумента X, причем воз-
возможные значения X принадлежат всей оси Ох, то
или
= J <p*(x)f(x)dx-lM[<?(X)]]*.
В частности, если все возможные значения X принадлежат ин-
интервалу (а, Ь), то
ь
D [Ф (X)] = J [Ф (*) -М [Ф(*)]]*/(х) d*.
а
ИЛИ
6
D [Ф(А)] - J Ф2 (х) / (х) dx-[Al [Ф (А)Ц«.
а
Начальный теоретический момент порядка k непрерывной слу-
случайной величины X определяется равенством
ю
Центральный теоретический момент порядка k непрерывной
случайной величины X определяется равенством
— 00
В частности, если все возможные значения X принадлежат ин-
интервалу (а, Ь), то
ь ь
v*= J х*/(х) dx. 11к=^ [х-М(А)]*/(х) dx.
а а
Очевидно, что если А=1, то vj = M(X), |ii=0; если А=2, то
96
Центральные моменты выражаются через начальные моменты по
формулам:
m = vt—v,,
H» = v3—:3v,v2 |-2v,,
t*4 = v4 —4v!Vai- 6v,v,—3vfr
275. Случайная величина X задана плотностью рас-
распределения f(x) — 2x в интервале @, 1); вне этого ин-
интервала f{x) = O. Найти математическое ожидание вели-
величины X.
Решение. Используем формулу
ь
Подставив а —0, fc=l, f(x) = 2x, получим
I 1 1
| =2/3.
о
276. Случайная величина X задана плотностью рас-
распределения f(x) = (l/2)x в интервале @; 2); вне этого
интервала f(x) = Q. Найти математическое ожидание ве-
величины X.
277. Случайная величина X в интервале (—с, с) за-
задана плотностью распределения f(x) — \\{nVcl—**); вне
этого интервала f{x) = 0. Найти математическое ожидание
величины X.
ь
Решение. Используем формулу Af (X) = \ xf (x) dx. Подста-
а
вив fl=— с, Ь — с, /(лг)=1/(я У<?—хг), получим
Учитывая, что подынтегральная функция нечетная и пределы интег-
интегрирования симметричны относительно начала координат, заключаем,
что интеграл равен нулю. Следовательно, М (Х) = 0.
Этот результат можно получить сразу, если принять во внима-
внимание, что кривая распределения симметрична относительно прямой
*=0.
278. Случайная величина X задана плотностью веро-
вероятности (распределение Лапласа) /(лг)=A/2)е-|д:1. Найти
математическое ожидание величины X.
4 Гмурман В. Е. 97
279. Случайная величина X задана плотностью рас-
распределения f(x)>mc(xi + 2x) в интервале @, 1); вне этого
интервала /(#)"•(). Найти: а) параметр с; б) математи-
математическое ожидание величины X.
280. Найти математическое ожидание случайной вели-
величины X, заданной функцией распределения
{0 при JC<0
х/4 при 0<х<4,
1 при х > 4.
Решение. Найдем плотность распределения величины X:
{0 при х<0,
1/4 при 0<*<4,
0 при х > 4.
Найдем искомое математическое ожидание:
4 4
* = 2.
281. Случайная величина X, возможные значения
которой неотрицательны, задана функцией распределения
F(x)^\—е~ах (а > 0). Найти математическое ожидание
величины X.
282. Случайная величина X задана плотностью рас-
распределения /(*)-• A/2) sin л: в интервале @, я); вне этого
интервала f(x)m*0. Найти математическое ожидание
функции Y «и ф (X) «¦ Хг (не находя предварительно плот-
плотности распределения Y).
Решение. Воспользуемся формулой для вычисления матема-
математического Ожидания функции <f(X) от случайного аргумента X:
ь
где а и &—'концы интервала, в котором заключены возможные зна-
значения X. Подставляя <p(x)=x2, f (x) = (l/2)sinx, а — О, Ь = л и ин-
интегрируя по частям, окончательно получим
п
М (X*) =» i- \x* sin х dx = (ла—4)/2.
283. Случайная величина X задана плотностью рас-
распределения /(*)=¦ cos л: в интервале @, я/2); вне этого
интервала /(х) — 0. Найти математическое ожидание
функции У — ф(Х)«вХ* (не находя предварительно плот-
плотности распределения Y).
98
284. Случайная величина X задана плотностью рас-
распределения f(x)**x-\-0,5 в интервале @, 1); вне этого
интервала / (х) = 0. Найти математическое ожидание функ-
функции У = Х3 (не находя предварительно плотности рас-
распределения Y).
285. Случайная величина X задана плотностью рас*
пределения /(х) «* 2 cos2х в интервале @, я/4); вне этого
интервала / (дг) = 0. Найти! а) моду; б) медиану X.
Решение, а) Легко убедиться, что функция /(х) = 2cos2x
в открытом интервале @, я/4) не имеет максимума, поэтому X моду
не имеет.
б) Найдем медиану М1(Х) = те, исходя из определения медианы.
Р (X < те)=*Р (X > те), или, что то же, Р (X < те) -= 1/2.
Учитывая, что по условию возможные значения X положительны,
перепишем это равенство так:
те
Р@ < X < те)=\/2, или 2 С cos2^dx«=sln2me=-l/2.
Отсюда 2/ne = arcsin 1/2= я/6. Следовательно, искомая медиана
/12
286. Случайная величина X в интервале B, 4) задана
плотностью распределения /(*)=— C/4) х* ¦+• (9/2) х—6,
вне этого интервала f(x)**O. Найти моду, математическое
ожидание и медиану величины X.
Решение. Представим плотность распределения в виде /(*)»•
= — C/4) (*—3J+3/4. Отсюда видно, что при *=3 плотность рас*
пределения достигает максимума; следовательно, М0(Х)=3. (Разу-
(Разумеется, можно было найти максимум методами дифференциального
исчисления.)
Кривая распределения симметрична относительно прямой х —3,
поэтому /И(Х)"=3 и Ме(Х)^3.
287i Случайная величина X в интервале C, 5) задана
плотностью распределения /(*)-•— C/4) х2 + 6х—45/4}
вне этого интервала /(х) = 0. Найти моду, математическое
ожидание и медиану X.
288. Случайная величина X в интервале (—1, 1) за»
дана плотностью распределения /(*)•= 1/(л 1/^1—л;4); вне
этого интервала /(х) = 0. Найти: а) моду; б) медиану X,
289« Случайная величина X при х^О задана плот-
плотностью вероятности (распределение Вейбулла)
/(л;) = 0 при #<0. Найти моду X.
А* 99
290. Доказать, что математическое ожидание непре-
непрерывной случайной величины заключено между наимень-
наименьшим и наибольшим ее возможными значениями.
Решение. Пусть X— непрерывная случайная величина, за-
заданная плотностью распределения /(*) на отрезке [а, Ь\\ вне этого
отрезка/U) = 0. Тогда а<Ж&. Учитывая, что f(x)^O, получим
af (*)<*/(xXbf (x). Проинтегрируем это двойное неравенство в
пределах от а до Ь:
ь ь ь
a J / <*) dx< J xf(x) dx<b J / (x) dx.
a a a
Принимая во внимание, что
/> ft
J / (*) d.v= 1, \xf(x)dx=M(X),
a a
окончательно получим а<М (Х)<Ь.
291. Доказать, что если ton [xF(x)\ = 0 и litn [x(l —
w 0
M(X)-*Ul— F(x)]dx- J F(x)dx.
Указание. Имеем
CD 0 (В
M (X) = 5 */ (x) d*= J x/ («) d*+J ^ (*) dx.
-*> -oo 0
Заменить f(x) в первом слагаемом на f (x), а во втором—на
292. Случайная величина X в интервале (—с, с) за-
задана плотностью распределения / (х) = 1/(я Кс2—х*), вне
этого интервала ^(^ssO. Найти дисперсию X.
Решение. Будем искать дисперсию по формуле
ь
а
Подставляя М (Х)=0 (кривая распределения симметрична относи-
относительно прямой х=0), а = —с, Ь=с, /(дс)=1/(л У с*—-Xs), получим
Г
- ' Г x*dx 2 f x*dx
-с О
Сделав подстановку *=csin/, окончательно имеем D(X)—c*/2.
100
293. Случайная величина X в интервале (—3, 3) за-
задана плотностью распределения / (х) = 1 /(я У 9 —х*)\ вне
этого интервала f(x) = O. а) Найти дисперсию X; б) что
вероятнее: в результате испытания окажется X < 1 или
Х>1?
294. Доказать, что дисперсию непрерывной случайной
величины X можно вычислить по формуле
ос
Указание. Воспользоваться формулой
» »
я равенствами V xf (х)йх-М(Х), V / <дг) djt = 1.
-»
295. Случайная величина X в интервале @, л) задана
плотностью распределения /(*) = ( 1/2)sin*; вне этого
интервала /(х) = 0. Найти дисперсию X.
Решение. Найдем дисперсию по формуле
ь
Подставив сюда М(Х) = л/2 (кривая распределения симметрична
относительно прямой х=л/2), а=0, 6=л, / (х) = A/2) sin x, получим
Дважды интегрируя по частям, найдем
я
V jr* sin дс <1дг=зг* —4. (••)
о
Подставив (••) в (•), окончательно получим ?>(Х) = (д*—8)/4.
296. Случайная величина X в интервале @, 5) задана
плотностью распределения / (х) = B/25) х; вне этого ин-
интервала f(x)=±O. Найти дисперсию X.
297. Найти дисперсию случайной величины X, задан-
заданной функцией распределения
0 при *<—2,
,4 + 1/2 при —2<л:<2,
1 при х > 2.
101
ем плотность
\ 0
5< (с) = | 1/4
V 0
Решение. Найдем плотность распределения:
О при Ж—2,
1/4 при —2 < х < 2,
при х > 2.
Найдем математическое ожидание
2 2
Л1(Х) = \ xf(x)&x= \ *.Td*=0
-2 -2
(подынтегральная функция нечетная, пределы интегрирования сим-
симметричны относительно начала коордннат).
Найдем искомую дисперсию, учитывая, что М(Х)—0:
2 2 2.
D (X) = [ [х—М (X)]* f(x)dx= [ X* dx=~4
-2 -2 (
298. Случайная величина задана функцией распреде-
распределения
1—xl/x* при х > х„ {х0 > 0),
0 при х < х0.
Найти математическое ожидание, дисперсию и среднее
квадратическое отклонение X.
Указание. Найти сначала плотность распределения, исполь-
использовать формулу
00
x*f(x)dx-lM(X)]*.
299. Случайная величина X в интервале @, л) задана
плотностью распределения /(*) = (l/2)sin*; вне этого
интервала / (х)~ 0. Найти диспероию функции К = <р(Х)=
—X*, не находя предварительно плотности распределе-
распределения Y.
Решение. Используем формулу
ь
D [Ф (X)] = J ф* (х) / (х) dA:— [Л1 [ф (Х)]]«.
а
Подставив у(х)=хг, f(x) = (l/2)sinx, o=0, Ь=п, М[<р(Х)]=
УИ[Х2](л2—4)/2 (см. задачу 282), получим
л
p^i]* (*)
Интегрируя по частям, найдем
я
f ж45тх<к = я4—12я* + 48. (**)
Подставив (*•) в (•), окончательно имеем D(X2) = (n*—16л*+80)/4-
102
300. Случайная величина X задана плотностью рас-
распределения f(x) = cosx в интервале @, л/2); вне этого
интервала / (х) = 0. Найти дисперсию функции Y = <р (Х)=
—X2, не находя предварительно плотности распределе-
распределения Y.
Указание. Использовать формулу
ь
D [ф (X)] = J ф* (*) / (х) dx- [М [Ф (X)]]2
а
и то, что Л*(Х2) = (л2—8)/4 (см. задачу 283).
301. Случайная величина X задана плотностью рас-
распределения / (х) «= хпе~*/п\ при x^sO; /(д:) = 0 при л:<0.
Найти: а) математическое ожидание; б) дисперсию X.
Решение, а) Найдем математическое ожидание:
00 00 00
М (X) = J xf (x) Ax=^ J x-x"e-*dx = -1- J xn+>e-* dx.
Воспользуемся так называемой гамма-функцией, которая опре-
определяется равенством
»
Г(л)=Л x»-4-*dx.
'"I
Как видим, аргумент (целое число л), стоящий под знаком гамма-
функции, на единицу больше показателя степени буквы х, стоящей
под знаком интеграла. Следовательно,
[ (**)
о
Подставив (**) в (*), получим
Г(^+2) (***)
Воспользуемся следующим свойством гамма-функции:
Г(л) = (л-1)!
Как видим, гамма-функция от целого аргумента равна факториалу
от аргумента, уменьшенного на единицу. Следовательно,
Г(л+2) =
Подставив (****) в (***), получим
М (Х) л! л!
б) Найдем дисперсию. Учитывая, что
00
103
получим
Итак, D(X)=n+l.
302. Случайная величина X при х^О задана плот-
плотностью распределения (гамма-распределение)
/(д:) = 0 при ,v<0. Найти: а) математическое ожидание;
б) дисперсию X.
Указание. Сделать подстановку y—xl$ и использовать
гамма-функцию.
303. Доказать, что для любой непрерывной случайной
величины центральный момент первого порядка равен
нулю.
Решение. По определению центрального момента первого
порядка,
ос а> »
IH- J [x-M(X)]f(x)&x~ J xf(x)<bc-M{X) J f(x)Ax.
-ж -» -в
Учитывая, что
» «
J xf(x)dx=*M{X) и ^ /(л-) dx=l,
получим
М,=.Л1 (Х)-М (Х)=0.
304. Доказать, что обычный момент второго порядка
имеет наименьшее значение, если с = М{Х).
104
Решение. Преобразуем fij так:
00 Л
ц,'=. J (x-c)>/(x)dx« J f(x-
— о» -л
+ (М (X) -с)}* f (х) Ах = J [х-М (X)l« f (х)
-at
+ 2[М(А:)-с1 J [jc—Ai {АГI / (лс) d* Ч {М (X)—^J" J f(x)dx.
Принимая во внимание равенства
получим
Отсюда видно, что ц« имеет наименьше* значение при с=-М (X),
что и требовалось доказать,
Заметим, что из (•) следует, что ц»=»ц»— [М(Х)—с]1, т.е.
центральный момент второго порядка меньше любого обычного мо-
момента второго порядка, если с Ф М (X).
305. Случайная величина X задана плотностью рас
пределения /(х) = 0,5х в интервале @, 2); вне этого ин-
интервала / (лг) = 0. Найти начальные и центральные мо-
моменты первого, второго, третьего и четвертого порядков.
Решение. По формуле
2
найдем начальные моменты:
2 2
v, = \х- @,5*) d*=»-i l v, = \ х* ¦ @,5*) d*=2;
2 2
v,= Сж».@.5л) djt=3,2; v4= С х»-@,5*) d* = j.
Найдем центральные моменты. Центральный момент первого порядка
любой случайной величины f*i==0.
105
Воспользуемся формулами, выражающими центральные моменты
через начальные:
Подставив в эти формулы ранее найденные начальные моменты,
получим: Ца = 2/9, fis = — 8/135, ц4= 16/135.
306. Случайная величина X задана плотностью рас-
распределения /(*) = 2* в интервале @, 1); вне этого интер-
интервала /(л:) = 0. Найти начальные и центральные моменты
первого, второго, третьего и четвертого порядков.
§ 4. Равномерное распределение
Равномерным называют распределение вероятностей непрерывной
случайной величины X, если на интервале (а, Ь), которому принад-
принадлежат все возможные значения X, плотность сохраняет постоянное
значение, а именно f(x) = l/(b—а); вне этого интервала f(x)—Q.
307. Плотность равномерного распределения сохраняет
в интервале (а, Ь) постоянное значение, равное С; вне
этого интервала f(x) = 0. Найти значение постоянного
параметра С.
308. Цена деления шкалы амперметра равна 0,1 А.
Показания округляют до ближайшего целого деления.
Найти вероятность того, что при отсчете будет сделана
ошибка, превышающая 0,02 А.
Решение. Ошибку округления отсчета можно рассматривать
как случайную величину X, которая распределена равномерно в
интервале между двумя соседними целыми делениями. Плотность
равномерного распределения f(x) = \/(b—а), где (Ь—а)—длина ин-
интервала, в котором заключены возможные значения А"; вне этого
интервала f(x)=Q. В рассматриваемой задаче длина интерпала,
в котором заключены возможные значения X, равна 0,1, поэтому
/ (дс) = 1/0,1 = 10. Легко сообразить, что ошибка отсчета превысит
0,02, если она будет заключена в интервале @,02, 0,08).
ь
По формуле Р (а < X < Ь) = С / {х) dx получим
а
0,08
Р @,02 < X < 0,08)= [ 10d*=0,6.
0,02
309. Цена деления шкалы измерительного прибора
равна 0,2. Показания прибора округляют до ближайшего
целого деления. Найти вероятность того, что прн отсчете
будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.
106
310. Автобусы некоторого маршрута идут строго по
расписанию. Интервал движения 5 мин. Найти вероят-
вероятность того, что пассажир, подошедший к остановке, будет
ожидать очередной автобус менее 3 мин.
311. Минутная стрелка электрических часов переме-
перемещается скачком в конце каждой минуты. Найти вероят-
вероятность того, что в данное мгновение часы покажут время,
которое отличается от истинного не более чем на 20 с.
312. Закон равномерного распределения задан плот-
плотностью вероятности f(x) = l/(b—а) в интервале (а, 6); вне
этого интервала /(*) = 0. Найти функцию распределе-
распределения F(x).
313. Найти математическое ожидание случайной вели-
величины X, равномерно распределенной в интервале (а, Ь).
Решение. График плотности равномерного распределения сим-
симметричен относительно прямой *=(а+6)/2, поэтому М (Х)=(а-{-Ь)/2.
Итак, математическое ожидание случайной величины, равномерно
распределенной в интервале (а, Ь), равно полусумме концов этого
интервала. Разумеется, этот же результат можно получить по фор-
формуле
В частности, математическое ожидание случайной величины R,
распределенной равномерно в интервале @, 1), равно
314. Найти математическое ожидание случайной вели-
величины X, распределенной равномерно в интервале B, 8).
315. Найти дисперсию и среднее квадратическое откло-
отклонение случайной величины X, распределенной равномерно
в интервале (а, Ь).
Решение. Используем формулу
ъ
а
Подставив /(*) = 1/(&—а), М(Х) = (а+Ь)/2 (см. задачу 313) и вы-
выполнив элементарные выкладки, получим искомую дисперсию
?>(*) = (*—aJ/12.
Среднее квадратнческое отклонение случайной величины X равно
квадратному корню из ее дисперсии:
В частности, дисперсия н среднее квадратическое отклонение
случайной величины/?, распределенной равномерное интервале @,1),
соответственно равны: D(R) = 1/12, о (Я) = 1/B У~Ъ)-
107
316. Найти дисперсию и среднее квадратическое откло-
отклонение случайной величины X, распределенной равномерно
в интервале B, 8).
317. Равномерно распределенная случайная величина X
задана плотностью распределения /(*) = 1/B/) в интервале
(а—/, а + 1); вне этого интервала /(*) = 0. Найти мате-
математическое ожидание и дисперсию X.
318. Диаметр круга х измерен приближенно, причем
a^Ars^fc. Рассматривая диаметр как случайную вели-
величину X, распределенную равномерно в интервале (а, Ь),
найти математическое ожидание и дисперсию площади
круга.
Решение. I. Найдем математическое ожидание площади
круга—случайной величины К = <р(/С)=лХ4/4—по формуле
ь
а
Подставив ф(ж)=ллс*/4, f(x) = l/(b—а) и выполнив интегрирование,
получим
М [яЯ*/4] = л {Ь* + аЬ + оа)/12.
2. Найдем дисперсию площади круга по формуле
ь
D [Ф(X)} = J ф*(х) f (х) dx-[M [ф<*)]]¦.
а
Подставив ф(х) = лд;г/4, }(х) = \/(Ь—а) и выполнив интегрирование»
получим
D [яХг/41 = (л1/720) (Ь—а)« (<№-\-7ab у 4аг).
319. Ребро куба х измерено приближенно, причем
а^лг<[&. Рассматривая ребро куба как случайную вели-
величину X, распределенную равномерно в интервале (а, Ь),
найти математическое ожидание и дисперсию объема куба.
320. Случайные величины X н Y независимы и рас-
распределены равномерно: X — в интервале (a, b), Y—в ин-
интервале (с, d). Найти математическое ожидание произве-
произведения XY.
Указание. Воспользоваться решением задачи 313.
321. Случайные величины X и К независимы и рас-
распределены равномерно: X — в интервале (a, b), Y — в ин-
интервале (с, d). Найти дисперсию произведения XY.
Решение. Воспользуемся формулой
Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий, поэтому
D(XY) = M(Xt)-M(Y*)-[M (X)M(Y)}*. (*)
108
Найдем М (X*) по формуле
ь
Подставляя ф(дг) = **, /(х) = 1/(*—а) и выполняя интегрирование,
получим
Аналогично найдем
Подставив M(X) = {a+b)/2, M(Y) = (c+d)/2, а также (*•) и
(¦*¦) в (*), окончательно получим
§ 5. Нормальное распределение
Нормальным называют распределение вероятностей непрерывной
случайной величины X, плотность которого имеет вид
где а—математическое ожидание, а—среднее квадрэтическое откло-
отклонение X.
Вероятность того, что X примет значение, принадлежащее ин-
интервалу (а, Р),
X
где Ф(дг) = . \ е"**'* Ах—функция Лапласа.
]Г2к \
X
. \
]Г2к \
Вероятность того, что абсолютная величина отклонения меньше
положительного числа б,
Р(\Х—а\ <б) = 2ФF/о-).
В частности, при а=0 справедливо равенство
Р(\Х\ <6)=2Ф(б/о).
Асимметрия, эксцесс, мода н медиана нормального распределе-
распределения соответственно равны:
AS=Q, Е*=0, М„ = а, Ме = а, где а = М(Х).
322. Математическое ожидание нормально распреде-
распределенной случайной величины X равно а — 3 и среднее квад-
ратическое отклонение а = 2. Написать плотность веро-
вероятности X.
323. Написать плотность вероятности нормально рас-
распределенной случайной величины X, зная, что М(Х) = 3,
D(X)=16.
109
324. Нормально распределенная случайная величина X
задана плотностью f(x) = —y=-e~ix~1)'/t<'- Найти матема-
тическое ожидание и дисперсию X.
325. Дана функция распределения нормированного
нормального закона F(x) = -^= J e-'l/2cU. Найти плот-
' * -00
ность распределения /(*).
326. Доказать, что параметры а и а—плотности
нормального распределения—являются соответственно
математическим ожиданием и средним квадратическим
отклонением X.
Указание. При нахождении М(X) и D(X) следует ввести
новую переменную г=(х—а)/о и использовать интеграл Пуассона
со
327. Доказать, что функция Лапласа
нечетна: Ф(—х) =—Ф(х).
Указание. Положить z=—t в равенстве
328. Математическое ожидание и среднее квадрэтичес-
квадрэтическое отклонение нормально распределенной случайной
величины X соответственно равны 10 и 2. Найти вероят-
вероятность того, что в результате испытания X примет значе-
значение, заключенное в интервале A2, 14).
Решение. Воспользуемся формулой
Подставив а=12, Р = 14, а=10 и а=2, получим Я A2 < X < 14) =
= ФB)—ФA). По таблице приложения 2 находим: Ф B) =0,4772,
Ф A)=0,3413. Искомая вероятность РA2 < X < 14)=0,1359.
329. Математическое ожидание и среднее квадратичес-
кое отклонение нормально распределенной случайной
по
величины X соответственно равны 20 и 5. Найти вероят-
вероятность того, что в результате испытания X примет значе-
значение, заключенное в интервале A5, 25).
330. Автомат штампует детали. Контролируется длина
детали X, которая распределена нормально с математи-
математическим ожиданием (проектная длина), равным 50 мм. Фак-
Фактически длина изготовленных деталей не менее 32 и не
более 68 мм. Найти вероятность того, что длина наудачу
взятой детали: а) больше 55 мм; б) меньше 40 мм.
Указание. Из равенства Р C2 < X < 68) = 1 предварительно
найти о.
331. Производится измерение диаметра вала без си-
систематических (одного знака) ошибок. Случайные ошибки
измерения X подчинены нормальному закону со средним
квадратическим отклонением а=10мм. Найти вероятность
того, что измерение будет произведено с ошибкой, не пре-
превосходящей по абсолютной величине 15 мм.
Решение. Математическое ожидание случайных ошибок равно
иулю, поэтому применима формула Р (\Х\< о)=2Ф(б/а). Положив
6=15, о=10, находим Р(|Х|< 15)=2ФA,5). По таблице прило-
приложения 2 находим: Ф A,5) =0,4332. Искомая вероятность
Р(\Х\ < 15)^2-0,4332 = 0,8664.
332. Производится взвешивание некоторого вещества
без систематических ошибок. Случайные ошибки взвеши-
взвешивания подчинены нормальному закону со средним квад-
квадратическим отклонением а = 20 г. Найти вероятность того,
что взвешивание будет произведено с ошибкой, не пре-
превосходящей по абсолютной величине 10 г.
333. Случайные ошибки измерения подчинены нор-
нормальному закону со средним квадратическим отклонением
а = 20 мм и математическим ожиданием а = 0. Найти
вероятность того, что из трех независимых измерений
ошибка хотя бы одного не превзойдет по абсолютной
величине 4 мм.
334. Автомат изготовляет шарики. Шарик считается
годным, если отклонение X диаметра шарика от проектного
размера по абсолютной величине меньше 0,7 мм. Считая,
что случайная величина X распределена нормально со
средним квадратическим отклонением а = 0,4 мм, найти,
сколько в среднем будет годных шариков среди ста из-
изготовленных.
Решение. Так как X—отклонение (диаметра шарика от про-
проектного размера), то М(Х)=а= 0.
111
Воспользуемся формулой Р (| X | < 6) - 2Ф F/о). Подставив
в —0,7, о«^0,4, получим
Р(\Х\< 0,7) = 2Ф (Й)=2Ф 0.75) = 2 0,4599 = 0,92.
Таким образом, вероятность отклонения, меньшего 0,7 мм, равна
0,92. Отсюда следует, что примерно 92 шарика из 100 окажутся
годными.
335. Деталь, изготовленная автоматом, считается год-
годной, если отклонение ее контролируемого размера от
проектного не превышает 10 мм. Случайные отклонения
контролируемого размера от проектного подчинены нор-
нормальному закону со средним квадратическим отклонением
а = 5мм и математическим ожиданием а = 0. Сколько
процентов годных деталей изготавливает автомат?
336. Бомбардировщик, пролетевший вдоль моста, длина
которого 30 м и ширина 8 м, сбросил бомбы. Случайные
величины X и У (расстояния от вертикальной и гори-
горизонтальной осей симметрии моста до места падения бомбы)
независимы и распределены нормально со средними квад-
ратическими отклонениями, соответственно равными 6 и
4 м, и математическими ожиданиями, равными нулю.
Найти: а) вероятность попадания в мост одной сброшен-
сброшенной бомбы; б) вероятность разрушения моста, если сбро-
сброшены две бомбы, причем известно, что для разрушения
моста достаточно одного попадания.
337. Случайная величина X распределена нормально
с математическим ожиданием а = 10. Вероятность попада-
попадания X в интервал A0, 20) равна 0,3. Чему равна веро-
вероятность попадания X в интервал @, 10)?
Решение. Так как нормальная кривая симметрична относи-
относительно прямой х = а—Ю, то площади, ограниченные сверху нор-
нормальной кривой и снизу—интервалами @, 10) и A0, 20), равны
между собой. Поскольку эти площади численно равны вероятностям
попадания X в соответствующий интервал, то
Р @ < X < 10) = /> A0 < X < 20)=--0,3.
338. Случайная величина X распределена нормально
с математическим ожиданием а = 25. Вероятность попа-
попадания X в интервал A0, 15) равна 0,2. Чему равна веро-
вероятность попадания X в интервал C5, 40)?
339. Доказать, что
1. е., что значение удвоенной функции Лапласа при за-
заданном / определяет вероятность того, что отклонение
112
X—а нормально распределенной случайной величины X
по абсолютной величине меньше at.
Указание. Использовать формулу Р (\ Х—а | < 6) =2Ф (в/о),
положив б/а-—/.
840. Вывести «правило трех сигм»: вероятность того,
что абсолютная величина отклонения нормально распре-
распределенной случайной величины будет меньше утроенного
среднего квадратического отклонения, равна 0,9973.
Указание. Использовать решение задачи 339, положив/ = 3.
341. Случайная величина X распределена нормально
е математическим ожиданием а =10 и средним квадра-
тическим отклонением о —5. Найти интервал, симмет-
симметричный относительно математического ожидания, в кото-
который с вероятностью 0,9973 попадет величина X в ре-
результате испытания.
342. Случайная величина X распределена нормально
со средним квадратическим отклонением а = 5 мм. Найти
длину интервала, симметричного относительно математи-
математического ожидания, в который с вероятностью 0,9973
попадет X в результате испытания.
343. Станок-автомат изготовляет валики, причем кон-
контролируется их диаметр X. Считая, что X—нормально
распределенная случайная величина с математическим
ожиданием а —10 мм и средним квадратическим откло-
отклонением о = 0,1 мм, найти интервал, симметричный отно-
относительно математического ожидания, в котором с веро-
вероятностью 0,9973 будут заключены диаметры изготовленных
валиков.
344. Нормально распределенная случайная величина X
задана плотностью
Найти моду и медиану X.
Решение. Модой М„ (X) называют то возможное значение X,
при котором плотность распределения имеет максимум. Легко убе-
убедиться, что при х*=а производная /' (а)=0; при х < а производная
/' (ж) > 0, при х > а производная /' (*) < 0; таким образом, точка
х = а есть точка максимума, следовательно, Afo(X) = a.
Медианой Ме (X) называют то возможное значение X, прн ко-
котором ордината fix) делит пополам площадь, ограниченную кривой
распределения. Так как нормальная кривая [график функции /(*)]
симметрична относительно прямой х — а, то ордината f (а) делит
1K
пополам площадь, ограниченную нормальной кривой. Следовательно,
Ме(Х) = а.
Итак, мода и медиана нормального распределення совпадают
с математическим ожиданием а.
345. Случайная величина X распределена нормально,
причем математическое ожидание а = 0 и среднее квад-
ратическое отклонение равно а. Найти значение а, при
котором вероятность того, что X примет значение, при-
принадлежащее интервалу (а, р") (а > 0, р* > а), будет наи-
наибольшей.
Указание. Воспользоваться формулой
Р (а < X < Р) = Ф (Р/а) —Ф (а/о) =
найти о из уравнения ф'(о)=0.
§ 6. Показательное распределение
и его числовые характеристики
Показательным (экспоненциальным) называют распределение ве-
вероятностей непрерывной случайной величины X, которое описы-
описывается плотностью
О при х < О,
где Я.—постоянная положительная величина.
Функция распределення показательного закона
0 при х < О,
Вероятность попадания в интервал (а, Ь) непрерывной случай-
случайной величины X, распределенной по показательному закону,
Р (а < X < 6) = e~^—e-w.
Математическое ожидание, дисперсия и среднее квадратическое
отклонение показательного распределения соответственно равны:
Таким образом, математическое ожидание и среднее квадрати-
квадратическое отклонение показательного распределения равны между собой.
346. Написать плотность и функцию распределения
показательного закона, если параметр Х = 5.
114
Решение. Подставив Л.™о в соотношения (*) п (**), получив*
. ( 0 при*<0,
tW \5e-5* при
\l-e-5* при
347. Написать плотность и функцию распределения
показательного закона, если параметр Х = 6.
348. Найти параметр Я показательного распределе-
распределения: а) заданного плотностью / (*)=0 при х < 0, / (х)=2е~г*
при х>0; б) заданного функцией распределения/г(х)=0
при л:<0 и F(x)=*l— е-»-** при *>0.
349. Доказать, что если непрерывная случайная вели-
величина X распределена по показательному закону, то вероят-
вероятность попадания X в интервал (а, Ь) равна е-*"—е~**.
Решение. Первый способ. Пусть величина X задана
функцией распределения F(*) = 1— e-te(x^sQ). Тогда вероятность
попадания X в интервал (а, Ь) (см. гл. VI, § 1)
Р (а < X < Ь) = F (Ь) — F (а) = [1 —e-W] _ [1 —е W
Второй способ. Пусть величина X задана плотностью рас-
распределения f(x) = ke-b*(x^sO). В этом случае (см. гл. VI, § 2)
ъ
( ) е-**
Р(а< X < 6) = Jе-** d*=A, •(- у) е
350. Непрерывная случайная величина X распреде-
распределена по показательному закону, заданному плотностью
вероятности /(д:) = 3е~3* при А'>0; при л:<0 /(д;) = 0.
Найти вероятность того, что в результате испытания X
попадает в интервал @,13, 0,7).
Решение. Используем формулу
Р(а<Х <Ъ) = е-**—e-W.
Учитывая, что, по условию, о=0,13, 6=0,7, Я, = 3, и пользуясь
таблицей значений функции е~*. получим
Р @,13 < X < 0,7) = е-з-о.»з_е-8-о.7 =е-°.з»—e~*.i =
=0,677—0,122 = 0,555.
351. Непрерывная случайная величина X распреде-
распределена по показательному закону, заданному при х^0
плотностью распределения /(Ar) = O,O4«e~OiMJC; при д;<0
функции /(д;) = 0. Найти вероятность того, что в резуль-
результате испытания X попадает в интервал A, 2).
115
352. Непрерывная случайная величина X распреде-
распределена по показательному закону, заданному функцией
распределения F(x)= Г— е~м* при х^О; при .v<0
F(x) = 0. Найти вероятность того, что в результате ис-
испытания X попадет в интервал B, 5).
353. Найти математическое ожидание показательного
распределения
(> = 0
Решение. Используем формулу
М (X) = J */ (х) dx.
— «о
Учитывая, что f (х) -=0 при х < 0 и / (дг) = Л.е~*^ при х^О, получим
Интегрируя по частям по формуле
о3 1° i
положив и = х, dv — e-*** dx и выполнив выкладки, окончательно по-
получим М(Х) = 1/Х.
Итак, математическое ожидание показательного распределения
равно обратной величине параметра X.
354. Найти математическое ожидание показательного
распределения, заданного при х^О: а) плотностью
f(x) = 5e-;*; б) функцией распределения F(x) — \—е~м*.
355. а) Доказать, что если непрерывная случайная
величина распределена по показательному закону, то
вероятность того, что X примет значение, меньшее мате-
математического ожидания М (X), не зависит от величины
параметра X; б) найти вероятность того, что X > М(Х).
356. Найти: а) дисперсию; б) среднее квадратическое
отклонение показательного распределения, заданного
плотностью вероятности: /(.г) = Яе-и при д:>0; /
при х < 0.
Решение, а) Используем формулу
116
Учитывая, что /(дс) = О при х < О, АЦХ) = \/\ (см. задачу 358), по-
получим
т
D{X) =xf x*e-b*dx
S
Интегрируя дважды по частям, найдем
Следовательно, искомая дисперсия
т. е. дисперсия показательного распределения равна величине, об-
обратной А.*.
б) Найдем среднее квадратическое отклонение:
т. е. среднее квадратическое отклонение показательного распределе-
распределения равно величине, обратной А..
357. Найти дисперсию и среднее квадратическое от-
отклонение показательного распределения, заданного плот-
плотностью вероятности /(*) = 10е~1в* (х^О).
358. Найти дисперсию и среднее квадратическое от-
отклонение показательного закона, заданного функцией
распределения F (х) = 1 —е~м* (х ^ 0).
359. Студент помнит, что плотность показательного
распределения имеет вид /(.v) = 0 при л:<0, /(л:) = Се~ь
при дс^гО; однако он забыл, чему равна постоянная С.
Требуется найти С.
Указание. Использовать свойство плотности распределения:
360. Найти теоретический центральный момент третьего
порядка ря = М[Х — М(Х)]* показательного распределе-
распределения.
Указание. Использовать решения задач 353 и 356.
361. Найти асимметрию As = \i3/o*(X) показательного
распределения.
Указание. Использовать решения задач 356 и 360.
117
862. Найти теоретический центральный момент четвер-
четвертого порядка ц4 = М [X — М (X)]4 показательного распре-
распределения.
363. Найти эксцесс Ек— а^Х)—3 показательного рас-
распределения.
364. Доказать, что непрерывная случайная величина
Т — время между появлениями двух последовательных
событий простейшего потока с заданной интенсивностью %
(см. гл. IV, § 2)—имеет показательное распределение
lu(tO)
Решение. Предположим, что в момент t0 наступило событие Ai
потока. Пусть ti=t(>-rt (рекомендуем для наглядности начертить
ось времени н отметить на ней точки tt и t{).
Если хотя бы одно событие потока, следующее за событием Аи
произойдет в интервале, заключенном внутри интервала (to, tx)>
например, в интервале (/0, '*)> то время Т между появлениями двух
последовательных событий окажется меньшим /, т. е. окажется, что
Т <t.
Для того чтобы найти вероятность Р (Т < /), примем во вни-
внимание, что события — «внутри интервала (/0, t{) появилось хотя бы
одно событие потока» и «внутри интервала (t0, i{) не появилось ни
одного события потока»—противоположны (сумма их вероятностей
равна единице).
Вероятность непоявления за время t ни одного события потока
Pt(®)=——-fif—i = e-*'. Следовательно, интересующая нас веро-
вероятность противоположного события Р (Т < 0 — 1—е-*-', или [по оп-
определению функции распределения F(t) = P (T < t)] имеем F(t) =
=1—е-*', что и требовалось доказать.
365. Задана интенсивность простейшего потока >- = 5.
Найти: а) математическое ожидание; б) дисперсию; в) сред-
среднее квадратическое отклонение непрерывной случайной
величины Т—времени между появлениями двух последо-
последовательных событий потока.
Указание. Использовать решение задачи 364.
366. На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти
математическое ожидание и среднее квадратическое от-
отклонение случайной величины Т — времени ожидания
очередной машины контролером,— если поток машин про-
простейший и время (в часах) между прохождениями машин
через контрольный пункт распределено по показатель-
показательному закону /(/) = 5е~8'.
Указание. Время ожидания машины контролером и время
прохождения машин через контрольный пункт распределены одинаково.
118
§ 7. Функция надежности
Элементом называют некоторое устройство, независимо от того,
«простое» оно или «сложное». Пусть элемент начинает работать в мо-
момент времени /о —0, а в момент t происходит отказ. Обозначим
через Т непрерывную случайную величину—длительность времени
безотказной работы элемента, а через Я,—интенсивность отказов (сред-
(среднее число отказов в единицу времени).
Часто длительность времени безотказной работы элемента имеет
показательное распределение, функция распределения которого
F(t) = P(T< 0 = 1— е-*' (А,>0)
определяет вероятность отказа элемента за время длитель-
длительностью t.
Функцией надежности R (/) называют функцию, определяющую
вероятность безотказной работы элемента за время
длительностью t:
Я@=е-«.
367. Длительность времени безотказной работы элемента
имеет показательное распределение F (t)=1 —е~0<01' (t > 0).
Найти вероятность того, что за время длительностью
2 = 50 ч: а) элемент откажет; б) элемент не откажет.
Решение, а) Так как функция распределения F (/) = 1 —е-"-01'
определяет вероятность отказа элемента за время длительностью t,
то, подставив /=50 в функцию распределения, получим вероятность
отказа:
F E0) = 1 — e-o.oi-50^ 1 — е-**. = 1 —0,606 = 0,394;
б) события «элемент откажет» и «элемент не откажет»—противо-
откажет»—противоположные, поэтому вероятность того, что элемент не откажет
Р = 1—0,394=0,606.
Этот же результат можно получить непосредственно, пользуясь
функцией надежности #@ = е-х', которая определяет вероятность
безотказной работы элемента за время длительностью /:
R E0) = e-».eiso==e-o.5 =0,606.
368. Длительность времени безотказной работы эле-
элемента имеет показательное распределение F (/)= 1—е-03'.
Найти вероятность того, что за время длительностью
2 = 100 ч: а) элемент откажет; б) элемент не откажет.
369. Испытывают два независимо работающих эле-
элемента. Длительность времени безотказной работы первого
элемента имеет показательное распределение Ft (i) =
= 1 —е~0'02*, второго Fa(t) = l— е~°«вм. Найти вероят-
вероятность того, что за время длительностью 2 = 6 ч: а) оба
элемента откажут; б) оба элемента не откажут; в) только
один элемент откажет; г) хотя бы один элемент откажет.
119
Решение, а) Вероятность отказа первого элемента
^1 = ^1 F)= 1 — е-».««= 1 — е-*1* = 1 -0,887-0,113.
Вероятность отказа второго элемента
ptr^ | _е-в.»»« - 1 — е-»-» 1 —0,741 ==-0.259.
Искомая вероятность того, что оба элемента откажут, по теореме
умножения вероятностей
PtPt- 0,113 0,259=0.03.
б) Вероятность безотказной работы первого элемента
qt = R, F)x=e-e.<«« = e-«>.»=0,887.
Вероятность безотказной работы второго элемента
,fc = tftF) = e-<M>slt--=e-e.s = 0,741.
Искомая вероятность безотказной работы обоих элементов
<?!•<?» =0,887 0,741 =0,66.
в) Вероятность того, что откажет только один элемент
Pi<?2 :-/>i<?i = 0,1130,741-J- 0,259 0,887 = 0,31.
г) Вероятность того, что хотя бы один элемент откажет
Р ¦-, 1 —(/,G,-1 —0,66 = 0,34.
370. Испытывают три элемента, которые работают
независимо один от другого. Длительность времени без-
безотказной работы элементов распределена по показатель-
показательному закону: для первого элемента Ft (/) = 1—e~Ot"; для
второго F2(t) — — e~0'", для третьего элемента F,(*) ¦¦
— 1 —е~0-". Найти вероятности того, что в интервале
времени @, 5) ч откажут: а) только один элемент; б) только
два элемента; в) все три элемента.
371. Производится испытание трех элементов, работаю-
работающих независимо один от другого. Длительность времени
безотказной работы элементов распределена по показа-
показательному закону: для первого элемента /i(^) = 0,le~e'ut
для второго /,(/) = 0,2е~0'", для третьего элемента /,(/)-¦
=0,Зе~0>". Найти вероятности того, что в интервале
времени @, 10) ч откажут: а) хотя бы один элемент;
б) не менее двух элементов.
Указание. Воспользоваться результатами, полученными при
решении задачи 370.
372. Показательным законом надежности называют
функцию надежности, определяемую равенством R (/j»e~wf
где положительное число Я,—интенсивность отказов. Дока-
Доказать характеристическое свойство показательного закона
120
надежности: вероятность безотказной работы элемента
в интервале времени длительностью t не зависит от вре-
времени предшествующей работы до начала рассматривае-
рассматриваемого интервала, а зависит только от длительности ин-
интервала / (при заданной интенсивности отказов X).
Решение. Введем обозначения событий: Л — безотказная работа
элемента в интервале (О, t0) длительностью to; В—безотказная ра-
работа элемента в интервале (/„, /0 —/) длительностью /.
Тогда АВ—безотказная работа в интервале @, ioi-t) длитель-
длительностью /в — I.
По формуле R (О --¦¦ е-*' найдем вероятности этих событий:
Найдем условную вероятность того, что элемент будет работать
безотказно в интервале (tt, tt-\-() при условии, что он уже прора-
проработал безотказно в предшествующем интервале @. /„):
Так как в полученной формуле не содержится ta, а содержится
только i, то это и означает, что время работы в предшествующем
интервале не влияет на величину вероятности безотказиой работы
иа последующем интервале, а зависит только от длины I последую-
последующего интервала (tf+t), что и требовалось доказать.
Другими словами, условная вероятность Рд (б) безотказной ра-
работы в интервале времени длительностью /, вычисленная в предполо-
предположении, что элемент проработал безотказно на предшествующем
интервале, равна безусловной вероятности Р (В).
Глава седьмая
РАСПРЕДЕЛЕНИЕ ФУНКЦИИ ОДНОГО
И ДВУХ СЛУЧАЙНЫХ АРГУМЕНТОВ
§ 1. Функция одного случайного аргумента
Если каждому возможному значению случайной величины X
соответствует одно возможное значение случайной величины Y, то Y
называют функцией случайного аргумента X и записывают У = <р (Л).
Если X — дискретн а я случайная величина н функ-
функция К=<р(Л) монотонна, то различным значениям X соответствуют
различные значения V, причем вероятности соответствующих зна-
значений X и Y одинаковы. Другими словами, возможные значения Y
находят нз равенства
где дс/—возможные значения X; вероятности возможных значений Y
находят из равенства
Р(К=и)=Я(Х-х/).
Если же Y = fp(X)—немонотонная функция, то, вообще говоря,
различным значениям X могут соответствовать одинаковые значе-
121
ния У (так будет, если возможные значения X попадут в интервал,
в котором функция <р (X) не монотонна). В этом случае для отыска-
отыскания вероятностей возможных значений У следует сложить вероятности
тех возможных значений X, при которых У принимает одинаковые
значения. Другими словами, вероятность повторяющегося значения Y
равна сумме вероятностей тех возможных значений X, при кото-
которых У принимает одно и то же значение.
Если X—непрерывная случайная величина, за-
заданная плотностью распределения /(*), и если #=<p(jr)—дифферен-
#=<p(jr)—дифференцируемая строго возрастающая или строго убывающая функция,
обратная функция которой дс=а|) (у), то плотность распределения g (у)
случайной величины Y находят из равенства
Если функция у=<р(х) в интервале возможных значений X не
монотонна, то следует разбить этот интервал на такие интервалы,
в которых функция <р(дг) монотонна, и найти плотности распределе-
распределений gi(y) для каждого нз интервалов монотонности, а затем пред-
представить g(y) в виде суммы:
2
Например, если функция <р(х) монотонна в двух интервалах, в ко-
которых соответствующие обратные функции равны ф4 (у) и а|)г (у), то
g (y) = f N>f (У)] -I *I (У) \+f H* (У)] I Ь (У) I-
373. Дискретная случайная величина X задана зако-
законом распределения:
X 1 3 5
р 0,4 0,1 0,5
Найти закон распределения случайной величины Y = ЗХ.
Решение. Найдем возможные значения величины Y = 3X.
Имеем: yi=3• 1 = 3; уг=3-3 = 9; уя=3-5=15. Видим, что различным
возможным значениям X соответствуют различные значения У. Это
объясняется тем, что функция у=<р(х)=3х монотонна. Найдем
вероятности возможных значений У. Для того чтобы У = У| = 3
достаточно, чтобы величина X приняла значение хх = 1. Вероятность
же события Х=1 по условию равна 0,4; следовательно, и вероят-
вероятность события y = yt = 3 также равна 0,4.
Аналогично получим вероятности остальных возможных значе-
значений У:
Напишем искомый закон распределения У:
У 3 9 15
р 0,4 0,1 0,5
374. Дискретная случайная величина X задана зако-
законом распределения:
X 3 6 10
р 0,2 0,1 0,7
122
Найти закон распределения случайной величины Y —
= 2Х + 1.
375. Дискретная случайная величина X задана зако-
законом распределения:
X —1 —2 1 2
р 0,3 0,1 0,2 0,4
Найти закон распределения случайной величины Y = Х*.
Решение. Найдем возможные значения У:
Итак, различным значениям X соответствуют одинаковые значе-
значения Y. Это объясняется тем, что возможные значения X принадле-
принадлежат интервалу, на котором функция Y — X* не монотонна.
Найдем вероятности возможных значений У. Для того чтобы
величина Y приняла значение У = 1, достаточно, чтобы величина X
приняла значение Х=—1 или Х = 1. Последние два события не-
совместиы, их вероятности соответственно равны 0,3 н 0,2. Поэтому
вероятность события Г = 1 по теореме сложения
= 1)=0,3+0,2=0,5.
Аналогично найдем вероятность возможного значения У =4:
Напишем искомый закон распределения величины Y:
Y 1 4
р 0,5 0,5
376. Дискретная случайная величина X задана зако-
законом распределения:
X л/4 л/2 Зл/4
р 0,2 0,7 0,1
Найти закон распределения случайной величины K=sin X.
377. Задана плотность распределения /(*) случайной
величины X, возможные значения которой заключены
в интервале (а, Ь). Найти плотность распределения слу-
случайной величины Y = ЪХ.
Решение. Так как функция у=3дс дифференцируемая н строго
возрастает, то применима формула
где i|)(i/)—функция, обратная функции y—Zx.
Найдем а|) (у):
Найдем / [г|) (у)]:
/1Ф(У)]=/(У/3). (••)
123
Найдем производную \|)' (у):
Очевидно, что
|Ч>' (У) 1 = 1/3. С")
Найдем искомую плотность распределения, для чего подставим
(*•) и (***) в (*): g(jr) = (l/3)/|(y/3).
Так как х изменяется в интервале (в, 6) и у — Здг, то Зв < у < 36.
378. Задана плотность распределения f(x) случайной
величины X, возможные значения которой заключены
в интервале (а, Ь). Найти плотность распределения g(y)
случайной величины Y, если: а) К — — ЗХ; б) Y= АХ+В.
379. Случайная величина X распределена по закону
Коши
Найти плотность распределения случайной величины Y—
380. Задана плотность распределения f(x) случайной
величины X, возможные значения которой заключены
в интервале @, оо). Найти плотность распределения g(у)
случайной величины Y, если: а) К = е~*; б) К = 1пХ;
в) К = Х»; г) К=1/Х»; д) Y = VX.
381. Задана плотность распределения f(x) случайной
величины X, возможные значения которой заключены
в интервале (— оо, оо). Найти плотность распределе-
распределения g(y) случайной величины Y, если: a) Y = X*;
б) У = е-*'; в) К = |Х|; г) K = cosX; д) K = arctgX;
е) К.1/A+Х»).
382. В прямоугольной системе координат хОу из точки
А D; 0) наудачу (под произвольным углом /) проведен луч,
пересекающий ось Оу. Найти дифференциальную функцию
g(y) распределения вероятностей ординаты у точки пере-
пересечения проведенного луча с осью Оу.
Решение. Угол / можно рассматривать как случайную вели-
величину, распределенную равномерно в интервале (—л/2, л/2), причем
в этом интервале плотность распределения
л/2—(—л/2)~л"
вне рассматриваемого интервала /(/) = 0.
Из рис. 7 следует, что ордината у связана с углом / следующей
зависимостью: y=4igt. Эта функция в интервале (—л/2, я/2) моно-
монотонно возрастает, поэтому для отыскания искомой плотности
124
рвспределения g(y) применима формула
где * (у) —функция, обратная функции у — 4tg/.
Найдем $()
Найдем if' (у):
Следовательно,
ts'(y)| = 4/A6-i-y«). (**) V
/ И (У))- Так как f(t) = \/n, _S
9\
1
Найдем / [*(у)]. Так как f(t) = \/n,
то Т
Подставив (**) и (••*) в (•), оконча-
окончательно получим
г (у) 4
AM)
ЯA6-т-у*) ' РиС. У
причем — оо < у < оо (последнее следует из того, что y = A\.gt
и —я/2 < / < я/2).
Контроль:
<к «е х
*L__A.of АУ _4-2л_,
383. Саучайная величина X равномерно распределена
в интервале (—я/2, я/2). Найти плотность распределе-
распределения g(y) случайной величины K = sinX.
Решение. Найдем плотность распределения /(*) случайной
величины X. Величина X распределена равномерно в интервале
<—я/2, я/2), поэтому в этом интервале
_
n/2—(— л/2)~я :
вне рассматриваемого интервала f(x)=O.
Функция y = sinx в интервале (—я/2, я/2) монотонна, следова-
следовательно, в этом интервале она имеет обратную функцию x—\f{y) =
— arcsiny. Найдем производную ^' (У)'-
Найдем искомую плотность распределения по формуле
Учитывая, что f(x) — \fn (следовательно, / [я|) (у)] = 1/я) и
*' (У) 1 = 1/^1 —Уг. получим
= 1/(л V\-y*).
125
Так как y = s\nx, причем — л/2 < дс < л/2, то — 1 < у < I.
Таким образом, в интервале (—1, 1) имеем g {у) = 1/(я V 1—у2); вне
этого интервала g(y)==0.
Контроль:
= 2/л-я/2=1.
384, Случайная величина X распределена равномерно
в интервале @, л/2). Найти плотность распределения g(y)
случайной величины Y—
-=sinX.
385. Задана плотность
распределения случайной ве-
величины X: f(x) = 1/я в интер-
0
271 X вале (— Я/2' п/2У> вне ЭТОГО
интервала / (х) = 0. Найти
плотность распределения g (у)
рис в случайной величины К«=
g
386. Случайная величина X распределена равномерно
в интервале @, 2я). Найти плотность распределения g(y)
случайной величины K = cosX.
Решение. Найдем плотность распределения /(*) случайной
величины X: в интервале @, 2л) имеем
вне этого интервала /(*) = 0.
Из уравнения y = cosx найдем обратную функцию x=ty(y)
Так как в интервале @, 2л) функция у = cos л: не монотонна, то
разобьем этот интервал на интервалы @, я) н (л, 2л), в которых
эта функция монотонна (рис. 8). В интервале @, я) обратная функ-
функция i|5i(y) = arccoay; в интервале (я, 2л) обратная функция ifjW =
=—arc cos 1/. Искомая плотность распределения может быть найдена
из равенства
Найдем производные обратных функций:
^(у) = (arccosу)' = — 1/У 1— у2, fy(у) = (— arccosу)'
Найдем модули производных:
h'i(y)\=WT=F, \b(y)\=i/VT=i?. (**)
Учитывая, что /(х)=1/2л, получим
126
Подставляя (**) и (***) в (*), имеем
8(У) ±
Так как y = cos#, причем 0 < х < 2л, то — 1 < у < 1. Таким обра-
образом, в интервале (—1, 1) искомая плотность распределения ()
¦я 1/(я }Л—у2); вне этого интервала g(y)=0.
Контроль:
= 2/я-л/2=1.
387. Случайная величина X распределена равномерно
в интервале (—я/2, я/2). Найти плотность распределе-
распределения g(y) случайной величины K = cosX.
388. Случайная величина X распределена нормально
с математическим ожиданием, равным а, и средним квад-
ратическим отклонением, равным а. Доказать, что линей-
линейная функция Y = АХ + В также распределена нормально,
причем
M(Y) = Aa+B, a(Y) = \A\o.
Решение. Напишем плотность распределения случайной вели-
величины X:
Функция у = Ах-\-В монотонна, поэтому применима формула
Найдем дс=о|)(#) из уравнения у=Ах+В:
Найдем /N, (у)]:
1(у-В)/А-ау
Найдем а|/ (у):
V (У) = 1(У
Найдем | а|/ {у) |:
|я))'(у)| = 1/|Л|. (•*¦)
Подставляя (**) и (***) в (*), имеем
Отсюда видно, что линейная функция Y=AX + B распределена
нормально, причем М (Y) = Аа+ В н а (К) = | А | а, что и требовалось
доказать.
127
389. Задана плотность / (х) = ' е-**''», (— °о<х<оо)
V 2л
нормально распределенной случайной величины X. Найти
плотность распределения а {у) случайной величины
Y = X*.
Решение. Из уравнения у=х* найдем обратную функцию.
Так как в интервале (—ее, ее) функция у — хг не монотонна, то
разобьем этот интервал на интервалы (— оо, 0) и @, оо), в которых
рассматриваемая функция монотонна. В интервале (— оо, 0) обрат-
обратная функция i\'\(y) = — V~y\ в интервале @, оо) обратная функция
y)Vy
Искомая плотность распределения может быть найдена из ра-
равенства
g (у)=/ 1Ь Ш -I Ь(у) I + / № (у)) -\ъ(у) I- С)
Найдем производные обратных функций:
Чч {У) - -1/B VI). *» (У) = 1/B }П,).
Найдем модули производных:
I Ч>1 (У) 1-1/B VI), I Ч* (У) I =» 1/B VD- С»)
Учитывая, что /(^)=_—e-*'/J, $t(y)^
получим
Подставляя (**) и (***) в (*), имеем
Так как у =жа, причем — оо<лс<ее, тоО<у<оо.
Таким образом, в интервале @, ее) искомая плотность распре-
распределения
вне этого интервала g((/)=0.
Контроль:
Положив у = /* и, следовательно, dy=2/d/, получим
128
ев
Учитывая, что интеграл Пуассона 1 e~/>/l2 d<= . ' , найдем
о
390. Задана плотность /(.t) = ...^ е~*>/2 нормально
К 2л
распределенной случайной величины X. Найти плотность
распределения случайной величины К = A/2)Х*.
391. Задана плотность распределения /(*) =
= ——=-е *'/-°*. Найти плотность распределения g(y)
о У 2я
случайной величины «/ = A/4) X*.
392. Случайная величина X задана плотностью рас-
распределения /(*) = ( 1/2) sin* в интервале @, п); вне этого
интервала /(,v) = 0. Найти математическое ожидание слу-
случайной величины К = ф(Х) = Х2, определив предвари-
предварительно плотность распределения g(Y) величины Y.
Решение. Найдем сначала плотность g (у) случайной вели-
величины Y. Так как функция у=у(х)=х* для рассматриваемых зна-
значений х @ < х < л) строго возрастающая, то плотность g (у) будем
искать по формуле
где ty(y)=V~y—функция, обратная функции К = дгг. Подставляя
*(*)= VJ и учитывая, что / (х) -A/2) sin х, | ф' (у) | | ( /"?)' |
= 1/B ]^у), получим
У у).
Найдем искомое математическое ожидание величины У, учитывая,
что возможные значения Y заключены в интервале @, л2) [так как
у =х* иО<дс<л, тоО<у< л*]:
Пользуясь подстановкой y = t2, получим
л
M(Y)<=—[t* sin tdt.
о
Интегрируя дважды по частям, окончательно имеем
5 Гмурмаи Б. Е. 129
Замечание. Решение, приведенное выше, преследует учебные
цели. Гораздо быстрее ведет к цели формула
я
1 f
М [Я2] = -д- ^JC2sin jc djf = (л2—4)/2.
о
Это же замечание относится и к задаче 393.
393, Случайная величина X задана плотностью рас-
пределекия /(x) = cosjc в интервале @, я/2); вне этого
интервала Дд;) = 0. Найти математическое ожидание
функции К = ф(Х) = Х2.
394. Случайная величина X задана плотностью рас-
распределения /(*)«= A/2)sin* в интервале @, я); вне
этого интервала /(х) = 0. Найти дисперсию функции
К = ф(Х) = Х2, используя плотность распределения g(y).
Решение. Используем формулу
d
с
где с я d—концы интервала, в котором заключены возможные зна-
значения Y. Подставляя g(y) = sin V~ylA V~y, M (У) = (ла—4)/2 (см.
задачу 392) и учитывая, что с=0 и rf=n4 (так каку=дсг н 0<*<я,
то 0 < у < я2), получим
Г)
Интегрируя сначала с помощью подстановки y = t%, а потом
четырежды по частям, имеем
У '
Подставив (**) в (*), окончательно получим
(л4—16яа + 80)/4.
395. Случайная величина X задана плотностью рас-
распределения /(x) = cqsx в интервале @, л/2); вне этого
интервала /(х) = 0. Найти дисперсию функции
У к а з а н_и е. Предварительно найти плотность распределения
cos Y у/2 VI) величины У<^Хг; использовать формулу
я«/4
[
130
где М(У) = (л2—8)/4 (см. задачу 393). При вычислении интеграла
сначала воспользоваться подстановкой у =>¦<*, а затем интегрировать
по частям.
396. Ребро куба измерено приближенно, причем
а^х^Ь. Рассматривая ребро куба как случайную ве-
величину X, распределенную равномерно в интервале
(а, Ь), найти: а) математическое ожидание объема куба;
б) дисперсию объема куба.
Указание. Предварительно найти плотность распределения
8(У)=3(Ь-а)у*>*
случайной величины у = Х3. Использовать формулы
ft5 б»
М (Y) = [ yg (у) йу, D(Y)=[ y*g {у) dy-W (Y)}*.
397. Задана функция распределения F(x) случайной
величины X. Найти функцию распределения G{y) слу-
случайной величины У = ЗХ + 2
Решение. По определению функции распределения, G(y) =
= Р (У < у). Поскольку функция у=3*-{-2—возрастающая, то не-
неравенство Y < у выполняется, если имеет место неравенство X < х,
поэтому
Из уравнения у=Зх-]-2 выразим дс:
х = (у-2)/3. (**)
Подставив (**) в (*), окончательно получим
398. Задана функция распределения F(x) случайной
величины X. Найти функцию распределения G(y) слу-
случайной величины У*=— B/3) X + 2.
Решение. По определению функции распределения,
G(y)=P(Y <y).
Поскольку функция у — — B/3)jc+2—убывающая, то неравенство
Y < у выполняется, если имеет место неравенство X > х, поэтому
G() P(Y)P(X>)
) (y)()
События X < х к X > х противоположны, поэтому сумма веро-
вероятностей этих событий равна единице: Р (X < х)-\-Р(Х > *) = 1.
Отсюда
P{X>x) = l-PiX<x)-l-F(x))
следовательно,
G(y) = l-F(x). (•)
5* 131
Из уравнения у—— B/3)дг+2 выразим х:
*=3B-у)/2. (**)
Подставив (**) в (*), окончательно получим
399. Задана функция распределения F (х) случайной
величины X. Найти функцию распределения G(y) слу-
случайной величины Y, если: а) К = 4X4-6; б) Y-— 5Х + 1;
в) Y = X b
§ 2. Функция двух случайных аргументов
Если каждой паре возможных значений случайных величии X
и У соответствует одно возможное значение случайной величины Z,
то Z называют функцией двух случайных аргументов X и Y и пишут
Если X и Y—дискретные независимые случайные вели-
величины, то, для того чтобы найти распределение функции Z=X-\-Y,
надо найти все возможные значения 2, для чего достаточно сложить
каждое возможное значение X со всеми возможными значениями Y;
вероятности найденных возможных значений Z равны произведениям
вероятностей складываемых значений X и Y.
Если X н Y—непрерывные независимые случайные вели-
величины, то плотность распределения g(z) суммы Z = X-\-Y (при усло-
условии, что плотность распределения хотя бы одного нз аргументов
задана в интервале (— оо, оо) одной формулой) может быть найдена
по формуле
fi(x)ft(?-
либо по равносильной формуле
где fi и ft—плотности распределения аргументов; если возможные
значения аргументов неотрицательны, то плотность распределения
g(z) величины Z=X + Y находят по формуле
либо по равносильной формуле
О
В том случае, когда обе плотности /i(x) и ft(y) заданы иа
конечных интервалах, для отыскания плотности g(z) величины
Z = X-{-Y целесообразно сначала найти функцию распределения
132
G(z), а затем продифференцировать ее по г:
Если X и Y—независимые случайные величины, заданные соот-
соответствующими плотностями распределения /i(;c) и ft(y), то вероят-
вероятность попадания случайной точки (X, Y) в область D равна двойному
интегралу по этой области от произведения плотностей распреде-
распределения:
Р \(Х, У)сО] = J J /, (.г)/,(у)d* Ay.
ID)
400. Дискретные независимые случайные величины X
и Y заданы распределениями:
X 1 3 К 2 4
Р 0,3 0,7: Р 0,6 0,4
Найти распределение случайной величины Z = X + K.
Решение. Для того чтобы составить распределение величины
Z~X-\-Y, надо найти все возможные значения Z и их вероятности.
Возможные значения Z есть суммы каждого возможного значе-
значения X со всеми возможными значениями Y:
г, = 1+2=3; га = 1-|-4 = 5; *,=3-i-2 = 5; z4 = 3-f4 = 7.
Найдем вероятности этих возможных значений. Для того чтобы
Z=3, достаточно, чтобы величина X приняла значение *j = l и
величина К—значение yi=2. Вероятности этих возможных значе-
значений, как следует из данных законов распределения, соответственно
равны 0,3 и 0,6. Так как аргументы X и Y независимы, то события
Х = \ и Y=2 независимы н, следовательно, вероятность нх совмест-
совместного наступления (т. е. вероятность события Z = 3) no теореме умно-
умножения раина 0,30,6=0,18.
Аналогично найдем:
Я B=!-f4 = 5) = 0,3 0,4 = 0,12;
P(Z = 34-2 = 5) =0,7 0.6 = 0,42;
P(Z = 3-Й = 7) =0,7-0,4 = 0.28.
Напишем искомое распределение, сложив предварительно веро-
вероятности несовместных событий 2 = га = 5, Z=zs = 5 @,12+0,42=0,54):
Z 3 5 7
Р 0,18 0,54 0,28
Контроль: 0,18 + 0,54+0,28 = 1.
401. Дискретные случайные величины X и К заданы
распределениями:
а) X 10 12 16 К 1 2
Р 0,4 0,1 0,5' Р 0,2 0,8'
б) X 4 10 К 1 7
Р 0,7 0,3* Р 0,8 0,2'
Найти распределение случайной величины Z = X-\-Y.
133
402. Независимые случайные величины X и Y заданы
плотностями распределений:
М*) = е-* @<*<оо), Ш
Найти композицию этих законов, т. е. плотность распре-
распределения случайной величины Z**X + Y.
Решение. Так как возможные значения аргументов неотри-
неотрицательны, то применима формула
Z
= U
Следовательно,
Выполнив элементарные преобразования, получим
Здесь z^sO, так как Z=X-\-Y и возможные значения X и Y
неотрицательны.
Итак, g(z)=e~2/2 [1—е~2/2] в интервале @, оо), вне этого
интервала g(z) — 0.
00
Рекомендуем для контроля убедиться, что \ g(z)dz = l.
о
403. Независимые случайные величины X и Y заданы
плотностями распределений:
Д (х) = A/3) е-*/» @<х < оо), /, (у) = A/5) е-»/» @<«/< оо).
Найти композицию этих законов, т. е. плотность распре-
распределения случайной величины Z = X + Y.
404. Независимые нормально распределенные случай-
случайные величины X и Y заданы плотностями распределений:
Л (*) = A/K2S) е-*''2, /, (у) - A/К2Й) е-^/2.
Доказать, что композиция этих законов, т. е. плот-
плотность распределения случайной величины Z — X + Y,
также есть нормальный закон.
Решение. Используем формулу g(z)= С fi(x)ft(z—x) dx.
Тогда
05
()
134
Выполнив элементарные выкладки, получим
Дополнив показатель степени показательной функции, стоящей
под знаком интеграла, до полного квадрата, вынесем ег'^4 за знак
интеграла:
05
— 00
Учитывая, что интеграл Пуассона, стоящий в правой части равен-
равенства, равен У~л , окончательно имеем в (г)=—7=.Р~2*^1,
У1л
Рекомендуем для контроля убедиться, что \ ?(г)<1г = 1, Для
— 00
этого следует воспользоваться подстановкой г=У~2 4 и принять во
00
внимание, что интеграл Пуассона \ e~/tyf2d/= У~2л~.
-00
Заметим, что в рассматриваемой задаче легко убедиться, что
Можно доказать, что эти формулы справедливы и при композиции
общих нормальных законов (т. е. если математическое ожидание
отлично от нуля и среднее квадратическое отклонение ие равно
единице).
405. Заданы плотности распределений независимых
равномерно распределенных случайных величин X и Y:
fx (х) = 1/2 в интервале @, 2), вне этого интервала
Л(*) = О;
/а (У) = 1/2 в интервале @,2), вне этого интервала
Ш) = 0.
Найти функцию распределения и плотность распределе-
распределения случайной величины Z = X-\-Y. Построить график
плотности распределения ()
Решение. По условию, возможные значения X определяются
неравенством 0 < х < 2, возможные значения У—неравенством
О < у < 2. Отсюда следует, что возможные случайные точки {X; Y)
расположены в квадрате О ABC (рис. 9, а).
По определению функции распределения,
135
Неравенству х-\-у < г удовлетворяют те точки (х; у) плоскости хОу,
которые лежат ниже прямом х-\-у—г (эта прямая отсекает на осях
Ох и Оу отрезки, равные г): если же брать только возможные зна-
значения х н у, то неравенство х-\-у<г выполняется только для
точек, лежащих в квадрате О ABC ниже прямой х-\-у = г.
3
г
V
[
г\
{
0
А
ч
к ч
Ш
ч
ч
к
Ш
г
к
к ч
\\
? 2
S
С
У
ч
А
0
ч
ч
ч
ч
ч
F \
\ ч
\
\
як
й
\
ч
к
щ
8
ч
\
К \
V
Ч X
Рис. 9
С другой стороны, так как
О (г) = f J /г (х) /, (у) dx Ay
f J
0)
величины
i
X и Y независимы, то
Ax Ay = 1S,
где S—величина той части площади квадрата О ABC, которая лежит
ниже прямой х-\-у=*г. Очевидно, величина площади S зависит от
значения г.
Если г<0, toS=0. т. е. 0(г) = A/4H=0.
Если 0 < г < 2, то (рис. 9, о) 0 (г) =A/4) SA 0DE = 1/4-гг/2=г*/8.
Если 2 < г < 4, то (рис. 9, б) G (г) = A/4) S0AHKC= I —D—г)*/8.
Площадь фигуры ОАНКС найдена как разность между площадью
квадрата ОАВС, которая, очевидно, равна 2- —4, и площадью прямо-
прямоугольного треугольника НВК: S^ нвк = НВг/2, причем НВ=2 —
— АН =2 — AF = 2—(г—2) =4—г.
Если г > 4, то G (г) = ( 1/4) 50ДЛС =1/4-4 = 1.
Итак, искомая функция распределения такова:
0 при г<0,
!*/8 при 0 < г < 2,
'V*'S прн 2 < г < 4,
при г > 4.
Найдем плотность распределения:
О при г<0,
г/4 при 0 < г < 2,
• — г/4 при 2 < г < 4,
О при г > 4.
1
График плотности распределения g(z) изображен на рис. 10.
Рекомендуем для контроля убедиться, что площадь, ограничен-
ограниченная кривой распределения g(z), равна единице.
406. Заданы плотности равномерно распределенных
независимых случайных величин X и Y: ft (х) = 1 в интер-
интервале @, 1), вне этого интервала /, (х) = 0; /, (у) — 1 в интер-
интервале @, 1), вне этого интервала ft(y) = O.
0,5
о г ч г
Рис. 10
Найти функцию распределения и плотность распре-
распределения случайной величины Z — X-\-Y. Построить гра-
график плотности распределения g(z).
407. Заданы плотности распределений равномерно
распределенных независимых случайных величин X и Y:
fl(x)=*\l2 в интервале A,3), вне этого интервала
ft(x) — 0\ /s(j/) = l/4 в интервале B,6), вне этого интер-
интервала ft(y) = O. Найти функцию распределения и плот-
плотность распределения случайной величины Z — X + Y.
Построить график плотности распределения ?(г).
Глава восьмая
СИСТЕМА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
§ 1. Закон распределения двумерной случайной
величины
Двумерной называют случайную величину (X, Y), возможные
значения которой есть пары чисел (лг, у). Составляющие X и Y,
рассматриваемые одновременно, образуют систему двух случайных
величин.
Двумерную величину геометрически можно истолковать как слу-
случайную точку М (X; Y) на плоскости хОу либо как случайный
вектор ОМ.
Дискретной называют двумерную величину, составляющие кото-
которой дискретны.
Непрерывной называют двумерную величину, составляющие
которой непрерывны.
Законом, распределения вероятностей двумерной случайной вели-
величины называют соответствие между возможными значениями в их
вероятностями.
137
Закон распределения дискретной двумерной случайной величины
может быть задан: а) в виде таблицы с двойным входом, содержа-
содержащей возможные значения и их вероятности; б) аналитически, напри-
например в виде функции распределения.
Функцией распределения вероятностей двумерной случайной
величины называют функцию F (х, у), определяющую для каждой
пары чисел (х, у) вероятность того, что X примет значение, меньшее
х, н при этом Y примет значение, меньшее у:
F(x, у)=Р(Х<х, Y <у).
Геометрически это равенство можно истолковать так: F (х, у) есть
вероятность того, что случайная точка (X, Y) попадет в бесконеч-
бесконечный квадрант с вершиной (*, у), расположенный левее н ниже этой
вершины.
Иногда вместо термина «функция распределения» используют
термин «интегральная функция».
Функция распределения обладает следующими свойствами:
Свойство 1. Значения функции распределения удовлетворяют
двойному неравенству
Свойство 2. Функция распределения есть неубывающая
функция по каждому аргументу:
F (*а. У) Зг F (*„ у), если хг > Xi,
F (х, уг) Ss F (х, yt), если уг > yt.
Свойство 3. Имеют место предельные соотношения:
I) F(-*>, у)=0, 2) F(x, -oo)=0,
3) F(—v>, -ео) = 0, 4) F(oo, ео) = 1.
Свойство 4. а) При у=ао функция распределения системы
становится функцией распределения составляющей X:
F(x, *>) = F1(x).
б) При х = ео функция распределения системы становится
функцией распределения составляющей Y:
f(«>, y) = F*(y)-
Используя функцию распределения, можно иайти вероятность
попадания случайной точки в прямоугольник *i < X < хг,
Vi <Y < уг:
Р (*j < X < дга, у! < Y < уг) = [F (хг, уг) —F (xit уг)\ —
-[F(xit yi)-F(xu у,)].
Плотностью совместного распределения вероятностей (двумерной
плотностью вероятности) непрерывной двумерной случайной вели-
величины называют вторую смешанную производную от функции распре-
распределения:
Пх.У)- дхду •
Иногда вместо термина «двумерная плотность вероятности»
используют термин «дифференциальная функция системы».
Плотность совместного распределения можно рассматривать как
предел отношения вероятности попадания случайной точки в прямо-
138
угольник со сторонами Ах и Ау к площади этого прямоугольника,
когда обе его стороны стремятся к нулю; геометрически ее можно
истолковать как поверхность, которую называют поверхностью рас-
распределения.
Зная плотность распределения, можно найти функцию распре-
распределения по формуле
v *
\ f(x,y)dxdy.
— 00 —00
Вероятность попадания случайной точки (X, У) в область D
определяется равенством
(D)
Двумерная плотность вероятности обладает следующими свой-
свойствами:
Свойство 1. Двумерная плотность вероятности неотрица-
неотрицательна:
{(х, у) 5=0.
Свойство 2. Двойной несобственный интеграл с бесконеч-
бесконечными пределами от двумерной плотности вероятности равен единице:
00 00
f(x,y)dxdy = l.
.•00—00
В частности, если все возможные значения (X, Y) принадлежат
конечной области D, то
408. Задано распределение вероятностей дискретной
двумерной случайной величины:
у
4
5
0.
0,
3
17
10
0
0
X
10
,13
.30
12
0,25
0,05
Найти законы распределения составляющих X и Y.
Решение. Сложив вероятности «по столбцам», получим веро-
вероятности возможных значений X: р C) =0,27, р A0) =0,43, р A2) =0,30.
Напишем закон распределения составляющей X:
X 3 10 12
р 0,27 0,43 0,30
Контроль: 0,27+0,43+0,30 = 1.
Сложив вероятности «по строкам», аналогично найдем распре-
распределение составляющей Y:
К 4 5
р 0,55 0,45
139
Контроль: 0,55+0,45=1.
409. Задано распределение вероятностей дискретной
двумерной случайной величины:
2,
2,
3
1
2
0
о,
05
09
0
0
X
30
,12
.30
0
0
41
,08
.11
0
0
50
.04
.21
Найти законы распределения составляющих.
410. Задана функция распределения двумерной слу-
случайной величины
fsinx-sin*/ при
F()
Найти вероятность попадания случайной точки (X, К)
в прямоугольник, ограниченный прямыми х = 0, х = 4
у = п,6, # = л,3.
Решение. Используем формулу
/>(*, < X <хг, у, < Y < yt) = lF(xt, y?—F(xu y2)] —
Положив *i=0, л-8=л/4, у,=л/6, уг = л/3, получим
Р — [sin (л/4) -sin (л/3) —sin 0 sin (я/3)| —
— |sin(n;4)-siu(n/6)—sinO-sin(.x-6)]=(/5"—Кг2~)/4=0,2б.
411. Найти вероятность попадания случайной точки
(X, Y) в прямоугольник, ограниченный прямыми х=\,
х = 2, у = 3, у = 5, если известна функция распределения
| 1—2"*—2~*-f-2~*~1' при х^О, у^О,
F (х, У) = | 0 при л < 0 или у < 0.
412. Задана функция распределения двумерной слу-
случайной величины
| 1 — 3-*—3-» +3-*-* при *>0, 1/>0,
| 0 при х < 0 или t/ < 0.
Найти двумерную плотность вероятности системы.
дхду
Решение. Используем формулу / (х, у)
ные производные:
ЯР Л2Е-
-=1п83-3-*-*.
. Найдем част-
част" дхду'
140
Итак, искомая двумерная плотность вероятности
-*-* при *S=0,
' \ О при х < О или у < 0.
Рекомендуем читателю для контроля убедиться, что
о о
413. Задана функция распределения двумерной слу-
случайной величины
A_е-**)A-е-»») при х>0, у>0,
О при *<0, у<0.
Найти двумерную плотность вероятности системы (X, К).
414. Задана двумерная плотность вероятности системы
случайных величин (X, Y)
20
Найти функцию распределения системы.
Указание. Использовать формулу
>-{
х
f(x, y)dxdy.
415. Задана двумерная плотность вероятности системы
двух случайных величин: f{x, y) = (l/2)-s'm(x+y) в квад-
квадрате 0<*<л/2, 0<^<п/2; вне квадрата f(x,y) = O.
Найтн функцию распределения системы (X, У).
416. В круге **+#*<#* двумерная плотность веро-
вероятности /(*, y) = C(R—Vхг-\-у*)\ вне круга f(x,y) = Q.
Найти: а) постоянную С; б) вероятность попадания слу-
случайной точки (X, Y) в круг радиуса г = 1 с центром
в начале координат, если /? = 2.
Решение, а) Используем второе свойство двумерной плот-
плотности вероятности:
С J с (R— V х*+ у*) dx dy = l.
^_ Ф)
Отсюда
С = 1 /С \ (R— У х*+у%) Ах йу.
(О)
141
Перейдя к полярным координатам, получим
2л R
о о
б) По условию, R = 2; следовательно, С = 3/(8л) и
f(x, y) = C/8.i)B-VlMV)-
Вероятность попадания случайной точки (X, Y) в круг радиуса
1 с центром в начале координат (область Dt)
Р 1(Х, К) с D,] = C/8л) J J B - V^TP) dx Ay.
Перейдя к полярным координатам, окончательно получим искомую
вероятность:
2л 1
Р = C/8я) J dtp J B-р) р dp = 1/2.
о о
417. Поверхность распределения системы случайных
величин (X, Y) представляет собой прямой круговой
конус, основание которого—круг с центром в начале
координат. Найти двумерную плотность вероятности
системы.
Указание. Перейти к полярным координатам.
418. Задана двумерная плотность вероятности f(x, у)—
—С/\(9 + хг)A6-\-у2)] системы (X, Y) двух случайных
величин. Найти постоянную С.
419. Задана двумерная плотность вероятности f{x,y)=
=С/(л:2+#* + 1K системы случайных величин {X, Y).
Найти постоянную С.
Указание. Перейти к полярным координатам.
420. В первом квадранте задана функция распреде-
распределения системы двух случайных величин: F(x, у) =
= 1+2~*—2~у + 2~х~у. Найти: а) двумерную плотность
вероятности системы; б) вероятность попадания случайной
точки (X, Y) в треугольник с вершинами Л A; 3), В C; 3),
С B; 8).
§ 2. Условные законы распределения вероятностей
составляющих дискретной двумерной случайной
величины
Пусть составляющие X и Y дискретны и имеют соответственно
следующие возможные значения: xt, xt хп\ уи у2, ..., у,„.
Условным распределением составляющей X при Y = yj (/ сохра-
сохраняет одно и то же значение при всех возможных значениях X) на-
142
зывают совокупность условных вероятностей
Р (*1 \У/), Р (НI У/) Р (*„ | У/).
Аналогично определяется условное распределение Y.
Условные вероятности составляющих X и Y вычисляют соответ-
соответственно по формулам
Р (*/. у/) р (*,-, у/)
Для контроля вычислений целесообразно убедиться, что сумма
вероятностей условного распределения равна единице.
421. Задана дискретная двумерная случайная вели-
величина (X, Y):
Y
У! = 0,4
У* = 0,8
*.
0
0
= 2
,15
,05
X
дг,=5
0,30
0,12
*.
0
0
= 8
.35
,03
Найти: а) безусловные законы распределения состав-
составляющих; б) условный закон распределения составляющей
X при условии, что составляющая Y приняла значение
#! = 0,4; в) условный закон распределения Y при условии,
что Х = х2 = 5.
Решение, а) Сложив вероятности «по столбцам», иапишем
закон распределения X:
X 2 5 8
р 0,20 0,42 0,38
Сложив вероятности «по строкам», найдем закон распредзления у:
у 0,4 0,8
р 0,80 0,20
б) Найдем условные вероятности возможных значений X при
условии, что составляющая У приняла значение ^ = 0,4:
Уд = Р (Xi, Vi)IP (yi) = 0,15/0,80=3/I6,
Р (Xi \yi) = P (*2, УхIР (yi) =0,30/0,80 = 3/8,
P (xs | Vi) = P (x3, yi)/P (y,)=0,35/0,80 = 7/16.
Напишем искомый условный закон распределения X:
X 2 5 8
p(X\yi) 3/16 3/8 7/16
Контроль: 3/16+3/8+7/16=1.
в) Аналогично найдем условный закон распределения У:
Y 0,4 0,8
Р(у\хь) 5/7 2/7
Контроль: 5/7+2/7 = 1.
143
422. Задана дискретная двумерная случайная вели-
величина (X, Y):
У
10
14
18
0
0
0
3
,25
,15
,32
X
6
0,10
0,05
0,13
Найти: а) условный закон распределения X при усло-
условии, что Y =10; б) условный закон распределения Y при
условии, что Х = 6.
§ 3. Отыскание плотностей и условных законов
распределения составляющих непрерывной
двумерной случайной величины
Плотность распределения одной из составляющих равна несобст-
несобственному интегралу с бесконечными пределами от плотности совмест-
совместною распределения системы, причем переменная интегрирования со-
соответствует другой составляющей:
*. у)
(У)
/ (X, У) UX.
Здесь предполагается, что возможные значения каждой из состав-
составляющих принадлежат всей числовой оси; если же возможные значе-
значения принадлежат конечному интервалу, то в качестве пределов ин-
интегрирования принимают соответствующие конечные числа.
Условной плотностью распределения составляющей X при задан-
заданном значении Y- у называют отношение плотности совместного рас-
распределения системы к плотности распределения составляющей У:
/ (X, У)«
Аналогично определяется условная плотность распределения
составляющей Y:
fix, У) Ay
Если условные плотности распределения случайных величин X
и Y равны их безусловным плотностям, то такие величины незави-
независимы.
Равномерным называют распределение двумерной непрерывной
случайной величины (X, Y), если в области, которой принадлежат
144
все возможные значения (х, у), плотность совместного распределения
вероятностей сохраняет постоянное значение.
423. Задана плотность совместного распределения не-
непрерывной двумерной случайной величины (X, Y)
f(x, у) = — е-<i/*> <*'+«*+»*•>.
Найти: а) плотности распределения составляющих; б) ус-
условные плотности распределения составляющих.
Решение, а) Найдем плотность распределения составляющей X:
Л W= J / (х, у) йу= ~
-ж —<к
Вынесем за знак интеграла множитель е~х'^, не зависящий от
переменной интегрирования у, и дополним оставшийся показатель
степени до полного квадрата; тогда
xd
Учитывая, что интеграл Пуассона \ е~а*йи— У^л, окоичатель-
— 06
но получим плотность распределения составляющей X:
/,(*)=/lA^Oe-M*2.
Аналогично найдем плотность распределения составляющей Y:
б) Найдем условные плотности распределения составляющих.
Выполнив элементарные выкладки, получим:
424. Плотность совместного распределения непрерыв-
непрерывной двумерной случайной величины (X, Y)
Найти: а) постоянный множитель С; б) плотности рас-
распределения составляющих; в) условные плотности распре-
распределения составляющих.
425. Плотность совместного распределения непрерыв-
непрерывной двумерной случайной величины {(х, y) = cosx'Cosy
145
в квадрате 0<л:<я/2, 0<</<я/2; вне квадрата
f (х, у) = 0. Доказать, что составляющие X и У независимы.
Указание. Убедиться, что безусловные плотности распреде-
распределения составляющих равны соответствующим условным плотностям.
426. Непрерывная двумерная случайная величина
(X, Y) распределена равномерно внутри прямоугольника
с центром симметрии в начале координат и сторонами
2а и 26, параллельными координатным осям. Найти:
а) двумерную плотность вероятности системы; б) плот-
плотности распределения составляющих.
427*. Непрерывная двумерная случайная величина
(X, Y) распределена равномерно внутри прямоугольной
трапеции с вершинами 0@; 0), Л @; 4), 5C; 4), С F; 0).
Найти: а) двумерную плотность вероятности системы;
б) плотности распределения составляющих.
428. Непрерывная двумерная случайная величина
(X, Y) равномерно распределена внутри прямоугольного
треугольника с вершинами 0@; 0), Л @; 8), 5(8;0). Най-
Найти: а) двумерную плотность вероятности системы; б) плот-
плотности и условные плотности распределения составляющих.
429*. Непрерывная двумерная случайная величина
(X, Y) равномерно распределена внутри трапеции с вер-
вершинами А(— 6;0), В(— 3; 4), СC;4), ?>F;0). Найти:
а) двумерную плотность вероятности системы; б) плотно-
плотности распределения составляющих.
§ 4. Числовые характеристики непрерывной системы
двух случайных величин
Зная плотности распределения составляющих X и Y непрерыв-
непрерывной двумерной случайной величины (X, Y), можно найти их матема-
математические ожидания и дисперсии:
ОО «О
М(Х)= J */,(*) d*. М<У)= J yhiy)Ay;
— 00 — X
00 00
D(X)= J [x- J
— 00 — в
00 00
Иногда удобнее использовать формулы, содержащие двумерную
плотность вероятности (двойные интегралы берутся по области воз-
146
можных значений системы):
М (X) = J J xf (х, у) Ах Ay, M (Y) = J $ у/ (*, у) dx dy;
Г Г (* Г
J J J J
= ^ [У—Л* (К)]2/ (*, у) d* Ay = f f y2f (x, y) Ax Ay — [Af (K)]2.
Начальным моментом vk, s порядка k-\-s системы (X, Y) назы-
называют математическое ожидание произведения XkYs:
В частности,
Центральным моментом fiks порядка k + s системы (X, Y) на-
называют математическое ожидание произведения отклонений соответ-
соответственно k-й и s-й степеней:
В частности,
|ii, t = M [Х-М (X)] =0, щ, 1-М [Y-M (У)] =0;
2
Корреляционным моментом \ixy системы (X, Y) называют цент-
центральный момент (ii 1 порядка 1 +1:
РхУ=М {[Х-М (Х)]-[У-М (К)]}.
Коэффициентом корреляции величин X я Y называют отношение
корреляционного момента к произведению средних квадратнческих
отклонений этих величин:
уу
Коэффнциент корреляции—безразмерная величина, причем | гху |
Коэффнциент корреляции служит для оценки тесноты линейной
связи между X и Y: чем ближе абсолютная величина коэффициента
корреляции к единице, тем связь сильнее; чем ближе абсолютная
величина коэффициента корреляции к нулю, тем связь слабее.
Коррелированными называют две случайные величины, если их
корреляционный момент отличен от нуля.
Некоррелированными называют две случайные величины, если нх
корреляционный момент равен нулю.
Две коррелированные величины также и зависимы; если две ве-
величины зависимы, то они могут быть как коррелированными, так и
некоррелированными. Из независимости двух величин следует их
некоррелированность, но из некоррелированности еще нельзя сделать
вывод о независимости этих величин (для нормально распределенных
величин из некоррелированности этих величин вытекает их незави-
независимость).
Для непрерывных величин X и Y корреляционный момент может
быть найден по формулам:
00 00
Нл-i, = J J [х-М(Х)] [у-М (К)] / (х, у) Ах dy,
— <в -»
X 00
\хху = J J xyf (х, у) d* dy-M (X) М (К).
— во -»
147
430. Задана плотность совместного распределения не-
непрерывной двумерной случайной величины (X, Y):
fix irt-l 4**е"*'"'" (*>0,у>0),
п"у' \ 0 (*<0 или у<0).
Найти: а) математические ожидания; б) дисперсии состав-
составляющих X и Y.
Решение, а) Найдем сначала плотность распределения состав-
составляющей X:
\f(x,y)&y 4.te * \уе У ду 2хе * (х > 0).
Аналогично получим
Найдем математическое ожидание составляющей X:
00 <
M(X) = \jxfl(x)Ax = \
о 6
09
Интегрируя по частям и учитывая, что интеграл Пуассона V e~x'dx=
_ о _
= Уп/2, получим М (X) = Уп/2. Очевидно, что М (Y) = У л/2.
б) Найдем дисперсию X:
00
D (X) = J х2/! (Jt) d*— [,M (X)|s =
О
00
Очевидно, что 0 (Y) — 1 —л/4.
431. Задана плотность совместного распределения дву-
двумерной случайной величины (X, У)
| 36хуе-<х'+Уг) (дг>0, у>0),
/(*.У) = | о (А.<0 или у<0).
Найти математические ожидания и дисперсии составля-
составляющих.
432. Задана плотность совместного распределения не-
непрерывной двумерной случайной величины {X, Y): f(x, y)=
= 2cosatcos</ в квадрате 0<!л:^л/4, 0^^^л/4; вне
квадрата f(x,y) = O. Найти математические ожидания
составляющих.
148
433. Задана плотность совместного распределения не-
непрерывной двумерной случайной величины (X, Y): f(x, у) =
= (l/2)sin(jc-t-у) в квадрате 0<х<л/2, 0<</<я/2;
вне квадрата f(x, у) = 0- Найти математические ожидания
и дисперсии составляющих.
434. Задана плотность совместного распределения не-
непрерывной двумерной случайной величины (X, Y):
f(x,y) = (l;4)s\nxs\ny в квадрате 0<а<!л, 0<</<!я;
вне квадрата f(x,y) — Q. Найти: а) математические ожи-
ожидания и дисперсии составляющих; б) корреляционный
момент.
435. Заданы плотности распределения независимых
составляющих непрерывной двумерной случайной вели-
величины (X, У):
| 0 при х<0, ( 0 при у<0,
tl(X> = \ 5е-°* при .v > 0; '2 {у) ~ \ 2e~v при у > 0.
Найти: а) плотность совместного распределения си-
системы; б) функцию распределения системы.
Указание. Пели составляющие системы иезаиисимы, то дву-
двумерная плотность вероятности равна произведению плотностей со-
составляющих, а функция совместного распределения системы равна
произведению функций распределения составляющих.
436. Непрерывная двумерная случайная величина
(X, Y) распределена равномерно в круге радиуса г с цент-
центром в начале координат. Доказать, что X и Y зависимы,
но некоррелнрованны.
Указание. Сравнить безусловные и условные плотности рас-
распределения составляющих; убедиться, что корреляционный момент
равен нулю.
437. Доказать, что если двумерную плотность вероят-
вероятности системы случайных величин (X, Y) можно пред-
представить в виде произведения двух функций, одна из
которых зависит только от х, а другая— только от у, то
величины X и Y независимы.
Решение. По условию,
/(*, У) = ф(*)-Ф(*г). (*)
Найдем плотности распределения составляющих:
/iW= 5 f(x,y)dy = <f(x) J ${у)ду, (**)
-00
h (У) = 5 / (х, у) <3*= Ч> (У) J <р (х) dx. (***)
-» —00
149
Выразим ф(лс) из (**) и ty(y) из (***):
ф W = Л (*)/ J * (У) dy. * @ = /• (У)/ J Ф <*) d*.
—» -»
В силу (*)
@0 00 ч
J *to)dy J 9(*)d*).
— 00 —» /
Учитывая, что, по второму свойству двумерной плотности вероят-
00 00
ности, \ \ f(x,y)dxdy=l и, следовательно,
— <в —ж
(jc)
окончательно получим /(x, y)=fj(x)-/a(y)-
Таким образом, двумерная плотность вероятности рассматривае-
рассматриваемой системы равна произведению плотностей вероятности составляю-
составляющих. Отсюда следует, что X и Y независимы, что и требовалось
доказать.
438. Доказать, что если X и Y связаны линейной за-
зависимостью Y — aX-\-b, то абсолютная величина коэффи-
коэффициента корреляции равна единице.
Решение. По определению коэффициента корреляции,
где
Найдем математическое ожидание Y:
(**)
Подставив (**) в (*), после элементарных преобразований получим
рху=аМ [X—M(X)\% = aD(X)=a<j\.
Учитывая, что
Y—M (Y)= (аХ + Ь)—(аМ (X) +Ь) =а [X—М (X)],
найдем дисперсию Y:
D(Y) = M [У—М(У)]*=а*М [X—Л1(Х)]а=а8а|.
Отсюда Оу — \а\ох. Следовательно, коэффициент корреляции
_ Ц*у ао| а
Г*« ~ охоу~ох (\а\ ох)~~Щ '
Если а > 0, то гху — \\ если а < 0, то гху = — 1.
Итак, \гху\ = 1, что и требовалось доказать.
Часть третья
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Глава девятая
ВЫБОРОЧНЫЙ МЕТОД
§ 1. Статистическое распределение выборки
Пусть для изучения количественного (дискретного или непре-
непрерывного) признака X из генеральной совокупности извлечена выборка
Xi, хг хк объема п. Наблюдавшиеся значения дг,- признака X
называют вариантами, а последовательность вариант, записанных
в возрастающем порядке,—вариационным рядом.
Статистическим распределением выборки называют перечень
вариант *,• вариационного ряда и соответствующих им частот гц
(сумма всех частот равна объему выборки п) нли относительных ча-
частот wi (сумма всех относительных частот равна единице).
Статистическое распределение выборки можно задать также в виде
последовательности интервалов и соответствующих им частот (в ка-
качестве частоты интервала принимают сумму частот вариант, попавших
в этот интервал).
439, Выборка задана в виде распределения частот:
Xi 2 5 7
п( 1 3 6
Найти распределение относительных частот.
Решение. Найдем объем выборки: л = 1 +3 + 6 = 10. Найдем
относительные частоты:
Wl= 1/10 = 0,1; 102 = 3/10=0,3; 108=6/10 = 0,6.
Напишем искомое распределение относительных частот:
ж,- 2 5 7
wt 0,1 0,3 0,6
Контроль: 0,1+0,3+0,6=1.
440. Выборка задана в виде распределения частот:
х, 4 7 8 12
и,- 5 2 3 10
Найти распределение относительных частот.
151
§ 2. Эмпирическая функция распределения
Эмпирической функцией распределения (функцией распределения
выборки) называют функцию F* (х), определяющую для каждого зна-
значения х относительную частоту события X < х:
где пх—число вариант, меньших х; п—объем выборки.
Эмпирическая функция обладает следующими свойствами.
Свойство 1. Значения эмпирической функции принадлежат
отрезку [0; 1].
Свойство 2. F* (х) — неубывающая функция.
Свойство 3. Если Xi—наименьшая варианта, а х*—наиболь-
х*—наибольшая, то F*(x)=0 при Ж*1 и F*(x) = \ при * > ж*.
441. Найти эмпирическую функцию по данному рас-
распределению выборки:
х, 1 4 б
tii 10 15 25
Решение. Найдем объем выборки: п = 10-Ь15-|-25=50.
Наименьшая варианта равна единице, поэтому F*(*)=0 при
Значение X < 4, а именно хх = \, наблюдалось 10 раз, следо-
следовательно, f* (jc) = 10/50 =0.2 при 1 < лс<4.
Значения х < 6, а имен-
именно: *i=«! и х% — 4, наблюда-
наблюдались 10-|-15=25 раз; следо-
/| ) вательно, F*(x)= 25/50 =0,5
при 4 < дг<6.
Так как ж=6—наи-
ж=6—наибольшая варианта, Tof*{*)=
= 1 при х > 6.
Напишем искомую эм-
эмпирическую функцию:
@ при *<1,
0.2 при К,<4
0,5 при 4 <*<6
1 при ж>6.
График этой функции изображен на рис. П.
442. Найти эмпирическую функцию по данному рас-
распределению выборки:
а) *(- 2 5 7 8 б) х{ 4 7 8
п,- 1 3 2 4 и, 5 2 3
§ 3. Полигон и гистограмма
А. Дискретное распределение признака X. Полигоном частот
называют ломаную, отрезки которой соединяют точки (хи nt), (*,, п2),
.... (хк, я*), где лс,—варианты выборки и щ—соответствующие им
частоты.
162
0,5
0.1
Полигоном относительных частот называют ломаную, отрезки
которой соединяют точки (jci; wrf, (хг; wt) (хк; wk), где х,—
варианты выборки и w;—соответствующие нм относительные частоты.
Б. Непрерывное распределение признака X. При непрерывном
распределении признака весь интервал, в котором заключены все
наблюдаемые значения признака, разбивают на ряд частичных ин-
интервалов длины Л и находят л,-—сумму частот вариант, попавших
в i-й интервал. Гистограммой частот называют ступенчатую фигуру,
состоящую из прямоугольников, основаниями которых "служат ча-
частичные интервалы длины А, а высоты равны отношению «,7А (плот-
(плотность частоты). Площадь частичного /-го прямоугольника равна
Л(л//Л)=я,-—сумме частот вариант, попавших в /-й интервал. Пло-
Площадь гистограммы частот равна сумме всех частот, т. е. объему
выборки п.
Гистограммой относительных частот называют ступенчатую
фигуру, состоящую из прямоугольников, основаниями" которых
служат частичные интервалы длины Л, а высоты равны отношению
with (плотность относительной частоты). Площадь частичного /-го
прямоугольника равна Л (ш,-,'Л)=и;,—относительной частоте вариант,
попавших в »-й интервал. Площадь гистограммы относительных
частот равна сумме всех относительных частот, т. е. единице.
443. Построить полигон частот по данному распре-
распределению выборки:
xt 1 4 5 7
п, 20 10 14 б
Решение. Отложим на оси абсцисс варианты х,-, а на оси
ординат—соответствующие им частоты л,-; соединив точки (*,-, л,-)
отрезками прямых, получим ис-
искомый полигон частот (рис. 12).
щ
¦Иг
Рис. 12
2 4 5 7 10
Рис. 13
444. Построить полигон частот по данному распре-
распределению выборки:
а) г, 2 3 5 6 б) х, 15 20 25 30 35
щ 10 15 5 20 п, 10 15 30 20 25
445. Построить полигон относительных частот по дан-
данному распределению выборки:
а) *, 2 4 5 7 10
w, 0,15 0,2 0,1 0,1 0,45
б) X/ 1 4 5 8 9
Ш/ 0,15 0,25 0,3 0,2 0,1
153
в) xt 20 40 65 80
wt 0,1 0,2 0,3 0,4
Решение, а) Отложим иа оси абсцисс варианты ж/, а на оси
ординат—соответствующие относительные частоты w/. Соединив точки
(xj, w{) отрезками прямых, получим искомый полигон относительных
частот (рис. 13).
446. Построить гистограмму частот по данному рас-
распределению выборки объема п =100:
Номер
интервала
i
1
2
3
4
5
Частичный
интервал
xrxi+i
1—5
5-9
9—13
13—17
17—21
Суыма частот
вариант интервала
"/
10
20
50
12
8
Плотность
частоты
nilh
2,5
5
12,5
3
2
Решение. Построим на оси абсцисс заданные интервалы длины
й = 4. Проведем над этими интервалами отрезки, параллельные оси
абсцисс и находящиеся от нее на расстояниях, равных соответст-
соответствующим плотностям частоты л,-/Л. Например, над интервалом A, 5)
построим отрезок, параллельный оси абсцисс, на расстоянии я//й =
= 10/4=2,5; аналогично строят остальные отрезки.
л
13
12
3 13
Рис. 14
17
21 X
Искомая гистограмма частот изображена на рис. 14.
447. Построить гистограмму частот по данному рас-
распределению выборки:
154
a)
Номер
интервала
Частичный
интервал
xrxi+i
Сумма частот
вариант интервала
Плотность
частоты
1
2
3
4
5
2—7
7—12
12—17
17-22
22-27
5
10
25
6
4
б)
Номер
интервала
1
1
2
3
4
5
6
7
Частичный
интервал
*/-*,-+»
3—5
5—7
7-9
9—11
11—13
13—15
15—17
Сумма частот
вариант интервала
4
6
20
40
20
4
6
Плотность
частоты
V*
Указание. Найти предварительно плотность частоты л,-/Л
для каждого интервала н заполнить последний столбец таблицы.
448. Построить гистограмму относительных частот по
данному распределению выборки:
Номер
интервала
1
2
3
Частичный
интервал
*Г*1+1
0-2
2—4
4—6
Сумма частот вариант
частичного интервала
"<
20
30
50
п=2я4 = 100
Решение. Найдем относительные частоты:
Wi=20/100=0,2, и;8=30/100=0,3, ю, =50/100 =0,5.
155
Найдем плотности относительных частот, учитывая, что длина
интервала Л=2:
ю,/Л = 0,2/2 = 0,1, wt/h =0,3/2 = 0,15, w3/h = 0,5/2=0,25.
Построим на оси абсцисс данные частичные интервалы. Прове-
Проведем няд этими интервалами отрезки, параллельные оси абсцисс н
находящиеся от нее на расстояниях, равных соответствующим плот-
плотностям относительной частоты. Например, над интервалом @, 2)
пронедем отрезок, параллельный оси абсцисс и находящийся от нее
иа расстоянии, равном 0,1; аналогично строят остальные отрезки.
Искомая гистограмма относительных частот изображена на
рис. 15.
449. Построить гистограмму относительных частот по
данному распределению выборки:
а)
Номер
интервала
1
2
3
4
5
Частичный
интервал
'Г'1 + 1
10—15
15—20
20—25
25—30
30—35
Сумма частот вариант
частичного интервала
"/
2
4
8
4
2
n=2n,=20
156
б)
Номер
интервала
1
2
3
4
Частичный
интервал
*!-*/+1
2—5
5-8
8-11
11—14
Сумма частот вариант
частичного интервала
6
10
4
5
Указание. Найти сначала относительные частоты, соответ-
соответствующие плотности относительной частоты для каждого интервала.
Глааа десятая
СТАТИСТИЧЕСКИЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
§ 1. Точечные оценки
Статистической оценкой 6* неизвестного параметра в теорети-
теоретического распределения называют функцию f(Xx, X2, ..., Х„) от
наблюдаемых случайных величин Ль Хг, •••> Х„-
Точечной называют статистическую оценку, которая определяется
одним числом 6* = /(*1, Xi х„), где xt, хг, .... х„—резуль-
х„—результаты п наблюдений над количественным признаком X (выборка).
Несмещенной называют точечную оценку, математическое ожи-
ожидание которой равно оцениваемому параметру при любом объеме
выборки.
Смещенной называют точечную оценку, математическое ожида-
ожидание которой не равно оцениваемому параметру.
Несмещенной оценкой генеральной средней (математического
ожидания) служит выборочная средняя
•41,
П,Х1 /Я,
где Х(—варианта выборки, я,-—частота варианты х/, я=2я« —
i= i
объем выборки.
Замечание 1. Если первоначальные варианты х/—большие
числа, то для упрощения расчета целесообразно вычесть из каждой
варианты одно и то же число С, т. е. перейти к условным вариантам
u,=Xi~C (в качестве С выгодно принять число, близкое к выбо-
выборочной средней; поскольку выборочная средняя неизвестна, число С
выбирают «на глаз»). Тогда
15?
Смещенной оценкой генеральной дисперсии служит выборочная
дисперсия
( 2 ni(xi-;
Г
эта оценка является смещенной, так как
М \DK] = D,
п
Более удобна формула
Замечание 2. Если первоначальные варианты ж;—большие
числа, то целесообразно вычесть из всех вариант одно и то же
число С, равное выборочной средней или близкое к ней, т. е. перейти
к условным вариантам и/ = дг,-—С (дисперсия при этом не изменится).
Тогда
Г 2"Г
Замечание 3. Если первоначальные варианты являются де-
десятичными дробями с k десятичными знаками после запятой, то,
чтобы избежать действий с дробями, умножают первоначальные ва-
варианты на постоянное число С =10*, т.е. переходят к условным
вариантам «,-=Сж,\ При этом дисперсия увеличится в С2 раз.
Поэтому, найдя дисперсию условных вариант, надо разделить ее
на С2:
Несмещенной оценкой генеральной дисперсии служит исправлен-
исправленная выборочная дисперсия
2
п
s —K=i'Db7Г
Более удобна формула
А. 2".*Н2"/
sx _
В условных вариантах она имеет вид
, 2 «.«М
s=
причем если «г=дг/—С, то 5л = $?1; если «,- = Сх/, то s\ = syc2.
Замечание 4. При большом числе данных используют метод
произведений (см. гл. XI, § 1) или метод сумм (см. гл. XI, § 2).
450. Из генеральной совокупности извлечена выборка
объема п = 50:
варианта х{ 2 5 7 10
частота nt 16 12 8 14
Найти несмещенную оценку генеральной средней.
158
Решение. Несмещенной оценкой генеральной средней является
выборочная средняя
451. Из генеральной совокупности извлечена выборка
объема п = 60:
*,. 1 3 6 26
п, 8 40 10 2
Найти несмещенную оценку генеральной средней.
452. Задано распределение первоначальных вариант
выборки объема п:
xi xl хг • • • хк
tij nt п2 ... nk
Доказать, что
*В = С+B «,",)/«,
где условные варианты щ=>х1—С.
Решение. Так как щ=х{—С, то л,-«/=я;(дс{—С); суммируя
левую и правую часта равенства по всем значениям i, получим
Sniui =2n/(*i— С), или 222 2
Отсюда
2
2//
Следовательно,
B"'*')/" = C + Bn'"')/n> или *в=
что и требовалось доказать.
453. Найти выборочную среднюю по данному распре-
распределению выборки объема п = 10:
xi 1250 1270 1280
nt 2 5 3
Решение. Первоначальные варианты—большие числа, поэтому
перейдем к условным вариантам «;=*,•—1270. В итоге получим
распределение условных вариант:
и/ —20 0 10
щ 2 5 3
Найдем искомую выборочную среднюю:
12.= .270-1 = .269.
454. Найти выборочную среднюю по данному распре-
распределению выборки объема /г = 20:
xt 2560 2600 2620 2650 2700
/г, 2 3 10 4 1
Указание. Перейти к условным вариантам и;=.г,—2620.
455. По выборке объема /г = 41 найдена смещенная
оценка DB = 3 генеральной дисперсии. Найти несмещен-
несмещенную оценку дисперсии генеральной совокупности.
Решение. Искомая несмещенная оценка равна исправленной
дисперсии:
456. По выборке объема п = 51 найдена смещенная
оценка Dtt = o генеральной дисперсии. Найти несмещен-
несмещенную оценку дисперсии генеральной совокупности.
457. В итоге пяти измерений длины стержня одним
прибором (без систематических ошибок) получены сле-
следующие результаты (в мм): 92; 94; 103; 105; 106. Найти:
а) выборочную среднюю длину стержня; б) выборочную
и исправленную дисперсии ошибок прибора.
Решение, а) Найдем выборочную среднюю:
х„=92+@+2+11 + 13 + 14)/5=92+8 = 100.
б) Найдем выборочную дисперсию:
?>в = 2j *i— *¦>> ^{(92—100)' + (94—100J + A03—100J]/5+
+ [A05 —100J+A06 — 100)г]/5 = 34.
Найдем исправленную дисперсию:
а П 5
s — я_| • в—4" — •¦ •
458. В итоге четырех измерений некоторой физической
величины одним прибором (без систематических ошибок)
получены следующие результаты: 8; 9; 11; 12. Найти:
а) выборочную среднюю результатов измерений; б) выбо-
выборочную и исправленную дисперсии ошибок прибора.
459. Ниже приведены результаты измерения роста
(в см) случайно отобранных 100 студентов.
Рост
Число
сту-
студентов
154—158
10
158—162
14
162—166
26
166—170
28
170—174
12
174-178
8
178—182
2
Найти выборочную среднюю и выборочную дисперсию
роста обследованных студентов.
Указание. Найти середины интервала и принять их в ка-
качестве вариант.
160
460. Найти выборочную дисперсию по данному рас-
распределению выборки объема »=10:
х, 186 192 194
щ 2 5 3
Решение. Варианты—сравнительно большие числа, поэтому
перейдем к условным вариантам «,=*/—191 (мы вычли из вариант
число С = 191, близкое к выборочной средней). В итоге получим
распределение условных вариант:
и/ —5 1 3
л,- 2 5 3
Найдем искомую выборочную дисперсию:
— [B(-5)+51+3-3)/10]2=8,2—0,16=8,04.
461. Найти выборочную дисперсию по данному рас-
распределению выборки объема я =100:
х, 340 360 375 380
я,- 20 50 18 12
Указание. Перейти к услозным вариантам «/=»*/—360.
462. Найти выборочную дисперсию по данному рас-
распределению выборки объема »=100:
х, 2502 2804 2903 3028
п, 8 30 60 2
Указание. Перейти к услозным вариантам «/=*/—2844.
463. Найти выборочную дисперсию по данному рас-
распределению выборки объема я =10:
xt 0,01 0,04 0,08
я, 5 3 2
Решение. Для того чтобы избежать действий с дробями,
перейдем к условным вариантам и,-= 100*,-. В итоге получим рас-
распределение
и,- 1 4 8
л,- 5 3 2
Найдем выборочную дисперсию условных вариант:
Подставив в эту формулу услозные варианты и их частоты, получим
Ов(ы) = 7,21.
Найдем искомую выборочную дисперсию первоначальных вариант:
DB (X) = DB (ы)/1002 =7,21/10000=0,0007.
6 Гмурман В. Е. 161
464. Найти выборочную дисперсию по данному рас-
распределению выборки объема я = 50:
х{ 0,1 0,5 0,6 0,8
я, 5 15 20 10
Указание. Перейти к условным вариантам и/= 10*/.
465. Найти выборочную дисперсию по данному рас-
распределению выборки объема я = 50:
х{ 18,4 18,9 19,3 19,6
я, 5 10 20 15
Указание. Перейти к условным вариантам uj=\Oxj—195.
466. Найти исправленную выборочную дисперсию по
данному распределению выборки я = 10:
х, 102 104 108
п, 2 3 5
Решение. Перейдем к условным вариантам u/=x/—104.
В итоге получим распределение
«,—2 0 4
л/ 2 3 5
Найдем исправленную выборочную дисперсию условных вариант;
Подставив в эту формулу условные варианты, их частоты и объем
выборки, получим slu— 6,93.
Все первоначальные варианты были уменьшены на одно и то же
постоянное число С = 104, поэтому дисперсия не изменилась, т. е.
искомая дисперсия равна дисперсии условных вариант: sx = Su = 6,93.
467. Найти исправленную выборочную дисперсию
по данному распределению выборки объема я = 100:
xt 1250 1275 1280 1300
я, 20 25 50 5
Укааание. Перейти к условным вариантам "/=*,•—1275.
468. Найти исправленную выборочную дисперсию по
данному распределению выборки объема я =10:
х{ 0,01 0,05 0,09
я, 2 3 5
Решение. Для того чтобы избежать действий с дробями, пе-
перейдем к условным вариантам ui=100x/. В итоге получим распре-
распределение
щ 1 5 9
л/ 2 3 5
162
Найдем исправленную выборочную дисперсию условных вариант
Подставив в эту формулу данные задачи, получим
s«= 10,844.
Найдем искомую исправленную дисперсию первоначальных
вариант:
s2x = si = /100* = 10,844/10 000 as 0,0085.
469. Найти исправленную выборочную дисперсию по
данному распределению выборки объема я = 20:
Х[ 0,1 0,5 0,7 0,9.
^6 12 1 1
Указание. Перейти к условным вариантам и,-=10*/.
470. Найти исправленную выборочную дисперсию по
данному распределению выборки объема я =10:
xt 23,5 26,1 28,2 30,4
п, 2 3 4 1
Указание. Перейти к условным вариантам ui = 10xi—268.
§ 2. Метод моментов
Метод моментов точечной оценки неизвестных параметров
заданного распределения состоит в приравнивании теоретических
моментов соответствующим эмпирическим моментам того же порядка.
Если распределение определяется одним параметром, то
для его отыскания приравнивают одни теоретический момент одному
эмпирическому моменту того же порядка. Например, можно при-
приравнять начальный теоретический момент первого порядка началь-
начальному эмпирическому моменту первого порядка: vI = M1. Учитывая,
что Vi=M(X) и Mi=xB, получим
М (*)=*„. (*)
Математическое ожидание является функцией от неизвестного па-
параметра заданного распределения, поэтому, решив уравнение (*)
относительно неизвестного параметра, тем самым получим его точеч-
точечную оценку.
Если распределение определяется д ° у м я параметрами, то
приравнивают два теоретических момента двум соответствующим эм-
эмпирическим моментам того же порядка. Например, можно прирав-
приравнять начальный теоретический момент первого порядка начальному
эмпирическому моменту первого порядка и центральный теорети-
теоретический момент второго порядка центральному эмпирическому моменту
второго порядка:
vl = M1, ца=/яа.
6* 163
Учитывая, что vi=Af(X), Mi = xB, nt=D(X), m2 = DB, имеем
[М(Х)=!В, ,,«
\D(X) = DB. y
Левые части этих равенств являются функциями от неизвестных
параметров, поэтому, решив систему (**) относительно неизвестных
параметров, тем самым получим их точечные оценки. _
Разумеется, для вычисления выборочной средней хв н выбо-
выборочной дисперсии DB надо располагать выборкой хи х хп.
471. Случайная величина X распределена по закону
Пуассона
Р()
где т—число испытаний, произведенных в одном опыте;
х{—число появлений события в i-м опыте.
Найти методом моментов по выборке xv хг, ..., хп
точечную оценку неизвестного параметра "к, определяю-
определяющего распределение Пуассона.
Решение. Требуется оценить один параметр, поэтому доста-
достаточно иметь одно уравнение относительно этого параметра. Прирав-
Приравняем начальный теоретический момент первого порядка vt началь-
начальному эмпирическому моменту первого порядка М\:
Приняв во внимание, что \\ = М(Х), Mi = x~B, получим M(X) = x[t.
Учитывая, что математическое ожидание распределения Пуассона
равно параметру А. этого распределения (см. задачу 207), оконча-
окончательно имеем Х=хв.
Итак, точечной оценкой параметра к распределения Пуассона
служит выборочная средняя: Х*=хв.
472. Случайная величина X (число семян сорняков в
пробе зерна) распределена по закону Пуассона. Ниже
приведено распределение семян сорняков в я =1000 про-
пробах зерна (в первой строке указано количество xt сор-
сорняков в одной пробе; во второй строке указана частота
tij—число проб, содержащих xt семян сорняков):
^0123456
щ 405 366 175 40 8 4 2
Найти методом моментов точечную оценку неизвест-
неизвестного параметра распределения Пуассона.
Указание. Использовать решение задачи 471.
473. Случайная величина X (число нестандартных
изделий в партии изделий) распределена по закону Пу-
164
ассона. Ниже приведено распределение нестандартных
изделий в п = 200 партиях (в первой строке указано
количество х( нестандартных изделий в одной партии;
во второй строке указана частота я,—число партий,
содержащих лг, нестандартных изделий):
xt 0 1 2 3 4
п, 132 43 20 3 2
Найти методом моментов точечную оценку неизвест-
неизвестного параметра А, распределения Пуассона.
474. Найти методом моментов по выборке хх, хг, ....
х„ точечную оценку параметра р биномиального распре-
распределения
где Xj — число появлений события в i-m опыте (» = 1, 2,
..., п), т — количество испытаний в одном опыте.
Указание. Приравнять начальный теоретический момент пер-
первого порядка начальному эмпирическому моменту первого порядка.
475. Случайная величина X (число появлений собы-
события А в т независимых испытаниях) подчинена биноми-
биномиальному закону распределения с неизвестным парамет-
параметром р. Ниже приведено эмпирическое распределение
числа появлений события в 10 опытах по 5 испытаний
в каждом (в первой строке указано число х{ появлений
события А в одном опыте; во второй строке указана
частота щ — количество опытов, в которых наблюдалось
X; появлений события А):
л;,- 0 1 2 3 4
«,-52111
Найти методом моментов точечную оценку параметра р
биномиального распределения.
Указание. Использовать решение задачи 474.
476. Найти методом моментов по выборке хх, х2, ....
хп точечную оценку неизвестного параметра Я показа-
показательного распределения, плотность которого f(x) = )&-**
0
477. Случайная величина X (время работы элемента)
имеет показательное распределение f(x) = ke~Xx (х^О).
Ниже приведено эмпирическое распределение среднего
времени работы п — 200 элементов (в первой строке при-
165
ведено среднее время х,- работы элемента в часах; во вто-
второй строке указана частота nt—количество элементов,
проработавших в среднем х, часов):
Xl 2,5 7,5 12,5 17,5 22,5 27,5
щ 133 45 15 4 2 1
Найти методом моментов точечную оценку неизвест-
неизвестного параметра показательного распределения.
Указание. Использовать решение задачи 476.
478. Найти методом моментов точечную оценку пара-
параметра р (вероятности) геометрического распределения
Р(Х — х1) = (\—р)х<-1-р, где .г, —число испытаний, про-
произведенных до появления события; р—вероятность по-
появления события в одном испытании.
Указание. Принять во внимание, что М(Х)=1/р (см. за-
задачу 222).
479. Найти методом моментов оценку параметра р
геометрического распределения Р(Х = X;) = A —р)*''1 •/»,
если в четырех опытах событие появилось соответственно
после двух, четырех, шести и восьми испытаний.
480. Найти методом моментов по выборке xlt x
хп точечные оценки неизвестных параметров аир гам-
гамма-распределения, плотность которого
*"е"Л1 <«>-!. Р>0.*>0).
Решение. Для отыскания двух неизвестных параметров не-
необходимо иметь два уравнения; приравняем начальный теоретический
момент первого порядка Vi начальному эмпирическому моменту пер-
первого порядка Mi и центральный теоретический момент второго по-
порядка щ центральному эмпирическому моменту второго порядка /я2;
Vi = Mi, цг=/яг.
Учитывая, что V! = M(X), М^ = хв, цг = й(Х), /n2=DB, имеем
(М(Х)=ТВ, m
\D(X) = DB. ()
Математическое ожидание и дисперсия гамма-распределения со-
соответственно равны М (Х) = (а+1) р\ D(X)=(a+l)pa (см. зада-
задачу 302), поэтому (*) можно записать в виде
Решив эту систему, окончательно^ получим искомые точечные
оценки неизвестных параметров: a* = {xB)*/DB—l, $* = DB/xB.
166
481. Случайная величина X (уровень воды в реке по
сравнению с номиналом) подчинена гамма-распределению,
плотность которого определяется параметрами аир
(а>-1, р>0):
Ниже приведено распределение среднего уровня воды по
данным л = 45 паводков (в первой строке указан сред-
средний уровень воды xt (см); во второй строке приведена
частота п,-—количество паводков со средним уровнем
воды х,):
xt 37,5 62,5 87,5 112,5 137,5 162,5 187,5 250 350
«,136 7 7 5 484
Найти методом моментов точечные оценки неизвестных
параметров аир рассматриваемого гамма-распределения.
Решение. Используем точечные оценки параметров гамма-
распределения (см. задачу 480):
а* =(!„)*/Д.-1. P* = DB/*B. (*)
По заданному распределению легко найдем выборочную среднюю
и выборочную дисперсию: Зёв = 166, DB=6782.
Подставив эти числа в формулы (*), окончательно получим
искомые точечные оценки неизвестных параметров рассматриваемого
гамма-распределения: а* =3,06, Р* =40,86.
482. Устройство состоит из элементов, время безот-
безотказной работы которых подчинено гамма-распределению.
Испытания пяти элементов дали следующие наработки
(время работы элемента в часах до отказа): 50, 75, 125, 250,
300. Найти методом моментов точечные оценки неизвест-
неизвестных параметров аир, которыми определяется гамма-
распределение.
Указание. Использовать решение задачи 480. Учесть, что
объем выборки л = 5 мал, поэтому в формулах для вычисления па-
параметров аир вместо выборочной дисперсии подставить исправлен-
исправленную дисперсию sa = 2n,-(*/—хв)г/(п—1).
483. Найти методом моментов по выборке xt, хг
хп точечные оценки неизвестных параметров а и о нор-
нормального распределения, плотность которого
Указание. Приравнять начальный теоретический момент
первого порядка и центральный теоретический момент второго по-
порядка соответствующим эмпирическим моментам.
167
484. Случайная величина X (отклонение контролируе-
контролируемого размера изделия от номинала) подчинена нормаль-
нормальному закону распределения с неизвестными параметрами
а и а. Ниже приведено эмпирическое распределение от-
отклонения от номинала п = 200 изделий (в первой строке
указано отклонение xt (мм); во второй строке приведена
частота п,—количество изделий, имеющих отклонение *,):
х, 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,2 2,3
я, 6 9 26 25 30 26 21 24 20 8 5
Найти методом моментов точечные оценки неизвестных
параметров а и а нормального распределения.
Указание. Использовать задачу 483.
485. Найти методом моментов по выборке xv хл, ...,
хп точечные оценки параметров а и Ь равномерного рас-
распределения, плотность которого f(x) = l/(b—a) (b>a).
Указание. Использовать решения задач 313, 315.
486. Случайная величина X (ошибка измерения даль-
дальности радиодальномером) подчинена равномерному за-
закону распределения с неизвестными параметрами а и Ь.
Ниже приведено эмпирическое распределение средней
ошибки я = 200 измерений дальности (в первой строке
указана средняя ошибка х,-; во второй строке указана
частота я,-—количество измерений, имеющих среднюю
ошибку X/):
X/ 3 5 7 9 11 13 15 17 19 21
я, 21 16 15 26 22 14 21 22 18 25
Найти методом моментов точечные оценки неизвестных
параметров а и Ь равномерного распределения.
Указание. Использовать задачу 485.
487. Найти методом моментов по выборке ху, хг, ...,
хп точечные оценки неизвестных параметров Xt и А,а
«двойного распределения» Пуассона
PiXx)
где х(—число появлений события в п,- испытаниях A,t и
К2—положительные числа, причем Kt > A,,.
Решение. Если случайная величина Z распределена по закону
Пуассона с параметром к, то ее начальные теоретические моменты
168
первого и второго порядка соответственно равны (см. задачи 207,
227):
Найдем начальные теоретические моменты первого и второго
порядка рассматриваемой случайной величины X, учитывая соотно-
соотношения (*):
)=¦ A/2) (Хж
Отсюда
Решив эту систему относительно неизвестных параметров, приняв
во внимание, что ла > ^i> получим:
Aii=vt—Kvt—vi—vj, Xs = v1 + Kv8—v, — vj.
488. Случайная величина X распределена по «двой-
«двойному» закону Пуассона:
Ниже приведено эмпирическое распределение числа
появлений события в я = 327 испытаниях (в первой
строке указано число xt появлений события; во второй
строке приведена частота п,-—количество испытаний,
в которых появилось X; событий):
X/ 0123456789 10
п, 28 47 81 67 53 24 13 8 3 2 1
Найти методом моментов точечные оценки неизвест-
неизвестных параметров Я, и Я2 «двойного распределения» Пу-
Пуассона.
Указание. Использовать решение задачи 487. Вычислить по
выборке начальные эмпирические моменты первого и второго по-
порядков:
(?)/ Мг= B щх)Iп.
§ 3. Метод наибольшего правдоподобия
Метод наибольшего правдоподобия точечной оценки неизвестных
параметров заданного распределения сводится к отысканию макси-
максимума функции одного или нескольких оцениваемых параметров.
А. Дискретные случайные величины. Пусть X—дискретная слу-
случайная величина, которая в результате л опытов приняла возмож-
возможные значения xlt x2, ¦¦¦, х„. Допустим, что вид закона распреде-
распределения величины X задан, но неизвестен параметр в, которым оп-
169
ределяется этоу закон; требуется найти его точечную оценку
е*=9*(*1. хг *„).
Обозначим вероятность того, что в результате испытания вели-
величина X примет значение х,- через р (*,-; в).
Функцией правдоподобия дискретной случайной величины X
называют функцию аргумента в:
L(xu хг хп; 6) = р(а;1; в)-р(х2; Ь)...р(х„\ в).
Оценкой наибольшего правдоподобия параметра в называют
такое его значение в*, при котором функции правдоподобия дости-
достигает максимума.
Функции L и In L достигают максимума при одном и том же
значении 9, поэтому вместо отыскания максимума функции L ищут,
что удобнее, максимум функции In L.
Логарифмической функцией правдоподобия называют функцию In/..
Точку максимума функции In L аргумента в можно искать, на-
например, так:
. ,, , d In/.
1. Найти производную ,Q .
2. Приравнять производную нулю и найти критическую точку
в*— корень полученного уравнения (его называют уравнением
правдоподобия).
3. Найти вторую производную ,ft2 ; если вторая производная
при 9 = 9* отрицательна, то в*—точка максимума.
Найденную точку максимума в* принимают в качестве оценки
наибольшего правдоподобия параметра в.
Б. Непрерывные случайные величины. Пусть X—непрерывная
случайная величина, которая в результате л испытаний приняла
значения х\, х2, ..., х„. Допустим, что вид плотности распределе-
распределения—функции f (х)—задан, но неизвестен параметр в, которым оп-
определяется эта функция.
Функцией правдоподобия непрерывной случайной величины X
называют функцию аргумента в:
L(xu х *„; в) = /(*1; в)-/(*а; в).../(*„; в).
Оценку наибольшего правдоподобия неизвестного параметра
распределения непрерывной случайной величины ищут так же, как
в случае дискретной случайной величины.
Если плотность распределения f(x) непрерывной случайной
величины определяется двумя неизвестными параметрами 9i и в2,
то функция правдоподобия есть функция двух независимых аргумен-
аргументов в| и в2:
L = f(xi, в,, в2)-/(*2; eIf в2).../(*„; 01, в2).
Далее находят логарифмическую функцию правдоподобия и для
отыскания ее максимума составляют и решают систему
d\nL
Ж" '
489. Найти методом наибольшего правдоподобия то-
точечную оценку неизвестного параметра р (вероятность
170
появления события в одном испытании) биномиального
распределения:
где х{ — число появлений события в t-м опыте, т—коли-
т—количество испытаний в одном опыте, п—число опытов.
Решение. Составим функцию правдоподобия:
L = p(Xi, e)p(x2; в)...р(хп; в).
Учитывая, что 9=р и Р (X=xi)=Cx\pxi (\ — р)т~ч, получим
L=[О*1 A -р)т-х'\[схт'Рх' A -р)т-х>).. .[c*«p*«(i -р)т-х»\,
или
L = (C*lCXl ... C*n)pXl+Xt+-+Xn(l— р)Я"«-(*1+*« + .»+«в).
Напишем логарифмическую функцию правдоподобия:
In L = ln[С*'С? ... С*«] + B*/) In р + (ят-2*/) »п A -р).
Найдем первую производную по р:
d In L 2j *i i V \ 1
dp p ^ " 1 — p
Приравняв первую произеодную нулю и решив получеиное урав-
уравнение, получим критическую точку
2
Найдем вторую производную по р:
dMnZ. 2*/ , пт— 2J
dp2 р2 ' A— рJ '
Легко убедиться, что при р = B*/)Лят) ВТ°рая производная
отрицательна; следовательно, эта точка есть точка максимума и ее
надо принять в качестве оценки наибольшего правдоподобия неиз-
неизвестной вероятности р биномиального распределения:
Очевидно, что если х; появлений события наблюдалось в л/
опытах, то
490. Случайная величина X (число появлений собы-
события А в т независимых испытаниях) подчинена бино-
биномиальному закону распределения с неизвестным пара-
параметром р. Ниже приведено эмпирическое распределение
числа появлений события А в 1000 испытаний (в пер-
первой строке указано число х{ появлений события в одном
опыте из т=10 испытаний, во второй строке приведена
частота п,—число опытов, в которых наблюдалось х{
171
появлений события А):
Х/012 34 5 67
п, 2 3 10 22 26 20 12 5
Найти методом наибольшего правдоподобия точечную
оценку неизвестного параметра р биномиального распре-
распределения.
Указание. Использовать задачу 480.
491. Случайная величина X (число появлений собы-
события А в т независимых испытаниях) подчинена закону
распределения Пуассона с неизвестным параметром X:
Pm(X = Xl) = Xxi-e-4xi\,
где т—число испытаний в одном опыте, xt—число по-
появлений события в 1-м опыте (» = 1, 2, ..., п).
Найти методом наибольшего правдоподобия по вы-
выборке xlt х2, ..., хп точечную оценку неизвестного пара-
параметра А, распределения Пуассона.
492. Случайная величина X (число поврежденных
стеклянных изделий в одном контейнере) распределена
по закону Пуассона с неизвестным параметром К. Ниже
приведено эмпирическое распределение числа повреж-
поврежденных изделий в 500 контейнерах (в первой строке
указано количество X; поврежденных изделий в одном
контейнере, во второй строке приведена частота п,- —
число контейнеров, содержащих х{ поврежденных изде-
изделий):
*, 0 1 234567
щ 199 169 87 31 9 3 1 1
Найти методом наибольшего правдоподобия точечную
оценку неизвестного параметра А. распределения Пуас-
Пуассона.
Указание. Использовать задачу 401.
493. Найти методом наибольшего правдоподобия по
выборке xlt x2, .... хп точечную оценку неизвестного
параметра А, показательного распределения, плотность
которого f(x) = te~u (*>0).
Решение. Составим функцию правдоподобия
*.=/(*i; в)/(л:2; в).../(*„; в),
учитывая, что в=А, и, следовательно, f (x\ &)=f(x\ K) — 'kt~^x:
172
Найдем логарифмическую функцию правдоподобия:
In L=n lnA—Х_2 */•
Найдем первую производную по А:
din/. ,, \л
Запишем уравнение правдоподобия, для чего приравняем первую
производную нулю: л/А—2-*,- = 0. Найдем критическую точку, для
чего решим полученное уравнение относительно А:
Найдем вторую производную по А:
d'lnL
{
Легко видеть, что при А = 1/хв вторая производная отрицательна;
следовательно, эта точка есть точка максимума и, значит, в каче-
качестве оценки наибольшего правдоподобия надо принять величину,
обратную выборочной средней: А* = 1/жв.
494. Случайная величина X (время безотказной работы
элемента) имеет показательное распределение f(x) = Ke~Xx
(х^О). Ниже приведено эмпирическое распределение
среднего времени работы 1000 элементов (в первой строке
указано среднее время xt безотказной работы одного
элемента в часах; во второй строке указана частота
п.;—количество элементов, проработавших в среднем xt
часов):
х, 5 15 25 35 45 55 65
я, 365 245 150 100 70 45 25
Найти методом наибольшего правдоподобия точечную
оценку неизвестного параметра Я показательного рас
пределен ия.
Указание. Использовать задачу 403.
495. Найти методом наибольшего правдоподобия по
выборке xv xs, ..., х„ точечную оценку параметра р* гамма-
распределения (параметр а известен), плотность которого
496. Устройство состоит из элементов, время безот-
безотказной работы которых подчинено гамма-распределению.
Испытания пяти элементов дали следующие наработки
173
(время работы элемента в часах до отказа): 50, 75, 125,
250, 300. Найти методом наибольшего правдоподобия
точечную оценку одного неизвестного параметра р гамма-
распределения, если второй параметр этого распределе-
распределения а = 1,12.
Указание. Использовать задачу 495.
497. Найти методом наибольшего правдоподобия по
выборке хх, х
геометрического распределения:
где х{— число испытаний, произведенных до появления
события; р—вероятность появления события в одном
испытании.
498. Найти методом наибольшего правдоподобия по
выборке xv хг, ..., хп точечную оценку параметра а
(параметр а известен) распределения Кэптейна, плот-
плотность которого
ау2п
где g(x)—дифференцируемая функция.
499. Найти методом наибольшего правдоподобия по
выборке х1г хг, ..., хп точечную оценку параметра а
(параметр а известен) распределения Кэптейна (см.
задачу 498).
500. Найти методом наибольшего правдоподобия по
выборке xlt х2, ..., хп точечные оценки параметров а и
а нормального распределения, плотность которого
L
/(*) = —L-ea
а у 2л
Указание. Составить и решить систему
dlnL . d\nL n
0 0
§ 4. Интервальные оценки
Интервальной называют оценку, которая определяется двумя
числами—концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надеж-
надежностью у покрывает заданный параметр.
1. Интервальной оценкой (с надежностью у) математического
ожидания а нормально распределенного количественного признака X
по выборочной средней хв при известном среднем к в а д-
174
ратическом отклонении а генеральной совокупности слу-
служит доверительный интервал
~хв—t (a/ V"n) <а< *в+ t (о/ УК),
где t (а/У~п)=б— точность оценки, я—объем выборки, /—значе-
/—значение аргумента функции Лапласа Ф (/) (см. приложение 2), при кото-
котором Ф (/) = у/2; при неизвестном а (и объеме выборки л < 30)
где s—«исправленное» выборочное среднее квадратическое отклоне-
отклонение, / находят по таблице приложения 3 по заданным пну.
2. Интервальной оценкой (с надежностью у) среднего квадра-
тического отклонения а нормально распределенного количественного
признака X по «исправленному» выборочному среднему квадрати-
ческому отклонению s служит доверительный интервал
s (I — q)< a < s A+ q) (при q < 1),
0 < а < s(\+q) (при q > 1),
где q находят по таблице приложения 4 по заданным я и у.
3. Интервальной оценкой (с надежностью у) неизвестной вероят-
вероятности р биномиального распределения по относительной частоте w
служит доверительный интервал (с приближенными концами pt и р2)
Р] < р < pit
где
где л—общее число испытаний; т—число появлений события; w —
относительная частота, равная отношению m/л; t — значение аргу-
аргумента функции Лапласа (приложение 2), при котором Ф(?) = у/2
(у—заданная надежность).
Замечание. При больших значениях п (порядка сотен)
можно принять в качестве приближенных границ доверительного
интервала
. -, fwA—w) . . -*fw{,\—w)
Pl=w—t у -*-^—'. p2=w+l у -i-^—'-.
501. Найти доверительный интервал для оценки
с надежностью 0,95 неизвестного математического ожи-
ожидания а нормально распределенного признака X гене-
генеральной совокупности, если генеральное среднее квад-
квадратическое отклонение а = 5, выборочная ередняя *„=14
и объем выборки я = 25.
Решение. Требуется найти доверительный интервал
xt<a<x+t (•)
175
Все величины, кроме t, известны. Найдем t из соотношения
Ф(/) = 0,95/2 = 0,475. По таблице приложения 2 находим / = 1,96.
Подставив ^ = 1,96, х„ = 14, а=5, л=25 в (»), окончательно полу-
получим искомый доверительный интервал 12,04 < а < 15,96.
502. Найти доверительный интервал для оценки
с надежностью 0,99 неизвестного математического ожи-
ожидания а нормально распределенного признака X гене-
генеральной совокупности, если известны генеральное сред-
среднее квадратическое отклонение^ о, выборочная средняя
хв и объем выборки»: а) а = 4, хв=10,2, я =16; б) о = 5,
*в=16,8, я = 25.
503. Одним и тем же прибором со средним квадра-
тическим отклонением случайных ошибок измерений
а = 40 м произведено пять равноточных измерений рас-
расстояния от орудия до цели. Найти доверительный интер-
интервал для оценки истинного расстояния а до цели с на-
надежностью v = 0,95, зная среднее арифметическое резуль-
результатов измерений хв — 2000 м.
Предполагается, что результаты измерений распреде-
распределены нормально.
504. Выборка из большой партии электроламп содер-
содержит 100 ламп. Средняя продолжительность горения
лампы выборки оказалась равной 1000 ч. Найти с надеж-
надежностью 0,95 доверительный интервал для средней про-
продолжительности а горения лампы всей партии, если
известно, что среднее квадратическое отклонение про-
продолжительности горения лампы <т = 40ч. Предполагается,
что продолжительность горения ламп распределена нор-
нормально.
505. Станок-автомат штампует валики. По выборке
объема п=100 вычислена выборочная средняя диаметров
изготовленных валиков. Найти с надежностью 0,95 точ-
точность б, с которой выборочная средняя оценивает мате-
математическое ожидание диаметров изготовляемых валиков,
зная, что их среднее квадратическое отклонение а — 2 мм.
Предполагается, что диаметры валиков распределены нор-
нормально.
506. Найти минимальный объем выборки, при кото-
котором с надежностью 0,975 точность оценки математиче-
математического ожидания а генеральной совокупности по выбороч-
выборочной средней равна 6 = 0,3, если известно среднее квад-
квадратическое отклонение о= 1,2 нормально распределенной
генеральной совокупности.
176
Решение. Воспользуемся формулой, определяющей точность
оценки математического ожидания генеральной совокупности по
выборочной средней: б = to/ У~п. Отсюда
По условию, y=°.975; следовательно, Ф(/)= 0,975/2 = 0,4875. По
таблице приложения 2 найдем /=2,24. Подставив /=2,24, о=1,2
и 6=0,3 в (*), получим искомый объем выборки я = 81.
507. Найти минимальный объем выборки, при кото-
котором с надежностью 0,925 точность оценки математиче-
математического ожидания нормально распределенной генеральной
совокупности по выборочной средней равна 0,2, если
известно среднее квадратическое отклонение генеральной
совокупности а =1,5.
508. Из генеральной совокупности извлечена выборка
объема п— 10:
варианта X; —2 12 3 4 5
частота п,- 2 12 2 2 1
Оценить с надежностью 0,95 математическое ожида-
ожидание а нормально распределенного признака генеральной
совокупности по выборочной средней при помощи дове-
доверительного интервала.
Решение. Выборочную среднюю и «исправленное» среднее
квадратическое отклонение найдем соответственно по формулам:
,—*вJ
Подставив в эти формулы данные задачи, получим хв=2, s = 2,4.
Найдем ty. Пользуясь таблицей приложения 3, по у =0,95 и
« = !0 находим /?=2,26.
Найдем искомый доверительный интервал:
*в - t vs/ Vn < а < ~хв +1 ?s/ Vn.
Подставляя хв=2, ty=2,26, s=2,4, n = 10, получим искомый дове-
доверительный интервал 0,3 < а < 3,7, покрывающий неизвестное мате-
математическое ожидание а с надежностью 0,95.
509. Из генеральной совокупности извлечена выборка
объема я= 12:
варианта х{ —0,5 —0,4 —0,2 0 0,2 0,6 0,8 1 1,2 1,5
частота п{ 1 2 1111112 1
Оценить с надежностью 0,95 математическое ожидание а
нормально распределенного признака генеральной сово-
совокупности с помощью доверительного интервала.
177
510. По данным девяти независимых равноточных
измерений некоторой физической величины найдены сред-
среднее арифметическое результатов измерений лгв = 30,1 и
«исправленное» среднее квадратическое отклонение s = 6.
Оценить истинное значение измеряемой величины с по-
помощью доверительного интервала с надежностью у = 0,99.
Предполагается, что результаты измерений распределены
нормально.
Решение. Истинное значение измеряемой велнчины равно ее
математическому ожиданию а. Поэтому задача сводится к оценке
математического ожидания (при неизвестном а) при помощи довери-
доверительного интервала
Все величины, кроме ty, известны. Найдем ty. По таблице прило-
приложения 3 по y=0.99 и я=9 находим ?„=2,36.
Подставив *в = 30,1, / =2,36, s=6, л=9 в (»), получим иско-
искомый интервал: 25,38 < а < 34,82.
511. По данным 16 независимых равноточных изме-
измерений некоторой физической величины найдены среднее
арифметическое результатов измерений *в=42,8 и «исправ-
«исправленное» среднее квадратическое отклонение s = 8. Оце-
Оценить истинное значение измеряемой величины с надеж-
надежностью 7 = 0,999.
512. По данным выборки объема я =16 из генераль-
генеральной совокупности найдено «исправленное» среднее квад-
квадратическое отклонение s=l нормально распределенного
количественного признака. Найти доверительный интер-
интервал, покрывающий генеральное среднее квадратическое
отклонение а с надежностью 0,95.
Решение. Задача сводится к отысканию доверительного ин-
интервала
s(l— q)<a <s(l+q) (если q < 1), (»)
или
0 < а < s A + q) (если q > 1).
По данным y=0>95 и л = 16 по таблице приложения 4 найдем
<7=О,44. Так как q<l, то, подставив s — \, <?=0,44 в соотноше-
соотношение (*), получим искомый дорерительный интервал 0,56 < а < 1,44.
513. По данным выборки объема п из генеральной
совокупности нормально распределенного количествен-
количественного признака найдено «исправленное» среднее квадра-
квадратическое отклонение s. Найти доверительный интервал,
178
покрывающий генеральное среднее квадратическое откло-
отклонение о с надежностью 0,999, если: a) n=10, s = 5,1;
б) я = 50, s= 14.
514. Произведено 12 измерений одним прибором (без
систематической ошибки) некоторой физической вели-
величины, причем «исправленное» среднее квадратическое
отклонение s случайных ошибок измерений оказалось
равным 0,6. Найти точность прибора с надежностью 0,99.
Предполагается, что результаты измерений распределены
нормально.
Решение. Точность прибора характеризуется средним квад-
ратнческим отклонением случайных ошибок измерений. Поэтому
задача сводится к отысканию доверительного интервала, покрываю-
покрывающего а с заданной надежностью у = 0,99:
По данным y=0,99 и я = 12 по таблице приложения 4 найдем
9=0,9. Подставив s=0,6, <?=0,9 в соотношение (•), окончательно
получим 0,06 < а < 1,14.
515. Произведено 10 измерений одним прибором (без
систематической ошибки) некоторой физической вели-
величины, причем «исправленное» среднее квадратическое
отклонение s случайных ошибок измерений оказалось
равным 0,8. Найти точность прибора с надежностью 0,95.
Предполагается, что результаты измерений распределены
нормально.
516. Производятся независимые испытания с одина-
одинаковой, но неизвестной вероятностью р появления собы-
события А в каждом испытании. Найти доверительный интер-
интервал для оценки вероятности р с надежностью 0,95, если
в 60 испытаниях событие А появилось 15 раз.
Решение. По условию, л = 60, т = 15, у = 0,95. Найдем отно-
относительную частоту появления события A: w=m/n = 15/60 = 0,25.
Найдем / из соотношения Ф(/) = 7/2=0,95/2 = 0,475. По таб-
таблице функции Лапласа (см. приложение 2) находим / = 1,96.
Найдем границы искомого доверительного интервала:
Подставив в эти формулы л=60, ш=0,25, f = 1,96, получим
Pl=0,16, р2=0,37.
Итак, искомый доверительный интервал 0,16 < р < 0,37.
179
517. Производятся независимые испытания с одина-
одинаковой, но неизвестной вероятностью р появления собы-
события А в каждом испытании. Найти доверительный интер-
интервал для оценки вероятности р с надежностью 0,99, если
в 100 испытаниях событие А появилось 60 раз.
518. Изготовлен экспериментальный игровой автомат,
который должен обеспечить появление выигрыша в одном
случае из 100 бросаний монеты в автомат. Для про-
проверки пригодности автомата произведено 400 испытаний,
причем выигрыш появился 5 раз. Найти доверительный
интервал, покрывающий неизвестную вероятность появ-
появления выигрыша с надежностью 7 = 0.999.
Решение. Найдем относительную частоту появления выиг-
выигрыша: ш = т/л=5/400=0,0125. Найдем / из соотношения Ф(/) =
= у/2 = 0,999/2=0,4995. По таблице функции Лапласа (см. прило-
приложение 2) находим /=3,3.
Учитывая, что п = 400 велико, используем для отыскания гра-
границ доверительного интервала приближенные формулы:
pl=w—t Yw(\—w)ln, pt=
Подставив в этн формулы w =0,0125, /=3,3, л=400, получим
Pi=— 0,0058, р„=0,0308.
Итак, искомый доверительный интервал 0 < р < 0,0308.
519. Произведено 300 испытаний, в каждом из кото-
которых неизвестная вероятность р появления события А
постоянна. Событие А появилось в 250 испытаниях.
Найти доверительный интервал, покрывающий неизвест-
неизвестную вероятность р с надежностью 0,95.
520. В 360 испытаниях, в каждом из которых вероят-
вероятность появления события одинакова и неизвестна, собы-
событие А появилось 270 раз. Найти доверительный интер-
интервал, покрывающий неизвестную вероятность р с надеж-
надежностью 0,95.
521. Среди 250 деталей, изготовленных станком-авто-
станком-автоматом, оказалось 32 нестандартных. Найти доверитель-
доверительный интервал, покрывающий с надежностью 0,99 неиз-
неизвестную вероятность р изготовления станком нестандарт-
нестандартной детали.
522. При испытаниях 1000 элементов зарегистриро-
зарегистрировано 100 отказов. Найти доверительный интервал, покры-
покрывающий неизвестную вероятность р отказа элемента
с надежностью: а) 0,95; б) 0,99.
180
Глава одиннадцатая
МЕТОДЫ РАСЧЕТА СВОДНЫХ ХАРАКТЕРИСТИК ВЫБОРКИ
§ 1. Метод произведений вычисления
выборочных средней и дисперсии
А. Равноотстоящие варианты. Пусть выборка задана в виде рас*
пределения равноотстоящих вариант и соответствующих им частот.
В этом случае удобно находить выборочные среднюю н дисперсию
методом произведений по формулам
где А—шаг (разность между двумя соседними вариантами); С—лож-
С—ложный нуль (варианта, которая расположена примерно в середине
вариационного ряда); и,- = (дс;—С)/А—условная варианта; Ai[ =
= B Я|И,-)/я—условный момент первого порядка; М%= B я,-и?)/я —
условный момент второго порядка.
Как практически использовать метод произведений, указано
в задаче 523.
523. Найти методом произведений выборочную сред-
среднюю и выборочную дисперсию по заданному распреде-
распределению выборки объема п = 100:
варианта х,- 12 14 16 18 20 22
частота п, 5 15 50 16 10 4
Решение. Составим расчетную табл. 1; для этого:
1) запишем варианты в первый столбец;
2) запишем частоты во второй столбец; сумму частот A00) по-
поместим в нижнюю клетку столбца;
3) в качестве ложного нуля С выберем варианту A6), которая
имеет наибольшую частоту (в качестве С можно взять любую вари-
варианту, расположенную примерно в середине столбца); в клетке треть-
третьего столбца, которая принадлежит строке, содержащей ложный
нуль, пишем 0; над нулем последовательно записываем —1, —2,
а под нулем 1,2, 3;
4) произведения частот л,- на условные варианты щ запишем
в четвертый столбец; отдельно находим сумму (—25) отрицательных
чисел и отдельно сумму D8) положительных чисел; сложив эти
числа, их сумму B3) помещаем в нижнюю клетку четвертого столбца;
5) произведения частот на квадраты условных вариант, т. е. пщ,
запишем в пятый столбец (удобнее перемножить числа каждой стро-
строки третьего и четвертого столбцов: и,'-я/и,-=я/и?); сумму чисел
столбца A27) помещаем в нижнюю клетку пятого столбца;
6) произведения частот на квадраты условных вариант, увели-
увеличенных на единицу, т. е. л,(и,+ 1J, запишем в шестой контроль-
контрольный столбец; сумму чисел столбца B73) помещаем в нижнюю клетку
шестого столбца.
В итоге получим расчетную табл. 1.
181
Для контроля вычислений пользуются тождеством
2 «/(«/+1J = 2 «/«' + 22 я/«/+п.
Контроль:
2 «/ (и/ + 1 J = 273, 2 я/«* +22 «№ + я =
= 127+2-23+100=273.
Совпадение контрольных сумм свидетельствует о правильности вы-
вычислений.
Вычислим условные моменты первого и второго порядков:
Ml = B п/и,)/п = 23/100 = 0,23; Ait = B п,и?)/п = 127/100 = 1,27.
Найдем шаг (разность между любыми двумя соседними вариан-
вариантами): А= 14—12 = 2.
Вычислим искомые выборочные среднюю и дисперсию, учитывая,
что ложный нуль (варианта, которая имеет наибольшую частоту)
С = 16:
хв = лО» + С=0,23-2+ 16= 16,46;
DB = [Л*!-(МIJ] А2 = [ 1,27-0,23*]-2* = 4,87.
Таблица 1
1
XI
12
14
16
18
20
22
2
п{
5
15
50
16
10
4
/1=100
3
«1
-2
—1
0
1
2
3
4
л/и,-
—10
—15
-25
16
20
12
48
2л/«/ = 23
5
щи\
20
15
16
40
36
2п/и?=127
6
n,-(u/+l)«
5
—
Е0
64
SO
64
2n,(«, + lJ = 273
524. Найти методом произведений выборочную сред
нюю и выборочную дисперсию по заданному распреде-
распределению выборки:
18,6 19,0
4 6
а) варианта xt
частота nt
19,4 19,8 20,2 20,6
30 40 18 2
б) варианта
частота п
65 70 75 80 85
2 5 25 15 3
182
Б. Неравноотстоящие варианты. Если первоначальные варианты
не являются равноотстоящими, то интервал, в котором заключены
все варианты выборки, делят на несколько равных, длины h, час-
частичных интервалов (каждый частичный интервал должен содержать
не менее 8—10 вариант). Затем находят середины частичных интер-
интервалов, которые и образуют последовательность равноотстоящих ва-
вариант. В качестве частоты каждой середины интерпала принимают
сумму частот вариант, которые попали в соответствующий частич-
частичный интервал.
При вычислении выборочной дисперсин для уменьшения ошибки,
вызванной группировкой (особенно при малом числе интервалов),
делают поправку Шепиарда, а именно вычитают из вычисленной
дисперсии 1/12 квадрата длины частичного интервала.
Таким образом, с учетом поправки Шеппарда дисперсию вычис-
вычисляют по формуле
i
525. Найти методом произведений выборочную сред-
среднюю и выборочную дисперсию по заданному распреде-
распределению выборки объема п = 100:
*,- 2 3 7 9 11 12,5 16 18 23 25 26
п, 3 5 10 6 10 4 12 13 8 20 9
Решение. Разобьем интервал 2—26 на следующие четыре
частичных интервала длины А = 6:2—8; 8—14; 14—20; 20—26.
Приняв середины частичных интервалов в качестве новых вариант
У1, получим равноотстоящие варианты: yi=5, Уг = и,у3—17, у4 = 23.
В качестве частоты п, варианты yt = 5 примем сумму частот
вариант, попавших в первый интервал: «1 = 3 + 5+10=18.
Вычислив аналогично частоты остальных вариант, получим рас-
распределение равноотстоящих вариант:
У1 5 11 17 23
гц 18 20 25 37
Пользуясь методом произведений, найдем уе= 15,86, ?>в = 45,14.
Принимая во внимание, что число частичных интервалов D)
мало, учтем поправку Шеппарда:
D'B = DB—A/12) Л2 = 45,14—62/12 = 42,14.
526. При вычислении дисперсии распределения не-
неравноотстоящих вариант выборка была разбита на пять
интервалов длины /г =12. Выборочная дисперсия равно-
равноотстоящих вариант (середин частичных интервалов)
?>в = 52,4. Найти выборочную дисперсию, учитывая по-
поправку Шеппарда.
527. а) Найти методом произведений выборочную
среднюю и выборочную дисперсию по заданному распре-
распределению неравноотстоящих вариант выборки объема п=50:
л:,- 6 8 11 13 15,5 17,5 20 23,5 24,5 26
п,- 19664 6 85 4 1
183
б) найти выборочную дисперсию с учетом поправки
Шеппарда.
Указание. Разбить интервал 6—26 на пять частичных интер-
интервалов длины А = 4.
528. а) Найти методом произведений выборочную
среднюю и выборочную дисперсию по заданному распре-
распределению неравноотстоящих вариант выборки объема
п=100:
xt 10 13 15 17 19 23 24 26 28 32 34 35
п, 2 4 6 8 9 6 20 15 10 8 7 5
б) найти выборочную дисперсию с учетом поправки
Шеппарда.
Указание. Разбить интервал 10—35 на пять частичных ин-
интервалов длины А=5. Частоту варианты дс=15, т. е. частоту 6, рас-
распределить поровну между первым и вторым частичными интервалами
(так как варианта 15 попала на границу интервала).
§ 2. Метод сумм вычисления
выборочных средней и дисперсии
Пусть выборка задана в виде распределения равностоящих ва-
вариант и соответствующих им частот. В этом случае, как было ука-
указано в § 1, выборочные среднюю и дисперсию можно вычислить по
формулам:
l ['(ГJ]
При использовании метода сумм условные моменты первого и вто-
второго порядков находят по формулам:
где di=al—bi, sl = a1+b1, sa = a2-f Ьг. Таким образом, в конечном
счете надо вычислить числа аи аъ bu b2. Как практически вычис-
вычислить эти числа, указано в задаче 529.
529. Найти методом сумм выборочную среднюю и вы-
выборочную дисперсию по заданному распределению вы-
выборки объема п=100:
варианта х( 48 52 56 60 64 68 72 76 80 84
частота п, 2 4 6 8 12 30 18 8 7 5
Решение. Составим расчетную табл. 2, для этого:
1) запишем варианты в первый столбец;
2) запишем частоты во второй столбец; сумму частот A00) по-
поместим в нижнюю клетку столбца;
3) ь качестве ложного нуля С выберем варианту F3), которая
имеет наибольшую частоту (в качестве С можно взять любую ва-
варианту, расположенную примерно в середине столбца); в клетках
строки, содержащей ложный нуль, запишем нули; в четвертом
134
столбце над и под уже помещенным нулем запишем еще по одному
нулю;
4) в оставшихся незаполненными над нулем клетках третьего
столбца (исключая самую верхнюю) запишем последовательно накоп-
накопленные частоты: 2; 2+4 = 6; 6+6=12; 12 + 8=20; 20+12 = 32;
сложив все накопленные частоты, получим число bi = 72, которое
поместим в верхнюю клетку третьего столбца. В оставшихся неза-
незаполненными под нулем клетках третьего столбца (исключая самую
нижнюю) запишем последовательно накопленные частоты: 5; 5+7= 12;
124-8 = 20; 20+18=38; сложив все накопленные частоты, получим
число ai = 75, которое поместим в иижнюю клетку третьего столбца;
5) аналогично заполняется четвертый столбец, причем сумми-
суммируют частоты третьего столбца; сложив все накопленные частоты,
расположенные над нулем, получим число 6а = 70, которое поместим
в верхнюю клетку четвертого столбца; сумма накопленных частот,
расположенных под нулем, равна числу а*, которое поместим в ниж-
нижнюю клетку четвертого столбца.
В итоге получим расчетную табл. 2.
Найдем dt, sx, sa:
dt = ai—bt = 75—72 = 3;
129.
Таблица 2
*/
48
52
56
60
64
68
72
76
80
84
2
1|
2
4
6
8
12
30
18
8
7
5
/1=100
3
*, = 72
2
6
12
20
32
0
38
20
12
5
a, = 75
4
b, = 70
2
8
20
40
0
0
0
37
17
5
aa = 59
185
Найдем условные моменты первого и второго порядков:
Ml = dlln = 3/100 = 0,03;
Вычислим искомые выборочную среднюю и выборочную диспер-
дисперсию, учитывая, что шаг (разность между двумя соседними вариан-
вариантами) А = 4 и ложный нуль С = 63:
Г„ = МГА + С = 0,03-4 + 68 = 68,12;
О„ = [Л*2—(Л*;J]А* = [4,05—0,032]-42 ~ 64,78.
530. Найти методом сумм выборочную среднюю и вы-
выборочную дисперсию по заданному распределению вы-
выборки объема п = 100:
а)
варианта xt 30 35 40 45 50 55 60 65 70 75
частота п{ 4 6 8 15 25 20 8 7 5 2
б)
варианта xt 122 128 134 140 146 152 158 164 170 176
частота п, 7 8 12 16 4 20 13 10 7 3
в)
варианта х( 12 14 16 18 20 22
частота п,- 5 15 50 16 10 4
г)
варианта л:,- 10,2 10,4 10,6 10,8 11,0 11,2 11,4 11,6 11,8 12,0
частота п, 2 3 8 13 25 20 12 10 6 1
§ 3. Асимметрия и эксцесс эмпирического распределения
Асимметрия и эксцесс эмпирического распределения определя-
определяются соответственно равенствами
я$=/Яз/0в> в? = /я4/Св—3;
здесь ав—выборочное среднее квадратическое отклонение; т9 и/и4 —
центральные эмпирические моменты третьего и четвертого порядков:
Эти моменты в случае равноотстоящих вариант с шагом Л (шаг
равен разности между любыми двумя соседними вариантами) удоб-
удобно вычислять по формулам:
ms = [Ml — ЪМ\м1 + 2 (Л*ГK] А3,
где M*k= B пщ)/п—условные моменты k-то порядка «,-=(*,•—С)/А —
условные варианты. Здесь х,-—первоначальные варианты; С—лож-
С—ложный нуль, т. е. варианта, имеющая наибольшую частоту (либо лю-
любая варианта, расположенная примерно в середине вариационного
ряда).
186
Итак, для отыскания асимметрии и эксиесса необходимо вычис-
вычислить условные моменты, что можно сделать методом произведений
или методом сумм.
А. Метод произведений
531. Найти методом произведений асимметрию и экс-
эксцесс по заданному распределению выборки объема п = 100:
варианта *,- 12 14 16 18 20 22
частота п, 5 15 50 16 10 4
Решение. Воспользуемся методом произведений. Составим
расчетную табл. 3. В § 1 этой главы при решении задачи 523 уже
было указано, как заполняются столбцы 1—5 расчетной таблицы,
поэтому ограничимся краткими пояснениями.
Для заполнения столбца 6 удобно перемножить числа каждой
строки столбцов 3 и 5. Для заполнения столбца 7 удобно перемно-
перемножать числа каждой строки столбцов 3 и 6. Столбец 8 служит для
контроля вычислений с помощью тождества
2 п/ <«/+1L = 2 «/«* + 4 2 «/и*+ 6 2 «<«? + 4 2 пт+п.
Приведем расчетную табл. 3.
Таблица 3
1
XI
12
14
16
18
20
22
2
5
15
50
16
10
4
/г = 100
3
«i
о
—1
0
1
2
3
4
Ч|И/
—10
—15
-25
16
20
12
48
2"i«f =
5
л/uf
20
15
—
16
40
36
2я/«4 =
= 127
6
—40
—15
-55
16
80
108
204
2«-«?=
= 149
7
80
15
—
16
160
324
2лд4=
=595
8
л/(и/+1)«
5
—
50
256
810
1024
=2145
Контроль:
2
2 п,и*+42 "i"! + 6 2 "«и?+4 2 "/«/+" =
= 595+4-149 + 6-127+4-23+100=2145.
187
Совпадение контрольных сумм свидетельствует о правильности
вычислений.
Найдем условные моменты третьего и четвертого порядков (ус-
(условные моменты первого и второго порядков вычислены в задаче
523: Л*1=0,23, Л*?=1,27):
..3. IЛО . \* „ ...4 дог
Найдем центральные эмпирические моменты третьего и четвер-
четвертого порядков:
ms= [Ml — ЗМ\м!+2 (MiK\ A»,
Подставляя Л = 2 и М1=О,23, ЛЙ = 1,27, Л*^ = 1,49, ^ = 5,95, по-
получим т3 =5,104, «4 = 79,582.
Найдем искомые асимметрию и эксцесс, учитывая, что ?>д=4,87
(см. задачу 523):
as= m3/a%=5,124/( / 4,87)» = 0,47;
еЛ = т4/ав—3 = 79,582/A^4,87)*—3 = 0,36.
532. Найти методом произведений асимметрию и экс-
эксцесс по заданному распределению выборки объема п= 100:
а) х, 2,6 3,0 3,4 3,8 4,2 б) лг,- 1 6 11 16 21
п, 8 20 45 15 12 ' nt 5 25 40 20 10
Б. Метод сумм
533. Найти методом сумм асимметрию и эксцесс по
заданному распределению выборки объема п=100:
х, 48 52 56 60 64 68 72 76 80 84
п, 2 4 6 8 12 30 18 8 7 5
Решение. Воспользуемся методом сумм, для этого составим
расчетную табл. 4. В § 2 этой главы при решении задачи 529 уже
было указано, как заполняются столбцы 1—4 расчетной таблицы,
поэтому ограничимся краткими пояснениями.
Для заполнения столбца 5 запишем нуль в клетке строки, со-
содержащей ложный нуль F8); над этим нулем и под ним поставим
еще по два нуля.
В клетках над нулями запишем накопленные частоты, для
чего просуммируем частоты столбца 4 сверху вниз; в итоге
будем иметь следующие накопленные частоты: 2; 2+8=10; 2+8 +
+ 20 = 30. Сложив накопленные частоты, получим число Ь3 = 2-\-10 +
+ 30 = 42, которое поместим в верхнюю клетку пятого столбца.
В клетках под пулями запишем накопленные частоты, для
чего просуммируем частоты столбца 4 с н и з у вверх; в итоге будем
иметь следующие накопленные частоты: 5; 5+17=22. Сложив на-
накопленные частоты, получим число о3 = 5+22 = 27, которое поместим
в нижнюю клетку пятого столбца.
Аналогично заполняют столбец 6, причем суммируем частоты
столбца 5. Сложив накопленные частоты, расположенные над нуля-
188
ми, получим число <>4 = 2+12=14, которое запишем в верхнюю
клетку шестого столбца. Сложив числа, расположенные под нулями
(в нашей задаче есть лишь одно слагаемое), получим число а4=5,
которое поместим в нижнюю клетку шестого столбца.
В итоге получим расчетную табл. 4.
Контроль: сумма чисел, расположенных непосредственно над
нулем третьего столбца, слева от него и под ним, должна быть равна
объему выборки C2+30+38= 100); сумма двух чисел, расположен-
расположенных над двумя ступеньками ступенчатой линни (обведены жирными
отрезками), должна быть равна соответственно числам Ь,; стоящим
над предшествующей ступенькой (при движении по «лесенке»
вверх): 32 + 40 = 72=61; 40+30 = 70 = 6s; 30+12 = 42 = 6s. Анало-
Аналогично проверяется совпадение сумм двух чисел, стоящих под «сту-
«ступеньками лесенки», ведущей вниз: 38+37=75=а,; 37+22 = 59 = Оа;
22+5=27 = as. При несовпадении хотя бы одной из указанных
сумм следует искать ошибку в расчете.
Найдем di («=1, 2, 3) и s,- (i=l. 2, 3, 4):
, = ai—61 = 75—72=3,
2—6„ = 59—70 = — 11,
1
«i
48
52
56
60
64
68
72
76
80
84
2
Л/
2
4
6
8
12
30
18
8
7
5
п = 100
3
ft, = 72
2
6
12
20
32
0
38
20
12
5
ах = 75
4
fr, = 70
2
8
20
40
0
0
0
37
17
5
^=59
T
5
ft, = 42
2
10
30
0
0
0
0
0
22
5
«,=27
абл ица 4
6
bt=\4
2
12
0
0
0
0
0
0
0
5
a4 = 5
rfs=e,,—fcs=27—42 = —15;
75+72=147; «2=02+68=59+70 = 129,
as+6s=27+42=69, s4=a4+fc4 = 5+14= 19.
189
Найдем условные моменты первого, второго, третьего и четвер-
четвертого порядков:
М* di 3 ппч и* '' +2*g 147+2129
Ml=—=Тоо==0'03- Мг п Шо—=4>05>
. ^ + 6^+64, 3+6(-11)+6(-15) _„
М3 = - = Joo =- ' -53'
Д1» si+14s2+36s3+24s4 147+14-129+36-69+24-19_10 g3
Найдем центральные эмпирические моменты третьего и четвер-
четвертого порядков:
= [_ 1,53—ЗО.ОЗ^.Об+г^О.ОЗK] 48 = -121,245,
ntA, = lMi — 4Л]1Л1з + О \Mi) Л12 — O^/Wi/ Jft* =
= [48,93—40,03(— 1,53)+
+ 6 @,03)a.4,05—3 @.03L] -4* = 12578,679.
Найдем искомые асимметрию и эксцесс, учитывая, что сгв =
= У Db = 1^64,78 (дисперсия DB была найдена ранее, см. задачу
629):
«5= тг/а% = —121,245/(}/4J8)s = -0,25,
еЛ=т4/аЬ—3= 12578,679/( /64J8L—3=26,97.
534. Найти методом сумм асимметрию и эксцесс по
заданному распределению выборки объема п=100:
а) х{ 10,2 10,4 10,6 10,8 11,0 11,2 11,4 11,6 11,8 12,0;
п, 2 3 8 13 25 20 12 10 6 1
б) *, 12 14 16 18 20 22.
п{ 5 15 50 16 10 4
Глава двенадцатая
ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ
§ 1. Линейная корреляция
Если обе линии регрессии Y на X и X на Y—прямые, то кор-
корреляцию называют линейной.
Выборочное уравнение прямой линии регрессии Y на X имеет вид
ov
Ух—У=гв — (х—х), (»)
где Ух—условная средняя; х и ^—выборочные средние признаков
X и Y; ах и о«—выборочные средние квадратические отклонения;
гв—выборочный коэффициент корреляции, причем
гв = B nxvxy—nxy)l(naxau).
190
Выборочное уравнение прямой линии регрессии X на Y имеет вид
Если данные наблюдений над признаками X и Y заданы в виде
корреляционной таблицы с равноотстоящими вариантами, то целе-
целесообразно перейти к условным вариантам:
vj=(y/—Ct)/ha,
где С,—«ложный нуль» вариант X (новое начало отсчета); в ка-
качестве ложного нуля выгодно принять варианту, которая располо-
расположена примерно в середине рариационного ряда (условимся прини-
принимать в качестве ложного нуля парианту, имеющую наибольшую
частоту); hi—шаг, т. е. разность между двумя соседними вариантами
X; Сг—ложный нуль вариант Y; ht—шаг вариант Y.
В этом случае выборочный коэффициент корреляции
/•„ = B navuv—nuv)/(nauav),
причем слагаемое 2 "о»' удобно вычислять, используя расчетную
табл. 7 (см. далее решение задачи 535).
Величины п, v, aa, av могут быть найдены либо методом произ-
произведений (при большом числе данных), либо непосредственно по фор-
формулам:
Зная эти величины, можно определить входящие в уравнения рег-
ресенн (*) и (**) селичины по формулам:
Для оценки силы линейной корреляционной связи служит вы-
выборочный коэффициент корреляции /„.
Для обоснованного суждения о наличии связи между количест-
количественными признаками следует проверить, значим ли выборочный ко-
коэффициент корреляции (см. гл. XIII, § 12).
535. Найти выборочное уравнение прямой линии рег-
регрессии Y на X по данным, приведенным в корреляцион-
корреляционной табл. 5.
Таблица 5
У
16
26
36
46
56
%
X
20
4
__
_
_
4
25
6
8
_
_
—
14
30
10
32
4
46
35
_
3
12
I
16
40
9
6
5
20
nv
10
18
44
22
6
л = 100
191
Решение. Составим корреляционную табл. 6 в условных ва-
вариантах, выбрав в качестве ложных нулей Сх=30 и С2=36 (каж-
(каждая из этих вариант расположена в середине соответствующего
вариационного ряда).
Т аблица 6
V
—2
—1
0
1
2
пи
и
-2
4
—
—
—
—
4
-1
6
8
—
—
—
14
0
—
10
32
4
—
46
I
—
—
3
12
1
16
2
—
—
9
6
5
20
%
10
18
44
22
6
/1=100
Найдем и и v:
-0+22-1 + 6-2)/100=— 0,04.
Найдем вспомогательные величины ы2 и Vя:
F=(Sn««2)/n= D-4 +141 +16-1+20-4)/100= 1,26;
^ = B«г,«*)/п=A0-4+18-1+22-1+6.4)/100 = 1,04.
Найдем <т„ и <т„
—0,342= 1,07;
,02.
о„ = KU1—Й2 = 1^1,04—0,04*
Найдем 2пвоИ1'> лля чег0 составим расчетную табл. 7.
Суммируя числа последнего столбца табл. 7, находим
Для контроля вычислений находим сумму чисел последней
строки:
2 и.V =2««,««= 82.
и
Совпадение сумм свидетельствует о правильности вычислений.
Пояснения к составлению табл. 7.
1. Произведение частоты яио на варианту и, т. е. nuvu, записы-
записывают в правом верхнем углу клетки, содержащей значение частоты.
Например, в правых верхних углах клеток первой строки записаны
произведения: 4(—2)=—8; 6(—1)=—6.
192
VI
Ю
и -2
—1
о
¦
2
-2
—8
—
—8
16
-
—12
6
—6
Q
-8
—
—20
20
0
—1
[о
[о
чо 1
0
—
—6
0
0
12
2
Г
1
11
12
Ll
14
14
2
0
6
10
9 '
с
12
16
32
—14
—8
21
24
11
и
Таблица 7
v-U
28
8
0
24
22
0 ° t
—Контроль
2. Складывают все числа, помещенные в правых верхних углах
клеток одной строки, и их сумму помещают в клетку этой же стро-
строки «столбца U». Например, для первой строки ы=— 8+(—6)=—14.
3. Наконец, умножают варианту v на U и полученное произве-
произведение записывают в соответствующую клетку «столбца vll». Напри-
Например, в первой строке таблицы v = —2, U = —14, следовательно,
t;f/ = (—2) (—14) = 28.
4. Сложив все числа «столбца vU», получают сумму ^vU, ко-
V
торая равна искомой сумме ^navuv. Например, для табл. 7
2 vU = 82, следовательно, искомая сумма VnBO«y=82.
V
Для контроля аналогичные вычисления производят по столбцам:
произведения nuvv записывают в левый нижний угол клетки, содер-
содержащей значение частоты; все числа, помещенные в левых нижних
углах клеток одного столбца, складывают и их сумму помещают в
«строку V»; наконец, умножают каждую варианту и на V и резуль-
результат записывают в клетках последней строки.
Сложив все числа последней строки, получают сумму ^uV,
и
которая также равна искомой сумме V navuv. Например, для табл. 7
2«V=82, следовательно, ^n^uv=82.
и
Найдем искомый выборочный коэффициент корреляции:
^nuvuv-rum 82—100-0,34 • (-0,04)
ЮО-1,07-1,02
Найдем шаги hi и Л2 (разности между любыми двумя соседннми
вариантами):
Ai = 25—20=5; Л2 = 26—16=10.
Найдем хну, учитывая, что Сх=30, С2 = 36:
х = й-Л1+С1=0,34-5+ 30=31,70;
y=Z-h»+Ct = (—0,04)-10 + 36=35,60.
Найдем ах и ау:
ax=hi-aa = 5-1,07 = 5,35; сту=Ла-стг, = 10-1,02= 10,2.
Подставив найденные величины в соотношение (*), получим
искомое уравнение прямой линии регрессии Y на X:
— 10 2
«/ж-35,60=0,76 -gi (*-31,70),
или окончательно ух=1,45х—10,36.
194
536. Найти выборочные уравнения прямых линий
регрессии К на X и X на Y по данным, приведенным
в следующих корреляционных таблицах:
а)
У
100
120
140
160
180
пх
X
5
2
3
—
—
—
5
10
1
4
—
—
—
5
15
—
3
5
—
—
8
20
—
—
10
1
—
11
25
—
—
8
—
—
8
30
—
—
—
6
—
6
35
—
—
—
1
4
5
40
—
—
—
1
1
2
%
3
10
23
9
5
я=50
б)
У
125
150
175
200
225
250
X
18
—
1
—
—
—
—
1
23
1
2
3
—
—
—
6
28
—
5
2
1
—
—
8
33
—
—
12
8
—
—
20
38
—
7
3
—
10
43
—
—
—
—
3
1
4
48
—
—
—
—
—
1
1
ПУ
1
8
17
16
6
2
л=50
195
в)
У
100
120
140
160
180
пх
X
б
—
—
—
3
2
5
10
—
—
—
4
1
5
15
—
—
8
3
—
11
20
—
—
10
—
1
11
25
—
—
5
—
—
5
30
6
4
—
—
—
10
36
1
2
—
—
—
3
7
6
23
10
4
п = 50
§ 2. Криволинейная корреляция
Если график регрессии—кривая линия, то корреляцию назы-
называют криволинейной. В частности, в случае параболической корре-
корреляции второго порядка выборочное уравнение регрессии У на X
имеет вид
ух = Ах* + Вх+С.
Неизвестные параметры А, В и С находят (например, методом Га-
Гаусса) из системы уравнений:
B л**4) А + B пхх>) В + B пхх*) С=2 пх1}хх*,
B пхх*) А + B пхх*) В + B«**) С=2 пхЦхх, (•)
B я**1) А + B я**) В +яС=2«*?*•
Аналогично находится выборочное уравнение регрессии X на У:
Для оценки силы корреляции У па X служит выборочное корре-
корреляционное отношение (отношение межгруппового среднего квадрэти-
квадрэтического отклонения к общему среднему квадратическому отклонению
признака У)
Чу* ==о"межгр/°"об1и>
или в других обозначениях
1
Здесь
196
где л—объем выборкн (сумма всех частот); пх—частота значения х
признака X; пу—частота значения у признака У; ух—условная
средняя признака К; у—общая средняя признака К.
Аналогично определяется выборочное корреляционное отношение
X к Y:
; рх-
537. Найти выборочное уравнение регрессии ух =
— Ах2 + Вх + С по данным, приведенным в корреляцион-
корреляционной табл. 8.
Оценить силу корреляционной связи по выборочному
корреляционному отношению.
Таблица 8
Y
25
45
ПО
я*
X
. | з
20
—
—
20
—
30
1
31
5
—
1
48
49
nV
20
31
49
/1=100
Решение. Составим расчетную табл. 9.
Таблица 9
X
2
3
5
2
"х
20
31
49
100
25
47,1
108,67
40
93
245
378
пхх*
80
279
1225
1584
169
837
6125
7122
пхх*
320
2511
30 625
33 456
"хУх
500
1460
5325
7285
пхУх*
1000
4380
26 624
32004
2000
13141
133 121
148262
Подставив числа, содержащиеся в последней строке табл. 9,
в (*), получим систему уравнений относительно неизвестных коэф-
коэффициентов А, В, С:
33456 А + 7122 В+1584 С= 148262,
7122 А +1584 В+ 378С= 32004,
1584 А + 378 В + 100 С= 7285.
197
Решив эту систему (например, методом Гаусса), найдем: А =2,94,
В = 7,27, С=—1,25. Подставив найденные коэффициенты в уравне-
уравнение регрессии у~х = Ахг-\-Вх-\-С, окончательно получим
ух =2,94*а+7,27*— 1,25.
Для того чтобы вычислить выборочное корреляционное отноше-
отношение i[yX, предварительно найдем общую среднюю у~, общее среднее
квадратическое отклонение оу н межгрупповое среднее квадратиче-
ское отклонение а- :
у
-45+49-1!0)/100 = 72,85;
^B0B5—72,85J+31 D5—72,85)' + 49 A10—72,85>8>/100 =37,07;
= ^B0B5—72,85J+31 D7,1— 72,85J + 49A08,67— 72,85)*)/100
=35,95.
Найдем искомое выборочное корреляционное отношение:
г)ух = о- 1оу= 35,95/37,07 = 0,97.
ух1
538. Найти выборочное уравнение регрессии ~ух=Ах2+
В + С и выборочное корреляционное отношение т\уХ
по данным, приведенным в корреляционной таблице:
а)
У
0
3
5
10
17
X
0
18
1
3
22
1
1
20
5
26
2
1
10
7
18
3
2
12
14
4
20
20
%
20
21
20
19
20
/1=100
198
б)
У
7
13
40
80
200
«*
X
0
19
2
21
4
1
14
3
18
6
1
22
23
7
2
15
17
10
21
21
"у
21
16
27
15
21
/1=100
в)
У
1
35
50
X
0
50
50
4
5
44
5
54
5
1
45
46
"у
56
44
50
/1 = 150
г)
У
10
И
20
35
50
«*
X
0
20
7
27
1
5
15
3
23
2
3
17
8
28
3
1
4
13
5
23
4
7
42
49
"у
25
26
24
28
47
л = 150
199
д)
У
200
300
400
«*
X
7
41
1
42
8
7
52
8
67
9
1
40
41
пУ
48
54
48
/1=150
539. Найти выборочное уравнение регрессии ху=Ау*+
+Ву+С и выборочное корреляционное отношение г\ху
по данным, приведенным в корреляционной таблице:
а)
У
1
3
4
X
б
15
1
16
30
14
2
16
60
18
18
пу
15
15
20
п=50
б)
У
0
2
3
X
i
13
2
1
16
9
10
1
11
19
23
23
"у
13
12
25
л=50
§ 3. Ранговая корреляция
А. Выборочный коэффициент ранговой корреляции Спирмеиа.
Пусть выборка объема п содержит независимые объекты, которые
обладают двумя качественными признаками: А я В. Под качествен-
качественным подразумевают признак, который невозможно измерить точно,
но он позволяет сравнивать объекты между собой и, следовательно,
расположить их в порядке убывания или возрастания качества.
Для определенности условимся располагать объекты в
порядке ухудшения качества.
Расположим сначала объекты в порядке ухудшения качества по
признаку А. Припишем объекту, стоящему на »-м месте, число—
ранг х/, равный порядковому номеру объекта: *,- = «. Затем распо-
расположим объекты в порядке убывания качества по признаку В и при-
припишем каждому из них ранг (порядковый номер) у/, причем (для
удобства сравнения рангов) индекс < при у по-лрежиему равен по-
порядковому номеру объекта по признаку А.
В итоге получим две последовательности рангов:
по признаку А Х\ хг ... хп,
по признаку В yi уз ... уп
Для оценки степени связи признаков А и В служат, в част-
частности, коэффициенты ранговой корреляции Спнрмена и Кендалла
(см. п. Б).
Выборочный коэффициент ранговой корреляции С пир мена нахо-
находят по формуле
где d,-=Xj—у;, п—объем выборки.
Абсолютная величина коэффициента ранговой корреляции Спир-
мена не превышает единицы: |рв|<1.
Для обоснованного суждения о наличии связи между качест-
качественными признаками следует проверить, значим ли выборочный
коэффициент ранговой корреляции Спирмена (см. гл. XIII, § 13).
540. Знания десяти студентов проверены по двум
тестам: А и В. Оценки по стобалльной системе оказались
следующими (в первой строке указано количество баллов
по тесту Л, а во второй—по тесту В):
95 90 86 84 75 70 62 60 57 50 ...
92 93 83 80 55 60 45 72 62 70 ( >
Найти выборочный коэффициент ранговой корреляции
Спирмена между оценками по двум тестам.
Решение. Присвоим ранги Х{ оценкам по тесту А. Эти оценки
расположены в убывающем порядке, поэтому их ранги xt равны
порядковым номерам:
ранги xi 123456789 10
оценки по тесту А 95 90 86 84 75 70 62 60 57 50
201
Присвоим ранги у,- оценкам по тесту В, для чего сначала рас-
расположим эти оценки в убывающем порядке и пронумеруем их:
123456789 10 ,**,
93 92 83 80 72 70 62 60 55 45 * '
Напомним, что индекс t при у должен быть равен порядковому
номеру оценки студента по тесту А.
Найдем ранг yv Индекс i = 1 указывает, что рассматривается
оценка студента, который занимает по тесту А в ряду (•) первое
место (эта оценка равна 95); из условия видно, что по тесту В сту-
студент получил оценку 92, которая в (•*) расположена на втором
месте. Таким образом, ранг yi=2.
Найдем ранг у2- Индекс (=2 указывает, что рассматривается
оценка студента, который занимает по тесту А в ряду (*) второе
место; из условия видно, что студент получил по тесту В оценку 93,
которая в (**) расположена на первом месте. Таким образом,
ранг ^2 = 1-
Аналогично найдем остальные ранги: j/s = 3, yt = 4, f/6=9,
Ув = 8, ^7 = 10. у8=5, 09 = 7. Ую=6.
Выпишем последовательности рангов х,- н у;:
Xi 1 2 3 4 5 6 7 8 9 10
у/213498 10 57 6
Найдем разности рангов: dt=xi—0i = l—2=—1; dt=x%—Уг=
= 2 — 1 = 1. Аналогично получим: da=Q, d4=0, db=—i, de=—2,
d, = -3, d8 = 3, de = 2, d,0 = 4.
Вычислим сумму квадратов разностей рангов:
16+4+9+9-1-4+16=60.
Найдем искомый коэффициент ранговой корреляции Спирмена,
учитывая, что л = 10:
6 2Х2 , 6-60 ой.
Итак, рв=0,64.
541. Два преподавателя оценили знания 12 учащихся
по стобалльной системе и выставили им следующие
оценки (в первой строке указано количество баллов,
выставленных первым преподавателем, а во второй —
вторым):
98 94 88 80 76 70 63 61 60 58 56 51
99 91 93 74 78 65 64 66 52 53 48 62
Найти выборочный коэффициент ранговой корреляции
Спирмена между оценками двух преподавателей.
542. Тринадцать цветных полос расположены в по-
порядке убывания окраски от темной к светлой и каждой
полосе присвоен ранг—порядковый номер. В итоге по-
получена последовательность рангов
х, 1 2 3 4 5 6 7 8 9 10 11 12 13
202
При проверке способности различать оттенки цветов,
испытуемый расположил полосы в следующем порядке:
у, 6 3 4 2 1 10 7 8 9 5 11 13 12
Найти коэффициент ранговой корреляции Спирмена между
«правильными» рангами х( и рангами y!t которые при-
присвоены полосам испытуемым.
543. Два товароведа расположили девять мотков
пряжи в порядке убывания толщины нити. В итоге были
получены две последовательности рангов:
xt 123456789
\ji 4 15326987
Найти коэффициент ранговой корреляции Спирмена
между рангами х{ и yt.
544. Специалисты двух заводов проранжировали
11 факторов, влияющих на ход технологического про-
процесса. В итоге были получены две последовательности
рангов:
х, 1 2 3 4 5 6 7 8 9 10 11
у, 1235498 11 6 7 10
Определить, согласуются ли мнения специалистов раз-
различных заводов, используя коэффициент ранговой кор-
корреляции Спирмена.
545. Три арбитра оценили мастерство 10 спортсменов,
в итоге были получены три последовательности рангов
(в первой строке приведены ранги арбитра А, во вто-
второй— ранги арбитра В, в третьей—ранги арбитра С):
х, 1 2345678 9 10
у, 3 10 7 2 8 5 6 9 1 4
г, 6 2139457 10 8
Определить пару арбитров, оценки которых наиболее
согласуются, используя коэффициент ранговой корреля-
корреляции Спирмена.
546. Два контролера А и В расположили образцы
изделий, изготовленных девятью мастерами, в порядке
ухудшения качества (в скобках помещены порядковые
номера изделий одинакового качества):
(A) 1 2 C, 4, 5) F, 7, 8, 9)
(B) 2 1 4 3 5 F, 7) 8 9
Найти выборочный коэффициент ранговой корреляции
Спирмена между рангами изделий, присвоенными им
двумя контролерами.
203
Решение. Учитывая, что ранги изделий одинакового качества
равны среднему арифметическому порядковых номеров изделий:
C + 4+5)/3 = 4, F + 7+8+9)/4 = 7,5, F+7)/2=6,5, напишем по-
последовательности рангов, присвоенные изделиям контролерами:
У1
1
2
2
1
4
4
4
3
4
5
7,5
6,5
7,5
6,5
7.5
8
7,5
9
Найдем выборочный коэффициент ранговой корреляции Спир-
мена, учитывая, что 2 4 = 8,5, л =9:
P==I~=1~irr==093
Итак, рв=0,93.
547. Два инспектора А и В проверили 12 водителей
на быстроту реакции и расположили их в порядке ухуд-
ухудшения реакции (в скобках помещены порядковые номера
водителей с одинаковой реакцией):
(A) 1 B, 3, 4) 5 F, 7, 8) 9 10 11 12
(B) 3 1 2 6 4 5 7 8 11 10 9 12
Найти выборочный коэффициент ранговой корреляции
Спирмена между рангами водителей, присвоенными им
двумя инспекторами.
Б. Выборочный коэффициент ранговой корреляции Кендалла.
Можно оценивать связь между двумя качественными признаками,
используя коэффициент ранговой корреляции Кеидалла. Пусть ранги
объектов выборки объема п (здесь сохранены все обозначения п. А):
по признаку A Xi х2 ... х„
по признаку В ух уг ... уп
Допустим, что справа от у\ имеется Rx рангов, больших у,;
справа от у2 имеется Rt рангов, больших ул; справа от yn-i имеется
#„_! рангов, больших уп-\. Введем обозначение суммы рангов:
Выборочный коэффициент ранговой корреляции Кендалла нахо-
находят по формуле
4/?
х1
где п—объем выборки, R—сумма рангов R/ (i = I, 2, .... п—1).
Абсолютная величина коэффициента ранговой корреляции Кен-
Кендалла не превышает единицы: | тв I «S 1.
Для обоснованного суждения о наличии связи между
качественными признаками следует проверить, значим ли
выборочный коэффициент ранговой корреляции Кендалла
(см. гл. XIII, § 14).
204
548. Знания 10 студентов проверены по двум тестам:
А и В. Оценки по стобалльной системе оказались сле-
следующими (в первой строке указано количество баллов
по тесту Л, а во второй—по тесту В):
95 90 86 84 75 70 62 60 57 50
92 93 83 80 55 60 45 72 62 70
Найти выборочный коэффициент ранговой корреляции
Кендалла между оценками по двум тестам.
Решение. При решении задачи 540, условие которой совпа-
совпадает с условием настоящей задачи, были получены две последова-
последовательности рангов (в первой строке приведены ранги по тесту А, во
второй — по тесту В):
Xi 1 2 3 4 5 6 7 8 9 10
yi 2 1 3 4 9 8 10 5 7 6
Справа от уг=2 имеется /?t = 8 рангов C, 4, 9, 8, 10, 5, 7, 6),
больших (/i=2; справа от (/2 = 1 имеется #2 = 8 рангов, больших
i/a = l. Аналогично получим: R3 = 7, #4=6, Rt = l, Rt = l, R7=0,
/?8=2, #,=0. Следовательно, сумма рангов
# = ?, + ?„+... + ?,=8 + 8+7+6+ 1 + 1 +2=33.
Найдем коэффициент рангоьой корреляции Кендалла, учитывая,
#=33, л = 10:
i 433 i па
) то^э «
Найдем коэффи
что #=33, л = 10:
Итак, т„=0,47.
549. Два контролера расположили 10 деталей в по-
порядке ухудшения их качества. В итоге были получены
две последовательности рангов:
*, 1234567 89 10
у, 1243657 10 9 8
Используя коэффициент ранговой корреляции Кен-
Кендалла, определить, согласуются ли оценки контролеров.
550. Найти выборочный коэффициент ранговой кор-
корреляции Кендалла по условию задачи 542.
551. По условию задачи 544, используя коэффициент
ранговой корреляции Кендалла, определить, согласуются
ли мнения специалистов различных заводов.
552. По условию задачи 545, используя коэффициент
ранговой корреляции Кендалла, определить пару арбит-
арбитров, оценки которых наиболее совпадают.
553. Найти выборочный коэффициент ранговой кор-
корреляции Кендалла по условию задачи 547.
205
Глава тринадцатая
СТАТИСТИЧЕСКАЯ ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
§ 1. Основные сведения
Статистической называют гипотезу о виде неизвестного рас-
распределения или о параметрах известных распределений.
Нулевой (основной) называют выдвинутую гипотезу Но.
Конкурирующей (альтернативной) называют гипотезу Нъ которая
противоречит нулевой.
Различают гипотезы, которые содержат одно н более одного
предположений.
Простой называют гипотезу, содержащую только одно предпо-
предположение.
Сложной называют гипотезу, которая состоит из конечного
или бесконечного числа простых гипотез.
В итоге проверки гипотезы могут быть допущены ошибки двух
родов.
Ошибка первого рода состоит в том, что будет отвергнута пра-
правильная нулевая гипотеза. Вероятность ошибки первого рода назы-
называют уровнем значимости и обозначают через а.
Ошибка второго рода состоит в том, что будет принята непра-
неправильная нулевая гипотеза. Вероятность ошибки второго рода обоз-
обозначают через р.
Статистическим критерием (или просто критерием) называют
случайную величину К, которая служит для проверки гипотезы.
Наблюдаемым (эмпирическим) значением /С„аЛл называют то зна-
значение критерия, которое вычислено по выборкам.
Критической областью называют совокупность значений крите-
критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (областью допустимых значений)
называют совокупность значений критерия, при которых нулевую
гипотезу принимают.
Основной принцип проверки статистических гипотез: если на-
наблюдаемое значение критерия принадлежит критической области,
то нулевую гипотезу отвергают; если наблюдаемое значение критерия
принадлежит области принятия гипотезы, то гипотезу принимают.
Критическими точками (границами) &кр называют точки, отде-
отделяющие критическую область от области принятия гипотезы.
Правосторонней называют критическую область, определяемую
неравенством К > &Кр> где &кр—положительное число.
Левосторонней называют критическую область, определяемую
неравенством К < *кр> где Акр—отрицательное число.
Двусторонней называют критическую область, определяемую
неравенством К < klt К > *2, гДе *2 > *i- В частности, если крити-
критические точки симметричны относительно нуля, то двусторонняя кри-
критическая область определяется неравенствами (в предположении,
что Акр > 0)
К < —kKp, К > *кр.
или равносильным неравенством
|*|>*кр-
206
Для отыскания критической области задаются уровнем значи-
значимости а и ищут критические точки, исходя из следующих соот-
соотношений:
а) для правосторонней критической области
P(K>kKp)=a (*кр>0);
б) для левосторонней критической области
в) для двусторонней симметричной области
Р (К > *кр) = (а/2) (*кР > 0), Р (К < -*кР)=а/2.
Мощностью критерия называют вероятность попадания крите-
критерия в критическую область при условии, что справедлива конкури-
конкурирующая гипотеза. Другими словами, мощность критерия есть веро-
вероятность того, что нулевая гипотеза будет отвергнута, если верна
конкурирующая гипотеза.
§ 2. Сравнение двух дисперсий
нормальных генеральных совокупностей
По независимым выборкам, объемы которых л1( п2, извлеченным
из нормальных генеральных совокупностей, найдены исправленные
выборочные дисперсии s\ и sy. Требуется сравнить эти дисперсии.
Правило 1. Для того чтобы при заданном уровне значимости а
проверить нулевую гипотезу Но: D(X) = D(Y) о равенстве генераль-
генеральных дисперсий нормальных совокупностей при конкурирующей гипо-
гипотезе Нг: D (X) > D (Y), надо вычислить наблюдаемое значение
критерия (отношение большей исправленной дисперсии к меньшей)
и по таблице критических точек распределения Фишера—Снедекора,
по заданному уровню значимости а и числам степеней свободы
*i=rti—1, Аа=л2—1 (k\—число степеней свободы большей исправ-
исправленной дисперсии) найти критическую точку FKV(a; ku k2). Если
^набл < Лср—нет оснований отвергнуть нулевую гипотезу. Если
^иабл > ^кр—нулевую гипотезу отвергают.
Правило 2. При конкурирующей гипотезе Ht: D(X) ф D (Y)
критическую точку FKP (a/2; klt k2) ищут по уровню значимости а/2
(вдвое меньшему заданного) и числам степеней свободы kt и kt
(*!—число степеней свободы большей дисперсии). Если ^Набл < ^кр —
нет оснований отвергнуть нулевую гипотезу. Если FHa6n > Fкр —
нулевую гипотезу отвергают.
554. По двум независимым выборкам, объемы которых
«х = 11 и п2=14, извлеченным из нормальных генераль-
генеральных совокупностей X и Y, найдены исправленные выбо-
выборочные дисперсии s2x = 0,76 и sy = 0,38. При уровне зна-
значимости а = 0,05, проверить нулевую гипотезу Но: D(X)~
=D(Y) о равенстве генеральных дисперсий, при конку-
конкурирующей гипотезе Нх: D(X)> D(Y).
207
Решение. Найдем отношение большей исправленной диспер-
дисперсии к меньшей:
Л.абл= 0,76/0,38=2.
По условию конкурирующая гипотеза имеет вид D(X)>D(Y),
поэтому критическая область—правосторонняя.
По таблице приложения 7, по уровню значимости о =0,05 и
числам степеней свободы *i=rti —1 = 11 —1=10 и k2 = n2—1=14—
— 1=13 находим критическую точку
FKp@,05; 10; 13) =2,67.
Так как Р„абл < FKp—нет оснований отвергнуть гипотезу о ра-
равенстве генеральных дисперсий. Другими словами, выборочные
исправленные дисперсии различаются незначимо.
555. По двум независимым выборкам, объемы которых
«! = 9 и п2= 16, извлеченным из нормальных генеральных
совокупностей X и Y, найдены исправленные выборочные
дисперсии s\ =34,02 и s\r= 12,15. При уровне значимо-
значимости 0,01, проверить нулевую гипотезу Я,: D(X) = D(Y)
о равенстве генеральных дисперсий при конкурирующей
гипотезе Ях: D(X)>D(Y).
556. По двум независимым выборкам, объемы которых
nt=14 и п2=10, извлеченным из нормальных генераль-
генеральных совокупностей X и Y, найдены исправленные выбо-
выборочные дисперсии s3c = 0,84 и Sy = 2,52. При уровне зна-
значимости а = 0,1, проверить нулевую гипотезу Н„: D(X)=
= D(Y) о равенс.ве генеральных дисперсий при конку-
конкурирующей гипотезе Нх: Г)(Х)фО(У).
Решение. Найдем отношение большей исправленной диспер-
дисперсии к меньшей:
=2,52/0,84 = 3.
По условию конкурирующая гипотеза имеет вид D (X) Ф D (Y),
поэтому критическая область—двусторонняя. В соответствии с пра-
правилом 2 при отыскании критической точки следует брать уровень
значимости, вдвое меньший заданного.
По таблице приложения 7, по уровню значимости а/2=0,1/2 =
= 0,05 и числам степеней свободы ^ = 10—1=9 и Л2 = 14—1=13,
находим критическую точку
FKP(O,O5; 9; 13)=2,72.
Так как ^На6л > ^кр — нулевую гипотезу о равенстве генераль-
генеральных дисперсий отвергаем.
557. По двум независимым выборкам, объемы которых
«1 = 9 и па = 6, извлеченным из нормальных генеральных
совокупностей X и Y, найдены выборочные дисперсии
DB(X)= 14,4 и DB(Y) = 20,5. При уровне значимости 0,1
проверить нулевую гипотезу //„:?> (X) = D (Y) о равенстве
208
генеральных дисперсий при конкурирующей гипотезе
Указание. Найти сначала исправленные дисперсии по фор-
формулам:
Л=-г^-г • DB (X), «*«--2S-r • DB (К).
558. Двумя методами проведены измерения одной и
той же физической величины. Получены следующие
результаты:
а) в первом случае *х = 9,6; *а=10,0; х, = 9,8;
*4=10,2; *6=10,6;
б) во втором случае */х=10,4; y2 = 9,7; уа = Ю,0\
*/4=10,3.
Можно ли считать, что оба метода обеспечивают оди-
одинаковую точность измерений, если принять уровень зна-
значимости а = 0,1? Предполагается, что результаты измере-
измерений распределены нормально и выборки независимы.
Решение. Будем судить о точности методов по величинам
дисперсий. Таким образом, нулевая гипотеза имеет вид Но: D(X)=
= D (Y). В качестве конкурирующей примем гипотезу Нх: D (X) ф
ФП(У)
()
Найдем выборочные дисперсии. Для упрощения вычислений
перейдем к условным вариантам:
и/ = Юле,-—100, vi = Юу/—100.
В итоге получим условные варианты
щ _4 0—226
vt 4—3 0 3
Найдем исправленные выборочные дисперсии:
.2 2?|2>/Г/я' A6 + 4 + 4 + 36)-23/5_,,о.
su —7l g—-{ 14,8,
Н2]г/ -4»/4
Сравним дисперсии. Найдем отношение большей исправленной
дисперсии к меньшей (каждая из дисперсий увеличилась в 10* раз,
но их отношение не изменилось):
По условию конкурирующая гипотеза имеет вид D (X) ф D (К),
поэтому критическая область двусторонняя и в соответствии с пра-
правилом 2 при отыскании критической точки следует брать уровень
значимости, вдвое меньший заданного.
По таблице приложения 7, по уровню значимости а/2 =0,1/2 =
= 0,05 и числам степеней свободы *i = ni—1=5—1=4 и k2 = n2—1 =
= 4—1=3 находим критическую точку Fkp^.OS; 4; 3)=9,12.
209
Так как /^абл < ^кр—нет оснований отвергнуть нулевую гипо-
гипотезу о равенстве генеральных дисперсий. Другими словами, исправ-
исправленные дисперсии различаются незначимо и, следовательно, оба
метода обеспечивают одинаковую точность измерений.
559. Для сравнения точности двух станков-автоматов
взяты две пробы (выборки), объемы которых «1=10 и
п2 = 8. В результате измерения контролируемого размера
отобранных изделий получены следующие результаты:
х,. 1,08 1,10 1,12 1,14 1,15 1,25 1,36 1,38 1,40 1,42
у. 1,11 1,12 1,18 1,22 1,33 1,35 1,36 1,38
Можно ли считать, что станки обладают одинаковой
точностью [Яо: D(X) = D(Y)], если принять уровень зна-
значимости а = 0,1 и в качестве конкурирующей гипотезы
Н,: D(X)^D(YO
Указание. Для упрощения вычислений перейти к условным
вариантам «/ = 100*,—124, vt = 1(%,—126.
§ 3. Сравнение исправленной выборочной дисперсии
с гипотетической генеральной дисперсией
нормальной совокупности
Обозначим через л объем выборки, по которой найдена исправ-
исправленная дисперсия s2.
Правило 1. Для того чтобы при заданном уровне значимости а
проверить нулевую гипотезу Н„: o'ssaj о равенстве неизвестной
генеральной дисперсии о2 гипотетическому (предполагаемому) зна-
значению о? при конкурирующей гипотезе Hji о2 > а\, надо вычислить
наблюдаемое значение критерия
2 (п—\)s*
Хнабл j
Со
и по таблице критических точек распределения X2, по заданному
уровню значимости а и числу степеней свободы k=n—1 найти
критическую точку Хкр (а; *)• Если Хнабл < X кр—нет оснований
отвергнуть нулевую гипотезу. Если /набл > ^—нулевую гипотезу
отвергают.
Правило 2. При конкурирующей гипотезе HL: о2 Ф а\ находят
левую Хлев. крA—а/2; k) и правую Хправ. кр (а/2; *) критические
точки. Если Хлев, кр < Хнабл < Хправ.кр — нет оснований отвергнуть
нулевую гипотезу. Если Хнабл < Хлев, кр или Хнабл > Хправ.кр —ну-
—нулевую гипотезу отвергают.
Правило 3. При конкурирующей гипотезе #t: о2 < 0о находят
критическую точку ХкрA—а; *)• Если Хнабл > ХкрО— а". к)—нет
оснований отвергнуть нулевую гипотезу. Если Хнабл < ХкрA—«; *)—
нулевую гипотезу отвергают.
210
Замечание. Если число степеней свободы k > 30, то крити-
критикую
ферти:
ческую точку Хкр(а". *) можно найти из равенства Уилсоиа—Гиль-
Хкр (a; k)=k [l -2/9*+ га /2/(9*)]8,
где га находят, используя функцию Лапласа (см. приложение 2),
из равенства
ф(га)=A-2а)/2.
560. Из нормальной генеральной совокупности извле-
извлечена выборка объема п — 21 и по ней найдена исправ-
исправленная выборочная дисперсия s8 = 16,2. Требуется при
уровне значимости 0,01 проверить нулевую гипотезу Я„:
о8 = Оо=15, приняв в качестве конкурирующей гипо-
гипотезы Ях: ajj> 15.
Решение. Найдем наблюдаемое значение критерия:
2 _(n-l)s' B1-1I6,2
Хнабл = г 15
По условию, конкурирующая гипотеза имеет вид а2 > 15, по-
поэтому критическая область—правосторонняя (правило 1). По таблице
приложения 5, по уровню значимости 0,01 и числу степеней свободы
k=n—1=21 —1=20 находим критическую точку xilp @,01; 20)=37,6.
Так как Хнабл < Хкр—нет оснований отвергнуть нулевую гипо-
гипотезу о равенстве генеральной дисперсии гипотетическому значению
о~о=15. Другими словами, различие между исправленной диспер-
дисперсией A6,2) и гипотетической генеральной дисперсией A5) незначимо.
561. Из нормальной генеральной совокупности извле-
извлечена выборка объема п= 17 и по ней найдена исправлен-
исправленная выборочная дисперсия s* = 0,24. Требуется при
уровне значимости 0,05 проверить нулевую гипотезу #„:
а2 = Оо = 0,18, приняв в качестве конкурирующей гипо-
гипотезы -Ht: os>0,18.
562. Из нормальной генеральной совокупности извле-
извлечена выборка объема п — 31:
варианты х, 10,1 10,3 10,6 11,2 11,5 11,8 12,0
частоты п, 1 3 7 10 6 3 1
Требуется при уровне значимости 0,05 проверить ну-
нулевую гипотезу Яо: aj) = aj| = 0,18, приняв в качестве
конкурирующей гипотезы Ях: а8 > 0,18.
Указание. Принять условные варианты u,- = 10x,-—ПО; вы-
21Г2Рл s
2 211Г2|'Р 2
числить сначала si= ; , а затем Sx^-rrrz .
П — 1 Ш
563. Точность работы станка-автомата проверяется по
дисперсии контролируемого размера изделий, которая не
211
должна превышать as = 0,1. Взята проба из 25 случай-
случайных отобранных изделий, причем получены следующие
результаты измерений:
контролируемый размер
изделий пробы х{ 3,0 3,5 3,8 4,4 4,5
частота щ 2 6 9 7 1
Требуется при уровне значимости 0,05 проверить,
обеспечивает ли станок требуемую точность.
Решение. Нулевая гипотеза Но: о2=0о=О,1. Примем в ка-
качестве конкурирующей гипотезы Ht: a2 > 0,1.
Найдем исправленную выборочную дисперсию. Для упрощения
расчета перейдем к условным вариантам. Приняв во внимание, что
выборочная средняя примерно равна 3,9, положим «, = 10x,-—39.
Распределение частот принимает вид
и, —9 —4—15 6
щ 2 6 9 7 1
Найдем вспомогательную дисперсию условных вариант:
подставив данные задачи, получим sj= 19,75.
Найдем искомую исправленную дисперсию:
Л== 4/Ю* = 19,75/100=0,2.
Найдем наблюдаемое значение критерия:
* л (n-\)s\ B5-1H,2
Хнабл = -5 = — =48.
0О 0,1
Конкурирующая гипотеза имеет вид о2 > оо. поэтому критиче-
критическая область—односторонняя (правило 1).
Найдем по таблице приложения 5 критическую точку xicp@,05; 24)=
=36,4. Имеем Хнабл > Хкр. следовательно, нулевую гипотезу отвер-
отвергаем; станок не обеспечивает необходимую точность и требует под-
наладки.
564. В результате длительного хронометража времени
сборки узла различными сборщиками установлено, что
дисперсия этого времени о, = 2 мин2. Результаты 20 наб-
наблюдений за работой новичка таковы:
время сборки одного
узла в минутах
частота
X,
56
1
58
4
60
10
62
3
64
2
Можно ли при уровне значимости 0,05 считать, что нови-
новичок работает ритмично (в том смысле, что дисперсия
212
затрачиваемого им времени существенно не отличается
от дисперсии времени остальных сборщиков)?
Указание. Нулевая гипотеза Но: 02=о;=2; конкурирующая
гипотеза Hj\ а2 ф с2,. Принять «/=*/—60 и вычислить s2u.
565. Партия изделий принимается, если дисперсия
контролируемого размера значимо не превышает 0,2.
Исправленная выборочная дисперсия, найденная по вы-
выборке объема п— 121, оказалась равной s* = 0,3. Можно
ли принять партию при уровне значимости 0,01?
Решение. Нулевая гипотеза Но: 0s=0o=O,2. Конкурирую-
Конкурирующая гипотеза Hi. a2 > 0,2.
Найдем наблюдаемое значение критерия:
Конкурирующая гипотеза имеет вид о2 > 0,2, следовательно,
критическая область правосторонняя. Поскольку в таблице приложе-
приложения 5 не содержится числа степеней свободы k =120, найдем крити-
критическую точку приближенно из равенства Уилсона—Гильферти:
ХкР(«; *) = *[1-2/(9*)+га J/!7(9A}]S.
Найдем предварительно (учитывая, что по условию a =0,01 )га =
= zo,oi из равенства
(l-2.0,00/2=0,49.
По таблице функции Лапласа (см. приложение 2), используя линей-
линейную интерполяцию, находим: г001 = 2,326. Подставив k =120, га =
= 2,326 в формулу Уилсона —Гильферти, получим Хкр@,01; 120) =
= 158,85. (Это приближение достаточно хорошее: в более полных
таблицах приведено значение 158,95). Так как Хнабл > Хкр—нуле-
Хкр—нулевую гипотезу отвергаем. Партию принять нельзя.
566. Решить задачу 565, приняв уровень значимости
a = 0,05.
§ 4. Сравнение двух средних генеральных
совокупностей, дисперсии которых известны
(большие независимые выборки)
Обозначим через пит объемы больших (п > 30, т > 30) неза-
независимых выборок, по которым найдены соответствующие выборочные
средние х и у. Генеральные дисперсии D(X) и D(Y) известны.
Правило 1. Для того чтобы при заданном уровне значимости
проверить нулевую гипотезу Но: М (л) = М (Y) о равенстве матема-
математических ожиданий (генеральных средних) двух нормальных гене-
генеральных совокупностей с известными дисперсиями (в случае больших
выборок) при конкурирующей гипотезе Нх: М {X) ф М (Y), надо
213
вычислить наблюдаемое значение критерия
z л - *—у
НабЛ VD(X)ln+D(Y)lm
и по таблице функции Лапласа найти критическую точку гкр из
равенства
Ф(гкр) = A-а)/2.
Если | ZHa6.i I < гкр—"б/п оснований отвергнуть нулевую гипотезу.
Если |?набл| > гкр—нулевую гипотезу отвергают.
Правило 2. При конкурирующей гипотезе Н\\ М (X) > М (К)
находят критическую точку zKp no таблице функции Лапласа из
равенства
Ф(гкр) = A-2а)/2.
Если 2„абл < гкр—нет оснований отвергнуть нулевую гипотезу.
Если Z],a6.<i > гкр—нулевую гипотезу отвергают.
Правило 3. При конкурирующей гипотезе Hi. М (X) < М (Y)
находят «вспомогательную точку* гкр по правилу 2. Если ZHa6.<i > —гкр—
нет оснований отвергнуть нулевую гипотезу. Если 2иабл'<—гкр —
нулевую гипотезу отвергают.
567. По двум независимым выборкам, объемы которых
п = 40 и т = 50, извлеченным из нормальных генеральных
совокупностей, найдены выборочные средние: х=130 и
у =140. Генеральные дисперсии известны: D(X) = 80,
О (Y) = 100. Требуется при уровне значимости 0,01 прове-
проверить нулевую гипотезу Но: М (X) = М (К) при конкури-
конкурирующей гипотезе Ях: М(Х) Ф M(Y).
Решение. Найдем наблюдаемое значение критерия:
Z *~~* = 13°-140 =_s
набл VD(X)ln+D(Y)lm /80/40+100/50
По условию, конкурирующая гипотеза имеет вид М (X) Ф М (Y),
поэтому критическая область—двусторонняя.
Найдем правую критическую точку из равенства
По таблице функции Лапласа (см. приложение 2) находим
гкр = 2,58.
Так как | Zna6]l \ > zKP, то в соответствии с правилом 1
нулевую гипотезу отвергаем. Другими словами, выбороч-
выборочные средние различаются значимо.
568. По выборке объема п = 30 найден средний вес
*=130 г изделий, изготовленных на первом станке; по
выборке объема т = 40 найден средний вес у = 125 г изде-
изделий, изготовленных на втором станке. Генеральные дис-
дисперсии известны: D(X) = 60ra, ?>(У) = 80га. Требуется,
214
при уровне значимости 0,05, проверить нулевую гипотезу
Яо: М (X) = М (Y) при конкурирующей гипотезе М (X) Ф
ФМ(У). Предполагается, что случайные величины X и
Y распределены нормально и выборки независимы.
569. По выборке объема п — 50 найден средний размер
х = 20,1 мм диаметра валиков, изготовленных автоматом
№ 1; по выборке объема т = 50 найден средний размер
у =19,8 мм диаметра валиков, изготовленных автоматом
№ 2. Генеральные дисперсии известны: D (X) = 1,750 мм2,
D (Y) = 1,375 мм2. Требуется, при уровне значимости
0,05, проверить нулевую гипотезу Но: М (X) = М (К) при
конкурирующей гипотезе М (X) фЬЛ (К). Предполагается,
что случайные величины X и Y распределены нормально
и выборки независимы.
§ 5. Сравнение двух средних
нормальных генеральных совокупностей,
дисперсии которых неизвестны
и одинаковы (малые независимые выборки)
Обозначим через пит объемы малых независимых выборок
(л < 30, т < 30), по которым найдены соответствующие выборочные
средние х и у и исправленные выборочные дисперсии sx и sy. Гене-
Генеральные дисперсии хотя и неизвестны, но предполагаются одинако-
одинаковыми.
Правило 1. Для того чтобы при заданном уровне значимости
а проверить нулевую гипотезу Но: М (X) = М (К) о равенстве мате-
математических ожиданий (генеральных средних) двух нормальных сово-
совокупностей с неизвестными, но одинаковыми дисперсиями (в случае
малых независимых выборок) при конкурирующей гипотезе Н^. М(Х) Ф
Ф M(Y), надо вычислить наблюдаемое значение критерия
Т х—у 1/rnm(n + w—2)
набл (n У
и по таблице критических точек распределения Стьюдента, по за-
заданному уровню значимости а, помещенному в верхней строке таб-
таблицы приложения 6, и числу степеней свободы k — n-\-m—2 найти
критическую точку *двуСт.кр(а; *)• ?сл« |Гна6л| < /двуСт.кр(а; А) —
нет оснований отвергнуть нулевую гипотезу. Если | Тнабл | >
> *двуст.кр («I *) — нулевую гипотезу отвергают.
Правило 2. При конкурирующей гипотезе М(Х) > M(Y) находят
критическую точку /„равост. кр («: *) яо таблице приложения 6 по
уровню значимости а, помещенному в нижней строке таблицы, и
числу степеней свободы k = n+m—2. Если Тяацл < /правост.кр—нет
оснований отвергнуть нулевую гипотезу. Если Тнабл > 'правост.кр—
нулевую гипотезу отвергают.
Правило 3. При конкурирующей гипотезе М (X) < M(Y) находят
сначала критическую точку /Правост.кр по правилу 2 и полагают
215
'левостр.кр 'правост.кр- Если Тиа$л >—/правост.кр—нет основа-
оснований отвергнуть нулевую гипотезу. Если Гнабл <—'праност.кр —
нулевую гипотезу отвергают.
570. По двум независимым малым выборкам, объемы
которых п=12 и т=18, извлеченным из нормальных
генеральных совокупностей X и Y, найдены выборочные
средние: jc = 31,2, у = 29,2 и исправленные дисперсии:
sx = 0,84 и Sy = 0,40. Требуется при уровне значимости
0,05 проверить нулевую гипотезу Но: М (X) = М (Y) при
конкурирующей гипотезе Н{. М(Х)фМ(У).
Решение. Исправленные дисперсии различны, поэтому про-
проверим предварительно гипотезу о равенстве генеральных дисперсий,
используя критерий Фишера—Снедекора (см. § 2).
Найдем отношение большей дисперсии к меньшей: /^абл —
= 0,84/0,40=2,1. Дисперсия sx значительно больше дисперсии sy, по-
поэтому в качестве конкурирующей примем гипотезу #,: D(X)>D(Y).
В этом случае критическая область—правосторонняя. По таблице
приложения 7, по уровню значимости а = 0,05 и числам степенен
свободы ki=n—1 = 12—1=11 и кг—т —1 = 18—1=17 находим
критическую точку FKp@,05; 11; 17) = 2,41.
Так как ^Набл < ^кр—нет оснований отвергнуть нулевую гипо-
гипотезу о равенстве генеральных дисперсий. Предположение о равенстве
генеральных дисперсий выполняется, поэтому сравним средние.
Вычислим наблюдаемое значение критерия Стьюдента:
,/п-
—у ,/п-т(п+т—2)
Подставив числовые значения входящих в эту формулу величин,
получим 7'„абл = 7,1.
По условию, конкурирующая гипотеза имеет вид М (X) Ф М (К),
поэтому критическая область—двусторонняя. По уровню значимости
0,05 и числу степеней свободы k = n-\-m—2=12+18—2=28 нахо-
находим по таблице приложения 6 критическую точку /ДВуст.кр @,05; 28) =
= 2,05.
Так как 7*набл > /ДВуст.кр — нулевую гипотезу о равенстве сред-
средних отвергаем. Другими словами, выборочные средние различаются
значимо.
571. По двум независимым малым выборкам, объемы
которых п = 10 и т = 8, извлеченным из нормальных
генеральных совокупностей, найдены выборочные средние:
х= 142,3, «/=145,3 и исправленные дисперсии: ^ = 2,7
и Sy = 3,2. При уровне значимости 0,01 проверить нуле-
нулевую гипотезу //„: M(X) = M(Y) при конкурирующей ги-
гипотезе Нг: М(Х)ФМ(У).
Указание. Предварительно проверить равенство дисперсий,
используя критерий Фишера—Снедекора.
216
572. Из двух партий изделий, изготовленных на двух
одинаково настроенных станках, извлечены малые вы-
выборки, объемы которых п=10 и т=12. Получены сле-
следующие результаты:
контролируемый размер
изделий первого станка х{ 3,4 3,5 3,7 3,9
частота (число изделий) щ 2 3 4 1
контролируемый размер
изделий второго станка у{ 3,2 3,4 3,6
частота т, 2 2 8
Требуется при уровне значимости 0,02 проверить гипо-
гипотезу //„: M(X) = M(Y) о равенстве средних размеров
изделий при конкурирующей гипотезе Ях: М (Х)фМ (Y).
Предполагается, что случайные величины X и Y распре-
распределены нормально.
Решение. По формулам
х = B л/*/) /я н у = B ЩУ(Iт
найдем выборочные средние: х=3,б, у = 3,5.
Для упрощения вычислений исправленных дисперсий перейдем
к условным вариантам и,-=10ж,-—36, и/=10у,-—35.
По формуалам
/л 2 2 "«/»*—[2'"it'iJV'n
и S
найдем Su = 2,67 и 5^ = 2,55. Следовательно,
2 = 2,67/100 = 0,0267, sy = 4/Ю* = 2,55/100 = 0,0255.
Таким образом, исправленные дисперсии различны; рассматри-
рассматриваемый в этом параграфе критерий предполагает, что генеральные
дисперсии одинаковы, поэтому надо сравнить дисперсии, используя
критерий Фншера — Снедекора. Сделаем это, приняв в качестве кон-
конкурирующей гипотезы Hi: D(X) ФБ(У) (см. § 2, правило 2).
Найдем наблюдаемое значение критерия: ^На6л =0,0267/0,0255 =
= 1,05. По таблице приложения 7 находим FKp@,01; 9; 11) = 4,63.
Так как Либл < Лср—дисперсии различаются незначимо и, следо-
следовательно, можно считать, что допущение о равенстве генеральных
дисперсий выполняется.
Сравним средние, для чего вычислим наблюдаемое значение
критерия Стьюдента:
х—у1/n-m(n+m—2)
Мбл К(л
Подставив в эту формулу числовые значения входящих в нее вели*
чин, получим Гнабл=1,45.
По условию, конкурирующая гипотеза имеет вид М {X) ф М (Y),
поэтому критическая область—двусторонняя. По уровню значимости
21?
0,02 и числу степеней свободы k = n+m— 2 = 10+ 12—2=20 находим
по таблице приложения 6 критическую точку /двуст.кр @,02; 20) =
= 2,53.
Так как Т„а^я < ^двуст.кр—нет оснований отвергнуть гипотезу
о равенстве средних. Таким образом, средние размеры изделий су-
существенно не различаются.
573. На уровне значимости 0,05 требуется проверить
нулевую гипотезу Но: М(Х) = М (Y) о равенстве гене-
генеральных средних нормальных совокупностей X и Y при
конкурирующей гипотезе Н^. М (X) > М (Y) по малым
независимым выборкам, объемы которых п= 10 и гп= 16.
Получены следующие результаты:
х, 12,3 12,5 12,8 13,0 13,5; у, 12,2 12,3 13,0
п, 1 2 4 2 1 т,- 6 8 2
Указание. Предварительно проверить нулевую гипотезу Но:
D(X) = D(Y) о равенстве генеральных дисперсий при конкурирую-
конкурирующей гипотезе Ях: D(X) > D(Y) (см. § 2).
§ 6. Сравнение выборочной средней
с гипотетической генеральной
средней нормальной совокупности
А. Дисперсия генеральной совокупности известна. Правило !•
Для того чтобы при заданном уровне значимости а проверить нуле-
нулевую гипотезу Но: а=а0 о равенстве генеральной средней а нормаль-
нормальной совокупности с известной дисперсией о3 гипотетическому (пред-
(предполагаемому) значению а0 при конкурирующей гипотезе Нг: а Ф а0,
надо вычислить наблюдаемое значение критерия
и по таблице функции Лапласа найти критическую точку икр дву-
двусторонней критической области из равенства
Если 11/Набл I < «кр—нет оснований отвергнуть нулевую гипо-
гипотезу. Если | инабл | > «кр—нулевую гипотезу отвергают.
Правило 2. При конкурирующей гипотезе Ях: a> а0 критическую
точку правосторонней критической области находят из равенства
Если 1/„абл < икр—нет оснований отвергнуть нулевую гипотезу.
Если ?/набл > "кр—нулевую гипотезу отвергают.
Правило 3. При конкурирующей гипотезе Нг: а < а0 сначала
находят вспомогательную критическую точку икр по правилу 2, а
затем полагают границу левосторонней критической области
«кр = — «кр-
Если инабл > —иКр—«em оснований отвергнуть нулевую гипо-
гипотезу. Если пиабл <—«кр—нулевую гипотезу отвергают.
218
Мощность критерия проверки нулевой гипотезы Но: а=а0 о ра-
равенстве генеральной средней гипотетическому значению а0 при
известном среднем квадратичее ком отклонении о
находят в зависимости от вида конкурирующей гипотезы.
При конкурирующей гипотезе Н^. а > а0 для гипотетического
значения генеральной средней a = ai > а0 мощность правостороннего
критерия
1р05
где и„р находят из равенства Ф(иКр) = A—2<х)/2, X = (ai—аа)Уп/а.
При различных значениях аг функция мощности одностороннего
критерия
ni(a1)=0,5—Ф(«Кр-Я).
При конкурирующей гипотезе Нх: а ф а0 для гипотетического
значения генеральной средней а = п\ мощность двустороннего кри-
критерия
1-р=1-[Ф(«кр-Я)+Ф(иКр+Я)], (¦¦)
где икр находят из равенства Ф(икр) = A—а)/2, Х = (а1—а0) Угг/о.
При различных значениях at функция мощности двустороннего кри-
критерия
В формулах (*) и (**)
г—функция Лапласа.
574. Из нормальной генеральной совокупности с из-
известным средним квадратическим отклонением a = 5,2
извлечена выборка объема п=100 и по ней найдена
выборочная средняя *= 27,56. Требуется при уровне
значимости 0,05 проверить нулевую гипотезу Н„: а =
= а„ — 26 при конкурирующей гипотезе Ях: аФ26.
Решение. Найдем наблюдаемое значение критерия:
6-26)- |/~i00/5,2 = 3.
По условию, конкурирующая гипотеза имеет вид а ф а„, по-
поэтому критическая область—двусторонняя.
Найдем критическую точку из равенства
ф(икр) = A— а)/2 = (!— 0,05)/2=0,475.
По таблице функции Лапласа (см. приложение 2) находим икр=1,96.
Так как инабл > «кр—нулевую гипотезу отвергаем. Другими
словами, выборочная и гипотетическая генеральная средние разли-
различаются значимо.
575. а) Из нормальной генеральной совокупности
с известным средним квадратическим отклонением a = 40
извлечена выборка объема п = 64 и по ней найдена вы-
выборочная средняя х= 136,5. Требуется при уровне зна-
219
чимости 0,01 проверить нулевую гипотезу Но: а = ао =
= 130 при конкурирующей гипотезе Нг: аф 130.
б) Решить эту задачу при конкурирующей гипотезе
Ht: a > 130.
в) Установлено, что средний вес таблетки лекарства
сильного действия должен быть равен а„ = 0,50 мг. Выбо-
Выборочная проверка 121 таблетки полученной партии лекар-
лекарства показала, что средний вес таблетки этой партии
jc = 0,53 мг. Требуется при уровне значимости 0,01 про-
проверить нулевую гипотезу #,: а = а„ = 0,50 при конкури-
конкурирующей гипотезе Ht: a > 0,50. Многократными предвари-
предварительными опытами по взвешиванию таблеток, поставляе-
поставляемых фармацевтическим заводом, было установлено, что вес
таблеток распределен нормально со средним квадрати-
ческим отклонением а = 0,11 мг.
576. а) По выборке объема п, извлеченной из нормаль-
нормальной генеральной совокупности с известным средним квад-
ратическим отклонением а, найдена выборочная средняя
х. При уровне значимости ос требуется: 1) найти крити-
критическую область, если проверяется нулевая гипотеза //„:
а = аа о равенстве генеральной средней а гипотетическому
значению а0 при конкурирующей гипотезе Ях: а > а0;
2) найти функцию мощности рассматриваемого критерия,
приняв в качестве аргумента гипотетическое значение
генеральной средней а = а1(а1>а0); 3) убедиться, что
увеличение объема выборки влечет увеличение мощности
критерия; 4) убедиться, что увеличение уровня значимо-
значимости влечет увеличение мощности критерия.
Решение. 1) Конкурирующая гипотеза имеет вид а > а0,
поэтому критическая область—правосторонняя. Используя правило 2,
найдем критическую точку ыкр из равенства Ф(«кр)=A—2а)/2. Сле-
Следовательно, правосторонняя критическая область определяется не-
неравенством U > ыкр, или подробнее -р— > икр. Отсюда
о у п
При этих значениях выборочной средней нулевая гипотеза отвер-
отвергается; в этом смысле лс = иКр (°/ Уп)-\-а0 можно рассматривать как
критическое значение выборочной средней.
2) Для того чтобы вычислить мощность рассматриваемого крите-
критерия, предварительно найдем его значение при условии справедливости
конкурирующей гипотезы (т. е. при а = ах), положив х = икр (а/ У~п) -f-
+ а0:
»/__?—?i u-KV(al V~n)+ ao—ai п\—аа
alVn o/fn P
220
Таким образом,
i/=uKP—Я,, где к = (аг—а0) У~п/а.
При U > икр—Я, нулевая гипотеза отвергается, поэтому мощ-
мощность рассматриваемого критерия при а = ах равна
1-Р = Я(?/ > «кр-Я.) = 1-Я (U < «„„-*.) =
= 1 —[Я(-оо <U <0)+P@<U <иКр — *-) =
= 1-[0,5+Ф(икр-Я.)]=0,5-Ф(«кр-Я.).
Каждому значению п\ соответствует определенное значение мощ-
мощности, поэтому мощность критерия есть функция от ад; обозначим
ее через щ (ai).
Итак искомая мощность правостороннего критерия
л1(а,) = 0,5-Ф(«кр—Я.),
где Ф(дс)—функция Лапласа, % = (а1—а0) У~п/а, икр находят нз ра-
равенства Ф(икр) = A—2а)/2.
3) Убедимся, что увеличение объема выборки влечет увеличе-
увеличение мощности критерия. Действительно, из соотношения Я, =
= (пг—а0) У~п/а видно, что увеличение объема выборки приводит
к увеличению величины Я,, а значит к уменьшению величины аргу-
аргумента "ко—^ и тем самым к уменьшению значения функции Лапласа
Ф(икр—л) (Ф(дс)—возрастающая функция) и, следовательно, к
увеличению мощности 1— 0=0,5—Ф(икр—А,).
4) Убедимся, что увеличение уровня значимости а влечет уве-
увеличение мощности критерия. Действительно, из соотношения
Ф((/кр) = A—2а)/2 видно, что увеличение а приводит к уменьше-
уменьшению «кр, а значит к уменьшению величины аргумента икр—К и в
итоге к увеличению мощности 1—р=0,5—Ф(икр—Я,).
б) По выборке объема п = 16, извлеченной из нор-
нормальной генеральной совокупности с известным средним
квадратическим отклонением о = 4, при уровне значимо-
значимости 0,05 проверяется нулевая гипотеза Яо: а = аа = 2
о равенстве генеральной средней а гипотетическому зна-
значению ао = 2 при конкурирующей гипотезе Ях: а > 2.
Требуется: 1) найти мощность правостороннего критерия
проверки рассматриваемой гипотезы для гипотетического
значения генеральной средней а = ^ = 3,2) найти объем
выборки п1( при котором мощность критерия равна 0,6.
Решение. 1) Используем формулу
1—Р=0,5—Ф(ИкР—Я,). (¦)
По правилу 2 найдем критическую точку правосторонней кри-
критической области «кр = 1,65.
Вычислим Я., учитывая, что, по условию, ai=3, ao—2, л = 16,
а = 4: _ _
Я, = (ах—а„) /я/а = C—2) /16/4 = 1.
Подставив «кр = 1,65 и Я. = 1 в формулу (•), получим
1—Р=0,5—Ф A,65—1)=0,5—Ф @,65).
221
По таблице функции Лапласа (см. приложение 2) находим Ф@,65)=
= 0,2422. Искомая мощность 1—0=0,5—0,2422=0,2578.
2) Для отыскания «нового» объема выборки пи при котором
мощность критерия равна 0,6, найдем «новое» значение параметра X
(обозначим его через XJ из соотношения 0,6=0,5—Ф A,65—Xj).
Отсюда
Ф(Я, —1,65)=0,1.
По таблице функции Лапласа (см. приложение 2) находим Хх —
— 1,65 = 0,253. Следовательно, Кг =j ,903.
Учитывая, 4ToXi = (ej—а„) Ynja, причем, по условию, ai = 3,
ао=2, а=4, получим 1,903 = C — 2) У/п/4. Отсюда искомый объем
выборки rtj =58.
в) По выборке объема п = 9, извлеченной из нормаль-
нормальной генеральной совокупности с известным средним
квадратическим отклонением о = 4, при уровне значимо-
значимости 0,05 проверяется нулевая гипотеза //„: а = ао=15
о равенстве генеральной средней а гипотетическому зна-
значению ао = 15 при конкурирующей гипотезе а > 15. Тре-
Требуется: 1) найти мощность правостороннего критерия
для гипотетического значения генеральной средней а =
= al = 17; 2) найти объем выборки л„ при котором мощ-
мощность критерия равна 0,8.
577. а) По выборке объема п, извлеченной из нор-
нормальной генеральной совокупности с известным средним
квадратическим отклонением о, найдена выборочная
средняя х. При уровне значимости а требуется найти
функцию мощности критерия проверки нулевой гипо-
гипотезы //„: а = ав о равенстве генеральной средней а гипо-
гипотетическому значению а0 при конкурирующей гипотезе
Решение. Конкурирующая гипотеза имеет вид афай, по-
поэтому критическая область—двусторонняя. Используя правило 1,
найдем критическую точку икр из равенства Ф(иКр) = 0—°0/2-
Следовательно, двусторонняя критическая область определяется
неравенством \U | > икр, или подробнее
а/ У п
Найдем мощность рассматриваемого критерия, т. е. вероятность
попадания критерия в критическую область при допущении, что
справедлива конкурирующая гипотеза а — ахфа^.
«up! а=аЛ.
Преобразуем выражение, стоящее под знаком модуля:
х-а0 x—aj, . at—gp .
QlVn ajYn o/ V n
222
где b= rA,'k=~—г?. Используя эти соотношения, получим
а/ \п а/ \п
икр) = Р (Ь+Х > uKV)+P(b+K <-икр)
=Р ф > икр—Х)+Р ф < —икр—Х) =
= [1-Я ф < икр-К)] + Р ф < -«кр-Я.) =
Таким образом, мощность двустороннего критерия при а =
равна
1Р 1
где X = (ai—a0) Vn/o-
Каждому значению ах соответствует определенное значение мощ-
мощности, поэтому мощность критерия есть функция от ац обозначим
ее через л2 (аз).
Итак, искомая мощность двустороннего критерия
Щ (а,) = 1 -[Ф («кр-Ь) + Ф («kP+^)],
где Ф(х)—функция Лапласа, A, = (ai—uq) V~n/o,uKp находят из ра-
равенства Ф(акр) = A—а)/2.
б) По выборке объема л = 16, извлеченной из нор-
нормальной генеральной совокупности с известным средним
квадратическим отклонением о = 5, при уровне значимо-
значимости 0,05 проверяется нулевая гипотеза #„: a = ao = 2O
о равенстве генеральной средней а гипотетическому зна-
значению а0 = 20 при конкурирующей гипотезе Нг: а Ф 20.
Найти мощность двустороннего критерия проверки рас-
рассматриваемой гипотезы для гипотетического значения
генеральной средней aj = 24.
Решение. Используем формулу
1_р = 1_[ф(Икр_Я,)+Ф(Икр+Я.)]. (,)
По правилу 1 найдем критическую точку икр = 1,96.
Вычислим К, учитывая, что, по условию, а,.=24, аа = 20,
я = 16, а—5:
к = (а!—а9) /я/а=B4—20)
Подставив «кр = 1,96 и Я,=3,2 в формулу (•), получим
1_Р=1-[ФA,96-3,2)+Ф A,96+3,2)] = 1 + фA,24)-Ф E,16).
По таблице функции Лапласа (см. приложение 2) находим
ФA, 24) =0,3925, ФE,16) = 0,5. Искомая мощность 1— Р = 1 +
+ 0,3925—0,5=0,8925.
в) По выборке объема л = 36, извлеченной из нор-
нормальной генеральной совокупности с известным средним
квадратическим отклонением о = 6, при уровне значи-
значимости 0,01 проверяется нулевая гипотеза Но: a = ae=15
223
при конкурирующей гипотезе Н{. афа0. Найти мощ-
мощность двустороннего критерия проверки рассматриваемой
гипотезы для гипотетического значения генеральной
средней а = ах= 12.
578. а) По выборочной медиане X при уровне значи-
значимости а проверяется нулевая гипотеза Яо: а — а0 о ра-
равенстве генеральной средней а гипотетическому значе-
значению а0 при конкурирующей гипотезе Нг: афа0. Найти
функцию мощности п3 (at) рассматриваемого двусторон-
двустороннего критерия.
Указание. При больших значениях объема выборки выбо-
выборочная медиана X распределена приближенно нормально с матема-
математическим ожиданием М (X) и средним квадратическим отклонением
—- /т-
б) По выборке объема п = 50, извлеченной из нормаль-
нормальной генеральной совокупности с известным средним
квадратическим отклонением a = 5, при уровне значимо-
значимости 0,05 проверяется нулевая гипотеза Яо: a = ao=l8 о
равенстве генеральной средней а гипотетическому зна-
значению ао=18 при конкурирующей гипотезе Я,: аф18.
Сравнить мощности двусторонних критериев я2(а,) и
я, (ax) при ax = 20. Можно ли предвидеть результат срав-
сравнения мощностей, не производя вычислений?
Б. Дисперсия генеральной совокупности неизвестна. Если дис-
дисперсия генеральной совокупности неизвестна (например, в случае
малых выборок), то в качестве критерия проверки нулевой гипотезы
принимают случайную величину
где S=l/ — —, исправленное среднее квадра-
тическое отклонение. Величина Т имеет распределение Стьюдента с
к = п—1 степенями свободы.
Правило 1. Для того чтобы при заданном уровне значимости а
проверить нулевую гипотезу Но: а=а0 о равенстве неизвестной ге-
генеральной средней а (нормальной совокупности с неизвестной дис-
дисперсией) гипотетическому значению а0 при конкурирующей гипо-
гипотезе Hi', а Ф а0, надо вычислить наблюдаемое значение критерия
и по таблице критических точек распределения Стьюдента, по за-
заданному уровню значимости а, помещенному в верхней строке таб-
таблицы, и числу степеней свободы k—n — l найти критическую точку
'двуст. кр (а> *)•
224
Если | Гнабл | < /двуст. кр—нет оснований отвергнуть нулевую
гипотезу. Если \ Т^авл! > 'двусг. кр—нулевую гипотезу отвергают.
Правило 2. При конкурирующей гипотезе Я,: а > а0 по уровню
значимости а, помещенному в нижней строке таблицы приложе-
приложения 6, и числу степеней свободы k=n—\ находят критическую
точку /Правоот. кр (я; k) правосторонней критической области. Если
7"набл < 'правост. кр—нет оснований отвергнуть нулевую гипотезу.
Если Тпз(,Л > /правост. кр—нулевую гипотезу отвергают.
Правило 3. При конкурирующей гипотезе Я,: а < а0 сначала
находят «вспомогательную» критическую точку (по правилу 2)
'правост. кр («; 6) и полагают границу левосторонней критической
Области 'лсвост.кр~—'правост.кр- Если /набл >—'правост.кр нет
оснований отвергнуть нулевую гипотезу. Если Тпа(,я < —'правост. кр —
нулевую гипотезу отвергают.
579. а) По выборке объема п=16, извлеченной из
нормальной генеральной совокупности, найдены выбо-
выборочная средняя х= 118,2 и «исправленное» среднее квад-
ратическое отклонение s = 3,6. Требуется при уровне
значимости 0,05 проверить нулевую гипотезу Но: а =
= ао=12О при конкурирующей гипотезе //,: аФ\20.
Решение. Найдем наблюдаемое значение критерия
_(х-а0) УИ_(\ 18,2-120) /Тб_
'иабл ; 3^ ""
По условию, конкурирующая гипотеза имеет вид а ф а^, поэтому
критическая область—двусторонняя.
По таблице критических точек распределения Стьюдента (см.
приложение 6), по уровню значимости а=0,05, помещенному
в верхней строке таблицы, и по числу степеней свободы k = n—1 =
= 16—1 = 15 находим критическую точку /ДВуСт. кр @,05; 15) = 2,13.
Так как | Г„абл | < /дяуСт. кр— нет основании отвергнуть нулевую
гипотезу. Другими словами, выборочная средняя х= 118,2 незна-
незначимо отличается от гипотетической генеральной средней ао = 12О.
а) Решить эгу задачу, приняв в качестве конкури-
конкурирующей гипотезы #„: а<ао=120.
580. Проектный контролируемый размер изделий,
изготовляемых станком-автоматом, а = ао = 35 мм. Изме-
Измерения 20 случайно отобранных изделий дали следующие
результаты:
контролируемый размер .v,- 34,8 34,9 35,0 35,1 35,3
частота (число изделий) л,- 2 3 4 6 о
Требуется при уровне значимости 0,05 проверить
нулевую гипотезу Но: а = ао = 35 при конкурирующей
гипотезе Я,: аФ35.
8 Гмурмаи В. Е. 225
Решение. Найдем средний размер изделий выборки:
- 2"'•*' 2-34,8+3.34,9+4.35,0+6-35,1+5-35,3 _og _
х — = 20 JOlU/<
Найдем исправленную дисперсию. Для упрощения расчета пе-
перейдем к условным вариантам щ= Юле/— 351. В итоге получим рас-
распределение:
и, —3 —2—10 2
щ 2 3 4 6 5
Найдем исправленную дисперсию условных вариант
л 2п'"Н2я'и']/'' „54-I-61V20
Н- —{ fg -2,747.
Следовательно, исправленная дисперсия первоначальных вариант
«JC =-2,747/10а =0,027.
Отсюда «исправленное» среднее квадратическое отклонение ty«*
=. /0^027=0,16.
Найдем наблюдаемое значение критерия:
(*-во) У~п C5,07-35,0) /20 „
- = 57Гб = 1>96'
По условию, конкурирующая гипотеза имеет вид а Ф а0, поэтому
критическая область—двусторонняя. По таблице критических точек
распределения Стьюдента (см. приложение 6), по уровню значимо-
значимости а = 0,05, помещенному в верхней строке таблицы, и по числу
степеней свободы к —п.—1=20—1 = 19 находим критическую точку
'явуст. кр @,05; 19) = 2,09. Так как Гиа6л < /двуст. кр—чет оснований
отвергнуть нулевую гипотезу. Другими словами, станок обеспечи-
обеспечивает проектный размер изделий.
§ 7. Сравнение двух средних нормальных
генеральных совокупностей
с неизвестными дисперсиями (зависимые выборки)
Пусть генеральные совокупности X и Y распределены нор-
нормально, причем их дисперсии неизвестны. Из этих совокупностей
извлечены зависимые выборки одинакового объема п, варианты ко-
которых соответственно равны *,- и щ. Введем следующие обозначения:
di—У!—разности вариант с одинаковыми номерами,
—средняя разностей варианте одинаковыми номерами,
— ¦—:— «исправленное» среднее квадрати-
квадратическое отклонение.
Правило 1. Для того чтобы при заданном уровне значимости а
проверить нулевую гипотезу Но: M(X) = M(Y) о равенстве двух
средних нормальных совокупностей X и Y с неизвестными диспер-
дисперсиями (в случае зависимых выборок одинакового объема) при конку-
конкурирующей гипотезе Н%: М (X) Ф М (К), надо вычислить наблюдаемое
226
j/
значение критерия:
и по таблице критических точек распределения Стьюдента, по за-
заданному уровню значимости а, помещенному в верхней строке таб-
таблицы, и числу степеней свободы k = n—1 найти критическую точку
'двуст.кр (<К Ю- Если |Гиабл| < ^двует.кр—нет оснований отверг-
отвергнуть нулевую гипотезу. Если \ТтбЛ\ > <дВуст. кр—нулевую гипотезу
отвергают.
581. Двумя приборами в одном и том же порядке
измерены шесть деталей и получены следующие резуль-
результаты измерений (в сотых долях миллиметра):
^i = 2, хЛж13, хя = 5, х4 = 6, хъ = о, х« = 10;
#1 = Ю> #» = 3, yg = 6, #4 = 1, уь=*7, #« = 4.
При уровне значимости 0,05 установить, значимо или
незначимо различаются результаты измерений, в пред-
предположении, что они распределены нормально.
Решение. Найдем разности d ,-=#,•—(/,¦; вычитая из чисел
первой строки числа второй, получим:
djas—8, d, = 0, ds=—1, d4=5, dt=l, de=6.
Найдем выборочную среднюю, учитывая, что 2jdi=3: d>
= 3/6 = 0,5.
Найдем «исправленное» среднее квадратическое отклонение
учитывая, что 2jd*=\27 и )
Найдем наблюдаемое значение критерия:
По таблице критических точек распределения Стьюдента (см. при-
приложение 6), по уровню значимости 0,05, помещенному в верхней
строке таблицы, и числу степеней свободы k=n—1=6—1 = 5 на-
находим критическую точку /двуСт. кр(°.О5; 5) = 2,57.
Так как Гнавл < 'двуст. кр—нет оснований отвергнуть нулевую
гипотезу. Другими словами, средние результаты измерений разли-
различаются незначимо.
582. На двух аналитических весах, в одном и том же
порядке, взвешены 10 проб химического вещества и по-
получены следующие результаты взвешиваний (в мг):
х, 25 30 28 50 20 40 32 36 42 38
у, 28 31 26 52 24 36 33 35 45 40
При уровне значимости 0,01 установить, значимо или
незначимо различаются результаты взвешиваний, в пред-
предположении, что они распределены нормально.
8* 227
583. Физическая подготовка 9 спортсменов была про-
проверена при поступлении в спортивную школу, а затем
после недели тренировок. Итоги проверки в баллах ока-
оказались следующими (в первой строке указано число бал-
баллов, полученных каждым спортсменом при поступлении
в школу; во второй строке—после обучения):
Xi 76 71 57 49 70 69 26 65 59
у, 81 85 52 52 70 63 33 83 62
Требуется прн уровне значимости 0,05 установить,
значимо или незначимо улучшилась физическая подго-
подготовка спортсменов, в предположении, что число баллов
распределено нормально.
584. Химическая лаборатория произвела в одном и
том же порядке анализ 8 проб двумя методами.
Получены следующие результаты (в первой строке
указано содержание некоторого вещества в процентах
в каждой пробе, определенное первым методом; во вто-
второй строке—вторым методом):
х{ 15 20 16 22 24 14 18 20
у( 15 22 14 25 29 16 20 24
Требуется при уровне значимости 0,05 установить, зна-
значимо или незначимо различаются средние результаты
анализов, в предположении, что они распределены нор-
нормально.
585. Две лаборатории одним и тем же методом, в
одном и том же порядке, определяли содержание угле-
углерода в 13 пробах нелегированной стали. Получены сле-
следующие результаты анализов *) (в первой строке указано
содержание углерода в процентах в каждой пробе, по-
полученное первой лабораторией; во второй строке—вто-
строке—второй лабораторией):
Х[ 0,18 0,12 0,12 0,08 0,08 0,12 0,19 0,32 0,27
yt 0,16 0,09 0,08 0,05 0,13 0,10 0,14 0,30 0,31
х{ 0,22 0,34 0,14 0,46
у, 0,24 0,28 0,11 0,42
Требуется при уровне значимости 0,05 установить,
значимо или незначимо различаются средние результаты
анализа в предложении, что они распределены нормально.
¦) См.: Налимов В. В. Применение математической статис-
статистики при анализе вещества. М., 1960.
228
§ 8. Сравнение наблюдаемой относительной частоты
с гипотетической вероятностью появления события
Пусть по достаточно большому числу п независимых испытаний,
в каждом из которых вероятность р появления события постоянна,
но неизвестна, найдена относительная частота m/л. Требуется прн
заданном уровне значимости а проверить нулевую гипотезу, со-
состоящую в том, что неизвестная вероятность р равна гипотетической
вероятности р0.
Правило 1. Для того чтобы при заданном уровне значимости
а проверить нулевую гипотезу //„: р = Ро ° равенстве неизвестной
вероятности р гипотетической вероятности р0 при конкурирующей
гипотезе Н\. р Ф р0, надо вычислить наблюдаемое значение критерия
__\(т!п)—рй\ УН
и пабл
УРоЯв
и по таблице функции Лапласа найти критическую точку мкр из
равенства
Ф() A
Если 11/на<$л | < ыкр —нет оснований отвергнуть нулевую гипо-
гипотезу. Если 11/цабл I > «кр—нулевую гипотезу отвергают.
Правило 2. При конкурирующей гипотезе Нг: р > р0 находят
критическую точку правосторонней критической области из ра-
равенства
Если 1/набл < "кр—не™ оснований отвергнуть нулевую гипотезу.
Если (Унабл > "кр—нулевую гипотезу отвергают.
Правило 3. При конкурирующей гипотезе Н-с. р < р0 находят
сначала «.вспомогательную» критическую точку икр по правилу 2, а
нашем полагают границу левосторонней критической области
и'кр — — нкр. Если и„збл>—"кр—нет оснований отвергнуть нуле-
нулевую гипотезу. Если (УНабл <—"кр—нулевую гипотезу отвергают.
Замечание. Удовлетворительные результаты обеспечивает
выполнение неравенства npoqo > 9.
586. По 100 независимым испытаниям найдена отно-
относительная частота /и/п = 0,14. При уровне значимости
0,05 требуется проверить нулевую гипотезу Яо: р = р„ =
= 0,20 при конкурирующей гипотезе //,: рф0,20.
Решение. Найдем наблюдаемое значение критерия, учитывая,
что q0 = 1 — Ро = 1 —0,20 = 0,80:
(т/п-р,,).^ @,14-0!20М^ШО
"в6Л V~P~M ^020080
По условию, конкурирующая гипотеза имеет вид р ф р0, по-
поэтому критическая область—двусторонняя. Найдем критическую
точку нкр по равенству
Ф (икр) = A —а)/2 = A —0,05)/2 ^0,475.
По таблице функции Лапласа (см. приложение 2) находим
"кр— 1.96-
229
Так как |?/Яабл I < «кр—иет оснований отвергнуть нулевую
гипотезу. Другими словами, наблюдаемая относительная частота 0,14
незначимо отличается от гипотетической вероятности 0,20.
587. Решить задачу 586 при конкурирующей гипо-
гипотезе Я^ р<р0-
Решение. По условию, конкурирующая гипотеза имеет вид
р < ро, поэтому критическая область—левосторонняя. Найдем сна-
сначала «вспомогательную» точку—границу правосторонней критиче-
критической области из равенства (правило 2)
) = 0— 2се)/2 = A— 2.0,05)/2=0,45.
По таблице функции Лапласа находим ыкр= 1,645, Следовательно,
граница левосторонней критической области иКр=—1,645.
Так как ?/набл > «кр —нет оснований отвергнуть нулевую ги-
гипотезу (правило 3).
588. Партия изделий принимается, если вероятность
того, что изделие окажется бракованным, не превышает
0,02. Среди случайно отобранных 480 изделий оказалось
12 дефектных. Можно ли принять партию?
Решение. Нулевая гипотеза Но имеет вид р = ро = 0,02.
Найдем относительную частоту брака:
т/п= 12/480 = 0,025.
Примем в качестве конкурирующей гипотезы Нх: р > 0,02
и уровень значимости а=0,05.
Найдем наблюдаемое значение критерия:
(т/п-Рл)-УИ @,025-0,02)-/480
Иа6Л=> РоЯ, У 0,020,98 =°>78-
По условию, конкурирующая гипотеза имеет вид р > р0, поэтому
критическая область—правосторонняя. Найдем критическую точку икр
правосторонней критической области из равенства (правило 2)
Ф («кр) = A —2 -0,05)/2=0,45.
По таблице функции Лапласа (см. приложение 2) находим
икр = 1,645.
Так как {/„аПл < икр—нет оснований отвергнуть гипотезу о том,
что вероятность брака в партии не превышает 0,02. Таким образом,
партию можно принять.
589. Партия изделий принимается, если вероятность
того, что изделие окажется бракованным, не превышает
0,03. Среди случайно отобранных 400 изделий оказалось
18 бракованных. Можно ли принять партию?
Указание. Принять нулевую гипотезу #0: р=ро=О,ОЗ,
а в качестве конкурирующей Hi. p > 0,03; уровень значимости
ос=0,05.
230
590. Завод рассылает рекламные каталоги возможным
заказчикам. Как показал опыт, вероятность того, что
организация, получившая каталог, закажет рекламируе-
рекламируемое изделие, равна 0,08. Завод разослал 1000 каталогов
новой улучшенной формы и получил 100 заказов. Можно
ли считать, что новая форма рекламы оказалась значимо
эффективнее первой?
Указание. Принять нулевую гипотезу Но: р = ро=0,08,
а в качесгве конкурирующей Н-с. р > 0,08; уровень значимости
а=0,05.
591. В результате длительных наблюдений установ-
установлено, что вероятность полного выздоровления больного,
принимавшего лекарство А, равна 0,8. Новое лекарство В
назначено 800 больным, причем 660 из них полностью
выздоровели. Можно ли считать новое лекарство значимо
эффективнее лекарства А на пятипроцентном уровне зна-
значимости?
Указание. Принять Н„: р = 0,8; Нц р^0,8.
§ 9. Сравнение нескольких дисперсий нормальных
генеральных совокупностей
по выборкам различного объема.
Критерий Бартлетта
Пусть генеральные совокупности Хл, Хг, ..., Xt распределены
нормально. Из этих совокупностей извлечены независимые выборки,
вообще говоря, различных объемов л/ (некоторые объемы могут быть
одинаковыми; если все выборки имеют одинаковый объем, то пред-
предпочтительнее пользоваться критерием Кочрена, который приведен
в следующем параграфе). По выборкам найдены исправленные выбо-
выборочные дисперсии s\, si, .... si Требуется при уровне значимости а
проверить нулевую гипотезу об однородности дисперсий, т. е. гипо-
гипотезу о равенстве между собой генеральных дисперсий:
Но: D(Xl)=D(X2)=..i=D(Xl).
Введем обозначения: */ = л/—I —число степеней свободы дисперсии sf;
•ж
$? k{—сумма чисел степеней свободы; *2=( 2 *'s' )/*—сРеД'
1ленных дисперсий, взв<
Г - ' ?1
няя арифметическая исправленных дисперсий, взвешенная по числам
степеней свободы;
V=2,303
231
B = V/C—случайная величина (критерий Бартлетта), которая
при условии справедливости гипотезы об однородности дисперсий
распределена приближенно как х2 с / — 1 степенями свободы, если
объем каждой выборки л,- Ss 4.
Правило. Для того чтобы при заданном уровне значимости а
проверить нулевую гипотезу об однородности дисперсий нормальных
совокупностей, надо вычислить наблюдаемое значение критерия Барт-
Бартлетта ВПЛ(,Я = У1С и по таблице критических точек распределения х2.
по уровню значимости а и числу степеней свободы I—1 G—число
выборок) найти критическую точку Хкр («; I—1) правосторонней
критической области). Если В„аця < Хкр—нет оснований отвергнуть
нулевую гипотезу. Если б„авл > Хкр—нулевую гипотезу отвергают.
Замечание 1. Не следует торопиться вычислять постоян-
постоянную С. Сначала надо найти V и сравнить с Хкр; если окажется, что
V < Хкр. то подавно (так как С > 1) B = V/C < Хкр и, следовательно,
С вычислять не нужно. Если же V > Хкр. то надо вычислить С и за-
затем сравнить В с Хкс-
Замечание 2. Критерий Бартлетта весьма чувствителен
к отклонениям распределений от нормального, поэтому к выводам,
полученным по этому критерию, надо относиться осторожно.
Замечание 3. При условии однородности дисперсий в ка-
качестве оценки генеральной дисперсии принимают среднюю арифме-
арифметическую исправленных дисперсий, взвешенную по числам степеней
свободы:
592. По трем независимым выборкам, объемы которых
п1 = 9, п2=13 и п3 = 15, извлеченным из нормальных
генеральных совокупностей, найдены исправленные выбо-
выборочные дисперсии, соответственно равные 3,2; 3,8 и 6,3.
Требуется при уровне значимости 0,05 проверить нулевую
гипотезу об однородности дисперсий.
Решение. Составим расчетную табл. 10 (столбец 8 пока за-
заполнять не будем, поскольку еще неизвестно, понадобится лн вы-
вычислять С).
Используя расчетную таблицу, найдем:
s*.= B*/s')/*= 150,4/34 = 4,688; lgs2=0,6709;
V=2,303 [* lg72-2 *,- Ig s?]=2,303 [340,6709-22,1886] = 1,43.
По таблице приложения 5, по уровню значимости 0,05 н числу
степеней свободы /—1=3—1=2 находим критическую точку
ХкР @.05; 2)= 6,0. ^
Так как V < Хкр. то подавно (поскольку С > 1) SHa6j,=V/C < Хкр
и, следовательно, отвергнуть нулевую гипотезу об однородности дис-
дисперсий нет оснований. Другими словами, выборочные дисперсии
различаются незначимо.
593. По данным задачи 592 требуется оценить гене-
генеральную дисперсию рассматриваемых генеральных сово-
совокупностей.
232
Таблица 10
1
Номер
выборки
i
1
2
3
2
2
Объем
выборки
9
13
15
3
Число
степеней
свободы
*/
8
12
14
А;=34
4
Исправ-
Исправленные
дисперсии
А
3,2
3,8
6,3
5
*,-?
25,6
45,6
88,2
159,4
о
Igs?
0,5051
0,5798
0,7993
7
*i 'в sf
4,0408
6,9576
11,1902
22,1886
8
Решение. Поскольку в результате решения предыдущей задачи
установлена однородность дисперсий, то в качестве оценки генераль-
генеральной дисперсии примем среднюю арифметическую исправленных дис-
дисперсий, взвешенную по числам степеней свободы:
D'r =Fa = B *!*?)/* = 159,4/34 =* 4,7.
594. Можно ли воспользоваться критерием Бартлетта
для проверки гипотезы об однородности дисперсий по
выборкам объема пх —3, ng = 2, пэ=20?
595. По четырем независимым выборкам, объемы кото-
которых п, = 17, «8 = 20, и„ = 15, л4 = 16, извлеченным из
нормальных генеральных совокупностей, найдены исправ-
исправленные выборочные дисперсии, соответственно равные 2,5;
3,6; 4,1; 5,8. Требуется: а) при уровне значимости 0,05
проверить гипотезу об однородности дисперсий; б) оце-
оценить генеральную дисперсию.
596. Четыре исследователя параллельно определяют
процентное содержание углерода в сплаве, причем первый
исследователь произвел анализ 25 проб, второй — 33, тре-
третий— 29, четвертый — 33 проб. «Исправленные» выбороч-
выборочные средние квадратические отклонения оказались соот-
соответственно равными 0,05; 0,07; 0,10; 0,08.
Требуется при уровне значимости 0,01 проверить гипо-
гипотезу об однородности дисперсий, в предположении, что
процентное содержание углерода в сплаве распределено
нормально.
Указание. Для упрощения вычислений принять/¦/ = 100s,-.
233
597. Сравниваются четыре способа обработки изделий.
Лучшим считается тот из способов, дисперсия контроли-
контролируемого параметра которого меньше. Первым способом
обработано 15, вторым —20, третьим—20, четвертым —
14 изделий. Исправленные выборочные дисперсии s* соот-
соответственно равны: 0,00053; 0,00078; 0,00096; 0,00062.
Можно ли отдать предпочтение одному из способов, при
уровне значимости 0,05? Предполагается, что контроли-
контролируемый параметр распределен нормально.
Указание. Для упрощения вычислений принять А = 100000s?-
598. Требуется сравнить точность обработки изделий
на каждом из трех станков. С этой целью на первом
станке было обработано 20, на втором—25, на третьем —
26 изделий. Отклонения X, У и Z контролируемого раз-
размера от заданного оказались следующими (в десятых
долях мм):
отклонения для изделий
первого станка xt 2 4 6 8 9
частота щ 5 6 3 2 4
отклонения для изделий
второго станка у, 1 2 3 5 7 8 12
частота mt 2 4 4 6 3 5 1
отклонения для изделий
третьего станка г/ 234 78 10 14
частота pt 3 5 4 6 3 2 3
а) Можно ли считать, что станки обеспечивают оди-
одинаковую точность при уровне значимости 0,05 в предполо-
предположении, что отклонения распределены нормально?
б) Исключив из рассмотрения третий станок (диспер-
(дисперсия отклонений этого станка—наибольшая), с помощью
критерия Фишера—Снедекора убедиться, что первый и
второй станки обеспечивают одинаковую точность обра-
обработки изделий.
§ 10. Сравнение нескольких дисперсий
нормальных генеральных совокупностей
по выборкам одинакового объема.
Критерий Кочрена
Пусть генеральные совокупности Хи Xit ..., Xt распределены
нормально. Из этих совокупностей извлечены / независимых выбо-
выборок одинакового объема п и по ним найдены исправленные выбороч-
234
мые дисперсии si, s-l s/, все с одинаковым числом степеней сво-
свободы к = п— 1. Требуется при уровне значимости а проверить нуле-
нулевую гипотезу сб однородности дисперсий, т. е. гипотезу о равенстве
между собой генеральных дисперсий:
В качестве критерия проверки нулевой гипотезы примем крите-
критерий Кочрена—отношение максимальной исправленной дисперсии
к сумме всех исправленных дисперсий:
Smax
sl + 4+...+sf
Распределение этой случайной величины зависит только от числа
степеней свободы к — п—1 и количества выборок /. Для проверки
нулевой гипотезы строят правостороннюю критическую область.
Правило. Для того чтобы при заданном уровне значимости а
проверить гипотезу об однородности дисперсий нормально распреде-
распределенных совокупностей, надо вычислить наблюдаемое значение критерия
и по таблице критических точек распределения Кочрена (см. при-
яожениед) найти критическую точку 0кр (а; к; I). Если ОНабл < 0кр —
нет оснований отвергнуть нулевую гипотезу. Если ОВабл > GKP —
нулевую гипотезу отвергают.
Замечание. При условии однородности дисперсий независи-
независимых выборок одинакового объема в качестве оценки генеральной
дисперсии принимают среднюю арифметическую исправленных дис-
дисперсий.
599. По четырем независимым выборкам одинакового
объема л = 17, извлеченным из нормальных генеральных
совокупностей, найдены исправленные выборочные дис-
дисперсии: 0,21; 0,25; 0,34; 0,40.
Требуется: а) при уровне значимости 0,05 проверить
нулевую гипотезу об однородности дисперсий (критиче-
(критическая область—правосторонняя); б) оценить генеральную
дисперсию.
Решение, а) Найдем наблюдаемое значение критерия Коч-
Кочрена—отношение максимальной исправленной дисперсии к сумме
всех дисперсий:
Онабл =0,40/@,21 +0,25 + 0,34+0,40) =у.
Найдем по таблице критических точек распределения Кочрена
(см. приложение 8) по уровню значимости 0,05, числу степеней сво-
свободы к—п—1=17—1=16 и числу выборок 1 = 4 критическую точку
Скр@,05; 16; 4)=0,4366.
Так как Ояабл < GKp—нет оснований отвергнуть нулевую гипо-
гипотезу. Другими словами, исправленные выборочные дисперсии раз-
различаются незначимо.
235
б) Поскольку однородность дисперсий установлена, в качестве
оценки генеральной дисперсии примем среднюю арифметическую
исправленных дисперсий:
?>? = (O,21-fO,25-|-O,34+O,4O)/4=O,3.
600. По шести независимым выборкам одинакового
объема « = 37, извлеченным из нормальных генеральных
совокупностей, найдены исправленные выборочные дис-
дисперсии: 2,34; 2,66; 2,95; 3,65; 3,86; 4,54.
Требуется проверить нулевую гипотезу об однород-
однородности дисперсий: а) при уровне значимости 0,01; б) при
уровне значимости 0,05.
601. Доказать, что наблюдаемое значение критерия
Кочрена не изменится, если все исправленные диспер-
дисперсии умножить на одно и то же постоянное число.
602. По пяти независимым выборкам одинакового
объема п = 37, извлеченным из нормальных генеральных
совокупностей, найдены «исправленные» средние квадра-
тические отклонения: 0,00021; 0,00035; 0,00038; 0,00062;
0,00084.
Требуется при уровне значимости 0,05 проверить нуле-
нулевую гипотезу об однородности дисперсий.
Указание. Умножить предварительно все средние квадратн-
ческие отклонения на 10s.
603. Четыре фасовочных автомата настроены на отве-
отвешивание одного и того же веса. На каждом автомате
отвесили по 10 проб, а затем эти же пробы взвесили на-
точных весах и нашли по полученным отклонениям ис-
исправленные дисперсии: 0,012; 0,021; 0,025; 0,032: а) можно
ли при уровне значимости 0,05 считать, что автоматы
обеспечивают одинаковую точность взвешивания? б) оце-
оценить генеральную дисперсию.
Предполагается, что отклонения зарегистрированного
веса от требуемого распределены нормально.
604. Каждая из трех лабораторий произвела анализ
10 проб сплава для определения процентного содержания
углерода, причем исправленные выборочные дисперсии
оказались равными 0,045; 0,062; 0,093: а) требуется при
уровне значимости 0,01 проверить гипотезу об однород-
однородности дисперсий; б) оценить генеральную дисперсию.
Предполагается, что процентное содержание углерода
в сплаве распределено нормально.
605. Проверяется устойчивость (отсутствие разладки)
работы станка по величине контролируемого размера
236
изделий. С этой целью каждые 30 мин отбирали пробу
из 20 изделий; всего взяли 15 проб. В итоге измерения
отобранных изделий были вычислены исправленные дис-
дисперсии (их значения приведены в табл. 11).
Таблица 11
Номер
пробы
2
3
4
5
Исправленная
дисперсия
0,082
0,094
0,162
0,143
0,121
Номер
пробы
6
7
8
9
10
Исправленная
дисперсия
0,109
0,121
0,094
0,156
0,110
Номер
пробы
11
12
13
14
15
Исправленная
дисперсия
0,112
0,109
0,110
0,156
0,164
Можно ли при уровне значимости 0,05 считать, что
станок работает устойчиво (разладка не произошла)?
Предполагается, что контролируемый размер изделий
распределен нормально.
Указание. Используя таблицу приложения 8, выполнить
линейную интерполяцию.
§ 11. Сравнение двух вероятностей
биномиальных распределений
Пусть в двух генеральных совокупностях производятся незави-
независимые испытания: в результате каждого испытания событие А может
появиться в первой совокупности с неизвестной вероятностью р,, а
во второй—с неизвестной вероятностью рг. По выборкам, извлечен-
извлеченным из первой и второй совокупностей, найдены соответственные
частоты:
wi(A)=m1/nl и
где /Пх, т%—числа появлений события A; n1( n2—количества испы-
испытаний.
В качестве оценок неизвестных вероятностей примем отно-
относительные частоты: p1^.w1 и pa=b.w2- Требуется при заданном уровне
значимости а проверить нулевую гипотезу, состоящую в том, что
вероятности pt и р± равны между собой: Но: Р\=Рг- Другими сло-
словами, требуется установить, значимо или незначимо различаются
относительные частоты wx и w2.
Предполагается, что выборки имеют достаточно большой объем.
Правило 1. Для того чтобы при заданном уровне значимости а
проверить нулевую гипотезу //0: Р\=Рг=Р о равенстве вероятно-
вероятностей появления события в двух генеральных совокупностях (имеющих
биномиальные распределения) при конкурирующей гипотезе Н^ рц?рг,
237
надо вычислить наблюдаемое знамение критерия
u no таблице функции Лапласа найти критическую точку икр по
равенству Ф(икр) = A—<х)/2. ?сл« | (/„абл1 < "кр—««я оснований
отвергнуть нулевую гипотезу. Если | f/набл I > "кр—нулевую гипо-
гипотезу отвергают.
Правило 2. При конкурирующей гипотезе Ht: рг > рг находят
критическую точку правосторонней критической области по равен-
равенству Ф(нкр) = A—2а)/2. Если Um6s< икр—нет оснований отверг-
отвергнуть нулевую гипотезу. Если (/Иабл > икр—нулевую гипотезу от-
отвергают.
Правило 3. При конкурирующей гипотезе Н^. р, < рг находят
критическую точку икр по правилу 2, а затем полагают границу
левосторонней критической области и'кр = — икр. Если ?/„абл >~"кр—
нет оснований отвергнуть нулевую гипотезу. Если 1/яабл <—"кр —
нулевую гипотезу отвергают.
606. За смену отказали 15 элементов устройства /,
состоящего из 800 элементов и 25 элементов устройства 2,
состоящего из 1000 элементов. При уровне значимости
а = 0,05 проверить нулевую гипотезу Н„: />i = p»=p
о равенстве вероятностей отказа элементов обоих устройств
при конкурирующей гипотезе Ях: рхфрг-
Решение. По условию, конкурирующая гипотеза имеет вид
Рг Ф Pi, поэтому критическая область двусторонняя. Найдем наблю-
наблюдаемое значение критерия:
U „,«, = ffii/n,—m2,/n2 ^
/J_ J_\
\ лх пг)
nt+nt
Подставив /п1 = 15, Л! = 800, т2=25, л2 = 1000, получим t/иабл =*
=—0,89.
Найдем критическую точку по равенству
Ф(«кР)=A—а)/2 = A—0,05)/2 =0,475.
По таблице функции Лапласа (см. приложение 2) находим
«кр=1.96- Так как |?/Иабл1 < мКр—нет оснований отвергнуть нуле-
нулевую гипотезу. Другими словами, вероятности отказа элемента обоих
устройств различаются незначимо.
607. В партии из 500 деталей, изготовленных первым
станком-автоматом, оказалось 60 нестандартных; из 600 де-
деталей второго станка 42 нестандартных. При уровне зна-
значимости 0,01 проверить нулевую гипотезу Яо: рх—р% = р
о равенстве вероятностей изготовления нестандартной
детали обоими станками при конкурирующей гипотезе
238
608. Для оценки качества изделий, изготовленных
двумя заводами, взяты выборки п, = 200 и я„ = 300 изде-
изделий. В этих выборках оказалось соответственно ml = 20
и /и, = 15 бракованных изделий. При уровне значимо-
значимости 0,05 проверить нулевую гипотезу Яо: p1 = pi = P
о равенстве вероятностей изготовления бракованного нз-
делия обоими заводами при конкурирующей гипотезе
Я,: рх > />,.
Указание. Построить правостороннюю критическую область.
609. Из 100 выстрелов по цели каждым из двух ору-
орудий зарегистрировано соответственно т1—12 и тг=8 про-
промахов. При уровне значимости 0,05 проверить нулевую
гипотезу Но: Pi = Pt = po равенстве вероятностей промаха
обоих орудий при конкурирующей гипотезе Ht: рхФрг.
§ 12. Проверка гипотезы о значимости
выборочного коэффициента корреляции
Пусть двумерная генеральная совокупность (X, Y) распределена
нормально. Из этой совокупности извлечена выборка объема л и по
ней найден выборочный коэффициент корреляции /¦„ ф 0. Требуется
проверить нулевую гипотезу Но: гг=0 о равенстве нулю генераль-
генерального коэффициента корреляции.
Если нулевая гипотеза принимается, то это означает, что X и Y
некоррелированы; в противном случае—коррелированы.
Правило. Для того чтобы при уровне значимости а проверить
нулевую гипотезу о равенстве нулю генерального, коэффициента кор-
корреляции нормальной двумерной случайной величины при конкурирую-
конкурирующей гипотезе Ях: гТ Ф 0, надо вычислить наблюдаемое значение кри-
критерия
и по таблице критических точек распределения Стьюдента, по
заданному уровню значимости а и числу степеней свободы k=n—2
найти критическую точку tKp (a; k) двусторонней критической
области. Если \ Т„„цл | < /кр—нет оснований отвергнуть нулевую
гипотезу. Если \ТаааЛ\ > tKp— нулевую гипотезу отвергают.
610. По выборке объема л =100, извлеченной из дву-
двумерной нормальной генеральной совокупности (X, Y),
найден выборочный коэффициент корреляции гв = 0,2.
Требуется при уровне значимости 0,05 проверить нуле-
нулевую гипотезу о равенстве нулю генерального коэффи-
коэффициента корреляции при конкурирующей гипотезе Нг :гГФ0.
Решение. Найдем наблюдаемое (эмпирическое) значение
критерия:
7\»6л *= гв Vn~=2lV\ — r\ = 0,2 У 100—2/ \ 1—0,2* = 2,02.
239
По условию, конкурирующая гипотеза имеет вид гт Ф О, по-
поэтому критическая область—двусторонняя.
По таблице критических точек распределения Стьюдепта
(см. приложение 6), по уровню значимости а=0,05, помещенному
в верхней строке таблицы, и числу степеней свободы k = n—2 =
= 100—2 = 98 находим критическую точку двусторонней критиче-
критической области /кр@,05; 98)= 1,99.
Так как Г„ацл > tKV—отвергаем нулевую гипотезу о равенстве
нулю генерального коэффициента корреляции. Другими словами,
коэффициент корреляции значимо отличается от нуля; следовательно,
X и Y коррелированы.
611. По выборке объема п = 62, извлеченной из нор-
нормальной двумерной генеральной совокупности (X, Y),
найден выборочный коэффициент корреляции г„ = 0,3.
Требуется при уровне значимости 0,01 проверить нуле-
нулевую гипотезу о равенстве нулю генерального коэффици-
коэффициента корреляции при конкурирующей гипотезе //,:гтф0.
612. По выборке объема п = 120, извлеченной из нор-
нормальной двумерной генеральной совокупности (X, Y),
найден выборочный коэффициент корреляции гв = 0,4.
Требуется при уровне значимости 0,05 проверить нулевую
гипотезу о равенстве нулю генерального коэффициента
корреляции при конкурирующей гипотезе Нх: ггф0.
613. По выборке объема л = 100, извлеченной из дву-
двумерной нормальной генеральной совокупности {X, Y),
составлена корреляционная табл. 12.
Таблица 12
у
35
45
55
65
75
пх
X
10
5
—
—
—
—
5
15
1
6
—
—
—
7
20
—
2
5
2
—
9
25
—
—
40
8
4
52
30
—
—
5
7
7
19
35
—
—
—
—
8
8
"у
6
8
50
17
19
п=100
Требуется: а) найти выборочный коэффициент корре-
корреляции; б) при уровне значимости 0,05 проверить нулевую
240
гипотезу о равенстве генерального коэффициента корре-
корреляции нулю при конкурирующей гипотезе Ht: гтФ0.
Решение, а) Для упрощения вычислений перейдем к услов-
условным вариантам
«, = (*,—С,)//'!, Vi = (yi—Ct)/ht,
где Ct и С2 —ложные нули (в качестве ложного нуля выгодно
взять варианту, расположенную примерно в середине вариационного
ряда; в данном случае принимаем Сх--25, С2 = 55); Ai = «/+i—и.[,
т. е. разность между двумя соседними вариантами (шаг); ft2 = u,-+i—у,\
Практически корреляционную таблицу в условных вариантах
составляют так: в первой строке вместо ложного нуля СУ~2Ь пи-
пишут нуль; слева от нуля пишут последовательно'—1, —2, —3,
а справа от нуля записывают 1, 2, 3. Аналогично, в первом столбце
вместо ложного нуля С2 = 55 записывают нуль; над нулем пишут
последовательно — 1, — 2, — 3, а под нулем 1, 2, 3. Частоты пе-
переписывают нз корреляционной таблицы в первоначальных вариан-
вариантах. В итоге получают корреляционную табл. 13.
Таблица 13
V
— 2
1
0
1
2
«а
и
-3
5
—
—
—
—
5
-2
1
6
—
—
—
7
-1
—
2
5
2
—
9
0
—
40
8
4
52
1
—
—
5
7
7
19
2
—
—
—
—
8
3
nv
6
8
50
17
19
л = 100
Воспользуемся формулой для вычисления выборочного коэффи-
коэффициента корреляции в условных вариантах:
гв = B navuv—nuv)/{nouov).
Вычислив входящие в эту формулу величины и, v, a,,, ov ме-
методом произведений или непосредственным расчетом, получим:
м = — 0,03; t>=0,35; ао= 1,153; а„= 1,062.
Пользуясь расчетной таблицей (см. задачу 535, табл. 7), найдем
2 nuvuv — 99.
Следовательно, выборочный коэффициент корреляции
2"'—"йц_99—100-(— 0,03) 0,35
_
в
/шцо„
100 1.153 1,062
~~ '
б) Проверим нулевую гипотезу о равенстве нулю генерального
коэффициента корреляции.
241
Вычислим наблюдаемое значение критерия:
У"п^2 __ 0,817-^100—2
7'набд = -
l -0,817»
= 14,03.
По условию, конкурирующая гипотеза имеет вид гт Ф 0, поэтому
критическая область—двусторонняя. По таблице критических точек
распределения Стьюдента (см. приложение 6), по уровню значимости
а=0,05, помещенному в верхней строке таблицы, и числу степеней
свободы k = n—2=100—2 = 98 находим критическую точку двусто-
двусторонней критической области /кр@,05; 98)= 1,99.
Так как Гнавл > /кр, нулевую гипотезу о равенстве нулю гене-
генерального коэффициента корреляции отвергаем. Другими словами,
коэффициент корреляции значимо отличается от нуля; следова-
следовательно, X и Y коррелированы.
614. По выборке объема я = 100, извлеченной из дву-
двумерной нормальной генеральной совокупности (X, Y),
составлена корреляционная табл. 14.
Таблица 14
У
ПО
120
130
140
150
я*
X
2
2
—
—
—
—
2
7
4
6
—
—
—
10
12
—
2
3
1
—
6
17
—
—
50
10
4
64
22
—
—
2
6
7
15
27
—
—
—
—
3
3
"и
6
8
55
17
14
п= 100
Требуется: а) найти выборочный коэффициент корре-
корреляции; б) при уровне значимости 0,01 проверить нуле-
нулевую гипотезу о равенстве нулю генерального коэффици-
коэффициента корреляции гг при конкурирующей гипотезе Ht: гтФ0.
Указание. Перейти к условным вариантам и, = (ж,—17)/5,
A30)/10
615. По выборке объема п = 100, извлеченной из дву-
двумерной нормальной генеральной совокупности (X, Y),
составлена корреляционная табл. 15.
242
Y
65
70
75
80
85
90
95
я*
T
а б л и ua 15
X
12
—
—
—
—
—
1
1
2
22
—
—
—
—
4
5
2
11
32
—
2
1
6
8
6
23
42
—
—
7
25
—
2
—
34
52
10
4
1
—
—
15
62
6
4
2
—
—
—
—
12
72
2
1
—
—
—
—
—
3
"»
18
5
15
26
11
16
9
«=10О
Требуется: а) найти выборочный коэффициент корре-
корреляции; б) при уровне значимости 0,001 проверить ну-
нулевую гипотезу о равенстве нулю генерального коэффи-
коэффициента корреляции гг при конкурирующей гипотезе
Указание. Перейти к условным вариантам «, = (x/—42)/10,
f; = (y,— 80)/5.
616. По выборке объема я =100, извлеченной из
двумерной нормальной генеральной совокупности (X, Y),
получена корреляционная табл. 16.
Таблица 16
Y
35
45
55
65
75
X
100
4
5
6
—
5
20
105
—
5
7
6
1
19
по
6
2
—
5
2
15
¦ ¦.
7
10
—
4
4
25
120
8
—
2
—
3
13
125
3
—
3
2
—
8
%
28
22
18
17
15
п=100
243
Требуется: а) найти выборочный коэффициент корре-
корреляции; б) при уровне значимости 0,05 проверить нуле-
нулевую гипотезу о равенстве нулю генерального коэффици-
коэффициента корреляции гг при конкурирующей гипотезе
Я 0
Указание. Перейти к условным вариантам «, = (*,-—115)/5,
р,- = (У,—45)/10.
§ 13. Проверка гипотезы о значимости
выборочного коэффициента ранговой корреляции
Спирмена
Пусть генеральная совокупность состоит нз объектов, которые
обладают двумя качественными признаками: А и В. Из этой
совокупности извлечена выборка объема п и по ней найден выбо-
выборочный коэффициент ранговой корреляции Спирмена р„ Ф 0
(см. гл. XII, § 3, А). Требуется проверить нулевую гипотезу Яо:
рг = 0 о равенстве нулю генерального коэффициента ранговой корре-
корреляции Спирмена.
Если нулевая гипотеза принимается, то это означает, что между
признаками А и В нет значимой ранговой корреляционной связи
(выборочный коэффициент рв незначим); в противном случае между
признаками имеется значимая ранговая корреляционная связь
(выборочный коэффициент (>в значим).
Правило. Для того чтобы при уровне значимости а проверить
нулевую гипотезу о равенстве нулю генерального коэффициента ран-
ранговой корреляции р,- Спирмена при конкурирующей гипотезе Ну.
рг Ф 0, надо вычислить критическую точку
где п —объем выборки; рв—выборочный коэффициент ранговой кор-
корреляции Спирмена; /кр(«. *)—критическая точка двусторонней
критической области, которую находят по таблице критических
точек распределения Стьюдента (см. приложение 6), по уровню
значимости а и числу степеней свободы k=n—2.
Если |рв| < Ткр — нет оснований отвергнуть нулевую гипотезу.
Ранговая корреляционная связь между качественными признаками
не значима. Если |р„| > 7"к])—нулевую гипотезу отвергают. Между
качественными признаками существует значимая ранговая корреля-
корреляционная связь.
617. В задаче 540 по выборке объема п = 10 вычислен
выборочный коэффициент ранговой корреляции Спирмена
р„ = 0,64 между оценками знаний студентов по двум
тестам. При уровне значимости 0,01 проверить нулевую
гипотезу о равенстве нулю генерального коэффициента
ранговой корреляции Спирмена. Другими словами, тре-
требуется проверить, является ли значимой ранговая кор-
корреляционная связь между оценками по двум тестам.
244
Решение. Найдем критическую точку двусторонней крити-
критической сбласти распределения Стьюдеита по уровню значимости
а -0,01 и числу степеней свободы k-=n—2— 10—2 = 8 (см. прило-
приложение 6): /Кр @,01; 8)^3,36.
Найдем критическую точку:
7-кр='кр(«; *) |А=§-=з,эб YX-^f =о,92.
Итак, Гкр~0,92, р„ = 0,64. Так как рв < Гкр—нет оснований
отвергнуть нулевую гипотезу о равенстве нулю генерального коэф-
коэффициента ранговой корреляции Спирмена. Другими словами, ранго-
ранговая корреляционная связь между оценками по двум тестам незна-
незначимая.
618. В задаче 541 по выборке объема и — 12 вычислен
выборочный коэффициент ранговой корреляции Спирмена
рв = 0,92 между оценками, выставленными одним и тем же
учащимся двумя преподавателями. При уровне значи-
значимости 0,05 проверить гипотезу о равенстве нулю гене-
генерального коэффициента ранговой корреляции Спирмена.
Другими словами, требуется проверить, является лн
значимой ранговая корреляционная связь между оцен-
оценками двух преподавателей.
619. В задаче 542 по выборке объема п — 13 вычислен
выборочный коэффициент ранговой корреляции Спирмена
рв = 0,75 между правильными рангами оттенков цветов
и рангами, которые им присвоил испытуемый. При уровне
значимости 0,02 проверить, значим ли найденный коэф-
коэффициент ранговой корреляции Спирмена.
620. В задаче 543 по выборке объема п —- 9 вычислен
выборочный коэффициент ранговой корреляции Спирмена
рв = 0,73 между двумя последовательностями рангов.
При уровне значимости 0,05 проверить гипотезу о ра-
равенстве нулю генерального коэффициента ранговой кор-
корреляции Спирмена.
621. В задаче 544 по выборке объема п — 11 вычислен
выборочный коэффициент ранговой корреляции Спирмена
рв = 0,82 между двумя последовательностями рангов,
установленными специалистами двух заводов при ран-
ранжировании факторов, влияющих на ход технологического
процесса. При уровне значимости 0,01 проверить, зна-
значима ли ранговая корреляционная связь между после-
последовательностями рангов.
622. По выборке объема п = 42 вычислен выборочный
коэффициент ранговой корреляции Спирмена р„ = 0,6
215
между двумя последовательностями рангов. При уровне
значимости 0,02 проверить, значим ли выборочный ко-
коэффициент ранговой корреляции Спирмена.
§ 14. Проверка гипотезы о значимости
выборочного коэффициента ранговой корреляции
Кендалла
Пусть генеральная совокупность состоит из объектов, которые
обладают двумя качественными признаками: А и В. Из этой
совокупности извлечена выборка сбъема я н по ней найден выбо-
выборочный коэффициент ранговой корреляции Кендалла тг ф 0 (см.
гл. XII, § 3, Б). Требуется проверить нулевую гипотезу Но: тг=0
о равенстве нулю генерального коэффициента ранговой корреляции
Кендалла.
Если нулевая гипотеза принимается, то это означает, что между
признаками А и В нет значимой ранговой корреляционной связи
(выборочный коэффициент т„ незначнм); в противном случае между
признаками имеется значимая ранговая корреляционная связь (выбо-
(выборочный коэффициент т„ значим).
Правило. Для того чтобы при уровне значимости а проверить
нулевую гипотезу о равенстве нулю генерального коэффициента ран-
ранговой корреляции Кендалла при конкурирующей гипотезе Hx: хТф$,
надо вычислить критическую точку
ГКр—гКр
9я(я—I)'
где п—объем выборки; гкр—критическая точка двусторонней кри-
критической области, которую находят по таблице функции Лапласа
по равенству Ф(гкр)=A—о)/2.
Если |т„| < Ткр—нет оснований отвергнуть нулевую гипотезу.
Ранговая корреляционная связь между качественными признаками
незначима. Если |тв| > 7"кр — нулевую гипотезу отвергают. Между
качественными признаками существует значимая ранговая корреля-
корреляционная связь.
623. В задаче 548 по выборке объема п = 10 вычислен
выборочный коэффициент ранговой корреляции Кендалла
тв = 0,47 между оценками знаний студентов по двум
тестам. При уровне значимости 0,05 проверить нулевую
гипотезу о равенстве нулю генерального коэффициента
ранговой корреляции Кендалла. Другими словами, тре-
требуется проверить, является ли значимой ранговая кор-
корреляционная связь между оценками по двум тестам.
Решение. Найдем критическую точку гкр:
Ф (гкР)=0-<х)/2 =A-0,05)/2=0,475.
По таблице Лапласа (см. приложение 2) находим гкр = 1,96.
246
Найдем критическую точку:
-,/2Bя + 5)' , оат/ 2B,10+5) . .о
Г"Р = Zl"> К 9«(я-1) = 1>96 К 9-10A0-1) " 0>49-
Итак, 71кр=0,49, тв=0,47. Так как тв < Ткр—нет оснований
отвергнуть нулевую гипотезу; ранговая корреляционная связь между
оценками по двум тестам незначимая.
624. В задаче 549 по выборке объема п= 10 вычислен
выборочный коэффициент ранговой корреляции Кендалла
тв = 0,78 между оценками качества деталей, которые
были выставлены двумя контролерами. При уровне зна-
значимости 0,01 проверить, является ли значимой ранговая
корреляционная связь между оценками двух контро-
контролеров.
625. По выборке объема п —13 найден выборочный
коэффициент ранговой корреляции Кендалла т„ = 0,54
между двумя последовательностями рангов. При уровне
значимости 0,05 проверить, является ли значимой ран-
ранговая корреляционная связь между последовательностями
рангов.
626. По выборке объема м = 20 найден выборочный
коэффициент ранговой корреляции Кендалла тв = 0,24
между двумя последовательностями рангов. При уровне
значимости 0,01 проверить, является ли значимой ран-
ранговая корреляция между последовательностями рангов.
§ 15. Проверка гипотезы об однородности двух выборок
по критерию Вилкоксона
Критерий Вилкоксона служит для проверки однородности не-
независимых выборок хи х2 хП| и(/ь(/2, ...,#„, в предположении,
что X и Y—непрерывные случайные величины.
Нулевая гипотеза состоит в том, что при всех значениях аргу-
аргумента (обозначим его через х) функции распределения равны между
собой:
Л (*) = f Не-
Неконкурирующие гипотезы:
*Ч (*) Ф Fi (х), f, (x) < Ft(x), f, (x) > f8 (x).
Заметим, что принятие конкурирующей гипотезы Ht: Ft (x)<Ft (x)
означает, что X > Y. Аналогично, если справедлива конкурирующая
гипотеза Я,: Ft (х) > Ft {х), то X < Y.
Далее предполагается, что объем первой выборки меньше (не
больше) второй: /!]<пг; если это не так, то выборки можно пере-
перенумеровать (поменять местами).
А. Проверка нулевой гипотезы в случае, если объем обеих
выборок не превосходит 25. Правило I. Для того чтобы при уровне
значимости а проверить нулевую гипотезу Но: Ft (x) = Fa (лс) об
247
однородности двух независимых выборок объемов п1 и nt (/ij < л2)
при конкурирующей гипотезе Нх: Ft(x) Ф F^(x), надо:
1) расположить варианты обеих выборок в возрастающем порядке
т. е. в виде одного вариационного ряда, и найти в этом ряду
№„зйл—сумму порядковых номеров вариант первой выборки;
2) найти по таблице нижнюю критическую точку
»иижи.кр(О. "i. "*)¦ где 0=а/2;
3) найти верхнюю критическую точку по формуле
«'верхн.кр = («l + If "Г 1 )«1 — ^иижи.кр-
Если а.'НИЖ1|.кр < WHa6a < и>Верхи.кр—н^т оснований отвергнуть
нулевую гипотезу. Если Г„абл < а'нижн.кр или Wna6]l > «.'„ер.хн.кр —
нулевую гипотезу отвергают.
627. При уровне значимости 0,01 проверить нулевую
гипотезу Яо: Fl(x) = Ft(x) об однородности двух выбо-
выборок, объемы которых п1~6, «а==7 (в первой строке
приведены варианты первой выборки; во второй строке —
варианты второй выборки):
х, 3 4 6 10 13 17
у, 1 2 5 7 16 20 22
Принять в качестве конкурирующей гипотезу Ht:
F()F()
Решение. Конкурирующая гипотеза имеет вид Fx(x) # Ft (x),
поэтому критическая область—двусторонняя. Расположим варианты
обеих выборок в виде одного вариационного ряда и пронумеруем их:
порядковый
номер 12 3 4 5 6 7 8 9 10 1112 13
варианта 1 2 3 4 5 6 7 10 13 16 17 20 22
Найдем наблюдаемое значение критерия Вилкоксона —сумму
порядковых номеров (они набраны курсивом) вариант первой выборки:
Найдем по таблице* нижнюю критическую точку критиче-
критической области, учитывая, что 0=0,01/2=0,005, «j=6, я2=7:
«'ияжн-кр @,005; 6, 7) =24. Найдем верхнюю критическую точку:
»верхи.кр = ( + я* + 1) «1 — «»ииж11.к1. F +7-1- 1N—24 = 60. По-
Поскольку ю„нжи.кр < Г„абл < вУвсрхн.кр B4 < 41 < 60)—нет оснований
отвергнуть нулевую гипотезу об однородности выборок.
628. Предложены два метода (А и В) увеличения
выхода продукции. При уровне значимости 0,05 прове-
проверить нулевую гипотезу об их одинаковой эффективности
по двум выборкам объемов «, = 6 и «2 = 9 (в первой
* При решении задач 627—630 использовать таблицу, помещен-
помещенную в книге: Гм урман В. Е. Теория вероятностей и математи-
математическая статистика. М., 1977.
248
строке приведены проценты прироста продукции в каж-
каждом опыте по методу А; во второй строке—по методу В):
х{ 0,2 0,3 0,5 0,8 1,0 1,3
у, 0,1 0,4 0,6 0,7 0,9 1,4 1,7 1,8 1,9
Принять в качестве конкурирующей гипотезу: эффек-
эффективность методов А и В различна.
629. Производительность труда двух смен завода
характеризуется выборками объемов ях = 9 и«2=10:
первая смена 28 33 39 40 41 42 45 46 47
вторая смена 34 40 41 42 43 44 46 48 49 52
Используя критерий Вилкоксона, при уровне значи-
значимости 0,1 проверить нулевую гипотезу об одинаковой
производительности обеих смен, приняв в качестве кон-
конкурирующей гипотезу: производительность труда смен
различна.
Указание. При вычислении наблюдаемого значения крите-
критерия Внлкоксона учесть, что ранги совпадающих вариант различ-
различных выборок равны среднему арифметическому порядковых
номеров вариант в общем вариационном ряде, составленном из ва-
вариант обеих выборок.
630. Эффективность каждого из двух рационов (А и В)
откорма скота характеризуется выборками объемов
/1!= 10 и я2 = 12 (в первой строке приведен вес (в кг)
животных, которых откармливали по рациону А, во
второй строке—по рациону В):
х, 24 26 27 27 30 32 33 34 35 36
у, 21 21 22 23 25 25 25 25 27 27 29 31
Используя критерий Вилкоксона, при уровне значи-
значимости 0,05 проверить нулевую гипотезу об одинаковой
эффективности рационов А и В, приняв в качестве кон-
конкурирующей гипотезу: рацион А эффективнее рациона В
(Ях: /ч(*)</%(*), т.е. Х>У).
Указание. Критическая область — правосторонняя.
Б. Проверка нулевой гипотезы в случае, если объем хотя бы одной
из выборок превосходит 25. 1. При конкурирующей гипотезе t\ (х) Ф
Ф F% (.r) нижняя критическая точка
№'• "l- "*) =
+ "г+'I .„.
12 J' ()
249
где Q=ot/2; гкр находят по таблице функции Лапласа с помощью
равенства Ф(гкр) = A—а)/2; знак \а\ означает целую часть числа а.
В остальном правило 1, приведенное в п. А, сохраняется.
2. При конкурирующих гипотезах Fj (х) < F2 (х) и F, (*) > Ft (x)
нижнюю критическую точку находят по формуле (*), положив
Q=a; соответственно гкр находят по таблице функции Лапласа
с помощью равенства Ф(гкр = A—2а)/2. В остальном правила
2 —3, приведенные в п. А, сохраияюгся.
631. При уровне значимости 0,05 проверить нулевую
гипотезу об однородности двух выборок объемов: «, = 40
и п, = 50 при конкурирующей гипотезе Ht: Ft (x) Ф F% (x),
если известно, что в общем вариационном ряду, состав-
составленном из вариант обеих выборок, сумма порядковых
номеров вариант первой выборки №„абл= 1800.
Решение. По условию, конкурирующая гипотеза имеет вид
р1(*) = Рг(х), поэтому критическая область—двусторонняя.
Найдем 2кр с помощью равенства
Ф (гкР) = A —а)/2 = A —0,05)/2=0,475.
По таблице функции Лапласа (см. приложение2) находим гкр=1,96.
Подставив я,=40, яг=50, гкр=1,96, 0=0,05/2=0,025 в формулу
12" J •
ПОЛУЧИМ й|мижн.кР = 1578.
Найдем верхнюю критическую точку: и.'верхн кР=(я1+я»+1) Щ—-
-sfHHWi..Kp=D0+5(H-l)-40- 1578=2062. Так как м>„Иж1..кр<»'набл<
< «|верхн.крA578 < 1800 < 2062), то нет оснований отвергнуть нулевую
гипотезу об однородности выборок.
632. При уровне значимости 0,01 проверить нулевую
гипотезу об однородности двух выборок объемов: пх = 40
и пг — 60 при конкурирующей гипотезе Я,: F, (х) Ф Ft (x),
если известно, что в общем вариационном ряду, состав-
составленном из вариант обеих выборок, сумма порядковых
номеров вариант первой выборки И7на6л = 3020.
633. При уровне значимости 0,05 проверить нулевую
гипотезу об однородности двух выборок объемов п., = 25
и п2 = 30 при конкурирующей гипотезе Ht: F1(x)^Fi{x):
варианты пер- 12 14 15 18 21 25 26 27 30 31 32 35 38
вой выборки 41 43 46 48 52 56 57 60 65 68 73 75
варианты вто- 11 13 16 17 19 20 22 23 24 26 28 29
рой выборки 33 34 36 37 39 40 42 44 45 47 49 51
53 55 58 61 63 66
250
§ 16. Проверка гипотезы о нормальном распределении
генеральной совокупности по критерию Пирсона
А. Эмпирическое распределение задано в виде последовательно»
сти равноотстоящих вариант и соответствующих им частот. Пусть
эмпирическое распределение задано в виде последовательности рав-
равноотстоящих вариант и соответствующих им частот:
nl ni па • • • nN-
Требуется, используя критерий Пирсона, проверить гипотезу
о том, что генеральная совокупность X распределена нормально.
Правило 1. Для того чтобы при заданном уровне значимости а
проверить гипотезу о нормальном распределении генеральной сово-
совокупности, надо:
1. Вычислить непосредственно (при малом числе наблюдений)
или упрощенным методом (при большом числе наблюдений)^напри-
наблюдений)^например методом произведений или сумм, выборочную среднюю хв и вы-
выборочное среднее квадратическое отклонение ав.
2. Вычислить теоретические частоты
nh
«/ = —
где п—объем выборки (сумма всех частот), h—шаг (разность между
двумя соседними вариантами),
«,-2=5. ,(„)—¦..—/..
ав
3. Сравнить эмпирические и теоретические частоты с помощью
критерия Пирсона. Для этого:
а) составляют расчетную таблицу (см. табл. 18J, по которой
находят наблюдаемое значение критерия
Хиабл= V
б) по таблице критических точек распределения %2, по задан-
заданному уровню значимости а и числу степеней свободы k = s—3 (s —
число групп выборки) находят критическую точку Хкр (a; k) право-
правосторонней критической области.
Если Хиабл < Хкр—нет оснований отвергнуть гипотезу о нор-
мольном распределении генеральной совокупности. Другими словами,
эмпирические и теоретические частоты различаются незначимо
(случайно). Если Хнабл > Хкр—гипотезу отвергают. Другими сло-
словами, эмпирические и теоретические частоты различаются значимо.
Замечание 1. Малочисленные частоты (п/ < 5) следует объе-
объединить; в этом случае и соответствующие им теоретические частоты
также надо сложить. Если производилось объединение частот, то
при определении числа степеней свободы по формуле k — s—3 .сле-
.следует в качестве s принять число групп выборки, оставшихся после
объединения частот.
251
634. Почему при проверке с помощью критерия Пир-
Пирсона гипотезы о нормальном распределении генеральной
совокупности число степеней свободы находят по фор-
формуле k = s—3?
Решение. Прн использовании критерия Пирсона число сте-
степеней свободы k—s—1—г, где г — число параметров, оцениваемых
по выборке. Нормальное распределение определяется двумя пара-
параметрами: математическим ожиданием а и средним квадратическим
отклонением о. Так как оба эти параметра оценивались по выборке
(в качестве оценки о принимают выборочную среднюю, в качестве
оценки а—выборочное среднее квадратическое отклонение), то г=~2
следовательно, к ¦ s — 1—2=s—3.
635. Используя критерий Пирсона, при уровне зна-
значимости 0,05 проверить, согласуется ли гипотеза о нор-
нормальном распределении генеральной совокупности X
с эмпирическим распределением выборки объема и = 200:
X; 5 7 9 11 13 15 17 19 21
п, 15 26 25 30 26 21 24 20 13
Решение I. Используя метод произведений, найдем выбо-
выборочную среднюю хв—12,63 н выборочное среднее квадратическое
отклонение ов-- 4,695.
2. Вычислим теоретические частоты, учитывая, что я = 200,
h = 2, ав — 4,695, по формуле
п'[ =---^-' Ф("<)=4695 ф("()^85'21)(и')'
Составим расчетную табл. 17 (значения функции ф(и) помещены
в приложении I).
Таблица 17
1
1
2
3
4
5
6
7
8
9
5
7
9
11
13
15
17
19
21
и Х'"*в
1 %
-1,62
—1,20
—0,77
—0,35
0,08
0,51
0,93
1,36
1,78
Ф(",)
0,1074
0,1942
0.2Р66
0,3752
0,3977
0,3503
0,2589
0,1582
0,0818
л^-85.г-ф (и.)
9,1
16,5
25,3
32,0
33,9
29,8
22,0
13,5
7,0
3. Сравним эмпирические и теоретические частоты,
а) Составим расчетную табл. 18, из которой найдем
наблюдаемое значение критерия
252
Таблица 18
i
1
2
3
4
5
6
7
8
9
2
15
26
25
30
26
21
24
20
13
n'i
9,1
16,5
25,3
32,0
33,9
29,8
22,0
13,5
7,0
200
П;-П.
5,9
9,5
—0,3
-2,0
—7,9
—8,8
2,0
6,5
6,0
34,81
90,25
0,09
4,00
62,41
77,44
4,00
42,25
36,00
3,8
5,5
0,0
0,1
1,8
2,6
0,2
3,1
5,1
Хнабл=22,2
Из табл. 18 находим Хнабл=22,2.
б) По таблице критических точек распределения х* (см. прило-
приложение 5), по уровню значимости о = 0,05 и числу степеней свободы
k = s—3 = 9—3=6 находим критическую точку правосторонней кри-
критической области
Хкр@,05; 6)= 12,6.
Так как Хнабл > Хкр—гипотезу о нормальном распределении ге-
генеральной совокупности отвергаем. Другими словами, эмпирические
и теоретические частоты различаются значимо.
636. Используя критерий Пирсона, при уровне зна-
значимости 0,05 проверить, согласуется ли гипотеза о нор-
нормальном распределении генеральной совокупности X
с эмпирическим распределением выборки объема п = 200:
Xf 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3
nt 6 9 26 25 30 26 21 24 20 8 5
637. Используя критерий Пирсона, при уровне зна-
значимости 0,01 установить, случайно или значимо расхож-
расхождение между эмпирическими частотами п,- и теоретическими
частотами п\, которые вычислены, исходя из гипотезы
о нормальном распределении генеральной совокупности X:
8
6
16 40
18 36
72 36
76 39
18
18
10
7
Решение. Найдем наблюдаемое значение критерия Пирсона:
Хиабл = 2^П("—пЪ*!п\. Составим расчетную табл. 19.
Из табл. 19 находим наблюдаемое значение
Хиабл = 3,061.
критерия:
253
По таблице критических точек распределения ха (см. приложе-
приложение 5), по уровню значимости 0,01 и числу степеней свободы k = s—
— 3 = 7—3 = 4 находим критическую точку правосторонней крити-
критической области Хкр@,01; 4)= 13,3.
Так как Хнабл < Хкр—нет оснований отвергнуть гипотезу о нор-
нормальном распределении генеральной совокупности. Другими сло-
словами, расхождение между эмпирическими и теоретическими частотами
незначимо (случайно).
Табл ица 19
(
1
2
3
4
5
6
7
2
nl
8
16
40
72
36
18
10
п=200
*\
6
18
36
76
39
18
7
пгп\
2
—2
4
—4
—3
3
4
4
16
16
9
__
9
("Г"()%/п1
0,667
0,222
0,444
0,211
0,231
1,286
Хнабл = 3,061
638. Используя критерий Пирсона, при уровне зна-
значимости 0,05 установить, случайно или значимо расхож-
расхождение между эмпирическими частотами п,- и теоретическими
частотами п\, которые вычислены исходя из гипотезы
о нормальном распределении генеральной совокупности X:
а) п, 5 10 20 8 7
n't 6 14 18 7 5
б) п, 6 8 13 15 20 16 10 7 5
п\ 5 9 14 16 18 16 9 6 7
в) п, 14 18 32 70 20 36
п\ 10 24 34 80 18 22
5 14 2 6
г) п
5 7 15 14 21 16
6 6 14 15 22 15
10
12
9 7 6
8 8 6
Б. Эмпирическое распределение задано в виде последовательно-
последовательности интервалов одинаковой длины и соответствующих им частот.
Пусть эмпирическое распределение задано в виде последовательности
интервалов (jc,-, */+i) и соответствующих им частот п,- (п/—сумма
частот, которые попали в i-й интервал):
/2j Яд Ms
Требуется, используя критерий Пирсона, проверить гипотезу
о том, что генеральная совокупность X распределена нормально.
254
Правило 2. Для того чтобы при уровне значимости а проверить
гипотезу о нормальном распределении генеральной совокупности, надо:
1. Вычислить, например методом произведений, выборочную
среднюю х и выборочное среднее квадратическое отклонение ав, при-
причем в качестве вариант х* принимают среднее арифметическое кон-
концов интервала:
2. Пронормировать X, т. е. перейти к случайной величине
(X—l?)/o*j_ и вычислить концы интервалов: г/ = (ж,-—х*)/о*,
(*/+i—х*/о*, причем наименьшее значение Z, т. е. гг, по-
полагают равным —со, а наибольшее, т. е. zs+l, полагают равным о».
3. Вычислить теоретические частоты
где п—объем выборки (сумма всех частот); Я/=Ф(г/+1) — Ф(г/) —
вероятности попадания X в интервалы (х,-, jc,-+1); Ф(?)—функция
Лапласа.
4. Сравнить эмпирические и теоретические частоты с помощью
критерия Пирсона. Для этого:
а) составляют расчетную таблицу (см. табл. 18), по которой
находят наблюдаемое значение критерия Пирсона
Хнабл =2 («/—"/)*/«'*;
б) по таблице критических точек распределения ха, по заданному
уровню значимости а и числу степеней свободы k=s—3 (s—число
интервалов выборка) находят критическую точку правосторонней
критической области %кр(а- k).
Если Хнабл < Х«Р—нет оснований отвергнуть гипотезу о нор-
нормальном распределении генеральной совокупности. Если Хнабл > Хкр—
гипотезу отвергают.
Замечание 2. Интервалы, содержащие малочисленные эмпи-
эмпирические частоты (я,- < 5), следует объединить, а частоты этих интер-
интервалов сложить. Если производилось объединение интервалов, то при
определении числа степеней свободы по формуле k=s—3 следует
в качестве s принять число интервалов, оставшихся после объеди-
объединения интервалов.
639. Используя критерий Пирсона, при уровне зна-
значимости 0,05 проверить, согласуется ли гипотеза о нор-
нормальном распределении генеральной совокупности X
с эмпирическим распределением выборки объема л. = 100,
приведенным в табл. 20.
Решение 1. Вычислим выборочную среднюю и выборочное
среднее квадратическое отклонение методом произведений. Для этого
перейдем от заданного интервального распределения к распределе-
распределению равноотстоящих вариант, приняв в качестве варианты х* сред-
255
Таблица 20
Номер
интер-
интервала
t
1
2
3
4
Граница
интервала
xi
3
8
13
18
*/ + !
8
13
18
23
Часто-
Частота л(.
6
8
15
40
Номер
интервала
i
5
6
7
Граница
интервала
*i
23
28
33
28
33
38
Частота
"i
Ifi
8
7
n=100
нее арифметическое концов интервала: **=(*,•+х/+1)/2. В итоге по-
получим распределение:
я,-
5,5 10,5 15,5 20,5 25,5 30,5 35,5
6 8 15 40 16 8 7
Выполнив выкладки по методу произведений, найдем выборочную
среднюю и выборочное среднее квадратическое отклонение: дс* = 20,7,
а» = 7,28. _
2. Найдем интервалы (г,-, z,-+i), учитывая, что ** = 20,7, а* =
= 7,28, 1/а*=0,137. Для этого составим расчетную табл. 21 (левый
конец первого интервала примем равным —со, а правый конец по-
последнего интервала со).
3. Найдем теоретические вероятности Р,- и теоретические частоты
/»i=rt-P/ = 100-P/. Для этого составим расчетную табл. 22.
Таблица 21'
1
1
2
3
4
5
6
7
Границы
интервала
ч
3
8
13
18
23
28
33
8
13
18
23
28
33
38
-12,7
— 7,7
— 2,7
2,3
7,3
12,3
Ч + 1-*
—12,7
— 7,7
— 2,7
2,3
7,3
12,3
—
Границы интервала
Х( X*
— 00
-1,74
—1,06
-0,37
0,32
1,00
1,69
-1+1 о*
-1,74
—1,06
—0,37
0,32
1,00
1,69
00
256
Таблица 22
i
1
2
3
4
5
6
7
2
Границы
интервала
3
-1
|
—0
0
1
1
,74
,06
.37
.32
,00
,69
-1.74
—1,06
—0,37
0,32
1,00
1,69
-о,
-о.
-о,
—0,
0,
0,
0,
*'
5000
4591
3554
1443
1255
3413
4545
—0
—0
—0
0
0
0
0
Ч+г
,4591
,3554
,1443
,1255
,3413
,4545
,5000
Р(.=Ф
0,
0,
0,
0,
0,
о,
0,
(z/+l)~
Ф(г,)
0409
1037
2111
2698
2158
1132
0455
1
4
10
21
26
21
11
4
100
ioopf
,09
,37
,11
,98
,58
.32
.55
4. Сравним эмпирические и теоретические частоты, используя
критерии Пирсона:
а) вычислим наблюдаемое значение критерия Пирсона. Для этого
составим расчетную табл. 23. Столбцы 7 и 8 служат для контроля
вычислений по формуле
Хнабл-
Вы-
ВыКонтроль: 2 (я?//»;)—п= 113,22— 100=13,22
числения произведены правильно;
б) по таблице критических точек распределения х2 (приложе-
(приложение 5), по уровню значимости а=0,05 и числу
Таблица 23
1
1
1
2
3
4
5
6
7
2
2
"|
6
8
15
40
16
8
7
100
3
4,09
10,37
21,11
26,98
21,58
11,32
4,55
100
4
nr"i
1.91
—2,37
-6,11
13,02
—5,58
—3,32
2,45
s
("г"*)*
3,6481
5,6169
37,3321
169,5204
31,1364
11,0224
6,0025
6
(nrn'iJln'i
0,8920
0,5416
1,7684
6,2833
1,4428
0,9737
1,3192
Х?,абл=13.22
7
«?
36
64
225
1600
256
64
49
8
пуп'.
8,8019
6,1716
10,6584
59,3052
11,8628
5,6537
10,7692
113,22
степеней свободы k=s—3 = 7—3 = 4 (s—число интервалов) нахо-
находим критическую точку правосторонней критической области
ХкР@.05; 4) = 9,5.
9 Гнурнав В. В. 257
Так как Хнабл > Хкр—отвергаем гипотезу о нормальном распре-
распределении генеральной совокупности X; другими словами, эмпириче-
эмпирические и теоретические частоты различаются значимо. Это означает,
что данные наблюдений не согласуются с гипотезой о нормальном
распределении генеральной совокупности.
640. Используя критерий Пирсона, при уровне зна-
значимости 0,05 проверить, согласуется ли гипотеза о нор-
нормальном распределении генеральной совокупности X с
заданным эмпирическим распределением.
а)
Номер
интер-
интервала
i
1
2
3
4
Граница
интервала
*1
—20
—10
0
10
—10
0
10
20
Частота
ni
20
47
80
89
Номер
интер-
интервала
1
5
6
7
Граница
интервала
*/
20
30
40
30
40
50
Частота
п1
40
16
8
я-300
б)
Номер
интер-
интервала
1
1
2
3
4
5
6
Границы
интервала
*/
1
3
5
7
9
11
3
5
7
9
11
13
Частота
п1
2
4
6
10
18
20
Номер
интер-
интервала
(
7
8
9
10
11
Границы
интервала
*/
13
15
17
19
21
15
17
19
21
23
Частота
"/
16
11
7
5
1
п=100
258
в)
Номер
интер-
интервала
i
1
2
3
4
5
Границы
интервала
*/
6
16
26
36
46
16
26
36
46
56
Частота
*1
8
7
16
35
15
Номер
интер-
интервала
1
6
7
8
Границы
интервала
xi
56
66
76
*. + 1
66
76
86
Частота
"/
8
в
5
rt=100
г)
Номер
интер-
интервала
i
1
2
3
4
5
Границы
интервала
Ч
5
10
15
20
25
Ч+i
10
15
20
25
30
Частота
"/
7
8
15
18
23
Номер
интер-
интервала
i
6
7
8
9
Границы
интервала
*/
30
35
40
45
35
40
45
50
Частота
ni
19
14
10
6
rt=120
б) Указание. Объединить малочисленные частоты первых
двух и последних двух интервалов, а также сами интервалы.
§ 17. Графическая проверка гипотезы
о нормальном распределении генеральной совокупности.
Метод спрямленных диаграмм
А. Сгруппированные данные. Пусть эмпирическое распределение
выборки из генеральной совокупности X задано в виде последова-
последовательности интервалов (х0, хх), (хи х2), ..., (*/s-i> •**) и соответст-
соответствующих им частот п,- (п;—число вариант, попавших в i'-й интервал).
Требуется графически проверить гипотезу о нормальном распреде-
распределении X.
Предварительно введем определенне р-квантили случайной вели-
величины X. Если задана вероятность р, то р-квантилью {квантилем) X
называют такое значение аргумента ир функцни распределения F(x),
для которого вероятность события X < ир равна заданному значе-
значению р. Например, если величина X распределена нормально и
р=0,975, то Иу, = ио.974= I'96- Это означает, что Р (X < 1,96)=0,975.
9* 259
Заметим, что поскольку функции распределения общего и нор-
нормированного нормальных распределений связаны равенством F (х) =
( \
/х д\
I ),
П
то F(Xj,)
р
(Хр — О\
I —-—) и,
б ф
следовательно, ир=(хр—а)/а.
„ ) 'V "\ о
Правило I. Для того чтобы графически проверить гипотезу о
нормальном распределении генеральной совокупности X по эмпири-
эмпирическому распределению, заданному в виде последовательности интер-
интервалов и соответствующих им частот, надо:
1. Составить расчетную табл. 24. Квантили находят по таб-
таблице (см. приложение 10).
Таблица 24
' 1 2
Номер
интервала
1
Правый
конец
интервала
*i
3
Частота
4
Накоп-
Накопленная
частота
Ж"'
s
Относи-
Относительная
накоп-
накопленная
частота
' л
С
Относи-
Относительная
накоп-
накопленная
частота. %
/>,-100%
7
Квантили
ир.
В столбце 6 табл. 24 относительные накопленные частоты умно-
умножены на 100, так как в таблице приложения 10 эти частоты указа-
указаны в процентах.
х-а
х-а
Рис. 16
2. Построить в прямоугольной системе координат (х; и) точки
(x-i, Ui), (х2; и2), ... (значок р при квантилях опущен для простоты
записи). Если эти точки лежат вблизи некоторой прямой, то нет
оснований отвергнуть гипотезу о нормальном распределении X; если
же построенные точки удалены от прямой, то гипотезу отвергают.
Замечание 1. Следует иметь в виду, что «начальные» и «ко-
«конечные» точки (*,•; и/) могут заметно отклоняться от прямой
и=(х—а)/а.
260
Замечание 2. Если построенные точки оказались вблизи
прямой, то легко графически оценить параметры а и о нормального
распределения. В качестве оценки математического ожидания о можно
принять абсциссу точки L(xi\ 0) пересечения построенной прямой
с осью Ох. В качестве оценки среднего квадратического отклонения
о можно принять разность абсцисс точки L(xL; 0) и точки M(xjf, — I)
пересечения построенной линии с прямой н = — I: o*=*Xf—х,\
(рис. 16).
Замечание 3. При наличии вероятностной бумаги надобность
в отыскании квантилей отпадает: на соответствующей оси отклады-
откладывают накопленные относительные частоты.
641. Пусть метод спрямленных диаграмм подтверждает
гипотезу о нормальном распределении генеральной сово-
совокупности X, т. е. точки (,v(-; и,-) оказались вблизи прямой
и = (х—а)/о. (*)
а) Почему в качестве оценки математического ожида-
ожидания а нормального распределения можно принять абс-
абсциссу xL точки L пересечения прямой (*) с осью Ох
(рис. 16,о)?
б) Почему в качестве оценки среднего квадратического
отклонения нормального распределения можно принять
разность абсцисс xL—xN (рис. 16,6)?
Решение, а) В точке L пересечения прямой (*) с осью Ох
ордината ы = 0, абсцисса x=xi (рис. 16, а). Положив в уравнении
(*) « = 0, x=xi, получим
0 = (xL—a)/a.
Отсюда a=Jtf
б) Обозначим через N такую точку прямой (*), ордината кото-
которой и=—1; абсциссу этой точки обозначим через *,у Подставим
координаты точки N в уравнение (*):
— 1=(*дг— а)/а.
Отсюда о = а—x/f. Учитывая, что а = лсд, окончательно получим
o = xL—xy.
642. Из генеральной совокупности X извлечена вы-
выборка объема п = 100, которая задана в виде последова-
последовательности интервалов одинаковой длины и соответствую-
соответствующих им частот nt (П(—число вариант, попавших в 1-й
интервал). Эмпирическое распределение приведено в
табл. 25.
261
Таблица 25
Номер
интер-
интервала
(
1
2
3
4
5
6
Границы
интервала
1
3
5
7
9
11
*/
3
5
7
9
11
13
Частота
"/
2
4
6
10
18
20
Номер
интер-
интервала
i
7
8
9
10
11
Границы
интервала
13
15
17
19
21
Х1
15
17
19
21
23
Частота
"/
16
И
7
5
1
я = 100
Требуется: а) методом спрямленных диаграмм прове-
проверить гипотезу о нормальном распределении генеральной
совокупности Х\ б) оценить графически математическое
ожидание и среднее квадратическое отклонение X.
Решение, а) 1. Составим расчетную табл. 26. Квантили для
столбца 7 взяты из таблицы приложения 10.
Таблица 26
Номер
интер-
интервала
1
1
2
3
4
5
6
7
8
9
10
11
Правый
конец
интервала
3
5
7
9
И
13
15
17
19
21
23
Часто-
Частота
2
4
6
10
18
20
16
И
7
5
1
Накоплен-
Накопленная часто-
частота
1
Жпг
2
6
12
22
40
60
76
87
94
99
100
От носитель-
мая накоп-
ПС1Л llunvll
ленная ча-
частота
0,02
0,06
0,12
0,22
0,40
0,60
0,76
0,87
0,94
0,99
1,00
Относитель-
Относительней накоп-
накопленная ча-
частота. %
Р,: 100
2
6
12
22
40
60
76
87
94
99
100
Квантили
и
—2,054
—1,555
—1,175
—0,772
—0,253
0,253
0,706
1.126
1,555
2,326
3,09
2. Построим в прямоугольной системе координат точки (х-,; арЛ
(рис. 17). Построенные точки лежат вблизи прямой, поэтому нет
оснований отвергнуть гипотезу о нормальном распределении X. Дру-
Другими словами, данные выборки согласуются с этой гипотезой.
262
б) Найдем графически оценки математического ожидания и сред-
среднего квадратического отклонения предполагаемого нормального рас-
распределения.
В качестве оценки математического ожидания а примем абсцис-
абсциссу Х?. = 12,1 точки L пересечения построенной прямой с осью Ох.
Оценим а, для чего проведем через точку М @; —1) вертикаль-
вертикальной оси прямую « =—1 до пересечения с построенной прямой
в точке N; опустим из точки N перпендикуляр на ось Ох; абсцисса
Fhc. 17
основания этого перпендикуляра jcjv=8. В качестве оценки среднего
квадратического отклонения примем разность абсцисс:
a* = xL—xN= 12,1—8 = 4,1.
Разумеется, полученные оценки грубые. В действительности
а = 12,04; 0 = 4,261.
643. Из генеральной совокупности X извлечена вы-
выборка объема п =120, которая задана в виде последова-
последовательности интервалов одинаковой длины и соответствую-
соответствующих им частот (табл. 27).
Требуется: а) методом спрямленных диаграмм прове-
проверить гипотезу о нормальном распределении X; б) оценить
графически математическое ожидание и среднее квадра-
ти чес кое отклонение X.
644. Из генеральной совокупности X извлечена вы-
выборка объема л =100, заданная табл. 28.
263
Таблица 27
Номер
интер-
интервала
1
1
2
3
4
5
Граница
нитеркала
-1
5
10
15
20
30
10
15
20
25
35
Частота
"i
7
8
15
18
23
Номер
интер-
интервала
1
6
7
8
9
Граница
интерпала
30
35
40
45
*/
35
40
45
50
Частота
"/
19
14
10
6
я =120
Таблица 28
Номер
интер-
интервала
1
2
3
4
Граница
интерпала
6
16
26
36
Ч
16
26
36
46
Частота
8
16
7
15
Номер
интер-
интервала
1
5
6
7
8
Граница
интервала
«/-1
46
56
66
76
*,¦
56
66
76
86
Частота
35
6
5
8
л = 100
Требуется методом спрямленных диаграмм проверить ги-
гипотезу о нормальном распределении X.
Б. Несгруппированные по интервалам данные. Пусть эмпириче-
эмпирическое распределение выборки задано в виде последовательности вари-
вариант Xj, расположенных в возрастающем порядке, т. е. в виде вариа-
вариационного ряда, и соответствующих им частот я,-. Требуется графи-
графически проверить гипотезу о нормальном распределении X.
Правило 2. Для того чтобы по несгруппированной по интерва-
интервалам выборке объема п проверить гипотезу о нормальном распределе-
распределении генеральной совокупности X, из которой извлечена выборка, надо:
1. Составить расчетную табл. 29. Сразу укажем, что при за-
заполнении столбца 4 принято из суммы частот вычитать 1/2; зна-
значения квантилей для заполнения столбца 7 находят по таблице (см.
приложение 10).
2. Построить в прямоугольной системе координат точки (хх; Uj),
(хг; ut), ..., (xk; и*) (значок р при и опущен для простоты записи).
Если эти точки лежат вблизи некоторой прямой (в случае справед-
справедливости гипотезы о нормальном распределении X уравнение этой
прямой и — (х—хIаь), то нет оснований отвергнуть гипотезу о нор-
264
Таблица 29
1
Номер
вари-
варианты
i
2
Вари-
Варианта
*/
3
Ча-
Частота
ni
*
Накоп-
Накопленная
частота
5
Относитель-
Относительная накоп-
накопленная ча-
частота
F» /* л=—L
1 1) а
6 1
Относитель-
Относительная накоп-
накопленная ча-
частота, %
P,.=F' (,,)x
хюо
7
Квантили
"Pt
мольном распределении генеральной совокупности X; в противном
случае гипотезу отвергают.
Замечание 4. Замечания 1 —3, приведенные выше для сгруп-
сгруппированной по интервалам выборки, остаются в силе.
645. Из генеральной совокупности X извлечена вы-
выборка объема п = 50, несгруппированная по интервалам
(в первой строке указаны варианты, а во второй —соот-
—соответствующие частоты):
Xt 1,40 1,52 1,63 1,69 1,73 1,78 1,89 1,92 1,95
п(. 1 1 1 1 2 1 1 1 1
х, 1,98 1,99 2,03 2,07 2,12 2,16 2,20 2,23 2,26 2,31
л, 1 12 1321 1 13
х, 2,36 2,40 2,44 2,47 2,50 2,52 2,55 2,60 2,64
Я; 3 3 1 1 1 1 1 1 3
х, 2,71 2,74 2,78 2,86 2,93 3,02 3,30
п, 1 1 2 1 2 1 1
Требуется: а) методом спрямленных диаграмм прове-
проверить гипотезу о нормальном распределении X; б) оценить
графически математическое ожидание и среднее квадра-
тическое отклонение X.
Решение. 1. Составим расчетную табл. 30.
2. Построим в прямоугольной системе координат точки (х/, и,-)
(рис. 18). Построенные точки лежат вблизи прямой, поэтому нет
оснований отвергнуть гипотезу о нормальном распределении X; дан-
данные выборки согласуются с этой гипотезой.
б) Найдем графически, используя рнс. 18, оценки математиче-
математического ожидания и среднего квадратического отклонения предпола-
предполагаемого нормального распределения.
В качестве оценки математического ожидания а примем абсциссу
л:^ = 2,30 точки L пересечения построенной прямой с осью Ох.
265
1
HoMip
вари*
аита
i
1
2
3
4
5-6
7
8
9
10
11
12
13—14
15
16—18
19—20
21
22
23
24—26
27-29
30—32
33
34
35
36
37
38
39—41
42
43
44—45
46
47—48
49
50
2
Вари-
Варианта
1,40
,52
,63
,69
,73
,78
,89
,92
,95
,S8
,99
2,03
2,07
2,12
2,16
2,20
2,23
2,26
2,31
2,36
2,40
2,44
2,47
2,50
2,52
2,55
2,60
2,64
2,71
2,74
2,78
2,86
2,93
3,02
3
,30
3
Ча-
Частота
ni
i
!
3
3
3
1
1
1
1
1
1
3
1
1
2
1
2
1
1
4
Накопленная
частота минус
1
Т
г=|
0,5
1,5
2,5
3,5
5,5
6,5
7,5
8,5
9,5
10,5
11,5
13,5
14,5
17,5
19,5
20,5
21.5
22,5
25,5
28,5
31,5
32,5
33,5
34,5
35,5
36,5
37,5
40,5
41,5
42,5
44,5
45,5
47,5
48,5
49,5
6
Относитель-
Относительная накоп-
накопленная ча-
частота
F* л \- "'
\ /7 п
0,01
0,03
0,05
0,07
0,11
0,13
0,15
0,17
0,>9
0,21
0,23
0,27
0,29
0,35
0,39
0,41
0,43
0,45
0,51
0,57
0,63
0,65
0,67
0,69
0,71
0,73
0,75
0,81
0,83
0,85
0.8Э
0,91
0,95
0,97
0,99
Табл и
6
Относитель-
Относительная накоп-
накопленная ча-
частота. %
1
3
5
7
11
13
15
17
19
21
23
27
29
35
39
41
43
45
51
57
63
65
67
69
71
73
75
81
83
85
89
91
95
97
99
на 30
7
Квантили
UPi
—2.326
__
—
__
_
1,881
1,645
1,476
1,227
1,126
1,036
—0,954
-0,878
-0,806
—0,739
—0,613
-0,553
—0,385
-0,279
-0,228
—0,176
-0,126
0,025
0,176
0,332
0,385
0,440
0,496
0,553
0,613
0,674
0,878
0.954
,036
,227
,341
,645
,881
2,326
Оценим а, для чего проведем через точку М @; —1) вертикаль-
вертикальной оси прямую и =—1 до пересечения с построенной прямой линией
в точке Л'; опустим из точки N перпендикуляр на ось Ох; абсцисса
основания этого перпендикуляра лдг=1,9Э. В качестве оценки
266
среднего квадратического отклонения а примем разность абсцисс:
o=xL—xN =2,30—1,90=0,40.
Рис. 18
646. Из генеральной совокупности X извлечена вы-
выборка объема я = 50. Составлены следующие таблицы
(в первой строке указаны варианты, а во второй—соот-
второй—соответствующие частоты):
х, —20,0 —17,0 —14,1 —11,5 —10,5
п, 1 1 1 1 1
xt —9,0 —8,0 —6,5 —5,5
я, 1 1 1 1 •
х, —4,0 —3,0 —1,5 —1,0 0,0 0,5
п, 1 1 1 112»
х, 1,0 1,5 2,0 2,5 3,5 4,0 4,5
п, 1 1 2 1 1 2 1 !
х, 5,0 6,0 6,5 7,0 7,5 8,5 9,5 10,0 10,5 11,0 12,0 12,5
п, 2 1 1 2 2 2 1 11 1 1 1
xt 13,0 14,0 14,5 17,0 18,0 19,0 19,5 21,0 23,5
rt, 1 1 1 1 1 1 1 1 1
Требуется: а) методом спрямленных диаграмм прове-
проверить гипотезу о нормальном распределении генеральной
совокупности X; б) оценить графически математическое
ожидание и среднее квадратическое отклонение X.
Указание. Использовать таблицу квантилей (см. прило-
приложение 10).
267
§ 18. Проверка гипотезы о показательном
распределении генеральной совокупности
Задано эмпирическое распределение непрерывной случайной
величины X в виде последовательности интервалов лс,-—лс/+1 и соот-
соответствующих им частот п-„ причем 2Я'=Я (объем выборки). Тре-
Требуется, используя критерий Пирсона, проверить гипотезу о том,
что случайная величина X имеет показательное распределение.
Правило. Для того чтобы при уровне значимости а проверить
гипотезу о том, что непрерывная случайная величина распределена
по показательному закону, надо:
1. Найти по заданному эмпирическому распределению выбороч-
выборочную среднюю хв. Для итого, приняв в качестве «представителя»
i-го интервала его середину x*i = (je,-+*/+1)/2, составляют последо-
последовательность равноотстоящих вариант и соответствующих им частот.
2. Принять в качестве оценки параметра К показательного рас-
распределения величину, обратную выборочной средней:
3. Найти вероятности попадания X в частичные интервалы
*/+,) по формуле
4. Вычислить теоретические частоты:
n'i = ni-Pt,
где я=2я/— объем выборки.
5. Сравнить эмпирические и теоретические частоты с помощом
критерия Пирсона, приняв число степеней свободы k = s—2, где s —
число первоначальных интервалов выборки; если же было произведено
объединение малочисленных частот, следовательно, и самих интер-
интервалов, то s—число интервалов, оставшихся после объединения.
647. Почему при проверке по критерию Пирсона
гипотезы о показательном распределении генеральной
совокупности число степеней свободы определяется равен-
равенством k = s—2, где s—число интервалов выборки?
Решение. При использовании критерия Пирсона число сте -
пеней свободы k=s—1—г, где г — число параметров, оцениваемых
по выборке. Показательное распределение определяется одним пара-
параметром к. Так как этот параметр оценивается по выборке, то г — \
и, следовательно, число степеней свободы k=s—1—1 =s—2.
648. В результате испытания 200 элементов на дли-
длительность работы получено эмпирическое распределение,
приведенное в табл. 31 (в первом столбце указаны ин-
интервалы времени в часах, во втором столбце—частоты,
т. е. количество элементов, проработавших время в пре-
пределах соответствующего интервала).
268
Таблица 31
0-5
5—10
10-15
133
45
15
*/"*/+1
15—20
20-25
25-30
4
2
1
Требуется, при уровне значимости 0,05, проверить
гипотезу о том, что время работы элементов распределено
по показательному закону.
Решение 1. Найдем среднее время работы всех элементов
(в качестве среднего времени работы одного элемента примем сере-
середину интервала, которому принадлежит элемент):
хв = A33-2,5+45-7,5+15-12,5+4-17,5+2.22,5+Ь27,5)/200 =
= 1000/200=5.
2. Найдем оценку параметра предполагаемого показательного
распределения:
Я, = 1/*в = 1/5=0,2.
Таким образом, дифференциальная функция предполагаемого пока-
показательного распределения имеет вид
3. Найдем вероятности попадания X в каждый из интервалов
по формуле
Например, для первого интервала
Р,=Р@ < X < 5) = е-°>2-°— е-°'8>» = 1-е-1 =
= 1—0,3679=0,6321.
Аналогично вычислим вероятности попадания X в остальные
интервалы: Рг =0,2326; Ps =0,0855; Р4 =0,0315; Р»=0,0116;
Р„ =0,0042.
4. Найдем теоретические частоты:
/ц' = пР,=200Р/,
где Р,— вероятность попадания X в 1-й интервал.
Например, для первого интервала
п[ =200 Pt = 200 0,6321 = 126,42.
Аналогично вычислим остальные теоретические частоты:
/4 = 46,52; яз = 17,10; п, =6,30; /te=2,32; n't=0,84.
5. Сравним эмпирические и теоретические частоты с помощью
критерия Пирсона. Для этого составим расчетную таблицу 32, при-
269
чем объединим малочисленные частоты D+2+1=7) и соответст-
соответствующие им теоретические частоты F,30+2,32+0,84=9,46).
Таблица 32
1
2
3
4
2
nl
133
45
15
7
л=200
-
126
46
17
9
(
.42
,52
,10
.46
пгп\
6,58
-1,52
—2,10
—2,46
43
2
4
6
,2964
,3104
,4100
,0516
(¦/-Л1
0,3425
0,0497
0,2579
0,6397
Хнабл = 1.29
Замечание. Для упрощения вычислений в случае объеди-
объединения малочисленных частот целесообразно объединить и самн интер-
интервалы, которым принадлежат малочисленные частоты, в один интервал.
Так, в рассматриваемой задаче, объединив последние три интервала,
иолучим один интервал A5, 30). В этом случае теоретическая
частота
n't = nP A5 < X < 30) =200-0,0473 = 9,46
совпадает с суммой теоретических частот (9,46), приведенной в табл. 32.
Из табл. 32 находим: Хиабл —1,29. По таблице критических
точек распределения хг (см. приложение 5), по уровню значимости
а=0,05 и числу степеней свободы * = s—2=4—2=2 находим крити-
критическую точку правосторонней критической области Хкр @,05; 2) =6,0.
Так как Хнабл < Хкр—нет оснований отвергнуть гипотезу о рас-
распределении X по показательному закону. Другими словами, данные
наблюдений согласуются с этой гипотезой.
649. В итоге испытания 450 ламп было получено
эмпирическое распределение длительности их горения,
приведенное в табл. 33 (в первом столбце указаны интер-
0—400
400—800
800—1200
1200—1600
121
95
76
56
*rxi+i
1600-2000
2000-2400
2400-2800
Таблица 33
ni
45
36
21
л = 450
270
валы в часах, во втором столбце—частота n!t т. е. коли-
количество ламп, время горения которых заключено в пределах
соответствующего интервала).
Требуется при уровне значимости 0,01 проверить
гипотезу о том, что время горения ламп распределено по
показательному закону.
650. В итоге испытаний 1000 элементов на время
безотказной работы получено эмпирическое распределение,
приведенное в табл. 34 (в первом столбце указаны интер-
интервалы времени в часах; во втором столбце—частота п,-,
т. е. количество отказавших элементов в i-м интервале).
Таблица 34
*t-xi+l
0—10
10-20
20-30
30-40
365
245
150
100
40—50
50-60
60-70
70
45
25
л = 1000
Требуется при уровне значимости 0,01 проверить
гипотезу о том, что время безотказной работы элементов
распределено по показательному закону.
651. В итоге регистрации времени прихода 800 посе-
посетителей выставки (в качестве начала отсчета времени
принят момент открытия работы выставки) получено
эмпирическое распределение, приведенное в табл. 35
(в первом столбце указаны интервалы времени; во втором
столбце—частоты п{, т. е. количество посетителей, при-
пришедших в течение соответствующего интервала).
Таблица 35
xi~*i+i
0-1
1—2
2-3
3-4
259
167
109
74
xr*i+i
4—5
5-6
6-7
7-8
70
47
40
34
800
271
Требуется при уровне значимости 0,01 проверить
гипотезу о том, что время прихода посетителей выставки
распределено по показательному закону.
§ 19. Проверка гипотезы о распределении
генеральной совокупности по биномиальному закону
Произведено п опытов. Каждый опыт состоит из N независимых
испытаний, в каждом из которых вероятность появления события А
одна н та же. Регистрируется число появлений события А в каж-
каждом опыте. В итоге получено следующее распределение дискретной
случайной пеличины л—числа появлений события А (ч первой
строке указано число лс,- появлений события А в одном опыте; во
второй строке—частота щ, т. е. число опытов, в которых зарегист-
зарегистрировано х/ появлений события А):
xi 0 1 2 ... N
я,- 0 1 2 ... п.ц
Требуется, используя критерий Пирсона, проверить гипотезу
о распределении дискретной случайной величины X по биномиаль-
биномиальному закону.
Правило. Для того чтобы при уровне значимости а проверить
гипотезу о том, что дискретная случайная величина X (число
появлений события А) распределена по биномиальному закону, надо:
1. Найти по формуле Бернулли вероятности Р/ появления ровно i
событий А в N испытаниях ((=0, 1, 2, ..., s, где s—максимальное
число наблюдавшихся появлений события А в одном опыте, m.e.s< N).
2. Найти теоретические частоты
n'i=n-Pi,
где п—число опытов.
3. Сравнить эмпирические и теоретические частоты по крите-
критерию Пирсона, приняв число степеней свободы k = s—1 (при этом пред-
предполагается, что вероятность р появления события А задана, т. е.
не оценивалось по выборке и не производилось объединение малочис-
малочисленных частот).
Если же вероятность р была оценена по выборке, то k = s—2.
Если, кроме того, было произведено объединение малочисленных
частот, то s—число групп выборки, оставшихся после объединения
частот.
652. Произведено п =100 опытов. Каждый опыт со-
состоял из N = 10 испытаний, в каждом из которых
вероятность р появления события А равна 0,3. В итоге
получено следующее эмпирическое распределение (в пер-
первой строке указано число xt появлений события А в одном
опыте; во второй строке—частота nt, т. е. число опытов,
в которых наблюдалось х{ появлений события А):
xs 0 1 2 3 4 5
nt 2 10 27 32 23 6
272
Требуется при уровне значимости 0,05 проверить
гипотезу о том, что дискретная случайная величина X
(число появлений события А) распределена по бино-
биномиальному закону.
Решение. 1. По формуле Бернулли
найдем вероятность Р;(»=0, 1, 2, 3, 4, 5) того, что событие А
появится в Л/= 10 испытаниях ровно i раз.
Учитывая, что р=0,3, 9 = 1—0,3=0,7, получим:
/>о = />ю@)=0,710=0,0282; Р,=РHA) = 10-0,3 0,7» =0,1211.
Аналогично вычислим: Р8=0,2335; Ps=0,2668; Р4= 0,2001; Р8 =
= 0,1029.
2. Найдем теоретические частоты щ = п-Р,-. Учитывая, что
л=100, получим: пЦ=2,82; п[ = \2,\\; /12 = 23,35; лз=26,68;
/ц =20,01; «5 = 10,29.
3. Сравним эмпирические и теоретические частоты с помощью
критерия Пирсона. Для этого составим расчетную табл. 36. Поскольку
частота яо=2 малочислеиная (меньше пяти), объединим ее с часто-
частотой /ti = 10 и в таблицу запишем 2+10 = 12; в качестве теоретиче-
теоретической частоты, соответствующей объединенной частоте 12, запишем
сумму соответствующих теоретических частот: /io+ «1 = 2,82 +
+ 12,11=14,93.
Таблица 36
1
2
3
4
5
2
¦/
12
27
32
23
6
я = 100
л'
14,93
23,35
26,68
20,01
10,29
пГп1
-2,93
3,65
5,32
2,99
-4,29
8,5849
13,3225
28,3024
8,9401
18,4041
0,5750
0,5706
1,0608
0,4468
1,7886
Хнабл = 4,44
Из табл. 36 находим Хнабл = 4,44.
По таблице критических точек распределения у} по уровню
значимости а=0,05 и числу степеней свободы А=5— 1 =4
находим критическую точку правосторонней критической области
Хкр@,05; 4) =9,5.
Так как Хнабл < Хкр—нет оснований отвергнуть гипотезу о бино-
биномиальном распределении X.
273
653. Опыт, состоящий в одновременном подбрасывании
четырех монет, повторили 100 раз. Эмпирическое рас-
распределение дискретной случайной величины X — числа
появившихся «гербов»—оказалось следующим (в первой
строке указано число х,- выпавших «гербов» в одном
бросании монет; во второй строке—частота п,-, т. е. число
бросаний, при которых выпало х, «гербов»):
х, 0 1 2 3 4
п, 8 20 42 22 8
Требуется при уровне значимости 0,05 проверить
гипотезу о том, что случайная величина X распределена
но биномиальному закону.
Указание. Принять вероятность выпадения «герба» р=0,5.
654. Отдел технического контроля проверил п=100
партий изделий по #=10 изделий в каждой партии и
получил следующее эмпирическое распределение дискрет-
дискретной случайной величины X — числа нестандартных изде-
изделий (в первой строке указано число х,- нестандартных
изделий в одной партии; во второй строке—частота п,-,
т. е. количество партий, содержащих х,- нестандартных
изделий):
0
2
1
3
2
10
3
22
4
26
5
20
6
12
7
5
Требуется при уровне значимости 0,01 проверить
гипотезу о том, что случайная величина X распределена
по биномиальному закону.
Указания. 1. Найти сначала относительную частоту появ-
появления нестандартных изделий и принять ее в качестве «оценки р*
вероятности того, что паудачу взятое изделие окажется нестандартным.
2. При составлении расчетной таблицы для сравнения эмпири-
эмпирических и теоретических частот с помощью критерия Пирсона сле-
следует объединить эмпирические частоты B+3=5) и соответствующие
им теоретические частоты @,60 + 4,03=4,63); учесть, что после
объединения частот число групп выборки s=7.
3. Один параметр (вероятность р) оценивался по выборке, поэтому
при определении числа степеней свободы надо вычесть из s не еди-
единицу, а два: s—2=7—2 = 5.
655. В библиотеке случайно отобрано 200 выборок
по 5 книг. Регистрировалось число поврежденных книг
(подчеркивания, помарки и т. д.). В итоге получено
следующее эмпирическое распределение (в первой строке
указано число X; поврежденных книг в одной выборке;
274
во второй строке—частота nh т. е. количество выборок,
содержащих х{ поврежденных книг):
х, 0 1 2 3 4 5
п, 72 77 34 14 2 1
Требуется, используя критерий Пирсона, при уровне
значимости 0,05 проверить гипотезу о том, что дискрет-
дискретная случайная величина X (число поврежденных книг)
распределена по биномиальному закону.
Указание. Принять во внимание указания к задаче 654.
§ 20. Проверка гипотезы о равномерном распределении
генеральной совокупности
Задано эмпирическое распределение непрерывной случайной
величины X в виде последовательности интервалов */_i—х,- и соот-
соответствующих им частот я/, причем 2Я/Г=Я (объем выборки). Тре-
Требуется, используя критерий Пирсона, проверить гипотезу о том,
что случайная величина Л распределена равномерно.
Правило. Для того чтобы проверить гипотезу о равномерном
распределении X, т. е. по закону
f \l(b—a) в интервале (а, Ъ),
\ 0 вне интервала (а, Ь),
надо:
1. Оценить параметры а и Ь—концы интервала, в котором
наблюдались возможные значения X, по формулам (через а* и Ь*
обозначены оценки параметров):
а* =ИВ—VJ ов, Ь*
2. Найти плотность вероятности предполагаемого распределения
f(x)=\l(b*-a*).
3. Найти теоретические частоты:
= ns-t = n-jz—-»(*/—*i-i). («=2. 3, .... s —1);
4. Сравнить эмпирические и теоретические частоты с помощью
критерия Пирсона, приняв число степеней свободы k = s—3, где s —
число интервалов, на которые разбита выборка.
656. Почему параметры а и Ь равномерно распреде-
распределенной случайной величины X оцениваются по формулам
a* =~xB-VJaB, b* = xB+V3~oBl
275
Решен и е. Известно, что в качестве оценок математического
ожидания и среднего квадратнческого отклонения случайной вели-
величины X можно принять соответственно выборочную среднюю ~хв и
еыбирочное среднее квадратическое отклонение ов.
Известно также (см. гл. VI, задачи 313, 315), что для равно-
равномерного распределения математическое ожидание и среднее квадра-
квадратическое отклонение соответственно равны:
М(Х) = (а-\-Ь)/2, а(Х)= VW{X)=V(b—aJ,12= (Ь—а)/2 У~3.
Поэтому для оценки параметров равномерного распределения полу-
получаем систему двух линейных уравнений
( (Ь*— а*)/2=~хв, | Ь9-\-а*=2х~в,
\ - или : _
\ (Ь*—а*I2 УЗ =ов, \ Ь*—а*=2 \Гз<5в.
Решив эту систему, получим а*=хв—У~3 ав, Ь* =хв-г Уз ав.
657. Почему при проверке с помощью критерия
Пирсона гипотезы о равномерном распределении гене-
генеральной совокупности X число степеней свободы опре-
определяется из равенства k = s—3, где s—число интервалов
выборки?
Решение. При использовании критерия Пирсона число сте-
степеней свободы k=s— 1— г, где г—число параметров, оцениваемых
по выборке. Равномерное распределение определяется двумя пара-
параметрами а и Ь. Так как эти два параметра оцениваются по выборке,
то г=2 и, следовательно, число степеней свободы?=8 — 1—2 = s—3.
658. Произведено п = 200 испытаний, в результате
каждого из которых событие А появлялось в различные
моменты времени. В итоге было получено эмпирическое
распределение, приведенное в табл. 37 (в первом столбце
указаны интервалы времени в минутах, во втором столбце—
соответствующие частоты, т. е. число появлений события
А в интервале). Требуется при уровне значимости 0,05
проверить гипотезу о том, что время появления событий
распределено равномерно.
Таблица 37
Интервал
*/_,-*/
2-4
4-6
6-8
8—!0
10-12
Частота
п1
21
16
15
26
22
Интервал
xi-\-*i
12-14
14-16
16—18
18—20
20—22
Частота
Л|
14
21
22
18
25
276
Решение. 1. Найдем оценки параметров а и b равномерного
распределения по формулам:
Для вычисления выборочной средней хв и выборочного сред-
среднего квадратического отклонения ов примем середины х\ интервалов
в качестве вариант (наблюдаемых значений X). В итоге получим
эмпирическое распределение равноотстоящих вариант:
х* 3 5 7 9 11 13 15 17 19 21
л,- 21 16 15 26 22 14 21 22 18 25
Пользуясь, например, методом произведений, найдем: х~в= 12,31,
ов = 5,81. Следовательно,
а* = 12,31—1,73-5,81=2,26, Ь* = 12,31 + 1,73-5,81 =22,36.
2. Найдем плотность предполагаемого равномерного распре-
распределения:
f(x) = \l(b*-a*)= 1/B2,36-2,26) =0,05.
3. Найдем теоретические частоты:
я;=п./(х)-(*1-а*)=200-0,05-D-2,26) = 17,4;
П2=200-0,05-(*2—*,) = 10-F —4) = 20.
Длины третьего—девятого интервалов равны длине второго
интервала, поэтому теоретические частоты, соответствующие этим
интервалам и теоретическая частота второго интервала одинаковы, т. е.
/tio = 2OO.O,O5-(&*— je,)=10-B2,36—20) =-23,6.
4. Сравним эмпирические и теоретические частоты, используя
критерий Пирсона, приняв число степеней свободы k = s—3 =
= ю—3 = 7. Для этого составим расчетную табл. 38.
Таблица 38
i
\
2
3
4
5
6
7
8
9
10
21
16
15
26
22
14
21
22
18
25
17,3
20
20
20
20
20
20
20
20
23,6
3,7
—4
—5
6
2
-6
1
2
—2
1,4
к-»;)8
13,69
16
25
36
4
36
1
4
4
1,96
0,79
0,80
1,25
1,80
0,20
1,80
0.05
0,20
0,20
0,08
277
Из расчетной таблицы получаем х5абл = ^''^
Найдем по таблице критических точек распределения х2 (см-
приложение 5) по уровню значимости а=0,05 и числу степеней
свободы k = s—3= 10—3 = 7 критическую точку правосторонией кри-
критической области ХкР(°>05; 7) = 14,1.
Так как Х^абл< ХкР~нет оснований отвергнуть гопотезу о
равномерном распределении X. Другими словами, данные наблюде-
наблюдений согласуются с этой гипотезой.
659. В результате взвешивания 800 стальных шари-
шариков получено эмпирическое распределение, приведенное
в табл. 39 (в первом столбце указан интервал веса
в граммах, во втором столбце—частота, т. е. количество
шариков, вес которых принадлежит этому интервалу).
Требуется при уровне значимости 0,01 проверить
гипотезу о том, что вес шариков X распределен равно-
равномерно.
Таблица 39
*l-t-*i
20,0—20,5
20,5—21,0
21,0—21,5
21.5—22,0
22,0—22,5
22,5—23,0
"/
91
76
75
74
92
83
"i-i-'i
23,0—23,5
23,5—24,0
24,0—24,5
24,5—25,0
79
73
80
77
п =- 800
660. В некоторой местности в течение 300 сут ре-
регистрировалась среднесуточная температура воздуха.
В итоге наблюдений было получено эмпирическое распре-
распределение, приведенное в табл. 40 (в первом столбце
указан интервал температуры в градусах, во втором
столбце—частота п{, т. е. количество дней, среднесу-
среднесуточная температура которых принадлежит этому интер-
интервалу).
Таблица 40
_40—(—30)
—30-(—20)
—20—(—10)
—10—0
25
40
30
45
0—10
10—20
20—30
30—40
40
46
48
26
278
Требуется при уровне значимости 0,05 проверить
гипотезу о том, что среднесуточная температура воздуха
распределена равномерно.
661. В течение 10 ч регистрировали прибытие авто-
автомашин к бензоколонке и получили эмпирическое рас-
распределение, приведенное в табл. 41 (в первом столбце
указан интервал времени в часах, во втором столбце —
частота, т. е. количество машин, прибывших в этом
интервале). Всего было зарегистрировано 200 машин.
Таблица 41
8—9
9—10
10—11
11—12
12-13
12
40
22
16
28
13—14
14—15
15—16
16—17
17—18
"i
6
11
33
18
14
Требуется при уровне значимости 0,01 проверить
гипотезу о том, что время прибытия машин распределено
равномерно.
§ 21. Проверка гипотезы о распределении
генеральной совокупности по закону Пуассона
Задано эмпирическое распределение дискретной случайной ise-
личины X. Требуется, используя критерий Пирсона, проверить ги-
гипотезу о распределении генеральной совокупности по закону Пуас-
Пуассона.
Правило. Для того чтобы при уровне значимости а проверить
гипотезу о том, что случайная величина X распределена по закону
Пуассона, надо:
1. Найти_по заданному эмпирическому распределению выбороч-
выборочную среднюю хв.
2. Принять в качестве оценки параметра к распределения
Пуассона выборочную среднюю Х = хв,
3. Найти по формуле Пуассона (или по готовым таблицам)
вероятности Pi появления ровно i событий в п испытаниях (»-=
= 0, 1, 2 г, где г—максимальное число наблюдавшихся со-
событий; п—объем выборки).
4. Найти теоретические частоты по формуле п\=-п-Р(.
5. Сравнить эмпирические и теоретические частоты с помощью
критерия Пирсона, приняв число степеней свободы k = s—2, л)е
s—число различных групп выборки (если производилось объединение
малочисленных частот в одну группу, то s—число оставшихся групп
выборки после объединения частот).
662. Отдел технического контроля проверил п = 200
партий одинаковых изделий и получил следующее эмпи-
279
рическое распределение (в первой строке указано коли-
количество Xf нестандартных изделий в одной партии; во
второй строке—частота «,-, т. е. количество партий,
содержащих xt нестандартных изделий);
я,- О 12 3 4
nt 116 56 22 4 2
Требуется при уровне значимости 0,05 проверить
гипотезу о том, что число нестандартных изделий X
распределено по закону Пуассона.
Решение. 1. Найдем выборочную среднюю:
2. Примем в качестве оценки параметра к распределения Пуас-
соиа выборочную среднюю: к — 0,6. Следовательно, предполагаемый
закон Пуассона
P(i) ki
имеет вид
/>гоо(')=(О.6)'е-».в/П.
3. Положив / = 0, 1, 2, 3, 4, найдем вероятности Р/ появле-
появления i нестандартных изделий в 200 партиях:
Л» = ^«00@)=0,5488; Р1=Рт@=0.3293; Р2=Р2ОоB)=0,0988;
Р3 = /W3) = 0,0198; Р4 = Р200 D) = 0,0030.
4. Найдем теоретические частоты по формуле
Подставив в эту формулу найденные в п. 3 значения вероят-
вероятностей Р/, получим п'а = 200 0,5488 = 109,76.
Аналогично найдем: п(=65,86; <= 19,76; п'3 =3,96; п'4 = 0,60.
5. Сравним эмпирические и теоретические частоты с помощью
критерия Пирсона. Для этого составим расчетную табл. 42. Учиты-
Учитывая замечание I (см. $ 16), объединим малочисленные частоты
D+2=6) и соответствующие им теоретические частоты C,96+0,60 =
= 4,56), результаты объединения частот запишем в табл. 42.
Таблица 42
1
i
0
1
2
3
2
г
-I
116
56
22
6
200
э
"l
109,76
65,86
19,76
4,56
4
Т
6.
-9.
2.
1,
24
86
24
44
с
38
97
2
б
-;,•
,9376
,2196
,0176
,0736
(V
0
1
0
0
xLc
в
-у/.;
,3548
,4762
,2539
,4547
.=2.54
280
Из расчетной таблицы находим наблюдаемое значение критерия
Пирсона: Х*абл=2,54.
По таблице критических точек распределения х2 (см- прило-
приложение 5), по уровню значимости а=0,05 и числу степеней свободы
Л- --= 4—2=2 находим критическую точку правосторонней критической
области: ХкР@.05; 2) = 6,0.
Так как Хнабл < Хкр—нет оснований отвергнуть гипотезу о
распределении случайной величины X по закону Пуассона.
663. В итоге проверки на нестандартность 200 ящи-
ящиков консервов получено следующее эмпирическое распре-
распределение (в первой строке указано количество xt нестан-
нестандартных коробок консервов в одном ящике; во второй
строке —частота и,, т. е. число ящиков, содержащих .г,-
коробок нестандартных консервов):
х,- 0 12 3 4
и, 132 43 20 3 2
Требуется при уровне значимости 0,05 проверить
гипотезу о том, что случайная величина X— число не-
нестандартных коробок — распределена по закону Пуассона.
Указание. Объединить малочисленные частоты двух послед-
последних групп.
664. Для определения засоренности партии семян
клевера семенами сорняков было проверено 1000 слу-
случайно отобранных проб и получено следующее эмпири-
эмпирическое распределение (в первой строке указано коли-
количество X/ семян сорняков в одной пробе; во второй
строке—частота щ, т. е. число проб, содержащих xt
семян сорняков):
х( 0 1 2 3 4 5 6
пх. 405 366 175 40 8 4 2
Требуется при уровне значимости 0,01 проверить ги-
гипотезу о том, что случайная величина X (число семян
сорняков) распределена по закону Пуассона.
Указание. Объединить малочисленные частоты последних
двух групп.
665. В результате эксперимента, состоящего из и =
= 1000 испытаний, в каждом из которых регистрирова-
регистрировалось число jc,- появлений некоторого события, получено
следующее эмпирическое распределение (в первой строке
указано количество jc,- появлений события; во второй
281
строке—частота я,, т. е. число испытаний, в которых
наблюдалось х( появлений события):
jc,- О 1 2 3 4 5
tit 505 336 125 24 8 2
Требуется при уровне значимости 0,05 проверить ги-
гипотезу о том, что случайная величина X—число появ-
появлений события — распределена по закону Пуассона.
Указание. Объединить частоты двух последних групп.
666. В результате проверки 500 контейнеров со стек-
стеклянными изделиями установлено, что число поврежден-
поврежденных изделий X имеет следующее эмпирическое распре-
распределение (в первой строке указано количество х{ повреж-
поврежденных изделий в одном контейнере; во второй строке
частота л,, т. е. число контейнеров, содержащих xt
поврежденных изделий):
дг,0 1 234567
nt 199 169 87 31 9 3 1 1
Требуется при уровне значимости 0,01 проверить
гипотезу о том, что случайная величина X—число по-
поврежденных изделий — распределена по закону Пуассона.
У казан и е. Объединить частоты трех последних групп.
667. Задача Борткевича. На основании 200 донесе-
донесений, полученных в течение двадцати лет о количестве
кавалеристов прусской армии, которые погибли в ре-
результате гибели под ними коня, было получено следую-
следующее эмпирическое распределение (в первой строке ука-
указано количество х( погибших кавалеристов, указанных
в одном донесении; во второй строке—частота и,-, т. е.
число донесений, в которых сообщено о гибели .v,- кава-
кавалеристов):
х, 0 12 3 4
я, 109 65 22 3 1
Требуется при урозне значимости 0,05 проверить
гипотезу о распределении случайной величины X (числа
погибших кавалеристов) по закону Пуассона.
Указание. Объединить малочисленные частоты 3 и 1 в одну.
282
Глава четырнадцатая
ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
§ 1. Одинаковое число испытаний на всех уровнях
Пусть на количественный нормально распределенный признак X
воздействует фактор F, который имеет р постоянных уровней Flt
Ft. •••, Fp. На каждом уровне произведено по q испытаний. Резуль-
Результаты наблюдений—числа(x/j, где i— номер) испытания (i = l, 2
..., q), I—номер уровня фактора (/ = 1, 2, .... р),— записывают
в виде таблицы (табл. 43).
Таблица 43
Номер испытания
1
1
2
Я
Групповая средняя хгр
Уровни фактора
F,
Хц
Хц
Xq\
*rpl
F,
X\t
Хм
Xqt
*гр*
...
...
• • •
х1р
Xtp
Xqp
xrvp
Ставится задача: на уровне значимости а проверить нулевую
гипотезу о равенстве групповых средних при допущении, что груп-
групповые генеральные дисперсии хотя и неизвестны, но одинаковы.
Для решения этой задачи вводятся: общая сумма квадратов откло-
отклонений наблюдаемых значений признака от общей средней
С (*,/-*)*;
"общ ¦
факторная сумма квадратов отклонений групповых средних от об-
общей средней (характеризует рассеяние «между группами»)
р _ _
5фа«ет=<7 S (*гр/—*)*:
остаточная сумма квадратов отклонений наблюдаемых значений
группы от своей групповой средней (характеризует рассеяние «внутри
групп»)
$ост = 2 (хп —*rpiJ
Практически остаточную сумму находят по формуле
Soei ==^общ—"факт*
283
Для вычисления общей и факторной сумм более удобны сле-
следующие формулы:
/ - [ Jj Я/]
= Jj R'i/Ч ~ [ Jj
где Р/= 2 Al~сумма квадратов наблюдаемых значений признака
на уровне Ff, Rj=2jX;j—сумма наблюдаемых значений признака
на уровне F/.
Если наблюдаемые значения признака—сравнительно большие
числа, то для упрощения вычислений вычитают из каждого наблю-
наблюдаемого значения одно и то же число С, примерно равное общей
средней. Если уменьшенные значения у//=дс;/—С, то
Q/=S !/Ь—
где Q/=S !/Ь—сумма квадратов уменьшенных значений признака
на уровне F/\ Т/= 2*Уи—сумма уменьшенных значений признака
на уровне Fj.
Разделив уже вычисленные факторную и остаточную суммы на
соответствующее число степеней свободы, находят факторную и оста-
остаточную дисперсии:
^ -i "ост
SocT p(q-l) '
Наконец, сравнивают факторную и остаточную дисперсии по
критерию Фишера—Снедекора (см. гл. XIII, § 2).
Если /'набл < ^кр—различие групповых средних незначимое.
Если /^найл > ^кр—различие групповых средних значимое.
Замечание 1. Если факторная дисперсия окажется меньше
остаточной, то уже отсюда непосредственно следует справедливость
нулевой гипотезы о равенстве групповых средних, поэтому дальней-
дальнейшие вычисления (сравнение дисперсий с помощью критерия F) из-
лишнн.
Замечание 2. Если наблюдаемые значения *//—десятичные
дроби с к знаками после запятой, то целесообразно перейти к це-
целым числам
где С—примерно среднее значение чисел \0kx,j. При этом фактор-
факторная и остаточная дисперсия увеличатся каждая в 102* раз, однако
их отношение ие изменится,
284
668. Произведено по четыре испытания на каждом
из трех уровней фактора F. Методом дисперсионного
анализа при уровне значимости 0,05 проверить нулевую
гипотезу о равенстве групповых средних. Предполагается,
что выборки извлечены из нормальных совокупностей
с одинаковыми дисперсиями. Результаты испытаний при-
приведены в табл. 44.
Таблица 44
Номер испытания
1
2
3
4
*гр/
Уровни фактора
/\
38
36
35
31
35
F,
20
24
26
30
25
F,
21
22
31
34
27
Решение. Для упрощения расчета вычтем из каждого наблю-
наблюдаемого значения х,у общую среднюю д-=29, т. е. перейдем к умень-
уменьшенным величинам: у/,=дс,/—29. Например, уп=хп—29=38 —
— 29 = 9; уи=хп— 29=36—29 = 7 и т. д.
Составим расчетную табл. 45.
Таблица 45
Номер
испытания
i
1
2
3
4
'V"
Уровни фактора
F,
«п
9
7
6
2
24
576
»8д
81
49
36
4
170
F,
«п
—5
—3
1
-16
256
у%
81
25
9
1
116
F,
»ts
—8
—7
2
5
-8
64
У\г
64
49
4
25
142
Итоговый
столбец
2Qy=428
Используя итоговый столбец табл. 45, найдем общую и фактор-
факторную суммы квадратов отклонений, учитывая, что число уровней
285
фактора р = 3, число испытаний на каждом уровне q — 4:
Найдем остаточную сумму квадратов отклонений:
Soct=So6iu—S«t>aKT = 428—224 = 204.
Найдем факторную дисперсию; для этого разделим 5факт на
число степеней свободы р—1=3—1=2:.
s|aKT=S.,,aKr/(p-l)=224/2 = 112.
Найдем остаточную дисперсию; для этого разделим S0CT на
число степеней свободы p{q —1) = 3D—1)=9:
«Зет = Soc ,/p (q -1) = 204/9=22,67.
Сравним факторную и остаточную дисперсии с помощью крите-
критерия Фишера—Снедекора (см. гл. XIII, § 2). Для этого сначала
найдем наблюдаемое значение критерия:
F „абл = 4жт/4ег = 112/22,67 = 4,94.
Учитывая, что число степеней свободы числителя #i=2, а зна-
знаменателя kt = 9 и что уровень значимости а=0,05, по таблице
приложения 7 находим критическую точку
FKp@,05; 2; 9) = 4.26.
Так как /^абл > ^кр—нулевую гипотезу о равенстве групповых
средних отвергаем. Другими словами, групповые средние «в целом»
различаются значимо.
669. Произведено по пять испытаний на каждом
из четырех уровней фактора F. Методом дисперсионного
анализа при уровне значимости 0,05 проверить нулевую
гипотезу о равенстве групповых средних xrvf. Предпо-
Предполагается, что выборки извлечены из нормальных сово-
совокупностей с одинаковыми дисперсиями. Результаты испы-
испытаний приведены в табл. 46.
Указание. Принять yij=x;j—58.
670. Произведено по восемь испытаний на каждом
из шести уровней фактора. Методом дисперсионного ана-
анализа при уровне значимости 0,01 проверить нулевую
гипотезу о равенстве групповых средних. Предполагается,
что выборки извлечены из нормальных совокупностей
с одинаковыми дисперсиями. Результаты испытаний при-
приведены в табл. 47.
Указание. Принять уц =*,•/—100.
286
Таблица 46
Номер
испытания
1
1
2
3
4
5
Ft
36
47
50
58
67
51,6
Уровни
F,
56
61
64
66
66
62,6
фактора
F,
52
57
59
58
79
61,0
Ft
39
57
63
61
65
57,0
Таблица 47
Номер
испытания
>
1
2
3
4
5
6
7
8
Ft
100
101
126
128
133
141
147
148
128
F,
92
102
104
115
119
122
128
146
116
Уровни
F,
74
87
88
93
94
101
102
105
93
фактора
F,
68
80
83
87
96
97
106
127
93
F.
64
83
83
84
90
96
101
111
89
F,
69
71
80
80
81
82
86
99
81
671. Произведено по четыре испытания на каждом из
трех уровней фактора F. Методом дисперсионного ана-
анализа при уровне значимости 0,05 проверить нулевую
гипотезу о равенстве групповых средних. Предполагается,
что выборки извлечены из нормальных совокупностей
с одинаковыми дисперсиями. Результаты испытаний при-
приведены в табл. 48.
287
Номер испытания
i
1
2
3
4
*.р/
Л
35
32
31
30
32
Т
абл
Уровни фактора
F,
30
24
26
20
25
ица 48
F,
21
22
34
31
27
Указание. Принять уу = ху—28.
672. Произведено по семь испытаний на каждом из
четырех уровней фактора. Методом дисперсионного ана-
анализа при уровне значимости 0,05 проверить нулевую
гипотезу о равенстве групповых средних. Предполагается,
что выборки извлечены из нормальных совокупностей
с одинаковыми дисперсиями. Результаты испытаний при-
приведены в табл. 49.
Таблица 49
Номер испытания
/
1
2
3
4
5
6
7
F,
51
59
53
59
63
69
72
60,9
Уровни
F,
52
58
66
69
70
72
74
65,9
фактора
F,
56
56
58
58
70
74
78
64,3
F,
54
58
62
64
66
67
69
62,9
Указание. Принять у^ = хц—63. Воспользоваться замеча-
замечанием 1.
673. Произведено по четыре испытания на каждом из
трех уровней фактора. Методом дисперсионного анализа
при уровне значимости 0,05 проверить нулевую гипотезу
о равенстве групповых средних. Предполагается, что
288
выборки извлечены из нормальных совокупностей с одина-
одинаковыми дисперсиями. Результаты испытаний приведены
в табл. 50.
Таблица 50
Номер испытания
'
1
2
3
4
*гр/
F,
27
23
29
29
27
Уровни фактора
F,
24
20
26
30
25
F,
22
21
36
37
29
Указание. Принять У1/=ху—27. Использовать замечание 1.
§ 2. Неодинаковое число испытаний
на различных уровнях
Если число испытаний на уровне Ft равно q\, на уровне F2—¦
— q%, ..., на уровне Fp—qp, то общую сумму квадратов отклонений
вычисляют, как и в случае одинакового числа испытаний на всех
уровнях (см. § 1). Факторную сумму квадратов отклонений находят
по формуле
р
У т)
'l i '2 , , 1р /=1
f \- • • • Н -— ,
где я = <7|+<7»+ ... +qp—общее число испытаний.
Остальные вычисления производят, как и в случае одинакового
числа испытаний:
«факт = 5факт/(Р —'). «ост = 50ст/(я — Р)-
674. Произведено 13 испытаний, из них 4—на пер-
первом уровне фактора, 4 — на втором, 3—на третьем и
2—на четвертом. Методом дисперсионного анализа при
уровне значимости 0,05 проверить нулевую гипотезу
о равенстве групповых средних. Предполагается, что
выборки извлечены из нормальных совокупностей с оди-
одинаковыми дисперсиями. Результаты испытаний приведены
в табл. 51.
10 Гмурмаи В. В.
289
Таблица 51
Номер испытания
1
2
3
4
*гр/
Уровни фактора
F,
1,38
1,38
1,42
1,42
1,40
F,
1,41
1.42
1,44
1,45
1,43
F,
1,32
1,33
1,34
1,33
F,
1,31
1,33
1,32
Решение. Используя замечание 2 (см. §1), перейдем к целым
числам yi/z=\0ixif—138. Составим расчетную табл. 52.
Номер
испытания
i
1
2
3
4
"И
0
0
4
4
8
64
•г.
0
0
16
16
32
1
/ровни фактора
F,
ч.
3
4
6
7
20
400
9
16
36
49
ПО
F,
•ft
—6
—5
—4
-15
225
4.
36
25
16
77
Т
F,
»п
—12
144
«и
49
25
74
а б л и и а 52
Итого выП
столбец
^](?у = 293
Используя итоговый столбец и нижнюю строку табл. 52, найдем
общую и факторную суммы квадратов отклонений:
r2r/J4/n = 293—^/13=293—0,08 = 292,92;
9 / /«
= 64/4 + 400/4+225/3+144/2—0,08=262,92.
Найдем остаточную сумму квадратов отклонений:
5ост=5общ—5факт = 292,92—262,92 = 30.
Найдем факторную и остаточную дисперсии:
4акт=S0aKT/(p -1) = 262,92/D— 1)=262,92/3=87,64;
Soct=Soct/(« —р) = 30/A3—4) = 30/9 = 3,33.
290
Сравним факторную и остаточную дисперсии с помощью крите-
критерия F (см. гл. XIII, § 2). Для этого сначала вычислим наблюдаемое
значение критерия:
^иабл = 4акт/ «ост=87,64/3.33 = 26,32.
Учитывая, что число степеней свободы числителя kt = p—1 =
=4—1=3, знаменателя k2 = n—/>=13—4 = 9 и что уровень значи-
значимости ос=О,О5, по таблице приложения 7 находим критическую точку
fKP@.05; 3; 9) = 3,86.
Так как FHafa > ^кр—нулевую гипотезу о равенстве групповых
средних отвергаем. Другими словами, групповые средние различа-
различаются значимо.
675. Произведено 14 испытаний, из них 5 — на первом
уровне фактора, 3—на втором, 2—на третьем, 3—на
четвертом и 1—на пятом. Методом дисперсионного ана-
анализа при уровне значимости 0,05 проверить нулевую
гипотезу о равенстве групповых средних. Предполагается,
что выборки извлечены из нормальных совокупностей
с одинаковыми дисперсиями. Результаты испытаний при-
приведены в табл. 53.
Таблица 53
Номер испытания
1
2
3
4
5
*гр/
Уровни фактора
г,
7,3
7.6
8.3
8,3
8.4
7,98
5.4
7.1
7.4
6,63
6,4
8,1
7,25
F,
7,9
9,5
9,6
9,0
7,1
7.1
Указание. Принять уц = Idx/j—78.
676. Произведено 13 испытаний, из них 4 — на первом
уровне фактора, 6—на втором и 3—на третьем. Методом
дисперсионного анализа при уровне значимости 0,01 про-
проверить нулевую гипотезу о равенстве групповых средних.
Предполагается, что выборки извлечены из нормальных
совокупностей с одинаковыми дисперсиями. Результаты
испытаний приведены в табл. 54.
10» 291
Номер
испытания
i
1
2
3
4
5
6
Т а бл
Уровни фактора
F,
37
47
40
60
46
Ft
60
86
67
92
95
98
83
и ц а 54
F,
69
100
98
89
У казанн е. Принять У(} = хц—73.
677. Произведено 14 испытаний, из них 7—на пер-
первом уровне фактора, 3—на втором и 4—на третьем.
Методом дисперсионного анализа при уровне значимости
0,01 проверить нулевую гипотезу о равенстве групповых
средних. Предполагается, что выборки извлечены из
нормальных совокупностей с одинаковыми дисперсиями.
Результаты испытаний приведены в табл. 55.
Таблица 55
Номер испытания
1
2
3
4
5
6
7
*гР/
Уровни фактора
F,
30,56
32,66
34,78
35,50
36,63
40,20
42,28
36,03
F,
43,44
47,51
53,80
48,25
F,
31,36
36,20
36,38
42,20
36,54
Указание. Принять у^ = 100лс,у—3900.
678. Произведено 26 испытаний, из них 7—на первом
уровне фактора, 5—на втором, 8—на третьем и 6—на
четвертом. Методом дисперсионного анализа при уровне
значимости 0,05 проверить гипотезу о равенстве груп-
292
новых средних. Предполагается, что выборки извлечены
из нормальных генеральных совокупностей с одинако-
одинаковыми дисперсиями. Результаты испытаний приведены
в табл. 56.
Таблица 56
Номер испытания
i
1
2
3
4
5
6
7
8
*гр/
F,
1600
1610
1650
1680
1700
1700
1800
1677
Уровни
F,
1580
1640
1640
1700
1750
1662
фактора
F,
1460
1550
1600
1620
1640
1660
1740
1820
1638
Л
1510
1520
1530
1570
1600
1680
1568
Указание. Принять уц
1 (см. § 1).
*хц —1630. Использовать замечание
Часть четвертая
МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН
Глава пятнадцатая
МОДЕЛИРОВАНИЕ (РАЗЫГРЫВАНИЕ)
СЛУЧАЙНЫХ ВЕЛИЧИН МЕТОДОМ МОНТЕ-КАРЛО
§ 1. Разыгрывание дискретной случайной величины
Сущность метода Монте-Карло состоит в следующем: требуется
найти значение а некоторой изучаемой величины. С этой целью вы-
выбирают такую случайную величину X, математическое ожидание
которой равно а: М(Х) = а.
Практически же поступают так: вычисляют (разыгрывают) п
возможных значений х/ случайной величины X, находят их среднее
арифметическое
B)
и принимают х в качестве оценки (приближенного значения) а*
искомого числа а:
а~а* —1с.
Таким образом, для применения метода Монте-Карло необходимо
уметь разыгрывать случайную величину.
В этом параграфе требуется разыграть дискретную случайную
величину X, т. е. вычислить последовательность ее возможных зна-
значений Xi(i—\, 2, ...), зная закон распределения X.
Введем обозначения: R—непрерывная случайная величина, рас-
распределенная равномерно в интервале @, 1); rj(j = \, 2, ...)—слу-
...)—случайные числа (возможные значения R).
Правило. Для того чтобы разыграть дискретную случайную ве-
величину X, заданную законом распределения
Л Х\ Х% * • * Xfi
Р Pi Pi «•• Рп
надо:
1. Разбить интервал @, 1) оси Or на п частичных интервалов:
Ai—@; Pi), А8—(РГ. Pi + Pt) Ав—(Р1 + Р2+ •••+Рп-1> О-
2. Выбрать (например, из таблицы случайных чисел) случайное
чиСЛО Tj.
Если Г] попало в частичный интервал Л/, то разыгрываемая
величина приняла возможное значение лс,-.
679. Разыграть шесть возможных значений дискретной
случайной величины X, закон распределения которой
задан в виде таблицы:
Л 2 10 18
р 0,22 0,17 0,61
294
Решение. Разобьем интервал @, 1) оси Or точками с коор-
координатами 0,22; 0,22+0,17=0,39 на три частичных интервала:
Д,-@; 0,22), Да-@,22; 0,39), Д3-@;39, 1).
2. Выпишем из таблицы приложения 9 шесть случайных чисел,
например 0,32; 0,17; 0,90; 0,05; 0,97; 0,87.
Случайное число Г\ =0,32 принадлежит частичному интервалу Д2,
поэтому разыгрываемая дискретная случайная величина приняла
возможное значение лс2=10; случайное число га=0,17 принадлежит
частичному интервалу Дх, поэтому разыгрываемая величина приняла
возможное значение дс1 = 2.
Аналогично получим остальные возможные значения.
Итак, разыгранные возможные значения таковы: 10; 2; 18; 2;
18; 18.
680. Разыграть восемь возможных значений дискрет-
дискретной случайной величины X, закон распределения кото-
которой задан в виде таблицы:
X 3 8 12 23
р 0,2 0,12 0,43 0,23
Указание. Для определенности принять случайные числа:
0,33; 0,18; 0,51; 0,62; 0,32; 0,41; 0,94; 0,15.
681. Разыграть пять опытов по схеме Бернулли: опыт
состоит из трех независимых испытаний, в каждом из
которых вероятность появления события А равна 0,4.
Указание, а) Составить сначала закон распределения ди-
дискретной случайной величины X—числа появлений события Л в трех
независимых испытаниях, если в каждом испытании вероятность по-
появления события А равна 0,4; б) принять для определенности слу-
случайные числа: 0,945; 0,572; 0,857; 0,367; 0,897.
682. Разыграть шесть опытов по схеме Бернулли:
опыт состоит из четырех испытаний, в каждом из кото-
которых вероятность появления события А равна 0,5.
Указание. Принять для определенности случайные числа:
0,1009; 0,7325; 0,3376; 0,5201; 0,3586; 0,3467.
§ 2. Разыгрывание полной группы событий
Требуется разыграть испытания, в каждом из которых наступает
одно из событий полной группы, вероятности которых известны.
Разыгрывание полной группы событий сводится к разыгрыванию
дискретной случайной величины.
Правило. Для того чтобы разыграть испытания, в каждом из
которых наступает одно из событий Аи А2, .... А„ полной группы,
вероятности которых р\, р2, ...,рп известны, достаточно разыграть
(по правилу § 1) дискретную случайную величину X со следующим
законом распределения:
X I 2 ... п
р Pi рг ... р„
295
Если в испытании величина X приняла возможное значение *,• = /,
то наступило событие Л/.
683. Заданы вероятности трех событий: Av Л2, А3,
образующих полную группу: р1 = Р(Л1) = 0,22, р3 =
= Р (Ах) = 0,31, р3 = Р(А3) = 0,47. Разыграть пять испы-
испытаний, в каждом из которых появляется одно из трех
рассматриваемых событий.
Решение. В соответствии с правилом настоящего параграфа
надо разыграть дискретную случайную величину X с законом рас-
распределения:
X 1 2 3
р 0,22 0,31 0,47
По правилу § 1 разобьем интервал @, 1) на три частичных ин-
интервала: Дх—(О; 0,22), Д2 —@,22; 0,43), Д3—@,43; 1).
Выберем из таблицы приложения 9 пять случайных чисел, на-
например 0,61; 0,19; 0,69; 0,04; 0,46.
Случайное число га = 0,61 принадлежит интервалу Д3, поэтому
Х = 3 и, следовательно, наступило событие А3. Аналогично найдем
остальные события. В итоге получим искомую последовательность
событий: А3, Ах, А3, А\, As.
684. Заданы вероятности четырех событий, образую-
образующих полную группу: р, = Р(Л1) = 0,15, р8 = Р(Л2) = 0,64;
Рз = Р(А3) = 0,05, Pi = P(A<) = 0,16.
Разыграть 10 испытаний, в каждом из которых появ-
появляется одно из рассматриваемых событий.
Указание. Принять для определенности случайные числа:
0,37; 0,54; 0,20; 0,48; 0,05; 0,64; 0,89; 0,47; 0,42; 0,96.
685. События А и В независимы и совместны. Разы-
Разыграть четыре испытания, в каждом из которых вероят-
вероятность появления события А равна 0,7, а события В—0,4.
Решение. Возможны четыре исхода испытания:
Ах = АВ, причем в силу независимости событий Р(АВ)=Р (А)Х
ХЯ(В)=0,7 0,4 = 0,28;
А2 = АВ, причем Р(АВ) = 0,7-0,6=0,42;
А3 = АВ, причем Р(ЛВ)=0,30,4 = 0,12;
At = AB, причем Р(ЛВ)=0,3-0,6 = 0,18.
Таким образом, задача сведена к разыгрыванию полной группы
четырех событий: Ai с вероятностью р1=0,28, Аз с вероятностью
рг=0,42, А3 с вероятностью ря = 0,12, Л4 с вероятностью pt=0,l8.
Эта задача в соответствии с правилом настоящего параграфа
сводится к разыгрыванию дискретной случайной величины X с за-
законом распределения
X 1 2 3 4
р 0,28 0,42 0,12 0,18
Выберем из таблицы приложения 9 четыре случайных числа,
например 0,32; 0,17; 0,90; 0,05.
296
Используя правило § 1, легко найдем искомую последователь-
последовательность результатов четырех испытаний: Ait Ait A4, A\.
686. События А и В независимы и совместны. Разы-
Разыграть пять испытаний, в каждом из которых вероятность
появления события А равна 0,6, а события В—0,8.
Указание. Составить полную группу событий: Ai=AB,
Ai — AB, А3=АВ, A4 = AB; для определенности принять случайные
числа: 0,69; 0,07; 0,49; 0,41; 0,38.
687. События А, В и С независимы и совместны. Разы-
Разыграть пять испытаний, в каждом из которых вероятность
появления события А равна 0,6, события В—0,2, собы-
события С—0,4.
У к а_з а н и е._Составить_ полную группу событий: Ai — ABC,
А2 = АВС, А3 = АЪС, А4 = АВС, Аь = АВС, Ай = АВС, А7 = АВС,
АВ = АВС; для определенности принять случайные числа: 0,541;
0,784; 0,561; 0,180; 0,993.
688. События А и В зависимы и совместны. Разыграть
пять испытаний, в каждом из которых заданы вероятно-
вероятности: Р(Л) = 0,5, Р (В) = 0,6, Р(АВ) = 0,2.
Указание. Составить полную группу событий: Ах = А В,
а = АВ, А3=~АВ, At=~AB. Учесть, что Р(Аг) = Р (А)-Р(АВ),
(А)Р(В)Р{АВ) РШ11Р(А) + Р(А) + Р(А)] Д
а 3, t (г) ()(),
Р(А3)=Р(В)-Р{АВ), РШ=1-1Р(А,) + Р(А2) + Р(Аа)]. Для
определенности принять случайные числа: 0,66; 0,06; 0,57; 0,47; 0,17.
§ 3. Разыгрывание непрерывной случайной величины
Известна функция распределения F (х) непрерывной случайной
величины X. Требуется разыграть X, т. е. вычислить последователь-
последовательность возможных значений *,•([ = I, 2, ...).
А. Метод обратных функций. Правило 1. Для того чтобы ра-
разыграть возможное значение х/ непрерывной случайной величины X,
зная ее функцию распределения F(x), надо выбрать случайное чис-
число г/, приравнять его функции распределения и решить относи-
относительно х/ полученное уравнение F (*,•) = г,-.
Если известна плотность вероятности / (х), т используют пра-
правило 2.
Правило 2. Для того, чтобы разыграть возможное значение X;
непрерывной случайной величины X, зная ее плотность вероятности
f (х), надо выбрать случайное число г; и решить относительно xi
уравнение
Х1
[ f(x)dx=rh
297
или уравнение
где а—наименьшее конечное возможное значение Х>
Б. Метод суперпозиции. Правило 3. Для того чтобы разыграть
возможное значение случайной величины X, функция распределения
которой
где Fk(x)—функции распределения {k—\, 2, .... п), С* > 0,
г + ... + Сп = \, надо выбрать два н й
й
k\, 2, .... п), С* > , t +
Сг + + п , р независимых случайных числа
Т\ и Ti и по случайному числу г, разыграть возможное значение
вспомогательной дискретной случайной величины Z (по правилу 1):
Z \ 2 ... л
р d С3 ... С„
Если окажется, что Z = k, то решают относительно х уравнение
f ft (*) = '*¦ , и
Замечание 1. Если задана плотность вероятности непрерыв-
непрерывной случайной величины X в виде
где /*(*)—плотности вероятностей, коэффициенты С к положительны,
их сумма рапна единице и если окажется, что Z=k, то решают (по
правилу 2) относительно *,• уравнение V fk(x)dx=ra или урав-
— ш
*/
нение \ f/t(x)dx=ri.
а
Замечание 2. Модифицированный метод суперпозиции, пред-
предложенный Г. А. Михайловым, выгоднее рассматриваемого метода,
так как использует лишь одно случайное число вместо двух (см.:
Соболь И. М. Численные методы Монте-Карло. М., 1973).
689. Найти явную формулу для разыгрывания непре-
непрерывной случайной величины X, распределенной равно-
равномерно в интервале (а, Ь), зная ее функцию распределе-
распределения F(jc) = (jc—a)l(b—a) (a<x<b).
Решение. В соответствии с правилом 1 приравняем задан-
заданную функцию распределения случайному числу /•,•:
Решив это уравнение относительно *,-, получим явную формулу
для разыгрывания возможных значений X: х/= (b—a) rt+a.
690. Разыграть четыре возможных значения непре-
непрерывной случайной величины X, распределенной равно-
равномерно в интервале D, 14).
Указание. Для определенности принять случайные числа:
0,74; 0,02; 0,94; 0,36.
691. Найти явную формулу для разыгрывания непре-
непрерывной случайной величины X, распределенной по пока-
показательному закону, заданному функцией распределения
F(x) = l—t-b<(x>0).
692. Найти явную формулу для разыгрывания непре-
непрерывной случайной величины, заданной плотностью веро-
вероятности f(x)=6/A + ах)а в интервале [0, 1/F—а)]; вне
этого интервала /(л:) = 0.
Решение. Используя правило 2, напишем уравнение
Ь \ l/(l+axJdx=rl.
о
Решив это уравнение относительно */, окончательно получим
693. Разыграть пять возможных значений непрерыв-
непрерывной случайной величины X, заданной плотностью веро-
вероятности /(*)= 10/A+2jcJ в интервале @, 1/8); вне этого
интервала f(x) = 0.
Указание. Для определенности принять случайные числа:
0,186; 0,333; 0,253; 0,798; 0,145.
694. Найти явную формулу для разыгрывания равно-
равномерно распределенной случайной величины X, заданной
плотностью вероятности f(x) = 2 в интервале @; 0,5);
вне этого интервала f(x) = 0.
695. Разыграть пять возможных значений непрерыв-
непрерывной равномерно распределенной случайной величины X,
заданной плотностью вероятности / (л:) = 0,1 в интервале
@; 10); вне этого интервала /(л:) = 0.
Указание. Для определенности принять случайные числа:
0,690; 0,749; 0,413; 0,887; 0,637.
696. Найти явную формулу для разыгрывания непре-
непрерывной случайной величины, распределенной по показа-
показательному закону, заданному плотностью вероятности
f(x) = Xt-u в интервале @, се); вне этого интервала
f(x) = 0.
697. Разыграть пять возможных значений непрерыв-
непрерывной случайной величины X, распределенной по показа-
показательному закону, заданному плотностью вероятности
299
f(x) = O,l е~0Лл в интервале @, оо); вне этого интервала
f() O
Указание. Для определенности принять случайные числа:
0,80; 0,33; 0,69; 0,45; 0,98.
689. Найти явную формулу для разыгрывания непре-
непрерывной случайной величины X, распределенной по за-
закону Вейбулла, заданного плотностью вероятности /(*)=
= (п/хо)хп-1е-*п"с° при х>0; /(jc) = O при л;<0.
699. Найти явную формулу для разыгрывания не-
непрерывной случайной величины X, распределенной по
закону Релея, заданного плотностью вероятности /(*) —
= (х/аг) е-**/2о« при jc>0; /(*) = 0 при х<0.
700. Найти явную формулу для разыгрывания непре-
непрерывной случайной величины X, заданной плотностью
вероятности /(л:) = А,[1— (кх)/2] в интервале @;2/Я); вне
этого интервала /(jc) = O.
701. Разыграть четыре возможных значения непрерыв-
непрерывной случайной величины X, заданной плотностью веро-
вероятности / (х) = 1 —х/2 в интервале @; 2); вне этого ин-
интервала /(л:) = 0.
Указание. Для определенности принять случайные числа:
0,35; 0,96; 0,31; 0,53.
702. Найти явную формулу для разыгрывания непре-
непрерывной случайной величины X, заданной плотностью
вероятности /(*) = G,)sinje в интервале @, я); вне этого
интервала /(л;) = 0.
703. Найти явную формулу для разыгрывания не-
непрерывной елучайной величины X, заданной плотностью
вероятности f(x) = ce-cx/(l—e-te) в интервале @,6); вне
этого интервала /(л;)=0.
704. Найти методом суперпозиции явные формулы
для разыгрывания непрерывной случайней величины X,
заданной функцией распределения F(x)=l — (V3)Be~2jl-(-
+e-**)@<x<oo).
Решение. В соответствии с правилом 3 яредставим заданную
функцию в виде
Функции, заключенные в скобках, являются функциями распределе-
распределения показательного закона, поэтому можно принять: Fi (х) = 1 —е~3*,
/•8(*) = 1-е-2*, C1=1/s, C2=a/.v
Введем в рассмотрение вспомогательную дискретную случайную
величину Z с законом распределения
Z 1 2
р 1/3 2/3
300
Выберем независимые случайные числа гг и г2. Разыграем Z
по случайному числу ги для чего по правилу § 1 построим частич-
частичные интервалы Д,—(О, V») и Д2—(Vs. О- Если гх < Vs. то Z=\;
если /^SaVa. то Z=2.
Итак, возможное значение X находят, решая относительно х
уразнение
1— е-3*=/-г, если /1 < Vs.
или
1— е-2* = г2, если
Решив эти уравнения, получим:
*=[ — In A — /-2)]/3, если /-1 < 1/3;
х=[ — \пA—гг)]/2, если
Приняв во внимание, что случайные величины R и I —R в ин-
интерпале @, 1) распределены одинаково, окончательно имеем более
простые формулы:
*=( —1п/-2)/3, если гг < 1/3,
*=(—lnra)/2, если
705. Найти методом суперпозиции явные формулы для
разыгрывания непрерывной случайной величины X, задан-
заданной функцией распределения F (х) = 1 — 0,25 (е~** +
+ 3e-*)@<*<oo).
Указание. Принять F1(x)=l—e~ix, Ft (x) = l— e~*.
706. Найти методом суперпозиции явные формулы
для разыгрывания непрерывной случайной величины X,
заданной функцией распределения F (х) = 1 — G6) Bе*+
+ 3е-«*)@<*<оо).
Указание. Принять Fl(x)= I— e"8*, Fg(x) = l —е~4*.
707. Найти методом суперпозиции явные формулы
для разыгрывания непрерывной случайной величины X,
заданной функцией распределения F(x) = I — (l/i)(e~* +
+ 2е~2* + 4е-»*) @ < х < со).
Указание. Принять F1(x)=l — е~*, F2 (д:) = 1 — е*,
F3(x)=l— е-3*.
708. а) Найти методом суперпозиции явные формулы
для разыгрывания непрерывной случайной величины X,
заданной плотностью вероятности /(*)=D/27)[l+(*—IK]
в интервале @, 3); вне этого интервала /(*) = 0.
б) Показать, что метод обратных функций требует
решения уравнения четвертой степени (х,-—\)* + 4х; —
-B7г,.+ 1) = 0.
Указание. Принять /х (*) = «/». /i (*) = (*/») (*—•)*. C, = V.i,
C2 = 2/s-
301
709. а) Найти методом суперпозиции явные формулы
для разыгрывания непрерывной случайной величины X,
заданной плотностью вероятности / (х) = E/12)[1+(*— l)'j
в интервале @, 2); вне этого интервала /(*) = 0.
б) Показать, что метод обратных функций требует
решения уравнения пятой степени (х{—1M + 5*,—(I2rt—
—1) = 0.
Ухазание. Принять h(x) = 1/t, /t (*)=(»/») (*—!)*. Сх = 6/«.
§ 4. Приближенное разыгрывание
нормальной случайной величины
Требуется приближенно разыграть нормальную случайную ве-
величину.
Правило. Для того чтобы приближенно разыграть возможное
значение х/ нормальной случайной величины X с параметрами а = 0
и о=1, надо сложить 12 независимых случайных чисел и из полу-
полученной суммы вычесть 6:
12
/—6=S;-6.
Замечание. Если требуется приближенно разыграть нор-
нормальную случайную величину Z с математическим ожиданием а н
средним квадратнческим отклонением о, то, разыграв возможное
значение х; по приведенному выше правилу, находят искомое воз-
возможное значение по формуле
г; = ох/ + а.
710. Разыграть четыре возможных значения нормаль-
нормальной случайной величины с параметрами: а) а = 0, а=1;
б) а = 2, о = 3.
Решение, а) В соответствии с правилом разыграем козмож-
ное значение Xj нормальной случайной величины X с параметрами
а=0 и о=1 по формуле
12
,-,_ 6=Si-6.
Выберем из второй строки таблицы приложения 9 первых 12 слу-
случайных чисел: 0,37; 0,54; 0,20; 0,48; 0,05; 0,64; 0,89; 0,47; 0,42;
0,96; 0,24; 0,80. Сложив эти числа, получим St =6,06. Искомое
возможное значение *i=Si—6=6,06—6=0,06.
Аналогично, выбрав из третьей, четвертой и пятой строк таб-
таблицы по 12 первых случайных чисел, получим; S2=4,90, S3=4,48,
S4=6,83. Следовательно, х2=4,90—6 =—1,10; xs = 4,48—6=—1,52}
х4=6,83—6=0,83.
б) Найдем возможные значения нормальной случайной величины Z
с параметрами а=2, а=3 по формуле г,-=ах,-|-а. Подставив воз-
возможные значения ху =0,06, а =2, а=3, получимгх=3-0,06+2 =2,18.
302
Аналогично найдем остальные возможные значения: га=—1,3,
га=— 2,56, 24 = 4,49.
711. Разыграть пять возможных значений нормаль-
нормальной случайной величины с параметрами: а)а = 0, а=1;
б) а=10, о = 2.
У к а з а и и е. Лля определенности выбрать по 12 первых дву-
двузначных чисел последних пяти строк таблицы приложения 9 и ум-
умножить каждое двузначное число на 0,01.
712. Разыграть пять возможных значений нормаль-
нормальной случайной величины с параметрами: а) а = 0, а—\;
б) а = 4, 0 = 0,1.
Указание. Лля определенности выбрать по 12 первых трех-
трехзначных чисел из первых пяти строк таблицы приложения 9 и умно-
умножить каждое трехзначное число иа 0,001.
713. Разыграть 50 возможных значений нормальной
случайной величины X с параметрами а = 0, а = 1 и оце-
оценить параметры разыгранной величины.
Указание. Лля определенности при разыгрывании возмож-
возможного значения х/ выбрать первые 12 двузначных чисел 1-й строки
таблицы приложения 9 и умножить каждое двузначное число на 0,01.
§ 5. Разыгрывание двумерной случайной величины
А. Дискретная двумерная случайная величина. Разыгрывание дис-
дискретной двумерной случайной величины (X, Y) сводится к разыг-
разыгрывай ню ее составляющих—одномерных дискретных случайных вели-
величин X и У.
Пусть задан закон распределения двумерной случайной вели-
величины (X, К). Если составляющие X и Y независимы, то нахо-
находят законы их распределения и по ним разыгрывают X и Y по пра-
правилу § 1.
Если составляющие зависимы, то находят закон распределе-
распределения одной из ннх, условные законы распределения другой и по ним
разыгрывают X и/по правилу § 1.
714. Дискретная двумерная случайная величина
(X, Y), составляющие которой независимы, задана законом
распределения:
Y
У\
Уг
0,
0,
18
12
0
0
X
*,
,30
,20
0
е
х,
.12
.08
Разыграть случайную величину (X, Y).
303
Решение. Найдем закон распределения составляющей X:
Ра=Р (*=*„)= 0,30+0,20 =0,50,
ра=Р (Х=*,)=0,12+0,08=0,20.
Таким образом, искомый закон распределения имеет внд
X *i xs х3
р 0,30 0,50 0,20
Аналогично найдем закон распределения У:
У У\ Уз
р 0,60 0,40
Составляющие X и У разыгрывают по правилу § 1.
715. Разыграть пять пар возможных значений дву-
двумерной случайной величины (X, Y), составляющие кото-
которой независимы, зная закон ее распределения:
Y
У\
У*
0
0
*¦
,20
,30
0
0
X
*t
,08
,12
0,
0,
г,
12
18
Указание. Для определенности принять при разыгрывании X
случайные числа: 0,98; 0,52; 0,01; 0,77; 0,67, а при разыгрывании
К—числа 0,11; 0,80; 0,50; 0,54; 0,31.
716. Дискретная двумерная случайная величина
(X, Y) задана законом распределения:
Y
У\
Уз
*
0,
0,
10
06
0
0
X
X,
,30
,18
0,
0,
с»
20
16
Разыграть пять пар возможных значений (X, Y).
Указание. Найти закон распределения составляющей X
и разыграть ее. Найти условные законы распределения p(yj\x/) =
р (х/, у,-)
= 7—т— составляющей У н разыграть ее. Для определенности
принять случайные числа, приведенные в задаче 715.
Б. Непрерывная двумерная случайная величина. Разыгрывание
непрерывной двумерной случайной величины (X, У) сводится к ра-
разыгрыванию ее составляющих—одномерных случайных величии X и У.
304
Пусть задан закон распределения двумерной случайной вели-
величины (X, У). Если составляющие X и Y независимы, то нахо-
находят законы их распределения и по ним разыгрывают X и Y по пра-
правилам § 3.
Если составляющие X иУ зависимы, то находят закон рас-
распределения одной из них, условный закон распределения другой
и по ним разыгрывают X и У по правилам § 3.
Замечание. Составляющие X и Y независимы, если гыпол-
няется любое нз условий:
1. Плотность совместного распределения равна произведению
плотностей составляющих.
2. Функция совместного распределения равна произведению
функций распределения составляющих.
3. Условные плотности распределения составляющих равны их
безусловным плотностям.
4. Плотность совместного распределения равна произведению
двух функций, одна из которых зависит только от *, а другая —
только от у (задача 437).
717. Найти явные формулы для разыгрывания непре-
непрерывной двумерной случайной величины (X, У), заданной
плотностью вероятности / (х, у) = C/4) ху* в области, огра-
ограниченной прямыми * = 0, у —0, дс=1, у = 2.
Решение. Составляющие X и Y независимы, так как совме-
совместную плотность вероятности /(*, у)=C/4)ху3 можно представить
в виде произведения двух функций, одна из которых зависит только
от *, а другая только от у.
Найдем плотность распределения составляющей X:
2 2
h(x)=\f (х, У) Ау = C/4)* \ у* Ау — 2х.
о о
Итак, /, (*)=2*@<*<1).
Разыграем X по правилу 2 (§ 3):
2 С х Ах=Г[.
о
Отсюда получим явную формулу для вычисления возможных значе-
значений X:
Найдем плотность распределения составляющей У:
1 1
ft Uf) = \ f (*. У) Ах = (»/4) Уг [х Ах = (»/„> у\
Итак, h(y) = C/8)y* ф<у< 2).
Разыграем Y по правилу 2 (§ 3):
(8/в)$ УгАу=г\.
305
Отсюда получим явную формулу для вычисления возможных
значений у: _
у,=2 Уг\.
718. Найти явные формулы для разыгрывания дву-
двумерной непрерывной случайной величины (X, Y), задан-
заданной плотностью вероятности f (х, у) = 4ху в области,
ограниченной прямыми * = 0, у = 0, х=1, у=\.
719. Найти явные формулы для разыгрывания непре-
непрерывной двумерной случайной величины (X, К), если
составляющая X задана плотностью вероятности /, (х) —
= х/2 в интервале @; 2); составляющая Y равномерно
распределена в интервале (x/tx,+3) с плотностью ft(y)= 1/3,
где Х(—разыгранное возможное значение X.
Решение. Разыграем составляющую X по правилу 2 (§ 3):
J (х/2) dx = rt.
о
Отсюда получим явную формулу для вычисления возможных зна-
значений X: _
*,=2 V7J. (*)
Найдем условную функцию распределения составляющей Y,
учитывая, что величина Y распределена равномерно в интервале
(*,, *,-+3).
Используем правило 1 (§ 3): (у,-—Xi)/3 = r'i, где г\—случайное
число.
Решив это уравнение относительно у/, получим явную формулу
для вычисления возможных значений у:
где х/ находят по формуле (¦).
720. Найти явные формулы для разыгрывания непре-
непрерывной двумерной случайной величины (X, Y), если со-
составляющая X задана плотностью вероятности /, (х)=Bх)/9
в интервале @, 3); составляющая Y равномерно распре-
распределена в интервале (*, —2, xt + 2) с плотностью /2 (у) = 1/4,
где х, —разыгранное возможное значение X.
721. Найти явные формулы для разыгрывания непре-
непрерывной двумерной случайной величины (X, Y), заданной
плотностью вероятности f(x, y) = 6y в области, ограни-
ограниченной прямыми у = 0, у = х, х=\.
Решение. Найдем плотность вероятности составляющей X:
X
306
Разыграем X по правилу 2 (§ 3):
Отсюда получим явную формулу для вычисления возможных
значений X:
Найдем условную плотность вероятности составляющей Yi
¦ (У I *)=/ (*. y)lh (х) = (
Разыграем Y по правилу 2 (§ 3):
Отсюда получим явную формулу для вычисления возможных зна-
значений Y:
где Х[ находят по формуле (*).
722. Найти явные формулы для разыгрывания непре-
непрерывной двумерной случайной величины (X, Y), заданной
плотностью вероятности f(x, у) = Ъу в области, ограни-
ограниченной прямыми * = 0, у = х, у=1.
Указание. Найти сначала плотность вероятности состав-
составляющей Y и разыграть К; найти условную плотность распределения
составляющей X и разыграть X.
723. Найти явные формулы для разыгрывания непре-
непрерывной двумерной случайной величины (X, Y), заданной
плотностью вероятности f(x, y) = 4x в области, ограни-
ограниченной линиями у = х2, у = 0, х=\.
§ 6. Оценка надежности простейших систем
методом Монте-Карло
724. Система состоит из двух блоков, соединенных
последовательно. Система отказывает при отказе хотя
бы одного блока. Первый блок содержит два элемента:
А, В (они соединены параллельно) и отказывает при
одновременном отказе обоих элементов. Второй блок со-
содержит один элемент С и отказывает при отказе этого
элемента, а) Найти методом Монте-Карло оценку Р* на-
надежности (вероятности безотказной работы) системы, зная
вероятности безотказной работы элементов: Р(А) = 0,8,
307
Р (В) = 0,85, P(C) = 0,6; б) найти абсолютную погреш-
погрешность \Р — Р*\, где Р—надежность системы, вычисленная
аналитически. Произвести 50 испытаний.
Решение, а) Выберем из таблицы приложения 9 три случай-
случайных числа: 0,10, 0,09 н 0,73; по правилу *' (если случайное число
меньше вероятности события, то событие наступило; если случайное
число больше илн равно вероятности события, то событие не насту-
наступило) разыграем события А, В, С, состоящие в безотказной работе
соответственно элементов А, В, С. Результаты испытания будем
записывать в расчетную табл. 57.
Поскольку Р (А) =0,8 н 0,10 < 0,8, то событие А наступило,
т. е. элемент А в этом испытании работает безотказно. Так как
р (В) =0,85 и 0,09 < 0,85, то событие В наступило, т. е. элемент В
работает безотказно.
Таким образом, оба элемента первого блока работают; следова-
следовательно, работает и сам первый блок. В соответствующих клетках
табл. 57 ставим знак плюс.
Таб л н ца 57
Номер
испытания
I
2
3
4
Блок
Первый
Второй
Первый
Второй
Первый
Второй
Первый
Второй
Случайные числа, мо-
моделирующие элементы
А
0,10
0,25
0,52
0,86
в
0,09
0,33
0,01
0,34
С
0,73
0,76
0,35
0,67
Заключение о работе
элементов
А
+
+
+
—
В
+
+
+
+
С
—
+
—
блоков
+
+
+
+
+
системы
—
—
+
—
Так как Р(С)=0,6 и 0,73 > 0,6, то событие С не наступило,
т. е. элемент С получает отказ; другими словами, второй блок, а
значит и вся система, получают отказ. В соответствующих клетках
табл. 57 ставим знак минус.
Аналогично разыгрываются и остальные испытания. В табл. 57
приведены результаты четырех испытаний.
Произведя 50 испытаний, получим, что в 28 из них система
работала безотказно. В качестве оценки искомой надежности Р при-
примем относительную частоту Р* = 28/50=0,56.
*> См.: Гмурман В. Е. Теория вероятностей и математическая
статистика. М., 1977, гл. XXI, § 5.
308
б) Найдем надежность системы Р аналитически. Вероятности
безотказной работы первого и второго блоков соответственно равны:
Р1 = \-Р(А)Р(В) = 1-0,2-0,15 = 0,97, Ра=Р(С)=0,6.
Вероятность безотказной работы системы
Р=Р,.рг = 0,97 0,6 =0,582.
Искомая абсолютная погрешность |Р — Р*|= 0,582—0,56 = 0,022.
725. Система состоит из двух блоков, соединенных
последовательно. Первый блок содержит три элемента:
А, В, С, а второй—два элемента: D, Е. Элементы каж-
каждого блока соединены параллельно, а) Найти методом
Монте-Карло оценку Р* надежности системы, зная вероят-
вероятности безотказной работы элементов: Р(А) = 0,8,
Р(В) = 0,9, Р (С) = 0,85, P(D) = 0,7, P(E) = 0,6; б) найти
абсолютную погрешность \Р—Р*\, где Р—надежность
системы, вычисленная аналитически. Произвести 20 ис-
испытаний.
Указание. Для определенности брать случайные числа из
таблицы приложения 9, начина» с шестой строки сверху.
726. Система состоит из трех блоков, соединенных
последовательно. Первый блок содержит два элемента:
А, В, второй—три элемента: С, D, Е, третий—один
элемент F. Элементы первого и второго блоков соединены
параллельно, а) Найти методом Монте-Карло оценку Р*
надежности системы, зная вероятности безотказной работы
элементов: Р (А) = 0,8; Р (В) = 0,9; Р (С) = 0,7; Р (D)=0,75;
/>(?) = 0,8; P(F) = 0,6;
б) найти абсолютную погрешность \Р — Р*\, где Р —
надежность системы, вычисленная аналитически. Произ-
Произвести 30 испытаний.
Указание. Для определенности брать случайные числа из
таблицы приложения 9, начиная с первой строки сверху.
727. Устройство состоит из двух узлов, соединенных
последовательно. Первый узел содержит два элемента:
А, В, которые соединены параллельно. Второй узел со-
содержит один элемент С. Время безотказной работы эле-
элементов распределено по показательному закону с пара-
параметрами, соответственно равными 0,04; 0,05; 0,10. Найти
методом Монте-Карло: а) оценку Р* вероятности безот-
безотказной работы устройства за время длительностью 10 ч;
б) среднее время безотказной работы устройства. Произ-
Произвести 50 испытаний.
309
Решение, а) Разыграем время (в ч) безотказной работы эле-
элементов по формулам:
*И= A/0,04) In Г!-25 (-In гх),
tB=— A/0,05) In rt=20 (— In /-г),
tc A/0,10) lnr8 = 10(-lnrs),
где ri, гг, ra—случайные числа. Например, для первого испытания
возьмем из таблицы приложения 9 три случайных числа: 0, 10, 0,09,
0,73 н по ним разыграем время безотказной работы элементов:
1А =25 (—1п 0,10) =25 -2,30=57,50,
/л=20(—In 0,09)=20-2,41 =48,20,
/с=10(— In 0,73) = 10 -0,32=3,2.
Элементы А, В первого узла соединены параллельно, поэтому
для его работы достаточно, чтобы работал хотя бы один элемент.
Следовательно, в первом испытании первый узел будет работать
max E7,50; 48,20) = 57,50 ч.
Первый и второй узлы соединены последовательно, поэтому
устройство работает, если оба узла работают одновременно. Следо-
Следовательно, в первом испытании устройство будет работать min E7,50;
3,2) = 3,2 ч.
Составим расчетную табл. 58.
Таблица 58
испыта-
1
2
3
4
Случайные числа,
мо-
делирующие элемент
0
0
0
о
А
10
25
52
86
в
0,09
0,33
0,01
0,34
0
0
0
0
С
,73
,76
,35
,67
57
34
16
3
Время
элементов
А
,50
,75
,25
,75
48
22
92
21
В
.20
.20
,00
,60
с
3,
2,
ю,
4,
безотказной
2
7
5
0
работы
узлов
первого
57
34
92
21
,50
,75
,00
.60
второго
3,2
2,7
10,5
4.0
устройства
3,2
2,7
10,5
4,0
В табл. 58 приведены результаты только четырех испытаний.
Если произвести 50 испытаний, то окажется, что в 18 испытаниях
устройство работало 10 ч (и более).
Искомая оценка надежности устройства (вероятности его без-
безотказной работы за время длительностью 10 ч) Р*~ 18/50 = 0,36.
Для сравнения приведем аналитическое решение. Вероятности
безотказной работы элементов:
'•4=0,67,
°-6 =0,61,
1 =0.37.
Вероятность безотказной работы первого узла за время длитель-
длительностью 10 ч
р, = 1 _A —0,67) A —0,61)=0,87.
Вероятность безотказной работы устройства за время длитель-
длительностью 10 ч
/>=Р1-/?сA0)=0,87 0,37=0,32.
310
Абсолютная погрешность \Р— Р*| = |0,32—0,361 = 0,04.
б) Найдем среднее время безотказной работы устройства, учи-
учитывая, что в 50 испытаниях оно работало безотказно всего 450 ч:
Г*=450/50 = 9.
Для сравнения приведем аналитическое решение. Среднее время
работы элементов: 7,4 = 1/0,04 = 25, 7В = 1/0,05=20, 7С = 1/0,10= 10.
Среднее время работы узлов: 7]=тахB5, 20)=25, /2=10.
Среднее время работы устройства: 7 = minB5, 10) = 10.
Абсолютная погрешность | Г—7* | = 10—9 = 1.
728. Устройство состоит из трех узлов, соединенных
последовательно. Первый узел содержит два элемента:
А, В, которые соединены параллельно. Второй узел со-
содержит один элемент С, третий узел—один элемент D.
Время безотказной работы элементов (в ч) распределено
по показательному закону с параметрами, соответственно
равными 0,02; 0,05; 0,08; 0,01. Найти методом Монте-
Карло: а) оценку Р* вероятности безотказной работы
устройства за время длительностью 6 ч; б) среднее время
безотказной работы устройства. Произвести 50 испытаний.
Указание. Для определенности брать случайные числа из
таблицы приложения 9, начиная с первой строки сверху.
729. Устройство состоит из двух узлов, соединенных
последовательно. Первый узел содержит три элемента:
А, В, С, а второй—два элемента: D, Е. Элементы каж-
каждого узла соединены параллельно. Время безотказной
работы элементов распределено по показательному закону
с параметрами, соответственно равными 0,01; 0,02; 0,04;
0,01; 0,05. Найти методом Монте-Карло: а) оценку Р*
вероятности безотказной работы устройства за время
длительностью 60 ч; б) среднее время безотказной работы
устройства. Произвести 50 испытаний.
Указание. Для определенности брать случайные числа из
таблицы приложения 9, начиная с первой строки сверху.
§ 7. Расчет систем массового обслуживания
с отказами методом Монте-Кгрло
730. В трехканальную систему массового обслужива-
обслуживания с отказами поступает пуассоновский поток заявок.
Время между поступлениями двух последовательных
заявок распределено по показательному закону/(т) = 5е~".
Длительность обслуживания каждой заявки равна 0,5 мин.
311
Найти методом Монте-Карло математическое ожидание а
числа обслуженных заявок за время Т = 4 мин.
Решение. Пусть Г] =0—момент поступления первой заявки.
Заявка поступит в первый канал и будет им обслужена. Момент
окончания обслуживания первой заявки Г1 + 0,5=0+0,5 = 0,5.
В счетчик обслуженных заявок записываем единицу.
Моменты поступления последующих заявок найдем по формуле
где т,-—длительность времени между двумя последовательными за-
заявками с номерами i — 1 и /.
Возможные значения т,- разыгрываем по формуле
т, = -A А) 1п /-,• = (!Л) (- In /•,).
Учитывая, что, по условию, \ = 5, получим т,- = 0,2(— 1пг,-).
Случайные числа л,- берем из таблицы приложения 9, начиная
с первой строки сверху. Для нахождения времени между поступле-
поступлениями первой и второй заявок возьмем случайное число г =0,10.
Тогда т2 = 0,2(—1п0,10) = 0,2-2,30 = 0,460. Первая заявка поступила
в момент Г1 = 0. Следовательно, вторая заявка поступит в момент
Г2= 71 + 0,460 = 0+0,460=0,460. В этот момент первый канал еще
занят обслуживанием первой заявки, поэтому вторая заявка посту-
поступит во второй канал и будет им обслужена. Момент окончания обслу-
обслуживания второй заявки Г2+0,5=0,460 + 0,5 = 0,960. В счетчик
обслуженных заяпок добавляем единицу.
По очередному случайному числу /- = 0,09 разыграем время тя
между поступлениями второй и третьей заявок:
т„ = 0,2(—1п0,09)=0,2-2,41 =0,482.
Вторая заявка поступила в момент Тг =0,460. Поэтому третья
заявка поступит в момент Tt = Tt +0,482=0,460+0,482 = 0,942.
В этот момент первый канал уже свободен н третья заявка поступит
в первый канал. Момент окончания обслуживания третьей заявки
Г»+0,5=0,942+0,5 = 1,442. В счетчик обслуженных заявок добав-
добавляем единицу.
Дальнейший расчет производят аналогично (табл. 59), причем
если в момент поступления заявки все каналы заняты (момент по-
поступлений заявки меньше каждого из моментов окончания обслу-
обслуживания), то в счетчик отказов добавляют единицу.
Заметим, что обслуживание 20-й заявки закончится в момент
4,148 > 4, поэтому эта заявка получает отказ.
Испытание прекращают (в таблице записывают «стоп»), если
момент поступления заявки Т > 4.
Из табл. 59 находим, что за 4 мин всего поступило 20 заявок;
обслужено Х] = 12 заявок.
Выполнив аналогично еще пять испытаний, получим: х2=\Ъ,
дс»= 14, *4 = 12, *6=13, д:,, = 15.
В качестве оценки искомого математического ожидания а числа
обслуженных заявок примем выборочную среднюю
а*=7=B-12+13+14+2-15)/6=13,5.
312
Но-
Номер
заяв-
заявки
i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Слу-
ное
чи-
число
ri
0,10
0,09
0,73
0,25
0,33
0,76
0,52
0,01
0,35
0,86
0,34
0,67
0,35
0,48
0,76
0,80
0,95
0,90
0,91
0,17
-In Г/
2,30
2,41
0,32
1,39
1,11
0,27
0,65
4,60
1,05
0.15
1,08
0,40
1,05
0,73
0,27
0,22
0,05
00,10
0,09
1,77
Время
между
двумя
последова-
последовательными
заявками
т,=
=0.2Aп г.)
0,460
0,482
0.064
0,278
0,222
0,054
0,130
0,920
0,210
0,030
0,216
0,080
0,210
0,146
0,054
0,044
0,010
0,020
0,018
0.354
Момент
поступле-
поступления заявки
7\=
' i
-г/-]+т/
0
0,460
0,942
1,006
1,284
1,506
1,560
1,690
2,610
2,820
2,850
3,066
3,146
3,356
3,502
3,556
3,600
3,610
3,630
3,648
4,002
(Стоп)
Момент
Т1
+ 0,5
окончания
обслужива
ния заявки
каналом
1
0,500
1,442
2,006
3,110
3,646
4,148
2
0,960
1,506
2,060
3,320
3,856
Табл
3
1,784
3,350
4,002
Ито-
Итого
и ца
59
Счетчик
обслу-
обслуженных
заявок
*, = 12
от-
ка-
казов
1
1
8
731. В трехканальную систему массового обслужива-
обслуживания с отказами поступает пуассоновский поток заявок.
Время между поступлениями двух последовательных за-
заявок распределено по показательному закону / (т) = 4е~4Т.
Длительность обслуживания каждой заявки равна 1 мин.
Найти методом Монте-Карло математическое ожидание
а числа обслуженных заявок за время Т = 5мин.
Указание. Произвести шесть испытаний. Для определенности
брать случайные числа из таблицы приложения 9 с двумя знаками
после запятой, начиная с первой строки сверху.
732. В одноканальную систему массового обслужи-
обслуживания с отказами поступает пуассоновский поток заявок.
313
Время между моментами поступления двух последова-
последовательных заявок распределено по закону /(т) = 0,8е~0>8Т;
время обслуживания заявок случайное и распределено
по закону f1(t) = l,5e~lM. Найти методом Монте-Карло
за время Г = 30мин: а) среднее число обслуженных
заявок; б) среднее время обслуживания одной заявки;
в) вероятность обслуживания; г) вероятность отказа.
Произвести шесть испытаний.
Решение. Время между моментами поступления двух после-
последовательных заявок распределено по закону /(т)=0,8е~°'8т, поэтому
значения т,- разыграем по формуле
т,-=— A/0,8) In /-,-= 1,25 (— In /•,).
Случайные числа г/ берем из таблицы приложения 9, начиная
с первой строки снизу.
Время обслуживания заявок распределено по закону fx (t) =
= 1,5е~1'4', поэтому значения t/ разыграем по формуле
/,=_ A/1,5) 1п #,-=0.67 (-
Случайные числа /?,• берем из той же таблицы, начиная с первой
строки сверху.
Пусть Г1 = 0—момент поступления первой заявки. По случай-
случайному числу ^1=0,10 разыграем длительность времени обслуживания
первой заявки (в мин):
/, =0,67 (—1п0,10)=0,67 -2,30= 1,54.
Момент окончания -обслуживания первой заявки Т1 = 1,54 —
= 0+ 1,54= 1,54. В счетчик обслуженных заявок записываем единицу.
По случайному числу /-2=0,69 разыграем время (в мии) между
моментами поступления первой и второй заявок *':
т2 = 1,25 (—1п 0,69) = 1,25 0,37 = 0,46.
Первая заявка поступила в момент Т, =0. Следовательно, вто-
вторая заявка поступит в момент 712 = 7'i+0,46=0+0,46=0,46.
В этот момент канал занят обслуживанием первой заявки
@,46 < 1,54), поэтому вторая заявка получит отказ. В счетчик
отказов записываем единицу.
По очередному случайному числу г3 = 0,07 разыграем время
между моментами поступления второй и третьей заявок:
т., = 1,25 (—In 0,07) = 1,25-2,66=3,32.
Вторая заявка поступила в момент Г2 = 0,46. Следовательно, третья
заявка поступит в момент Г3=Т2+3,32 = 0,46 + 3,32=3,78. В этот
момент канал уже свободен C,78 > 1,54), поэтому он обслужит
третью заявку. В счетчик обслуженных заявок добавляем единицу.
Дальнейший расчет ясен из табл. 60 и 61. Испытание заканчи-
заканчивают, когда момент поступления заявки Tj^s30. Например, в первом
испытании, как видно из табл. 60, 23-я заявка поступила в момент
*' У первого случайного числа намеренно поставлен индекс 2.
чтобы не вносить расхождений с обозначениями табл. 60.
314
7*83=31,35 > 30, поэтому эту заявку исключаем («Стоп») и первое
испытание заканчиваем.
Диалогично производят и остальные испытаиия.
Таблица 60
Номер
заявки
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Случайное
число
''
0,69
0,07
0,49
0,41
0,38
0,87
0,63
0,79
0,19
0,76
0,35
0,58
0,40
0,44
0,01
0,10
0,51
0,82
0,16
0,15
0,48
0,32
-In rj
0,37
2,66
0,71
0,89
0,97
0,14
0,46
0,24
1,66
0,27
1,05
0,54
0,92
0,82
4,60
2,30
0,67
0,20
1,83
1,90
0,73
1,14
Время между
дпумя после-
последовательными
заявками
= 1.2б('-1п г,)
0,46
3,32
0,89
1,11
1,21
0,18
0,58
0,30
2,08
0,34
1,31
0,68
1,15
1,02
5,75
2,88
0,84
0,25
2,29
2,38
0,91
1,42
Момент
поступления
заявки
0
0,46
3,78
4 67
5,78
6,99
7,17
7,75
8,05
10,13
10,47
11,78
12,46
13,61
14,63
20.38
23,26
24,10
24,35
26,64
29,02
29,93
31,35 (Стоп)
Аналогично производят и остальные испытания. В табл. 62
приведены результаты шести испытании, включая первое.
Используя табл. 62, найдем_искомые величины: а) среднее число
обслуженных за 30 мин заявок А'обсл = 93/6 = 15,5,
б) среднее время обслуживания одной заявки ?обсл = 4,49/6 =
= 0,748,
в) вероятность обслуживания Ровсл = 3,974/6=0,662,
г) вероятность отказа Ротк = 1—Робсл = 1—0,662=0,338.
Таким образом, примерно 66% заявок будут обслужены, а 34%
получат отказ.
733. В одноканальную систему массового обслужива-
обслуживания с отказами поступает пуассоновский поток заявок.
Время между моментами поступления двух последова-
последовательных заявок распределено по закону / (г) = 0,5е~0>",
315
Таблица 61
Номер
заявки
t
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
s
Слу-
Случайное
число
Я/
1
0,10
0,09
0,73
0,25
0,33
0,76
0,52
0,01
0,35
0,86
0,34
0,67
0,35
0,48
- In и,
I
2,30
2,41
0,32
1,39
1,11
0,27
0,65
4.60
1,05
0,15
1,08
0,40
1,05
0,73
Длительиост!
обслуживания
заявки
= 0,67('-1пЯ()
1,54
1,61
0,21
0,93
0,74
0,18
0,44
3,08
0,70
0,10
0,72
0,27
0,70
0,49
11,71
поступ-
поступления
заявки
0
0,46
3,78
4,67
5,78
6,99
7,17
7,75
8,05
10,13
10,47
11,78
12,46
13,61
14,63
20,38
23,26
24,10
24,35
26,64
29,02
29,93
Момент
начала
обслу-
жива-
живания
0
3,78
5,78
6,99
8,05
10,13
10,47
11,78
20,38
23,26
24,10
26,64
29,02
30,42
оконча-
окончания
обслу-
жива-
живания
1,54
5,39
5,99
7,92
8,79
10,31
10,91
14,86
21,08
23,36
24,82
26,91
29,72
Счетчик
обслу-
жен-
женных
зая вок
1
1
1
1
I
1
1
1
13
отказов
1
1
1
1
1
1
1
1
1
9
время обслуживания случайное и распределено по закону
/j@ = 2e~2'. Найти методом Монте-Карло за время
Т = 20 мин: а) ереднее число обслуженных заявок;
б) среднее время обслуживания одной заявки; в) веро-
вероятность обслуживания; г) вероятность отказа.
Указание. Произвести шесть испытаиий. Для определенности
брать случайные числа с двумя десятичными знаками после запятой
из таблицы приложения 9 при разыгрывании т/, начиная с первой
строки снизу, а при разыгрывании ti—начиная с первой строки
сверху.
316
Табл ица 62
Номер
испы-
испытания
1
2
3
4
5
6
2
Посту-
Поступило
заявок
/пост
22
25
24
22
20
27
140
Обслу-
Обслужено
заявок
"/обсл
13
17
16
15
13
19
93
Длитель-
Длительность
обслужи-
обслуживания
'/обсл
11,71
8,80
13,46
12,19
11,99
9,57
Среднее время
обслуживания
'/обсл=
^ '/обсл
/обсл
0,90
0,52
0,84
0,81
0,92
0,50
4,49
Вероятность
обслуживания
Р/обсл=
_^/обсл
/ПОСТ
0,591
0,680
0,667
0,682
0,650
0,704
3,974
Вероятность
отказа
Р! отк =
= '-''/обсл
0,409
0,320
0,333
0,318
0,350
0,296
§ 8. Вычисление интегралов методом Монте-Карло
А. Способ усреднения подынтегральной функции. В качестве
I)
оценки определенного интеграла / = V ф (*) dx принимают
а
2 <р (*,)
где п—число испытаний; *,— возможные значения случайной вели-
величины X, распределенной равномерно в интервале интегрирования
(о, Ь), нх разыгрывают по формуле xt=a-\-\b—а)г,-, где г,—слу-
чайиое число.
Дисперсия усредняемой функции <р(Х) равна
ь
J <р»
где М [(р (X)] = J ф (*) / (*) их, f (*)= 1/F—а).
а
Если точное значение дисперсии вычислить трудно или невоз-
невозможно, то находят выборочную дисперсию (при п > 30)
или исправленную дисперсию (при п < 30)
где и,-=(р(д:,).
317
Эти формулы для вычисления дисперсии применяют и при дру-
других способах интегрирования, когда усредняемая функция не сов-
совпадает с подынтегральной функцией.
В качестве оценки интеграла / = V w (х, у) Ах Ау, где область
о
интегрирования D принадлежит единичному квадрату @<*<1,
0<^<1), принимают
2 /(*/. Уд
/J=s'iiLLTv С)
где 5—площадь области интегрирования; N—число случайных
точек (х{, yd, принадлежащих области интегрирования.
Если вычислить площадь 5 трудно, то в качестве ее оценки
можно принять S*=tN/n; в этом случае формула (*) имеет вид
N
2
<1
¦1 n
где п—число испытаний.
В качестве оценки интеграла / = \ X \ / (х, у, г) Ах Ау Аг, где
область интегрирования V принадлежит единичному кубу @<*<1,
0<е,{/<1, 0<г<1), принимают
N
2 /(*'• У1> *•)
/[=у.{——^ , (¦•)
где V—объем области интегрирования, N—число случайных точек
(Х{, у{, г,), принадлежащих области интегрирования.
Если вычислить объем трудно, то в качестве его оценки можно
принять V*<=N/n; в этом случае формула (**) имеет вид
N
2
п
где п—число испытаний.
Б. Способ существенной выборки, использующий «вспомогатель*
ную плотность распределения». В качестве оценки интеграла / =
ь
V ф (х) Ах принимают
а
*_ 1
п
где п—число испытаний; }(х) — плотность распределения «вспомо-
ь
гательиой» случайной величины X, причем \/(*)dx = l; х/—воз-
а
318
можные значения X, которые разыгрывают по формуле
/(x)dx=/>
Функцию f(x) желательно выбирать так, чтобы отношение
f(x)/<p(x) при различных значениях х изменялось незначительно.
В частности, если /(х) = 1/F—а), получим оценку I*.
В. Способ, основанный на истолковании интеграла как площади.
Пусть подынтегральная функция неотрицательна и ограничена:
0<<р(х)<с, а двумерная случайная величина (X, К)распределена
равномерно в прямоугольнике D с основанием (Ь—а) и высотой с.
Тогда двумерная плотность вероятности /(х, у) =1/F—а) с для то-
точек, принадлежащих D; /(х, у)==0 вне D.
ь
В качестве оценки интеграла /= \ <p(x)dx принимают
а
1*з = (b—а) с (л,/я),
где я—общее число случайных точек (х/, yi), принадлежащих D;
пг—число случайных точек, которые расположены под кривой
(/=ф(Х).
Г. Способ «выделения главной части». В качестве оценки ин-
ь
теграла / = \ ф (х) dx принимают
а
п ь
.* Ъ—от1
~hi
где х/—возможные значения случайной величины X, распределен-
распределенной равномерно в интервале интегрирования (а, Ь), которые разы-
разыгрывают по формуле х/=а+F—a)rf, функция g (х) 2» <р (х), причем
ь
интеграл \ g (x) dx можно вычислить обычными методами.
а
734. Вывести формулу
л
2
где х( = а-\-ф—а) г{, для оценки определенного инте-
ь
грала / = ) ф (х) dx.
а
Решение. Введем в рассмотрение случайную величину X,
распределенную равномерно в интервале интегрирования (а, Ь) с
плотностью /(х) = 1/(Ь—а). Тогда математическое ожидание
ь ь
М [ф (Х)\ = j ф (х) / (х) dx=Tl7 J <р (х) dx.
а а
319
Отсюда
Заменив математическое ожидание М[у(Х)] его оценкой —выбороч-
—выборочной средней, получим оценку искомого интеграла
S Ф (*/)
где X/—возможные значения X. Так как случайная величина X
распределена равномерно в интервале (а, Ь) с плотностью f(x) =
ь
= 1/F —а), то Х{ разыгрывают по формуле \ (!* = /•; (см. § 3,
a
правило 2). Отсюда JC/ = a-j-(?> — a)/7, где Г{—случайное число.
735. Найти: а) оценку 1\ определенного интеграла
3
dx; б) абсолютную погрешность |/ — /*|;
i
в) минимальное число испытаний, которые с надежно-
надежностью 0,95 обеспечат верхнюю границу ошибки 6 = 0,1.
Решение, а) Используем формулу
21
По условию, а = \, 6=3, <р(лс) = *+1. Примем для простоты число
исяытаннй п=10. Тогда оценка
ю ю
2 (*/+*) 2 <*<+')
/i*=C-l).^-!_ = 2''-^Чо
где возможные значения х/ разыгрывают по формуле */=а + F—о) г,=
+ (), +a
Результаты десяти испытаний приведены в табл. 63. Случайные
числа г\ взяты из таблицы приложения 9.
Таблица 63
Номер
испытания I
10
0,1000,9730,253
1,200 2,9461,506
2,200 3,94бЬ,506 2,752 3,040 2
376 0,520 0,135 0,863 0,467 0,354 0,876
1,270 2,7261,9341,708 2,752
,270 3,726 2.934 2,708 3,752
0,
1,752 2,040
320
Из табл. 63 находим 2<Р (*/) =29,834. Искомая оценка
/1=2.B9,834/10) =5,967.
з
б) Приняв во внимание, что /= V (*+1) 6х=6, найдем абсо-
абсолютную погрешность 16—5,9671 =0,033.
в) Найдем дисперсию усредняемой функции <р(Х)=Х-\-1, учи-
учитывая, что случайная величина X в интервале интегрирования A, 3)
D(X) C l)a/12 l/3
распределена равномерно и ее дисперсия D(X) = C— l)a/12 = 1/3
(см. задачу 315):
a*=D (X+1) = D (X) = 1/3.
Найдем минимальное число испытаний, которые с надеж-
надежностью 0,95 обеспечат верхнюю границу ошибки 6=0,1. Из равен-
равенства Ф @=0,95/2=0,475 по таблице приложения 2 находим
/ = 1,96. Искомое минимальное число испытаний
л = (/а.аа)/6а=A,96а.A/3))/0,1а=128.
736. В качестве приближенного значения интеграла
i с j r* /t ч 2ч> (*/) гт *.
I = \ cosjtqa: принята оценка /" = (о—а) • — • Най-
ти минимальное число испытаний, при котором с на-
надежностью 0,95 верхняя граница ошибки 6 = 0,1.
Решение. Найдем дисперсию усредняемой функции <р (X) =
= cosX, учитывая, что случайная величина X распределена равно-
равномерно в интервале @,п/2) с плотностью / (*) =2/я:
Я/2 |- Я/2 -.*
аа=— С cosa*d*- — Г cos«d« =0,09.
Ч [Ч 1
Из равенства Ф @=0,95/2=0,475 по таблице приложения 2
находим / = 1,96.
Искомое минимальное число испытаний
л = (/».аа)/61' = A,96а.0,09)/0,1»=35.
737. В качестве приближенного значения интеграла
Я/2
/= [ sinхdx принята оценка /?. Найти минимальное
Is1
число испытаний, при котором с надежностью 0,99 верх-
верхняя граница ошибки 6 = 0,05.
738. Найти а) оценку 1{ определенного интеграла
х2 dx; б) дисперсию а* усредняемой функции <р(Х) = Хя;
в) минимальное число испытаний, которые с надежностью
0,95 обеспечат верхнюю границу ошибки б ==0,1.
11 Гмурман В. Е. 321
Указание*). Для определенности взять 10 случайных чисел
с тремя знаками после запятой нз таблицы приложения 9, начиная
с первой строки сверху.
739. Найти: а) оценку 1\ определенного интеграла
Ve*d.*; б) дисперсию а* усредняемой функции <р(Х) = ех;
в) минимальное число испытаний, при котором с на-
надежностью 0,95 верхняя граница ошибки 6 = 0,02.
740. Найти оценку определенных интегралов:
Л/4 4
741. Найти: а) оценку /J определенного интеграла
I
cos х dx; б) исправленную дисперсию усредняемой
функции K = cosX по данным 10 испытаний.
Решение, а) Разыграем 10 возможных значений X по формуле
*/=0+(я/2)/7=1,571/-,.
Результаты испытаний приведены в табл. 64.
Таблица 64
Номер
испытания }
10
n
*/=(Я/2)
=cos*j
0,100 0,973 0,263
0,167
1,529
0,988 0,042
0,976
0,002
0,398
0,922
0,850
0,376
0,591
0,830
0,689
0,520 0,135 0.863
0,817
0,684
0,468
0,212
1,356
0,9780.213
0,956
0,046
0,467
0,734
0,742
0,551
0,354
0,556
0,849
0.721
0,876
1,376
0,194
0,038
Учитывая, что 2u/=6,442, найдем искомую оценку интеграла:
/J = (я/2) F,442/10) = 1,01.
б) Найдем исправленную дисперсию усредняемой функции:
[ВД
Используя табл. 64, найдем: 2и/==6,442, 2 й? =5,296. Учитывая,
что п = 10, получим искомую дисперсию s* = 0,127.
*) Это указание относится ко всем последующим задачам,
в которых число испытаний не указано. Малое число испытании
взято для простоты.
322
Точное значение дисперсии усредняемой функции равно 0,09
(см. задачу 736),
742, Найти: а) оценку /J определенного интеграла
Я/2
\ sin л: (be; б) исправленную дисперсию усредняемой
функции K = sinX по данным 10 испытаний.
1 I
743. Найти оценку Г интеграла /
Произвести 10 испытаний.
Решение. Область интегрирования ограничена линиями
д=х, у = 1, х=0 и, очевидно, принадлежит единичному квадрату,
Площадь области интегрирования (прямоугольного треугольника)
S=(M)/2=0,5.
Используем формулу
2
^^ , (•)
где N—число случайных точек (х/, д/), которые принадлежат обла-
области интегрирования; у этих точек ffi^xi (при каждом испытании,
в котором это условие выполняется в счетчик N записывают еди-
единицу). Пары независимых случайных чисел (*/, gi) берем из таб-
таблицы приложения 9, начиная с первой строки сверху. Результаты
10 испытаний приведены в табл, 65.
Таблица 65
Номер
испытания 1
1
2
3
4
5
6
7
8
9
10
S
*/
0,100
0,253
0,520
0,863
0,354
0,809
0,911
0,542
0,056
0,474
Ч
0,973
0,376
0,135
0,467
0,876
0,590
0,737
0,048
0,489
0,296
Счетчнк
»t>*t
1
1
I
1
4
1,073
0,629
1,230
0,545
3,477
Из табл. 65 находим V = 4, 2 /(*/• 9t) =3,477. Подставив эти
323
числа в формулу («), получим искомую оценку:
/*=0,5. C,477/4) =0,435.
11»
Сравнительно большое расхождение полученной оценки с точ-
точным значением /=0,5 объясняется малым числом испытаний.
744. Найти оценку /* интегралов:
б) fd* f yi-x*-y*dy;
в)
l-x-y
y
д) Jcbcjch/ j xyzdz.
Произвести по 10 испытаний. Случайные числа брать из
таблицы приложения 9 с тремя знаками после запятой,
начиная с первой строки сверху.
745, Вывести формулу /J = 1^2-^ для оценки
ь
определенного интеграла / = $ <р (лс) Ах, где /(*)—плот-
а
ность распределения «вспомогательной» случайной вели-
величины X в интервале интегрирования (а, Ь); %,—возмож-
%,—возможные значения X, разыгранные по известной плотности
f(x); n—число испытаний.
Решение. Пусть /(*)—плотность распределения некоторой
случайной величины X в интервале интегрирования (а, Ь), т. е.
ь
{f(x)dx=\. Представим интеграл / так:
Таким образом, интеграл / представлен в виде математического
ожидания функции F(X)=<p(X)/f(X). В качестве оценки этого ма-
математического ожидания, а следовательно равного ему интеграла /,
примем выборочную среднюю
/*= 1 ()
где «/—возможные значения случайной величины X, которые разыг-
разыгрывают по известной плотности / (х); п—число испытаний. Искомая
оценка подучена.
824
Заметим, что желательно выбрать /(*) так, чтобы по возмож-
возможности отношение / (д)/| <р (х) | = const.
746. Найти оценку /J интеграла
Решение. Так как е* = 1+*+..., то в качестве плотности
распределения «вспомогательной» случайной величины X примем
функцию f(x)—C(\+x). Из условия cC(l+*)d* = l найдем
о
С =2/3. Итак, / (х) = B/3) (*+1).
Запишем искомый интеграл так:
1
Г е»
¦J B/3) (х+1)'
Таким образом, интеграл / представлен в виде математического
ожидания функции .. _. . . ... В качестве искомой оценки примем
выборочную среднюю (для простоты ограничимся десятью испы-
испытаниями):
,. 1 V «*' *'
где дс/—возможные значения X, которые надо разыграть по извест-
известной плотности /(*)=B/3)(*+l). По правилу 2 (см. § 3), имеем
B/3) f (x+l)dx=rt.
о
Отсюда находим явную формулу для разыгрывания возможных зна-
значений X:
В табл. 66 приведены результаты 10 испытаний.
Таблица 66
Номер
испытанна 1
п
Ф(х/)=е"
М
С
1
0, 100
0,140
1,150
1.140
1.009
2
0.973
0,980
2,664
1,980
1,345
3
0,253
0.326
1,385
1,326
1,044
4
0,376
0,459
1,582
1,459
1,084
5
0.520
0,600
1,822
1,600
1.139
6
0,135
0,185
1,203
1.185
1,015
7
0,863
0,894
2,445
1,894
1,291
8
0,467
0,550
1.733
1.550
1,118
9
0,354
0,436
1,546
1.436
1,077
10
0,876
0,905
2.472
1,905
1,298
325
10 e"
Сложив числа последней строки табл. 66, получим
(=1
=11,42 Искомая оценка в силу (*) равна /J =0,15'11,42 = 1,713.
747* Найти оценки /J определенных интегралов:
з i л/г
а) ^(x+l)dx', б) ^e**dx; в) j shutdx;
4
Указание, Принять в качестве «вспомогательной плотности»
fix) функцию, соответственно равную: а) A/4)*; б) 0,5A+2*);
в) (8/я*)ж; г) 1,092/A+*).
748. Вывести формулу 11 = (b—a)c(njri) для оценки
ь
определенного интеграла / — $ <р (лс) Ах, где подынтеграль-
ная функция неотрицательна и ограничена
исходя из истолкования интеграла как площади.
Решение. Введем в рассмотрение двумерную случайную ве-
величину (X, Y), распределенную равномерно в прямоугольнике D
с основанием (b—а) и высотой с, плотность вероятности которой
f(x, y)=\l(b—a)e. Составляющая Л распределена в интервале
(о, Ь) равномерно с плотностью \/(Ь—а); составляющая Y распре-
распределена в интервале @, с) с плотностью 1/с.
Если разыграно п точек (*/, у{), принадлежащих прямоуголь-
прямоугольнику D, из которых гц точек оказались под кривой y = q>(x), то
отношение площадл, определяемой интегралом /, к площади прямо-
прямоугольника D
ь
в «1
(b—a) en'
Отсюда
ь
Ф (*) 6x = (b—а) с(пгп).
a
Таким образом, в качестве оценки интеграла / можно принять
2
749. Найти оценку /J интеграла $D—х*)йх.
о
326
<p(x)=4—хг не-
не; следовательно,
Решение. Используем формулу
/J=(ft— a)o(ntfn).
В интервале @, 2) подынтегральная функция
отрицательна и ограничена, причем <р(х)<<р(О)
можно принять с=4.
Введем в рассмотрение двумерную случайную величину (X, Y),
распределенную равномерно в прямоугольнике D с основанием
о—а=2—0=2 и высотой с=4, плотность вероятности которой
/(*. У) = 1/B-4) = 1/8.
Разыграем л =10 случайных точек (*/, у/), принадлежащих пря-
прямоугольнику D. Учитывая, что составляющая X в интервале @, 2)
распределена равномерно с плотностью/,(*)= 1/2 и составляющая г
в интервале @, 4) распределена равномерно с плотностью /, (у) = 1/4,
разыграем координаты случайной точки (*/, у{), принадлежащей
прямоугольнику D, по паре независимых случайных чисел (г/, /?/):
Отсюда x/=2rf, y/
Если окажется, что у/ < 4—*?, то точка (*/, gj) лежит под
кривой у=ф (х) и в «счетчик nj» надо добавить единицу.
Результаты десяти испытаний приведены в табл. 67,
Таблица 67
Номер
испытания
1
1
2
3
4
5
6
7
8
9
10
rl
0,100
0,253
0,520
0,863
0,354
0,809
0,911
0,542
0,056
0,474
0,200
0,506
1,040
1,726
0,708
1,618
1,822
1,084
0,112
0,948
2
0,040
0,256
1,082
2,979
0,501
2,618
3,320
1,175
0,013
0,899
4-Х?
3,960
3,744
2,918
1,021
3,499
1,382
0,680
2.825
3,987
3.101
Rl
0,973
0.376
0,135
0,467
0.876
0,590
0,737
0,048
0,489
0,296
VI-4RI
3,892
1,504
0,540
1,868
3,504
2,360
2,948
0.192
1.956
1,184
1
1
1
1
1
1
Из табл. 67 находим Л( = 6. Искомая оценка интеграла
/J=F—o)c(ni/n)=2.4.F/10) = 4,8.
4
750« Найти оценку /J интеграла \—йх.
Указание. Для определенности взять 20 пар случайных
чисел с тремя знаками после запятой из таблицы приложения 9,
начиная с первой строки сверху.
327
1
751. Найти оценку /J интеграла $е*с!л:.
о
Указание*). Для определенности взять 10 пар случайных
чисел с тремя знаками после запятой из таблицы приложения 9,
начиная с первой строки сверху.
752. Вывести формулу
где Xi = a+(b—a)rv g(x)c*y(x), для оценки интеграла
ь
<р (я) их.
а
Решение. Введем в рассмотрение случайную величину X,
распределенную равномерно в интервале интегрирования (а, Ь)
с плотностью/ (*)=1/(Л—а).
Допустим, что найдена такая функция g(x), которая «мало
отличается» от <р (х) и интеграл от которой можно вычислить, не
прибегая к методу Монте-Карло. Тогда математическое ожидание
функции
ь
а
равно /•
Действительно, учтывая, что величина X распределена в интер-
интервале интегрирования (а, Ь) равномерно с плотностью 1/F—а),
получим
ь ь
М [F(X)) = ф-а) J [Ф (x)-g(х)] • jf^ - dx+Jfif W<**=
а
Таким образом, в качестве оценки математического ожидания
M[F(X)], а следовательно интеграла /, можно принять среднее
арифметическое п значений функции F(X):
._ п ь
i=l a
где xi—возможные значения X, которые разыгрывают по формуле
xi=a+(b—a)ri.
753. Найти оценку 1\ интеграла / = J V \ + хг Ах.
*) Это указание относится и к задачам 764, 766.
328
Решение. Так как \ 1+*2 =
«ем g(*) = l + (l/2)*2. Тогда, пш
ю
примем
имеем оценку
е
<=1
Выполнив элементарные преобразования, получим
ю
.то
полагая число испытаний л = 10,
/ i \
cbe.
Учитывая, что а=0, *=1, возможные значения х/ разыграем по
формуле Xj=a-\-(b—a)r{=r[. Результаты вычислении приведены
в табл. 68.
Таблица 68
Номер
испытания 1
4
1
0,100
0,010
1,010
1,005
2,000
2
0,973
0,947
1,947
1,395
1,843
3
0,253
0,064
1,064
1,032
2,000
4
0,376
0.U1
1,141
1,068
1,995
S
0,620
0,270
1,270
1,127
1,984
6
0, 13S
0,018
1,018
1,009
2.000
7
0,863
0.745
1,745
1,321
1,897
8
0,467
0,218
1,218
1,104
1,990
9
0,354
0,126
1,125
1.061
1.997
10
0,876
0,767
1,767
1,329
1,891
Сложив числа последней строки табл. 68, найдем сумму 19,597,
подставив которую в соотношение («), получим искомую оценку
интеграла
/1 = A9,597/20)+A/6) = 1,145.
Заметим, что точное значение / = 1,147.
754. Найти оценку /J интеграла
Указание. Принять функцию g(x) = l + x. так как е* =
755. Найти оценку II интеграла j e-*f/a dx.
Указание. Принять функцию g(x) = l— (x*/2), так как
**У» 1(»/2)+
Часть пятая
СЛУЧАЙНЫЕ ФУНКЦИИ
Глава шестнадцатая
КОРРЕЛЯЦИОННАЯ ТЕОРИЯ СЛУЧАЙНЫХ ФУНКЦИЙ
§ 1. Основные понятия. Характеристики случайных
функций
Случайной функцией X (t) называют функцню неслучайного аргу-
аргумента t, которая при каждом фиксированном значении аргумента
является случайной величиной.
Сечением случайной функции X(t) называют случайную вели-
величину, соответствующую фиксированному значению аргумента случай-
ной функции.
Реализацией случайной функции X (t) называют неслучайную
функцию аргумента t, которой может оказаться равной случайная
функция в результате испытания.
Таким образом, случайную функцию можно рассматривать как
совокупность случайных величин (X(t)}, зависящих от параметра /,
или как совокупность ее возможных реализаций.
Характеристиками случайной функции называют ее моменты,
которые являются неслучайными функциями.
Математическим ожиданием случайной функции X (/) называют
неслучайную функцию mx(t), значение которой при каждом фикси-
фиксированном значении аргумента равно математическому ожиданию сече-
сечения, соответствующего этому же фиксированному значению аргумента:
X
Свойства математического ожидания случайной функции. Свой-
Свойство 1. Математическое ожидание неслучайной функции <р (/) равно
самой неслучайной функции:
Свойство 2. Неслучайный множитель ф(t) можно выносить
ва знак математического ожидания:
M[<p(f)X(t)]=<p(()-M[X(i)]=<p(t).mx(t).
Свойство 3. Математическое ожидание суммы двух случай'
пых функций равно сумме математических ожиданий слагаемых:
M[X(t)+Y(t)]=mx(t)+mv(t).
Свойство можно обобщить на п слагаемых функций:
М 2 Xt(t) = 2 mx(t).
L< = I J !=1
Следствие. Если X(t) —случайная функция, ф(/)—неслу-
ф(/)—неслучайная функция, то
M[X(t)+<p(t)] = mx(t) +Ф(/).
Дисперсией случайной функции X(t) называют неслучайную не-
неотрицательную функцию Dx (t), значение которой при каждом фикси-
830
рованном значенни аргумента / равно дисперсии сечения, соответст-
соответствующего этому же фиксированному значению аргумента:
Ож (О-D [*</)].
Средним квадратическим отклонением случайной функции назы-
называют квадратный корень из дисперсии:
Свойства дисперсии случайной функции. Свойство 1. Дис-
персия неслучайной функции <р(<) равна нулю:
О[Ф(/)]=0.
Свойство 2. Дисперсия суммы случайной функции X (I) и
неслучайной функции q>(t) равна дисперсии случайной функции:
p
Свойство 3. Дисперсия произведения случайной функции X(/)
на неслучайную функцию <р @ равна произведению квадрата неслу-
неслучайного множителя на дисперсию случайной функции:
Центрированной случайной функцией называют разность между
случайной функцией и ее математическим ожиданием:
X(i) = X(t)-mx(t).
Корреляционной функцией случайной функции X(t) называют
неслучайную функцию Кх (t\, tt) двух независимых аргументов t\ и
tt, значение которой прн каждой паре фиксированных значений аргу-
аргументов равно корреляционному моменту сечений, соответствующих
этим же фиксированным значениям аргументов:
При равных между собой значениях аргументов ff=f2 =' К0Р*
реляционная функция случайной функции равна дисперсии этой
функции:
Kx{t, l)-Dx{t).
Свойства корреляционной функции. Свойство К При пере-
перестановке аргументов корреляционная функция не изменяется (свой-
(свойство симметрии):
KAU, h) = KAh, h).
Свойство 2. Прибавление к случайной функции X(/) неслу-
неслучайного слагаемого (f(t) не изменяет ее корреляционной функции:
если Y(t) = X(t)+<p(l), то
Свойство 3. При умножении случайной функции X(/) на
неслучайный множитель <р (/) ее корреляционная функция умножается
на произведение <p('i)-<p('a): если Y(t)=X(t)-q>(t), то
Свойство 4. Абсолютная величина корреляционной функции
не превышает среднего геометрического дисперсий соответствующих
сечений:
К Ah, ttX VDAWDAU.
331
Нормированной корреляционной функцией случайной функции
X (t) называют неслучайную функцию двух незавнснмых переменных
ti и t2, значение которой при каждой паре фиксированных значений
аргументов равно коэффициенту корреляции сечений, соответствую-
соответствующих этим же фиксированным значениям аргументов:
Kx(tu tt) _ Kx(h, tt)
Абсолютная величина нормированной корреляционной функции
не превышает единицы: \px(tlt <8)|<1.
Взаимной корреляционной функцией двух случайных функций X (/)
и Y (t) называют неслучайную функцию Rxy (tu t2) двух незавнсимых
аргументов /j н t2, значение которой при каждой паре фиксирован-
фиксированных значений аргументов равно корреляционному моменту сечений
обеих функций, соответствующих этим же фиксированным значениям
аргументов:
Коррелированными называют две случайные функции, если их
взаимная корреляционная функция не равна тождественно нулю.
Некоррелированными называют две случайные функции, взаим-
взаимная корреляционная функция которых тождественно равна нулю.
Свойства взаимной корреляционной функции. Свойство 1.
При одновременной перестановке индексов и аргументов взаимная
корреляционная функция не изменяется:
Rxy Oi. tt) = Ryx{tt, h)-
Свойство 2. Прибавление к случайным функциям Х({) и
К (t) неслучайных слагаемых ф (/) и гр (t) не изменяет их взаимной
корреляционной функции: если
то
Rxtyt{h. '.) = Я*Г(<1. h).
Свойство 3. При умножении случайных функций X(i) и
К (t) на неслучайные множители, соответственно ф(/) и гр (/), взаим-
ноя корреляционная функция умножается на произведение <р (tt) ty (tt):
если
X, @ - X @ -ф @, Yt @=К (Q • * (Q,
то
Свойство 4. Абсолютная величина взаимной корреляционной
функции двух случайных функций X (t) и К (t) не превышает среднего
геометрического их дисперсий:
\Rxyih. U)\<. VDx(h)Dy(tt).
Нормированной взаимной корреляционной функцией двух случай-
случайных функций X (t) и К @ называют неслучайную функцию двух
независимых аргументов ti и tt:
независимых аргументов ti и tt:
y v
Абсолютная величина нормированной взаимной корреляционной
функции не превышает единицы: \pXy(h, ^)|<Ь
332
756. Случайная функция X {t) = {t2+ 1I), где U —
случайная величина, возможные значения которой при-
принадлежат интервалу @,10). Найти реализации функции
X (t) в двух испытаниях, в которых величина U при-
приняла значения; a) «i = 2; б) и2 = 3,5.
757. Случайная функция X(t) = Usint, где (/—слу-
(/—случайная величина. Найти сечения X(t), соответствующие
фиксированным значениям аргумента: а) /,=я/6;б) ta =
= я/2.
758. Доказать, что неслучайный множитель можно вы-
выносить за знак математического ожидания:
ф (9 •«*(')•
759. Найти математическое ожидание случайной функ-
функции ХУ) = иег, где U—случайная величина, причем
M(U) 5
()
760. Доказать, что математическое ожидание суммы
двух случайных функций равно сумме математических
ожиданий слагаемых:
Указание. Принять во внимание, что при любом фиксиро-
фиксированном значении аргумента сеченне случайной функции есть случай-
случайная величина.
761. Найти математическое ожидание случайной функ-
функции: a) X(t) = Ut* + 2t + \; б) X@ = t/sin4* + Kcos4*.
где U и К—случайные величины, причем М (U) = М (V) =
= 1.
762. Доказать, что корреляционная функция случай-
случайной функции X (t) равна корреляционной функции цент-
центрированной случайной функции: X(t)=*X (t)—mx(t).
763. Доказать, что при равных между собой значениях
аргументов корреляционная функция случайной функции
X(t) равна ее дисперсии: Kx\t, t) = Dx(t).
Указание. Принять во внимание, что, по определению дис-
дисперсии случайной величины X, DX = M[(X— тх)*] = М [(Х)*].
764. Доказать, что от прибавления к случайной функ-
функции X(t) неслучайной функции <р(*) корреляционная
функция не изменяется: если Y (t) = X(t) + q>(t), то
Решение. Найдем математическое ожидание:
ту @ = М [X @+ф @1 = тх @+ф (/).
Найдем центрированную функцию:
333
Таким образом, ^(<) = л уч.
Найдем корреляционную функцию*1:
Kv = М [f (/,) ? (t2)] = М [X (/г) X (tt)] = Кх.
Итак, КУ = КХ>
765. Известна корреляционная функция Кх случай-
случайной функции X (/). Найти корреляционную функцию
случайной функции Y (t) = X(t) + t*.
766. Доказать, что при умножении случайной функ-
функции X (t) на неслучайный множитель <р (t) корреляцион-
корреляционная функция умножается на произведение <р(Л)*ф(*8).
767. Известна корреляционная функция Кх случайной
функции X(t). Найти корреляционную функцию случай-
случайной функции: a) Y(t) = X(t)-(t + 1); б) Z(t) = CX(t),
где С—постоянная.
768. Пусть X @—случайная функция, <р @—неслу-
@—неслучайная функция. Доказать: если Y(t) = X(t)-\-q>(t), то
Решение. Первый способ. При любом фиксированном
значении аргумента сечение X (t)—случайная величина, <р @—по-
@—постоянное число. Известно, что прибавление к случайной величине
постоянного числа не изменяет ее дисперсии, поэтому Dy (t) =
[()+()] x()
Второй способ. Прибавление к случайной функции неслу-
неслучайного слагаемого не изменяет корреляционной функции: К у d, tt) =
=Kx(tu tt). При равных значениях аргументов получим д„ (/, О =
= Kx\t, t), или окончательно Dy(t) = Dx(i).
769. Известна дисперсия Dx(t) случайной функции
X (t). Найти дисперсию случайной функции Y (t) —
Х@+2
@
770. Дано: X(t)—случайная функция, <р(/)—неслучай-
<р(/)—неслучайная функция. Доказать: если Y (t) = X (t)-q>(t), то Du(t)=
= <p*(t).Dx(t).
771. Известна дисперсия случайной функции X(t).
Найти дисперсию случайной функции Y (/) = (/ + 3)X(t).
772. На вход усилительного звена подается случайная
функция X(t), математическое ожидание и корреляцион-
корреляционная функция которой известны: тх(/) = /, Kx(tv tt) =
= е-а(/,-/,)» (а>0). Найти: а) математическое ожидание;
б) корреляционную функцию выходной случайной функ-
функции Y (t), если коэффициент усиления fe = 5.
Указание. Учесть, что выходная функция Y(t) = 5X(t).
*> В этой задаче и в ряде последующих задач для простоты
записи скобки (tt, /j) опущены.
334
773. Доказать, что корреляционная функция произве-
произведения двух центрированных некоррелированных случай-
случайных функций равна произведению корреляционных функ-
функций сомножителей.
Решение. Пусть Z(t) = k(/)?(/)• Математическое ожидание
произведения некоррелированных функций равно пронзведеиню мате-
математических ожиданий сомножителей, поэтому mz(/) = m.(/)m. (/).
Математическое ожидание любой центрированной функции равно
нулю, поэтому тг (/)=0-0 = 0 и, следовательно, i(t) = X(t)V (().
Искомая корреляционная функция
Kz=M [Z(tr) I(tt)] - М {[X (ti) f (tt)] [* {tt) ? (/2)},
Перегруппируем сомножители под знаком математического ожидания:
Кг = М {\X(h) k (/,)] [9 (Н) 9 «,)]}.
Учитывая, что заданные функции не коррелированы, получим
Кг= М [к (tx) к (/*)] М [l'(tt) •(«],
или Кг — КхКу
Корреляционная функция случайной функции равна корреля-
корреляционной функции центрированной функции (см. задачу 762), поэтому
окончательно имеем Кг=К»Кч
774. Доказать, что корреляционная функция произ-
произведения трех центрированных независимых случайных
функций равна произведению корреляционных функций
сомножителей.
775. Найти: а) математическое ожидание; б) корреля-
корреляционную функцию; в) дисперсию случайной функции
X (t) = U cos 2t, где 0—случайная величина, причем
M(U) = 5, D(U) = 6.
Решение, а) Найдем искомое математическое ожидание (неслу-
(неслучайный множитель cos It вынесем за зиак математического ожидания):
М [X @] = М [U cos 2/] = cos ItM (U) = 5 cos 2t,
б) Найдем центрированную функцию:
k(t) = X(t)—mx(t) = U cos2t—5cos2/ = (V— 5) cos 2/.
Найдем искомую корреляционную функцию:
Кх (tt, tt) =M[k (tt) k (/,)] = M {[(U -5) cos2tt] [(U - 5) cos 2t,]} =
— cos2/!COs2<sAl (U —5)*.
Учитывая, что M(U— 5)*= 0A/)=6, окончательно имеем
KxVi, <*)=6cos2/icos2<,.
в) Найдем искомую дисперсию, для чего положим t1 = tt — t:
776. Найти: а) математическое ожидание; б) корреля-
корреляционную функцию; в) дисперсию случайной функции
X{t)=*Usin3/, где О—случайная величина, причем
M(U) = 10, D(U) = 0,2.
777. Известна корреляционная функция Кх (h> **) —
= 'i*t + 5'!*i случайной функции X(t). а) Убедиться на
примере при t1=l, tt=2 что абсолютная величина корре-
корреляционной функции не превышает среднего геометри-
геометрического дисперсий соответствующих сечений; б) найти
нормированную корреляционную функцию и вычислить
коэффициент корреляции сечений, соответствующих зна-
значениям аргументов ^ = 1, /2 = 4.
778. Задана корреляционная функция Кх (к> Ч) ="
= t1tie-\''-bl случайной функции X(t). Найти нормиро-
нормированную корреляционную функцию.
779. Найти взаимную корреляционную функцию двух
случайных функций: X(t) — t2U и Y(t) = t*U, где U —
случайная величина, причем D(U) = 5.
Решение. Найдем математические ожидания:
тх (/) = М (W) = /2тя> ту (t) = M (t*U) = t*mai
Найдем центрированные функции:
X(t) = X(t)—mx(t) = tW—1*та = ^(и—ти),
my(t) = t3U—t*ma = t* (U —ma).
Найдем взаимную корреляционную функцию:
Rxy = М [X (h) ? (t2)] = M {[tl (U-ma)\ [t\ (U-ma)]\
Итак, Rxy = 5tltl
780. Доказать, что взаимная корреляционная функция
случайных функций X (t) и Y (t) равна взаимной корре-
корреляционной функции центрированных функций X (t) и
Y(t).
781. Доказать, что при одновременной перестановке
индексов и аргументов взаимная корреляционная функ-
функция двух случайных функций не изменяется: /?жу (/lf ?„) =
782. Задана взаимная корреляционная функция
RXy(ti> ^a) = cos (ot^i + P<2). Написать взаимную корреля-
корреляционную функцию RyX(ti, tt).
336
783. Найти нормированную взаимную корреляционную
функцию случайных функций X(t) = tU и Y(t) = (t + \)U,
где (/—случайная величина, причем дисперсия D(U) =
= 10.
§ 2. Характеристики суммы случайных функций
Теорема 1. Математическое ожидание суммы конечного числа
случайных функций равно сумме математических ожиданий слагаемых.
Следстви е. Математическое ожидание суммы случайной
функции и случайной величины равно сумме их математических ожи-
ожиданий.
Теорема 2. Корреляционная функция суммы двух коррелированных
случайных функций равна сумме корреляционных функций слагаемых
и взаимной корреляционной функции, которая прибавляется дважды
(с разным порядком следования аргументов): если Z(t) = X(t) +
+ Y @. то
Теорема обобщается на л попарно коррелированных функций:
если К (/)=2 */<0. то
i
= 2 Ki(d, /2)+ 2 я*, ли.
1=1 1Ф1 '/
2 2
1=1 1Ф1
где пары индексов («, /) второго слагаемого есть размещения из
чисел 1, 2, ..., л, взятых по два.
Следствие 1. Корреляционная функция суммы некоррелиро-
некоррелированных случайных функций равна сумме корреляционных функций сла-
слагаемых.
Следствие 2. Корреляционная функция случайной функции
и некоррелированной с ней случайной величины равна сумме корре-
корреляционной функции случайной функции и дисперсии случайной вели-
величины.
784. Заданы корреляционные и взаимные корреляци-
корреляционные функции случайных функций X (t) и Y (t). Найти
корреляционную функцию случайной функции Z(/) =
= X(t) + Y (t), если рассматриваемые функции: а) корре-
лированы; б) не коррелированы.
785. Известны математические ожидания тх (t) = 2t +
+ 1, my{t) — t — 1 и корреляционные функции Kx=tlB,
/Су = е-4(/«"'1'' некоррелированных случайных функции
X (/) и Y(t). Найти: а) математическое ожидание; б) кор-
корреляционную функцию случайной функции Z(t) = X (t) +
+ Y(th
786. Заданы корреляционные и взаимные корреляци-
корреляционные функции случайных функций X (t) и Y (/). Найти
12 Гмурыан В. Е. 337
взаимную корреляционную функцию случайных функций
U(i) = aX(t)+by(t) nV(t) = cX(() + dY (t), где с, b, с, d-
постоянные действительные числа.
787. Заданы корреляционные и взаимные корреляцион-
корреляционные функции случайных функций X (t), Y (t), Z(t). Найти
корреляционную функцию случайной функции U (/) =
= X(t) + Y(t) + Z(t), если рассматриваемые функции:
а) попарно коррелированы; б) попарно не коррелированы.
788. Доказать, что формулу К„ — 2tf*,+ 2 Rx*, для
отыскания корреляционной функции суммы Y (t) =
= 2 Я/ @ п коррелированных случайных функций можно
записать в виде /С„= 2 Rxx;
/=i
789. Найти математическое ожидание, корреляцион-
корреляционную функцию и дисперсию случайной функции X (t) =
— Ut+Vt2, где U к V—некоррелированные случайные
величины, причем M(U) = 4, M(V) = 7, D{U) = 0,1,
D(F) 2
Указание. Принять во внимание, что величины U и V не корре-
коррелированы, поэтому их корреляционный момент М [U—ти) (У—щ)\ —
— 0.
790. Найти математическое ожидание, корреляцион-
корреляционную функцию и дисперсию случайной функции X (t) =
= Usmt+Vcost, где U и V—некоррелированные слу-
случайные величины, причем M(U)—l, M(V) = 8, D(U) =
= D(V) = 4.
791. Найти математическое ожидание, корреляцион-
корреляционную функцию и дисперсию случайной функции X (t) —
= 0cos2t + Vsint + t, где U и V—некоррелированные
случай«ые величины, причем M(U)= I, M(V) = 2, D(U) =
= 3, D(V) = 4
Указание. Прибавление к случайной функции неслучайного
слагаемого t не изменяет ее корреляционной функции, поэтому дос-
достаточно найтн корреляционную функцию случайной функции Y (t) =
{/2/ + ViW
792. Заданы случайные функции X (t) = U cos t+Fsin t,
Y (t) = U cos 3t+Vsin 3t, где U и V—некоррелированные
случайные величины, причем M(U) = M(V) = 0, D(U) =
= D(V) = 5. Найти нормированную взаимную корреля-
корреляционную функцию рХу (tv tt).
793. Найти корреляционную функцию случайной
функции X (i)=(/<i^+^^fV'i/
338
где ©lt о>2—постоянные числа; (/„ U2, Vv Ka—попарно не-
некоррелированные случайные величины, причем их матема-
математические ожидания равны нулю, дисперсии величин Ut
и Vx равны ?)„ дисперсии величин Ut и Ка равны D2.
§ 3. Характеристики производной от случайной функции
Говорят, что последовательность случайных величин Х\, Хг,
..., Хп сходится в среднеквадратичном к случайной величине X,
если математическое ожидание квадрата разности Хп—X стремится
к нулю при л-»оо: М [(Хп—Х)'2\=0. Случайную величину X на-
называют пределом в среднеквадратичном последовательности случай-
случайных величин Хи Х.2 Х„, ... н пишут: Х = \Л.т. Хп.
Случайную функцию X (/) называют дифференцируемой, если
существует такая функция А" (/) (ее называют производной), что
Таким образом, производной случайной функции X' (t) называют
среднеквадратичный предел отношения приращения функции к при-
приращению аргумента Д* при Д* -* 0:
у (О-и.ш.
А10
Теорема 1. Математическое ожидание производной ХA)=х
от случайной функции X (/) равно производной от ее математиче-
математического ожидания:
m.(t)=mx(t).
X
Теорему 1 можно обобщить: математическое ожидание произ-
производной порядка п от случайной функции равно производной этого
же порядка от ее математического ожидания.
Теорема 2. Корреляционная функция производной от случайной
функции X (/) равна второй смешанной частной производной от ее
корреляционной функции:
Теорема 3. Взаимная корреляционная функция случайной функ-
функции ХA) и ее производной равна частной произеодной от корреля-
корреляционной функции по соответствующему аргументу [если индекс х
записан на первом (втором) месте, то дифференцируют по первому
(второму) аргументу]:
р и м Ж*<**'•> р и t\-dJS*lbJA
Rxx V* /а) 5?^ ' Rix(/l> '2) дп *
794. Задано математическое ожидание тх (t)=t3+2t+1
случайной функции X (t). Найти математическое ожида-
ожидание ее производной.
795. Задано математическое ожидание тхA) = Р + 4
случайной функции X(t). Найти математическое ожида-
ожидание случайной функции Y (t) = tX' (t) +1*.
12* 339
796. Доказать, что математическое ожидание второй
производной от дважды дифференцируемой случайной
функции X @ равно второй производной от ее матема-
математического ожидания.
797. Задана корреляционная функция /Cx = 5e-('«-'')f
случайной функции X(t). Найти корреляционную функ-
функцию ее производной.
798*. Задана случайная функция X(t) = Ueslcos2t,
где U — случайная величина, причем М (U) — 4, D(U) = l.
Найти: а) математическое ожидание; 6) корреляционную
функцию ее производной.
799. На вход дифференцирующего звена поступает
случайная функция X (t), корреляционная функция ко-
которой Кх = \ЬЖ cos © (t2—tfi)]/(*i+*2)- Найти корреляцион-
корреляционную функцию выходной функции Y (t) = Xr (t).
800. На вход дифференцирующего звена поступает
случайная функция X (t) с математическим ожиданием
тх (t)=5 sin /и корреляционной функцией Kx=3e~°Mtt-'i)i.
Найти: а) математическое ожидание; б) корреляционную
функцию выходной функции Y(t) = X' (/).
801. Доказать, что взаимная корреляционная функ-
функция случайной функции X (t) и ее производной равна
частной производной от корреляционной функции по
аргументу, который «соответствует производной» [если
индекс х стоит на первом (втором) месте, то надо диф-
дифференцировать по первому (второму) аргументу^
Решение, а) По определению взаимной корреляционной
функции,
Произведение под знаком математического ожидания можно
представить в виде частной производной по аргументу 1г:
dig 012
поэтому RX-X = M) dtt I"
Учитывая, что операции дифференцирования н нахождения ма-
математического ожидания можно переставлять, окончательно получим
дКх
dt,'
б) Рекомендуем доказать самостоятельно.
340
802. Заданы корреляционные функции: а)Кх = е~*''~'1)г',
б) Kx=t1t2e'l+'t. Найти взаимные корреляционные функ-
функции случайной функции X(t) и ее производной.
803. Известна взаимная корреляционная функция
Rxi случайной функции X(t) и ее производной. Найти
корреляционную функцию производной.
804. Известна взаимная корреляционная функция
Rxx — tiWi~^~ l)e'1+'' случайной функции X(t) и ее про-
производной. Найти корреляционную функцию производной.
805. Найти корреляционную функцию случайной функ-
функции Z(t)=X (t)+X' @> зная корреляционную функциюК'х-
Решение. В силу теоремы 2 (§ 2), Кг = Кх + К- +R .+#•
Учитывая, что корреляционная функция производной (теорема 2)
к - д*К*
и взаимные корреляционные функции (теорема 3)
окончательно получим искомую корреляционную функцию:
, дКх , дКх
806. Найти корреляционную функцию случайной функ-
функции Z(i) = X(t)-\-X' (/), зная корреляционную функцию
/<-x==5e-<'«-'')f.
Указание. Использовать задачи 797 и 805.
807. Доказать, что взаимная корреляционная функ-
функция случайной функции и ее второй производной равна
частной производной второго порядка от корреляцион-
корреляционной функции по аргументу, который «соответствует»
производной [если индекс х на первом (втором) месте,
то дифференцируют корреляционную функцию по пер-
первому (второму) аргументу]:
г> // /\ &2Кх в it 4\
808. Задана корреляционная функция /С, = е-<'«-'»'*.
Найти взаимные корреляционные функции случайной
функции X(t) и ее второй производной.
809*. Найти корреляционную функцию случайной
функции Y(t) = U(t)X(t) + V(t)X'(t), где X (t)—диф-
(t)—дифференцируемая случайная функция, корреляционная
341
функция которой известна; V (t) и V(t)—неслучайные
функции.
810*. Задана корреляционная функция случайной
функции X(t). Найги взаимную корреляционную функ-
функцию Ryz случайных функций Y(t) = aX{t) + ЬХ'(t) и
Z(t)=cX'(t) + dX(t), где a, b, с, d—постоянные дейст-
действительные числа.
§ 4. Характеристики интеграла от случайной функции
Интегралом от случайной функции X (/) по отрезку. [0, t] на-
называют предел в среднеквадратнчном интегральной суммы при стрем-
стремлении к нулю частичного интервала As,- макснмальной длины (пере-
(переменная интегрирования обозначена через s, чтобы отличить ее от
предела интегрирования t):
Y @ = l.i .m. Y.X (si) As/ = С X (s) ds.
Теорема 1. Математическое ожидание интеграла от случайной
функции равно интегралу от ев математического ожидания:
t t
если Y @ = J X (s) ds, то т„ (/) = J mx (s) ds.
о о
Теорема 2. Корреляционная функция интеграла от случайной
функции равна двойному интегралу от ее корреляционной функции:
t
если Y (/)= J X (s) ds, то К„= J $ Кх
0 0 0
ds2.
Теорема 3. Взаимная корреляционная функция случайной функ-
функции X (t) н интеграла Y (t) = \ X (s) ds равна интегралу от кор-
о
реляционной функции случайной функции X(t):
U
811. Зная математическое ожидание /пж(/) = 3/2+1
случайной функции X (t), найти математическое ожида-
ожидание интеграла Y (t) = j X (s) ds.
Решение. Искомое математическое ожидание
/ t
m,,(t)={ m*(s)ds=f
о
812. Найти математическое ожидание интеграла
Y (t) = С X (s) ds, зная математическое ожидание случай-
63
ной функции X(t): a) mx(t) = cost; б) mx(t) = 4cos* t;
в) mx(t) = t—cos 2/.
813. Задана случайная функция X (t) = Ueat cos fit,
где U—случайная величина, причем М@) = 5. Найти
математическое ожидание интеграла Y (t) = \ X (s) ds.
о
Указание. Найти сначала тх(/).
814. Найти математическое ожидание случайной функ-
функции Y (t) = С X (s) ds, зная случайную функцию X (/):
a) X(t) = Ueatsmt; б) X{t) = Usin4, где (У—случайная
величина, причем M(U) = 2.
815. Задана случайная функция X(t) = U cos2*, где
U—случайная величина, причем М (U) = 2. Найти мате-
математическое ожидание случайной функции
о
816. Задана корреляционная функция Кх (*i. t*) ~
= cos<o/1cos<b/2 случайной функции X(t). Найти: а) кор-
корреляционную функцию; б) дисперсию интеграла Y (t) =
= J X (s) ds.
Решение, а) Корреляционная функция интеграла Y(()
i
= V X (s) ds равна двойному интегралу от заданной корреляционной
о
кции:
Ку (<i, <а) = \ \ ^* («1. st) d«i dsa = \ \ cos ©Si со» (os2 dsx ds2 =
oo oo
о
функции:
= \ cos <osi ds1 \ cos cos2 ds2 = (sin ш/j sin ш/г)/<о2.
б) Найдем искомую дисперсию, для чего в найденной корреля-
корреляционной функции полежим /, = /2 = /:
Dj, (t)=Ky (/,/)=sin2 ш//(ва.
343
817. Задана корреляционная функция/С* = 1a
случайной функции X(t). Найти: а) корреляционную
t
функцию; б) дисперсию интеграла Y (t) = С X (s) ds.
Iх'
818. На вход интегрирующего устройства поступает
случайная функция X (t), корреляционная функция ко-
которой Kx='titi. Найти дисперсию на выходе интегратора.
Указание. Вычислить сначала корреляционную функцию
выходной функции Y (/) = V X (s) ds.
О
t
819. Найти дисперсию интеграла Y(t)= \ X(s)ds,
о
зная корреляционную функцию случайной функции X (t):
а) /С* = 2^1 + 3^,; б)/е*=М»е'|+'ч в) Kx=\/l+(ta—trf;
г) Кх = е» <'¦ + '•> cos 2 tx cos 2 tt.
820. На вход интегрирующего устройства поступает
случайная функция X (t), математическое ожидание и
корреляционная функция которой известны: tnx(t) = cosit,
Kx = cos(ut1cosata. Найти: а) математическое ожидание;
б) корреляционную функцию; в) дисперсию на выходе
интегратора.
821*. Задана случайная функция X (t) = l/e»' cos 2t,
где U—случайная величина, причем M(U)=5, D(U)=l.
Найти: а) математическое ожидание, б) корреляционную
функцию; в) дисперсию интеграла Y (t) == J X (s) ds.
о
Решение, а) Вычислим предварительно математическое ожи-
ожидание заданной функции, учитывая, что М (t/) = 5:
тх @ = М lt/e»' cos 2/J = Ue»' cos 2t¦ M (U) =5e« cos 2t.
Найдем искомое математическое ожидание:
ту (t) = \ тх (s) ds=5 С e»s cos 2s ds.
0 0
Интегрируя дважды по частям, окончательно получим
ту @ = E/13) [е*< Bsin2t +3cos 20—3].
б) Вычислим предварительно корреляционную функцию задан-
заданной функции. Приняв во внимание, что центрированная функция
X(t) = X (t) — mx @ = е" cos 2t— 5e3< cos 2/ =е3' cos 2t (U — 5),
имеем
Kx = Af {[e3' cos 2/t (U — 5)] [e3'. cos 2/2 (U —5)] ==
= es('«+'»)cos2/1cos2/2M(t/— 5)*.
344
По условию, D(U) = M (U— 5J = 1, следовательно,
Кх = е3 <». + '»> cos 2/, cos 2ta.
Найдем искомую корреляционную функцню:
'¦'•
Ку (<i. h) = \ \ е3 (*!+*») cos 2st cos 2s» dsj ds2,
о о
Выполнив интегрирование, окончательно имеем
Ky(tu /a) = A/169) [e3tt B sin 2/x +3 cos 2/x)—3] [e3t B sin 2/s +
+3cos2/2)—3].
в) Найдем искомую дисперсию:
Dy(t)=Ky(t, 0 = (l/169)[e3'Bsin2/+3cos20-3]2.
822. Найти дисперсию интеграла Y (t) — J X (s) ds,
зная случайную функцию: a) X(t) = U cos 2/, где U —
случайная величина, причем M(U) = 5, D(U) = f>;
б) X(t) = Usmt, причем М(?У) = 2, D(U) = 3.
823. Задана корреляционная функция /Cx = e-">+'»>.
Найти корреляционную функцию случайной функции
i
Y (t) = t J X (s) ds.
о
Указание. Найти сначала корреляционную функцию интег-
интеграла, а затем использовать свойство 3 корреляционной функции (§ 1).
824. Задана случайная функция X(t) = Ucos3t, где
U—случайная величина, причем М({/) = 1, D(U)=l.
Найти: а) математическое ожидание; б) корреляционную
функцию; в) дисперсию случайной функции
825*. Задана корреляционная функция Кх =
C'Jp^ cosp/j. Найти дисперсию случайной функ-
функции K(O=2
826*. Задана корреляционная функция /Сж = De-"*-'»!.
Найти: а) корреляционную функцию; б) дисперсию ин-
интеграла
о
345
Решение. Используем формулу
¦1!
= $ J Kx (Sl,st) dsx dst = D J dsx J e-'s'-s'l <fc2, (¦)
0 0
1. Пусть tt < i2- Тогда внутренний интеграл
'» Sl t,
J e-'s'-s«' ds8 = J e-(s'-s«>ds2 + 5 e-<s'-s«» dss.
0 0 s,
Выполнив интегрирование, найдем
'>
f e-ls«-sil ds2 = 2—e-*i— e-*i—e-('«"Sl). (**)
о
Подставив (**) в (*):
Ky(h, tt) = D $ [2-e-'.-e <'•-««)]ds,.
о
После интегрирования получим корреляционную функцию при ti<t2:
2. Пусть /2 < /,. Используя свойство симметрии (при переста-
перестановке аргументов корреляционная функция не изменится), сразу
получим корреляционную функцию интеграла при tt < tt:
Ky(t*, /1) = D[2/2+e-'» + e-'—e-«.-'»>—1].
3. Объединив эту формулу с формулой (***), окончательно име-
имеем для любых /х и tt
где min(/], /2)—наименьшее из чисел tt и /а.
Найдем искомую дисперсию:
827*. Заданы математическое ожидание тх @ = 3 + 4/,
корреляционная функция К.х= 10е~2!'•-'«I. Найти: а) ма-
математическое ожидание; б) дисперсию интеграла
J
о
828. Доказать, что если известна корреляционная
функция случайной функции X (t), то взаимные корре-
корреляционные функции случайных функций X (t) и У (t) =
346
= J X (s) ds выражаются интегралами:
о
U it
a) Rxu = J Кх (tv s) ds; 6) RyX = J Kx (s, /,) ds.
о о
Решение. По определению взаимной корреляционной функ-
функции» Rxy — M[X(ti)y(B)]. Найдем центрированную функцию:
/ t
t{f)-Y (/)-ту @ = С X (s) ds- f m, (s) ds =
О О
Следовательно,
[U
X(td\k(s)ds I
о J
Г'*. . 1
:М\
\\ \X(U)X(s)ds .
Операции нахождения математнческого ожндания и интегрирования
можно менять местами, поэтому
'• 't
Rxy = f M [X «J X (s)] ds=[Kx (h, s) ds.
о о
б) Доказать самостоятельно.
829. Найти взаимные корреляционные функции слу-
случайных функций X(t) и К (*) = $ X (s) ds, если известна
корреляционная функция Кх случайной функции X(t):
а) Кх = 2^+\; б) /C* = cos^cos^; в) /Сж = ^'+«
Глава семнадцатая
СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ
§ 1. Характеристики стационарной случайной функции
Стационарной называют случайную функцию X (t), математи-
математическое ожидание которой постоянно при всех значениях аргумента t
и корреляционная функция которой зависит только от разности
аргументов /»—t^. Отсюда следует, что:
347
1. Корреляционная функция стационарной случайной функции
есть функция одного аргумента т = /2—ti-
Kx(tl, /l) =**(/•-*!) = ** М-
2. Дисперсия стационарной случайной функции постоянна при
всех значениях аргумента t и равна значению корреляционной
функции в начале координат (x=0):Dx(t)=kx@).
Корреляционная функция стационарной функции обладает сле-
следующими свойствами.
Свойство 1. Корреляционная функция стационарной случай-
случайной функции —четная функция:кх(х)=кх(—1).
Свойство 2. Абсолютная величина корреляционной функции
стационарной случайной функции не превышает ее значения в начале
координат: \ kx (т) | < kx @).
Нормированной корреляционной функцией стационарной случай-
случайной функции называют неслучайную функцию аргумента т:
Абсолютная величина нормированной коорреляционной функции
не превышает единицы: |рх(?)|<1.
830. Задана случайная функция X(t) = cos(t-\-<f>),
где ф—случайная величина, распределенная равномерно
в интервале @,2 я). Доказать, что X(t)—стационарная
функция.
Решение. Найдем математическое ожидание X (/):
mx(t)=M [cos (t-\-<p)] = M [cos / coscp—sin / sin,(p] =
=cos t-M [coscp]—sin t-M [sinqj].
Учитывая, что (см. гл. VI, § 3)
2л 2л
М [cosq>] = (l/2n) V созфAф = 0, M[sin<p]=(\/2n) \ sin9d9=0,
0 0
окончательно получим тхA)=0.
Найдем корреляционную функцию случайной функции X (/).
Приняв во внимание, что центрированная функция X (t) = X(() —
— тх (/) =Х (/)— cos (/ +q>)t имеем
КХ = М [к (/х) X (tt)\ = M [cos(/,+V)cos (/а + ф)]-
Выполнив элементарные выкладки, найдем
Кх = A/2) cos (h-h)+A/2) М [cos (/2+f,+2cp)].
Легко убедиться, что математическое ожидание второго слагаемого
равно нулю, поэтому окончательно получим Кх — A/2) cos (tt—ti).
Итак, математическое ожидание функции X (/) постоянно при
всех значениях аргумента и корреляционная функция зависит только
от разности аргументов. Следовательно, X(t)—стационарная слу-
случайная функция.
831. Задана случайная функция X(t) = s\n(t + q>),
где ф—случайная величина, распределенная равномерно
348
в интервале @, 2я). Доказать, что Х(/)—стационарная
функция.
832. Доказать, что если X(t)—стационарная случай-
случайная функция, Y—случайная величина, не связанная
с X(t), то случайная функция Z(t) = X(t)-\-Y стацио-
стационарна.
833. Доказать, что если X(t)—стационарная случай-
случайная функция, Y — X(i0)—случайная величина, то слу-
случайная функция Z(t) =X{t) + Y нестационарна.
834. Стационарна ли случайная функция X (/) =
= Ucos2t, где U—случайная величина?
835. Является ли стационарной случайная функция
X(t) = Us\nt + Vcost, где U и V—некоррелированные
случайные величины, причем mu=mv = 0, Da=Dv=D?
836. Задана случайная функция X (t) = /* -f- V sin t+
+ Vcost, где U и V—случайные величины, причем
M(U) = M(V) = 0, M(UV) = 0; D(U) = D(V)= 10. Дока-
Доказать, что: а) X (t) — нестационарная функция; б) X(t) —
стационарная функция.
837. Будет ли стационарной случайная функция
X (l)= a sin ((at+ ({>), где а, а—положительные постоян-
постоянные числа: q>—случайная величина, плотность распре-
распределения которой /(ф) = соэф в интервале @, я/2)?
838*. Доказать нестационарность случайной функции
X(t)=asin(<at+<p), где а, ю—положительные числа;
Ф — нормально распределенная случайная величина, плот-
плотность вероятности которой /(ф) = A/)/г2я)е(-(')'/2)-
Решение. Найдем математическое ожидание заданной функции:
тх (I) = М [a sin (<o/ -f ф)] = a sin <ot ¦ М (cos ф) -f
+ acos<ot-M(sin<{i). (*)
Математическое ожидание
так как пределы интегрирования симметричны относительно начала
координат н подынтегральная функция—нечетная.
Найдем математическое ожидание:
I (cos ф) = -tL= Г cos фе~ (*!/г) dw.
V 2л J
М\
' '' У 2л J
— CD
349
Введем в рассмотрение интеграл, зависящий от параметра а:
/(а)=
Заметим, что при а=0 получим интеграл Пуассона /@) =
00 00
= $ е" «>>>/2) dq>= ^2я- При а= 1 имеем / A)= J cos фе"*1'*) <кр.
-00 —00
Следовательно,
Продифференцируем / (а) по параметру а:
00
Интегрируя по частям, приняв u = sin (сир), получим /' (а)=— а/ (а).
Общее решение этого дифференциального уравнения /(a)=Ce~(a*^.
Положив а=0, учитывая, что /@)= У^2л, имеем С— ^2я; следо-
вательно, _
/ (а) = У 2г. е"(а2/2), / A) = У~2И/ f e.
В силу (•**) _
M(cos<p) = /(l)/V2n=l/Y'e. {****)
Подставив (**) и (••••) в (*), окончательно получим
Таким образом, тх (/) зависит от аргумента /, поэтому X (t) —
нестационарная функция, что и требовалось доказать.
839*. Найти дисперсию случайной функции X(t) —
= asin(w/ + <p), где а и ©—положительные числа, <р —
нормально распределенная случайная величина с плот-
плотностью вероятности /(ф)=A/1/г5я)е~<ч>|/2>.
Указание. Использовать задачу 838. Принять го внимание,
что
840. Доказать, что корреляционная функция стацио-
стационарной случайной функции есть четная функция.
Решение. Корреляционная функция любой случайной функ-
функции при перестановке аргументов не изменяется. В частности, для
стационарной функции, корреляционная функция которой зависит
только от разности аргументов, поменяв местами аргументы, получим
*х С*—ti) = kx(ti—/2)- Положив v=ti—tu окончательно имеем
350
841. Известна корреляционная функция kx(x) стацио-
стационарной функции X(t). Доказать, что если Y (t) = aX(t),
то ku{T) = a*kx(x).
842. Известна корреляционная функция kx(x) = De~alxt
стационарной случайной функции X (t). Найти корреля-
корреляционную функцию случайной функции Y(t) = 4X(t).
843. Доказать, что дисперсия стационарной случайной
функции X (t) постоянна и равна значению корреляцион-
корреляционной функции в начале координат: Dx(t) = kx(O).
Решен и е. Дисперсия любой случайной функции равна значе-
значению ее корреляционной функции прн равных значениях аргументов.
В частности, для стационарной функции, корреляционная функция
которой зависит только от разности аргументов, получим
844. Доказать, что абсолютная величина корреляцион-
корреляционной функции стационарной случайной функции не пре-
превышает ее значения вначале координат: |&*()|^/О)
Указание. Использовать задачу 843 и свойство 4 корреля-
корреляционной функции (гл. XVI, § 1).
845. Найти нормированную корреляционную функцию,
зная корреляционную функцию стационарной случайной
функции X @: а) М*) ==3е-*'; б) М*) = А*е-1тЦ1+|Т|).
§ 2. Стационарно связанные случайные функции
Стационарно связанными называют две случайные функции X (f)
и Y(i), взаимная корреляционная функция которых зависит только
от разности аргументов т = /2—/^ Rxy = r(Ti).
Не всякие две стационарные функции стационарно связаны;
с другой стороны, две нестационарные функции могут быть стацио-
стационарно связанными.
846. Доказать, что взаимные корреляционные функции
двух стационарно связанных случайных функций X(t)
и Y (t), взятых в различных порядках, связаны равен-
равенством гху(х) = гух(х).
Указание. Использовать задачу 781.
847. Доказать, что для стационарных и стационарно
связанных случайных функций X(t) и Y (t) абсолютная
величина взаимной корреляционной функции не превы-
превышает среднего геометрического дисперсий этих функций:
351
Указание. Использовать свойство 4 взаимной корреляцион-
корреляционной функции (гл. XVI, § 1).
848. Заданы две стационарные случайные функции:
X(t) = cos(t + <p) и Y (t) = sin (t + q>), где ф—случайная
величина, распределенная равномерно в интервале @,2я).
Доказать, что заданные стационарные функции стацио-
стационарно связаны.
Указание. Использовать задачи 830, 831; Я*;,=0,5 sin (/» — /,).
849. Заданы случайные функции X(t) = Vcost —
— Usint, Y(t) = Ucost + Vsint, где V и V—некорре-
V—некоррелированные случайные величины, причем их математи-
математические ожидания равны нулю, а дисперсии равны 5.
Доказать, что заданные функции стационарны и стацио-
стационарно связаны.
850. Заданы стационарные случайные функции:
a) X(t) = U sin t+V cost, Y{t) = Wsin t + Vcost, где
U, V, W — некоррелированные случайные величины с ма-
математическими ожиданиями, равными нулю, и диспер-
дисперсиями, равными 6; б) X(t) = Ucost+Vs'm t, Y (t)=
^Ucos2t+Vsin2t, где U и V—некоррелированные слу-
случайные величины с математическими ожиданиями, равными
нулю, и дисперсиями, равными 3. Являются ли заданные
функции стационарно связанными?
851. Заданы стационарные и стационарно связанные
случайные функции X (t) = —U sin t+V cost, Y (t) —
— Ucost-\-V sin t, где U и V—некоррелированные слу-
случайные величины с математическими ожиданиями, рав-
равными нулю, и дисперсиями, равными единице. Найти
нормированную взаимную корреляционную функцию за-
заданных функций.
§ 3. Корреляционная функция производной
от стационарной случайной функции
Корреляционная функция производной X'(t)=x дифференци-
дифференцируемой стационарной случайной функции X (t) равна второй произ-
производной от ее корреляционной функции, взятой со знаком минус:
852. Доказать, что если известна корреляционная
функция kx(x) дифференцируемой стационарной случай-
случайной функции X(t), то корреляционная функция ее про-
производной к-х (т) =.—Ц'х (т).
352
Решение. Известно, что корреляционная функция производ-
производной любой дифференцируемой случайной функции равна второй сме-
смешанной производной от ее корреляционной функции:
*i <'>•'«>—dtldtt •
По условию, X (()—стационарная функция, поэтому, ее корреля-
корреляционная функция зависит только от разности аргументов: Кх (tlt t2)=
=kx (t). Из соотношения т=/8—/j находим
— —1 —-I (*)
Учитывая равенства (*), получим
Кх (tu li) ^duU^Wi \_~dh] =дГг [if ' ~дЦ\ =
Внднм, что искомая корреляционная функция зависит только от т,
поэтому К-х (tlt t2) — ki (т). Итак, *. (т) =— *;(т).
853. Доказать, что производные любого порядка (если
они существуют) от стационарной случайной функции
также стационарны.
Решение 1. Докажем, что первая производная стационарна.
Из задачи 852 следует, что корреляционная функция первой произ-
производной стационарной случайной функции зависит только от разности
аргументов.
Остается показать, что математическое ожидание производной
есть постоянная величина. Учитывая, что математическое ожидание
тх стационарной функции постоянно н что операции нахождения
математического ожидания н дифференцирования можно менять ме-
местами, получим
М [X' @] ={М [X @)}' = (тх)' =0.
Таким образом, математическое ожидание производной есть постоян-
постоянная величина.
Итак, первая производная X' (/)—стационарная функция.
2. Докажем, что вторая производная стационарна. Функция
X' (t) стационарна, поэтому по доказанному в п.1, ее производная
X" \t) также стационарна.
3. Рекомендуем методом математической индукции доказать
стационарность производной любого порядка от стационарной функ-
функции в предположении, что рассматриваемые производные существуют.
854. Задана корреляционная функция /гх(т) = 2е-°-6т1
стационарной случайной функции X(t). Найти: а) кор-
корреляционную функцию и дисперсию производной X' (t)=x;
б) отношение дисперсий функции X (t) и ее производной.
855. Задана корреляционная функция kx(x) =
= De"alTl(l -fa|x|), (a>0) стационарной случайной
353
функции X(t). Найти: а) корреляционную функцию
производной X'(t); б) доказать, что дисперсия произ-
производной пропорциональна параметру D и квадрату пара-
параметра а.
Решение, а) Используем для отыскания корреляционной
функции производной формулу (см. задачу 852) к. (т) = — k"x(x).
Допустим, что т^О и, следовательно, |т|=т; выполнив дифферен-
дифференцирование, получим
— ?(т) = ?>е-°"а2A— ат). (*)
Допустив, что т < 0 н, следовательно, |т|= — т, аналогично
найдем
Объединив (*) н (**), окончательно получим искомую корреля-
корреляционную функцию: к. =?>а2е~а|т|A—а|т|).
X
б) Найдем дисперсию производной: D [X' (/)] =к. @) = Da2.
х
Таким образом, дисперсия производной пропорциональна D н а2,
что н требовалось доказать.
856. На вход дифференцирующего устройства подается
стационарный случайный сигнал X (/), корреляционная
функция которого kx(x) = e-2txi(chx + 2shx). Найти:
а) корреляционную функцию на выходе устройства;
б) наибольшее ее значение.
857. Известна корреляционная функция kx(x) стацио-
стационарной случайной функции X (t). Доказать, что корре-
корреляционная функция второй производной kx-(x) = klxv (т).
Указание. Рассмотреть вторую производную как производ-
производную от первой производной н использовать задачу 852.
858*. Заданы математическое ожидание tnx(t) = 8 и
корреляционная функция kx(x) = 5е~'т' [cos2т +
+ 0,5 sin 21 т || нормальной стационарной случайной функ-
функции X(t). Найти вероятность того, что производная
Y(t) = X'(t) заключена в интервале @, 10).
Решение. По условию, функция X (t) распределена нормально,
поэтому ее производная Y(t)=X' (t), как известно, также распре-
распределена нормально. Вероятность попадания нормальной величины Y
в интервал (а, Р) (см. гл. VI, § 5)
Р(а < Y < Р) = Ф[(Р—а)/о] —1Ф(а—в)/о], (•)
где а—математическое ожидание Y, а—среднее квадратнческое от-
отклонение Y, Ф(/)—функция Лапласа.
Таким образом, задача сводится к отысканию параметров а н а
нормально распределенной случайной величины Y.
1. Найдем математическое ожидание производной: ту (t)~m'x(t)=
=(8f=0. Следовательно, параметр a=my(t)=Q.
354
2. Используем для отыскания корреляционной функции производ-
производной формулу (см. задачу 852) ky(i)= — kx(i). Допустив, что т^О,
найдем
— k"x(x) =25e"T [cos2т—0,5sin2т]. (**)
При т < 0
_ /г"ж(т) =25е~т [cos2т+0,5sin2т]. (*•*)
Объединив (**) и (***), получим корреляционную функцию произ-
производной:
ky (т) =25е~|тI [cos 2т—0,5 sin2|т|].
3. Найдем дисперсию производной: Dy = ky @) = 25. Отсюда
среднее квадратнческое отклонение оу — 5.
4. Найдем по формуле (*) искомую вероятность того, что про-
производная заключена в интервале @, 10), учитывая, чтоа=0, а„ =5,
а = 0, р = 10: "
Р @ < Y < 10) = Ф [A0—0)/5]— Ф f@—0)/5] =ФB) =0,4772.
859. Заданы математическое ожидание тх = 12 и кор-
корреляционная функция /5j(T) = 4e-|T;[cos2T + 0,5sin2|T|]
нормальной стационарной случайной функции X(t).
Найти вероятность того, что производная Y(t)=*X'(t)
принимает значения, большие, чем \fb.
860*. Заданы математическое ожидание тх — 6 и кор-
корреляционная функция кх(т)= 10e-iTlfcos3x + (l/3)sin3|T|]
нормальной стационарной случайной функции X(t).
Найти плотность вероятности производной Y (t) = X' (t).
§ 4. Корреляционная функция интеграла
от стационарной случайной функции
Корреляционную функцию и дисперсию интеграла Y (/) =
= \ X (s) ds от стационарной случайной функции находят соответ-
о
ственно по формулам:
861*. Задана корреляционная функция kx(r) стацио-
стационарной случайной функции X (t). Доказать, что корре-
355
ляционная функция интеграла Y (t) = J X (s) ds равна
о
t,-t,
о
Указание. При отыскании деойного интеграла Ки (tu t? =
= \ ^
о о
о о
перейти к новым переменным t=s2—s,,
Начертить новую область интегрирования, ограничен-
ограниченную прямыми т = |, т =—S,
т = |—2<,, т=— 6+2/2, и вы-
выполнить интегрирование по ?.
Двойной интеграл по области
OABD вычислить как разность
двойных интегралов по областям
ОАС и BDC. При интегриро-
интегрировании по области ODE пере-
переставить пределы интегрирова-
интегрирования по т и перейти к новой пе-
переменной интегрирования V —
= — г (рис. 19).
862*. Известна корре-
? ляционная функция kx (т)
стационарной случайной
функции X (t). Доказать,
что дисперсия интеграла
У
у (<) = J X(s)ds равна
о
Рис. 19
Первый способ. Положив tt = ta =т в формуле для вычи-
вычисления корреляционной функцни, приведенной в задаче 861, получим
требуемую формулу.
Второй способ. Известно, что корреляционная функция
ивтеграла Y (t) = V X (s) ds определяется формулой KyUi, tt) =
2. При ti = tt = i получим дисперсию Dy(t)=
U I,
о
8S6
'it
> и
kx(s2—S|) dsi ds2. Введем новые переменные: t=s2—s
6 б
» = S2+Si. Отсюда Si = F—т)/2, s2 = (|-|-t.)/2. Легко найти, что
модуль якобиана
дх д\
ds2 ds%
равен -д-. Учитывая, что новая область
интегрирования (рекомендуем начертить ее для определения новых
пределов интегрирования) ограничена прямыми т = |, т = —|,
х = 1—2/, i = — Ц-2/, получим
Выполнив интегрирование по | н сделав во втором интеграле за-
замену т = —i'', переставив в нем пределы интегрирования и вновь
обозначив переменную интегрирования через т, приняв во внима-
внимание, что kx(—i) = kx(x), окончательно получим
r.
863. Найти дисперсию интеграла Y (/) = ) х (s) ds, зная
о
корреляционную функцию стационарной случайной функ-
функции X(t): a) kx(x)= 1/A+та); б) &x(T) = De-alTl(a>0);
в) kx(т) = Ое~а'т|(Ч"а1т1)-
Указание. Использовать задачу 862.
864. Задана корреляционная функция kx (т)=10е-°-61т1х
ХA+0,5|т|). Найти отношение дисперсии случайной вели-
величины К= ^ X (s) ds к дисперсии случайной функции X (/).
о
§ 5. Взаимная корреляционная функция
дифференцируемой стационарной случайной функции
и ее производных
Ниже предполагается, что x = t2—t1.
Взаимные корреляционные функции стационарной случайной
функции X(t) н ее производных выражаются формулами:
rxx(i) = k'x(x), rxx(x)=—kx(x); rxx-(x)=rxx(x)=kx(x).
357
865. Доказать, что взаимная корреляционная функ-
функция дифференцируемой стационарной случайной функ-
функции X(t) и ее производной X'(t) = x равна первой про-
производной от корреляционной функции kx(x), взятой со
своим (противоположным) знаком, если индекс х стоит
на втором (первом) по порядку месте: а) тх'х (т) = /г'*(т);
б) пх(т) = — к'х(г).
Решение, а) По определению взаимной корреляционной функ-
цнн,
Операции нахождения математического ожидания и дифференциро-
дифференцирования можно переставить, поэтому
* dKx(tj, /г)
пхх~ dti dta
Так как X(t)—стационарная функция, то Kx(h> <*
где т = /г—h> и следовательно, -^-—=1. Таким образом,
Правая часть равенства зависит только от т; следовательно, и ле-
левая часть есть функция от т; обозначив ее через г . (т), получим
г . (т) = А' (т).
XX X
Подчеркнем, что поскольку взаимная корреляционная функция
зависит только от т, то стационарная случайная функция н ее про-
производная стационарно связаны.
866. Найти взаимные корреляционные функции ста-
стационарной случайной функции X (t) и ее производной,
зная корреляционную функцию /г*(тО = е-1т1A + |т|).
867. Доказать, что взаимная корреляционная функ-
функция стационарной случайной функции X (t) и ее произ-
производной изменяет знак при перемене местами аргументов
h и tt.
Решение. Используем задачу 865:
Изменив порядок следования аргументов во взаимной корреля-
корреляционной функции, получим R . (tt, /t). Индекс х стоит на втором
месте; следовательно, kx(x) надо дифференцировать по аргументу tlt
который расположен на втором месте. Учитывая, что т = /а—tlt
358
fa
•щ- = — 1, найдем
Ж kx
Сравнивая (*) и (•*), окончательно получим R . (tu t2) = R ¦ (/а. 'i)-
868. Известная корреляционная функция kx(x) ста-
стационарной функции X(t). Найти взаимные корреляцион-
корреляционные функции случайной функции X (t) и ее второй про-
производной.
Указание. Использовать задачу 807.
869. Задана корреляционная функция
kx (т) = De-«I' I [1 +а|т| + (а4/3) тг], а > 0,
стационарной случайной функции X (t). Найти взаим-
взаимную корреляционную функцию случайной функции X (t)
и ее второй производной.
У Казани е. Использовать задачу 868. Рассмотреть два слу-
случая: т^О и т < 0.
870. Найти корреляционную функцию случайной функ-
функции У (t) = X (t) + X'Ц), зная корреляционную функцию
kx (т) стационарной функции X (t).
Решение- Искомая корреляционная функция (§ 2, теорема 2)
К (tlt t ) = ? (x)-{-k. (т)+г .(х)-{-г. (т). Второе слагаемое равно
— kx (т), а сумма третьего и четвертого слагаемых равна нулю
(см. задачи 852, 865). Итак, Ky(t^, ti) = kx(i)—kx(i). Правая часть
равенства зависит только от т; следовательно, и левая часть есть
функция аргумента т: ky(-z) = kx(t) — kx(r).
871. Найти корреляционную функцию случайной функ-
функции Y (l)=*X(l) + X'(t), зная корреляционную функцию
kx(x) = e~x' стационарной функции X(t).
Указание. Использовать задачу 870.
872. Известна корреляционная функция стационарной
случайной функции X (t). Найти корреляционную функ-
функцию случайной функции Y(t), если: a) Y (t) — X(t) +
+ *"('); б) Y(t) = X'(t) + X'A).
873. известна корреляционная функция /гх(т) = е-1т1х
х[1 +|т.| + A/3)т2] стационарной случайной функции
X (t). Найти корреляционную функцию случайной функ-
функции Y{t) = X(t)-\-X"(t).
359
874*. Известна корреляционная функция стационар-
стационарной случайной функции X (t). Найти корреляционную
функцию случайной функции Y (t) = X(t) + X'(t) + X" (t).
875. Известна корреляционная функция стационарной
случайной функции X(t). Найти взаимные корреляцион-
корреляционные функции случайной функции X (t) и ее третьей про-
производной.
876. Известна корреляционная функция стационарной
случайной функции X(t). Найти взаимную корреляцион-
корреляционную функцию первой и второй производных.
Указание. Использовать задачи 852, 853 и 865.
§ 6. Спектральная плотность стационарной случайной
функции
Спектральной плотностью стационарной случайной функции
X{t) называют функцию sx(a>), которая связана с корреляционной
функцией kx(x) взаимно-обратными преобразованиями Фурье:
00 00
sx(ш) =^- j kx (т) e-w dx, kx (т) = j sx (<o)e'*>x do.
— 00 —00
Эти формулы называют формулами Винера—Хинчина. В действи-
действительной форме они представляют взаимнообратные косинус-преоб-
косинус-преобразования Фурье:
00
sx (<») = — I kx (т) cos ют dt, kx (т) =2 \ sx (<в) cos an d<o.
= — I
Я5
Нормированной спектральной плотностью стационарной слу-
случайной функции X (t) называют отношение спектральной плотности
к дисперсии случайной функции:
sx норн (<») = sx (<o)/Dx = sx (a>) I } sx (a) d<o.
— 00
Взаимной спектральной плотностью двух стационарных н ста-
стационарно связанных случайных функций Л (/) и У (/) называют
функцию sAy (ш), определяемую преобразованием Фурье:
00
^Г J"
— 00
Взаимная корреляционная функция выражается через взаимную
спектральную плотность с помощью обратного преобразования Фурье:
860
877. Доказать, что спектральная плотность стацио-
стационарной случайной функции—четная функция.
Указание. Использовать формулу
00
s, (со) =тг- \ kx (т) cos сот dr.
— 00
878. Доказать, что, зная спектральную плотность
стационарной случайной функции X(t), можно найти
00
дисперсию этой функции по формуле Dx= С sx(co)dco.
— 00
Указание. Принять во внимание, что
00
kx (т) = jj sx (со) е<«« dco, Dx = Ax @).
— 00
879. Найти дисперсию стационарной случайной функ-
функции X @» зная ее спектральную плотность sx (со) =
880. Доказать, что, зная спектральную плотность
дифференцируемой стационарной случайной функции,
можно найти спектральную плотность ее производной
по формуле Si (со) = co*sx (со).
Решение. Производная стационарной функции также ста-
стационарна (см. задачу 853), поэтому спектральная плотность произ-
производной
— 00
Учитывая, что к^(т)—— k"x(i),
со
кх (т) = С в,
х
— 00
и предполагая допустимость дифференцирования под знаком инте-
интеграла (**) по параметру т, имеем
00
kk (т) = - k"x (т) = ©* J s^ (©) е«« dx=©а Ах (т). (***)
— CD
Подставив (***) в (*), окончательно получим
CD
sx (со) = ©2 ¦— J ftx (т) е-<«« dx=<о\ (©),
— СО
361
881. Задана спектральная плотность sx (ю) = аг/((о* +
+ а*)а (а>0) дифференцируемой стационарной случай-
случайной функции X (t). Найти дисперсию производной X' (t).
882. Доказать, что, зная спектральную плотность
дважды дифференцируемой стационарной случайной функ-
функции X (t), можно найти спектральную плотность второй
производной Xя @ по формуле S'i((o) — (d*sx(a>).
Указание. Использовать задачи 853, 880.
883. Найти спектральную плотность стационарной
случайной функции X (t), зная ее корреляционную функ-
функцию kx(r) = l—|т| при |т|^1; корреляционная функ-
функция равна нулю при |т|> 1.
Решение. Используя формулу
00
sx(a)=— \ kx (x) cos ют dx
о
и учитывая, что |х|=т в интервале @, 1), имеем
i
1 р
sx(m) = — \ A —х) cos шт dx.
Интегрируя по частям, окончательно получим 8ж(й))=2з1па((в/2)/1Ио*.
884. Найти спектральную плотность стационарной
случайной функции X (t), зная ее корреляционную функ-
функцию fex(t)=l — A/5)|тг| при |т|^5; корреляционная
функция равна нулю при |т|> 5.
885. Найти спектральную плотность стационарной
случайной функции, зная ее корреляционную функцию
Л*(т) = е-1Ч.
Решение. Используем формулу sx(a)= у- \ *х(т)е-'*«(к.
— 00
Учитывая, что |т( = —т при т < 0, |т|=т при xSsO, получим
ftx(x)=et при т < 0; при т^О ftx(x)=e-t. Следовательно,
Выполнив выкладки, окончательно получим sx(«)
886. Найти спектральную плотность стационарной
случайной функции, зная ее корреляционную функцию
?х(т) = ?>е-«1*1 (а>0).
362
887. Найти спектральную плотность стационарной
случайной функции, зная ее корреляционную функцию
?() lT'
Решение. Учитывая, что |т| = —т при х < О, при т
|т|=т и используя формулу Эйлера cosx = (e«+e-'T)/2, имеем
ПРИ т
при
Следовательно,
— 00
О
— 00
со
_L f {e-[i-«
Выполнив выкладки, получим искомую спектральную плотность:
888*. Найти спектральную плотность стационарной
функции, зная ее корреляционную функцию kx(x) =
?>«lTlp (>0)
?ecospT (>0)
889*. Найти спектральную плотность стационарной
функции, зная ее корреляционную функцию kx(x)~
?>«lTl[p + f/p)ip||] (>0)
Указание. Раскрыть скобки и использовать задачу 888;
выразить тригонометрические функции через показательные по фор-
формулам Эйлера.
890*. Найти спектральную плотность стационарной
функции, зная ее корреляционную функцию kx (т) =
= ?>е-а'Л
Указание. Использовать формулу
00
— 00
дополнить показатель степени до полного квадрата и учесть, что
00
интеграл Пуассона V e~B*/l)dz= У~2п,
— со
363
891*. Найти спектральную плотность стационарной
функции, зная ее корреляционную функцию кх (т) =
01ЧA||) @)
Решение. Используем формулу
00
Подставив заданную корреляционную функцию, представим правую
часть равенства в виде суммы двух интегралов:
00
— О» —Об
Обозначим первое слагаемое через /; производная этого интеграла
но параметру о
00
Следовательно,
**(©) = /— а^Г'
Учитывая, что (см. задачу 886)
и подставив (•*) в (•), окончательно получим sx (<o) =2Da?/n (oa-f со2)8.
892. Найти спектральную плотность стационарной
функции, зная ее корреляционную функцию кх (т) =
1ООЦ| A+01||)
Указание. Использовать задачу 891.
893*. Найти спектральную плотность стационарной
функции, зная ее корреляционную функцию kx(x) =
i
Решение. Первый способ. Используем формулу
00
— 00
Подставив заданную корреляционную функцию, получим
Представим этот интеграл в виде суммы трех интегралов и выпол-
364
ним выкладки; окончательно имеем
sx (©) = 8?>а8/3л («*+ ш*)».
Второй способ. Введем обозначение
00
I е~а' Tle"W dT-
— CD
Найдем производную этого интеграла по параметру а:
Отсюда
о»
a/ d с
dot, 2я J
— 00
Аналогично найдем
3
— OD
Следовательно,
, . . а/ , а* дЧ
Учитывая (см. задачу 886), что /=Са/л (а2+«>*). найдя част-
а/ 6*1 , .
ные производные -г— , -^-j- и подставив их в соотношение (*), окон-
окончательно получим искомую спектральную плотность: sx (со) =
8/)&/З(а+!!K
Достоинство этого способа состоит в том, что вместо трех ин-
интегралов достаточно вычислить только одни, причем самый простой.
894*. Найти спектральную плотность случайной функ-
функции Y(t) = X(t) + X (t), зная корреляционную функцию
&х(т) = ?>е-а1т1A+а|т|) (а >0) стационарной диффе-
дифференцируемой случайной функции X (t).
Указание. Найдя
ky (т)=kx (т)-Wx(т) = De-«i *l [A + а*)+а0 — «*)Iт|],
использовать второй способ решения задачи 893:
sy (©) - /A + а») -о A -а») |j..
где
00
/ = ? f e-aixie-f—- Da
— 00
365
895*. Может ли функция kx(x) = е~1т|A + || + )
быть корреляционной функцией стационарной случайной
функции X(t)?
Решение. Проверим, выполняются ли все свойства корре-
корреляционной функции &х(т).
(.Свойство *х(т)—четная функция—выполняется: kx(— т) =
= ** (*)•
2. Свойство kx@) > 0 выполняется: Лх@) = 1 > 0.
3. Свойство |Ъх(т)|<kx@) не выполняется: например, kx(\) =
= 3/е>*х@) = Ь
4. Свойство
S* [<0)=-,
при всех значениях ш не выполняется. Действительно, допустив,
что заданная функция кх (т) является корреляционной функцией
некоторой стационарной случайной функции X (t), и выполнив вы-
выкладки, найдем функцию sx(©)=4(l— со2)/л A+ со2); при |ш| > 1
функция sx (©) < 0.
Итак, заданная функция kx(i) не является корреляционной
функцией никакой стационарной случайной функции. Разумеется,
это заключение можно было сделать, убедившись, что не выпол-
выполняется хотя бы одно свойство корреляционной функции.
896. а) Доказать, что функция &х(т) = 5е-2х' может
быть корреляционной функцией стационарной случайной
функции X(t).
б) Доказать методом от противного, что не сущест-
существует такой стационарной функции, корреляционная функ-
функция которой сохраняет постоянное значение в интер-
интервале (— тг, тх), симметричном относительно начала коор-
координат, и которая равна нулю вне этого интервала.
897. Задана спектральная плотность sx (ю) = 10а/я(а* +
-f cea) (а > 0) стационарной случайной функции. Найти
нормированную спектральную плотность.
Указание. Использовать задачу 878.
898. Задана спектральная плотность sx(a>) = Da/n(a* +
+ <»2) (а > 0) стационарной случайной функции. Найти
@
спектральную функцию Sx (ю) = $ sx (at) dee.
899. Доказать, что спектральная плотность равна
производной от спектральной функции: sx(<o) — S'x (ю).
900. Доказать, что для стационарных и стационарно
связанных случайных функций X (t) и Y (t) справедливо
366
соотношение, связывающее взаимные спектральные плот-
плотности: sxy(—a>) = syx{oi).
Решение. По определению взаимной спектральной плотности,
00
SXy («•) = ¦! J ГхуA)*Г
Следовательно,
со
Поскольку гхи(т) = гух(—х) (см. задачу 846), то
со
Сделаем замену переменной интегрирования, положив xj =—t
и, следовательно, ат! = —dx. Новый нижний предел интегрирова-
интегрирования равен о», а верхний —оо. Таким образом,
00
= h. I /"j/*(Ti)e~tot<dTi=v((i))-
— 00
901. Доказать, что взаимные спектральные плотности
дифференцируемой стационарной случайной функции и
ее производной связаны равенством s*i (©)=—six((a).
Указание. Использовать соотношение г . (х)= — г. (х).
902. Доказать, что, зная спектральную плотность
sx(<o) дифференцируемой стационарной случайной функ-
функции X(t), можно найти взаимную спектральную плот-
ность функции X(t) и ее производной по формуле
Решение. По определению взаимной спектральной плотности,
Известно (см. задачу 865), что Гд^(т)—~J^p • Учитывая, что
367
да
kx(x)= \ sx(e))e'T<ad(o, получим
d (* Р
^ . (х) =-т— \ s_(<o)e ш do)= to i
дглг dx J J
— O» —00
Следовательно,
00
— 00 —0»
Отсюда окончательно имеем s . (w) = ta>-sx(a>).
903. Известна спектральная плотность sx(w) =
= 2/>а3/я (ю*+а8)» дифференцируемой стационарной слу-
случайной функции X(t). Найти взаимную спектральную
плотность функции X (t) и ее производной.
Указание. Использовать задачу 902.
904. Найти взаимную спектральную плотность диф-
дифференцируемой стационарной случайной функции X(t)
и ее производной, зная корреляционную функцию
k() 2\
Указание. Найти сначала взаимную корреляционную функ-
функцию г ¦ (т) = *л(т), а затем искомую взаимную спектральную плот-
плотность. Можно поступить иначе: найти спектральную плотность (см.
задачу 890), а затем умножить ее на /со (см. задачу 902).
905. Найти корреляционную функцию стационарной
случайной функции X(t), зная ее спектральную плот-
плотность sx(<») = s0 в интервале —<ао^со^а>о; вне этого
интервала sx(a)) = O.
Решение. Используем формулу
00
kx (т)=2 \ sx (<o) cos ют d ш.
Учитывая, что sx(to)~s0 в интервале @; соо), получим
со
kx (т) = 2s0 \ cos ©т d to = 2s0 (sin а>от)/т.
о
906. Найти корреляционную функцию стационарной
случайной функции, зная ее спектральную плотность:
sx((o) = s0 в интервалах (—2ю0, —<оо) и (ю0, 2<оо); вне
этих интервалов sx(a>) = 0.
368
907. Найти корреляционную функцию стационарной
случайной функции, зная ее спектральную плотность
() ?>/(*+ *)
Решение. Первый способ. Из задачи 886 следует, что
корреляционной функции kx (т) = De~a'т' соответствует заданная
спектральная плотность. Поскольку кх (т) и sx (to) связаны взаимно-
обратными преобразованиями Фурье, то искомая корреляционная
функция кх (т) = De~a'г •.
Второй способ. Используем формулу
Известно, что
Следовательно, искомая корреляционная функция *Л(т)
908. Найти корреляционную функцию стационарной
случайной функции, зная ее спектральную плотность
(J4«)
ж()()
909. Найти корреляционную функцию стационарного
белого шума—стационарной случайной функции с посто-
постоянной спектральной плотностью sx(<») = se.
Решение. Используем формулу
Ая.(
(т)= С $х(ш)е'т<0 d© = se f
Примем во внимание, что я- \ е'та> d© = 6 (т), где б(т)—дель-
— 00
та-функция. Отсюда
OD
Г e/t(ada) = 2n6(T). (••)
— 00
Подставив (••) в (•), окончательно получим искомую корреляцион-
корреляционную функцию kx(i) — 2ns06(T).
§ 7. Преобразование стационарной случайной функцию
стационарной линейной динамической системой
Стационарной линейной динамической системой называют уст-
устройство, которое описывается линейным дифференциальным уравне-
уравнением с постоянными коэффициентами вида
()+ + n]()
Р*-»> @+ ¦ .. + *.) Х- @.
13 Гмурман В. Е.
где Х(/)—входная стационарная случайная функция (воздействие,
возмущение), К (/)—выходная случайная функция (реакция, отклик).
Если динамическая система устойчива, то при достаточно боль-
больших значениях t, т. е. по окончании переходного процесса, функцию
Y (t) можно считать стационарной.
Математическое ожидание выходной функции Y (/) находят по
формуле ту=(Ьт/а„)тх, где тх—математическое ожидание вход-
входной функцни X (t).
В операторной форме уравнение (•) имеет вид
aoPn-MiP"-4- ". +e,)K@-(ft»Pe+6iP"-*+ ••• +bm)X(t).
Передаточной функцией линейной динамической системы назы-
называют отношение многочлена относительно р при ХA) к многочлену
при Y @ в операторном уравнении (»*):
Частотной характеристикой линейной динамической системы
называют функцию, которая получается заменой аргумента р в пе-
передаточной функцни на аргумент i'co(w—действительное число):
Ф(Ш)
Спектральные плотности выходной н входной функций связаны
равенством sy (a) = sx (а) ¦ |Ф(ш) |г, т. е., чтобы найти спектраль-
спектральную плотность выходной функции, надо умножить спектральную
плотность входной функции на квадрат модуля частотной характе-
характеристики. Зная же спектральную плотность выходной функции, можно
найти ее корреляционную функцию
— *>
а следовательно, и дисперсию
— СО
910. На вход линейной стационарной динамической
системы, описываемой уравнением Y' (t) +2Y (t) — 5X'(t) +
-\-6X(t), подается стационарная случайная функция X (i)
с математическим ожиданием тх — Ъ. Найти математи-
математическое ожидание случайной функции Y (t) на выходе
системы в установившемся режиме (после затухания пе-
переходного процесса).
Реше-нне. Приравняем математические ожидания левой и пра-
правой частей заданного дифференциального уравнения:
или М [У"(/)Н-2/п„ =
По условию, X{t) и К @—стационарные функции, а математическое
сжидание производной стационарной функции равно нулю, поэтому
370
2гпц=6тх. Отсюда искомое математическое ожидание ту = 3тх=з
= 3'5 = 15.
911. На вход линейной стационарной динамической
системы, описываемой уравнением Y" (t) -f- ЗК' (/) + BY (/) =
= 4X'(t) + \0X (t), подается стационарная случайная
функция X(t) с математическим ожиданием тх = 2. Найти
математическое ожидание случайной функции Y(t) на
выходе системы в установившемся режиме.
912. На вход линейной стационарной динамической
системы, описываемой уравнением 3Y' (t) -f Y (/) = 4Л" (i)+
+ X(t), подается стационарная случайная функция X(t)
с корреляционной функцией Лх (т) = бе-2'т'. Найти дис-
дисперсию случайной функции Y(t) на выходе системы в
установившемся режиме.
Решение. I, Найти спектральную плотность sx (<о). Используя
решение задачи 886, при Dx = kx@) = Q и а—2, получим
) = 12/л (<
2. Найдем передаточную функцию системы. Для этого запишем
заданное дифференциальное уравнение в операторной форме:
(Зр+1)К(/)=Dр-!-1)Х(/). Отсюда К(/) = К4р+1)/<Зр+П]Х@-
Следовательно, передаточная функция Ф(р) = Dр+1)/(Зр+1)<
3. Найдем частотную характеристику системы, для чего поло-
положим p=coj:
4. Найдем спектральную плотность sy (со) на выходе системы,
для чего умножим спектральную плотность sx (со) на квадрат моду-
ля частотной характеристики:
s9 (©) = sx (©) | Ф (©01» = (lS/я ((о»-Ь 4) [
5. Найдем искомую дисперсию:
... 12
00
_24 f"
n J
Представим подынтегральную функцию в виде суммы простевших
дробен:
24[63P_d© 7 р do 1
«~л L35J w* + 4 35j9u)a-t-lJ '
О О
Выполнив интегрирование, получим искомую дисперсию DM —
= B4/я)(бя/12)=10.
13* 371
913. На вход линейной стационарной динамической
системы, описываемой уравнением У (t)-{-3Y(t) = X'(i) +
+ 4Х (/), подается стационарная случайная функция X (/)
с математическим ожиданием тх = 6 и корреляционной
функцией кх (т) = 5е-2|т1. Найти: а) математическое ожи-
ожидание; б) дисперсию случайной функции Y (t) на выхо-
выходе системы в установившемся режиме.
914. На вход линейной стационарной динамической
системы, описываемой уравнением Y" (t) -j- 5К' (/) -f 6К (/) —
= X' {t) + X(t), подается стационарная случайная функ-
функция с математическим ожиданием тх — 4 и корреляци-
корреляционной функцией /гл(т) = е-1т|. Найти: а) математическое
ожидание; б) спектральную плотность случайной функ-
функции Y (t) на выходе системы в установившемся режиме.
915*. На вход линейной стационарной динамической
системы, описываемой уравнением Y'" (/) -f-6K* (/) +
+ UY'(t) + 6Y{t) = 7X"(t)-\-5X(t), подается стационар-
стационарная случайная функция X (t) с известной корреляцион-
корреляционной функцией: а)Мт) = 4е-т;б) *д (т) = 2е-1т'| A+|т|).
Найти спектральную плотность случайной функции Y (t)
на выходе системы в установившемся режиме.
Указание. Использовать задачи 886 и 891. Разложить на ли-
линейные множители знаменатель передаточной функции:
<ИHН2)( + 3)
916. На вход линейной стационарной динамической
системы, описываемой уравнением Y' (t) -f Y (t) — X (/), по-
поступает стационарная случайная функция X{i) с постоян-
постоянной спектральной плотностью s0 (белый шум). Найти
дисперсию случайной функции Y (t) на выходе системы
в установившемся режиме.
917. На вход линейной стационарной динамической
системы, описываемой уравнением Y" (i) + 2hYr (t) +
+ k*Y(t) = X(t) (ft > 0), k^h), поступает стационар-
стационарная случайная функция X (t) с постоянной спектральной
плотностью s0 (белый шум). Найти спектральную плот-
плотность случайной функции Y (t) на выходе системы в уста-
установившемся режиме.
918*. Спроектированы две линейные стационарные
динамические системы, на вход которых поступает стацио-
стационарная случайная функция X(t). Передаточные функции
систем соответственно равны: Фг (р) = Dр -f-1 )/Cp +1),
Ф»(Р) — (Р + 1)/{Зр+1)- Спектральная плотность выход-
выходной функции известна: sx(<a)= 12,'л(©* + 4). Какая из
систем обеспечивает наименьшую дисперсию выходной
функции?
ОТВЕТЫ
Глава первая
3. а) Р = 1/90;б)Р = 1/81. 5. а) Р«1/6;б) Р = 1/18; в) Р = 1/2;
г) Р=1/18. 6. а) 0,384; б) 0,096; в) 0,008. 7. Р=3/4. 8. Р== 1/720.
10. Р = 1/С1о = 1/190. 12. P=Cfo/C?6=24/91. 13. P = CS^CJ8e=0,l.
14. a) P=Cjo/Ctoo ^ 0,65; б) Р=С*о/С*т ^ 0,00005. 15. Р=С1/Св=0,3.
16. Р = 1//4?„= 1/720.18. Р =CjCj/Clo=O,5. 19. Р =Cf0-Cj/Ciew0,4.
20. P = Cjci/C?i= 14/55. 21. а) Р=Сз-С?/С|«=0,6; б)Р=С|/С»=0,3;
в) Р=0,9. 22. Р=1/5«. 24. №=0,9. 25. 180 приборов. 26. Р = 1/2.
27. Р = 1/3. 28. P=r*/R*. 29. Р =Ba—2r)/Ba) = (a—r)/a. 30. Р =
= (а—2г)г/а2. 31. Р=F—2)/6=2/3. 32. Р=A0«—5»)/10*=0,75.
33. а) Р=2/л; б) Р=ЗКгЗ/Dл). 34. Р = 0,5л/?*/(л/?1|)=0,5. 36. Воз-
Возможные значения координат: 0<x<Z., 0<y<L; благоприятст-
благоприятствующие значения: у—х < х, у>х; х—у < у, у < х; р= 1/2.
37. Возможные значения координат: 0<.v<L; Q<y<L, y^x,
благоприятствующие значения координат: y—x<L/2; р=0,75.
38. Возможные значения координат: 0<x<L; 0«?y«?i.; благо-
благоприятствующие значения координат: у—х < L/2, у > х; х—у< L/2,
у < х; р=0,75. 42. Р = 7/16. 43. Возможные значения координат:
0<x<Z., 0<y<L; 0<z^Z.; благоприятствующие значения ко-
координат: х<у-\-г, у < г+х, г < х-\-у\ Р = 1/2. 44. Возможные
значения координат: (У<х<.2,_й <у<2; благоприятствующие зна-
ч.ния координат: 0<дс<|//2, 0<у<^л2 и ^2/2<*<2,
1/2<у</2; Р=A+31п2)/8г-0,38. 45. Возможные значения ко-
координат: 0<Ж1, Q <у<\; благоприятствующие значения коор-
координат: 0,1 <х<0,9, 0,1<у<0,9; Р~0,2.
Глава вторая
47. P = I—Cj/C?o = 5/6. 50. Р=0,14. 51. Р = 0,38. 52. Р=0,7.
кЗ. Р=0,18. 54. Р =0,432. 55. Р=0,384. 56. а) Р =0,188; б) Р =0,452;
в) Р =0,336. 57. а) Р=0,6976; б) Р=0,9572. 58. а) Р = 1/63; б) Р =
= 6A/63) = 1/36. 59. а)Р=С1A/6»-5/6)=5/72;б)Р = 5/12; в)Р = 5/9.
3!A/3K.65. Р = 5/100-4/99= 1/495.67. Р»6/10-5/9-4/8.3/7=
373
= 1/14. 68. a) P = l/5-l/41/3 = l/60; 6) P=O,1. 69. P=20/25-19/24X
X18/23»57/115. 70. a) P = l/10-l/9-l/8 = l/720; 6) P=0,001.
81. P-0,126. 821Pai0,95. 83. P=0,388. 85. Pa*0,76. 87. p=0,8.
где E[N]—целая часть числа N. 90. P =
. 91. P~0,89. 92. P= 0,85. 93. P = 0,78. 94. P=0,5.
95. P=0,4. 96. P=»0,87. 98. Вероятнее, что винтовка была без оп-
оптического прицела (вероятность того, что винтовка была без опти-
оптического прицела, равна 24/43; с оптическим прицелом—19/43).
99. Р=3/7. 100. Р=»1/3. 101. Р=5/11. 102. Р ~ 0,47. 104. РА (Bs)=
»1—@,6+0,3)«=0,l. 107. Р = 10/19. 109*. Р=0,039.
Глава третья
111. а) Вероятнее выиграть одну партию из двух: Р2A) = 1/2;
Р4B)=3/8; б) вероятнее выиграть не менее двух партий из четырех:
' ЛC)+Р»DН-
4()+4()+4() [4() + 4 ()] /
-И*6E)=8/16. 112. а) Р = Р6@)+Р8A)==3/16; б) Q [,()f
+Р6 AI=13/16. ИЗ. а) Р«C)+Р« D) =0,1792; б) Р,D)+Р5E)=0,74.
114. а)р3=0,729; б) Clp3q+Cip* =0,95; B)ClpV+C6p4<7+Cep6=0,99.
115. Искомые вероятности таковы: а) 0,31; б) 0,48; в) 0,52; г) 0,62.
116. Р4B)=С!B/3JA/3J = 8/27. 117. PeB)=C|(x/a)»[(e-*)/a]s.
118. P=C?CjC4Cl(l/4)8. 121. Р,оо G5) = 0,04565. 122. Р100E0) =
=0,5642/ VN. 124. PiN(N+m)= У~Ш х
Хф( YilNm). 126. a) P81Oo A470; 1500) =0,4236); б) Р21ОоA47О; 2100)=
•0,5; в) Р„оо @; 1469)=0,5. 127. Р21 A1; 21)=0,95945. 128. Р=
=ФA)—Ф(—1)=2ФA) = 0,6826. 130. п = 177. 132. Р=2ФA,2) =
«0,7698. 133. Р = 2Ф B,31)=0,979. 134. Р=2Ф@,877) =0,6196.
137. я =-661.138. «=6147.140. е=0,02. 141. е=0,01.143. 15<т<33.
144. 5<т<22. 146. /го=8. 148. Л, = 17, *e-f-1 = 18. 151. *0 = 7.
153. 100<п<102. 154. 28<л<29. 156. 0,625 < р<0,65.
158. а)А0=1; б) Р&A)=0,41; в) Р =0,0067. 160. а) РаB) =0,72;
б) Р,A) = 0,26; в) Р2@) = 0,02; г) Р,A) + Р,B)=0,98.161. а) Р,C)=
0612 б) РBH329 ) РAH056 ) Р@H003
) ,() , ) 2() , ) ,() + ,(),) ,()
-0,612; б) Р3B)=0,329; в) Р3A)=0,056; г) Р3@)=0,003;
д) Р== 1—^^3=0,997. 162. а) Р4D) = 0,006; б) Р4C)=0,065;
ж) Р4B) = 0,254; г) Р4A)=0.423; д) Р4@) = 0,252; е) Р4@) + Р4A)+
+Р4B)=0,929. 163. 0,325.
Глава четвертая
167. X 0 1 2 3 4 lfifiX012
р 0,6561 0,2916 0,0486 0,0036 0.000Г I68> p 1/4 1/2 1/4'
1вй X 0 1 2 ... X 0 1 2 3
1ВВ- р 9 16 6/16 1/16 * ш> р 0 1/5 3/5 1/5-
173* а) р 0,2 0,16 0,128 ... O.e*-1^ ...' б) **=I-
т- ? 0,7 0224 0,042 0,04144- «77. Р1в.„ C)=0,18. 178.РаооD)=О,О9.
180. а.)Р1000 B)=0,224; б)Р1Ово (О)-ЬР,0оо A)=0,1992; в)Р1Оов (А >2)=
=0,5768; г) P = l —Pieoo(O)=O,95. 181. б) Я=3. 186. а) Р4C)=0,0256;
6) Pt(k<3) =0,0123; в) Р, (k ^3)= 0,9877. 188. б) Л1(Х) = 0,535.
189. 6)A1(Z)=3O. 191. ^з=21; р,=0,2. 193. pt =0,2; ра=0,3;
Р,=0,5. 194. Ж(Х) = 3/5. 198. Ж(Х) = Л^С?1A/6)"> E/6)»-».
374
200. M (X) = 50-Cs-0,9«0,l ~ 16.209. D(Z)=61. 21!. a)D(X)a=8 545;
а(Х)^2,923; 6) D (X) as 248,95; a (X)s= 15,78. 214. D (X) = 0,9.
216. D(X) = 0,495. 217. Pl=0,3; p,=0,7. 219. f 0>2 „J.
22°- p о!з 0?2 0?5-228- а> Л/(*) = 10; б> OW-90. 229. V1 = 3,9;
v2 = 16,5;'v3 = 74,l. 23b ^ = 0; ^i2 = 0,64; ц3=—0,77; ц4 = 1,33.
Глава пятая
236. Р(|Х—М (Х)\ < 3a)Ss 1 —о2/(9о2) =8/9.
238.Р(|Х—М (X)|^2a)<a*/Do2)= 1/4. 239. Р (IX—Ж (Х)| < 0,2)^
Ss 1 —0,004/0,04 = 0,9. 240. е^О.З. 242. а) Я (X—161< 3) ^0,64;
б) Р{\Х— 16|^3)<0,361244.Р(|Х—200|<50)^1 —150/502 =0,94.
246. Р(\Х—0,441 < У,4)з» 1—0,0364/0,4=0,909. 248. Применима.
Математические ожидания Х„ конечны и равны —a.Bn-|-l); дис-
дисперсии равномерно ограничены числом аг. 249. а) С возрастанием
л дисперсии D(A'n) = Bn3-|-3n2-rn)/Bn-|- 1) неограниченно возрас-
возрастают; б) нельзя, так как требование равномерной ограниченности
дисперсий лишь достаточно, но не необходимо. 2S1. Применима:
М(Х„)=0; D(X,,)=2.
Глава шестая
253. Р @ < X < 1)=1/4. 254. Р(—1 < X < 1)=1/3. 255. Р (^)
= \—Р(Х < Т) = \—Р @ < X < Г) = 1/е.257.р=Р@,25<Х<0,75)
=0,5; Р4C)=С|р3<?=0,25. 259. A!=2)/~3. 261. F(x) =
0 при х<3,
0,2 при 3 < дс<4,
0,3 при 4 <ж<7, 263. /(ж) = 2cos2* в интервале @; я/4);
0,7 при 7 < дс< 10,
1 при х > 10.
вне этого интервала /(ж) = 0. 2*5. РA < X < 2) = (е« —1)/е5*.
266. р (?!)* *2
( 0 при х<0,
= ' 1— 0
\
( р <,
268. F (*) = ' 1— cos ж при 0<х<л/2, 269. F(x) =
\ 1 при х> я/2.
Г0 прнх<1, @ прих<я/6,
= ' A/2) (а-8— х) при 1 < х<2, 270. F(x)= ' —cos3x при я/6<*<л/3,
^1 при jf>2. U при х>я/3.
272. С = 1/2. 273. С=1. 274. С—4.'(л— 1п4). 276. Ж (X) = 4'3.
278. Л*(Х)=0. 279, а) с = 3/4; ^ М(Х)=11/16. 281. М(Х) = 1/а.
Я/2
283. Л1(Ха)= ? х2со8Ж<Зх = (л2—8)/4. 284.
287. M0(X) — M(X)=Me(X) = 4. 288. а) Моды X не имеет (плотность
распределения не имеет максимума); б) М (X) =0 (кривая распреде-
распределения симметрична относительно прямой х=0). 289. М9(Х) =
= Г ("—J)** |'/л. 293. a) D(X) = 4,5; б) Р (-3 < X < 1)=©,5 +
-)- (l/.-t)arcsin A/3); Р A < X < 3)=0,5— A/л) arcsin A/3). 296. D (Х)=
375
25/18. 298. M (A) -Зх«/2; D(X)^3xl'4: о (А)- ^Здгв/2.
300.О(Х*) = 20-2л*. 302. M(Л = (а11)в; б) D(A)-(a-r 1)р*.
ЗОв. Vi=2/3, v,:= 1/2, v3 = 2/5, v4= 1/3: ц, ==0, ц2= 1/18. ца-—1/135.
1». = 1/135. 307. C = l/(ft-o). 309. а) Р @ < X < 0.04)- Р @,16 <
< А < 20)=0.4; б)Р @,05 < А < 0,15) = 0.5. 310. ЯB <! X < 5)=0.6.
«I. Р @ < А < 1/3) -Р B/3) < А < 1) = 2/3. 312. F(х) ~
Г 0 при *<а,
= ' (х_в)/(*_а) при а<х<Ь, 314. Af(A) = 5. 316. D(A)=3;
\ _ I при х > Ь.
о(Х)— У~Ъ. 317. М{Х) — а («кривая» распределения симметрична
относительно прямой ж = а); D(A)=/s/3. 319. М (А3)=F-i а)(Ь*- +
^ [i^±lf±!l]3. 320.
_ e<Jf-3>>/s. 323.
324. Af(A)=l; D(A)=25. 325.
e . 329. P A5 < A < 25) =0,6826. 330. a) P E5 < A <
К 2л
< 68) =0,0823; 6) P C2 < X < 40) --= 0.0027. 332. P (| A | < 10) ----
= 2Ф70.5) =0,383. 333. P st 0,41. 335. Примерно 95%. 336. a) P (I A I<
< 15)P(|K|< 4)=2ФB,5)-2ФA)=0,6741;б)Р = 1—A-0,6741J^
0.8938. 338. PC5< A <40)=PA0 < A < 15)=0.2. 341. (в—За,
+3o) ( 5,25). 342. 6a =30 мм. 343. (9,7; 10,3). 345. a =--=
yflp) M7# /W*"** в интервале @. о», вне
«того интервала /(^)=0; f(^)-=l—е~'х в интервале @, оо), вне
«того интервала f (jt) =0. 348. а)Х^2;б) Х = 0,4. 351.РA < А< 2)~
= 0,038. 352. Р B < А < 5) =0,251. 354. а) М (А) =0,2; б) М (А) = 10.
855. а) Р[А< М(А)]==Р[0< А<AД)| = (е— 1)/е: б) 1 е.
3S7. D(A) = 0,01;a(A)=0.1.358. D (А) = 6,25; о (А) =2.5. 359. С = Я,
8Ю.и,=2/Х». 361. As^2. 362. nt=m*. 363. ?й=6. 365. а) М(Г)=0,2;
б) D (Г) =0,04; в) а (Г) =0,2. 366. М (Г)==а(Г)=0,2 ч. Контролер
» среднем будет ждать очередную машину 12 мнн. 368. а) F A00) ---
= 0,95; б) tf(IOO)=O.O5. 370. а) 0,292; 6H,466: вH.19. 371. аH,9975;
б) 0,656.
Глава седьмая
374. К 7 13 21 ,7„ К К2/2 1 „„
р 0,2 0.1 0,7- 37в- р 0,3 0,7- 378-
v<-3a); б) ?({,)=-• ^j
при /4>0, (АЬ+ В<у < /1а-|-б)при /1 < О.
в)
¦if(V7)x-f(-Vy)),@<y<°>r,6)g(y)=; ' ;
2y Kln(l/y)
X [f(Vln{l/y)) + f(-V ЩЦу)\ @<у<1)
@<y<oo); r)g(y)=? —TJ^l/^-farccosyH-/^* —
-arccosy)l (-1
J-
. ц(у)=21(лУ\—у*)ъ интервале @, 1), вне этого интервала
)Q 385 ()l/((l+2)) () 387 ()
(Уу) р (, ),
385. g(y)=l/(.t(l+»2)) (-оо<у<оо). 387.
= 2/(л 1^1—у*) в интервале @, 1), вне этого интервала g(y)=O.
390. g(y)=——=ге~У в интервале @, оо); вне этого интервала
о
g(y) — Q. 391. g (у) =— е-2у/о'- в интервале @, оо); вне этого
а у 1пу
интервала g(у) =0. 393. M(Y) = (n*— 8)/4. 395. ?>(Х2) = 20—2я2.
396. <fr)f^a> ^gI^»/>+^]'
399. a) G(y) = f l(y-6)/4J;6) G(y)-1-/[A-у)/5], в) (y)
= F[(y—ft)/a] при о >0, G(y) = l—f(y—ft)/aj при a < 0.
.ftl . Z 11 12 13 14 17 18 . ,. Z 5 11 17
401. a) p o,O8 0,32 0,02 0,08 0,10 0,40' 0) P 0,56 0.38 0,06 '
при
г<3,
3 < г < 5,
5 < г < 7,
7 < г < 9,
г>9;
3 < г < 5,
5 < г < 7,
7 < г < 9,
г>9.
Глава восьмая
409. X 26 30 41 . 50 Y 2,3 2,7 411. Р=3/128.
р 0,14 0,42 0,19' 0,25 р 0,29 0,71.
413. /(х, у)=8е-4*-** при х> 0, у > 0; /(ж, у) = 0 при ж < 0 или
у <0. 414. (larctg-i+i) (JLarctg|+l) . 415. F(x, у) -
377
. . . rx4-yi]
внутри круга радиуса R с центром в начале координат; вне этого
круга /(ж; у)-0. 418. С-12/я8. 419. С -2/я. 420. а) /(ж, у) =
= )пг2-2~х~У в первом квадранте; вне квадранта /(ж, у)=0;
б) /> = 5/3-218. 422. а) X 3 6 б) К 10 14 18
р (А-110) 5/7 2/7; pJY | 6) 5/14 5/28 13/28.
424. _а) С=/3/я; б) /х(ж) = /3/B /я)е-°.т***. /»(У) =
= (/ 3/ VH) е~»Л в) <р (ж | у) A/ /7) е-<*+Я\ ф (у | ж)=B/ /я)х
Xe-°t*H*+*yr. 426. /(ж, у)=1/Dо&) внутри заданного прямоуголь-
прямоугольника; вне его /(ж, у)—-О; б) Д (ж) =1/Bа) при |ж|<а, при | х\ >а
' ' )=0; при |у|«?б ft(у) = 11BЬ), при \у\>Ь /г(у) = О.
а) / (ж, у) = 1/18 внутри трапеции; вне её / (ж, у) = 0; б) Д (ж) =
О при ж < О,
2/9 при 0 < ж < 3,
(—2/27) ж+4/9 при 3 < ж < 6,
О при ж > 6;
ГО при у < О,
h (У) = { (~ 1 /24) у +1 /3 при 0 < у < 4, 429*. а) / (ж, у) = 1 /36;
V 0 при у > 4.
внутри трапеции; вне её /(ж, у) = 0; б) /](ж) =
/ 0 при ж < —6,
I ж/27 + 2/9 —6 < ж < —3, ( 0 при у < 0;
=Л 1/9 —3 < ж < 3, /г(у) = ' -у/24 + 1/3 при 0 < у < 4,
I -ж/27+2/9 3<ж<6 \о у>4.
V 0 ж>_6.
= М (К) = (я + 4-4 / 2)/4. 433. М (А) - М (Y) ~ л/4; D (A)=D (K)=
= (я8 -1-8я—32)/16. 434. а) М (Х)^=М (Y) = я/2; D (А) = D (К)=л^-4;
п 4чк «u(t ,л—} О при ж<0 или у < О,
, = 0. 435. а) / (ж, у) _ { ,Ое-„де+w п{;и ж > о, у > 0|
' " при ж < 0, или у < О,
при ж > 0, у > 0.
<Р(* I У) = 1 /2 //•* -у8; /»(у) -= 2 У гг—у
Глава девятая
7 8 12
0,10 0,15 0,50-
при х<2,
... при 2<ж«с5,
442. a) f*(x) = { 0,4 прн 5<ж<7,
при 7< ж<8,
при ж > 8.
*<4,
6tf*W-P'5 "Ри 4<ж<7,
°) ^ W-1 0 7 пп„ 7<ж<8,
ж>8.
4«7. s5f = 4= 168,88.469. s^ = s*/10» = 5,25/100 = 0,0525. 470. s^ =
-s»/100 = 489/100 = 4,89. 472. *•=*„= 0,9. 473. V=*B=0,5.
474.p = (S*/)/n»«. 475. р = (У «,*,)/( 10 5)=0,22. 476. Г=1/*в.
477. X» =T/3EB = 1 /5 = 0,2. 478Гр = 1 /Гв. 479. p*=0,2. 482. о» =
= (jcJ/s*—l = 160*/12062,5—1 = 1,12; p»=s*/x = 12062,5/160 = 75.4.
483. a*=3cB,_af= V"DB. 484. a»= 1,26, a*=0,5. 485. a»=JB—^ЗО^
ft»=xB+K3DB. 486. a*=2,24, ft»=22,38. 488. ХГ == 2,11, Я? = 3,57.
490. p»=Bn/*,-)/tOOO=0,4. 491. >.»=B*/)/п=*в- 492. 3l»=l.
94. X*=l/xB= 1/20=0,05. 496. p»=*„/(«+1). 496. p»=xB/(a+l)=
= 75,47. 497. p=l/ZB. 498. a»= 2>(х,Шя. 499. a» -
= l/ S lg(xi)-a]*/n. 500. a»=*B> a«= /Б^. 502. a) 7,63 < a <
< 12,77;" 6) 14,23 < a < 19,37. 503. 1964,94 < a < 2035,06.
504. 992,16 < a < 1007,84. 505. 6 = /-^== l,96-^==0,392MM.
507. n = 179. 509. -0,04 < a < 0,88. 511. 34,66 < a < 50,94.
513. a) 0 < a < 14,28; 6) 7,93 < a < 20,02. 515. 0,28 < a < 1,32.
517. 0,47 < p < 0,71. 519. 0,78 < p < 0,87. 520. 0,705 < p < 0.795.
521. 0,07 < p < 0,18. 522. a) 0,083 < p < 0,119; 6) 0,076 < p < 0,124.
Глава одиннадцатая
524. a) JcB=19,672, DB=0,169; 6) xB = 76,2, DB = 18,56.
526. DB=40,4. 527. a) yB = 15,68, DB=32; 6) DB = 30-|.
528. a) ?, = 23,85, DB=38,43; 6) DB=36,35^ 530. a) 3cB = 5i,l,
DB = 10!,29; 6) *B = 147,62, DB=212,3; в) жв = 16,46, DB = 4,87;
г)*„ = 11,П4; DB=0,14. 532. а) а,=0,135, <?* = -0,33l; б)а,=0,18,
ek = — 0,45. 534. a) a, = —0,01, e* = — 0,21; 6) as=0,47, еЛ=0,36.
Глава двенадцатая
536. а) ух = 1,92ж+100,9, ху=0,42у—38,3; ^)
0\931 ) 215+1818
у^
х„= 0,\9у-3,1; в) ух = -2,15дс+181.8, ж„ = -0,ЗЗу-)-65,7;
538. а) ух=0,6&с*+ 1,23ж + 1,07. т|,,х=0,96; б) ~ух=3,20х* —13,00*4-
4-^.07, т)ид:=0,99; в) ух = 1,48д:г + 2,4!дс, т)ух=0,93; г) ух =
= 1,59^4-3,33*4-9,4, т\их =0,93; д) ух = —1,52**4- 121,94х—576,61,
Т1ИЛ-=0,91. 539. а) *и=2,8у24-0.02у4-3,18, т»ди=0,96; б) *„ =
= 2,29у« —1,2504-1. Г)*»=0.92. 541. рв=0,92 542. рв=0,75.
543. рв=0,73. 544. рв=0,82. Мнения специалистов достаточно хо-
хорошо согласуются. 545. (>ав = — О.21. Рлс=0.64, рВг = —0,3.
Наиболее согласуются оценки арбитров А и С. 547. р„=0,89. 549.
т„=0,78. Оценки контролеров согласуются. 550. тв—0,54. 551.
тв = 0,67. Мнения специалистов согласуются удовлетворительно.
552. т/,в = —0,16, т^г==0,51, хвс =0,51. Наиболее совпадают оценки
арбитров А и С, б'и С. 553. т„ = 0,79.
379
Глава тринадцатая
555. Любл^Я.в; Л,,, @,01; 8; 15) = 4. Нет оснований отвергнуть
пулевую гипотезу. 557. fHa64==l,52; /^@,05; 5; 8) = 3,69. Таким
образом, нет оснований отвергнуть нулевую гипотезу о равенстве
генеральных дисперсий. 559. $« = 188,67; .4=124,84; Р„абл = 1,51;
Лер @,05; 9; 7) = 3,E8. Таким образом, нет оснований считать точ-
точность станков различной. 561. Хнабл = 21,33; Хкр@,05; 16)=26,3.
Нет оснований отвергнуть нулевую гипотезу. 562. sJ=0.27; Хпабл =
= 45,0; Хкр @,05; 30) = 43,8. Нулевая гипотеза отвергается. Исправ-
Исправленная выборочная дисперсия значимо отличается от гипотетической.
564. sl=s*x = 4; )йев. кр@,975; 19) =8,91; Хправ. кр@,025; 19) = 32,9;
Хнабл=38. Нулевая гипотеза отвергается; новичок работает нерит-
неритмично. 566. гв,оа= 1,645; Хкр @,05; 120)= 146,16. Партия бракуется.
568. ZHa6j, = 2,5; гкр = 1,96. Нулевая гипотеза отвергается. Средний вес
изделий различается значимо. 569. 2„айл = 1,2; гкр = 1,96. Данные
наблюдений согласуются с нулевой гипотезой; выборочные средние
различаются незначимо. 571. FBata — l,\9\ fKp@,01; 7;9)=5,62. Нет
оснований отвергнуть гипотезу о равенстве дисперсий. Имеем
|7"иа«л 1=3,7; /двуст. кр @.01; 16) =2,92. Нулевая гипотеза о ра-
равенстве средних отвергается. 573. х=12,8; ~у = 12,35; sx=0,ll; s\=
= 0,07; Л,абл = 1.57; fKp@,05; 9; 15) =2,59; 7"иайл = 3,83;
'правост. кр @,05; 24) = 1,71. Нулевая гипотеза отвергается.
575. а) 1/Иа6л = |>3. «кр=2,57. Нет оснований отвергнуть нулевую
гипотезу, б) икр = 2,33. Нет оснований отвергнуть нулевую гипо-
гипотезу, в) СНабл = 3. «кр=2,33. Средний вес таблетки значимо отли-
отличается от допустимого; давать лекарство больным нельзя.
576. в) 1) 1—0 = 0,5—Ф @,15) =0,4404; 2) я, =25. 577. в) 1— (J =
= 0,6664. 578. а) я3(в1) = 1 — [Ф(икр—Я.1)-)-Ф(ыкр + Я,,)], где Хг =
=(oi—а0)/[(о/ Уп) Уп/2], «„у находят из равенства Ф(икр)=A—а)/2;
б) При проверке нулевой гипотезы по выборочной средней мощность
л2 B0) =0,8078; при проверке нулевой гипотезы по выборочной ме-
медиане мощность п3B0) =0,6103. При уменьшении |Я| мощность
уменьшается; таккак|Х.]|= а' ~f? • , =|Х| «--==< I Я, I,
а/Уп Ул/2 /л/2
то мощность критерия проверки нулевой гипотезы по выборочиой
медиане меньше мощности критерия по выборочной средней. 579.
бO'вайл=:—2; —'правост. кр = —1,75. Нулевую гипотезу отвергаем.
582. d=—0,9;2 4 = 65; 5^ = 2,51; Гнайл=—1,13; /д„уст.кр @,01;
9) =3,25. Результаты взвешиваний различаются незначимо. 583. Нет
оснований считать, что физическая подготовка улучшилась. 584. d=—2;
24= 66; sd=/34/7; Г„а6л=-2,57;/двуС1.^р @,05; 7)=2,36. Ре-
зультаты анализов различаются значимо. 585. d=0,018; 2<*f =0,0177;
sd =0,034; Г„абл = 1,91; /ДВуСт. Кр(°.05; 12) =2,18. Результаты анализа
различаются незначимо. 589.1/Иабл = 1.76; икр=1,645. Партию принять
нельзя. 590. (/набл = 2,33; икр = 1,645. Нулевая гипотеза отвергается.
Новая форма рекламы значимо эффективнее прежней. 591. t/,,a6.i =
= 1,77; икр>в],9б. Нет основании считать новое лекарство значимо
эффективнее прежнего. 594. Нельзя (объем каждой выборки не дол-
должен быть меньше 4). 595. а) ?-64; 2*'s< =252,8;
380
= 36,9663; V =2,8; бна6л < 2,8; х*р@,05; 3) = 7,8. Нет оснований
отвергнуть гипотезу об однородности дисперсий; б) О? =3,95.
59в. * = 116; SV* = 7016; /3=60,48; У*/ Ig *¦*-=201.4344;
V = 12,0475; С = 1,0146; бна6л= 11,87; х*р @,01;3) = Н,3. Гипотеза
об однородности дисперсий отвергается. 597. ? = 65; г2 = 74,68;
2I*i Ig Л-= 121,0550; V = l,62; виа6л < 1,62; Хкр@.05; 3) = 7,8. Нет
оснований предпочесть один_из способов остальным. 598. a) sx =
= 7,12; sy = 7,92; s| = I3,92; «* = 9,902; У^! =673, 36; 2*/>gs?=
= 66,36; K = 3,ll; В„абл = 7,76; х2кр@.05; 2) = 6,0. Гипотеза об од-
однородности дисперсий принимается. Станки обеспечивают одина-
одинаковую точность; б) РцаЛл =2; FKP @,05; 24.19) =2,11. 600. fe = 36;
'•¦=6; GHaft. = 0,2270. а)'Скр@,01; 36; 6) = 0.28б8; б) GKp@.05;
36; 6) =0,2612. В обоих случаях нет оснований отвергнуть гипо-
гипотезу об однородности дисперсий. 602. *—-36; / = 5; Gaa^ —
=0,5036; Окр @,05; 36; 5) = 0,3066. Гипотеза об однородности ди-
дисперсий отвергается. 603. а) *=9; 1=4; GHa6.,=0,3556; СкрХ
X @,05: 9; 4) =0,5017. Автоматы обеспечивают одинаковую точность
взвешивания, б) 0*=О,О225. 604. а) * = 9; /=3; Она6л = 0,465;
Скр@,01; 9; 3> =0,6912. Нет оснований отвергнуть нулевую гипо-
гипотезу об однородности дисперсий; б) Dr=0,067. 605. fe = 19; / = 15;
GHa6.A°89; GKp @,05; 19; 15) =0,1386. Станок работает устойчиво.
607.'{/„абл = 2,85, «кр=2,57. Нулевая гипотеза отвергается. Отно-
Относительные частоты изготовленных станками нестандартных деталей
различаются значимо. 608. 1/„абл = 2,15; икр = 1,б5. Нулевая гипо-
гипотеза отвергается. Вероятность изготовления бракованного изделия
первым заводом больше, чем вторым. 609. 1/11абл=0,94; иКр = '.96.
Нет оснований отвергнуть нулевую гипотезу. 611. *=60; 7"набл ==
= 2,44; /кр@,01; 60) =2,66. Нет оснований отвергнуть нулевую ги-
гипотезу; X и К —некоррелированные случайные величины.
612. /г = 118; 7"„айл =4,74; /кр@,05; 118) = 1,98. Нулевая гипотеза
отвергается; X н К—коррелированные случайные величины.
614. а) 17=—0,11; о„=0,948, tT=0,25, о„ = 0,994, 2"и» = 73.
г„=0,8; б) Гна«л = 13,2; /кр@,01; 98) = 2,64. Нулевая гипотеза
отвергается: X и Y коррелированы. 615. а) и — — 0,03, а„= 1,321.
7=—0,09, а„ = 1,877; ^пи})т=— 206, гв = —0,83; б) Гна6л =
= —14.73. /кр@,001; 98)=_3,43. Нулевая гипотеза отвергается: X н
Y коррелированы. 616. а) « = —0,84, аи = 1.567, 7=-0,69, ov = 1,419;
2«вp«^' = -^4,'•в = -0,16;б) Г„а6л =—1.3, *кр @,05; 98)= 1,99. Нет
оснований отвергнуть нулевую гипотезу: X и V некоррелированы.
618. Гкр=0,28. Нулевая гипотеза отвергается. Ранговая корреляци-
корреляционная свявь между оценками двух преподавателей значимая.
610. Т1кр=0,54. Ранговая корреляционная связь значима.
620. Гкр=0,61. Нулевая гипотеза отвергается. Ранговая корреля-
корреляционная связь значима. 621. 7"кр=0,62. Ранговая корреляционная
связь значима. 622. 7кр=0,31. Выборочный коэффициент ранговой
корреляции значим. 624. Гкр=0,64. Ранговая корреляционная связь
значимая. 625. Гкр—0,41. Ранговая корреляционная связь значи-
значимая. 626. Гкр=0,42. Ранговая корреляционная связь незначимая.
628. ГН?6Л = 39, к»„Ижн. кр @,025; 6,9) = 31, суверх„.кр=65. Нет
оснований отвергнуть нулевую гипотезу об одинаковой эффектив-
381
иости методов А и В. 629. №на6., = 73, ш,11|Ж„. кр @,05; 9, 10) =-69,
и'верхп. кр = Ч1- Нет основании отвергнуть гипотезу об одинаковой
производительности труда смен. 630. №цаЛл = 156, а',|,,Ж11. кр@,05;
10, 12) = 89, к>ВСрХ„. кр = 141. Нулевая гипотеза отвергается: раци-
рацион А эффективнее рациона В. 632. ю„нж„. кр @,005; 40, 60) =
= 1654, ц'всрхи кр=2386- Нулевая гипотеза отвергается. 633. №„а6,=
= 730,5, а'пижв. кр @,025; 25, 30) = 584, и'верх11. Кр=816. Нет основа-
оснований отвергнуть нулевую гипотезу об однородности выборок.
636. * = 8; Х'^абл^7'711 ХкР@.°5; 8) = 15,5. Нет оснований отвер-
отвергнуть гипотезу о нормальном распределении генеральной совокуп-
совокупности. 638. а) Случайно; *=2, У.?111вл = 2,47, х?р@,05; 2)=6,0;
б) случайно; k = 6, y.Jufcl= 1,52, yt« @,05; 6)= 12,6; в) значимо;
fr = 4. Хгнабл = 13'93' Х*р@,05; 4)=§,5; г) случайно; *=6, yf,a&1 =
= 0,83, Хкр@,05; 6) = 12,6. 640. а) Согласуется;** =10,4; о* = 13,67;
* = 4; Хнабл = 5,4; -/кр@,05; 4)=9,5; б) Согласуется; х*=12,04;
о* = 4,261Ц k = 9-3 = 6; у?шбл = IЛ Х^ @,05; 6) = 12,6; в) не согла-
согласуется; **=42,5; о*=17Л7; * = 5; Х"абл = 14; у.кр@,05; 5) = 11,1;
г) согласуется; л*=27,54; а*=10,44; А=6;
Хкр @,05; 6) = 12,6. 643. а) Гипотеза о нормальном распределении X
согласуется с выборкой; б) о=27,5, о=10,4. 644. Гипотеза о нор-
нормальном распределении X не согласуется с выборкой. 646. а) Нет
оснований отвергнуть гипотезу о нормальном распределении гене-
генеральной совокупности X; б) а*=4,16, о* = 9,8. 649. *=5;х„ = 1000;
Х = 0,001; теор*етические частоты 148,36; 99,45; 66,64; 44,68; 29,97;
20,07; 13,46; Х?,абл= 33>84; ХЦР(О.&1; 5)== 15,1- Гипотеза о показа-
показательном распределении отвергается. 650. k = 5; 7a=20; Я. =0,05;
теоретические частоты: 393,47; 238,65; 144,75; 87,79; 53,26; 32,29;
19,59; у.*абл = 15,88; х?р@,01; Э) = 15,1. Гипотеза о показательном
распределении времени безотказной работы элементов отвергается.
«51. * = 6; ~хв = 2,5; Х=0,4; теоретические частоты: 263,76; 176,80;
118,48; 79,44; 53,28; 35,68; 23,92: 16*00; %*„*,=*UJX; Х?ф@,01; 6)==
= 16,8. Гипотеза о показательном распределении! отвергается.
653. * = 4; теоретические частоты: 6,25} 25,рО; 37,50; 25,00; 6,25;
Янабл3*2'8**' Xjp(°>OSi 4) =9,5. Нет оснований отвергнуть гипотезу
о биномиальном распределении X. 654. р* = 0,4; k — 5; теоретические
частоты: 0,60; 4,04; 12,24; 21,50; 25,05; 20,05; 11,15; 4,25; х?ибд= 0,68;
XiJp @,01; 5) = 15',1. Нет основан»* отвергнуть гипотезу о распреде-
распределении X по биномиальному закону. 683. р*-=0,2; At=»2; теоретичес-
теоретические частоты: 65,54; 81,92; 40,96; 10,24; 1,28; 0,06; Х^абл^4»6^
Х*р @,05; 2) =6,0. Нет оснований отвергнуть гипотезу о распреде-
распределении X по биномиальному закону. 659; хл=22,47; а„ = 1,44;
а* =19,98; *>• = 24,96; /(*)=0,2; * = 7; *?,«&,= 4.39> X^j». @,01; 7) =
= 18,5. Нет оснований отвергнуть гипотезу о равномерном распре-
распределении X. 660. FB=1,5; ав=21,31;о*=—35,37; 6* = 38,37; /(*) =
= 0,014; * = 5; х?1абл"=7-71: С @>05: 5) = n''- Нет основвиий от-
отвергнуть гипотезу о равномерном распределении температуры.
661. It=12,71; ов = 2,86; й* = 7,76; Ь*=17,66; /(^) = 0,101; * = 7;
382
3$ 53,43; Хкр @.01; 7) = 18,5. Гипотеза о равномерном распре-
распределении времени отвергается. Данные наблюдений не согласуются
с этой гипотезой. 663. k — 2; А.=хв=0,5; теоретические частоты:
122,30; 60.66; 15,16; 2,52; 0,32; х?абл=9'27; Х2кр @.05; 2)=6,0. Нет
оснований отвергнуть гипотезу о распределении X по закону Пуас-
Пуассона. 664. *=4; A,=*U = 0,9; теоретические частоты: 406,6; 365,9;
164,7; 49.4; 11.1; 2.3; Х^а«5л=9'26: 4р@,01; 4) = 13,3. Нет основа-
оснований отвергнуть_гипотезу о распределении X по закону Пуассона.
665. *=3; А,=*в=0,7; теоретические частоты: 496,6; 347,6; 121,7;
28,4; 5,0; 0,7; х*а6л=4,5; х?р@,05; 4)=9,5. Нет оснований отверг-
отвергнуть^ гипотезу о распределении X по закону Пуассона. 666. k=4;
X=*i = l; теоретические частоты: 183,95; 183,95; 92,00; 30,65; 7,65;
1,55; 0,25; 0,05; Хнабл = 8>32; ХкР(°.01; 4) = 13,3. Нет оснований от-
отвергнуть гипотезу о распределении X по закону Пуассона. 667. Д=2;
A,=JB=0,61; теоретические частоты: 108,7; 66,3; 20,2; 4,1; 0,7;
Янабл'32* Якр@>05; 2) = 6,0. Нет оснований отвергнуть гипотезу
о распределении X по закону Пуассона.
Глава четырнадцатая
669. Soeu,= !851; S$aKT=360,55; SOCT = 1490,45; s|aKT = 120;
sSct=93; Fu<b = l,29; FKp@,05; 3; 16)=3,24. Нет оснований отверг-
отвергнуть нулевую гипотезу о равенстве групповых средних. 670. S06m —
= 22426; 5факт = 12960; SOCT=9466; 4акт=2592; &т=225; Fm6a =
= 11,5; FKp@,01; 5; 42) =3,49. Нулевая гипотеза о равенстве груп-
групповых средних отвергается. 671. 50бщ=296; 5факт = 104; SOCT = 192;
4акт=52; sScr=21,3; fHa^=2,44; FKp@,05; 2; 9) =4,26. Нет осио-
ваний отвергнуть нулевую гипотезу о равенстве групповых средних.
672. So6u,= 1541; 5факт=95; SOCT = 1446; 4акт=31,67; s2cr=60,25.
Нет оснований отвергнуть нулевую гипотезу о равенстве групповых
средних. 673. So6ul=334; 5факт=32; SOCT=302; 4акт = 16; 4ст =
= 33,56. Нет оснований отвергнуть нулевую гипотезу о равенстве
групповых средних. 675. So6lu = 1619,43; 5факт =961,46; S0CT =657,97;
4акт=240,36; 4ст = 73,П; ^„,64=3,29; FKV @,05; 4; 9)=3,63. Нет
оснований отвергнуть нулевую гипотезу о равенстве групповых сред-
средних. 676. Soeiu = 6444; 5факт=4284; SOCT=2l60; 4акт=2142; sgcT =
= 216; FHaea=9,92; FKp@,01; 2; 10) = 7,56. Нулевая гипотеза от-
отвергается. Групповые средние различаются значимо. 677. 50лш =
= 5533442; S*aKT = 3399392; S0CT=2134050; sL,KT = 1699696; <&т =
-=194004; ^Иабл = 8,76; FKp@,0l; 2; 11) = 7,20. Нулевая гипотеза
отвергается. Групповые средние различаются значимо. 678. 50вш =
-=192788; 5ф1КТ = 42695; S0CT = 150093; 4акт= 14232; 5^=0822;
/•на6л=2,09; fKP@,05; 3; 22)=3,05. Нет оснований отвергнуть ну-
нулевую гипотезу о равенстве групповых средних.
Глава пятнадцатая
680. 8, 3, 12, 12, 8, 12, 23, 3. 681. а р 0 2,6 0 432 0>288 0>064 ;
б) 3, 1,2, 1,2. 682. 1, 3, 2, 2, 2, 2. 684. А%, Л», Ла, А1г А„ Л4, Аг,
383
At, AA. 686. Ая, Au At, Au Av 687. .4S, А,, Аъ, Ая, At. 688. A3,
Аи At, Аг, Л- 690. 11,4; 4,2; 13,4; 7,6. 691. *, = (- In /¦,-);*,.
693. 0,019: 0,036; 0,027; 0,095; 0,015. 694. x; = 0,5r,-. 695. 6,90; 7,49;
4,13; 8,87; 6.37. 696. xt = (— 1п/у)/Я. 697. 2,232; 11,087:3,711; 7,985;
0,202. 698. *,= У —i0 In /-/ . 699. Xj = a Y~—2\nri. 700. *,• =
= 2A— V~n)/X. 701. 0,388; 1,600; 0,338; 0,628. 702. x,- = arccos(l —
— 2r,). 703. *, = -(l/c)ln[l— /7A— e-»01: .*,= — (l/c)ln [/•,• +
4-A—/¦/)*-**]- 705. * = (— ln/-2)/2, если rx < 0,25, x=(—ln/-8),
если rjSsO.25. 706. * = (— ln/-2)/3, если /•, < 2/5, д: = (—In/-2)/4,
если ^^2/5. 707. x — — In г2, если rt < 1.7, x = (— In /-2)/2, если
1/7<Г!<3/7, x=(—ln/-2)/3, если г,rs3/7. 708. * = (9r2)/4, если
ri < 1/3, *=J/l8/-2-f 1 +1, если /-!S!l/3. 709. a=2/-2, если /-t <
<5/6, x = \-\-\/2rt— 1 , если г,5*5/6. 711. a) 0,84; —0,14; 0,31;
— 1,27; 0,21; 6) 11,68; 9,72; 10,62; 7,46; 10,42. 712. a) 0,316; 0,045;
— 1,232; ^,357; —0,930; 6)_4,O3I6; 4,0045; 3,8768; 4,0357; 3,9070.
713. a*—xB = — 0,1; o*= VDa =1,3. 715. (дг3, yi), (*2, y2), («i, y2),
(Jfs. Уг)> (Xtj_ Vi)- 716^ (x3> у,), (хг, yj, (xlt yt), (*,, yt), (x3, {/,)•
718. X( = ]/ri, yt-Vr',. 720. x,- = 3I/'/'I-, «,=4/- ',+xi—2. 722. i/,=
У;, Xi = y{-r'u. 723. */=*//-,•, у,=дг^;. 725. а) Я»=0,95,
б) |Р—Р*|=0,07. 726. а) Р* = 0.5; б) \Р—Я*| =0,079. 728. а) Р* =
= 0,5; б) /• = 10,17. 729. а) Р^=0,4б; б) /* = 66. 731. *,=9, хг =
= x3=xt=Xb = \0, л-« = 11; а* = ^ = Ю. 733. a) 8,5; б) 4,96; в) 0,85;
г) 0,15. 737. 238. 738. а) 38,63; б) 37,2; в) 14291. 739. а) 1,711;
б) о« = A/2)(е2— 1)-(е—1)* = 0,242; в) 2324. 740. а) 0,164; б) 0,479;
742. а) 0,97; б) 0,096. 744. а) 0,253; б) 0,491; в) 0,413; г) 0,658.
д) 0,104. 747. а) 5,988; б) 3, 173; в) 1,001; г) 0,477. 750. 5,2.
751. 1,903. 754. 1,719. 755. 0,857.
Глава шестнадцатая
756. а) *,@ = 2(**+1); б) *4(/)=3,5(г2+1). 757. а) Х и/2;
б) Xt = U. 759. т*(О = 5е'. 761. а) тх(/) = (/+1)г; б)
i4/ + 4/ 765 KK 767 ) tf (+1) /
*(О ) х() (+); )
= sin4/ + cos4/. 765. KV=KX. 767. a) tf,, = (/i+1) (/a-f i)Kx;
б) Кг=С*Кх. 769. Dyy(t) = Dx(t). 771. Ъу (/) = (/ + 3)*?>*(/).
772. a) mv(t)=bt, ^j,=25e-a(''-'l)i. 776. a) mx @ = 10sin3/;
6) ^JC = 0,2sin3/1sin3^; в) Dx @=0,2 sin4 3/. 777. a) Kx A, 2) = 22,
?>x(l) = 6, ?>жB) = 84; б)рх(/„ <a)=(l + 5/1/2)/(l/'l-f 5/f J/T+57f) ,
(e-l'i-Mt если аргументы одного
знака
— е'»"'1', если аргументы раз-
разных знаков.
782. Ryx(tt, it) = Rxu(tt, /1) = cos(a?2+p/1). 783. рху=\, если /,
и /j+Г одного знака; рхв = — 1, если tt и 1г-\-1 разных знаков.
784. )К(/ t)KV )+K(t /L/?(' ^)+/?(/ ')
y у у
u- 785. а)тг@ = 3/; А:г = /,/2 + е-4 <'«-'«>'. 787. а)/(„=
г/ /?г/+/?!//?/?/?!//?у; б) KV = KX +
Кг- 789. М
+ 790.
791.
384
v() ! 792. pxv = cosCt2 —/,). 793. Kx—
= Dl cos <o, (tt - /,) ~ Dt cos oL (^ -/t). 794. mx (/) = 3<* -f- 2.
795. /ny@ = 3/2. 797. ^ = 10e" "•-'•>' [I —2(/,—/f)*J. 798. а) И;(/>=
= 4es'C cos 2/—2 sin 2/); 6) Kx =es ('1+'«> Ccos2/,—2sin2/,)x
XCcos2/2-2sin2/8). 799. Ky = Dx ^i±^tB cos o> (/,-/,).
800.a) mj,(O=5cos/; 6) ^=3e-o.5(/.-/L^
==/ге/1+'*('1-г1)- 803.^Щ
80в. ^г = 5 [3-4 (/,-/!>*] e-«»-'.>*. 808.
/,J-I]e-<'»-'.'*. 809*. K
V (tJV A*)Кх + U (IJV (tt)???+U (tt)V (tj^. 810*.
6) my(/) = 2/-f sin2/, в) mj,(/) = 0,5(/2—sin2/). 813. my(t) =
= I5/(as+ P!)) Ie°" (P sin B/ + a cos 6/) — a]. 814. a) my (/) =
= 2/(H-a*)[ee'(<xsin/— cos /)+I), 6) mu(t) = t— 0,5 sin it.
815. mJ/(/) = (/!+l)(/ + 0>5sin2/). 817. a) ЛСу = (cos <o/i — 1) x
X(cos(o/2 — 1)/©*; 6) D«(/) = (cos<b/ — IJ/<b*. 818. Du(t) = t*/4.
819. a) Du{()=t* 12<*/i9)+C/4)|; б) ?>„(/) = [е' (/ — 1)+IJ»;
в) Dy(t)=b arctg / — ln(l+/s); r) Dj.(O = (l/169) [2e»' sin2/ +
-f 3Be«cos2/ —1I. 820. a) mj,(/)>=0,5[/4-(sin2//2)]; б) К» =
=(sin o)/, sin <B/2)/<o-; в) Dy (/) = (sin*w/)/oJ. 822. а) ?>у (/) = 1,5 sin* 2Л
6) ?>„(/)= 3A —cos/)*. 823. Ky—ttt» (e-'•—1) (e~'«-l). 824. а) т„ (/)=
= (sin 3/)/3/; 6) tfy = (sin 3/, sin 3/2)/9/, tt; в) Dtf(/)=(sin*3/)/9 /*.
825*. Dy (l) = e20" F sin 6/-fa cos B/—a)*/4/4 (а*+Р2J.827*. a) «„(/)=
= 3/4-2/*; 6) ?>g,(/) = 5B/-fe-«-l). 829. a) /?x»=/j/f+/,;
6) /?xv = sip/ilcos/I; в) /?*?, = /, e'.[(/,—l)e'»+1f, /? =
= /2e'.J(/l-l)e'.+ lj.
Глава семнадцатая
функция: тхA)=а V sin (м/+ф)со5ф Aф. 839*.
831. тхA)=0, ^ = (l/2)cos(/s—/,). 834. *(/)—нестацнонар-
иая функция: тж (/) = mB cos 2/ Ф const. 835. -Y(/)—стационарная
функция: /ях@ = 0, ^x = ?)cos(/a—^). 837. Л (О—нестационарная
л/2
V
= а* [0,5—A /2 е*)я] cos*w/+o* [0,5—A/е)—A/2е2)] sin*<o/. 842.
*?(T) = 16?>e-att>. 845. а) рж(т) = е-т'; б) рж(т) = е- 1х|A + |х|).
849. тх (/) = «„@ = 0, /(x=^y = 5cos(/a—/0; /?xy=5sin(/,—/j).
850. Нет. a) Rxy = &cofitAcosi%; 6) /?xy = 3cosB/4—/,). 851.
pxy(x) = sinx. 854. a) *л.(т)=2е-°-5х'A-т»), ?>. =A^ @) = 2;
6) Dx/Di=l. 856. a) *i(T)=3e-2l1[l(chT-2sh|T|);
885
б)*,.@) = 3. 859. Р (^5<K<oe)=0,5—P @ < К <
= 0,5-0,1915=0,3085. 860*. /(у) = A/10»^2я) е" ("'/200>. 863.
a) Dy(O=2/arotg<—1пA + /г); б) Dy @ = 2?>(a/+e-a'-l)/ct»;
в) ?>y(O=B?>/a*)[(a/ + 3)e-°" + Ba<-3)]. 864. Dy/kx@) =
= 1360/10=136.866. г^(т)=-|т|е11
I — 1 при т < 0,
где signT = <J 0 при т=0, 868. г .. (т) = г.. (т)=**(т).
{ 1 при т > 0. ** ** *
869. ^»(т)—(?ta*e-a |х 1/3) (а*т*—а |т|—1). 871. ку (т)—C-4т«) в"*' •
872. a) ky(T)=kx(x)+2k'x'(x)+k]cv(-t);6)ky(T)^-ki'(i)+klxV(t).
873. Л(т) = D/3) е~ I * I (т*-|тЦ-1). 874*. *„(т)=*ж(т)+кх' (т) +
Г(т). 875. гя^)-*Г (т), гж~(т)—-*;"(т). 876. ^.. (т) =
). 879. Ол=10. 881. ^ = яо*/2 . 884. «ж (
s. 886. *ж(<»)=?>а/л(а2+<о*). 888*. sx(w)=(
P)*+as] [(<o+p)»+a*J. 889*. sx (<o)=BDa/n)
*-4р*©*]. 890. sx(©)=?>e-(w'/4aV »^J. 892.
=A/5)/(<о*+0,01)* я. 894*. sv (<в) = 2?»а3 A + <o*)/j
897. s,HopM (<в) =а/я (а8-]-©2). 898. Sx (<o)=D [(l/л)arctgj(w/a)+0,5].
903. «<;.(<в)=ш2/)а3/л(<в*+а11)*- 904. s^. (w) = ((<»//л) e" (w'/4).
906. ^t(i)=Bse sin©eT)Bcos<B0T—l)/x. 908. A,(T) = e~2'Tl. 911.
/п„=4.913.а)т#=8;б)О#=22/3. 914. a)/ntf = 2/3;6) sy(<o)=(l/n)X
+(-©*)*]. 915. a)sv(©)=4E—7©*)»/я(<в»+1)*(<в*+4)Х
); б) sv(w) = 4E—Ш)г1л (<в»+1)»(<в«+4) (©*+9). 916.
. 917. Sj,(w) = so/(fe*—©s)8+4A*<b*. 916*. Вторая система:
D l0/7
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1
Таблица значений функции <р (х)--
/2Н
0.0
0,1
0.2
0.3
0.4
0.5
0.6
0.7
0,8
0.9
1.0
1,1
1,2
1,3
1,4
1,5
0
0,3989
3970
3910
3814
3683
3521
3332
ЗШ
2887
2661
0,2420
2179
1942
1714
1497
1295
1
3989
3965
3902
3802
3668
3503
3312
ЗИМ
2874
2637
2396
2155
1919
1691
1476
1276
2
3989
3961
3894
3790
3652
3485
3292
3079
2850
2613
2371
2131
1895
1669
1456
1257
3
3988
3956
3885
3778
2637
3467
3271
3056
2827
2589
2347
2107
1872
1647
1435
1238
3986
3951
3876
3765
3621
3448
3251
3034
2803
2565
2323
2083
1849
1626
1415
1219
5
3984
3945
3867
3752
3605
3429
3230
ЗОН
2780
2541
2299
2059
1826
1604
1394
1200
6
3982
3939
3857
3739
3589
3410
3209
2989
2756
2546
2275
2036
1804
1582
1374
1182
7
3980
3932
3847
3726
3572
3391
3187
2732
2492
2251
2012
1781
1561
1354
1163
8
3977
3925
3836
3712
3555
3372
3166
2943
2709
2468
2227
1989
1758
1539
1334
1145
9
3973
3918
3825
3697
3538
3352
3144
2920
2685
2444
2203
1965
1736
1518
1315
1127
387
1.6
1.7
1.8
1.9
2.0
2,1
2.2
2.3
2.4
2.5
2.6
2.7
2,8
2.9
3,0
3.1
3.2
3.3
3.4
3,5
3.6
8.7
3.8
3.9
0
1109
0940
0790
0656
.0540
0440
0355
0283
0224
0175
0136
0104
0079
0060
0,0044
0033
0024
0017
0012
0009
0006
0004
0003
0002
-
1092
0925
0775
0644
0529
0431
0347
0277
0219
0171
0132
0101
0077
0058
0043
0032
0023
0017
0012
0008
0006
0004
0003
0002
2
1074
0909
0761
0632
0519
0422
0339
0270
0213
0167
0129
0099
0075
0056
0042
0031
0022
0016
0012
0008
0006
0004
0003
0002
3
1057
0893
0748
0620
0508
0413
0332
0264
0208
0163
0126
0096
0073
0055
0040
0030
0022
0016
ООП
0008
0005
0004
0003
0002
4
1040
0878
0734
0608
0498
0404
0325
0258
0203
0158
0122
0093
0071
0053
0039
0029
0021
0015
ООП
0008
0005
0004
0003
0002
Продолжение
s
1023
0863
0721
0596
0488
0396
0317
0252
0198
0154
0119
0091
0069
0051
0038
0028
0020
0015
0010
0007
0005
0004
0002
0002
6
006
0848
0707
0584
0478
0387
0310
0246
0194
0151
0116
0088
0067
0050
0037
0027
0020
0014
0010
0007
0005
0003
0002
0002
7
0989
0833
0694
0573
0468
0379
0303
0241
0189
0147
0113
0086
0065
0048
0036
0026
0019
0014
0010
0007
0005
0003
0002
0002
прилож. 1
8
0973
0818
0681
0562
0459
0371
0297
0235
0184
0143
ОНО
0084
0063
0047
0035
0025
0018
0013
0009
0007
0005
0003
0002
0001
9
0957
0804
0669
0551
0449
0363
02<Ю
0229
0180
0139
0107
0081
0061
0043
0034
0025
0018
0013
0009
0006
0004
0003
0002
0001
ПРИЛОЖЕНИЕ 3
л
Таблица значений функции Ф (х)~ , ( е~**/2Л
V2n\
X
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,20
0,21
0,22
0,23
0,24
0,25
0,26
0,27
0.28
0,29
0,30
0.31
Ф (х)
0,0000
0,0040
0,0080
0.0120
0,0160
0,0199
0,0239
0,0279
0.0319
0,0359
0,0398
0.0438
0,0478
0,0517
0.0557
0,0596
0,0636
0,0675
0,0714
0,0753
0,0793
0,0832
0,0871
0,0910
0,0948
0,0987
0,1026
0,1064
0,1103
0,1141
0,1179
0.1217
X
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,44
0,45
0.46
0,47
0,48
0,49
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0.58
0,59
0,60
0,61
0,62
0,63
Ф (ДО
0,1255
0.1293
0,1331
0,1368
0,1406
0,1443
0,1480
0,1517
0,1554
0,1591
0,1628
0,1664
0,1700
0,1736
0,1772
0,1808
0,1844
0.1879
0,1915
0,1950
0,1985
0,2019
0,2054
0,2088
0,2123
0,2157
0,2190
0,2224
0.2257
0,2291
0,2324
0,2357
*
0,64
0,65
0,66
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,80
0,81
0,82
0.83
0,84
0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
Ф U) *
II
0,2389
0,2422
0,2454
0,2486
0,2517
0,2549
0,2580
0,2611
0,2642
0,2673
0,2703
0,2734
0,2764
0,2794
0,2823
0,2852
0,2881
0,2910
0,2939
0,2967
0,2995
0,3023
0,3051
0,3078
0,3106
0,3133
0.3159
0,3186
0,3212
0,3238
0,3264
0,3289
0,96
0,97
0.98
0,99
,00
,01
.02
,03
,04
,05
,06
.07
,08
,09
,10
,П
,12
.13
,14
.15
1.16
1,17
1,18
1,19
1.20
1,21
1,22
1,23
1.24
1,25
Ф <*)
0.3315
0,3340
0.3365
0,3389
0,3413
0,3438
0,3461
0,3486
0,3508
0,3531
0,3554
0,3577
0,3599
0,3621
0,3643
0,3665
0,3686
0,3708
0,3729
0,3749
0.3770
0,3790
0,3810
0,3830
0,3849
0,3869
0,3883
0,3907
0,3925
0,3944
38»
Продолжение прилож. 2
Ф(дг)
ф(дс)
*(*)
1,26
1.27
1,28
1,29
1,30
1.31
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,40
1,41
1,42
1,43
1,44
1.45
1,46
1,47
1,48
1,49
1,50
1,51
1,52
1,53
1,54
1,55
1.56
1,57
1,58
390
0,
0,
0,
0.
0,
0,
о,
0,
0,
о,
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
3962
3980
3997
4015
4032
4049
4066
4082
4099
4115
4131
4147
4162
4177
4192
4207
4222
,4236
4251
,4265
,4279
,4292
,4306
,4319
,4332
,4345
,4357
,4370
,4382
,4394
,4406
,4418
,4429
1.
1,
1.
1,
1
1,
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
59
60
61
62
63
64
65
66
67
68
69
70
71
72
,73
,74
.75
.76
.77
,78
,79
,80
,81
,82
,83
,84
,85
,86
,87
,88
,89
.90
,91
0,
0.
0.
0.
0,
0,
0.
0,
0,
0,
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4441
4452
4463
4474
4484
4495
4505
4515
4525
4535
4545
4554
4564
4573
4582
4591
4599
4608
,4616
,4625
,4633
,4641
,4649
,4656
,4664
,4671
,4678
,4686
,4693
,4699
,4706
,4713
,4719
,92
,93
,94
,95
,96
,97
1,98
1,99
2,00
2,02
2,04
2,06
2,08
2,10
2,12
2,14
2,16
2,18
2,20
2,22
2,24
2,26
2,28
2,30
2,32
2,34
2,36
2,38
2,40
2,42
2,44
2,46
2,48
0,4726
0,4732
0.4738
0,4744
0,4750
0,4756
0,4761
0,4767
0,4772
0,4783
0,4793
0,4803
0,4812
0,4821
0,4830
0,4838
0,4846
0,4854
0,4861
0,4868
0,4875
0.4881
0,4887
0,4893
0,4898
0,4904
0,4909
0,4913
0,4918
0,4922
0,4927
0,4931
0,4934
2,50
2,52
2,54
2,56
2,58
2,60
2,62
2,64
2,66
2,68
2,70
2,72
2,74
2,76
2,78
2,80
2,82
2,84
2,86
2,88
2,90
2,92
2,94
2,96
2,98
3,00
3,20
3,40
3,60
3,80
4,00
4,50
5,00
0,4938
0,4941
0,4945
0,4948
0,4951
0,4953
0,4956
0,4959
0,4961
0,4963
0,4965
0,4967
0,4969
0,4971
0,4973
0,4974
0,4976
0,4977
0,4979
0,4980
0.4981
0,4982
0,4984
0,4985
0,4986
0,49865
0,49931
0,49966
0,499841
0,499928
0,499968
0,499997
0,499997
ooooooooo
СО4>4*,*>Ъ^СЛСЛСЛ
OOOOOOOOO
S285S3S8SS8
О О О О —¦ *—
82g8S3
— •— — •— какэ
OMUOOO
e
,95
e
,99
e
666'
55 SeS 5
55 SeS 5 SC OS *¦* ЯЭ 5Л *> л. со со ic
o — )«uais!goouoi>-sa<sao
ra
1
064
045
032
023
016
009
001
996
991
987
СЛ О
^ 4 ^
г.* ej е*э лл гл с л е*э t*5 о? Со со со со со
,418
,403
,392
374
.291
.527
745
59
00
58
27
п
X
S
ПРИЛОЖЕНИЕ 5
Число
степеней
свободы
к
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Критические точки распределения
0,01
6,6
9,2
11,3
13,3
15,1
16,8
18,5
20,1
21,7
23,2
24,7
26,2
27,7
29,1
30,6
32,0
33,4
34,8
36,2
37,6
38,9
40,3
41,6
43,0
44.3
45,6
47,0
48,3
49,6
50,9
0.025
5,0
7,4
9,4
11,1
12,8
14,4
16,0
17,5
19.0
20,5
21,9
23,3
24,7
26,1
27,5
28,8
30,2
31,5
32,9
34,2
35,5
36,8
38,1
39,4
40,6
41,9
43,2
44,5
45,7
47,0
Уровень значимости а
0,05
3,8
6,0
7,8
9,5
11.1
12,6
14.1
15,5.
16,9
18,3
19.7
21,0
22,4
23,7
25,0
26,3
27,6
28,9
30,1
31,4
32,7
33,9
35,2
36,4
37.7
38,9
40,1
41,3
42,6
43,8
0,95
0,0039
0,103
0,352
0,711
1.15
1,64
2,17
2,73
3,33
3,94
4.57
5,23
5,89
6,57
7,26
7,96
8.67
9.39
10,1
10,9
11,6
12.3
13,1
13,8
14.6
15,4
16,2
16,9
17.7
18.5
X*
0,975
0,00098
0.051
0,216
0,484
0,831
1,24
1,69
2,18
2,70
3,25
3,82
4,40
5,01
5,63
6,26
6,91
7,56
8,23
8,91
9,59
10,3
11,0
П.7
12,4
13,1
13.8
14,6
15,3
16,0
16,8
0,99
0,00016
0,020
0,115
0,297
0,554
0,872
1,24
1,65
2,09
2,56
3,05
3,57
4,11
4,66
5.23
5.81
6,41
7,01
7,63
8,26
8,90
9.54
10,2
10,9
11,5
12,2
12.9
13.6
14,3
15.0
g3.fi
?3
I
О
5
§1
a 5
¦es
S B>
IS
3
о
g
о
о
i
о
8
• N3 tOI>9 tOO
e
о
M ^ M M bO M to M N3 to N3 N3 N3 Is5 N5 Ю КЗ N3 N3 N5 »O N5 КО N3 N3 N5 to КЗ КЗ CO *• N3
: — OOlNOOOoO
e
о
ел ел Ъ> да
soDON
I
CO
M00
8
s
1
!
X
s
I
ПРИЛОЖЕНИЕ 7
Критические точки распределения F Фишера — Снедекора
fkl—число степеней свободы большей дисперсии,\
\k}—число степеней свободы меньшей дисперсии )
X
*. \
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
4052
98,49
34,12
21,20
16,26
13,74
12,25
11,26
10,56
10,04
9,86
9,33
9,07
8,86
8,68
8,53
8,40
2
4999
99,01
30,81
18,00
13,27
10,92
9,55
8,65
8,02
7,56
7,20
6,93
6,70
6,51
6,36
6,23
6,11
3
5403
90,17
29,46
16,69
12,06
9,78
8,45
7,59
6,99
6,55
6,22
5,95
5,74
5,56
5,42
5,29
5,18
Уровень значимости а —
4
5625
99,25
28,71
15,98
11,39
9,15
7,85
7,01
6,42
5,99
5,67
5,41
5,20
5,03
4,89
4,77
4,67
5
5764
99,33
28.24
15,52
10,97
8,75
7,46
6,63
6,06
5,64
5,32
5,06
4,86
4,69
4,56
4.44
4,34
6
5889
99,30
27,91
15,21
10,67
8,47
7,19
6,37
5,80
5,39
5,07
4,82
4,62
4,46
4.32
4,20
4,10
7
5928
99,34
27,67
14,98
10,45
8,26
7,00
6,19
5,62
5,21
4,88
4,65
4,44
4,28
4,14
4,03
3,93
0.01
8
5981
99,36
27,49
14,80
10,27
8,10
6,84
6,03
5,47
5,06
4,74
4,50
4,30
4,14
4,00
3,89
3,79
9
6022
99,36
27,34
14,66
10,15
7,98
6,71
5.91
5,35
4,95
4,63
4,39
4,19
4,03
3,89
3,78
3,68
10
6056
99,40
27,23
14,54
10,05
7,87
6,62
5,82
5,26
4,85
4,54
4,30
4,10
3,94
3,80
3,69
3,59
п
6082
99,41
27,13
14,45
9,96
7,79
6,54
5,74
5,18
4,78
4,46
4,22
4,02
3,86
3,73
3,61
3,52
12
6106
99,42
27,05
14,37
9,89
7.72
6,47
5,67
5,11
4,71
4,40
4,16
3,96
3,80
3,67
3,55
3,45
*.\
,
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
161
18,51
10,13
7,71
6,61
5,99
5,59
5,32
5,12
4,96
4,84
4,75
4.67
4,60
4,54
4,49
4,45
2
200
19,00
9,55
6,94
5,79
5,14
4.74
4,46
4,2.6
4.Г0
3,98
3,88
3,80
3,74
3,68
3,63
3,59
3
216
19,16
9,28
6,59
5,41
4,76
4,35
4,07
3,86
3,71
3,59
3,49
3,41
3,34
3,29
3,24
3,20
Уровень значимости « =
4
225
19,25
9,12
6,39
5,19
4,53
4,12
3.84
3,63
3,48
3,36
3,26
3,18
3,11
3,06
3,01
2,96
5
230
19.30
9,01
f>,26
5,05
4,39
3,97
3,69
3,48
3,33
3,20
3,11
3,02
2,96
2,90
2,85
2,81
6
234
19.33
8,94
6,16
4,95
4,28
3,87
3,58
3,37
3,22
3,09
3,00
2,92
2,85
2,79
2,74
2,70
7
237
19,36
8,88
6,09
4,88
4.21
3,79
3,50
3,29
3,14
3,01
2,92
2,84
2,77
2,70
2.66
2,62
0.05
8
239
19,37
8,84
6,04
4,82
4,15
3,73
3,44
3,?3
3,07
2,95
2,85
2,77
2,70
2,64
2.59
2,55
9
241
19.38
8,81
6,00
4,78
4,10
3,68
3.39
3,18
3,02
2,90
2,80
2,72
2,65
2,59
2,54
2,50
10
242
19,39
8,78
5,96
4,74
4,06
3,63
3,34
3,13
2,97
2,86
2,76
2,67
2,60
2,55
2,49
2,45
п
243
19,40
8,76
5,93
4,70
4,03
3,60
3.31
3,10
2,94
2,82
2,72
2,63
2,56
2,51
2,45
2,41
12
244
19,41
8,74
5,91
4,68
4,00
3,57
3,28
3,07
2,91
2,79
2,69
2,60
2,53
2,48
2,42
2,38
894
ПРИЛОЖЕНИЕ 8
Критические точки распределения Кочрена
число степеней свободы, /—количество выборок)
Уровень значимости а= 0,01
\ ft
/ \^
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
0,9999
9933
9676
0,9279
8828
8376
0,7945
7544
7175
0,6528
5747
4799
0,4247
3632
2940
0,2151
1225
0000
2
0,9950
9423
8643
0,7885
7218
6644
0,6152
5727
5358
0,4751
4069
3297
0,2871
2412
1915
0,1371
0759
0000
3
0,9794
8831
7814
0,0957
6258
5685
0,5209
4810
4469
0,3919
3317
2654
0,2295
1913
1508
0,1069
0585
0000
4
0,9586
8335
7212
0,6329
5635
5080
0,4627
4251
3934
0,3428
2882
2288
0,1970
1635
1281
0,0902
0489
0000
5
0,9373
7933
6761
0,5875
5195
4659
0,4226
3870
3572
0,3099
2593
2048
0,1759
1454
1135
0,0796
0429
0000
6
0,9172
7606
6410
0,5531
4866
4347
0,3932
3592
3308
0,2861
2386
1877
0,1608
1327
1033
0,0722
0387
0000
т
0,8988
7335
6129
0,5259
4608
4105
0,3704
3378
3106
0,2680
2228
1748
0,1495
1232
0957
0,0668
0357
0000
\ *
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
00
8
0,8823
7107
5897
0,5037
4401
3911
0,3522
3207
2945
0,2535
2104
1646
0,1406
1157
0898
0,0625
0334
0000
Уровень значимости а = 0.
9
0,8674
6912
5702
0,4854
4229
3751
0,3373
3067
2813
0,2419
2002
1567
0,1338
1100
0853
0,0594
0316
0000
10
0,8539
6743
5536
0,4697
4084
3616
0,3248
2950
2704
0,2320
1918
1501
0,1283
1054
0816
0,0567
0302
0000
16
0,7949
6059
4884
0,4094
3529
3105
0,2779
2514
2297
0,1961
1612
124«
0,1060
0867
0668
0,0461
0242
0000
01
36
0,7067
5153
4057
0,3351
2858
2494
0,2214
1992
1811
0,1535
1251
0960
0,0810
0658
0503
0,0344
0178
0000
144
0,6062
4230
3251
0,2644
2229
1929
0,1700
1521
1376
0,1157
0934
0709
0,0595
0480
0363
0,0245
0125
0000
0,5000
3333
2500
0,2000
1667
1429
0,1250
1111
1000
0,0833
0667
0500
0,0417
0333
0250
0,0167
0083
0000
395
Продолжение прилож. 8
Ч ft
/ Ч^
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
09
1
0,9985
9669
9065
0,8412
7808
7271
0,6798
6385
6020
0,5410
4709
3894
0,3434
2929
2370
0,1737
0998
0000
Уровень значимости а = 0,
2
0,9750
8709
7679
0,6338
6161
5612
0,5157
4775
4450
0,3924
334G
2705
0,2354
1980
1576
0,1131
0632
0000
3
0,9392
7977
6841
0,5981
5321
4800
0,4377
4027
3733
0,3624
2758
2205
0,1907
1593
1259
0,0895
0495
0000
4
0,9057
7457
6287
0,5440
4803
4307
0,3910
3584
3311
0,2880
2419
1921
0,1656
1377
1082
0,0765
0419
0000
95
5
0,8772
7071
5895
0,5063
4447
3974
0,3595
3286
3029
0,2624
2195
1735
0,1493
1237
0968
0,0682
0371
0000
6
0,8534
6771
5598
0,4783
4184
3726
0,3362
3067
2823
0,2439
2034
1602
0,1374
1137
0887
0,0623
0337
0000
г
0,8332
6530
5365
0,4564
3980
3535
0,3185
2901
2666
0,2299
1911
1501
0,1286
!061
0827
0,0583
0312
0000
\ *
1 Ч.
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
ее
8
0,8159
6333
5175
0,4387
3817
3384
0,3043
2768
2541
0,2187
1815
1422
0,1216
1002
0780
0,0552
0292
0000
Уровень значимости а = 0,
9
0,8010
6167
5017
0,4241
3682
3259
0,2926
2659
2439
0,2098
1736
1357
0,1160
0958
0745
0,0520
0279
0000
10
0,7880
6025
4884
0.4118
3568
3154
0,2829
2538
2353
0,2020
1671
1303
0,1113
0921
0713
0,0497
0266
0000
16
0,7341
5466
4366
0,3645
3135
2756
0,2462
2226
2032
0,1737
1429
1108
0,0942
0771
0595
0,0411
0218
0000
M
36
0,6602
4748
3720
0,3066
2612
2278
0,2022
1820
1655
0,1403
1144
0879
0,0743
0604
0462
0,0316
0165
0000
144
0,5813
4031
3093
0,2013
2119
1833
0,1616
1446
1308
0,1100
0889
0675
0,0567
0457
0347
0,0234
0120
0000
0,5000
3333
2500
0,2000
1667
1429
0,1250
1111
1000
0,0833
0667
0500
0,0417
0333
0250
0,0167
0083
0000
896
ПРИЛОЖЕНИЕ 9
Равномерно распределенные случайные числа
10 09 73 25 33 76 52 01 35 86 34 67 35 48 76 80 95 90 91 17
37 54 20 48 05 64 89 47 42 96 24 80 52 40 37 20 63 61 04 02
08 42 26 89 53 19 64 50 93 03 23 20 90 25 60 15 95 33 47 64
99 01 90 25 29 09 37 67 07 15 38 31 13 11 65 88 67 67 43 97
12 80 79 99 70 80 15 73 61 47 64 03 23 66 53 98 95 11 68 77
66 06 57 47 17 34 07 27 68 50 36 69 73 61 70 65 81 33 98 85
31 06 01 08 05 45 57 18 24 06 35 30 34 26 14 86 79 90 74 39
85 26 97 76 02 02 05 16 56 92 68 66 57 48 18 73 05 38 52 47
63 57 33 21 35 05 32 54 70 48 90 55 35 75 48 28 46 82 87 09
73 79 64 57 53 03 52 96 47 78 35 80 83 42 82 60 93 52 03 44
98 52 01 77 67 14 90 56 86 07 22 10 94 05 58 60 97 09 34 33
1I 80 50 54 31 39 80 82 77 32 50 72 56 82 48 29 40 52 42 01
83 45 29 96 34 06 28 89 80 83 13 74 67 00 78 18 47 54 06 10
88 68 54 02 00 86 50 75 84 01 36 76 66 79 51 90 36 47 64 93
99 59 46 73 48 87 51 76 49 69 91 82 60 89 28 93 78 56 13 68
65 48 11 76 74 17 46* 85 09 50 58 04 77 69 74 73 03 95 71 86
80 12 43 56 35 17 72 70 80 15 45 31 82 23 74 21 11 57 82 53
74 35 09 98 17 77 40 27 72 14 43 23 60 02 10 45 52 16 42 37
69 91 62 68 03 66 25 22 91 48 36 93 68 72 03 76 62 II 39 90
09 89 32 05 05 14 22 56 85 14 46 42 75 67 88 96 29 77 88 22
91 49 91 45 23 68 47 92 76 86 46 16 28 35 54 94 75 08 99 23
80 33 69 45 98 26 94 03 68 58 70 29 73 41 35 53 14 03 33 40
44 10 48 19 49 85 15 74 79 54 32 97 92 65 75 57 60 04 08 81
12 55 07 37 42 11 10 00 20 40 12 86 07 46 97 96 64 48 94 39
63 60 64 93 29 16 50 53 44 84 40 21 95 25 63 43 65 17 70 82
61 19 69 04 46 26 45 74 77 74 51 92 43 37 29 66 39 45 95 93
15 47 44 52 66 95 27 07 99 53 59 36 78 38 48 82 39 61 01 18
94 55 72 85 73 67 89 75 43 87 54 62 24 44 31 91 19 04 25 92
42 48 11 62 13 97 34 40 87 21 16 86 84 87 67 03 07 11 20 59
23 52 37 83 17 73 20 88 98 37 68 93 59 14 16 26 26 22 96 63
04 49 35 24 94 75 24 63 38 24 45 86 25 10 25 61 96 27 93 35
00 54 99 76 54 64 05 18 81 59 96 I1 96 38 96 54 69 28 23 91
35 96 31 53 07 26 89 80 93 54 33 35 13 54 62 77 97 45 00 24
59 80 80 83 91 45 42 72 68 42 83 60 94 97 00 13 02 12 48 92
46 05 88 52 36 01 39 09 22 86 77 28 i4 40 77 93 91 08 36 47
32 17 90 05 97 87 37 92 52 41 05 56 70 70 07 86 74 31 71 57
69 23 46 14 06 20 11 74 52 04 15 95 66 00 00 18 74 39 24 23
19 56 54 14 30 01 75 87 53 79 40 41 92 15 85 66 67 43 68 06
45 15 51 49 38 19 47 60 72 46 43 66 79 45 43 59 04 79 00 33
94 86 43 19 94 36 16 81 08 51 34 88 88 15 53 01 54 03 54 56
397
Продолжение прилож. 9
98 08 62 48 26
33 18 51 62 32
80 95 10 04 06
79 75 24 91 40
18 63 33 25 37
74 02 94 39 02
54 17 84 56 11
11 66 44 98 83
48 32 47 79 28
69 07 49 41 38
45 24 02 84 04
41 94 15 09 49
96 38 27 07 74
71 96 12 82 96
98 14 50 65 71
77 55 73 22 70
80 99 33 71 43
52 07 98 48 27
31 24 96 47 10
87 63 79 19 76
44 99 90 88 96
89 43 54 85 81
20 15 12 33 87
69 86 10 25 91
31 01 02 46 74
97 79 01 71 19
05 33 51 29 69
59 38 17 15 39
02 29 53 68 70
35 58 40 44 01
39 09 47 34 07
88 69 54 19 94
25 01 62 52 98
74 85 22 05 39
05 45 56 14 27
52 52 75 80 21
56 12 71 92 55
09 97 33 34 40
32 30 75 75 46
10 51 82 16 15
ПРИЛОЖЕ НИ Е 10
Квантили нормального распределения ир
(перед всеми значениями квантилей в этой части таблицы
нужно поставить знак минус)
Ю0Р1
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0
1 ;
2 S
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
>,326 2
J.054 2
,881
,751
,645
,555
,476
,405
,341
1,282
1,227
1,175
1,126
1,080
1,036
0,994
0,954
0,915
0,878
0,842
806
772
739
706
674
643
613
583
553
$.090 г
>,290 5
>,034 2
,866 1
,739 1
,635
,546
,468
,398
,335
1,276
1,221
1,170
1,122
1,076
1,032
0,990
0,950
0,912
0.874
0,838
803
769
736
703
671
640
610
580
550
>,878 2
',257 i
',014
,852
,728
,626
,538
,461
,392
,329
1,270
1,216
1,165
1,117
1,071
1,028
3,986
3,946
3,908
3,871
0,834
800
765
732
700
668
637
607
577
548
>,748 2
!,226 5
,995
,838
,717
,616
,530
,454
,385
,323
1,265
1,211
1,160
1,112
1,067
1,024
0,982 i
3,942
9,904
0,867
0,831
796
762
729
697
665
634
604
574
545
',652 2
2,197 5
,977
,825
,706 1
,607
,522
,447
1,379
1,317
1,259
1,206
1,155
1,108
,063
1,019
3,978 (
3,938
3,900
3,863 (
0,827
793
759
726
693
662
631
601
571
542
!,576 2
!,170 \
,960 1
,812
,695
,598
,514
,440
,372
,311
1,254
1,200
1,150
1.103
1,058
1,015
3,974
3,935
1,896
3,860
0,824
789
755
722
690
659
628
598
568
539
!,512 2
г, 144 5
,943
,799
.685
,589
,506
,433
,366
,305
1,248
1,195
1,146
,098
,054
1,011
3,970 (
0,931
3,893
3,856
0,820
786
752
719
687
656
625
595
565
536
',457 i
!,120 i
,927
,787
,675
,580
,499
,426
,359
,299
1,243
1,190
,141
,094
,049
,007
3,966 (
3,927
3,889 (
3,852
0,817
782
749
716
684
653
622
592
562
533
>,409 '.
>,097 '.
,911
,774
,665
,572
,491
,419
.353
,293
1,237
1,185
,136
3,089
,045
1,003
3,962
3,923
3,885
3,849
0,813
779
745
713
681
650
619
589
559
530
2,366
2,075
,896
.762
,655
.563
,483
,412
,347
1,287
1,232
1,180
1,131
1,085
1,041
3,999
0,958
0,919
0,882
0,845
0,810
776
742
710
678
646
616
586
556
527
398
Продолжение прилож. 10
юор,-
%
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
0,0
0,524
496
468
440
412
385
358
332
305
279
0,253
228
202
176
151
126
100
075
050
025
0,1
0,522
493
465
437
410
383
356
329
303
277
0,251
225
199
174
148
123
098
073
048
023
0
0,
0,
,2
519
490
462
434
407
380
353
327
300
274
248
222
197
171
146
121
095
070
045
020
0,3
0,516
487
459
432
404
377
350
324
298
272
0,246
220
194
169
143
118
093
068
043
018
0,4
0,513
485
457
429
402
375
348
321
295
269
0,243
217
192
166
141
116
090
065
040
015
0,5
0,510
482
454
426
399
372
345
319
292
266
0,240
215
189
164
138
ИЗ
088
063
038
013
0,6
0,507
479
451
423
396
369
342
316
290
264
0,238
212
187
161
136
111
085
060
035
010
0.7
0,504
476
448
421
393
366
340
313
287
261
0,235
210
184
159
133
108
083
058
033
008
0,8
0,502
473
445
418
391
364
337
311
285
259
0,233
207
181
156
131
105
080
055
030
005
0.9
0,499
470
443
415
388
361
335
308
282
256
0,230
204
179
154
128
103
078
053
028
003
Квантили нормального распределения ир
(все значения квантилей в этой части таблицы—положительные)
ЮОР/
50
51
52
53
54
55
56
57
58
59
0,0
0,025
050
075
100
126
151
176
202
228
0,1
0,003
028
053
078
103
128
154
179
204
230
0,2
0,005
030
055
080
105
131
156
181
207
233
0,3
0,008
033
058
083
108
133
159
184
210
235
0,4
0,010
035
060
085
111
136
161
187
212
238
0,5
0,013
038
063
088
ПО
138
164
189
215
240
0.6
0,015
040
065
090
116
141
166
192
217
243
0,7
0,018
043
068
093
118
143
169
194
220
246
0,8
0,020
045
070
095
121
146
171
197
222
248
0.9
0,023
048
073
098
123
148
174
199
225
251
399
Продолжение прилож. 10
юор,-
60 С
61
62
63
64
65
66
67
68
69
70 С
71
72
73
74
75
76
77
78
79
0,0
),253 (
279
305
332
358
385
412
440
468
496
),524 (
553
583
613
643
674
706
739
772
806
80 0,842 (
81 0.878 (
82 0.915 (
83 (
),954 (
84 0,994 (
85
86
87
88
89 1
90 1
91
92
93
94
95
96
97
98 5
99 I
,036
,080
.126
,175
,227
,282
.341
,405
,476
,555
,645
,751
,881
>,054 1
2,326 i
0,1
).256С
282
308
335
361
388
415
443
470
499
),527 С
556
586
616
64S
678
710
742
776
810
),845 (
),882 (
),919 (
),958 (
),999
.041
1,085
,131
,180
,232
,287 1
.347
,412
,483
,563
,655
,762
,896
?,075 i
г, 366 i
0,2
),259 (
285
311
337
364
391
418
445
473
502
),530 (
559
589
619
650
681
713
745
779
813
),849 (
),885 (
),923 (
),962 (
,003
,045
,089
,136
,185
,237
,293
,353
.419
.491
,572
,665
,774
,911
г,097:
>,409 !
0,3
),261 (
287
313
340
366
393
421
448
476
504
),533 (
562
592
622
653
684
716
7J9
782
817
),852 (
),889 (
3,927 (
3,966 (
,007
,049
,094
,141
,190
1,243
,299
,359
,426
1,499
,580
,675
,787
,927
2,120 !
2,457 !
0.4
3,264 <
290
316
342
369
393
423
451
479
507
0,5
3,266 (
292
319
345
372
399
426
454
482
510
),536 0.539 (
565
595
625
653
687
719
752
786
820
3,856 (
3,893 (
3,931 (
3,970 (
1,011
.054
,098
1,146
.195
,248
,305
,366
,433
,506
,589
,685
,799
,943
2,144 I
2,512 5
568
598
628
659
690
722
755
789
824
3,860 (
3,896 (
3,935 (
3,974 (
1,015
,058
,103
,150
,200
,254
.311
.372
,440
,514
,598 !
.695
,812
,960
2,170 2
2,576 2
0,6
3.269
295
321
348
375
402
429
457
485
513
3,542 (
571
601
631
662
693
726
759
793
827
3,863 (
3,900 (
3,938 (
3,978 (
,019
,063
,108
,155
,206
,259
.317
,379
,447
,522
,607
.706
,825
,977
>,197 i
2,652 \
0,7
0,272
298
324
350
377
404
432
459
487
516
3,545
574
604
634
665
697
729
762
796
831
3,867
3,904
3.942 (
3.982 (
,024
,067
,112
,160
1.211
1.265
1.323
1.385
,454
,530
,616
,717
,838
.995!
2,226 !
2,748 !
0.8
0,274
300
327
353
380
407
434
462
490
519
0,548
577
607
637
668
700
732
765
800
834
0,871
3,908
3,946
3,986
1,028
,071
,117
1,165
1,216
1,270
1,329
1,392
1,461
,538
,626
,728
,852
2,014 !
2,257 !
2,878 ;
0,9
0,277
303
329
356
383
410
437
465
493
522
0,550
580
610
610
671
703
736
769
803
838
0,874
0,912
3,950
3,990
,032
,076
,122
1,170
1.221
1,276
1,335
,398
,468
,546
,635
,739
,866
2,034
2,290
5,090