Author: Фрайфельд А.В. Брод Г.Н.
Tags: инженерное дело техника в целом электроника электротехника электропоезда издательство транспорт контактная сеть
ISBN: 5-277-00796-2
Year: 1991
Text
I
г,?
А.В.Фрайфельд
Г. Н. Брод
ПРОЕКТИРОВАНИЕ
КОНТАКТНОЙ СЕ1И народ- спорта. не про- предо- движе-
ИЗДАНИЕ ТРЕТЬЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ е мате- рящих-
тивные ведший проек- щвшие- .IX коп- >дборов
ваииях гования зличин, ми раз- in ьютон он-метр ть (Па>
ко, вы- еча.чий,
и с бла- Цосква,
МОСКВА «ТРАНСПОРТ» 1991
УДК 62 i .332.3.001.63
Фрайфельд Л, В, Брод Г Н. Проектирование контактной сети
3-е изд., перераб. и доп. - М: Транспорт, 1991. 335 с
В книге приведены методы проектирования контактной сети и
воздушных линий электрифицированных железных дорог; выбор ти-
пов контактных подвесок и их расчеты; расчеты и подборы опорных,
поддерживающих и фиксирующих устройств: составление схем пита-
ния н секционирования; разработка планов контактной седи на стан
пнях и иепсгона<; л-тны примеры расчетов и подборов различных Оте-
ментов контактной сети и воздушных .линий
Второе издание вышло в 3984 г.
Книга рассчитана на инженерно-технических работников, за-
нятых проектированием, сооружением и эксплуатацией контактной
сети и воздушных линий электрифицированных .•кс-летных дорог.
Управление учебных гавсдсний МПС рекомендует се для использо-
вания в качестве учебного пособия для студентов вузов железнодо-
рожного транспорта.
Ил 138, табл. 77, библиогр 16 иазв.
л и и г у н л и и с а л и. капд техн. наук. А. В Фрайфельд -
г.таны 1—5, § 6.1 -6.4, 7.1—7.5, 8.'1, 8.3 8.5, главы 9 и 10; инж
Г. IL Брод- § 6.5, 7.6, 8.2, 8.6 п 8.7.
р i цензе и т инж. В. М, f цепко
3 а в е д у ю щ и й р е д а к ц и е й 11. 71. Немцова
Р е д а к т о р И. К. Петушкова
3202030000-065
ф---------------
049(01) -91
84-90
ISBN 5-277-00796-2
© Издательство «Транспорт», 5984
© А В. Фнайфельд, Г. Я. Брод, 1991.
с изменениями и дополнениями
ОТ АВТОРОВ
Третье издание книги выходит в период перестройки всего народ-
ного хозяйства страны, в том числе и железнодорожного транспорта.
В этом издании авторы стремились отразить совершенствование про-
ектирования контактной сети, надежность которой во многом предо-
пределяет бесперебойность перевозок и соблюдение графика движе-
ния поездов.
Сохранив прежнее название книги, авторы включили в нее мате-
риалы по проектированию различных воздушных линий, относящих-
ся к электрифицированной железной дороге.
В 3-м издании учтены все изменения, внесенные в нормативные
документы и типовые проекты контактной сети, за период, прошедший
со времени выхода 2-го издания. Отражены передовые методы проек-
тирования, сооружения и эксплуатации контактной сети, появившие-
ся в последние годы. Приведены новые методы подбора типовых кон-
струкций, переработаны и дополнены примеры расчетов и подборов
параметров и устройств контактной сети и воздушных линий.
В нормативных документах имеются разночтения в наименованиях
отдельных величин. Авторы использовали в книге ге наименования
и размерности, которые рекомендованы Перечнем физических величин,
подлежащих применению в строительстве (ОН 528-80). Основными раз-
мерностями приняты: для сил - деканьютон (даН) и килоньютон
(кН), для моментов деканьютон-метр (даН-м) и килоныотон-метр
(кН-м), для механических напряжений н давлений паскаль (На)
и мегапаскаль (МПа).
Авторы выражают свою признательность инж. В. М. Гиенко, вы-
сказавшему при рецензировании рукописи ряд полезных замечаний,
которые способствовали улучшению содержания книги.
Все предложения и отзывы по книге будут приняты авторами с бла-
годарностью. Их следует направлять по адресу: 103064, г. Москва,
Басманный туп , ба, издательство «Транспорт».
3
Глава 1
МЕТОДЫ ПРОЕКТИРОВАНИЯ УСТРОЙСТВ
КОНТАКТНОЙ СЕТИ И ВОЗДУШНЫХ ЛИНИЙ.
РАСЧЕТНЫЕ УСЛОВИЯ
§ 1.1. Организация проектирования
К устройствам контактной сети относятся все провода контакт-
ных подвесок, поддерживающие и фиксирующие конструкции, опоры
с деталями для их крепления в грунте, к устройствам воздушных ли-
ний — провода различных линий (питающих, отсасывающих, для
электроснабжения автоблокировки и прочих нетяговых потребителей
и др.) и конструкции для их крепления на опорах.
Устройства контактной сети и воздушных линий, подвергаясь
воздействиям различных климатических факторов (значительные пе-
репады температур, сильные ветры, гололедные образования), долж-
ны успешно им противостоять, обеспечивая бесперебойное движение
поездов с установленными весовыми нормами, скоростями и интерва-
лами между поездами при требуемых размерах движения. Кроме того,
в условиях эксплуатации возможны обрывы проводов, удары токо-
приемников и другие воздействия, которые также нужно учиты-
вать в процессе проектирования.
Контактная сеть не имеет резерва, что обусловливает повышенные
требования к качеству ее проектирования.
Проектные работы по электрификации участков железных дорог,
строящихся или переводимых на электрическую тягу, а также при
усилениях и переустройствах на действующих электрифицированных
участках, выполняют транспортные проектно-изыскательские инсти-
туты и проектные организации на железных дорогах.
Задание на конкретный проект обычно выдается управлением же-
лезной дороги или Министерством путей сообщения. Проектирование,
как правило, начинается с технико-экономического расчета (ТЭР),
в котором обосновываются основные решения, определяется пример-
ная стоимость строительства и его эффективность. Дальнейшие работы
обычно осуществляются в две стадии: на первой выполняется проект
электрификации заданного участка, на второй разрабатывается ра-
бочая документация. При проектировании электрификации неболь-
ших и несложных участков выполняется только одна стадия -....ра-
бочий проект.
По каждому проекту электрификации назначается главный ин-
женер проекта, координирующий выполнение различных разделов,
отвечающий за качество проекта и все принципиальные технические
решения, а также за правильное определение сметной стоимости
строительства, технико-экономические показатели, соблюдение норм
4
проектирования и установленных сроков разработки проекта. В про-
цессе строительства главный инженер проекта контролирует соблю-
дение принятых решений, согласовывает отдельные изменения, если
в этом возникает необходимость, и участвует в сдаче участка в экс-
плуатацию.
Раздел контактной сети (в нем рассматриваются и воздушные
линии, закрепленные на ее опорах) является одной из основных ча-
стей проекта электрификации железнодорожного участка; его выпол-
няют, соблюдая требования и рекомендации руководящих докумен-
тов по разработке проектов и смет для промышленного и железнодорож-
ного строительства, а также нормативных документов, регламенти-
рующих сооружение и эксплуатацию контактной сети и воздушных
линий.
В разделе контактной сети проекта электрификации железнодорож-
ного участка устанавливают: расчетные условия климатические
и инженерно-геологические; тип контактной подвески (все расчеты по
определению необходимой площади сечения проводов контактной
сети выполняют в разделе электроснабжения проекта); длину про-
летов между опорами контактной сети на всех участках трассы; типы
опор, способы их закрепления в грунте и типы фундаментов для тех
опор, которым они необходимы; виды поддерживающих и фиксирую-
щих конструкций; схемы питания и секционирования; объемы работ
по установке опор на перегонах и станциях; основные положения по
организации строительства и эксплуатации; потребности в основ-
ных материалах и оборудовании с оформлением .заказных специфика-
ций па оборудование, для изготовления которого требуется длитель-
ное время.
В состав рабочей документации включают: планы контактной сети
па станциях и перегонах с приложением принятых условных обозна-
чений; чертежи нетиповых опор (например, для установки иа мостах
с ездой поверху), фундаментов, узлов конструкций и деталей; схемы
нетиповых сопряжений анкерных участков; воздушные линии напря-
жением выше 1000 В; планы самостоятельных трасс питающих и от-
сасывающих линий; полную схему питания и секционирования с рас-
положением постов секционирования, пунктов параллельного соеди-
нения подвесок путей, а при системе 2 X 25 кВ - - еще и автотранс-
форматорных пунктов; планы пунктов группировки на станциях
стыкования; схемы плавки гололеда, дистанционного управления сек-
ционными разъединителями, рельсовых цепей и групповых заземле-
ний; чертежи искусственных сооружений и прохода в них контактной
подвески, а также устройства контактной сети внутри электродепо;
чертежи габаритных ворот и учебных полигонов контактной сети;
границы районов контактной сети; основные данные для производст-
ва строительных и монтажных работ; полные заказные спецификации;
перечень примененных типовых проектов; сметную документацию.
В рабочем проекте, выполняемом обычно по типовым и повторно
применяемым индивидуальным проектам, указанная рабочая доку-
5
ментация дополняется пояснительной запиской, в которой приводятся
обоснования принятых решений, технико-экономические показатели,
основные объемы строительных и монтажных работ, основные поло-
жения по организации сооружения и эксплуатации контактной сети,
перечень изменений и дополнений к типовым проектам, вызванных
привязкой к конкретным условиям.
При проектировании контактной сети необходимо иметь следую-
щие данные:
для установления климатических и инженер но-геологических рас-
четных условий подробные сведения о средних и экстремальных
температурах воздуха (желательно с распределением по суткам го-
да): об интенсивности гололедных и снеговых образований; о ветро-
вых воздействиях при отсутствии и наличии гололеда; о шероховато-
сти подстилающей поверхности на разных участках; о сейсмичности
района; о температурах, при которых наблюдаются гололед и ветры,
о расположении лесозащитных полос и не защищенных от ветра от-
крытых мест; характеристики грунтов на всей протяженности элек-
трифицируемой линии с указанием «больных» участков; сведения о
наличии грунтовых вод и их агрессивности, о степени загрязненности
воздуха и о местах хранения горючих веществ и минеральных удоб-
рений;
для выбора типа контактной подвески — площадь ее сечения и
марки проводов па ближайший период и на перспективу, максималь-
ные и длительные тяговые токи в отдельных элементах трассы, наи-
большие скорости движения различных поездов (существующие и пла-
нируемые), сведения о наличии автоколебаний на воздушных линиях,
расположенных в районе электрифицируемого участка;
для выбора типов опор, фундаментов, поддерживающих и фикси-
рующих устройств, помимо указанных выше, нужно иметь еще данные
об усиливающих, питающих и отсасывающих проводах и линиях элек-
троснабжения для нетяговых потребителей (ВЛ 6—10 кВ или ДПР),
а также о других воздушных линиях и устройствах, которые будут
крепиться на опорах контактной сети;
для трассировки контактной сети и воздушных линий на перего-
нах и станциях — подробный продольный профиль электрифицируе-
мой линии, данные о верхнем строении пути, точные места установки
и габариты всех сигналов, сведения о конструкциях и габаритах
всех искусственных сооружений (существующих и намечаемых на
перспективу), а также о воздушных линиях, пересекающих железно-
дорожные пути или иначе влияющих на условия установки опор;
планы всех станций, разъездов и обгонных пунктов (желательно
в масштабе I : 1000, но не менее 1 : 2000) с указаниями о их последую-
щем развитии, перечнем путей, электрифицируемых в различные
периоды эксплуатации, схемами подземных устройств и коммуника-
ций, обозначениями мест расположения тяговых подстанций, электро-
депо, экипировочных устройств, постов секционирования, пунктов
параллельного соединения, пунктов группировки, автотрансформа-
ь
торных пунктов и других технических сооружений и служебных зда-
ний.
Перед разработкой рабочих чертежей перечисленные выше ма-
териалы уточняют и дополняют; например, к планам станций (масшта-
бом не менее 1 : 1000) прилагают поперечные профили, в данные о
путевых переустройствах включают проекты средних и капитальных
ремонтов путей, на чертежах искусственных сооружений приводят
деталировку отдельных элементов, связанных с креплениями кон-
струкций контактной сети, и т. д.
Если разрабатывается проект усиления, реконструкции или мо-
дернизации ранее электрифицированного участка, то необходимо
иметь все данные о существующей контактной сети.
Перед выполнением проекта по контактной сети для получения
некоторых из указанных выше данных производят соответствующие
обследования и изыскания.
При общем обследовании устанавливают строительно-монтажные
организации, которые будут вести работы, и их производственные
возможности; определяют наличие путей подъезда к железной дороге
для организации работ по сооружению контактной сети «с поля»;
выявляют участки трассы, особо подверженные гололедным образо-
ваниям и ветровым воздействиям; отмечают особо сильно снегозано-
симые выемки и «больные» места земляного полотна; выявляют места
расположения промышленных предприятий, загрязняющих атмосфе-
ру отходами производства, и складов минеральных удобрений; уста-
навливают примерный объем работ, необходимых для прокладки но-
вых дорог, устройства мостов и гатей; определяют сроки работ, пред-
шествующих электрификации, и т. д.
В процессе топографо-геодезических изысканий производят съемки
перегонов и проходящих вдоль них линий электропередачи и связи;
трасс подземных коммуникаций; искусственных сооружений, по ко-
торым проходят железнодорожные пути или их пересекающие; если
нет планов станций, то съемки их путевого развития и технических
обустройств; съемки самостоятельных трасс питающих и отсасываю-
щих линий, площадок под тяговые подстанции, районы контактной
сети, дистанции электроснабжения и другие сооружения.
При инженерно-геологических изысканиях выявляют качество грун-
тов в местах установки опор, уровень грунтовых вод и их агрессив-
ность, глубину промерзания и др.
Обычно такие обследования и изыскания выполняют один раз до
начала проектирования, но если имеется возможность, то при проек-
тировании в две стадии перед разработкой рабочих чертежей нужно
произвести дополнительные изыскания с целью уточнения условий,
необходимых для выполнения рабочих чертежей с высоким качеством.
При проектировании контактной сети широко используют типо-
вые проекты отдельных ее устройств, «привязывая» последние к кон-
кретным условиям. Типовое проектирование осуществляют государст-
венные проектно-изыскательские институты Трансэлектропроект и
Гипропромтрансстрой, а по отдельным вопросам — институт Гипро-
транссигналсвязь. Типовые проекты разработаны почти для всех
конструкций, узлов и деталей контактной сети и воздушных линий,
их применение существенно повышает качество, ускоряет и удешевля-
ет проектирование, сооружение и эксплуатацию этих устройств.
§ 1.2. Методы проектирования
Расчеты всех конструкций контактной сети должны выполнятвся
по методу расчетных предельных состояний, предусматривающему
производство расчетов на такие (предельные) состояния, при которых
конструкция перестает удовлетворять предъявляемым к ней требова-
ниям эксплуатации. Расчеты осуществляют по одному, двум или трем
предельным состояниям. Первое предельное состояние характеризует
несущую способность конструкции, т. е. ее прочность, устойчивость
и выносливость; второе — возможные деформации, перемещения и ко-
лебания конструкции; третье — подверженность железобетонной или
бетонной конструкции образованию трещин.
При расчетах конструкций по первому предельному состоянию
должно выполняться условие
2 A'max (11)
где 2Wmax — суммарные максимальные внешние воздействия;
Ф1П1п — минимальная несущая способность конструкции.
В расчетах по второму предельному состоянию проверяют выпол-
нение условия
Дщах <1 Ддош (1-2)
где Дтах — максимальная деформация или перемещение;
Ддоп — допускаемая деформация или перемещение.
Расчеты металлических конструкций контактной сети всегда вы-
полняют по первому, а иногда и по второму предельному состоянию.
Железобетонные конструкции рассчитывают еще и по третьему пре-
дельному состоянию (трещиностойкости).
Для практических расчетов по методу предельных состояний долж-
ны быть известны установленные нормами коэффициенты надежности
по материалу К, по нагрузке п, условий работы т и сочетаний пс.
Коэффициент надежности по материалу характеризует возмож-
ное уменьшение сопротивления данного материала. Поэтому расчет-
ное сопротивление деформации i определяется делением установ-
ленного нормативного сопротивления Р" на коэффициент 1:
Rt — R*/К. (1.3)
Например, в СНиП 11-23-81 для стального проката и труб реко-
мендуются значения коэффициента надежности по материалу от
1.025 до 1,15.
8
Коэффициент надежности по нагрузке характеризует возможное
увеличение нормативной нагрузки. Расчетная нагрузка Nj опреде-
ляется произведением нормативной (V" на коэффициент /г > 1:
(1.4)
Например, в СНиП 2.01.07-85 рекомендуется в отдельных слу-
чаях для гололедных нагрузок учитывать коэффициент надежности
по нагрузке, равный 1,3, для ветровых нагрузок-- 1,4 (см. §2.1).
Коэффициент условий работы т < 1 характеризует особенности
работы данной конструкции в общем комплексе. На этот коэффи-
циент следует умножать расчетные сопротивления. Например, сог-
ласно ВС11 141-84 коэффициент условий работы для фиксаторов и
фиксаторных кронштейнов следует принимать равным 0,85, а для
анкеровочных устройств и анкерных болтов- 0,75 (подробнее см.
§2.1).
Коэффициент сочетаний /(,.•<! вводят в расчет при одновременном
действии нескольких нагрузок, чтобы учесть несовпадение их макси-
мальных значений. Этот коэффициент принимают равным 0,8 0,9,
если нет оснований применять более низкое значение.
Кроме указанных, при расчете опорных, поддерживающих и фик-
сирующих устройств контактной сети учитывают установленный Гос-
строем (XLCP коэффициент надежности по назначению, равный 0,95.
На этот коэ(|х|ящиент нужно делить предельные .значения несущей
способности, расчетные значения сопротивлений, предельные значе-
ния деформаций и раскрытия трещин пли умножать расчетные зна-
чения нагрузок, усилий и воздействий.
Отметим следующее. Отнесение опорных, поддерживающих и фиксирую-
щих конструкций контактной сети электрифицированных участков к устройст-
вам, для которых установлен коэффициент надежности но назначению, равный
0,95, по мнению автора, является спорным. Контактная сеть работает в особен-
но трудных условиях, без резерва. Представляется, что более правильным,бы-
ло бы отнести конструкции контактной сети к устройствам, для которых коэф-
фициент надежности но назначению равен единице.
Расчеты но первому предельному состоянию на прочность и устой-
чивость выполняют применительно к упругой стадии работы материа-
ла исходя из расчетных нагрузок, а на выносливость исходя из
нормативных нагрузок. Расчеты по второму предельному состоянию
выполняют па нормативные нагрузки также применительно к упру-
гой стадии работы материала. Расчеты но третьему предельному сос-
тоянию проводят исходя из нормативных или расчетных нагрузок.
Расчет на растяжение какого-либо элемента конструкции по
первому предельному состоянию можно выполнить по условию
|> HIB X 111 Ку ^'нт, (1.3)
где/Vp ,Hax. —- максимальная расчетная растягивающая сила;
/?р — расчетное сопротивление растяжению;
SHr — площадь поперечною сечения элемента нетто (с учетом возмож-
ного ослабления).
9
Аналогичный расчет на изгиб осуществляют по условию
Мтах ''С т Rm . (1 • 6)
где Minax — максимальный расчетный изгибающий момент от внешних сил;
/?„ — расчетное сопротивление на изгиб;
й'нт — момент сопротивления элемента нетто (с учетом возможного ослаб-
ления).
Расчет на сжатие выполняют по условию
Л'с inax т Re Sf,p; (1 .7)
расчет на устойчивость при центральном сжатии — по условию
где iVc тих — максимальная расчетная сжимающая сила;
<р — коэффициент продольного изгиба;
/?(., — расчетное сопротивление на сжатие;
S г,р — площадь поперечного сечения элемента брутто (без учета воз-
можного ослабления).
При расчетах по методу допускаемых напряжений определяют
напряжение о в расчетном элементе и сравнивают его с допускаемым
(о|:
о •• |о| Опр/к-з. (1.9)
где аир — предельно допускаемое напряжение;
к'з — номинальный коэффициент запаса прочности.
В расчетах проводов и тросов в качестве о,|р принимают временное
сопротивление разрыву ст,,р, умноженное на поправочный коэффициент,
учитывающий возможное снижение (тп|| (для проводов контактных
подвесок и воздушных линий этот коэффициент можно принять рав-
ным 0,95). Выполняя расчеты всех проводов (кроме контактных и по-
перечных несущих тросов гибких поперечин), для медных, бронзовых,
сталемедных и алюминиевых принимают к-л 2; для контактных и
сталеалюминиевых проводов /с, 2,5, а для стальных тросов кл 3.
При расчетах поперечных несущих тросов для сталемедных проводов
принимают к.л $- 3, а для стальных тросов к., > 4. Рассчитывая сталь-
ные конструкции, в качестве о||(| принимают обычно предел текуче-
сти от, а коэффициент запаса к:, 1,5.
Выражение (1.5) можно представить в виде
/?"
п .V" т —— S,lr.
А'
Приняв /?р --- оцР. пК/т \ и выполнив соответствующие пре-
образования, это выражение можно привести к виду
л<аП1)/Л. (1-Ю)
Сравнивая условия (1.10) и (1.9), видим, что расчет по первому
предельному состоянию более полно раскрывает возможности работы
материала, чем расчет по допускаемым напряжениям; расчеты по вто-
10
рому, а для железобетонных конструкций и по третьему предельным
состояниям дают дополнительные гарантии надежной работы рассчи-
тываемой конструкции в эксплуатации.
При проектировании контактной сети в тех случаях, когда необ-
ходимые для расчетов по методу предельных состояний коэффициенты
Д', п, т и пс установлены соответствующими нормами, расчеты выпол-
няют по этому методу. Если же указанные коэффициенты еще не оп-
ределены, то расчеты производят по методу допускаемых напряжений,
используя номинальный коэффициент запаса прочности к3. Расчеты
типовых железобетонных опор, ригелей и всех конструкций для за-
крепления опор в грунте выполняют по методу предельных состояний,
а типовых металлических опор, консолей, кронштейнов и фиксато-
ров — по методу допускаемых напряжений. Последний используется
также при расчетах проводов и тросов.
В практике проектирования контактной сети многие конструкции
не рассчитывают, а лишь подбирают типовые, «привязывая» их к ме-
стам конкретной установки (см. гл. 8).
§ 1.3. Учет климатических условий
Расчетные климатические условия. Эти условия принимают на
основании соответствующих нормативных документов и долголетних
наблюдений метеорологических станций, расположенных в непосред-
ственной близости от железной дороги, для которой выполняется про-
ектирование контактной сети и воздушных линий. Желательно эти
данные получить не только от железнодорожных метеорологических
станций, но и от станций других организаций. Следует учесть опыт
эксплуатации существующих в данном районе линий электропереда-
чи и связи, а также наблюдения местных работников и жителей. Все
полученные значения нужно учитывать только в тех случаях, когда
они превышают указанные в нормативных документах.
Поскольку воздействия климатических факторов носят случай-
ный характер, то для определения их пределов и обусловленных ими
нагрузок применяют вероятностно-статистические методы. В норма-
тивных документах приводится повторяемость различных климатиче-
ских воздействий не реже одного раза в определенное число лет, ко-
торая должна учитываться в расчетах по определению нормативных
нагрузок.
Основными нормативными документами для установления расчет-
ных экстремальных температур воздуха, интенсивности гололедных
и снеговых образований, а также ветровых воздействий являются
СНиП 2.01.07-85 (Нагрузки и воздействия), СНиП 2.01.01—82
(Строительная климатология и геофизика), СНиП 11-23-81 (Стальные
конструкции), ГОСТ 16530—83 (Климат СССР. Районирование и ха-
рактеристики климатических параметров для промышленных изде-
лий), ВСН 141-84 (Нормы проектирования конструкций контакт-
ной сети), ВНТП-81 (Нормы технологического проектирования элек-
трификации железных дорог), а также другие нормативные докумен-
ты, ведомственные инструкции и технические условия. Поскольку в
расчетах контактной сети принимают повторяемость не реже одного
раза в 10 лет, далее приводятся данные только для этого значения.
Наиболее неблагоприятные условия работы отдельных конструк-
ций контактной сети могут возникнуть при различных сочетаниях
климатических факторов во время монтажа и эксплуатации этих кон-
струкций. Указанные сочетания могут складываться из четырех основ-
ных компонентов: минимальной температуры воздуха, максимальной
температуры воздуха; максимальной интенсивности гололедных об-
разований на проводах и массы снега на поддерживающих устройст-
вах; максимальной скорости ветра. Однако принятие в качестве рас-
четных самых неблагоприятных сочетаний (например, наличие голо-
ледных образований при минимальной температуре воздуха в усло-
виях эксплуатации или максимальной скорости ветра при монтаже)
приведет к неопределенному усложнению и удорожанию конструк-
ций. Поэтому на основании многолетнего опыта эксплуатации кон-
тактной сети в качестве расчетных приняты следующие режимы:
минимальной температуры без учета дополнительных нагрузок
от гололеда и ветра;
максимальной температуры при отсутствии ветровых нагрузок;
максимальной интенсивности гололедных образований с одновре-
менным воздействием ветра;
максимальной скорости ветра без гололедных образований.
Нагрузки от гололедных образований. Для расчетов этих нагру-
зок сначала устанавливают гололедный район, к которому относится
местность, где находится проектируемое устройство. По интенсивно-
сти гололедных отложений территория СССР разделена па пять райо-
нов, границы которых указаны на карте № 4 приложения 5 к СНиП
2.01.07-85. Толщина стенки льда в различных гололедных районах:
Гололедный район ............I 11 III IV V
Толщина стеики льда, мм .... 5 10 15 20 25
Условно считают, что гололедные отложения имеют цилиндриче-
скую форму и плотность, равную 900 кг/м3. Значения толщины стенки
льда приведены для проводов диаметром 10 мм, расположенных на
высоте 10 м над поверхностью земли. В других условиях расчетную
толщину стенки льда следует определять, умножая эти значения на
поправочные коэффициенты, приведенные в СНиПе: при диаметрах
провода 5, 20 и 30 мм — соответственно на 1,1; 0,9 и 0,8; при высотах
от поверхности земли 5, 20, 30 и 50 м — соответственно на 0,8; 1,2:
1,4 и 1,6.
Применительно к конкретным условиям для учета высоты распо-
ложения проводов ВСН 141-84 рекомендуют следующие поправочные
коэффициенты при расположении проводов:
12
на насыпях —
Высота насыпи, м . . 5 10
Поправочный коэф-
фициент . .. 1,10 1,30
15 20 25 30 и более
1,35 1,45 1,55 1,60
в выемках глубиной 5 и 7 м (и более) — соответственно 0,75 и 0,60;
в незащищенной от ветра, открытой и ровной местности- - 1,1;
в лесах или среди зданий при высоте деревьев или построек, боль-
шей, чем высота подвеса проводов, — 0,8.
Для промежуточных значений диаметров и высот расположения
проводов поправочные коэффициенты могут определяться методом ли-
нейной интерполяции.
Нагрузки от воздействий ветра. При расчетах этих нагрузок преж-
де всего определяют, к какому ветровому району относится местность,
в которой находится проектируемое устройство. Вся территория СССР
разделена на восемь районов, различающихся нормативными ветро-
выми давлениями или по терминологии установленной СН 528-80, рас-
пределенными поверхностными нагрузками (в ВСН 141-84 применяет-
ся еще термин «скоростной напор»). Границы этих ветровых районов
указаны на карте №3 приложения 5 к СНиП 2.01.07-85.
Необходимые для расчетов значения нормативных величии приве-
дены в табл. 1.1 (для ветрового района 1а ориентировочные).
При учете динамического воздействия ветра нормативную распре-
деленную поверхностную нагрузку В (Па) для определения статиче-
ской составляющей ветровой нагрузки на провода и конструкции
контактной сети (см. §2.2 и 2.3) находят по следующей формуле:
Д Во (0,2381п z/z0)2 fi0, (1.11)
где - нормативная распределенная поверхностная нагрузка, Па, опре-
деляемая по табл. 1.1;
Кд - коэффициент, учитывающий изменения этой нагрузки в зависимо-
сти от местных условий;
z — высота, на которой определяется скорость ветра, м;
г„ - параметр шероховатости поверхности, над которой определяется
скорость ветра, м.
Таблица 11
Нормативные величины Значения нормативных величин в ветровых районах
III I II III IV V VI VII
Распределенная поверхностная на- грузка Ви, Па 250 310 400 <510 ьзо 800 1000 (970) 1250 (1140)
Скорость ветра, м/с 19 22 25 29 42 36 40 (39) 45 (43)
П р и меч а н и е. принимать при расчетах В ско( провод 5ках да ов конт< пы значения и жтиой сети. ормативных ве; ичин. которые нужно
13
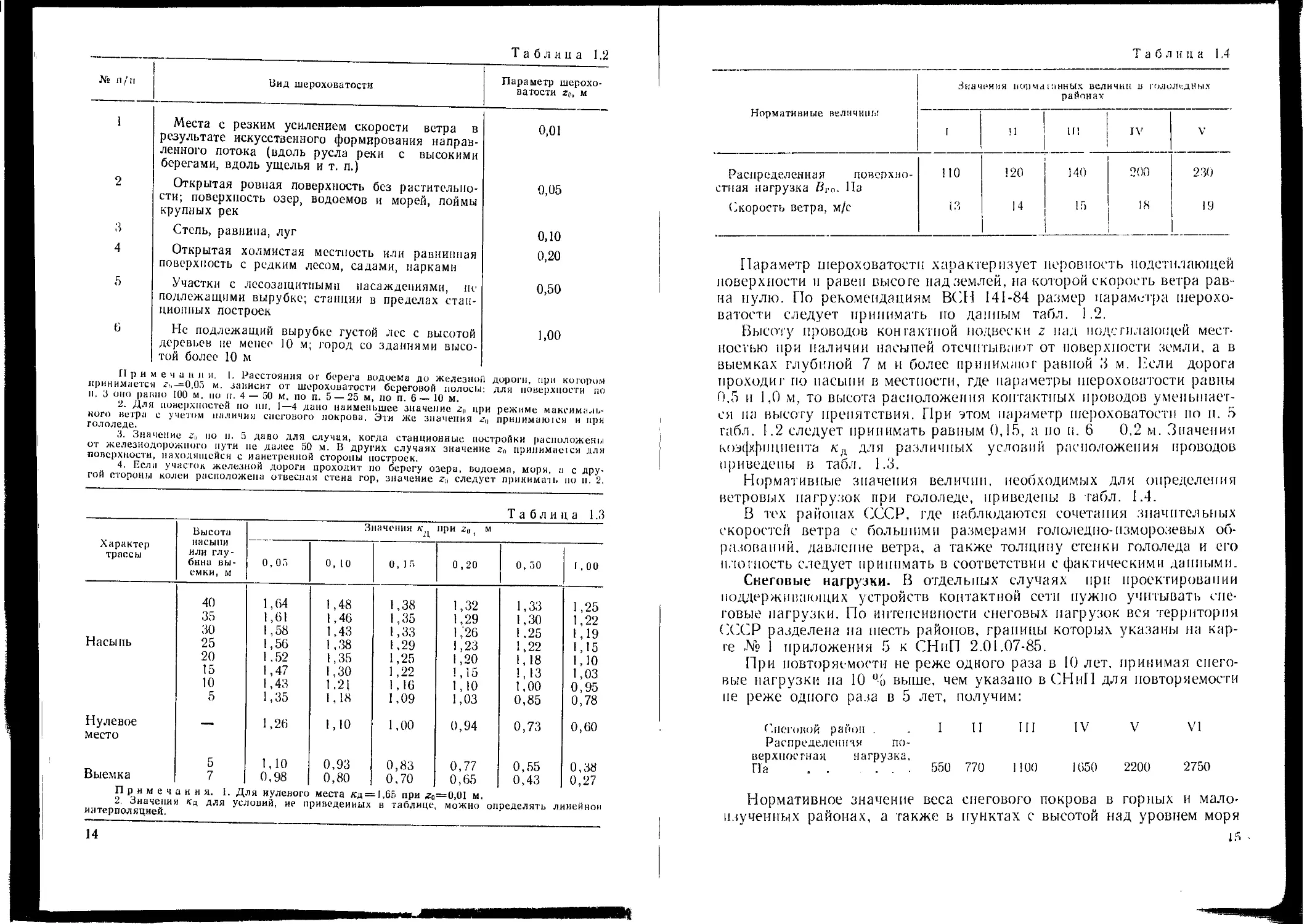
Таблица 1.2
№ п/п Вид шероховатости Параметр шерохо- ватости го, м
1 Места с резким усилением скорости ветра в результате искусственного формирования направ- ленного потока (вдоль русла реки с высокими берегами, вдоль ущелья и т. л.) 0,01
2 Открытая ровная поверхность без растительно- сти; поверхность озер, водоемов и морей, поймы крупных рек 0,05
3 Степь, равнина, луг 0,10
4 Открытая холмистая местность или равнинная поверхность с редким лесом, садами, парками 0,20
5 Участки с лесозащитными насаждениями, не подлежащими вырубке; станции в пределах стан- ционных построек 0,50
6 Не подлежащий вырубке густой лес с высотой деревьев не менее 10 м; город со зданиями высо- той более 10 м 1,00
Примечания. 1. Расстояния ог берега водоема до железной дороги, при котором
принимается z(1—0,05 м, зависит от шероховатости береговой полосы: для поверхности по
и. 3 оно равно 100 м, по и. 4 — 50 м. по п. 5 — 25 м, по п. 6—10 м.
2. Для поверхностей по пн. 1—4 дано наименьшее значение z(l при режиме максималь-
кого ветра с учетом наличия снегового покрова. Эли же значения г0 принимание» и пря
гололеде.
3. Значение z(l по и. 5 дано для случая, когда станционные постройки расположены
от железнодорожного пути не далее 50 м. В других случаях значение принимался для
поверхности, находящейся с иаиетренвой стороны построек.
4. Если участок железной дороги проходит по берегу озера, водоема, моря, а с дру-
гой стороны колеи расположена отвесная стена гор, значение г() следует принимай* по п. 2.
Таблица 1.3
Характер трассы Высота насыпи или глу- бина вы- емки, м Значения к При Z(J, М
0,05 0, 10 0, 1 г> 0,20 0, 50 I , 00
40 1,64 1,48 1,38 1,32 1,33 1,25
35 1,61 1,46 1,35 1,29 1,30 1,22
30 1,58 1,43 1,33 1,26 1 ,25 1,19
Насыпь 25 1,56 1,38 1,29 1,23 1,22 1,15
20 1.52 1,35 1,25 1,20 1,18 1,10
15 1,47 1,30 1,22 1,15 1,13 1,03
10 1,43 1,21 1,16 1,10 1,00 0,95
5 1,35 1,18 1,09 1,03 0,85 0,78
Нулевое —. 1,26 1,10 1,00 0,94 0,73 0,60
место 5 1,10 0,93 0,83 0,77 0,55 0,38
Выемка 7 0,98 0,80 0,70 0,65 0,43 0,27
Примечания. 1. Для нулевого места кд=-1,65 при Zo=0,01 м,
2. Значения кд для условий, ие приведенных в таблице, можно определять линейной
интерполяцией.
14
Таблица 1.4
Нормативные величины Значения порча пшных величин в гололедных районах
1 п 11! IV V
Распределенная поверхно- стная нагрузка Дгп. Па но 120 140 200 230
Скорость ветра, м/с 13 14 15 IS 19
Параметр шероховатости характеризует неровность подстилающей
поверхности и равен высоте над землей, на которой скорость ветра рав-
на нулю. По рекомендациям ВСН 141-84 размер параметра шерохо-
ватости следует принимать по данным табл. 1.2.
Высоту проводов контактной подвески z над подстилающей мест-
ностью при наличии насыпей отсчитывают от поверхности земли, а в
выемках глубиной 7 м и более принимают равной 3 м. Если дорога
проходит по насыпи в местности, где параметры шероховатости равны
0,5 и 1,0 м, то высота расположения контактных проводов уменьшает-
ся на высоту препятствия. При этом параметр шероховатости по п. 5
табл. 1.2 следует принимать равным 0,15, а но и. 6 0,2 м. Значения
коэффициента кд для различных условий расположения проводов
приведены в табл. 1.3.
Нормативные значения величин, необходимых для определения
ветровых нагрузок при гололеде, приведены в табл. 1.4.
В тех районах СССР, где наблюдаются сочетания значительных
скоростей ветра с большими размерами гололедно-изморозевых об-
разований, давление ветра, а также толщину стенки гололеда и его
Илогпость следует принимать в соответствии с фактическими данными.
Снеговые нагрузки. В отдельных случаях при проектировании
поддерживающих устройств контактной сети нужно учитывать сне-
говые нагрузки. По интенсивности снеговых нагрузок вся территория
СССР разделена на шесть районов, границы которых указаны на кар-
ге № 1 приложения 5 к СНиП 2.01.07-85.
При повторяемости не реже одного раза в 10 лет, принимая снего-
вые нагрузки па 10 % выше, чем указано в СНиП для повторяемости
не реже одного раза в 5 лет, получим:
('.иеговой район . . I II III IV V VI
Распределенная по-
верхностная нагрузка.
Па .............. 550 770 1100 1650 2200 2750
Нормативное значение веса снегового покрова в горных и мало-
изученных районах, а также в пунктах с высотой над уровнем моря
15
более 1500 м и в местах со сложным рельефом местности, следует уста-
навливать по дополнительным данным.
Расчетные температуры воздуха. Учет всех приведенных выше
климатических факторов при расчетах контактной сети и воздушных
линий производится при определенных значениях температуры возду-
ха — экстремальных для данного района, а также имеющих место при
гололедах и ветре максимальной интенсивности.
Нормативное значение минимальной температуры воздуха, °C,
определяют по формуле
-G-Аг-б,
(1.12)
где многолетняя среднемесячная температура в январе, принимаемая
по данным СНиП 2.01.01—82 и карте №5 приложения 5 к СНиП
2.01.07............85;
Л( — отклонение средней температуры наиболее холодных суток от Z,,
принимаемое поданным карты № 7 приложения 5 к СНиП
2.01.07- 85.
При наличии многолетних (не менее 20 лет) данных местных ме-
теорологических станций нормативное значение минимальной темпе-
ратуры
0,5 Пср-Нпщ), (1.13)
| ле /Д средняя температура наиболее холодных суток;
/|Н1П абсолютная минимальная температура воздуха.
Расчетное значение минимальной температуры воздуха может
быть принято равным абсолютной минимальной температуре. Норма-
тивное и расчетное значения максимальной температуры воздуха при-
нимают равным сумме значения абсолютной максимальной температу-
ры и добавки, вносимой нагревом проводов солнечной радиацией:
0,0162Ч,П1Ях,
(1-14)
где q>mnx максимальное значение, суммарной (прямой и рассеянной) солнеч-
ной радиации, Вт/м2, принимаемое по данным СНиП 2.01.01-82.
Для районов, расположенных между 46 и 56й с. ш., значение tv
может быть принято равным 14 °C.
Температуру воздуха при расчетах с учетом гололедных образова-
ний принимают равной: —15 °C в горных районах с отметкой выше
2000 м; - 10 °C в горных районах с отметкой от 1000 до 2000 м; - 5 °C
для всей остальной территории СССР (при высоте сооружения до
100 м).
При отсутствии достоверных метеорологических наблюдений нор-
мативную температуру воздуха во время максимальных ветровых воз-
действий в соответствии с рекомендацией ВСН 141-84 следует прини-
мать равной —5 °C.
16
Пример. Задание и исходные данные. Определить нор-
мативные и расчетные значения экстремальных температур воздуха для проек-
тирования контактной сети при электрификации участка Псков — Великие Лу-
ки.
Решение. Нормативные значения минимальных температур определим
по формуле (1.12). Среднемесячная температура января по СНиП 2.01.01-82
для Пскова равна — 7,5 °C и для Великих Лук — 8,2 °C. Отклонение темпера-
туры наиболее холодных суток от среднемесячной январской по карте № 7 при-
ложения 5 к СНиП 2.01.07-85 в районе рассматриваемого участка составляет
20 Г’С. Следовательно:
для Пскова *”..п — —7,5—20—6 - —33.5 С;
для Великих Лук “ —Я,2 — 20—6 —.34,2 "С.
Расчетное значение минимальной температуры принимается ранным ее аб-
солютному значению, которое по СНиП 2.01.01-82 составляет —41 С для Пско-
ва и —46 °C для Великих Лук
Абсолютные значения максимальных температур по этому же СНиПу рав-
ны для Пскова 36 °C и для Великих Лук 35 'С. Эквивалентные увеличения мак-
симальных температур в результате нагрева солнечной радиацией найдем по фор-
муле (1.14). Псков находится примерно на 58° с. ш., а Великие Луки на 56°.
Для этих мест максимальные значения суммы значений прямой и рассеянной сол-
нечной радиации по СНиП 2.01.01-82 равны соответственно 796 и 817 Вт м'-.
Следовательно-
для Пскова /р 0,0162-796 12,9 °C;
для Великих Лук /р 0,0162-817 13,2 С.
Суммируя полученные значения tv с абсолютными получим для Пскова мак-
симальную температуру равной 48,9 °C, а для Великих Лук 48,2 ‘С.
Округляя полученные результаты до 5е принимаем для всего электрифици-
руемого участка: -35 ПС нормативное значение минимальной температуры и
45 °C расчетное; ! 50 'С нормативное и расчетное значения максимальной
температуры.
§ 1.4. Основные данные для расчетов
Расчетные данные проводов, тросов и проволок, а также их фи-
зико-механические характеристики принимают по соответствующим
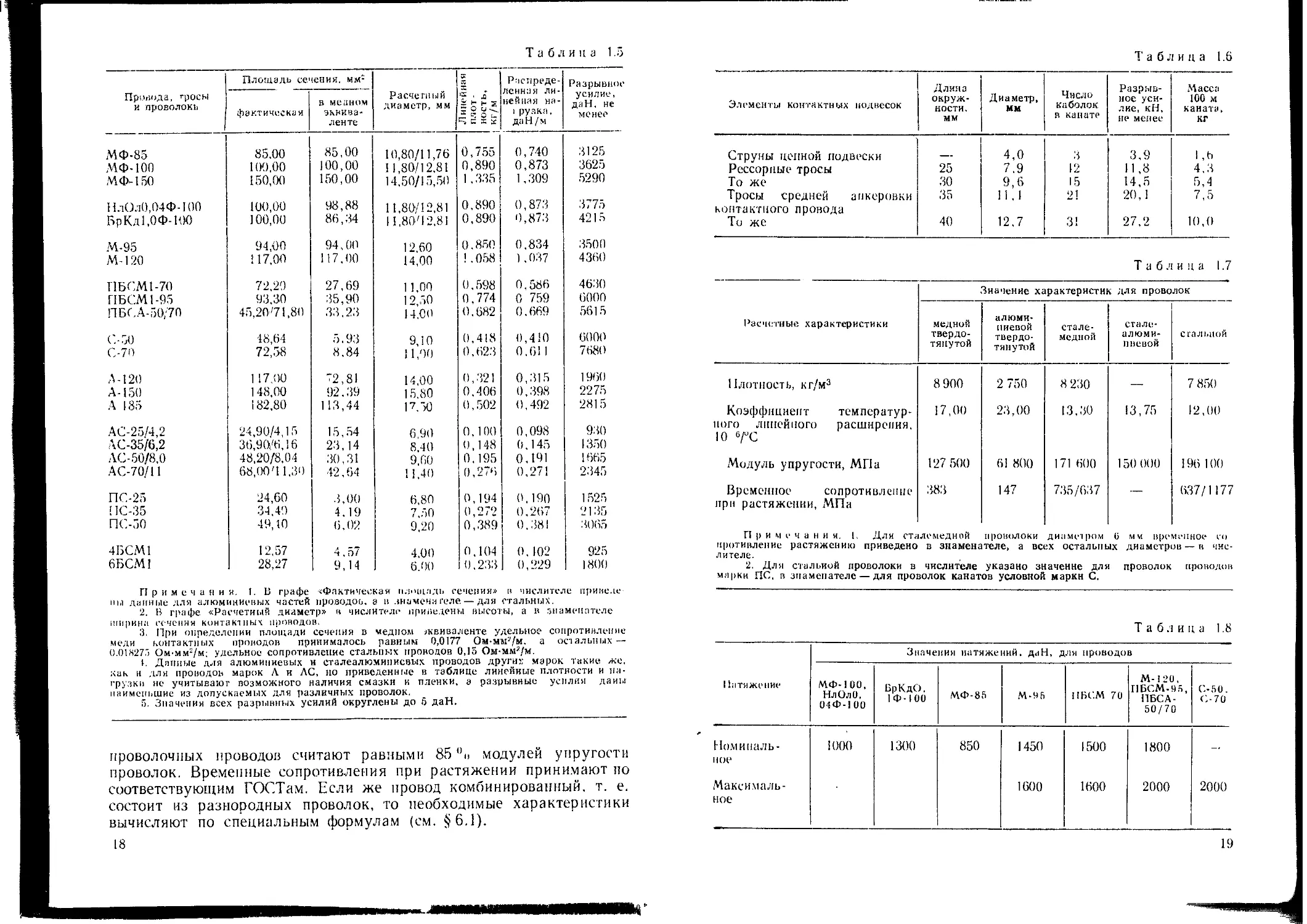
ГОСТам или техническим условиям. Для примера в табл. 1.5 приведе-
ны данные для изделий, применяемых в устройствах контактной сети
и воздушных линий.
В устройствах контактной сети все шире применяют различные
полимерные материалы. Для примера в табл. 1.6 приведены характе-
ристики капроновых канатов, используемых в контактных подвесках.
Некоторые физико-механические характеристики отдельных про-
волок, из которых изготовляют многопроволочные провода, в раз-
ных документах немного различаются, а для биметаллической сталеа-
люминиевой проволоки вообще отсутствуют. В табл. 1.7 приведены
значения, которые обычно учитывают при проектировании контактной
сети и воздушных линий.
При расчетах многопроволочных проводов, состоящих из однород-
ных проволок, физико-механические характеристики, кроме времен-
ного сопротивления при растяжении, принимают те же, что указаны
в табл. 1.7 для отдельных проволок. Иногда модули упругости много-
.• 17'
Таблица 1.5
Провода, гросы и проволоки Площадь сечения, мм- Расчетный диаметр, мм Ли нейная плот- ность, ! кг/м Распреде- ленная ли- нейная на- । рузка, даН/м Разрывши усилие, даН, не менее
фактическая в мепно.м эквива- ленте
МФ-85 85.00 85,00 10,80/11,76 0,755 0,740 3125
МФ-100 100,00 100,00 11,80/12,81 0,890 0,873 3625
МФ-150 150,00 150,00 14,50/15,50 1, .3.35 1,309 5290
НлОл(),04Ф-100 100,00 98,88 11,80/12,81 0,890 0,87.3 3775
БрКд1,ОФ-100 100,00 86,34 11,80'12,81 0,890 0,873 4215
М-95 94,00 94,00 12.60 0.850 0,834 3500
М-120 117,00 117,00 14,00 1 .058 ), 037 4360
Г1БСМ1-70 72,20 27,69 11,00 0.598 0.586 4630
ПБСМ1-95 93,80 35,90 12,50 0,774 0 759 6000
ПБСА-50/70 45,20'71,80 .33.23 14.00 0.682 0.669 5615
('.•50 48,64 5.93 9,10 0,418 0,410 6000
С-70 72,58 8.84 11,90 0,623 0.61 1 7680
Л-120 1 17,00 72,81 14.00 0,321 0,315 1960
А-150 148,00 92.39 15.80 0,406 0,398 2275
А 185 182,80 113,44 1Т50 0,502 0,492 2815
АС-25/4,2 24,90/4,15 15,54 6,90 0,100 0,098 930
АС-35/6,2 36,901'6,16 23,14 8,40 0,148 0,145 1350
ЛС-50/8,0 48,20/8,04 30,31 9,60 0.195 0.191 1665
АС-70/11 68,00'11,30 42,64 11.40 0,276 0,271 2345
ПС-25 24,60 3,00 6.80 0,194 0.190 1525
! 1С-.35 .34.49 4. 19 7.50 (1,2'72 0.267 21.35
ПС-50 49,10 6,02 9.20 0,389 0,381 3065
4БСМ1 12,57 4.57 4.00 0,104 0, 102 925
6БСМ1 28,27 9,14 6.00 0.233 0,229 1800
П р и м е ч а я и я. 1. В графе '•«Фактическая площадь с учения» в числителе п р и в е д е -
ны данные для алюминиевых частей проводощ а в знамена геле. — для стальных.
2. В графе «Расчетный диаметр» в числителе приведены высоты, а в знаменателе
ширина сечения контактных проводов.
3. При определении площади сечения в медном эквиваленте удельное сопротивление
мели контактных проводов принималось равным 0,0177 Ом«мм?/м, а остальных--
0.018275 Ом«мм2/м; удельное сопротивление стальных проводов 0,15 Ом-мм*/м.
I. Данные для алюминиевых и сталеалюмннисвых проводов других марок такие же,
как и для проводов марок Л и АС, но приведенные в таблице линейные плотности и на-
грузки не учитывают возможного наличия смазки и пленки, а разрывные усилия даиы
наименьшие из допускаемых для различных проволок.
б. Значения всех разрывных усилий округлены до 5 даН.
проволочных проводов считают равными 85 "о модулей упругости
проволок. Временные сопротивления при растяжении принимают по
соответствующим ГОСТам. Если же провод комбинированный, т. е.
состоит из разнородных проволок, то необходимые характеристики
вычисляют по специальным формулам (см. §6.1).
18
Т аблица 1.6
Элементы контактных подвесок Длина окруж- ности, мм Диаметр, мм Число каболок в канате Разрыв- ное уси- лие, кН, не менее Масса 100 м каната, кг
Струны цепной подвески 4,0 3 3,9 1 ,ь
Рессорные тросы 25 7.9 12 11 ,8 4.3
Го же 30 9,6 15 14,5 5,4
Тросы средней анкеровки .35 11,1 2! 20,1 7,5
контактного провода То же 40 12,7 31 27,2 10,0
Таблиц а 1.7
Расчетные характеристики Значение характеристик для проволок
медной твердо- тянутой алюми- ниевой твердо- тянутой стале- медной стало- алюми- ниевой стальной
Плотность, кг/м3 8 900 2 750 8 230 — 7 850
Коэффициент температур- ного линейного расширения. 10 6/°С 17,00 23,00 13,30 13,75 12,00
Модуль упругости, МПа 127 500 61 «00 171 600 150 000 196 100
Временное сопротивление при растяжении, МПа 383 147 735/637 — 637/1177
Примечания, I, Для сталемедной проволоки диаметром б
противление растяжению приведено в знаменателе» а всех остальных
л и теле.
мм временное со
диаметров — в чис-
2. Для стальной проволоки в числителе указано значение для проволок проводов
марки ПС, в знаменателе — для проволок канатов условной марки С.
Таблица 1.8
1 Ьтяжение Значения натяжений. даН, для проводов
МФ-100, НлОлО, 04Ф-100 БрКдО. 1Ф-100 МФ-85 М-95 НБС.М 70 М-120, ПБСМ-9,5, ПБСА- 50/70 С-50. С-70
Нсшиналь- юе 1000 1300 850 1450 1500 1800 -
Максималь- ное 1600 1600 2000 2000
19
Для всех контактных проводов (медных, низколегированных и
бронзовых) физико-механические характеристики, кроме временного
сопротивления, учитывают аналогично указанным в табл.1.7 для мед-
ной проволоки. Временные сопротивления при растяжении контакт-
ных проводов принимают в соответствии с ГОСТ 2584—86.
В табл. 1.8 представлены обычно принимаемые в расчетах макси-
мальные и номинальные натяжения некоторых проводов и тросов.
Натяжения большие, чем 2000 даН, в таблице не приводятся, так как
указанное значение является предельным для отдельных деталей кон-
тактной сети и превышать его не разрешается.
В практических расчетах проводов и тросов часто возникает не-
обходимость вычислять произведения 24а и aES, а также обратные
им величины (а — коэффициент температурного линейного расши-
рения материала провода или троса; Е - модуль упругости; S —
фактическая площадь сечения). В целях облегчения расчетов значе-
ния указанных величин для некоторых проводов, тросов и проволок
приведены в табл. 1.9.
Таблица 19
Провода, тросы и проволок» 24а. 1 0—• 1 /°C 1/(24а), “С даН/°C l/(a/-.S') “С/да11
МФ-85 18,42 0,0543
МФ-100 21,68 0,0461
МФ-150 408 2451 32,51 0,0308
М-95 20,37 0,0491
М-120 25,36 0,0394
Г1БСМ-70 16,48 0,0607
ПБСМ-95 319 3135 21,29 0,0470
4БСМ 2,87 0,3484
6БСМ 6,45 0,1550
ПБСА-50/70 330 3030 24,13 0,0414
С-50 11,45 0,0874
С-70 17,08 0,0585
ПС-25 288 3472 5,79 0,1727
ПС-35 8,10 0,1235
ПС-50 11,62 0,0860
А-120 16,63 0,0601
А-150 552 1812 21,04 0,0475
А-185 25,98 0,0385
АС-2 5/4,2 4,52 0,2213
АС-35/6,2 461 2169 6.70 0,1493
АС-50/8,0 8,75 0,1143
АС-70/11 12,33 0,0811
Примечания. 1. Для проводов марки АС приняты следующие расчетные зна-
чения: а = 19,2-10-* I/"; ООО МПа.
2. Данные для низколегированных и бронзовых контактных проводов такие же, как
и для медных одинаковой площади сечения.
20
«ааамммм
Для изготовления стальных конструкций контактной сети и воз-
душных линий обычно используют листовую и фасонную прокатные
углеродистые стали марок 18сп (спокойную), 18 пс (полуспокойную)
и 18 кп (кипящую), а также ВСтЗспб, ВСтЗпсб и ВСтЗкп2, выпускаемые
по ТУ 14-1-3023-80 и ГОСТ 380-88*.
В марках сталей, изготовляемых по упомянутым ТУ, через дефис
указывают группу прочное™ (1 или 2). Для конструкций контактной
сети рекомендуется использовать стали 1-й i руины прочности. В рай-
онах с расчетными температурами ниже —40 °C (но не ниже -.65 °C)
применяют низколегированные стали марок 09Г2, 09Г2С, 15ХСНД
и др., выпускаемые по ТУ 14-1-3023-80, а также по ГОСТ 19281—89.
Расчетную температуру принимают по СНиП 2.01.01-82 как среднюю
для наиболее холодной пятидневки. Кроме того, применяют также
полосовую и круглую стали по ГОСТ 535—88.
Использование той или иной марки стали применительно к различ-
ным конструкциям контактной сети и воздушных линий подробно
указано в ВСН 141-84. В более ответственных конструкциях, как пра-
вило, применяют спокойную и полуспокойную стали, а в менее от-
ветственных -- полуспокойную и кипящую. В соответствии со СНиП
11-23-81 применение углеродистой стали по ГОСТ 380- 88* и низ-
колегированных сталей марок 09Г2 и 09Г2С. допускается только
в том случае, если невозможно получить изделия в соответствии с
ТУ 14-1-3023-80.
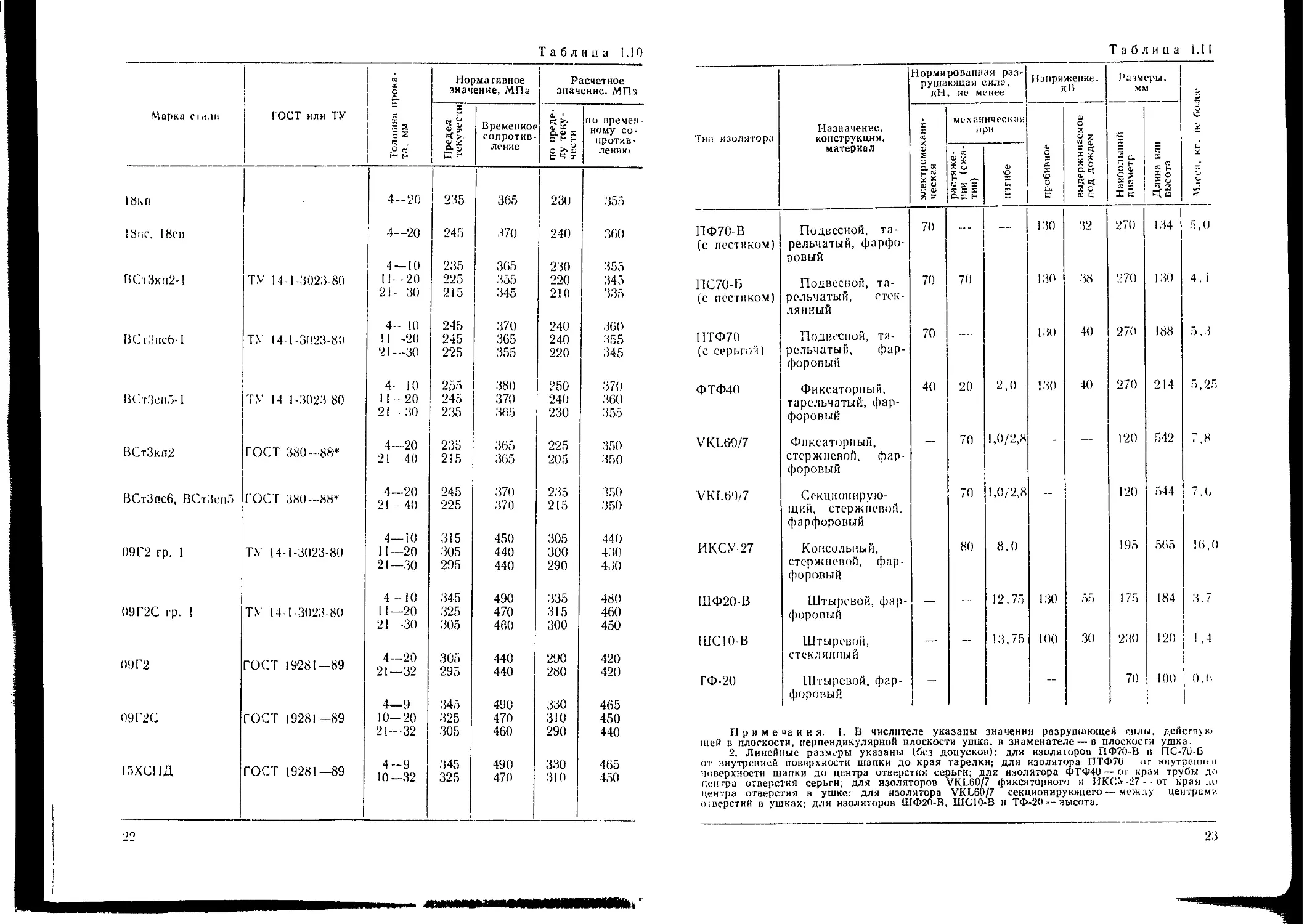
Для примера в табл. 1.10 приведены нормативные и расчетные со-
противления фасонного проката, наиболее часто используемого в кон-
струкциях контактной сети и воздушных линий. За толщину проката,
указанную в этой таблице, для изделий с полками следует принимать
толщину полки. Модуль упругости прокатной стали принимают рав-
ным 206 ГПа, модуль сдвига - 78 ГПа, а плотность и коэффициент
температурного линейного расширения те же, что указаны в табл.
1.7 для стальной проволоки.
В устройствах контактной сети и воздушных линий широко исполь-
зуют различные изоляторы. Некоторые данные для наиболее часто
применяемых изоляторов приведены в табл. 1.11.
Для подвешивания несущих тросов, питающих и усиливающих
проводов обычно применяют гирлянды из двух изоляторов ПФ70-В
на участках постоянного тока и не менее трех изоляторов ПС70-Б
на участках переменного тока. В условиях повышенного загрязнения
при переменном токе в гирлянды включают четыре (иногда пять) изо-
лятора. При подвеске на изолированных гибких поперечинах постоян-
ного тока допускается применение одного изолятора Г1Ф70-В или
Г1ТФ70.
Отсасывающие провода, тросы группового заземления и провода
обратного тока (на участках переменного тока с отсасывающими транс-
форматорами) подвешивают на одном изоляторе с пестиком или серь-
гой .
21
Таблица 1.10
Марка ci ал и ГОСТ или ТУ Толщина прока- та , мм Нормативное значение, МПа Расчетное значение. МПа
Предел текучести Временное сопротив- ление по преде- лу теку- чести но времен- ному со- против- лению
1 &КП 4-20 235 365 230 355
18пс, 18сп 4—20 245 370 240 360
4 — 10 235 365 230 355
ПС', Зкп2-1 ТУ 14-1-3023-80 11- -20 225 355 220 345
21- 30 215 345 210 335
4 - 10 245 370 240 360
11(2 гЗпсб-1 ТУ 14-1-3023-80 И -20 245 365 240 355
21--30 225 За5 220 345
4- 10 255 380 250 370
ВСтЗсп5-1 ТУ 14 1-3023 80 11-20 245 370 240 360
21 30 235 365 230 355
ВСтЗкп2 ГОСТ 380-88* 4--20 21 -40 235 215 365 365 225 205 350 350
ВСтЗпсб, ВСтЗсиб ГОСТ 380—88* 4—20 21 - 40 245 225 370 370 235 215 350 350
4—10 315 450 305 440
09Г2 гр. 1 ТУ 14-1-3023-80 11—20 305 440 300 430
21—30 295 440 290 430
4 - 10 345 490 335 480
09Г2С гр. 1 ТУ 14-1-3023-80 11—20 325 470 315 460
21 -30 305 460 300 450
09 Г2 ГОСТ 19281—89 4—20 21—32 305 295 440 440 290 280 420 420
4—9 345 490 330 465
09Г2С ГОСТ 19281-89 10-20 325 470 310 450
21 — 32 305 460 290 440
15ХС11Д ГОСТ 19281—89 4-9 10—32 345 325 490 470 330 310 465 450
тпмага ЛММММ
шшшшь'
Таблица 1.11
Гии изолятора Назначение, конструкция, материал Нормированная раз- рушающая сила, кН, ие менее Напряжение, кВ Размеры, мм ! | Масса, кг. не более
электромехани- ческая механическая при пробивное выдерживаемое под дождем Наибольший диаметр S S « £ = о ® С-1 d к
растяже- нии (сжа- тии) 1 изгибе
ПФ70-В (с пестиком) Подвесной, та- рельчатый, фарфо- ровый 70 -- 130 32 270 134 5,0
ПС70-Б (с пестиком) Подвесной, та- рельчатый, стек- лянный 70 70 130 38 270 130 4.1
ПТФ70 (с серьгой) Подвесной, та- рельчатый, фар- форовый 70 — 130 40 270 188 5,3
ФТФ40 Фиксаторный, тарельчатый, фар- форовый 40 20 2,0 130 40 270 214 5,25
VKL60/7 Фиксаторный, стержневой, фар- форовый — 70 1,0/2,8 - — 120 542 7.8
VKI.6O/7 Секционирую- щий, стержневой, фарфоровый 70 ! ,0/2,8 120 544 7.(,
ИКСУ-27 Консольный, стержневой, фар- форовый 80 8.0 195 505 !(>,(
ШФ20-В Штыревой, фар- форовый — 12,75 130 55 175 184 3.7
ШС10-В Штыревой, стеклянный — - 13.75 100 30 230 120 1 ,4
ГФ-20 Штыревой, фар- форовый - - 70 100 о.о
Примечания. I. В числителе указаны значения разрушающей силы, действую
щей и плоскости, перпендикулярной плоскости ушка, в знаменателе — в плоскости ушка.
2. Линейные размеры указаны (без допусков): для изоляюров ПФ70-В и ПС-70-Б
от внутренней поверхности шапки до края тарелки; для изолятора ПТФ70 от внутреши н
поверхности шапки до центра отверстия серьги; для изолятора ФТФ40 — or края трубы до
центра отверстия серьги; для изоляторов VKL60/7 фиксаторного и ИКСА-27--от края .го
центра отверстия в ушке: для изолятора VKL60/7 секционирующего — между центрами
о;верстий в ушках; для изоляторов ШФ20-В, ШС10-В и ТФ-20--высота.
23
В анкеруемые ветви проводов контактных подвесок, питающих
и усиливающих проводов включают гирлянды, в которых на один изо-
лятор больше, чем в подвесных. Обычно такие гирлянды состоят из
одного изолятора 11ТФ70 и двух ПФ70-В на участках постоянного то-
ка и из четырех ПС70-Б при переменном токе. Начато применение раз-
личных полимерных изоляторов (например, со стеклопластиковыми
стержнями и ребрами из кремнийорганического эластомера), выпус-
каемых пока опытными партиями. В анкеруемых ветвях отсасываю-
щих линий и проводов обратного тока используют одни из упомянутых
выше — фарфоровый или стеклянный изолятор.
В кронштейнах изолированных консолей устанавливают изолятор
ИКСУ-27, а в тягах и подкосах VKL60/7 (фиксаторный).
В прямых и обратных сочлененных фиксаторах постоянного тока
обычно применяют два соединенных последовательно изолятора
ФТФ40, а при переменном токе- один VKL60/7 (фиксаторный).
Для усиленных фиксаторов постоянного тока, а также для фиксато-
ров проводов, отводимых на анкеровку, используют консольные изо-
ляторы ИКСУ-27. В тросы гибких фиксаторов включают гирлянды
из одного изолятора ПТФ70 и одного ПФ70-В (при постоянном токе)
и из трех 11С70-Б (при переменном токе). Применяют также и полимер-
ные изоляторы.
В фиксирующие тросы гибких, жестких и фиксирующих попере-
чин для обеспечения поперечного секционирования контактных под-
весок включают два соединенных последовательно изолятора 11Ф70-В
и ПТФ70 на участках постоянного тока и один VKL60. 7 (секционирую-
щий) па участках переменного тока.
Провода линий ДПР подвешивают аналогично приведенному выше
для несущих тросов на участках переменного тока, а провода ВЛ
6 10 кВ па участках постоянного тока крепят па штыревых изолято-
рах ШФ20-В или ШС10-В. Провода напряжением до 1000 В и волно-
водные закрепляют па штыревых изоляторах ТФ-20.
Глава 2
РАСЧЕТЫ НАГРУЗОК, ДЕЙСТВУЮЩИХ НА УСТРОЙСТВА
КОНТАКТНОЙ СЕТИ И ВОЗДУШНЫХ ЛИНИЙ
§ 2.1. Виды нагрузок и их сочетания
В соответствии со СНиП 2.01.07-85 все нагрузки разделяют на
постоянные, действующие всегда, и временные, которые в отдельные
периоды сооружения и эксплуатации могут отсутствовать. Временные
нагрузки в свою очередь делят на длительные, кратковременные
и особые.
Применительно к условиям работы контактной сети и воздушных
линий к постоянным относят нагрузки от собственного веса всех
конструкций и проводов (с арматурой и изоляторами), а также от сил,
вызываемых натяжениями и изменениями направления проводов (не-
компенсированных - при среднегодовой температуре). Длительными
временными нагрузками являются, например, снеговые и температур-
ные, принимаемые с пониженными относительно нормативных зна-
чениями. В расчетах контактной сети такие нагрузки обычно не учи-
тывают. К кратковременным относят нагрузки, возникающие при
экстремальных температурах воздуха, воздействиях ветра, гололедных
и снеговых образованиях, при транспортировке и установке опор и
других конструкций, монтаже проводов контактной сети и воздуш-
ных линий. К особым относят нагрузки, появляющиеся при обрывах
проводов, сейсмических и взрывных воздействиях, в некоторых дру-
гих необычных условиях.
В практических расчетах обычно рассматривают несколько дейст-
вующих одновременно нагрузок в сочетаниях, оказывающих наибо-
лее неблагоприятное воздействие на проектируемые устройства. Раз-
личают основные сочетания постоянных и кратковременных нагрузок
и особые, при которых к указанным добавляется одна из особых
нагрузок.
При расчетах устройств контактной сети и воздушных линий в
основные сочетания включают следующие нагрузки:
от веса опор, поддерживающих и фиксирующих устройств;
от веса проводов с арматурой и изоляторами;
натяжения анкеруемых проводов;
усилия от изменения направления проводов в кривых пути;
то же при отводах проводов в сторону для анкеровки или других
целей;
то же вследствие зигзагов проводов на прямых участках пути;
от веса гололеда и снега па поддерживающих и фиксирующих уст-
ройствах;
25
от веса гололеда на проводах;
от давления ветра на опоры;
то же на провода;
нагрузки, возникающие при монтаже и эксплуатации контактной
сети (например, от веса электромонтера, поднимающегося на опору,
или усилие, передающееся на консоль при переводе раскатанного по-
низу несущего троса в рабочее положение, и др.).
В особые сочетания включают усилия, возникающие при обрыве
одного из проводов и оказывающие наиболее существенное влияние
на напряженное состояние рассчитываемого элемента конструкции,
а также возможные в этих условиях нагрузки основных сочетаний.
При этом вводят различные допущения, например учитывают гололед-
ные образования, но при отсутствии ветра, и др.
В расчетах на основные сочетания нагрузок, включающие одну
кратковременную нагрузку, коэффициент сочетаний щ. (см. §1.2)
принимают равным единице, а при двух кратковременных нагрузках
расчетные значения этих нагрузок (или соответствующих им усилий
в конструкциях) следует умножать на пг -- 0,9. В расчетах на осо-
бые сочетания для кратковременных нагрузок следует принимать
и,. ~ 0,8 (за исключением случаев, оговоренных в нормах на проек-
тирование для сейсмических районов). Такой же коэффициен! соче-
таний вводят в расчет при определении усилий от дополнительного
натяжения или изменения направления некомпенсированных прово-
дов, обусловленных температурными воздействиями при максимальном
ветре.
Далее (см. § 2.2 и 2.3) приводятся расчеты только нормативных
нагрузок. Для расчетов проводов контактных подвесок и различных
воздушных линий, гибких и фиксирующих поперечин, выполняемых
но методу допускаемых напряжений, другие на!рузкн и не требуются.
Что же касается нагрузок па опорные, поддерживающие и фиксирую-
щие устройства, то их расчетные значения получают, умножая норма-
тивные значения нагрузок на соответствующие коэффициенты надеж-
ности по нагрузке п (см. § 1.2).
В р а с ч е т а х и а прочность эти коэффициенты со-
гласно ВСН 141-84 составляют:
Для нагрузок от веса проводов с арматурой и изоляторами,
конструкций, от натяжений компенсированных проводов, пе-
редаваемых па устройства контактной сети . .1.1
То же, если уменьшение нагрузок от веса может ухудшить
условия работы конструкции........................(),()
Для нагрузок от гололеда на проводах контактной сечи и
воздушных линий в гололедных районах 1—III . . .1 .3
То же н гололедных районах IV и V.................1.4
» во всех гололедных районах для проводов, на кото-
рых предусмотрена плавка гололеда . . . . . . .1.0
Для нагрузок от гололеда на опорных, поддерживающих
и фиксирующих конструкциях но всех гололедных районах 1.3
Для ветровых нагрузок, передающихся с проводов, покры-
тых гололедом, на опорные, поддерживающие и фиксирующие
конструкции.......................................... 1,25
Для нагрузок от воздействия ветра иа провода в ветровых
районах 1—V............................................1,2
То же в ветровых районах VI и VII....................1,15
Для нагрузок от воздействия ветра на опорные, поддержи-
вающие и фиксирующие устройства в ветровых районах I—V 1,15
То же в ветровых районах VI и VII....................1,1
Для нагрузок, передающихся на конструкции контактной
сети при температурных воздействиях от некомпенсированных
несущих тросов.........................................1,1
То же от одиночных проводов воздушных линий . . 1.2
При расчетах по деформациям коэффициенты на-
дежности по нагрузке принимают равными:
Для нагрузок от гололеда на проводах в гололедных райо-
нах I -III.............................................0.5
То же в гололедных районах IV и V....................0,7
Для ветровых нагрузок, передающихся с проводов, покры-
тых гололедом, на опорные, поддерживающие и фиксирующие
конструкции .... ..................0.8
Для ветровых нагрузок на провода во всех ветровых райо-
нах ......................................... . . 0,9
Для остальных указанных выше воздействий .1,0
Значения некоторых коэффициентов условий работы т (см. § 1.2),
которые следует вводить и расчет различных элементов конструкций
согласно ВСН 141-84, следующие:
Для сжатых и растянутых элементов поясов и растянутых
элементов решетки.....................................0,95
Для продольных и поперечных оттяжек из круглой стали 0,9
Для фиксаторов и фиксаторных кронштейнов . 0,85
Для сжатых основных элементов решетки при гибкости их
60 и более; для оттяжек из стальных канатов; для сжато-
изогнутых элементов консолей и фиксаторов при гибкости их
200 и более............................................
Для анкеровочных устройств и анкерных болгов . 0,75
Для стяжных болтов, работающих па растяжение 0.65
§ 2.2. Расчеты нормативных нагрузок на провода и тросы
Нагрузки на провода и тросы принимают равномерно распределен-
ными по длине пролета и называют распределенными линейными,
так как относят их к 1 м длины провода. В данной книге для измере-
ния распределенных линейных нагрузок принята размерность даН/м
(см. табл. 1.5). Нагрузки, действующие на провода контактной сети,
разделяют на вертикальные (от собственного веса проводов или под-
весок и от веса гололеда на проводах или подвесках), горизонтальные
(от воздействия ветра на свободные от гололеда провода и на покрытые
гололедом) и результирующие (определяемые совместным действием
вертикальных и горизонтальных нагрузок). Рассмотрим определение
всех указанных нагрузок применительно к некоторому проводу. При
определении той или иной нагрузки к условным обозначениям нагру-
зок для несущего троса будем добавлять индекс «н», для контактного
провода — индекс «к», для провода воздушной линии — индекс «пр».
Нагрузку от собственного веса проводов и тросов g определяют по
соответствующим ГОСТам (см. табл. 1.5). При отсутствии данных
распределенная линейная нагрузка провода или троса, даН/м,
g~ 9,815 у л;'- 10-т, (2.1)
где S — площадь поперечного сечения провода или троса, мм2;
у — плотность материала провода или троса, кг/м:!;
к' — коэффициент, учитывающий конструкцию провода (для однопрово-
лочных проводов/г' == I, для многопроволочных, если приближен-
но учесть увеличение длины проволок при их скрутке, k' = 1,025).
Для комбинированных проводов, состоящих из проволок раз-
личных материалов, определить нагрузку от собственного веса при
двух материалах, даН/м, можно по формуле
g-=9,81x:' (51Т1-| S„Y2) 10 (2.2)
где Sj и S., — площади поперечного сечения проволок из материалов I и 2,
мм2;
Yi и Уг плотности материалов 1 и 2, кг/мя
Нагрузки от собственного веса контактных подвесок g (даН.м)
находят, суммируя нагрузки отдельных проводов, из которых состоит
подвеска, струн и зажимов для их крепления. Нагрузку от рессорного
троса, струп и зажимов учитывают приближенно, относя ее к 1 м дли-
ны подвески в размере 0,1 даН/м при одном контактном проводе и
0,2 даН/м при двух. Таким образом,
ff-gn-l-Пк Uk-H’J)- (2.3)
где цк — число контактных проводов.
Нагрузки от веса гололеда на I м длины провода или троса gr,
даН/м, принимая гололед цилиндрической формы плотностью 900 кг,м3,
определяют по формуле
gr--=2.776r (</ <-Ьг) 10-Л (2.4)
где — расчетная толщина стенки гололеда, мм-
d — диаметр провода (для контактных проводов среднее арифметическое
значение из высоты и ширины его сечения), мм.
Расчетное значение толщины стенки гололеда в формуле (2.4)
Д. -Д’ к,.,
где йн —толщина стенки гололеда в соответствии с данными § 1.3, мм;
кг — коэффициент, учитывающий действительные диаметр провода и вы-
соту его подвешивания.
При определении нагрузки от веса гололедных образований на
контактных проводах расчетную толщину стенки льда, учитывая уда-
28
ление его токоприемниками и эксплуатационным персоналом, условно
принимают в размере 50 % расчетного значения для других проводов.
Необходимо отметить следующее. Приведенная условность определения го-
лоледных нагрузок на контактных проводах представляется недостаточно обо-
снованной для подвесок станционных и тракционных путей. При расчете раз-
личных поддерживающих устройств и опор нагрузки на них в режиме, который
часто определяет их несущую способность, окажутся заниженными. Поэтому,
по мнению автора, уменьшение гололедных нагрузок на контактные провода ука-
занных путей нужно принимать в меньших размерах относительно нормативных
или не учитывать вообще.
Нагрузку от веса гололеда на несущем тросе вследствие затруднен-
ных условий гололедообразования (по сравнению со свободно висящи-
ми проводами) ВСН 141-84 рекомендуется учитывать с поправочным
коэффициентом, равным 0,8, к весу отложения, определяемому форму-
лой (2.4). Можно эту нагрузку, даН/м, вычислить и по формуле
.Чгн- = 2,226г !-br) IO "3. (2.5)
Распределенную линейную нагрузку от веса гололеда па цепной
подвеске получают, суммируя такие нагрузки на все провода подвески
и добавляя вес гололедных отложений па струцах и зажимах, отнесен-
ный к длине пролета. Приближенно, даН/м,
^,=5,0 489/^(1 i'-iZ,.) 10-». (2 6)
где dc — диаметр струны, мм.
Ветровая нагрузка на провод определяется как сумма статической
и динамической составляющих. Статическая составляющая ветровой
нагрузки на провод, свободный от гололеда, даН/м,
рс- BCxd-U) 4, (2.7)
где В — распределенная поверхностная нагрузка, Па, определяемая по фор-
муле (1.11);
C.v — аэродинамический коэффициент лобового сопротивления;
d — диаметр провода (для контактных проводов — вертикальный раз-
мер диаметрального сечения), мм.
По ВНТП-81 значения аэродинамических коэффициентов лобово-
го сопротивления Сх, отнесенные к площади сечения одного провода,
рекомендуется принимать следующими:
Одиночные провода и троен диаметром 20 мм и более . . 1,10
То же диаметром меиее 20 мм, а также провода и тросы,
покрытые гололедом . .. .................. , 1,20
Одиночные контактные, провода и тросы контактной под-
вески с учетом зажимов и струн...................1,25
Двойные контактные провода при расстоянии между ними
40 мм . . ............ I ,85
По экспериментальным данным значение Сх при двух контакт-
ных проводах МФ-100 и расстоянии между ними 40 мм составляет 1,55
для нулевых мест и насыпей высотой до 5 м, для более высоких насы-
пей— 1,85. При расстоянии между контактными проводами 100 мм
29
значения Сх соответственно равны 1,85 и 2,15; для контактного провода
МФ-150 Сх ----- 1,30.
Динамическая составляющая ветровой нагрузки в тех же условиях,
даН/м,
рд~0,88р(. 1] ft L (2.8)
где Г| и 6 — коэффициенты, учитывающие пульсацию ветра;
5 — коэффициент динамичности
Значения коэффициента т; находят в зависимости от длины проле-
та Z:
I, м........................ 30 40 50 60 70 75
I].......................... 0,74 0,70 0,65 0.60 0,56 0,51
Коэффициент 6 определяется скоростью ветра v:
с, м/с ... 10 15 20 25 30 35 40 45 50
ft.......... 0.10 0.13 0,16 0,18 0.20 0,22 0,24 0,25 0,26
Значения £ определяются распределенной линейной нагрузкой от
веса провода g (при гололеде — с учетом его веса):
g, даН/м 0,4 0.6 0,8 1,0 1,2 1,4 1,6 1,8 2,0иболее
5 . . . 0,80 0,86 0,90 0,93 0,96 0,98 1,00 1.02 1,03
Для параметров, не соответствующих приведенным выше, значения
коэффициентов т), 6 и ё определяются линейной интерполяцией.
Статическая составляющая ветровой нагрузки на провод, покрытый
гололедом, даН
р,-с нгсх (<И 2М 10-ц (2.9)
динамическая составляющая
Ргд :0,88р|-с п ft 5, (2.10)
где /3|, - распределенная поверхностная нагрузка на провод с гололедом, Па
(см. табл. 1.4), определяемая по формуле (1.11).
Для вычисления статической составляющей ветровой нагрузки на
покрытые льдом контактные провода, учитывая приведенную выше ус-
ловность принятия гололедной нагрузки, формулу (2.9) можно пред-
ставить в виде
/’гск ВГСХ (Лк-! М Ю-1, (2.11)
где — высота сечения контактного провода, мм
При определении статической составляющей ветровой нагрузки
на несущий трос с гололедом надо учесть снижение гололедной нагруз-
ки, что может быть выполнено введением в расчет уменьшенной тол-
щины стенки льда на этом проводе. Условная толщина стенки льда
f’гн ••-= - °. МН ]/~0,2бЛ Ч o’,8^ (4 +.6г)" , (2.121
где ф, — диаметр несущего троса, мм.
30
мшшмьг
Расчеты проводов контактной сети и воздушных линий, а также оп-
ределение длин пролетов при гололеде с ветром согласно ВСН 141-84
рекомендуется выполнять по нормативным значениям только статиче-
ских составляющих ветровых нагрузок, вычисляемых по формулам
(2.7) и (2.9).
Результирующие нагрузки на отдельный провод при отсутствии
гол оледн ы х обра зоваi1 и й
q I Д’Ч /Л' > (2.13)
при наличии гололеда на проводе
qr I г Sr)2 1-Ргс • (2.14)
Результирующие нагрузки на несущий трос цепной подвески опре-
деляют без учета ветровой нагрузки на контактные провода, гак как
значительная часть последней воспринимается фиксаторами, а часть,
передающаяся па несущий ipoc через струны, невелика. Поэтому ре-
зультирующая нагрузка при ветре без гололеда на проводах
</и I S/'ей ,
а при соьмесню.м действии гололеда и ветра
Чгп ! (Si Sr)2 I рб-и •
(2 J5)
(2.16)
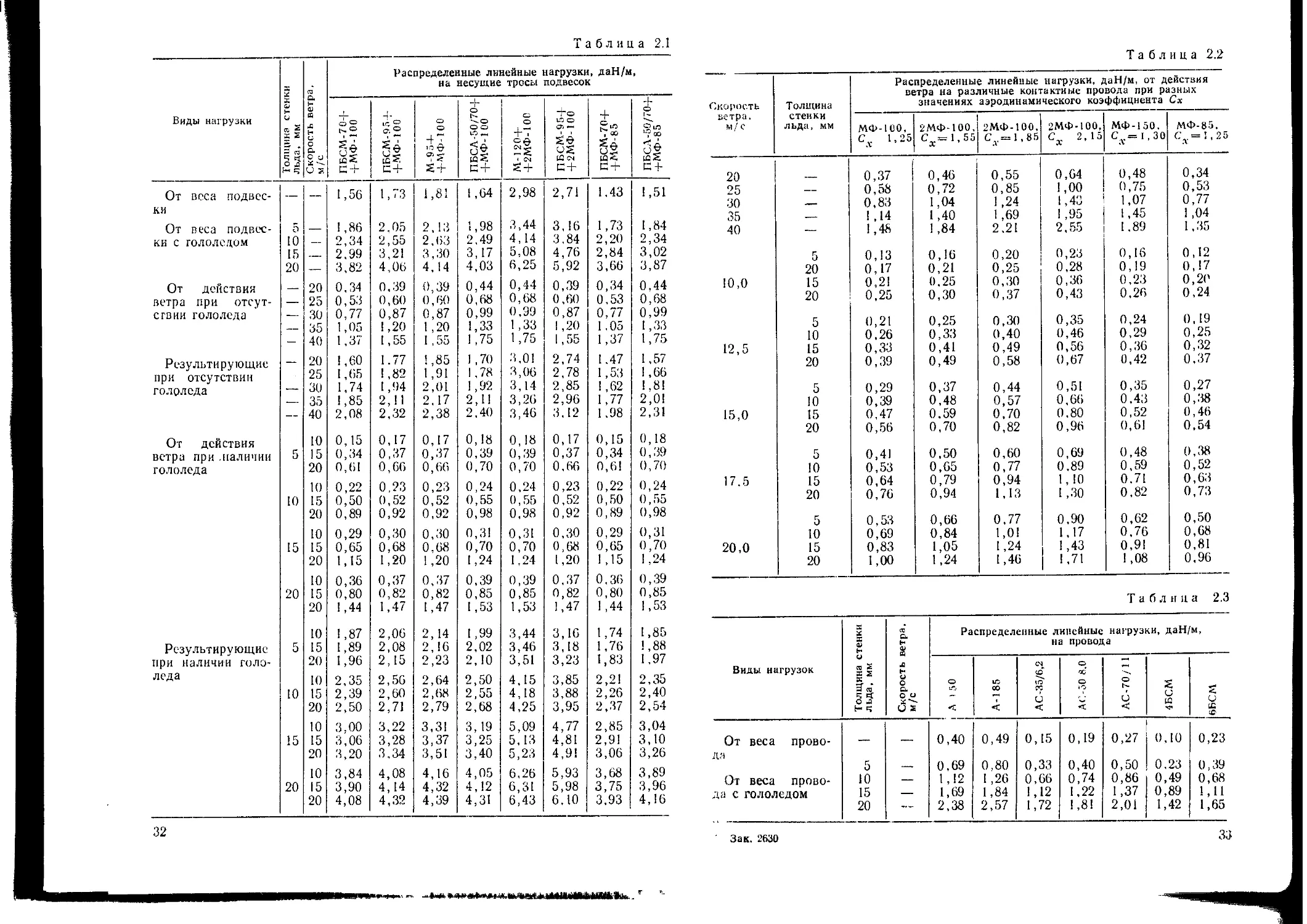
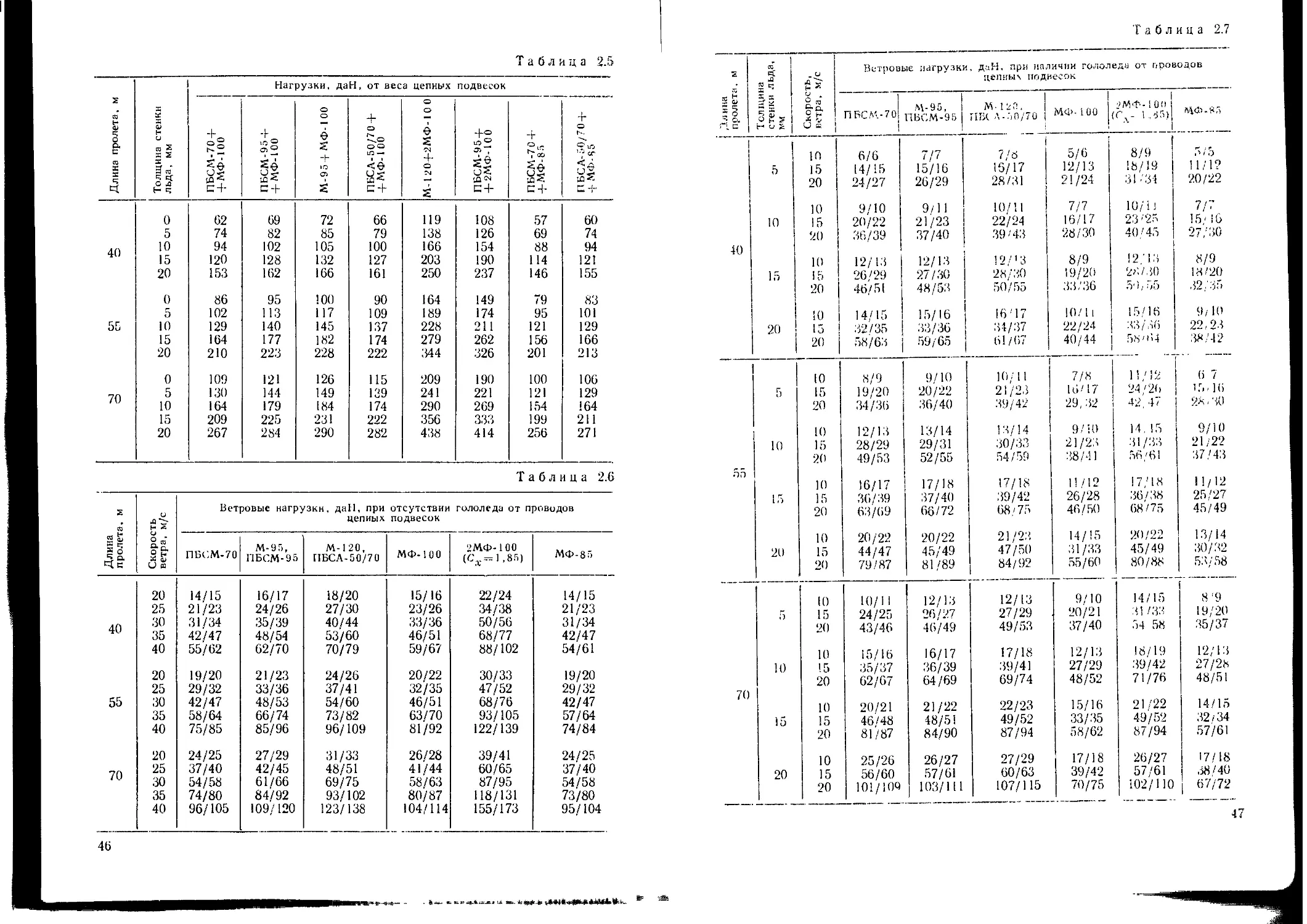
Значения распределенных чиненных нагрузок для наиболее часто
применяемых цепных подвесок приведены в табл. 2.1 по откорректи-
рованным данным Трансэлектропроекта. Нагрузки на несущие тросы
подвесок с низколегированными и бронзовыми контактными провода-
ми равны приведенным в таблице для подвесок с медными контактны-
ми проводами. Нагрузки для подвески С-70 |- МФ-85 в таблице от-
сутствуют. их можно принимать такими же. как для подвески
ПБСМ-70 -) МФ-85.
В табл. 2.2 приведены значения распределенных линейных нагру-
зок от ветровых воздействий на контактные провода марки МФ при
различных значениях аэродинамического коэффициента лобового со-
противления Сл (включая экспериментальные). Ветровые нагрузки па
низколегированные и бронзовые контактные провода такие же, как
и на медные. Значения различных распределенных линейных нагру-
зок для наиболее часто применяемых проводов воздушных липин при-
ведены в табл. 2.3. Там же указаны аналогичные нагрузки на биметал-
лические сталемедные проволоки.
При пользовании табл. 2.1— -2.3 переход от известной нормативной
распределенной поверхностной нагрузки Вх. Па. к нормативной ско-
рости ветра их, м/с следует- выполнять по формуле
щ. ---- 1, 6/Тх . (217)
Если скорость ветра в конкретном расчете отличается от приведен-
ных в табл. 2.1.2.3, то требуемые данные для горизонтальных нагру-
31
Таблица 2.1
Распределенные линейные нагрузки, даН/м,
S га на несущие тросы подвесок
Виды нагрузки Й О) О Л 70+ 00 С.® G) О 50/70+ :оо © 001- +S6- 1 + +
£ Ня- 5 О Q. О у ПБСМ- +МФ-1 5СМ- МФ-1 4 7 Ф о 5* БСА-! МФ-1 < сч ge og id сч gs о®
О J2 г- с; О ?. С + г-: С + £ + с+ с + С -Ь
От веса подвес- — — 1,56 1,73 1,81 1 ,64 2,98 2,71 1.43 1,51
КМ
От веса подвес- л 1,86 2,05 2,13 1,98 3,44 3,16 1,73 1,84
ки с гололедом 10 — 2,34 2, 55 2,63 2,49 4,14 3,84 2,20 2,34
15 2,99 3,21 3,30 3,17 5,08 4,76 2,84 3,02
20 — 3,82 4,06 4,14 4,03 6,25 5,92 3,66 3,87
От действия 20 0,34 0,39 0,39 0,44 0,44 0,39 0,34 0,44
ветра при отсут- — 25 0,53 0,60 0,60 0,68 0,68 0,60 0,53 0,68
с гв ии гололеда 30 0,77 0,87 0,87 0,99 0,99 0,87 0,77 0,99
35 1,05 1,20 1,20 1,33 1 ,33 1,20 1.05 1,33
— 40 1,37 1,55 1,55 1,75 1,75 1,55 1,37 1,75
Результирующие при отсутствии гололеда — 20 25 30 1,60 1,65 1.74 1.77 1 ,82 1,94 1,85 1,91 2,01 1,70 1,78 1,92 3,01 3,06 3,14 2,74 2,78 2,85 1,47 1,53 1,62 1,57 1,66 1,81
35 1,85 2,11 2,17 2,11 3,26 2,96 1,77 2,01
— 40 2,08 2,32 2,38 2,40 3,46 3,12 1,98 2,31
От действия 10 0,15 0,17 0,17 0,18 0,18 0,17 0,15 0,18
ветра при .наличии 5 15 0,34 0,37 0,37 0,39 0,39 0,37 0,34 0,39
гололеда 20 0,61 0,66 0,66 0,70 0,70 0,66 0,61 0,70
10 0,22 0,23 0,23 0,24 0,24 0,23 0,22 0,24
10 15 0,50 0,52 0,52 0,55 0,55 0,52 0,50 0,55
20 0,89 0,92 0,92 0,98 0,98 0,92 0,89 0,98
10 0,29 0,30 0,30 0,31 0,31 0,30 0,29 0,31
15 15 0,65 0,68 0,68 0,70 0,70 0,68 0,65 0,70
20 1,15 1,20 1,20 1,24 1,24 1,20 1,15 1,24
10 0,36 0,37 0,37 0,39 0,39 0,37 0,36 0,39
20 15 0,80 0,82 0,82 0,85 0,85 0,82 0,80 0,85
20 1,44 1,47 1,47 1,53 1,53 1,47 1,44 1,53
10 1,87 2,06 2, 14 1,99 3,44 3,16 1,74 1,85
Результирующие 5 15 1,89 2,08 2,16 2,02 3,46 3,18 1,76 1,88
при наличии голо- 20 1,96 2,15 2,23 2,10 3,51 3,23 1,83 1,97
леда 10 2,35 2,56 2,64 2,50 4,15 3,85 2,21 2,35
10 15 2,39 2,60 2,68 2,55 4,18 3,88 2,26 2,40
20 2,50 2,71 2,79 2,68 4,25 3,95 2,37 2,54
10 3,00 3,22 3,31 3,19 5,09 4,77 2,85 3,04
15 15 3,06 3,28 3,37 3,25 5,13 4,81 2,91 3,10
20 3,20 3,34 3,51 3,40 5,23 4,91 3,06 3,26
10 3,84 4,08 4,16 4,05 6,26 5,93 3,68 3,89
20 15 3,90 4,14 4,32 4,12 6,31 5,98 3,75 3,96
20 4,08 4,32 4,39 4,31 6,43 6,10 3,93 4,16
.***<мым»М«мшн^кШММииМШМШ^ г
32
Таблица 2.2
Скорость Толщина Распределенные линейные нагрузки, даН/м, от действия ветра на различные контактные провода при разных значениях аэродинамического коэффициента Сх
ветра. стенки
м/с льда, мм МФ-100, Ст 1,25 2МФ-100, Сж=1,55 2МФ-100. Сг=1,85 2МФ-100, сх 2'15 МФ-150. I , 30 МФ-85. С\.= 1,25
20 0,37 0,46 0,55 0,64 0,48 0,34
25 0,58 0,72 0,85 1,00 0,75 0,53
30 0,83 1,04 1,24 1,43 1,07 0,77
.35 — 1,14 1,40 1,69 1 ,95 1,45 1,04
40 — 1,48 1,84 2.21 2,55 1.89 1,35
5 0,13 0,16 0,20 0,23 0,16 0,12
20 0,17 0,21 0,25 0,28 0,19 0,17
10,0 15 0,21 0.25 0,30 0,36 0,23 0,20
20 0,25 0,30 0,37 0,43 0,26 0,24
5 0,21 0,25 0,30 0,35 0,24 0,19
10 0,26 0,33 0,40 0,46 0,29 0,25
12,5 15 0,33 0,41 0,49 0,56 0,36 0,32
20 0,39 0,49 0,58 0,67 0,42 0,37
5 0,29 0,37 0,44 0,51 0,35 0,27
10 0,39 0,48 0,57 0,66 0,43 0,38
15,0 15 0,47 0,59 0,70 0.80 0,52 0,46
20 0,56 0,70 0,82 0,96 0,61 0,54
5 0,41 0,50 0,60 0,69 0,48 0,38
10 0,53 0,65 0,77 0,89 0,59 0,52
17.5 15 0,64 0,79 0,94 1,10 0.71 0,63
20 0,76 0,94 1,13 1,30 0,82 0,73
5 0,53 0,66 0,77 0,90 0,62 0,50
10 0,69 0,84 1,01 1,17 0.76 0,68
20,0 15 0,83 1,05 1,24 1,43 0,91 0,81
20 1,00 1,24 1,46 1,71 1,08 0,96
Таблица 2.3
Виды нагрузок | Толщина стенки : льда, мм Скорость ветра, м/с Распределенные линейные нагрузки, даН/м, на провода
о А-185 АС-35/6,2 О о АС-70/11 4БСМ 6БСМ
От веса прово- — — 0,40 0,49 0,15 0,19 0,27 0,10 0,23
Д') 5 0,69 0.80 0,33 0,40 0,50 0.23 0,39
От веса прово- 10 — 1,12 1,69 1,26 0,66 0,74 0,86 0,49 0,68
да с гололедом 15 — 1,84 1,12 1,22 1,37 0,89 1,11
20 —- 2,38 2,57 1,72 1,81 2,01 1,42 1,65
Зак. 2630
33
П родолжение табл. 2.3
я и н ветра, Распределенные линейные нагрузки, даН/м, на провода
Виды нагрузок сс S я 2 я —
Я о Iff iff'
d « с КС а ю ад iff и
~ £ С 2 < ъ А*
От 1СЙСТВИЧ 20 0,47 0,52 0,25 0 28 о’ 15 0.34 0,12 9 18
остра при отсуг- — 25 0,74 0,81 0,39 0,59 0,19 0,27
стоим гололеда — 30 1,07 1,18 0,57 0, сь 9,77 0,26 0,41
— 35 ! ,44 1,61 0,77 0,87 1 ,05 0.37 0,55
— 40 1 ,88 2,20 1,0! 1,15 1 /Х 0,48 0,72
Результнрующщ 20 0,02 0,71 0,29 0,34 <•) / ' 0,16 0.29
при отсутствии 23 0,84 0,95 0,42 0,49 О , 0. ‘ 9.22 0.36
гололеда — 30 1,14 1,28 0,59 0,68 0,82 0,28 0.47
35 1,49 1,68 0,78 0,89 1 ,08 0,38 0,6^:
40 1 ,92 2,25 1,02 1,17 1,39 0,49 0,76
От действия 10 0,20 0,20 0,14 0,15 0,16 0,11 0,12
четра при налипни О 15 0,44 0,46 0,30 0,33 0,36 0,24 0,26
гололеда 20 0,77 0,81 0,55 0,59 0,64 0,43 0,48
10 0,26 0,27 0,21 0,22 0,24 0,18 0,20
10 15 0,61 0,62 0,48 0,50 0,53 0,41 0,44
20 I ,08 1,12 0,84 0,88 0,93 0,73 0, 77
10 0,34 0,36 0,28 0,29 0,30 0,25 0,26
15 i5 0,77 0,79 0,65 0,67 0,70 0,57 0,61
20 1, об 1.42 1,15 1,19 1,25 1,02 1,09
10 0,42 0,93 0,43 0,36 0,37 0,39 0,33 0,35
20 15 0,97 0,81 0,83 0,86 0,74 0,77
20 1,67 1,73 1 ,45 1 ,48 1,54 1,31 1.38
Результирующие 10 0,72 0,82 0,36 0,42 0,52 0,25 0,4!
при наличии го- О f 0,82 0,92 0,45 0,62 0,32 0,47
поледа 20 1,03 1,14 0,64 0,71 0,81 0,49 0,62
10 1,15 1,28 0,70 0.76 0,89 0,52 0,71
10 15 1,28 1,40 0,82 0,89 1,01 0,64 0,81
20 1,56 1,69 1 ,07 1 . 15 1,27 0,88 1,03
10 1,72 1,87 1,15 1.26 1,40 0,92 1,14
15 15 1,86 2,00 1.29 1,39 1,54 1,06 1 ,27
20 2,17 2,32 1,61 1.70 1,85 1,35 1,56
10 2,42 2,61 1,76 1,85 2,05 1,46 1,69
20 15 2,56 2,75 1,91 1,99 2,19 1,60 1.82
20 2,91 3,10 2,25 2,34 2,53 1,93 2,15
^Дшь. «-аймМима.
им ш ыиммиШиИЫЬ*..
34
зок можно получить методом линейной интерполяции, а при необхо-
димости более высокой точности — с учетом квадратичной зависимо-
сти этих нагрузок от скорости ветра. В табл. 2.1—2.3 представлены
только -статические составляющие ветровых (и связанных с ними) на-
грузок. Поэтому в тех случаях, когда для расчета требуются полные
ветровые нагрузки, необходимо учесть дополнительно еще их динами-
ческие составляющие.
Пример. .3 а д а и и е ч и с х о д и ы е д а н н ы е. Определить нор-
мативные распределенные линейные результирующие нагрузки при режимах
1 ололеда с ветром и максимального ветра для расчета несущего троса цепной
подвески М-120 (-2МФ-100. Подвеска находится в гололедном районе III и вет-
ровом IV в степной местности на насыпи высотой 12 м.
Р е ш е н и е. Определим нагрузку от собственного веса подвески по фор-
муле (2.3) и данным табл. 1.5:
К 1.037 (-2(0,873 ( 0.1) -2,983 даН/м.
В гололедном районе HI толщина стенки льда составляет 15 мм. Поскольку
диаметр провода М-120 равен 14 мм, то первый поправочный коэффициент
(см § 1.3) равен 0,96. Для насыпи высотой 12 м, второй поправочный коэффици-
ент равен 1,32. Таким образом, расчетная толщина стенки льда
5Г- 15-0,96.1,32 19 мм.
Нагрузка от веса гололеда на несущем тросе по формуле (2.5)
2,22-19 (14 1-19) К) » - 1,392 даН/м.
Нагрузку от веса гололеда на контактные провода найдем но формуле (2,4),
учитывая, что толщина стенки льда равна 50 % принятой для несущего троса.
Расчетный диаметр контактного провода определим как полусумму высоты и
ширины его площади сечения
0,5(11,8 + 12,8) 12,3 мм.
Следовательно, для одного контактного провода
2,77-9,5(12,3 (-9,5) 10--» =0,574 даН/м.
Нагрузку от веса гололеда на струнах найдем по формуле (2.6). Учитывая,
что струны выполнены из проволоки 4БСМ диаметром 4 мм, эта нагрузка при
одном контактном проводе
.0,489-19 (1,15-19 (-4) 10-» 0,024 даН/м.
Полная нагрузка от веса гололеда на ценной подвеске
Я,..-- 1,392 (-2-0.574 -2-0,1)24 2,588 даН,м.
Для расчета несущего троса достаточно иметь только статические состав-
ляющие ветровых нагрузок. Принимая нормативную распределенную поверх-
ностную нагрузку В-,-,, при гололеде но табл. 1.4 равной 140 Па, определим нуж-
ное для дальнейших расчетов значение Вг но фефмуле (1.11). Коэффициент кд
найдем при параметре шероховатости для стенной местности по табл. 1.2, рав-
ном 0,1. Интерполируя данные табл. 1.3, для насыпи высотой 12 м получим ка
1,246. Тогда
Вг--- 140-1,2462--=21 7 Па.
По формуле (2.12) определим условную толщину стенки льда на несущем
тросе
6™ = — 7 - [- У 49 (- ()78“11~Т4+'1Щ“ =16,46 мм.
2*
38
Принимая значение Сх — 1,25 по формуле (2.9) найдем статическую состав-
ляющую ветровой нагрузки при гололеде
рге = 217-1,25 (14+2-16,46) 10-*= 1,273 даН/м.
Искомая результирующая нагрузка на несущий трос при гололеде с ветром
по формуле (2.16)
qra = }/(2,983 + 2,588)4-1,273^ = 5,715 даН/м.
При максимальном ветре нормативная распределенная поверхностная на-
грузка для ветрового района IV по табл. 1.1 равна 630 Па. Учитывая, что кл-
-- 1,246, по формуле (1.11) получим
£ = 630-1,2462 = 978 Па.
Статическая составляющая ветровой нагрузки на несущий трос при макси-
мальном ветре но формуле (2.7)
= 978-1,25-14-10-* = 1,712 даН/м;
искомая результирующая нагрузка определяется по формуле (2.15)
q„ ---У 2.983'2 1,7122 3,439 даН/м.
§ 2.3. Расчеты нормативных нагрузок
на опорные устройства
Нагрузки от собственного веса опор, поддерживающих и фикси-
рующих устройств определяют исходя из конкретных размеров, мате-
риалов и конструкций расчетных устройств. В тех случаях, когда точ-
ные размеры заранее не известны, указанные нагрузки принимают по
аналогии с нагрузками для существующих конструкций.
Нагрузка от веса проводов с изоляторами и арматурой G! при
закреплении их на одном изоляторе или на одной гирлянде
Gj- 2«/+-(+, (2 18)
где 2 dl — суммарная нагрузка от веса цепных подвесок или каких-либо про-
водов (усиливающих, питающих и др.), закрепленных на одном изо-
ляторе или гирлянде, даН;
ц — нагрузка от собственного веса ценной подвески или провода, даН/м;
/ - расчетная длина пролета, принимаемая равной средней арифмети-
ческой из длин двух пролетов, прилегающих к расчетному устройст-
ву, м;
GH -- нагрузка от веса изолятора или гирлянды изоляторов е арматурой,
даН.
Если цепные подвески закреплены на консолях или на жестких
поперечинах, то нагрузки от собственного веса
Gj-^Gj + Gfc, (2.19)
где Сф .. часть веса фиксаторов, передающаяся на расчетное опорное уст-
ройство, даН.
При закреплении цепных подвесок или каких-либо проводов на
гибких поперечинах равномерно распределенную нагрузку от собствен-
36
NBbihiiu ««< » ел йА-илм ..сш-ЧмнИ* тИЖИИТКЙУ'.*. .
Таблица 2.4
Система тока Нагрузка gn, даН/м Нагрузка gn+grn, даН/м, при толщине стенки льда, мм
5 10 15 20
Переменный 7,0 8,5 10,0 12,5 16,0
Постоянный 6,0 7,5 9,0 11,5 15,0
ного веса поперечины можно приближенно учесть несколькими сосре-
доточенными нагрузками, приложенными в точках крепления подве-
сок или проводов. Тогда полная нагрузка в одной из указанных точек
G'i-Zgl -НА'н/нМп, (2.20)
где Дп - часть веса гибкой поперечины (с учетом веса изоляторов, струн, фик
саторов и арматуры), приходящаяся на 1 м длины поперечного проле-
та, даН/м (табл. 2.4);
/П — длина поперечного пролета, м;
«и - число нагрузок на гибкой поперечине.
Нагрузки от веса гололеда на проводах учитывают совместно с на-
грузками от собственного веса проводов. Нагрузку от гололеда па фик-
саторах и изоляторах ввиду ее незначительности для указанных
элементов обычно не определяют. Таким образом, нагрузки от веса
проводов с гололедом при закреплении их на одном изоляторе или гир-
лянде изоляторов
о,. V (к ; ДГ) / i Сг,.,, (2.21)
где gr - нагрузка от гололеда на проводах, даН/м.
При закреплении цепных подвесок на консолях искомая нагрузка
G^-.-Gr-|- о;. (2.22)
Если же ценные подвески или провода закреплены на гибких попе-
речинах, то по аналогии с формулой (2.20) нагрузка от веса проводов
с гололедом может быть определена как
G;.' = v (йЧ-йг) (-1- (ffn-1-ffrn) !и/пп, (2.23)
где Дсп - часть веса гололеда на гибкой поперечине, ери ходящая! я па I м
длины поперечного пролета, даН/м.
При перекрытии гибкими поперечинами от 8 до 16 путей вклю-
чительно нагрузки gj, и gn -|- grn можно принимать по данным
табл. 2.4. Значения, приведенные в табл. 2.4, получены для ширины
междупутий 5,3 м, габаритов опор 4,5 м на линиях переменного и
4,1 м на линиях постоянного тока; вес изоляторов, включенных в
37
тросы гибких поперечин непосредственно у опор, не учтен; результа-
ты округлены до 0,5 даН/м.
Нагрузки от веса гололеда и снега на других поддерживающих
устройствах и настилах опорных устройств G'r можно определить ис-
ходя из фактической площади элементов, на которых возможно обра-
зование гололеда или снега, и нагрузки g'r (см. § 1.3), характерной
для данного района,
Gr — S' gr,
где S' — фактическая площадь элементов, которые могут быть покрыты голо-
ледом или снегом, в которую включают и зазоры меньше 4 см меж-
ду параллельными элементами, м2.
Нагрузку на провода от ветра, передающуюся на опорные устрой-
ства, принимая направление действия ветра перпендикулярным к про-
водам, для одного провода определяют:
при максимальном ветре
(2.24)
при гололеде с ветром
Рг (Р Ргс + Ргд) (’ (2.25)
где рс и ргс,1 — соответственно статические и динамические составляющие
Рц и ргд| ветровых нагрузок. даН/м;
Р — коэффициент, учитывающий неравномерность действия ветра
на провод по пролету.
Значение р принимают в зависимости от распределенной поверх-
ностной нагрузки В:
В, Па .• до 400 400 - 650 660 -ЮОО более 1010
Р . . . . . 0,85 0,75 0,70 0,65
При резких изменениях направления проводов на опорах (напри-
мер, на угловых опорах питающих линий) направление ветра прини-
мают соответствующим биссектрисе внутреннего угла 2а, образуемо-
го проводом. В этом случае ветровая нагрузка, передающаяся на
опору,
Рв — pl sin а.
Нагрузка от ветра на опоры, даН.
Pon=0,lBCxSon, (2.26)
где В — распределенная поверхностная нагрузка, Па, принимаемая в со-
ответствии с расчетным режимом;
Сх — аэродинамический коэффициент лобового сопротивления, прини-
маемый для плоских элементов конструкций равным 1,4, а для ци-
линдрических и конусных — 0,7;
Son — площадь поверхности опоры, на которую действует ветер, м2.
38
При вычислении ветровой нагрузки на металлические опоры с ре-
шеткой обычно пользуются приближенной формулой
Роп = 0,1ВСХ Son коп, (2.27)
где •— площадь опоры, определенная по периметру, м2;
кои — коэффициент, учитывающий заполнение площади Son; его прини-
мают равным 0,5—0,6.
Усилия от изменения направления проводов в кривых в том
случае, когда полеты по обе стороны от расчетной опоры целиком рас-
положены в пределах кривой и зигзаги проводов у опор одинаковы,
определяют как
Pi — Hl/R, (2.28)
где Н — натяжение провода, соответствующее режиму, для которого опреде-
ляется нагрузка, даН;
R — радиус кривой, м.
Если же зигзаги проводов на соседних опорах не равны зигзагу
на расчетной опоре (рис. 2.1), то
\ 2R Z,
-«г
/’
(2.29)
В тех случаях, когда один из пролетов, соседних с расчетным опор-
ным устройством, расположен в кривой, а другой — частично на пря-
мом участке пути (рис. 2.2), расчетное усилие
Р + {2.30)
12 |_ 2R li J
где 1К — длина пролета на кривом участке пути, м;
It — длина пролета, частично находящегося на прямом участке пути, м;
к — отношение части пролета, расположенной на прямом участке пути,
ко всей длине пролета /у,
а — зигзаг провода на кривом участке пути, м;
at — зигзаг провода на прямом участке пути, м;
ст — смещение оси токоприемника от оси пути на высоте подвешивания
расчетного провода, м.
Знак «—» в последнем члене формулы (2.30) относится к зигзагам,
имеющим одностороннее направление от оси пути, знак «+» — к зиг-
загам разностороннего направления.
39
I
I
Рис. 2.2. Расчетная схема для определения нагрузок Р12 и Pis
Смещение оси токоприемника от оси пути ст на высоте h опреде-
ляют в зависимости от разности у уровней головок рельсов на кривой
при расстоянии между осями рельсов ар:
ст -hi//ар.
(2.31)
Если пролет Ц целиком расположен на прямом участке пути, то
формула (2.30) примет вид
(2-32)
В тех случах, когда один из соседних с расчетным опорным уст-
ройством пролетов расположен на прямом участке пути, а другой
частично на кривой (см. рис. 2.2), расчетное усилие
<2.33)
I ‘2 «I I
где /2 —• длина пролета, находящегося на прямом участке пути, м.
Остальные обозначения и условия применения знаков те же, что
и в формуле (2.30).
Если рассчитываемое опорное устройство расположено на кривой
таким образом, что два соседних пролета частично находятся на пря-
мых участках пути (рис. 2.3), то расчетное усилие
(2.34;
40
Если же расчетное опорное устройство расположено на прямом
участке пути так, что оба соседних пролета частично находятся на кри-
вых (рис. 2.4), то расчетное усилие
( 1 — К-, ) /, U j - - С-г > t Ч (1 — Л.'о) Е (Та — Ст2 ~4~ ч!
» -А-----------‘-L-----1 Г..-.. . _Д--AI—L-----г_ w- (2 ;й)
1 2Rt I, 2R2 l2 ]
Все обозначения, принятые в формулах (2.34) и (2.35), указаны
па рис. 2.3 и 2.4. Условия применения знаков перед величинами a, at
и </г те же, что и в формуле (2.30).
При определении расчетных нагрузок от усиливающих, дополни-
тельных и других проводов расчетные усилия можно определять по
формуле (2.28). а при сопряжении прямых и кривых участков пути
по формулам (2.30) и (2.32)—(2.35), принимая в них значения а, а,,
и2, ст, Cti и с’т2 равными пулю.
Усилия, обусловленные изменением направления проводов при их
отводах, Р2, если провод подвешен без зигзагов (например, при от-
воде несущего троса полукосой ценной подвески па анкеровку), для
прямых участков пути
Pt-Hz/l. (2.36)
При наличии зигзагов у проводов, изменяющих свое направле-
ние, усилие, вызванное отводами,
/ г ! а а I а, \
т~+ ~77-) <2-37)
Все линейные размеры в формулах (2.36) и (2.37) показаны на
рис. 2.5.
41
Рис 2.6. Расчетная схема для определения нагрузки Ри
Знаки « г» в формуле (2.37) относятся к случаю, когда зигзаг
а на расчетной опоре направлен от нее, а знаки «—», — когда он на-
правлен к опоре. Если зигзаги а и аг имеют одностороннее направле-
ние, знак « ! » в числителе второго члена скобки в формуле (2.37)
должен быть заменен па «---».
При отводах на анкеровку без учета возможного наклона опоры
z—Г [-0,5.5,
где Г — габарит установки опоры (расстояние от оси пути до передней грани
опоры на уровне головок рельсов), м;
6 - ширина опоры на уровне головок рельсов, м.
В случае отвода усиливающих или каких-либо других проводов
усилие, передающееся на опору,
/>22 -llz'/l- (2..38)
Величина z Сем. рис. 2.5) определяется как
г’ Г' \ 0,55.
где Г' — расстояние от грани опоры до провода на уровне головок рельсов, м
На кривых участках усилия, передающиеся на опорные устройст-
ва при отводах проводов, определяют как результирующие усилий от
изменения направления проводов, вызванных кривизной пути, и от
изменения направления проводов, вызванных отводами. Результи-
рующее усилие Р2,{ может быть для проводов цепных подвесок опре-
делено следующим образом (рис. 2.6):
при анкеровке на опору, расположенную с внешней стороны кри-
вой (показано сплошной линией),
zj-' ст — -а
(2.39)
при анкеровке на опору, расположенную с внутренней стороны кри-
вой (показано штриховой линией),
а
^2 —
' 2R
11
(2.40)
42
i пнипИйMlft т. -
при анкеровке с опоры, расположенной на кривом участке пути,
на опору, находящуюся на прямом участке пути (показано штрих-
пунктирной линией),
Ргя=Н
/к + (1 — к2) /л _ г + ст —а
2А> ' /1
(2.41)
при анкеровке с опоры, расположенной на прямом участке
на опору, находящуюся на кривой (на рис. 2.6 не показано),
,, Г - “2 [ (1— к)2 4 _ ±г±«! ]
' аз —
пути.
2R
(2.42)
Все обозначения те же, что н в формулах, приведенных выше
(см. рис. 2.2 и 2.6).
Знак «4-» перед величиной z в числителе последнего члена формулы
(2.42) относится к случаю установки анкерной опоры с внешней сто-
роны кривого участка пути, а «знак «—» — к установке ее с внутрен-
ней стороны этого участка. Величину г принимают в зависимости от
места установки анкерной опоры равной zt или z.2. Условия применения
знаков перед величинами аг и а.2 в формуле (2.42) те же, что и в фор-
муле (2.30).
В случае анкеровки усиливающих, питающих или других проводов
без пересечения оси пути по схемам, показанным на рис. 2.7, расчет-
ные усилия определяют по формулам:
при анкеровке на опорах, расположенных с внешней стороны кри-
вой (показано сплошной линией),
(2.43)
при анкеровке на опорах, расположенных с внутренней стороны
кривой (показано штриховой линией),
(2-44>
\ 2R /1 /
при анкеровке с опоры, расположенной на кривой, на опору, на-
ходящуюся па прямом участке пути (показано штрихпунктирной ли-
нией),
при анкеровке с опоры, расположенной на прямом участке пути,
на опору, находящуюся на кривой (на рис. 2.7 не показано),
Р21 = //
(I—к)3
г'-ЬГ
2R
(2.46)
где Л/' — разница в габаритах установки опор на прямых и кривых участках
пути.
43
Верхние знаки в формулах (2.45) и (2.46) относятся к расположе-
нию опор на внешней стороне кривого участка пути, а нижние знаки -
к расположению на внутренней стороне кривого участка пути. Вели-
чину z' в этих формулах принимают в зависимости от места установки
опор равной z( или z(>.
Усилия от изменения направления проводов при зигзагах на пря-
мых участках Р3, если на соседних опорах выполнены равные, но раз-
носторонние зигзаги а, и все пролеты по длине равны,
М, (2.47)
При неравных зигзагах и разных пролетах (рис. 2.8) усилие от
зигзага провода на средней опоре
(и + а, . а +- а., \
(2-48'
Знаки « г» в этой формуле относятся к разносторонним зигзагам,
знаки « -» — к односторонним.
Результирующие нагрузки на опорные устройства могут быть оп-
ределены при отсутствии гололеда как
Q (2.491
при наличии гололеда с ветром
<?Г • Р Gr -PPv- (2.50)
В формулах (2.49) и (2.50) величины Р и Рг представляют собой ал-
гебраическую сумму всех горизонтальных нагрузок, действующих
соответственно ври отсутствии и наличии гололеда.
Для облегчения трудоемких вычислений нормативных нагрузок
при расчетах различных конструкций контактной сети и воздушных
линий в табл. 2.5-2.12 приведены вспомогательные материалы
К этим данным необходимы следующие пояснения
В табл. 2.5 указаны вертикальные нагрузки без учета веса изоля-
торов с арматурой и части веса фиксаторов, передающихся на несущий
трос, которые следует определять в соответствии с конкретными усло-
виями расчета. Эти дополнительные нагрузки зависят от вида поддер-
живающего устройства, рода тока (числа изоляторов), числа контакт-
ных проводов и типа фиксатора. Например, при закреплении несуще-
го троса на неизолированной консоли на прямом участке пути постояв
ного тока (при двух контактных проводах и двух изоляторах в подвес-
ной гирлянде) и на таком же участке переменного тока (при одном кон-
тактном проводе и трех изоляторах в гирлянде) эти дополнительные на-
грузки примерно равны и составляют в среднем около 30 даН.
Аналогичные дополнительные нагрузки к указанным в табл. 2.8
для проводов воздушных линий меньше, так как отсутствуют фикса-
торы. Для одного провода, закрепленного на подвесных изоляторах,
эта нагрузка может быть принята равной 15 даН при постоянном токе
(два изолятора в гирлянде) и 20 даН при переменном (три изолятора).
Для каждого следующего провода, подвешиваемого на этих же изоля-
торах, значения нагрузок надо увеличивать на 2 даН.
В табл. 2.6, 2.7, 2.9 и 2.10 в числителях указаны статические
составляющие ветровых нагрузок, а в знаменателях — полные (т. о
суммы статической и динамической составляющих). Статические со-
ставляющие рассчитаны при коэффициенте, учитывающем неравно-
мерность воздействия ветра по пролету, равном единице. Введение
в расчет любого другого значения этого коэффициента осуществляется
умножением на это значение соответствующей нагрузки (статической
или полной). При определении ветровых нагрузок на металлические
опоры (см. табл. 2.11) для промежуточных опор принят коэффициент
заполнения равным 0,5, а для анкерных опор — 0,6.
Во всех таблицах нагрузки округлены до 1 даН. Нагрузки, соот-
ветствующие условиям, отличающимся от принятых в таблицах, мо-
гут быть определены линейной интерполяцией. Для других скоростей
ветра интерполяцию следует применять с учетом квадратичной зави-
симости ветровых нагрузок от скорости ветра.
Пример. Задание и исходные да н н ы е. Определить верти-
кальную и горизонтальную расчетные нагрузки на консоль от цепной подвески
М-120 (-2МФ-100 на участке постоянного тока при гололеде с ветром. Подвеска
находится на прямом участке пути в условиях, указанных в примере к § 2.2, дли-
на пролета равна 70 м. Результаты, полученные в примере к § 2.2: распределен-
ная линейная нагрузка от собственного веса подвески 2,983 даН/м, от веса голо
леда на подвеске 2,588 даН/м, от веса несущего троса с гололедом 2,429 даН/м;
статическая составляющая ветровой нагрузки на несущий трос при гололеде
1,273 даН/м; нормативная распределенная по поверхности нагрузка в этих усло-
виях 217 Па.
Решение. Примем нагрузку от веса изоляторов с арматурой и части
веса фиксаторов, передающуюся нг несущий трое, равной 30 даН.
45-
Т а блица 2.7
Таблица 2.5
Длина пролета, м Толщина стенкн льда, мм Нагрузки, даН, от веса цепных подвесок
ПБСМ-70-F 4-МФ-юо ПБСМ-95 4- + МФ-100 М-95 + МФ-100 ПБСА-50/70 + + МФ-100 М-1 204-2МФ-1 0 0 ПБСМ-95 + + 2.МФ-100 ПБСМ-70 4- -{-МФ-8 5 1 3® С 4
0 62 69 72 66 119 108 57 60
5 74 82 85 79 138 126 69 74
40 10 94 102 105 100 166 154 88 94
15 120 128 132 127 203 190 114 121
20 153 162 166 161 250 237 146 155
0 86 95 100 90 164 149 79 83
5 102 113 117 109 189 174 95 101
55 10 129 140 145 137 228 211 121 129
15 164 177 182 174 279 262 156 166
20 210 223 228 222 344 326 201 213
0 109 121 126 115 209 190 100 106
70 5 130 144 149 139 241 221 121 129
10 164 179 184 174 290 269 154 164
15 209 225 231 222 356 333 199 211
20 267 284 290 282 438 414 256 271
Таблица 2.6
2 Й} Я £ 5 Q Ч сх ч? Скорость ветра, м/с Ветровые нагрузки, даН, при отсутствии гололеда от проводов ценных подвесок
ПБСМ-70 М-95, ПБСМ-95 М-120, ПБСА-50/70 МФ-100 2МФ-100 (Сж-1 ,85) МФ-8 5
20 14/15 16/17 18/20 15/16 22/24 14/15
25 21/23 24/26 27/30 23/26 34/38 21/23
40 30 31/34 35/39 40/44 33/36 50/56 31/34
35 42/47 48/54 53/60 46/51 68/77 42/47
40 55/62 62/70 70/79 59/67 88/102 54/61
20 19/20 21/23 24/26 20/22 30/33 19/20
25 29/32 33/36 37/41 32/35 47/52 29/32
55 30 42/47 48/53 54/60 46/51 68/76 42/47
35 58/64 66/74 73/82 63/70 93/105 57/64
40 75/85 85/96 96/109 81/92 122/139 74/84
20 24/25 27/29 31/33 26/28 39/41 24/25
70 25 37/40 42/45 48/51 41/44 60/65 37/40
30 54/58 61/66 69/75 58/63 87/95 54/58
35 74/80 84/92 93/102 80/87 118/131 73/80
40 96/105 109/120 123/138 104/114 155/173 95/104
46
2 зЕ ® § Я Толщина стенки льда, мм Скорость, ветра, м/с Ветровые нагрузки, даН, при наличии гололеду от проводов цепных подвесок
ПБСМ-70 М-95, ПБСМ-95 М-120. | П1Х А---.0/70 ! 1 МФ-100 | 1 ->МФ-10(8 1 (<\- 1,-/5 1 МФ - 8 Ъ
1 10 6/6 7/7 f 7/6 5/6 8/9 5 / 5
5 15 14/15 15/16 15/17 12/13 18/19 11/1?
20 24/27 26/29 28/31 ! 21/24 31 -'34 20/22
10 9/10 9/11 10/11 7/7 10/и 7/7
10 15 20/22 21/23 22/24 16/17 23'25 15' 16
20 36/39 37/40 39'43 28/30 40/45 27/30
40 10 12/13 12/13 1 9 / 1 3 8/9 12'13 8/9
15 15 26/29 27/30 28/30 19/20 28,/30 18/20
20 46/51 48/53 50/55 33/36 ; ’/.) 32/35
10 14/15 15/16 16'17 Ю/li 15/16 9/10
20 15 32/35 33/36 31/37 22/24 40/44 33/,/б 22,23
20 58/63 59/65 6! /67 58'114 38/-12
10 8/9 9/10 10/11 7/8 11/12 6 7
5 15 19/20 20/22 21/23 16/17 24/26 15,16
20 34/36 36/40 39/42 29,32 42, 4/ 28.30
10 12/13 13/14 13/14 9/10 14, 15 9/10
10 15 28/29 29/31 30/33 21/23 31/33 21/22
20 49/53 52/55 54/59 38/41 56 / 61 37/43
10 16/17 17/18 17/18 11/12 17/18 11/12
15 15 36/39 37/40 39/42 26/28 36/38 25/27
20 63/69 66/72 68/ 75 46/50 68/75 45/49
10 20/22 20/22 21/23 14/15 20/22 13/14
20 15 44/47 45/49 47/50 31/33 45/49 30/32
20 79/87 81/89 84/92 55/60 80/88 53/58
10 10/11 12/13 12/(3 9/10 20/21 14/15 8 '9
15 24/25 26/27 27/29 3] /33 19/20
20 43/46 46/49 49/53 37/40 .’>4 58 35/37
10 15/16 35/37 16/17 17/18 12/13 18/19 12/13
10 15 36/39 39/41 27/29 39/42 27/28
20 62/67 64/69 69/74 48/52 71/76 48/51
70 10 20/21 21/22 22/23 15/16 21 /22 14/15
15 15 46/48 48/51 49/52 33/35 49/52 32,34
20 81/87 84/90 87/94 58/62 87/94 57/61
10 25/26 26/27 27/29 17/18 26/27 57/61 102/110 17/18
20 15 56/60 57/61 60/63 39/42 38/40
20 101/109 103/111 107/115 70/75 67/72
47
. ш 4* Шк..
Т а б л и ц а 2.8
Длина пролета, м Толщина стенки льда, мм Нагрузки, даН, от веса проводов и проволоки
Л-150 Л-185 ЛС-35/6,2 АС-50/8,0 ЛС-70/1 1 6БСМ
0 16 20 6 8 11 9
5 28 32 13 16 20 16
40 10 45 50 26 30 34 27
15 68 74 45 49 55 44
20 95 103 69 72 80 66
0 22 27 8 10 15 13
5 38 44 18 22 28 21
55 10 62 69 36 41 47 37
15 93 10! 62 67 75 61
20 131 141 95 100 111 91
0 28 34 11 13 19 16
5 48 56 23 28 35 27
70 10 78 88 46 52 60 48
15 118 129 78 85 96 78
20 167 180 120 127 141 116
Таблица 2.9"
I Д.:ьн<1 1 пролета, • м Скорость ветра. м/с Ветровые нагрузки, даН, при отсутствии гололеда от проводов
А-150 А-185 АС-35/6.2 АС-50/8,0 АС-70/11
20 19/20 21/23 10/11 11/12 14/15
40 25 30/32 32/35 16/17 18/20 24/26
30 43/47 47/52 23/25 26/28 31/34
35 58/64 64/72 31/34 35/38 42/46
40 75/84 88/99 40/45 46/51 54/61
20 26/28 29/31 14/15 15/17 19/20
55 25 41/44 45/48 21/23 25/27 32/35
30 59/64 65/71 31/34 36/39 42/46
35 79/87 89/98 42/46 48/53 58/64
40 103/115 121/135 56/64 63/70 75/83
20 33/35 36/39 18/19 20/21 24/25
25 52/55 57/61 27/29 32/34 41/44
70 30 75/81 83'89 40/43 46/49 54/58 74/80
35 101/109 113/122 54/58 61 /66
40 132/144 154-'!68 71/77 81/87 95/104
Шип»»#'««>•»»./is- №. fe»*..»
18
Таблица 2.10
Длина Толщина Ветровые нагрузки, даН, при наличии гололеда от проводов
пролета, стенки льда, мм ветра, м/с
А-150 Л-185 АС-35/6,2 АС-50/8.0 ЛС-70/ 1 1
10 8/8 8/9 6/6 6/6 6/7
5 15 18/19 18/20 12/13 13/14 14/15
20 31/33 32/35 22/24 24/26 26/28
10 10/11 11/12 8/9 9/9 9/10
10 15 24/26 25/27 19/21 20/21 21/23
лп 20 43/47 45/49 34/37 35/38 37/41
4 и 10 14/15 14/15 11/12 11/12 12/13
15 15 31/33 32/34 26/28 27/29 28/30
20 54/6! 57/63 46/50 48/52 50/55
10 17/18 17/18 14/15 15/16 16/17
20 15 37/40 39/42 32/35 33/36 34/37
20 67/74 69/75 58/64 59/65 62/68
10 11/12 11/12 8/8 8/9 9/9
5 15 24/26 25/27 17/18 18/19 19/20
20 42/46 45/48 30/33 32/35 35/38
10 14/15 15/17 1 1/12 12/13 13,14
10 15 34/36 34/37 26/28 27/29 29/31
ее 20 59/65 62/67 46/50 48/53 51 /56
DD 10 19/20 20/21 15/16 16/17 17/18
15 15 43/46 43/47 36/38 37/40 39/41
20 75/82 78/86 63/69 65/71 69/75
10 23/25 24/26 20/21 20/22 22/23
20 15 51/56 53/58 45/48 46/49 47/51
20 92/101 95/104 80/87 81/89 85/93
10 14/15 14/15 10/10 10/11 11/12
5 15 31/33 32/34 21/22 23/24 25/26
20 54/58 57/62 39/41 41/44 45/48
10 18/19 19/20 15/15 15/16 17/18
10 15 43/45 43/46 34/35 35/37 37/39
70 20 76/8! 78/84 59/63 62/67 65/70
i \/ 10 24/25 25/26 20/21 20/21 21/22
15 15 54/57 55/59 46/48 47/50 49/52
20 95/103 99/107 81/86 83/89 88/94
10 29/31 30/32 25/26 26/27 27/29
20 15 65/69 68/72 57/60 58/62 60/64
20 117/126 121/131 102/109 104/112 108/116
4 Я
Таблица 2.11
j Скорость вен
Ветреные нагрузки, даН. на опоры
Oj CO 1 MH 4 5 - i | MH - I 05 4 3 25 10
66 c 1S|L 15 M 15 ’ ! M “T”' м J±J
1 HW 1 1 MH - 65 15' MH | MH- 1 50 20 M- i 5 M' i J 5 7." 111
Поперек пути
10 15 19 46 49 70 79 79 28 61
15 34 43 103 11! 158 177 177 61 138
20 61 77 134 197 280 315 315 114 245
25 95 120 237 308 438 493 492 178 383
30 ! 36 17? 4 ! 'i 443 6. if j 705 709 25'1 552
35 136 234 563 tn»3 858 965 965 348 751
40 243 306 735 788 1120 1260 1260 455 981
liPuJIb tllJTI!
10 15 19 , -3 66 1(!5 123 59 43 44
15 34 43 113 148 236 276 1зз 96 9!)
20 6! 77 210 263 420 490 236 171 175
05 95 120 328 410 656 766 369 267 274
30 136 172 471 591 945 1103 53? 384 395
136 234 643 304 1286 1501 724 523 537
40 243 306 840 1050 1680 196(1 945 683 701
Таблица 2.12
Радиус i кривой, M 1 I Длина пролета. м Нпгрузкк. даН. от излом.) пронмдов па кривых при натяжения х , даН,
•1 5 0 G00 851) 1 000 1 500 ! 80 0 2000
300 30 35 60 85 100 150 180 200
40 47 80 113 133 200 240 266
400 35 3! 53 74 88 131 158 175
45 39 68 96 1 13 169 203 225
500 40 28 48 68 80 120 144 160
50 35 60 85 100 150 180 200
700 45 23 39 55 64 96 116 129
55 28 47 67 79 118 141 157
1000 50 18 30 43 50 75 90 100
60 21 36 5! 60 90 108 126
1500 55 13 22 31 37 55 66 73
65 15 26 37 43 65 78 87
2000 60 11 18 26 30 45 54 60
70 12 21 30 35 53 63 70
50
Вертикальную расчетную нагрузку на консоль рассчитаем, используя фор
мулу (2.21) и принимая коэффициенты надежности по нагрузке равными для соб-
ственного веса 1.1 и для веса гололеда 1,3 (см. § 2.1):
Gf = (2,983-70-ЬЗО) 1,1+2,588-70-1,3 498 даН.
С учетом коэффициента надежности по назначению, равного 0,95 (ем. § 1.2).
искомая расчетная цщрузка
G, -- 498-0,95: 473 даН.
Для определения горизонтальной расчетной нагрузки сначала нужно най-
ти статическую составляющую ветровой нагрузки, передающуюся на консоль.
Руководствуясь рекомендациями § 2.2. принимаем 0 0.85 при В 100 Па.
Используя формулу (2.25) получим
I ,273-70-0,85 75,74 даН.
Динамическую составляющую ветровой нагрузки определим по формуле
(2.I0).
/>1Д - 0,88-75,74-0,56-0,152•1,03 5,84 даН.
Здесь коэффициент q 0,56 для пролета длиной 70 м. коэффициент J; для
веса несущего троса с гололедом более 2 даН/м 1,03. По формуле (2.17) вычи-
слим скорость ветра
и [/ 1,6-217 18,6м/с,
для которой методом интерполяции найдем б 0,152.
Полная нормативная горизонтальная нагрузка па консоль
/'" -75,74 , 5,81 81,58 даН;
расчетная нагрузка при коэффициенте надежности по нагрузке 1,25 и коэффи
циенте надежности по назначению 0,95 (см. § 2.1)
Р -81,58-1,25-0,95 97 даН.
§ 2.4. Расчеты нагрузок,
возникающих при сооружении и эксплуатации
Рассчитывая опоры, поддерживающие и фиксирующие устройства
контактной сети, необходимо, кроме приведенных в §2.3, учитывать
также кратковременные нагрузки, возникающие при транспортиров-
ке и установке опор, монтаже контактных подвесок и проводов воз-
душных линий, а также нагрузки, возможные в эксплуатации (кроме
особых, рассмотренных в § 2.5).
Дополнительной и при сооружении и при эксплуатации контактной
сети может быть нагрузка от веса человека, поднимающегося на опору
или находящегося на поддерживающем либо фиксирующем устройст-
ве. Эту нагрузку учитывают при расчетах горизонтальных и наклонных
элементов решеток металлических опор и жестких поперечин при угле
их наклона 30° и менее, а также при расчетах консолей и фиксаторных
кронштейнов; в расчетах гибких и фиксирующих поперечин ее, как
правило, не учитывают. Обычно нагрузку от веса одного человека при-
нимают равной 100 даН (с учетом веса инструмента и деталей, которые
51
Рис 2.9 Схемы укладки опор при их
транспортировке
Рис. 2.10. Схемы установки опор кра-
ном
могут быть при нем). Для учета возможных в условиях эксплуата-
ции отклонений в натяжениях проводов, определяя расчетные нагруз-
ки основных сочетаний для расчетов анкерных опор и их оттяжек,
натяжения анкеруемых проводов увеличивают на 15 %.
Кратковременные нагрузки в процессе транспортировки опор нуж-
но учитывать в зависимости от способа их укладки при перевозке
(рис. 2.9). Для схем а, б и « на рис. 2.9 нагрузки определяют как рав-
номерно распределенные от веса опор. Если подпорка находится в се-
редине панели металлической опоры, имеющей решетку (рис. 2.9, с),
то пояса опоры следует проверять на местную нагрузку, определяе-
мую в зависимости от числа и мест расположения подпорок.
Дополнительные нагрузки, возникающие при установке опор, за
висят оттого, как организованы соответствующие работы. При уста-
новке опор крапом возможны расчетные схемы, приведенные па
рис. 2.10, а, б и в. Схема рис. 2.10, в может быть применена и при
установке опор с помощью падающей стрелы.
Чтобы определить нагрузки от собственного веса конструкций
при их погрузке, выгрузке и транспортировке, применяют коэффи-
циенты, учитывающие возможность динамических воздействий: 1,25
при подъеме кранами, 1,6 при перевозке. Опоры и ригели, уложен-
ные в несколько вертикальных рядов, проверяют на воздействие веса
вышележащих конструкций на расположенные в нижнем ряду.
В процессе монтажа цепных подвесок непосредственно в рабочее
положение обычно не возникают дополнительные нагрузки, которые
следовало бы учитывать в расчетах опорных устройств. Если же мон-
таж производится комбинированным методом или сборка цепной
подвески выполняется у основания опор, а затем ее поднимают в ра-
бочее положение (монтаж понизу), то возникают дополнительные на-
грузки, которые нужно учитывать.
52
»—• «. s; • йг. :.адв чгв**
При комбинированном методе монтажа цепной подвески несущий
трос раскатывают понизу, придают ему необходимое натяжение, ан-
керуют, устанавливают струны и рессорные тросы, а затем переводят
в седла. Как правило, несущий трос поднимают ни консоли, разверну-
тые вдоль пути. В этом случае на консоль будет действовать верти-
кальная нагрузка G„ (рис. 2.11, й):
G^ (бя F 7 м h// ) Кд, (2 .) 1 I
где Тм -натяжение несущего троса во время монтажа, даН:
6’,, — нагрузка от веса пролета несущего троса, даН;
- коэффициент, учитывающий возможность динамического нощей
ствия нагрузки (обычно его принимают равным 1,25);
I/ и 1' — размеры, показанные на рис. 2.11, а:
Длина _______
/' -']/ 2TMh!uH , (2.52)
где g распределенная линейная нагрузка от веса нест щего троса, даН м
Для уменьшения монтажной нагрузки подъем несущего троса иног-
да производят сразу на нескольких опорах. При этом размер h в фор-
мулах (2.51) и (2.52) должен соответствовать конкретным условиям.
В отдельных случаях неизолированные консоли располагают- не
вдоль пути во время монтажа, а перпендикулярно опорам, т. е. в ра
бочем положении. Тогда при переводе несущего троса на консоль, кро-
ме вертикальной нагрузки См, увеличенной на нагрузку от веса чело-
века, находящегося на консоли, будет действовать еще горизонта п>
ная нагрузка Рм (рис. 2.11,6):
I’m 'I м Кд Т ’ (2 -1:)
где г расстояние но горизонтали между точками крепления несуinei о грога
на соседней опоре и па расчетной консоли, м:
/ длина пролета, м.
На кривых участках пути при любых положениях консолей надо
еще учитывать дополнительное усилие от изменения направления
троса, определяемое по формулам (2.28)- (2.35).
В процессе монтажа цепной подвески методом понизу, что допус-
кается только па неизолированных консолях, подъем собранной вни-
зу подвески при одном контактном проводе производят сразу в седла
на развернутые вдоль пути консоли (показано сплошной линией на
рис. 2.12), а при двух подвеску сначала поднимают к месту крепления
тяги на опоре (показано штриховой линией) и затем уже переводят
в седла. При этом действует вертикальная нагрузка Оф
I . . Ф .1
Gm G ; (?м + ^) Кд б’.,, (2.54)
1 ' 1 'к I
где О' - нагрузка от веса пролета подвески, даН:
К — натяжение контактного провода (проводов), даН;
G4 — нагрузка от веса одного человека с инструментом, даН;
— расстояние от оси опоры до точки крепления несущего троса на кон-
соли, м;
ф высота, па которую поднимается подвеска, м.
Рис ii.11 Схема нагрузок при подъеме
несущего троса
Рис 2 12. Схема нагрузок при полис
ме контакт ной подвески
Как и при комбинированном методе монтажа, для уменьшения мон-
тажной нагрузки па консоль при монтаже понизу иногда подъем под-
вески производят одновременно па двух и более опорах. В этом слу-
чае шачеиие ht в формуле (2.54) выбирают и соответствии с конкрет-
ными условиями монтажа.
Подъем цепной подвески с двумя контактными проводами, а также
подвески с одним контактным проводом на внутренней стороне кривой
иногда осуществляют сначала под пяты всех консолей анкерного уча-
ciKa. а затем переводят в седла (показано штрихпунктнрной линией
на рис. 2.12). При этом вертикальную монтажную нагрузку можно
определи!ь по формуле (2.54), заменив размер на /и. Если подвес-
ку переводят на консоли, находящиеся в рабочем положении, то .зна-
чение в формуле <2.54) необходимо принять равным пулю, а гори-
юнтальную монтажную нагрузку определять по формуле (2.53), учиты-
вая в ней суммарное натяжение всех проводов подвески. При монтаже
в кривых следует также учесть усилия от изменения направления про
водов аналогично указанному для несущего троса.
Нагрузки G4 и G,', при некоторых монтажных условиях приведе-
ны в габл. 2.13, где значения 7\, и 7\, • А' приняты округленными;
пользуясь ими, возможно определять нагрузки при других условиях
путем интерполяции.
При вычислениях этих нагрузок принималось: h h, 7,5 м:
h., 3 м: 3,5 м.
Нагрузки Р„ на каждые 100 даН натяжения монтируемых прово-
дов в зависимости от габаритов установки опор на прямых участках
пути Г и длины пролета / следующие:
/’, ,м 3.1 3.5 4.9 5.7
Рм. даН, при /, м:
50 . .... 7,75 8,75 12,25 14,25
60 . . 6,45 7,30 10,20 11 .90
70 5.55 6.25 8.75 10,20
54
При вычислении нагрузок Рм принимали z Г
Пример. Задание и исходные дан и ы е. Определить нагрузку
на консоль, находящуюся в рабочем положении (перпендикулярно оси путик
при переводе раскатанного понизу несущего троса ПБСМ-95 н седло на прямом
участке пути с пролетами длиной 65 м. Габарит установки опоры 3.3 м.
Р е ш е н и е. Натяжение троса при монтаже примем равным 600 даН.
Вертикальную нагрузку на консоль определим по формуле (2.51). Распреде-
ленная линейная нагрузка троса по табл. 1.5 составляет 6.759 даН м. Размер h
(см. рис. 2.1 1) примем равным 7,5 м. а Г найдем по формуле (2.52)
Г - V2-600.7,5/07759-- (08.9 м
Следовательно, вертикальная нагрузка
(0,759-65-1 600-7,5; 108.9) 1,25 113.3 даН
Коэффициент динамичности принят равным 1,25.
Горизонтальную нагрузку иа консоль определим но формуле (2.53)
Рм-----ООО-3,3-1.25-65 -38 даН
Полная нагрузка на консоль
ум - У П3.3~18“ 120 даН
Если во время подъема несущего троса на консоли будет находиться ч-л..-
век, то вертикальная нагрузка на нес увеличится на 100 даН, тогда полная на-
грузка
4?м j/213.32 : 38:Г 217 даН.
Табл и ц а 2,13
Несущие тросы и подвески 7. м Hi гречки (1м И (ГМ\ 7 даН, к ©ответственно при Гм и М 'А - Д«Н
500 1000 1 500 2 000 2 30 0 300(|
ПБСМ-70 50 80 120 160 __
70 95 135 175 — —
ПБСМ-95 и М-95 50 100 145 195 245 —
70 120 105 215 265 --
М-120 50 120 175 230 290 —
70 145 200 255 310 —
ПБСМ-70 МФ-100 50 160/305 550/340 635 >375 -
70 — 4.30/315 490/340 555'365 —
ПБСМ-95 -- МФ-100 50 .... 170/315 560/350 645/385 7.35/445
70 — 435/330 505/355 570 380 6.15/405
ПБСМ-95+2МФ-100 50 535/375 620/410 710/445 795/480
70 — —- 530/415 59,5/440 645/465 720/490
М-12О+2МФ-100 50 550/390 635/425 725/460 810/495
70 555/440 615/465 680/490 745/515
Примечание В числителе указань» нагрузки яри переводе нодмч’ок в седла от
низа опоры (ft, «.-7,5 м), в знаменателе--при переводе подвесок от пяты консоли (Н? —
- л и).
55
§ 2.5. Расчеты особых нагрузок
В условиях эксплуатации устройств контактной сети и воздушных
линий наибольшую опасность для их нормальной работы представляют
особые нагрузки, возникающие при обрыве проводов и воздействиях,
возможных в районах с высокой сейсмичностью.
По рекомендациям ВСН 141-84 на нагрузки, возникающие при
обрыве проводов контактной подвески, нужно рассчитывать консоль-
ные опоры, жесткие поперечины, консоли и фиксаторы. Опоры гибких
поперечин на эти усилия не проверяют. Расчет консольных опор и
других конструкций па особые сочетания нагрузок, включающие уси-
лия при обрыве проводов, следует выполнять только по несущей спо-
собности (первому предельному состоянию). Для металлических кон-
струкций расчетное сопротивление стали следует принимать равным
нормативному при наличии гололедных образований и 95 % норма-
тивного при отсутствии гололеда. Для железобетонных опор расчет-
ное сопротивление стали может быть повышено па К) %, а бетона
па 25 %.
Анкерные опоры следует проверять па максимальные натяжения
анкеруемых проводов, увеличенные еще на 15 "о, для учета динамиче-
ского воздействия нагрузки при обрыве несущего троса или контакт-
ного провода. Силу, направленную вдоль пути и действующую на опо-
ру средней анкеровки компенсированной подвески, определяют с уче-
том максимального натяжения в дополнительном тросе и 40 % натяже-
ния в несущем тросе.
При проверке консольных опор и консолей на нагрузку, возникаю-
щую вследствие обрыва проводов, обычно учитывают обрыв только
одного несущего троса, что создает наиболее неблагоприятные усло-
вия. В этом случае считают, что на конце консоли приложена верти-
кальная нагрузка, которую можно определить как
б’д =GlliaxKn, (2.55)
i.le Glll!i4 -нагрузка от веса максимального пролета ценной подвески при
расчетном режиме, даН;
Кд — динамический коэффициент, принимаемый равным 1,9.
Если расчетным является режим гололеда, то, учитывая сброс
гололедных образований при обрыве подвески за время с начала обры-
ва до момента достижения наибольшей динамической нагрузки, рас-
четную толщину стенки льда можно принимать равной 50 % норма-
тивной для статических условий.
Изгибающие моменты, действующие па консольную опору при
обрыве проводов, — полный Л4Д, вдоль пути Л4Ж и поперек пути Му -
можно определить следующим образом:
Л1;1 -- (6'д-|- Gu) n,;4-GH а,; (2.56)
Л1.х--Л1д sin р; (2.57)
ЛЕ -AEcosp, (2.58)
56
Ь ... -i. si.
где 6'и — нагрузка от веса изоляторов, даН;
— расстояние от оси опоры до точки крепления несущего троса, м;
GK — нагрузка от веса консоли, даН;
di — расстояние от оси опоры до центра тяжести консоли, м;
р — угол между повернувшейся консолью и линией, перпендикулярной
к оси пути:
sin Р Ь/ак\
b — проекция консоли на ось пути, которую принимают равной конструк-
тивной высоте цепной подвески (независимо от длины пролета), м.
Для опор с жесткими поперечинами продольные нагрузки на ноне-
речипу рекомендуется определять исходя только из условий заделки
несущего троса в седле
Т’об | 1Г, (2.59)
где 7’об - усилие, действующее на поперечину вдоль пути, даН;
лс — коэффициент сопротивления перемещению несущего троса в
седле (7гс 0,75 для троса ПБСМ-95: /г(. 0,7 для М-120;
kc 0,2 для С-70);
//" дополнительная сила сопротивления выдергивания троса, зажа-
того в седле плашками, даН (77' 150 даН для тросов ПБСМ-95
и М-120; /7' 210 даН для С-70);
''-'max то же, что в формуле (2.55).
Для примера в табл. 2.14 приведены рекомендуемые ВСН 141-84
максимальные вертикальные силы и изгибающие моменты, определен-
ные для основных контактных подвесок на участках постоянного и
переменного тока при наибольших длинах пролетов и самых неблаго-
приятных погодных условиях.
При определении продольной нагрузки на жесткие поперечины ди-
намический коэффициент не вводится, так как максимальная динами-
та б л и ц а 2.14
Габарит установки опоры, м Расчетные данные без гололеда Расчетные данные при гололеде
дан Мд. ДаН • м МХ. да Н • м М„, даН-м 7 об . да Н сд. ДаН Мд. да Н • м ЛГу, даН м м,/. даН • м 7 об. ДаН
Подвеска М-120-\-2МФ-100, длина пролета 75 м
3,1 420 1530 1030 изо 315 672 2370 1600 1750 415
3,5 420 1720 1035 1370 315 672 2660 1600 2130 415
4,9 420 2440 1040 2200 315 672 3735 1600 3380 415
5,7 420 2860 1060 2660 315 672 4340 1620 4050 415
Подвеска ПБСМ-95-\-МФ-100, длина пролета 7 2 м
3,1 236 870 590 640 250 415 1470 990 1085 320
3,5 236 970 590 780 250 415 1650 990 1320 320
4,9 236 1390 590 1250 250 415 2320 995 2090 320
5,7 236 1770 650 1640 250 415 2870 1060 2700 320
57
ческая нагрузка не совпадает с моментом проскальзывания. В расчете
жесткой поперечины на вертикальную нагрузку от обрыва проводов
подвески, которую определяют по формуле (2.55), действие продоль-
ной силы не учитывают. При наличии на жесткой поперечине стоек
с поворотными консолями место приложения вертикальной нагрузки
определяют с учетом поворота консоли на угол р.
Нагрузки в случае обрыва проводов на опорах с питающими или
другими воздушными линиями (при отсутствии на них консолей с цеп-
ной подвеской) определяют исходя из того, что оборвался один из
подвешенных проводов, обусловливающий наибольший изгибающий
или крутящий момент на опору. Продольную силу, действующую на
опору вдоль линии и приложенную в точке крепления оборванного про-
вода, принимают равной 50 % наибольшего натяжения провода, под-
вешенного на металлических опорах, и 30 % при подвеске на железо-
бетонных. Нагрузки, возникающие в случае обрыва проводов, на кон-
цевые, угловые и анкерные опоры определяют из условий обрыва 1/3
проводов одного пролета, создающих максимальный изгибающий или
крутящий момент для опоры.
При проектировании устройств контактной сети и воздушных
линий в районах с высокой (8- -9 баллов) сейсмичностью осуществля-
ют ряд мероприятий для устранения или существенного снижения сей-
смически?; воздействий. Например, применяют только компенсирован-
ные контактные подвески, при которых уменьшаются направленные
вдоль пути сейсмические нагрузки на опоры и изоляторы. Стараются
не устанавливать штыревые и опорные изоляторы; на конструкциях с
некомпенсированными проводами предусматривают дополнительные
крепления Фундаменты, опоры и соединенные с ними жестко ригели
рассчитывают с учетом сейсмических воздействий в соответствии со
специальными нормами. При расчетах консолей, фиксаторов и других
конструкций, соединенных с опорой шарнирно, сейсмические нагрузки
не учитывают.
Расчеты опор контактной сети и воздушных линий выполняют для
двух направлений распространения сейсмических волн. Если они на-
правлены перпендикулярно проводам, то проверку опор контактной
сети производят по прочности и деформациям, а опор воздушных ли-
ний, - кроме того, с учетом дополнительного момента от массы про-
водов, получающегося в результате наклона опоры. Если же направ-
ления сейсмических волн и проводов совпадают, то определяют дефор-
мации опор на уровне подвешивания проводов; затем но разности де-
формаций опор находят изменение натяжения проводов (вследствие
изменения длины пролета некомпенсированных проводов, начиная
с анкерной опоры). По этим данным определяют продольную силу
в точках крепления проводов к изоляторам, по которой и проверяют
прочность всех креплений.
В расчетах на сейсмостойкость опору рассматривают как систему
е двумя степенями свободы и массой, сосредоточенной в вершине и в
середине опоры. Расчетные изгибающие моменты вычисляют только
.58
для первой формы колебаний. Коэффициент динамичности при оп-
ределении сейсмических сил увеличивают ь 1,5 раза.
Поимео. Задание. Определить вертикальную силу и изгибающие мо-
менты₽ которые нужно учитывать в расчете консоли на обрыв несущею троса
’.ТТЛ I
тока расположен в гололедном районе 1\. Длина пролета / < опораi. i
соль которой приходится натяжение оборвавшс! ot я р >е« ,
ВеТ°р е ш'е 'н Уе Вертикальную нагрузку, приложенную к концу консоли при
обпывеНесущего троса, определим по формуле (2.55) Распределенную линейную
нагрузку от веса подвески с гололедом (учитывая толщину стенки ль ла в разм<И
50 % нормативной в гололедном районе IV. г. е. 10 мм) находим по шол. р<.
ной 2,34 даН/м. Тогда
Од 2,34-70-1,9 - 311 даН.
ра в*
веса
Принимая нагрузку от веса изоляторов е деталями равной лаН,
стояние от оси опоры До точки крепления несущего троса о,Эм, на i узку or
консоли 80 даН и расстояние от оси опоры до центра тяжести коне >ли . ,
определим полный изгибающий момент, действующий на консоль при обрыве
несущего троса, но формуле (2.56)
Л4д -- (311 Ч-30) 5,9 -1-80.3.5 - 2292 даН-м.
Если принять проекцию консоли на ось пути равной конструктивной высо-
те подвески, которая при переменном токе составляет 1,8 м, ь-
sm [5 -1,8/5,9 -0,305; cos (5 0,952.
Следовательно,
--2292-0,305 -700 даН-м;
М .2292-0,952 2180 даН-м.
Глава 3
РАСЧЕТЫ ВЕТРОВЫХ ОТКЛОНЕНИЙ ПРОВОДОВ И ДЛИН
ПРОЛЕТОВ МЕЖДУ ОПОРАМИ КОНТАКТНОЙ СЕТИ
§ 3.1. Общие положения
Длина пролета между опорами контактной сети во многом опре-
деляет ее надежность и экономичность. Чем больше длина пролета,
тем меньше число опор и, следовательно, существенно меньше строи-
тельная стоимость контактной сети (стоимость опор и фундаментов
достигает 40 % общей стоимости сети). Но с увеличением длины про-
лета увеличиваются отклонения проводов под действием ветра (их
называют ветровыми отклонениями), в результате чего при определен-
ных условиях контактный провод может сойти с полоза токоприемни-
ка и попасть под пего. Это приводит к разрушению токоприемника и
повреждению струн и фиксаторов, а в отдельных случаях - к обрыв)
контактного провода. Кроме того, увеличение длины пролета повы-
шает неравномерность эластичности (жесткости) контактной подвески
вдоль пролета, что может затруднить нормальный токосъем (см. гла-
вы 4 и 5). При слишком большой длине пролета труднее выдержать
установленные нормами экстремальные значения положения контакт-
ных проводов но высоте от уровня головок рельсов. Ветровые откло-
нения проводов с увеличением длины пролета растут в квадратичной
зависимости, что может привести к нежелательным и даже опасным
приближениям проводов к заземленным конструкциям.
Для токоприемников, эксплуатируемых в СССР, ширина рабочей
части которых составляет около 1,3 м, установлены максимальные
допускаемые ветровые отклонения контактных проводов Ькдп от оси
токоприемника: 0,5 м для прямых участков пути и 0,45 м для кривых.
Эти значения необходимо соблюдать, учитывая возможную порывис-
тость ветра, влияние отклонения несущего троса, а также дополнитель-
ного (под действием ветра) прогиба опор на уровне контактного про-
вода.
При проектировании контактной сети максимальную допускае-
мую длину пролета определяют из условия
Ьц шах *к дг. • (31)
где Ьк max - максимальное ветровое отклонение контактного провода в про-
лете.
При двух контактных проводах величины Ьктах и Ькяп относят
к дальнему от оси токоприемника проводу. Для выполнения условия
(3.1) необходимо очень тщательно соблюдать параметры контактной
сети, заданные проектом, при ее эксплуатации.
60
ЦЯНЯ»*--- --
.. i—1. ь. .
---------Ось токоприемника.
—------ Контактный пробод
Рис, 3 1. Расположение в плане контактного провода (сплошные линии) при раз-
личных зигзагах относительно оси токоприемника (штрихпуиктирные)
Максимальное ветровое отклонение контактных проводов обычно
наблюдается при ветре наибольшей интенсивности и отсутствии голо-
леда, но в отдельных случаях может возникнуть и при воздействии
ветра меньшей силы на провода, покрытые гололедом. При расчетах
ветровых отклонений контактных проводов не учитывают их возмож-
ный износ, так как в этом случае ветровые отклонения уменьшаются.
Скорость ветра имеет постоянную и переменную составляющие,
поэтому и полное отклонение провода под действием ветра можно опре-
делить как сумму статической п динамической составляющих. Стати-
ческая составляющая перемещения провода определяется по обычно
применяемым формулам, но с учетом изменения натяжения провода,
вызванного его колебаниями. Так как пульсации скорости ветра слу-
чайны, то динамическая составляющая перемещения провода опреде-
ляется средним квадратичным отклонением значения этого перемеще-
ния. Точные расчетные формулы для практического проектирования
довольно сложны. Поэтому в § 3.2 приводятся только упрощенные
расчетные формулы, погрешность которых не превышает 5% (по срав-
нению с результатами расчетов по точным формулам).
Обычно зигзаги контактных проводов на прямых участках пути
принимают разносторонними на смежных опорах и равными 0,3 м,
но в необходимых случаях (например, на воздушных стрелках или
сопряжениях анкерных участков) их заменяют. На кривых участках
нормальный односторонний зигаг принимается равным 0,4 м. В этом
случае контактный провод образует хорду по отношению к оси токо-
приемника (рис. 3.1, а). Однако при больших радиусах кривых такие
зигзаги могут вызвать нежелательное расположение контактного
провода (рис. 3.1, в). Поэтому при максимальной длине пролета на
прямом участке /пр в таких же расчетных условиях для кривых при-
нимают зигзаг а 0,4 м, если радиус кривой R < /,21р/3,2; при R >
> /пр/3,2 используют формулу
а = /пр/(8«). (3.2)
В последнем случае контактный провод в середине пролета будет
располагаться по касательной к оси токоприемника (рис. 3.1,6).
Предельные радиусы кривых /?пр, при которых еще допустимы
зигзаги контактных проводов, равные 0,4 м, в зависимости от длины
пролета на прямых участках /пр той же трассы, следующие:
iup, м.......... 35 40 45 50 55 60 65 70 75
/?пр, м......... 383 500 633 781 945 1125 1320 1531 1758
61
Длина пролета Znj, должна быть определена при нормальных раз-
носторонних зигзагах контактного провода. Если принять длину, до-
пустимую при отсутствии зигзагов (т. е. расположить провод, по оси
пути), то вследствие того, что йвд., для кривых участков пути меньше,
чем для прямых, радиус превышение которого обусловливает
зигзаги, меныпие 0,4 м, будет вычислен неправильно.
При проектировании контактной сети на конкретном участке для
определения максимальной допускаемой длины пролета можно вос-
пользоваться номограммами, приведенными в ВСН 141-84 и в выпус-
ке 2-86 Инструктивно-методических указаний Трансэлектропроекта.
Эти номограммы построены для многих контактных подвесок постоян-
ного и переменного тока, закрепленных на изолированных и неизоли-
рованных консолях, расположенных на прямых участках пути и в
кривых радиусами от 300 до 2000 м. Расчеты для построений выпол-
нены по методике, учитывающей динамические нагрузки, для раз
личных ветровых нагрузок и интенсивностей гололедных образований.
Чтобы пользовагься номограммами, достаточно знать только норма-
тивные скорость ветра и толщину стенки льда па проводах подвески
на данном участке трассы.
В ВСН 141-84 указано, что при необходимости максимальную до-
пускаемую длину пролета, определенную по номограмме, корректи-
руют по режиму гололеда с ветром. Принимают меньшее из двух зна-
чений, полученных ври расчетных режимах ветра максимальной ин-
тенсивности и гололеда с ветром.
Отмстим следующее. Выполненными нами исследованиями установлено, что
длина пролета в случае гололеда с ветром меньше, чем при максимальном ветре
без гололеда, только в районах со значительной интенсивностью гололедных об-
разований. Но при наличии большого гололеда на контактных проводах не смо-
жет осуществляться движение поездов и, следовательно, не нужно опасаться
схода токоприемника с контактного провода. Л после того как гололед, даже
частично, будет удален (планкой или механическими средствами) или образова-
ние его будет предотвращено профилактическим подогревом проводов, ветровое
отклонение контактного провода станет меньше, чем при ветре максимальной ин -
тенсивности. Таким образом, уменьшение длины пролета из-за ветровых откло
нений контактного провода при режиме гололеда в ряде случаев приведет к не-
оправданному увеличению строительной стоимости контактной сети По нашему
мнению, максимальную допускаемую длину пролета следует определять только
при режиме ветра наибольшей интенсивности независимо от размеров гололед-
ных образований.
В местностях с особо сильными ветровыми воздействиями целе-
сообразно проектировать контактные подвески повышенной ветро-
устойчивости. К ним относятся подвески косые, ромбовидные при
двух контактных проводах и с оттяжными тросами ври одном контакт-
ном проводе. Косые подвески очень сложны в эксплуатации, для них
требуются специальные поддерживающие устройства, вследствие чего
их практически не применяют. Подвески с оттяжными тросами в СССР
пока также не получили распространения вследствие конструктивных
затруднений, но в дальнейшем применение их вполне вероятно. Наи-
более широко используют ромбовидные подвески. Так как при ромбо-
62
Рис. 3.2. Схемы расположения в
плане контактных проводов ромбо-
видных подвесок
видных подвесках увеличивается износ средней части контактных
пластин токоприемников, то их общая протяженность в пределах уча-
стка обслуживания не должна превышать 20 %.
Повышение ветроустойчивости ромбовидных подвесок (рис 3.2),
как и подвесок с оттяжными тросами (рис. 3.3), достигается путем
уменьшения свободной длины пролета и увеличения поперечной жест-
кости подвесок
Контактные подвески, выполненные по схемам рис. 3.2. а и 3.3. а,
характеризуются высокой ветроустойчивостью, ио при лом требуется
устанавливать обратные фиксаторы на всех опорах. На двухпутных
участках расстояния между стержнями основных фиксаторов сосед-
них путей могут оказаться меньшими, чем. требуется правилами тех-
ники безопасности. Поэтому на эксплуатируемых электрифицирован-
ных линиях могут быть смонтированы подвески по схемам рис. 3.2, б
и 3.3. б, в которых устройство ромбов или установка оттяжных тросов
поедусмотрены не на каждой опоре, а через одну там. где уже
имеются обратные фиксаторы. Однако такие подвески обладают мень-
шей ветроустойчивостью, чем при схемах рис. 3.2. а и 3.3, а, и вызы-
вают повышенный износ средней части контактных пластин токоприем-
ников. Кроме того, на опорах, где пег ромбов или оттяжных тросов,
необходимо устанавливать жесткие распорки между основными фик-
саторами и консолями, чтобы предотвратить раскрытие этих фикса-
торов, которое в рассматриваемых условиях более вероятно, чем при
наличии зигзагов контактных проводов.
Скрепления контактных проводов в пролете ромбовидных подвесок
могут быть шарнирными и жесткими. При шарнирных скреплениях,
обеспечивающих полное и всестороннее взаимное перемещение контакт-
ных проводов, их натяжения в случае воздействия ветра будут неиз-
менными. При жестких скреплениях натяжения проводов в случае
воздействия ветра будут различными: в первом по направлению ветра
Рис 3.3. Схемы расположения в
плане контактных проводов подве-
сок с оттяжными тросами*
I контактные провод»: 2 оттяжные
। росы: ? -- ролики
проводе натяжение будет больше, чем во втором. Это обусловит мень-
шие ветровые отклонения, чем при шарнирных скреплениях. Следо-
вательно, для вновь электрифицируемых линий целесообразно приме-
нять ромбовидную подвеску по схеме рис. 3.2, а с жесткими скрепле-
ниями контактных проводов; такая подвеска обеспечивает наибольшую
ветроустойчивость. При этом на двухпутных линиях необходимо уста-
навливать опоры не в створе, а со сдвигом друг относительно друга
вдоль линии на 5 м. Если же требуется применить ромбовидную под-
веску на уже эксплуатируемой линии, т. е. при заданных длинах про-
летов, то в каждом конкретном случае нужно выполнить соответст-
вующие расчеты, выбрать схему и скрепления, которые обеспечат не-
обходимую ветроустойчивость подвески.
Основными параметрами, определяющими ветроустойчивость рас-
сматриваемых подвесок при уже выбранной схеме, являются расстоя-
ние X от оси опор до точек скрепления контактных проводов в ромбо-
видных подвесках или до точек крепления оттяжных тросов к контакт-
ному проводу, а также смещения а и b проводов или оттяжных тросов
на опорах относительно оси пути.
Расстояния от оси опор до мест скрепления контактных проводов
ромбовидной подвески для удобства монтажа можно принимать рав-
ными расстоянию до второй от опоры простой струны на несущем
тросе, а от оси опор до мест крепления к контактному проводу оттяж-
ного троса - до околоопориой струны. Зигзаги контактных прово-
дов ромбовидной подвески обычно принимают нормального размера,
т. е. 0,3 м, но при необходимости повышения ветроустойчивости под-
вески их допустимо увеличить до 0,4 м. Расстояния между контакт-
ными проводами в средней части пролета устанавливают минимальные
возможные по конструктивным условиям. Узлы крепления оттяжных
тросов к контактному проводу желательно располагать от оси пути на
расстоянии 0,1 м, а ролики на фиксаторах — на расстоянии около J м.
Статические составляющие ветровых нагрузок на провода кон-
тактных подвесок, необходимые для расчетов ветровых отклонений
контактных проводов и максимальных допускаемых длин пролетов,
могут быть приняты по данным табл. 2.1 и 2.2.
Для облегчения пользования материалами данной главы приведем
принятые основные условные обозначения и размерности:
I — длина пролета, м;
цк нагрузка от веси контактного провода (проводов), даН/м;
t> нагрузка от веса цепной подвески, даН/м;
рк, Ри ~ нагрузки от ветра соответственно на контактный провод (провода)
и несущий трос обычной (см. § 3.2) подвески, даН/м;
рк1 нагрузка от ветра на один контактный провод ромбовидной подвес-
ки, даН/м;
рК2 — нагрузка на два контактных провода ромбовидной подвески с уче-
том их взаимного экранирования, даН/м;
</н — результирующая нагрузка на несущий трос, даН/м;
ра — эквивалентная нагрузка, заменяющая часть ветровой, передающей-
t ся с контактного провода (проводов) на несущий трос обычной под-
вески, даН/м;
рэн, Рэи —то же при разных схемах ромбовидной подвески, даН/м;
а—зигзаг контактного провода, одинакового размера на соседних
опорах, м;
а. — больший зигзаг контактного провода, м;
а3 — меньший зигзаг контактного провода, м;
R — радиус кривой пути, м;
ук, Vh — изменения прогиба опор под действием ветра па уровнях соответст-
венно контактного провода и несущего троса, м;
h0 — конструктивная высота цепной подвески, м;
йи — длина гирлянды подвесных изоляторов или крепежных деталей для
несущего троса, м;
сСр, Сер —средняя длина струн в средней части пролета равной соответствен-
но половине и 4/5 его длины, м;
X — расстояние от оси опоры до места скрепления контактных проводов
ромбовидной подвески или до места крепления оттяжного троса, м;
d — расстояние между контактными проводами ромбовидной подвески
в средней части пролета, м;
К' — натяжение неизношенного контактного провода (проводов), даН;
Т„, Т'г — натяжения несущего троса соответственно при ветре максимальной
интенсивности и гололеде с ветром, даН;
То — натяжение несущего троса при беспровесном положении контакт-
ного провода, даН;
/ /Л>т — модули упругости материалов соответственно контактного провода
и оттяжного троса, МПа;
5',.-. ,S’0T — площади поперечного сечения соответственно контактного провода
и оттяжного троса, м2.
§ 3.2. Расчеты для обычных подвесок
i 1од обычными понимаются одинарные цепные подвески, со смещен-
ными от осн опор простыми струнами и с рессорными тросами, полу-
компенсированные и компенсированные, вертикальные и полукосые.
Определение ветровых отклонений контактных проводов. Полное
отклонение проводов под действием ветра складывается из статиче-
ской и динамической составляющих (см. §3,1).
В общем случае статическая составляющая максимального ветро-
вого отклонения контактного провода от оси токоприемника
> (Рк —РэТ А'//?) /2 , (flj—а2)^ С!Щ
:'"ах 8К 2 (Рк-Рэ+ K!R) /2 ± 2 ''Vk’ ( ’
Верхние знаки перед дробью K./R соответствуют направлению
ветра от центра кривой, нижние знаки — к ее центру. Верхний знак
перед полусуммой «j и а2 относится к односторонним зигзагам. При
разносторонних зигзагах переда! или а2 надо изменить знак на обрат-
ный и принять ту комбинацию знаков, которая обусловит наибольшее
значение дктах.
На прямых участках пути ветровое отклонение
контактных проводов от оси токоприемника на расстоянии х от опоры
(ряс. 3.4)
. (Рк — Рэ) (/- Х)х а(1—2х) . аг-а2
6кх=----------------+---------+ —-------+ Yk> (3.4)
Зак, 2630
65
где средний размер зигзага
а = 0,5 (ai + а2). (3.5)
Максимальным ветровое отклонение Ьктах будет в точке при
I 2a К
х —--------------.
2 (рк—ря) I
Подставляя это выражение в формулу (3.4), получим
I (Рк- Рэ) , 2a* К , щ Т аг
ктах " ' 8Х + (ри-ря)Р + 2 ”'1’Тк- ( Ь)
Верхние знаки в формулах (3.5) и (3.6) относятся к разносторонним
зигзагам а} и а2, а нижние — к односторонним.
Формула (3.6) является универсальной. Если нет несущего троса,
т. е. если определяются ветровые отклонения одиночных проводов,
принимают рэ - 0. Аналогично поступают, определяя ветровое от-
клонение контактного провода цепной подвески без учета влияния не-
сущего троса. При одинаковых разносторонних зигзагах контактных
проводов на соседних опорах предпоследний член формулы (3.6) об-
ращается в нуль.
На кривых участках пути ветровое отклонение кон-
тактных проводов бывает максимальным в центре пролета и при оди-
наковых зигзагах определяется по формуле
, (Рк~Р») I'2 । 7.
Ьк inav----—------ГIYk- (3.7)
ОЛ ОЛ
Эта формула получена при определенном направлении ветра —
к центру кривой, что является наиболее опасным при нормальном
расположении контактного провода по хорде относительно оси токо-
приемника (см. рис. 3.1, а). Положение контактного провода, показан-
ное на рис. 3.1, в, в эксплуатации нежелательно; предельным явля-
ется положение, приведенное на рис. 3.1,6 (по касательной к оси токо-
приемника). Поэтому в формуле (3.7) отсутствуют знаки, соответствую-
щие направлению ветра от центра кривой, так как оно при нормаль-
ном положении контактного провода не определяет его максимально-
го отклонения к оси токоприемника, а при расположении провода
по касательной к ней дает тот же результат, что и в случае направле-
ния ветра к центру кривой.
При неодинаковых зигзагах контактных проводов на смежных опо-
рах в кривой можно считать, что наибольшим ветровое отклонение
будет в середине пролета (как и при одинаковых односторонних зиг-
загах), поэтому расчетное значение а в формуле (3.7) в этом случае вы-
числяется по выражению (3.5), но знак «+» в последнем нужно отно-
сить к односторонним, а «—» — к разносторонним зигзагам. Формула
(3.7), как и (3.6), универсальна.
66
Рис. 3.4. Схема, поясняющая вет-
ровое отклонение контактного про-
вода от оси пути
Эквивалентная нагрузка р.г входящая в формулы (3.3), (3.4), (3.6),
(3.7),
Рк Т~Рн К—8КТ [h„ Рп/дн + Ун —Ук1У'2
f>'' Т + ЛЧ-Ю.б^р КТ/(£К1*) ’ ’
где Т — натяжение несущего троса, соответствующее расчетному режиму (для
компенсированных подвесок — номинальное натяжение).
Значение еср (рис. 3.5) в средней части пролета, равной 0,5/, при
заданной конструктивной высоте подвески /г0 можно определить как
Г(;р “Л,,— 0 , 1 15Д/“ / 7 о .
(3.9)
Значение ук и ун для типовых железобетонных опор можно прини-
мать в зависимости от расчетной скорости ветра ир:
Чр, м/с
Ун, м
Ун, м
до 25 30 35 40
0,010 0.015 0,022 0,030
0.015 0,022 0,030 0,040
Более точно эти величины следует определять по формулам §6.5.
Конструктивную высоту подвески /ц, при одном контактном прово-
де на участках переменного тока обычно принимают равной 1,8 м
(иногда 1,6 м), а при двух контактных проводах на участках постоян-
ного тока — 2 м (иногда 2,2 м).
В случаях применения изолированных консолей /г„ -- 0,16 м; при
гирляндах из подвесных изоляторов ПФ70-В (1-3 шт.) и ПТФ70
(1 шт.) принимают следующие значения /г„:
Число изоляторов в гирлянде .2 3 4
Ли. м . .............. 0,42 0.55 0,68
При подвесных изоляторах других
h„ необходимо скорректировать.
Рис. 3.5. Расчетная схема для оп-
ределения средней длины струны
Сер в средней части пролета
типов приведенные значения
3*
67
I
Неизвестное на данном этапе расчета натяжение несущего троса
полукомпенсированной подвески в режиме максимального ветра 7\
ориентировочно можно принять равным при медном тросе 70 %, а при
сталемедном и стальном тросах —• 75 % максимального. Натяжение
несущего троса в случае беспровесного положения контактных прово-
дов То приближенно можно считать равным 80 % максимального не-
зависимо от материала несущего троса.
Формула (3.8) может быть представлена в виде
Рк т — рп К— KTAJI*
р ч —--------------------, (3.10)
Т + К + <?сРТЯэ//2
где (йиРн/^н ЬУн—Тк): «я-- 10,6/(7gK.
Значения коэффициентов Д., для некоторых расчетных условий
приведены в табл. 3.1, данные которой могут быть использованы как
для определения статической составляющей эквивалентной нагрузки,
так и полной в соответствии с тем, какие приняты значения р„ и q„.
Т а б лица 3.1
Кош а ктн ые ш»дв“ски Л„. и Значения Л», м, при скоростях ветра, м/с
20 25 <0 5.» 10
НБСМ-704-МФ-100 0. 16 0.312 0,451 0,622 0,779 0,923
0.55 0.9/5 1.453 2,003 2,521 2,978
0,68 1,196 1,787 2,463 3,102 3,663
11БСМ-95+МФ-100 0,16 0,322 0,462 0,630 0,792 0,935
0,55 1 .009 1,491 2,029 2,566 3,020
0.68 1.239 1,833 2.496 3,158 3.714
\4-95<-МФ-100 0, 16 0.310 0,442 0,610 0,772 0,914
0.55 0.968 1,422 1,960 2,497 2,946
0,68 1,187 1,749 2,411 3,072 3,623
ПБСА-50/70Н-МФ-100 0,16 0,371 0,590 0,716 0,871 1 ,013
0,55 1,179 1,721 2,325 2,837 3,288
0,68 1,448 2,118 2,861 3,493 4,047
М-120±2МФ-Ю0 0,42 0.531 0,787 1,115 1,435 1,779
ПБСМ-95+2МФ-100 0,42 0,518 0,765 1,082 1,426 1,749
ПБСМ-70+МФ-85 0,42 0,817 1.204 1 ,653 2,057 2.405
0.55 1,058 1,564 2, 147 2,674 3,124
0,68 1,298 1,924 2 ,(>42 3,291 3,844
ПБСА-50/70+МФ 85 0,42 0.982 1,416 1,894 2,287 2,625
0,55 1,273 1,842 2,463 2,975 3,413
0,68 1,565 2,268 3,031 3.664 4.201
П р и м е ч а н и е. Данные для подвесок с низколегированными и бронзовыми кон-
тактными проводами такие же. как с медными.
68
Коэффициент В3 равен 12 145 м для подвесок с компенсированными
контактными проводами МФ-100 и МФ-150 и 12 175 м при проводе
МФ-85.
Динамическая составляющая ветрового отклонения контактного
провода
,д 3 (Рк-Р;,) /2 t
= ----nfit. (З.И)
где коэффициенты т], 6 и § те же, что в формуле (2.8).
Таким образом, на прямых участках пути полное ветровое откло-
нение контактного провода от оси токоприемника на расстоянии х от
опоры аналогично формуле (3.4) может быть определено выраже-
нием
, (Рк -Р-.PfJ- х)х «(/- 2х) , а, — а2
(>|.> —---57?------- О ! 3i|6g) |----------1---------| ylf. (3.12)
хЛ 12
Максимальное ветровое отклонение /?К111ах на прямых участках
пути определится по формуле, аналогичной (3.6),
Условия применения знаков в формуле (3.13) те же, что и в форму-
лах (3.5) и (3.6).
Максимальное ветровое отклонение контактного провода от оси
токоприемника в середине пролета в кривых (при одинаковых одно-
сторонних зигзагах на смежных опорах) аналогично формуле (3.7)
определяется как
max ' ЗГ|Л~а I V«- (3.14)
ОД ОА
Формулы (3.12) -(3.14) справедливы как для компенсированных,
гак и для полукомпеисированных подвесок.
Определение максимальных допускаемых длин пролетов. Макси-
мальное ветровое отклонение контактного провода приравнивают до-
пускаемому (см. §3.1); при этом длина пролета в ф°РмУлах Для
расчета ветровых отклонений становится максимальной допускаемой.
Без учета динамической составляющей ветровой нагрузки искомая
длина пролета после преобразования формулы (3.3) определяется как
. 1/ 2 Л' , .----------,
£,пах "V Р;~ p.tk/r |лч 1’
(3.15)
где /V - 2 (&кдп —ук) Т (в1 F вг)> условия применения знаков перед дробью
K/R аналогичны приведенным для формулы (3.3).
Для прямых участков пути формула (3.15) может быть преобразо-
вана к виду
(щах -2~\/ КАпр/(Рк~~Рэ) >
(3.16)
69
I
ВПр = *кдп--01 ga~— 7к + р/ ^кдп-------—у/ — a2 . (3.17>
Условия применения знаков в формуле (3.17) те же, что и в фор-
муле (3.6). При одинаковых разносторонних зигзагах на смежных
опорах формула (3.17) принимает вид
5пр = Ькдп — Ук + "И (^кдп—Ук)2— О2 (3.18)
Для кривых формула (3.15) может быть преобразована (учитывая
только направление ветра к центру кривой) в следующую:
/щах = 21/---^Е_, (3.19)
т Рк — Рэ 'гК/R
где ^кр = ^кдп — Ук + а-
В тех случаях, когда на соседних опорах прямых участков пути
применены одинаковые разносторонние зигзаги контактных проводов,
равные 0,3 м, а на кривых одинаковые односторонние зигзаги, равные
0,4 м, значения и Вкр в зависимости от ук следующие:
у„, м ......... 0,010 0,015 0,022 0,030
Впр, м . . . 0,877 0,866 0,850 0,832
Вкр, м .... 0,840 0.835 0,828 0,820
Формулы (3.16) и (3.19) являются универсальными и используют-
ся так, как указано для формул (3.6) и (3.7). Однако при определении
величины р,} необходимо знать длину пролета, вследствие чего приме-
няют метод последовательных приближений. Сначала определяют дли-
ну пролета без учета влияния несущего троса (т. е. принимая р, - 0),
а затем, получив при найденной длине пролета значение ри, вычисляют
Лпах по формуле (3.16) или (3.19). Указанные действия повторяют до
тех нор. пока разность между пролетами, определенными без учета
и с учетом влияния несущего троса, не станет менее 5 м. При этом
необходимо помнить, что пролеты длиной более 70 м для новых
линий не проектируют.
Пользуясь формулой (3.19), обычно принимают а = 0,4 м. При
этом на кривых больших радиусов длина пролета может получиться
больше, чем для прямых участков. Это значит, что контактный провод
займет положение, показанное па рис. 3.1, в. Но такое положение про-
вода нежелательно, поэтому обычно принимают длину пролета на та-
ких кривых равной длине пролета на прямом участке. В этом случае
действительные зигзаги должны иметь значения, вычисленные в соот-
ветствии с условиями, приведенными в §3.1.
С учетом динамической составляющей ветровой нагрузки макси-
мальная допускаемая длина пролета на прямых участках пути (при
одинаковых разносторонних зигзагах на смежных опорах)
Апах —2 1/Л^пр/(рк — Рэ) >
(3.20)
70
на кривых (при одинаковых односторонних зигзагах на смежных
опорах)
^тах = 2 V 2КВкр/(ркк1-р3+А//?) • (3.21)
В этих формулах все обозначения (кроме коэффициента х4) те же,
что и в формулах (3.16) и (3.19). Значение коэффициента к4 определя-
ется выражением
л-1 = к2-|-2т]65, (3.22)
где к, — коэффициент, учитывающий упругие деформации провода при
его отклонении;
г], 6, £ —то же, что в формулах (3.11) и (2.8).
Значение коэффициента кг определяется выражением
К2 Кд Кд Кд . (3.23)
Коэффициент кя определяется в зависимости от длины пролета I.
', м............ 30 40 50 60 70 80
кя ............. 0,72 0.70 0,68 0,66 0,64 0,52
Значения коэффициента /с4 зависят от скорости ветра и:
V, м/с . . . 10 15 20 25 30 35 40 45 50
к4........1,50 1,50 1,49 1,45 1,41 1.35 1,29 1,22 1,14
Коэффициент к5 находят в зависимости от типа контактного прово-
да (проводов):
Тип провода . . МФ-85 МФ-100 МФ-150 2МФ-100
к6 . . .... 0,99 1,00 1.04 1,075
Значения кя, /с4 и х5 для параметров, не соответствующих приве-
денным выше, определяются линейной интерполяцией.
Как и раньше, следует применять метод последовательных при-
ближений — сначала определить значение длины пролета без учета
влияния натяжения несущего троса на ветровые отклонения контакт-
ных проводов (т. е. принимать рэ — 0). Коэффициент х4 в первом рас-
чете можно задавать равным единице. Затем следует уточнить его зна-
чение по формуле (3.22) и определить новую ориентировочную длину
пролета при этом значении после чего вычислить нагрузку р3 по
формуле (3.8) и, введя ее в выражение (3.20) или (3.21), учесть влия-
ние несущего троса.
Пример. Задание и исходные данные. Определить для
электрифицированных участков, расположенных в ветровом районе IV на откры-
той холмистой местности:
А. Наибольшее ветровое отклонение контактных проводов от оси токоприем-
ника для полукомпенсированной подвески М-120+2МФ-100 на неизолированных
консолях в пролете длиной 70 м на прямом участке пути;
Б. Максимальную допускаемую длину пролета по режиму максимального
ветра для компенсированной подвески ПБСМ-704-НлОлО, 04Ф-100 на изолиро-
ванных консолях в кривой радиусом 950 м.
71
Решен» е. Л. По табл. 1.1 для ветрового рйона IV находим распреде-
ленною поверхностную нагрузку Вп — 630 Па. Для открытой холмистой мест-
ности из табл. 1.2 получаем z0 - 0,2 м, а по табл. 1.3 коэффициент k:i - 0,94
(для нулевого места).
Следовательно, по формуле (1.11) В 0,942-630 557 Па; скорость ветра
для данного района по формуле (2.17)
v = У ТДГ55Т SS 30 м / с.
Распределенные линейные нагрузки для несущего троса найдем по табл. 2.1,
а для контактных проводов — по табл. 2.2 (принимая Ся 1,85):
от веса подвески - 2,98 даИ/м;
статическая составляющая ветровой нагрузки на контактные провода —
— 1.24 даН/м, на несущий трос — 0,99 даН/м;
результирующая нагрузка на несущий трос — 3,14 даН/м.
Принимая конструктивную высоту подвески 2 м, а натяжение несущего
троса при беепровссном положении контактных проводов равным 80 % макси-
мального допускаемого, указанного в табл. 1.8, т. с. Т0 ~ 0,8-2000 1600 даН,
найдем размер с,.р по формуле (3.9):
е(;р -2- 0,115-2,98-702/1600 --0,95 м .
Нагрузку р., определим по формуле (3.10), принимая h„ 0,42 м и натяже-
ние несущего троса при максимальном ветре равным 70 % максимального допу-
скаемого (см.§3.2), т. е. Т 0,7-2000 - 1400 даН.
Используя данные табл. 3.1, получим
1,24-1400 — 0,99-2000—1400 • 2000 -1,115/ 70»
р.,------------------------------------------—0,132 даН/м.
' 1400-}-2000 (-0,95-1400-12 145/70»
Искомое ветровое отклонение контактных проводов определим по формуле
(3.13). Для учета динамической составляющей ветровой нагрузки коэффици-
енты принимаем следующие: 4 0,56 для пролета длиной 70 м, 6 = 0,2 для
скорости ветра 30 м/с и 5 = 1,015 (получено методом интерполяции) для
веса двух контактных проводов 1,746 даН/м; тогда
(1,24 (-0,132 ) 702 (1 (.3.0.56-0,2-1,015)
^ктах 8.2000 +
2-0,32-2000
(1 ,24 1-0,132) 702
( 0,015 — 0,632 м.
Результат расчета показывает, что для заданных условий ветровое отклоне-
ние контактных проводов превышает допустимое равное 0,5 м. Поэтому необ-
ходимо принять меры к снижению ветрового отклонения, переоборудовав под-
веску в ромбовидную или уменьшив длину пролета.
Р е ш с н и е Б. Для вычисленной выше скорости ветра 30 м/с по табл. 2.1 и
2.2 найдем распределенные линейные нагрузки;
Й = 1,56 даН/м; рк -0,83 даН/м; ри—0,77 даН/м; </н=1,74 даН/м.
Длину пролета рассчитаем по формуле (3.21), сначала не учитывая влияние,
несущего троса, т. е. принимая рэ = 0. Считаем, что — 1. Ориентировочное
значение длины пролета определим, принимая Вкр = 0,835:
Лпах
I'
2
2.1000.0,835
0,834-1000/950 ~
Определим значение коэффициента для пролета длиной 60 м по формуле
(3.22):
Kj -0,66-1.41 • 1 4-2-0,56-0,2-0,911 — 1,135.
72
Здесь приняты значения кл~ 0,66 для пролета длиной 60 м, = 1,41 для
скорости ветра 30 м/с, =- 1 для провода НлОлО,04Ф-100 (такой же, как для
МФ-100), Т] и 6 — те же, что и выше; £---0,911 (по интерполяции) для £ -=
0,873 даН/м.
С учетом найденного значения коэффициента К] получим
I max
-:2
2-1000-0,835
0,83• 1,135 1000,'950
57,87 58 м.
Теперь - 0,664-1,41 • 1 f 2-0,61-0,2-0,911 1.159.
Принимая конструктивную высоту подвески равной 1,8 м, определим но
формуле (3.9)
еср --1,8 -0,115-1,56-58»/1500 -1,4 м.
Принимая 0,16 м и используя данные табл. 3.1. рассчитаем но форму-
ле (3.10)
0,83 -1500 -0,77-1000 - 1000 -1500 -0,622 /58»
р;, --------------------------------------- 0,02 даН 'м.
1500-1 1000 । 1,4-1500-12 145/58'-
Искомую длину пролета найдем по формуле (3.21)
58 м.
Дальнейшие уточнения не требуются. Окончательно принимаем максималь-
ную допускаемую длину пролета на кривой радиусом 950 м равной 58 м.
§ 3.3 Расчеты для подвесок
с повышенной ветроустойчивостью
Расчеты приводятся для двух подвесок с повышенной ветроустой-
чивостью: ромбовидной (при двух контактных проводах) и с оттяж-
ными тросами (при одном контактном проводе). Каждая из подвесок
рассматривается в двух вариантах: с ромбами или оттяжными троса-
ми на всех опорах и через опору, а ромбовидные подвески, — кроме
того, с шарнирными и жесткими скреплениями контактных проводов
(см. §3.1). Ветровые нагрузки в расчетных формулах для обеих под-
весок следует учитывать полные, т. е. сумму статической и динамиче-
ской составляющих.
При шарнирных скреплениях контактных прово-
дов ромбовидных подвесок могут быть использованы формулы, при-
меняемые для расчетов ветровых отклонений в обычных подвесках.
Необходимо только учитывать, что ветровая нагрузка вдоль про-
лета неравномерна (неодинаково расстояние между контактными
проводами), и в средней части пролета будет проявляться эффект
экранирования.
Неравномерную нагрузку вдоль пролета можно заменить равно-
мерной эквивалентной p.iK (штриховая линия на рис. 3.6)
/>эк=--2рв1-(2pK)-pKiS) (1—47- /-)
(3.24)
73
Ветровое отклонение любого из контактных проводов от его нор-
мального положения при отсутствии ветра (рис. 3.7) в месте скрепле-
ния проводов
, о (Рэк-Рэн)^(.1-—М .
--------—--------- I Тк; (3.25)
2Л
в середине пролета
, О (Рэк — Рэн) (2 , „„
- Р-----—------- t Y к, (3.26)
ОЛ
где Р коэффициент, учитывающий степень шарнириости скрепления кон-
тактных проводов; на основании опытных данных можно принять
Р =•- 0,85.
Эквивалентную нагрузку рможно рассчитать по формуле (3.8),
в которую вместо рк нужно подставить величину вычисленную по
формуле (3.24).
Чтобы определить ветровые отклонения контактных проводов от
оси пути, значения, подсчитанные по формулам (3.25) и (3.26), для
первого по направлению действия ветра провода необходимо умень-
шить, а для второго увеличить на половину расстояния d между кон-
тактными проводами в средней части пролета.
Максимальное ветровое отклонение контактного провода па уча-
стке между фиксатором и местом скрепления проводов (см. рис. 3.7)
Лк max Л' Yu- (3 27)
Здесь а, 0,5 (a t bv). Величина Ь' определяется по формуле
(3.6), как для провода с одинаковыми разносторонними зигзагами,
Л' ... | 2«с2рКг /I (3.28)
где Л’2 натяжение второго но направлению ветра контактного провода;
щ.р — условный средний зигзаг; а(.р 0,5 (а -• Лг) при а > Л(. и а,.р
0.5 (Лс а) при а < Л(..
При жестких скреплениях контактных проводов
ромбовидных подвесок, обусловливающих невозможность продоль-
ного смещения одного провода относительно другого, в случае воз-
-- Л
Рис. 3.6. Расчетная схема для оп-
ределения эквивалентной нагрузки
на контактный провод Р;,
74
Рис. 3.7. Расчетная схема для оп-
ределения ветровых отклонений
контактных проводов ромбовидной
подвески при шарнирных скреп-
лениях
действия ветра в первом по его направлению контактном проводе на-
тяжение будет увеличиваться, а во втором уменьшаться по сравнению
с натяжениями (одинаковыми) проводов до появления ветра. Опреде-
лить перемещение места скрепления контактных проводов можно ме-
тодом разнесения нагрузок в узлы. Для этого распределенные вдоль
пролета нагрузки должны быть заменены сосредоточенными (рис. 3.8).
В соответствии со схемой рис. 3.8. учитывая обычно применяемые
допущения, ветровое отклонение узла жесткого скрепления можно
определить но формуле, предложенной Г. Г. Энгельсом,
РХ______
'к 1 2a’!lzKSKi'№
4 Yk
(3 29)
Сосредоточенная сила Р. заменяющая равномерно распределен-
ную нагрузку на контактные провода, определяется как
Р --0.5 (2рка — Р«н) Х+(рК2-р!)н) <0,5/-X). (3.30)
Максимальное ветровое отклонение второго по направлению ветра
контактного провода от оси пути в середине пролета
Ькшак =&с С (РК2 —P.ni) (1 —2X)--i/(«K) po,5d. (3.31)
Ветровое отклонение контактного провода на участке между фик-
сатором и местом скрепления проводов можно определять аналогич-
но изложенному по формуле (3.27), принимая при вычислении Ь'
коэффициент р — 1.
При подвеске с оттяжными тросами на каж-
дой опоре (рис. 3.9) смещение под действием ветра узла крепления
оттяжного троса к контактному проводу может быть найдено по фор-
муле
(Phi ~Рэн) ^ ( 1 X)
2 [К На -Н)2/(А--'Р)]
(3.32)
где р-= 1/(£к ,S1() ) 1/(£От‘%т)-
75
Рис. 3.8. Расчетная схема для определения
ветровых отклонений контактных проводов
ромбовидной подвески при жестких скреп-
лениях
Рис. 3 9. Расчетная схема для определения
ветровых отклонений контактного провода
подвески с оттяжными тросами на всех
опорах
Рис, 3.10 Расчетные схемы для определения
ветровых отклонений контактных проводов
подвесок с ромбами или оттяжными тро-
сами, установленными через опору
Величину рЭ)1, входящую
в эту формулу, следует оп-
ределить по выражению (3.8),
в котором вместо нагрузки
рк нужно принимать на-
грузку pKi.
Принимая, что макси-
мальным ветровое отклоне-
ние контактного провода бу-
дет в середине пролета, его
можно найти по формуле
Л|(1пах-=^ 1 (Рщ —Ргш)Х
.< (/--2Х)2/(8К). (3.33)
Ветровые отклонения кон-
тактных проводов ромбовид-
ной подвески с ромбами че-
рез опору (рис. 3.10, а) в
месте скрепления проводов
I, _ (Р1<2 I Рэи) I I .
' 2 (Л' ! 2а‘-Sh-/X2) П *”
(3.34)
в середине пролета
1>к max 0,55с | (/)кз ( Рэп) X
X (/ Z)2;(«K) | 0,5d. (3.35)
Ветровые отклонения кон-
тактного провода подвески
с оттяжными тросами через
опору (рис. 3.10,6) в месте
крепления оттяжного троса
Ье =____________________-1-ук;
2 К (н-|-6)2/(Х2р)|
(3.36)
в середине пролета
*1! шах -0,5 (ic : а')
г(рк1 I /•’эн) (I — ^)2/(8К), (3.37)
где а' — расстояние от оси пути
до узла крепления от-
тяжного троса к кон-
тактному проводу.
Эквивалентную нагрузку
р')Н в формулах (3.34) (3.37)
находят из выражения, полу-
76
ценного при допущении, что контактный провод и несущий трос взаи-
модействуют друг с другом в части пролета, равной 4/5 его длины.
}' — Р» К—Рк X) 7’ -|-8КТ (ХиРн/<7нН~Тц—Yk)/U—М ,
₽эн-' K(l + M+T(l X) | 8,34еср KT/[gK (/—Aj] ' " ’
Значение рк в формуле (3.38) для расчетов подвесок с оттяжными
тросами принимается равным рк1, для расчетов ромбовидных подве-
сок — 2р1П, так как в последнем случае экранирование контактных
проводов на длине X не учитывается. Величина е(р определяется
как
еср -ho-O,O985g/2/To. (.3.39)
Несмотря на ряд допущений, принятых при выводах расчетных
формул для ветроустойчивых подвесок, результаты расчетов достаточ-
но близки к экспериментальным данным, что позволяет применять
эти формулы для практических целей.
При ромбовидных контактных подвесках с
ромбами на каждой опоре (см. рис. 3.2, а) и шарнирными скрепления-
ми контактных проводов, если наибольшим ветровое отклонение кон-
тактных проводов будет в середине пролета, максимальная допусти-
мая по ветровым отклонениям длина пролета
2 V » ) (^доп-Хк--0,5Д) (3.40)
Величины р:.,к и /?,)И определяют методом последовательных при-
ближений. Вычислив длину пролета по формуле (3.40), необходимо
проверить ветровое отклонение на участке между фиксатором и ме-
стом скрепления контактных проводов, пользуясь выражением (3.27).
Если это отклонение больше допустимого, то /тах следует соответ-
ственно уменьшить или изменить расположение мест скрепления
проводов.
Максимальная допустимая по ветровым отклонениям длина про-
лета при жестких скреплениях контактных проводов и наибольшем
отклонении в середине пролета
Коэффициенты, входящие в формулу (3.41), имеют следующие зна
чения:
А [2 (рм — Щэн) а.1 : (рК2-Рэи) (0.25 - <ха) |:
В -2(р112 -р,,и) (0,5- a)2a2£lt Slt — 2№а2 (Ьи Д()11 ук-О,5Д);
С—4К и2 S),-(&к доп—)’ц -О,5<7)
Для определения искомой длины пролета необходимо задаться
значением а — X/Z или знать его. Определив /111Н, но формуле (3.41),
проверяют соответствие ветрового отклонения допускаемому на уча-
77
стках между фиксаторами и местами скреплений проводов аналогич-
но тому, как это было указано для шарнирных скреплений.
При ромбовидных подвесках с ромбами через опору (см. рис. 3.2, б),
используя формулу (3.35), максимальную допускаемую длину про-
лета можно определить как
Лпнх "Х--!-2 Г К (26к доц Ь(.—d)/(pv.2-\ рэн) , (3.42)
где величину Ь,. рассчитывают по формуле (3.34).
Для подвесок с оттяжными тросами, если эти
тросы расположены на каждой опоре (см. рис. 3.3, а), максимальная
допускаемая длина пролета на основании формулы (3.33)
^ШЯХ 2|Х V" )/2Д^ ( д,,]! — i^(’) / (Рк J-Рэн) I, (3.43)
где величина bv определяется по формуле (3.32).
Если оттяжные тросы расположены через опору (см. рис. 3.3, б),
то максимальную допускаемую длину пролета, принимая наиболь-
шее ветровое отклонение в середине пролета и используя формулу
(3.37), можно определить как
бнах А 21/ --------[2tKA0U-(/v. !«')]. (3.44)
у Ркг ! Рэн
где величина bt. определяется по формуле (3.36).
Поскольку для определения Ьс необходимо знать длину пролета,
при расчетах по формулам (3.42) — (3.44) применяют метод последо-
вательных приближений.
Пример. Исходи ы е д а н и ы е. На электрифицированном участке
постоянного тока, расположенном в открытой незащищенной от ветра местно-
сти, смонтирована компенсированная подвеска ПБСМ-95 1-2МФ-100 с пролетами
на прямых участках пути длиной 75 м. Вследствие строительства гидроэлектро-
станции вблизи железной дороги образовалось искусственное море и местная ме-
теорологическая станция зарегистрировала увеличение скорости порывов ветра
до 33 м/с.
3 а д а н и е. Проверить, сохранилась ли достаточная ветроустойчивость
обычной подвески и в случае отрицательного ответа выбрать схему ромбовидной
подвески и способ скрепления ее контактных проводов, которые позволят из-
бежать нереразбивки пролетов.
Р е in е и и е. Сначала определим необходимые для расчета нагрузки. По
табл. 2.1 найдем, что распределенная линейная нагрузка от веса цепной подвески
равна 2,71 даЬРм. Статические составляющие ветровых нагрузок, даН/м, при-
мем по табл. 2.1 и 2.2, определяя их методом интерполяции для заданной ско-
рости ветра:
Рнс 1.07; р1пс 1,03; рК2С = 1,26 (при Сл = 1,55).
Динамические составляющие этих нагрузок, даН/м, вычислим но формуле
(2.8):
/Л1д==0,11; Ршд=0,10; Рк2д = 0,13.
Полные ветровые нагрузки, даН/м, с округлением до 0,05 даН/м:
рн = 1,2; р,а=1,15; рм=1,4.
78
Результирующую нагрузку на несущий трос определим по формуле (2.1 Л;
</„=.-= У2,7Г2+1,22 =2,96 даН/м.
По формуле (3,9) определим значение вСр, принимая hn -= 2 м,
еср = 2—0,115-2,71*75®/1800 =1.026 м.
Эквивалентную нагрузку рэ найдем по формуле (3.10). принимая
0,42 м, и используя данные табл. 3.1 для скорости ветра 35 м/с:
1,4-1800 —1,2- 2000 — 2000 -1800 • 1,426 /753
Ра~ 1800 4-2000+ 1,026-1800-12 145/752 ~0, Юг даН/м .
Максимальное ветровое отклонение контактных проводов обычной полни
еки определим по формуле (3.6), принимая а 0,3 м:
max
(1.4 j 0,102) 752 ,___2-0^2000
8-2000 ~Г (1,4-:-0,102) 75“
0,022 = 0,593 м.
Очевидно, что ветроустойчивость обычной подвески недостаточна, так как
ветровое отклонение превышает допускаемое. равное 0.5 м
Проверим ветровое отклонение контактных проводов при ромбовидной под-
веске с ромбами через опору (см. рис. 1 2, б) и жестким скреплением, для ново
сначала вычислим нагрузку рэя по формуле (3.38), приняв л 17.8:' м d
0,04 м и а 0,3 м,
1.2 (75 + 17.85) 2000 - 1.4 (75-- 17.85) 1800 ,
I 8-2000.1800 (0,42-1,2/2,96 : 0,008) , (75 — 17,85)
--------------------------------------------------- 0.26.1 даН, и
;'эн 2000 (75 -1-17,85)+ 1800 (75- 17,85) +
I- 8,34-1.17- 2000 1800 /[2-0.873(75 — 17,85)]
Здесь значение Сер определено по формуле (3.39)
ес'р = 2 — 0,0985-2,71 -75+1800 1,17 м.
Наибольшее ветровое отклонение узла скрепления контактных проводов
пандем по формуле (3.34)
(1.4-1-0,263) 75-17,85
b с ..........—1-------------------------I- 0,022 --0.346 м
2 ( 2000 4 2-0,32-12 750-200/17,852) 1
максимальное ветровое отклонение второго по направлению ветра контактного
провода от оси пути в середине пролета — по формуле (3.35)
йя„„-1х - 0,346/2-| - (1,4 +0,263) (75-17,85)2/(8-2000) 4-0,04'2 0,532 м.
Как показывает результат расчета, при такой ромбовидной подвеске нуж-
ная ветроустойчивость не обеспечивается. Проверим, что даст применение ром-
бовидной подвески с ромбами на всех опорах (см. рис. 3.2. а) и шарнирными
скреплениями контактных проводов.
Вычислим нагрузку рэк по формуле (3.24)
рэк = 2-1,14 —(2-1,14-1,4) (1-4-17,852/752) =1,6 даН/м.
Эквивалентную нагрузку рэ11 найдем по формуле (3.10)
1,6-1800 -1,2- 2000 — 2000 • 1800 • 1,426/75®
Р',и~‘ 1800 4-2000-1 1,026-1800-12 1 45/752 0,0оЬ даН/м -
79
Наибольшее ветровое отклонение контактных проводов в местах их скреп-
лений, принимая - 0,85, определим по формуле (3.25)
0,85 (1,6 + 0,056) 17,85 (75—17,85)
Ь.. = —--1:---------------5----------- + 0,022 = 0,381 м;
2-2000 г
+ max
максимальное ветровое отклонение контактных проводов от оси пути в середине
пролета - по формуле (3.26)
0,85(1,64-0,056)752 0,04
——Л_-—:-------------+ о, 022 4------- 0,5.37 м .
8-2000 2
Очевидно, что и эта подвеска не обеспечивает нужной ветроустойчивости.
Проверим такую же. подвеску, но с жесткими скреплениями контактных прово-
дов. По формуле (3.30) рассчитаем
Р 0,5 (2-1,14 : 0,056) 17,85 )-(1,44-0,056) (37,5—17,85) - 49,46 даН.
Наибольшее ветровое отклонение контактных проводов в местах их скрепле-
ний найдем по формуле (3.29)
49,46-17,85
{-0,022 0,279 м.
2000 1-2-0,32-12 750-200/17,852
Для второго по направлению ветра контактного провода от оси пути рас-
считаем по формуле (3.31)
(1,4 ; 0,056) (75- 2-17,85)2 0,04
0.279 ——!—1--------------------!_2_+ _... опм,
к 8-2000
2
Проверим ветровое отклонение контактного провода на участке между
фиксатором и местом скрепления проводов. Поскольку &с as а, можно принять
«,,р 0. Задаваясь /(2 800 даН, определим по формуле (3.28)
(1,14-10,056)17,852
b .---------------------- 0,06 м .
8-800
Ветровое отклонение контактного провода на рассматриваемом участке
найдем но формуле (3.27)
ftKnu.x 0,06 { 0,5 (0,3 | 0,279) |-0,022 =0,372 м,
что меньше, чем в середине пролета.
Таким образом, для обеспечения нужной ветроустойчивости подвески без
персразбивкн прологов необходимо перемонтировать ее в ромбовидную с ромба-
ми на всех опорах и жесткими скреплениями контактных проводов.
§ 3.4. Проверка длины пролета по соблюдению
высотных положений 1 контактных проводов
и в условиях эксплуатации
Максимальную длину пролета, определенную по ветровым откло-
нениям контактных проводов, необходимо еще проверить по соблю-
дению их высотных положений. В обычных условиях минимальная
допустимая высота контактного провода от уровня головок рель-
1 Высотное положение — расстояние от уровня головки рельса до контакт-
ного провода
80
Рис. 3.11. Расчетная схема для опреде-
ления максимальной допустимой длины
пролета при компенсированной подвеске
(штриховая линия — нормальное положе-
ние контактного провода при отсутствии
дополнительных нагрузок)
сов (у.г.р. на рис. 3.11) в эксплуатации составляет 5,75 м на перего-
нах и станциях, максимальная допустимая высота hmax 6,8 м.
Проверяемая длина пролета при компенсированных подвесках
допустима, если выдержаны следующие условия:
у опоры
А Ьдн 7г—7-j Л ।
у околоопорной струны
А йди 7 г — 7 г А ЛИ1. | Л hj \-f;
в середине пролета при А/г,. > /
А ЛЯ11 ' Fv -7’-|-ЛЛц,.-|-АЛс,
где Ft- — вертикальная проекция стрелы провеса несущего троса при
гололеде с ветром;
/•', f — нормальные стрелы провеса соответственно несущего троса
и контактного провода (при отсутствии дополнительных на-
грузок);
Л/111Г — изменение высоты положения контактного провода при ветре
во время гололеда вследствие поворота гирлянды подвесных
изоляторов (при неизолированных консолях и без учета не-
значительного влияния фиксаторов);
Л/?„, ЛЛ|. АЛ,- —соответственно подъемы контактных проводов токоприем-
ников у опоры, у околоопорной струны и в середине про-
лета, определяемые по формулам, приведенным в § 4.4. (Па
рис. 3.11 они не показаны.)
Очевидно, что при Д/г,. > \h„ f и при Д/i,. > \h} / расчет
следует вести для середины пролета; если же \h0 + f >• А/г,. или
A/ii /> Д/гс, то более неблагоприятные условия будут соответст-
венно у опор или у околоопорных струн.
Введем условные обозначения:
у опоры
\ йдп А /1дц A 7i|ir— А hn
у околоопорной струны
АЛдп, -АЛдп- АЛ,п-—Ahi —/:
в середине пролета
А ЬдПр - А Ьди — Л hllr - Л hc.
Я1
Тогда для максимального допускаемого по габаритным условиям
пролета предельным будет значение
= Sr бпах __Sr (^iiiax —2с)~ А
д" 8Т ” 8 (TH А') Т ’
где с расстояние от оси опоры до околоопорной струны.
Решая это уравнение относительно /П1ах, получим
/шах -0,5/1 г У'О^ДЧ’Я', (3.45)
где Л irK/Г; Н -.4с* К./Т 8 (7’ i К) \h^‘gv.
Поскольку величины A/i0, A/i, п Vi(., а также A/i(ll. н / зависят от
неизвестной на данном этапе длины пролета, для практических рас-
четов можно принимать при одном контактном проводе Мц,, 0,85 м.
а при двух контактных проводах на 0,05 м больше, не уточняя, для
какого места пролета ведется расчет.
Для середины пролета при компенсированных подвесках выраже-
ние (3.45) приводится к виду
Onax 2 I 27 Лц!|/-Уг * (3 46)
При полукомненсироваппых подвесках для середины пролета
проверку его длины можно осуществить но приближенной формуле
Onax J 2А ЬЛп/(W.2/Z2 — IV3/ZJ , (3 47)
где W., и Z2 соответственно приведенные линейная нагрузка и натяжение не-
сущего троса для режима, при котором возможна максимальная
стрела провеса несущего троса (определение приведенных пагру
зок и натяжений см. в гл. 6);
U7, н Z, то же для режима, при котором минимальна стрела провеса не-
сущего троса.
Вели в результате проверки окажется, что длина пролета I, оп-
ределяемая условиями соблюдения высотных положений контактных
проводов, будет меньше длины по ветровым отклонениям, то при
дальнейшем проектировании нужно принимать значение I, обеспечи-
вающее соблюдение нормированных высот.
При проектировании контактной сети детально выясняют усло-
вия ветровых воздействий в данном районе (см. § 1.3) и поэтому пра-
вильно сооруженная сеть обеспечивает нужную ветроустойчивость.
Однако в процессе эксплуатации климатические условия могут из-
мениться и тогда возникает необходимость проверки и повышения вет-
роустойчивости контактной сети. Текущая проверка необходима и для
определения правильности эксплуатационного содержания сети. Прак-
тически на линии возможно измерить только длину пролета и разме-
ры зигзагов контактных проводов, а для ромбовидных подвесок — еще
и расстояния от осей опор до мест скреплений контактных проводов.
Эти параметры и подлежат проверке.
Если возникает сомнение в допустимости какой-либо длины про-
лета, то для проверки можно воспользоваться графиками, приведен-
82
ними в Правилах технического обслуживания и ремонта контактной
сети электрифицированных железных дорог, или номограммами, о
которых было сказано в §3.1. Допустимы ли измеренные зигзаги
контактных проводов, можно установить, пользуясь Инструктивны-
ми указаниями по регулировке контактных подвесок, где приведе-
ны предельные зигзаги, необходимые для обеспечения требуемой вет-
роустойчивости контактной сети для различных подвесок и клима-
тических условий. Там же для двух видов ромбовидных подвесок
указаны расстояния от оси опоры до места скрепления контактных
проводов, обеспечивающие требуемую ветроустойчивость сети.
Если же при измеренной длине пролета или размерах зигзагов
ветроустойчивость обычной контактной подвески ниже требуемой,
возможно осуществить следующие мероприятия (приводятся в по-
рядке их сложности): изменение зигзагов контактных проводов; по-
вышение их натяжения (в допускаемых пределах); переоборудование
обычной контактной подвески в подвеску повышенной ветроустойчи-
вости (при двух контактных проводах — в ромбовидную, при одном
контактном проводе — подвеску с оттяжными тросами или в косую);
установка дополнительных (фиксирующих) опор в середине пролетов
или переразбивка пролетов, если нельзя добиться нужной ветроустой-
чивости другими мерами.
Усилить ветроустойчивость ромбовидной контактной подвески
возможно, заменив шарнирные скрепления жесткими, приблизив ме-
ста скреплений к опорам и выполнив ромбы на каждой опоре, если они
были установлены через опору.
Пример. 3 я дани е. Проверить допустимость максимальной длины про-
лета, равной 68 м, вычисленной но условию соблюдения ветрового отклонения для
компенсированной подвески ПЬСМ-95 ! МФ-100 на прямом участке пути, но
условию соблюдения нысотных положений контактны о провода в случае гололе-
да при толщине стенки льда 20 мм.
Р е ш е н и е. По табл. 2.1 найдем распределенную линейную нагрузку от
веса гололеда на подвеске
4,06—1,73 2,33 даН/м.
Принимая с - 10 м и ЛЛд(1 0,85 м, получим следующие значения коэф-
фициентов для уравнения (3.45):
А = 4-10-1000/1800=- 22,2;
В 4-102.1000/1800 + 8 (1800+ 1000) 0,85/2.33 8394.
Максимальную допускаемую длину пролета по условиям соблюдения вы-
сотных положений контактного провода определим по формуле (3.45)
/max -11.1 ! V 11,12+8394' -=81.2 м.
Таким образом, длину пролета, равную 68 м. определенную по условию соб-
людения ветрового отклонения контактного провода, можно принять в качестве
максимальной.
Глава 4
РАСЧЕТЫ ВЗАИМОДЕЙСТВИЯ
КОНТАКТНЫХ ПОДВЕСОК С ТОКОПРИЕМНИКАМИ
§ 4.1. Методы исследований
В процессе проектирования контактных подвесок и токоприемни-
ков для высоких скоростей движения поездов необходимо оценивать
качество токосъема при различных вариантах исполнения взаимо-
действующих конструкций, чтобы правильно выбрать их оптималь-
ные параметры. Для этого нужно или строить траектории токопри-
емников и кривые их контактных нажатий, или определять экстре-
мальные значения вертикальных перемещений точки контакта поло-
<а токоприемника с контактным проводом и контактных нажатий,
вызывающих эти перемещения, а иногда только устанавливать воз-
можность отрыва полоза токоприемника от контактного провода.
Расчеты но статической методике не могут обеспечить решение та-
ких задач; для этого необходимо учесть динамику взаимодействия
контактной подвески с токоприемниками в процессе токосъема.
В связи с ростом скоростей движения поездов расчеты, учитываю-
щие динамику, приобретают все большее значение и непрерывно со-
вершенствуются. Основная цель таких расчетов — обеспечение вы-
сокого качества токосъема путем стабилизации контактного нажатия
каждого из участвующих в процессе токосъема токоприемника около
оптимального уровня. Это приведет к снижению износа контактных
проводов и токосъемных пластин, а также к уменьшению помех ра-
диоприему, возникающих при искрении и отрывах токоприемников.
Выполнение необходимых расчетов на ЭВМ позволит существен-
но расширить границы исследований, а при необходимости экспери-
ментов — сократить их объем и затраты на них.
Взаимодействие контактной подвески с токоприемниками пред-
ставляет собой очень сложный колебательный процесс, в котором уча-
ствуют разнородные колебательные системы: две из них с распреде-
ленными параметрами (железнодорожный путь и контактная подвес-
ка) и несколько систем с условно сосредоточенными параметрами
(локомотивы с токоприемниками). Таким образом, интересующие нас
точки контакта полозов токоприемников с контактным проводом со-
вершают колебания, обусловленные параметрическим возбуждением
со стороны контактной подвески вследствие периодического изменения
ее параметров, а со стороны локомотива — воздействием колеблю-
щихся токоприемников, на основании которых передаются колеба-
ния пути и электроподвижного состава. Кроме того, вдоль контактной
подвески в обе стороны от точки приложения контактного нажатия
м
каждого из токоприемников распространяются волны колебаний,
влияющие на взаимодействие подвески с другими токоприемниками.
Сказанное можно пояснить схемой, приведенной на рис. 4.1, для слу-
чая, когда один токоприемник движется со скоростью и в направле-
нии, указанном верхней стрелкой.
Методы исследований взаимодействия контактной подвески с то-
коприемниками можно разделить на аналитические, моделирующие и
экспериментальные. Такое разделение весьма условно, так как все эти
методы тесно связаны. Результаты расчетов аналитическим или мо-
делирующим методом не могут быть достоверными без эксперимен-
тального подтверждения, а моделирующие и экспериментальные методы
должны базироваться на определенных теоретических предпосылках.
Аналитические методы можно разделить на две основные группы:
учитывающие и не учитывающие динамические процессы; модели-
рование может быть физическим и математическим (с помощью уни-
версальных ЭВМ и на специально разработанных электроаналого-
вых установках); эксперименты проводят либо в лабораторных усло-
виях, либо на действующих линиях или на специальных полигонах.
Для проектирования контактной сети основной интерес представ-
ляют аналитические методы исследований. Принципиально возмож-
но на стадии проектирования использовать специальные электро-
аналоговые установки, в которых моделировался бы процесс взаимо-
действия контактной подвески с токоприемниками. Однако подобных
установок нет и поэтому в дальнейшем подробно рассматриваются
только аналитические методы расчетов, учитывающие динамические
процессы. Для выполнения подобных расчетов обычно используют
универсальные ЭВМ.
Расчеты, учитывающие динамику, можно базировать на резуль-
татах анализа процессов, возникающих при токосъеме, принимая их
детерминированными или случайными. И в том и в другом случае
развитие методик расчета идет по различным путям в зависимости от
того, учитывается или не учитывается распространение колеба-
ний вдоль контактной подвески.
Не менее важен учет влияния на
токосъем колебаний пути и локо-
мотива. Воздействия этих колеба-
ний, а также ветра (действие его
допустимо учитывать совместно с
аэродинамическими силами) всегда
являются случайными. Можно счи-
тать случайными и некоторые дру-
гие факторы, например кривые про-
висания контактных проводов, на-
тяжения проводов подвески и т. д.
Поэтому исследования динамики
взаимодействия контактной подвес-
ки с токоприемниками методами
Рис. 4.1. Схема, поясняющая взаимо-
действие токоприемника с контактной
подвеской
85
теории вероятностей являются более строгими. Одиако учет случайных
явлений существенно усложнит решение поставленной задачи. По-
этому в первую очередь были разработаны методики расчетов взаимо-
действия контактной подвески с токоприемниками, базирующиеся
на анализе детерминированных процессов.
В большинстве современных методик расчета, разработанных в раз-
личных странах, не принимается во внимание распространение волн
колебаний в обе стороны от точки контакта вдоль контактной подвес-
ки. Такие методики применяют лишь для расчетов взаимодействия
контактной подвески с одним токоприемником. При взаимодействии
же контактной подвески с несколькими работающими одновременно
токоприемниками без учета распространения колебаний вдоль кон-
тактной подвески точно решить задачу нельзя. Влияние на процесс
токосъема колебаний локомотива необходимо учитывать, так как
иначе результаты расчетов могут существенно разойтись с действи-
тельными перемещениями или нажатиями.
Из сказанного следует, что решить поставленную задачу анали-
тически на основе анализа детерминированных процессов достаточ-
но трудно. Колебания даже одиночного провода описываются диффе-
ренциальными уравнениями в частных производных четвертого по-
рядка со сложными граничными условиями. Колебания каждого из
токоприемников должны быть представлены обыкновенными нели-
нейными дифференциальными уравнениями, которые нужно решать
совместно с уравнением колебаний контактной подвески и уравнения-
ми, описывающими колебания крыши локомотива. Последние про-
исходят с переменной амплитудой и спектром частот, зависящими
от типа локомотива, состояния пути, скорости движения. Колебатель-
ная система, в которой учтены все участвующие в процессе токосъе-
ма компоненты, обладает бесконечным числом степеней свободы. Все
это делает практически невозможным аналитические решения си-
стем таких уравнений без принятия каких-либо упрощающих допу-
щений. Однако каждое из вводимых допущений должно быть тщатель-
но обосновано. Критерием приемлемости тех или иных допущений явля-
ется соответствие результатов аналитических расчетов эксперимен-
тальным данным с достаточной для практических целей точностью.
В Советском Союзе вопросами динамического взаимодействия кон-
тактной сети с токоприемниками и разработкой соответствующих ме-
тодик расчета занимаются многие научные организации. Ниже при-
водится разработанная в МИИТе под руководством автора методика
динамического расчета, результаты которого подтверждены экспери-
ментальными исследованиями, выполненными совместно с лаборато-
рией контактной сети ВНИИЖТа (см. §4.4).
Несмотря на то что указанная методика не учитывает распро-
странения колебаний вдоль контактной подвески, она рекомендована
для практического применения в проектных организациях, так как
позволяет не только достаточно просто моделировать процесс взаимо-
действия контактной подвески с токоприемником, но и производить
86
необходимые расчеты на ЭВМ. Создание соответствующих вычисли-
тельных программ для различных ЭВМ не представляет затруднений.
С целью облегчения пользования материалами данной главы при-
ведем принятые в ней основные условные обозначения и единицы из-
мерения различных величин:
Р - полное контактное нажатие, даН;
Р(.— постоянная составляющая контактного нажатия, даН:
Рл сила нажатия подъемных пружин токоприемника, приведенная к оси
верхних шарниров подвижных рам, даН;
Pi - вертикальная составляющая сила аэродинамического воздействия (при
необходимости с учетом ветра) на элемент I, даН;
Q — переменная составляющая контактного нажатия, даН:
Q-- ± Р-л ±
Ра — инерционная составляющая контактного нажатия, даН;
Р-л — инерционная сила, возникающая при разности ускорений верхних шар-
ниров подвижных рам и центра их масс, при передаче колебаний крыши
локомотива на ось верхних шарниров, даН;
т.) — условная приведенная масса элемента I, кг;
гг- — коэффициент вязкого трения элемента I, даН-с/м;
— сила сопротивления сухого трения в элементе Г, даН;
Ж[ - - жесткость элемента (, даН^м;
h — длина пружин кареток токоприемника в свободном состоянии, м;
У; — ордината точки на элементе i при наличии нажатия токоприемника, м;
г,- — то же при отсутствии нажатия токоприемника, м;
у, — скорость перемещения точки на элементе i, м/с;
У/ — ускорение точки на элементе i, м/с2;
0 — круговая частота изменения параметров контактной подвески. рад'С'
О =2л и/1\
v — скорость поезда, м/с;
I — длина пролета между опорами контактной сети, м,
Т — натяжение несущего троса, даН;
К — натяжение контактного провода (иронодон), даН;
Н —натяжение рессорного троса, даН;
Л.ч — амплитуда колебаний крыши локомотива, м;
<о,, — основная круговая частота колебаний крыши локомотива, ряд/с;
<р — угол сдвига начала колебаний крыши локомотива относительно начала
пролета контактной подвески, рад.
В зависимости от того, какой элемент подлежит рассмотрению,
индекс i заменяется на соответствующий: н — несущему тросу; к, —
контактному проводу; к — контактной подвеске; т — токоприемни-
ку; п — полозу токоприемника; р—подвижным рамам токоприем-
ника; 1 — элементам, расположенным между полозом и подвижны-
ми рамами токоприемника; 2 — элементам, находящимся между верх-
ними шарнирами подвижных рам токоприемника и крышей локомо-
тива; л — крыше локомотива. Массы тк и тн приводятся к точке
контакта полоза токоприемника с контактным проводом, а масса
tnv — к оси верхних шарниров подвижных рам токоприемника.
87
§ 4.2. Критерий и показатели качества токосъема
Критерием оптимального качества токосъема для проектируемо-
го участка являются минимальные суммарные приведенные затраты
на контактную сеть и токоприемники, позволяющие обеспечить при
их взаимодействии заданные режимы работы всех устройств электри-
ческой тяги. Указанные затраты определяются известным выражением
Н - кя[Кк + КТ\+[Эк \ЭТ]. (4.1)
где // — приведенные затраты на контактную сеть и токоприемники,
руб./год;
/<к и К-г — капитальные затраты па соответственно контактную сеть и то-
коприемники, руб.;
к;, — коэффициент эффективности капитальных затрат, 1/год;
Эг и — годовые эксплуатационные расходы соответственно на контакт-
ную сеть и токоприемники (включая амортизационные отчис-
ления), руб./год.
Основной частью связанных с процессом токосъема расходов на
содержание контактной сети и токоприемников являются затраты на
замену изношенных контактных проводов и токосъемных пластин
токоприемников. Интенсивность износа контактирующих элементов
находится в определенной зависимости от контактного нажатия. Эту
зависимость для конкретных условий взаимодействия контактной
подвески с токоприемником можно представить кривой, показанной
на рис. 4.2. По оси ординат этого графика могут быть отложены зна-
чения износа контактных проводов (либо токосъемных пластин или
суммарного) в мм-/км или в кг/км. Минимум кривой на рис. 4.2 опре-
делит оптимальное значение контактного нажатия Р011Т, обусловли-
вающего наименьший износ контактирующих элементов.
Обычно пользуются различными техническими показателями, ко-
торые позволяют дать качественную оценку токосъема при сравнениях
вариантов исполнения тех или иных конструкций контактных подве-
сок и токоприемников или при сопоставлениях их взаимодействия
в различных условиях работы.
Наиболее объективной функцией для определения показателей
оценки качества токосъема является контактное нажатие. Чем ста-
Рис 4.2. Зависимость износа контакт-
ных элементов от нажатия токопри-
емника
О х
Рис 4 3. Примерное изменение нажатия
токоприемника вдоль пролета контакт-
ной подвески
ЯК
Рис. 1.4. Гистограмма нажатий то
коприемника в пролете контакт-
ной подвески
бильнее контактное нажатие, тем меньше изнашиваются контактные
провода и токосъемные пластины и, следовательно, лучше качество
токосъема. При этом необходимо, чтобы нажатие было стабилизиро-
вано па оптимальном уровне, который должен быть установлен с
возможно большей точностью.
Располагая кривыми изменения контактного нажатия вдоль про-
лета контактной подвески Р (х) или экстремальными значениями на-
жатия в пролете, при проектировании контактных подвесок и токо-
приемников можно использовать следующие показатели (рис. 4.3).
Коэффициент относительного изменения контактного нажатия п,
который выбирается из двух значений:
«1 Ршах/Ре—1 и л2"’Рт1п/Рс *1> (4.2)
где Р1Пах и Р|П!и — экстремальные значения контактного нажатия в одном и
том же пролете.
Токосъем считается удовлетворительным, если |n| с 0,3 4- 0,5.
Чем больше скорость движения, тем меныпим следует принимать
предельное значение п.
Максимальная переменная составляющая контактного нажатия
Q, которая выбирается из следующих двух значений:
Ох- Рmax — Ре и Ог-'-РтН, — Ре- (4.3)
Исходя из сказанного токосъем можно считать удовлетворитель-
ным при условии
IQImaxC (0,3 = 0.5) Рс. (4.4)
При наличии кривых изменения контактного нажатия вдоль про-
лета можно построить гистограмму (рис. 4.4) и определить среднее
квадратичное отклонение нажатия
о [Р] |/ £ [Pi-»HP)JS-^-. (4.5)
tli
где т (Р) У Pi----;
i = l п
Pl — среднее значение контактного нажатия в интервале г.
щ — число случаев с нажатием Р р
п — общее число случаев (интервалов).
Чем меньше величина ст (Р), тем лучше качество токосъема.
Кроме указанных, при проектировании контактных подвесок и то-
коприемников могут быть использованы показатели оценки качест-
89
Рис. 4.5. Примерная траектория
токоприемника (сплошная линия)
и положение контактного провода
при отсутствии нажатия токопри-
емника (штриховая)
ва токосъема, характеризующие вертикальные перемещения точки
контакта полоза токоприемника с контактным проводом (рис. 4.5).
Максимальный размах (двойная амплитуда) вертикальных пере-
мещений точки контакта
24 ук п1ах — Ук mln , (4-6)
fAe Ук щах j —экстремальные значения высоты точки контакта в одном и том
Miimln < же пролете.
Чем меньше значение показателя 2/1, тем ближе к прямолинейной
траектория токоприемника и тем лучше качество токосъема. Чтобы
определить этот показатель, нужно иметь или кривые траектории
токоприемника в пролете ук (х), или экстремальные значения высоты
точки контакта в пределах данного пролета.
Отжатие контактного провода в заданной точке
укх=ук г —гк х, (4.7)
гДе Укл )---ординаты контактного провода па расстоянии х от опоры соответсг-
и х> вечно при наличии и отсутствии нажатия токоприемника.
Этот показатель имеет значение для сравнительной проверки
качества токосъема при проходе контактной подвески в искусст-
венных сооружениях и в других условиях (например, под фиксато-
рами).
В тех случаях, когда при сравнении качества токосъема возмож-
но определить длительность отрыва полоза токоприемника (или его
отдельных пластин) от контактного провода, может быть использо-
ван коэффициент отрыва токоприемника (в %)
Кот -23— 100, (4.8)
т
где т01. суммарное время отрыва токоприемника (или его пластин) за время т.
Токосъем считается удовлетворительным, если кот 0,3 %.
Определение длительности отрыва полоза токоприемника от кон-
тактного провода при аналитических расчетах представляет слож-
ную задачу. На стадии проектирования контактных подвесок и токо-
приемников в ряде случаев достаточно только установить возможность
такого отрыва, что достигается фиксированием точки, в которой
нажатие токоприемника становится отрицательным.
Таким образом, при проектировании контактных подвесок и то-
коприемников можно использовать только показатели |Q|max или
90
2/1 (обычно они дают однозначные решения), а в тех случаях, когда
этого недостаточно, определять возможность отрыва полоза токо-
приемника от провода. При необходимости нужно еще устанавливать
отжатия контактных проводов в тех точках, где может возникнуть не-
допустимый подъем контактного провода. Помимо этого, следует про-
верять соответствие экстремальных значений контактного нажатия
допускаемым. Поскольку последние нормами не установлены, ори-
ентировочно можно принимать для токоприемников серии Л допусти-
мые изменения контактного нажатия в пределах от 4 до 20 даН, а для
токоприемников серии Т — в пределах от 6 до 36 даН.
§ 4.3. Расчеты для построения траектории токоприемника
и кривой его нажатия вдоль пролета
Искомые кривые строятся для одного (обычно максимального на
проектируемом участке) пролета. Этот пролет делят на определенное
число отдельных интервалов, внутри которых все параметры контакт-
ных подвесок и токоприемников принимают неизменными. Распреде-
ленные параметры контактной подвески заменяют сосредоточенными
и приведенными к точке контакта с полозом токоприемника.
Как уже указывалось, при взаимодействии контактной подвески
и токоприемника общая колебательная система обладает бесконечным
числом степеней свободы. Рассмотрим, как
это принято, взаимодействие отдельных
элементов системы исходя из приведенных
к соответствующим точкам масс (что для
пути и контактной подвески условно) и
учтем связи между этими массами в виде
жесткостей, вязкого и сухого трения. При-
нимая во внимание только наиболее су-
щественные перемещения в вертикальной
плоскости и значительно упростив колеба-
тельные системы пути и локомотива, мож-
но при наличии контакта полоза токопри-
емника с контактным проводом предста-
вить для каждого интервала пролета об-
щую колебательную систему с шестью сте-
пенями свободы (рис. 4.6).
Колебания пути передаются на локо-
мотив, масса которого значительно боль-
ше массы токоприемника. Поэтому, не
принимая во внимание обратное воздействие
токоприемника на локомотив, колебания
последнего можно учесть, введя в схему
вертикальные перемещения крыши. Эти
колебания имеют определенный спектр
Опоры
| Несущий трос
Контактный провод'
Полоз токоприемника
I Рамы токоприемника
Локомотив
Путь
Рис. 4.6. Колебательная си-
стема с шестью степенями
свободы
91
частот и переменную амплитуду. Для упрощения расчеты производят
при постоянной амплитуде Лл и основной круговой частоте гало-
пирования или подпрыгивания локомотива сол, принятых по экспе-
риментальным данным и усредненных для различных скоростей дви-
жения. В этом случае колебания крыши локомотива могут быть
описаны функцией
Ул -Ллео8 (ыл Н ф). (4.9)
Не учитывая незначительных колебаний опор (вследствие их
большой массы), допустимо от системы с шестью степенями свободы
перейти к системе с тремя степенями свободы (рис. 4.7, а). На рис. 4.7, а
контактная подвеска представлена с разделением условных приве-
денных масс отдельных проводов, благодаря чему можно рассматри-
вать несинфазные колебания несущего троса н контактного провода.
Такие колебания могут возникнуть при наличии рессорных струн,
обычно применяемых в условиях высоких скоростей движения,
а также при разгрузке отдельных простых струн. Последнее возмож-
но в случае существенного увеличения контактного нажатия, выз-
ванного ростом его аэродинамической составляющей при увеличении
скорости движения или близком расположении токоприемников на
электроподвижном составе. Кроме того, схема рис. 4.7, а позволяет
учитывать наличие в струнах демпфирующих устройств.
Токоприемник с обычно применяемым подрессор Иванием полоза
представлен на рис. 4.7, а системой с двумя степенями свободы. При
специальных конструкциях может понадобиться рассмотреть токо-
приемник и с большим числом степеней свободы, но это не представит
принципиальных затруднений.
Особенностью схемы рис. 4.7, помимо разделения колебаний про-
водов контактной подвески и учета колебаний локомотива перемеще-
ниями его крыши, является также разделение трения во всех элемен-
тах на вязкое и сухое. Это позволяет оценивать влияние различных
видов трения на процесс токосъема независимо друг от друга. Кроме
того, отдельно учтено воздействие аэродинамических сил на полоз
и рамы токоприемника, что позволяет более точно оценить влияние
этих воздействий.
Жесткость подъемных пружин токоприемника при составлении
схемы рис. 4.7. а (и последующих) не учтена, так как в каждом пра-
вильно отрегулированном аппарате изменения жесткости этих пру-
жин при вертикальных перемещениях токоприемника в пределах ра-
бочей высоп,1 не должны отражаться на силе их воздействия Ри,
приведенной к оси верхних шарниров подвижных рам. Поэтому до-
статочно ввести в расчетную схему силу Ро, приняв ее неизменной
Штриховыми линиями показаны положения отдельных элементов
колебательной системы при отсутствии нажатия токоприемника.
Расчетные уравнения для одного интервала пролета получим
в удобной для практических целей подвижной системе координат,
начало которой перемещается вдоль пути вместе с токоприемником.
92
а горизонтальная ось абсцисс расположена на произвольной высоте.
Составим расчетную схему (рис. 4.7. б), на которой реакции отдельных
связей заменены эквивалентными силами Р„, Рк1, Рг и Р2. а фик-
тивные силы инерции обозначены Рая, Рак1 и Рар. Направления дей-
ствия всех сил, кроме инерционных, указаны в соответствии с при-
нятыми в данный момент времени перемещениями всех масс снизу
вверх и при соотношении отдельных перемещений уп > ук > ур > ул.
Направления действия инерционных сил показаны условно.
В соответствии с принципом Даламбера справедливы следующие
уравнения, если принять за положительное направление сил вверх:
— Раи — Р и — Рк1 - 0;
—Рак1—Pj 'Г Рк1-1~ Рп '0;
~ Рар- Р2 + Р14- Р„ Ра + Рп ----- о.
(4.10)
Входящие в эти уравнения силы определяются выражениями:
Ран -тяун- Ра1п --(гпк1 Ь«п) Ук-.
Рн <и 1/ц-Ь-Жн (Ун —гп) i и>н;
Phi ~Гк1(Уи - Ук) t“ (Ун Ук -At)
Р1 Г} (ук — ур) -Г iWj ((/„ — ;/р — h) -I- ;
Рар- - Ир Ур:
Р2 r2 G/p _ У;1) “4^2-
(4.1П
Подставив значения всех сил из выражений (4.11) в уравнения
(4.10) и выполнив соответствующие преобразования, получим иско-
мую систему дифференциальных уравнений:
тн Ун+гнУк \-жа (уи--гн) -1-ьан + гК1(ун—Ук)
+ жю (Уц--Ук—’О;
(ик1 4-/пп) Ук+ ri (ук—Ур) -Т--Ж1 (Ук— Ур —Я) 4-
г ЬУ) — rni (.Ун ~Ук)~ ЖК1 (Ун— У к — Я) — Шк1--Рп>
Ир Ур + Г1 (.Ур—Ул) -I- а<г— (ук—Ур) ~
- жг (Ук — Ур — Я) — - /’о -1-Ра + Рр. 1
Решив для всех интервалов пролета систему уравнений (4.12)
с помощью любой универсальной ЭВМ, можно построить кривую
траектории токоприемника в пролете ук (х), а также кривые переме-
щений несущего троса уи (х), и верхних шарниров подвижных рам
токоприемника ур (х).
93
Рис. 4.7 Колебательная система с тремя
степенями свободы (а) и ее расчетная
схема (б)
Рис 4.8. Колебательные системы с
двумя (а) и одной (б) степенями сво-
боды и их расчетные схемы
Кривую изменения вдоль пролета контактного нажатия Р (х) стро-
ят. решив для всех интервалов пролета уравнение, полученное для
условий равновесия массы mKI на рис. 4.7, б,
Р "»К1 Ук+ ГК1 (ь'к — Ун) + жк1 (Ук — Ун + hi) 4
(4.13)
Практические решения получены пока для систем с двумя
(рис. 4.8, а) и одной (рис. 4.8, б) степенями свободы.
Аналогично изложенному в той же системе координат для систе-
мы е двумя степенями свободы справедливы выражения:
-РаК-^-/\ + Рп=0, 1 (4л4)
— Ра р- Рг + /'1 + Р о + Ра 4- Рр О, I
где значения Ряр. Рг и Р2 те же, что и выше, а
Рак"-; (mK + m„) у'к;
₽к=-: гк 1/к-Ь^к (.«к —гк) 4-шк.
(4.15)
94
Выполнив соответствующие преобразования, получим искомую
систему дифференциальных уравнений в виде:
(/пк + тп) ук±гку'к 4-жк (|/к—гк)-|-“’к +
4-/-1 (.Ук--.Ур) + ж! (ук — у?-h) -I- W-i -=Рп', (4 |6)
Я1р Ур+ г-1 (</р — Г-^2 — 'j Gk —Ур) —
— Ж'1 Ок—Ур - h) — w1 = Р„ 4- Ра -I- Рр.
Для системы с одной степенью свободы справедливо уравнение
Рак - Рк - Рт 4- Ро + Ра Р Рт'-О, (4.17)
где значение Plt то же, что и выше, и
Рак--(лчгт-тт) ,'/к; | .. ..
„ / (4.18)
”т гт \Ук У и) Ь М<т 1
Искомое дифференциальное уравнение
Ик : тт) 1/к + гц i/к (Ук гк)
!-гт (ук—Ул) I ®т - Рч [-Ра+Рт’, (4.19)
Контактное нажатие Р для систем с двумя и одной степенями
свободы в каждый момент времени будет определяться выражением,
полученным для условий равновесия массы тк в схемах рис. 4.8,
Р--тк ук-\ |/к+ жк (ук — z,:) а’к (4.20)
При разработке алгоритма решения для ЭВМ задают шаг инте-
грирования, т. е. время прохода одного интервала из тех, на которые
будет разделен расчетный пролет. Сравнительные расчеты показали,
что достаточная точность результатов достигается при длине интер-
валов, равной 1 м. Длительность шага определится в зависимости от
заданной расчетной скорости движения.
Решение дифференциальных уравнений выполняется по стандарт-
ной программе, постоянно хранящейся в долговременном запоминаю-
щем устройстве ЭВМ. Обращение к этой программе осуществляется
с помощью условного кода (команды). Расчетные дифференциальные
уравнения (4.16) и (4.19) приводят к виду:
для системы с двумя степенями свободы (см. рис. 4.8, а)
Ук Ь At Ук -1-Л2 Ур 4 А3 Ук : Ур --Л5; ( ('
Ур h Pi Ур Р% Ук Е>з Ур ' F Pt Ук I
для системы с одной степенью свободы (см. рис. 4.8, б)
Ук ^- Pi Ук~1~ ^2 Ук~- Рз- (4.22)
95
Значения коэффициентов в уравнениях (4.21) и (4.22) в каждом
интервале пролета определяются следующими выражениями:
д гк д _____________________д ЖцЧ-Жл
1 ткт^п' 2 ткА-то' 3 тк-\-та ’
А. ; Л5-_-------(Рп — wH — ®j + «|(2K 1-Ж! й);
mK h тп тк -f- тп
---06- ---------------(Ри 1/4+ />р + ^1— «Ъ k ) r2y,fl);
W р ГП р
i/iK тТ
1 , . .
1>з---------{р0 I-. /V! Рт — wK— Шт + жк гк 1-ГтУл).
тк znT
Обычно задают условную начальную высоту контактного провода
у опор равной 6 м. Необходимые для решения дифференциальных
уравнений исходные данные вводятся в ЭВМ принятым для этой ма-
шины способом. Изменения расчетных параметров по интервалам про-
лета могут быть заданы в табличной форме или соответствующими
формулами. Определение параметров, необходимых для выполнения
расчетов, а также рекомендуемые значения и законы изменений от-
дельных параметров вдоль расчетного пролета приведены в § 4.4.
Силы сопротивления сухого трения для упрощения в приведенных
формулах обозначены Более строго было бы их обозначить
Wj sign у,. Чтобы автоматически изменялся знак силы сопротивления
сухого трения при перемене направления скорости движения дан-
ного элемента в вертикальной плоскости, а также были устранены в рас-
четах разрывные функции, в уравнениях для ЭВМ вместо w, sign yj
можно задавать wt th (10z/y), а вместо w: sign (y} — yn) — выражение
U>; th (10 (У) — yn)l.
Если необходимо учесть одностороннее действие каких-либо дем-
пфирующих устройств, оказывающих воздействие только при пере-
мещениях токоприемника вниз, то, принимая результирующую ско-
рость со знаком «—». коэффициенты вязкого трения следует задавать
в виде
0.5 11 —- ify/P y}]rt или 0,5 11 —(t/j—tjujll (1/j —i/n)3] гг.
Инерционная сила г*а незначительна и в практических расчетах
ее допустимо не учитывать.
Поскольку совпадение начала колебаний крыши локомотива с на-
чалом пролета контактной подвески — явление случайное, то для
96
получения более точных результатов расчеты следует выполнять
для нескольких пролетов, учитывая колебания крыши локомотива
при различных значениях угла ф в формуле (4.9), а затем определять
искомые значения как средние из полученных для отдельных проле-
тов. При этом надо задать расчетную круговую частоту колебаний
крыши локомотива таким образом, чтобы полный цикл колебаний за-
нял принятое к расчету число пролетов, а значение частоты не выхо-
дило за пределы, установленные при экспериментальных исследова-
ниях (8,8—10,7 рад/с). Для соблюдения этого условия расчетная
круговая частота «>., должна быть определена по формуле
<«л — 1.75so/(ml) (4.23)
где т — принятое к расчету число пролетов;
s — любое целое число, не кратное т.
Расчетные значения s определяются выражением
S 3,б/Щ/((0.585 0.7J5) о|, (4.24)
в котором скорость поезда и принята в километрах в час, а. период
колебаний локомотива установлен по опытным данным в пределах
0,585—0,715 с.
Сравнительные расчеты показали, что достаточно принять т = 5.
Однако полное число расчетных пролетов должно быть большим, чем
т, так как начальные условия для первого пролета могут быть зада-
ны лишь приближенно (например, по статическому расчету), вследст-
вие чего данные по начальным пролетам нельзя считать достоверны-
ми. Полное число расчетных пролетов можно задать равным 10 (2m),
а необходимые значения величин вычислять как средние для проле-
тов с 6-го по 10-й включительно.
В тех случаях, когда не требуется высокая точность, расчеты
можно упростить, не учитывая несколько различных форм колебаний
крыши локомотива. При этом в каждом пролете следует принимать
Ф -- 0 (или л/2), а результаты расчетов выводить па печать ЭВМ тог-
да, когда начальные и конечные значения для расчетного пролета
совпадут с заданной точностью.
§ 4.4. Определение расчетных параметров
Рассмотренные выше расчеты можно выполнить, если имеются
следующие исходные данные:
по контактной подвеске — жесткость условная
приведенная масса тк; параметры вязкого и сухого трения гк и
провес контактного провода в свободном состоянии (задаваемый орди-
натой г„). Необходимо знать законы изменения всех этих параметров
вдоль пролета. Тип подвески, натяжения ее проводов и стрела про-
веса контактного провода должны быть известны;
1 Зак. 2630 97
по гок с п р и е м н и к а м — нажатие подъемных пружин,
равнее среднему статическому нажатию P!t; аэродинамические силы
Pj, ч действующие соответственно на полоз и на подвижные ра-
мы: приведенные массы полозов и подвижных рамтп нт?; жесткость
пружин, подрессоривающих полоз, ж,; параметры вязкого и сухого
трения в верхнем узле (rt и и в подвижных рамах (г., и ио) с уче-
том демпфирующих устройств, если они установлены, Если полоз не
подрессорен или это не учитывается, нужно знать суммарные пара-
метры. указанные выше отдельно для полозов и подвижных рам
(Р’г. тг. г,т, цу);
<i о э л е к т р о и о д вижп о му составу-- с’мплшп- да
,1и основная частота колебаний ы.,,. которые принимают по опытным
данным.
Рассмотрим определение всех перечисленных вып ? параметров.
Длч вычисления жесткости (или эласшчносзи) контактной под-
вески достаточно знать подъем контактного провода в онгедеденпой
точке пролета и силу Рх, вызвавшую его. Тогда в этой точке
жесткость подвески и эластичность определяют соответственно как:
ж.к , /\/А йк :v; (4.25)
Чкх A/lK.v7\. (4.26)
Точно определить подъем контактного провода весьма сложно,
гак как. помимо зависимости от силы нажатия токоприемника (опре-
деляется конструкцией токоприемника, скоростью движения и дрТ
и параметров контактной подвески (натяжений проводов, геометриче-
ских размеров и др.), этот подъем зависит от состояния струн, а так-
же от числа рабочих токоприемников и их взаимного расположения.
Когда нажатие токоприемника невелико, струны, находящиеся вбли-
зи точки приложения силы, как правило, не разгружаются, г. е. про-
должают выполнять свою функцию. При значительных нажатиях стру-
ны ослабляются и могут разгрузиться совсем. Полностью разгружен-
ные струны перестают выполнять свое назначение, а нагрузка от кон-
тактного провода передается па струны, более удаленные от точки
приложения силы. Чем больше нажатие токоприемника, тем больше
струн разгружается по обе стороны от точки его приложения. Осо-
бенно сложно определять юдъем контактного провода в опорных уз-
лах рессорных подвесок, где к перечисленным факторам прибавля-
ется еще влияние изменения положения и натяжения рессорного тро-
са. Этим же объясняется и то, что нельзя определять подъем контакт-
ного провода ь различных частях пролета рессорной подвески но
одним и гем же формулам.
В проектной практике для этих целей применяют достаточно про-
стую методику, которая излагается ниже.
При расчетах по этой методике, в пролете контактной подвесхч
различают гр и расчетные зоны (рис, 4.9). Зоны .4 и Б относятся к
опорным узлам подвески, зона В - к средней части пролета. Каж-
дой из зон соответствуют определенные расчетные формулы. Для опор-
98
I
Рис. 4 9 Расчетные зоны пролета рессорной контактной подвески-
: рентный трос; 2- нолрессорпая струпа: .4 околоопорная струна
ных узлов подвесок с рессорными тросами имеются значения величин,
полученные на основании обработки результатов массовых экспе-
риментальных исследований, выполненных под руководством авто-
ра. При этих исследованиях в широком диапазоне менялись все пара-
метры контактных подвесок (пролет, натяжения проводов, геометри-
ческие размеры опорных узлов и др.); нажатие токоприемника изме-
нялось через каждые 2 даН до 30 даН включительно. Однако приво-
димые далее опытные соотношения проверены только для подвесок с
положительными стрелами провеса контактного провода (проводов).
Поэтому их можно применять без ограничений лишь для компенси-
рованных подвесок, а для полукомпенсированных только при тем-
пературах, равных температуре бесировесного положения контакт-
ного провода (проводов) или больших ее.
Выбор расчетной формулы производи гея в зависимости от места
расположения токоприемников в пролете и от соотношения между
силой их нажатия и силой, при которой происходит разгрузка струн.
Если токоприемник находится под струной, тс его нажатие может либо
не вызывать разгрузку данной струны, либо вызывать разгрузку ее.
но не разгружать соседние, либо разгружать и данную и соседние
струны. Когда токоприемник расположен между струнами, надо раз-
личать условия подъема проводов до ч после разгрузки этих струн.
Примем следующие обозначения: - сила при которой начи
нается разгрузка подрессорных струп; R, - то же околоопорной
струны; - тс же струн, соседних с указанной; Rc то же любой
струны в средней части пролета. Расчетные варианты, которые могут
встретиться в практических условиях, классифицируем так, как это
показано в табл. 4.1 применительно к схеме на рис. 4.9.
Примерные значения сил, при которых начинается разгрузка раз-
личных струн, могут быть определены по формулам, полученным на
основании обработки данных экспериментальных исследований:
Кв- «кйк (с-l-ax)-)-i?p-2a ;-лсбс4-Лф б‘ф '-2/V; (4 27)
:f •-лк.Ск-0.5 (с—а,-'-Cj) -!-бс i Л'-,: (4 28)
99
Р' Пк gI{ (с 1-1,5cj) Зб£ 1- N1; (4.29)
/?<•• («Kg.Hc-1-Gc—Vj (Т + Ю/Т, (4.30)
где N 4/ К/(/ — 2с); (4.31)
/V. -= /V [1 —Ci/(Z—2с)]; (4.32)
V) ---V [1 -Зс1/(/--2с)]; (4.33)
Л'с -8/ К cc/(Z —2г)2. (4.34)
В формулах (4.27) — (4.34), помимо условных обозначений, при-
веденных в §4.1 и показанных на рис. 4.9, применены следующие:
gp — нагрузки соответственно от контактного провода и рессорного
троса длиной 1 м, даН м;
б’с - нагрузка от струнового зажима вместе с частью струны, воспри-
нимаемая при ее разгрузке, даН;
О’ф часть нагрузки от фиксатора, передающаяся на контактный про-
вод при воздействии токоприемника, даН;
п,.. nt.. лц) - число соответственно контактных проводов, струн и фиксаторов.
Т а б л ина 1.1
Условия расчета Соотношения сил в точках (см. рис. 4.9)
о 01 и '»() 1 и 5
До разгрузки дайной струны — — Р Ri
До разгрузки сосед- них струн р < /?„ н/?1 Rt<P^ R't
После разгрузки со- седних струн Р > Ra Р > R\
Продолжение табл. 4.1
Соотношения сил в точках (см. рис. 4.9)
Условия расчета 12 и45 •* И 4 22 и 2 4
До разгрузки данной струны Re —
До разгрузки сосед- них струн P^Ri 1 Re Re < P < 3Re P < 2Kn
После разгрузки со- седних струн Pz>Ri г Rc 3R( <.P <=.5tfc 2/?c < P < 4Re
100
Таблица 4.2
1. м с{. , м Л М Значения различных сил. даН
Л» Л,
Один контактный провод площадью сечения 100 мм2
.50 7,5 0,01 0,03 0,05 0,07 18,0 23,5 29,0 34,0 8,0 10,0 12,0 14,0 20,0 20,5 21,0 22,0 10,5/9,5 8,0/7,5 6,0/5,5 3,5/3,5
0,02 19,5 9,0 21,0 11,0/10,0
60 8.0 0,04 23,5 10,5 21,5 9,5/9,0
0,06 27,5 12,0 22,5 8,0/7,5
0,08 31,5 13,5 23,5 7,0/6.5
0,03 20,5 9,0 20,5 9,5/9,0
70 7.14 0,05 23,5 10,5 21,0 9,0/8,5
0,07 26,5 11,5 22,0 8,0/7,5
0,09 30,0 13,0 23,0 7,5/7,0
Два контактных провода площадью сечения по 100 мм2 каждый
50 3,75 0,01 0,03 0,05 0,07 34,0 45,0 55,5 66,0 16,0 20,0 24,0 28,0 38,5 40,0 41,5 42,5 14,5/13,0 11,5/10,0 8,0/7,5 5,0/4,5
0,02 37,0 17,5 41.0 15,0/13,5
60 4.0 0,04 45,0 20,5 42,5 13,0/12,0
0,06 53,0 24,9 44,0 11,5/10,5
0,08 61,0 27,0 45,5 9,5/8,5
0,03 38,5 17,5 40,0 13,5/12,5
70 3,57 0,05 45,0 20,5 41,5 12,5/11,5
0,07 51,0 23,0 43,5 11,5/10,5
0,99 57,5 26,0 45,5 10,5/9,5
п и именам* е. В числителе приведены значения сил пои Г 1500 даН. а в ша
менателе •• • при Т- = 1800 даН.
Результаты расчетов по формулам (4.27)—(4.34) приведены в
табл. 4.2 с округлением до 0,5 даН. При этом учитывались следую-
щие значения отдельных параметров: с = 10 м; а --- 6 м при одном
и 7 м при двух контактных проводах; аг ~ 2 м; G(. — 0,3 даН; Оф =
— 1,7 даН. Количество струн и фиксаторов учитывалось в соответ-
ствии с числом контактных проводов.
Основные формулы для определения подъемов контактных прово-
дов в зонах А и Б выводятся с обычными для статических расчетов
допущениями. Кроме того, не учитываются подъемы контактных про-
водов и изменения натяжений рессорных тросов на опорах, сосед-
101
Рис. 4.10. Расчетная схема для определения величины \Нп
пих с той, для которой рассчитывается опорный узел. Однако введе-
ние в эти формулы опытных величин у компенсирует допущения, при-
нятые при выводе, и результаты расчетов по ним весьма близки к
эксперим ентал ьны м да н ны м.
Для определения подъема контактного провода в точках О (см.
рис. 4.9). если нажатие токоприемника не вызывает разгрузки под-
рессорпых струн, составим расчетную схему, представленную на
рис. 4.10. и. Здесь половина силы нажатия токоприемника Р отнесе-
на к рассматриваемому пролету, а вторая половина — к соседнему
(левому) пролету. Определив сумму моментов всех сил относительно
точки Б сначала до. а татем после воздействия токоприемника и вы-
чтя первую сумму из второй, получим
0.5 (1Д \'Л)1- 0,5/' 1 — (К ' IP) A/i0 (Н'—П)1> 0.
Пренебрегая незначительными горизонтальными перемещениями,
рассмотрим уравнения равновесия сил в узле А до и после воздейст-
вия токоприемника (рис. 4.10. б). Вычтя первое уравнение для поло-
вины вертикальной составляющей опорной реакции из второго, по-
лучим
0,5 I'.,) - (T—fP) &haiu — (IP — H) t/я/а. (6)
Подставив значение полуразности вертикальной составляющей
опорной реакции из выражения (б) в (а) и выполнив соответствующие
преобразования, найдем
P-2(T-fP) bh„;a-2(H'-H)(ya!u-b/l)
X h.. —------------------------------. /н)
Обозначив отношение подъемов проводов Л/ги/Д/гп -= получим
расчетную формулу
. hn (4 35)
° 2 (Т-Н') уРа \-2 (K-lH')p
102
Для определения подъема контактного провода в точке 1 (см.
рис. 4.9), если нажатие токоприемника не вызывает разгрузки данной
струны, составим расчетную схему рис. 4.11. Вызванное нажатием
токоприемника изменение момента от вертикальных сил
А Л1верг---Р б' — с) сП- (г)
а изменение момента от горизонтальных сил
А МРоР - Г \ hj -j-K (A hj~- A — //' Л Ло (Н' -Н) 1> (д)
Приравняв выражения (г) и (д) и выполнив соответствующие
преобразования, получим
. Л .U„,.tlT (А- : ДА,, (Н'-Н)Ь
Обозначив отношение подъемов проводов \hai\hA получим
расчетную формулу
Pc Ы
Х'п, ---------—-— -----—. (4.36)
' {T+K-fK-t-H) уз! I
Определение подъемов контактных проводов в основных точках
пролета может быть выполнено по формулам, приведенным в табл. 4.3.
Формулы для зон А и Б даны без учета влияния изменений натяжения
рессорного троса, а формулы для зоны В составлены по работам
д-ра техн, наук И. И. Власова и канд. техн, наук 10. И. Горошко-
ва. Там же указаны эмпирические формулы для вычислений значе-
ний у.
При натяжениях рессорных тросов до 150 даН для подвесок с од-
ним и двумя контактными проводами и совмещенными струнами экс-
периментально были получены следующие результаты: подъемы про-
водов в точках 01 н 50 (см. рис. 4.9) до разгрузки соседних струн на
10 %, а после разгрузки этих струи на 25 % выше, чем в точках 0 и 0'.
В точках 12 и 45 до разгрузки соседних струп подъемы проводов на
35 %, а после разгрузки соседних струп на 65 % выше, чем в точках
/ и 5. У подвесок с двумя контактными' проводами и шахматным рас-
положением струн в точках 01, 50, 12 и 45 будут находиться струны,
подъемы проводов в точках 01 и 50 будут примерно такими же. как
в точках 0 и б', а в точках 12 и 45 - на 10 % выше, чем в точках 1 и 5.
При расчетах подвесок с шахматным расположением струн рас-
стояния с и Cj в соответствующих формулах нужно принимать по то-
му из контактных проводов, у которого подрессорная струна ближе
к опоре, а расстояния сс учитывать но несущему тросу.
Для практических расчетов можно принять, что жесткость кон-
тактной подвески вдоль пролета распределяется по кривой, показан-
ной на рис. 4.12. Для построения этой кривой необходимо определять
только жесткости подвески в точках 0 и 1 (см. рис. 4.9) и в центре про-
лета. Закон изменения жесткости между точками би/ (5 и 0) может
быть принят линейным, а между точками / и 5 -..- параболическим.
ЮЗ
Расчетные формулы при условиях
Расчет-_______________________________________________________2-------------—-----------------------
ные зоны
(точки) ч после Разгрузки данной струны, пачгп^ки сосрлних стпун
на рнс. 4.9 до Разгрузки данной струны н0 до разгрузки соседних струн после разгрузки соседних струн
о
О
S
X
W
Я"
<и
S
X
о.
с
Рис. 4.11. Расчетная схема для опре-
деления величины ДЯ|
Рис 4.12. Расчетные распределения жест-
кости подвески (а) и расположение кон-
тактного провода (б) в пролете
При этом на участках между точками Ок! (5 и 0) допустимо прини-
мать жесткость подвески, равной среднему из двух значений для
этих точек, а жесткость в центре пролета, если неизвестно, будет ли
в этом месте струна, - среднему из значений при наличии й отсутст-
вии струны. Как показали сравнительные расчеты, такие упрощения
незначительно отражаются на конечных результатах.
Таким образом, при 0 ^ги / - с х I имеем ж1(Х - Жко,
а при с < х I — с
жц ж' I (1--2х)~. (4.52)
кс 1 (/ — 2с)2
Для определения условной приведенной массы контактной под-
вески предложено большое число различных формул. Результаты рас-
четов по ним в отдельных случаях дают значения, существенно раз-
личающиеся для одних и тех же условий. Поэтому были выполнены
специальные эксперименты, в результате которых удалось установить
необходимые для расчетов значения приведенной массы контактной
подвески. Используя формулу (4.20), можно написать
Р—гкУк — жк(ук—гк) wKsigni/l( , г„,
т 5 ------------------------------------. (4.53)
Ук
Представим выражение (4.53) в виде
— ж к (Хк- гк)
тк-------------------, (4.54)
Ук
где жк — жесткость контактной подвески, определенная экспериментально,
с учетом трения в подвеске.
Экспериментальные исследования по определению тк были вы-
полнены совместно с д-ром техн, наук В. А. Вологиным на скорост-
ном испытательном полигоне ВНИИЖТа Белореченская — Майкоп.
Для определения опытной величины ж”к (х) было совершено несколь-
104
105
ко поездок со скоростями, не превышающими 10 км/ч. Одни из этих
поездок были осуществлены с очень малым нажатием токоприемника
испытательного вагона Р', а другие — с нормальным контактным
нажатием Рх. При этом непрерывно записывались значения контакт-
ных нажатий и соответствующих им вертикальных перемещений кон-
тактных проводов у\ и Поскольку при указанных скоростях дина-
мические и аэродинамические воздействия отсутствуют, искомое зна-
чение Жк в каждой точке пролета
Жк Р') '(yi — 1/ih (4.55)
После поездок с малыми скоростями были выполнены поездки со
скоростями от 100 до 160 км/ч, во время которых синхронно осцилло-
графировалнсь значения Р, ук и у,.. Обработка полученных данных
показала, что искомая приведенная масса контактной подвески из-
менялась в пределах, мало влияющих на результаты расчетов. Это
позволило принять приведенную массу данной подвески неизменной
вдоль пролета и подобрать следующую эмпирическую формулу для
определения условной массы, кг:
»/,. /1К А4Н | 22, (1.56)
где И1( - маесд 10-метрового отрезка контактного провода, кг;
- число контактных проводов.
Параметры трения контактной подвески определяются следую-
щим образом. Вязкое трение в подвеске несколько больше в средней
части пролета, чем у опор, а сухое трение сильнее проявляется в опор-
ных узлах, где имеются шарнирные конструкции (фиксаторы). Ана-
литические данные по этим параметрам отсутствуют, поэтому прихо-
дится ориентироваться на экспериментальные исследования. По опыт-
ным данным, полученным д-ром техн, наук В. А. Вологиным и канд.
Табл и и а 4.4
Параметры Средние значения параметров контактных подвесок
ПБСМ-70+МФ-100 компенсированная М-1204-2МФ-100
компенсированная лолукомпенси- ровавная
К, даН 1000 2X1000 2Х Ю00
Г, даН 1500 1800 2000/1000
//, даН 150 150 150
.«ко, даН/м 205 310 350/250
ж,(с, даН/м 145 215 230/170
тк, кг 30 40 40
гк, даН-с/м 0,8 1,5 1,5
а>к, даН 0,8 1,2 5 1,2
/, см 5 -5/10
Примечание. В числителе приведены данные для режима минимальной темпе-
ратуры, в знаменателе — для режима максимальной температуры.
106
Рис 4.13 Кривые изменений контактных нажатий по длине пролета, рассчитанные
на ЭВМ (сплошные; и полученные экспериментально (штриховые) с усреднени-
ем результатов трех поездок со скоростями 160 км/ч
техн, наук А. Ф. Дроботенко, учитывая незначительное влияние
изменений вязкого и сухого трения подвески вдоль пролета на ре-
зультаты расчетов, для практических целей можно принимать по-
стоянные значения, указанные в табл. 4.4.
Как показали неоднократные эксперименты автора совместно
с В. А. Вологиным при различных скоростях движения, применение
описанной в §4.3 методики расчета взаимодействия контактной под-
вески с токоприемником обусловливает удовлетворительное совпаде-
ние результатов расчетов и опытных данных (рис. 4.13).
Показатели оценки качества токосъема (см. § 4.2), вычисленные
по этим кривым, незначительно различаются, что и дало основание
рекомендовать методику расчета, не учитывающую распространение
колебаний вдоль подвески, для практических расчетов. Отсутствие
существенных расхождений между расчетными и экспериментальны-
ми данными позволило отказаться от уточнения путем учета нели-
нейности тех отдельных функций, которые принимались линейными.
Значения ординаты гк (л-) для выполнения расчетов могут зада-
ваться в зависимости от стрелы провеса контактного провода / по
кривой, приведенной на рис. 4.12, б. При О^х^си/ с < х < /
имеем zKX -= г1(0, а при с sj х < Z — с
а -?ьс Н 77 ~~V(2"0— 2х)2- (4.57)
(I — ZC) ‘
Если значение zK1) принято равным 6, то гке -- 6 — /.
Средние значения основных параметров наиболее часто применяе-
мых компенсированных контактных подвесок ПБСМ-70 4- МФ-100 на
линиях переменного тока и различных подвесок М-120 4- 2МФ-100
на линиях постоянного тока приведены в табл. 4.4, где значения ж
и f указаны для пролета длиной 70 м, а величина Н для полукомпенси-
107
рованной подвески дана при температуре беспровесного положения
контактных проводов.
Параметры токоприемников, необходимые для практических рас-
четов, приводятся в различной литературе.
Если нет конкретных данных, можно принять средние параметры,
указанные в табл. 4.5, для токоприемников легкой серии Л (электро-
подвижной состав переменного тока и электропоезда постоянного
тока) и тяжелой серии Т (электровозы постоянного тока).
Если необходимо разделить силу Pi на Р'„ и /%, можно исходить
из того, что аэродинамическая сила, действующая на полоз, Р'„ со-
ставляет 70—75 % полной силы Р\. Соответственно аэродинамическая
сила Рр, действующая на рамы, составит 25—30 % полной. Приведен-
ная масса токоприемника тт может быть принята равной сумме при-
веденных масс полоза т„ и подвижных рам тр. При наличии каких-
либо демпфирующих устройств коэффициенты вязкого трения г,
и г2 следует принимать в соответствии с конкретными конструкциями
и местами их установки.
Некоторые данные наиболее часто применяемых токоприемников
приведены в табл. 4.6.
Большое значение для обеспечения хорошего качества токосъема
при нескольких рабочих токоприемниках имеет правильный выбор
расстояния между ними. Для этого нужно учитывать статическое и
динамическое воздействия токоприемников друг па друга. Как показа-
ли экспериментальные исследования, взаимное статическое влияние со-
седних токоприемников практически не ощущается при расстояниях
между ними более 40 м. При меньших расстояниях увеличение отжа-
тий контактных проводов в результате статического взаимодейст-
вия имеет линейный характер. Это позволило В. А. Вологину пред-
ложить для определения дополнительного отжатия контактного про-
вода приближенную формулу
A .VK х - 1>е1 (1 /./40)/жкт. (4.58)
где /\.1 — постоянная составляющая контактов нажатия одного из токоприем-
ников;
жкх — жесткость контактной подвески на расстоянии х от опоры, где оп-
ределяется Аукл.
Аналогично может быть вычислено условное нажатие Русл, ко-
торое должен был бы иметь один токоприемник, чтобы вызвать подъем
контактного провода, равный подъему под воздействием каждого
из токоприемников с учетом их статического влияния друг на друга:
Pycni-Pi + Pei (1 — Е/40). (4.59)
В результате испытаний со скоростями до 200 км/ч на линии с про-
летами длиной 70 м было рекомендовано выбирать расстояния Lr
между токоприемниками скоростного электропоезда исходя из усло-
вия 40 < Ет < 70.
108
Таблица 4.5
Параметры Средние значения параметров токоприемников серий
л т
Р(>, даН 7,35 11,30
даН 2,00/3,50 3,00/5,50
ГПа, КГ 10 20
тр, кг 15 20
Ж), даН/м 600 800
гт, даН-с/м 0,50 1,00
о/1, даН 0,25 0,50
о/2, даН 0,50 1,00
Примечание. В числителе приведены данные при скорости движения поездов
100 км/ч. в знаменателе— 160 км/ч.
Таблица 4.6
Тип токо- приемника Допу- стимая скорость движе- ния, км/ч Число рычагов подвиж- ной си- стемы Число полозов Материал контактных вставок полоза Тип ЭПС, иа кото- ром устанавлива- ется токоприемник
Переменный ток
П-1 В 120 4 1 Уголь ВЛ60
Л-13У П-7А 160 140 2 1 » ВЛ80, ВЛ85. ЭР9П. ЭР9М
2SLS-1 160 4 1 » ЧС4. ЧС4Г
3SLS-1 160 4 1 » ЧС8
Постоянный ток
П-ЗА 110 4 2 Уголь ВЛ23, ВЛ8
Т-5 НО 4 2 Металлокерамика ВЛ10У, ВЛ 11
Л-13У П-7А 160 140 2 1 У голь ЭР2, ЭР22М
Сн-6М 200 4 1 Медь ЭР200, ЧС200
10РР 160 4 1 Металлокерамика ЧС2, ЧС2Т
17РР 160 4 1 Металлокерамика ЧС6, ЧС7, ЧС200
Примечания. Допустимая скорость движения указана для токоприемников; у
электроподвижного состава, на котором они устанавливаются, эта скорость может быть
ниже.
2. На электровозах ЧС200 токоприемники типа Сп-6М применяются е металлокерами-
ческими вставками; при замене таких токоприемников устанавливают токоприемники типа
17РР.
109
Амплитуда колебаний крыши локомотива Ал по опытным данным
может достигать 0.02—0,03 м. При отсутствии более достоверных све-
дений величину Дл в расчетах допустимо принимать равной 0,025 м.
Основная круговая частота галопирования или подпрыгивания
электроподвижного состава <ол по экспериментальным данным на-
ходится в пределах 8,8—10,7 рад/с. Определять расчетную круговую
частоту необходимо с помощью формул (4.23) и (4.24).
Пример. 3 а д а н и е и и с х о д н ы е д а н н ы е Построить эпюры
эластичности и жесткости в пролете длиной 68 м для компенсированной рессор-
ной подвески ПБСМ-95-1-МФ-100 (рис. 4.14, а) при расчетных нажатиях токопри-
емника 10 и 16 даН, а также для компенсированной рессорной подвески М-120
• 2МФ-100 (рис. 4.14, б) при расчетном нажатии токоприемника 20 даН. Рес-
сорные тросы выполнены из проволоки 6БСМ с натяжением 150 даН. Необхо-
димые данные для всех проводов приведены в табл. 1.5 —1.8.
Решение. В дальнейшем подвеску ПБСМ-95-(-МФ-100 будем именовать
подвеска 1 (индекс п1), а М-120 | 2 МФ-100 — подвеска 2 (индекс п2).
Чтобы выбрать формулы для определения подъема контактных проводов в
точках 0 (см. рис. 4.14), надо сравнить заданные нажатия токоприемников с си-
лами /?0, при которых начинается разгрузка гюдрессорпых струн. Значения
N для обеих подвесок находим по формуле (4.31):
hi
4-0,06.1000
----------- .5,00 даН и А',,.,
68 --2.Ю
4-0,04-2000
68-2-10
6,67 даН.
Значения /?0 определим по формуле (4.27). Часть нагрузки от веса одного до-
полнительного фиксатора с фиксирующим зажимом Оф, передающуюся на кон-
тактный провод при воздействии на него токоприемника, примем равной 1,7
даН, а часть нагрузки от веса одной струны Gc, воспринимаемую при ее разгруз
ке, - 0,3 даН:
/?„„] -=0,873 (10 । 2) 1-0,229-2-6 |-2-0,3 | 1,7 | 2-5 --25,5 даН;
- 2-0,873 (10 I 2) 1-0.229-2-8-|-4-0,3 | 2-1,7 | 2-6,67 42,6 даН
Поскольку значения /?0 в обоих случаях больше, чем максимальные расчет-
ные нажатия токоприемников, то разгрузки подрессорпых струн не произой-
Рис. 4.14. Расчетные схемы контактных подвесок ПБСМ-95+МФ-100 (а) и
М-120+2МФ-100 (б) в половинах пролетов
110
дет, и значения АЛ» для обеих подвесок следует определять но формуле
(4. >7).
Значения у, находим по формуле (4.39s
(>• 1000
- -0|/
1/ 3-2000
' 0,34'3 И Т|1|2 I/--
10.1890----------------------------------К 1С-1800
Для подвесок 1 (при Р
-- 10 даН) г> 2 (при Р 20 даН!:
A 1 '
10-1000
2 (1800 — 150) 0,346: (> -|- 2 (1000
150) : 08
20-1000_________________
2 <' 1800 — 150 ) 0.566 :8 • 1 2 (2000 - ! 50) : 68
Значения эластичностей г)0 и жесткостей эго будут равны:
Г)(.„, 45.10 4.50 мм даН. ,w0II1 - 10:0,'45 222 даН,'м:
г)011-2 07:20 3,35 мм,'даН: jk0U2 20'0,007 299 даН м
Чтобы выбрать нужные формулы для определения подьем:> контактных пре
волов в точках / (сл рис. 4.14). сравним заданные нажатия токоприемников с си-
лами Rt, при которых начинается разгрузка струн в этих точках, и с силами Rj.
при которых начнется разгрузка соседних с этой точкой струн. Сш-чала опреде-
лим значения V, по формуле (4.32) и 'V,' по формуле (4.33):
8 \ , i 3 8
Л'пн 5(1- ------------4.17 дат! и /Viol - 5 1 ---------
",l I 68-2-10' ' 08 2-10
Значения R, определим по формуле (4.28), a R { — по формуле (4.29). Для
подвески 1
Rini - 0,873 (10 — 2-1-8) : 2 0.3 4,17 11.5 даН;
Ri',,1 0,873(10 1-1,5-8) 3-0,3 ! 2.5 22.fi даН,
для подвески 2
/<„2 2-0,873 (10 —2-|-8) • 2 (-0,3 ! 5.56 1.9.8 даН.
Поскольку для подвески 2 значение R, незначительно отличается от 20 даН,
величину /?{ можно не определять.
Таким образом, для подвески 1 при нажатии токоприемника 10 даН и для
подвески 2 при нажатии 20 даН значения Л/ц следует определять по формуле
(4.41), я для подвески 1 при нажатии токоприемника 16 даН - по формуле
(4.42).
Значения у3 определим по формуле (4.44):
т.,П1 = 6 (1-0,05-6) : 10=.---0,42;
Y3H2 =8 (1-0,05-8) : 10.- 0,48.
Для подвески 1 величина A/i, при Р 10 даН
________10-10 (68—Ю) 1000________
~|Ш)0~’ 1000 - (1000 | 150) 0,42 ] 68 37 мм •
111
а при P ~ 16 даН
37-16 , (16—11,5)2 2,333-1000
А л । и 1 — - г „ « —л л хч "" м м,
8-0,873-1000
Здесь значение у4 определено по формуле (4.45)
Тип - 1-4-6: (16- 11,5) 2,333.
Для подвески 2 при Р 20 даН
20-10 (68--10) 1000
1ГГ2 [1800 I 2000— (2000-4-150 ) 0,48[68
- 62 мм.
Значения эластичностей г], и жесткостей составят для подвески I при Р
10 даН и Р ..........
16 даН соответственно:
•Inn
37 : 10
3.70 даН/мм;
ж,,и 10 :0.037 =.-270 даН/м;
Пни
66: 16-
4,13 мм/даН;
ж1П! - 16:0,066 242 даН/м,
и для подвески
2 при Р
20 даН;
6 П12- 62:20
3.10 мм/даН;
.w1U8 20:0,062 323 даН/м.
Чтобы выбрать нужные формулы для определения подъемов контактных
проводов в точках 2, 3 и 4 (см. рис. 4.14), найдем сначала по формуле (4.30) зна-
чения Rc, при которых начнется разгрузка струн в этих точках. Значения Nr
определим по формуле (4.34);
8-0,06-1000-8
8-0.04-2000-4
---------------1.11 даН.
(68- 2-К))2
dll-----------------1,67 даН и Л’,
(68 —2-I0)2
Величины /?,. будут
/?(-,„ (0.873-8'0.3 1 ,67) (1800-1-1000)/1800 8.7 даН;
Р,.112 (2-0.873-4-1 0,3—1,11) (I860 | 2000)/1800 =13.0 даН.
Очевидно, что разгрузка струн в точках 2, 3 и 4 будет происходить при всех
заданных нажатиях токоприемников. Так как 3/?,. > 20 даН, то подъемы кон
тактных проводов в указанных точках следует рассчитывать по формуле (4.48).
Рис. 4.15. Эпюры эластичности (а)
-95+МФ-100 (сплошные кривые)
жесткости (б) контактных подвесок
и М-1204-2МФ-100 (штриховые)
лете
пьсм-
в про-
и
112
Таблица 4.7
Подвеска Расчетная величина Р. даН Значения расчетных величин в точках (см. рис. 4.14)
0 / 2 .7 4
ПБСМ-95+ г], мм/даН 10 4,50 3,70 5,10 6,07 6,41
+ МФ-100 16 4,13 5,88 6,91 7,25
ж, даН/м 10 222 270 196 165 156
16 242 170 145 138
М-120 + 2МФ-100 Т), мм/даН 20 3,35 3,10 3,65 4,39 4,64
ж, даН/м 20 299 323 274 228 2)6
Например, в точке 2 на расстоянии 18 м от опоры для подвески 1 при Р
----- 10 даН и Р - 16 даН соответственно:
10.18 ( 68—18)1000 , 8-1800 (10 — 8,7)1000
ДЛ,п1 ------------------------г ------------------- - 51 ми;
2П| 68 (1800 I 1000) 2-1000(1800+1000)
16-18 ( 68—18)1000 , 8-1800 (16 — 8,7)1000
А Л»п1 ----------------------t"---------------------'94 мм ,
2 68 (1800+1000) 2-1000 (1800+1000)
для подвески 2 при Р ~ 20 даН
20-18 (68—18)1000 . 4-1800 (20—13)1000
Л Л.,,,,,--------------------+---------------------- 73 мм.
22 68 (1800 + 2000) 2-2000 (1800 + 2000)
Значения эластичностей т]2 и жесткостей ж2 будут:
i)2Ul — 51 : 10 — 5.10 мм/даН; .ж2щ -10:0,051 = 196 даН/м;
г)2п1--94: 16- 5,88 мм/даН; .ж2п1 -16:0,094 170 даН/м;
•12112 73 : 20 3,65 мм/даН; як2Па—20 : 0,073 —274 даН/м .
Результаты расчетов для всех точек приведены в табл. 4.7.
Эпюры эластичности и жесткости обеих подвесок построены на рис. 4.15 без
учета изменений этих величин между струнами.
ИЗ
Глава 5
ВЫБОР ТИПОВ КОНТАКТНЫХ ПОДВЕСОК
И ИХ ОПТИМАЛЬНЫХ ПАРАМЕТРОВ
ПО УСЛОВИЯМ ТОКОСЪЕМА
§ 5.1. Влияние параметров контактной сети
на качество токосъема
Качество токосъема, как указывалось в гл. 4, тем выше, чем мень-
ше отклонения контактного нажатия от установленного оптималь-
ного уровня. Очевидно, этому должна способствовать соответствующая
траектория токоприемника Экспериментальные данные показывают,
что чем ближе траектория токоприемника к прямолинейной, тем
меньше изменяется контактное нажатие.
Хорошее качество токосъема обеспечивает контактная подвес-
ка. обладающая следующими свойствами:
изменения -кесткости (эластичности) подвески вдоль пролета ми-
нимальны (нанлучшин токосъем обеспечит подвеска, обладающая
равномерной жесткостью; чем больше различается жесткость у опор
н в средней части пролета, тем труднее обеспечить хорошее качество
токосъема):
стрела провеса контактного провода позволяет получить траекто-
рию токоприемника, наиболее близкую к прямолинейной:
возникающие в процессе взаимодействия < токоприемником коле-
бания подвески имеют небольшую амплитуду и быстро затухают, что
существенно улучшает качество токосъема при одновременной работе
нес кол ь к их то ко пр нем! i и ков;
число жестких точек и сосредоточенных масс на подвеске мини-
мально (каждый проход токоприемника в таких точках, как известно,
сопровождается ударом) Если невозможно устранить жесткие точки
и сосредоточенные массы, нужно принять меры для облегчения про-
хода токоприемника в этих местах,
ветроустойчивость подвески достаточно высока и надежный токо-
съем обеспечивается при наибольших ветровых отклонениях контакт-
ных проводов.
Кроме того, желательно, чтобы контактная подвеска, обладаю-
щая указанными свойствами, имела возможно меньшую строительную
стоимость, обеспечивала достаточный срок службы и требовала наи-
меньших затрат па эксплуатационное содержание. Состояние подвес-
ки в условиях эксплуатации должно соответствовать расчетному, а от-
клонения от заданных положений не должны выходить за пределы,
установленные проектом и нормативными документами, регламенти-
рующими эксплуатацию электрифицированных железных дорог. Реко-
мендации по применению различных типов контактных подвесок,
приводимые в документах, в основном сводятся к следующим.
114
При скоростях движения от 120 до 160 км/ч на главных путях
перегонов и станций следует применять одинарную компенсирован-
ную рессорную подвеску с сочлененными фиксаторами. На действую-
щих линиях с разрешения МПС допускается аналогичная пол у компен-
сированная подвеска, которая обычно применяется при скоростях
до 120 км/ч.
Таким образом, одинарную рессорную подвеску с сочлененными
фиксаторами (компенсированную и полу компенсированную) можно
считать типовой для главных путей электрифицированных железных
дорог Советского Союза.
На станционных путях (кроме главных), на которых скорость
движения не превышает 70 км/ч, рекомендуется применять одинарную
полукомпенсировакную подвеску с простыми опорными струнами; па
второстепенных станционных путях, а также на путях депо при ско-
рости до 50 км/ч допускается использовать существующую простую
компенсированную подвеску без несущего троса.
На главных путях перегонов и станций линий переменного тока
применяют один контактный провод площадью сечения 100 мм2, а при
постоянном токе или два таких провода, или в отдельных случаях
один -• 150 мм2. При движении на линии постоянного тока только
электропоездов с небольшим числом вагонов может быть подвешен
один контактный провод с площадью сечения 100 мм2. На станцион-
ных путях, кроме главных, обычно используют один контактный про-
вод с площадью сечения 85 мм2, учитывая, что контактные подвески
этих путей обычно соединяют параллельно (см. §9.1).
Несущие тросы при переменном токе, как правило, применяют
сталемедные (ПБСМ-70 и ПБСМ-95), а при постоянном - медные
(М-120 и М-95). В отдельных случаях используют медный несущий
трос при переменном токе и сталемедный при постоянном. С целью
экономии меди в качестве несущих тросов па дорогах переменного то-
ка начали применять биметаллический сталеалюминиевый провод
ПБСА-50/70 (в числителе указана номинальная площадь сечения алю-
миниевой, в знаменателе — стальной части провода в мм2). На стан-
ционных путях, кроме главных, применяют несущие тросы ПБСМ-70
и ПБСА-50/70.
Рессорные тросы выполняют из сталемедной проволоки диаметром
6 мм, а звеньевые струны -- из такой же проволоки диаметром 4 мм.
Оптимальными считают такие параметры контактной сети (гео-
метрические размеры подвески и натяжения проводов), которые при
заданных условиях (скорость движения, тип токоприемника) обеспе-
чивают возможно лучшее качество токосъема.
Для того чтобы при проектировании выбрать соответствующую
контактную подвеску и ее оптимальные параметры, необходимо пра-
вильно представлять степень влияния изменений отдельных пара-
метров подвески на распределение ее жесткости вдоль пролета и
на качество токосъема. Введем условные обозначения параметров,
показанные на рис. 5.1, и следующие обозначения жесткости кон-
115
тактной подвески в характерных точках пролета: жк0 — жесткость
подвески у опоры; ж^— то же у околоопорной струны; жкс — тоже
в центре пролета.
Основное влияние на изменение жесткости подвески в опорных уз-
лах жк0 и Жк! оказывают длина рессорного троса 2а, расстояние от
оси опоры до околоопорной струны с, натяжения несущего троса
Т и контактного провода К. Изменение жесткости подвески в середи-
не пролета жкс в основном зависит от длины пролета I, а также натя-
жений Т и Л. Некоторое влияние оказывает расстояние между стру-
нами в средней части пролета сс.
Для того чтобы проследить, как влияет изменение различных па-
раметров подвесок на распределение жесткости вдоль пролета, введем
понятие коэффициент жесткости:
жко/жке, (5.1)
где жко — среднее арифметическое значение жесткостей жко и .жк1.
Основное влияние на распределение жесткости подвески вдоль
пролета (т. е. изменение к.к) оказывают длина пролета I (рис. 5.2),
длина рессорного троса 2а и расстояние от оси опоры до околоопор-
ной струны с. Изменения натяжений несущего троса и контактного
провода (проводов) влияют на величину кж незначительно. Такое же
заключение можно сделать и о влиянии изменений других параметров.
Если принять для оценки качества токосъема показатель |Q|max
(см. §4.2), то влияние изменения коэффициента жесткости кт можно
характеризовать кривыми рис. 5.3. Анализ этих кривых показывает,
что наилучшим качество токосъема будет при сочетании определен-
ных значений кж и /. В условиях, принятых для построений графи-
ков на рис. 5.3, оптимальная стрела провеса равна примерно 4 см.
Как следует из рис. 5.3, для стрел провеса, меньших оптимальной,
качество токосъема ухудшается с увеличением коэффициента кт.
При оптимальной стреле провеса наблюдается некоторый минимум
IQImax- В случае отклонения значений |Q|max от минимума каче-
ство токосъема ухудшается как при уменьшении, так и при увеличе-
нии к.к.
Таким образом, кроме параметров подвески Z, 2а и с, определяю-
щих в основном значение на качество токосъема существенно вли-
яет стрела провеса контактных проводов. Это подтверждается много-
численными отечественными и зарубежными экспериментальными
исследованиями, на основании которых рекомендуется оптимальную
задаваемую стрелу провеса контактных проводов компенсированных
рессорных подвесок определять, м, как
/опт = Q—2с)/1000. (5-2)
Более точное определение величины /опт с учетом скорости дви-
жения и коэффициента жесткости подвески приведено в § 5.2.
Показатель IQImax изменяется в зависимости от расстояния с
(рис. 5.4, а). Наименьшее значение |Q|inax> а следовательно, и наи-
116
Рис 5.2. Влияние различных параметров контактных подвесок на изменения ко-
эффициента Кт при взаимодействии:
/-- подвески ПБСМ-70+МФ-100 с токоприемником серии Л (верхняя шкала); 2--подвес-
ки М-120+2МФ-100 с токоприемником серии Т (нижняя шкала)
Рис 5.3 Расчетные кривые Ю|>»«к
(Кж) при разных стрелах провеса
контактных проводов f и сырости
200 к.м'ч для условий линий перемен-
иото (i.J я постоянно,о (б) том
Рис. 5.4. Зависимости показателя |Q |>пая
от расстояния < (а) н соотношения
ж,^жх> (5) при скорости 200 км/ч
в пролете длиной 70 м при /=5 см и
к.к-1.6 для линий переменного (кривая
/) н постоянного (кривая 2) тока
лучшее качество токосьемз при условиях, для которых построены
кривые рис. 5.4, а, соответствует значению с ж 10 м. Изменения
этого расстояния без соответствующих изменений / и к.1( приводят
к ухудшению качества токосъема как при сдвижке околоопорных струн
к опорам, так и при удалении их от опор.
Отклонение соотношения жесткостей подвески ак1(0 и жкл в любую
сторону от единицы приводит к увеличению |Q|vlj<x (рис. 5.4,6), а
значит, и к ухудшению качества токосъема. Поэтому следует стре-
миться к выравниванию жесткости подвески в пределах опорных узлов.
На основании приведенных материалов можно сделать заключе-
ние о возможности улучшения качества токосъема путем правильного
выбора параметров контактной подвески, оказывающих основное
влияние на качество токосъема. Поскольку длину пролета / выбирают
исходя из необходимости обеспечить требуемую ветроустойчивость
контактной сети (см. гл. 3), рассчитывать нужно такие взаимосвязан-
ные параметры подвески, как длину рессорного троса 2а, расстояние
от оси опоры до околоопорпой струны с и стрелу провеса контактного
провода f.
§ 5.2. Определение оптимальных параметров
компенсированных контактных подвесок
При проектировании контактной сети оптимальные значения ос-
новных параметров компенсированной подвески (2а, с, f) можно опре-
делить, используя методику расчета взаимодействия контактной под-
вески и токоприемника, изложенную в §4.3. Задаваясь определенны-
ми сочетаниями искомых параметров, устанавливают условия, при
которых показатель, принятый для оценки качества токосъема, имеет
наилучшее значение. Параметры, сочетание которых обусловит ука-
118
занное значение показателя, и будут оптимальными. В качестве при-
мера на рис. 5.5 показаны определенные таким образом оптимальные
стрелы провеса контактных проводов, которые увеличиваются при
повышении значений кЯ(.
В тех случаях, когда выполнить расчеты, учитывающие динамиче-
ские процессы, затруднительно или объем необходимых вычислений
незначителен, для определения основных оптимальных параметров
можно применить разработанную автором методику, основанную на
использовании статических подъемов контактного провода в характер-
ных точках пролета (у опор, у околоопорных струн и в центре
пролета), обеспечивающих траекторию токоприемника, близкую к
прямолинейной. При такой траектории влияния инерционной со-
ставляющей контактного нажатия и сил трения в шарнирах незначи-
тельны и расчетное контактное нажатие допустимо определять как
сумму силы нажатия подъемных пружин токоприемника и аэроди-
намической составляющей, т. е. принимать равным постоянной со-
ставляющей контактного нажатия Рг.
Таким образом, расчетное контактное пажа>не будет зависеть от
конструкции токоприемника и заданной скорости движения, так как
аэродинамическая составляющая определяется значением скорости.
Конкретное значение аэродинамической составляющей следует опре-
делять по экспериментальным данным, полученным для заданного
типа токоприемника или аналогичного ему при расчетной скорости
движения. Если таких данных нет, при токоприемниках серий Л и Т
в расчетах по выбору оптимальных параметров контактных подве-
сок могут быть использованы значения, приведенные в табл. 5.1.
Токоприемники серий Л и Т применяют для скоростей движения
до 160 км/ч включительно. При более высоких скоростях используют
специальные токоприемники. В этом случае расчетное контактное на-
жатие следует принимать соответствующим конкретной конструкции
Рис. 5.5. Расчетные кривые |Q|max (f) при различных значениях км для линий
переменного (с) и постоянного (б) тока при скорости 200 км/ч (/=70 м; 2а=12м;
с —10 м)
119
Таблица 5.1
Значение Рс, даН, при скоростях движения, км/ч
Серия токоприемника 100 120 140 160
л 10 11 13 16
т 15 17 21 27
(например, для токоприемника Сп-бМ при скорости 200 км/ч, по дан-
ным канд. техн, наук И. А. Беляева, Рс « 20 даН).
Оптимальные значения 2а и /, если известны длина пролета и дру-
гие параметры подвески, можно определить графоаналитическим
способом, основанным на обеспечении равенства (см. рис. 5.1)
ЛЛо-’-ЛЛ! --ДЛГ —/. (5.3)
где ДЛ() — подъем контактного провода у опор;
— то же у ближайших к опорам простых струн, закрепленных на не-
сущем тросе;
Л/г(. — то же в середине пролета.
Эластичность подвески и провес, контактного провода в средней
части пролета между околоопорными струнами изменяются по пара-
болам, вершины которых направлены в разные стороны. Можно ожи-
дать, что при выполнении равенства (5.3) траектория токоприемника
будет близка к прямолинейной вдоль всего пролета.
Необходимые построения выполняются следующим образом. Для
расчетного пролета проектируемого участка намечают несколько зна-
чений а и /. Примерные пределы их изменений для различных усло-
вий расчета при обычно применяемых натяжениях проводов подвес-
ки приведены в табл. 5.2.
Вычислив для принятых значений а и / величины Ай0 и строят
кривые A/ir,(a) и (а) так, как это показано для примера на левых
графиках рис. 5.6. Точкам пересечения указанных кривых (при од-
Таблица 5.2
Число контактных проводов Расчетное нажатие, даН а, м Значении /, см, при пролетах длиной, м
65-70 55-60
1 До 12 13-16 2 6 4-8 2—6 3-7 1-5 1-6
2 До 27 4-8 2-6 1-5
120
6) Aft
—X—АЛ0 -Aft;-Aft„-Aft'
Рис 5.6 Определение значе-
ний Поит и /опт при отсутст-
вии разгрузки струн в опор-
ном узле (а), при разгрузке
только околоопорной стуны
(б) и при разгрузке всех
струн в опорном узле (в)
них и тех же значениях /) соответствует равенство Л/10--Д/ь — Aho-
Эти точки надо перенести на правый график и построить кривую
A/io (/). Обозначив A/ic — / — &h'c, на правом графике строят кри-
вую A/ic (/), вычислив предварительно значения А/1С для принятых
к расчету значений /. Точка пересечения кривых на втором графике
соответствует оптимальному значению стрелы провеса контактного
провода /опт, а подъем провода в этой точке, перенесенной на кривую
&h0(a) левого графика при полученном значении /, определит полови-
ну оптимальной длины рессорного троса (йоггг).
Все необходимые вычисления подъемов контактных проводов
в различных точках пролета могут быть выполнены по формулам,
приведенным в § 4.4. При этом в каждом случае необходимо сначала
сравнить расчетное нажатие токоприемника с силами, при которых
наступает разгрузка струн, азатем уже выбирать необходимые расчет-
ные формулы. Если расчетное нажатие не вызывает разгрузки струн,
кривые различных подъемов контактного провода будут иметь вид,
показанный на рис. 5.6, а. При разгрузке только околоопорных струн
каждой из принятых к расчету стрел провеса контактного прово-
да (/i. /2, /з) будет соответствовать определенная кривая A/tj (а)
(рис. 5.6, б). Если же произойдет разрузка и подрессорных струн,
кривые A/i0 (а) также будут различными — в зависимости от значений
/. В этом случае для определения аопт необходимо построить еще кри-
вую A/i0 (а) при /опт (рис. 5.6, в).
121
Оптимальная длина рессорных тросов может быть определена
только для максимального пролета проектируемого участка и задана
такой же для всех остальных пролетов. Оптимальную стрелу провеса
контактного провода обязательно выбирают отдельно для каждого
из пролетов следующим образом. Для определенного пролета, зада-
ваясь несколькими значениями / по табл. 5.2, при уже известной
длине рессорных тросов вычисляют зависимости Л/г0 (/), Л/гх (/) и
ЛЛс' <0 и строят их на одном графике так, как это показано на рис. 5.7
применительно к условиям, принятым для рис. 5.6, б. Оптимальной
стрела провеса контактного провода для этого пролета будет в том
месте, где значения A/i„, г\/гг и Л/г<'- ближе всего друг к другу.
Оптимальная длина рессорного троса различна для разных ско-
ростей движения, длин пролетов и натяжений контактных проводов,
снижаемых по мере их износа или повышаемых с целью усиления вет-
роустойчивости. Изменять длину рессорных тросов в условиях экс-
плуатации практически невозможно. Поэтому целесообразно устано-
вить для всех возможных условий единую длину, при которой ухуд-
шение качества токосъема в случае изменения этих условий будет ми-
нимальным. Исследования показали, что при с 10 м и скоростях
движения до 160 км'ч на линиях переменного тока с подвесками, имею-
щими один контактный провод, можно принять 2а 12 м, а на ли-
ниях постоянного тока при подвесках с двумя контактными проводами
2а - 1-1 м. В условиях более высоких скоростей значения 2а и с целе-
сообразно увеличить (см. ниже).
Таким образом, для эксплуатационной проверки состояния кон-
тактной сети и приведения ее геометрических размеров к значениям,
обеспечивающим улучшение качества токосъема и снижение износа,
при правильных размерах а и с достаточно измерить и отрегулировать
только стрелу провеса контактного провода / и размер 6, т. е. расстоя-
ние между иесушим и рессорным тросами на опоре (см. рис. 5.1).
Во всех пролетах, кроме переходных
Рис. ЪЛ. Определение значе-
ния /[1Пт при заданной дли-
не рессорною троса
при сопряжениях анкерных участков в
трех пролетах, значения оптимальных
стрел провеса контактного провода поло-
жительны. В переходных пролетах жест-
кость в средней части пролета (там, где
токоприемник взаимодействует с двумя
контактными подвесками), как правило,
бгиьше, чем у опор, вследствие чего для
выравнивания траектории токоприемника
оптимальные стрелы провеса контактного
провода должны быть отрицательными.
Изменение жесткости сопрягаемых подве-
сок вдоль переходного пролета описывает-
ся более сложной кривой, чем в промежу-
точных пролетах, что не дает возмож-
ности определять оптимальные параметры
122
Т а бл кца 53
Число контакт- ных про- водов МФ-100 Длина проле- та, м Размер Ь, мм Стрелы провеса контактных прородор, мм при скоростях движения, км/ч, до
90 140 90 140
Во всех фОЛСЧЪХ, В переходных
кроме переходных пролетах
40 400 10 20 —15 -25
1 50 425 15 25 -10 -20
1 60 450 25 35 -10 -20
70 500 35 50 —5 —20
40 575 0 10 -20 -30
о 50 625 5 15 -15 —25
60 700 15 25 -15 -25
70 750 25 40 -10 —25
Примечание. Значения стрел провеса контактных провозом округлены до Ь мм»
а размера Ь —до 25 мм.
подвесок графоаналитическим расчетом. В этом случае необходимые
результаты могут быть получены при учете динамических процессов,
т. е. с помощью методики, изложенной в § 4.3.
В качестве примера в табл. 5.3 приведены выдержки из инструк-
тивных указании по вертикальной регулировке компенсированных
контактных подвесок, применяемых на линиях переменного и по-
стоянного тока, при размерах а и с, указанных выше.
Расстояния между струнами в средней части пролета компенси-
рованных подвесок желательно иметь 7 м при одном контактном про-
воде и 4 м (по несущему тросу) при двух контактных проводах и шах-
матном расположении струн. Натяжение рессорных тросов целесо-
образно установить равным 150 даН.
Выравнивание жесткости рессорной подвески вдоль пролета наи-
более эффективно может быть достигнуто подбором параметров 2г- и г.
Так, при одновременном увеличении длины рессорного троса с 12
до 18 и, а расстояния с с 10 до 14 м значения «п, значительно снизи-
лись (рис. 5.8), что способствует улучшению качества токосъема. Од-
нако допустимое снижение жесткости подвески в опорных узлах
ограничивается возрастающим отжатием контактного провода, что
в конкретных условиях может привести к нарушению нормального
токосъема под фиксаторами и на сопряжениях анкерных участков.
Установлено, что оптимальную стрелу провеса контактного про-
вода. используя условие (5.3), можно более точно, чем по выражению
(5.2), определить как
^кс
123
Рис. 5.8. Расчетные кривые
(I) для условий перемен-
ного (штриховые линии) и
постоянного (сплошные) то-
ка при 2п=12 м, с=10 м
(кривые /) и 2а = 18 м. с =
— 14 м (кривые 2)
Если на проектируемом участке ско-
рости движения различны, то значение
/опт следует выбирать исходя из значения
Рс, соответствующего максимальной ско-
рости. В этом случае обеспечивается луч-
шая стабилизация контактного нажатия
при всех реализуемых скоростях и, следо-
вательно, минимальный возможный износ
контактных проводов и токосъемных пла-
стин.
При нескольких токоприемниках зна-
чение Рс следует вычислять как Рус^,
по формуле (4.59).
В связи с тем что в условиях эксплуа-
тации неизбежны различные отклонения
от расчетного значения /опт, желательно
при проектировании установить допусти-
мые пределы таких отклонений.
Кроме параметров, определение кото-
рых рассмотрено выше, для обеспечения
расчетного натяжения рессорного троса
нужно правильно задавать длину подрес-
сорных струн h'.
Ее определяют в зависимости от конструктивной высоты цеп-
ной подвески й0 (см. рис. 5.1):
h' — hu—b,
(5.5)
где
* = ф; (5.6)
На -н|.£;/-(щ1-2йр)ы-ЬнфОф|/[2(7'-//)]; (5.7)
i|-==- (a—щ) Qp/(2//). (5.8)
Значения Q(, вычисляют как
(?р=-лк£к (c-l-flj)-J-gp (e+fli) Т пс Gc + пф бф. (5.9)
В формулах (5.7) и (5.9) Gc — нагрузка от веса струны с зажимами,
даН; Оф — часть нагрузки от веса фиксатора, передающаяся на
рессорный трос, даН. Остальные обозначения те же. что на рис. 5.1
и в § 4.4.
Для струн, закрепленных на рессорном тросе в шахматном поряд-
ке (при двух контактных проводах), размер для ближайшей к
опоре подрессорной струны определяется также по формуле (5.8). но
значение Qp изменится. Принимая нагрузки подрессорных струн
одинаковыми и обозначив через а2 расстояние от оси опоры до даль-
ней от нее струны, получим
Qp--2.Vp (2 — ——— )+gp(a+ai).
\ а— аг ;
124
Нагрузка подрессорной струны
.'Vp =-0,5gK (с + а2) “Ь£'с4-0,5бф.
Стрела провеса дальней от опоры подрессорной струны
а2) Qpl(2H), (5.10)
где Qp = 4,VP4-gp (а + а2).
В общем случае
бф = 0,5СфД-|- Офз—77фЛ/^-фд> (5.11)
где Сфд — нагрузка от веса дополнительного фиксатора, даН;
Офз — то же от веса фиксирующего зажима, даН;
Нф — горизонтальная составляющая реакции фиксатора, определяемая
на прямых участках пути по формуле (2.42). в кривых — по формуле
(2.28), даН;
h — расстояние по вертикали от контактного провода до шарнира до-
полнительного фиксатора, м;
£фд — шарнирная длина дополнительного фиксатора, м.
При точной регулировке фиксатора компенсированной контакт-
ной подвески можно принять 6ф = 0.
Пример. Задание и исходные данные. Выбрать оптималь"
ную длину рессорного троса и стрелу провеса контактного провода для компен*
сированной рессорной подвески ПБСМ-70 -I- Нл0л0,04Ф-100 на линии перемен-
ного тока при наибольшей скорости движения поездов 160 км/ч в пролете дли-
ной 70 м (рис. 5.9, а) и оптимальную стрелу провеса контактного провода в про-
лете длиной 55 м (рис. 5.9, б) при длине рессорного троса, оптимальной для про-
лета длиной 70 м. Материал и натяжение рессорных тросов такие же, как в
примере к § 4.4. Необходимые данные всех проводов приведены в табл. 1.5
и 1.8.
Решение для пролета длиной 70 м. В соответствии с дан-
ными табл. 5.1 расчетное нажатие токоприемника типа Л для заданной скорости
Рис. 5.9. Схемы расположения струн в пролетах длиной 70 м (а) и 55 м (б)
125
движения составляет 16 даН. Зададимся половинами длины рессорного троса 4:
6 и 8 м и стрелами провеса контактного провода 3: 5 и 7 см (см табл 5.2). Чтобы
выбрать нужные расчетные формулы для построения кривой АЛ0 (а), сначала оп-
ределим но формуле (4.27) минимальное значение силы Rfl> при которой наступа-
ет разгрузка подрссеорвь.>. струн. Величины 6ф и Gc примем равными соответ-
ственно 1,” и 0,3 даН
Минимальной сиди /?0 будет при а 4 м н f - 3 см
R(l п-.Р. 0,873 (IO-i-2) 1-0,229-2-4-;-2-0,Л-<- 1,74-
Поскольку п <' Ro щщ, то разгрузка подрессор вых струн не произойдет и
искомые значения V8I( надо определять ио формуле (4.37) Кривая ДА0 (а) будет
единственной, так кяк \hn не зависит от значений/в принятых пределах:
16-1000 16 000
Д --------------- ---—--------------—----------------мм,
’ 2 (1500— 150) v, ,а+2 (1000-J 150):70 2700?,:М 32.9
где значение у, должно вычисляться по формуле (4.39)
у. -.--0,6 уЛобо^ТТТб'ЛббоГ ---0,6 У'^Тб'
Значения ДА0 в зависимости от величины а следующие:
а, м . . . . 4 6 8
Mio, мм ... 66,1 78,6 88.5
Чтобы выбрать формулы для построения кривых ДА, (а), определим макси-
мальное значение силы Rt и минимальное R- соответственно но формулам (4.28)
и ('4.29):
R< 0,873 ( I (> - 2 - 7,14) : 2 0,3
7,14 \
— —-------- -6.914 68,6
70.-2-10/
R-, - 11,7 даН будет при /та;;
при Anin.. б см:
4-0,03-1000 , 3-7,14
1.5-7.14) I 3-0,3 ! ----------! 1 —----------
_4£-_1000_
70-2-10
Ма ксимал ьны м знамени е
мальве - значение Л?,' наступит
ем, мини-
70-2-10
МО/
ы
Поскольку при полученных значениях /?1гаал и A’Jmili имеет место соотноше-
ние 7;инах »nitn- то вычислять ЛА,’ нужно по формуле 14.42)
16-10 (70-10) 1000 . (16 —/?-)г 1000
д _______________;__-______________——------------------
' 1 ' 15 50'.) -I 1000-. (1000-1-150) ys[ 70
--J- (Я>—
2500—1150-
8-0,873-1090
6,984
где значение у-, следует определять по формуле (4.44)
Уя —« (1 —0,05а) : 10,
а у4 — по формуле (4.45)
?4= Н-« : (16 —/?±)
Результаты этих расчетов приведены в табл. 5.4.
126
Т а б л и ц а 5.4
Значения Afti, мм, при f, ем
I
3 5 | 7
75,4 72,1 | 69,4
81,1 77,4 ! 74,3
85 5 81,5 | 77,9
Чтобы выбрать формулы для построения зависимости Лй( / от 7 опреде-
лим сначала экстремальные значения силы R,. по формуле (4. 1'0):
/?с -={0,873-7,15 1-0,3 —1000-7,15 : <70 --2-IO)“J (1500 1000) : 1500-.
(6,54—22 9,') i,67 даН.
Максимальное значение .‘?cnia^-8 даН (при ,pl(1in 3 ем/, минималь-
ное Rc m>n 8,2 даН (при/шач 7 <’м), Поскольку расчетное иа.котие токопри-
емника меньше, чем 2Ре то '.Л,, нужно вычислять по формуле <4.50):
10-35-1000 , 16-15-1500-1000
\ hi ----------------г -------------------- (29 2 мм.
70 -1500 4 10ОО J 4-1000 (1500 |-1000)
Разность Лйс - [ в зависимости от / имеет следующие значения:
Ь см ............. 3 5 7
5/.-C--Z, мм ... 99,2 79,2 59.2
В соответствии с рекомендациями, приведенными в §5.2, шпелпим построе-
ния. показанные ча сне. 5.10 Округ чая найденное (начсние до 0,5 м я
font 4° 0-5 ем, получим, что для заданных условий оптимальная длина рессорно-
го троса составляет 1! м, оптимальная стрела провеса контактного провода
5,5 ем.
Длину подреееорных струн определим по формуле (5.5), Примем нагрузку на
рессорный трое от веса одной струны с зажимами, равной 0,6 даН, а от части
веса дополнительного фиксатора с фиксирующим зажимом, передающуюся на
рессорный трос, равной нулю. Провес несущего троса в точке крепления рессор-
кого троса £/,, найдем по формуле (5.7)
иа --5,5 [1,56-70—(0,586 — 2-0,229 ) 5,5] . {2 (150/' — 150)] -0.221 м
Стрелу провеса рессорного троса ф определим но формуле (5.8), вычислив
значение Qp по формуле (5.9),
С?р- = е 87 НИ) 1-2) 1-0 229 (5,5 2) 2-0,6 13,4 даН-,
ф f о, 5 — 2) 53.4 . (2 -1 м0) -=(.<, 156 м.
При конструктивной высоте подвески, равной ! .8 м (с..,. j 3.2), длина поц
рессорных <-тру<<
/('--1,8-.(0 221 i-0,156) ! ,4.23 м.
Р е ш е н и е д ля пр о л е т а дли н о й 55 м. Размер а принимаем
равным оптимальному для пролета длиной 70 м, т. е. 5,5 м. В соответствии е
127
табл. 5.2 задаемся значениями /, равными 1; 3 и 5 см. Величину Дй0, которая не
зависит от принятых значений f, определим по формуле (4.37)
16-1000
Д hn --------------------------------------------==72,7 мм,
0 2 (1500—150) 0,363 : 5,5 + 2 (1000 + 150) : 55
где по формуле (4.39)
у 1 = 0,6 V 5,5-1000: (10-1500)- ==0,363.
Величины Дй' вычислим по формуле (4.42) для различных значений /, от
которых зависит сила RIf
________16-10 (55—10) 1000__________(16 —RJa 1000
ЛЙ1 " [1500+1000 —(1000+150) 0,3991 55 ‘ 8-0,873-1000 71’
где по формуле (4.44) у3 = 5,5 (1-0,05-5,5) : 10=0,399, а по формуле (4.45)
у4= 1 -5,5 : (16— Rj). По формуле (4.28)
4/-1000 / 7 \
/?х = 0,873 (10-2-1-7)-.2 + 0,3 - - 1 -- =6,85 + 91.4/ даН.
Величина Дй] в зависимости от f имеет следующие значения:
f, см ................................ 1 3 5
Ай], мм............................ 80,4 75,1 70,7
Определим mln (при /тах~ см) и Rp max (при / 1 см) по формуле
(4.30)
Rc-.—[0,873-7+0,3—8/-1000-7: (55 —2-10)*] (1500+1000) : 1500==
==(6,41-45,7/) 1,67 даН.
В результате расчетов получим Rc пдп 6,89 даН и RCmax“ 9,94 даН. Так
как искомая стрела провеса контактного провода явно меньше 5,5 см (оптималь
Рис. 5.10. Построения для определения аОпт и /опт в пролете длиной 70 м
128
ное значение для пролета длиной 70 м).
то соседние струны не разгрузятся и ве-
личину Дйс' можно определять по фор-
муле (4.50):
, 16-27.5-27.5-1000
Айс — 4-
55 (1500 - 1000) 1
. 16-7-1500-1000
Н----------------------_=Ю4,8 мм.
4 -1000 (1500-1- 1000)
Разность :Vit —/ в зависимости от
/ имеет следующие значения:
}, см . . 1 3 5
Aftc-f, мм 94,8 74,8 54.8
В соответствии с рекомендациями,
приведенными в § 5.2. выполним по-
строения, показанные на рис. 5.11,
Округляя найденное значение f до
0,5 см, получим, что для заданных ус-
ловий оптимальная стрела провеса кон-
тактного провода равна 3 см.
Длину подрессорных струн определим аналогично приведенному выше для
пролета длиной 70 м
t/e^5.5 [1,56-55 — (0,586 — 2-0,229) 5,5]: |2 (1500— 150)| =--•= 0.1?3 м.
Поскольку значения Qp и ф не изменятся, то искомая длина струн
h' 1.8 —(0,173-1-0,1,56) 1.471 м.
§ 5.3. Определение оптимальных параметров
полукомпенсированных контактных подвесок
Правильным выбором оптимальных параметров обеспечить оди-
наково хорошее качество токосъема при любых изменениях темпера-
туры в случае полукомпенсированных подвесок нельзя. При таких
подвесках натяжение несущего троса и стрелы провеса всех проводов
в течение года существенно изменяются, поэтому можно обеспечить
хорошее качество токосъема лишь в течение некоторой части года.
Очевидно, что и оптимальные параметры полукомпенсированной под-
вески следует выбирать для условий, сохраняющихся наиболее про-
должительное время в течение года.
Назовем температуру, при которой определенные параметры полу-
компенсированной подвески должны иметь оптимальные значения.
температурой оптимальных параметров tum. Одним из основных
параметров, оказывающих существенное влияние на качество токо-
съема, является стрела провеса контактного провода (см. §5.1). В
полукомпенсированных подвесках стрелы провеса контактных про-
водов зависят от принятой температуры их беспровесного положения
5 Зак 2630
129
Правильный выбор этой температуры и предопределит качество токо-
съема в различных температурных условиях в течение года.
Таким образом, определение оптимальных параметров полуком-
пенсиронанных подвесок можно производить при f0)!T так же, как для
компенсированных подвесок (см. §5.2), а чтобы обеспечить соответст-
вующую стрелу провеса контактных проводов при нужно пра-
вильно выбрать температуру их беспровесного положения. Значение
/ОТ1Т можно установить, анализируя кривую распределения темпера-
туры в течение года в районе, для которого проектируется контакт-
ная сеть. Эту кривую строят по результатам многолетних наблюдений
метеорологических станций. Для выбора нужно составить гисто-
грамму, показывающую, сколько суток в течение года на участ-
ке сохраняется среднесуточная температура (,• (рнс. 5.12). Величину
/оит можно определ ить как математическое ожидание температуры дан-
ного района
где п - число интервалов, принятых при построении гистограммы.
Поскольку математическое ожидание температуры района незна-
чительно отличается от его среднегодовой температуры, то допустимо
принимать ?0!,г равной среднегодовой температуре.
Для определения температуры беспровесного положения контакт
него провода которая обеспечит при температуре (n,i> опти-
мальную стрелу провеса провода, нужно построить зависимость
f (/0) при /.„it (рис. 5.13). Эта зависимость, практически представляю-
щая собой прямую линию, строится по формулам, приведенным в
§6.3. Далее, по известному значению оптимальной стрелы провеса
контактного провода, которое можно определить но формуле (5.4;.
находят значение .,„т так, как показано на рис. 5.13.
Поскольку величина /'оит зависит от скорости движения, типов
контактной подвески и токоприемника, длины пролета п других фак-
Рис. 5 12. Гистограмма для оп
ределения значения
Рис. 5.13, Графическое опреде-
ление значения „„т
130
торов, значение /()Опт также зависит от этих факторов. Однако не-
возможно установить различные значения t„ для разных скоростей
движения или отличающихся по длине пролетов одного и того же
анкерного участка. Поэтому, учитывая сравнительно небольшое влия-
ние на качество токосъема отклонений t„ от оптимального значения,
допустимо определять /!)011.г для наибольшей скорости движения и по
максимальному пролету данного участка (обеспечить токосъем в боль-
ших пролетах труднее, чем в малых). Если число таких пролетов не-
значительно, то учитывают пролет, длина которого наиболее часто
встречается на участке. Влияние же типов контактных подвесок и то-
коприемников нужно учитывать в соответствии с конкретными усло-
виями. Например, для Московской области, где /,,11Т -- •|-5°С, зна-
чения /()|)11Т при электровозах с токоприемниками 10РР для скоро-
стей до 80 км/ч составляют 5 4- 10 °C, а при скоростях до
160 км/ч на 10 'С ниже.
Пол у компенсированные контактные подвески, отрегулированные
в соответствии с приведенными рекомендациями, обеспечат наилуч-
шее качество токосъема (а еледовагелыю. и наименьший износ кон-
тактных проводов) примерно в течение ЮОеутв году, а при отклоне-
ниях от /0[1Т -1 5 °C на ±15 4- 20 °C качество токосъема будет хо-
рошим в течение более чем ЗОН сут в году.
Обеспечение наилучшего качества токосъема при температуре
оптимальных параметров может вызвать нарушение токосъема в ус-
ловиях экстремальных температур в данном районе. Поэтому необ-
ходимо проверить качество токосъема при экстремальных температу-
рах соответствующими расчетами, учтя динамические процессы. Вслед-
ствие небольшой длительности экстремальных температур можно оце-
нивать качество токосъема не так. как обычно, а считать его приемле-
мым, если не происходит отрыва полоза токоприемника от контакт-
ного провода. В противном случае значение г0„,п необходимо изме-
нить соответствующим образом, если происходит нарушение токо-
съема при минимальной температуре, значение /0О11Т должно быть
снижено, а при максимальной - повышено.
Таким образом, выбор оптимальных параметров полукомпепси-
рованнон рессорной подвески можно выполнять в такой последова-
тельности:
установление чиста суток в году с одинаковой среднесуточной
температурой и определение температуры оптимальных параметров;
выбор оптимальных значений параметров ‘2и, с и / при г,,Г1Т ана-
логично тому, как эго делается для компенсированных подвесок
(СМ. § 5.2);
предварительное определение температуры беснровосного поло-
жения контактного провода, обеспечивающей оптимальное значение
стрелы провеса этого провода при /0П1,
проверка токосъема при экстремальных температурах; оконча-
тельный выбор температуры беспровееногс положения контактных
проводов.
Г)*
13!
Аналогично тому, как было указано в § 5.2 для компенсированных
подвесок, разработаны инструктивные указания по вертикальной
регулировке полукомпенсированных подвесок. В этом случае потре-
бовалось вводить в рассмотрение изменения натяжения несущих
тросов и усреднять результаты. Длины рессорных тросов при подвес-
ках с одним контактным проводом на линиях переменного тока для
скоростей движения до 120 км/ч были приняты равными 10 м, а на
линиях постоянного тока при двух контактных проводах и скоростях
до 160 км/ч — 12 м. Расстояние от оси опор до околоопорных струн
составляют 10 м. Поскольку оптимальные стрелы провеса / и размер
b (см. рис. 5.1) возможно установить только при одной температуре
(принята равной среднегодовой температуре данного района), значе-
ния / и Ъ при других температурах были определены соответствую-
щими расчетами и указаны в таблицах применительно к среднегодо-
вым температурам, равным —5, 0, 45 и 4-10 ‘С.
В качестве примера в табл. 5.5 приведена выдержка из инструк-
тивных указаний по вертикальной регулировке полукомненсирован-
пой контактной подвески ПБСМ-70 4 МФ-100 при среднегодовой
температуре, равной 0 ’С, и размерах а, с и сс (см. рис. 5.1), равных
соответственно 5; 10 и 9 м.
Так же, как было указано в § 5.2 для компенсированных подве-
сок, при полукомпенсированных подвесках с рессорными тросами
оптимальные стрелы провеса контактных проводов в прреходных
пролетах при среднегодовой температуре имеют отрицательные зна-
чения. В тех случаях, когда рессорные тросы не устанавливают (па
кривых участках пути радиусом менее 800 м, изолирующих сопряже-
ниях анкерных участков и др.) вследствие повышенной жесткости
опорных узлов, оптимальные стрелы провеса контактных проводов
в переходных пролетах могут иметь и положительные значения при
с р едн е годовой температуре.
Расстояния между струнами в средней части пролета иолукомпен-
сированпых подвесок желательно иметь около 9 м независимо от
числа контактных проводов (при двух контактных проводах применяют
совмещенные струны). Натяжение рессорного троса, равное при-
мерно 100 даН, должно соответствовать температуре оптимальных
параметров. На кривых участках пути радиусом менее 800 м, где
рессорные тросы не применяют, ближайшие к опорам простые струны
можно устанавливать на расстоянии 3 м.
Параметры рессорного троса и длину подрессорных струн при
режиме беспровесного положения контактного провода определяют по
формулам (5.5)—(5.9), принимая Бф 0.
Пример. 3 а д а и и е и и с х о д н ы с д а н и ы е. Выбрать темпера-
туру беспровесного положения контактных проводов для полукомпенсирован-
ной подвески ПБСМ-95 ! 2НлОл0,04Ф-Ю0 на линии постоянною тока, где ско-
рость движения поездов будет достигать 140 км/ч. Длина наибольшего принта
равна 70 м, минимальная температура воздуха—40 °C, максимальная ; 40 С,
среднегодовая 5 "С Рессорные тросы аналогичны принятым в примере к
§ 4.4. Необходимые данные для проводов подвески приведены в табл. 1.5—-1.8.
132
Таблица 5.5
Темпера- Стрелы провеса контактного провода, мм,
тура при регу- лировке. Длина Размер />. при скоростях, км/ч, до
пролета, м мм
°C 90 140 90 140
Во всех пролетах, В переходных
кроме переходных пролетах
40 325 5 15 -25/0 35/10
50 350 5 15 25/0 35/10
10 (10 375 5 15 30/ 10 40/0
70 425 10 25 30/- 10 —45/5
40 350 10 20 20/10 • 30/20
о 50 375 15 25 15/15 —25/25
60 400 20 30 -15/15 -25/25
70 450 30 45 10/20 - -25/35
40 350 15 25 15/20 25/30
10 50 400 25 35 5/30 15/40
60 425 35 45 0/40 10/50
70 475 50 65 10/50 -5/65
20 40 .375 20 30 10/30 20/40
50 425 35 45 5/45 -5/55
60 475 50 60 15/65 5/75
70 500 70 85 30/80 15/95
П р и м е ч а п и 1. В числителе указаны стрелы провеса при наличии рессорных
1 рогов для любых схе м сопряжений ликерных участков, в знаменателе )ри отсутствии
рессорного ?•) ков. троса в р 'Июней Ветви подвески на изолирующем сопряжении анкерных уча-
2 .Значения стрел провеса контакшого провода округлены до 5 мм. а размера
до 25 мм.
Р е in е и и е. Примем температуру, которой должны . соответствовать оп
гнмальные параметры подвески, равной среднегодовой, т. е. 1 5 'С, Для пред
нарительного выбора температуры бссировесного положения контактных прово
дов /0.нужно построить зависимость /,. (/„).
Задаваясь натяжениями несущего троса при беспровесном положении кон-
тактных проводов 7’0, рапными 1900 и 1700 да)), ио формуле (6.31) определим со-
ответствующие этим натяжениям значения 1в. Полагая, что максимальным патя
хкеиие несущего троса будет при минимальной температуре, и учитывая, что на-
грузка от веса подвески составляет 2.7! даП-м (см. табл. 2.1), определим коэф
фициенты уравнения 1'6.31). При этом используем данные табл. 1.9;
/1, - 40 — 2,71-• 70-’. 3I35/20002 ! 2000/21,29 25,7;
Во- 2,712.702-3135 112,8- 10»
Значения tn составят:
при 7’’ 1900 даН
! •= 25,7 -i- )] 2,8 10»' 19002 — j 900/21,29 - •= — 32,3° С;
при Т" -- 1700 даН
Z" : 25,7 Н 112,8 • 10» /17002 - 1700/21,29— 15,10 С.
133
Чтобы определить стрелы провеса контактных проводов при температуре
4-5 “С, сначала по формуле (6.36) вычислим соответствующее этой температуре
натяжение несущего троса Г-,. Поскольку значения коэффициентов Ло и Вх в.
уравнении (6.36) такие же, что и полученные выше .4, и BL,, искомое натяжение
определим методом интерполяции.
Задаваясь Т'ъ — 1600 даН, получим
^-=25,7 4-112,8 • 10« /16002 — 1600 /21,29 - - о, 4° С.
Если принять 1400 даН, то
i"x --=25,74-112,8•10е/I4002— 1400/21,29 - 17,5° С.
Интерполируя для tx ~ 5'С, получим Т5 --- 1510 даН.
Стрелы провеса контактных проводов при fx = 5 ПС определим по формуле-
(6.40), принимая с10 м:
при tg ---- - 32,3 °C (Т;~- 1900 даН) (70-2-10)2 / 1510 \ г .... >— 2,71-2.71 = 0,05 м, 8 (1510-; 2000) \ 1900 /
а при Гц - -15,1 °C (Т'и - 1700 даН) (70-2-10)2 1 , 1510 X п 1 .. —5 1— 2,71- 2,71) ^0.027 м. 8 (15104 -2000) \ 7 1700 /
Зависимость / (/0) приведена на рис. 5.14.
Оптимальную стрелу провеса контактных проводов определим, как для компен-
сированной подвески, по формуле (5.4) при температуре, равной среднегодо-
вой, т. е. '--5 °C. Принимая длину рессорного троса равной 14 м (а 7 м), его
натяжение при этой температуре 100 даН и используя формулы (4.25) и (4.371.
вычислим значение жесткости подвески у опор
жко==-2 (1510—100) 0.578/74-2 (2000 ф-100)/70 .292.9 даН/м,
где по формуле (4.39) - 0.64/7-2000/(10-1510) -0,578.
Жесткость подвески в середине пролета, считая, что разгрузки струн не бу-
дет. определим, используя формулы (4.25) и (4.47):
жкс =-70 (1510 42000)/352 = 200,6 даН/м.
Значение коэффициента кж,
формуле (5.1): к)( 292,9/20045
Рис. 5.14. Построения для опреде-
ления t0 опт
принимая Жк| '«[;=> вычислим ио
1,46.
Приняв расчетное нажатие токоприем-
ника типа Т равным 21 даН (см. табл
5.1), по формуле (5.4) определим оптималь-
ную стрелу провеса контактных проводов
/опт -(1,46—1) 21/(1,46-200,6) 0,033 м.
Выполнив построения, показанные на
рис. 5.14, получим, что для обеспечения
при температуре :-5”С стрелы пронеси
контактных проводов, равной 3.3 см, необ-
ходимо беспровесное положение контакт-
ных проводов иметь при температуре
tn - - 20 °C.
Чтобы принять окончательное реше-
ние, необходимо проверить, будет ли обес-
печено безотрывное следование токопри-
емника по контактным проводам при
экстремальных температурах. Для опреде-
ления стрел провеса контактных проводов
134
2000 \
-----—0,03 m;
1750 )
в этих условиях вычислим значения натяжений несущего троса при t0 и /тах
Опуская аналогичные приведенным выше расчеты по формулам (6.31) и (6.36).
получим:
при (0 — —20 JC — 7’0 •— 1750 данН; при /тах : 40 °C — Тт1п -=
1250 данН.
Стрелы провеса контактных проводов определим по формуле (6.40).
при (inin -- — 40 °C (?'rliax 2000 ДаН)
(70-2-10)2 /
f mll, =--5--------------2,71 —2,71
8 (2000 1-2000) \
при Gnax = i-40 C (7’rnin 1250 даН)
(70-2-10)2 I
^nax 8 (1250-I- 2000) (2’7!“ ’71
1250 \
----- . 0,075 m.
Проверка безотрывного следования токоприемника при этих стрелах прове-
са контактных проводов для скорости движения поездов 140 км^ч должна быть
выполнена с учетом динамических процессов при токосъеме по рекомендациям
§ 4.3.
§ 5.4. Основные направления совершенствования
контактных подвесок и токоприемников
Обеспечение хорошего качества токосъема зависит от правильно
выбранного сочетания типов токоприемников и контактных подвесок.
Улучшение качества токосъема и снижение износа контактирующих
элементов достигаются в основном совершенствованием конструкций
токоприемников и применением самосмазывающихся токосъемных
материалов. Однако использованы далеко не все возможности и кон-
тактных подвесок; совершенствовать их возможно следующими спо-
собами.
Выравнивание жесткости подвески в пролете. Это один из основ-
ных способов улучшения качества токосъема, так как чем равномер-
нее жесткость подвески вдоль пролета, тем меньше параметрические
колебания, передающиеся на точку контакта со стороны подвески. Вы-
равнивание жесткости осуществляют различными путями. Наиболь-
шее распространение получили рессорные подвески, которые вследст-
вие уменьшения жесткости в опорных узлах обеспечивают более рав-
номерную жесткость, чем подвески с простыми опорными струнами
(рис. 5.15). Широко применяют и двойные подвески, в которых вырав-
нивание жесткости достигается увеличением ее в средней части про-
лета.
Однако ни применение двойных подвесок с рессорными опорными
струнами, ни установка двойных рессорных тросов в опорных узлах
одинарных подвесок (осуществлена в ФРГ) не позволяют получить
коэффициент жесткости подвески ниже 1,2. Для очень высоких ско-
ростей движения при таком значении не всегда обеспечивается
нужное качество токосъема.
135
В некоторых странах для выравнивания жесткости подвески сни-
жали длину пролета, что явно неэкономично. Были предложены спе-
циальные конструкции контактных подвесок (рис. 5.16) — равно-
мастичные, так как для них можно принять коэффициент к.к - 1.
К ним относят, например, подвески тройные (Япония), с упругими
струнами (ФРГ, Италия, СССР) и др. Близко к таким подвескам стоит
и двойная вантовая (СССР).
Тройные подвески — весьма сложные и дорогие, нигде, кроме
Японии, не применяются, да и там эту подвеску смонтировали лишь
для испытаний. Конструкции вантовых подвесок также сложны, и
пока они находятся в стадии опытных проработок.
Подвески с упругими струнами в разных странах имеют различ-
ное устройство. Принципиальная особенность подвески с упругими
струнами, предложенной в СССР, работа несущего троса на кру-
чение, что осуществляется рычагами, закрепленными на тросе в трех
крайних струнах с обеих сторон каждого пролета, В средней части
пролета рычаги не устанавливают и рессорные струны в опорных уз-
лах не применяют. Рычаги имеют различную длину; самые длинные
расположены ближе к опорам, самые короткие — ближе к середине
пролета. Благодаря этому жесткость рычажной подвески можно из-
менять в любом нужном соотношении вдоль пролета. Очень важно,
что струны подвески под воздействием токоприемника не будут раз-
гружаться, а это обусловит хорошее качество токосъема при различ-
ных скоростях движения. Кроме того, удлинится срок службы
звеньевых струп. Можно также с помощью рычагов выравнивать
жесткость в двойных и ромбовидных подвесках.
Рис. 5.16. Схемы равноэластичпых
контактных подвесок: тройной (а), с
упругими струнами (б) и двойной
вантовой (fl)
Рис. 5.15 Схемы подвесок: с простыми
опорными струнами (а), с рессорными
тросами (б) и двойной (в) и кривые рас-
пределения жесткости этих подвесок
вдоль пролета (а):
/, 2, .7 соответственно для схем а, б н в
136
Рис. 5.17 Расчетные кри-
вые |Q|max (Д() ДЛИ ЛИ-
ТИЙ переменного (а) и
постоянного (б) тока при
скорости 200 км/ч
Было выполнено сравнение качества токосъема но показателю
IQIma х- (рис. 5.17) при обычной рессорной (кж 1,6) и равноэластич-
пой (кж -- 1) подвесках. Если стрелы провеса контактных проводов
отклоняются от оптимальных значений, качество токосъема при равно-
эластичных подвесках ухудшается не так интенсивно, как при обыч-
ных. Кроме того, при равноэластичных подвесках проще осуществить
более точную регулировку, так как для оптимальных условий нужно
обеспечить беспровесное положение контактных проводов, что сделать
значительно легче, чем правильно установить их заданную стрелу
провеса при обычных подвесках.
На рис. 5.18 приведены результаты расчетов по взаимодействию
токоприемников серий Т и Л с обычной и равноэластичной компенси-
рованными подвесками М-120 1 2А4Ф-100. Равноэластичная подвес-
ка исследовалась в двух вариантах: при нормальных номинальных
натяжениях проводов (жи 215 даН/м) и при повышенных в сумме
до 5400 даН (жГ! - 315 даН.м). Эти варианты можно рассматривать
и так, что в первом случае жесткость подвески вдоль пролета
выравнена путем се уменьшения в опорных узлах, а во втором — в
результате увеличения в середине пролета.
Из кривых рис. 5.18, а следует, что при равноэластичной под-
веске с нормальной жесткостью (215 даН/м) токоприемник серии Л
обеспечивает лучшее качество токосъема, чем серии Т, как при бес-
провеспом положении контактных проводов, так и при отклонениях
провода в обе стороны от этого положения. При взаимодействии же
с подвеской повышенной жесткости (315 даН м) нарушения беспро-
весного положения приводят к более резким ухудшениям качества
токосъема (при стреле провеса, равной 7 см, токоприемник серии Л
отрывается от контактного провода). Аналогичные выводы можно сде-
лать, рассмотрев кривые рис. 5.18, б, где для сравнения приведены
еще данные для обычной рессорной подвески (к.к - 1,6). Таким об-
разом, при меныпей жесткости равноэластичной подвески и возмож-
ных в условиях эксплуатации отклонениях от оптимального режима
легче обеспечить нужное качество токосъема, чем при равиоэластич-
ной подвеске с повышенной жесткостью. Это необходимо учитывать
в тех случаях, когда по тем или иным причинам потребуется увели-
чивать жесткость равноэластичных подвесок.
137
Рис. 5.18. Расчетные
Кривые |Q|max (f) и
IQImax (А/) для под-
вески М-120 + 2МФ-100 и
токоприемников серий Т
(кривые 1) и Л (кри-
вые 2) при подвесках
О6ЫЧИОЙ С Кж -- 1,6
(штрихпунктирные ли-
нии) и равноэластичны-
ми с ж„ = 215 даЬРм
(сплошные) и 315 даН м
(штриховые); / = 70 м,
о = 250 км'ч
Обеспечение оптимальных параметров подвесок. Оно может су-
щественно улучшить качество токосъема и при обычно применяемых
рессорных подвесках (см. §5.2 и 5.3). В ряде случаев даже при вы-
соких скоростях движения может оказаться неоправданным проек-
тирование равноэластичных или каких-либо других сложных подв(
сок.
Таким образом, при определенных условиях, которые должен уста-
новить проектировщик, надежный токосъем и снижение износа кон-
тактных проводов и токосъемных пластин могут быть обеспечены не
усложнением и удорожанием контактной подвески, а значительно
более экономичным путем.
Экспериментальные исследования взаимодействия с токоприемни-
ком одинарной компенсированной рессорной контактной подвески
с одним контактным проводом, выполненные В. А. Болотиным, по-
казали, что при оптимальных параметрах подвески, заданных в со-
ответствии с приведенной выше методикой (см. §5.2). возможно осу-
ществить надежный токосъем при скоростях движения до 200 км/ч
включительно. Неравномерность жесткости подвески, которая при
испытаниях была в середине пролета длиной 70 м на 75 % ниже, чем
в опорных узлах, не явилась препятствием для получения траектории
токоприемника, близкой к прямолинейной (размах вертикальных
перемещений точки контакта не превышал 4 см)
При этих испытаниях было также установлено, что изменения
длины пролета практически не отражаются на затухании колебаний.
Основное влияние на размеры вертикальных перемощений проводов
оказывает неравномерность жесткости подвески вдоль пролета, уве-
личивающаяся с ростом его длины. Однако, как показали теоретиче-
ские исследования и опытные поездки, при правильном выборе оп-
тимальных параметров подвески траектория токоприемника близки
к прямолинейным независимо от длины пролета.
Выравнивание и увеличение натяжений проводов контактной под-
вески. Выравнивание натяжений проводов при колебаниях темпера-
туры осуществляется применением компенсированных подвесок, ко
торые в этих условиях обеспечивают лучшее качество токосъема, чем
полукомпенсированные. В определенных условиях, особенно при вза-
138
имодействии контактной подвески с несколькими рабочими токопри-
емниками, повышение натяжений проводов подвески существенно
улучшает качество токосъема. Это объясняется не только увеличе-
нием жесткости подвески и снижением вертикальных перемещений
точки контакта, но п ростом скорости распространения фронта бе-
гущей волны вдоль контактной подвески (при сохранении массы под-
вески). Чем больше разность между скоростью движения поездов и
скоростью распространения фронта бегущей волны, тем лучше ка-
чество токосъема при нескольких токоприемниках Кроме того, с
увеличением натяжений проводов растет так называемая критиче-
ская скорость, при которой возникают резонансные явления, нарушаю-
щие токосъем. Таким образом, увеличив натяжение проводов, по
возможности сохранив их суммарную плотность, можно добиться
устранения резонансных явлений, так как критическая скорость
станет выше реализуемых скоростей движения. Увеличение натяже-
ний проводов подвески, особенно контактных, существенно повышает
и ее ветроустойчивость.
Возможности для повышения качества токосъема создает приме-
нение бронзовых проводов, так как увеличение их натяжения не со-
провождается ростом плотности. Однако вследствие пониженной элек-
трической проводимости и высокой стоимости бронзовых проводов
целесообразность их применения следует определять технико-эконо-
мическим расчетом, учитывая увеличение срока службы проводов,
если они использованы в качестве контактных.
Возможность повышения натяжений проводов необходимо прове-
рять расчетами, учитывая динамические процессы, применительно
к конкретным токоприемникам. Как указывалось выше, при более
жесткой подвеске и слишком легких токоприемниках качество токо-
съема может оказаться неприемлемым.
Следует отметить, что в зарубежной практике часто применяют
более высокие натяжения рессорных тросов, чем в СССР.
Обеспечение быстрейшего затухания колебаний, возникаю-
щих при взаимодействии контактной подвески с токоприемником.
Снижение амплитуды этих колебаний может быть достигнуто спе-
циальным демпфированием. Например, в Японии для этого включают
в некоторые струны между несущим и вспомогательным тросами двой-
ной подвески пружинно-воздушные демпферы. Большое число таких
устройств требует значительных расходов на содержание их в экс-
плуатации. В дальнейшем от применения их отказались.
Осуществить демпфирование в колебательной системе значитель-
но проще на токоприемниках.
Применительно к контактным подвескам следует указать на уст-
ройство, которое предложил для снижения размаха автоколебаний
подвесок И. А. Беляев. В опорных узлах совместно с рессорными
струнами устанавливают еще и простые. Не препятствуя подъему
контактного провода у опор, простые струны не позволяют ему опу-
ститься ниже определенного уровня, что существенно уменьшает
139
вертикальные перемещения подвески не только при автоколебаниях,
но и при колебаниях, возникающих в результате взаимодействия
с токоприемниками. Такие струны сравнительно просто применить
в компенсированных подвесках; в полукомпенсированных подвесках
требуется принимать специальные меры для сезонной регулировки
длины простых струн, что существенно осложнит эксплуатацию под-
весок.
Устранение жестких точек и сосредоточенных масс на контакт-
ной подвеске или уменьшение жесткости подвески в таких местах.
Из осциллограммы контактного нажатия (рис. 5.19), снятой в пролете
длиной 70 м, в котором на расстоянии 7,5 м от опоры сосредоточена
масса 7,5 кг, следует, что в месте нахождения ее контактное нажатие
увеличилось более чем вдвое и затем довольно быстро установилось
нормальным. Таким образом, в месте расположения сосредоточенной
массы проявилось ударное воздействие токоприемника, которое хотя
и не привело в данном случае к потере контакта, но при повторных
проходах токоприемника вызовет усиленный местный износ контакт-
ного провода.
Основные жесткие точки и сосредоточенные массы на контактной
подвеске обусловлены наличием фиксаторов, стыковых зажимов и др.
При высоких скоростях движения особенно важно совершенствовать
конструкции фиксаторов и облегчать их (например, применять алю-
миниевые сплавы) с тем, чтобы нагрузка на контактный провод от
дополнительного фиксатора в момент прохода токоприемника была
возможно ниже. Устранить стыковые зажимы контактных проводов
можно, применяя специальную сварку. Для монтажа контактной
подвески следует так подбирать барабаны с контактным проводом.
Рис. 5.19 Осциллограмма контактного нажатия, полученного при проходе токо
приемника Сп-1М со скоростью 165 км/ч по контактной подвеске М=120 + МФ =
— 100 с беспровесным положением контактного провода н наличием на нем со
средоточеннои массы
140
чтобы длина его на барабане соответствовала длине монтируемого
анкерного участка.
Совершенствование конструкций токоприемников. В основном оно
идет по пути снижения их приведенной массы. Это при прочих рав-
ных условиях приводит к увеличению ускорений, реализуемых токо-
приемником, что способствует улучшению качества токосъема. Тео-
ретические и экспериментальные исследования показывают, что при
скоростях движения более 100 км/ч снижение приведенной массы
токоприемника заметно стабилизирует контактное нажатие.
Уменьшать приведенную массу токоприемника можно, облегчая
полозы и подвижные рамы. Однако масса полоза, определяемая в зна-
чительной мере массой контактных элементов, зависит от снимаемого
тока и особенно при постоянном токе не может быть снижена без уче-
та этого. Масса подвижных рам, которую можно уменьшить, приме-
няя более тонкие трубы, в обычных токоприемниках уже достигла
минимального значения, обусловленного требованиями механической
прочности, необходимой поперечной жесткости и проводимости. По-
этому параметры отечественных токоприемников можно считать близ-
кими к оптимальным.
За рубежом некоторое уменьшение приведенной массы достиг-
нуто в результате применения асимметричных токоприемников (Фран-
ция, Великобритания, ФРГ), а значительное снижение ее — путем со-
кращения рабочего хода токоприемника (Япония). В последнем слу-
чае требуется ограничить изменения высоты подвески контактного
провода (в Японии принято 0,5 м).
Необходимость снижения приведенной массы токоприемника бе <
уменьшения его рабочего хода привела к разработке двухъярусного
токоприемника, в котором подвижная система расчленена на две ча-
сти. Нормально токосъем осуществляет только верхняя подвижная
система токоприемника, нижняя вступает в работу лишь при значи-
тельных изменениях высоты контактного провода (например, при
проходе искусственного сооружения). Двухъярусный токоприемник,
разработанный во ВНИИЖТе, существенно отличается от подобных
зарубежных конструкций наличием авторегулирования, при кото-
ром даже в переходном режиме (когда нижняя подвижная система на-
чинает изменять свое положение) приведенная масса токоприемника
определяется только массами верхней подвижной системы и полоза.
В ряде стран для снижения амплитуды колебаний и быстрейше-
го их затухания, а также для стабилизации контактного нажатия
применяют демпфирование токоприемников. Демпфирующие устройст-
ва включают или между подвижными рамами и основанием токоприем-
ника (СССР. Италия и др.), или между подвижными рамами и поло-
зом (ФРГ). Демпфирование, выполняемое обычно гидравлическими
устройствами с вязкой жидкостью, может быть двусторонним и одно-
сторонним (в последнем случае оно осуществляется только при сни-
жениях полоза токоприемника). Коэффициент вязкого трения для
гидравлических демпферов двустороннего действия, включаемых в
145
отечественных токоприемниках между подвижными рамами и осно-
ванием, составляет около 4,5 даН-с/м (приведенный к оси верхних
шарниров подвижных рам). Эффект демпфирования зависит от жест-
кости пружин кареток, что нужно учитывать при выборе оптималь-
ного коэффициента вязкого трения.
Исследования показали, что применение демпфированных токо-
приемников с приведенной массой 25—35 кг позволяет обеспечить
хорошее качество токосъема с одинарных компенсированных рессор-
ных подвесок при скоростях движения до 250 км/ч. Оказывается воз-
можным при токоприемниках с приведенной массой 25 кг в определен-
ных климатических условиях после соответствующей перерегулиров-
ки оставлять в эксплуатации рессорную полукомпенсированную под-
веску с двумя контактными проводами для скоростей движения до
200 км/ч. При одном контактном проводе в этом случае скорость дви-
жения не должна быть выше 160 км/ч.
При эксплуатации локомотивов или электропоездов с нескольки-
ми рабочими токоприемниками следует предусмотреть их параллель-
ное электрическое соединение, что практически исключит появление
электродуговых процессов в случае нарушения контакта между по-
лозом одного из них и контактным проводом. В частности, эти реко-
мендации реализованы на электровозах ЧС6, ЧС200 и электропоезде
ЭР200.
Глава 6
РАСЧЕТЫ ПРОВОДОВ ВОЗДУШНЫХ ЛИНИЙ
И КОНТАКТНЫХ ПОДВЕСОК ПРИ ИЗМЕНЕНИЯХ
КЛИМАТИЧЕСКИХ УСЛОВИЙ
§ 6.1. Общие положения
Расчеты проводов воздушных линий выполняют е целью получе-
ния необходимых данных для производства монтажа и регулировки
проводов в различных температурных условиях и для проверки со-
блюдения вертикальных и горизонтальных габаритных размеров
Кроме того, вычисляют натяжения проводов, которые могут быть опре-
деляющими нри расчете пли подборе поддерживающих устройств и
опор. Как правило, провода рассчитывают так, чтобы полностью ис-
пользовать их механические свойства, но иногда для облегчения под
держиваюших устройств или опор снижают максимальное натяжение
провода, вводя в расчет повышенный коэффициент занасч прочности,
Поскольку все провода воздушных линий не имеют комненсаю-
ров, принятое в качестве допустимого максимальное' натяжение при-
вода будет только в одном (очень редко в двух) режиме работы Чтобы
не превысить это натяжение в условиях эксплуатации и не допустить
слишком больших провесов провода вследствие понижения натяже-
ния, необходимо правильно смой тировать провод, т. е. придать ему
во время монтажа определенное натяжение. Для этого составляют iак
называемые монтажные таблицы. Б них указывают натяжения и стре-
лы провеса провода, которые нужно задавать при температуре, со-
ответствующей времени производства монтажных работ. Но этим же
таблицам проверяют параметры провода нри температуре в момент
регулировки его в условиях эксплуатации.
В процессе расчета определяют также максимальные перемещения
провода в вертикальной и горизонтальной плоскостях, проверяя, не
будут ли нарушены в каких-либо гонках пролета нормированные вы-
соты положения провода или допускаемые расстояния его до заземлен-
ных элементов. Особенно важно проверять это при возникновении
гололедных образований, воздействии ветра на провод без гололеда,
а также при его наличии. В отдельных случаях провод может чрезмер-
но провиснуть в результате нагрева его электрическим током при
максимальной температуре воздуха.
Расчеты контактных подвесок по определению данных, необхо-
димых при их монтаже и эксплуатации, производят после того, как
уже определены все основные параметры, способствующие достиже-
нию возможно лучшего качества токосъема в заданных условиях
(см. главы 4 и 5). При этом широко используют различные ЭВМ.
ИЗ
Расчеты простых контактных подвесок, применяемых на желез-
ных дорогах только в виде компенсированных так же, как и компенси-
рованных цепных подвесок, производят, чтобы определить изменения
стрел провеса проводов при дополнительных нагрузках и отклонения
проводов от нормального положения для проверки соблюдения тре-
буемых расстояний до заземленных частей.
Полукомпенеированные цепные подвески рассчитывают е целью
проверки прочности несущего троса, определения соответствующих
данных для правильного монтажа троса в разгруженном состоянии
(без контактного провода) и стрел провеса всех проводов, что необ-
ходимо знать при монтаже и эксплуатации. Кроме того, как и для
проводов воздушных линий, определяют натяжения несущего троса,
необходимые для расчета или подбора поддерживающих устройств
и опор.
Поскольку некомпенсированные цепные подвески па железных
дорогах не применяют, их расчеты не приводятся.
При расчетах проводов воздушных линий и несущих тросов полу-
компеисировапных подвесок нужно определять режимы, которым со-
ответствует максимальное натяжение или наибольшая стрела провеса.
Максимальное натяжение в проводе может возникнуть в режиме или
минимальной температуры, или максимальных дополнительных на-
грузок, возникающих при гололеде с ветром. Для выбора между этими
режимами пользуются понятиями критического пролета или крити-
ческой нагрузки.
Критическим называют такой пролет, при котором натяжение
провода равно максимальному в обоих указанных режимах. Если
расчетный пролет I меньше критического /кр, максимальным натя-
жение будет при минимальной температуре Zmiu, а если то
натяжение возникает при наибольших дополнительных нагруз-
ках. Для провода воздушной линии
б<р F 24а (/г-/,,.!,,g2) , (61)
где а темперитурнын коэффициент линейного расширения материала про-
вода;
/г расчетная температура гололедных образований;
с/р — результирующая распределенная линейная нагрузка на привод
при гололеде с ветром;
а линейная нагрузка от веса провода.
Для несущего троса лолукомпепсированной цепной подвески
б;р ^гпах Iх 24(Хц(/г — —МДпПр)" (6.2)
। jc Zmax — максимальное приведенное натяжение подвески:
Wи - приведенные линейные нагрузки на подвеску соответственно
при гололеде с ветром и минимальной температуре;
а» температурный коэффициент линейного расширения материала
несущего троса.
I 1-1
Приведенные величины Zx и Wх для реж ша х вычисляют по фор-
мулам, предложенным д-ром техн, наук И. И. Власовым:
Z.x^Tx\-qxK: (6.3)
). (6 4)
\ S.x ‘о 1
Здесь gx, (/д. — соответственно вертикальная и результирующая нагрузки на
несущий трос в режиме х;
К — натяжение контактного провода (проводов), принимаемое по-
стоянным вследствие наличия компенсаторов;
Та — натяжение несущего троса при беспровссном положении кон-
тактного провода;
ф.х — конструктивный коэффициент цепной подвески, определяемый
по формуле, предложенной автором:
X
ь и-(1 ык/тх '
где X - (/ —2г.)2//3 (6 6)
Величина с в выражении (6.6) означает расстояние от оси опоры
до околоогюрной струны (см. рис. 4.9). Таким образом, при заданных
значениях I и с величина X неизменна.
Формула (6.2) является приближенной, так как, во-первых, на
данном этапе неизвестна величина Та (ее можно принять только ори-
ентировочно по данным, приведенным в §3.2), во-вторых, не ясно,
для какой длины I определять X и ф. Обычно эти коэффициенты нахо-
дят для расчетного пролета. Если длины расчетного и критического
пролетов существенно различны, то получаемая ошибка не имеет
значения (режим максимального натяжения все равно будет выбран
правильно), а если расчетный и критический пролеты близки, то при-
нятое к расчету значение ip мало отличается от истинного.
Для режима гололеда с ветром:
ZpТг -j - фр А; (67)
для режима ветра максимальной интенсивности:
Zu - Тп ) фв Ад (6.9)
^в=--<7в (1 1-фвК/Г0) (6.10)
и для любого режима без дополнительных нагрузок при температуре /:
Z;---I фц А; (6.11)
1Г'г -2(И-Ф/ К/Та). (6.12)
В формулах (6.8) и (6.10):
gr — линейная нагрузка от веса гололеда на подвеске.
£/в — результирующая линейная нагрузка при максимальном ветре.
145
В каждом случае при определении конструктивных коэффициен-
тов гр,.. ср,, и ф( по формуле (6.5) следует учитывать соответствующие
натяжения несущего гроса Тг. Т,_ и Тt.
Удовлетворительные результаты расчета длины критического про-
лета могут быть также получены по приближенной формуле, предло-
женной ипж. Э. /А. Мазурским,
‘кр " (''’шах + р К) | 24ан(Гг- /т1п) ,'(<7г — g2)- (6 13}
В этой формуле коэффициент р для подвесок с простыми опорны-
ми струнами при одном контактном проводе рекомендуется принимать
равным 0,5, а при двух проводах — 0,4. Как показали сравнитель-
ные расчеты, для подвесок с рессорными тросами коэффициент р мо-
жет быть принят равным 0,15 при одном контактном проводе и 0,1
при двух проводах.
К ритичсекий называют такую нагрузку в режиме гололеда с вет-
ром. при которой натяжение провода становится максимальным и рав-
ным натяжению при минимальной температуре. Если нагрузка при
гололеде с ветром у, меньше критической й|!Г), то натяжение Нтлх
будет при минимальной температуре, а если нагрузка в режиме го-
лоледа с ветром больше критической, то и наибольшее патяжени*
возникнет в этом режиме. Критическая нагрузка для провода воздуш-
ной ЛИНИН
,/кр | / 4ц2. !(> 14!
а для несущего трота полукомнежированной цепной подвески (при-
ближенно, так как принято ориентировочное значение Т„)
<?кр I . -Jjlll’L(.IT / n,iг, -- ZVrA (6 15J
I 1- тй
Максимальная стрела провеса провода может возникнуть при ре-
жиме максимальной температуры или при наибольших дополнитель-
ных нагрузках. Для выбора между этими режимами пользуются по-
нятием критической температуры. Критической называют такую
температуру, при которой стрела провеса провода без гололеда рав-
на его стреле провеса при гололеде. Если максимальная расчетная
температура б11:1, меньше критической /к)1. то наибольшей стрела про-
веса будет в режиме гололеда, а если т,па1, > twp, то она возникнет при
максимальной температуре.
Для проводов воздушных линий
• frт т.тг 1 1 — “ , (6.16|
\ gr J
где //]. — натяжение провода при гололеде с ветром.
aES — произведение температурного коэффициента линейного расширения
материала проводов а. его модуля упругости Е и площади поперс
чногч сечения S (см. табл. 1.9).
146
Для несущих тросов полукомпенсированных ценных подвесок
/кр ~tT-' t ) / (Я.)! Г-н SH)
Здесь произведение a„EltSn относится к мггериялу несущего
гроса, а Т1кр— к режиму критической температуры. Поскольку зна-
чение Ttf(p заранее неизвестно, то вычисления можно осуществить
только методом последовательных приближений: задавшись 7\р. опре-
делить /кр; затем проверить соответствие натяжения несущего троса
вычисленной температуре и т. д., пока не будет достигнута нужная
точность. Если расчеты производят не на ЭВМ, то из-за указанной их
сложности при цепных подвесках предпочтительнее для определения
максимальной стрелы провеса несущего троса выполнить два расчета
в искомых режимах, не вычисляя значение 7кр.
Если различны уровни закрепления провода воздушной линии на
соседних опорах, в расчет можно ввести условный пролет
/' I , 211 h/(</ /), (0 17)
i.’je h — разность уровней подвески провода;
//, с/ -соответственно натяжение я результирующая линейн!? нагрузка
на провод при одном и том же режиме:
I — фактическая длина пролета.
Для несущего троса полукомпепсировапной ценной подвески
/' I [-27.h/(W I), (6 IM
где Z и № - приведенные значения соответственно натяжения и нагрежи
подвески
Использование формул (6.17) и (6.18) при одном и том же режиме
работы провода или троса не внесет ошибку в результаты расчетов,
но при переходах от одного режима к другому пользоваться условным
пролетом не следует.
Расчеты проводов воздушных линий и контактных подвесок обыч-
но производят для анкерных участков, в которых могут быть пролеты
различной длины. В этом случае необходимо для каждого анкерного
участка выбрать какой-то один пролет, для которого будут выпол-
няться расчеты. Расчетный пролет выбирают в зависимости от спо-
соба закрепления проводов (жесткое или шарнирное) на опорах. Шар-
нирным закрепление получается для несущих тросов цепных подве-
сок и проводов воздушных линий на подвесных изоляторах. Жестким
закреплением становится при использовании штыревых изоляторов на
неповоротных кронштейнах.
При шарнирном закреплении провода расчетным является эк-
вивалентный пролет, в котором натяжение провода меняется по тому
же закону, что и во всем анкерном участке. Длина эквивалентного
пролета
Г п
]/ 5} , (6.19)
\41
где /а — длина анкерного участка;
п — число пролетов в анкерном участке;
i — номер пролета.
В случае жесткого закрепления провода на опорах в качестве рас-
четных выбирают один или оба экстремальных пролета анкерного
участка, определив сначала длину /1(р по формуле (6.1) и значение /Кр
по формуле (6.16). При этом исходят из следующих условий:
если наибольший пролет анкерного участка меньше критического,
расчетным является минимальный пролет анкерного участка;
если наименьший пролет анкерного участка больше критическо-
го. то при температурах ниже критической расчетным является мак-
симальный пролет анкерного участка, а при температурах выше кри-
тической — минимальный;
если критический пролет находится в пределах между экстремаль-
ными, то выполняют два расчета (для минимального и максимального
пролетов) и в качестве расчетного при данной температуре принимают
меньшее из полученных натяжений. Если начинать с минимальной
температуры, получим, что расчетным окажется максимальный про-
лет. При некоторой температуре расчетным окажется минимальный
пролет. Далее вычисления для максимального пролета производить
не надо, так как он уже расчетным не будет.
Расчеты биметаллических проводов выполняют так же, как и од-
нородных, учитывая физические характеристики основного металла.
Для комбинированных проводов, состоящих из проволок с различны-
ми физическими харак геристиками, тоже можно использовать форму-
лы для расчета однородных проводов, принимая в этом случае пло-
щадь сечения равной сумме площадей сечения проволок из отдельных
металлов и заменяя температурный коэффициент линейного расшире-
ния а и модуль упругости Е эквивалентными значениями:
ОС:. | as/:2 5.2)/(/:i Sj | /:'2>S'2);
(/ц .S\| /:2 S2) / (.S', |.........$2).
(6.20)
(6.21)
Здесь индексы 1 и 2 относятся к различным материалам проволок,
из которых изготовлен провод (например, 1 - алюминий, 2 - сталь)
Длина критического пролета для комбинированного провода
где относится к материалу, имеющему большие деформации (на-
пример, при сталеалюминиевых проводах — к алюминию).
Максимальные допускаемые натяжения провода в режимах гололеда
с ветром Wniai г и минимальной температуры A/,liax t в формуле (6.22)
определяют как
Нmax I [Щ (ОЦ ОЦ)) ((ииг — Е) ^;л| $/£],
(6.23)
где /изг — температура при которой был изготовлен провод (обычно 15 "С);
Е —- температура искомого режима;
О| н /•', — соответственно допускаемое напряжение и модуль упругости для
материала с большими деформациями.
148
§ 6.2. Расчеты проводов воздушных линий
На подготовительном этапе расчета анкерного участка провода
воздушной линии (питающей, усиливающей, ДПР и др.) выполняют
следующие вычисления:
1. Определяют или задают максимальное допускаемое натяжение
провода. Это натяжение, даже если механические качества провода
будут использованы не полностью, для данного расчета является пре-
дельным; превышение его недопустимо ни при каких условиях;
2. Вычисляют все распределенные линейные нагрузки на провод
(от собственного веса, веса провода с гололедом, ветровые нагрузки
на провод без гололеда и при его наличии, результирующие нагрузки
при максимальном ветре без гололеда и при гололеде с ветром) по
формулам, приведенным в § 2.2 или по данным табл. 2.3.
3. Определяют длину критического пролета по формуле (6.1) и,
если закрепление провода жесткое, критическую температуру по
формуле (6.16).
4. Выбирают расчетный пролет в соответствии с рекомендациями,
приведенными в §6.1.
5. Определяют режим, которому соответствует принятое в расче-
те максимальное натяжение провода. Если закрепления провода на
опорах шарнирные, то это делается путем сравнения эквивалентно-
го расчетного пролета с критическим; если же закрепления жесткие,
то режим максимального натяжения уже определен ранее в и. 4.
После подготовительного этапа выполняют расчеты, необходимые
для построения монтажной кривой. Эта кривая представляет собой
зависимость натяжения провода от температуры (рис. 6.1). Пользо
ваться графиками во время работы на линии неудобно, поэтому на
основании монтажной кривой составляю! монтажную таблицу по
форме, аналогичной табл. 6.1 (см. с. 153). Кривые швисимостей стрел
провеса провода от температуры не сгроят, а вычисляют значения этих
стрел и заносят их в монтажную таблицу.
Монтаж и регулировку проводов производят по их стрелам про-
веса, поэтому расчеты стрел провеса выполняют для всех пролетов,
входящих в состав анкерного участка. Натяжение в монтажной таб-
Рис. 6.1. Примерные монтажные кривые при максимальном натяжении в режиме
минимальной температуры (и) и при гололеде с ветром (о)
яйце указывают для расчетного пролета, так как оно будет одинаковым
во всех пролетах анкерного участка. Температуры в монтажной табли-
це приводят через 5 или 10 °C для всего диапазона между экстремаль-
ными расчетными температурами.
Расчеты натяжений проводов, если задаваться значениями темпе-
ратур, можно выполнить, решая уравнение
//v -/Ц.7/; - В,, (6.24)
ме 4; И, - I* fiS'(24Н&ЯХ) a ES .
Все величины с индексом 1 относят к режиму, при котором будет
максимальным натяжение провода, с индексом х - к любому дру-
гому режиму. При этом исключается возможность превышения натя-
жения, принятого в качестве максимального, в других режимах.
Обычно предпочитают решать не кубическое уравнение (6.24),
а линейное, задаваясь натяжением провода н определяя температуру,
при которой будет возникать это натяжение.
-'2 . //max Ч2 I2
где 4, -=/,-------;----1---—: ЛЛ-- —------.
24а //.“„ах а1 s ••4«
Вначале следует проверить правильность вычисленных коэффициен-
те А я В. Если задаться температурой и нагрузкой при режиме мак-
симального натяжения, то это натяжение должно получиться в ре-
тультате решения уравнения (6.24), а если задаться максимальным
натяжением и соответствующей нагрузкой, то по уравнению (6.25)
получают температуру, при которой возникает указанное натяжение.
Полученные при решении уравнения (6.25) температуры опреде-
ляют точки для построения кривой Нх (/х). Стрелы провеса провода
при температуре 1Х вычисляют для каждого из пролетов анкерного
участка I-,:
к-1 <М//(«/Л). (6.26)
После этого находят натяжения провода в режимах с дополнитель-
ными нагрузками: при гололеде с ветром (если этот режим не обуслов-
ливал максимальное натяжение) и при ветре максимальной интенсив-
ности (см. соответствующие точки на рис. 6.1). Расчеты выполняют
также по уравнению (6.24) или (6.25), но в последнем случае прихо-
дится задаваться натяжениями дважды, чтобы стало возможным опре-
делить искомую (фиксированную) температуру интерполяцией. При
этом величина qx должна быть равна результирующей нагрузке для
Таиного режима.
Чтобы определить вертикальные и горизонтальные перемещения
провода на расстоянии х от опоры, используют формулы:
150
для расчета вертикальной составляющей стрелы провеса провода
//'=-g'.v (/—Л')/(2//); (6.27)
для определения его горизонтального отклонения
х(1 — х)!(2Н). (6.28)
В этих формулах, значения нагрузок g' (вертикальной) и р* (го-
ризонтальной), а также натяжений И должны соответствовать тем
расчетным режимам, при которых определяются отклонения.
Пример. Задачи е. Составить монтажную таблицу для комбинирован
кого провода АС-50/8,0, который будут крепить к штыревым изоляторам на
неповоротных кронштейнах; определить наибольшие провисание провода и его
горизонтальное отклонение.
Исходныеданпы е. Провод будут монтировать на равнине без на
сыпей и выемок (нулевое место). Гололедный район II, ветровой район III. экс.
тремальные температуры — 50 и 40 С Длина минимального пролета 50 м
максимального 70 м.
Определение распределен и ы х л и н е и п ы х н я г |! х
з о к н а н р о в о д.
По табл 1.5 нагрузка от собственного веса д 0 I9i anН м
Нагрузку от веса ! ололеда с толщиной стенки 10 мм определяют по фор>.п н-
(2.4|. Диаметр провода равен 9,6 мм (см. табл. 1.5). тогда
gr- 2,77 10(9,6 1 10) 10-s 0.54.3 даН/м.
Чтобы определит! статические составляющие ветровых нагрузок найдем
сначала распределенные поверх постные н.-чрузки для заданных условий П"
табл. 1.3 значение коэффициента для равнины (z0 0.1 м) и нулевою мес
равно 1,1. Следовательно, принимая по табл I 4 для гололедного района II тк,
чение В|-о • 120 Па. а по табл. 1 1 для ветрового района III Д„ 510 Па
формуле (1.11) получим
В,. 1,Г:-120 145 Па, /? 1.р.510 М? Па
Нагрузку от давления ветра на провод, покрытый, гололедом, определим по
формуле (2.9), приняв коэффициент аэродинамического лобового сопротивления
равным 1,2,
ргс 145-1.2(9.64-2.10) 10~4 0.515 даН/м.
Результирующую нагрузку на провод при гололеде с ветром найдем но фор-
муле (2,16)
qr У(0719Г^017543)5:МГ515“' --0,89 даН/м
Статическую составляющую нагрузки на провод от ветра максимальной ин
теш явности определим но формуле (2.7)
рс -= 617-1.2- 9,6-10 40,711 даН /м ,
результирующую нагрузку при максимальном ветре — по форму ie (2.15)
qn - ]/0,1912 |-0,7I Г2 -0,74 даН/м.
Выбор р а с ч е т н о г о п роле г а. Для этого нужно знать д^инх
критического пролета. Поскольку провод АС-50/8,0 комбинированный, то сняч:»
ла вычислим ряд вспомогательных данных. Эквивалентное значение коэффици-
ента линейного расширения провода найдем по формуле (6.20). Площадь сече-
ния алюминиевой части провода равна 48.2 мм2, стальной — 8,04 мм'-’ (см
15)
В-
табл. 1.5). Характеристики провода принимаем по табл. 1.7; после перевода раз-
мерности модулей упругости в даН/мм2 по формуле (6.20) получим
23-10- «.6180-48,2-1 12-10-«-19 610-8,04
-----------------:1-----------------------= 19,2-10-“
6180-48.2 -! 19 610-8,04
Значение эквивалентного модуля упругости найдем по формуле (6.21)
6180-48,2+ 19 610 8,04
48,2 +-8,04
8100 даН/мм2.
Значения максимальных допускаемых натяжений провода нри гололеде
с ветром и минимальной температуре определим по формуле (6.23), принимая Oj
и Ei для алюминиевой части провода равными соответственно 7,35 даН/мм2 (см.
табл. 1.7 и учитывая коэффициент запаса прочности, равный 2) и 6180 даН/мм^
8100-56,24
/Лнахг 1 + 35- (23-10-«—19,2-10~«) (15+5) 6180----------------=507 ДаН;
6180
8100-56,24
Нтах, [7,35 - (23-10-»—19.2-10-«) (15 |-50)6180]----------:--- 430 даН .
6180
Длину критического пролета определим по формуле (6,22)
/|ф- м
* V (0.89/507)'-— (0,191/430)2
Поскольку все пролеты заданного участка меньше критического, то в каче
ствс расчетного принимаем минимальный пролет, т е. 50 м.
П о с т р о е и и с м о и т а ж н о й к р и в о й. Расчеты ведем по
формуле (6.25). Коэффициенты в этом уравнении, принимая за исходный ре-
жим минимальной температуры и учитывая характеристики а., и Е.,, определи
ем как
0.191й-502 , 430
4. 50--------------------------------------------- 1,92;
' 24 19,2-10 “-4302 19,2-10 “-8100-56.24
/1
0,19 Г2 502
24-19.2-10 “
0,2-10“.
Проверим правильность полученных коэффициентов. Зададимся натяже-
нием провода, равным 430 даН. Тогда
1Х --1,92 )-0,2-Ю«/430« — 430/8,75 ~ — 50°C.
Следовательно, коэффициенты А и
расчеты дали следующие результаты.
В определены правильно. Дальнейшие
Нх, да 11...................
/х. С.......................
430 300 200 150 100 80 65
—50 -34 -20 10 7 20 38
Монтажная кривая Нх (1Х) построена на рис. 6.2.
Подготовим монтажную таблицу табл. 6.1 и перенесем в нее значения Нх,
соответствующие принятым в таблице температурам, с монтажной кривой (ок-
ругление до 5 даН).
Значения стрел провеса провода определим по формуле (6.26), например,
при натяжении 350 даН
f 0.191-502/(8-350) ==-0,171 м s 17 см.
152
Рис. 6.2. Монтажная кривая для провода
ЛС-л0'8,6 и значения натяжений Нг, //„ при
дополнительных нагрузках
Определение и а и б о л ьш их значении провиса-
ния провода и его горизонтал ьиого отклонения.
Для этого сначала нужно найти значения натяжений провода при дополнитель-
ных нагрузках. Принимая, что гололеде ветром и максимальный ветер без голо-
леда возможны при температуре воздуха - 5 °C, выполним расчеты по фор-
муле (6.25).
При гололеде с ветром
йг
0,89- 502
24-19,2-10-6
4,29-10».
Задаваясь натяжением Нг
300 даН, получим
l't- 1.92 i 4,29-10»/3002 - 300/8,75 11,5°С.
Натяжение занижено. Задаемся Hi - 350 даН, тогда
/г — 1.92-I-4.29-10«/3502 —350/8,75 - 6,9"С.
Путем интерполяции определяем Нг 345 даН.
Нри ветре максимальной интенсивности
0,742-502
--2,97-10®
«в
“ 24-19,2-10-е
Задаемся натяжением Нп 330 даН, нри этом 2,97.10» 330 /в —1,92 ! — ЗЗО2 8.75 Натяжение завышено. Если Нп 300 даН. то терполянии найдем Нп 305 даН. - 10.55 °C. /» -3,21 Т С Путем ин 1 б л и ц а 6.1
Параметры х £ г О 10 Зн 30 ачения 20 шрамет --10 эов при 0 темпера ! 0 турах, 20 °C 30 4(1
Нх. даН — 350 275 200 150 120 100 80 70 60
/ С М 50 70 17 33 22 43 30 58 40 78 50 97 60 117 75 146 85 167 100 195
Вертикальную составляющую стрелы провеса провода при гололеде с вет-
ром в середине пролета длиной 70 м определим (условно) по формуле (6.27)
(0,1914-0,543) 70»
8-345
1,3 м,
а горизонтальную составляющую •- по формуле (6.28)
0.515-702
Горизонтальное отклонение провода при максимальном ветре в середине то-
го же пролета определим по формуле (6.28)
0,711-70»
8-305
1,43 м.
Таким образом, наибольшим провисание провода будет при максимальной
1смпсратуре (1,95 м), а горизонтальное отклонение — при максимальном ветре
без гололеда (1,43 м). Эти данные могут быть использованы для проверки соот-
ветствия допускаемому нормами расстояния от провода до поверхности земли и
его приближения к заземленным элементам, расположенным и середине про-
лета.
§ 6.3. Расчеты контактных подвесок
Полукомпенсированные контактные подвески. Расчеты таких
подвесок заключаются в определении натяжений и стрел провеса не-
сущего троса, а также в установлении стрел провеса контактных про-
водов и их вертикальных перемещений у опор во всех необходимых
расчетных режимах.
Приведем получившую наибольшее распространение в проектной
практике методику расчета д-ра техн, наук И. И. Власова с исполь-
зованием выражения (6.5); не являясь абсолютно строгой, эта мето-
дика позволяет достаточно просто рассчитывать различные конструк-
ции полу компенсированных контактных подвесок по одним и тем же
формулам
На подготовительном этапе выполняют следующие расчеты:
1. Определяют длину эквивалентного пролета по формуле (6.19),
поскольку закрепление несущего троса на поддерживающих устройст-
вах всегда можно считать шарнирным.
2. Задаются максимальным допустимым натяжением несущего тро-
са и номинальным натяжением контактного провода (проводов)
К, которое принимают в расчете постоянным.
3. Вычисляют все распределенные линейные нагрузки на несущий
грос (от собственного веса подвески, веса подвески с гололедом, вет-
ровые нагрузки без гололеда, и при его наличии, результирующие
нагрузки при максимальном ветре без гололеда и при гололеде с вет-
ром) по формулам, приведенным в §2.2, или по данным табл. 2.1.
4. Выбирают режим, при котором максимально натяжение не-
сущего троса, сравнивая длину эквивалентного пролета с длиной
критического, определенной по формуле (6.2) или (6.13), либо резуль-
тирующую нагрузку при гололеде с ветром с критической, вычислен-
ной но формуле (6.15).
5. Определяют температуру, при которой контактный провод
(провода) должен занимать беспровесное положение.
По рекомендациям ВСН 141-84 температуру беспровесного поло-
жения контактных проводов определяют как
/0 - t'v - i', (6.29)
где /г - среднегодовая температура воздуха, принимаемая П'.' данным СНиП
2.01.01-82,
/' - поправка, равная 20—25 °C при одном и 15—20 °C при двух контакт-
ных проводах.
Значение поправки более точно можно определить исходя из соот-
ношения tr и (“р, где /"р — средняя нормативная температура воз-
духа, равная полусумме максимальной и нормативной минимальной
температур (см § 1.3). Если /,' =сс (после округления до 5 °C), то
/'равно 20 °C при одном и 15 °C при. двух контактных проводах; если
же // > /“р> то поправка f соответственно равна 25 и 20 °C.
В практических расчетах обычно принимали значение /„ ниже
/срна 10-—15 °C при одном и на 5 -10 °C при двух контактных про-
водах. Температура /,.,, определялась как полусумма принятых для
расчета экстремальных температур воздуха.
Представляется, что такие способы определения температуры беспровес
кого положения контактных проводов допустимы лишь iij-h сравнительно не-
больших скоростях движения поездов (до 120 км'ч). Для обеспеченья высокого
качества токосъема при более высоких скоростях движения значение /0 следует
вычислять в соответствии с рекомендациями, приведенными в § 5 3.
6. Определяют натяжение и стрелу провеса шсущего троса при
беспровеспом положении контактных проводов. Натяжение Та «
этом режиме может быть найдено, например, из следующих ураь
нений:
W* 1э , ? max S6 ^3
где
Решение уравнений вида (6.30) без применения ЭВМ сопряжено
с некоторыми неудобствами: каждый раз, задаваясь натяжением,
надо определять соответствующие ему значения ср, W и Z.
Однако в практике проектирования широко используют ЭВМ, и до-
статочно составить необходимую программу вычислений (как это
’ 55
сделано в Трансэлектропроекте), чтобы не испытывать затруднений
при расчетах любых полукомпенсированных подвесок.
Обычно в расчеты вводят следующие упрощения: для подвесок с про-
стыми опорными струнами принимают гр - Л (т. е. величину ср неиз-
менной для данного пролета), а при расчетах рессорных подвесок
считают ср =- 0, что приводит уравнение (6.30) к виду, аналогичному
(6.25) для провода воздушной линии
7 (; а„ /:и Дн
97 , Тщах /э
ГДе 1 ' ‘ -24а„ 7’2,.,/ ' //’ 0 24а,,
В формулах (6.30) и (6.31) величины с индексом 1 относят к исход-
ному расчетному режиму максимального натяжения несущего троса,
а с индексом «п» — к материалу несущего троса. Величина g0 пред-
ставляет собой нагрузку от собственного веса подвески, так как бес-
провесное положение контактного провода реализуется при отсутст-
вии дополнительных нагрузок. Задаваясь несколькими значениями 'Г„
(начиная с указанного в §3.2) и воспользовавшись интерполяцией,
определяют значение этого натяжения, которое точно соответствует
ранее выбранной температуре tn.
Стрела провеса несущего троса при беспровесном положении кон-
тактного провода для подвесок с рессорными тросами в пролете I
определяется по формуле
где //„ — натяжение рессорного троса при данном режиме:
Л(|, - расстояние между несущим и рессорным тросами по оси оноры при
том же режиме (рис. 6.3).
Формула (6.32) получена из условий равновесия половины про-
лета рессорной подвески при беспровесном состоянии контактного
провода (см. рис. 6.3) Обычно принимают /•/„ < 150 даН. а значение
but вычисляют как сумму размеров //<„• И1|-„г, определение которых было
описано в § 5.2.
Для подвесок с простыми опорными струнами значение стрелы про-
веса несущего троса при беспровесном положении контактного провода
определяется первым слагаемым формулы (6.32).
После подготовительного этапа расчеты могут быть выполнены в та-
кой последовательности.
Монтируя несущий трое без контактного провода, необходимо
иметь монтажную кривую и таблицу, аналогичные описанным в
§6.2, для провода воздушной линии. Построение монтажной кривой
Трх (Q. показанной на рис. 6.4, ведут, задаваясь натяжениями раз-
груженного (т. е. без контактного провода) несущего троса Т},х и оп-
156
Рис 6.3, Расчетные схемы полукомпенсиро-
ванной подвески с рессорными тросами при
беспровесном положении контактного про-
вода (штриховые линии) и н режиме л
(сплошные)
Рис. 6.4. Примерные зависимости
изменений натяжения несущего
троса полукомпенсированной под-
вески от температуры
ределяя соответствующие этим натяжениям температуры по урав-
нению
/3„ 7‘п V
= + -------(6 33)
рл С4ц d ||
г,» а / _ -4- « .. дй
(Де Яц — !0— — — Т ----------——— , Dp .
24ап Т аилп5н ^4а,1
Здесь величина g„ представляет собой нагрузку от собственного
веса несущего троса. Значение коэффициента Ап в формуле (6.33)
равно значению коэффициента Аг в формуле (6.31). Поэтому, если
известен один из них. вычислять второй нет необходимости.
Стрелы провеса разгруженного несущего троса Fp при температу-
рах 1Л в конкретных пролетах 1; анкерного участка
fp хГ йв А-
(6.341
При монтаже цепной подвески и для проверки ее состояния в ус-
ловиях эксплуатации необходимо иметь еще одну таблицу, рассчи-
танную для несущего троса в рабочем положении (т. е. при наличии
контактного провода) В этой таблице указывают также значения стре.i
провеса контактного провода fxl и его перемещений относительно
беспровесного положения у опор .\hx, по форме, аналогичной табл. 6.3
(см. с. 167). Стрелы провеса контактного провода и его перемещения
у опор, направленные вниз от беспровесного положения, указывают
в таблице со знаком «-(-», а вверх -- со знаком «—».
Изменения натяжения нагруженного несущего троса при измене-
ниях температуры рассчитывают, задаваясь натяжениями и опреде-
ляя соответствующие им температуры на основании уравнений:
1”
дли любых подвесок (кроме специальных1)
в; т,
'Х-- />о-1 ------------------~т—. (Ь. $5>
где В.,.- U7f/,5 /(2}ап>; Ло — то же, что в форм)ле (6.33s:
для упрощенных расчетов рессорной подвески
|де Вv Ло — то же, что и выше.
Здесь величина qx представляе! собой результирующую нагрузку
на несущий трос, которая в данном случае равна gft.
В результате расчетов по формуле (6.35) или (6.36) строят кривую
Тх (tx). показанную на рис. 6.4.
Вертикальная составляющая стрелы провеса несущего троса в про
лете It
F'xi W-'Г... l-/^Zx<). (6.37)
Значения и Zxf определяются выражениями- (6.4) и (6.3).
Стрела провеса контактного провода в этом же пролете
I xi ’ 4xi(FXj —f«i), (6.381
я вертикальное перемещение контактного провода у опоры
Д Л.г/ -•(!' (Г xi) (Fxi " ' Fn i) • г‘^1пх!. (6.39)
Значения fxi и :\hx/ можно также найти., подставив в формулы
(6.38) и (6.39) выражение по формуле (6.5). После соответствующих
преобразова ви й пол учим:
_ТХ_ 1
ix'~ Г(ТХ )-/<) йл' Г
Их Но
I Ьх1 —— — 'W ---— !- л hu х/,
* Л ‘ 6
где Н.\ и //0- натяжения рессорного троса соответственно нри режиме х и при
беспровесном положении контактного провода,
(; — расстояние от оси опоры до околоопорной струны в пролете /;
Вследствие большой сложности точного определения значения Н х
в практических расчетах не учитывают изменения отношения натяже-
ния рессорного троса к натяжению несущего троса и принимают это
отношение таким же. как при бесг.ровесном положении контактного
! К специа.'ьны и относя гея косые, рычажные, вангоные и другие сложные
подвески
J58
провода (т е. Нх/Тх -- Тогда формула (6.41) упрощается и
после преобразований может быть представлена в виде
. . _ Г Тх I 7’о , . . ....
Ал»:» ----—------;g.v— А’о — Т-------77-’f Л Л« (6.42)
2 / V L 1 о J ‘ •) — ' о
Перемещение \hilXi, обусловленное изменением угла наклона изо-
пяторов, на которых подвешен несущий трос, не учитывая влияние
фиксаторов, можно определить как
1 Де , А 1;
б(>; и Qo;
(Jx! и Qx,
"i Qxi Qoi Г .....
длина гирлянды изоляторов;
соответственно вертикальная и результирующая нагрузка
па изоляторы в режиме беспровееного положения контакт
поп, провода в пролете
та же при режиме с температурой 'х.
Определи 1ь значение ViMX/ с учетом влияния фиксаторов можно
по материалам приведенным в §7.6. Учитывать величину \й„ А,
особенно важно для кривых при подвеске несущего троса па. неизо-
лированных консолях или на изолированных с двойной изоляцией.
Стрелу провеса несущего троса в вертикальной плоскости F'xt для
рессорной подвески можно найти, рассмотрев условия равновесия по-
ловины пролета этой подвески в режиме х (см. рис. 6.3):
F К Нх
F- /1,--------------- bxi------. И> 44;
8Гv 1Х !\
; 3? ; A hyi ((> 45»
Значения hnj вычисляют но формулам, приведенным в § 5.2. а
\/щ,- по формуле (6.42) Учитывая сказанное, отношение Н (‘Т, в
последнем члене формулы (6.44) заменяют на 7/(|. Г„.
Для подвесок с простыми опорными струнами вертикальная со-
ставляющая стрелы провеса несущего троса
(6 4бу
Расчеты натяжений несущего троса при режимах с дополнитель-
ными нагрузками производят решая уравнение (6.35) или <6 'Д. в ко-
торых все величины с индексом х относят к искомому режиму (гололе-
да с ветром и пн ветра максимальной интенсивности). Полученные
результаты обычно показывают точками на графике Тх (см. рис.
6.4). Стрелы провеса проводов и вертикальные перемещения кон-
тактного провода у опор вычисляют но формулам (6.37) -(6 46). При
необходимости стрелу 'провеса несущего троса в плоскости действия
результирующей нагрузки можно определить с достаточной точностью
как
Fxi Fyi^x^x, Ki 471
где !>х и д,- - соответственно вертикальная и результирующая на, pv-iK.i на н<-
сущий трое.
При расчетах полукомпенсированных подвесок для линий постоян-
ного тока иногда требуется учесть, что для первого периода экс-
плуатации подвешивают один контактный провод, а через некоторое
время добавляют другой без перерегулировки несущего троса. В этом
случае расчет несущего троса на прочность выполняют исходя из
наличия двух контактных проводов: рассчитывают разгруженный
трос и составляют монтажные таблицы, как было описано выше. Но
для того чтобы правильно осуществить монтаж подвески с одним кон-
тактным проводом и ее эксплуатационную проверку, рассчитывают
еще натяжения несущего троса при различных температурах, решая
соответствующее уравнение:
для любых подвесок (кроме специальных)
‘Ле 02 ° 24аи7’-(г ' «„Д',! ’ х' 24(Хц
для упрощенных расчетов рессорной подвески
/щ, 7\.
/.v Д02-1—----------. («49)
‘XI КцЛцОи
|Де Bxl '(^4ан); Д02 — то же, что в формуле (6.48).
В уравнениях (6.48) и (6.49) все величины с индексом 02 относят-
ся к режиму беспровесного положения двух контактных проводов,
а величины с индексом х! — к искомому режиму при одном контакт-
ном проводе. После построения кривой ТХ1 (tx) (см. рис. 6.4) вычис-
1яют соответствующие стрелы провеса обоих проводов, вертикальные
перемещения контактного провода и составляют таблицу по форме,
указанной выше для несущего троса цепной подвески. Расчеты стрел
провеса и вертикальных перемещений контактных проводов выпол-
няют по формулам (6.37)—(6.46), в которые подставляют нагрузки
и натяжения при одном контактном проводе. Расчеты натяжений не-
сущего троса в режимах с дополнительными нагрузками ври одном
контактном проводе не производят, так как поддерживающие уст-
ройства и опоры выбирают исходя из наличия двух контактных про-
водов.
Двойные полукомненсированные подвески в СССР применяют очень
редко, только на электрифицированных участках постоянного тока,
где изношенный контактный провод приподнимали и использовали в
качестве вспомогательного троса. При этом и старый и новый кон-
тактные провода снабжали компенсаторами. Поскольку эти провода
расположены в непосредственной близости друг от друга, рассчиты-
вают несущий трос двойной подвески по приведенным выше форму-
лам для одинарной, учитывая все нагрузки от вспомогательного троса
и принимая везде вместо натяжения контактного провода сумму натя-
ни)
жений вспомогательного троса и контактного провода. Такой расчет
обусловливает некоторую неточность получаемых результатов, но
в пределах, допустимых для практических целей.
Изменения высоты контактного провода у опор А/г ,., и у ближайших
простых струн A/i.y.j при двойной подвеске определяют как:
A ftx-f - Z7;,—^--1 Чгв.г - По; (6 50)
F|)i) I 4% х—Ч'до, (6.5lj
где 'I’b.v и <|’i,o -- стрелы провеса вспомогательною провода соответственно в ре-
жиме х и при бсспровесном положении контактного провода.
Стрела провеса вспомогательного провода
Нх СгСс/(2(/х-). (6.52)
Здесь Се — расстояние между струнами контактного провода;
Ux — натяжение вспомогательного провода;
Рх — сосредоточенная нагрузка на вспомогательный провод:
Ру I 0.75Й11Д.се I щ,
1 де gB — нагрузка от веса 1 м вспомогательного провода;
нк, fin и gc — то же. что и ранее.
При некомпенсированном вспомогательном проводе его
ние можно определить на основании следующей формулы:
Л k1 4aBl/f aH£HSn I
Р* ux
j X л
4a B U~ a. B E B S B
Задаваясь натяжением вспомогательного провода UY при темпе-
ратуре /1 и подставляя в уравнение (6.54) различные значения Ux,
взятые через произвольные интервалы, находят соответствующие зна-
чения tx и строят кривую Uх (Iд.).
Простые и цепные компенсированные подвески. Расчеты их за-
ключаются только в определении стрел провеса проводов и вертикаль-
ных перемещений у опор контактных проводов при отсутствии и на-
личии дополнительных нагрузок.
Стрелу провеса контактных проводов компенсированных под-
весок в пролете устанавливают исходя из условий обеспечения воз-
можно лучшего качества токосъема в соответствии с материалами,
приведенными в §5.2. Стрела провеса контактного провода цепной
компенсированной подвески в том же пролете при наличии гололеда
(6.53)
натяже-
(6.54)
де gr — линейная нагрузка от веса гололеда на проводах подвески;
С;- — расстояние от оси опоры до ближайшей простой струны, закрепленной
на несущем тросе в пролете
Зак. 2630
161
Изменение высоты контактного провода у опоры (без учета изме-
нения натяжения рессорного троса)
Л — С-}
’ Л>Г г — —- >j- /lup I .
' 2(7’ -Z/)
Изменение высоты провода вследствие поворота гирлянды
торов можно определить по формуле, аналогичной (6.43).
Л Т, ((;•- ; t'Ql'i ~ Gi Qi) .
где i>H - длч,,;: изоляторной гирляндьг
G; и Gri вертикальные нагрузки на изоляторы соотнетстьенно
лоледя ч ири наличии его;
Q,- и Qr/ результирующие нагрузки на изоляторы соответственно без
гололета и ветра и при наличии их.
Если при отсутствии гололеда гирлянда изоляторов располага-
лась вертикально. >’о выражение (6.57) преобразуется к виду
\ (Gr t/Qr i — И • (6. 5b)
Стрелу провеса несущего троса рессорной подвески в пролете /,
при отсутствии дополнительных нагрузок можно определить по фор-
муле, аналогичной (6.44),
(6.ob s
ИЗОЛ Я -
(6.57;
бе: го
при простых опорных струнах по формуле, аналогичной выра-
жению (6.46),
l:i - -/; . (0.60)
Вертикальная проекция стрелы провеса несущего троса при голо-
леде с ветром в пролете I, для рессорной подвески
(Р 1 /2 К -- /Г( 1 bv i —(6.61) КТ Т Т
при простых опорных струпах t —г~. (6.62т
В плоскости действия результирующей нагрузки стрела провеса
несущего троса рессорной подвески
С/г If Cjf (Л' (г j— ^г Ьг j) ZR К'.. Fr i -- — - - • , (Ь.Ьо
87 (Д ; йг) Т
при простых опорных струнах
4г'7 f _ _К ____у_г_
'«г '""'f' g+gr
(6.64)
162
В формулах (6.63) и (6.64) величина qr представляет собой резуль-
тирующую нагрузку на несущий трос при гололеде с ветром. Значе-
ние bri может быть определено по формуле (6.45).
Расчеты стрел провеса контактного провода при простой компен-
сированной подвеске выполняют по формулам, приведенным в §6.2
для проводов воздушных линий.
Пример. 3 -'1 д а и я е а исход п ы е д а н и ы е. Выполнить расчет
анкерного участка полукомиенсированной рессорной контактной подвески
ПБСМ-70 • •НлОлО,04Ф 100 тля линии переменного тока. В анкерном участке
длиной 1290 м четыре пролета по 70 м, 10 по 65 м и шесть по 60 м. Электрифици-
руемая линия расположена в степной местности с редкими садами в гололед-
ном районе II и ветроном районе II. Минимальная температура —40 "С, макси-
мальная 40 °C. среднегодовая— i 5 l’C.
О п р е д о л е н и е д л и и ы экий в а л е н т н о г о и р о лета.
Длину эквивалентного продета определим по формуле (6.19)
Г ГтоЧТб ЩТГГЩМР
I . I /-------------------- 64 . К м
|/ 1290
В ы б о р м а к с и и а л ь и о ; о д о п у с каем о г о н а т я ж е-
н и я н е с v ш с ; о р оса и ч о м и и а л ь н о г о н а т я ж е и и я
конт а к 1 в о г о и р о в о д а В соответствии е данными табл. 1.8 прини-
маем 7|Щ1Х 1600 даН и А 1000 даН.
О пред е л с |> и е р а с и р е д е л е н н ы х л н н е й н ы х натру-
з о к и а н е с у щ и й т р о с. Для заданной местности параметр шерохова-
тости примем равным 0.15 м (см. табл. 1.2). При этом для нулевого места кЛ 1
(см. табл. 1.3). Таким образом, скорости ветра для расчета могут быт;, приняты
равными 25 м/с (см. табл. ’ 1) при максимальном ветре к 14 м с (см. табл. 1.4) при
гололеде с ветром.
Необходимые для расчеса нагрузки найдем но габл. 1.5 и 2.1: 0,586 даН/м
от веса несущего троса, 1.56 даН/м от веса подвески без гололеда, 2,34 даН/м
от веса подвески е гололедом, 2.38 дч'Рм (но интерполяции) результирующая
при гололеде с ветром. ! .65 даН м результирующая при максимальном негре
В ы б о р р е ж и м а с м а к с и м а л ь н ы м н аг я ж е н и с м н е-
с у щ е г о л р о с а. Будем исходит» из сравнения эквивалентного пролета с
критическим, длину которого определим ио формуле (6.2). Необходимое для
расчета натяжение несущего троса при беспровесном положении контактного
провода примем равным 80 % максимального допускаемого (см 3.2)-
т;, 0,8.160(1 1280 даН.
Конструктивный коэффициент подвески q , принимая с 10 м. определим
по формуле (6 5)
0,48
и ------------------------ 0,362,
' I , (I— 0,48) 1000Н600
где значение л вычислено по формуле (6.6)
Z ---(64,8---2-10)?.64,8-
Значения Zllta. и W'r определим гоогвегственно но формулам (6 II),
(6.12) и (6.8).
Z,,.aK -г 1600 j 0,362-1006 1962 даН;
6*
163
Длину критического пролета найдем по формуле (6.2):
, Z24-13,3-10- в ( — 5-4-40)
Z„p =- 1962 I /---:-----------:=- 10.3,6 м ,
р у 2,83'- — 22
по приближенной формуле (6.13)
/“*319-10 "-35
Тзда^ТйбГ -102’9м'
что незначительно отличается от вычисленного по более точной формуле (6.2).
Так как критический пролет оказался больше эквивалентного, то макси-
мальным натяжение несущего троса будет при минимальной температуре.
Поставленную задачу можно также решить, сравнивая нагрузку при голо-
леде с ветром с критической, определяемой по формуле (6.15):
/ 319-10~“. 19622--35 1,56-0,362-1000
У)!Р |/ ---------’ 22 - ---------------------------- З.ЗЗдаН,м.
Поскольку критическая нагрузка оказалась больше, чем при гололеде с вет-
ром (2,38 даН'м), вывод будет тот же.
Выбор тем п ер а т у р ы б е с провес н о г о н о л о ж е н и я
контакта о г о п р о в о д а. При полукомпепсированиой подвеске с од-
ним контактным проводом скорость движения поездов не превышает 120 км/ч.
Поэтому рассчитываем искомую температуру по формуле (6.29). Поскольку сред-
негодовая температура примерно равна средней нормативной (с учетом увеличе-
ния заданной максимальной температуры за счет солнечной радиации), то /0 6 -
- 20 ....15 ‘С.
Опре д е л е н и е н а т я ж е и и я несу ш, е г о т р о с а и р и
б е с п р о в е с н о м положении к о н т а к т н о г о и р о в о д а.
Расчет выполним по формуле (6.31). задаваясь искомым натяжением, 7'/,
1280 даН. Используя данные табл. 1.9. получим:
д, — 40—-1,5(Р-64,8-’-.3135 ' I6002 ; 1600/16,48 44.57:
/)„ 1.56*.64.82-3135 - 32,04-10";
.44,57-832,04-10" 12802 —1280/16,48 -=—13,54 ‘С.
Очевидно, что принятое значение 7’,', немного занижено. Повторим расчет,
принимая 7’" 13.30 даН. В этом случае
44,57 । 32.04-10" I3302- -1330,16,48 18,02 “С
Путем интерполяции получим Т1,, 1296 даН.
Р а с чет р а з г р у ж ё п и о г о н е с у ш. е г о т р о е а. Вычисления
выполним по формуле (6.33). задаваясь натяжениями разгруженного троса и оп-
ределяя соответствующие им температуры. При этом
Дп —|Г>-- I ,56*.64,х2 •3135/12962 4- 1296/16,48 Л,;
/Зр 0,586-’ • 64,8-’ - 3135 4,52 • 10».
При значении Тух, равном, например, 1400 даН. получим
tx- 44,57 1-4,52-10"/14002— 1400/16,48 .-—38,1 'С.
Результаты подобных расчетов:
Tnt. даН.................. 1400 1200 1000 800 650 550 450
tx\ С.................... -38.1 —25,1 -11,6 3,1 15,1 26,1 39,6
164
Рис. 6.5. Монтажные кривые нагру-
женного и разгруженного несущего
гроса и значения натяжений нагру-
женного несущего троса при допол-
нительных нагрузках
По этим данным на рис. 6.5 построена кривая Fpx. (/т). Принимая различ-
ные значения Трх, по формуле (6.34) определим стрелы провеса разгруженного
несущего троса для всех пролетов анкерного участка. Например, для пролета
длиной 70 м при натяжении разгруженного несущего троса 1430 даН его стрела
провеса
F„ 0.586-70*/8-1430 0.251м.
Результаты таких расчетов приведены в табл. 6.2 с округлением до 0,5 см.
Подобная таблица при меньших интервалах температур является монтажной для
разгруженного несущего троса.
Р а с чет в а г р у ж е н н о г о несу щ е г о т р о с а б е з а о-
п о л п и т е л ь н ы х н а г р у з о к. Для построения зависимости ТЛ. (/д.)
используем формулу (6.36). Коэффициент Ло 44,57, R 32,04-IO11 (такой же,
как полученный выше коэффициент б0). Например, при
Тх- И 50 даН
М 44,57 |-32.04 I01’/11502-—1150/1б,48 —1 ’С.
Результаты подобных расчетов:
Ту. даН................ 1600 1450 1296 1150 1000 850
/д., С.................—40.0 28,2 -15.0 —1.0 15,9 37,3
По этим данным на рис. 6.5 построена зависимость 7'Л.(/Х.). Принимая по
этому графику различные значения Тх, соответствующие определенным темпера
турам, определим стрелы провеса обоих проводов подвески и вертикальные пере
мощения контактного провода у опор для всех пролетов анкерного участка.
Т а б л и ц а 6.2
Парамет- ры Длина пролета, м Значения параметров при температурах, ’С
—40 —20 0 20 40
Ffl v, см 60 18,5 23,5 31,5 43,0 59.0
65 21,5 27,5 37,0 50,5 69,5
70 25.0 32,0 42,5 59,0 80,5
Tf)x. даН ... 1430 1120 840 610 145
J65
Например, при 1Х О °C получим Тх — 1130 даН. Для этих условии
в пролете длиной 70 м стрелу провеса контактного провода найдем по формуле
(6.40):
1,56(70-2.10)2 /, ИЗО \
/--------------------1 -........।и ,и29 м.
«(1130+1000) 1296 /
По данным § 5.3 для рассматриваемой подвески а '5 м. г - 10 м и а- - 2 м.
Натяжение рессорного троса при беспроврсном положении контактного провода
примем равным 150 даН, Gc 0,6 и Лф • 0.
Значение ЛЛЛ определим по формуле (6.42) без учета величины ААИХ:
1,56.10 (70—10) / ИЗО \ 1296
Л/1 -------1-------— 1 •• ------------------0,06м.
2-ИЗО 1. 1296 / 1296—150
Размер i/,,„ найдем по формуле (5.7)
у„„ ----------~ 11.56 70 - (0,586—2-0.229) 5] . 0,237 м;
J 2 (1296 -150) 1
по формуле (5.8)
ф0 (5 — 2) 13,28/2-150-+). 133 м.
По формуле (5.9) определено значение величины Qp, входящей в выражение
(5.8):
Qp 0,873 (10 I-2)+0.229 (5 + 2) | 2-0.6 13,28 даН.
1аким образом.
+ 0.237 ) 0,133- 0,37 м,
по формуле (ь.45)
бу = 0.37 ' •() ,06 0,43 м.
(лрелу провеса несущего троса определим по формуле (6.44)
л;
1,56-70'- 1000 150
— 0.03 0,43 —
8-1130------------------------------ИЗО-1296
0,869 м.
Рснультаты таких расчетов приведены в табл. 6.3 с округлением до 0,5 см.
Подобные таблицы, составленные обычно для меньших интервалов темпера-
туры. используют при монтаже контактного провода и для проверки состояния
подвески в условиях эксплуатации.
О п р е д с л е в и е и а 1 я ж е и и й н е с у щ е г о т р о с а и р и
д о н о л н и т с л ь и ы х н а г р у з к а х. Расчеты выполним по формуле
(6.36), -«алана ясь различными значениями натяжений несущего троса и доби-
ваясь их соответствия температурам, при которых имеют место гололед с вет-
ром и ветер максимальной интенсивности (в обоих случаях -5 °C).
При гололеде е ветром коэффициент /40 44,57 (см. выше)
- 2.382-64.«г-3135 -74,6-10''.
Задаемся Г, 1400 даН. Тогда но формуле (6.36)
t; 44 .57 1 74,6-!0"/14002 — 1400/16,48 — 2,32 °C.
Следовательно, искомое натяжение больше. Примем Тг - 1500 даН. При
этом
t; - х 44,57 >-74.6-10" ’ 1500'2 _ [ 500 /16,48 — — 13,29 ° С.
166
Таблица 63
I la ри - метры 40 Значения параметров. см. нри температуре, °C
-20 0 20 40
60 /л 49,5 3,0 6,5 57,0 -1,0 1.5 65,0 2.0 5,0 74,0 4.0 11.5 83,0 6.0 18,5
65 fx X hx 57,0 -3,5 7.0 66.0 0.5 - 1.5 75.5 2,5 5.5 85,5 5,0 12,5 96.0 7,5 20,5
70 Fx 1 X A/la. 66.5 -4,5 8.0 76,0 1,5 1.5 87,0 3,0 6.0 98,0 6,0 13,5 109,5 9,5 22,0
Tx. даН 1600 1350 ИЗО 970 840
Путем интерполяции найдем, что Тг — 1425 даН.
При максимальном метре коэффициент .40 не меняется
/*„ 1,652-64,8а-3135 35,8-10«.
Задаемся Т'г - 1250 даН. По формуле (6.36)
z(, 44.57 .35.8-10й/12502—1250/16,4.4 -.8.37 °C.
Принятое натяжение завышено. Зададимся 7'в - 1200 даН; тогда
44,57 35.8-106/12002—1200/16,48 -3.39 "С.
Путем интерполяции найдем Тв - 1215 даН.
Полученные значения Тг и 7'и показаны точками на рис. 6.5.
§ 6.4. Расчеты длин анкерных участков цепных подвесок
Определение длины анкерных участков нолукомленсированной
цепной подвески производят, учитывая реакции от наклона струн
и поворота фиксаторов, а также расположение кривых в пределах
конкретного анкерного участка. Колебания натяжения контактного
провода в заданных условиях экстремальных температур воздуха
не должны превышать + 15 % номинального натяжения, создавае-
мого компенсаторами. Излагаемая ниже методика предложена
И. И. Власовым.
Изменение натяжения контактного провода (проводов) на кривых-
участках пути может быть определено как
д д.______________________________________
1-2 ( \КС-- АКф) /[3£к SK (ак А/—ё)] ’
где А К с -- L (L 4- /) (е — ак А/) / (2е);
(6.65)
167
L(L — l) (e —акЛг) , 2ДКС \
Л Л ф • - I К о. I
Ф 2/Мф—0,5Z. (L--/) (г—ак A/) \ 3 /
i де АЛ' — полное изменение натяжения контактного провода:
ДЛ'С - изменение натяжения, вызванное влиянием струн подвески;
ААф — изменение натяжения, вызнанное влиянием фиксаторов:
1. - расстояние от компенсатора до средней анкеровки;
Дф — шарнирная длина фиксатора:
е — средняя длина струны;
Д/ — отклонение температуры от среднего значения
Коэффициент е рассчитывают как
где/и/Л. • стрелы провеса контактного провода соответственно при средней
температуре и при температуре 1Х.
По формуле (6.65) строят кривые приращений натяжения кон-
тактного провода у средней анкеровки в зависимости от длины анкер-
ного участка, исходя из принятых параметров цепной подвески, при
крайних значениях расчетных температур воздуха для прямых и
кривых участков пути всех радиусов на данном участке. Пользуясь
такими зависимостями и учитывая, что наибольшее изменение натя-
жения контактного провода не должно превосходить указанного выше
значения, можно определить допустимую длину анкерного участка в
конкретных условиях. В тех случаях, когда эти условия меняются,
общее приращение натяжения определяется как сумма приращений
натяжения в разных условиях.
Для примера па рис. 6.6 показаны изменения натяжения кон-
тактного провода полукомпенсированной подвески ПБСМ-70 i МФ-100
при конструктивной высоте подвески 1,8 м; шарнирной длине сочле-
ненных фиксаторов 1,2 м, гибких — 2,5 м. Сравнение кривых / и 3 по-
казывает влияние кривизны пути, а кривых 2 и 3 — преимущества
установки гибких фиксаторов. При допустимом изменении натяжения
контактного провода 150 даН наибольшая длина анкерного участка
при расположении подвески целиком на кривой радиусом 600 м равна
1300 м при гибких фиксаторах и 1000 м при сочлененных (с двусторон-
ней компенсацией).
В компенсированных цепных подвесках длина анкерных участ-
ков должна быть такой, чтобы, кроме соблюдения указанных выше
допускаемых изменений натяжения контактного провода, колебания
натяжения несущего троса не превышали ±10 % номинального.
Изменения натяжения несущего троса на кривых участках
-f- L (L — /) а.. \tT „ „
\Т, ----------------—u-------, (6.66)
1 2RdK ± 0,5L (L- /) ан Л(
1 де <•/,< горизонтальная проекция поворотной консоли, считая отточки креп-
ления несущего троса на консоли до оси шарнирного крепления кон-
соли на опоре.
J6S
Рис. 6.6. Зависимости приращений на-
тяжения контактного провода \К от
расстояния до средней анкеровки L
при 7'та1=40°С и Тппп = —40°С:
I прямой участок пути, сочлененные
фиксаторы; 2 — кривая радиусом 60и м.
|Ибкне фиксаторы; 3 — то же, сочленен-
ные фиксаторы
Верхние знаки в формуле (6.66) относятся к случаю расположения
консолей с внешней стороны кривой, нижние - к расположению их
на внутренней ее стороне. С учетом поправки па упругие деформации
несущего троса
1 —2АГ1 /СЗс-,, 5„ А/)
(6.67)
Для расчетов длины анкерного участка несущего троса компенси-
рованной подвески строят кривые приращения его натяжения по
формуле (6.67) аналогично описанному ранее для контактного про-
вода.
Значения приращений натяжения несущего троса в пределах ан-
керного участка, на котором имеются кривые различных радиусов,
находят так же. как приращения натяжения контактного провода.
Когда опоры расположены на внутренней стороне кривой, прираще-
ния l\T имеют знак, обратный величинам \Т при нахождении опор
с внешней стороны кривой; суммарное приращение определяется с
учетом этих знаков. Таким образом можно найти наибольшую длину
анкерных участков для различных условий трассы.
Для определения приращений натяжения контактного провода
компенсированной подвески можно пользоваться теми же формулами,
что и для полукомпенсированной. Необходимо только правильно
учесть изменение влияния наклона струн на натяжение контактного
провода. Если несущий трос и контактный провод выполнены из
материалов, имеющих одинаковые коэффициенты температурного ли-
нейного расширения, можно считать, что струны будут располагать-
ся вертикально и на изменения натяжения контактного провода ока-
жут влияние лишь отклонения фиксаторов. Таким образом, при ис-
пользовании формулы (6.65) значение \Ке принимают равным нулю.
Если же несущий трос и контактный провод имеют разные коэффи-
циенты линейного расширения, то при определении значений \Л"(. по
формуле (6.65) вместо ак надо подставлять разность коэффициентов
температурного линейного расширения контактного провода и несу-
щего троса, а величиной в можно пренебречь.
169
Рис. 6.7. Зависимости \7'(Л) на внешней (<») н внутренней (б) сторонах кривой
Пример. Задание. Определит >. приращения натяжения несущего тро-
са компенсированной подвески М 120 2.ЧФ-100 дли участка длиной 700 м.
состоящего из следующих моментов трассы, начиная от средней анкеровки:
прямая длиной 200 м; внешняя сторона кривой радиусом 300 м и длиной 200 м;
прямая длиной 100 м; внутренняя сторона кривой радиусом 500 м и длиной
200 м. Экстремальные температуры воздуха j 40 ’С.
’ Р е ш с н н о. На рис. 6.7 приведены зависимости, построенные ио формуле
(6.67) для различных сторон кривых заданных радиусов. Первый прямой участок
пути отмечен как 0а, кривая радиусом 300 м - uh. второй прямой уча-
сток Ьс и кривая радиусом 500 м - cd.
Изменение натяжения несущего троса при температуре 40 определяется;
сложением отрезков ец и тп ( 63 130 67 даН), при температуре —40 С -
сложением отрезков c'g' и т'п' (74 134 — 60 даН). И в том и в друюм слу-
чае значение нвиращення натяжения несущего троса щ превышает допускаемо
го (180 даН).
§ 6.5. Особые случаи расчета
Расчеты провода в отдельном пролете. П р о в о д н а г р у ж е п
двумя р а с п р е д е ле и ны м и лине й ны ми на -
груз к а м и р а а и о й и и т о н с и в н о е т и . например под-
веска шлейфов разъединителя на проводе в части пролета (рис. 6.8. и).
Натяжение провода при любом режиме может быть определено
из уравнения
“7«| «:,6, Нл- //, HI (6.68)
24/А"; 24///f ES
170
или
i ; Н. \ Чгах^Ьх Нх
G--' G—-------------------- • -----------—------;— . (6.69)
1 24a///J a.ES / 24а///;. aES ’
. k1 b 3b
где d -- l-i---, — <l-f E)2: k qifb^qaa).
a I
В этих формулах q.A и qfj распределенные линейные нагрузки
провода соответственно на участках а и b (см. рис. 6.8. а). Все осталь-
ные обозначения те же, что и выше. Величины с индексом 1 относятся
к извес ному (заданному) режиму работы провода.
Формулы (6.68) и (6.69) справедливы для случая, когда нагрузки
qa и qi4 действуют в одной плоскости как в определяемом, так и в за-
данном режиме; плоскости действия нагрузок в разных режимах мо-
гут и не совпадать.
1 Провесы провода на участке и могут быть определены как
*/« ЧХ lt 2.Н ! ч—. _/у [ о H i (6.70)
на участке 1) Ча а (/—.г) " 2Н Г k (х —о> L т Ц (6.711
на границе участков и и b У ‘/(1 Ча Л . (6.72)
( 1 (i 21Н }
При расчетах но формулам (6.70) и (6.71) значение х отсчитывает-
ся от опоры Л.
11ро в о д нагружен сосредоточенно й с и -
л о й, например при подвеске изолятора, поддерживающего другие
провода (рис. 6.8, б). Натяжение //к можно определить из уравнения
и- al' Нх-Н.
~~^Г <z'- -/ J <3 7:°
или
/ h\<ib и \ fl
\ 2al2H- ' aES / 2а/-’-//| aES ' ’ '
ricGtHCj — сосредоточенные силы соответственно в определяемом и в задан-
ном режимах.
Рис 6.8 Расчетные схемы провода при наличии двух распределенных линейны*,
нагрузок разной интенсивности (а) и соередоти диной силы /61
17!
Рис. 6.9. Расчетная схема кони-
ческой железобетонной опоры
(а). а также эпюры изгибаю-
щего момента (б. а)
Рис. 6.10. Зависимости жесткости EJ коничес-
ких железобетонных опор от высоты It для
опор с нормативным моментом 79 кН-м (кри-
вая 1). а также 44 и 59 кН-м (кривая 2)
Приведенными уравнениями можно пользоваться в тех случаях,
когда собственной распределенной линейной нагрузкой провода до-
пустимо пренебречь, если она значительно меньше нагрузки от со-
средоточенной силы.
Стрела провеса провода в точке приложения сосредоточенной силы
/ -Gab/(IH).
(6.75)
В частном случае при расположении сосредоточенной силы в се-
редине пролета формулы (6.73)- (6.75) упрощаются:
'х р! Gf Н,-Н. - »/// и «>.7в> 8a//'f al'S ) 8а/7'(. aES 1 67/(4/71. (6.78)
Определение прогиба железобетонных опор. Конические железо-
бетонные опоры имеют переменную по высоте жесткость. Однако для
практических расчетов прогибы таких опор можно определить с до-
статочной точностью, если заменить опору трехступенчатой фигурой
(рис. 6.9, а), каждая ступень которой имеет длину, равную 1/3 высо-
ты опоры, и жесткость, соответствующую среднему сечению данной
ступени. Для расчета прогибов опор можно использовать графики
рис. 6.10, выбирая нужную часть по высоте опоры в соответствии со
схемой нагружения.
172
При треугольной эпюре изгибающего момента (рис. 6.9, б) на
расстоянии а от вершины прогиб опоры
I 9л /ЗЛ'-—I 3 5 у 1 7 19 ]
7 = 81 1.2 ( EJi ~ EJ2 ” EJ3 } EJj'1 EJ2 1 EJ3 J’ <6'9)
где h — высота крепления провода от уровня заделки;
Е — модуль упругости материала опор;
Jt, J.< Лэ — моменты инерции среднего сечения каждой из трех равных ча-
стей, на которые разделена опора от уровня заделки до уровня
крепления провода (см. рис. 6.9, а);
А. U /Л .
Жесткости отдельных ступеней EJt, EJ2 и EJ3 нужно опреде-
лить по графику рис. 6.10, разделив на три равные части размер
h, взятый на принятом участке опоры по высоте.
В частном случае на вершине опоры (X 0) прогиб
Если эпюра изгибающего момента прямоугольная (рис. 6.9, в),
прогиб опоры на расстоянии а от вершины
а на вершине опоры
Утах
Л12/Г2 /I 3 5 \
—-------- -------: ------- I ------- •
18 EJt EJ2 EJ3 /
(6.82)
Формулы (6.79) и (6.81) справедливы при условии а < Л/3.
Если опора имеет по высоте постоянную жесткость, т. е. EJ L -
EJEJ.t= EJ. то при треугольной эпюре изгибающего момента:
У (1~М2(2 i Л); Утах Mth^/(3EJV. (6.83); (6.84)
6/:./
при прямоугольной эпюре изгибающего момента (см. рис. 6.9, в):
Л1., h-
У (1-М1: Утах= Л12й2/(2/?./). (6.85); (6.86)
Натяжение провода Нх с учетом прогибов железобетонных опор
при любом режиме может быть определено из уравнения
<7? С’ q~i I- ,1 у' \
-----//,)-------------------------1- J— |а(/к —/,) (6.87)
24//; 24/7‘f ' ' ’ ’ ES I I '
или
qv /I у'
‘ 24а//2, 1 ( aES ' al
ix - /
173
где у' суммарный единичный прогиб обеих опор на высоте крепления от на-
тяжения. равного 1 даН:
, 2й3 I 1 7 19 \
у —-------------1- ---------- . (о. 69 >
81 I Е,!г EJ2 EJ3 ./
Если одна из опор не может иметь прогиба (например, при нали-
чии оттяжки, закрепленной на уровне провода), то в расчет следует
ввести единичный прогиб, равный 0,5/.
Определение длины анкерных участков проводов воздушных ли-
ний. При кронштейнах, жестко закрепленных на опорах в горизон-
тальной плоскости, длина анкерного участка может быть ограничена
только по удобству монтажа и восстановления провода после обрыва.
Практически применяют различные по конструкции кронштейны,
имеющие ограниченную подвижность на опорах. В этом случае при
ветре вдоль провода происходит смещение всех кронштейнов, ветро-
вая нагрузка с кронштейнов передается на провод, в результате чего
натяжение провода вдоль анкерного участка становится неодинако-
вым. Поэтому длину анкерного участка следует выбрать исходя из
необходимости соблюдения следующих условий: натяжение провода
в наиболее нагруженном пролете не превышает максимального, при-
нятого для данного провода; натяжение провода в наиболее разгружен-
ном пролете не становится ниже определенного значения, при кото-
ром вследствие увеличения стрел провеса нарушаются допустимые рас-
стояния от провода до земли и сооружений; максимальное смещение
кронштейнов не превышает значения, исчерпывающего возможную
подвижность кронштейна, обусловленную конструкцией его закреп-
ления на опоре; при максимальном смещении кронштейнов, па кото-
рых подвешены провода разных фаз (например. ДПР), горизонталь-
ное расстояние между ними не снижается до значения, недопустимо-
го для линии данного напряжения и условий подвешивания.
В рассматриваемом случае расчетным для определения длин ан-
керных участков является режим ветра максимальной интенсивности
или режим ветра при гололеде; в обоих режимах направление ветра
принимается вдоль проводов. Натяжение провода Н vll в наиболее на-
груженном пролете /, расположенном в конце анкерного участка с на
ветренной стороны (рис. 6.11), может быть определено из уравнения
.е; Ph, («) яЛ|, I- нг\ 0.5 (n-1) l>
~~'еГ 'ЕЁ
(6.901
где п число пролетов в анкерном участке;
//j — натяжение провода до появления ветра;
Е — часть ветровой нагрузки на кронштейн, передающаяся на провод,
(а) — безразмерная величина, определяемая для ц пролетов по графи
ку рис 6.12 в зависимости от соотношения а = Р'Нха.
Поскольку перед началом расчета натяжение Нхи неизвестно, то
задача решается методом последовательных приближений. Сначала
следует задаться значением Нхн - (1,03 ч- 1,10) 1/7г •- 0,5 (п -- I) Р].
Рис 6.1! Расчетная схема анкерного участка провода на
I
i
определить а и fn (а), а затем из уравнения (6.90) найти значение Н хн.
Если полученное значение отличается от принятого более чем на 2 %,
то расчет можно повторить для нового значения Нх1).
Передаваемая на провод ветровая нагрузка Р определяется в со-
ответствии со схемой, приведенной на рис. 6.13:
Р (Ркр А-(-/>„ щ)/(2«), (6.91)
где Ркр и соответственно нагрузки от ветра на кронштейн и подкос (тя-
гу). определяемые по формуле (2.28).
Принимается, что сила 0,5 Ри приложена в точке крепления под-
коса (тяги) к кронштейну. Давление ветра на тягу из круглой стали
можно не учитывать. Натяжение провода НХ1> в разгруженном проле-
те п, расположенном в конце анкерного участка с подветренной сторо-
ны,
//др //а>, -(« (6.92)
При известном НЛ|, смещение вдоль провода точки подвеса т-го
кронштейна
Здесь (а) определяется по рис. 6.12 для т пролетов.
Расчеты по формуле (6.93) показывают, что максимальное смеще-
ние получают кронштейны, расположенные несколько дальше сере-
дины анкерного участка в подветренную сторону.
Угол поворота т-го кронштейна может быть определен как Р
arc sin а расстояние между двумя проводами разных фаз при
повернутом т-м кронштейне с’ с„ cos P„t. где с„ — расстояние меж-
ду проводами до поворота кронштейна.
При подвеске на одном кронштейне двух проводов различных фаз
с достаточной
ние Ь 13. Расчет-
ная схема хля оп-
ределения пагргз-
кп Р
точностью расчет можно вести, принимая во внимание
один провод, имеющий двойные вес, площадь се-
чения, натяжение и подвешенный посередине
между действительными точками подвеса про-
водов.
В кривых также происходит смещение крон-
штейнов под действием ветровых нагрузок. Одна-
ко при повернутом кронштейне усилие от измене-
ния направления провода па кривой дополнитель-
но изменяет натяжение провода. При направле-
нии усилий,обусловленных изменением направле-
ния провода в сторону опоры, натяжение изме-
няется больше, а при направлении в сторону от
опоры—меньше, чем на прямом участке пути. Ана-
логично изменяются и смещения кронштейнов.
176
Состояние провода в анкерном участке при направлении усилий,
обусловленных изменением направления провода, в сторону опоры
описывается системой уравнений:
H3-i (2а' R—l&i) — 2a' RP
где i — номер пролета (кронштейна): i 1,2, 3.......п;
При п пролетах в анкерном участке можно составить одно уравне-
ние (6.94) и по п — I уравнений (6.95) и (6.96), а всего 2п — -1 уравне-
ний. Общее число неизвестных также будет 2/1— 1 (натяжения в п про-
летах и смещения п — I кронштейнов). Таким образом, в результате
решения системы уравнений (6.94) — (6.96), которое нужно выпол-
нять на ЭВМ, определятся все необходимые величины.
Для анкерного участка при направлении усилий от изменений на-
правления проводов в сторону от опоры уравнения (6.94) и (6.96) не
изменяются, а уравнение (6.95) принимает вид
Hxi (2а'R | /Л;) -2а'' RP
---------------------- (6.9/1
2(1'/? -/Д;
Давление ветра на кронштейны при достаточно большой длине ан-
керного участка неравномерно. Это будет сказываться сильнее в кри
вых, где направление ветра не может совпадать с направлением линии
на значительных расстояниях. Поэтому на прямых участках пути и в
кривых радиусом более 2000 м при определении длин анкерных участ-
ков следует расчетную скорость ветра для данного района снижать на
10 %, а в кривых радиусом менее 2000 м на 10— 15 %, принимая
большее снижение для кривых меньшего радиуса
Ч (+1
Глава 7
РАСЧЕТЫ ПОДДЕРЖИВАЮЩИХ
И ФИКСИРУЮЩИХ УСТРОЙСТВ
§ 7.1. Поддерживающие и фиксирующие устройства
К поддерживающим устройствам контактной сети относятся кон-
соли для цепных подвесок, жесткие и гибкие поперечины, а также крон-
штейны для различных проводов; к фиксирующим — фиксаторы,
фиксирующие поперечины, фиксаторные стойки и кронштейны В дан-
ной главе рассматриваются .вопросы опредетення геометрических раз-
меров и ра-четц т.еех поддерживающих и фиксирующих устройств,
кроме жестких поперечин, которые при проектировании контактной
сети тольк" подбирают из типовых конструкции (см. § 8.2).
Выбор гипо» поддерживающих и фиксирующих устройств во многом
определяется условиями установки опор. 11а однопутных и двухпутных
перегонах применяют однопутные ксчсо.'ш. Установка на двухпутных
перегонах двухпутных консолей нежелательна н допускается только
как исключение.
Основными поддерживающими устройствами контактной сети на
многопутных перегонах и станциях являются жесткие иопермпны
перекрывающие до восьми путей включительно.
На небольших еппшиях при широких междупутьях а также на
отдельно расноложо-шых путях могут быть применены однопутные
консоли. На крупных станциях с числом путей более восьми при отсут-
ствии междупутий шириной, достаточной для установки стоек жестких
поперечин, а также в случае невозможности или нецелее собранности
раздвижки или снятия пути допускае.тсч применять гибкие поперечи-
ны. Желательно, чктбы одна поперечина перекрывала не более 10 пу-
тей, но в отдельных случаях допускается перекрытие и большего числа
путей.
Однопутные изолированные и неизолированные консоли применяют
наклонные с рас положенными горизонт п. но илы под углом к опоре
тягами (см. рис. 7.2, а) На опорах высотой более i 1 м иногда устанав-
ливают горизонтальные консоли, на которых можно разместить и уси-
ливающие или другие провода (см рпс 7.2, а). Двухпутные консоли
применяют только горизонтальные (см. рис. 7.4)
Наклонно однопутные консоли проектируют с тягами, работаю-
щими на растяжение или сжатие в зависимости от места установки
опоры, на которой крепится консоль, и направления проводов поддер-
живаемой подвески. Консоли с растянутыми тягами устанав-
ливают на промежуточных и переходных (для рабочих ветвей подвес
ки) опорах на прямых и с внешней стороны кривых. Сжатые тяги при-
меняют в консолях на промежуточных опорах, устанавливаемых с
внутренней стороны кривых, н на всех переходных опорах для анкеру-
емых ветвей подвески. Кроме того, консоли со сжатыми тягами уста-
навливают на опорах, расположенных на прямых участках пути, но
перед началом кривых, где усилия от изломов проводов ценно”! подвес-
ки и ветра могут быть направлены в сторону оноры, а также в некото-
рых других случаях (см. §8.1).
Исюгнцтые консоли (см. рис. 7.2. б) ранее использовались широко
Для крепления фиксаторов на утих консолях у.аьлпвали специ-
альные фиксаторные стойки При строительстве новых линий га кие
консоли не применяют.
Для подвески дополнительных, усиливающих, играющих и отса-
сывающих проводов применяют горизонтальные крлпнтейны с под-
косами или с тягами (см. рис. 8.1) Выполняют эш кронштейны нор
мальной длины и удлиненные из швеллерной или уiясной стали. При
креплении на одном кронштейне двух дополнительных проводов его
располагают горизонтально или наклоном относительно опоры.
Провода ВЛ 6 10 кВ крепят на деревянных кронштейнах из двух
связанных одна с другой горизонтальных частей- на верхней креня!
на штыревых изоляторах два провода, на нижней один провод.
Эти кронштейны также бывают нормальной длины в удлиненные.
В стесненных условиях на станциях провода можно крешпь в ряд па
горизонтальном деревянном кронштейне, расположенном над жен
кой поперечиной.
Различные низковольтные провода закрепляют е помощью штыре-
вых изоляторов на горизонтальных кронштейнах с подкосами и тя-
гами при установке на металлических опорах и с подкосами при уста-
новке- на железобетонных опорах.
При размещении липни электроснабжения устройств автоблоки-
ровки на самостоятельных опорах все провода кренят на штыревых
изоляторах. Высоковольтные провода располагают на деревянных
траверсах, рассчитанных на два или четыре провода, а сигнальные про-
вода -- на траверсах, на каждой из которых можно поместить до вось-
ми проводов. Все траверсы усиливают подкосами из полосовой стали.
Фиксатор — один из основных элементов контактной сети, влияю-
щий на качество токосъема и износ контактных проводов. Обеспечивая
надежное закрепление контактных проводов в нужном положении от-
носительно оси пути, фиксаторы не должны существенно снижать
эластичность опорных узлов ценных подвесок.
При подвеске па консолях и жестких поперечинах на всех главных
путях и тех приемо-отправочных, на которых скорость движения
превышает 50 км/ч, проектируют сочлененные фиксаторы с возможно
более легкими элементами, которые крепят непосредственно к кон-
тактным проводам. На фиксирующих тросах жестких и гибких попе-
речин устанавливают фиксаторы из полосовой стали и труб, в нор-
мальных условиях работающие на растяжение.
При действии в самых неблагоприятных условиях растягивающего
усилия не менее 20 даН на фиксатор его выжлняют гибким (Онреле-
Таблица 7.1
Длина пролета, м Марка кон- тактного провода Наибольшие радиусы кривых, м, на внешней стороне которых допустимо применение гибких фиксаторов при скорости ветра, м/с
до 25 30 35 40 45 50
МФ-100 900 750 600 500 400 350
40 2МФ-100 1150 1000 800 700 600 550
450
1050 850 750 600 500
50 МФ-100 1000 800 650 500 450 350
2МФ-100 1200 1100 900 750 650 550
550 450
1150 950 800 650
МФ-100 1100 850 650 550 — —
60 2МФ-100 1450 1200 950 800 650
550
1250 1050 850 700
МФ-100 1150 900 — — —
70 2МФ-100 1550 1350 1200 1100 1000 850 — — —
Примечания. 1. В знаменателе указаны радиусы для насыпей высотой более
Г» м, расположенных в местах с сильными ветрами; в числителе для всех остальных мест.
2. Тире в таблице означают, что при таких скоростях ветра указанные длины проле-
тов не могут быть реализованы.
3. Все радиусы кривых округлены до 50 м.
ление усилия, действующего на фиксатор, рассмотрено в § 2.2.) Усло-
вия применения гибких фиксаторов приведены в табл. 7.1. На кривых
радиусом 600 м и менее устанавливают двойные фиксаторы, разнося
точки их крепления к контактному проводу на 2 м.
При двух контактных проводах, чтобы обеспечить возможность
взаимного их продольного перемещения на 100—150 мм, каждый из
них фиксируют самостоятельными дополнительными фиксаторами
одинаковой длины. Гибкие фиксаторы применяют отдельно для каждо-
го провода.
Почти по всем рассматриваемым в данной главе конструкциям име-
ются типовые решения и может возникнуть вопрос: нужны ли методи-
ки расчета таких конструкций? Конечно, наличие типовых консолей,
кронштейнов или фиксаторов, как правило, избавляет проектировщи-
ка от необходимости каждый раз выполнять соответствующие расчеты.
Однако при проектировании, а особенно при строительстве контакт-
ной сети всегда возможны отклонения от положений, принятых в ти-
повых проектах. Это вызывает потребность в различных проверках:
выдержит ли принятая конструкция возникающие нагрузки или не
180
будут ли чрезмерными какие-либо смещения и т.д. В условиях эксплу-
атации также вполне вероятны изменения принятых в проекте расчет-
ных предпосылкой (например, наличие в отдельных местах непреду-
смотренных скоростей ветра или интенсивности гололедных образова-
ний, необходимость подвески на типовой конструкции дополнитель-
ных проводов и т.д.). В этих случаях дальнейшие материалы данной
главы окажутся весьма полезными.
§ 7.2. Расчеты консолей
Определение геометрических размеров. Для этого необходимо
сначала найти координаты крайних точек крепления несущих тросов
и усиливающих проводов на консоли. Под координатами в данном слу-
чае подразумевают расстояния от передней грани опоры на уровне го-
ловки рельса до наиболее близкой и наиболее удаленной возможных
точек крепления несущих тросов НТ или других проводов, если их под-
вешивают па этой же консоли (рис. 7.1).
Указанные на рис. 7.1, а координаты ХП)1П и находятся в оп-
ределенной зависимости от типа цепной подвески (вертикальная, по-
лукосая или косая), места установки опорного устройства (определя-
Рис. 7,1 Расчетные схемы для определения координаты X на прямом :а) участке
пути и в кривой (б)'
I ось пути; 2 - ось токоприемника
18!
ющего его габарит), назначения консоли (промежуточная или переход-
ная), схемы сопряжения анкерных участков (неизолирующее или изо-
лирующее), «исла пролетов сопряжения (четыре, три или два) н конст-
рукции консоли (неизолированная или изолированная).
Рассмотрим для примера определение координат Х„11(1 и Хгоах у
консолей, предназначенных для закрепления только несущих тросов
вертикальных и полукосы-. ценных подвесок.
Искомые координаты для промежуточных консолей находят оп-
ределяя точную координату л мест? крепления несущего троса и учи-
тывая допуск на чоочисютъ установки опор и консолей. Координата X
на прямых участках пути при шдиикальном расположении изоляторов
несущею о.оса численно равна габариту установки опоры Г (см.
рис. 7.1 ц), а при наклонном расположении изоляторов ('по применя-
ют на линиях переменного тока) она больше или меньше габарита Г на
щаченнс сдвига точки креитеннч изоляторов от оси пути.
На кривых, принимая, что несущий трек расположен над контакт-
ным приводом или при двух контактных проводах -....... над серединой
расстояния vumj проводами. к<х>рдинату X (рис. 7.1,6) определяют
К Cj
\ гь,; (7.1)
: ;к .. 5 . мина пне оси токоприемника но отношению к оси пути на вчсотс кон-
'L"kt ног'« провода кривой. вьг-нь’.’гтем.е оо формуле (2.3!),
j диг jar контактного проводи от оси токоприемника п ли при дплх
контактн.ык яр о ио да к расстояние от оси т»-коп р нем ни к а до середины
ППССГОЯНИЯ М(‘-К.л;, П рОВОДа М И
। оризон: ильная пр'н’кнья или со кл jichhoi о и’-еляь'рнсти 3i>"‘ia, нои
гирлянды изол я горсч нрн it-.-!-? и и «юн ан и ы \ кон» о,?чх. или л-': ал.ш
крепления при Идолнроюс'.н К'*н-илчх:
/!,, е. l/Tf ; ?? (7-2)
Здесь йц - шарнирная мн на или язолягярпшо звена. или гирлянды <<зо..ч<г .о-
рон, пли дегачей крепления
6', • вертикальная нагрузка от цепной подвески:
/у гс р изч итг-.ч r> ri.i я нагрузка от изменения направления г,('е\
гроса на кривы' >. ч-нл к а >. пути, определяемая по формулам,
приведенным в § 2..’-
Верхние знаки в формуле (7.1) относятся к случаям установки
опор с внешней стороны кривых, нижние - с внутренней. Расчеь
иое натяжение несущего троса полукомпенсированпых ценных под-
весок, определяя горизонтальные нагрузки, условно принимаю': рав-
ным натяжению троса при бееировееиом положении кошактпых (урово-
дов. При установке консолей в местах сопряжений прямых н кривых
участков пути координату X определяют также на основании формул
(7.1) и (7.2), вычисляя усилие Рг с учетом конкретных условий.
Координаты Хш1п н ХП)а,, для переходных консолей зависят от схе-
мы сопряжения анкерных участков. При неизолирующих сопряжени-
ях несущий трос располагают над серединой расстояния между кон-
тактными проводами различных участков и определяют искомые коор-
i S2
динаты так, как рассмотрено выше, т. е. находят точную координа-
ту X и учитывают допуск на неточность установки опор и консолей.
При изолирующих сопряжениях несущие тросы располагают над кон-
тактными проводами соответствующих им участков. В этих случаях для
определения координат Хт1п и ХГО8Х находят значения Хг для бли-
жайшей к опоре точки подвеса несущего троса и Х& для наиболее уда-
ленной от опоры точки подвеса. Затем Xj уменьшают, а Х2 увеличива-
ют на величину допусков.
Если на консоли, кроме несущих тросов, размещены усиливающие
или другие провода, координату точки подвеса X' каждого из них
можно определить, вычитая из X (или Xj) принятое для конкретны,
условий расстояние между проводами подвески и другими проводами
и учитывая разность в наклоне поддерживающих изоляторов.
Обычно во избежание применения большого числа различных кон-
солей их объединяют исходя из значений координат Л'т111 и Хта •
полученных для различных случаев установки консолей. После того
как А,.и,, и Хтах определены окончательно, геометрические размеры
консолей находят в зависимости от их конкретных схем
О д н о п у т н ы е к о н с о л и б е з ф и к с а т о_ р ь ы х
с т о е к (рис. 7.2). Для уменьшения в точке крепления пяты консолв
горизонтальной составляющей реакции, действующей на опору как
местная нагрузка, размер Л целесообразно выбирать достаточно боль-
шим. Однако с увеличением его растет длина консоли. Па внутрен-
ней стороне кривых в том случае, когда размер h превышает определен-
ное значение, может произойти запрокидывание консоли на опору. По
этому для консолей, устанавливаемых на внутренней стороне кривых
малых радиусов н на опорах с большим габаритом относительно пути
следует проверять, не происходит ли запрокидывания к<шсол'-й при
принятом значении й. Это исключается, если применены кон-.оли «.
фиксаторными стойками.
Размер т' при консолях всех типов определяют как расстояние
между передней гранью опоры па уровне головок рельсов (на рис.7 2
она показана штриховой линией) и концом стрелы консоли расстояние
до которого зависит от конструкции пяты и сбега опоры. Ос сальные
размеры определяют следующим образом.
Для наклонной консоли (рис. 7.2, а) точку крепления i ?п п устанав-
ливают, определив место крепления изолятора пли деталей, поддер-
живающих несущий трос. Точки крепления тяги п изолятора (или де-
талей) должны находиться в непосредственной близости друг от друга.
Полная длина консоли этого типа
I. _ (A)liaV-' d т') cos а < 7
Длина тяги определяется значением угла (5 (т. е. высотой опоры н
положением точки крепления тяги к подкосу) и способом крепления
гяги к опоре. Для изогнутой консоли (рис. 7.2. (Л
-V Л’1П1|1 (</, /;! т' . (7.11
fJ п.а- 1 d. - d-, . \1 01
183
Здесь приближенно р -- 2л7?'а/.36О. Размеры d и выбирают
ио конструктивным соображениям. Полную длину заготовки консоли
/ определяют как
Л « Л'/cosа + р' I- Б, (7.6)
где !>' - р2/(2/?'|
Длину тяги находят в зависимости от размеров A,h и принято-
го способа крепления тяги к опоре.
Геометрические размеры горизонтальной консоли определяют по
разным формулам в зависимости от места закрепления тяги. Напри-
мер, для горизонтальной консоли, схема которой изображена на
рис. 7.2, в:
'Gnin— (7.7)
-^"max ^min (7.8)
Рис. 7.2 Расчетные схемы для опре
деления геометрических размеров од-
нопутных конс<ыей без фиксаторных
стоек наклонной («) изогнутой (б)
и юризонтальной (и)
Полная длина консоли при
показанном расположении тяги
г -Х'п.ах I (7.9)
Длину тяги определяют в
зависимости от тех же факто-
ров, что и для изогнутой кон-
сол и.
Однопутные кон-
соли с фиксаторны-
ми стойками. На рис. 7.3
показан только конец консоли,
на которой закрепляется фикса-
торная стойка, так как все ос-
тальные размеры консоли опре-
деляют аналогично изложенно-
му выше (тип фиксаторной стой-
ки на рис. 7.3 показан условно).
Рис. 7.3 Расчетная схема для опреде-
ления геометрических размеров одно-
путной консоли с фиксаторной стой-
кой
Для изогнутых и горизонтальных консолей
Е~- hT-}- hu— -Лф 1 dj. (7 10)
где Лт — расстояние от консоли до несущего троса;
ha - высота ценной подвески;
/»ф - разность между высотами контактного провода и креплением фикса-
тора на стойке;
а, — конструктивный размер для учета возможных неточностей установки.
Размер С во всех случаях выбирают в зависимости от конструкции
фиксаторной стойки так, чтобы обеспечить возможность закрепления
на стойке фиксатора, работающего на растяжение, с шарнирной дли-
ной, принятой для данной системы цепной подвески. Размер Л" при-
нимают исходя из необходимости размещения на стойке соответствую-
щего числа фиксаторов того или иного типа. Размеры d2, d:t и вы-
бирают по конструктивным соображениям.
Полная длина консолей по сравнению с длиной их без фиксатор-
ных стоек увеличивается для изгогнутых и горизонтальных консолей
на С d -1 с/4. На наклонных консолях фиксаторные стойки не уста-
навливают.
Двухпутные консоли (рис. 7.4). Размер h выбирают на
основании технико-экономических расчетов, в которых сравниваются
стоимости опорных устройств в целом. Для типовых металлических
опор размер h принят равным 3 м при высоте опор 13 м и 5 м при высо-
те 15 м. Геометрические размеры консолей в зависимости от места за-
крепления тяг определяются различными выражениями.
Расстояние от пяты консоли до точки закрепления первой тяги для
положения, показанного на рис. 7.4 сплошной линией.
.4 Л'шах rd ] ill' , (7.11)
для положения, показанного штриховой линией,
4 '^mtn-~dz tm' • <7,12)
Размер т' определяют так же. как ранее. Расстояние М между точ-
ками крепления тяг зависит от места закрепления второй тяги. На-
пример, если обе тяги расположены так, как показано на рис. 7.4
сплошными линиями, это расстояние можно в отдельных случаях при-
нять равным ширине междупутья с небольшим запасом. В этом слу-
чае полная длина консоли
1. A-t-M-L-di. (7.13)
Размеры d, и d2 выбирают по конструктивным соображениям.
Длину тяг определяют в зависимости от размеров А, М, h и принято-
го способа крепления тяг к опоре.
Поверочные расчеты. Расчеты консолей обычно выполняют как по-
верочные, т. е. сначала выбирают сортаменты для изготовления всех
элементов, а затем рассчитывают по двум предельным состояниям.
Можно построить расчет и иначе: сначала определить необходимые
параметры отдельных элементов консоли (моменты сопротивления.
18.3
Рис. 7 4, Расчетная схема для опреде-
ления геометрических размеров двхх
путной консоли
Рис 7.5 Расположение элементов консо-
ли. состоящей из двух швеллеров или
уголков
площади поперечного сечения и др.), затем подобрать соответствую-
щие сортаменты. При проектировании консолей необходимо также
производить поверочный расчет на нагрузки, возникающие при об-
рыве несущего троса.
Для из! отопления кронштейнов консолей применяют швеллерную,
двутавровую или угловую сталь, а также стальные трубы. При швел-
лерной или угловой стали кронштейны консолей обычно выполняют
из двух элементов, соединяемых привариваемыми через определенные
расстояния планками. Расстояние Lo между скрепляющими планками
для сжатых участков кронштейна целесообразно выбирать так, чтобы
гибкость отдельного элемента относительно оси наименьшей жестко-
сти была не больше, чем гибкость всего кронштейна относительно оси х
(рис. 7.5). Для этого достаточно, чтобы соблюдалось условие
бо < .nsu Сх,
(7.14)
где l-с длина сжатого участка кронштейна:
;.т — радиус инерции кронштейна относительно оси х;
'min ' минимальный радиус инерции элемента кронштейна.
Зазор с' между отдельными элементами, определяемый обычно по
конструктивным соображениям, при кронштейнах из двух швеллеров
или неравнополочных уголков, расположенных, как показано на
рис. 7.5. должен быть проверен по условию обеспечения наиболее пол-
ного использования материала кронштейна при работе на продольный
изгиб. Это условие выполняется в тех случаях, когда момент инерции
сечения кронштейна относительно оси у больше или равен моменту
инерции относительно оси х. Для этого величина с' должна удовлетво-
рять соотношению
с 2 ( V (Ух 7 ц) / г о г п),
(7.15)
где моменты инерции сечения элемента кронштейна соответственно
относительно осей х0 и у0;
F„ — площадь поперечного сечения элемента кронштейна:
— расстояние от наружной грани элемента до центра тяжести.
186
Для изготовления растянутых тяг обычно применяю'1' круглую
сталь, сжатых — трубы и угловую сталь. При расчете консолей учи-
тывают наличие шарнирного закрепления их на опорах.
Чтобы определить максимальные расчетные нагрузки при их основ-
ных сочетаниях, следует рассматривать работу контактной сети в ре-
жимах гололеда е ветром и ветра наибольшей интенсивности В тех
случаях, когда некомпенсированные провода, закрепленные на кон-
солях. изменяют направление (на кривых, при отводах на анкеровку
и т.д.), кроме указанных, надо рассмотреть еще режим минимальной
температуры. Направление ветра принимают таким, при котором соз-
даются наиболее неблагоприятные условия для работы рассчитывае-
мого элемента консоли.
О д н о п у т н ы е к о н с о л и без ф и к с а т о р н ы х
стое к. На расчетных схемах рис. 7.6 приведено условное (для при-
мера) число внешних нагрузок и их взаимное расположение. На схе-
мах рис. 7.6, а и б показаны усилия Р()1. которые следует учитывать в
расчетах при закреплении фиксаторов на подкосах консолей. Часть
нагрузки от веса фиксаторов, передающуюся в этих случаях на кон-
соль, можно учесть, прибавляя ее к расчетной нагрузке.от веса консо-
ли. Направление горизонтальных нагрузок (кроме ветровых) учиты-
вают в соответствии с конкретными условиями их воздействия.
Для расчета консолей должны быть определены наибольшие из воз-
можных значения изгибающих моментов Мд и Aflt растягивающего
усилия Т и сжимающего усилия N. Максимальными моменты А1д и
/Mi чаще всего будут в режиме гололеда с ветром. Наибольшие усилия
N для схем рис. 7.6, а и б обычно также возникают при гололеде с вет-
ром. Значения усилия N для схемы рис. 7.6, в и усилий Т для всех
трех схем могут стать максимальными при различных условиях. По-
этому, определяя эти условия, надо рассматривать все указанные выше
режимы.
Изгибающий момент в месте крепления тяги к кронштейну:
для схем рис. 7.6. а и в
Мл Gj t> । />, \h i 0.5G„ 8, (7 16)
где Gj, — нес вылета консоли с учетом (в необходимы* случаях) веса гололеда
и снега;
для схемы рис. 7.6, б
МА --G, bt 4 G2 Ьг - (/>, -г Л2) ЛЛ 0-5<7„ В. 17.17)
Знаки перед моментами от горизонтальных сил в этих и последу-
ющих формулах приняты в соответствии с условным направлением
сил, указанных на рис. 7.6.
Изгибающий момент /Vfj для консолей всех рассматриваемых типов
может быть определен путем построения суммарной эпюры моментов,
действующих па участках О — А .
187
Усилие в тяге Т, учитывая приближенно влияние веса консоли,
можно определить для схемы рис. 7.6, а как
т. - '------[G, й1-|-С2 «2-1-0,5Glf (/Н-В) г^фе); (7.18)
п cos cq
для схемы рис. 7.6, б
Т —---------|Gj (Д+Ш О2 (Д ; Ьг)4 0,5О„ (Д-| В) 1
h cos а,
| (/', /<,) М-Рф е|; (7.19)
для схемы рис. 7.6, в (без учета сил и Р2).
Т —----------[О\«! i G2«2-(-0,5GK (Д-(-В)]. (7.20)
h ecu, a
Сжимающее усилие (V с достаточной точностью для схем рис. 7.6.»
и б определяют как
.V J\x cos a-) Nц sin а.
(7.21)
где .V.v 7'cosa, Р, Р2 —Рф! Gj ! G2 ! О’ц-т-7’ sin at.
Для схемы рис. 7.6, в (при отсутствии фиксаторной стойки)
При расчете изолированной
консоли, схема нагрузок кото-
рой подобна представленной на
рис. 7.6, а, необходимо еще
определить изгибающий момент
в месте соединения подкоса
консоли с изолятором для про-
верки прочности консольного
изолятора. Для схемы, представ-
ленной на рис. 7.7, искомый
момент в точке Б
м h - ь (/’ф л(|) i о; Ukои Ои—
S, - /’| 6’[ В, -( hi)/L.
(7.23)
где GK - нагрузка от веса консоли
без изолятора в подкосе;
6'и нагрузка от веса консоль
ного изолятора;
«к 0,5 (/ — 6) cos а;
ац (L 0,5Л) cos а.
Рис 7 7. Схема расположения нагрузок
для расчета наклонной изолированной
консоли
Расположение нагрузок G1? Gj, Pt, Р\ на рис. 7.7. показано услов-
но. При наличии нагрузок Gj и PL не может быть нагрузок GJ, Р{ (и
наоборот). Если любая лара этих нагрузок будет приложена в точке
А (а вторая пара отсутствует), изгибающий момент в точке Б
ЛД /’(РфЛф : С'«к-< Оипи)/В. (7.24)
Расчеты стержневых консольных изоляторов приведены в § 7.6.
Поверочные расчеты по первому предельному состоянию выполня-
ют следующим образом:
1. Кронштейн консоли проверяют на совместное действие изгиба
и растяжения или сжатия в месте крепления тяги (точка Л), исполь-
зуя условие (для схемы рис. 7.6, а приближенно)
МА
mWxlir
l’i- 1'2
niFIIT
(7.25)
i де т - коэффиииен! условий работы (см. § 1.2):
/'пт площадь поперечного сечения кронштейна с учетом ослабления се-
чения;
Р — расчетное сопротивление материала кронштейна при работе на рас-
тяжение, сжатие и изтиб.
Для консолей, кронштейны которых выполнены из элементов,
обладающих меньшей жесткостью относительно оси у, чем относитель-
но осн х (например, при одном швеллере или двутавре), необходимо
еще учесть действие косого изгиба (при пеповоротных консолях).
В этом случае проверяют, выполняется ли неравенство:
У ч т
Е.
b-os-ip-j.
♦h
(7.261
U t|,r. V'"/; нт—моменты сопротивления сечения кронштейна огноснтсльно
о<ей у и у г: учетов ослабления сечения;
ii- - угоч который чоетиг.ляе! плоскость дейстующей нагрузки
с вертикальной плоскостью.
2. Кронштейн консоли проверяют па совместное действие изгиба
и сжатия в месте действия максимального момента Л4/.
(7.27}
Согласно рекомендации ВСН 14)-84 в сжато-изогнутых элементах
консолей допускается гибкость в подкосах консолей до 350, а в сжатых
тягах - до 500. Прочность сжато-изогнутых и растянуто-изогнутых
сплошных стержней, имеющих гибкость более 200, проверяют, исполь-
зуя неравенство
А' /И:г Мч
г 1 . У Д- г
mJ хнт mJ Ч11т
(7.28)
г \ . И,, /V/,, - pat четные значения соответственно продольной силы и из-
гибающих моментов относительно осей х я у,
ГН1. площадь поперечного сечения нетто;
J к ит- А; нт " моменты инерции сечения стержни нетто относительно осей
х и у;
г. у координаты рассматриваемой точки сечения относит-.и.но
его главных ои.-й.
3. Проверяют сжатый участок кронштейна на устойчивость. Если
। ибкемть кронштейна консоли не превышает 200, то расчет следует вы-
полнять по рекомендациям СНиП П-23-81. Однако изложенная там
методика весьма сложна и для данного случая возможно использовать
менее строгий, но более простой способ расчета.
Проверку можно произвести, определив, выполняются ли следую-
щие условия в плоскости действия изгибающих моментов и ЛЕ:
для схем рис 7,6, н е
где Гд момент сопротивления сечения кронштейна относительно оси х без
учета ослабления сеченая;
/•' — площадь поперечного сечения кронштейна без учета ослабления се-
чения;
фА. — коэффициент продольного изгиба, принимаемый по табл. 7.2 в за-
висимости от гибкости сжатой части кронштейна, вычисленной для
рассматриваемой плоскости
<90
Т а б л и и а 7.2
Л л Зна«ення (р для элементов из era пи с расчетным сопротивлением, МПа
О * s 200 1 1 240 •280 J20 i ,»60 | !')0 НО i «0
20 0.967 0,962 0,959 0.955 0.952 0,949 0,946 0.943
•10 0.906 ! 0,894 0.883 0,873 0.863 0.854 0,846 0,83.9
00 0.827 | 0.805 0,785 0.766 0,749 0,721 0.696 0.672
80 0.734 | 0.686 0.641 0,602 0.566 0,532 0.501 0.47!
100 0,599 1 0,542 0,493 0,448 0.408 0,369 0.335 0,309
«20 0.479 0.419 0,366 0.321 0,287 0,260 0.237 0.219
140 0.376 i 0,315 0.272 0,240 0.215 0.195 0, 178 0.164
160 0.290 i 0,244 0,212 0.187 0 167 0. 152 0,139 0.129
180 0.233 i 0.196 0,170 0. 150 0,135 0.123 0. ! 12 0.104
200 0.191 i 0.161 0 140 0. 124 0.111 0.10! 0.093 0 086
220 0 160 1 0,135 0,118 0,104 0.094 0.086 0,077 0.073
для рис. 7.6, б при отсутствии закрепленного на подкосе консоли
фиксатора
0.6А1,. д/
---7 1-----Д'. < 7 .'30)
mw у---------------------------------------m<pv F
При действии усилия Рф необходимо еще учесть создаваемый им
изгибающий момент, что приближенно можно выполнить, прибавляя
(или вычитая) этот момент к 0,6 Мд.
В случае необходимости коэффициент <р для промежуточных зна-
чений гибкости элемента X, не указанных в табл. 7.2, можно опреде-
лить линейной интерполяцией. В общем случае для ежа i ой части крон-
штейна
л Zp/i', (7-ЗЩ
1 де /р расчетная длина сжатой части;
; радиус инерции сечения кронштейна относительно гой оси. для кото-
рой определяется гибкость.
Расчетну?» длину сжатых элементов /р в зависимости от способа
их закрепления и нагрузки принимают по рекомендациям СНиП
i 1-23-81.
Например, гибкость относительно оси х
V i-v/ix, (7.32)
где Ц,. - то же, что в формуле (7.11);
«х — радиус инерции относительно оси х:
ix V-ix/F', <7 33)
’х — момент инерции сечения кронштейна относительно осп х (и>ч учета
ослабления сечения,
191
Кронштейны, обладающие меньшей жесткостью относительно оси
I/, можно проверить на устойчивость в этой плоскости (не совпадаю-
щей с плоскостью действия моментов Л4л и М,). используя неравенст-
во
। де <р;; коэффициент продольного изгиба, значение которого определяется
гибкостью относительно оси у.
Если необходимо проверить элемент кронштейна, состоящего из
двух стержней, на устойчивость в плоскости наименьшей жесткости,
не совпадающей с плоскостью дейовия моментов Мд и Mt, применяют
неравенство
где /'„ .то же. что в формуле (7.15);
<р0 - коэффициент продольного изгиба, значение которого определяется
гибкостью ЛО -
1„ — расстояние между осями скрепляющих планок;
/,„1П минимальный радиус инерции сечения элемента кронштейна:
'mln - VAnln/Fn ’> (7.36)
•Лп1п минимальный момент инерции сечения элемента кронштейна.
Отдельный элемент кронштейна, состоящего из двух стержней,
проверяют на устойчивость, только если гибкость одного стержня на
длине между скрепляющими планками относительно оси наименьшей
жесткости больше, чем гибкость целого кронштейна относительно
оси х.
Сжатые и сжато-изогнутые элементы консолей, имеющих гибкость
более 200, проверяют на устойчивость по коэффициенту устойчивости
п„ PK/N, (7.37)
где Рк — критическая (Эйлерова) сила.
Для случая, когда оба конца кронштейна закреплены шарнир-
но,
Р„ л»/-Уп11п//.;т, (7.38)
где Е — модуль упругости материала кронштейна.
Не допускается коэффициент устойчивости п;/ < 2. При 2 < п„
<4 максимальный изгибающий момент сжато-изогнутых стержней с
гибкостью более 200 следует определять построением эпюры моментов в
соответствии с рекомендациями ВСН 141-84. Для n,d > 4 построение
такой эпюры не обязательно.
Подкосы консолей, на которых предусматривается крепление фик-
саторов или фиксаторных стоек, проверяют по второму предельному
состоянию. При этом горизонтальная составляющая прогиба подкоса
192
11
консоли от кратковременных нагрузок в точке крепления фиксатора
или фиксаторной стойки не должна превышать 35 мм.
4. Проверяют растянутую тягу на растяжение
Т'тах/бн^тнт) 7?. (7.39)
где 7'тах — максимальное усилие в тяге;
/•'гнт — площадь поперечного сечения тяги с учетом ослабления сечения.
Сжатые тяги консолей, применяемые, когда растягивающее усилие
в тяге может стать менее 20 даН, рассчитывают как сжато-изогнутые
стержни, сжимаемые продольной силой и изгибающим моментом от
собственного веса и продольной силы.
5. Проверяют валик диаметром dY, крепящий тягу к кронштейну
консоли, на изгиб
Tm.AXc'/(m-Q,4d't)<R, (7.40)
(7.42)
где с' — увеличенное на 5 % расстояние с между элементами, из которых со-
стоит кронштейн, или между планками, приваренными для крепления
тяги к кронштейну, состоящему из одного элемента.
Затем производят проверку на срез
2TIllax/(mnd*t) </?ср, (7.41)
где — расчетное сопротивление материала валика при работе на срез.
Кроме того, проверяют на смятие полки элементов кронштейна или
поддерживающих планок
Лпах г,
6m СМ ’
где 6 — толщина полок или планок;
/?см — расчетное сопротивление при работе на смятие.
6. Проверяют валик, крепящий кронштейн консоли к пяте, анало-
гично тому, как это изложено для валика, крепящего тягу к кронштей-
ну. Расчетным в данном случае будет усилие
N' . (7.43)
Это же усилие /V" считают расчетным для проверки на смятие полок
элементов кронштейна или крепительных планок по формуле (7.42).
Если расчет консоли ведется так. что сначала определяют основные
параметры консоли, а затем подбирают соответствующие сортаменты,
то. например, для выбора сортамента для изготовления кронштейна
неизолированной консоли определяют минимальный необходимый мо-
мент сопротивления сечения в месте крепления тяги, а при выборе ди-
аметра круглой стали для изготовления растянутой тяги— минималь-
ную потребную площадь поперечного сечения тяги.
Для выбора диаметров валиков, крепящих тягу к кронштейну dr и
кронштейн к пяте d2, определяют минимальные необходимые диа-
метры:
7 Зак 2630
dimin = 1 Тс'/(0,4mRj;
4smin = T N' c'/(0,4mR).
(7.44)
(7.45)
193
Рис 7.Й. Схема расположения на-
грузок для расчета однопутной кон-
соли с фиксаторной стойкой
саторными стойками будет отлг
После того как подобраны
соответствующие сортаменты, для
каждого элемента консоли произ-
водят остальные поверочные рас-
четы.
Однопутные консо-
ли с фиксаторными
стойками. Примем в каче-
стве расчетной схему, приведен-
ную на рис. 7.8. Аналогичные
схемы могут быть составлены
для различных горизонтальных
консолей. Расчет консолей с фик-
(аться от изложенного выше зна-
чениями расчетных нагрузок Л4д, Alj, Т и N.
Для рассматриваемой схемы изгибающий момент
МА Gb + РДЛ 4 Рф Л2 4- 0,5GB В -у- Оф Вх, (7.46)
где - вес вылета консоли;
Оф — вес фиксаторной стойки с учетом части веса фиксатора.
Растягивающее усилие
i
Т _--------|G (Д.Ь6)..-рд у.Рф/1 +о,50к (А-1--В)4-Оф (А -I В,)}, (7.47)
п cos а,
где GK — вес консоли без учета фиксаторной стойки и передающейся на стойку
части веса фиксатора.
Составляющие усилий V и N't
\’х =- Т c.os а; 4- Р -|-Рф; (7.48)
N}l -= G-f- GK 4’бф Tsincxj. (7.49)
Расчет самих фиксаторных стоек не дается, так как при конструк-
циях, приведенных на рис. 7.8 и 7.9, их расчетная схема и последова-
тельность расчета подобны изложенному выше для изогнутых консолей
без стоек. Если же фиксаторные стойки выполняют из одного элемента,
расчет их прост и не требует отдельных пояснений.
Двухпутные консоли. Одна из возможных расчетных
схем двухпутной консоли приведена на рис. 7.9. Для расчета консоли,
нагруженной согласно этой схеме, необходимо знать изгибающие мо-
менты /И5, М2. /Ив, /Ис, растягивающие 7\, Т2 и сжимающие A/\,
JV2 усилия. Кроме того, для расчета крепления консоли к пяте нужно
знать расчетное усилие N^. Чтобы определить указанные изгибающие
моменты и усилия, можно рассматривать данную консоль как двух-
пролетную неразрезную балку с опорами, находящимися на одном
уровне, которая имеет с одной стороны вылет. Собственный вес вылета
консоли допустимо учитывать не как равномерно распределенную, а
как сосредоточенную нагрузку GE. В отдельных случаях для упроще-
194
ния расчета вес консоли на участках АВ и ВС также можно учиты-
вать как сосредоточенную нагрузку.
Для определения расчетных нагрузок делят схему консоли на ряд
элементарных схем. Частные значения изгибающих моментов, опор-
ных реакций и перерезывающих сил для каждой элементарной схемы
могут быть определены по формулам, приведенным в соответствую-
щих справочниках. Затем находят их суммарные значения. Расчет-
ные опорные реакции Va, Vb> Ус, опорные моменты Мв и Л4С и пере-
резывающие силы Q.i, Qb, Qb, Qc определяют путем сложения част-
ных значений, полученных для одной и той же точки. Расчетные изги-
бающие моменты и Л4а могут быть получены как наибольшие из
суммарных эпюр моментов, построенных для каждого расчетного уча-
стка.
По известным вертикальным составляющим опорных реакций УА,
У в, У'с нетрудно определить все необходимые расчетные усилия:
7-j=VB/sinai; (7.50)
7'2=--Hc/sina2; . (7.51)
.V,-.. lzH/tgar4-Pt-j-/V2; (7.52)
.vn-(7.53)
V8 Ис./1й a, . P* i- + (7.54)
где ...\ф tgf).
Дальнейшие расчеты, заключающиеся в проверке ослабленных се-
чений кронштейна консоли на изгиб в точках В и С, проверке крон-
штейна на совместное действие изгиба и сжатия на участках АВ и ВС,
проверке тяг на растяжение и кронштейна на устойчивость, не требу-
Рис. 7.9. Схема расположения нагрузок для расчета двухпутной консоли
у*
195
юг особых пояснений, так как производятся аналогично изложенному
выше для однопутных консолей.
Проверку кронштейна консоли на устойчивость в плоскости дейст-
вия изгибающих моментов Мг и М2 на участках АВ и ВС для упро-
щения расчета можно производить раздельно для каждого участка ис-
ходя из тех моментов и усилий, которые действуют на данном участке,
и не учитывая влияние соседнего участка. Если необходимо проверить
кронштейн на устойчивость в плоскости, не совпадающей с плоскостью
действия изгибающих моментов, расчетную длину можно принимать
равной /х + /2, а расчетное усилие равным усилию Nv Содержание
расчетов аналогично изложенному.
При проектировании единичных конструкций для упрощения до-
пустимо рассчитывать двухпутные консоли как разрезные балки.
Пример. С ища и и я. На электрифицировааном участке постоянного
тока долгое время осуществлялось движение только электропоездов и пол у ком-
пенсированная контактная подвеска состояла из несущею троса М-120 и кон-
гакт.чого провод;; МФ-100. В связи с переводом па электрическую тягу грузовых
и пассажирских поездов решено было снять изношенный контактный провод
и подвесить к тому же несущему тросу два контактных провода НлОл0,04Ф-100.
Возник вопрос: можно ли оставить без усиления устройства контактной сйти и, в
частности, консоли? Особое беспокойство вызывала прочность консолей на опо-
рах, установленных с внутренней стороны кривых участков пути.
3 а д а н и е. Выполнить поверочный расчет консоли с обратной фиксатор-
ной стойкой, установленной на опоре с внутренней стороны кривой радиу-
сом 700 м, для крепления полукомпенсированной цепной подвески М-120 |-
i 2НлОлО,04Ф-ЮО.
Исходные данны е. Длина пролета равна 55 м. Экстремальные тем-
пературы воздуха ±40 °C. Рассматриваемый участок дороги проходит по откры-
той холмистой местности с насыпями высотой до 13 м и находится в гололедном
районе II и ветровом II. Расчет несущего троса М-120, нагруженного двумя кон-
тактными проводами НлОлО,04Ф-ЮО* дал следующие результаты: натяжение не-
сущего троса при минимальной температуре 2000 даН, при гололеде с ветром
1700 даН, нри максимальном ветре 1450 даН.
Консоль изогнутого типа выполнена из днух швеллеров № 10. Сталь марки
ВСтЗкп2 с расчетным сопротивлением по пределу текучести 225 МПа (ем.
табл. 1.10). Тяга выполнена из круглой стали диаметром 16 мм, валики для креп-
ления тяги к подкосу и подкоса к пяте имеют диаметр 22 мм. Длина подкоса
3,78 м, расстояние между швеллерами 5 см. между осями скрепляющих планок
1,2 м.
Схема нагрузок консоли соответствует представленной на рис. 7.8. Угол а
составляет 37°30', угол а, ~ 10°30'; необходимые для расчета размеры состав-
ляют: А - 3 м; В 2 м; Я, 1.4 м: b 0,5 м; h — 1,75 м: я, - 1,7 м; /г2 —
— 2,8 м; hs — 0,55 м; АЛ — 0,6 м.
Определение расчетных нагрузок. Сначала найдем все
нормативные нагрузки. Для этого определим скорости ветра, при которых необ-
ходимо искать такие нагрузки. Местность, в которой находится электрифициро-
ванный участок, характеризуется параметром шероховатости, равным 0,2 м (см.
табл. 1.2). Для заданных условий коэффициент кя -- 1,13 (см. табл, 1.3). Следо-
вательно, искомые скорости ветра на основании формулы (1.11) равны 1,13s?-;
Х25 --32 м/с при максимальном ветре и 1,13s-14—18 м/с при гололеде с ветром.
Нормативные значения распределенных линейных нагрузок на несущий
трос найдем по табл. 2.1, учитывая, что при низколегированных контактных
проводах нагрузки такие же, как и при медных: 2,98 даН/м от собственного веса
цепной подвески, (4,14—2,98) - 1,16 даН,м от веса гололеда на подвеске;
196
0,81 даН/м—статическая составляющая нагрузки от ветра нри гололеде и
1,13 даН/м —то же при максимальном ветре.
Статические составляющие распределенных линейных нагрузок на контакт'
ные провода от действия ветра найдем по табл. 2.2, принимая Сх - 1,85. при
гололеде с ветром 0,64 даН/м и при максимальном ветре 1,42 даН/м.
Динамические составляющие ветровых нагрузок па несущий трос опреде-
лим по формулам (2.8) и (2.10):
при гололеде с ветром 0,88-0,81 -0,625-0,148-0,997—0,066 даН/м;
при максимальном ветре 0,88-1,13-0,625-0,208-0,936--0,12! даН/м.
Принятые в этих вычислениях коэффициенты определены по данным § 2 2
г) 0,625 для пролета длиной 55 м, 6 0,148 для скорости ветра при гололеде
18 м/с и 6 0,208 для максимальной скорости ветра 32 м;с.
Чтобы определить значение коэффициента $ при гололеде, найдем нагрузку
от веса несущего троса с гололедом с помощью формулы (2.5),
gHr 1.037 [-2,22-10 (14 - 10) 10-» 1,57 даН/м.
Для этой нагрузки коэффициент 5 0,997, при максимальном ветре нри
нагрузке от несущего троса 1,037 даН/м получим £ 0,936.
Динамические составляющие ветровых нагрузок па контактные провода
определим аналогично приведенному выше для несущего троса:
при гололеде с ветром 0,88-0,64-0,625-0,148-1,03 0.054 даН'м.
при максимальном ветре 0,88-1,42-0,625-0,208-1,015 0,165 даН м
Здесь коэффициенты г( и 6 те же, что раньше, а коэффициент Е, . I 03 дли
нагрузки от веса контактных проводов с гололедом, определенной г помыцио
формулы (2.4), так как
йкг 2 [0.873 2,77-5 (12,.3 {-5) К)"3] -2.23даН,м.
При максимальном ветре и нагрузке от веса контактных проводов равной
1,746 даН/м, коэффициент & 1,015.
Полные нормативные нагрузки от действия ветра будут.
на несущий трос при гололеде с ветром 0,8! ' 0.066 0,«76 даН м
то же при максимальном ветре 1,13 I 0,121" 1,251 даН м,
на контактные провода при юлоледе с ветром 0.6-1 0,054 0,694 да!0м;
то же при максимальном негре 1,42 , 0,165 1.585 даН .м.
Нормативные нагрузки па консоль и на фиксаторную стойку
от собственного веса подвески при н.прузке от изоляторов и части веса
фиксаторов, передающейся на несущий трт 30 даН
</“ 2.98-55 1 30 194 даН;
от веса гололеда на подвеске <7^ 1,16-55 64 даН.
Принимая р 1, по формулам (2.25) и (2.24) получим нагрузки
от давления ветра на несущий трос при гололеде и при максимальном нет
ре соответственно'
P*t 0,876-55 48даН и Р"я 1.251-55 - 69 даН;
то же на контактные провода:
Р",.-- 0,694-55 -38 даН и Р"в 1.585-55-=87 даН.
Усилия от излома несущего троса на кривой определим но формуле (2 28)
нри гололеде с ветром Р*р 1700-55/700 - 134 даН;
при максимальном ветре 1450-55/700 -'114 даН:
при минимальной температуре Р*р --- 2000-55/700 157 даН,
от излома контактных проводов при всех режимах РфР -- 2 1000-55/700-
157 даН.
Ж
Таблица 7.3
Расчетные режимы 6. даН Р, даН Рф, даН
Ветер от пути на опору Ветер от опоры на путь Ветер от пути на опору Ветер от опоры на путь
Гололед с вет- 300 200 75 205 по
ром Максимальный ветер 215 195 30 260 55
Минимальная температура 215 155 155 155 155
Расчетные нагрузки на консоль и фиксаторную стойку с учетом коэффи-
циентов надежности по нагрузке, приведенных в § 2.1:
вертикальная нагрузка от веса подвески с изоляторами и арматурой G'—
= 194-1,1 = 213 даН;
от веса гололеда на подвеске Gr = 64-1,3=83 даН;
от веса подвески с гололедом G = 213+83=296 даН.
Горизонтальные нагрузки при гололеде с ветром:
134 ± 48-1,25= 134 + бОдаН и Рф= 157 ± 38-1,25= 157 ± 48 даН.
Верхние знаки соответствуют направлению ветра от пути на опору, ниж-
ние — от опоры на путь.
Горизонтальные нагрузки при максимальном ветре:
Р---114 + 69-1.2= 114 + 83 даН и Рф = 154 + 87-1,2 = 157 ± 104 даН;
при минимальной температуре
Р = Рф- 157 даН.
Значения всех расчетных нагрузок для разных режимов и при различных
направлениях ветра приведены в табл. 7.3 с небольшим округлением.
Нагрузку от веса консоли без гололеда примем равной 180 даН, а с гололе-
дом — 230 даН; от веса вылета консоли — соответственно 60 и 80 даН; от веса
фиксаторной стойки — соответственно 25 и 30 даН.
Значение изгибающего момента Мд определим по формуле (7.46) при на-
иболее опасном направлении ветра от пути на опору:
при гололеде с ветром
Мл = 300-0,5 + 200-0,6 + 205-2,8 + 0,5-80-2 + 30-1,4 = 966 даН-м;
при максимальном ветре
Л4Л =215-0,5+195-0,6+260-2,8 t-0,5-60-2+25-1,4 = 1048 даН-м.
Значение этого момента при минимальной температуре не определяем, так
как оно будет явно меньше полученных.
Усилия в тяге Т рассчитаем по формуле (7.47) при наиболее тяжелом для
данного случая режиме гололеда с ветром:
при ветре от пути на опору
300 ( 3 + 0,5)—200-1,7-)-205-0,55 + 0,5-230 ( 3 + 2) +30 ( 3+1,4)
198
при ветре от опоры иа путь
Г 300 (3+о,5) —75-i,7+-110.0,55+0,5-230 (3 + 2)4-30 (3+1,4) _
1,75-0,983
= 985 даН.
Составляющие расчетных усилий N и Д' определим по формулам (7.48)
и (7.49):
при ветре от пути на опору:
Дх = 890•0,983 + 200 + 205 = 1280 даН;
Д у = 300 + 230 + 30 + 890 - 0,182 -- 720 да Н;
при ветре от опоры на путь:
Л'ж = 985-0,983-1 75+110— 1150 даН;
Д у = 300 + 230 4- 30 + 985 • 0,182 -= 740 даН.
Очевидно, что большие значения усилий Д и Д" будут при ветре от пути
на опору. Усилие Д определим по формуле (7.21)
Д = 1280 0.793+720 - 0,609 - --- 1454 да Н,
усилие Д' — по формуле (7.43)
Л'' = 1/12802 + 7204' = 1470даН.
Для дальнейших расчетов примем, округлив до 5 даН, наибольшие из рас-
четных значений:
МА 1050даН-м; 7’=985даН; Л -1455 даН; Д'-1470 даН
Поверочные расчет ы. Для удобства выпишем из сортамента
необходимые для расчетов данные швеллера № 10: h — 10 см;б — 0,45 см; Fo -
— 10,9 см2; 7х0 - 174 см4; Wx ~ 34,8 см3; ix 3,99 см; J= 20,4 см4; iv - •
— 1,37 см; z0 = 1,44 см.
Проверим, соответствует ли условию (7.15) расстояние Между швеллерами
с и условию (7.14) расстояние между осями скрепляющих плаиок Lo.
с = 2 [ 1/(174 — 20,4)/10,9 — 1,441-4,63 с м < 5;
+ -= 3,78-1,37/3,99 - 1,3 м > 1,2 м .
Результаты расчетов показывают, что расстояния с и Lo можно оставить
без изменений. Дальнейшие проверки выполним, принимая коэффициент ус-
ловий работы т — 1.
Проверим кронштейн консоли на прочность в точке .4, воспользовавшись
формулой (7.25),
105 000/69,4 + 200/19,64 = 1523 даН /см2 = 152 МПа.
Здесь значения И7ЖНТ и Аит определены с учетом диаметра отверстий для ва-
лика, крепящего тягу, равного 2,4 см:
2 (7Х0 —б</3/12) 2 (174-0,45-2,43/12) ,
№хнт =-----——-------=----------X ; --------— 69,4 см»;
0,5Л 0,5-10
+нт =2 (f0—6d) =2 (10,9—0,45-2,4) ==19,64 см4.
Проверку кронштейна на совместное действие изгиба и сжатия выполним
по формуле (7.27).
105 000 1470
+ ——— = 1576даН/см2= 158 МПа,
199
проверку кронштейна на устойчивость — по формуле (7.29), так как его
гибкость, определяемая выражением (7.3i), меньше 200,
= (3,78/3,99) 100 -95.
Пользуясь данными табл. 7.2, путем интерполяции найдем значение коэф-
фициента продольного изгиба (рг. -- 0,628. Тогда искомое напряжение
0,6-105 000 1455
----------- I --------— - ’012 даН/см2 = 101 МПа.
2-34,8 1 0.628-2-10,9 '
Результаты проверок показывают, что полученные напряжения во всех слу-
чаях ниже допускаемого значения, которое с учетом коэффициента надежности
по материалу 1,025 и коэффициента надежности по назначению 0,95 (см. § 1.2)
составляет
225/(1,025-0,95) -231 МПа.
Выполним проверку тяги консоли на растяжение по формуле (7.39)
4-985/(3,14-1,62) -490 даН/см2 = 49 МПа.
Проверим на прочность валик, крепящий кронштейн консоли к пяте. На из-
гиб проверку выполним по формуле (7.40)
1470- 1,05-5/(0,4-2,2-’) = 1812 даН/см2 = 181 МПа,
на срез — по формуле (7.41)
2-1470/(3,14-2,2“) -= 193даН/см«= 19МПа.
Проверим полки швеллеров кронштейна на смятие по формуле (7.42)
1470/(2-2,2-0.45) •• 742 даН /см2 = 74 МПа.
Валик, крепящий тягу консоли к кронштейну, на прочность не проверяем,
так как диаметр валика такой же, как у проверенного, а усилие в этом месте
меньше, чем в точке крепления кронштейна к пяте.
Все полученные напряжения ниже допускаемых, следовательно, данная кон-
соль может быть использована без усиления и при двух контактных проводах в
цепной подвеске
§ 7.3. Расчеты кронштейнов для проводов
воздушных линий
Определение геометрических размеров. Кронштейны для усилива-
ющих, питающих, отсасывающих, дополнительных и некоторых дру-
гих проводов, как правило, применяют горизонтальные с подкосом
и с тягой. Длина горизонтальной части кронштейна с подкосом
(рис. 7.10, а)
L=A' ч (7.55)
где .4' - наименьшее установленное нормами допустимое расстояние от
отклоненного провода до подкоса с учетом запаса на неточность
установки,
й/ горизонтальная проекция отклоненной гирлянды изоляторов,
определяемая для условий, вызывающих наибольшее отклонение;
и - размеры, выбираемые по конструктивным соображениям.
200
Рис. 7.10. Расчетные схемы для определения геометрических размеров кронштейн
нов с подкосом (а), с тремя проводами ВЛ 6 и 10 кВ (б) и с проводами под на-
пряжением до 1000 В (в)
Если усилие, отклоняющее гирлянду изоляторов, имеет постоян-
ное направление, вызывающее отклонение гирлянды в сторону от опо-
ры, то знак «+» перед в формуле (7.55) следует изменить на «—»,
а значение h’K рассчитывать для условий, определяющих наименьшее
отклонение гирлянды изоляторов.
Длину подкоса Ln находят в зависимости от размера С, угла а и
принятого способа крепления к опоре, определяющего конструктив-
ный размер d;t:
Ln -С/cos а. (7.56)
Геометрические размеры кронштейна с тягой определяют анало-
гично изложенному в § 7.2 для горизонтальной консоли с тягой (см.
рис. 7.2, в).
Геометрические размеры кронштейна, применяемого для крепле-
ния трехфазной ВЛ 6 и 10 кВ (рис. 7.10, б), могут быть определены сле-
дующим образом:
для верхнего элемента
La A" h В j (7.57)
для нижнего элемента
LH-.= -А" -j-0,5B-j df— Дз, (7.58)
где А" — наименьшее, установленное нормами допустимое расстояние
от провода до грани опоры с учетом запаса на неточность уста-
новки;
В — расстояние между проводами, установленное нормами в за-
висимости от напряжения и гололедного района;
Jj, d-j. d”3 — размеры, выбираемые по конструктивным соображениям.
Длину подкоса определяют аналогично длине кронштейна, пока-
занного на рис. 7.10, б, в зависимости от угла а' и размеров h” и б4.
Длина кронштейна с подкосом для п проводов линий напряжением до
1000 В, которые обычно располагают горизонтально (рис. 7.10, в),
L' = A" (п— 1) B+Jj—Дз . (7.59)
201
Рис. 7.!!. Схеме: расположения изгрузок для расчета кронштейнов с подкосом
(а), с тягой (б) и без подкоса или тяги (в)
Размеры горизонтальных кронштейнов без подкосов или тяг опре-
деляют в зависимости от допускаемого расстояния от опоры до бли-
жайшего к ней провода, числа проводов, принятого между ними рас-
стояния и конструктивных размеров, аналогично тому, как было по-
казано выше. При закреплении кронштейна на металлической опоре
следует учитывать ширину опоры на уровне нахождения кронштейна.
Расчеты кронштейнов. Для рассмотрения расчетных условий опи-
санные кронштейны можно представить тремя схемами, показанными
на рис. 7.11.
Расчет кронштейна с приваренным подкосом обычно выполняют,
допуская, что горизонтальный элемент кронштейна и подкос соедине-
ны шарнирно. На рис. 7.11, а в качестве примера показана одна из
возможных расчетных схем кронштейна с подкосом и двумя провода-
ми с вертикальными нагрузками GL и G2 и горизонтальными нагрузка-
ми Pj и Р2. Необходимые нагрузки для этой схемы определяют по сле-
дующим формулам:
Мд G2b-\ Р2 c-|-0,5GB В; (7.60)
Т ~ [G, а -I 6'2(Д -I (й' I е) г 0,3Ge (Д !-В) | 0,5Gu4J; (7.61)
h
А\ т-Pi-P,-, (7.62)
Nn - 6'i+6'2-|-GC + G'„. (7.63)
где Gc — нагрузка от веса горизонтального элемента;
GB,Gn — нагрузка от веса соответственно вылета кронштейна и подкоса.
Расчетный изгибающий момент Mi может быть определен как мак-
симальный по суммарной эпюре моментов, построенной для участка
БА. Дальнейшие расчеты горизонтального элемента производят ана-
логично изложенному в § 7.2 для однопутной горизонтальной консоли
несущего троса. Расчеты подкоса выполняют так же, как (см. § 7.2)
подкоса однопутной изогнутой консоли для несущего троса, но без
учета действия изгибающего момента
Расчет горизонтального кронштейна с тягой, нагруженного по схе-
ме рис. 7.11, б, аналогичен изложенному в § 7.2 для такой же консоли
несущего троса. В тех случаях, когда провода крепят на штыревых
202
изоляторах, необходимо при определении расчетного момента Ма
учитывать дополнительный момент от силы Р'.
Расчет горизонтального кронштейна без подкоса или тяги
(рис. 7.11, в) заключается в проверке (или выборе) площади сечения
кронштейна в месте его закрепления на опоре. Определение расчет-
ного момента /Ио выполняется по формуле
Мо = 2 Сгсн-пр;н-0,50к£к, (7.64)
i -+ 1
где п — число проводов на кронштейне.
Последующий расчет не представляет затруднений и поэтому не
приводится.
§ 7.4. Расчеты гибких поперечин
Общие сведения. Гибкие поперечины, как и все другие провода,
рассчитывают по допускаемым напряжениям. Расчеты обычно вы пол-
няют как поверочные, т. е. сначала задаются определенным числом
поперечных несущих и фиксирующих тросов и площадью их сечения,
а затем проверяют соответствие максимальных возникающих напря-
жений допускаемым по нормам. Поперечные несущие и фиксирующие
тросы рассчитывают независимо друг от друга. Это возможно потому,
что каждый из тросов гибких поперечин воспринимает определенные
нагрузки, обычно не передающиеся с одного троса на другой. Если же
между тросами имеется жесткая связь (системы с фиксаторными стой-
ками), то для расчета все нагрузки можно распределить между соот-
ветствующими тросами.
Поперечные несущие тросы рассчитывают на вертикальные нагруз-
ки от всех проводов, закрепленных на гибкой поперечине, и от самой
поперечины, верхний фиксирующий трос — на все горизонтальные
нагрузки от несущих тросов цепных подвесок и от усиливающих и дру-
гих проводов: нижний фиксирующий трос — на все горизонтальные
нагрузки от контактных проводов.
Поперечные несущие и фиксирующие тросы выполняют из биметал-
лических или стальных проводов. Для увеличения надежности попе-
речные несущие тросы выполняют не менее чем из двух проводов с тем,
чтобы при обрыве одного из них оставшиеся могли выдержать всю на-
грузку с достаточным запасом прочности. Обычно для поперечных не-
сущих тросов применяют провода, площадь сечения которых не менее
70 мм2, а для фиксирующих тросов — не менее 50 мм2. В последнее
время поперечные несущие тросы выполняют из проводов ПБСМ-95,
а фиксирующие — из проводов ПБСМ-70 и ПБСА-50/70.
'Ниже приводится расчет гибкой поперечины при одинаковой высо-
те точек закрепления поперечного несущего троса. Расчет этого тро-
са при разной высоте его крепления на опорах изложен в § 7.6.
203
Рис. 7 12. Схемы расположения нагрузок
при расчете гибкой поперечины для по-
перечного несущего троса (а), для опре-
деления места действия наибольшего из-
гибающего момента (б) и для фиксирую-
щего троса (в)
Расчет поперечных несущих тросов. Определение необходимой
суммарной площади сечения поперечного несущего троса или про-
верку прочности заранее выбранного троса производят но максималь-
ному усилию Тп 111ах, возникающему в тросе при гололеде:
Sn Т„ max/l^pJ или Т’пшах^
(7.65); (7.66)
где (Стр) — допускаемое напряжение материала троса на растяжение;
пп — число проводов в поперечном несущем тросе;
Гр — разрывное усилие для одного провода;
к3 — коэффициент запаса прочности.
Максимальное усилие в тросе при гололеде
Ти max -- ^max 'i ^п,
(7.67)
где Vmax — наибольшая из вертикальных составляющих опорных реакций;
На — горизонтальная составляющая натяжения троса.
Одну из вертикальных составляющих опорных реакций определя-
ют по формуле (рис. 7.12, а)
(7.68)
где /п — расстояние между точками закрепления поперечного несущего троса
на опорах (длина поперечного пролета);
п — число вертикальных нагрузок, в каждую из которых включают соот-
ветствующую часть нагрузки от веса гибкой поперечины (см. § 2.3);
О, — нагрузка, расположенная на расстоянии /г от второй опоры.
Вертикальную составляющую опорной реакции на второй опоре
можно определить аналогично первой или, что проще, по формуле
п
VA- 2 G~vs
1= I
(7.69)
204
Горизонтальная составляющая натяжения поперечного несущего
троса
Нп Л4тах//П тах, (7.70)
где Л1тах — максимальный момент от вертикальных сил;
/п max —максимальная стрела провеса поперечного несущего троса.
Место действия момента Л4шах от вертикальных сил можно опре-
делить путем построения эпюры перерезывающих сил: оно соответст-
вует точке перехода через нуль. Для схемы нагрузок, представленной
на рис. 7.12, б, это место находится в точке приложения четвертой на-
грузки.
Наибольшую стрелу провеса поперечного несущего троса, если не
задана высота опор, выбирают на основании технико-экономического
расчета, сравнивая стоимости опорных устройств и фундаментов при
различных стрелах провеса, по не менее ’/Щ длины поперечного проле-
та, чтобы свести к минимуму влияния изменения внешней температуры
на изменения стрелы провеса троса. Если же высота опор задана, то
значение /п тах определяют по формуле
/ятах-^оп—(Л1 + -j-Ди -\-h2-\-h9) 0,1/п. . (7.71)
Все размеры показаны на рис. 7.13. Величина Л2 должна быть не
менее 300 мм.
Необходимая для монтажа стрела провеса поперечного несущего
троса в ненагруженном состоянии
/п —к'"|/3 (Ln— /и) 1ц/И , (7.72)
где — полная длина поперечного несущего троса;
к’ ..коэффициент, учитывающий последующее удлинение троса и прогиб-
опор: к' = 0,85 4- 0,9.
Полная длина поперечного несу-
щего троса может быть подсчитана
путем сложения длин отдельных от-
резков ломаной линии, образуемой
тросом в нагруженном состоянии.
Длина каждого такого отрезка (см.
рис. 7.12, а)
(7.73)
Провес поперечного несущего
троса под каждой из нагрузок
У1 --Mt/Иа, (7.74)
где Mi —момент от вертикальных сил,
действующих в точке приложе-
ния нагрузки О;.
Площадь сечения струн между
поперечным несущим и верхним фик-
сирующим тросами рассчитывают ис-
ходя из той нагрузки, которая пере-
Рис. 7.13. Схема, поясняющая оп-
ределение величины /п mar
205
дается через данную струну. При биметаллических сталемедных
струнах их диаметр принимают не менее 6 мм.
Для ускорения расчетов при большом числе нагрузок может быть
применен приближенный способ определения натяжения поперечного
несущего троса. С целью уменьшения погрешности, получаемой при
использовании приближенного расчета, расчетное число нагрузок нуж-
но установить, расположив действительные нагрузки следующим об-
разом. Нагрузки, находящиеся друг от друга на расстояниях, боль-
ших половины средней ширины междупутья между электрифициро-
ванными путями, принимают за основные и никуда не перемещают.
Нагрузки, расположенные от основных на расстояниях, меньших по-
ловины средней ширины междупутья, смещают в сторону ближайших
основных нагрузок и учитывают совместно с основными. Если рассто-
яния между нагрузками превышают в 1,5 раза и более среднюю шири-
ну междупутья, то на этих расстояниях располагают соответствующее
число условных нагрузок, которые в последующих расчетах принима-
ют равными нулю.
Вертикальные составляющие опорных реакций определяют как:
п'
п
V^-G— + > (Gi-G)K/-
I 1
V.^G (n-n')-k 2
i = l
(7.75)
(7.70)
где n — число расчетных нагрузок (включая условные);
G — значение нагрузки, принятое за эталон;
п' — число нагрузок, отличающихся от принятой за эталон;
i — номер нагрузки, отличающейся от эталонной, отсчитываемый от той
опоры, для которой определяется опорная реакция;
к'. — коэффициент, учитывающий место расположения нагрузки G;.
В качестве эталонной следует принимать одну из тех нагрузок, чис-
ло которых составляет большинство для данной гибкой поперечины.
Коэффициент Kt (табл. 7.4) может быть определен по формуле
К; - 1 —(7(п4-1). (7.77)
Определение горизонтальной составляющей натяжения попереч-
ного несущего троса производят исходя из приведенного расстояния
а между нагрузками
где 1а — длина поперечного пролета;
Ьг и bn+i — расстояние между крайними нагрузками и опорами (см. рис.
7.12, а);
п — то же, что и в формуле (7.75).
206
Таблица 7.4
к Коэффициент при числе нагрузок п
Номер 1 нагруз» 7 8 9 10 1 1 12 13 14 1 5 16 17 1 8
1 0,88 0,89 0,90 0,91 0.92 0,92 0,93 0,93 0.94 0.94 0,95 0,95
о 0,75 0,78 0,80 0,82 0,83 0.84 0,86 0,87 0,88 0,88 0,89 0,90
3 0,63 0,67 0,70 0,73 0,75 0,77 0,79 0,80 0,81 0,82 0,83 0,84
4 0.50 0.56 0,60 0,64 0,67 0,69 0,71 0,73 0,75 0,76 0,78 0,79
5 0,37 0,44 0,50 0,55 0.58 0,62 0,64 0.67 0,69 0.71 0 72 0,74
б 0,25 0,33 0,40 0,45 0,50 0,54 0,57 0.60 0,63 0.65 0,67 0,68
7 0. 0,22 0,30 0.36 0,42 0,46 0,50 0,53 0.56 0,59 0,61 0,63
8 —- 0,11 0,20 0,27 0,33 0,38 0,43 0,47 0.50 0,53 0,55 0,58
9 — — 0,10 0,18 0.25 0,31 0.36 0,40 0,44 0,47 0,50 0,53
10 — — — 0,09 0,17 0,23 0,29 0,33 0.37 0,41 0,45 0,47
11 — — — — 0,08 0,16 0,21 0,27 0,31 0,35 0,39 0,42
12 ... — — 0,08 0.14 0,20 0,25 0,29 0,33 0,37
13 — — — — 0.07 0,13 0,19 0,24 0.28 0,32
14 — -- — 0.07 0, 12 0,18 0,22 0,26
15 16 0,06 0,12 0,06 0.17 •(), 11 0.21 0.16
17 — ... — — — — - 0,05 0,10
18 — .... — — --- 0.05
Горизонтальная составляющая натяжения поперечного несущего
троса
1 де и ь'2 — коэффициенты;
t номер нагрузки, отсчитываемый от левой опоры;
пх - число нагрузок, которые отличаются от эталонной и расположе-
ны между левой опорой и местом нахождения Д, шах;
/ номер нагрузки, отсчитываемый от правой опоры;
zz.j — число нагрузок, которые отличаются от эталонной и расположены
между правой опорой и местом нахождения /цтах-
Значения коэффициентов с} и с2 определяют по формулам:
-----п (п-I 1)/4—тп/‘2 — с; (7.ЙО)
с- =0,5 -|- т/(п-\-1), (7.81)
где т — число пролетов между нагрузками, па которые смешена точка с /’umux
от средней нагрузки при нечетном п или от середины расстояния между
средними нагрузками при четном п;
с — сумма ряда простых чисел, число членов которого равноО,5 (n- 11 - т
Место нахождения /п тах определяют так, как изложено выше
(см. рис. 7.12, б).
Формула (7.80) для определения ct при четном числе нагрузок спра-
ведлива только для значений т, равных 0,5; 1,5; 2,5 и т. д. Если при
четном числе нагрузок т - 0. то коэффициент q имеет то же значение.
207
Таблица 7.5
Значения коэффициента Ci при числе нагрузок п
ЧП 7 8 9 10 11 12 13 14 15 16 1 7 18
0 8,0 10,0 12,5 15,0 18,0 21 ,0 24,5 28,0 32,0 36,0 40,5 45,0
0,5 — 10,0 — 15,0 '— 21,0 — 28,0 — 36,0 45,0
1 7,5 — 12,0 — 17,5 — 24,0 — 31,5 . 40,0
1,5 — 9,0 — 14,0 20.0 — 27,0 — 35,0 — 44,0
2 6,0 — 10,5 — 16,0 — 22,5 — 30,0 — 38,5 —,
2,5 — 7,0 — 12,0 — 18,0 — 25,0 — 33,0 — 42,0
3 3,5 — 8,0 — 13,5 — 20,0 — 27,5 — 36,0 —
3,5 — 4,0 — 9,0 — 15,0 — 22,0 — 30,0 — 39,0
4 — — 4,5 — 10,0 — 16.5 — 24,0 — 32.5 —-
4,5 — — — 5,0 — 11,0 — 18,0 — 26,0 . 35,0
5 — — — — 5,5 — 12,0 — 19,5 — 28,0 —
5,5 — — —. — — 6,0 — 13,0 — 21,0 — 30,0
6 —. — — — - — 6,5 — 14,0 — 22,5 —
6,5 — — — — 7,0 — 15,0 — 24,0
7 — — — — — — — 7,5 — 16,0 —
Таблица 7.6-
Значения коэффициента с2 при числе нагрузок п
HI 7 к 9 10 11 12 13 11 15 16 17 18
0 0,50 0,50 0,50 0,50 0.50 0,50 0,50 0,50 0,50 0,50 0,50 0,50
0,5 — 0,55 — 0,54 — 0,54 — 0,53 — 0,53 — 0,53
1 0,63 —_ 0,60 — 0,58 — 0,57 — 0,56 0,55 —
1,5 — 0,67 — 0,64 — 0,62 — 0,60 — 0,59 — 0,58
2 0,75 — 0,70 — 0,67 — 0.64 — 0,63 — 0,61
2,5 0,78 -— 0,73 0,69 — 0,67 — 0,65 — 0,63
3 0,87 — 0,80 — 0,75 0,71 — 0,69 —. 0,67 —
3.5 — 0,89 ' 1 0,82 — 0,77 — 0,73 — 0,71 — 0,68
4 — — 0,90 — 0,83 —. 0,79 — 0,75 — 0,72 —
4,5 — — — 0,91 — 0,85 0,80 — 0,77 — 0,74
5 -— — — — 0,92 — 0,86 — 0,81 — 0,78 —
5,5 — — — — 0,92 0,87 — 0,82 — 0,79
6 — — — 0,93 — 0,87 — 0,83 --—.
6,5 — — — — — — 0,93 — 0,88 — 0,84
7 — — — — — — - - — 0,94 — 0,89 —
что и при т - 0,5. Значения коэффициентов Cj и с2 для различного
числа нагрузок приведены в табл. 7.5 и 7.6.
В тех случаях, когда точка, в которой стрела провеса поперечного
несущего троса максимальна fa max, находится под средней (средними}
нагрузкой (т - 0), имеем
Г п '
Яп = 7-2— Gci + 0,5 V (Gj-G)/
/ п max I
(7.82)
208
где / — номер нагрузки, отличающейся от принятой за эталонную, отсчиты-
ваемый от той опоры, к которой эта нагрузка ближе.
Пользоваться приближенным способом расчета целесообразно при
числе нагрузок более шести, но в отдельных случаях он может дать
неточность до 3 %. Чем больше число действительных нагрузок, тем
меньше получаемая погрешность.
При ориентировочных расчетах горизонтальную составляющую на-
тяжения поперечного несущего троса допустимо определять по форму-
ле (7.82) независимо от места нахождения /п тах. Точность расчета
при смещении /п тах от средней нагрузки меньше, чем при пользова-
нии формулой (7.79), но при большом числе нагрузок она вполне при-
емлема.
Расчет фиксирующих тросов. Определение необходимой площади
поперечного сечения фиксирующего троса 5ф или проверку прочности
при заранее выбранной площади сечения производят исходя из макси-
мального усилия в тросе Нф тах
>//ф max/l^pl (7.83)
или
Нф >п а \ 7/ф р /л. (7.84)
где //фР - разрывное усилие для данного провода.
Максимальным усилие Нф 1Пах может быть в одном из следующих
режимов работы фиксирующих тросов: при минимальной температуре,
гололеде с ветром или ветре максимальной интенсивности.
Ввиду незначительных стрел провеса фиксирующих тросов при рас-
чете их влияние не учитывают. Для уменьшения изменений натяже-
ния фиксирующего троса в зависимости от изменений температуры
внешней среды в наиболее ослабленное звено троса рекомендуется
включать пружинный компенсатор.
В расчетной схеме рис. 7.12, в направление внешних горизонталь-
ных нагрузок принято условно. В конкретных условиях каждое из го-
ризонтальных усилий, кроме ветровых, учитывают в соответствии с его
действительным направлением. Направление усилий от воздействия
ветра следует принимать такое, при котором создаются наиболее не-
благоприятные условия работы фиксирующего троса.
Натяжение троса в наиболее нагруженном звене при данном режи-
ме работы
Яф + V Pi, (7 85)
i -1
где Нф — натяжение троса в наиболее ослабленном звене;
п и i - соответственно число и номер горизонтальных нагрузок.
Натяжение фиксирующего троса в наиболее ослабленном звене
Нф для режима, характеризуемого величинами с индексом х, при на-
209
личии компенсатора с достаточной точностью можно определить
как
0,5 / У Рц— У Ptx j -! «<ь £ф Зф ulnax — tx)
flmin1П 6£ф S,J, ’
где Hmin — минимальное допускаемое натяжение в наиболее ослаблен-
ном звене при режиме максимальной температуры (обычно
принимается равным 100 даН);
/г' — расстояние между точками закрепления фиксирующего тро-
са на опорах;
Хф и £ф —температурный коэффициент линейного расширении и модуль
упругости материала троса;
6 - гибкость пружины компенсатора, м/даН:
/И1а,, - максимальная расчетная температура;
1Х - температура, соответствующая расчетному режиму;
/’;1 и l''ix — внешние горизонтальные усилия соответственно при режиме
максимальной температуры и при расчетном режиме.
Если компенсаторов в фиксирующих тросах нет, натяжения тро-
сов необходимо определять с учетом изменений „погибов опор. При
этом в наиболее ослабленном звене троса
яфл- i Ям ) ! Яф£ф Зф (/„,ах /., ) -
' •’ 1 i i /
! /-'ф ^‘ф (7[- (7,87)
где у, - сумма прогибов обеих опор на уровне крепления рассчитываемого
фиксирующего троса при максимальной температуре, м;
Yv — то же при расчетном режиме.
Прогибы некоторых металлических опор проекта 1973 г., подсчи-
танные для единичной силы, равной 10(.) даН, приведены в табл. 7.7
(прогибы железобетонных опор рассмотрены в § 6.5). В тех случаях,
когда опоры, па которых закреплены фиксирующие тросы, имеют от-
тяжки или нагружены с обеих сторон примерно одинаково, изменение
прогибов этих опор можно не учитывать. Если же нагрузки с обеих
сторон опоры ре.зко неравномерны, то отказываться от учета влияния
прогиба опоры не следует.
Для фиксирующих тросов без компенсаторов, закрепленных па
опорах, прогибы которых не учитывают, усилие в ослабленном звене
/7фх /;min '°,5( 2 «ф£фЗф (/,„.)Х —/х). (?.««)
\ i 1 11
Поскольку формулы (7.86) — (7.88) являются приближенными, в
отдельных случаях величины Н^ф, определяемые по ним, могут полу-
читься отрицательными, что в реальных условиях невозможно. Такой
результат означает, что натяжение в ослабленном звене фиксирующе-
го троса снижается почти до нуля, и, следовательно, натяжение Нф в
210
Т а б л и ц а 7.7
Место приложения СИЛЫ Прогиб на уровне Прогиб, мм, опор типа
35 мн--—' 1ф ?. | 65 I мн-ДГ 65 МН-— 10 5 1 1 150 45 — 25 м_—— 7k ‘Д
В вершине опоры Приложения силы (15 или 20 м) 6.73 4,25 3,12 5,79 3, К) 2.28 2,75 1 .95
То же Между фикси- рующими троса- ми (8,7 м) 1.98 1,31 1.12 0.99 0,57 0.41 0.75 0,61
Между фиксиру- ющими тросами Приложения силы (8,7 м) 0,93 0.59 0,44 0,32 0, 18 0, 12 0,33 0,27
Примем фиксирующими а и и е. Прогибы на уровне вершины опоры от силы, приложенной между тросами, определяют по среденй строке таблицы.
наиболее нагруженном звене будет определяться только суммой всех
внешних горизонтальных сил, действующих на трос.
Расчеты фиксирующих тросов жестких и фиксирующих поперечин
приведены в § 7.6.
Пример. 3 а д а и и е и и с х о д и ы с д а и и ы е. Выполнить расчет
гибкой поперечины, закрепленной на металлических опорах высотой 15 м. План
путей, перекрываемых поперечиной, показан на рис. 7.14, где / и II — сланные
пути, нал которыми расположены компенсированные подвески М-120 [-2МФ-
100, 3—8 станционные пути, над которыми находятся щ>лукомпепсирован-
ные подвески ПБСМ-70 | МФ-85. Пути 7 и 8 расположены па кривой радиу-
сом 1000 м; над путем 6 фиксируется воздушная стрела для стрелочного пере-
вода е маркой крестовины 1/Ц. Станция расположена в гололедном районе
II и в защищенной от ветра местности ветрового района Ill. Минимальная
температура в районе 35 'С, максимальная '-40 "С. Длина продольного
пролета 65 м.
Р е in е н и с. Расчет выполним применительно к гибкой поперечине с по-
перечным несущим тросом из двух проводов ПБСМ-70 и фиксирующими троса-
ми из провода ПБСМ-50 каждый. Расчетное направление ветра примем совпада-
ющим е направлением усилий, вызванных кривизной путей 7 и 8. т. е. от опоры
А к опоре Б.
Для заданного расчета необходимо иметь вертикальные и горизонтальные
нормативные нагрузки в четырех расчетных режимах: гололед с ветром, макси-
мальный ветер, минимальная и максимальная температуры. Определение таких
Рис. 7.14 План расположения путей под гибкой поперечиной
211
Таблица 7.8
Путь Вертикальные нагрузки, даН. при гололеде Горизонтальные нагрузки. даН, при режиме
гололеда с ветром максималь- ного ветра минималь- ной темпе- ратуры максималь- ной темпе- ратуры
/ и !/ 320 60/55 60/75 -/ /
3, 4 н 5 200 55/40 50/50 / - -/-
6 350 25/-10 10/20 145/—80 75/ 80
7 н 8 200 145/90 120/105 105/55 55/55
нагрузок рассматривалось и примерах гл. 2 и др.; поэтому, опуская подробные
вычисления, вес нужные для расчета нагрузки приводим в табл. 7.8. В числителе
указаны горизонтальные нагрузки от несущих тросов, в знаменателе — от кон-
тактных проводов. Знаки «—» перед цифрой соответствуют силам, направление
которых обратно принятому расчетному направлению ветра.
Р а с ч е т н о п е р е ч н о г о н е с у щ е г о т р о с а. Составляем
расчетную схему, показанную на рис. 7.15, а. Вертикальную реакцию на опоре
/> определим по формуле (7.68):
Vti |320 (9,1 1 14,4)-(-200 (3,1 - 5,1 -j 20,7 | 31,()-( 36,0) |
350-25,71: 40 892 даН ,
вертикальную реакцию на опоре А - по формуле (7.69)
VA 320-2 |-200-5 j 350 — 892 1098даН.
Примем следующие размеры (см. рис. 7.13): 0,5 м; hK 6,6 м; Ло
2 м: 0,6 м; 0,3 м; h:l 0. По формуле (7.71) определим максималь-
ную стрелу провеса поперечного несущего троса:
/птах 15—(0,5 1 6,6 1-2,0 |-0,6-1-0,3) 5>40.10м.
Установив, что максимальный момент от вертикальных сил действует над
путем 5 (см. рис. 7.14), определим горизонтальную составляющую натяжения
поперечного несущего троса но формуле (7.70)
//„ |1098-20.7 — 20()(17.6-| 15,6) — 320 (11 ,(> 1 6,3)]:5 2072даН.
Максимальное натяжение поперечного несущего троса (у опоры Л) опреде-
лим по формуле (7.67)
'/'птах 1/I098--: | 2072“ - 2345 даН .
Напряжение в поперечном несущем тросе о„ 23450:(2-72,2• 10-“) 163
МНа, что ниже допускаемого нормами.
Повторим произведенный расчет упрощенным способом. Для этого совме-
стим нагрузки путей 3 и 4 в одну, расположенную над путем 4, и составим рас-
четную схему, показанную на рис. 7.15, б. За эталонные примем нагрузки 4, 6 и
7, равные 200 даН.
Но формуле (7.75), определив коэффициент к, ио табл. 7.4, вычислим
200-7:2 ) 200-0.88 , 120 (0,75 1 0,63) ( 150-0,37 1097 даН.
212
Приведенное расстояние между нагрузками определим по формуле (7.78)
Поскольку величина т == 0, горизонтальная составляющая натяжения по-
перечного несущего троса определится по формуле (7.82). Для п 7 и т - О
по табл. 7.5 коэффициент q -- 8; тогда
Ца - 4,64 [200-8 [-0,5 (200-1 ( 120-2 |• 120-3-[- 150-3)1: 5 2065 даН.
Полное максимальное натяжение поперечного несущего троса ио формуле
(7.67):
Sninax V 1097« । 20658 |2338даН.
Как видно, полученные в приближенном расчете ошибки незначительным
Расчет верхнего фиксирующего т р о с а. Составим
расчетную схему (рис. 7.15, в). Задаваясь минимальным натяжением троса нрн
максимальной температуре, равным 100 даН, найдем натяжения в наиболее ос
лабленном звене троса при других режимах по формуле (7.88) без учета про-
гибов опор. Характеристики троса принимаем по данным табл. 1.7.
При гололеде с ветром (1Г — 5 ’С)
7/ф( 100 0,5 (35 - 550)-: 1:1,3-К)-"-17 160-49,5 (40 ; 5) 352 да11.
При максимальном ветре (/в - - 5 "С)
Рис. 7.15. Расчетные схемы для поперечного несущего (а, б) и фиксирующего
(в) тросов
213
При минимальной температуре — — 35 °C)
Н’ 100н 0,5 (35—65)4 11,3 (40-4-35) 933 даН,
‘r'min
Натяжения в наиболее нагруженном звене троса определим по формуле
(7.85):
при гололеде е ветром Н$г 352-;-550-902 даН;
при максимальном ветре 7/фВ 377-1 500 — 877 даН;
при минимальной температуре 77ф/1П)п — 933-1 65— 998 даН.
Проверку фиксирующего троса на прочность выполним по наибольшему из
полученных натяжений
Оф (9980/49,5) 10—®--- 202 МПа ,
что чиже допускаемого.
Таким образом, при проверке нет необходимости учитывать прогибы опоры,
так как усилия будут меньше полученных. Если же натяжения фиксирующих
тросов необходимо знать для подбора типовых опор, то следует учитывать про-
гибы опор, иначе получаемые натяжения будут завышены, что приведет к выбору
более мощных опор, чем это необходимо. Например, если принять разность про-
гибов обеих опор на уровне между креплениями фиксирующих тросов в режимах
максимальной температуры и гололеда с ветром в размере 12 мм, то по форму-
ле (7.87)
//ф, 100 ’ 0.5 (35—-550) , 11.3(40 ; 5)-| 17 160-49,5 (- 0,012)/42 108 даН;
//ф1. 108-1550.. 658 даН.
Р а с ч с т н и ж н е го фиксирую щ его троса. Этот расчет
не приводим, так как он аналогичен расчету верхнею фиксирующего троса (раз-
личие только в значениях нагрузок).
§ 7.5. Расчеты фиксаторов и фиксирующих поперечин
Расчеты фиксаторов. Геометрические размеры
фиксаторов и поддерживающих их элементов определяют в за-
висимости от назначения фиксаторов и мест их установки исходя из
следующих основных соображений.
Для уменьшения воздействия на натяжение контактного провода
шарнирная длина фиксаторов (расстояние от оси штифта фиксирую-
щего зажима до точки шарнирного крепления фиксатора) при полуком-
пенсированных цепных подвесках должна не менее чем в 3 раза пре-
вышать возможные перемещения провода вдоль железнодорожного
пути. В указанных подвесках шарнирная длина дополнительного
фиксатора установлена равной 1.2 м, Такая же длина принята и в ком-
пенсированных подвесках.
Форму фиксатора выбирают с учетом его максимального возмож-
ного подъема при изменениях температуры и под воздействием токо-
приемника. Уклон фиксатора в сторону провода (определяется по ли-
нии, соединяющей точку шарнирного крепления фиксатора с точкой
крепления на нем контактного провода) не должен превышать 0,2 при
гемпературе, соответствующей беспровесному положению контактного
провода.
214
Передняя грань опоры нп
I уровне головок рельсов
Рис. 7.16. Расчетные схемы для определения геометрических размеров фиксато
ров- сочлененного прямого (а), сочлененного обратного (б) и одиночного ("<;) на
прямых участках пути
Рис 7.17, Расчетные схемы для определения геометрических размеров фикса го
ров одиночного (а) и сочлененного обратного (б) на кривых участках пути-
/ ось пути; 2 ось токоприемника
Рис. 7.18. Схемы расположения нагрузок для расчета .прямых фиксаторов оди
ночного (а) и сочлененного (б)
Рис. 7 19. Схема расположения на-
грузок для расчета обратного сочле-
ненного фиксатора
2)5
Рассмотрим несколько случаев определения длины фиксатора и его
элементов. Длину основных стержней сочлененных фиксаторов, кото-
рые закреплены на опорах, установленных на прямых участках пути,
определяют по формулам:
при зигзаге к опоре (рис. 7.16, а)
Ln Г \ т"-В-с1-1.ф Н: (7.К9)
при зигзаге от опоры (рис. 7.16, б)
1.и Г-\-т"В-\-а \-L^+d, (7.90)
|де пГ — размер, обусловленный сбегом и уклоном опоры на высоте крепления
фиксаторного кронштейна;
В — расстояние от грани опоры до точки шарнирного крепления фикса-
тора;
d — размер, выбираемый по конструктивным соображениям;
7ф — принятая шарнирная длина дополнительного фиксатора.
Шарнирная длина одиночных прямых фиксаторов, закрепленных
на опорах, которые установлены на прямых участках (рис. 7.16, в).
/.ф Г\-т" — В + а. (7.91)
При закреплении одиночного прямого фиксатора на подкосе на-
клонной консоли, установленной с внешней стороны кривой
(рис. 7.17, а), значениях т' и с’т тех же, что и в § 7.2, его длина
/.ф Г-\-т'— В — а ст. (7 92)
Расстояние от оси шарнира поддерживающего элемента обратного
фиксатора до оси шарнира фиксатора Lu в случае его закрепления на
опоре, установленной с внутренней стороны кривой (рис. 7.17, б).
/-и Г-\ т' — В ! и—ст--|-Дф. (7.93)
Крепление основного фиксатора к несущему тросу цепной подвес-
ки осуществляют двумя наклонными поддерживающими струнами или
жесткими распорками. При расчете фиксатора считают, что оба его
конца закреплены шарнирно и находятся в состоянии равновесия при
действии всех внешних сил. Сила G, указанная на рис. 7.18 и 7.19, -
это результирующее вертикальное усилие, установившееся в со-
стоянии равновесия и препятствующее дальнейшему подъему фиксато-
ра. Оно зависит от горизонтальной силы Р, веса поддерживаемого
фиксатором участка контактного провода и положения фиксатора.
Расчет растянутых фиксаторов заключается
или в проверке выбранного сортамента на совместное действие изги-
ба и растяжения, или в подборе необходимого сортамента по мини-
мальному моменту сопротивления в ослабленном нарезкой или отвер-
стиями сечении с. последующей проверкой на совместное действие из-
гиба и растяжения. Для растянутого фиксатора, схема которого приве-
дена на рис. 7.18, а, приближенно учитывая влияние его веса, который
216
41
условно принимается сосредоточенным, проверку можно произвести
по условию
И>1 + О,256ФДФ (7 94)
mlV'nT ffiF11T
где Р — наибольшая возможная в эксплуатации растягивающая сила;
6’ф — нагрузка от веса фиксатора с учетом (в необходимых слу-
чаях) веса гололеда;
^нт — соответственно момент сопротивления и площадь попереч-
ного сечения фиксатора с учетом ослабления сечения;
ft] • наибольшее расстояние от линии ОА до оси фиксатора.
Здесь и ниже силу, действующую вдоль фиксатора, можно прини-
мать равной внешней силе Р, пренебрегая небольшим углом между
направлениями действия сил. (Погрешность, получаемая при этом
допущении, не превышает 2 %.)
Для растянутого основного фиксатора (рис. 7.18, б), принимая те
же допущения, что и раньше, и не учитывая незначительный момент
от вертикальной силы G, приложенной в точке С, проверку в точке А
производят по условию
РЬ -г (),25С<ь L Р-р Pt
----1-----2— j !—-^R, (7 95)
mWUT mFHf
где Pi —- горизонтальная составляющая натяжения //,. в поддерживающих
струнах:
Р, 0,5 (Сф : G)/tga. (7.96)
Натяжение определяют по формуле
//с 0,5 (6’ф j 6’),.sin а. (7.97)
Расчеты сжатых элементов обратных со-
члененных фиксаторов заключаются в проверке выб-
ранного сортамента на изгиб и сжатие и по условиям устойчивости.
При X < 200 расчет производят аналогично изложенному выше для
однопутных консолей. В этом случае для фиксатора но схеме рис. 7.19
проверку на прочность следует производить по изгибающему моменту
в точке А с учетом сжимающей силы
Здесь
Pb-PGa
rnWur
Pb - Ga
L
etga.
(7.98)
(7.99)
Проверка на устойчивость основного фиксатора, выполненного по
схеме рис. 7.19, должна производиться на длине ОА с учетом дефор-
мации проверяемого элемента.
По ВСН 141-84 максимальная гибкость сжато-изогнутых стержней
фиксаторов должна быть не более 550, а коэффициент устойчивости
при этом (см. § 7.2) - не менее 2. Расчеты на прочность и устойчи-
вость фиксаторных стержней с гибкостью более 200 следует произво-
217
дить так же, как при расчетах консолей. Для дополнительных фикса-
торов из алюминиевых сплавов эти расчеты выполняют при гибкости
более 150.
Влияние собственного веса фиксатора бф при проверке на устой-
чивость можно не учитывать, так как эта нагрузка облегчает условия
работы сжатого участка основного фиксатора, что в некоторой степе-
ни компенсирует влияние не учитываемой в расчете начальной кри-
визны фиксатора, которая может ухудшить эти условия работы. Натя-
жения в поддерживающих струнах (см. рис. 7.19)
Нс Р}/со&а. (7.100)
Если поддерживающие элементы обратных сочлененных фиксато-
ров выполняют из двух швеллеров или неравнополочных уголков, то
выбор расстояния между ними и между скрепляющими планками про-
изводят так же, как при расчете однопутных консолей.
В расчетах сочлененных фиксаторов нужно проверять значение
внешней нагрузки Р при ветре максимальной интенсивности, дейст-
вующем встречно по отношению к расчетному направлению сил. Если
при этом сила Р становится отрицательной, то обычно растянутые
стержни надо проверить на устойчивость и предусмотреть дополни-
тельное крепление фиксагоров.
Сочлененные фиксаторы в необходимых случаях должны иметь ог-
раничительные упоры на стойках, а при компенсированных подвес-
ках ограничительные струны. Устройства от опрокидывания сле-
дует применять при одном контактном проводе всегда, а при двух про-
водах МФ-100 (или одном МФ-150)—в открытых местах. При ограничи-
тельных струнах длину основных прямых фиксаторов увеличивают по
сравнению с определяемой выражением (7.89). На прямых участках
пути, в кривых радиусом более 500 м, во всех поймах рек, на насыпях
высотой более 5 м от поверхности земли или деревьев, а также в местах
возможных автоколебаний проводов вместо поддерживающих струн ус-
танавливают жесткие распорки между основным фиксатором и несу-
щим тросом. Эти распорки выполняют из труб с внутренним диаметром
15 мм или из уголков 32>'32> 4 (табл. 7.9). Последние не применяют в
местах, где возникают колебания проводов и на насыпях высотой 10 м и
более.
Т а б л и ц а 7.9
Конструктив- ная высота подвески, мм Длина рас порки, мм Распорки из труб Распорки из уголков
Обозначение Масса, кг Обозначение Масса, кг
1400 1700 1800 Т-1 2.3 У-1 3,6
1701-2100 2100 т-п 2,7 У-11 4,1
2101 -2400 2400 Т-111 3,1 У-111 4,7
2401 2600 2600 T-IV 3,4 У-IV 5,1
218
При расчетах фиксаторных кронштейнов следует учитывать воз-
можность обрыва несущего троса, для чего нужно принимать верти-
кальную нагрузку, приложенную в точке крепления фиксатора, рав-
ной весу контактных проводов в пролете наибольшей длины.
Расчеты фиксаторов по второму предельному состоянию произво-
дят, определяя перемещения основного и дополнительного стержней
под воздействием внешних нагрузок и нажатия токоприемника.
Расчет тросов фиксирующих поперечин. Задачи этих расчетов те
же, что и расчетов фиксирующих тросов гибких поперечин (см. § 7.4).
Если фиксирующая поперечина находится недалеко от несущих опор,
то в ней обычно монтируют два фиксирующих троса: один - для фик-
сации положений несущих тросов контактных подвесок, другой --
контактных проводов. В этом случае каждый из фиксирующих тросов
может быть рассчитан аналогично одноименному тросу гибкой попере-
чины. При установке фиксирующих опор в средней части пролета, как
правило, монтируют один фиксирующий трос -- общий для несущих
тросов и контактных проводов. Расчет общего троса может быть выпол-
нен аналогично расчету нижнего фиксирующего троса гибкой попере-
чины или с учетом жесткости железобетонных стоек по материалам
§7.6.
§ 7.6. Особые случаи расчетов поддерживающих
и фиксирующих устройств
Определение перемещений элементов опорных узлов контактных
подвесок. Для определения размеров консолей, фиксаторов и других
деталей, а также перемещений узлов контактной подвески при измене-
нии нагрузок необходимо знать взаимное расположение этих узлов в
конкретных условиях установки опор. Решение такой задачи затруд-
няется неопределенностью расположения подвесной гирлянды изоля-
торов. В отличие от подобной гирлянды воздушных линий на гирлянду
для подвешивания несущего троса дополнительно действуют усилия
от контактного провода, передающиеся через фиксаторы. Взаимное
узлов контактной подвески определяется системой
расположение
уравнений:
щ <р. -
tga -
р __р 4
Gi + V'c -i-O.SG; ’ “т “г— S1П ф:
йп + h + Ли cos <р /г,-, cos а
Чп + чг— Ап sin а
«к -=чп — (Лц+Лк -(-Лфсова) ctg а—Лф sin а;
, „ Рк (+ Лк ± Леф cos Р) ± (Ск-!-0,5Сфд) Чд
Рк (Чк ~F чд -f- Лсф s i n Р)
219
яф Нк 4* йд 4- Лсф sin 0 i Пр cos 0;
Л1ф б'и ыи-|-Офос «фос + Сц ик4"6фд (ак -+- 0,5«д) -}- Осф X
X («,: + «д Т 0,5ЛСф sin 0) =Г- Рк hK;
р -^Иф ( Г оф Т ок —«т)
«ф \ h— hr. + (<?к + от) tg 0]
V Л1ф (h~-hK + “Ф tgft)
Оф [h — hK 4- (uK 4- лт) tg 0]
где (J, - нагрузка от веса пролета ценной подвески;
О’фое нагрузка от веса основного фиксатора без учета веса фиксатор-
ного изолятора би;
б,;,д — нагрузка от веса дополнительного фиксатора;
бсф - нагрузка от веса фиксаторной стойки;
Оц нагрузка от веса фиксирующего зажима и половины веса контакт-
ных проводов на участке между ближайшими к фиксатору стру-
нами;
/ф и 1ф соответственно горизонтальная и вертикальная составляющие
натяжения струн, передающих нагрузку от фиксатора на несущий
трос.
Остальные обозначения величин, входящих в систему уравнений
(7.101), показаны на рнс. 7.20.
При расчете угла наклона основного фиксатора принято, что ре-
гулировка фиксатора выполнена таким образом, что шарнир дополни-
тельного фиксатора поднят над уровнем контактного провода на высо-
ту, при которой с учетом действия горизонтальной нагрузки Рк фик-
сатор воспринимает полностью усилия СфЛ и Сн. Верхние знаки в урав-
нениях (7.101) относятся к узлам с прямым фиксатором, нижние
к узлам с обратным фиксатором.
Для узлов подвески с гибким фиксатором следует использовать си-
стему (7.101) со знаками, относящимися к узлам с прямым фиксато-
ром. В этом случае ввиду отсутствия основного фиксатора и фиксатор-
ной стойки значения Оф0с. и /гсф нужно принять равными нулю.
Кроме того, так как струны, передающие нагрузку от фиксатора па не-
сущий трос, прикреплены непосредственно к фиксаторному изолято-
ру, шестое уравнение системы (7.101) надо заменить на -с cos 0.
где а известное расстояние от шарнира фиксатора до места креп-
ления струн (изоляторное звено). Для узлов с гибким фиксатором угол
0 получается отрицательным, что соответствует фактическому положе-
нию узла с гибким фиксатором.
Обычно при определении размеров консолей и фиксаторов раз-
меры бугеля Лб и детали крепления фиксатора Лф известны. Неизвест-
ны момент Л4ф, силы Рк и Ус, размеры ат (или аг), ак, аф, углы ср. а и
0. Если точка крепления гирлянды на бугеле должна быть отнесена от
оси пути, то av известно, но в этом случае неизвестно ат. Если же от-
носить гирлянду от оси пути не требуется, то задано ат, определяю-
220
Щее положение несущего троса по отношению к контактному проводу
в плане, а аг неизвестно.
Систему уравнений (7.101) нужно решать методом последователь-
ных приближений. Исходя из того, что натяжение в струнах, прикре-
пляющих фиксатор к несущему тросу, является второстепенным фак-
тором для положения гирлянды изоляторов, можно определять угол
Рт
<р ее наклона без учета влияния фиксатора: ср - arctg ~ Най-
дя значение ср, которое рассматривают как первое приближение,
решают систему (7.101). Проще всего это выполняется в той последо-
вательности, в которой уравнения записаны в системе. Получив силы
и Гс, можно из первого уравнения системы определить значение уг-
ла ср, являющееся вторым приближением. Обычно оно не нуждается в
дальнейшем уточнении, по при необходимости можно получить третье
приближение и т.д. Влияние прямого и гибкого фиксаторов па положе-
ние гирлянды изоляторов существенно меньше, чем обратного фикса-
тора, поэтому второе приближение угла ср, как правило, является окон-
чательным.
Поскольку конструктивные размеры подвески и установочные раз-
меры фиксаторов обычно относятся к беспровесному положению кон-
тактного провода, все нагрузки следует определять для этого режима.
Если нужно найти расположение узлов при добавочных нагрузках
(например, приближение подвесных изоляторов и деталей подвески не-
сущего троса к заземленной консоли при максимальном ветре или при
гололеде с ветром), то поступают следующим образом. Сначала реша-
ют систему уравнений (7.101), как изложено выше, и получают дли-
ну консоли и ее положение (угол ос), а также длину фиксатора, кото-
рые при переходе к режиму добавочных нагрузок не изменяются. Не
изменится также длина струп, передающих нагрузку от фиксатора на
Рис. 7.20. Расчетные схемы для определения отклонений гирлянды подвесных изо-
ляторов при обратном (а) и прямом (б) сочлененных фиксаторах
221
несущий трос. Затем решают следующую систему уравнений, опреде-
ляющую положение узлов в режиме добавочных нагрузок:
'‘КВ Ф* ^И0'"'Лкв« ^КО" ‘^КВт
^КГ "ISO. "ГЛ* "го rt ЛК1< "’!’х "ГЛ''—SH1 фх:
cos р,-
"<t>.v "фс —:
( ; «Ф,- ± ••>;< "та-)2-! (Л-—-/»Кл =F Офл tg ₽.,.)«
1 Т "Фо ! "р»—"то)‘е(Й йцо -₽ "фо tg Ро)“;
"i.a I + "c Icos Px ± "сФ sm P> rt Яд:
\ eos px /
Л... Г 1 1 + ar 1 sin /ic,()cospx; CDS ₽,• /
Мфд Ии ‘ йфос "фосН 'бсФ ("КА "д Ч- О.БЛсф sl,! Р
• 0,5Сфд ("кд + ад) i-Pkt (^kx I Лфакл/ад);
Мфг (-i- "фд + "кх — "tt)_____
афх{Л -h^x—(±"кх — атхМёРх
v- (h — hKx T афт tgfia.) _
"ф.т ^Kx—G.t "к.х — "tx) tg Pad
PTA--Pe.v
Щ <b----------------------.
6'LS.-! vcx-i-o,5g;
л ,i>- Хф - изменение высоты шарнира дополнительною фиксатора;
\,(i, и Лкг изменения положения контактного провода соответственно но
вертикали и по горизонтали.
Остальные обозначения те же, что и в системе (7.101).
Be |ичины с индексом 0 относятся к режиму беспровесного положе-
ния контактного провода, с индексом х — к режиму добавочных на-
грузок. Знак« • » у вертикальных перемещений Лф и ДИв соответствует
перемещению вверх, знак « — » - вниз. Для горизонтального сме-
щения Л „г знак «-) » соответствует перемещению от опоры, знак «—»
к опоре (для фиксаторов любого типа). В системе (7.102) принято,
что перемещения узлов невелики, вследствие чего можно пренебречь
изменением конструктивной высоты подвески, а также горизонтальной
проекции дополнительного фиксатора. При расчете угла наклона ос-
новного фиксатора принимаем во внимание усилия, передающиеся на
него, е учетом перемещений узлов.
Система уравнений (7.102) также решается методом последователь-
ных приближений. При известном из очередного приближения значе-
нии q восьмое уравнение системы после преобразований приводится к
виду
№+Б2+Ва---Г
Sin (S— Рх) =--- -----,
2А Уб^+В'2
где угол б и остальные величины определяются уравнениями;
sin 6 = Б!УБг-j - В3’, cos 6 — Bi l/fi24- S2:
.4--- T «фо/cos p0; Б «го «ко~sin фЛ.,
В - h—hKS)-i~h„ (cos <p0—cos <рЛ);
' = i + «фо ± «ко—«го)а I —Лко-F «ф0 la !-
Определив из выражения (7.103) угол рл., можно решить все урав-
нения системы (7.102).
Расчеты консольных и фиксаторных стержневых изоляторов. Кон-
сольные и фиксаторные стержневые изоляторы находятся иод дейст-
вием сложной системы нагрузок, которые могут быть приведены к про-
дольной и поперечной силам и изгибающему моменту. Продольная и
поперечная силы несущественно влияют па напряженное сосюяпие
изолятора вследствие того, что при реальных значениях Э1их сил и гео-
метрических размеров сечения изолятора напряжения в фарфоре не-
значительны. Во многих случаях, например в изолированных консо-
лях, продольная сила является сжимающей, что облегчает работу изо-
лятора (сжимающие напряжения для фарфора .менее опасны, чем рас-
тягивающие; кроме того, сжимающие напряжения уменьшаю! растя-
гивающие, вызываемые другими силовыми факторами). Поэтому основ-
ной нагрузкой, определяющей напряженное состояние изолятора, яв-
ляется изгибающий момент. Это подтверждается результатами испы-
таний, которые показали, что разрушение фарфора стержневых изо-
ляторов происходит обычно в сечениях, где развивается наибольший
изгибающий момент.
Для изолированной консоли без подкоса (рис. 7.21, а) п шибающий
момент в опасном сечении фарфора консольного изолятора (у кромки
шапки, примыкающей к кронштейну консоли)
~ 'J’uh бф^ 1 <»,5 (L —«) cos-х (Ок , О‘„)
' 0,5 (Z. —<0 sin- а | Вк (/. - а; !• Н.л с„ «|; н ПИ)
ле G'l( — нагрузка от веса кронштейна консоли;
Оф и би — нагрузка от веса соответственно фиксатора и изолятора;
и - распределенные поверхностные нагрузки от ветра, действующие
iответственно на консоль и изолятор, с учетом аэродинамиче-
ских коэффициентов;
с,{ и сп горизонтальные размеры соответственно консоли и изолятора,
определяющие их поверхность, подверженную действию ветра.
Остальные обозначения показаны на рис. 7.21.
При расчетах в режиме гололеда все вертикальные нагрузки следу-
ет определять с учетом веса гололедных образований.
В формуле (7.104) не учтены вертикальные нагрузки от лепной под-
вески и горизонтальные от несущего троса, которые создают в нзоля-
223
торе лишь продольную силу. Не внося существенной погрешности,
можно пренебречь тем, что давление ветра на консоль и изолятор не-
одинаково, и принять Вн — Вк и си —- ск. В этом случае
М -- [Рк h !-бф d + 0,5 (L— и) cos а (G'K |
4-0,5L (L—a) BifcK sin2aj. (7. )05>
На кривых достаточно малого радиуса изгибающий момент опре-
деляется в основном силой Рк. В этих случаях можно не учитывать точ-
но вес изолятора, считая его частью веса кронштейна консоли, что
позволит еще больше упростить расчетную формулу:
М - \PKh । Оф d , U.5 (L—a) (G* cos a + Bfi cK /- sin2 a) |. (7.106)
где G{. — нагрузка от веса кронштейна консоли при длине /..
При расчете по формулам (7.104) -(7.106) все усилия следует учи-
тывать с определенными знаками. Например, знак«4-» можно прида-
вать силам, вызывающим при изгибе растяжение нижних и сжатие верх-
них волокон изолятора, а знак «—» — силам, вызывающим сжатие
нижних и растяжение верхних волокон. Приняв такое правило знаков,
вес консоли и изолятора, а также усилие от излома контактного про-
вода па внешней стороне кривой следует считать положительными, а
усилие от излома контактного провода на внутренней стороне кри-
вой отрицательным. Давление ветра на консоль и изолятор, оче-
видно. может быть и положительным и отрицательным.
Изгибающий момент на консольном изоляторе для консоли с под-
косом определяют, рассчитывая консоль как неразрезную балку на
грех шарнирных опорах (рис. 7.21, б). Если средний шарнир (точка
Рис 7 21 Расчетные схемы для изоляторов консолей без подкоса (а) и е под
косом (б)
224
крепления подкоса) находится выше места установки фиксатора на
мшсоли, то изгибающий момент на изоляторе
«г (/.
а 1 „ , Г /, — а,
-у-----L
G I L ь — и,
!Л —^)2 Г * [ ^i + u)2 (L-—н),£ \ I
• (ql; cos a j- Вк ск sin- а)---------| 1 -----------------------(------------I -|-
2 [ 4/. \ /, 1 — /|
, 2/1 —а I а (‘МЛ — а2) 1]
1 (G„cos а . «испо sin2 а) — ------------- 1 - --——---------—-1 . (7.107)
2 | 4/./|(2/]- «) j)
При расположении среднего шарнира ниже места крепления фик-
сатора расчетная формула имеет вид
/, , L — at \ |
а (
м ... — Л
Т (qK COS а ; Вк СК sin- а)----- 1 - — ---------------1 -,т----~
2 | 4/. \ /, (/1—«Н /]
(6'и cos а ) Ли си а sin2 а) —-—— II- --------------—(; (7.103)
2 L 4/./1(2/1-<0 II
Обозначения в формулах (7.107) и (7.108). а также правило зна-
ков те же, что для консолей без подкоса. Положение среднего шарнира
на рис. 7.21, б показано условно, конструктивно этот шарнир может на-
ходиться и выше и ниже точки крепления как прямого, так и обратно-
го фиксаторов. Изгибающие моменты на изоляторе консоли с подкосом
получаются значительно меньшими, чем моменты для такой же консо-
ли без подкоса. По этой причине формулы (7.107) и (7.108), не внося
заметной погрешности, упростить не удается.
Расчеты фиксаторных изоляторов выполняют в соответствии со
схемами, приведенными на рис. 7.22. Опасным является сечение фар-
фора у кромки шапки, примыкающей к основному фиксатору. Из-
гибающие моменты в этом сечении определяют по формулам:
для прямого фиксатора (рис. 7.22, а)
М ——[В,; (ci b sin fl) \-Gb ' 0.5 (/ф a) (Оф f 0и)]; (7.109)
/ф
для обратного фиксатора (рис. 7.22, б)
М-= ——[ - Р„ (С I- b sin Р) Gb 0,5 (/ф а) (<?ф + би)—
‘ф
—0,5 (Л —/ф) Оф].
(7.110)
В этих формулах G - нагрузка от веса фиксаторной стойки с уче-
том части веса дополнительных фиксаторов и контактных проводов,
передаваемого на стойку. Знаки сил нужно учитывать по правилу,
указанному для консольных изоляторов. В формулах (7.109) и (7.110)
знаки даны в соответствии с направлениями сил, приведенными на схе-
мах рис. 7.22.
я
Зак -МО
225
Рис i 22 Схемы расположения нагрузок для расчета изоляторов прямою (а > и
обратного (б) фиксаторов
Формулы для расчета изгибающих моментов на фиксаторных изо-
ляторах являются приближенными, но при 8 «с 10-.- 12" результаты
получаются достаточно точные. Стержневые изоляторы гибких фикса-
торов. а также фиксаторов анкеруемых ветвей ценной подвески, на-
груженных в основном растягивающей или сжимающей силами, па из-
гиб не рассчитывают.
Расчет поперечного несущего троса при разной высоте ею закреп-
ления на опорах. В случае крепления поперечного несущего греха
в разных уровнях вертикальные составляющие опорных реакций за-
висят от горизонтальной составляющей натяжения троса; место дей-
ствия максимального момента и наибольшего провисания троса не мо-
жет быть определено построением эпюры перерезывающих сил от за-
данных вертикальных си,л, ибо оно зависит еще от горизонтальной со-
ставляющей натяжения троса, которая в начале расчета неизвестна.
Поэтому при заданной высоте точек подвеса троса расчет следует на-
чинать с определения горизо»iалыюй составляющей его натяжения.
Принимая, что точка Б находится ниже точки А (см. рис. 7.12, а) на
величину \h. искомую составляющую можно определить но одной из
формул:
_2<К____
/игГ';к 711
(7.1)1!
(7.112)
где Мк ' изгибающий момент от известных вертикальных сил в сечении,
где расположена точка максимального провеса троса;
шах наибольшая стрела провеса троса по отношению к высокой опоре’
П1ах - то же по отношению к низкой опоре;
Ч и />" ' горизонтальные расстояния от места наибольшего провисания
троса соответственно до высокой и низкой опоры.
Расчет ведется подбором путем определения На для различных то-
чек расположения нагрузок. Максимальным значение Н а будет в точ-
ке наибольшего провисания троса. Чтобы быстро найти эту точку, не-
226
H„\h ,
(7.113)
(7.И4)
(7.117)
расположения на-
(7.120)
(7.115)
(7.116)
(7 ИЗ)
(7.119)
к —• /1) 1 7/ H \h
обходимо учитывать следующее. При одинаковых вертикальных на-
грузках и равномерном расположении их вдоль поперечного пролета
искомая точка может быть в середине пролета, если там находится од-
на из нагрузок, или смещается от середины пролета в сторону более низ-
кой точки подвеса (это смещение тем больше, чем больше разность
уровней А/г). Если имеются отдельные большие, чем остальные, вер-
тикальные нагрузки или места с более частым расположением нагру-
зок. точка максимального провеса троса смещается в сторону таких
нагрузок.
При известной горизонтальной составляющей натяжения попереч-
ного несущего троса вертикальные составляющие опорных реакций:
V’
‘ H
Монтажные стрелы провеса ненагруженного поперечного несущего
гроса
по отношению к опорам А и Б:
/пд к' ( I Д/>)«/(4а);
К' (<! — ДД)'!/(4и) .
]/ 6/~'(Т.~'М“
и д' — то же, что и в формуле (7.72).
где it
Л в
Полную длину поперечного несущего троса в данном случае также
определяют по формуле (7.73). Провесы нагруженного поперечного не-
сущего
можно
троса нод каждой из нагрузок 7 но отношению к обеим опорам
определить как-
ii:A \hH„ -I-М/ 77»:
.У,-/; —(Л| — (;) ЛЛ//ц
где Л1;
!«згиб4и<>|ци й момент <)1 нертикальнь'х сил в
I рузки €:.
Определенная по формуле (7.117) величина а имеет физический
смысл учетверенной стрелы провеса ненагруженного поперечного не-
сущего троса в пролете 1Ц при одинаковой высоте точек закрепления
гроса на опорах и натяжении, определенном, для троса при разной вы-
соте указанных точек. Это натяжение
И -•(>' Г~/('2а).
Точка максимального провисания разгруженного троса находится
в пределах пролета, если а > АЛ, чему соответствует условие
>2М2,(3/п) (-.121)
227
Точка максимального провисания находится за пределами пролета,
если а < iMi, что получается при соотношении
A/i2/(2/„) < <2Л/^/(3/п). (7.122)
Левая часть неравенства (7.122) установлена из условия, что раз-
ность Ln — 1п не может быть равна A/i2/(2Z„), что соответствовало бы
невесомому тросу с длиной, равной расстоянию между точками подве-
са по прямой.
Точка максимального провисания троса совпадает с точкой креп-
ления его на более низкой опоре при a i\h:
2Л^(3/И).
(7 1231
Положение точки максимального провисания ненагружениого тро-
са определяется расстояниями по горизонтали от опор А и Б до ис-
комой точки-
1Л 0.5Z., (I ' Лй.н); C-Vn (1 - \л.«)
Положительное значение соответствует положению точки мак-
симального провисания в пределах пролета, отрицательное за его
пределами.
Расчеты изменения натяжения поперечного несущего троса. Для
выбора параметров опор гибких поперечин, в частности высоты и жест-
кости, для проверки изменений вершкальных габаритов контактного
провода и решения других задач необходимо определить натяжение
поперечного несущею троса при изменениях температуры внешней
среды и нагрузок. Наиболее просто расчетное уравнение можно полу-
читьпри условии, что все вертикальные нагрузки равны и равномерно
размещены вдоль гибкой поперечины, т. е. расстояние от опоры до
первой нагрузки и все расстояния между нагрузками одинаковы.
В этом случае для одного поперечного несущего троса справедливы
следующие уравнения:
а, (В - '। ;
К'т! . 1 , Т* ят । п
24<х., //»! а, \ .$” /м / 24а... Ду,.
г.’н 6,
X.li
226
В этих формулах:
у,.,- -- распределенная линейная вертикальная нагрузка от всех тросов гибкой
поперечины (включая фиксирующие), приходящаяся на один поперечный
несущий трос;
а, — сосредоточенная вертикальная нагрузка на одном пути от веса пенной
подвееки (в необходимых случаях с гололедом), гирлянды изоляторов
с арматурой, фиксаторов и струн;
/7П число сосредоточенных нагрузок (число путей);
пг — число поперечных несущих тросов;
S’r площадь сечения одного поперечного несущего троса.
Все величины в формулах (7.124) и (7.125) с индексом 1 относятся
к известному режиму, а с индексом х - к любому искомому режиму.
Величины с индексом i относятся и к известным и к искомым режимам.
Единичный прогиб обеих опор па высоте крепления поперечного не-
сущего троса у' при трехступенчатых опорах может быть определен по
формуле (6.89), при двухступенчатых
и при четырехетупенчатых опорах
_2Лу_ 1 7 19 37 \
V 192 \ /:У, /7'4 /'
В случае нечетного числа путей максимальной стрела провеса по-
перечного несущего троса будет у средней подвески (в середине попе-
речины)
/ Umax;
i !
Ля /
При четном числе путей максимальной стрела провеса троса также
получается в середине поперечины
<7 129>
а у ближайшей к середине ценной подвески определяется по формуле
В" l'ii П1. («II____________2)
11 к//,1? (пп i)-
: 1
«п
I !
(7.130)
Все обозначения в формулах (7.126)—(7.130) те же, что и выше.
Расчеты фиксирующих тросов жестких и фиксирующих попере-
чин. При расчете фиксирующего троса жесткой поперечины необходи-
мо учитывать температурные деформации металлической поперечины,
имеющей температурный коэффициент линейного расширения, близ-
кий к соответствующему для фиксирующего троса. Сечение поперечи-
ны во много раз больше сечения троса; поперечина расположена близ-
ко от фиксирующего троса но высоте. Все это приводит к тому, что стоп-
229
I
I
I
I
I
i
I
i
I
I
i
I
Рис. 7.23. Расчетные схемы жесткой
(а) и фиксирующей (б) поперечин
ки на уровне крепления троса получают значительные деформации при
изменениях температуры воздуха. Заметно влияют на натяжение тро-
са также прогибы стоек, вызванные действием этого натяжения.
Для жестких поперечин балочного типа, которые рассчитывают,
принимая защемление стоек в грунте и шарнирное соединение попере-
чины со стойками, уравнение состояния фиксирующего троса при оди-
наковых стойках и отсутствии компенсатора имеет вид
I
I
i
I
I
I
I
//Д "iin °-5 ( £ V PiT) : р/:ф5ф(/111ах-/г). (7.131)
'Г - 1 11 /
к «Ф~«р 2B/D j
где Р 1з. () (Д_Bi/D) ’ (7.132)
/> - 4С /ф Sp). I
В этих формулах:
О 2й»/:ф 5ф/(81Л,), (7Л З.З)
। де /;р -- модуль упругости материала жесткой поперечины;
суммарное сечение нижних поясов жесткой поперечины;
<хр температурный коэффициент линейного расширения материала ри-
гел я;
It высота стоек, считая от поверхности грунта до шарнира прикрепле-
ния ригеля к стойкам.
Остальные обозначения те же. что в формулах (7.85) и (7.86).
Буквы А, В и С в формулах (7.132) обозначают величины, характе-
ризующие жесткость стоек. Если в качестве стоек применены типовые
конические железобетонные опоры, то при тех же допущениях, кото-
рые были приняты в §6.5, и схеме поперечины по рис. 7.23, а указан
ные величины можно определить по формулам:
(I-3X):l 27X(I—-X)—7 27^-45X4-19
----------_. --------------— - -----------------; (/. ! )
А,/ ]
(I — ЗХ)г (2 +ЗА.) 14—27А. 38— 45А. ,7 i
EJ, г EJ., EJ*
С \,(EJir 7/(£V2) 3 19/(/:./3) , (7.1361
236
где X ah:
Е — модуль упругости материала стоек;
Д, /а— моменты инерции каждой части стоек.
В случае постоянной по высоте жесткости стоек формулы (7.134)—
(7.136) упрощаются:
4 = 27 (1— k)U(EJ): {7 137)
В---27 (2 — 3X + X:')/(/-V);
(7.138)
С =27 ЦЕ J). (7 139)
Величина Р в формуле (7.131) имеет размерность температурного
коэффициента линейного расширения, но зависит не только от тем-
пературного расширения материалов ригеля и фиксирующего троса,
а еще от упругих свойств их и железобетонных стоек и геометриче-
ских размеров поперечины. Допустив незначительную погрешность
расчета, натяжение фиксирующего троса по формуле (7.131) можно оп-
ределить без учета упругих деформаций ригеля. Тогда
в КФ —«Р д/<2С)
Р 14 0 [Д— Й2/(4С)|'
Расчет натяжения фиксирующего троса в наиболее ослабленном
звене фиксирующей поперечины (рис. 7.23, б) может быть произведен
также по формуле (7.131), но в этом случае
(7.140)
Р аф/(1+0С). (7.141)
Здесь значение С вычисляется по формулам (7. 136) и (7.139). Жест-
кости отдельных ступеней железобетонных опор можно определить по
кривым рис. 6.10.
231
Глава 8
ПОДБОР ТИПОВЫХ КОНСТРУКЦИИ
§ 8.1. Подбор консолей, кронштейнов и фиксаторов
Подбор типовых поддерживающих и фиксирующих устройств вы-
полняют при проектировании контактной сети путем привязки раз
работанных конструкций к конкретным условиям их установки. Если
же эти условия не соответствуют принятым в типовых проектах, то не-
обходимые расчеты могут быть произведены по материалам в гл. 7.
Подбор консолей. Типовые консоли для компенсированных и полу-
компенсированных ценных подвесок разработаны в проектном инсти-
туте Трансэлектропроект и на Люберецком электромеханическом заво-
де треста Трансэлектромонтаж.
Одно п у т пы е неизолиров а нн ы е наклонные
к о н соли выполняют с кронштейнами из двух швеллеров или из
труб, с растянутыми и сжатыми тягами, с подкосами и без них, имею-
щих разные геометрические размеры.
Консоли с кронштейнами из швеллеров маркируют буквой Н (на-
клонная) с добавлением букв Р (растянутая тяга) или С (сжатая тяга).
Кроме того, в маркировку вводят римские цифры, соответствующие
различным длинам кронштейнов консолей (0 — 3630, мм, 1 - 4730.
1 1 5230, 111 —6230 и IV — 7130 мм), и арабские цифры, обозначаю-
щие номера швеллеров, из которых изготовлены кронштейны (№ 5 и
6,5); наличие подкоса в конкретном типе консоли отмечают буквой II
Примеры маркировки:
HP-1-5—неизолированная наклонная консоль с растянутой тя-
гой. кронштейном из швеллеров № 5, длина кронштейна 4730 мм;
НС-111-6,5-П-- неизолированная наклонная консоль со сжатой тя-
гой и подкосом, кронштейном из швеллеров № 6.5 длиной 6230 м.
Консоли с кронштейнами из швеллеров устанавливают на переход-
ных опорах сопряжений анкерных участков, на промежуточных опо-
рах с габаритом 4,9 и 5,7 м. в отдельных случаях на станциях.
Консоли с кронштейнами из труб маркируют буквами НТ (наклон-
ная, трубчатая) и обозначениями, аналогичными для консолей с крон-
штейнами из швеллеров. Трубчатые консоли предусмотрены с тремя
длинами кронштейнов (0 ..-3865 мм, 1 —4615 мм, И — 5115 мм).
Иногда в маркировке есть буква И. что указывает на применение
укороченного бугеля. Например:
ИТРИ-0 неизолированная наклонная консоль с растянутой тя-
гой и кронштейном из трубы длиной 3865 мм, укомплектована укоро-
ченным бугелем;
232
HTC-II-П — неизолированная наклонная консоль со сжатой тягой
и подкосом, кронштейн из трубы длиной 5115 мм.
Трубчатые консоли устанавливают на промежуточных опорах с
габаритами от 3,1 до 3,5 м. Консоли с укороченным бугелем применя-
ют только на прямых участках пути и на внешней стороне кривых.
Наклонные неизолированные консоли используют и для крепления
на специальных стойках под ригелями жестких поперечин. При этом
существенно уменьшается длина кронштейнов, которые выполняют из
одного швеллера № 5. Такие консоли предусмотрены трех типов:
ЖНР-I, ЖНР-П и ЖНС-1. Буква Ж свидетельствует о предназначе-
нии для установки на жестких поперечинах, Р и С обозначают соот-
ветственно растянутую и сжатую тяги, цифра I длину кронштейна
2520 мм, цифра II -- 2880 мм.
О д н о п у т н ы е изолированные консоли из-
готовляют с кронштейнами из двух швеллеров №5 или из труб. Кон-
соли с кронштейнами из швеллеров маркируют ИР (изолированная
с растянутой тягой) и ИС (изолированная со сжатой тягой). Консо-
ли типа ИР выполняют с кронштейнами различной длины, чему в их
маркировке соответствуют цифры II, III, IV, V и VI (3700 , 4200,
4700, 5200 и 5900 мм), а консоли типа ИС, кроме того, еще с' крон-
штейнами длиной 6400 мм (цифра VII в маркировке). Наличие подкоса
в этом случае отмечается строчной буквой «п». Если консоль предна-
значена для крепления контактной подвески с усиленной (двойной)
изоляцией, то вводится строчная буква «у». Примеры маркировки:
HP-IV-5-п — изолированная наклонная консоль с растянутой тя-
гой и подкосом, кронштейн из швеллеров № 5 длиной 4700 мм;
ИС-11у-5 — изолированная наклонная консоль со сжатой тягой и
кронштейном из швеллеров № 5 длиной 3700 мм для установки с уси-
ленной изоляцией контактной подвески.
Консоли с кронштейнами из труб имеют в маркировке букву Т
(ИТР и ИТС). Консоли типа ИТР (с растянутой зягой) выполняют с
кронштейнами только одного размера II (3700 мм), а типа ИТС (со
сжатой тягой), кроме того, с кронштейнами размера III (4200 мм). Как
и в маркировке консолей ИР и ИС, здесь также применяют буквы
«п» и «у». Примеры маркировки:
ИТР-I 1-у — изолированная наклонная консоль с растянутой тя-
гой и кронштейном из трубы длиной 3700 мм для установки с усилен-
ной изоляцией контактной подвески;
ИТС-Ш-п — изолированная наклонная консоль со сжатой тя-
гой и подкосом, кронштейн из трубы длиной 4200 мм.
Изолированные консоли для установки на жестких поперечинах
предусмотрены трех типов: ЖР-I и ЖР-П (с растянутой тягой и дли-
нами кронштейнов 1950 и 2310 мм), ЖС-1 (со сжатой тягой и крон-
штейном длиной 1950 мм).
Изолированные консоли используют на дорогах переменного тока
при высоких скоростях движения, в береговых зонах морей и океанов,
в местах с загрязненной атмосферой. В таких случаях, а также в ме-
233
стах выгрузки минеральных удобрений применяют изолированные
консоли, предусматривающие крепление контактной подвески с уси-
ленной изоляцией. На дорогах постоянного тока при особо загрязнен-
ной атмосфере применяют изолированные консоли с усиленной изоля-
цией контактной подвески. В этих случаях кронштейны консолей мо-
гут быть изготовлены из швеллеров № 6,5.
Подбор консолей в различных условиях установки осуществляют
в соответствии с таблицами, разработанными в Траисэлектропроекте
для районов с нормативной толщиной стенки гололеда до 20 мм вклю-
чительно и скоростью ветра до 35 м.с при повторяемости климатиче-
ских нагрузок не реже одного раза в 10 лет. Все данные определены
для габаритов установки опор от 3,1 до 3.5 м (через каждые 0,1 м),
4.9 и 5,7 м.
Подбор типовых неизолированных и изолированных консолей для
линий постоянного и переменного тока выполняют в зависимости от
типа опор и места их установки, а при подборе переходных консолей
учитывают еще наличие или отсутствие секционирования сети, распо-
ложение рабочей и анкеруемой ветвей подвески относительно опоры и
то, какая ветвь крепится на данной консоли. Кроме того, для линий
постоянного тока па прямых участках пути необходимо учитывать га-
барит установки анкерных опор.
Области применения сжатых тяг консолей типов НС, НТС, ИС и
ИТС определены для нормальных условий работы контактной подвес-
ки с двумя контактными проводами на линиях постоянного тока и с
одним контактным проводом на линиях переменного тока. Во всех
случаях, когда может возникнуть дополнительное сжимающее усилие
в растянутой тяге (например, при расположении пролета частично па
прямой и частично на внутренней стороне кривой или при скорости
ветра более 35 м/с), возможность применения растянутых тяг следует
проверить расчетом исходя из условия, что в самых неблагоприятных
случаях растягивающее усилие в тяге должно быть не менее 20 даН.
(Расчет усилия в тяге см. § 7.1.)
В целях повышения ветроустойчивости подвески в местах, подвер-
женных особо сильным ветровым воздействиям (например, поймы
рек, насыпи высотой более 5 м от поверхности земли или при располо-
жении подвески выше вершин деревьев в лесистой местности, а также
в местах, где могут возникнуть автоколебания проводов), возмож-
ность применения растянутых тяг на линиях постоянного тока также
необходимо проверить расчетом исходя из того, что при самом небла-
гоприятном сочетании нагрузок растягивающее усилие в тяге должно
быть не менее 50 даН. На линиях переменного тока в указанных усло-
виях растянутые тяги из круглой стали должны быть заменены более
жесткими (за исключением участков пути на внешней стороне кривых
радиусом менее 1000 м). В отдельных случаях сжатые тяги из труб за-
меняют выполненными из угловой стали (например, на консолях ан-
керуемой ветви подвески переходных опор на внутренней стороне кри-
вых радиусом 600 м и менее при габарите опор 3,5 м и менее).
234
Однопутные неизолированные горизон-
тальные консоли с одной тягой маркируют буквами Г
(горизонтальная), В (устанавливается в выемке за кюветом), Ф (уком-
плектована обратной фиксаторной стойкой), П (устанавливается за
пассажирской платформой). Кроме того, римскими цифрами указыва-
ют длину кронштейна консоли, арабскими — номера швеллеров, из
которых он изготовлен. Буква «а» указывает, что данная консоль снаб-
жена прямой фиксаторной стойкой, буква «п», т. е. что она предназна-
чена для установки на переходной опоре с усиленной фиксаторной
стойкой. Горизонтальная консоль типа П имеет кронштейн только од-
ной длины (1 — 5700 мм), типа Г — двух (I — 2650 мм, II — 3300 мм),
типа ГФ — одной (II—4500 мм), типа ВГ — одной (II — 5200 мм)
и типа ВГФ - одной (II — 5900 мм). Пример маркировки:
ВГ-П-8-а — однопутная горизонтальная консоль для установки за
кюветом в выемке, кронштейн из швеллеров № 8 длиной 5200 мм,
укомплектована прямой фиксаторной стойкой;
ГФ-11 п-10 — однопутная горизонтальная консоль с усиленной об-
ратной фиксаторной стойкой для установки на переходной опоре,
кронштейн из швеллеров № 10 длиной 4500 мм.
Двухпутные неизолированные горизон-
тальные консоли с двумя тягами предусмотрены типов Д-11
(двухпутная с длиной кронштейна 9770 мм) и Д-VII (длина кронштей-
на 12 000 мм). Консоли типа Д-VIl могут быть вида Д-VII-C (с одной
фиксаторной стойкой) и Д-УП-2С (с двумя фиксаторными стойками).
Все эти консоли имеют различные геометрические размеры и массы в
зависимости от того, на каких опорах предполагается их устанавли-
вать. Двухпутные консоли могут быть установлены на металлических
опорах высотой 13 м и более, а также на спаренных железобетонных
стойках обычной длины, но закрепленных на фундаментах.
Подбор кронштейнов для проводов воздушных линий. Типовые
кронштейны разработаны металлические и деревянные. На металличе-
ских подвешивают провода линий ДПР, усиливающие, питающие, от-
сасывающие и провода обратного тока (на участках с отсасывающими
трансформаторами). На деревянных кронштейнах крепят провода воз-
душных линий 6 и 10 кВ напряжением до 1000 В и волноводные.
В маркировках металлических кронштей-
нов используют буквы К (кронштейн), Ф (фидерный), У (удлинен-
ный), П (прямой), Д (для подвески двух линий в одной горизонталь-
ной плоскости), И (для подвески питающего провода при системе
2x25 кВ), а также цифры 5 и 6,5 (номера швеллеров, из которых изго-
товлены кронштейны), 50 и 63 (размеры полок уголков в миллиметрах,
из которых состоят кронштейны). Кроме того, в маркировках метал-
лических кронштейнов используется буква С, которая в кронштейне
типа КФС-6,5 означает, что данная конструкция разработана в проект-
ном институте Сибгипротранс. а типа КФДС указывает на наличие
сжатой тяги:
23;
КФУ-6,5 — металлический фидерный кронштейн, удлиненный, из
швеллеров №6, 5;
КФДСИ — металлический фидерный кронштейн со сжатой тягой
для подвески двух проводов при системе 2 х 25 кВ (питающего и одно-
го ДПР).
Области применения металлических кронштейнов следующие:
КФ и КФУ — для подвески питающих проводов напряжением
27.5 кВ;
КФ, КФУ, КФП и КФПУ — для подвески питающих проводов
напряжением 3,3 кВ и отсасывающих;
КФ, КФУ, КФД и КФДС — для подвески усиливающих прово-
дов напряжением 27,5 кВ;
КФ, КФУ. КФП и КФПУ - для подвески усиливающих прово-
дов напряжением 3,3 кВ;
КФ, КФУ, КФС, КФД и КФДС для подвески проводов линий
ДПР;
КФП и КФПУ - для подвески проводов обратного тока.
Кронштейны КФД всегда устанавливают горизонтально, типа
КФДС — иногда с наклоном (в выемках, на станциях при наличии на
опоре линии освещения и в других случаях). Кронштейны КФДС при-
меняют в местах со значительными скоростями ветра — в поймах рек.
на насыпях - высотой более 5 м от поверхности земли, в местах, где
наблюдаются автоколебания проводов, а также при расположении опор
с внешней стороны кривых участков пути и установке кронштейнов
с тягами, наклоненными вверх от опоры. На опорах, расположенных
с внешней стороны кривых радиусом менее 1000 м, кронштейны типа
КФДС устанавливают только горизонтально. Удлиненные кронштей-
ны применяют при установке па анкерных опорах, на опорах с секци-
онными разъединителями и разрядниками и в других случаях, ког.,а
нужно отдалить провода от опор.
Чтобы выбрать тин кронштейна, в соответствии со схемами рис. 8.1
нужно определить наиболее невыгодные сочетания суммарных норма-
Рис. 8.1 Схемы нагрузок кронштейнов КФ, КФУ, КФС (а); КФП. КФПУ (6),
КФД, КФДС (ь); Г-образной стойки (е); Т-образной надставки '()); надставки
с подкосом (е)
236
Рис 8 2. Допустимые нормативные нагрузки на кронштейны КФ-5, КФ-6,5 н КФС
(а); КФУ 5, КФ-V-6,5 и Г-образную стойку (б)
тивных нагрузок Q и Р (последние с учетом их знака) и найти точку
их пересечения на соответствующем графике (рис. 8.2). Указанная точ-
ка должна быть ниже линии допустимой нормативной нагрузки для
кронштейна данного типа. Определяют нагрузки Q и Р в соответствии
с материалами, приведенными в § 2.3. При расчете конструкций по ме-
тоду предельных состояний расчетные нагрузки Qp и Рр по данным
ТраИСЗ^;тоо'1роекта можно получить умножением нормативных
значений Q и Р на коэффициент
В маркировке деревянных кронштейнов
ИСНи;; QViC: буквы Д (деревянный), О (облегченный из бруска шириной
80 мм"и"высО1м»7 (низковольтный, т. е. для крепления про-
водов напряжением до /м*' (удлннеН’пЫи;. а !ачже цифры 11 и
III, указывающие расстояния мел.,Д' "бородами разных фаз (соответ-
ственно 1000 и 1250 мм). Например:
ДОУ-Н — деревянный облегченный удлиненный [^општейн для
крепления проводов с расстояниями между ними 1000 мм;
ДНО — деревянный облегченный кронштейн для крепления про-
водов напряжением до 1000 В.
Кронштейны ДО, ДНО и ДНОУ оснащены ограничительными шты-
рями, которые предотвращают прикосновение провода к опоре, если он
сорвется с изолятора. Кронштейны ДНО и ДНОУ рассчитаны для
крепления до четырех проводов включительно. Для крепления пятого
провода на кронштейнах может быть применен крюк, который ввора-
чивается в подкос кронштейна. Допускается на ограничительном шты-
ре располагать волноводный провод, при этом изолятор крепится на
промасленной пеньке.
Условия применения удлиненных деревянных кронштейнов анало-
гичны приведенным выше для металлических кронштейнов.
При прохождении проводов над пассажирскими платформами и
переездами провода линий напряжением выше 1000 В имеют двойное
крепление для чего в процессе монтажа на кронштейны ДО устанав-
ливают дополнительные штыри с изоляторами на расстоянии 245 мм
в сторону опоры от основного штыря.
237
Подбор деревянных кронштейнов для закрепления на штыревых
изоляторах трех проводов воздушной линии 6 и 10 кВ выполняют в за-
висимости от требуемых расстояний, на которые провода должны от-
стоять от опоры, и от расстояний между проводами разных фаз. Под-
бор ведут по графикам допустимых нагрузок вида приведенных на
рис. 8.2, рассчитанным для таких кронштейнов. Аналогично выбирают
деревянные кронштейны для крепления проводов напряжением до
1000 В.
Подбор надставок и стоек. Надставки и стойки применяют в тех
случаях, когда высота опор недостаточна для установки необходимого
кронштейна, а также если требуется расположить провода над жест-
кой поперечиной.
Типовые надставки для жестких поперечин запроектированы двух
видов: Т-образпые (для установки над ригелем) и с подкосом (для креп-
ления кронштейна выше опоры с полевой стороны). Основные данные
Т-образных надставок приведены в табл. 8.1.
Надставки для крепления металлических и деревянных кронштей-
нов с полевой стороны опор жестких поперечин предусмотрены типов
Р-1 и Р-П (для ригелей шириной соответственно 450 и 740 мм). Р-1у и
Р-Пу (удлиненные). Их выполняют из угловой стали.
Надставки па железобетонные опоры высотой 9,6 м (их обычно на-
зывают стойками) запроектированы вертикальные (для крепления
кронштейна) и Г-образные (для подвески проводов па них). Верти-
кальные стойки предусмотрены типов I и II, их изготовляют но швел-
леров №6,5; Г-образные стойки также бывают типо« I '(для подвески
двух проводов Л-185) и 11 (для одного пг,£>°°Да)- Они выполнены из
швеллеров № 10 (вертикальная часть) и № 6,5 (горизонтальная).
Стойки типа 1 применяли «а участках постоянного тока, типа II при
переменном токе. В последнее время эти стойки не используют, пред-
почитая для усиления надежности применять более высокие опоры.
Надставки и стойки подбирают в зависимости от назначения, в не-
обходимых случаях их проверяют па конкретные нагрузки аналогии
Таблица 8.1
Размеры ригеля, мм Тип надстав- ки Число и номер швеллеров для элементов Размеры крепитель- ных уголков, мм Масса, кг
вертикаль- ного горизон- тального Ширина полок и толщина Длина
700X450 I II 2; № 5 2; .№ 8 2; № 5 80X80X8 570 91,5 101,7
1200X740 III IV 2; № 5 2; № 8 2; № 5 80X80X8 860 102,7 115,9
238
Т а б л я ц
Длина основного стерев Ч, MN|, фИК :атор.?в типов
Размеры ФП-3, ФО-Й, ФЛ-25.
ФП-26, ФПИ ФО-25 ФОН УФН УФО ФА >, Ф1--5 ФТ-25 ’Г ХИ ФТИ
I 1200 30(Ю „.. 3000 , . - г- 'I/O 1300
(кроме
ФО И)
II 1600 3400 1630 4000 1675 1800
III 2000 3800 4300 2175 2300
IV 2400 4200 2675 2800
V 3000 4600 3000 — 3175 3300
VI 360.» 5000 - 3675 3800
(только ! только
ФПИ) ФА-3)
VII 5409 4300
(только ('только
ФОИ) ФАИ и
ФТИ)
но изложенному выше для кронштейнов (схемы нагрузок показаны на
рис. 8.1, с, д, е).
Подбор фиксаторов. Типовые сочлененные фиксаторы, разрабо-
шиныс в Трансэлектропроекте, подбирают в зависимости от типа коп-
солей и места их установки, а для переходных опор — с учетом распо-
ложения рабочей и анкеруемой ветвей подвески относительно опоры
Кроме того, учитывают, для какой из них предназначен фиксатор.
В обозначениях типовых фиксаторов применяют буквы Ф (фикса-
тор), II (прямой), О (обратный), А (контактного провода анкеруемой
ветви), Т (троса анкеруемой ветви), Г (гибкий). И (для изолированных
консолей), С (воздушных стрелок), К (комбинированный), Р (ромбо-
видных подвесок) и У (усиленный). В маркировке имеются цифры 3
(для линий постоянного тока) и 25 (для линий переменного тока), ука-
зывающие напряжение в киловольтах, а также римские цифры 1, 11
и т. д., характеризующие длины основных фиксаторов (табл. 8.2).
Пример маркировки:
ФП-11-3- прямой фиксатор для неизолированной консоли на ли-
нии постоянного тока, длина основного стержня 1600 мм;
ФОИ-1У-25 обратный фиксатор/ для изолированной консоли на
пинии переменного тока, длина основного стержня 4200 мм;
ФГ-25 — гибкий фиксатор для линий переменного тока;
ФГ2-3 — гибкий фиксатор, двойной (с разнесением мест фиксации
на кривых R < 600 м), для линий постоянного тока;
ФА-111-3— фиксатор контактного провода анкеруемой ветви для
неизолированной консоли на линии постоянного тока, длина основ-
ного стержня 2175 мм;
239
Т а б л и ц а 8.3
Тип изолятора (число их) Типы фиксаторов (всех размеров)
прямых обратных гибких для анке- руемых проводик специаль- ных
ФГФ40 (два) ФП-З ФО-З ФР 3
ФПС-3 ФОС-3 — ФКС-3
VKL-60/7 (фик- ФП 25 ФО-25 — ФТ-25 ФКС-25
еаторный) ФПС-25 ФО2-25 ФА-25 —
ФОС-25 —
ИКСУ-27 У ФП-З УФО-3 ФГ-3
— УФО2 3 ФА-3 —•
ПТФ70+ПФ70-В ФГ-3 ..
ФГ2-3 -- —
ПТФ70+ПФ70 В ФГ-25 — —
(два) или ПС70-Б (три) — ФГ2-25
ФТИ-Ц-25 — фиксатор несущего троса анкеруемой ветви для изо-
лированной консоли на линии переменного тока, длина основного
стержня 1800 мм;
УФО-1-3 усиленный обратный фиксатор для неизолированной
консоли на линии постоянного тока, длина основного стержня
3000 мм.
К фиксаторным кронштейнам, опорам и неизолированным консолям
фиксаторы кренят через изоляторы. Типы изоляторов, обычно при-
меняемых для различных фиксаторов, приведены в табл. 8.3.
Подбор фиксаторов выполняют по таблицам, имеющимся в типо-
вом проекте. Эти таблицы разработаны для участков постоянного и
переменного тока, неизолированных и изолированных консолей, про-
межуточных и переходных опор (при неизолирующих и изолирующих
сопряжениях анкерных участков), разных мест установки опор на
прямых участках пути (при зигзагах, направленных на опору и от нее)
и в кривых различных радиусов (для опор, находящихся с внешней и
внутренней сторон кривой), разных габаритов опор (от 3,1 до 5,7 м)
и других условий установки фиксаторов.
Пример. 3 а д а н н е и и с х о д н ые д а и н ы е. Подобрать типовой
кронштейн для подвески двух усиливающих проводов А-185 в пролете длиной
58 м на полевой стороне опоры, установленной с внешней стороны кривой радиу-
сом 800 м. Максимальная скорость ветра без гололеда 30 м/с, при гололеде с тол-
щиной стенки 20 мм — 18 м/с. Натяжение провода при максимальном ветре 900
даН, при гололеде с ветром — ! 150 даН.
Р е ш е н и е. По табл. 2.3 найдем нормативные распределенные линейные
нагрузки на провод: от собственного веса проводя — 0,49 даН/м; от веса провода
с гололедом — 2.57 даН/м; статическую составляющую ветровой нагрузки на
240
провод при максимальном ветре — 1.18 даН/м: то же при гололеде с ветром (пуп-
дем интерполяции) — 1,41 даН/м.
Динамические составляющие нормативных распределенных линейных нет
ровых нагрузок определим по формулам (2.8) и (2.10):
при максимальном ветре Ря - 0,88 1,18-0.59-0,2-0,828 0.10! даН.-м,-
при гололеде с. ветром РГд ~ 0,88-1,41 -0,59-0,148-1,03 0,116 даН м.
Коэффициент т] определен интерполяцией: он равен 0,59, коэффициенты 6
для скоростей ветра 30 и 18 м/с равны соответственно 0,2 (интерполяция) и
0,148; коэффициенты ; для провода без гололеда 0,828 (интерполяция) и нри го-
лоледе 1,03.
Таким образом, нормативные распределенные линейные ветровые нагрузки
на провод будут:
при максимальном ветре рв 1,18 1-0,101 1,281 даН/м;
при гололеде с ветром рг 1.41 : 0,116 1,526 даН м.
Горизонтальные нагрузки на кронштейн от излома проводов на кривой оп-
ределим по формуле (2.28):
при максимальном ветре Ркр 2-900-58.800 131 даН;
при гололеде с ветром Рг кр 2-1150-58/800 - 167 даН.
Вертикальные нагрузки па кронштейн:
нри максимальном ветре Q 2-0,49-58 57 даН;
нри гололеде е ветром Qr 2-2,57-58- 298 даН;
горизонтальные нагрузки па кронштейн:
при максимальном ветре Р 2-1,281-58 ; 131 280 даН:
при гололеде с ветром Рг — 2-1,526-58 167= 344 даН.
Так как обе. нагрузки при гололеде с ветром больше, чем при максимальном
ветре, то, учитывая, что Q,- 298 даН и Рг - 344 даН, по графику рис. 8.2,о вы-
бираем кронштейн КФ-6,5.
§ 8.2. Подбор жестких поперечин
Типовые жесткие поперечины балочного тина представляют собой
сквозные фермы прямоугольного сечения, состоящие из отдельных
блоков. Решетка раскосная: направленная в вертикальных плоскостях
и ненаправленная в горизонтальных. Поперечины в обычном исполне-
нии, предназначенные для районов с расчетной температурой до
—40 “С, изготовляют из стали ВСтЗнсб 1-й и 2-й групп прочности
Для районов с расчетной температурой от —40 до 65 JC изготовля-
ют поперечины в северном исполнении из стали 09Г2 1-й и 2-й групп
прочности; категория стали 6 при расчетной температуре до —50°C и
12 при температуре от —50 до --65 X.. Поперечины длиной до 22,5 м
имеют ширину ферм 450 мм, высоту 700 мм, длину основной панели
800 мм; поперечины длиной 30,3; 34,0; 39,2; 44,2 м - соответствен-
но 740, 1200, 1250 мм. Поперечины длиной 30,3 м и более могут быть
изготовлены без учета установки приборов освещения и при наличии
освещения: в последнем случае поперечины снабжают настилом, пе-
рильным ограждением, а также лестницей для обслуживающего
персонала.
Поперечины комплектуют из двух, трех или четырех блоков в за-
висимости от длины расчетного пролета. Стыки блоков поперечин в
обычном исполнении сварные, в северном исполнении — на болтах
Маркировка блоков поперечин в б чн м i нении - ЬК (край-
241
Рис *3. Схемы расположения путей (а) и нагрузок (б) для подбора жесткой
поперечины:
»ные личщ главные пути и соответствующие им t огруби, чоикне линии - оеталь
оьь с^нциомыс нуги и нагрузки; расстояния указаны в метрах
ний). БС (средний), и северном исполнении —- DKC, БСС. К буквен-
ному обозначению через черточку добавляется порядковый номер бло-
ка, например Б КС-29.
Маркировка поперечин буквенно-цифровая, например 11320-34,0-1
сто обозначение поперечины в обычном исполнении с несущей спо-
собностью 320 j.l i • м при расчетном пролете 34,0 м. из стали I-й груп-
пы прочности1 ПСЗЮ-34,0-1 — то же в северном исполнении. Для по-
перечин с освещением в обозначении добавляется буква О. например
0(1320-34,0-1.
Длина основного пролета поперечины в необходимых случаях мо-
жет быть уменьшена путем уменьшения числа панелей в крайних
блоках симметрично или только в одном из блоков, за исключением
усиленных панелей. Основные данные некоторых жестких поперечин
приведены в табл. 8.4 и 8.5.
При подборе же< гких поперечин приходится выполнять достаточно
громоздкие расчеты, для чего обычно используют ЭВМ. Вспомогатель-
ные материалы, используемые в этих расчетах, приведены далее не
полностью, а лишь в качестве примеров, поясняющих выполнение по-
добных работ (для поперечин обычного исполнения из стали 1-й груп-
пы).
Методика подбора типовых жестких поперечин разработана в про-
ектном институте Гипропромтрансстрой и заключается в следующем.
Составляется расчетная схема поперечины (рис. 8.3. а), по которой ус-
танавливается ее фактическая длина. Применительно к этой длине за-
даются типовой поперечиной с определенной несущей способностью и
проверяют пригодность ее. сопоставляя действующие изгибающие мо-
менты от внешних сил с допускаемыми моментами, предназначенными
только для подбора поперечин. Рассматривают три режима: аварий-
ный— обрыв несущего троса при гололеде, ветер отсутствует, два нор-
мальных -.- гололед с ветром вдоль пути при скорости, в 2 раза меньшей
максимальной, и ветер максимальной интенсивности вдоль пути, голо-
лед отсутствует. Конкретную поперечину рассчитывают только в тех
режимах, для которых в типовом проекте заданы несущие способно-
сти — максимальный момент М (табл. 8.6) Например, все поперечи-
ны длиной 30,3 м и более рассчитывают только в нормальных режи-
242
II
Табл и ц а 8.4
Марка поперечины Несущая слое об- ность. кН «и Масса попере- чины, кг 1 Несуща я Марка ! способ поперечины | чоегь, ! к Н м Масса лопере чины
Обычное исполнение Севепкое исполнение
11180-22.5-1 11130-22,5-1 И100-22,5-1 1180-22,5- i 11360-30,3-1 11320-30,3-1 П 180-30,3-1 П38О-34.0-1 11320-34,0-1 11280-34,0-1 11220-34,0-1 ОПЗбО 30.3-1 ОП320-30.3-1 011220-30,3-11 ОП380-34.0-1 011320-34,0-1 ОП 280-34,0-1 ОП250-34,0-1 182 134 102 82 355 318 176 377 318 282 923 355 318 224 377 318 282 250 903.2 75! ,6 703.7 685,3 1543.2 139,3,0 1181,1 i 82 i , 7 169) ,6 1490.5 1350,1 2046,1 1895.9 1684,1 2386,0 2255.8 2034,8 1914,4 ПС 180-22.5-1 । 176 ПС.140-22,5-1 138 ПС 110-22,5-1 115 ПС90-22.5-1 91 ПСЗ 10-30,3-1 j 'W 11С280-30.3-1 275 ПС190-30.3-1 ’9() ПС390-34.0-1 ПС'350-34,0 1 I ПС310-34,0-1 1 307 ПС240-34.0-! । 244 ОПС310-30,3 1 1 307 ОПС280-30.3-! ; 275 011С25О-30,3- i 250 ОПС390-34.0-) 390 ОПС350-34.0-1 346 ОПСЗ 10-34,0-1 307 ОПС270-34.0-1 275 821.9 738,3 716,5 697.6 137b,2 1283,3 1202,9 1750,0 1625.3 ’ 1485,2 18,63.8 1881,1 178fj, 2 1705,8 2314,3 2189,7 2049,4 1928,0
Расчетная длина основной попере- чины, м Число блоков Табл и и а 8.5 Допускаемая расчетная длина поперечины, м. при уменьшении числа панелей
22,515 30,260 34,010 39,165 44,165 2 3 3 4 4 21,715; 20,915; 20,115; 19,315 17,715; 16,915; 16,115; 15,31 13,715; 12,915 29,010; 27,760 32,760, 31,510; 30,260 37,915; 36,665; 35,415 42,915; 41,665; 40,415; 39,165 18,515; 5; 14,515;
поперечин могут быть уменьшены при
Приме ч а и и е. Расчетные длины
...... ___„. „________ .... ...... измене-
нии места опирания с пределах крайних усиленных панелей для поперечин с основной
длиной до 22.5 м на величину до 0,8 м. а для остальных на величину до 1,25 м.
243
мах. Изгибающие моменты от внешних сил в аварийном режиме опре-
деляют нормативные, а в нормальных режимах — расчетные. Про-
верки поперечин на изгиб выполняют в середине пролета (крайние
блоки двухблочных поперечин п средние блоки трех- и четырехблоч-
ных), в 1/3 пролета (крайние блоки трехблочных поперечин) и в 3 ,
пролета (крайние блоки четырехблочных поперечин). Изгибающие мо-
менты рассчитывают с учетом фактической длины поперечин, т. е.
возможного укорочения. Если моменты от внешних сил оказались су-
щественно меньше допустимых, следует либо принять более легкую
поперечину, либо, если возможно, увеличить расстояние между по-
перечинами (пролет подвески). При моментах, превышающих допуска-
емые. нужно принять более тяжелые поперечины или уменьшить рас-
стояние- между поперечинами. Во всех случаях необходимо снова оп-
ределить моменты от внешних сил и повторить все указанные про-
верки.
г\б,'ДД дугибающие моменты от внешних сил значительно меньше
несущих способное;ей сойтЗете।вующих блоков, типовой проект разре-
шает замену отдельных и.'!пков, которые можно взять из более легких
поперечин. При этом должны сои.пОД>пься 1зсе необходимые условия в
отношении размеров поперечного сечения Д’’ины> расположе-
ния панелей с перекрестными раскосами, расположении .?"•’Онего уз-
ла в пределах усиленных панелей. Например, средний блок четырел-
Г а б л и и а 8.5
Марка поперечины Средний блок Крайний блок
И И Их н и й ПОЯС Верхний пояс Нижний пояс Верхний иояс
WP, кН м б. кН • м б. кН • м мР, к Н м 'и ,мн, к Н • м ,ЧР, кН -м 'в I , 14 1.18 1,06 1,00 1 ,28 1 .29 1.12 1 ,28 1,33 1,26 1.18 1,28 1,29 1,12 1,28 1,33 1,26 1,18
11180-22,5-1 (1130-22,5-1 11100-22.5-1 1180-22,5-1 11360-30,3-1 11320-30,3-1 11180-30,3-1 11380-34,0 1 11320-34,0-1 11280-34,0-1 П220-34,0-1 ОП360-30.3-1 ОП320-30.3-1 ОП220-30,3-1 011380-34,0-1 ОП320-34.0-1 ОП280-34.0-1 ОП250-34.0-1 355 318 224 377 318 282 250 355 318 224 377 318 282 250 0,78 0,79 0.82 0,74 0.67 0,76 0,82 0,78 0,79 0,82 0,74 0,67 0,76 0,82 391 340 176 482 441 302 222 475 413 252 556 54! 381 292 1,22 1,21 1,18 1,26 1,33 1,24 1,18 1,22 1,21 1,18 1,26 1,33 1.24 1,18 134 134 135 182 318 250 225 355 281 250 224 318 250 225 355 281 250 224 0,86 0,82 0,94 1,00 0,72 0,71 0,88 0.72 0.67 0.74 0,82 0,72 0,71 0,88 0,72 0.67 0,74 0,82 । ! 1 1 1 ! . i ! U : 1 1 gg1 : 197 145 392 303 131 48! 392 261 176 476 382 209 556 476 347 252
244
Т а б л и и а 8.7
Коэффи- циент В середине пролета В конце крайнего блока
слева справа слева | справа
Трехблочная Четырехблочная
поперечина поперечина
а 0,5 0.167 (3+е) 0,167 (3 е) 0,2.5 (24-,') 0,25(2- е)
р 0,5 0.167 (3 -с) 0.167 (3-4-е) 0.25(2 >•) ; <1.25 (2—<->
блочной поперечины не может быть заменен средним блоком трехблоч-
ной поперечины вследствие несоответствия расположения панелей с
’ ОПС> Hfii >Т1 Г 5
! I V 1 J LU j»i ’« i.»ux rtWH.H* . .
Несущая способность блоков поперечин в обычном исполнений й-
стали 1-й группы прочности в качестве примера приведена в табл. 8 6
Расчетная схема для подбора поперечин составляется с учетом
фактического расположения путей, габаритов установки сгоек,- уве
личения их вследствие неточности установки, размера междупутий
(рис. 8.3, б). Вначале определяют изгибающие моменты в необходимых
сечениях от веса подвесок
•И ((}) а 2 ' Г' 2 Gjaj (X 1>
(1 / I
и от веса гололеда на подвесках
а т
/И |Ор) а 2 бг; 2 GVjiij. |К 2}
i ’ / '
.v <х и 3 коэффициенты, принесенные и табл. 8 7 и учи i ываияние поло
жение расчетного сечения, а также отличие фактической дли
ны поперечины 1..,р от расчетной длины основной поперечины
Лр. е - Lpl/.ф:
>t т число нагрузок, расположенных соответственно слева и справа
от расчетного сечения.
О’.-. (jj нагрузки от собственно! о веса подвесок расположенных соот
вегственно слева (<) и справа (/) <л расчетного сечения, считая
от опор (нагрузке попадающею в сечение читывшот один рал,
даН;
(ф (iv s -то же от веса гололеда па подвесках, даН:
a,-. n j плечи натру :ок <.оотвегс1венно от собственного aec.i или н<- а
гололеда на подвесках / и / м.
Нагрузка от собственного веса подвески i (или /)
б; lift । <?г, (8.J)
। де ц, - распределенная линейная нагрузка от веса I м подвески (см
табл. 2.1), даН/м;
I длина пролета подвески, м,
О'т нагрузка от веса конструкции в точке подвеса, даН.
245
Нагрузка Gr при подвешивании на консольной стойке принимает-
ся 127,5 даН для промежуточных опор и 245 даН для переходных; при
фиксаторных стойках — на переменном токе 103 даН для промежуточ-
ных опор и 206 даН для переходных, на постоянном — соответственно
98 и 21 i даН; при фиксирующих тросах — на переменном токе для
промежуточных опор 41 даН, для переходных 83,5 даН, на постоян-
ном токе —- соответственно 39 и 88 даН.
Нагрузка от веса гололеда на подвеске i (или /)
<Jrj - grl l.
тзе gr; распределенная линейная нагрузка от гололеда на 1 м подвески
(см. табл. 2.11, даН/м.
Затем вычисляют изгибающие моменты от всех внешних сил. Для
проверки блоков двухблочпых поперечна и средних блоков остальных
поперечин применяют следующие формулы;
при аварийном режиме
У1' О.!25Лф(<.р >-йрр) t 938Лф h/b '-55 ((?) I Л! (Gr);
при нормальном режиме гололеда с ветром
.. h
11»-- (1 I,17gPr)-l 0,135РРГ £ф —/-г-ЫЛ4 (G) 1
-г 1, 1755 (Оф); 53.4)
ппи нормальном режиме ветра максимальной интенсивности
УУ 0 13Н/-Ф Др-1-0,15Рр /.ф-у/•!•!, IM (G). (6.5)
. gp я распределенная линейная нагрузка спотвегсгвшпю от
собственного леса и ui гололеда на 1 м поперечины
Набл 8.8);
а b - расчетные соответственно высота и ширина нопсречи-
ны; rub ! ,56 для поперечин длиной до 22,5 м и
1,62 для более длинных поперечин;
/н или - коэффициенты соответственно для верхнего или ниж-
него пояса, учитывающие распределение давления вет-
ра вдоль пути между горизонтальными плоскостями
поперечины за счет различной жесткости поясов (см.
табл. 8.6):
/’р1. — нагрузка на поперечину от ветра при гололеде,
даН/м:
Ррг “ т (0,5i.'liiax)2; (8.6)
lJv - нагрузка на поперечину от ветра максимальной интен-
сивности, даН/м:
рр = 7С,х; (8-7)
чгпах—скорость ветра максимальной интенсивности, м/с.
Значения коэффициента у приведены в табл. 8.8.
Коэффициент 1,17 к нагрузкам от гололеда на ригеле и на подвес-
ках в нормальном режиме здесь и ниже принимают для районов голо-
ледности I. II, Ill, для районов IV и V принимают коэффициент 1,26.
246
Т а б л икс 8.8
Марка поперечины Кр, дпН/ч £Р1’, даН/м, при гололеде, мм V
5 10 г; го
Ill 80-22,5-i ГИЗО-22,5-1 П100-22,5-1 1180-22,5-1 40,12 33,38 31 ,25 30,44 4,79 9,58 14,37 19.1ь 0,025
П360-30.3-1 П320-30,3-1 П180-30,3-1 51,00 46,03 39.03 6.27 12.54 18,81 25,08 0.034
11380-34,0-1 П320-34.0-1 П280-34,0-1 П220-34.0-1 53,56 49,74 43,83 39.70 6.29 12,58 25,17 0.034
ОП360-30.3-1 01.1320-30,3-1 ОП220-30.3-1 6.7,59 62.62 55,62 8.75 17.49 26,24 34,99 .0,048
ОП380-34.0-1 ОП320-34.0-1 ОП280-34.0-1 011250-34,0-1 70,1 1 66,29 60,38 56.25 8,77 17.53 26.30 35,06 0.048
Для проверки крайнего блока в одной трети пролета (трехблоч-
ные поперечины) применяют формулы.
при нормальном режиме гололеда с ветром
'И1' 0,0139 (9—г4) £ф (I, )gp j-1,17gpr)
f 0.015(9-e*)/'pr4y Z-I-I.IAJ (G) 4 -1, J7M (GP). (8.8}
нри нормальном режиме ветра максимальной интенсивности
Л4Р—-0.0153 (9—е«) Ugp-l-1.0167 (9 -е«) Рр Ц,— i t 1.1М (G) 18.9)
Для проверки крайнего блока в ’Д пролета (четырехблочные по-
перечины) пользуются формулами:
при нормальном режиме гололеда с ветром
Л7Р -0.0313 (4—е«> £ф (1,lg-р Д 1,17gpr) -
0,03.38 (4- й“) Ррг Ьф~ I 1, IM (G) + 1,17Л1 (GP);
при нормальном режиме ветра максимальной интенсивности
Л1!’ -0.0344 (4-Д /.«Др . о ,0375 (4- е«) Pf, 4 у t -f l.l.M (G).
247
i.. ._ «v _ё ti Jl-jS- j.
Сгл
21.05
Сгл
С,
S555_
_ ййГТ
17551
р/й5
20'95
15,55
8.66 '
1/Зпролета 1/2 пропета 1/3 пропета
50.5
25,55
Моменты от веса цепных под-
весок и гололеда на них для
проверки крайних блоков в \3
и пролета определяют слева
и справа, т. е. для каждого
крайнего блока, и для подбора
принимают больший момент.
Рис 8.4 Расчетная схема для подбора
Пример. 3 а д а пне и ис-
ходные д а н в ы е. Подобрать
типовую жесткую поперечину с фик-
сирующим тросом и устройствами
жесткой поперечины освещения для перекрытия шести
путей на линии постоянного тока
по схеме, приведенной на рис. 8.4.
Поперечина промежуточная. Подвески на главных путях М-120 2МФ-100.
на станционных — ПБСМ-70 ! МФ-85. Расчетная толщина стенки гололеда
15 мм, скорость ветра максимальной интенсивности 30 м.с, Нагрузки
от веса подвесок iданных путей 178 даН, от веса гололеда на этих путях -
129 даН. Соответственно нагрузки от подвесок станционных путей составляют
86 и 91 даН. Поперечина обычного исполнения из стали марки ВСт.Зпсб 1-й
группы прочности по ТУ 14—1 —3023—80.
Р е ш е и и е, Фактическая длина поперечины, определенная с учетом уве
личения габарита стоек по 0,15 м с каждой стороны 30,5 м. Для проверки выби-
раем поперечину 011250-34,0-1, имеющую основную длину 34.0м. Фактическая
длина 30,5 м получается путем исключения по одной панели в крайних блоках и
смещения точек опирания на 0,5 м с каждой стороны 34.0—1,25-2- 0,5-2 -
— 30,5 м. Вертикальные нагрузки'
от подвесок главных путей G, 178 !-39 -217 даН:
от гололеда 6п-.> - 129 даН.
Соответственно нагрузки от подвесок станционных путей:
О’ст -.89-1-39 125да11; 6’п.т- 91 да!I
Нормативные на) рузки от собственного веса поперечины и гололеда на пен
(по табл. 8.8): gp 56,3 даН/м; £рг 26.3 даН/м.
Нагрузки па поперечину от ветра максимальной интенсивности и от ветра
при гололеде определяем по формулам (8.6) и (8.7) и данным табл. 8.8:
/>р 0,048-30-’ 43,2 даН/м: Ррг 0,048 (0,5-30)2 10,8 даН/м.
Коэффициент е 34,0/30,5 1,115.
Для принятой поперечины, состоящей из трех блоков, необходимо выпол-
нить расчет среднего блока в середине пролета и крайних блоков в 1/3 пролета
(рис. 8.4) в нормальных режимах'.
Определим изгибающие моменты 44 (G) и .44 (Сг) в середине пролета по фор-
мулам (8.1) и (8.2)
44(G) 0,5 [125-3.45 г217 (9,55-I-14,85)] 1-0,5У
/, 125(13,15 ; 8,65ч 4,85)-"-4528.7;
М (Gr) 0,5[91-3,45 [-129 (9,554 14,85)] {-0,5-91 (13,15-{-8,65-]-4,85)-=2943,4.
Моменты в 1/;, пролета:
слева:
41(G) - 0,167 ( 34-1,115) (125-3,45 4-217.9.55)4-0,167 (3--1,115) '...
:< [217 • 15.65 -|- 125 (13,15 8,65- ‘.4,85)] =-= 3838,2;
248
'И (GP) -0.167 (3 г 1,110) (91.3.45 H 129-9,55) ;-(). 1G7 (3— 1,115)
(129-15,65 -91 (1.3.15 7-8,65 1 4,85.)] 2461,3;
справа:
Л1 (G) 0,167 (3-1.115) |125 (3.45 I- 17,35)4217 (9,55 f- 14.85) | t-
i-0.167 (3 + 1.115) 125(8,65 1- 4,35) -- 3644,9;
M (Gr) -0.167 (3...-1,115) 191 (3.45 ( 17.35) । 129 (9,55-| 14,85)] ,
-1-0,167 (3 , 1.115) 91 (3.65 j-4.35) 2430,9.
Для дальнейших расчетов принимаем максимальные нагибающие моменты в
1 з пролета, т. е. 3838,2 и 2461,3 даН-м.
Изгибающие моменты от внешних сил в середине пролета определим:
при нормальном режиме гололеда с ветром для нижних поясов по формуле
(8.4)
/ИР -0, 125-30.5» (1,10-56,3 ] 1.26-26,3) !- 0,135 10.8-30.5--1 .62-0,82 !
( 1.10-4528.7 i-1 ,26-2943,4 = 21546,6даН-м:
то же для верхних поясов по той же формуле
,И1> --0,125-30.541,10-56,3 , ' ,26-26,3) 1-0,135-К),8-30,52 1.62 1.18
1,10-4528.7 1.26-2943,4--223.37,6 даН-м.
при нормальном режиме ветра максимальной интенсивности для нижних
поясов по формуле (8.5)
/ИР 0,138-30.5“-56,3 0, 15-43.2-30.5'-=-1,62-0.82 1.10-4528,7
20216.7 даН • м;
то же для верхних поясов
.ИР -0,138-30.5--56.3 0.15-43,2-30,52-1.62-1 .18
. 1.1-4528.7 23732.2 даН-м.
Изгибающие моменты от внешних сил в Ъ3 пролета определим:
при нормальном режиме гололеда с ветром для нижних поясов по формуле
(8.8)
ИР 0.0139 ( 9 - 1.115*) 30.5* (1,1-56.3 1,26-26.3 ) 0.015 ( 9 1,115*) <
10.8- 30.52-1,62-0.82 1,1-3838,2 1,26-2461.3 18 411 .3 даН•м;
то же для верхних поясов
ИР 0,0139(9 1,115») 30,541,1-56.3 1,26-26,3) 0.015 (9 - 1 .1 15*)
10.8.30.а2-1,62-1,18 , 1.1-3838,2 ; 1,26-2461,3 19093,3 даН-м;
при нормальном режиме петря максимальной интенсивности для нижних по-
ясов по формуле (8.9)
Ир 0.0153(9- 1.115*) 30.52.56.3 0,0167 (9 - 1,115») 43.2-30,5*. 1,62-0.82 ,
, 1,1-3838,2 17352,9даН-м:
то же для верхних поясов
,ИР- 0,0153 (9— 1.115*) 30,5-’-56,3 , 0.0167 (9—1 ,115)2-43.2-30,52-1,62-1,18 ]
, 1,1-3838,2 20388,8 даН-м.
Сравнивая максимальные значения полученных изгибающих моментов от
внешних сил с допускаемыми, приведенными в табл. 8.6, можно сделать вывод о
том, что несущая способность принятой жесткой поперечины ОП250-34.0-1 удов-
летворяет заданным условиям, так как для среднего блока:
/ИР -2154b, «<25045,2 даН-м и Л4Р
22 337,6 <29 198,7 даН-м;
Л1₽ -20216.7 <25045,2 даН-м и УИР—23 732,2 < 29 198,7 даН-м;
для крайнего блока-
;И₽ - 18411,3 < 22437,6 даН-м и /ИР
ЛГ<> 17352,9 <22437,6 даН-м и МР
-19 093,3 <25 193,8 даН • м;
20 388,8 < 25 193.8 даН-м.
Поскольку крайние блоки принятой поперечины по несущей способности
имеют значительный запас, целесообразно заменить их крайними блоками по-
перечины 011220-30,3-1 основной длины, имеющими достаточную несущую спо-
собность. Одновременная замена и среднего блока невозможна вследствие недо-
статка длины.
§ 3.3. Опоры контактной сети и их закрепление в грунте
Классификация опор. Опоры контактной сети могут быть разделе-
ны на две основные группы: несущие, на которых имеются какие-либо
поддерживающие устройства (консоли, кронштейны, жесткие или гиб-
кие поперечины), и фиксирующие, на которых крепят только фиксиру-
ющие устройства (фиксаторы или фиксирующие поперечины) В пер-
вом случае опоры воспринимают и вертикальные и горизонтальные
нагрузки, во втором - лишь горизонтальные.
В зависимости от типа поддерживающего устройства различают не-
сущие опоры консольные (с однопутными или двухпутными консо-
лями), стойки жестких поперечин (одиночные и спаренные) и опоры
гибких поперечин Консольные опоры обычно разделяют на промежу-
точные (на них крепится одна контактная подвеска) и переходные, ус-
танавливаемые на сопряжениях анкерных участков и воздушных
стрелках (на них крепятся две контактные подвески).
Помимо нагрузок в плоскости, перпендикулярной к оси пути, опо-
ры могут воспринимать усилия от анкеровки тех или иных проводов,
создающих нагрузки в плоскости, почти параллельной оси пути. В этом
случае опоры называют анкерными. Как правило, опоры контактной
сети выполняют одновременно несколько функций, например пере-
ходная консольная опора может быть анкерной и, кроме того, поддер-
живать еще питающие провода.
Опоры, на которых подвешиваются только провода питающих или
отсасывающих линий, называю! фидерными. Различают фидерные опо-
ры: промежуточные, угловые (на которых осуществляется изменение
направления проводов), анкерные (устанавливаемые с двух сторон
пересекаемых линией железнодорожных путей или автомобильных
дорог) и концевые (на которых производится конечная анкеровка про-
водов) .
Опоры контактной сети могут быть выполнены железобетонными и
металлическими (стальными). Наибольшее распространение в СССР
250
нашли железобетонные опоры, так как на них затрачивается значитель-
тельно меньше металла, чем на металлические опоры. Последние при-
меняют в тех случаях, когда по мощности или геометрическим разме-
рам невозможно использовать железобетонные (например, для круп-
ных гибких поперечин) или в прибрежных зонах морей и океанов, где
создаются условия для усиленной коррозии арматуры железобетон-
ных опор. Металлические опоры устанавливают также на мостах с ез-
дой поверху, если длина моста больше расчетной длины пролета между
опорами контактной сети.
Железобетонные опоры. Для установки на вновь электрифицируе-
мых линиях проектируют опоры типа С для участков переменного тока
и типа СО для участков постоянного тока. Эти опоры представляют со-
бой изготовленные методом центрифугирования полые конические бес-
стыковые трубы из предварительно напряженного железобетона с. ар-
мированием высокопрочной проволокой. Такие опоры называют пру-
нобетонными.
Типовые опоры с высотой надземной части 9,6 м от условного обре-
за фундамента запроектированы длиной 13,6 и 10,8 м, опоры с высотой
11,6 м ---длиной 15,6 м. Первые из них рассчитаны на нормативные
изгибающие моменты относительно уровня условного обреза фунда-
мента 44; 59; 79 и 98 кН-м (4,5; 6,0; 8,0 и 16,0 тс-м), вторые (длиной
15,6 м) — на 49; 66; 88 и 111 кН-м (5,0; 6,7; 9,0 и 11,3 тс-м). Опоры
мощностью более 88 кН-м можно применять только с разрешения
МПС. При недостаточной несущей способности одной опоры устанав-
ливают спаренные, т. е. две рядом, располагая нх вдоль пути. Изгиба-
ющие моменты поперек пути, которые могут быть допущены на спа-
ренные опоры, вдвое больше приведенных выше для одиночных опор.
Опоры типа С длиной 13,6 и 10,8 м могут быть изготовлены из бе-
тона обычной и повышенной прочности. Опоры типа й. 1 в нижней части
имеют дополнительную ненапрягаемую арматуру, рассчитанную на
восприятие нормативного момента, если основная арматура потеряет
несущую способность вследствие коррозии Эти опоры предусмотрены
длиной только 13,6 и 10,8 м.
В районах с сейсмичностью не более 8 баллов опоры мощностью до
88 кН-м включительно могут применяться без ограничений. Опоры
мощностью 98 и 111 кН-м допустимо устанавливать только ь районах,
где сейсмичность не превышает 7 баллов. В районах с сейсмичностью
9 баллов опоры мощностью 44 и 49 кН-м применять не рекомендуется.
Основные данные разработанных в Гипропромтрансстрое типовых
железобетонных опор приведены в табл. 8.9.
В соответствии с ГОСТ 19330—81* типовые железобетонные опоры
именуют стойками и маркируют буквенно-цифровыми группами. Пер-
вая группа содержит обозначение типа стойки и номинальные габарит-
ные размеры — длину стойки в дециметрах и толщину стенки в сан-
тиметрах (с округлением до целого числа). Во второй группе приво-
дится порядковый номер стойки, соответствующий ее несущей способ-
ности, т. е. определенному нормативному изгибающему моменту отно-
Г5!
Табл и ц и 8.9
Типоразмеры стоек Номера стоек Норматив- ные изгиба- ющие моменты, кН-м (тс-м) Длини стоек, мм Диаметр стоек, мч Толщина стенки, М*1 При- мерна» масса.
С (СО) 108.6 1 2 44 (4,5) 59 (6,0) К) 800 450/432 60 1 ,57
С (СО) 108.7 3 4 79 (8,0) 98 (10,0) 10 800 450/432 75 1 .КВ
С (СО) 136.6 1 2 44 (4,5) 59 (6,0) 13 600 492/432 60 2. 10
с (СО) 136.7 3 4 79 (8.01 98 (10,0) 13 600 492/432 75 2,52
С 156.6 5 6 49 (5,0) 66 (6,7) 15 000 524/464 60 2.75
С 156.7 7 8 88 (9,0) 111 (11,3) 15 600 524/464 75 3.10
Примечания L В числителе приведены диаметры стоек у основания. в зна
мен а теле -- на > ровне условного обреза фундамента: диаметр всех стоек у вершин рати
290 мм.
2. Толщина стенок для опор тина С пз бетона повышенной прочности составляет
55 мм при мощности 44 кН-м. 60 мм — при 59 и 79 кН«м и 70 мм* при 98
сителыю уровня условного обреза фундамента (см. табл. 8.9). В треть-
ей группе указывают: буквой П - изготовление стойки из бетона по-
вышенной прочности, буквой М — пригодность для установки в рай-
онах с расчетной температурой наружного воздуха ниже -40 °C (но
не ниже -..65 °C) и буквой К - для применения в газовой среде со
среднеагрессивным воздействием на железобетонные конструкции.
Отсутствие букв М и К означает, что данные опоры предназначены
для применения в районах с расчетными температурами - 40 С и
выше при неагрессивном и слабоагрессивном воздействии газовой сре-
ды на железобетонные конструкции. Например:
С 108.6-1 стойка тина С длиной 10 800 мм с толщиной стенки
60 мм, первой несущей способности (44 кН-м) для применения в рай-
онах с расчетной температурой 40 "С и выше при неагрессивном и
слабоагрессивном воздействии газовой среды;
С 108.6-1П — то же, но стойка изготовлена из бетона повышенной
прочности с толщиной стенки 55 мм;
СО 136.7-4-М — стойка типа СО длиной 13 600 мм с толщиной стен-
ки 75мм, четвертой несущей способности (98 кН-м) для применения в
районах с расчетной температурой ниже —40 °C при неагрессивном н
слабоагрессивном воздействии газовой среды;
252
С 156.6-7-К — стойка типа С длиной 15 600 мм с толщиной стенки
60 мм, седьмой несущей способности (88 кН-м) для применения в рай-
онах с расчетной температурой —40°С и выше при среднеагрессив-
ном воздействии газовой среды;
СО 108.6-2-МК — стойка типа СО длиной 10 800 мм с толщиной
стенки 60 мм, второй несущей способности (59 кН-м) для примене-
ния в районах с расчетной температурой ниже - -40 °C при среднеаг-
рессивном воздействии газовой среды.
Ранее типовые железобетонные опоры маркировали по схеме
А-М-Н. где А — характеристика конструкции опоры, М — норматив-
ный изгибающий момент относительно уровня условного обреза фун-
дамента, тс-м, Н - длина опоры, м. Например, СКЦ-6,0-13,6 — стру-
нобетонная коническая центрифугированная опора мощностью 6 тс-м
длиной 13.6 м.
Крепление консолей и кронштейнов ко всем типовым опорам пре-
дусмотрено болтовое, применяются закладные детали. Для болтов вы-
полнены цилиндрические отверстия в опорах под изолирующие втул-
ки из полиэтилена.
Опоры длиной 15.6 м широко используют при электрификации
БАМа. На полевой стороне опор можно установить кронштейны для
крепления проводов ВЛ 35 кВ с треугольным или горизонтальным рас-
положением. В первом случае питающие или усиливающие провода
подвешивают над контактной подвеской, а во втором • над проводами
ВЛ 35 кВ. При отсутствии контактной сети эти опоры могут быть ис-
пользованы для подвески двух трехфазных ВЛ 10 и 35 кВ с разных сто-
рон опор.
В опытном порядке начат выпуск железобетонных опор тина СОК
(стойка обратной комичности). Это опоры из центрифугированного же-
лезобетона; их надземные части такие же, как и у обычных опор, а
подземные, начиная с расстояния 3,5 м от основания, имеют комич-
ность, обратную верхней. На указанной длине подземной части сбег
вдвое больше, чем в остальной части до вершины. Для участков пере-
менного тока эти опоры обозначают СОКВ. для участков постоянного
тока .СОКО. Котлованы под опоры СОК выштамповываются спе-
циальным механизмом (лидером). Предполагается, что надежность за-
делки таких опор в грунте будет выше, чем обычных.
Конические железобетонные опоры могут быть закреплены в грун-
те различными способами. Опоры длиной более 10,8 м закапывают
на глубину около 4 м, обеспечивающую требуемую устойчивость.
Иногда эта устойчивость достигается установкой одного верхнего или
одновременно верхнего и нижнего лежней (рис. 8.5, а). Опоры длиной
10,8 м устанавливают на железобетонные трехлучевые стаканные
фундаменты типа ТС (рис. 8.5, б). Это делают и тогда, когда несущая
способность грунта недостаточна для обеспечения нужной устойчиво-
сти опор даже при наличии лежней (например, в болотистой местности
или на насыпях.). В отдельных случаях, если необходима рабочая вы-
piu b.5 Схемы заделки и грхнт железобетонных опор
/ опора. - верхней .se.'VHb; 3 нижний лежень; •? фундамент ТС. 5 - свая, ( слож-
ном 7 леревянш”; короб* К --оттяжки; 9 - анкер ТЛ; (0 • опорная плита
сота опор более 9.6 м, на фундаменты типа ТС устанавливают и опоры
длиной 13,6 м.
При необходимости на насыпях опоры длиной 10,8 м устанавли-
вают па сваях длиной 8 10 м (рис. 8.5, в). В пуччнистых грунтах и в
районах вечной мерзлоты опоры устанавливают в котлованы, ограж-
денные деревянными коробами (рис. 8.5, г), засыпая пазухи в верхней
части дренирующим грунтом, а в сильно обводненных грунтах, кроме
кого, применяя специальные обмотки.
Анкерные железобетонные опоры образуют из опор с нормативным
изгибающим моментом 79 кН-м и более, усиленных продольными от-
тяжками (одной или дв)мя). Закрепление в грунте анкерных опор осу-
ществляют так, как это показано на рис. 8.5, д. Для крепления оття-
жек применяют спениальпый трехлучевой фундамент (анкер) типа ТА,
а под опоры устанавливают опорные плиты. Стрелками в подземной
части опор на рис. 8.5 показаны реакции грунта, возникающие при
внешнем изгибающем моменте М.
Кроме показанных на рис. 8.5, применяют еще блочные фундамен-
ты с уширенной полкой типа ЗФ-1. Они имеют размер вдоль пути, рав-
ный 1.3 м, что обеспечивает необходимую устойчивость опоры при срав-
нительно небольшой глубине заделки (2,5 м). Эти фундаменты исполь-
зуют для установки в иольдиевых глинах (с присыпкой), в разборно-
скальных грунтах и в местах, где имеются карстовые образования.
Опоры, устанавливаемые в грунт непосредственно, называют
цельными, а .закрепленные на фундаментах — раздельными. Раздель-
ные опоры после соединения с фундаментами типа ТС становятся не-
разъемными. Опоры, закрепленные на фундаментах другого типа ан-
керными болтами, называют разъемными.
Металлические опоры. Такие опоры применяют обычно сквозного
типа; они представляют собой пространственные фермы с четырьмя
стойками из угловой стали, соединенными треугольной решеткой.
Эти опоры (рис. 8.6) имеют пирамидальную форму со сбегом в обеих
254
имно перпендику-
выпуска типового
рассчитанная на
плоскостях. Например, для опор гибких поперечин сбег составляе!
53—68 мм/м в рабочей плоскости и 27-.40 мм/м в нерабочей. Опоры вы-
полняют из отдельных поясов высотой 5—7 м, соединенных болтам)!
или сваркой (на рис. 8.6 показана схема металлической опоры из двух
поясов).
С целью экономии металла стойки разных поясов мо«-ут быть изго-
товлены из профилей различного сечения, а элементы, работающие
только па растяжение, принимают меныпеги размера, чем аналогич-
ные, работающие на сжатие с продольным изгибом. При этом эконо-
мия металла составляет в среднем 4—5 % массы опоры. Такие опо-
ры называют направленными и обозначают буквами МН Опоры, до-
пускающие анкеровки каких-либо проводов, т. е. нагруженные в двух
взаимно перпендикулярных плоскостях, выполняют ненаправленными
и обозначают одной буквой М.
Типовые металлические опоры маркируют ио схеме А --Д.
где А — характеристика конструкции опоры (направленная или не:
направленная); М - значение нормативного изгибающего момента,
тс-м, относительно основания опоры (при опорах, допускающих анке-
ровку проводов, указывают два значения во вза
.тарных плоскостях); Н — длина опоры, м; Д год
проекта (две последних цифры). Например:
МН-рг-73- металлическая направленная опора.,
изгибающий момент 45 тс-м, длиной 15 м, типо-
вой проект 1973 г.;
t)5 *-°5
М-—-—-73 ... ненаправленная металлическая
опора, рассчитанная на изгибающие моменты 65 и
25 тс-м, длиной 15м, типовой проект 1973 г.
Основные данные типовых металлических опор,
разработанных в Трансэлектропроекте, приведены
в табл, а.10. Кроме того, в Трансэлектропроекте
разработаны консольные металлические опоры
для применения в северных районах (марки МО)
и в промышленных районах с агрессивными сре-
дами (марки М). Эти опоры рассчитаны на те же
нормативные изгибающие моменты, что и железо-
бетонные марки СКЦ, г. е. 4,5; 6; 8 и ’0 тс-м при
высоте 9,6 м и на 6; 8 и 10 тс-м при высоте 11.6м.
Анкерные опоры рассчитаны на нормативные изги-
бающие моменты поперек пути б; 8 и 10 тс-м при
высоте 9,6 м, 8 и 10 тс-м при высоте 11.6 м.
На этих опорах устанавливают одну или две
оттяжки, расположенные в плоскости анкеровки.
Конструктивно опоры выполнены решетчатыми с
поясами из швеллеров от № 14 до 18 и ре-
Рис. 8 б Схема ме-
таллической опо-
ры:
i рпсьос решетки;
- стойки пояса I.
<7 - соединительные
накладки; 4- диаф-
рагмы; 6-- стойки
пояса И
255
щеткой из уголков 32 X 32 X 4. Закрепление металлических опор в грун-
те осуществляют с помощью фундаментов различных типов. Для лег-
ких консольных опор могут быть применены призматические или дву-
тавровые железобетонные фундаменты (рис. 8.7, «). Мощные металли-
ческие опоры обычно устанавливают на раздельные железобетонные
Т а б л и ц а 8.10
Тип опоры Назначение Норма- тивные изгиба- ющие моменты, кН-M Базы в плоскости большего момента, мм Масса, кг, при стыках
внизу наверху болто- вых свар- ных
мн .----—73 1 5 Для гибких 11(1- .34,3 1200 400 782 765
мн 45 -73 15 перечни без анке- ровки 441 1500 500 851 834
мн - 73 15 637 150(1 500 1041 101 1
мн (>."> . -73 637 1800 600 1284 1252
мн 105 „ / 3 20 1030 2000 800 1779 1722
мн 150 _ 73 20 1471 2000 800 2127 2059
М- 45-25 -73 15 То же с анке- ровкой 441 и 245 1500 500 1194 1 176
м- —'—-73 15 637 н 245 1500 500 1520 1486
м- 10 -7-3 1.3 Для тухну 1 • пых консолей 98 1000 500 Не приме- няют 482
м- 15 -7.3 13 147 1000 500 То же 559
м- 10-40 -7.3 10 Для однопут- ных консолей 98 и 392 1500 835 » 790
10-10
Примечание. Па опоре М- । 7.1 можно осуществить анкеровку одной пере-
гонной подвески с двумя контактными проводами или двух станционных подвесок с одной
пороны опоры прн одновременной нагрузке в плоскости поперек пути. При отсутствии
«той нагрузки можно анкеровать вместе перегонную и станционную подвески с одной сто-
роны опоры, а также использовать эту опору в качестве угловой для питающей линии.
256
Рис. 8.7. Схемы заделки в грунт металлических опор на призматическом фхнда
менте (а), на раздельных блоках (б), на ростверке со сваями (я/ и на монолит
ном ступенчатом фундаменте (?)
блоки, один из которых работает на погружение, а другой на вы-
дергивание (рис. 8.7, б), или применяют ростверк со сваями, часть ко-
торых работает на погружение, а часть — на выдергивание (рис. 8.7.щ
Если окажется целесообразным выполнять бетонные работы на месте,
для мощных опор можно применить монолитные ступенчатые фунда-
менты (рис. 8.7, а). Стрелками в подземной части опор на рис. 8.7 пока-
заны реакции грунта, возникающие при наличии внешнего изгибаю-
щего момента Л1.
Для установки металлических опор в северных районах и в райо-
нах с агрессивными средами разработаны специальные железобетон-
ные и свайные фундаменты, рассчитанные на применение при расчет-
ных температурах до —65 °C.
Соединение оснований металлических опор с фундаментами во
всех случаях осуществляют с помощью анкерных болтов, закладыва-
емых в тело фундаментов. Для заделки опор в скальных грунтах, а
также в вечномерзлых грунтах или с большой глубиной сезонного про-
мерзания и в других случаях, когда требуемая устойчивость опор и
долговечность фундаментов не обеспечиваются описанными выше спо-
собами, разрабатывают специальные конструкции.
Для удобства пользования дальнейшими материалами приведем
принятые ниже основные условные обозначения:
G — вертикальная нагрузка;
— горизонтальная нагрузка от давления ветра;
7*из —- горизонтальная нагрузка от излома проводов;
На — горизонтальная составляющая натяжения поперечного несущего троса
гибкой поперечины;
Нф — натяжение фиксирующего троса;
г — расстояние от оси опоры до точки приложения вертикальной нагрузки,
h высота точки приложения горизонтальной нагрузки относительно уров
ня условного обреза фундамента для железобетонных опор или от
носительно основания металлических опор.
Кроме того, применены различные индексы, обозначающие рас-
четную величину; п — контактная подвеска и поперечный несущий
С) Зак 2631> 25"
трос; н — несущий трос; к — контактный провод (провода); у -
усиливающий провод; пр — любой воздушный провод (кроме усилива-
ющего); оп — опора; кн — консоль; кр — кронштейн; пт - пята кон-
соли: ф — фиксирующий трос.
§ 8.4. Подбор консольных и фиксирующих опор
Поскольку для железобетон пых опор контактной сети, как пра-
вило, лимитирующими ио трещиностойкости являются нормативные
изгибающие моменты, опоры подбирают по этим моментам. Для опор,
устанавливаемых в сейсмических районах, необходимо учитывать до-
полнительные моменты от сейсмических воздействий в соответствии с
данными, приведенными в типовых проектах опор. Сумм;: моментов oi
конкретных нагрузок и от сейсмических воздействий не должна пре
вышать расчетные моменты, выдерживаемые опорой
При подборе типовых консольных и фиксирующих опор необходи-
мо правильно выбрать расчетный режим, расчетное направление в<ч-
ра и расчетное сечение опоры. В табл. 8.11 приведены условия, кото-
рые нужно учитывать при подборе указанных опор в случаях исполь
ювания нолукомиенсированных подвесок и однопутных консолей.
'Чтобы подобрать консольную опору. например переходную с полу-
компенсированными подвесками, нужно определить изгибающие
моменты от внешних сил 10 раз (три расчетных режима, при двух и ••
Т а б .1 и и а 8.11
Тип опор Место установии •»цор Расе! и ые режим и Расчетные направо»1 ния негра Расчетные сечения опоры
Консоль- Прямая Гололед с нет- От опоры Условный об-
ныс про- ром; максималь- на путь рез фундамента
меж\точны е Внешняя ныя ветер Гололед с вот- То же иди основание То же
сторона кривой Внутрец- ром; максима,зь- IIып ветер; мини- мальная темпера- тура То же От опоры Условный об
Консоль- нчя сто- рона кривой Везде ,> на путь; от пути на опору То же рез фундамента или основание уровень пяты кон соли То же
мыс пере- ходные Фикси От опоры Условный обрез
рующие на путь фундамента
И8
Рис О. Графическое определение -,квивалешпого радиуса кривой
иях два различных направления ветра и во всех случаях два расчет-
ных сечения опоры), после чего выбрать из них .максимальные для рас
четных сечений опоры. При компенсированных подвесках число рас-
четов для определения изгибающих моментов от внешних сил сокраща-
ется. так как отпадает необходимость проверки режима минимальной
1емпературы. В этом случае для подбора переходной консольной опо-
ры достаточно выполнить восемь расчетов (два режима, два направле-
ния ветра и два расчетных сечения опоры). Определение необходимых
нагрузок прок «водят в соответствии с материалами, приведенными ",
гл. 2
При расположении опоры ла сопряжении прямого и кривого участ-
ков пути для определения действующих па опору нагрузок можно не-
иолыовать формулы, приведенные г § 2.3. или способ, который пред-
ложен в Транеэлектропроекте. Этот способ предусматривает графиче-
ское оирелд лс-ние жвнвалентного радиуса кривой при котором
нагрузка от излома проводов, определяемая по формуле (2.28). будет
равна пагру же при действительном расположении опоры. Для выбора
жачепия которое нужно подставить в формулу (2.28), разрабо-
!.-'.ны вспомогательные графики. Часть одного из них для примера по-
намиа на рис 8 8. где приняты следующие условные обозначения:
/? радиус кривого участка пути, м; /(! длина пролета в сторону
кривого участка пути, м: /и - то же в сторону прямого участка пути,
м: д,. расстояние от начала кривой до расчетной опоры при ее рас-
положении на кривом участке пути, м; х.. - расстояние от качала
кривой де расчетной опоры при ее расположении на прямом участке
пути, м
Штриховой линией на рис. 8.8 показана последовательность опре-
деления А’Э1{П при* R 600 м, /к — 50 м. /„ 60 м, хп 15 м. Иско-
мо!1 значение /?.,кв --- 1100 м.
На линиях е электрической тягой для грузовых поездов в соответ-
ствии с ВНТП-81 опоры контактной сети должны быть рассчитаны на
Q* 959
sjfrm т ги nwnr и
Рис. 8.9. Примерные расчетные схемы для подбора промежуточных н переход-
ных консольных опор на линиях переменного ot) и постоянного (б) тока
участках переменного тока па подвеску одного усиливающего провода
А-185, а иа участках постоянного тока — на подвеску двух таких же
проводов. В последнем случае в межподстанциопных зонах с расчетны-
ми подъемами па '/* расстояний от тяговых подстанций опоры должны
быть рассчитаны на подвеску трех усиливающих проводов А-185.
Чтобы подвесить указанные усиливающие провода на тех же опорах,
которые использованы для закрепления кронштейнов для проводов ВЛ
6 К) кВ или ДПР, необходимы специальные надставки. Такие над-
ставки разработаны в Трансэлектропроекте для электрифицированных
яинпй постоянного и переменного тока (см. §8.1).
На рис. 8.9 показаны примерные расчетные схемы для подбора про-
межуточных и переходных опор на участках переменного и постоян-
ного тока для тех случаев, когда на этих опорах, кроме проводов ли-
ний питания нетяговых потребителей, подвешены еще и усиливающие
провода.
При отсутствии усиливающих проводов над контактной под-
веской эти же схемы можно использовать для подбора опор, прини-
мая все нагрузки от усиливающих проводов равными нулю.
На расчетных схемах рис. 8.9 горизонтальные силы условно обо-
шачены одной буквой; каждая из них определяется выражением
/'<--+^±24 (а-10)
2Ы)
где P‘t — нагрузка от ветра;
SP‘3 — суммарная нагрузка от излома проводов на кривых участках
пути, отводах ла анкеровку и др.
Знаки «-1-» в выражении (8.10) принимают при направлении дей-
ствия нагрузок от опоры на путь, знаки «--» • от пути на опору.
Точки приложения нагрузок на рис. 8.9 соответствуют действи-
тельному положению проводов. Это не позволяет при подвесных изо-
ляторах точно определить длину плеч для вычислений изгибающих
моментов, так как не учитывается наклон гирлянд изоляторов. Одна-
ко получаемая ошибка незначительна, вследствие чего указанное
уточнение в расчеты не вводят. При необходимости углы наклона изо-
ляторных гирлянд в различных условиях могут быть определены с по-
мощью материалов § 7.6.
Равномерно распределенные нагрузки от веса консолей и кронштей-
нов для упрощения расчета обычно заменяют сосредоточенными и при-
ложенными на половине длины горизонтальной проекции данной кон-
струкции. Такое допущение не дает заметной погрешности в резуль-
татах расчетов, так как определяемые этими нагрузками изгибающие
моменты незначительны по сравнению с другими Равномерно распре-
деленную нагрузку от ветра на опору также заменяют сосредоточен-
ной и приложенной в середине рассматриваемой части опоры.
Наличие двух подвесок и консолей на переходных опорах учитыва-
ют соответствующим увеличением вертикальных п горизонтальных
нагрузок. Например, для переходной опоры на кривой в нормальных
условиях горизонтальная нагрузка от проводов цепной подвески
4- 2Рг
— *• и <.кр
где
Г)’
‘ н <.анк
усилие от излома провода i па кривой (« • » — при установке
опоры с внешней стороны кривой, « —» - г внутренней).
усилие от излома провода i при отводе его на анкеровку
С учетом указанных условий и допущений суммарный изгибающий
мо’лент относительно условного обреза фундамента для схемы рис. 8.9
при режиме /
W,1;-= Hn6u;Zu-j /гкц 9’кн / 2нн 1 «у GyZy -I GKpy; гКру —
,гпр
। Gnp/ гПрг “Льр Gh-р/zKp ± Д- ±
”пр
J- ^пр{ Лпрг ± fly Pyj hy 4 7’01Jy hon,
< = 1
/Н.12)
а изгибающий момент относительно уровня крепления пя ты консо
ли при том же режиме /
261
’Ж Ф^ВГМ.1 йи♦ a.Ji .«At *abifcfc&
Миту" Gn_; гп-Н«кн <Jkh7 гкнЧ-«у Gyj ?y-l Glipyy ?upv —
"np
— У*1 G’np/Ztipf—nKp Оцр; гкр ± ^n,z (fllt — Лпт) i /’к? (hu — Лит) ±
i -- I
"rip
± 2 ^rip; (^npJ -Giur) ± hy Pyj (lij—-Лнт) 4: Pnnj (h- h-nr)i/(2h) (8.13)
i - 1
В формулах (8.12) и (8.13) nn, пКу, Пу и /гПр — соответственно число под-
весок, консолей, кронштейнов и проводов
Если на опорах имеются какие-либо провода, не показанные на
схемах рис. 8.9. изгибающие моменты от нагрузок, создаваемых этими
проводами и их кронштейнами, учитывают при определении суммар-
ных моментов /Ио и /И11Т аналогично тому, как это сделано в формулах
(8.12) и (8.13) для величин с индексами «пр» и «кр».
Допускаемый нормативный изгибающий момент для железобетон-
ных опор на уровне пяты консоли обычно принимают равным 50 %
шачений, указанных в табл. 8.9. Примерная эпюра допускаемых нор-
мативных моментов показана на рис. 8.10.
При подборе фиксирующих опор и фиксации проводов двух кон-
1яктных подвесок одной оттяжкой (рис. 8.11, а) усилие, действующее
н.-1 опору в месте крепления оттяжки,при любом числе фиксируемых
подвесок определяется выражением
/’<»> ± Иц Р'я ±- Иц ± «и I* ± l*s-
(8 14)
При фиксации контактной подвески двумя оттяжками, т е. отдель-
но несущего троса и контактного провода (рис. 8.Н, б), каждое и <
цзух усилий определяют ио формуле (8.10).
Рис 8.10 Примерная
чиюра допустимых нор-
мативных моментов на
железобетонную опору в
зависимости от высоты
опоры
Знаки « ---» в формулах (8.10) и (8.141 н
случае подбора фиксирующих опор для одной
подвески учитывают, лишь проверяя усилия
в оттяжке, которая должна работать только
па растяжение. Если фиксируется несколько
подвесок, знаки « --» рассматривают при ис-
пользовании фиксирующих поперечин, чтобы
выяснить наиболее неблагоприятные условия
нагрузки каждой из опор поперечины.
Изгибающие моменты относительно услов-
ного обреза фундамента для схемы рис. 8.11, а
определяют как
/Ио Рф кф f /’on ^оп- (8.15)
а для схемы рис. 8.11, б (при нескольких под-
весках)
М„ -- - п„ Ptl h„ 4- пк Рк ht: 1 Роа Лоп • (8 16)
где /гк и пк -- соответственно число несущих тро-
сов и контактных проводов
262
Уровень условного обреза фундамента
Рис 8.11 Примерные расчетные схемы для подбора фиксирующих опор при
одном (а) и двух (б) фиксирующих тросах
Подбор консольных и фиксирующих опор может быть также осу-
ществлен но методике, разработанной в Трансэлектропроекте. Эта
методика использует ряд вспомогательных материалов, в которых для
различных условий приведены изгибающие моменты в расчетных се-
чениях опоры от отдельных нагрузок. Суммарный изгибающий момент
относительно нужного расчетного сечения
(Я.171
где Л1, - момент от веса подвески с гололедом:
/И2 — момент от давления ветра на провода контактной подвески;
Л13 — момент от излома на кривой проводов контактной подвески.
М4 — момент от излома проводов подвески при их отводах на анкеровку,
М5 — момент от веса усиливающих или других проводов,
,Мв — момент от давления ветра на усиливающие или другие провода,
М7 - момент от излома ла кривой усиливающих или других проводов
Мк - момент от зигзагов контактных проводов (учитывается только при
определении момента относительно условною обреза фундамента)
Анкерные железобетонные опоры, которые применяют только с от-
тяжками (рис. 8. |2). подбирают для нормального режима работы ана-
логично промежуточным опорам и проверяют для аварийного режима
при обрыве несущего троса В последнем случае происходит косой из-
гиб. при котором должно быть соблюдено условие
J Л/*-1
(Я.18»
где М' - допускаемый момент при косом изгибе:
,ИП — изгибающий момент поперек пути:
/VI h - то же вдоль пути.
В качестве примера в табл. 8.12 приведены значения моментов М’
для опор длиной 13,6 и 10,8 м из обычного бетона. Там же указаны
формулы для вычисления момента Л1п.
263
Рис 8.12, Схемы установки оттяжек на анкерных опорах-
а при совместной анкеровке проводов компенсированной подвески: б при разделений
анкеровке проводов цепных подвесок: в—для опор средней анкеровки компенсированном
подвески и при анкеровке усиливающих проводов
Расстояние А от оси опоры до оси анкера (см. рис. 8.12) принимают
в зависимости от типа анкера, ширины земляного полотна и условий
установки опор. Например, при трехлучевом анкере и ширине земля-
ного полотна 5,8 м это расстояние составляет: 7 м при габаритах ус-
тановки опор 3,3—3,6 м, 8 м при габарите 4,9 м и 8,5 м при габарите
5,7 м и установке в междупутьях.
Максимальный изгибающий момент в плоскости поперек пути оп-
ределяют так же, как и для промежуточных или переходных опор,
в соответствии со схемой нагрузок опоры в этой плоскости.
Данные оттяжек из круглой стали, применяемых в различных ус-
ловиях на анкерных железобетонных опорах, приведены в табл. 8.13.
Для подбора опоры с двухпутной консолью можно использовать
схему рис. 8.13. Как правило, такие опоры выполняют металлически-
Таблица 8.12
Расчетное сечение опоры Значение М', кН-м, для опор с нормативным моментом, кН-м Мв. кН • м
4 4 59 79 98
__ Условный обрез фундамента 76,5 85,7 115,1 129,9 hit Н -hi К’
Уровень крепле- ния нижней от- тяжки 44, 1 45.5 60,8 77,7 (hit-hii) Н
П ри меча ние. Расстояния h н и Лк
показаны
на рис. 8.12, б, // — натяжение ан-
керуемых проводов со стороны, противоположной анкеровке несущего троса; К' — натяже-
ние контактного провода при обрыве несущего троса
264
Таблица 8.13
П рнчечани е. Оттяжки для опор с анкеровкой усиливающих проводов такие же,
как при анкеровке компенсированной подвески.
ми (см. табл. 8.10). но в отдельных случаях применяют и спаренные
железобетонные опоры длиной 13,6 м, устанавливая их на фундамен-
ты типа ТС. В последнем случае допускаемые изгибающие моменты от-
носительно уровня обреза фундамента для каждой опоры могут быть
увеличены по сравнению с указанными в табл. 8.9: примерно на 20 %
для опор с нормативным моментом 44 кН-м, на 15 % для опор с нор-
мативным моментом 59 кН-м и на 10 % для опор с нормативным мо-
ментом 79 кН- м.
Изгибающий момент у основания металлической опоры (или об-
реза фундамента железобетонной опоры) определяют как
"и "у
/О() 2 Оц; Z||j f У GyjZyj j Оьи О(. |. г<.т 4;
I I / 1
,!н "к "у
ft(l t Рк; htr + , Pyj hy ± P0[i Лоп > 16.19)
I I i I /1
а изгибающий момент относительно уровня крепления пяты консоли
"11 "у
Л4цт=-; Он,-гп; GyjZyj ОК1| г((н т Ост г(.| j Роп (h -hUT)2, (2h), (8.20)
i ----- 1 / I
где Пу — число мест подвеса усиливающих проводов.
265
Число и расположение прово-
дов на рис. 8.13 показаны услов-
но. При ином числе или располо-
жении проводов формулы (8.19) и
(8.20) следует соответствующим
образом откорректировать.
Пример. 3 а дани с. Подобрать
типовые железобетонные опоры для ус-
тановки их в качестве, консольных про-
межуточных на прямых участках пути,
с внешней и внутренней сторон кривой
радиусом 900 м, а также в качестве
консольных переходных при сопряже-
ниях анкерных участков в трех проле-
тах на прямых участках пути. Подбор
выполнить по нормативным нагрузкам
и моментам.
И с х о д и ы с д а н в ы е. Кон
Рис «13 Примерная расчетная схема тактная |юдисска М-120 : 2НлОЛО.
ьля подоора опоры с двухпутной коп 04Ф-100 компенсированная на пеизоля'
и,л,>10 роваиных наклонных консолях. С поло-
вой стороны опор находится трехфазная
В.1 10 кВ. выполненная проводами ЛС-50/8,0. Па промежуточных опорах пря-
мых участков пути на надставках подвешены два усиливающих провода Л-185.
Наибольшая длина пролета на прямых участках пути составляет 68 м. Эту
же длину пролета следует принять и для подбора переходных опор, так как опа
может быть реализована при иеизолирующих сопряжениях анкерных участков,
что обусловит большие нагрузки опор, чем при изолирующих сопряжениях, кот
да длина пролета между переходными опорами хмепьшается. Па кривых рядну
сом 900 м наибольшая длина пролет 60 м Промежуточные и переходные опоры
устанавливают с габаритом 3.1 и, анкерные с габаритом 3.3 м.
Поскольку определение необходимых для расчетов нормативных нагрузок
иеодпокра 1 но рассматривалось в примерах к предыдущим главам, в данном слу
'Г а б л и п а 8.1 4
Значения нагрузок. лиН. на опоры '> н а че пн я нагрузок. даН на пипры
1.П рузк» Наг
промежуток ную и пере- ходную на прямой промежутки ную на кривой ручки Промеж > ч <*ч ную па прямой промежуточ ную на кривой ПГреЧОДНу ю IJ.I Прямой
<>„ 316 233 282/209 I'i, 7. >/96 / /
б‘п р G'y 151’39 171/67 134/33 /' /'и, 118/118 91/91
п 72/81 63/71 /Ж из 35/35 131/131 101/101
1* 67/99 60/89 рпр }И / 27/20 !
рпр в 60/53 53/47 /'on 61/165 61/165 61/165
чае эти нагрузки просто приведены в табл. 8.14 (в числителе указаны нагрузки
при режиме гололеда с толщиной стенки 10 мм и ветром, в знаменателе — при ре-
жиме максимального ветра). Нагрузки для режима минимальной температуры в
габл. 8.14 не приводятся, так как при компенсированной контактной подвеске
этот режим не может быть определяющим для подбора опор.
Р е ш е н и е. Принимаем для установки железобетонные опоры СО 136.6
без фундаментов и составляем расчетную схему, показанную на рис. 8.14. Под-
бор опор будем вести отдельно для каждого из заданных типов опор. Изгибаю-
щие моменты для промежуточных опор определим только относительно уровня
условного обреза фундамента, а для переходной опоры, -- кроме того, еще и от-
носительно уровня крепления пяты консоли. Расчетное направление ветра для
опор на прямых участках пути и на внешней стороне кривой примем от опоры па
путь, для опоры с внутренней стороны кривой - от пути на опору, а для пере-
ходной опоры выполним расчеты для обоих направлений ветра. Изгибающие
моменты относительно уровня условною обреза фундамента определим по форму-
ле (8.12), а относительно уровня пяты консоли но формуле (8.13).
11 р о м е ж j го ч и а я о п о р а и а н р я м о м у ч а с т к е.
Нормативный изгибающий момент относительно уровня условного обреза фунда-
мент-
Рис. 8.14. Расчетная схема для подбора промежуточной и переходной консоль-
ных опор
267
при режиме гололеда с ветром
/Иог.--=316-3,3-Н00-1,8+171-0,94 '-50-0,47— 151 1,7-70-1,3 ;-72-9 :
I (67 +35) 7 + 2-60.9,7 + 60-8,85 + 75-10,7 61-4,8-= 5212 даН-м 52,1 кН-м;
при режиме максимального ветра
УИОВ -233-3,3 |-60-1,8 ф-67-0,94-I-30-0,47 —39-1,7-40-1.3-| 81-9 I-(99 35) '
Гх 7-| 2-53-9,7 ! 53-8,85 | 96-10,7 | 165-4,8 5819 даН-м 58,2кН-м.
Поскольку наибольший изгибающий момент равен 58,2 кН-м, то в соответ-
ствии с табл. 8.9 выбираем типовую опору СО 136.6-2.
Промежуточная опора на вне ш н е й с т о р о не
кривой. Нормативный изгибающий момент относительно уровня условного
обреза фундамента:
при режиме гололеда с негром
Мог 282-3,3 ; 100-1,8 134-1,7- 70-1,3 j-(6.3 | 118) 9-[-(60 131)7|-
| 2 (53! 27) 9,7 ) (53 [ 27) 8,85 (-61 -4.8 6311 даН-м 63.1 кН-м;
при режиме максимального ветра
М()|1 --209-3,3 !-60-1,8 —35-1,7- 40-1,34 (71 ; 118)9 (89-|-131) 7 ।
| 2 (47 1 20) 9,7 (47 ] 20) 8,85 4-165-4,8 6612даН-м 66,1к11-м.
Выбираем типовую опору СО 136.6-3.
П рои е ж у то ч п а я о п о р а н а в н утре п и е й с т о р о -
не криво й. Нормативный изгибающий момент относительно уровня услов-
ного обреза фундамента:
при режиме гололеда с ветром
А401. 282-3.3 j 100-1,8—134-1,7 —70-1 ,3—(63 118)9 (60 (-131)7 —
— 2(53 |-27)9,7— (5.3 27) 8.85- -61 • 4,8 -4727 даН-м -47,3к11-м;
при режиме максимального ветра
Мов 209-3,3 I--60-1 .8 -35-1.7 —40-1 ,3- (71 ! 1 18) 9—(89-)-131) 7 —
— 2(47 | 20) 9,7—(47 |-20 ) 8,85— 165-1,8 — 5240даН-м — 52,4кН-.м.
Выбираем опору СО 136.6-2.
П е р е х о д н а я о п о р а н а прямом у ч а с т к е. На этой опо-
ре крепят две контактные подвески, каждую на отдельной консоли. Подвеска,
отходящая па анкеровку, передает на опору усилия от изменения направления
проводов, действующие от пути на опору. Провода ЛЭН 10 кВ крепят па переход-
ной опоре без изменения их направления.
Нормативный изгибающий момент относительно уровня условного обреза
фундамента:
при режиме гололеда с ветром
Л1()Г 2-316-3,3 -2-100-1.8—151-1,7 —70-1,3 И 4 2-72 —91) 9 [
|-( h 2-67— 101) 7 к 2-60-9,7 ± 60-8.85 + 61 -4,8 (572 ± 4222) даН-м;
при режиме максимального ветра
<ИП|1 -2-233-3,3 j-2• 60-1,8 —39-1, 7 —40-1,3 -[ ( ± 9-81 — 91) 9 :
; (±2-99—101) 7 ± 2-53-9,7 ± 53-8,8г. ± 165-4,8 - (109 ± 5135) даН-м.
В случае направления ветра от опоры на путь (знаки « +) изгибающие мо-
менты составят при режиме гололеда с ветром 47,9 кН-м, а при режиме макси-
мального ветра —52,4 кН-м. Если ветер будет направлен от пути на опору
268
(знаки «—»), то изгибающие моменты равны соответственно — 36,5 и
-50,3 кН-м.
Нормативные изгибающие моменты относительно уровня крепления пяты
консоли:
при режиме гололеда с ветром
Мцг 2*316*3,3 1-2-100.1,8—151-1,7 -70-1.3 ; (± 2-72—91) (9—6,75)-;--
1 ( + 2-67—101) (7 — 6,75) ±2*60 (9.7-6,75) ±60(8.85 -6,75) ±
+ 61 -2,852: (2-9,6) (1670 + 864) даН-м;
при режиме максимального ветра
М11в 2-233-3,3 2-60-1,8-—39-1,7 —40-1,3 :-( .±2-81—91) (9 —6,75) I-
I ( щ 2-99 — 101) (7 — 0,75) 4 2-53 (9,7 — 6,75) ± 53 (8,<85 —6,75) +
+ 165*2,85s: (2*9,6) (1406 + 909) даН*м,
При направлении ветра от опоры на путь (знаки « < ») изгибающие моменты
составят для режима гололеда с ветром 27,3 кН-м, а для режима максимального
ветра 23.2 кН-м. Если ветер будет направлен от пути на опору (знаки «—»),
то изгибающие моменты соответственно равны 10,1 и 5 кН-м. Так как макси-
мальный изгибающий момент на уровне условного обреза фундамента получил-
ся равным 52,4 кН-м (при режиме максимального ветра), а па уровне крепления
пяты консоли 27,3 кН-м (при режиме гололеда с ветром), то в соответствии с
табл. 8.9 выбираем опору СО 136.6-2.
§ 8.5. Подбор опор для гибких поперечин
В соответствия с расчетной схемой (рис. 8.15) изгибающий .момент
от внешних сил относительно основания опоры определится как
Л1() 11п hu 7/ф Лиф 7/ф /1нф -| 7-01|/i0i|.
(8.21)
Значения усилий /7„ (горизонтальная составляющая натяжения по-
перечного несущего троса), /7” (натяжение верхнего фиксирующего
троса) и Нф (натяжение нижнего фикси-
рующего троса) должны быть подсчитаны
по материалам § 7.4. Расчетным для под-
бора опор гибких поперечин, как прави-
ло, является режим гололеда с ветром,
определяющий максимальное усилие в по-
перечном несущем тросе. В отдельных слу-
чаях (при небольшом поперечном проле-
те) расчетным может быть режим макси-
мального ветра. Расчетным сечением всегда
является основание опоры.
В Трапсэлекгропроекте применяют спо-
соб подбора опор гибких поперечин, осно-
ванный на использовании специально раз-
работанных для этой цели вспомогатель-
ных материалов, позволяющих существен-
Рпс. 8.15. Примерная рас
четная схема для подбора
опоры гибкой поперечины
269
ln ~ 3_Z м_
3,3» /Дл 5,9м
Рис 8 16 Схема расположения путей в поперечном пролете а) и условная рас
четная схема (б) для подбора опор гибкой поперечины:
толщенные линии главные пути и соответствующие им нагрузки, топкие линии ос
тальные станционные пути и нагрузки
ио сократить время, необходимое для определения изгибающего мо
мента от внешних сил. Сначала подготавливают условную расчетную
схему, для чего определяют среднее междупутье по формуле
«ср- 61 (« > !)• (8.22)
где /,1 длина поперечного пролета, м;
п — число нагрузок.
Для схемы расположения путей (рис. 8.16, а) среднее междупутье
составляет 5,33 м. При расстояниях между нагрузками, меньших
0,5 о(.р. нагрузки совмещаются, а при расстояниях, превышающих
1.5 а,. р, вводится фиктивная нагрузка (крайняя справа на схеме
рис. 8.16. б). Каждой из нагрузок расчетной схемы, включая фиктив
ные, присваивается номер, начиная с нагрузок, расположенных на-
иболее близко к опорам. Таким образом нагрузки в средней части про-
лета получают наибольшие номера, а при нечетном числе нагрузок на-
ибольший номер имеет средняя из них.
Суммарный изгибающий момент от всех внешних сил относитель-
но основания опоры определяют как
Мп I УИ5, (8.23)
где /И, -момент от вертикальных нагрузок, кН-м;
М., момент от действия ветра на провода, кН-м;
Мх - суммарный момент от затяжки фиксирующих тросов и от дей
стиия ветра на опору, кН-м;
.И4 — момент от излома проводов на кривых участках пути, кН-м:
Л15 — момент от излома проводов при изменении их направления. кН м
Изгибающий момент от вертикальных нагрузок
\М(аглт1.;л | aCTm(..r I апрИцр). (8.24)
1 де ЛЛ1 — удельный изгибающий момент, кН-м;
сс.,-.,, а,.,., аНр поправочные коэффициенты для подвесок главных и сган
ционных путей или других проводов;
Мрл, шС|. тир - сумма номеров нагрузок на главных и станционных путях
(без учета фиктивных).
Удельный изгибающий момент ДЛ4 определяют в зависимости от
размера агр по специально подготовленным графикам, один из которых
для примера приведен на рис. 8.17. Такие графики имеются для стан-
ционных подвесок линий переменного и постоянного тока при различ-
ных условиях гололедных образований. Поправочные коэффициенты а
27(1
находят по графикам, один из которых показан на рис. 8.18 (для ус-
ловий, принятых при построении графика на рис. 8.17). Значения по-
правочных коэффициентов зависят от типа подвески и длины продоль-
ного пролета I. Аналогичные графики могут быть построены и для лю-
бых других проводов, закрепленных на поперечном несущем гросс
гибкой поперечины.
Изгибающий момент от действия ветра на провода
Л1. .+ I (М'л пгл | лст) 10-
iк 25}
где и -Vlt'T изгибающие моменты от давления ветра на I м подвески *-о
ответственно главных и станционных путей даН-м м.
«’/гл н • число подвесок соответственно на главных и иашоннт
путях.
Изгибающие моменты Л4,'л и МА находят но специально подгото-
вленной таблице, составленной для различных подвесок и различных
ветровых и гололедных условий. Некоторые данные из нес приведены
для примера в табл. 8.15. Суммарный изгибающий момент от затяжки
фиксирующих тросов и действия ветра па опору .И., также находя;
по специально подготовленной таблице, выдержки из которой для при-
мера приведены в табл. 8.I6.
И и’ибающий момент от излома проводов на кривых участках пути
1.11 'Г, II Л,
/'НФ и 'Ci.i.
'О
'к
уч / >,
А14 ’ < Т; Йнф Hi Kj ft,i(p П; I -—10 •- 13 26)
.•*-'] Л>
шпяжения cooi веге) ненио несущего [рост и котактпою нр*
иода подвески синя /. даН.
высота крепления соответственно верхнего и нижнего фик- и
рующих тросов относигелI.но основания опоры, м:
число подвесок типа I на кривой радиусом R.
длина пролета на кривом участке пути, м.
ион подвески ПБСМ-70-1-МФ-85
при толщине стенки гололеда 10 мм.
двух (сплошные линии) и четырех
(штриховые) поперечных несущих
коэффициента а от длины пролета
/ для различных подвесок, закреплен-
ных на поперечном несущем тросе,
при толщине стенки гололеда 10 мм
тросах
271
Таблица 8.15
Скорость ветра, м/с Толщина стенки гололеда, мм Изгибающие моменты М', даН’М/м, для подвесок
M-I20+ 4-2МФ-Ю0 ПБСМ-95+ 1-2МФ-100. М-95+ Г2МФ-100 ПБСМ-70+ + МФ-100 ПБСМ-70Т (-МФ-85, С-70+ +МФ-85
25 11,94 11,24 9,49 9,09
30 17,26 16,19 13,65 13,14
35 .. 23,42 22,07 18,55 17,87
> 5,95 5,76 5,06 4,92
10 8.15 7,89 7,14 7,09
14 15 10,29 10,11 9,10 9,04
20 12.52 12.25 11,20 11,07
Изгибающий момент от излома проводов при изменениях их на-
правления
.Иг, J_ У < Г1 Л1 <*"'/; Л’i Л»ф "4'1 р-10 2, (8.27)
। де rrtj -число подвесок типа /, меняющих свое направление;
р -уге1 между прежним и новым направлением провода.
Знаки « » в формулах (8.25) — (8.27) применяют при направле-
ниях усилий от подбираемой опоры к пути, а «—» - от путей к этой
опоре.
Анкерные опоры гибких поперечин но моментам, действующим по-
перек путей, подбирают аналогично изложенному выше, а вдоль пути
допускают анкеровку одной станционной подвески. Если несуща»! спо-
собность опоры поперек пути полностью не используется, допускае-
мый изгибающий момент вдоль пути можно увеличить.
Табл и и а 8.16
Суммарный момент М& жП-м, для опор ттюн
Расчетный по ж им 45 мн 1.) <5 Ml! ~~ 1 э b5 мн- 1S 65 МН 105 МН —, 1 50 мн — 15 2 5 М 9 , <>5 --25 М 1 5
Максимального негра скоростью J0 м/с 59.82 66,69 71 ,59 9! .20 97.09 76.49
Гололеда с вет- ром скоростью 14 м/с 15,38 28.20 35.03 36 73 39,30 36,73
Рис. 8.19 Расчетная схема для подбора опор с гибкой поперечиной:
Гл — главные пути; & — другие станционные пути
Пример. Задание и исходные дан н ы е. Подобрать типо-
вые металлические опоры для гибкой поперечины, рассчитанной в примере к
§7.4.
Р е ш е н и е. Расчетную схему опоры примем по рис. 8.15. Значения Л1(,
Л1(ф, Л„ф и Лпп зададим соответственно равными 15; 9,6; 7,4 и 7,5 м. Учитывая
результаты расчетов гибкой поперечины, определим значение Л1П по формуле
(8.21) для режима гололеда с ветром
Мо 2072-15 658-9,6-|-(>58-7,4-1-95-7,5—42 979 даН-м - 430 кН-м.
Здесь натяжение нижнего фиксирующего троса условно принято таким же,
как и верхнего (658 даН), а ветровая нагрузка на опору определена по формуле
(2.27)
/>оп 0,1-120-1,4 (14-0,5) 15-0,5/2.95 даН.
Таким образом, в соответствии с данными табл. 8.10 для заданной гибкой по-
перечины могут быть установлены опоры МН-45/15-73.
Выполним подбор опор для этих же условий упрощенным способом, при-
меняемым в Трансэлектронроекте. Составим расчетную схему (рис 8.19) и оп-
ределим среднее междупутье по формуле (8.22)
«ср - 40/(8-| 1) 4,44 м.
Значение изгибающего момента в основании опоры от вертикальных нагру-
зок найдем но формуле (8.24). Для этого сначала определим удельный изгибаю-
щий момент л.VI по кривой рис. 8.17, учитывая высоту опор, равную 15 м, и два
провода в поперечном несущем тросе: ДЛ4 = 15,6 кН-м.
Поправочные коэффициенты для подвесок главных и станционных путей по
графику на рис. 8.18 соответственно составят 1,48 и 0,9 (при заданной длине про-
дольного пролета 65 м'. Сумма номеров нагрузок от главных путей равна 7 (3 --
4), а от станционных путей 13(1 |-2-|-4-| 34-2-/1). Тогда по формуле (8.24)
Л4,-- 15,6 (1,48-7 4 0,9-13) — 344,1 кН-м.
Изгибающий момент от воздействия ветра на провода подвесок определим по
формуле (8.25). Для этого сначала найдем значения моментов от давления ветра
на 1 м подвесок по табл. 8.15. Эти моменты: для главных путей (число подве-
сок 2) — 8,15 даН м/м, а для станционных путей (число подвесок 7)- 7,09 даН • м/м
При длине пролета, равной 65 м, по формуле (8.25)
4!г -65 (8,15-2 1-7,09-7) !(')-- 42.9 кН-м .
Суммарный изгибающий момент от затяжки фиксирующих тросов при ре-
жиме гололеда с ветром для опоры МН-45/15-73 поданным табл. 8.16.
Д43 —28.2 кН-м.
Принимая натяжения несущих тросов равными 1400 даН (см. пример к
§7 4) и контактных проводов МФ-85 850 даН (см. табл. 1.8), получим изгибающий
момент от излома двух подвесок станционных путей на кривой радиусом 1000 м
по формуле (8.26)
/И4--2 (1400-9,64-850-7,4) 65-10—“/1000 - 25,6кН-м.
273
I
Il Изгибающий момент от излома проводов одной подвески станционного nj
! ти на стрелке с маркой крестовины 1'11 найдем по формуле (8.27)
JHS - (1400-9,« !-850-7,4) I0-* 11 -17.9кН-м
Суммарный изгибающий момент от всех внешних сил относительно основа
ния опоры определим ио формуле (8.23)
Мо 344.1 -< 42,9-! 2H.2-i-25.6-17.9 423 кН-м
Различие между результатами, полученными точным и приближенным рае
четами, незначительно. Для заданной гибкой поперечины по приближенному
расчету также могут быть приняты опоры МН-45'15-73
i |
§ 8.6. Подбор стоек для жестких поперечин
j В качестве стоек для жестких поперечин используют типовые же-
лезобетонные опоры контактной сети. Подбор опор выполняется по
) нормативному изгибающему моменту на уровне условного обреза
1 фундамента, определяемому в двух режимах- ветер максимальной
। интенсивности в направлении поперек пути и вдоль пути. Онора под-
бирается по наибольшему моменту.
Для поперечин с фиксирующим тросом изгибающий момент в
режиме ветра поперек пути
I 'И.., ЛД,- 1-Л7, 3i,. I И„„ , Л1„„ (8 28)
Момент от контактных проводов
Л(к 0,25Л-х//фл. -0.25/ф//^. (8.29)
! Здесь а 4 (I - X) - - В'/С\ [3 /3/С; X ah (см. рис 7.23).
.! Натяжения фиксирующего троса в наиболее ослабленном звене Н ,j,,
определяют по формуле (7.131), в нагруженном звоне - по форму к
(7.85), величины В и С - по формулам (7.135) и (7.136)
Изгибающий момент от несущих тросов
Мт 6,511 V (8 Д(Н
I Т*|
тде /<|.,- - горизонтальные усилия от несущих тросов в рассмаiриваемом р.-
; жиме- давление ветра на трое, усилия от изменения направлен i
троса в плаче (на кривых и при отводах на анкеровку)
Момент от давления ветра на одиночную опору, даН-м,
Мс 0 566f4, (8 31)
j где е - скорость ветра, м с
। Выражения для расчета изгибающих моментов /Ипп от давления
ветра поперек пути на поперечину в зависимости от скорости ветра
расчетной длины Lp основной поперечины приведены в табл 8 17
Момент от давления ветра на цепную подвеску освещения. даН-м
Моп 1,675 10-* v-l, (8 .32)
'де > пролет подвески контактной сети
ИХ
Табл и ца 8.17
Изгибающие мименгы от давления негра на поперечину,
Рмчр гная даН м (на одну опор;,)
длш-.а ,'.р м М ' п и Л1 П)!
22.515 0.857н2 ' 2 ,859с2 '
30,260 1.604и2/2,265сг 5,350с2/7,55 Щ2
34,010 1,80.3у2/9,545щ 6.01 L?2/8.483с2
39,165 2.259с2/3,115:.'2 7,532»* /10,380-е2
2.75ёу’/3.719;.'-' 9,184с2/12,396с2
П р и ч е ч <i 11 и я. 1. В чиг'щк’ле приведены моменш >ля поперечин без освещения
к .шаменсио.’и- • с ocv( щг лие^
2 Нели фактическим ллино поперечины /ф меньше расчетной цлииы основной чопер<
чины /,р. r<i цриве и нньь в таблице мом.чны следует умножить на отношение Лф/Lp.
В режиме ветра вдоль иуш изгибающий момент
11, М, Л1П„. (8 ло
rje /И11в - момент (л дянления вира вдоль пути на поперечину (су,. та*'л 8 17;
Для гюперечии с фиксаторными стойками изгибающий момып i
режиме ветра поперек пути
ЛТ4 Ик НИ.,. 1-Л7с I Л(„„.
Момент от контактных проводов
0,.^ /\-ь
i i
। де РК1 - горизонтальные усилия от контактных проводов я рас<-м;нривж--
мом режиме: давление ветра на провода, усилия or изменения на
правления проводов в плане на кривых и при отводе нм анке
ровку
Моменты Л4Т, Мг и Мпп определяют так же, как для поперечин
< фиксирующим тросом.
Изгибающий момент в режиме ветра вдоль пути определяют, как
и для поперечин с фиксирующим тросом, по формуле (8.33).
В типовом проекте жестких поперечин приведены таблицы изги-
бающих моментов па уровне условного обреза фундамента стоек для
различных условий применения: поперечин с фиксирующим тросом и с
фиксаторпыми стойками, без освещения и с освещением, для перемен
кого и постоянного тока, для различных скоростей ветра, на прямых
и в кривых участках, для различных пролетов подвесок и длин попе-
речин.
Если на жесткой поперечине или на стойках, кроме цепных подве-
сок, подвешены другие провода, то изгибающие моменты от соответ
275
Рис. 8 20. Расчетные схемы приложения горизонтальных нагрузок от проводов,
подвешенных на жесткой поперечине:
а~ нагрузки на поперечине; б - нагрузка на одной стойке; в - нагрузка на повышенной
стойке
ствующих нагрузок необходимо дополнительно учесть в режиме ветра
поперек пути. Для схемы рис. 8.20, а
/VI д — ;иЛ- — {),пРП-,
для схемы рис. 8.20, б:
МА 0,25haI>, Мь -- 0,25/фР;
для схемы рис. 8.20, в:
МА 0,25/’й (2-| 4А—9М/С); МБ 0,25/Vi (2 } 9W/C).
В приведенных формулах Р - суммарная горизонтальная нагруз-
ка от давления ветра на провода, от изменения направления проводов
в плане на кривых и при отводах на анкеровку. Величины а, р, X, В, С
определяют соответственно по формулам (8.29), (7.135), (7.136) в со-
ответствии с рис. 7.23
1 3 5
I)-------I- --- ;------.
/:71 1-J2 EJ:l
Пример. 3 а д а н и е и исходи ы с д а и и ы с. Подобрать типовые
железобетонные опоры для жесткой поперечины с фиксирующим тросом и уст-
ройствами освещения на линии переменного тока, перекрывающей семь путей по
схеме, приведенной на рис. 8.21. Поперечина образована из основной с расчет-
ной длиной /.р 39,165 м. Контактные подвески на главных путях ПБСМ-70-+-
I МФ-100, на остальных станционных путях ПБСМ-70 } МФ-85; подвески полу-
компенсированные. Натяжение несущих тросов станционных путей 1176 даН,
контактных проводов — 833 даН. Фиксирующий трос выполнен из провода
ПБСМ-70. На надставке, закрепленной на поперечине, подвешен провод А-185.
Расчетная скорость ветра 30 м/с, максимальная температура | 40 ,:С, при мак-
симальном ветре —5“С. Длина пролета подвески 60 м.
А-!д5 Ст Ст Гл. Гл Ст Ст Гт.
Ы I Т I I ( (
i .. 35.8м._
Рис. 8.21. Схема расположения путей
для подбора стоек жесткой попере-
чины (стрелками указано направление
ветра)
Решение. Определим нормативные горизонтальные нагрузки от прово-
дов:
давление ветра на несущий трос подвески 1 по формуле (2.24) и табл. 2.1]
ртв= 0,77-60 = 45,6 даН;
на контактный провод главного пути (по табл. 2.2)
Рнвг.-, 0.83-60 = 49,2 даН;
на контактный провод станционного пути (по табл. 2.2)
р,.к ст — 0,77-60 -45.6 даН;
на провод А-185 (по табл. 2.3)
Р„ 1.18-60 69,6 даН;
усилие от изменения направления несущего троса на кривой [по формуле
(2.28)]
РтК 1176-60/1000 70,6 даН;
то же от контактного провода
PkR - 833-60/1000 50,0 даН.
Для расчета фиксирующего троса примем/г 10 м. по рис 6.10 для опоры с
нормативным моментом 79 кН - м получим;
EJt 14,5; EJ2 24,5; -37,5 МПа• м'1;
Л -2.5,100,25;
но формулам (7.134), (7.135) и (7.136):
л I1"-ЗА 25)” _ 27-0,25 (I -0,25) - 7 27-0,252 45-0,25 . 19
14,5-10® “ 24,5-10® .37,5-10®
0.332-10 -“Па-'-м
й (1—3-0,25)2(2 3-0,25) 14- 27-0,25 . 38 - 45-0,25
14,5-10® ' 24.5-10® 37,5 10“
-.1,021-10-® Па '-и 4;
1 7 19
С...........4------------ [ ---------- 0,861 • 10—6 па 1. м- “
14,5-10® 24,5-10® 37.5-10®
Для фиксирующего троса из провода ПБСМ-70 по табл. 1.5 получим
Зф 72,2 мм2 72,2-10-® м2,
по табл. 1.7 Еф 171 600 МПа; по формуле (7.133) определим
9 - 2-103-17 1 600-10®.72,2-10-6/(81-35,8) =- 8,545-10“ Па-м“,
ио табл. 1.7; аф - 13,3-10-® 1/"С; ар 12-10-® 1Л'С; по формуле (7.140)
u 13,3-10-“ - 12-10-®-1 ,021-10-«/(2-0,861-ю-®)
К --------------------------------------:--------------__- л дик. Ю-“ 1 / °C
18,545-106 [0,332-10-6—1,0212-10-12/(4-0,861 -10-6) j ’ 7
Натяжение в ослабленном звене фиксирующего троса (у опоры 5) при вет-
ре по стрелке / но формуле (7.131)
'7фх'- 100 "I 0,5[50-2— (49,2-2.; 45,6-5 50-2)
-Ь-4,946- 10--в. 171 600-)0«.72.2-10-« (404-5) 10 1 --212,6даН.
Натяжение в наиболее нагруженном звене фиксирующего троса определим
по формуле (7.85): /7ф., 212,6- 49,2-2 ! 45,6-5 1-50,0-2- 639 даН.
Для стойки А изгибающий момент от контактных проводов — по формуле
-18.29). предварительно рассчитав а и fk
а -- 4 (1 -- 0,25) — ), 021 • 10- »/ (0, ЙЪI -10-«) 1,614;
В 1 .021 • 10- «/(0,861 • 10-~«) -1.166;
,И,. 0,25-10 1 ,«14.639-0,25-Ю-1,166-212,(Ь- 2268 даН-м.
Изгибающий момент от несущих тросов найдем ио формуле (8.30)
31,. 0,5-10 (45,6-7 । 70,6-2) 2302 даН м;
давления ветра на одну опору - но формуле (8 31)
M,L- 0,566- 302 5)0 даН • м;
чт давления ветра на поперечину с учетом укорочения основной поперечины —
-ю габл 8.17
Иип 3,115-302-35.8/39,17 -2562 ДаН-м,
от давления ветра на ценную подвеску освещения - - по формуле (8.32)
Л10„ 1.67j.3()2.(;() Ю- 2 905 даН-м
Суммарный изгибающий момент определим но формуле (8 28)
МЛ 2268-1-2302 6 510 4 2562 । 905 8547 даН м
Дополнительный изгибающий момент от провода А-185, подвешенного по
схеме рис 8 20, и,
Мц 0,5-69,6-10 348 даН-м.
Полный момент стойки А в плоскости поперек нуги
ИЛ 8547 | 348 8895даН-м.
Изгибающий момент при ветре вдоль пути с учетом укорочения поперечины
найдем по формуле (8.33)
,ИА 510 , К),38-302-35,8/39,17 - 9048даН-м
В соответствии с табл (8.9) для данной поперечины в качестве стойки А сле-
дует принять спаренные опоры С 136.6-2 или е разрешения МПС одиночную оно
ру С 136.7-4. При спаренной опоре изгибающий момент при ветре поперек пути
увеличится вследствие давления ветра на вторую опору па М(. 510 даН-м, т е
момент в плоскости поперек пути
Мд -8895 1 510- 9405даН-м.
278
Окончательно для стойки Л принимаем по моменту поперек пути спаренную
опору С 136.6-2. поскольку 9405 < 2-5300 даН-м (см. табл. 8.9).
Подбор опор для стопки .5 следует провести при двух направлениях ветра
поперек, пути и при ветре вдоль пути Рассмотрим нагрузки стойки Б при ветре
по стрелке /. Выше были получены натяжения фиксирующего троса /?'фл
- 212.6 даН и Нл,л 639 даН, Следовательно.
Afb 0.25-10-1,814-212.6 - 0.25 10-1.186-639 .901 даП-м.
Знак « говорит о том, что момент направлен к полю. Изгибающие моменты
Мт, Л4С, Л4||н. Л1((П. AJn остаются по величине такими же, как для стойки А.
но получают знак поскольку направлены к полю. Полный момент
Mh - ...901- 2302- 510 -2562 -905 318- - 7328 даН-м
Определим изгибающий момент стойки Б при ветре поперек пути но стрел
ке II
II' 100 0,3(50-2 ( 49.2-2 -45.6-5 - 50-2)j
ф-
‘ 4.496-IO-11-171 600-10'672.2 к) •• (40 . 5) !<)-’ 589 даН:
7/фд 589 -49,2-2- 45,6 5,50-2 ЗЬ2.6даН,
Л4к 0.25 10-1.814-589 - 0,25-10-1.186-362.6 1596 даН-м.
.-И., 0,5-10(45,6-7 70,6-2) 890 даП-м
Изгибающие моменты от давления ветра Л1... М,,,,. ,ИОц. Мд сохраняют
свои значения, по направление изменяют на противоположное (ио стрелке //)
Л4(, 1596 । 890 ,510-4 2562 905 , 348 68Н даН м
Значит, для стойки Б изгибающий момент поперек пути оказался большим
при ветре по стрелке .4. Значение изгибающего момента при ветре вдоль пу и.
изменится М 1; 9048 даН-м
По табл. 8.9 следует принять спаренную стойку из опор С 136.6-2 и.о •
разрешения МПС одиночную опору С 136.7 4. При спаренной стойке момен' но
перек пути увеличивается
М/; --7528 1510 8038 даН-м.
но остается меньше момента от ветра вдоль пути. Таким образом, стойка Б доля
на быть также выполнена спаренной и т опор С 1,36.6-2.
§ 8.7. Подбор конструкций для закрепления опор в грунте
Условия закрепления в грунте типовых железобетонных опор вы
бирают такими, чтобы максимальный нормативный изгибающий мо-
мент А1ф на уровне условного обреза фундамента (не выше допустимо
io момента для принятой опоры) не превышал допускаемого норма
тонного момента ,-И'у, обеспечивающего необходимую устойчивость
опоры нгрунте
2“ч
Цельные опоры могут закрепляться в грунте как без лежней, так и с
лежнями для увеличения устойчивости. Число лежней указывают
арабскими цифрами, тип лежней — римскими, например 1-П. Обыч-
но применяют только верхние лежни, но иногда (в слабых грунтах)
и нижние. При моменте, действующем в направлении к пути, верхние
лежни устанавливают со стороны пути, нижние — со стороны поля.
Если момент действует в направлении к полю, то верхние лежни уста-
навливают со стороны поля, нижние — со стороны пути. При дейст-
вии момента вдоль пути (стойки жестких поперечин) лежни устанавли-
вают перпендикулярно пути с обеих сторон стойки. Лежни применя-
ют шириной 500 мм следующих типов: I — длиной 1000 мм, II -
1800 мм, IV — также длиной 1800 мм, они предназначены для устано-
вки на спаренных опорах; лежни типа III имеют размеры 600 ''-:800 мм.
Подбор конструкций для закрепления консольных опор в грунте
выполняют по таблицам, в которых приведены значения Л4"р, рас-
считанные для различных условий: ширина земляного полотна 5,8 и
7,0 м; установка на насыпи различной высоты и в выемке различной
глубины; габариты опор 3,1; 3,4; 4,9; 5,7 м; различное направление
нагрузки (к пути, к полю); грунты с расчетными сопротивлениями
0,10; 0,15; 0.20 МПа; без лежней и с лежнями разных типов; опоры
цельные и па фундаментах ТС длиной 3,5; 4,0 и 4,5 м.
Аналогичные таблицы составлены для подбора условий закрепле-
ния в грунте стоек жестких поперечин. В этом случае дополнительно
даны условия для одинарных и спаренных опор, а также для нагру-
зок вдоль пути. В качестве примера в табл. 8.18 и 8.19 приведены зна-
чения Л4"р для спаренных опор жестких поперечин при ширине зем-
ляного полотна 5,8 м.
Приведенные в табл. 8.18 и 8.19 значения УИ",, определены при рас-
четном заглублении опор и доле постоянной нагрузки, равной 35 %
полной нагрузки, при действии обеих нагрузок в одном направлении.
Если заглубление меньше расчетного, допускаемый момент необходи-
мо пересчитать. При другой доле постоянной нагрузки табличные зна-
чения УИ"Р следует умножить на поправочные коэффициенты:
Доля постоян-
ной нагрузки, % Ю 20 35 50 60 80 100
Поправочный
коэффициент . 1.49 1,24 1.00 0,83 0,765 0,65 0,57
Если моменты от постоянной нагрузки Мп и временной ?ИВ дей-
ствуют в противоположных направлениях и Ма<Ми, поправочный
коэффициент принимают 1,49; если же Л4(1 > ?ИВ, коэффициент при-
нимают равным 0,57, но учитывается только момент Л4П.
Указанные в табл. 8.18 и 8.19 расчетные сопротивления (при за-
сыпке котлованов до плотности окружающего грунта с учетом послой-
ного уплотнения) относятся к следующим видам грунтов: 0,1 МПа —
пески пылеватые, глины, суглинки и супеси мягкопластичные; 0,15
280
Таблица 8.18
Габарич опоры, м Направ- ление действия момента Расчетное сопротивление грунта. МПа Моменты At гр. кН м, для опор
без лежней с лежнями bIV/2-IV 1 л й ! без лежней с лежнями MV/2-IV без лежней с лежнями 1-IV/2-IV
//пае < 1 М //нас 1 -? 2 м ^пае >2 м
к пути 0,10 143 192/220 126 169/192 101 135/155
0,15 194 262/298 170 229/262 318/ 136 184/210
3,1 и 3,4 (с присып- 0.20 207 362/- 233 188 255/290
79/93
кой)
к ПОЛК) 0.10 118 147/173 85 106/125 64
0.15 159 199/233 115 144/170 86 108/127 149'175
0,20 219 275/323 159 199/234 1 19
к п\ ги 0.10 117 159/172 103 140'150 84 115/124
0,15 158 217/232 138 190/204 114 156/168
3.4 (без 0,20 217 299/- 190 263/282 156 216/231
к ПОЛЮ 0,10 106 133/147 77 97/107 55 70/76
присыпки)
0,15 143 180/198 104 132/145 75 94/104
0,20 196 249/275 143 182/201 102 129/143
Примечание. Значения рассчитаны дли опор, установленных на насыпи
при направлении нагрузки поперек пути: //н;ц высота насыпи, м
Таблица 8.19
1 кшрав- Габарит опоры, м И Моменты Л1Гр» кП’м, при расчетном сопротивлении грунта. МПа
ление нагрузки U. ! U, I 5 0,2 0, 1 0. 15 0.2 0, 1 0 . 1 5 0,2
Без лежней Лежень /./ Лежень 1-Н
Вдоль пути 3,1 и 3,4 (с присып- кой) 76 103 143 101 138 192 122 167 232
3.4 (без присыпки) 4.9 1,4 108 86 148 120 206 85 142 116 195 160 273 101 170 138 233 192 328
5.7 144 198 279 188 260 364 226 312
!! ;> и ч е ч а и и я. 1- Нагрузке направлена вдоль пути.
Прочерк в таблице означает, что допускаемые моменты больше максимальных
норма 1НЯНЫХ .Iliy.X ОПОр.
,. Нее моменты округлены до I кН-ч. ____ __________________
281
Т.П Г I Т ПИП
МПа пески мелкие, глины, суглинки и супеси тугопластичные;
0,2 МПа - пески крупные и средней крупности, глины, суглинки
и супеси твердые.
Для металлических консольных опор, применяемых в северных
районах и промышленных районах с агрессивными средами, разрабо-
таны условия установки железобетонных и свайных фундаментов в
различных грунтах (благоприятных, условно благоприятных и не-
благоприятных). Эти условия приведены в таблицах, аналогичных
табл. 8.18 и 8.19. В районах, где наблюдаются сейсмические явления,
рекомендуется при сейсмичности 7 баллов расчетный момент, действу-
ющий на опору, увеличить на К) %, при 8 баллах- 18 % и при 9 бал-
лах па 35 %.
Опорные плиты, выпускаемые трех типов (тин 1 диаметр 0,75 м
для установки в котлованы, образованные буровой машиной, тип 2
размер 0,65'- 0,65 м, тип 3 размер 0,65 1,2 м), устанавливают под
консольные анкерные опоры. Обычно при усилиях в оттяжках до
50 кН и одиночных стиках применяю! или гы типов 1 или 2. при спа-
ренных стойках тина 3.
Трехлучевые анкеры к оттяжкам анкерных опор, применяемых на
благоприятных участках земляного полотна, выполняют двух типов:
ТА-4 длиной 4 м и ТА-4,5 длиной 4,5 м. Ликеры п опорные плиты под-
бирают в зависимости от усилий в оттяжках и расчетного сопротивле-
ния грунта. При ширине земляного полотна 5,8 и 7 м подбор может
быть осуществлен по табл. 8.20 таким образом, чтобы усилия в оттяж-
ках не превышали приведенных в пей значений.
Таблиц а 8.20
Чести уста Габарит опор, м Порматниные усилия в оттяжках. кН. при условном расчетном сопротивлении грунта . МПа
новкя анкера 0.1 Мб и, 2 0,1 0,15 и 0,2
Насыпь .3.3 3.11 Анкеры ТА-4,0 55 70 1 70 46 | 64 | 68 Анкер 70 60 ы Г Л-4,5 70 70
Выемка 4.9 5.7 45 51 (46) 62 69 (64) 66 69 (68) 58 65 (60) 70 70 (70)
Междупутье 56 70 70 70 70
Примечание. В выемках при габарите опор 5,7 м цифры без скобок относятся
к ширине лимляпого полотна 5.S м. о скобках '-7 м.
282
На условно благоприятных и неблагоприятных участках земляного
полотна применяют стоечные анкеры длиной 4,5 м типов СА-4,5-1 и
САЛ,5-2, а также свайные анкеры длиной !0 м типа СА-10.
Металлические опоры для гибких поперечин устанавливают па
фундаменты из двух раздельных блоков типа ФР. После букв в марке
блока указывают две цифры: первая означает тип блока ио опалубоч-
ным размерам, вторая (через черточку) тип армирования. Напри-
мер, ФР1-2 это фундамент (блок) раздельный типа 1 с армирова-
нием типа 2. Всего имеется четыре вида опалубочных размеров и два
вида армирования. Типовые блоки подбирают в зависимости от марки
и места установки опор, их габарита, характера работы блока (растя-
нутый или сжатый) и расчетного сопротивления грунта.
Металлические опоры с двухпутными консолями (М-10'13-73 и
М-15'13-73) устанавливают на фундаменты типа Ф1-1 одноблочные
прямоугольного сечения. Значения цифр в марке фундамента анало-
гичны приведенным выше для фундаментов типа ФР.
Пример. 3 а д а и и е и и е х о д и ы с д а и а ы е. Выбрать способ
закрепления в грунте стоек жесткой поперечины г. соответствии с данными § 8.6
и необходимые типовые конетрх кипи, (дойки устанавливают на насыпи ныспгон
до I м при габарите 3.1 м, расчешое сопротивление грунта 0,15 МПа.
Р е in е и и е. Поскольку допускаемый момент по грунту суыестненпо зави-
сит от доли постоянной нагрузки в суммарной, а также от направления дей-
ствия нагрузок, необходимо выполнить дополнительные расчеты Рассмотрим
стойку А (см. рис. 8.21).
Постоянные нагрузки, передаваемые на стойки от контактных проводов, мо-
гут быть получены путем решения уравнения состояния фиксирующего троса в
режиме отсутствия Петра при температуре 5 С. Натяжение звена троса у
стойки И
11^. 100 I 0,5 (й()-2 50-2) | 4,946-10 «-171600 '
' 10«-72,2-10 -»-(40 I 5) 10 1 -375ш шН.
Натяжение звена троса у стойки А
Ифг 375.8 | 50.0-2 475.8 даН.
Изгибающий момент от контактных проводов
Мк- 0.25-10 -1,814-475,8--0,25-10-1,186.375.8 1044 даН-м.
Пренебрегая изменением натяжения несущих тросов в рассматриваемом
режиме, определим постоянную нагрузку от несущих тросов
4!.,. 0,5-10-70,6-2 706 даН-м.
Изгибающие моменты от давления ветра на стойку, поперечину, цепную под-
веску освещения, провод A-I85 отсутствуют.
Полный момент поперек пути от постоянных нагрузок
/Ии -1044-1 706 - 1750 даН-м.
При ветре по стрелке / направления действия постоянных и временных на-
грузок совпадают (к пути); поэтому доля постоянных нагрузок в суммарной
1 750'9 405 v 0,186 18,6 %.
283
ай it | iwMMiitiH и ни ма
Поправочный коэффициент по интерполяции составит 1,275, и допускаемый
момент по табл. 8.18 даже без лежней составит 19400- 1,275 > 9 405 даН-м, т. е,
закрепление спаренной стойки обеспечивается с большим запасом.
Изгибающий момент к нолю будет максимальным при ветре по стрелке//.
Момент от контактных проводов (см. § 8.6)
ЛД{ —0,25-10-1 ,«14.362,6 — 0,25-10-1,186-589-= - 102 даН-м.
Момент от несущих тросов
Л4Т 0.5-10 (70.6-2 —45.6-7) — 890 даН-м.
Напомним, что отрицательное значение момента соответствует направлению
его действия к полю. Моменты Л4С, М ш), Л4ол и Л4Д сохранят те же значения, что
в примере к§ 8.6, но будут действовать к полю. Тогда полный момент
Мл — 102 —890 — 510 —2562 —905 —348 —510 -• — 5827 даН-м.
Допускаемый момент, действующий в сторону ноля, следует уточнить с уче-
том доли постоянной нагрузки в суммарной. Выше был определен изгибающий
момент в стойке /1 от постоянных нагрузок Мп 1750 даН• м, действующий к пу-
ти. Момент от временных нагрузок при ветре по стрелке 11 действует к полю
причем Л4И < Л1В. Допускаемый момент к полю 15 900-1,19 > 5827 даН-м (см.
табл. 8.18). т. е. закрепление в грунте обеспечивается и в этом случае.
При ветре вдоль пути изгибающий момент Л4Н 9048 да.Н-м является вре-
менной нагрузкой, постоянная нагрузка отсутствует. По табл. 8.19 Л4” -
10 300-1,49 > 9048 даН-м. Закрепление стойки А обеспечивается с запасом.
Устойчивость в грунте стойки Б проверяется аналогично. В данном случае
условия закрепления в грунте такие же, как и стойки А. изгибающие нагрузки
меньше или равны (см. §8.6); поэтому дополнительная проверка ее устойчивости
не требуется.
284
Глава 9
ПРОЕКТИРОВАНИЕ СХЕМ СЕКЦИОНИРОВАНИЯ
КОНТАКТНОЙ сети и прохода
контактной подвески
В ИСКУССТВЕННЫХ СООРУЖЕНИЯХ
§ 9.1. Принципы питания и секционирования.
Рекомендуемые схемы
Схема питания и секционирования контактной сети должна быть
спроектирована так, чтобы были обеспечены возможно меньшие потери
напряжения и энергии в сети при нормальном режиме работы и мини-
мальные нарушения графика движения поездов при выходе из работы
какой-либо секции контактной сети. При этом на станциях необходи-
мо обеспечить максимальную самостоятельность маршрутов.
На однопутных и двухпутных электрифицируемых линиях приме-
няют схемы одностороннего (рис. 9.1. а) и двустороннего (рис. 9.1, б)
питания контактной сети. В последнем случае для обеспечения более
надежной защиты сети от гоков короткого замыкания между тяго-
выми подстанциями обычно имеются посты секционирования ПС
(рис. 9.1, в), наличие которых, кроме защиты, обусловливает снижение
потерь напряжения и энергии в контактной сети. Для достижения
этой же цели на двухпутных линиях устанавливают пункты параллель-
ного соединения ППС (рис. 9.1, г, где число таких пунктов условно).
Схема параллельного соединения контактных подвесок разных путей
предусматривает автоматическое отключение сети поврежденного пу-
ти на участке между соседними тяговыми подстанциями (или между
подстанцией и постом секционирования) при сохранении напряжения
на контактной сети всех остальных, неповрежденных участков.
Как правило, для участков контактной сети, расположенных
между двумя тяговыми подстанциями, используется схема двусторон-
него питания. Схема одностороннего питания может быть допущена для
небольших но длине участков, расположенных за крайними тяговыми
подстанциями главной линии, и для малодеятельных линий незначи-
тельной протяженности, примыкающих к ней.
На линиях переменного тока, чтобы уменьшить неравномерность
нагрузки фаз энергосистемы, питание к отдельным участкам контакт-
ной сети подводят от разных фаз. При этом участки сети, которые на-
ходятся между соседними тяговыми подстанциями, получают питание
от одной и той же фазы.
При проектировании схем питания и секционирования контакт-
ной сети и воздушных линий необходимо знать, какие секционные изо-
ляторы и секционные разъединители будут устанавливаться в конкрет-
ных местах на станциях или перегонах. Основные данные наиболее
часто применяемых секционных изоляторов приведены в табл. 9.1, сек-
ционных разъединителей и приводов к ним — в табл. 9.2.
285
При условии выполнения требования о минимальном нарушении
графика движения поездов в результате отключения какой-либо сек-
ции в схеме секционирования контактной сети используют возможно
ценьшее число секционных изоляторов и секционных разъединителей.
В схемах низания и секционирования контактной сети обычно при-
меняют следующие основные условные обозначения:
ГдиТ]
П
изолирующее сопряжение анкерных участков:
изолирующее сопряжение с нейтральной вставкой,
с е к п и о 11 н ы ii и з и л я то р:
однополюсный секционный разъединитель г диш а
тельным приводом и с телеуправлением нормально
включенный 1-1 нормаль н о от кл юч е н н i я й.
двухполюсный секционный разъединитель е двн1я
гельным приводом и с телеуправлением нормально
включенный и нормально отключенный;
однополюсный секционный разъедини гель с ручным
приводом нормально включенный и нормально (пклю
чинный,
двухполюсный гекцнонпын разъединитель е ручным
приводом нормально включенный и нормально
ключенный:
однополюсный секционный разьедишиель с ручным
приводом и заземляющим ножом нормально включен
ный и нормально отключенный;
пункт параллельного соединения;
автотрансформаторпый пункт (при системе 2> 25 кВ)
ЕВ процессе проектирования предусматривают продольное и попе-
речное секционирование, а также секционирование с обязательным за-
землением отключаемой секции.
Uродильное секционирование - это разделение контактной сети
вдоль электрифицированной линии у каждой тяговой подстанции и
каждого поста секционирования. Кроме того, выделяют в отдельные
продольные секции контактные сети перегонов и станций по схемам,
приведенным ниже. На станциях, имеющих несколько электрифициро-
ванных парков или групп путей, каждый парк или каждую группу пу-
тей обычно выделяют в самостоятельные продольные секции. На очень
больших станциях в отдельные секции иногда выделяют контактные
сети в обеих горловинах станции. Если на линии имеются крупные тон-
нели или мосты с ездой понизу, их контактные сети иногда выде-
2Н6
ляют в самостоятельные продоль-
ные секции.
Для обеспечения питания ли-
нии при отключении контактной
сети станции или искусственного
сооружения на участках с односто-
ронним питанием проектируют
шунтирующие (обходные) линии /
(рис. 9 2), что позволяет не пре-
рывать питание контактной сети
участков, примыкающих к станции
или сооружению, в случае повреж-
дения или вывода из работы их
контактной сети.
При поперечном секционирова-
нии в первую очередь предусмат-
ривают разделение контактных се-
тей каждого из главных путей как
на перегонах, гак я на станциях,
разъездах и обгонных пунктах.
Кроме того, на станциях с числом
путей, примыкающих к каждому
из главных, более трех проекти-
руют дополнительное поперечное
секционирование. Число попереч-
ных секций на таких станциях
определяется не только количест-
вом, но и назначением отдельных
путей.
Для обеспечения условий плав-
ки гололеда на проводах контакт-
ной сети электрическим током во
всех гололедных районах, кроме
первого, контактная сеть по каж-
дому главному пути в пределах
цепи тока (включая станции и
сопряжения анкерных участков)
должна иметь одну эквивалентную
площадь сечения, обеспечивающую
равномерный прогрев проводов
ври оплавлении гололеда. Парал-
лельное соединение подвесок глав-
ного пути и соседнего станционного
допускают только в том случае,
когда суммарная площадь сечения
обеих контактных подвесок равна
площади сечения подвески на
дг-м шиммша mat
Т а блица 9 Л
Тип секци-
онного
изолятора
Допустимая
скорость
[Еижения,
км/ч
Число
контактных
проводов
Число изо-
лирующих
вставок
Масса, кг
общая средняя ! м
Переменный и постоянный ток
ЦНИИ-7МА ИСМ-1М 130 160 1: 2 1: 2 2 1; 2 36,0 28,0 12,4 18,1
Переменный юк
ЦНИИ-12 100 1 2 34,7 9.3
Постоянный ток
СИ 2У 70 1 '2 46,7 28,5
'.И-4 70 1. 2 2, 4 46,6: 64,4 24,8; 34,3
СИ-6 70 2 4 64,5 39,8
ЦНИИ-7М 80 1; 2 2 39,5 15,0
Т а б л и ц а 9.2
Секционный разъединитель Привод
1 НН 11<|.минальное напряже- ние. кВ Номиналь- ный ток, А Масса, кг Двигательный (мото рный) Ручной
Тин Масса, кг Тип Масса, кг
Контактная сеть переменного тока и ВЛ 27,5 кВ
PH Д-35/1000 РНДЗ 16-35/1000 (с заземляющим НОЖиМ 1 35 1000 66,0 74,0 УМП-11 58.0 ПР-90 ПР-ЭОЛ 23,0 28,0
Контактная сеть постоянного тока
РС-ЗООО-З.З РС-ЗООО.'З.З с «аземля клип м 10ЖОМ 3 .3000 85,0 90,0 УМП-11 .58,0 ПР-1 10,0
н,ц Ю кВ
РЛ ИД-10/400 I К) 400 46.0 УМП-11 58.0 ПРИ-ЮМ 8 .2
Рис. 9.3. Схемы установки разъединителя
с заземляющим контактом при ручном
(а) и двигательном (б) приводах
перегонах. Если это не выполняется, то на промежуточных стан-
циях нужно врезать секционные изоляторы в контактные подвески
станционных путей в одной из горловин станции и включить по одно-
му секционирующему изолятору в фиксирующие тросы жестких и гиб-
ких поперечин или выделить главные пути в самостоятельные попе-
речные секции.
'Поперечное секционирование выполняют также в парках или
группах путей в тех случаях, когда число путей в каждом парке или
группе более пяти. При электрификации только головной части путей
парка в одной секции может быть и более пяти путей. Число путей в
секции зависит также от их назначения и объема работы.
Секционирование с обязательным заземлением отключенной сек-
ции осуществляют для следующих путей вне зависимости от общего
числа электрифицируемых путей станции: каждого из погрузочно-
разгрузочных, снабжения пассажирских составов водой и налива ем-
костей, осмотра крышевого оборудования и отстоя электроподвижно-
го состава (э.п.с.), электродепо и пунктов экипировки. Обязательное
заземление отключенной секции осуществляется секционным разъе-
динителем с ручным приводом и заземляющим ножом (рис. 9.3, а'
При необходимости дистанционного управления подачей напряжения
и заземления отключенной секции по условиям обеспечения безопас-
ности работы на крыше э. п. с. (например, при экипировке) на лини-
ях переменного тока устанавливают два секционных разъединителя
(рис. 9.3, б). Приводы обоих разъединителей сблокированы так, что
одновременно включить их невозможно.
Число питающих линий, отходящих от тяговой подстанции, зави-
сит от числа путей на станции и от места расположения подстанции.
Если тяговая подстанция находится в пределах станции, то при опре-
деленном числе путей для питания контактной сети станции преду-
сматривают отдельную линию, которая одновременно является резерв-
ной для питающих линий перегонов. На крупных станциях, имеющих
отдельные парки, число питающих линий для станционной сети мо-
жет быть увеличено. Если на данной станции находится депо, то для
питания его контактной сети предусматривают самостоятельную ли-
нию.
В местах соединения продольных секций контактной сети, получа-
ющих питание при различных напряжениях, проектируют нейтраль-
10 Зак. 2630 2 89
#»%
IWM
шяе вставки. В отдельных случаях (см §9.4), когда подвеску контакт-
ной сети в негабаритном искусственном сооружении осуществляют с
ее заземлением, по обоим концам такого сооружения также делают
нейтральные вставки. Длину рабочей части нейтральной вставки при-
нимают такой, чтобы все поднятые в самой невыгодной комбинации то-
коприемники электровозов (с учетом кратной тяги) или электропоез-
дов помещались на нейтральной вставке. Места расположения нейт-
ральных вставок выбирают с проверкой по тяговым расчетам возмож-
ности безостановочного проследования вставки поездом на электротя-
ге со скоростью входа на нее 20 км/ч у сигнала «Отключить ток». Мо-
жет быть также применено несколько пос ледова гель но включенных
коротких нейтральных вставок, длину которых выбирают такой, при
которой невозможно замыкание разных секций контактной сети под-
нятым и токоприем»и ками.
Для соединения отдельных секций контактной сети одна с другой и
питающими линиями, а также для разделения их предусматривают
секционные разъединители. На схемах питания и секционирования
указывают нормальное положение (включенное и отключенное) каж-
дого из разъединителей. Продольные разъединители обозначают
обычно первыми буквами русского алфавита: поперечные - буквой
/7; разъединители, устанавливаемые в питающих линиях, буквой
Ф; разъединители с заземляющим ножом - буквой 3; прочие разъе-
динители - буквой Р. К каждой из указанных букв в случае необхо-
димости добавляют цифровой индекс, соответствующий номерам путей
и направлений.
Нумерацию разъединителей в питающих линиях принимают сле-
дующей: на двухпутных участках четные номера 2 и 4 дают разъеди-
нителям. подключенным к подвескам над четными путями; нечетные
1 и 5 — к подвескам над нечетными путями; разъединителю, подклю-
ченному к станционным путям, присваивают помер 3; на однопутных
участках применяют только нечетные номера разьединителей; разъ-
единителю линии, питающей электроцепо, дают номер, следующий за
последним номером на главных путях. Номера разъединителей воз-
растают ио направлению движения четных поездов.
Пигаюшие линии переменного тока го всех случаях присоединя-
ют к контактной сети линейными разъединителями с двигательными
приводами, а питающие линии постоянного тока — линейными разъ-
единителями только при длине воздушных питающих линий более
150 м и наличии разъединителей с двигательными приводами у типо-
вых подстанций. В последнем случае линейные разъединители на ли-
ниях длиной более 750 м оборудуют двигательными приводами, а на
линиях длиной 750 м и менее (до 150 м) — ручными.
Все поперечные разъединители, кроме оперативных, оборудуют
ручными приводами и предусматривают их установку с таким расче-
том, чтобы расстояние от разъединителя до наиболее удаленного сек-
ционного изолятора не превышало 1000 м. При наличии на станции
оперативных разъединителей с двигательными приводами в указан-
290
ных выше условиях поперечные разъединители с ручными приводами
не устанавливают.
В станционных питающих линиях используют разъединители с
двигательными приводами. Все разъединители, применяемые для сбор-
ки схем плавки гололеда электрическим током, тоже должны иметь
двигательные приводы. Секционные разъединители с двигательными
приводами располагают возможно ближе к месту, где установлены
пульты управления Управляет часто переключаемыми разъедините-
лями энергодиспетчер по телеуправлению. Разъединители, отключе-
ние- которых должно обеспечивать безопасность производства работ па
отключенных ими путях, применяют с заземляющими ножами.
Для подачи напряжения в контактную сеть погрузочно-разгрузоч-
ных путей устанавливают разъединители нормально отключенные, а
дл/i подачи напряжения в контактную сеть путей, па которых возмо-
жен осмотр крышевою оборудования электроподвижпого состава, -
нормально включенные.
На схемах питания и секционирования показывают: тяговые под-
etaiiuHn и посты секционирования: питающие и отсасывающие линии;
линии продольного электроснабжения; линии электропередачи и для
автоблокировки; секционные разъединители с присвоенными им буква-
ми (литерами) и номерами - -с указанием нормального положения разъ-
единителя; изолирующие сопряжения анкерных участков и нейтраль-
ные вставки, секционные изоляторы и их номера: пересечения контакт-
ной сети воздушными линиями; искусственные сооружения, пересе-
кающие контактную сеть, и некоторые другие данные.
На станциях с >яговыми подстанциями при переменном токе пре-
дусматривают раздел фаз, устраивая для каждого из главных путей
с одной стороны станции изолирующее сопряжение анкерных участ-
ков с нейтральной вставкой. На другой стороне таких станций по
каждому пути осуществляют изолирующее сопряжение без нейтраль-
ной вставки. При этом на станциях с числом электрифицированных пу-
тей пять и более (кроме главных) проектирую! схему с отдельной пита-
ющей линией для станции. (В число электрифицируемых путей вхо-
дят электрифицируемые тупики и части путей-.)
Если на станции двухпутной линии переменного тою.) электрифици-
рованных путей пять и более, кроме главных (рис. 9.4, а), то для кон-
тактной сети каждого из путей обоих примыкающих к станции пере-
гонов проектируют самостоятельные питающие липин. При числе элек-
трифицированных путей менее пяти (кроме главных) контактные сети
одною из перегонов получают питание через контактные сети стан-
ционных путей (рис. 9.4, б).
Для создания цепи юка при плавке гололеда па проводах контакт-
ных подвесок каждую нейтральную вставку оборудуют двумя телеуп-
равляемыми секционными разъединителями, которые включают на вре-
мя производства плавки Сем. рис. 9.4 и 9.7).
На станциях с тяговыми подстанциями при постоянном токе про-
ектируют по изолирующему сопряжению анкерных участков (для
10* 291
5)
Рис, 9,4. Схемы питания и секционирования контактной сети станций на двух
путной линии переменного тока при наличии тяговой подстанции
Рис. 9.5 Схема питания и секциони
рования контактной сети станции на
двухпутной линии постоянного тока
при наличии тяговой подстанции
Рис. 9.6. Схемы секционирования контактной сети станций без тяговых подстан-
ций на двухпутной линии (а), на однопутной (б) и с продольным расположени-
ем путей (в)
Рис. 9.7. Схемы питания и секционирования контактной сети станций с тяговыми
подстанциями на однопутной линии переменного (а) и постоянного (б) тока
292
Ряс. 9.8. Схемы разделения кон-
тактных сетей у постов секциони-
рования на однопутной (а) и двух-
путной (б) линиях
каждого из главных путей) с двух сторон станции. На двухпутных
линиях применяют схему, приведенную на рис. 9.5, независимо от
числа электрифицированных путей на станции. На станциях двухпут-
ных линий без тяговых подстанций независимо от системы тока и чис-
ла электрифицированных путей устанавливают продольные секцион-
ные разъединители с двигательными приводами на обеих сторонах
станции (рис. 9.6, а).
Схемы питания и секционирования многопутных линий проек-
тируют аналогично схемам двухпутных линий, соответственно уве-
личивая число секционных изоляторов, осуществляющих поперечное
секционирование, а также число питающих линий и разъединителей.
Питание и секционирование станций с тяговыми подстанциями на
однопутных линиях переменного тока осуществляют по схеме
рис. 9.7, а, а на линиях постоянного тока по схеме рис. 9.7, б при
любом числе электрифицированных путей. Секционирование станций
без тяговых подстанций па однопутных линиях проектируют независи-
мо от системы тока и числа электрифицированных путей по схеме
рис. 9.6, б. На станциях с продольным расположением путей также
применяют схему рис. 9.6, б, а иногда устраивают секционирование
в середине станции (рис. 9.6, в). В местах расположения постов
секционирования продольное разделение контактных подвесок одного
или двух путей осуществляют по схемам рис. 9.8, а, б.
§ 9.2. Секционирование контактной сети при стыковании
линий постоянного и переменного тока
Стыкование линий, электрифицированных на постоянном и перемен-
ном токе, в СССР осуществляют на так называемых станциях стыко-
вания или с помощью специальных электровозов двойного питания.
В контактной сети станций стыкования выделяют соответствующее
число переключаемых секций, на которые может быть подано напря-
жение как постоянного, так и переменного тока. Выбор числа и мест
расположения переключаемых секций контактной сети зависит от
схемы путевого развития станции, спецификации путей, организации
работы и т. д. При любой схеме станции должно быть обеспечено при-
бытие поездов с электровозами одной системы тока и отправление этих
293
же поездов с тех же путей с электровозами другой системы тока, а так-
же проход электровозов обеих систем тока из одного парка в другой
и на пути отстоя.
Основным аппаратом, осуществляющим подачу на переключае-
мую секцию напряжения переменного или постоянного тока, явля-
ется переключатель рода тока. Число таких переключателей, постоян-
но находящихся в рабочем состоянии, должно соответствовать числу
переключаемых секций. Для удобства обслуживания несколько пере-
ключателей рода тока размещают в одном месте, называемом пунктом
группировки. Эти пункты, как правило, проектируют открытого типа
(без зданий). На типовом пункте группировки предусмотрено 10 яче-
ек, одна из которых предназначена для резервного переключателя
рода тока. Здесь же размещают секционные разъединители, через ко-
торые подается напряжение на соответствующие шины. С этих тин по-
ступает питание к переключателям рода тока и от них через секцион-
ные разъединители к переключаемым секциям контактной сети.
Пункты группировки получают питание от тяговой подстанции по-
стоянного и переменного юка, расположенной на станции стыкова-
ния (рис. 9.9). От этой подстанции прокладывают кольцевые питаю-
Рие. 9.9. Упрощенная схема питания и секционирования станции стыкования:
/—тяговая подстанция постоянного н переменного тока; 2- - кольцевые питающие линии;
пункты группировки; 4 переключатель рода тока
29
щие линии постоянного и переменного тока, ооеспечивая при этом
100 %-ное резервирование питания. На каждом пункте группировки
имеются три шины: постоянного тока, переменного тока и резервная,
на которую может быть подано напряжение любого рода тока. Кроме
того, па каждом пункте устанавливают резервный переключатель ро-
да тока, что позволяет быстро заменить один из рабочих выключателей
в случаях его повреждения или вывода в плановый ремонт.
Места расположения пунктов группировки выбирают так, чтобы
расстояния до переключаемых секций контактной сети, обслуживае-
мых с данного пункта, было минимальным. Число таких пунктов на
станции стыкования выбирают наименьшее из возможных, но так, что-
бы было обеспечено питание всех переключаемых секций. Желатель-
но как можно полнее использовать число рабочих ячеек на типовых
пунктах группировки.
Между маршрутом, подготовленным для следования электровоза,
и родом напряжения, подаваемого на соответствующие секции кон-
тактной сети, обеспечивают автоматическую зависимость. Для этого
переключатели, через которые подается питание на переключаемые
секции, блокируют с маршрутными устройствами централизации стре-
лок. Включение переключателей производится одновременно с приго-
товлением стрелочного маршрута и установкой в нужное положение
сигналов. Кроме того, если на пути с переключаемой секцией контакт-
ной сети находится электровоз, то переключение ее на другое напря-
жение не должно осуществляться до тех пор, пока электровоз не уй-
дет с этой секции. Показания сигналов, разрешающие переезд элект-
ровоза с одной секции на другую, появляются только при наличии
на обеих секциях одинакового напряжения.
Для примера рассмотрим схему рис. 9.9, где условно показаны два пункта
группировки, питание переключаемых секций приведено только для одной из
них, не показана резервная шина. Маневры поездных локомотивов могут быть
организованы, например, так. Электровозы постоянного тока, прибывающие с
поездами в нарк А или на главный путь /, отцепляют и направляют в тупик 2.
Затем их переводят в отстойный тупик 2', откуда подают под составы, отправля-
ющиеся на участок постоянного тока. Электровозы переменного тока из парка Б
или с главного пути II направляют в тупик /, затем в отстойный тупик /' и к по-
ездам, уходящим на участок переменного тока.
На рис. 9.9 показано только питание переключаемых секций контактной
сети, так как схемы питания и секционирования каждой из частей станиии, нахо-
дящихся постоянно под одним и тем же родом напряжения, проектируют ана-
логично тому, как это было рассмотрено выше.
Разъединители пунктов группировки оборудуют блокировками,
которые не позволяют переключить разъединители при включенном
переключателе, а также включить заземляющий нож при включенном
одном из разъединителей и наоборот.
Стоимость станций стыкования очень высока, поэтому их целесо-
образно применять только в тех случаях, когда стыкуемые участки
имеют значительные размеры движения и большую протяженность,
что вызывает необходимость иметь значительное число электровозов
двойного питания. Если же один из стыкуемых участков небольшой
295
протяженности, то используют электровозы, способные работать и
при постоянном и при переменном токе.
Секционирование контактной сети при использовании специальных
электровозов осуществляется гораздо проще, чем на станциях сты-
кования. В контактной сети главных путей, на которых выполняют
стыкование, при движении поездов с большими скоростями необходи-
мо предусмотреть изолирующие сопряжения с нейтральными вставка-
ми, а в контактной сети путей, по которым осуществляется движение с
невысокими скоростями, — секционные изоляторы с нейтральными
вставками.
§ 9.3. Рельсовые цепи и отсасывающие линии.
Размещение заземлений и разрядников
Рельсовые цепи. На линиях, оборудованных автоблокировкой с
двухниточными цепями, рельсовые нити соединяют параллельно уста-
новленными у изолированных стыков дроссель-трансформаторами,
средние точки которых соединены с дроссель-трансформаторами дру-
гих путей через два стыка на третий. На станциях с однониточными
рельсовыми цепями электротяговые нити соединяют в горловинах у
выходных сигналов, в пунктах присоединения отсасывающих проводов
и через каждые 400 м. На участках, где рельсовые нити не использу-
ются для цепей автоблокировки или электрической централизации,
устанавливают между рельсовые и междупутные соединения через
каждые 300 и 600 м на станциях и через вдвое большие расстояния
на перегонах.
Отсасывающие линии. При двухниточных рельсовых цепях отса-
сывающие липни подключают к средним точкам ближайших дроссель-
трансформаторов, при однониточных цепях — к электротяговым рель-
совым нитям всех электрифицированных путей. Отсасывающие ли-
нии переменного тока (кроме подстанций на стыковых станциях) вы-
полняют двумя параллельными линиями: одной от заземленных выво-
дов тяговой обмотки трансформатора до рельсов главных путей и вто-
рой по рельсам подъездного тупика, соединенным с контуром заземле-
ния тяговой подстанции. На подстанциях, расположенных на станциях
стыкования двух систем тока, отсасывающие линии на 3 и 25 кВ вы-
полняют раздельно, не используя рельсы подъездного тупика и контур
заземления подстанции.
Подключение к рельсовой цепи отсасывающих линий должно увя-
зываться с проектом СЦБ, и в экономически обоснованных случаях в
целях уменьшения длины отсасывающих линий следует предусматри-
вать дополнительные дроссель-трансформаторы.
На участках, где отсутствует автоблокировка, отсасывающие ли-
нии подсоединяют к рельсовым нитям ближайших электрифицируе-
мых путей, связанных с другими путями поперечными соединителями
в месте устройства отсасывающего пункта.
296
Заземления. Все металлические опоры и конструкции, исполь-
зуемые для крепления проводов контактной сети, а также другие ме-
таллические конструкции, расположенные на расстоянии менее 5 м
от частей контактной сети, находящихся под напряжением, оборуду-
ют заземлениями. Заземляют также арматуру и все металлические кон-
струкции крепления изоляторов контактной сети, линий электропере-
дачи и продольного электроснабжения, расположенные на железобе-
тонных опорах и искусственных железобетонных или других неметал-
лических сооружениях. У оттяжек на железобетонных опорах заземля-
ют хомуты. На линиях переменного тока заземляют также все рас-
положенные в зоне влияния контактной сети металлические сооруже-
ния, на которых могут возникнуть опасные наведенные напряжения.
Заземления проектируют индивидуальные и групповые, присое-
диняемые к средним точкам ближайших дроссель-трансформаторов
или к электротяговым рельсовым нитям. Заземляющие проводники
между опорами и рельсами изолируют от земли.
В заземляющие цепи в необходимых случаях устанавливают защит-
ные устройства, препятствующие утечке тягового и сигнального тока.
К таким устройствам относятся искровые промежутки и различные
специальные схемы, например, с диодными заземлителями.
Искровые промежутки устанавливают при двухпиточных рельсо-
вых цепях автоблокировки на линиях постоянного и переменного то-
ка на опорах с индивидуальным заземлением при сопротивлении цепи
заземления менее 100 Ом; в спусках группового заземления катодных
юн на линиях постоянного тока и при сопротивлении цепи заземле-
ния менее 6 Ом км на линиях переменного тока; па всех опорах с про-
водами воздушных линий независимо от сопротивления цепи заземле-
ния и в некоторых других случаях.
Искровые промежутки не включают в заземления опор, на которых
расположены трубчатые разрядники, приводы секционных разъеди-
нителей и спуски групповых заземлений, а также опор на пассажир-
ских платформах и в других общедоступных местах. В этих случаях
проектируют двойные заземления, которые также устанавливают на мо-
стах, путепроводах, пешеходных и сигнальных мостиках без искровых
промежутков. На линиях постоянного тока между узлами контактной
сети, находящимися под напряжением, и конструкциями крепления
на искусственных сооружениях и пешеходных мостах, а при необходи-
мости и на опорных устройствах рекомендуется дополнительно устраи-
вать нейтральные вставки. Эти вставки следует присоединять к рель-
сам наглухо проводом, изолированным от конструкции сооружения.
Опоры, на которых подвешивают провода питающих или отсасы-
вающих линий и расположенные вдали от железнодорожных путей, за-
земляют через искровые промежутки на отсасывающие провода или
при их отсутствии с помощью группового заземления. Групповое за-
земление применяют также для опор контактной сети, стоящих на
перегонах в выемках за кюветами (с большим габаритом), для опор
на пассажирских платформах или за платформами, для опор изоли-
297
рующих сопряжений и в горловинах станций, в зоне которых установ-
лены секционные разъединители с двигательными приводами. Груп-
повые заземления осуществляют, если подряд находится не менее
трех опор, подлежащих заземлению.
Наибольшая длина провода группового заземления на линиях по-
стоянного тока при Т-образной схеме подключения не должна превы-
шать 1200 м (2 600) для железобетонных опор и 600 м (2 300) для ме-
таллических опор. При Г-образной схеме указанные длины соответст-
венно в 2 раза меньше. На линиях переменного тока максимальная
длина провода группового заземления не должна превышать 400 м
(2-200) при Т-образной схеме подключения и 200 м при Г-образной.
Диодные заземлители устанавливают на линиях постоянного тока
в спусках групповых заземлений анодных и знакопеременных зон при
сопротивлении цепи заземления менее 25 Ом на 1 В среднего положи-
тельного значения потенциала рельс -земля. На участках с двухни-
точными рельсовыми цепями автоблокировки при сопротивлении цепи
заземления менее 6 Ом/км последовательно с диодным заземлителем
в каждый провод спуска со стороны рельса устанавливают искровой
промежуток.
На линиях постоянного тока в заземления мостов, путепроводов,
пешеходных и сигнальных мостиков, на которых крепятся конструк-
ции контактной сети, включают два последовательно соединенных ис-
кровых промежутка с пробивным напряжением каждого 400 В или
один с пробивным напряжением 800 В. На линиях переменного тока
металлические конструкции креплений контактной сети па железобе-
тонных искусственных сооружениях не должны касатося арматуры, н
заземление их на дроссель-трансформатор или тяговый рельс осуще-
ствляется без искровых промежутков. Перила и друше металличе-
ские элементы железобетонных искусственных сооружений, соединен-
ные с арматурой, следует заземлять через искровые промежутки, как
для линий постоянного тока.
Разрядники. На линиях постоянного тока устанавливают роговые
разрядники с двумя последовательными воздушными промежутками
по 5 мм каждый. На линиях переменного тока применяют аналогич-
ные разрядники с воздушными промежутками ио 45 мм каждый, а так-
же трубчатые разрядники па напряжение 35 кВ. Разрядники устанав-
ливают не далее двух пролетов от защищаемых ими мест на любых
опорах, кроме анкерных с оттяжками.
Роговые разрядники на линиях постоянного тока устанавливают:
в местах анкеровок проводов контактной сети (в том числе и средних
для компенсированных подвесок): на одной из переходных опор пе-
изолирующих сопряжений анкерных участков; на переходных опорах
изолирующих сопряжений анкерных участков — для каждой подве-
ски при нормально разомкнутых секционных разъединителях и для
одной из подвесок при нормально замкнутых разъединителях; по
каждому пути у мест присоединения постов параллельного соедине-
ния; у искусственных сооружений при анкеровках на них контактной
298
сети — с обеих сторон сооружения при длине его 80 м и более и с од-
ной стороны при меньшей длине сооружения; на питающих линиях у
мест их присоединения к контактной сети или к пунктам группировки
переключателей (на станциях стыкования), а также на расстояния
не более 100 м от тяговой подстанции при длине этих линий более
150 м и через каждые 1 —1,5 км при более длинных питающих линиях.
Роговые разрядники на линиях переменного тока устанавливают:
с обеих сторон изолирующих сопряжений анкерных участков; по
каждому пути у мест присоединения постов параллельного соедине-
ния; у обоих выводов первичной обмотки отсасывающих трансформа-
торов, присоединенной к контактной сети на расстоянии не менее 5 м;
на конце консольных участков контактной сети, состоящих из двух
или более анкерных участков.
Трубчатые разрядники с внешним искровым промежутком 100 мм
устанавливают у мест присоединения питающих линий к контактной
сети, а на станциях стыкования — в конце линии и у первого ответв-
ления ее к пункту группировки переключателей и, кроме того, на рас-
стоянии не более 200 м от тяговой подстанции, если длина питающих
линий превышает 300 м.Такие же разрядники, ио с внешним искровым
промежутком 60 мм устанавливают на линиях ДПР у мест их пересече-
ния с контактной подвеской — с одной стороны от места пересечения.
В местах, подверженных частым грозовым разрядам, следует ус-
танавливать дополнительные разрядники у неизолирующих сопряже-
ний анкерных участков.
§ 9.4. Выбор способа прохода контактной подвески
в искусственных сооружениях
Выбор способа прохода контактной подвески в искусственных со-
оружениях производят в зависимости от типа и конструкции сооруже-
ния, от высоты его над уровнем головок рельсов и длины в направле-
нии вдоль электрифицированных путей. Принятый способ прохода
должен обеспечивать движение поездов с установленной скоростью,
определенную равномерность эластичности контактной подвески и ее
необходимую надежность в эксплуатационных условиях, для чего обя-
зательно выдерживают габаритные расстояния, приведенные в§ 10.1.
На подходах к искусственным сооружениям контактные провода
следует располагать с уклонами, не превышающими 0,004.
Под искусственными сооружениями (пешеходные и сигнальные мо-
стики, однопутные и двухпутные путепроводы и т.п.), длина которых
вдоль пути меньше расстояния между струнами цепной подвески
(8—12 м) или равна ему, может быть осуществлен один из следующих
основных способов прохода контактной подвески:
использование искусственного сооружения в качестве опоры;
пропуск подвески без крепления к искусственному сооружению и
без разрезания несущего троса;
2<»
Рис. 9.10. Схемы прохода контактной подвески под искусственным сооружением
с использованием его в качестве опоры (а) и без крепления к нему (б)
включение под искусственным сооружением в несущий трос изоли-
рованной штанги.
П е р в ы й способ прохода ^ожет быть применен в тех слу-
чаях, когда расстояние от головки рельса до нижнего края искусствен-
ного сооружения h удовлетворяет следующему условию (рис. 9.10, а):
h Лк п>1л-|-/к111пх 'b^-inln I'^max I Ли
(9.1)
где Лк min — минимальная допустимая высота контактных проводов над уров-
нем головок рельсов;
fniax — максимальная стрела провеса несущего троса;
/к max — наибольшая местная стрела провеса контактных проводов при
условиях, определяющих наличие Fmax’.
Crnin — минимальное расстояние между несущим тросом и контактными
проводами в середине пролета;
йи — длина изоляторного звена или гирлянды.
Если конструкция искусственного сооружения позволяет осуще-
ствить крепление изолятора несущего троса над нижним краем соору-
жения, то величину /ги в формуле (9.1) можно принять равной /гт1п,
т. е. минимальному расстоянию от частей, находящихся под напря-
жением, до заземленных частей, допустимому при данном напряже-
нии контактной сети (см. рис. 9.12). При компенсированных подве-
сках крепление несущего троса па искусственном сооружении должно
обеспечивать возможность продольных перемещений троса; при этом
может оказаться необходимым увеличение размера Ли.
Для компенсированных подвесок можно принять emln -- 0,3ч
4-0,5 м. При нолукомпенсированных подвесках без скользящих струн
величину emln принимают в зависимости от расстояния между дайной
струной и средней анкеровкой такой, чтобы угол наклона в плоскости
подвески не превысил 30°. При скользящих струнах величину emill вы-
бирают по конструктивным соображениям.
300
Если условие, установленное выражением (9.1), выполнимо ври
нормальной длине пролета, то ближайшие к искусственному сооруже-
нию опоры располагают на расстоянии, равном длине этого пролета.
Если же габарит искусственного сооружения не позволяет реализо-
вать нормальную длину пролета, то следует проверить, возможно ли
использовать сооружение в качестве опоры при уменьшенной длине со-
седних пролетов. Для этого сначала определяют стрелу провеса несу-
щего троса Fmax. допускающую осуществить подвеску его к сооруже-
нию,
^'max ‘"mln (итак- (9.2)
Расстояния, на которых должны быть ближайшие к искусственно-
му сооружению опоры, определяются выражениями (рис. 9.11):
I- щ,5 (/„ + /'): (9.3)
(9.4)
где /0 - длина нормального пролета;
Z и W — приведенные соответственно натяжение подвески и нагрузка при
режиме, определяющем наличие Fj„ax.
Если подвеска несущего троса к искусственному сооружению по-
требует значительного уменьшения длины пролетов, целесообразнее
остановиться на способе прохода контактной подвески под таким со-
оружением без крепления к нему (рис. 9.10, б). Это возможно, если
Л ^кпПп г/ктах4~ст1П4-F|Пах ^mln ^min (9.5)
где бт1п — стрела провеса несущего троса при температуре flnin;
Ht mln ~ подъем несущего троса при минимальной температуре на рас-
стоянии х от середины пролета;
hf mtn — подъем несущего троса под воздействием токоприемника при ми-
нимальной температуре;
Лгп1п — минимальное допустимое расстояние от частей, находящихся под
напряжением, до заземленных частей.
Ближайшие к искусственному сооружению опоры контактной сети
в данном случае устанавливают так, чтобы было выдержано расстоя-
ние hmin с учетом всех факторов, указанных в выражении (9.5). Если
это условие не удается выполнить, то следует проверить возможность
прохода подвески под искусственным сооружением с установкой на
нем отбойников (рис. 9.12. а). При наличии отбойников величина h
может удовлетворять условию
h ЙнтИН’/ншах I ^’niax _’/‘min-|"t’nitti 4- J/Onln ‘ (9.6)
где h„ - высота отбойника, не меньшая, чем Л1пщ-
Если имеется возможность закрепить отбойник над нижним краем
сооружения (.рис. 9.12, б), го в выражении (9.6) можно принять, что
/i(, hinj п.
При отсутствии данных о стрелах провеса Fmax и Fmlll расчеты
по формулам (9.1) (9.6) можно выполнить приближенно относи-
30!
Рис. 9.11. Схема расположения бли-
жайших к искусственному сооруже-
нию опор
Рис. 9.12. Схемы крепления отбойника
снизу искусственного сооружения (а) и
над его пнжним краем (б)\
!- провод; 2-- отбойник
телыю беепровесиого положения контактных проводов, принимая
вместо hlt П1Н, величины, приведенные в § 10.1. Значение Та для опре-
деления F„ принимают поданным, приведенным в §3.1.
Втор о й с и о с о б прохода контактной подвески под искус-
ственным сооружением с установкой отбойника для несущего троса
пояснен на рис. 9.13, а.
Третий способ (с включением в несущий трос изолирован-
ной штанги) осуществим в тех случаях, когда
Z1 2^ ^Kinln !*Ляпах 1'^от l_^inln’ (9-7)
где /от допускаемое расстояние от контактного провода до отбойника (см.
§ 10.1).
При компенсированных подвесках обеспечивают свободное пере-
мещение изолированной штанги вдоль пути (рис. 9.13. б, в). Для вос-
полнения ослабленного сечения контактной подвески монтируют об-
Рис. 9.13. Схемы прохода контактной подвески под искусственным сооружением
без изолированной штанги (а) и с нею (б, в):
] —- отбойник контактного провода; 2 — поперечный электрический соединитель; 3 сколь
зящая струна; 4 — щит ограждения; 5—отбойник несущего троса; б и полированная
штанга; 7 •-обводной электрический соединитель (на схеме б не показан)
302
Рис 9 14 Схема прол ода контактней подвеска под путепроводом:
; - отбойник контактного провота; ,? анкеровка несуще, о троса- 5* -- шит ограждения; 4 - -
г><?(!рречч1»!й электрический соедини tел./. 7 - о) раничигель подъеме контактно, о нророда. 6 - •
про меж V оч пая т очка подвеса
водной электрический соединитель (ем. рис. 9 13, в) В тех случаях,
когда не предусматривается плавка гололеда, допускается умень-
шение площади сечения контактной сети ня 20 %.
Проход контактной подвески под сигнальными и пешеходными мо-
стиками. а также под путепроводами может быть осуществлен по одной
из схем, приведенных на рис. 9.13. иод путепроводами, длина которых
вдоль путей превышает 15 м, по схеме рис. 9.14. Эта схема при ком-
пенсированной денной подвеске применима только, если путепровод
расположен в середине анкерного участка. Выбор той или иной схемы
рис 9 13 определяется вертикальным габаритом искусственного‘со-
оружения Промежуточную точку подвеса контактного провода при
(-.''•мс рис. 9.14 получаю» обычно, применив скользящую струну. При
проходе подвески по схеме рис. 9.14 недостающее сечение троса вос-
иолняки. применяя специальное обводное электрическое соединение,
которое рас полагают в стороне от пути, пли, если скорость движения
не превышает 70 км ч. закрепляют на контактном проводе (см,
pile 9.13. л) При анкеровках несущего vpoca на сооружении для
уменьшения о!жатия контактных проводов иногда устанавливают or
рапичите'1Ы1ые кольца (см. рис 9.14).
В (ом случае, когда пя электрифицируемой линии имеются мосты
с ездой поверху, следует устанавливать на них возможно меньшее чис-
то опор. Вели имеются мосты с ездой понизу, тоннели или путепрово-
ды жачптелыюй длины, проход контактной подвески .может быть
осуществлен или цепной подвеской с малой конструктивной высотой,
или простой подвеской.
Цепная подвеска с малой конструктивной высотой образуется зна-
чительным сближением точек подвеса несущего троса. Расстояние
между точками крепления несущего троса в данном случае определя-
ют по формуле (9 4) в зависимости от возможной стрелы провеса троса,
вычисляемой по формуле (9.2). При этом расстояние emlI1 может быть
уменьшено до определяемого конструкцией скользящих зажимов или
струн.
На мостах с ездой понизу при низко расположенных верхних вет-
ровых связях моста устанавливают специальные конструкции для
подвески несущего гроса (рис. 9.15). Размещение этих конструкций
должно быть увязано с. расположением ветровых связей моста, а мини-
Рис, 9.15, Схемы установки на мостах
с, ездой понизу П-образной конструк-
ции (а) и поворотной консоли (б)
мальная необходимая высота /г'т1п для схем рис. 9.15, а и б может быть
определена соответственно по формулам:
fynjn~ 1 ^Kinln h/кгпах • г cmlr. ’ 1 • Fmax ^ii l — (9-8}
^niin 1^‘Kmlii 1 /кгпах’I" einln + ^niax'l'0,3] h. (9.9)
На мостах с ездой понизу полукомпенсированная подвеска с малой
конструктивной высотой может быть применена и в тех случаях, ког-
да габарит порталов моста не позволяет пропустить несущий трос, но
ветровые связи расположены так, что на них можно закрепить изоля-
торы для несущего троса. Тогда основной несущий трос / (рис. 9.16,а)
анкеруют с обеих сторон моста на порталах, а в его средней части под-
вешивают дополнительный отрезок троса 3. соединяемый с основными
электрическими соединениями 2,
В сводах тоннелей для увеличения высоты точек крепления несу-
щего троса могут быть устроены ниши. В двухпутных тоннелях, если
позволяет очертание свода, по оси междупутья укрепляют специаль-
ную конструкцию, на которой размещают консоли для контактных под-
весок обоих путей.
При смешанной тяге для уменьшения воздействия на изоляторы ды-
ма и газов изоляторы смещают в сторону от оси пути, располагая их
вне габаритов токоприемника. Контактный провод также смещают на
30- 40 см в сторону от оси пути, а при двух контактных проводах рас-
полагают их на указанном расстоянии по обе стороны от оси пути.
Применение более тяжелой контактной подвески улучшает каче-
ство токосъема, вследствие чего желательно подвешивать под искус-
ственным сооружением второй контактный провод, если на участке
применена подвеска с одним проводом сечением 100 мм2.
Рис. 9.16 Схемы контактных подвесок цепной с малой конструктивной высотой
(я) и простой с двумя контактными проводами (б)
304
В тех случаях, когда устройство цепной подвески с малой конструк-
тивной высотой невозможно, применяют простую подвеску с двумя
контактными проводами сечением по 100 мм2 каждый или с одним сече-
нием 150 мм2. При одном контактном проводе в основной подвеске до-
полнительный контактный провод анкеруют на опорах, расположен-
ных по обе стороны от искусственного сооружения (обычно на вторых,
считая от сооружения). Несущий трос закрепляют на искусственном
сооружении с обеих сторон (при компенсированных подвесках в слу-
чае необходимости через компенсатор), а контактные провода для уве-
личения эластичности подвешивают или на поперечных тросах
(рис. 9.16, б), или на специальных кронштейнах, укрепленных на ис-
кусственном сооружении. Расстояния между точками подвеса контакт-
ных проводов принимают в зависимости от местных условий, но не бо-
лее 12 м. Крепления контактных проводов должны обеспечивать воз-
можность их перемещений вдоль пути при изменениях температуры.
В тоннелях также применяют специальные контактные подвески
(пространственно-ромбовидную, шинную и др.), размещение которых
возможно при любом вертикальном габарите тоннеля.
Приближение контактных проводов к элементам искусственных
сооружений должно быть проверено при максимальных нажатиях
токоприемников, зависящих от их типа и скорости движения поездов
на участках трассы, где расположены эти сооружения. При отсутствии
достоверных данных о максимальных нажатиях токоприемников Рта*
можно пользоваться примерными значениями, приведенными в
табл. 9.3.
Если ни один из описанных способов прохода контактной подвески
в искусственном сооружении нельзя применить и невозможно или не-
экономично опускание путей, сооружение подлежит переустройству.
Как исключение, когда позволяют условия движения поездов, можно
принять решение о пропуске подвески без ее изоляции от сооружения
с устройством по обеим его сторонам нейтральных вставок.
Пример. Задание и исходные да н и ы е. Выбрать способы
прохода полукомпенсированпон подвески ПБСМ-70-|-НлОл0,04Ф-100 под дву-
мя пешеходными мостиками на станции и такой же компенсированной подвески
на мосту с ездой понизу на перегоне линии переменного тока. Длина пролета на
станции 65 м. Пешеходные мостики имеют высоту 7,6 и 6,35 м от уровня голо-
Т а б л и ц а 9.3
Серия токоприемника Ртах, даН, при скоростях движения, км/ч
100 120 140 i 160
л 13 14 16 19
т 20 22 26 32
Примечав и е. Значения Нтах при других скоростях движения могуч быть оп-
ределены линейной интерполяцией.
305
вок рельсов. Моет с ездой понизу на перегоне длиной 300 м прямоугольного сече-
ния с высотой порталов 0,2 м от уровня головок рельсов. Необходимые данные
для полукомпенсированной подвески приведены в примере § 6.3.
Р е ш е и и с. Проверим по формуле (9.1), возможно ли использовать более
высокий пешеходный мостик в качестве опоры. Примем fcKmin -- 5,75 м, Fmax
0,96 м (см. табл. 6.3): ?lnin -- 0,8 м; /'н 1Па\ —0,075 м и h„ -.0,55 м (три изоля-
тора). При -лих данных
5,75-1- 0,0754-0,96 4-0,8 > 0,55 =. 8,135 > 7,6 м.
Использовать мостик в качестве опоры нельзя. Проверим возможность про-
хода подвески по схеме рис. 9.10. Принимая, что мостик расположен в середине
пролета, расчет ведем по формуле (9.5). Значение Ftnit) - 0,57 м (см табл 6.3),
ht п,|г1 0,15 м. h0 - 0,35 м; при закреплении отбойников выше нижнего края
мостика (ем. рис. 9.12. б)
5,75 1 0,075 40.8 40,96 — 0.57 i-0,15 : 0,35 7,51-м.
Таким образом, для пешеходного мостика высотой 7,6 м можно осу шествии,
проход подвески л о схемам рис. 9.10 и 9 12.
При расчете относиюльно бесировег ноге положения коптактного провода,
учитывая, что ht.f, 6,5? м, Ьп 0,37 м и /-4 - 150 даН. получим
/•„ 1 ,56-652/(8-1290) л,37- 150/1 >9Г, 0 679 м.
По формуле (9 1) pat считаем
6,2 1-0,8 1-0.6794 0.55 -8,229ч,
по формуле <9.51
6,2 |-О,8 I 0, 15 [ (), 35 7.5 м .
что пезначип'льно отличается от значении, полученных более точным» расчета
ми. Очевидно, что и вывод о способе прочода подвески под мостиком высотой 7,6 м
изменится.
Для пешеходной; мостика высотой 6.35 м примем способ прохода подвески
с включением и не, yuiin'i трос изолированной шышк (см. рис. 9.13). Проверим
это по формуле (9.7), принимая 0.1-5 м,
5,75-]-0,075 - • - •,). 15 40,35 6,325м.
Следовательно, указанный способ прохода подвески прием тем.
Если мост с ездой понизу на перегоне находится в сродней части анкерного
участка, го для крепления несмцего троса на мосту можно применить П-образ-
пые конструкции (см. рис 9,13. и). Примем, что таких конструкций семь; тогда
расстояние между ними будет равно 50 м Определим минимальную высоту ука-
занных конструкций по формуле (9.8). Для этого вычислим стрелу провеса не-
сущего троса но формуле (6 44). принимая о -- 0,3 м, -= 0,03 м, Н„
150 даН и Г = 1500 даН;
F -- 1,56 • 5(Г-’ / (8 • 1500) — о, 03 • 100( । /1М (-0.3-150 /1500 - О, .34 м .
По формуле (9.8) найдем
/i,'niI1- 3,75-40,03-1 0,8 1 0,34 40,55—6,2 1.27м.
Если же мост находится не в средней части анкерного участка, нужно уста-
новить изолированные поворотные консоли но схеме рис. 9.15, б, а необходимую
для этого минимальную высоту стоек определить по формуле (9.9)
5,75-! О.ОЗ-'-0,84 0,34-1 0,3-.6,2 1,02 м.
Такой способ прохода подвески может быть осуществлен и при расположе-
нии моста в средней части анкерного участка.
Глава 10
РАЗРАБОТКА ПЛАНОВ КОНТАКТНОЙ СЕТИ
НА СТАНЦИЯХ И ПЕРЕГОНАХ
§ ЮЛ. Основные габариты устройств контактной сети
Высота подвески контактного провода в любой точке пролета над
уровнем головки рельса установлена Г1ТЭ не менее 5750 мм как на
перегонах, так и на станциях. В исключительных случаях с разреше-
ния МПС на существующих линиях это расстояние в пределах искус-
ственных сооружений, расположенных на путях станций, где не пре-
дусматривается стоянка подвижного состава, а также на перегонах
может быть уменьшено до 5550 мм на линиях постоянного тока и до
5675 мм па линиях переменного тока. Высота подвески контактного
провода не должна превышать 6800 мм.
Основные наименьшие габаритные размеры проводов контактных
подвесок принимают в соответствии с ГОСТ 9238 -83 (рис. 10.1 и
табл. 10.1).
Во всех случаях, когда это не связано с экономически нецелесооб-
разными затратами или длительными перерывами движения, пере-
устройство существующих искусственных сооружений для размеще-
ния контактной сети производят для напряжения 25 кВ или другого
максимально возможного в перспективе на данной липин, чтобы избе-
жать еще одного переустройства в том случае, если напряжение будет
повышено. Минимальные допускаемые размеры, приведенные в
табл. 10.1, применяют с разрешения Министерства путей сообщения и
только в исключительных случаях на существующих искусственных
Рис. 10.1. Допускаемые расстояния между искусственным сооружением и кон-
тактным проводом, токоприемником и подвижным составом:
/ - граница приближения искусственных сооружений: 2 — контур, соответствующий по
ложениям токоприемника при его смещениях по высоте и в стороны; <3 —габарит подвиж-
ного состава
307
сооружениях, переустройство которых признано в данное время неце-
лесообразным.
Расстояние от рабочего контактного провода при его беспровесном
положении до нижнего фиксирующего троса, фиксирующей оттяжки,
пересекающей анкеровочной ветви другого пути, а также до основного
стержня обратного фиксатора должно быть не менее 450—400 мм
(первая цифра относится к прямым и кривым радиусом более 2000 м,
вторая — к кривым радиусом 2000 м и менее). При скоростях поездов
выше 120 км/ч и в местах с особо сильными ветровыми воздействиями
указанные расстояния увеличивают на 50 мм. Расстояние от контакт-
ного провода до расположенных над ним заземленных частей опор-
ных устройств и искусственных сооружений (жестких поперечин, пу-
тепроводов, мостов и т.п.) принимают при двух контактных проводах
не менее 500 мм и при одном — не менее 650 мм. Меныпие расстояния
могут быть допущены, если установлены изолированные отбойники, ис-
ключающие опасное приближение контактного провода к заземленным
частям.
Расстояние от контактного провода до нижней грани отбойника
(без учета отжатия токоприемником) на линиях, где скорость движе-
ния поездов превышает 120 км/ч, принимают не менее 150 мм при оди-
ночном и не менее 100 мм при двойном контактном проводе. На лини-
ях, где скорость не более 120 км/ч. эти расстояния могут быть соот-
ветственно снижены до 100 и 70 мм. При скорости движения не более
50 км/ч па станционных путях расстояние до отбойника должно быть
не менее 50 мм. Расстояние от нижней грани отбойника до нижней гра-
ни жесткой поперечины или мостика принимают в соответствии с ука-
занными в табл. 10.1 допускаемыми расстояниями до заземленных
частей.
Расстояние от токоведущих частей секционных разъединителей
до заземленных конструкций должно быть не менее 800 мм на линиях
постоянного тока и 1000 мм на линиях переменного тока. Не донуска-
Таблица 10.1
мм А, ММ ММ 6, мм
- для станци-1 *й, где пре- 1 стоянка 1 ) состава ] для перегонов и станционных путей, где не предусмотрена стоянка подвижного состава я а? без несущего троса с несущим тросом
Напряжен! в контактн сети. кВ 5 с Q.S и < о S 2 3sa О. X U rf О X >. о X О Г.? с нормаль- j ное j мини- 1 мальное | допус- ’ каемое | нормально* минимальн допускаемс 1 | нормально* минимальн допускаем* нормаль- । 1 ное ' 1. 1 ! МИНИ- i j мальное ! допус 1 каемое • нормаль- 1 ное i О 1 ' х О О 2 5 S П X ф я га о то 2 2 «
1,5-4 6—12 25 950 950 950 450 450 450 250 300 375 200 250 350 150 200 300 200 220 250 150 180 200 150 150 150 100 100 100 300 300 300 250 250 250
ЗОЯ
Рис 10.2. Расчетные схемы к определению увеличения горизонтального расстоя-
ния от оси пут до внутреннего края опор (Г — габарит установки опор на пря-
мом участке пути)
ется размещать какие-либо провода, изоляторы и другие конструкции
на расстоянии менее 3 м над рогами разъединителей.
Фиксаторные изоляторы, изоляторы в апкеровочных ветвях про-
водов и в фиксирующих тросах гибких и жестких поперечин, а также
изоляторы усиливающих и других проводов при постоянном токе ус-
танавливают на таком расстоянии от опор, чтобы части контактной
сети, находящиеся под напряжением, были удалены от ближайшей гра-
ни опоры на расстояние не менее 8000 мм. Аналогичное расстояние при
переменном токе для изоляторов в анкеровочных ветвях и различных
проводах принимают не менее 1000 мм.
Габарит опор или расстояние от оси пути до внутренней грани опор
на уровне головок рельсов на прямых участках пути перегонов и стан-
ций принимают не менее 3100 мм, а для анкерных опор — не менее
3300 мм В особо сильно снегозаносимых выемках (кроме скальных)
и на выходах из них на длине 100 м расстояние от оси крайнего пути до
внутреннего края опор контактной сети принимают, как правило, рав-
ным 5700 мм. В особо трудных условиях габарит опор разрешено
уменьшать до 2750 мм на перегонах и 2450 мм на станциях (кроме
крайних путей).
Все указанные размеры даны для прямых участков пути. На кри-
вых эти расстояния увеличивают в соответствии с габаритным ушире-
нием, установленным для опор контактной сети.
Увеличение горизонтальных расстояний ог оси пути до внутренне-
го края опор на кривых участках пути, прилегающих к прямым, мо-
жет быть определено по данным Трансэлектропроекта следующим
обр.’.ьом:
на внешней стороне кривой при наличии переходной кривой п воз-
вышения наружного рельса (рис. 10.2, о)
Av = -Ai:(/u : 10--х)/(/п 1 10);
ЗОЙ
на внутренней стороне кривой (рис. 10.2, б)
\х- ’ -'к Uu-f- Ю — х)/1^'.
ца внешней стороне кривой при отсутствии переходной кривой и
возвышения наружного рельса (рис. 10.2, в)
\v -Ак (15—,v)/15;
на внутренней стороне кривой (рис. 10.2, а):
ДЛ. ... л„ (10— х)/15;
(10-: Л-')/15.
В этих формулах:
tn - длина переходной кривой, м;
Лк -- увеличение габарита опоры на кривой м,
' величение габирита опоры на расстоянии х от начала круговой кри-
вой, м.
Результаты ренетов но этим формулам приведены в табл. 10.2, где
в числителе даны размеры для главных путей перегонов и станций,
а в знаменателе для остальных станционных путей (кроме главных).
Таблица 10.2
Увеличения горизонтальных расстояний от оси пути
до внутреннею края опор, мм, при условиях
Радиусы ривых, м 2
I /’—2450 м г? . :’7оо-~;иао мм i57(jo мм
4000 10 140/40 105/25 25/10
3000 10 205/40 150/30 40/15
2500 15 260/70 190/50 55/20
2000 20 320/75 235/55 70/29
1800 20 375/75 275/55 85/25
1500 25 430/110 320/80 100/25
1200 30 440/140 325/105 105/35
1000 35 445/175 330/130 110/50
800 45 450/210 340/160 120/65
700 50 460/240 345/185 125/75
600 60 465/250 355/195 135/85
500 70 480/265 365/205 145/95
400 90 500/280 385/225 165/115
350 105 510/295 400/240 180/130
300 120 525/310 415/255 195/145
250 140 535/340 445/285 225/175
200 180 585/370 475/315 255/205
180 200 605/390 495/335 275/225
Приме чан и я. Условие — на внешней стороне кривой при любых возвышениях
наружного рельса и любых габаритах опор на прямых участках пути, а также во всех
случаях, когда возвышение наружного рельса не предусмотрено; условие 2 —па внутрен-
ней стороне кривой при расчетном возвышении наружного рельса и различном габарите
опор на прямых участках пути.
310
При расположении опор на пассажирски?: платформах расстояние
между краем платформы и ближайшей гранью опоры должно быть нс
менее 2 м. В обоснованных случаях, например при наличии на плат-
форме какого-либо строения, это расстояние уменьшают, по не менее
чем до 3,1 м от оси пути. Если ширина боковой платформы меньше 4 м.
опоры следует устанавливать за пределами платформы. Размещать
опоры контактной сети в пределах пассажирских платформ, вблизи
зданий вокзалов, павильонов и сходов с пешеходных мостов следует
так, чтобы не нарушались внешний вид сооружений и устройств и
условия обслуживания пассажиров.
Опоры, гибкие п жесткие поперечины, устанавливаемые перед
сигналами, располагают с такими габаритами, чтобы не ухудшалась
видимость сигналов. Расстояние от сигналов до частей контактной
подвески, находящихся под напряжением, принимают не менее 2 .м
для постоянного тока и 2.5 м для переменного.
Опоры контактной сети (а также анкеры их оттяжек). расположен-
ные непосредственно у главных путей перегонов и станций и находя-
щиеся вблизи железнодорожных переездов, следует устанавливать
на расстоянии нс менее 25 м от края проезжей части иерее да но на-
правлению движения поездов. На двухпутных участках допи кается
размещать опоры пе в створе Для опор, расположенных j воздушных
стрелок. указанное расстояние можно уменьшить но условиям распо-
ложен’! я воздушных стрелок. Во всех случаях опоры и анкеры их от-
тяжек должны находиться на расстоянии не менее 5 м от края проезжей
части переездов.
Опоры, размещаемые вдоль тупикового пути, на которых подвеши-
ваю! кон1иктны<. подвески других путей, на протяжении 100 м уста-
навливают с габаритом не менее 4 м от оси тупика. Анкерные опоры и
анкеры оттяжек в копие тупика за упором располагают так. чтобы
расстояние от упорного бруса до ближайшей грани опоры или оттяж-
ки было не менее 20 м, что снижает вероятность наезда па упорный
брус с последующим повреждением опоры. В обоснованных случаях
это расстояние может быть уменьшено. Все указанные требования не
относятся к опорам, устанавливаемым за туниками или вдоль тупико-
вых путей отстоя электроподвижного состава.
Наименьшие расстояния от проводов питающих, отсасывающих
и других воздушных линий при пересечении и сближении е другими
проводами или сооружениями приведены в табл. 10.3. Эти расстоя-
ния должны быть выдержаны при наибольшем провисании проводов
с учетом нагрева их током или отложений гололеда, а также отклоне-
ний под действием ветра. Наименьшие расстояния до поверхности зем-
ли от проводов различных линий в табл. 10.3 приведены в зависимости
от характера местности, в которой расположена данная линия
Территории станций обычно относят к населенной местности, .пере
гоны к ненаселенной, откосы насыпей и выемок к труднодоступ-
ной (для транспорта) местности.
11
Таблиц a 10.3
Объекты сближения или пересечения Наименьшие расстояния, м, от проводов
отсасываю- щих. обрат- ного тока, волновода, до 1 кВ усиливающих, питающих продольного электроснаб- жения напряжением. кВ
3—10 25—35
До поверхности земли в населенной местности 6,0 7,0 7,0
То ж в ненаселенной местности и в пределах искусственных сооружений 5,0 6,0 6,0
То же в труднодоступной местности 4,0 5,0 5,0
До недоступных склонов гор. скал, утесов До полотна автомобильных дорог1: 1,0 2,5 3,0
категории 1 7,0 7,0 7,0
категории II 6,0 7,0 7,0
До поверхности пассажирских плат- форм (при двойном креплении прово- дов) 4,5 7,0 7,0
До головок рельсов неэлсктрнфици- ровапных путей 7,5 7,5 7,5
До несущих тросов или верхних про- водов линий, подвешенных на опорах контактной сети 2,0 2,0 2,0
До верхних проводов трамвайных и троллейбусных линий До проводов воздушных линий (кро- ме указанных выше) при напряжении: 1,5 3,0 3.0
менее 1 кВ 1,0 2,0 3.0
6 10 кВ 2,0 2,0 3,0
20 110 кВт 3,0 3,0 3,0
150 220 кВ 4,0 4,0 4,0
330—500 кВ До проводов или подвесных кабелей линий связи и радио: 5,0 5,0 5,0
по вертикали 1,5 2,0 ...
по горизонтали 2,0 2,0
До пастила пешеходных мостиков (при устройстве над ними предохрани- тельных щитов) 4,0 4,5 5,0
До крыши несгораемых производст- венных зданий и сооружений (при за- земленных металлических крышах) До ближайших частей зданий по го- ризонтали: 3,0 3,0 3,0
до балконов, террас, окон 1,5 2,0 4,0
до глухих степ 1,0 2,0 4,0
До кроны деревьев 1,0 2,0 3.0
1 В пределах переездов (между габаритными воротами) наименьшие расстояния уста-
навливаются в соответствии с габаритами контактных проводов; расстояние по вертикали
от проводов группового заземления до поверхности земли должно быть .не менее 5 м.
312
Пересечение воздушных линий электропередачи с электрифициро-
ванными железными дорогами производят под углом, близким к 90°,
но не менее 40°. Расстояние от опоры пересекающей линии до оси опор
контактной сети принимают не менее высоты опоры, увеличенной на
3 м. В особо стесненных условиях это расстояние может быть снижено
на величину, зависящую от напряжения пересекающей линии, но не
менее чем до 3 м. Опоры для перехода устанавливают металлические
или железобетонные анкерного типа, В горловинах станций пересече-
ния электрифицированных путей воздушными линиями запрещены.
Пересечения линий связи и радиофикации с контактными сетями
выполняют подземным кабелем. При числе проводов на междугород-
ных линиях связи до 16, а на других линиях связи до восьми допуска-
ется пересечение этих линий с контактной сетью постоянного тока в
пределах между опорами. Эти пересечения нельзя располагать над
сопряжениями анкерных участков, па станциях, над пассажирскими
платформами, на остановочных пунктах, над переездами и пешеход-
ными мостиками. Угол пересечения принимают близким к 90°, но не
менее 45°. Воздушные пересечения выполняют только биметалличе-
скими проводами площадью сечения не менее 25 мм2.
§ 10.2. Принципы составления планов
Составление планов контактной сети на раздельных пунктах, име-
ющих путевое развитие, и на перегонах электрифицируемой линии
является одной из наиболее ответственных работ, производимых
при проектировании контактной сети. На основании этих планов оп-
ределяют объемы работ, составляют заявки на оборудование и мате-
риалы, устанавливают стоимость сооружения контактной сети и вы-
полняют строительные и монтажные работы. Поэтому, составляя пла-
ны контактной сети при условии удовлетворения всех требований по
обеспечению ее надежной работы в эксплуатации, необходимо выбрать
наиболее экономичные решения и создать возможно более благопри-
ятные условия для производства работ по сооружению сети.
Планы контактной сети составляют для каждой станции, разъезда
и обгонного пункта и для каждого перешла. В дальнейшем для упро-
щения будем все раздельные пункты, имеющие путевое развитие, име-
новать станциями. Поскольку условия разбивки опор крайних сопря-
жений анкерных участков на станциях несколько сложнее, чем на пе-
регонах, целесообразно сначала составлять планы контактной сети на
станциях, а затем приступать к разработке планов сети на перегонах,
увязывая их с соответствующими станциями. Наиболее подробные
планы контактной сети составляют на стадии рабочих чертежей.
При составлении планов контактной сети выполняют следующие об-
щие требования.
Пролеты между опорами контактной сети проектируют по возмож-
ности максимальными допускаемыми в данной местности в данных
3)3
конкретных условиях (см. гл. 3). Максимальную длину пролетов со-
кращают на 10 % в местах устройства средних анкерных контактных
проводов и в случаях, когда опоры располагают на кривых участках
пути в пучиниетых местах, на свежеотсыпанных насыпях и в других
местах, где может образоваться перекос пути, ле соответствующий
расчетному.
Длину переходных пролетов изолирующих сопряжений анкерных
участков снижают по отношению к максимальным допускаемым: на
25 % в прямых и кривых радиусом более 1500 м; па 20 % -- в кри-
вых радиусом от 1000 до 1500 м; на 15 % в кривых радиусом от
500 до 1000 м; на 10 % - в кривых радиусом менее 500 м. Снижения
длин пролетов указаны для расстояний между проводами различных
анкерных участков 500 мм на линиях переменного тока и 400 мм при
постоянном токе. В случаях раздвижки проводов до 550 мм длины
переходных пролетов должны быть определены соответствующим рас-
четом
Длину пролетов уменьшают также в тех случаях, когда требуется
снизить нагрузки на опорные и поддерживающие конструкции или
увязать зигзаги контактных проводов в соседних пролетах. (Допусти-
мые длины про,тегов при различных .значениях и направлениях зиг-
загов могут быть определены по справочнику или графическими по-
строениями с помощью специальных лекал.) Разница в длине двух
соседних пролетов при полукомпенеированных подвесках не должна
превышать 25 % длины большего пролета.
Длину анкерных участков устанавливают по методике, приведен-
ной в § 6.4. Наибольшая допускаемая длина анкерного участка кон-
фетного провода при нолукомпенсированной и компенсированной под-
весках па прямых участках пути равна 1600м и в виде исключения мо-
жет быть увеличена до 1S00 м. Длину анкерного участка некомпен-
сированного несущего троса не ограничивают.
Средние анкеровки размещают таким образом, чтобы обеспечить
примерно одинаковые условия компенсации обеих половин анкерного
у чистка 1а:.га анкерный участок целиком находится на прямой, то
среднюю анкеровку располагают в его середине. Если же в преде-
лах анкерного участка имеются кривые, то среднюю анкеровку сме-
щают в сторону расположения кривых. Получившиеся по условиям
разбивки анкерные участки длиной, равной половине максимально
допускаемой в данных местах или меньшей, устраивают с односто-
ронней компенсацией бе.з средней анкеровки.
Нормальные зигзаги контактных проводов принимают в соот-
ветствии с указаниями, приведенными в § 3.1. Зигзаг несущего тро-
са при полукосых цепных подвесках па прямых участках пути ра-
вен нулю, а на кривых при вертикальных подвесках его принима-
ют таким же, как у контактных проводов.
Сопряжения анкерных участков на перегонах и станциях произво-
дят в трех пролетах. На станционных путях как исключение допуска-
ют двухпролетные сопряжения при условии, что скорость движения
31-1
по этим путям не превысит 70 км/ч. Сопряжения анкерных участков
следует по возможности располагать на прямых участках пути. Распо-
ложение сопряжений на кривых радиусом менее 1000 м нежелательно
вследствие трудностей монтажа и эксплуатации, а на кривых радиу-
сом менее 600 м возможно лишь на жестких поперечинах. Устройство
сопряжений под искусственными сооружениями не допускается без
соотве i ствующего обое нова н и я.
На линиях, расположенных во всех гололедных районах, кроме рай-
она 1, сопряжения анкерных участков должны быть смонтированы с
учетом возможности плавки гололеда электрическим тиком.
На главных путях перегонов и станций желательно применять од-
нотипные контактные подвески. При наличии на перегоне компенсиро-
ванной, а на станции полукомпенсироваиной подвесок их сопряжение
осуществляют анкерным участком, в котором одна половина подвески
работает как полукомпенсированная, а другая - как компенсирован-
ная. Для этого устанавливают среднюю анкеровку компенсированной
подвески, а конечные анкеровки осуществляют в соответствии с типом
проектируемой подвески.
При изменении направления контактных проводов угол между от-
клоненной ветвью провода и первоначальным его направлением не
должен превышать 6° (тангенс угла отклонения не более 0,1). На егаи
ционных путях (кроме главных), а также в следующих после первого
пролетах угол излома контактных проводов может быть увеличен до
10° (тангенс угла J7i().
Уклон контактного провода при переходе от одной высоты к другой
при бес провесном положении и скоростях до 120 км/ч не должен пре-
вышать 0,004, а на линиях, где скорости движения больше 120 км/ч,
— 0,002; при этом по обоим концам каждого участка с основным укло-
ном устраивают вставки длиной не менее одного пролета с уклоном,
равным половине основного. На станционных путях, где скорости дви-
жения не превышают 50 км/ч, допускаемый уклон может быть увели-
чен, но не более чем до 0,01.
На планах контактной сети применяют следующие основные услов-
ные обозначения:
рабочие ветви контактных подвесок нал электрифицируемым
путем;
нерабочие ветви контактных подвесок-
пути и устройства, сооружаемые в перспективе,
иеэлектрифицируемые пути:
воздушные усиливающие провода;
питающие провода напряжением 50 кВ;
воздушные питающие линии,
воздушные отсасывающие линии;
провода линий продольного электроснабжения;
—w
V — у— провода групповых заземлений; железобетонные консольные и фиксирующие опоры;
6
О—<1 о=< анкерные железобетонные опоры с одной и двумя оттяжка- ми;
• существующие железобетонные и металлические опоры;
о □ устанавливаемые железобетонные и металлические опоры;
железобетонные и металлические опоры, устанавливаемые
£2 по другим чертежам;
ор жесткие поперечины с фиксирующим тросом на железобе-
ф со тонных одиночных и спаренных опорах;
1ибкая поперечина на металлических опорах;
"И------- врезной изолятор в контактных подвесках или тросах жест
ких и гибких поперечин;
ф-------секционный изолятор;
анкеровка компенсированной цепной подвески;
------- анкеровка пол у компенсирован ной цепной подвески;
жесткая анкеровка цепной подвески;
жесткая анкеровка питающей линии;
средняя анкеровка компенсированной подвески;
средняя анкеровка полукомпенсированпой подвески;
электрическое соединение на неизолирующем сопряжении ан-
керных участков, предусматривающем плавку гололеда;
анкеровка и обвод усиливающего провода на анкерной опоре
неизолирующего сопряжения анкерных участков;
длина и номер анкерного участка-
нормальный зигзаг контактного провода и поперечное элект-
рическое соединение;
316
27 у jfe 0*23
зигзаг контактного провода, отличающиеся от нормального,
ем;
длина пролета, м, номера опор, направления зигзагов;
пересечение проводов на воздушной стрелке;
роговой разрядник с двумя разрывами;
трубчатый разрядник;
сигнальный знак «Отключить ток»;
сигнальный знак «Включить ток на электровозе»;
сигнальный знак «Включить ток на электропоезде».
Условные обозначения секционных разъединителей, пунктов па-
раллельного соединения и автотрансформаторных пунктов аналогичны
приведенным в § 9.1.
§ 10.3. Составление планов контактной сети станций
Основные положения. Планы контактной сети станций составляют,
увязывая их с существующими и выполняемыми проектами: путевого
развития станций, сооружаемых мостов и путепроводов, переходов
вновь сооружаемых линий электропередачи и переустройства сущест-
вующих, СЦБ и связи, укладки или переустройства водопровода и
канализации и других подземных коммуникаций, тяговых подстан-
ций, постов секционирования и электродепо.
Для выбора наиболее правильного решения необходимо сравнить
несколько возможных вариантов разбивки опор с учетом удовлетво-
рения всех технических требований, предъявляемых к контактной се-
ти, и выбрать самый экономичный.
Работы по составлению планов контактной сети на станциях удоб-
но производить в такой последовательности: подготовка плана станции,
наметка мест, где необходима фиксация контактных проводов; раз-
бивка опор в горловинах, по концам станции, в средней части станции:
разбивка анкерных участков; разбивка зигзагов; трассировка питаю-
щих. отсасывающих и других проводов; обработка плана контактной
сети; подбор типов опор, фундаментов, консолей и пр.
Рассмотрим выполнение каждой из перечисленных выше работ от-
дельно, хотя некоторые из них настолько связаны друг с другом, что
такое разделение является условным.
31"
Подготовка плана станции. Обычно используют план в масштабе
1:1000; он наиболее удобен для производства разбивки опор. На плане
топкими вертикальными линиями наносят условные станционные пике-
ты, располагаемые через каждые 100 м по обе стороны от оси пассажир-
ского здания станции, принимаемой за нулевой пикет. В дальнейшем
для упрощения ось пассажирскою здания станции будем называть
осью станции.
На плане указывают оси всех подлежащих электрификации
путей, число которых зависит от размеров движения, рода поездов,
переводимых на электрическую гиту организации движения поездов
и типа маневрового локомотива. На промежуточных станциях при
грузовом движении в отсутствии маневровых автономных локомоти-
вов контактную сеть монтируют над всеми путями. На крупных стан-
циях, обслуживаемых автономными маневровыми локомотивами, кон
тактную сеть подвешивают на путях, предназначенных для непосред-
ственного приема или отправления с них поездов на электрифициро-
ванные участки, на путях электровозного и моторвагонного депо, пу-
тях подачи п уборки электровозов, в отдельных случаях на некоторых
других. Пути, которые используют только для отправления поездов
па электрифицированные участки, можно оборудовать контактной
сетью лишь в головной части на 150—200 м полезной длины.
Кроме электрифицируемых, на плане станции показывают все ос-
тальные неэлектрифицируемые пути, а также пути, поедполагаемыс
к укладке пли передвижке в егклветствии с дальнейшим развитием
станции и примыканием других линий.
Размеры всех '"'ждунутий указывают цифрами между соотвегсь
вующнми путями через каждые 100 м На планах показывают все кри-
вые, их радиусы, начало и конец, отмечают разные уровни насыпи,
выемки, кюветы и другие водоотводные сооружения, а также центры
стрелочных переводов, которые отмечают буквами ЦП. Около каждого
центра должна быть указана марка крестовины стрелочного перевода.
На план наносят все оказывающие влияние на расположение уст-
ройств контактной сети здания, сооружения, платформы, подземные
коммуникации, воздушные и кабельные линии, сигналы и т. п., от-
мечая их местонахождение относительно оси станции и ближайших
путей.
По возможности во избежание ошибок желательно выполнять пла-
ны контактной сети непосредственно на генпланах станций.
Наметка мест, где необходима фиксация контактных проводов.
Устройства для фиксации контактных проводов необходимо преду-
сматривать на всех стрелочных переводах электрифицированных пу-
тей, над которыми должны быть расположены воздушные стрелки, па
переходных стрелочных кривых и в других местах, где контактные про-
вода изменяют направление. В дальнейшем некоторые из намеченных
мест, возможно, не будут оборудованы фиксирующими устройствами,
однако до разбивки опор необходимо отмечать все без исключения ме-
ста. в которых требуется фиксировать контактные провода. Отметку
318
Рис. 10.3, Схема расположения фиксированной воздушной стрелки над обыкно-
венным стрелочным переводом:
' остряк сIреличло) о перевода; 2 -.нкррусмзн пегвь подвески; .7 область ноилучш ч о
расположения фиксир у ’ощей опоры; / ючка пересечения контакт пых проводов; а мал
магический центр крестовины: t - центр стрелочного перевода
производят тонкой вертикальной линией, около которой указывают
пикет (расстояние от оси станции) того места, где требуется фиксиру-
ющее устройство. При окончательной обработке плана эти липин сти-
рают.
На одиночных стрелочных переводах наилучшие условия прохода
токоприемника по воздушной стрелке во всех направлениях получают-
ся при расположении фиксирующих устройств на расстоянии 1 2 м
от точки пересечения контактных проводов в сторону остряка стрелки.
Наплучшим расположение контактных проводов, обра>ующих воз-
душную стрелку для обыкновенных стрелочных переводов (рис. 10.3),
будет тогда, когда точка пересечения проводов находится, между ося-
ми прямого и отклоненного путей и отстоит от каждого из них па 360 —
400 мм, г. е. там, где расстояние между внутренними гранями голо-
вок соединительных рельсов крестовины равно 730- 800 мм.
Расстояния до наилучшего места установки фиксирующих уст-
ройств от центра стрелочного перевода принимают в зависимости or
марки крестовины:
Марка крестовины . . 1,« 1/9 1/li 1 /!8
Расстояние, м . . . 3,Г- Л,0 7.5 10.8
На перекрестных стрелочных переводах контактные провода долж-
ны иметь двойное (ромбовидное) пересечение. При глухом пересече-
нии путей точку перекрещивания контактных проводов располагают
над его центром
Зигзаги контактных проводов а и b (рис. 10.4) выбирают в зависи-
мости от расстояния опоры до центра стрелочного перевода (табл. 10.4).
Размеры в табл. 10.4 приведены для случая, когда зигзаги а и b рав-
ны. Если в соответствии с зигзагами в соседних пролетах зигзаги и и
b требуется изменить, их можно выполнить разными но величине, но
сумма их должна быть равна 2a.
Таблица 10.4
Расстоя- ние, м, от оси опоры до центра перевода Зигзаги, см, при марке крестовины Расстоя- ние, м, от оси опоры до центра перевода Зигзаги, см, при марке крестовины
1/9 1/и 1/18 1/9 1/11 1/18
1 25 22 25 6 42 37 33
2 28 25 26 7 47 40 34
3 31 27 28 8 51 44 36
4 35 30 29 9 56 47 38
5 38 33 30 10 61 51 40
Разбивка опор в горловинах. Наиболее трудно разместить опоры в
горловинах, так как здесь имеется большое число стрелочных пере-
водов. Как правило, расстояния между намеченными ранее местами, в
которых необходима фиксация контактных проводов, не совпадают с
максимальными пролетами, возможными для данной местности. Если
в частных случаях получится такое совпадение или расстояния между
местами фиксации незначительно меньше допускаемых пролетов, то
наиболее целесообразно в каждом месте, где требуется фиксация кон-
тактных проводов, поставить несущие опоры. Если же установка
только несущих опор приведет к значительному уменьшению длин
пролетов (и, следовательно, к удорожанию контактной сети), необхо-
димо определить, возможно ли выполнить часть воздушных стрелок
нефиксированными. Это допускается для стрелок, не примыкающих к
главным путям. В местах расположения воздушных стрелок у главных
путей и в других случаях, когда
контактные провода изменяют на-
правление, нужно установить не-
сущие или фиксирующие опоры.
У главных путей желательно уста-
навливать несущие опоры.
Все воздушные стрелки подвесок
на главных путях выполняют с
пересечением контактных проводов
и подвеской несущих тросов на
опоре. Пересечения на воздушных
стрелках главных путей станции
компенсированной и полукомпен-
сированной подвесок не допуска-
ют. Фиксацию пересекающихся
Рис. 10.4. Схема для определения зиг-
загов контактных проводов на воз-
душной стрелке
проводов желательно производить
с одной стороны, для чего подвес-
ки в плане надо располагать так,
320
*“41
чтобы усилия от изменения направления проводов были направлены
в одну сторону.
Нефиксированные стрелки применяют в тех случаях, когда на
опорных конструкциях, расположенных не далее 20 м от стрелочного
перевода, возможно крепление проводов, обеспечивающих монтаж воз-
душной стрелки без фиксаторов. Это может быть выполнено или сме-
щением анкерных опор па такое расстояние, чтобы анкеруемые прово-
да проходили без излома (рис. 10 5. а), или закреплением пересекаю-
щихся проводов на фиксирующих тросах гибких или жестких попере-
чин так, чтобы эти провода на стрелках не изменяли направления
(рис. 10.5, б).
Если место расположения воздушной стрелки находится недалеко
от консольной опоры, нефиксированная стрелка может быть образова-
на путем соответствующего расположения пересекающихся несущих
тросов на консоли и установкой специальных фиксаторов для контакт-
ных проводов. В необходимых случаях при одиночных стрелочных
переводах можно смещать место установки несущих или фиксирую-
щих опор от наилучшего в сторону центра перевода на расстояние. 1-
2 м от него, однако это несколько ухудшит условия работы воздуш-
ной стрелки.
При выборе мест расположения фиксирующих опор желательно од-
ну опору использовать для фиксации нескольких точек, а при разносто-
роннем направлении усилий, действующих на фиксаторы, надо уста-
навливать две опоры с одним или двумя фиксирующими тросами
(фиксирующие поперечины). Сжатые фиксаторы на воздушных стрел-
ках не применяют.
При разбивке опор в горловинах необходимо учитывать возмож-
ность анкеровок всех проводов путей, заканчивающихся (или начина-
ющихся) в горловинах, без установки дополнительных анкерных опор
и стремиться к максимальному совмещению опор различного назначе-
ние. 10 5 Схемы нефиксированных воздушных стрелок, получаемых вследствие
соответствующего габарита анкерной опоры (а) и при отсутствии изменения на-
правления пересекающихся проводов на жесткой поперечине (б):
7 нефиксированные воздушные стрелки; 2 фиксированные
11 Зак. 2630
321
ния (несущих, анкерных и фиксирующих). Нежелательны пересече-
ния различных ветвей контактных подвесок.
Положение опор контактной сети на плане определяется, как пра-
вило, расстоянием от оси ближайшего пути и расстоянием от оси пас-
сажирского здания, измеряемым по оси базисного пути, за который
обычно принимают главный путь.
Разбивка опор по концам станции. Основная задача при разбивке
опор по концам станции — увязка мест установки опор для устройства
сопряжений анкерных участков контактных сетей станции и примыка-
ющих к ней перегонов с местами расположения входных сигналов. Воз-
душные промежутки изолирующих сопряжений анкерных участков
размещают между входным сигналом и первой (со стороны перегона)
стрелкой, примыкающей к данному пути. При этом необходимо преду-
смотреть возможность перестановки сцена двух электровозов с одного
пути станции на другой при снятии напряжения с контактной сети пере-
гона, т. е. без заезда на переходный пролет сопряжения.
Желательно, чтобы входной сигнал был расположен не далее 300 м
от центра крайнего стрелочного перевода пути прибытия. Если по ус-
ловиям размещения изолирующих сопряжений анкерных участков это
расстояние не выдерживается, то входной сигнал переносят в сторону
перегона с обязательной проверкой расстояния до следующего сигна-
ла на перегоне по условиям движения поездов. Крайняя со стороны
перегона анкерная опора может быть установлена и до входного сиг-
нала.
На главных путях двухпутных и многопутных участков изолирую-
щие сопряжения размещают по возможности в створе друг с другом.
Длину пролетов между переходными опорами следует выбирать в
соответствии с рекомендациями, приведенными в § 10.2. В тех случа-
ях, когда не удается выполнить все требования, предъявляемые к ме-
стам расположения изолирующих сопряжений при максимальной до-
пускаемой длине пролетов, можно во избежание переноса сигналов
уменьшить длину пролетов.
Разбивка опор в средней части станции. Условия разбивки опор в
средней части станции обычно значительно проще, чем в горловинах
или по концам, поэтому размещение опор здесь производят в послед-
нюю очередь. В отдельных случаях при усложнении этих условий
указанная последовательность разбивки опор может быть изменена.
Если в пределах станции расположены какие-либо искусственные
сооружения, то сначала выбирают способ прохода контактной сети
через них (см. §9.4). В соответствии с принятым способом намечают ме-
ста установки ближайших к сооружениям опор. Кроме того, намеча-
ют места установки опор у пассажирских зданий, пакгаузов и т.д
После этого на оставшихся частях станции, по возможности применяя
максимальные допускаемые пролеты, намечают места для опор жест-
ких или гибких поперечин. Отдельные парки и группы путей и с уче-
том схемы секционирования желательно оборудовать поперечинами,
механически не связанными. Там, где это выполнить не удается, сле-
.322
дует исходя из технико-экономической целесообразности рассмотреть
вопрос о раздвижке путей для установки опор в междупутьях или о
снятии одного из путей.
Если необходимо перекрыть жесткой поперечиной более восьми
путей, то при наличии (или создании) междупутья достаточной ширины
устанавливают две поперечины. Эти поперечины сдвигают вдоль стан-
ции таким образом, чтобы внутренние стойки были установлены в од-
ном и том же междупутье, а каждая из поперечин перекрывала не
больше восьми путей.
Длину одного-двух пролетов, расположенных примерно в середи-
не анкерного участка подвески главного пути станции, снижают на
10 % относительно максимальной в данном месте, чтобы разместить
среднюю анкеровку. При симметричном расположении станционных
путей в этих пролетах можно выполнить средние анкеровки и других
анкерных участков. Если же это недопустимо по условиям компен-
сации, то для других средних анкеровок следует также предусмотреть
соответствующее число уменьшенных пролетов.
Пролеты между двумя-тремя жесткими или гибкими поперечинами
вблизи горловин станции следует принимать короче максимально-до-
пускаемых, не увеличивая общего числа опор. Это позволит проще
увязать зигзаги на воздушных стрелках, расположенных в разных
концах станции.
После того как все опоры контактной сети на станции установлены
окончательно, необходимо для каждой из них указать габарит отно-
сительно оси ближайшего пути и расстояние (пикет) от оси станции.
Разбивка анкерных участков. После разбивки опор по всей дли-
не станции производят разбивку анкерных участков и окончательно
выбирают места установки анкерных опор. Для анкеровок стараются
использовать намеченные ранее опоры и только в отдельных случаях
добавляют специальные анкерные опоры, не воспринимающие других
нагрузок.
Над главными путями, но которым возможно движение поездов с
высокими скоростями, по всей длине должна быть контактная сеть то-
го же чипа и сечения, что и на перегоне. Анкерные участки подвесок
главных путей обычно располагают от крайних в сторону перегона ан-
керных опор сопряжений в одном конце станции до таких же опор на
другом конце.
Если длина анкерных участков станционных путей превышает до-
пустимую, то проектируют дополнительные сопряжения, размещая их
по возможности на крайних путях. Не допускается объединять в один
анкерный участок съезды между главными путями в обеих горловинах
станции.
При разбивке анкерных участков желательно все воздушные стрелки
выполнять с одиночным пересечением контактных проводов. Если же
по каким-либо причинам это сделать не удается, то воздушные стрел-
ки проектируют с двойным пересечением проводов, разнесенным на
пролет (рис. 10.6, а). Двойное пересечение без разнесения на пролет
11 * 323
Рис. 10.6. Схемы расположения кон-
тактных проводов с двойным их пе-
ресечением на одной воздушной
стрелке (а) и двух встречных стрел-
ках с двойным (б) и тройным (а) пе-
ресечением
не рекомендуется, а «открытые» воздушные стрелки, т. е. выполнен-
ные без пересечения проводов, вообще недопустимы.
Встречные простые стрелки, если они расположены на незначи-
тельном расстоянии одна от другой, могут быть образованы одной и той
же парой проводов. Между опорами, фиксирующими провода на стрел-
ках, оба контактных провода располагают на рабочей высоте. При
этом воздушные стрелки выполняют или с двойным пересечением кон-
тактных проводов (рис. 10.6, б), или, если это требуется по условиям
разбивки анкерных участков, с тройным (рис. 10.6, в). Контактные
провода главных путей или путей преимущественного направления
движения на воздушных стрелках располагают снизу.
На металлических опорах без оттяжек размещают не более двух
анкеровок цепных подвесок с каждой стороны опоры при условии
установки опоры соответствующего типа и возможности размещения
компенсаторов. На железобетонных опорах можно выполнять анкеров-
ки с компенсаторами только со стороны, противоположной той, на ко-
торой размещают оттяжки. Расположение анкеровочных ветвей под-
весок над пассажирскими платформами, навесами и крышами зданий
допускают как исключение при условии, что эти ветви будут изолиро-
ваны от частей контактной сети, находящихся под напряжением, и за-
землены.
По окончании разбивки анкерных участков подсчитывают их дли-
ну, у начала и конца каждого из участков указывают ее и номер участ-
ка и составляют спецификацию. Когда окончательно определены на-
чало и конец каждого из анкерных участков, отмечают места располо-
жения средних анкеровок на тех участках, для которых они необходи-
мы. При этом, если средние анкеровки не попадают в намеченные ра-
нее уменьшенные пролеты, производят соответствующую переразбивку
опор с корректировкой отметок длин пролетов и габаритов опор.
Разбивка зигзагов. Размещение зигзагов следует начинать с воз-
душных стрелок. Величины зигзагов в зависимости от места распо-
ложения фиксирующего устройства приведены в табл. 10.4. После
того как намечены зигзаги на всех воздушных стрелках, производят
увязку зигзагов между близко расположенными стрелками, для че-
го иногда уменьшают их нормальную величину на соответствующих
опорах.
Затем намечают зигзаги на опорах, расположенных на кривых, пос-
ле чего их увязывают с намеченными ранее зигзагами. Размечают
324
зигзаги проводов у опор сопряжений анкерных участков в соответствии
с принятой ранее схемой. Для удобства присоединения проводов от
продольных секционных разъединителей к контактным подвескам эти
разъединители желательно располагать на переходных опорах с «от-
крытой» стороны изолирующих сопряжений, где отходящие на анке-
ровку подвески ближе к опоре.
Трассировка питающих, отсасывающих и других проводов. Пита-
ющие и отсасывающие линии от тяговых подстанций к контактной се-
ти обычно выполняют воздушными и только в исключительных случа-
ях (с соответствующим обоснованием) кабельными. Если эти линии
кабельные, трассировку выполняют по кратчайшим расстояниям меж-
ду тяговыми подстанциями и местами присоединения линий к контакт-
ной или рельсовой сети с учетом возможности производства земляных
работ.
Воздушные питающие н отсасывающие линии, как правило, подве-
шивают на опорах контактной сети. Для подвода линий от здания тя-
говой подстанции до ближайших опор контактной сети устанавливают
самостоятельные опоры.
Питающую и отсасывающую линии, идущие вдоль станции, как
правило, подвешивают с полевой стороны опор контактной сети. Та-
кне линии желательно располагать вдоль одной стороны станции, ос-
тавляя другую для подвески проводов линий продольного электро-
снабжения, дистанционного управления и др. На опорах гибких попе-
речин высотой 15 м с полевой стороны размещают не более двух воз-
душных линий. На консольных опорах и опорах жестких поперечин
высотой до 10 м с полевой стороны может быть размещено не более од-
ной питающей или отсасывающей линии. Если имеются надставки, на
этих опорах можно подвесить и две линии.
При большом числе проводов отсасывающей линии устанавливают
дополнительные опоры. На таких опорах высотой до 10 м может быть
подвешено не более двух различных линий (по одной на противополож-
ных сторонах опор), а на специальных опорах высотой 15 м — не бо-
лее четырех (по две на противоположных сторонах опор).
До полотна железной дороги, как правило, питающие и отсасыва-
ющие линии выполняют так, чтобы число их проводов в одной точке
подвеса не превышало четырех. Длину пролетов выбирают из условия
сохранения допускаемых вертикальных габаритов при наибольших
стрелах провеса проводов. Отсасывающие линии размещают ниже пи-
тающих. Расположение проводов над пассажирскими платформами,
навесами и крышами зданий допускают при условии соблюдения га-
баритов, приведенных в табл. 10.3. При этом провода в местах прохо-
да над платформами должны иметь двойные крепления.
Переходы проводов питающих и отсасывающих линий через кон-
тактные сети путей осуществляют, применяя специальные опоры, ус-
тановленные по обе стороны путей, с анкеровкой проводов воздушных
линий на этих опорах.
325
Станционные питающие линии к контактной сети присоединяют
через секционные разъединители в соответствии с принятой схемой
секционирования по возможности ближе к тяговой подстанции.
Присоединения перегонных питающих линий к контактной сети
при расположении тяговой подстанции в пределах станции осуществ-
ляют в местах изолирующих сопряжений анкерных участков (жела-
тельно па ближайших к оси станции переходных опорах1). При рас-
положении тяговой подстанции на перегоне за пределами изолирую-
щего сопряжения анкерных участков такие присоединения выполня-
ют непосредственно у подстанции. Если тяговая подстанция располо-
жена далеко в стороне от железнодорожных путей и питающие и от-
сасывающие линии проходят вне полосы отвода, трассировку выполня-
ют в соответствии с требованиями Правил устройства электроустано-
вок.
Трассировку линий продольного энергоснабжения, как правило,
выполняют на одних чертежах с планами контактной сети.
По окончании трассировки питающих, отсасывающих и других
проводов подсчитывают длину их анкерных участков и приводят ее,
указывая марки проводов или кабелей, в отдельных спецификациях.
Обработка плана контактной сети. Обрабатывая план контактной се-
ти станции, в соответствии с принятой схемой секционирования на нем
отмечают места установки секционных изоляторов, указывая их типы
и места включения секционирующих изоляторов в тросы жестких и
гибких поперечин и в нерабочие ветви цепных подвесок.
На план наносят все секционные разъединители, изображаемые у
тех опор, на которых они должны быть установлены. (На анкерных
опорах для контактных подвесок секционные разъединители не уста-
навливают). Проверяют наличие обозначений продольных электриче-
ских соединителей на воздушных стрелках и обводных соединений в
тех местах, в которых они должны быть (с учетом обеспечения плавки
гололеда там, где это предусмотрено). Показывают электрические сое-
динители в местах пересечения цепных подвесок и между проводами
подвесок путей, входящих в одну общую секцию станционной контакт-
ной сети (через 300—400 м друг от друга и в местах трогания электро-
возов), а также заземления и места установки разрядников (см. § 9.3).
Все опоры, установленные на станции (включая для питающих и от-
сасывающих линий), нумеруют в направлении счета километров, начи-
ная с первой анкерной опоры сопряжения анкерных участков в одном
конце станции и кончая последней на другом конце. Желательно, что-
бы опоры, расположенные со стороны четных путей, имели четные
номера, а со стороны нечетных путей — нечетные.
Нумерацию анкерных участков по возможности рекомендуется да-
вать в соответствии с номером пути, над которым расположена под-
веска. Анкерные участки главных путей следует нумеровать римскими
цифрами, прочих станционных путей — арабскими.
Подсчитывают и указывают на плане суммарную длину всех элект-
рифицированных путей. Длину главных путей учитывают на рассто-
326
яяии между крайними в сторону перегонов анкерными опорами со-
пряжений анкерных участков, а длину станционных путей — на рас-
стояниях между центрами соответствующих стрелочных переводов.
Вдоль всего плана станции могут быть размещены таблицы, анало-
гичные применяемым на планах перегонов (см. рис. 10.8). Если таких
таблиц нет. все необходимые данные должны быть указаны в соответ-
ствующих местах плана (см. рис. 10.7).
Подбор типов опор, фундаментов и консолей. Типы опор подбира-
ют по максимальным значениям изгибающих моментов у оснований или
в других расчетных сечениях в соответствии с рекомендациями, при-
веденными в гл. 8. Перед этим выявляют группы опор, имеющих оди-
наковые схемы и значения расчетных нагрузок, необходимые расчеты
производят только для опор, представляющих каждую из указанных
групп. Для подбора опор с жесткими и гибкими поперечинами пред-
варительно производят расчеты соответствующих поперечин и опре-
деляют наибольшие усилия, передающиеся на опоры. Анкерные кон-
сольные опоры, как правило, устанавливают железобетонные с от-
тяжками. В тех стучаях, когда невозможно разместить оттяжки,, не
обеспечивается предотвращение случайных повреждений оттяжек или
необходимо выполнить несколько анкеровок, устанавливают метал-
лические анкерные опоры без оттяжек. После подбора всех опор про-
веряют возможность установки тех опор, которые были намечены в
междупутьях.
По максимальным значениям моментов или сил у оснований опор
подбирают соответствующие типы фундаментов для всех опор, которые
предусмотрены к установке с фундаментами. Для опор, устанавливае-
мых без фундаментов, подбирают лежии и опорные плиты, а для от-
тяжек — анкеры.
Подбор типов консолей и фиксаторов производят в зависимости от
места их расположения, габарита опор, значения и схемы приложен-
ных нагрузок. Все тины опор, фундаментов, жестких поперечин и пр.
указывают или в графах специальных таблиц, или непосредствен-
но на плане контактной сети около соответствующих опор; для каждо-
го вида этих устройств составляют спецификацию.
Для примера на рис. 10.7 показан участок плана контактной сети
на станции линии переменного тока вблизи условного станционного пи-
кета 600 м. На участке приведены два пролета по 65 м, ограниченн ые
тремя жесткими поперечинами. Одна из них, перекрывающая семь пу-
тей, имеет стойки из двух железобетонных опор каждая; две другие,
перекрывающие по шесть путей, имеют стойки из одиночных опор.
Поперечное секционирование выполнено только между подвесками
главных путей i н //. Контактные подвески остальных станционных
путей находятся в одних секциях с подвеской главного: нечетных
путей с подвеской пути /, а четных -• //. С одной стороны электрифи-
цированных путей расположены идущие от тяговой подстанции на
перегон две питающие линии, выполненные проводами А-185 каждая,
327
Рис. 10 7 Учш-гок плана контактной сети на станции линии переменного ток..
а с другой стороны чугей линия ДПР из двух проводов АС-35/6.2
Около каждой опоры показаны: ее номер, гид. условный станционный
пикет и габарит установки относительно ближайшего пути. Сведения
о консолях, фиксаторах, кронштейнах, деталях заделки опор в грунт
на рис. 10.7 не приведены.
§ 10.4. Составление планов контактной сети перегонов
Основные положения. Планы контактной сети перегонов состав-
ляют в увязке с существующими и выполняемыми проектами мостов
и путепроводов, переходов вновь сооружаемых линий электропередачи
и переустройства существующих, СЦБ и связи, укладки или переуст-
ройства различных подземных коммуникаций. Работы по составлению
планов контактной сети на перегонах удобно выполнять в следующем
порядке: подготовка плана перегона; разбивка опор; разбивка анкер-
ных участков и зигзагов; трассировка усиливающих и других прово-
дов; обработка плана контактной сети; подбор типов опор, фундамен-
тов, консолей и пр.
Подготовка плана перегона. План перегона подготавливают для
разбивки опор контактной сети в схематическом виде (см. рис. 10.8)
на основании данных, указанных в § 1.1, выполняют его в масштабе
1:2000.
Число параллельно идущих прямых линий, на которых будет про-
изводиться разбивка опор, соответствует числу имеющихся и проек-
тируемых главных путей. Под этими линиями вычерчивают спрямлен-
ный план перегона, а на нем условными обозначениями указывают
328
километровые знаки, направления, радиусы и длину кривых, насыпи
и их высоту, выемки и их глубину.
Искусственные сооружения, переезды, путевые здания, пересече-
ния различных линий и места установки сигналов показывают на ус-
ловных прямых линиях. Вдоль всего перегона размещают таблицы,
в графах которых приводят все необходимые данные (см. рис. 10.8).
Между километровыми знаками тонкими вертикальными линиями
наносят проектные пикеты, нумеруемые в направлении счета ки-
лометров. Пикеты осей или границ искусственных сооружений, нача-
ла и конца кривых и т.п. отмечают в таблице двумя цифрами, показы-
вающими расстояния от соседних пикетных линий.
Разбивка опор. Поскольку планы контактной сети на станциях
составляют до начала разбивки опор на перегонах, то прежде всего
переносят на план перегона опоры крайних сопряжений анкерных
участков с планов соответствующих станций. Увязку станционных
и перегонных пикетов производят по отметке оси пассажирского зда-
ния станции. Сначала отмечают на плане перегона одну (любую) из
опор крайнего сопряжения анкерных участков и определяют ее от-
метку по пикетам перегона. После этого, руководствуясь указанной на
плане станции длиной пролетов, переносят на план перегона все
остальные опоры сопряжения и отмечают зигзаги проводов, принятые
на станции.
На однопутных линиях опоры устанавливают со стороны, про-
тивоположной предполагаемой укладке второго пути. На двухпут-
ных участках опоры располагают в створе по обоим путям, за исключе-
нием опор для ромбовидной подвески и переходных опор сопряже-
ний анкерных участков, которые иногда смещают одну относительно
другой на 5 м.
Сначала примерно намечают места расположения всех анкеровок,
а затем расставляют опоры. Разбивку ведут пролетами, по возможно-
сти равными максимальным допускаемым на данном участке пути и
местности, за исключением районов, в которых возможно возникнове-
ние автоколебаний проводов. В этих районах разбивку опор произво-
дят с непериодическим чередованием длин пролетов, различающихся
на 7 -10 м. При пересечении железной дорогой оврагов, балок и дру-
гих зон небольшой ширины с повышенным ветровым воздействием
опоры устанавливают в середине таких зон. Определив ориентировоч-
но возможное расположение анкерных участков, соответствующее
число пролетов уменьшают по длине на 10 % для последующего раз-
мещения средних анкеровок. Если по схеме секционирования на дан-
ном перегоне предусматривается устройство изолирующих сопряже-
ний анкерных участков, то учитывают необходимое уменьшение дли-
ны пролетов между переходными опорами.
Опоры у переездов располагают таким образом, чтобы расстояние
от проезжей части переезда до края опоры (или ее оттяжки) было, как
правило, не менее 25 м (см. § 10.1). Указанное расстояние до опоры вы-
329
держивают также от края каменных или железобетонных труб и дру-
гих подобных сооружений, если высота насыпи не позволяет осущест-
вить заделку опоры над сооружением. Если на перегоне имеются тон-
нели, путепроводы или мосты с ездой понизу, то при разбивке опор учи-
тывают принятые способы прохода контактной подвески в этих соору-
жениях (см. § 9.4).
Разбивка анкерных участков и зигзагов. Длину анкерных участ-
ков принимают возможно большей по условиям трассы, чтобы число
анкерных опор было минимальным Сопряжения анкерных участков
проектируют в трех пролетах.
После окончательного выбора мест установки анкерных опор и дли-
ны анкерных участков там, где это необходимо, отмечают места распо-
ложения средних анкеровок. Если средние анкеровки не попадут в на-
меченные ранее пролеты, в этих местах производят переразбивку опор,
добиваясь размещения средних анкеровок в уменьшенных по длине
пролетах. Анкерные участки нумеруют в направлении счета километ-
ров (на двухпутных линиях участкам по четному пути присваивают
четные номера, а по нечетному нечетные). Около анкерных опор
указывают номера и длины анкерных участков и составляют их спе-
цификацию.
Для всех опор, кроме опор сопряжений анкерных участков по кон-
цам перегонов, которые относят к станционным, в соответствующих
графах таблиц проставляют пикеты и габариты их установки.
Разбивку зигзагов проводов следует начинать с кривых, после че-
го производят разбивку зигзагов па прямых участка?; и увязку с на-
меченными ранее зигзагами проводов на опорах сопряжений анкер-
ных участков по концам перегона. При этом может получиться, что
на двух смежных опорах зигзаги имеют одностороннее направление.
Во избежание этого на одной из опор контактные провода размещают
над ( ,'ью пути, а на соседних опорах зигзаги устанавливают в соответ-
ствии с принятыми в этом месте длинами пролетов.
Во всех случаях, когда возникает сомнение в возможности примене-
ния той или иной длины пролета при зигзагах проводов, отличающих-
ся от нормальных (особенно в местах сопряжений прямых и кривых
участков пути), следует проверить эти пролеты так, как было указано
в § 10.3.
Трассировка усиливающих и других проводов. Усиливающие про-
вода обычно располагают на специальных кронштейнах, установлен-
ных на опорах с полевой стороны, или (реже) над консолями, на кото-
рых крепится несущий трос. В местах сопряжений анкерных участ-
ков усиливающие провода, сечение которых меньше или равно сече-
нию нерабочей ветви подвески, анкеруют на анкерных опорах со сто-
роны, противоположной анкеровке цепных подвесок, и устраивают
обводные электрические соединения. Остальные усиливающие про-
вода ведут без анкеровки. На железобетонных опорах анкеровка двух
усиливающих проводов со стороны, противоположной анкеровке цеп-
330
ной подвески, допустима только при двойном контактном проводе или
одном МФ-150. При одном контактном проводе МФ-100 со стороны, об-
ратной анкеровке цепной подвески, можно заанксровать только один
усиливающий провод.
Если необходимо обеспечить возможность плавки гололеда элект-
рическим током, усиливающие провода в местах сопряжений анкер-
ных участков следует пропускать с учетом сохранения эквивалентного
сечения сети.
Комплектные трансформаторные подстанции располагают вблизи
железной дороги. Расстояние до них выбирают с учетом профиля зем-
ляного полотна и возможности установки их с пути крапом.
На планах контактной сети усиливающие и другие провода обыч-
но показывают только в местах сопряжений анкерных участков, пере-
ходов с одной стороны пути на другую, отходов к комплектным транс-
форматорным подстанциям и т. д. После окончания трассировки усили-
вающих и других проводов составляют их спецификации с указанием
марок проводов и длин анкерных участков.
Обработка плана контактной сети, подбор типов опор, фундамен-
тов, консолей и пр. При обработке плана контактной сети на перегоне
обозначают места расположения разрядников (см. § 9.3). электричес-
ских соединителей, секционных разъединителей и т.д. Производят ну-
мерацию всех опор (кроме опор
крайних сопряжений анкерных
участков, относящихся к стан-
циям) в направлении счета кило-
метров, причем на двухпутных
линиях опорам со стороны четного
пути присваивают четные номера,
а со стороны нечетного пути не-
четные.
11одбор типов опор, фундамен-
тов, консолей и т.д., а также со-
ставление спецификаций произво-
дят так, как было указано в § 10.3.
Данные, характеризующие тины
опор, фундаментов, консолей, фик-
саторов, и условия их установки
указывают в таблицах для каждой
опоры.
Для примера на рис. 10.8 пока-
зан участок плана контактной сети
на двухпутном перегоне линии
постоянного тока между пикетами
ПК-3 и ПК-4 На участке распо-
ложен один пролет длиной 60 м
и четыре консольные опоры. Со
стороны нечетного пути подвешен
1 ~ Ф0-1-д~ ' ’ ФП-]Г-з"
7 HP-1-5______________НР-1-~5 ___
j ______________________
s соТж.в-z________ ~с01зе.б-г
в_______а, ю______________з. ю
пк-з " ПК-J
" А-М м
7 " ' во
Л---------j-i--------- н------------
16Q ЗАС-50/8,0ПЬ1»(^
— w -А—--— у.....-з-/-- л 4-
7
8________СО 13В. 6-Z ’Сб 1366-7
3 _______--______________-__________
io 1-1_________________________;
11 HP-I-S " HP-I-5
12 ФП-Л-3~ ФО-Щ-З
13 SIS
____
План линии
Рис 10 8. Участок плана контактной
сети на перегоне тинин постоянного
тока
331
усиливающий провод А-185, а со стороны четного — трехфазная
линия 10 кВ из проводов АС-50/8,0. Около каждой опоры указан
ее номер (15 -18), все остальные сведения приводятся в графах таб-
лиц, расположенных вдоль всего перегона. В верхней таблице даны
сведения, относящиеся к пути 1, в нижней аналогичные данные
для пути //.
В строках 1 и 12 указываются типы фиксаторов, в 2 и 11 — типы
консолей (или ригелей, если они имеются), в 3 и 10 — число и типы
верхних лежней, в 4 и 9 — число и типы нижних лежней (при необхо-
димости в строках 3, 4, 9 и 10 указывают типы фундаментов и анке-
ров), в строках 5 и 8 — типы опор, 6 и 7 -- расстояния от оси пути до
ближайшего края опоры, м. В строке 13 указывают расстояние опор,
м, от соседних пикетов и в строке 14 — то же для искусственных со-
оружений, кривых и т.д.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
И ОСНОВНЫХ НОРМАТИВНЫХ ДОКУМЕНТОВ
Беляев И. А., Вологин В. А. Взаимодействие токоприемников и кон-
тактной сети. М.: Транспорт, 1983 192 с.
Брод Г. Н. О расчете стоек жестких поперечин контактной сети / Экспресс-
информация. Серия: Проектирование. Строительство. Выи. 1, 1986. С. 16—23.
Горошков Ю. И., Б о идарев Н. А. Контактная сеть. Изд. 2-е, перераб.
и доп. М.: Транспорт, 1981. 400 с
Марков А. С. Монтаж контактной сети железных дорог ' Справочник М:
Транспорт, 1985. 240 с
Фрайфельд А. В Проектирование контактной сети Изд. 2-е, перераб. и
доп. М.: Транспорт, 1984. 327 с.
Ф р а й ф е л ь д А. В., Бондарев Н. А., Марк о в А. С. Устройство, со-
оружение и эксплуатация контактной сети и воздушных линий. Изд. 2-е, перераб
и доп. / Под род А. В. Франфельда. М.: Транспорт, 1987. 335 с
Инструктивные указания по регулировке контактных подвесок / МНС СССР
М.: Транспорт, 1981. 63 с.
Нормы проектирования конструкций контактной сети. ВСН 141-84 / Минтранс-
строй СССР. М., 1985 170 с.
Нормы технологического проектирования электрификации железных дорог
ВНТП-81 / МПС СССР. М„ 1981. 73 с.
Перечень единиц физических величин, подлежащих применению в строитель-
стве. С-Н 528-80. М.: Стройи.здат, 1981 33 с.
Правила техники безопасности при эксплуатации контактной сети электри-
фицированных железных дорог и устройств электроснабжения автоблокировки '
МПС СССР. М.: Транспорт, 1988. 61 с.
Правила технического обслуживания и ремонта контактной сети и воздуш-
ных линий / МПС СССР. М : Транспорт, 1981. 72 с.
Правила технической эксплуатации железных дорог Союза ССР / МПС СССР
М.: Транспорт, 1989. 160 с.
Строительные нормы и правила. Нагрузки в воздействия. СНиП 2.0107-85
М.: Госстрой СССР, 1987. 35 с 4 7 карт.
Строительные нормы и правила. Стальные конструкции СНиП П-23-81. М.:
Стройнздат, 1982. 93 с.
Строительные нормы и правила. Строительная климатология н геофизика
СНиП 2 01.01-82. М : Госстрой СССР, 1983 136 с
O't ЗН'ЮрОВ
ОГЛАВЛЕНИЕ
Глава I
Методы проектирования устройств контактной сети
и воздушных линий. Расчетные условия
§ 1.1. Организация проектирования 4
§ 1.2. Методы проектирования .... 8
§ 1.3 Учет климатических условий................................... Н
§ I 4 Основные данные для расчетов . ... 17
Г л а в а 2
Расчеты нагрузок, действующих на устройства контактной сети
и воздушных линий
>5 2.1. Виды нагрузок и их сочетания..............................25
§ 2.2. Расчеты нормативных нагрузок на провода и тросы...........27
« 2.3. Расчеты нормативных нагрузок на опорные устройства . . . 3(1
2.4. Расчеты нагрузок, возникающих при сооружении и эксплуатации 5)
4 2.5 Расчеты особых нагрузок ... . ... 5(>
Глава 1
Расчеты ветровых отклонений проводов и длин пролетов
между опорами контактной сети
§ 3.1. Общие положения................................ . (/’
§ 3.2. Расчеты для обычных подвесок............................ .65
§ 3.3. Расчеты для подвесок с повышенной ветроустойчивостью. . . . 73
§ 3.4. Проверка длины пролета по соблюдению высотных положений
контактных проводов и в условиях эксплуатации .... 80
Глава 4
Расчеты взаимодействия контактных подвесок с токоприемниками
$ 4.1. Методы исследований...................................... 84
§ 4.2. Критерий и показатели качества токосъема..................88
§ 4.3. Расчеты для построения траектории токоприемника и кривой его
нажатия вдоль пролета.......................................... .91
4 4.4. Определение расчетных параметров .... 97
Глав а 5
Выбор типов контактных подвесок и их оптимальных параметров
по условиям токосъема
§ 5.1. Влияние параметров контактной сети на качество токосъема ... 114
§ 5.2. Определение оптимальных параметров компенсированных контакт-
ных подвесок..................................................118
§ 5 3. Определение оптимальных параметров полукомпенсированных
контактных подвесок . . ................................129
334
§ 5,4. Основные направления совершенствования контактных подвесок
и токоприемников..................... . • 135
Г л а в а 6
Расчеты проводов воздушных линий и контактных подвесок
при изменениях климатических условий
§ 6.1. Общие положения......... ............. 143
§ 6.2. Расчеты проводов воздушных линий . . 149
§ 6.3. Расчеты контактных подвесок ............................. 154
§ 6.4 Расчеты длин анкерных участков ценных подвесок . . . 167
§ 6.5. Особые случаи расчета................................... 170
I' л а в а 7
Расчеты поддерживающих и фиксирующих устройств
S 7.! Поддерживающие и фиксирующие устройства . . 178
§ 7.2. Расчеты консолей . . .181
§ 7.3 Расчеты кронштейнов для проводов воздушных линий . 200
§ 7.4. Расчеты гибких поперечин................................. 203
§ 7.5. Расчеты фиксаторов и фиксирующих поперечин....... 214
§ 7.6. Особые случаи расчета поддерживающих и фиксиру ющих ycipoiiem ‘>19
Глава 8
Подбор типовых конструкций
§ 8.1 Подбор консолей, кронштейнов и фиксаторов . .. 23'2
§ 8.2. Подбор жестких поперечин................................. 241
§ 8.3. Опоры контактной сети и их закрепление в грунте ... . 250
§ 8.4. Подбор консольных и фиксирующих опор......... . 258
§ 8.5. Подбор опор для гибких поперечин ....................... . 269
§ 8.6. Подбор стоек для жестких поперечи-........................274
§ 8.7. Подбор конструкций для закрепления опор в грунте . . 279
Глав а 9
Проектирование схем секционирования контактной сети
и прохода контактной подвески в искусственных сооружениях
§ 9.1. Принципы питания и секционирования. Рекомендуемые схемы . . 285
§ 9.2. Секционирование контактной сети при стыковании липин по-
стоянного и переменного тока................................... 293
§ 9 3. Рельсовые цени и отсасывающие линии. Размещение заземлений
и разрядников ..................................................296
§ 9.4. Выбор способа прохода контактной подвески в искусственных со-
оружениях ................................................. ... 299
Г л а в а 10
Разработка планов контактной сети на станциях и перегонах
§ 10.1. Основные габариты устройств контактной сети . . 307
§ 10.2. Принципы составления планов............................ . 313
§ 10.3. Составление планов контактной сети станций............. 317
§ 10.4. Составление планов контактной сети перегонов............ 328
Список использованной литературы и основных нормативных докумен-
тов ....................... . ............... . . 333
335
Производственное издание
фрапфе.нх) Александр Владимирович. Ирод Герц Наумович
ПРОЕКТИРОВАНИЕ КОНТАКТНОЙ СЕТИ
Переплет художника //. Волкова
Технический редактор //. Л Муравьева
Корргктор-вычитчик И. М. Лукина
Корректор Л1. В. Лжалнашвили
И Б № 4364
Сдано в набор 15.12.89. Подписано в печать 30.01.91.
Формат bOX88‘/tf. Бум . офс. № 2. Гарнитура литературная. Офсетная печать.
*'сл. печ л 21. Усл. кр.-отт. 21. Уч.-изд. л. 23,91. Тираж 3000 экз Заказ 2630
Цена 3 руб. Изд. № 1-3-1/5 № 5240
Орлена «Знак Почета» издательство «ТРАНСПОРТ»,
103064, Москва. Басманный туп., 6а
Московская типография № 4 Госкомпечати СССР
129041. Москва. Б Переяславская 46