4	ОГЛАВЛЕНИЕ
ОТДЕЛ II.
СЛОЖНЫЕ СЛУЧАИ РАСТЯЖЕНИЯ И СЖАТИЯ.
Глава IV. Расчёт статически неопределимых систем по допускае-
допускаемым напряжениям	 72
§19. Статически неопределимые системы		72
§ 20. Влияние неточностей изготовления на усилия в элементах
статически неопределимых конструкций		79
§ 21. Расчёт на растяжение и сжатие стержней, состоящих из
разнородных материалов		83
§ 22. Напряжения, возникающие при изменении температуры ....	85
§ 23. Одновременный учёт различных факторов 		88
§ 24. Более сложные случаи статически неопределимых кон-
конструкций		90
§ 25. Примеры		91
Глава V. Расчёт статически неопределимых систем по допускае-
допускаемым нагрузкам	 95
§ 26. Понятие о расчёте по допускаемым нагрузкам. Применение
к статически определимым системам	 95
§ 27. Расчёт статически неопределимых систем по способу до-
допускаемых нагрузок	 97
§ 28. Применение способа допускаемых нагрузок к расчёту же-
железобетонных стержней	101
Глава VI. Учёт собственного веса при растяжении и сжатии. Рас-
Расчёт гибких нитей.		102
§ 29. Подбор сечений с учётом собственного веса (при растяже-
растяжении и сжатии)		102
§ 30. Деформации при действии собственного веса		107
§ 31. Гибкие нити		108
§ 32. Примеры		115
Глава VII. Сложное напряжённое состояние. Напряжения и де-
деформации	118
§ 33. Напряжения по наклонным сечениям при осевом растяжении
или сжатии (линейное напряжённое состояние)	118
§ 34. Понятие о главных напряжениях. Виды напряжённого со-
состояния материала	120
§ 35. Примеры плоского и объёмного напряжённого состояний.
Расчёт цилиндрического котла. Понятие о контактных
напряжениях	122
§ 36. Напряжения при плоском напряжённом состоянии	125
§ 37. Графическое определение напряжений (круг Мора)	128
§ 38. Нахождение главных напряжений при помощи круга	132
§ 39. Нахождение наибольших напряжений для объёмного напря-
напряжённого состояния	135
§ 40. Вычисление деформаций при плоском и объёмном напряжён-
напряжённом состояниях	136
§ 41. Потенциальная энергия упругой деформации при сложном
напряжённом состоянии	139
Глава VIII. Проверка прочности материала при сложном напря-
напряжённом состоянии		142
§ 42. Понятие о теориях прочности		142
§ 43. Проверка прочности по различным теориям		144
§ 44. Примеры проверки прочности		151

ОГЛАВЛЕНИЕ	О
Глава IX. Контактные напряжения	152
§ 45. Общие понятия. Формулы для контактных напряжений .... 152
- § 46. Проверка прочности соприкасающихся тел	153
ОТДЕЛ III.
СДВИГ И КРУЧЕНИЕ.
Глава X. Практические примеры деформации сдвига. Чистый
сдвиг	.	158
§ 47. Понятие о сдвиге. Расчёт заклёпок на перерезывание		158
§ 48. Проверка заклёпок на смятие и листов на разрыв		160
§ 49. Примеры		166
§ 50. Расчёт сварных соединений		168
§ 51. Примеры		175
§ 52. Расчёт врубок	 .	176
§ 53. Чистый сдвиг. Определение главных напряжений и проверка
прочности		178
§ 54. Связь между напряжениями и деформацией при чистом
сдвиге. Потенциальная энергия сдвига		183
Глава XI. Кручение. Проверка прочности и вычисление дефор-
деформаций		186
§ 55. Понятие о крутящем моменте		186
§ 56. Вычисление моментов, передаваемых на вал		188
§ 57. Определение напряжений при кручении круглого вала		189
§ 58. Вычисление полярных моментов инерции и моментов сопро-
сопротивления сечения вала		195
§ 59. Условие прочности при кручении		197
§ 60. Определение деформаций при кручении	* ....	197
§ 61. Напряжения при кручении по сечениям, наклонённым к оси
стержня		199
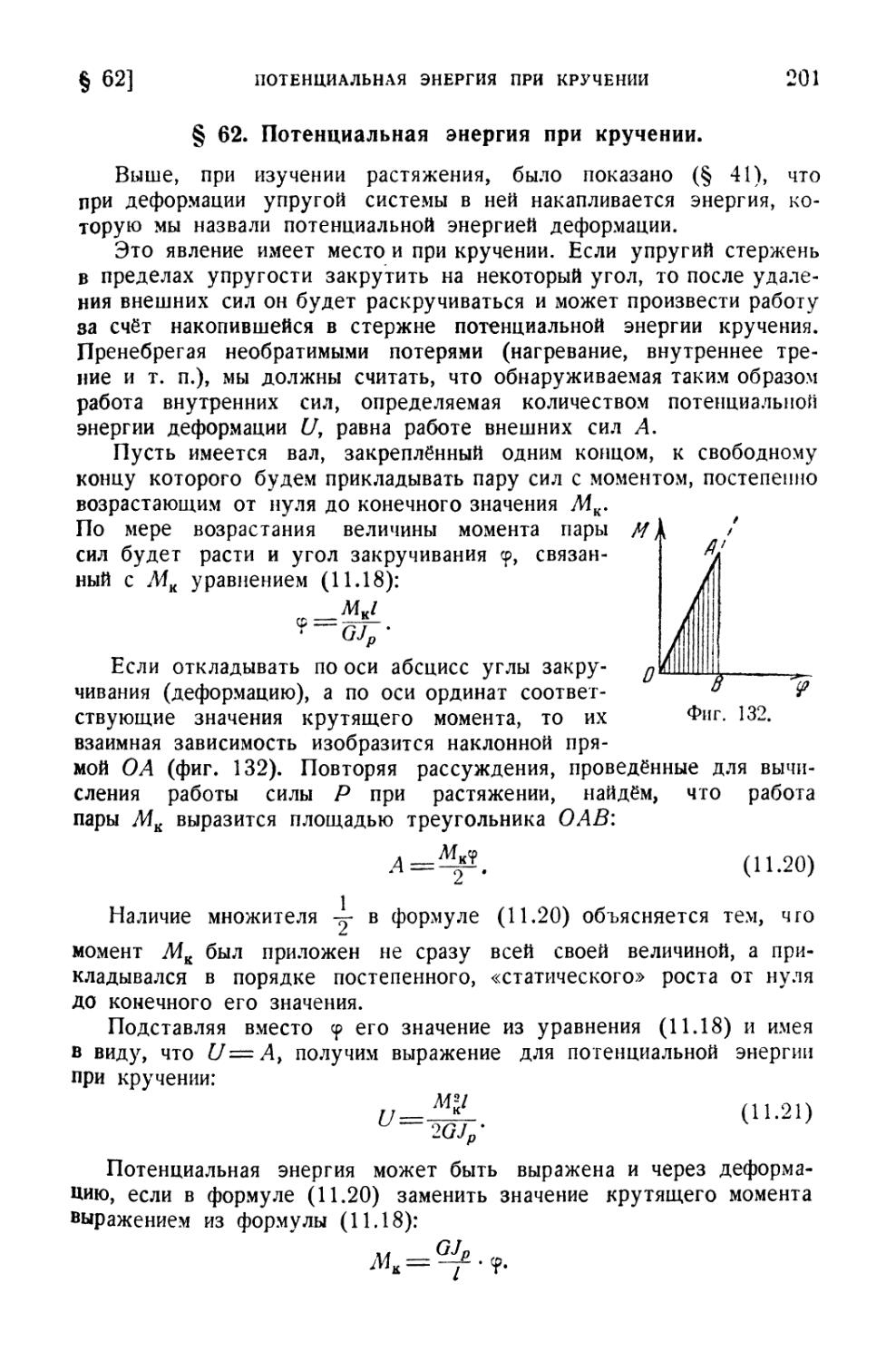
§ 62. Потенциальная энергия при кручении 		201
§ 63. Определение предельной грузоподъёмности скручиваемого
стержня		202
§ 64. Примеры		204
§ 65. Напряжения и деформации в винтовых пружинах с малым
шагом 		206
§ 66. Примеры		210
§ 67. Чистое кручение стержней некруглого сечения. . . *		212
§ 68. Примеры		218
ОТДЕЛ IV.
ИЗГИБ. ПРОВЕРКА ПРОЧНОСТИ БАЛОК.
Глава XII. Постановка задачи о проверке прочности при изгибе
и метод её решения	 221
§ 69. Общие понятия о деформации изгиба. Устройство опор
балок	221
§ 70. Характер напряжений в балке. Изгибающий момент и попе-
поперечная сила	226
§ 71. Дифференциальные зависимости между интенсивностью
сплошной нагрузки, поперечной силой и изгибающим мо-
моментом 	231
§ 72. Построение эпюр изгибающих моментов и поперечных сил. . 232
§ 73. Построение эпюр Q и М для более сложных случаев
нагрузки	240

6	ОГЛАВЛЕНИЕ
§ 74. Контроль правильности построения эпюр Q и М		250
§ 75, Способ сложения действия сил при построении эпюр ......	252
§ 76. Графический метод построения эпюр изгибающих моментов
и поперечных сил		254
Глава XIII. Вычисление нормальных напряжений при изгибе и про-
проверка прочности балок	258
§ 77. Экспериментальное изучение работы материала при чистом
изгибе	258
§ 78. Вычисление нормальных напряжений при изгибе. Закон Гука
и потенциальная энергия при изгибе	261
§ 79. Применение полученных результатов к проверке прочности
балок	267
Глава XIV. Вычисление моментов инерции плоских фигур	 . 270
§ 80. Вычисление моментов инерции и моментов сопротивления
для простейших сечений	270
§ 81. Общий способ вычисления моментов инерции сложных сече-
сечений 	274
§ 82. Зависимость мез::ду моментами инерции относительно парал-
параллельных осей, из которых одна — центральная	275
§ 83. Зависимость между моментами инерции при повороте осей. . 277
$ 84. Главные оси инерции и главные моменты инерции	280
§ 85. Наибольшее и наименьшее значения центральных моментов
инерции	284
§ 86. Распространение формулы для вычисления нормальных на-
напряжений на случай несимметричного сечения балки	285
§ 87. Эллипс инерции	286
§ 88. Приближённый метод вычисления моментов инерции пло-
площади	288
§ 89. Пример расчёта балки несимметричного сечения	290
§ 90. Примеры	293
ОТДЕЛ V.
ПОЛНАЯ ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ.
Глава XV. Вычисление касательных и главных напряжений в
балках	298
§ 91. Касательные напряжения в балке прямоугольного сечения
(формула Журавского)	298
§ 92. Касательные напряжения в балке двутаврового сечения.... 304
§ 93. Касательные напряжения в балках круглого профиля и пу-
пустотелых 	307
§ 94. Проверка прочности но главным напряжениям	309
§ 95. Направления главных напряжений	314
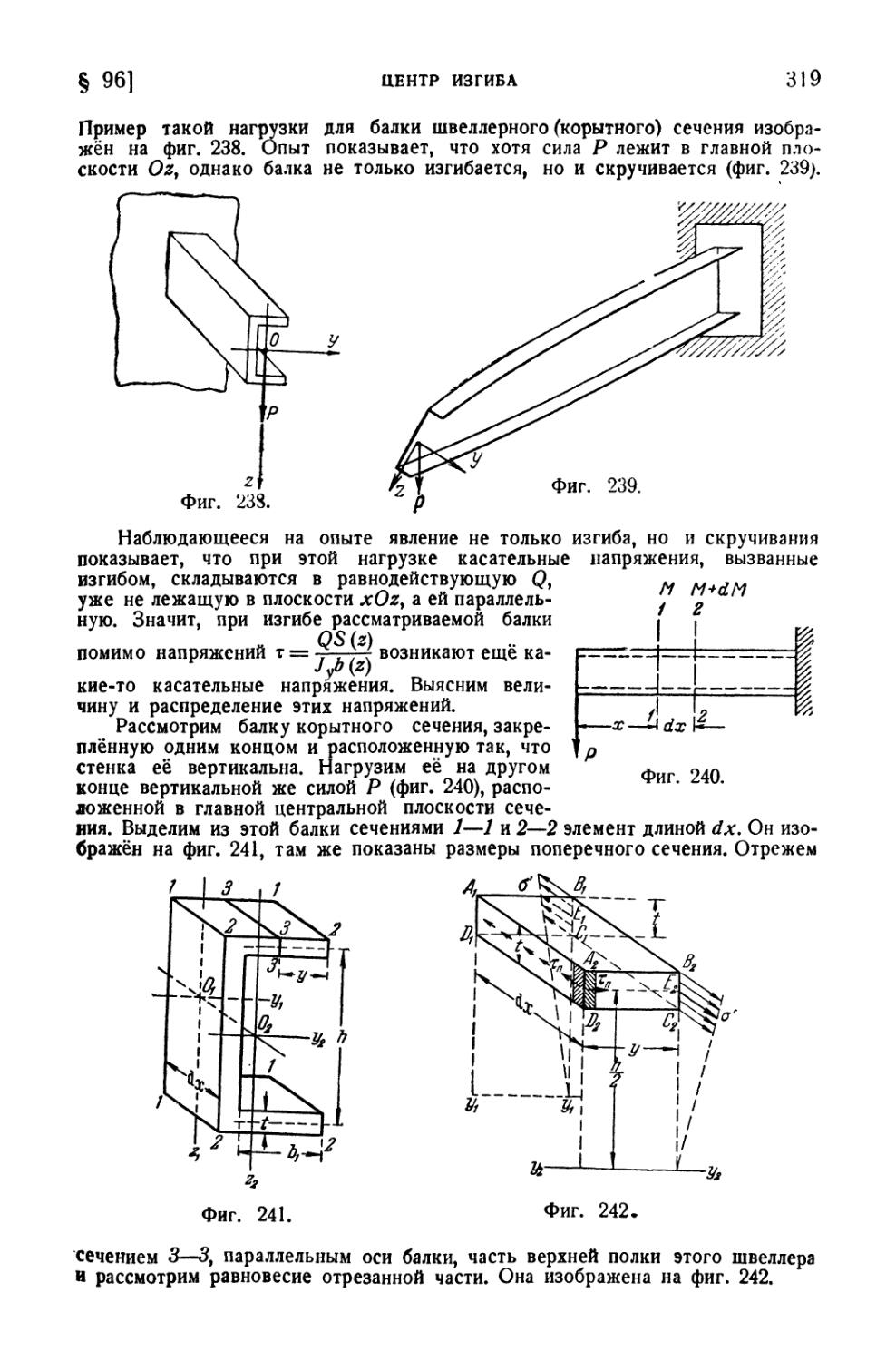
§ 96. Центр изгиба	318
§ 97. Подбор сечения балок но допускаемым нагрузкам ........ 323
Глава XVI. Расчёт составных балок	 328
§ 98. Подбор сечения клёпаных балок		328
§ 99.	Проверка прочности балки по нормальным напряжениям. . .	332
§ 100.	Проверка прочности балки по касательным напряжениям . .	336
§ 101. Проверка прочности балки по главным напряжениям		337
§ 102. Расчёт заклёпок в балке		338
§ 103.	Подбор сечения и проверка прочности сварной балки ....	340
§ 104. Расчёт деревянных составных балок 		342

ОГЛАВЛВНИВ	7
Глава XVII. Расчёт железобетонных балок		344
§ 105. Расчёт железобетонной балки по допускаемым напряжениям	344
§ 106. Расчёт железобетонной балки по допускаемым нагрузкам. .	347
§ 107. Развитие теории изгиба		349
ОТДЕЛ VI.
ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ БАЛОК ПРИ ИЗГИБЕ.
Глава XVIII. Аналитический способ определения деформаций....	351
§ 108. Прогиб и поворот сечения балки		351
§ 109. Дифференциальное уравнение изогнутой оси		353
§ ПО. Интегрирование дифференциального уравнения изогнутой
оси балки, защемлённой одним концом		355
§ 111. Интегрирование дифференциального уравнения изогнутой
оси балки на двух опорах		359
§ 112. Интегрирование дифференциального уравнения изогнутой
оси балки при двух участках		361
§ 113. Приёмы составления и интегрирования дифференциального
уравнения при нескольких участках		366
§ 114. Интегрирование дифференциального уравнения для случая
балки с шарниром		370
§ 115. Сложение действия сил		372
§ 116. Дифференциальные зависимости при изгибе		374
Глава XIX. Графоаналитический и графический методы вычисле-
вычисления деформаций при изгибе		375
§ 117. Графоаналитический метод		375
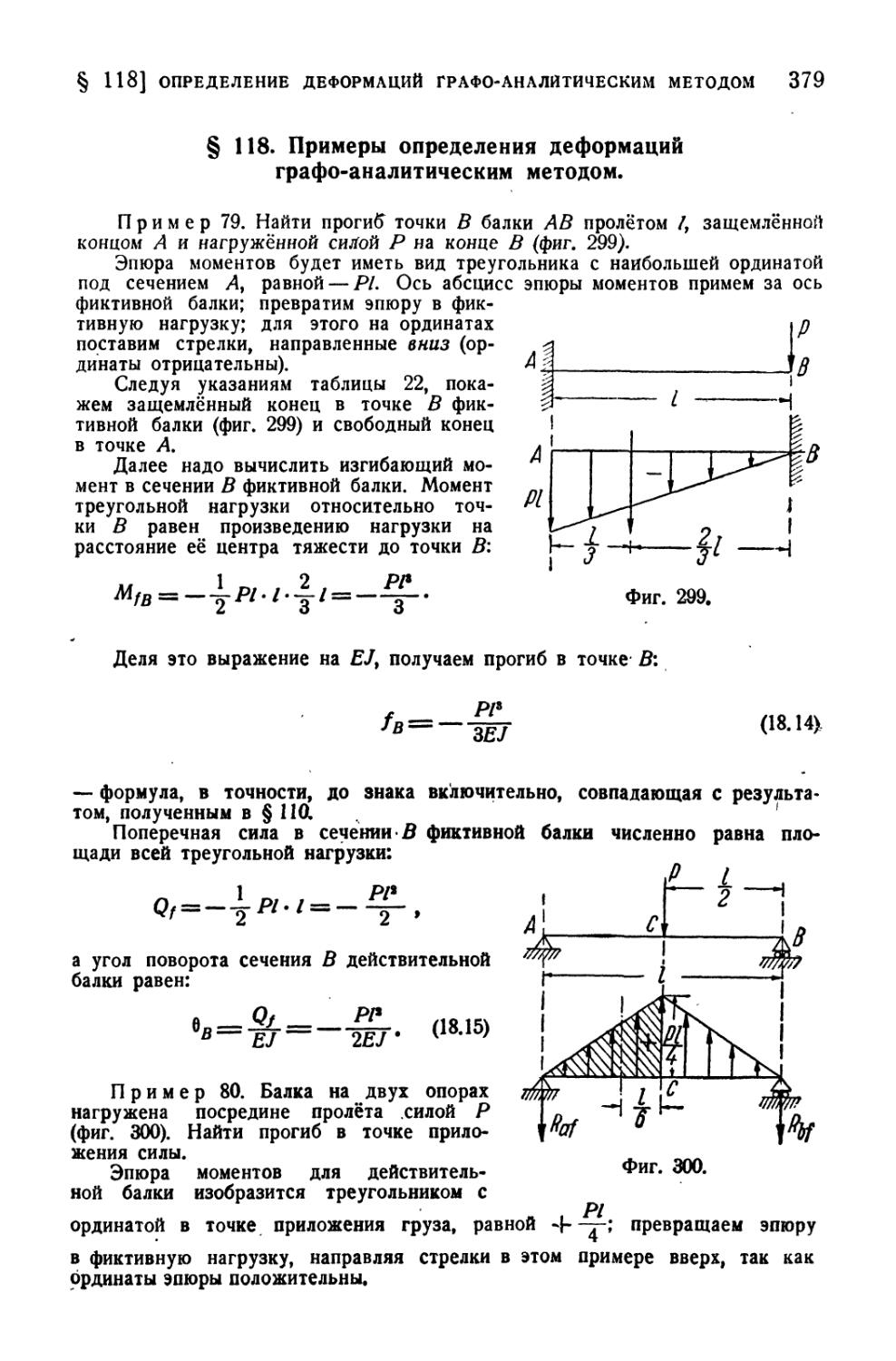
§118. Примеры определения деформаций графоаналитическим
методом		379
§ 119. Графоаналитический метод при криволинейных эпюрах
изгибающего момента.		382
§ 120. Графический метод построения изогнутой оси балки		384
Глава XX. Балки переменного сечения		383
§ 121. Подбор сечений балок равного сопротивления		388
§ 122. Практические примеры балок равного сопротивления		390
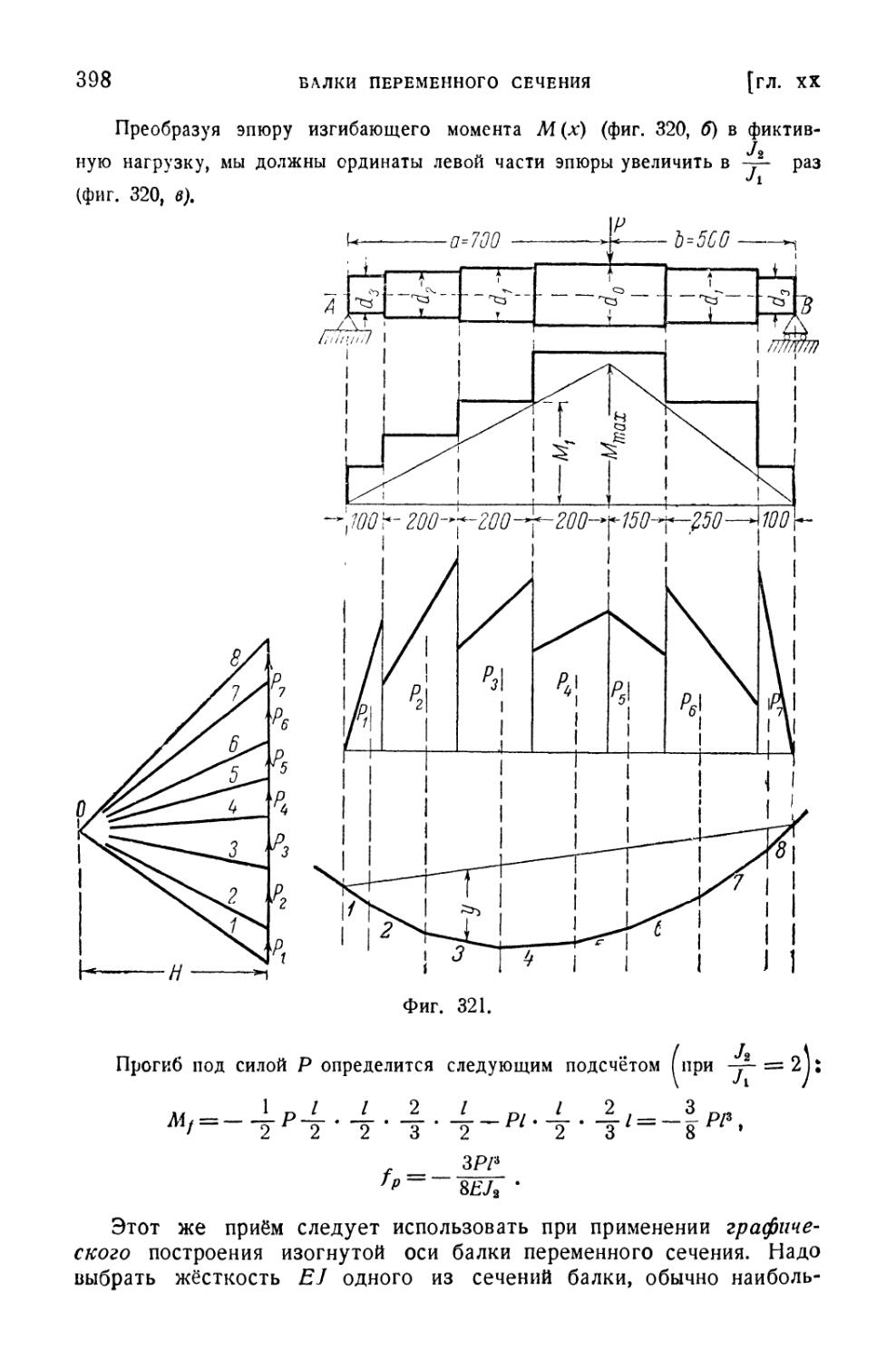
§ 123. Определение деформаций балок переменного сечения ....	395
ОТДЕЛ VII.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ.
Глава XXI. Применение понятия о потенциальной энергии к опре-
определению деформаций		400
§ 124. Постановка вопроса		400
§ 125. Вычисление потенциальной энергии		402
§ 126. Теорема Кастильяно		405
§ 127. Примеры приложения теоремы Кастильяно		409
§ 128. Приём введения добавочной силы		411
§ 129. Теорема о взаимности работ		413
§ 130. Теорема Максвелла — Мора		415
§ 131. Способ Верещагина		417
§ 132. Прогибы балок от действия поперечной силы 		419
§ 133. Примеры		422

8	ОГЛАВЛЕНИЕ
Глава XXII. Приближённое уравнение изогнутой оси балки	427
§ 134. Приближённый приём вычисления прогибов	427
§ 135. Разложение уравнения изогнутой оси в тригонометриче-
тригонометрический ряд	430
Глава XXIII. Статически неопределимые балки 	433
§ 136. Общие понятия и метод расчёта	433
§ 137. Способ сравнения деформаций	435
§ 138. Применение теоремы Кастильяно, теоремы Мора и способа
Верещагина	437
§ 139. Выбор лишней неизвестной и основной системы	439
§ 140. План решения статически неопределимой задачи	441
§ 141. Примеры расчёта статически неопределимых систем	443
§ 142. Определение деформаций статически неопределимых балок. 447
§ 143. Расчёт неразреэных балок	448
§ 144. Теорема о трёх моментах	450
§ 145. Вычисление опорных реакций и построение эпюр для нераз-
неразрезных балок	456
§ 146. Неразрезные балки с консолями. Балки с защемлёнными
концами 	460
§ 147. Примеры расчёта неразрезных балок	463
§ 148. Влияние неточного расположения опор по высоте	465
Глава XXIV. Расчёт статически неопределимых балок по допускае-
допускаемым нагрузкам	467
§ 149. Общие понятия. Расчёт двухпролётной балки	467
§ 150. Расчёт трёхпролётной балки	470
§ 151. Пример	471
Глава XXV. Балка на упругом основании	473
§ 152. Общие понятия		473
§ 153. Расчёт бесконечно длинной балки на упругом основании,
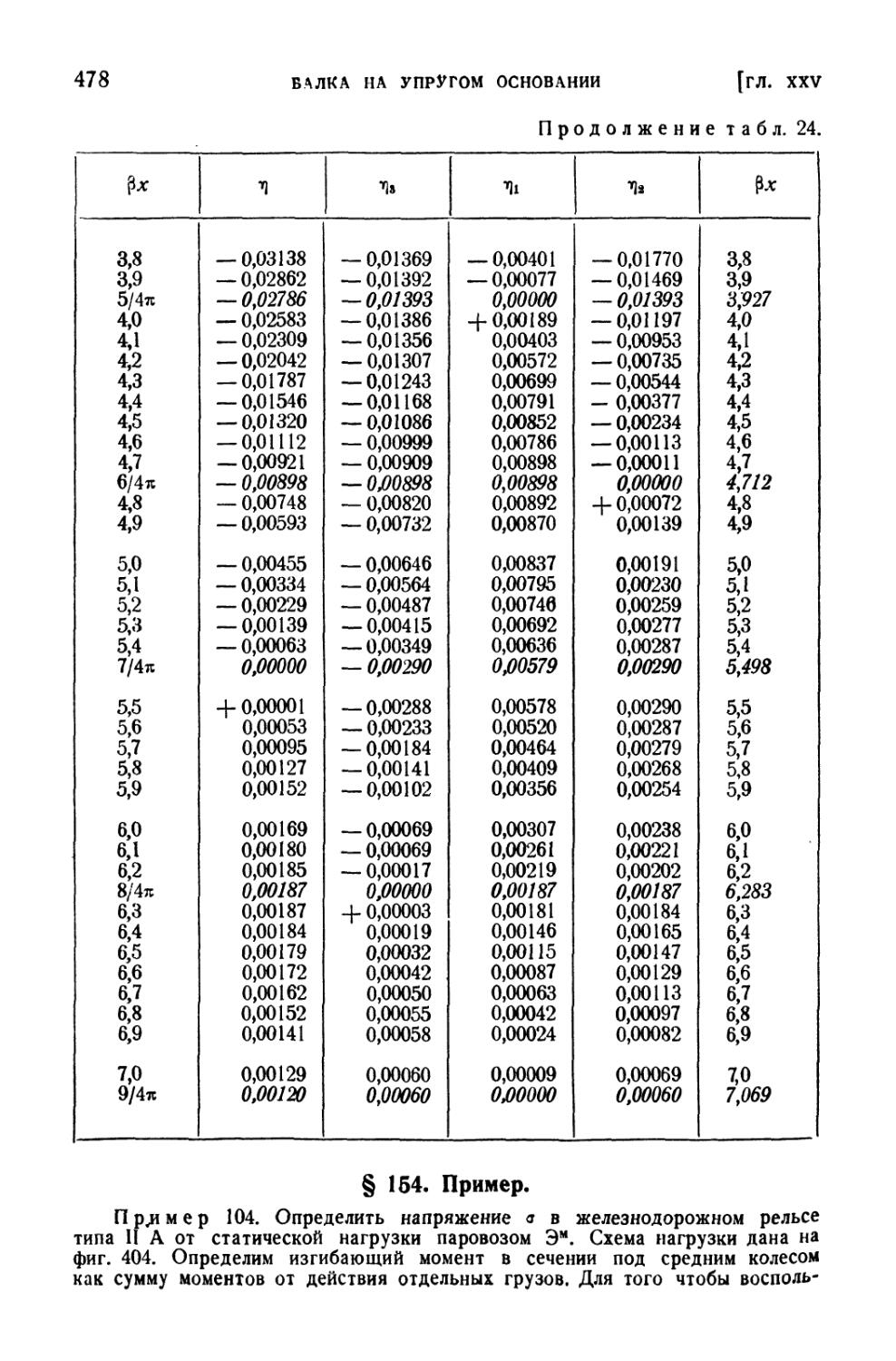
загружённой одной силой Р . . . . .		475
§ 154. Пример		478
§ 155. Расчёты балок конечной длины		479
ОТДЕЛ VIII.
СЛОЖНОЕ СОПРОТИВЛЕНИЕ.
Глава XXVI. Косой изгиб	483
§ 156. Основные понятия		483
§ 157. Косой изгиб. Вычисление напряжений		483
§ 158. Определение деформаций при косом изгибе		490
§ 159. Примеры расчётов при косом изгибе		492
Глава XXVII. Совместное действие изгиба и растяжения или
сжатия	495
§ 160. Изгиб балки при действии продольных и поперечных сил. . 495
§ 161. Учёт деформаций балки	497
§ 162. Примеры	.- . 498
§ 163. Внецентренное сжатие или растяжение	499
§ 164. Ядро сечения	 	504
§ 165. Примеры	, . 507

ОГЛАВЛЕНИЕ	9
Глава XXVIII. Совместное действие кручения и изгиба		510
§ 166. Определение изгибающих и крутящих моментов		510
§ 167. Определение напряжений и проверка прочности при изгибе
с кручением		512
§ 168. Примеры		516
Глава XXIX. Общий случай сложного сопротивления		517
§ 169. Вычисление напряжений и деформаций		517
§ 170. Расчёт простейшего коленчатого вала		522
Глава XXX. Основы расчёта тонкостенных стержней на кручение
и изгиб		528
§ 171. Введение		528
§ 172. Понятие о свободном и стеснённом кручении		529
§ 173. Внутренние усилия в сечениях стержня при стеснённом кру-
кручении. Гипотезы		532
§ 174. Деформация тонкостенного стержня, связанная с неравно-
неравномерной депланацией сечений 		537
§ 175. Секториальные нормальные напряжения. Секториальные ха-
характеристики сечения		541
§ 176. Дифференциальные аависимости между силовыми величи-
величинами 	,		546
§ 177. Дифференциальное уравнение деформаций при стеснённом
кручении. Определение силовых факторов		548
§ 178. Вычисление касательных напряжений в сечении тонкостен-
тонкостенного стержня		555
§ 179. Вычисление секториальных площадей. Построение секто-
риальных эпюр	 .	556
§ 180. Определение секториальных геометрических характеристик
сечения		561
§ 181. Примеры вычисления секториальных геометрических харак-
характеристик сечения		564
§ 182. Вычисление напряжений в общем случае сложного сопро-
сопротивления тонкостенного стержня		570
§ 183. Примеры вычисления напряжений в тонкостенных стержнях	573
Глава XXXI. Кривые стержни		580
§ 184. Общие понятия	'		580
§ 185. Вычисление изгибающих моментов, нормальных и попереч-
поперечных сил		581
§ 186. Вычисление напряжений от сил Q и N		583
§ 187. Вычисление напряжений от изгибающего момента		584
§ 188. Определение радиуса кривизны нейтрального слоя при прямо-
прямоугольном сечении		590
§ 189. Вычисление радиуса кривизны нейтрального слоя для круга
и трапеции		592
§ 190. Приближённый способ определения положения нейтраль-
нейтрального слоя		593
§ 191. Анализ формулы нормальных напряжений в кривом стержне	596
§ 192. Дополнительные замечания к формуле нормальных напря-
напряжений	*		598
§ 193. Примеры определения напряжений в кривых стержнях . . .	600
§ 194. Деформации кривых стержней		602
§ 195. Вычисление деформаций с учётом кривизны стержня		604
§ 196. Примеры расчёта кривых стержней		606

10	ОГЛАВЛЕНИЕ
Глава XXXII. Расчёт толстостенных и тонкостенных сосудов ....	609
§ 197. Расчёт толстостенных цилиндров		609
§ 198. Напряжения в сферических толстостенных сосудах		615
§ 199. Расчёт тонкостенных сосудов		616
ОТДЕЛ IX.
УСТОЙЧИВОСТЬ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ.
Глава XXXIII. Проверка сжатых стержней на устойчивость		619
§ 200. Введение. Понятие об устойчивости формы сжатых стерж-
стержней		619
§ 201. Формула Эйлера для критической силы		622
§ 202. Влияние способа закрепления концов стержня		626
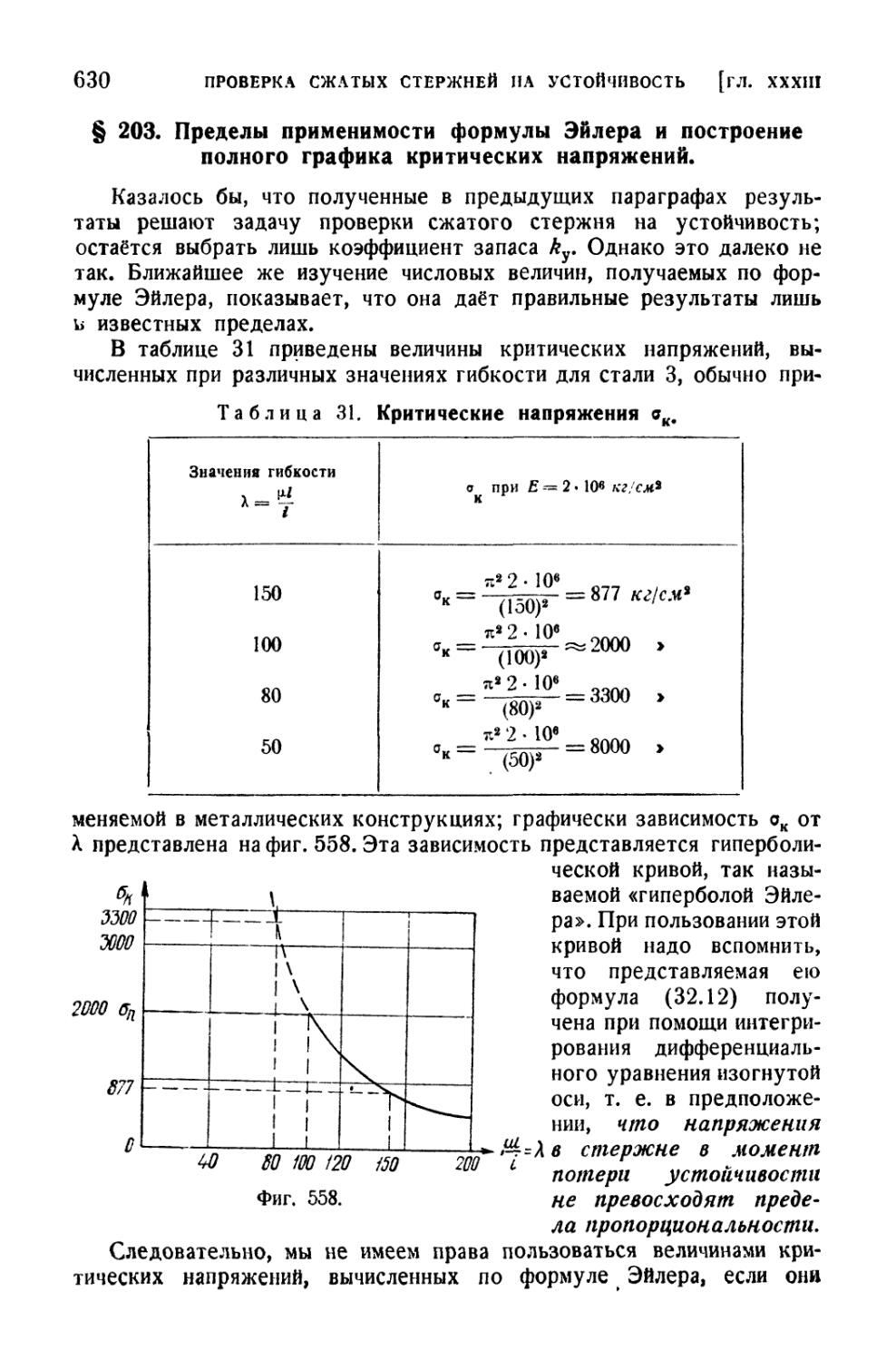
§ 203. Пределы применимости формулы Эйлера и построение
полного графика критических напряжений	: . . .	630
§ 204. Проверка сжатых стержней на устойчивость		634
§ 205. Выбор типа сечения и материала		637
§ 206. Примеры		640
§ 207. Практическое значение проверки на устойчивость		644
Глава XXXIV. Более сложные вопросы проверки элементов кон-
конструкций на устойчивость		645
§ 208. Устойчивость плоской формы изгиба балок		645
§ 209. Проверка прочности стержней на совместное действие про-
продольных и поперечных сил (с учётом деформаций)		652
§ 210. Влияние эксцентриситета -приложения сжимающей силы и
начальной кривизны стержня		658
§ 211. Обоснование расчёта соединительной решётки в составных
стержнях		661
§ 212. Примеры расчёта сжато-изогнутых стержней		663
§ 213. Проверка тонкостенных стержней открытого профиля на
устойчивость 		665
§ 214. Развитие расчётов на устойчивость		670
отдел х.
ДИНАМИЧЕСКОЕ ДЕЙСТВИЕ НАГРУЗОК,
Глава XXXV. Учёт сил инерции и колебаний		674
§ 215. Введение		674
§ 216. Вычисление напряжений при равноускоренном движении . .	676
§ 217. Расчёт вращающегося кольца (обод маховика)		677
§ 218. Напряжения в спарниках и шатунах		678
§ 219. Вращающийся диск постоянной толщины		681
§ 220. Диск равного сопротивления		685
§ 221. Влияние резонанса на величину напряжений		686
§ 222. Вычисление напряжений при колебаниях		687
§ 223. Учёт массы упругой системы при колебаниях		692
§ 224. Примеры		697
Глава XXXVI. Напряжения при ударе		700
§ 225. Основные положения		700
§ 226. Общий приём вычисления напряжений при ударе		701
§ 227. Частные случаи вычисления напряжений и проверки проч-
прочности при ударе		706
§ 228. Напряжения при продольном ударе стержня о неподвиж-
неподвижную плоскость		710

ОГЛАВЛЕНИЕ	11
§ 229. Напряжения в стержнях переменного сечения при ударе . .	712
| 230. Практические выводы из полученных результатов		713
§ 231. Учёт массы упругой системы, испытывающей удар		715
§ 232. Примеры		717
§ 233. Испытания на удар до разрушения. Ударная проба		720
§ 234. Влияние различных факторов на результаты ударной пробы	723
Глава XXXVIL Проверка прочности материала при переменных
напряжениях		726
§ 235. Основные понятия о влиянии переменных напряжений на
прочность материала	 726
§ 236. Составление условия прочности при переменных напряже-
напряжениях 	728
§ 237. Определение предела выносливости при симметричном
цикле	730
§ 238. Предел выносливости при несимметричном цикле	734
§ 239. Местные напряжения	738
§ 240. Влияние размеров детали на величину предела выносли-
выносливости 	745
§ 241. Практические примеры разрушения при переменных нагруз-
нагрузках. Механизм появления и развития трещин усталости. . . 747
§ 242. Установление допускаемых напряжений	752
§ 243. Примеры	758
§ 244. Проверка прочности при переменных напряжениях и слож-
сложном напряжённом состоянии	762
§ 245. Практические меры по борьбе с изломами усталости	764
§ 246. Развитие вопроса о сопротивлении материалов динамиче-
динамическим нагрузкам	769
Глава XXXVIII. Прочность материалов	772
§ 247. Основные понятия		772
§ 248. Сопротивление пластическим деформациям		773
§ 249. Сопротивление разрушению. Отрыв и срез		776
§ 250. Теории прочности		779
§ 251. Обобщённая теория прочности Мора		784
§ 252. Объединённая теория прочности Давиденкова-Фридмана . .	787
Глава XXXIX. Основы расчётов на ползучесть	792
§ 253. Влияние высоких температур на механические свойства
металлов		792
§ 254. Явление ползучести и релаксации		794
§ 255. Кривые ползучести и релаксации		796
§ 256. Основы расчётов на ползучесть		802
§ 257. Примеры расчётов на ползучесть		806
Приложения	818
Указатель имён	844
Предметный указатель	846

6.05
Б 43
УДК 620.10.
Николай Михайлович Беляев
Сопротивление материалов
М., 1965 г., 856 стр. с илл.
Редактор Я. К* Снитко
Техн. редактор А. П. Колесникова	Корректор О. А. Сигал
Печать с матриц. Подписано к печати 21/V 1965 г. Бумага бОХЭФ'/м. Физич. печ. л. 53,5.
Усл. печ. л. 53,5. Уч.-изд. л. 60,65. Тираж 75 000 экз. Т-06947 Цена книги 1 р. 92 к.
Заказ № 1687.
Издательство «Наука»
Главная редакция физико-математической литературы
Москва, В-71 Ленинский проспект. 15»
Ленинградская типография JS& 1 «Печатный Двор» им. А. М. Горького Главполиграфпро-
ма Государственного комитета Совета Министров СССР по печати, Гатчинская, 26.

ИЗ ПРЕДИСЛОВИЯ К ТРЕТЬЕМУ ИЗДАНИЮ.
При составлении книги в первую очередь имелось в виду прак-
практическое значение сопротивления материалов для инженера. Поэтому
обращено особое внимание на правильную последовательность распо-
расположения материала.
При решении основной задачи сопротивления материалов — выбора
материала и поперечных размеров для элементов сооружений и
машин — необходимо, помимо умения вычислять напряжения, знание
механических свойств реальных материалов. Это влечёт за собой
необходимость экспериментальных исследований в лаборатории. В свя-
связи с этим в книге отведено значительное место изучению механиче-
механических свойств материалов и рассмотрению физической картины явления
при различных деформациях. В конце книги помещён ряд подробных таб-
таблиц, заключающих в себе данные о механических свойствах материалов.
Описание же лабораторных работ, являющихся неотъемлемой частью
прохождения курса сопротивления материалов, вынесено в отдельное
руководство, так как программа и объём их определяются в значи-
значительной степени местными условиями оборудования лабораторий.
Принятое в настоящей книге совместное рассмотрение аналити-
аналитических и физических вопросов должно приучить студента видеть
в формулах отражение физической стороны явления при разных
деформациях и одновременно ознакомить его с сопротивлением реаль-
реальных материалов. Глубокое знание прочности применяемых материа-
материалов и не менее глубокое и ясное представление о распределении
напряжений в элементах конструкций — вот что должно дать сопро-
сопротивление материалов инженеру, чтобы достаточно вооружить его
при решении практических задач.
Книга предназначена для студентов и аспирантов. Она имеет
целью дать не только теоретический материал, но и показать при-
применение полученных результатов на примерах и дать материал для
самостоятельной домашней работы. Поэтому каждый раздел сопро-
сопровождается задачами; приведены также выдержки из существующих
технических условий.
Данные во всех задачах приведены в алгебраической и числовой
форме. Студент никогда не должен торопиться с использованием

ПРЕДИСЛОВИЯ	13
чисел при решении задач. Как правило, надо стремиться к тому,
чтобы решить задачу до конца в алгебраическом виде. Однако
доведение её до числового результата обязательно; при этом все
арифметические выкладки надо вести, сохраняя не более трёх-четы-
рёх значащих цифр, считая от левой руки к правой.
Проф. Н. Беляев
18 мая 1939 г.
ИЗ ПРЕДИСЛОВИЯ К ПЯТОМУ ИЗДАНИЮ.
Настоящее пятое издание курса проф. Н. М. Беляева выходит
в свет через пять лет после смерти автора и через четыре года
после опубликования предыдущего издания, подготовленного к пе-
печати ещё самим Н. М. Беляевым.
Наиболее существенные изменения курса, внесённые в книгу,
состоят в следующем.
Значительно полнее отражена роль отечественных учёных в раз-
развитии науки о сопротивлении материалов. Глава о материалах, при-
применяемых в инженерном деле, заменена таблицами в приложении.
В связи с необходимостью отразить современное состояние науки
о сопротивлении материалов, значительно переработано изложение
вопросов прочности, расчёта сварных соединений и устойчивости
элементов конструкций.
Чтобы удовлетворить программно-методическим требованиям и
из-за необходимости значительного сокращения, пришлось частично
переработать следующие разделы курса: основания для выбора коэф-
коэффициента запаса прочности; гибкие нити; сложное напряжённое со-
состояние; контактные напряжения; сдвиг и кручение; расчёт составных
балок; определение деформаций при изгибе; кривые стержни; напря-
напряжения при ударе. Существенно дополнены главы, в которых рас-
рассмотрены: общий случай определения напряжений при сложном дей-
действии сил; устойчивость плоской формы изгиба; расчёт вращающихся
дисков; вопросы колебаний упругих систем.
Коллектив, подготовивший настоящее издание, состоит из сотруд-
сотрудников кафедр сопротивления материалов Ленинградского института
инженеров железнодорожного транспорта и Ленинградского политех-
политехнического института им. М. И. Калинина, т. е. кафедр, возглавлявшихся
проф. Н. М. Беляевым; этот коллектив старался сохранить порядок
изложения, методику и стиль предыдущих изданий курса.
Между авторами переработки проделанная работа распределяется
следующим образом: доц. Л. А. Белявскому принадлежит перера-
переработка глав XV—XXV и глав XXXI—XXXII; доц. Я. И. Кипнису —
глав VII—XIV и XXXIII—XXXIV; доц. Н. Ю. Кушелеву — глав I—VI
и приложений; доц. А. К. Синицкому — глав XXVI—XXIX и
XXXV—XXXVIII *).
*> Нумерация глав дана по седьмому и восьмому изданиям.

14	ПРЕДИСЛОВИЯ
Общее руководство переработкой и редактирование проведены
проф. В. К. Качуриным.
Ученики и сотрудники Николая Михайловича Беляева надеются,
что и для этого издания, подготовленного ими к печати, будут спра-
справедливы слова покойного академика Б. Г. Галёркина, которыми он за-
закончил своё предисловие к предыдущему изданию настоящей книги:
«Вместе с задачником по сопротивлению материалов и руковод-
руководством к лабораторным работам по сопротивлению материалов того
же автора настоящий курс охватывает полностью данный предмет.
Все эти книги связаны общей идеей — идеей практических расчётов
на прочность, производимых на строгой научной основе. В этом духе
всегда воспитывал Николай Михайлович своих многочисленных уче-
учеников и сотрудников, и в этом же духе после его смерти будет
воспитывать их и его курс».
Проф. В. К. Качурин
ПРЕДИСЛОВИЕ К СЕДЬМОМУ ИЗДАНИЮ.
В седьмое, вновь переработанное издание курса проф. Н. М. Бе-
Беляева, по сравнению с пятым изданием, внесены следующие измене-
изменения и дополнения. Определение деформаций по методу Мора — Вере-
Верещагина изложено несколько полнее. Добавлена глава о расчёте
тонкостенных стержней. При расчётах на усталость введён учёт мас-
масштабного фактора. Даны методы технических расчётов на ползучесть.
Кроме того, заново просмотрен весь текст, который местами сокра-
сокращён, а местами дополнен и обновлён.
Распределение работы между авторами переработки сохранено
таким же, как и в пятом издании. Новая глава (XXX по новой нуме-
нумерации) о расчёте тонкостенных стержней написана доц. Я. И. Кипни-
сом, XXXIX глава о расчётах на ползучесть — доц. А. К. Синицким.
Авторы переработки выражают свою благодарность проф.
А. Н. Митинскому, а также всем другим лицам, сообщившим свои
замечания по предыдущему изданию курса.
Проф. В. К. Качурин
В четырнадцатом издании сортамент прокатной стали в приложе-
приложении заменён на современный. В соответствии с этим пересчитаны все
примеры в курсе, связанные с данными старого сортамента.
Проф. В. К. Качурин

ОТДЕЛ I.
ВВЕДЕНИЕ. РАСТЯЖЕНИЕ И СЖАТИЕ.
ГЛАВА Г.
ВВЕДЕНИЕ.
§ 1. Задачи сопротивления материалов.
При проектировании сооружений и машин инженеру приходится
выбирать материал и поперечные размеры для каждого элемента
конструкции так, чтобы он вполне надёжно, без риска разрушиться
или исказить свою форму, сопротивлялся действию внешних сил,
передающихся на него от соседних частей конструкции, т. е. чтобы
была обеспечена нормальная работа этого элемента. Основания для
правильного решения этой задачи даёт инженеру наука о сопроти-
сопротивлении материалов.
Эта наука изучает поведение различных материалов при действии
на них сил и указывает, как подобрать для каждого элемента кон-
конструкции надлежащий материал и поперечные размеры при условии
полной надёжности работы и наибольшей дешевизны конструкции.
Иногда сопротивлению материалов приходится решать видоизме-
видоизменённую задачу — проверять достаточность размеров уже запроекти-
запроектированной или существующей конструкции.
Требования надёжности и наибольшей экономии противоречат
друг другу. Первое обычно ведёт к увеличению расхода материала,
второе же требует снижения этого расхода. Это противоречие
является важнейшим элементом научной методики, обусловливающей
развитие сопротивления материалов.
Часто наступает момент, когда существующие материалы и методы
проверки прочности не в состоянии удовлетворить потребностям
практики, ставящей на очередь решение новых задач (в наше время
сюда относятся использование больших скоростей в технике вообще,
в воздухоплавании в частности, перекрытие больших пролётов,
•динамические задачи и др.). Тогда начинаются поиски новых мате-
материалов, исследование их свойств, улучшение и создание новых мето-
методов расчёта и проектирования. Прогресс науки о сопротивлении
материалов должен поспевать за общим прогрессом техники.
В некоторых случаях инженеру, помимо основных требований —
надёжности и наибольшей экономии, — приходится при выполнении
конструкции удовлетворять и другим условиям, например- требова-
требованиям быстроты постройки (при восстановлении разрушенных соору-

16	ВВЕДЕНИЕ	[ГЛ. I
жений), минимального веса (при конструировании самолётов) и т. п.
Эти обстоятельства также отражаются на выборе материала, разме-
размеров и форм частей конструкции.
Начало развития сопротивления материалов как науки иногда
относят к 1638 г. и связывают с именем Галилео Галилея, знамени-
знаменитого итальянского учёного. Галилей был профессором математики
в Падуе. Он жил в период разложения феодального строя, развития
торгового капитала, международных морских сношений и зачатков
горной и металлургической промышленности.
Новая экономика того времени поставила на очередь решение
ряда новых технических проблем. Оживление внешних торговых сно-
сношений поставило задачу увеличения тоннажа судов, а это повлекло
за собой необходимость изменения их конструкции; одновременно
стал вопрос о реконструкции и создании новых внутренних водных
путей сообщения, включая устройство каналов и шлюзов. Эти техни-
технические задачи не могли быть решены простым копированием суще-
существовавших раньше конструкций судов и сооружений; оказалось
необходимым научиться путём расчёта оценивать прочность элемен-
элементов конструкции в зависимости от их размеров и величины дей-
действующих на них нагрузок.
Значительная часть работ Галилея была посвящена решению
задач о зависимости между размерами балок и других стержней и
теми нагрузками, которые могут выдержать эти элементы конструк-
конструкции. Он указал, что полученные им результаты могут «принести
большую пользу при постройке крупных судов, в особенности при
укреплении палуб и покрытий, так как в сооружениях этого рода
лёгкость имеет огромное значение». Исследования Галилея опубли-
опубликованы в его книге «Discorsi e Dimostrazioni matematiche» A638, Лей-
Лейден, Голландия).
Дальнейшее развитие сопротивления материалов шло параллельно
развитию техники строительства и машиностроения и связано с целым
рядом работ выдающихся учёных-математиков, физиков и инженеров.
Среди них значительное место занимают русские и советские учёные.
Большой вклад в науку о сопротивлении материалов внёс
в XVIII веке действительный член Петербургской Академии наук
Леонард Эйлер, решивший задачу об устойчивости сжатых стер-
стержней.
В XIX веке мировую известность приобрели работы Д. И. Журав-
ского и X. С. Головина. В связи с проектированием и постройкой
ряда мостов на строившейся Николаевской, ныне Октябрьской, же-
железной дороге между Петербургом и Москвой Д. И. Журавский
решил ряд важных и интересных вопросов, связанных с прочностью
балок при их изгибе. X. С. Головин впервые правильно решил задачу
о прочности кривых стержней. В мировую науку прочно вошли
работы Ф. С. Ясинского по вопросам устойчивости элементов кон-
конструкций, вызванные к жизни изучением причин разрушения неко-

§2] КЛАССИФИКАЦИЯ СИЛ, ДЕЙСТВУЮЩИХ НА КОНСТРУКЦИИ 17
торых мостов. Проф. П. И. Собко организовал крупнейшую лабора-
лабораторию по испытанию материалов в Петербургском институте инжене-
инженеров путей сообщения.
С начала XX века роль русских учёных в сопротивлении мате-
материалов стала ведущей. Проф. И. Г. Бубнов явился основоположником
современной науки о прочности корабля. Академик А. Н. Крылов,
помимо дальнейшего развития задач о расчёте корабля, известен
крупнейшими исследованиями в области динамических расчётов. Проф.
Н. П. Пузыревский создал новую методику расчёта балок на упру-
упругом основании.
Из многочисленных трудов академика Б. Г. Галёркина достаточно
упомянуть работы по развитию вариационных методов механики,
общему решению пространственной задачи теории упругости и рас-
расчёту плит. Многих вопросов расчёта на прочность касались и работы
С. П. Тимошенко.
В советское время передовая роль нашей страны закрепилась ещё
в большей степени. Продолжали работать академики А. Н. Крылов
и Б. Г. Галёркин. Академик А. Н. Динник опубликовал ряд крупных
работ по устойчивости элементов конструкций. Проф. Н. М. Герсе-
ванов плодотворно работал в области механики грунтов, науки,
решающей задачи прочности и устойчивости оснований и фундамен-
фундаментов сооружений и машин.
Профессора П. Ф. Папкович и Ю. А. Шиманский стали во главе
школы учёных, занимающихся вопросами прочности кораблей. Проф.
Н. Н. Давиденков создал, совместно со своими учениками, нсвую
теорию, объясняющую причины разрушения материалов. Большое зна-
значение имеют и его труды по вопросам динамической прочности и
разрушения при ударе. Усилиями наших инженеров разработана новая
теория расчёта железобетонных конструкций, которая более правильно,
чем теории, принятые за границей, отражает действительный характер
работы этих конструкций и при обеспеченной прочности даёт значи-
значительную экономию размеров.. Академик Н. И. Мусхелишвйли развил
современные методы теории функций комплексного переменного и
теории сингулярных интегральных уравнений и применил их к реше-
решению ряда задач. Проф. В. 3. Власов создал новую оригинальную тео-
теорию расчёта тонкостенных оболочек и тонких стержней, имеющих
широкое применение в различных конструкциях.
§ 2. Классификация сил, действующих на элементы
конструкций.
При работе сооружений и машин их части воспринимают внеш-
внешние нагрузки и действие их передают друг другу. Плотина восприни-
воспринимает свой собственный вес и давление удерживаемой ею воды и пе-
передаёт эти силы на основание. Стальные фермы моста воспринимают

18	ВВЕДЕНИЕ	[ГЛ. I
от колёс через рельсы вес поезда и передают его на каменные
опоры; последние, в свою очередь, передают нагрузку на грунт
основания. Давление пара в цилиндре паровой машины передаётся
на шток поршня. Сила тяги паровоза передаётся поезду через стяжку,
соединяющую тендер с вагонами. Таким образом, силы, восприни-
воспринимаемые элементами конструкции, представляют собой либо объемные
силы*, действующие на каждый элемент объёма (собственный вес),
либо силы взаимодействия1) между рассматриваемым элементом и
соседними или этим элементом и прилегающей к нему средой (вода,
пар, воздух). Говоря, что к той или другой части конструкции при-
приложена внешняя сила, мы будем понимать под этим термином пере-
передачу давления (движения) на рассматриваемую часть от окружающей
её среды или от соседних частей конструкции.
Классификацию сил можно произвести по нескольким приз-
признакам.
Мы различаем силы.. сосредоточенны^ и распределённые.
Сосредоточенными силами называется[давления, передающиеся на
элемент конструкции через площадку, размеры которой очень малы
по сравнению с размерами всего элемента, например давление колёс
подвижного состава на рельсы.
При расчётах, благодаря малости площадар,, предающей давление,
обычно считают сосредоточенную сийу^риЛбженной Ы точке. Надо
помнить, что это — приближённое представление, вводимое лишь для
упрощения расчёта; через точку никакого давления фактически
передать нельзя. Однако неточность, вызываемая таким приближён-
приближённым представлением, настолько мала, что ею обычно на практике
можно пренебречь.
Р^2<^лёнными нагрузками называются силы, приложенные
непрерывно на протяжении некоторой длины или площади конструк-
конструкции. Слой песка одинаковой толщины, насыпанный на тротуар моста,
представляет собой нагрузку, равномерно распределённую по некото-
некоторой площади; при неодинаковой толщине слоя мы получим неравно-
неравномерно распределённую сплошную нагрузку. Собственный вес балки
какого-либо перекрытия представляет собой нагрузку, распределён-
распределённую по длине элемента.
Сосредоточенные нагрузки измеряются в единицах силы (тоннах,
килограммах); распределённые по площади нагрузки выражаются
в единицах силы, отнесённых к единице площади (т/м%, кг/см*
и т. п.); распределённые по длине элемента — в единицах силы, отне-
отнесённых к единице длины (кг/м).
Далее нагрузки можно разделить н&м??шоянныен временные.
Первые действуют во всё время существования конструкции,
например собственный вес сооружения. Временные нагрузки
*) Строго говоря, вес тела есть также сила взаимодействия между те-
телом и землёй.

$ 2] КЛАССИФИКАЦИЯ СИЛ, ДЕЙСТВУЮЩИХ НА КОНСТРУКЦИИ 19
действуют на конструкцию лишь в течение некоторого проме-
промежутка времени. Примером может служить вес поезда, идущего по
По характеру действия нагрузки можно разделить на статичес-
статические и динамические.
Статические нагружают конструкцию постепенно; будучи при-
приложены к сооружению, они не меняются или меняются незначительно;
таково большинство нагрузок в гражданских и гидротехнических
сооружениях. При передаче статических нагрузок на конструкцию
все её части находятся в равновесии; ускорения элементов кон-
конструкции отсутствуют или настолько малы, что ими можно пре-
пренебречь.
Если же эти ускорения значительны и изменение скорости элемен-
элементов машины или другой конструкции происходит за сравнительно
небольшой период времени, то мы имеем дело с приложением дина-
динамических нагрузок.
Примерами таких нагрузок могут служить внезапно приложенные
нагрузки, ударные и повторно-переменные.
Внезапно приложенные нагрузки передаются на сооружение
сразу полной своей величиной. Таковы давления колёс паровоза,
входящего на мост.
Ударные нагрузки возникают при быстром изменении скорости
соприкасающихся элементов конструкции, например при ударе бабы
копра о сваю при её забивке.
Повторно-переменные нагрузки действуют на элементы конструк-
конструкции, повторяясь значительное число раз. Таковы, например, повтор-
повторные давления пара, попеременно растягивающие и сжимающие шток
поршня и шатун паровой машины. Во многих случаях нагрузка пред-
представляет собой комбинацию нескольких видов динамических воз-
воздействий.
В дальнейшем мы в первую очередь займёмся вопросом о сопро-
сопротивлении материалов статическому действию сил, когда вопрос
о подборе сечения и материала для каждой части конструкции
решается наиболее просто.
В отделе X будут рассмотрены некоторые случаи действия дина-
динамических нагрузок, которые на практике встречаются не менее часто,
чем статические, и требуют особого изучения, так как и резуль-
результаты воздействия таких нагрузок на элемент конструкции оказы-
оказываются иными, чем статических, и материал иначе сопротивляется
этим воздействиям.
Заканчивая классификацию сил, действующих на элемент кон-
конструкции, можно выделить воздействие тех её частей, на которые
этот элемент опирается; эти силы называются реакциями; в начале
расчёта они оказываются неизвестными и определяются из условия,
что каждая часть конструкции находится в равновесии под действием
всех приложенных к ней сил и реакций.

20	ВВЕДЕНИЕ	[ГЛ. I
§ 3. Понятие о деформациях и напряжениях.
В теоретической механике (статике) изучается равновесие абсо-
абсолютно твёрдого тела; этого представления о материале достаточно
для решения поставленной в статике задачи — определения условий,
при которых возможно взаимное уравновешивание приложенных
к телу сил. При изучении сопротивления материалов действию этих
сил такого грубо приближенного представления о свойствах мате-
материала уже недостаточно; мы должны учесть, что абсолютно твёрдых
тел в природе не существует.
Как элементы конструкций, так и конструкции в целом при дей-
действии внешних сил в большей или меньшей степени изменяют свои
размеры и форму и в конце концов могут разрушиться. Это изме-
изменение носит общее название — деформация.
Величины и характер деформаций связаны со структурой, строе-
строением применяемых нами материалов. Все эти материалы могут быть
разбиты на два класса: кристаллические и аморфные.
Кристаллические материалы состоят из громадного количества
очень малых кристаллических зёрен. Каждое из этих зёрен пред-
представляет собой систему атомов, размещённых на весьма близких
расстояниях друг от друга правильными рядами. Эти ряды образуют
так называемую кристаллическую решётку. В аморфных материа-
материалах мы не имеем правильного расположения атомов. Атомы удер-
удерживаются в равновесии силами взаимодействия. Деформация тел
происходит за счёт изменения расположения атомов, их сближения
или удаления.
Деформации, разделяются на упругие и остаточные. Упругими
деформациями называются такие изменения формы и размеров эле-
элементов, которые исчезают после удаления вызвавших их сил, — тело
полностью восстанавливает свою прежнюю форму. Эти деформации
связаны лишь с "упругими искажениямй~~рёшётки~ атомов. Опыт пока-
показывает, что упругие деформации наблюдаются, пока величина внеш-
внешних сил не превзошла известного предела.
Если же внешние силы перешли этот предел, то после их
удаления форма и размеры элемента не восстанавливаются в перво-
первоначальном виде; оставшиеся разности размеров называются оста-
остаточными деформациями. Эти деформации в кристаллических мате-
материалах связаны с необратимыми перемещениями одних слоев кри-
кристаллической решётки относительно других. При удалении внешних
сил сместившиеся слои атомов сохраняют своё положение.
Смещение атомов при деформации материала под действием
внешних сил сопровождается изменением сил взаимодействия между
атомами — сил притяжения и отталкивания.
В элементах конструкции под действием внешних сил возникают
дополнительные внутренние силы, сопровождающие деформацию
материала. Эти внутренние силы сопротивляются стремлению внеш-

§ 3]	ПОНЯТИЕ О ДЕФОРМАЦИЯХ И НАПРЯЖЕНИЯХ	21
них сил разрушить элемент конструкции, изменить его форму, отде-
отделить одну его часть от другой. Они стремятся восстановить преж-
прежнюю форму и размеры деформированной части конструкции. Чтобы
численно характеризовать степень воздействия внешних сил на дефор-
деформированный элемент, нам необходимо научиться измерять и вычис-
вычислять величину внутренних междуатомных сил, возникших как резуль-
результат деформации, вызванной определёнными внешними силами.
Для этого в сопротивлении материалов пользуются так называе-
называемым методом сечений, который мы поясним на следующем примере.
Представим себе стержень (фиг. 1) под действием двух равных и
прямо противоположных сил Я и	j	j.
мысленно разделим его на две	(\	\		\_^
части I и II плоскостью тп. Под р~*~ч	М	^j ^
действием сил Р обе половины
стержня стремятся разъединиться	Фиг. 1.
и удерживаются вместе за счёт
сил взаимодействия между атомами, находящимися по обе стороны
плоскости тп. Равнодействующая этих сил взаимодействия назы-
называется усилием, передающимся через сечение тп от одной части
стержня на другую, и обратно. Внутренняя сила взаимодействия,
приходящаяся на единицу площади, выделенную у какой-либо точки
сечения тп, называется напряжением в этой точке по проведённому
сечению. Напряжения, действующие от части // на / и от / на //,
по закону равенства действия и противодействия равны между
собой.
Через одну и ту же точку стержня можно провести целый ряд
сечений, разделяющих стержень различным образом на две части.
Величина и направление напряжений, передающихся в рассматри-
рассматриваемой точке от одной части на другую, будут различными в зави-
зависимости от того, как проведён разрез.
Таким образом, нельзя говорить о напряжении, не указывая
сечения, через которое происходит передача этого напряжения. По-
Поэтому говорят о «напряжении по такой-то площадке, по такому-то
сечению». Так как напряжение представляет собой силу, приходя-
приходящуюся на единицу площади, то оно измеряется в единицах силы,
отнесённых к единице площади: кг/см*, кг/мм*, т/см*, т/м* и т. д.
Обозначать напряжения в дальнейшем мы будем буквами р, о и
Ч обозначение р применяется при любом наклоне напряжения к рас-
рассматриваемой площадке, буквой а обозначают напряжение нормаль-
нормальное к площадке, а т — лежащее в её плоскости, так называемое
касательное напряжение.
Величина напряжений в каждой точке и является мерой вну-
внутренних сил, которые возникают в материале как результат дефор-
деформации, вызванной внешними силами. Усилие, передающееся от части
' стержня на // (фиг. 1), удерживает часть // в равновесии, т. е.
уравновешивает систему внешних сил, приложенных к части IL

22	введение	[гл. [
Усилие же может быть выражено через искомые напряжения; если
мы выделим элемент площади dF в проведённом сечении, то элемен-
элементарное усилие, действующее на эту часть площади, будет равно р dFf
при этом р — напряжение в той точке, где выделен элемент пло-
площади. Сумма .этих элементарных усилий и даст полное усилие,
.передающееся через проведённое сечение.
Таким образом, для вычисления напряжений надо мысленно раз-
разделить рассматриваемый элемент конструкции сечением на две части
и составить условия равновесия для системы сил, приложенных
к одной из отсечённых частей; эта система будет включать в себя
внешние силы, приложенные к выделенной части стержня, а также
усилие, передающееся через проведённое сечение и выраженное
через искомые напряжения. В этом и состоит метод сечений, кото-
которым в дальнейшем мы будем постоянно пользоваться.
Заметим, что в сопротивлении материалов термин «напряжение»
применяется очень часто вместо термина «внутренние силы взаимо-
взаимодействия между частями стержня», поэтому мы будем говорить
о «равномерном или неравномерном распределении напряжений по
сечению», об «усилии как сумме напряжений»; надо помнить, что
эти выражения являются в известной мере условными; например, для
вычисления усилия нельзя просто суммировать напряжения в разных
точках; надо, как это указано выше, вычислить в каждой точке
сечения элементарное усилие, передающееся через малую площадку
dF, а потом суммировать уже эти слагаемые. Резюмируя изложен-
изложенное, можно сказать, что результатом действия внешних сил на эле-
элементы конструкции является возникновение в них деформаций, сопро-
сопровождаемых напряжениями.
Сопротивление материалов, изучая зависимость между внешними
силами, с одной стороны, и вызванными ими деформациями и напря-
напряжениями— с другой, даёт возможность решить стоящую перед
инженером задачу — противопоставить действию внешних сцл стер-
стержень достаточных размеров и из наиболее подходящего материала.
В следующем параграфе изложен план этого решения.
§ 4. План решения основной задачи сопротивления материалов.
При выборе размеров и материала для того или иного элемента
конструкции мы должны обеспечить известный запас против воз-
возможности его разрушения или остающегося изменения формы. Эле-
Элемент должен быть так спроектирован, чтобы наибольшие напряже-
напряжения, возникающие в нём при его работе, были во всяком случае
меньше тех, при которых материал разрушается или получает оста-
остаточные деформации.
Величина напряжений, достижение которых обусловливает разру-
разрушение материала, называется пределом прочности или временным
сопротивлением; его мы будем обозначать теми же буквами, что и

I 4]	ПЛАН РЕШЕНИЯ ОСНОВНОЙ ЗАДАЧИ	23
напряжения, но с индексом «в». Величина же напряжений, при пре-
превышении которых материал получает незначительные, заранее обу-
обусловленные, остаточные деформации, называется пределом упруго-
упругости. Эти величины являются механическими характеристиками сопро-
сопротивления материала разрушению и остаточному изменению формы1).
Чтобы обеспечить сооружение от риска разрушения, мы должны
допускать в его элементах напряжения, которые будут по своей
величине составлять лишь часть предела прочности материала.
Величину допускаемых напряжений обозначают той же буквой,
что и напряжение, но заключённой в прямые скобки; она связана
с пределом прочности ръ равенством
где k — так называемый коэффициент запаса прочности — число,
показывающее, во сколько раз допущенные нами в конструкции
напряжения меньше предела прочности материала. Коэффициент k
будем в дальнейшем называть просто коэффициентом запаса. Вели-
Величина этого коэффициента колеблется на практике в пределах от
1,7—1,8 до 8—10 и зависит от условий, в которых работает кон-
конструкция. Подробнее этот вопрос разобран в §§ 17 и 18.
Обозначая наибольшие напряжения, которые возникнут при дей-
действии внешних сил в проектируемом элементе, буквой /?тах» мы мо-
можем выразить основное требование, которому должны удовлетво-
удовлетворять материал и размеры этого элемента, неравенством
Это — так называемое условие прочности: действительные на-
напряжения должны быть не больше допускаемых.
Теперь мы можем составить план решения задач сопротивления
материалов. Необходимо:
1)	выяснить величину и характер действия всех внешних сил,
приложенных к проектируемому элементу, включая и реакции;
2)	выбрать материал, наиболее отвечающий назначению конструк-
конструкции и характеру действия внешних сил, и установить величину допу-
допускаемого напряжения;
3)	задаться размерами поперечного сечения элемента в числовой
или алгебраической форме и вычислить величину наибольших дей-
действительных напряжений pmix, которые в нём возникнут;
4)	написать условие прочности Рт&х^[р] и> пользуясь им, найти
величину поперечных размеров элемента или проверить достаточ-
достаточность уже принятых.
В последнее время эта схема решения задач сопротивления мате-
материалов в некоторых случаях видоизменяется; встречаются конструк-
') Уточнение понятий «предел прочности! и «предел упругости» сделало
• § 11.

24	ВВЕДЕНИЕ	[ГЛ. I
ции, в которых запас прочности для всей конструкции в целом
оказывается большим, чем для материала в наиболее напряжённом
месте. Исчерпание грузоподъёмности материала в этом месте иногда
не влечёт за собой исчерпания грузоподъёмности всей конструкции
в целом.
Условие прочности для материала ртах^[р] заменяется в этих
случаях условием прочности для всей конструкции в целом:
где Р — нагрузка, действующая на конструкцию, Рдоп — её допускае-
допускаемая величина, а Рв — предельная, разрушающая всю конструкцию
нагрузка. Таким образом, расчёт по допускаемым напряжениям заме-
заменяется расчётом по допускаемым нагрузкам.
В этом случае необходимо:
1)	выяснить величину и характер действия всех внешних сил,
приложенных к конструкции;
2)	выбрать материал, наиболее отвечающий назначению конструк-
конструкции и характеру внешних сил, и установить величину коэффициента
запаса;
3)	задаться размерами поперечных сечений элементов сооруже-
сооружения в числовой или алгебраической форме и установить допускае-
допускаемую нагрузку;
4)	написать условие прочности: Р^Ряоп и, пользуясь им, найти
величину поперечных размеров элементов конструкции или прове-
проверить достаточность уже принятых.
В ряде случаев, как мы увидим дальше (§ 27), оба метода ре-
решения дают совпадающие результаты.
Мы будем, как правило, пользоваться общепринятым пока мето-
методом расчёта по допускаемым напряжениям, но параллельно будем
излагать и способ расчёта по допускаемым нагрузкам в особенности
там, где он даёт отличные от первого способа результаты.
В большинстве случаев условие прочности должно быть допол-
дополнено поверками на устойчивость и жёсткость. Первая поверка
должна обеспечить невозможность общего изменения элементами
конструкции намеченной для них формы равновесия, вторая —
должна ограничить их деформации.
При решении задач сопротивления материалов приходится при-
применять и методы теоретической механики, и экспериментальные
методы. При определении внешних сил приходится основываться на
уравнениях статики; в случае статически неопределимых конструк-
конструкций необходимо производить, как это будет показано ниже (§ 19),
вычисление деформаций материала, что возможно лишь при нали-
наличии надёжных результатов лабораторных опытов, в которых опре-
определялись зависимости между деформациями и силами или напря-
напряжениями.

§ 5]	ТИПЫ ДЕФОРМАЦИЙ	2&
Установление допускаемых напряжений требует знания предела
прочности материала и других его механических характеристик,
что может быть получено также при помощи экспериментальных
исследований материала в специальных лабораториях испытания
материалов. Наконец, вычисление действительных напряжений требует
как применения методов математического анализа и механики, так
и использования опытных данных. Таким образом, сопротивление
материалов включает в себя две области: одну — аналитическую,
основанную на механике и математике, другую — экспериментальную.
Обе эти области тесно между собой переплетаются.
Сопротивление материалов нельзя рассматривать как дисциплину,
которая занимается только теоретическим вычислением напряжений
в каком-то однородном упругом теле. Решение задач, изучаемых
в сопротивлении материалов, возможно лишь при наличии резуль-
результатов экспериментального исследования механических свойств
реальных материалов в связи с их структурой, методами их изго-
изготовления и обработки. Поэтому в настоящем курсе этой стороне
отведено достаточное внимание. Работы в лаборатории составляют
один из важнейших элементов обучения и должны непременно
выполняться студентами параллельно с изучением курса. Описание
этих работ, разработанное применительно к существующему обо-
оборудованию механических лабораторий, выделено в особое руко-
руководство *).
Хотя при самом возникновении сопротивления материалов вопрос
о прочности был поставлен в связи с чисто практическими зада-
задачами, в дальнейшем сопротивление материалов развивалось в значи-
значительной степени по линии теоретической, что и вызывало иногда
разрыв между результатами исследований и их приложениями на
практике. Лабораторное изучение материалов шло особняком, глав-
главным образом по линии установления норм для приёмки разных
материалов. В настоящее время сопротивление материалов изучает
реальные материалы с точки зрения их работы в конструкциях
путём широких экспериментальных и теоретических исследований,
что открывает возможность решения ряда новых практических задач.
Таковы задачи изучения прочности новых материалов, условий их
разрушения, задачи определения напряжений не только в пределах,
но и за пределами упругости, и другие.
§ 5. Типы деформаций.
Установив общий план решения задач сопротивления материалов,
мы можем теперь перейти к отдельным видам этих задач. Их можно
рйВбить на несколько групп в зависимости от типа деформаций.
l) H. М. Беляев, Лабораторные работы по сопротивлению материалов,
Гостехиздат, 1951.

26
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. П
Основными типами деформаций являются (фиг. 2):
1) растяжение или сжатие (а и б); примеры — работа цепей,
канатов, тросов, растянутых и сжатых стержней в фермах, колонн;
2) перерезывание (в) — работа болтов, заклёпок; 3) кручение — ра-
работа валов (г); 4) изгиб — работа всякого рода балок (д). Эти
четыре типа деформаций назы-
называются простыми.
В конструкциях встречается
и более сложная работа эле-
элементов, когда они испытывают
два и более типов деформаций
одновременно, например, ра-
растяжение или сжатие с изги-
изгибом, изгиб с кручением и т. д.;
в этих случаях мы имеем дело
с так называемой сложной
деформацией. Для каждого
из этих видов деформаций
мы установим способы для
вычисления напряжений, под-
подбора материала и поперечных
размеров элементов конструк-
конструкции, а также способы для
вычисления деформаций.
Для простоты мы будем
сначала рассматривать лишь
те элементы сооружений и
машин, которые представляют собой так называемые призматиче-
призматические стержни с прямой осью. Таким стержнем мы будем называть
тело, все поперечные сечения которого одинаковы; центры тяжести
этих сечений лежат на одной прямой, называемой осью стержня.
В дальнейшем мы рассмотрим стержни и с переменным сечением и
с криволинейной осью.
Фиг. 2.
ГЛАВА II.
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ
В ПРЕДЕЛАХ УПРУГОСТИ. ПОДБОР СЕЧЕНИЙ.
§ 6. Вычисление напряжений по площадкам,
перпендикулярным к оси стержня.
Решение основной задачи сопротивления материалов мы начнём
с простейшего случая растяжения или сжатия призматического стержня.
Центральным растяжением или сжатием этого стержня назы-
называется деформация его под действием двух равных и прямопротиво-

§6]
ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ
27
положных сил, приложенных к концевым сечениям и направленных
по оси стержня. Если эти силы направлены наружу от концевых
сечений, то мы имеем pa-	Q	$
стяжение (фиг. 3, а), в про р |	——1 Р Р
тивном случае — сжатие "*l!	 I
(фиг. 3, б).
По общему плану ре-	Фиг. 3.
шения всякой задачи со:
противления материалов мы прежде всего должны найти величину
этих внешних сил Р, растягивающих стержень. Величина сил Р обычно
может быть определена из условий взаимодействия рассматриваемого
стержня с остальными частями конструкции.
В качестве простейшего примера можно рассмотреть винт вагон-
вагонной стяжки (фиг. 4). При равномерном движении поезда сила тяги
Фиг. 4.
паровоза Р, передающаяся через стяжку, уравновешивается с сопро-
сопротивлением движению остальной части поезда. Сила тяги паровоза (она
иногда достигает 25 т) передаётся на винт стяжки при помощи
винтовой нарезки так, что силы Р направлены по оси винта. Стер-
Стержень винта подвергается растяжению. Нашей задачей будет подо-
подобрать поперечные размеры винта таким образом, чтобы прочность
его была обеспечена.
Внешние силы, действующие на винт, равны силе тяги. Далее
необходимо найти вызванные этими силами напряжения, установить
Для них допускаемую величину и выбрать так размеры поперечного
сечения стержня, чтобы действительные напряжения не превосхо-
превосходили допускаемых.
Для вычисления напряжений необходимо выбрать те разрезы,
которыми мы будем разделять стержень на две части. Для про-
верки прочности следует отыскать опасное сечение, ;т% $. то, через
которое передаётся наибольшее напряжение. Мы установим формулы

28	НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. П
для вычисления напряжений сначала по сечениям, перпендикулярным
к оси стержня, а в дальнейшем и по наклонным сечениям; таким
путём мы сумеем отыскать наиболее опасное сечение.
Возьмём растянутый стержень и разделим его на две части попе-
поперечным сечением тп (фиг. 5), перпендикулярным к оси. Отбросим
вторую часть; тогда, чтобы равновесие первой не было нарушено,
мы должны заменить действие отброшенной части силами, передаю-
передающимися на оставшуюся часть через сечение (фиг, 6). Заменяющие
т
/т 1- )р?р
п
Фиг. 5.	Фиг. б.
силы будут уравновешивать внешнюю силу Р, поэтому они должны
сложиться в равнодействующую1) Рн, равную Р, направленную по
оси стержня в сторону, противоположную внешней силе (фиг. 6).
Эта равнодействующая Рн будет усилием, действующим в стержне.
Таким образом, условия равновесия оставшейся части дают нам
лишь величину равнодействующей внутренних сил, передающихся
по сечению тп, её направление и точку приложения, но не могут
указать, как распределяются напряжения по площади сечения, т. е.
какие силы будут передаваться через различные квадратные еди-
единицы этой площади. Между тем, для оценки опасности, угрожаю-
угрожающей прочности материала, необходимо найти наибольшее напряже-
напряжение, отыскать ту квадратную единицу площади, через которую
передаётся наибольшая сила.
Опыты с растяжением стержней из различных материалов пока-
показывают, что если растягивающие силы достаточно точно совпадают
с осью стержня, то удлинения прямых линий, проведённых на по-
поверхности стержня параллельно его оси, будут одинаковы. Отсюда
возникает предположение о равномерном распределении напряже-
напряжений по сечению. Лишь у концов стержня, там, где происходит не-
непосредственная передача сил Р на стержень, растяжение распреде-
распределяется неравномерно между отдельными участками площади сече-
сечения: те участки, к которым непосредственно приложена сила Р,
перегружаются; но уже на небольшом расстоянии от концов работа
материала выравнивается, и наступает равномерное распределение
напряжений по сечению, перпендикулярному к оси. Эти напряжения
направлены параллельно силе Р, т. е. нормально к сечению; поэтому
их называют нормальными напряжениями и обозначают буквой а.
*) Значок <Н> при Р (Рн) означает, что эта величина является равно-
равнодействующей распределённых по сечению сил, выражаемых через напря-
напряжения.

§ 7]	ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. ПОДБОР СЕЧЕНИЙ	29
Так как они распределены равномерно по площади сечения, то
ptt = oF, с другой стороны, РН = Р; отсюда получаем
« = •?•	B-1)
Эта формула позволяет нам вычислить напряжение с, если из-
известны растягивающая сила и размеры сечения стержня. С другой
стороны, если мы зададимся допустимой величиной нормального
напряжения, из этой же формулы можно будет найти необходимую
площадь поперечного сечения /\
§ 7. Допускаемые напряжения. Подбор сечений.
Чтобы выяснить, какую величину напряжений мы можем считать
допустимой при работе стержня из выбранного материала, необхо-
необходимо опытным путём установить зависимость между прочностью
стержня и возникающими в нём напряжениями. Для этого изготовим
из данного материала образец (обычно круглого или прямоугольного
поперечного сечения), заложим концы его в захваты машины, по-
позволяющей осуществить растяжение стержня, и начнём постепенно
увеличивать силы Р. Образец будет растягиваться и, наконец,
разорвётся.
Пусть наибольшей нагрузкой, которую выдержал образец до
разрыва, будет Рв. Величина нормальных напряжений, вызванных
этой нагрузкой, равная
..=4,
называется пределом прочности или временным сопротивлением
испытываемого материала на растяжение. Она выражается обычно
в кг/мм* или кг/см*.
Как указано в § 4, в стержнях конструкции приходится допу-
допускать при работе на растяжение нормальные напряжения [о], в не-
несколько раз меньшие, чем предел прочности ов; допускаемое напря-
напряжение получается делением предела прочности св на коэффи-
коэффициент запаса k. Величина этого коэффициента определяется целым
рядом соображений, которые подробно будут изложены дальше
(§ 17). Во всяком случае она должна быть такова, чтобы при нор-
нормальной работе стержня не только не произошло разрыва, но чтобы
не образовалось и остающихся деформаций, могущих изменить схему
сооружения или машины. Коэффициент запаса меняется в зависи-
зависимости от характера применяемого материала, способа действия сил
на элемент, экономических условий и ряда других факторов.
Ввиду важности правильного выбора коэффициента запаса и
величины допускаемых напряжений эти величины для многих кон-
конструкций даются нормами, обязательными для составителей проектов

30	НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. l{
и расчётов. Таким образом, величины допускаемых напряжений [а]
для каждого случая можно считать известными. Тогда для опреде-
определения необходимой величины площади поперечного сечения растя-
растянутого стержня можно, пользуясь формулой B.1), написать условие
прочности; это условие должно выразить, что действительное на-
напряжение а в растянутом стержне при действии аил Р не должно
превосходить допускаемого напряжения [а]:
° = ?<М-	B-2)
Из этого условия определяется наименьшая необходимая площадь
стержня;
F>?.	B.3)
Пользуясь формулой B.3), мы можем производить подбор сече-
сечения стержня.
Иногда площадь поперечного сечения является заданной. Тогда,
решая формулу B.3) относительно Я, мы производим определение
допускаемой силы
F[].	B.4)
Возвращаясь к расчёту стержня вагонной стяжки (§ 6, фиг. 4),
мы должны установить род материала, идущего для изготовления
этой детали, и допускаемое напряжение. Стержень стяжки делается
из стали с пределом прочности около 50 кг/мм*. Такой выбор ма-
материала определяется тем, что винт стяжки должен быть не очень
тяжёлым, — это требует материала повышенной прочности; с другой
стороны, в этом направлении нельзя итти слишком далеко, чтобы
материал винта мог хорошо сопротивляться ударам и толчкам. Если
применить сталь со слишком высоким пределом прочности, она ока-
окажется хрупкой.
Винт стяжки не только не должен давать обрыва, но в нём не
должно быть даже незначительных остаточных деформаций, чтобы не
произошло заедания в нарезке. Предел упругости для выбранного
материала составляет примерно 0,60 от предела прочности ав. Как
мы увидим дальше, при внезапном приложении сил (трогание с места)
напряжения увеличиваются примерно вдвое по сравнению со спокой-
спокойным, статическим растяжением, при котором определяют механиче-
механические характеристики материала в лаборатории. Поэтому величина
допускаемых напряжений не должна превышать
0,5-0,60 ав = 0,30 ав.
Это даёт коэффициент запаса

7]
ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. ПОДБОР СЕЧЕНИЙ
31
Таким образом, в данном случае допускаемое напряжение может
быть принято равным
[о] = Ь- = 0,3 ав = 50.0,3. = 15 кг/мм* = 1500 кг/см\
Необходимая, площадь при Р=25 т рарна
Р 25000 1С _ «
167см
Диаметр d стержня стяжки определяется условием
откуда
d
- = 4,55 см ъ* 4,5 см.
Полученный диаметр определён по дну нарезки для наименьшей
площади поперечного сечения. В тех случаях, когда площадь отдель-
отдельных сечений стержня меньше других, например из-за наличия отвер-
отверстий для болтов или заклёпок, наружных выкружек или канавок
(нарезки), определяется эта наименьшая площадь сечения, назы-
называемая площадью нетто и обозначаемая FHeTT0 или FH. Площадь
поперечных сечений, не имеющих ослаблений, называется площадью
брутто и обозначается /брутто или ^бр- Определив расчётом сече-
сечение FH, размеры F6p получаем уже из конструктивных соображений.
Выведенные выше формулы относились к случаю растяжения
стержня. Без всяких изменений они могут быть применены и к тому
случаю, когда мы встречаемся с деформацией сжатия. Разница будет
лишь в направлении нормальных напряжений и в величине допускае-
допускаемого напряжения [о]; при сжатии
стержней явление осложняется
Растяжение
/—Ц^ о
Л-
Сжатие
31	Г
Фиг. 7.
тем, что такие стержни могут н
оказаться неустойчивыми, — они
могут внезапно искривиться. Ра-
Расчётам на устойчивость будет р ,1 /
посвящен отдел IX.	*—
На фиг. 7 изображено распре-
распределение нормальных напряжений,
действующих по сечению, перпендикулярному к оси стержня, для
случая растяжения и сжатия. Для ряда материалов (сталь) величина
Допускаемого напряжения может быть принята одинаковой как при
растяжении, так и при сжатии (коротких стержней, т. е. таких,
У которых длина превышает размеры поперечного сечения не более
чеи в 5 раз). В других случаях (чугун) приходится назначать раз-
различные величины допускаемых напряжений для растяжения и сжатия
в аависимости от величины предела прочности при этих деформациях.

32	НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. II
В ряде конструкций мы встречаемся со случаем передачи сжи-
сжимающих напряжений от одного элемента другому через сравнительно
небольшую площадь, по которой соприкасаются между собой эти
элементы. Подобные напряжения называют обыкновенно напряже-
напряжениями смятия или контактными напряжениями. Распределение
напряжений около места соприкасания весьма сложно.и поддается
определению лишь методами теории упругости. При обычных расчё-
расчётах рассматривают в большинстве случаев эти напряжения просто
как сжимающие и ограничиваются лишь назначением для них спе-
специального допускаемого напряжения. В главе IX дан метод вычи-
вычисления этих напряжений и проверки прочности.
§ 8. Деформации при растяжении и сжатии. Закон Гука.
Для того чтобы иметь полную картину работы растянутого или
сжатого элемента, необходимо иметь возможность вычислить, как
будут меняться его размеры.
Соответствующие законы можно получить лишь на основании
опытов с растяжением и сжатием образцов изучаемого материала; эти
же опыты дают возможность изучать и прочность материала, опре-
определять его предел прочности и другие характеристики (§ 11).
Для осуществления подобных опытов в лабораториях пользуются
специальными машинами, позволяющими деформировать образцы и
доводить их до разрушения, измеряя требуемую для этого величину
усилий.
Одновременно при помощи достаточно точных измерительных
приборов — тензометров — производят измерения деформаций образ-
образцов. Предельные нагрузки, которые можно в настоящее время осу-
осуществлять при помощи испытательных машин и точно измерять, до-
достаточно велики. Существуют испытательные прессы, силой до 5000 т,
на которых можно испытывать на сжатие целые части конструкций
(колонны, части стен); что касается испытаний на растяжение, то
лаборатории располагают машинами, позволяющими осуществлять
растягивающие усилия до 1500 т. В большинстве современных лабо-
лабораторий пользуются машинами гораздо меньшей силы — от 5 до 100 г
на растяжение и до 200-f-500 т на сжатие.
Подробное описание подобных машин и приборов, в частности, очень
известной русской машины — пресса Гагарина, можно найти в нашей
книге «Лабораторные работы по сопротивлению материалов» и в спе-
специальных руководствах по механическим испытаниям материалов.
Пользуясь такими машинами и приборами, можно установить, как
будут меняться размеры образцов материала при растяжении и сжа-
сжатии. Если мы будем наблюдать, как изменяется расстояние / между
двумя точками А и В (фиг. 8) при растяжении образца, то увидим,
что по мере увеличения нагрузки увеличивается и расстояние между
намеченными точками.

§ 8]
ДЕФОРМАЦИЙ ПРИ РАСТЯЖЕНИИ И СЖАТИИ
33
В таблице 1 даны результаты одного из опытов, произведённых
в механической лаборатории Ленинградского института инженеров
путей сообщения; растяжению подвергался стержень, вырезанный из
рельса; нагрузка, при которой было
произведено первоначальное изме-
рение длины между двумя наме-
ценными точками, равнялась 0,5 г.
Далее эта нагрузка увеличивалась
ступенями тоже по 0,5 г. При
каждом увеличении нагрузки изме-
измерялось специальным точным при-
прибором, называемым тензометром, приращение Д длины / A00 мм) между
намеченными точками. Таким образом, например, при увеличении от
1 о А
1,5 до 2,0 т эта длина увеличилась на ^Шмм% ^еличины этих ПРИ-
ращений А при каждой ступени нагрузки даны в таблице 1*
ф
Нагрузки
в тоннах
0,5
1,0
1,5
2,0
2,5
3,0
3,5
4,0
4,5
Таблица
Удлинения
от каждой
ступени
нагрузки
91ШММ
14,5
13,7
13,4
13,5
13,7
13,4
13,6
13,9
1. Данные
Полные
удлинения
BW "*
14,5
28,2
41,6
55,1
68,8
82,2
95,8
109,7
опытных наблюдений.
Нагрузки
в тоннах
4,5
5,0
5,5
6,0
6,5
7,0
7,5
8,0
8,5
Удлинения
от каждой
ступени
нагрузки
* Тооо"**
13,7
13,6
14,4
14,6
17,5
36,3
328,2
361,0
Полные
удлинения
1
В Шю~мм
123,4
137,0
151,4
166,0
183,5
219,8
548,0
909,0
Примечание. Расчётная длина / = 100 мм. Площадь поперечного
сечения F=* 191,2 жж8.
Рассматривая эту таблицу, мы видим, что:
1) в начале опыта увеличение длины идёт пропорционально уве-
увеличению нагрузки; каждому приращению нагрузки в 0,5 г соответ-
соответствует приращение длины примерно на одну и ту же (в пределах
in/»
точности опыта) величину, а именно -щ^ мм (в среднем);
2) эта пропорциональность нарушается, когда нагрузка достигла
известного предела, в данном случае 5,5 т; за этим пределом де-
деформации (удлинение образца) растут быстрее, чем нагрузки.
Если мы полученные в этом опыте результаты изобразим графи-
графически, откладывая нагрузки по вертикали, а соответствующие удли-
2 Н,м, Беляев

34
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [гл. II
нения участка АВ — по горизонтали, то в известных пределах (в дан-
данном случае до нагрузки в 5,5 т) получим прямую, показывающую
пропорциональность между силой и вызванным ею удлинением (фиг. 9).
Нагрузка, после достижения которой нарушается пропорциональ-
пропорциональность между приращением нагрузки и приращением удлинения, назы-
называется нагрузкой, соответствующей пределу пропорциональности.
Напряжение же, вызванное этим грузом, называется пределом про-
пропорциональности. Оно полу-
получается делением величины это-
этого груза на площадь попереч-
ного сечения растягиваемого
7>° ~t	образца.
6,0 —-f~		Если мы, повторяя опыт,
будем измерять увеличение
длины между двумя другими
точками С и Д нанесёнными
2,0
2,0
%0
т
у
/
/
/
"л
/
f
Р—
——"
=="
¦О—
яг:
.——
>
ЛЬ
0,200 0>Ш 0,600
Фиг. 9.
на расстоянии, вдвое мень-
меньшем длины АВ, то прира-
приращения длины CD от тех же
ступеней нагрузки будут
вдвое меньше приращений
длины АВ.
Если же мы повторим опыты
со стержнями из того же ма-
материала, но с иной площадью поперечного сечения, то увидим, что
удлинения меняются обратно пропорционально площади.
Таким образом, опыты приводят к заключению, что пока нагрузка
на образец не достигла известного предела, удлинение прямо про-
пропорционально растягивающей силе Р, длине образца / и обратно
пропорционально площади поперечного сечения F. Обозначая через Д/
приращение длины образца от силы Р> можем написать формулу,
связывающую между собой эти опытные данные:
Pl
B.5)
где Е — коэффициент пропорциональности, различный для разных
материалов. Величина А/ называется абсолютным удлинением стержня
от силы А Формула B.5) носит название закона Гуна, по имени
ученого, впервые открывшего этот закон пропорциональности в 1660 г.
Зависимость B.5) можно представить в ином виде. Разделим обе
части этой формулы на первоначальную длину стержня /:
А/_ Р
А/
отношение -у — абсолютного удлинения к первоначальной длине —
называется относительным удлинением; оно обозначается буквой г.

§ 8]	ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ	35
Относительное удлинение является отвлечённой величиной, как
отношение двух длин А/ и /, и по своему числовому значению равно
удлинению каждой единицы длины стержня. Подставив в предыду-
Д/	Р
ихую формулу вместо -у величину е, а вместо -=г — величину нор-
нормального напряжения о, получаем иное выражение закона Гука:
« = ¦?	B-6)
или
а = еЕ.	B.7)
Таким образом, нормальное напряжение при растяжении или сжа-
сжатии прямо пропорционально относительному удлинению или укоро-
укорочению стержня.
Коэффициент пропорциональности Е, связывающий нормальное
напряжение и относительное удлинение, называется модулем упру-
гости при растяжении материала. Чем больше эта величина, тем менее
растягивается стержень при прочих равных условиях (длине, пло-
площади, силе Р). Таким образом, физически модуль Е характеризует
сопротивляемость материала упругой деформации при растяжении.
Так как е — относительное удлинение — является отвлечённой ве-
величиной, то из формулы B.7) следует, что модуль выражается в тех
же единицах, что и напряжение а, т. е. в единицах силы, делённых
на единицу площади.
Для стали мы можем вычислить величину этого модуля, пользуясь
результатами опыта, приведёнными в таблице 1. Среднее удлинение
образца до нарушения пропорциональности от нагрузки 0,5 г рав-
равнялось 0,0136 мм, длина / была равна 100 мм, наконец, площадь F
равнялась 191,2 мм%. Из формулы B.5) получаем следующее выра-
выражение для Е:
Е Pi .
подставляя Р = 500 кг, /=100 мм, А/=0,0136 мм, /7= 191,2 мм*9
получаем:
^!^}Ш = 19 200 кг/мм* = 1 920 000 кг/см\
Надо заметить, что величина модуля упругости материала Е даже
Для одного и того же материала не является постоянной, а несколько
колеблется. Для некоторых материалов величина модуля оказывается
одинаковой как при растяжении, так и при сжатии (сталь, медь),
в других случаях — различной для каждой из этих деформаций.
В обычных расчётах этой разницей пренебрегают и принимают для
громадного большинства материалов одно и то же значение Е как
ПР* растяжении, так и при сжатии.
2*

36
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. II
Надо иметь в виду, что закон Гука представлен формулой, которая
только приближённо отражает результаты опытов, схематизируя их;
поэтому он не представляет собой совершенно точной зависимости.
Все материалы при растяжении или сжатии дают величины дефор-
деформаций, более или менее отклоняющиеся от этого закона. Для неко-
некоторых материалов (большинство металлов) эти отклонения ничтожно
малы, и можно считать, что осуществляется полная пропорциональность
между деформацией и нагрузкой; для других (чугун, камень, бетон) —
отклонения значительно больше.
Однако для практических целей мы можем пренебречь наблю-
наблюдающимися небольшими отклонениями от формул B.5) и B.6) и
пользоваться ими при вычислении деформаций стержней.
Средние величины модуля Е для ряда материалов даны в таб-
таблице 2. Более подробные данные приведены в таблице в конце книги.
Таблица 2, Значения модуля упругости.
Наименование материала
Сталь
Чугун (серый, белый)
Медь и её сплавы (латунь, бронза)
Алюминий и дуралюмин
Каменная кладка:
из гранита
>	известняка
>	кирпича
Бетон
Дерево:
вдоль волокон
поперёк волокон
Каучук
Целлулоид
Е
в миллионах
кг/см*
2,0
, 1,60
1,0
0,7
0,09
0,06
0,03
0,10 + 0,30
0,1
0,005
0,00008
0,0193 + 0,0174
Из рассмотрения формулы B.5) ясно, что чем больше её зна-
знаменатель, тем менее растяжим (податлив) или, как говорят, тем более
жёсток стержень, поэтому знаменатель формулы B.5), величина EF,
называется жёсткостью стержня при растяжении или сжатии.
Мы видим, что жёсткость при растяжении или сжатии зависит,
с одной стороны, от материала стержня, характеризуемого величи-
величиной его модуля упругости Е, а с другой стороны, от размеров по-
поперечного сечения стержня, характеризуемых величиной площади
его поперечного сечения F. Иногда бывает удобно пользоваться
EF
понятием относительной жёсткости, которая равна —, т. е. от-
отношению жёсткости к длине стержня.
Формулы B.5) и B.6) позволяют определить удлинения и укоро-
укорочения, которые получает тот или иной стержень конструкции при

ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ
37
растяжении или сжатии. Обратно, зная эти удлинения, размеры и
материал стержня, можно вычислить нормальные напряжения, кото-
которые в нём возникают. Таким образом, для вычисления напряжений а
мы имеем два пути: если известны внешние силы Р, растягивающие
или сжимающие стержень, то а вычисляется по формуле
* = -?-;	B.1)
если же внешние силы неизвестны, а можно измерить удлинение
стержня, то а определяется формулой
а = е?.	B.7)
Величина относительного удлинения может быть
вычислена, если мы измерим абсолютное удлинение А/
участка стержня длиной / и применим формулу
Вторым приёмом определения напряжений прихо-
приходится пользоваться довольно часто при решении це-
целого ряда задач, как это будет показано ниже.
Для иллюстрации метода подбора сечения и опре-
определения деформаций решим два примера.
Фиг. 10.
П р и м е р 1. Трубчатая чугунная колонна с наружным диаметром D=25 см
сжата силой Р = 50 г. Допускаемое напряжение на сжатие [а] = 300 кг/см*,
длина колонны / = 3,5 м. Найти толщину стенок и абсолютное укорочение
колонны; модуль Е= 1 200000 кг/см3.
Величина рабочей площади колонны (заштрихованное кольцо на фиг. 10)
определится из формулы B.3):
„^ Р 50000 1Л7 ш
FS^-r-r——ojvv— = 167 см*.
{о] 300
Площадь кольца равна
где d— внутренний диаметр колонны.
Тогда
— ~^ = 20,2 см.
Толщина стенок будет равна
,= ^ = 2Ц20!2=2Lяа25а{
и окончательно d = 20 см. Абсолютная величина укорочения колонны опре-
определяется формулой B.5)
где
/?=-*(D* — (/8) = ^B5' — 203) = 177 см*,

38	НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. II
следовательно,
Т3^ =0'082
Подученное укорочение оказывается весьма малым по сравнению с дли-
длиной колонны. Можно было бы думать, что для инженера такие изменения
размеров конструкции не имеют практического значения. Однако это не так.
Небольшие изменения длины колонны под нагрузкой могут вызвать, как это
будет показано дальше, значительные изменения напряжения в частях кон-
конструкции, поддерживаемых этой колонной.
Пример 2. При испытании моста возникла необходимость в измерении
напряжений, появившихся в элементе фермы моста при нагружении его
поездом. Для этого измерялось увеличение длины / между двумя точками,
отмеченными на данном элементе. Измерение производилось прибором, уве-
увеличивающим действительные деформации в л =1000 раз. Длина /=10 ел*;
модуль Е =в 2 • 10е кг/см9. Перемещение стрелки прибора по шкале при на-
нагружении моста равнялось а = 20 мм. Найти напряжение.
Для вычисления напряжения в этом случае придётся воспользоваться
формулой B.7):
р
применить формулу сгг=~ невозможно, так как сила Р неизвестна.
Относительное удлинение t равно
А/
— т.
Абсолютное же удлинение равно перемещению а стрелки прибора, раз-
разделённому на коэффициент увеличения прибора я:
Таким образом,
§ 9. Коэффициент поперечной деформации.
Стержни, работающие на растяжение или сжатие, испытывают
помимо продольных деформаций и поперечные.
Как показывает опыт, при растяжении бруска (фиг. 11) длина
его увеличивается на величину А/, ширина же уменьшается на вели-
величину ЬЪ = Ь — Ь\. Относительная продольная деформация равна
д/
относительная поперечная деформация равна
При сжатии бруска продольной деформацией является укороче-
укорочение, поперечной — удлинение. Опыты показывают, что для большин-
большинства материалов et в 3-ь4 раза меньше» чем е.

§ 9]	КОЭФФИЦИЕНТ ПОПЕРЕЧНОЙ ДЕФОРМАЦИИ	39
Абсолютная величина отношения относительной поперечной де-
деформации et к относительной продольной е называется коэффи-
коэффициентом поперечной деформации или коэффициентом Пуассона \х:
1* = -у.	B.8)
Коэффициент поперечной деформации ц, так же как и модуль
упругости Е, является характеристикой упругих свойств мате*
риала. Для материалов, упругие свойства которых
одинаковы во всех направлениях, упругие постоянные
Е и р. полностью характеризуют эти свойства. Такие
материалы называют изотропными. С достаточной
для целей практики точностью к ним могут быть
отнесены сталь и другие металлы, большинство есте-
естественных камней, бетон, каучук, неслоистые пласт-
пластмассы.
Наряду с материалами изотропными существуют и
анизотропные материалы, т. е. такие, свойства кото-
которых в различных направлениях различны. К таким
материалам относятся в первую очередь дерево, слои-
слоистые пластмассы, некоторые камни, ткани и другие. Фиг. 11.
Одно значение ? и р. не может охарактеризовать их
упругие свойства, для них необходимо иметь ряд значений упругих
характеристик в различных направлениях.
Для измерения числовой величины р. необходимо при растяжении
или сжатии бруска измерять одновременно продольные и поперечные
деформации. Обычно эти измерения производятся при растяжении
образца, взятого в виде длинной и широкой пластинки (металлы),
или при сжатии призматических образцов (камень).
Рассмотрим определение коэффициента поперечной деформации
в следующем примере.
Пример 3. При растяжении стального образца с поперечным сече-
сечением в виде узкого прямоугольника со сторонами 80 мм и 3 мм продоль-
продольное удлинение, измеренное на длине 100 мм, равнялось 0,05 мм; поперечное
сжатие на длине 60 мм нри той же нагрузке было равно 0,0093 мм. Опре-
Определим коэффициент поперечной деформации.
Относительная продольная деформация равна
1
1
i
4-4 -п
( |
г:1
+•-0 -н
1	1
f
¦-?
е- loo -5
относительная поперечная деформация равна
Абсолютное отношение — даёт величину коэффициента поперечной де-
деформации р;
=-!#> =о,31.

40 НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [гл 11
Величины коэффициента поперечной деформации для различных
материалов при деформировании их в пределах упругости даны
в таблице 3.
Таблица 3.
Название материала
Сталь
Медь
Бронза .
Чугун
Свинец
Латунь
Алюминий
Цинк
Значения коэффициента поперечной
деформации.
0,25 — 0,33
0,31 — 0,34
0,32 — 0,35
0,23 — 0,27
0,45
0,32 — 0,42
0,32 — 0,36
0,21
Название материала
Золото
Серебро
Стекло
Камни
Бетон
Каучук
Пробка
Фанера
Целлулоид
0,42
0,39
0,25
0,16 — 0,34
0,08 — 0,18
0,47
0,00
0,07
0,39
Зная [х, можно вычислить изменение объёма образца при растя-
растяжении или сжатии. Длина образца после деформации равна /(l-f-?)«
Площадь после деформации равна F(l—tp)\ Объём после дефор-
деформации равен
Ц = Fl{\ + е) A -1«)« = V(l + е) A - ре)*.
где V—первоначальный объём.
Так как е до предела пропорциональности — малая величина, то
квадратами её пренебрегаем. Тогда объём V\ равен
Относительное изменение объёма равно
П р и м е р 4. Вычислим относительное увеличение объёма для растянутого
стержня из малоуглеродистой стали. Модуль упругости ? = 2-10* кг/см2;
коэффициент поперечной деформации |х = 0,3; напряжение растяжения равно
допускаемому для малоуглеродистой стали, а именно о = 1400 кг/см3. Увели-
Увеличение объёма равно
- 2 • 0,3] = 2,8-10-* =О,О28о/о
— очень малая величина.
Если коэффициент поперечной деформации [х = 0,5, то объём
при деформации не меняется. Так как для большинства материалов
то растяжение сопровождается увеличением, а сжатие —

§ 10]	примеры	41
уменьшением объёма. Для резины |ая«0,5, и объём её при растя-
растяжении почти не меняется.
Практическое значение появления поперечных деформаций в связи
с продольными чрезвычайно велико. Это значение в дальнейшем
будет подробно освещено.
§ 10. Примеры.
Пример 5. Цепь, служащая для подъёма грузов Р = 4 г, сделана
(фиг. 12) из круглой стали с пределом прочности ов = 37 кг/мм*. Коэффи-
Коэффициент запаса k = 6. Найти необходи-	.
мый диаметр звена */, ограничившись		\
учётом усилий растяжения в ветвях /, /^	**=>
цепи. В закруглённых частях возник- -?-Г~( в j | i
нут напряжения от их изгиба, метод °—\^w ^т,
определения которых будет изложен		т
в главе XXXI.	•
Так как сила Р действует по оси	Фиг. 12.
звена, то она распределяется поровну
между обеими его сторонами. Условие, определяющее площадь . каждой
ветви звена, имеет вид
Р
Допускаемое напряжение [а] равно
[а] = ^ = =61
Таким образом, площадь сечения ветви будет равна
^_2000
Г-"[с]--"б1Т 'Z4 '
а диаметр стержня звена равен
л=уц=Vй?-=2'°з ~ 2>1 см-
Пример 6. К кронштейну ABC, состоящему из деревянного стержня АС
и железной тяги АВ, подвешен в точке А груз Q = 4 т (фиг. 13). Сечение
тяги АВ — круглое, стержня АС — квадратное. Каковы должны быть диа-
диаметр d стержня АВ и стороны квадрата а (стержень АС\ если допускаемые
напряжения для дерева [а_[ = 25 кг/см*, а для стали [оч.[ = 900 кг/см9
(Iе-] — допускаемое напряжение на сжатие, [а+] — на растяжение); найти
вертикальное и горизонтальное перемещения точки А. Длина АС равна
^ = 1 м.
Усилия Nx и Л^а в стержнях АВ и АС находим из условия равновесия
шарнира А, к которому приложена известная сила Q и неизвестные уси-
усилия Nt и N*.
Построив треугольник равновесия для этих сил (фиг. 14), получаем
^ =	2Q = 8 г; JV2

НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [гл. U
Фш. 13.
Фиг 14.
Фиг. 15.

А Ю]	ПРИМЕРЫ	43
Потребные площади сечений стержней АВ и АС равны
ft - |о+) - goo - »,«* « , г, _ ^ — ^ - ^// с* .
Диаметр тяги равен
сторона квадрата равна
/277« 16,6 смъ* 17
обе величины приняты с округлением — для стального стержня до целых мм%
для деревянного до см.
Для определения перемещения / точки А разъединим в ней стержни и
изобразим их новые длины ВАХ и СЛ2, увеличив и уменьшив старые на
д/, s=AAi и A/j = AAt, не меняя пока направления стержней (фиг. 15, а).
Для того чтобы найти новое положение точки А, сведём вместе деформи-
деформированные стержни, вращая их около точек В и С. Точки Ai и At будут
перемещаться по дугам А%Аг и А2А*, которые по их малости могут быть
приняты за прямые, перпендикулярные к ВАи и CAt. Тогда горизонтальное
перемещение точки А будет равно
/2 5= АА% es Atif
а вертикальное (фиг. 15, б)
Отрезок
AtAA as i4i4j «в Д/t sin л,
а
ИИ, = >М4 —.
Но AiA4 = >4И5 + /45Л4 = ДЛ cosa-+-A/f, так что
Тогда
Л COS1 а 4- 4/, COS a	i/, -+¦ Д/, COS a
iJ^	=
Деформации стержней определяются формулами
6930- 100
?л 1&тг'4 ™ см'
Л/,/,	8000- 100-2	.„, ,Л ,
^ ==5,07 • 10"» см.
2 • 10» • " "
Таким образом, горизонтальное перемещение точки А равно t% = 0,24 мм,
вертикальное
А , . А ,	О.507 4 0»24 ~
A/, -f A/, COS a	2	„о тялт
fl-	ШГа
а полное перемещение АА9 равно
+ 0,24* == 1,45

44
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. II
Пример 7. Найти допускаемую нагрузку Р для цепи, составленной из
четырёх пластинок, каждая толщиной * = 4,5 мм, шириной h = 65 мм и
Я = 40 мм с отверстием для болта tf = 30 мм (фиг. 16). Допускаемое на-
напряжение [а] = 800 кг/см2.
Опасным сечением пластинки является сечение цепи, ослабленное отвер-
отверстием для болта, так как ширина её в этом месте, за вычетом отверстия,
будет 65 — 30 = 35 мм, что меньше ширины посредине её длины, равной
40 мм. Рабочая площадь цепи в опасном месте равна
F = 4 • 4,5 [65 — 30] = 630 мм* = 6,30 см К
Допускаемая нагрузка Р=800 • 6,3 = 5040 кг ^5 т.
Фиг. 16.
Пример 8. Трубчатая чугунная колонна проходит через два этажа.
Диаметр её (наружный) ? = 25 см; толщина стенок * = 2,5 см. Верхняя
часть её имеет длину /4 = 3,0 м, нижняя /, = 4,0 лс. На верхнее сечение
центрально действует нагрузка Pt = 25 г, на высоте /, на колонну добав-
добавляется нагрузка от междуэтажного перекрытия Р8 = 35 т. Найти напряже-
напряжения в сечениях верхней и нижней частей колонны и найти общее укорочение
её при модуле упругости Е = 1,3 • 10е кг/см2.
Проведём сечение в пределах длины 1Х\ верхняя отсечённая часть нахо-
находится в равновесии под действием силы Pi и нормальных напряжений о',
действующих по проведённому сечению. Условие равновесия имеет вид
i
р
Отсюда с' = -тт-; площадь сечения колонны равна
г
тогда
= i6(D — t)* *==* • 22,5-2,5=177 см2;
о, = 25000 = 141
Проводим сечение в пределах длины /2; верхняя отсечённая часть ко-
колонны находится в равновесии под действием напряжения а" и силы Pt + Р2;
отсюда
a"F=P1 + P, и 0'.=-^ = -^=340«г/с*>.
Так как напряжения в нижней и верхней частях колонны различны, то
её полное укорочение может быть вычислено как сумма укорочений обеих

§ Н ]	ДИАГРАММА РАСТЯЖЕНИЯ	45
частей. Для верхней части, сжатой силами Ри укорочение равно
_ РА _ 25000-300
Л/1 - "ЯГ~ 1,3- 10». 177 - °'33 **'
для нижней, сжатой силами Рх + Р%, укорочение равно
60000-400 1Q4u,f
/f	EF	1,3.10*
Полное укорочение равно
0,33+1,04 = 1,37^1,4 ММ.
Это укорочение можно подсчитать и иначе. Сила Рх и вызываемая ею
реакция сжимают колонну по всей её длине / = 1Х + /2, сила же Ра и вызы-
вызываемая этой силой реакция сжимают колонну лишь на длине /2. Полное
укорочение получится как сумма укорочений, вызываемых каждой из сил
в отдельности, и будет равно
EF "^ EF~ EF "t" EF #
Как и следовало ожидать, пришли к выражению, уже полученному ранее.
ГЛАВА III.
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ
РАЗЛИЧНЫХ МАТЕРИАЛОВ И ОСНОВЫ ВЫБОРА
ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ.
§ 11. Диаграмма растяжения. Механические характеристики
материала.
В предыдущей главе при определении размеров поперечного
сечения и вычислении деформаций мы встретились с рядом величин,
характеризующих материал не только в пределах пропорциональ-
пропорциональности (модуль упругости, предел пропорциональности), но и в ста-
стадии разрушения (предел прочности). Для полного представления
о механических свойствах материала при его растяжении и сжатии
до разрушения необходимо изучение на опыте явлений, которые при
этом процессе происходят.
С точки зрения различия в механических качествах при простом
растяжении и сжатии и при обычной температуре материалы могут
быть хрупкими или пластичными. Хрупкие материалы разрушаются
при очень малых остаточных деформациях. У пластичных же мате-
материалов разрушение наступает лишь после значительной остающейся
Деформации. К первому типу материалов относятся, например, чугун,
камень, бетон и др. К пластичным материалам относятся малоугле-
малоуглеродистая сталь, медь и др.
Выясним сначала поведение обоих типов материалов в опыте на
Растяжение вплоть до разрушения. Для этого опыта изготовляется
°бразец призматической формы круглого или прямоугольного сече-

46
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [ГЛ. Ш
Фиг. 17.
ния. На рабочей части образца наносят деления через каждый санти-
сантиметр или доли сантиметра, чтобы иметь возможность после опыта
судить об изменении длины образца. Образец помещают в машину и
закрепляют его концы. Медленно перемещая один конец образца
в направлении его оси, стержень растя-
растягивают нагрузкой, которая возрастает
постепенно, без толчков и ударов. При
опыте отмечают ряд последовательных
величин нагрузки и измеряют соответ-
соответствующее им увеличение длины /, на-
намеченной на образце.
Результаты измерений нагляднее все-
всего можно представить в виде так назы-
Д1 ваемой диаграммы растяжения; на боль-
большинстве машин имеется приспособление,
автоматически зачерчивающее эту диа-
диаграмму при растяжении образца. При
вычерчивании диаграммы по вертикальной оси откладываются в опре-
определённом масштабе нагрузки, а по горизонтальной — абсолютные уд-
удлинения.
При разрыве образца из пластичного материала—малоуглеро-
материала—малоуглеродистой стали — диаграмма имеет вид, показанный на фиг. 17. Пер-
Первая, часть диаграммы до точки Л, соответствующей
пределу пропорциональности, представляет собой
прямую линию.
Ордината OAt представляет собой величину рас-
растягивающей силы, соответствующую пределу пропор-
пропорциональности ап, т. е. тому наибольшему напряжению,
превышение которого вызывает отклонение от закона
Гука; для малоуглеродистой стали величина ап равна
примерно 2000 кг/см\
При увеличении растягивающей силы за величину
ОАХ деформация начинает расти быстрее нагрузки,—-
диаграмма имеет криволинейный вид с выпуклостью
вверх. Далее наблюдается резкое изменение в работе
материала; при некотором значении растягивающей
силы OCi материал «течёт»; для увеличения дефор-
деформации почти не нужно увеличивать растягивающую
силу. На диаграмме образуется горизонтальная (или
почти горизонтальная) площадка. Напряжение, при
котором происходит это течение материала—рост деформаций
при постоянной (примерно) нагрузке,—называется пределом текуче-
сти от. Для изучаемого материала эта величина равна около 2400 кг/см*.
Во время течения материала на поверхности образца появляются
в более или менее резкой степени так называемые линии Людерса,
которые легко обнаружить путём протравливания образца. Эти линии
Фиг. 18.

с
ДИАГРАММА РАСТЯЖЕНИЯ	47
вызываются взаимными перемещениями частиц материала при насту-
наступлении значительных деформаций образца.
После образования площадки текучести материал вновь начинает
сопротивляться дальнейшему растяжению, и для увеличения удли-
удлинения Д/ приходится увеличивать силу. Точка D диаграммы соот-
соответствует наибольшей величине нагрузки.
В этот момент поведение образца ещё раз резко меняется. До
этого в удлинении участвовал весь стержень; каждая единица его
длины удлинялась примерно одинаково; точно так же во всех сече-
сечениях было одинаковое уменьшение поперечных размеров образца.
С момента, когда нагрузка достигает величины ODXy деформа-
деформация в основном сосредоточивается в одном месте образца; неболь-
небольшой участок образца около этого места подвергается в дальнейшем
наибольшему напряжению; это влечёт за собой местное
сужение поперечного сечения, образуется так называемая
«шейка» (фиг. 19).
Вследствие уменьшения площади в деформирующейся
части для дальнейшего удлинения бруска нужна всё
меньшая и меньшая сила. Наконец, при нагрузке ОКХ
происходит разрыв.
Если мы приостановим опыт при нагрузке, меньшей ОАи
и разгрузим образец, то при разгрузке зависимость между
силой и удлинением будет выражаться той же прямой, что
и при нагрузке ОА. После удаления груза удлинение
исчезает, — мы имели лишь упругую деформацию.
и
Если мы произведём разгрузку образца от некоторой Фиг jg
точки Z диаграммы, лежащей между С и D, то при раз-
разгрузке диаграмма будет изображаться прямой ZOit примерно парал-
параллельной прямой ОА. Таким образом, образец в этом случае не
вернётся к первоначальным размерам; отрезок О{О^ будет пред-
представлять упругое удлинение, попрежнему меняющееся пропорцио-
пропорционально нагрузке с прежним модулем упругости; отрезок ООХ —
остающееся удлинение и отрезок 00^ — полное удлинение при
нагрузке OZV Можно найти такую нагрузку OBlt до которой мы
будем иметь лишь упругие деформации. Соответствующая точка В
диаграммы обычно лежит выше, но очень близко к точке Л, отве-
отвечающей пределу пропорциональности. Напряжение, превышение
которого вызывает незначительные (порядка 0,001 -f-0,003%) оста-
остаточные деформации, называется пределом упругости ау; на диа-
диаграмме (фиг. 17) нагрузка, вызывающая это напряжение, измеряется
ординатой ОВХ.
Точки А и В настолько близки друг к другу, что обычно счи-
считают предел упругости и предел пропорциональности совпадающими.
Поэтому зачастую говорят, что материал следует закону Гука, пока
Не достигнет предела упругости, хотя правильнее было бы сказать —
пРедела пропорциональности.

48
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [ГЛ. Щ
Наибольшая величина растягивающей образец силы изображается
ординатой ODX\ она часто называется разрушающей нагрузкой, так
как необходима для того, чтобы началось разрушение; окончатель-
окончательное же разрушение происходит при нагрузке, изображаемой на
диаграмме ординатой точки К» Напряжение, вызванное наибольшей
нагрузкой, носит название предела прочности или временного
сопротивления ов. Предел прочности, полученный как частное от
деления наибольшего груза на первоначальную площадь
поперечного сечения образца, характеризует величину тех
сил, которые необходимы, чтобы довести стержень из рассматри-
рассматриваемого материала до разрушения при растяжении; для малоугле-
малоуглеродистой стали эта величина достигает ~ 4000 кг/см\
Изучая диаграмму, мы наметили на ней целый ряд ординат,
выражающих величину нагрузок, связанных с различными механи-
механическими характеристиками материала. В таблице 4 дана сводка этих
нагрузок и соответствующих им характеристик (напряжений) с их
обозначениями. Для получения любого из указанных в таблице
пределов соответствующая нагрузка делится на первоначальную
площадь поперечного сечения.
Таблица 4. Механические характеристики материалов.
Нагрузка
Нагрузка, соответствующая концу
прямолинейного участка OAi
Нагрузка, соответствующая появле-
появлению остаточных деформаций ОВХ
Нагрузка, соответствующая явлению
текучести (возрастание деформа-
деформации при постоянной нагрузке) OCt
Наибольшая нагрузка ODi
Название соответствующего
напряжения и его обозначение
Предел пропорциональности ?п
Предел упругости <sy
Предел текучести ат
Предел прочности или временное
сопротивление ав
Все эти механические характеристики (пределы пропорциональ-
пропорциональности, упругости, текучести и прочности) характеризуют способ-
способность материала сопротивляться стремлению внешних сил деформи-
деформировать и разрушать образец при растяжении.
Абсциссы диаграммы испытания характеризуют иное свойство
материала, а именно, его способность в большей или меньшей сте-
степени деформироваться, прежде чем наступит разрушение.
Отрезок ОгОк (фиг. 17) даёт нам величину упругой деформации
образца к моменту разрыва, исчезающей в тот же момент, как
разрушение произошло. Длина же ОО3 = А/0 представляет собой
величину остающихся удлинений участка / образца после разрыва.
Эта величина тем больше, чем больше длина выбранного для изме-
измерений участка и чем пластичнее материал.

.л И]	ДИАГРАММА РАСТЯЖЕНИЯ	49
Отношение удлинения А/о к первоначальной длине участка /
принимается за меру пластичности материала, т. е. его способ-
способности испытывать большие деформации при разрушении.
Величина этого отношения, выраженная в процентах, обозна-
обозначается буквой 8 и называется остаточным относительным удли-
удлинением образца после разрыва и для обычно применяемых сортов
стали колеблется в пределах от 8 до 28%. Таким образом,
8 = ^. 100.
Следует отметить, что величина остаточного относительного
удлинения образца в значительной степени зависит от формы об-
образца, главным образом от отношения его длины к площади попе-
речного сечения. Поэтому в лабораторной практике принято изме-
измерять, после разрыва образца, остаточное удлинение не на всей его
длине, а лишь на некоторой ее части, называемой расчётной. В об-
образцах с круглым поперечным сечением расчётная длина чаще всего
назначается равной 10d, иногда 5d. В образцах с прямоугольным
поперечным сечением расчётная длина назначается так, чтобы при
круглом поперечном сечении той же площади F, что и прямоуголь-
прямоугольное, отношение длины к диаметру оставалось прежним. Например,
соответственно принятой для образца круглого сечения длине в 10tf,
для образца с прямоугольным поперечным сечением за расчётную
длину следует принять 11,3|//\ Образцы изготовляются так, что
их длина между головками несколько превышает принятую рас-
расчётную.
Для оценки пластичности материала при испытании на растяже-
растяжение служит и другая величина, так называемое остаточное отно-
относительное сужение. После достижения наибольшей нагрузки на
одном из участков стержня начинается образование «шейки», и
сечение образца в месте разрыва обычно имеет меньшую площадь,
чем первоначальное (фиг. 19). Назовём первоначальную площадь
сечения Fo, а площадь в месте разрыва Ft; величина
(в процентах) носит название относительного сужения после раз-
разрыва. Чем эта величина больше, тем материал пластичнее.
Наконец, диаграмма на фиг. 17 даёт нам возможность устано-
установить ещё одну механическую характеристику материала, связанную
с его сопротивлением ударам *). Это сопротивление оказывается тем
ббльшим, чем больше работа, которую нужно затратить, чтобы
разорвать образец. Поэтому в качестве характеристики способности
материала сопротивляться действию внезапного приложения нагрузки
-—	±
*) Подробнее см. § 233.

60
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [гл. Щ
можно взять величину работы, которую надо затратить на растя-
растяжение образца до предела упругости или до разрыва. Оказывается,
что эта работа в определённом масштабе
выражается площадью диаграммы растяже-
растяжения (фиг. 17).
Рассмотрим часть этой диаграммы в пре-
	. .	_.	делах применимости закона Гука (фиг. 20).
Т rf^T/p T	При растяжении закреплённого одним кон-
• Г ¦ 7ША	цом образца перемещение другого его конца
кяжи--	под действием постепенно возрастающей
I / /^ф^-dbl	силы Р равно тоже постепенно растущему
	*2вда	=*- удлинению A/=-w; эта зависимость вы-
выражается прямой ОВ.
Фиг. 20.	Какому-либо значению силы Р (отре-
(отрезок ВХВ%) соответствует удлинение А/
(отрезок ОВъ на фиг. 20). Увеличим нагрузку на dP\ удлинение
увеличится на dAl и растягивающая сила, средняя величина кото-
рой при этом равна Я-j-ydP, совершит работу
-dP'dAl.
Отбрасывая малую величину второго порядка -к dP • tf Д/, получаем
Графически работа dA изображается площадью заштрихованного
Прямоугольника высотой Р и основанием dAl.
Рассматривая постепенное возрастание силы Р, как ряд последо-
последовательных прибавлений элементарных нагрузок dPt получим, что
работа, производимая внешними силами при постепенном растяже-
растяжении образца, представится суммой элементарных прямоугольников
(фиг. 20). При непрерывном увеличении Р, т. е. при dP и dAl
бесконечно малых, эта сумма для определённых значений Р и А/
обратится в площадь треугольника ОВХВ%, равную
1	1
2	12' « 2
Таким образом, величина работы, совершённой при упругом
удлинении бруска на величину А/, выразится формулой
А = \РМ	C.1)
и графически представится площадью соответствующей части диа-
диаграммы растяжения.
Такие же рассуждения можно применить и к полной площади
диаграммы (фиг. 17). Вся площадь выражает собой полную работу Ал,
затраченную для разрыва образца длиной / и площадью F.

с 12]	ДИАГРАММА НАПРЯЖЕНИЙ	51
Чтобы получить величину, характеризующую с одной стороны
лишь материалу а не образец, принято делить работу Л на объём
образца. Отношение а = yj называется удельной работой упругой
деформации растяжения.
Аналогично можно определить полную удельную работу
aB=z ~рг? это та работа, которую необходимо затратить, чтобы
разорвать образец. Чем эта величина больше, тем надежнее воспри-
воспринимает материал ударное и внезапное действие нагрузки.
Выше мы видели, что материал образца после перехода за пре-
предел текучести продолжает испытывать упругие деформации, следую-
следующие по-прежнему закону Гука; к ним лишь добавляются остаточные
деформации. Это обстоятельство обнаруживается при разгрузке
образца после перехода за предел текучести (точка Z диаграммы
на фиг. 17).
Если образец после такой разгрузки сразу начать вновь растя-
растягивать, то диаграмма при нагрузке изобразится почти той же пря-
прямой O\Zy параллельной ОА, что и при разгрузке, а после точки Z—
той же кривой ZDKj которая была бы при отсутствии разгрузки.
Таким образом, если сравнить диаграмму растяжения OCZDK для
образца, не подвергавшегося разгрузке, с диаграммой O\ZDK для
образца из того же материала, предварительно нагружённого до
точки Z и разгружённого до точки Oit то мы видим, что предел
пропорциональности повышается до того напряжения, на которое
предварительно был нагружен образец, а остаточная деформация
после разрыва уменьшается на величину OOiy т. е. на ту величину
остаточной деформации, которая была приобретена при предвари-
предварительном нагружении.
Такое повышение предела пропорциональности и уменьшение
остаточной деформации после разрыва, вызванное предварительным
нагружением за предел текучести с последующей разгрузкой, носит
название наклёпа. При наклёпе как бы отрезается соответствующая
часть диаграммы растяжения, что понижает и полную удельную
работу ав. В действительности явление происходит много сложнее
описанной здесь упрощённой схемы. В частности, если после раз-
разгрузки дать образцу «отдохнуть», не сразу начать нагружение, а
спустя один-два часа, то соответствующая часть диаграммы ZDK
пройдёт несколько выше, чем при отсутствии отдыха.
§ 12. Диаграмма напряжений.
Приведённая на фиг. 17 диаграмма иллюстрирует поведение мате-
материала при данных размерах образца; поэтому для получения гра-
графика, характеризующего непосредственно изучаемый материал, диа-
диаграмму растяжения несколько видоизменяют.

52
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [ГЛ. Ill
Ординаты кривой фиг. 17, изображающие нагрузки, делят на
первоначальную (до опыта) площадь сечения образца Fo, а абсциссы
А/ — на расчётную длину /. Таким образом, в новой диаграмме по
вертикали откладываются
I
0*1
напряжения
Р_
Фиг. 21.
а по горизонтали — относи-
относительные удлинения
_ А/
е-"Г* ^
Такая диаграмма изобра-
изображена на фиг. 21; она носит
название диаграммы напря-
напряжений при растяжении для
данного материала. По очертанию она подобна диаграмме фиг. 17:
на ней нанесены все величины напряжений, характеризующие меха-
механические свойства материала: пределы пропорциональности оп, теку-
текучести от, прочности ов.
Если мы будем рассматривать часть этой диаграммы ОА до пре-
предела пропорциональности, то при некотором напряжении о и соот-
соответствующем ему относительном удлинении е
площадь треугольника ОАВ (фиг. 22), равная
~, будет выражать удельную работу дефор-
деформации при растяжении материала до напря-
напряжения о. В самом деле,
Зная, что s = -=, можно представить вы-
выражение для удельной работы деформации
в пределах упругости в таком виде:
C.2)
2Ет
Фиг. 22.
По аналогии вся площадь диаграммы
фиг. 21 представляет собой удельную работу
деформации ав при разрыве образца изучаемого материала. Эту
величину можно представить себе как произведение длины диа-
диаграммы 8 на наибольшую ординату ов и на некоторый коэффициент ij,
характеризующий отношение площади диаграммы к площади прямо-
прямоугольника со сторонами 8 и ов:
в. = Ч°Л	C.3)

с 12]	ДИАГРАММА НАПРЯЖЕНИЙ	53
Таким образом, удельная работа при разрыве до известной
степени характеризуется произведением предела прочности на
относительное удлинение после разрыва. Поэтому часто оценивают
способность материала сопротивляться ударам по величине произве-
произведения <зв8.
Из диаграммы фиг. 22 видно, что
Таким образом, модуль Е графически изображается тангенсом
угла наклона к оси абсцисс прямолинейной части диаграммы рас-
растяжения.
Величина предела прочности при разрыве пластичных материалов
в известной степени связана с их свойством, называемым твёрдостью.
Твёрдость — это свойство материала сопротивляться проникновению
в него других тел.
Одним из наиболее распространенных методов является опреде-
определение твёрдости по Бринелю. При этом способе характеристикой
твёрдости является так называемое «число твёрдости», определяе-
определяемое при помощи вдавливания в материал шарика из закалённой
стали. «Числом твёрдости по Бринелю» называется частное от деле-
деления величины вдавливающей силы Р на шаровую поверхность лунки
отпечатка:
Н = Р =	W
где D — диаметр шарика, d — диаметр отпечатка, h — глубина его. Для
малоуглеродистой стали это число равно Яв = 100 ч-120 кг/мм*,
для рельсовой стали //в = 200 -f- 220 кг/мм*, для твёрдой закалён-
закалённой стали //в достигает 400 -ь 450 кг/мм*. Между числом твёрдости
по Бринелю и величиной предела прочности стали при разрыве уста-
установлена довольно отчётливая эмпирическая зависимость:
ов ъ* 0,36#в.
Таким образом, определение предела прочности стали путём
изготовления специальных образцов и разрыва их можно заменить
определением твёрдости — «бринелированием». Этим способом широко
пользуются на практике.
Из прочих методов определения твёрдости упомянем тоже до-
довольно распространённый метод Роквелла. Он состоит во вдавлива-
вдавливании в материал алмазного конуса или закалённого шарика диамет-
Ром 1,59 мм.
Характеристикой твёрдости в этом способе является глубина
вдавливания при повышении нагрузки от начальной (небольшой) ве-
величины до окончательной.

54
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [гл. III
§ 13, Истинная диаграмма растяжения.
Диаграмму напряжений при растяжении, показанную на фиг. 21,
можно рассматривать как характеризующую свойства данного мате-
материала при растяжении.
Эта характеристика механических свойств материала является
однако условной. Если в начале испытания площадь поперечного
сечения образца почти не изменяется, то, начиная с напряжений,
равных пределу текучести, наступает заметное уменьшение этой
площади, сначала равномерное по всей длине, а с момента перехода
за предел прочности — местное. Таким образом, ординаты кривой
фиг. 21 на участке за пределом текучести представляют собой услов-
условные напряжения, отнесённые не к действительной площади сече-
сечения, а к первоначальной.
Точно так же абсциссы диаграммы фиг. 21 до достижения пре-
предела прочности зависят лишь от способности материала удлиняться;
после же образования шейки величина относительного удлинения
зависит и от соотношения размеров образца (длины и диаметра) и,
таким образом, не является уже характеристикой только материала.
Поэтому, чтобы получить график, более точно характеризующий
свойства самого материала, строят так называемую диаграмму истин-
истинных напряжений. Она иллюстрирует связь между напряжениями и
деформациями в том сечении образца, где происходит разрыв.
Для построения диаграммы истинных напряжений необходимо
отмечать в разные моменты опыта величину силы, растягивающей
образец, и одновременно измерять попе-
поперечные размеры образца в наиболее су-
суженном месте.
По этим размерам вычисляем действи-
действительную площадь образца для каждого мо-
момента измерений. Пусть эта площадь равна
Ft, а растягивающая сила Pt\ первоначаль-
первоначальная же площадь образца пусть была Fr
По оси абсцисс откладываем в процентах
величину относительного сужения
а на соответствующей ординате — вели-
величину истинного напряжения
0,1 02 0,3 0,4 0,5
Фиг. 23.
На фиг. 23 представлена такая диа-
диаграмма истинных напряжений для образца
рельсовой стали. Как видно из этой диаграммы, напряжение ой воз-
возрастает до самого разрыва, сначала быстро, после же достижения

С 14]	ДИАГРАММЫ РАСТЯЖЕНИЯ	55
наибольшего груза (точка А) менее резко. В момент разрыва на-
напряжение, отнесённое к действительной площади сечения, оказы-
оказывается ббльшим предела прочности, вычисленного обычным спосо-
способом. В приведённом примере предел прочности равен 67,7 кг/мм*9
а напряжение при разрыве 102,1 кг\мм%.
Однако было бы ошибкой использовать эту последнюю величину
для вычисления тех наибольших сил, которые может выдержать
стержень до разрыва, что для нас и интересно с практической точки
зрения. Это видно из обычной диаграммы растяжения фиг. 17; наи-
наибольший груз, выдерживаемый образцом, соответствует не моменту
разрыва, а более раннему; величина этого груза для образца данной
площади и характеризуется пределом прочности. Повышение же
действительных напряжений между точками, соответствующими наи-
наибольшему грузу и моменту разрыва, связано с резким уменьшением ра-
рабочей площади образца, т. е. практически с процессом его разрушения.
Пользуясь диаграммой истинных напряжений, можно установить
ряд новых механических характеристик.
Ординаты истинной диаграммы характеризуют способность
материала сопротивляться пластической деформации.
Для продолжения пластической (остаточной) деформации нам при-
приходится давать материалу веб большее и большее напряжение; по
мере роста пластической деформации материал оказывает ей веб
большее сопротивление. Это явление называется упрочнением.
Способность материала к упрочнению характеризуется крутизной
подъёма истинной диаграммы.
Ордината в точке А в момент достижения наибольшего груза
называется истинным пределом прочности или истинным времен-
временным сопротивлением. Ордината в конце кривой при разрыве об-
образца называется напряжением при разрыве:
Абсциссы истинной диаграммы характеризуют способность мате-
материала к пластической деформации, выраженной относительным суже-
сужением. До точки А это сужение площади по всей длине образца
может считаться одинаковым; оно называется равномерным суже-
сужением и характеризует способность материала к общей деформации
при разрыве. Разность между полным сужением и равномерным
характеризует способность материала к местным деформациям (шейка)
и называется местным сужением.
§ 14. Диаграммы растяжения для пластичных
и хрупких материалов.
В предыдущих параграфах рассмотрена физическая картина явле-
явлений при растяжении образцов из пластичного материала типа мало-
малоуглеродистой стали. Для других видов материалов, дающих при
растяжении пластическую деформацию, получаются диаграммы напря-
напряжений примерно того же вида, что и на фиг. 21.

56
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [гл. Щ
Некоторые сорта стали (специальные), медь, бронза не имеют
площадки текучести. Прямая часть диаграммы переходит непосред-
непосредственно в криволинейную. Для примера диаграммы напряжений литой
стали (а), бронзы (б), никелевой стали (в) и марганцевой стали (г)
показаны на фиг. 24.
+6
кг/см
9000
8000
WOO
6000
6000
то
3000
2000
@00
t
у
9i56ktjc
ti*29y99ji
л
ф-22,6% lKTJ^CNm
0m0Jfi7»
<-
'
1
0 . ,10 1. 20
3578нг1см*
^^$
^2471кг/смК
;
\
\ . 3D \ Ш*/о . +*
w го so 40 so 60%
Фиг.
24.
Для материала, диаграмма растяжения которого не имеет площадки
текучести, за величину предела текучести условно принято считать
то1
0,№ 0,200 0J00
Фиг. 25.
напряжение, при котором остаточное
относительное удлинение образца дости-
достигает примерно такой же величины, как
при наличии ясно выраженной площадки
текучести. За эту величину остаточного
относительного удлинения принимают
обычно 0,2%-
Хрупкие материалы характеризуются
тем, что разрушение происходит уже при
небольших деформациях. При растяже-
растяжении образца из такого типично хрупко-
хрупкого материала, как чугун, мы до самого
момента разрыва наблюдаем лишь незна-
незначительные деформации; разрушение про-
происходит внезапно; относительное удли-
удлинение и относительное сужение после
разрыва оказываются очень малыми. Диа-
Диаграмма напряжений при растяжении для
чугуна дана на фиг. 25. Обращаем внимание на то, что по сравне-
сравнению с диаграммами фиг. 24 горизонтальный масштаб диаграммы

ДИАГРАММА СЖАТИЯ
57
§15]
жиг. 25 увеличен примерно в 40 раз, а вертикальный — примерно
в 6 раз.
Как правило, хрупкие материалы плохо сопротивляются растя-
растяжению; их предел прочности на разрыв оказывается малым по
сравнению с пределом прочности пластичных материалов.
Зависимость деформаций от напряжений при растяжении хрупких
материалов обычно плохо изображается законом Гука; на диаграмме
вместо прямолинейного участка мы уже при низких напряжениях
получаем слегка искривлённую линию, т. е. не наблюдается строго
линейной пропорциональности между силой или напряжением и со-
соответствующей деформацией.
Таким образом, модуль упругости Е,
равный (§ 12) тангенсу угла наклона отно-
относительно оси абсцисс касательной к диа-
диаграмме напряжений, собственно говоря,
нельзя считать для таких материалов по-
постоянной величиной; он меняется в зависи-
зависимости от величины того напряжения, для
которого мы вычисляем деформацию. Чем эти
напряжения больше, тем модуль меньше
или больше, в зависимости от того, куда
направлена выпуклость кривой диаграммы— -г
вверх или вниз.
Однако в пределах тех напряжений, при
которых материал обычно работает в со-
сооружениях, наблюдающиеся отклонения от закона Гука незначи-
незначительны. Поэтому при практических расчетах заменяют криво-
криволинейную часть диаграммы соответствующей хордой (фиг. 26) и счи-
считают модуль Е постоянным. Это тем более допустимо, что механи-
механические характеристики хрупких материалов изменяются для отдельных
образцов в более широких пределах, чем характеристики пластичных
материалов; поэтому нет смысла пользоваться более точными выра-
выражениями зависимости между напряжениями и деформациями.
§ 15. Характер разрушения при сжатии пластичных
и хрупких материалов. Диаграмма сжатия.
При изучении сопротивления материалов сжатию приходится
пРименять образцы в виде кубика или цилиндра с высотой, немного
большей диаметра. Для более длинных образцов в опытах трудно
избежать искривления.
Размеры образцов для разных материалов различны и колеб-
?*отся в пределах (ребро кубика) от 2 см (дерево) до 20—30 см
(бетон).
. При сжатии цилиндрика из пластичного материала при напряже-
я* ниже предела пропорциональности или текучести материал
Фиг. 26.

58
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [гл. щ
ведёт себя так же, как при растяжении. Величины предела пропори
циональности (а также текучести для стали) и модуля упругости
для пластичных материалов при сжатии и
растяжении примерно одинаковы.
После перехода за предел
\	нальности появляются заметные
I	деформации, выражающиеся в
1~"\ образца и увеличении диаметра.
г
Г
пропорцио-
остаточные
укорочении
Благодаря
..Л-J—-—»-zi.../ трению между опорными плитами пресса и
I	основаниями образца затрудняются попереч-
Фиг. 27.	ные деформации материала у торцов образца;
он принимает бочкообразную форму (фиг. 27).
По мере увеличения площади поперечного сечения приходится
для дальнейшей деформации всё увеличивать нагрузку, образец
продолжает сжиматься, обращаясь в лепёшку. Напряжения, ана-
аналогичного пределу прочности при разрыве, наблюдать не прихо-
приходится.
Типичная диаграмма напряжений при сжатии для пластичного
материала (малоуглеродистая сталь) показана на фиг. 28. При сжа-
сжатии пластичных материалов, как и при их растяжении, имеет место
явление наклёпа.
куем?
7500
5000
2500
600
0,f
Фиг. 28.
Фиг. 29.
Хрупкие материалы — камень, чугун, бетон — при сжатии разру-
разрушаются так же, как и при растяжении, при весьма малых дефор-
деформациях. На фиг. 29 показана диаграмма напряжений при сжатии ка-
каменного образца (кубик размерами ШХ^ХЮ см, гранит).
На фиг. 30 дана диаграмма напряжений при сжатии чугуна. Здесь
также обращаем внимание на то, что масштабы диаграмм фиг. 29

3000 -
с 15]	ДИАГРАММА СЖАТИЯ	59
я 30, в особенности горизонтальный, значительно увеличены по
сравнению с масштабом диаграммы фиг. 28.
Характер разрушения образцов камня показан на фиг, 31; раз-
раздробленный образец представляет собой усечённые пирамиды, сое-
соединённые меньшими осно-
основаниями. Эта форма разру- кг/см*\о
шения зависит от наличия
при опыте сил трения между
образцом и опорными пли-
плитами пресса. Если уничто-
уничтожить это трение, например,
путём смазывания парафи-
парафином торцов кубика, то ха-
характер разрушения камня
будет иным: камень будет
разделяться на части тре-
трещинами, параллельными дей-
действию сжимающей силы
(фиг. 32). Разрушающая на-
нагрузка для такого кубика
будет меньше, чем для
кубика, испытанного обыч-
обычным путём, без смазки. Та-
Таким образом, при испыта-
испытании на сжатие величина предела прочности оказывается в значи-
значительной мере условной характеристикой прочности материала. Эхо
500
цбоо то Jm
Фиг. 30.
Фиг. 31.
Фиг. 32.
°бстоятельство приходится учитывать при назначении коэффициента
запаса.
При медленном ведении опыта на сжатие для образцов призма-
тнческой формы из бетона или из каменной кладки подмечено, что
Разрушение начинается с появления продольных, параллельных на-
пРавлению силы трещин. Таким образом, можно сказать, что материал

60
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [ГЛ. щ
сжимаемого образца разрушается, повидимому, от нарушения
сопротивления отрыву отдельных его частей.
Для чугуна характер разрушения близок к тому, который на-
наблюдается для камня. Вид раздробленного сжатием вдоль оси чу-
чугунного цилиндра показан на фиг. 33. Необходимо отметать,
что хрупкие материалы обычно сопротивляются сжатию гораздо
лучше, чем растяжению.
I Д В долы
I	Поперек
Фиг. 33.
Фиг. 34.
При сжатии образцов дерева получаются резко различные ре-
результаты в зависимости от направления сжатия по отношению
к волокнам; дерево — материал, называемый анизотропным, т. е.
обладающим разными свойствами в разных направлениях. При сжа-
сжатии дерева вдоль волокон предед прочности оказывается примерно
в 10 раз больше, чем при сжатии поперёк волокон, а деформация
значительно меньше. На фиг. 34 показаны диаграммы сжатия дере-
деревянного кубика вдоль и поперёк волокон. В таблице 5 приведены
данные о пределах прочности при растяжении и сжатии важнейших
материалов.
Таблица 5. Пределы прочности в кг/см3.
Наименование материала
Сталь для конструкций (в мостах, зданиях)
Сталь машиноподелочная (углеродистая) .
Рельсовая сталь
Специальные стали для машиностроения .
Чугун (серый)
Сплавы меди (латунь, бронза)
Дерево (сосна)
Естественные камни
Бетон
При
растяжении
3800— 4200
3200— 8000
7000— 8000
7500—19000
1700— 2500
2200— 5000
800
При сжатии
6000- 10000
400
100 — 5000
50— 350
Более подробные сведения даны в приложении в конце книги.

§ 16]
СРАВНИТЕЛЬНАЯ ХАРАКТЕРИСТИКА МЕХАНИЧЕСКИХ СВОЙСТВ
61
§16. Сравнительная характеристика механических свойств
пластичных и хрупких материалов.
Основная разница между хрупкими и пластичными материалами
заключается в том, что хрупкие материалы разрушаются при очень
неболыиих деформациях, в то время как окончательное разрушение
пластичных материалов происходит лишь после значительных изме-
изменений формы. В связи с этим площади диаграмм для пластичных
материалов значительно больше, чем для хрупких.
Для разрушения пластичных материалов необходимо затратить
гораздо больше работы, чем для хрупких. Поэтому в тех случаях,
где задачей конструкции является поглощение возможно большей
кинетической энергии удара без разрушения, пластичные материалы
оказываются более подходящими.
Хрупкие материалы очень легко разрушаются при действии удара
именно потому, что их удельная работа деформации очень мала.
При спокойной же, постепенно возрастающей сжимающей нагрузке
те же хрупкие материалы способны иногда безопасно брать на себя
значительно ббльшие напряжения, чем пластичные, благодаря своей
способности давать очень малые изменения формы до напряжений,
близких даже к пределу прочности.
Вторым характерным признаком, разделяющим оба типа мате-
материалов, является тот признак, что для пластичных материалов можно
считать почти одинаковым их поведение в первых стадиях дефор-
деформации при растяжении и сжатии. Громадное же
большинство хрупких материалов сопротив-
сопротивляется растяжению много хуже, чем сжатию.
Это в значительной мере ограничивает область
применения хрупких материалов или требует
специальных мер при работе их на растяже-
растяжение, например усиления бетона сталью в растя-
растянутых элементах.
Резкая разница между пластичными и хруп-
хрупкими материалами обнаруживается в их пове-
поведении по отношению к так называемым мест-
местным напряжениям. Под местными напряже-
напряжениями мы подразумеваем такие, которые рас-
распространяются на сравнительно малую часть
поперечного сечения элемента. Обычно эти на-
напряжения вызываются каким-либо резким из-
изменением размеров или формы поперечных
Учений по длине стержня.
Так, если мы будем растягивать стержень, ослабленный отвер-
отвергнем (фиг. 35), то в сечении 2—2, достаточно удалённом от
°ТВеРстия, распределение напряжений будет равномерным: о=-^-#
Фиг. 35.

62
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [гл. Щ
Фиг. 36.
Это распределение показано на фиг. 36. Если же мы возьмём се-
сечение /—/, наиболее ослабленное, то, в случае достаточно боль-
большой ширины стержня, в нём распределение нормаль-
ffiffifftffiTTff ных напРяжений будет таким, как показано на фиг. 37,
1111111111111,-1 т. е. в частях сечения около отверстия напряжение
будет примерно равно Зо; однако такое резкое по-
повышение напряжений распространяется на весьма
небольшую часть сечения, лишь около отверстия.
На всей остальной площади сечения напряже-
напряжения остаются равными о, как будто ослабления не
было. Таким образом, наличие небольшого отвер-
отверстия в стержне вызывает очень большие местные
напряжения, захватывающие, однако, очень малую часть площади
поперечного сечения. Подобные же местные перенапряжения вызы-
вызываются всякими надрезами, выточками и царапинами на поверхности
стержня, винтовой нарезкой, следами от обработки резцом и т. п.
У дна этих нарезок и царапин материал испытывает значительно
большие напряжения, чем по всему прочему сече-
сечению. Эти выводы верны, пока материал следует
закону Гука, а деформации, сопровождающие напря-
напряжения, малы.
Коэффициент повышения наибольших местных
напряжений по отношению к общим называется ко-
коэффициентом концентрации и обозначается ак:
Так как у хрупких материалов мы не получаем
значительных деформаций почти до самого разру-
разрушения, то изображённая картина распределения на-
напряжений будет иметь место при сжатии или растя-
растяжении стержня из такого материала всё время, т. е. пока наиболь-
наибольшие напряжения не достигнут предела прочности *). В связи с этим
стержень из хрупкого материала при наличии местных напряжений
разрушится или даст хотя бы трещины при значительно меньших
р
величинах средних нормальных напряжений о = -^, чем такой же
стержень при отсутствии местных напряжений. Последние, таким
образом, резко понижают прочность хрупких материалов.
Пластичные материалы гораздо менее восприимчивы к влиянию
этих местных перенапряжений. Представим себе, что мы будем растя-
растягивать стержень, показанный на фиг. 35, при условии, что материал
его — малоуглеродистая сталь. Пока местные напряжения, равные Зз,
будут ниже предела текучести, будет сохраняться та (или почти та-^
1) Мы рисуем несколько упрощённую схему работы стержня.

? 16] СРАВНИТЕЛЬНАЯ ХАРАКТЕРИСТИКА МЕХАНИЧЕСКИХ СВОЙСТВ	63
а протяжении между пределами пропорциональности й текучести)
картина распределения напряжений, которая показана на фиг. 37.
Как только наибольшие напряжения у краёв отверстия дойдут до
предела текучести, тотчас же в этих точках начнут появляться оста-
остаточные деформации, — некоторое время материал будет деформиро-
деформироваться без дальнейшего повышения напряжений. После того как
эти деформации достигнут определённой величины, иначе говоря,
после того как будет пройдена площадка текучести, — начнётся
упрочнение, напряжения вновь начнут увеличиваться, но медленнее,
чем до наступления текучести.
В остальной части сечения, работающей при напряжениях ниже
предела текучести, эти напряжения при дальнейшем увеличении на-
нагрузки будут расти и догонять остановившиеся на некоторое время
в своём росте напряжения у краёв отверстия. Таким образом,
к тому моменту, когда средние напряжения достигнут предела теку-
текучести, при условии достаточно длинной площадки текучести, дей-
действительные напряжения в значительной степени выравнятся, — не
будет резкой разницы в их величине у края отверстия и по осталь-
остальному сечению. При короткой площадке текучести такое выравнива-
выравнивание будет менее значительным из-за явления упрочнения, так как
напряжения у края отверстия вновь начнут расти ещё до того, как
в остальной части сечения будет достигнут предел текучести.
При дальнейшем растяжении стержня частичное выравнивание
напряжений отчасти сохранится, и наибольшие грузы для стержней,
ослабленного и не ослабленного отверстием, для пластичного мате-
материала, будут значительно менее разниться, чем для подобных стер-
стержней из хрупкого материала. Таким образом, в стержнях из пла-
пластичного материала местные перенапряжения значительно слабее
отзываются на прочности при статической нагрузке, чем в стержнях
из хрупкого материала. Поэтому, например, при испытании образцы
из углеродистой (менее пластичной) стали требуют гораздо более
тщательной отделки поверхности, чем образцы из малоуглеродистой
стали. Роль пластичности по отношению к местным напряжениям
заключается в том, что она как бы выравнивает эти напряжения.
Нами описана значительно упрощённая схема работы стержня
с отверстием. На самом деле, выравниванию напряжений препятствует
ие только явление упрочнения, но и изменение напряжённого состоя-
состояния в месте концентрации, переход его из линейного напряжённого
состояния в объёмное. Такое сложное напряжённое состояние будет
исследовано в дальнейшем в гл. VII.
Наконец, ещё одно обстоятельство обусловливает выбор того
или другого типа материала при практическом применении. Зачастую
пРи сборке конструкции бывает необходимо несколько погнуть или
исправить искривлённый элемент. Так как хрупкие материалы выдер-
выдергивают без разрушения лишь очень малые деформации, то подобные
°иерации с ними обычно ведут к появлению трещин. Пластичные же

64	ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [гл. щ
материалы, имеющие способность принимать значительные деформа-
деформации без разрушения, обычно без всяких затруднений допускают
такие изгибы и исправления.
Таким образом, хрупкие материалы плохо сопротивляются
растяжению и ударам, очень чувствительны к местным напряже-
напряжениям и не переносят исправлений формы изготовленных из них
элементов.
Пластичные же материалы этими недостатками не обладают;
таким образом, пластичность является одним из самых важных
и желательных качеств материала.
У хрупких материалов имеется то достоинство, что они обычно
дешевле и зачастую обладают высоким пределом прочности сжатию,
что может быть использовано при спокойной нагрузке.
Таким образом, хрупкие и пластичные материалы обладают резко
разнящимися, противоположными свойствами в отношении их сопро-
сопротивления простому сжатию и растяжению. Однако эта разница
является лишь относительной. Хрупкий материал может получить
свойства пластичного, и наоборот. Эти свойства — хрупкость и пла-
пластичность— зависят от способа обработки материала, от вида напря-
напряжённого состояния и температуры. Камень, являющийся при простом
сжатии типично хрупким материалом, можно заставить деформиро-
деформироваться как пластичный; в некоторых опытах это удавалось при
действии на цилиндрический образец камня давлений, приложенных
не только по основаниям цилиндра, но и по его боковой поверх-
поверхности. С другой стороны, малоуглеродистую сталь, пластичный ма-
материал, можно поставить в такие условия работы, например при
низких температурах, что она даёт совершенно хрупкое разру-
разрушение.
Таким образом, характеристики «хрупкий», «пластичный», кото-
которые мы даём материалам на основании опытов на растяжение и
сжатие, относятся лишь к поведению этих материалов при обычных
температурах и лишь при сопротивлении указанным видам де-
деформаций. Вообще же хрупкий материал может перейти в пластич-
пластичный, и наоборот. Поэтому правильнее говорить не о «хрупком» и
«пластичном» материале, а о хрупком или пластичном состояниях
материала.
Необходимо отметить, что уже сравнительно небольшое повыше-
повышение пластичности хрупкого материала (хотя бы до 2°/0 относитель-
относительного удлинения при разрыве) позволяет применять его в целом
ряде случаев, исключавшихся для хрупких материалов (в частях
машин).
Поэтому работа над повышением пластичности таких мате-
материалов, как бетон, чугун, заслуживает самого серьёзного вни-
внимания.
Подробнее вопрос о причинах хрупкого и пластичного состояния
материала рассмотрен в главе XXXVIII.

с 17] ОСНОВАНИЯ ДЛЯ ВЫБОРА КОЭФФИЦИЕНТА ЗАПАСА ПРОЧНОСТИ	65
с 17. Основания для выбора коэффициента запаса прочности.
д. В предыдущих параграфах подробно изучены способы вычи-
вычисления напряжений, определения механических свойств материалов
при растяжении и сжатии и даны указания о выборе того или иного
типа материала (пластичного или хрупкого) в зависимости от усло-
условий работы конструкции.
Для установления величины допускаемых напряжений, пригодных
в разных случаях действия нагрузки, приведённых пока данных все
же не вполне достаточно. Все величины, характеризующие механиче-
механические свойства материала (предел прочности, относительное удлинение,
предел пропорциональности и т. п.), получаются из опытов в лабора-
лаборатории при действии статической нагрузки, т. е. возрастающей посте-
постепенно, без толчков, ударов и перемен знака. Точно так же формулы,
связывающие величину нормальных напряжений с с величиной сжи-
сжимающих или растягивающих сил Р, выведены для случая статического
действия этих сил; предполагалось, что внешние силы и напряжения,
приложенные к отсечённой части стержня, взаимно уравновешиваются.
Между тем в целом ряде случаев приходится иметь дело с нагруз-
нагрузками, действующими ударно или систематически меняющимися.
Влияние ударно приложенной нагрузки сказывается двояко по
сравнению со статической: с одной стороны, хрупкие и пластичные
материалы различно реагируют как материалы на ударное действие
нагрузок; с другой стороны, и напряжения оказываются в этом
случае другими*, чем при статических нагрузках. Подробнее этот
вопрос будет разобран в главах о динамическом действии нагрузок.
Здесь мы обратим внимание только на то обстоятельство, что при
динамическом действии нагрузок напряжения обычно будут ббль-
шими, чем при статическом действии тех же нагрузок. Это поло-
положение подтверждается опытами и может быть доказано теоретически,
что и будет сделано в отделе X.
Отношение напряжения од, вызванного динамическим действием
нагрузки, к напряжению о, вызванному статическим действием той
же нагрузки, носит название динамического коэффициента и обо-
обозначается А'д:
Величина динамического коэффициента зависит от характера
Динамичности нагрузки и в ряде случаев достигает весьма больших
значений.
Б. Сопротивление материалов действию нагрузок, систематически
вменяющих свою величину или величину и знак, значительно отли-
отличается от сопротивления материалов статическому и ударному дей-
действию нагрузок.
Если, например, стальной стержень мы будем подвергать боль-
больше число раз попеременно растяжению и сжатию, то обнаружим,
3 Н. М. Беляев

66	ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [ГЛ. Щ
что после определённого количества перемен напряжений стержень
в некоторых случаях даст трещину и затем разрушится при напря-
напряжениях, значительно меньших предела прочности. Даже в случае
пластичного материала остаточная деформация образца, разрушен-
разрушенного подобным образом, оказывается весьма незначительной — про-
происходит хрупкий излом.
Явление разрушения материала при действии переменных напря-
напряжений, меньших, чем предел прочности, называется явлением уста-
усталости. Это название не отвечает физической природе явления, однако
оно настолько укоренилось, что применяется и в настоящее время.
Опыты показывают, что при переменном растяжении и сжатии,
по мере понижения величины, действующей силы возрастает число
перемен этой силы, необходимое для того, чтобы вызвать разруше-
разрушение образца. Для каждого материала существует такое максималь-
максимальное значение нормального напряжения с, при котором образец вы-
выдерживает практически неограниченное число перемен усилий, не
разрушаясь. Это напряжение обозначается ок и называется пределом
выносливости или пределом усталости. Пока действительные на-
напряжения в элементе не превзошли этого предела, разрушения не
произойдёт, сколько бы раз напряжение не меняло свою величину.
Таким образом, в случае систематически меняющихся нагрузок
оказывается необходимым установить новую механическую характе-
характеристику материала — предел выносливости; эта величина определяет
способность материала сопротивляться переменным • напряжениям.
Подробное изучение вопросов усталости материала при разных
видах нагрузок будет дано в главе XXXVII.
Всё изложенное необходимо учитывать при выборе допускаемых
напряжений на растяжение и сжатие или, что всё равно, при опре-
определении коэффициента запаса k в формуле (см. §§ 4 и 7):
М=*.	C-4)
Этот коэффициент должен быть выбран с тем расчётом, чтобы
величина нормальных напряжений, действующих по всему сечению,
не превосходила предела упругости (или текучести) материала, иначе
наш стержень получит остаточные деформации, а при действии
переменных нагрузок не превосходила предела выносливости, кото-
который обычно ниже предела текучести.
При ударной нагрузке следует учесть, что напряжения обычно
повышаются. Так как и в этом случае напряжения всё же обычно
вычисляют в предположении статического действия сил, то влияние
динамического действия нагрузки приходится учитывать соответ-
соответствующим увеличением коэффициента запаса.
В. Что касается местных напряжений (см. § 16), то можно мириться
с переходом их за предел упругости и текучести в пластичных
материалах при отсутствии переменных нагрузок. В этом случае мы

с 17] ОСНОВАНИЯ ДЛЯ ВЫБОРА КОЭФФИЦИЕНТА ЗАПАСА ПРОЧНОСТИ	67
получаем остаточные деформации лишь на протяжении такой неболь-
небольшой части стержня, что на работе конструкции это обстоятельство
не скажется. За счёт появления остаточных деформаций местные
напряжения прекращают своё увеличение, отчасти выравниваются.
В хрупких материалах этого преимущества нет (§ 16): для них при-
приходится коэффициент запаса назначать повышенным, тем более, что
и в отношении сопротивления ударам они стоят значительно ниже
пластичных.
При переменных нагрузках, когда мы вынуждены считаться
с возможностью развития трещин усталости, учёт величины местных
напряжений необходим и может очень резко сказаться на выборе
коэффициента запаса даже для пластичных материалов. Для появле-
появления трещин усталости необходимо, чтобы в каком-либо месте стержня
действительные напряжения перешли за предел выносливости. Так
как местные напряжения выше общих (действующих по большей
части сечения), то опасность появления трещины и вызывается тем,
что именно местные напряжения перейдут за предел выносливости.
Так как подбор сечения мы ведём, исходя из величины наибольших
общих напряжений по условию
то коэффициент запаса для допускаемых общих напряжений в этом
случае надлежит выбрать так, чтобы местные напряжения не пре-
превосходили предела выносливости. Это во многих случаях требует
значительного увеличения коэффициента k по сравнению со случаем
статической нагрузки.
Для пластичных материалов в тех случаях, когда предел вы-
выносливости лежит выше предела текучести, можно не учитывать
местные напряжения, так как явление текучести уменьшает воз-
возможность их распространения, играет как бы роль буфера.
Для хрупких материалов, не имеющих площадки текучести,
опасность появления трещин усталости при переменных нагруз-
нагрузках остаётся в полной мере, что требует соответствующего уве-
увеличения коэффициента запаса по сравнению со статической на-
нагрузкой.
Таким образом, поскольку выбор коэффициента запаса обуслов-
обусловливается свойствами материала и способом приложения внешних
сил, хрупкие материалы требуют обычно больших коэффициентов
запаса, чем пластичные; точно так же эти коэффициенты приходится
выбирать большими при динамических и переменных нагрузках, чем
пРи статических.
Г. При выборе допускаемых напряжений приходится учитывать
е1Дё ряд других обстоятельств. Величины сил, входящих в наши
расчёты, известны нам не вполне точно; механические свойства
материалов дают на практике зачастую значительные колебания;
3*

68	ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [гл. Щ
методы наших расчётов, наши представления о взаимодействии
отдельных частей конструкций являются обычно упрощёнными и
приближёнными. Коэффициент запаса должен покрыть все эти не-
неточности, неизбежные в наших расчётах.
Чем неоднороднее материал, чем хуже мы знаем действительные
нагрузки, чем упрощённее мы представляем себе соединение отдель-
отдельных элементов конструкции, тем большим этот коэффициент при-
приходится выбирать. Части машин в работе изнашиваются, поэтому
во многих случаях приходится давать «запас на износ». Точно так же
в металлических и деревянных инженерных сооружениях приходится
учитывать возможность коррозии и загнивания.
С другой стороны, имеются конструкции (самолёты), где необ-
необходимо итти до крайнях пределов снижения коэффициента запаса
с целью уменьшения веса. Точно так же инженеру приходится
снижать коэффициент запаса при выполнении работ в обстановке
военного времени.
Таким образом, правильный выбор допускаемых напряжений
представляет собой весьма сложную задачу, связанную и с методами
расчётов, методами исследования материалов, с хозяйственно-эконо-
хозяйственно-экономическими и некоторыми другими факторами. Выбор той или инрй
величины допускаемого напряжения определяет и расход данного
материала, и формы его применения в конструкции; этот выбор ре-
регулирует и продолжительность использования сооружений, и область
применения тех или других материалов. Поэтому ясно, что в Со-
Советском Союзе вопрос о допускаемых напряжениях тесно связан с
вопросами регулирования и планирования хозяйственной жизни
страны.
Для многих конструкций нормы допускаемых напряжений уста-
устанавливаются законом, и инженер должен лишь уметь правильно
применять их. В исключительных же обстоятельствах, например
в обстановке военного времени, инженеру приходится в некоторых
случаях отступать от этих норм; тогда он может руководствоваться
общими соображениями, изложенными в настоящем параграфе и
в главе XXXVII.
Д. Подводя итог всему сказанному выше, можно формулировать
следующие основные соображения.
Коэффициент запаса надо выбирать с тем расчётом, чтобы был
обеспечен известный запас против появления так называемого опас-
опасного состояния материала, которое будет угрожающим для работы
конструкции.
При статической или ударной нагрузке для пластичных материа-
материалов такое состояние характеризуется появлением больших остаточ-
остаточных деформаций (явление текучести), для хрупких — появлением
трещин, разрушением материала. При повторно-переменной нагруз-
нагрузке опасное состояние характеризуется появлением и развитием
трещины усталости. Напряжение, соответствующее наступлению

с {71 ОСНОВАНИЯ ДЛЯ ВЫБОРА КОЭФФИЦИЕНТА ЗАПАСА ПРОЧНОСТИ
69
опасного состояния, мы будем называть условно а0. Это напряже-
напряжение равно:
ат — пределу текучести — при наступлении
текучести пластичного материала,
ав — пределу прочности — при разрушении
(трещины) хрупкого материала,
ок — пределу выносливости — при появлении
трещины усталости.
Таким образом, формула C.4) может быть теперь уточнена и
заменена тремя формулами в зависимости от характера опасного
состояния материала:
где йт, кВУ kK — соответствующие коэффициенты запаса. Эти три
форму:ш можно обобщить в виде
Г 1	а°
подразумевая под о0 либо ат, либо ав, либо ак, а под k либо kT9
либо kB, либо kK.
Однако наша первоначальная формула C.4) не утратила своего
практического значения. Так как пределы текучести и выносливости
в известной мере связаны с пределом прочности, то можно для
всех видов опасного состояния установить коэффициент запаса и по
отношению к пределу прочности ов.
Таковы, в общем, исходные соображения, положенные в основу
решения задачи о выборе допускаемых напряжений.
Е. Переходя к вопросу о назначении величины коэффициента
запаса, пока ограничимся весьма краткими указаниями. Неоднород-
Неоднородность материала, неточность при определении величин сил, неточ-
неточность расчёта, т. е. общие факторы, учитываются так называемым
основным коэффициентом запаса k0. Для пластичных материалов
(сталь) он принимается обычно равным kT= ko= 1,4-f- 1,6, для
хрупких материалов и дерева ?в = &0 = 2,5-?-3,0. Остальные фак-
факторы, т. е. динамичность нагрузок, переменность их действия и
влияние местных перенапряжений, учитываются дополнительными
коэффициентами, на которые умножается основной.
При этом надо помнить, что полученное по формуле C.4) до-
допекаемое напряжение [о] должно сопоставляться с действующим в
Детали конструкции статическим напряжением без учёта динамич-
динамичности нагрузки и прочих дополнительных факторов.
Если при назначении допускаемого напряжения учитываются
только общие факторы, т. е. коэффициент запаса принимается

70
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ РАСТЯЖЕНИЯ И СЖАТИЯ [ГЛ. Щ
равным одному лишь основному, то динамику и местные напряже-
напряжения учитывают, когда это возможно, в величине действительного
напряжения, умножая основное статическое напряжение на коэффи-
коэффициенты динамики и концентрации. Нетрудно убедиться, что в обоих
случаях результаты будут одинаковыми.
Примерные значения общего коэффициента запаса по отноше-
отношению к пределу прочности для различного состояния материала и
для различного характера действия нагрузок со включением в него
обычной величины влияния динамичности нагрузки и местных на-
напряжений показаны в таблице 6.
Таблица 6. Коэффициенты запаса.
Характер нагрузки
1. Статическая нагрузка >
2. Ударная нагрузка
3. Переменная нагрузка (рас-
(растяжение-сжатие одинако-
одинаковой величины)
Состояние материала
Пластичный материал
Хрупкий материал
Пластичный материал
Пластичный материал (сталь)
2,4 ч- 2,6
3,0-ь 9,0
2,8-5- 5,0
5,0 4-15,0
Эта таблица имеет лишь ориентировочный характер; она даёт
представление об изменении коэффициента в зависимости от раз-
различных обстоятельств. Подробнее о коэффициентах запаса для
ударных и переменных нагрузок будет сказано в главах XXXVI
и XXXVII.
§ 18. Допускаемые напряжения на растяжение и сжатие
для различных материалов.
В предыдущем параграфе нами были выяснены те многочислен-
многочисленные обстоятельства, которые влияют на выбор величины коэффи-
коэффициента запаса прочности и, следовательно, на значение допускаемого
напряжения. Ниже, в таблице 7, приводятся ориентировочные вели-
величины основных допускаемых напряжений на растяжение и сжатие
некоторых главнейших материалов, применяемых в инженерном деле
и в машиностроении. Эта таблица составлена на основании дей-
действующих в настоящее время в СССР норм. Она не охватывает
всего многообразия материалов и условий их работы. В каждом
частном случае расчётной практики следует устанавливать допуска-
допускаемые напряжения в соответствии с официальными техническими
условиями и нормами проектирования данной конкретной конструк-
конструкции или, при их отсутствии, на основании соображений, изло-
изложенных в предыдущем параграфе.

ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ НА РАСТЯЖЕНИЕ И СЖАТИЕ
71
Таблица 7. Ориентировочные величины основных допускаемых
напряжений.
Наименование материала
Допускаемое напряжение
в кг/см^
на растяжение
Чугун серый в отливках
Сталь ОС и ст. 2
Сталь ст. 3
Сталь ст. 3 в мостах
Сталь углеродистая конструкционная в ма-
машиностроении
Сталь легированная конструкционная в ма-
машиностроении
Медь
Латунь
Бронза
Алюминий
Алюминиевая бронза
Дюралюмин
Текстолит
Гетинакс
Бакелизованная фанера
Сосна вдоль волокон
Сосна поперёк волокон
Дуб вдоль волокон
Дуб поперёк волокон
Каменная кладка
Кирпичная кладка
Бетон
280—800 1200—1500
1400
1600
1400
600—2500
1000—4000 и выше
300—1200
700—1400
600—1200
300— 800
800—1200
800—1500
300— 400
500— 700
400— 500
70—100
90—130
до 3
до 2
1—7
100—120
15- 20
130—150
20— 35
4— 40
6— 25
10- 90
Материалы, перечисленные в таблице, должны удовлетворять
требованиям и нормам (в отношении механической прочности, пла-
пластичности, технологии изготовления, химического состава и пр.),
содержащимся в соответствующих стандартах (см. приложение в
конце книги).

ОТДЕЛ II.
СЛОЖНЫЕ СЛУЧАИ РАСТЯЖЕНИЯ И СЖАТИЯ.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ч
ГЛАВА IV.
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
ПО ДОПУСКАЕМЫМ НАПРЯЖЕНИЯМ.
§ 19. Статически неопределимые системы.
Умение вычислять деформации стержней при растяжении и сжатии
да?т нам возможность установить, насколько изменяются формы и
размеры частей конструкций при действии внешних сил. Обычно
эти изменения формы настолько незначительны, что кажутся лишён-
лишёнными практического значения.
Однако есть целый класс конструкций, для которых проверка
прочности и определение сечения отдельных элементов невозможны
без умения определять деформации;
это так называемые статически не-
определимые конструкции (системы);
нахождение усилий в их элементах
представляет собой статически неопре-
неопределимую задачу.
Во всех примерах, которые мы
рассматривали до сих пор, усилия,
растягивающие или сжимающие стерж-
стержни, определялись из условий статики
твёрдого тела.
Так, в случае подвески груза Q на
двух стержнях (фиг. 38) АВ и АС мы
находим усилия Nx и N2, растягиваю-
растягивающие эти стержни, из условия равно-
равновесия точки Л. Три силы, приложенные в точке Л, должны удовле-
удовлетворять двум уравнениям равновесия, а именно: сумма проекций
этих сил на каждую из двух координатных осей должна равняться
нулю. Таким образом, число неизвестных (два) равно числу
уравнений (два), и усилия Nx и iV2 из этих уравнений могут быть
найдены. Эта задача — статически определимая.
Иначе будет обстоять дело, если груз Q будет подвешен на
трех стержнях (фиг. 39). В этом случае точка А находится в равно-
Фиг. 38.

§
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
73
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\^^^
весии под действием четырёх сил: Q, 7V3, Nt и Nb причём три
последние являются неизвестными. Уравнений же равновесия можно
написать по-прежнему лишь два. Таким образом, число неизвестных
на единицу больше числа уравнений — конструкция однажды ста-
статически неопределима, и задача не может быть решена только с
помощью уравнений статики.
Необходимое для решения задачи дополнительное уравнение
ложно составить, пользуясь теми представлениями о свойствах ма-
материалов, которые мы получили, переходя от теоретической меха-
механики к сопротивлению материалов. Речь идёт об учёте деформи-
деформируемости материала. Дополнительное уравнение мы сможем найти,
изучая те деформации, которые испы-
испытывает конструкция. Оказывается, что
всегда можно найти столько дополни-
дополнительных уравнений, сколько нам нужно,
чтобы полное число уравнений вместе
с условиями статики равнялось числу
неизвестных.
Эти дополнительные уравнения со-
составляются на основании одного об-
общего принципа, они должны выразить
условия совместности деформаций
системы.
Всякая конструкция деформируется
так, что не происходит разрывов
стержней, разъединения их друг от
друга, или не предусмотренных схемой сооружения перемещений
одной части конструкции относительно другой. В этом и заклю-
заключается совместность деформаций элементов системы.
Общий метод расчёта статически неопределимых систем таков.
Сначала следует выяснить, какие усилия необходимо определить;
затем написать все уравнения статики твёрдого тела; после этого —
составить дополнительные уравнения в таком числе, чтобы можно
было найти все неизвестные усилия.
Ход решения выясним на взятом частном примере (фиг. 39).
Пусть крайние стержни, имеющие равные площади поперечных се-
сечений,— стальные, средний же стержень — медный. Длина среднего
стержня /3, крайних lt; допускаемые напряжения для стали пусть
будут [ос], а для меди [ам]. Требуется установить прочные размеры
поперечных сечений этих стержней под действием подвешенного к
ним груза Q.
Прежде всего установим силы, действующие на каждый из трёх
Стержней. Так как в точках Л, В, С и D имеются шарниры, все
тРи стержня могут подвергаться только осевым усилиям. Считаем
ЭТи усилия растягивающими; для их определения мы должны рас-
рассмотреть равновесие точки Л, к которой приложена единственная
Фиг. 39.

74
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
[ГЛ. [V
///////////////////////////////У///////////
известная сила Q. Схема действия сил на точку и расположение
координатных осей даны на фиг. 40. Приравниваем нулю суммы
проекций на координатные оси сил, дей-
действующих на точку А:
N% sin a — Nt sin а = 0,
Q — 7V3 — iVj cos а — Nt cos а = 0.
Из первого уравнения получаем Л^ = Л^;
подставляя вместо iV2 во второе уравне-
уравнение величину Nx> получаем:
Д	N3 + 2М cos а = Q-	D- О
Теперь у нас осталось одно уравнение
у	с двумя неизвестными.
Для получения дополнительного урав-
Фиг. 40.	нения мы должны обратиться к изуче-
изучению деформаций нашей конструкции. Под
действием силы Q все три стержня удлинятся, и точка А опустится.
Так как усилия Nt и N2 равны между собой и стержни / и 2 из
одного материала, то при равных длинах стержней их удлинения
Ых и Д/2 будут одинаковы, точка А опустится по вертикали вниз.
Удлинение третьего стержня назо-
назовём Д/?.
Изменения длин всех трёх стерж-
стержней будут совместны, т. е. и после
деформации стержни остаются соеди-
соединёнными в точке А. Для нахождения
нового положения этой точки разъеди-
разъединим в ней стержни и изобразим на
чертеже (фиг. 41) новые длины край-
крайних стержней СС% и ВВ%, увеличив
их старую длину на величины A/j =
= ЛВ2 и Д/2 = АС2. Для того чтобы
найти новое положение точки А,
необходимо свести вместе удлинён-
Фиг. 41.	ные стержни СС^ и ВВ& вращая их
вокруг точек В и С. Точки В% и Са
совпадут в точке Аи двигаясь по дугам С^АХ и В%Аи которые
вследствие малости деформаций можно принять за прямые отрезки,
перпендикулярные к СС^ и ВВ%.
Новое положение крайних стержней ВАХ и САХ показано пун-
пунктиром. Так как конец среднего стержня тоже прикреплён к шар-
шарниру, то и он перейдёт в точку Ах, и удлинение А/3 будет равно
отрезку ААХ.
Удлинения всех трёх стержней A/t, «A^ и А/3 по закону Гука
будут пропорциональны усилиям, растягивающим эти стержни.

§ 19]	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ	75
Найдя из чертежа зависимость между этими удлинениями, мы по-
получим добавочное уравнение, связывающее между собой неизвест-
неизвестные усилия в стержнях. Из треугольника А\АВ^ имеем:
АВ% = AAi cos а или А^ = Д/3 cos а.	D.2)
Выразим Д/х и Д/3 через усилия Л^ и Nz. Для этого необходимо
знать площади этих стержней. Здесь мы подходим к важной осо-
особенности статически неопределимых систем: для нахождения уси-
усилий в стержнях необходимо предварительно задаваться разме-
размерами их поперечных сечений или их отношениями.
Пусть площади сечений стержней будут Fx и F3; модуль упру-
упругости стали обозначим Ес и модуль упругости меди ?м. Тогда
Л/ — N^ . Л/ _ ^з/з	(А оч
Подставляя эти значения A/t и А/3 в уравнение D.2), получаем:
Так как из треугольника ABD (фиг. 41) следует, что
/3 = lx cos a,
то
Wi=W3f?-cos*a.	D.4)
Таким образом, путём рассмотрения совместности деформаций
системы получено дополнительное уравнение, связывающее Л^ и N3.
Условие совместности деформаций имело место и в статически
определимых конструкциях, но там оно не налагало никаких огра-
ограничений на распределение усилий; для таких конструкций возможна
только одна система усилий, удовлетворяющая условиям равновесия;
так как там число неизвестных равно числу уравнений статики,
соответствующая система деформаций удовлетворяет и условиям со-
совместности. Например, для конструкции, изображённой на фиг. 38,
усилия в стержнях вполне определяются при малых деформациях из
условий равновесия точки А\ оба стержня могут получить вызы-
вызываемые этими усилиями удлинения без нарушения связи их друг
с другом, — условие совместности деформаций будет выполнено
автоматически.
Наоборот, в статически неопределимых конструкциях может
быть сколько угодно систем усилий, для которых выполнены
Уравнения равновесия, так как число неизвестных больше числа
этих уравнений; условие совместности деформаций отбирает из всех
этих возможных комбинаций усилий ту комбинацию, которая будет
иметь место в действительности.

76	РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ	[ГЛ. IV
В статически неопределимой системе (фиг. 39) положение точ-
точки А после деформации связывает между собой удлинения всех
трёх стержней; чтобы была соблюдена совместность деформаций,
необходимо, чтобы эти удлинения находились между собой в опре-
определённом отношении; это условие и даёт добавочное уравнение
D.4) для определения неизвестного усилия.
Продолжая решение нашей задачи, подставляем из D.4) значе-
значение Nx в уравнение D.1) и получаем:
Отсюда
1 + 2 jp?±- cos3 a
и из D.4)
Q ttV- cos2 a
1 4- 2 fsil cos' a
Из полученных формул видно, что величина усилий N зависит
не от абсолютных величин площадей F и модулей Е, а от их отно-
тений. Задаваясь различными соотношениями # = ^-, мы будем
получать различные комбинации усилий Л^, 7V2, N3.
По величинам этих усилий и допускаемым напряжениям можно
теперь найти и сами величины Fx и Fz из условий, что
Ff<l«e]. %<К].	D-7)
Определив из первого условия Ft и зная выбранную нами вели-
чину п = -^-у находим /73 = ~« Затем проверяем, удовлетворяет
ли она второму из условий D.7); если нет, то из этого условия
находим ^з, а Fx определяем формулой
Ft = nF%.	' D.8)
Таким образом, в статически неопределимой системе при дан-
данной нагрузке мы можем осуществить много вариантов распределе-
распределения усилий между стержнями, меняя соотношение площадей попе-
поперечных сечений стержней. Для дальнейшего разъяснения возьмём
числовой пример.
Пусть Q = 4 т; a = 30°; [ос] = 1000 кг\см\ ?с = 2.106 кг\см\
(ом] = 600 кг\см\ ?м=1 • Ю6 кг/см\

§ 19]	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ	77
Для предварительного подсчёта выбираем
Тогда
4FT?cos230°
Nt = Nt =	4^05	= 1,67 г,
=1'U г"
Из условий прочности получаем:
Г*~ [acj — 1000— 1'0/ СМ*
Так как мы приняли, что /71 = /73, то /73=1,67 см*.
Проверим, будет ли при таких условиях удовлетворено условие
прочности для среднего стержня:
^==1*^ = 667 яг/<г**>600 кг/см*.
Принятая площадь F$ мала; необходимо взять
Г3— [аи]— 600— 1>*0СМ-
Для того чтобы было	соблюдено положенное в основу нашего
расчёта условие Fl = FZy	мы должны принять /71==/73= 1,85 см*
вместо необходимой из	первого условия величины 1,67 см*.
Таким образом, в крайних стержнях мы имеем дополнительный
запас.
Если бы мы захотели	избежать этого излишнего запаса и при-
приняли бы
/?1 = Fa=l,67 см*\ /73=1,85 см\	D.9)
то сейчас же изменились бы усилия Л^, N% и iV3; отношение -—•
было бы равно уже не 1, как было раньше принято, а 0,9. В фор-
формуле D.5) знаменатель уменьшится и 7V3 увеличится; в формуле же
D-6) знаменатель уменьшится в меньшей степени, чем числитель,
поэтому Nt и N2 уменьшатся.
Уменьшая площади крайних стержней по отношению к площади
среднего, мы уменьшаем усилия в этих крайних элементах и уве-
увеличиваем усилие в среднем стержне.

78	РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ [ГЛ. IV
Здесь отражается общий закон, характеризующий распределение
усилий между стержнями в статически неопределимых системах,—
эти усилия распределяются соответственно жёсткости стержней;
чем больше площадь данного стержня, тем большую долю усилия
он на себя берёт, и наоборот.
Если мы будем площади Fx и F% приближать к нулю, то и уси-
усилия Nx и Ni будут приближаться к нулю, a iV3 к Q. Если же будем
уменьшать площадь Fd, то N3 будет уменьшаться, a Nt и N% —
увеличиваться.
При отношении п = 0,9 [формула D.8)] N1 = Ni=l,60 г,
yV3=l,20 г. Это потребует /73 = 2,0 см* и /71 = 1,8 см* вместо
требуемой по условию прочности для стальных стержней 1,6 см*.
Если бы мы приняли для крайних стержней Fi=\fi см*, то
отношение п вновь уменьшилось бы, и средний стержень оказался
бы опять перенапряжённым. Поэтому приходится опять мириться
с запасом в крайних стержнях. Из формулы D.4) вытекает, что
подобрать соотношение площадей п = -^ так, чтобы напряжение во
всех стержнях было равно допускаемому, можно лишь при опреде-
определённом значении угла а. В самом деле, если бы нам удалось назна-
назначить площади F точно по допускаемым напряжениям, то мы имели
бы соотношения
Nt = Fx [ac]; N3 = F3 [ам].	D.10)
Подставляя эти величины в равенство D.4), получаем:
F1[az) = Fz[au]^cos%a.	D.11)
Отсюда имеем:
cos2 a = |^| .|К	D.12)
т. е. для возможности подбора сечений стержней без излишнего
запаса при всяком п необходимо, чтобы cos а удовлетворял усло-
условию D.12).
При наших данных получаем:
2 1000. 1 . 10е	пЛО
CQS а= 600 . 2. 10' и а = 24'
Так как в нашей конструкции а = 30°, то при всяком п мы вы-
вынуждены будем или давать запас в одной группе стержней или
итти на перенапряжение для другой группы. Самую же величину п
надо выбирать так, чтобы получить наиболее экономичное решение.
В таблице 8 даны результаты подсчёта для различных п. Зная пло-
площади, длины и материал стержней, можно выбрать комбинацию,
дающую наиболее экономичное решение в зависимости от стоимо-
стоимости материала.

к 20J	ВЛИЯНИЕ НЕТОЧНОСТЕЙ ИЗГОТОВЛЕНИЯ	79
Таблица 8. Результаты расчётов при различных значениях я.
0,8
0,9
1,0
1,2
1,5
1т %
1,56
1,60
1,67
1,75
1,83
т
1,30
1,20
1,11
0,97
0,82
Fx—F% см*
необходимая
1,56
1,60
1,67
1,75
1,83
принятая
1,74
1,80
1,85
1,94
2,06
Fs см*
2,17
2,00
1,85
1,62 '
1,37
§ 20. Влияние неточностей изготовления на усилия в элементах
статически неопределимых конструкций.
В предыдущих параграфах мы установили особенности работы и
расчёта статически неопределимых систем.
1.	Недостающие для определения усилий уравнения могут быть
получены только при помощи изучения совместности деформаций
данной системы.
2.	Распределение усилий между элементами статически неопре-
неопределимой конструкции зависит от соотношения между площадями,
модулями упругости и длинами этих элементов.
3.	Чем более жёсток данный элемент, т. е. чем меньше его
длина и больше площадь и модуль упругости, тем сравнительно
ббльшую долю усилия он принимает на себя.
В настоящем параграфе мы рассмотрим ещё одно важное для
практики свойство статически неопределимых конструкций.
При изготовлении всякого рода сооружений нельзя обеспечить
абсолютно точного выполнения размеров их частей; всегда надо
считаться с возможностью тех
или иных небольших неправильно-
неправильностей при их изготовлении. Если
мы имеем дело со статически опре-
определимой системой, то такие неточ-
неточности не вызовут никаких напря-
напряжений в этой системе. Так, напри-
например, если стержень АВ (фиг. 38)
будет сделан немного короче, чем
предполагалось по чертежу, то это
поведёт за собой лишь лёгкое иска-
М(
'//////////////////////////////////////////А
\\
\\
\\
\\
\\
/\\
\ \
fc
/7
//
//
з ''
А > Г
* / /к
30°
УЧ-
Фиг. 42.
жение треугольника CAB. При от-
отсутствии силы Q усилия в стержнях
АВ и АС будут равны нулю неза-
независимо от того, с какой точностью
исполнены длины этих стержней.
Совсем иначе поведёт себя статически неопределимая конструк-
конструкция, изображённая на фиг. 39. Пусть средний стержень будет сделан
короче, чем следует на длину ЛЛ0 = 8 (фиг. 42). Чтобы соединить

80	РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ	[гл. IV
конец среднего стержня Ло с концами А крайних стержней где-то
в точке Аи необходимо средний стержень растянуть на длину
А/3 = Л0Л1, а крайние сжать на длину Д/1 = Л?2 = ЛС2. Проводя
в точках С2 и В% перпендикуляры к первоначальным положениям
крайних стержней, как описано в § 19, получаем точку соединения
концов всех трёх стержней Аг. Из чертежа получаем уравнение
совместности деформаций стержней:
А0А = AqAx -f- АХА,
или
Так как внешних нагрузок нет и усилие Nt — сжимающее,
а Л;3 — растягивающее, то уравнение равновесия D.1) принимает вид
N3 — 2iVj cos a = 0.	D.14)
Заменяя в уравнении D.13) величины A/j й А/3 их значениями
« л/ N& N*!l cosа
и решая совместно D.13) и D.14), получаем:
\ I E*F* I 9
]+2EcFlcos*a\
2 cos а
Знак плюс перед значениями усилий 7V3 и Л^ показывает, что
наши предположения об их направлении правильны.
Отметим, что в формулу D.3) можно подставлять взамен длины
среднего стержня величину /3, а не /3 — 8, ввиду малобти 8 по
сравнению с /3. Это упрощение всегда следует применять при рас-
расчёте на неточность изготовления.
Приведённый расчёт показывает, что неточности изготовления
влекут за собой напряжения в стержнях даже при отсутствии
внешних воздействий на конструкцию. Таким образом, возможность
появления так называемых начальных напряжений тоже является
основным свойством статически неопределимых конструкций.
Если все три стержня будут сделаны из одного материала и
одинаковой площади, то при действии груза Q (фиг. 39) растяги^
вающее усилие в среднем стержне будет больше, чем в крайних
D.4); наличие рассмотренной неточности изготовления вызывает
добавочное растягивающее усилие в среднем и ужимающие усилия
ь крайних стержнях; в этом примере наличие начальных напряжений

§20]
ВЛИЯНИЕ НЕТОЧНОСТЕЙ ИЗГОТОВЛЕНИЯ
81
усиливает неравномерность работы стержней и является поэто-
му вредным.
Если бы мы сделали средний стержень длиннее, чем следовало,
на величину 8, то начальные напряжения изменили бы знак и не-
несколько выраеняли бы неравномерность распределения усилий между
средним и крайними стержнями под нагрузкой Q. В этом случае
Фиг. 43.
рассмотренное свойство статически неопределимых систем было бы
использовано для улучшения работы конструкции.
Другим примером целесообразного использования начальных на-
напряжений является посадка бандажей на колёса подвижного состава.
Эти колёса состоят из двух частей: средней отливки — колёсного
центра, и стального кованого кольца, надеваемого* на центр, — бан-
бандажа (фиг. 43, а и б). Для закре-
закрепления бандажа на центре приме-
применяют специальные приспособле-
приспособления; кроме того, его внутренний
диаметр а?2 делают несколько
меньше диаметра dx\ обычно эта
разница составляет — dx—около
2qqqG?!. При надевании бандажа
на колёсный центр его нагревают
настолько, чтобы внутренний диа-
диаметр его стал больше диаметра
Центра; надетый бандаж, охла-
охлаждаясь, будет стремиться сжаться и будет стягивать центр. В бандаже
возникнет растягивающее усилие Nt а между бандажом и центром —
Реакция р (фиг. 43, б). Если мы разрежем бандаж по диаметру
(фиг. 44), то две силы TV должны уравновешивать сумму давлений
на внутреннюю поверхность отрезанной части бандажа. Составим
Условие равновесия, проектируя все силы на ось у (фиг. 44); на
элемент длины бандажа ds действует давление р ds\ его проекция

на ось у равна —р ds sin a = — р -у sin а da, так как ds= -^
82	РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ	[гл.
на ось у равна —р ds sin a = — /
Условие равновесия принимает вид
С d	pd С
— j /?ysina a— , или -^Isina a= ,
ABC	0
Отсюда
27V—pd = 0 и N=^-, или /? = —.
Таким образом, для двух неизвестных N и р мы имеем одно
уравнение статики; задача статически неопределима. Для нахожде-
нахождения неизвестных усилий необходимо учесть совместность деформаций
конструкции.
Растяжение бандажа и сжатие центра должны быть таковы, чтобы
уравнялась разница в диаметрах d1 и d2. Пренебрегая деформацией
центра ввиду его массивности по сравнению с бандажом, получаем,
что всё уравнивание разницы в диаметрах пойдёт за счёт удлинения
бандажа. Если эта разница составляет — долю диаметра бандажа,
то относительное удлинение еп диаметра, а стало быть, и всего
бандажа будет тоже —.
N
Относительное удлинение бандажа от усилия N будет zN = -pp9
где F—площадь поперечного сечения бандажа. Приравнивая эти
значения ел = е^, получаем добавочное уравнение
М 1	FF	9FF
N Е
Напряжение в бандаже равно о = -=г=:—.
В формулу D.16) вместо d можно подставлять (вместо началь-
начального диаметра бандажа d%) диаметр центра du так как обе эти ве-
величины отличаются друг от друга чрезвычайно мало.
Возьмём числовой пример (бандаж товарного вагона шириной
13 см и толщиной 7,5 см). Пусть
11	о
А—Л —QDD м м* ——		• Р	9. 1 Пь W? гм**
It 	 U-J	 <J\J\J JnAVy 	 	 1 f\f\(\ '			fvCj bJn ,
F=7,5- 13 = 97,5 cm\
Тогда получаем:
o = ^^-" = 2000 кг/с.м*; N = ^-^^-==195 000 кг=195 г,

21]
РАСЧЁТ СТЕРЖНЕЙ ИЗ РАЗНОРОДНЫХ МАТЕРИАЛОВ
83
§ 21. Расчёт на растяжение и сжатие стержней,
состоящих из разнородных материалов.
Этот вид стержней относится к категории статически неопреде-
неопределимых. В качестве примера разберём определение размеров железо-
железобетонной колонны квадратного поперечного сечения
со стороной а см и высотой Нм (фиг. 45). Колонна
сделана из бетона и снабжена продольными сталь-
стальными прутьями, расположенными вблизи поверх-
поверхности колонны, так называемой арматурой.
Обозначим: F6 — площадь поперечного сечения
бетонной части колонны; Fz — площадь всех стерж-
стержней арматуры; [аб] — допускаемое напряжение на
сжатие для бетона; [<зс]— то же для стали; ?б —
модуль упругости для бетона; Ес — то же для
стали.
Пусть требуется определить размеры колонны
так, чтобы она могла взять на себя нагрузку А
Заметим, что F6 -\- Fc = а2.
Найдём напряжения аб и ос, возникающие от на-
нагрузки Р по площадям F6 и Fc, и составим условия
прочности.
На колонну действует приложенная в центре
тяжести верхнего сечения сила Я, уравновеши-
уравновешивающаяся такой же (собственным весом колонны. пренебрегаем)
реакцией фундамента Р. Часть Р6
сжимающих колонну сил пере-
передаётся через бетон, часть Рс —
через арматуру (фиг. 46). Для на-
нахождения этих двух сил, вызываю-
вызывающих напряжения в бетоне и арма-
арматуре, мы имеем одно условие ста-	^	II	^
тики | | (| |>
DЛ7)	§	1	|
Задача является статически не-
неопределимой; второе уравнение по-
получается из рассмотрения совмест-
совместности деформаций по условию, что
как бетонная, так и стальная части
колонны- (фиг. 46) укоротятся на
одну и ту же величину А/, так
как верхние и нижние плоскости обеих частей совпадают. По закону
гУка имеем:
D.18)
Фиг. 45.
Фиг. 46.

84	РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ	[ГЛ. [у
это и будет второе уравнение, связывающее Рб и Рс. Из D.18)
находим
подставляя это значение Рс в уравнение D.17), получаем:
>^с
О
D.20)
Распределение усилий между элементами в статически неопреде-
неопределимых системах зависит от отношения площадей этих элементов и
их модулей упругости. Из уравнения же D.18), учитывая, что
получаем, что отношение напряжений в бетоне и стали зависит лишь
от отношения модулей
напряжения распределяются прямо пропорционально модулям упру-
упругости. Допустив, что при сжатии Ес = 2 • 106 кг/см* и ?1б = 2Х
X Ю5 кг/см*, получим -^-=10, и напряжения в стали всегда ока-
^б
жутся лишь в 10 раз большими, чем напряжения в бетоне. До-
Допускаемые же напряжения для стали примерно в 20 раз больше, чем
допускаемые напряжения для бетона на сжатие. Поэтому напряжения
в арматуре всегда будут ниже допускаемых.
Размеры колонны определяются из условия прочности бетона на
сжатие:

С 22] НАПРЯЖЕНИЯ, ВОЗНИКАЮЩИЕ ПРИ ИЗМЕНЕНИИ ТЕМПЕРАТУРЫ	85
Необходимо теперь лишь задаться отношением ¦—-. Обычно пло-
* б
уцадь арматуры выражают в процентах от полной площади колонны
р J^-F6 и задаются процентом армирования, не меньшим, чем
0,4% 4-0,2%.- р	^
Обозначим р с^ = — ; так как площадь арматуры мала по
сравнению с площадью бетона, то
m F6'
Подставляя эту величину в условие D.21), получаем
Р
- = [аб] и F6=-
р
Площадь арматуры будет равна
Пусть Р = 30 г; m =100 (арматуры 1 «/о); 1^ = 10; [зв] = 45 кг/см3 и
[»с]=1250 кг/см*. Тогда
=605 см3> Fc=ш=6>05 см2; Fб+Fс=611 см*-
Берём колонну квадратного сечения 25 X 25 см и ставим 4 стержня
диаметром d = 14 мм с общей площадью 6,28 см2.
Вычисление деформаций для таких конструкций ведётся по общим
правилам. Так как укорочение бетонной и стальной частей колонны
одинаково, то безразлично, какой формулой в равенстве D.18)
воспользоваться для вычисления А/.
§ 22. Напряжения, возникающие при изменении температуры.
В статически неопределимых системах возникают напряжения
при отсутствии внешних нагрузок не только от неточностей изго-
изготовления и сборки, но и от изменения температуры.
Довольно значительные напряжения этого типа получаются в рель-
Сах> сваренных в одну непрерывную линию. При изменении темпе-
Ратуры рельсов по отношению к той, при которой была произведена
Сварка, в них возникают либо растягивающие, либо сжимающие на-
напряжения. Эту задачу можно схематизировать в таком виде: дан
Стержень, защемлённый неподвижно концами при температуре tx\

86	РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ	[ГЛ. IV
найти, какие возникнут в нём напряжения при изменении темпера-
температуры до t<i (фиг. 47). Длина стержня /, площадь поперечного сече-
сечения F, модуль упругости Е.
Выясним, какие силы будут действовать на стержень, если тем-
температура повысится от tx до t%. Стержень в таком случае стремится
удлиниться и будет распирать опоры Д
" и В. Со стороны этих опор на стержень
. будут действовать реакции, направлен-
° ные, как показано на чертеже. Эти силы
——/	^\ и будут вызывать сжатие стержня.
Фиг. 47.	Их величины нельзя найти из усло-
условий статики, так как единственное усло-
условие равновесия даёт нам, что реакции опор в точках А и В
равны и прямо противоположны. Величина же реакций Р остаётся
неизвестной, и конструкция оказывается статически неопределимой.
Для составления дополнительного уравнения учтём, что длина /
стержня, закреплённого концами, остаётся и при нагревании неиз-
неизменной; значит, укорочение Д//>, вызываемое силами Р, равно по
абсолютной величине тому температурному удлинению Д/^, которое
стержень получил бы, если бы опора А осталась на месте, а конец В
стержня был бы освобождён и мог бы перемещаться при нагревании.
Значит,
А/, —Д/Р=0.	D.22)
Это и будет условие совместности деформаций; оно указывает
на то, что и после повышения или понижения температуры длина
стержня не изменилась, — он не оторвался от неподвижных опор.
Так как
~ и Ы< = аЦЬ-Ь)9
где а — коэффициент линейного температурного расширения мате-
материала стержня, то
— tx),	D.23)
т. е. напряжение, вызванное изменением температуры в стержне
постоянного сечения с жёстко защемлёнными концами, зависит лишь
от модуля упругости материала, его коэффициента линейного рас-
расширения, разности температур и не зависит ни от его длины, ни от
площади поперечного сечения.
Сила Р равна

§22]
НАПРЯЖЕНИЯ, ВОЗНИКАЮЩИЕ ПРИ ИЗМЕНЕНИИ ТЕМПЕРАТУРЫ
87
В рассматриваемом примере при t^^>tx напряжение а будет
сжимающим, так как направление реакций Р внутрь стержня здесь
принято положительным. Если придерживаться обычно применяемого
обозначения сжимающих напряжений знаком минус, а растягивающих
знаком плюс, то для автоматического получения знака напряжений
формула D.23) должна быть написана так:
о =
У/////////////Л/////////////Л
У///,
Когда поперечное сечение стержня не постоянно по его длине
или он сделан из разных материалов, когда конструкция опор даёт
ему возможность несколько изменить свою длину, или если эти усло-
условия имеют место одновременно, метод
определения температурных напряжений,
в основе своей оставаясь прежним, имеет
всё же ряд особенностей.
Переменность сечения и различие
в материалах необходимо учесть при
подсчёте А/, определяя его суммирова-
суммированием подсчётов, сделанных по каждому
отдельному участку. Возможность для
стержня несколько изменить свою длину
отразится в уравнении совместности
деформаций D.22); разность деформа-
деформаций, температурной и вызванной силами,
в этом случае не будет равна нулю,
а будет равна той величине, на которую
наш стержень имеет возможность удли-
удлиниться.
Пример 9. Стальной стержень состо-
состоящий из двух частей длиной /t=40 см и
1% = 60 см и площадью соответственно Ft =
*= Ю см2 и F2 = 20 см2, защемлён одним кон-	фш • 48-
ном; другой конец не доходит до опоры на
величину До = 0,3 мм (фиг. 48). Найти напряжения в обеих частях при повы-
повышении температуры на г = 50° С, если а = 125 • 10~7.
Повышение температуры вызывает удлинение стержня Mt> а сжатие
*го реакциями опор Р—укорочение Д/р. Разность этих двух деформаций (по
абсолютной величине) равна До (см. фиг. 48):
А// — Д/Р=АО;
**о и будет условие совместности деформаций. Величины Mt и Д/р соответ-
соответственно равны

88	РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ	[ГЛ. IV
Огсюда
[125 • 1О-' • 100 • 50-0,03] 2 • 10' ¦ 10 _
Напряжение в верхней части равно
о1== Р==9
ГI	1U
Р 9300
в нижней части о" = — = -^- = 465 кг/см2 (оба напряжения — сжимающие).
Если бы зазора До не было, то усилие и напряжения возросли бы
в 1,92 раза.
§ 23. Одновременный учёт различных факторов.
Иногда в статически неопределимых конструкциях приходится
одновременно учитывать влияние внешней нагрузки, изменения тем-
температуры и неточности изготовления. Решение таких задач возможно
двумя путями: первый путь — это одновременный учёт всех факторов.
В этом случае в уравнение совместности деформаций должны быть
включены члены, отражающие влияние всех этих обстоятельств
(нагрузки, температуры, неточности изготовления). Полученные в ре-
результате расчёта усилия и напряжения являются окончательными.
Второй путь расчёта подобных конструкций заключается в раз-
раздельном учёте усилий и напряжений, вызванных нагрузкой, темпе-
температурой, неточностью изготовления. Решается как бы несколько
отдельных задач, в каждой из которых учитывается только один из
этих факторов. Окончательные усилия и напряжения определяются
путём алгебраического суммирования этих-величин, полученных при
решении каждой из задач. Последний путь часто является более
ясным и удобным, вызывая лишь небольшое увеличение количества
выкладок. Он носит название способа сложения действия сил.
Рассмотренные до сих пор частные примеры расчёта статически
неопределимых конструкций учитывали влияние лишь одного какого-
нибудь фактора — внешней нагрузки, изменения температуры или
неточности сборки. Для ознакомления с приёмом одновременного
учёта всех этих обстоятельств решим следующий числовой пример.
Пример 10. Три параллельных вертикальных стержня одинаковой
длины / = 2 м поддерживают жёсткий брус АВ, к коюрому приложена сила
Р = 4 т (фиг. 49). Расстояния между стержнями и от среднего стержня до
силы Р соответственно равны: а = 1,5 ж, Ь=\ м и с = 0,25 м. -Средний
стержень выполнен короче проектного размера на 5 = 0,2 мм. Данные
о стержнях помещены в таблице 9.

23]	ОДНОВРЕМЕННЫЙ УЧЁТ РАЗЛИЧНЫХ ФАКТОРОВ
Таблица 9. Данные к примеру 10.
89
„чуй стержней
1
2
3
Материал
медь
сталь
сталь
F см*
2
1
3
Е кг/см*
Ы0в
2-10е
2.10е
а
17-10-*
13-10-*
13 10~в
Температура конструкции во время её эксплуатации может повыситься
на 20° С.
Определить напряжения в каждом из трёх стержней.
Предположим, что усилия во всех стержнях Nu jV2 и Ns будут растяги-
растягивающими. Равные им реакции точек подвеса стержней показаны на фиг. 49.
Уравнений равновесия ввиду параллельности всех сил мы можем составить
два. Первое — сумма проекций на вертикаль — имеет следующий вид:
#i + ^2 + N8 — Р = 0.	D.24)
Для составления второго уравнения возьмём сумму моментов всех сил
относительно точки подвеса второго стержня:
Nxa — Nzb + Рс = 0.	D.25)
Для определения трёх неизвестных усилий этих двух уравнений равно-
равновесия недостаточно. Необходимо обратиться к рассмотрению деформаций.
На фиг. 50 показана схема деформаций нашей конструкции, составленная
/
п
1
I
L,
Ш///////////////А
1
—— a —^
—^-
л
V///////////A
Z
c\
t
p
N3
3
T	¦
-4-
Фиг. 49.
Фиг. 50,
в предположении растягивающих усилий во всех стержнях. Из рассмотрения
ьшй схемы можно составить следующее условие совместности деформаций:
А/,-А/. _а+Ь
Значения входящих в это уравнение деформаций (с учётом влияния
температуры) будут следующими:
Подставим эти значения деформаций в уравнение D.26):
N'J
D.27)

90
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
1гл.
Совместно решая уравнения D.24), D.25) и D.27), определяем Nlt #f
и N3. Они будут равны:
Ni = 792 кг, Ns = 1020 кг и Ns = 2188 кг.
Если бы наше предположение о направлении усилий для какого-нибудь
стержня оказалось ошибочным, то мы получили бы отрицательное значение
этого усилия.
Теперь находим соответствующие напряжения:
в первом стержне 0! = ^- = — = 396 кг/см*,
во втором стержне а2 = =е=—т—=
N* 2188
и в третьем стержне а, = —.==——=
729 кг/см*.
Эта же задача могла бы быть решена при раздельном учёте влияний
нагрузки, температуры и неточности изготовления с последующим алгебраи-
алгебраическим суммированием напряжений. Результат был бы, конечно, такой же.
§ 24. Более сложные случаи статически неопределимых
конструкций.
Во всех рассмотренных статически неопределимых задачах число не-
неизвестных усилий на единицу превышало число уравнений статики; это —
задачи однажды статически неопределимые; одно из неизвестных усилий
может быть принято, как говорят, за лишнюю, не определяемую из уравне-
уравнений статики, неизвестную.
Могут быть случаи, когда таких лишних неизвестных будет несколько;
тогда придётся составить столько же дополнительных уравнений, рассматри-
Фиг. 51.
вая совместность деформаций системы. Это всегда возможно. Как пример
можно указать конструкцию, изображённую на фиг. 51; очень жёсткий
стержень шарнирно прикреплён к неподвижной опоре, подвешен на трёх
стержнях и нагружён силой Р.
Для стержня АВ можно написать три уравнения равновесия; число же
неизвестных будет пять: усилия в трёх подвесках и вертикальная и горизон-
горизонтальная составляющие реакции в шарнире Л.
Дополнительные уравнения можно написать, рассматривая деформацию
системы. Так как стержень АВ мы считаем очень жёстким, то его собствен-

с 25]
примеры
91
нъ»ми деформациями можно пренебречь. Тогда он, оставаясь прямым, зай-
займет положение ABt. Из подобия треугольников можно найти соотношения
между A/i, А/, и А/3, что и даёт два дополнительных уравнения, а именно:
= ^1 и
А/, '
cos 45°
Дальнейший ход решения задачи подобен рассмотренному выше (§ 19).
§ 25. Примеры.
Пример И. Стержень, защемлённый концами А и #, состоит из двух
равных половин длиной -у (фиг. 52, а); верхняя половина изготовлена из
стали, нижняя — из меди. Площади обеих частей стержня одинаковы и равны
/^ = 20 см2. К среднему сечению приложена сила Р=б г, направленная по
оси стержня сверху вниз от конца А к концу В. Найти напряжения в мед-
медной и стальной частях при повышении температуры на f = 30° С. Модули
упругости равны Ес = 2 • 10е кг/см2, Ем =
s= 106 кг/см2. Коэффициенты линейного тем-
температурного расширения ас = 125 • 10~7,
ом = 165 . 10-7.
Реакции опор стержня принимаем на-
направленными вверх и обозначаем Ра и Рь
(фиг. 52, а). Условие статики приводит к
тому, что
¦5-
Для того чтобы лучше разобраться в
имеющих место деформациях, предполо-
предположим, что нижний конец стержня свободен,
опора отсутствует (фиг. 52, б). Это предпо-
предположение не изменит работы конструкции
при условии, что перемещение этого конца
равно нулю и что действие опоры учтено
наличием приложенной к нижнему концу реакции данной опоры — силы Р&.
Полученный путём отбрасывания «лишнего» (против количества уравнений
равновесия) закрепления статически определимый стержень называется
основной системой нашей статически неопределимой конструкции. Заметим
попутно, что мы могли бы выбрать и другую основную систему, хотя бы
путём отбрасывания верхней опоры (фиг. 52, в). Основную систему при этом
пришлось бы. загрузить, конечно, помимо силы Р ещё и реакцией этой верх-
верхней отброшенной опоры.
Основная система, загруженная всеми нагрузками и реакциями всех опор,
сохранённых и отброшенных, совершенно эквивалентна той статически не-
неопределимой конструкции, из которой она получена при условии, что удовле-
удовлетворены уравнения совместности деформаций. Эти уравнения составляются,
Исходя из тех ограничений, которые опоры статически неопределимой системы
накладывают на деформации. Совместное их решение с уравнениями равно-
Весия и определяет величины всех неизвестных.
В нашем случае условие совместности выражает ту мысль, что удлине-
Ние стержня от повышения температуры (при свободном нижнем конце)
плюс удлинение верхней его части от силы Р должно быть численно равно

92	РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ	[гл.
укорочению стержня от силы Рь:
IIP! Phi Phi
или
"сП ¦ °м
2 I +^
Отсюда находим реакцию Рь, а из условия статики и Ра:
Обе реакции состоят из двух слагаемых — первого, вызванного силой Р9
и второго, вызванного действием температуры; мы могли бы изменить поря-
порядок решения задачи и находить отдельно реакции и напряжения от силы Ръ
и от повышения температуры, а потом их суммировать (способ сложения
действия сил).
Реакции от силы Р обе направлены вверх, а от действия температуры —
реакция опоры В вверх, а опоры А — вниз (минус в формуле для Ра). Таким
образом, весь стержень будет сжат температурными реакциями, и кроме того,
верхняя часть будет растянута, а нижняя сжата силами:
Поэтому, обозначая растягивающие напряжения знаком +, а сжимаю-
сжимающие —, получаем:
i+&
6000	30.125.10-41+^12.10.
2 • 10"
= 2U0 — 580 = — 380 кг/см2

с 25]	примеры	93
для сечений верхней части и
•-[•+5:1
¦?\F
6000
[¦+'-#]
. — 580 = — 680
20
для сечений нижней части. Необходимо обратить внимание на то, что при
решении задачи удобно преобразовывать формулы так, чтобы в них входили
отношения больших величин (Е) или малых (а); это упрощает числовые
расчёты.
Пример 12. Стержень защемлён верхним концом Л и не доходит до
нижней опоры В на величину Д/о = 1,25 мм; верхняя часть стержня мед-
медная, длиной /м = 1,6 м9 площадью FM = 10 см2; нижняя часть — стальная,
площадью Fc = 20 см2 и длиной /с = 0,8 м. Сила Р= 10 т приложена по
оси стержня вниз в месте раздела обеих частей. Найти напряжения в сече-
сечениях стальной и медной части.
Для нахождения напряжений определим реакции РА и Р в; предполагаем
их направленными вверх. Условие равновесия даёт:
Условие совместности деформаций выражает ту мысль, что разность величин
удлинения верхней части и укорочения нижней равна зазору Д/о:
Д/м — Д/с = Д/о
или
F~F Т1Г
ии1 м ^z1 с
Заменяя Рв через Р—РА> получаем:
°"
F F ' F F	F F
'-'м1 и ^cl с '-'С1 с
Отсюда
с1 PU . А/
р	{	 р	1м

94
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
[гл.
Подставляя числовые значения, имеем:
1 ОС
.20. 2- 10»
=805°
80 • 10 • 10°
о„ = -рг- = —гтг- = 805" кг/см* (растяжение);
гтг
Ю 000 -
РВ=
10.10-
80 Ш 10»
160-20-2- 10е
1950
в
(сжатие).
Пример 13. Определить начальные напряжения в трёх полосах звена
цепи висячего моста (фиг. 53), если средняя полоса будет короче крайних на
^ = 2ббб' ГДе /"~длина ПОЛ°С
Материал полос—сталь. Полосы
соединены болтами, проходя-
проходящими через проушины. Дефор-
Деформацией болтов можно прене-
пренебречь. Схема конструкции и
картина деформации даны на
-/-
щи
тт
[ | 1 i.
V
-I
Фиг. 53.
if фиг. 54.
, j j | '	Сжимающие усилия в край-
. ULlU них полосах обозначаем Nt и
	^	Nz, растягивающее усилие в
средней iV2; условия статики
приводят к уравнениям
-64,
I
Фиг. 54.
Обозначая длину полос /, а их площадь F, получаем:
или
Условие совместности дефор-
деформаций выражает, что сумма
числовых значений удлинения
средней полосы и укорочения
крайней равна Ь (фиг. 54):
Ь = A/x + Д/2.
EF*
Так как
= -—, то
' 2EF ~ EF~ 2EF '

* 26]	ПОНЯТИЕ О РАСЧЁТЕ ПО ДОПУСКАЕМЫМ НАГРУЗКАМ
оТСК)да напряжение в средней полосе равно
N* 2ЬЕ 2 • 2 • 10е
- = 667 кг/см2 (растяжение).
95
3/
3-2000
Напряжения в крайних полосах будут вдвое меньшими и сжимающими.
Пример 14. Стальной болт диаметром dx = 30 мм
проходит внутри чугунной трубки (фиг. 55), внутренний
диаметр которой равен
наружный
tfз == 32 мм,
= 62 мм.
Гайка болта завинчена настолько, что головка и шайба
соприкасаются с концами трубки, но болт ещё не на-
натянут. Длина трубки / = 500 мм, ?"с = 2« 10е кг/см2,
?ч = 1,2 • 10е кг\см2. На какую длину надо навернуть
гайку на болт, чтобы вызвать в нём натяжение Р= 12 г?
Какие напряжения будут в чугунной трубке?
Навинчивание гайки вызовет реакции между шай-
шайбой и торцом трубки. Эти реакции будут сжимать
трубку и растягивать болт; надо добиться, чтобы они	Фиг. 55.
были равны 12 т. Укорочение трубки плюс удлинение
болта и составят то перемещение Л, на которое надо навернуть гайку, чтобы
вызвать заданное натяжение болта.
Площадь сечения трубки равна
Рт = ~ (d2 — df) = ~ F,22 — 3,22) = 22,1 см\
Площадь сечения болта равна
Необходимое перемещение гайки равно
PI , PI PI
12 000» 500
: 2 - 10е
2- 10е- 7,07
*»*
ГЛАВА V.
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
ПО ДОПУСКАЕМЫМ НАГРУЗКАМ.
§ 26. Понятие о расчёте по допускаемым нагрузкам. Примене-
Применение к статически определимым системам.
В предыдущем изложении методов расчёта на растяжение и сжа-
сжатие как статически определимых, так и неопределимых конструкций
}*ы исходили (§§ 4 и 19) из основного условия прочности огаах^[а].
Это неравенство требует выбора размеров конструкции с таким рас-
ч?том, чтобы наибольшее напряжение в самом опасном месте не
пРевосходило допускаемого.

96
РАСЧЁТ ПО ДОПУСКАЕМЫМ НАГРУЗКАМ
[гл.
Но можно стать на другую точку зрения (§ 4). Можно задать
условие, чтобы действительная нагрузка на всю конструкцию не
превосходила некоторой допускаемой величины. Условие это можно
выразить таким неравенством:
За допускаемую нагрузку надо выбрать некоторую -г- часть той
нагрузки, при которой конструкция перестанет функционировать
правильно, перестанет выполнять свой
назначение. Такая нагрузка обычно
называется предельной, иногда—раз-
иногда—разрушающей в широком смысле слова
(под разрушением конструкции подра-
подразумевают прекращение её нормальной
работы).
В качестве примера возьмём си-
систему из двух стальных стержней АВ
и АС (фиг. 56), нагружённых си-
силой А Рассчитывая эту систему обыч-
обычным путём, найдём усилия NX = N% по
формуле
N N	N
Л^ Тс
Фиг. 56.
2 cos а
(из равновесия узла Л). Отсюда площадь каждого из стержней
равна
р
[а] ~ 2[ajcosa #
По способу допускаемых нагрузок имеем
Введя в качестве коэффициента запаса для конструкции в целом
ту же величину kt которая была принята в качестве коэффициента
Р
запаса для напряжений, мы получим, что величина Рдоп= —j*-.
Предельной, опасной величиной Рпр будет та, при которой напря-
напряжения в стержнях дойдут до предела текучести:
Япр = 2/4jtcos a.	(a)
Таким образом, допускаемая величина Р равна
cos a

ft 27]	РАСЧЁТ ПО СПОСОБУ ДОПУСКАЕМЫХ НАГРУЗОК
Условие прочности (а) принимает вид
а учитывая, что -jr ¦
Отсюда
97
получаем
P<2/7[a]cosa.
2 1<j| cos a
Таким образом, расчёт по допускаемым нагрузкам привёл в дан-
данном случае к тем же результатам, что и расчёт по допускаемым
напряжениям. Это всегда имеет место для статически определимых
конструкций при равномерном распределении напряжений, когда
материал по всему сечению используется полностью.
§ 27. Расчёт статически неопределимых систем
по способу допускаемых нагрузок.
Совсем другие результаты мы получим, если будем применять
способ допускаемых нагрузок к статически неопределимым систе-
системам, стержни которых изготовлены из
материала, обладающего способностью
к большим пластическим деформа-
деформациям, например из малоуглеродистой
стали.
В качестве примера рассмотрим
систему из трёх стержней, нагружён-
нагружённых силой Q (фиг. 57), Пусть все
стержни сделаны из малоуглероди-
малоуглеродистой стали с пределом текучести ат.
Длины крайних стержней, как и выше,
обозначим 4, длину среднего /3. До-
л\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\*
Фиг. 57.
пускаемое напряжение [о] = -?-. Как
и раньше, при расчёте этой статически
неопределимой системы зададимся отношением площадей стержней;
примем, что все три стержня будут иметь одинаковую площадь F.
Тогда, решая задачу так, как это указано в § 19, получим:
l+2cos8
Так как Nd^>Nu средний стержень напряжён больше, чем
крайние; поэтому подбор площади сечения F надо произвести по
Формуле
4 Н. М. Беляев

98
РАСЧЁТ ПО ДОПУСКАЕМЫМ НАГРУЗКАМ
[гл. v
Ту же величину площади надо дать и боковым стержням; в них
получается некоторый дополнительный запас.
Применим способ допускаемых нагрузок; условием прочности будет:
i -Ceil
доп— k •
Что в данном случае следует понимать под предельной нагруз-
нагрузкой конструкции? Так как конструкция выполнена из материала,
имеющего площадку текучести, то, по аналогии с простым растяже-
растяжением стержня из такого материала, за предельную нагрузку следует
взять груз, соответствующий достижению состояния текучести для
всей конструкции в целом. Назовём эту нагрузку Q?. Пока сила Q
не достигла этого значения, для дальнейшей деформации (опуска-
(опускания точки А) требуется возрастание нагрузки. Когда же Q сде-
сделается равным Q*, дальнейший рост деформаций будет происходить
уже без увеличения нагрузки, — конструкция выйдет из строя.
Для определения величины ©J рассмотрим постепенный ход де-
деформации нашей стержневой системы. Так как средний стержень
напряжён сильнее крайних, то в нём раньше, чем в других, напря-
напряжение дойдёт до предела текучести. Нагрузку, соответствующую этому
моменту, обозначим QT; она будет равна
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\^
где Nl = FoT — усилие в среднем стержне, соответствующее его
пределу текучести.
Напряжения в крайних стержнях, имеющих ту же площадь,
в этот момент ещё не дойдут до предела текучести, и эти стержни
будут упруго сопротивляться дальней-
дальнейшей деформации. Для того чтобы эта
деформация происходила, необходимо
дальнейшее увеличение нагрузки до
тех пор, пока в крайних стержнях
напряжения тоже не дойдут до пре-
предела текучести. Лишь тогда будет до-
достигнута предельная грузоподъёмность
конструкции QJ.
Так как при нагрузке QT напряже-
напряжения в среднем стержне дойдут уже до
предела текучести от, то при дальней-
дальнейшем возрастании груза они, а стало
быть и усилие Af3, останутся без
увеличения. Наша статически неопре-
неопределимая система превратится в статически определимую, состоящую
из двух стержней АВ и АС и нагружённую в точке А силой Q,
направленной вниз, и известным усилием NJ, равным Fo7 (фиг. 58).
Фиг. 58.

§ 27]	РАСЧЁТ ПО СПОСОБУ ДОПУСКАЕМЫХ НАГРУЗОК	99
Такая схема работы нашей конструкции будет иметь место, пока
Для иллюстрации хода деформации рассматриваемой конструкции
изобразим графически зависимость между силой Q и перемещением /
точки А (фиг. 59). Пока Q^QT,
опускание точки А равно удлине-
удлинению среднего стержня и опреде-
определяется формулой
/oi — А 4 —;
Как только Q будет заклю-
заключаться в промежутке QT ^ Q ^ Q?,
перемещение точки А должно быть
вычислено, как опускание этого
узла в системе двух стержней АС
и АВУ нагружённых в точке А силой (Q — FoT). Из фиг. 41 мы
видим, что это опускание равно
Фиг. 59.
/=
A/i .
COS a '
в свою очередь
Отсюда
2 cos a
2EFcosa
Jn =
2?^cosa<x -~ 2?Fcos*a '
Для /,2 (на втором участке) получаем уравнение прямой, но уже
не проходящей через начало координат. После достижения нагруз-
нагрузкой Q значения Q* напряжения в крайних стержнях достигнут
предела текучести, и система будет деформироваться без увеличе-
увеличения нагрузки. График перемещения идёт теперь параллельно оси
абсцисс.
Для определения предельной грузоподъёмности всей системы Q*
мы должны для системы двух стержней, нагружённых силой (Q — FoT),
найти то значение Q, при котором напряжения и в крайних стерж-
стержнях дойдут до предела текучести. Такая задача решена в предыду-
предыдущем параграфе; подставляя в выражение (а) § 26 вместо Р величину
Я — FoT, получаем:
(Q — Лт)Вр = 0? — F°i = 2/4 cos a.

100	РАСЧЁТ ПО ДОПУСКАЕМЫМ НАГРУЗКАМ	[ГЛ, V
Отсюда
Q? = /7aT(
Допускаемая нагрузка будет равна
v*on—' k ~ k
а учитывая, что -^- = [с], получаем
Qm = F[o](l
Окончательно:
Эта величина меньше, чем полученная обычным методом расчёта,
т. е.
Q
М A+2 COS3 а)'
При Q = 4 г, а = 30°, [ас] = 1000 кг /см* (сталь) получаем:
по обычному способу
р—	4000	_ 1 74 rf-
г ~ 1000 A+2 cos8 30°) ~" >' сж '
по способу допускаемых нагрузок
F4000	 4R 9
F
t ~ 1000 A+2 cos 30°)
Таким образом, метод расчёта по допускаемым нагрузкам по-
позволяет спроектировать статически неопределимую систему из мате-
материала, обладающего площадкой текучести, экономичнее, чем при
расчёте по допускаемым напряжениям. Это понятно: при способе
расчёта по допускаемым напряжениям мы считали за предельную
нагрузку нашей конструкции величину QT, при которой до предела
текучести доходил лишь материал среднего стержня, крайние же
были недонапряжены. При методе расчёта по допускаемым нагруз-
нагрузкам предельная грузоподъёмность определяется величиной Q?^>QT-
При нагрузке Q? полностью используется материал всех трёх
стержней.
Таким образом, новый метод расчёта позволяет реализовать
скрытые при старом способе запасы прочности в статически неопре-
неопределимых системах, добиться повышения их расчётной грузоподъём-
грузоподъёмности и действительной равнопрочности всех частей конструкции.
Не представит никаких затруднений распространить этот метод на
случай, когда соотношение площадей среднего и крайних стержней
не будет равно единице.

с 28]	ПРИМЕНЕНИЕ СПОСОБА ДОПУСКАЕМЫХ НАГРУЗОК	101
Изложенные выше теоретические соображения проверялись не-
неоднократно на опыте, причём всегда наблюдалась достаточно близ-
близкая сходимость величин предельной нагрузки — вычисленной и
определённой при эксперименте. Это даёт уверенность в правиль-
правильности теоретических предпосылок метода допускаемых нагрузок.
§ 28. Применение способа допускаемых нагрузок к расчёту
железобетонных стержней.
В § 21 показан расчёт железобетонной колонны на сжатие по методу
допускаемых напряжений. Как мы видели, в этом случае не удалось добиться
равнопрочности: напряжения в бетоне достигли допускаемых, а в арматуре —
не достигли.
Применим способ допускаемых нагрузок. Условие прочности имеет вид:
Для установления Рдоп надо найти предельное значение Рпр для всей
колонны и разделить его на коэффициент запаса.
Опыты показали, что при сжатии железобетонных колонн бетон после
достижения напряжениями предела прочности на сжатие начинал сдавать;
появлялась своеобразная «текучесть> бетона, постепенно разрушающегося,
но поддерживаемого арматурой; колонна продолжала укорачиваться при
постоянных напряжениях в бетоне и возрастающих в арматуре; разрушение
наступало, когда в арматуре напряжения доходили до предела текучести.
Такая картина разрушения наблюдалась в колоннах с арматурой из малоуг-
малоуглеродистой стали, хорошо укреплённой хомутами против бокового выпу-
выпучивания.
Проделанные в СССР в большом количестве опыты показали, что для
железобетонных колонн указанного выше типа предельная нагрузка равна
сумме предельных нагрузок бетонной и стальной частей:
где F$ — площадь бетона; Fc — площадь арматуры; ав — предел прочности
бетона при сжатии; от — предел текучести стали. В таком случае
Условие прочности принимает вид
р ^ (F6 Ы + Fc Ы) = р« (ы + tel 75J
Задаваясь отношением -~ или процентом армирования, получаем:
* б
Применим этот способ к примеру, рассмотренному в § 21. Имеем:
Р == 30 г; Ы = 45 кг/см*; К] = 1250 кг/см*; р- =

102
УЧЁТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИИ И СЖАТИИ [гл. VI
Следовательно,
30 000
45+таг1250
- = 522,5 см*,
т. е. меньше, чем полученная в § 21 величина F05 см2).
Благодаря работам советских учёных нроф. Лолейта, проф. Гвоздева
и др. этот метод расчёта прежде, чем в других странах, был введён в СССР
и принят некоторыми нашими нормами.
ГЛАВА VI.
УЧЁТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИИ И СЖАТИИ.
РАСЧЁТ ГИБКИХ НИТЕЙ.
§ 29. Подбор сечений с учётом собственного веса
(при растяжении и сжатии).
При установлении внешних сил, растягивающих или сжимающих
элементы конструкций, мы до сих пор игнорировали собственный
вес этих элементов. Возникает вопрос, не вносится ли этим упро-
упрощением расчёта слишком большая погрешность? В связи с этим
подсчитаем величины напряже-
напряжений и деформаций при учёте
влияния собственного веса растя-
растянутых или сжатых стержней.
б(х>	Пусть вертикальный стер-
стержень (фиг. 60, а) закреплён своим
Т^ верхним концом; к нижнему его
I концу подвешен груз Р. Длина
*? стержня /, площадь поперечного
I сечения F, удельный вес мате-
-* риала 7 и модуль упругости Е.
Подсчитаем напряжения по се-
сечению АВ, расположенному на
Qx	0j	расстоянии х от свободного конца
стержня.
<^>иг* 60-	Рассечём стержень сечением
АВ и выделим нижнюю часть
длиной х с приложенными к ней внешними силами (фиг. 60, б) — гру-
грузом Р и её собственным весом -\Fx. Эти две силы уравновешиваются
напряжениями, действующими на площадь АВ от отброшенной части.
Эти напряжения будут нормальными, равномерно распределёнными
по сечению и направленными наружу от рассматриваемой части
стержня, т. е. растягивающими. Величина их будет равна
о\х) — р — р -J- \х.	\v.ij
\
Р
В

.1.

§ 291	ПОДБОР СЕЧЕНИЙ С УЧЁТОМ СОБСТВЕННОГО ВЕСА	103
Таким образом, при учёте собственного веса нормальные напря-
напряжения оказываются неодинаковыми во всех сечениях. Наиболее на-
напряжённым, опасным, будет верхнее сечение, для которого х дости-
достигает наибольшего значения /; напряжение в нём равно
Условие прочности должно быть выполнено именно для этого
сечения:
[ol.	F.3)
Отсюда необходимая площадь стержня равна
F^ . ,Р ..	F.4)
От формулы, определяющей площадь растянутого стержня без
учета влияния собственного веса, эта формула отличается лишь тем,
что из допускаемого напряжения вычитается величина fl.
Чтобы оценить значение этой поправки, подсчитаем её для двух
случаев. Возьмём стержень из мягкой стали длиной 10 м\ для
него [о] = 1400 кг/см\ а величина f/=7,85 . Ю~3 • 103 = 7,85 кг/см*.
Таким образом, для стержня из мягкой стали поправка составит
7 85
щд, т. е. около 0,6%. Теперь возьмём кирпичный столб высотой
тоже 10 м\ для него [а] = 12 кг) см1, а величина ?/= 1,8 • 10~3 • 103 =
= 1,8 кг/см*. Таким образом, для кирпичного столба поправка
1 8
составит -т~, т. е. уже 15%-
Вполне понятно, что влиянием собственного веса при растяжении
и сжатии стержней можно пренебрегать, если мы не имеем дела
с длинными стержнями или со стержнями из материала, обладаю-
обладающего сравнительно небольшой прочностью (камень, кирпич) при
достаточном весе. При расчёте длинных канатов подъёмников, раз-
различного рода длинных штанг и высоких каменных сооружений
(башни маяков, опоры мостовых ферм) приходится вводить в расчет
и собственный вес конструкции.
В таких случаях возникает вопрос о целесообразной форме
стержня. Если мы подберём сечение стержня (фиг. 60) по формуле
F.4) и дадим одну и ту же площадь поперечного сечения по всей
Длине, то материал стержня будет плохо использован; нормальное
напряжение в нём дойдёт до допускаемого лишь в одном верхнем
сечении; во всех прочих сечениях мы будем иметь запас в напря-
напряжениях, т. е. излишний материал. Поэтому желательно так запроек-
запроектировать размеры стержня, чтобы во всех его поперечных сечениях
(перпендикулярных к оси) нормальные напряжения были постоянны.

104	УЧЁТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. VI
Такой стержень называется стержнем равного сопротивления
растяжению или сжатию. Если при этом напряжения равны допу-
допускаемым, то такой стержень будет иметь наименьший вес.
Возьмём длинный стержень, подверженный сжатию силой Р и
собственным весом (фиг. 61). Чем ближе к основанию стержня мы
будем брать сечение, тем больше будет сила, вызывающая напря-
напряжения в этом сечении, тем ббльшими придётся
брать размеры площади сечения. Стержень
получит форму, расширяющуюся книзу. Пло-
Площадь сечения F будет изменяться по высоте
в зависимости от х, т. е. F=f(x).
| /	|		Установим этот закон изменения площади
F/krfFf в зависимости от расстояния сечения х от
\ (xj+a (х) верХа СТержня.
Площадь верхнего сечения стержня F9
,	определится из условия прочности:
У///////////////У
Фиг. 61.	77 = [°] и /7° = М>
где [а] — допускаемое напряжение на сжатие; напряжения во всех
прочих сечениях стержня также должны равняться величине
Чтобы выяснить закон изменения площадей по высоте стержня,
возьмём два смежных бесконечно близких сечения на расстоянии х
от верха стержня; расстояние между сечениями dx\ площадь верх-
верхнего назовём F(x), площадь же смежного F (x) -\- dF (х).
Приращение площади dF(x) при переходе от одного сечения
к другому должно воспринять вес ^F(x)dx элемента стержня между
сечениями. Так как на площади dF{x) он должен вызвать напряже-
напряжение, равное допускаемому [а], то dF(x) определится из условия
Отсюда
dF(x)_ 7
F(x) — [о] ах*
После интегрирования получаем
js]x.	F,6)
При х=0 площадь F(x) = Fb; подставляя эти значения в (Ь.Ь),
имеем:

§ 29] ПОДБОР СЕЧЕНИЙ С УЧЁТОМ СОБСТВЕННОГО ВЕСА 105
Отсюда
-г
1
Если менять сечения точно по этому закону, то боковые грани
стержня получат криволинейное очертание (фиг. 61), что усложняет
и удорожает работу. Поэтому обычно такому сооружению придают
лишь приближённую форму стержня равного сопротивления, напри-
например в виде усечённой пирамиды с плоскими гранями. у/////////
Приведённый расчёт является приближённым. Мы уpf\ ]
предполагали, что по всему сечению стержня рав-
равного сопротивления передаются только нормальные
напряжения; на самом деле у краёв сечения напря-
напряжения будут направлены по касательной к боковой
поверхности.
В случае длинных канатов или растянутых штанг
форму стержня равного сопротивления осуществляют
тоже приближённо, разделяя стержень по длине на
ряд участков; на протяжении каждого участка сечение ^ IP
остаётся постоянным (фиг. 62) — получается так назы- Фиг. 62.
ваемый ступенчатый стержень.
Определение площадей Fl9 Fit ... при выбранных длинах произ-
производится следующим образом. Площадь поперечного сечения первого
снизу участка будет по формуле F.4) равна
F = Р
Чтобы получить площадь поперечного сечения второго участка,
надо нагрузить его внешней силой Р и весом первого участка
Для третьего участка к внешней силе добавляются веса первого
и второго участков. Подобным же образом поступают и для других
участков.
Для того чтобы сравнить выгодность применения брусьев рав-
ного сопротивления, ступенчатых и постоянного сечения, рассмотрим
^еловой пример.
Пример 15. Опора высотой Л = 42 м подвергается сжатию центрально
пРиложенной силой Р = 400 г, принимая объёмный вес кладки 2,2 т/мь,
а Допускаемое налряжение на сжатие 12 кг/см2, сравнить объёмы кладки
Аля случаев:
опоры постоянного сечения,
опоры из трёх призматических частей равной длины,
опоры равного сопротивления сжатию.

106	УЧЕТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. VI
Расчёт ведём в тоннах и метрах.
Для первого случая площадь поперечного сечения равна
/7== [aj^^ ==120 —42.2,2==1415 МК
Объём равен
V = F
Во втором случае площадь сечения верхней части равна
Fi=SS~ h ^Ш —14-2,2
Площадь сечения второго участка равна
¦~	h
120-14-2,2
Площадь сечения на третьем участке равна
р	-3+^'Т _400 + 2,2-4,48-14 + 2,2-6,04-14 _
м	*	120-14-2,2
И—дТ
Полный объём кладки равен
V «(Ft + F8 + F,) у = D,48 + 6,04 + 8,12) 14 = 261 м\
Этот же ответ можно получить из условия, что усилие внизу третьего
участка, равное P-f-G (где Сг — вес всей опоры), одновременно равно
(о)/7,; тогда
Для опоры равного сопротивления сжатию площадь верхнего сечения равна
Fo ="Й — 120 =
Площадь нижнего сечения равна
1Л
1
Fh = Foe[<l1 = 3,33 е 12° = 3,33 *0'77 = 7,15 лс».
Вес опоры равного сопротивления G определится из условия
отсюда
G = [a]/^ —Р= 120- 7,15 — 400 = 460 г.
Объём опоры равен
^_460_
v- ^ -22-лт м ,
что меньше объёма ступенчатой опоры на 20»/, и примерно втрое меньше
опоры постоянного сечения.

I 30]	ДЕФОРМАЦИИ ПРИ ДЕЙСТВИИ СОБСТВЕННОГО ВЕСА	107
§ 30. Деформации при действии собственного веса.
При определении влияния собственного веса на деформацию при
растяжении и сжатии стержней придётся учесть, что относительное
удлинение различных участков стержня будет переменным, как и
напряжение о(х). Для вычисления полного удлинения стержня по-
постоянного сечения определим сначала удлинение бесконечно малого
участка стержня длиной dx, находящегося на расстоя-
яии х от конца стержня (фиг. 63). Абсолютное удлине-
удлинение этого участка (формула B.5)) равно
а л (P + ixF)dx dx\ P
Полное удлинение стержня А/ равно
Помножим и разделим второе слагаемое на F и учтём, что
fFl=Q есть полный вес стержня. Тогда удлинение от одного соб*
ственного веса (второе слагаемое формулы) равно
тс в — 2EF >
т. е. оно в два раза меньше удлинения от приложенной к концу
стержня внешней силы Q, равной собственному его весу.
Что же касается деформаций стержней равного сопротивления,
то, так как нормальные напряжения во всех сечениях одинаковы
и равны допускаемым [о], относительное удлинение по всей длине
стержня одинаково и равно
В— Б9
Абсолютное же удлинение при длине стержня / равно
ы — и— Е — EFq,
где обозначения соответствуют фиг. 61.
Деформацию ступенчатых стержней следует определять по
частям, выполняя подсчёты по отдельным призматическим участкам.
При определении деформации каждого участка учитывается не
только его собственный вес, но и вес тех участков, которые
влияют на его деформацию, добавляясь к внешней силе. Пол-
Полная деформация получится суммированием деформаций отдельных
Участков.

108
УЧЕТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. V\
Пример 16. Трос шахтного подъёмника длиной 120 м имеет два
участка по 60 м каждый. Площадь поперечного сечения верхнего участка
равна 4 см*, нижнего — 3 см2. Объёмный вес материала троса 7,85 г/см*,
его модуль упругости Е= 1,5* 10е кг/см2. Вес клети, поднимаемой тро-
тросом, равен 1500 кг. Определить удлинение троса.
Вес нижней части троса составит.
<?! = 7,85 • 10-» • 3 • 60 • 10» = 141,3 кг,
и вес верхней части
Q2 = 7,85 • 10"» • 4 • 60 • 10* = 188,4 кг.
Удлинение нижней части троса будет равно
K-fr)'
a удлинение верхней части
(
1,5 . 10« • 3
1500+141,:
- = 2,10 см,
: 1,74 СМ.
2~~	EF2	~~	1,5-10е-4
Полное удлинение троса будет равно
А/ = Д/Л + А/2 = 2,10 + 1,74 = 3,84 см.
§ 31. Гибкие нити.
А. В технике встречается ещё один вид растянутых элемен-
элементов, при определении прочности которых важное значение имеет соб-
собственный вес. Это — так называемые гибкие нити. Таким термином
обозначаются гибкие элементы
*	°	в линиях электропередач, в
канатных дорогах, в висячих
мостах и других сооружениях.
Пусть (фиг. 64) имеется гиб-
гибкая нить постоянного сечения,
нагружённая собственным ве-
весом и подвешенная в двух
точках, находящихся на разных
уровнях. Под действием соб-
собственного веса нить прови-
провисает по некоторой кривой АОВ.
Горизонтальная проекция расстояния между опорами (точками
её закрепления), обозначаемая /, носит название пролёта.
Нить имеет ностоянное сечение, следовательно, вес её распре-
распределён равномерно по её длине. Обычно провисание нити невелико
по сравнению с её пролётом, и длина кривой АОВ мало отличается
(не более чем на 10%) от длины хорды АВ. В этом случае с до-
достаточной степенью точности можно считать, что вес нити равно-
Фиг. 64.

& 31]	гибкие нити	109
церно распределён не по её длине, а по длине её проекции на
горизонтальную ось, т. е. вдоль пролёта I. Эту категорию гибких
нитей мы и рассмотрим. Примем, что интенсивность нагрузки, равно-
равномерно распределённой по пролёту нити, равна q. Эта нагрузка,
имеющая размерность сила/длина, может быть не только собствен-
собственным весом нити, приходящимся на единицу длины пролёта, но и
весом льда или любой другой нагрузкой, также равномерно рас-
распределённой. Сделанное допущение о законе распределения нагрузки
значительно облегчает расчёт, но делает его вместе с тем при-
приближённым; если при точном решении (нагрузка распределена вдоль
кривой) кривой провисания будет цепная линия, то в приближённом
решении кривая провисания оказывается квадратной параболой.
Начало координат выберем в самой низшей точке провисания
нити О (фиг. 64), положение которой, нам пока неизвестное, оче-
очевидно, зависит от величины нагрузки q, от соотношения между
длиной нити по кривой и длиной пролёта, а также от относитель-
относительного положения опорных точек. В точке О касательная к кривой
провисания нити, очевидно, горизонтальна. По этой касательной
направим вправо ось х.
Вырежем двумя сечениями — в начале координат и на расстоянии
х от начала координат (сечение т — п) — часть длины нити. Так как
нить предположена гибкой, т. е.
способной сопротивляться лишь
растяжению, то действие отбро-
отброшенной части на оставшуюся воз-
возможно только в виде силы, на-
направленной по касательной к кри-
кривой провисания нити в месте раз- И
реза; иное направление этой силы J*- о\
невозможно.
На фигуре 65 представлена
вырезанная часть нити с действую-	*	Фиг. 65.
щими на неё силами. Равномерно
распределённая нагрузка интенсивностью q направлена вертикально
вниз. Воздействие левой отброшенной части (горизонтальная сила Н)
направлено, ввиду того, что нить работает на растяжение, влево.
Действие правой отброшенной части, сила Г, направлено вправо
по касательной к кривой провисания нити в этой точке.
Составим уравнение равновесия вырезанного участка нити.
Возьмём сумму моментов всех сил относительно точки приложения
силы Т и приравняем её нулю. При этом учтём, опираясь на при-
приведённое в начале допущение, что равнодействующая распределён-
распределённой нагрузки интенсивностью q будет qx, и что она приложена
посредине отрезка х (фиг. 65). Тогда
H*y — qX'Y = Q> откуда У = -<^*	F-8)

110	УЧЁТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИЙ И СЖАТИИ [ГЛ. VI
Отсюда следует, что кривая провисания нити является параболой.
Когда обе точки подвеса нити находятся на одном уровне, то
/1=/2=/. Величина / в данном случае будет так называемой
стрелой провисания. Её легко определить из уравнения F.8); так
как в этом случае, ввиду симметрии, низшая точка нити находится
посредине пролёта, то а = Ь = -^\ подставляя в уравнение F.8)
значения х = Ь=-^ и y=f, получаем:
Из этой формулы находим величину силы Н:
Н=$.	F.10)
Величина И называется горизонтальным натяжением нити.
Таким образом, если известны нагрузка q и натяжение //, то по
формуле F.9) найдём стрелу провисания /. При заданных q и /
натяжение Н определяется формулой F.10). Связь этих величин
с длиной 5 нити по кривой провисания устанавливается при помощи
известной из математики приближённой формулы1)
F.П)
Вернёмся к рассмотрению фиг. 65. Составим ещб одно условие
равновесия вырезанной части нити, а именно, приравняем нулю сумму
проекций всех сил на ось х:
Из этого уравнения найдём силу Т—натяжение в произвольной
точке
Из формулы F.12) видно, что сила Т увеличивается от низшей
точки нити к опорам и будет наибольшей в точках подвеса — там, где
касательная к кривой провисания нити составляет наибольший угол
с горизонталью. При малом провисании нити этот угол не достигает
*) Элемент длины кривой ds — dx 1/ 1 + \-^~] J так как из формул F.8)
и F.10) следует, что -р = z_ = J-. ? то ds = d~ , * -,- -- 4 ,
32/2л:2\	Х
-\	ji— J. После интегрирования в пределах от х = 0 до х = 1/2 и удваива-
удваивания приходим к формуле F.11),

§ 31]
ГИБКИЕ НИТИ	111
больших значений, поэтому с достаточной для практики степенью
точности можно считать, что усилие в нити постоянно и равно ев
натяжению Н. На эту величину обычно и ведется расчёт проч-
прочности нити. Если всё же требуется вести расчёт на наибольшую
силу у точек подвеса, то для симметричной нити её величину опре-
определим следующим путём. Вертикальные составляющие реакций опор
равны между собой и равны половине суммарной нагрузки на нить,
т. е. \. Горизонтальные составляющие равны силе //, определяемой
по формуле F.10). Полные реакции опор получатся как геометри-
геометрические суммы этих составляющих:
Условие прочности для гибкой нити, если через F обозначена
площадь сечения, имеет вид:
Заменив натяжение Н его значением по формуле F.10), получим:
Из этой формулы при заданных /, q> F и [а] можно определить
необходимую стрелу провисания /. Решение при этом упростится,
если в q включён лишь собственный вес; тогда q = *[*Ff где f —
вес единицы объёма материала нити, и
т. ef. величина F не войдёт в расчёт.
Б. Если точки подвеса нити находятся на разных уровнях, то
подставляя в уравнение F.8) значения х = — а и х = Ь, нахо-
находим fx и U
FЛЗ>
Отсюда из второго выражения определяем натяжение
Н=Ч~,	F.14)
а деля первое на второе, находим:

1 12	УЧЕТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИИ И СЖАТИИ [гл. Vl
Имея в виду, что b-\-a = l, получаем:
или 0 = -
Подставив это значение Ъ в формулу F.14), окончательно опре-
определяем *):
,_	9JL
F.15)
Два внака в знаменателе указывают на то, что могут быть две
основные формы провисания нити. Первая форма при меньшем зна-
значении И (знак плюс пе-
перед вторым корнем) даёт
нам вершину параболы
между опорами нити
(фиг. 64 и пунктирная
кривая АО^В на фиг. 66).
При большем натяже-
натяжении Н (знак минус пе-
перед вторым корнем) вер-
вершина параболы располо-
расположится левее опоры А
(сплошная кривая 0%АВ
на фиг. 66). Получаем
вторую форму кривой.
Возможна и третья
(промежуточная между
двумя основными) форма
провисания, соответствующая условию /, = 0; тогда начало коор-
координат О3 совмещается с точкой А. Та или иная форма будет полу-
получена в зависимости от соотношений между длиной нити по кривой
провисания АОВ (фиг. 64) и длиной хорды АВ.
Если при подвеске нити на разных уровнях неизвестны стрелы
провисания /, и /2, но известно натяжение Н, то легко получить
значения расстояний а и Ъ и стрел провисания ft и /2.
Разность h уровней подвески равна (фиг. 64 и 66):
А =/,-/,.
Подставим в это выражение значения /t и /2, согласно F.13), и
преобразуем его, имея в виду, что a-\-b = l:
Фиг. 66.
1) Впервые формула для Н в таком примерно виде была указана проф.
Штаерманом И. Я. («Наука и Техника>, журнал Одесского политехни-
политехнического института 1925).

§ 311	гибкие нити	113
откуда
b~a=~jr>
а так как a-\-b = l, то
/ Hh	, / , Hh
Следует иметь в виду, что при я^>0 будет иметь место первая
форма провисания нити (фиг. 66), при а<^0 — вторая форма про-
провисания и при а = 0 — третья форма. Подставляя значения а и b
в выражения F.13), получаем величины fx и /2:
г __qt* , Hh* h
fi ~ 8Я "Г 2^/а 2
в
f ^/2 , Hh* , /г
В. Теперь выясним, что произойдёт с симметричной нитью,
перекрывающей пролёт /, если после подвешивания её при темпе-
температуре tx и интенсивности нагрузки qx температура нити повысится
до /2, а нагрузка увеличится до интенсивности ^2 (например, из-за
её обледенения). При этом предположим, что в первом состоянии
задано или натяжение Ни или стрела провисания fx. (Зная одну из
этих двух величин, по формуле F.10) всегда можно определить
другую.)
При подсчёте деформации нити, являющейся по сравнению с дли-
длиной нити малой величиной, сделаем два допущения: длина нити
равна её пролёту, а натяжение постоянно и равно Н. При пологих
нитях эти допущения дают небольшую погрешность.
В таком случае удлинение нити, вызванное увеличением темпе-
температуры, будет равно
As1 = a(t% — t1)I9	F.16)
где а — коэффициент линейного температурного расширения мате-
материала нити.
При повышении температуры нить удлиняется. В связи с этим
увеличится её стрела провисания и, как следствие, в соответствии
с формулой F.10) уменьшится её натяжение. С другой стороны»
из-за увеличения нагрузки, как видно из той же формулы F.10),
натяжение увеличится. Допустим, что окончательно натяжение
увеличивается. Тогда удлинение нити, вызванное увеличением
натяжения, будет, согласно закону Гука, равно:
=

114	УЧЁТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. VI
Если Н% окажется меньше, чем Hit то величина Asa будет от-
отрицательной. При понижении температуры будет отрицательной
величина As1#
Таким образом, длина нити во втором её состоянии будет равна
длине при первом ей состоянии с добавлением тех деформаций,
которые произойдут от повышения температуры и натяжения:
s% = sx -f- A$! + A s2.	F.18)
Изменение длины нити вызовет изменение и ее стрелы провиса-
провисания. Вместо fx она станет /9.
Теперь заменим в уравнении F.18) sx и s9 их выражениями по
формуле F.11), а деформации As, и As2 — их значениями по форму-
лам F.16) и F.17). Тогда уравнение F.18) примет следующий вид:
- FЛ9)
В этом уравнении заменим fx и /2 их значениями по формуле F.9):
Тогда, после некоторых преобразований, уравнение F,19) может быть
написано в виде
^-'i>-^]^-^=°- F-20)
Определив из уравнения F.20) натяжение //„ можно найти по
формуле F.9) и стрелу /2.
В случае, если при переходе от первого ко второму состоянию
нагрузка не изменяется, а изменяется лишь температура, то в урав-
уравнении F.20) интенсивность q% заменяется на qx. В случае, если
при переходе от первого ко второму состоянию не изменяется
температура, а изменяется лишь нагрузка, то в уравнении F.20)
средний член в квадратной скобке равен нулю.
Уравнение F.20) пригодно, конечно, и при понижении темпера-
температуры и уменьшении нагрузки.
В тех случаях, когда стрела провисания не является малой по
сравнению с пролётом, выведенные выше формулы, строго говоря,
неприменимы, так как действительная кривая провисания нити, цеп-
цепная линия, будет уже значительно отличаться от параболы, получен-
полученной нами благодаря предположению о равномерном распределении
нагрузки по пролёту нити, а не по ее длине, как то имеет
место в действительности.

§ 32]
ПРИМЕРЫ
115
Точные подсчёты показывают, что значение погрешности в вели-
величине натяжения Н, вызванной этим предположением, таково: при от-
/1	f \
ношении y<Coo погРешность не превосходит 0,3%, при у = т?\
ошибка составляет уже 1,3%, а при y=-g- погрешность несколько
превосходит 5%.
§ 32. Примеры.
Пример 17. Многожильный медный провод, сечением F'= 120 мм2,
симметрично подвешен к опорам, отстоящим одна от другой на /=100 м.
Температура провода зимой может понизиться до —40° С, а при темпе-
температуре — 5° С имеет место обледенение провода при одновременном давлении
на него ветра.
Определить натяжение провода и выяснить, при каких из указанных
условий состояние его будет опаснее.
В соответствии с сортаментом проводов многожильный медный провод
F=\20 мм2 имеет диаметр 14,2 мм и погонный метр его весит 1,090 кг.
Модуль упругости материала провода равен Е =
= 1,3 • 104 кг/мм2, коэффициент линейного температур-
температурного расширения равен а = 17- 10~в. Допускаемое на-
напряжение примем равным [а] = 8 кг/мм2.
Из условия прочности -р ^ [а] находим наиболь-
наибольшее допустимое натяжение:
Ядоп = F [а] = 120 • 8 = 960 кг.
Теперь предположим, что при температуре —40° С
натяжение будет наибольшим — равным допускаемому,
т. е. 960 кг. Проверим, каково будет натяжение во
втором случае, при обледенении, ветре и температуре
— 5° С. Для этого сначала подсчитаем в этих условиях
погонную нагрузку провода.
Толщина обледенения принята равной 10 мм, В нашем случае площадь
поперечного сечения льда (фиг. 67) будет равна:
FA = iji C,42* — 1,422) = 7,58 см2.
10мм
При объёмном весе льда 0,9 г/см3 нагрузка от льда на погонный метр
провода составит:
Нагрузка от собственного веса и льда получится суммированием. Она
будет равна:
Д = 1,090 + 0,682 = 1,772 кг/м.
дсл =
Давление ветра определяется на диаметральное сечение провода. Интен-
Интенсивность давления принята равной 24 кг/м2, направление ветра — горизон-
горизонтальным. При этих условиях нагрузка от ветра будет равна:
дв = 24 • 1 . 0,0342 = 0,822 кг/м.

116	УЧЁТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИИ И СЖАТИИ [ГЛ. VI
Суммирование нагрузок от собственного веса провода и веса льда с вет-
ветровой нагрузкой производится геометрически. Тогда полная нагрузка на
погонный метр провода будет равна:
+ 41 =У 1,772^ + 0,8222 = 1,950 кг/м.
Теперь мы можем приступить к определению натяжения провода при этой
нагрузке. Нам надо перейти от состояния первого, когда t\ = — 40° С, qx =
= 1,090 кг/м (только собственный вес) и #i = 960 кг (допускаемое натяже-
натяжение) к состоянию второму, когда ^а = — 5° С, #8= 1,950 кг/м, а натяжение
#2 неизвестно. Напишем, соблюдая размерность, при этих данных и ранее
приведённых значениях Ef Fy l и а уравнение F.20):
щ
+ 1>3.10М20,1^
1,3.10** 120» 1,95» • 100» _А
24	~0'
или
Щ + 805Я1 — 2,47- 10° = 0.
Единственно нас интересующий положительный рациональный корень
этого уравнения проще всего определить подбором, путём последовательных
попыток. Он равен
Оказалось, что при температуре —5° С, обледенении и ветре натяжение
больше, чем при температуре — 40° С и нагрузке только от собственного
веса. * Таким образом, приходится за опасное состояние при заданных усло-
условиях задачи принимать наличие обледенения и ветра. В этом случае,
а не в случае * = —40° С, натяжение должно быть равно допускаемому,
т. е. 960 кг. Производить обратную проверку нет смысла, так как проде-
проделанный выше расчёт уже показал, что при обледенении и ветре натяжение
больше, чем при низкой температуре. Сама же величина натяжения при
низкой температуре нас не интересует, важно лишь то, что она меньше
допускаемой.
Пример 18. Провод, рассмотренный в предыдущем примере, подве-
подвешивается к опорам при температуре +15° С. Определить необходимую
стрелу провисания провода при условии, что в опасном состоянии натяжения
в нём равны допускаемым.
В предыдущем примере было выяснено, что опасное состояние имеет
место при обледенении. Приняв это состояние за исходное и назвав его
сейчас первым, примем (согласно данным примера 17) ti = —5° С, qt =
= 1,950 кг/м и #i = 960 кг и перейдём ко второму состоянию, во время
монтажа, при ?2 = -j-15°C, q2 = 1,090 кг/м и неизвестном #2. Опять напишем
для этого случая уравнение F.20):
1,3» 10*. 120» 1,092 • 1002_
24	-
или
Щ + 2250#! — 7,72 • 108 = 0э
откуда #а = 527 /сг.

§ 321	примеры	117
Стрелу провисания мы найдём из формулы F.9):
«?,/»_ 1,090-100»
/а "" 87/7"- 8-527 ~ Z>
а длину провода из формулы F.11):
Пример 19. Определить необходимую высоту точек подвеса провода,
рассмотренного в предыдущих примерах. Для обеспечения проезда под
проводом расстояние от земли до низшей его точки не должно быть менее
6 м. Наибольшее провисание провода может иметь место летом при темпе-
температуре +40? С, а также во время его обледенения при температуре —5° С,
но в отсутствии ветра.
Для того чтобы определить высоту точек подвеса, надо узнать величину
наибольшей стрелы провисания. Для этого следует перейти от какого-либо
известного нам состояния провода к тем состояниям, когда возможна
наибольшая стрела провисания.
Этот переход может быть сделан как от опасного, так и от монтажного
состояний. Мы возьмём за исходное состояние в обоих случаях опасное.
Определим сначала стрелу провисания при наличии обледенения без
ветра. В первом состоянии примем *,= —5° С, qx = 1,950 кг/м, #t = 960 кг;
во втором состоянии *2 = *i и #2 = 1,772 кг/м (собственный вес и обледене-
обледенение). Напишем уравнение F.20), но без среднего члена в квадратной скобке,
так как не происходит изменения температуры:
,3-104'120. 1,95». 100»	1	1,3.10*. 120 . 1,772». 1002 _п
24 • 960»	УЬ0Г2	24
откуда #2 = 885 кг.
Стрела провисания определяется из формулы F.9):
1,772. 100» _
7	Z01 M
7~ 8-885 -Z'01 M'
Теперь определим стрелу провисания при наивысшей температуре. Пер-
Первое состояние прежнее, при втором состоянии *2<=-|-40оС и q2 = 1,090 кг/м.
Для этого случая уравнение F.20) имеет вид:
1,3. 10^. 120- 17.
Стрела провисания будет равна
1,09.100»
7 8-478 -z'
Следовательно, наибольшая стрела провисания имеет место при наивыс-
наивысшей температуре и равна
Для того чтобы был соблюдён габарит проезда 6 м% необходимо точки
подвеса взять на высоте 6 + 2,85 = 8,85 м.

118
СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ
[гл. vn
ГЛАВА VII.
СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ.
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ.
§ 33. Напряжения по наклонным сечениям при осевом
растяжении или сжатии (линейное напряжённое состояние).
перпендикулярному
Р
т
h
т
I
Л
В предыдущих параграфах, проверяя прочность растянутого или
сжатого стержней, мы определяли напряжения только по сечению,
к его оси. Но правильно оценить опасность,
угрожающую прочности стержня, можно, лишь
зная полностью его напряжённое состояние, а
это требует уменья вычислять напряжения не
только по сечению, перпендикулярному к оси,
а по любому.
Вычислим напряжения, действующие по
какому-либо наклонному сечению. Возьмём
призматический стержень, растянутый силами Р
(фиг. 68). Разделим его на две части: / и
// сечением тп, составляющим угол а с по-
поперечным сечением mk, перпендикулярным
к оси. Тот же угол составляют между собой
и нормали к этим сечениям.
За положительное направление отсчётов
этого угла возьмём направление против ча-
часовой стрелки. Нормаль ОЛ, направленную
наружу по отношению к отсечённой части стержня, будем назы-
называть внешней нормалью к сечению тп. Площадь сечения mk обо-
обозначим Fo, площадь же сечения тп обозначим Fa.
Для нахождения напряжений, передающихся через намеченное
сечение от верхней (/) части на нижнюю (//), отбросим мысленно
верхнюю часть и заменим действие её на нижнюю напряжениями ра.
Для равновесия нижней части напряжения ра должны уравновеши-
уравновешивать силу Р и быть направлены параллельно оси стержня. В данном
случае напряжения уже не перпендикулярны к той площадке, по
которой они действуют. Величина их тоже будет иной, чем для
площадки mk.
Делая предположение, как и ранее для поперечного сечения (§ 6),
что напряжения ра равномерно распределены по площади проведён-
проведённого разреза, найдём:
Р
Фиг. 68.
Но так как Fn=-
COS a
то
Pcosa
Р* = —р— = a0cosa,

33]
НАПРЯЖЕНИЯ ПО НАКЛОННЫМ СЕЧЕНИЯМ
119
и величина полных напряжений
площадке, и угол наклона их
где с0 = -р	нормальное напряжение по площадке mk> перпенди-
перпендикулярной к растягивающей силе.
При изменении угла а меняется
р^ действующих по проведённой
(90° — а) к этой площадке.
Для того чтобы при любом угле наклона а иметь дело всегда
с одними и теми же видами напряжений, разложим напряжения рх
на две составляющие: в плоскости тп и перпендикулярно к ней
(фиг. 69). Таким образом, напряжение ра, действующее в точке А
площадки тп, мы заменяем двумя взаимно перпенди-
перпендикулярными напряжениями: нормальным напряже-
напряжением оа и касательным напряжением тв. Вели-
Величины этих двух напряжений будут меняться в зави-
зависимости от изменения угла а между нормалью к
площадке и направлением растягивающей силы.
Из фиг. 69 имеем:
, = р„ cos a = а0 cos2 а,	G.1)
cos2 а,
та = ра sin а = о0 sin а cos а = -^ а0 sin 2а. G.2)
Установим следующие условия относительно зна-
знаков напряжений оа и та. Растягивающие напря-
напряжения оа, т. е. совпадающие с направлением внешней нормали, бу-
будем считать положительными; нормальные напряжения обратного
направления — сжимающие — будем принимать со знаком минус.
Касательные напряжения будем считать положительными, если
ях направление таково, что внешняя нормаль для совмещения с ними
должна повернуться по часовой стрел-
стрелке. Обратное направление та будем счи-
считать отрицательным. Можно руковод-
руководствоваться и таким правилом знаков:
если касательное напряжение % дает мо-
момент по часовой стрелке относительно
Центра рассматриваемого элемента, то
оно считается положительным; против
часовой стрелки — отрицательным.
На фиг. 70 показаны принятые усло-
условия относительно знаков а, о и т.
При любом угле наклона площадки а
иы всегда будем иметь дело лишь с
двумя видами напряжений, действую-
действующих в каждой точке проведённого	Фиг. 70.
Разреза: с нормальным и касательным
напряжениями. Эти два вида напряжений соответствуют двум видам
Деформаций, которые испытывает материал стержня.

120	сложное напряжённое состояние	[гл. vii
Выделим (фиг. 71) из растянутого стержня двумя наклонными
параллельными сечениями /—1 и 2—2 тонкий слой материала: этот
слой на фиг. 71 заштрихован. На обе плоскости, ограни-
ограничивающие этот слой, будут действовать и нормальные
и касательные напряжения, аа и та. Как видно из чер-
чертежа, нормальные напряжения соответствуют растя-
растяжению выделенного слоя; напряжения же та соот-
соответствуют стремлению сечений /—/ и 2—2 сдвинуться
параллельно одно другому.
Значит, наличие этих двух видов напряжений соот-
соответствует наличию двух видов деформаций: продольной
деформации (удлинение или укорочение) и деформации
сдвига.
Фиг. 71.	Этому соответствуют и два вида разрушения ма-
материала: путём отрыва и путём сдвига.
Для того чтобы убедиться в достаточном сопротивлении мате-
материала стержня разрушению, необходимо установить наибольшие зна-
значения величин оа и та в зависимости от положения площадки тп.
Из формул G.1) и G.2) следует, что оа достигает своего наи-
наибольшего значения, когда cos2 а будет равен единице и угол а = 0.
Максимум же та получится при sin 2а =1, т. е. при 2а = 90° и
а = 45°. Величины этих наибольших напряжений будут равны:
тахоа==а0 = _-; тахта = |-.	G.3)
Таким образом: наибольшие нормальные напряжения действуют
в данном случае по площадкам, перпендикулярным к оси стержня;
наибольшие касательные напряжения действуют по площадкам,
составляющим угол 45° с направлением оси стержня, и равны
половине наибольших нормальных напряжений.
Возникает вопрос, по отношению к какому из этих видов напря-
напряжений следует производить проверку прочности, какому из них при-
приписать решающую роль в нарушении прочности материала. Это под-
подробно освещено в главе VIII (§ 43).
§ 34. Понятие о главных напряжениях. Виды напряжённого
состояния материала.
В предыдущих главах мы ознакомились с поведением материала
при осевом (или, как его часто называют, простом) растяжении и
сжатии. На практике, однако, возможны случаи, когда под действием
внешних сил элемент материала подвергается растяжению или сжа-
сжатию по двум и трём направлениям, т. е. находится в условиях слож-
сложного напряжённого состояния.
В § 33 было показано, что и при простом растяжении возможны
напряжения двух видов — нормальные о и касательные т. Из фор-

34]	ПОНЯТИЕ О ГЛАВНЫХ НАПРЯЖЕНИЯХ	121
у G.1) и G.2) следует, что по сечениям, перпендикулярным к оси
растянутого стержня (а = 0), возникают только нормальные напря-
напряжения (х = 0), а по сечениям, параллельным его оси (а ==90°) нет
ни нормальных, ни касательных напряжений (а = 0 и т = 0).
Такие площадки, по которым нет касательных напряжений, назы-
называются главными; нормальные напряжения, действующие по этим
площадкам, называются главными напряжениями.
В теории упругости доказывается, что в каждой точке любого
напряжённого тела можно провести три взаимно перпендикулярные
главные площадки, через которые передаются три главных (нор-
(нормальных) напряжения] из них два имеют экстремальные значения:
одно является наибольшим нормальным напряжением, другое — наи-
наименьшим, третье — промежуточное. В каждой точке напряжённого
тела можно выделить элементарный
кубик, гранями которого служат глав-
главные площадки. Материал кубика растя-
растягивается или сжимается тремя взаимно
перпендикулярными главными напря- б2 -«¦
жениями, передающимися через эти
грани (фиг. 72).	А
В случае простого растяжения б3
(§ 33) одна главная площадка в ка-
каждой точке перпендикулярна к оси	Фиг. 72.
стержня (а = 0°), а две другие па-
параллельны этой оси (а = 90°). Так как по первой главной пло-
площадке нормальное напряжение не равно нулю (аа ф 0), а по двум
другим оно обращается в нуль, то при простом растяжении и сжатии
в каждой точке стержня из трёх главных напряжений только одно
не равно нулю; оно направлено параллельно растягивающей силе и
оси стержня. Такое напряжённое состояние материала называется
линейным. Выделенный из стержня элемент растягивается лишь
в одном направлении.
На практике встречаются случаи, когда элемент материала, в виде
кубика, подвергается растяжению или сжатию по двум взаимно пер-
перпендикулярным направлениям или по всем трём (фиг. 72). Такой
случай работы материала, когда два главных напряжения не равны
нулю, называется плоским напряжённым состоянием.
Если же все три главных напряжения не равны нулю в рассмат-
рассматриваемой точке, то налицо самый общий случай распределения
напряжений в материале — объёмное напряжённое состояние] эле-
элементарный кубик будет подвергаться растяжению или сжатию по
*сем трём взаимно перпендикулярным направлениям.
Главные напряжения условимся в дальнейшем обозначать буквами
°ь о2> аг. Нумерацию главных напряжений установим таким образом,
чтобы aj обозначало наибольшее по алгебраической величине, а с3 —
наименьшее напряжение. Сжимающие напряжения условимся, как и

122
СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ
[ГЛ. VII
прежде, считать отрицательными; поэтому, если, например, главные
напряжения будут иметь значения -j-1000 кг/см*, —600 кг/см%,
+ 400 кг/см*, то нумерация должна быть такой:
кг\см%\ о3 = —600 кг\см*\
условие 01^>с9^>аз будет выполнено.
Таким образом, мы различаем три вида напряжённого состояния:
1)	объёмное напряжённое состояние — когда все три главных
напряжения не равны нулю (например, случай растяжения или сжа-
сжатия по трём взаимно перпендикулярным направлениям);
2)	плоское напряжённое состояние — когда одно главное напря-
напряжение равно нулю (случай растяжения или сжатия по двум на-
направлениям);
3)	линейное напряжённое состояние — когда два главных на-
напряжения равны нулю (случай растяжения или сжатия в одном
направлении).
В § 33 мы рассмотрели распределение напряжений при линейном
напряжённом состоянии; ниже будут приведены примеры плоского
и объёмного напряжённых состояний и изучено распределение на-
напряжений по различным площадкам в этих случаях.
§ 35. Примеры плоского и объёмного напряжённого состояний.
Расчёт цилиндрического котла. Понятие о контактных
напряжениях.
В качестве примера сложного напряжённого состояния рассмот-
рассмотрим напряжения, которым подвергается материал цилиндрической
части тонкостенного резервуара (котла), внутри которого находится
газ, пар или вода при давлении q am, т. е. q кг/см*. Боковые стенки
и днища резервуара
подвергаются равно-
равномерно распределённо-
распределённому давлению q. Соб-
Собственным весом жидко-
жидкости в резервуаре пре-
пренебрегаем.
Давление на днища
будет стремиться ра-
разорвать цилиндриче-
цилиндрическую часть по поперечному сечению; давление же на боковые стенки вы-
вызовет в них стремление разорваться по образующим цилиндра. Таким
образом, если мы выделим из цилиндрической части резервуара пря-
прямоугольный элемент ABCD, то этот элемент будет подвергаться
растяжению в двух направлениях: напряжениями о' по сечениям,
перпендикулярным к образующим, и напряжениями о" по сечениям
вдоль образующих (фиг. 73).
Фиг. 73.

§ 35] ПРИМЕРЫ ПЛОСКОГО И ОБЪЁМНОГО НАПРЯЖЁННОГО СОСТОЯНИЙ 123
Вычислим эти напряжения. Обозначим через D диаметр цилин-
цилиндрической части резервуара, / — её длину, t — толщину её стенок
(будем считать, что t мало по сравнению с D (^^оп^/г
Силы, действующие на днища и растягивающие цилиндрическую
часть резервуара вдоль образующей, равны
Площадь, воспринимающая эти силы, представляет собой кольцо
толщиной t и диаметром D (поперечное сечение цилиндрической
части). Величина этой площади (как полоски
шириной t и длиной kD)	N	а	У
Отсюда напряжение равно
Q,_P_/ 4 _qP
Напряжение о" мы найдём, разрезав резервуар	Фиг. 74.
диаметральной плоскостью и отбросив верхнюю
часть (фиг. 74). На диаметральную поверхность жидкости или газа
в оставленной части действует давление q. Оно уравновешивается
силами N, растягивающими материал резервуара в направлении, пер-
перпендикулярном к образующим. Условие равновесия нижней части будет
qDl=2N,
отсюда
и напряжения о" равны
««—?L—i?L9R
~tl~ 2tl~ 2t*
Напряжения по площадкам, параллельным образующим цилиндри-
цилиндрической поверхности резервуара, в два раза больше, чем в направле-
направлении перпендикулярном. Элемент ABCD, вырезанный из стенки
резервуара, испытывает растяжение по двум взаимно перпендику-
перпендикулярным направлениям. Напряжения а' и о" являются главными, так
как по соответствующим им сечениям отсутствуют, вследствие сим-
симметрии нагрузки и деформации элемента, касательные напряжения.
Третье главное напряжение, перпендикулярное к а' и о", равно
нУлю. (Давлением газа по плоскости ABCD и атмосферным давле-
давлением на поверхность стенки котла, соответствующим этому глав-
главному напряжению, пренебрегаем по его малости, сравнительно с </
^ о'.) Таким образом, мы здесь имеем дело с плоским напряжённым
состоянием. Применяя правило нумерации главных напряжений, имеем
о1==а" = §; os = a' = ??; о3 = 0.	G.4)

124
СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ
[гл. vii
Примером объёмного напряженного состояния может служить
работа материала при передаче давления в шариковом подшипнике
от шарика на обойму или при передаче давления от колёс подвиж-
подвижного состава на рельсы.
Так как соприкасание поверхностей головки рельса и бандажа
представляет собой соприкасание двух цилиндров разных радиусов
с образующими, расположенными накрест, то эти две поверхности
должны касаться друг друга в точке.
Нормальные напряжения, возникающие в точке соприкасания
при передаче давления от одного тела на другое, называются кон-
контактными напряжениями.
Фиг. 75.
При передаче нагрузки материал рельса и бандажа у этой точки
деформируется, и передача давления происходит по площадке сопри-
соприкасания, имеющей эллиптическую форму. Величина этой площадки
зависит от величины передаваемого давления и соотношения радиу-
радиусов соприкасающихся поверхностей. Если мы в центре площадки
давления вырежем из материала рельса маленький кубик (например,
с ребром 1 мм), грани которого параллельны и перпендикулярны
к оси рельса (фиг. 75), то на грани этого кубика будут действовать
лишь нормальные сжимающие напряжения *). Таким образом (фиг. 76),
в данном случае мы имеем дело с тремя взаимно перпендикуляр-
перпендикулярными площадками, по которым действуют главные напряжения о*,
о" и о"'.
Появление боковых напряжений о" и о"' объясняется тем, что
под действием напряжений ог, перпендикулярных к площадке давле-
давления, материал выделенного нами кубика стремится раздаться в сто-
стороны и вызывает реакции о" и о"' со стороны окружающего кубик
материала рельса.
*) Вычисление этих напряжений приводится в курсах теории упругости;
результаты соответствующих расчётов приведены в главе IX.

§ 36]
НАПРЯЖЕНИЯ ПРИ ПЛОСКОМ НАПРЯЖЁННОМ СОСТОЯНИИ
125
Подсчёты величин этих напряжений *) показывают, что они до-
достигают в действительности весьма больших величин. Так, при со-
соприкасании бегунка паровоза серии Л с рельсом мы получаем такие
величины для с/, о", о"': J = 110 кг/мм\ о"=90 кг/мм*, о'"=80 кг/мм*.
Правило нумерации главных напряжений в рассмотренном при-
примере даёт:
01=зг" = — 80 kzjmm*\ с2=а"=— 90 кг/мм*\ <jz=J=— ПО кг/мм*.
В данном случае мы сразу нашли такой кубик, по граням кото-
которого действуют только нормальные напряжения, т. е. сразу полу-
получили и величины главных напряжений и положение тех площадок,
по которым они действуют. В общем случае по граням вырезанного
кубика будут действовать и нормальные и касательные напряжения.
Однако и тогда можно, меняя направление плоскостей, ограничиваю-
ограничивающих элементарный кубик, подыскать три взаимно перпендикулярные
площадки, по которым«. действуют лишь нормальные, т. е. главные
напряжения. Это самый общий случай распределения напряжений
в материале — объёмное напряжённое состояние; все три главные
напряжения не равны нулю.
§ 36. Напряжения при плоском напряжённом состоянии*
Для проверки прочности материала при плоском и объёмном
напряжённом состояниях необходимо найти наибольшие значения
нормальных и касательных на-
напряжений.
Начнём с плоского напряжён-
напряжённого состояния. Представим себе
прямоугольный параллелепипед,
на боковые грани которого дей-
действуют главные напряжения ot и а2
(фиг. 77). Оба эти напряжения бу-
будем считать растягивающими. По
фасадным граням элемента ника-
никаких напряжений нет; следователь-
следовательно, третье главное напряжение
равно нулю. Если одно из напря-
напряжений аи о2 или оба будут сжи-
сжимающими, то в дальнейшие фор-
формулы придётся вводить значение
соответствующего напряжения со	фЙГ 77.
знаком минус и менять нумера-
нумерацию главных напряжений в соответствии с условием § 34. Так, если
°дно из главных напряжений будет растягивающим, а другое сжи-
*) Н. М. Беляев, Вычисление наибольших расчётных напряжений при
с*атии соприкасающихся тел, Сборник Ленинградского института инжене-
Р°в путей сообщения, вып. 99 и 102, 1929.

126	СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ	[гл. VII
мающим, то первое придётся называть о1э а второе о3; если оба
напряжения будут сжимающими, то меньшее по абсолютной вели-
величине придётся назвать а2, а большее о3.
Поставим задачу отыскания наибольших нормальных и касатель-
касательных напряжений по сечениям, перпендикулярным к фасадным
граням.
Проведём такое сечение, нормаль к которому составит с напра-
направлением / угол 04 (фиг. 77). С направлением // та же нормаль со-
составит угол а2. По этому сечению будут действовать и нормаль-
нормальные оа и касательные та напряжения, зависящие и от ot и от о,.
Величину их мы получим, рассматривая действие ох и о2 отдельно
и складывая результаты. Та доля нормальных напряжений, которую
вызывают ах> выразится по формуле G.1) так: ах cos2 04; другая же
часть напряжений оа, вызванная а2, выразится по той же формуле
в виде o2cos2a2. Полное нормальное напряжение аа равно
оа = ах cos2 04 -{- о2 cos2 а2 = ах cos2 04 -\- о2 cos2 @4 -f- 90°)
или
аа = ах cos2 04 -f- a2 sin2 04.	G.5)
Таким же рассуждением при помощи формулы G.2) находим
величину касательных напряжений ча по проведённой площадке:
ха = у [ох sin 204 + о2 sin 2&2] = ~ [ох sin 2<хх + а2 sin 2 (а! + 90°)]
или
Та = -^"У Sin 2(Х1-	G-6)
В этих формулах ах — угол, отсчитанный против часовой стрелки
от направления оси / (напряжения ах) до нормали к рассматриваемому
сечению. Знаки для оа и та, а также для углов ах и аа будем при-
принимать по правилу, установленному выше, в § 33.
В дальнейшем в формулах для оа и та угол ах будем обозна-
обозначать через а, отсчитывая этот угол всегда от направления наиболь-
наибольшего (алгебраически) главного напряжения против часовой стрелки.
Пользуясь формулами G.5) и G.6) для напряжений по площадке
а — а (фиг. 78), легко находим напряжения по площадке Ь — Ь, ей
перпендикулярной, имеющей нормаль п , составляющую с направле-
направлением наибольшего главного напряжения угол p = a-f-90°:
a^ = qx cos2 p -f a2 sin2 p = ot cos2 (a + 90°) + o2 sin2 (a + 90°),l
0=0! sin2 a-j-a2 cos2 a;	J
G.60

36]
НАПРЯЖЕНИЯ ПРИ ПЛОСКОМ НАПРЯЖЁННОМ СОСТОЯНИИ
127
Из полученных формул выясняются свойства напряжений, дей-
действующих по взаимно перпендикулярным площадкам. Для нормальных
напряжений имеем:
оа == al cos2 а -}- <*з sin2 а»
а = at sin2 а -f- o2 cos2 а.
Складывая, получим:
оа + °з = ai + °2 = const., G.7)
t# e. сумма нормальных напряжений по <h
двум взаимно перпендикулярным пло-
площадкам постоянна и равна сумме глав- ^ "
ных напряжений.
Для касательных напряжений, сопо-
сопоставляя формулы G.6) и G.6'), получим:
тв = -та.	G.8)
Следовательно, касательные напря-
напряжения по двум взаимно перпендику-
перпендикулярным площадкам равны по величине и противоположны по
знаку. Это свойство обычно называют «законом парности каса-
касательных напряжений»у причем оно имеет место во всех случаях,
когда имеются касательные напряжения.
Из формул G.5) и G.6) видно, что величины нормальных и каса-
касательных напряжений по любой площадке зависят от угла наклона
этой площадки.
Чтобы найти наибольшее значение нормального напряжения, ис-
исследуем выражение G.5) на maximum. Взяв производную и при-
приравняв её нулю, получим:
а« — — 2oj cos a sin а -f- 2o2 sin а cos а = О
Фиг. 78.
или
G.9)
Сопоставляя полученное выражение G.9) с формулой G.6), видим,
что условие максимума для оа совпадает с условием равенства нулю
касательных напряжений по соответствующим площадкам. Из этого же
выражения следует, что аа = at cos2 a -f- a9 sin2 a получит наиболь-
наибольшее значение либо при a = 0, либо при a = 90°. Так как ai^>aa> т°*
тгхаа = сх	(при а = 0),
min аа = о9	(при а = 90°),
т» е. наибольшее и наименьшее нормальные напряжения в дан-
ной точке — это главные напряжения ot и о2, действующие по
*заимно перпендикулярным площадкам, свободным от касатель-
н**х напряжений.

128
СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ
[гл. у*
Наибольшее значение касательных напряжений, как это видно
из формулы G.6), будет:
тахт,,
! — <Ja
(при sin 2a =1, т. е. при а = 45°). G.10)
Следовательно, наибольшие касательные напряжения равны полу*
разности главных напряжений и действуют по площадкам, наклонён-
наклонённым к главным площадкам на угол 45° и перпендикулярным к пло-
плоскости чертежа. По площадкам, параллельным о2, наибольшее
касательное напряжение будет:
§ 37. Графическое определение напряжений (круг Мора).
Вычисление оа и та по формулам G.5) и G.6) может быть заме-
заменено графическим построением (фиг. 79).
Возьмём систему прямоугольных координат с осями с и т. Поло-
Положительную ось о направим вправо. Отложим на оси о отрезки ОА
и ОВ, изображающие
в определённом мас-
масштабе числовые вели-
величины напряжений ох и
о2 (ось о удобно рас-
располагать параллельно
наибольшему главному
напряжению at).
На фиг. 79 оба эти
напряжения приняты
растягивающими и от-
отложены на оси а в по-
Фиг. 79.	ложительном напра-
направлении. Если бы одно
или оба эти напряжения были сжимающими, мы отложили бы их в
противоположном направлении. Построим на отрезке ABf как на диа-
диаметре, круг с центром С, который назовём кругом напряжений»
Тогда для нахождения нормального оа и касательного напряжения
та по площадке, нормаль к которой составляет с наибольшим глав-
главным напряжением at угол а, надо построить при точке С централь-
центральный угол 2а, откладывая его положительные значения от оси а
против часовой стрелки. Точка D круга напряжений будет соответ-
соответствовать выбранной площадке; её координаты ОК и DK соответ-
соответственно равны оа и та. Это легко доказать. Из чертежа находим
радиус круга напряжений:
СР=:АС = ВС — АВ= ОА — °В — qi-"cr».

§ 37]	ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ	129
из прямоугольного треугольника KDC имеем:
DK— CD sin 2а = ^=^ sin 2а = та.
Далее:
ОК= ОВ+ВС + СК = Ч +^Чр + ^~ cos 2a =
= о3 -j- ах cos2 а — а2 cos2 а = ох cos2 а -|~ а2 sin2 а = за.
Таким образом, координаты точек окружности определяют напря-
напряжения. Величины аа измеряются отрезками по оси а. Положитель-
Положительные аа отложены в положительном направлении оси о. Величины та
измеряются отрезками, параллельными оси т. Положительные тв на-
направлены вверх, так как при принятых нами условиях значениям а
от 0 до 90° соответствуют положительные величины v> это же
видно и из формулы
*„ = *=!• sin 2а,
в которой за ах выбрано наибольшее из главных напряжений.
Определив построением круга напряжения аа и та, изобразим их
на чертеже выделенного элемента, учитывая знаки этих напряжений
(фиг. 79). Напомним, что мы условились отсчитывать угол а, опре-
определяющий положение внешней нормали к рассматриваемой площадке,
всегда от линии действия наибольшего (алгебраически) главного
напряжения. Совместим поэтому линию действия наибольшего глав-
главного напряжения ах с осью а на круге; тогда линия BD, наклонён-
наклонённая к оси о под углом а, будет параллельна нормали к рассматри-
рассматриваемой площадке, а значит, параллельна оа; линия ВМ будет па-
параллельна та.
Как видно из фиг. 79, наибольшее значение касательных напря-
напряжений равно отрезку CD0, т. е. радиусу круга напряжений
соответствующий угол 2а равен 90° и угол a = 45°. В круге напря-
напряжений величина тах^а изображается ординатой CD0, абсциссой для
которой служит OC = CTl ^ 2, т. е. на той площадке, где ta = ^max>
нормальное напряжение является средним.
Точно так же из фиг. 79 видно, что наибольшее нормальное
напряжение изображается отрезком ОА и равно аи а наименьшее —
отрезком ОВ и равно о4. Отсюда следует, что величины нормаль-
нормальных напряжений по любой из рассматриваемых площадок с углом а
заключаются между значениями главных напряжений ах и а2.
5 II. М. Беляев

130
СЛОЖНОЕ НАПРЯЖЁНЙОЕ СОСТОЯНИЕ
[гл. vii
Так, зная главные напряжения для плоского напряжённого состоя-
состояния, мы можем с помощью круга напряжений всесторонне изучить
напряжённое состояние материала в точке.
Пример 20. Графически найдём напряжения аа и та для пло-
площадки с углом а = — 30°; главные напряжения равны а3 = — 700 кг\см%
и oj = -f- 300 кг/см*. Построение дано на фиг. 80:
Пользуясь кругом напряжений, можно найти по известным глав-
главным напряжениям ах и о2 напряжения по двум взаимно перпендику-
Фиг. 80.
лярным площадкам а — а и b — b> нормали к которым (фиг. 81)
составляют углы а и р с направлением наибольшего главного напря-
напряжения а у.
В круге напряжений (фиг. 81) при точке С построим угол 2а.
Точка Da будет соответствовать площадке а — а, а отрезки DaKa и
ОКа представят собой напряжения та и оа по этой площадке.
Для нахождения напряжений по площадке b — b надо построить
угол 2р, т. е. прибавить 180° к углу 2а. Для этого надо лишь
продолжить радиус CDa\ точка D соответствует площадке b — b.
Напряжения т и а представляются отрезками DJK* и ОКЬ* Из
чертежа ясно, что ^о = — та> a
о„ + оя = oi 4- Oa =
Напряжения, действующие по граням элемента, вырезанного
плоскостями а и плоскостями Ь, показаны на фиг. 81 справа и на
фиг. 82.
Совмещая на круге напряжений линию действия наибольше-
наибольшего (алгебраически) главного напряжения ах с осью о (фиг. 81),

§37]
ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ
131
Фиг. 81.
Фиг. 83.

132
СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ
[ГЛ. VII
получаем, что линия BDa1 соединяющая левую крайнюю точку круга
с точкой Dat параллельна напряжению аа; линия BD —напряжению
о ; стрелки поставлены в соответствии с полученными знаками
напряжений.
На фиг. 83 изображено построение для случая, когда оба глав-
главных напряжения сжимающие.
§ 38. Нахождение главных напряжений при помощи круга.
Иногда приходится решать задачу, обратную рассмотренной
в предыдущем параграфе, т. е. по напряжениям аа, та и о , т нахо-
находить главные напряжения. Проще всего это сделать, пользуясь кру-
кругом напряжений.
Пусть (фиг. 84) мы знаем нормальные и касательные напряже-
напряжения по площадкам аир, перпендикулярным к плоскости чертежа
и составляющим между собой прямой
угол. Нормальные напряжения обозна-,
чим оа и а , а касательные та и z ; при
этом та = — т . Условимся значки аир
/сс ставить так, чтобы оа^>а (алгебраи-
(алгебраически). Примем для определённости,
и #
Нанесём напряжения оа, о , та и т
на систему координат искомого круга
напряжений (фиг. 84):
Так как точки Da и D , соответ-
соответствующие взаимно перпендикулярным
площадкам а и Ь, должны лежать на
противоположных концах диаметра
Фиг. 84.	круга, то точка пересечения линии
DaD с осью о даст центр круга С.
Описывая из точки С круг радиусом CDa или CD., получим на оси
о отрезки О А и ОВ, изображающие главные напряжения: ОА = о1
Направление оа на круге напряжений изображается прямой BDa,
наклонённой к оси о на положительный угол а. Следовательно,
чтобы перейти в круге напряжений от линии ог к линии оа, надо
отложить угол а против часовой стрелки, двигаясь от точки А
к точке Da. В нашем примере известным считается направление са.
Значит, чтобы на ^чертеже рассматриваемого элемента изобразить
искомое направление оь надо от направления оа отложить угол а
в обратную сторону, по часовой стрелке; относительное располо-

§ 38] НАХОЖДЕНИЕ ГЛАВНЫХ НАПРЯЖЕНИЙ ПРИ ПОМОЩИ КРУГА	133
экение напряжений о{ и ая, изображаемых на чертеже круга линиями
ОА и BlJay должно быть сохранено и на чертеже элемента.
Можно дать и на круге напряжений истинное направление главного
напряжения аи совпадающее с получаемым, как сейчас описано, на
чертеже элемента; для этого нужно от оси а, параллельной напра-
направлению са, отложить угол а из крайней левой точки В круга по
часовой стрелке, иначе говоря, снести точку Da в точку D'a. Напра-
Направление BD'a теперь совпадёт с направлением аи а направление ai
будет к нему перпендикулярно. При изображении главных напряже-
напряжений (в нашем примере ах и с2) необходимо помнить об их знаках,
полученных при построении круга, а также соблюдать правила нуме-
нумерации главных напряжений.
Заметим, что в рассматриваемых задачах при плоском напряжён-
напряжённом состоянии третье главное напряжение равно нулю. В соответ-
соответствии с этим, если при построении круга оба главных напряжения
получатся положительными (фиг. 84), то большее будет сь а мень-
меньшее с.2; если одно положительное, а другое отрицательное, то пер-
первое будет с1у а второе с3; наконец, если оба отрицательны, то
большее по абсолютной величине будет о3, а меньшее са.
Величина угла а определяется формулами (фиг. 84):
С*-	'"V	G.11)
Знак минус ставится потому, что при положительных значениях аа
и та угол а (угол поворота направления aa в главное направление)
отсчитывается по часовой стрелке.
Пользуясь фиг. 84, можно получить формулы для вычисления
главных напряжений, изображаемых отрезками ОА и ОВ} при пло-
плоском напряжённом состоянии. Из чертежа имеем
ОА = ОС-\-СА и ОВ = ОС — СВ.
Далее:
Радиусы круга напряжений СЛ = СВ, равные CDa = CD., равны:
с а=св = cd, = vcia + кМ = У ^'"'"^ + < =
Таким образом,

134
СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ
[ГЛ. VII
В практике часто приходится встречаться с такими случаями
плоского напряжённого состояния, когда о0 = О. Тогда формулы для
главных напряжений примут вид:
G.13)
Здесь наименьшее главное напряжение обозначено через о3, так как
оно отрицательно (поскольку подкоренное выражение больше оа).
Угол наклона 1-го главного напряжения к оси о определяется
формулами, вытекающими из G.11):
tg 2a = — —«¦
или
GЛ4)
Ниже па примерах показано нахождение главных напряжений
с помощью круга напряжений.
Фиг. 85.
Пример 21. Дано: са = + 400 Агг/с.н2; та = ~ 300 кг/см2; с9 =
= — 200 кг/см2; z, = + 300 кг/см2;
На фиг. 85 показано нахождение величин и направлений главных напря-
напряжений: о1== + 530 кг/см2; с3 = — 330 кг/см2; о = 22° (между оа и о,).
П	22 Д	1000 /	400	2	0
1 +	/; 3	/;	(у а ,)
Пример 22. Дано: ста = 1000 кг/см-; za = 400 кг/см2; ^ =0, ^ =
= — 400 кг /см2. Построение показано на фиг. 86. ^ = 1140 кг/см2; са =
= —140 IK

§ 39]
НАХОЖДЕНИЕ НАИБОЛЬШИХ НАПРЯЖЕНИЙ
135
а)
§ 39. Нахождение наибольших напряжений для объёмного
напряжённого состояния.
Для случая объёмного напряжённого состояния напряжения по
любой площадке можно представить также графически.
Пусть мы имеем выделенный из тела элемент кубической формы,
на грани которого действуют три главных напряжения: аь о^, а3
(фиг. 87). Поставим задачу нахождения нормального и касательного
напряжений по любой площадке, пере-
пересекающей выделенный кубик.
Сначала будем искать эти напря-
напряжения по площадкам, параллельным
одному из главных напряжений, напри-
например Of. На фиг. 87, а эта площадка
заштрихована.
Как мы видели выше (§ 34), глав-
главное напряжение, параллельное прове-
проведённой площадке, не вызывает по ней
ни нормальных, ни касательных напря-
напряжений. Поэтому напряжения по рас-
сматриваемым площадкам будут зави-
зависеть лишь от а3 и а3— для них мы
будем иметь дело с плоским напряжён-
напряжённым состоянием. Тогда этим пло-
площадкам будут соответствовать точки
круга напряжений, построенного на
главных напряжениях о2 и а3 (фиг. 87, б).
Точно так же напряжения по пло-
площадкам, направленным параллельно о2>
будут изображаться координатами то-
точек круга, построенного на напряже-
напряжениях а1 и о3; для площадок, парал-
параллельных а3, — на напряжениях ах и а2.
Таким образом, координаты точек трёх кругов напряжений
(фиг, 87, б) изображают нормальные и касательные напряжения по
сечениям кубика, параллельным одному из главных напряжений.
Что же касается площадок, пересекающих все три оси главных
напряжений, то в теории упругости показано, что для них напряже-
напряжения о и х изображаются координатами точек D заштрихованной на
Фиг. 87, б площади.
Значения этих напряжений могут быть вычислены по формулам:
aa = oi cos* ^-\-о% cos2a2-{-a3 cos* a3,	G.15)
xa = Yo\ cos2 aA -|- o\ cos* a* -j- o\ cos*2 a3 — <з%.	G.16)
Здесь ai9 a2 и a3 — углы, составленные нормалью к площадке
с направлениями соответствующих главных напряжений oit a3 и as.

136	СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИИ	[ГЛ. VII
Из фиг. 87 ясно, что в случае объёмного напряжённого состоя-
состояния наибольшее и наименьшее нормальные напряжения равны соот-
соответственно наибольшему и наименьшему главным напряжениям.
Наибольшее касательное напряжение равно радиусу наибольшего
круга, следовательно, полуразности наибольшего и наименьшего
главных напряжений. Оно действует по площадкам, наклонённым
под углом 45° к направлению этих главных напряжений, причем
нормальные напряжения на таких площадках равны полусумме
наибольшего и наименьшего главных напряжений (ох ^> а2 ^> а3).
Таким образом, в общем случае напряжённого состояния мате-
материала, когда в рассматриваемой точке все три главных напряжения
не равны нулю, получаем:
= аз5 тахТа ~ ' * 2 *'	G.17)
По площадкам, параллельным одному из главных напряжений и
наклонённым к двум другим на угол 45°, касательные напряжения
будут: тахт по формуле G.17), далее
°J, 2
G.17')
§ 40. Вычисление деформаций при плоском и объёмном
напряжённом состояниях.
При проверках прочности элемента (фиг. 87), на грани кото-
которого действуют напряжения alt a.2, o3, нам придётся столкнуться
с вопросом о величинах соответствующих деформаций. Называя
ребро, параллельное главному напряжению ci9 первым, а рёбра,
параллельные главным напряжениям с2 и о3, вторым и третьим,
определим относительные продольные деформации элемента в напра-
направлении этих рёбер, отдельно рассматривая влияние каждого из
напряжений и складывая результаты.
Под действием напряжений а{ элемент в направлении первого
ребра получит относительное удлинение, равное
В то же время по отношению к напряжениям о2 и а3 первое
ребро является поперечным размером, а потому под действием на-
напряжений а2 и отдельно а3 элемент в направлении первого ребра
испытывает относительные укорочения, равные (см. § 9):
Полная относительная деформация элемента в направлении первого
ребра выразится суммой

с 40]	ВЫЧИСЛЕНИЕ ДЕФОРМАЦИЙ	137
Подобные же выражения получим и для деформаций в двух дру-
других направлениях; в результата имеем:
е — -^- — J *2 4-
Если какие-либо из напряжений alt о2, a3 будут сжимающими,
то соответствующие числовые« значения их необходимо ввести
в формулы G.18) со знаком минус.
Из формулы G.18) можно сейчас же получить выражения для
случая растяжения или сжатия по двум направлениям, — тогда одно
из главных напряжений следует положить равным нулю. Например,
для случая, показанного на фиг. 81, имеем:
=-r
G.19)
Вычислим изменение объёма прямоугольного параллелепипеда со
сторонами, равными a, b и с, в общем случае напряжённого состоя-
состояния. До деформации объём его равен VQ — abc. После деформации,
вследствие изменения длины рёбер, объём его станет
V, = (а + А«) (Р + Ад) (с + Ас),
или, пренебрегая произведениями малых деформаций:
\\ = abc -\-ab • &с-{-ас * &b -j- be • Да = Vo (I -j- ?i + ?a + ?з)«
Относительное изменение объёма равно:
Ь^^^^^ + ^ + ц.	G.20)
Подставляя в эту формулу вместо гг> е2, е3 их значения из формул
G.18), получим:
Заметим, что если коэффициент Пуассона \х равен -к-% то отно-
относительное изменение объёма равно нулю. Это мы уже л ол учи ли
в § 9 для случая линейного напряжённого состояния.

138	СЛОЖНОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ
Если С| = а2 = о3 = о, то
1гл.
Величину 3 j _2 называют модулем объёмной деформации и
обозначают буквой К» Тогда, вводя это обозначение в G.21),
находим:
6 = e1+e2 + e3 = -^-±|^L.	G.22)
Мы видим, что изменение объёма зависит лишь от суммы глав-
главных напряжений, а не от их соотношения. Поэтому кубик получит
одно и то же изменение объёма, будут ли по его граням действо-
действовать различные по величине главные напряжения
си оа и о3 или одинаковые напряжения:
в последнем случае все рёбра кубика получат оди-
одинаковую деформацию:
3
за: •
G.23)
П р и м е р 23. Бетонный кубик со стороной а =» 20 см
плотно помещён в абсолютно жёсткую обойму и центрально
сжимается силами Р = 24 т (фиг. 88).
Найти давление на стенки обоймы и напряжения в бе-
бетоне. Коэффициент Пуассона для бетона jx = 0,18.
При продольном сжатии бетона он стремится раздаться
в стороны и давит при этом на стенки обоймы с силой, рав-
Фиг. 88.	ной реакциям стенок. Обозначим реакции стенок Nx и Nf
(силы Р направлены по оси z). Ввиду симметрии оси х9
у и z совпадают с направлениями главных напряжений. Поскольку все дей-
действующие на кубик силы пересекаются в одной точке, уравнения статики
не могут быть использованы, так как обращаются в тождества вида 0 = 0.
Обратимся к рассмотрению упругих деформаций. В силу жёсткости
обоймы поперечные деформации (в направлениях осей х и v) невозможны.
Следовательно, е^ = гу = 0. Выразим относительные удлинения через наири-
и с.:
Здесь
••—?- и о„ = —
а2	' аг
Решая уравнения деформаций совместно, найдём;

41]	ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 3ГПРУГОЙ ДЕФОРМАЦИИ
Подставляя значения, найдём:
Л^ = Ny = —	• Р или Л^ = Ny = -j—' 1Я • 24 =
Напряжения в бетоне будут:
ау = аа == — 13,2 кг/см2,
Р	24 000
~60 кг/см*.
§ 41. Потенциальная энергия упругой деформации при сложном
напряжённом состоянии.
Потенциальной энергией деформации называется энергия, нака-
накапливаемая в материале в результате упругой деформации, вызванной
действием внешних сил.
Для вычисления потенциальной энергии, накопленной упругой
системой, можно воспользоваться законом сохранения энергии.
Рассмотрим сначала случай простого растяжения (фиг. 89). Если
мы будем нагружать стержень статически, путём постепенного под-
подвешивания очень малых грузов АР, то при добавлении каждого
такого груза подвешенная часть нагрузки опустится и*
потенциальная энергия , её уменьшится, а потенциальная
энергия деформации растянутого стержня возрастёт.
При медленном, постепенном возрастании нагрузки,
скорость перемещения свободного конца стержня будет
весьма мала. Поэтому силами инерции перемещающихся
масс можно пренебречь, и, значит, можно считать, что
деформация стержня не будет сопровождаться измене-
изменением кинетической энергии системы.
При этих условиях потенциальная энергия груза
при его опускании преобразуется в потенциальную энер-
энергию упругой деформации стержня (рассеиванием энергии за счет
тепловых и электромагнитных явлений, сопровождающих упругую
деформацию, — пренебрегаем). Таким образом, упругую систему
при статическом действии сил можно рассматривать как своеобразную
машину, преобразующую один вид потенциальной энергии в другой.
Так как количество потенциальной энергии, потерянной грузом,
численно равно работе, произведённой им при опускании, то задача
°6 определении потенциальной энергии деформации сводится к вы-
вычислению работы внешних сил. При простом растяжении (§ 11)
Али работы внешних сил было получено
А = ¦??-.	C.1)

140	сложное напряжённое состояние	[гл. vn
(Р1
При A/=-grrr
Количество потенциальной энергии, накапливаемое в единице
объёма C.2):
и = я = -^г —4р.	G.25)
Теперь перейдём к определению количества потенциальной энер-
энергия, накапливаемой в единице объёма материала, находящегося
в условиях сложного (объёмного и плоского) напряжённого состоят
ния. Пользуясь принципом независимости и сложения действия сил
и предполагая постепенное возрастание главных напряжений, под-
подсчитаем потенциальную энергию, как сумму энергий, накапливаемых
в единице объёма материала под действием каждого из главных
напряжений сх, о2 и а3 по формуле G.25)
и —а— 2-t-2i-2,
где elf e^ и е3 — относительные удлинения, вычисляемые по фор-
формулам G.18). Следовательно, удельная энергия деформации в этом
случае будет:
или, после раскрытия скобок,
11	[а' + °* +
Таким образом, полная энергия деформации, накапливаемая
в единице объёма материала (кубик со сторонами, равными единице
длины), может быть определена по формуле G.26). Эта энергия
может рассматриваться как состоящая из двух частей: 1) энергии
uv, накапливаемой за счёт изменения объёма v рассматриваемого
кубика (т. е. одинакового изменения всех его размеров без изме-
изменения кубической формы) и 2) энергии иф, связанной с изменением
формы кубика (т. е. энергии, расходуемой на превращение кубика
в параллелепипед).
Такое разделение потенциальной энергии на две части оказы-
оказывается удобным при дальнейшем рассмотрении вопроса о прочности
материала при объёмном напряжённом состоянии.

§41]	ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ	141
Подсчитаем величину обеих составляющих удельной потенциаль-
потенциальной энергии. Выше было показано (§ 40), что при одинаковой
деформации рёбер кубика, т. е. при изменении только объёма,
относительное удлинение каждого ребра равно (формула 7.23):
п ~ зк *
где ап = gl ""*"а*"* Стз , а объёмный модуль упругости К= о,» _о V •
Тогда энергия изменения объёма будет:
~ 2АГ ""	18ДГ
или
Потенциальная энергия, соответствующая изменению формы вы-
выделенного элемента материала, теперь найдётся как разность:
Произведя вычисления, получим:
При простом растяжении, когда а, == а = -^-, о2 = 0 и а3 = 0,
удельная потенциальная энергия, связанная с изменением объёма
элементарного кубика
а потенциальная энергия формоизменения
иЪ——ЗЯ	'	G'dU)
Разумеется, сумма их даёт полную удельную энергию растя-
растяжения:

142	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА	[ГЛ. VIU
ГЛАВА VIII.
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА ПРИ СЛОЖНОМ
НАПРЯЖЁННОМ СОСТОЯНИИ.
§ 42. Понятие о теориях прочности.
В § 33 был поставлен вопрос о проверке прочности материала
при линейном напряжённом состоянии, при простом растяжении,
когда главные напряжения имеют значения
°1 = 7Г' 02 = 0, 33 = 0,
или при сжатии коротких стержней, когда
а1==0, о2 = 0 и а3 = ——-.
В этом случае проверка прочности производится по условиям
ai<ja] или ||]
(растяжение)	(сжатие)
Буквой [<з] обозначена допускаемая величина напряжений при
растяжении или сжатии. Для большинства пластичных материалов
эти значения одинаковы, для хрупких — различны.
В § 17 указано, что допускаемое напряжение определяется
с таким расчётом, чтобы был обеспечен известный запас k против
наступления опасного состояния:
где а0 — напряжение, характеризующее опасное состояние. При ста-
статической нагрузке для пластичного материала достижение такого
состояния характеризуется появлением больших остаточных дефор-
деформаций, а для хрупкого — появлением трещин, разрушением мате-
материала. Тогда в первом случае а°з=от, а во втором a° = aB.
При линейном напряжённом состоянии эти величины получаются
непосредственно из лабораторных опытов на растяжение или сжатие.
Подобный вид действия сил легко осуществить в лаборатории
и можно непосредственно установить величину предела текучести
и предела прочности для испытываемого материала.
Рассмотрим теперь, как производить проверку прочности в тех
случаях, когда два или все три главных напряжения аь а2, а3 не
равны нулю.
В этом случае наступление опасного состояния материала может
быть вызвано, вообще говоря, различными числовыми значениями
главных напряжений о,, а2, о3 в зависимости от величины отноше-
отношении их друг к другу. Каждой комбинации этих отношений будут

421
ПОНЯТИЕ О ТЕОРИЯХ ПРОЧНОСТИ
142
соответствовать определённые опасные величины главных напряже-
напряжений о\, 0°, о°, ПРИ которых наступят опасное состояние материала
(появление больших остаточных деформаций или трещин).
Таким образом, для нахождения этих опасных значений напря-
напряжений аи о2, <?3 пришлось бы в лаборатории подвергать образцы
материала действию главных напряжений при разных соотношениях
Л±-, —. Практически осуществить такие опыты невозможно ввиду
трудности их постановки и громадного объёма испытаний.
Поэтому необходимо найти способ составления условия прочности
при сложном напряжённом состоянии, пользуясь величинами от и ов,
полученными при опытах для линейного напряжённого состояния.
Таким образом, задача проверки прочности материала в общем
случае, когда все три главных напряжения не равны нулю, ста-
ставится так:
1)	определены расчётом три главных напряжения: Oi^>o2^>o3>
2)	выбран материал,
3)	для этого материала при помощи опытов в лаборатории най-
найдена при простом растяжении или сжатии величина опасных напря-
напря°	°
= ав и установлено допускаемое напряжение*
<*>
1
— 1
I
прочности?
известно:
Фиг. 90.
жений о" = аг или <г
Требуется составить
условие прочности для
общего случая напря-
напряжённого состояния,
зная а1э оа и а3 и со-
сохраняя тот же коэф-
коэффициент запаса k
(фиг. 90).
Поставленная зада-
задача может быть решена
лишь на основании
предположения (гипотезы) о том, каков вид функции, связывающей
прочность материала с величиной и знаком главных напряжений,
каким фактором вызывается наступление опасного состояния ма-
материала.
Таких факторов можно наметить несколько. В самом деле, даже
при простом растяжении стержня из пластичного материала можно
поставить вопрос: что является причиной текучести?
Можно предположить, что текучесть появится тогда, когда
наибольшие нормальные напряжения в стержне дойдут до предела
текучести ст. Однако можно было бы стать и на другую точку
зрения и высказать предположение, что явление текучести наступит
тогда, когда наибольшее удлинение материала достигнет определён-
определённого значения. Можно сделать и третье предположение, а именно,
что появление больших остаточных деформаций связано с тем, что
касательные напряжения достигнут определённой величины.

144	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА	[ГЛ. Vll|
Таким образом, мы можем высказать ряд гипотез, построить ряд
так называемых теорий прочности. Как мы увидим дальше, при
простом растяжении или сжатии, при линейном напряжённом состоя-
состоянии результаты проверки прочности оказываются одинаковыми,
какую бы из гипотез мы ни приняли. Это объясняется тем, что
в этом случае проверка прочности основывается непосредственно
на опыте.
Совсем иначе будет обстоять дело при сложном напряжённом
состоянии. В следующих параграфах будет показано, как меняется
условие прочности в зависимости от принятой теории. Выбор для
практического применения той или иной теории окончательно опре-
определяется проверкой её на опыте для случая сложного напряжён-
напряжённого состояния.
Прежде чем перейти к изложению теорий прочности, заметим,
что опасное состояние как для пластичных материалов (момент
появления больших остаточных деформаций), так и для хрупких
(момент появления трещин) лежит на границе применения закона
Гука (с известным, достаточным для практики приближением). Это
позволяет при всех дальнейших вычислениях, относящихся к про-
проверкам прочности, пользоваться формулами, выведенными в преды-
предыдущих параграфах при условии применимости закона Гука.
§ 43. Проверка прочности по различным теориям.
Первое, наиболее простое, предположение заключается в том,
что опасное состояние материала наступает в тот момент, когда
наибольшее по абсолютной величине нормальное напряжение до-
достигает опасного значения. Эта гипотеза носит название теории
наибольших нормальных напряжений, или первой теории проч-
прочности.
Таким образом, и в общем случае, когда все три главных
напряжения ои о.2 и о3 не равны нулю, при проверке по этой теории
необходимо учитывать величину лишь наибольшего растягивающего
или наибольшего сжимающего напряжений. Величина же двух дру-
других главных напряжений не имеет при этом как бы никакого
влияния на прочность материала, на достижение им опасного состоя-
состояния, и о них при проверке прочности можно забыть. Тогда теряется
в известной степени различие между проверкой прочности при
линейном напряжённом состоянии и при объёмном.
Если в случае простого растяжения или сжатия мы для напря-
напряжений ах и о3 допускаем величину [о], то и в общем случае, когда
все три главных напряжения clf о2, о3 не равны нулю, для наиболь-
наибольшего из них мы должны допустить ту же величину [о]. При этих
условиях коэффициент запаса по отношению к возможности появле-
появления опасного состояния будет одинаков как в случае простого
растяжения, так и в общем случае.

§ 43] ПРОВЕРКА ПРОЧНОСТИ ПО РАЗЛИЧНЫМ ТЕОРИЯМ	145
Условие прочности для обоих случаев напишется одинаково:
ci<[s] или |o3|*S[cj].	(8.1)
При проверке указанной гипотезы опытами, однако, обнаружи-
обнаружилось несоответствие её выводов с результатами опытов на все-
всестороннее сжатие не только пластичных материалов, но и хрупких.
Это можно видеть из приведённых в § 35 напряжений при сопри-
соприкосновении колёс и рельсов. В этом случае а3^110 кг)мм*, что далеко
превышает величину предела текучести рельсовой стали D0 кг/мм*)
при простом растяжении или сжатии. Лишь для случая растяжения
хрупких материалов эта теория согласуется с опытами. Так как
обычно эта теория даёт либо излишние, либо недостаточные размеры
сечений элементов конструкций при сложном напряжённом состоянии,
ею избегают пользоваться.
Выдвинутая позднее первой, и до известной степени в противовес
ей, вторая гипотеза принимает, что наступление опасного состояния
определяется не наибольшим напряжением, а величиной наибольшего
относительного удлинения или укорочения.
Если это так, то проверку прочности следует производить по
наибольшим относительным деформациям. Сохраняя тот же коэф-
коэффициент запаса, мы должны для наибольшей относительной про-
продольной деформации в общем случае (все главные напряжения не
р^вны нулю) допускать ту же величину, что и при простом растя-
растяжении.
Для общего случая мы имели формулы G.16) для главных
линейных деформаций (§ 40). В зависимости от соотношения вели-
величин главных напряжений одна из этих деформаций будет численно
наибольшей. Пусть это будет е1# Тогда
1 г
Для случая же линейного напряжённого состояния мы знаем
величину допускаемого напряжения [а]. Тем самым для наибольших
относительных деформаций допускаем величину
Условие прочности выразится так:
?max^L?J»	\°.1)
т. е.
тогда
fa — Iх (а2 + аз)] ^ М-	(8.3)
Таким образом, принимая теорию наибольших относительных
Удлинений, необходимо сравнивать с допускаемым напряжением,

146	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА	[ГЛ. \Лц
установленным для простого растяжения или сжатия, не то или
другое главное напряжение, а их совокупность, так называемое
приведённое (расчётное) напряжение, определяемое формулой:
Эта гипотеза также стоит в противоречии с некоторыми опытами
по исследованию прочности пластичных материалов. Если бы она
была для таких материалов верна, то образец, растягиваемый в двух
или трёх направлениях, был бы прочнее образца, растягиваемого
линейно; опыт этого не подтверждает. Не подтверждается эта
гипотеза и при всестороннем равномерном сжатии.
Для хрупкого состояния материала теория наибольших относи-
относительных деформаций даёт обычно согласующиеся с опытом резуль-
результаты.
Третья гипотеза возвращает нас опять к. представлению о том,
что главную роль в наступлении опасного состояния материала
играет наибольшее напряжение, но уже не нормальное, а касатель-
касательное, равное полуразности наибольшего и наименьшего главных
напряжений:
При этом предположении проверку прочности надо вести по
касательным напряжениям. Условие прочности имеет вид:
*тах ^ М.
Что касается величины допускаемого напряжения [х], то, считая,
что наступление опасного состояния зависит лишь от наибольших
касательных напряжений, мы и при объёмном напряжённом состоя-
состоянии должны для этих напряжений допускать ту же величину, что
и при простом растяжении. Степень безопасности по отношению
к наступлению опасного состояния в обоих случаях будет тогда
одинаковой.
Если при простом растяжении мы допускаем для нормальных напря-
напряжений величину [а], то тем самым для наибольших касательных мы до-
допускаем значение [х]=|~| [см. формулу G.3)]; эти касательные на-
напряжения, как известно, действуют по площадке, наклонённой под
углом в 45° к направлению растягивающей силы.
Условие прочности для объёмного напряжённого состояния прини-
принимает вид:
-max —	2^2 » ИЛИ (°1~°зХМ-	С8'4)
Таким образом, принимая указанную гипотезу, приходится при
проверке прочности сравнивать с допускаемым напряжением на растя-

§ 43] ПРОВЕРКА ПРОЧНОСТИ ПО РАЗЛИЧНЫМ ТЕОРИЯМ	147
жение или сжатие не наибольшее нормальное напряжение, а разность
между наибольшим и наименьшим нормальными (главными) напряже-
напряжениями. Величина расчётного (приведённого) напряжения в этом
случае равна
сг3 = сх — а3.
Теория наибольших касательных напряжений стоит в доста-
достаточно близком согласии с результатами опытов, особенно для пла-
пластичных материалов; она подтверждается опытами на всестороннее
сжатие. Обычно эта теория обеспечивает прочные размеры рассчи-
рассчитываемых элементов конструкций; иногда эти размеры оказываются
даже несколько завышенными.
В том простом виде, как оно дано формулой (8.4), условие
прочности может быть написано лишь для тех материалов, для ко-
которых допускаемые напряжения на растяжение и сжатие могут
быть приняты равными: например, для стали. Для таких материалов,
как чугун, камень и т. д., в условие (8.4) необходимо внести изме-
изменения, изложение которых сделано в главе XXXVII.
Недостатком теории наибольших касательных напряжений, бро-
бросающимся сразу в глаза, является то обстоятельство, что она совер-
совершенно не учитывает влияния на работу материала среднего по вели-
величине главного напряжения. Выходит, что при постоянных наиболь-
наибольшем ot и наименьшем о3 главных напряжениях мы можем, не изме-
изменяя условий работы материала, как угодно менять величину
среднего напряжения <з2, лишь бы оно было меньше о{ и больше
о3. Это обстоятельство представляется сомнительным, и опыты
подтверждают, что величина напряжения а2 всё же оказывает влия-
влияние на прочность материала. Недооценивается этой теорией и опас-
опасность нарушения прочности элементов, испытывающих примерно
равные растягивающие напряжения в трёх главных направлениях.
В связи с недостатками старых теорий возникли новые идеи
относительно того, какой фактор вызывает наступление опасного
состояния.
Рядом авторов было высказано предположение, что опасное
состояние материала зависит не от величины деформаций или напря-
напряжений в отдельности, а от совокупности тех и других — от вели-
величины потенциальной энергии или от численно ей равной удельной
работы деформации. Величина этой работы выражается через все
три главных напряжения.
Если сделать предположение, что причиной опасного состояния
является накопление полной удельной потенциальной энергии дефор-
деформации, то прочность материала будет обеспечена при условии, что
и^[н]. Здесь и — потенциальная энергия деформации при объёмном
напряжённом состоянии, выражающаяся формулой G.26):

148	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА	[гл. VIII
а [и] — допускаемое количество потенциальной энергии, которое
(по условию равнопрочности материала при сложном и линейном
напряжённых состояниях) может быть получено из выражения G.25)
для полной энергии деформации при простом растяжении:
	 с2
«р — /Г •
При простом растяжении мы допускаем для нормальных напряжений
величину [о], тем самым для удельной работы деформации мы допу-
допускаем
Для соблюдения той же степени безопасности в общем случае
мы для удельной работы деформации должны допускать не больше
чем [и]. Условие прочности принимает вид:
или
V< + °i + < - ^ (°1°* + ^1^3 Т~*^) < И	(8-5)
Расчётное напряжение равно
Эта гипотеза опытами не подтвердилась и имеет сейчас только
историческое значение. Но зато она явилась базой для создания
новой энергетической теории прочности, обычно хорошо согла-
согласующейся с опытами.
Эта теория, которую обычно называют четвёртой теорией (или
гипотезой) прочности, предполагает, что причиной возникновения
опасной пластической деформации является не вся потенциальная
энергия деформации, а только та часть её, которая связана с изме-
изменением формы элементарных объёмов материала. Следовательно,
прочность материала будет обеспечена, если
Здесь г/ф — потенциальная энергия формоизменения при сложном
напряжённом состоянии, равная G.28):
Величина же допускаемой потенциальной энергии изменения формы
для случая простого растяжения равна G.30):

§ 43] ПРОВЕРКА ПРОЧНОСТИ ПО РАЗЛИЧНЫМ ТЕОРИЯМ 149
Условие прочности по энергетической теории получит вид:
al +
а приведённое напряжение будет 1):
Л/—2	i	2	(	2
Условие прочности (8.6) можно представить и в ином виде, иногда
более удобном для вычислений:
Формулы (8.6) и (8.7) представляют условие прочности по так назы-
называемой теории наибольшей потенциальной энергии изменения формы.
Можно показать, что расчётное напряжение аг4 по этой теории
пропорционально касательному напряжению по площадке, равно накло-
наклонённой к направлениям главных напряжений. Поэтому этот вид энер-
энергетической теории тоже может быть отнесён к категории теорий,
основывающих проверку прочности для пластичных материалов на
величине касательных напряжений (глава XXXVIII). Опыты очень
хорошо подтверждают результаты, получаемые по этой теории для
пластичных материалов.
На основании формул G.17) условие прочности (8.7) может
быть написано ещё и так:
Подводя итог рассмотрению теории прочности, мы можем написать
условие прочности при объёмном напряжённом состоянии в таком виде:
а,«?М,	(8.9)
где сг — расчётное (приведённое) напряжение; [а] — допускаемое на-
напряжение при простом растяжении или сжатии. Расчётное напряже-
напряжение аг может быть истолковано как растягивающее напряжение при
линейном напряжённом состоянии, эквивалентном рассматриваемому
объёмному в отношении опасности для прочности материала.
Выбор теории прочности, а значит и формулы для оп таким
образом, отвечает на вопрос: какой критерий прочности материала
столь же надёжен для рассматриваемого объёмного напряжённого
состояния, как и для линейного?
Что касается приложения теорий прочности к практическим рас-
расчётам, то надо иметь в виду, что под «разрушением» мы подразу-
1) К такому же результату придё\м, положив р. = 0,5 в формуле (8.5), что
отвечает неизменяемости объёма.

150	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА	[гл. Щц
меваем для материала, находящегося в пластичном состоянии, на-
наступление заметных остаточных деформаций — текучесть, а для мате-
материала в хрупком состоянии — появление трещин, отделение, отрыв
одной части материала от другой.
Так как в зависимости от условий работы и характера напряжён-
напряжённого состояния всякий материал может находиться и в хрупком
и в пластичном состояниях, то, вообще говоря, следует принять для
практического применения две теории прочности — одну, пригодную
для проверки прочности материала при его пластичном состоянии,
другую — при хрупком. Опыты показывают, что для пластичного
состояния материала наиболее оправдываема опытами энергетическая
теория прочности; несколько, но незначительно, расходится с опы-
опытами теория наибольших касательных напряжений.
Для хрупкого состояния материала, повидимому, может иногда
применяться теория наибольших удлинений; имеются опыты, которые
показывают, что в ряде случаев подтверждается для такого состоя-
состояния материала и теория наибольших нормальных напряжений; ею
пользуются на практике при проверке прочности таких материалов,
как чугун, камень и т. д.
В последнее время советскими учёными Н. Н. Давиденковым
и Я. Б. Фридманом предложена новая «объединённая теория проч-
прочности», обобщающая современные воззрения на вопросы прочности
материалов в их хрупком или в пластичном состоянии. Эта теория
подробно рассматривается в главе XXXVIII.
Все изложенные соображения по теориям прочности относятся к
материалам, которые с достаточной степенью точности могут счи-
считаться изотропными. Для анизотропных материалов, например
дерева, приведённые выше формулы неприменимы; здесь прихо-
приходится учитывать направление усилий по отношению к волокнам
(в дереве)»
Необходимо остановиться на вопросе о переходе в практических
расчётах от одной теории прочности к другой. В первой четверти
нашего века в практике проектирования, особенно в машинострое-
машиностроении, широко применялись формулы, основанные на теории наиболь-
наибольших деформаций. Вполне оправданным оказался переход к более
правильным для пластичных материалов теориям наибольших каса-
касательных напряжений и наибольшей потенциальной энергии. Надо
помнить, что этот переход нельзя осуществлять механически — путём
простой замены в условии прочности одного выражения для расчёт-
расчётного напряжения другим. Необходимо изменить и правую часть нера-
неравенства— величину допускаемого напряжения [о]. Дело в том, что,
уточняя расчёт, вводя в практику более правильную теорию проч-
прочности, мы должны во многих случаях изменить и коэффициент за-
запаса ky а значит и [а]. Если этого не сделать, то можно впасть и
ошибку. Ниже, на примерах в отделах сдвига и изгиба, это будет
разъяснено детально.

§ 44J	ПРИМЕРЫ ПРОВЕРКИ ПРОЧНОСТИ	151
§ 44. Примеры проверки прочности.
Пример 24. Возьмём приведённый выше (§ 35) случай передачи давле-
давления от бегунка паровоза на рельс. На кубик с рёбрами длиной 1 мм, выре-
вырезанный в центре той площадки, через которую передаётся давление колеса
на рельс, действуют сжимающие главные напряжения: <st = — 80 кг/мм*:
ojsss — 90 кг/мм%\ а3 = —110 кг/мм*. Подсчитаем по каждой из теорий проч-
прочности величину расчётного напряжения, которое следует сравнивать с допу-
допускаемым, имея при этом в виду, что вычисление расчётных напряжений ио
первым двум теориям производится лишь с целью сопоставления результа-
результатов. Эти теории, как уже указывалось, неприменимы для пластичного ма-
материала.
По теории наибольших нормальных напряжений расчётным напряжение л
будет
\ол\ = ПО кг/мм*.
По теории наибольших деформаций расчётное напряжение равно
На, —pi(сг2 + а0] | = |-110 + 0,3(90 + 80)| =59/сг/жл^.
По теории наибольших касательных напряжений расчётное напряжение равно
('1 — <*з) = ~ 80 + 110 = 30 кг/мм*.
Наконец, по энергетической теории
l + ai + Ql — °ia2 — *Л — Vt = 26,4 кг/мм*.
Так как для обычной рельсовой стали предел текучести близок к 40 кг/мм3,
а предел упругости около 30 кг/мм*, то лишь две последние теории указы-
указывают на то, что напряжения находятся в допускаемых пределах; это подтвер-
подтверждается опытом эксплуатации рельсового пути.
Пример 25. Сделаем проверку напряжений в стенке резервуара (§ 35).
Как выяснено при решении этой задачи, на прямоугольный элемент, выре-
вырезанный из цилиндрической стенки двумя смежными образующими и двумя
поперечными сечениями (фиг. 91), действуют главные
напряжения в-двух направлениях, а4 и о2; третье глав-
главное напряжение равно нулю. Величина напряжений вы-
выражается формулами	|
а. = —— в« = —— ст. = О
Фиг. 91.
где р — внутреннее давление в кг/см2; ?—толщина
стенок резервуара; D — диаметр цилиндрической части.
Для котла все теории дают мало отличные друг от друга результаты.
Сравним результаты теорий наибольших касательных напряжений и энерге-
энергетической. По теории касательных напряжений
01 — аз ^ М или 9/ ^ [3]«
По энергетической теории прочности
j/ jj 4~ ai — °ia2^M или
даёт
л ол pD .
0,86^. ^[з

152	контактные напряжения	[гл.
IX
Условия прочности по этим теориям в данном случае дают результаты,
отличающиеся на 14%; Ддя расчёта толщины стенок котла из пластичной
стали лучше воспользоваться формулой (8.10).
Пример 26. Проверим прочность чугунной детали (работающей на
сложное напряжённое состояние), если главные напряжения в опасной точке
сечения: Qt = 240 кг/см2', аа = 0; с3 = — 360 кг/см2.
Допускаемое напряжение на растяжение [з] = 350
>	>	> сжатие [асж] = 1200
Для проверки прочности чугуна на растяжение следует применить теорию
наибольших относительных удлинений. Коэффициент Пуассона примем
ц = 0,25. Тогда
ar2 = cj — jj.<j, = 240 -f 0,25 • 360 = 330 кг/см*.
Расчётное напряжение близко к допускаемому на растяжение.
Если бы мы воспользовались для расчёта теорией касательных напря-
напряжений (неприменимой для хрупкого состояния материала), то получили бы
ошибочные результаты:
Qri = О! — а3 == 240 -}- 360 = 600 кг/см2
(близко к разрушающему при растяжении).
ГЛАВА IX.
КОНТАКТНЫЕ НАПРЯЖЕНИЯ.
§ 45. Общие понятия. Формулы для контактных напряжений.
При определении понятия «сосредоточенная сила> (§ 2) было уже ука-
указано, что передача давления от одной части конструкции на другую проис-
происходит обычно по очень небольшой по сравнению с размерами соприкасаю-
соприкасающихся элементов площадке. Материал около этой площадки испытывает
объёмное напряжённое состояние, причём распределение напряжений оказы-
оказывается весьма сложным и поддаётся исследованию лишь методами теории
упругости. Эти напряжения, возникающие при нажатии одной части кон-
конструкции на другую (работа шариковых и роликовых подшипников, катков,
зубчатых колёс и т. д.), называются контактными напряжениями. Величина
их очень быстро убывает при удалении от площадки соприкасания; поэтому
иногда эти напряжения называются местными.
Ниже приводятся результаты определения контактных напряжений, по-
полученные в теории упругости. Возникающие при контакте силы трения
в расчётах не учтены.
Поверхность контакта для рассмотренных ниже случаев первоначального
касания в точке ограничена эллипсом, уравнение которого
Ах2 + By2 = С = const.;	(9.1)
здесь А и В — величины, зависящие от главных радиусов кривизны *) ка-
каждого из соприкасающихся тел, а С — величина сближения соприкасающихся
тел, вызванного упругой деформацией по площадке касания.
*) Главными кривизнами являются наибольшая и наименьшая кривизны,
лежащие в двух взаимно перпендикулярных плоскостях, проходящих через
центр кривизны. Кривизна считается положительной, если центр кривизны
находится внутри тела.

§46]
ПРОВЕРКА ПРОЧНОСТИ СОПРИКАСАЮЩИХСЯ ТЕЛ
153
Напряжения по площадке соприкасания распределяются по закону эллип-
эллипсоида и могут быть найдены из уравнения:
"Г • ™Ь = Р> ИЛИ amax = "о" Z^u*
(9.2)
Здесь Р—величина давления при касании, a -^ъаЬ • атах— объём полуэл-
полуэллипсоида напряжений, имеющего в основании эллипс с полуосями а и Ь, вели-
величина которых зависит от отношения -^.
Величина наибольших напряжений в центре эллипса касания может быть
выражена формулой
f7	(9.3)
где a — коэффициент, зависящий от отношения -щ . Значения коэффициента a
в функции -щ даны в табл. 10.
Таблица 10. Значения коэффициента а в формуле (9.3).
А
~В
а
1,0
0,388
0,9
0,400
0,8
0,420
0,7
0,440
0,6
0,468
0,5
0,490
0,4
0,536
0,3
0,600
Л
а
0,2
0,716
0,15
0,800
0,10
0,970
0,05
1,280
1
0,02
,800
0,01
2,271
0,007
3,202
Эллипс контакта обращается в круг при касании двух шаровых поверх-
поверхностей или шара с плоскостью и в прямоугольник шириной 2ЬУ если перво-
первоначальное касание происходит не в точке, а по прямой (например, при каса-
касании цилиндрических катков с параллельными осями).
В таблице 11 даны формулы коэффициентов А и В и наибольших напря-
напряжений в центре касания ошах для наиболее часто встречающихся форм по-
поверхностей соприкасания.
§ 46. Проверка прочности соприкасающихся тел.
Как уже было показано в § 35, материал соприкасающихся тел в центре
площадки касания находится в условиях объёмного напряжённого состояния
и может поэтому надёжно работать при очень больших сжимающих напря-
напряжениях. Сталь, например, может безопасно выдержать очень высокие давле-
давления, порядка 35 000 4- 40 000 кг/см9.
Чтобы проверить прочность материала при объёмном напряжённом
состоянии, нужно знать величину главных напряжений в опасной точке и
составить условие прочности по одной из* теорий.

154
КОНТАКТНЫЕ НАПРЯЖЕНИЯ
[гл.
8
00
00
00
сГ
3
Jn.
00
8
О*
а
о
s
4>
X
о
3
>
о
•в-
"л
+
2
а
a,
gs
4
Си
II
§.&Л
Л Ч Q.

§40]
ПРОВЕРКА ПРОЧНОСТИ СОПРИКАСАЮЩИХСЯ ТЕЛ
155
гэ
(U
"Z
о
к
с
1=1
о
ex
rx
?
шря
a
i
л
о
к
tn
ce
о
a
«=i
ее
Я
<u
равн
ния
нты у]
каса
(У
я
я
•&
•в"
(Т>
о
я тел
ющихс
саса
с.
о
те
S
Си
О
•6-
X
Е
°
ев
К
Я
3
ев
О
са
Р
о
о
азмерь
о.
ания
ге
S
о
1
S:
«^\.
-
—* 0^
^	-'
— :сч
1 1 1 s~v
cus o-s;
» «=1 та Я
со а с
S СчЗк
се Ч С
s Q^
си о 2 ' *
СО СО CQ ei
с
\
ее
С
^
О
|
ь
о.
{
^_
N
•"*
S
сов R
радиу
ч—
*<.
"^
^5
о?
—.
-
см
с?
	"
<N
со
о
аЗ
со со
круго
диусо
% \
в
СМ
ICNJ
О
р,
« S
та
я
!|^
Т
I
ос
о"
_L
i
та си
Си
та
и
5 S аз
§||
^-^ ^—~ч
У Ml
ее
о*
*~ :сч
1
1
S
/	ч
и
CU О
1ЛИНД
плоек
ч

156
КОНТАКТНЫЕ НАПРЯЖЕНИЯ
[ГЛ. IX
Можно показать *), что опасная точка лежит на некоторой глубине кон-
контактирующих тел, и по соответствующим формулам найти главные напря-
напряжения.
Оказывается, что расчётное напряжение в опасной точке внутри мате-
материала по энергетической теории прочности аг4 =^ 0,6?тах. Ha поверхности
соприкасания расчётные напряжения по той же теории прочности соответ-
соответственно равны:
в центре эллипса касания ^4 = /2iJmax>
на конце большой полуоси аД = п^т^г
Коэффициенты nt и п2 в функции отношения ^ даны на графике (фиг. 92).
Таким образом, для определения расчётных напряжений, которые сле-
следует сравнивать с допускаемыми нормальными напряжениями при про-
простом сжатии, надлежит:
1)	вычислить А и В, принимая за А меньшую из этих двух величин по
формулам таблицы 11;
2)	по отношению ~= найти а (таблица 10);
3)	вычислить по формуле таблицы 11 величину сгшах;
4)	для проверки прочности в точках площадки соприкасания умножить
атах на коэффициент п (фиг. 92);
5)	для проверки же прочности в наиболее опасной точке умножить сгаах
на 0,60; величины расчётных напряжений надлежит сравнить с допускае-
допускаемыми напряжениями при
ПГ»ГкГ»ТГк!
П
0,0
0,5
0,4
6,3
1 i
1 ' I
^ !
!
\ пз
ПТ; Г
"
•SB.

Д
В
простом растяжении • или
с пределом текучести (упру-
(упругости).
Заметим, что на вид фор-
формул для контактных напря-
напряжений существенно отли-
отличается от обычных формул
для напряжений при про-
простом растяжении или сжа-
сжатии. Раньше во всех слу-
случаях мы получали вели-
величину напряжений прямо
пропорциональной величи-
величине силы и не зависящей
от упругих постоянных ма-
материала. Из приведённых
в табл. 11 формул мы ви-
видим, что контактные напряжения зависят от модуля упругости материала
и растут медленнее силы.
Подробно вопрос о вычислении контактных напряжений излагается в кур-
курсах теории упругости и в специальной литературе2). Ценные исследования
в этой области выполнены советским учёным И. Я. Штаерманом, давшим
принципиально новое решение контактной задачи 3).
0/1 0,3 0,'4 0,S 0,6 0,7 0,8 0,9 1ч0 1,1
Фиг. 92.
х) См. Н. М. Беляев, О вычислении наибольших расчётных напряже-
напряжений при сжатии соприкасающихся тел, Сборник Ленинградского института
инженеров путей сообщения, вып. 99, 1920 г. и вып. 102, 1929 г.
2) См., например, А. Н. Д и н н и к, Удар и сжатие упругих тел.
ь) И. Я. ill т а е р м а н, Контактная задача теории упругости, ГТТИ,
1949.

§ 46] ПРОВЕРКА ПРОЧНОСТИ СОПРИКАСАЮЩИХСЯ ТЕЛ > 157
Пример 27. Подсчитаем напряжения, возникающие в рельсе с радиу-
радиусом головки г = 300 мм в месте соприкасания с ним переднего бегунка
паровоза радиусом /? = 470 мм\ нагрузка на рельс Р=7300 кг\ модуль
упругости стали ? = 2 • 104 кг/мм2.
'Имеем (по таблицам 10 и 11):
^	;	^ 064 и а = 0,456.
Таким образом,
расчётное напряжение внутри рельса равно
сг4 = 0,60 . 108 = 65 кг!мм2.
На поверхности соприкасания расчётное напряжение равно
0;4 = 0,24 . 108 = 26,0 кг/мм9.
Здесь л = 0,24 взято но графику (фиг. 92) средним между значениями пх и п2.
На поверхности соприкасания расчётные напряжения близки к пределу
текучести, внутри же превышают его; это показывает, что остаточные дефор-
деформации, правда захватывающие небольшой объём материала, неизбежны в го-
головке рельса.

ОТДЕЛ III.
СДВИГ И КРУЧЕНИЕ.
ГЛАЗА X.
ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА.
ЧИСТЫЙ СДВИГ.
§ 47. Понятие 6 сдвиге. Расчёт заклёпок на перерезывание.
Мы видим в предыдущем отделе (§ 33), что при простом растя-
растяжении или простом сжатии две части стержня, разделённые наклон-
наклонным сечением, стремятся не только оторваться друг от друга, но
и сдвинуться одна относительно другой. Растяжению сопротивляются
нормальные, а сдвигу — касательные напряжения.
На практике целый ряд деталей и элементов конструкций рабо-
работает в таких условиях, что внешние силы стремятся их разрушить
именно путём сдвига.
В соответствии с этим при проверке прочности таких элементов
на первый план выступают касательные напряжения. Простейшими
примерами подобных деталей являются болтовые и заклёпочные со-
соединения. Заклёпки во многих случаях уже вытеснены сваркой;
однако они имеют ещё очень большое применение для соединения
частей всякого рода металлических
конструкций: стропил, ферм мостов,
кранов, для соединения листов в
котлах, судах, резервуарах и т. п.
Для образования заклёпочного
соединения в обоих листах про-
просверливают или продавливают от-
отверстия. В них закладывается на-
нагретый до красного каления стер-
стержень заклёпки с одной головкой;
другой конец заклёпки расклёпывается ударами специального молотка
или давлением гидравлического пресса (клепальной машины) для
образования второй головки. Мелкие заклёпки (малого диаметра —
меньше 8 мм) ставятся в холодном состоянии (авиационные кон-
конструкции).
Для изучения работы заклёпок рассмотрим простейший пример
заклёпочного соединения (фиг. 93). Шесть заклёпок, расположенных
в два ряда, соединяют два листа внахлёстку. Под действием сил Р
(о)!

§ 47] ПОНЯТИЕ О СДВИГЕ. РАСЧЁТ ЗАКЛЁПОК НА ПЕРЕРЕЗЫВАНИЕ	159
эти листы стремятся сдвинуться один по другому, чему препятствуют
заклёпки, на которые и будет передаваться действие сил Р1).
Для проверки прочности заклёпок применим общий порядок
решения задач сопротивления материалов.
На каждую заклёпку передаются по две равные и прямо проти-
противоположные силы: одна — от первого листа, другая — от второго.
Опытные исследования показывают, что одни из заклёпок ряда
нагружаются больше, другие — меньше. Однако к моменту разру-
разрушения усилия, передающиеся на различные заклёпки, более или
менее выравниваются за счёт пластических деформаций. Поэтому
принято считать, что все заклёпки работают оди-
одинаково. Таким образом, при п заклёпках в соеди-
соединении, изображённом на фиг. 93, на каждую из
них действуют по две равные и противоположные п \
Р	''
силы Рх = — (фиг. 94); эти силы передаются на п
заклёпку путём нажима соответствующего листа
на боковую полуцилиндрическую поверхность
стержня. Силы Рх стремятся перерезать заклёпку
но плоскости tnk раздела обоих листов.
Для вычисления напряжений, действующих по	Фиг. 94.
этой плоскости, разделим мысленно заклёпочный
стержень сечением mk и отбросим нижнюю часть (фиг. 94). Внутрен-
Внутренние усилия, передающиеся по этому сечению от нижней части на
верхнюю, будут уравновешивать силу Ри т. е. будут действовать
параллельно ей в плоскости сечения, и в сумме дадут равнодей-
равнодействующую, равную Рг. Следовательно, напряжения, возникающие
в этом сечении и действующие касательно к плоскости сечения,
это — касательные напряжения т. Обычно принимают равномерное
.распределение этих напряжений по сечению. Тогда при диаметре
заклёпки d на единицу площади сечения будет приходиться напря-
напряжение
р.	р
Определение величины допускаемого касательного напряжения [т]3,
или, как говорят, допускаемого напряжения на срез, дано в § 53.
,3ная [т]3, мы напишем условие прочности заклёпки на перерезывание
в таком виде:
^ = ?=-5i<Ww	00.2)
т- е. действительное касательное напряжение т в материале заклёпки
Должно быть равно допускаемому [х]3 или меньше его.
О Сопротивление трения не учитывается.

160 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [гл. X
Из этого условия можно определить необходимый диаметр заклё-
заклёпок, если задаться их числом, и наоборот. Обычно задаются диаметром
заклёпочных стержней d в соответствии с толщиной t склёпываемых
частей (обычно d я^ 2t) и определяют необходимое число заклёпок п:
Знаменатель этой формулы представляет собой ту силу, которую
безопасно может взять на себя каждая заклёпка.
Пусть Р = 72 000 кг; d = 2 см\ [т]3=Ю00 кг/см*; тогда
_ Р	72000
•Мз
3,14 • 4
. 1000
""Л
I
Фиг. 95.
При выводе формулы A0.2), помимо оговорённых, допущена
ещё одна неточность. Дело в том, что силы Ри действующие на
заклёпку, не направлены по одной пря-
прямой, а образуют пару. Эта пара уравно-
уравновешивается другой парой, образую-
образующейся из реакций соединённых листов
на головку заклёпки (фиг. 95) и ведёт
к появлению нормальных напряжений,
действующих по сечению mk.
Кроме этих нормальных напряже-
напряжений, по сечению mk действуют ещё
нормальные напряжения, вызванные
тем, что при охлаждении заклёпочный
стержень стремится сократить свою
длину, чему мешает упор головок за-
заклёпки в листы. Это обстоятельство, с одной стороны, обеспечивает
стягивание заклёпками листов и возникновение между ними сил трения,
с другой — вызывает значительные нормальные напряжения по сече-
сечениям стержня заклёпки. Особых неприятностей эти напряжения при-
принести не могут. На заклёпки идёт сталь, обладающая значительной
пластичностью; поэтому даже если бы нормальные напряжения до-
достигли предела текучести, можно ожидать некоторого пластического
удлинения стержня заклёпки, что вызовет лишь уменьшение сил тре-
трения между листами и осуществление в действительности той схемы
работы заклёпки на перерезывание, на которую она и рассчиты-
рассчитывается. Поэтому эти нормальные напряжения расчётом не учитываются.
§ 48. Проверка заклёпок на смятие и листов на разрыв.
В § 47 рассмотрены условия прочности, ограждающие заклёпоч-
заклёпочное соединение от разрушения путём срезывания заклёпок. Однако
заклёпкам и соединяемым листам в конструкции, показанной на
фиг. 93, угрожают и иные опасности.

§ 48]
ПРОВЕРКА ЗАКЛЁПОК НА СМЯТИЕ И ЛИСТОВ НА РАЗРЫВ
161
Так как передача сил на заклёпочный стержень происходит путём
нажатия стенок заклёпочного отверстия на заклёпку, то необходимо
установить, не произойдёт ли наружное обмятие этого стержня или
стенок отверстия, — произвести проверку на смятие.
На фиг. 96 указана примерная схема передачи давлений на стер-
стержень заклёпки. Закон распределения этих давлений по цилиндриче-
цилиндрической поверхности нам
неизвестен; он во мно-
многом зависит от непра-
неправильностей формы за-
заклёпочного отверстия и
стержня, вызванных усло-
условиями изготовления кон-
конструкции. Поэтому ра-
расчёт производится услов-
условно. Принято считать, что
неравномерное давление,
передающееся на поверх-
поверхность заклёпки от листа,	Фиг. 96.
распределяется равномер-
равномерно по диаметральной плоскости сечения заклёпки (фиг. 96). При этом
напряжение по этой диаметральной плоскости оказывается примерно
равным наибольшему сминающему напряжению ос в точке А поверх-
поверхности заклёпки.
Чтобы вычислить это условное напряжение смятия, необходимо
разделить силу, приходящуюся на заклёпку, на площадь диаметраль-
диаметрального сечения ВСС'В' (фиг. 96). Эта площадь представляет собой
прямоугольник, одной стороной которого служит диаметр заклёпки,
другая же равна толщине листа, передающего давление на стержень
заклёпки.
Р
Так как давление на одну заклёпку равно —, то
условие прочности на смятие будет иметь вид:
A0.5)
где [ос] — допускаемое напряжение на смятие. Отсюда необходимое
число заклёпок
п^	A06)
Допускаемое напряжение на смятие принимают обычно в 2—2,5
раза больше основного допускаемого напряжения на растяжение и
сжатие [а], так как расчёт на смятие по существу является упро-
упрощённой проверкой прочности по контактным напряжениям.
6 Н. М. Беляев

162 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [ГЛ. X
Таким образом, число заклёпок, необходимое для прочного
соединения листов, определяется формулами A0.3) и A0.6). Из
двух полученных значений п, конечно, надо взять большее.
Если мы вернёмся к рассмотренной выше задаче (фиг. 93) и при-
примем Р = 72 000 кг\ t=lcM\d = 2 см; [ас] = 2400 кг/см*, то получим:
72 000
= 2 • 1 .2400
= 15.
Таким образом, условие прочности заклёпок на перерезывание
требует постановки двадцати четырёх заклёпок; условие же проч-
прочности на смятие — пятнадцати заклёпок. Очевидно, необходимо
поставить двадцать четыре заклёпки. В этом примере работа заклё-
заклёпок на срез оказывается опаснее работы их на смятие. Это обычно
бывает в соединениях с так называемыми односрезными заклёпками,
в которых каждая заклёпка перерезывается в одной плоскости.
Р i&
Фиг. 97.
Фиг. 98.
В несколько других условиях будут работать заклёпки соедине-
соединения, показанного на фиг. 97. Здесь стык двух листов осуществлён
при помощи двух накладок. Сила Р при помощи первой группы
заклёпок передаётся от левого листа обеим накладкам, а от по-
последних при помощи второй группы заклёпок передаётся правому
листу.
Называя через п число заклёпок, необходимое для передачи
усилия Р от листа на накладки и от накладок на другой лист,
получаем, что на каждую заклёпку передаётся усилие от основного
листа Р/п. Оно уравновешивается усилиями Р/2п, передающимися
на заклёпку от накладок (фиг. 98).
Стержень заклёпки теперь подвергается перерезыванию уже
в двух плоскостях; средняя часть заклёпки сдвигается влево. Допу-
Допускают, что срезывающая сила Р/п равномерно распределяется по двум
сечениям, mk и gf. Напряжение т определяется формулой
и • 2 \-

§ 48J	ПРОВЕРКА ЗАКЛЁПОК НА СМЯТИЕ И ЛИСТОВ НА РАЗРЫВ	163
и условие прочности для двухсрезной заклёпки принимает вид:
П ~2	-2~[т]з
Таким образом, при двойном перерезывании число заклёпок по
срезыванию оказывается в два раза меньше, чем при одиночном
перерезывании [формула A0.3)].
Переходим к проверке на смятие. Толщина склёпываемых листов t;
толщина накладок tx не должна быть меньше 0,5/, так как две
накладки должны взять от основного листа всю силу Р. Поэтому
0,
Сила Р/п сминает и среднюю часть заклёпки и верхнюю с ниж-
нижней. Опаснее будет смятие той части, где площадь смятия меньше.
Так как толщина среднего листа не больше суммы толщин обеих
накладок, то в худших условиях по смятию будет средняя часть
заклёпки. Условие прочности на смятие A0.5) останется таким же,
как и при односрезных заклёпках:
Таким образом, для рассматриваемой конструкции число заклё-
заклёпок в первой и во второй группах определится из условий A0.7)
и A0.6).
Пусть Р=72 000 кг; d = 2 см; t=\ см; ^ = 0,8 см; [т] =
= 1000 кг/'см2; [ас] = 2400 кг/см*. Тогда
Р	72000	. Р	72000
-2400
В этом случае при двухсрезных заклёпках условия их работы
на смятие тяжелее, чем на срезывание; следует принять я =15.
На двух рассмотренных примерах мы установили общие методы
проверки прочности заклёпочных соединений. В металлических кон-
конструкциях иногда приходится склёпывать целые пакеты соединяемых
элементов. В таких пакетах заклёпки могут работать и на большее
число срезов. Однако методы расчёта многосрезных заклёпок не
отличаются от изложенных. Для вычисления касательных напряжений
следует разделить силу, относящуюся к одной заклёпке, на сум-
суммарную площадь среза, воспринимающую эту силу. Для вычисле-
вычисления же напряжений смятия следует найти ту часть заклёпки, которая
находится в наиболее опасных условиях, т. е. воспринимает наи-
наибольшую силу на наименьшем протяжении. Напряжения смятия полу-
получаются делением этой силы на площадь диаметрального сечения
наиболее напряжённой части заклёпки. Затем останется написать
Два условия прочности и получить п,
6»

164 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [ГЛ. X
Наличие заклёпок вносит некоторые изменения и в проверку
прочности на растяжение или сжатие самих склёпанных листов.
Опасным сечением каждого листа (фиг. 99) будет теперь сечение,
проходящее через заклёпочные отверстия; здесь рабочая ширина
Фиг. 99.
листа будет наименьшей; принято говорить, что это сечение ослаб-
лено заклёпочным отверстием. Называя полную ширину листа Ьу
получаем для него такое условие прочности:
Р
t (b — md)
A0.8)
где т — число отверстий, попадающих в сечение (в нашем слу-
случае — два).
Отсюда можно найти величину Ь, задавшись толщиной листа t.
Площадь (b — md) t ослабленного сечения называется площадью
нетто, площадь же полного сечения листа Ы называется площадью
брутто.
Этот учёт влияния заклёпочных отверстий на прочность склёпы-
склёпываемых листов общепринят, но является весьма условным. На самом
деле, влияние отверстия в листе вызывает у его краёв, на концах
диаметра, перпендикулярного к направлению растяжения, значитель-
значительные местные напряжения, которые могут достичь предела теку-
текучести материала и вызвать остаточные деформации, захватывающие,
однако, весьма небольшой объём материала листа.
Некоторую опасность в отношении образования трещин эти
местные напряжения могут представить лишь при действии пере-
переменных нагрузок в материале, имеющем низкий предел усталости
(§ 17). Однако в обычных условиях работы заклёпочных соеди-
соединений эта опасность может считаться исключённой. Во избежа-
избежание возможности разрушения листов заклёпками заклёпки разме-
размещаются на определённых расстояниях друг от друга и от края
листа.
Расположение заклёпок в плане производится как по условиям
обеспечения прочности и плотности соединения, так и по чисто
производственным соображениям. Расстояния между центрами заклё-

§ 48]	ПРОВЕРКА ЗАКЛЁПОК НА СМЯТИЕ И ЛИСТОВ НА РАЗРЫВ	165
пок принимаются не менее 3d и не более Id. Расстояния до края
листов должны быть не менее A,5 -~- 2) d (фиг. 100). Чтобы длина
стыка была возможно меньше, берут a = C-j-4)d, а в целях мень-
меньшего ослабления сечения расстояние е берут возможно бблыним (до
Td), что позволяет умень-
уменьшить число рядов, а следо- j	j—j	\	1-
вательно, и ослабление.
При проектировании за- Р^
клёпочных соединений для
котлов и резервуаров, где
добиваются плотных швов,
помимо расчёта на срез про-
производят проверку сопроти-
сопротивления скольжению за счёт
трения. Однако допускаемое напряжение по скольжению даётся в кг/см*
поперечного сечения заклёпки; таким образом, проверка на трение
при односрезных заклёпках сводится к проверке на срез лишь
с другим допускаемым напряжением. При двухсрезных заклёпках
в расчёт на трение вводится, конечно, одна площадь сечения за-
заклёпки, но зато повышается почти вдвое допускаемое напряжение
на трение за счёт двух накладок.
Поэтому так называемый расчёт заклёпок на трение является,
по существу, проверкой прочности на срез с другими лишь допу-
допускаемыми напряжениями на квадратный сантиметр площади попе-
поперечного сечения заклёпки.
Правильнее было бы сохранить лишь один метод проверки за-
заклёпочных соединений на смятие и срез, учитывая влияние сил
трения при назначении допускаемых напряжений в зависимости
от способа клёпки, качества отверстий и требований, предъявляе-
предъявляемых ко шву в отношении плотности.
В заклёпочных соединениях для котлов принимают обычно до-
допускаемое напряжение на скольжение (на 1 см* площади заклёпки):
от 500 до 700 кг/см* при швах внахлёстку,
» 900 » 1200 » » » с двумя накладками.
При проверке по этим данным, очевидно, надо вести расчёт, как
при заклёпках одиночного перерезывания, с допускаемым напряже-
напряжением от 500 до 700 или от 900 до 1200 кг/см*.
В таблице 12 приведены допускаемые величины касательных на-
напряжений [т] для стали 3 (ав = 38ч-45 кг\мм\ а также допускае-
допускаемые напряжения на смятие [ос] для заклёпок по существующим
нормам. Таблица относится к гидротехническим и промышленным
сооружениям при условии действия статической нагрузки.
В авиастроении употребляют обычно дюралюминовые заклёпки
(с пределом прочности на разрыв — около 40 кг\мм*)\ допускаемые

166 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [гл. X
напряжения для них колеблются в пределах [т]=18-ь25 кг/мм*,
[ос]=60-ь70 кг/мм* (Т. У. Министерства авиапромышленности
345 СМТУ).
Таблица 12. Допускаемые напряжения в заклёпочных
соединениях.
Объект
Основные элементы
3 а к л ё п к и:
Класс В — в рассверленных дырах ......
Класс С — в продавленных дырах
Напряжения
кг/см*
\ [а] = 1600
\ [т] = 1000
| [т] = 1400
1 [ас] = 3200
/ [т] = 1000
1 [сс] = 2800
§ 49. Примеры.
Пример 28. Проверить прочность заклёпок в продольном шве листов
котла, сомкнутых впритык; шов перекрыт двойными накладками. Диаметр
котла /)= 1500 мм; толщина листов t = 18 мм; толщина накладок t\ = 10 мм;
диаметр заклёпок d = 22 мм; [т]3 = 800 кг/см2; [ас] = 2000 кг/см2. За-
Заклёпки расположены в два ряда в шахматном порядке (фиг. 101), расстоя-
Фиг. 101.
ние между рядами Ъ = 75 мм; шаг заклёпок а = 90 мм. Давление пара # = 9 am.
Напряжение в стенках котла (§ 35) а = %г- ; вырежем из котла кольцо
длиной по образующей, равной 2 шагам заклёпок: 2а = 180 мм. Концы
этого кольца соединены через накладки четырьмя двухсрезными за-
заклёпками по две с каждой стороны стыка. Кольцо растягивается-силой
P 2t D

§ 49]
ПРИМЕРЫ
167
Проверяем прочность заклёпок на срез:
дРа _9 • 150- 9
Х~о *d* 0 3,14.2,2»*
; 800 кг/см* = [х]3.
На смятие:
_ gDa _ 9 ¦ 150 • 9 _	. .
: = ~Ш - 2 • 2,2 • 1,8 - 152° / СЖ < l'cJ-
Проверка на смятие оказывается благоприятнее, чем на срез, несмотря
на то, что здесь заклёпки двойного перерезывания. Это объясняется весьма
большой толщиной листов.
Пример 29. Болт скрепляет проушину с двумя накладками (фиг. 10_'а).
Толщина стержня проушины г=15жж; найти диаметр болта d и ширину
Фиг. 102а.
Фиг. 1026.
стержня Ь\ стержень растянут силой Р= 12 г, [а] = 800 кг/см*\Ы = 600 кг/см\
[ас]= 1600 кг/см2. Схема работы соединения дана на фиг. Шо.
Ширина стержня определяется из условия прочности на растяжение;
12 000
1,5 -800
= 10 см;

168 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [ГЛ. X
диаметр болта определяется из условий прочности на срез и смятие:
2 • 12 000
12 000
1,5- 1600 -" "~#
Диаметр должен быть принят равным 5 см.
§ 50. Расчёт сварных соединений.
А. При изготовлении металлических конструкций часто приме-
применяется сварка с помощью электрической дуги.
Впервые электрическая дуга была открыта русским учёным
проф. В. В. Петровым в 1802 г. Обнаружив плавление металла
в пламени полученной им электрической дуги, проф. Петров ука-
указал на возможность использования этого явления в технике. Одна-
Однако электрическая дуговая сварка была изобретена лишь в кон-
конце XIX века русскими инженерами Н. Н. Бенардосом A882 г.)
и Н. Г. Славяновым A888 г.) и получила впоследствии широкое
распространение во всём мире.
Сущность электросварки по методу Славянова заключается в том,
что, расплавляя электрической дугой материал электрода (сталь),
заполняют им стык соединяе-
ДерЖатель Д	мых элементов, также про-
jvj^A^&flil/^	-4-ff i	греваемых дугой до темпера-
улектрод туры плавления. В результате,
после остывания расплавлен-
Сдаридаемыа ного металла, образуется шов,
" прочно соединяющий стыкуе-
	U мые элементы.
Схема сварки показана на
Фиг. 103.	фиг. 103. Электрическая дуга
горит между металлическим
электродом и свариваемым металлом, расплавляя электрод и кромки
соединяемых элементов металла, между которыми образуется так
называемая сварочная ванна.
Для защиты плавящегося металла от попадания вредных включе-
включений из окружающего воздуха на поверхность электрода наносится
толстая защитная обмазка, выделяющая при плавлении электрода
большое количество шлака и газов, благодаря чему плавящийся ме-
металл изолируется от окружающего воздуха.
Этим обеспечивается высокое качество металла сварного шва,
механические свойства которого могут резко ухудшиться под влия-

50]
РАСЧЁТ СВАРНЫХ СОЕДИНЕНИЙ
169
нием кислорода и азота воздуха (при отсутствии обмазки или при
тонкой обмазке). С той же целью автоматическая сварка произво-
производится под слоем флюса, защищающим плавящийся металл от попа-
попадания кислорода и азота воздуха.
При правильном выборе конструкции соединений, материалов
и технологии сварки сварные соединения по надёжности не усту-
уступают заклёпочным при действии как статических, , так и динами-
динамических нагрузок (в том числе ударных и знакопеременных). В то же
время электросварка имеет ряд преимуществ перед клёпкой, из
которых важнейшими являются меньшая трудоёмкость сварочных
работ и отсутствие ослабления сечений соединяемых элементов
отверстиями. Это даёт значительную экономию средств и металла,
помимо экономии, получаемой за счёт большей компактности со-
соединений. Большие экономические выгоды, приносимые электро-
электросваркой, и даваемое ею упрощение конструкций привели в послед-
последнее время к постепенному вытеснению заклёпочных соединений
сварными.
Значительное развитие электросварка получила в СССР благо-
благодаря трудам советских учёных Патона, Вологдина, Никитина,
Хренова и др., разработавших новые методы сварки, обеспечиваю-
обеспечивающие высокую прочность соединений.
Б. Расчёт сварных соединений, как и заклёпочных, условно ве-
ведётся в предположении равномерного распределения напряжений по
сечению швов. При этом он тесно связан с технологией сварки;
в частности, это находит отражение в величине допускаемых напря-
напряжений для материала швов, назначаемых в зависимости от способа
сварки (ручная или автоматическая), а также от состава и толщины
защитной обмазки электродов.
В таблице 13 приведены допускаемые напряжения для сварных
швов в конструкциях из стали марки ст. 3 по существующим нормам
Таблица 13. Допускаемые напряжения при сварке.
Вид
напряжения
Растяжение. .
Сжатие ....
Срез
Обозначения
} Ы
Ручная сварка
электроды с
тонкой обмазкой
1000 кг!см2
1100 »
800 >
электроды с
толстой обмазкой
1300 кг!см*
1450 »
1100 >
Автоматическая
сварка
1300 кг!см2
1450 '»
1100 >
(ГОСТ-960-46). При проверке прочности сварных швов учиты-
учитывается возможный непровар в начале шва и образование кратера
в конце. Поэтому расчётная длина шва принимается меньшей, чем
действительная или проектная (по техническим условиям 1946 г.
на 10 мм).

170 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ. [ГЛ. X
В. Наиболее простым и надёжным видом соединения является
соединение встык, образуемое путём заполнения зазора между тор-
торцами соединяемых эле-
элементов наплавленным
металлом. Соединение
встык осуществляется,
в зависимости от тол-
толщины соединяемых эле-
элементов, по одному из
типов, показанных на
фиг. 104. Проверка проч-
прочности производится на
растяжение или сжатие
по формуле
*. = -?< [<>.]•	(Ю.9)
Фиг. 104.
Здесь /t—FB—услов-
/t—FB—условная рабочая площадь
сечения шва, где рас-
расчётная длина шва / =
= Ъ—10 мм, а вы-
высота шва h принимается
равной толщине свари-
свариваемых элементов t.
Поскольку допускае-
допускаемое напряжение для
сварного шва ниже,
чем для основного ме-
металла, стремятся к уве-
увеличению длины стыко-
стыкового шва. С этой целью
применяют соединение
встык с косым швом
(фиг. 105). Исследования
таких соединений, про-
произведённые Институтом электросварки Академии наук УССР, по-
показали, что равнопрочность их с основным металлом всегда обес-
обеспечивается.
Проверка прочности косых швов производится и по нормальным
и по касательным напряжениям, возникающим по сечению шва тп:
Фиг. 105.
=/?a C0S a = /Г * C0S a«
* a

§ 50]
РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ
171
Имея в виду, что Fa = tt (фиг. 106), получим:
р
оэ = — • sina<[o9],
A0.10)
L
Здесь расчётная длина шва по техническим условиям прини-
принимается равной /=-	10 мм.
*	Sin a
Как установлено опытом, наиболее рациональным углом наклона
шва к линии действия сил является 2. 45 -т- 50°. Недостатком со-
соединения косым швом является неудобство центрировки стыкуемых
элементов при сварке,
поэтому его применяют
редко.
Г. Иногда соедине-
соединение листов произво-
производится внахлёстку или
встык с перекрытием
накладками. Это вы-
вызывает необходимость сваривать листы, не лежащие в одной пло-
плоскости, что осуществляется при помощи так называемых валиковых
(или угловых) швов — лобовых или торцевых (перпендикулярных
к направлению действующей	h=07t
р
Фиг. 106.
Л
1
b
1
1 1
силы) и боковых или флан-
фланговых (параллельных ей), р
Валиковый шов в сече- "^
нии имеет довольно не-
неопределённую форму (фиг.
106, а). В теоретических
расчётах на прочность се- ?+
чение шва принимается в
виде равнобедренного тре-
треугольника (очерченного
пунктиром) с расчётной вы- р
сотой /г1).	~"
Соединения торцевыми
(лобовыми) швами показаны
на фиг. 107. Разрушение
таких швов происходит по
наиболее слабому сечению АВ, как это установлено опытами.
Как это видно из фиг. 106, б, полное напряжение, возникаю-
возникающее в сечении АВ, может быть разложено на нормальную и каса-
касательную составляющие. Поскольку сопротивление стали сдвигу ниже,
J) Иногда лобовые швы делают вогнутыми с высотой h < 0,7*. Катет
шва может быть и меньше толщины листа.
Р
Р
Фиг. 107.

172 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИЙ СДВИГА. ЧИСТЫЙ СДВИГ [ГЛ. X
чем при растяжении, расчёт лобовых швов производится условно
на срез в предположении равномерного распределения касательных
напряжений по площади сечения АВ. Имея в виду, что на восприя-
восприятие силы Р в этих соединениях (фиг. 107) работают два лобовых
шва, верхний и нижний, получим:
_ Р_
т*"" 2/V
Так как площадь сечения шва Fb — hl = t cos 45°/^0,7 tlt а расчёт-
расчётная длина l = b—10 мм, то условие прочности примет вид:
1,4- tl"
A0.11)
В действительности, материал шва испытывает сложное напря-
напряжённое состояние, причём напряжения по сечению АВ распреде-
распределяются неравномерно. Исследования, произведённые методами теории
упругости и подтверждённые экспериментально, показали, что в углах
шва имеет место высокая концентрация напряжений.
Кроме того, вследствие укорочения швов при остывании в зоне
сварки возникают дополнительные напряжения не только в материале
швов, но и в основном металле, вызывающие переход его в сложное
напряжённое состояние.
Это обстоятельство может повести к снижению пластичности
металла в стыке, что делает такое соединение (с лобовыми швами)
менее надёжным, особенно при ударных и переменных нагрузках,
чем соединение встык без накладок.
Д. Соединение фланговыми (или боковыми) швами показано на
фиг. 108, а. Разрушение шва, показанное на фиг. 108, б, происходит
Р
4
1
л
Ь
Фиг. 108.
на значительном его протяжении путём срезывания наплавленного
металла в направлении, параллельном шву по наиболее слабой пло-
плоскости АВ. Условие прочности для двух симметрично расположен-
расположенных швов таково:
Р ^г ,
2 • 0,7 . *. /
A0.12)

§ 50]
РАСЧЁТ СВАРНЫХ СОЕДИНЕНИЙ
173
Если стык перекрыт двухсторонними накладками, число швов
удвоится и условие прочности примет вид:
Из формул A0.12) и A0.12г) обычно определяют необходимую
расчётную длину / фланговых швов. Проектная же длина каждого
шва принимается равной /0 === / —}— 10 мм.
Как показали опыты, разрушение фланговых швов происходит
по типу разрушений пластичных материалов со значительными оста-
остаточными деформациями. Это делает работу фланговых швов более
благоприятной, чем работу лобовых швов. Однако следует иметь
в виду, что у концов фланговых швов также имеет место высокая
концентрация напряжений.
При проектировании часто стремятся обеспечить большую на-
надёжность соединения, применяя вместо сварки встык, или в допол-
дополнение к ней, перекрытие стыка накладками, которые привариваются
фланговыми или торцевыми швами, а иногда и теми и другими
вместе. Как уже указывалось, при переменных и ударных нагрузках
такое «усиление» стыка может принести больше вреда, чем пользы.
Что касается расчёта такого комбинированного стыка, то при
одновременном применении лобовых и фланговых швов считают,
что сопротивление соединения равно сумме сопротивлений всех
швов, т. е. Р=Рт-\-Рф, где сопротивление торцевого шва при
расчётной длине /т равно Рт = 0,7 t • /т [т9], а сопротивление двух
фланговых швов Рф = 2 • 0,71 • /ф [т9], причём /т = Ь, где b — ши-
ширина накладки. В результате подстановки получаем:
Р = @,7 tlr + 1,4 */ф) [xj.	A0.13)
Зная длину торцевого шва, определяют длину фланговых швов /ф.
При двухсторонних накладках число швов удваивается, т. е. пра-
правую часть формулы A0.13)
следует удвоить.
Так как торцевые швы бо-
более жёстки, то при совместной
работе с фланговыми они пере-
перегружаются, что ведёт к не-
неравномерной работе соедине-
соединения. Если учесть, что в таком
соединении и термические на-	Фиг. 109.
пряжения достигают больших
значений, то устройства такого стыка следует избегать.
Е. Иногда при соединении внахлёстку в дополнение к флан-
фланговым швам применяют прорезные швы, осуществляемые путём
наплавки металла в узкую прорезь, сделанную в одном из соеди-
соединяемых элементов параллельно действующему на соединение уси-
усилию (фиг. 109).
Р

174 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ. [ГЛ. X
При длине прорезного шва /п и ширине прорези d сопротивление
такого шва срезу равно:
где рп — усилие, приходящееся на прорезной шов.
В "комбинированном соединении с фланговыми швами для записи
расчётного условия принимают, что Р = Рф -\- Рп, или
Задавшись размерами одного из швов (обычно флангового), на-
находят необходимую длину другого. При этом ширина прорези d
принимается равной двойной толщине прорезанного металла, длина —
не более двадцати толщин.
Недостатками соединения с прорезными швами являются: 1) ослаб-
ослабление сечения прорезями вследствие неизбежного непровара и
2) высокая концентрация напряжений в основном металле в зоне
сварки, могущая повести в некоторых случаях к возникновению тре-
трещин около углов прорезного шва. Поэтому такое соединение может
применяться лишь в случаях, когда стык не предназначен для работы
при переменных и ударных нагрузках.
В заключение заметим, что в том случае, когда приходится
прибегать к соединению внахлёстку, лучше всего ограничиться
одними фланговыми швами,
избегая комбинированных
соединений.
Ж. При сварке элемен-
Ш	 тов металлических конст-
1 рукций встречается необхо-
необходимость приварки элемен-
элементов, например уголков, для
которых линия действия
силы не проходит посре-
посредине привариваемой полки. В этом случае приходится применять
два фланговых шва разной длины или разной высоты. Общая длина
швов определяется величиной передаваемого усилия, соотношение
же их длин зависит от положения линии действия усилия.
На фиг. НО изображено прикрепление уголка к листу; сумма
длин фланговых швов 1а и 1С определяется уравнением
Фиг. ПО.
Отсюда
^-,7 tla + OJ tlс
— 0,7 tUn\ — '*
С другой стороны, усилия, приходящиеся на каждый из двух швов,
распределяются обратно пропорционально расстояниям от линии

§51]
ПРИМЕРЫ
175
действия силы Р9 проходящей через центр тяжести сечения уголка;
поэтому
la
Зная сумму длин и их отношение, определяем рабочую длину
каждого шва. Проектные длины швов принимаются на 10 мм больше.
§ 51. Примеры.
Пример 30. Рассчитать растянутый сварной стык двух листов сече-
сечением 12 X 250 мм, перекрытый двумя накладками, из условия равнопрочности
соединения с основным металлом при допускаемых напряжениях:
на растяжение основного металла [а] = 1600 кг/см2,
> срез металла швов	[т9]=1100 >
Допускаемая нагрузка на стык из условия прочности листов на растя-
растяжение:
/>=[*]/*= 1600- 1,2-25 = 48 000 кг.
Прикрепление накладок лучше всего осуществить
с помощью фланговых швов (фиг. 111).
Для размещения фланговых швов примем
ширину накладок ^ = 220 мм. Так как, по усло-
условию равнопрочности, площадь сечения двух
р
\Lf8\t=t2 p
Г
, j; м I и 1111:11!
Фиг. 111.
накладок должна быть не менее площади сечения листа, т. е. 2b^ti > F, то
толщина накладки:
Примем tfi = 8 мм. Необходимая рабочая длина фланговых швов [фор-
аула A0.12)]
Р _ 48 000 _1nR
/^4.0,7^1[ха]~" 2,8-0,8. 1100 "" 1У'° см'
Полная длина флангового шва по техническим условиям должна быть при-
принята:
/0 = / + 10 мм = 195 + 10 мм = 205 мм.
Примем /о = 200 мм.
Пример 31. Определить необходимую длину фланговых швов для
прикрепления стержня фермы, состоящего из двух равнобоких уголков
?§ х 75 х 8 (фиг. 112). Растягивающее усилие N = 32 т. Допускаемое напря-
напряжение на срез швов [та] = 1100 кг/см3.

176 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [гл. X
Усилие, приходящееся на один уголок и приложенное в-центре тяже-
тяжести сечения, Рх=0,5-32 = 16 т. Расстояние от обушка уголкового сечения
до его центра тяжести (по сортаменту) а = 20 = 2,15 см, а от края полки
с = Ь — z0 = 7,5 — 2,15 = 5,35 см.
Общая длина фланговых швов, необходимая для прикрепления уголка
к косынке:	D	i^nnr»
	/i/ 	 " 	 lo 000 	9fi
/-'a-We- o,7*. [тэ] "",7.0,8.1100 ° CMt
Имея в виду, что отношение /a//c=c/a, получим:
с	5 35
la = — ' h = 2^5 1с>
ИЛИ
la =
С\Г*
Зная сумму 1а-\-1с и их отношение, находим:
2,49/с + /с = 26 см, откуда lc = j^ = 7,45 см,
1а = 2,49/с = 2,49. 7,45 = 18,55 см.
Так как размещение швов столь различной длины вызывает иногда кон-
конструктивные неудобства, то можно уменьшить длину шва со стороны обушка 1а%
увеличив соответственно его толщину. Приняв высоту катета шва ta = 12 мм,
можно уменьшить длину его в отношении -—= —= 1,5. Тогда
* о
Учитывая возможные непровары, примем проектные размеры швов:
1а = 140 мм
ta = 12 мм
§ 52. Расчёт врубок.
С напряжениями скалывания и смятия приходится встречаться при
расчётах прочности деревянных сопряжений — врубок.
Дерево, как материал неоднородный, оказывает различное сопро-
сопротивление одним и тем же деформациям в зависимости от направле-
направления сил по отношению к волокнам. В отношении смятия и срезыва-
срезывания обычно различают сопротивление этим двум деформациям вдоль
волокон и поперёк волокон.
В таблице 14 приведены в качестве примера данные о сопро-
сопротивлении дерева скалыванию. Допускаемые напряжения для дерева
Таблица 14. Предел прочности при скалы-
скалывании в кг/см2.
Порода
Сосна
Дуб
Вдоль
волокон
60
90
Поперёк
волокон
30

§ 52]
РАСЧЁТ ВРУБОК
177
во врубках зависят от породы дерева и характера конструкции.
Применительно к нормам их можно назначать по данным таблицы 15.
Отклонения в ту или другую сторону (на 25—30%, о чём подробно
сказано в нормах) стоят в зависимости от сорта дерева, степени
влажности, условий работы конструкций и пр.
Таблица 15. Данные о допускаемых напряжениях в кг/см*.
Вид напряжения
Обозна-
Обозначения
Сосна
Дуб
Растяжение	,
Сжатие вдоль волокон и смятие торца
Смятие во врубках вдоль волокон
Смятие перпендикулярно к волокнам (на длине
>10 см)
Скалывание во врубках вдоль волокон
Скалывание во врубках поперёк волокон
Изгиб
Скалывание при изгибе
А
Мю
Ы
100
120
80
24
5—10
6
120
20
130
150
110
48
8—14
8
150
28
При смятии (или скалывании) под углом а к направлению воло-
волокон допускаемое напряжение имеет промежуточное значение между
[°см] и [асм]эо или М и Мэо и определяется по условной формуле:
	Км]	_
[".]=¦
1_l| Км]	A. sin3 a '
A0.15)
При действии скалывающих сил в тангенциальной плоскости под
углом а к напраэвленрио волокон допускаемое напряжение опреде-
определяется по подобной же фор-	м,
муле, где вместо [асм] бе- ^ч^ JP\
у,
рётся [т].
Приёмы проверки ггроч-
ности врубки поеджем на
примере.
Пример 32. Стропиль-
Стропильная нога (фиг. 113) упирается
в затяжку под углом a = 30°;
усилие в ноге Р = 5 т\ опре-
определить размеры врубки ноги
в затяжку и длину выпущен-
выпущенного за врубку конца затяжки.
Материал — сосна. Размеры бру-	Фиг. 113.
сьев 20 х 15 см.
Конец затяжкп испытывает скалывание вдоль волокон горизонтальной
проекцией /^ силы Р:
РХ = Р cos 30° == 5 . 0,865 = 4,325 т.

178 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [>Л. X
При ширине затяжки Ь = \5см и длине скалывания а условие проч-
прочности имеет вид:
у- ^ [-с], или а ^ ~рр = ~—г77 = 29 ел*.
Та же сила Л производит смятие вертикальной плоскости врубки. Для
затяжки это будет смятие вдоль волокон, для ноги же — смятие по сечению
под углом а = 30° к направлению волокон. Вычислим допускаемое напряжение:
i^	llsin3a I 4- (|j — 1)sins 30°
Глубина врубки h определится из условия, чтобы сминающая сила была
меньше или равна сопротивлению врубки смятию. Площадь смятия — прямо-
прямоугольник высотой Л, шириной Ъ\ условие прочности имеет вид:
—Pl	h Pi — 4325
Необходимо далее проверить смятие затяжки перпендикулярно к волок-
волокнам силой Р2 — вертикальной проекцией силы Р\
1
= 5 • -~- = 2,5 т.
Р*
Длина площади смятия с определится из условия сСМво = -^- ^ [зсм]8о>
откуда
Ps	2590
^ "лТт Г~ ~" 1 ^ . 94. "^
С/ [эсм190	*'-' ^^
§ 53. Чистый сдвиг. Определение главных напряжений
и проверка прочности.
В предыдущих параграфах мы рассмотрели ряд широко приме-
применяющихся на практике соединений, работающих на сдвиг (заклёпоч-
(заклёпочные, болтовые, сварные соединения, врубки).
Расчёт таких соединений, как это уже указывалось, в значи-
значительной мере является условным. Проверка прочности на сдвиг
обычно производится в предположении равномерного распределения
касательных напряжений по площади сечения по формуле
т = ?<[т].	A0.2)
Чтобы установить величину допускаемого напряжения [т], нам
нужно было бы найти, руководствуясь опытом, величину предела
прочности и предела текучести для стержня, в сечениях которого
возникали бы только касательные напряжения, и, задавшись затем
коэффициентом запаса, назначить величину допускаемого касатель-
касательного напряжения [т]. Однако такой опыт поставить нельзя, так
как при испытании на срез соединительного элемента (болт, за-
заклёпка и т. п.) в поперечных его сечениях будут возникать не только

63]
ЧИСТЫЙ СДВИГ. ОПРЕДЕЛЕНИЕ ГЛАВНЫХ НАПРЯЖЕНИЙ
179
касательные, но и нормальные напряжения (§ 47), и деформация
будет сложной.
Это заставляет нас исходить при установлении величины допу-
допускаемого напряжения [т] в общем случае не из рассмотрения до-
достаточно сложных действительных условий
работы заклёпочных или иных вилов соедине-
соединений, а из некоторых общих теоретических со-
ображений. Теоретическое значение [т] при
установлении норм, конечно, корректируется
данными опытов.
Пусть мы имеем малый элемент материала,
по граням которого действуют только ка-
касательные напряжения (фиг. 114). Такой вид
плоского напряжённого состояния называется
чистым сдвигом. Пусть, кроме того, допус-
допускаемое нормальное напряжение [а] для мате-
материала известно, и требуется найти величину
допускаемого касательного напряжения [т],
написав условие прочности для рассматри-
рассматриваемого элемента.
Как известно (см. главы VII и VIII), для
любой точки напряжённого материала можно
найти главные площадки и главные напря-
напряжения (§ 34); поэтому задачу расчёта на
сдвиг можно свести к задаче проверки проч-
прочности при сложном напряжённом состоянии
(§ 42).
Для решения поставленной задачи найдём
величины главных напряжений и проследим
применение рассмотренных в § 43 теорий
прочности.
Заметим, что по закону парности касатель-
касательных напряжений [§ 36, формула G.8)] каса-
касательные напряжения, действующие по верти-
вертикальным и горизонтальным граням элемента,
одинаковы. По фасадной грани abed нет ни-
никаких напряжений. Следовательно, это — одна из главных площадок,
на которой главное напряжение равно нулю.
Для определения направления и величины двух других главных
напряжений воспользуемся построением круга напряжений, что можно
сделать, если известны напряжения, действующие по двум взаимно
перпендикулярным площадкам (фиг. 115, б). От точки О, поскольку
нормальные напряжения при гранях элемента (фиг. 114) равны нулю,
отложены: вверх — отрезок ODa, равный таЬ = т, и вниз — OD^
равный tbc = — т. Так как точки Da и D лежат на круге, то радиус
его равен ODa = iz.
а.)
Фиг. 115.

180 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [ГЛ. X
Отрезки О А и ОВ определяют величины главных напряжений
°i и °з и равны радиусам круга, а направление BD^ составляющее
угол 45° с нормалью к площадке be, совпадает с направлением о1#
Следовательно, применяя обозначения § 34, имеем:
Напряжение по фасадной грани abed о2 = 0.
Таким образом, если рассечь наш элемент (при условии, что
грань abed-—квадрат) диагональными плоскостями, то по сечению
ас будут действовать растягивающие напряжения аг = т, а по сече-
гию bd— сжимающие: а3== — т (фиг. 115, а). Это можно было бы
доказать и иначе, не
пользуясь построением
круга напряжений, а
рассматривая условия
равновесия- отсечённой
части (фиг. 116). Такое
доказательство рекомен-
рекомендуется читателям выпол-
выполнить самостоятельно.
Следовательно, чи-
сны* сдвиг эквивален-
Фиг. 116.	тен комбинации двух
ршыых. по числовой ве-
величине нормальных напряжений — одного растягивающего и дру-
другого сжимающего. Каждое из этих напряжений равмо по числовой
величине касательному напряжению, вызывающему чистый сдвиг;
площадки, по которым действуют главные (моршлыше) налряжения,
составляют угол 45° с площадками действия только касательных
напряжений.
Если мы выделим элемент из параллелепипеда abed плоскостями,
перпендикулярными к диагоналям ас и bd (фиг. 115, а), то этот
элемент будет подвергаться растяжению в направлении bd напря-
напряжениями аг и сжатию в направлении ас напряжениями а3.
В § 33 мы выяснили, с какими видами деформаций связаны нор-
нормальные и касательные напряжения. Первым соответствовало удли-
удлинение или укорочение, вторым — сдвиг. Теперь мы видим, что такого
резкого разграничения провести нельзя. Деформация сдвига непре-
непременно сопровождается и деформациями растяжения и сжатия.
Как видно по фиг. 115, а, из элемента, подвергающегося по его
граням действию только касательных сил, можно выделить новый
элемент, по граням которого действуют только нормальные напря-
напряжения. Таким образом, весь элемент, изображённый на фиг. 114,
испытывает деформацию чистого сдвига, а материал этого элемента
в то же время претерпевает в некоторых направлениях растяжение
или сжатие.

§ 53]	ЧИСТЫЙ СДВИГ. ОПРЕДЕЛЕНИЕ ГЛАВНЫХ НАПРЯЖЕНИЙ	181
Зная главные напряжения olf o2 и о3 и допускаемое напряжение
для материала нашего элемента при простом растяжении [о], мы
можем составить условие прочности для этого элемента, применяя
ту или иную из изложенных выше теорий. По теории наибольших
нормальных напряжений проводить проверку прочности не следует,
так как она устарела. Поэтому мы начнём решение вопроса о про-
проверке прочности при чистом сдвиге с применения теории наиболь-
наибольших относительных удлинений, которая применялась в машинострое-
машиностроении более полувека, хотя, строго говоря, она неприменима к пла-
пластичным материалам.
В этом случае (§ 43) условие прочности принимает вид:
Подставляя значения ах = т, а2 = 0 и с3 = — т, получаем:
[т - {х (- т)] < [о], или т A + {х) < [а].
Отсюда величина касательных напряжений при чистом сдвиге должна
удовлетворять условию:
Дробь, стоящая в правой части неравенства, представляет собой
допускаемую величину касательного напряжения [х] при чистом
сдвиге. Для стали (j.^0,3, поэтому
М = @,7-*-0,8) [а].
Если же мы возьмём за основу третью теорию прочности (наи-
(наибольших касательных напряжений), то получим:
К — *з] < М или [т — (— т)] < [а].
Отсюда
х<И = [т] и [Т] = 0,5[о].	A0.17)
Наконец, по четвёртой теории прочности (энергетической) имеем:
4 — а^ — о2а3 — а^ < [а],
или
отсюда
[т] = 0,57 [а] я^ 0,6 [о].	A0.18)
Мы видим, что результаты, полученные по различным теориям
прочности, существенно отличаются друг or друга. Поэтому вопрос

182 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [ГЛ. X
о выборе той или иной теории приобретает важное практическое
значение.
Прежде расчётные формулы составлялись по теории наибольших
удлинений; тогда за допускаемое касательное напряжение принимали
величину [т] = 0,8 [о]. В настоящее время надо считать для пла-
пластичных материалов наиболее достоверной энергетическую теорию,
по которой соотношение между [т] и [о] выражается формулой
[т] = 0,6[о].
Значит ли это, как иногда думают, что применение энергетиче-
энергетической теории должно вызвать снижение допускаемой величины каса-
касательных напряжений и увеличение расхода материала? Такое пред-
предположение совершенно неверно; наоборот, правильное применение
новой теории прочности должно привести к повышению допускаемого
напряжения, к ещё лучшему использованию материала.
Это легко показать на следующем примере. Сравним нормы до-
допускаемых напряжений для металлических конструкций в период
широкого применения теории наибольших относительных удлинений
(примерно 1910—1912 гг.) и современные нормы.
Наряду с применением специальных сталей (ДС, малолегирован-
малолегированные и др.) для изготовления металлических конструкций и теперь
часто применяется та же сталь, которая применялась и в 1912 г.
(ст. 3 — с пределом прочности около 4000 кг/см* и пределом теку-
текучести около 2400 кг/см*).
Допускаемые напряжения в 1912 г. имели следующие значения:
для нормальных напряжений [а] = 1000 кг/см*, для касательных
напряжений [т] = 0,8 [о] ==800 кг/см*. Как надлежит изменить эти
нормы в настоящее время, когда мы применяем энергетическую
теорию прочности? Следует ли считать, что, принимая за основное
допускаемое напряжение значения [о] = 1000 кг/см*, мы для [т]
должны принять величину [т] = 0,6 [а] = 600 кг/см*?
Это было бы грубой ошибкой. Величина [т] = 800 -кг/см* оправ-
оправдана практикой, опытом проектирования конструкций, поэтому
снижать её мы не имеем никаких оснований. А если это так, значит
занижены были основные допускаемые напряжения на растяжение [о].
Переход к новой, более совершенной энергетической теории
прочности позволяет вскрыть излишний запас прочности в величине
нормальных напряжений. В настоящее время для стали 3 величина
допускаемых напряжений на растяжение и сжатие повышена до
1600 кг/см* (ГОСТ-960-46), а допускаемых напряжений на сдвиг —
до 1000 кг/см*у что и составляет примерно 0,6 [о].
Таким образом, правильное, не схоластическое, опирающееся на
практику применение новых теорий прочности не только не вызы-
вызывает снижения допускаемых напряжений, а наоборот, даёт метод
для их повышения, для дальнейшего использования излишних запа-
запасов прочности.

§ 54]
СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЕЙ
183
-
	_
AVWVAVAy
Что касается величины допускаемых напряжений на срез заклё-
заклёпок, условия работы которых не отвечают рассмотренному случаю
чистого сдвига, то на практике эта величина колеблется довольно
сильно ([х] = 0,6 -т-0,8 [а]), в зависимости от способа изготовления
заклёпочного соединения. Правильный выбор допускаемых напряже-
напряжений для заклёпок может быть сделан только с учётом эксперимен-
экспериментов над целыми заклёпочными соединениями.
§ 54. Связь между напряжениями и деформацией при чистом
сдвиге. Потенциальная энергия сдвига.
В дальнейшем, при изучении кручения, нам придётся встретиться
с вопросом о деформациях, которые возникают в элементах мате-
материала при действии на него касательных напряже-
напряжений. Пока речь идёт о расчёте заклёпок и болтов,
изучение этих деформаций практического значения не
имеет и осложняется вдобавок тем, что во всех этих
соединениях мы имеем в действительности гораздо
более сложное распределение касательных напряже-
напряжений, чем то, которое было положено в основу наших
расчётов по проверке прочности.
Однако общий характер этой деформации может
быть выяснен и на примере хотя бы той же заклёпки.
Выделенный из стержня заклёпки очень тонкий слой
материала (фиг. 117) стремится при действии на него
касательных напряжений перекоситься; этот перекос и является
характерным для деформации сдвига. Изучить связь этого перекоса
с напряжениями т в заклёпке невозможно, ибо мы не знаем дей-
действительного закона распределения касательных напряжений по
поперечному сечению заклёпки. Поэтому
мы будем изучать деформацию при дей-
действии касательных напряжений на эле-
элементе, испытывающем чистый сдвиг
(фиг. 118).
Если мы закрепим грань АВ этого
элемента неподвижно, то под действием
касательных напряжений грань CD сдви-
сдвинется параллельно АВ на некоторую ве-
величину DDt = ССХ = As, называемую
абсолютным сдвигом. Элемент ABCD
перекосится, пряхмые углы обратятся в острые или тупые, изме-
изменившись на величину у. Этот угол называется относительным
сдвигом, или углом сдвига, и служит мерой искажения (пере-
(перекоса) углов прямоугольника. Поскольку в конструкциях мы имеем
дело лишь с упругими деформациями, этот угол будет весьма
малым.
Фиг. 117.
18.

184 ПРАКТИЧЕСКИЕ ПРИМЕРЫ ДЕФОРМАЦИИ СДВИГА. ЧИСТЫЙ СДВИГ [гл. X
Относительный сдвиг связан по своей величине с абсолютным
сдвигом и расстоянием а между плоскостями ЛВ и CD:
т. е. относительный сдвиг равен абсолютному, делённому на рас-
расстояние между сдвигающимися плоскостями; выражается он в ра-
радианах.
Можно показать, что величина относительного сдвига будет про-
пропорциональна напряжениям г, таким образом, именно относительный
сдвиг, величина перекоса элемента, и является тем, что характери-
характеризует числовым образом деформацию сдвига.
Для установления зависимости между -у и т рассмотрим фиг. 118.
При перекосе нашего элемента диагональ AD удлиняется. Это
удлинение можно связать, с одной стороны, с действующими напря-
напряжениями, с другой — с относительным сдвигом; комбинируя обе
зависимости, найдём связь между т и f,
На фиг. 118 абсолютное удлинение диагонали мы получим, если
из точки А радиусом, равным AD, сделаем засечку на новом поло-
положении этой диагонали — ADV Тогда получаем прямоугольный тре-
треугольник DDtDiy в котором сторона DDX — абсолютный сдвиг As,
сторона D^Di — удлинение диагонали А/; угол при точке Dx может
быть по малости деформаций принят равным 45°. Тогда
A/=Ascos 45°.
Относительное удлинение диагонали
Следовательно,
Д/	r
= Т' где / =
е = ^ cos 45° sin 45°;
As
так как — = f> a cos 45° sin 45° = 0,5, то
С другой стороны, относительное удлинение диагонали, вызван-
вызванное действием главных напряжений oj = tho3 = — т (§ 53, фиг. 115),
может быть выражено формулой G.18):
Подставив это значение е в формулу A0.20), получим:
откуда
'-HITS*	<10-21)

§ 54]	СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЕЙ	185
Таким образом, относительный сдвиг f и касательное напряже-
напряжение т друг другу пропорциональны, т. е. и при сдвиге напряжение
и соответствующая ему относительная деформация связаны законом
Гука.
Величину 2(\л- \ обозначают буквой G и называют модулем
упругости при сдвиге или модулем сдвига. Числовые величины О
для различных материалов приведены в таблице в конце книги
(Приложение VII).
Формула A0.20) принимает вид:
x = TG,	A0.2Г)
и мы имеем полную аналогию в формулах, связывающих напряже-
напряжение и относительную деформацию при растяжении и сдвиге:
Величину G можно вычислить по формуле
G	<1022>
но можно найти и прямым путём в опыте на кручение.
Величина абсолютного сдвига зависит не только от величины
касательных напряжений, но и от размеров выделенного элемента.
Назовём площадь граней, по которым действуют касательные напря-
напряжения, F; расстояние между параллельными гранями обозначено
через а (фиг. 118). Абсолютный сдвиг равен:
Hs = a4=^} где * = j?>
следовательно,
As = gj.	A0.23)
Абсолютный сдвиг прямо пропорционален сдвигающей силе, рас-
расстоянию между сдвигаемыми гранями и обратно пропорционален
площади сечения этих граней и модулю упругости при сдвиге т. е.
мы имеем формулу, выражающую закон Гука для деформации сдвига,
вполне подобную формуле для вычисления абсолютного удлинения
при растяжении:
M-Pl
Так как в формуле A0.22) для модуля сдвига из трёх так называе-
называемых упругих постоянных Е, (J- и G независимыми являются лишь две,
третья может быть выражена через первые. Эта особенность является
характерной для изотропного материала, свойства которого во всех
направлениях одинаковы.
Заметим, что при деформации сдвига изменение объёма элемента
материала равно нулю. Это следует из формулы G.19) § 40, так как
при чистом сдвиге сумма главных напряжений равна нулю.

186
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
[ГЛ. XI
Теперь можно подсчитать также и потенциальную энергию при
чистом сдвиге. Считая, что сила Q приложена статически, можем
выразить работу этой силы на перемещении As:
(половина вошла в формулу для Л, так как сила возрастает от нуля
до конечного значения постепенно, — работа выражается площадью
треугольника). Подставив значение As A0.23), получим:
-^-
2GF
2G
A0.24)
Поделив на объём v = aF, найдём значение удельной потенци-
потенциальной энергии при чистом сдвиге:
« = 7 = Й-	A0>25)
К такому же результату можно было притти на основании фор-
формулы G.26) § 41, рассматривая чистый сдвиг как сложное напря-
напряжённое состояние при главных напряжениях: ох = чу о2 = 0, а3 = — т.
ГЛАВА XI.
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ И ВЫЧИСЛЕНИЕ
ДЕФОРМАЦИЙ.
§ 55. Понятие о крутящем моменте.
Результаты, которые получены при изучении деформации сдвига,
позволяют перейти к решению задачи о проверке прочности при
кручении. С кручением на практике приходится встречаться очень
часто: оси подвижного состава, трансмиссионные валы, элементы про-
пространственных кон-
конструкций, пружины и
даже обыкновенный за-
замочный ключ — всё это
примеры стержней, ра-
работающих на круче-
кручение.
Рассмотрим сначала
задачу о скручивании
валов круглого попе-
поперечного сечения.
Представим себе
(фиг. 119) вал С/7, на
который насажены два шкива / и //. Вал поддерживается подшип-
подшипниками С, D, Е и 771). Шкив / передаёт валу вращение при помощи
х) Подшипники считаем расположенными так, что изгибом вала можно
пренебречь.
Фиг. 119.

§ 55]
ПОНЯТИЕ О КРУТЯЩЕМ МОМЕНТЕ
187
ремённой передачи от электромотора. Шкив // передаёт это враще-
вращение станку, с которым он соединён тоже при помощи ремня.
К шкиву / приложены силы натяжения ведущей и набегающей
ветвей ремня, Тх и tlf лежащие в плоскости, перпендикулярной
к оси вала. Аналогично, к шкиву // приложены силы натяжения
ремня Г2 и ?2.
Эти силы, с одной стороны, создают давление на подшипники
(как и собственный вес шкивов), а с другой — образуют пары сил,
лежащие в плоскости, перпен-	^
дикулярной к оси вала.	Ми	/т\	„
Момент, передающийся от	^ т'" х ° - 9 Мз
шкива / на вал (фиг. 119),
будет:
Аналогично, от шкива // на вал
передаётся момент М2, напра-
направленный в противоположную
сторону и равный
При равномерном ходе ма-	Фиг. 120.
шины все силы, действующие
на вал, находятся в равновесии; вращающий момент (Tt — tx) Ri всё
время уравновешивается сопротивляющимся: (Г2 —1%) R%, т. е.
Участок вала между центрами шкивов подвергается действию
двух равных и противоположных пар сил, лежащих в плоскостях,
перпендикулярных к оси вала: он скручивается. Деформация кру-
кручения, таким образом, вызывается парами сил, лежащими в пло-
плоскостях, перпендикулярных к оси стержня.
Момент пар, скручивающих вал, называется крутящим моментом.
В рассмотренном случае величина его выражается формулой A1.1);
но так как натяжения Tut обычно неизвестны, то для вычисле-
вычисления Мк применяется иной путь (§ 56).
Мы рассмотрели тот случай, когда на валу имеются лишь два
шкива, передающих ему равные и противоположно направленные
моменты Мк; тогда часть вала между шкивами скручивалась этим
моментом Мк.
Бывают более сложные случаи, когда на валу насажено несколько
шкивов; один — ведущий, остальные — ведомые; каждый шкив пере-
передаёт валу свой момент, и при равномерном ходе машины сумма
всех моментов, действующих на вал, равна нулю.
На фиг. 120 показан вал, на который действуют моменты Mv
Мъ МЪ} Мб М^ — в одну сторону (от ведущего шкива), М2, Жа,

188	КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ	[ГЛ. XI
Mi — в другую сторону (от ведомых шкивов). При равномерном
ходе вала
Здесь крутящий момент на разных участках вала будет иметь
различную величину. Часть вала слева от сечения /—/ будет нахо-
находиться в равновесии под действием момента Л14 и касательных на-
напряжений по сечению /—/; таким образом, для этого сечения Мк
будет равен Ж4. Если же мы возьмём сечение 2—2 между шкивами
7 и 2, то напряжениям по этому сечению придётся уравновешивать
сумму моментов, передаваемых на отсечённую левую часть шкивами
/ и 4, т. е. крутящий момент равен Мк = УИ4 — Мх.
К той же величине крутящего момента для сечения 2—2 мы
пришли бы, если бы рассматривали равновесие правой отсечённой
части, на которую действуют моменты Мъ и /И2. В этом случае
Мк = Мг -f- М%> но из условия равновесия
Таким образом, крутящий момент Мк в сечении 2—2 является
одним и тем же по величине, будем ли мы рассматривать равнове-
равновесие правой или левой части вала. Он равен сумме моментов, дей-
действующих на вал справа или слева от проведённого сечения, Знак
крутящего момента будем считать по знаку внешних моментов,
действующих слева от сечения, т. е. при взгляде слева вдоль оси
вала момент, действующий по часовой стрелке, считаем положительным.
Величину крутящего момента на различных участках вала можно
изобразить графически, построив так называемую эпюру крутящих
моментов. Для этого под чертежом вала располагаем ось абсцисс
и от неё откладываем ординаты, изображающие величину крутящего
момента на каждом участке.
Пусть в предыдущем примере Mt = -\- 600 гсгм; М% = — 300 кгм\
Мг = —100 кем; Л14 = — 200 кгм. На фиг. 120 изображено рас-
распределение крутящих моментов по длине
вала.
§ 56. Вычисление моментов, передаваемых
на вал.
Для вычисления крутящих моментов
необходимо знать моменты, передаваемые
на вал каждым шкивом.
Эти моменты можно определить, если нам
Фиг- 121«	известны число оборотов вала и передавае-
передаваемая шкивом мощность. Пусть (фиг. 121) на
шкив действует пара сил с моментом М. Эту пару можно себе
представить состоящей из двух сил Р, приложенных к окружности
шкива. При вращении шкива она производит работу, величина

§ 57]	ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ ПРИ КРУЧЕНИИ	189
которой в единицу времени равна мощности, передаваемой
шкивом.
Вычислим работу пары М при вращении шкива. При повороте
его на угол а каждая сила пары пройдёт путь /?а, где R — радиус
шкива; вся пара произведёт работу
Таким образом, работа пары сил при повороте на угол а равна
моменту пары, умноженному на угол поворота (в радианах).
Если вал совершает т оборотов в единицу времени, то работа
момента будет равна А = М • 2тш. С другой стороны, работа в еди-
единицу времени — это мощность W. Следовательно, крутящий момент
может быть выражен через известные мощность и число оборотов
вала:
Если мощность задана в лошадиных силах W = N л. с, или
W = 75N кгм/сек, а число оборотов в минуту т = п об/мин.гили
в секунду ~, то
., 75.7V-60 2250- N плас, N
Ж = - 2*. я =-^7Г = 716>2'1Г
Мощность может быть задана также в киловаттах W = /f кзт. Так
как 1 кет равен приближённо 102 кгм/сек, то
М = ^|^ .^кгм = 973,6 ¦? кгм.	A1.4)
Из этих формул мы получаем по данным jV (или К) и п величину
момента, передаваемого каждым шкивом, в килограммометрах,
после чего находим сечение вала с наибольшим крутящим моментом
и по нему определяем необходимые размеры вала (§§ 57 и 59).
§ 57. Определение напряжений при кручении
круглого вала.
А. Построив эпюру крутящих моментов, мы можем найти вели-
величину крутящего момента в любом сечении вала. Чтобы найти напря-
напряжения, вызываемые крутящим моментом в сечении, воспользуемся
основным методом решения задач сопротивления материалов — мето-
методом сечений.
Однако прежде чем приступить к решению поставленной задачи,
обратимся к рассмотрению результатов опытных исследований.

190
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
[ГЛ. XI
Опыты показывают, что при скручивании вала круглого сечения
парами Мк (фиг. 122) происходит следующее.
Все образующие поворачиваются на один и тот же угол у, а
квадраты, нанесённые на поверхность вала, перекашиваются, обра-
обращаясь в 4>омбы, т. е. подвергаются деформации сдвига.
Каждое поперечное сечение поворачивается относительно дру-
другого вокруг оси вала на некоторый угол, называемый углом закру-
закручивания. Величина этого угла пропорциональна величине крутящего
момента и расстоянию между сечениями.
Торцевое сечение остаётся плоским, а контуры всех проведён-
проведённых сечений не искажаются (круги остаются кругами).
Фиг. 122.
Радиусы, нанесённые на торцевом сечении, после деформации
не искривляются.
Расстояния между смежными сечениями практически не меняются,
т. е. сечения 1—1 и 2—2, поворачиваясь друг относительно друга
на угол Дер, сохраняют между собой расстояние Ад;.
Таким образом, результаты опытов показывают, что при круче-
кручении стержень-представляет как бы систему жёстких кружков, наса-
насаженных центрами на общую ось ОХО^. При деформации все эти
кружки, не меняя своего вида, размеров и взаимных расстояний,
поворачиваются один относительно другого.
Перечисленные опытные наблюдения дают основание для при-
принятия следующих гипотез:
1.	Все поперечные сечения остаются плоскими.
2.	Радиусы, проведённые в них, остаются прямыми.
3.	Расстояния между сечениями не изменяются.
Приемлемость этих гипотез подтверждается тем, что формулы,
полученные на их основе, хорошо согласуются с результатами
опытов.
Б. Теперь перейдём к отысканию напряжений, действующих по
сечениям, перпендикулярным к оси вала. Разрежем мысленно
(фиг. 123) скручиваемый стержень ОуО^ на две части I и II сече-
сечением 1—7, перпендикулярным к оси вала и находящимся на рас-
расстоянии х от сечения О^. Отбросим часть // стержня и оставим

57]
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ ПРИ КРУЧЕНИИ
Г91
часть /; на нее действует из внешних сил лишь один момент Мк,
приложенный в сечении Ot.
Оставленная часть стержня находится в равновесии под дей-
действием этого момента и сил в сечении /—/, передающихся от от-
отброшенной отсечённой части на оставленную (фиг. 123).
Так как силы в сечении уравновешивают внешнюю пару Жк,
лежащую в плоскости, перпендикулярной к оси вала, то они также
должны приводиться к паре, лежащей в плоскости, перпендикуляр-
перпендикулярной к оси Ох, т. е. в плоскости сечения /—/. Следовательно, эти
силы и соответствующие напряжения касательны к сечению и пер-
перпендикулярны к радиусам
(фиг. 123).
Составим условие рав-
равновесия оставленной ча-
части / в форме уравнения
моментов всех сил отно-
относительно оси Ofi:
или
Для вычисления ?МТ—
суммы моментов сил, дей-
действующих в сечении /—/,
возьмём любую точку
сечения в расстоянии р
от центра круга и выде-
выделим вокруг неё элемен-
элементарную площадку dF.
Тогда усилие, приложенное к ней, будет <1Р = р	р
тельное напряжение в рассматриваемой точке. Момент же этого уси-
усилия относительно точки О равен:
Фиг. 123.
где тр — каса-
касаСчитая площадку dF бесконечно малой, можно найти сумму мо-
моментов всех сил, как определенный интеграл, распространённый по
площади сечения:
2 Л1Т =
или, используя составленное ранее уравнение равновесия, получим:
.p.dF = MK.	(.11.5)

192
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
[ГЛ. XI
Однако найти из полученного уравнения величину т мы пока не
можем, так как ещё не знаем, как распределяются касательные на-
напряжения по сечению.
В. Уравнения статики не дают возможности довести до конца
решение задачи определения напряжений по сечению 7—/. Задача
оказывается статически неопределимой, и для окончания её реше-
решения нам придётся обратиться к рассмотрению деформаций стержня,
показанных на фиг. 122 и 124.
Выделим (фиг. 124) на поверхности скручиваемого стержня до
его деформации двумя смежными образующими ab и cd и двумя
контурами смежных сечений 7—7 и 2—2 прямоугольник ABDC.
!/ \2
Фиг. 124.
После деформации оба сечения, 1—1 и 2—2, повернутся отно-
относительно защемлённого конца на углы <рх (сечение 1—1) и <р* + <*Р
(сечение 2—2). На основании принятых гипотез оба сечения оста-
останутся плоскими, радиусы О2? и OtAy OtC и O^D останутся пря-
прямыми, а расстояние dx между сечениями 1—1 и 2—2 останется
без изменения. При таких условиях весь элемент ABDCOXO^ сме-
сместится и перекосится, так как его правая грань, совпадающая с се-
сечением 2—2, повернётся на угол dy относительно левой, совпа-
совпадающей* с сечением 7—7. Прямоугольник ABDC займёт положение,
показанное на фиг. 124 штриховкой. Перекошенный элемент
AiB^xCxOxOt показан на фиг. 125; там же пунктиром изображён
вид этого элемента, если бы он не испытал перекоса, т. е. если бы
его левая и правая грани обе повернулись на один и тот же угол.
Перекос, вызванный неодинаковым поворотом сечений 7—7 и
2	2, обращает прямые углы прямоугольника ABDC в тупые и
острые; материал нашего элемента испытывает деформацию сдвига
(фиг. 122 и 124). Величина этой деформации будет характеризо-
характеризоваться углом перекоса — относительным сдвигом; на поверхности
стержня в прямоугольнике AiBxDxCi этот угол будет равен ВАхВ»
он обозначен на фиг. 125 буквой f.

§ 57]
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ ПРИ КРУЧЕНИИ
193
Как известно, деформация сдвига сопровождается возникнове-
возникновением касательных напряжений по граням перекашиваемого элемента
(§ 54).
На фиг. 125 изображены эти напряжения, действующие на пло-
площадки, выделенные на правой грани (поперечное сечение 2—2) и
горизонтальной поверхности элемента AiBiDxCiOxO^ Величину этих
напряжений мы можем выразить через относительный сдвиг f> харак-
характеризующий перекос прямо-
прямоугольника ^BjDjCi, по фор-
формуле A0.21): t = 7g-
Так как абсолютный
сдвиг элемента на поверх-
поверхности вала равен BBf = r dy,
а относительный сдвиг f==
В Б' rdv
= -г-н = -т- , то напряжение
AiB dx 9	r
у точки /?! будет;
Найдём теперь напряже-
напряжение т в какой-нибудь дру-
другой точке сечения Lu от-
отстоящей от центра на рас-
расстоянии р (фиг. 125). Для
этого нужно найти величину относительного сдвига, который испы-
испытывает материал у точки Lv На фиг. 125 показан относительный
сдвиг-г-угол перекоса LKLU обозначенный fp, Он будет меньше,
чем относительный сдвиг f на поверхности стержня. Повторяя те же
рассуждения, что и при вычислении f, мы	г
найдём, что y ==р#-г7, и получим:
<zp = 9G^t.	A1.6)
Относительный сдвиг и касательное на-
напряжение в каждой точке поперечного се-
сечения скручиваемого стержня прямо про-
пропорциональны расстоянию р этой точки
от центра сечения. Графически этот за-
закон изменения касательных напряжений	Фиг. 126.
выражается прямой линией (фиг. 126).
Наибольшего значения т достигают в точках, лежащих у самого
края сечения, и обращаются в нуль в центре.
Таким образом, найден закон распределения касательных напря-
напряжений по поперечным сечениям скручиваемого стержня.
7 11. М. Беляев

194	КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ	[ГЛ. XI
Г. Величина касательных напряжений теперь может быть найдена
из уравнения A1.5), выражающего условие равновесия отсечённой
части.
Подставляя вместо т его значение A1.6) и вынося за знак ин-
теграла величину О -^-, постоянную при интегрировании по площади,
получим:
¦у.
\ p*«?F, т. е. сумма произведений из элементарных площадок на
г
квадраты расстояния их до точки О, называется полярным моментом
инерции и обозначается Jp. Тогда
ОЙ-*-А
откуда угол закручивания на единицу длины вала (относительный
угол закручивания) равен:
Подставляя это в уравнение A1.6), получим:
т=^р.	A1.8)
Наибольшего значения напряжения достигнут в точках сечения
у поверхности вала при р ===== ртах = г:
7
Jp
Формулу для ттах можно представить в ином виде:
jp
A1.10)
Pmax/
Отношение —?-= Wp называется моментом сопротивления при
Ртах
кручении; так как момент инерции Jp выражается в единицах длины
в четвёртой степени, то момент сопротивления Wp измеряется в еди-
единицах длины в третьей степени.

ВЫЧИСЛЕНИЕ ПОЛЯРНЫХ МОМЕНТОВ ИНЕРЦИИ
195
§ 58. Вычисление полярных моментов инерции и моментов
сопротивления сечения вала.
Для вычисления Л== 1 р2 dF выделим в сечении кольцевую пло-
площадку радиусами р и p-f-rfp (фиг. 127). В пределах этого кольца
выделим маленькую площадку dF. Просуммируем
произведения р* dF сначала для кольцевой пло-
площадки, а потом сложим полученные величины
для всех кольцевых площадок, на которые можно
разделить сечение. Так как все площадки внутри
кольца находятся на одном и том же расстоя-
расстоянии р от центра, то для них
Но ? dF для кольца, как площадь узкой по-	фиг# 127и
лоски, равна 2jdF=2izpdp и, следовательно,
p2?dF=2np*dp. Тогда, суммируя эти величины для всего сече-
сечения, получаем:
A1.11)
или, выражая через диаметр,
Это и будет полярный момент инерции для круга. Момент сопро-
сопротивления при кручении для круга равен:
Ртах
2 • г
A1.12)
Из формулы A1.8) видно, что напряже-
напряжения т в точках сечения, близких к центру
(р мало), невелики. Крутящий момент урав-
уравновешивается, главным образом, напряже-
напряжениями, действующими в части сечения,	Фиг. 128.
близкой к поверхности стержня; мате-
материал же средней части вала принимает очень слабое участие в этой
работе. Поэтому с целью облегчения валов иногда делают их труб-
трубчатыми (фиг. 128). При этом удаляется и наиболее загрязненная
посторонними примесями центральная часть поковки, из которой
Изготовляют вал.
7*

196
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
[ГЛ. XI
Вычислим момент инерции и момент сопротивления такого труб-
трубчатого сечения. Радиус наружного очертания назовём Ry внутрен-
внутреннего г. Тогда
R
или
A1.13)
)
Момент сопротивления
2R
\6D
Если задаться отношением диаметров -*- = а, или
получим:
^— 16 ^
A1.14)
: а/5, то
(ИЛУ)
A1.14')
При малой толщине t стенок трубчатого сечения
юзначив средний радиус трубы го = —^— и имея в виду, что
— г = /, получим:
Заменяя /? = го-}-у и г = г0 — у и пренебрегая квадратом малой
толщины, после возведения в квадрат получим для полярного мо-
момента инерции:
A1.25)
Точно так же для момента сопротивления найдём:
Wp^2v:rlt	A1Л 6)
Эти приближённые формулы очень удобны для практических рас-
расчётов.
Как видно, для каждого поперечного сечения полярные момент
инерции и момент сопротивления Jp и Wp имеют только одно
вполне определённое значение, зависящее от поперечных размеров
вала.

§ 60]	ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ ПРИ КРУЧЕНИИ	197
§ 59. Условие прочности при кручении.
Зная величину полярного момента сопротивления сечения, можем
найти тахт по формуле A1.10).
По условию прочности наибольшее касательное напряжение не
должно превышать допускаемого, т. е.
Л/Т
maxT = -gb<[x].	A1.17)
W P
Отсюда при известном крутящем моменте и выбранном допускае-
допускаемом напряжении можно определить необходимый момент сопротив-
сопротивления сечения, а затем и необходимый радиус или диаметр вала.
Что касается величины допускаемого напряжения [т], то, как
выяснено выше (§ 53), его следует принимать от 0,5 до 0,6 основ-
основного допускаемого напряжения на растяжение.
На практике величина [т] колеблется для мягкой стали от 200
до 1000 кг/см*, для твёрдой — от 300 до 1200 кг\см%, в зависимости
от характера нагрузки (постоянная, переменная, ударная) и величины
местных напряжений, возникающих в тех местах вала, где в нём
имеются гнезда для шпонок, выкружки и другие изменения формы
сечения.
Применение условия прочности A1.16) для подбора сечения вала
покажем на примере.
Пример 33. Найдём диаметр стального вала, передающего мощность
yV=150 л. с. при л = 60 об/мин. Допускаемое касательное напряжение
(т] = 400 кг/см*.
Из формулы A1.3) получаем:
м 2250-150
Из формулы A1.15) имеем:
:=^ = ?4!* <-[tl.
Отсюда
2.179000
Диаметр вала ^^13,2 см.
§ 60. Определение деформаций при кручении.
Как мы видели в § 57, при скручивании цилиндрического стержня
с круглым поперечным сечением парами сил М&, приложенными по
его концам, деформация состоит в повороте сечений стержня ошо*
сительно неподвижного опорного сечения.

198	КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ	[ГЛ. XI
Для сечения на расстоянии х от опорного сечения этот угол
поворота мы обозначали (фиг. 122) буквой ух и называли углом за-
закручивания. Для определения его воспользуемся равенством A1.7):
г-г-, или dv ¦=
dx GJPт GJP
Интегрируя по х, получаем (при постоянном Мк):
X
iMKdx	Мкх
GJn —~^г~'
При длине стержня / наибольший угол закручивания будет между
крайними сечениями (при х = 1):
Формула A1.18) имеет вид, вполне аналогичный соответствующей
формуле при растяжении или сжатии.
71Г1
Здесь уместно указать на физический смысл величины Jp=z—-~9
Как видно из формулы A1.18), величина угла закручивания <р тем
меньше (при данном Мк), чем больше произведение GJp — так на-
называемая жёсткость при кручении. Таким образом, Jp отражает
влияние размеров поперечного сечения на деформируемость стержня
при кручении.
Если мы будем иметь вал с несколькими шкивами, делящими
его на участки, скручиваемые различными моментами Мю то по
формуле A1.18) можно вычислить для каждого участка угол закру-
закручивания одного его конца по отношению к другому. Суммируя
алгебраически эти углы закручивания для всех участков, получим
полный угол закручивания для всего вала.
Вычисление углов закручивания имеет двоякое практическое зна-
значение: во-первых, оно необходимо для определения опорных реакций
скручиваемых стержней в статически неопределимых системах, —
это редкий случай; во-вторых, умение вычислить угол закручивания
необходимо для проверки жёсткости вала.
Практикой выработаны высшие допустимые пределы для угла ср»
которых нельзя переходить, чтобы не получить нарушения работы
машины. Эти пределы таковы: в обычных условиях [ср] = О,3° на
каждый метр длины вала; при переменных нагрузках [<р] = 0,25°;
для внезапно (с ударом) меняющихся нагрузок [ср] = 0,15°. Иногда
для обычных условий принимают [<р] = 1° на длину, равную 20 диа-
диаметрам вала *).
!) В последнее Bpei\w в советском машиностроении допускаемый угод
закручивании [f] принимается до 2° на погонный метр длины вала.

§ 611 НАПРЯЖЕНИЯ ПО СЕЧЕНИЯМ, НАКЛОНЁННЫМ К ОСИ СТЕРЖНЯ
199
Таким образом, размеры вала следует определять не только из
условия прочности A1.15), но и из условия жёсткости:
Р].	(H.I9)
Это условие часто выдвигается на первое место при длинных
валах. Проверку жёсткости вала покажем на примере.
П р и м е р 34. Для задачи, решённой в § 59 (пример 33), проверим вели-
величину угла закручивания вала на длине /=1 м\ модуль упругости примем
равным G = 8 • 10* лгг/слс2. По формуле A1.19) получаем:
7 = 17900°-^ = о,ОО75 радиана = 0,43%
8 . ю» g'D
что превышает допустимую норму 0,3° на 1 лс. Чтобы соблюсти условие
жёсткости, следует определить радиус вала из неравенства A1.19):
МК1
яг4.
откуда
4Г2М.1 ¦ Г 2 • 179000- 100- 180
г ли [ср] f те . 8 • 10* • я • 0,3
Диаметр должен быть равен d = 14,5 ел*.
§ 61. Напряжения при кручении по сечениям,
наклонённым к оси стержня.
Изучая напряжения при скручивании стержня круглого сечения
(§ 57), мы видели, что по сечениям, перпендикулярным к оси,
в каждой точке действуют касательные напряжения т. По закону
парности касательных напряже-
напряжений такие же напряжения (фиг. 125
и 130) будут действовать и по
продольным граням вырезанного
нами из стержня элемента. Эти
напряжения будут также наиболь-
наибольшими в точках у поверхности
стержня и дойдут до нуля в точ-
точках оси.
Таким образом, если мы про-
проведём сечение через ось скру-
скручиваемого стержня диаметральной
плоскостью (фиг. 129), то в точ-
точках, расположенных по прямой АВУ перпендикулярной к оси стер-
стержня, касательные напряжения будут изменяться по закону прямой
линии. Нормальных напряжений по этим плоскостям не будет.
Фиг. 129.

200
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
[ГЛ. XI
Они действуют по наклонным сечениям и достигают наиболь-
наибольшего значения по сечениям, наклонённым к оси стержня под
углом 45°.
В самом деле, элемент ABCD, вырезанный у поверхности вала
(фиг. 130), подвергается по своим боковым граням действию лишь
касательных напряжений; он находится в тех же условиях, что и
элемент abed на фиг. 115, т. е. в условиях чистого сдвига. Поэтому
по площадкам, наклонённым на угол 45° к оси стержня, касательных
напряжений не будет; это — главные площадки, по которым действуют
рястягивающие и сжимающие главные напряжения Oj и о3, равные
в каждой точке напряжению т (см. фиг. 115).
К
Ж
6'-
m
m
ж
щ
%
в 6)
Фиг. 130.
Фиг. 131.
Величина их для всех точек сечения меняется пропорционально
расстоянию до центра и равна т. Хрупкие материалы, например
чугун, разрушаются (фиг. 131) при кручении от разрыва по наклон-
наклонным сечениям ВС (фиг. 130), т. е. по тем, где действуют наиболь-
наибольшие растягивающие напряжения.
Зная величину и направление главных напряжений в любой точке,
мы можем найти нормальные и касательные напряжения по какой
угодно наклонной площадке из круга напряжений или по форму-
формулам G.5) и G.6). Что касается проверки прочности, то, так как
при кручении наибольшие нормальные и касательные напряжения
равны по абсолютной величине, допускаемые же величины для
касательных напряжений меньше, чем для нормальных, то понятно,
что при кручении, как и вообще при чистом сдвиге, можно огра-
ограничиться проверкой лишь по отношению к касательным напря-
напряжениям.

§ 62]
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ КРУЧЕНИИ
201
§ 62. Потенциальная энергия при кручении.
Выше, при изучении растяжения, было показано (§ 41), что
при деформации упругой системы в ней накапливается энергия, ко-
которую мы назвали потенциальной энергией деформации.
Это явление имеет место и при кручении. Если упругий стержень
в пределах упругости закрутить на некоторый угол, то после удале-
удаления внешних сил он будет раскручиваться и может произвести работу
за счёт накопившейся в стержне потенциальной энергии кручения.
Пренебрегая необратимыми потерями (нагревание, внутреннее тре-
трение и т. п.), мы должны считать, что обнаруживаемая таким образом
работа внутренних сил, определяемая количеством потенциальной
энергии деформации U, равна работе внешних сил А.
Пусть имеется вал, закреплённый одним концом, к свободному
концу которого будем прикладывать пару сил с моментом, постепенно
возрастающим от нуля до конечного значения Жк.
По мере возрастания величины момента пары М)
сил будет расти и угол закручивания ср, связан-
связанный с Мк уравнением A1.18):
MJ
I
В
Фиг. 132.
Если откладывать по оси абсцисс углы закру-
закручивания (деформацию), а по оси ординат соответ-
соответствующие значения крутящего момента, то их
взаимная зависимость изобразится наклонной пря-
прямой О А (фиг. 132). Повторяя рассуждения, проведённые для вычи-
вычисления работы силы Р при растяжении, найдём, что работа
пары Мк выразится площадью треугольника ОАВ:
A1.20)
1
Наличие множителя у в формуле A1.20) объясняется тем, что
момент Мк был приложен не сразу всей своей величиной, а при-
прикладывался в порядке постепенного, «статического» роста от нуля
до конечного его значения.
Подставляя вместо ср его значение из уравнения A1.18) и имея
в виду, что U=A} получим выражение для потенциальной энергии
при кручении;
М1	A1.21)
М*1
2GJP
Потенциальная энергия может быть выражена и через деформа-
деформацию, если в формуле A1.20) заменить значение крутящего момента
выражением из формулы A1.18):

202
Тогда
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
[гл. xi
A1.22)
Из формул A1.21) и A1.22) видим, что потенциальная энергия при
кручении, так же как и при растяжении, является функцией второй
степени от силы или от деформации.
§ 63. Определение предельной грузоподъёмности
скручиваемого стержня.
В предыдущих параграфах мы определяли необходимые размеры
скручиваемого стержня, выполняя условие, чтобы наибольшие каса-
касательные напряжения в точках у контура поперечного сечения не
превысили допускаемого напряжения [т]. Таким образом, не считаясь
с неравномерностью в распределении напряжений по сечению, мы
вели расчёт по допускаемым напряжениям.
В этом способе расчёта, так же как и при решении статически
неопределимых систем, мы не используем полностью предельной
Mr
грузоподъёмности стержня. В предыдущих главах мы считали опас-
опасным то состояние стержня, при котором лишь в контурных точках
сечения напряжения достигнут предела текучести материала (стали)
при сдвиге тт (фиг. 133, а). Величина хт по энергетической теории
прочности должна быть равна 0,6от. Крутящий момент при этом
будет равен:
а угол закручивания
_ЛМ_
2С?Т
_ V
— ~GF
Для дальнейшего увеличения угла закручивания необходимо воз-
возрастание крутящего момента, так как материал внутри стержня
находится ещё в упругом состоянии. При увеличении деформации
рост напряжения у краёв сечения остановится (явление текучести).

ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОЙ ГРУЗОПОДЪЁМНОСТИ
203
и при некотором М^>МТ распределение напряжений будет соот-
соответствовать графику, изображённому на фиг. 133, б. Внутри неза-
штрихованной окружности радиуса ОВ материал будет, по-прежнему
в упругом состоянии.
Предельным состоянием, соответствующим полному исчерпанию
грузоподъёмности стержня, будет то распределение напряжений,
когда упругая зона исчезнет, — по всему се-
сечению напряжения будут равны пределу теку-
текучести тт (фиг. 133, в) *).
Крутящий момент Мпр в этом случае можно
вычислить, составляя сумму моментов всех
внутренних сил относительно центра круга.
Для этого разобьём площадь нашего сечения
концентрическими кругами на бесконечно ма-
малые (кольцевые) площадки.
Напряжения, действующие на каждую та-
такую площадку, в предельном состоянии имеют
постоянное значение и равны тт (фиг. 133, в).
Внутренние усилия, приложенные к элементар-
элементарной площадке радиуса р, будут равны (фиг. 134) тт • dF, а момент
внутреннего усилия тт . dFp. Суммируя элементарные моменты вну-
внутренних сил по площади кольца, получим:
ВН	ТГ лша!	ТГ	Г	Г*
Составляя теперь условие равновесия внешних и внутренних
моментов, найдём:
г
У7ИЛ = 0; М — 1 2тгтар2йр = 0.
о
Отсюда
М —~тг*х	И1 23^
Фиг. 134.
Допускаемый крутящий момент при коэффициенте запаса k будет
равен:
откуда
>УШ;
1) Эта схема работы сечения в предельном состоянии является лишь
приближённой. В действительности, в центре вала напряжения растут не
скачком, хотя и очень резко, и на поверхности не остаются равными тт, а воз-
возрастают вследствие упрочнения материала.

204	КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ	[ГЛ. Х(
в то же время по обычному расчёту мы имеем:
В результате переход к расчёту по допускаемым нагрузкам по-
позволяет уменьшить диаметр вала в отношении
2.2 — v'*x#
Таким образом, вследствие неравномерного распределения на-
напряжений по сечению при упругом состоянии стержня, переход
к методу расчёта по допускаемым нагрузкам может дать экономию
материала.
Надо, однако, помнить, что приведённый расчёт мог бы иметь
силу лишь при статической нагрузке, когда опасным состоянием
является состояние текучести материала. Скручиваемые же стержни,
валы, в подавляющем большинстве случаев работают на переменную
нагрузку в условиях, когда проверка прочности должна производиться
из расчёта на возможность появления трещин усталости. Поэтому
применение изложенного способа к валам, повидимому, в большин-
большинстве случаев невозможно. Иначе будет обстоять дело, как *увидим
дальше, при расчётах балок на изгиб.
Приведённый результат интересен потому, что даёт возможность
проверить его на опыте. Опыты показали, что величина напряже-
напряжения тт, получаемого из формулы A1.23), по предельному моменту,
определённому экспериментально, достаточно близка к 0,6 ат, что
и следует ожидать на основании энергетической теории прочности.
§ 64. Примеры.
Пример 35. Заменить сплошной вал диаметром d = 300 мм полым
валом наружного диаметра ?> = 350 мму эквивалентным в отношении проч-
прочности. Найти внутренний диаметр полого вала d? сравнить веса этих валов.
Наибольшие касательные напряжения в обоих валах должны быть равны
между собою:
.МК_2МК_ 2МК
Отсюда получаем формулу для вычисления а:
Внутренний диаметр равен di = aD = 0,78 • 350 = 273 мм. Отношение
весов равно отношению площадей поперечных сечений; поэтому вес полого
вала составляет
—~
веса сплошного вала.

§ 64]	примеры	205
Пример 36. Определить диаметр стального вала, передающего мощ-
мощность 450 л, с. при 300 об/мин. Допускаемое напряжение [т] = 800 кг/см2:
допускаемый угол закручивания 0,3° на метр длины; модуль <3 = 8 • 10* кг/см*.
Крутящий момент равен Мк == 716,2— = 716,2 |^= 1075 кгм. Необ-
ходимый диаметр определяется формулами
9 л/~Ш* 9 У/ • 1075 • 100
2 У м^г=2 У —Т8бо— =8-82
2ЛУ -,У 2 . 1075 . 100 • 100 ¦ 180"
2 V * . 8 • 10» . « . 03 = 12>8
откуда
10» . « . 0,3
Таким образом, диаметр вала определяется из условий жёсткости и дот-
жен быть принят равным d = 12,8 см.
Пример 37. Для стального вала, рассмотренного в § 55 (фиг. 120),
определить диаметр и полный угол поворота третьего шкива относительно
четвёртого; расстояния между шкивами равны соответственно:
1п =1,0 м; /Х2 = 0,9 м; /2а = 1,5 м.
Допускаемое напряжение равно [т) = 400 кг/см2; допускаемый угол закручи-
закручи1	025°; 0 = 8 • 10*' /2
Ду	р	р [)	/;
вания на 1 м равен 9доп = 0,25°; 0 = 8 • 10*' кг/см2.
Величины моментов, скручивающих вал, даны на фиг. 120. Наибольший
крутящий момент будет на участке между шкивами 1 и 2; он равен 400 кгм.
Определим диаметр вала из условия прочности:
тахт = -
По условию жёсткости:
__ МК1 __
Так как допускаемый угол закручивания на 1 м равен 0,25 у^ = 4,36
радиана, то получаем:
10»
Полярный момент инерции равен Jp = -^ • 5,2* = 1145 см*. Углы закручива-
закручивания отдельных участков вала равны:
MuUt 20 000-100
20000. 100
8. 10» • 1145"""'	'
_
Mtilit_ 40000.90
~S^	8 • 10». 1145
Мп1гг ЮООО-150

206
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
[ГЛ. XI
Так как угол <р41 направлен по часовой стрелке, а углы 91а и <р2$ — против
часовой стрелки, то полный угол поворота третьего шкива относительно
четвёртого равен:
9з4 = C,98 + 1,64 — 2,18) • К)"8 = 3,44 • 10"8 радиана = 0,197°.
пружин
т
§ 65. Напряжения и деформации в винтовых пружинах
с малым шагом.
В рессорах вагонов, в клапанах и в других деталях механизмов
применяются винтовые пружины, подвергающиеся действию сил, сжи-
сжимающих или растягивающих пружину. При проектировании таких
необходимо уметь вычислять наибольшее напряжение (для
проверки прочности) и определять деформа-
деформацию пружины — её удлинение или осадку.
Последнее необходимо, так как на прак-
практике регулируют нагрузки, приходящиеся
на пружину, давая ей большие или меньшие
деформации сжатия или растяжения.
Таким образом, необходимо по разме-
размерам пружины уметь вычислить зависимость
между её деформацией и силой. Оказы-
Оказывается, что материал пружины испыты-
испытывает напряжения кручения, как это будет
показано ниже.
Представим себе (фиг. 135, а) цилин-
цилиндрическую пружину, растянутую силами Р,
приложенными по её оси. Назовём: R —
радиус винтовой оси (витка) пружины,
п — число витков, г — радиус поперечного сечения стержня пру-
пружины, G — модуль сдвига. Наклоном витков пренебрегаем.
Для вычисления напряжений разрежем эту пружину на две
части сечением, проходящим через ось цилиндра, образован-
образованного пружиной. Верхнюю часть отбросим
и рассмотрим равновесие нижней части (фиг.
135, б).
На эту часть действует внешняя сила Р
и напряжения по сечению стержня пружины.
Чтобы выяснить, какие это напряжения,
приложим в точке О, центре поперечного
сечения пружины, две силы Pt и Я2, равные
по величине Р и направленные по вертикали
в разные стороны (фиг. 136).
Так как и сила Р2, и пара сил P=Pt
с моментом Мк = Р • R лежат в плоскости
то они должны уравновеситься касательными
Фиг. 135.
136.
проведённого разреза,
напряжениями.

§ 66]]
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ВИНТОВЫХ ПРУЖИНАХ
207
Сила Р2 сдвигает отсечённую часть пружины вниз и вызы-
вызывает появление касательных напряжений, показанных на фиг. 137, а
и равных:	MH=PR
Момент пары MK =
вызывает скручивание стер- /J
жня пружины и является
причиной возникновения
второй' группы касательных
напряжений A1.8):
Фиг. 137.
Эти напряжения будут меняться по своей величине пропорционально
расстоянию от центра (фиг. 137, б) и достигают наибольшего значе-
значения по площадкам, расположенным у контура сечения; их величина
равна:
Накладывая обе группы напряжений друг на друга, получаем
полное распределение напряжений по сечению.
Опасной точкой будет та из точек контура, в которой направле-
направления тх и тахт2 совпадут. Такой точкой будет А — у внутреннего
края сечения; в ней полное касательное напряжение равно (фиг. 137):
w==-^+?*?==-?-(l 4-—).	(И.25)
Так как в большинстве случаев второе слагаемое в скобках зна-
значительно больше единицы, то обычно пренебрегают первым слагае-
слагаемым — напряжением от про-
простого перерезывания — и учи-
учитывают лишь кручение стержня
парами PR. Тогда
*»о = ^?. (Н.26)
При таком упрощении очень
легко вычислить деформацию
растяжения пружины, которую
мы обозначим X.
Вырежем из пружины от-
отрезок длиной ds двумя смеж-	фиг- 138#
ными сечениями — СОХ и СО^
проходящими через ось пружины (фиг. 138). Так как эти сечения
мы выбираем весьма близко, то можно принять, что до деформации

208	КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ	[ГЛ. XI
радиусы R, идущие от оси пружины к центрам проведённых сечений,
лежат в одной плоскости и образуют треугольник ОХСО<>.
После деформации второе сечение, вследствие скручивания
участка стержня dsy повернётся относительно первого на угол
db = к s . Тогда радиус О.2С повернётся относительно радиуса ОХС
тоже на угол dd, и точка С переместится в положение Сь что по-
повлечёт опускание конца пружины на величину
Если мы учтём, что все элементы ds стержня пружины деформи-
деформируются таким же образом, то полное опускание нижнего конца пру-
пружины, т. е. её удлинение, выразится суммой величин dh
1
Здесь /= \ ds — полная длина стержня пружины, а ^	взаим-
ный угол закручивания концов стержня пружины, определённый
в предположении, что стержень распрямлён.
Пренебрегая наклоном витков к горизонтали и принимая число
их пу получаем, что полная длина винтового стержня равна:
тогда
Формулы A1.25) и A1.28) дают возможность проверить проч-
прочность и определить деформацию пружины.
Чем выше допускаемое напряжение на срез [т], тем более гиб-
гибкой будет пружина, тем большую осадку она даст при том же
грузе Р, так как её можно сделать из стержня меньшего попереч-
поперечного сечения.
Так как рессоры должны быть достаточно гибкими, то для них
берётся закалённая сталь с очень высоким пределом упругости; допу-
допускаемое напряжение на срез достигает здесь 40 кг/мм* и даже
80 кг/мм*. Для хромованадиевой стали допускаются напряжения
в растянутых пружинах до 70 кг/мм* при г от 6 мм до 8 мм. Для
фосфористой бронзы при G = 4400 кг\мм% и г до 8 мм допускают
1т] = 13 кг\мм\
Эти напряжения могут быть допущены при спокойной нагрузке.
Для изменяющейся нагрузки они понижаются примерно на 1/3, а при

§65]
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ВИНТОВЫХ ПРУЖИНАХ
209
непрерывно работающих пружинах (пружины клапанов) примерно
на */3. В этих случаях большую роль играет возможность развития
трещин усталости (см. § 17). Кроме того, клапанные пружины часто
работают при высоких температурах, что также требует снижения
основных допускаемых напряжений.
На практике при расчёте пружин в формулу A1.25) вводят поправочный
коэффициент к, учитывающий как влияние перерезывания, так и ряд других,
не учтённых выше факторов (изгиб стержня пружины, продольные деформации
и т. д.); величина этого коэффициента тем больше, чем больше отношение -=?¦,
т. е. чем более жестка в геометрическом отношении пружина.
Вместо формулы A1.25), учитывающей помимо кручения только допол-
дополнительное влияние перерезывания сечения пружины силон Р% ведут расчёт
по формуле:
= *§*=*^?;	A1.29)
поправочный коэффициент k может быть взят по таблице 16.
При расчёте пружин иногда заданной является не сила, сжимающая или
растягивающая пружину, а энергия Г, которая должна быть ею поглощена.
Подобно тому, как это было при растяжении или сжатии стержня, потен-
потенциальная энергия деформации пружины U измеряется работой внешних сил.
Таблица 16. Поправочные коэффициенты к.
г
k
3
1,58
4
1,40
5
1,31
6
1,25
7
1,21
8
1,18
9
1,16
10
1,14
Так как для пружины зависимость между X и Р прямолинейна (формула
A1.28), потенциальная энергия деформации пружины равна:
A1.30)
Из формулы A1.26) имеем:
Подставляя это выражение в формулу A1.30), получим:
2т. Rn 0_2
4G %Г"^'
Так как 2r.Rn — длина стержня пружины, а т.г2— площадь сечения, то
где V—объём пружины; из A1.31), учитывая, что U = T, находим:
01.31)
(П.32)

210
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
XI
Таким образом, задавшись предельной величиной напряжения т = [г],
мы можем вычислить объём пружины, необходимый для поглощения задан-
заданной величины энергии T = U с тем, чтобы не были
превышены допускаемые напряжения [т]. При этом
необходимо проверить осадку пружины при напряже-
напряжениях [т]; она должна быть такой, чтобы не произошло
закрытия зазоров между витками.
Кроме цилиндрических винтовых пружин на прак-
практике приходится встречаться с коническими пружинами
(фиг. 139). Радиусы верхнего и нижнего витков обо-
обозначены соответственно Rt и /?2; величина промежу-
промежуточного радиуса R определяется формулой
Фиг. 139.
где п — число витков, а о — угол, образованный рас-
рассматриваемым радиусом с верхним радиусом Rt и от-
отсчитываемый по виткам пружины.
Проверка прочности для конической пружины
производится по формулам A1.25) или A1.26) с заме-
заменой в них величины R её наибольшим значением R*.
Что касается осадки X, то при её вычислении, как и
раньше, надо суммировать элементарные деформации
л MKRds
(JJD
где Мк — теперь переменная величина PR.
Таким образом,
2zn
х =
Рп
A1.33)
Иногда пружины делают из стержня не круглого, а прямоугольного сече-
сечения; тогда приходится для вычисления напряжений и деформаций пользоваться
формулами, приведёнными в § 67 (таблица 17).
§ 66. Примеры.
Пример 38. Предохранительный клапан диаметром D = 75 мм должен
открываться при давлении пара ^ = 6 ат. Пружина клапана сделана из круг-
круглой стали диаметром ?/=12 мм; диаметр витка пружины 2R = 60 мм. При
отсутствии нагрузки расстояние между осями смежных витков по вертикали
(шаг пружины) равно 2=17 мм.
Требуется найти необходимое число витков пружины я, предполагая,
что при максимальном поднятии клапана должно оставаться не менее
Х2 = 35 мм в запас на дальнейшее сжатие пружины (до соприкасания витков),
а также определить начальное сжатие пружины Хх и напряжение х при пол-
полном открытий клапана; модуль упругости G = 8 • 105 кг/см2.
Определим силу, поднимающую клапан:

§ 66]	ПРИМЕРЫ	211
Для того чтобы только при этой силе пружина начала сжиматься, надо ей
дать первоначальную осадку:
Xi = -OF" = 8.1У. 0,6*
Полная длина пружины в ненагружённом состоянии (считая.по её вер-
вертикальной оси) будет складываться из Хх и запаса Х2.
Эта сумма должна равняться предельному сжатию пружины l9 = (? — d) n:
или
0,276/г + 3,5 = A,7 — 1,2) л,
откуда
«=о|з4=16ви1КОВ-
Предварительная осадка пружины равна:
Х1== 0,276- 16 = 4,4 см.
Наибольшее напряжение в пружине при полном открытии клапана мы вычи-
вычислим, связав X с х; с одной стороны,
с другой стороны,
Из второго равенства имеем:
подставляя это значение Р в первое равенство, получаем:
Tmax — 2/?2лл#
При полном открытии клапана имеем:
X = Xt + Х2 = 4,4 + 3,5 = 7,9 мм; max т = ^З^У^и = 4°7°
Пример 39. Винтовая пружина сделана из проволоки диаметром
d = 4 жж. Диаметр образующего цилиндра равен D = 46 жж. В ненапряжённом
состоянии зазор в свету между витками равен ?=1,0 мм. Какой силой надо
сжать пружину, чтобы зазор исчез? G = 8 • 105 кг/см2 = 8 • 103 кг/мм2.
Диаметр витка пружины Z) = 2/? равен сумме диаметров образующего
цилиндра и стержня пружины: 2R = D\ + d = 50 жле. Чтобы зазор закрылся,
надо, чтобы осадка одного витка равнялась зазору. Тогда
_ p_Qr«<_8.10'.2«.lt0
И P-W~	4Т255	-2.0а «к?.,
Напряжения при этой нагрузке равны:
AfK Р^ „2,05-25
= 4,1 кг/мм-.

212
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
[ГЛ. XI
Фиг. 140.
§ 67. Чистое кручение стержней некруглого сечения.
На практике довольно часто встречаются случаи, когда скручиванию
подвергаются стержни некруглого сечения. В таких стержнях поперечное
сечение после деформации не остаётся плоским, а коробится, и касательные
напряжения распределяются по
более сложному закону, чем для
круглого сечения (фиг. 140).
Чистым (или свободным) круче-
кручением называется кручение стержня,
не сопровождающееся возникно-
возникновением нормальных напряжений в
его поперечных сечениях, что воз-
возможно лишь при условии беспре-
беспрепятственной депланации (коробле-
(короблении) всех сечений. При чистом
кручении распределение и вели-
величины касательных напряжений во
всех поперечных сечениях стержня
одинаковы.
Чистое кручение возможно
лишь для стержня постоянного
сечения по всей длине при скру-
скручивании его парами сил, прило-
приложенными к его концам 1).
Из сказанного выше ясно, что
основная гипотеза сопротивления
материалов — гипотеза плоских сечений — неприменима к расчёту на кручение
стержней некруглого сечения. Поэтому расчёт таких стержней на кручение
может быть выполнен лишь методами теории упругости.
Общий метод решения задачи о чистом кручении стержня некруглого
сечения впервые был дан Сен-Венаном в 1864 г. Им же был разобран и ряд
случаев решения этой задачи (прямоугольник, эллипс и др.). В 1865 г. рус-
русским учёным А. Соколовым было дано оригинальное решение ряда задач на
кручение стержней некруглого сечения.
Впервые были исследованы многие задачи чистого кручения стержней
сложного очертания советскими учёными В. Г. Галёркиным, Н. И. Мусхе-
лишвили, Л. С. Лейбензоном, А. Н. Динником и др. Общее решение задачи
о кручении тонкостенных стержней дал проф. В. 3. Власов.
Решение этих задач приводится в курсах теории упругости и в специаль-
специальной литературе.
Для иллюстрации на фиг. 141 показано распределение напряжений для
эллиптического и прямоугольного сечений. На основании закона парности
касательных напряжений легко доказывается, что при кручении стержней
любого сечения касательные напряжения в точках контура сечения напра-
направлены вдоль контура (по касательной); составляющие, перпендикулярные
к контуру, требуют появления равных им составляющих касательных напря-
напряжений на боковой поверхности; но так как боковая (внешняя) поверхность
свободна от них, в поперечном сечении нет касательных напряжений, пер-
перпендикулярных к контуру.
По этим соображениям можно считать, что касательные напряжения
образуют сплошной поток, направленный вдоль контура сечения, как это
видно из фиг. 141.
1) Подробнее вопрос о чистом и стеснённом кручении изложен в
главе XXX.

§ 67]
КРУЧЕНИЕ СТЕРЖНЕЙ НЕКРУГЛОГО СЕЧЕНИЯ
213
Некоторые результаты, полученные теорией упругости, приведены в таб-
таблице 17. При пользовании таблицей 17 следует иметь в виду некоторые новые
обозначения. Для всех видов сечений угол закручивания и наибольшее
касательное напряжение
могут быть выражены
формулами, подобными
формулам для круглого
сечения; только вместо
полярного момента инер-
инерции Jp будет входить ве-
величина Ук, выражающаяся
тоже в единицах длины
в четвёртой степени и за-
зависящая от размеров се-
сечения, а вместо Wp — ве-
величина WK той же размерности, что и Wp. Эти геометрические характеристики
сечения условно названы моментом инерции при кручении Ук и моментом
сопротивления при кручении WK.
Для некоторых форм сечения (круг, кольцо)
jk — J pi w к— w p.
Для пользования таблицей 17 имеем следующие формулы:
I max
Фиг. 141.
WK
• 	<—
A1.34)
A1.35)
Если имеет место кручение стержня сложного сечения, которое может быть
разбито на части из тонкостенных элементов, то для него;
-г • •. = aj Лея*
где п = 1, 2, 3,...— номера тех простейших частей, на которые разбито
сечение.
Так как угол закручивания для всего сечения и всех его частей один
и тот же:
G/K G/Ki "# GJKn *
то крутящий момент распределяется между отдельными частями сечения
пропорционально их жёсткостям:
Соответственно наибольшее касательное напряжение в каждой части {п)
сечения будет равно:
Мкп	М«
№к

214
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
[ГЛ. XI
«в
о
о.
с
S
I
>>
а.
о
с
о
3
X
X
«я
ю
о4
аэ-
К
со
О
ieHi
к
p
1?!
о
о;
д
а>
CtJ
со
в
Q
*^~
со.
в
Q
•5*
Я
со
о
о
о
г-
ю
Й
о
о
о>
о
со
со
о
S
о
со
ю
S
о
S
о
00
со
о
сч
ю
о"
г
о
со
ю
*~"
00
о
о
о
I
Ё
о
\о
.Е
О
S
S
о
СО
S
и
о
|8
н S. I
8S
8
1§
о
s
-	§
О	О)
a	a
з	s
О
14
со
_ *г
1

§ 67]
КРУЧЕНИЕ СТЕРЖНЕЙ НЕКРУГЛОГО СЕЧЕНИЯ
215
с
»=¦
с
а.
:§
#о О S
SS.S
Sow
s g ^
§ и °
« 3 5 = «
I S 2
О Он ej
SCO
- I ?J
о
§
790
о
00
о
с
о
х
о
II >§
I s
s
CO
Is
p il
о
>>
О
с
о
о
53
о> о
Си г-
се Я
е- m
и. а
а
S, !
Мом
s,

216
КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
ГЛ. XI
s
а:
ах
II
0,743
1,789
1,789
6,0
0,742
2,456
2,456
8,0
0,742
3,123
3,123
10,0
о S
S
X
о к s
И О О
_ О* Я
щ О S
н о
я я х ^
s о я^
о s н
я * ^
о о II
О
о
|3
If
о
II'
(N .
[И
н о. 1
я с «
о ?

§ 67]	КРУЧЕНИЕ СТЕРЖНЕЙ НЕКРУГЛОГО СЕЧЕНИЯ	217
Наибольшего значения т достигает для того элемента, у которого -~~
будет максимальным. Тогда
где
В дополнение к таблице 17 приведём формулы Ук и т для сечений,
составленных из узких и длинных прямоугольников, как-то: уголковых, тав-
тавровых, двутавровых, корытных и т. п.
В этом случае можно принять
^^'т^^3'	(П*36)
где Ь — короткие, a h — длинные стороны прямоугольников, на которые
можно разбить сечение.
Коэффициент у\ зависит от формы сечения и равен:
для уголкового сечения		^ = 1,00,
>	двутаврового » 		yj = 1,20,
>	таврового » 		yj = 1,15,
>	корытного » 		г, = 1,12.
Угол <р попрежнему выразится формулой
Наибольшего касательного напряжения можно ожидать в наиболее
широком из прямоугольников, на которые мы разбиваем наш профиль. Это
напряжение можно вычислить по формуле
т	— К Ша*	Л] Q7\
где Втах — наибольшая толщина из всех толщин фигуры.
Для расчёта на кручение трубчатых стержней некруглого сечения при
малой толщине стенок можно воспользоваться формулами, полученными для
круглого кольцевого сечения. Момент сопротивления тонкостенного кольце-
кольцевого сечения по формуле A1.16) равен:
где Fq — площадь круга, ограниченная средней линией кольца, at — его тол-
толщина. Считая, что касательные напряжения равномерно распределены по се-
сечению кольца, получим:
Этой формулой можно пользоваться для расчёта тонкостенных стержней
некруглого замкнутого сечения.

218	КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ
Для угла закручивания имеем:
[ГЛ. XI
т/
Умножив и поделив на 2ъг0 = S, получим:
A1.39)
где S — длина осевой линии трубчатого сечения, a Fo—площадь, ограни-
ограниченная средней линией рассматриваемого замкнутого профиля.
§ 68. Примеры.
Пример 40. Найти наибольшее касательное напряжение и угол закру-
закручивании для рельса типа II Л длиной 12 м иод действием моментов
Мк = 0,1 тм, приложенных к
обоим концам рельса.
Для вычисления напряже-
напряжений и деформаций в рельсе при
кручении профиль рельса надо
разбить, как показано на фиг.
142; размеры этих частей даны
на чертеже в миллиметрах.
Наибольшее напряжение и
угол закручивания выразятся
формулами A1.34) и A1.35):
Фиг. 142.
где WK=
к—мо-
мент инерции всего сечения при
кручении; WK — момент сопротивления при кручении; (Лся/^кя^ах — отно-
отношение соответствующих моментов, вычисленных для той из частей сечения,
JJ^{J'' + /?'
ущ	,	,
для которой эта величина достигает максимума; JK=:J^-{-J'K' + /?', где ка-
каждое из слагаемых в правой части — момент инерции при кручении, вычис-
вычисленный для каждой из трёх частей сечения, изображенных на фиг. 142, с
округлением размеров.
Головка рельса: /^ = 68 мм; ?1 = 40 мм; т^ = 1,7; У^ = а?{ — как для
прямоугольника (таблица 17, случай 5) а = 0,359; 7^ = 0,359 -44 = 91,9 см*;
W'K = $bs; р = 0,405; WK = 0,405 -43 = 25,9 мъ;
трг = o^q = 3,55 см.
VvK ZO,y
Шейка рельса: h2 = 71 мм; Ь2 = 13 мм; m = -— = 5,46;> 4 (таблица 17,
случай 6)
/к = — (ш — 0,63) № = 4,6 см*; -тт^т = b = 1,3 c.w.

§ 68]	примеры	219
Г* ;=» 17 мм; т = -- = -¦--
Подошва рельса (таблица 17, случай 6): b т Г* ;=» 17 мм; т = -- = -¦-- =
= 6,72>4; У^" = ~-(ш —0,63) = 19,1 см*.
lv к
JK = 91,9 + 4,6 + 19,1 = 115,6 см*.
Наибольшее JK/WK — для головки; поэтому наибольшее х в головке посре-
посредине её ширины — наверху:
у; ^ — з,55
х -^-
AV 10000-1200 Л1„о ,	180 П1ОО „„„,
^-077 = 8- 10*. 115,6 ~0'128 p^"aWe; ? = ^Г ' °'128 = 7 33-
^Пример 41. При допускаемом напряжении |т] = 50 кг/см2 вычислить
наибольший крутящий момент для стальных стержней, имеющих следующие
поперечные сечения: а) прямоугольник 18 X 30 мм; б) эллипс с диаметрами
18 и 30 мм; в) круг с диаметром 30 мм; г) квадратная труба со сторонами
а = 30 см и толщиной стенок т = 6 мм.
Определим для прямоугольного сечения величину /л= г^= 1,67; соот-
ветствующие значения аир возьмём из таблицы 17 (по интерполяции); {J =
= 0,39*6; а = 0,3493; тогда
Ук = аЬ* = 0,3493 . 1,8* = 3,66 см'; WK = ф = 0,396 . 1,83 = 2,315 см\
При наибольшем напряжении хтах = 500 кг/см2 допускаемый крутящий
момент для прямоугольного сечения равен Л1а = хтах \\7К = 2,315 • 500 =
= 1157 кгсм= 11,57 кем.
Для эллиптического сечения
16""—	[б	-1'91 см
и допускаемый крутящий момент Mq = 5
Для круглого сечения диаметром cf = 30 мм
1V_ тег3
WK = -к- =
= 500 • 1,91 =955 кгсм = 9,55 кгм.
мм
7t • L53
и допускаемый момент Мъ = 500 • 5,31 = 2655 кгсм = 26,55 кгм.
И, наконец, для трубчатого квадратного сечения по формуле A1.38) имеем:
где
F9 = (а — tJ = C0 — 0,6)* = 860 см\
Мк = 500 . 2 . 860 . 0,6 = 516 000 кгсм.

220	КРУЧЕНИЕ. ПРОВЕРКА ПРОЧНОСТИ	[ГЛ. XI
Пример 42. Стальной стержень прямоугольного сечения передаёт
крутящий момент Мк = 100 кгм при допускаемом напряжении [т] = 400 кг-см3;
толщина стержня г = 2,8 см. Найти ширину Ь. Определим:
_МК_10 000
Отсюда находим коэффициент
WK__25_
По таблице 17 определяем т (по интерполяции):
/« = 3,96 и ? = */л = 2,8. 3,96=11,1 см.

ОТДЕЛ IV.
ИЗГИБ. ПРОВЕРКА ПРОЧНОСТИ БАЛОК.
ГЛАВА XII.
ПОСТАНОВКА ЗАДАЧИ О ПРОВЕРКЕ ПРОЧНОСТИ ПРИ ИЗГИБЕ
И МЕТОД ЕЁ РЕШЕНИЯ.
§ 69. Общие понятия о деформации изгиба.
Устройство опор балок.
Деформация изгиба призматического стержня с прямой осью про-
происходит, если к нему будут приложены в плоскостях, проходящих
через ось стержня, пары сил или силы, перпендикулярные к его оси.
Стержень, работающий на изгиб, обычно называется балкой. Опыт
показывает, что при указанном действии сил ось балки искривляется*
балка изгибается. На фиг. 143 изображена в качестве примера
система сил, изгибающих балку прямо-
прямоугольного сечения; силы расположены
в плоскости симметрии балки. Если
плоскость действия сил не является
плоскостью симметрии, помимо из-
изгиба может наблюдаться скручивание j
стержня.
Балки являются наиболее часто
встречающимися элементами сооруже-
сооружений и машин, принимающими давле-
давления от других элементов конструкции
(например, силы Ри Р2, Рг на фиг. 143) и передающими их тем
частям, которые поддерживают балку (например, силы Я4, Р5 на
фиг. 143).
Таким образом, на балку действуют приложенные силы и реак*
щи опор. Для решения задачи сопротивления материалов необхо-
необходимо знать и те и другие.
Внешние приложенные силы можно вычислить, если известно,
какие части конструкции опираются на балку. Эти нагрузки сво-
сводятся к сосредоточенным силам Я (г, кг), парам сил м{тм, кгм)
и равномерно и неравномерно распределённым по длине балки
нагрузкам.
Равномерно распределённые нагрузки измеряются их интенсив-
интенсивностью <7, т. е. величиной нагрузки, приходящейся на единицу длины
балки, и выражаются в т/м и кг/м.
г*
Фиг. 143.

222
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
[ГЛ, XII
Интенсивность неравномерно распределённых нагрузок меняется
по длине балки и обозначается через q(x). В этом случае q(x)
равна величине нагрузки, приходящейся на единицу длины балки
в рассматриваемой точке*). Иначе: q (x) равно пределу отношения
величины нагрузки, лежащей на длине dx в рассматриваемой точке
балки, к этой длине.
Некоторые примеры балок изображены на фиг. 144, а, б> в. Пер-
Первая из них, балка междуэтажного перекрытия, загружена равномерно
распределённой на-
1 1 1 Uj 1 I 11 1 1 SpTv	грузкой q = 200 кг/м;
J^J -* т ¦ т т I I ¦ ¦ IД ^Г \	вторая — стойка пло-
гМгу	\	тины, загружённая тре-
треугольной нагрузкой
(давление воды) с ин-
интенсивностью q (x), ме-
Р-Ют	'""'" Г	\	няющейся от 0 до qo=
= 1200 кг/м; третья—
главная балка моста,
загружённая давле-
давлением колёс паровоза.
Вагонная ось пред-
представляет собой балку,
Фиг. 144.
опирающуюся на колёса и загружённую давлением букс; балки,
входящие в состав крыла самолёта, изгибаются давлением воздуха*
Будем пока рассматривать лишь балки, удовлетворяющие следую-
следующим двум ограничениям:
1)	сечение балки имеет хотя бы одну ось симметрии (фиг. 145);
2)	все внешние силы лежат в этой плоскости симметрии балки.
z	„	Опорные реакции,
уравновешивая прило-
1
1
I
\
I I I . 1 женные к балке силы,
Фиг. 145.
будут расположены в
той же плоскости.
Для вычисления
опорных реакций не-
необходимо рассмотреть
устройство опор балок. Эти опоры относятся обычно к одному
из следующих трёх типов:
а)	шарнирно-неподвижная опора;
б)	шарнирно-подвижная опора;
в)	защемлённый конец.
Шарнирно-неподвижная опора схематически изображена в точке
А на фиг. 146. Она позволяет опорному сечению балки свободно
1) Обозначение q(x) означает, что интенсивность нагрузки в этом случае
является функцией х.

§ 69}	ОБЩИЕ ПОНЯТИЯ О ДЕФОРМАЦИЙ ИЗГИБА	223
поворачиваться вокруг шарнира, расположенного в центре тяжести А
опорного сечения, но не допускает поступательного перемещения
этого конца. Это сопротивление выражается реакцией, которая пере-
передаётся от опоры через шарнир на конец балки и лежит в плоскости
действия внешних сил.
Нам известна только точка приложения этой реакции — шарнир —
как единственная точка, в которой происходит соприкосновение
балки и опоры, но неизвестны ни величина реакции, ни её напра-
направление. Поэтому будем всегда заменять эту реакцию двумя её соста-
составляющими: одной Яд, направленной по оси балки, и другой А9 ла-
правленной перпендикулярно к оси. Шарнирно-неподвижная опора
даёт, с этой точки зрения, две неизвестные по величине реакции
(Л и НА).
\
мПш
Фиг. 146.	Фиг. 147.
Шарнирно-подвижная опора допускает, помимо поворотов, также
свободное перемещение в соответствующем направлении (фиг. 146,
точка В). Таким образом, рассматриваемая опора препятствует лишь
перемещению, перпендикулярному к определённому направлению.
В соответствии с этим реакция такой опоры проходит через центр
шарнира и направлена перпендикулярно к линии свободного переме-
перемещения опоры — обычно оси балки. Шарнирно-подвижная опора
даёт лишь одну неизвестную реакцию В.
Наконец, при защемлённом конце балки опора препятствует вся-
всяким перемещениям этого конца в плоскости действия сил. Она мо-
может быть получена из шарнирно-неподвижной опоры путём уничто-
уничтожения шарнира (фиг. 147).
Уничтожая шарнир, мы препятствуем вращению концевого сече-
сечения балки — вводим новую реакцию, которая должна помешать этому
вращению; такой реакцией может быть только пара сил. Поэтому
защемлённый конец балки даёт три неизвестные реакции: состав-
составляющую На> параллельную оси балки, составляющую Л, перпенди-
перпендикулярную к оси, и опорный момент Ма-
Балка может опираться на ряд опор указанных типов. Так, на
фиг. 147 изображена балка, защемлённая одним концом; на фиг. 146 —
балка, опёртая шарнирно-неподвижно на одном конце и подвижно
на другом; на фиг. 148, а — та же балка, подпертая посредине ещё
одной шарнирно-подвижной опорой; на фиг. 148, б—балка, защемлён-
защемлённая одним концом и подпертая шарнирно-подвижной опорой в одном
из промежуточных сечений.

224
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
[гл. хн
На всех этих фигурах изображены реакции опор, которые могут,
в связи с конструкцией опорных частей, возникнуть при действии
на балки внешних нагрузок; эти нагрузки на чертежах не показаны.
Для определения неизвестных реакций нам придётся в первую
очередь использовать уравнения статики, выражающие условие, что
В
<%
с
4
Ф
•в7
Фиг. 148.
балка в целом при действии всех сил и реакций, приложенных к ней,
находится в равновесии. Так как все эти силы лежат в одной пло-
плоскости, то уравнений равновесия для них можно написать три. По-
Поэтому задача определения реакций из условий статики разрешима
при наличии лишь трёх неизвестных реакций.
Таким образом, балки с устройством опор, дающим три реакции
(фиг. 146—147), являются статически определимыми. К стати-
статически определимым балкам относятся также многопролётные (много-
(многоопорные) балки с промежуточными шарнирами; такие балки могут
быть расчленены на основные статически определимые балки (А — /
и 2—3) и подвесные (/—2 и 3 — D), опирающиеся на первые через
шарниры (фиг. 149).
^ 1 ^ \в' \с ШШг
Фиг. 149.
Прочие балки относятся к категории статически неопределимых,
вопросам расчёта которых посвящены специальные главы.
Устройство опор балок в действительности далеко не всегда со-
соответствует схемам, изображённым на фиг. 146 и 147, Поэтому,
приступал к решению задачи по расчёту балки, надо прежде всего
рассмотреть, как запроектировано устройство опор этой балки, и
отнести эти опоры к тому или иному виду из изображённых на
фиг. 146 и 147.

§ 69]
ОБЩИЕ ПОНЯТИЯ О ДЕФОРМАЦИИ ИЗГИБА
225
Так как деформации балок обычно весьма малы и напряжения ле-
лежат в пределах упругости, надо установить, допускает ли устрой-
устройство опор балки хотя бы небольшой поворот или перемещение;
этого уже достаточно, чтобы считать опору шарнирной или подвиж-
подвижной. Если конец металлической или деревянной балки заложен в кир-
кирпичную стену на небольшую глубину, то можно считать вполне
возможным незначительные повороты этого конца и, стало быть,
принять его при расчёте за шарнирный.
Таким образом, приступая к определению опорных реакций балки,
необходимо схематизировать опорные части, заменяя действительную
конструкцию наиболее прибли-
приближающейся к ней схемой (фиг.
146 и 147).
В качестве примера рассмот-
рассмотрим работу вагонной оси (фиг.
150, а). В точках Л и В на ось пе-
передаются давления Р от кузова
вагона; в точках же С и D эти
давления передаются рельсам. Мы
можем рассматривать ось как бал-
балку (фиг. 150, б)у нагружённую си-
силами Р в точках А и В и имею-
щую опоры в точках С и D. Спра-
Спрашивается, к какой типовой схеме
следует отнести эти опоры?
Необходимо выяснить, чему мешает и что разрешает конструк-
конструктивное устройство этих опор. Пренебрегая трением между колесом
и рельсом в поперечном направлении и учитывая наличие реборд,
можем сказать, что эти опоры:
1)	препятствуют перемещениям точек С и D оси в вертикальном
направлении;
2)	препятствуют перемещениям всей оси в горизонтальном на-
направлении;
3)	допускают относительное сближение или удаление этих точек;
4)	допускают повороты опорных сечений оси.
Этим условиям можно удовлетворить, поставив в одной из точек
С и D шарнирно-неподвижную, а в другой — шарнирно-подвижную
опору, как схематически показано на фиг. 150, б.
Для определения опорных реакций в статически определимых
балках мы будем пользоваться тремя уравнениями равновесия. При
этом за ось х будем принимать ось балки, за начало координат —
центр одного из опорных шарниров, а ось у будем направлять вер-
вертикально вверх.
Сначала составляем условие равенства нулю суммы проекций
«сех сил на ось х— для определения горизонтальной составляющей
опорной реакции.
8 Н. М. Беляев
Фиг. 150.

226	ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ	[ГЛ. XII
Вертикальные составляющие и опорный момент определяем, со-
составляя два условия равенства нулю суммы моментов всех сил от-
относительно двух каких-либо точек балки, обычно относительно
центров тяжести опорных сечений балки. Условие равенства
нулю суммы проекций сил на ось у лучше оставить для проверки
правильности вычислений: оно должно обращаться в тождество
при подстановке в него определённых уже величин опорных
реакций.
Для балок с промежуточными шарнирами рассматриваем сначала
равновесие подвесных балок, как двухопорных балок, и находим их
реакции. Эти реакции уравновешивают давления, передающиеся через
шарниры от подвесных балок на основные. Зная давления, находим
реакции основных балок (см. § 73).
§ 70. Характер напряжений в балке. Изгибающий момент
и поперечная сила.
Выбор расчётной схемы и вычисление опорных реакций завер-
завершают первую часть задачи о расчёте балки — определение внешних
сил, действующих на балку.
Теперь можно перейти к отысканию напряжений в сечениях
балки; это будет следующим шагом в решении задачи об изгибе.
В качестве объекта для рассуждений возьмём балку (фиг. 151),
шарнирно-опёртую по концам и нагружённую силами Ри Р2, Р3-
Реакция На при заданной системе
j \-а,-А \р \р . нагрузок равна нулю, реакции же
у |/77 \ 12 т \В А и В определяются из уравне-
.	-j	<L~_^j?ii-sL -2^Ав ний моментов; таким образом,
-I	^—'	ум7 внешние силы известны.
I	При вычислении напряжений
2	/	л необходимо отыскать опасное
сечение балки, через которое
^1-	передаются наибольшие напряже-
напряжения. Для этого мы должны полу-
получить формулы, позволяющие вычислить напряжения по любому
сечению (например, наклонному сечению 2—2); после этого можно
будет найти и опасное сечение и наибольшие напряжения.
Сначала научимся вычислять напряжения по сечениям, перпенди-
перпендикулярным к оси; затем — по сечениям, параллельным оси, и уже по-
потом— по любым сечениям. Возьмём перпендикулярное к оси сечение
тп с центром тяжести О на расстоянии х от левого опорного
конца. Для вычисления напряжений по этому сечению отбросим одну
часть балки и заменим действие её на оставшуюся часть искомыми
напряжениями. Оставить следует, для упрощения вычислений, ту
часть балки, к которой приложено меньше сил, в нашем случае—•
левую.

70]
ХАРАКТЕР НАПРЯЖЕНИЙ В БАЛКЕ
227
На оставленную левую часть балки (фиг. 152) в каждой точке
сечения тп будут действовать напряжения, которые можно представить
составляющими: нормальными с и касательными т. Эти напряжения бу-
будут уравновешивать внешние силы А и Plt приложенные к оставленной
части. Внешние силы и напряжения вместе п Dx
образуют систему сил в пространстве, для
которой можно составить шесть уравнений
равновесия.
Пытаясь из этих уравнений найти напря-
напряжения сих, мы должны были бы для каждого
сечения (при изменении х) заново составлять
уравнения равновесия, так как система внешних сил, приложенных к
рассматриваемой части, не была бы одинаковой. Например, для сече-
сечения между силами Р2 и Рг к левой части были бы приложены не
две, а уже три силы.
Чтобы получить для о и х общие формулы, годные при любом
значении х, удобно, чтобы система внешних сил, действующих на
оставленную часть, была всегда единообразного, стандартного
вида.
Так как эта система состоит из сил, лежащих в одной плоскости,
то её всегда можно заменить силой, приложенной в какой-либо точке,
центре приведения, и парой сил; в частном случае сила может об-
обратиться в нуль. Это и будет достаточно простой и в то же время
единообразный вид, к которому всегда можно привести систему
внешних сил, действующих
на оставленную часть балки. f n t %-q]
За центр приведения
обычно берут центр тяжести \ ^	t	fa—#/
рассматриваемого сечения, п
что, как мы увидим дальше,
значительно упрощает фор-
формулы для вычисления а и т.
В рассматриваемой ле-
левой части балки заменим	Фиг. 153.
силы А и Р^ эквивалент-
эквивалентной системой стандартного типа, приведя их к точке О (фиг. 153).
Приложим в этой точке две силы А — вверх и вниз. Тогда
система из реакции А и этих двух сил сведётся к сосредоточенной
силе А (на фиг. 153, б дважды перечёркнута), приложенной в точ-
точке О, и к паре из сил А (один раз перечёркнута) с плечом лг.
Момент этой пары равен Ах. Таким же образом поступаем и
с силой Рх.
Складываем все дважды перечёркнутые силы, приложенные
в точке О, и моменты всех пар, составленных из однажды перечёрк-
перечёркнутых сил. При сложении положительными будем считать направле-
направления для сил — вверх, а для моментов — по часовой стрелке.
8*
/
о л
О

228	ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ	[ГЛ. XII
В результате сложения вместо сил А и Рх мы получим силу Q,
приложенную в центре тяжести сечения, и пару с моментом Ж; ве-
величины М и Q определяются формулами:
М = Ах — Л (лг — а{),
Q=A-Pl.
Момент пары, приложенной к оставленной части балки, назы-
называется изгибающим моментом в выбранном сечении; можно также
считать, кчто изгибающий момент — это момент системы сил, заме-
заменяющих в данном сечении действие отброшенной части балки на её
оставшуюся часть.
Изгибающий момент М равен сумме моментов всех внешних сил,
приложенных к рассматриваемой части балки, относительно центра
тяжести проведённого сечения. Сила Q, стремящаяся сдвинуть оста-
оставленную часть балки относительно отброшенной, называется попе-
поперечной (или перерезывающей) силой в данном сечении.
Поперечную силу Q можно также рассматривать как проекцию
на плоскость сечения равнодействующей системы сил, заменяющих
в данном сечении действие отброшенной части балки на оставшуюся
её часть.
Поперечная сила Q равна сумме проекций всех внешних сил,
приложенных к оставленной части балки, на нормаль к её оси.
Таким образом, М и Q совместно заменяют систему внешних сил,
приложенных к рассматриваемой части балки, и уравновешивают
систему усилий, передающихся через проведённое сечение со сто-
стороны отброшенной части балки.
Заметим, что при действии на балку только сил, перпендику-
перпендикулярных к её оси, можно говорить о поперечной силе, как об алге-
алгебраической сумме сил, приложенных к оставленной части балки.
Важно отметить, что М и Q надо рассматривать при этом опре-
определении вместе, ибо они представляют собой систему стандарт-
стандартного вида, заменяющую систему А и Ри приложенную к рассматри-
рассматриваемой части балки. Эти определения дают ответ на вопрос, как
вычислить М и Q по данным внешним силам.
При вычислении М и Q в приведённом примере мы рассматри-
рассматривали левую часть балки, но во многих случаях будет удобнее для
вычислений рассматривать правую часть и отбросить левую. Устано-
Установим связь между значениями М и Q для левой и правой частей
балки.
По фиг. 154 на часть балки слева от сечения тп действует си-
система внешних сил Л, Рх\ на правую часть — система Р2, Ръ и В.
Так как вся балка в целом (фиг. 154) находится в равновесии,
то система сил А и Рх должна уравновешивать систему сил Яа, Я3
и В. Первая система заменена силой Q, приложенной к точке О и
направленной вверх, и парой М, вращающей по ходу часовой стрелки;
поэтому система Ръ Рг н В после приведения к центру тяжести

§ 70]
ХАРАКТЕР НАПРЯЖЕНИЙ В ВАЛКЕ
229
рассматриваемого сечения должна замениться такой же силой Q,
приложенной в точке О, но направленной вниз (фиг. 154), и па-
парой М, вращающей против хода часовой стрелки.
Значит, если мы рассматриваем правую часть балки, то получим
для М и Q те же величины, что и при рассмотрении левой части,
но направления их бу-	,
дут противоположны. А*	\ч
Чтобы получать для 1 	L
изгибающего момента
и поперечной силы
одни и те же значения
не только по величине,
но и по знаку, незави-
независимо от выбора правой
или левой части балки,
мы условимся считать
положительными: М-
по часовой стрелке и
Q — вверх, если при
вычислениях рассма-
рассматривается левая часть балки, и обратно, М — против часовой стрелки
и Q — вниз, если рассматривается правая часть. Это условие пока-
показано на фиг. 154. При таком выборе знаков мы будем для каждого
сечения балки получать одинаковые значения М и Q, независимо
от выбора при вычислениях левой или правой половины балки.
Знаки для М и Q можно связать с характером деформации балки
при действии внешних сил. Если изгибающий момент в сечении тп
положителен, то балка в этом сечении гнётся выпуклостью вни*
(фиг. 155, а)\ если же он отрицателен, то балка гнётся выпуклостью
вверх (фиг. 155, б). В сечении, где М переходит через нуль, кри-
кривизна балки меняет своё направление, т. е. ось балки в этом сече-
сечении имеет точку перегиба.
На фиг. 156 изображён характер деформаций в сечении тп при
действии положительной и отрицательной поперечных сил.
Теперь мы можем перейти к вопросу о выражении напряжений а
и х через М и Q. На фиг. 157 вновь изображена часть балки,
раньше показанная на фиг. 152 и 154. Разница в том, что вместо

230	ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ	[ГЛ. XII
внешних сил А и Р к рассматриваемой части приложены пара М и
сила Q. Напряжения а и т, заменяющие действие правой отброшен-
отброшенной части, должны уравновесить эту систему внешних сил.
Нормальные напряжения о не могут уравновесить силы Q, так
как направлены перпендикулярно к ней. Но они могут сложиться
в пару, уравновешивающую изгибающий момент Ж, так как направ-
направлены параллельно плоскости симметрии балки, в которой лежит М.
Таким образом, нормальные напряжения а зависят только от М.
С другой стороны, касательные напряжения т не могут уравно-
уравновесить пару Му так как они лежат в плоскости тп, перпендикуляр-
перпендикулярной к плоскости действия изгибающего момента; силу же Q они мо-
могут уравновесить, так как лежат в той же плоскости тп, что и она.
Таким образом, приходим к выводу: поперечная сила Q уравнове-
уравновешивается только касательными усилиями, сумма которых должна быть
равна и противоположна силе Q. Следовательно:
°=/i(Al),	A2.1)
t=/2(Q).	A2.2)
Вывод формул A2.1) и A2.2) достаточно произвести только один
раз для какого-нибудь сечения балки. В дальнейшем этими выраже-
выражениями можно пользоваться для любого сечения, стоит только найти
для него значения М и Q.
Напряжения а и х будут тем большими, чем больше М и Q; так
как для проверки прочности материала необходимо найти наиболь-
наибольшие значения этих напряжений, то мы должны отыскать те сечения
балки, для которых значения изгибающего момента и поперечной
силы достигают максимума. Отысканию этих опасных сечений очень
помогает построение так называемых эпюр изгибающих моментов и
поперечных сил, т. е. графиков, которые показывают, как меняются
для различных сечений балки величины М и Q в зависимости от
изменения переменной х.
Таким образом, поперечная сила Q{x) и изгибающий момент
М (х) являются функциями от х. Для краткости в дальнейшем будем
их обозначать Q и Ж, сохраняя значок (х) лишь в тех случаях,
когда необходимо подчеркнуть, что Q и М — величины переменные,
зависящие от х. При построении эпюр откладывают под каждым се-
сечением от оси абсцисс, проведённой параллельно оси балки, орди-
ординаты, которые в выбранном масштабе изображают величину изгибаю-
изгибающего момента или поперечной силы в этом сечении. Ниже (§ 72)
мы покажем построение этих эпюр на примерах.
Построение эпюр Q и М может быть облегчено, если будут
установлены некоторые зависимости между значениями поперечной
силы и изгибающего момента в любом сечении балки, а также связь
этих величин Q и М с приложенной к балке нагрузкой.
Отыскание этих зависимостей между нагрузкой, поперечной силой
и изгибающим моментом дано и следующем параграфе.

§ 71]
ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ
231
§ 71. Дифференциальные зависимости между интенсивностью
сплошной нагрузки, поперечной силой и изгибающим моментом.
Мы выяснили (§ 70), что внешние силы в любом сечении балки
приводятся к силе Q и паре с моментом М. Следовательно, для
равновесия отсечённой части необходимо, как мы уже установили,
чтобы и внутренние силы
привелись к такой же силе
Q и моменту М.
Поэтому, если из балки
(фиг. 158) вырезать элемент
бесконечно малой длины dx,
то он должен находиться
в равновесии под действием
части сплошной нагрузки
с интенсивностью q (кото-
(которую на длине dx можно
считать постоянной), а так-
также сил Q и Qt и моментов
М и Ж1э заменяющих дей-
действие на него соответствен-
соответственно левой и правой отбро-
отброшенных частей J). Заметим,
что Qt = Q-\-dQ и МА =
= M~\-dM, так как приращения этих величин при переходе от
сечения тп к бесконечно близкому сечению тхпх — также беско-
бесконечно малые величины.
Условия равновесия выделенного элемента напишутся так:
Из первого уравнения имеем:
q dx — dQ = Q,
откуда
A2.3)
т. е. производная от поперечной силы по абсциссе сечения равна
интенсивности сплошной нагрузки в том же сечении.
Из второго уравнения, пренебрегая бесконечно малыми второго
порядка малости, получим:
= 0, или ^=0,	A2.4)
!) В пределах участка dx не приложено сосредоточенной силы или
пары сил.

232	ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ	[ГЛ. XII
т. е. производная от изгибающего момента по абсциссе сечения
равна поперечной силе в том же сечении.
Взяв производную от обеих частей равенства A2.4), получим:
d4\ dQ dM	,1ОКЧ
1~ъ = -г или -J—5 = <7,	A2.5)
dx2 dx	dx* ч*	v '
т. е. вторая производная от изгибающего момента по абсциссе
равна интенсивности сплошной нагрузки. Если q направлено вниз,
d2M
то уравнение A2.5) будет: ^ = — q<
Полученные зависимости могут быть использованы при построе-
построении эпюр Q и Ж, особенно если учесть, что производная функции
геометрически представляет собой тангенс угла наклона, образуе-
образуемого с осью абсцисс, касательной в данной точке кривой. Иначе
говоря, поперечная сила в данном сечении может рассматриваться
как тангенс угла наклона касательной к эпюре М в точке, соответ-
соответствующей этому сечению. Поэтому надо иметь в виду, что если
ось х направлена справа налево, то ~т- = — Q, так как угол наклона
касательной меняет знак при изменении направления оси абсцисс.
Из уравнения A2.3) следует, что в том сечении, где интенсив-
интенсивность нагрузки # = 0, поперечная сила Q — QmaLX или Q = Qmin>TaK
как если q = -—- — 0, то касательная к эпюре Q параллельна оси
абсцисс. По той же причине из формулы A2.4) следует другое, более
важное заключение, что изгибающий момент достигнет максимума
(или минимума) в том сечении, где Q = -j- = 0, т. е. в сечении, где
поперечная сила переходит через нуль.
Хотя уравнение A2.4) даёт возможность получить выражение
для Q, как производной от М, однако при построении эпюр сле-
следует определять Q независимо, используя уравнение A2.4) только
для проверки. Так же для проверки правильности построения эпюры М
может быть использовано уравнение A2.5), поскольку знаком второй
производной определяется направление выпуклости кривой, по кото-
которой очерчена эпюра М. Указания о проверке правильности построе-
построения эпюр Q n M даны ниже (§ 74).
§ 72. Построение эпюр изгибающих моментов и поперечных сил.
Пример 43. Построить эпюры моментов и поперечных сил для
балки, лежащей на двух опорах и нагружённой силой Р (фиг. 159).
Для вычисления М и Q в любом сечении этой балки прежде всего
необходимо отыскать реакции. На фиг. 159 намечено предполагаемое
направление этих реакций Л, На и В.
Из условия равенства нулю суммы проекций всех сил на ось
балки получаем, что

§ 72]
ЭПЮРЫ ИЗГИБАЮЩИХ МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ
233
Этот результат можно было предвидеть заранее, так как нагрузки
перпендикулярны к оси балки.
Составляя сумму моментов сил относительно точки В, получаем:
и
Точно так же
и
Для проверки правильности полученных результатов составим
сумму проекций всех сил на вертикальную ось у:
А — Р -f- В = 0, или A -f- В = Р.
Подставляя значение найденных реакций, получим:
РЬ . Ра _ Р(а + Ь) _р
I ' /	/	'
что удовлетворяет условию равновесия. Такую проверку всегда не-
необходимо производить, так как ошибка в определении реакций
неизбежно поведёт к ошибкам и в по-
построении эпюр Q и М,
Для получения выражений, дающих
нам величины поперечной силы и из-
изгибающего момента в любом сечении
балки, возьмём какое-либо сечение
/ — / между точками Л и С на рас-
расстоянии хх от конца А, Заметим, что
выражение «взять сечение» требует не
только обозначить это сечение на чер-
чертеже, но и обязательно отметить
его расстояние от выбранного начала
координат. Центр тяжести проведён-
проведённого сечения обозначен через Ох.
Для вычисления поперечной силы Q
в этом сечении удобнее рассмотреть
левую отсечённую часть, так как к
ней приложено меньше сил (только
сила А). Рассматривая часть балки слева от сечения Ох и проекти-
проектируя приложенные к ней внешние силы на перпендикуляр к оси
балки, получаем выражение для поперечной силы Qx в сечении на
расстоянии хх от опоры А:
Qx = JrA = ~.	A2.6)
И

234	ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ	[ГЛ. XII
Поперечная сила в сечении с абсциссой хх не зависит от этого рас-
расстояния. Таким образом, пока хх меняется в пределах от 0 до а,
поперечная сила остаётся постоянной, и её эпюра на этом участке
изобразится прямой F^D^ параллельной оси абсцисс А^В^ (фиг. 159).
Выражение A2.6) для Qx будет справедливым, пока взятое нами
сечение не перешло за точку С, т. е. пока О^л^^а. Если х^^хх,
в левую часть балки попадут уже две силы А и Р\ следовательно,
сумма проекций сил, приложенных к левой отсечённой части балки,
изменится.
Чтобы найти величину поперечной силы на втором участке, при-
придётся взять ещё одно сечение между точками В и С с центром тя-
тяжести О2. Расстояние его х% будем отсчитывать от правой опоры В.
В этом случае нам будет выгоднее рассматривать правую часть балки,
так как на неё действует лишь сила В.
Рассматривая правую отсечённую часть балки, получим выражение
для поперечной силы в сечении 2—2:
Q^ = — B = — ^.	A2.7)
Знак минус взят потому, что сила В, приложенная к правой отсе-
отсечённой части, направлена вверх.
Нетрудно видеть, что если бы мы рассматривали левую отсечён-
отсечённую часть, то получили бы то же значение для Q2:
Qz = A — P— — B (так как А-\- В = Р).
Выражение A2.7) пригодно при любом значении хъ не выходя-
выходящем за пределы участка ВС, т. е. при О^х^^Ь, и показывает,
что Qa от х<ь не зависит.
График для поперечной силы на протяжении второго, участка
представляет собой прямую ?"аО2, параллельную оси абсцисс. Эпюра
поперечных сил имеет разрыв — скачок в месте приложения силы Рх\
в этом месте поперечная сила переходит через нуль и не равна от-
отрезку ZJ?2 = A В сечении непосредственно слева от С
«= + ?;
в сечении же непосредственно справа
—
Отметим, что абсолютная величина скачка равна величине
приложенной в этом сечении сосредоточенной силы А
Такое очертание эпюры поперечных сил (фиг. 159) есть следствие
того, что мы при расчёте считаем сосредоточенную силу Р приложенной
в одной точке С. В действительности передача давления Р на балку

§ 72]
ЭПЮРЫ ИЗГИБАЮЩИХ МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ
235
происходит через очень малую площадку, имеющую некоторую длину
вдоль балки (фиг. 160). Поэтому на самом деле поперечная сила на
протяжении этой длины постепенно изменяется
. РЬ Ра
от величины -)- — до	, переходя через
нуль.
Наибольшим значением поперечной силы по
абсолютной величине
будет
в данном примере (при
Опасными в отношении касательных напряжений
будут все сечения участка балки СВ.
Для построения эпюры изгибающих момен-
моментов воспользуемся теми же сечениями /—/
(с началом координат в точке А) для левой
части балки и 2—2 (с началом координат в
точке В) для правой части балки.
Рассматривая левую отсечённую часть, найдём значение момента
в сечении /—7, как сумму моментов приложенных к ней сил отно-
относительно центра тяжести сечения О{.
Ml = A*xl = j^-xlt	A2.8)
причём М1 — функция первой степени от хи Следовательно, если-мы
будем передвигать наше сечение, менять хь то Мх будет меняться по
закону прямой линии. Полученное выражение A2.8) для Жх будет
пригодным, пока наше сечение не перешло за точку С, т. е. пока
0 ^ хх ^ а.
Как только хг станет больше а, на левую часть балки попа-
попадут уже две силы: А и Ру и формула A2.8) окажется непригодной.
Так как этот график — прямая линия, то хх достаточно дать лишь
два значения для получения двух точек эпюры моментов. При Х\ = 0
получаем Мх = 0 — это ордината под точкой А. Точно так же при
.. , РаЬ	~
х1 = а получим М1 = -\—	ордината под сечением С.
При построении эпюр условимся откладывать положительные
ординаты вверх (в сторону положительной оси у)> а отрицатель-
отрицательные — вниз; другими словами, все ординаты эпюры моментов от-
откладываются на вогнутой стороне балки. Иногда принимают и
обратное расположение ординат, что часто практикуется при ра-
расчёте рам.
Отложив от оси абсцисс вверх (положительный момент!) отре-
отрезок QDi, выражающий в масштабе ординату —у-, и соединив точку
Dx и Ах прямой, получаем первый участок эпюры моментов. Для
построения эпюры на втором участке составим выражение момента

236
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
[ГЛ. XI!
сил, приложенных к правой отсечённой части балки, относительно
точки О2:
Рп
М2 = ?*2 == ™ • х2.	A2.9)
Момент и на этом участке получился положительным, так как
мы рассматривали правую часть, и сила В вращала её относительно
точки О2 против часовой стрелки. Полученное выражение A2.9)
представляет собой уравнение прямой линии и пригодно при
О
Ь. При лг2 = Ьу
= -]—— и при
= О, М2 = 0.
Таким образом, второй участок эпюры моментов изображается
прямой DA. На всём протяжении балки изгибающий момент поло-
положителен и достигает максимума в сечении С — в месте приложения
силы Р, где он равен
Жтах = ^.	A2.10)
В этом сечении будут наибольшие нормальные напряжения.
При a = b = -j (сила приложена посредине пролёта) получаем:
A2.10')
Рассмотрим ещё несколько примеров построения эпюр М и Q
при различных видах загружения балки.
Пример 44. Построим эпюры моментов и поперечных сил для
балки, изображённой на фиг. 161. Так как у этой балки правый
конец свободен, то при построении эпюр
можно обойтись без предварительного
определения опорных реакций, если мы
всё время будем рассматривать правую
часть балки.
Взяв сечение на первом участке
между точками С и В> мы видим, что
на оставшуюся правую часть ОХВ не
действует никаких сил. Поэтому в се-
сечении Ох изгибающий момент и попе-
поперечная сила равны нулю. Это относится
ко всем сечениям между 5и С. Эпюры
М и Q для этого участка совпадают с
осью абсцисс. Для участка АС получаем:
М = — Ялг2.
М
Фиг.
Эпюры изображены на фиг. 161; из них видно, что
Мт[п= — Р{1— а) и Qmai = P.

ЭПЮРЫ ИЗГИБАЮЩИХ МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ
237
§ 72]
Отметим, что для этой балки мы построили эпюры Q и М без
определения опорных реакций.
Пример 45. Построим эпюры моментов и поперечных сил для
балки, изображённой на фиг. 162, нагружённой сплошной равномерно
распределённой нагрузкой интенсив-
интенсивности ^(выражаемой в кг/МуТ/ми т.п.).
Здесь необходимо начать с опре-
определения опорных реакций.
Реакция Н равна нулю, реакции
же Л и В по симметрии равны;
каждая из них равна половине всей
лежащей на.балке нагрузки:
Возьмём сечение О на расстоя-
расстоянии х от левого конца балки. Оста-
Оставим для вычисления Q и М левую
часть. На неё действуют реакция А
и равномерно распределённая по
длине х нагрузка q.
Для определения поперечной	Фиг. 162.
силы в сечении О нужно взять
сумму сил, приложенных к левой отсечённой части балки. Слева от
сечения лежит сила Л = у, направленная вверх, и равнодействую-
равнодействующая равномерно распределённой нагрузки, расположенной на длине х,
равная qx и направленная вниз. Следовательно,
Поперечная сила меняется с изменением х по закону прямой линии,
для построения которой дадим переменной х два значения:
при х =
) = %- и при х = / Q == —
Эпюра поперечных сил дана на фиг. 162; maxQ = y.
Для построения эпюры М составим сумму моментов тех же сил,
приложенных к рассматриваемой части балки, относительно точки О.
Имея в виду, что равнодействующая qx приложена посредине от-
X
резка длиной х и плечо относительно точки О равно у, получим:
Это уравнение моментов пригодно для вычисления изгибающего
момента в любом сечении балки.

238
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
[гл. хп
В данном случае величина изгибающего момента зависит от
квадрата абсциссы лг, следовательно, очертание эпюры представляет
собой кривую — квадратную параболу. Для построения этой кривой
наметим по крайней мере три-четыре точки её. Имеем:
при х = О М = 0;
/	ql
/ 4 ) ~~ 32 ;
» х = 1 М = 0.
Эпюра моментов получает вид, показанный на фиг. 162.
Для нахождения Жтах найдём абсциссу лг0 соответствующего
сечения, приравнивая нулю производную от М по х:
dM	ql 2qx0	п
откуда
= + ?у('-*о) = + Х
Наибольший изгибающий момент имеет место посредине про-
пролёта, т. е. в том сечении, где Q = 0, что является следствием
установленной выше (§ 71) зависимости между М(х) и Q(x).
Пример 46. Построить эпюры для балки, нагружённой равно--
мерно распределённой нагрузкой q и защемлённой одним концом
в стену.
Таблица 18. Данные к примеру 46.
X
х—0;
Х = ~2
х — 1
Q (х)
<?=0;
Q = -ql
М(х)
М = 0;
Фиг. 163.
Здесь можно построить эпюры Q и М без определения опор-
опорных реакций. Рассматривая левую отсечённую часть (фиг. 163),
получим:
Q = — qx, M = -q-?.
Результаты вычислений сведены в таблицу 18.

§ 72]
ЭПЮРЫ ИЗГИБАЮЩИХ МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ
239
Эпюры даны на фиг. 163; из неё видно, что
= — Y ®min = ~~ ?'
В этом случае наибольшее по абсолютной величине значение
изгибающего момента соответствует не аналитическому макси-
максимуму ( —=0],а имеет место в заделке, как это видно из эпюры
моментов.
Это, однако, не противоречит дифференциальной зависимости
A2.4), так как поперечная сила Q==— равна нулю именно в том
сечении, где кривая моментов имеет аналитический максимум (вер-
(вершина параболы с уравнением М(х)=:
Пример 47. Рассмотреть балку, на-
нагружённую парой сил с моментом М
(фиг. 164).
Реакция Н равна нулю. Реакции А и В
образуют пару с плечом /, уравновеши- М_
вающую момент М\ они равны по вели- Т
чине и направлены в разные стороны:
В этом нетрудно убедиться из урав-
уравнений статики, взяв, например, сумму
моментов относительно точки В:
?Мд = 0; Л-/ —М = 0.
Выражения для Q(x) и М(х) составим отдельно для каждого
участка. Для первого участка между сечениями Л и С
М.
Фиг. 164.
при лг1 = О Mi = 0\ при хх = а 1
Для второго участка между сечениями С и В
Ai
м
при дг2 = 0 Ж2 = 0; при х.2 = Ь М% =	j
Эпюры Q и М показаны на фиг. 164; из них получаем:
Mb ,
n=	^-(при
Л1

240
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
[гл.
Обратим внимание на то, что в	сечении, где приложена пара
сил, на эпюре изгибающих моментов	получается скачок на величину
момента этой пары:
., Ma ,	Mb
§ 73. Построение эпюр Q и М для более сложных случаев
нагрузки.
Изучив общий метод построения эпюр и их свойства, перейдём
к решению более сложных задач.
Рассмотрим, как вычислить Q и Ж, когда на балку действует
сплошная неравномерно распределённая нагрузка, интенсивность ко-
которой меняется по длине балки
в зависимости от х (фиг. 165).
Иначе говоря, q есть функция от
х или q = q (x). Поперечная сила
и изгибающий момент также будут
некоторыми функциями от х:
М = М(х) и Q = Q(x).
Фиг. 165.	Кривая adceb, показывающая за-
закон изменения q(x), называется
грузовой линией, а площадь, ограниченная этой кривой, — грузовой
площадью.
Вычислим Q и М в любом сечении балки, взятом на расстоя-
расстоянии хг от свободного конца. Рассматривая поперечную силу как
сумму элементарных сил q (дг) • dx, приложенных к левой отсечён-
отсечённой части балки, и заменяя суммирование интегрированием, найдём:
Xt	Xi
Q(Xl) = — \ q(x)dx = — \ du = —
о	о
A2.12)
Здесь через со (хг) обозначена часть грузовой площади, располо-
расположенная левее взятого сечения с—С. Следовательно, поперечная
сила Q(Jti), равная равнодействующей Rq сплошной нагрузки, лежа-
лежащей на участке ЛС = лг1, может быть вычислена как грузовая пло-
площадь (о (xi)f лежащая по одну сторону от сечения.
Изгибающий момент в том же сечении, равный сумме моментов
элементарных сил q (x) dx, действующих на отсечённую часть балки,
относительно точки С, может быть вычислен и как момент равно-
равнодействующей Rgi т. е.
= — Rq-xr = —
A2.13)
Иначе говоря, изгибающий момент от неравномерно распреде-
распределённой нагрузки равен произведению грузовой площади, лежащей

§ 73] ПОСТРОЕНИЕ ЭПЮР Q И М ДЛЯ БОЛЕЕ СЛОЖНЫХ СЛУЧАЕВ	241
по одну сторону от сечения, на расстояние от центра тяжести
этой площади до рассматриваемого сечения (плечо равнодействую-
равнодействующей).
Пример 48. Рассмотреть построение эпюр при действии сплош-
сплошной нагрузки, изменяющейся по длине балки по закону треуголь-
треугольника (фиг. 166).
Под такой нагрузкой работают балки, поддерживающие давле-
давление воды или земли, например, стойки плотин, стойки, подкрепляю-
подкрепляющие стенки резервуаров, предназна-
предназначенных для хранения жидкостей. По-
Подобным же образом нагружаются си-
силами инерции шатуны паровых машин
и двигателей внутреннего сгорания.
Величина этой нагрузки опреде-
определяется ординатой q0 — наибольшей ин-
интенсивностью нагрузки (в кг/м). Реак-
Реакция На = 0; определим реакции А и В.
Для нахождения А составим урав-
нение моментов относительно точки В.
Момент нагрузки равен моменту её
равнодействующей, т. е. площади всей
а I
^-
на
нагрузки ^-, умноженной
ние до её центра тяжести от конца В. -	i j-
Равнодействующая изображена на фиг.	^ У
166 пунктиром; этим подчёркивается,	фиг \§§
что сосредоточенная сила, равная
грузовой площади со = -~- qol, в действительности к балке
ложена и что мы ею пользуемся для вычисления суммы
всей нагрузки только при определении реакций.
Уравнения моментов будут иметь вид:
ПЕЙ
не при-
примоментов
Таким образом, на опору А передаётся две трети всей нагрузки
(о = Щ-, а на опору В — одна треть.
Для построения эпюр возьмём сечение на расстоянии х от пра-
правого конца балки. Ордината нагрузки в этом сечении q(x) опре-
определяется из подобия треугольников:

242	ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ	[ГЛ. XII
Для вычисления Q и М будем рассматривать правую часть
балки, так как на неё действуют сосредоточенная сила и треуголь-
треугольная нагрузка, в то время как на левую часть действуют сила и
трапецоидальная нагрузка, что даст более сложные вычисления.
Поперечная сила Q будет равна сумме проекций на верти-
вертикаль реакции В и заштрихованной нагрузки ш (х) = -у q {х)х =
В данном случае эпюра поперечных сил изображается кривой
второго порядка, причём
при х = 0 Q = — 7F =: — В\
Очертание эпюры Q дано на фиг. 166. Из этой фигуры видно,
что наибольшее значение (по абсолютной величине) поперечная сила
получает в сечении А (у опоры):
Vmax = ~Г А = -) g- •
Через нуль поперечная сила переходит при xQ, определяющемся
из уравнения
О	о	*Ы:(\ 	Зл:о\ . v 	 I 	о FV77/
Это значение лг0 будет использовано нами для определения макси-
максимума М. Наконец, аналитического минимума поперечная сила дости-
достигает в точке В, где интенсивность сплошной нагрузки равна нулю.
Как это следует из уравнения A2.3), касательная к эпюре попе-
поперечных сил в этом сечении параллельна оси абсцисс.
Перейдём к построению эпюры М, для чего опять рассмотрим
правую отсечённую часть балки. Момент относительно точки О
равнодействующей заштрихованной (фиг. 166) треугольной нагрузки
X
равен её грузовой площади, умноженной на плечо -~ :
(х)х q(x)x ^
Изгибающий момент в проведённом сечении равен:

§ 73] ПОСТРОЕНИЕ ЭПЮР Q И М ДЛЯ БОЛЕЕ СЛОЖНЫХ СЛУЧАЕВ	243
Это выражение для М пригодно на всём протяжении балки.
Эпюра М представляет кривую третьего порядка. Для построения
кубической параболы по точкам найдём несколько ординат:
при х = 0 М=0;
ЛГ=тг
48
16-
Наибольшее значение изгибающий момент получит в сечении,
где Q = 0, т. е. при хо = -^=; он равен
A2.14)
Эпюра показана на фиг. 166. Как видно из формулы A2.14),
наибольший изгибающий момент весьма мало отличается от момента
посредине пролёта, равного $?-. При практических подсчётах для
балки, загружённой треугольной на-
нагрузкой, всегда можно вместо Жтах
вводить в вычисления момент посре-
посредине пролёта ^~; ошибка не превы-
превышает 2,6%.
Пример 49. Рассмотреть построение
эпюр Q и М для шарнирно-опёртой балки
на двух опорах (фиг. 167), загружённой ^
сплошной нагрузкой, интенсивность кото- ^
рой изменяется по параболическому за- °~
кону, выражаемому уравнением:
,(*>=4* (?-?).	фиг-167-
Вследствие симметрии опорные реакции равны между собой:
Здесь со — грузовая площадь, определяемая из условия A2.12):
0
Следовательно, реакции опор равны
= 4-^[{ xdx--j-
A2.15)

244	ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ	[ГЛ. XII
Теперь перейдём к составлению выражений Q (х) и М (х) для сече-
сечения 1—7, взятого на расстоянии xi от левой опоры А. Обозначив грузовую
площадь, расположенную на длине х^ через <о (л:), получим:
а) Для поперечной силы Q (х) = А — <*> (х).
Грузовая площадь, лежащая слева от сечения, равна:
или
(О \Х) = — I -~	;
I | Z	<
Подставляя найденные значения Л и <о (л:) в уравнения для Q (х), найдём:
ц; ^лг^ = —тг	— (о/ — ?Xi).	(i z. I о)
м б) Для изгибающего момента, имея в виду, что элементарная сила q (x) dx
даёт относительно центра тяжести сечения 7—1 момент, равный:
dM = q (x) dx (xt — х),
найдем:
о
Первый интеграл равен
Второй интеграл даёт:
§q(x)dx- J ?(*)* dx].
о	о
После подстановки получим:
М (х) = & xt - [4 2?! C/ _ 2*0 - д-ф D/ - 3x0] =
= ^х1-[^- F/-4*!-
или после выполнения действий:
М (х) = ^Xi-g-^- B1 - Xi).	A2.17)
Из уравнений A2.16) и A2.17) видно, что поперечная сила изменяется
по закону кубической параболы, а изгибающий момент — по параболе четвер-
четвертой степени.

§ 73] ПОСТРОЕНИЕ ЭПЮР Q И М ДЛЯ БОЛЕЕ СЛОЖНЫХ СЛУЧАЕВ	245
Для построения этих кривых по точкам дадим переменной х значения:
* = -н-;
л: = /;
3 '
Соответствующие эпюры Q и М построены на фиг. 167. Наибольшие значе-
значения Q и М соответственно равны:
= ^- и
Пример 50. Рассмотреть построение эпюр Q и М для балки, нагру-
нагружённой сосредоточенной силой Р = 2 г, равномерно распределённой нагруз-
нагрузкой q = 2 т/м и парой сил с моментом Мо = 16 тм. Размеры показаны на
чертеже (фиг. 168).
11,3тм
8тм
Фиг. 168.
Для вычисления опорных реакций составим уравнения моментов относи-
относительно точек А и В:
|l+i + e] —Af,

246	ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ	[ГЛ. ХЛ
Отсюда
Аналогично
= 0; Л • /—^ • у
Для проверки правильности полученных результатов составим уравнение
проекций на ось у:
? Y = 0; А + 5 — 0 (Ь + с) — /> = 7,2 + 14,8 — 2 (8 + 2) — 2 = 0.
Реакции найдены верно. Теперь, когда все внешние силы известны, перейдём
к построению эпюр Q и М.
Нам придётся рассмотреть три участка между силами AD, DB, BE.
Расстояние до сечений 1—1 и 2—2 будем отсчитывать от левой опоры Л,
а для 3-го сечения от точки Е (фиг. 168). Рассматривая левую отсечённую
часть, получим выражение для поперечной силы в сечении /—/: Qi — A
(уравнение прямой, параллельной оси х). Это уравнение справедливо, пока
О ^ *i ^ а.
Для сечения 2—2, определяемого значениями а ^ х2 ^ /, получим:
Q2 = А — q (x2 — а).
Это — уравнение прямой, построение которой производим по двум точкам:
при х2 = л Q2 = Л = 7,2 г,
> л-2 = / ^2 = Л — ?(/ — а) = 7,2 — 2.A0 — 2) = — 8,8 г.
Наконец, для 3-го участка, рассматривая правую отсечённую часть,
получим:
0
Эпюра изобразится прямой, пригодной для 0 -^ х3
при х3 = 0 03 = Р = 2 г,
+ q	+ 2 = б г.
Полная эпюра поперечных сил, построенная по полученным трём урав-
уравнениям, изображена на фиг. 168. Из эпюры видно, что max Q = 8,8 т (по
абсолютной величине) в сечении у опоры В, слева.
Перейдём теперь к построению эпюры изгибающих моментов, для чего
воспользуемся теми же тремя сечениями. Момент сил, приложенных к левой
отсечённой части, относительно центра тяжести сечения 1—/:
Mi = Ахх (уравнение прямой).
Прил:1 = 0 Afi =0; прилг! = а Mt = Аа = 7,2 • 2 = 14,4 тм.
Для второго участка (а ^ х2 ^ /):
{aJ -MQ. A2.18)

§ 73] ПОСТРОЕНИЕ ЭПЮР Q И М ДЛЯ БОЛЕЕ СЛОЖНЫХ СЛУЧАЕВ	247
Зто уравнение параболы, для построения которой необходимо дать пере-
переменной лга не менее трёх значений:
при лг2 = а Ма = Аа — Мо = 7,2 - 2 — 16 = — 1,6 тм\
при лга = / Ма = Л/ —Мо — g(/~gJ=7,2 • 10 — 16 — 2 '(Ш2~~2)8 = — 8 тм.
Теперь вычислим М% для того значения лг2, при котором Л12 достигает
наибольшей величины, т. е. для точки, где эпюра Q переходит через нуль.
Исследуя уравнение моментов на максимум, найдём:
^==<?а = Л--?(л:о--я)==0, или д;0 = А + а = ^ + 2 = 5,6л*.
Подставляя это в уравнение для М2, получим:
max М% = Ах0 — Мо — q (*° ~ "^ = 7,2 • 5,6 — 16,0 — 2 ' ^ ~ 2)* =11,3 тм.
По полученным трём значениям момента строим параболическую кривую,
выражающую закон изменения моментов в пределах второго участка (для
большей точности построения можно найти и нулевые точки эпюры, поло-
положив М2 = 0).
Чтобы получить выражение изгибающего момента для третьего участка,
рассмотрим правую отсечённую часть балки. Момент правых сил относи-
относительно центра тяжести сечения 3—3 будет:
М3 = -Рх3--^.	A2.19)
Это уравнение (парабола) справедливо для значений 0
при хь = 0 Мг = 0;
с ..	Рс qc2	2 • 2 2 • 22
лг2	2 ¦ 22
> лг3 = с М,=— Рс — ^- = — 2-2 — =~y~ =—S тм.
Значение Mz для сечения над опорой В совпадает с ранее найденным зна-
значением М2 для того же сечения.
Эпюра изгибающих моментов построена на фиг. 168. Как это видно из
эпюры, max M = 14,4 г (больше, чем аналитический максимум, найденный
для Л12). Заметим, что, как и на фиг. 164, в сечении, где приложена пара
сия Мо, в эпюре М имеется скачок на величину Мо.
Пример 51. Рассмотреть построение эпюр М и Q для системы балок
(фиг. 169), состоящей из основной консольной балки ABC и подвесной
балки CD, соединённых шарниром С. Нагрузки и длины участков балки
показаны на чертеже.
Для построения эпюр найдём реакции балок. Как видно из фиг. 169,
система балок может иметь четыре опорные реакции Л, НД1 В и D. Уравне-
Уравнений же равновесия для всей балки AD мы можем написать только три. Чет-
Четвёртое уравнение определяется условием, что шарнир С (по свойству кон-
конструкции) не может передать момента, так как позволяет взаимно повора-
поворачиваться одной части балки (АС) относительно другой (CD).
Последнее условие требует, чтобы сумма моментов относительно точки С
сил, приложенных слева или справа от этого шарнира, равнялась нулю.

248
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
[ГЛ. XII
Другими словами, для соблюдения равновесия балки изгибающий момент
в шарнире должен равняться нулю. Это добавочное требование делает
балку AD статически опре-
определимой.
Определение реакций на-
начинаем с вычисления И
о
А,
Приравнивая нулю сумму
проекций всех сил на ось бал-
балки, убеждаемся, что НА = 0.
Далее мы могли бы на-
написать три уравнения мо-
моментов, а именно:
1)	приравнять нулю сум-
му моментов всех сил отно-
относительно точки Л;
2)	приравнять нулю сум-
му моментов всех сил стно-
сительно точки В или D\
3)	приравнять нулю мо-
момент относительно точки С
сил, расположенных слева
или справа от этого шар-
шарнира.
Решая систему этих трёх
уравнений, можно получить
все три неизвестные реакции: Л, В и D. Однако проще определить эти
реакции путём разложения балки AD на простейшие. Подвесная балка CD
опирается в точке С шарнирно на конец консоли ВС> а в точке D—на
шарнирную подвижную опору. Поэтому всю балку AD мы можем рас-
рассматривать (фиг. 170) как
Р	В комбинацию из двух ба-
лок. Подвесная балка
воспринимает в шарни-
шарнире С реакцию С от кон-
конца консоли и в свою
очередь давит на этот
конец с такой же си-
силой С.
Рассматривая сна-
сначала равновесие под-
подвесной балки, находим
силу С к концу кон-
конФиг. 169.
3*6м—-J
Фиг.
её реакции D и С, а прикладывая уже известную
соли, находим реакции А и В. В нашем примере:
После определения реакций изображаем вновь балку как одно целое
со всеми силами и реакциями и определяем моменты и поперечные силы,
как для обычного случая. Проверкой будет служить равенство нулю момента
в шарнире С. Следует обратить внимание на то, что шарнир С не является
точкой раздела участков, если в нём не приложена внешняя сила. Эпюры
элементов и поперечных сил показаны на фиг. 169.

§ 73] ПОСТРОЕНИЕ ЭПЮР Q И М ДЛЯ БОЛЕЕ СЛОЖНЫХ СЛУЧАЕВ	249
Болеее удобно после определения опорных реакций строить эпюры Q
и М отдельно для каждой подвесной и основной балки, откладывая значе-
значения полученных величин Q и М от общей оси х.
Пример 52. Построить эпюры Q и М для балки с ломаной осью,
обычно называемой рамой (фиг. 171).
Горизонтальный стержень ВС называют ригелем, а вертикальный — стой-
стойкой рамы. Ригель и стойка соединены жёстким узлом С, образуя сплошную
систему. Рамы с жёсткими узлами имеют
широкое распространение в инженерном
деле.
Порядок построения эпюр Q и М
для таких систем остаётся прежним.
Для определения опорных реакций со-
составим уравнения равновесия:
или
д=2тш
НА = qh = 2 • 4 = 8 г,
или
"- 2/ -Т2=О '•
Для ригеля, 0 ^ х ^ /, поперечная сила Q (х)
щий момент М (х) = Вх = %- - х.
^Tf7f)}/fjf
Фиг. 172.
Для стойки — поперечная сила Q (y) = q * у; изгибающий момент М {у) -
Значения ординат эпюр Q и М приведены в таблице 19.
Соответствующие эпюры Q и М построены на фиг. 172.

250
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
Таблица 19. Данные к фиг. 172.
r/i к и
Л' В М
—
у в м
Q в г
Q (х) = — 5 = — 8
<? (л;) = — 5 = — 8
М в глс
М(л-) = О
§ 74. Контроль правильности построения эпюр Q и М.
Дифференциальные зависимости между изгибающим моментом,
поперечной силой и интенсивностью сплошной нагрузки определяют
связь между эпюрами М и Q,
построенными при любой на-
нагрузке. Эта взаимная связь
имеет важное практическое
значение для контроля пра-
правильности выполненного по-
построения. Приведём некоторые
заключительные замечания, мо-
могущие быть полезными и при
построении эпюр Q и М.
1. Уже было указано (§71),
что каждая ордината эпюры
~ dM
поперечных сил Q = -,— гео-
геометрически представляет со-
Фиг. 173.	бой тангенс образуемого с
осью х угла наклона касатель-
касательной к эпюре М в соответствующей точке (фиг. 173). Подобные же
геометрические соотношения имеются и между эпюрами q и Q
(фиг. 173).
2.	Если на некотором участке:
а)	Q^>0, т. е. tga^>0, то момент возрастает;
б)	Q<^0, т. е. tga<^0, то момент убывает;
в)	Q переходит через нуль, меняя знак с -f- на —, то М =
= Мтах; при изменении знака с — на -\-М = Мт'т\
г)	Q = 0, т. е. tga = O, to Л1 = const.
3.	Если # = 0, т. е. -~=0, то Q = const. Следовательно, на
участках, свободных от сплошной нагрузки, эпюра Q ограничена
прямыми, параллельными оси х\ эпюра же моментов изобразится

§ 741
КОНТРОЛЬ ПРАВИЛЬНОСТИ ПОСТРОЕНИЯ ЭПЮР Q И М
251
наклонными прямыми, если только Q -ф О (см. п. 2, г). Если
т. е. tg3<^0, то поперечная сила убывает.
4.	На участках балки, загруженных сплошной равномерно рас-
распределённой нагрузкой, эпюра М ограничена параболической кривой,
а эпюра Q — наклонной прямой. При неравномерно распределённой
нагрузке обе эпюры Q и М будут ограничены кривыми, характер
которых зависит от типа нагрузки.
5.	В сечениях под сосредоточенными силами в эпюре Q имеется
скачок (на величину силы), а в эпюре М резкое изменение угла
наклона (излом) смежных участков эпюры (см., например, сечение В
на фиг. 168).
Вёерх
6.	Если сплошная нагрузка направлена вниз, т. е. -~г-$ =
иначе, если вторая производная, характеризующая кривизну линии М,
отрицательна, то эпюра
М очерчена кривой,
имеющей выпуклость
кверху. Наоборот, если
д^>0 (нагрузка на-
направлена вверх), то
эпюра М на соот-
соответствующем участке
имеет выпуклость кни-
книзу (фиг. 174).
7.	На концевой шар-	Фиг. 174.
нирной опоре попе-
поперечная сила равна реакции этой опоры, а изгибающий момент равен
нулю, если в опорном сечении не приложена пара сил.
8.	На свободном конце балки (консоль) изгибающий момент ра-
равен нулю, если там нет сосредоточенной пары сил. При отсутствии
в концевом сечении консоли сосредоточенной силы поперечная
сила Q также равна нулю.
9.	В защемлённом конце (заделка) Q и М соответственно равны
опорной реакции и опорному моменту.
10.	В сечениях, где приложена пара сил, эпюра М имеет ска-
скачок на величину момента этой пары. На эпюре Q это не отра-
отражается.
Указанные в § 71 дифференциальные зависимости и приведённые
здесь замечания служат не только для проверки правильности эпюр,
но будут использованы нами в дальнейшем (§§ 116, 117 и др.).
Пример 53. Фигура 175, а представляет собой эпюру поперечных сил
для балки AFy шарнирно опёртой в сечениях В и Е. Определить нагрузку,
лежащую на балке, и построить эпюру моментов.
Вид эпюры показывает, что в точках А, С и D приложены сосредото-
сосредоточенные силы, в точках В и Е—реакции, а на участке EF — равномерно
распределённая нагрузка.

252
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
[ГЛ. XII
Prim
Разность алгебраических величин ординат эпюры поперечных сил в сече-
сечении с сосредоточенной силой равна величине этой силы. В точке А прило-
приложена сосредоточенная си-
сила 2 г, направленная, как
показывает знак попереч-
поперечной силы, вниз; в точке В
приложена реакция б1/» г,
направленная вверх; в
точках С и D приложены
направленные вниз со-
сосредоточенные силы 5 Т
и 4 г; в точке Е на-
направлена вверх реакция
102/з г, наконец, равно-
равномерно распределённая на
участке EF нагрузка q
равна ^д = 6,67 т/м.
Построение эпюры
изгибающих моментов за-
затруднений не встречает.
На протяжении АЕ она
будет изображаться мно-
многоугольником со следую-
следующими ординатами:
1
9П
/И
Фиг. 175.
Сечения по длине балки
Ординаты эпюры М
А
0,0
В
-1,2
С
5,3
D
4,3
Е
-2,7
На участке EF эпюра М должна изобразиться параболической кривой
с аналитическим максимумом в точке F, где Q = 0> при абсолютном значе-
значении момента в этой точке Mf = 0 (свободный конец балки).
Соответствующая эпюра изгибающих моментов приведена на фиг. 175, б,
§ 75. Способ сложения действия сил при построении эпюр.
Рассматривая выражения для М и Q, полученные нами в послед-
последних задачах, мы видим, что внешние нагрузки входят в эти выра-
выражения в первой степени; М и Q линейно зависят от нагрузок.
Рассматривая, например, уравнение A2.19) (стр. 247) для М6:
мы видим, что ординаты изгибающего момента в сечениях этого
участка складываются из двух: — Рх и — q у; первая из них пред-
представляет собой изгибающий момент, вызванный в выбранном сече-
сечении силой Р, а вторая — нагрузкой q.

§ 75]
СПОСОБ СЛОЖЕНИЯ ДЕЙСТВИЯ СИЛ
253
Мы могли бы построить отдельно эпюры моментов от силы Р
и от нагрузки q, а потом ординаты этих эпюр алгебраически сло-
сложить. Это было бы применением так называемого способа сложе-
сложения действия сил.
Пример 54. Эпюра Mq для консоли от распределённой нагрузки имеет
вид параболы с наибольшим (по абсолютной величине) значением момента
в защемлении min Mq = — ^г- (см. § 72).
От сосредоточенной силы, приложенной на свободном конце балки,
изгибающий момент Мр — — Рх изменяется по закону прямой:
при х = О Мр = О,
Чтобы сложить ординаты двух графиков одинакового знака, следует
приложить их один к другому, как это показано на фиг 176а, для чего
у	один из графиков (М) отложен вверх.
1
1
m
г
if
n
It
/
HI
'ТТТТъч.
Ш
Щ
(Mq) i
III ||||||jj]]Jil^W*'
PPJ^ j
IIIIIIIIIITnTh>wj
один из графиков (М^) отложен вверх.
Изгибающий момент в любом сечении
складывается из моментов
qx*
Если сила Р направлена вверх, то
изменяется знак Мр. Для сложения двух
Фиг. 176а.
Фиг. 1766.
графиков, имеющих разные знаки, достаточно наложить один график на
другой (фиг. 1766).
Пусть по абсолютному значению mm Mq > max тр, т. е.

254
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
[гл. хн
При наложении графиков ординаты автоматически вычтутся, и в данном
случае мы получим в защемлении отрицательную ординату, в пролёте же на
некотором протяжении ординаты будут положительными.
Разумеется, для графического суммирования необходимо оба графика
строить в одном и том же масштабе. Аналогично можно построить эпюру Q.
Этот приём сложения эпюр удобен при расчёте статически неопределимых
неразрезных балок.
Для приведения эпюры к обычному виду можно полученные суммарные
ординаты отложить от горизонтальной оси х (фиг. 1766).
§ 76. Графический метод построения эпюр изгибающих
моментов и поперечных сил.
Если на балку действует много нагрузок, как сосредоточенных,
так и распределённых, то часто с успехом можно применить гра-
графический способ построения эпюр. При известной аккуратности
в построении чертежа
решение оказывается
достаточно точным для
целей практики.
Рассмотрим балку
АВУ нагружённую вер-
вертикальными силами Рь
Ръ Ръ (фиг. 177). Ана-
Аналитические выраже-
выражения для изгибающего
момента и поперечной
силы будут для сече-
сечения / — 1 такими:
Q = A, Mt = ЛлГ|.
Для сечения 2 — 2 по-
получаем:
М%=Ах% —Рх (х2—а).
Для графического
определения М и Q в
Фиг. 177.	этих же сечениях по-
построим силовой и ве-
верёвочный многоугольники при произвольно выбранном полюсном
расстоянии Н. Полюсное расстояние в плане сил откладывается
в том же масштабе, что и силы Ри Р2, Р3 (например, в 1 см f кг).
Верёвочный же многоугольник, непосредственно связанный с черте-
чертежом балки, имеет тот же масштаб ординат, в каком изображена
балка (например, в 1 см п пог. м).
Так как силы, действующие на балку (включая и реакции), на-
находятся в равновесии, то оба многоугольника (силовой и верёвоч-

§ 76] ГРАФИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ ЭПЮР М И Q 255
ный) должны быть замкнуты. Поэтому, вычертив в поле сил ли-
линии, параллельные лучам силового многоугольника, проводим, как
этого требуют известные правила механики, между крайними ли-
линиями а — 1 и 3 — р замыкающую верёвочного многоугольника
А —В.
Проводя затем в многоугольнике сил луч АВУ параллельный за-
замыкающей, получим отрезки ab и be, представляющие в масштабе
сил опорные реакции А и В.
Если провести вертикаль через сечение балки /—/ до пересечения
со сторонами верёвочного многоугольника, то получим ординату т]ь
образующую со сторонами а — 1 и АВ треугольник, подобный тре-
треугольнику ОаЬ в силовом многоугольнике. Из подобия треугольни-
треугольников можно написать:
Ц. = ^1 или Ахх = И • v,
но произведение Axt = M\. Следовательно,
Нетрудно также доказать (из рассмотрения треугольников, обра-
образуемых продолжением вертикали 2—2 со сторонами верёвочного
многоугольника и подобных им в многоугольнике сил), что
Ах% — Pi (лг2 — ах) = Н • т]2 или М2 = Н • т]2
и вообще
Н-т\.	A2.20)
Иначе говоря, изгибающий момент в любом сечении балки равен
произведению полюсного расстояния Н, взятого в масштабе сил,
на ординату i\ верёвочного многоугольника в том же сечении,
измеренную в масштабе длин. Значит, верёвочный многоугольник
представляет собой эпюру Ж, ординаты которой у\ отсчитываются
М
по вертикали от наклонной замыкающей и равны -ц = —-%
Чтобы придать эпюре М обычный вид, можно её перестроить,
откладывая те же ординаты t\ от горизонтальной нулевой оси. Если
опорные реакции А и В подсчитаны аналитически, то, поместив
полное на горизонтали, отделяющей А от В в многоугольнике сил,
сразу получим замыкающую горизонтальной (параллельной горизон-
горизонтальному лучу Л — В).
Построение эпюры Q ясно из чертежа. Проведя прямую, парал-
параллельную нулевой оси, на расстоянии (в масштабе, сил), равном край-
крайней левой силе (реакции Л), сносим затем (сохраняя масштаб) все
остальные силы по линии и по направлению их действия, как это
показано на фиг. 177. Получим ступенчатую эпюру поперечных сил,

256
ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ
[гл хи
каждая ордината которой t]q==Q(x) имеет тот же масштаб, что и
многоугольник сил.
В случае, если балка загружена сплошной нагрузкой (фиг. 178),
графическое построение эпюр М и Q может быть выполнено лишь
приближённо. Разделяя сплошную нагрузку вертикалями на несколько
частей и заменяя каждую часть равнодействующей (равной соответ-
соответствующей грузовой
площади (о), строим
эпюры М и Q с по-
помощью силового и ве-
верёвочного многоуголь-
многоугольников для системы со-
сосредоточенных СИЛ (Oj,
оо.2, оK и т. д., как это
было сделано выше.
Эпюра Q получится
ступенчатой, а эпюра
М — в виде ломаного
многоугольника.
Чтобы привести по-
полученные графики к
виду, отвечающему
истинному очертанию
эпюр М и Q, следует:
а) для эпюры М
вписать в верёвочный
многоугольник кри-
кривую, так как в пре-
пределе, при бесконеч-
бесконечном увеличении числа
равнодействующих сил
(о, верёвочный многоугольник обращается в верёвочную кривую
и касается многоугольных участков в точках деления;
б) для эпюры Q заменить ступенчатую эпюру одной линией,
проходящей через точки, в которых горизонтальные участки
эпюры Q пересекаются с вертикалями, разбивающими нагрузку на
части.
Особенностью графического построения эпюры изгибающего мо-
момента для консоли является то, что замыкающая АВ заменяется
продолжением первого луча а—1, от которого и ведутся отсчёты
ординат т] (фиг, 178). Выбрав в этом случае положение полюса О
так, чтобы первый луч был горизонтален, сразу получаем эпюру М,
приведённую к горизонтальной оси.
Пример 55. Построить графическим способом эпюры М и Q для
балки, изображённой на фиг. 179. Найденные графическим путём значении
max M и max Q проверить аналитическим подсчётом.
Фиг. 178.

§ 76]
ГРАФИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ ЭПЮР М И (J
257
Для графического построения эпюр М и Q вычертим балку в масштабе.
По удобству размещения чертежа примем масштабы:
длин — в 1 см-
сил — в 1 см-
> 1 м;
>2 т.
Полюсное расстояние принято равным 3 см. Следовательно, в масштабе
сил Н = 6 т. В принятых масштабах вычерчена балка, силовой и верёвоч-
верёвочный многоугольники и
эпюра поперечных сил
(фиг. 179).
Наибольшая ордина-
ордината верёвочного много-
многоугольника ifjmax располо-
расположена в сечении под си-
силой Р2. Измерив её в
масштабе длин, находим:
*lmax= 1,75 ж. Отсюда
наибольший изгибающий
момент:
max М = Н • Y]max =
= 6 • 1,75=10,5 тм.
Наибольшая попереч-
поперечная сила равна реакции
левой опоры А, которая,
будучи измерена в мас-
масштабе сил, оказалась рав-
равной А = 5,3 г.
Чтобы оценить точ-
точность графического по-
построения эпюр М и (J,
проверим аналитически
величины тахМ и maxQ.
Составив уравнение мо-
моментов относительно точ-
точки В, найдём:	Фиг. 179.
v мв = 0; Al—Piil — а,) — Р2 (/ — а%) — Р8 (/ — аг) = 0.
Отсюда:
= ~[2 • 5 + 5 • 3,5+3 • 1,5] =5,34 г.
Расхождение с графическим решением составляет Л '- 100 = 0,80/*
Изгибающий момент в сечении под силой Ра равен:
max М = А . а% — Р1 (а2 — ах) = 5,34 -2,5 — 2 B,5 — 1,0) = 10,75 тм.
Расхождение против графического решения 2,3%. Такая точность для прак-
практических целей достаточна.
9 Н. М. Беляев

Фиг. 180.
258	ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ	[ГЛ. XIII
ГЛАВА XIII.
ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ
И ПРОВЕРКА ПРОЧНОСТИ БАЛОК.
§ 77. Экспериментальное изучение работы материала
при чистом изгибе.
После изучения эпюр изгибающих моментов и поперечных сил
можно вернуться к вопросу о вычислении нормальных и касатель-
касательных напряжений по выбран-
выбранному сечению. Выше мы выяс-
выяснили, что нормальные напря-
напряжения зависят лишь от изги-
изгибающего момента, касатель-
касательные — лишь от поперечной
силы:
o=/,(M), A2.1)
*=/«(<?)• A2.2)
Это позволяет нам упро-
упростить вычисление а, а именно,
провести его для частного случая изгиба балки, когда Q = Q.
Полученная формула будет справедлива и в остальных случаях.
Изгиб балки, при котором поперечная сила равна нулю, вполне
возможен, если пренебречь собственным весом балки. Для этого
необходимо, чтобы система внешних сил, приложенных к отсечённой
части балки, приводилась к одной лишь паре сил.
Как пример можно привести изгиб оси железнодорожного вагона
(см. § 69). Схема действия сил дана на фиг. 180. Если мы будем
брать сечения между точками С и D, то для любого из этих сечений
изгибающий момент и поперечная сила соответственно равны
М (х) = Рх — Р (х — а) = Ра = const., Q (х) = Р — Р = 0.
Таким образом, во всех сечениях средней части оси CD изги-
изгибающий момент постоянен, а поперечная сила равна нулю (вспомним,
что Q=j-\. Такой случай изгиба называется чистым изгибом.
Разрежем эту балку (фиг. 180, а) сечением на расстоянии х от
левого конца. На отсечённую часть (фиг. 180, б) будут действовать
изгибающий момент М = Ра и одни только нормальные напряже-
напряжения о. Условие равновесия отсечённой части требует, чтобы эти
напряжения а приводились к паре, лежащей в плоскости действия
внешних сил — плоскости симметрии балки. Но чтобы найти наибо-
наиболее напряжённую часть материала, необходимо уметь вычислять
напряжения в каждой точке сечения, знать распределение напря-
напряжений по сечению.

§ 77]
ИЗУЧЕНИЕ РАБОТЫ МАТЕРИАЛА ПРИ ИЗГИБЕ
259
Фиг. 181.
Условия равновесия нам этого не дают, задача оказывается ста-
тячески неопределимой, и мы вынуждены обратиться к эксперимен-
экспериментальному исследованию деформации балки.
Рассмотрим результаты опыта с чистым изгибом балки парами
сил, лежащими в плоскости симметрии балки (фиг. 181).
Проведём до деформации балки на её боковой поверхности
близко друг к другу две линии /—/ и 2—2, перпендикулярно
к оси балки. Это будут следы
двух смежных поперечных сече-
сечений, отстоящих друг от друга
на Ах. Проведём между этими
сечениями линии ab и cd, парал-
параллельные оси балки: одну — близко
к верхнему, другую—к нижнему
краю балки. До деформации
ab = cd = Ax.
Опыт показывает, что после
деформации (фиг. 181, б):
1)	линии /—/ и 2—2 остались прямыми, но наклонились друг
к другу и образуют угол Да;
2)	отрезок ab укоротился, а отрезок cd удлинился;
3)	ширина балки в сжатой зоне увеличилась, а в растянутой —
уменьшилась (фиг. 181, в).
Эти экспериментальные результаты позволяют сделать следующие
«выводы о характере деформаций балки при чистом изгибе. Так как
линии /—/ и 2—2 после деформации остались прямыми, то можно
думать, что соответствующие поперечные сечения балки остались
плоскими и лишь повернулись одно относительно другого на
угол Да.
Судя по изменению длин отрезков ab и cd, можно заключить,
что (при М положительном) верхние волокна сжаты, а нижние
растянуты. Так как деформация волокон меняется непрерывно, то
на каком-то уровне по высоте балки мы встретим слой волокон,
не изменивших своей длины, так называемый нейтральный слой,
т. е. поверхность, разделяющую сжатую зону от растянутой.
На фиг. 181, б нейтральный слой изображён пунктиром; отрезок
О{О,г сохранил прежнюю длину Ах.
Наша балка симметрична относительно плоскости внешних сил.
Поэтому обе её половины деформируются симметрично относительно
^Д"Ой плоскости. Это позволяет сделать предположение, что дефор-
деформация волокон любого слоя, параллельного нейтральному, не зави-
зависит от их положения по ширине балки.
Нейтральный слой перпендикулярен к плоскости симметрии
балки и пересекает плоскость каждого поперечного сечения балки
по прямой, называемой нейтральной осью сечения. Эта ось также
перпендикулярна к плоскости симметрии балки.
9*

260	ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ [ГЛ. XIII
Повороты сечений происходят вокруг их нейтральных осей,
изображённых на фиг. 181 точками Oj и О2. Если бы поворот
сечений происходил не около осей, лежащих в нейтральном
слое, то отрезок ОгО.2 не мог бы сохранить своей первоначальной
длины.
Так как сечения поворачиваются вокруг нейтральных осей, пер-
перпендикулярных к плоскости действия сил, точки этой плоскости
останутся в ней и после деформации; следовательно, ось балки оста-
останется в плоскости действия сил, обратившись в плоскую кривую.
Изгиб, при котором ось балки после деформации остаётся в пло-
плоскости действия внешних сил, называется плоским изгибом.
Наконец, деформации материала балки в направлении её ширины
показывают, что волокна её испытывают обычное растяжение или
сжатие, при котором имеет место явление, учитываемое коэффици-
коэффициентом Пуассона: в сжатой зоне ширина сечения балки увеличивается,
в растянутой — уменьшается (фиг. 181, в).
Экспериментальные исследования изгиба балок дают основание
для ряда допущений, положенных в основу дальнейших выво-
выводов:
1.	При чистом изгибе поперечные сечения, бывшие плоскими до
деформации, остаются плоскими и во время деформации (так назы-
называемая гипотеза плоских сечений).
2.	Продольные волокна друг на друга не давят и, следовательно,
под действием нормальных напряжений испытывают простое линей-
линейное растяжение или сжатие.
3.	Деформации волокон не зависят от их положения по ширине
сечения. Следовательно, и нормальные напряжения, изменяясь по
высоте сечения, остаются по ширине одинаковыми.
Помимо этих допущений, введём ещё три ограничения:
1.	Балка имеет хотя бы одну плоскость симметрии, и все внеш-
внешние силы лежат в этой плоскости.
2.	Материал балки подчиняется закону Гука, причём модуль
упругости при растяжении и сжатии одинаков.
3.	Соотношения между размерами балки таковы, что она рабо-
работает в условиях плоского изгиба без коробления или скручи-
скручивания.
Из опыта известно, что балки с малой шириной сечения легко
теряют устойчивость плоской формы при изгибе (скручиваются).
При отношении высоты прямоугольного сечения балки к её про-
пролёту y^>-g- она работает не как балка, а как пластинка, и усло-
условия её расчёта изменяются.
Сделанные выше предположения в обычных случаях изгиба верны
только приблизительно. Однако вытекающие из них погрешности
теории так невелики (за исключением особых случаев), что ими
можно пренебречь.

м
^	 	^
2
2
§ 78]	ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ	261
§ 78. Вычисление нормальных напряжений при изгибе.
Закон Гука и потенциальная энергия при изгибе.
А. Возьмём балку, подвергающуюся чистому изгибу парами М
(фиг. 182). Пользуясь методом сечения, разрежем балку сечением 1—1
на 2 части и рассмотрим условия равновесия одной из отсечённых
частей, например левой,
показанной на фиг. 182
внизу. Для простоты чер-
чертежа балка взята прямо-
прямоугольного сечения. Так как
практически искривления
балки ничтожны по сравне-
сравнению с её размерами, то от-
отсечённая часть изображена
недеформированной.
Линия пересечения пло-
плоскости симметрии балки с
плоскостью сечения при-
принята за ось z (положитель-
(положительное направление взято вниз); нейтральная ось сечения принята за
ось у, причём положение её по высоте балки пока неизвестно.
Ось х взята вдоль нейтрального слоя перпендикулярно к осям
у и z.
В каждой точке поперечного сечения действуют нормальные на-
напряжения с. Выделив вокруг любой точки с координатами у и z
элементарную площадку dF, обозначим действующую на неё силу
dN=a dF.
Отсечённая часть балки находится в равновесии под действием
внешних сил, образующих пару Му и нормальных усилий dN, заме-
заменяющих отброшенную часть балки. Для равновесия эта система сил
должна удовлетворять шести уравнениям статики. Напишем сначала
уравнения проекций на 3 координатные оси х, у, z.
Так как проекция пары М на любую ось равна нулю, то эти
уравнения дадут равенство нулю суммы проекций нормальных уси-
усилий dAr на оси. Заменяя суммирование этих усилий по всей площади
сечения интегрированием, получим:
?Х = 0; i\adF=0.
A3.1)
=0 и ?Z = 0 обращаются в тождества вида 0 = 0, так как
усилия dN=adF проектируются на эти оси в точку.
Составим теперь уравнения моментов относительно осей х, у и z.
Заметим при этом, что пара М лежит в плоскости xOz и потому
моментов относительно осей Ох и Oz не даёт.

262
ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ [ГЛ. ХТП
= 0 обращается в тождество, так как усилия dN =
параллельны оси х:
= 0 или M—
откуда
\
= 0 или
$
A3.2)
A3.3)
Таким образом, из шести уравнений равновесия можно исполь-
эовать только три:
A3.П
A3.20
A3.3')
%Х = 0 или С adF=0,
= 0 или I о zdF= M,
aydF = 0.
= 0 или
Однако полученных трёх уравнений статики недостаточно для опре-
определения величины нормальных напряжений, так как с изменяется
в зависимости от расстояния z площадки
dF до нейтральной оси по неизвестному
пока закону. Это расстояние B) тоже не-
неизвестно, так как неизвестно положение
нейтральной оси у.
Б. Обратимся к рассмотрению дефор-
деформаций балки, для чего двумя бесконечно
близкими сечениями /—/ и 2—2 выде-
выделим из неё элемент длиной dx. Вид этого
элемента до и после деформации показан
на фиг. 183.
Для ясности чертежа деформация эле-
элемента показана с сильным преувеличением.
Оба поперечных сечения, оставаясь плос-
м кими, повернутся вокруг нейтральных осей
(на фасаде точки Ох и О3) и образуют угол
da. Нейтральный слой показан пунктиром.
Линия OxOiy принадлежащая нейтральному
слою, после деформации сохранит свою
первоначальную длину dx. Все волокна, лежащие выше нейтраль-
нейтрального слоя, укорачиваются, а ниже — удлиняются.
Фиг. 183.

§78]
ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ
263
Найдём удлинение какого-либо волокна АВ, расположенного
в расстоянии z от нейтрального слоя и растянутого напряжениями а.
Первоначальная длина этого волокна равна dx = ^ O1O% = pda.
После деформации его длина по дуге АВ стала ^AB = (p-\-z)d<x.
Абсолютное удлинение рассматриваемого волокна А/ = (р -j- z) do.—
— pd7. = zdz. Относительное удлинение равно
"р doi
т. е. удлинения волокон пропорциональны их расстояниям до ней-
нейтрального слоя.
Здесь р — радиус кривизны нейтрального слоя, величину кото-
которого для выделенного (бесконечно малого по длине) элемента можно
считать постоянной. Допустив, что при изгибе волокна друг на друга
не давят и что каждое волокно испытывает простое (линейное)
растяжение или сжатие, — для вычисления напряжений можем вос-
воспользоваться законом Гука при растяжении:
или
E-Z
Р
A3.4)
Уравнение A3.4) показывает, что величина нормальных напря-
напряжений при изгибе меняется прямо пропорционально расстоянию z
рассматриваемой точки сечения от нейтрального слоя. Значит, напря-
напряжения распределены по вы-
высоте сечения по линейному
закону.
На нейтральной оси при
z = 0 и а = 0; при пере-
переходе в сжатую зону (выше
нейтральной оси) а вместе
с z меняет знак на минус
(сжатие) и вновь растёт по	Фиг. 184.
абсолютному значению по
мере удаления от нейтральной оси. Следовательно, наибольшего
значения напряжения достигнут у верхнего и нижнего краев сече-
сечения при z = zmax. Характер распределения напряжений показан на
фиг. 184.
Уравнение A3.4) даёт только характер распределения нормаль-
нормальных напряжений по сечению, но им нельзя воспользоваться для
вычисления величины их, так как ни р, ни z неизвестны, поскольку
неизвестно расположение нейтрального слоя по высоте сечения.
В. Для определения а в зависимости от изгибающего момента
обратимся к совместному решению полученного из рассмотрения
деформаций уравнения A3.4) и уравнений статики A3.1), A3.2)
и A3.3).

264	ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ [гл. XIII
Подставляя значение о из выражения A3.4) в уравнение A3.1),
получим:
VA' = 0 или $-
$--zdF=
Так как — = const. 7^0, то
A3.5)
Этот интеграл представляет собой статический момент площади
сечения относительно нейтральной оси. Так как он равен нулю, то,
следовательно, нейтральная ось проходит через центр тяжести
сечения. Так как центр тяжести лежит и на оси симметрии Oz, то
точка пересечения этих двух осей О является центром тяжести
сечения, а ось Ох— осью стержня.
Таким образом, положения нейтральной оси и нейтрального слоя
вполне определены. Нейтральный слой заключает в себе центры
тяжести всех сечений стержня.
Теперь подставим то же выражение A3.4) в уравнение A3.3):
У\М2 = 0, [~zydF=0 или
Р Р
Отсюда следует, что
$zydF=0.	A3.6)
Полученный интеграл — сумма произведений из элементарных пло-
площадок на расстояния их до координатных осей — называется цен-
центробежным моментом инерции относительно осей у и z. Центробеж-
Центробежный момент инерции может быть положителен, может быть и величиной
отрицательной, а следовательно, может и обратиться в нуль, так
как координаты элементарных площадок могут иметь разные знаки.
По условию A3.6), в нашем случае центробежный момент инер-
инерции, который обычно обозначается символом
Jzy=\zydF>
Р
должен обратиться в нуль.
Так как сечение симметрично относительно оси Oz, то для
каждой площадки dF с координатами г, у слева от оси z мы мо-
можем подыскать такую же, симметрично расположенную, площадку
справа от оси z. Координаты z для этих площадок будут одинако-
одинаковыми и по величине и по знаку, координаты же у окажутся одина-

§ 78]	ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ	265
новыми по абсолютной величине, но обратными по знаку. Поэтому
сумма
\zydF
F
разобьётся на две суммы, равные по величине и противополож-
противоположные по знаку. Таким образом, этот интеграл для симметричных
сечений всегда равен нулю, и уравнение A3.6) обращается в то-
тождество.
Наконец, используем последнее уравнение A3.2); подставив
в него выражение A3.4), получим:
= M или — \
Обозначим
J=[z*dF.	A3.7)
Этот интеграл, т. е. сумма произведений из элементарных пло»
щадок на квадраты расстояний их до оси, называется осевым или
экваториальным моментом инерции площади относительно оси у
и обозначается символом Jy. Так как ось у — нейтральная ось, то Уу
есть момент инерции площади сечения балки относительно нейтраль-
нейтральной оси1). Тогда из преобразованного только что уравнения A3.2)
получаем:
f = M или | = у-.	A3.8)
Подставляя найденное значение — в уравнение A3.4), находим:
а = ^.	A3.9)
Таким образом, нормальные напряжения в любой точке сече-
сечения прямо пропорциональны величине изгибающего момента и
расстоянию точки от нейтральной оси и обратно пропорцио-
пропорциональны моменту инерции сечения относительно нейтральной оси.
Нейтральная ось проходит через центр тяжести сечения и перпен-
перпендикулярна к плоскости действия сил.
Момент инерции сечения, как видно из формулы A3.7), изме-
измеряется в единицах длины в четвёртой степени и зависит от формы
1) В дальнейшем, при обозначении момента инерции относительно ней-
нейтральной оси у, мы часто будем опускать индекс уу обозначая его для крат-
краткости просто У, вместо Jy.

266	ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ [ГЛ. XIII
и размеров сечения. Практические приёмы его вычисления для раз-
различных сечений будут показаны далее.
Для установления физического смысла этой величины видоизме-
видоизменим формулу A3.8):
Отсюда видно, что чем больше при данном изгибающем моменте
момент инерции сечения J, тем большим окажется радиус кривизны
нейтрального слоя, а стало быть, и оси балки, т. е. тем меньше
балка искривится.
Величина момента инерции характеризует способность бал-
балки сопротивляться искривлению в зависимости от размеров и
формы поперечного сечения балки. Модуль упругости Е харак-
характеризует ту же способность балки сопротивляться искривлению,
но уже в зависимости от материала балки. Произведение EJ на-
называется жёсткостью балки при изгибе, и чем оно больше, тем
меньше искривится балка при действии данного изгибающего мо-
момента.
Г. С искривлением оси балки связан взаимный поворот сечений;
длина отрезка O(J = dx, как это видно из чертежа (фиг. 183),
равна р dz. Отсюда угол поворота двух смежных сечений
. dx
doL = —.
Р
1	М
Подставляя вместо — его значение -р-т, получим:
л М dx	, А о Л Л ч
d* = —gj-,	A3.11)
т. е. деформации при изгибе — поворот сечений den, как и кривизна
оси балки —, прямо пропорциональны величине изгибающего момента
и обратно пропорциональны жёсткости балки.
Повторяя рассуждения, приведённые в § 62, легко подсчитать
потенциальную энергию, накопленную балкой при изгибе. При
изгибе бесконечно малого отрезка балки, длиной dx} работа изги-
изгибающего момента на угловом перемещении den будет:
dA = ~ М da..
Подставляя da из уравнения A3.11), получим

§ 79]	ПРОВЕРКА ПРОЧНОСТИ ВАЛОК
Просуммировав по всей длине балки, найдём:
i
= Г
и=
M*dx
2EJ
267
A3.12)
При чистом изгибе балки (М = const.) и постоянном сечении еб
по всей длине (?= const.) потенциальная энергия выразится так
/7— мч
2EJ '
§ 79. Применение полученных результатов
к проверке прочности балок.
Формула A3.9) решает вопрос о величине и распределении нор-
нормальных напряжений по сечению. Она выведена в предположении
наличия чистого изгиба, когда сечения остаются плоскими.
Исследования показали, что когда Q не равно нулю, сечения не
только поворачиваются, но и несколько искривляются под влиянием
касательных напряжений. Однако это искривление для двух смежных
сечений таково, что оно не меняет установленного выше закона
распределения деформаций волокон, заключающихся между этими
сечениями. Поэтому фор-
формула A3.9) может быть при-
применена и в том случае, ко-
когда Q не равно нулю.
Далее следует отметить,
что пока мы имеем право
применять эту формулу лишь
в том случае, когда сечения
балки имеют ось симметрии
и внешние силы располо-
расположены в этой плоскости сим-
симметрии.
Нейтральная ось в каж-
каждом сечении, от которой от-
считывается г, проходит че-
через центр тяжести перпенди-
перпендикулярно к оси симметрии.
На фиг. 185 приведены
примеры распределения на-
напряжений при различных формах сечений балки: прямоугольник, тавр,
Треугольник. Во всех точках, одинаково удалённых от нейтральной
оси, нормальные напряжения одинаковы. По одну сторону нейтраль-
нейтральной оси мы получаем сжимающие, а по другую сторону — растяги-
растягивающие напряжения. Наибольшие напряжения получаются в точках,
наиболее удалённых от нейтральной оси. При выбранных условиях
Фиг. 185.

268	ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ [ГЛ. ХШ
относительно знаков Muz формула A3.9) автоматически даёт пра-
правильный знак для о, плюс — для растягивающих и минус — для сжи-
сжимающих напряжений.
При положительном изгибающем моменте балка гнётся выпукло-
выпуклостью вниз, верхние волокна сжимаются (г<^0), нижние растяги-
растягиваются. При отрицательном изгибающем моменте получается обрат-
обратная картина. Поэтому при решении практических задач для выбора
знака нормальных напряжений можно руководствоваться правилом:
если точка рассматриваемого сечения находится в растянутой зоне,
то а следует брать со знаком плюс, а если в сжатой — со знаком
минус. Разумеется, в этом случае в формулу A3.9) следует под-
подставлять абсолютные значения Миг.
Для проверки прочности материала балки по отношению к нор-
нормальным напряжениям необходимо найти наиболее напряжённые на
растяжение и сжатие площадки. Для этого необходимо применить
формулу A3.9) к опасному сечению, т. е. подставить в неё вместо М
его наибольшее значение Afmax, а вместо z подставить zmSLX — рас-
расстояние от нейтральной оси до наиболее удалённых от неё точек.
Тогда для наибольшего нормального напряжения получаем формулу
Обычно эту формулу преобразовывают, деля числитель и знаме-
знаменатель на ^max:
Величина 	 называется осевым моментом сопротивления
сечения и обозначается буквой W. Так как J выражается в едини-
единицах длины в четвёртой степени, то W измеряется единицами длины
в третьей степени, например смъ. Таким образом,
М
атах=-^,	A3.13)
где
W = — .	A3.14)
При симметричном относительно нейтральной оси сечении, на-
например прямоугольном, расстояния до крайних растянутых и сжатых
волокон одинаковы и такое сечение имеет одно вполне определён-
определённое значение момента сопротивления относительно оси у. Так, при
высоте прямоугольника (фиг. 186, а), равной h.
h	ЛЛГ, J
Zm*T—-X- И W =

§ 791
ПРОВЕРКА ПРОЧНОСТИ БАЛОК
269
Если сечение несимметрично относительно нейтральной оси —
тавр, мы получим два момента сопротивления: один для волокон А
(фиг. 186, б): №,=^идру-	ь_^
' Т Ф
-У h
гой для волокон В: W* —
J	c
= т-. Теперь в формулу

A3.13) следует . вводить:
Wx — при вычислении на-
напряжений в точке А и W%—
при вычислении напряжений
в точке В,
Переходим к составле-
составлению условия прочности по
напряжениям растяжения или сжатия. Это условие выражает ту
мысль, что наибольшее действительное напряжение должно быть
не больше допускаемого:
атах = ^-х<[о].	A3.15)
Фиг. 186.
Отсюда находим, что
A3.16)
т. е. необходимый по условию прочности момент сопротивления
сечения балки должен быть больше или равен наибольшему изги-
изгибающему моменту, делённому на допускаемое напряжение.
Так как W зависит от формы и размеров сечения балки, то,
выбрав форму (прямоугольник, тавр, двутавр), мы сможем подобрать
размеры балки так, чтобы её сечение имело момент сопротивления,
равный полученному из формулы A3.16). Как это делается практи-
практически, будет показано ниже. Для прокатных профилей значения J
и W даются в таблицах сортамента (см. приложение IX).
При применении формул A3.15) и A3.16) следует различать
два случая.
Первый случай, наиболее часто встречающийся при изгибе,—
когда материал одинаково сопротивляется растяжению и сжатию;
в этом случае допускаемые напряжения для того и другого вида
деформации равны между собой:
Ы = Кж] = М-
Тогда при симметричном сечении безразлично, проверять ли
прочность растянутых или сжатых волокон, ибо для тех и других
момент сопротивления W и наибольшие действительные напряжения
будут иметь одну и ту же величину. При несимметричном сечении
в формулы A3.15) и A3.16) вместо W надо подставить то значение
W\ или 1F2, которое меньше; оно будет относиться к более уда-
удалённому волокну.

270	ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
Второй случай имеет место, когда материал балки различно
сопротивляется растяжению и сжатию; тогда (подробнее см. в § 90)
вместо одного условия прочности мы получаем два: одно — для
растянутых, другое — для сжатых волокон:
м	м
В зависимости от того, чему лучше сопротивляется материал,
что больше, [а] или [асж], приходится соответствующим образом
конструировать сечение, выбирая его форму и размеры так, чтобы
Wx и W% удовлетворяли условию прочности.
Таким образом, формулы A3.15) и A3.17) дают нам возмож-
возможность при вычисленной величине Мтах и выбранном материале
(допускаемом напряжении) подобрать необходимую величину мо-
момента сопротивления балки. Для того чтобы от этой величины
перейти к размерам сечения, необходимо научиться вычислять
J и W для любых форм поперечных сечений. Методы вычисления
J и W даны в следующем параграфе.
Что касается физического смысла момента сопротивления, то он
ясен из формулы A3.13); чем больше W, тем больший изгибающий
момент может принять на себя балка, не подвергаясь опасности
разрушения. Таким образом, величина момента сопротивления
характеризует влияние формы и размеров принятого сечения на
прочность балки при напряжениях, не превосходящих предела
пропорциональности.
При напряжениях, превышающих предел пропорциональности
материала, формулы A3.13) и A3.17) перестают быть справедливыми.
ГЛАВА XIV.
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР.
§ 80. Вычисление моментов инерции и моментов сопротивления
для простейших сечений.
В § 78 мы назвали моментом инерции сечения относительно
нейтральной оси интеграл такого вида:
J= [z*dF.	A3.7)
Здесь z — расстояние элементарной площадки dF от нейтраль-
нейтральной оси; суммирование охватывает всю площадь сечения. Покажем
в качестве примера вычисление этого интеграла для прямоугольника
(фиг. 187) высотой h и шириной Ь. Проведём через его центр тя-
тяжести О оси симметрии Oz и Оу. Если внешние силы, действующие

§80]
МОМЕНТЫ ИНЕРЦИИ ДЛЯ ПРОСТЕЙШИХ СЕЧЕНИЙ
271
на балку, лежат в плоскости Oz> то нейтральной осью будет ось Оу.
Найдём относительно этой оси сначала момент инерции, а потом
и момент сопротивления площади прямоугольника.
Площадки dFy на которые следует разбить всю площадь сечения,
выберем в виде узких прямоугольников шириной b и высотой dz
(фиг. 187). Тогда
и интеграл J принимает вид:
Jy={ bz* dz.
Чтобы взять интеграл по всей площади прямоугольника, следует
z менять от —-j- до -fy. Тогда
A4.1)
Момент же сопротивления относительно нейтральной оси Оу
мы получим, разделив Jy на zmax=-^:
"а :
2
6 *
- A4.2)
Если бы нам нужно было вычислить момент инерции и момент
сопротивления прямоугольника относительно оси Oz, то в получен-
полученных формулах следо-
следовало бы b и h поме-
поменять местами:
12
6
= -^-. A4.3)
Фиг. 187.
Заметим, что сумма
произведений z%dF не
изменится, если мы
сдвинем все полоски dF = bdz (фиг. 187) параллельно самим себе
так, что они расположатся в пределах параллелограмма ABCD
(фиг. 188),

272
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
Таким образом, момент инерции параллелограмма ABCD отно-
относительно оси у равен моменту инерции равновеликого ему прямо-
прямоугольника ABGE:
Jy = fi-	О4- О
При вычислении момента инерции круга радиуса г (фиг. 189)
также разбиваем площадь на узкие полоски размером dz вдоль
оси Oz\ ширина этих полосок b = b(z) тоже будет переменной
по высоте сечения. Элементарная
площадка
dF = b(z)dz.
Момент инерции равен:
J= Г z*b(z)dz.
Так как верхняя и нижняя поло-
половины сечения одинаковы, то вы-
вычисление момента инерции доста-
достаточно провести для одной нижней
и результат удвоить. Пределами
для изменения z будут 0 и г:
г
J=2 [z4(z)dz.
Введем новую переменную интегрирования — угол а (фиг. 189);
тогда
z = г cos у; dz = — у г sin у dz,
b(z) = 2r sin у.
Пределы: при z = 0 a = ir, при z = r a = 0, следовательно,
О
= — 2 f
те
2y .yda = y f sin2a tfa=:~-4 A4.4)
A4.5)
Для круга всякая ось, проходящая через центр тяжести, есть ось
?имметрии. Поэтому формулы A4.4) и A4.5) годны для любой
такой оси.

§80]
МОМЕНТЫ ИНЕРЦИИ ДЛЯ ПРОСТЕЙШИХ СЕЧЕНИЙ
273
Для треугольника (фиг. 190) момент инерции относительно оси
АВ равен
с ' z \ i bh?i Ъкъ	bh}
В следующей главе будет показано, как вычислять момент инер-
инерции для сечения любой сложной формы относительно любой оси.
На практике из симметричных сечений встречаются чаще всего:
для дерева — прямоугольник и круг, для металлов — двутавровое и
тавровое сечения (фиг. 191). Для прокатных профилей можно пользо-
пользоваться таблицами ОСТ (сортамент), в которых помещены размеры и
Фиг. 190.
Фиг. 191.
Фиг. 192.
величины J и W для профилей, выпускаемых заводами. Эти таблицы
помещены в приложении IX и пользование ими показано на примере
в следующем параграфе.
В балках, из металла обычно применяются сложные поперечные
сечения, потому что в них материал может быть использован эконо-
экономичнее, чем в таких сечениях, как прямоугольник и круг.
Мы видели (§ 58), что валы делают полыми, чтобы удалить
ту часть материала, которая слабо работает. При изгибе балок
материал около нейтральной оси принимает на себя малые нормаль-
нормальные напряжения [формула A3.9)] и также не может быть исполь-
использован полностью. Поэтому целесообразнее переделать прямоугольное
сечение так, чтобы удалить материал у нейтральной оси и часть
его сэкономить, а часть перенести в верхнюю и нижнюю зоны
балки, где он будет работать более интенсивно. Так получается
(фиг. 192) из прямоугольного сечения профиль двутавра, обла-
обладающего той же прочностью и меньшим весом. Применение двутавра
целесообразно при материалах, одинаково сопротивляющихся растя-
растяжению и сжатию (большинство металлов).
Сечения в виде тавра применяются или в случаях, вызываемых
специальными конструктивными обстоятельствами, или для таких
материалов, как чугун, бетон, у которых сопротивления растяжению

274
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
и сжатию резко разнятся между собой; последнее обстоятельство
требует, чтобы напряжения в крайних волокнах были различными.
Как видно из изложенного, при решении вопроса о наиболее
экономичном проектировании сечения следует стремиться к тому,
чтобы при одной и той же площади F получить наибольший момент
сопротивления и момент инерции. Это
ведёт к размещению большей части мате-
материала подальше от нейтральной оси.
Однако для некоторых сечений можно
увеличить момент сопротивления не до-
добавлением, а, наоборот, путём срезки
некоторой части сечения, наиболее уда-
удалённой от нейтральной оси.
Так, например, для круглого сече-
сечения срезка заштрихованных сегментов
(фиг. 193) несколько увеличивает мо-
так как при этом мы уменьшаем
Фиг. 193.
мент сопротивления
инерции сечения в меньшей степени, чем расстояние до крайнего
волокна zmax.
§81. Общий способ вычисления моментов инерции
сложных сечений.
При проверке прочности частей конструкций нам приходится
встречаться с сечениями довольно сложной формы, для которых
нельзя вычислить момент инерции таким простым путём, каким мы
пользовались для прямоугольника и круга в § 80.
Таким сечением может быть, например, тавр (фиг. 194, а),
кольцевое сечение трубы, работающей на изгиб (авиационные кон-
Фиг. 194.
Фиг. 19о.
струкции) (фиг. 194, б), кольцевое сечение шейки вала или ещё более
сложное сечение (фиг. 194, в). Все эти сечения можно разбить на
простейшие, как-то: прямоугольники, треугольники, круги и т. д.
Можно показать, что момент инерции такой сложной фигуры яв-
является суммой моментов инерции частей, на которые мы её разбиваем.

§ 82] МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ	275
Возьмем (фиг. 195) какую угодно фигуру, изображающую попе-
поперечное сечение балки; в её плоскости проведена ось у —у. Момент
инерции этой фигуры относительно оси у—у равен A3.7):
Jv= f z*dFf
где z — расстояние элементарных площадок dF до оси у—у.
Разобьём взятую площадь на четыре части: Fit F2, Fd и Fk.
Теперь при вычислении момента инерции по формуле A3.7) можно
сгруппировать слагаемые в подинтегральной функции так, чтобы
отдельно произвести суммирование для каждой из выделенных
четырёх площадей, а затем эти суммы сложить. Величина интеграла
от этого не изменится.
Наш интеграл разобьётся на четыре интеграла, каждый из кото-
которых будет охватывать одну из площадей Fl9 F%9 Ръ или F&
Jy= \z*dF= f z*dF+ \#dF+ f z*dF + \z*dF.
P	ft	ft	ft	ft
Каждый из этих интегралов представляет собой момент инерции
соответствующей части площади относительно оси у—у\ поэтому
,.	О4-6)
где j\ — момент инерции относительно оси у—у площади Fl9 Jy —
то же для площади F% и т. д.
Полученный результат можно формулировать так: момент
инерции сложной фигуры равен сумме моментов инерции состав-
составных её частей. Поэтому, чтобы вычислить, например, момент инерции
сечения, изображённого на фиг. 194, в, относительно оси Оу, необ-
необходимо найти моменты инерции прямоугольников и треугольников
относительно оси Оу и затем сложить их. Таким образом, нам не-
необходимо уметь вычислять момент инерции любой фигуры отно-
относительно любой оси, лежащей в её плоскости.
Решение этой задачи и составляет содержание настоящей главы.
§ 82. Зависимость между моментами инерции относительно
параллельных осей, из которых одна — центральная.
Задачу — получить наиболее простые формулы для вычисления
момента инерции любой фигуры относительно любой оси — мы
решим в несколько приёмов. Если взять серию осей, параллельных
друг другу, то оказывается, что можно легко вычислить моменты
инерции фигуры относительно любой из этих осей, зная её момент
инерции относительно оси, проходящей через центр тяжести фигуры
параллельно выбранным осям.
Оси, проходящие через центр тяжести, мы будем называть цен-
центральными осями. Возьмём (фиг. 196) какую-нибудь фигуру.

276
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
Проведём центральную ось Оу, момент инерции относительно этой оси
назовём Jy. Проведём в плоскости фигуры ось yt параллельно оси
у на расстоянии а от неё. Найдём зависимость между Jy и J'y — мо-
моментом инерции относительно оси yv Для этого напишем выражения
для Jy и Jy. Разобьём площадь фигуры на площадки dF\ расстояния
каждой такой площадки до осей у и ух назовём z и z^. Тогда
л = С z* dF и у;=
Но из чертежа имеем:
следовательно:
= z
f z*dF-\- 2a \zdF-\-a* f
?	f	P
dF.
Первый из этих трёх интегралов — момент инерции относительно
центральной оси Оу. Второй — статический момент относительно
той же оси; он равен нулю, так как ось у проходит через центр
2	тяжести фигуры. Наконец, третий интеграл
равен площади фигуры F. Таким образом,
j; = Jy + a*F,	A4.7)
У т. е. момент инерции относительно любой
оси равен моменту инерции относительно
центральной оси, проведённой параллельно
данной, плюс произведение площади фигуры
на квадрат расстояния между осями.
Значит, наша задача теперь свелась к вы-
вычислению только центральных моментов инер-
инерции; если мы их будем знать, то по формуле A4.7) сможем вы-
вычислить момент инерции относительно любой другой оси. Из
формулы A4.7) следует, что центральный момент инерции является
наименьшим среди моментов инерции относительно параллельных
осей и для него мы получаем:
Фиг. 195.
Найдём также центробежный момент инерции J'y2 относительно
осей yxzu параллельных центральным, если известен Jyz= \yzdF
F
(фиг. 196). Так как по определению

§ 83]	ЦЕНТРАЛЬНЫЕ МОМЕНТЫ ИНЕРЦИИ	277
где у\ —у -\-b, zi=z-\-ai то
= ^yzdFA-ab [
F	F
dF + a \ydF-\rb
F	F
Так как два последних интеграла представляют собой статиче-
статические моменты площади относительно центральных осей Оу и Oz,
то они обращаются в нуль и, следовательно:
Jy'g = Jyg-\-ab -F.	A4.8)
Центробежный момент инерции относительно системы взаимно
перпендикулярных осей, параллельных центральным, равен цен-
центробежному моменту инерции относительно этих центральных
осей плюс произведение из площади фигуры на координаты её
центра тяжести относительно новых осей.
§ 83. Зависимость между моментами инерции при повороте осей*
Центральных осей можно провести сколько угодно. Является
вопрос, нельзя ли выразить момент инерции относительно любой
центральной оси в зависимости от момента инерции относительно
одной или двух определённых осей. Для
этого посмотрим, как будут меняться мо-
моменты инерции относительно двух взаимно
перпендикулярных осей при повороте их
на угол а.
Возьмём какую-либо фигуру и прове-
проведём через её центр тяжести О две взаимно
перпендикулярные оси Оу и Oz (фиг. 197).
Пусть нам известны осевые моменты инер-
инерции относительно этих осей Jy, J2, а также
центробежный момент инерции Jyz. На-	Фиг- 197.
чертим вторую систему координатных осей
ух и zu наклонённых к первым под углом а; положительное направле-
направление этого угла будем считать при повороте осей вокруг точки О
против часовой стрелки. Начало координат О сохраняем. Выразим
моменты относительно второй системы координатных осей Jy и J'z
через известные моменты инерции Jy и Jz.
Напишем выражения для моментов инерции относительно этих
осей:
A4.9)

278	ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
Из чертежа видно, что координаты площадки dF в системе по-
повернутых осей у1Ог1 будут:
у1 = ОЕ+ЕС = ОЕ-\-ВО=у cos a.-\-z sin a, 1
zx = AD — DC = AD — BE = zcosa — у sm ol. J
Подставляя эти значения ух и гг в формулы A4.9), получим:
Jy = I (z cos a —у sin аJ с//7 =
= 1 (г2 cos2 а -{-у* sin2 а — 2yz sin а cos а) dF9
или
;= cos2а f г*rfF-J- sin2а f j/2 rfF— sin 2а С _yzofF. A4.11)
Аналогично:
Jz = I (у cos a -f- * sin aJ dF
или
"y</F+sin2a \ yzdF. A4.12)
Первые два интеграла выражений A4.11) и A4.12) представляют
собой осевые моменты инерции Jv и Jz, а последний — центробеж-
центробежный момент инерции площади относительно этих осей Jyz. Тогда:
J'=J cos2 a 4-Л sin2 a—Л, sin 2a, )
>	(Л А 1
Для решения задач могут понадобиться формулы перехода от
одних осей к другим для центробежного момента инерции. При
повороте осей (фиг, 197) имеем:
где j^i и z, вычисляются по формулам A4.10); тогда
Sy9 s= i (z sin a -f- j; cos a) (z cos a —у sin a)dF =
=sinacosal z2dF—sin a cos a \y* dF -{- cos2ai yzdF—sin2a \yzdF.
После преобразований получим:
fyg = i- (iy — 7J sin 2a -f Jyg cos 2a.	A4.14)

§ 83]	ЦЕНТРАЛЬНЫЕ МОМЕНТЫ ИНЕРЦИИ	279
Таким образом, для того чтобы вычислить момент инерции
относительно любой центральной оси yt, надо знать моменты инерции
Jy и Jz относительно системы каких-нибудь двух взаимно перпенди-
перпендикулярных центральных осей Оу и Ог, центробежный момент инер-
инерции Jyz относительно тех же осей и угол наклона оси у1 к оси у.
Для вычисления же величин Jy) JZ) JyZ приходится так выбирать
оси у и z и разбивать площадь фигуры на такие составные части,
чтобы иметь возможность произвести это вычисление, пользуясь
только формулами перехода от центральных осей каждой из состав-
составных частей к осям, им параллельным. Как это сделать на практике,
будет показано ниже на примере. Заметим, что при этом вычислении
сложные фигуры надо разбивать на такие элементарные части, для
которых по возможности известны величины центральных моментов
инерции относительно системы взаимно перпендикулярных осей.
Заметим, что ход вывода и полученные результаты A4.13) и
A4.14) не изменились бы, если бы начало координат было взято
не в центре тяжести сечения, а в любой другой точке О. Таким
образом, формулы A4.13) и A4.14) являются формулами перехода
от одной системы взаимно-перпендикулярных осей к другой, повёр-
повёрнутой на некоторый угол а, независимо от того, центральные это
оси или нет.
Из формул A4.13) можно получить ещё одну зависимость между
моментами инерции при повороте осей. Сложим выражения для
Jy и J^ A4.13); получим
^	+cos2a) = 7:v+J(?, A4.15)
т. е. сумма моментов инерции относительно любых взаимно перпен-
перпендикулярных осей у и z не меняется при их повороте. Подставляя
в формулу A4.15) вместо Jy и Jz их значения из A4.9), получаем:
y*dF
= Jp> A4.16)
где p — ^y^-^z*— расстояние площадок dF от точки О. Величина
Jp = i p2 dF является, как уже известно, полярным моментом инерции
сечения относительно точки О (§ 58).
Полярный момент инерции сечения относительно какой-либо
точки равен сумме осевых моментов инерции относительно
взаимно перпендикулярных осей, проходяшдх через эту точку.
Поэтому эта сумма и остаётся постоянной при повороте осей. Зави-
Зависимостью A4.16) можно пользоваться для упрощения вычисления
моментов инерции. Так, для круга мы уже имели (§ 58)
Jp— 2 #

280	ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
Так как по симметрии для круга Jz = Jyy то
что было получено выше путём интегрирования (§ 80).
Точно так же для тонкостенного кольцевого сечения на основании
формулы A1.15) можно получить:
§ 84. Главные оси инерции и главные моменты инерции.
Формулы A4.7) и A4.13) решают поставленную в § 81 задачу:
зная для данной фигуры центральные моменты инерции Jyy Jz и
Jzy, мы можем вычислить момент инерции и относительно любой
другой оси.
При этом можно за основную систему осей принять такую систему,
при которой формулы A4.13) упрощаются. Именно, можно найти
систему координатных осей, для которых центробежный момент
инерции равен нулю. В самом деле, моменты инерции Jy и J2 всегда
положительны, как суммы положительных слагаемых, центробеж-
центробежный же момент
может быть и положительным и отрицательным, так как слагаемые
zydF могут быть разного знака в зависимости от знаков z и у
для той или иной площадки. Значит, он может быть равен нулю
(см. § 78, п. В).
Те оси, относительно которых центробежный момент инерции
обращается в нуль, называются главными осями инерции. Если
начало такой системы помещено в центре
тяжести фигуры, то это будут главные
/; ^ центральные оси. Эти оси мы будем обо-
' значать у0 и г0; для них
Найдём, под каким углом а0 накло-
наклонены к центральным осям у и z (фиг. 198)
главные оси. В формуле перехода A4.14)
от осей yz к осям yxzx для центробежного
момента инерции дадим углу а значение <х0; тогда оси ух и zx совпадут
с главными, и центробежный момент инерции будет равен нулю:
Jyz при
ИЛИ
C0S 2а° =

§ 84]	ГЛАВНЫЕ ОСИ И МОМЕНТЫ ИНЕРЦИИ	281
откуда
tg2a0 = T?4y.	A4.17)
Этому уравнению удовлетворяют два значения 2а0, отличающиеся
на 180°, или два значения а0, отличающиеся на 90°. Таким образом,
уравнение A4.17) даёт нам положение двух осей, составляющих
между собой прямой угол. Это и будут главные центральные оси
у0 и zQ, для которых Jyozo = 0.
Пользуясь формулой A4.17), можно по известным Jy, Jz и Jyz
получить формулы для главных моментов инерции Jyo и JZr Для этого
опять воспользуемся формулами A4.13); они дадут нам значения
Jy0 и JZq, если вместо а подставить а0:
A4.18)
о = Jy sin « а0 -f- Л cos2 ao + Jyz sin 2ao- /
Этими формулами вместе с формулой A4.17) можно пользоваться
при решении задач. В § 85 будет показано, что одним из главных
моментов инерции является /тах, другим /min.
Формулы A4.18) можно преобразовать к виду, свободному от
значения а0. Выражая cos2 a0 и sin2 a0 через cos 2a0 и подставляя их
значения в первую формулу A4.18), получим, делая одновременно
замену Jyz из формулы A4.17):
_
cos2a0*
Заменяя здесь из формулы A4.17) дробь—^ на ±/l+tg22a0 =
min
A4.18')
К этой же формуле можно прийти, делая подобное же преобразо-
преобразование второй формулы A4.18).
За основную систему центральных осей, от которых можно
переходить к любой другой, можно взять не Оу и Oz, а главные
оси OyQ и OzQ; тогда в формулах вида A4.13) не будет фигуриро-
фигурировать центробежный момент инерции C/yozo = O). Обозначим угол,
составленный осью у{ (фиг. 199) с главной осью Оу0, через 3. Для
вычисления Jy, J's и Jyz, переходя от осей у0 и zQ9 нужно в формулах

232
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
A4.13) и A4.14) заменить угол а через р, a Jy} Jz и Jyz — через
/ Л J	Q В результате получаем:
о' Л© Jyozo — Q*
J.vo-J.
2
г°
sin
A4.19)
По своему виду эти формулы совершенно аналогичны формулам
для нормальных оа и касательных та напряжений G.5) и G.6) по
двум взаимно-перпендикулярным площадкам в элементе, подвергаю-
подвергающемся растяжению в двух направлениях (§ 36). Поэтому мы и
здесь можем применить построение круга Мора; следует лишь по
горизонтальной оси откладывать экваториальные моменты инерции,
по вертикальной — центробежные. Построение круга и анализ его
рекомендуется сделать самостоятельно. Укажем лишь формулу,
позволяющую из двух значений угла а0 (формула A4.17)) выделить
то, которое соответствует отклонению первой главной оси (дающей
max J) от начального положения оси у.
tgao=. JV , .	A4.170
Эта формула полностью аналогична формуле G.11).
Теперь можно окончательно формулировать, что надо сделать,
чтобы получить возможность простейшим образом вычислять момент
инерции фигуры относительно любой оси. Необходимо через центр
тяжести фигуры провести оси Оу и Oz так, чтобы, разбивая фигуру
на простейшие части, мы могли легко вычислить моменты Jy, Jz и
Jzv. После этого следует найти по фор-
формуле A4.17) величину угла а0 и вычис-
вычислить главные центральные моменты инерции
0 по формулам A4.18).
Далее, можно найти момент инерции
относительно любой центральной оси Оух
(фиг. 199), наклонённой к Оу0 под углом р,
по формуле A4.19):
2 p
Jyo и
fy = Jyo cos2
z0
sin2
199.
Зная же центральный момент инер-
инерции Jyy можно сейчас же найти момент
инерции относительно любой параллельной ей оси уь проходящей
на расстоянии а (фиг. 199) от центра тяжести по формуле A4.7):
Во многих случаях удаётся сразу провести главные оси фигуры;
если фигура имеет ось симметрии, то это и будет одна из главных

§ 841
ГЛАВНЫЕ ОСИ И МОМЕНТЫ ИНЕРЦИИ
283
осей. В самом деле, при выводе формулы о = -у мы уже имели
дело с интегралом \ yz dF, представляющим собой центробежный
?
момент инерции сечения относительно осей у и z\ было доказано,
что если ось Oz является осью симметрии, этот интеграл обра-
обращается в нуль.
Стало быть, в данном случае
оси Оу и Oz являются главными
центральными осями инерции сече-
сечения. Таким образом, ось симмет-
симметрии — всегда главная центральная
ось; вторая главная центральная
ось проходит через центр тяже-
тяжести перпендикулярно к оси сим-
симметрии.
я
г,
\
By
/45°
//
п-госм
Фиг. 200.
Пример 56. Найти моменты инер-
инерции прямоугольника (фиг. 200) отно-
относительно осей ух и zx и центробежный момент его относительно тех же
осей.
Центральные оси у и z как оси симметрии будут главными осями; мо-
моменты инерции сечения относительно этих осей равны:
4 . 153 . 20 _„_
см » Л =	Го	^ 5625 см •
20» • 15
</у =	12— =
Центральные моменты относительно повёрнутых осей у0 и z0 равны:
уо — Jy C0S2 45° + J2 sin2 45° = i- [ 10 000 + 5625] = 7813 см4 = Pz.
Центробежный момент инерции относительно осей у0 и z0 равен:
•in 90»- 10000-5625 = + 21,88 см*.
Координаты центра тяжести прямоугольника относительно осей yt и zx равны:
34 = АВ + BD = 7,5 У2 + 2,5 • 0,7 = 12,35 см,
zl~OD = BD = 2,5 . 0,7 = + 1,75 см.
Моменты инерции относительно осей yt и zt равны:
Уу = у* + Fz\ = 7813 + 300 . 1,752 = 8734 см\
J'2 = J° + Fy\ = 7813 + 300 . 12,35s = 53 616 смК
Центробежный момент инерции равен:
Ууг = Pyz + Fy^ = 2188 + 300 • 1,75 • 12,35 = + 8678 см*.

284	ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
§ 85. Наибольшее и наименьшее значения
центральных моментов инерции.
Как мы уже знаем, центральные моменты инерции являются
наименьшими из всех моментов относительно ряда параллельных
осей.
Найдём теперь крайние значения (максимум и минимум) для
центральных моментов инерции. Возьмём ось ух и начнём её вра-
вращать, т. е. менять угол а; при этом будет изменяться величина
Jfy, = Jy cos2 a -\- Jz sin2 а — Jyz sin 2а.
Наибольшее и наименьшее значения этого момента инерции
соответствуют углу аь при котором производная -^- обращается
в нуль. Эта производная равна:
-—¦ = — 2Jy cos a sin a -j- 2JZ sin a cos а — 2Jyz cos 2а.
Подставляя в написанное выражение а = 04 и приравнивая его
нулю, получаем:
(Jz — Jy) sin 2ах — 2Jyz cos 2а4 = 0;
отсюда
Таким образом, осями с наибольшим и наименьшим центральными
моментами инерции будут главные центральные оси. Так как при
повороте центральных осей сумма соответствующих моментов
инерции не меняется, то
Когда один из центральных моментов инерции достигает наиболь-
наибольшего значения, другой оказывается минимальным, т. е. если
Следовательно, главные центральные оси инерции — это такие
взаимно перпендикулярные оси, проходящие через центр тяжести
сечения, относительно которых центробежный момент инерции
обращается в нуль, а осевые моменты инерции имеют наибольшее
и наименьшее значения.
В дальнейшем будем обозначать главные оси инерции у и z
и главные моменты инерции сечения Jy и Jz, Осью х по-прежнему
будет обозначаться ось балки по её длине.

§ 86] СЛУЧАЙ НЕСИММЕТРИЧНОГО СЕЧЕНИЯ БАЛКИ	285
§ 86. Распространение формулы для вычисления нормальных
напряжений на случай несимметричного сечения балки.
Пользуясь равенством нулю центробежного момента инерции
относительно главных осей, можно показать, что формулы § 78
применимы при известных условиях и к несимметричным сечениям.
При выводе формулы для нормальных напряжений (§ 78) вве-
введённое нзхми ограничение, что балка симметрична относительно
плоскости действия внешних сил xz, понадобилось нам прежде
всего для: 1) установления перпендикулярности нейтральной оси у
к плоскости zx, 2) доказательства того, что сумма моментов усилий
dN относительно оси z равна нулю:
' %Mg = 0, —[zydF=09 {zydF = 0.	A3.6)
Но условия перпендикулярности осей z и у и равенства нулю
zydF могут быть выполнены и для несимметричного сечения
балки; для этого достаточно, чтобы ось z, лежащая в плоскости
действия сил, и нейтральная ось у были главными центральными
осями инерции поперечного сечения балки. Тогда и условие пер-
перпендикулярности соблюдается, и интеграл i zydF, как центробеж-
центробежный момент инерции сечения относительно главных осей, снова
будет равен нулю.
Значит, вместо условия совпадения плоскости внешних сил
с плоскостью симметрии сечений балки можно ввести другое:
чтобы плоскость действия внешних сил совпадала с одной из двух
плоскостей, содержащих главные оси инерции поперечных сечений.
Эти две плоскости в балке называются главными плоскостями
инерции.
Тогда нейтральной осью будет вторая главная ось, перпендику-
перпендикулярная к плоскости внешних сил, и условие \ zydF=0 будет ав-
Г zydF=0
томатически удовлетворено.
Так как при всякой форме поперечного сечения балки мы можем
найти главные центральные оси инерции, то для балки любого
поперечного сечения можно пользоваться выведенными формулами
A3.9) и A3.13)
Mz	max M
Q — ~]~ и °тах = —^Г~
при условии, что внешние силы лежат в одной из главных плоско-
плоскостей инерции балки; J и W берутся относительно другой главной

286	ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
оси, перпендикулярной к плоскости действия внешних сил и являю-
являющейся нейтральной осью.
Как пример, можно указать балку зетового сечения (фиг. 201)
с главными осями z и у. Приведённые выше формулы применимы
к ней, если внешние силы будут лежать в плоскости
z или у; нейтральной осью в первом случае будет у,
во втором z. Так как нейтральные оси сечений и в
этом случае перпендикулярны плоскости действия
/а	- внешних сил, то ось балки при деформации будет
//	оставаться в этой плоскости. Таким образом, располо-
s^	жение внешних сил в одной из главных плоскостей
инерции балки и будет общим случаем плоского
изгиба.
Надо заметить, что в некоторых случаях в балках
несимметричного (относительно оси, лежащей в пло-
плоскости действия сил) сечения появляется дополнительная система
нормальных и касательных напряжений (§ 96), связанная с добавоч-
добавочным кручением балки *).
§ 87. Эллипс инерции.
Помимо аналитического, можно дать графическое изображение изменения
моментов инерции при помощи построения так называемого эллипса инерции.
Введём новую величину — радиус инерции фигуры относительно ка-
какой-либо оси. Радиусом инерции относительно оси v называется величина
A4.20)
где 7V — момент инерции относительно оси v, a F—площадь фигуры.
Если Jy и Jz — главные моменты инерции, то
называются главными радиусами инерции.
Построим на главных осях инерции фигуры (оси у и г) эллипс с полу-
полуосями iv и iZt отложив радиус iy перпендикулярно к оса у и радиус i2
перпендикулярно к оси z (фиг. 202). Этот эллипс называется центральным
эллипсом инерции фигуры; уравнение его будет
где у и z — координаты точек эллипса.
Если iy = ig = it то эллипс инерции обращается в круг инерции с урав-
уравнением:
;> См. главу XXX, Основы расчёта тонкостенных стержней на кручение
и изгиб.

§87]
ЭЛЛИПС ИНЕРЦИИ
287
При помощи эллипса инерции можно графически найти радиус инер-
инерции ix для любой оси х, составляющей с главной осью у угол р (фиг. 202),
а затем, следовательно, вычислить и момент
инерции Jx по формуле
	 /2/7
A4.21)
Для нахождения радиуса инерции ix надо
провести к эллипсу касательную, параллель-
параллельную оси х; расстояние от центра эллипса до
этой касательной (отрезок О А) и будет радиу-
радиусом инерции ix. Действительно, напишем выра-
выражение для Jx\
Разделив обе части этой формулы на Ft полу-
получим зависимость
Фиг. 202.
Теперь напишем уравнение касательной к
эллипсу инерции, составляющей с осью у
угол р, и вычислим длину перпендикуляра О А,
опущенного из центра эллипса на эту ка-
касательную. Уравнение эллипса в параметрической форме имеет вид:
у = i2 cos cp; z = iy sin ср.
Координаты точки касания С отметим значком с:
ус = iz cos cpc; zc = iy sin <pc.
Уравнение касательной напишем в виде
z = ау + Ь.
Угловой её коэффициент равен:
с другой стороны, из уравнения эллипса
Ординату Ь найдём, подставляя в уравнение касательной координаты
точки С; после некоторых преобразований, получим:
cosp
Квадрат длины перпендикуляра ОА, опущенного из центра О на каса-
касательную, равен:
cos2P(l+tg2P) ¦
что мы и хотели доказать.
Кроме указанного графического построения, изображающего зависимость
между моментами инерции относительно различных осей, имеется ещё ряд
графических приёмов, из которых рассмотрим лишь применение верёвочного
многоугольника.

288
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
§ 88. Приближённый метод вычисления моментов
инерции площади.
В некоторых случаях очертание поперечного сечения оказывается на-
настолько сложным, что его трудно разбить на простые элементы, особенно
если это очертание криволинейно. Тогда можно
при\. :пъ следующий приближённый метод
вычк ^ч момента инерции этой фигуры
относше.^но какой-нибудь оси у (фиг. 203).
Ра?т.еляем фигуру на полоски линиями,
параллельными оси у\ ширину полосок t вы-
выбираем малой по сравнению с размерами фи-
фигуры. Тогда каждую из этих полосок можно
принять за прямоугольник высотой t и пере-
переменной шириной Ь. Момент инерции каждой
такой полоски относительно оси .у будет равен:
Фиг. 203.	/за
Так как мы выбрали высоту полосок t малой, то слагаемым -г^ можно
пренебречь по сравнению с a2 tb. Тогда полный момент инерции фигуры
будет равен:
	 		A4.22)
Чтобы оценить точность этого метода, вычислим момент инерции отно-
относительно центральной оси прямоугольника, изображённого на фиг. 204;
прямоугольник взят потому, что для него легко
подсчитать точное значение Jy. Так как мы вы-
вычисляем момент инерции относительно оси сим-
симметрии, то достаточно вычислить момент инерции
для верхней половины сечения и результат удвоить.
Разделим верхнюю половину площади сечения на
5 полосок высотой по ? = 2 см\ ширина всех по-
полосок одинакова. Тогда
1
2см
\
0
20см
J =
у
я2 = 2 . 10 • 2 A2 + З2 + 5» + 72 + 92) =
=6600 см\
Точная величина этого момента инерции равна:
. bh* 10. 20* fififi_
Jy = —= ——— = 6667 смК
Разница
6667 — 6600 _ 67
6667 — 6667 ^ /о*
Мы видим, что даже при таком грубом делении площади на полоски
результат получается достаточно точным. В пределе мы и приходим к точ-
точному выражению для момента инерции.
При неправильном или криволинейном очертании фигуры кроме число-
числового подсчёта по формуле A4.22) можно применить графический метод —
построение верёвочного многоугольника. Начертим (фиг. 205) какую-либо
фигуру в линейном масштабе я/1, проведём ось у и разделим рассматривае-
рассматриваемую площадь на элементарные полоски bt. Приложим в центре тяжести
каждой п-й полоски условную (фиктивную) силу Fm равную по числовой
величине площади полоски; направление сил возьмём параллельно оси у.

§ 88] ПРИБЛИЖЁННЫЙ МЕТОД ВЫЧИСЛЕНИЯ МОМЕНТОВ ИНЕРЦИИ
289
Построим силовой многоугольник в масштабе 1// с произвольным по-
полюсным расстоянием //, проведём лучи и построим верёвочный много-
многоугольник.
Возьмём в силовом многоугольнике какую-нибудь силу Fn; продолжим
стороны верёвочного многоугольника, пересекающиеся на линии этой силы в
точке о, до пересечения их с осью у в точках к и т. Расстояние силы Fn до
Фиг. 205.
оси у обозначим ап. Заштрихованному на верёвочном многоугольнике тре-
треугольнику okm соответствует подобный ему треугольник ОКМ в силовом
многоугольнике. Из подобия этих треугольников имеем:
ап	km
7ТТ
Произведение средних и крайних даёт нам
Умножим обе части этого равенства на дЛ:
Произведение
ап • km =
2- -
km . Н.
1 —
FT <*п ' km
равно удвоенной площади заштрихованного треугольника okm.
Таким образом, момент инерции я-й площадки (Fn = bt) относительно
оси у численно равен площади заштрихованного треугольника okm, умно-
умноженной на удвоенное полюсное расстояние //.
* Надо помнить, что Н входит в силовой многоугольник и, стало быть,
выражается, как и силы Fnt в единицах площади. Если проделать эти вычи-
вычисления для всех сил Fn и просуммировать полученные результаты, то мо-
момент инерции фигуры /v, равный ^па%, будет графически изображаться
произведением полюсного расстояния Н на удвоенную площадь ABCDA,
ограниченную верёвочным многоугольником и продолжениями его крайних
сторон. Называя величину этой площади <о, имеем формулу:
Jy = 2H*.	A4.23)

290	ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
При вычислениях надо учитывать масштабы. Площадь <о измеряется на
чертеже, изображённом в линейном масштабе я/1 (см/см), а полюсное рас-
расстояние Н измеряется в масштабе сил -j (см/см2). Поэтому если мы на
чертеже измерили площадь ABCDA равной <о см2, а полюсное расстоя-
расстояние Н см, то
Jy = 2//<о/ . п2.
Удобно выбирать высоту полосок одинаковой, тогда все Fn будут про-
пропорциональны ширинам полосок. Площадь <о может быть измерена плани-
планиметром. Нет нужды гнаться за большим числом полосок; мы видели выше,
что достаточная точность получается при сравнительно широких полосках.
Надо помнить, что описанный способ основан на пренебрежении собствен-
собственными центральными моментами инерции полосок.
Применим теперь полученные в этой главе результаты к решению задач
по проверке прочности балок с более сложным сечением.
§ 89. Пример расчёта балки несимметричного сечения.
Пример 57. Определить величину допускаемого изгибающего
момента для балки, защемлённой одним концом в стену, если пара
сил расположена на другом конце в главной плоскости инерции.
Размеры сечения в мм показаны на фиг. 206. Пролёт балки /=
= 0,6 м. Допускаемое напряжение [а] = 1600 кг/см*.
Прежде всего необходимо найти положение центра тяжести
сечения. Для этого выбираем произвольную систему координатных
осей yxzx\ удобно, чтобы вся фигура лежала в положительном
квадранте. Расстояния центра тяжести сечения до этих осей най-
найдутся по формулам:
Sz	Sy
Ус = т? и *c = f9
где Sy и S'z — статические моменты площади относительно осей ух
и zx.
Для подсчёта статических моментов разобьём площадь нашей
фигуры на 2 прямоугольника — вертикальный / и горизонтальный II.
Площадь фигуры равна F=\ • 12 -|- 7 • 1 = 19,0 см*. Статические
моменты !):
; = Л^1,1 + ^1.2= 12-0,5+ 7 A + 3,5) = 37,5 См*;
2 = 12.6,o4-7- 11,5=152,5 см\
Координаты центра тяжести:
Л = Н|=1,97 см ъ* 2,0 см;
ге=*^ = 8,00 см.
*) Здесь индексы при координатах площадок указывают: первый — ось
i; *i), а второй — номер площадки.

§891
ПРИМЕР РАСЧЁТА БАЛКИ НЕСИММЕТРИЧНОГО СЕЧЕНИЯ
291
Теперь наметим систему центральных осей у9 и z0. Проще
всего эти оси направить параллельно сторонам фигуры, что облег-
облегчит вычисление моментов инерции пло-
площади сечения относительно этих осей.
Моменты инерции отдельных пря-
прямоугольников относительно осей у0
и 20 вычисляются по формулам пере-
перехода к параллельным осям A4.7) и
A4.8), а собственные моменты инерции
прямоугольников по формулам A4.1).
Вычисления ведём по схеме, по-
показанной в таблице 20 (см. фиг. 206),
пользуясь которой можно найти угол
наклона главных осей с осью Оу0:
..»-	2У-	2-97 __109.
**о—/о_/о —100-278
2а; = — 47°40' и а^ = — 23°50\
Фиг. 206.
Знак минус показывает, что угол а^
следует отложить по часовой стрелке:
sin а^ = — 0,404; cosa; = 0,915; sin 2а^ = —0,74; cos 2a^ = 0,673.
Главные моменты инерции будут:
Jy = 7° cos2 a0 -f- Jl sin2 a0 — J^ sin 2a0 =
= 278 • 0,9152+ 100 • 0,4042-f-97 . 0,74 = 320 см\
Jz = Гу sin2 a0 -f- Jl cos2 a0 -f J% sin 2a0 =
= 278 . 0,4042+ 100 . 0,9152 —97 . 0,74 = 58 смК
Произведём проверку правильности вычислений:
y\z	{	;+|=378 см1,
2) Jyz = 1 (J5 — Л) sin 2a -j- j;z cos 2a = — -i B78 —100) • 0,74 -\-
+ 97-0,673 = 0.
Расчёт показал, что Jy = 7max,
a Jg = Jmin. Следовательно, изги-
изгибающую пару выгоднее располо- м0
жить в плоскости Oz так, чтобы
ось Оу была нейтральной осью -*—
(фиг. 207).
Теперь найдём момент сопро-
сопротивления сечения. Для этого не-
необходимо найти расстояние zmax
от нейтральной оси Оу до наиболее удалённого волокна. Проще
всего это сделать графически, вычертив в масштабе сечение и
10*
\к
Фиг. 207.

292
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
I
S
а
о
2
О
S
о
сг
2
СО
О)
•я
о
с
к
о.
0)
ЕС
2
ас
а>
Мом
о
if
a
II
+
Q
W0 В
iqieuuirdoo)]
4-1
V
•с i
О
{1Э±ЭВЬ И1ГВГОО1Г1]
И31ЭВЬ Bd9K0]J
со
СО
О
см
+
00
см
г-
см
II
II
п
см
1,(
II
09
см
см
192
00
II
II
¦
см
II
1
см
1
см
2,0
ют
см
-
со
1!
|)
ю
00
ю
г-
+
см
ОС
<го
JI
см*
со
28,
II
ее
см
со
00
со^
00
II
ю
00
со
о
1
ее
1
см
ю
00
ю
см
см
+
100
70,8
со^
см
278
со
33,
•—•
со

§ 90]	примеры	293
изобразив на нем главные оси*). Для нашего сечения измеренное
расстояние оказалось равным «zmax = 8,l см. Момент сопротивле-
сопротивления сечения относительно оси у, следовательно, равен:
Из условия прочности2) находим величину допускаемого изгибаю-
изгибающего момента
= max [Ж] ^1600- 39,5 = 63 200 кгсм^ОЯЗ тм.
откуда
Если пару сил расположить в плоскости Оу> то при расстоя-
расстоянии от оси z до крайнего волокна j/max = 4,12 см момент сопротив-
J	СО
ления сечения был бы равен Wz = —— = т-пг=14Д смъ, и мы
¦Ушах 4»^
могли бы безопасно приложить нагрузку в виде пары с моментом:
М\ = max[iWi] ^ 1600 • 14,1 = 22 560 кгсм я« 0,226 тле,
что почти втрое меньше, чем при расположении пары в плоско-
плоскости О,г.
Заметим также, что если пара будет расположена в какой-либо
другой, не главной плоскости, например параллельно полке уголка,
то и изгиб в этом случае не будет плоским изгибом и условие
прочности примет другой вид (§ 157).
§ 90. Примеры.
Пример 58. Найти момент инерции треугольника (фиг. 190, § 80) от-
относительно центральной оси у, параллельной основанию.
Для оси АВ, проходящей через основание треугольника, выше были
получено (§ 80): /A5 = -jy.
Применяя формулу перехода для параллельных осей, имеем;
Го Г	Fh2 bh* l hh h% Ш
J Jm	bh
Пример 59. Определить диаметр d оси железнодорожного вагона,
представляющей балку с двумя консолями, нагружённую силами Р = 6,25 г
на концах консолей (фиг. 150, § 69). Длина пролёта /=1,58 ж; длина консо-
консолей а = 0,267 л(, допускаемое напряжение на изгиб [<j] = 600 кг/см*.
1) Для аналитического определения zm&x или ушах можно воспользоваться
формулами A4.10).
*) В примере не учитываются дополнительные нормальные напряжения,
возникающие в рассматриваемом случае вследствие стеснённого кручения
(см. главу XXX).

294	ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР	[ГЛ. XIV
Наибольший изгибающий момент равен
Мтах=:Ра = 6,25 • 0,267 = 1,67 тм.
Момент сопротивления сечения № = ^—. Из условия прочности W^ га*
61	[а\
получаем:
32-167 000
— ^—- = 14,2
Пример 60. Двутавровая балка № 45 пролётом / = 6 м шарнирно
опёрта по концам и несёт равномерно распределённую нагрузку q = 2 т/м
(включая и собственный вес).
Какой сосредоточенный груз Р можно дополнительно приложить к этой
балке на расстоянии д = —- от левой опоры при допускаемом напряжении
[а] == 1400 кг/см2?
Для определения величины добавочного груза Р необходимо найти ве-
величину наибольшего изгибающего момента в функции от Р и q. Сечениями,
где M = Mmix, предположительно могут быть: сечение в точке приложения
силы Р, где изгибающий момент от этого груза достигает максимума; сече-
сечение посредине пролёта, где мы имеем Мтпх от распределённой нагрузки,
и, наконец, сечение 3—5, расположенное между первыми двумя.
Опорные реакции будут:
ql P(l — a) ql . 3 _
i\ — О	/	— 9 ' 4
D ql , Pa ql . P
правая B=^ + T = f + -T.
Изгибающий момент в сечении 1 — 1 под силой
В сечении 2 — 2 посредине пролёта:
.. [ql . P\ I ql I ql2 PI /
Для промежуточного сечения 3 — 5, проведённого в расстоянии х от правой
Взяв производную от Af3 по х и приравняв её нулю, найдём абсциссу
х = х0 сечения, где Мг = MmSLX:
^„qXo + !L = o, охкуда ,.=4 + $.
Подставляя полученное значение х0 в выражение для Mt, получим:
+) [+
l,P\[qt

§ 90]
примеры
295
Величина допускаемого изгибающего момента должна быть:
[М] ^ [а]. W= 1400 • 1220 = 17,1 . 105 кгсм = 17,1 тм.
Приравнивая это значение момента полученным выражениям для ми
i и Mtt находим три значения силы Р:
17,1-6,75
_
17,1 -9,0
2" 0,75 ~~ ' "
Р3 = (/Щ —3).8 = 9,1 г.
Наименьшее из этих значений и будет допустимым: Р = 9,1 т.
Пример 61. Подобрать двутавровое сечение балки на двух опорах
пролётом /=4 Mt загруженной равномерно распределённой нагрузкой q=2 т\м
и сосредоточенной силой посредине пролёта Р = 5,3 г при допускаемом
напряжении [с] = 1600 кг/см2.
Вследствие симметрии изгибающий момент будет иметь наибольшее зна-
значение посредине пролёта. Величину его найдём по методу сложения дейст-
действия сил, пользуясь выражениями A2.10') и A2.11):
., . ., Р1 . а/2	1
-4 2 ¦
= 9,3 тм = 9,3 • 10* кгсм.
Из условия прочности необходимый момент сопро-
сопротивления сечения балки:
930000
580'
Мт
Ближайший по сортаменту (ГОСТ 8239—56) номер
профиля, удовлетворяющий этому условию, двутавр
№ 33; № = 597 см* (СМ# приложение IX, табл. 3).
Пример 62. Какую равномерно распределённую
нагрузку можно приложить к мостовой балке пролё-
том /=10 м, свободно лежащей на двух опорах, при
допускаемом напряжении [а] = 1400 кг/см2"? Сечение
балки состоит из двутавра № 60, усиленного двумя
приваренными к нему листами 200 X 20 мм (фиг. 208).
М	б	й
Фиг. 208.
варенными к му листами 200 X 20 мм (фиг. 208).
Момент инерции сечения балки относительно нейтральной оси у опре-
определяется как сумма моментов инерции двутавра и двух листов полок. Для
определения момента инерции полок воспользуемся формулой перехода
к параллельным осям; для двутавра — по сортаменту (ГОСТ 8239—56):
[20.23	1
-J2- +20.2C0+1L = 152500 см*.
Момент сопротивления сечения равен:
Jv 152 500
5о
32
««4770 см9.
Наибольший изгибающий момент Mmax=if. Из условия прочности

296
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ ФИГУР [ГЛ. XIV
отк\'да
,8 [о]-Ц?_ 8-1400-4770
/2 ~~ 102-1002
;53,5 kz'jCM = 5,35 т'м.
Имея в виду, что вес двутавра составляет 104 кг\см (см. приложение IX,
табл. 3), а двух листов 2 • 20 • 2 • 100 • 0,00785 = 63 кг/м, получаем собствен-
собственный вес балки 104 -j-63 =167 кг\м\ тогда допу-
допускаемая (полезная) нагрузка будет:
q = 5350— 167 = 5183 кг/м*
s 5,2 т\М.
Пример 63. Определить момент инерции
и момент сопротивления сечения, изображённого
на фиг. 209, относительно центральной оси у.
Так как момент инерции представляет собой
сумму вида Jy=\z2dF, то для вычисления мо-
F
мента инерции'можно воспользоваться формулами
A4.1) и A4.6):"
12
12 *
W — Уу —
у ~~ ~
Момент сопротивления сечения:
—
ТГ 6Я
12-—-
"" 6Я [
Фиг. 210.
Обращаем внимание на то, что момент сопро-
сопротивления подобного сечения нельзя считать как
разность вида W= Wt — W2 или W = -g	g-,
360 что противоречит самому определению понятия о
моменте сопротивления сечения балки, как об от-
отношении 	.
max
Пример 64. Определить грузоподъёмность
чугунной балки, изображённой на фиг. 210.
Допускаемое напряжение на растяжение [а] =
=300 кг1см2> на сжатие [асж] = 800 кг/см2.
Д
1>	[сж]	/
Допустить, что ограничения, перечисленные в
§ 77, строго соблюдаются и изгибающий момент действует в плоскости
симметрии балки.
Найдём положение центра тяжести сечения. Статический момент отно-
относительно края узкой полки равен
St = 36 • 3.34,5 + 30. 3 • 18 + 9 • 3 • 1,5 = 5385 см3.
Площадь сечения равна
F= 36 • 3 + 30.3 + 9 • 3 = 225 см2.
Расстояние до центра тяжести от края узкой полки равно
z1 = ~ = -y^r = 23,9 см ^ 24 см.
Расстояние до центра тяжести от края широкой полки равно
*, = 36 —24=12 см.

§ 90]	примеры	297
Момент инерции сечения относительно нейтральной оси уу равен сумме мо-
моментов инерции трёх прямоугольников, на которые разбита фигура:
^ = §^ + 36. 3.10,5»+ 2^ + 30. 3.6^+^ + 3.9. 22,5» =
= 35 640 см4.
Моменты сопротивления сечения будут:
для волокон у края узкой полки Wi = —кг— = 1485 смъ,
„	TV7 35 640 оп_л
> >	» > широкой > W2 = —щ— = 2970 см9.
Так как центр тяжести расположен ближе к широкой полке, то в её
крайних волокнах напряжения будут но абсолютному значению меньше, чем
в крайних волокнах узкой полки; поэтому сечение должно быть расположено
так, чтобы широкая полка чугунной балки была растянута, а узкая сжата.
Допустимый изгибающий момент определяется формулами:
Mt = Wi [асж] = 1485 . 800 = 1 120 000 кгсм,
М2 = Wt [а] = 2970 • 300 = 891 000 кгсм.
Допускаемая грузоподъёмность равна М2. Чтобы балка имела одинако-
одинаковую грузоподъёмность по растяжению и сжатию, надо, чтобы расстояния
*	[а] 3
центра тяжести от краев широкой и узкой полок относились, как т^-— s= -=-,
1асж1 ъ
что может быть достигнуто путем изменения размеров сечения, например
ширины одной из полок.

ОТДЕЛ V.
ПОЛНАЯ ПРОВЕРКА ПРОЧНОСТИ ПРИ ИЗГИБЕ.
ГЛАВА XV.
ВЫЧИСЛЕНИЕ КАСАТЕЛЬНЫХ И ГЛАВНЫХ НАПРЯЖЕНИЙ
В БАЛКАХ.
§ 91. Касательные напряжения в балке прямоугольного
сечения (формула Журавского).
Касательные напряжения при изгибе, уравновешивающие попе-
поперечную силу Q, достигают, как мы увидим дальше, более или
менее значительной величины в балках, сечение которых имеет
форму узкого прямоугольника или составлено из прямоугольников
(двутавр). Поэтому мы займёмся в первую очередь вопросом о вы-
вычислении касательных напряжений по сечениям, перпендикулярным
к оси балки, в том случае, когда эти сечения имеют форму прямо-
прямоугольника (фиг. 211) высотой h и шириной Ь.
Пусть на левую отсечённую часть балки действует положитель-
положительная поперечная сила Q, направленная вверх. Она уравновешивается
касательными напряжениями т, передающимися
от правой части и как-то распределёнными по
сечению.
Относительно распределения напряжений
Журавским A855 г.) были сделаны следующие
предположения:
1)	направление всех касательных напря-
напряжений параллельно уравновешиваемой ими
силе Q;
2)	касательные напряжения, действующие
по площадкам, расположенным на одном и том же
расстоянии z от нейтральной оси у, равны
между собой.
г- 211.	Как показывает теория упругости, оба ука-
указанных предположения оказываются достаточно
правильными для балок прямоугольного сечения, если высота балки
будет больше её ширины.
Перейдём к вычислению величины и распределения касательных
напряжений по поперечному сечению балки.
Возьмём балку прямоугольного сечения, подвергающуюся пло-
плоскому изгибу. Проведем какое-нибудь сечение 2—2 и рассмотрим

§ 91]
ФОРМУЛА ЖУРАВСКОГО
299
левую часть балки. На неё будут действовать изгибающий момент М
и поперечная сила Q, уравновешивающиеся нормальными и каса-
касательными напряжения-
напряжениями. Примем, что М
и С? положительны
(фиг. 212).
Нормальных напря-
напряжений изображать не
будем; касательные же
напряжения будут на-
направлены по прове-
проведённому сечению вниз.
Проведём очень близ-
близкое смежное сечение
/—/ на расстоянии
dx от 2—2. Относя
выделенный элемент /—/—2—2 то к левой, то к правой части
балки, получаем, что по сечению /—/ действуют такие же каса-
касательные напряжения т, как и по сечению 2—2, но направленные
в другую сторону.
Разницей в величине сил Q для
сечений /—/ и 2—2, которая имеет
место при наличии сплошной нагрузки,
пренебрегаем но её малости.
По свойству парности касательных
напряжений [гл. VII, § 36, формула
G.8)] следует ожидать появления та-
таких же касательных напряжений по
площадкам, перпендикулярным к сече-
сечениям балки, т. е. параллельным оси х.
Поэтому, если мы на расстоянии z и
z-\-dz от нейтральной оси проведём
два горизонтальных сечения балки и
таким образом выделим элемент с
рёбрами dz> dx, b (фиг. 213), то на
этот элемент будут действовать каса-
касательные напряжения т по вертикаль-
вертикальным граням и равные им по вели-
величине касательные напряжения т' по
горизонтальным граням.
Так как продольные волокна балки при деформации не давят
друг на друга, то по сечениям балки, параллельным оси, нормаль-
нормальных напряжений не будет, а будут одни касательные т\ Заменим
вычисление касательных напряжений т по сечению, перпендикуляр-
перпендикулярному к оси, вычислением равных им напряжений т' по сечению,
параллельному оси, взятому на том же уровне (фиг. 214).
Фиг. 214.

300
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В ВАЛКАХ	[ГЛ. XV
w
б)
На первый взгляд кажется странным появление касатель-
касательных напряжений по этим (параллельным оси балки) сечениям.
Однако сейчас же можно привести пример, поясняющий это
явление.
Представим себе балку состоящей из двух одинаковых брусков
прямоугольного сечения, положенных друг на друга (фиг. 215, а)\
будем пренебрегать трением между ними.
Предположим, что эта балка изгибается
хотя бы силой Я, приложенной посредине
пролёта. Вид балки после искривления в
сильно преувеличенном масштабе показан
на фиг. 215, б. Нижние волокна верхней
балки Афх растянулись, а верхние во-
волокна нижней балки А^В^ сократились по
сравнению со своей первоначальной дли-
длиной АВ.
Если же балка является цельным брус-
бруском, то она изогнётся так, как показано
на фиг. 215, в. Волокна АВ окажутся в ней-
нейтральном слое и не изменят своей длины.
VZJV/
Фиг. 215.
Фиг. 216.
Следовательно, при изгибе цельной балки по нейтральной пло-
плоскости от верхней половины балки на нижнюю, и обратно, будут
передаваться касательные напряжения т' = т, удерживающие верхнюю
и нижнюю половины балки от сдвига по нейтральному слою
(фиг. 215, г).
Изобразим на фиг. 216 нижнюю часть фасада балки прямоуголь-
прямоугольного сечения, испытывающей плоский изгиб. Проведём два очень
близких сечения 1—1 и 2—2 на расстоянии dx друг от друга.
Проведём ещё горизонтальное сечение на расстоянии z от ней-
нейтрального слоя.

§ 91]	ФОРМУЛА ЖУРАВСКОГО	301
Таким образом из балки выделится элемент ABCD размерами
dx, -к- — z и Ь. Вид этого элемента в аксонометрической проекции
показан на фиг. 217. Пусть изгибающий момент в сечении /—1
равен Ж, а в смежном сечении 2—2 равен
M-\-dM. Тогда по боковым граням элемента dT-
будут действовать нормальные напряжения
о — слева меньшие, справа ббльшие. По гори-
зонтальному сечению будут действовать каса-
касательные напряжения ir.
Касательные напряжения т по сечениям
/—/ и 2—2 в условие равновесия выделен-
выделенного элемента не войдут, так как мы используем равенство нулю
суммы проекций всех сил на ось балки; поэтому мы их на чертеже
и не изображаем.
Для составления уравнений равновесия вычислим все силы, дей-
действующие на наш элемент, параллельные оси балки. Элементарное
касательное усилие dT по площадке bdx будет равно
Нормальные напряжения, действующие по боковой бесконечно ма-
малой площадке dF на уровне zx от нейтральной оси, будут равны:
_Мгх
°— J *
Усилие dNu приходящееся на эту площадку, будет равно:
На всю боковую грань AD будет действовать сила Nt (фиг. 217):
Интеграл 1 zxdF представляет собой статический момент
1
относительно нейтральной оси у части площади сечения GFAD,
/расположенной от уровня z до края балки (фиг. 218). Обозначим
его S(z). Знак z показывает, что S(z) меняется в зависимости от
того, на каком расстоянии z от нейтральной оси мы вычисляем на-
напряжение т. Таким образом,
^>	A5.1)
Аналогично на грань ВС нашего элемента действует сила

302
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ [ГЛ. XV
Разность нормальных усилий
Л', N1= dM's(z)
Jy
уравновешивается при проектировании на ось Ох (фиг. 217) каса-
касательным усилием dT. Отсюда
Но ^. = Q, поэтому
_Ш_ S(z)
~~~~ dx Jyb *
_ QS(z)
Jvb
A5.3)
а значит, этой же формулой выражается и касательное напряжение
на уровне z по сечению, перпендикулярному к оси балки.
Выведем формулу S(z) для случая балки прямоугольного сече-
сечения (фиг. 218) высотой h и шириной Ь. Статический момент пло-
площади QFAD относительно оси ОХОХ будет равен величине этой
расстояние zk от её центра тяжести до
оси OxOi. Площадь GFAD равна
Н_
2
площади, умноженной на
расстояние zk
— z
равно
— -Z
Фиг. 218.
= *?(!-
Л2
A5.4)
При вычислении статического момента части площади сечения
безразлично, брать ли ту часть площади сечения, что расположена
ниже уровня z, или большую, так как по абсолютному значению оба
статических момента будут равны. Берут обычно статический момент
той части площади, вычисление которого более просто. Так как для
прямоугольника Jy=-^-f то формула A5.3) принимает вид:
8
Таким образом, величина касательного напряжения т меняется по
высоте прямоугольного сечения по закону параболы. У верхнего
и нижнего краёв сечения при z = zhhj2 касательное напряжение х
обращается в нуль, что находится в строгом соответствии с законом
парности касательных напряжений. Максимума оно достигает в точках

ФОРМУЛА ЖУРАВСКОГО
303
на нейтральной оси (там, где нормальное напряжение равно нулю)
при z = Q п притом в сечении, где Q (х) = Qmax:
„. _ 3 Qmax
A5.6)
Таким образом, наибольшее касательное напряжение при прямо-
прямоугольном сечении будет в 11/2 раза больше среднего значения этого
напряжения. На фиг. 219
изображена картина рас-
распределения касательных
напряжений при положи-
положительной поперечной силе.
Наличие касательных
напряжений в балке не-
несколько искажает при-
принятую нами раньше схему
деформации балки. Мы
считали, что под дей-
действием изгибающих мо-
моментов поперечные се-	фиг- 219-
чения, оставаясь плоски-
плоскими, поворачиваются (фиг.
220, а). Под действием
касательных напряжений
элементы материала ме-
между двумя сечениями пе-
перекашиваются; этот пе-
перекос, в соответствии с
изменением величины ка-
касательных напряжений,
возрастает от краёв бал-	Фиг. 220.
_ки к нейтральной оси.
Поэтому сечения искривляются (фиг. 220, б). Однако это искривле-
искривление почти не отражается на продольных деформациях волокон, что поз-
позволяет пользоваться формулой с = ~ и при наличии поперечной силы.
Поэтому кроме проверки прочности материала по наибольшим
нормальным напряжениям A3.15)
<*тах = уу ^ [а|
производится проверка прочности материала и по наибольшим каса-
касательным напряжениям
п я
?[т].	A5.7)
"max— yy? ^=L4'
Значения допускаемого напряжения |т] были даны выше.

304
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ
[гл. xv
= 22 кг! см2.
cmax
max —
1 'max
w
ibh
240 000 • 6
18 • 27*
3 • 2400
" 2 -27 • 18
Для того чтобы получить представление о порядке величины т в балках
прямоугольного сечения, рассмотрим числовой пример.
Найдём наибольшие нормальные и касательные напряжения для балки
прямоугольного сечения при следующих данных: балка лежит на двух
опорах и по всей длине 1=4 м несёт равномерную нагрузку при ^=1,2 т/м;
Mmax = 2>4 ™> Qmaxz=2^ Т> п = 27 см; b = \8 см; [*]= ПО кг/см2; [xj =
= 109,5 кг!см- < 110 кг!см2;
— 7,5 кг/см2 < 22 кг/см*.
Балка прямоугольного сечения, подобранная при нормальных напряже-
напряжениях, равных допускаемым, имеет большое недонапряжение по касательным.
Однако на практике может встретиться и обратное явление; оно имеет
место в случае, когда при большой поперечной силе изгибающий момент
невелик. В этих случаях и при прямоугольном сечении величина касательных
напряжений может оказаться решающей для определения размеров балки.
Формула касательных напряжений в балке прямоугольного сечения
впервые была выведена русским инженером Д. И. Журавским при проекти-
проектировании *) им деревянных мостов для железной дороги Петербург — Москва
в 1855 г. Журавский воспользовался несколько иным и более трудным приёмом
для получения этой формулы, не применяя зависимости —^— = Q, с которой
иногда совершенно напрасно связывают имя Шведлера.
§ 92. Касательные напряжения в балке двутаврового сечения.
Так как сечения двутавровых и тавровых балок можно рассмат-
рассматривать как составленные из прямоугольников, то с известным при-
приближением можно распространить на них теорию, изложенную в
предыдущем парагра-
параграфе. Таким образом, ка-
касательные напряжения
в точке на расстоянии z
от нейтральной оси для
двутаврового сечения
(фиг. 221) выражаются
также формулой
Фиг. 221.
нейтральной
балки. Что
Здесь 5 (z) — по-
прежнему статический
момент относительно
оси у части площади сечения между уровнем z и краем
касается величины b(z) — ширины сечения, то ей в дан-
*) Д. И. Журавский, О мостах раскосной системы Гау, часть И, при-
приложение III. Замечания относительно сопротивления брус#а, подверженного
силе, нормальной к его длине, стр. 130.

§ 92]	БАЛКА ДВУТАВРОВОГО СЕЧЕНИЯ	305
ном случае приписан значок z\ это означает, что в знаменатель
формулы A5.3) следует подставлять ширину сечения на уровне z.
Как видно из вывода формулы A5.3), величина b входила мно-
множителем в слагаемое i'b dxt т. е. была поперечным размером пло-
площадки, по которой действовало напряжение тг; таким образом, вели-
величина b была шириной балки на уровне z. Поэтому при применении
формулы A5.3) к двутавровому сечению следует, вычисляя каса-
касательные напряжения на уровне zn (фиг. 221, б)у т. е. на площадках,
попадающих в пределы полки, подставлять в знаменатель ширину
пояса Ьп. В этом случае формула A5.3) принимает вид:
При вычислении же касательных напряжений на уровне zc> т. е.
на площадках, находящихся в пределах стенки, надо вместо Ьг под-
подставлять толщину стенки ?с. Формула тоже видоизменится: придётся
брать статический момент двух прямоугольников (штриховка на
фиг. 221, а). Если произвести вычисления, то получим:
-f)]. A5.9)
В обоих случаях т меняется по параболической кривой.
Так как для двутаврового сечения толщина стенки обычно бывает
незначительной, то в этом профиле касательные напряжения дости-
достигают довольно большой величины, и поэтому проверка их всегда
является необходимой.
В месте перехода от полки (пояса) к стенке ширина Ьг меняется
скачком; в знаменатель формулы A5.9) можем подставить значе-
значения и Ьа и Ьс. Для величины касательного напряжения мы на этом
уровне получаем два значения. График распределения напряже-
напряжений по оси стенки z — z получает вид, изображённый на фиг.
221, в и 222, а.
Надо помнить, что это результат подсчётов, сделанных в предполо-
предположении, что формула A5.3) применима и к вычислению напряжений у места
перехода от пояса к стенке. На самом деле резкое изменение ширины сече-
сечения вызывает местное перераспределение напряжений.
Более точные исследования показывают, что по линии, совпадающей
с осью симметрии сечения, распределение касательных напряжений будет
с достаточной точностью изображаться графиком фиг. 222, б\ по линии же
2—2, проходящей у самого края стенки, — кривой, показанной на фиг. 222, в;
последний график показывает, что в точках у входящих углов сечения
касательные напряжения теоретически достигают очень большой величины;
на практике эти входящие углы скругляются, напряжения падают и их рас-
распределение в точках линии 2—2 примерно представляется кривой фиг. 222, г.
Наибольшая ордината графиков фиг. 222, а, б и г примерно одинакова
и относится к точкам на нейтральной оси.

306
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ	[ГЛ. XV
Внесённые поправки не изменяют двух основных следствий, вытекающих
из графика фиг. 222, д, а именно:
1)	наибольшее касательное напряжение будет в точках нейтраль-
нейтральной оси;
2)	большая часть поперечной силы уравновешивается касательными
напряжениями в стенке.
Поэтому пользование условным графиком (фиг. 222, а) допустимо. Надо
лишь помнить, что он не даёт правильного представления о распределении
Фиг. 222.
касательных напряжений как вблизи места перехода от полок к стенке, так
и в пределах самих полок.
Результаты исследования распределения напряжений в двутавровом се-
сечении позволяют высказать следующее заключение о работе различных эле-
элементов этого профиля.
Пояса балки, или полки, попадают в область наибольших нормальных
напряжений; так как их ширина большая, а толщина незначительна, они
всей своей площадью воспринимают нормальные напряжения, близкие к наи-
наибольшим; таким образом, они берут на себя главную долю сопротивления
сечения изгибающему моменту. Касательные напряжения в них очень малы,
а потому пояса принимают на себя сравнительно небольшую часть попереч-
поперечной силы.
Наоборот, на долю стенки приходится малая часть сопротивления изги-
изгибающему моменту, так как её наибольший размер расположен по высоте, а
по мере приближения к нейтральной оси нормальные напряжения быстро
падают. С другой стороны, величина S (z) для различных значений z в пре-
пределах стенки меняется слабо (средняя часть кривой на фиг. 222, я), а ши-
ширина Ьс мала. Поэтому касательные напряжения по всей высоте стенки
обычно достаточно велики, и почти вся поперечная сила ими и урав-
уравновешивается.
Таким образом, в двутавровом сечении пояса работают главным обра-
образом на уравновешивание изгибающего момента, а стенка — поперечной силы.
Проверим на касательные напряжения балку, испытывающую действие
поперечной силы 0 = 2,4 г, приняв [т] = 1000 кг/см2. Профиль двутавра
№ 18 в схематизированном виде показан на фиг. 223. Момент инерции
./,, = 1290 еж4.
Найдём касательные напряжения в точках на уровне 1, 2, 3. Статиче-
Статические моменты равны:
52	= 9 • 0,81 • 8,595 = 62,6 см*,
53	= 62,6 + 0,51 • 8,19 • 4,095 = 79,7 см9.

§ 93] КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ КРУГЛОГО ПРОФИЛЯ	307
Касательные напряжения равны:
т1==0,
„ 2400-62,6 оол
- —	=226
2400.62,6
1290-9
2400 • 79,7
= 12,9 кгIсм*,
= 292 кг1см2.
*2 "" 1290. 0,51 - ~" ""'*" ' wg - 1290 • 0,05
Условный график распределения касательных напряжений показан на
фиг. 223. Как видно, наибольшее касательное напряжение значительно ниже
допускаемого. Это произошло пото-
потому, что мы взяли прокатный профиль,	к-	дд-
у которого стенка сделана достаточно J^	/_
толстой. Как мы увидим дальше, для
составных балок, клёпаных и свар-
сварных, можно добиться значительно
большего использования материала
стенки. Определим ту долю попе-
поперечной силы, которая соответственно
условной эпюре воспринята стен-
стенкой. Умножим ординаты эпюры каса-
касательных напряжений на площадь стен-	_ ,&
ки двутавра Qc = 226 • 0,51.16,38 +
+ B92—226) * 0,51. у • 16,38 = 1890 +
+ 368 = 2258 кг, что составляет 94°/о	f
от всей силы Q.	фиг 223.
Приведённый в настоящем пара-
параграфе способ определения касатель-
касательных напряжений для двутавра может быть применён и к другим подобным
сечениям (полый прямоугольник, тавр и др.).
§ 93. Касательные напряжения в балках круглого профиля
и пустотелых.
Принимая ранее сделанное для прямоугольного сечения предположение,
что касательные напряжения постоянны по ширине профиля и параллельны
поперечной силе, что для круга не вполне
справедливо, можем пользоваться фор-
формулой A5.3):
*=Щу	A5.3)
которая определит ту составляющую
касательного напряжения, которая па-
параллельна Q.
Здесь S (z) будет по-прежнему ста-
статическим моментом части площади от
уровня z до края и будет выражаться
формулой (фиг. 224)
b (zt) • dzv
Для вычисления S(z) лучше ввести новую переменную — угол уг1; г —
радиус сечения. Тогда
z = г • sin oz; zt = r • sin уг1; b (zt) = 2r cos cpzl;
dzt = r cos срг1 • d^gi, b (z) = 2r cos yz.

308	КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ	[ГЛ. XV
Ограничим свою задачу нахождением величины ~тах*.
max °тах	,,,-7\
1С
Т
5max = J 2r cos Ъг • r sin ?2i • г cos -f,! • dbl =
2r8
2
2rs
3 ™ TZ, i - ., .	A5.10)
Ttr1
Так как /=—— и #,_0 = d = 2r, то получаем:
_ Q ¦ 2r3 . 4 __ 4Q
Tmax — 3 • 2r • т:г4 "" ^"
Таким образом, для круглого сечения
т. е. tmax в 1х/з раза больше среднего значения т.
Так как уже для прямоугольного сечения, где ттах в 17а раза больше
среднего значения, проверка по касательным напряжениям часто бывает
излишней, то тем более это относится к круглому сечению. Надо отметить,
однако, что для балок трубчатого сечения касательные напряжения могут
достигнуть более значительной величины.
Пример 65. Определить наибольшие касательные напряжения в чугун-
чугунной трубе наружным диаметром d = 10 см с толщиной стенок t = 1 см\
<?ш«=2*.
Наибольшее касательное напряжение имеет место в точках нейтральной
плоскости и будет выражаться формулой
Jy.b
05.7)
здесь Jy —момент инерции трубчатого сечения; Sfflax — статический момент
полукольца; b = 2t — удвоенная толщина стенок трубы
где Го — средний радиус трубы.
Статический момент полукольца будет равен разности статических мо-
моментов относительно диаметра наружного и внутреннего полукругов; формула
статического момента для полукруга:
S(z)=2?~.	A5.10)
Искомый статический момент полукольца равен

309
Наибольшее касательное напряжение для кольцевого сечения в два раза
больше среднего; напомним, что для прямоугольника это соотношение
равно 1,5, а для сплошного круга 1,33;
§ 94]	ПРОВЕРКА ПРОЧНОСТИ ПО ГЛАВНЫМ НАПРЯЖЕНИЯМ
Таким образом,
Q.2r\t Q	2Q
2 «2000
я . 9 • 1
= 141,4 кг/см*.
Пример 66. Определить для уровня аЪ
нормальные и касательные напряжения в балке
пустотелого профиля, загружённой в проверяе-
проверяемом сечении изгибающим моментом Af = 1,2 тм
и поперечной силой Q = 4 т. Плоскость дей-
действия М и Q — xOz. Форма поперечного сечения
балки представлена на фиг. 225.
Момент инерции сечения
8 • 14» 4 • 10* , 4 • 23
12
4-2*
12
12 ^ 12 ~"
B • 7* —58 + 1) = 1500 см\
Фиг. 225.
Статический момент части сечения, лежащей
выше уровня аЬ, где можно ожидать значи-
значительных нормальных и касательных напряжений (при г = 5 см\ равен
= 2. 8E+1)== 96 см%.
Ширину сечения Ь(г) следует принять равной сумме толщин двух стенок
Ь (z) = 2 + 2 = 4 см.
Напряжения по уровню аЪ будут:
Mz
= 400 кг/см*,
120000 . 5
1500
4000 . 96
1500 . 4
§ 94. Проверка прочности по главным напряжениям.
В предыдущем изложении были введены две проверки прочности
материала балки при изгибе — по нормальным A3.15) и касательным
A5.7) напряжениям:
М
o*ax=-iiFL<[o]>	A3.16)
Cmax^rr
A5.7)
Выясним, прочность каких элементов балки мы проверяем по
этим формулам.

310
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ
[ГЛ. XV
7Ш
max
Фиг. 226.
На фиг. 226 показана часть фасада изучаемой балки в том
месте, где расположены сечения с наибольшим изгибающим моментом
и наибольшей поперечной си-
силой. На чертеже изображены
элементы, прочность которых
мы проверяем по условиям
A3.15), A5.7). Первое отно-
относится к элементам, расположен-
расположенным у верхнего и нижнего
	краёв сечения с Мтах. Эти эле-
элементы подвергаются простому
растяжению или сжатию. Вто-
Второе условие прочности A5.7)
относится к элементу, располо-
расположенному у нейтрального слоя в
сечении с Qmax» — этот эле-
элемент испытывает чистый сдвиг.
Таким образом, производя
принятую в обычной практике
расчёта проверку прочности по наибольшим нормальным и касатель-
касательным напряжениям, мы на самом деле проверяем прочность мате-
материала балки лишь в трёх указанных на фиг. 226 элементах.
Нет никакой уверенности, вообще говоря, в том, что эти три
элемента находятся в наиболее опасном состоянии. Поэтому мы
должны научиться проверять прочность каждого элемента балки,
взятого в любом сечении на любом расстоянии z от нейтральной
оси. Только тогда мы сумеем среди этих элементов разыскать
наиболее напряжённый и сможем проверить его прочность.
Возьмём какой-нибудь элемент материала (фиг. 226) в произволь-
произвольном сечении на расстоянии z от нейтрального слоя. На этот элемент
будут действовать нормальное на-
напряжение а по граням, перпендику-
-я-лярным к оси балки, и касательные
напряжения т по всем четырём бо-
боковым граням. Фасадные грани эле-
элемента будут свободны от напряже-
напряжений (фиг. 227).
Напряжения о и т выразятся сле-
следующими формулами:
Фиг. 227.
A5.12)
где М — изгибающий момент и Q — поперечная сила в том сечении,
где мы выделили элемент.
Возьмём случай, когда о и х положительны. Так как этот эле-
элемент подвергается сложному напряжённому состоянию, то для его

§941
ПРОВЕРКА ПРОЧНОСТИ ПО ГЛАВНЫМ НАПРЯЖЕНИЯМ
311
проверки придётся применить теории прочности; вычисления надо
начать с нахождения главных напряжений.
Так как по фасадной грани ABCD элемента (фиг. 227) и по
параллельным ей не действуют касательные напряжения, то это будет
одна из главных площадок; так как по ней отсутствуют и нормаль-
нормальные напряжения, то соответствующее ей главное напряжение равно
нулю. Таким образом, мы имеем дело с плоским напряжённым
состоянием.
Нам теперь нужно найти оставшиеся два главных напряжения,
зная нормальные и касательные напряжения по двум взаимно
перпендикулярным площадкам, параллельным и перпендикулярным
к оси балки (фиг. 226). Подобную задачу мы уже решали в § 38
путём построения круга напряжений. Там этот приём был применён
к более общему случаю напряжённого состояния, когда по двум
взаимно перпендикулярным площадкам с нормалями аир действо-
действовали напряжения оа, о , та, ^ =— V Условимся теперь относить
значок а к грани нашего элемента, перпендикулярной к оси балки,
а р — к грани, параллельной этой оси (фиг. 228).
Фиг. 228.
Отложим от точки О в положительном направлении величину
а, =а — отрезок ОКа\ на перпендикуляре к оси а в точке Ка отло-
отложим вверх отрезок KaDat равный т. Точка Da лежит на круге
напряжений, соответствует площадке, перпендикулярной к оси балки.
Для площадки, параллельной оси балки, о =0; значит, точка
К9 совпадает с точкой О. Отрезок K*Dp отложенный вниз, изобра-
изобразит касательное напряжение х = — т и даст вторую точку круга Ь..
Соединяя их, получаем центр круга — точку С — и радиусы СиЛ
и CD . Построение круга даёт нам отрезки ОА и 05, изображаю-
изображающие искомые главные напряжения. Из чертежа ясно, что эти напря-
напряжения — разных знаков. Поэтому нумерация главных напряжений
должна быть выбрана такой:

312	КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ	[ГЛ. XV
Пользуясь данными в § 38 формулами G.13), получим:
Формулы для ах и а3 могут быть сведены в одну:
= у [о ± V^ -Г 4^2 ]•	A5.13)
Построение и вычисление мы провели, когда и с и х положительны.
При отрицательном значении того или иного из этих напряжений
следует изменить его знак в формулах A5.13). Соответственное
изменение построений пришлось бы сделать и при графическом
определении ох и а3 с помощью круга напряжений.
Имея величину всех трёх главных напряжений, мы можем соста-
составить расчётные условия по всем теориям прочности.
По первой теории — наибольших нормальных напряжений:
ах^[о] или сг1 = 1[а+1/а* + 4^]<{а].	A5Л4)
По второй теории — наибольших относительных удлинений:
Подставляя значения ait а2, а3, находим:
ji(e /O
[у О
Принимая (л = 0,3, получаем:
cr3 = [0,35a + 0,65 ТЛ^ + Фс»] < [о].	A5.15)
По третьей теории — наибольших касательных напряжений:
[at —o,]<[o]t или |[a+|/a« + 4x^ - a + Y<fi + 4х2 ] < [a];
окончательно
.	A5.16)
Наконец, по четвёртой теории — наибольшей потенциальной энергии
изменения формы:
K*i - **? + («• - ^зJ + (а, - аО2] ^ 2 [о]«,
откуда
• + (а - V^+Wf + B /О2 + 4х«)«] < 2 la]».

§ 94]	ПРОВЕРКА ПРОЧНОСТИ ПО ГЛАВНЫМ НАПРЯЖЕНИЯМ
После преобразований получаем:
313
Фиг. 229.
A5.17)
Теперь надо выяснить, в каких точках балки следует произво-
производить проверку прочности на главные напряжения.
Так как расчётное напряжение аг зависит и от а и от т, то про-
проверке подлежит тот элемент материала балки, для которого с и х
будут одновременно возможно
ббльшими; это осуществимо при	б.	__._ г
наличии, скажем, двух таких ус-
условий: 	!_
1)	изгибающий момент и по-
поперечная сила достигают наиболь-
наибольшей величины в одном и том же [
сечении;
2)	ширина балки резко ме-
меняется вблизи краёв сечения (на-
поимер в двутавре или пустотелом прямоугольном профиле); эпюры
напряжений для таких профилей (фиг. 229) показывают, что на
уровне перехода от полки к стенке (точки а и *) касательные и
нормальные напряжения имеют величину, близкую к максимальной.
Указанные два условия, таким образом, определяют и необходи-
необходимость дополнительной проверки прочности, и тот элемент, для кото-
которого эта проверка должна быть сделана; может случиться, что эти
условия не имеют места; тогда ограни-
ограничиваются выбором нескольких точек,
могущих дать наиболее высокие значе-
значения сг Что же касается выбора расчёт-
расчётной формулы, то наиболее правильным
было бы применить теорию наиболь-
наибольшей потенциальной энергии A5.17).
На практике, однако, при расчёте
балок до сих пор сохранилось приме-
применение теории наибольших нормальных
напряжений A5.14), дающей часто бо-
более экономичные размеры.
Пример 67. Балка АВ (фиг. 230), ле-
лежащая на двух опорах, нагружена симме-
симметрично расположенными силами Р = 6,4 г,
ii	P
Фиг. 230.
		двутавровое сечение и про-
проверить прочностГматериала у места перехода от полки к стенке.
Наибольшие значения Ми <? будут в одном сечении-под грузом.
AL
: А* = 0,5 • 6,4 = 3,2 /л/,

314
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ [ГЛ. XV
Подбираем сечение:
ш — тах
М
320000

1400
Надо взять двутавровую балку №22; №=232 см9; J =2550 см*. Размеры
поперечного сечения балки показаны схематично на фиг. 231. При выбран-
выбранном профиле
320000
110-
1
5ft
232
-=1380 кг 1см2.
Дополнительная проверка прочности должна
быть сделана при 2=10,13 см.
320000-10,13
= 1271 кг/см2.
2550
Статический момент равен
S(z) =11.0,87 • 10,565 = 101 см\
Касательные напряжения
6400 • 101
Фиг. 231.
0,54 • 2550
= 469 кг/см2.
Условие прочности по первой теории прочности A5.14):
~ [1271 + )/'12712 + 4 • 4692 ] = 1426 кг\см2 > 1400 кг/см*.
Условие прочности по четвёртой теории прочности A5.17):
У 12712 + 3-4692 = 1510 кг/см2 > 1400 кг\см2.
Так как расчётные напряжения по четвёртой теории прочности на 8°/о
превышают допускаемые напряжения, размер сечения следует увеличить,
приняв двутавр № 22а. Для этого профиля после пересчёта получим:
ome« 1260 кг/см2 и при 2 = 10,11 см о= 1158 кг/см2 и х = 482 кг/см2. Рас-
Расчётные напряжения: по первой теории прочности аГ1 = 1329 кг\см2 и по чет-
четвёртой теории прочности аг^ = 1423 кг/см2.
§ 95. Направления главных напряжений.
В предыдущем параграфе мы определили лишь величину главных
напряжений для произвольно взятого элемента балки и не интересо-
интересовались их направлением. С точки зрения проверки прочности мате-
материалов, одинаково сопротивляющихся растяжению и сжатию, полу-
полученных результатов было достаточно. Для таких же материалов, как
железобетон, крайне существенно знать направления растягивающих
напряжений в каждой точке, чтобы в этом направлении расположить
стержни арматуры.
Определение положения главных напряжений может быть сделано
при помощи кругл напряжений (фиг. 232). Пусть в рассматриваемом

§95]
НАПРАВЛЕНИЯ ГЛАВНЫХ НАПРЯЖЕНИЙ
Я15
случае оа и та по сечению, перпендикулярному к оси балки, будут
положительны:
,	Mz
Строим круг; взаимное расположение линий действия напряжений aa
и наибольшего (алгебраически) главного напряжения cj совпадает
с относительным расположением на чертеже круга напряжений ли-
линии BDa и оси абсцисс, составляющих между собой угол а (фиг. 232).
Фиг. 232.
Чтобы на чертеже элемента построить линию действия о,, надо
от направления оа отложить угол a no часовой стрелке. При пере-
перемещении выбранного элемента в пределах сечения направление глав-
главных напряжений меняется. У краёв балки одно из главных напря-
напряжений нуль, а другое направлено параллельно оси балки, у нейтраль-
нейтрального слоя главные напряжения составляют углы 45° с осью балки.
На фиг. 233 изображены круги напряжений и направления глав-
главных напряжений в различных точках сечения. Направление сжимаю-
сжимающих напряжений показано на фасаде балки жирными линиями, растя-
растягивающих — тонкими. Принято, что изгибающий момент и поперечная
сила в сечении положительны.
Получив направление главных напряжений в какой-либо точке
проведённого сечения, продолжаем направление одного из них до
пересечения с соседним сечением. В полученной точке определяем
новое направление рассматриваемого главного напряжения и продол-
продолжаем его до пересечения со следующим сечением. Поступая таким
образом, получим ломаную линию, которая в пределе обратится
в кривую, касательная к которой совпадает с направлением рассма-
рассматриваемого главного напряжения в точке касания. Эта кривая на-
навивается траекторией главного напряжения. Направление траек-
траекторий главных напряжений зависит от вида нагрузки и от условий

316
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В ВАЛКАХ	[ГЛ. XV
Фиг. 233.

§ 951
НАПРАВЛЕНИЯ ГЛАВНЫХ НАПРЯЖЕНИЙ
317
опирания балки. Через каждую точку балки можно провести две
траектории главных напряжений — растягивающих и сжимающих
(фиг. 234). Для сжимающих напряжений траектории показаны пункти-
пунктиром, для растягивающих — сплошной линией.
Фиг. 234.
В железобетонных балках надо располагать арматуру так, чтобы
она шла примерно в направлении траекторий главных растягиваю-
растягивающих напряжений. Для примера на фиг. 235 показано расположение
арматуры в простой балке.
//72
Фиг. 235.
Пример 68. Балка прямоугольного сечения высотой h = 160 мм и
шириной Ь = 80 мм, пролётом /=0,80 м нагружена силой Р = 2 г посредине
пролёта. Найти величину и направление главных напряжений в точке на
расстоянии 2 = 2 см вверх от нейтрального слоя в сечении на расстоянии
лго = О,3 м от левой опоры.
Реакции балки А и В равны 1000 кг; изгибающий момент во взятом
сечении равен М=А*го=1000- 30=30000 кгсм. Поперечная сила 0=1000 кг.
Момент инерции сечения
Статический момент части сечения выше уровня г равен (фиг. 236, а)
Sz = 8 • 6 • 5 = 240 см*.
Нормальное напряжение в рассматриваемой точке равно
30 000 • 2
а = ~-г=-
2730
. = — 22 кг/см2.
Касательное напряжение равно
ggfr) . 1М0-240 ... , s
т==~Л~в + 2730-8 ~+И Нг/СМ-

318	КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ	[ГЛ. XV
Главные напряжения равны:
с3 I ~2 ~~	2	~"	~~"
I — 26,6 J
Для определения направления главных напряжений изобразим выде-
выделенный у рассматриваемой точки элемент материала и построим круг
напряжений.
Фиг. 236.
На фиг. 236, в линия BDa соответствует направлению напряжения 9t. Вели-
Величина угла а определяется формулой
DaK
ВК
	 	* *		 * * _ О QQO.
~ 26,6-22~р~"А аД
§ 96. Центр изгиба.
| = 67°15'.
При изучении случая плоского изгиба балок мы предполагали, что все
внешние силы лежат в одной из главных плоскостей инерции балки. Возьмём
балку, имеющую симметричное сечение (например,
прямоугольник), и посмотрим, что будет, если мы
нагрузим её силами, лежащими в плоскости, парал-
параллельной главной плоскости симметрии (фиг. 237).
Пусть для этой балки сила Р будет приложена к
концу стержня OiO, лежащего в плоскости торца
балки и с ним скреплённого. Прикладывая в центре
тяжести торцевого сечения О две равные и прямо
У* противоположные силы Р, мы видим, что балка
будет изгибаться в плоскости главной оси Oz
силой Р, однажды перечеркнутой на чертеже, и
скручиваться парой сил с моментом Р • ОХО. Здесь
мы будем иметь случай совместного действия
плоского изгиба и кручения. Для того чтобы из-
избежать кручения, которому балка такого сечения,
как вытянутый прямоугольник, сопротивляется
плохо, в рассматриваемом случае необходимо приложить силу Р в точке О,
в плоскости симметрии сечения Oz. Опыт показывает, что, действительно,
при загрузке балки симметричного сечения силами в плоскости симметрии
кручения не происходит; балка испытывает плоский изгиб.
Несколько иначе будет обстоять дело, если мы нагрузим балку сосредото-
сосредоточенной силой в плоскости главной оси, не являющейся осью симметрии.
Фиг. 237.

§961
ЦЕНТР ИЗГИБА
319
Пример такой нагрузки для балки швеллерного (корытного) сечения изобра-
изображён на фиг. 238. Опыт показывает, что хотя сила Р лежит в главной пло-
плоскости Oz, однако балка не только изгибается, но и скручивается (фиг. 239).
Фиг. 23S.
Фиг. 239.
Наблюдающееся на опыте явление не только изгиба, но и скручивания
показывает, что при этой нагрузке касательные напряжения, вызванные
М
1
изгибом, складываются в равнодействующую Q,
уже не лежащую в плоскости xOz, а ей параллель-
параллельную. Значит, при изгибе рассматриваемой балки
помимо напряжений т = J v ' возникают еще ка-
кие-то касательные напряжения. Выясним вели-
величину и распределение этих напряжений.
Рассмотрим балку корытного сечения, закре-
закреплённую одним концом и расположенную так, что
стенка её вертикальна. Нагрузим её на другом	ф 240
конце вертикальной же силой Р (фиг. 240), распо-
расположенной в главной центральной плоскости сече-
сечения. Выделим из этой балки сечениями 1—1 и 2—2 элемент длиной dx. Он изо-
изображён на фиг. 241, там же показаны размеры поперечного сечения. Отрежем
M+dM
г
U
Фиг. 242-
сечением 3—3, параллельным оси балки, часть верхней полки этого швеллера
в рассмотрим равновесие отрезанной части. Она изображена на фиг. 242.

320
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ	[ГЛ. XV
По граням AiBiCiDi и A2B2C2D2 этого элемента действуют нормальные
напряжения с, в нашем случае растягивающие; величина их зависит от
изгибающих моментов М \\M-\-dM в сечениях 1 — 1 и 2— 2. Сумма JV2
нормальных усилий по площади A2B2C2D2 больше суммы Nu действующей
по площади AiBidDu поэтому для равновесия выделенного элемента полки
должны возникнуть касательные напряжения тп по площади DiAiA2D2.
Сумма напряжений тп должна уравновешивать разность нормальных уси-
усилий, т. е.
rnt dx = N2 —
Обозначим среднее значение нормального напряжения, действующего по
площадке торца полки A2B2C2D2} т. е. напряжение в точках Е2у через a", a
соответствующее среднее напряжение в точках Ei сече-
сечения AtBidDi — через а' (фиг. 242).
Тогда
где величина напряжения а" равна
Следовательно,
M + dM h
N* ~ J	2 ey'
j Подобным же образом
—! rflH	VZ Отсюда
М h
.. .r dM h .
= ЛГ2 — ЛГ1== -j-. — ty,
или
Фиг. 243.
	d™ h 	4,ij,	/ie; iq\
~" лчГ • o7^— "o7«	A0.18)
По свойству парности касательных напряжений наличие тп по площадке
AiA^D^Di сейчас же влечёт за собой появление такого же по величине и
обратного по знаку касательного напряжения в точках у ребра Л2^2 по
площадке А^В&С2й2 (фиг. 242). (Надо помнить, что масштаб чертежа иска-
искажён: отрезок DiD2 = dx очень мал, а отрезок А*В2=у — конечная величина.)
Таким образом, по сечению 2 — 2 в точках верхней полки будут дей-
действовать горизонтально направленные касательные напряжения тл, меняю-
меняющиеся по закону прямой в зависимости от у (фиг. 243):
Qh
Подобным же образом можно показать, что такие же напряжения, но
обратного направления, будут действовать в точках нижней полки.
Касательные напряжения тп, действующие на каждую полку, дадут
в сумме равнодействующее усилие Ти которое можно вычислить так. Сила,
действующая на заштрихованную площадку t dy} равна (фиг. 243):

§96]	ЦЕНТР ИЗГИБА
суммируя все такие силы, получаем:
321
Эти усилия показаны на фиг. 244. Кроме касательных напряжений т„, по
сечению действуют вертикально направленные касательные напряжения:
T_QS(z)
7- Jt>(z)-
Условная эпюра распределения этих напряжений показана на фиг. 245.
Соответствующие усилия сложатся в равнодействующее усилие Г2, которое
с достаточной степенью точности можно считать равным поперечной силе
Q и приложенным в центре тяжести стенка Са (фиг. 244); таким образом,
здесь пренебрегают вертикальными касательными напряжениями в полках
(по сравнению с касательными напряжениями в стенке)').
1*1-
4*1»
¦Г
И'
и
ТТ"
ft
И.
¦ ¦¦
-
Г
к
Фиг. 244.
Фиг. 245.
Полная система касательных усилий, состоящая из усилия Г, и пары
усилий Ти может быть заменена одним усилием Г2, приложенным з точке
Kit в расстоянии е от центра тяжести стенки С2.
Плечо пары усилий Тг измеряется расстоянием h (фиг. 243 и 244). Для
определения расстояния е приравняем нулю сумму моментов трёх сил отно-
относительно точки /fa:
отсюда
A5.19)
Таким образом, при изгибе швеллера сосредоточенной силой Р, приложенной
в центре тяжести сечения, помимо обычных напряжений т, возникают ещё
касательные напряжения т„. Суммирование всех этих напряжений даёт нам
касательное усилие, проходящее уже не через центр тяжести сечения О,
а через точку ДГ2, так называемый центр изгиба (иногда именуемый центром
жёсткости или центром скалывания).
1) Все выводы этого параграфа можно считать достаточно точными,
если толщины станки и полки составляют менее 1:20 соответствующего
второго размера. В противном случае расчёт нуждается в уточнении: при
определении, например, положения усилия Г* следует учесть и вертикаль-
вертикальные касательные усилия в полках.

322
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В ВАЛКАХ1	[ГЛ. XV
Если мы расположим силу Р в плоскости xOz, то отрезок балки длиной
х (фиг. 246) не может быть в равновесии; поперечная сила Q в сечении 2
проходит через точку О2, тогда как полное касательное усилие 7У—через
точку /Са- Для равновесия необходимо, чтобы в проведённом сечении воз-
возникли ещё касательные напряжения кручения, которые дадут пару, уравно-
уравновешивающую совместно с усилием Г3 поперечную силу Q в сечении 2.
Если же мы хотим избежать кручения нашей балки, то надо силу Р
приложить в точке Ki хотя бы при помощи приваренного отрезка уголка,
как схематически показано на фиг. 247. Тогда поперечная сила в сече-
сечении 2 пройдёт тоже через точку Д,
и равновесие по отношению к ка-
2^ ^ ^	сательным напряжениям будет обес-
обеспечено.
Фиг. 246.
Фиг. 247.
Формулу для вычисления е можно преобразовать. Подставим в неё
приближённое значение момента инерции J; последний будем вычислять,
принимая момент инерции полки равным её площади, умноженной на квадрат
половины расстояния h. Тогда (фиг. 243)
где tc — толщина стенки. Называя площадь стенки
полки bit = Fa, получаем:
= Fc, а площадь
=т"'г
и, далее,
A5.20)
?п
" Эта формула показывает, что расстояние е будет тем больше, чем
больше площадь пояса по отношению к площади стенки; но во всяком
случае

§ 97]	ПОДБОР СЕЧ5НИЯ БАЛОК ПО ДОПУСКАЕМЫМ НАГРУЗКАМ	323
Для сечений типа двутавра при изгибе поперечными силами мы также
будем иметь наличие горизонтальных касательных напряжений в поясах
(фиг. 248). Однако благодаря симметрии сечения эти напряжения взаимно
уравновешиваются в пределах каждой полки, и центр изгиба совпадает с
центром тяжести сечения. Совпадение центра изгиба с центром тяжести
сечения имеет место, если сечение имеет две оси симметрии или центр
антисимметрии (зетобразная форма); в этом случае скручивание при дейст-
действии нагрузки в плоскости, проходящей через, ось стержня, исключено. Кроме
того, из формул A5.18) и A5.19) следует, что скручивание
балок при нагрузке их в главной плоскости, не являющейся .
плоскостью симметрии, связано с наличием в сечениях попе- t^:
речной силы. Впрочем, для тонкостенных стержней несимме-
несимметричного профиля (см. главу XXX) скручивание балки может
возникнуть и при отсутствии поперечных сил.
Практическое значение рассмотренного явления доста-
достаточно велико. Балки корытного, уголкового и тому подобных г— ^
сечений скручиваются весьма легко; поэтому расположение I'""** I -——*
плоскости действия внешних сил вне центров изгиба может
повести к значительным дополнительным деформациям в этих Фиг. 248.
балках. Более точные исследования показывают, что в неко-
некоторых случаях кручение балок таких профилей сопровождается
появлением дополнительных нормальных напряжений, достигающих иногда
значительной величины. Надо, однако, помнить, что для развития этих до-
дополнительных напряжений необходимо, чтобы деформация кручения — и до-
довольно значительная — произошла. Поэтому наличие связей, соединяющих
балку с соседними элементами конструкции и препятствующих кручению,
может предотвратить появление этих добавочных напряжений даже и при
несовпадении плоскости внешних сил с плоскостью центров изгиба.
Пример 69. Швеллер № 40 изгибается сосредоточенными силами,
расположенными в плоскости, параллельной стенке. Определить расстояние
этой плоскости от оси стенки при условии, что кручение балки должно
быть исключено.
Плоскость действия сил должна проходить через линию центров изгиба.
Расстояние этой линии от оси стенки определяется формулой A5.20)
c
4У "
Для нашего профиля (см. таблицу в приложении IX) bt = b — d=115 — 8 =
= 107 мм; Л = 400 —13,5 = 386,5 мм; 7=15220 см*. Отсюда
_ 38,65*. 10,72-1,35 _OQ
е~~ 4-15220	"" ''
т. е. плоскость нагрузки должна проходить вне сечения на расстояний
е = 3,8 см от оси стенки.
§ 97. Подбор сечения балок по допускаемым нагрузкам.
Всё предыдущее изложение было построено на методе подбора
сечения и поверки прочности балок по допускаемым напряжениям.
Но уже на примере скручиваемого стержня мы видели, что при
неравномерном распределении напряжений по сечению метод подбора
размеров сечения по допускаемым нагрузкам дает иной результат.
Подобный же случай мы имеем и при изгибе.

324
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ
[ГЛ. XV
В методе расчёта по допускаемым напряжениям мы пользовались
для подбора сечения балок условием
W
Здесь [о] для материалов, имеющих площадку текучести (мягкая
сталь), было равно
где от — предел текучести, a kT — соответствующий коэффициент
запаса.
Таким образом, опасным мы представляем себе здесь то состояние,
когда наибольшее напряжение в опасном сечении балки дойдёт
до предела текучести. Изгибающий момент при этом состоянии назо-
назовём Мт; он соответствует достижению грузоподъёмности материала
в наиболее напряженных волокнах опасного сечения балки. Однако
этому состоянию не будет отвечать исчерпание грузоподъёмности
всей балки, как конструкции.
df
if
а)
б)
\
1
^
г)
д)
Возьмём стальную балку симметричного (например, прямоуголь-
прямоугольного или двутаврового) сечения (фиг. 249, а и б). При моменте,
равном Мт, распределение напряжений в опасном сечении показано
на фиг. 249, в\ напряжение дошло до предела текучести лишь
в крайних волокнах, вся же остальная часть балки находится в уп-
упругом состоянии. Поэтому для дальнейшей деформации балки необ-
необходимо новое увеличение нагрузки и изгибающего момента: грузо-
грузоподъёмность балки ещё не исчерпана.
При увеличении момента зона текучести будет распространяться
внутрь балки, эпюра напряжений примет вид, показанный на фиг. 249, г,
и в пределе, когда материал по всей высоте сечения потечёт и
грузоподъёмность балки будет полностью исчерпана, эпюра напря-
напряжений примет форму двух прямоугольников (фиг. 249, д). Изгибаю-
Изгибающий момент на этой стадии работы балки и будет предельным,
разрушающим для балки в целом. Дальнейшая деформация балки

§ 97]	ПОДБОР СЕЧЕНИЯ ВАЛОК ПО ДОПУСКАЕМЫМ НАГРУЗКАМ .	325
пойдет уже без увеличения момента; в опасном сечении образуется
так называемый пластический шарнир.
Определим величину этого предельного момента М*. Он будет
равен сумме моментов относительно нейтральной оси усилий по
фиг. 249, д. На площадку dF на расстоянии z от нейтральной оси
будет действовать сила oTdF; момент этой силы относительно ней-
нейтральной оси равен aTdF • z. По симметрии сечения достаточно вы-
вычислить сумму моментов этих сил для верхней или нижней поло-
половины сечения и результат удвоить; тогда
I
2
где F—площадь всего сечения. Так как от постоянно для всех точек
сечения, то
М* = 2ат С zdF=2Gx
i
2
поскольку интеграл
представляет собой статический момент половины сечения относи-
относительно нейтральной оси.
Условие прочности имеет вид
при коэффициенте запаса kT получаем:
хТогда условием прочности будет:
Жтах<25тахЬ1 и 2Smax^^p.	A5.21)
Следовательно, при расчёте по допускаемым нагрузкам вместо
подбора сечения симметричной балки по ее моменту сопротивления
W приходится подбирать размеры по величине удвоенного статиче-
статического момента полусечения балки. Для прямоугольного сечения вы-
высотой h и шириной b
9С 	9h~h 	^! —1 5 —	1 5 W
Подставляя это значение в формулу A5.21), получаем:

326
КАСАТЕЛЬНЫЕ И ГЛАВНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ	[ГЛ. XV
Таким образом, при расчёте по допускаемым нагрузкам необхо-
необходимый момент сопротивления балки прямоугольного сечения полу-
получается в 1,5 раза меньшим, чем при расчёте по допускаемым напря-
напряжениям.
Можно для любого симметричного сечения представить вели-
величину 25тах как произведение момента сопротивления на некоторый
коэффициент п, зависящий от формы сечения:
A5.22)
тогда формула A5.21) примет вид
Фиг. 250.
Для прямоугольника я = 1,5; ^ для двутавровых сечений нашего
сортамента п колеблется от 1,13 *до 1,17; в среднем можно принять
л=1,15. Таким образом, переход на метод расчёта по допускаемым
нагрузкам для стальных балок наиболее употребительного профиля
может дать возможность поднять грузоподъёмность на 15%, что
равносильно ^повышению допускаемых напряжений. Такое повышение
допускаемых напряжений потребует более
тщательного исследования (при проверке
прочности) запаса против других возмрж-
ных видов разрушения балки.
Опыт показывает, что стальные дву-
двутаврового профиля балки никогда не мо-
могут быть разрушены только в результате
наступления текучести по всему сече-
сечению. Чаще наблюдается потеря устойчивости пояса (фиг. 250) или
устойчивости стенки. Таким образом, повышение допускаемых на-
напряжений, к которому сводится в данном случае применение метода
расчёта по допускаемым нагрузкам, требует особого внимания к про-
проверкам устойчивости элементов балок.
При действии повторной нагрузки следует иметь в виду возмож-
возможность разрушения материала за счёт развития трещин усталости.
Это требует дополнительной про-
проверки прочности для обеспечения кон-
конструкции от подобного вида разру-
разрушения.
Для балок, сечения которых имеют лишь
одну ось симметрии, например балок тавро-
таврового профиля, расчёт по допускаемым
нагрузкам несколько осложняется.
На фиг. 251 изображены сечение та-
такой балки и эпюра распределения нор-
нормальных напряжений при исчерпании гру-
грузоподъёмности балки. Здесь надо сначала
определить положение нейтральной оси; в рассматриваемой стадии работы
балки эта ось уже не проходит через центр тяжести сечения.

§ 97]
ПОДБОР СЕЧЕНИЯ БАЛОК Пв ДОПУСКАЕМЫМ НАГРУЗКАМ
327
Назовём площадь сжатой части сечения Flt а растянутой F8. Усло-
Условие равенства между собой сумм растягивающих и сжимающих напря-
напряжений даёт
GjFi = <sTF2 или Ft = F2.
Нейтральная ось делит площадь сечения на две равновеликие части. При
изгибе в пределах упругости это же условие привело нас к равенству стати-
статических моментов сжатой и растянутой части сечения, в силу чего нейтраль-
нейтральная ось проходила через центр тяжести сечения. Здесь же она делит пло-
площадь сечения пополам.
Найдя положение нейтральной оси, определяем величину
kl
где Si и S2— статические моменты верхней и нижней половин площади
сечения относительно нейтральной оси. Условие прочности принимает вид
A5.23)
Изложенные соображения относятся к случаю чистого изгиба; наличие
поперечных сил несколько осложняет расчёт.
Пример 70. Определить коэффициент п для круглого сечения ра-
радиуса г.
Статический момент полукруга относительно нейтральной оси равен (§ 93)
2г8	яг*
Smах=-о-; момент сопротивления W = —г, следовательно,
о	4
4г8 - 4
W
= 1,7.
Пример 71. Определить по методу допускаемых нагрузок величину до-
допускаемой силы Р, приложенной посредине пролёта / = 2 м к шарнирно-опёр-
той балке. Сечение балки — тавр 70 х 70 х 8 мм
(фиг. 252). Допускаемое напряжение
[а] = 1600 кг/см2.
Величина допускаемого изгибающего момента
определяется формулой
Для нахождения Sx и S* надо отыскать
положение нейтральной оси так, чтобы она
делила площадь сечения пополам и была перпен-
перпендикулярна к оси симметрии. Называя через zt расстояние нейтральной
оси от края полки, получаем уравнение
7.^ = 6,2
отсюда гх = 0,75 см.
Статические моменты равны
k =t 7,0 ^ = 1,98 см\ S2 = 7,0 • ^ + 6,2 . 0,8 . 3,15 = 15,61 см*.

328
РАСЧЁТ СОСТАВНЫХ БАЛОК
[ГЛ, XVI
Изгибающий момент равен
Мтах = A,98 + 15,61) • 1600 = 28 160 кгсм.
Допускаемое значение силы Р равно
rpi _ 4Л1тах __ 4.28160
[ * ~~ I ~~ 200
= 563 кг.
ГЛАВА XVI.
РАСЧЁТ СОСТАВНЫХ БАЛОК.
§ 98. Подбор сечения клёпаных балок.
Наибольший прокатный профиль двутавровой балки № 706 имеет
момент сопротивления №=5010 смъ (см. стр. 837). Момент сопро-
сопротивления самого большого балочного широкополочного профиля
(ГОСТ 6183—52) № Ю0Б7 достигает 20 440 смъ. Однако прокатные
профили больших размеров изготовляются лишь по специальным за-
заказам при больших поставках,
а потому очень часто прихо-
приходится прибегать к составным
сечениям — к клёпаным и свар-
сварным балкам.
Клёпаная балка состоит
(фиг. 253, а) из вертикального
листа /, нескольких пар гори-
горизонтальных листов 2 и четырех
уголков 3; уголки и листы сое-
соединяются заклёпками.
Сварная балка (фиг. 253, б)
J
| состоит из вертикального и го-
горизонтальных листов, соединён-
соединённых сварными швами.
Фиг. 253.	Покажем на примере ход
подбора сечения клёпаной бал-
балки. Допускаемые напряжения примем следующие: на растяжение и
сжатие [а] = 1600 кг/см\ на срезывание [т] = 1000 кг/см\ на смя-
смятие в заклёпках [ос] = 2800 кг/см\ на срезывание в заклёпках
[т]3=1000 кг/см\
Схема выбранной для расчёта балки и нагрузок показана на
фиг. 254. Опасными сечениями являются:
а)	сечение посредине пролёта балки: Мтах= 177,6 тм\ Q = 0;
б)	сечения над обеими опорами: М = 174,2 тм\ Qmax = 94 т.
Необходимый момент сопротивления равен
«7 ^гаах 17 760 000 ц щи а
W=-w- = —Ym-=U 100 см\

§ 98}
ПОДБОР СЕЧЕНИЯ КЛЁПАНЫХ БАЛОК
329
Определение необходимых размеров поперечного сечения балки
будет требовать выполнения следующих операций:
1. Прежде всего необходимо установить основной размер попе-
поперечного сечения — высоту вертикального листа ft.
Практика проектирования показала, что достаточно хорошие ре-
результаты дают следующие эмпирические формулы:
ft =1,2/W
при
10000 смъ
(ft в см)
30 000 см\
ft = 1,0 У W при
Для нашего случая можно принять промежуточное значение
й=1,18уТГПH = 1,18-105,7 = 124,7 см.
Примем высоту стенки ft =124 см.
2. Далее необходимо определить толщину вертикального листа Ъ
(толщину стенки балки). При предварительном подборе толщины
стенки будем в запас
прочности считать, что p*eomA=W6jSm	iB хР=30т
вся поперечная сила вое-	|	g^ttfm/M
принимается только стен-
стенкой, т. е. прямоугольным
сечением высотой А и
шириной Ь. Тогда усло-
условие прочности по каса-
тельным напряжениям по-
получит вид:
2bh
откуда
3-94000
2 • 124 -1000
= 1,13
Фиг. 254.
По техническим условиям
для обеспечения устойчи-
устойчивости стенки (сопротивления короблению) толщина её должна быть
не менее Ъ ^ 0,08 ]/"А (см), или для нашего примера
Ъ S* 0,08 /124 = 0,89 см.
Обычно толщину стенки принимают в пределах от 8 до 12 и
более мм: назначаем '? = 1,0 см =10 мм.

330	РАСЧЁТ СОСТАВНЫХ БАЛОК	[ГЛ. XVI
3. Для определения размера поясов балки, состоящих каждый
из двух уголков и горизонтальных листов, необходимо выяснить,
какой же момент инерции должна иметь балка.
Выше мы нашли величину необходимого момента сопротивления
W=\\ 100 см3; это — так называемый момент сопротивления нетто,
рабочий момент сопротивления балки, или момент сопротивления
ослабленного заклёпочными отверстиями сечения балки.
Перейдём к моменту инерции:
унет _ ^
здесь zmax — расстояние от нейтральной оси до наиболее удалённого
волокна балки. Величина zmSLX превышает половину высоты верти-
вертикального листа на толщину пакета горизонтальных листов; принимая,
что эта толщина колеблется в обычных балках от 1 до 3 см, по-
получаем:
h
В нашем случае примем zmax = 62 -}- 2 = 64 см. Если мы при этом
ошибёмся на 1 — 2 см, то относительная ошибка будет весьма ма-
малой. Далее находим
Лет = ^нет ^шах = 11 100 • 64 ^ 711 000 СМ\
Практика проектирования показала, что ослабление момента инер-
инерции за счёт заклёпочных отверстий составляет обычно от 12 до
18%.
Полный момент инерции сечения, включающий в себя и моменты
инерции площадей заклёпочных отверстий, будем называть J брутто
и обозначать Уб . Следовательно, Уб =A,12-5-1,18) Унет.
Примем Убр = 1,15 Унет= 1,15-711000^ 818 000 см*.
' 4. Далее следует определить момент инерции поясов. Так как
размеры стенки нам известны, то мы можем вычислить её момент
инерции. Он равен
Г
I
г
fy На долю обоих поясов (горизонтальные
J листы и уголки) остаётся момент инерции:
— 159 000 =
= 659 000 см*.
	I	1
Фиг. 255.	g теперЬ можно найти приблизительную
величину площади пояса Fn по его моменту
инерции, предположив, что центр тяжести пояса обычно лежит на
уровне верха вертикального листа (фиг. 255).

§ 98]
ПОДБОР СЕЧЕНИЯ КЛЁПАНЫХ БАЛОк
331
Пренебрегая собственным центральным моментом инерции пло-
площади пояса, можно считать, что
Отсюда
2-659000
_860 ,
Площадь пояса состоит из площади двух уголков и пакета гори-
горизонтальных листов.
Площадь уголков обычно составляет 0,3-ь 0,5 от площади пояса,
т. е. в нашем случае от 26 до 43 см*. Выпишем из сортамента
уголки, дающие нам приблизительно нужную площадь. Это уголки:
90 X 90 X 8 площадь двух уголков 27,8 см2
90 X 90 X 9
100 X ЮО X 8
100ХЮ0Х10
100 X ЮО X 7
100 X ЮО X IS
125 X 125 X 8
»
»
31>2
31,2
38,4
30,4
34,4
39,4
. Тогда на долю
Выберем из этой таблички уголки 100 X 100 X
площади пакета горизонтальных листов остаётся
86,0 — 38,4 = 47,6 ^^48 см\
Приняв, что в поясе должно быть два листа, и назначая толщину
48
листов 10 мм, мы должны взять ширину b = y = 24 сл* = 240 мм.
Брать листы толщиной 12 мм в данном
случае не можем, так как при этом ширина
окажется равной 20 сму листы не будут за-
закрывать уголков, не будут иметь свесов над
ними. ^
Ставить один лист 480 X Ю невозможно,
так как будут большие свесы листа, не поддер-
поддержанные уголками; эти свесы могут коробиться
при работе сжатого пояса балки. Обычно свесы
допускаются в пределах от 5 до 30 мм\ верхний
предел определяется требованием, чтобы расстояние от оси вертикаль-
вертикальной поясной заклёпки до края листа не превышало 88, где Ь — тол-
толщина листа. При листах 240 X Ю свес получается (фиг. 256) равным
15 мм, что допустимо.
Фиг. 256.

332
РАСЧЁТ СОСТАВНЫХ ВАЛОК
[гл. xvi
§ 99. Проверка прочности балки по нормальным напряжениям.
Задавшись размерами составных частей сечения, приступаем к про-
проверке прочности балки по формулам A3.15) и A5.7), для чего сле-
следует вычислить более точно значения У, W, S. Вычисление всех
этих величин удобно проводить в табличной форме. Таблица 21 по-
подобных вычислений дана на стр. 333. Поясним произведённые в таб-
таблице подсчёты и записи.
Момент инерции уголков равен учетверённому моменту инерции
одного уголка (фиг. 257). Этот момент инерции равен собственному
центральному моменту инерции уголка (берём из таблиц сортамента)
плюс произведение площади его на квадрат расстояния а от центра
тяжести уголка до нейтральной оси; расстояние zQ от края уголка
до его центра тяжести дано в таблицах сортамента.
А
-оси
-ОСЬ
Фиг. 257.
Фиг. 258.
Подобным же образом вычисляется момент инерции обеих пар
горизонтальных листов (фиг. 258).
Момент инерции выбранного нами сечения равен Убр = 811 000 см*.
Как мы видим, несмотря на приближённость подбора, мы получили
искомую величину момента инерции очень близкой к той, которую
хотели получить. Разница составляет всего
811000 — 818 000	nQ0/
	8Г8000	Ю0 = -0,9о/0.
Теперь необходимо вычислить уменьшение момента инерции
балки вследствие наличия заклёпочных отверстий.
Расположение Ьаклёпок на фасаде балки показано на фиг. 259,
260, 261.
Заклёпки в вертикальных и горизонтальных полках поясных
уголков располагаются в шахматном порядке. Расстояние между
заклёпками а называется шагом заклёпок. Определение величины
шага заклёпок в поясных уголках приведено ниже, в § 102. Шаг
заклёпок в уголках жёсткости расчётом обычно не устанавливается,
а берётся равным bd-t-ld, где d— диаметр заклёпки.

99] ПРОВЕРКА ПРОЧНОСТИ БАЛКИ ПО НОРМАЛЬНЫМ НАПРЯЖЕНИЯМ 333
I
п
и
О5
ю
см
9
IN
ю
8
8
8
СМ	~*
О
ас
S
8
?
с^ +
ю
2
см ~	~
^ см	см
4 см	см
сч	см
и
О.
СО
Я
S
Eg
О
са
Н
1
S
s о
?&
я
1
2 S §
СМ
2
«s
3
зз
л
ч
н
о.
0Q
8
8
2
S
в
X
us
о
р.
|
U
к
о
с
3
н
О
&
О
S
X
о
sr
о
S
§
см
см
о

334
РАСЧЁТ СОСТАВНЫХ БАЛОК
[ГЛ. XVI
Вид по 1-1
Фиг. 259.
Г
а
L
625
SS5
300
180
Фиг. 261.
УголоМ
\
ти
1
Фиг
+
+
/
|
•¦-
+
+
+
ч-
/1
. 260.
2
/
/
с 700x700* 70
1.80*80*3

§ 99] ПРОВЕРКА ПРОЧНОСТИ БАЛКИ ПО НОРМАЛЬНЫМ НАПРЯЖЕНИЯМ 335
Диаметр заклёпок принимается примерно равным удвоенной тол-
толщине применённых в конструкции листов; стандартные диаметры за-
заклёпок: rf=14, 17, 20, 23, 26 мм.
Для предотвращения коробления и выпучивания тонкой верти-
вертикальной стенки её укрепляют, приклёпывая через промежутки, при-
примерно равные высоте балки, уголки жёсткости.
На фиг. 259 показана часть фасада и разрез клёпаной балки,
на которой уголки жёсткости присоединены с постановкой прокла-
прокладок между ними и стенкой балки. Прокладки на фасаде отмечены
тонкой штриховкой.
На фиг. 260 показан другой приём прикрепления уголков жёсткости.
Для того чтобы перевести уголок жёсткости из плоскости стенки балки
в плоскость поясных уголков, концы уголка жёсткости «высаживаются».
В обоих случаях уголок жёсткости прикрепляется к балке заклёпками.
В нашем примере выбран диаметр заклёпок 20 мм и шаг
а =120 мм. Расположение заклёпок, прикрепляющих уголок жёст-
жёсткости, показано на фиг. 259, 260 и 261.
При вычислении величины ослабления момента инерции учиты-
учитывают, что отдельные элементы сечения балки ничем, кроме заклёпок,
не соединены. Поэтому вычисляют наибольшее возможное ослабление
для каждого из этих элементов. Так, для стенки берут сечение /—/
(фиг. 260) — по заклёпкам, прикрепляющим уголок жёсткости; для
горизонтальных листов — сечение 2—2 — через вертикальные заклёпки;
для уголков — тоже сечение 2—2, так как отверстия в горизонталь-
горизонтальных полках уголков сильнее ослабляют балку, чем отверстия в вер-
вертикальных: они дальше расположены от нейтральной оси.
Поэтому отверстие для заклёпки, присоединяющей поясной уголок
к стенке, учитывается при вычислении ослабления стенки (заштрихо--
ванный прямоугольник на фиг. 261) и не учитывается при вычисле-
вычислении ослабления уголка (два белых прямоугольника).
Влияние отверстий на прочность балки принято учитывать, вычи-
вычитая из момента инерции всего сечения Убр момент инерции АУ за-
заштрихованных площадей заклёпочных отверстий. Этот способ учёта
влияния заклёпочных отверстий является условным; он просто отра-
отражает тот факт, что балка, составленная из нескольких элементов,
слабее сплошной, цельной балки.
При вычислении момента инерции площадей заклёпочных отвер-
отверстий пренебрегают их собственными центральными моментами инер-
инерции, так как размеры этих отверстий малы по сравнению с разме-
размерами балки. Тогда А/ просто равен сумме произведений величины
каждой заштрихованной площадки на квадрат её расстояния до ней-
нейтральной оси.
Подсчёт моментов инерции заклёпочных отверстий производим
в графе 3 таблицы 21. Действительное ослабление оказалось равным
118 500
щ-_. 100 = 14,7% вместо принятых нами 15%.

336	РАСЧЁТ СОСТАВНЫХ БАЛОК
Момент инерции сечения балки равен:
[ГЛ. XVI
см
Момент сопротивления нетто
YV7 	 Унет
w нет	 _
692 500
= 10 800 см\
Zmax	64
и действительное напряжение получается равным
17 760 000
°
°тах— 10 800
Перенапряжение составляет
= 1645
1600 кг\см\
1645—1600
1600
100% = 2,8%.
Обычно практикой допускается перенапряжение (или недона-
пряжение) до 5%. Таким образом, принятое сечение может быть
оставлено.
Если бы перенапряжение оказалось более 5%, то сечение балки
следовало бы усилить. Это проще всего достигается увеличением
24Q , ,..	ширины полок с последующей повтор-
повторной проверкой прочности усиленного
таким образом сечения.
§ 100. Проверка прочности балки
по касательным напряжениям.
Полученное сечение надо проверить
по касательным напряжениям по фор-
5
муле A5.7):
	 Q
max Smax
При пользовании этой формулой обыч-
обычно возникает вопрос, помещать в зна-
знаменатель Убр или Унет. Очевидно, в пер-
первом случае пришлось бы в числителе
иметь 5бр, а во втором 5нет. Отношение -~
ФИГ. 262.	-	5нет г,
примерно то же, что и j—. Поэтому
принято обе величины вводить в формулу, не учитывая осла-
ослабления, т. е. брутто.
Вычисление статического момента полусечения (фиг. 262) вы-
выполнено в пятой графе таблицы 21. Условие прочности по касатель-
касательным напряжениям:
Г\ А АЛЛ *7П t />
= 835 кг!сл

§ 101] ПРОВЕРКА ПРОЧНОСТИ БАЛКИ ПО ГЛАВНЫМ НАПРЯЖЕНИЯМ 337
§ 101. Проверка прочности балки по главным напряжениям.
Проверку прочности по главным напряжениям производим в сече-
сечении над опорой, где М= 174,2 тм и Qmax=94 г (фиг. 254).
Принимают, что в клёпаной балке уголки ниже заклёпки совсем
не связаны со стенкой. Утрируя это предположение, можно изобра-
изобразить поперечное сечение балки, как показано на фиг. 263.
Тогда в наиболее опасном положении по высоте сечения оказы-
оказываются элементы материала стенки, лежащие на уровне горизон-
горизонтальных поясных заклёпок; в этом
уровне и принято проводить проверку
прочности. Величину нормальных на-
напряжений следует вычислять по фор-
формуле
АЛ ~
62 см
а касательных — по формуле
где. be — толщина стенки, а 5П — ста-
статический момент пояса (заштрихо-	Фиг# 2t^'
ванная площадь) плюс части стенки
выше поясных заклёпок (перечёркнутый прямоугольник). Другими
словами, считают, что переход от широкой части балки к узкой
происходит на уровне оси поясных заклёпок. Делаем вычисления:
_ 17 420000.56,5 _	, ,
0 — 692500 ~ *^U Кг1СМ '
5П = 3024 + 2270 + 1-5,5 F2 — 2,75) = 5620 см\
94 000-5620
1-811000
= 652 кг/см\
Что касается формулы для расчётных напряжений, то на практике
ещё удержалась проверка по первой теории прочности (наибольших
нормальных напряжений):
ог1 = у[о + /о2 + 4т* ] < [о].	A5.14)
Эта формула A5.14) даёт более экономичное решение, а полу-
полувековой опыт пользования ею даёт удовлетворительные результаты.
В результате имеем:
1
1
O/.1===JL[i420+ /1420* +4-6522] = уA420+1926)= 1673 кг/см*.
При [о] = 1600 kzJcm* перенапряжение составляет всего лишь 4,5%.

338
РАСЧЁТ СОСТАВНЫХ ВАЛОК
[гл. х\л
Надо сказать, что для составных балок, работа которых в дей-
действительности гораздо сложнее, эта поверка носит в значительной
мере условный характер, чем и объясняется сохранение до сих пор
указанной расчётной формулы.
§ 102. Расчёт заклёпок в балке.
Совместная работа всех элементов клёпаной балки обусловлена
наличием заклёпок. Поэтому необходимо разместить поясные заклёпки,
установить расстояние между ними и проверить их прочность. Рас-
1 п	X)	смотрим сначала гори-
горизонтальные поясные
заклёпки.
Вырежем сечения-
сечениями / и 2 (фиг. 264)
из балки часть пояса
длиной а между двумя
вертикальными за-
заклепками. Пусть изги-
изгибающий момент в се-
сечении / будет Ж, а в
сечении 2 М-\- ДУИ.
	Тогда вырезанный эле-
элемент пояса окажется в
равновесии под дей-
6)
Фиг. 264.	Фиг. 265.
ствием разности сумм (Л^ и N\) нормальных напряжений, пе-
передающихся на него слева и справа, и реакции заклёпки N
(фиг. 264, в и г).
Нормальное усилие Nl9 действующее на торец выделенного эле-
менга пояса (фиг. 265), будет равно статическому моменту заштри-

§ 102]	,	РАСЧЁТ ЗАКЛЁПОК В ВАЛКЕ	339
хованной площади, пояса относительно нейтральной оси, умножен-
умноженному на у (сравнить с формулой A5.1) стр. 301):
Точно так же.
Усилие, перерезывающее заклёпку (так называемая сдвигающая сила)
Но -г- =Q и dM=Qdx\B нашем случае можно заменить dx на а
и dM на ДМ, следовательно, LM = Qa и
A6.1)
Эта формула впервые была выведена Д. И. Журавским.
В свою очередь, обе стенки пояса (вертикальные полки угол-
уголков) будут передавать на заклёпку силы -^ уравновешивающиеся
реакцией стенки балки N (фиг, 264, г); заклёпка подвергается двой-
двойному перерезыванию. Условие прочности заклёпки на перерезыва-
перерезывание имеет вид:
N	QSna
'•d*\ =о,™*з^[т]3.	A6.2)
Т) 2JT
Условием прочности на смятие служит:
_ N _QSna
где d — диаметр заклёпки; Ьс — толщина стенки балки; [т]3 — до-
допускаемое напряжение на срезывание; [ос] — допускаемое напряже-
напряжение на смятие.
Проверку надо вести в сечении, где Q — максимум. В нашем
примере:
Qmax = 94 г, J= 811 000 см*\ Sa = 3024 -f- 2270 = 5294 см*\
d = 2 см; bc=l см.

340
РАСЧЁТ СОСТАВНЫХ БАЛОК
[ГЛ. XV!
Расстояние между заклёпками определится из условий прочности
на перерезывание A6.2):
[т]37тц/* 	 100Q.811 000-3,14.4
а^ 2QSn ~ 2.94000-5294
или на смятие A6.3):
'°c]Jbcd 2800.811000 • 1 -2
а
• = 9,2 см.
QSn	94 000-5294
Следовательно, шаг поясных заклёпок необходимо принять равным
а = 90 мм.
Таким же путём можно проверить прочность заклёпок, соеди-
соединяющих горизонтальные листы с уголками. Однако такой проверки
никогда не делают, так как эти заклёпки находятся в лучших усло-
условиях, чем горизонтальные заклёпки пояса.
§ 103. Подбор сечения и проверка прочности сварной балки.
Ход подбора размеров сечения сварной балки тот же, что
и клёпаной. Не приходится лишь вычислять ослабления сечения.
Уголки жёсткости заменяются рёбрами, привариваемыми к стенке
(фиг. 266). Для примера рассмотрим вариант расчёта балки, изучен-
и
Фиг. 266.
ной в §§ 98—102. Принимаем ту же высоту стенки, что и для
клёпаной балки, й=1240 мм; предполагая толщину пояса / равной
2 см, получаем необходимую величину момента инерции:
J=W-zmax = 11 100-64^711000 смК
Вычитая момент инерции стенки, получаем момент инерции
поясов:
Jn = 7U 000 —159 000 = 552 000 смК

§ 103]
ПРОВЕРКА ПРОЧНОСТИ СВАРКОЙ ВАЛКИ
341
Плоиладь пояса
'{h
2-552 000
: 1262
= 69,5 см*.
Пояс делаем из одного толстого листа. Для соблюдения нормаль-
нормальных пропорций между шириной пояса Ь и высотой балки h обычно
принимают
?с^0,2/г-ь-0,3/г и b < 30 t.
При толщине листов t = 2 см получаем необходимую ширину
пояса 6 = 35 см, что удовлетворяет всем поставленным ограни-
ограничениям.
Фиг. 267.
Фиг. 268.
Вычислим величину момента инерции поясов при принятых разме-
размерах (фиг. 267 и 268):
ja _ 2.
63*-35.2l = 2 B3 -f 277 830) ^ 555 700 смК
Момент инерции всего сечения равен
У = 159 000 -f 555 700 = 714 700 смх.
Момент сопротивления
W =1Ц™'= П 150 см\
64
Наибольшие напряжения
17 760 000
= 1592 кг/см2,
т. е. всего на 0,5% меньше допускаемых.
Вместо заклёпок приходится назначать сварные швы, прикреп-
прикрепляющие пояс к стенке. Можно сделать как сплошной шов, так и
прерывистый (фиг. 266, 267 и 268).
Примем следующие обозначения: т — расчётная высота сечения
шва; с — расчётная длина участка шва (шпонки); а — расстояние
между серединами шпонок; KJ — допускаемое напряжение на сре-
срезывание в материале шва.

342	РАСЧЁТ СОСТАВНЫХ ВАЛОК	[ГЛ. XVI
Шпонки в сварной балке играют ту же роль, что заклёпки
в клёпаной балке. Поэтому размеры шпонок и расстояние между
ними следует определять так же, как это сделано в предыдущем
параграфе. Каждая пара шпонок (слева и справа от вертикального
листа) берёт на себя силу, равную
Условие прочности шпонки на срезывание имеет вид
^ ^[x.J.'	A6.4)
Отсюда
¦^~QS7~'	A6'0)
Задаваясь высотой шва т, находим отношение —. Величина т не
должна быть меньше 4 мм.
Наибольшее расстояние в свету между шпонками должно быть
не больше 168 и во всяком случае не больше 250 мм (8 — наимень-
наименьшая толщина свариваемых листов). Длина же шпонки должна удо-
удовлетворять условию
?min^4/tf И ВО ВСЯКОМ Случае tfminS^O ММ.
Каждая шпонка шва является очагом крнцентрации местных напря-
напряжений, что при хрупком состоянии материала в зоне сварки очень
нежелательно. Прерывистые швы не допускают применения автомати-
автоматической сварки. Поэтому Т. У. на ответственные металлические конст-
конструкции рекомендуют применение сплошных швов по всей длине
соединяемых элементов.
При сплошном шве условие прочности на срез по ломаному
сечению / — / напишется так:
откуда
m—rw:y	A6J)
§ 104. Расчёт деревянных составных балок.
В § 91 мы рассмотрели работу деревянной балки, составленной из двух
одинаковых, положенных друг на друга брусьев.,
На практике для соединения частей деревянной балки часто применяют
шпонки, играющие ту же роль, что заклёпки и сварные шпонки в металли-
металлических балках. Сейчас применяется очень большое число различных типов

§104]
РАСЧЁТ ДЕРЕВЯННЫХ СОСТАВНЫХ БАЛОК
343
шпоночных соединений, но все эти типы развились из наиболее простого,
проверочный расчёт которого мы и рассмотрим.
Представим себе балку, составленную из двух сосновых брусьев прямо-
прямоугольного сечения, соединённых дубовыми шпонками и стянутых болтами
Фиг. 269.
(фиг. 269). При работе балки каждая шпонка воспринимает от одного брус-
бруска и передаёт другому силу
д, QSna
J >
A6.8)
Фиг. 270.
где Sn — статический момент половины сечения шпоночной балки относи-
относительно нейтральной оси. Характер действия сил N на шпонку показан на
фиг. 269.
Сила Nt стремящаяся сдви-
сдвинуть верхний брус относи-
относительно нижнего, передаётся на
шпонку и вызывает появление
следующих напряжений (обо-
(обозначения размеров даны" на
фиг. 269 и 270):
а)	смятия балки о шпонку
на площадке db, где Ь — ширина
балки, *2d — высота шпонки;
б)	скалывания балки на участке между шпонками по площадке (а — с) Ь;
в)	смятия шпонки о балку по, площадке db\
г)	скалывания шпонки по площадке cb.
Для допускаемых по этим площадкам напряжений можно принять сле-
следующие значения:
[аСм] = на смятие вдоль волокон = 70 кг/см2
[х] = на скалывание вдоль во-
волокон	= 12 кг)см*
[аСм]9о = на смятие поперёк во-
волокон	= 50 кг/си2
[xJ90 = на скалывание поперёк во-
волокон в тангенциальном на-
направлении = 10 кг/см*
Условия прочности для указанных четырёх площадок напишутся так:
для ш-териала
балки (сосна);
для материала
шпонок (дуб).
Чъ
N
(а — с) Ь
N
М;
A6.9)
A6.10)
A6.11)
A6Л2)

344	РАСЧЁТ ЖЕЛЕЗОБЕТОННЫХ БАЛОК	[ГЛ. XVII
Балка в целом должна удовлетворять условию прочности
°=	7	= -r-^W'
где [а] — допускаемое напряжение на растяжение или сжатие при изгибе
балки, принимаемое равным 80 кг/см2.
Величину J в данном случае следовало бы вычислять с учётом ослабле-
ослабления сечения шпонкой по формуле:
J=-^lh*-Bd)*].	A6.13)
Так как глубина врубок d составляет обычно 1/10 -ь 1/20 Л, то ослабление
сечения врубками, вычисленной по этой формуле, получается порядка 0,10/с
Между тем, многочисленные опыты показывают, что за счёт податливости
соединений балка составного сечения значительно слабее цельной балки.
Некоторые технические условия предлагают поэтому расчётный момент
сопротивления W определять как для цельного бруса с умножением его
затем на понижающий коэффициент 0,8, если балка состоит из двух брусьев
или на 0,7, если она состоит из трёх брусьев.
Пример 72. Проверить напряжения в деревянной балке по следующим
данным: нагрузка равномерно распределена по длине балки и равна (j = 1,25 т/м;
пролёт балки / = 6 м (фиг. 269); высота балки h = 42 см; ширина Ь = 30 см;
ширина шпонки с =12 еж, толщина шпонки 2*/ = 4 см; расстояние между
осями шпонок (шаг шпонок) а = 22 см. Допускаемые напряжения приведены
на стр. 343.
Наибольшие нормальные напряжения от изгиба A3.15):
Мтят ?/3-6	3.1,25.6*. 105
*«"BWBT5B3ir- 3,2.30.42*
Сила взаимодействия между шпонкой и балкой A6.8):
_ QSa _ qlbh'a 12 _3-1,25-6-22 _
/V~ J "~ 2-8.bh* — 4-42 -
Напряжения смятия проверяются для дуба поперёк волокон, так как
для сосны вдоль волокон значение допускаемого напряжения на смятие
значительно больше:
осм^ = -N- = |^ = 49,2 кг/см' < 50 кг/см*.
Напряжения скалывания [формулы A6.11) и A6.12)]:
N	2950
в балке: т = —	г- = ОЛ 1А = 9,8 кг/см% < 12 кг/см2;
о (а — с) 30» 10
N 2950
в шпонке: % = -т- = -о?гТо в 8,2/сг/сж2 < Юкг/см2.
so ос ои* 1.2,
Заданные размеры балки удовлетворяют всем условиям прочности.
ГЛАВА XVII.
РАСЧЁТ ЖЕЛЕЗОБЕТОННЫХ БАЛОК.
§ 105. Расчёт железобетонной балки по допускаемым
напряжениям.
На практике довольно часто встречаются балки, составленные	из разно-
разнородных материалов. Деревянную балку можно укрепить снизу	стальным
листом. В железобетонных балках в растянутую зону помещают	стальную
арматуру.

§ 105]
РАСЧЁТ ПО ДОПУСКАЕМЫМ НАПРЯЖЕНИЯМ
345
В этих случаях предполагается, что разнородные элементы, из которых
изготовлена балка, соединены друг с другом так, что обеспечена их совмест-
совместная работа. Считает, что поперечные сечения такой сложной балки при
деформации остаются плослшми и поворачиваются вокруг нейтральных осей.
Как следствие из этого положения вытекает линейный закон распределения
удлинений и укорочений по высоте балки:
z
е = —.
Р
Формула для вычисления нормальных напряжений имеет вид
Е Е
при этом в расчётах, конечно, приходится учитывать разные значения моду-
модулей Е для материалов такой сложной балки.
Схема железобетонной балки показана на фиг. 271. В нижней (растяну-
(растянутой) части балки помещена арматура в виде трёх стальных прутьев.
Фиг. 271.
При расчёте такой балки принято считать, что:
1)	бетон не берёт на себя растягивающих напряжений;
2)	арматура благодаря крюкам и сцеплению с бетоном работает совме-
совместно с последним и воспринимает все растягивающие усилия;
3)	сечения балки остаются плоскими.
В целях получения расчётных формул для рассматриваемой балки надо
повторить в основном вывод, изложенный в §§ 78 и 79. Верхние волокна
балки сжаты, нижние растянуты, нейтральный слой проходит на некотором
расстоянии 20 от верхнего края балки. Принимая, что сечения при изгибе
остаются плоскими, получаем, что относительные удлинения и укорочения
меняются по закону прямой линии (фиг. 272). Умножая относительную деформа-
деформацию в каждой точке на модуль упругости соответствующего материала, полу-
получаем эпюру распределения нормальных напряжений (фиг. 273).
М
Фиг. 272.
Фиг. 273.
Напряжения в стальной арматуре будут значительно больше, чем в бетоне,
так как модуль упругости стали Ес примерно в 10 4-15 раз больше модуля
упругости бетона Е$. Можно в среднем считать
Ес = 2 .106
) Еб = 140 000 -f- 200 000 кг\см\

346
РАСЧЁТ ЖЕЛЕЗОБЕТОННЫХ ВАЛОК
[гл. xvn
Наибольшие сжимающие, напряжения в бетоне обозначим fy. Растягива-
Растягивающие напряжения в стали можно считать одинаковыми по всей площади
арматуры, так как её диаметр мал по сравнению с высотой сечения; эти
напряжения обозначим ас.
Назовем расстояние от сжатого края сечения до центра тяжести арма-
арматуры hx; площадь сечения арматуры Fa; высоту сечения h\ ширину Ь; отно-
Ez
шение модулей упругости -=~ =л= 10 -М5. Рас-
Еб
стояние нейтральной оси от верха балки z0 и ве-
величину напряжений определим из условия равно-
равновесия отсечённой части балки под действием нор-
нормальных напряжений и изгибающего момента.
Эти условия приводятся к двум: 1) сумма
сжимающих напряжений равна сумме растяги-
растягивающих и 2) сумма моментов внутренних усилий
относительно нейтральной оси О равна изгибаю-
изгибающему моменту.
Сжимающее усилие D можно вычислить
приёмом, аналогичным вычислению усилия Nt
На площадку Ъ dz в расстоянии z от нейтральной оси (фиг. 274) дей-
дейсила ab dz; вся сумма сжимающих усилий равна
Фиг. 274.
/)= \ abdz;
в § 91.
ствует
но по линейному закону для напряжений
	 z
отсюда
Растягивающее усилие в арматуре равно
Первое уравнение равновесия принимает вид (фиг. 273):
=0, или D = ZC9
или
A7.1)
Напряжение <jc можно выразить через <sd.
Из линейного закона для деформаций (фиг. 272) имеем:
Но
следовательно,
==Ес?с и а^ =

§ 106]	РАСЧЁТ ПО ДОПУСКАЕМЫМ НАГРУЗКАМ	347
Уравнение равновесия A7.1) принимает вид
Преобразуя, получаем:
Fa«	2Fanhl
Из этого уравнения находим положение нейтрального слоя zQ:
(П.2)
Зная г0, можем составить второе уравнение равновесия. При этом сле-
следует учесть, что усилие D приложено в центре тяжести соответствующего
треугольника; расстояние усилия D от верха балки равно -^, а плечо пары
усилий D и Z равно hx — •—. Второе уравнение имеет вид:
о
или
Отсюда получаем формулу напряжений в бетоне:
2М
Зная arf, находим и ос, т. е. напряжение в арматуре:
Zc D __ d0 ^
Проверка прочности в этом случае должна быть произведена по формулам
maxcd^[acj и тахсс^[а],
где [асж] — допускаемое напряжение для бетона на сжатие, а [а] — для стали
на растяжение.
§ 106. Расчёт железобетонной балки по допускаемым нагрузкам.
Описанный выше способ предполагает, что опасным состоянием балки
будет такое, при котором либо наибольшие напряжения в бетоне дойдут до
предела прочности ав, либо напряжения в арматуре — до предела текучести от.
Крайне редко может случиться, что оба эти обстоятельства наступят одно-
одновременно; обычно раньше наступает явление текучести в арматуре; бетон
же имеет ещё некоторый запас по отношению к пределу прочности.

348	РАСЧЁТ ЖЕЛЕЗОБЕТОННЫХ БАЛОК	[ГЛ. XVII
Опыты показывают, что при этом состоянии балки её грузоподъёмность
ещё не исчерпана полностью. Хотя бетон и является, вообще говоря, хруп-
хрупким материалом, но железобетонная балка ведёт себя как балка из свое-
своеобразного пластичного материала.
После достижения напряжениями
в арматуре предела текучести
для увеличения деформации балки
надо увеличивать нагрузку. Арма-
Арматура продолжает течь при по-
постоянном напряжении ат> а напря-
' жения в бетоне у края балки воз-
возрастают, пока не дойдут до пре-
-	дела прочности на сжатие <*в.
Тогда бетон в сжатой зоне вы-
выкалывается, и балка в целом раз-
разрушается, теряя свою грузоподъёмность. Распределение нормальных на-
напряжений в балке в этот момент показано на фиг. 275.
Изгибающий момент при этой стадии работы балки и будет предельным,
разрушающим; его величину М* можно вычислить как момент пары из сжи-
сжимающего усилия D в бетоне и растягивающего Zc —- в арматуре. Усилия D
и Zc выражаются теперь так:
Расстояние z0 найдётся опять из условия равновесия:
Теперь
ат^а
Назовём величину —тг- буквой а (отвлечённое число); тогда
CB0#i
Л*; = а„*Л?«A— 0,67а).	A7.6)
При проверке балки по допускаемым нагрузкам надо написать
Мк
^тах^^дош величина же допускаемого момента будет равна: Мдоп =	I,
k
где к — коэффициент запаса.
При выводе формулы A7.6) мы предположили, что в момент достиже-
достижения балкой предельной грузоподъёмности эпюра распределения напряжений
в бетоне будет треугольником с наибольшей ординатой ов. На самом деле
предельная грузоподъёмность балки оказывается ещё выше.
Бетон в сжатой зоне обычно усилен хомутами и при сжатии испытывает
своеобразное явление текучести, постепенно разрушаясь (как и в сжатой
колонне, § 28). Таким образом, как крайний случай можно принять, что

107}
РАЗВИТИЕ ТЕОРИЙ ИЗГИБА
349
предельная грузоподъёмность балки будет достигнута в тот момент, когда
во всей сжатой зоне напряжения в бетоне дойдут до предела прочности св,#
Эпюра напряжений получит вид, показанный на фиг. 276. Усилия (фиг. 277)
будут равны
Расстояние z0 будет равно
2л =
«.*
Разрушающий момент М* выразится формулой
-±-z0 j^
-0,5 «). A7.7)
Таким образом, два крайних предположения — треугольная и прямоуголь-
прямоугольная эпюры — дают при а (в скобках) коэффициенты 0>67 или 0,5. С опытами
L
гигх ^
Фиг. 276.
Фиг. 277.
хорошо согласуется величина 0,53, которая вошла в окончательно принятую
расчётную формулу:
М« = oBbhlос A — 0,53 а).	A7.8)
Изложенный метод расчёта железобетонных балок по допускаемым
нагрузкам был впервые предложен в СССР проф. Лолейтом в 1932 г. Ряд
опытов подтвердил правильность этого метода.
§ 107. Развитие теории изгиба.
Основные положения теории плоского изгиба, подтверждающиеся опытом
и изложенные в §§ 78, 91, 93, кажутся нам теперь почти очевидными. Однако
потребовалось много времени и труда, чтобы установить эти положения.
В 1638 г. в связи с задачами судостроения Галилей пытался связать
величину разрушающего груза для балки, защемлённой одним концом и
нагружённой на другом, с размерами её сечения. Галилей ошибочно считал
при этом, что все волокна балки подвергаются растягивающим усилиям и
не меняют своей длины.
В 1680 г. Мариотт произвёл опыты, которые привели его к заключению
о том, что часть волокон балки растянута, а часть сжата. В 1705 г. Яков Бер-
нулли высказал гипотезу плоских сечений, но сомневался в применимости
закона Гука к сжатию. В 1776 г. Кулон дал теорию изгиба, уже близко стоя-
стоящую к современной. К этому времени рядом опытов было уже доказано
существование сжатой зоны в балке при изгибе. Потребовалось 138 лет,
чтобы подойти к решению задачи, поставленной Галилеем.
Опыты последующих за этим лет отличались более тщательной поста-
постановкой, более точными измерениями деформаций. На помощь опыту Навье

350	РАСЧЁТ ЖЕЛЕЗОБЕТОННЫХ ВАЛОК	[ГЛ. XVII
привлёк уравнения теории упругости A824 г.). Его продолжателем был Сен-
Бенан, развивший более точно теорию изгиба.
Многочисленные теоретические исследования, касающиеся действия попе-
поперечной силы и касательных напряжений, как уже указывалось, принадлежат
Д. И. Журавскому. Им же подробно исследовалась работа связей при
изгибе составных балок и даны расчётные формулы, сохранившие значение
и по сие время. Работы Д. И. Журавского были опубликованы в 1855—1876 гг.
Теоретические исследования, касающиеся главных напряжений при изгибе
(«косых напряжений») и приводящие к современным расчётным формулам,
впервые были приложены к расчёту мостовых балок Н. А. Белелюбским,
опубликовавшим свои работы в 1870—1876 гг.
Исследования по изгибу тонких пластинок выполнялись в течение ряда
лет, начиная с 1&21 г., академиком Б. Г. Галеркиным. Глубокие теоретические
исследования вопросов изгиба балок тонкостенного профиля принадлежат
проф. В. 3. Власову; они публикуются, начиная с 1939 г. Он же возглавил
обширные опытные работы по изучению тонкостенных стержней.
Дальнейшее развитие строительной техники, появление новых материалов,
новых представлений о работе материала в конструкции, расширение воз-
возможностей более точного опытного изучения материалов в связи с привле-
привлечением в лабораторную технику новых методов исследований требовали
пересмотра и развития методов расчётов в области изгиба. Исторические
ссылки по этим вопросам (железобетон, расчёт по допускаемым нагрузкам)
приведены параллельно с их изложением в соответствующих разделах курса.

ОТДЕЛ VI.
ДЕФОРМАЦИИ БАЛОК ПРИ ИЗГИБЕ.
ГЛАВА XVIII.
АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ.
§ 108. Прогиб и поворот сечения балки.
При действии внешних сил, расположенных в одной из главных>
плоскостей инерции балки, наблюдается искривление её оси в той же
плоскости, происходит так называемый плоский изгиб.
На фиг. 278 изображена в искажённом масштабе искривлённая
ось балки, защемлённой одним концом и нагружённой на другом конце
сосредоточенной силой. Центр тяжести О какого-либо сечения
с абсциссой х перемещается" в точку О\.
Перемещение ОО\ центра тяжести сечения по направлению,
перпендикулярному к оси балки, называется прогибом балки в этом
Фиг. 279.
сечении или прогибом этого сечения балки. Прогиб будем обозна-
обозначать буквой у.
Строго говоря, так как ось балки, лежащая в нейтральном слое,
не меняет при изгибе своей длины, то точка О\ сместится несколько
в сторону от перпендикуляра к оси балки. Однако обычно прогибы у
малы по сравнению с длиной балки, и указанное смещение в сто-
сторону является величиной уже 2-го порядка малости по отношению
к длине балки, — им поэтому пренебрегают.
При деформации балки сечение, оставаясь плоским, поворачивается
по отношению к своему прежнему положению. На фиг. 279 изобра-
изображено сечение / до и после деформации. Угол 0, на который каждое
сечение поворачивается по отношению к своему первоначальному
положению, называется углом поворота сечения. Для практических
целей необходимо уметь вычислять прогибы и повороты для любого
сечения балки.

352	АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
Величина наибольшего прогиба может служить мерилом того,
насколько искажается форма конструкции при действии внешних сил.
Обычно с целью сохранения соединений частей балки от расшаты-
расшатывания и уменьшения колебаний под действием подвижной нагрузки
ограничивают величину наибольшего прогиба балки под нагрузкой.
Так, для стальных балок в зависимости от назначения их ставят
условием, чтобы прогиб не превосходил ппп -н -^^ доли пролёта.
1UUU Zk)\)
Кроме того, знание деформаций балки нам потребуется при
решении статически неопределимых задач, когда число опорных
реакций превышает число уравнений статики. Дополнительные урав-
уравнения могут быть написаны лишь путём изучения деформаций кон-
конструкции. Для того чтобы полностью знать деформацию балки, не-
необходимо уметь вычислить для каждого сечения его прогиб у и угол
поворота 9. Оба они будут функциями от х — расстояния сечения
от начала координат; между у и 0 для каждого сечения имеется
определённая зависимость.
Выберем систему координат, которой будем в дальнейшем поль-
пользоваться. Начало координат расположим в одной из точек первона-
первоначальной оси балки, которую всегда будем выбирать за ось лг; ось у
будем направлять перпендикулярно первоначальной оси балки вверх.
При таких условиях уравнение
У=/\х)	A8.1)
представит собой уравнение кривой, по которой изогнётся ось балки
под нагрузкой; это будет уравнение изогнутой оси балки.
Касательная к изогнутой оси балки (фиг. 279) в точке О\ соста-
составит с осью х угол; равный 6, т. е. углу поворота поперечного сече-
сечения относительно первоначального положения. С другой стороны,
тангенс угла, образованного касательной к кривой-у=/(дг) с осью лг,
как известно, равен
tg6 = -g..	A8.2)
Так как на практике прогибы балки обычно малы по сравнению
с пролётом, то б бывают очень малыми углами, обычно не больше
1°. Для таких углов можно считать, что тангенс угла равен углу,
выраженному в радианах. Отсюда следует, что
¦« = ?.	08-3)
т. е. угол поворота сечения равен первой производной по х от
прогиба у в этом сечении.
Таким образом, задача изучения деформации балки сводится
к получению уравнения изогнутой оси у=/(х); зная его, мы можем
вычислить дифференцированием и угол поворота для любого сечения
балки.

§ 109]
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ
353
§ 109» Дифференциальное уравнение изогнутой оси.
Для того чтобы получить у как функцию от х, надо установить
зависимость деформации балки от внешних сил, изгибающих её, от
ее размеров и материала. Такая зависимость была нами получена
уже раньше в § 78.
Используем формулу A3.10), полученную нами при рассмотрении
чистого изгиба. Распространяя её на общий случай изгиба, то есть
пренебрегая влиянием поперечной силы на деформации балки, можем
написать
1 _ М(х)
9{х) — EJ '
где р(дг) — радиус кривизны участка изогнутой оси балки между
двумя смежными сечениями на расстоянии х от начала координат;
М(х) — изгибающий момент в том же
сечении; EJ—жёсткость балки. Влия-
Влияние Q(x) на деформации балки обычно
невелико; метод его учета дан в § 132.
На фиг., 280 изображено изменение
радиусов кривизны по мере изменения
изгибающего момента. Для получения
уравнения изогнутой оси необходимо
использовать математическую зависи-
зависимость между радиусом кривизны оси и
координатами её точек х я у:
dx*
Подставляя это значение для кривизны	Фиг* 80*
в формулу A3.10), получаем дифференциальное уравнение,
связывающее у% х, М (х) и EJ:
d2y
Эх*
_М(х)
;~ EJ
A8.5)
Это — так называемое дифференциальное уравнение изогнутой оси,
или, как его часто называют, «дифференциальное уравнение упругой
линии».
Для громадного большинства практически встречающихся задач
величина^, представляющая собой угол поворота сечения балки,

354	АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
очень малая величина, квадратом которой можно пренебречь по
сравнению с единицей; тогда уравнение A8.5) упрощается:
или
Это уравнение называется приближённым дифференциальным
уравнением изогнутой оси балки.
Правило знаков для изгибающего момента установлено независимо
от направления координатных осей, вторая же производная, как
известно, положительна, если в сторону поло-
положительной оси у обращена вогнутость кривой,
и отрицательна,— если выпуклость (фиг. 281).
Таким образом, знак изгибающего момента М (х)
% не зависит от расположения координатных осей;
>0	знак же второй производной — зависит.
При направлении оси у вверх в уравне-
уравнении A8.6) следует оставить знак -J-, а при
направлении вниз знак —.
Условимся в дальнейшем всегда ось у на-
направлять вверх и дифференциальное уравне-
pi<0 X ние A8.6) писать в виде
Фиг. 281.	. EJ-^-==M(x).	A8.7)
Знак изгибающего момента при этом будем ставить по прежним
правилам.
Для получения из дифференциального уравнения изогнутой оси
уравнения прогибов y=f(x) необходимо произвести интегрирование
уравнения A8.7). Выражение для М(х) является функцией от х\
поэтому, интегрируя, получаем:
интегрируя второй раз, имеем
EJy—
Таким образом, мы получили уравнение углов поворота:
и уравнение прогибов:
[§ J	\	A8.9)
В эти уравнения входят постоянные интегрирования С и D.
Порядок вычисления этих постоянных будет показан на примерах.

§ 110] УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ, ЗАЩЕМЛЁННОЙ КОНЦОМ	355
Прежде чем перейти к практическим примерам, необходимо ещё
раз подчеркнуть, что уравнение A8.7) является приближённым] та
ошибка, которую мы допустили, пренебрегая величиной f -j- \ по
сравнению с единицей, практически мала только в тех случаях,
когда деформаций" балок малы по сравнению с их размерами. Если же
это условие не соблюдено и углы поворота сечений балок таковы,
что квадратом их величины нельзя пренебречь по сравнению с еди-
единицей, то приходится обращаться к интегрированию уже полного
уравнения A8.5).
Такие случаи могут быть при изучении деформаций тонких пру-
пружин, тонкой фанеры, вообще при изгибе гибких балок.
§ ПО. Интегрирование дифференциального уравнения
изогнутой оси балки, защемлённой одним концом.
Пример 73. Рассмотреть балку, защемлённую концом А и
нагружённую на другом конце силой Р (фиг. 282); пролёт балки
назовём /, жёсткость EJ. Начало ко-
координат назначим в точке Л; ось у
направим вверх, ось х— вправо. На-
Напишем дифференциальное уравнение
изогнутей оси A8.7):
EJ2L
Фиг. 282.
для вычисления изгибающего момента
возьмём произвольное сечение на расстоянии х от начала коорди-
координат; изгибающий момент в этом сечении равен М (х) = — Р (/ — х).
Тогда
EJy" = — P{1 — х).
Это уравнение интегрируем два раза:
EJy' = — P^lx — ~^-)+С.	A8.10)
A8.11)
Для определения С и D отыщем в балке сечения, для которых
мы заранее знаем величины прогиба и угла поворота. Таким является
опорное сечение Л; для него при х = 0
Подставляя эти значения сначала в уравнение A8.10), а затем
fe A8.11), получаем:
С = 0 и ?> = 0.
12'

356	АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
Как видно из уравнений углов поворота и прогибов, произвольные
постоянные Си/), делённые на жёсткость балки EJ, дают значения
соответственного угла поворота и прогиба сечения балки в начале
координат. Постоянные С и D — именованные числа, с размерностью:
С—[сила X длина2] и D — [сила X длина3].
Постоянные интегрирования обратились в нуль, что является
следствием выбора начала координат в защемлённом сечении балки.
При построении эпюр мы отсчитывали абсциссу х от нагружённого
конца балки; здесь оказывается более выгодным для уменьшения
вычислений при определении С и D отсчитывать х от защемлённого
конца, что несколько усложняет выражение для изгибающего момента,
но облегчает нахождение деформаций.
Определив постоянные С и D, мы можем преобразовать выра-
выражения для у и б таким образом, чтобы в скобках остались лишь
отвлечённые числа, это упрощает в дальнейшем вычисления прогибов
и углов поворота. Производим преобразования:
— dx — 2EJ L / J '
Пользуясь этими выражениями, найдём наибольшие значения для
у и 0; так как инженера интересует наибольшее по абсолютной
величине значение прогиба, то следует отыскивать как аналитиче-
аналитический максимум функции у при 0 = ~^-=О, так и наибольшее её
значение на границе участка. В нашем примере наибольшего по абсолют-
абсолютной величине значения у достигает в точке В> где б не равно нулю.
Прогибы, вычисляемые в отдельных точках, будем обозначать
буквой / с индексом, указывающим место прогиба. Для рассматри-
рассматриваемого случая в точке В при х = 1
/	<18Л4>
Знак минус означает, что прогиб направлен вниз. Наибольший угол
поворота будет, очевидно, в том же сечении; он равен
2EJ*
A8.15)
Знак минус означает, что сечение повернулось по часовой стрелке.
Для того чтобы оценить числовую величину деформаций балки,
возьмём Р= 2 Ту /= 2 му допускаемое напряжение [а] = 1400 кг/см*
и подберём сечение двутавровой балки по сортаменту. Условие
прочности имеет вид:
ту/^ мт*х 2 . 2 . 10» . 10»
W^"W=	ибо

§ 110] УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ, ЗАЩЕМЛЁННОЙ КОНЦОМ	357
Возьмём балку № 24; для неё №=289 см* и У =3460 см*;
принимая Е=2-106 ягг/сж2, получаем:
3 • 2.106 • 3460
2 -103 -22 • 104
1
2-2". 10е • 3460	173 Радиана ~ з
Из этого подсчета видно, что действительно деформации обычных
балок малы; наибольший прогиб составляет
0,78
200:
:2бо долю пР°лета;
квадрат же величины наибольшего угла поворота равен
" зоооо •
Этой величиной, конечно, можно пренебречь по сравнению с еди-
единицей (см. формулу A8.5)).
Пример 74. Рассмотреть балку, защемлённую концом, нагру-
нагружённую сплошной нагрузкой q т/м
(фиг. 283).
Повторяя ход вычислений, имеем:
4-
2
Фиг. 283.
Возведя (/ — х) в квадрат и интегри-
интегрируя трёхчлен почленно, как и в пре-
дьщущем примере, мы получили бы для произвольных постоянных
нулевые значения. Рекомендуя это проделать самим учащимся, при-
применим здесь другой приём- интегрирования, представляющий особый
интерес при решении задач с более сложной нагрузкой на балке.
Так как dx = — d(l — х\ то, не раскрывая выражения (/ — xf и
интегрируя первый раз по [—d(l — х)], получаем:
или
Интегрируя первое слагаемое правой части по [—d(l — х)\ а вто-
второе по dxt находим:
При таком методе интегрирования- постоянные С и D не опреде-
определяют непосредственно угла и прогиба в начале координат и в нуль
не обращаются.

358	АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
Вычисляем произвольные постоянные:
при х = 0 ® = ~dJ~®> C =	q-*>
при лг = О у = 0;	О = -2д.
Окончательные уравнения углов поворота и прогибов будут:
соответ-
соответA8.19)
Для пояснения действий при ином расположении начала координат и
ином направлении координатных осей рассмотрим эту же балку с той же на-
нагрузкой q9 т/м; однако начало коорди-
координат возьмём в правом свободном кон-
конце. Ось х направим влево, ось у—•
попрежнему вверх (фиг. 284). Диф-
Дифференциальное уравнение и его инте-
интегралы:
Наибольшие деформации на правом конце балки при лг =
ственно равны: '
4
I
г
1
п
У
EJy' = —
Фиг. 284.
24
A8.20)
К A8.21)
В сечении А угол поворота и прогиб равны нулю, т. е.
при х = / У = в = 0;
при jc=/ .у = 0'
Отсюда следует, что
Окончательные уравнения углов поворота и прогибов примут следующий вид:
Т + Т*	{18'22)
Задавшись значением х = 0 и вычисляя наибольшие значения 0тах и
/шах в сечении В, получим:
л/3
A8.18)
A8.19)

§ 111]	УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ НА ДВУХ ОПОРАХ	359
Как видно, и в этом случае постоянные С и D, делённые на жёсткость
балки Я/, дают значения угла поворота и прогиба балки в начале координат.
В выбранной .системе координат угол Ьв имеет положительное значение.
В системе же координат, принятой ранее (фиг. 283), этот же угол имел
отрицательное значение. На знаке fB изменение в направлении оси х не
отразилось.
§111. Интегрирование дифференциального уравнения
изогнутой оси балки на двух опорах.
Пример 75. Разберём вычисление деформаций для балки, свободно
лежащей на двух опорах и загружённой на всём пролёте сплошной нагруз-
нагрузкой q (фиг. 285). Начало координат вы-
берем в левом опорном сечении, ось
х направим вправо. В этой задаче, в от-
личие от двух предыдущих, для соста-
составления выражения М (х) надо найти
опорные реакции.
По симметрии А = ?
а //д=0.
L.i
Последовательно вычисляем:
Фиг. 285.
= + -f х —*f = + ±
A8.25)
Нам известны следующие значения прогибов:
на опоре А, то есть при х = 0 прогиб .у = 0
» > В, > > > х = 1 > У=0.
Применяя формулу A8.25) сначала к сечению А, имеем:
D = 0;
применяя же её к сечению В, получаем следующее уравнение:
A826)
откуда
.9L
24 *
dv
dv
Формулы для у и -~- принимают теперь вид:

360
АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
Для отыскания наибольшего значения прогиба надо найти сечение,
в котором 0=0; по симметрии это будет среднее сечение; при подстановке
в формулу A8.27) значения ~=-^- угол в = -р- обращается в нуль; при
= 384Ё
этом
Наибольшие значения 0 получаются для опорных сечений при х = 0 и
л- = /:
&	08-30)
И в этом примере при определении произвольных постоянных интегри-
интегрирования мы устанавливаем, что -prj- есть прогиб балки в начале коорди-
Q
нат, а -р-т-— угол поворота опорного сечения Д совпадающего с началом
координат.
Подберём сечение прокатной балки и определим величину её деформа-
деформаций при следующих условиях: д = 2 т/пог. м; / = 4 м\ [а] = 1400 кг/см2; се-
сечение— двутавровое; ? = 2» 10е кг/см2. Так как наибольший изгибающий
момент равен
__$/2__2-42
•^тах — ~g~ — ~~g — ™>
как и в примере §110, то опять пригодна балка №24; для неё N7 = 289 еж3
и 7 = 3460 см*;
__ 5 • 20 ¦ 4* * 108
/max— 384-2.10°. 3460"" ' °Му
384-2.10°. 3460"
20.48.10е
1
__ 1
U*ax- -1- 24-2- 10е • 3460	1Э0 Радиана'
Во всех рассмотренных примерах, если мы направляем ось у вверх, а
ось х вправо, то отрицательное значение 0 соответствует вращению се-
сечения по часовой стрелке, положитель-
положительное— против часовой стрелки.
Пример 76. Разберём ещё один слу-
случай вычисления деформаций для балки,
свободно лежащей на двух опорах с пролё-
пролётом /. Нагрузим эту балку парой сил 7W,
приложенной к правому опорному сечению
(фиг. 286). Реакции А и В образуют пару
с моментом М и равны
А = В = ~-.
Фиг. 286.
Расположим начало координат на левой опоре; тогда получим
!

§ 112] УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ ПРИ ДВУХ УЧАСТКАХ	361
Постоянные интегрирования определяются из условий, выражающих
равенство нулю прогибов на опорах А и В:
при х = О прогиб у = О, откуда D = 0;
Ml
> х = 1 у ;У = 0, откуда С =	g- .
Таким образом,
rfy _ Ml Г	*М
Af/x
Сечению с наибольшим прогибом соответствует -—• = 0, поэтому
1-3^=0;
абсцисса этого сечения х0 равна
,. = ^ = 0,577/.
Наибольший прогиб равен
Г "" 6 уТЕ/ I- "^2 J "" 9 JT3EJ ~~
прогиб же посредине пролёта равен
М/2 Г 1 /8 1 М/2
I	J
/8 1 _
4/2J""
2
Разница с наибольшим прогибом составляет всего 2,5%; таким образом,
даже при таком резко несимметричном случае нагрузки за наибольший про-
прогиб для балки на двух опорах можно с достаточной точностью принимать
прогиб посредине пролёта.
§ 112. Интегрирование дифференциального уравнения
изогнутой оси балки при двух участках.
Если изгибающий момент на различных участках балки выра-
выражается различными формулами, приходится составлять столько диф-
дифференциальных уравнений, сколько участков на балке.
Возьмём балку на двух опорах пролётом /, нагружённой силой Р
на расстоянии а от левого и b от правого конца; пусть
(фиг. 287). Опорные реакции балки у i	j	\n II
равны
Начало координат возьмём на левой
опоре и ось х направим вправо.
Изгибающие моменты на первом	Фиг. 287,
и втором участках будут выражаться
различными формулами; поэтому придётся взять два произвольных
сечения с абсциссами Xi и дг2 и написать два дифференциальных

3G2
АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
уравнения. Величины у, М9 С, D и абсциссу сечения будем помечать
индексом 1 для первого участка и индексом 2 для второго.
При составлении выражения моментов для обоих участков будем
рассматривать левую часть балки; тогда для сечения Ох на первом
участке:
ал л РЬ
Mi = Ахх = -j хг;
для второго же участка (сечение О2):
РЬ
i
Интегрирование слагаемых вида Р(дга — а) будет производить, не
раскрывая скобок, как это сделано в примере 74. При этих условиях
вычисления располагаются следующим образом:
Первый участок
EJy{ = — хх\
A8.31)
¦\-CtXi-\-Di. A8.32)
Второй участок
5 — Mt = Лдг, — Р (дг, — а);
. A833)
A8.34)
В выражения для прогибов и углов поворота вошли четыре по-
постоянных интегрирования, вдвое больше, чем число участков. Для
определения этих постоянных надо написать четыре уравнения. Эти
уравнения всегда можно составить, как и в предыдущих случаях,
рассматривая сечения балки, для которых нам что-либо известно
о прогибе и угле поворота. Такими сечениями в рассматриваемой
задаче являются: сечение раздела между первым и вторым участками —
сечение С и опорные сечения Л и В.
Сечение С, расположенное на границе двух участков, может быть
отнесено как к первому, так и ко второму из них. Поэтому величину
прогиба и угла поворота сечения С можно вычислить как из формул
для первого участка, так и из формул для второго:
т. е. при
полученные величины для у и
yi=y.2 и 61 = 6а или
6 должны быть одинаковы, т. е.
(a)
(b)

§ 112] УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ ПРИ ДВУХ УЧАСТКАХ
363
Таким образом, точка раздела участков всегда даёт нам два уравне-
уравнения. Два других условия получим по данным на опорах:
В сечении А при хх = О прогиб Ух = О,
(с)
(d)
Подставляя в формулы A8.31) и A8.33) вместо ху и хй вели-
величину а и приравнивая правые части, получаем по условию (а):
откуда
7У т м — "ТТ	2 » 2*
Cj = С3.
A8.35)
Подобным же образом из формул A8.32) и A8.34) получаем но
условию (Ь):
РЬ
-у
x = — -^ — Р
откуда
A8.36)
Таким образом, постоянные интегрирования для обеих участков
оказались одинаковыми. Это произошло благодаря принятому методу
составления и интегрирования дифференциальных уравнений.
Применяя формулу A8.32) к опорному сечению А, получим на
основании (с) D| = 0, а следовательно, и De = 0. Применяя же
формулу A8.34) к опорному сечению В, на основании (d) получаем
Теперь формулы для j; и 0 получают вид:
Первый участок	Второй участок
EJ[ I 2

364 АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [гл. XVHI
Выясним величину наибольшего прогиба/. Он будет в сечении,
для которого 6 = 0. Из формулы для 6t видим, что при х1 = 0,
т. е. в сечении Л,
б_
в сечении же С при х^ = а
так как Ь<^а, то величина ^
Таким образом, дг между точками А и С меняет знак, т. е. пе-
переходит через нуль. Значит, наибольший прогиб будет на первом
участке. Чтобы найти абсциссу х\ соответствующего сечения, под-
подставим это значение х\ в выражение для Ь1 и приравняем его нулю;
Подставляя в формулу для уи получаем:
Щ* A8 37)
— 2Ж
Расстояние сечения с наибольшим прогибом от левой опоры будет
меняться с изменением положения груза. Если сила Р находится
посредине пролёта, то
^==~2~; •^о==="» /max== 4SEJ '	(lo.oo)
если же мы будем отодвигать силу Р к правой опоре и приближать
в пределе расстояние Ь к нулю, то
при b -> 0; ха = -1р=. = 0,577/.
v	° ут
Таким образом, при перемещении Р
\*—0,5771	i	от середины пролёта до опоры между
точками D и В (фиг. 288) абсцисса
точки с наибольшим прогибом меняется
всего от 0,5/до 0,577/между точками D
и F. Практически часто условно считают, что при действии любых на-
нагрузок, изгибающих балку в одну сторону, наибольший прогиб для
балки на двух опорах будет посредине пролёта. В частности, при
расположении груза по фиг. 287 прогиб посредине пролёта равен
f 	 го го/2	4/>21
*1_	АШ 1°	J-	A8.39)
Числовыми подсчётами легко убедиться в малой разнице между
/шах и f i •

§ 112] УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ ВАЛКИ ПРИ ДВУХ УЧАСТКАХ
365
Пример 77. Подобрать сечение стальной двутавровой балки, нагру-
нагружённой сплошной нагрузкой q = 4 т/м на полупролёте (фиг. 289), если до-
допускаемое напряжение [а] = 1000 кг/см2, a
допускаемый прогиб не должен превышать
1000
пролёта, равного / = 2,0 м.
Поместим начало координат в точке Л,
ось х направим вправо, ось у — вверх. Ну-
Нумерация участков показана на чертеже. Со-
Составляем дифференциальные уравнения изо-
изогнутой оси, отсчитывая х на обоих участ-
участках от точки Л, и интегрируем.
Первый участок
dx\
Фиг. 289.
Второй участок
dx\
~ 2 Г3 2 ) *
Постоянные интегрирования определяются из условий:
При лг3 = /	должно быть -~^
Первые два условия дают:
48 '	16*24	384 *
Из третьего и четвёртого условий следует:
„ 	q 	 , д1ъ ~ 	~ 	 7ql*
Так как наибольший прогиб будет на конце балки, напишем в оконча-
окончательном виде уравнение прогибов лишь для первого участка:
1 Г . ql* Iql* I
i==Ej[+lSXl	38TJ
ql*
384?/
Наибольший прогиб равен (при л: = 0) / =
чадр г *
Теперь из условия жёсткости мы можем определить /:
/ ~ 384 EJ' J~
lf\
384-2.10»
Необходимо поставить двутавр № 24 с моментом инерции У = 3460 см*.

366	АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
Определим момент сопротивления из условия прочности:
АГтах *"8 40-4-
w:
¦ = 200 см3.
[а]	[а]	8-10»
Достаточно было бы поставить двутавр № 20а с №=203 см*. Следовательно,
сечение определяется из условия жёсткости.
§ 113. Приёмы составления и интегрирования
дифференциального уравнения при нескольких участках.
А. Метод уравнивания произвольных постоянных. Разобранные
в § 112 примеры показывают, что при определённом порядке соста-
составления и интегрирования дифференциальных уравнений изогнутой
оси балки можно достигнуть сокращения числа произвольных по-
постоянных до двух: С и D.
При большом числе участков загружения балки такое сокраще-
сокращение значительно упрощает подсчёты. Равенство между собой произ-
произвольных постоянных (d = С2 =... = С и Dt = D2 =... = D) воз-
возможно при соблюдении следующих условий:
а)	отсчёт абсцисс всех участков должен вестись от одного на-
начала координат — крайней левой (или правой) точки ос» балки;
б)	все составляющие выражения изгибающего момента предыду-
предыдущего участка должны сохраняться неизменными в выражении изги-
изгибающего момента последующего участка балки: это условие может
быть соблюдено, если при вычислении моментов будет рассматри-
рассматриваться та часть балки, которая содержит начало координат;
в)	все вновь вводимые в последующих участках составляющие
выражения изгибающего момента должны содержать множитель —
скобку {х — а), где
а — сумма длин всех
предыдущих участков;
г) интегрирование
д и ф ф е р е нциального
уравнения должно ве-
вестись без раскрытия
скобок.
При наличии рас-
распределённой нагрузки
для выполнения усло-
условия б) нагрузка не
должна обрываться: если по условию задачи распределённая нагрузка
оканчивается (фиг. 290, конец второго участка), — её следует продол-
продолжить до конца балки, добавив одновременно той же интенсивности
нагрузку другого знака (см. третий участок).
При наличии сосредоточенного момента М (фиг. 290) условие
и) окажется выполненным, если в выражении М(х) величина^ будет
Фиг. 290.

§ ИЗ]
УРАВНЕНИЕ ПРИ НЕСКОЛЬКИХ УЧАСТКАХ
367
умножена на величину (лг — сH, где с — часть длины балки от начала
координат до сечения, где приложен момент М.
Поясним выполнение перечисленных условий на примере фиг. 290.
.Первый участок
2
IT
Второй участок
Ej? = -P^ + A^^-q{^-^ + ^
Третий участок
Определяем произвольные постоянные
dVt dy* r> s>
при X\=== d ¦— Xa -?— '-—" -f~ \ C\ === C\
dy^ dy% ^ ^
при x% = с = x$ -j— = t— ; Cg = С
при xt = d 3/! = 0; — P |- -f- Cd -f- Z) = 0,
— Cg —— С»з — С,

36$	АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
Произвольные постоянные С и D определяются из этих двух
выражений. Дальнейшее решение примера трудностей не пред-
представляет.
Б. Метод начальных параметров. Рассматривая уравнения (§§ 110—
112) и сопровождающие их пояснения, нетрудно подметить, что эти
уравнения могут быть видоизменены так, что смогут служить для
решения задач при любом из рассмотренных здесь видов загру-
жения.
Сосредоточенные силы Рг, Р2, ... , расположенные в расстояниях
/i, /2 ...от начала координат, дадут в уравнение прогибовA8.9) члены
(д.-/,)» ^	(*-/,)'.
Сосредоточенные моменты Ми М2, ... с теми же расстояниями
от начала координат дадут в уравнение A8.9) слагаемые
Равномерно распределённая нагрузка qu q%> *.. , начинающаяся
в расстояниях lit /2, ... , от начала координат и расположенная далее
непрерывна, даст выражения:
24 » 24 » •*•
Произвольные постоянные при принятом выше порядке составле-
составления выражений М(х) и порядке интегрирования будут на всех
участках одинаковы и могут быть заменены через увеличенные в EJ
раз прогиб ув и угол поворота 60 в начале координат.
Рассмотрев, наконец, значения коэффициентов в знаменателях,
можно подметить, что они раскладываются на следующие первона-
первоначальные множители:
24 = 1-2.3.4 = 4!
6=1-2.3 =3!
2=Ь2 =2!
1 = 1	=1!
Располагая члены уравнения A8.9) по восходящим степеням х>
заменяя 1и /2, ... через /0 и суммируя все однотипные члены, можем
составить следующие общие уравнения упругой линии.
Уравнение углов поворота:

§ 113]	УРАВНЕНИЕ ПРИ НЕСКОЛЬКИХ УЧАСТКАХ	369
Уравнение прогибов:
[18.9']
Применим эти уравнения к нахождению прогиба и угла поворота
балки, защемлённой одним концом и загружённой силой Р на другом
конце (фиг. 282). Учитывая, что yQ = 0; 60 = 0; q = 0 и рассматривая
силы, расположенные слева, т. е. опорный момент М = — Р1 и
реакцию А = Р, получим вместо уравнений A8*. 10) и A8.11)
+ ??/>
Деформации на конце балки под силой Р при х = 1
v -_^1- б —-?!-
уР— 3EJ' Р— 2EJm
Рассмотрим балку на двух опорах, загружённую сплошь равно-
равномерно распределенной нагрузкой интенсивностью q (фиг. 285).
В этом случае уй = 0у а 0О определится из условия, что при дг = /
j/ = 0. Уравнение прогибов будет:
откуда при лг =
Подставим полученное значение 60 в уравнение прогибов:
ql% \ x 4- qlx% gx*
24EJ )X~r~l2	2Г#
Найдём теперь прогиб / посредине пролёта (при лг== -2")г
_ 41х . Я? ч*.
f_	5_ _^
3	384 # EJ '

[/J
370	АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
§ 114. Интегрирование дифференциального уравнения
для случая балки с шарниром.
В предыдущих примерах участки при составлении уравнения
изогнутой оси соответствовали участкам эпюры изгибающих моментов.
При нарушении непрерывности оси балки шарниром для инте-
интегрирования уравнения оси участок с шарниром придётся разделить
на два, хотя выражение для изгибающего момента по обе стороны
от шарнира будет одним и тем же.
Hi ¦	м .	В шарнире должны быть равны между
м	собой лишь прогибы соединяемых ча-
' НА 1	п	В х стей; углы же поворота сечений, примы-
,_	_^—>- кающих к шарниру, будут различны.
fl	^	^—*- Поэтому уравнение изогнутой оси бу-
I	дет различным для участков балки,
ф 291	разделённых шарниром.
Рассмотрим балку, изображённую
на фиг. 291; в сечении С поме-
помещён шарнир; для простоты вычислений нагрузим балку только парой
сил М в сечении 5. Реакцию В легко определить, приравняв нулю
сумму моментов относительно шарнира С всех сил, расположенных
справа от шарнира (т. е. сил В и М). Получим Б = у.
Реакция А определится из суммы проекций на вертикаль всех
сил, действующих на балку АСВ (т. е. сил А и В). Получим A = -j.
Реактивный момент МА равен сумме моментов относительно точки А
сил Ж и В:
М А = — М т.
А	I
Начало координат выберем в точке А Изгибающий момент
в любом сечении балки .между А и В выражается формулой
Для получения же уравнения изогнутой оси надо рассмотреть
участка АС и СВ. Дифференциальные уравнения и их интегралы
имеют вид:
Первый участок
Второй участок

§ 114]	УРАВНЕНИЕ ДЛЯ СЛУЧАЯ БАЛКИ С ШАРНИРОМ	371
Для определения постоянных интегрирования имеем четыре условия:
сечение А при х = О величина -?- = О и ух = 0,
» С » х = а	»	У1=Уъ
» В » х = а-\-1	»	д^=0.
Из первых двух получаем:
С, = 0; Dx = 0.
Из двух последних
^/^
Отсюда
При этих условиях прогибы обеих частей балки в шарнире одина-
одинаковы, углы же поворота отличаются на величину С2.
При решении этой задачи общим уравнением поступаем так. В начале
координат у0 =s б0 = 0; Мо = — М -у и Qo = А = -у. В месте стыка I и II уча-
участков происходит разрыв непрерывности (скачок) для угла поворота, который
обозначаем 6С. Тогда по A8.9') для. II участка получаем:
М л* . М л
a +
для уi следует отбросить последний член правой части. Назначая х = 1+а
и ^2 = 0 (условие на правой опоре), получаем для 6С выражение, совпадаю-
совпадающее с С2.
Пример 78. Для балки, показанной на фиг. 292, наметить решение
задачи по определению прогибов.
Балка имеет шесть участков, и, следовательно, при решении задачи по
определению деформаций мы получим 12 произвольных постоянных. Не-
Нетрудно проследить, что сече-
сечения раздела нагрузки, опоры и
шарниры дадут нам необходи-
необходимые 12 уравнений. Защемлён- 4
ный конец А даёт два уравне-
> 0B) (Z)
ния: прогиб равен нулю и угол	я BCD
поворота равен нулю. Шар-
нирно-опёртый конец G — одно	фиг 292.
уравнение: прогиб равен нулю.
Шарниры В и D по одному
уравнению: прогибы лев(ого и правого участков в сечениях шарниров равны
между собой.
Сечения раздела нагрузки (сечение С, где обрывается распределённая
нагрузка, и сечение F, где приложена сосредоточенная сила Р) дадут по два
Уравнения: прогибы левого и правого участков в этих сечениях равны между
собой, и углы поворота тех же участков равны между собой. Шарнирная

372	АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XVIII
промежуточная опора Е даёт три условия: равенство прогибов между собой,
равенство углов поворота между собой и равенство любого из прогибов
в этом сечении нулю.
На фиг. 292 в кружках указано количество уравнений в каждом рас-
рассмотренном сечении.
§ 115. Сложение действия сил.
Закон Гука справедлив не только для материала, но и для всей балки
в целом; прогибы и углы поворота прямо пропорциональны нагрузкам.
Это — следствие линейной зависимости изгибающего момента от нагру-
нагрузок, а кривизны — от изгибающего момента. Для балки, защемлённой кон-
концом и нагружённой сплошной нагрузкой q и сосредоточенной силой Р на
свободном конце, изгибающий момент в сечении на расстоянии х от за-
защемления выражается линейной по отношению к нагрузкам формулой
) = — />(/ — х) — q(l~~2f ;
зависимость же кривизны от момента тоже линейна.
поэтому после интегрирования по х получаем линейную зависимость
прогиба от нагрузок:
У	l3
т. е. сумму ординат изогнутой оси балки от силы Яи от нагрузки q
отдельно (см. § ПО, формулы A8.13)
лттттъ	г и {18Л7))-
д] 1111t1 ig—_	? gT0 обстоятельство позволяет в
случае сложной нагрузки получать
уравнение изогнутой оси как сумму
ординат кривых, соответствующих
частным нагрузкам. Особенно упро-
упрощается в некоторых случах вычисле-
вычисление наибольшего прогиба.
Рассмотрим применение метода сло-
сложения действия сил для определения
деформации конца консоли А однопро-
лётной балки ABC (фиг. 293). Заменив
влияние на участок балки ВС нагрузки q,
расположенной на консоли АВ, момен-
Фиг. 293.	. ЯЛ	па*
том Мо = — ^к" , мы можем, пользуясь
формулой § 111 (фиг. 286), вычислить угол поворота сечения балки
на опоре В:
n	MQl
Прямая ось консоли АВ при повороте сечения В наклонится на

§ 115]	СЛОЖЕНИЕ ДЕЙСТВИЯ СИЛ	373
тот же угол 0#, и величина прогиба конца консоли А составит:
Консоль АВ под действием нагрузки q не останется прямой, а
изогнётся, заняв положение Аф (не изменив, однако, угла поворота
6# у точки В), и прогиб на конце консоли А при этом изгибе со-
составит, как для балки, защемлённой одним концом (см. § 110, фор-
формула A8.19)):
Полный прогиб конца консоли А будет:
Ta—Ja i JA — ~-bE] Ш —'
Определение деформаций балок с шарнирами может быть прове-
проведено также с применением метода сложения действия сил. Для этого
балку нужно расчленить на несколько составляющих её балок, рас-
рассмотреть их порознь и просуммиро-
просуммировать вычисленные раздельно дефор-
деформации.
Так, например, схему балки
§ 114 (фиг. 294, а) можно заменить
схемой фиг. 294, б. В этой схеме
«подвесная» балка СВ опирается
левым концом С на правый конец С
«основной» балки АС Действие шар-
шарнира С может быть заменено сила-
силами С (фиг. 294, в, г).
Определение величины силы С
нужно произвести, рассмотрев рав- г)
новесие балки СВ; для этой балки
сила С является силой пассивной —
реакцией балки АС На балку АС
будет действовать той же величины А™—r^-^--_~ ^ -У-^^'Ч'
активная сила С — давление балки	/f°^ ~	*~ ~ * \
СВ на балку AC	f*	U
Прогиб балки СВ, показанной	Фиг. 294.
отдельно на фиг. 294, в, опреде-
определится в любой точке по формулам примера 76 (см. стр. 361). Про-
Прогиб балки АС, показанной на фиг. 294, г, можно вычислить по фор-
формулам A8.13) и A8.14) (см. стр. 356).
Деформация заданной балки АСВ показана на фиг. 294, д. Уча-
Участок АС балки АСВ имеет на всем протяжении те же прогибы,

374
АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ [ГЛ. XV1IT
что и отдельно рассмотренная балка АС. Прогибы же участка СВ
балки АСВ представят суммы двух прогибов: прогиба fu соста-
составляющего часть прогиба fc (прямо пропорциональную удалению от
точки В) и прогиба /2, вычисленного для схемы балки СВ
(фиг. 294, в).
§ 116. Дифференциальные зависимости при изгибе.
В §§ 71 и 109 были получены дифференциальные зависимости
для сплошной нагрузки q(x)> поперечной силы Q(x), изгибающего
момента М(х\ угла поворота сечения б и прогиба у:
dM (х)
Эти зависимости, после некоторого
преобразования, можно расположить
последовательно:
d
dx
dx*
=<?(*).
ШР^
Фиг. 295.	Из этих уравнений видно, что,
зная нагрузку q (x) и устройство
опор балки, можно последовательным интегрированием получить
величины Q(x)9 M(x), ЕЛ и EJy; обратно, зная уравнение изогну-
изогнутой оси, можно путем последовательного дифференцирования по х
из функции EJy получить ?78, М(х), Q(x) и q(x). Для графи-
графического изображения этих зависимостей условимся положительные
значения всех перечисленных величин откладывать вверх, а отри-
отрицательные — вниз; положительное направление оси х примем вправо,
поворот сечения по часовой стрелке — отрицательным, а против —
положительным. На рис. 295 в качестве примера изображены гра-
графики изменения всех величин, характеризующих изгиб, для балки
шарнирно-опбртой и загружённой неравномерно распределенной
нагрузкой q(x) (отрицательной, направленной вниз).

§117]	ГРАФОАНАЛИТИЧЕСКИЙ МЕТОД	375
ГЛАВА XIX.
ГРАФОАНАЛИТИЧЕСКИЙ И ГРАФИЧЕСКИЙ МЕТОДЫ
ВЫЧИСЛЕНИЯ ДЕФОРМАЦИЙ ПРИ ИЗГИБЕ.
§ 117. Графо-аналитический метод.
Метод интегрирования дифференциального уравнения изогнутой
оси даёт уравнения прогибов и уравнения углов поворота, при по-
помощи которых можно вычислить прогиб и угол поворота в любом
сечении балки.
Когда мы имеем дело с большим числом участков, а также
в случае сложной нагрузки, вычисления при применении этого спо-
способа делаются достаточно громоздкими. В этих случаях наиболее
удобным может оказаться графический способ.
С другой стороны, при решении целого ряда задач (статически
неопределимые балки, вычисление наибольшего прогиба) достаточно
уметь найти прогиб и угол поворота лишь для некоторых опреде-
определённых сечений. В этих случаях уместно применение графо-аналп-
тжеского метода. Этот способ основан на сходстве дифферен-
дифференциальных зависимостей, связывающих прогиб, изгибающий момент
и интенсивность сплошной нагрузки.
.Пусть мы имеем какую угодно балку с произвольной нагрузкой
Т
а)
V гтЛЛТП
T^j
Фиг. 296.
(фиг. 296). Дифференциальным уравнением изогнутой оси этой
балки является (§ 109):
= М(х).	A9. *)
Под нашей балкой изобразим вторую балку той же длины, на-
нагруженную некоторой, пока неизвестной, сплошной нагрузкой qf%
положительное направление которой принято вверх; устройство
опор этой балки тоже оставим пока неопределенным; отметим лишь,
что опорные реакции будут уравновешивать нагрузку qf. Эту
вторую балку назовём воображаемой, фиктивной; v все величины,
относящиеся к ней, будем обозначать значком /. Для этой вооб-
воображаемой балки вычислим величину изгибающего момента Mf
в каждом сечении тоже путем интегрирования, пользуясь

376	ГРАФОАНАЛИТИЧЕСКИЙ И ГРАФИЧЕСКИЙ МЕТОДЫ	[ГЛ. XIX
дифференциальным уравнением, связывающим изгибающий момент
и интенсивность сплошной нагрузки (§ 116):
A9.2)
Проведём сопоставление уравнений A9.1) и A9.2). Если принять
qf = М (лг),
т. е. загрузить фиктивную балку фиктивной нагрузкой, меняющейся
по закону изгибающего момента действительной балки, то
d2 (EJy) _ d*Mf
dx* ~ dx* *
Если при интегрировании обеих сторон уравнения добиться ра-
равенства произвольных постоянных левой и правой частей уравнения,
т. е. Сл = Сп и Ол = Dn, то получим:
я	„ У	dx	dx *
dMf
Учитывая, что -—t-==Q^ и решая эти вы-
выражения относительно у и В, получим фор-
формулы:
y = -^j->	A9-3)
*=%.	A9-4)
Прогиб сечения действительной балки
(от заданной нагрузки) равен изгибающему
*	к моменту в том же сечении фиктивной балки
Фиг. 297.	(от фиктивной нагрузки), делённому на жёст-
жёсткость действительной балки.
Угол поворота действительной балки (от заданной нагрузки)
равен поперечной силе в том же сечении фиктивной балки (от
фиктивной нагрузки), делённой на жёсткость действительной
балки.
В аналитическом способе определения деформаций произвольные
постоянные находились по условиям на границах, т. е. по условиям
равенства нулю прогибов в опорных сечениях и равенства дефор-
деформаций между собой в сечениях, общих для двух смежных участков
балки.
В рассматриваемом способе добиться равенства между собой
произвольных постоянных при интегрировании уравнений A9.1)
и A9.2) можно путём такого закрепления концов (или промежу-
промежуточных сечений) фиктивной балки, которое удовлетворяло бы еле-

§ 117]
ГРАФОАНАЛИТИЧЕСКИЙ МЕТОД
377
дующим условиям, непосредственно вытекающим из выражений
A9.3) и A9.4):
1)	если прогиб действительной балки / равен нулю, то в том же
сечении фиктивной балки фиктивный изгибающий момент должен
быть равен нулю;
2)	если угол поворота действительной балки 0 равен нулю, то
в том же сечении фиктивной балки фиктивная поперечная сила
должна быть равна нулю;
3)	если прогиб или угол поворота действительной балки не ра-
равен нулю, то соответствующие им Mf или Qy также не должны
быть равны нулю.
В таблице 22 приводятся условия для всех случаев опирания
действительной балки с указанием соответствующих этим условиям
закреплений тех же сечений фиктивной балки. Действительная и
фиктивная балки, связанные условиями этой таблицы, называются
сопряжёнными. На фиг. 297 для наиболее распространённых стати-
Таблица 22. Условия образования фиктивных балок.
Действительная балка
Наименование опоры
Шарнирная концевая
опора (прогиба нет; по-
поворот сечения возможен)
Защемлённый конец
балки (нет прогиба и нет
поворота)
Свободный конец балки
(возможны и прогиб и
поворот сечения)
Промежуточная опора
(прогиба нет; поворот се-
сечения возможен)
Промежуточный шар-
шарнир (возможны и прогиб
и поворот сечения)
Условия
для у и 8
у = 0
jr = o'
0 = 0
уфЪ
6^:0
jr = O
6^:0
уфО
Фиктивная балка
Требуемые
условия для
Mfu Qf
Mf = 0
0/ = o
Mf = 0
Отвечающее этим условиям
опирание фиктивной балки
Шарнирная концевая
опора (момента нет, воз-
возможна опорная реакция)
Свободный конец балки
(отсутствуют и сосредо-
сосредоточенная сила и момент)
Защемлённый конец
балки (имеются момент
защемления и реакция)
Промежуточный шар-
шарнир (момента нет; шар-
шарнир передаёт давление)
Промежуточная опора
(в опорном сечении воз-
возможны и момент и реак-
реакция)

378	ГРАФО-АНАЛЙТИЧБСКИЙ И ГРАФИЧЕСКИЙ МЕТОДЫ	[ГЛ. Х!Х
чески определимых балок показаны сочетания действительных и
фиктивных балок. В каждой паре сопряжённых балок любая может
быть принята за действительную, тогда вторая из них будет фи-
фиктивной, что легко можно проверить, обратившись к таблице 22.
Для многопролётных балок с шарнирами выбор сопряжённой
балки можно проследить по фиг. 298.
Следует заметить, что статически определимой действительной
балке всегда соответствует статически определимая фиктивная балка.
Таким образом, для того чтобы найти прогиб у или угол 0
поворота какого-либо сечения заданной (действительной) бал-
балки, нужно последовательно выполнить следующие операции:
а)	вычертить схему заданной балки с заданной нагрузкой;
б)	построить эпюру изгибающего момента М (х);
V/Я.	V77ft
Фиг. 298.
в)	принять нулевую линию эпюры М(х) за ось фиктивной
балки, а эпюру М(х) за фиктивную нагрузку qf\ при положитель-
положительных значениях изгибающего момента ординаты нагрузки qf напра-
направить вверх, при отрицательных — вниз.
г)	показать опоры фиктивной балки в соответствии с условийми
таблицы 22 и фиг. 297 или 298;
д)	подсчитать величину опорных реакций фиктивной бал-
балки от фиктивной нагрузки (т. е. фиктивных опорных реак-
реакций); для балок, защемленных одним концом, этого можно не
делать;
е)	подсчитать величину изгибающего момента Mf в сечении фи-
фиктивной балки с той же абсциссой, что и сечение, где отыски-
отыскивается прогиб /;
ж)	подсчитать величину поперечной силы Qf в сечении фиктив-
фиктивной балки с той же абсциссой, что и сечение, где отыскивается
угол поворота 0;
з)	определить / и 0 по формулам A9.3) и A9.4).
Графо-аналитический метод определения деформаций освобо-
освобождает нас от необходимости нахождения произвольных постоянных
в каждом частном случае, и сразу, при использовании данных
табл. 22 и схем фиг. 297 или 298, даёт решение, согласованное
с определёнными начальными условиями.
Фиктивные моменты имеют размерность [сила X длина3]; фиктив-
фиктивные поперечные силы — [сила X длина9]; интенсивность фиктивной
нагрузки измеряется в единицах — [сила X длина].

§ 118] ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ ГРАФОАНАЛИТИЧЕСКИМ МЕТОДОМ 379
§ 118. Примеры определения деформаций
графо-аналитическим методом.
Пример 79. Найти прогиб точки В балки АВ пролётом /, защемлённой
концом А и нагружённой сил^ой Р на конце В (фиг. 299).
Эпюра моментов будет иметь вид треугольника с наибольшей ординатой
под сечением Л, равной — Pi, Ось абсцисс эпюры моментов примем за ось
фиктивной балки; превратим эпюру в фик-
фиктивную нагрузку; для этого на ординатах
поставим стрелки, направленные вниз (ор-
(ординаты отрицательны).
Следуя указаниям таблицы 22, пока-
покажем защемлённый конец в точке В фик-
фиктивной балки (фиг. 299) и свободный конец
в точке А
Далее надо вычислить изгибающий мо-
момент в сечении В фиктивной балки. Момент
треугольной нагрузки относительно точ-
точки В равен произведению нагрузки на
расстояние её центра тяжести до точки В:
Фиг. 299.
Деля это выражение на EJ, получаем прогиб в точке В:
A8.14).
— формула, в точности, до знака включительно, совпадающая с результа-
результатом, полученным в § 110.
Поперечная сила в сечении В фиктивной балки численно равна пло-
площади всей треугольной нагрузки:
а угол поворота сечения В действительной
балки равен:
.-&—*
Фиг. 300.
В
A8.15)
Пример 80. Балка на двух опорах
нагружена посредине пролёта силой Р
(фиг. 300). Найти прогиб в точке прило-
приложения силы.
Эпюра моментов для действитель-
действительной балки изобразится треугольником с
ординатой в точке приложения груза, равной +-J-1 превращаем эпюру
в фиктивную нагрузку, направляя стрелки в этом примере вверх, так как
ординаты эпюры положительны.

380	ГРЛФО-АНАЛИТИЧЕСКИЙ И ГРАФИЧЕСКИЙ МЕТОДЫ	[ГЛ. XIX
Устройство опор фиктивной балки определим по данным табл. 22 из
условий закрепления действительной балки. Реакции опор фиктивной балки
по симметрии будут равны между собой, и каждая равна половине всей
нагрузки:
1 1 PI PI2
Изгибающий момент в сечении С равен моменту реакции (со знаком
минус) плюс момент половины треугольной нагрузки (с плечом-^-):
АЛ
Отсюда
n
(кА/
I .
2 "•"
1 1
2 2
PI
4
f
/
' 6
PI*
/>/3
16
, Pl% I
1 16 ' 6 ""
48
Угол поворота сечения на левой опоре будет равен
A "~ EJ "" ^У —
так как поперечная сила в опорном сечении равна опорной реакции (в на-
уу шем случае со знаком минус, поскольку RAf на-
направлена вниз). Для опоры В:
В	гл.*
Ъ.
Как видно из рассмотренных примеров,
при выбранных условиях для знака фи-
фиктивных нагрузок, изгибающих моментов и
поперечных сил знак минус в формуле для
прогибов соответствует, как и раньше,
Фиг. 301.	направлению вниз, а в формуле для углов
поворота — вращению по часовой стрелке;
знак плюс соответствует обратным направлениям:
Пример 81. Найти графо-аналитически угол поворота концов балки АВ,
изображённой на фиг. 301.
Фиктивная балка с нагрузкой моментной площадью показана на чертеже.
Угол поворота для левой опоры 8д равен:
А,	Т 2 м _ Ml
А~ EJ ~	EJ ~~
Для правой опоры:
-2.1-М/
_ BJ _ 3 2 _ Ml
В~~Ё7	?7 - 3EJ '

§ 118] ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИИ ГРАФО-АНАЛЙТЙЧЕСКИМ МЕТОДОМ 381
Пример 82. Найти графо-аналитически прогиб посредине пролёта и на
концах консолей для балки (фиг. 302).
Зпюра изгибающих моментов имеет вид трапеции с наибольшими орди-
ординатами М = — Ра. Превращаем эпюру в грузовую площадь, направляя на-
нагрузку вниз. Фиктивная балка бу-
будет состоять из двух балочек, за-
Р\	tp щемлённых концом и поддержи-
I	I	вающих подвесную балку АВ.
Прогиб посредине пролёта (точ-
(точка F) равен фиктивному моменту
в этой точке от равномерно рас-
распределённой нагрузки, делённому
/71
SSs?)?S/,
I
на жёсткость:
а
в
Pal2
'" SEJ •¦
Прогиб в точке С найдём, вычи-
вычисляя фиктивный момент в этом
Ра,
Ра
А
Фиг. 302.
Фиг. 303.
сечении; он будет вызываться треугольной нагрузкой, расположенной на бал-
балке СА% и реакцией подверной балки Л/ = -^2— (Фиг-
pfl.fl 2
РаЧ Ра*
Отсюда прогиб сечения С
Пример 83. Для балки, изображённой на фиг. 303, найти графо-анали-
графо-аналитически прогиб сечения В.
Построим эпюру изгибающих моментов. В сечении С момент равен + М;
в точке В он равен нулю. На всём протяжении балки момент меняется по
закону прямой. Превращаем эпюру М в фиктивную нагрузку и устраиваем
фиктивную балку в соответствии с таблицей 22. Рассматривая консоль АВ,
находим фиктивный момент в точке В:
м * луг/ 2 / Ш* •
Щв = ~ fMl 'Т	3~'
соответствующий прогиб равен:
х 		Ml2

382
ГРАФО-АНАЛИТИЧЕСКЙЙ И ГРАФИЧЕСКИЙ МЕТОДЫ	[ГЛ. XIX
§ 119. Графо-аналитический метод при криволинейных
эпюрах изгибающего момента.
Пример 84. Найти величину прогиба посредине балки, загружённой
сплошной нагрузкой и показанной на фиг. 304.
Площадь эпюры изгибающих моментов определится выражением
о
Следовательно, площадь данной квадратной параболы составляет 2/3 пло-
площади описанного прямо-
прямоугольника
2 ql* , ql%
У
Фиктивные опорные
реакции будут:
а4 — В* — — — gP
Af — Bf- 2 - 24".
Фиг. 304.
Фиг. 305.
Фиктивный изгибаю-
изгибающий момент в середине
пролёта равен сумме ста-
статических моментов фик-
фиктивных сил, расположен-
расположенных по одну сторону от
среднего сечения балки, допустим, по левую сторону; слева располагаются фи-
фиктивные силы: Af и левая половина площади параболы. Плечо Л/ равно по-
половине пролёта; плечо же половины площади параболы ( у
лится следующим выражением (фиг. 305):
хЛ опреде-
опредеМ (х) • dx • х
384
ql*
(О
т
т. е. центр тяжести половины данной квадратной параболы находится в рас-
5	3
стоянии -у^-/ от опоры балки и в -^/ от середины пролёта балки. Следо-
Следовательно, в середине пролёта
Мг-
— ~~" **f • Г* ~Г" ~7Г * * г» * —• ~~~ ~7ГГ *
16
24
2 "*" 24.' 16 384 дГ'
а прогиб посредине пролёта равен:
f - J-HL
L~ 384 EJ'

§ 119] ГРАФО-АНАЛИТИЧЕСКИЙ МЕТОД ПРИ КРИВОЛИНЕЙНЫХ ЭПЮРАХ 383
Пример 85. Рассмотреть балку, защемлённую одним концом и за-
загружённую равномерно распределённой нагрузкой (фиг. 306, а). Опреде-
Определить величину прогиба свободного конца. Эпюра действительных изги-
изгибающих моментов и схема фиктивной балки показаны на фиг. 306, б.
Изгибающий момент . в заще-
защемлении А фиктивной балки равен
произведению площади а> всей а) д
эпюры на расстояние до её центра
тяжести. Площадь эпюры равна
i
С qxi . qlb
» —- 1	с\ ыл 	 О 9
т. е. одной трети, площади описан*
ного прямоугольника
1 я/2 . qlb
Абсцисса центра тяжести равна:
т. е. центр тяжести данной квад-
квадратной параболы расположен в 3 //4
А	m
i-H*j ^ г
Фиг. 307.
от свободного конца действительной балки и в //4 от места её защемления.
Фиктивный изгибающий момен» в сечении А будет:
гм	Я1Ь 3 .	ql*
а прогиб сечения Л действительной балки равен:
fA=s~~sEJ*
Пример 86. Применяя приём расчленения эпюр и метод сложения
результатов действия сил, определить прогиб и угол поворота в сечении С
балки АВС9 лежащей на двух опорах^ с консолью ВС (фиг. 307, а). Равно-

384	ГРАФО-АНАЛЙТИЧЕСКИЙ И ГРАФИЧЕСКИЙ МЕТОДЫ	[ГЛ. XIX
мерно распределённая нагрузка лежит по всей длине балки. Возможный вид
эпюры изгибающих моментов показан на фиг. 307, б. Заменяем эту эпюру
её составляющими: от нагрузки q на пролёте / (фиг. 307, в) и от нагрузки q
на консоли а (фиг. 307, г). Ординаты двух последних" эпюр могут быть легко
подсчитаны или взяты из ранее решённых задач или из справочника. Харак-
Характерные ординаты надписаны на фиг. 307, *, г. На фиг. 307, д показана фи-
фиктивная балка. Выделим фиктивную балку ВС: на неё действуют давление Bf
от подвесной балки ЛВ и нагрузка параболой с наибольшей ординатой -—
(фиг. 307, е).
Из рассмотрения фиктивной балки АВ, взяв сумму моментов всех фи-
фиктивных сил относительно опоры Л, находим (фиг. 307, ж), что
°f~3 2 2* 2 12 ~6qal 24*
Возвращаясь к схеме фиг. 307, е, вычисляем:
Искомые деформации в сечении С будут:
§ 120. Графический метод построения изогнутой оси балки.
В предыдущем параграфе мы получили зависимость A9.3):
у EJ '
из которой следует, что ординаты изогнутой оси основной балки
пропорциональны ординатам эпюры моментов фиктивной балки;
эта эпюра непосредственно представляет в некотором масштабе
изогнутую ось. Таким образом, задача определения прогибов основ-
основной балки может быть сведена к построению эпюры изгибающего
момента фиктивной балки, т. е. к графическому решению.
Возьмём балку АВ (фиг. 308) пролёсом /, защемлённую концом
и нагружённую на другом парой сил М. Вычертим её с соблюде-
соблюдением- линейного масштаба: в I см чертежа п см балки.
Эпюра изгибающего момента изобразится в виде прямоугольника
с положительной ординатой М\ принимаем эпюру за фиктивную на-
нагрузку. Фиктивная балка будет иметь в точке А свободный конец
и в точке В — защемлённый.
Для графического построения эпюры фиктивного момента за-
заменяем равномерно распределённую нагрузку фиктивной балки

§ 120] ГРАФИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ ИЗОГНУТОЙ ОСИ БАЛКИ 385
четырьмя равными сосредоточенными фиктивными силами, прило-
приложенными в центрах тяжести соответствующих грузовых площадей.
Все эти силы шА, оK,
^ А С	д
«>з
4 будут равны
л*-] каждая.
Выбрав, как будет
указано ниже, полюс
О, построим много-
многоугольник сил и верё-
верёвочный многоуголь-
многоугольник (фиг. 308).
Ранее (§ 76) было
доказано, что М =
= Я-т], где И—по-
люсное расстояние, от-
отложенное в масштабе сил, а т\ — ордината верёвочного многоуголь-
многоугольника, измеренная в масштабе балки (в масштабе длин).
Так как это справедливо и для балки, загружённой фиктивной
нагрузкой, то, сохраняя приведённые только что обозначения, имеем
Фиг. 308.
С другой стороны, нам известно, что
Отсюда — если бы можно было в масштабе фиктивных сил отложить
H=EJr то прогиб действительной балки / равнялся бы ординате
верёвочного многоугольника т], измеренной в масштабе балки.
Но так как EJ обычно велико по сравнению с фиктивными
силами, то выполнить построение многоугольника сил в одинако-
одинаковом масштабе по вертикали (где отложены а>и а>2, а>3, • • •) и по
горизонтали (где откладываем Н) нельзя. Полюс оказался бы очень
удалённым от линии сил о> и прогибы вышли бы на чертеже очень
EJ
малыми. Поэтому принимают // = —, где k — любое положитель-
положительное целое число, выбираемое по только что указанным соображе-
EJ
ниям удобства построения. Отсюда следует, что Mf= ~-r- • % а
прогиб f=\ .
F1
Следовательно, если отложить —г- в том же масштабе, в каком отло-
отложены о)!, со2, <о3,..., то ордината верёвочного многоугольника % изме-
измеренная в масштабе балки, даст увеличенную в k раз величину прогиба/.
Если же принять n = k, то прогибы изобразятся в натуральную
величину.
В приведённом на фиг. 308 построении видим, что многоуголь-
многоугольник сил замкнут, верёвочный же многоугольник не замкнут; это

386
ГРАФОАНАЛИТИЧЕСКИЙ И ГРАФИЧЕСКИЙ МЕТОДЫ	[гл. Х\Х
означает, что заданные силы а)ь аJ, ... уравновешиваются фиктив-
фиктивной опорной реакцией в защемлении В (причём /?? = 2Ш) и фик-
фиктивным опорным моментом. Первый луч построения, проведённый
до пересечения с линией действия оI5 является замыкающим лучом:
он пересекается также и с линией действия силы RB и представ-
представляет прямую ось балки, а крайний левый его участок и лучи 2, 3,
4У 5 дают верёвочную ломаную линию, стремящуюся при дроблении
сил со в пределе к изогнутой оси балки.
Предположим, что / = 4 м, М = 4 тм, [а] = 1400 к г; см2, Е = 2 • 10° кг! см2.
Необходимый момент сопротивления будет
примем для расчёта двутавр № 24:7 = 3460 еж4, W = 2&9 см9.'
При делении балки на четыре равные части получаем (фиг. 308):
coj = со2 = со3 = <о4 = 4 ТМ2.
Вычертим балку в масштабе 1:п= 1:100; длина балки изобразится отрез-
отрезком в 4 см; k примем равным 100:
^ = 6,92 тм2.
(	EJ\
Для изображения многоугольника сил (со и -г- \ выберем масштаб в
1 см — 2 тм2.
Каждая сила со изобразится отрезком в 2 сму а полюсное расстояние
EJ
И = -г	отрезком 3,46 см. После построения верёвочного многоугольника
ордината ц, измеренная в сечении В, дает прогиб / в натуральную величину
(в данном примере y]=/=4,6 cm, что предлагается проверить построением).
Фиг. 309.
Рассмотрим в качестве второго примера балку на двух опо-
опорах А и В с произвольной нагрузкой (фиг. 309).

§ 120] ГРАФИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ ИЗОГНУТОЙ ОСИ ВАЛКИ	387
Фиктивная балка тоже будет шарнирно-опёртой на две опоры;
деля площадь фиктивной нагрузки на несколько частей, строим
верёвочный многоугольник и проводим замыкающий луч О.
Ординаты верёвочного многоугольника, измеренные от замыкаю-
замыкающей, будут пропорциональны изгибающим моментам для фиктивной
балки, а следовательно, прогибам основной балки.
Изложенный выше способ решения задачи должен быть упро-
упрощён; нет необходимости изображать фиктивную балку и решать
вопрос об её конструкции.
Для изогнутой оси балки осью абсцисс служит первоначальная
прямая ось; следовательно, в рассмотренных примерах верёвочный
многоугольник изображал изогнутую ось, а та сторона, от которой
шёл отсчёт ординат,— первоначальную ось балки.
Поэтому достаточно построить эпюру моментов для основной
балки, не определяя условий опирания фиктивной балки, заме-
заменить эпюру распределённой фиктивной нагрузки (эпюру qf) фик-
фиктивными сосредоточенными силами, построить для них верёвоч-
верёвочный многоугольник при соответственно выбранном полюсном рас-
расстоянии, а затем так провести ось абсцисс, чтобы она заняла
относительно верёвочного многоугольника такое же положение,
какое первоначальная ось балки занимает относительно изогну-
изогнутой.
В первом примере (фиг. 308) первоначальная ось балки касалась
изогнутой под сечением Л, поэтому и ось абсцисс должна касаться
верёвочного многоугольника в том же сечении, т. е. совпадать с
продолжением его первой стороны; во втором примере (фиг. 309)
прогибы балки в точках А и В должны быть равны нулю, поэтому
ось абсцисс (замыкающая) пересекает верёвочный многоугольник
под точками А и В.
Покажем применение графического способа ещё на одном при-
примере. Возьмём балку, защемлённую концом, поддерживающую под-
подвесную балку с консолью (фиг. 310).
Проведём ось абсцисс и построим эпюру моментов. Заменим
эпюру М(х)у как нагрузку qfi силами и построим силовой и вере-
веревочный многоугольники, не забывая о знаках фиктивных сил. Так
как конец А защемлён, то ось абсцисс для балки АВ надо прове-
провести так, чтобы она коснулась верёвочного многоугольника под
этим сечением, т. е. являлась бы продолжением первой стороны;
ось абсцисс для второй балки BD определится тем, что в точ-
точке С прогиб равен нулю, а в шарнире В обе балки имеют
один и тот же прогиб; поэтому ось абсцисс второй балки пройдёт
через точку с пересечения верёвочного многоугольника с вер-
вертикалью опоры С и через точку Ь — точку пересечения пер-
первой оси абсцисс с вертикалью шарнира В. В нижней части
фиг. 310 ординаты прогибов отложены от общей горизонтальной
оси абсцисс.
13'

388
БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ
[гл. хх
Описанный в настоящем параграфе графический метод имеет
ряд преимуществ: он приложим при любой системе нагрузок; по-
\Р
Фиг. 310.
строения при сложной системе грузов требуют почти столько же
времени, что и при простой; легче заметить ошибку; точность этого
способа для практических целей почти всегда достаточна.
ГЛАВА XX.
БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ.
§ 121. Подбор сечений балок равного сопротивления.
Все предыдущие расчёты относились к балкам постоянного сече-
сечения. На практике мы имеем часто дело с балками, поперечные раз-
размеры которых меняются по длине либо постепенно, либо резко.
Ниже рассмотрено несколько примеров подбора сечения и опре-
определения деформаций балок переменного профиля.
Так как изгибающие моменты обычно меняются по длине балки,
то, подбирая её сечение по наибольшему изгибающему моменту, мы
получаем излишний запас материала во всех сечениях балки, кроме
того, которому соответствует Мтгх. Для экономии материала, а
также для увеличения в нужных случаях гибкости балок применяют
балки равного сопротивления. Под этим названием подразумевают
балки, у которых во всех сечениях наибольшее нормальное напря-
напряжение одинаково и равно допускаемому (или не превышает его).

§ 121]
ПОДБОР СЕЧЕНИЙ БАЛОК РАВНОГО СОПРОТИВЛЕНИЯ
Условие, определяющее форму такой балки, имеет вид
М(х) _,_,
°max
W(x) =
М(х)
389
B0.1)
B0.2)
Здесь М{х) и W{x) — изгибающий момент и момент сопроти-
сопротивления в любом сечении балки; W(x) для каждого сечения балки
должен меняться пропорционально изгибающему моменту.
Условия B0.1) и B0.2) справедливы и для сечения с наиболь-
наибольшим изгибающим моментом; если обозначить Wo — момент сопроти-
сопротивления балки в сечении с наибольшим изгибающим моментом Мтах,
то можно написать:
,].	B0.3)
Wo ~ W (х) L J#
Покажем ход вычислений на примере. Рассмотрим балку пролё-
пролётом /, защемлённую концом А и нагружённую на другом конце
силой Р (фиг. 311 и 312). Выберем сечение этой балки в виде
min
Фиг. 311.
Фиг. 312.
прямоугольника; задачу о надлежащем изменении момента сопроти-
сопротивления можно решать, меняя высоту или ширину балки или тот и
другой размер вместе.
Пусть высота балки будет постоянной h = hQy а ширина пере-
переменной— Ь(х). Момент сопротивления в сечении на расстоянии х
от свободного конца будет W (х) == —Цг— , а изгибающий момент
М = — Рх\ момент сопротивления опорного сечения WQ = °6 , а
наибольший изгибающий момент в опорном сечении Мтах = \Р1\.
В расчёте имеют значения лишь абсолютные величины М (х) и Мтах.
По формуле B0.3) получаем:
PI • 6	РХ • 6
=Tp- 0ТКУда *(*> = *• Т»

390	БЛЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ	[ГЛ. XX
т. е. ширина меняется по линейному закону в зависимости от х.
При лг = / ширина равна bQ.
Вид балки в фасаде и плане показан на фиг. 311. Такое очерта-
очертание балки получается, если учитывать её прочность только по отно-
отношению к нормальным напряжениям; ширина b (x) в сечении В обра-
обращается в нуль.
Однако необходимо обеспечить прочность и по отношению
к касательным напряжениям. Наименьшая ширина балки, требуемая
этим условием, определится из уравнения
О	^с ГПЗХ	г т
тах 2 hbm[n L J
или, так как Qmax = P9
Ь - - ЗР
Исправленное очертание балки показано на фиг. 312.
§ 122. Практические примеры балок равного сопротивления.
Только что рассмотренный пример имеет применение на прак-
практике при проектировании рессор. Рессору, пренебрегая её доста-
достаточно слабой кривизной, можно рассматривать как балку на двух
опорах (фиг. 313, а), нагружённую силой Р посредине пролёта и
р
реакциями -у по концам.
Запроектируем этот стержень как балку равного сопротивления
с постоянной высотой /г0 и переменной шириной Ьх\ по симметрии
достаточно ограничиться рассмотрением одной половины пролёта.
Моменты сопротивления W(x) и Wo будут выражаться также,
как и в первом примере. Наибольший изгибающий момент — посре-
посредине пролёта — равен
_Р1_
max	4 *
Изгибающий момент в любом сечении
Решая задачу, как и в первом примере, получим:
Ширина балки, необходимая для обеспечения сопротивления попе-
/ Р \
речной силе [ -о-), определяется формулой

§ 122] ПРАКТИЧЕСКИЕ ПРИМЕРЫ БАЛОК РАВНОГО СОПРОТИВЛЕНИЯ
391
Вид рессоры в фасаде и плане показан на той же фиг. 313, б
и 0. Подобная конструкция рессоры была бы крайне неудобной на
практике; поэтому ей придают несколько другую форму, не меняя
характера её работы. Представим себе, что в плане лист рессоры
разделён на узкие полоски, как показано на фиг. 313, г. Если мы
расположим эти полоски не рядом друг с другом, а одну над
ю -
-d2-
¦
t
— d—
Фиг. 313.
Фиг. 314.
другой, то, если пренебречь трением между ними, работа балки не из-
изменится, а рессора получит вид, изображённый в плане на фиг. 313, д
и в фасаде — на фиг. 313, е.
Конечно, на практике каждый лист рессоры, 1-й, 2-й и т. д., изго-
изготовляют цельным, а не состоящим из двух половинок.
Балки переменного сечения применяются и в машиностроении;
например, валы часто конструируются как балки равного сопроти-
сопротивления.
Пример 87. Возьмём вал, опёртый по концам (фиг. 314, а) и нагру-
нагружённый весом маховика в расстоянии а от левой и Ъ от правой опоры. Про-
Пролёт вала /.
Найдём форму балки равного сопротивления для вала. Реакции вала
равны
А™' В^

392
БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ
[ГЛ. XX
Наибольший изгибающий момент (под силой Р)
Мтах = Р /" •
Момент сопротивления в этом сечении (фиг. 314)
Размер d может быть определён из условия прочности вала в этом сечении
^ах ^ М; d = 1/ ^ ^ .
Для левой части вала имеем условия:
тогда
Pab 32
32
I	n[d (jc) J3
или
для правой части вала получаем:
~ Xf.
Наименьший диаметр у концов вала может быть определён по условию
прочности на касательные напряжения:
4
"8 '
4
АРЬ
\Ра
: [т] для левой части
: [х] для правой части.
Отсюда
или
,/:
Ра
3*/[т1 *
Этот диаметр, однако, приходится обычно значительно увеличивать из
условий проверки цапф вала на нагревание. Теоретическая форма вала пока-
показана на фиг. 314, б.
Практически диаметр вала меняют ступенчатым образом. Разницу между
d и dmin разбивают на несколько частей; таким образом, отдельные участки
вала будут иметь диаметры rf, du dit ... Длину каждого участка проще всего
определить графически, пользуясь эпюрой моментов. Вычисляем для этого
моменты сопротивления, соответствующие диаметрам d, dlt d%1 ...; они будут
wmax =="oo">^i в ~о9 и т* д* ^множая эти моменты сопротивления на допу-
допускаемое напряжение [а], получаем величину допускаемого изгибающего

§ 122] ПРАКТИЧЕСКИЕ ПРИМЕРЫ БАЛОК РАВНОГО СОПРОТИВЛЕНИЯ 393
момента для каждого участка вала. Проводим на эпюре моментов ряд гори-
горизонтальных линий с ординатами ^шах[с?], Wx [a], W2 [а], ... (фиг. 314, в);
точки пересечения этих линий с эпюрой моментов определяют длины участков
вала. Действительная форма вала дана на фиг. 314, г.
Возьмём числовой пример. Пусть /=1,2 м; а =0,7 м; ? = 0,5 м;
р = 5 т; [а] = 400 кг/см2; [т] = 250 кг/см2.
5000 • 0,5
:2100 кг; В-.
5000 • 0,7
1,2
«^2900 кг.
Тогда
-'Y~
5000 -50-70
'я/[о1	У " я • 120 • 400
rf ¦ =4l/"^~=4l/" 5000.70 =4,
К 3^R	К 3*. 120-250 '
15,5 см ^з 16 см%
Зл/[х
Принимая из условий проверки на нагревание диаметр цапф равным
10 см, берём диаметры участков вала равными
d = 16 еж, g?i = 14 см,
d% = 12 еж, </8 = 10 еж.
Вычислив для этих диамет-
диаметров соответствующие допускае-
допускаемые изгибающие моменты по
формуле W[q], проводя соот-
соответствующие горизонтали на
эпюре моментов (фиг. 315) и
округляя полученные длины
участков, окончательно уста-
устанавливаем форму вала.
Эпюра действительно до-
допускаемых изгибающих момен-
моментов для ступенчатого вала по-
показана на фиг. 315 ступенча-
ступенчатой линией. Она нигде не пересекает треугольную эпюру моментов от на-
нагрузки Р; всюду мы имеем некоторый запас.
Для сравнения в сечениях, где изменяется диаметр, вычислены ординаты
этой эпюры по формуле М (х) = Ах и сопоставлены с допускаемыми момен-
моментами (Wfal) для этих же сечений:
Фиг. 315.
32
32
7ll23
400 = 160 000 кгсм > 2100 . 70 = 147 000 кгсм%
400 = 107600 > > 2100- 50= 105000 >
W, [а] = -~f- • 400 = 67 800 > > 2100 • 30 = 63000 »
№8ы = Д|^. 400 = 39 200 > > 2100-10 = 21000 >
о/
При конструировании клёпаной или сварной балки нет необхо-
необходимости тянуть все горизонтальные листы по всей длине балки.
По мере уменьшения изгибающего момента можно обрывать сначала
наружный горизонтальный лист пояса, а потом и внутренний.

394
ВАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ
[ГЛ. XX
Умножая моменты сопротивления балки с одним листом и без
листов на допускаемое напряжение, получаем величины допускаемых
изгибающих моментов для этих сечений.
Пользуясь эпюрой действительных изгибающих моментов так же,
как и для случаев вала, получаем возможность определить необходи-
необходимую длину горизонтальных листов балки. Определим значения W[g]
для клёпаной балки, подробно разобранной в §§ 98—102. Исходные
данные берём из таблицы 21. Подсчёты ведём согласно таблице 21а.
Таблица 21а. Допустимые изгибающие моменты.
т
J_
т
j
L Балка полного сечения
г Балка с одной парой ли-
L стов
г
L Балка без поясных листов
У„ет
см*
692 500
531 200
374 900
Z
max
см
64
63
62
w
см*
10 800
8400
6050
[М]
тм
173,0
135,0
96,5
На фиг. 316 заштрихована эпюра действующих изгибающих момен-
моментов. Ступенчатая линия — эпюра допустимых изгибающих моментов.
\30rn
12,5m/м
166,2m
\3Om
173,0m
	135,0/m
Фиг. 316.
Надо заметить, что на практике обычно избегают оставлять сече-
сечение балки совсем без горизонтальных листов для улучшения связи
между уголками.

§ 123] ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ БАЛОК ПЕРЕМЕННОГО СЕЧЕНИЯ	395
§ 123, Определение деформаций балок переменного сечения.
При определении прогибов и углов поворота для балок с пере-
переменным сечением надлежит иметь в виду, что жёсткость такой
балки является функцией от х. Поэтому дифференциальное уравне-
уравнение изогнутой оси принимает вид
где J(x) — переменный момент инерции сечений балки.
До интегрирования этого уравнения можно выразить J(x) над-
надлежащей подстановкой через У, т. е. через момент инерции того
сечения, где действует Almax» после этого вычисления производятся
так же, как и для балок постоянного сечения (§ 109).
Покажем это на примере, разобранном выше. Определим прогиб
балки равного сопротивления (фиг. 311), защемлённой одним кон-
концом, нагружённой на другом конце силой Р и имеющей постоянную
высоту. Начало координат выберем на свободном конце балки.
Тогда'
^=*§-±=jlr, B0.6)
Дифференциальное уравнение принимает вид:
= — — = - Р/.	B0.7)
х	v '
Интегрируем два раза:
Для определения постоянных интегрирования имеем условия:
в точке А при х = 1 прогиб j/ = 0 и угол поворота -~ = 0, или
\J 	 	 Л. If ^ V-/	И	V 		q
отсюда
С=Р1* и D = — ^-.
Выражения для j/и 0 принимают вид:
t/л:	f/ ~^~ EJ ?"У L	' .г
Plx* Pl2x PP	PI* Г	«^
1-2т+"? г
Наибольший прогиб на свободном конце балки В получится при
= 0; он равен
f __^L

396	БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ	[ГЛ. XX
Если бы мы всю балку сделали постоянного сечения с моментом
инерции J, то наибольший прогиб был бы
/max = op г »
т. е. в Л у раза меньше.
Таким образом, балки переменного сечения обладают большей
гибкостью по сравнению с балками постоянной жёсткости при оди-
одинаковой с ними прочности. Именно поэтому, а не только ради эконо-
экономии материала, они и применяются в таких конструкциях, как рессоры.
Уравнение B0.7) показывает, что в рассмотренном примере кри-
кривизна балки постоянна, т. е. ось балки должна изогнуться по
дуге круга. Между тем в результате интегрирования мы получили
уравнение параболы; предлагаем учащимся объяснить, почему это
произошло.
Применение графо-аналитического метода определения деформа-
деформаций к балкам переменного сечения также не представляет затрудне-
затруднений. Вместо того чтобы для вычислений / и 0 делить на жёсткость
EJ изгибающий момент и поперечную силу в фиктивной балке,
можно за фиктивную нагрузку принять
Р	f эпюру моментов для основной балки, раз-
^gj	3 делив её ординаты на EJ. Тогда
EJ
^	"	CJ	J	J
\ Обобщая этот способ на балки переменного
сечения, полагаем
Фиг. 317.	, _ М (х) .
загружаем этой нагрузкой фиктивную балку и получаем искомые
прогибы и углы поворота как изгибающие моменты и поперечные
силы в сечениях фиктивной балки.
,п Для рассмотренного выше примера q} =
J"	pxi	pi
jR =——— =— —, т. е. фиктивная балка
должна быть загружена сплошной уже не тре-
треугольной, а равномерно распределённой на-
нагрузкой (фиг. 317). Прогиб сечения В, равный
изгибающему моменту в защемлении фик-
I I I I I | I" тивной балки, выразится формулой
Фиг. 318.
Тот же результат мы получили бы, предполагая, что наша балка
имеет постоянную жёсткость EJ, а её эпюра изгибающих моментов
преобразована путём умножения каждой ординаты на отношение

§ 123] ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ БАЛОК ПЕРЕМЕННОГО СЕЧЕНИЯ
EJ
397
EJ(x)
; преобразованная эпюра моментов имела бы ординаты
Рх-^—— РхЕП — PL
~ ИХ EJ (х) — ~ ИХ ЁТх — ~ ИС
(фиг. 318); тогда по общему правилу графо-аналитического метода
/	Р/3	р/3
АЛ	 Р/ . /_	л * ы <1 		? 1
Mf— Hi l2— 2 *У — — <1ЕГ
Таким образом, определение прогибов балки переменного сече-
сечения можно привести к той же операции для балки постоянной
EJ
жёсткости, но с преобразованной умножением на EJ( ^ эпюрой
моментов.
Пример 88. Определить графо-аналитически прогиб под грузом Р
для балки, свободно лежащей на двух опорах и нагружённой посредине
пролёта / сосредоточенным грузом Р (фиг. 319, а). Момент инерции сечений
левой половины балки равен /, правой -у. Преобразуем эпюру моментов
(фиг. 319, &), умножая ординаты правой половины на отношение /://2 = 2;
•¦	1
Y '
1
1т z
Z
1
Z
Фиг. 319.
фиктивная балка с преобразованной нагрузкой изображена на фиг. 319, в.
Левая фиктивная реакция равна
фиктивный изгибающий момент в сечении С и прогиб точки С соответственно
будут:
Л1/с = -л/у
2 2
4 6
24 "*" 96
32
Р/3
2ЕУ
Пример 89. Определить прогиб балки, защемлённой одним концом
и загружённой сосредоточенной силой на другом конце (фиг. 320, а). Одна
половина балки имеет сечение больших размеров, причём
Л > Л.

398
БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ
[гл. хх
Преобразуя эпюру изгибающего момента М(х) (фиг. 320, б) в фиктив-
фиктивную нагрузку, мы должны ординаты левой части эпюры увеличить в ~- раз
(фиг. 320, в).
Фиг. 321.
Прогиб под силой Р определится следующим подсчётом (при -^- =
/~~" ^~~ ~ г>	о	О	О	О ^^	О	Q ~~~	Q	'
J,	?	?	о	Z.	?>	о	о
= ЗР/3
Этот же приём следует использовать при применении графиче-
графического построения изогнутой оси балки переменного сечения. Надо
выбрать жёсткость EJ одного из сечений балки, обычно наиболь-

§ 123] ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ БАЛОК ПЕРЕМЕННОГО СЕЧЕНИЯ 399
шего, за основную, преобразовать эпюру моментов и для неб построить
верёвочный многоугольник с полюсным расстояниехМ (§ 120), равным
#= — . Ординаты построенного обычным порядком многоугольника
изобразят прогибы нашей балки.
Метод преобразования эпюры особенно удобен, если сечение
балки меняется ступенчатым образом, а не непрерывно. Применим
этот способ к построению изогнутой оси вала, рассмотренного
в предыдущем параграфе. Построение показано на фиг. 321. Эпюра
моментов имеет вид треугольника с наибольшей ординатой, равной
РаЪ 5000.70.50.==145500кг^
Диаметры d участков вала и соответствующие моменты инерции
- имеют следующие значения:
1СТКИ
0
1
2
3
Диаметр
см
16
14
12
10
Момент инерцш
еж4
3217
1886
1018
491
Ордината эпюры моментов, соответствующая переходу от участка
с диаметром 16 см к участку с диаметром 14 см, равна Мх = Ах{=з
= 2100 • 50= 105 000 кгсм\ после преобразования она будет равна
4917
105 000 • -jgjg- = 180 000 кгем.
Подобным же образом преобразуются все прочие граничные
ординаты. Части полученной грузовой площади заменены сосредото-
сосредоточенными силами; далее известным уже образом построен верёвочный
многоугольник, изображающий изогнутую ось вала.

ОТДЕЛ VII.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ.
ГЛАВА XXI.
ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
К ОПРЕДЕЛЕНИЮ ДЕФОРМАЦИЙ.
§ 124. Постановка вопроса.
Кроме рассмотренных способов вычисления прогибов и углов по-
поворота сечений балок существует более общий метод, пригодный
для определения деформаций любых упругих конструкций. Он осно-
основан на применении закона сохранения энергии.
При статическом растяжении или сжатии упругого стержня
происходит превращение потенциальной энергии из одного вида
в другой; часть потенциальной энергии действующего на стержень
груза полностью переходит в потенциальную энергию деформации
стержня. Действительно, если мы будем нагружать стержень путём
постепенного подвешивания к его нижнему концу очень
малых грузов dP (фиг. 322), то при добавлении каждого
такого груза подвешенная уже часть нагрузки опустится
и её потенциальная энергия уменьшится, а потенциальная
энергия деформации стержня соответственно увеличится.
Это явление имеет место при любом виде деформации
всякой упругой конструкции при статической нагрузке;
такую конструкцию можно рассматривать как своеобраз-
своеобразную машину, преобразующую один вид потенциальной
энергии в другой.
Фиг. 322. эды уСЛОВИЛИСЬ (§ 2) называть «статической» такую
нагрузку, которая возрастает постепенно и таким обра-
образом, что ускорениями элементов конструкции можно пренебречь;
передача давлений (сил) от одной части конструкции на другую не
меняет характера движения этих частей, т. е. их скорость остаётся
постоянной и ускорение отсутствует.
При этих условиях деформация конструкции не будет сопрово-
сопровождаться изменением кинетической энергии системы, и будет иметь
место лишь преобразование потенциальной энергии из одного вида
в другой. При этом мы пренебрегаем магнитными, электрическими
и тепловыми явлениями, сопровождающими упругие статические де-
деформации тела лишь в очень слабой мере.

§ 124]	постановка вопроса	401
Так как характер движения всех элементов конструкции с те-
течением времени не меняется, то в каждый момент времени будет
иметь место равновесие как для каждой части конструкции в целом
под действием внешних сил и реакций, так и для каждого элемента
этой части под действием внешних сил и напряжений, приложенных
к этому элементу. Деформации конструкции, напряжения в её частях
и реакции, передающиеся от одной части на другую, успевают
следовать за ростом нагрузки.
Таким образом, можно сказать, что полное преобразование одного
вида потенциальной энергии в другой имеет место, если деформа-
деформация происходит без нарушения равновесия системы. Мерой энер-
энергии, превратившейся в другой вид, является величина работы,
произведённой силами, действующими на конструкцию.
Обозначим величину накопленной потенциальной энергии дефор-
деформации через U, а уменьшение потенциальной энергии внешних на-
нагрузок UP. Тогда величина UP измеряется положительной работой
этих нагрузок Ар; с другой стороны, накоплению потенциальной
энергии деформации U соответствует отрицательная работа вну-
внутренних, междучастичных сил Л, так как перемещения точек тела
при деформации происходят в обратном по отношению к внутренним
силам направлении.
Закон сохранения энергии при деформациях упругих систем при-
принимает вид:
UP=U\	B1.1)
заменяя в этой формуле величины Up и U численно равными им
значениями работ Ар и —А, получаем иную формулировку этого
закона:
Ар= — А или ЛР + Л = 0.	B1.2)
Эта формулировка закона сохранения энергии совпадает с так
называемым «началом» возможных перемещений в применении к уп-
упругим системам; равенство B1.2) выражает ту мысль, что при
перемещениях без нарушения равновесия сумма работ всех сил,
приложенных к точкам тела, равна нулю.
Таким образом, начало возможных перемещений в применении
к упругим системам является следствием закона сохранения энергии.
Из формулы B1.1) следует, что потенциальная энергия деформа-
деформации U численно равна работе внешних сил Ар, проделанной ими
при этой деформации:
U=Ap.	B1.3)
Совершенно неправильным является истолкование этого равенства,
иногда встречающееся в учебниках по строительной механике:
«работа внешних сил при деформации стержня переходит в потен-
потенциальную энергию деформации»; переходить в потенциальную энер-

402
ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ [ГЛ. XXI
гию деформации может только другой вид энергии; как правило,
это — потенциальная энергия внешних нагрузок. Величина же ра-
работы, производимой при этом переходе внешними силами, является
лишь числовой мерой превратившейся части энергии.
§ 125. Вычисление потенциальной энергии.
А. При вычислении потенциальной энергии мы будем предпо-
предполагать, что деформации не только материала, но и всей конструкции,
следуя закону Гука, пропорциональны нагрузкам, т. е. линейно
с ними связаны и растут постепенно вместе с ними.
Мы знаем (§ И), что при статическом растяжении или сжатии
стержня силами Р величина работы Ар, а следовательно, и вели-
величина энергии U равняется:
В случае сдвига (§ 54)
При кручении (§ 62)
2?/
Q4
~ 2Gt
МЦ
2ШР
Д 20F
? 2fl
ф2ОУп
2/ '
B1.4)
B1.5)
B1.6)
Так же как и при кручении, может быть вычислена потенциаль-
потенциальная энергия при чистом изгибе.
Концевые сечения балки под действием изгибающих моментов
(фиг. 323) повернутся на угол 0 =
Ж
где <р— центральный угол
изогнувшейся по дуге радиусом р оси балки.
Тогда
Фиг. 323.
Ap^L^!L^L B171
= |, а | = ^ A3.10)(см. §78).
Из формул B1.4) — B1.7) следует, что
потенциальная энергия деформации равна
половине произведения силы или пары сил
на перемещение по её направлению того
сечения, где эта сила приложена. Условимся
называть термином «обобщённая сила» всякую нагрузку, вызы-
вызывающую соответствующее нагрузке перемещение, т. е. и сосредо-
сосредоточенную силу, и пару сил, и т. п.; перемещение же, соответ-
соответствующее этой силе, будем называть «обобщённой координатой».
«Соответствие» заключается в том, что речь идёт о перемещении
того сечения, где приложена рассматриваемая сила, причём о таком

§ 125]
ВЫЧИСЛЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
103
перемещении, что произведение его на эту силу даёт нам величину
работы; для сосредоточенной силы это будет линейное перемеще-
перемещение по направлению действия силы — прогиб, удлинение; для пары
сил — это угол поворота сечения по направлению действия пары.
Теперь мы можем формулы B1.4) — B1.7) обобщить: потен-
потенциальная энергия деформации численно равна половине произве-
произведения обобщённой силы на соответствующую ей координату:
U=-
B1.8)
где Р — обобщённая сила, В— обобщённая координата.
Формулы B1.4) — B1.7) показывают, что потенциальная энергия
является функцией второй степени от независимых внешних сил,
так как в эти формулы не входят реакции, зависящие от прило-
приложенных к элементу сил и связанные с ними уравнениями равнове-
равновесия. Из тех же формул видно, что величина потенциальной энергии
деформации является функцией второй степени от «обобщённых
координат» системы и вполне ими определяется. Таким образом,
порядок приложения нагрузок в этом отношении безразличен,
важна лишь окончательная форма деформированного элемента.
Поэтому, хотя результаты этого параграфа получены в предполо-
предположении, что нагрузка возрастает статически, при сохранении равно-
равновесия в течение всего процесса нагружения, однако выведенные
формулы сохраняют силу и при любом способе приложения нагру-
нагрузок, лишь бы значения сил и деформаций были связаны линейной
зависимостью и относились к тому моменту, когда установится
равновесие конструкции.
Б. В общем случае изгиба изгибающий момент М(х) является
величиной переменной. В любом сечении ему будет сопутствовать
поперечная сила Q(x). Поэтому рассматривать следует уже не всю
балку в целом, а лишь бесконечно малый элемент балки длиной dx.
А
Qix)
I
О,
2
М[Х) MlXL
В G
del h& П do
/ z
!J(X)
Л
\оГ"ог
^—dx-
а.)
/1
J4(x)
It-1-^-) Q(*>
>v /
dx—s-1
6)
Фиг. 324.
\П
Под действием изгибающих усилий сечения элемента поворачи-
поворачиваются и образуют между собой угол dB (фиг. 324, б). Касательные
же усилия стремятся вызвать (фиг. 324, в) перекос элемента; таким

404	ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ	[ГЛ. XXI
образом перемещения от нормальных напряжений идут перпендику-
перпендикулярно к направлению касательных напряжений, и наоборот. Это по-
позволяет независимо вычислять работу изгибающих и касательных
усилий.
Обычно работа касательных усилий оказывается малой по срав-
сравнению с работой нормальных, поэтому мы пока ею будем пренебре-
пренебрегать. Элементарная работа нормаль-
РЬ	ных усилий (как и в случае чистого
^	р	| _Ра изгиба) равна:
|
? B1.9)
или
Фиг. 325.	aU ——2E7~f B1-9)
Вся потенциальная энергия изгиба получится суммированием по
длине балки
Знак предела интегрирования условно указывает, что интегриро-
интегрирование должно охватить всю балку; в тех случаях, когда для М(х)
мы имеем несколько участков, интеграл B1.9") приходится разбивать
на сумму интегралов.
Вычислим потенциальную энергию балки на двух опорах, нагру-
нагружённой силой Р (фиг. 325). Эпюра моментов имеет два участка;
поэтому
а	Ъ
?M\dx , С M\dx
U — J 2EJ "» J 2EJ
о	о
о
., if
iff (Pb\* °j i Г (Р
=m[ J (t) ^i^+j (т
В. Зная величину потенциальной энергии и пользуясь тем, что из внеш-
внешних сил только сила Р совершает работу при деформации балки, можем найти
величину прогиба под этой силой из следующих зависимостей:
1	Р22Ь2
откуда

§ 126]
ТЕОРЕМА КАСТЙЛЬЯНО
405
В частном случае
значение прогиба:
при а = ? = — получаем хорошо известное уже
PI*
48EJ
Иногда, при малом количестве внешних активных сил, определение ве-
величины потенциальной энергии при изгибе можно производить, минуя фор-
формулу B1.8), путём вычисления работы внешних сил.
Рассмотрим, например, балку (фиг. 326), защемлённую концом Л. и на-
нагружённую на конце В сосредоточенной силой Р. Пролёт балки /. На балку
действует заданная сила Р и вызванные ею реакции Л, МА и //д. Так как
опорное сечение неподвижно, то реакции работы при деформации балки не
производят. Работу даёт лишь сила Р\ прогиб конца балки при постепенном
возрастании силы Р связан с ней линейной зависимостью:
SEJ
или F =
работа сила Р
D2/3
— П	 _ DP— Г L
-и- 2 /у- 6?У—
Если на элемент конструкции будет действовать несколько сил, то пол-
полная потенциальная энергия получится суммированием таких произведений,
вычисленных при совместном действии на конструкцию всех этих сил,
так как каждое перемещение будет зависеть от всей нагрузки.
Т
л Л
А Ь
Л
• А
И
Фиг. 326.
Фиг. 327.
Например, при действии на балку, защемлённую концом (фиг. 327),
силы Р и пары Му приложенных на свободном конце В, потенциальная
энергия будет равна:
a -n-lpf . ±М8 -±P(f<L-M^\ \_ (Ш W\
лр— и — 2 Пв~Г 2 м*в— 2 ^\ЗЕУ 2EJ ) ^ 2 т \EJ ~~2EJ1~~
_Р2/3 МЧ PMI2
oEj 2EJ 2EJ
В двух последних примерах для определения величины работы внешних
сил Лр= U требовалось знать величину прогиба или угла поворота в сече-
сечении приложения внешней силы.
§ 126. Теорема Кастильяно.
Установим теперь метод определения перемещений, основанный
на вычислении потенциальной энергии деформации. Поставим себе
задачу нахождения перемещений точек упругой системы по направ-
направлению действия приложенных к этой системе внешних сил.

406 ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ [ГЛ. XXI
Будем решать эту задачу в несколько приёмов; сначала рас-
рассмотрим более простой случай (фиг. 328), когда на балку в сече-
сечениях /, 2, 3,... действуют только сосредоточенные силы Ри Р2,
Рд, ... и т. д. Под действием этих сил балка прогнётся по кривой /
и останется в равновесии.
Прогибы сечений /, 2, 3, ..., в которых приложены силы Ри
Р%> Р3> • • • > обозначим У\,Уъ,Уз>.-* и т- Д- Найдём один из этих
прогибов, например уг — прогиб сечения, в котором приложена
сила Pt.
Переведём балку, не нарушая равновесия, из положения /
в смежное положение //, показанное на фиг. 328 пунктиром. Это
можно сделать различными приёмами:
добавить новую нагрузку, увеличить
уже приложенные и т. д.
Мы представим себе,, что для пе-
перехода к смежному деформированному
состоянию // к силе Рх сделана беско-
бесконечно малая добавка dPx (фиг. 328);
чтобы при этом переходе не нарушать
Фиг. 328.	равновесия, будем считать, что эта
добавка прикладывается статически, т. е. возрастает от нуля до
окончательного значения медленно и постепенно.
При переходе от состояния / балки к состоянию // все нагрузки
Р опустятся, значит, их потенциальная энергия уменьшится. Так как
равновесие не нарушалось, то уменьшение энергии нагрузок dUp
целиком преобразовалось в увеличение потенциальной энергии де-
деформаций балки dU. Величина dUp измеряется работой внешних
сил при переходе балки из положения / в положение //:
dU = dAP.	B1.10)
Изменение dU потенциальной энергии деформации, являющейся
функцией сил Рь Pif Р3> ..., произошло за счёт очень малого при-
приращения одной из этих независимых переменных /у, поэтому диф-
дифференциал такой сложной функции равен:
dU=d^dP,.	B1.11)
Что касается величины dApy то эта работа в свою очередь яв-
является разностью работы нагрузок Р для положений II и /:
Работа Ах при одновременном и постепенном возрастании сил Р
равна:
А = j Р1У1 +  Р^ +

§ 126]	ТЕОРЕМА КАСТИЛЬЯНО	407
При вычислении работы Л2 учтём, что её величина всецело опре-
определяется окончательной формой деформированной балки (§ 125)
и не зависит от порядка, в котором производилась нагрузка.
Предположим, что мы сначала нагрузили нашу балку грузом dPx\
балка очень немного прогнётся (фиг. 329, положение ///), и про-
прогибы её в точках /, 2, 3 будут dyb
&Уъ 4Уг- Работа статически прило-	\Р/ \р? \Рз
женной нагрузки dPx будет равна	\	\	»
1	! Щ I	'
Y dP1dy1, После этого начнём посте- ф 1/	h Ф^З
пенно нагружать балку одновременно ^^^-s-.^_ftyA 111--\''/ф*17
возрастающими грузами Ри Р2, Р3«	-^.^ ^1 // ^у
К первоначальным прогибам dyv
dy%, dyd добавятся прогибы уи уъ уъ	Фиг. 32а
(фиг. 329). При этой стадии нагруже-
ния силы Р1У Ръ Р3 произведут работу у Рхух + у /\Уз + у РзУъ=Ах\
кроме этого, произведёт работу уже находившийся на балке груз dPx\
он пройдёт путь уи и так как при втором этапе нагружения он
оставался постоянным, то его работа равна dP^y^ Балка займёт
положение //, показанное на фиг. 329 пунктиром.
Таким образом, полная работа, проделанная внешними нагрузками
при переходе балки из недеформированного состояния в положение
//, будет равна (фиг. 329)
Теперь вычислим
Пренебрегая слагаемым второго порядка малости, получаем:
B1.12)
Подставляя полученные значения dU B1.11) и dAp B1.12) в урав-
уравнение B1.10), находим
или
Уг = дщ.	B1.13)
Таким образом, в рассмотренном случае прогиб точки приложе-
приложения сосредоточенной силы Р] равен частной производной потен-
потенциальной энергии деформации по этой силе.

408	ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ	[гл. XXI
Полученный результат можно обобщить. Пусть на балку, помимо
сосредоточенных сил Р, действуют в разных сечениях ещё пары сил
М (фиг. 330). Мы можем повторить
предыдущие рассуждения, считая, что
балка переводится из положения / в по-
положение // путём добавки dMt к паре
М{. Весь ход рассуждений остаётся
без изменений, надо будет лишь при
Фиг. 330.	вычислении работы моментов Ми
М%, ... умножать их не на прогибы,
а на углы поворота 6Ь 02, ... тех сечений, где эти пары прило-
приложены. Тогда dU будет равно jTrdMu dAp станет ^ШД, и фор-
формула B1.13) примет вид:
Так как^ — это перемещение, соответствующее силе Рь а б4 —
перемещение, соответствующее силе Mlt то полученные нами ре-
результаты можно формулировать так: производная потенциальной
энергии деформации по одной из независимых внешних сил равна
перемещению, соответствующему этой силе. Это и есть так на-
называемая теорема Кастильяно, опубликованная в 1875 г.
Заметим, что присутствие на балке сплошной нагрузки не меняет
предыдущих выводов, так как всякую сплошную нагрузку можно
рассматривать как состоящую из большого числа сосредоточен-
сосредоточенных сил.
Предыдущий вывод был сделан для балки, но совершенно ясно,
что его можно повторить для любой конструкции, деформации ко-
которой следуют закону Гука.
Для случая изгиба нами была получена формула, связывающая
величину потенциальной энергии U с изгибающими моментами:
;_ CM*(x)dx
и — J 2EJ '
Изгибающий момент является линейной функцией нагрузок Pl9
2, ..., Ml9 Ж2, ..., q, приложенных к балке:
в этом легко убедиться, просмотрев формулы для вычисления изги-
изгибающих моментов при построении эпюр (§§ 72, 73); следовательно,
потенциальная энергия является функцией второй степени от незави-
независимых внешних нагрузок.
Вычислим частную производную от U по одной из внешних сил,
например Рх. Получаем:
2EJ

§ 127]	ПРИМЕРЫ ПРИЛОЖЕНИЯ ТЕОРЕМЫ КАСТИЛЬЯНО	409
Здесь мы имеем дело с так называемым дифференцированием опре-
определённого интеграла по параметру, так как М(х) — функция и Р1
и х\ интегрирование производится по х, а дифференцирование — по
параметру Рг. Как известно, если пределы интеграла постоянны, то
следует просто дифференцировать подинтегральную функцию.
Таким образом, прогиб в точке приложения сосредоточенной
силы Рх равен;
dU С M(x)dx дМ(х)	,91 -.
а угол поворота сечения с парой Alj
fi _ dU С M(x)dx дМ(х)
i
Напомним, что знак предела / условно показывает, что интеграл
должен быть распространён на всю длину балки.
§ 127. Примеры приложения теоремы Кастильяно.
Определим (фиг. 331) прогиб свободного конца В балки, защемлённой
другим концом А. Балка нагружена сосредоточенной силой, приложенной
в точке В. В данном случае возможно непосред-
непосредственное применение теоремы Кастильяно, так
как отыскивается прогиб сечения, где приложена
сосредоточенная сила Р
__ dU f М (х) dx дМ(х)
Ув~д'Р ) EJ дР '
Начало отсчёта абсциссы х сечения можно	иг*
выбирать произвольно, лишь бы формула для
М (х) была возможно проще. Отсчитывая х от точки В, получаем для
момента в любом сечении балки
дМ (х)
—. —_ Рх И 	v '	 г
Подставляя эти значения в формулу для ув и интегрируя, чтобы охва-
охватить всю длину балки от 0 до /, получаем:
С
- J
о
_ рх) dx , . Р f 8J , Р/8
{x) = j x*dx = +
EJ
Получилась уже известная нам формула с той лишь разницей, что ув
оказался положительным. Мы определили перемещение, соответствующее
той силе, по которой производилось дифференцирование. Соответствие заклю-
заключается в том, что произведение из силы на соответствующее перемещение
Даёт нам работу. Если перемещение имеет знак плюс, то работа будет тоже
положительна, а это значит, что направления перемещения и силы совпадают.
Если же прогиб или поворот сечения получаются со знаком минус, то ия
направление противоположно направлению соответствующей силы. Таким
образом, в этой задаче прогиб точки В направлен вниз.

410	ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ	[ГЛ. XXI
Рассмотрим пример, где для вычисления М(х) необходимо определение
реакций.
Найдем угол поворота опорного сечения В балки на двух опорах про-
пролётом / (фиг.* 332), нагружённой парой сил М в этом опорном сечении и
равномерно распределённой нагрузкой q.
Искомый угол поворота равен:
М (х) dx дМ(х)
-дМ—)
EJ дМ '
Изгибающий момент (фиг. 332) определяется уравнением
При нахождении производной от М (х) по М надо в формуле для М(х)
оставить лишь независимые внешние силы, которые и учитываются теоремой
Н
/>и щи м щ ми inn мттг
ь—z
V
'I-
Фиг. 332.	Фиг. 333.
Кастильяно. Поэтому реакция А обязательно должна быть выражена через
М и <7, в противном случае легко впасть в ошибку и при дифференцировании
упустить из вида, что А — функция от М. Реакция равна:
тогда
ql qx2 , Мх
) = ^x — 4-Y + -r.
Производная будет
дМ(х)_ х
дМ ~+ / '
Пределы интегрирования определяются тем, что формула изгибающего
момента годится на протяжении всей балки. Искомый угол поворота равен:
x	qP Ml
йх	+
__^__ f I W r qx*Mx
о
В тех случаях, когда изгибающий момент на разных участках балки
выражается различными функциями от ху необходимо и интегрирование раз-
разбить по участкам. Перемещение будет выражаться суммой интегралов, число
которых равно числу участков балки. При решении подобных задач суще-
существенным является вопрос о назначении пределов интегрирования.
Возьмём в качестве примера балку длиной /, защемлённую одним концом
(фиг. 333) и нагружённую моментом М в точке С на расстоянии а от оиоры
и силой Р на свободном конце В. Найдём угол поворота сечения С.
Точка приложения момента М делит балку на два участка: первый ВС
и второй АС. Поэтому угол поворота сечения С будет равен:
— ди — f
EJ a:.\ + J EJ дМ

§ 128]	ПРИЁМ ВВЕДЕНИЯ ДОБАВОЧНОЙ СИЛЫ	411
Здесь Mi и М2 — изгибающие моменты для сечений первого и второго
участков. Пределы интегрирования можно будет установить лишь после того,
как мы решим, от каких точек отсчитывать координату х каждого сечения
для того или другого участков.
Для первого участка возьмём произвольное сечение на расстоянии х от
конца В балки. Изгибающий момент в этом сечении равен:
=0;
Mi=-p-v и ж
пределы интегрирования для этого участка будут 0 и / — а.
При вычислении изгибающего момента в сечении второго участка можно
продолжать отсчитывать х от точки В] тогда
, дМ» . л
и ш- = +1;
пределы интегрирования будут 1 — а и /. Но гораздо проще начать отсчиты-
отсчитывать х для второго участка с тем расчётом, чтобы нижний предел интегри-
интегрирования был бы нуль, — это упростит вычисления. Очевидно, за начало от-
отсчётов тогда надо взять начало второго участка — точку С. В этом случае
мы имеем:
Пределами интегрирования будут Она.
Останавливаясь на втором варианте, получаем:
'~q Mtdx dMt f M2dx дМ2
dM+)
о
EJ дМ ^ J EJ dM
первый интеграл равен нулю, и
6 -¦ * fГ Р(х 1 / a) M]dx = pBi — a)a Ma
с EJ л	2EJ	EJ
Искомый угол поворота является суммой двух слагаемых — одного, вы-
вызванного силой Р и направленного по часовой стрелке (против направления М),
и второго, определяемого моментом М и направленного против часовой
стрелки.
§ 128. Приём введения добавочной силы.
Возьмём балку пролётом /, защемлённую концом Л и нагружённую
силой Р на свободном конце В. Найдём угол поворота сечения В.
Непосредственно применить теорему Кастильяно нельзя, так как в этом
сечении нет обобщённой силы, соответствующей углу поворота, — нет пары
сил. Для того чтобы решить задачу,
приложим в точке В дополнительно пару
сил (фиг. 334), направленную как угодно, A
хотя бы против часовой стрелки. При
такой нагрузке мы можем найти угол
поворота сечения В при помощи тео-
теоремы Кастильяно.	ф о34
Этот угол выразится формулой,
состоящей из двух слагаемых — одного,
зависящего от Р, а другого — от Мп. Эта формула будет верна при любых
числовых значениях Р и МА% в том числе и при МЛ = 0; поэтому, полагая

4i a.
ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ [ГЛ. XXI
в полученном выражении Л4д = 0, получим значение угла поворота, вызван-
вызванного лишь силой Р. Проведём это вычисление:
Mdx дМ
пределы интегрирования 0 и /; тогда
i
B1.17)
можно было бы произвести интегрирование, и в полученном результате по-
положить Мд равным нулю. Однако результат не изменится, если мы при-
приравняем Мд нулю уже в формуле A2.17). Дополнительная сила нужна нам
только для вычисления частной производной от изгибающего момента по
этой "дополнительной силе; после этого её можно положить равной нулю.
Таким образом, угол поворота сечения В от силы Р равен:
"" 2EJ '
Знак минус показывает, что этот поворот происходит против направления
пары Мд, т. е. по часовой стрелке.
При вычислении прогиба такого сечения балки, где нет сосредоточенной
силы, следует подобным же образом приложить в этом сечении добавочную
силу Яд и после составления фор-
формулы для прогиба дать этой силе
частное значение, равное нулю.
Найдём прогиб конца В кон-
консоли балки, изображённой на фиг.
335. Балка нагружена равномерно
распределённой нагрузкой. Для вы-
вычисления прогиба точки В прило-
Фиг. 335.	жим в этом сечении дополнитель-
дополнительную силу Яд. Балка имеет два
участка: первый ВС и второй СЛ. Поэтому прогиб точки В предста-
представится суммой двух интегралов:
\А
! ]
Ы
1—.Z-
11
•о\
0
1
1 1
II
с
V
ц
в
1
\
—^
||
II
-а ¦
II
Pi
в
__ dU _ С Mjdx <Ш, Г
Реакции балки равны:
--Р а
21
2/
I
2/
При определении реакций никогда не следует забывать о добавочной
силе. Мы решаем усложнённую задачу, где добавочная сила должна учиты-
учитываться так же, как и все активные силы.
Отсчёт координаты х для обоих участков показан на фиг. 335.

129]	ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ	413
Для первого участка имеем:
пределы интегрирования: х = 0 и х = а. Для второго участка
±х + И?=1х-!,
пределы интегрирования: х = О и л; = /. Тогда
TJ
а
=TJI (~ Р«* ~ ?) (~ х) dx
1
О
Полагая Рд = 0, получаем:
1. {idx	- (\lS?=l±x,-2l
Ej) 2 пХ EJ J L 2/*	21
о	о
Первое из слагаемых отражает влияние деформаций консоли, второе же —
междуопорной части.
§ 129. Теорема о взаимности работ.
Пользуясь понятием о потенциальной энергии, можно установить
следующую зависимость между деформациями в различных сечениях
балки.
Если к балке, нагружённой силой Ри приложить затем ста-
Ц
\[ У12
Фиг. 336.
тически силу Р2 в сечении 2, то к прогибу точки приложения
силы Рх от этой же силы ух{ прибавится (фиг. 336) прогиб от
силы Р2, равный уп; первый значок у буквы у указывает точку,
Для которой вычисляется прогиб; второй — обозначает силу, вы-
вывающую этот прогиб.

414 ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ [ГЛ. XXI
Полная работа внешних сил составится из трёх частей: рабо-
работы силы Рх на вызванном ею прогибе уп, т. е. у Р\Уп\ работы силы Р%
на вызванном ею прогибе её точки приложения у^ъ т. е. у Р%У^\
наконец, работы силы Рх на прогибе её точки приложения от си-
силы Ръ т. е. Р^уп.
Таким образом, накопленная в стержне при действии обеих сил
энергия будет равна:
±	Ру+Ру	B1-18)
Это количество энергии деформации зависит лишь от конеч-
конечных значений сил и прогибов и не зависит от порядка нагру-
жения.
Если к балке, загружённой силой Ръ приложить затем силу Ри
то, повторив цепь вычислений, получим:
U РУ +
у	у	<21Л'8'>
Сравнивая оба значения U, получаем:
B1.19)
т. е. работа силы Рх (или первой группы сил) на перемещениях,
вызванных силой Р2 (второй группой сил), равна работе сил Р9
на перемещениях, вызванных силой Рх»
Это и есть теорема о взаимности работ. Её можно сформулиро-
сформулировать и иначе: работа первой силы (Рх) при действии второй (Р%)
ПрогиВомерь,	РЗВНа Раб0Те ВТ0Р0Й
~	ствии первой.
?сли Взять частный случай, когда
Pi = PSt то получим теорему о взаимно-
взаимности перемещений: уц=У2и т. е. прогиб
точки 7, вызванный силой, приложенной
в точке 2, равен прогибу точки 2, вызван-
вызванному такой же силой, но приложенной в
точке 1,
Пользуясь этим свойством взаимности,
можно, например, упростить производство
Фиг. 337.	опытов по определению деформаций.
Пусть мы хотим опытным путём найти
прогибы в сечениях Д 2, 3, 4 балки, защемлённой одним концом Л
и нагружённой на другом (В) силой Р (фиг. 337). Вместо того чтобы ста-
ставить для каждой точки свой прогибомер (фиг. 337, а) или переносить прибор,
что всегда очень неудобно и может повлечь ошибки, можно поступить иначе.
Поставим прогибомер в точке В, а силу Р будем последовательно прикла-
прикладывать в сечениях /, 2, 3, 4 (фиг. 337, б); измеренные в точке В прогибы
и будут по теореме о взаимности перемещений равны прогибам точек 1, 2, 3, 4
от силы Р, приложенной в точке В.

§ 130]	ТЕОРЕМА МАКСВЕЛЛА —МОРА	415
§ 130. Теорема Максвелла — Мора.
Прогиб балки в точке приложения сосредоточенной силы Р равен:
y=CM(x)dxdM(x).	B1Л5)
о
аналогичное выражение мы имеем и для угла поворота с заменой
производной dp на ш . Выясним, что представляют собой эти
производные.
Если на балке расположена какая угодно нагрузка из сосредо-
сосредоточенных сил Ри Ръ Р3, ... , моментов Ми Мъ ... у сплошных
нагрузок qlt qb ... , то момент М (х) в любом сечении такой балки
выражается линейной функцией от нагрузок:
Л4{х) = a^Pi -f- а2Ра~Ь ••• ~\~b\M\ -\-b^M^ -f- ... -\-cxqx-\- ... B1.20)
Коэффициенты аъ аъ ... , bt, Ьъ ... , съ съ ... являются функциями
пролёта балки, расстояний точек приложения сил и моментов от опор
и абсциссы х взятого сечения. Пусть мы отыскиваем прогиб точки
г.	дМ(х)
приложения силы /у, тогда -37> = аь	кР
так как Pif Р3, , Ми Мъ ... , ^'^ ... . ' 1111111 i 11111111111 ll
al9 а2, ... , bu bb ... у съ с9) ... при этом А Ц " " " " ''' " " " "тл
дифференцировании постоянны. Но аА мож- бу
но рассматривать как численную вели- ьщ	\
чину момента М в любом сечении бал-	^	н*— х -
ки от действия так называемой единич-	фиг 338
ной нагрузки, т. е. силы Р1 = 1; действи-
действительно, подставляя в формулу B1.20)
вместо Pt его частное значение, единицу, и приравнивая все осталь-
остальные нагрузки нулю, получаем М = ах.
Например, для балки, изображённой на фиг. 338, а, изгибающий
момент равен:
Производная —/*р* — — х\ но эт0 как Раз и будет выражение
изги-
изгибающего момента нашей балки, если мы её нагрузим силой /, при-
приложенной в той же точке Ву где расположена сила Р (фиг. 338, б),
и направленной в ту же сторону.
Аналогично, производная изгибающего момента М (х) по паре сил
Mt численно представляет собой изгибающий момент от пары
с моментом, равным единице, приложенной в том же сечении^ где
Имеется пара Mlf и направленной в ту же сторону. Таким образом,
вычисление производных изгибающего момента можно заменить

416	ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ	[ГЛ. XXI
вычислением изгибающих моментов от единичной нагрузки. Эти
моменты мы будем обозначать буквой М°.
Таким образом, для отыскания перемещения В (прогиба или угла
поворота) любого сечения балки, вне зависимости от того, прило-
приложена или не приложена в этом сечении соответствующая сила, не-
необходимо найти выражение для изгибающего момента М от задан-
заданной нагрузки и момента А1° от соответствующей единичной нагрузки,
приложенной в сечении, где
ищем перемещение 8; тогда
а)	это перемещение выразится
формулой
б)	8= fed*. B1.21)
Эта формула была пред-
S) ложена Максвеллом в 1864 г.
,	-	и введена в практику рас-
м\ 	 ]м ма\ 	 \м° чёта °* М°Р°М в 1874 г-
^J	1^ ^J	|^	?СЛИ мы в формуле B1.21)
v под 8 подразумеваем прогиб,
Фиг. 339.	то момент Ж0 надо вычис-
вычислять от сосредоточенной
единичной силы, приложенной в той точке, где мы отыскиваем
прогиб; при вычислении же угла поворота в качестве единичной
нагрузки прикладывается пара сил с моментом, равным единице.
Для примера фиг. 338 имеем:
УИ = — Р- х — ^(фиг. 338, а),
М° = —1 .х = — х (фиг. 338, E),
Знак плюс означает, что направление перемещения совпадает
с направлением единичной нагрузки, знак минус — наоборот.
Если при определении изгибающих моментов придётся делить
балку на участки, то соответственно и интеграл в формуле распа-
распадётся на сумму интегралов.
Сравнивая формулу Кастильяно B1.15) и B1.16) с формулой
Мора B1.21), нетрудно заметить, что они отличаются лишь одним
множителем. В теореме Кастильяно --ш или ^хг > в теореме Мора Ж0.
Or	OiViq
Следовательно, производная от изгибающего момента по обобщённой
силе — это то же самое, что изгибающий момент от силы Р° = 1.

§ 131]
СПОСОБ ВЕРЕЩАГИНА
417
Формулы B.5), A0.23), A1.19) и A3.11) с точки зрения применения тео-
теоремы Мора можно переписать так:
А/ = Р-^г, где 1=Р° (растяжение — фиг. 339, а),
As = S -~ , где 1 = S0 (сдвиг — фиг. 339, б),
1 • /
<р = Мь -jjj-, где 1 = Mg (кручение — фиг. 339, в),
6 = М -^j-, где 1 = М° (чистый изгиб — фиг. 339, г).
Для простейших стержневых систем формула Мора приобретает вид
'^,	B1.21")
где S — усилие в^стержнях от заданной нагрузки, а 5° — усилия в стержнях
от силы Р°=1, приложенной в точке, где определяется перемещение.
Если стержень испытывает переменное по его длине усилие ^V(jc), to его
удлинение по Мору может быть вычислено по следующей формуле:
1_ f N(x)N°dx
~	EF
-j-
B1.21'")
§ 131. Способ Верещагина.
Способ Максвелла — Мора в настоящее время в значительной сте-
степени вытеснил на практике непосредственное применение теоремы
Кастильяно. В справочниках обычно приводятся таблицы интегралов
1 MMQdx для наиболее часто встречаю-
щихся типов нагрузки.
Наш соотечественник А. К. Верещагин
в 1924 г. предложил упрощение вычис- ]
лений по формуле B1.21). Так как единич-
единичной нагрузкой бывает обычно либо со-
сосредоточенная сила, либо пара сил, то
эпюра М° оказывается ограниченной
прямыми линиями. Тогда вычисление
I MM\dx при любом очертании эпюры
М можно произвести следующим образом.
Пусть эпюра М (фиг. 340) имеет криволинейное очертание, а
эпюра Ж0 — прямолинейное. Произведение Mdx можно рассма-
рассматривать, как элемент dm площади эпюры М, заштрихованный на
чертеже.
Так как ордината М° равна M° = xtga, то произведение
= du)xtg<xt а весь интеграл 1 MMQdx = tg<x. \da)X пред-
Фиг. 340.

418
ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ [гл. XXI
ставляет собой статический момент площади эпюры Ж относительно
точки Л, умноженный на tga. Но этот статический момент равен
всей площади о> эпюры Ж, умноженной на расстояние от её центра
тяжести хс до точки Л. Таким образом,
\
но величина jtrc teca равна ординате Mq эпюры Ж0 под центром
тяжести эпюры Ж. Отсюда
MM» dx — o)Mbc,
и искомое перемещение равно
i
EJ
B1.22)
Таким образом, для определения перемещения В надо вычислить
о) — площадь эпюры Ж, умножить её на ординату М°с эпюры от
единичной нагрузки под центром тяжести площади ш и разделить
на жёсткость балки.
Определим этим способом угол поворота сечения D балки,
изображённой на фиг. 341, а\ балка загружена моментом Ж, при-
приложенным в сечении В к консоли АВ. Эпюра Ж показана на фиг. 341, б.
Прикладываем в сечении D еди-
единичную пару, выбирая её напра-
направление произвольно (фиг. 341, i?).
Эпюра моментов от единичной на-
нагрузки показана на фиг. 341, г.
Так как Ж на участках DC и СВ
а)
б)
равен нулю, то остаётся лишь
один интеграл для участка АВ.
Площадь со равна -\~ Ж/; орди-
ордината эпюры Ж0 под центром тя-
тяжести площади со равна -Ьоа»
отсюда искомый угол поворота
0# райен
Фиг. 34i.
Знак плюс показывает, что вращение происходит по направлению
единичной пары, т. е. по часовой стрелке.
Формула B1.22) может быть распространена и на тот случай, когда не-
необходимо учесть влияние осевых сил Л^(л), поперечных сил Q (х) или крутя-
крутящих моментов Mk.
Вместо жёсткости балки ?/, в формулу B1.22) будут подставляться: EF —
при растяжении или сжатии, QF — при чистом сдвиге и G7Kp — при кручении.

§ 132]
ПРОГИБЫ ВАЛОК ОТ ДЕЙСТВИЯ ПОПЕ1>ЕЧНОЙ СИЛЫ
419
§ 132. Прогибы балок от действия поперечной силы.
При вычислении деформаций балок мы до сих пор учитывали лишь
влияние изгибающих моментов. Но поперечные силы в свою очередь тоже
вызывают прогибы. Задача учёта поперечной силы при определении дефор-
деформаций балок была решена русским профессором И. Г. Бубновым.
Рассмотрим балку, закреплённую одним концом и нагружённую на дру-
другом силой Р. Под действием касательных напряжений два смежных сечении
Qibi и а*Ь* (фиг. 342, я), расположенные на расстоянии dx друг от друга,
Фиг. 342.
искривятся; наибольший перекос будет у нейтральной оси; элементы же,
расположенные у верха и низа балки, не будут перекашиваться, Первоначаль-
Первоначальные плоскости сечений займут какие-то средние положения (пунктир CiOidt
и CiQtd^y повернувшись относительно прежних на некоторый малый угол 7а
(фиг. 342, б). Так как в данном случае касательные напряжения во всех
сечениях одинаковы, то все эти сечения повернутся на один и тот же угол 7о
и балка под действием только касательных напряжений, займёт положе-
положение, показанное на фиг. 342, б; конец В опустится по отношению к опоре А.
Деформация, производимая изгибающим моментом и заключающаяся во вза-
взаимном повороте смежных поперечных сечений, на фиг. 342 не показана.
Прогиб второго сечения по отношению к смежному первому будет по
абсолютной величине равен отрезку О^О'21 т. е.
\dyQ\ = 0i0i	B1.23)
В более общем случае, когда поперечная сила Q(x) не одинакова в различ-
различных сечениях балки, углы поворота 7о будут переменными; однако общая
картина деформации сохранится, лишь dyq будут разными для различных
элементов dx балки.
Абсолютную величину» прогиба второго сечения по отношению к первому
I ^Уа I мы определим из условия, что при деформации балки от сдвига потен-
потенциальная энергия, накопленная в элементе длиной dx, равна работе внешних
сил, приложенных к этому элементу: dU q~dAp%
Для рассматриваемой деформации балки такими внешними силами будут
касательные усилия, равные поперечной силе Q (л*); при постепенном возра-
возрастании нагрузки и деформаций балки работа этих сил на относительном
перемещении | dyq | равна
=± Q(x)\dyQ\.
B1.24)
Так как касательные напряжения распределены неравномерно по сече-
сечению, то для вычисления потенциальной энергии, накопленной в балке при
действии этих напряжений, применим дифференциальный путь.

420	применение понятия о потенциальной энергии [гл. xxi
Вырежем из балки прямоугольного сечения (или составленного из пря-
прямоугольников) на расстоянии х от начала координат и на расстоянии z от
нейтральной оси (фиг. 342, а) малый элемент размерами dx, dz, b (z). По
боковым граням элемента будут действовать, кроме нормальных, касательные
напряжения
Q(x)S(z)
Л (г) '
Потенциальная энергия сдвига для этого элемента выразится формулой
(таблица 22)
[b(z)dzz]*dx I 2A
Энергия в элементе балки длиной dx и высотой h будет равна
- ' Q4x)dx rffl(z)rf*
-2Q J* J b{z) '
Интегрирование производится по z, и пределы интеграла надо взять такими,
чтобы охватить всё сечение.
Выражение это можно представить в несколько ином виде, умножая и
деля его на площадь сечения балки F:
_Q*(x)dx F С S*(z)dz _kQ*(x)dx
dUQ~ 2GF Т ) b(z) - 2GF '	BШ)
где через k обозначено отвлечённое число, зависящее только от формы и
размеров сечения балки, равное
*=4(^.	B1-25)
Приравнивая значения dUq и dAp, получаем:
kQ4x)dx 1 л/
2GF =yQW
Отсюда
Знак прогиба */у<? определится тем, что (фиг. 342, б) при переходе	от левого
сечения к правому (dx > 0) и при положительной поперечной силе Q (х)
относительный прогиб dyQ отрицателен, если направлять ось	у вверх.
Значит,
k^	B1.26)
Полный прогиб любого сечения с абсциссой х получаем,	интегри-
получаем,	интегрируя B1.26)
§^	B1.26')
Постоянная интегрирования Cq зависит от устройства опор балки. Так
„ _ *М(х)
„, ч dM(x)
как Q(x)= -^-, то

§ 132]	ПРОГИБЫ БАЛОК ОТ ДЕЙСТВИЯ ПОПЕРЕЧНОЙ СИЛЫ	421
т. е. прогибы балки от действия поперечной силы пропорциональны орди-
ординатам эпюры изгибающих моментов с обратным знаком; ординаты отсчи-
тываются от определённой оси абсцисс.
Величина к может быть определена для- каждого вида поперечного сече*
ния балки. Для прямоугольника
5(г) = -g-( 1 — --p-j; Jz=~Y2'
Тогда
F C
А	А
S*(z)dz_9 ГЛ_4^у	6
Применим полученные результаты к определению прогибов балки длиной /,
защемлённой левым концом в точке А и нагружённой на свободном конце В
сосредоточенной силой Р.
Располагая начало координат в точке Л, получаем:
М(х)=-РA-х) и yQ = + kP(lQ~X) + CQ= 6P^X)+CQ.
6P/
При jc = O прогиб J^q = 0; следовательно, CQ = —g-^.
Прогиб yq равен
Наибольший прогиб будет на конце балки в точке В (при х = /)
_ 6Р/
Полный прогиб точки В
f___Pl___b_ PI ___J^Fi
f~~3EJ 5 GF "" 3^7 [
Так как для прямоугольника -^ = тк, то
3EJ 5 GF~~ 3EJ I ~ blWF J '
12'
3EJ L Ю/2 G J *
Принимая отношение -^ Равным для металлов -^-, а для дерева 20, получаем:
(дерево)-

422
ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ [ГЛ. XXI
зависит от
Таким образом, дополнительный прогиб, вызванный поперечной силой,
(-г-); поэтому для сравнительно коротких балок, особенно де-
деревянных, он может достигнуть большой величины. Так, при -— = — для
[h2 \
1 -j- 6 -g- = 1,375, т. е. прогиб от поперечной силы составляет 37,5%
от прогиба, вызванного изгибающими моментами.
Надо отметить, что в ряде курсов величина коэффициента к считается
равной 1,5, а не 1,2 (для прямоугольного сечения). Это получается, если
предположить, что прогибы балки от по-
поперечной силы определяются величиной от-
относительного сдвига у нейтрального слоя,
что неверно.
-'у
§ 133. Примеры.
Пример 90. Найти вертикальное /
и горизонтальное А перемещения, а так-
также поворот в сечения А стержня ABC
(фиг. 343). Момент инерции J во всех сече-
сечениях одинаков.
Для определения / надо дифференци-
дифференцировать потенциальную энергию по силе Р\
для вычисления Д и 0 надо это диффе-
дифференцирование производить соответственно
по горизонтальной добавочной силе и добавочному моменту Мл. При вычис-
вычислении изгибающих моментов стержень надо разделить на два участка; от-
отсчёт абсцисс показан на чертеже.
Величины /, А и 0 определяются формулами:
Фиг. 343.
f — ЛИ — С
Ml dx dMl
EJ dp
C M±d?dAU
* EJ др
А=-т^- =
A1A dx дМх
EJ
I
х Г Ма дх дМ* и
A + J EJ дРл '
Mjdx дМх
EJ дМа f J EJ дМл '
Вычисляем изгибающие моменты и их производные:
дР —
. \ =0,
дм]
дМл
= -1.
дРж
дМг
"" л"*;

133]
ПРИМЕРЫ
423
Полагаем теперь в формулах для Mt и М2, что Рл=0и М3 = О и про-
производим интегрирование:
Знак плюс показывает, что все перемещения направлены соответственгю
по силам Р, Рд и Мл.
Пример 91. Найти угол поворота 6 сечения С и горизонтальное
перемещение А точки D конструкции, изображённой на фиг. 344.
г
-рэ
Фиг. 344.
Для определения 6 и А необходимо приложить в точке D горизонталь-
горизонтальную добавочную силу Рд, а в сечении С добавочный момент Л^д.
Определим реакции из условий статики:
?Л- = 0; Рд — // = 0; #=РД; ЕК = 0; -Л+^ = 0; ?> = Д;
+Рл * 2а ^
Изгибающие моменты и их производные:
дМя
~2а'
= 0;
Мг =
дМл
0.

424
ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ [ГЛ. XXI
Горизонтальное перемещение точки D равно
2а	а	а
О
Е/|_2д~з ]rMa2+ ~Tj ~6~~?7#
>та сечения С равен
2а	а	с
Г Г дМ\	С dAU
\ Mi зтт- dx 4- \ М2 -Т1ГГ dx -
.«=0:
=0
Угол поворота сечения С равен
2а	а
1
М BаУ_2Ма
1
EJ
Найдём угол поворота 8 сечения С и горизонтальное перемещение А
точки D той же конструкции, пользуясь теоремой Мора. Изобразим три
	г-ж
5)
Фиг. 345.
6)
состояния загружения: а, б и в (фиг. 345). Определим реакции и изгибающие
моменты для всех трёх состояний, показанных на фиг. 345:
а) От заданной нагрузки:
б)	От единичной силы:
в)	От единичного момента:
Я 0 DA

56\
Вычислим
а) и б)
деформации:
2а
Д = 4у [ f MiA
EJ4
2а
ПРИМЕРЫ
а
\\dx + i M2M?2dx +
а
а
\
0
425
а) и в)
2a	a	a
"О
2а
— х >^dx
Мы получили те же выражения, что и при помощи теоремы Кастильяно.
М
Фиг. 346.
При решении этой же задачи способом Верещагина нужно для схем
загружения а, б и в фиг. 345 построить эпюры изгибающего момента, что
сделано на фиг. 346, и по ним определить:
toj = Ma', tt>2 = Ма\
_ 4 м, _ 3 а
Af^=-|-; Af?2=0; Л
Искомые перемещения равны:
ОK =
0
0
- 0]
(фиг.
(фиг.
(фиг.
346, а);
346, б);
346, в).
17

426
ПРИМЕНЕНИЕ ПОНЯТИЯ О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ	[ГЛ. ХХГ
Пример 92. Определить прогиб сечения D балки АВ (фиг. 347). Пролёт
балки / = 6 м; сечение двутавровое № 20а с моментом инерции У = 2370 см1;
сила Р = 2 г; пружина имеет п = 10 витков; радиус её витков ^ = 5 еж; диа-
диаметр стержня пружины d = 2 ел; материал — сталь.
Искомый прогиб можно представить как сумму двух прогибов: / = /( -(-
f	б	D	/
р	р
где fi — прогиб сечения
просадки опоры,
D под влиянием
(
а /2—
изгиба
D под влиянием
прогиб сечения
балки А В.
Прогиб /i равен половине осадки пру-
пружины под опорой В. На пружину действует
сила ? = 0,5Р; по формуле A1.28) имеем:
/ — А. 4 ¦ 0,5 Р . R*n __ PRvi
/l "- 2" '	Gr*	~~ ~GrT~'
Прогиб /8 находим по способу Верещагина,
построив эпюры М и М° (фиг. 347):
L
4 2/\3 4/~48?У
подставляя численные значения, находим:
2000 • 600* , 2000 . 5* . 10
^:
48 • 2 . 10е . 2370
Фиг. 347.
8 • 10s • I* —
= 1,9 + 3,1=5,0 см.
Пример 93. Определить прогиб от
поперечной силы для деревянной балки,
шарнирно-опёртой, пролётом /=1,2 м, нагружённой посредине пролёта
силой Р=10г; сечение балки — прямоугольник с размерами 30 х 20 см;
G = 5500 кг/см*; Е= 100000 лгг/сж*.
Пользуемся зависимостью между прогибом
в сечениях балки:
_ kM (x)
yQ~ GF
и изгибающим моментом
B1.27)
Отсчитывая абсциссы от левого конца балки, получаем для её левой
половины:
_ Р х	_ k Рх
при х = 0 прогиб }>q равен нулю; поэтому Cq = 0 и
_	Рх
Наибольший прогиб, как известно, будет посредине пролета
Р/	6 10000- 120
B1.28)
/
max }'q = — I
- = — 0,11 см.
5 4-5500-30-20"
Знак минус показывает, что прогиб направлен вниз (положительная ось у
направлена вверх). Вычислим прогиб от действия изгибающих моментов:
Р/5	10 000 • 120*
48- 100000-
30» . 20
12
= — 0,08 см;
он меньше, чем от действия поперечной силы. Это объясняется тем, что

§ 134]
ПРИБЛИЖЁННЫЙ ПРИЁМ ВЫЧИСЛЕНИЯ ПРОГИБОВ
427
h
1
балка сравнительно короткая: -—= — п поперечная сила велика при срав-
сравнительно небольшом изгибающем моменте.
Пример 94. Определить вертикальное (f) и горизонтальное (А) пере-
перемещения узла В кронштейна ЛВС под действием силы Р (фиг. 348); Р=4 т.
11
i \ -.
i ' '
i .'• '¦
\ v
Щ
/c
150—
/
/z
/ ^
S)
Фиг. 348.
Фиг. 349.
Поперечное сечение стальных стержней: АВ — круглое, d = 2 см, ВС — дву-
двутавр № 12 с площадью сечения 14,7 см2.
Усилия в стержнях от заданной нагрузки (фиг. 348)
Sx = 0,75 Р; 52==— 1,25 Р.
Загружаем ту же систему: силой Pf = l, направленной вертикально (для оп-
определения /), и силой Pf, = 1, направленной горизонтально (для определе-
определения Л). Усилия в стержнях от единичной нагрузки
5J = 0,75; SJ = 1,25 (фиг. 349, a); «SJ = 1; S" = 0 (фиг. 349, б).
Искомые перемещения (см. 21.22м):
у S.SQ./_0,75P.Q,75.150 - 1,25Р . (- 1,25) ¦ 250 _
J~~jL EF ~~ 2- 10е- 3,14 ~г	2 • 106 • 14,7	~~ и»!| «--••
0,75Р • 1 • 150
А =
S-
/
EF
= 0,07 см.
2 • 10е . 3,14
Узел В переместится, следовательно, на 0,11 см вниз (по направлению
силы Р?) и на 0,07 см вправо (по направлению силы Р?,).
ГЛАВА XXII.
ПРИБЛИЖЁННОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ.
§ 134. Приближённый приём вычисления прогибов.
При аналитическом вычислении прогибов мы получали для каждого
участка балки своё уравнение изогнутой оси. Но можно представить изо-
изогнутую ось балки, лежащей, например, на двух опорах, одной кривой,
сколько бы участков ни было на балке.
Уравнение этой кривой можно в известной мере выбрать произволь-
произвольно, лишь бы были удовлетворены условия для прогибов, углов поворота,

428
ПРИБЛИЖЕННОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ [ГЛ. XXII
изгибающих моментов и поперечных сил в тех сечениях балки, где эти вели-
величины заранее известны. Определённым условиям должны удовлетворять как
сама функция уу так и её производные. Например, изогнутую ось балки,
изображённой на фиг. 350, можно представить, направляя положительную
ось у вниз, в виде синусоиды:
y = aisin^f;	B2.1)
это уравнение удовлетворяет условиям на опорах А и В. Действительно,
в этих сечениях прогибы и изгибающие моменты равны нулю, а углы поворотов
и поперечные силы не обращаются в нуль, т. е.
при
х =
> = 0,/' = 0, а/ и
В уравнении B2.1) sin —	безразмерная функция от х, которой мы зара-
заранее задаёмся, a at — прогиб в середине пролёта. Достаточно найти aif чтобы
получить возможность прибли-
I
•Р
жённого вычисления прогибов
балки. Для нахождения ах на-
напишем условие превращения
части потенциальной энергии
внешних нагрузок в потенци-
потенциальную энергию деформации
балки при переходе её в смеж-
смежное положение равновесия, по-
показанное на фиг. 350 пункти-
пунктиром. Этот переход может быть
вызван, например, небольшим
статическим увеличением dP приложенной силы. Тогда уменьшение потен-
потенциальной энергии независимых внешних сил будет измеряться их работой:
Фиг. 350.
d(Jp= dAp = -7r dP ddi + Pda^
С другой стороны,
Но так как
г f M*(x)dx
U~) 2EJ •
(ось у направлена в сторону выпуклости балки, см. § 109), то
/	i
\r'ydx=—~ \ f(x)dx.
При переходе балки во второе положение, т. е. при изменении обоб-
обобщённой координаты ах на daif получаем:
= jjjt daL = at, dax EJ f /"* (*) dx.

§ 134]	ПРИБЛИЖЁННЫЙ ПРИЁМ ВЫЧИСЛЕНИЯ ПРОГИБОВ	429
По закону сохранения энергии
и
Pdai = ах dat EJ \ / (х) dx.
Отсюда
B2.2)
EJ ^f
8
Примем
Л»	. тъХ
х) = sin —»
Тогда
7t4
р/з
48,7?/'
что чрезвычайно близко к точному значению прогиба посредине пролёта
Р /3
рассматриваемой балки: ^п =^. Достаточная точность получилась благодаря
тому, что выбранная форма кривой / (л:) удовлетворяет в опорных сечениях
не только условиям для прогибов yf но и для изгибающих моментов, про-
пропорциональных у".
Если бы на балке было расположено несколько сил Ри Р2, Рг> • • • на
расстояниях си с2у c3f ..• от начала координат (левого конца балки), то работа
dAp выразилась бы формулой
и для ах мы получили бы выражение
EJ.[f"*(x)dx
Рассматривая сплошную нагрузку как сумму отдельных элементарных
сил, мы можем путём интегрирования получить ах и для этого вида загру-
зкения балки. При действии пар сил М\у М2, УИ3» ..» множителями при них
бУ/'()/'Ы

430
ПРИБЛИЖЁННОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ [ГЛ. ХХП
§ 135. Разложение уравнения изогнутой оси
в тригонометрический ряд.
Изложенный в предыдущем параграфе приём замены изогнутой оси бал-
балки одной синусоидой не при всех случаях нагрузки может дать такой удовле-
удовлетворительный результат, как в рассмотренном примере.
В этих случаях целесообразно представить изогнутую ось балки в виде
суммы ряда синусоид, т. е. разложить уравнение изогнутой оси в беско-
бесконечный тригонометрический ряд, ко-
который обычно быстро сходится и в
пределе даёт точное решение.
Общее выражение для изогнутой
оси в случае балки на двух опорах
принимает вид:
у = ах sin
ТТЛ-	. 2т.х ,
_- -f «* sin +.
...+am sin
. -t- an sin
тт.х
B2.3)
Фиг. 351.
Последовательные синусоиды изобра-
изображены на фиг. 351. Каждый член этого
ряда и его производные удовлетворяют
условиям на опорах Аи В. При выборе
формы ряда надо иметь в виду, что так как в выражение dU входит квадрат вто-
второй производной от у, то удовлетворение условий для этой производной очень
важно; в противном случае можно получить большую погрешность. Условие
же для третьей производной от у (для поперечной силы) может быть нару-
нарушено без особого влияния на точность результатов. Для определения коэф-
коэффициентов аь а%, а»,..., ап следует применить, как и в предыдущем при-
примере, закон сохранения энергии.
Формула для вычисления потенциальной энергии деформации принимает вид:
Ь
U
tmzx
л л а"
При возведении в квадрат мы получим под интегралом слагаемые двух видов:
а пт.х
2апа,
п /4	/
я2/я2я4 . пт.х . тъх
Интегрируя, находим:
. пт.х . тт.х , Л
sin —— sin —-- dx = 0.

135]	РАЗЛОЖЕНИЕ УРАВНЕНИЯ ИЗОГНУТОЙ ОСИ В РЯД	431
Таким образом, выражение для потенциальной энергии деформации при-
примет вид:
мет вид
^~
Потенциальная энергия деформации выражена в функции обобщённых
координат ап и представляет собой сумму количеств потенциальной энер-
энергии, накапливающихся при изгибе балки отдельно по каждой синусоиде.
Переведём балку в смежное, очень близкое, положение равновесия и
составим уравнение сохранения энергии. Мы можем перевести балку в смеж-
смежное положение равновесия, изменяя на dan только один какой-либо из коэф-
коэффициентов аю оставляя остальные без перемен. Тогда в выражения B2.3)
вместо слагаемого ап sin —— войдет величина (ап + dan) sin 	, а все
остальные слагаемые сохранят своё значение. При этом изменится потен-
потенциальная энергия деформации, соответствующая только изгибу балки по си-
. пъх
нусоиде ап sin —-.
Таким образом, приращение потенциальной энергии деформации балки
за счёт изменения коэффициента ап будет равно
OU	"К CjJ
Это приращение должно быть численно равно уменьшению потенциальной
энергии внешних независимых сил при вариации координаты ап.
Рассмотрим случай нагрузки балки на двух опорах сосредоточенной си-
силой Р, приложенной на расстоянии с от левой опоры (фиг. 351). Прогиб под
этой силой равен
. тгс , . 2пс , , . ппс
Ус == Я1 sin ~Т "Т" Л2 Slfl ~~~,	Г • • • "Г ап S*n Т~ •
При увеличении этого прогиба за счёт изменения координаты ап на dan
потенциальная энергия нагрузки уменьшится на величину dUp, равную ра-
работе dA силы Р при изменении прогиба
dU~dA = P dyc\ dUp = Р dan sin -~ .
Составляем уравнение сохранения энергии:
dU — dUp, или
-^ n*andan = Р dan sin —,
откуда
«Л = -гг—	.	B2.5)
Тогда уравнение прогибов получает вид:
Р/3 Г . ™ . пх , 1 . 2тсс . 2icjc ,
,in — sin у -|- щ- sin — • sin •— -\- ,
Р1Ъ \У 1 . ППС . ППХ	.ООг\
	 7 т sin Т~ sin —Г *	B2.Ь)
-EJ А П	'	1
СЛ *-'«' /1=1

432
ПРИБЛИЖЁННОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ [гл. XXII
Отметим, что при вычислении dU безразлично, за счёт добавления
каких сил происходит вариация координаты ап, лишь бы эта вариация была
мала; соответствующая сила тоже будет мала, её работа окажется величиной
2-го порядка малости и не войдёт в уравнение сохранения энергии, как это
было показано в § 126.
Применяя формулу B2.6) к случаю, когда сила приложена посредине
пролёта, и отыскивая прогиб в этом же сечении, получаем при с = —
И X — -?г- *
V	= ¦
-'шах
Р/8
-к-U п==\> з, 5, ...
Этот ряд сходится очень быстро, достаточно сохранить только первый член.
Пример 95. Дать приближённое выражение для изогнутой оси
балки, представленной на фиг. 352. Сплошную нагрузку можно заменить
системой элементарных сосредоточенных сил q dc. Прогиб dy в любом сече-
do
f/TiVT
f f I ! f
i —
Фиг. 352.
нии с абсциссой л' от такой силы, расположенной на расстоянии с от начала
координат, можно вычислить по формуле B2.6), заменяя Р на q dc. Тогда
п = оо
qd clb \^ 1
1 . mzc . пкх
Я4	/	/
Для вычисления полного прогиба у надо проинтегрировать этот ряд по с от
О до -^-; интегрируя общий член ряда, получаем:
L	L
f 4^1 sin 5?-с sin ^ = -?^-1 sin 5H f sin^dc.
0 "	0
Интеграл
I
'2
J

§ 136]	ОБЩИЕ ПОНЯТИЯ И МЕТОД РАСЧЁТА	433
Разность, стоящая в скобках, равна
при п = 1	1
» п = 2	2
» я = 3	1
> я. = 4	О и т. д.
Таким образом, у будет выражаться формулой
>-ч?в[ 1 >~+ 1 >=?]¦ <^>
п= 1, 3, 5, ...	/1 = 2, 6, 10, ...
Оба ряда, стоящие в скобках, быстро сходятся. Сохраняя лишь первые сла-
слагаемые, вычислим прогибы посредине и в четвертях пролёта:
,	~ 153,0?/
вместо точного значения
~-153,
__ ql* Г . т,1 2 . 2тг/1 __ 0,769 ^/4
— 0,5«* ЯУ L 8Ш 47 + 2^ ЗШ ~4f\ - 0,5*5 EJ '>
. 3nl . 2 . 2л . 3/1 0,645 J/4
mT7 + ^sin--4r~J = "o^
ГЛАВА XXIII.
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ.
§ 136. Общие понятия и метод расчёта.
До сих пор мы рассматривали только статически определимые
балки, у которых три опорные реакции определялись из условий
равновесия. Очень часто, по условиям работы конструкции, оказы-
оказывается необходимым увеличить число опорных закреплений; тогда
мы получаем так называемую статически неопределимую балку.
В
Фиг. 353.	Фиг. 354.
Например, для уменьшения пролёта балки АВ на двух опорах
(фиг. 353, а) можно поставить опору ещё посредине (фиг. 353, б);
Для уменьшения деформаций балки, защемлённой одним концом
(фиг. 354, а), можно подпереть её свободный конец (фиг. 354, б).

434	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ	[ГЛ. XXIII
Для подбора сечения таких балок, так же как и в рассмотренных
ранее задачах, необходимо построить обычным порядком эпюры
изгибающих моментов и поперечных сил, а стало быть, определить
опорные реакции.
Во всех подобных случаях число опорных реакций, которые
могут возникнуть, превышает число уравнений статики, например,
для балок фиг. 355, а и б четыре опорные реакции, а для бглки
М;
У
Фиг. 355.
фиг. 355, в — пять. Поэтому необходимо составить дополнительные
уравнения, выражающие условия совместности деформаций, кото-
которые вместе с обычными уравнениями равновесия и дадут возмож-
возможность определить все опорные реакции.
Определим опорные реакции и построим эпюру моментов для
балки, находящейся (фиг. 356) под действием равномерно распреде-
распределённой нагрузки q. Сначала изобразим все реакции, которые по
устройству опор могут возникнуть в этой балке. Таких реакций
может быть на опоре А три: вертикальная Л, горизонтальная На
и опорный момент Жд; на опоре В воз-
можно появление лишь одной реакции В.
Таким образом, число опорных реакций на
одну больше, чем уравнений статики.
Одна из реакций является добавочной,
Фиг. 356.	как говорят, «лишней» неизвестной. Этот
термин прочно укоренился в технической
литературе; между тем, принять его можно лишь условно. Действи-
Действительно, добавочная реакция и соответствующее ей добавочное опорное
закрепление являются «лишними» только с точки зрения необходимости
этих закреплений для равновесия балки как жёсткого целого. С точки
же зрения инженера добавленное закрепление во многих случаях
не только не является лишним, а наоборот, позволяет осуществить
такую конструкцию, которая без него была бы невозможна. Напри-
Например, балка фиг. 353, б могла бы в некоторых случаях перекрыть
пролёт АВ лишь при наличии добавочной опоры в точке С. Поэтому
мы будем пользоваться термином «лишняя опорная реакция», «лиш-
«лишняя неизвестная» лишь условно.

§ 137]	СПОСОБ СРАВНЕНИЯ ДЕФОРМАЦИЙ	435
Составим все уравнения статики для нашей балки, приравнивая нулю
сумму проекций всех сил на направление оси балки, на перпендикуляр
к ней, и сумму моментов относительно точки Л. Получим систему:
Из первого уравнения сразу определяется опорная реакция Яд:
для определения трёх других остаются лишь два уравнения.
За лишнюю реакцию можно взять любую из этих трёх: попро-
попробуем взять реакцию опоры В, В таком случае мы должны считать,
что рассматриваемая балка получилась из статически определимой
балки АВ, защемлённой концом А (фиг. 357), у которой потом
поставили добавочную опору в точке В. Эта ^
статически определимая балка, которая ^-1	——J
получается из статически неопределимой I
при удалении добавочного, лишнего опор-	Фш. 357.
ного закрепления, называется основной
системой. Выбрав какую-либо из реакций л	q
за лишнюю неизвестную, мы тем самым вы- А Ц \ и i 1 и и ! I u I! III1 ?•?
бираем основную систему.	^	?—.г—-f«
Попробуем теперь превратить основную h	f- 	'
систему (фиг. 357) в' систему, полностью	Ф»г- 358.
совпадающую с заданной статически неопре-
неопределимой балкой (фиг. 356). Для этого загрузим её сплошной на-
нагрузкой q и в точке В приложим лишнюю реакцию В (фиг. 358).
Однако этого мало: в балке, изображённой на фиг. 358, точка В
может перемещаться по вертикали под действием нагрузок q и В;
между тем, в нашей статически неопределимой балке (фиг. 356)
точка В не имеет этой возможности, она должна совпадать с опор-
опорным шарниром. Поэтому, чтобы привести к окончательному совпа-
совпадению фиг. 356 и 358, надо к последней добавить условие, что
прогиб точки В основной системы под действием нагрузок q и В
должен быть равен нулю:
/я = 0.	B3.2)
Это и будет добавочное уравнение, определяющее реакцию В; оно
является условием совместности деформаций в рассматриваемом слу-
случае: конец В балки не отрывается от опоры.
Решение этого добавочного уравнения возможно несколькими
способами.
§ 137. Способ сравнения деформаций.
Выполняя решение составленного в § 136 уравнения B3.2)
/в = 0, названного уравнением совместности деформаций, можно
рассуждать следующим образом.
Прогиб точки В основной системы под действием нагрузок q
н В складывается из двух прогибов: одного /вя, вызванного лишь

436
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ
[ГЛ. XXIII
нагрузкой q, и другого fBB> вызванного реакцией В. Таким обра-
8ОМ,
а) о	/в=/вд+/вв = 0.	B3.3)
Остаётся вычислить эти прогибы. Для
^, этого загрузим основную систему одной
^^ нагрузкой q (фиг. 359, а). Тогда прогиб
•* ^ точки В будет равен:
При нагружении основной системы реак-
реакцией В (фиг. 359, б) имеем:
Подставляя эти значения прогибов в уравнение B3.3), получаем:
Отсюда
B3.4)
....... ....... .\
1 I 1 1 1 1 1 N 1 1 1 I 1 1 I \\В
В этом способе мы сначала даём возможность основной системе
деформироваться под действием внешней нагрузки q, а затем под-
ь	 / 	^ бираем такую силу В, которая бы
й	i	! вернула точку В обратно. Таким
образом, мы подбираем величину не-
неизвестной дополнительной реакции В
с тем расчётом, чтобы уравнять про-
прогибы от нагрузки q и силы В. Этот
способ и называют способом сравне-
сравнения деформаций.
Подставляя значение лишней реак-
реакции В в уравнения статики B3.1),
JLQl2	\ получаем
!Zd \	I
\	. /7/
I
1
gQ	'	Выражение изгибающего момента
получаем, рассматривая правую часть
балки (фиг. 358) и подставляя значение В:
2 14

138]	ПРИМЕНЕНИЕ ТЕОРЕМЫ КАСТИЛЬЯНО
Поперечная сила Q выражается формулой
437
Эпюры моментов и поперечных сил изображены на фиг. 360. Сече-
Сечение с наибольшим положительным моментом соответствует абсциссе
х0, определяемой равенством
dM л	. Sql
т.е. ^-**. =
3/
Отсюда xo=-Q-t соответствующая ордината эпюры моментов, равна:
м —м —
/Wmax — МХо —
3/
g — уТб!" ' 128 9 *
§ 138. Применение теоремы Кастильяно, теоремы Мора
и способа Верещагина.
Раскрытие статической \ неопределимости для балки, рассмотрен-
рассмотренной в §§ 136 и 137, может быть произведено и при помощи теоремы
Кастильяно (§ 127).
«Лишнюю» опорную реакцию В (фиг. 361, а) заменяем «лишней»
неизвестной силой В, действующей вместе с заданной нагрузкой q
на основную статически определимую балку АВ (фиг. 361, б).
Дифференцируя по силе В потенциальную энергию и вычисляя
таким образом прогиб /#, сле-
Дует /в приравнять нулю; урав-
уравнение B3.2) станет следующим:
С MdxdM
EJ дВ
= 0. B3.5)
Остаётся вычислить М и ^5-, уста-
устаем»
новить пределы интеграла и взять
его:
ЛГ2
B3.6)
Фиг. ЗС1.
Будем считать, что сечение балки не меняется по длине; уравнение
B3.5) примет вид:
отсюда
= 0 или ?-? = <

438
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ВАЛКИ
[гл. ххш
Далее решение не отличается от описанного в способе сравнения
деформаций.
Раскрытие статической неопределимости возможно выполнить
также и по теореме Мора. При решении по Мору, кроме пер-
первого состояния нагружения ос-
основной балки заданной нагрузкой
и лишней неизвестной силой
(фиг. 362, я), следует показать
ту же балку во втором состоя-
состоянии загружения — силой Р° = 1
(фиг. 362, б).
Вычисления при обозначениях,
о принятых на фиг. 362, дают:
Фит. 362.
т. е. то же, что и при пользова-
пользовании теоремой Кастильяно B3.6).
2) При решении того же при-
примера по способу Верещагина к
двум схемам состояний загру-
загружения (фиг. 362, а и б) следует
л» построить эпюры моментов: от
нагрузки q (фиг. 362, в), от
силы В (фиг. 362, г) и от силы
Р°=1 (фиг. 362, д).
Величина моментных площадей:
от нагрузки q: u>^ =— у^
от нагрузки В: и>я = т^-В*
Ординаты эпюр единичной нагрузки:
для умножения на юд:
для умножения на (%:
Прогиб в точке В
/2
1
Отсюда
ВР
Дальше решение идёт, как указано в § 137.

§ 139]
ВЫБОР ЛИШНЕЙ НЕИЗВЕСТНОЙ И ОСНОВНОЙ СИСТЕМЫ
439
I
§ 139. Выбор лишней неизвестной и основной системы.
В предыдущем примере мы выбрали за лишнюю неизвестную
реакцию ?. Мы могли бы выбрать и момент Жд. Соответственно
изменилась бы основная система и
ход решения. Окончательный же
результат, конечно, получился бы
прежним.
Возьмём за лишнюю неизвестную м/
опорный момент Мд (фиг. 363, а).
Какой будет основная система?
Чтобы получить её, надо отбро-
отбросить то опорное закрепление, ко-
которое создаёт момент Жд, т. е.
защемление конца А. Чтобы на
конце А не было опорного момента,
там следует поставить шарнирно-
неподвижную опору.	дг
Основной системой будет балка,
изображённая на фиг. 363, б. За-
Загрузим её внешней нагрузкой и
опорным моментом Мд (фиг. 363, в).
Чтобы балки фиг. 363, айв работали одинаково, надо для
балки фиг. 363, в написать дополнительное условие, что сечение А
под действием изображённых нагрузок не может поворачиваться;
накладываем это ограничение на перемещение, соответствующее
выбранной лишней неизвестной:
Фиг. 363.
Далее, применив для решения уравнения Од = 0 теорему Кастиль-
яно, имеем
л dU С Mdx dM
EJ дМА
следовательно,
Для нахождения М и
Mdx дМ
= 0.
дМ
дМА
EJ дМА
выразим реакцию В основной системы
(фиг. 363, в) через Ма и произведём все обычные вычисления:
МАх
дМ
дМА
X

440	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ
Подставляя полученные данные в B3.7), находим:
[гл. ххш
Отсюда
т. е. той же величине, которая была получена раньше. Дальнейший
ход решения не отличается от разобранного выше.
Решение той же основной системы (фиг. 363, в и 364, а) с при-
применением способа Верещагина потребует изображения второго со-
состояния загружения основной
системы моментом М° = 1 (фиг.
364, б) и построения эпюр изги-
изгибающего момента: от заданной
нагрузки q (фиг. 364, в), от мо-
момента МА (фиг. 364, г) и от еди-
единичной нагрузки М°=1 (фиг.
364, д). Пользуясь формулой
S) B1.22),' вычисляем ВА:
()(
-<<) ЮН-
Как видно, уравнение для
определения Мл полностью
г) совпадает с найденным по Ка-
стильяно.
Сравнивая два варианта реше-
решения поставленной задачи с лишней
8) неизвестной Лис лишней не-
неизвестной Ма, видим, что при
Фиг. 364.	применении способа Кастильяно
первый вариант менее сложен
по вычислениям. Это объясняется тем, что основной системой
в первом варианте является балка, защемлённая одним концом,
во втором же —балка на двух опорах; для второй — вычисления
сложнее Таким образом, лишнюю неизвестную и, следовательно,
основную систему надо выбирать с таким расчётом, чтобы выкладки
(вычисление изгибающих моментов и т. д.) были проще.

§ 140] ПЛАН РЕШЕНИЯ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ ЗАДАЧИ	441
Если бы мы выбрали за лишнюю неизвестную реакцию А, то
основную систему следовало бы так устроить, чтобы опора Л не
давала возможности поворота сечения и горизонтальных перемеще-
перемещений, но допускала бы вертикальные движения.
На фиг. 365 показано соответствующее устройство балки: в точ-
точке Л к концу балки наглухо прикреплён ползун, скользящий без
трения в вертикальных направляющих. Тогда опора Л будет пере-
передавать момент и горизонтальную составля-
составляющую, но не будет давать вертикальной
реакции.
Дополнительное уравнение получим, при- | |	тЬ
равнивая нулю перемещение (в основной
системе), соответствующее реакции Л, т. е.
вертикальный прогиб точки А.
За лишнюю неизвестную нельзя брать лишь ту реакцию, при
отбрасывании которой мы получим изменяемую, неустойчивую основ-
основную систему; в нашем примере такой была бы реакция Яд, но она
и определилась из уравнения статики.
§ 140. План решения статически неопределимой задачи.
Общий метод решения, показанный в предыдущих параграфах,
распадается на ряд отдельных этапов, которые даны в сводном
виде в таблице 23.
В этой таблице даны два варианта решения задачи: с лиш-
лишней реакцией В и с лишней реакцией Жд. Для развёртыва-
развёртывания добавочного условия даны также два варианта решения:
хпособом сравнения деформаций и с применением теоремы Ка-
стильяно.
Если бы число реакций статически неопределимой балки было
не четыре, как в рассмотренном примере, а больше, то соответ-
соответственно увеличилось бы число лишних неизвестных; загрузив основ-
основную систему внешней нагрузкой и этими лишними неизвестными, мы
можем написать дополнительные условия, ограничивающие деформа-
деформации балки в тех сечениях, где эти лишние реакции приложены.
/Таким путём будет получено столько же дополнительных уравнений,
сколько лишних неизвестных.
Следовательно, общий метод определения добавочных опорных
реакций в статически неопределимых балках основан на том, что
всякая дополнительная опора, вводя лишнюю неизвестную реакцию,
в то же время накладывает дополнительное ограничение в основной
Статически определимой системе на перемещение, соответствующее
Лишней неизвестной реакции. Выражая уравнением это ограничение,
•ил получаем столько дополнительных уравнений, сколько добавлено
йовых опорных закреплений.

442	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ВАЛКИ	[ГЛ. XXII:
Таблица 23. План решения однажды статически неопределимой задачи.
1. Для заданной схемы балки
указываются все реакции, соста-
составляются уравнения статики и из
них определяются статически опре-
определимые реакции
За лишнюю неиз-
неизвестную выбрано В
А
В
2. Из остальных реакций
выбрать одну за лишнюю и
изобразить основную систему
За лишнюю неиз-
неизвестную выбрано МА
JMIIIIIIIHIIJIHIIII
ШМП11М |
\-xAi
3. Загрузить основную си-
систему внешней заданной на-
нагрузкой и лишней неизвестной
4. Написать добавочное условие, ограничивающее
деформации основной системы и выражающее условие
совместности деформаций статически неопределимой
системы
ел=о
Дальнейшее решение задачи можно вести
способом сравнения деформаций
применением теоремы Кастильяно
5. Развернуть
добавочное
условие
М(л-)
дМА
6. Вычисляются значения деформа-
деформаций. Они подставляются в добавоч-
добавочное условие, которое затем решается
6. Вычисляются: изгибающий мо-
момент, производная и весь интеграл
в целом. Находится лишнее неизве-
неизвестное
7. Из уравнений статики определяются остальные реакции; эпюры изги-
изгибающего момента и поперечной силы строятся обычными приёмами

§ 141] ПРИМЕРЫ РАСЧЁТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ 443
§ 141. Примеры расчёта статически неопределимых систем.
Пример 96. Балка, защемлённая одним концом и опёртая другим,
загружена сосредоточенной силой Р (фиг. 366, а).
Проведём расчёт по методу сравнения деформаций. Опорных реакций —
четыре. Имеем уравнения статики:
B3.7)
За лишнюю неизвестную выбираем реак-
цию В, Основная система изображена на фиг.
366, б. Загружаем основную систему задан-
заданной нагрузкой Р и лишней неизвестной В
(фиг. 366* в). При таком загружении прогиб
в точке В должен быть равен нулю
>
-Q
Загружаем теперь основную систему раз-
раздельно: силой Р, вызывающей прогиб fBPi и
силой В, вызывающей прогиб fBB (фиг. 366, А
г и е); тогда:	г)
:0.	B3.8)	j
(фиг. 366, д):
Прогиб /gjj известен из предыдущего
^	B3.10)
Определим прогиб fBp графо-аналитически sjY
Внося полученные выражения в уравне-
иие B3.8), получаем:
Отсюда
Изгибающий момент на первом участке
$>иг. 366, з) равен
При xi = b имеем:
2)
^fetbJ^
!
l-Mllll
ЕШ!^
Фиг. 36b.

444	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ	[ГЛ. ХХШ
Для второго участка
При х2 = / имеем:
Поперечная сила для первого участка (фиг. 366, и) равна:
Дла второго
В частном случае при a — b =~f В = -f- — Р; Д = -}- — Р;
Пример 97. Балка АВУ нагружённая силой Р (фиг. 367), защем-
защемлена концом А, конец В опирается на упругую опору (пружину).
Податливость пружины, т. е. её осадку от
единичной силы, обозначим а [см/кг]; эта вели-
,	чина может быть вычислена по формуле A1.28)
л	*~ . д (§ 65); полагая
|	получаем:
111' "	За лишнюю неизвестную выбираем реакцию В
между балкой и упругой опорой. Ход решения
остаётся таким же, что и в предыдущем примере: изменится лишь уравне-
уравнение совместности. Прогиб конца В балки будет равен уже не нулю, а осадке
пружины от силы В, т. е.
знак минус перед \ поставлен потому, что положительное направление
прогибов принято вверх. Подставляя в уравнение B3.13) значения fBp и fBB
(см. пример 96) и величину X = <хВ, получаем:
Отсюда
При абсолютно жёсткой пружине a = 0 и формула для В совпадает
с полученной выше в предыдущем примере B3.12).
Определим наибольшие напряжения в балке и пружине при следующих
числовых данных: балка двутавровая № 20, /= 1840 см*, W= 184 см3, про-

Я 141] ПРИМЕРЫ РАСЧЁТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ	445
лёт / = 4 м\ а = Ь — 2 м\ Р = 2 т. Радиус витка пружины /? = 5 см, ра-
радиус её стержня г=\ см; число витков п = 6. Модули: ? = 2-10е кг/см*,
G = 8» 105 кг/см2. Податливость пружины равна:
4 • 53 • 6
а= 8-10»-1« СМ1К2'
Вычисляем отношение к формуле B3.14) и реакцию:
_
Опасными являются сечение в защемлении и сечение под грузом. В первом
из них
МА = В1 — Р y = 378 • 400 — 2000 . 200 = — 248 800 кгсм\
во втором
Мс=+В ~ = 378 • 200 == 75600 кгсм.
Наибольшее нормальное напряжение в балке равно:
I max M I 248 800
W	184
- = 1343 кг/см*.
Наибольшее касательное напряжение в пружине
2BR 2-378-5 1ПЛЛ
max т = —^ =	— == 1200 /
Пример 98. Построить эпюру моментов для рамы (фиг. 368, а) при
нагрузке силой Р. Жёсткость стержня EJ постоянна.
Обозначая реакции через Л, Я, МА и С, составляем уравнения статики:
Лишних неизвестных одна; пусть это будет реакция С. Основная си-
система с нагрузкой силой Р и лишней неизвестной показана на фиг. 368, б.
Применим теорему Кастильяно. В уравнении совместности деформаций
потенциальная энергия U является суммой величин энергии для первого
участка СВ и второго В А. Уравнение /с = 0 принимает вид:
о	о
Вычисляем моменты и их производные:
Ml = + Cxu -gjj-=xu M2 =
Подставляя в уравнение совместности
а	а
\ Cxi dx+ \ (Ca — Px2) adx =
б	о

446	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ	[ГЛ. ХХШ
и вычисляя интегралы, получаем:
Изгибающие моменты будут: на первом участке Mi = -^ Рхи на втором уча-
о
о
стке Mt = -^- Ра — Рлг*. Эпюра моментов показана на фиг. 368, в.
1
При решении того же примера способом Верещагина изображаем два
состояния нагрузки: заданными силами и опорной реакцией С (фиг. 368, г)
и единичной силой, действующей по направлению реакции С (фиг. 368, д);
строим эпюры М и М°. Площади эпюр М первого состояния загружения
(фиг. 368, е и ж):
—
Ц = + Са • а =
Ра2
Ординаты единичных эпюр, соответствующие центрам тяжести эпюр первого
состояния загружения (фиг. 368, з)\
Условие совместности деформаций (по сокращении ?7):
Са* 2 , ^ .	Ра3	л
откуда C=-^-Pt как и в решении, показанном выше,
о

§ 142] ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК 447
§ 142. Определение деформаций статически неопределимых балок.
После того, как определены опорные реакции, построены эпюры изги-
изгибающих моментов и поперечных сил, подобраны сечения статически не-
неопределимой балки, определение её деформаций ничем не отличается от
таких же вычислений для статически определимой балки.
Необходимо лишь отметить, что в этом случае мы будем иметь избы-
избыточное число уравнений для определения постоянных интегрирования. Этот
избыток равен числу лишних неизвестных. Избыточные уравнения при пра-
правильно найденных реакциях обратятся в тождества, ибо они уже и были
использованы при нахождении лишних неизвестных. Так, для балки, изобра-
изображённой на фиг. 356, получим следующее дифференциальное уравнение изо-
изогнутой оси:
EJ%L = Bx-2f.
dx2	2
Интегрируем:
(b)
Постоянных интегрирования две, условий же для их определения можно
написать три, а именно:
dv
в точке А при х = / прогиб ji = 0 и угол поворота -~- = 0;
>>.?>jts=O> ^ = 0.
Третье из этих уравнений обратится в тождество, ибо оно уже было нами
использовано при составлении дополнительного уравнения, из которого мы
нашли для В значение -g- qL Заметим, что мы могли бы использовать урав-
уравнение изогнутой оси балки для нахождения лишней неизвестной. Приняв за
лишнюю неизвестную реакцию В, соста-
составим и проинтегрируем дифференциальное а]
уравнение изогнутой оси; получим фор- >
мулы (а) и (Ь). Используя граничные уело- " \ -
вия в точках А и В, получим три урав-
уравнения, из которых найдём реакцию В и
постоянные интегрирования С и D.
При применении графо-аналитиче- gj
ского метода к вычислению деформаций
статически неопределимых балок мы
получим для фиктивной балки недо-
недостаточное число опор; это обстоятель-
обстоятельство соответствует избыточному числу
Уравнений для определения постоян-	Фпг« 369.
Hbix интегрирования при аналитическом
методе. Так, в примере 96 (фиг. 366) мы получим фиктивную балку, изобра-
изображённую на фиг. 369, б; конец А свободен, конец В опёрт шарнирно.
Однако эпюра нагрузки фиктивной балки такова, что балка находится
в равновесии. Можно проверить, что фиктивный момент в сечении В равен
йУлю; это обстоятельство служит контролем правильности вычислений.
Дальнейший ход определения прогибов остаётся прежним; найдём, на-
например, прогиб /с в сечении под грузом; фиктивный момент Mjq равен

448	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ	[ГЛ. XXIII
моменту от треугольной нагрузки а^сс^ направленной вверх, и моменту от
прямоугольной нагрузки ас^сф^ направленной вниз (фиг. 369, б); получаем:
1М + М\а\а-МАа\а = ^ [Мс-2МА],
Прогиб в точке С равен
Mfr	РаЧ*
При а = # = -^- прогиб
если бы не было защемления левого конца, этот прогиб был бы в два с лиш-
рп
ним раза больше; /г = ~-
§ 143. Расчёт неразрезных балок.
Очень важным с практической точки зрения типом статически
неопределимых конструкций является неразрезная балка, проходя-
проходящая, не прерываясь, над рядом промежуточных опор, с которыми
она соединена шарнирно. Крайние опоры могут быть или шарнир-
шарнирными или защемлёнными. Сначала мы разберём случай шарнирных
опор. Одна из опор неразрезной балки делается обычно шарнирно-
неподвижной, прочие — шарнирно-подвижными. Нумерацию опор и
/7+2
]f U	I	\п-1 \п
1 А Ж B
i А 1г А Ж Bh in Шп+im
Фиг. 370.
пролётов будем вести от левой руки к правой, обозначая крайнюю
левую опору номером 0 и крайний левый пролёт номером 1. Длины
пролётов будем обозначать буквой / с соответствующим номеру
пролёта значком. Сечения балки во всех пролётах будем считать
одинаковыми и, следовательно, жёсткость балки EJ—постоянной.
На фиг. 370 изображена неразрезная балка, указаны принятые
обозначения и изображены возможные реакции опор. Как легко
видеть, число лишних опорных реакций равно числу промежуточ-
промежуточных опор.
Применяя описанный выше приём решения задачи, следовало бы
взять за дополнительные неизвестные реакции промежуточных опор,

с 143J	РАСЧЁТ FIEPA3PE3HbIX БАЛОК	449
а за основную систему — балку, шарнирно-опёртую в точках 0 и
я-|-2. Дополнительными уравнениями служили бы условия равенства
нулю прогибов в точках основной системы, соответствующих про-
промежуточным опорам; в этом случае все неизвестные входили бы во
все уравнения. Однако более простым и распространённым является
другой способ, связанный с иным видом основной системы и допол-
дополнительных неизвестных; при этом способе в каждое из уравнений
входит не больше трёх неизвестных.
Операции выбора лишней неизвестной и основной системы нераз-
неразрывно связаны друг с другом; основная статически определимая систе-
система получается из статически неопределимой путём отбрасывания опор-
опорных закреплений, вызывающих опор-
опорные реакции, принятые за лишние.	Q
Можно поступить иначе: пре- >*.	II11 И 1111
вратить каким-либо способом рас- /7W7 	. М?*
сматриваемую статически неопреде-
лимую конструкцию в статически
определимую, а затем посмотреть,
какие усилия или реакции приш- А
лось бы при этом отбросить. Эти лщ
величины и будут лишними неиз- I 1~
вестными в нашей статически не-
неопределимой системе.
Так, в двухпролётной нераз-
неразрезной балке (фиг. 371, а) можно аг
принять за лишнюю неизвестную ^f7
хотя бы реакцию средней опоры
В; тогда основной системой будет	Фиг. 371.
балка на двух опорах Л и С; но
можно превратить рассматриваемую балку в статически определимую
путём устройства дополнительного шарнира в точке D (фиг. 371, б).
Тогда получится основная система, состоящая из консольной балки
CBD и подвесной AD. Постановка шарнира в сечении D требует,
чтобы изгибающий момент, а значит, и вызываемые им нормальные
напряжения в этом сечении были равны нулю. Таким образом, при
переходе к основной системе мы отбросили эти нормальные напря-
напряжения в сечении Д передающиеся от левой части на правую, и
наоборот; они суммируются в пары сил, равные изгибающему моменту
в сечении Д эти пары, вновь приложенные к основной системе,
показаны на фиг. 371, в.
Превращая нашу балку в статически определимую путём введе-
введения шарнира Д мы за лишнюю неизвестную выбираем не внешнюю
силу — одну из опорных реакций, а величину изгибающего момента
* этом сечении.
Положение сечения D может быть взято произвольно; вычисле-
вычисления получаются наиболее простыми, если совместить точку D

450	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ВАЛКИ	[ГЛ. ХХТМ
с опорным сечением над промежуточной опорой — точкой В, т. е. взять за
лишнюю неизвестную опорный момент в сечении В. Тогда основная
система будет представлять собой две простые балки, шарнирно
опёртые в точках А, В и С, имеющие общую опору в точке В.
Именно так и выбирают основную систему при расчёте неразрез-
неразрезных балок. За лишние неизвестные выбирают величины опорных
изгибающих моментов Мь М^ ..., Мп_и Мп, Мп+1 над всеми
промежуточными опорами.
При таком выборе лишних неизвестных уравнения для их опре-
определения упрощаются и могут быть составлены в общем виде при
помощи теоремы о трёх моментах.
§ 144. Теорема о трёх моментах.
Для вывода теоремы о трёх моментах возьмём неразрезную
балку с рядом пролётов различной длины 1Х и /2 и т. д. и с какими
угодно вертикальными нагрузками (фиг. 372, а). Сначала изобразим
все реакции, которые могут быть в данном случае; из условий
равновесия ясно, что горизонтальная реакция //ft = 0.
jf . \ jf/тттп Ь птп \з\ \ L/lrm fiiiliiijL/l
МР' 1 VW7 2 /mfr	7Щ7	ШШ? Л /flW faf Ш17
*™Г	гЩг МП	Mr	1%Г	^7 A Mr У
Фиг. 372.
Для того чтобы получить основную систему (фиг. 372, б), распо-
расположим в опорных сечениях шарниры. Добавочными неизвестными
окажутся опорные моменты над промежуточными опорами Мх, М&
Мг, ... и т. д. Моменты над крайними опорами равны нулю. Загру-
Загрузим основную систему внешними нагрузками и опорными моментами
(фиг. 372, в). Так как направление опорных моментов нам неиз-
неизвестно, то примем их положительными. При решении знак резуль-
результата покажет, правильно ли наше предположение.
Теперь необходимо составить условие, вносящее то же ограниче-
ограничение на деформации основной системы, которое имеется в неразрезной

§ 144]
ТЕОРЕМА О ТРЁХ МОМЕНТАХ
451
балке. В основной системе обе стороны п-го опорного сечения, раз-
разделённые поставленным в балку шарниром (фиг. 373), могут пово-
поворачиваться под нагрузкой независимо одна от другой. Угол поворота
сечения на опоре п левого примыкающего к данной опоре пролёта
обозначим Ь'п, а угол поворота сечения на опоре п для правого
примыкающего пролёта назовём 0„. Эти возможные углы поворота
опорных сечений смежных пролётов показаны
на фиг. 373. В неразрезной балке оба опор-
опорных сечения совпадают, представляют собой
лишь разные стороны одного и того же опор-
опорного сечения, поэтому в этом случае условием
совместности деформаций будет:
в;-е; = о.	B3.15)
Ш+1
Фиг. 373.
Это и есть то ограничение, которое мы
должны ввести для опорных сечений смежных
балок над опорой п в нашей основной системе, загружённой внешни-
внешними силами и опорными моментами. Такое условие мы можем составить
для каждой из промежуточных опор, и, значит, написать столько доба-
добавочных уравнений, сколько мы имеем неизвестных опорных моментов.
Л
..111111111 111111 I I Ш
о)
Фиг. 374.
Поясним составление условия B3.15) примером. Возьмем двух-
пролётную неразрезную балку (фиг. 374, а), загружённую различ-
различными сплошными нагрузками в обоих пролётах qx и q^
Основная система, нагружённая только внешней нагрузкой, пока-
показана на фиг. 374, б. Для ясности чертежа оба смежных пролёта
представлены несколько раздвинутыми на опоре /; на самом деле
шарниры /' и Г' совпадают.
Обе стороны опорного сечения 1 повернутся, как показано
на чертеже. В неразрезной балке деформации должны совпадать;
16»

452
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ
[ГЛ. ХХШ
ФИГ. 375.
этого можно добиться, загружая основную систему отрицательным
опорным моментом Мх (фиг. 374, в) и подбирая его величину так,
чтобы достигнуть этого совпадения; но отсюда и следует, что для
указанного совпадения деформации основной системы должны удо-
удовлетворять условию B3.15):
о; — е;'=о.
Следуя далее плану расчёта статически неопределимой балки по
методу сравнения деформаций и возвращаясь к схеме фиг. 372, мы
должны развернуть
уравнение B3.15), вы-
вычислив величины де-
деформаций, входящие
в него.
Углы поворота се-
сечений в основной си-
системе на опоре п за-
зависят от деформаций
только двух смежных
пролётов 1п и /ль1. Вы-
Выделим эти два пролёта
со всеми действую-
действующими на них нагрузками (фиг. 375). На пролёг 1п действуют внешние
силы, расположенные на нём, и опорные моменты Мп_х и Мп\ на
пролёт /Л+1 действуют помимо внешних нагрузок опорные моменты
Мп и Жл+1. Для ясности чертежа оба смежных пролёта представлены
несколько раздвинутыми на опоре п\ на самом деле шарниры ri и
п" совпадают.
Для вычисления углов 6Л и 6„ воспользуемся графо-аналитиче-
ским методом. Фиктивные балки, изображённые под чертежом рас-
рассматриваемых пролётов, представляют собой тоже балки шарнирно-
опёртые. Фиктивной нагрузкой левого пролёта 1п служит:
а)	эпюра изгибающего момента от внешних нагрузок с грузо-
грузовой площадью а)„ и расстоянием центра тяжести этой площади от
левой опоры ап\ так как эпюра положительна, то ставим на орди-
ординатах стрелки вверх; если ординаты этой эпюры будут отрицатель-
отрицательными, то при вычислениях величину «)д придётся вводить с минусом;
б)	треугольная эпюра изгибающего момента от положительного
опорного момента Мп_х>
в)	треугольная эпюра изгибающего момента от положительного
опорного момента Мп.
На правую фиктивную балку пролёта /я+1 действуют нагрузки:
а)	эпюра изгибающего момента от внешних сил с грузовой
площадью а>л+1 и расстоянием центра тяжести от правой опоры Ьп+Х\
б)	треугольная эпюра изгибающего момента от положительного
опорного момента Мп\

§ 144]	ТЕОРЕМА О ТРЁХ МОМЕНТАХ	453
в) треугольная эпюра изгибающего момента от положительного
опорного момента Л1п+1.
Угол поворота опорного сечения пг левого пролёта равен делён-
делённой на жёсткость поперечной силе на этой опоре для соответствую-
соответствующей фиктивной балки:
поперечная же сила в опорном сечении равна опорной реакции фи-
фиктивной балки R'n.
Вычислим эту реакцию; грузовая площадь со^ распределяется
между опорами фиктивной балки по закону рычага, передавая на
опору п' часть нагрузки, равную и>п-~) треугольная нагрузка с наи-
большей ординатой Мп передаёт на эту опору две трети своей
величины, а треугольная нагрузка с ординатой Мп_г — одну треть.
Таким образом,
f
Фиктивная поперечная сила Q'n равна этой реакции со знаком -J-:
Q'n = R'n.
Угол поворота Ь'п равен
Подобным же образом получаем для правого пролёта:
R" = ш«* fe + Т М^ + Т М*«1**'
Поперечная сила в этом случае равна опорной реакции со знаком
минус:
Ql = -R"n,
а угол поворота Ь„ равен:
6« = - Ш
Подставляя значения Ь'п и % в уравнение Q'n — Ь"п = 0, сокращая
на QEJ, получаем:
ИЛИ
МпЛ1п -}- 2Мп (/„ + /eti)
Г^4-№"!А+'1- B3.16)

454
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ
[гл. ххш
Это и есть уравнение трёх моментов.
Таких уравнений мы можем написать столько, сколько имеем
промежуточных опор, т. е. сколько имеем неизвестных опорных мо-
моментов. После вычисления опорных моментов задача сводится к ра-
расчёту ряда шарнирно-опёртых балок, нагружённых уже известными
опорными моментами и внешней нагрузкой.
Уравнение B3.16) можно представить в более краткой форме,
удобной для запоминания. Подставим в уравнение B3.15) вместо
углов б их выражения через Q', а затем и через R:
Qn Qn Rn 	Rn
EJ EJ EJ EJ
или
Rln-\~R^ = 0.	B3.17)
Величины R'n и Rn представляют собой реакции на опоре п
левого и правого пролётов фиктивной балки; таким образом, теорема
о трёх моментах кратко может быть сформулирована так: сумма
фиктивных реакций на каждой промежуточной опоре должна
быть равна нулю.
Представляют уравнение трёх моментов и в следующем виде:
Под Rn подразумевается при этом фиктивная опорная реакция
средней опоры (п) от эпюр М(х) заданной нагрузки на обоих
смежных пролётах.
B3.16) к расчёту неразрезной трёхпролёг-
сечения, загружённой, как показано на
фиг. 376. Перенумеруем
q	опоры от левой руки к
]«? правой. Уравнение трёх
моментов следует напи-
написать 2 раза: для опоры
1 и опоры 2.
Нам понадобятся пло-
площади эпюр изгибающих
моментов от внешней
нагрузки для основной
системы. Эти эпюры
уравнение трёх моментов
Применим уравнение
ной балки постоянного
Фиг. 376.
построены на фиг. 376, б. Напишем
для опоры /. Полагаем я=1; тогда
= ^о = 0; соя = о)! = 0;
1 P/t , , Pl\ и
Уравнение имеет вид:
B3.19)

1441
ТЕОРЕМА О ТРбХ МОМЕНТАХ
455
Переходим к опоре 2; полагаем л = 2; тогда Мп±\ = Ж3 = 0;
, P/L	, 2 , „ П .all.
Y
h
Второе уравнение трёх моментов получает форму
Лишние неизвестные М{ и Ж2 определятся решением уравнений
B3.19) и B3.20).
В частном случае, если принять /1 = /2==/3==/, эти два уравне-
уравнения сведутся к следующим:
Шх-\-Мъ = — ^Р1,	B3.21)
= —J/V--?.	B3.22)
Решая их, получаем:
—- 40^~Т
B3.23)
B3*24)
Зная величины опорных моментов, можно легко построить эпюру
моментов для неразрезной балки, не делая дополнительных вычис-
вычислений. Для этого вычерчиваем в основной системе эпюры изгибающего
3 3
!		И ?L Y
6) \ •—	 ! *
Фиг. 377.
момента от заданной нагрузки (фиг. 377, б). Эпюры изгибаю-
изгибающего момента от опорных моментов Мх и jW2 (фиг. 377, в) на-
наносятся пунктиром на фиг. 377, б\ для сложения пограничных

456	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ВАЛКИ	[гл. ХХШ
ординат и ординат перелома эпюр следует все эпюры изображать
в одном масштабе.
Суммарная эпюра с вычислением характерных ординат показана
на фиг. 377, г. Всё построение можно производить и без раздвигания
опорных сечений; в данном случае это было сделано лишь в целях
большей наглядности.
§ 145. Вычисление опорных реакций и построение эпюр
для неразрезных балок.
Возьмём /2-й пролёт (фиг. 378); в основной системе он пред-
представляет собой шарнирно-опёртую балку, на которую действует
какая-то внешняя нагрузка и уже известные опорные моменты
Мп_\ и Мп. Воспользуемся способом сложения действия сил; тогда
опорные реакции я-го пролёта, левая R%_i и правая R", будут со-
содержать в себе по три слагаемых: первое, отражающее влияние
внешней нагрузки, мы обозначим А\ и В%\ два других будут вы-
вызваны опорными моментами Мп_\ и Мп.
*п-1
Mri-ir I МШИМ!
I	сп	и	п
Фиг. 378.	Фиг. 379.
Индексы у буквы R (фиг. 378 и 379) означают: верхний —
номер пролёта, нижний — номер опоры.
Каждая пара сил, приложенная к шарнирно-опёртой балке, вы-
вызывает равные и противоположно направленные реакции, равные
моменту пары, делённому на пролёт. Считая опорные моменты
^п~\ и Мп положительными, получим:
Rnn_x = А°п — Щ=± _J- ёи t	B3.25)
«л 'я
Rn = Вп -\	j- .	B6.20)
Эти формулы дают опорные реакции лишь одного пролёта; чтобы
найти полные реакции каждой промежуточной опоры неразрезной
балки, надо суммировать реакции смежных пролётов. Так, называя
полные реакции буквой R с одним индексом внизу — номером
опоры — получим для п-й опоры (фиг. 379):
Rn = RnnJrRnnJ^\	B3.27)

§ -Мб]
ПОСТРОЕНИЕ ЭПЮР ДЛЯ НЕРАЗРЕЗНЫХ БАЛОК
457
Поперечная сила в любом сечении п-го пролёта неразрезной
балки будет отличаться от поперечной силы Q0 (х) простой балки
только за счёт влияния реакций, вызванных опорными моментами;
тогда (фиг. 380)
Q(X) — Q (х)	;	Г~Г'	B3.28)
Заметим, что поперечные силы у опор я-го пролёта равны
ответствующими знаками) опорным реакциям Rn~i и Rn (см.
как для всякой шарнирно-опёр-
той балки.
Ордината изгибающего момен-
момента в рассматриваемом сечении бу-
будет равна (фиг. 381) сумме ординат
трёх эпюр: от внешней нагрузки
(фиг. 381, б) и от опорных мо-
моментов (фиг. 381, в и г). Первая
(с со-
выше),
Г
щгптп.
V
I/?-
г)
Фиг. 380.
Фиг. 381.
нами обозначена М°(х) и вычисляется по обычным правилам, как
для балки, опёртой по концам; ординаты же треугольных эпюр
равны Мпт* и Л*я-1/лТЛ/1
1	1
М (х) = М° (х) + М„_,
B3.29)
Формулы B3.25) — B3.29) полностью решают вопрос об опре-
определении реакций, поперечных сил и изгибающих моментов для
неразрезных балок.
При вычислении опорных реакций, поперечных сил и изги-
изгибающих моментов для отдельно взятого пролёта балки вместо
применения формул B3.28) и B3.29) можно (и это часто ока-
оказывается проще) пользоваться обычным способом вычисления
М(х) и Q(x), применяемого для балок, свободно лежащих
нз двух опорах с известными уже нагрузками в пролёте и на
°порах.

458
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ВАЛКИ
[ГЛ. XXIII
Пример 99. Определить опорные моменты, найти реакции опор и
построить эпюры изгибающего момента и поперечной силы для балки, изо-
изображённой на фиг. 382, а. Первый
q I	U	Ш \Р N пролёт загружён равномерно рас-
~]/ \	2 I у $ 3 пределённой нагрузкой q, а тре-
^ »	*-*-!	» тий — сосредоточенной силой Р
посредине пролёта, причём Р по
числовой величине равно ql;
пролёты балки одинаковы и
равны /.
Эпюры изгибающего момен-
момента от внешней нагрузки для ос-
основной системы показаны на
фиг. 382, б.
Фиг. 382.
Фиг. 383.
Уравнения трёх моментов имеют вид:
Отсюда
24
B3'30)
B3.31)
Рассматриваем далее отдельные балки. Сначала выделяем балку 0—/
с действующей на ней нагрузкой q и Mi.
Вычисляем реакции, как для простой балки:
~+1
24''
24 24
Поперечная сила в сечении с абсциссой xt (фиг. 383) равна:
Q Mi = /?i — ^i = 25 ql ~~ qXl*
Изгибающий момент в том же сечении

§ 145]
ПОСТРОЕНИЕ ЭПЮР ДЛЯ НЕРАЗРЕЗНЫХ ВАЛОК
459
Выделяем второй пролёт в виде отдельной балки /—2 (фиг. 384); он загружён
только опорными моментами Mi и М2. Повторяем весь ход вычислений:
Mi л Ml
» - _ Mi л. Ml - # _ 91 _ _ Si.
l~~ / "*" / 24 2"" 24'
__ Мх __ NW ^__Ч1 I Я1 __ Я1.
'2 I Г	24"^" 12 24'
-1 ¦ h
Фиг. 384,	Фиг. 385.
Последний третий пролёт 2—3 имеет два участка (фиг. 385),
Р
* ~* 2
2 12
Полные опорные реакции определятся суммированием опорных реакций
на каждой опоре, вычисленных выше раздельно:
24
24
з з 12^ *
•Сумма всех реакций равна заданной нагрузке: P-\-ql = 2qf.
Построенные по вычисленным данным эпюры изгибающего момента и
Поперечной силы показаны на фиг. 382, виг. Наибольшими будут ордината
АЛ	г,	V2
"^rnax под грузом Р, равная -5т-, и максимальная ордината в первом про-
пролёте, которая получится при д: = ^/, и будет равна п*5 ^* ^ Тп ^8*f

460
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ
[ел, ххш
§ 146. Неразрезные балки с консолями. Балки
с защемлёнными концами.
Теорему о трёх моментах легко распространить на те случаи,
когда неразрезная балка имеет консоли или когда концы балки
(один или оба) защемлены.
При наличии консоли длиной а (фиг. 386) в уравнении трёх
моментов опорный момент М2 следует считать известным и равным
не пулю, а моменту в защемлении для консоли; т. е. в приведён-
;
1ТПЛ МИНИН
ном примере
qa*
Wv	I
надо забывать о знаке этого мо-
момента. При вычислении реакций еле-
дует учесть влияние нагрузки, распо-
расположенной на консоли, т. е. рассматри-
рассматривать балку пролётом /2 с консолью а.
Для примера рассмотрим балку ABCD, нагружённую, как указано
на фиг. 387, а\ ^ = 6 м\ /2 = 5 м\ а = 2 м\ # = 4 tjm.
Фиг. 38G.
В) ttt
Фиг. 387.
Для составления уравнения трёх моментов имеем:
Л1Я_1 = Жо = 0; М п = Aij = ?; Л!n+i = Ж2 = — ~9 ; /г = 1;
Уравнение имеет вид:
12 2
ИЛИ
откуда
f4 = —3,86 гж.

§ 146]
НЕРАЗРЕЗНЫЕ БАЛКИ С КОНСОЛЯМИ
461
<*>иг-
а)
При определении реакций опор рекомендуется отдельно рассмо-
рассмотреть балку АВ и отдельно балку с консолью BCD. Эпюры изги-
изгибающего момента и поперечной силы по-
построены на фиг. 387, б> в.
Чтобы выяснить, как следует поступить
при наличии защемлённого конца балки,
рассмотрим конструкцию этого защемления
(фиг. 388). Защемлённый конец можно рас-
рассматривать как подпертый снизу в точке А
и сверху б точке В, или наоборот.
Подобное защемление не будет абсо-
абсолютно жёстким, ибо участок балки между
точками А и В длиной 1Х имеет возможность несколько деформиро-
деформироваться, вследствие чего сечение балки, совпадающее с лицевой гранью
стены, сможет поворачиваться. Чем
короче будет участок 1Ь чем больше
его момент инерции и чем непо-
неподатливее стена, тем более жёстким
будет защемление. Вполне защем-
защемлённый конец балки мы получим,
полагая в пределе 1Х равным нулю
(или 71 = оо). При расчёте неразрез-
неразрезной балки с защемлённым концом
необходимо вместо защемления до-
добавить ещё пролёт, составить урав-
уравнения трёх моментов и перейти к
пределу, полагая /х равным нулю
(или J1 = oo).
Рассмотрим балку с двумя за-
защемлёнными концами, нагружён-
нагружённую силой Р на расстояниях а
и Ъ от левой и правой опор
(фиг. 389, а). Предполагается, что
опоры А и В не препятствуют
продольным деформациям балки.
Вместо защемлённых концов до-
добавляем слева и справа по пролёту
и, таким образом, переходим к ра-
расчёту трёхпролётной неразрезной
балки (фиг. 389, б).
Данные к составлению уравнения
ь)
9*Р&
Фиг. 389.
трёх моментов
	t_^L. I i
Уравнение получает вид:
для опоры
Ъ
/;
= - 6
B3.32)

462	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ	[ГЛ. XXIII
Данные к уравнению трёх моментов для опоры 2 (п = 2);
Тогда
B3.33)
Теперь в уравнениях трёх моментов B3.32) и B3.33) положим
/1 = /3=:0, а 4 = /; тогда получаем систему
У = — РаЪ\\ +у),
= — Pab [\ +т)«
Решая эту систему, находим:
РаЬ2
Pa2b
/2 •
Момент под грузом Мр равен при х = а:
лл r,<*b , Mtb , М2а
МР\\
опоры /:
При действии на балку с защемлёнными концами равномерно
распределённой нагрузки q (фиг. 390, а) опорные моменты М\ и Ж2
равны; заменяя защемление добавочным пролётом, составляем урав-
уравнение трёх моментов для
—«•
Полагая 1Х = 0, 4 = А М\ =
= Ж2, получаем:
Фиг. 390.	^f1 = _9L.#
Наибольший положительный изгибающий момент будет посредине
пролёта; он равен
Mi =
12
	 i 1L
	 194 •
Эпюра моментов показана на фиг. 390, &

§ 147]
ПРИМЕРЫ РАСЧЁТА НЕРАЗРЕЗНЫХ БАЛОК
463
§ 147. Примеры расчёта неразрезных балок.
Пример 100. Рассмотрим балку (фиг. 391, а). Единственной лишней
неизвестной будет опорный момент Afb Эпюрой от внешней нагрузки дли
основной системы будет парабола на протяжении второго пролёта с наи-
/2
большей ординатой q -^. Уравнение трёх моментов имеет вид
Реакции опор равны:
D	ql2	ql
^° ^ Тб7= ~ Тб •
_ql ql' _
Вычисляем поперечные силы и изгибающие моменты:
Q (хJ = - /?2 + qx = - ^ G/ - 1 6лг),
Изгибающий момент во втором пролёте обращается в нуль при х = -н- / и пе-
О
I ,1	jr(ll
в)
Фиг. 391.
Фиг. 392.
реходит через максимум при x~jxl\ максимальное значение момента равно
Эпюры момента и поперечной силы показаны на фиг. 391, бив.
Пример 101. Возьмём балку с нагрузкой q на обоих пролётах
(фиг. 392, а).
Выдерживая тот же порядок вычислений, получим:

464
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ
[ГЛ. XXIII
естественно, что против предыдущего примера момент удвоился. Опорные
реакции имеют значения:
а;
Поперечные силы и изгибающие
моменты для левого пролёта выразятся
формулами:
Q Mi = #d — tf* = -§- ?/ — ?*;
Для правого пролёта решение ана-
аналогично.
При А' = 3//8, т. е. при Q(at) = O,
моменты будут иметь наибольшее по-
положительное значение:
MmaY = 1Tt5 ql2 ?__ y- ql2.
max 128 ^ 14^
т. е. наибольшим по абсолютной вели-
величине будет изгибающий момент над
опорой Mv Эпюры показаны на фиг. 392,
б я в.
Пример 102. Двухпролётная с
Г" консолью на левом конце балка загру-
загружена силой Р на конце консоли и мо-
моментом М в двух третях первого пролёта
! . (фиг. 393, а). Построить эпюры М{х) и
ш. л/«у Числовые значения такие:
Фиг. 393.
р = 2 г; М = 6 тм; а = 2 м;
Ь = 4 м; с = 2 ж; */ = 5 ж.
Составляем уравнение трёх моментов, пользуясь фигурой 393, б:
MA* + c) + Wi{b + c + d)=-6\^--~f±),
ИЛИ
— Ра F + с) + 2М1 (Ь + с + d) -.
Подставляя числовые значения
1 1 .,
7-Т-3 ЛЬ
________
-2.2.6 + 2^
и, решая, получаем
1Х = 0,545 тм ____; 0,55

§
ВЛИЯНИЕ НЕТОЧНОГО РАСПОЛОЖЕНИЯ ОПОР ПО ВЫСОТЕ 465
' Эпюра опорных моментов показана на фиг. 393, в. Ордината этой эпюры
1	2
под сечением, где приложен момент М, равна—^ Мо + у Mi = —¦ 0,97 тм.
Складывая ординаты эпюр изгибающего момента от М (фиг. 393, б) и от
совместного действия Р и Mi (фиг. 393, в), получаем суммарную эпюру
изгибающего момента (фиг. 393, г). В сечении, где приложен заданный
2
момент М, ординаты эпюры: положительная -^ М — 0,97 = 3,03 тм и отри-
о
цательная у М + 0,97 = 2,97 тм.
Опорные реакции находим, рассматривая схему фиг. 393, д:
_
Hi = — -~- = — 0,11 г; /<js=4---i=o,ll г.
Полные реакции равны:
#а = 3,76 т) /?i = — 1,87 г; #а = 0,11 г.
Эпюра поперечной силы на фиг. 393, е>
§ 148. Влияние неточного расположения опор по высоте.
Изложенный выше метод расчёта неразрезных балок предполагает, что
все опоры расположены на одном уровне. Практически при установке балки
нельзя добиться совершенно точного выполнения этого требования; часть
опор может оказаться несколько выше, часть — ниже проектного уровня.
Иногда расположение опор в разных уровнях может явиться следствием
неодинаковой осадки опор. Иногда такое расположение может оказаться
выгодным, и его делают умышленно. В статически определимой балке, на-
например, в балке на двух опо-
опорах или* с шарнирами в пролёте,	а/ц п ^Щ
такие неточности сборки не	\\ Г/
вызовут сколько-нибудь суще-	\\ \/
ственного изменения напряже- J}d	^Ап' п'Ж^	~т-
ний; в неразрезной же балке,
как статически неопределимой
системе, можно ожидать воз-
возникновения довольно значи-
значительных начальных напряже- ^	~~ In		l-n+f"
ний от неточности расположе-	ф , ,>q.
ния опор или от их неравно-	'
мерной осадки.
Выясним, как отразится осадка или повышение одной из опор, напри-
например л-й, на моментах и напряжениях в балке. Величину смещения л-й опоры
будем обозначать Ьп. На фиг. 394 изображено влияние повышения л-й опоры
на деформации основной системы в л-м и (п -\- 1)-м пролётах. На остальные
пролёты основной системы влияние этого повышения не распространяется.
Как видно из чертежа, повышение л-й опоры вызывает в основной
системе над л-й опорой такие же углы поворота а, какие появились бы при
изгибе этих пролётов положительными изгибающими моментами с площадями

4бб	СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ	[ГЛ. XXIII
эпюр о)л и с1>л+1. Углы поворота опорных сечений (§ 144) от действия таких
внешних нагрузок выражались формулами
Так как углы поворота опорных сечений вызываются повышением п-й
опоры, то, составляя уравнение трёх моментов для этой опоры, мы должны
вместо слагаемого <оя ^ поставить anEJ и вместо <оя+1 -^ величину ая+1 EJ, т. е.
Мп^1п + 2Мп (/„ + /л+1) + Mn+iin+l = - 6EJ (ап
Тангенсы углов ап и ая+1 по своей величине соответственно равны (фиг. 394)
= г и
вследствие малости этих величин принимаем тангенсы равными углам; тогда
уравнение трёх моментов B3.16) для опоры п принимает вид
1п + 2Мп Aп + /я+1) + Мя+1/я+1 = - (>ЕЛп (-L + J
Vn 'л
Для смежных опор п — 1 и п +1 мы будем иметь понижение Ьп
этих опор по сравнению с опорой п; в соответствии с этим уравне-
уравнения трёх моментов (от разницы уровней) для этих опор получат вид:
для опоры п — 1
Фиг. 395.
Уравнения трех моментов для остальных опор не будут зависеть от Ьп.
Определим опорные моменты от повышения Ь средней опоры двухпро-
лётной неразрезной балки (фиг. 395) постоянного сечения. Достаточно напи-
написать одно уравнение для опоры 1:
2Mi .2/ = — 6?/у,
Отсюда
наибольшее напряжение равно
_\Mt\ _ЗЕЛ _ о
°max— w — /2^r—6C i
Ясно, что при понижении опоры / на Ь опорный момент был бы равен
Ji—72~* Так как в такой балке от внешней нагрузки опорный момент обычно
бывает отрицательным, то искусственное понижение средней опоры могло бы
снизить расчётную величину опорного момента и уравнять его с моментами
в пролётах. Однако этот приём ещё не получил широкого распространения.

ОБЩИЕ ПОНЯТИЯ. РАСЧЁТ ДВУХПРОЛЁТНОЙ БАЛКИ
467
§ 149]
Величина дополнительного момента от разницы уровней опор пропор-
пропорциональна жёсткости балки и может достигнуть большой величины. Так, для
пвухпролётной балки профиля № 60а с пролётами 6 м при повышении сред,
ней опоры по сравнению с крайними на 1/200 пролёта дополнительное на-
напряжение	Я. 2.
Таким образом, для неразрезных балок возможно более точное выпол-
выполнение проектного расположения опор имеет очень большое значение.
ГЛАВА XXIV.
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК
ПО ДОПУСКАЕМЫМ НАГРУЗКАМ.
§ 149. Общие понятия. Расчёт двухпролётной балки.
При расчёте по допускаемым напряжениям мы считаем опасным то
состояние балки, когда наибольшие нормальные напряжения в наибо-
наиболее напряжённом сечении дойдут до предела текучести отах = аТ. Одна-
Однако даже для статически определимой
балки это состояние не будет соот-
соответствовать исчерпанию грузоподъ-
грузоподъемности балки; необходимо, чтобы
в опасном сечении образовался «пла-
«пластический шарнир», передающий из-
изгибающий момент Ж? = 2ат5шах =
= №#от. В этом случае при стати-
статически определимой балке дальней-
дальнейшая деформация будет происходить
без повышения нагрузки (§ 97).
В -статически неопределимой бал-
балке образования одного пластиче-
пластического шарнира недостаточно для
исчерпания грузоподъёмности балки;
для этого необходимо появление
ещё по крайней мере одного пласти-
пластического шарнира. Покажем это на
примере.
Рассмотрим двухпролётную не-
неразрезную балку постоянного сече-
сечения (фиг. 396, а); эпюра моментов
Для неё при упругой работе
(фиг. 396, б) представляет собой разность эпюр от груза Р и от
опорного момента Ж, = — ^ PL Пунктиром показано графическое
вычитание эпюр. Результирующая эпюра заштрихована. Наиболее
Фиг. 396.

468	РАСЧЁТ ВАЛОК ПО ДОПУСКАЕМЫМ НАГРУЗКАМ	[ГЛ. XXIV
напряжёнными являются сечения под грузом с моментом Мр=
Pi Я	13	3
==Т— 64^ = 64^ и на сРедней 0П0Ре с моментом Мх= t^PI <]
13
п/. При возрастании накрузки напряжение дойдёт до предела
текучести ат прежде всего в крайних волокнах сечения под грузом
при величине силы Рт, определяемой уравнением
= .„ „хкуд, *_
При дальнейшем увеличении нагрузки в этом сечении образуется
пластический «шарнир», когда изгибающий момент (§ 97) станет
равным
Однако при такой нагрузке балка не утратит грузоподъёмности.
Она обратится в статически определимую систему с шарниром
в точке Д через который передаётся момент Ж? (фиг. 397); такая
балка способна принять и дальнейшее
\рг* и*	увеличение нагрузки. При этом увели-
0 *мл\ т 1	2 чении момент в сечении D останется
,я^ Jj}\. ?Г	jjV постоянным, а момент над опорой будет
увеличиваться, пока не дойдёт тоже
Фиг. 397.	д0 величины Ж?; в опорном сечении
образуется второй пластический шар-
шарнир, левый пролёт обратится в подвижную систему, и грузо-
грузоподъёмность балки будет исчерпана при нагрузке Р?. Эпюра момен-
моментов для этого состояния балки показана на фиг. 396, в — это будет
эпюра разрушающих моментов. Она представляет собой разность
рк/
ординат треугольника adb с наибольшей ординатой под грузом —~
и ординат треугольника aek с ординатой на опоре Ж? и под гру-
К
зом ~2~. Величина разрушающего груза Рт определяется из условия,
что отрезок сау равный —	^-, тоже должен быть равен Мт:
Отсюда
и p* = -Jl = —rL.	B4.1)

§ 149]	ОБЩИЕ ПОНЯТИЯ. РАСЧЁТ ДВУХПРОЛЙТНОЙ БАЛКИ	469
Условие прочности имеет вид (§ 27)
Р^?[Р],	B4.2)
где Р — заданная, а [Р]— допускаемая нагрузки.
Для получения [Р] делим обе части равенства B4.1) на коэффи-
коэффициент запаса k:
[Р* — пг—~w—~w—~i
Подставляя это значение [Р] в B4.2), получаем
Отсюда
W^J?L==-^f	B4.4)
"^ 6/г [а] п [а] '	v '
PI
где Mr=-sr — расчётный изгибающий момент в сечениях 1 и Z>.
Таким образом, подбор сечения балки в этом примере следует вести
Р1
по расчётному моменту Мг = -?г и по допускаемому напряжению п[а].
Pi	к Р*1
Как видно из формул для Мг = -?г и Мт=-о-, ординаты эпюры
расчётных моментов (фиг. 396, г) пропорциональны ординатам эпюры
разрушающих моментов и получаются из них заменой разрушающего
груза Р* действующей нагрузкой А
Если вести расчёт по допускаемым напряжениям, то расчётный
13	1
момент следовало бы взять (по фиг. 396, б) Л1тах = ^тР/^>-^Р/, а за
допускаемое напряжение -— [о]. Таким образом, для статически неопре-
неопределимых балок переход на расчёт по допускаемым нагрузкам даёт
двойную выгоду, — повышается, как и для статически определимых
балок, допускаемое напряжение и видоизменяется расчётная эпюра
изгибающего момента в сторону снижения её ординат.
Полное повышение расчётной грузоподъёмности характеризуется
отношением
Р^ 6n<tTW -13/ 78
П
Принимая я = 1,15 (для двутавровых балок, § 97), получаем, что
расчётная грузоподъёмность балки возрастёт при переходе на новый
метод расчёта в 1,4 раза, т. е. на 40%.
В рассмотренном примере расчётная эпюра моментов (фиг. 396, в)
характеризовалась равенством изгибающих моментов в двух наиболее
напряжённых сечениях. Поэтому этот способ расчёта при балке по-
постоянного сечения иногда называют способом уравнивания моментов.

470
РАСЧЁТ БАЛОК ПО ДОПУСКАЕМЫМ НАГРУЗКАМ	[ГЛ. XXIV
6)
Фиг. 398.
Имея это в виду, мы могли построить расчётную (по допускае-
допускаемым нагрузкам) эпюру моментов графически: сначала изобразить
эпюру от груза Р для разрезной
балки (Ladb)> а затем построить
 ~&2 линию опорных моментов aek так,
l\	z3? чтобы be = cd\ для этого разделим
отрезок db пополам в точке / и
проведём прямую afe.
Если бы к рассмотренной балке
был приложен ещё груз Р посредине
второго пролёта, то расчётная эпюра
моментов (фиг. 398, б) не изменилась
бы, т. е. добавление этого груза не потребовало бы усиления балки.
Изменился бы лишь порядок появления пластических шарниров:
сначала такой шарнир
образовался бы в сече-
сечении над средней опорой,
а уже потом — под обо-
обоими грузами.
§ 160. Расчёт трёхпро-
лётной балки.
Рассмотрим теперь бал-
балку, имеющую и средний про-
промежуточный пролёт (фиг.
399, а). Эпюра моментов
для этой балки при упру-
~А 3 гой работе изображена на
Щг, фиг. 399, б. При постепен-
Г ном возрастании нагрузки
пластические шарниры обра-
образуются сначала над сред-
средней опорой / и посре-
посредине (приблизительно) сред-
среднего пролёта (фиг. 399, в);
однако балка сможет и даль-
дальше воспринимать увеличе-
увеличение нагрузки, пока не обра-
образуется третий шарнир на опоре 2. Выравненная эпюра разрушающих мо-
моментов показана на фиг. 399, г. Предельный момент равен
Фиг. 399.
а расчётный
2 8
16
Необходимый момент сопротивления равен
'л [о]" 16л [а]'

§
ПРИМЕР
471
Таким образом, при возможности разрушения промежуточного пролёта
должны образоваться три пластических шарнира, моменты в которых будут
одинаковы. Если бы на-
нагрузка была расположена
на всех пролётах нашей
балки, то следовало бы
рассмотреть возможность
разрушения каждого из про-
пролётов, построить соот-
соответствующие эпюры рас-
расчётных моментов (путём
уравнивания их величин в
опасных сечениях) и по- Т"!
добрать W по наиболь--.' •
шему из полученных Мп
В качестве примера загру-
загрузим трёхпролётную балку
(фиг. 400) равномерной на-
нагрузкой q в среднем про-
пролёте и сосредоточенными
силами P = 2fl/ в середи-
серединах крайних пролётов. Опре-
Определение расчётных моментов Мг для всех трех пролетов показано на
чертеже пунктиром; они равны
Фиг. 400.
Мг1 = '
ql*
Подбор сечения балки следует вести по Моменту Мг = ^\ момент сопро-
2гп/м
тивления равен
Подобным же образом q
следует проводить расчёт
любой многопролётной не- ,
разрезной балки, оценивая |
возможность разрушения
каждого лз пролётов.
§ 151. Пример.
Пример 103. Подо-
Подобрать двутавровое сечение
по методу допускаемых на-
напряжений и допускаемых
нагрузок для трёхпролёт-
ной неразрезной балки
(фиг. 401, а) постоянного
сечения с равными про-
пролётами / = 4 м; балка на-
нагружена в среднем пролёте
сосредоточенной силой Р =
= 10 г на расстоянии а =
= 1 м от левого конца
среднего пролёта.
Фиг. 401.
Крайний правый пролёт загружён сплошной нагрузкой q = 2 цпог, м;
= 1600 кг/см2.

472	РАСЧЁТ БАЛОК ПО ДОПУСКАЕМЫМ НАГРУЗКАМ	[ГЛ.
1. Расчёт по допускаемым напряжениям. Составляем уравнения трёх
моментов
- 6 ^
Подставляя числовые значения, имеем:
16М! + 4Af2 = — 10 *4] ' 3D + 3) = — 52,5,
AM, + 16М2 = - Ю 'I ' 3D+ 1)-^ = -69,5;
откуда Mi = — 2,32 тм; Af2 = — 3,77 тм.
Ординаты эпюр моментов для основной системы под грузом и посредине
крайнего правого пролёта
%л Pab 10 • 1 • 3 _ R	.. ql* 2 • 42 .
Мр= — ~	^	= 7,5 тм; Mq = ^ = —g— = 4 тм.
Эпюра изгибающих моментов показана на фиг. 401, б. Наибольший изги-
изгибающий момент
485 000
ЛГшах = 7,50 — 2,65 = 4,85 тм, М ^ ^^ = 303
Необходимо поставить двутавр № 24а с № = 317 см*.
2. Расчёт по допускаемым нагрузкам. Предельное состояние среднего
пролёта будет при
Расчётный момент в сечении под силой находим из уравнения:
м РаЬ ла
отсюда
Mr- 2/ .
Условие прочности
Mr^nW[a)
приводит к ответу:
Pab	10000.100.300
Ш [а] -" 2 • 400 • 1,16 • 1600
Необходимо поставить двутавр № 20а с W = 203 си3.
Расчётный момент для крайнего пролёта определяется из условия, что
Мтза в пролёте равен моменту на опоре; их величина и будет Мг% Выраже-
Выражение для М(х) при предельном состоянии имеет вид

I 152]	общие понятия	473
Приравнивая производную от этого выражения нулю, находим абсциссу х%
сечения с моментом, равным Afmax
Уравнение для определения Мг имеет вид
/К1тах — 2	2
Подставляя числовые данные, имеем:
Мг = 3,39 тм < !~ = 3,75 тм.
Сечение должно быть подобрано по Мг для среднего пролёта.
Описанный способ расчёта неразрезных балок требует ряда оговорок
и ограничений. Во-первых, он относится к статическим нагрузкам. Во-вто-
Во-вторых, физическая картина разрушения балки и при статической нагрузке
гораздо сложнее той, весьма упрощённой, схемы образования пластических
шарниров, о которой речь шла выше. Пластическая деформация не сосредо-
сосредоточивается в одном сечении, а распространяется и по длине балки. Затем
исчерпание грузоподъёмности может произойти не только за счёт пласти-
пластических деформаций, а и за счёт потери устойчивости как всей балки в целом,
так и листов сжатого пояса или стенки балки. Таким образом, попытки
перейти к практическому приложению этого метода расчёта даже при
статических нагрузках требуют повышения внимания к проверкам балки на
устойчивость.
Опыты над разрушением статически неопределимых балок при стати-
статической нагрузке показывают, что в тех случаях, когда исключается разру-
разрушение балок от потери устойчивости, величины разрушающей нагрузки,
полученные экспериментально и теоретически описанным выше способом,
сходятся очень хорошо.
ГЛАВА XXV.
БАЛКА НА УПРУГОМ ОСНОВАНИИ.
§ 152. Общие понятия.
К числу статически неопределимых балок может быть отнесена балка
на упругом основании. Так называется балка, опирающаяся по всей своей
длине (фиг. 402) на упругое основание, оказывающее в каждой точке на балку
реакцию, пропорциональную у — прогибу балки в этой точке. Коэффициент
пропорциональности обозначается бук-
вой ft.	,	Л ,р2
Введение предположения о пропор- Т'	¦ f
ииональности реакций прогибу является WAyy^^^f^^f^f^^^^^^
приближением, хотя и достаточно близ- *	' ' 1	' ' '
ким к действительным условиям.	фиг 402.
Предложение ввести в расчёт коэф-
коэффициент пропорциональности kt име-
именуемый «коэффициентом постели», было впервые сделано русским академи-
академиком Николаем Ивановичем Фуссом в 1801 году. Принимая это предположе-
предположение, получаем, что интенсивность реакции основания в каждой точке
равна ky и измеряется в единицах ——; размерность коэффициента Л при

474	ВАЛКА НА УПРУГОМ ОСНОВАНИИ	[ГЛ. XXV
этом будет Сила (kzjcm*). Будем считать, что основание оказывает реакцию
длина
при прогибах балки как вниз, так и вверх.
На практике задачи о расчёте балки на упругом основании встречаются
в железнодорожном деле (рельс, шпала), в строительстве — фундаменты раз-
различных сооружений, передающие нагрузку на грунт.
Статически неопределимой такая балка будет потому, что условие ста-
статики — сумма нагрузок равна всей реакции основания — не даёт возможности
установить распределение этой реакции по длине балки, а значит, вычислить
изгибающие моменты и поперечные силы.
Интенсивность реакции в каждой точке связана с прогибами балки.
Поэтому для решения задачи необходимо найти сначала уравнение изогнутой
оси^=/(лг), а уже затем формулы для вычисления изгибающего момента
и поперечной силы. Ход решения оказывается обратным обычному.
Найдём уравнение изогнутой оси для балки постоянного сечения, лежа-
лежащей на упругом основании и нагружённой сосредоточенными силами Ри Р2,...
(фиг. 402). Начало координат возьмём в любой точке, ось х направим вправо,
ось у вертикально вверх. Направление нагрузок вверх будем считать поло-
положительным. Напишем обычное дифференциальное уравнение
Так как М(х) нам неизвестен, то постараемся связать прогибы непо-
непосредственно с нагрузкой, для этого дифференцируем дважды предыдущее
уравнение:
EJ^ = q(x),	B5.1)
где q(x) — интенсивность сплошной нагрузки, действующей на балку в се-
сечении с абсциссой х.
Сплошной нагрузкой для нашей балки является лишь реакция упругого
основания. Интенсивность её пропорциональна прогибам; эта нагрузка на-
направлена вверх, т. е. положительна, когда прогибы идут вниз, т. е. отри-
отрицательны, и наоборот. Таким образом, эта нагрузка имеет знак, обратный
знаку прогибов:
Тогда
EJ^=-ky,	B5.2)
или
0 + ^ = 0.	B5.3)
,у—y~
Если обозначить I/ -^— = р, то общий интеграл уравнения B5.3) имеет вид:
у = еЧх (A sin рлг + В cos $x) + е'$* (С sin $x + D cos рис).	B5.4)
Постоянные А, В, С, D должны быть определены в каждом частном
случае нагрузки и длины балки. Величина р имеет измерение
длина

§ 153] РАСЧЁТ БЕСКОНЕЧНО ДЛИННОЙ ВАЛКИ НА З'ПРУГОМ ОСНОВАНИИ 475
§ 153. Расчёт бесконечно длинной балки на упругом
основании, загружённой одной силой Р.
Наиболее просто решается задача об изгибе бесконечно длинной балки,
нагружённой одной сосредоточенной силой (фиг. 403). Помимо непосред-
непосредственного практического
значения решение этой за-
задачи позволит путём после-
последовательных приближений
рассчитывать и балки ко-
конечной длины.
Начало координат рас-
расположим в точке приложе-
приложения силы Р. Определим
постоянные Л, В, С и D.
Так как вся реакция осно-	фиг-
вания, равная силе Р,
должна быть конечной величиной, то прогибы балки в точках, бесконечно
удалённых от точки приложения силы, должны обращаться в нуль:
vy =0.	B5.5)
При бесконечно больших значениях х два вторых слагаемых в правой
части формулы B5.4) обращаются в нуль благодаря множителю e~Pxt два же
первых могут обратиться в нуль лишь при
Л = 0 и # = 0;
таким образом,
у = *-р* (С sin px + D cos pjc).	B5.6)
Далее, по симметрии нагрузки и реакции основания, касательная к изо-
изогнутой оси в точке приложения силы должна итти параллельно оси абсцисс:
Дифференцируя B5.6), получаем:
¦Q = 6 = — р*~Р* [sin рд: (C + D)+ cos рд: (D — С)].
Подставляя в это выражение д: = 0 и приравнивая результат нулю, находим:
D — С = 0 и C = D;
таким образом, уравнения будут:
у = е-р* С (sin рл: + cos Рлг),	B5.7)
?L = 6 = — 2е-$* Ср sin рл:.	B5.8)
Для определения последней постоянной С имеем ещё одно уравнение:
нам известна величина поперечной силы в начале координат.
Разрезав балку сечением в точке О справа от силы Р и рассматривая
пРавую часть балки, видим, что поперечная сила в этом сечении равна
Реакции основания, действующей на правую половину балки со знаком минус;

476	БАЛКА НА УПРУГОМ ОСНОВАНИИ	[ГЛ. XXV
так как реакция направлена вверх (для правой половины) и вся реакция осно-
основания равна Р, значит, поперечная сила в сечении при л* = О равна
Но, с другой стороны,
С Т У Г\ / v\	/0^ Q\
C.J -z—г = V \'^/«	DО.У)
Таким образом,
d2v dzv
Вычисляем, пользуясь B5.8), -~~ и -~:
F [ cos $х — sin pjcj,	B5.11)
cos px	B5.12)
Подставляя B5.12) в B5.10) и приравнивая х нулю, получаем:
B5-13)
Теперь значения у и её производных получают вид
у = ~ Ж/W е~*х (sin ?'v + cos ?х) = "" "S^F'% B5Л4)
^sin ^ = + W'ri3'	B5Л5)
x- sin W = J. • 4l>	B5.16)
^ |	—y .tj2.	B5.17)
Таким образом, напряжённое состояние и деформации балки на упругом
основании всецело определяются нагрузкой и коэффициентом р, зависящим
от соотношения жёсткостей балки и упругого основания.
Значения величин у\, rilt yj2, tj3 в функции аргумента $х приведены
в таблице 24.
Значения коэффициента k колеблются довольно сильно в зависимости
от рода основания; называя ширину балки Ь, можем представить этот коэф-
коэффициент в виде k = kibf где kL — так называемый коэффициент податливости
основания; он равен силе, которую надо приложить к единице площади
основания, чтобы дать ему осадку, равную единице длины.
Для грунта средней плотности kL колеблется в пределах от 0,5
до 5 кг/смь; для плотного грунта от 5 до 10 kzjcmz\ для каменной кладки,
как основания под балку, от 400 до 600 кг/см9 и для бетона от 800
до 1500 кг/см9. Так как в выражение для р входит V k, то даже значитель-
значительные колебания величины кл отражаются сравнительно слабо на результатах
расчёта.

§ 153] РАСЧЁТ БЕСКОНЕЧНО ДЛИННОЙ ВАЛКИ НА УПРУГОМ ОСНОВАНИИ 477
Таблица 24. Значения функций *?, щ, ъ и rtt.
y) = е~Ъх (cos рл: + sin рл:); % = <rF cosfrv,
^ = <?-р* (cos рл: — sin Рл:); yj, = <rP* sin рл:.
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
1/4*
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1/2*
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
3/4тс
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
7С
3,2
3,3
3,4
3,5
3,6
3,7
•ч
1,0000
0,9907
0,9651
0,9267
0,8784
0,8231
0,7628
0,6997
0,6448
0,6354
0,5712
0,5083
0,4476
0,3899
0,3355
0,2849
0,2384
0,2079
0,1959
0,1576
0,1234
0,0932
0,0667
0,0439
0,0244
0,0080
0,0000
— 0,0056
— 0,0166
— 0,0254
— 0,0320
— 0,0369
— 0,0403
— 0,04226
— 0,04314
— 0,04321
— 0,04307
— 0,04224
— 0,04079
— 0,03887
— 0,03659
— 0,03407
о,оооо
(- 0,0903
-0,1627
-0,2189
-0,2610
- 0,2908
- 0,3099
-0,3199
- 0,3224
- 0,3223
-0,3185
- 0,3096
- 0,2967
- 0,2807
- 0,2626
-0,2430
- 0,2226
-0,2079
-0,2018
-0,1812
-0,1610
-0,1415
У 0,1231
-0,1057
-0,0896
- 0,0748
-0,0670
-0,0613
[-0,0491
- 0,0383
- 0,0287
- 0,0204
-0,0132
+ 0,00703
+ 0,00187
+ 0,00000
— 0,00238
— 0,00582
— 0,00853
— 0,01059
— 0,01209
— 0,01310
1J00O0
0,8100
0,6398
0,4888
0,3564
0,2415
0,1431
0,0599
0,0000
— 0,0093
— 0,0657
— 0,1108
— 0,1457
— 0,1716
— 0,1897
— 0,2011
— 0,2068
— 0,2079
— 0,2077
— 0,2047
— 0,1985
— 0,1899
— 0,1794
— 0,1675
— 0,1548
— 0,1416
— 0,1340
— 0,1282
— 0,1149
— 0,1019
— 0,0895
— 0,0777
— 0,0666
— 0,05632
— 0,04688
— 0,04321
— 0,03831
— 0,03060
— 0,02374
— 0,01769
— 0,01241
— 0,00787
\-1,0000
-0,9003
- 0,8024
- 0,7077
-0,6174
-0,5323
- 0,4530
- 0,3708
-0,3224
-0,3131
- 0,2527
-0,1988
-0,1510
-0,1091
-0,0729
-0,0419
- 0,0158
0,0000
— 0,0059
— 0,0235
— 0,0376
с- 0,0484
— 0,0563
— 0,0618
— 0,0652
— 0,0668
— 0J0670
— 0,0669
— 0,0658
— 0,0636
— 0,0608
— 0,0573
— 0,0534
— 0,04929
— 0,04501
— 0,04321
— 0,04069
— 0,03642
— 0,03227
— 0,02828
— 0,02450
— 0,02097
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,785
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,571
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,356
2,4
2,5
2,6
2,7 n
2,8
2,9
3,0
3,1
3,142
3,2
3,3
3,4
3,5
3,6
3,7

478
ВАЛКА НА УПРУГОМ ОСНОВАНИИ	[ГЛ. XXV
Продолжение табл. 24.
3,8
3,9
5/4*
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
6/4*
4,8
4,9
5,0
5,1
5,2
5,3
5,4
7/4*
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
8/4*
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
9/4*
— 0,03138
— 0,02862
— 0,02786
— 0,02583
— 0,02309
— 0,02042
— 0,01787
— 0,01546
— 0,01320
— 0,01112
— 0,00921
— 0,00898
— 0,00748
— 0,00593
— 0,00455
— 0,00334
— 0,00229
— 0,00139
— 0,00063
0,00000
+ 0,00001
0,00053
0,00095
0,00127
0,00152
0,00169
0,00180
0,00185
0,00187
0,00187
0,00184
0,00179
0,00172
0,00162
0,00152
0,00141
0,00129
0,00120
— 0,01369
— 0,01392
— 0,01393
— 0,01386
— 0,01356
— 0,01307
— 0,01243
— 0,01168
— 0,01086
— 0,00999
— 0,00909
— 0J00898
— 0,00820
— 0,00732
— 0,00646
— 0,00564
— 0,00487
— 0,00415
— 0,00349
— 0,00290
— 0,00288
— 0,00233
— 0,00184
— 0,00141
— 0,00102
— 0,00069
— 0,00069
— 0,00017
0,00000
+ 0,00003
0,00019
0,00032
0,00042
0,00050
0,00055
0,00058
0,00060
0,00060
— 0,00401
— 0,00077
0,00000
+ 0,00189
0,00403
0,00572
0,00699
0,00791
0,00852
0,00786
0,00898
0,00898
0,00892
0,00870
0,00837
0,00795
0,00740
0,00692
0,00636
0,00579
0,00578
0,00520
0,00464
0,00409
0,00356
0,00307
0,00261
0,00219
0,00187
0,00181
0,00146
0,00115
0,00087
0,00063
0,00042
0,00024
0,00009
0,00000
— 0,01770
— 0,01469
— 0,01393
— 0,01197
— 0,00953
— 0,00735
— 0,00544
- 0,00377
— 0,00234
— 0,00113
— 0,00011
0,00000
+ 0,00072
0,00139
0,00191
0,00230
0,00259
0,00277
0,00287
0,00290
0,00290
0,00287
0,00279
0,00268
0,00254
0,00238
0,00221
0,00202
0,00187
0,00184
0,00165
0,00147
0,00129
0,00113
0,00097
0,00082
0,00069
0,00060
3,8
3,9
3,927
4,0
4,1
4,2
4,3
4,4
4,5
4,6
V
4,712
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,498
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,283
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,069
§ 154. Пример,
П р^и м е р 104. Определить напряжение а в железнодорожном рельсе
типа II А от статической нагрузки паровозом Эм. Схема нагрузки дана на
фиг. 404. Определим изгибающий момент в сечении под средним колесом
как сумму моментов от действия отдельных грузов. Для того чтобы восполь-

§ 155]
РАСЧЁТЫ БАЛОК КОНЕЧНОЙ ДЛИНЫ
479
зоваться формулой B5.16), необходимо при учёте влияния каждого колеса
располагать начало координат под ним, а за абсциссу х принимать расстоя-
расстояот этого колеса до
8,90т
МО
ЦОЗт 8,05т д,90т
\-~ttfO—-4— то-*+- *
CD Ф Ф
8,72т
mm
ние от этого колеса до
того сечения, где вычис-
вычисляется момент.
Коэффициент k мо-
может быть принят рав-
равным 300 кг/мм2. Жёст-
Жёсткость рельса EJ = 2 X
X 10е -1223 кг-см2; тогда
Р = лт • \/см. Изгибающий момент в сечении рельса под третьим колесом
равен
Фиг. 404.
расстояния х от этого сечения до каждого колеса и, соответственно, вели-
величины $х равны
хг = 289 см; х% = 143 см; хъ = 0; лг4 = 143 см; хъ = 289 см;
= 5,9; $хь = 12,0.
^	*8 = — = 5,9; рл:8 = 0;
При (Зле >> 7 величинами т^ практически можно пренебречь.
Таким образом^ давление крайних колёс не вызывает напряжений в рас-
рассматриваемом сечении. Влияние остальных колёс характеризуется величи-
величинами
7]{1 = 0,00356 = 7]}V; т]Ш = 1Д
Таким образом,
94
М = ~ [(8720 + 8050) . 0,00356 + 8900 . 1] = 53 800 кгем.
Наибольшее воздействие оказывает колесо, стоящее над рассматривае-
рассматриваемым сечением; смежные колёса, даже сравнительно близко расположенные,
оказывают ничтожное влияние на
напряжение в этом сечении.
Так как W"= 180 см\ то а =
= 299 кг/см*.
§ 155. Расчёты балок
конечной длины.
Для решения вопроса, в какой
мере полученные выше результаты
могут быть применены к балкам
конечной длины, рассмотрим изо-
изображённую на фиг. 405 половину
изогнутой оси бесконечно длин-	Фиг. 405.
ной балки, нагружённой сосредо-
сосредоточенной силой Р. Эта ось представляет собой волнообразную кривую с по-
постепенно затухающими ординатами. Для большей общности по горизонтали
отложены отвлечённые величины $х вместо абсцисс х.
Длина полуволны этой кривой равна /О = тс/Р; из таблицы 24 мы видим,
что уже на расстоянии двух полуволн 2/0 от начала координат наибольший

480*	балка на упругом основании	[гл. xxv
прогиб равен всего ^0,2% от прогиба под грузом. Таким образом, практи-
практически прогибы обращаются в нуль не при х = оо, а при х = 2/0.
Поэтому полученными формулами можно смело пользоваться при ра-
расчётах симметричных балок с длиной /^4/0, а если учесть, что при л: = /в
прогиб равен 4°/0 от наибольшего, то и для балок при /^=2/0 часто ими
пользуются.
Для более коротких балок можно применить метод последовательных
приближений. Для этого нам потребуется уметь вычислять М(х) и Q (х)
в бесконечно длинной балке, нагружённой на одном конце силой Р% и
Q
Фиг. 406.
парой Мо. Начало координат принимаем на нагружённом конце, направление
осей координат оставляем прежним (фиг. 406).
Начальными условиями, определяющими постоянные в выражении B5.4)
будут;
1)	при л: == оо прогиб у = 0; отсюда А = В = 0;
2)	при х = 0 изгибающий момент М (х) = EJ ~т~ = + Мо\
3)	при х = 0 поперечная сила Q (х) = ?У -pg- = — Ро.
Опускаем промежуточные вычисления; при помощи второго условия полу-
получаем
г- М»
а из третьего условия
Тогда
М (х) = — ~ [Ро sin р* - Мор (cos рл- + sin рх)] = — у [Рв^-М^^],B5.18)
Q (х) = — ^-р* [Ро (cos pjc — sin (U) + 2M03 sin ^x] = — [Ротц + 2M0SriS].B5.19)
Теперь готов весь аппарат для расчёта балки любой длины на упругом
основании под сосредоточенной нагрузкой.
Рассмотрим балку АВ длиной /<2/0, нагружённую сосредоточенной
силой Р на расстоянии а от левого и Ь от правого конца (фиг. 407, а).
Для расчёта такой балки заменим её бесконечно длинной балкой (фиг. 407, б).
Для такой балки мы можем найти напряжения в любом сечении, в том
числе и в сечениях At и Biy соответствующих концам нашей короткой
балки.
Таким образом, средняя часть А^ВХ (фиг. 407, в) бесконечно длинной
балки окажется под действием силы Р и усилий по сечениям Ах и В% —

§ 155]	расчёты валок конечной длины	481
Mat Мь и Qa* Qb't показанные на чертеже направления усилий соответ-
соответствуют их положительным значениям.
Чтобы работа выделенной части балки AiBi совпала с работой заданной
балки АВ, надо к сечению Ai приложить внешние: силу — Qa и пару — Ма,
а к сечению Вх: —Qb и —Мь, так как в действительной балке в сечениях
А и В напряжений нет.
Таким образом, в первом приближении напряжения в балке АВ могут
быть вычислены как сумма напряжений в точках участка AtBi трёх балок
/ //, /// (Фиг. 407). Изгибающие моменты и поперечные силы в сечениях
*	Р	Р
правой части балки / равны М'х = + ж г<ь Q*== —§" ^2» для сечении левой
части должен быть изменён знак у tj2. Для подсчёта М" (х) и Q" (х) во вто-
второй балке можно воспользоваться формулами B5.18) и B5.19), положив
po = --Qbt M0 = — Mb и переменив знак в выражении для О" (л*), так как
изменено направление оси
х по сравнению с фиг. 406,
к которой относятся эти
формулы. Таким образом,	тмтт
Г4 Qi)МВт1 б)	^
Q" (jc) = —
Для третьей балки еле-	Af с\		Д	^
дует положить АГ0 = -~ Ма	г) гшшш!!тпт}/шш}^ш1///п/^;1тшш//Л!Ш1Ш1/^ -
и Ро = + Qa> таким обра-
образом,	^
у^/////////////////////////////////////щ////// х """
Что касается величин	фиг 407.
усилий в сечениях А и В,
то они численно равны изги-
изгибающим моментам и поперечным силам в этих сечениях. Если при их
вычислениях пользоваться таблицей 24, то для поперечной силы в сечении А
придётся переменить знак.
Таким образом, вычисляя поправки М" (х\ М'" (х), Q" (х) и Q'" (х) при
помощи таблицы 24, надо для основной балки вычислить по этой же
таблице Мш Qa при х = а и М^, Qb при х = Ь, а затем воспользоваться
формулами B5.18) и B5.19), положив Мо = — Ма или — Mb} a PQ = — Qa
или — Qb. Так как при подсчёте поправок мы допустим новую по-
погрешность—в сечении At балки //ив сечении BL балки /// усилия полу-
получаются, хотя и малыми, но не равными нулю, то указанным путём
можно внести и дальнейшие поправки, однако это обычно уже является
излишним.
Задача расчёта балок на упругом основании изучалась многими совет-
советскими учёными, в том числе академиком А. Н. Крыловым, профессорами
Н. П. Пузыревским, П. Л. Пастернаком, В. В. Кречмером, доцентом
':. Д- Дутовым, профессорами Н. К. Снитко, Б. Г. Кореневым, В. А. Кисе-
Киселёвым, А. А. Уманским, С. С. Голушкевичем, Л. В. Канторовичем,
К- С. Завриевым, П. Ф. Папковичем, Я. А. Пратусевичем, А. П. Коробо-
Коробовым и др.

482	ВАЛКА НА УПРУГОМ ОСНОВАНИИ	[ГЛ. XXV
Был разработан A923 г.) эффективный метод расчёта, позволяющий
обойтись без описанного здесь приёма последовательных приближений; он
назван методом начальных параметров и позволяет через четыре начальных
параметра у09 60, Мо и Qo, действующих в выбранном начале коорди-
координат, выразить прогиб у (х), угол поворота 6 (л:), момент М (х) и поперечную
силу Q (х) для любого сечения.
Приведём лишь уравнение у (х), так как остальные легко получить диф-
дифференцированием
B5.20)
Исследования изгиба балок, не следующих закону B5.20), принадлежат
профессорам Г. Э. Проктору, Н. М. Герсеванову, Я. А. Мачерету,
Б. Н. Жемочкину, М. И. Горбунову-Посадову, А. П. Филиппову,
И. Г. Альперину, М. М. Филоненко-Бородичу и др.

ОТДЕЛ VIII.
СЛОЖНОЕ СОПРОТИВЛЕНИЕ.
ГЛАВА XXVI.
КОСОЙ ИЗГИБ.
§ 156. Основные понятия.
До сих пор мы рассматривали задачи, где стержни конструкции
испытывали одну из простейших деформаций: осевое растяжение или
сжатие, кручение, плоский изгиб. На практике же большинство эле-
элементов конструкций и машин подвергается действиям сил, вызываю-
вызывающих одновременно не одну из указанных деформаций, а две и более.
Валы машин подвергаются действию кручения и изгиба; стержни
ферм (стропильных, мостовых, крановых), помимо растяжения или
сжатия, испытывают ещё и изгиб, вызываемый устройством в узлах
сварных или клёпаных соединений взамен шарниров, предполагаю-
предполагающихся при выполнении расчётов. Все такие случаи сопротивления
стержней, когда мы имеем дело с комбинацией простейших дефор-
деформаций, называются сложным сопротивлением.
При расчётах на сложное сопротивление обычно исходят из так
называемого принципа независимости действия сил, т. е. предпола-
предполагают, что влиянием деформаций, вызванных одной из приложенных
к упругой системе нагрузок, на расположение, а следовательно, и
на результаты действия остальных нагрузок можно пренебречь. Опыт
показывает, что пока деформации системы малы этот принцип мо-
может быть использован (исключительные случаи, когда он вообще не
применим, будут рассмотрены ниже); а поэтому для нахождения пол-
полных напряжений и деформаций, возникающих в упругой системе в
результате действия на неё любой сложной системы нагрузок, можно
применять способ сложения действия сил, т. е. геометрически сумми-
суммировать напряжения и перемещения, соответствующие различным видам
простейших деформаций.
Вначале рассмотрим решение частных задач сложного сопротивле-
сопротивления, а затем и самый общий случай действия сил на упругую систему.
§ 157. Косой изгиб. Вычисление напряжений.
Для вычисления нормальных напряжений при изгибе мы до сих
Mz
П(>Р пользовались формулой: а = -г-. Однако нормальные напряже-
у
Ния в каком-либо сечении балки полностью определяются по этой
16*

484
КОСОЙ ИЗГИБ
[гл. xxvi
*z
формуле только в случае плоского изгиба *), когда искривление оси
балки происходит в плоскости действия сил и нейтральной осью яв-
является главная ось инерции поперечного сечения, перпендикулярная
к плоскости нагрузки.
На практике часто встречаются случаи, когда плоскость действия
сил, перпендикулярных оси стержня," не совпадает ни с одной из
двух плоскостей, проходящих через ось стержня и главные оси инер-
инерции поперечных сече-
ч 1-	ний стержня. Опыт по-
jL^	казывает, что изогну-
тая ось стержня при
этом уже не будет ле-
лежать в плоскости дей-
действия сил, и мы будем
иметь случай так назы-
называемого косого изгиба.
Обрешетины кров-
кровли обычно подверга-
подвергаются нагрузкам, плоскость действия которых составляет довольно
значительный угол с главными осями (фиг. 408); довольно часто встре-
встречаются и случаи, когда направление нагрузок лишь слегка откло-
отклоняется от главных осей
инерции.
Покажем на при-
примере метод проверки
прочности и вычисле-
вычисления деформаций балок
при косом изгибе.
Рассмотрим балку,
защемлённую одним
концом и нагружённую
на другом силой Р,
лежащей в плоскости
торца балки и направ-
направленной под углом ср
фиг- 40а	к главной оси Bz
(фиг. 409). Вторая глав-
главная ось By пойдёт перпендикулярно к первой; направления этих осей
выберем так, чтобы сила Р проходила в первом квадранте коор-
координатной системы.
Для проверки прочности необходимо найти точку с наибольшим
нормальным напряжением. Выведем сначала формулу для вычисления
1) Говоря более точно, это будет иметь место, когда все силы лежат в
одной из главных плоскостей инерции стержня, проходящей через центр
изгиба; в целом ряде случаев последний совпадает с центром тяжести попе-
поперечного сечения (§ 96).

§ 157]
КОСОЙ ИЗГИБ. ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ
485
нормального напряжения в любой точке произвольного сечения, отсто-
отстоящего в расстоянии х от свободного конца балки.
Разложим силу Р на составляющие Рг и Руу направленные по
главным осям инерции сечения Bz и By. Величины этих составляю-
составляющих определяются формулами
Рг = Р cos ср и Ру = Р sin <p.
Таким образом, мы привели случай косого изгиба к комбинации
двух плоских изгибов, вызванных силами Р2 и Ру> расположенными
в главных плоскостях инерции балки. Суммируя напряжения и дефор-
деформации, соответствующие каждому из этих изгибов, мы получим ре-
решение и для косого изгиба.
Изгибающие моменты в сечении с абсциссой х от сил Рг и Ру
будут равны
| Му | = Р2х = Рх cos <p =
\ = Рух = Рх sin <p =
cos
sin
p, 1
p. J
B6.1)
Значки у и z при М обозначают главные оси, относительно которых
берутся моменты; буквой М обозначен изгибающий момент в пло-
плоскости действия силы Р, для прове-
проведённого сечения равный Рх. Применяя
векторное изображение моментов, ви-
видим, что для вычисления изгибающих
моментов Му и Мг можно было непо-
непосредственно разложить полный изгибаю-
изгибающий момент М по главным осям
(фиг. 410).
Для установления знаков изгибаю-
изгибающих моментов следовало бы ввести
дополнительные условия, определяю-
определяющие эти знаки в связи с переходом к
пространственной задаче. Это и будет
сделано ниже; сейчас же ограничимся
лишь вычислением абсолютной вели-
величины изгибающих моментов, влияние же направления моментов на
знаки напряжений учтём при вычислении последних.
Вычислим напряжения в какой-либо точке С (с координатами у
и z), расположенной в первом квадранте (фиг. 409). Мы имеем
возможность вычислить для этой точки нормальные напряжения,
вызванные отдельно моментами Му и Mz, изгибающими балку в глав-
главных плоскостях xz и ху\ в этом случае применимы формулы, полу-
полуденные для плоского изгиба.
Нормальное напряжение в точке С от изгиба моментом Mv
является сжимающим (отрицательным) и выражается формулой

КОСОЙ ИЗГИБ	[ГЛ. XXVI
т~^ cos 9» где Jy — момент инерции относительно оси у,
J у	J у
которая при изгибе моментом Му будет нейтральной осью. Момент
М2 вызывает в этой точке тоже сжимающее напряжение, равное
	f? =	? sin 9; Jg — момент инерции сечения относительно
оси z. Полное напряжение в точке С находим как алгебраическую
сумму полученных напряжений:
(^ ^У B6.2)
В данном случае этой формулой можно пользоваться при вычи-
вычислении напряжений в любой точке каждого сечения балки. Так как
формула выведена для точки с положительными координатами у и
z9 то, подставляя в неё значения координат с соответствующими зна-
знаками, будем всегда получать по формуле B6.2) правильный знак
напряжения.
Так, для точки D (фиг. 409) координата у будет положительна,
г z — отрицательна; в соответствии с этим первое слагаемое в фор-
формуле B6.2) представит собой положительное (растягивающее) напря-
напряжение, а второе — попрежнему сжимающее.
Хотя формула B6.2) и получена из рассмотрения частного слу-
случая косого изгиба балки, защемлённой одним концом и нагружённой
на другом сосредоточенной силой Р, однако, как нетрудно заметить,
она является общей формулой для вычисления напряжений при косом
изгибе. Для балок иначе нагружённых и закреплённых нужно лишь
договориться о правиле знаков. Если положительное направление
главных центральных осей инерции поперечного сечения балки всегда
выбирать так, чтобы след плоскости действия сил в сечении прохо-
проходил через первый квадрант, то знак перед правой частью форму-
формулы B6.2) необходимо назначать по тому действию, которое из-
изгибающий момент М (или, что равноценно, его компоненты) ока-
оказывают на любую площадку первого квадранта (при растяжении
ставить плюс, при сжатии — минус). Тогда для получения по фор-
формуле B6.2) правильного знака напряжения на любой другой
площадке поперечного сечения достаточно учитывать знаки коор-
координат у и z.
Для нахождения наибольшего нормального напряжения надо
отыскать опасное сечение балки и в нём наиболее напряжённую
точку. Из формулы B6.2) видно, что опасным сечением будет то,
где изгибающий момент М достигнет наибольшей величины.
Для нахождения опасной точки учтём, что при плоском изгибе
деформация, соответствующая нормальным напряжениям, сводится к
относительному повороту сечений вокруг нейтральных осей. При ко-
косом изгибе, являющемся комбинацией двух плоских изгибов, мы имеем

§ 157]
КОСОЙ ИЗГИБ. ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ
487
одновременный относительный поворот сечений вокруг двух осей,
пересекающихся в центре тяжести сечения.
Из кинематики известно, что вращение фигуры вокруг двух пере-
пересекающихся осей может быть заменено вращением вокруг оси, про-
проходящей через точку пересечения. Таким образом, и при косом из-
изгибе мы в каждом сечении будем иметь линию, проходящую через
центр тяжести, вокруг которой будет происходить поворот сечения
при деформации балки. Эта ось и будет нейтральной; волокна, распо-
расположенные в её плоскости, не будут удлиняться или укорачиваться, и
нормальные напряжения в точках нейтральной оси будут равны нулю.
При относительном повороте сечений наибольшую деформацию (растя-
(растяжение или сжатие) ис-
испытывают волокна,
наиболее удалённые от
нейтральной оси.
Поэтому нахожде-
нахождение опасных точек при
косом изгибе сводит-
сводится к определению по-
положения нейтральной
оси и отысканию то-
точек, наиболее далеко
от неё отстоящих.
Уравнение ней-
нейтральной оси получим
из условия, что нор-
нормальные напряжения
и
411.
в точках, лежащих на этой оси, равны нулю.
Обозначим координаты этих точек j/0 и z0; подставив эти величины
вместо у и z в формулу B6.2), мы должны получить для с значение,
равное нулю:
М cos <р . zit М sin ср • у0
Сокращая на —Ж, имеем:
COS ср •
¦+
J,
sin Т • >'о _
—
B6.3)
Это и есть уравнение нейтральной оси; она является прямой, про-
проходящей через центр тяжести сечения (при у0 = О и zQ = 0).
На фиг. 411 изображены два поперечных сечения балок; оси
У и z являются главными осями инерции. В предположении, что
балки нагружены по схеме фиг. 409, на каждом сечении показана
проекция силы Р и для каждого квадранта сечения приведены знаки
нормальных напряжений; знаки выше и ниже сечения относятся
к напряжениям от изгиба моментом Mv знаки справа и слева от
сечения — к напряжениям от изгиба моментом Мг. Для балки, иным

488
КОСОЙ ИЗГИБ
[гл. xxvi
образом нагружённой и закреплённой (фиг. 412), знаки напряжений
соответственно будут другими.
На фиг. 411 нанесено примерное расположение нейтральной оси.
Так как она проходит через центр тяжести сечения, то для опреде-
определения её положения достаточно
знать угол а, составленный ею
с осью у. Из фиг. 411 видно, что
тангенс этого угла равен абсолют-
абсолютной величине отношения zQ к у^:
tga =
Уо
Из уравнения B6.3) получаем:
tga =
B6.4)
Таким образом, положение ней-
нейтральной оси не зависит от вели-
величины силы Р, а лишь от угла на-
наклона плоскости внешних сил к оси
z и от формы сечения.
Вычислив по формуле B6.4) ве-
величину угла а, строим на чертеже
нейтральную ось, а проводя к се-
сечению касательные, параллельно
ей, находим наиболее напряжённые точки, как наиболее удалённые
от нейтральной оси (точки / и 2 на фиг. 411).
Подставляя в формулу B6.2) координаты этих точек (у1 и zt
или j/2 и г%) с учётом их знаков, находим величины наибольшего
растягивающего и наибольшего сжимающего напряжений. Условие
прочности получает такой вид:
Фиг. 412.
sin
i]^W,
B6.5)
где у^ и zx (или уъ и z^) — координаты точки (в системе главных
центральных осей), наиболее удалённой от нейтральной оси.
Для поперечных сечений с выступающими углами, у которых обе
главные оси инерции являются осями симметрии (прямоугольник,
двутавр)
формула B6.5) упрощается; для о(Ь2) имеем:
sin ф\ , М I
^Д) = ± w (cos f
sin <p). B6.6)

§ 157]
КОСОЙ ИЗГИБ. ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ
489
Условие прочности для таких сечений принимает вид:
W
B6.7)
При подборе сечений приходится задаваться отношением ^Л и,
зная [а], Мтах и угол ср, путём последовательных попыток искать
значения Wy и W2, удовлетворяющие условию прочности B6.7).
В случае несимметричных сечений, не имеющих выступающих углов,
т. е. при использовании условия прочности B6.5), при каждой новой
попытке подбора сечения необходимо предварительно вновь найти
положение нейтральной линии и координаты наиболее удалённой
точки (у{ и Zi). В случае прямоугольного сечения т^<у = -т ; поэтому,
задаваясь отношением -г-, из условия B6.7) без затруднений можно
найти величину Wy и размеры поперечного сечения.
Фиг. 413.
На фиг. 413 изображены эпюры распределения напряжений для
балки прямоугольного сечения.
Уравнение B6.4) показывает, что углы а и ср не равны, т. е.
нейтральная линия не перпендикулярна к плоскости внешних сил,
как это было при плоском изгибе. Эта перпендикулярность имеет
место лишь при
Jy = Jg,	B6.8)
но в этом случае все оси главные, и косой изгиб невозможен; в ка-
какой бы плоскости ни была расположена нагрузка, мы будем иметь
Дело с плоским изгибом. Это будет соблюдаться для сечений квад-
квадратного, круглого, являющихся правильными фигурами, и любых
Других, для которых будет выполнено условие B6.8).

490
КОСОЙ ИЗГИБ
1гл. xxvi
Что касается касательных напряжений, то и их можно вычислить
тем же приёмом, которым мы пользовались при вычислении нормаль-
нормальных; суммарное напряжение будет равно геометрической сумме каса-
касательных напряжений от изгиба в каждой из главных плоскостей. Прак-
Практического значения определение этих напряжений обычно не имеет.
§ 158. Определение деформаций при косом изгибе.
Для определения прогибов в различных сечениях балки при косом
изгибе опять применим способ сложения действия сил. Возвращаясь
к примеру, рассмотренному в предыдущем параграфе, находим сна-
сначала прогиб точки В (свободного конца балки) только от действия
силы Р/у этот прогиб fz будет направлен по оси z и равен
, _ /у3 _ />cos у /3
f*—'SEJy~ 3EJy '
где /—пролёт балки. Аналогично прогиб точки Sot одной силы Ру
будет направлен по оси у и выразится формулой
Полный прогиб / конца балки будет представлять собой гео-
геометрическую (фиг. 414) сумму обоих этих прогибов; он равен
B6.9)
При этом
:tga B6.10)
sin a
COS a *
что угол, соста-
состаОтсюда следует	у
вленный полным прогибом / с осью z,
равен углу а, т. е. прогиб / направлен
перпендикулярно к нейтральной оси. Из-
Изгиб балки происходит не в плоскости дей-
действия внешних сил, а в плоскости, перпен-
перпендикулярной к нейтральной оси (фиг. 414).
Условимся принимать за ось у главную ось с наибольшим момен-
моментом инерции; тогда плоскость xOz будет плоскостью наибольшей
жёсткостНу поскольку прогибы при изгибе балки в этой плоскости
будут наименьшими. Так как при Jy^>Jz, как в рассмотренных
примерах, и а^><р, то плоскость изгиба отклоняется от плоскости
наибольшей жёсткости больше, чем плоскость внешних сил. Эта
разница будет тем большей, чем больше отношение -/. Значит, для
узких и высоких сечений, у которых отношение главных моментов

§ 158]
ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ ПРИ КОСОМ ИЗГИБЕ
491
инерции может быть весьма велико, уже небольшое отклонение
плоскости действия внешних сил от плоскости наибольшей жёсткости
вызывает весьма значительное отклонение плоскости изгиба балки.
Пока для балки такого сечения внешние силы расположены
в плоскости наибольшей жёсткости х Oz, прогибы будут лежать в той
же плоскости и будут небольшими, так как момент инерции Jy будет
значительным. Стоит дать плоскости внешних сил отклонение от оси
Oz на небольшой угол <р, как сейчас же возникнут уже большие
прогибы в направлении оси у, на которые очень часто конструктор
и не рассчитывает. Прогибы же в направлении оси z будут оставаться
почти без изменения. Для оценки этого явления рассмотрим чис-
числовой пример. Возьмём деревянную балку с сечением (фиг. 409),
имеющим высоту h = 20 см, ширину Ь = Ъ см\ тогда
203 -6
б3 -20
= ?^ = 4000 с**; Jg = ^f = 3b0cMK
Отношение моментов инерции равно
Л 4000
Тогда при отклонении плоскости действия внешних сил от оси z
всего на 5° будем иметь;
= 0,0875- 11=0,963
а ^44°.
Прогибы в направлении
будут почти равны прогибам
в направлении оси z:
/ Плоскость нагрузил
Фиг. 415.
Вместе с тем, при отклонении
силы от плоскости наиболь-
наибольшей жёсткости произойдёт
и значительное повышение
нормальных напряжений. Так, в рассмотренном выше примере наи-
наибольшие нормальные напряжения (по сравнению со случаем плоского
изгиба при 9 = 0) увеличатся в отношении (см. формулу 26.6):
М /
кг
cos 9
=/ sin
М
, on * \
A+^0,0875) 1 = 1,29.
На фиг. 415 изображено относительное расположение плоско-
плоскостей нагрузки, изгиба и нейтральной.
Балки, главные моменты инерции сечений которых значительно
отличаются друг от друга, будут хорошо работать при изгибе в пло-
плоскости наибольшей жёсткости (высокие прямоугольники, двутавры,

492	косой изгиб	[гл. xxvi
швеллеры), но окажутся невыгодными при косом изгибе. Поэтому
в тех случаях, когда трудно рассчитывать на достаточно точное
совпадение плоскости внешних сил с главной плоскостью балки,
^	конструктор должен избегать применения подоб-
*	ных сечений или принимать дополнительные
конструктивные меры (постановка связей),
\и ^ чтобы воспрепятствовать боковым деформа-
-—	.-IV"-" циям балок при наличии косого изгиба.
Особенно опасным может явиться неосто
рожное усиление существующих конструкций.
Нам известен случай, когда балка швеллер-
ного сечения из листа и двух уголков (фиг.
Фиг. 416.	416, а), работавшая на нагрузку, расположен-
расположенную в плоскости х Oz, была усилена привар-
приваркой дополнительного уголка (фиг. 416, б). Это вызвало наклон главных
осей к плоскости внешних сил и совершенно непредусмотренные
деформации балки в боковом направлении.
§ 159. Примеры расчётов при косом изгибе.
Пример 105. Подобрать сечение деревянной обрешетины высотой Л и
шириной Ь и определить перемещение середины её пролёта; принято отно-
отношение h/b = 2; пролёт обрешетины (расстояние между стропильными фер-
фермами) равен /s=4 ж, а угол наклона кровли к горизонту 25°; нагрузка от
снега и собственного веса перекрытия является равномерно распределённой
с интенсивностью q = 400 кг/м. Обрешетина устроена как балка, шарнирно-
опёртая по концам. Допускаемое напряжение равно 100 кг/см2, модуль упру-
упругости материала ?=105 кг/см2.
Наибольший изгибающий момент Мтах будет посредине пролёта; он равен
= 800 Кгм.
Так как угол ср равен углу наклона кровли, т. е. 25°, то из формулы B6.7)
и условия hfb = 2 следует, что
Отсюда h^ |/l2. 1402 = 25,6^26 см и ?=13 см.
Наибольший прогиб обрешетины будет посредине пролёта. Моменты инер-
инерции сечения равны
, Ь№ 13-26* 1ПЛСЛ . , b*h 13*. 26 „„ .
Jy = -j2 =	12— = 19 050 см » Л = -J9" =	J9— = 4760 см '
Угол наклона нейтральной оси а определится условием
tg а =tg?? = tg25°. ^=1,865;
отсюда а = 61° 50' и угол, составленный плоскостью изгиба с плоскостью
внешних сил, равен а — <р = 61° 50' — 25° = 36° 50'.
Прогиб в плоскости наибольшей жёсткости равен
_ 5g/4cosу _ 5 - 4 . 4' . 10s ¦ 0,906
h~~	~~ 384. 19050- Ю5 "~U>04 CM'

§ 159]
ПРИМЕРЫ РАСЧЁТОВ ПРИ КОСОМ ИЗГИБЕ
493
Полный прогиб равен
f _ fz _ 0,64
7~~ cos a — 0,472"
: 1,35 см.
^Плоскость
0 нагрузок
Прогиб в направлении оси у (параллельно стороне Ь) равен
/у =/z tg a = 0,64 • 1,865 = 1,19 см.
Таким образом в рассмотренном случае прогиб в 'направлении оси Оу
гораздо больше, чем в направлении оси Oz, и почти равен полному прогибу.
Пример 106. Уголок раз-
размерами 160 X 160 X 16 мм рабо-
работает как балка, шарнирно опёртая
по концам (фиг. 417). Он нагру-
нагружен двумя одинаковыми силами
р = 1000 кг, расположенными сим-
симметрично в третях пролёта, рав-
равного 1 = 3 м; плоскость действия
сил параллельна одной из сторон
уголка и проходит через центр
тяжести сечения. Найдём наиболь-
наибольшие сжимающие и растягивающие
напряжения в уголке.
Так как средняя часть угол-
уголка с наибольшим изгибающим мо-
моментом испытывает чистый изгиб, то на результатах вычисления напря-
напряжений не отразится то обстоятельство, что плоскость действия нагрузок не
проходит через центр изгиба, расположенный на пересечении средних линий
обеих полок.
Наибольший изгибающий момент равен
/ «— 100= 105 кгсм.
Фиг. 417.
Вследствие симметрии сечения главные оси составляют углы 45е с направ-
направлениями полок. Следовательно:
Фиг. 418.
нУю вблизи
от неё точку
= U,3 см;
= 105.0,707 = 7,07 -10* кгсм.
По сортаменту главные моменты инерции рав-
равны: Уу= 1866 см* и /2 = 485 см*. Угол а опре-
определяется формулой
tga = ^tgcp = l^. 1=3,85 и а = 75°26\
Положение нейтральной линии показано
на фиг. 418; из неё видно, что опасными точ-
точками, наиболее удалёнными от нейтральной
оси, являются AY и С. Для упрощения расчё-
расчётов вместо точки Ах в качестве опасной
точки допустимо рассматривать расположен-
А. Координаты точек А и С равны:
Здесь 20 = 4,55 см — расстояние от центра тяжести уголка до наружных
кромок (по сортаменту).

494	косой изгив
Напряжения определяются формулой
[гл. xxvi
y
Для точки А напряжения от обоих изгибов представляют сжатие:
= L 7,07 • 10» ( »J + *g) — 1143 кг,**.
В точке С будет растяжение
ас = + 7,07 .
64
:gg = + 933 кг!см\
Так как точка С лежит на одной из главных осей инерции, то второе
слагаемое в формуле для напряжений равно нулю.
Пример 107. Стержень зетобразного сечения пролётом / = 3л1шар-
нирно опёрт по концам; он нагружён равномерно распределённой нагрузкой
^=500 kzjm\ размеры поперечного сечения и расположение грузовой пло-
плоскости даны на фиг. 419. Главные моменты инерции
сечения равны Jy = 2765 смА, Jz = 160 смА; угол,
составленный плоскостью наибольшей жёсткости со
стенкой зета, равен 18°. Толщина стенки 1 см. Найти
наибольшие нормальные напряжения и наибольший
прогиб.
и * *л ЦР 500-З2
Наибольший момент тахМ = ~- =—^	=
= 562 кгм. Угол ср = 18% sin <р = 0,309; cos ср== 0,951.
Положение нейтральной оси определяется отклоне-
отклонением её от оси у на угол а:
Фиг. 419.
а = 80°27\
Построение показывает, что опасными точками
являются ki и k2. Вычислим координаты этих точек zk и yk:
zk — 10 cos 18° — 0,5 sin 18° = 9,51 — 0,5 .0,309 = 9,36 см;
yk = 10 sin 18° + 0,5 cos 18° = 3,09 + 0,5 .0,951 = 3,57 см.
Наибольшее напряжение равно
1
=
0>95Ь9,36 0,309.3,57
2765 +	Г60
= ± 56 200 [0,0032 + 0,0069] = ± 568 кг/см9.
Прогиб в направлении оси z равен
mo = ± max M —j—*- -\
_ bql* cos у _ 5.5 • З4 ¦ 10' . 0,951
'*— 'ылрт — 384• 2 . 10е • 2765	'
Полный прогиб

§ 160] ИЗГИБ БАЛКИ ПРИ ДЕЙСТВИИ ПРОДОЛЬНЫХ И ПОПЕРЕЧНЫХ СИЛ 495
ГЛАВА XXVII.
СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И РАСТЯЖЕНИЯ
ИЛИ СЖАТИЯ.
§ 160. Изгиб балки при действии продольных и поперечных сил.
На практике очень часто встречаются случаи совместной работы
стержня на изгиб и на растяжение или сжатие. Подобного рода
деформация может вызываться или совместным действием на балку
продольных и поперечных сил, или только одними продольными
силами.
Первый случай изображён на фиг. 420. На балку АВ действуют
равномерно распределённая нагрузка q и продольные сжимающие
силы Р. Предположим, что прогибами балки по сравнению с разме-
размерами поперечного сечения можно пренебречь; тогда с достаточной
для практики степенью точности можно считать, что и после дефор-
деформации силы Р будут вызывать лишь осевое сжатие балки.
Применяя способ сложения действия сил, мы можем найти нор-
нормальное напряжение в любой точке каждого поперечного сечения
балки как алгебраическую сумму напряжений, вызванных силами Р
и нагрузкой q.
Сжимающие напряжения оР от сил Р равномерно распределены
по площади F поперечного сечения и одинаковы для всех сечений:
нормальные напряжения от изгиба в вертикальной плоскости в сече-
сечении с абсциссой х, которая отсчитана, скажем, от левого конца
балки, выражаются формулой
_М(х)г
Таким образом, полное напряжение в точке с координатой z (считая
от нейтральной оси) для этого сечения равно

496 СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ [ГЛ. XXVII
На фиг. 421 изображены эпюры распределения напряжений в рас-
рассматриваемом сечении от сил Ру нагрузки q и суммарная эпюра.
Наибольшее напряже-
напряжение в этом сечении
будет в верхних во-
волокнах, где оба вида
деформации вызывают
сжатие; в нижних во-
волокнах может быть
или сжатие или рас-
растяжение в зависимо-
зависимости от числовых вели-
величин напряжений аР и од. Для составления условия прочности най-
найдём наибольшее нормальное напряжение.
Так как напряжения от сил Р во всех сечениях одинаковы и
равномерно распределены, то опасными будут волокна, наиболее
напряжённые от изгиба. Такими являются крайние волокна в сечении
с наибольшим изгибающим моментом; для них
Фиг. 421.
Таким образом, напряжения в крайних волокнах 1 \\ 2 (фиг. 421)
среднего сечения балки выражаются формулой
р м
и расчётное напряжение будет равно
1 w
Если бы силы Р были растягивающими, то знак первого слагае-
слагаемого изменился бы, опасными были бы нижние волокна балки.
Обозначая буквой N сжимающую или растягивающую силу, можем
написать общую формулу для проверки прочности:
»|—	/- 4 °тах - ± LF + 
Фиг. 422.
р^-
При составлении формулы B7Л)
предполагалось, что сечение симме-
симметрично относительно нейтральной оси
и материал одинаково сопротивляется
растяжению и сжатию.
Описанный ход расчёта применяется и при действии на балку
наклонных сил (фиг. 422); такую силу можно разложить на нормаль-
нормальную к оси, изгибающую балку, и продольную, сжимающую или
растягивающую.

§ 161]	УЧЁТ ДЕФОРМАЦИЙ БАЛКИ	497
§ 161. Учёт деформаций балки.
Если прогибами балки нельзя пренебречь по сравнению с размерами
сечения, то следует учитывать не только равномерно распределённые на-
напряжения сжатия или растяжения, но и изгиб от продольных сил. На фиг. 423
изображена изогнутая ось балки, рассмотренной в предыдущем параграфе;
наибольший прогиб посредине пролёта обозначен буквой /.
Фиг. 423.	Фиг. 424.
Разрежем балку в опасном сечении посредине пролёта, оставим левую
часть (фиг. 424) и вычислим изгибающий момент. На отсечённую часть
помимо сплошной нагрузки q и вызванной ею реакции А будет действовать
приложенная в точке А горизонтальная сила Р. Прикладывая в центре
тяжести О проведённого сечения две равные и противоположные силы Р,
получаем, что однажды зачёркнутая сила Р вызывает в проведённом сече-
сечении уравновешивающую силу, создающую осевое сжатие, а две дважды
перечеркнутые силы Р дают пару с плечом /, добавляющуюся к изгибаю-
изгибающему моменту А1о, вызванному поперечной нагрузкой. Таким образом, полный
изгибающий момент в рассмотренном сечении равен
.P/.	B7.2)
Наибольшее нормальное напряжение выражается формулой
max — p —	yy
Прогиб / зависит от изгибающих моментов, вызванных не только попе-
поперечными нагрузками, но и продольными силами Р; поэтому для его опреде-
определения следует составить и интегрировать дифференциальное уравнение
изогнутой оси с учётом всех сил, действующих на стержень.
Здесь мы встречаемся с тем случаем, для которого принцип независи-
независимости действия сил уже неприменим. Более подробно этот вопрос рассматри-
рассматривается ниже, в § 209. Однако на практике необходимо уметь оценить, следует ли
учитывать добавочный изгибающий момент от продольных сил или им можно
пренебречь и ограничиться проверкой прочности, описанной в предыдущем
параграфе.
Принимая во внимание, что момент Р/ является лишь поправкой, можно
её вычислить путём последовательных приближений. Сначала найдём про-
прогиб / от одной только поперечной нагрузки; в рассматриваемом примере он
будет равен
B7.3)
48/V
так как МОшах = ^-; вычислим теперь Afmax = МOmax + Pf и подставим по-
полученное значение вместо MOmSLX в формулу B7.3); получим улучшенное
значение прогиба /; при желании эту операцию можно повторить ещё раз.
Таким образом можно приближённо оценить влияние добавочного изги-
изгибающего момента Pf.

498 СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ [ГЛ. XXVII
§ 162. Примеры.
Пример 108. Консольный кран (фиг. 425), состоящий из двутавровой
балки АВ и тяги АС, несёт груз Р = 2,5 г, расположенный посредине про-
пролёта балки АВ. Пролёт балки ра-
равен / = 2,6 мм, угол между тягой
и балкой а = 30°. Подберём сече-
сечение балки АВ.
Балка АВ подвергается дей-
действию изгибающих и сжимающих
усилий. Наибольший изгибающий
момент для балки АВ в точке D
только от Р равен
"JOmax = "у =	4	= l № ™.
Балка АВ находится в равно-
равновесии под действием трёх сил: Р,
реакции опоры В и усилия 52
Фиг. 425.	в тяге АС. Сумма моментов всех
сил, действующих на балку At,
относительно точки В должна быть равна нулю:
= Р-тс	S2 / sin a = О,
откуда 52 = Р. .
Стержень АВ будет сжиматься усилиями Si9 равными горизонтальным
составляющим В и 52:
Si == S2 cos 30° = Р cos 30° = 2,5. ^~ = 2,16 г.
Допускаемое напряжение [о] возьмём равным 1000 кг/см2. Тогда, пре-
пренебрегая в первом приближении сжимающей силой, получаем для момента
сопротивления балки величину
Этому соответствует профиль двутавр №20 с 7^=26,8 см2 и W= 184 смг.
Вычислим теперь наибольшее нормальное напряжение в балке этого про-
профиля с учётом как изгибающего момента Afmax, так и нормальной силы St:
Таким образом, сечение балки можно оставить без изменения.
Определим теперь, какую погрешность мы допустили, пренебрегая мо-
моментом от продольных сил. Прогиб балки от одной поперечной нагрузки
2500.2,6«. 1Ое
~~ ' ~~
" 5Ш — 48 • 2 • 10е. 1840 ~~ '	~~ 12Я/ *
Наибольший изгибающий момент приблизительно равен по B7.2):
M
Omax
= 162 500 + 2160 • 0,249 == 163 040 кгсм.

§ 163]	ВНЕЦЕНТРЕННОЕ СЖАТИЕ ИЛИ РАСТЯЖЕНИЕ
Исправленное значение прогиба
" = /о
499
X2EJ
'ощах
= 0,250,,
Изгибающий момент от продольных сил
5^ = 2160 • 0,250 = 540 кгсм,
что составляет всего Ve°/o 0T изгибающего момента, вызванного одними попе-
поперечными нагрузками. Таким образом, в данном случае этой величиной вполне
можно пренебречь.
Пример 109. Наклонная балка (фиг. 426) нагружена посредине своей
длины силой Р = 2,5 г; найти наиболь-
наибольшее сжимающее напряжение в балке.
Верхняя половина балки только из-
изгибается; нижняя изгибается и сжимает-
сжимается. Изгиб вызывает сила Р cos 30°, а сжа-
сжатие— сила Р sin 30°. Наибольший изги-
изгибающий момент равен
Р cos 30°
I l
\cos 30е
4
- =2^=1,875 тм.
P[
4
Фиг. 426.
Момент сопротивления сечения и
площадь поперечного сечения соответственно равны:
Щ 1^^ == 2400 см\ f = 16.30 = 480 см*.
Наибольшие сжимающие напряжения (в верхних волокнах балки, в сечении
слева от силы) равны:
Р sin 30°
2500 187 500
W
2-480
2400
= — 2,6 — 78,1 = — 80,7 kzjcm\
§ 163. Внецентренное сжатие или растяжение.
Вторым практически важным случаем сложения деформаций от
изгиба и от продольных сил является так называемое внецентренное
сжатие или растяжение, вызываемое одними продольными силами.
Этот вид деформации получается при действии на стержень двух
равных и прямопротивоположных сил Я, направленных по прямой Л Л,
параллельной оси стержня (фиг. 427). Расстояние точки А от центра
тяжести сечения ОА=е называется эксцентриситетом.
Рассмотрим сначала случай внецентренного сжатия, как имеющий
большее практическое значение.
Нашей задачей явится нахождение наибольших напряжений
в материале стержня и проверка прочности. Для решения этой
задачи приложим в точках О по две равные и противоположные

500 СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА Й РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ [ГЛ. ХХУП
силы Р (фиг. 428). Это не нарушит равновесия стержня в целом
и не изменит напряжений в его сечениях.
Силы Я, зачёркнутые один раз, вызовут осевое сжатие, а пары
сил Я, зачёркнутые дважды, вызовут чистый изгиб моментами Мо = Ре.
Расчётная схема стержня показана на фиг. 429. Так как плоскость
действия изгибающих пар ОА может не совпадать ни с одной из
главных плоскостей инерции стержня, то в общем случае имеет
место комбинация продольного сжатия и чистого косого изгиба.
Так как при осевом сжатии и чистом изгибе напряжения во всех
сечениях одинаковы, то проверку прочности можно произвести для
любого сечения, хотя бы С — С
(фиг. 429).
Отбросим верхнюю часть
стержня и оставим нижнюю (фиг.
430). Пусть оси Оу и Oz будут
о*.
Мо'-Ре
М0=Ре
Фиг. 427. Фиг. 428. Фиг. 429.
Фиг. 430.
главными осями инерции сечения. Координаты точки А, — точки
пересечения линии действия сил Р с плоскостью сечения, — пусть
будут уР и zP. Условимся выбирать положительные направления
осей Оу и Oz таким образом, чтобы точка А оказалась в первом
квадранте. Тогда уР и zP будут положительны.
Для того «чтобы отыскать наиболее опасную точку в выбранном
сечении, найдём нормальное напряжение о в любой точке В с ко-
координатами z и у. Напряжения в сечении С — С будут складываться
из напряжений осевого сжатия силой Р и напряжений от чистого
косого изгиба парами с моментом Ре, где е = ОЛ. Сжимающие на-
Р
пряжения от осевых сил Р в любой точке равны -р-, где F — пло-
площадь поперечного сечения стержня; что касается косого изгиба, то

§ 163]	ВИЁЦЕНТРЕННОЕ СЖАТИЕ ИЛИ РАСТЯЖЕНИЕ	501
заменим его действием изгибающих моментов в главных плоскостях.
Изгиб в плоскости хОу вокруг нейтральной оси Ог будет вызы-
вызываться моментом РуР и даст в точке В нормальное сжимающее на-
РуР -у
лряжение —-г—.
Точно так же нормальное напряжение в точке В от изгиба в глав-
главной плоскости х Ozy вызванное моментом Pzp, будет сжимающим
Pzp- z
и выразится формулой —-—.
_	v
Суммируя напряжения от осевого сжатия и двух плоских изги-
изгибов и считая сжимающие напряжения отрицательными, получаем
такую формулу для напряжения в точке В:
Эта формула годится для вычисления напряжений в любой точке
любого сечения стержня, стоит только вместо у и z подставить
координаты точки относительно главных осей с их знаками.
В случае внецентренного растяжения знаки всех составляющих
нормального напряжения в точке В изменятся на обратные. Поэтому
для того, чтобы по формуле B7.4) получать правильный знак напря-
напряжений как при внецентренном сжатии, так и при внецентренном
растяжении, нужно, кроме знаков координат у и г, учитывать также
и знак силы Р; при растяжении перед выражением
должен стоять знак плюс, при сжатии — минус.
Полученной формуле можно придать несколько иной вид; выне-
р
сем за скобку множитель -рг; получим:
Здесь 1г и 1у — радиусы инерции сечения относительно главных
осей (вспомним, что Jz = il. F и Jy = i^ * F).
Для отыскания точек с наибольшими напряжениями следует так
выбирать у и z, чтобы а достигло наибольшей величины. Перемен-
Переменными в формулах B7.4) и B7.5) являются два последних слагаемых,
отражающих влияние изгиба. А так как при изгибе наибольшие на-
наряжения получаются в точках, наиболее удалённых от нейтральной
°си, то здесь, как и при косом изгибе, надо отыскать положение
нейтральной оси.

502 СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ [ГЛ. XXVII
Обозначим координаты точек этой линии через j/0 и <г0; так как
в точках нейтральной оси нормальные напряжения равны нулю, то
после подстановки в формулу B7.5) значений у0 и zQ получаем:
или
1+^ + ^ = 0.	B7.6)
Это и будет уравнение нейтральной оси; очевидно, мы получили
уравнение прямой, не проходящей через центр тяжести сечения.
Чтобы построить эту прямую, проще всего вычислить отрезки,
отсекаемые ею на осях координат. Обозначим эти отрезки ау и az.
Чтобы найти отрезок ау, отсекаемый на оси Оу, надо в уравнении
B7.6) положить
*о = 0; уь = ау;
тогда мы получаем:
^ = 0 и -, = -?;	B7.7)
подобным же образом, полагая
получаем:
<*, = --?-.	B7.8)
zp
Если величины ур и zp положительны, то отрезки ау и аг будут
отрицательны, т. е. нейтральная ось будет расположена по другую
сторону центра тяжести сечения, чем точка А (фиг. 430).
Нейтральная ось делит сечение на две части — сжатую и растя-
растянутую; на фиг. 430 растянутая часть сечения заштрихована. Проводя
к контуру сечения касательные, параллельные нейтральной оси,
получаем две точки Dx и Dif в которых будут наибольшие сжимаю-
сжимающие и растягивающие напряжения.
Измеряя координаты у и z этих точек и подставляя их значения
в формулу B7.4), вычисляем величины наибольших напряжений
в точках Ъх и ?>2:
[^^ ^]	B7.9)
Если материал стержня одинаково сопротивляется растяжению
и сжатию, то условие прочности получает такой вид:
+ ^]<№	B7.10)

ИНЕЦЕНТРЕННОЕ СЖАТИЕ ИЛИ РАСТЯЖЕНИЕ
503
§ 163]
Для поперечных сечений с выступающими углами, у которых обе
главные оси инерции являются осями симметрии (прямоугольник,
двутавр и др.) ух=утах и zl = zmiK; поэтому формула B7.10) упро-
упрощается, и мы имеем	t
?[о].	B7.11)
Если же материал стержня неодинаково сопротивляется растяжению
и сжатию, то необходимо проверить прочность стержня как в рас-
растянутой, так и в сжатой зонах.
Однако может случиться, что и для таких материалов будет до-
достаточно одной проверки прочности. Из формул B7.7) и B7.8)
видно, что положение точки А приложения силы и положение
нейтральной оси связаны: чем ближе подходит точка А к центру
сечения, тем меньше величины j/ри Zp и тем больше отрезки ау и аг.
Таким образом, с приближением точки А к центру тяжести сечения
нейтральная ось удаляется от него, и з	^
наоборот. Поэтому при некоторых по- , \ н\ \
ложениях точки А нейтральная ось
будет проходить вне сечения и всё се
чение будет работать на напряжения ^
одного знака. Очевидно в этом случае 1
всегда достаточно проверить проч- г"
ность материала в точке Dv
Разберём практически важный слу-
случай, когда к стержню прямоугольного
сечения (фиг. 431) приложена внецентренно сила Р в точке Л, ле-
лежащей на главной оси сечения Оу. Эксцентриситет ОА равен е, раз-
размеры сечения bud. Применяя полученные выше формулы, имеем:
сь у
е- I
-н/
фиг 431.
Напряжение в любой точке В равно
B7.12)
так как
\2bd 12
Jz ~ ЪЧ
Напряжения во всех точках линии, параллельной оси Oz, одинаковы.
Положение нейтральной оси определяется отрезками
ь*
12* ;
B7.13)

504 СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ [ГЛ. XXVII
Нейтральная ось параллельна оси Oz\ точки с наибольшими рас-
растягивающими и сжимающими напряжениями расположены на сторо-
сторонах 1—1 и 3—3.
Значения атах и omin получатся, если в формулу B7.12) подста-
подставить вместо у его значения ± -у. Тогда
§ 164. Ядро сечения.
При конструировании стержней из материалов, плохо сопротив-
сопротивляющихся растяжению (бетон, камень), весьма желательно добиться
того, чтобы всё сечение работало лишь на сжатие. Этого можно
достигнуть, не давая точке приложения силы Р слишком далеко
отходить от центра тяжести сечения, ограничивая величину эксцен-
эксцентриситета.
Конструктору желательно заранее знать, какой эксцентриситет
при выбранном типе сечения можно допустить, не рискуя вызвать
в сечениях стержня напряжений разных знаков. Здесь вводится по-
понятие о так называемом ядре сечения. Этим термином обозначается
некоторая область вокруг центра тяжести сечения, внутри
которой можно располагать точку приложения си ли Р, не вызы-
вызывая в сечении напряжений разного знака.
Пока точка А располагается внутри ядра, нейтральная ось не
пересекает контура сечения, всё оно лежит по одну сторону от
нейтральной оси и, стало быть, работает лишь на сжатие. При уда-
удалении точки А от центра тяжести сечения нейтральная ось будет
приближаться к контуру; граница ядра
определится тем, что при расположении
точки А на этой границе нейтральная
ось подойдёт вплотную к сечению, коснёт-
коснётся его.
Таким образом, если мы будем пере-
перемещать точку А так, чтобы нейтральная
Фиг. 432.	ось катилась по контуру сечения, не
пересекая его (фиг. 432), то точка А
обойдёт по границе ядра сечения. Если контур сечения имеет
«впадины», то нейтральная ось будет катиться по огибающей кон-
контура.
Чтобы получить очертание ядра, необходимо дать нейтральной
оси несколько положений, касательных к контуру сечения, опреде-
определить для этих положений отрезки ау и аг и вычислить коорди-
координаты уР и zP точки приложения силы по формулам, вытекающим

§ 164]	ЯДРО СЕЧЕНИЯ
из зависимостей B7.7) и B7.8):
505
B7.15)
это и будут координаты точек контура ядра у$ и z%.
При многоугольной форме контура сечения (фиг. 433), совме-
совмещая последовательно нейтральную ось с каждой из сторон,много-
сторон,многоугольника, мы по отрезкам ау и а2 определим координаты у% и z% точек
границы ядра, соответствующихэтим сторонам.
При переходе от одной стороны контура
сечения к другой нейтральная ось будет вра-
вращаться вокруг вершины, разделяющей эти
стороны; точка приложения силы будет пе-
перемещаться по границе ядра между получен-
полученными уже точками. Установим, как должна
перемещаться сила Я, чтобы нейтральная ось
проходила всё время через одну и ту же точ-
точку В(уву Zb) — вращалась бы около неё.
Подставляя координаты этой точки ней-
нейтральной оси в уравнение B7.6)
Фиг. 433.
видим, что координаты ур и zp точки А приложения силы Р свя-
связаны линейно. Таким образом, при вращении нейтральной оси
около постоянной точки В тонка
А приложения силы движется
по прямой. Обратно, перемеще-
перемещение силы Р по прямой связано с вра-
щением нейтральной оси около
постоянной точки.
На фиг. 434 изображены три
положения точки приложения силы
на этой прямой и соответственно
три положения нейтральной оси.
Таким образом, при многоуголь-
ной форме контура сечения очерта-
очертание ядра между точками, соответ-
соответствующими сторонам многоуголь-
многоугольника, будет состоять из отрезков
прямых линий.
Если контур сечения целиком
или частично ограничен кривыми линиями, то построение границы
ядра можно вести по точкам (формулы 27.15), Рассмотрим несколько
простых примеров построения ядра сечения.

506 СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ [ГЛ. XXVII
При выполнении этого построения для прямоугольного попереч-
поперечного сечения (фиг. 431 и 435) воспользуемся формулами, выведен-
выведенными в конце предыдущего параграфа.
Для определения границ ядра сечения при движении точки А по
оси Оу найдём то значение е = е0, при котором нейтральная ось.
займёт положение HxOi (фиг. 435). Имеем по формуле B7.13):
2
откуда
B7.16)
Таким образом, границы ядра по оси Оу будут отстоять от центра
сечения на 1/6 величины Ь (фиг. 435, точки 1 и 3)\ по оси Oz
\Hf	2	xu	границы ядра определятся рас-
расстояниями -^-(точки 2 и 4).
Для получения очертания ядра
целиком изобразим положения ней-
нейтральной оси Н\Ох и //2О2, соответ-
соответствующие граничным точкам / и 2.
При перемещении силы из точ-
точки/в точку 2 по границе ядра
нейтральная ось должна перейти
из положения HxOi в положение
Я2О2, всё время касаясь сечения,
т. е. поворачиваясь вокруг точ-
точки D. Для этого сила должна двигаться по прямой /—2. Точно так же
можно доказать, что остальными границами ядра будут линии 2—3,
3—4 и 4—1.
Таким образом, для прямоугольного сечения ядро будет ромбом
с диагоналями, равными одной трети соответствующей стороны
\Р
0
Фиг. 435.
р
Фиг. 436.
сечения. Поэтому прямоугольное сечение при расположении силы по
главной оси работает на напряжения одного знака, если точка при-
приложения силы не выходит за пределы средней трети стороны сечения.

165]
ПРИМЕРЫ
507
Эпюры распределения нормальных напряжений по прямоугольному
сечению при эксцентриситете, равном нулю, меньшем, равном и
большем одной шестой ширины сечения, изображены на фиг. 436.
Отметим, что при всех положениях силы Р напряжение в центре тя-
р
жести сечения (точка О) одинаково и равно -^ и что сила Р не имеет
эксцентриситета по второй главной оси.
Для круглого сечения радиуса г очертание ядра будет по сим-
симметрии кругом радиуса г0. Возьмём какое-либо положение нейтраль-
нейтральной оси, касательное к контуру. Ось Оу расположим перпендику-
перпендикулярно к этой касательной. Тогда в , С	в \ с
У Я — го =
4 • кг*
Фиг. 438.
Таким образом, ядро предста-
представляет собой круг с радиусом, вчет-
вчетверо меньшим, чем радиус сечения.
Для двутавра нейтральная ось Фиг. 437.
при обходе контура не будет пе-
пересекать площади поперечного сечения, если будет касаться прямо-
прямоугольного контура ABCD, описанного около двутавра (фиг. 437).
Следовательно, очертание ядра для двутавра имеет форму ромба,
как и для прямоугольника, но с другими размерами.
Для швеллера, как и для двутавра, точки /, 2, 3, 4 контура
ядра (фиг. 438) соответствуют совпадению нейтральной оси со сто-
сторонами прямоугольника ABCD. Расстояния определятся по фор-
формулам B7.15).
§ 165. Примеры.
Пример 110. Разрезанное звено цепи (фиг. 439) сделано из стального
стержня диаметром d = 50 мм; a = 60 мм. Если допускаемое напряжение
на растяжение в сечении А принято равным [а] = 1200 кг/см2, какую ве-
величину можно допустить для силы Р1
Материал стержня в рассматриваемом сечении будет испытывать
внецентренное растяжение. Эксцентриситет е равен а + d/2. Выбирая

608 СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ fГЛ. XXVtl
ось Оу в плоскости, проходящей через силы Р и ось прямой части стержня,
имеем:
. d
Напряжение в любой точке сечения равно
Подставляя вместо у его крайние значения it -к-, находим наибольшее и наи-
наименьшее напряжения:
ffmax
mm
Условие
отсюда
1 4Р -ь
J ъй% ~~
прочности
Ар 1
64 Pde 4P
2itrf« *<Р
имеет вид:
1 d
3,14 • 53 • 1200
4(8 .6 + 5-5)
• 1610 кг.
Пример 111. Длинная подпорная стенка высотой й = 3 м и толщиной
Ь = 2 м (фиг. 440) поддерживает земляную насыпь. Давление земли на по-
погонный метр длины стены равно # = 3 т и
h	^
приложено на высоте -^ от основания. Объ-
Объёмный вес кладки y равен 2 т/ж3. Найти
крайние значения напряжений в сечении по
обрезу фундамента.
Выделив из стены по её длине участок
в 1 м (фиг. 440), мы можем рассматривать
эту часть стены как стержень, защемлён-
защемлённый концом, изгибаемый давлением земли
и сжимаемый собственным весом. Так как
наиболее напряжённым будет сечение в за-
защемлении, по обрезу фундамента, то не-
необходимо лишь его и проверить. Опреде-
Определение напряжений в этом сечении можно
свести к задаче одновременного сжатия и
изгиба. Силы, передающиеся через это се-
сечение, сводятся к собственному весу вы-
выделенной части стены N— 1 . 2 • 3 • 2 =
= 12 т и давлению земли # = 3 т. Из-
Изгибающий момент от силы Н в этом се-
сечении равен М = /У-п- = 3 • — = 3 тм.
Для вычисления наибольших нормальных
напряжений в сечении по обрезу фунда-
фундамента воспользуемся формулой B7.1). Проверяемое сечение имеет пря-
прямоугольную форму с размерами Ь = 2 м и d=*\ м; поэтому наибольшие

§ 165]	ПРИМЕРЫ
сжимающие напряжения в точках на стороне /—/ этого сечения равны
_ Н М_ 12 6-3_ л
"max — ~р деГ — 2T1	\ . 22 — — — ' —
= — 10,5 г/ж2 = — 1,05 л:г/слс2.
Сжимающие напряжения в точках на стороне 2—2 сечения равны
509
*min
= -^+-^- = -6 +4,5 =-1,5 т/м2 = -0,15 кг/см*.
Пример 112. Рама клепальной машины (фиг. 441) подвергается дей-
действию двух сил Р, равных каждая 1000 кг. Найти напряжения в точках А и
В сечения (фиг. 442).
' 200
Ч	В
-А
//////////////////////////////////////////А
Фиг. 441.
Фиг. 442.
Расстояние z^ центра тяжести сечения от края полки равно
9 _ Ftat + F&% _ 2,5 . 10 ¦ 1,25 + 2,5 . 20 ¦ 12,5
zi—	""	2,5 • 10 + 2,5 • 20	-
Расстояние zt = 22,5 — 8,75 = 13,75 см.
Момент инерции сечения относительно оси у равен
10 9 ^3	9 ^ 9ПЗ
Jy = iU '^ + 25 (8,75 — 1,25J + Z>J^ + 50 A3,75 — 10J = 3788 см\
Эксцентриситет е = а + zt = 40 -f- 8,75 = 48,75 см. Напряжения равны
, Р , Pezx 1000 , 1000 • 48,75 • 8,75 . 1О- . 2 .
*А = + у + -у-1 = 5" 4	37§8	— = + 125 кг/см2 (растяжение),
, Р Pezs 1000 1000 • 48,75 . 13,75
aBS + F--7r==T	3788	— = -
163 кг'см (сжатие)*

510
СОВМЕСТНОЕ ДЕЙСТВИЕ КРУЧЕНИЯ И ИЗГИБА	[ГЛ. XXVIII
ГЛАВА XXVIII.
СОВМЕСТНОЕ ДЕЙСТВИЕ КРУЧЕНИЯ И ИЗГИБА.
§ 166. Определение изгибающих и крутящих моментов.
В главе XI была разобрана задача проверки прочности при кру-
кручении. Однако такие части машины, как валы, редко работают на
чистое скручивание. Даже прямой вал при работе изгибается соб-
собственным весом, весом шкивов, натяжением ремней. Таким образом,
большинство скручиваемых элементов машин работает на совместное
действие кручения и изгиба. К числу подобных же деталей отно-
относятся и коленчатые валы.
При расчёте элементов, работающих одновременно на изгиб и
кручение, в первую очередь надо выяснить расчётные значения изги-
изгибающих УИИ и крутящих Мк моментов.
Покажем это на примере прямого вала круглого сечения со шки-
шкивом и кривошипом. Схема вала изображена на фиг. 443 и 444. На
Фиг. 443.
Фиг. 444.
левом конце вала расположен шкив весом Q; на него действуют
натяжения ремня Т и t (T^>t)\ на правом конце на палец криво-
кривошипа действует горизонтальная сила Р; рассмотрим момент, когда
кривошип расположен вертикально. Размеры конструкции даны на
чертеже.
Определим изгибающие и крутящие моменты для вала AD. Силы
Tat (натяжения ремня), действующие на шкив, заменяем силой
T-\-t, приложенной в центре шкива, и парой (Т — t)RQi где RQ—
радиус шкива. Сила T-\-t вместе с весом шкива Q производит
изгиб вала; пара же (Г — t) Ro> скручивая вал, уравновешивается
парой, приложенной к его правому концу.
Заменяем силу Р9 действующую на палец кривошипа, такой же
силой Р, приложенной к валу на продолжении его оси в точке N,
и парой с моментом Ph0. Таким образом, к концам вала приложены
пары PhQ и (Г — t)RQ; при равновесии, равномерном ходе машины,
моменты этих пар равны и дают скручивающий момент Мк = PhQ==
= (T-t)RQ.
Если известны число оборотов вала в единицу времени п и
передаваемая шкивом мощность N, то величина крутящего момента УИК

ОПРЕДЕЛЕНИЕ ИЗГИБАЮЩИХ И КРУТЯЩИХ МОМЕНТОВ
§ 166]
может быть найдена по формуле A1.3) § 56:
511
716,2 N
тогда Р = -^
Т—
1 —
М«
/?оA—да)
где тп —
Что же касается изгиба, то на вал действуют и вертикальные (Q)
и горизонтальные (T-\-t, P) силы. Поэтому построим эпюр>ы момен-
моментов для тех и других (фиг. 445, а
и б), считая опоры вала в подшип-
подшипниках В и С шарнирными; одна
из них имеет продольную под-
подвижность.
Имея эпюры моментов от верти-
вертикальных и горизонтальных нагру-
нагрузок, можем для каждого сечения
вала найти полный изгибающий мо-
момент Мп как геометрическую сум-
сумму обеих составляющих; на фиг. 446
показано такое геометрическое сло-
сложение векторов, изображающих
изгибающие моменты для сечения
В; для него полный изгибающий
момент будет равен
Фиг. 445.
Для каждого сечения мы будем
иметь свою плоскость действия
изгибающего момента; но так как
вал имеет круглое поперечное сечение, у которого моменты со-
сопротивления относительно всех центральных
осей одинаковы, то без влияния на резуль-
результаты расчёта мы можем совместить плоскости
изгибающих моментов для всех сечений и по-
построить суммарную эпюру, располагая её в
плоскости чертежа. Это и сделано на фиг.
445, в. Не приводя доказательства, заметим,
что между сечениями В и С эпюра пол-
(T+t)b
Плоскость
изгиба
ного изгибающего момента Жи будет огра-
Фиг. 446.
ничена кривой, не имеющей максимума.
Из очертания эпюры видно, что опасное сечение будет либо
в подшипнике В> либо в подшипнике С в зависимости от соотно-
соотношения числовых данных.

512
СОВМЕСТНОЕ ДЕЙСТВИЕ КРУЧЕНИЯ И ИЗГИБА	[гл. XXVIII
Фиг. 447.
§ 167. Определение напряжений и проверка прочности
при изгибе с кручением.
Вычислив наибольший изгибающий момент Мп и крутящий Жк,
можем теперь найти наибольшие напряжения в материале вала и
составить условие прочности. Предполагая, что опасным является
сечение С, разрежем вал в этом сечении (фиг. 447) и воспользу-
воспользуемся способом сложения действия сил. Вычислим напряжения в попе-
поперечном сечении от действия изгибающего момента и присоединим
к ним напряжения от скручивания.
Изгибающий момент действует в
горизонтальной плоскости; нейтраль-
нейтральная ось будет вертикальна, а наиболь-
наибольшие нормальные напряжения ои будут
в точках сх и г2 на концах горизон-
горизонтального диаметра. Крутящий момент
вызывает лишь касательные напряже-
напряжения, которые достигнут наибольшего
значения тк в точках у контура.
Таким образом, в точках сх и г2
будут действовать по плоскости се-
сечения и наибольшие нормальные и наибольшие касательные напря-
напряжения. В точках сг и с4 на концах вертикального диаметра
к наибольшим касательным напряжениям от кручения добавятся
касательные напряжения от изгиба; однако эти напряжения будут
невелики и результаты подсчётов показывают, что напряжённое
состояние материала будет опаснее в точках сх и с2. Выделим
у этих точек элементы материала кубической формы (фиг. 447);
по четырём граням этих элементов будут действовать касательные
напряжения хк; к двум из этих четырёх будут приложены ещё нор-
нормальные напряжения, две грани кубика будут свободны от напря-
напряжений (фиг. 448). Таким образом, выделенный
элемент материала испытывает плоское напряжён-
напряжённое состояние. Как известно (§§ 43 и 94), для
проверки прочности материала в этом случае не-
необходимо найти главные напряжения ох и а3 и
подставить их в условие прочности, соста-
составленное на основе той или иной теории проч-
прочности.
Подобное плоское напряжённое состояние
испытывает элемент материала, вырезанный в изо-
изогнутой балке на расстоянии z от нейтральной
оси. Проверку прочности такого элемента мы рассмотрели выше (§ 94),
при решении задачи о полной проверке прочности балки. Разница
лишь в том, что в балке и нормальные о и касательные х напря-
напряжения вызывались лишь изгибом.
Фиг. 448.

§ 167]	ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ПРОВЕРКА ПРОЧНОСТИ
513
Для проверки прочности элемента, вырезанного из вала, мы
можем прямо применить выведенные в § 94 формулы, подставляя
в них вместо а и т величины аи и тк. Тогда получим следующие
условия прочности (по четырём теориям):
Теория наибольших нормальных напряжений: 1
Теория наибольших удлинений:
[0,35аи-
0,65 У< + Щ < М-
Теория наибольших касательных напряжений:
К
Энергетическая теория:
B8.1)
]/*S + 3t*< [о].
Чтобы связать эту проверку прочности с величинами моментов М&
и Ми и размерами вала, надо вычислить напряжения ои и тк. Напря-
Напряжение аи, как наибольшее нормальное напряжение при изгибе мо-
моментом Жи, равно
Ми
где для вала круглого сечения 1^=—-; буквой г обозначен радиус
поперечного сечения вала.
С другой стороны, наибольшее напряжение при скручивании
вала лк равно
	ЛТК	Мк	 Мк 	Мк
к	W	тсгЗ	тггЗ	ОШ •
W р	У>Г	су 7СГ	Z VV
Подставляя эти значения напряжений в первую из формул B8.1),
получаем:
Подобным же образом могут быть получены расчётные формулы и
по другим теориям прочности. Нетрудно заметить, что все эти фор-
формулы могут быть заменены одной:
Т^-<И>	B8.2)
где Мр—расчётный момент, величина которого зависит как от
17 Н. М. Беляев

514	СОВМЕСТНОЕ ДЕЙСТВИЕ КРУЧЕНИЯ Й ЙЗГЙВА	[ГЛ.
Ми и Мк, так и от принятой теории прочносяш. Он равен по тео-
теории наибольших нормальных напряжений:
по теории наибольших удлинений:
М^ = 0,35 Мв + 0,65 У Mi + Ml,
по теории наибольших касательных напряжений:
по энергетической теории:
B8.3)
Формула B8.2) по своей структуре совершенно совпадает
с обычной формулой проверки прочности по нормальным напряже-
напряжениям при изгибе моментом Мр. Поэтому проверка прочности круг-
круглого вала на совместное действие кручения и изгиба может быть
заменена проверкой на один изгиб с изгибающим моментом Мр.
В некоторых конструкциях валы, помимо скручивания и изгиба,
растягиваются или сжимаются продольными силами N. Влияние этих
добавочных сил на прочность вала может быть учтено добавкой
к наибольшим напряжениям от изгиба о напряжений ort от продоль-
N
ных сил: о0 = -^г, где F — площадь поперечного сечения вала.
Из формулы B8.2) получаем
отсюда радиус вала равен
Для использования этой формулы остаётся лишь установить,
какой теорией прочности следует пользоваться, а следовательно, по
какой из формул B8.3) вычислять расчётный момент.
Так как валы обычно делаются из стали и вообще из пластич-
пластичных металлов, то при выборе теорий прочности сразу отпадает
теория наибольших нормальных напряжений (см. § 43). До сих пор
в машиностроении пользовались формулой, основанной на второй
теории (наибольших удлинений), называемой иногда формулой Сен-
Венана:	:
~ [0,35 Ми + 0,65 Ум*н + МЦ *? [о],
несмотря на то, что для пластичных металлов эта теория безусловно
неверна; в последнее время при расчётах применяются либо фор-

§167]
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ПРОВЕРКА ПРОЧНОСТИ
615
мулы, основанные на третьей теории (наибольших касательных на-
напряжений), либо — на четвёртой (энергетической) теории:
В таблице 25 сопоставлены результаты определения диаметра
вала при разных отношениях Ми к Мк при одном и том же допу-
допускаемом напряжении с учетом различных теорий прочности. Вели*
чина диаметра, полученная при применении теории наибольших
удлинений (формула Сен-Венана), принята за единицу.
Таблица 23. Сравнение диаметров вала.
Отношение
ми=о
Диаметры вала при применении
П
теории
1
1
1
III
теории
1,15
1,07
1,03
. IV
теории
1,10
1,03
1,01
Из этой таблицы видно, во-первых, что разница в размерах вала в зави-
зависимости от выбора той или иной теории сравнительно невелика; во-вто-
во-вторых, что формула Сен-Венана даёт во всех случаях меньшую величину диа-
диаметра, чем остальные две формулы. Этим и можно объяснить тот факт, что
на практике до сих пор иногда пользуются формулой Сен-Венана, хотя она
основана на заведомо непригодной для применяемого материала теории.
Инженер-практик должен понимать, что переход к расчёту по
новым формулам, основанным на более правильных теориях, был
бы всё же практически неприемлем при сохранении старых норм
допускаемых напряжений. Это заставило бы требовать постановки
валов большего диаметра там, где при расчёте по старой формуле
Сен-Венана благополучно работали валы более тонкие.
Выход заключается в том, что при переходе к новым формулам
нельзя сохранить прежний коэффициент запаса, прежнее допускае-
допускаемое напряжение. Повышение точности расчёта, углубление наших
знаний о работе материала требует, как правило, снижения коэф-
фициента запаса и повышения допускаемого напряжения [а].
Поэтому, вводя на практике вычисление расчётного момента по
новым формулам, необходимо поднять допускаемое напряжение [о]
настолько, чтобы диаметры валов, благополучно работающих на
практике, были оправданы новыми методами расчёта и достаточно
надежными опытными исследованиями.

516
СОВМЕСТНОЕ ДЕЙСТВИЕ КРУЧЕНИЯ И ИЗГИБА	[ГЛ. XXVIII
I
т
Pf =500 иг
§ 168. Примеры.
Пример 113. На вал, изображённый на фиг. 449, насажены два зубча-
зубчатых колеса, на которые действуют тангенциальные усилия Рх = 500 кг и
Р2 == 1000 кг; найти диа-
П"ёЩП 1=300 -4?s/lWH	метР вала "Ри Д°пУска"
I	емом напряжении [<j] =
I	= 1000 кг)см2. Вал шар-
[	/^ ^^ нирно опёрт в подшип-
подшипниках А и D.
Переносим силы Pt
и Р2 на ось вала, за-
заменяя каждую из них
силами, приложенными в
точках В и С, и парами
. ААЛ	сил РМ2 и РМ2.
Фиг. 449.	Обе пары, взаимно
уравновешиваясь, будут
скручивать среднюю часть вала между сечениями В и С; крутящий момент
будет равен
14 ,,-	Ц
J	= 500 . 15 = 75 500 кгсм.
На фиг. 450 изображены схемы
нагрузки вала вертикальными и гори-
горизонтальными силами и соответству-
соответствующие эпюры моментов, а также ре-
результирующая эпюра изгибающих мо-
моментов и эпюра крутящих моментов.
Изгибающие моменты в сече-
сечении В равны: изгибающий момент от
вертикальных сил
Л
изгибающий момент от горизонталь-
горизонтальных сил
полный изгибающий момент в сече-
сечении В
М? =
Фиг. 450.
Точно так же для сечения С:
' 1 + 2а
* 6760 кгсм.
V Р\
PI а* =
Л*и =

§ 169]	ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ	517
Опасным будет сечение С; вычисляя по энергетической теории прочности
расчётный момент, получаем:
р	75002= 13 120 кгсм.
Искомый диаметр вала равен
Пример 114. Сплошной вал диаметром d = 80 мм передаёт мощность
N=800 л. с. при числе оборотов п = 2000 об/мин. Продольное усилие
Р = 20 г. Найти расчётное напряжение в вале по третьей и четвёртой тео-
теориям прочности.
Крутящий момент вычисляется по формуле:
Мк = 716,2 ~ = 716,2 Ж = 286,5 кгм.
Наибольшее касательное напряжение равно (в точках у поверхности вала)
Наибольшее нормальное напряжение (равномерно распределённое)
Наиболее напряжённым будет материал в точках на поверхности вала. Рас-
Расчётные напряжения равны:
по третьей теории
<jr3 = ]/о2 + 4х2 = У 3982 + 4 . 2852 = 695 кг/см2;
по четвёртой теории
ГЛАВА XXIX.
ОБЩИЙ СЛУЧАЙ СЛОЖНОГО СОПРОТИВЛЕНИЯ.
§ 169. Вычисление напряжений и деформаций.
А. Приёмы определения напряжений и деформаций, использованные при
решении отдельных частных задач сложного сопротивления, могут быть рас-
распространены и на более сложные случаи действия сил на тело. Ограничи-
Ограничиваясь рассмотрением призматических брусьев, у которых центр изгиба совпа-
совпадает с центром тяжести поперечного сечения, допустим, что такой брус
(фиг. 451) находится в равновесии под действием приложенной к нему
системы сил, как угодно расположенных в пространстве. На фиг. 451 для
простоты чертежа показаны только сосредоточенные силы; однако внешними
силами могут быть также распределённые нагрузки и пары сил — дальнейшие
рассуждения от этого не меняются.	•
Для нахождения напряжений в некотором сечении „ mnf перпендикуляр-
перпендикулярном к оси бруса и разделяющем его на две части (I и II), выясним сначала,
какими усилиями эти напряжения могут быть вызваны.

518
ОБЩИЙ СЛУЧАЙ СЛОЖНОГО СОПРОТИВЛЕНИЯ
[гл.
Отбросим одну часть бруса, например правую, и рассмотрим равнове-
равновесие оставленной левой части. Используем систему прямоугольных координат;
начало координат расположим
в центре тяжести поперечного
сечения тп — точке О, ось х
направим вдоль оси бруса в
сторону внешней нормали к се-
сечению mnt а оси у и г совме-
стим с главными осями сече-
ния так, как это показано на
фиг. 451 (левовинтовая система
координат).
Перенесём последователь-
последовательно все внешние силы, действую-
действующие на левую (I) часть бруса,
в начало координат. При пере-
переносе любой силы Рк мы полу-
получим приложенную в центре тя-
тяжести сечения силу Рк, в об-
общем случае не совпадающую
ни с одной из координатных
осей, и пару сил Мк = Ркак,
действующую в плоскости, в
общем случае наклонённой ко
всем координатным плоскостям.
Изображающий эту пару век-
вектор 1К направлен перпендику-
перпендикулярно к плоскости действия па-
пары. Так же поступаем при пе-
переносе в точку О и всех дру-
других сил. Сложим теперь гео-
геометрически все силы Рк, при-
приложенные к центру тяжести
сечения тп, в одну равнодей-
равнодействующую /?, а векторы LK —
в один равнодействующий век-
вектор LR.
Проектируя затем силу R
(фиг. 452, а) на оси координат,
получим составляющие: Rx, Ry
и Rz; проектируя таким же об-
образом вектор Ьц (фиг. 452, б),
получим векторы: Lxt Z.y и Lz%
изображающие моменты во-
вокруг всех трёх осей: Mxt My и
М2. Силы RXi Ry и R2 в дан-
?м сечений бруса будем счи-
считать положительными, если на-
направления их ' совпадают с по-
положительными направлениями
Фиг. 452. w	координатных осей. Моменты
Мх, My и Mz условимся счи-
считать положительными в том случае, когда вокруг соответствующих осей они
действуют в направлении движения часовой стрелки.

§ 169]
ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ
619
Таким образом, в результате переноса сил мы можем заменить систему
внешних сил Рк, действующую на оставленную левую часть бруса, статиче-
статически эквивалентной ей системой из шести составляющих: трёх сил, приложен-
приложенных к центру тяжести выбранного сечения и направленных вдоль координат-
координатных осей, и трёх моментов, действующих вокруг этих же осей.
Из предыдущего известно, какое действие на левую часть бруса оказы-
оказывает каждая из этих шести составляющих. В рассматриваемом сечении поло-
положительная составляющая /?^(=УУ)— нормальная сила — вызывает сжатие
левой части бруса; изгибающий момент My и поперечная сила Q? (=/?*) —
соответственно изгиб и сдвиг бруса в плоскости xz; изгибающий момент Mt
и поперечная сила Qy(=fty)— изгиб и сдвиг в плоскости ху\ момент Мх
вызывает кручение бруса вокруг оси х.
Таким образом, в самом общем слу-
случае действия сил на брус в нём возни-
возникают четыре простых деформации:
осевое растяжение -или сжатие, два пло-
плоских изгиба и кручение.
Б. Составим формулы для вычисле-
вычисления нормальных и касательных напря-
напряжений в какой-либо точке А с коорди-
координатами у и г, расположенной в первом
квадранте сечения тп (фиг. 453). При
этом будем считать, что все шесть со-
составляющих системы внешних сил яв-
являются положительными (фиг. 452). В се-
сечении тп возникают уравновешиваю-
уравновешивающие эту систему нормальные и каса-
касательные напряжения. Нормальные напряжения обусловлены действием про-
продольной силы N и изгибающих моментов Му и М?. От положительной про-.
	 её равномерно распределён-
с' = —=¦ (фиг. 453). Положитель-
Фиг. 453.
дольной силы N возникают
ные по сечению сжимающие
ные изгибающие моменты Л1«
мальными напряжениями с" и о"';
в точке А возникает сжимающее
уравновешивающие
напряжения <* = — -р:
и Мг соответственно уравновешиваются нор-
»'"; при этом от положительного момента My
напряжение «"=: — —?—, а от
положитель-
положительного момента Мг — растягивающее напряжение от'" = -f-
Суммируя эти составляющие нормального напряжения, получаем такую
формулу для вычисления полного нормального напряжения в точке А:
^
Jy
B9.1)
Для вычисления полного нормального напряжения в любой другой точке
поперечного сечения бруса достаточно подставить в формулу B9.1) значе-
значения Nt My и MZf а также и координат у и zt с их знаками; при этом мы
всегда будем получать надлежащие величину и знак полного нормального
напряжения.
Полагая в формуле B9.1) напряжение з равным нулю и обозначая коор-
координаты точек нулевой линии через у0 и zOt для нахождения положения этой
линии получаем такое уравнение:	/
N

520
ОБЩИЙ СЛУЧАЙ СЛОЖНОГО СОПРОТИВЛЕНИЯ
[гл. xxix
Отрезки, отсекаемые нулевой линией на осях координат у и z, соответственно
равны (фиг. 454):
^ и «, = _?.?-.	B9.2)
.?. N
У
Тангенс угла наклона (fi) нейтральной линии к оси у равен:
B9.3)
Нейтральная линия в общем случае делит поперечное сечение бруса на две
области: растянутую и сжатую (фиг. 454). Проводя линии, параллельные ней-
нейтральной и касательные к контуру поперечного сечения, находим в той и
другой области наиболее удалённые от нейтральной линии точки 1 и 2
с наибольшими растягивающими и сжимающими
напряжениями. Подставляя координаты этих точек
(yi и Zt или у2 и 22) с их знаками в формулу
B9.1), находим наибольшие значения растягиваю-
растягивающих, и сжимающих напряжений:
аA,2) = - /г ~ 7%. 2) + -^У^У <29'4)
Касательные напряжения в сечении тп воз-
возникают вследствие кручения бруса вокруг оси х
и сдвига его в плоскостях ху и xz.
Крутящий момент Мх уравновешивается каса-
касательными напряжениями тк. Для бруса с попереч-
поперечным сечением в виде круга или кольца эти напря-
напряжения вычисляются (§ 57) по формуле:
B9.5)
г
Фиг. 454.
Для брусьев с поперечным сечением любой другой формы должна быть
использована формула, приведённая в § 67 (таблица 17):
то*« = 4г-.	<29-6)
Во всех случаях наибольшие касательные напряжения возникают на кон-
контуре поперечного сечения и направлены вдоль касательной к контуру.
Касательные напряжения от сдвига, уравновешивающие силы Qy и Q2$
как правило, играют второстепенную роль; они находятся * по форму-
формулам (§ 91):
Г\ С /«Л	П С /-Л
B9.7)
и тг= ^
Jyb(z)'
Для прямоугольного и круглого сечений касательные напряжения B9.7)
достигают максимума на соответствующих главных осях инерции: zy — на
noch г, a iz — на оси у. Суммарные касательные напряжения от двух плоских
изгибов наибольшего значения достигают в центре тяжести сечения, т. е.
как раз там, где касательные напряжения от кручения и нормальные напря-
напряжения от изгиба равны нулю. Благодаря этому определение этих напряжений
часто не имеет практического значения.
В связи с тем, что нормальные напряжения от изгиба и касательные
напряжения от кручения наибольших значений достигают на контуре попе-
поперечного сечения, именно там обычно приходится искать наиболее напряжён-

§ 169] ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ	521
ные точки и производить проверку прочности материала бруса. Точки с наи-
наибольшими касательными напряжениями не всегда совпадают с точками, в ко-
которых возникают наибольшие нормальные напряжения. Поэтому в наиболее
тяжёлых условиях материал бруса находится у тех точек контура, в которых
получается наиболее неблагоприятное сочетание нормальных и касательных
напряжений. Такими точками могут быть: точки с наибольшими нормальными
напряжениями, точки с наибольшими касательными напряжениями и какие-
либо промежуточные точки контура сечения. В случае надобности могут
быть учтены также и касательные напряжения от изгиба; тогда полное каса-
касательное напряжение должно быть найдено путём геометрического суммиро-
суммирования тк, ъу и iz.
Для проверки прочности материала в самом общем случае действия сил
на брус должны быть использованы расчётные формулы § 94 [формулы
A5.14——15.17)] или § 167 [формулы B8.1)], выведенные на основе той или иной
теории прочности. Сравнивая величину расчётного напряжения, вычисленного
по одной из формул A5.14—15.17) или B8.1), с величиной допускаемого на-
напряжения, получаем возможность решить одну из двух практически важных
задач: определить размеры поперечного сечения бруса или проверить проч-
прочность материала при известных размерах сечения бруса.
В. Для вычисления перемещений призматического бруса, Загружённого
системой сил, как угодно расположенных в пространстве, применяем прин-
принцип независимости действия сил (ограничение см. § 161). Это может быть
выполнено с помощью приёмов, изложенных ранее в соответствующих раз-
разделах курса.
Не останавливаясь на других приёмах, напомним использование теоремы
Кастильяно (§ 126). Потенциальную энергию деформации при сложном сопро-
сопротивлении рассматриваемого здесь бруса можно представить в виде суммы
количеств энергий от всех шести составляющих: N, Qyy Q2, MXi Afy и Mz.
Пренебрегая энергией касательных напряжений от изгиба, имеем:
.	B9.8)
Полагая, что нормальное усилие N и крутящий, момент Мх в общем случае
не остаются постоянными на протяжении всей длины бруса, для энергии
в элементе бруса длиной dx следует написать такие выражения:
А78 Их	Щ
и аи^
а для энергии на участке бруса длиной /:
С N* dx
$ и
Для энергии нормальных напряжений при плоском изгибе соответственно
имеем (§ 125):
M*dx
^h и
В связи с этим формула B9.8) получает теперь такой вид:
l^.^.J^L + J^L. + J^\ax.	B9.9)
Значок / показывает, что интегрирование распространяется на длину такого
Участка бруса, на протяжении которого функции координаты х, т. е. N, Мх,

522
ОБЩИЙ СЛУЧАЙ СЛОЖНОГО СОПРОТИВЛЕНИЯ
[гл. xxix
My и Мг остаются непрерывными. При наличии в брусе нескольких таких
участков вмест одного интеграла нужно вычислить интегралы по каждому
участков вместо одного интеграла
из участков и взять их сумму..
Применяя теорему Кастильяно, искомое
какой-либо из сил Р находим из выражения:
N dN , Мх дМх , Mv
перемещение в направлении
М2 дМ
Под Р и Ь здесь, конечно, понимается обобщённое усилие и соответствующее
этому усилию обобщённое перемещение. Аналогично составляются формулы
Мора и Верещагина.
Напоминаем, что все рассуждения в этом параграфе велись в предполо-
предположении, что центр изгиба совпадает с центром тяжести поперечного сечения
бруса. Выведенные здесь формулы должны быть несколько изменены для тех
случаев, когда такое совпадение не имеет места (см. гл. XXX).
§«170. Расчёт простейшего коленчатого вала.
Рассмотрим расчёт коленчатого вала, некоторые части которого подвер-
подвергаются одновременному действию продольных сил, крутящих и изгибающих
моментов. Исследуем наиболее простой случай работы вала, имеющего только
одно колено (фиг. 455).
Фиг. 455.
Части вала А и В называются коренными шейками; они расположены
в подшипниках, которые мы будем считать шарнирными опорами; одна из
них допускает горизонтальные перемещения. Шейка С вала называется
мотылёвой. Шейки имеют круговое поперечное сечение с диаметром й\ части
вала, соединяющие коренные шейки с мотылёвой, называются щеками вала
и имеют прямоугольное сечение шириной b и высотой h.
На мотылёвую шейку от шатуна передаётся давление Р, вращающее
вал; момент этого давления относительно оси вала уравновешивается
парой Мо, передающейся на вал от шкива, насаженного около коренной
шейки В. Чтобы найти изгибающие и крутящие моменты во всех частях
вала, разложим силу Р на две взаимно перпендикулярные составляющие:
Р2 в плоскости колена и Pi перпендикулярно к ней. Соответственно
разлагаем на такие же составляющие и реакции подшипников А и В. Их
можно найти из условия, что все силы, лежащие в плоскости колена, должны
уравновешиваться между собой, так же как и силы, лежащие в перпендику-
перпендикулярной плоскости. При вычислениях будем считать, что реакции подшипни-

§ 170)
РАСЧЁТ ПРОСТЕЙШЕГО КОЛЕНЧАТОГО ВАЛА
523
ков А и В и давление на мотылёвую шейку С приложены посредине длины
соответствующих шеек.
На фиг. 456 изображена схема вала со всеми действующими на него
силами. Разбивая вал на ряд участков (I—VII), при вычислении нормальных
сил, изгибающих и крутящих моментов отнесём каждый из этих участков
к своей прямоугольной системе координат xit yit гь. Системы координат рас-
расположи^ так, как это показано на фиг. 456. Начало координат каждой системы
поместим в центре тяжести рассматриваемого сечения. Тогда силы Pxi для
Фиг. 456.
каждого из участков будут нормальными силами, моменты вокруг осей xt
везде будут крутящими моментами, а моменты вокруг осей у^ и z-x — изги-
изгибающими моментами: Myi — в плоскости колена, а М21 — в плоскости, пер-
перпендикулярной к плоскости колена.
Проводя ряд сечений вала и рассматривая все время левую отсечённую
часть, вычисляем значения нормальных сил, изгибающих и крутящих момен-
моментов для каждого участка вала. Эти вычисления сведены в таблицу 26. По
данным таблицы 26 без затруднений могут быть построены эпюры измене-
изменения Ny МХ1 Afy и Af-f для всего вала.
При проверке прочности, а равно и при определении размеров попереч-
поперечных сечений, для каждого из участков вала необходимо установить опасное
сечение, а в этом сечении — наиболее напряжённые точки.
Для шейки вала опасным сечением является сечение bt на участке VI
(см. таблицу 26), в котором к наибольшим изгибающим моментам
и М2 = -
Добавляется ещё и крутящий момент
Результирующий изгибающий момент Мн равен:
»=±у pi+л =

524
ОБЩИЙ СЛУЧАЙ СЛОЖНОГО СОПРОТИВЛЕНИЯ
[гл. xxix
сё
се
я
г
о
н
се
сг
•лен
се
н
tr
о
о.
2
s
S
<о
см
ев
К
VD
сЗ
3
S
5*
S
с?
m
ев
О,
м
К
. S
I
и
ю
ДЛЯ
2
ч
>>
Фор
л- аинзьвнд
эинэьээ
нохэвь^
ев
ние
вал;
се
Ю S
ев и
Ч 5
см о (х
1
*
П !СМ О Q^
4-
1 ""
Н °
1 ^
ГЗ
t=5
СЗ
03
СЗ
3
(N
CM Q^
СМ О ?L
1
^|см
СМ "^	"
см
+
1
СЗ
(*>
4-
см
в « о
to* 1 «' со!
СЗ
- EJ
0?
сз
Лев
СМ -(-- ^
см
см
см
+
о;
.* •*
i

—ч
см
4 +
l +
см ^
см
•-—\ v»
см
^ +
г ^
см ^_^-
см
о
1
1
1
см ^
см
СЗ
<v
в
а
ш
ej
о
1

§ 1701
РАСЧЁТ ПРОСТЕЙШЕГО КОЛЕНЧАТОГО ВАЛА
525
s
г?
о
со
CJ
s
Я
<D
r-
C
P(
О
о.
С
X
3
Я
лич
CQ
rt
03
s
**в
s w
s
4
ЧИС
3
n
я
2
ч
a
a.
о
дг эияэьвн?
эинэьээ
ЯОХЭВЬД
о *
аз «в
Назва
части
1
см
I >о Н~
4- w
сС
см

1
"~^
см
1 ^«^
W JCM ~t" ^
+ ^-оГ
см
1
^^^^^-Q^ CM —|—
см +'
4-
о
1
1
? О * о
см
1 О Ц
>
со
В
СС
Мотылёва
н
~Ь *^ о
см с?
1
*
см
+
см
1 -
1
1
Ч О ^
1 г- to
>
•
СО
a
Правая щ
н
¦^ 1см в
I
сС
СМ
1
1
см «
+ ^ |
о*1 'см
о
1
1
1 ~ аз I
-
СО
Ч
Шейка ва
1
1
о
1
——" '¦" ч
1
О «*
—-^ *
>
СО
Шейка ва

526
ОБЩИЙ СЛУЧАЙ СЛОЖНОГО СОПРОТИВЛЕНИЯ
[гл. xxix
Наибольшие касательные и нормальные напряжения в шейке вала возникают
в точке пересечения окружности вала со следом плоскости действия результи-
результирующего изгибающего момента. Уело*
вие прочности (например, по теории
наибольших касательных напряжений)
получает такой вид:
5 =
16
- (О
Для мотылёвой шейки опасным
сечением является сечение С, в ко-
котором к наибольшим (на участках Ш
и IV) изгибающим моментам
Фиг. 457.
добавляется ещё и крутящий момент
Мх =	—- re. Результирующий изгибающий момент Ми равен:
Условие прочности для мотылёвой шейки по той же теории имеет такой вид:
Из условий 1 и 2 определяется диаметр вала d.	'	• *
Из двух щёк вала в худших условиях (см. таблицу 26) находится правая
щека в сечении &8. В этом сечении она подвергается действию продольной
силы ЛГ=	~, крутящего момента Мх =	<г(л + ~2") и изгибающих мо~
ментов Му = -|- -fr- (в + "о" 1 и Мг = + ^iro« При проверке прочности мате-
риала щеки необходимо произвести исследование напряженного состояния
в трёх точках: 7, 2 и 3 (фиг. 457).
В точке 1, где т^ = 0, условие прочности имеет такой вид:
=—JL — MyZi jl. м*у± —
(+т)
12
+ (""
(а)
12

§ 1701	РАСЧЁТ ПРОСТЕЙШЕГО КОЛЕНЧАТОГО ВАЛА	527
В точке 2, где нормальные напряжения от момента Мг равны нулю, имеем:
а
(Значения коэффициента Р для прямоугольного сечения см. в таблице 17 § 67.)
Условие прочности для точки 2 напишется так:
= -L |/р§ (За + 2*)» + Pf (« + у)У~ ^ [о]. F)
В точке 3, где нормальные напряжения от момента Му равны нулю,
¦	N
(Значения коэффициента 7 см. в таблице 17 § 67.)
Условие прочности в этом случае получает такой вид:
р?2 J ^ М- {¦)
Задаваясь отношением h к Ь, определяем размеры щеки вала по ка-
каждому из условий: (а), (б) и (в); из трёх вариантов выбираем тот, в котором
эти размеры получились наибольшими.
На практике очень часто встречаются многопролётные коленчатые валы
(у двигателей внутреннего сгорания). * Они представляют собой своеобразную
неразрезную балку, для которой можно составить в два раза больше допол-
дополнительных уравнений, аналогичных обычным уравнениям трёх моментов, чем
мы имеем дополнительных опор (в пространстве каждая опора даёт две
реакции). Вывод этих уравнений требует умения вычислять углы поворота
сечений коленчатого вала, расположенных над центрами подшипников. Эти
вычисления не представляют собой ничего принципиально трудного; их
можно произвести, применяя теорему Кастильяно или формулу Верещагина.
Пусть, например, нужно найти угол поворота <р сечения D шейки вала
относительно сечения С мотылёвой шейки. Применяя теорему Кастильяно,
искомый угол поворота найдём по формуле
аи
? дМо*
Так как от Мв зависит только величина силы Рх = —-, входящей лишь
в выражения Мх и М2, то
'М^^^М^ШЛ dx ^'yjf !МХ дМх Мг &Mz\dx

528	ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XXX
Подставляя сюда значения Mxi, Mzb -^ и -^ (см. таблицу 26) и
выполняя интегрирование, находим искомую величину <р.
Для решения этой задачи по Верещагину следует построить эпюры мо-
моментов (пользуясь таблицей 26); составить затем единичное состояние (в ко-
котором необходимо нагрузить сечения С и D двумя равными, но обратно
направленными крутящими моментами ± М^ = 1), построить эпюру М° и
произвести подсчёты по формуле B1.20).
ГЛАВА XXX.
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
НА КРУЧЕНИЕ И ИЗГИБ.
§ 171. Введение.
Развитие техники и особенно авиации вызвало в последние де-
десятилетия широкое применение в инженерных конструкциях тонко-
тонкостенных оболочек и стержней; благодаря этому достигается суще-
существенное снижение собственного веса систем. Тонкостенные кон-
конструкции получили распространение как в авиастроении, так и в ряде
других отраслей инженерного дела (кораблестроение, вагонострое-
вагоностроение, строительство высотных зданий и пр.).
Разработка и применение новых конструктивных форм привели
к созданию новой теории расчёта тонкостенных стержней и оболо-
оболочек. Ведущее место в создании и развитии новой теории занимают
советские ученые и в первую очередь дважды лауреат Государственной
премии профессор В. 3. Власов, положивший прочное основание
этой отрасли науки в своих выдающихся работах1).
Важную роль в развитии теории расчёта тонкостенных конструк-
конструкций сыграли также работы А. А. Уманского2), Д. В. Бычкова3),
Г. Ю. Джанелидзе4), А. Р. Ржаницына8) и др.
В настоящее время создана стройная теория расчёта тонкостен-
тонкостенных конструкций, оформившаяся как новый раздел строительной
механики, являющейся предметом изучения в специальных курсах вузов.
!) Власов В. 3., Тонкостенные упругие стержни. Стройиздат, 1940 г.
Его же, Строительная механика тонкостенных конструкций, 1950 г. Его же,
Новый метод расчёта призматических складчатых покрытий и оболочек, 1933 г.
*) У м а н с к и й А. А., Кручение и изгиб тонкостенных авиаконструкций,
1939	г. Его же, О нормальных напряжениях при кручении крыла самолёта,
1940	г.
») Б ы ч к о в Д. В. и Мрощинский А. К., Кручение металлических
балок, 1944 г. Б ы ч к о в Д. В., Расчёт балочных и рамных систем из тонко-
тонкостенных элементов, 1948 г.
4) Джанелидзе Г. Ю. иПановко Я. Г., Статика упругих тонко-
тонкостенных стержней, 1948 г.
') Ржаницын А. Р., Сложное сопротивление тонкостенных профилей
в пределах и за пределами упругости, 1942 г.

§ 172] ПОНЯТИЕ О СВОБОДНОМ И СТЕСНЁННОМ КРУЧЕНИИ 529
Теория тонкостенных стержней вводит ряд новых важных пред-
представлений, определений и выводов, с которыми целесообразно озна-
кбмить учащихся уже в курсе сопротивления материалов. В настоящей
главе рассматриваются лишь те вопросы теории кручения и изгиба
тонкостенных стержней незамкнутого профиля, изучение которых
позволит учащимся усвоить основы теории и получить понятие
о новых силовых факторах и геометрических характеристиках сече-
сечения. Совершенно не затрагиваются здесь вопросы расчёта тонкостен-
тонкостенных стержней замкнутого сечения, впервые разработанные проф.
А. А. Уманским. Не освещаются и вопросы расчёта рамных систем
и неразрезных тонкостенных балок, разобранные в работах Д. В. Быч-
Бычкова, Б. Н. Горбунова1) и др. Из теории устойчивости тонкостен-
тонкостенных стержней в § 213 приведены некоторые окончательные резуль-
результаты без выводов.
Таким образом, эту главу следует рассматривать лишь как вве-
введение в теорию расчёта тонкостенных стержней при работе их
в пределах упругости.
§ 172. Понятие о свободном и стеснённом кручении.
Приведённые в § 67 формулы для расчёта на кручение стержней
некруглого профиля относятся к случаю так называемого свободного
кручения. Под свободным, нестеснённым кручением разумеется
такой вид кручения, при котором элементы скручиваемого стержня
не испытывают изгиба. Опытные и теоретические исследования пока-
показывают, что если усло-
условия закрепления и нагру-
жения стержня таковы,
что не создаётся препят-
препятствий свободной депла-
нации (т. е. короблению)
сечений, то изгиба при
кручении не происходит.
Поясним это на лри-
мере. Пусть стержень	Фиг. 458.
двутаврового сечения со
свободными (незакреплёнными) концами скручивается парами, при-
приложенными к нему по торцам в плоскостях, перпендикулярных к его
оси (фиг. 458), Как показано на фиг. 458, б, полки двутавра изменяют
своё положение по отношению друг к другу, но остаются прямыми.
Продольные оси полок лишь поворачиваются друг относительно друга
на некоторый угол. Перпендикулярные к ним торцы полок АВ и CD,
поворачиваясь вместе с полками, перестают быть параллельными,
*) Горбунов Б. Н. и С т р е л ь 6 и ц к а я А. И., Теория расчёта рам
из тонкостенных стержней, ГТТИ, 1948.

530
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
выходят из плоскостей концевых сечений, сечения перестают быть
плоскими, коробятся или, как говорят, депланируют.
Таким образом, свободное, или нестеснённое, кручение име?т
место при свободной, нестеснённой депланации сечений, причём
в этом случае распределение касательных напряжений во всех сече-
сечениях остаётся одинаковым. Расстояния между сечениями вдоль любой
образующей при свободном кручении не изменяются, и, следова-
следовательно, в сечениях не возникает нормальных напряжений.
Если по условиям закрепления или загружения стержня свобод-
свободная депланация сечений (при скручивании его) становится невоз-
невозможной, то такой вид кручения сопровождается изгибом отдельных
элементов стержня и носит название стеснённого или изгибного
кручения.
Поясним это на примере того же двутавра. Пусть условия загру-
загружения останутся внешне такими же (две пары сил, приложенные
яо концам стержня), но условия закрепления изменятся (фиг. 459).
Левый конец двутавра бу-
Q\	дем считать жёстко заще-
'Мл млённым, правый — сво-
свободным.
По условию закрепле-
закрепления, защемлённое конце-
концевое сечение стержня не
коробится, остаётся пло-
плоским, и, следовательно,
препятствует свободной
депланации смежного с
ним сечения. Очевидно,
чем дальше расположено
сечение от места защемле-
защемления, тем свободнее его де-
депланация. Таким образом, в случаях стеснённого кручения стержня
депланация соседних сечений различна. Поэтому и расстояния между
отдельными точками этих сечений изменяются, т. е. изменяются
длины продольных волокон. Значит, стеснённое кручение сопрово-
сопровождается возникновением соответствующих этим деформациям нор-
нормальных напряжений.
На фиг. 459, б изображен^ деформация стержня двутаврового
профиля, защемлённого одним концом и нагружённого парой сил
с моментом Мо на другом конце. В этом случае полки двутавра не
остаются прямыми, так как защемлённые концы их остаются непо-
неподвижными в то время, как свободные концы под действием крутя-
крутящего момента смещаются в противоположные стороны. Таким обра-
образом, под действием крутящего момента MQ полки двутавра изги-
изгибаются, поэтому такой вид кручения называют изгибным кру-
кручением.
Фиг. 459.

172]
ПОНЯТИЕ О СВОБОДНОМ И СТЕСНЁННОМ КРУЧЕНИЯ
531
Фиг. 460.
Разумеется, свободное торцевое сечение, как и все промежуточные се-
сечения Между защемлением и концом стержня, перестаёт быть плоским.
Аналогичную картину изгиба полок мы прлучили бы для дву-
двутавра, опёртого *) по концам и нагружённого парой сил, приложен-
приложенной в серединном се-
сечении т—п (фиг. 460).
Вследствие симмет-
симметрии сечение т — п по-
посредине пролёта долж-
должно остаться плоским, /зг
При повороте же его '
под действием момен-
момента пары, полки дву-
двутавра подвергнутся де-
деформации изгиба. Де-
Депланация различных се- ш
чений по длине, стерж-"
ня будет неодинакова,
причём в среднем сече-
сечении её не будет вовсе.
Стеснённое кручение имеет место как в том случае, когда
имеется препятствие для свободной депланации хотя бы одного се-
сечения, так и тогда, когда депланация различных сечений неодина-
неодинакова. Так, например, если к торцам двутавра, изображённого на
фиг. 458, приварить достаточно жёсткие диафрагмы большой тол-
толщины, препятствующие де-
депланации торцевых сечений,
то вместо свободного кру-
кручения мы будем иметь кру-
кручение изгибное.
Точно так же, если за-
загрузить стержень несколь-
несколькими парами по длине (фиг.	.
461, а), то кручение будет а'
стеснённым, так как вслед-
вследствие различия bn величине
углов закручивания на раз-
разных участках стержня де-
депланация разных сечений не будет одинаковой. Неодинакова будет и
депланация смежных сечений, если сечение стержня меняется по
его длине (фиг. 461, б).
Напомним, что ранее в теории изгиба стержней несимметрич-
несимметричного сечения мы встречались с явлением кручения при изгибе (§ 96).
*) Предполагается, что опоры препятствуют повороту концевых сечений
относительно продольной оси балки, но не препятствуют их свободной де-
депланации.
Фиг. 461.

532
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
Здесь же, рассматривая случай стеснённого кручения тонкостенных
стержней, мы сталкиваемся с явлением изгиба.
Одна из задач стеснённого кручения была изучена ещё в 1905 г.
проф. С. П. Тимошенко при рассмотрении вопроса об устойчивости
плоской формы изгиба двутавровой балки!). Вопросами изгибного
кручения занимался ряд советских и иностранных учёных в после-
последующий период (Губер — 1924, Б. Г. Галёркин — 1927, Вагнер — 1928,
П. М. Знаменский—1934, Л. С. Лейбензон —1935, Блейх—1936,
Каппус —1937). Однако в общем виде задача об изгибном кручении
тонкостенных стержней открытого профиля была решена профессором
В. 3. Власовым в уже упомянутых его работах 1936—1939 гг.
§ 173. Внутренние усилия в сечениях стержня
при стеснённом кручении. Гипотезы.
Как было показано выше (§ 67), при свободном кручении стержня
в поперечном его сечении вблизи контура возникают касательные
напряжения, направленные вдоль контура (см. фиг. 141 § 67).
Поэтому на противоположных сторонах прямоугольника или
эллипса, показанных на фиг. 141, касательные напряжения напра-
направлены в разные стороны.
При чистом кручении стержней с сечениями из тонкостенных
элементов касательные напряжения распределяются по такому же
F3
(Ц
I-Г);
ii
MK
I
а)
б)
Фиг. 462.
закону, они параллельны контуру и направлены в противоположные
стороны (фиг. 462). Здесь касательные усилия приводятся к парам,
складывающимся в сумму моментов внутренних сил, как это пока-
показано на фиг. 462, г:
Очевидно, чем меньше толщина стенок стержня, тем меньше плечи
внутренних пар, а следовательно, тем больше величина касательных
^напряжений, уравновешивающих внешний момент. Отсюда следует,
что чем тоньше стенки скручиваемого стержня открытого профиля,,
тем хуже он сопротивляется крутящему моменту, так как даже при
1) Известия Спб. Политехнического Института, т. 4 и 5, 1905—1906 гг.

§ 173]
ВНУТРЕННИЕ УСИЛИЯ В СЕЧЕНИЯХ СТЕРЖНЯ
533
сравнительно небольшой величине Мк в сечениях будут возникать
большие касательные напряжения.
Заметим ещё, что поскольку касательные напряжения в пределах
толщины стенки профиля направлены в противоположные сторойы
(фиг. 463), по средней линии сечения
они должны быть равны нулю. Значит,
серединные поверхности скручиваемого
стержня свободны также от сдвигов;
элементарные прямоугольники, взятые
на серединной поверхности в любом
месте по длине стержня, при свободном
кручении не перекашиваются.
Перейдём теперь к рассмотрению
стеснённого (изгибного) кручения.
Как это ниже будет показано, при
стеснённом кручении, в изгибаемых
элементах профиля, помимо указанных
на фиг. 462—463, появляются дополни-
дополнительные касательные напряжения от
действия поперечных сил. Хотя эти дополнительные напряжения
на серединной линии сечений и не равны нулю, однако, как это
установлено расчётом, сдвиги, вызываемые ими в серединной по-
поверхности профиля, малы и ими можно пренебречь. Поэтому в тео-
теории расчёта тонкостенных стержней принято допущение, что мате-
материал на серединных поверхностях элементов тонкостенного
профиля при стеснённом кручении не претерпевает сдвигов.
Фиг. 463.
Фиг. 464.
Для ознакомления с характером деформации стержня, находя-
находящегося в условиях изгибного кручения, обратимся снова к рассмотрен-
рассмотренному выше (§ 172) примеру стержня двутаврового профиля (фиг. 464).
Заметим, что выводы, получаемые при этом, могут быть обобщены
и на несимметричные сечения, например изучаемые далее в § 174.

534
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
Вырезав элемент стержня длиной dx (заштрихованный на
фиг. 464, 6), выясним, какие напряжения возникают по сечениям
этого элемента. Будем при этом считать, что контуры поперечных
сечений стержня не деформируются. Эта основная гипотеза теории,
принятая взамен гипотезы плоских сечений, предполагает, что в де-
деформированном состоянии, несмотря на депланацию сечения при
кручении, контуры двутавра сохраняют свою форму, т. е. проекция
сечения, претерпевшего депланацию, на плоскость сечения остаётся
дсутавром (как это показано на фиг. 464, в).
На практике неизменяемость контура сечения обычно обеспечи-
обеспечивается постановкой диафрагм в нескольких сечениях по длине стержня,
препятствующих могущим иметь ме-
место искажениям формы контура.
Полки двутавра, как это видно
из фиг. 464, г, изгибаются в разные
стороны моментами М, направлен-
направленными в противоположные стороны;
при переменном изгибающем моменте
можно считать, что в сечениях полок
возникают дополнительно к изгибаю-
изгибающим моментам М поперечные силы Q,
Фиг. 465.
направленные в противоположные стороны (фиг. 464, г и 465). Под
действием этих силовых факторов в сечениях элемента, выделенного
из двутавра, возникают три группы напряжений, показанных на фиг. 466./
а) Касательные напряжения тк (фиг. 466, а), зависящие от той части
внешнего момента, которую мы назовём моментом чистого кручения:
Эти напряжения могут быть подсчитаны по формулам § 67
(глава XI), которыми мы пользовались при чистом кручении стержней
некруглого сечения:
Мк *

§ 173] ВНУТРЕННИЕ УСИЛИЯ В СЕЧЕНИЯХ СТЕРЖНЯ	535
Здесь JK — геометрическая характеристика сечения при кручении,
условно названная моментом инерции при кручении; 8 — толщина
стенки сечения в рассматриваемой точке; Мк — момент чистого
кручения, величина которого остаётся пока неизвестной.
б)	Дополнительные (вторичные) касательные напряжения т, воз-
возникающие в полках двутавра под действием поперечных сил Q
(фиг. 466, б). Эти касательные напряжения для рассматриваемого
случая можно подсчитать и по методу Журавского, если величина
поперечных сил станет известной. Заметим, что силы Q приводятся
к паре с моментом M^^Qh (фиг. 465); этот момент, вызываю-
вызывающий появление вторичных касательных напряжений, мы назовём
изгибно-крутящим моментом, а соответствующие касательные
напряжения — секториальными касательными напряжениями (т^).
Смысл этих терминов\ выяснится ниже.
в)	Нормальные напряжения в полках двутавра; поскольку внешние
силы приводятся к паре, вращающей вокруг оси х, эти напряжения
образуют статически уравновешенную систему внутренних усилий
(фиг. 466, в). Они пропорциональны относительным удлинениям во-
волокон, вызванным неравномерной депланацией сечений, называются
секториальными нормальными напряжениями и обозначаются аш.
Очевидно, что при депланации сечений одни волокна будут
удлиняться, другие укорачиваться, а значит, будут и нейтральные
волокна, не подвергающиеся ни растяжению, ни сжатию. Следова-
Следовательно, в сечении будут точки, в которых нормальные напряжения ат
обратятся в нуль, так называемые нулевые точки сечения. Так как
при изгибе и кручении тонкостенных стержней сечения не остаются
плоскими, то нулевые точки обычно не лежат на одной прямой,
нейтральные волокна не группируются в нейтральный слой. Оты-
Отыскание нулевых точек сечения, как мы увидим ниже, имеет суще-
существенное значение для определения секториальных нормальных на-
напряжений аш.
Так как действие трёх рассмотренных выше групп напряжений
(хк» т« и а») эквивалентно действию внешнего момента Мх = Жо,
составим для их определения уравнения равновесия (фиг. 466):
?* = 0, tomdF=0;	(ЗОЛ)
^dF-z^O;	C0.2)
= 0, t
dF-y = 0;	C0.3)
К	ш = 0 или Мл + Мт = Мш. C0.4)
Суммы проекций на оси у \\ z тождественно обращаются в нуль.

536	ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ [гл. XXX
Из шести уравнений статики два обратились в тождества, а урав-
уравнения (ЗОЛ), C0.2) и C0.3) выражают условие, что нормальные
напряжения (а^) приводятся к полностью уравновешенной системе
внутренних усилий. В рассматриваемом нами случае изгибного кру-
кручения двутавра система внутренних нормальных усилий, действую-
действующих в поперечных сечениях полок, может быть приведена к двум
парам Ж, направленным в противоположные стороны (фиг. 465 и 466, в).
Совокупность двух таких пар, лежащих в параллельных пло-
плоскостях, называется бипарой. Величина бипары может быть оценена
новым силовым фактором — моментом второго порядка, равным про-
произведению моментов М на расстояние между ними h (плечо бипары):
Эта новая обобщённая сила *), связанная с неравномерной деплана-
цией сечений и эквивалентная статически уравновешенной системе вну-
внутренних нормальных усилий, называется изгибно-крутящим бимомен-
том. Следовательно, вместо отыскания изгибающих моментов, прило-
приложенных к отдельным элементам скручиваемого стержня, можно поста-
поставить задачу определения величины изгибно-крутящего бимомента В.
Таким образом, для вычисления касательных и нормальных напря-
напряжений в сечении стержня необходимо найти величины МКУ Мф и В.
Составленные выше уравнения равновесия (ЗОЛ), C0.2) и C0.3)
пока не могут быть использованы, так как закон изменения секто-
риальных нормальных напряжений нам неизвестен и не один из
интегралов не может быть взят; лишь одно уравнение C0.4) свя-
связывает внутренние усилия с внешними. Задача определения напря-
напряжений в сечении тонкостенного стержня оказывается статически
неопределимой. Для её решения нам необходимо будет обратиться
к рассмотрению упругих деформаций.
Заметим, что в рассмотренном примере стеснённого кручения
стержня двутаврового сечения изгибу подвергаются только полки
двутавра, причём осью кручения стержня является его централь-
центральная ось х и центр кручения сечения совпадает с его центром
тяжести. В случае несимметричного сечения, либо сечения с одной
осью симметрии, повороты сечений будут происходить не вокруг
центральной оси стержня, а вокруг оси, проходящей через центры
изгиба сечений (см. "§ 96). Центр изгиба в этом случае будет
и центром кручения*). При стеснённом кручении подобных
стержней будет иметь место не только изгиб полок, но и изгиб
стенок профиля. Однако общие результаты выводов могут быть
сведены к тем же уравнениям (ЗОЛ) — C0.4).
*) Понятие «обобщённая сила> связывают с соответствующим ей поня-
понятием «обобщённое перемещение> тем условием, что обобщённая сила равна
работе на обобщённом перемещении, равном 1.
2) См. например, Бычков и Мрощинский, Кручение и изгиб ме-
металлических балок, Стройиздат, 1944, стр. 64.

I 174]
ДЕФОРМАЦИЯ ТОНКОСТЕННОГО СТЕРЖНЯ
537
§ 174. Деформация тонкостенного стержня, связанная
с неравномерной депланацией сечений.
В предыдущем параграфе было показано, что задача определения
.напряжений в сечениях тонкостенного стержня при стеснённом кру-
Фиг. 467.
чении статически неопределима. Для раскрытия статической неопре-
неопределимости рассмотрим деформацию тонкостенного стержня с открытым
сечением произвольной формы,
контур которого очерчен кри-
кривыми линиями (фиг. 467). Кон-
Контуры поперечных сечений счи-
считаем недеформируемыми (см.
§ 173) в своей плоскости, а сече-
сечения, не остающимися плоскими.
Теоретические выводы о де-
деформации тонкостенного стер-
стержня, рассматриваемые ниже» хо-
хорошо согласуются с данными
опытов.
Пусть к свободному концу
тонкостенного стержня, заще-
защемлённого одним концом, прило-
приложен момент MQ, вызывающий
нзгибное кручение (фиг. 467).
Так как стержень взят несимме-
несимметричного профиля, то повороты	Фиг. 468.
сечений происходят вокруг их
Центров изгиба А. При повороте произвольного сечения на угол dB и
депланации его точка л, принадлежащая любому продольному волокну,
перемещается в новое положение пг (фиг. 468, 469)*). Это перемещение
*) Вследствие малой толщины стенок профиля можно считать, что инте-
интересующие нас продольные перемещения и соответствующие им нормальные
Напряжения по толщине стенки одинаковы. Поэтому можно ограничиться
рассмотрением деформаций волокон серединной поверхности.

538
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
можно рассматривать как состоящее из трёх составляющих: одной —
вдоль касательной к серединной линии сечения в точке п, (п — п%),
второй — вдоль образующей (перпендикулярной к плоскости чертежа
и потому на фиг. 468 невидимой) и третьей — (я2 — пг), перпендику-
перпендикулярной к касательной п — л2; последняя нас не интересует, так как
мы ищем удлинение волокна (вдоль образующей), связанное с депла-
нацией сечения.
Сначала определим тангенциальную составляющую перемещения
(п — п%), а затем продольную, которую можно связать с танген-
тангенциальной. Для определения танген-
тангенциальной составляющей перемещения
воспользуемся гипотезой о недеформи-
недеформируемости контура сечения. На основа-
основании этой гипотезы, при определении ка-
касательного перемещения, лежащего в
плоскости сечения, можно рассматри-
рассматривать перемещение сечения в новое поло-
положение как поворот жёсткого диска во-
вокруг центра изгиба (точка А на фиг. 468
и 469), лежащего в плоскости сечения.
Ограничимся рассмотрением пово-
поворота на бесконечно малый угол dB, счи-
считая его за угол поворота одного се-
сечения относительно другого, смежного
с ним, отстоящего на расстояние dx. При этом повороте точка п
опишет радиусом р дугу п — пи равную a = pd6.
Опустив перпендикуляр r — AD из точки А на продолжение ка-
касательной nD> получим при вершине А угол а, равный углу между
сторонами п — щ и п — п% треугольника пгпп%. Перемещение п-*~щ
по касательной равно
dv = a cos a.
Фиг. 469.
Имея в виду, что r= p cos а, получим:
dv = p db cos а = г d9.
C0.5)
Перейдём к отысканию продольной составляющей перемещения,
которую обозначим du. Рассмотрим два бесконечно близких сечения
ВС и DE с расстоянием между ними dx (фиг. 469).
При повороте сечения ВС относительно DE на угол db и пере-
переходе точки п в новое положение пг образующая kn повернётся на
угол у» равный, как видно из чертежа,
• у — dJL — —r<®-
1 dx	dx
dx
-
dxm
Знак минус взят потому, что отрицательному направлению угла dB
(если смотреть от начала координат вдоль оси х — против часовой

§174)
ДЕФОРМАЦИЯ ТОНКОСТЕННОГО СТЕРЖНЯ
539
стрелки) соответствует положительный угол т (по часовой стрелке,
если смотреть от полюса вдоль радиуса г), и наоборот (фиг. 469 —
470).
Выделим на серединной поверхности стержня около рассматри-
рассматриваемой точки п элементарный квадрат, одна из сторон которого
является элементом дуги ds (фиг. 470).
На основании гипотезы об отсутствии сдви-
сдвигов на серединной поверхности этот квадрат
при перемещении точки п в новое поло-
положение #i не перекосится, прямые углы его
останутся прямыми. Вследствие этого эле-
элемент дуги ds выйдет из плоскости попе-
поперечного сечения. Нижний конец элемента ds
сместится вдоль оси стержня относительно
верхнего на величину:
du — ds* sin
ds • у.
Подставляя вместо f его значение, найдём элементарное продоль-
продольное перемещение:
du = — ds • rr.
Полное перемещение, накопленное как сумма перемещений на эле-
элементарных отрезках ds, будет
Фиг. 471.
Здесь г — перпендикуляр, опущенный из
центра изгиба А на направление касатель-
касательной к серединной линии сечения, проведён-
проведённой через рассматриваемую точку п. Нетрудно
видеть (фиг. 471), что произведение rds
равно удвоенной площади заштрихованного
треугольника Ankt с основанием ds, кото-
которую обозначим flfco = 2 • пл. • Д Ankx. Сум-
Суммируя эти элементарные площади по длине дуги sf найдём некото-
некоторую удвоенную площадь:
a)=Crds.	C0.7)
s
Эта площадь названа секториальной площадью или секториаль-
рой координатой точки п, соответствующей дуге длиной 5, отсчи-
отсчитываемой от главной нулевой точки, для которой (о0 = 0. Методы
вычисления секториальных площадей для различных сечений приве-
приведены ниже (§ 179).

540
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
Заменив интеграл в выражении C0.6) секториальной площадью,
найдём величину полного продольного перемещения точки п, связан-
связанного с депланацией сечения:
и = — -j- • со.
dx
C0.8)
Из формулы C0.8) видно, что величина продольного перемещения
точки п пропорциональна её секториальной координате со. Следова-
Следовательно, секториальные площади являются мерой депланации рас-.
сматриваемого сечения. По длине стер-
стержня депланация зависит от относитель-
относительна
ного угла кручения -т-.
Теперь можно найти удлинение во-
волокна тп, длиной dx (фиг. 472). Если
при скручивании стержня точка п пере-
переместилась вдоль оси на величину м, то
точка т, отстоящая от неё на расстоя-
расстояние dx> вследствие неодинаковой депла-
депланации смежных сечений, получит переме-
перемещение щ = и-\- du. Значит, расстояние между точками пят изме-
изменится на величину, равную абсолютному удлинению отрезка dx:
kdx = щ — и = du.
Так как и = — -т- • со, где о> от х не зависит, а б является
функцией только одной переменной х, то относительное удлинение
волокна будет
Adx du
dx dx	dx2
е = — сов".
Фиг. 472.
;W,
или
C0.9)
Считая, что волокна друг на друга не	давят1), можем найти
закон изменения нормальных напряжений	по сечению, пользуясь
законом Гука:
au) = ?s = — ?u>8".	C0.10)
Таким образом, величина нормальных напряжений при стеснённом
кручении зависит от второй производной по х от угла закручивания
и следует закону секториальных площадей. Поэтому эти напряжения
и названы секториальными нормальными напряжениями. Гипотеза
плоских сечений, обычно принятая в курсе сопротивления материа-
материалов, может рассматриваться как частный случай гипотезы секториаль-
секториальных площадей.
*) Этой гипотезы В. 3. Власов не вводит, поэтому в полученных им урав-
уравнениях вместо модуля упругости Е стоит ?i = -j	g.

§ 175]	СЕКТОРИАЛЬНЫЕ НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ	541
§ 175. Секториальные нормальные напряжения.
Секториальные характеристики сечения.
В §§ 173 и 174 нами были составлены уравнения равновесия
выделенной части стержня и рассмотрена деформация некоторого
продольного волокна, возникшая в результате неравномерной де-
планации смежных сечений. Теперь остаётся использовать совмест-
совместное решение уравнений C0.1), C0.2), C0.3) и C0.10) для опреде-
определения величины о^.
Подставляя значение аш C0.10) в уравнения равновесия и имея
при этом в виду, что при суммировании по площади б" = -т-^
остаётся постоянным, получим:
?6". Г corf/7 =0 или Г corfF =0;	C0.11)
. ?б" . С uz dF= 0 » С <oz dF= 0;	C0.12)
P	P
?6" - XaydF=0 » С coy dF= 0.	C0.13)
Условие приведения нормальных напряжений к самоуравнове-
самоуравновешенной системе внутренних нормальных усилий потребовало обра-
обращения в нуль трёх интегралов.
Первый из этих, интегралов носит название секториального ста-
статического момента площади сечения и обозначается
5Ф= f corfF;	C0.14)
размерность его — единицы длины в четвёртой степени (напри-
(например, см*).
Два других интеграла называются секториально-линейными ста-
статическими моментами сечения и соответственно обозначаются:
\	C0.15)
= (coj/rfF;	C0.16)
размерность их — единицы длины в пятой степени (например, смъ).
Чтобы связать секториальные нормальные напряжения с внеш-
внешними силовыми факторами, расширим понятие об изгибно-крутящем
бимоменте как об обобщённой силе; соответствующим ей обобщён-

542
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
ным перемещением является -т-*). По данным таблицы 26а (см.
фиг. 473) составляем условия равенства работ внешних и внутрен-
внутренних сил на единичных перемещениях; в результате можно получить
выражение для изгибно-крутящего бимомента:
В= f a^-corf/7.	C0.17)
Вид дефор-
деформации
Растяже-
Растяжение (фиг.
473, а)
Изгиб
(фиг.
473, б)
Изгибное
кручение
(фиг.
473,*)
Таблица 26а. Обобщённые координаты и
Для работы внешних сил
обобщён-
обобщённая сила
Растяги-
Растягивающая
сила Р
Изгибаю-
Изгибающий мо-
момент М
Изгибно-
крутящий
бимо-
мент(мо-
мент(момент би-
пары)
В = МН
обобщён-
обобщённое пере-
перемещение
Удлине-
Удлинение
Д/=1
Угол по-
поворота
сечения
6=1
Относи-
Относительный
угол за-
кручива-
кручивания
db x
dx~
Для работы внутреннего
усилия
элементар-
элементарное вну-
внутреннее
усилие
a *dF
• dF
*<»dF
соответствующее
ему перемещение
Удлинение волок-
волокна при растяже-
растяжении Д/ = 1
Удлинение волок-
волокна при повороте
сечения 0 • г = 1 *z
Удлинение волок-
волокна при депланации
сечения
работа.
Условия равенства
работ внешних и
внутренних сил
Р= f <sdF
М= f vdF- z
Подставляя сюда значение oa) = — EQ"w из выражения C0.10),
получим:
;¦
] — _ ЕЪ" f
Интеграл i aPdF зависит только от формы и размеров сечения
и имеет такую же структуру, как и интеграл i z%dF, выражаю-
		V
%) Обращаясь к фиг. 470 и 473, устанавливаем, что момент бипары на
перемещении ^ совершает работу, равную А = 2М? = 2Mh -j- = B j~.
г ' h	dv	. л	л В dv D db
Так как y^7"» а 1~d~* то Ра"ота бимомента Л = ~ • ^"^^^Т*

175]
СЕКТОРЙАЛЬНЫЕ НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ
543
щий величину момента инерции при изгибе балки. Полученный новый
интеграл, т. е. сумма произведений из элементарных площадок
на квадраты их секториальных координат называется секториаль-
ным моментом инерции сечения и
обозначается Jm.
Следовательно, изгибно-крутя- а)\
щий бимомент равен:
B = — E6rrJ^ C0.18)
Подставив теперь в выражение
C0.10) j- вместо — ?6", найдем:
°<о=А^. C0.19)
Полученная формула по своему
виду совершенно аналогична фор-
формуле для нормальных напряжений
яри изгибе (о = -^). Таким обра-
обраФиг. 473.
зом, для вычисления секториальных
Напряжений необходимо изучить ме-
методы вычисления величин, входя-
входящих в формулу C0.19): изгибно-крутящего бимомента В, сектори-
ального момента инерции Jm и секториальных координат со.
' В целях развития представления об изгибно-крутящем бимоменте,
рассмотрим один приём вычисления внешних бимоментов*).
1 Пусть мы имеем в плоскости zOy ломаный стержень ABC, за-
защемлённый одним концом, к другому концу которого приложена
цара сил, лежащая в некоторой
плоскости, параллельной оси х
(фиг. 474).
Взяв сечение в расстоянии у
от начала координат, приложим в
точке А две равные и противопо-
противоположно направленные пары Af0 (в
плоскости, параллельной заданной
паре). В результате переноса пары	фиг> 474.
в точку А мы получили пару Мо задан-
заданного направления и совокупность двух противоположных пар Жо с рас-
расстоянием г между плоскостями их действия, т. е. бипару с бимоментом
' В = Мь-г. т	C0.20)
0 См. Б ы ч к о в Д. В., Расчёт рам, Стройиздат, 1948; П р а т у с е в и ч Я. А.,
Вариационные методы в строительной механике, ГТТИ, 1948.

544
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[ГЛ. XXX
Если к свободному концу того же стержня приложена не пара
сил, а сила Р, перпендикулярная к плоскости ЛВС (фиг. 475), то, пере-
перенеся силу в точку В, получим силу и пару сил с моментом М = Ре.
Опустив теперь из некоторой точки А перпендикуляр г на пло-
плоскость этой пары, получим (в соответствии с формулой C0.20))
значение изгибно-крутящего бимомента (момента бипары):
В = М-г = Рег.	C0.20')
Таким образом, изгибно-крутящий бимомент В относительно
точки А есть произведение изгибно-крутящей пары Ре на плечо —
Фиг. 475.
перпендикуляр г, опущенный из точки А на плоскость этой пары.
Выражение C0.20') можно представить и в другой форме. Как видно
из чертежа, произведение ет предста-
представляет собой удвоенную площадь тре-
В угольника ABC. Обозначим эту площади
через ш. Тогда
В = Рш.	C0.21)
Для ломаного стержня, состоящего из
трёх прямых отрезков, изображённого на
фиг. 476, после переноса силы в точки В
и О получим величину бимомента как сумму бимоментов двух пар
Мг = Рег (перечёркнута двумя чёрточками) и М$ = Ре2 (перечёрк-
(перечёркнута тремя чёрточками):
Фиг. 477.
Но e1r1 = u>i, т. е. удвоенной площади треугольника ACD, a efa —
удвоенной площади треугольника ABC и, окончательно,
В = Р (о)! -f- щ) = Рш,	C0.22)
где со — удвоенная площадь, заштрихованная на фиг. 476 !).
1) Формулой C0.22) можно пользоваться для определения внешних
изгибно-крутящих бимоментов лишь в случаях, когда жёсткостью стержня
при кручении можно пренебречь (см. § 177).

§ 1751
СЕКТОРИАЛЬНЫЕ НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ
545
Если плоский стержень имеет вид, показанный на фиг. 477, то
очевидно, что изгибно-крутящий бимомент, соответствующий дей-
действию приложенной силы Р, будет равен:
В = Рсо,
где (о — удвоенная заштрихованная площадь ABC.
Для перехода к вычислениям внешних изгибно-крутящих бимо-
ментов в тонкостенном стержне представим себе, что ломаные ли-
линии, рассмотренные выше (фиг. 474—477), изображают собой не ось
стержня, а среднюю линию его поперечного сечения, связанную
с полюсом А, а также, что точка Л,
в которую производился перенос сил,
является центром изгиба сечения. В
таком случае о> — это та же секто-
риальная площадь, о которой шла
речь в § 174. Действительно, если
в некоторой точке п поперечного
сечения стержня (фиг. 478) приложе-
приложено усилие dP=o(adF, то после пере-
переноса его в точку My оно приводится
к силе dP = a^dF и паре сил
Фиг. 478.
Опустив из точки А перпендикуляр на плоскость этой пары,
получим, в соответствии с формулой C0.20), изгибно-крутящий
бимомент
dB — dM • г = оф dF • 5 • г;
здесь 5 • г (удвоенная площадь треугольника АМп) и, следовательно:
Тогда величина изгибно-крутящего бимомента, действующего в се-
сечении, будет
Фиг. 479.
что совпадает с формулой C0.17),
полученной из других сообра-
соображений.
Бимомент иногда обозначаю^ как показано на фиг. 479, Усло-
Условимся относительно знака бимомента. Изгибно-крутящий бимомент
будем считать положительным, если при взгляде со стороны по-
полюса А вдоль радиуса г мы видим, что изгибно-крутящая пара вра-
вращает против часовой стрелки. В соответствии с этим на фиг. 478
бимомент положителен, а на фиг. 477 — отрицателен.
18 Н. М, Беляев

546
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ	[гл. XXX
§ 176. Дифференциальные зависимости между
силовыми величинами.
Уравнением C0.4) определяется связь между внешним моментом
и составляющими моментами внутренних касательных усилий.
Как было показано в § 173, при стеснённом кручении тонко-
тонкостенного стержня возникают соответственно и два вида касатель-
касательных напряжений:
1) касательные напряжения чистого кручения (фиг. 480, а)
2) секториальные касательные напряжения (фиг. 480, 6)> скла-
складывающиеся в сдвигающие усилия dT=ijlF и дающие момент Жш
относительно центра кру-
кручения А:
AL =
C0.23)
где г — перпендикуляр,
опущенный из точки А
на направление касатель-
касательного усилия. Складывая
эти компоненты полного
касательного напряжения,
получим (фиг. 480, в):
Для установления связи между действующими в сечении сило-
силовыми факторами, рассмотрим условия равновесия элемента длиной
dx, вырезанного из стержня, показан-
ного на фиг. 467. Этот элемент стер-
стержня находится в равновесии под дей-
действием нормальных и касательных напря-
напряжений, приложенных в сечениях / — /и
//_// (фиг. 481).
Нормальные усилия, действующие в
сечениях / — / и // — //, приводятся к би-
моментам В и B-\-dB. Приращение би-
момента dB должно равняться бимоменту
касательных усилий dT=*zdF относи-
тельно центра кручения Л. Соответст-
Соответствующий элементарный бимомент может
быть вычислен как произведение пары
Фиг. 481.
на плечо г (перпендикуляр, опущенный из точки А на плосцос^ь,
пары).

§ 176] ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ В, Ма И Ш	547
Имея в виду, что усилия dT возникают на каждой элементарной
площадке сечения, получим:
dB = i dM • г= 1 т dF • djc • г = dx i (tK -{- тс
или
Первый интеграл 1 zKrdF обращается в нуль, что легко дока-
доказать, воспользовавшись формулой интегрирования по частям1). Что
касается второго интеграла \ ij dFf то по формуле C0.23) он пред-
представляет собой изгибно-крутящий момент М^ Следовательно,
dB = dx- Мш или ~ » Мт.	C0.24)
Мы получили дифференциальную зависимость, аналогичную изве-
известной дифференциальной зависимости между изгибающим моментом
и поперечной силой при изгибе
Рассмотрим случай нагружения стержня непрерывно переменным
внешним моментом по длине стержня. Так будет, например, при
изгибе стержня равномерно распреде-
распределённой нагрузкой q, лежащей в пло-
плоскости, не совпадающей с линией
центров изгиба.
В этом случае внешний момент
Mq = Mx, создаваемый сплошной на-
нагрузкой, изменяется по длине стер-
стержня. Мерой изменения величины мо-
момента Мх является интенсивность
сплошной моментной нагрузки, кото-
которую обозначим т. Если нагрузка q неравномерно распределена
по длине, то и /п будет переменной величиной т = ()
^Действительно, представив r = «t a zKdF—dv и интегрируя
\TKrdF~ iudv= | uv\ — ivdu, получаем: i>= I x^dF^O, так как
сумма касательных усилий от чистого кручения zKdF по сечению F равна нулю.
Пк	F0
Поскольку « = 0, tqh[uv
от чистого кручения zK
— I tn/a] = 0rT. e. 1

548	ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ [ГЛ. XXX
Выделив из стержня элемент длиной dx и составив условие
его равновесия (фиг. 482), получим:
C0.25)
— (Мх-\- dMJ + т dx 4- Мх = О
или
Мы снова получили дифференциальную зависимость, аналогичную
dQ
соответствующему уравнению -^- — д9 выражающему связь между
поперечной силой и интенсивностью сплошной нагрузки.
§ 177. Дифференциальное уравнение деформаций при
стеснённом кручении. Определение силовых факторов.
На основании полученных в § 176 зависимостей между сило-
силовыми факторами В, М^ Мх и т можно составить дифференциальное
уравнение углов закручивания, подобное дифференциальному уравне-
уравнению изогнутой оси стержня.
Так как внешний крутящий момент равен
'	. C0.4)
то формулу C0.25) можно написать в таком виде:
^к + ^.=от>	(Зо.26)
Из теории чистого кручения известно, что
,0 MKdx	%я ~. dQ
dQ = -^j— или Мк = OJK -г-;
GJK	к к dx'
продифференцировав, получим:
dx	Kdx2	K
С другой стороны, имея в виду, что М0) = -г-, получим:
=	в
dx dx2
Если выразить В через 0 по формуле C0.18), т. е. В = —
то В" •= — EJ<tfllw, и уравнение C0.26) примет вид:
Окончательно:
?/j}iv — GJJ" + т = 0.	C0.27)
Это и есть дифференциальное уравнение углов закручивания
для случая изгибного кручения. Проинтегрировав его и определив

§ 177] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СТЕСНЁННОГО КРУЧЕНИЯ	549
произвольные постоянные из начальных условий, можем найти вели-
величину угла закручивания б в любом сечении стержня, чем решается
задача определения всех силовых факторов:
: = — EJj";	C0.28)
Для проверки вычислений можно воспользоваться уравнением C0.4).
Уравнение C0.27) может быть упрощено, если учесть, что для ряда
случаев практики вторым членом дифференциального уравнения
можно пренебречь вследствие малой жёсткости тонкостенного
стержня при чистом кручении. Положив OJkp^0, получим:
Уравнение равновесия C0.27) может быть представлено и в дру-
другом виде, как дифференциальное уравнение бимоментов. Так как
из формулы C0.18) 0" = —дгу- и значит, 6IV = — -=y-t то взамен
C0.27) получим:
Обозначая отношение жёсткостей через а* = -^, имеем
m.	C0.29)
Общий интеграл уравнения C0.29) имеет вид:
В = Q sh out -f C2 ch сих -\- Во.
Здесь а=1/ -^~ — изгибно-крутильная характеристика стержня, а
В9 — частный интеграл, удовлетворяющий дифференциальному уравне-
уравнению C0.29). При т, изменяющемся по линейному закону, Во = — -^*
Произвольные постоянные Q и С2 определяются для каждого
частного случая загружения стержня в зависимости от условий его
закрепления и условий сопряжения смежных участков (при наличии
нескольких участков).
Общий интеграл неоднородного дифференциального уравнения
C0.27) может быть представлен в форме:
6 = Z?! -f- D^x -f- ZK sh ax -f- Dk ch ax -f- бл (х),
где Du ZJ, Dd и D4 — произвольные постоянные, определяемые из

550	основы расчёта тонкостенных стержней	[гл. ххх
граничных условий; 9А (х) — частное решение неоднородного уравне-
уравнения C0.27), подбираемое в зависимости от вида загружения1).
Для определения постоянных D всегда имеются четыре условия
закрепления концов стержня. Так например, для стержня на двух
опорах, конструкция которых препятствует .повороту концевых
сечений, но допускает свободную их депланацию, можно написать:
при х = 0 0О = О и в;' = 0 (иначе Б0 = 0);
» х = 1 е/ = 0 и e/ = 0 (иначе Bt = 0).
Для 0алки, абсолютно защемлённой одним концом, другой конец
которой свободен и незагружен, условия на границах имеют вид:
при х = 0 6 = 0 и 6' = 0
> х = 1 У = 0 и MX = OJKV — EJJT" = 0.
Таким образом, из уравнений C0.28) могут быть найдены все
силовые и деформационные факторы:
C0.28')
= Dt + DiX + Dz sh ax \ ?>4 ch clx + bA;
6"f _ _ ^ _ аздз ch ад; _j_ азд4 sh ад. _|_ e?.
Применив метод начальных параметров, т. е. считая, что в выбран-
выбранном начальном сечении все геометрические и силовые факторы имеют
вполне определённые значения 80, в'о, Во и Мо и предполагая, что
стержень находится под действием только этих начальных факто-
факторов, можем получить из уравнений C0.28') при х = 0:
в0 = Dx + ?>4; % = As + aD3; ?0 = — G/KD4; M% =
откуда
'(Бычков Д. В. и М рощи не кий А. К., Кручение металлических
балок, Стройиздат, 1944 г. § 16.

§ 177] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СТЕСНЁННОГО КРУЧЕНИЯ	551
Подставив эти значения произвольных постоянных в уравне-
уравнения C0.28') и имея в виду, что при отсутствии внешней нагрузки
частный интеграл 6д (х) равен нулю, получим*):
C0.30)
Если, кроме начальных факторов, на стержень действуют геомет-
геометрические и силовые факторы, приложенные в некотором сечении
jt=/, то изгибно-крутильные факторы для x^t по методу нало-
наложения будут зависеть также и от Bti 6J, Bt и Mt.
Первая из формул C0.30) в этом случае примет вид:
shajc
(заз(Г)
Аналогично црлучаются и остальные формулы. Формулы C0.30)
позволяют решить задачу о стеснённом кручении стержня при любом
характере действия нагрузок и потому имеют весьма важное значе-
значение для практических расчётов.
В таблице 27 приведены результаты решения уравнения C0.27)
для часто встречающихся схем загружения t балок и даны выраже-
выражения изгибно-крутящих бимоментов В, изгибно-крутящих моментов Мш
и крутящих моментов Жк2). Через е обозначено расстояние от
плоскости действия сил до линии центров изгиба сечения, показан-
показанной на каждой из схем.
Через Во обозначено выражение для сосредоточенного бимомента,
возникающего от действия пары сил Мо, приложенной в плоскости,
параллельной главной центральной плоскости, на расстоянии е от
центра изгиба. Величина Во зависит от способа приложения внешней
пары: если Мо образован действием пары поперечных сил, то Во =
= Мое; если же Мо реализуется в виде пары продольных сил Р, то
*) См. Власов В. 3., Упругие тонкостенные стержни, 1940, §11.
*) Б ычков Д. В. и Мрощинский А. К., Кручение металлических
балок, 1944.

552
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
X
o
2
X
X
1
X
0)
s
er>
s
s
s
s
руче
as
S
Q.
a
ров
2
•8-
ВЫХ
о
*?
X
о
к
улы дл
Форм;
со
И
«=;
СО
Е-
к
s
в
о
V
>>
сх
м
о
и
о
н
и
S
tf
енты
я
О
S
:
3
в
оме
я
о
н
>>
И
-01
\о
Я
{_
S
«Э
3
к
<и
Я
о
S
to
ящие
*бно-крут
Изп
S
и
irpys
в
S
>алки
СО
5
X
и
^ fch
t
1
о
х:
1
1
•»»
ел
1
^»
II
max
о
||
II
"в s
XJ С
з
и
1
о
II
х: s
max В
1
ко -
1
и
т
'С
»
х:
о
и
х:
ел
в
*:)ch
н
о
х:
С/)
в
х;
и
х:
х:
о
»
i +
§.-
•s
" 1
i
1
I
¦*
•*-
II'
v>
при j
и
сЗ
в
о
II
Н
при
3
стз
В
, о
II
при
max В
I
в
xt
ел
С
«
х:
ел
е
1
1
о
х:
е
i
/
7Т
1
Т
X
^*
"о
а
"а
II
s
max
||
и
3
•и
S
1
при
max В
^ \
СО
х:
4
в
х:
х:
ел
о
¦5 S.
С
:^- ^
<м и
i
II
II
*Jr 1
з
И
Гв
В
1
(N
\
II
CM 0Q
И
cd
В
—j
а, /
г
съ
7~
Т
г
U

§ 177] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СТЕСНЁННОГО КРУЧЕНИЯ 553
К
о
ex
С
ее
5
сручея
о
чистог
3
ент
Мом
3
3
X
ящие моме
н
>ч
CU
бно-к
К
1*
т
5
«3
3
н
мен
о
Я
S
ю
н
о.
о
S
VO
S
и,
m
S
S
сч
>»
О.
t_
ЛКИ И Hi
<0
VO
cd
Cxei
t
1
1
-|<N
x:
CO
V
о
-5 II
ч
s
и
cd
1 1
8.
1
Cft
О
II
в
м s.
3
1 .
i 1
1
1
«
x:
о
Си
с
03
*-ч CO
Г ! С
1
1
1
?
¦*.
¦>¦
?
"Г
	1
,—
—1
X
1
1
в
•С
в
JC
со
1—.—1
о?
о
Я"
1
1
W
х:
CJ
в
о
1
1
в
с/э
1
в
со
о
в
х:
со
Т
t
о
II
ч
ж
с
X
в
о
II
Ч
S
с
3
max
о
и
при х-
X
1
Г»
А 1
-о
со
Г
(Л
j
1
в
¦S
|
ся
1
1
в
со
—г-
•S
1 '
On 1
^	^
ч '¦*
1
8
х:
о
1
8
Peli
||
и
Ч
СО jg
(N ^
X
В '
j
и
II
8
X
(У
S
о
^ II
о* й
3
?
II
II
Ч
X
V
SS
ЕМ О
II
С
03
max
f
? ?
jui

554	ОСНОВЫ РАСЧЕТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ	(ГЛ. XXX
/?0 = Я (coj-f-<*>«)> где а>А и а>2—секториальные координаты точек при-
приложения сил Р.
Полученные выше дифференциальные уравнения позволяют про-
провести аналогию между теорией изгибного кручения и плоского
изгиба. Дифференцируя по х уравнение C0.18), получим:
EJJ" = —1
~ ^ '	C0.31)
Здесь т^ — интенсивность изменения изгибно-крутящего момента.
Уравнения C0.31) аналогичны равенствам A2.3) — A2.5). Однако
между этими двумя группами дифференциальных уравнений имеется
принципиальная разница. Если из второй системы уравнений путём
интегрирования их можно найти значение у, так как при заданной
нагрузке q величины Q и М известны, то из первой группы уравнений
C0.31) величину 6 найти нельзя, так как при заданной внешней
нагрузке величина тш сама неизвестна.
В случае, когда в уравнении C0.27) можно пренебречь жёсткостью при
кручении, последняя строка системы C0.31) преобразуется и примет вид:
Поскольку интенсивность т изменения внешнего момента известна,
аналогия вступает в свои права, и легко сраз/ найти все неизвест-
неизвестные величины.
Так, например, если для балки на двух опорах, загружённой по
всему пролёту равномерно распределённой нагрузкой, известно, что
тахМ = ^- и max f^^ET*
то при изгибном кручении той же балки можно написать по аналогии:
о ml2,	л 5т/4
тах/* = -тр и тах0 = -
Точно так же для консоли, загружённой сплошной нагрузкой q,
имея в виду, что
я/2	г л/4
тахМ = 22~" и шах/=-
можно написать:
->_я*/2 и 	* ю/4
— 2
В обоих случаях m = qe, где е — плечо нагрузки относительно
линии центров изгиба.
Следует иметь в виду, что эти результаты являются приближён-
приближёнными и что приведённая выше аналогия справедлива при OJK весьма
малом. По данным Д. В. Бычкова ошибка будет не более 5% в слу-
случае, если а/ не превосходит следующих значений:
' для консоли	при а/<0,5,
для балки на двух опорах	при а/< 0,75,
для балки, защемлённой обоими концами при а/ < 1,50.

§ 173]
ВЫЧИСЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
555
§ 178. Вычисление касательных напряжений
в сечении тонкостенного стержня.
Теперь, когда все силовые факторы определены, остаётся про-
произвести вычисление касательных напряжений, возникающих в се-
сечении стержня под действием внешнего крутящего момента
м.=мж+мт.
О касательных напряжениях от чистого кручения уже было
сказано в §§ 173, 176 и 67 [формулы A1.37)]. Для определения
секториальных касательных на-
напряжений воспользуемся той - /~
же методикой, какая была при-
принята при выводе формулы Жу-
равского (§ 91).
Вырежем из рассматривае-
рассматриваемого стержня (фиг. 467) эле-
элемент длиной dx, одна из гра-
граней которого (например, ниж-
нижняя) свободна от касательных
напряжений (фиг. 483). Эле-
Элемент находится в равновесии
под действием секториальных
нормальных и касательных напряжений. Обозначим нормальные напря-
напряжения, действующие на левую грань /—/ и на правую 2—2 соот-
соответственно;
°«> 1 = —
Фиг. 483.
И Om(q\ =
По этим же граням действуют секториальные касательные напря-
напряжения т^. По закону парности касательные напряжения т^ действуют
также по площадке, параллельной оси х. Эти касательные напря-
напряжения должны сложиться в усилие, уравновешивающее разность
нормальных усилий, действующих в сечениях /—/ и 2—2 по тор-
торцевым площадкам отсечённого элемента.
Величины нормальных усилий соответственно равны:
^OT
и W2 =
1
Так как интеграл \ mdF представляет собой секториальный стати-
ческий момент отсечённой площади торца элемента [см, форму-
формулу C0.14)], то
BSl	B + dB «в
и Nt = —j-'—Sl»

556
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
а сдвигающая сила, уравновешиваемая секториальными касательными
напряжениями, равна:
Отсюда величина искомых секториальных касательных напряже-
напряжений будет:
dN dB Si
C0.32)
J Г}
Имея в виду, что -г- = М(О C0.24), получим:
Структура полученной формулы совершенно аналогична струк-
структуре формулы Журавского для вычисления касательных напряже-
напряжений при поперечном изгибе. Заметим, что величина секториальных
касательных напряжений сравнительно невелика. Однако, несмотря
на это, они принимают на себя значительную долю внешнего мо-
момента, так как плечи соответствующих касательных усилий обычно
велики (см., например, фиг. 466, б).
В формулы для секториальных напряжений C0.19) и C0.32)
входят секториальные координаты и новые секториальные геоме-
геометрические характеристики сечения, методы определения которых
приводятся ниже (см. §§ 179 и 180).
§ 179. Вычисление секториальных площадей.
Построение секториальных эпюр.
Выше было показано, что секториальная нлощадь равна C0.7):
со = V г ds,
s
где г — перпендикуляр, опущенный из полюса А на направление
касательной к средней линии сечения, проведённой через данную
точку (фиг. 484). Пределы
интегрирования определяют-
определяются выбором начала коорди-
координат, т. е. того луча AM, от
которого ведутся отсчёты.
Точка М, лежащая на сред-
средней линии сечения, назы-
называется началом отсчёта.
Как известно (§ 174), ин-
интеграл \ rds равен удвоен-
S
ной площади заштрихованного на фиг. 484, а сектора, ограниченного
лучами AM, An и контуром средней линии сечения. Для контура,
Фиг. 484.

§ 179]
ВЫЧИСЛЕНИЕ СЕКТОРЙАЛЬНЫХ ПЛОЩАДЕЙ
557
ограниченного прямыми линиями, секториальная площадь равна удвоен-
удвоенной площади треугольника, заключённого между линией контура и
лучами AM и An (фиг. 484, б).
Нетрудно видеть, что каждой точке сечения соответствует своя
секториальная площадь. Поэтому секториальную площадь можно
рассматривать как секториальную координату данной точки.
Если вычислять значения секториальных площадей для каждой
точки сечения и откладывать их в определённом масштабе по нор-
нормали к средней линии сечения, то мы получим так называемую
эпюру секториальных площадей, т. е. график, показы-
показывающий закон изменения со по контуру сечения.
При криволинейном контуре сечения длина перпендикуляра ri
а значит и величина секториальных площадей о), изменяется по
длине контура, в зависимости от его очертания [a) = co(s)]. В этом
случае эпюра секториальных площадей будет криволинейной.
Если контур сечения представляет собой ломаную линию, то
для всех точек каждого прямолинейного участка величина, г будет
иметь одно и то же значение и эпюра секториальных координат
(фиг. 484, б) будет состоять из отдельных прямолинейных участков.
Условимся о знаках. Знак секториальной координаты о> для не-
некоторой точки п считаем положительным, если подвижной радиус-
'вектор при переходе от выбранного начального радиуса AM в по-
положение An поворачивается по часовой, стрелке (фиг. 485, а). В об-
обратном случае величина <d считается отрицательной (фиг. 485, б).
Если радиус-вектор пересекает контур сечения, то секториальная
площадь определяется как алгебраическая сумма двух площадей
разных знаков (фиг. 485, в):
ш = — гф -\- г^а = — ®\-\- <*>2»
Как это видно из сопоставления чертежей (фиг. 485, а и
фиг. 485, г), если начало отсчётов взять не в точке Ж, а в другой
какой-нибудь точке Мь то секториальная площадь (координата) для
той же точки получит другое значение и по величине, и по знаку.
м
Фиг. 485.	N
Нетрудно видеть, что величина секториальной площади зависит
также и от положения полюса А, из которого ведётся построение.

558	ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ [т. XXX
До сих пор во всех выводах мы исходили из предположения, что
секториальные площади строятся из центра изгиба, положение кото-
которого считалось известным. Однако иногда построение эпюры секто-
риальных площадей выполняют, пользуясь произвольным полюсом,
что даёт новые значения секториальных координат.
Условимся относительно выбора положения полюса и начала отсчё-
отсчётов при построении секториальных эпюр следующим образом.
Главным векториальным полюсом будем считать центр изгиба
сечения А, пользуясь которым в дальнейшем мы и будем вести
построение секториальных эпюр.
Начало отсчётов секториальных площадей будем вести от опре-
определённой точки сечения, называемой главной нулевой секториальной
точкой. Как уже указывалось (§ 173), в 'сечении тонкостенного
стержня, подвергающегося стесненному кручению, имеются точки,
где о^ = 0 (нулевые точки).
Главной кнулевой секториальной точкой М назовём нулевую
точку, которая находится в кратчайшем расстоянии от центра
изгиба Л.
Радиус А-М назовём главным начальным радиусом, а секто-
риальную эпюру, построенную от него — эпюрой главных секто-
секториальных площадей.
В дальнейшем для определения положения главного секториаль-
ного полюса и главной нулевой точки, нам придётся предварительно
строить секториальные эпюры при произвольном выборе этих точек
(подобно тому, как для отыскания положения главных центральных осей
инерции сечения балки приходится сначала вести отсчёты от произвольно
выбранных осей). Чтобы затем перейти к глав-
главным секториальным точкам, удобно воспользо-
воспользоваться приводимыми ниже формулами перехода
к новой системе секториальных координат.
а) Изменение накала отсчёта дуги $ равносиль-
равносильно изменению пределов интегрирования функции
W= i
Фиг. 486.	что веД?Т к изменению значения секториальной
площади на постоянную величину. Это видно из
фиг. 486; при перенесении начала отсчётов из точки Мх в точку М,
секториальная координата какой-либо точки получит значение:
а> = (о' — (oM,	C0.33)
где о/ — секториальная координата точки п при исходном начале
отсчётов в точке Mi9 a wM— удвоенная площадь сектора AMiMf
т. е. секториальная координата новой начальной точки М, отсчитан-
отсчитанная от прежнего начала отсчётов Mt.

179]
ВЫЧИСЛЕНИЕ СЕКТОРИАЛЬНЫХ ПЛОЩАДЕЙ
559
б) Формула перехода при перенесении полюса из точки А9
в точку А может быть получена из следующих соображений
(фиг, 487).
Возьмем на средней линии сечения любую точку п(у, z) (начало
координат у и z для простоты взято в точке А9). Для точки Лв эле-
элементарная секториальная площадь имеет значение dm9 = ds*r9.
Если мы теперь перенесём полюс в точку А(уА, zA), то
элементарная секториальная
площадь для той же точк» п h*	у
будет:
Длина перпендикуляра гА
может быть выражена через I ^^ /
г0 так:	1	\l^J2S1^J*
= r0 — zA sin a —yA cos a,
где sina=—-—-, a cosa=
dz
«=-г-; следовательно:
гл =ro + zA^ — yAg.	фиг- 487-
Или, умножив на ds и имея в виду, что dwA =ds • гА% получаем:
da>A = <fo>t -|- гд dy —^д • dz.
Проинтегрировав, находим:
-С.	C0.34)
Это и есть формула перехода к новому полюсу. Здесь ш0 — секто-
секториальная площадь, полученная из произвольного полюса Ло; ул>
zA—координаты нового полюса А; С — произвольная постоянная,
зависящая от выбора начала отсчёта дуги $.
Полученные формулы C0.33) и C0.34) позволяют перейти от
произвольных исходных точек — полюса и начала отсчётов —
к главным секториальным точкам: центру изгиба и
к главной нулевой секториальной точке. Отыскав таким образом
положение главных секториальных точек для сечения тонкостенного
стержня, мы сможем построить эпюру главных секториальных пло-
площадей (координат).
Имея в виду, что 0^ = -^ и что для данного сечения отноше-
В
Ййе 7- = const, т. е. имеет вполне определённое значение, можно

560
ОСНОВЫ РАСЧ&ТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
рассматривать эпюру секториальных координат как график нормаль-
нормальных напряжений с^, изображённый в некотором масштабе.
Пример 115. Построить эпюру секториальных координат для корыт-
ного профиля, изображённого на фиг. 488.
Расстояние от средней линии контура до центра изгиба А обозначим ау.
Начало отсчётов ведём от луча AM; точка М лежит на оси симметрии Оу.
Построение эпюры секториальных площадей для рассматриваемого сече-
сечения начнём с определения се кториальной координаты для точки 1 — пере-
пересечения полки со стенкой. Пово-
Поворачивая радиус-вектор от поло-
положения AM до А — Д получим
.	треугольник с основанием
Si = -я- и высотой Гх =
. Зна-
Знаб)
* чит, для рассматриваемой точ-
точки / секториальная координата
равна:
щ=-ау^. C0.35)
Знак минус взят потому, что
радиус-вектор был повёрнут
против часовой стрелки от на-
начала отсчётов. Найденную вели-
величину «л откладываем в некото-
некотором масштабе в точке 1 нор-
нормально к средней линии стенки швеллера наружу (влево). Так как точка 1
принадлежит как стенке, так и полке швеллера, то такую же ординату ык
откладываем также наружу (вверх) нормально к средней линии стенки.
Теперь повернём радиус-вектор А — 1 в положение А—2. При переходе
от точки / к точке 2, радиус-вектор вращается по часовой стрелке. Зна-
Значит, к отрицательной ординате <oi следует прибавить удвоенную площадь тре-
треугольника А —1 — 2 с высотой г2 =
h	и
A/	i =г— и основанием s2 = #
Фиг. 488.
¦ 2 — ау 2 + 2 ~~
~!L(b—.aл C0.36)
б)
Фиг. 489.
Откладываем ординату <о2 нормально
к полке вниз (в сторону, противопо-
противоположную (йг).
Аналогична определяются орди-
ординаты эпюры со для точек 3 и 4 ниж-
нижней части сечения. В пределах ка-
каждого участка профиля со изменяется
по закону прямой линии.
Пример И6. Построить эпюру секториальных координат для стержня
двутаврового сечения (фиг. 489).
Вследствие симметрии сечения центр изгиба совпадает с центром тяже-
тяжести сечения. Так как в этом случае расстояние от полюса до оси стенки
профиля г = 0, то и секториальные координаты для всех точек, принадлежа-
принадлежащих стенке двутавра, также равны нулю.

§ 180] ОПРЕДЕЛЕНИЕ СЕКТОРЙАЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК 561
Для полок, выбрав начало отсчётов в точке М, легко найдём значения
секториальных координат. Для точки 1 удвоенная площадь треугольника
А— М — 1 с высотой г = -тг и основанием s = -~- будет:
h Ь	bh	л _
о)!= — у •-2- = — ".	C0.37)
Знак минус взят потому, что радиус-вектор повёрнут от. начала отсчёта
против часовой стрелки (из положения AM в положение А — /). Такую же
величину получат ординаты других трёх точек а>2, <о3 и о>4. Знаки опреде-
определяются в зависимости от направления вращения подвижного радиуса-вектора
от начала отсчётов. Эпюра ш показана на фиг. 489, б.
Как мы видим, для профилей, имеющих ось симметрии, эпюры секто-
секториальных площадей оказываются обратно симметричными (или, иначе, косо
симметричными).
§ 180. Определение секториальных геометрических
характеристик сечения.
Для- расчёта тонкостенных стержней помимо вычислений, свя-
связанных с определением главных центральных моментов инерции,
необходимо:
а)	Найти положение главного секториального полюса, т. е. центра
изгиба сечения А.
б)	Отыскать положение главной нулевой секториальной точки
Ж, т. е. начало отсчёта секториальных координат.
в)	Построить эпюру главных секториальных координат а>.
г)	Подсчитать величины секториальных статических моментов
5да и главного секториального момента инерции сечения J^.
Укажем порядок выполнения соответствующих расчётов.
А. Отыскание положения центра изгиба сечения производится
на основании уравнений C0.12) и C0.13), полученных в § 175 из
условия, что повороты сечений происходят вокруг центра кручения,
совпадающего с центром изгиба
Здесь о) = а>л-секториальная координата точек сечения относи-
относительно главного секториального полюса, положение которого нам
пока неизвестно, а у и z — линейные координаты тех же точек
в системе главных центральных осей сечения.
Подставим значение и>д = о> из выражения C0.34) в уравнения
C0.12) и C0.13). Тогда:
f ®A.zdF=
где (o0 — секториальная координата, отсчитанная от произвольного
полюса Ло; уА и zA — координаты центра изгиба. Так как Оу и

562 ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ [гл. XXX
Oz— главные центральные оси сечения, следует положить равными
нулю центробежный момент инерции и статический момент площади
сечения:
Jzy= tzydF=0; [
Заметив, что
получим:
откуда
ул = —.—;	C0.38)
Jy
Jy
аналогично
1 (лоу dF
C0.39)
Таким образом, для определения координат центра изгиба в си-
системе главных центральных осей сечеция надо подсчитать секто-
риально-линейные статические моменты сечения относительно про-
произвольного полюса А и главных центральных осей инерции и поде-
поделить их на соответствующие моменты инерции, т. е.
уа=^; * = -V.	C0.40)
Конструкция гэтих формул ничем не отличается от аналогичных
формул для определения центра тяжести сечения:
Координаты центра изгиба не зависят от величины С [в формуле
C0.34)], т. е. от выбора того или иного начала отсчётов секториаль-
д	д	 ных площадей. Таким образом, для оты-
	» екания величин уА и zA начало отсчётов
II
может быть взято произвольно.
Если сечение имеет оси симметрии,
то отыскание центра изгиба упрощается.
При наличии двух осей симметрии центр
изгиба лежит в: центре тяжести сечения.
Фиг. 490.	Если сечение имеет только одну ось сим-
симметрии, то центр изгиба лежит на ней.
В случае, если сечение состоит из прямоугольников, пересе-
каклцихся в одной точке (тавр, уголок и т. п.), то центр изгиба
лежит в точке их пересечения (фиг. 490).

§ 180] ОПРЕДЕЛЕНИЕ СБКТОРЙАЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК 663
Б* Положение главной нулевой секториальной точки опреде-
определяется уравнением C0.11)
Здесь секториальные площади отсчитываются от полюса А,
являющегося центром изгиба, с началом отсчёта от главной нулевой
секториальной точки, положение которой нам пока неизвестно.
Как было показано в § 179, при перенесений начала отсчётов
секториальная координата любой точки может быть определена по
формуле C0.33)
где «/ — секториальная координата точек при начале отсчётов
от произвольной точки Ми а <*>м — секториальная координата иско-
искомой.нулевой секториальной точки. Подставляя а> в формулу C0.11),
получим:
ИЛИ
откуда
= С w'dF— ^u>MdF=0
I
C0.41)
Таким образом, выбрав произвольное начало отсчётов, мы
по формуле C0.41) можем определить секториальную координату
нулевой точки, удовлетворяющую условию C0.11). Вообще говоря,
этому условию может удовлетворить не одна, а несколько нулевых
точек профиля. В таком случае, главной секториальной нулевой
точкой, как уже указывалось, мы будем считать ту, которая нахо-
находится в кратчайшем расстоянии от главного секториального полюса.
Если сечение имеет ось симметрии, то главная нулевая секториаль-
секториальная точка лежит на пересечении этой оси со средней линией
сечения.
Теперь, когда положение центра изгиба и начала отсчётов опре-
определено, можно построить эпюру главных секториальных координат
и перейти к вычислению тех секториальных геометрических харак-
характеристик сечения из перечисленных ниже в таблице 28, какие
понадобятся в дальнейших расчётах. Мы здесь ограничимся вычи-
вычислением их для наиболее распространённых профилей1).
1) Общие методы вычисления секториальных характеристик см. Вла-
Власов В. 3. Упругие тонкостенные стержни, ГСИ, 1940.

564
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
Таблица 28. Секториальные геометрические характеристики
тонкостенных профилей.
Наименование
Секториальный статический
момент
Секториально-линейный стати-
статический момент относительно
полюса А и оси у
То же — относительно оси z
Секториальный момент инер-
инерции сечения
Обозначение
Sa = С со dF
P
Jm = ^ <** dF
Размер-
Размерность
CM4
CM*
см*
CM9
Для прокатных профилей секториальные характеристики по ОСТ
приведены в таблицах (см. приложение IX, табл. 5).
§ 181. Примеры вычисления секториальных геометрических
характеристик сечения.
1) Корытное сечение (фиг. 491).
Для определения положения центра изгиба выберем вспомогательный
полюс в точке Ао на оси у, от которого построим эпюру секториальных
Эпюра ш0 Эпюра у
У ~(
б) в)
Фиг. 491.
Эпюра г
J.
иниашнн л
координат оH. Эта точка принята за начало отсчётов для построения вспо-
вспомогательной эпюры секториальных площадей (фиг. 491, б).

§ 181]	ПРИМЕРЫ ВЫЧИСЛЕНИЯ СЕКТОРИАЛЬНЫХ ХАРАКТЕРИСТИК	565
Чтобы воспользоваться формулами C0.40), остаётся вычислить секто-
риально-линейные статические моменты S и Swz:
с*
о>0у==
Эти интегралы могут быть вычислены по способу Верещагина (см. § 131)
путём умножения площади эпюры щ на ординаты эпюр у или z, лежащие
под центром тяжести площади <о0. Построение эпюр у и z не требует пояс-
пояснений: откладываются расстояния точек средней линии контура сечения от
осей Oz (эпюра у) и Оу (эпюра z). Соответствующая эпюра расстояний z
приведена на фиг. 491, г. Построение эпюры у выполнено на фиг. 491, в.
Таким образом, интеграл 5Ш г = 1 uozdF= I a>0 zb • ds может быть заме-
0 г J
нён произведением:
„	п b bh . h
Поделив рЩг на момент инерции сечения относительно оси у, найдём
Имея в виду, что Jy — -—- -|- 2 • bt-jr Jt получим окончательно:
QA2/
Ь	;
<30-42)
= 0, так как Seft)f=
= I
(в силу того, что эпюра <а0 обратно симметрична, а эпюра у — симметрична).
Знак минус у пу показывает, что полученную величину ау следует отложить
от точки Ло влево.
Теперь, используя формулу C0.41), перейдём к отысканию главной нуле-
нулевой секториальной точки на контуре сечения. Как уже указывалось, для
сечения, имеющего ось симметрии, нулевая точка лежит на пересечении
этой оси со средней линией сечения, т. е. в данном случае на середине
высоты стенки. В целях ознакомления с методикой отыскания главной нуле-
нулевой секториальной точки, будем считать положение её неизвестным'и вос-
воспользуемся для её нахождения общим решением по формуле C0.41).
Для этого из главного полюса А (положение которого уже найдено)
построим эпюру секториальных координат а>', взяв за начало отсчётов произ-
произвольную точку /. Секториальные координаты будут (фиг. 492, а):
для точки 2(о2' = у^;
>	> 3 о>з = uyh\
>	» 4 ^ = ayk-b± = -^(b-2ay).
1) Собственными моментами инерции полок, за малостью, пренебрегаем.

566
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл.
Соответствующая эпюра секториальных координат построена на фиг. 492, б.
Секториальный статический момент 5Ш= i u'hds может быть подсчитан
теперь как сумма произведений площадей эпюры <о' на соответствующие
толщины полок (t) и стенки (bt):
Теперь, пользуясь формулой C0.41), определяем секториальную коорди-
координату нулевой точки от выбранного начала отсчётов:
Как видно из построенной эпюры <о', найденная координата соответствует
трём точкам: одной, лежащей посредине высоты стенки (средняя линия
треугольника), и двум другим, лежащим на полках на расстоянии ау от стенки.
Так как первая точка (М) является ближайшей к центру изгиба, то она
является главной нулевой секториальной точкой сечения.
(Ь.ау)
е)
Теперь строим эпюру главных секториальных координат, руководствуясь
указаниями § 179. Эпюра <о построена на фиг. 492, в.
Остаётся вычислить секториальный момент инерции сечения:
7Ш == 1 <о2 dF= 1 оJ ds ¦ Ь = 1 « . Ms.
Выполняя интегрирование по способу Верещагина| получаем:
2 h
 ' 3 " 2
hHa
y (b~ayfh4
* "~ 12 + 6 *	Ъ
подставляя вместо ау найденное выше его значение C0.42), получим:
12
C0.43)

§ 181]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ СЕКТОРИАЛЬНЫХ ХАРАКТЕРИСТИК
567
Наконец, пользуясь эпюрой главных секториальных координат, легко
Подсчитать и величину секториального статического момента отсечённой
части сечения
f
«dF=
этот интеграл равен площади отсечённой части эпюры «, умноженной на
соответствующие толщины стенок профиля. Закон изменения секториального
статического момента (эпюра SJ, а следовательно, и секториальных каса-
касательных напряжений, изображён на фиг. 493.
Наибольшая ордината эпюры ?ш равна площади треугольника, лежащего
правее нулевой точки эпюры <о (фиг. 492, в):
C0.43')
На фиг. 493 стрелками показано направление касательных напряжений,
приводящихся к изгибно-крутящему моменту Мю.
2) Двутавровое сечение (фиг. 494). Вследствие симметрии центр изгиба
сечения находится в центре тяжести. Нулевые точки, по той же причине,
«ежат посредине полок.
Эпюра главных сек-
секториальных координат
была построена ранее „„	,,,,„
(§179) и приводится здесь sJ**1-^*	I	ГЩШ ЬЬ
(фиг. 494) для вычисления
главного секториального
момента инерции сечения
Считая толщину
постоянной & = *,
<ads.
= I <*4ds.
Фиг. 493.
Фиг. 494.
Используя графо-аналитический способ интегрирования по Верещагину,
получим, учетверяя результат подсчёта в пределах одного из треугольников:
b*h bh\d
TS---6T
C0.44)
где последний множитель в скобках — ордината, а предпоследний — площадь
треугольника.
Подсчитаем также наибольший секториальный статический момент пло-
площади сечения, равный:
Наибольшее значение секториальный статический момент подучит для
середины полки и может быть подсчитан путём умножения площади тре-
треугольника эпюры © на толщину полки ?
b л
maxSw»~.^.
C0.45)

568
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
Для стенки
сумма I a>dF =
F
равно нулю, так как эпюра со обратно симметрична и
Значит, в стенке отсутствуют секториальные касательные
напряжения тш.
3) Тавровое сечение. Так как главный секториальный полюс лежит в точке
пересечения полки со стенкой, то секториальная координата любой точки
л	обращается в нуль (со = 0), а следовательно, и /ш = 0.
Изгибно-крутильная жёсткость профиля равна нулю,
вследствие чего при скручивании подобного профиля
бимомент, а равно и секториальные нормаль-
нормальные и касательные напряжения не возни-
возникают. Сечение работает на чистое кручение.
	I .	Г/з	4) Уголковый профиль также не обладает изгиб-
:! 2	' но-крутильной жёсткостью, так как эпюра со = 0.
5) Для составных сечений, состоящих из эле-
элементов, имеющих общую ось симметрии (фиг. 495),
координата центра изгиба, лежащего на оси симме-
симметрии, отсчитанная от центра изгиба Ах какого-либо из
элементов (I), равна *):
L2.3
Фиг. 495.
C0.46)
где У2) г и /3j г — осевые моменты инерции каждого из остальных элементов
относительно оси симметрии z\ Jz — общий момент инерции всего сечения
относительно той же оси, а величины с2, i и сь> х — расстояния от центров
изгиба отдельных элементов до центра изгиба элемента (I). Секториальный
момент инерции такого составного сечения равен:
Л, = -Л, „ + Л,
C0.47)
где Jtf а, У2) Q,, /3, со — секториальные моменты инерции отдельных элементов
сечения относительно собственных центров изгиба; Jly z, J2f Zr Л, z — осевые
моменты инерции отдельных элементов сечения отно-
относительно оси симметрии г; с1? 2, сь 8, c2j 8 — рас-
расстояния между центрами изгиба соответствующих
элементов 1 и 2, 2 и 3 и т. д.
Применим эти формулы для определения центра
изгиба и секториального момента инерции двутавра,
рассмотренного выше. Пронумеруем полки и стенку,
как показано на фиг. 496. За начало отсчёта примем
iz"	'/,* центр изгиба верхней полки (I). Пренебрегая соб-
| ственным моментом инерции стенки относительно
И /3 j J оси z, получим:
Фиг. 496.	,- о г	и	h
так как Зг = 2/3, г> а расстояние с3) i = /г, то а2 = — •
Секториальный момент инерции сечения по формуле C0.47) будет (по-
(поскольку У2) г = 0 и Jly о, = Л, <о = Л, <о = 0):
•'ш —	7
l) См. Бычков Д. В. и Мрощинский А. К., Кручение металли-
металлических балок, § 24.

ПРИМЕРЫ ВЫЧИСЛЕНИЯ СЕКТОРЙАЛЬНЫХ ХАРАКТЕРИСТИК
569
так как
—~j2"» то -'со—
24
что было получено ранее другим путём (формула C0.44)).
Формулами C0.46) и C0.47) особенно удобно пользоваться при расчёте
составных профилей, состоящих из элементов, секториальные характеристики
которых даны в таблицах ОСТ (клёпаная и сварная балка, прокатные
профили, усиленные листами, и т. п.).
6) Рассмотрим ещё случай антисимметричного зетового сечения (фиг. 497).
Центр тяжести сечения О лежит посредине высоты стенки. Главные цен-
центральные оси инерции у и z наклонены на угол а к соответствующим линиям
контура сечения.
Фиг. 497.
Для определения положения центра изгиба и главной нулевой сектори-
альной точки, построим вспомогательную эпюру секториальных площадей о>0,
приняв за полюс и начало отсчётов точку Л. Эта эпюра показана на фиг. 497, б.
Для определения координат центра изгиба графо-аналитическим методом
Верещагина построим эпюры расстояний точек контура сечения до главных
осей у\\ z.
Для точек 1 и 3 профиля значения координат ух; zx и уъ\ z3 соответ-
соответственно будут:
. h .	_ h
аналогично, для точек 2 и 4, имеем:
У% =^4 = ± \Ь COS а —у Sin aj ; z2 = ZA = =ь (у COS a + Ь sin a J .
Соответствующие эпюры у и z приведены на фиг. 497, виг.
Обе эпюры оказались обратно симметричными. Поэтому сумма произве-
произведений <о0 на .у dF и на z dF обратится в нуль, т. е. в нуль обращаются секто-
риально-линейные статические моменты S^y и 5шг. Следовательно, а^ = 0 и
вг = 0и центр изгиба сечения совпадает с центром его тяжести.
Для определения положения главной нулевой секториальной точки
воспользуемся формулой C0.41):
где Sa =
= \

570
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ	[гл. XXX
При постоянной толщине полок b = t интеграл может быть заменён произ-
произведением из площади эпюры о>0 на толщину t, т. е.
S -2.1
ш— 2
Поделив 5Ш на площадь F=
bh f__b4t
, найдём
b*ht
2 Bbt
Зная. <оМ из подобия треугольников, находим расстояние с до
неё от оси стенки (фиг. 497, б):
bh
2
откуда
ьч
2bt + hb}
. C0.48)
Фиг. 498.
ную на
считать
Тенерь мы, имея в виду, что
2@=0, можем построить эпюру
главных векториальных координат
от начального радиуса AM, показан-
фиг. 498. Имея эпюру главных секториальных площадей, легко под-
величину секториального момента инерции
сосой ds,
Применяя метод Верещагина, получим:
гЧ
6
C0.49)
§ 182. Вычисление напряжений в общем случае сложного
сопротивления тонкостенного стержня.
А. Выше, в §§ 172 —178 был рассмотрен случай стеснённого
(или изгибного) кручения тонкостенного стержня и получены фор-
формулы для вычисления сек-
секториальных нормальных и
касательных напряже-
напряжений.
Секториальные напря-
напряжения могут возникнуть
в сечениях тонкостенно-
тонкостенного стержня и в других
случаях действия сил.
работу такого
(фиг. 499).
стержня при
Рассмотрим, например,
внецентренном приложении сия

§ 182] ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ В СЛУЧАЕ СЛОЖНОГО СОПРОТИВЛЕНИЯ 571
Условия равновесия, выраженные формулами (ЗОЛ), C0.2), C0.3)
и C0.17), для этого случая примут вид (сравнить с фиг. 469):
j cdF=P;
•?
С о dFz = PzP;
lodFm
C0.50)
Здесь у, z и (о — линейные и секториальная координаты любой
точки сечения, а ур, zP и шР — линейные и секториальная коорди-
координаты точки приложения силы Р. Интегралы левой части уравнений
C0.50) представляют собой нормальную силу, моменты относи-
относительно осей z h'j/ и изгибно-крутящий бимомент.
Каждый и^ этих силовых факторов вызывает нормальные на-
напряжения. Поэтому формула для нормальных напряжений при
принятом для общего случая действия сил (глава XXIX) правиле
знаков примет вид:
Р
о — — -ргj
i	f у
Последний член формулы C0.51) представляет собой нормаль-
нормальные напряжения аш, возникающие вследствие закручивания стержня.
Изгибно-крутящий бимомент В в произвольном сечении по длине
стержня выражается формулой:
где Вц— бимомент для сечения в месте приложения силы, равный:
Следовательно, если продольная сила будет приложена в такой
точке поперечного сечения, для которой секториальная координата
«о равна нулю, то и изгибно-крутящий бимомент В также обратится
в нуль. Только в этом частном случае внецентренного приложения
растягивающей силы Р(при шр=0), гипотеза плоских сечений будет
справедливой: сила вызовет лишь растяжение и чистый косой изгиб
стержня, не сопровождающийся его закручиванием. В прочих слу-
случаях (при сор ф 0) внецентренное растяжение тонкостенного стержня
открытого профиля, будет сопровождаться его закручиванием.
В некоторых случаях закручивание стержня может произойти
(^только при внецентренном приложении продольной силы, но и
яри осевом еб действии. Так, например, для зетового профиля,

572
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[гл. ххх
рассмотренного выше (§ 180), эпюра секториальных площадей
имеет вид, показанный на фиг. 498. Секториальная координата
точки О, лежащей в центре тяжести сечения, отлична от нуля.
Поэтому если приложить в центре тяжести сечения зет сосредо-
сосредоточенную силу или равномерно распределённую по
длине стенки нагрузку с равнодействующей Р, про-
проходящей через центр тяжести сечения, то В = РтР ф 0,
и стержень будет закручиваться, как это показано на
фиг. 500 пунктиром.
Нормальные напряжения в точках сечения стержня
зетового профиля при центральном приложении про-
продольной силы должны определяться по формуле:
Сечения такого стержня после деформации не оста-
остаются плоскими, даже если закрепление его концов
не препятствует свободной депланации концевых
сечений.
Б. Изгибное кручение имеет место также и при
поперечном изгибе стержня силами, лежащими в глав-
главных плоскостях инерции, не проходящих через центр изгиба сечения.
При плоском поперечном изгибе нормальные напряжения опре-
определяются по формуле:
о =	т"Т"Т~у	C0.53)
Jy J<»
в более общем случае изгиба (косой изгиб, или изгиб в двух
главных направлениях):
Фиг. 500.
Myz . Мгу , В<*
^ у 2 J О)
C0.54)
Величины изгибно-крутящих бимоментов в этих случаях зависят
от эксцентриситета внешних сил относительно линии центров
изгиба и определяются путём интегрирования дифференциальных
уравнений C0.27) и C0.29) или по данным таблицы 27 (§ 177).
Наконец, для случая совместного действия продольных и по-
поперечных сил, сопровождающегося изгибным кручением, формула
для нормальных напряжений примет вид:
N Myz , М2у , Bi
Т	Г + Т + 7"
Г	Jy	Jz Joi
C0.55)
Здесь изгибно-крутящий бимомент В является функцией как
поперечных, так и продольных сил.
В. Касательные напряжения в этих случаях возникают как под
действием поперечных сил, так и вследствие закручивания стержня.

§ 183]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ НАПРЯЖЕНИЙ
573
может
C0.56)
Величина касательных напряжений от сил Q и от
быть определена по формуле:
Первыми двумя членами формулы определяются касательные
напряжения от составляющих поперечной силы Q, а третьим —
секториальные касательные напряжения от действия изгибно-крутя-
щего момента. Надо иметь в виду, что и те и другие касательные
напряжения действуют вдоль контура сечения. Величина 8 во всех
членах формулы — толщина стенки, измеряющаяся нормально к кон-
контуру; Sy и SI — статические моменты отсечённой части сечения
относительно главных осей инерции; Jy и Jz — моменты инерции
всего сечения относительно тех же осей; S% — секториальный стати-
статический момент той же .части сечения; Jm — главный секториальный
момент инерции сечения.
Кроме того, к касательным напряжениям, вычисляемым по фор-
формуле C0.56), добавляются ещё касательные напряжения от чистого
кручения, достигающие наибольших значений посредине краёв
стенок и вычисляемые по формуле A1.37) [см, §§ 67, 173 и 176].
§ 183. Примеры вычисления напряжений
в тонкостенных стержнях.
Пример 117. Тонкостенный стержень корытного профиля, защемлённый
одним концом в стену*), скручивается моментом Мо = 6 кгм. Найти вели-
величину касательных и нормальных на-
напряжений в опасном сечении стер-
стержня, размеры которого показаны на
фиг. 501: /= 1 м; h = 200 мм; Ь =
= 100 мм; Ь = 1 мм.
Для решения задачи необходи-
необходимо прежде всего найти значения
геометрических характеристик сече-
сечения. Площадь сечения
= 4 см*
Фиг. 501.
Расстояние центра тяжести сечения от оси вертикальной стенкк:
b
_Ь~2 _2- 10-0,1 -5_og
Ус — ~р —	^	— ' СМ'
Моменты инерции сечения относительно главных центральных осей:
Jy=%
• 4
12
^A\J см\
1) В защемлении предположено отсутствие депланации.

ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ	[ГЛ, XXX
ентра изг
6>i0CM-
Пользуясь формулой C0.42), найдём координату центра изгиба:
_ ЗЬН __ . 3 - 10» - 0,1
а
F. 10 + 20). 0,1
Строим эпюру секториальных координат (фиг. 502), значения которых
будут:
f aJx 3,75 • 20	О7 - t
для точки / <о1= —<о,=	|- =	!—^	= — 37,5 см*9
h	CH\
для точки 2 <о8 = — оL = у(^~Лу)=—A0 — 3,75) = 62,5 см*.
Секториальный момент инерции сечения (по формуле 30.43):
10» - 20» • 0,1 B - 20 + 3 . 10)
12^6.10 + 20). 0,1
Момент инерции сечения при кручении
Наибольший секториальный статический момент отсечённой части (см.
формулу 30.43'):
Подсчитаем упругую изгибно-крутильную характеристику стержня:
62,5 «/ = 0,00132 • 100 = 0,132 < 0,5 (см. § 177).
Вследствие весьма малой жёсткости при чистом
кручении (GJK) можно принять, что внешняя нагрузка
целиком воспринимается стержнем лишь за счёт изги-
изгиба полок и стенки. В таком случае изгибно-крутя-
щий бимомент в защемлении может быть определён
на основании аналогии, о которой сказано в кон-
конце § 177:
= 600 • 100 = 60000 кгсм*.
Фиг. 502.	р целях ознакомления с методикой точного решения
дифференциального уравнения C0.29) выполним его.
Имея в виду, что внешний момент MQ = const и значит т = --— = 0,
общий интеграл уравнения C0.29) имеет вид:
В = d sh ax + С2 Ch ax.	C0.57)
Произвольные постоянные интегрирования определяются из условий
закрепления концов стержня.
В защемлении при лг = О 6' = 0. Следовательно, нулю равен момент
чистого кручения MKf так как в' = -^ = 0. Имея в виду, что Afe = Л4К + Мш
можем это условие записать иначе, а именно;
1)лри*=0 ^ = Mw = Afo;

183]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ НАПРЯЖЕНИЙ
575
2) при х = 1 Z?=0 .(это вытекает из условия беспрепятственной депла-
нации свободного конца стержня).
Подставив эти условия в уравнение C0.57), получим:
при д: = 0 # =
откуда
откуда
~
==~; при
Подставив найденные значения произвольных постоянных в C0.57),
подучим:
В = — (shах—-th a/chour). При лг = 0 max # = — — tha/.
Так как*а = 0,00182, tha/=th0,132 = 0,131, то
Изгибно-крутящий момент в том же сечении, как было показано, равен:
) = Af0 = —600 кгсм.
Переходим , теперь к определению напряжений. Наибольшие секториаль-
ные нормальные напряжения в опасном сечении возникнут в крайних точках
полок (т. i> 2 и 4, фиг. 502):
¦
Секториальные касательные напряжения:
Пример 118. Определить величину нормальных и касательных напря-
напряжений в опасном сечении стержня, рассмотренного в примере 117, при
Фиг. 503.
загружении его парой сил, лежащей в главной плоскости Ог и равной
Afe=100 кгм (чистый изгиб, фиг. 503). Считать, что момент Мо образован
парой поперечных сил.
Выпишем значения геометрических и упругих характеристик: ус = 2,5 см;
«7=3,75 см; Jy = 2№,7 см4; /* = 41,7 см*; 7^ = 2920 см9; /*=0,0133 смА;
= 19,6 см"; /=100 см; о
0,00132—; а/=0,132.
Эксцентриситет (плечо) приложенной пары относительно центра изгиба
сечения (фиг. 503)
е =ус + ау = 2,5 + 3,75 = 6,25 см.

576
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[ГЛ. XXX
Выражения для силовых факторов Д М^ и Мк возьмём по данным
таблицы 27 (§ 177). Изгибно-крутящий бимомент
В = -z~f ch ах; max В = В0 (при д: = /).
Принятый в таблице знак минус изменён на плюс, так как эксцентриситет г
отложен в другую сторону (см. таблицу 27, схема 3).
Изгибно-крутящий момент
Me
Мш = -~~. а • sh ax; max Мш = аМ9е • th al (при х = /).
,,-	Л	.,	., ' aMoeshax
Крутящий момент Мк = — М^ =	~-—;—.
СП al
По этим данным на фиг. 504 построены эпюры В, Мю и AfK; подсчитаем
наибольшие числовые значения:
max В = 10 000 • 6,25 = 62 500 кгсм2;
max Мш = 1000.6,25.0,00132 - 0,131 = 10,8 кгсм;
max Мк = — max Мш = —-10,8 /сгсж.
Нормальные напряжения в опасном сечении (свободный конец стержня)
получат наибольшее значение в точке 2
(фиг. 502):
М
тахс =
,В*<&
\~ -j— =
_(— 10000)(— 10) 62 500» 62,5 _
~	266,7	+ 2920 ~"
= 1715 кг/см*.
Касательные напряжения:
а) От изгибно-крутящего момента Мш
т _ М^ш _ 10,8 ^ 19У6 _
ш "" /а, • Ь ~ 2920 -0,1 -"" tl г{ т
б) От крутящего момента
_ МКЬ _ 10,8 • 0,1
Тк~~ JK ~~ 0,0133
= 81 кг/см2.
t%eathocl
Фиг. 504.
Как и в предыдущем примере, ре-
решающее значение имеют секториаль-
ные нормальные напряжения (а^ =з
= 1340 кг/см2). Секториальные каса-
касательные напряжения всегда малы и ими
можно пренебречь. Касательные же на-
напряжения от чистого кручения в данном случае тоже малы. Однако они
могут достичь и весьма существенных значений, как это показано ниже.
Пример 119. Балка двутаврового профиля №206 (ОСТ 10016—39)
пролётом / = 4 м несёт нагрузку Р = 3 г, приложенную посредине пролёта
с эксцентриситетом е = 2 см (фиг. 505).
Найти величину наибольших нормальных и касательных напряжений
в опасном сечении балки, считая, что на концах балки невозможны пово-
повороты сечений относительно нейтральной оси, но возможна депланация.

§ 183]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ НАПРЯЖЕНИЙ
577
Геометрические характеристики сечения для двутавра № 206 взяты из
таблицы 5 (приложение IX):
Jy = 2500 см4;
5 = 0,9 см;
= 16,9 см;
Уш = 13 857 см«;
t = 1,14 см; о>тах = 47,05 см2;
bt
JK = 17,85 см4; max S,, = -^ = 67 еж4.
Изгибно-крутильная характеристика стержня (при отношении -^- = 2,6)
а = i/~5Zk_ I,/" 17>85 -
К Ша— У 2,6- 13857~
= 0,022 см~\
Наибольшие изгибающий момент
и поперечная сила:
Р1 3000 . 400
Р1
max — =
= 3 • 105
max 0 = ^ = ^=1500/гг.
Вследствие эксцентриситета силы,
помимо изгиба в главной плоскости,
Фиг. 505.
Фиг. 506.
балка работает на изгибное кручение под действием момента Мо = Ре, при-
приложенного посредине пролёта. По данным таблицы 27 (случай 4) имеем;
изгибно-крутящий бимомёнт
Ре • sh ах	п Ре ж, а/
; maxfi	th
изгибно-крутящий момент
,, Рг спал:	а_ Р^
"== Т —^Г; max ш = "
ch
крутящий момент
Ре
\; max Мк = ~ (\ — ¦
Соответствующие эпюры В, Мш и Мк построены на фиг. 506. Произведя
вычисления, получим:
а/ = 0,022 • 400 = 8,8; ± = Ц = 4,4;
sh 4,4 = 40,72; ch 4,4 = 40,73; th 4,4 ^ 1,0.
19 Н. М. Беляев

578
ОСНОВЫ РАСЧЁТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
[ГЛ. XXX
Подставляя ch — и th -~- в выражения для В, Мф и Мк, получим:
max i9=^ 136 000 кгсм2; max Мш = 3000 кгсм; max Мк ^ 2920 кгсм.
Теперь подсчитаем величины напряжений.
а) Нормальные напряжения возникают от действия изгибающего момента М
и изгибно-крутящего бимомента В, причём М > 0 и В > 0.
Напряжения от изгибающего момента в верхней полке сжимающие,
в нижней — растягивающие. Знак напряжений от изгибно-крутящего бимо-
1660 кг/см2
А
1200 кг/см2
740 кг/см г
Фиг. 507.
мента определяется знаком секториальной координаты (фиг. 507, а). Поэтому
наибольшие растягивающие напряжения будут в точке 3 опасного сечения
max M • zmaT max В • <ort
maxa = -
> = 1200 + 460= 1660 кг/см2.
Соответствующая эпюра распределения нормальных напряжений по сече-
кию показана на фиг. 507, б.
б) Касательные напряжения от действия Мш, Мк и Q соответственно
равны:
х„ = ^уф- = 12,7 кг/см2; тк == ™А = 150 кг/см2; т = ^ = 99 кг/см*.
УШ1	JK	JyO
Наибольшие касательные напряжения от изгиба и чистого кручения в се-
сечении над опорой
max т = 150 + 99 = 249 кг/см2.
Из рассмотренного примера видно, что и в не очень тонкостенных стерж-
стержнях открытого профиля (прокатные профили) дополнительные (секториальные)
нормальные напряжения от изгибного кручения могут иметь существенное
значение. В нашем примере они составляют:
Af\C\
100 = 38% от основных напряжений изгиба и
1200
460
1660
100 = 23% от суммарного значения напряжения.
Касательные напряжения от крутящего момента почти вдвое больше
таких же напряжений от действия поперечной силы. Секториальными каса-
касательными напряжениями (как и в предыдущих примерах) можно пренебречь.

§ 183]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ НАПРЯЖЕНИЙ
579
Пример 120. Рассмотрим ещё случай внецентренного растяжения тон-
тонкостенного стержня корытного профиля, изображённого на фиг. 508. Размеры
сечения (по средним линиям контура): Ь = 30 мм; h = 60 мм: 5 = 1 мм.
Растягивающая сила приложена по краю полки и равна Р= 150 кг.
a)
Площадь сечения F = BЬ + К) Ъ = B • 3 + 6) • 0,1 = 1,2 см2. Расстояние
от средней линии стенки до центра тяжести сечения:
Ш
Моменты инерции сечения относительно главных центральных осей:
Jy =
Jz = 2
+ ЬЬ(Ь-ycf] + bhy; =1,125 ем*.
Расстояние от оси стенки до центра изгиба C0.42):
гь2 з • з2
6
= 1,125 см.
Главный секториальный момент инерции сечения C0-43):
__bbh4 2/г + 3? __ З3 • б2 ¦ 0,1 B - 6 + 3 • 3) , в
Уа)-~-~ПГ* 6b + h ""	12F-3 + 6)	~~ ' СМ '
Эпюра секториальных площадей приведена на фиг. 509, а. Ординаты эпюры
соответственно равны:
аЛ 1,125 -6	о , _ „.	h ,, ^ ч 6
5,6см\

580
КРИВЫЕ СТЕРЖНИ
[гл. xxxi
Наибольшие нормальные напряжения возникают у кромки растянутой
полки и равны:
. , Р , Mvz , Mz_
1= F
где
= 450 кгсм;
Mz = P (b — yc) = 150 C — 0,75) = 338 кгсм;
В = Р(*р= 150 • 5,6 = 840 кгсм2.
Подставляя координаты точки 2 сечения z2 = -k- и у2 = Ь — ус, получим:
150 ¦ 450 . 3 , 338 - 2,25 ¦ 840 • 5,6 _
атах— 1?2+ 7,2 + 1,125 *" 7,1 "
= 125 + 188 + 677 + 660 = 1650 кг/см2.
Заметим, что дополнительные секториальные напряжения составляют от
основных q^: • 100 = 67%, а от полных: -т^т\ • 100 = 40%.
Для сопоставления на фиг. 509, бив построены эпюры распределения
нормальных напряжений: слева — по обычной формуле внецентренного растя-
растяжения B7.4), справа — с учётом изгибно-крутящего бимомента.
ГЛАВА XXXI.
КРИВЫЕ СТЕРЖНИ.
§ 184. Общие понятия.
Кроме стержней с прямой осью в конструкциях часто встречаются
элементы, у которых ось, т. е. линия, проходящая через центры
тяжести поперечных сечений, яв-
является кривой. К ним относятся
звенья цепей, проушины, крюки,
арки, своды, станины подъёмных
кранов и т. п. (фиг. 510). Кроме
того, на практике строго прямых
стержней не встречается; все стер-
стержни, рассчитываемые нами как пря-
прямые, имеют в той или иной степени
небольшую кривизну. Поэтому изуче-
изучение влияния кривизны оси стержня на
распределение напряжений позволит
нам, с одной стороны, проверять
прочность явно кривых стержней, а с другой — оценить влияние
небольших отступлений от прямолинейной формы на прочность
прямых стержней.
При проверке прочности подобных стержней введём следующие
ограничения:
Фиг. 510.

§ 185]
ВЫЧИСЛЕНИЕ ИЗГИБАЮЩИХ МОМЕНТОВ
581
а)	сечения стержня имеют ось симметрии;
б)	ось стержня представляет собой плоскую кривую, лежа-
лежащую в плоскости симметрии]
в)	внешние силы лежат в той же плоскости.
Тогда, вследствие симметрии, и деформация оси стержня будет
происходить в той же плоскости; ось стержня останется плоской
кривой, лежащей в плоскости внешних сил; мы будем иметь случай,
аналогичный плоскому изгибу балки.
Принимая при расчёте указанные выше ограничения, мы охваты-
охватываем почти все встречающиеся на практике случаи работы кривых
стержней. Нашей задачей будет отыскание наибольших напряжений,
проверка прочности и вычисление деформаций кривых стержней.
Решение этой задачи мы проведём совершенно аналогично тому,
как мы поступили в подобном случае для прямой балки.
Фиг. 511.
§ 185. Вычисление изгибающих моментов,
нормальных и поперечных сил.
уПредставим себе кривой стержень (фиг. 511), нагружённый внеш-
внешними силами Ри Р2, Р3> Pi и т» Д-> расположенными, как указано
в § 184, в плоскости симметрии попереч-
поперечных сечений. В той же плоскости будут
лежать и опорные реакции стержня.
Для выяснения напряжений по сечениям,
перпендикулярным к оси стержня, проведём
одно из таких сечений тпу делящее стер-
стержень на две части / и //. Отбросим одну
из них, например //, и рассмотрим равно-
равновесие оставленной. На неё будут действовать
внешние силы Ри Р2, Р3, атто сечению тп бу-
будут передаваться напряжения а и т.
Систему внешних сил, приложенных к оставленной части, можно
заменить в общем случае одной силой, в частном — парой сил.
Рассмотрим общий случай (фиг. 512). За-
Заменим силы Ри Р2, Р3 их равнодействую-
равнодействующей R\ затем приложим в центре тяже-
тяжести О сечения тп две противоположные
силы R! и R", равные R. Силы R и R"
образуют пару с моментом М\ силу же R!
разложим на нормальную к сечению N, и
лежащую в плоскости сечения Q. Таким
образом, система внешних сил Рь Р2, Р8,	Фиг. 512.
действующая на оставленную часть стержня,
заменена статически эквивалентной системой из пары сил М (изги-
(изгибающего момента), нормальной силы N и поперечной силы Q.

582
КРИВЫЕ СТЕРЖНИ
[ГЛ. XXXI
Эти три величины совместно заменяют действие внешних сил, при-
приложенных к оставленной части стержня. В частном случае, когда эти
внешние силы приводятся к паре, силы N и Q обращаются в нуль.
Величины сил М, N и Q определяются из условия статической экви-
эквивалентности этой системы сил Pl9 Я2, Ръ\ моменты относительно любой
точки и проекции на любую ось обеих систем сил равны между собой.
Составляя суммы моментов сил обеих систем относительно центра тя-
тяжести проведённого сечения, получаем, что изгибающий момент М равен
сумме моментов всех сил, приложенных к оставленной части стержня:
М = ^т(Рь />2, Ра)в.	C1.1)
Проектируя силы обеих систем на направления N п Q, получаем,
что нормальная и поперечная силы равны суммам проекций всех сил,
приложенных к оставленной части стержня, соответственно на на-
направление нормали к сечению и на плоскость самого сечения:
W = 2nP(A, Р* Р*)н,	C1.2)
<? = 2„р(А, я.. Pi)q.	C1.3)
Изгибающий момент будем считать положительным, если он уве-
увеличивает кривизну оси стержня. Нормальную силу будем считать
положительной, если она будет стремиться оторвать оставленную
часть стержня от отброшенной.	,'
Поперечную силу считаем поло-	/у
жительной, когда она получается
из положительного направления
Фиг. 513.
Фиг. 514.
нормальной силы поворотом по часовой стрелке на 90° (фиг. 513).
Так же, как и для балки, при вычислении величин М9 N и Q
можно рассматривать как левую, так и правую части стержня, раз-
разделённые проведённым сечением; выбор той или другой части опреде-
определяется условием наибольшей простоты вычислений.
Приведённые выше правила знаков для изгибающего момента,
нормальной и поперечной сил не зависят от того, правую или левую
часть стержня мы оставляем для их вычисления.
Рассмотрим пример вычисления М, Л/ и Q. Возьмём стержень,
представляющий собой четверть окружности радиуса RQ) зещемлён-

§ 186]
ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ ОТ СИЛ Q И N
583
ный одним концом и нагружённый на другом силой Р (фиг. 514);
проведём какое-нибудь сечение с центром тяжести О. Положение
сечения определим углом ср, составленным им с вертикалью. Для
вычисления М, N и Q рассмотрим правую часть стержня. Этим мы
избавляемся от вычисления реакций в сечении С.
Изгибающий момент будет равен моменту силы Р относительно
точки О:
М = + Р • OD = + PR<> sin <p.
Проектируя силу Р на нормаль к сечению и на само сечение, получаем:
N= — Р sin ср; Q = -}- Я cos ср.
Таким образом, наибольший изгибающий момент и нормальная
сила будут при ср = 90°, т. е. в опорном сечении.
в)
На фиг. 515 показаны эпюры М, N и Q. --За нулевую линию
принята ось стержня. Ординаты отложены по радиусам кривизны
стержня.
§ 186. Вычисление напряжений от сил Q и N.
Напряжения о и т по проведённому нами сечению пгп урав-
уравновешивают систему внешних сил (Р1э Р2, Я3), приложенных к
оставленной части, или, что всё равно, систему сил Ж, N и Q
(фиг. 511 и 512).
Сила Q, лежащая в плоскости сечения, может быть уравновешена
лишь касательными напряжениями т, сумма которых должна быть
равна и противоположна силе Q. Нормальная сила N и изгибающий
момент М, приложенные к оставленной части, могут быть уравно-
уравновешены лишь нормальными напряжениями.
Условия равновесия оставленной части позволяют найти лишь
суммарные внутренние усилия, передающиеся от отброшенной части
на оставленную; само же распределение напряжений по сечению

584	КРИВЫЕ СТЕРЖНИ	[ГЛ. XXXI
таким путём получено быть не может, — мы имеем дело со стати-
статически неопределимой задачей, для решения которой необходимо
рассмотрение деформаций стержня.
Однако в отношении напряжений, вызванных силами Q и N,
искомый результат можно получить проще. Теоретические исследо-
исследования показывают, что распределение касательных напряжений в кри-
кривых стержнях близко к тому, что мы имеем для прямых. Поэтому
обычно и для кривых стержней пользуются формулами, выведенными
для прямых балок:
т= 2 •	A5.3)
Это не точно; применяя те же методы, что и при вычислении
касательных напряжений в балках, можно вывести и для кривых
стержней более точные формулы для вычисления т. Однако практи-
практически вполне допустимо пользование формулой
A5.3).
Условие прочности по отношению к касатель-
"tT^ I ds I *]? ным напряжениям в таком случае для кривых
стержней имеет вид A5.7):
Фиг. 516.	@maAiax_. .
T	< I T|
Определим теперь напряжения, вызываемые нормальной силой М
Рассматривая элемент кривого стержня длиной ds под действием
усилий N (фиг. 516), видим, что эти силы, приложенные в центрах
тяжести поперечных сечений, соответствуют простому осевому растя-
растяжению или сжатию выделенного элемента. Поэтому и соответствую-
соответствующие напряжения будут нормальными к сечению и равномерно рас-
распределёнными по его площади F:
N
Знак напряжений определится знаком силы N.
§ 187. Вычисление напряжений от изгибающего момента.
Изгибающий момент М может быть уравновешен, как и в пря-
прямой балке, только нормальными напряжениями, приводящимися к паре,
расположенной в плоскости действия внешних сил, по направлению
обратной, а по величине равной моменту М. Задача нахождения
закона распределения напряжений по сечению и формул для их
вычислений является статически неопределимой и требует, как это
было и при изучении изгиба прямой балки, помимо составления и
решения уравнений статики, рассмотрения соответствующих дефор-
деформаций и составления дополнительных уравнений. При определении
напряжений от сил Q и N мы обошлись без подобных вычислений,

§ 187] ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ ОТ ИЗГИБАЮЩЕГО МОМЕНТА
585
так как воспользовались уже готовыми решениями; для нормаль-
нормальных же напряжений, уравновешивающих изгибающий момент М, мы
проделаем весь ход вычислений, который в своё время был изло-
изложен при определении нормальных напряжений в прямых балках (§ 78).
Рассмотрим условия равновесия оставленной части стержня АВ
(фиг. 517) под действием изгибающего момента М и системы напря-
напряжений о, передающихся через проведённое сечение. Изобразим
(фиг. 518) оставленную часть с действующими на неё силами. Поло-
М
Фиг. 517.
Фиг. 518.
жение нейтрального слоя по высоте сечения нам заранее неизвестно
и подлежит определению; будем в общем случае считать, что он
не проходит через центры тяжести сечений. Начало координат пока-
покажем в точке С, расположенной на нейтральной оси у и вне центра
тяжести сечения О, причём расстояние ОС оставим пока неизвест-
неизвестным. Ось z является осью симметрии; ось х направлена перпен-
перпендикулярно к плоскости сечения. В плоскости симметрии xCz рас-
расположен изгибающий момент М\ по каждой площадке dF с коор-
координатами у и z действует сила о dF. Для системы сил М и a dF,
под действием которых оставленная часть сохраняет равновесие,
можно написать шесть уравнений равновесия.
На ось х внешние силы дают проекцию, равную нулю; сумма же
проекций сил a dF выразится интегралом, охватывающим всю пло-
площадь поперечного сечения:
= 0; \odF=
= 0.
C1.4)
Уравнения проекций всех сил на оси у и z:
обращаются в тождества, так как напряжения о перпендикулярны
к осям у и z. Обращается в тождество и уравнение моментов отно-
относительно оси х
так как не дают момента ни силы adF, параллельные оси дг, ни
пара Ж, лежащая в плоскости xCz.

586
КРИВЫЕ СТЕРЖНИ
[ГЛ. XXXI
По этой же причине момент пары М относительно оси z тоже
равен нулю; что же касается сил odF, то их момент относительно
этой оси равен интегралу \ adFy.
Пятое уравнение равновесия, следовательно, будет
= 0,	C1.5)
но этот интеграл равен нулю вследствие симметрии сечения относи-
относительно оси z.
Остаётся приравнять нулю сумму моментов всех сил относи-
относительно оси у. Это уравнение запишется так:
= 0', M—i\odFz =0.
C1.6)
Итак, условия статики требуют рассмотрения двух уравнений:
0,	C1.4)
= 0.	C1.6)
Закон изменения нормальных напряжений по высоте сечения
остался пока неизвестным. Поэтому переходим к рассмотрению
деформаций.
Как и для случая изгиба прямого стержня, будем пользоваться
гипотезой плоских сечений, подтверждаемой опытами и для кривых
стержней. Будем предполагать, что
при действии изгибающего момента
сечения, перпендикулярные к оси,
j.\ остаются плоскими и лишь повора-
поворачиваются одно относительно дру-
другого (фиг. 519). Так как при сде-
сделанных выше предположениях (§ 184)
ось бруса остаётся при деформации
в той же плоскости, в которой она
лежала до деформации, то эти по-
повороты будут происходить вокруг нейтральных осей СХС\ и
С^С'ъ перпендикулярных к плоскости внешних сил, заключающей
в себе и ось стержня. Тогда удлинения и укорочения, а стало
быть и напряжения для волокон, отстоящих на одно и то же
расстояние от нейтральной оси, будут по ширине сечения одинако-
одинаковыми. Установим зависимость между углом относительного поворота
двух смежных сечений и деформациями волокон. Выделим из кривого
Фиг. 519.

§ 187] ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ ОТ ИЗГИБАЮЩЕГО МОМЕНТА
587
стержня, подвергающегося действию только изгибающих моментов
(фиг. 520), элемент, ограниченный двумя очень близкими сечениями,
составляющими угол rfcp. Этот элемент изображён на фиг. 521.
Oj—О2 — ось стержня; Q—С2 — нейтральный слой.
Нормальные напряжения, действующие по проведённым сечениям,
образуют пары; под их действием угол между смежными сечениями
М
Фиг. 520.
Фиг. 521.
/—1 и 2—2 изменится на величину 8 dcp вследствие относительного
поворота этих сечений вокруг нейтральных осей Сх и С2.
Найдём нормальные напряжения а, действующие по сечениям
в точках Ах и А% на расстоянии z от нейтральных осей. Положи-
Положительное направление оси z выберем в сторону наружных волокон.
Волокно AtAq получит удлинение A<JD<? соответствующее напря-
напряжение о будет равно
где е — относительное удлинение волокна A^AV Оно равно отно-
отношению абсолютного удлинения A^D^ к первоначальной длине во-
волокна АХА^:
p_A1D1.
ЛИ.'
называя буквой р радиус кривизны волокна АХАЪ имеем:
±^1
р d<?
C1.7)
Формула C1.7) даёт закон распределения по высоте сечения нор-
нормальных напряжений, вызванных изгибающим моментом Ж.
Так как для каждого сечения величины
и Е постоянны, то
изменение а зависит лишь от изменения координаты z и радиуса
кривизны р волокна ЛИ2, причём p — r-\-z9 где г — радиус кри-
кривизны нейтрального слоя.

588
КРИВЫЕ СТЕРЖНИ
[ГЛ. XXXI
В то время как для прямой балки мы имели линейный закон
распределения напряжений, для кривого стержня напряжения а
меняются по гиперболическому закону (фиг. 522). Из формулы C1.7)
видно, что в наружных от нейтрального
слоя волокнах напряжения растут мед-
медленнее, чем z\ во внутренних же, благо-
благодаря изменению знака z с положитель-
положительного на отрицательный, они растут бы-
быстрее, чем г.
Таким образом, в кривом стержне
нормальное напряжение во внутреннем
крайнем волокне больше, а в наружном
меньше, чем в тех же волокнах прямого
стержня того же сечения. Это понятно:
первоначальная длина внутреннего волокна
в кривом стержне значительно меньше, чем наружного; в прямом
же стержне эти длины равны. Поэтому и получается указанная
выше разница в относительных деформациях, а стало быть, и в напря-
напряжениях для этих волокон.
Перейдём к решению уравнений статики C1.4) и C1.6) с учёт<5м
зависимости, полученной из рассмотрения деформаций C1.7). В урав-
уравнение C1.4) подставим C1.7):
Фиг. 522.
Вынося постоянные для рассматриваемого сечения величины за знак
интеграла и сокращая их, получаем:
C1.8)
Это уравнение позволяет найти положение нейтральной оси.
Из равенства C1.8) ясно, что равен нулю не интеграл \ zdF,
представляющий собой статический момент сечения относительно
нейтральной оси, как это было для прямого стержня, а другой
интеграл. Это показывает, что при изгибе кривого стержня ней-
нейтральная ось действительно не проходит через центр тяжести сече-
сечения. Заменяя в C1.8) z = p — г (фиг. 521), находим:
"-?=0,
откуда следует, что
C1.9)

§ 187] ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ ОТ ИЗГИБАЮЩЕГО МОМЕНТА	589
Ход вычислений величины г для каждого частного вида попереч-
поперечного сечения будет различен. Подставив теперь зависимость C1.7)
в уравнение C1.6), получим:
M-Eb-^yidF = 0,	C1.10)
где М — изгибающий момент, а интегрирование охватывает всю
площадь поперечного сечения. Интеграл, входящий в это уравнение,
преобразуем следующим образом:
последний из полученных двух интегралов равен на основании C1.8)
нулю, а первый представляет собой статический мбмент 5 площади
поперечного сечения относительно нейтральной оси. Эта величина
может быть вычислена как произведение площади сечения F на рас-
расстояние её центра тяжести до нейтральной оси, т. е. на zQ (фиг. 522):
S = FzQ.	C1.11)
Таким образом, уравнение C1.10) получает вид:
p = 0;	C1.12)
отсюда
«*Р — IS '	F1Л6)
и формула для нормальных напряжений напишется так:
М Z
б
/9 1 1 ЛЧ
В уравнении C1.12) мы находим подтверждение того, что здесь
статический момент 5 площади сечения относительно нейтральной
оси не равен нулю, т. е. нейтральная ось при изгибе кривого стержня
не проходит через центр тяжести сечения, г несколько (на вели-
величину zQ) смещена. На фиг. 522 мы изобразили это смещение в сто-
сторону к центру кривизны стержня. Результаты определения величины г
из уравнения C1.9) для различных сечений показывают, что ней-
нейтральная ось действительно смещается в указанном направлении.
Это смещение связано с условием равенства между собой сумм
сжимающих и растягивающих напряжений, действующих по сечению.
Так как напряжения от изгибающего момента у наружного края
сечения меньше, а у внутреннего — больше, чем в соответствующих
волокнах прямого стержня того же сечения (фиг. 522), то для
равенства указанных сумм нейтральная ось должна сместиться от
центра тяжести сечения в сторону внутренних волокон.

590
КРИВЫЕ СТЕРЖНИ
[ГЛ. XXXI
Добавляя к полученным напряжениям найденные в предыдущем
параграфе напряжения от нормальной силы, получаем формулу для
вычисления полных нормальных напряжений в кривом стержне:
N , М z
C1.15)
Наибольшие по абсолютной величине растягивающие и сжимающие
напряжения будут иметь место в крайних волокнах / и 2 (фиг. 522),
§ 188. Определение радиуса кривизны нейтрального
слоя при прямоугольном сечении.
Для определения величины г служит уравнение C1.9):
F
С dF *
1т
Развернём это уравнение для случая прямоугольного сечения стержня.
Назовём (фиг. 523) h — высоту, b — ширину сечения, Ro — радиус
кривизны стержня, Rx — радиус кривизны наружных волокон, R% —
радиус кривизны внутрен-
внутренних волокон, г — радиус
кривизны нейтрального
слоя.
Разделим сечение на
—Ъ
Г
О
dz
полоски dF = bdp; тогда
уравнение C1.9) примет
вид:
bh h
т = ¦
)
'
i
In
р
C1.16)
R%
отсюда
Фиг. 523.
h
Формулы C1.16) и C1.17) позволяют вычислить г и zQ} а следо-
следовательно и 5, для прямоугольного сечения.
1) Натуральный логарифм равен десятичному, умноженному на 2,303.

§ 188] ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ НЕЙТРАЛЬНОГО СЛОЯ	691
Решение можно провести приближённо, разложив In ^ в ряд:
, #t , ° 2 i
отсюда
1+Т
45
В первом приближении, ограничившись двумя первыми членами ряда
C1.18), получим:
C1.19)
Г2/?о
12/?о""/?о*
C1.21)
Сохраняя и третий член ряда C1.18), полу-
получаем:
г = Ло\ 1 —
12У?о
C1.22)
C1.23)
C1.24)
Фиг. 524.
где /—момент инерции сечения относительно оси, проходящей через центр
тяжести сечения.
Положение нейтрального слоя для сечений, образованных из прямо-
прямоугольников, определяется так же, как и в случае прямоугольного сечения
кривого стержня: формула C1.16) приобретает лишь более сложный вид.
Рассмотрим двутавровое сечение с полками разных размеров (фиг. 524).
Знаменатель уравнения C1.9) определится следующим образом:
dF
btd
R*
R,
Радиус кривизны нейтрального слоя будет:
+ bbhb
г = -

592
КРИВЫЕ СТЕРЖНИ
[ГЛ. XXXI
§ 189. Вычисление радиуса кривизны нейтрального слоя
для круга и трапеции.
Для вычисления радиуса нейтрального слоя для кругового сечения,
имеющего диаметр d, разбиваем площадь круга на элементарные площадки dF
линиями, параллельными нейтральной оси (фиг. 525).
LL__L LJLJI
Фиг. 525.
Фиг. 526.
Выразим dF и р в функции центрального угла у. Предварительно вы-
вычисляем:
р = /?0 -J- — sin <p; dF = bz dp; но Ьг = d cos <р и dp = -у cos <p лГ«р.
Тогда dF=Y cos2 cp cfcp. Знаменатель уравнения C1.9) принимает вид:
)dJF С ^cos'
р ^ J 2/?0 + 6
C1.25)
Интегрируя, получаем:
подставляя полученное значение в уравнение C1.9) и заменяя F через —т-у
находим:
==т.	C1-26)
4 рЯо —
Для трапецеидального сечения (фиг. 526) снова воспользуемся уравне-
уравнением C1.9). Площадь трапеции равна
F-h±h.h

§ 190] ПРИБЛИЖЁН. СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ НЕЙТРАЛЬН. СЛОЯ 593
Ширина сечения трапеции на расстоянии р от центра кривизны
Интеграл
dF
имеет значение (опускаем промежуточные выкладки):
dF
? -(*.-*!)•
Теперь по уравнению C1.9) получаем:
h-
г =
h
C1.27)
In § -(**-
При Ь2 = Ьи т. е. для прямоугольника, эта формула переходит в фор-
формулу C1.16).
При #1=0 получим формулу для определения положения нейтральной
оси при треугольном сечении:
hb
Г=	7	R	 ¦
§ 190. Приближённый способ
определения положения нейтрального
слоя.
С dF
Вычисление 1 — может быть заменено
J Р
приближённым суммированием. Для этого
площадь любой фигуры, изображённой строго
в масштабе, должна быть разделена линиями,
параллельными нейтральной оси, на полоски
площадью AF. Величины AFi, AF2, Д^з,.. •,
равно как и расстояние полосок от центра
кривизны р,, р2, р8, ..., могут быть измерены
Фиг. 527.
AF
в масштабе чертежа. Суммирование отношений — даёт возможность
определить радиус кривизны г нейтрального слоя по формуле
r = -^J-.	C1.28)
Покажем применение этого способа на примере трапеции. Разделим трапе-
трапецию (фиг. 527) на 12 полосок, параллельных нейтральному слою, высотой
по 1 см каждая. Площадь каждой полоски, делённая на средний радиус
Ролоски, просуммируется следующим образом:
см.
18,5 " 17,5 "*" 16,5 "*" 15,5 "*" 14,5 "
+ 13,5 + 12,5 + 11,5 ^ 10,5 ^ 9,5
8,5

594
КРИВЫЕ СТЕРЖНИ
[ГЛ. XXXI
I
О.
О
н
о
X
со
s
о
О
Q
О.
н
X
к
s
X
ф
о
г?
о
о
S
I
Си
со
00ОЭО500С5ЮСО—«OOXNO00O
сотрсосос
OOTf»—' О5 0
^^ »"-* *—< ^5
смгоо^ооос
СО C^J '~н ¦"-"• »"~^
С0СЧ — С
CD С5 С5 С
ГСОЮ
OOO
OOOO
СМ-^-
	О СМ СО С
CD lO ^ ^f 00 С
ооо оо<
OCiiO
а со г^- со см
J — О QO
> о о о©

§ 190] ПРИБЛИЖЕН. СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ НЕЙТРАЛЬН. СЛОЯ 595
СО 00
jSioS^fn —oo
>оооооооо
жжш
WM
ш
T
T.i
\\~**
Х^Ж)$
1L
?г
^зт

596	КРИВЫЕ СТЕРЖНИ	[ГЛ. XXXI
Радиус кривизны нейтрального слоя
вместо 12,26 см по точной формуле C1.27) (см. пример 122, стр. 599).
Если разделить трапецию не на 12, а только на 6 частей, то вычисления
будут короче:
/3,42 4,25 5,08 5,92 6,75 7,58\
lT9" + T7" + "T5+T3- + "TT + "9~J:=
Радиус кривизны г = 66 :5,36 = 12,30 см.
Таким путём, как показано выше в §§ 188—189 для прямоугольного,
круглого и трапецоидального сечений, можно вычислить величины г и z0 для
сечения любой формы. При сложном очертании контура сечения может быть
применён приближённый способ вычисления, изложенный в настоящем пара-
параграфе. Результаты таких вычислений для некоторых форм сечения даны
в таблице 29.
В этой таблице приведены значения z0 в долях радиуса Ro в зависимости
от отношения R0/c, где с — расстояние от центра тяжести сечения до внут-
внутренних волокон.
В крайней левой и крайней правой графах указаны значения отноше-
отношения (^о • с).
В верхней части всех средних граф изображена форма сечения кривого
стержня. Величина z0 определяется умножением соответствующего таблич-
табличного числа <къ на R0} т. е.
z0 = kR0.
Из этой таблицы видно, что с увеличением отношения RQ/c отношение
быстро приближается к нулю, т. е. нейтральная ось приближается к
центру тяжести сечения, а это значит, что уничтожается разница между
работой материала в кривом и прямом стержнях. Отсюда же следует, что
нейтральная ось в пределе пройдёт через центр тяжести сечения. Таким об-
образом, при значительных величинах отношения RQ/c положение нейтральной
оси и величина напряжений в кривом стержне определяются с небольшой
погрешностью теми же формулами, что и в прямом.
Уже при отношении R0/ct равном десяти, можно считать величину г0
практически равной нулю.
§ 191. Анализ формулы нормальных напряжений
в кривом стержне.
Подставляя в формулу нормальных напряжений C1.15) коорди-
координаты наиболее удалённых точек сечения (фиг. 522):
точки / ... zl и R{ (наружные волокна),
точки 2 ... — z2 и R% (внутренние волокна),
можем написать условие прочности кривого стержня

§ 191] АНАЛИЗ ФОРМУЛЫ НОРМАЛЬН. НАПРЯЖЕНИЙ В КРИВОМ СТЕРЖНЕ 597
Если материал различно сопротивляется растяжению и сжатию,
величины [о] будут иметь различные значения. Что же касается
отыскания опасного сечения, то благодаря наличию двух факто-
факторов, вызывающих нормальные напряжения, М и N, этот вопрос
более сложен, чем для прямого стержня. В некоторых случаях
(см. пример § 185) М и N достигают наибольшей величины
в одном и том же сечении, тогда оно и будет опасным. Если же
это не имеет места, то приходится проверять прочность матери-
материала в ряде сечений, отыскивая вычислением наиболее напря-
напряжённое.	/
Если значение радиуса кривизны стержня /?0 велико по сравне-
сравнению с высотой* сечения h (а именно, R^^>bh)y то отношения z\p%
или Zx/Ri, или z^jRb становятся незначительными, и нормальные
напряжения, зависящие от изгибающего момента, будут мало чем
отличаться от напряжений, определяемых по формулам прямого
бруса. Это легко установить при помощи данных §§ 187 и 188.
Возьмём, например, уравнения C1.10) и C1.7). Исключая из них
Е -^ и заменяя р через r-\-z, получаем:
Если пренебречь здесь величиной —, то формула C1.30) обратится
в формулу напряжений в прямом стержне:
Mz
0
Определим, какова будет погрешность при вычислении наиболь-
наибольших нормальных напряжений от изгибающего момента по формуле
прямого стержня при значении
на примере стержня прямоугольного сечения. Радиус кривизны
нейтрального слоя в этом случае равен:
r—	h	_ h _	h —AQRWh
r— /?q +0,5ft ~t 5,5 "" 0,20067 —*>****n-
/?o — 0,5ft Ш4,5
Тогда
г0==Я0 — г = 0,0167ft и го = О,ОО334#о,
т. е. нейтральная ось отстоит всего на 1/60 высоты от центра
тяжести сечения.

598	КРИВЫЕ СТЕРЖНИ	[ГЛ. XXXI
Напряжения изгиба по формулам кривого стержня составляют:
_М zt __ М- 0,5167/г _ 0,5167 ¦ М • 6 _ ft Qqg M
0| ~ 5 ' #! ~~ bh • 0,0167/г . 5,5Л ~" 0,551 Ш2 ~ U> UP '
— М ** — М ' °»4833/*	_ °>4833 ' ^ • 6 _ 1 Q71 М . '
°*~ S ' Ra~ bh - 0,0167/i . 4,5Л ~ 04509^/г2 ~" >U
т. е. величина напряжений отличается на ±7% от определяемой
по формуле прямого стержня.
Это обстоятельство является причиной того, что для проверки
прочности кривые стержни разделяют часто на две категории.
п
К первой относят стержни большой кривизны с -—• ^ 5; для них под-
подсчёт нормальных напряжений следует вести по формуле
КГ	АЛ %\ 9
^=4±?'^М.	C1-29)
На практике это будет иметь место, главным образом, для частей
машин, крюков, звеньев цепей, колец и т. д. Ко второй категории
относят стержни малой кривизны^ у которых радиус оси велик по
сравнению с размерами сечения, т. е. -^^>5; для таких стержней
при вычислении напряжений от изгиба можно пользоваться форму-
формулой прямого стержня
oi,2 = ^zt-^<[o].	C1.31)
Эта категория обычно включает в себя кривые стержни, встречаю-
встречающиеся в различных инженерных сооружениях, — арки, своды и т. д.
§ 192. Дополнительные замечания к формуле
нормальных напряжений.
Проверяя прочность кривых стержней, мы очень часто полу-
получаем весьма значительные напряжения у внутренних волокон. Надо
иметь в виду, что эти напряжения (фиг. 522) падают весьма резко
уже на небольшом расстоянии от края сечения. Таким образом, они
носят явно выраженный характер местных напряжений, а потому при
оценке их влияния на прочность детали следует иметь в виду ука-
указания § 16: при статической нагрузке и при пластичном материале
(мягкая сталь) переход этих напряжений за предел текучести опас-
опасности не представляет.
Основы изложенной в § 187 теории расчёта кривых стержней
были даны русским академиком А. В. Гадолиным в 1856—1860 гг.
Точная теория изгиба кривых стержней прямоугольного сечения
впервые была изложена русским учёным X. С. Головиным в 1880 году;
полученные им результаты устанавливают, что сечения прямоуголь-

§ 192]
ЗАМЕЧАНИЯ К ФОРМУЛЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ
599
ной формы при изгибе кривого стержня остаются плоскими. Экспери-
Экспериментальные работы по проверке изложенной теории показывают
достаточно удовлетворительное совпадение результатов опыта и вы-
вычислений.
Гиперболический закон распределения напряжений отчётливо
виден при просвечивании напряжённой прозрачной модели кривого
стержня поляризованным одноцветным светом. В этом случае внутри
контура модели можно видеть ряд тёмных и светлых полос; чем
резче изменяются напряжения, тем эти полосы делаются уже и рас-
располагаются чаще. На фиг. 528 показано это распределение полос
Фиг. 528.
для чистого изгиба модели, имеющей и прямую и кривую части.
В пределах прямого участка полосы располагаются равномерно, так
как напряжения меняются по линейному закону, т. е. равномерно;
в кривой части наблюдается сгущение полос у вогнутой стороны
и обратная картина у выпуклой, что соответствует резкому и не-
неравномерному росту напряжений в первой зоне и значительно более
медленному — во второй.
При исследовании распределения нормальных напряжений в кри-
кривых стержнях мы пренебрегли наличием нормальных напряжений,
радиально направленных, т. е. давлением волокон друг на друга.

600
КРИВЫЕ СТЕРЖНИ
[гл. xxxi
Для кривых стержней эти напряжения имеют большее значение, чем
для прямой балки, как это показали исследования, произведённые
на гипсовых (хрупких) моделях. Особенно значительную величину
получают эти напряжения для сечений, ширина которых резко ме-
меняется (двутавр).
§ 193. Примеры определения напряжений в кривых стержнях.
Пример 121. Изогнутая рама машины (фиг. 529) подвергается дейст-
действию двух сил Р по 800 кг каждая. Найти краевые напряжения в сечении АВ.
Радиус оси Ro = 80 мм; сечение прямоугольное 80 X 30 мм.
Г)
Так как -— < 5, то следует
применить формулы для стержней
большой кривизны. Находим ра-
радиус нейтрального слоя п
,1
г =
¦¦$
Фиг. 529.
в нашем случае h = 80 мм, Ri =
= 120 мм, ^2 = 40 мм; следова-
следовательно,
, 120 — 1,099 •***
1П4О
Отсюда необходимые данные для расчёта:
zo = Ro — г = 80 — 72,8 = 7,2 жл* = 0,
S = F . z0 = 8 . 3 . 0,72 = 17,3 см";
см;
y	^ *а = .*. — *0 = 4 — 0,72 = 3,28 см.
Изгибающий момент относительно центра тяжести сечения равен
М = — 800 • 25 = — 20 000 кгсм.
Нормальная сила N=-{-$00 кг. Площадь поперечного сечения
Нормальные напряжения в точках A (j2) и В (sj) равны
24 см*.
Если бы мы воспользовались таблицей для вычисления г0, то имели бы
|	^ ^	= О,О9. 8 = 0,72 см,

§ 193] ПРИМЕРЫ ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ В КРИВЫХ СТЕРЖНЯХ	601
т. е. то же самое значение z0. Если бы мы пренебрегли кривизной стержня
и вычислили напряжения по формуле
то. получили бы
,+„„»-{-»}
Мы получили бы напряжения во внутреннем волокне на
981—658
981
= ЗЗо/о
80
меньше, не в запас прочности. Таким образом, подбор сечения без учёта
кривизны стержня может повлечь за собой значительные перенапря-
перенапряжения.
Пример 122. Проверить	"
прочность крюка грузоподъём-
грузоподъёмностью 10 т. Размеры крюка
приведены на фиг. 530. Опас-
Опасным сечением, для которого
М и N достигают максимума,
будет сечение АВ. Форма его —
трапецоидальная, что вызвано
желанием усилить зону наи-
наибольших напряжений, приле- о
гающую к внутренним волок-
волокнам. Площадь сечения
12 = 66 см2.
Фиг. 530.
Расстояние центра тяжести*от внутренних волокон равно
с =А . 2а + ?=12 6 + 8
а от наружных,
-Ь — 3 3 + 8"
^ = 6,91 см.
Воспользуемся формулой C1.27):
12 • 5,5
г =
66
^jln^-5 54.0,9163-5
/?0 = 8 + 5,09 =13,09 см;
zo = 13,09— 12,26 = 0,83 см;
S = 66 . 0,83 = 54,8 еж3;
z1 = 6,91+0,83 = 7,74 еж;
22 = 5,09 — 0,83 = 4,26 см.
= 12,26 см%

602	КРИВЫЕ СТЕРЖНИ	[ГЛ. XXXI
Нормальная сила для сечения А В равна N=P=+10000 кг. Изги-
Изгибающий момент М = — р./?0 = — 10000- 13,1 =— 131 000 кгсм.
Напряжения в крайних волокнах будут:
. 10 000 131000-7,74 1КО Л_.	то
" = + ~66	54,8 ¦ 20 = 152 - Ш = " 772
, 10 000 , 131000-4,26 ^0.1070 улол
§ 194. Деформации кривых стержней.
При решении статически неопределимых задач по расчёту кон-
конструкций, куда входят кривые стержни (арки, своды, звенья цепи и
кольца), необходимо уметь вычислять деформации кривых стержней.
Опыт и расчёты показывают, что если при определении напряжений
необходимо для стержней большой кривизны учитывать влияние
этой кривизны, то при вычислении деформаций в подавляющем
большинстве случаев можно пренебречь этим влиянием.
Рассмотрим, как определяется количество потенциальной энергии при
изгибе кривого стержня.
Вырежем из стержня двумя поперечными сечениями элемент длиной ds
(.|)иг. 531). На него будут действовать по обоим сечениям касательные на-
напряжения, складывающиеся в усилие Q, и нор-
нормальные, складывающиеся в усилия N и М.
Для определения количества потенциальной
энергии, накапливающейся в этом элементе, надо
подсчитать работу всех этих усилий, приложен-
приложенных к элементу. Уже в балках при подобных вы-
вычислениях мы пренебрегали работой касательных
усилий; в кривом стержне это тем более возможно,
так как влияние поперечных сил будет ещё меньше.
Остаётся подсчитать работу усилий N и М. Если мы пренебрежём
влиянием кривизны стержня, то это будет эквивалентно предположению, что
деформация выделенного элемента под действием пар М происходит так же,
как в балке; тогда количество потенциальной энергии, связанной с этой де-
M2ds
формацией, будет равно	; разница по отношению к балке лишь в дру-
другом обозначении длины элемента — вместо dx написано ds.
Так как мы пренебрегаем кривизной стержня, то нейтральная ось про-
проходит через центр тяжести сечения; поэтому при повороте сечения под дей-
действием пар М центры тяжести сечений Oi и О2 не перемещаются, и уси-
усилие N работы не производит. Поэтому мы можем вычислить его работу
независимо от действия пар М и результат прибавить к полученному выше.
Усилия N, действующие на элемент, производят простое растяжение
или сжатие; количество потенциальной энергии, накопленной при этом, будет
N*ds
равно	; вместо длины / растянутого или сжатого стержня подставлена
длина элемента ds.
Количество потенциальной энергии, накопившейся в выделенном эле-
элементе, равно
... M2ds . N*ds

§ 194]
ДЕФОРМАЦИИ КРИВЫХ СТЕРЖНЕЙ
603
потенциальная энергия, накопившаяся во всём стержне, выразится интегра-
интегралом от этой величины, охватывающим всю длину стержня:
„_ С M*ds С N*ds
J 2EJ + J 2EF •
C1.32)
Пользуясь теоремой Кастильяно, мы получим, что производная этой
величины по сосредоточенной силе Р даст нам линейное перемещение
центра тяжести того сечения, где эта сила приложена; точно так же произ-
производная от U по моменту Мо будет равна углу поворота соответствующего
сечения:
f__dU__ С Mds dM.CNds^ dN
Г~~дР~~) EJ 'дР + ) EF * дР'
s	s
dU С Mds дМ . f Nds dM
~~ OMq ~~ J EJ dM0 •" J EF дМ0'
s	s
C1.33)
Для вычисления деформаций кривого стержня удобно восполь-
воспользоваться способом Мора.
Возьмём кривой стержень, представляющий собой четверть
окружности (фиг. 532), защемлённый концом в точке А, Радиус
оси назовём /?0. Нагрузим этот стержень вертикальной силой Р на
свободном конце и найдём верти-
вертикальное перемещение точки В.
Нужно изобразить стержень
в двух состояниях:
а)	при загружении заданной
нагрузкой и
б)	при загружении единичной
силой, приложенной в том сечении,
где определяется перемещение.
Так, для определения верти-
вертикальной составляющей перемеще-
перемещения конца стержня В (фиг. 532) нужно приложить в этом сечении
единичную вертикальную силу Р° = 1 (фиг. 532, б).
Для определения вертикального перемещения будут служить
формулы B1.2 Г) и B1.2 Г") с заменой в них длины элемента dx
длиной оси криволинейного элемента ds
_ f M(x)M°ds
EJ
N(x)N°ds
EF
Вычислим M(x)9 M\ N{x)t jV°:
M = -f- PRb sin cp; M° =
N = — Я sin cp;	A7° =
ds = RQ d<$.
/?o sin cp;
— sin <f>;

604	КРИВЫЕ СТЕРЖНИ	[гл. XXXI
Подставляя полученные величины в формулу C1.33), получаем:
тс	тс
1 С	1 С
f= -pj \P sin2 <?Rl dy -j- -рГр \ P sin2 cp/?0 dcp =
~ J Р sin ?Я; </7 + -L
— AEJ
где / — радиус инерции сечения.
Первое слагаемое в скобках отражает влияние на прогиб изгибаю-
изгибающего момента, второе — нормальной силы. Так как в большинстве
i2
случаев отношение -^- — малая величина, то роль нормальной силы
при деформации кривых стержней в ряде случаев сравнительно
невелика.
Если бы мы хотели найти горизонтальное перемещение точки В,
то следовало бы приложить в этой точке горизонтальную силу
ро=1. Подобным же образом надо было бы поступить при оты-
отыскании угла поворота этого сечения; следует ввести М°=1.
Если при вычислении М и N приходится разбивать стержень на
участки, то соответственно этому каждый из интегралов в формулах
C1.33) распадается на сумму интегралов с соответственно выбран-
выбранными пределами.
§ 195. Вычисление деформаций с учётом кривизны стержня.
При рассмотрении деформаций элемента кривого стержня длиной ds мы
исходили из предположения о том, что деформация этого элемента происходит
так же, как в прямом стержне. Решим эту задачу более точно. Деформация
рассматриваемого элемента (фиг. 531) от действия усилий М и N состоит
из удлинения A ds отрезка ds оси элемента
и из относительного поворота 5 dy сечений,
ограничивающих наш элемент. Относитель-
Относительный поворот сечений, вызванный парами М
(фиг. 533), получается из формулы C1.13)
равным
М	Mds /о1 ол.
d	C1.34)
Но и усилия N, действующие на элемент,
Фиг. 533.	вызывают дополнительный поворот сечений
1—1 и 2—2 на угол bdy".
Нормальные напряжения, соответствующие усилию АГ, распределяются
по сечению равномерно, но длины волокон нашего элемента увеличиваются
от вогнутой к выпуклой стороне пропорционально расстояниям от центра
кривизны; в том же отношении возрастают и их абсолютные удлинения и,
таким образом, сечение 2—2 перемещается относительно 1—/ не парал-

§ 195] ВЫЧИСЛЕНИЕ ДЕФОРМАЦИЙ С УЧЁТОМ КРИВИЗНЫ СТЕРЖНЯ	605
лельно самому себе, а поворачиваясь вокруг центра кривизны элемента на
некоторый угол В dcp". Величина угла поворота В cfy" равна, как видно из фиг. 534,
удлинению осевого волокна, делённому на радиус
кривизны Ro:
КГ Но
CL35)
Удлинение осевого волокна A ds вырезанного
элемента в первую очередь зависит от нормальных
усилий N; эта доля удлинения будет равна
A ds' = рр .	C1.36)
Изгибающий момент М, вызывая относительный	Фиг. 534.
поворот сечений вокруг нейтральных осей на
угол В dy', влечёт за собой дополнительное удлинение осевого волокна,
как это видно из фиг. 533, на величину
Mds Mds	/о1 07Ч
\6i.Ol)
Таким образом, деформация элемента стержня свелась к относительному
повороту сечений 1—1 и 2—2 на угол
^ ? C1.38)
и к удлинению осевого волокна на
4	^	CL39)
Подсчитаем теперь работу, производимую усилиями М и N при посте-
постепенном их возрастании. Постепенно и пропорционально этим усилиям будут
возрастать и деформации В dy и A ds.
Количество потенциальной энергии, накопленной в элементе при этой
деформации, будет численно равно
dudAMbd+
1 „(Nds , Mds\ M*d$ , №ds , MNds
Вся энергия, накопленная в стержне, выразится суммой трёх интегралов:
M*ds С N'ds С MNds
C1.41)
Теперь на примере прямоугольного сечения легко установить погреш-
погрешность, допущенную нами при применении упрощённой формулы C1.32)
С
N2ds
2EF '
s
Как видим, упрощение заключается в замене произведения SRQ величиной
момента инерции У и в отбрасывании третьего слагаемого.
Мы имели для прямоугольного сечения
CL24)
таким образом, принимая SRQ = У, мы делаем относительную погрешность

606
КРИВЫЕ СТЕРЖНИ
[гл. xxxi
Л*
порядка ггбг'у даже при R0 = h (крюк) эта погрешность не превысит
6 -f- 7%; при —г— = 5 она упадёт до О,3°/о- Что же касается отбрасывания
третьего слагаемого, то относительная погрешность при этой операции зави-
зависит от соотношения изгибающего момента и продольной силы и, вообще
говоря, невелика.
§ 196. Примеры расчёта кривых стержней.
Пример 123. Рассчитать круговое кольцо под действием двух сил Р
(фиг. 535). Радиус оси кольца назовём /?0. Найдём напряжения в каком-
нибудь сечении кольца тп, наклонённом под углом ср к горизонту; для этого
разрежем стержень в этом сечении. Этот разрез
не разделяет кольцо на две независимые друг от
друга части, как это мы имели, например, в слу-
случае растянутого стержня. О величине напряжений
мы из условий статики ничего узнать не можем, —
задача, как говорят, внутренне статически не-
\_А определимая, хотя внешние силы, действующие на
кольцо, известны.
С другой стороны, если мы найдём напряжения,
действующие по какому-либо сечению, например Л,
и складывающиеся в общем случае в пару Ма%
нормальную и касательную силы Na и Qa, то для
каждого другого сечения тп мы сможем вычислить
изгибающий момент М, нормальную и попереч-
поперечную силы N и Q и найти потом напряжения. Для
этого надо будет выделить из кольца заштрихованную
часть между сечениями А и тп (фиг. 535) и уравновесить действующие на
неё по сечению Л силы Мау Na и Qa системой М, N н Q для сечения тп.
Считая Ма> Na и Qa положительными и обозначая угол между сече-
сечениями А и тп через ср, получим:
C1.42)
М = + а + aR0 (	y) +
+ QaR0 sin cp,
N = Na cos cp — Qa sin cp,
Q = Qa COS cp + Na Sin cp.
Таким образом, задача сводится к на-
нахождению трёх статически неопредели-
неопределимых величин внутренних усилий в ка-
каком-либо сечении А кольца: изгибаю'
щего момента Ма, нормальной силы Na
и поперечной силы Qa.
Разрезав кольцо сечениями в точ-
точках Л и С на две половины (фиг. 536),
мы видим, что по симметрии нормальные
усилия в сечениях Л и С равны Р/2, а касательные равны нулю. Таким образом,
из трёх лишних неизвестных остаётся только усилие Ма. Далее, тоже по
симметрии, сечения Б и Л при деформации полукольца не поворачиваются;
поэтому четверть кольца АВ мы можем рассматривать как кривой стержень,
защемлённый в сечении В и нагружённый на свободном конце силой* —
Фиг. 536.

§ 196]
ПРИМЕРЫ РАСЧЁТА КРИВЫХ СТЕРЖНЕЙ
607
и моментом Ма; условие же для нахождения Ма получится, если записать,
что поворот сечения А равен нулю, т. е.
Л/f/Vfe //о
™±р- = о.	C1.43)
Здесь М° ==\ — момент, приложенный в сечении А по направлению дей-
действующего неизвестного момента Ма. Изгибающий момент [формула C1.42)]
равен
далее,
М° = + 1 и ds = Ro dy.
Подставляя эти значения в уравнение C1.43), получаем:
я/2
^7 ( [+Ма + ? A - cosT)
Отсюда
( [
я/2
те/2
или
у/?§у - y*s=о.
--J)=~ 0,182 Р/?о
Отсюда
Таким образом, изгибающий момент Ма получился отрицательным.
Теперь для сечения В при <р =	у
у находим:
М-
= — 0,182 PRQ + 0,5 PRo = + 0,318 PROi
_Р_
Таким образом, для кольца опасным яв- *^г
ляется сечение В, хотя нормальная сила
в этом сечении и равна нулю.
Пример 124. Найти изгибающие
моменты и нормальные силы в кри-
кривом стержне (фиг. 537) под действием пары М. Обозначая реакции через
НА, Л4д, А и В, составляем уравнения статики:

608	КРИВЫЕ СТЕРЖНИ	[ГЛ. XXXI
Задача статически неопределима; за лишнюю неизвестную выбираем
реакцию В; за основную систему примем стержень, защемлённый концом Д.
Из условия равенства нулю прогиба в точке В имеем:
dU
М9 дМ9
Вычисляем изгибающий момент М9 и его производную по В; получаем:
М9 = Ва sin <р — М;	*" = a sin ?; ds = a • dy.
Тогда уравнение для определения реакции В принимает вид:
grv 1
-grv 1 (Ва sin <f — М) a2 sin ср сГ«р = 0, или Ва \ sin2 у dy—M I sin <р сГср = 0.
\ sin2 у dy—M I sin
Выполняя интегрирование и решая полученное уравнение относительно В,
находим:
Подставляя это значение В в выражение для М^ получаем:
М? =	sin <р — М = М I — sin <р — 1 ).
Таким образом, имеем: при <р = 0 момент М^ = — М, при <р = те/4 момент
Фиг. 538.
: — 0,11 М, при <р = те/2 момент М^
N<p = — В sin <р = -
Следовательно, при <р = 0 N« = 0,
р
равна
Фиг. 539.
= + 0,27 М. Нормальная сила N?
	sin <p.
Эпюры Мер и Мр показаны на фиг. 538 и 539.

§ 197]
РАСЧЁТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ
609
ГЛАВА XXXII.
РАСЧЁТ ТОЛСТОСТЕННЫХ И ТОНКОСТЕННЫХ СОСУДОВ.
Фиг. 540.
§ 197. Расчёт толстостенных цилиндров.
В тонкостенных цилиндрических резервуарах, подвергнутых внутреннему
давлению, вполне возможно при вычислениях считать напряжения равно-
равномерно распределёнными по толщине стен-
стенки (§ 35). Это допущение очень мало от-
отзывается на точности расчёта.
В цилиндрах, у которых толщина
стенок не мала по сравнению с радиусом,
подобное предположение повело бы к
слишком большим погрешностям. Расчёт
таких цилиндров дан Ляме и Гадолиным
в 1852—1854 гг. Работы русского акаде-
академика А. В. Гадолина в области расчёта
кривых стержней в применении к расчёту
прочности артиллерийских орудий создали
ему мировую известность. Отечественные
артиллерийские заводы (и многие зару-
зарубежные) до сих пор проектируют и из-
изготовляют орудия, пользуясь исследова-
исследованиями Гадолина.
На фиг. 540 изображено поперечное
сечение толстостенного цилиндра с наруж-
наружным радиусом ri, внутренним г2; цилиндр подвергнут наружному pt и вну-
внутреннему давлению р2.
Рассмотрим очень узкое кольцо материала радиусом г внутри стенки
цилиндра. Толщину кольца обозначим dr. Пусть АВ (фиг. 540) изображает
небольшую часть этого кольца, соответству-
соответствующую центральному углу db.
Размер выделенного элемента, перпен-
перпендикулярный к плоскости чертежа, возьмём
равным единице. Пусть аг и ar-\-dor будут
напряжения, действующие по внутренней и
наружной поверхностям элемента АВ, a Qt —
напряжения по его боковым граням. По
симметрии сечения цилиндра и действующей
нагрузки элемент АВ перекашиваться не бу-
будет, и касательные напряжения по его гра-
граням будут отсутствовать. По граням эле-
элемента АВ, совпадающим с плоскостью чер-
чертежа, будет действовать третье главное на-
напряжение ог, вызванное давлением на днище
цилиндра. Это напряжение можно считать
постоянным по всем точкам поперечного се-
сечения цилиндра.
На элемент АВ действуют в плоскости чертежа две силы a^dr • 1, со-
составляющие между собой угол dbt и радиальная сила, равная
(<гг + dsr) (г + dr) dti • 1— or rdb . 1.
Эта сила направлена в сторону наружной поверхности. Уравновешиваясь,
эти три силы составляют замкнутый треугольник abc (фиг. 541).
20 Н. М. Беляев
Фиг. 541.

610
РАСЧЕТ ТОЛСТОСТЕННЫХ И ТОНКОСТЕННЫХ СОСУДОВ [ГЛ. XXXII
Из него следует, что радиальная сила, изображаемая отрезком аЬл связана
с силой Qtdr (отрезок со) соотношением
~ab = 1а лГ0,
или
[(<jr + dsr) (r + dr) — crr] db = Qt dr </8;
пренебрегая малыми высшего порядка, получаем:
cr dr -+- darr = <st dr;
отсюда
i
C2.1)
Условие равновесия дало только одно уравнение для нахождения двух не-
неизвестных напряжений. Задача статически неопределима, и необходимо
обратиться к рассмотрению деформаций.
Деформация цилиндра будет заключаться
в его удлинении и в радиальном перемеще-
перемещении всех точек его поперечных сечений. На-
Назовём радиальное перемещение точек вну-
внутренней поверхности рассматриваемого эле-
элемента через и (фиг. 542). Точки наружной
поверхности переместятся по радиусу на
другую величину u-\-du\ таким образом,
толщина dr выделенного элемента увеличится
на du, и относительное удлинение материала
du
в радиальном направлении будет ег = —.
В направлении напряжений <*t относи-
относительное удлинение tt будет равно относи-
относительному удлинению дуги ад, занявшей поло-
положение cd; так как относительное удлинение дуги таково же, как относитель-
относительное удлинение радиуса г, то ?; = —. По закону Гука [формулы G.16) § 40]
Фиг. 542.
du
dr
и
г
C2.2)
Так как с^ и tr определяются одной и той же функцией и, то они связаны
условием совместности. Дифференцируем zt по г:
dr
г—
'< = Т; !F = -
C2.3)
Это и будет условие совместности деформаций; заменяя в нём значения
tr и tt no C2.2), получим второе уравнение, связывающее <st и аг:
rfrl
или
dr r
C2.4)

§ 197]	РАСЧЁТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ	Gil
Подставляя в это уравнение значение разности <sr— <^ из C2.1), находим:
dr
или
Для совместного решения уравнений C2.1) и C2.5) продифференцируем
первое по г и подставим в него значение -~ из второго; получим:
*?> _ *L*± 4- г ^L 4-^ — 0-
dr dr'rT dr* ~*~ dr~~ *
отсюда дифференциальное уравнение задачи:
^ + JLfe=0.	C2.6.
dr2 ' r dr	v
Интеграл этого уравнения будет
C2.7)
что можно проверить подстановкой.
Постоянные А и В определятся из условий на внутренней и наружной
поверхностях цилиндра:
Знак минус в правых частях этих формул поставлен потому, что положи-
положительными сг мы приняли растягивающие напряжения (фиг. 541)"
Из условий C2.8) получаем:
я
Л~ rf —rl • ^- rf-rj '
Пользуясь этими значениями и уравнением C2.7), получаем окончатель-
окончательные формулы для <sr и а/*.
_
_Ptr§—pArf (р2 — Pi)rfrf
_Р2Г1 p,r\ (PtPi)r\r\
t	rf_rf "t- Г2(Г?_Г|) -J
Как видно из этих формул, сумма <rr + <J/ не зависит от г, т. е. относи-
относительная деформация вдоль оси цилиндра во всех точках сечения одинакова
(так как и а2 одинаково), и сечение остаётся плоским.
Представляет очень большой практический интерес случай, когда имеет
место только одно внутреннее давление р*, тогда
C2.10)

612
РАСЧЁТ ТОЛСТОСТЕННЫХ И ТОНКОСТЕННЫХ СОСУДОВ [ГЛ. XXXII
ное
График, изображающий распределение напряжений по толщине цилиндра
в случае рх = 0, дан на фиг. 543. Так как по абсолютной величине продоль-
напряжение аг обычно значительно меньше аг и ati то
прочность цилиндра определяется этими
последними. Применяя третью теорию
прочности (наибольших касательных на-
напряжений), получаем, что наибольшая
разность главных напряжений, равная
(для случая pi = 0)
растягивающее
в
-°r)max = J|IZ7|
C2.11)
будет иметь место в точках внутренней
поверхности цилиндра и всегда будет
по абсолютной величине значительно
больше внутреннего давления.
Таким образом, остаточные деформа-
деформации появятся прежде всего у внутрен-
внутренней поверхности цилиндра, когда (j^ — CTr)max будет равно пределу текучести
материала; борьба с их появлением путём увеличения наружного радиуса п
практически безнадёжна, — с увеличением ri растут и числитель, и знамена-
знаменатель формулы C2.11); поэтому разность главных напряжений (з/— ar)max хотя
и убывает, но очень медленно. Однако момент появления пластических де-
деформаций у внутренней поверхности цилиндра далеко не соответствует ис-
исчерпанию грузоподъёмности конструкции; для правильной оценки прочности
цилиндра необходимо пе-
ф__	рейти к расчёту по допу-
допускаемым нагрузкам.
Полное исчерпание
грузоподъёмности про-
произойдёт тогда, когда коль-
кольцевая пластическая зона,
распространяясь от вну-
внутренней поверхности ци-
цилиндра, дойдёт до наруж-
наружной; состояние разруше-
разрушения наступит тогда, когда
материал у наружной по-
поверхности достигнет со-
состояния, при котором
произойдёт разрыв. По-
Подробное исследование ра-
работы толстостенных ци-
цилиндров при наличии
остаточных деформаций
дано в нашей работе *).
На фиг. 544 показано
2.2
2,0
iS
F
12
4
/
/
/
15
г
Фиг. 544.
2,5
отношение внутреннего
давления р2, при котором
пластическая зона охватывает всё сечение, к давлению, соответствующему
началу пластических деформаций р\. Оказывается, что действительная грузо-
грузоподъёмность значительно выше получаемой при обычном методе расчёта.
4) Беляев Н. М. и С и н и ц к и й А. К., Напряжения и деформации
в толстостенных цилиндрах при упруго-пластическом состоянии материала.
«Известия Отделения технических наук Академии Наук СССР», 1938.

РАСЧЁТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ
613
Упругая грузоподъёмность толстостенных цилиндров может быть под-
поднята путём создания начальных напряжений. Для этого необходимо изгото-
изготовить цилиндр, составленный из двух цилиндров, вставленных один в другой;
наружный диаметр внутреннего цилиндра делается несколько больше вну-
внутреннего диаметра наружного цилиндра; после надевания наружного цилиндра
в нагретом состоянии на внутренний и его остывания по поверхности сопри-
соприкасания возникнут реакции, сжимающие внутренний и растягивающие внеш-
внешний цилиндры. Наличие этих начальных напряжений улучшает работу состав-
составного цилиндра при внутреннем давлении, как видно из приведённого ниже
расчёта.
На фиг. 545 изображён составной цилиндр после
остывания. Напряжения в тангенциальном напра-
направлении а^ будут равны: для наружного цилиндра
(растяжение)
„'_ Р*Г1	Ръг\г1
Г2 I Г2
— ' з	'
2 	 Г%\ '
для внутреннего цилиндра (сжатие)
Г2	*-2 />2
Фиг. 545.
На фиг. 546 показаны кривые распределения этих начальных напряжений.
при следующих числовых данных:
гх = 11,50 см; г2 = 5,70 см; гг = 8,25 см; рг = 280 кг/см*.
Для наружного цилиндра напряжения у наружной поверхности равны:
у внутренней поверхности
°к = + Р> ^Щ = + 895
Для внутреннего цилиндра напряжения
у внутренней поверхности равны:
а;; = -ps -3^1— = - 1080 кг/см";
у наружной
аГ = - р3 0-±^| = - 800
W бнутреннещ
Ва&аеиия
Предположим теперь, что цилиндр	Фиг. 546.
подвергается внутреннему давлению
рш = 3400 кг[см2; тогда распределение напряжений с^ без учёта начальны*
усилий рь представится формулой C2.10)

614	РАСЧЁТ ТОЛСТОСТЕННЫХ И ТОНКОСТЕННЫХ СОСУДОВ [ГЛ. XXXII
Крайние значения этих напряжений равны:
у наружной поверхности аа = + 2245 кг/см*,
> внутренней >	ai2 = + 5620 >
Соответствующая кривая изображена на фиг. 546. При совместном дей-
действии внутреннего давления и начальных усилий напряжения выразятся сум-
суммой ординат кривых <st + o't и а, + а"; кривая, изображающая эти суммарные
напряжения, имеет зубчатое очертание; она тоже представлена на фиг. 546.
Вид результирующей кривой показывает, что при наличии начальных уси-
усилий рг напряжения в наружном цилиндре повышаются, а во внутреннем —
понижаются; таким образом, материал работает более равномерно; наиболь-
наибольшее напряжение падает до 5620— 1080 = + 4540 кг/см2у а наименьшее повы-
повышается до 2245 + 613 = 2858 кг/см2. Конечно, это распределение напряжений
имеет место при работе материала в пределах упругости.	*
Установим, какую разницу в радиусах Дг8 = r'l — г'г надо дать, чтобы
осуществить желательное начальное усилие р8; г$ — это начальный наруж-
наружный радиус внутреннего цилиндра, а г'ь — начальный внутренний радиус на-
наружного цилиндра.
При остывании наружной трубы происходит выравнивание этих радиусов
за счёт уменьшения r'l на Аг? и увеличения г\ на Аг'8; сумма абсолютных
величин этих деформаций должна быть равна Дг8:
Относительное тангенциальное удлинение материала на внутренней по-
поверхности наружного цилиндра равно
в эту формулу вместо г8 подставлена величина общего для обоих цилиндров
радиуса rs = r's — ДГд, так как Ьг'8 — малая величина и такая замена вводит
очень небольшую погрешность. Относительное увеличение радиуса г[ будет
тоже ej; поэтому
Относительное тангенциальное сжатие материала на наружной поверх-
поверхности внутренней трубы равно:
укорочение радиуса rl будет равно:
Сумма абсолютных величин ArJ и Дг?' равна по предыдущему
Р»г» И + rj ¦ 1 .ftr.rrj + n ,/|-2/>sr| r\~r\
Таким образом, чтобы обеспечить наличие принятого нами начального
усилия ph необходимо дать разницу диаметров Де/3, равную
??!_?
Е (r«-

§ 198] НАПРЯЖЕНИЯ В СФЕРИЧЕСКИХ ТОЛСТОСТЕННЫХ СОСУДАХ 615
Минимальная температура *°, до которой надо нагреть наружный цилиндр
при надевании его на внутренний, определяется уравнением
отсюда
(при наших числовых данных: а = 125 • 10~7; Е= 2 • 10е кг/смг;
0,0137 см).
§ 198. Напряжения в сферических толстостенных сосудах.
На фиг. 547 изображён элемент, вырезанный из толщи стенки толсто-
толстостенного сферического сосуда; внутренний радиус этого элемента равен г, а на-
наружный r+dr; напряжения, действующие на
этот элемент, изображены на чертеже.
Составляя уравнения равновесия и совме-
совместности, получаем для <зг и <st значе-
значения:
В
C2.12)
Постоянные А к В могут быть
определены из условий на внутренней
и внешней поверхностях сосуда при
соответственно, где rt и г2 — наружный и
внутренний радиусы.
Так, при действии внешнего pi и вну-
внутреннего р» давлений А и В определяются	Фиг. 547.
из условий:
с,. = Л +-y = — p2 на внутренней поверхности,
- —= — pi на внешней поверхности.
Отсюда
Тогда
r\rl
rj —
Г1
4?f
П r%
C2.13)

616
РАСЧЁТ ТОЛСТОСТЕННЫХ И ТОНКОСТЕННЫХ СОСУДОВ [ГЛ. XXXII
§ 199. Расчёт тонкостенных сосудов.
Если толщина стенок цилиндра t = п — г2 мала по сравнению с радиу-
радиусами rv и г2, то из формулы C2.10) мы получаем:
т. е. величину, определённую нами раньше (§ 34).
Для тонкостенных резервуаров, имеющих форму поверхностей вращения
и находящихся под внутренним давлением /?, распределённым симметрично
относительно оси вращения, можно вывести общую формулу для вычисления
напряжений.
Выделим (фиг. 548) из рассматриваемого резервуара элемент двумя
смежными меридиональными сечениями и двумя сечениями, нормальными
<Jmdstt
Фиг. 548.
к меридиану. Размеры элемента по меридиану и по перпендикулярному к нему
направлению обозначим соответственно dsm и tfs/, радиусы кривизны мери-
меридиана и перпендикулярного к нему сече-
,	ния обозначим рт и р^; толщину стенки
5tdsmt назовём t.
1	По симметрии по граням выделенного
элемента будут действовать только нор-
нормальные напряжения ат в меридиальном
направлении и at в направлении, перпенди-
перпендикулярном к меридиану. Соответствующие
усилия, приложенные к граням элемента,
будут amdstt и atdsmt. Так как тонкая обо-
оболочка сопротивляется только растяжению,
подобно гибкой нити, то эти усилия бу-
будут направлены по касательной к мери-
меридиану и к сечению, нормальному к мери-
меридиану.
Усилия atdsmt = ас = be (фиг. 549)
дадут в нормальном к поверхности эле-
элемента направлении равнодействующую aby равную
6tdsmt
Фиг. 549.
tdsmt.
?t
Подобным же образом усилия vmdstt дадут в том же направлении равнодей-

§ 199]
РАСЧЁТ ТОНКОСТЕННЫХ СОСУДОВ
617
ствующую *mdstdsm —. Сумма этих усилий уравновешивает нормальное дав-
ление, приложенное к элементу
Отсюда
Р dsmdst = °mdstdsm — + ct dsmdst —.
vm	Yt
Pm Pt
C2.14)
Это основное уравнение, связывающее напряжения ат и at для тонкостенных
сосудов вращения, дано Лапласом.
Так как мы задались распределением (равномерным) напряжений по
толщине стенки, то задача статически определима; второе уравнение равно-
равновесия получится, если мы рассмотрим рав-
равновесие нижней, отрезанной каким-либо па-
параллельным кругом, части резервуара.
Рассмотрим случай гидростатической
нагрузки (фиг. 550). Меридиональную кри-
кривую отнесём к осям х и у с началом ко-
координат в вершине кривой. Сечение про-
проведём на уровне у от точки О. Радиус
соответствующего параллельного круга
будет х.
Каждая пара усилий omtfs^, действу-
действующих на диаметрально противоположные
элементы dst проведённого сечения, даёт
вертикальную равнодействующую bct рав-
равную
be = 2ab cos 6 = 2ат dstt cos 0;
сумма этих усилий, действующих по всей
окружности проведённого сечения, будет
равна 2nx<smt cos 6; она будет уравнове-
уравновешивать давление жидкости p = f (h —у)
на этом уровне плюс вес жидкости в отре-
отрезанной части сосуда Ру
Отсюда
2nxamt cos 8 = пх2р -
рх
* 2t cos 6 ~ 2nxt cos 6'
C2.15)
Зная уравнение меридиональной кривой,
можно найти Q, х и Ру для каждого значе-
ния у, и стало быть, найти am, a из урав-
уравнения C2.14) и of.
Например, для конического резервуара с углом при вершине ?
ненного жидкостью с объёмным весом y на высоту Л, будем иметь:
напол-
напол= oo; x=y\ga; Ру == —
tr	• \	•'/*	» i: t	РПЧ Я

618	РАСЧЁТ ТОЛСТОСТЕННЫХ И ТОНКОСТЕННЫХ СОСУДОВ [ГЛ. XXXII
югда
j Trcy8tg8a _T (ft — У).У tg « . Г V8 tg a ^
' впу tg a ^COS a	2* COS a	'
j
2* COS a	' впу tg a ^COS a	2* COS a	'6/ COS a
t	t COS ct
Для сферического сосуда радиусом г0, находящегося под внутренним
давлением pQi по симметрии а^ = ат = а; тогда из уравнения C2.14), так как
?т = Р* = го»
Если меридиональная кривая будет иметь переломы с разрывом непре-
непрерывности угла 0, то равновесие тонкой оболочки у места перелома может
быть обеспечено лишь наличием реакций, приложенных к оболочке по окруж-
окружности в этом месте. Появление таких реакций обеспечивается устройством
специальных колец, способных брать на себя усилия, возникающие в них
в связи с неуравновешенностью напряжений ат по обе стороны точки
перелома.

ОТДЕЛ IX.
УСТОЙЧИВОСТЬ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ.
глава хххш.
ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ.
§ 200. Введение. Понятие об устойчивости формы
сжатых стержней.
Во всём предыдущем изложении мы определяли поперечные раз-
размеры стержней из условий прочности. Однако разрушение стержня
может произойти не только потому, что будет нарушена прочность,
но и оттого, что стержень не сохранит той формы, которая ему при-
придана конструктором; при этом изменится и характер напряжённого
состояния в стержне.
Наиболее типичным примером является работа стержня, сжатого
силами Р. До сих пор для проверки прочности мы имели условие
* = ?<М> где [а1 = 2 или tal = ^.
Это условие предполагает, что стержень всё время, вплоть до
разрушения его напряжениями ат или ов, работает на осевое сжатие.
Уже простейший опыт показывает, что далеко не всегда возможно
разрушить стержень путём доведения напряжений сжатия до пре-
предела текучести или до предела прочности материала.
Если мы подвергнем продольному сжатию тонкую деревянную
линейку, то она может сломаться, изогнувшись; перед изломом сжи-
сжимающие силы, при которых произойдёт разрушение линейки, будут
значительно меньше тех, которые вызвали бы при простом сжатии
напряжение, равное пределу прочности материала. Разрушение
линейки произойдёт потому, что она не сможет сохранить придан-
приданную ей форму прямолинейного, сжатого стержня, а искривится,
что вызовет появление изгибающих моментов от сжимающих сил Р
и, стало быть, добавочные напряжения от изгиба; линейка потеряет
устойчивость.
Поэтому для надёжной работы конструкции мало, чтобы она
была прочна; надо, чтобы все её элементы были устойчивы: они
должны при действии нагрузок деформироваться в таких пределах,
чтобы характер их работы оставался неизменным. Поэтому в целом
ряде случаев, в частности, для сжатых стержней, помимо проверки
на прочность, необходима и проверка на устойчивость. Для осу-
осуществления этой проверки надо ближе ознакомиться с условиями,

620	ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [ГЛ. ХХХШ
при которых устойчивость прямолинейной формы сжатого стержня
нарушается.
Возьмём достаточно длинный по сравнению с его поперечными
размерами стержень, шарнирно-прикрепленный к опорам (фиг. 551),
и нагрузим его сверху центрально силой Р, постепенно возрастаю-
возрастающей. Мы увидим, что пока сила Р сравнительно мала, стержень
будет сохранять прямолинейную форму. При попытках
отклонить его в сторону, например путём приложения
кратковременно действующей горизонтальной силы, он
будет после ряда колебаний возвращаться к первона-
первоначальной прямолинейной форме, как только будет уда-
удалена добавочная сила, вызвавшая отклонение.
При постепенном увеличении силы Р стержень
будет всё медленнее возвращаться к первоначаль-
первоначальному положению при проверках его устойчивости; на-
наконец, можно довести силу Р до такой величины,
при которой стержень после небольшого отклоне-
/ ния его в СТОрОНу уЖе не выпрямится, а останется
• н искривлённым. Если мы, не удаляя силы Р, выпря-
Фиг. 551. мим стержень, он уже, как правило, не сможет со-
сохранить прямолинейную форму. Другими словами, при
этом значении силы Р, называемом критическим, Рк, прямолиней-
прямолинейная форма перестаёт быть устойчивой формой равновесия сжатого
стержня !).
Переход к критическому значению силы Р происходит внезапно;
стоит нам очень немного уменьшить сжимающую силу по сравнению
с её критической величиной, как прямолинейная форма равновесия
вновь делается устойчивой.
С другой стороны, при очень небольшом превышении сжимаю-
сжимающей силой Р её критического значения прямолинейная форма стержня
делается крайне неустойчивой] достаточно при этом небольшого
эксцентриситета приложенной силы, неоднородности материала по
сечению, чтобы стержень искривился, и не только не вернулся
к прежней форме, а продолжал искривляться под действием всё
возрастающих при искривлении изгибающих моментов; процесс
искривления заканчивается либо достижением совершенно новой
(устойчивой) формы равновесия, либо разрушением.
Исходя из этого, мы должны практически считать критическую
величину сжимающей силы Рк эквивалентной нагрузке, «разрушаю-
«разрушающей» сжатый стержень, выводящей его (и связанную с ним конструк-
конструкцию) из условий нормальной работы, Конечно, при этом надо
помнить, что «разрушение» стержня нагрузкой, превышающей кри-
*) Исследования показывают, что потеря устойчивости становится возмож-
возможной при значениях Р, превышающих критическое на величину второго по-
порядка малости.

§ 200] ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ ФОРМЫ СЖАТЫХ СТЕРЖНЕЙ	621
тическую, может происходить при непременном условии беспрепят-
беспрепятственного возрастания искривления стержня; поэтому если при боко-
боковом выпучивании стержень встретит боковую опору, ограничивающую
его дальнейшее искривление, то разрушение может и не наступить.
Обычно подобная возможность является исключением; поэтому
практически следует считать критическую сжимающую силу низшим
пределом «разрушающей» стержень силы.
Явление потери устойчивости при сжатии можно по аналогии
иллюстрировать следующим примером из механики твёрдого тела
(фиг. 552). Будем вкатывать цилиндр на наклонную плоскость ab,
которая потом переходит в короткую гори-
горизонтальную площадку be и наклонную пло-
плоскость обратного направления cd. Пока мы
поднимаем цилиндр по плоскости ab, под-
поддерживая его при помощи упора, перпенди-
перпендикулярного к наклонной плоскости, он будет	фИг. 552.
в состоянии устойчивого равновесия; на
площадке be его равновесие делается безразличным; стоит же нам
поместить цилиндр в точку с, как его равновесие сделается не-
неустойчивым—при малейшем толчке вправо цилиндр начнёт дви-
двигаться вниз.
Описанную выше физическую картину потери устойчивости сжа-
сжатым стержнем легко осуществить в действительности в любой
механической лаборатории на очень элементарной установке *). Это
описание не является какой-то теоретической, идеализированной
схемой, а отражает поведение реального стержня под действием
сжимающих сил.
Потерю устойчивости прямолинейной формы сжатого стержня
иногда называют «продольным изгибом», так как она влечёт за со-
собой значительное искривление стержня под действием продольных
сил. Для проверки на устойчивость сохранился и до сих пор термин
«проверка на продольный изгиб», являющийся условным, так как
здесь речь должна итти не о проверке на изгиб, а о проверке на
устойчивость прямолинейной формы стержня.
Установив понятие о критической силе как о «разрушающей»
нагрузке, выводящей стержень из условий его нормальной работы,
мы легко можем составить условие для проверки на устойчивость,
аналогичное условию прочности.
Критическая сила Рк вызывает в сжатом стержне напряжение,
называемое «критическим напряжением» и обозначаемое буквой
Р
QK = -rr. Критические напряжения являются опасными напряжениями
Для сжатого стержня. Поэтому, чтобы обеспечить устойчивость пря-
*) См. Н. М. Беляев, Лабораторные работы по сопротивлению матери-
материалов, § 85, Гостехиздат, 1951.

622	проверка сжатых стержней на устойчивость [гл. хххш
молинейной формы стержня, сжатого силами Р, необходимо к условию
прочности fo = -p-^[a]J добавить ещё условие устойчивости:
* = ?<Ы	C3.1)
где [<зу] — допускаемое напряжение на устойчивость, равное кри-
критическому, делённому на коэффициент запаса на устойчивость,
т. е. [<*,] = ?.
Ку
Для возможности осуществить проверку на устойчивость мы дол-
должны показать, как определять ок и как выбрать коэффициент запаса ky.
§ 201. Формула Эйлера для критической силы.
Для нахождения критических напряжений ак надо вычислить кри-
критическую силу Рк, т. е. наименьшую осевую сжимающую силу, спо-
способную удержать в равновесии слегка искривлённый сжатый стержень.
Эту задачу впервые решил академик Петербургской Академии
наук Л. Эйлер в 1744 году.
Заметим, что самая постановка задачи иная, чем во всех ранее
рассмотренных отделах курса. Если раньше мы определяли дефор-
деформацию стержня при заданных
внешних нагрузках, то здесь
ставится обратная задача: за-
задавшись искривлением оси сжа-
сжатого стержня, следует опреде-
определить, при каком значении осе-
осевой сжимающей силы Р такое
искривление возможно.
Рассмотрим прямой стер-
стержень постоянного сечения,
шарнирно опёртый по концам;
одна из опор допускает возможность продольного перемещения
соответствующего конца стержня (фиг. 553). Собственным весом
стержня пренебрегаем.
Нагрузим стержень центрально приложенными продольными сжи-
сжимающими силами Р=РЕ и дадим ему весьма небольшое искривление
в плоскости наименьшей жёсткости; стержень удерживается в искри-
искривлённом состоянии, что возможно, так как Р = РК.
Деформация изгиба стержня предположена весьма малой, поэтому
для решения поставленной задачи можно воспользоваться прибли-
приближённым дифференциальным уравнением изогнутой оси стержня (§ 109).
Выбрав начало координат в точке А и направление координатных
осей, как показано на фиг. 553, имеем A8.7):
Фиг. 553.

§ 201]	ФОРМУЛА ЭЙЛЕРА ДЛЯ КРИТИЧЕСКОЙ СИЛЫ	623
Возьмём сечение на расстоянии х от начала координат; ордината
изогнутой оси в этом сечении будет у, а изгибающий момент равен
М(х) = — Ру.
По схеме, изображённой на фиг. 499, изгибающий момент полу-
получается отрицательным, ординаты же при выбранном направлении
оси у оказываются положительными. (Если бы стержень искривился
выпуклостью книзу, то момент был бы положительным, а у — отри-
отрицательным и М(х) =— Ру.)
Приведённое только что дифференциальное уравнение A8.7) при-
принимает вид:
EJ% = -Py\	C3.2)
р
деля обе части уравнения на EJ и обозначая дробь yj через k%,
приводим его к виду:
fg	O.	C3.3)
Общий интеграл этого уравнения имеет вид:
у = a sin kx -f- b cos kx.	C3.4)
Это решение заключает в себе три неизвестных: постоянные
интегрирования а и b и значение ?=1/-=у, так как величина кри-
критической силы нам неизвестна.
Условия на концах стержня дают два уравнения:
в точке А при х = 0 прогиб у = 0,
» » В » х = 1 » _у = 0.
Из первого условия следует (так как sin^x = 0 и cos^y=l)
0 = ».
Таким образом, изогнутая ось является синусоидой с уравнением
у = a sin kx.	C3.5)
Применяя второе условие, подставляем в это уравнение
у = 0 и х = /;
получаем:
0 = asinkl.	C3.6)
Отсюда следует, что или а или kl равны нулю.
Если а равно нулю, то из уравнения C3.5) следует, что прогиб
в любом сечении стержня равен нулю, т. е. стержень остался пря-

G24	ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIII
мым. Это противоречит исходным предпосылкам нашего вывода. Сле-
Следовательно, sin&/=0, и величина kl может иметь следующий бес-
бесконечный ряд значений:
*/=0, т., 2т:, Зт:, ..., Пт.}	C3.7)
где п — любое целое число.
Отсюда А = ~, а так как k=y -=j, то
^ ^	?М\	C3.8)
Иначе говоря, нагрузка, способная удержать слегка искривлён-
искривлённый стержень в равновесии, теоретически может иметь целый ряд
значений. Но так как отыскивается, и интересно с практической точ-
точки зрения, наименьшее значение осевой сжимающей силы, при ко-
которой становится возможным продольный изгиб, то следует при-
и /i 1 о /* ¦ /¦¦mill •
Первый корень п = 0 требует, чтобы Рк было равно нулю, что
Fie отвечает исходным данным задачи; поэтому этот корень должен
быть отброшен и наименьшим корнем принимается значение л=1.
Тогда получаем:
Pk = J^#	C3.9)
(Здесь J—минимальный момент инерции поперечного сечения стерж-
стержня.) Это — так называемая формула Эйлера для сжатого стержня
с шарнирно-опёртыми концами. Значению критической силы C3.9)
соответствует изгиб стержня по синусоиде с одной полуволной [фор-
[формула C3.5)]
y = asin~.	C3.10)
Значениям критической силы высших порядков соответствуют искрив-
искривления по синусоидам с двумя, тремя и т. д. полуволнами (фиг. 554):
2т.	. 2ъх \
Таким образом, чем больше точек перегиба будет иметь синусо-
синусоидально-искривлённая ось стержня, тем большей должна быть крити-
критическая сила. Более полные исследования показывают, что формы
равновесия, определяемые формулами C3.11), неустойчивы; они пе-

201]
ФОРМУЛА ЭЙЛЕРА ДЛЯ КРИТИЧЕСКОЙ СИЛЫ
625
реходят в устойчивые формы лишь при наличии промежуточных
опор в точках В и С (фиг. 554).
Таким образом, поставленная задача решена; для нашего стержня
наименьшая критическая сила определяется формулой
а изогнутая ось представляет синусоиду
Величина постоянной интегрирования а осталась неопределённой;
физическое значение её выяснится, если в уравнении синусоиды по-
положить х = 1/2; тогда Xv=//2 (т. е. посредине длины стержня)
получит значение:
Значит, а — это прогиб стержня в сечении по-
посредине его длины. Так как при критическом
значении силы Р равновесие изогнутого стержня
возможно при различных отклонениях его от пря-
прямолинейной формы, лишь «бы эти отклонения
йытг малыми,, то естественно, что прогиб /
остался неопределённым.
Он должен быть при этом настолько малым,
чтобы мы имели право применять приближённое
-дифференциальное уравнение изогнутой оси, т. е.
чтобы \-dr~) было мало по сравнению с едини-
единицей A8.5).
Получив значение критической силы, мы можем сейчас же най-
найти и величину критического напряжения ок, разделив силу Рк на
площадь сечения стержня F\ так как величина критической силы
определялась из рассмотрения деформаций стержня, на которых мест-
местные ослабления площади сечения сказываются крайне слабо, то в
формулу для Рк входит момент инерции J^ = i^F^\ поэтому при-
принято при вычислении критических напряжений, а также при состав-
составлении условия устойчивости вводить в расчёт полную, а не осла-
ослабленную, площадь поперечного сечения стержня F6?. Тогда
= -7Г- = -7ТТТ = ТГ.	(ЗЗЛ2)
Фиг. 554.
Таким образом, критическое напряжение для стержней данного
материала обратно пропорционально квадрату отношения длины
стержня к наименьшему радиусу инерции его поперечного сечения.

626
ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [ГЛ. ХХХШ
Это отношение Х = /// называется гибкостью стержня и играет
весьма важную роль во всех проверках сжатых стержней на устой-
устойчивость.
Из формулы C2.12) видно, что критическое напряжение при тон-
тонких и длинных стержнях может быть весьма малым, ниже основного
допускаемого напряжения на прочность [а]. Так, для стали 3 с пре-
пределом прочности ав^4000 кг/см% допускаемое напряжение может
быть принято [а] = 1600 кг/см*; критическое же напряжение для
стержня с гибкостью X = 150 при модуле упругости материала
Е=2 • 106 кг/см* будет равно
Таким образом, если бы площадь сжатого стержня с такой гибко-
гибкостью была подобрана лишь по условию прочности, то стержень
разрушился бы от потери устойчивости прямолинейной формы.
§ 202. Влияние способа закрепления концов стержня.
Формула Эйлера была получена путём интегрирования прибли-
приближённого дифференциального уравнения изогнутой оси стержня при
Р определённом закреплении его концов (шарнирно-опёр-
тых). Значит, найденное выражение критической
силы справедливо лишь для стержня с шарнирно-
опёртыми концами и изменится при изменении условий
закрепления концов стержня.
Закрепление сжатого стержня с шарнирно-опёр-
тыми концами мы будем называть основным случаем
закрепления. Другие виды закрепления будем приво-
приводить к основному случаю.
Если повторить весь ход вывода для стержня,
жёстко защемлённого одним концом и нагружённого
осевой сжимающей силой на другом конце (фиг. 555),
то мы получим другое выражение для критической
силы, а следовательно, и для критических напря-
напряжений.
Предоставляя учащимся проделать это во всех
подробностях самостоятельно, подойдём к выяснению
fu	критической силы для этого случая путём следующих
простых рассуждений.
Пусть при достижении силой Р критического зна-
Фиг. 555. чения колонна будет сохранять равновесие при слабом
выпучивании по кривой АВ. Сравнивая фиг. 551 и 555,
видим, что изогнутая ось стержня, защемлённого одним концом,
находится совершенно в тех же условиях, что и верхняя часть
стержня двойной длины с шарнирно-закреплёнными концами.

§ 202]
ВЛИЯНИЕ СПОСОБА ЗАКРЕПЛЕНИЯ КОНЦОВ СТЕРЖНЯ
627
Значит, критическая сила для стойки длиной / с одним защем-
защемлённым, а другим свободным концами будет та же, что для стойки
с шарнирно-опёртыми концами при длине 21:
C3.13)
к B/J 4/8 '
Если мы обратимся к случаю стойки, у которой оба конца заще-
защемлены и не могут поворачиваться (фиг. 556), то заметим, что при выпу-
выпучивании, по симметрии, средняя часть стержня, длиной -к-, будет ра-
работать в тех же условиях, что и стержень при шарнирно-опёртых
концах (так как в точках перегиба С и D изгибающие
моменты равны нулю, то эти точки можно рассматри-
рассматривать как шарниры).
Поэтому критическая сила для стержня с защем-
защемлёнными концами, длиной /, равна критической силе
для стержня основного случая длиной у:	( •,
•&EJ ArJEJ
тFf
\2
Формулы C3.13) и C3.14) можно объединить с
формулой для критической силы основного случая
*EJ
*EJ
= —-~ и записать:
Фиг. 556.
C3.15)
здесь |х — так называемый коэффициент длины, равный:
при шарнирных концах (основной случай) (х = 1,
» одном свободном, другом защемлённом (х = 2,
» обоих защемлённых	(х = */2.
Для стержня, изображённого на фиг. 557, с од-
одним защемлённым, а другим шарнирно-опёртым кон-
концами, коэффициент [х Называется примерно равным
1
--^=^0,7, а критическая сила:
""" ^2^.	C3.16)
Величина (х/ называется приведённой (свободной)
длиной] при помощи коэффициента длины любой случай устройства
опор стержня можно свести к основному; надо лишь при вычисле-
вычислении гибкости вместо действительной длины стержня ввести в расчёт

628	ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIII
приведённую длину \xl. Понятие о приведённой длине было впервые
введено профессором Петербургского института инженеров путей
сообщения Ф. Ясинским *).
На практике, однако, почти никогда не встречаются в чистом
виде те закрепления концов стержня, которые мы имеем на наших
расчётных схемах (фиг. 551, 556, 557).
Вместо шаровых опор обычно применяются цилиндрические шар-
шарниры. Подобные стержни следует считать шарнирно-опёртыми при
выпучивании их в плоскости, перпендикулярной к оси шарниров;
при искривлении же в плоскости этих осей концы стержней следует
считать защемлёнными (с учётом оговорок, приведённых ниже для
защемлённых концов).
В конструкциях очень часто встречаются сжатые стержни, кон-
концы которых приклёпаны или приварены к другим элементам, часто
ещё с добавлением в месте прикрепления фасонных листов. Такое
закрепление, однако, трудно считать защемлением, так как части кон-
конструкции, к которым прикреплены эти стержни, не являются абсо-
абсолютно жёсткими.
Между тем, достаточно возможности уже небольшого пово-
поворота опорного сечения в защемлении, чтобы оно оказалось в
условиях, очень близких к шарнирному опиранию. Поэтому на
практике недопустимо рассчитывать такие стержни, как стойки
с абсолютно защемлёнными концами. Лишь в тех случаях, когда
имеет место очень надёжное защемление концов, допускается
небольшое (процентов на 10—20) уменьшение свободной длины
стержня.
Наконец, на практике встречаются стержни, опирающиеся на со-
соседние элементы по всей плоскости опорных поперечных сечений.
Сюда относятся деревянные стойки, отдельно стоящие металлические
колонны, притянутые болтами к фундаменту, и т. д. При тщатель-
тщательном конструировании опорного башмака и соединения его с фунда-
фундаментом можно считать эти стержни имеющими защемлённый конец.
Сюда же относятся мощные колонны с цилиндрическим шарниром
при расчёте их на выпучивание в плоскости оси шарнира. Обычно
же трудно рассчитывать на надёжное и равномерное прилегание пло-
плоского концевого сечения сжатого стержня к опоре. Поэтому грузо-
грузоподъёмность таких стоек обычно мало превышает грузоподъёмность
стержней с шарнирно-опёртыми концами.
Значения критических нагрузок могут быть получены в виде
формул типа эйлеровой C3.15) и для стержней переменного сече-
сечения, а также при действии нескольких сжимающих сил. Результаты
решения некоторых задач теории упругой устойчивости, имеющих
практическое значение, приведены в таблице 30.
*) Известия собрания инженеров путей сообщения, Петербург, 1892.

§ 202]
ВЛИЯНИЕ СПОСОБА ЗАКРЕПЛЕНИЯ КОНЦОВ СТЕРЖНЯ
629
[Ы.
к
s
ф
1
ев
ПИВ
±
3
s
'й
иты
Z
о
ев
узк
а,
3
к
ев
О
ритич
тержня
о
ев
3
0)
и
я
Вид нагрузк
1'р
и
II а?
^ч 0
м
3? о"
II и
Г.*
С*
и— **	Hs
преде-
тержня
ее) q
авномерно рас
иная по длине с
^собственный в
ч
Ю
о"
п
11
II 5
^ 2*
11 11
I
тч^»- 	<^^\
То же
8
§
СМ
iO
Is-
*-•
,50
1—•
ю
см
,00
S /
/
/ с
82
о
00
о
о*
00
о
S
о
о?
о
о
8
|
1
!
1
СО
о
о
о
,02
S
S
«с
л
S
а>
ю
&
II
+
О
00
о
«—'
«—1
со
'—'
см
8
см
&
\О
а
и
о
с
Г" VI
[—}
о
—•
00
о
. о
CM
о
_.
о
о
о
о
см
о
см
00
см
см
см
см
см
25
со
й
« s
<г^ ч
^ \о
^^ н
1 §
II
g я ^>
«У Я С
2 о н <л
я ж II о о s
oj s ., с о rt
5 § - ^ II a
<u Ю Я ^^ ^^
0,0 о ^
О СО Ч -w-
о w С
я

630
ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [гл. ХХХШ
§ 203. Пределы применимости формулы Эйлера и построение
полного графика критических напряжений.
Казалось бы, что полученные в предыдущих параграфах резуль-
результаты решают задачу проверки сжатого стержня на устойчивость;
остаётся выбрать лишь коэффициент запаса ky. Однако это далеко не
так. Ближайшее же изучение числовых величин, получаемых по фор-
формуле Эйлера, показывает, что она даёт правильные результаты лишь
v> известных пределах.
В таблице 31 приведены величины критических напряжений, вы-
вычисленных при различных значениях гибкости для стали 3, обычно при-
Таблица 31. Критические напряжения ек.
Значения гибкости
А = —т"
150
100
80
50
о при Е = 2. 1
к v
Ок— A50J ~~
*к A00J '
тс2 2 • 10е
(80)«
и» 2 • 10е
E0)*
Об кг/см*
877 исг/сл*1
2000 >
3300 >
8000 >
меняемой в металлических конструкциях; графически зависимость ок от
X представлена на фиг. 558. Эта зависимость представляется гиперболи-
гиперболической кривой, так назы-
\
3300
то
2000 бп
877
ваемой «гиперболой Эйле-
Эйлера». При пользовании этой
кривой надо вспомнить,
что представляемая ею
формула C2.12) полу-
получена при помощи интегри-
интегрирования дифференциаль-
дифференциального уравнения изогнутой
оси, т. е. в предположе-
предположении, что напряжения
в стержне в момент
потери устойчивости
не превосходят преде-
предела пропорциональности.
Следовательно, мы не имеем права пользоваться величинами кри-
критических напряжений, вычисленных по формуле Эйлера, если они
U0
-±-LTZ
I I
Li
t0 100 120
Фиг. 558.
150
200

§ 203] ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРА	631
получаются выше этого предела для данного материала. Иначе говоря,
формула Эйлера применима лишь при соблюдении условия:
или -^<вп.	C3.17)
Если из неравенства C3.17) выразить гибкость X, то условие
применимости формул Эйлера получит иной вид:
.	C3.18)
П
Подставляя соответствующие значения модуля упругости и
предела пропорциональности для данного материала, находим наи-
наименьшее значение гибкости, при которой ещё можно пользоваться
формулой Эйлера. Для стали 3 предел пропорциональности может
быть принят равным ап = 2000 кг/см*, поэтому, как видно из таб-
таблицы 31 и из формулы C3.18), для стержней из этого материала
можно пользоваться формулой Эйлера лишь при гибкости
1UU'
2000
т. е. большей, чем 100.
Для стали 5 при оп я« 3000 кг/см* формула Эйлера применима при
гибкости Х^:85; для чугуна — при Xs==80, для сосны — при Х^ИО
и т. д. Если мы на фиг. 558 проведём горизонтальную линию с орди-
ординатой, равной оп = 2000 кг/см*, то она рассечёт гиперболу Эйлера
на две части; пользоваться можно лишь нижней частью графика,
относящейся к сравнительно тонким и длинным стержням, потеря
устойчивости которых происходит при напряжениях, лежащих не
выше предела пропорциональности.
Теоретическое решение, полученное Эйлером, оказалось приме-
применимым на практике лишь для очень ограниченной категории стерж-
стержней, а именно, тонких и длинных, с большой гибкостью. Между тем,
в конструкциях очень часто встречаются стержни с малой гибкостью.
Попытки использовать формулу Эйлера для вычисления критических
напряжений и проверки устойчивости при малых гибкостях вели
иногда к весьма серьёзным катастрофам, да и опыты над сжатием
стержней показывают, что при критических напряжениях, больших
предела пропорциональности, действительные критические силы зна-
значительно ниже определённых по формуле Эйлера.
Таким образом, надо найти способ вычисления критических на-
напряжений и для тех случаев, когда они превышают предел пропор-
пропорциональности материалов, например, для стержней из мягкой стали
при гибкостях от 0 до 100.
Необходимо сразу же отметить, что в настоящее время важ-
важнейшим источником для установления критических напряжений
за пределом пропорциональности, т. е. при малых и средних гиб-
гибкостях, являются результаты экспериментов. Имеются попытки

632	проверка сжатых стержней на устойчивость [гл. хххш
и теоретического решения этой задачи, но они скорее указывают
путь к дальнейшим исследованиям, чем дают основания для прак-
практических расчётов.
Прежде всего надо выделить стержни с малой гибкостью, от О
примерно до 30—40; у них длина сравнительно невелика по отно-
отношению к размерам поперечного сечения. Например, для стержня
круглого сечения гибкости 20 соответствует отношение длины
к диаметру, равное 5. Для таких стержней трудно говорить о
явлении потери устойчивости прямолинейной формы всего стержня
в целом в том смысле, как это имеет место для тонких и длинных
стержней.
Эти короткие стержни будут выходить из строя главным обра-
образом за счёт того, что напряжения сжатия в них будут достигать
предела текучести ат (при пластичном материале) или предела проч-
прочности ов (при хрупких материалах). Поэтому для коротких стерж-
стержней, до гибкости примерно 30-4-40, критические напряжения будут
равны, или немного ниже (за счёт наблюдающегося всё же неко-
некоторого искривления оси стержня), соответственно или от (сталь),
или ов (чугун, дерево).
Таким образом, мы имеем два предельных случая работы сжатых
стержней: короткие стержни, которые теряют грузоподъёмность в
основном за счёт разрушения материала от сжатия, и длинные,
для которых потеря грузоподъёмности вызывается нарушением устой-
устойчивости прямолинейной формы стержня. Количественное измене-
изменение соотношения длины и поперечных размеров стержня меняет и
весь характер явления разрушения. Общим остаётся лишь внезап-
внезапность наступления критического состояния в смысле внезапного
резкого возрастания деформаций.
В сжатых стержнях большой гибкости, для которых применима
формула Эйлера, после достижения силой Р критического значения
обычно наблюдается резкий рост деформаций. До этого момента
прогибы, как правило, растут с ростом нагрузки, но остаются незна-
незначительными. Теоретически можно было бы ожидать, что до крити-
критической силы стержень будет оставаться прямым; однако ряд неиз-
неизбежных на практике обстоятельств — начальная кривизна стержня,
некоторый эксцентриситет приложения нагрузки, местные перенапря-
перенапряжения, неоднородность материала — вызывают небольшие прогибы
и при сжимающих силах, меньших критических.
Подобный же характер имеет и зависимость укорочений от на-
напряжения при сжатии коротких стержней; мы имеем ту же внезап-
внезапность роста деформаций при определённой величине напряжений
(когда а = от).
Нам остаётся теперь рассмотреть поведение сжатых стержней
при средних величинах гибкости, например для стальных стержней
при гибкостях от 40 до 100; с подобными значениями гибкостей
инженер чаще всего встречается на практике.

§ 203] ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРА	633
По характеру разрушения эти стержни приближаются к катего-
категории тонких и длинных стержней; они теряют свою прямолинейную
форму и разрушаются при явлениях значительного бокового выпу-
выпучивания. При опытах для них можно отметить наличие ясно выра-
выраженной критической силы в «эйлеровом» смысле; критические напря-
напряжения получаются выше предела пропорциональности и ниже предела
текучести для пластичных и предела прочности для хрупких материалов.
Однако потеря прямолинейной формы и понижение критических
напряжений по сравнению с короткими стержнями для этих стерж-
стержней «средней» гибкости связаны с такими же явлениями нарушения
прочности материала, какие вызывают потерю грузоподъёмности в ко-
коротких стержнях. Здесь комбинируются и влияние длины, понижающее
величину критических напряжений, и влияние значительного роста
деформаций материала при напряжениях за пределом пропорцио-
пропорциональности.
Экспериментальное определение критических сил для сжатых
стержней производилось неоднократно как у нас, так и заграницей.
Особенно обширный опытный материал собрал проф. Ф. Ясин-
Ясинский, составивший таблицу критических («ломающих») напряжений
в зависимости от гибкости для целого ряда материалов и положив-
положивший начало современным методам расчёта сжатых стержней на
устойчивость 1).
На основании полученного опытного материала можно считать,
что при критических напряжениях, меньших предела пропорциональ-
пропорциональности, все эксперименты подтверждают формулу Эйлера для любого
материала.
Для стержней средней и малой гибкости были предложены раз-
различные эмпирические формулы, показывающие, что критические
напряжения при таких гибкостях меняются по закону, близкому
к линейному *):
ок = а — Ь\	C3.19)
где а и Ъ — коэффициенты, зависящие от материала, а Х==^-—
гибкость стержня. Для литого железа Ясинский получил: а =
= 3387 кг/см*, #=14,83 кг/см*. Для стали 3 при гибкостях от
Х = 40 до X ===== 100 коэффициенты а и Ь могут быть приняты:
а = 3360 кг/см*; Ь=\Ь,7 кг/см*. Для дерева (сосна): а = 293 кг/см*\
?=1,94 кг/см*.
Данные о коэффициентах а и Ъ для прочих материалов при-
приводятся в справочниках (см., например, Справочник под ред. А. Н.
Динника, Москва, 1949).
Иногда удобны эмпирические формулы, дающие для неупругой области
изменение критических напряжений по закону квадратной параболы; к ним
относится формула
ск = а0 — а\*.	C3.20)
') Ясинский, Собрание сочинений, т. 1. Петербург, 1902 г.

634
ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ (гл. ХХХШ
Здесь при X = 0 считают ак = с0 = ат для пластичного и ак = о?0 = ав для
хрупкого материала; коэффициент я, подобранный из условия плавного
сопряжения с гиперболой Эйлера, имеет значение:
для стали с пределом текучести ст = 2800 кг/см* а = 0,09 кг/см*
> сосны ь » прочности ав = 300 > а = 0,008 >
» чугуна > >	> св = 4200 > а = 0,44 >
При наличии приведённых здесь данных может быть построен
полный график критических напряжений (в зависимости от гиб-
гибкости) для любого материала. Ка фиг. 559 приведён такой график
для строительной стали с пределом текучести ат=2400 кг/см*
и пределом пропорциональ-
пропорциональности ап = 2000 кг/см*.
График состоит из трёх
частей: гиперболы Эйлера при
Х^> 100, наклонной прямой при
100 ^> X ^> 40 и горизонталь-
горизонтальной, или слабо наклонной, пря-
прямой при Х<^40. Подобные же
графики можно построить,
комбинируя формулу Эйлера
с результатами экспериментов,
и для других материалов.
Таким образом, можно счи-
считать, что задача определения
критических напряжений для стержней любой гибкости решена
с достаточной для практических целей точностью.
80 100 120
Фиг. 559.
§ 204. Проверка сжатых стержней на устойчивость.
В § 200 мы отметили, что для сжатых стержней должны быть
произведены две проверки:
на прочность
на устойчивость
где 1а =•?,
где
Величина критического напряжения ак найдена в предыдущем
параграфе; для установления допускаемого напряжения на устой-
устойчивость нам остаётся теперь выбрать только коэффициент запаса к.
В нашей практике этот коэффициент колеблется для стали
в пределах от 1,8 до 3,0. Коэффициент запаса на устойчивость вы-
выбирается выше коэффициента запаса на прочность ?0, равного для
стали 1,6.

§ 204]	ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ	635
. Это объясняется наличием ряда обстоятельств, неизбежных па
практике (начальная кривизна, эксцентриситет действия нагрузки,
неоднородность материала и т. д.) и почти не отражающихся на
работе конструкции-ври других видах деформации (кручение, изгиб,
растяжение).
Для сжатых же стержней, ввиду возможности потери устой-
устойчивости, эти обстоятельства могут сильно снизить грузоподъёмность
стержня. Для чугуна коэффициент запаса колеблется от 5,0 до 5,5,
для дерева —от 2,8 до 3,2.
Чтобы установить связь между допускаемым напряжением на
устойчивость [ау] и допускаемым напряжением на прочность [а], возь*
мём их отношение:
Ы = ТТ или К!= Г" ' 1г [°1-
Обозначая
получим:
[ау] = ?[а];	C3.22)
здесь ср — коэффициент уменьшения основного допускаемого напря-
напряжения для сжатых стержней.
Имея график зависимости ок от X для данного материала, зная
о9=:оТ или ао = ав и выбрав коэффициенты запаса на прочность ?0
и на устойчивость Ау, можно составить таблицы значений коэффи-
коэффициента ср в функции от гибкости. Такие данные приводятся в наших
технических условиях на проектирование сооружений; они сведены
в таблицу 32.
Пользуясь этой таблицей, можно произвести подбор сечения сжа-
сжатого стержня. Так как величина площади сечения зависит от [оу],
а это напряжение в свою очередь через коэффициент ср связано
с гибкостью стержня X, т. е. с формой и размерами его сечения, то
йодбор приходится осуществлять путём последовательных прибли-
приближений в таком, например, порядке.
Выбираем форму сечения и задаёмся его размерами; вычисляем
наименьший радиус инерции и гибкость; находим по таблице коэф-
коэффициент <р и вычисляем допускаемое напряжение на устойчивость
[ау] = ср [о]; сравниваем действительное напряжение о = -р— с вели-
* бр
чиной [оу]; если условие устойчивости
о=-^^ср[о]	C3.23)

636	ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [ГЛ. ХХХЩ
Таблица 32. Коэффициенты ср.
Гибкость
1
0
10
20
30
40
50
60
70
80
90
100
ПО
120
130
140
150
160
170
180
190
200
Значения ср для
стали марок
4, 3, 2, ОС
1,00
0,99
0,96
0,94
0,92
0,89
0,86
0,81
0,75
0,69
0,60
0,52
0,45
0,40
0,36
0,32
0,29
0,26
0,23
0,21
0,19
стали марки 5
1,00
0,98
0,95
0,92
0,89
0,86
0,82
0,76
0,70
0,62
0,51
0,43
0,36
0,33
0,29
0,26
0,24
0,21
0,19
0,17
0,16
стали СПК
1,00
0,97
0,95
0,91
0,87
0,83
0,79
0,72
0,65
0,55
0,43
0,35
0,30
0,26
0,23
0,21
0,19
0,17
0,15
0,14
0,13
чугуна
1,00
0,97
0,91
0,81
0,69
0,57
0,44
0,34
0,26
0,20
0,16
.—
—
—
—
—
—
—
—
дерева
1,00
0,99
0,97
0,93
0,87
0,80
0,71
0,60
0,48
0,38
0,31
0,25
0,22
0,18
0,16
0,14
0,12
0,11
0,10
0,09
0,08
не удовлетворено, или удовлетворено с большим запасом, меняем
размеры сечения и повторяем расчёт. Конечно, окончательно вы-
выбранное сечение должно удовлетворять и условию проч-
прочности
В практических расчётах условие устойчивости иногда
записывается так:
В левой части ар представляет собой расчётное (услов-
(условное) напряжение.
Фиг. 560. Ход вычислений покажем на примере.
Пример 125. Подобрать двутавровое сечение стойки с
одним защемлённым концом, сжатой силами Р = 35 т; длина
стойки /=15 м. Основное допускаемое напряжение [а] = 1600 кг/см*
(фиг. 560).	Р
Так как в условии устойчивости o=i-—— ^[aj нам не известно ни
Тбр
р, ни <р, одной из этих величин необходимо задаться. Примем для первого

§ 205]	ВЫБОР ТИПА СЕЧЕНИЯ И МАТЕРИАЛА	637
приближения tp = 0,5. При этом значении ср необходимая площадь попереч-
поперечного сечения должна быть:
Р __ 24000 ...ар ¦
6РГМ~~ 0,5-1600
По сортаменту (ГОСТ 8239—56) выбираем I № 22 с площадью сечения
/?=30,6 см2. Наименьший радиус инерции сечения /min = 2,27 см; соответ-
соответствующая гибкость стойки Х=-^— = -——==132; коэффициент ср (табл.32)
1тт 1>п
но интерполяции между значениями для X = 130 и X = 140 равен ср = 0,392.
расчётное напряжение оказывается равным:
Сечение не удовлетворяет условию устойчивости. Для второго прибли-
приближения попробуем I № 24 с площадью сечения /^=34,8 см2; /min=2,37 см;
2 • 150
А = -	= 127; коэффициент <р = 0,415. Расчётное напряжение будет:
Р	24 000
Р-~ «р/7""" 0,415, 34,8 "
Перенапряжение составляет	г^~—• 100 = 3,75 °/о, что допустимо.
§ 205. Выбор типа сечения и материала.
А. Так как в сопротивлении стержней продольному изгибу (нару-
(нарушению устойчивости) основную роль играет гибкость стержня, а
стало быть, величина наименьшего радиуса инерции сечения, то
очень существенным является вопрос не только о величине площади
стержня, как при расчёте на прочность, но и о форме поперечного
сечения.
Для наиболее экономичного решения вопроса необходимо кон-
конструировать сечение, у которого при определённой площади величина
Наименьшего радиуса инерции была бы возможно большей. Для этого
йрежде всего следует стремиться к тому, чтобы наименьший радиус
инерции был равен наибольшему, т. е. чтобы все центральные моменты
инерции сечения были равны, эллипс инерции обратился бы в круг.
Такой стержень будет оказывать одинаковое сопротивление потере
Устойчивости в любом направлении.
Если свободная длина стержня (§ 202) при возможном искривле-
йии в обеих главных плоскостях будет различна, то и главные момен-
моменты инерции тоже целесообразно выбрать разными с таким расчётом,
коэффициенты у были бы в обоих случаях одинаковыми.

638
ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [гл. ХХХШ
Далее необходимо стремиться к получению при данной площади
наибольших центральных моментов инерции. Для этого необходимо
разместить материал сечения по возможности дальше от центра
тяжести. Обоим поставленным условиям вполне удовлетворяет, напри-
например, трубчатое сечение (фиг. 561, а), которое очень часто и при-
применяется для сжатых колонн и стоек.
Низший предел толщины стенок такого сечения определяется или
возможностью конструктивного выполнения отливки (чугун), или тем,
б)
чтобы при работе стержня не произошло
S) местных деформаций тонкой стенки — её
коробления.
Для предотвращения таких местных
повреждений, чтобы обеспечить при ра-
работе стержня сохранение принятой фор-
формы сечения (кольцо), внутри трубчатого
\г стержня располагают систему усилений,
Фиг. 561.	например, на некотором расстоянии друг
от друга ставят так называемые диа-
диафрагмы, придающие жёсткость тонкостенному профилю (фиг. 561, б).
Вообще при правильном конструировании сжатых стержней устрой-
устройство дополнительных креплений играет весьма большую роль.
Некоторые виды сечений, прекрасно сопротивляющиеся изгибу
в одной плоскости, как это бывает при работе балок, оказываются
очень невыгодными при применении их для сжатых стержней; такими,
например, являются двутавровое сечение, сечение из двух швеллеров,
стенки которых примкну ты вплотную одна к другой (фиг. 561, б).
—r~
i
I
Фиг. 562.
Невыгодность подобных сечений при работе на продольный изгиб
обусловливается большой разницей в величинах их главных момен-
моментов инерции. Чтобы избежать этого недостатка, можно раздвинуть
обе половинки сечения из двух швеллеров, как это показано на

§ 205]	ВЫБОР ТИПА СЕЧЕНИЯ И МАТЕРИАЛА	639
фиг. 562, в; для того чтобы заставить все сечения работать как одно
целое, их соединяют при помощи так называемой соединительной
решётки (фиг. 562).
Необходимым условием безопасной работы таких составных стерж-
стержней является устройство достаточно мощного крепления (решётки,
планки), чтобы действительно заставить обе половины работать
совместно, как один целый стержень; только в этом случае мы будем
иметь право вводить в расчёт момент инерции относительно оси у —у.
Если же два мощных швеллера скрепить очень слабой решёткой,
то она не сможет заставить их работать совместно *). Каждая поло-
половина стержня будет работать самостоятельно, устойчивость её ока-
окажется во много раз меньше устойчивости стержня, в котором обе
половины представляют собой одно целое.
Недостаточное внимание к устройству надёжных креплений в со-
составных стержнях было причиной серьёзных катастроф (разрушение
Квебекского моста в Америке).
При конструировании составного стержня расстояние Ь, на
которое надо раздвинуть обе половины стержня, определяется
тем, чтобы моменты инерции относительно обеих главных осей
у и z были приблизительно равны. Обычно даже стремятся мо-
момент инерции относительно оси, перпендикулярной к плоскости
решётки, сделать несколько большим, так как решётка не
может обеспечить совместную работу обеих половин стержня
так же хорошо, как если бы сечение представляло собой одно
целое.
Б. Что касается выбора материала сжатых стержней, то это
обусловливается следующими соображениями. Пока критические
напряжения не превосходят предела пропорциональности материала,
единственной механической характеристикой, определяющей сопро-
сопротивляемость стержня потере устойчивости, является модуль упру-
упругости Е.
Между тем для стержней средней и в особенности малой гиб-
гибкости величина критических напряжений зависит в значительной
степени от предела текучести или предела прочности материала.
Этими обстоятельствами и следует руководствоваться при вы-
выборе материала для сжатых стержней большой и малой гиб-
гибкости.
Так, например, применение специальных сортов стали повышен-
повышенной прочности для тонких и длинных сжатых стержней не имеет
смысла, так как модуль Е для всех сортов стали примерно один
и тот же.
Наоборот, применение высокосортных сталей окажется очень
уместным для стержней с критическими напряжениями, превышаю-
*) Ниже, в § 212 приведены приёмы расчёта и методы определения раз-
размеров соединительной решётки и планок.

640
ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [ГЛ. ХХХ1Ц
щими предел пропорциональности, ибо для таких стержней увеличе-
увеличение предела текучести вызовет рост критических напряжений, а
стало быть, повысит сопро-
сопротивление нарушению устой-
устойчивости.
На фиг. 563 изображено
примерное расположение
графиков зависимости ак от
гибкости для малоугле-
малоуглеродистой стали и стали
повышенного качества с
пределом текучести ат =
= 3000 кг)см*.
Из графиков видно, что
критические, а следова-
3000
то
то
W00
Сталь высокосортная
родисйа^^
i4
1
40
160 200
80 100 120
Фиг. 563.
тельно, и допускаемые на-
напряжения для обоих сортов стали будут одинаковыми для стерж-
стержней с гибкостью Х^>100. И, наоборот, они будут существенно
отличаться для стержней с меньшими гибкостями.
§ 206. Примеры.
Пример 126. Пустотелая шарнирно-опёртая чугунная колонна длиной
h = 5 Mf с наружным диаметром d = 2г = 45 см должна'нести груз Р= 120 г.
Найти необходимую толщину t стенок колонны при основном допускаемом
напряжении [а] = 1000 кг/см2.
Пользуемся следующими приближёнными выражениями для момента
инерции и площади трубчатого сечения (см. §-93):
где r0 — средний радиус стенки:
Радиус инерции будет равен:
Полагаем в первом приближении го«»г =
гибкость будет равна
см. Тогда /=14,1 см и
соответствующее значение ср равно (таблица 32):
? = 0,81+0,69 =
Площадь сечения колонны определяется условием
Р	Р
F^-r-, или F = 2nrat = -r-;

§ 206]	примеры	641
отсюда
Р	120000	__1О7
'"¦2«riTW - 2«.20-0,75-1000
1 3
Проводим вторично расчёт, полагая го = 2О	^- = 19,35 еж. Радиус инер-
инерции / = 0,707.19,35 = 13,7 см; гибкость равна -~ = т^ = 37 и <р = 0,72; тол-
l 1о,7
щина * определится формулой
Р	120000
1=Ъ^Щ = 2*. 19,35.0,72
Дальнейшие пересчёты излишни; минимальная толщина стенок колонны
должна быть принята 14 иш.
Пример 127. Стержень фермы из двух равнобоких уголков (фиг. 564),
склёпанных вместе (с прокладками толщиною 10 мм), сжат силами Р = 32 т;
длина стержня / = 3,5 м. Считая концы
шарнирно опертыми, подобрать размеры
уголков при [а] = 1400 кг/см2.
Площадь сечения брутто определяется
формулой:
Принимая для первого приближения о = 0,5,
получим:
32 000
//////77///SA
0,5-1400
По сортаменту (ГОСТ 8509—57) подходят	Фиг* 564'
два уголка 100 X 100 X 12. Площадь сече-
сечения F = 2 • 22,8 = 45,6 см3. Наименьший момент инерции будет относи-
относительно оси г (фиг. 564). Соответствующий радиус инерции (см. приложе-
приложение IX, табл. 1) /^ = 2,91 см; гибкость стержня X = -J-—== ?т1гг = 120; коэф-
*min АУ1
фициент ер = 0,45.
Расчётное напряжение равно:
ср = —!~ = ;г 7^ = 1560 кг/см9 > 1400.
р ?-^бР 0,45-45,6
„ 1560—1400 1ЛЛ лл Ал. _
Перенапряжение составляет 	щд	100= 11,4%- Сечение следует
увеличить.
Возьмем два уголка 125 X 125 X 8; F6p = 2 • 19,7 = 39,4 см2; rmin = 3,36 см;
350
Х = —— =104; <р = 0,568. Расчётное напряжение:
о,оо
Р 49 ПОП
п	A430—1400). 100 ОЛ.
Перенапряжение составляет 			^2%, что вполне допустимо.
Проверим сечение на прочность, имея в виду, что оно ослабляется
Двумя заклепочными отверстиями диаметром d = 20 мм.
/?нет = /?бр-2.*.</ = 39,4-2-0,8.2 = 36,2 смК
'21 Н. М. Беляев

642	ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIII
Действительное напряжение равно:
Р	39 ООП
а = ¦=/-— = Ц~ = 885 кг/см2 < 1400 кг!см2.
^netto 36>2
Прочность стержня обеспечена.
Пример 128. Стержень прямоугольного сечения, расположенный боль-
большей стороной вертикально, сжат силой Р=Ют; размер большей верти-
вертикальной стороны сечения h = 8 см; найти второй размер Ь сечения, считая
концы стержня шарнирно-опёртыми при выпучивании в вертикальной пло-
плоскости и защемлёнными при выпучивании в горизонтальном направлении
(fi1 = l; р.2 = 0,5). Влиянием собственного веса пренебречь. Длина / = 2 м.
Основное допускаемое напряжение с учётом динамики [а] = 700 кг/см2; ма-
материал— сталь 5.
Расчётные гибкости стержня будут: при выпучивании в вертикальной
плоскости	,	,
f1
при выпучивании в горизонтальной плоскости
Если добиваться равноустойчивости стержня в обоих направлениях, то надо,
чтобы	, ,	/ 0,5/
xi = x2 или -у- = -у-;
отсюда
b = -y- = 4 см.
Проверим стержень при этой величине Ь. Расчётная гибкость
_\1 __ 200 __200
1- h~Wb~*» *
10 000
tp = 0,64; расчётное напряжение о = 4 8 4 = 488 kzjcm2 < 700 кг/см*.
Сечение имеет запас; можно уменьшить ширину Ь примерно до
Так как при уменьшении Ь уменьшается не только площадь, но и радиус
инерции /2> в то время как it остаётся без изменений, то решающей будет
проверка на выпучивание в горизонтальной плоскости. Радиус инерции равен
3	100
|'2 = --^= = 0,87 сму а гибкость ^г=115; «р = 0,40; расчётное напряжение
Op z=.	== 1040 кг/см2 > 700 кг/см2. Ширину Ь надо увеличить; она
будет заключаться между 3 и 4 еж. Примем Ь = 3,5 см.
Проверим устойчивость стержня при этом значении Ь. Радиус инерции
ОС	1 QQ
/2= '_ =1,01 см; гибкость равна ттгг^ W0; ср = 0,51. Расчётное напря-
жение равно	р
Сечение подобрано точно.

§ 206]
ПРИМЕРЫ
643
Пример 129. Сравнить предельные, допускаемые по условиям устой-
устойчивости нагрузки (грузоподъёмности) двух стоек, изготовленных каждая
из двух швеллеров № 30, с одинаковым основным допускаемым напряже-
напряжением [а] = 1600 кг/см2; длины стоек / = 4 м; концы стоек шарнирно закре-
закреплены; одна из стоек имеет оба швеллера с вплотную поставленными
и скреплёнными по всей длине стенками в виде двутавра, а в другой
швеллеры расставлены так, что моменты инерции относительно обеих
главных осей одинаковы (фиг. 561, в и 562, в).
Наименьший момент инерции составного сечения в первом (без просвета)
случае будет 7min = yz = 2 [327+ 40,5-2,522] = 1168 см* (по сортаменту -^
см. приложение). Так как F = 2 «40,5 = 81 см2, то
ТГ68
81
Гибкость X2 = — = _ = 105,3; ей соответствует «р = 0,558. Грузоподъём-
Грузоподъёмность Рх = F<p [а] = 81 • 0,558 • 1600 = 72 300 кг = 72,3 т.
Момент инерции составного сечения во втором (с просветом) случае
будет Уу = /^ = 2 - 5810 = 11 620 см*; /у =
400
400
~\2 ^ 33f3; ? = °)933# ГРУ30П°Дъёмн0СТЬ рг =
12 см; X„ = 4- =
h
= 81 ' °»933 * 1600 =
= 120 900 /сг = 120,9 т. Грузоподъёмность во втором случае в 1,67 раза
больше, чем в первом.
Совместная работа составного стержня из двух ветвей (два швеллера)
будет обеспечена лишь при надежном соединении их с помощью решётки
или планок (фиг. 562, а и б). Расстояния а
между соединительными элементами должны
быть выбраны так, чтобы отдельная ветвь не
выпучилась в плоскости наименьшей жёстко-
жёсткости сечения ветви. Это условие будет обеспе-
обеспечено, если гибкость отдельной ветви (в дан-
ком случае одного швеллера) на длине а
будет не больше гибкости всей стойки. Сле-
Следовательно:
'min
стойки*
Для одного швеллера наименьший радиус
инерции равен ijmin = 2,84 см. Следовательно:
а = Vmin = 33>3 • 2>84 = 94>6 см.
Значит, расстояние между соединительными
планками должно быть не более 94,6 см.
Что касается расстояния b между швел-
швеллерами в сечении (фиг. 565), то оно найдётся
из условия, что Jz ^ Jy> где
•t
к 6 -
Фиг. 565.
лера,
Здесь /J и J\
собственные центральные моменты инерции одного швел-
— его площадь. Таким образом:
с =
Так как & = 2 (с—у0), а по сортаменту дго =
*= 18,2 см.
= 11,6 см.
см, то ^ = 2A1,6 — 2,52)=-

644	ПРОВЕРКА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIII
§ 207. Практическое значение проверки на устойчивость.
Для инженера-практика значение проверки на устойчивость гро-
громадно. Можно сказать, что почти все значительные катастрофы ин-
инженерных сооружений произошли вследствие нарушения устойчиво-
устойчивости сжатых элементов сооружений. Хотя с подобными катастрофами
инженеры встречаются давно, однако не всегда правильно оценивают
их причины. Это показывает, что инженеры-практики часто не вполне
ясно представляют себе, какую роль могут играть маловажные,
казалось бы, обстоятельства при работе сжатых стержней.
Особая опасность потери устойчивости заключается в том, что
обычно она наступает внезапно. Почти до наступления критического
значения сжимающей силы деформации сооружения не бросают-
бросаются в глаза и не вызывают опасения. Далее, как уже указывалось,
ряд обстоятельств — эксцентриситет нагрузки, начальная кривизна
стержня, местные повреждения материала — может весьма значитель-
значительно понизить сопротивление сжатых стержней, в то время как
те же факторы почти не отражаются на работе других элементов
конструкции.
Особенно следует обратить внимание на достаточность и тща-
тщательность соединения частей сжатого стержня при составных сече-
сечениях. Недооценка этого фактора вела к тягчайшим катастрофам —
разрушение Квебекского моста, выпучивание сжатых раскосов моста
через Мозырь при испытании расчётной нагрузкой ') и др.
Современный инженер имеет в своём распоряжении все сред-
средства для того, чтобы при внимательном проектировании и тщатель-
тщательном выполнении конструкции подобные аварии были исключены.
Теория расчёта при проверке устойчивости, как это показано выше
(§§ 201—205), разработана достаточно надёжно.
В несколько особом положении находятся расчёты на устойчи-
устойчивость в машиностроении. Здесь особое значение приобретает вопрос
о выборе основного допускаемого напряжения [о]. При назначении
его величины не следует забывать о том, что такие детали машин,
как штоки, шатуны, подвергаются интенсивной динамической нагрузке.
Поэтому в формуле для вычисления допускаемого напряжения на
устойчивость
[°у\= ? М
под [а] следует подразумевать допускаемое напряжение па прочность
при динамической нагрузке (см. следующий отдел — глава XXXVII).
Уже в § 203 указывалось на аналогию между внезапным ростом
деформаций при переходе напряжений за предел текучести и столь
же внезапным увеличением прогибов при переходе за критическое
напряжение. Эта аналогия приводит к мысли, что в статически не-
') Г о л о в А. Д., Деформация раскосов ферм Мозырьского ж.-д. моста,
1925, Киев.

§ 208]	устойчивость плоской формы изгиба бллок	645
определимых конструкциях появление критических напряжений
в сжатом стержне может ещё не вызвать разрушения конструкции,
особенно если эти напряжения лежат в пределах упругости.
Подобный случай мы имеем в старых многорешётчатых фермах
мостов при работе их под современную более тяжёлую нагрузку.
Часть раскосов в таких фермах может оказаться сжатой эйлеровыми
критическими силами и находиться в состоянии упругого выпучива-
выпучивания. Работу этих раскосов возьмут на себя встречные растянутые
раскосы. По удалении нагрузки конструкция вернётся к первона-
первоначальному виду.
Такие же случаи имеют место в самолётостроении и судострое-
судостроении, где приходится иметь дело с потерей устойчивости не только
стержней, но и балок, пластинок и оболочек. Таким образом, на
практике могут быть исключительные случаи, когда можно допу-
допустить в сжатом элементе критические напряжения, если они не
превышают предела упругости при условии, что конструкция ста-
статически неопределима, и работу выбывшего из строя элемента возь-
возьмут на себя другие части.
Ниже мы рассмотрим некоторые более сложные задачи проверки
элементов конструкций на устойчивость.
ГЛАВА XXXIV.
БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ ЭЛЕМЕНТОВ
КОНСТРУКЦИЙ НА УСТОЙЧИВОСТЬ.
§ 208. Устойчивость плоской формы изгиба балок.
С явлением потери устойчивости мы встречаемся на практике
не только в случае простого сжатия стержней. Потерять устойчи-
устойчивость заданной формы равновесия может и балка, работающая на
изгиб, например двутаврового
сечения (фиг. 566).
Нижний пояс такой балки
представляет собой стержень,
сжатый продольным усилием и
прикреплённый к стенке балки.
Это прикрепление не позволяет
поясу выпучиться в плоскости
стенки; но возможно такое со-
соотношение размеров балки, при
котором сжатый пояс сможет
выпучиться в сторону, что влечёт за собой повороты сечений и
скручивание балки (фиг. 566). Вместо работы на изгиб в плоскости
наибольшей жёсткости, как это было назначено конструктором,
балка в целом ряде сечений начнёт работать на косой изгиб, что

646 БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА 3ТСТОЙЧИВОСТЬ [ГЛ. XXXIV
вызовет резкий рост деформаций, а в дальнейшем — полное раз-
разрушение конструкции.
Устойчивость балки зависит от размеров поперечного сечения и
от её свободной длины. Поэтому на практике ограничивают эту
длину, устраивая связи между балками. Недостаточное внимание
к этим боковым креплениям при длинных одиночных балках даже
малой высоты может повести к серьёзным катастрофам (например,
обрушение моста близ Тарба во Франции).
Потеря устойчивости может грозить и сжатым тонким пластин-
пластинкам, т. е. тем элементам конструкции, у которых один размер мал
по сравнению с другими. Так может покоробиться тонкий и широ-
широкий лист сжатого пояса двутавровой балки, может выпучиться не-
недостаточно укреплённая уголками жёсткости стенка и др.
Приведём приближённое определение величины критического груза для
балки, при котором плоская форма изгиба становится неустойчивой и даль-
дальнейшее увеличение которого ведёт к разрушению балки за счёт бокового
выпучивания. Рассмотрим балку на двух опорах с поперечным сечением
в виде узкого прямоуголь-
прямоугольника (фиг. 567) под дейст-
действием поперечной силы Р.
Пусть сила достигла кри-
критического значения и балка
t слегка выпучилась вбок, как
' это показано в плане и в раз-
разрезе на фиг. 567; не ухо-
уходят из начальной плоскости
балки А и В,
образом за-
заФиг. 567.
только концы
надлежащим
креплённые.
С появлением боковые
деформаций потенциальная
энергия балки должна воз-
возрастать за счёт деформации изгиба в боковом направлении и деформации
кручения (энергию деформации изгиба в вертикальной плоскости можно счи-
считать неизменной). Одновременно с этим потенциальная энергия груза умень-
уменьшается вследствие опускания точки его приложения.
Обозначим потенциальную энергию бокового изгиба Uu кручения U2
и работу при дополнительном опускании груза за счёт бокового выпучива-
выпучивания балки Up. Так как при действии критической силы переход от плоской
формы изгиба к боковому выпучиванию сопровождается переходом энергии
груза в потенциальную энергию деформации балки, то можем считать, что
= ?/„.	C4.1)
Потенциальная энергия бокового изгиба (относительно оси zx) равна
М2 (х) dx
Г
2EJ,
здесь изгибающий момент в произвольном сечении, взятом в расстоянии х от
левой опоры, будет (по малости угла поворота сечения ср):
М(х) = ~ х
Р
1>'Х

§ 208]	УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА БАЛОК
647
Подставляя значение изгибающего момента, получим:
и>= шт.-$
C4.2)
Потенциальную энергию кручения также выразим через угол ср. Работа кру-
крутящего момента на длине dx будет:
> где d*=
MKdx
Имея в виду, что
получим:
K = GJK^-, a dv^^
K Kdx* T dx
2 dx dx	2 [dx
Потенциальная энергия кручения, накопленная при боковом выпучивании
балки, равна:
C4.3)
Чтобы найти работу, совершаемую грузом Р при его опускании, найдём
вертикальное перемещение точки его приложения (фиг. 568). Заметим при
этом, что смещение точки О в положение О\
вызывается совокупностью двух причин: поворо-
поворотом сечения вокруг точки О на угол <р и боко-
боковым перемещением в направлении оси Оу±.
Так как при повороте сечения опускания
точки О не происходит, то, очевидно, причиной
опускания точки приложения силы Р является
боковой изгиб балки из плоскости xOz.
Величину вертикального перемещения точки
О найдём по теореме Кастильяно из выраже-
выражения C4.2):
2
дР 1Ыг I
C4.4)
Фиг. 568.
Отсюда работа силы Р (достигшей в момент начавшегося бокового переме-
перемещения значения Рк) на перемещении 5 будет:

648	БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [гл* XXXIV
Подставляя теперь значения Uu U% и Up в исходное уравнение C4.1),
получим: г	t	г
Т	У	Т
Р2 (*
откуда
О	О
Обозначая жёсткость при изгибе EJZ — CU а при кручении G7K = Ci,
получим для критического значения /^
J = AC xCs 2-j	.	C4.5)
Под интегралами — две переменных <$> и х, связанных между собой, так
как углы поворота сечений <р изменяются по длине jcy т. е. у = <р (л:). Закон
изменения ср в зависимости от х нам неизвестен. Пользуясь методами при-
приближённого решения, зададимся для ср каким-либо уравнением, связывающим
его с х так, чтобы были удовлетворены условия закрепления концов балки.
Положим, например:
ср = k • sin ^~.	C4.6)
При х = 0 ср = 0, при х = //2 ср = сртах и при х = / «f = 0. Таким образом,
эта функция обращается в нуль на опорах (где углы поворота сечений равны
пулю по условиям закрепления) и достигает максимума посредине пролёта,
т. е. удовлетворяет условиям деформации нашей балки.
Подставляя значение <р и её производной под знаки интегралов в урав-
уравнение C4.5), получим:
cost^dx
2
Проинтегрировав, найдём:
C4.7)
Точное значение критической силы для балки на двух опорах с прямо-
прямоугольным поперечным сечением (фиг. 567)х) выражается формулой:
_ 16,93
') Тимошенко, Устойчивость упругих систем, Гостехиздат, 1946.

§208]
УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА БАЛОК
649
Ошибка приближённого решения составляет около 1,5%. Величина критиче-
критической силы зависит от произведения жёсткости при боковом изгибе балки
Ct = EJZ и жёсткости при кручении С2 = GJK.
Если нагрузка равномерно распределена по длине осевой линии, то её
критическое значение равно
сю О
\.	C4.8)
Для консоли длиной /, загружённой по длине равномерно распределён-
распределённой нагрузкой, получим:
1 <Л ОС
:2.	C4.9)
Для консоли, несущей груз, приложенный к оси балки на свободном
копне:
C4.10)
В случае двутавровой балки формулы для критических нагрузок имеют
такой же вид, как и для прямоугольного сечения с той разницей, что число-
числовой коэффициент при jACiCs не является постоянной величиной, а зависит
от сопротивления полок боковому изгибу и определяется отношением
Здесь h — высота двутавра.
Таким образом, для двутавровой балки
C4.11)
где Э определяется для каждого значения а. Значения коэффициентов (J опре-
определены для разных видов нагрузки и приведены ниже в таблице 33.
Таблица 33. Значения g в формуле C4.11).
а С'- ( ' У
1
0,1
1,0
2,0
4,0
6,0
8,0
12,0
Р.
2
31,6
9,76
8,03
6,73
6,19
5,87
5,36
82
3
86,4
31,9
25,6
21,8
20,3
19,6
18,8
4
143,0
53,0
42,6
36,3
33,8
32,6
31,5
cAh)
1
16
20
32
50
70
90
100
Pi
су
5,08
—
.—
—
—
4,04
4,04
3
18,3
18,1
17,9
17,5
17,4
17,2
17,2
Рз
4
30,5
30,1
29,4
29,0
28,8
28,6
28,6
в графе 2 — для консоли, нагружённой силой на конце;
>	> 3 — » балки на двух опорах с силой посредине;
>	» 4 — * » > >* » равномерно нагружё
(агружённой.

650 БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
Как видно из таблицы, значения коэффициента р, по мере увеличения
отношения —, приближаются к значениям коэффициентов для балки прямо-
прямоугольного сечения. Для а =100, р почти точно совпадает с числовыми коэф-
коэффициентами для прямоугольных балок.
Для расчёта на устойчивость плоской формы изгиба необходимо, чтобы
возникающие при изгибе нормальные напряжения не превышали допускае-
допускаемых напряжений на устойчивость, равных [ау] = т^, где ky — коэффи-
циент запаса.
Зная величину критической нагрузки для каждого случая загружения
балки, мы легко можем определить величину критических напряжений:
где Mfnux — наибольший изгибающий момент от критической нагрузки, a Wy —
момент сопротивления сечения изгибу в плоскости стенки.
Полученные результаты справедливы лишь при условии, что критические
напряжения при выпучивании балок не превосходят предела пропорциональ-
пропорциональности материала.
Если ак > ап, то выведенные формулы будут давать преувеличенные
значения критических напряжений, как и формулы Эйлера для сжатых стер-
стержней малой гибкости. Для нахождения действительных
критических напряжений при выпучивании балок,
когда ак > оп, следует руководствоваться опытными
данными. Можно воспользоваться, по предложению
проф. Ф. Ясинского, аналогией со стержнями и пола-
полагать, что действительные напряжения находятся в
том же отношении с определёнными по формулам этого
параграфа, в каком находятся действительные с эйлеро-
эйлеровыми при ок > ап для сжатых колонн.
Пример 130. Балка двутаврового профиля № 60
(ГОСТ 8239—56) пролётом 1 = 6 м, лежащая на двух
опорах, загружена равномерно распределённой нагрузкой
q = 9 т/м. Проверить прочность балки и устойчивость
плоской формы изгиба при основном допускаемом напря-
напряжении [а]== 1600 кг/см2 и коэффициенте запаса на проч-
прочность и устойчивость k=\J.
Размеры сечения по сортаменту (фиг. 569) и геометрические характери-
характеристики профиля равны:
Л = 60 еж; Ь = 19 см;
&j = 1Д см; Ь2 = 1,8 см; ht = 56,4 см;
Jy = 75 450 см4; Jz = 1720 еж4;
см*; Лс= П8 еж4.
Фиг. 569.
Момент инерции при кручении JK подсчитан по формуле A1.36) /к =
= тг]—-Л Л53, где для двутавра yj = 1,2. Следовательно:
Ук = L? (hfil + 2ЬЦ) = 0,4 E6,4 • 1,13 + 2 • 19 • 1,83) = 118 см\

§ 208]	устойчивость плоской формы изгиба балок	651
а) Проверка на прочность.
Мт&х = X = Ц^~ = 40»5 ™ = 405 •
^тах 4О5'*°4
2510
=1615 кг/см2^ 1600 кг/см2.
Однако прочность балки можно считать обеспеченной лишь при условии,
что при изгибе не произойдёт бокового выпучивания.
б) Проверка на устойчивость плоской формы изгиба.
Для проверки на устойчивость воспользуемся формулой C4.11). Крити-
Критическая нагрузка:
где р — коэффициент, зависящий от отношения жёсткостей и от l/h; Сг = EJZ\
Принимая величину модуля упругости для стали ? = 2 «10е кг/см2,
а модуля сдвига
G== 2A+ц)=р>
получим:
1720-118 _p
2,6 -
Для определения коэффициента р найдём отношение
CiyQJ*	118 F00\2
2,6-1720 Uoj ~A
По таблице 33 (столбец 4) находим величину р == 40,5 (по интерполя-
интерполяции между значениями a = 2 и a = 4). Следовательно, критическая, т. е.
наименьшая, нагрузка для данной балки, при которой становится возможным
боковое её выпучивание, равна:
<?« = №)к = 279 р g- = 279 40^ог2 Ш = 62 600 кг.
Допускаемая нагрузка (при коэффициенте запаса k =1,7)
R	1, /
Значит, по условию устойчивости допускаемая интенсивность нагрузки
9 = .=_
Таким образом, надежная работа балки может быть обеспечена лишь при
условии уменьшения заданной нагрузки 9 т/м примерно в полтора раза,
либо при условии постановки поперечных связей, препятствующих боковому
выпучиванию балки (если это по конструкции возможно).
Выясним, как изменится величина критической нагрузки при закрепле-
закреплении середины пролёта с помощью поперечной связи. Это равносильно
Уменьшению свободной длины балки вдвое, что приводит к изменению

652 БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
коэффициентов а и Р:
_ С2 /0,5/4» _ Gh 0 О5 ft \2 _ П8 •0,25 /600\* _
а —C7V~7TJ ~E? ' UTJ ",6.1720 Uo) -0|ЬЬ'
Р = 59 (графическая интерполяция между а = 0,1 и а = 1,0). Критическая
нагрузка
|5^^
кг.
Это соответствует критическим напряжениям:
_ Ок/ _
8-2510 '
Полученное значение <тк значительно выше предела пропорциональности
материала, вследствие чего формула C3.11) уже неприменима. Найденному
значению ак в действительности соответствует предел текучести материала.
Значит, в этом случае достаточно ограничиться проверкой на прочность.
§ 209. Проверка прочности стержней на совместное действие
продольных и поперечных сил (с учётом деформаций).
Пользуясь приближённым методом определения прогибов (§ 134), мы
можем закончить начатое в § 161 рассмотрение сопротивления прямого
стержня действию поперечных нагрузок и продольных сил *).
В этом случае изгибающий момент в каждом сечении балки будет состав-
составляться из момента от поперечных нагрузок MQ и момента от продольных сил Р,
равного Ру, где у — абсолют-
а	J^pnx	+\AW- ная величина прогиба в рас-
' б" о сматриваемом сечении при со-
совместном действии обеих си-
^"^ шЩ стем сил (фиг. 570). Вычислим
величину у для случая шарнир-
уно-опёртой балки, сжатой
ф rj~	продольными силами Р и нагру-
' °	жённой силой Ро в расстоянии
а от левой опоры (фиг. 570).
Под действием постепенно возрастающих сил Р и Ро балка ЛВ изгибается,
и точки Л и В сближаются на величину А.
Применим приближённый метод и примем кривую изогнутой оси за
синусоиду, уравнение которой удовлетворяет условиям закрепления концов
балки
Тогда потенциальная энергия изгиба балки будет равна
y')srf.v = ^/»-	C4.12)
1) Эта задача впервые была решена профессором И. Г. Бубновым.

§ 209] СОВМЕСТНОЕ ДЕЙСТВИЕ ПРОДОЛЬНЫХ И ПОПЕРЕЧНЫХ СИЛ 653
Сближение концов балки А равно разности между длиной изогнутой оси
и хорды, или А = \ (ds — dx). Имея в виду, что ds~ Ydx2 + dy2 =
0
= dx 11 -f- (-jr) I или, приближённо, ds = dx\ 1 + -я-СУI I» получим для А:
i	/
A= Udx\l+±(y'r\--dx} = ~-{(yydx = ^. C4.13)
Дадим балке дополнительный прогиб так, чтобы середина её получила
бесконечно малое перемещение df. Тогда точка приложения силы Ро полу-
получит добавочное перемещение dy = df sin^-, или при x = ady = df sin . .
Точка же приложения силы Р переместится на </А = *~ df.
Потенциальная энергия изгиба балки при этом увеличится на
а энергия грузов уменьшится на величину:
dUp = dAp = Pody +
или
так как dU = dC/py то
OIK)
Отсюда величина / может быть выражена так:
n*EJ
Обозначив ^-^- = Рк, получим:
/=	^7	*пТ.	С3415)
При отсутствии продольной силы (Р = 0) величина прогиба посредине
пролёта была бы равна:
2РО/3 sin ^
/=	,ipi

654 более сложные вопросы проверки на устойчивость [гл. xxxiv
В частном случае, когда сила Ро приложена посредине пролёта, т. е. при
а = -у и Р = 0, получаем:
_ 2/у_3 _ Р/3
48,7'EJ'
что мало отличается от точного значения прогиба. При совместном же дей-
действии сил Ро и Р находим:
. . ял;
/о Sin —
>> =	7j- = % = Су0,	C4.16)
1 -—"р-	А	р~
где j'o—прогиб от поперечной нагрузки; таким образом, продольные сжи-
сжимающие силы вызывают увеличение прогибов, учитываемое множителем
С = —Ц_.	C4.17)
Формула C4.17) показывает, что если сжимающая сила Р достигает
критического значения, то прогиб теоретически становится бесконечно
большим.
Полученный выше (формула 34.15) результат можно распространить на
случай равномерно распределённой по всему пролёту нагрузки q\ заменяя
ее элементарными грузами q da, подставляя эту величину вместо Ро в фор-
формулу C4.15) и интегрируя по а от 0 до /, получим / для случая сплошной
равномерно распределённой нагрузки и сжимающих сил Р (фиг. 423) равный
q da sin™ P
лт	-т~=—^т—5-г	<34Л8>
При отсутствии продольных сил Р прогиб посредине пролёта был бы
равен
/0	те* 384 EJ '
значит, и в этом случае при совместном действии q и Р
/oSinT	v
. у =	/-=—V = c^
1	1

§ 209] СОВМЕСТНОЕ ДЕЙСТВИЕ ПРОДОЛЬНЫХ И ПОПЕРЕЧНЫХ СИЛ 655
Таким образом, для шарнирно-опёртой балки прогибы при совместном
действии поперечных нагрузок и сжимающих продольных сил Р равны про-
прогибам от одних поперечных сил, умноженным на
с— '
этот множитель С отражает влияние продольных сил.
Теперь можно произвести вычисление изгибающего момента для рассма-
рассматриваемых случаев нагрузки балки. Для стержня с шарнирно-опёртыми кон-
концами под действием сжимающих сил Р и поперечной равномерно распреде-
распределённой нагрузки q наибольший изгибающий момент будет посредине пролёта
и достигнет величины
так как
f- /о ^5^	1
7~~ . Р "84ЕУ , Р '
1 —-р-	1 —рг
то
"'max— 8 ^ 384?/ . Р	8 \	i P
Наибольшее напряжение будет в крайних волокнах балки; оно склады-
складывается из напряжений сжатия и изгиба:
max	p	ур *
отбрасывая знак минус, обозначающий сжатие, и подставляя вместо Мтах
его значение, получаем:
при практических расчётах, конечно, можно положить 1,028 «^1,00.
Как видно из этой формулы, напряжения в рассматриваемом случае не
пропорциональны внешним силам, а растут быстрее их. При увеличении
at2
нагрузок Р и qt например в два раза, дробь j^,, сама увеличившись вдвое,
будет умножаться ещё на возросший множитель в скобках. Таким образом,
полная величина напряжения возрастёт более чем вдвое. Это требует пере-
перехода от проверки прочности по допускаемым напряжениям к расчёту по
допускаемым нагрузкам.
В самом деле, условие прочности по допускаемым напряжениям имеет
вид:

656	БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
где [g] = ~; здесь ао = ст для пластичного состояния материала и <jo = cb —
для хрупкого.
Это условие обеспечивает коэффициент запаса k для наибольших напря-
напряжений, вызванных действующей на стержень нагрузкой, по отношению к их
опасному значению ст или св; чтобы получить это опасное состояние мате-
материала, необходимо увеличение действующих в стержне напряжений в k раз.
Но для этого в рассматриваемом случае потребуется увеличение нагрузки
меньше, чем в k раз. Значит, коэффициент запаса для действующей нагрузки
но отношению к предельной, вызывающей опасное состояние, будет меньше
чем kt а значит, расчёт по допускаемым напряжениям в рассматриваемом
случае не сможет обеспечить нам принятого коэффициента запаса k для
грузоподъёмности всего стержня в целом. Чтобы достигнуть этого, необхо-
необходимо перейти к расчёту по допускаемым нагрузкам. В этом случае, как
известно, условие прочности имеет вид
где Q — нагрузка конструкции; QT — предельная нагрузка, соответствующая
опасному состоянию конструкции.
Для стержней из хрупких материалов опасное состояние будет соответ-
соответствовать достижению наибольшим напряжением опасной величины а0 = ав;
что же касается стержней из пластичных материалов, то можно было бы
считать, что опасным состоянием для них, как и при простом изгибе, будет
распространение текучести материала на всё сечение. Однако опыты и теоре-
теоретические исследования показывают, что при таком распространении пласти-
пластических деформаций грузоподъёмность стержня, работающего на изгиб и сжа-
сжатие, падает; поэтому более осторожно и при применении пластичных мате-
материалов опасным состоянием стержня считать также достижение наибольшим
напряжением опасной величины ао = ат.
Таким образом, предельные нагрузки Рт и qT определяются формулой
/ 1,028^
T + wl'+TI^H-	C4-2O)
ч	рк /
Допускаемые нагрузки [Р] и [q] будут в к раз меньше предельных:
или
PT = {P]k и qT = [q]lrt
подставляя эти величины в формулу C4.20) и учитывая, что а0 = k
получаем:

§ 209] СОВМЕСТНОЕ ДЕЙСТВИЕ ПРОДОЛЬНЫХ II ПОПЕРЕЧНЫХ СИЛ	657
сокращаем обе части на к,
Так как действительные нагрузки Р и q должны удовлетворять условиям
Р^[Р] и q^lq],
то условие прочности для рассматриваемого стержня будет иметь вид:
1,028 *?\
р«
<34-21>
При применении формулы C4.21) надо иметь в виду, что величина Р& вошла
...	'+ ъ-EJ ..	~г
в наш расчет формально, как замена дроби —д-', жесткость же EJ появилась
здесь из формулы для вычисления потенциальной энергии при изгибе.
Таким образом, во всех этих вычислениях момент инерции / представляет
собой не наименьший центральный момент инерции сечения, как это было
при проверке устойчивости, а момент инерции относительно нейтральной
оси г при изгибе балки поперечной нагрузкой. Так как при изгибе выгодно
располагать сечение балки так, чтобы нейтральной осью была ось с наиболь-
наибольшим моментом инерции, то при вычислении РК в формуле C4.21) обычно
именно этот момент инерции и следует принимать в расчёт. Зная величину Л,
мы можем вычислить Рк но формуле
где Jz — момент инерции сечения относительно нейтральной оси г.
При помощи формулы C4.21) мы произвели проверку стержня на проч-
прочность', эта проверка должна быть дополнена проверкой на устойчивость, тем
более, что искривление стержня под действием поперечных нагрузок обычно
происходит в плоскости не наименьшей, а наибольшей жёсткости. Поэтому
стержню угрожает выпучивание, потеря устойчивости в боковом направле-
направлении. Значит, обычная проверка такого стержня на устойчивость под действием
только сил Р и проверка устойчивости плоской формы изгиба (§ 208) обяза-
обязательны.
Если бы на балку пролётом /, шарнирно-опёртую по концам, действовала
продольная сжимающая сила Р и сосредоточенная сила Ро посредине про-
пролета, то ход расчёта, подобный изложенному выше, привёл бы нас к сле-
следующей формуле для вычисления прогиба посредине пролёта:

658	БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
наибольший изгибающий момент был бы равен
Р0/3 1

4SEJ'
1 —
Дальнейший расчёт ясен.
Для балок с шарнирно-опёртыми концами изложенный здесь приём мо-
может быть распространён на любые комбинации поперечных нагрузок; если
эти силы действуют в одном направлении, то можно с достаточной точ-
точностью считать, что наибольший прогиб будет посредине пролёта. Подобные
же вычисления применимы и для балок, защемлённых одним концом.
Если продольные силы будут не сжимающими, а растягивающими, то
знак перед Р придётся изменить на обратный. Тогда, например для балки
на двух опорах с равномерно распределённой нагрузкой, условие прочности
будет иметь вид:
C4.23)
Влияние продольных растягивающих сил будет уменьшать напряжения
от изгиба.
§ 210. Влияние эксцентриситета приложения сжимающей силы
и начальной кривизны стержня.
Пользуясь таким же методом, как и в § 209, можно легко учесть влия-
влияние начального эксцентриситета силы при продольном сжатии (фиг. 571).
(Влиянием собственного веса пре-
пренебрегаем.)
Приняв уравнение изогнутой
оси в форме у =/sin — и имея в
виду, что сближение точек приложе-
приложения сил в этом случае будет равно
I
т. е.
Фиг. 571.
составим выражения для dU и dUp\
, где 6в=
= ^ + 2еу./'), C4.24)
С	712/2
Здесь, как и в § 197, Д= 1 (ds — dx) = -j-т-, а 2еу'—дополнительное
сближение концов, вследствие поворота опорных сечений на угол 0В.

§ 210] ВЛИЯНИЕ ЭКСЦЕНТРИСИТЕТА ПРИЛОЖЕНИЯ СЖИМАЮЩЕЙ СИЛЫ 659
Из равенства dU = d(Jp найдем величину наибольшего прогиба:
- 4е Р	1
C4.25)
Здесь Рк — эйлерова сила, равная Рк = —— ,
Формула C4.25) позволяет найти прогибы стержня в зависимости от
возрастания силы Р.
Мы видим, что лишь при приближении силы Р к критическому, эйлеро-
вому значению, которое мы получили для прямого стержня, прогибы нашего
стержня быстро возрастают, что ведёт за собой резкое увеличение напряже-
напряжений; эта эйлерова величина критической силы и при наличии эксцентриси-
эксцентриситета должна считаться разрушающей. Таким образом, можно считать, что
наличие эксцентриситета не отражается на величине разрушающей силы
при продольном сжатии стержня, пока явление происходит в пределах
упругости.
Поэтому проверка на устойчивость и в этом случае остаётся в силе;
изменится лишь проверка на прочность, так как ещё до достижения силами
Р критического значения мы бу-
будем иметь вместо сжатия совмест-
совместное действие сжатия и изгиба
моментами Р(е-\-у\ т. е. тот
случай, который был рассмотрен
выше (§ 209).
Совершенно аналогично мы
можем подойти к оценке влия-
влияния начальной (обычно очень
небольшой) кривизны сжатого
стержня (фиг. 572). Уравнение
оси стержня до приложения силы примем: .yi=^osin—. После приложе-
приложения силы, вследствие эксцентриситета е, стержень получит дополнительное
искривление, и мы можем принять:
Фиг. 572.
C4.26)
Потенциальная энергия изгиба балки определяется этим дополнительным
искривлением и будет равна, как и в предыдущих случаях,
4/3 Т '
Сближение же концов искривлённого стержня после приложения сил Р выра-
выражается формулой
Варьируя изогнутую ось и составляя уравнение
dU = dUp,
получаем:
2/3

660	БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
отсюда
ЕЛ'-
Р
Р
Учг
C4.27)
Таким образом, уравнение изогнутой оси имеет вид:
Р	. .-
. *х У°5тТ
C4.28)
Наибольшее значение у получает при дг = -- а именно:
•Ушах
	Уо
1—-рг
C4.29)
Как и в предыдущем случае, прогибы резко возрастают лишь при прибли-
приближении Р к Рк.
Резюмируя, можно сказать на основании теоретических соображений,
что при напряжениях в пределах пропорциональности ни эксцентриситет,
ни начальная кривизна не оказывают влияния на величину разрушающей
силы при продольном*сжатии стержня.
Иначе обстоит дело со стержнями малой и средней гибкости. При кри-
критических напряжениях, превосходящих предел пропорциональности, оба ука-
указанных обстоятельства значительно снижают величину ак. Это показывают
опыты и подтверждают теоретические попытки подсчитать величину крити-
критических деформаций. Из опытов следует, что для стержней малой и средней
гибкости влияние эксцентриситета весьма значительно; оно отражается на
устойчивости и длинных стержней, но в значительно меньшей степени.
Влияние добавочных обстоятельств, изученных в настоящем параграфе,
заставляет увеличивать коэффициент запаса при переходе к средним и
малым гибкостям, а также выбирать несколько больший, чем при проверке
на прочность, коэффициент запаса и для длинных стержней. Для оценки
влияния эксцентриситета и начальной кривизны на прочность и устойчивость
сжатых стержней необходимо дать себе отчёт о числовых величинах е и у0.
В тщательно изготовленных стержнях можно ожидать начального про-
прогиба v0 no крайней мере в у^- длины; при менее тщательном изготовлении
1UUU
3^0 может достигать вдвое большей величины.
Эксцентриситет при хорошей центрировке может быть оценён в 1/750
длины. Далее, следует принять во внимание допуски в размерах попереч-
поперечного сечения; можно считать, что они эквивалентны эксцентриситету разме-
размером Л/40 и начальной стрелке той же величины. Здесь h — размер попе-
поперечного сечения в плоскости возможного выпучивания. Для составных сече-
сечений следует иметь в виду добавочный эксцентриситет величиной около h/160
в связи с возможной разницей в площадях отдельных ветвей стержня (§211).

§ 211}
ОБОСНОВАНИЕ РАСЧЁТА СОЕДИНИТЕЛЬНОЙ РЕШЁТКИ
661
Таким образом, для стержней со сплошным сечением следует считать
возможными следующие минимальные величины е и у0:
— A-JlJL	— l _l_ h
е~~ 750 + 40 И Л>0~Т000 + 40*
Кроме эксцентриситета и начальной кривизны, имеется ещё целый ряд
обстоятельств, всегда возможных на практике и гораздо сильнее влияющих
на грузоподъёмность сжатых стержней, чем на прочность балок и растяну-
растянутых деталей, Сюда относятся: влияние наклёпа, величина начальных напря-
напряжений, вызванных изготовлением частей стержня, местные дефекты в отлив-
отливках, сучки в дереве. Для стальных конструкций влияние этих добавочных
обстоятельств учитывается некоторым (процентов на 10—20) повышением
коэффициента запаса на устойчивость (см. § 204).
§ 211. Обоснование расчёта соединительной решётки
в составных стержнях.
Как было показано выше (§ 205), соединение двух отдельно расположен-
расположенных частей сжатого стержня в одно целое при помощи решётки или планок,
сильно повышает грузоподъёмность стержня. Таким образом, роль этих допол-
дополнительных креплений исключительно серьёзна; они должны
быть достаточно мощными, чтобы обеспечить совместную
работу обеих половин стержня, — не допустить потери устой-
устойчивости каждой из этих половин в отдельности.
Расчёт этих дополнительных креплений обычно основы-
основывается на следующих соображениях. Пока сжатый составной
стержень из двух половин, соединённых решёткой или план-
планками, остаётся прямым, эта решётка не работает или почти
не работает. При искривлении же стержня в его сечениях
появляется поперечная сила, вызывающая усилия в стержнях
решётки.	~°
Так как в действительных конструкциях добиться того,
чтобы сжатый стержень оставался совершенно прямым, не-
невозможно из-за начальной кривизны, эксцентриситета на-
нагрузки и т. д., то всегда следует считаться с неизбежностью
возникновения усилий в креплениях составного стержня.
Пусть сжатый стержень с шарнирно-опёртыми концами
искривится, как показано на фиг. 573. Кривая изгиба, как мы
видели (§ 201), является синусоидой
y=f sm^%	фцГ# 573.
Разрежем стержень сечением на расстоянии х от одного из концов и вычи-
вычислим поперечную силу Q, проектируя все силы, приложенные к одной поло-
половине стержня, на направление сечения (фиг. 573). Получаем:
Q = Р sin <p,
где ср — угол между нормалью к сечению и силой Р. По малости этого угла
dv
синус его можно заменить тангенсом, а последний — производной -~ % /Таким
образом,

662 БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
Зная поперечную силу Q, можно найти усилия в элементах решётки;
проводя сечение тп (фиг. 574), отбрасывая одну часть стержня и проектируя
все силы, приложенные к оставленной части, на направление сечения, нахо-
находим усилие в раскосе Si.
<? -4- Q •
проводя сечение mitiu подобным же образом определяем усилие в стойке:
S* = Q.
Наибольшее значение поперечная сила получает у концов стержня при х = О
и х = /:
По этому значению поперечной силы и следует вести расчёт элементов
решётки. Для нахождения 0тах надо знать стрелу изогнутой оси /.
Искривление оси стержня при рабочей нагрузке зависит, главным обра-
образом, от эксцентриситета е и начальной стрелки у0. Наибольший прогиб, вы-
вызванный влиянием обоих факторов, будет (§§ 209 и 210):
C4.30)
Считая коэффициент запаса равным примерно 2,5, т. е. Рк = 2,5Р, получаем:
/= 1,67 Ь>0 +0,506*];
принимая (§ 210) для е значение =—, а для у0 значение tqqq, получаем
для /:
/= 0,00167/ + 0,00112/ = 0,00279/ ^ 0,003/.
Тогда Qmax = P-y • 0,003/= О,ОО95Р = О,95о/о от сжимающей силы Р.
В наших нормах для этой величины принимают в среднем около 1,5%.
В § 205 было уже указано, что при размерах элементов ^соединительной
решётки и планок, выбранных в соответствии с только что изложенными
соображениями, можно считать обе половины составного
стержня работающими совместно относительно оси уу
(фиг. 572). Однако благодаря неизбежным упругим дефор-
мациям соединительной решётки под действием попереч-
ной силы, действительный момент инерции обеих половин
сечения стержня относительно оси уу будет меньше тео-
теоретического.
Вместо того чтобы учитывать уменьшение момента
инерции относительно этой оси уу, перпендикулярной
к плоскости решётки, можно при проверке устойчивости
относительно этой оси вводить в расчёт несколько уве-
увеличенную длину стержня, т. е. умножать действительную
Фиг 574	Длину на коэффициент длины, больший единицы. Формулы
для вычисления этого коэффициента, полученные теоре-
теоретически, приводятся ниже.
Если решётка состоит из распорок и диагоналей (фиг. 575, а), то коэф-
коэффициент длины равен:
coss a sin

§ 212]
ПРИМЕРЫ РАСЧЁТА СЖАТО-ИЗОГНУТЫХ СТЕРЖНЕЙ
663
Здесь /^—площадь сечения диагонали; Fp — площадь сечения распорки;
а—угол между диагональю и распоркой; /—момент инерции обеих половин
сечения стержня относительно оси, перпендикулярной к плоскости решётки;
если стержень имеет две соединительные решётки, то в формулу для fi надо
вводить двойную площадь диагоналей и распорок; при решётках с двойными
(перекрёстными) диагоналями надо вводить в
расчёт вместо FK сумму площадей обеих
диагоналей.
Если обе половины стержня (фиг. 562, б)
соединены планками, то коэффициент длины
выражается формулой:
,=/;
Здесь J — собственный центральный момент
инерции всего сечения стержня относительно
оси, перпендикулярной к плоскости планок;
Ji — момент инерции полусечения относитель-
относительно его центральной оси; Jn — момент инерции
сечения планки относительно оси, проходящей
через центр тяжести сечения стержня перпен-
перпендикулярно к плоскости планки; а — расстояние
между осями планок вдоль стержня; Ь — рас-
расстояние между центрами тяжести половин се-
сечения.
Для обычно встречающихся на практике
размеров решётки и планок эти формулы могут
быть приведены к более простому виду; для
системы по фиг. 562, а и 575, а
C4.31)
для системы по фиг. 575, б
= У 1
+ 0,83 (-х?J; C4.32)
г*
здесь Fo — площадь половины сечения стерж-
ня; X — гибкость всего стержня относительно
оси, перпендикулярной к плоскости решётки или планок; Хр — гибкость одной
половины стержня между планками. По существующим нормам вместо 0,83
принято 1,0.
§ 212. Примеры расчёта сжато-изогнутых стержней.
Пример 131. Шарнирно опертая по концам двутавровая балка проле-
пролетом / = 8 м изгибается равномерно распределённой нагрузкой q = 1 т/м и
сжимается продольными силами Р = 80 т. В боковом направлении пролёт
разделён связями пополам. Подобрать поперечное сечение балки при допу-
допускаемом напряжении [а] = 1400 кг/см* и коэффициенте запаса k =1,6.
Так как продольные силы во много раз больше поперечных, подбор
сечения целесообразно произвести из условия устойчивости на сжатие. Сво-
Свободная длина стержня в боковом направлении /х = 0,5 / = 4 м. Принимая

664
БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
для первого приближения ер = 0,5, находим:
_ Р	80 000
= 114,4 см2.
"~VM"~" 0,5-1400
По сортаменту (см. приложение IX, табл. 3) подходит двутавр Ms 55
с площадью F= 114 см2; наименьший радиус инерции imin = 3,44 см; гибкость
А = —— = —- = 116; коэффициент у = 0,48. Расчётное напряжение равно:
'rain
3,44
80 000
= 1460 к г! см* < 1400 кг/см*.
V'y-F 0,48-114
Перенапряжение составляет около 4%, что допустимо. Произведём теперь
проверку прочности сечения на сжатие и изгиб в плоскости стенки двутавра.
Условие прочности имеет вид C4.21):
Р
М
1,028
kP_\
Vy\
Изгибающий момент
М = Ц- = ~ = 8 тм = 8• 10* кг'см*.
о о
Геометрические характеристики сечения (ГОСТ 8239—56): /^=114 см2;
7^ = 55150 см4; 1^ = 2000 смд. Входящая
v	в формулу эйлерова 4критическая» сила:
1
8002
= 1700 000 л:г=1700 т.
Подставляя, получим:
/	]68°\
у/////
80 000 8-10s
114
2000
1700
У////)У////77/
800а / ~~
= 1135 кг/см2 < 1400.
Таким образом, по условию устойчивости
сечение подобрано в обрез; по условию же
прочности имеется значительный запас.
Пример 132. Стержень уголкового
профиля размером 100 х 100x10 мм> шар-
нирно закреплённый по концам, сжимается
продольными силами Р=10 г, приложен-
приложенными с эксцентриситетом г = 3 мм в плоскости наименьшей жёстко-
жёсткости уголка (фиг. 576). Кроме того, стержень имеет начальную кривизну
в той же плоскости /0 = 2 мм. Найти величину прогиба и наибольших на-
напряжений в сечении посредине пролёта, если длина стержня / = 1 м. Прогиб
в средине сечения может быть вычислен по формуле C4.30) § 212:
Фиг. 576.
/=
f i4e
р\
где
«*?/
По сортаменту Jy = 74,1 см*. Следовательно,
"г -2 • 10е • 74 1
Р =	' = 146 300 кг.

§ 213] ПРОВЕРКА ТОНКОСТЕННЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ	666
Прогиб / равен:
146 300
Полный эксцентриситет сжимающей силы равен:
е0 = / + е = 0,242 + 0,3 = 0,542 см.
Изгибающий момент в сечении посредине пролёта:
Мтах = Р -е0 = 10 000.0,542 = 5420 кгсм.
Напряжения в этом сечении будут:
	 г * max
Здесь F=\9j2 см2,	a z — расстояния до крайних точек сечения.
До обушка:	,-—	г —
у	Zl = z0V2 = — 2,83/2 = — 4 см;
до края полки:
z% = Ь cos 45* — 12j | = 10.0,707 — 4,0 = 3,07 см.
Напряжения:
Onm = -i™*> +^--521+292 = 223 кг^,
10 000 5420-3 СО1 ООЛ
amin-- 19|2 ~74Д~"" ^1—Л-и—/41 лгг/^*.
§ 213. Проверка тонкостенных стержней открытого профиля
на устойчивость.
В главе XXX были приведены выводы основных формул теории В. 3. Вла-
Власова для вычисления нормальных и касательных напряжений при кручении
и изгибе тонкостенных стержней.
Особую проблему представляют расчёты на устойчивость сжатых
тонкостенных стержней незамкнутого (открытого) сечения, применяющихся
в авиационных и других конструкциях (фиг. 577). Теория упругой устойчи-
вости таких стержней излагается в специальных курсах устойчивости упругих
систем. В настоящем параграфе приводятся лишь некоторые окончательные
результаты, полученные В. 3. Власовым при исследовании устойчивости
тонкостенных стержней.
В § 182 было показано, что явление закручивания тонкостенного стержня
может иметь место не только при кручении или изгибе его поперечными
силами (не проходящими через центр изгиба сечения), но также и в случае
Действия только продольных сил, приложенных по концам стержня.
Из этого следует, что кручение, связанное с неравномерной депланацией
сечений и возникновением секториальных нормальных напряжений, может
играть важную роль и в случаях потерн устойчивости тонкостенным стержнем.

666	БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
Действительно, решения, полученные В. 3. Власовым при исследовании
устойчивости тонкостенного стержня, показывают, что в самом общем
случае потеря устойчивости его происходит в смешанной изгибно-кру-
тильной форме.
Для случая центрального (осевого) сжатия
дольными силами дифференциальные уравнения
веденные В. 3. Власовым, имеют вид (фиг. 578):
тонкостенного стержня про-
его искривлённой оси, вы-
Z" +агРЪ"=0;
,iv
C4.33)
EJJIW+ (Pr* — GJJ 6" + агР?* — ауРг[' = 0.
В этих уравнениях величины, связанные с изменением основной формы
равновесия стержня, имеют значения: EJy и EJ2 — жёсткости стержня
главных плоскостях инерции; EJ^ и GJK — секториальная и крутильная
жёсткости стержня; ? и у\ — дополнительные пере-
перемещения (прогибы) в направлениях осей у и 2, возни-
возникающие вследствие потери устойчивости плоской
формы изгиба при продольном сжатии; 0 — угол за-
кручивания сечения; а
изгиба сечения; г2 =
аг — координаты центра
-f- а*- + а\ — новая гео-
у
сечения
тонкостенного
метрическая характеристика
стержня.
Из уравнений C4.33) видно, что если ау и а2 не
равны нулю, то во всех трёх уравнениях члены,
содержащие 0, не обращаются в нуль и потеря устой-
устойчивости таких стержней сопровождается их закручи-
закручиванием. Следовательно, тонкостенные стержни не-
несимметричного профиля, у которых центр изгиба не
лежит ни на одной из главных осей инерции (ауф$
и а2ф0), всегда теряют устойчивость в смешанной
Фиг. 578.	изгибно-крутильной форме, характеризующейся по-
поворотом сечений относительно линии мгновенных
центров вращения. Чисто изгибная (эйлерова) форма потери устойчивости
для таких стержней вообще оказывается невозможной.
Из решения уравнений C4.33) следует, что критическая сила тонкостенных
стержней меньше, чем это получается по формуле Эйлера, применение которой
может повести к грубым просчётам.
Это обстоятельство, имеющее большое практическое значение, может
быть объяснено и физически. В теории Власова гипотеза плоских сечений
не используется; в эйлеровой же теории, по существу, предположено нали-
наличие как бы дополнительных связей по всей длине стержня (что соответствует
принятию гипотезы плоских сечений), устраняющих кручение стержня и
увеличивающих его жёсткость.
Отсюда следует, что критические силы, вычисленные по формулам
Эйлера, будут обычно больше, чем найденные по теории Власова, что под-
подтверждается и опытом.
В случае, если ау = 0и сг = 0, то-есть когда центр изгиба совпадает
с центром тяжести сечения, уравнения C4.33) принимают вид:
C4.34)
EJJ1

§ 213] ПРОВЕРКА ТОНКОСТЕННЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ 667
В этом случае в первых двух уравнениях члены, содержащие 6, обрати-
обратились в нуль. Эти уравнения соответствуют потере устойчивости в изгибной
форме. Третье уравнение не зависит от величин $ и •*) и потому соответствует
потере устойчивости в чисто крутильной форме.
При шарнирном опирании концов стержня, в результате интегрирования
и использования граничных условий, вычисленные корни этой системы
уравнений имеют значения:
P, = P.= «%L;
C4.35)
Pv и Pz — эйлеровы критические силы, соответствующие выпучиванию
стержня в той и другой главной плоскости инерции. Рш — критическая сила,
соответствующая потере устойчивости в чисто крутильной форме.
Для сечения, имеющего одну ось симметрии (например, ось у)} корни
дифференциальных уравнений В. 3. Власова C4.33) будут:
rJEJ
Pt = Pz = —-—- — эйлерова критическая сила;
*2
Р*\ (Ру + PJ г2 ± У(РУ + РшУг* - 4РуРт (г» -
В этом случае формы потери устойчивости будут: одна — чисто изгибная
и две — изгибно-крутильные с центрами вращения на оси симметрии сечения.
Из трёх корней дифференциальных уравнений В. 3. Власова (т. е. сил
Ри Р% и Pz) критической силой следует считать наименьшую. Теория и опыт
показывают, что для тонкостенного стержня, сечение которого имеет одну
ось симметрии, наименьшее значение обычно имеет сила РЬу под дей-
действием которой стержень теряет устойчивость в изгибно-крутильной форме,
причём в этих случаях Р3 оказывается значительно меньше эйлеровой
силы Рг.
Для сопоставления величин критической силы, вычисленных по формуле
Эйлера и по формуле Власова, и в целях сравнения полученных результатов
с опытными данными в таблице 34 приведены данные испытаний тонко-
тонкостенных металлических стержней на сжатие осевыми продольными силами,
выполненных в лабораториях ЦАГИ и ЦНИИ ПС.
Как видно из таблицы, опытные значения критических сил для всех
испытанных стержней хорошо согласуются с результатами, полученными по
теории В. 3. Власова, причём величины власовских критических сил значи-
значительно меньше эйлеровых.
Следует, однако, иметь в виду, что приведённые здесь результаты
В. 3. Власова получены из условия свободной депланации концевых сечений.
На практике же, закрепление концов сжатого стержня обычно в той или иной
мере препятствует депланации концевых сечений, что может существенно
снизить влияние крутильного эффекта при действии продольных сил. Кроме
того, наличие соединительных планок и решёток во многих случаях практики
приближает тонкостенный открытый профиль к замкнутому, что также ведёт
к уменьшению опасного влияния закручивания при продольном сжатии

668	БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА З'СТОЙЧИВОСТЬ [гл. XXXIV
Таблица 34. Опытные данные о критических силах.
Форма и размеры
сечений в' мм
Длина
стержня
Расчётные критические
силы в кг
по формуле
Эйлера
по теории
Власова
Опытное
значение
критической
силы в кг
\ is
1000
750
500
1423
2531
5694
412
654
1318
90
400
630
1200
1000
750
500
4026
7158
16105
461
744
1550
480
780
1420
2000
2000
18750
18750
14850
14850
14000
14000
стержня. Эти обстоятельства могут резко уменьшить разницу между вели-
величинами критических сил, подсчитан-
подсчитанных по формуле Эйлера и по тео-
теории Власова.
Ход вычислений при определении
величины критической силы но фор-
формулам В. 3. Власова покажем на
примере.
Пример 133. Подсчитать вели-
величину критической силы для тонкостен-
тонкостенного стержня корытного сечения
(фиг. 579) при следующих его раз-
размерах: длина /=100 см; высота
j\-—¦— w--:	дуд^д^^^здсржч сечения Л = 39 мм; ширина полки
#$wv9/,	|^ Ул ! ус	# = 30,5 мм; толщина стенок о = 1 мм.
(Размеры сечения даны по середин-
Г^— i uy _^ i	ной линии — фиг. 580.) Концы стер-
f	жня считать шарнирно-опёртыми.
z/	Прежде всего вычислим значения
геометрических характеристик сече-
сечеФиг. 579.
Фиг. 580.
ния. Площадь сечения
Г = (>1> + h) • о = 2 C,05 + 3,9) 0,1 = 1 см\

§ 213] ПРОВЕРКА ТОНКОСТЕННЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ	6€9
Расстояние от оси zQ до центра тяжести сечения
^	2ЬЧ _ Ь* _ 3,05*
Ус F
0
"~2. 3,05 + 3,9 '
Моменты инерции сечення относительно главных центральных
осей Jy и Jz:
= 3,9 . 0,1 • 0,932 + 2r°>L^W ^з,05 . 0,1 (Щ- — 0,93JH = 1,027 см*.
Расстояние от оси z0 до центра изгиба сечения (см. § 181, фор-
формула C0.42)):
ЗЬ2	3 • 3,052 , о_
У Л = ^FTh = 6.3,05 + 3,9^ ]-°7 СМ-
Расстояния от главной центральной оси до центра изгиба:
а у =уА + ус = 1,257.+ 0,93 = 2,187 см.
Новая характеристика сечения
Главный секториальный момент инерции сечения, подсчитанный для корытного
профиля (см. § 181),
3,05» • 3,9^ ¦ 0,1 B > 3,9 + 3 . 3,05)
12F-3,05 + 3,9)	-
Момент инерции при кручении:
JK = « У ^ = Ц?. B^ + Л) о* = Jili B . 3,05 + 3,9) . 0,13 = 0,00373 см*.
Величины, зависящие от жёсткости стержня (силовые факторы):
Эйлерова сила в плоскости наибольшей жёсткости
7i*EJv 9,87 • 2 • 10е • 2,815 ,Г,Л
Сила, соответствующая крутильному эффекту,
1 /*»?/„ , \_ 1 /9,87.2.10е.2,748 ,	0ППЯ7^ 07^ .
= Н\—7T" + 0/V 8^§1	Г00^	+ 810».0,00373J = 975 ^.
Таким образом, все величины, входящие в формулу В. 3. Власова, опре-
определены.

670 БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
Величина критической силы по Власову C4.36):
(Ру + PJ • г* - У [(Ру + Рш)*г* - 4РуРш (г* -
_ E550+ 97 5)- 8,625
— 2(8,625 — 2,1872)
	У [E550 + 975J • 8,625 — 4-5550-975 (8,625 — 2,1872)] 8,625 __
2 (8,625 — 2,1872)	"~~ *85 кг'
Для сопоставления подсчитаем величину критической силы по Эйлеру:
р -р _ **EJZ _ 9,87» 2 • 10». 1,027
Для рассмотренного примера величина критической силы по Власову
2025
оказалась в -qqh- = 2,3 раза меньше эйлеровой. Это значит, что опасное
ооО
состояние для рассчитываемого стержня наступит при гораздо меньшей
нагрузке, чем можно было бы предполагать на основании формулы Эйлера.
§ 214. Развитие расчётов на устойчивость.
Есть указания, что первым из занимавшихся вопросом об устой-
устойчивости сжатых стержней был знаменитый художник и учёный
Леонардо да Винчи A452—1519 гг.).
Теоретическое исследование вопросов о величине продольной
силы, при которой прямой сжатый стержень, кроме прямолинейной,
может иметь и искривлённую форму, принадлежит члену петер-
петербургской академии наук Леонарду Эйлеру (работы 1759—1780 гг.).
Простота и чёткость полученной им формулы привели к широкому
распространению её не только в России, но и на континенте Европы.
Явления, наблюдавшиеся при опытах со стойками средней и малой
гибкости, несколько затемнили в представлении инженеров идею
потери устойчивости; возникла мысль, что для вычисления крити-
критических сил может быть получена формула, рассматривающая выпу-
выпучивание стержня при действии продольных сил только как след-
стиие обычного нарушения прочности материала при совместном
действии изгиба и сжатия. На основе подобных соображений была
выведена Ренкином A858 г.) недостаточно обоснованная формула,
имеющая в настоящее время только историческое значение; её при-
применение за границей может быть объяснено лишь консерватизмом.
Из экспериментальных работ надо отметить довольно обширные
опыты Тетмайера (Цюрих). Это были опыты, поставленные весьма
тщательно в отношении обеспечения шарнирности опорных закре-
закреплений, охватывали широкий круг материалов (мягкая сталь, чугун,
дерево). Единственным недостатком были сравнительно небольшие
поперечные размеры образцов. Формулы типа «прямой линии», по-

§ 214]	РАЗВИТИЕ РАСЧЁТОВ НА УСТОЙЧИВОСТЬ	671
лученные Ф. Ясинским на основе этих и некоторых других работ
для критических напряжений, превышающих предел пропорциональ-
пропорциональности, получили большое распространение.
Надо заметить, что развитие методов расчётов на устойчивость
было самым тесным образом связано с практическими задачами,
которые возникли перед конструкторами, главным образом по линии
предупреждения разрушений. Потеря устойчивости сжатыми эле-
элементами конструкции очень часто вела к катастрофам, сопровождав-
сопровождавшимся большим материальным ущербом и человеческими жертвами.
Таковой была, например, катастрофа с Менхенштейнским мостом
в Швейцарии, когда потеряла устойчивость сжатая стойка фермы
при нагрузке поездом с двумя паровозами. При разрушении этого
моста пострадало около 200 человек. Опыты Тетмайера относились
как раз к этому времени A896 г.).
Развитие мостостроения в связи с постройкой железных дорог
потребовало пересмотра методов проектирования сооружений. Необ-
Необходимость этого пересмотра показала катастрофа с мостом через
реку Кевду на Моршанско-Сызранской железной дороге. Сжатый
пояс фермы этого моста был так слабо укреплён, что потерял
устойчивость под самой небольшой нагрузкой. В связи с изучением
этой катастрофы Ясинский разработал метод расчёта сжатых поясов
открытых мостов. К этому периоду относятся важнейшие теорети-
теоретические и экспериментальные исследования вопросов устойчивости.
Огромный вклад в науку об устойчивости элементов конструкций
внесли русские и советские учёные.
В 1892 г. Ф. Ясинский опубликовал свои первые работы об
устойчивости сжатых колонн1), а в 1902 г. был опубликован сборник
его трудов об устойчивости. Им был впервые решён ряд сложных
задач (об устойчивости стержня на упругих опорах; об устойчивости
сжатого стержня в упругой среде; определение критической на-
нагрузки, неравномерно распределённой по длине колонны; об устой-
устойчивости колонн ступенчатой формы при сжатии одной и двумя
силами и мн. др.). Ещё в 1892 г. Ф. Ясинским было введено понятие
о приведённой длине и о коэффициенте длины. Им же была со-
составлена таблица критических напряжений в зависимости от гиб-
гибкости, положенная в основу современных методов расчёта сжатых
стержней.
Методы расчёта сжатых колонн переменного сечения были даны
академиком А. Н. Динником2). Заметим, что только одна из частных
задач подобного рода была решена ранее Лагранжем. А. Н. Дин-
нику принадлежит также решение задачи об устойчивости арки
переменного сечения и многие другие3).
1)	Известия собрания инженеров путей сообщения, 1892.
2)	Известия Горного института, Екатеринослав, 1914, Изв. Донского
политехи, инст., 1925 г.
а) Труды Академии наук УССР, 1933 г. Устойчивость арок, 1947 г.

672 БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ ПРОВЕРКИ НА УСТОЙЧИВОСТЬ [ГЛ. XXXIV
Задачи об устойчивости плоской формы изгиба двутавровых
балок решены проф. С. П. Тимошенко1). Им же исследован целый
ряд задач об устойчивости кривых стержней, пластин и случаев
продольно-поперечного изгиба. Эта последняя задача была впервые
рассмотрена проф. Бубновым для неразрезной балки на упругих
опорах2). Им же были решены некоторые задачи об устойчивости
пластин. Ряд задач об устойчивости упругих плит был впервые
решён академиком Б. Г. Галёркиным3). Его общий метод прибли-
приближённого решения задач устойчивости упругих систем получил ши-
широкое распространение в СССР и за границей. Задача о формах
равновесия сжатых стержней была подробно исследована академиком
A.	Н. Крыловым4). Вопросы ¦ устойчивости скручиваемого вала под
действием продольных сжимающих сил были исследованы проф.
Е. Л. Николаи, которым были решены и другие задачи об устой-
устойчивости (арка с защемлёнными пятами и др.).
Некоторые вопросы устойчивости были впервые решены К. С. За-
вриевым, П. Ф. Папковичем, Е. П. Поповым, И. М. Рабиновичем,
Н. К. Снитко, И. Я. Штаерманом, Н. В. Корноуховым и другими.
Из этого краткого очерка видно, какое большое значение при-
принадлежит нашей отечественной науке в развитии всех разделов
общей теории устойчивости упругих систем. В последнее время,
в связи с широким применением лёгких тонкостенных конструкций
в разных областях техники (самолётостроение, судостроение, вагоно-
вагоностроение и т. д.), возникла потребность в исследовании устойчивости
тонкостенных стержней и тонких оболочек.
В 1935—1940 гг. были опубликованы уже цитированные работы
B.	3. Власова, в которых дана общая теория изгиба, кручения и
устойчивости тонких оболочек и тонкостенных стержней с незам-
незамкнутым профилем сечения5).
Теория Власова охватывает исследования упругой устойчивости
стержней, пластин, балок, оболочек, причём формулы Эйлера,
Тимошенко и др. могут рассматриваться как частные решения,
вытекающие из общей теории, предложенной В. 3. Власовым. Таким
образом, теория упругой устойчивости получила своё завершение
в трудах проф. В. 3. Власова, создавшего мощный аппарат, приме-
применимый к решению задач проверки устойчивости во всех случаях,
когда критические напряжения ниже предела упругости.
Исследования вопросов устойчивости систем за пределами упру-
упругости материала ожидают дальнейшего развития.
Приоритет в этой области принадлежит Ф. Ясинскому. Разра-
Разработав на базе огромного экспериментального материала общие
х) Известия Политехнич. ин-та, С. Петербург, 1904, 1908, 1915 гг.
*) Строительная механика корабля, С. Петербург, 1912 г.
*) Расчёт плит, Москва, Госстройиздат, 1934 г.
*) Известия Академии наук СССР, 1931 г.
5) В. 3. Власов, Тонкостенные упругие стержни, ГОНТИ, 1940 г.

§ 214]	РАЗВИТИЕ РАСЧЁТОВ НА УСТОЙЧИВОСТЬ	673
методы расчёта сжатых стержней на устойчивость, Ясинский наметил
также и пути теоретического решения задачи об устойчивости стержня
в неупругой области.
Предложив заменить модуль упругости Е переменным модулем Т
(в зависимости от гибкости), Ясинский показал, что таким путём
можно будет определить критическую силу при напряжениях, пре-
превосходящих предел пропорциональности материала. Эта идея Ясин-
Ясинского была развита Энгессером A899 г.) и Карманом A910 г.),
получившими теоретическим путём формулу типа эйлеровой для
неупругой области (с переменным модулем Т).
С тех пор, однако, теория неупругой устойчивости развивалась
мало и существенные успехи сделала лишь в СССР. Здесь надо
упомянуть работу А. А. Ильюшина *), в которой разработана теория
устойчивости плит и оболочек. Однако методы расчёта сжатых стерж-
стержней малой и средней гибкости базируются в основном пока на
экспериментальных исследованиях и формулах, выведенных в резуль-
результате обработки опытных данных.
Надо остановиться ещё на развитии вопроса о расчёте креплений
в составных стержнях. Потребность в исследованиях этого рода
возникла, когда попробовали применять сжатые стержни гораздо
ббльших размеров, чем это было раньше (постройка Квебекского
моста). Здесь обнаружилось, что применявшиеся раньше размеры
решётки, соединяющей обе половины стержня, оказались недоста-
недостаточными и вызвали катастрофу. Это побудило инженеров как экспе-
экспериментально, так и теоретически исследовать вопрос о роли соеди-
соединительной решётки и планок в сопротивлении стержней продоль-
продольному изгибу.
Рассмотрение этого вопроса имеется, например, в работах проф.
С. П. Тимошенко 2), акад. А. Н. Динника и других. Значительным
шагом вперёд здесь являются исследования А. Р. Ржаницына 3).
*) А. А. Ильюшин, Пластичность, Гостехиздат, 1948.
2)	С. П. Тимошенко, Об устойчивости упругих систем, Киев, 1910,
Теория упругости, т. 2, Петроград, 1916.
3)	Прикладная механика и математика, т. IV, в, 3, 1940.
22 Н, М, Беляев

ОТДЕЛ X
ДИНАМИЧЕСКОЕ ДЕЙСТВИЕ НАГРУЗОК-
ГЛАВА XXXV.
УЧЁТ СИЛ ИНЕРЦИИ И КОЛЕБАНИЙ»
§ 215. Введение*
До сих пор мы решали основную задачу сопротивления материа-
материалов, определяли размеры поперечных сечений частей конструкции
и выбирали для них материал лишь при статическом действии
нагрузок.
Как уже было указано в § 2, статическое действие нагрузок имеет
место, когда при передаче давления от одной части конструкции на
другую или при действии объёмных сил механическое движение этих
частей не меняется с течением времени. В этом случае каждый элемент
конструкции находится в равновесии под действием внешних нагру-
нагрузок и напряжений.
Постоянство движения характеризуется тем, что скорость рас-
рассматриваемых деталей и каждой их части не меняется — отсутствует
ускорение частиц этих элементов. Наличие же ускорения частиц
рассматриваемого тела или соприкасающихся с ним деталей харак-
характеризует уже воздействие динамической нагрузки. Так, давление
земли на подпорную стенку будет статической нагрузкой, так как
ни стенка, ни земляная масса не движутся, — скорость их постоянна
и равна нулю.
Точно так же статическим будет действие поднимаемого груза на
канат при постоянной скорости подъема груза. Наоборот, это дей-
действие будет динамическим, если груз поднимается с ускорением.
Динамическую нагрузку испытывают шатуны паровых машин и дви-
двигателей внутреннего сгорания, так как отдельные элементы их дви-
движутся с переменной скоростью. В качестве других примеров кон-
конструкций, работающих на динамическую нагрузку, можно указать
на фундамент машины, имеющей вращающиеся части, расположенные
внецентренно относительно оси вращения, — они будут испытывать
центростремительное ускорение; можно указать на фундамент и
шток парового молота, так как боёк молота при ковке теряет свою
скорость за очень короткий период времени, что связано с сообще-
сообщением ему весьма больших ускорений.
Уже из этих примеров видно, что на практике мы можем встре-
встречаться с различными видами ускорения рассматриваемой детали или

§ 215]	ВВЕДЕНИЕ	675
соприкасающихся с ней тел; оно может быть постоянным по величине и
направлению или только по направлению; может быть знакопеременным.
При переменных и знакопеременных напряжениях мы встречаемся
с явлением разрушения от постепенно развивающейся трещины —
с явлением усталости. При резком изменении скорости движения
элемента конструкции в зависимости от передачи на него давлений
от соседних деталей, когда имеет место явление ударау может обна-
обнаружиться хрупкость в таких материалах, которые при статическом
действии нагрузок оказывались пластичными. Поэтому при проверке
прочности деталей конструкций, подвергающихся действию динами-
динамических нагрузок, приходится интересоваться влиянием этих нагрузок
не только на величину напряжений в детали, но и на сопротивляе-
сопротивляемость материала.
Влияние ускорений точек деталей конструкции на напряжённое
состояние материала может быть учтено следующим образом. Если
какое-либо тело движется с ускорением, то это значит, что на него
передаются (к нему приложены) силы (давления) от других тел;
по закону равенства действия и противодействия оно передаёт на эти
тела равные приложенным силам и противоположно направленные
реакции, называемые силами инерции. Это рассуждение применимо
также и к каждому элементу движущегося с ускорением тела; этот
элемент будет передавать на прилегающие части материала усилия,
равные силе инерции этого элемента.
Таким образом, при ускоренном движении частей конструкции
в них возникают добавочные вполне реальные напряжения, которые
эквивалентны статическим напряжениям, вызванным силами инер-
инерции; от каждого элемента стержня на соседние части материала
будут передаваться такие напряжения, как будто бы к нему была
приложена соответствующая сила инерции.
Отсюда получаем практическое правило для определения напря-
напряжений в части конструкции, точки которой испытывают ускорения:
надо вычислить эти ускорения и в дополнение к внешним силам,
действующим на рассматриваемый элемент конструкции, нагрузить
его соответствующими силами инерции. Дальше следует вести расчёт
так, как будто на стержень действует статическая нагрузка.
Здесь надо различать три случая. Если величина и расположение
внешних сил, приложенных к рассматриваемому элементу, не зависят
от его деформаций, если эти деформации не изменяют характера
движения стержня, то ускорения его точек вычисляются по правилам
кинематики твёрдого тела, и учёт динамических воздействий сводится
к добавочной статической нагрузке соответствующими силами
инерции. Это имеет место в большинстве практически важных слу-
случаев (за исключением удара).
Если при этом ускорение будет меняться, то, как правило, воз-
возникнут колебания рассматриваемой части конструкции, которые могут
в некоторых случаях дать явление резонанса, связанное с резким

676
УЧЁТ СИЛ ИНЕРЦИИ И КОЛЕБАНИЙ
[ГЛ. XXXV
г
?
увеличением деформаций и напряжений. Эти напряжения могут до-
достигать весьма большой величины и будут прибавляться к тем,
которые учитываются путём введения в расчёт статической нагрузки
силами инерции.
Наконец, могут быть случаи (удар), когда величина ускорений,
а значит, и соответствующих сил инерции будет зависеть от дефор-
деформируемости рассматриваемых элементов; в этом случае при вычис-
вычислении сил инерции приходится использовать и данные сопротивления
материалов.
Способ проверки прочности для каждого из указанных случаев
покажем на примерах.
§ 216. Вычисление напряжений при равноускоренном движении.
Решение задачи о проверке прочности при динамических напря-
напряжениях мы начнём с простейшего случая, когда точки рассматриваемой
части конструкции имеют постоянное ускорение, не вызывающее
колебаний; примером возьмём равноускоренный подъём груза Q, под-
подвешенного на стальном тросе площадью F; объёмный вес материала
троса равен -у; груз поднимается с уско-
бц	рением а смjсек* (фиг. 581). Найдём
напряжения в каком-либо сечении на
расстоянии х от нижнего конца троса.
Разрежем трос в этом сечении и рас-
ffa смотрим нижнюю отсечённую часть.
Она будет двигаться вверх с ускоре-
—| нием а\ значит, на неё от верхней
6J	части троса будет передаваться помимо
силы, уравновешивающей её вес, ещё
	I направленная вверх сила, равная произ-
q	ведению её массы на ускорение я, т. е.
Q +iFx
fl> где g—ускорение силы
тяжести.
Фиг. 581.	По закону равенства действия и
противодействия на верхнюю часть
от нижней будет передаваться такая же сила, но направленная вниз.
Таким образом, динамические напряжения од, действующие по про-
проведённому сечению на нижнюю часть, будут уравновешивать не только
статическую нагрузку Q-\-'{Fx9 но и добавочную силу	—а;
чтобы вычислить эти напряжения, надо рассмотреть равновесие выде-
выделенной нижней части под действием ад, статической нагрузки Q-\-^Fx
а, направленной вниз (фиг. 581). Тогда
I П'СМ
L сек''
7№
Г
и силы инерции
g
±l

§ 217] расчёт вращающегося кольцл (обод млховикл)	677
дробь	-р—— представляет собой статическое напряжение ас в про-
проведённом сечении; поэтому
()	C5.1)
т. е. динамическое напряжение равно статическому, умноженному на
коэффицие
фициентом
коэффициент 1-р~. Эта величина называется динамическим коэф-
оя = Кмрс.	C5.2)
Такой вид формулы для динамических напряжений объясняет нам,
почему мы главным образом уделяли внимание вычислению напря-
напряжений при статическом действии нагрузки; в очень многих случаях
динамические напряжения могут быть выражены через статические
путём умножения на соответствующий динамический коэффициент.
Условие прочности получит вид:
1 g
Отсюда
Ы	fa]
°сmax ^	~—7г~ •	you.о)
g
Таким образом, можно в ряде случаев динамический расчёт
заменить статическим, понизив только допускаемое напряжение
делением его на динамический коэффициент Кж.
Так поступают в тех случаях, когда при расчёте оказывается
затруднительным теоретическое определение динамического коэффи-
коэффициента, а приходится пользоваться его значениями, полученными из
экспериментов. Подобным образом, например, учитывается динамич-
динамичность временной нагрузки, действующей на мосты.
§ 217. Расчёт вращающегося кольца (обод маховика).
В качестве второго примера рассмотрим вычисление напряжений
в быстро вращающемся кольце постоянного сечения (фиг. 582, а).
С известным приближением в подоб-	а)
ных условиях, если пренебречь влия j?ds
нием спиц, находится обод маЯовика.
Обозначим через F — площадь
поперечного сечения кольца; т — М
объёмный вес материала; п — число
оборотов в единицу времени; ш—
угловая скорость вращения; D —
диаметр оси кольца.
Выделим элемент кольца длиной ds. При вращении кольца этот
элемент движется по окружности с постоянной угловой скоростью ш.

678
УЧЁТ СИЛ ИНЕРЦИИ И КОЛЕБАНИЙ
[ГЛ. XXXV
Угловое ускорение е равно нулю, поэтому тангенциальное ускорение
элемента равно wt = e-^==0; радиальное же (центростремительное)
ускорение элемента равно wn = ^-7y- и направлено к центру кольца.
Чтобы вычислить напряжения ад, надо к каждому выделенному элементу
кольца приложить его силу инерции. Она направлена наружу и равна
wn-^ds = -^i^Y-ds = qdsi
где q — интенсивность сил инерции на единицу длины обода. Таким
образом, в кольце разовьются такие напряжения, как будто оно было
загружено радиальной нагрузкой интенсивности q на единицу длины
(фиг. 582, б). Усилия Р, растягивающие обод, равны (§ 20):
Напряжение ад равно
2F
DFi
g
D
где г; = а)-^- — окружная скорость точек кольца. Таким образом,
напряжение в ободе маховика зависит лишь от объёмного веса ма-
материала и линейной скорости частей обода. Чтобы отдать себе отчёт
в возможной величине этих напряжений, сделаем подсчёт при сле-
следующих числовых данных:
я = 360 об/мин; ?) = 4 м\ f = 7,5 г\смъ.
ЛТ	2пп 2% -360 1 о
Угловая скорость в секунду о)=-^-==—^—=12гс; напряжение равно:
4g
7,5
60
144*2 . 16 • 10*

4 • 103 • 981
= 435 кг/см*.
§ 218. Напряжения в спарниках и шатунах.
Проверим прочность спарника АВ, соединяющего две оси па-
паровоза (фиг. 583); на ось Ои ведущую, передаётся вращающий
момент от машины паровоза.
В точках Л и В спарник
прикреплён к колёсам при по-
помощи цилиндрических шарниров,
расстояния АО$ и BOt равны г,
диаметр колёс D, длина спар-
спарника /, паровоз движется с по-
постоянной скоростью v.
Фиг. 583.	Так как спарник движется, то
для проверки его прочности надо
прежде всего установить, будет ли движение иметь ускорение, т. е.
решить чисто кинематическую задачу. Спарник движется сам отно-
D

§ 218]
НАПРЯЖЕНИЯ В СПАРНИКАХ И ШАТУНАХ
679
сительно паровоза и участвует вместе с ним в переносном движении
со скоростью v.
Так как переносное движение является поступательным с по-
постоянной скоростью, то ускорение может появиться лишь в отно-
относительном движении. Так как в этом движении спарника две его
точки А и В движутся одинаково, описывая в одной плоскости
окружности радиуса г, то это движение будет плоским и поступа-
поступательным, следовательно, все точки спарника будут иметь те же ско-
скорости и ускорения, что и точки А и В.
Точка А движется вместе со вторым колесом, описывая окруж-
окружность радиуса г. При постоянной скорости движения паровоза угло-
угловая скорость вращения колёс w будет постоянна, значит, угловое
ускорение равно нулю, а следовательно, равно нулю и тангенциаль-
тангенциальное ускорение точки А, т. е. w( — 0; остаётся центростремительное
ускорение wn, направленное от А к О2 и равное wV. Любая точка
спарника, например К, тоже будет испытывать такое же ускорение,
направленное параллельно О2Л.
Чтобы проверить прочность спарника, надо добавить к его соб-
собственному весу ещё нагрузку силами инерции. На каждую единицу
длины спарника будет действовать сила инерции
1 • F .
F-t
направлена эта сила инерции параллельно радиусу О.2А в сторону,
противоположную ускорению.
При изображённом на чертеже положении спарника собственный
вес его вызывает изгиб в сторону, противоположную изгибу от сил
инерции. Наиболее опасным будет крайнее нижнее положение спар-
спарника AiBl9 когда обе нагрузки будут действовать в одном направле-
направлении. Тогда полная нагрузка дж на единицу длины спарника будет равна:
Спарник надо рассматривать как балку, шарнирно-опёртую в
точках А и В и нагружённую равномерно рас-
распределённой нагрузкой qv Наибольший изгибаю-
изгибающий момент будет посредине пролёта:
м — ^ — 7/7/2h 1 Ю>Г1
- о	о I	? I
Наибольшие напряжения в этом сечении
Од max = Hjj^-" = ^ -g" I + — L
Размеры в м#
Фиг. 584.
Пример 134. Исследовать два варианта поперечного сечения спар-
спарника: а) прямоугольное сечение и б) двутавровое сечение (фиг. 584), при

680
УЧЁТ СИЛ ИНЕРЦИИ И КОЛЕБАНИЙ
[ГЛ. XXXV
следующих данных:
со = 30 \!сек, 7 = 7,86 г/см\ г = 50 см и /=150 см.
В этом случае
0,00786 . 1502 Г. , 50^
8	L	98
Для прямоугольного сечения:
F=10. 4,5 = 45 см*, W = i5_lJ
^г = ~ = 0,6 \/см и здтах=0,6 • 1036 = 622 кг/см2.
Для двутаврового сечения:
F= 10. 4,5 — 2- 6. 1,5 = 27 еж2, И7 = 4'5 ' 10>ГГ2- !>° ' 6* =64,2 см\
= 75 ел»,
^ = ^ = 0,42 Цсм и *дтах=0,42 • 1036 = 435
Таким образом, несмотря на уменьшение момента сопротивления сечения
(почти на 15°/о), наибольшие напряжения во втором случае, благодаря зна-
значительному уменьшению веса спарника, понижаются почти в 1,5 раза.
Кроме изгиба спарник испытывает ещё сжатие или растяжение
силами Pt передающими вращение от колеса Ох колесу О2. В поло-
положении AiBi спарник будет сжат. Тогда, пренебрегая влиянием про-
прогиба на величину изгибающего момента, получаем условие прочности:
Кроме проверки на прочность, спарник следует проверить на
устойчивость, как стержень с шарнирно-опёртыми концами, в пло-
плоскости изгиба нагрузкой qx и, как стержень с защемлёнными кон-
концами, в перпендикулярной
плоскости. В первом случае
при вычислении гибкости в
расчёт следует вводить наи-
наибольший, а во втором слу-
случае — наименьший радиусы
инерции.
Подобным же образом
\
может быть выполнен и
расчёт шатуна АВ, шар-
нирно-скреплённого в точ-
Фиг. 585.	ке А с кривошипом 6И,
вращающимся вокруг точки
О с угловой скоростью о) (фиг. 585). При вращении кривошипа
с постоянной угловой скоростью точка А шатуна испытывает
только одно центростремительное ускорение, а точка В — только
тангенциальное ускорение. Все точки шатуна, расположенные

§ 219]
ВРАЩАЮЩИЙСЯ ДИСК ПОСТОЯННОЙ ТОЛЩИНЫ
681
между точками А и В, имеют и то и другое ускорения. Ограничи-
Ограничиваясь здесь учётом сил инерции, возникающих в шатуне в резуль-
результате одного только центростремительного ускорения, рассмотрим
такое положение шатуна, в котором он перпендикулярен кривошипу,
а следовательно, направление центростремительного ускорения
в точке А перпендикулярно к оси шатуна. Предположим, что центро-
центробежные силы инерции q везде перпендикулярны оси шатуна и по
длине его меняются по линейному закону от q = q0 в точке А до
д = 0 в точке В. Это предположение будет тем ближе к истине,
чем больше длина шатуна по сравнению с длиной кривошипа. Шатун
будем рассматривать как балку А В на двух шарнирных опорах А
и В. Изгибающий момент достигает наибольшего значения при х =
— —-=? (х отсчитывается от точки В) и равен (см. § 73):
Уз"
9/3"'
Так как qo =
_/?-7' 1
о
и адтах =
-, то
§ 219. Вращающийся диск постоянной толщины.
Значительный интерес представляет задача о напряжениях и деформа-
деформациях в быстро вращающихся валах и дисках. Высокие скорости вращения
валов паровых турбин обусловливают по-
появление в валах и дисках значительных
центробежных усилий. Вызванные ими на-
напряжения распределяются симметрично от-
относительно оси вращения диска.
Рассмотрим наиболее простую задачу
о расчёте диска постоянной толщины. Рас-
Расчёт такого диска положен в основу не-
некоторых приближённых способов расчёта
дисков любого профиля. Воспользуемся не-
некоторыми результатами, полученными при
выводе формул для расчёта толстостенных
цилиндров (§ 197). Предположим, что по
толщине диска, принимаемой равной еди-
единице, напряжения аг и с/ не меняются; осе-
осевое напряжение az будем считать равным
нулю.
Составим условия равновесия элемента
АВУ выделенного из диска двумя меридио-
меридиональными сечениями и двумя концентри-
концентрическими цилиндрическими поверхностями (фиг. 586). В данном случае, кроме
сил, действующих по граням элемента АВ, необходимо принять во внимание
также и силу инерции
9ir-l-drdb
Фиг. 586.

682	УЧЁТ СИЛ ИНЕРЦИИ И КОЛЕБАНИЙ	[ГЛ. XXXV
направленную вдоль радиуса от центра к внешнему контуру диска. Вместо
уравнения C2.1), выведенного в § 197, будем иметь:
^ + ~ = °-	С35-4)
Уравнение C2.4) того же параграфа (условие совместности деформаций)
остаётся в силе и для данной задачи, т. е.
-"^	Co-5)
Подставляя в это уравнение значение разности ar — zt из C5.4), находим:
dp = — -^ — L+Ji ТоJг.	C5.6)
dr	dr g '	х '
ds*
Дифференцируя уравнение C5.4) по г и подставляя в него вместо -~ его
значение из формулы C5.6), получаем линейное дифференциальное уравнение
г -т~ + 3 -р- + Х 1<*-г == О
dr- ' dr ' g l
или
d \ \ d Л 3 + fi oJr==0
dr\ r dr^ *r)\ "* g T0>
Интегрируя это уравнение, находим:
°г = ^ + ^ ~ ^г^ Т002''2-	C5.7)
Из C5.4) и C5.7) следует, что
В формулах C5.7) и C5.8) А и В — постоянные интегрирования, которые
должны быть определены из условий на контуре диска. При определении
постоянных рассмотрим два случая: 1) диск с отверстием в центре и 2) сплош-
сплошной диск. При этом вначале предположим, что края диска свободны от
внешних усилий.
Для диска с центральным отверстием напряжение <зг должно быть равно
нулю как при г = г1у так и при г = г2 (фиг. 586). Эти условия на контуре
при подстановке их в формулу C5.7) приводят к уравнениям:
В 3-f-fA g о
откуда
и B = -
Подставляя значения А и В в формулы C5.7) и C5.8), получаем:
«/ = Т^ [C +1*) ^1 + ri + Щ - A + 3F) г2 ].

§ 219]	ВРАЩАЮЩИЙСЯ ДИСК ПОСТОЯННОЙ ТОЛЩИНЫ
Полагая для краткости
683
•=а> >т=р-
7<o2rf=/? и
можем написать:
и
C5.9)
C5.10)
Замечаем, что напряжение аг обращается в нуль при р = 1 и р = а, т. е.
внутреннем и наружном контурах диска; при значениях р между 1 и а
б
на
напряжение о
шей величины при
; р	р	у
г положительно и, как нетрудно убедиться, достигает наиболь-
наиболь= У~а=~у —. При этом
('г)шах=/'A-аK-	C5-11)
Напряжение <st при всех значениях р также положительно и наибольшей
величины достигает у внутреннего края диска, где р = а:
(а/)шах = /> [2 + A — /и) а*].	C5.12)
Сравнивая C5.11) и C5.12), убеждаемся, что (s,)max всегда больше (зг)тах.
Поэтому при проверке прочности диска как по теории наибольших каса-
касательных напряжений, так и по .„ ..
энергетической теории условие °ruOt
прочности должно быть напи- ? Л	$
сано в таком виде:
C5.13)
= — вдоль радиуса диска
На фиг. 587 представлены
кривые изменения значений
Р
для разных а от 0 до 1 при
ц = 0,3. Там же приведена кри-
кривая для о° = — — при а=0,2. За-
Замечаем, что наибольшие зна-
значения напряжения ot C5.12)
(у внутреннего края диска)
мало меняются с изменением
радиуса отверстия, т. е. вели-
величины а (кривая ab). При <*«^0,
т. е. при очень маленьком ра-
радиусе центрального отверстия,
у края отверстия имеет место резкое изменение напряжения ^ — концен-
концентрация напряжений (кривая acd). При этом
Ыгаах = 2Р = ^Р^ 1<**г1	C5.14)
max	4g
О
1,0
Фиг. 587.

684
УЧЁТ СИЛ ИНЕРЦИИ И КОЛЕБАНИЙ
[гл. xxxv
Для очень тонкого кольца, при rL
g
C5.15)
что совпадает с выводом § 217. В этом случае наибольшее напряжение а/
C5.15) всего только на 20% больше C/)тах для диска с весьма малым отвер-
отверстием C5.14).
Из формул C5.9) и C5.10) видно, что напряжения аг и а^ очень быстро
растут с увеличением окружной скорости диска t> = <ori. Отметим, что, кроме
скорости v и характеристик материала (х и ;, эти напряжения зависят только
от безразмерных величин р и а. Таким образом, в геометрически подобных
дисках при одних и тех же значениях р напряжения аг и at будут одинаковы.
Это обстоятельство позволяет заменить заводские испытания дисков большого
диаметра лабораторными испытаниями их моделей.
В случае сплошного диска напряжения <зг и at в центре диска, т. е. при
г = 0, должны быть равны друг другу. Сравнивая формулы C5.7) и C5.8),
убеждаемся, что для выполнения этого условия постоянная В должна быть
равна нулю. Постоянная Л найдётся из условия: при г = гА| т. е. у наруж-
наружного края диска, напряжение аг равно нулю. Имеем:
Подставляя это значение Л, а также В = 0 в формулы C5.7) и C5.8),
получаем:
*г = />0-р2)	C5.16)
/=p(l —mf).
C5.17)
Соответствующие кривые изменения а° = —— и aj = —— вдоль радиуса
приведены на фиг. 587 (кривые fh и fed). Оба напряжения положительны
при всех значениях р и увеличиваются но мере уменьшения р, т. е. по
мере приближения к центру диска. При р = О
о>2Г|.	C5.18)
Таким образом, в диске с весьма малым центральным отверстием напряже-
напряжение Qf у края отверстия за счёт концентрации напряжений вдвое больше,
чем в центре сплошного диска [см. формулу C5.14)].
Все рассуждения велись до сих пор в предположении, что края диска
свободны от действия внешних усилий. Это предположение обычно не соот-
соответствует действительности. Посадка диска на вал выполняется в горячем
состоянии или с помощью гидравлического пресса с таким натягом, чтобы
деформация отверстия диска, вызванная центробежными усилиями, всегда
была меньше, чем обратная ей по знаку деформация при посадке диска,
т. е. чтобы в рабочем состоянии диск плотно сидел на вале. Наружный край
диска обычно снабжается ободом для закрепления в нём лопаток турбины,
при вращении которого возникают дополнительные центробежные усилия,
передающиеся на диск. Таким образом, по наружному и внутреннему краю
диска обычно действуют некоторые равномерно распределённые растягиваю-
растягивающие или сжимающие усилия. Вызванные этими усилиями напряжения в диске
могут быть вычислены по формулам, выведенным для расчёта толстостен-
толстостенных цилиндров (формулы C2.9) § 197). Складывая напряжения по формулам
C2.9), а также C5.9) и C5.10), получаем возможность построить полную кар-
картину распределения напряжений во вращающемся диске.

§ 220]
ДИСК РАВНОГО СОПРОТИВЛЕНИЯ
6S5
6tzur
§ 220. Диск равного сопротивления.
Как показывают формулы предыдущего параграфа и кривые фиг. 587,
изменение напряжений qt и at вдоль радиуса диска постоянной толщины
весьма значительно. Наиболее не-
неравномерное распределение напря-
напряжений имеет место в дисках по-
постоянной толщины с отверстием в
центре. При расчёте подобных дисков
приходится ориентироваться на наи-
наибольшее напряжение ^ у внутреннего
края диска, что сильно ограничивает
возможность повышения предельных
скоростей. Для достижения высоких
скоростей вращения диски прихо-
приходится делать с переменной толщи-
толщиной, уменьшающейся от центра к
окружности диска. Наиболее выгод-
выгодным является такой профиль диска,
в котором напряжения во всех точ-
точках диска сохраняют постоянное зна-
значение. Подобные диски называются
дисками равного сопротивления. При
расчёте этих дисков исходят из предположения, что по толщине диска напря-
напряжения не меняются, что обычно влечёт за собой небольшие погрешности
в величинах напряжений.
Основные формулы для расчёта дисков переменной толщины попреж-
нему могут быть выведены из рассмотрения условий равновесия элемента
диска abed (фиг. 586 и 588). Переменную толщину диска, являющуюся неко-
некоторой функцией радиуса г, обозначим через z. На элемент abed по меридио-
меридиональным сечениям ad и be действуют две силы atz dry составляющие между
собой угол db\ по грани dc на этот элемент действует радиальное усилие
arzrddt направленное к центру диска, а по грани ab — радиальное усилие
crzr db-\-d (arzr db), направленное от центра к наружной поверхности диска.
К этим усилиям должна быть присоединена ещё и сила инерции массы
элемента
zdr • г db <
g '
направленная от центра к окружности диска.
Проектируя все перечисленные выше усилия на направление радиуса,
получаем такое дифференциальное уравнение равновесия диска переменной
толщины:
или
g
= 0.
При z = const, это уравнение обращается в уравнение C5.4) предыдущего
параграфа.
В случае диска равного сопротивления напряжения аг и а/ всюду посто-
постоянны и равны между собой. Приравнивая их величине допускаемого напря-
напряжения [а], можем так переписать уравнение равновесия:

Г)86	УЧЁТ СИЛ ИНЕРЦИИ И КОЛЕБАНИЙ	[ГЛ. XXXV
ИЛИ
1	dz = т<о«г =
2	rfr	[а] • ?
где
7С02
Интегрируя это уравнение, находим:
где С — постоянная интегрирования. Если диск не имеет отверстия в центре,
то из условия, что при г = О z = z0, следует: С = г0. Толщина диска в цен-
центре B0) определяется из условий на контуре диска.
Сплошной диск равного сопротивления может быть применён даже при
очень высоких окружных скоростях. Однако по конструктивным соображе-
соображениям на практике обычно применяются диски переменной толщины с отвер-
отверстием в центре, профиль которых, близкий к профилю диска равного сопро-
сопротивления, обеспечивает наиболее^ выгодное распределение напряжений вдоль
радиуса. Методы расчёта таких дисков рассматриваются в специальных
курсах *).
§ 221. Влияние резонанса на величину напряжений.
В двух первых задачах, рассмотренных в §§ 216—218, ускорение
не меняло своего направления по отношению к элементу мате-
материала, на который оно действовало; в последнем же примере за
один оборот колеса ускорение непрерывно меняло своё направление
на 360°. В этом случае напряжения и деформации периодически
меняют свой знак, начинаются так на-
называемые вибрации, колебания стержня.
Подобный же случай будет иметь
место, если на балке расположена ма-
машина с вращающимся грузом, имеющим
Фиг. 589.	эксцентриситет по отношению к оси вра-
вращения (фиг. 589). Сила инерции груза
будет вызывать в балке напряжения и деформации, периодически ме-
меняющие свой знак. Балка будет совершать колебания с периодом,
равным периоду вращения груза. Это будут так называемые выну-
вынужденные колебания. Если период вынужденных колебаний совпадёт
с периодом свободных колебаний стержня, то мы получим явление
резонанса, при котором амплитуда (размах) колебаний будет резко
расти с течением времени. Наличие сил трения, сопротивление воз-
воздуха и т. д. ограничивают на практике рост этой амплитуды; однако
она может достичь очень большой величины, значительно превышаю-
l) M а л к и н Я. Ф., Профилирование турбинных дисков в связи
с расчётом их на прочность и вибрацию, ОНТИ, 1937; М. И. Яновский,
Конструирование и расчёт паровых турбин, изд-во В.-Морской академии,
1931 г.; Жирицкий Г. С, Паровые турбины, Укрполиграфобъединение,
1931 г. и др.

§ 222] ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ ПРИ КОЛЕБАНИЯХ	687
щей те деформации, которые испытывала бы конструкция под дей-
действием ускорений той же величины, но не меняющих знака.
Известен случай, когда при резонансе угол закручивания вала
увеличился в шесть раз по сравнению с тем углом, который был
до наступления резонанса, — это был случай поломки коленчатых
валов двигателей «Цеппелина» при первом его перелёте через
Атлантический океан.
Таким образом, явление резонанса, если оно длится некоторое
время, а не сбивается немедленно по возникновении, ведёт к посте-
постепенному росту деформации и пропорциональных им напряжений
в конструкции, что может вызвать поломку. Поэтому, как правило,
при проектировании конструкций, испытывающих переменные уско-
ускорения с постоянным периодом, необходимо избежать возникновения
явления резонанса.
Так как период раскачивающих (возмущающих) сил обычно
является заданным, то в распоряжении проектировщика остаётся лишь
период собственных свободных колебаний конструкции, который
надо подобрать так, чтобы он в должной мере отличался от периода
изменений возмущающей силы.
Вопросы, связанные с определением периода, частоты и ампли-
амплитуды свободных и вынужденных колебаний, рассматриваются в кур-
курсах теоретической механики *). Поэтому ниже (§ 222) мы ограни-
ограничимся лишь приложением полученных там выводов к определению
напряжений и проверке прочности элементов конструкции при
колебаниях.
§ 222. Вычисление напряжений при колебаниях.
А. Упругая система, выведенная каким-либо путём из равновесия,
приходит в колебательное движение. Колебания происходят около
положения упругого равновесия, при котором в нагружённой системе
имели место статические деформации 8С и соответствующие им
статические напряжения ре (ос или тс — в зависимости от вида дефор-
деформации). При колебаниях к статическим деформациям добавляются
динамические, зависящие от вида колебательного движения и от
величины размаха (амплитуды) колебаний. В связи с этим изменяются
и напряжения рс. Таким образом, при расчёте колеблющейся системы
на прочность необходимо уметь вычислять динамические добавки
к статическим деформациям и соответствующим им напряжениям.
Во многих случаях характер колебаний системы может быть
определён одной какой-нибудь величиной (одной координатой).
Такие системы называются системами с одной степенью свободы;
*) Лойцянский Л. Г. и Лурье А. И., Курс теоретической механики,
1940 г., часть И, §§ 91, 92, 150—154; Николаи Е. Л., Теоретическая меха-
механика, 1939 г., часть II, §§ 32, 33, 35, 36, 37; и др.

638
УЧЕТ СИЛ ИНЕРЦИИ II КОЛЕБАНИЙ
[ГЛ. XXXV
г
таковы, например, растянутая или сжатая незначительного веса
пружина с грузом на конце, совершающая продольные колебания;
небольшого (сравнительно с грузом Q) собственного веса балка,
изображённая на фиг. 590,
колеблющаяся в направ-
направлении, перпендикулярном
к её оси, и т. п.
При колебаниях си-
систем с одною степенью
свободы полные дефор-
|	мации системы в каком-
либо сечении могут быть
Фиг. 590.	найдены путём сложения
статической деформации
с добавочной деформацией при колебаниях. Для проверки проч-
прочности системы, очевидно, необходимо найти наиболее опасное сече-
сечение с «наибольшей в процессе колебаний суммарной величиной дефор-
деформации. В простейших случаях для этого потребуется сложить наи-
наибольшую статическую деформацию Scmax с наибольшей амплитудой
колебаний Л, т. е.
&д = &с max ~Г ^ — ^с max I -j- J	! = КЛК max-	C5.19)
\	лс шах У
Пока система деформируется в пределах упругости, напряжения
пропорциональны деформациям. Поэтому
А \
где
C5.20)
C5.21)
— коэффициент динамичности при колебаниях. Условие прочности
в этом случае должно иметь такой вид:
Рж
C5.22)
Таким образом, как при учёте сил инерции, не меняющих своего
направления, задача нахождения динамических напряжений и про-
проверки прочности при колебаниях может быть сведена к опре-
определению статических напряжений и коэффициента динамичности /Гд.
Так как последний зависит от величины Л, то нужно уметь
определять наибольшее значение амплитуды колебаний в разных
случаях.
Как известно, дифференциальное уравнение движения колеблю-
колеблющегося груза Q в случае свободных колебаний можно представить
в виде уравнения равновесия, в котором, кроме внешней силы (веса

§ 222]	ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ ПРИ КОЛЕБАНИЯХ	689
груза Q) и силы упругого сопротивления системы, учитывается также
и сила инерции:
-О- х" 4~ Р — Q = — х" 4- Рх = SL х» * сх = 0. C5.23)
g l	g ' * g ~	K
Здесь x — координата, полностью определяющая положение груза Q
во время колебаний (см., например, фиг. 590); Р—полное упругое
сопротивление системы при колебаниях; Р—Q = Pt — так называе-
называемая восстанавливающая сила (добавочное упругое усилие, возникаю-
возникающее в системе в результате перемещения точки приложения груза Q
на расстояние х при колебаниях), которую в пределах упругости
можно считать пропорциональной координате х (Pt = сх); с — коэф-
коэффициент пропорциональности, представляющий собой усилие, необ-
необходимое для того, чтобы вызвать равную единице статическую
деформацию системы в направлении действия груза Q. Если стати-
статическая деформация от груза Q равна 8q, то с = ~.
Решение уравнения C5.23) приводит к таким формулам для вычи-
вычисления частоты оH и периода tQ свободных колебаний:
Свободные колебания невесомого тела суть простые гармонические
колебания с частотой (периодом), равной частоте (периоду) колеба-
колебаний математического маятника, длина которого равна статической
деформации системы от груза Q. Так, например, если груз Q растя-
растягивает призматический стержень,
при изгибе балки на двух шарнирных опорах грузом Q посредине
пролёта
«о
И Т. Д.
Б. Если на упругую систему, кроме груза Q и силы упругого
сопротивления системы Р, в том же направлении действует перио-
периодически меняющаяся возмущающая сила 5 и сила сопротивления
среды R, то дифференциальное уравнение движения груза Q при
колебаниях также может быть представлено в виде уравнения равно-
равновесия, подобного уравнению C5.23):
J^'^cx_S4-/? = 0. C5.24)

690	УЧЁТ СИЛ ИНЕРЦИИ И КОЛЕБАНИЙ	[ГЛ. XXXV
Силу сопротивления среды R на практике в довольно большом
числе случаев можно считать пропорциональной первой степени
скорости колебательного движения, т. е. R=:rxf. Если возмущаю-
возмущающая сила 5 меняется по синусоидальному закону:
S = H sin <
где //=Smax> а со — частота возмущающей силы, то уравнение C5.24)
может быть переписано так:
-^- х" 4-rx'4-cx = H sin orf
g ~ ~
или
хГ + <2пх? + <* = Щ- sin arf.	C5.25)
Здесь п = у?г-—так называемый коэффициент затухания колебаний,
а аH — найденная выше частота свободных колебаний системы, воз-
возникающих при отсутствии как возмущающей силы 5, так и силы
сопротивления R.
Решение уравнения C5.25) приводит к такому выражению для
амплитуды А вынужденных колебаний при наличии сил сопротив-
сопротивления:
= ,	"		 C5.26)
~ш I \	I Cd \ I	/ Tl \, / to \
Здесь
— статическая деформация системы от наибольшей величины воз-
возмущающей силы 5 (Smax = //). Отношение амплитуды вынужденных
колебаний А к величине деформации 8Я называется коэффициентом
нарастания колебаний (J:
Q	А 	1	/ос Q74
•	R	f~r	i \ а то	/ \ а~? \ о * •	^	'
Таким образом, формула C5.21) для динамического коэффициента
Кж получает теперь такой вид:
В этом выражении не учтена амплитуда собственных колеба-
колебаний системы, которая может иметь сколько-нибудь существенное

§ 222]
ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ ПРИ КОЛЕБАНИЯХ
691
значение лишь в самом начале процесса колебаний; при наличии
сил сопротивления она довольно быстро уменьшается с течением
времени.
На фиг. 591 приведены графики изменения коэффициента нара
стания колебаний р в зависимости от величины отношении — при
разных значениях коэффициента затухания колебаний п (отношения —).
Если частота изменения возмущающей силы близка к частоте сво-
свободных колебаний системы, т. е.
о)	л
— я^ 1, и если величина коэф-
коэффициента затухания колебаний
сравнительно невелика, то зна-
знаменатели формул C5.26) и
C5.27) для Лир будут очень
малыми, амплитуда колебаний
и коэффициент нарастания ко-
колебаний будут очень большими
(фиг. 591). В этом случае даже
небольшая возмущающая сила
может вызвать высокие напря-
напряжения (явление резонанса).
С увеличением сил сопро-
сопротивления явление резонанса
становится всё менее замет-
заметным. Заметим, однако, что силы
сопротивления значительно
уменьшают величину ампли-
амплитуды вынужденных колебаний
только вблизи от резонанса @,75
Фиг. 591.
1,25);
при других вели-
величинах отношения — влияние сил сопротивления незначительно.
Из формул C5.26), C5.27) и C5.28) и фиг. 591 видно, что
если частота со изменения возмущающей силы 5 очень мала, то
амплитуда колебаний приближается к величине Ьн, коэффициент
нарастания колебаний стремится к единице и наибольшие напряже-
напряжения в системе могут быть вычислены как статические напряжения
от груза Q и наибольшего значения возмущающей силы 5 (Smax = //).
При очень большой частоте изменения возмущающей силы S ампли-
амплитуда колебаний и коэффициент нарастания колебаний стремятся
к нулю, груз Q можно рассматривать как неподвижный; поэтому
наибольшее напряжение в системе равно статическому напряже-
напряжению от груза Q.
Это обстоятельство имеет очень большое практическое значение;
оно используется при конструировании разного рода поглотителей

692	УЧЁТ СИЛ МНЕРШШ И КОЛЕБАНИЙ	[ГЛ. XXXV
колебаний, сейсмографов, вибрографов и других приборов. В ма-
машиностроении амортизаторы, предохраняющие основания машин от
усилий, возникающих при колебаниях, подбираются так, чтобы ча-
частота собственных колебаний машины на амортизаторах была зна-
значительно меньше частоты изменения возмущающей силы.
§ 223. Учёт массы упругой системы при колебаниях.
А. Если колеблющаяся система, несущая груз Q, обладает
довольно значительной распределённой массой (число степеней сво-
свободы, следовательно, велико), упрощённые расчёты, приведённые
в предыдущем параграфе, будут иметь уже значительную погреш-
погрешность. В этом случае дифференциальные уравнения движения соста-
составляются с учётом массы системы. При решении подобного рода
задач удобнее исходить не из условий равновесия, на основе кото-
которых составлены уравнения C5.23) и C5.24), а из закона сохранения
энергии.
Полагая, что количество энергии, сообщённое системе при выве-
выведении её из положения равновесия и представляющее собой сумму
кинетической и потенциальной энергии груза и упругой системы,
при свободных колебаниях остаётся постоянным, получаем уравнение
U-\- T — const.	C5.29)
Это уравнение показывает, что при колебаниях происходит непре-
непрерывный процесс преобразования энергии из одного вида в другой,
не сопровождающийся какими-либо потерями энергии. Когда упругая
система достигает одного из крайних положений, в котором ско-
скорость колебательного движения равна нулю, а следовательно, равна
нулю и кинетическая энергия G = 0), потенциальная энергия груза
и системы достигает наибольшего значения U=Ulflux; наоборот,
в положении равновесия U=0 и Г=Гтах.
Заметим, что принцип, положенный в основу уравнения C5.29),
применим лишь для систем с одной степенью свободы, так как
закон сохранения энергии не учитывает обмена энергии, происходя-
происходящего в системах с несколькими степенями свободы. Таким образом,
решение задачи о колебаниях системы с большим числом степеней
свободы здесь сводится к простейшей задаче, разобранной в § 222,
и мы сможем приближённо найти лишь одну (первую) частоту сво-
свободных колебаний.
Рассмотрим теперь некоторые примеры использования уравне-
уравнения C5.29).
Б. В качестве первого примера исследуем колебания груза Q,
подвешенного к нижнему концу призматического стержня длиной /,
площадью поперечного сечения F и удельным весом f (фиг. 592).
Выведенный из положения равновесия и затем предоставленный
самому себе груз начнёт совершать продольные колебания около

§ 223]
УЧЁТ МАССЫ УПРУГОЙ СИСТЕМЫ ПРИ КОЛЕБАНИЯХ
693
положения равновесия. Составим выражения для U и Т колеблю-
колеблющейся системы: груз — стержень.
Потенциальная энергия системы по сравнению с положением
равновесия изменится naU=[/t—?/0, где UQ — потенциальная энер-
энергия системы в начальный момент (в положении
равновесия), a Ut — в момент t.
Потенциальную энергию груза Q в начальный
момент обозначим через Uq\ потенциальная энер-
(?Д/С
гия стержня в тот же момент равна ——-
2
где
Д/с — статическая деформация стержня от груза Q.
Таким образом,
n=Uo-\-
<?А/С
2
х
Ah
х
В момент /, когда груз переместится на расстоя-	Ь	if
ние л" и стержень получит такую же дополни-
дополнительную деформацию х, потенциальная энергия	Фиг. 592.
груза уменьшится на Qx, а сила упругого сопро-
сопротивления стержня и статическая деформация его увеличатся в отно-
отношении с Л~Л . Поэтому
л/,
I
=*.+&
Qx*
Ж'
C5.30)
Кинетическая энергия системы складывается из кинетической
энергии груза Т{ и стержня 7V Кинетическая энергия груза
7\ = ;~(хг)*. При вычислении кинетической энергии стержня учтём,
что в некоторый момент t скорость груза и нижнего конца стержня
равна х\ а верхнего — нулю. Скорости промежуточных сечений
будут иметь значения, заключающиеся между этими двумя.
Предположим, что при колебаниях перемещения всех сечения
стержня по отношению к закрепленному концу меняются по тому же
закону, что и при статическом растяжении, т. е. пропорционально рас-
расстоянию от закреплённого сечения. Таким образом (фиг. 592), если ниж-
нижнее сечение стержня переместилось на величину х} то сечение, отстоя-
отстоящее от места защемления на ?, переместится на величину х~г*

694	учёт сил инерции и колебаний	[гл. xxxv
скорость этого сечения будет равна х'-г. Живая сила элемента стерж-
стержня длиной *#, отстоящего на Е от закреплённого конца, будет равна:
Кинетическая энергия всего стержня будет равна сумме величин
dT.2, т. е.
_ У
2~~
o 4 l*~2g 3 '
Таким образом, живая сила стержня равна живой силе груза,
т/7
имеющего массу 4с—, т. е. равную трети массы стержня, и двигаю-
двигающегося с той же скоростью х\ что и груз Q. Полная же кинети-
кинетическая энергия системы груз — стержень будет:
Подставляя 7 и выражение U C5.30) в уравнение C5.29), диффе-
дифференцируем последнее по t и находим:
или
YfT 4~ % .	Q	у.	 ГТГ I ^ ^	Л
VT^ з
Здесь Д/пр — статическая деформация от груза Q + ^g-. Получен-
Полученное нами дифференциальное уравнение движения с учётом массы ко-
колеблющегося стержня отличается от уравнения C5.23) только величи-
величиной множителя при х и полностью совпадает с ним, если прене-
пренебречь массой стержня. Поэтому поправка на массу стержня, которую
нужно ввести в расчёты предыдущего параграфа, состоит в том,
что при определении частоты свободных колебаний стержня стати-
статическая деформация его вычисляется не от груза Q, но от груза Q,
сложенного с одной третью веса стержня. Таким образом, учёт
массы колеблющегося стержня уменьшает частоту свободных коле-
tFl
баний и увеличивает их период. Величину ¦—- называют приведён-
приведённой массой стержня.
В. В качестве второго примера рассмотрим балку на двух шар-
шарнирных опорах с грузом Q посредине пролёта (фиг. 593).
О/8-
Обозначим через f=-~prj наибольший статический прогиб балки
под действием груза Q, а через z — переменный добавочный про-

§ 223]	УЧЁТ МАССЫ УПРУГОЙ СИСТЕМЫ ПРИ КОЛЕБАНИЯХ	695
гиб среднего сечения балки при колебаниях. Предположим, что при
свободных колебаниях добавочные прогибы балки меняются по её
длине по тому же уравнению, что и
при статической нагрузке силой Q; r	~
это последнее имеет вид (см. § 112): I	|Ц#
= f(bPx-Ax% C5.31)
Таким образом, если при ко-	Фиг. 593.
лебаниях среднее сечение балки
дополнительно переместится на z от положения статического равно-
равновесия, то сечение на расстоянии х от левого конца переместится на
Скорость колебаний э9ого сечения будет
Живая сила элемента балки длиной dx выразится формулой
f-r -tFdx /л C
а 1 о * —(Z—~ z \~
а кинетическая энергия всей балки будет равна:
Щ	C5.32)
О
Кинетическая энергия груза равна:
Так как потенциальная энергия при изгибе балки вычисляется по
С М2 dx	d2v
формуле U= \ ^EJ , a M = EJjp, то
Но при перемещении среднего сечения балки на расстояние z от
d	24
положения статического равновесия -~^ = — -^ zx\ поэтому
'Ч?
2
EJfd^yY2^ _9 EJ С /24^лг\2 ___ 24Е7 ^

696	УЧЁТ СИЛ ИНЕРЦИИ И КОЛЕБАНИЙ	[гл. XXXV
• Подставляя выражения для U и Т= 7\-j- T2 в уравнение C5.29)
и дифференцируя его по /, имеем:
7
Отсюда ясно, что для учёта массы балки при определении частоты
и периода свободных колебаний следует её считать невесомой,
а к весу груза Q прибавить — = 0,486 веса балки. Величина ~-—
называется приведённой массой балки.
Заметим, что если за изогнутую ось балки приближённо взять
синусоиду y=f sin '-j-f то приведённая масса получилась бы равной
не о=^—9 a -w-—, что достаточно близко к более точному значению,
¦w g z g
Определённая таким образом величина приведённой массы балки
получена всё же в предположении, что масса балки невелика по
сравнению с массой груза Q, так как мы пренебрегаем влиянием
собственного веса балки на кривую изгиба её оси; уравнение же
изогнутой оси C5.31) соответствует случаю приложения одного
сосредоточенного груза посредине пролёта.
Г. Возьмём теперь другой крайний случай, когда масса балки
очень велика по сравнению с грузом Q или когда колеблющаяся
балка загружена сплошной, равномерно распределённой нагрузкой q
(в которую включён и собственный вес балки). Тогда кривая изо-
изогнутой оси будет иметь уравнение (см. § 111):
где /— прогиб посредине пролёта.
Живая сила элемента балки длиной dx, находящегося на рас-
расстоянии х от левой опоры, выразится через скорость среднего
сечения балки zr такой формулой:
Вся кинетическая энергия балки будет равна:
Я у-2 / 16 \2 ? //3^ О/^З ! ИЧ2 А ^	Ч± уП 3968
Z [	}\tX UxtX) ax	2
l — TgZ [SF
¦2* \EF J v* —"•* -г-^ -*—2ff* 7875*
о
Потенциальная энергия балки равна:
FJ nd*y\*.EJ PN92 г . ,
№2EJz*
: 125 /3 '

§ 224]	примеры	697
Подставляя выражения для U и Т в уравнение C5.29) и дифферен-
дифференцируя его по t, имеем:
(I")"
Приведённая масса балки в этом случае равна: ^^- = 0,492^-.
Таким образом, при подсчёте периода собственных колебаний
уравнение кривой изгиба играет весьма малую роль, лишь бы был
сохранён общий характер изогнутой оси балки.
Для шарнирно-опёртой балки при изгибе её по кривой без точек
перегиба можно всегда принимать за уравнение изогнутой оси урав-
уравнение синусоиды с одной полуволной y=f sin'-— и приведённую массу
балки считать равной 0,5—.
Итак, при определении первой частоты свободных колебаний
системы с распределённой массой можно считать систему невесо-
невесомой, а к массе сосредоточенного груза добавлять приведённую
массу системы; операция «приведения» имеет силу и в том случае,
если Q = 0.
§ 224. Примеры.
Пример 135. Стержень длиной / переменного сечения, несущий на
одном конце груз Q (фиг. 594), вращается с угловой скоростью о вокруг
оси, к которой он прикреплён другим концом. Расстояние центра тяжести
груза Q от оси вращения равно г.
Найти зависимость площади сечения стержня Fx от расстояния сечения
х от свободного конца стержня при условии, что напряжения во всех сече-
сечениях равны [<т]. Объёмный вес материала 7.
Каждая точка стержня с абсциссой х испытывает центростремительное
ускорение, равное <о2(/— х)\ поэтому для определения напряжений надо на-
нагрузить все элементы стержня силами
инерции, направленными от центра и
равными массе элемента, умноженной
на со2 (/ — х). Элемент длиной dx между
двумя смежными сечениями с абсцис-
абсциссами х и x + dx, площади которых
равны Fx и Fx-\~dFx, нагружён силой
Fx-{dx ,, ч 9
инерции ——	(/ — х) оJ, где g — уско-
ускорение силы тяжести.
Сечения стержня должны меняться
таким образом, чтобы эта сила инер-	ф
ции вызвала на площади dFx напряже-
ние [а] (см. расчёт для стержня равного
сопротивления при растяжении и сжатии в § 29). Таким образом, получаем
дифференциальное уравнение для Fx:

698	учёт сил инерции и колебаний	[гл. xxxv
Разделяя переменные и интегрируя, получаем:
Для определения постоянной С полагаем х = 0, тогда Fx — F0 — пло-
площади на конце стержня. Эта площадь определяется в зависимости от силы
инерции груза Q, растягивающей концевой элемент стержня:
* 0	i	Г •
gl\
Подставляя в уравнение для Fx значение In Fo = С, получаем:
J^-Bl^-x)x
и F*=a
Пример 136. Двигатель весом С? = 500 кг укреплён (посредине) на
двух деревянных балках прямоугольного поперечного сечения, каждая из
которых лежит на двух опорах и имеет пролёт /=160 см (фиг. 590). Сече-
Сечение каждой балки 12 X 20 см, вес Qi=23 кг, материал — сосна с модулем
упругости ? = 8'104 кг/см2 и допускаемым напряжением \а] = 100 кг',см2.
Неуравновешенные массы двигателя условно могут быть заменены вращаю-
вращающимся грузом 02 = 5 кг, с радиусом вращения #=10 см и угловой ско-
скоростью вращения <*, равной скорости вращения вала двигателя. Двигатель
должен работать при п0 = 1500 об/мин. Требуется установить, является ли
это число оборотов безопасным для прочности балок. Силами сопротивления
при колебаниях можно пренебречь.
Определим частоту свободных колебаний балки:
48-8-101-12-203-981 1ЛО
= 168
Критическое значение угловой скорости вращения вала двигателя, при кото-
котором амплитуда колебаний балки неограниченно возрастает, будет
<окр==Шо = 168^(
что соответствует
пкр=^о)кр=^. -168 = 1605 об/мин.
Найдём наибольшие напряжения в балках при заданном числе оборотов
двигателя п0 = 1500 об/мин или при <оо = —? = ———г	= 143 . Из
уравнений C5.20) и C5.28) § 222 следует, что
Так как
'<2 ~ 96EJ ~*~ 384ЯУ
ю
fu iQ^H	8-5- 10- «о'
'/8 - 4<Э+5& п
_
D.500 + 5-23)981

§ 224]	примеры	699
Коэффициент нарастания колебаний равен:
а 1	cog __ 168*
Р	2 0J — 0J	1682 	 0J'
Наибольшее статическое напряжение в балке от груза —• и собственного
веса Qt равно:
а (Q + Qi)t_ E00 + 23I60-6 _
*с =	Ш	 	8 • 12 • 20*	~ 13'1 кг1емК
Поэтому при о) = (о0 = 143 — получаем:
С€К
? = 0,0001928оJ = 0,0001928 . 1432 == 3,95, р = *68* = 3>68
сд = 13,1 A + 3,95 • 3,68) = 203 кг/см2 > [<г] = 100 кг/см*.
Таким образом, при заданном числе оборотов двигателя наибольшее напря-
напряжение в балке оказывается значительно выше допускаемого. Установим
безопасный для прочности балок режим работы двигателя, исходя из усло-
условия, чтобы при колебаниях наибольшие динамические напряжения в балках
не превышали величины допускаемого напряжения. Из уравнений C5.22) и
C5.28) § 222 следует, что
Подставляя в это условие найденные выше выражения для р и т- и значе-
ния [з] и <хс, получаем уравнение для определения допускаемых значений
угловой скорости вращения вала двигателя [©]:
или
@,2356 ± 0,1928) [со]2 = 6634.
Отсюда [он] = 124— или [n\i = 1190 об/мин и [о)]3 = 394— или [я]2 =
евк	сек
= 3760 об/мин. Если п = [n]i и п = [я]2, наибольшие напряжения в балках
равны допускаемым. При заданных размерах балок безопасный режим работы
двигателя будет при я ^1190 об/мин и я ^3760 об/мин. Так как двигатель
должен работать при п0 = 1500 об/мин, то опасный для работы двигателя
диапазон можно сдвинуть увеличением или уменьшением размеров сечений
балок. Задавшись размерами 15 X 24 см и 12 X 12 см и повторяя последова-
последовательно все проделанные выше вычисления, получаем результаты, приведён-
приведённые в таблице 35.
В обоих вновь рассмотренных вариантах ад < [а]. Однако во втором
варианте при пуске и остановке двигателя, когда частота возмущающей
силы должна будет пройти через критическое значение (пкр = 750 об/мин),
*) При <о>168 следует брать минус, при со < 168 следует брать плюс.

700	напряжения при ударе	[гл. xxxvi
Таблица 35. Результаты расчёта балок примера № 136.
Размеры
балок
в см
20 X 12
15 X 24
12 X Г2
Вес
Qi
в кг
23
34,5
13,8
<т
с
к г.'см'
13,1
7,42
35,7
д-р
об/мин
1605
2330
750
[n\i
об/мин
1190
1690
580
\п\,
об/мин
3760
7260
1320
при п~пь
3,68
1,524
0,432
з кг см*
при n = nli
203
51
98
в балке могут возникнуть сотрясения. Поэтому опасный диапазон следует
проходить достаточно быстро, чтобы амплитуда колебаний не успела
'безопасный, диапазон
Опасный диапазон
Фиг. 595.
значительно увеличиться. Лучше поэтому размеры балок назначить по
первому варианту.
На'фиг. 595 приведены графики, иллюстрирующие произведённые выше
подсчёты.
ГЛАВА XXXVI.
НАПРЯЖЕНИЯ ПРИ УДАРЕ.
§ 225. Основные положения.
Явление удара получается в том случае, когда 'скорость рассма-
рассматриваемой части конструкции или соприкасающихся с ней частей
изменяется в очень короткий период времени.
При забивке свай тяжёлый груз падает с некоторой высоты на
верхний торец сваи и погружает ее в грунт; баба останавливается

§ 226J
ОБЩИЙ ПРИЁМ ВЫЧИСЛЕНИЯ НАПРЯЖЕНИЙ ПРИ УДАРЕ
701
почти мгновенно, вызывая удар. Аналогичные явления происходят
при ковке; удар испытывают и проковываемое изделие и шток
молота с бойком, так как последний очень быстро
останавливается при соприкосновении с изделием. Во
время удара между обеими ударяющимися деталями
возникают весьма большие взаимные давления. Ско-
Скорость ударяющего тела за очень короткий проме-
промежуток времени изменяется и в частном случае падает
до нуля; тело останавливается. Значит, на него от
ударяемой детали передаются очень большие ускоре-
ускорения, направленные в сторону, обратную его движе-
движению, т. е. передаётся реакция Рд, равная произведению
массы ударяющего тела на это ускорение.
Обозначая это ускорение через а, можно написать, что
реакция Рж=~а> где Q — вес ударяющего тела. По за-
|
Фиг. 596.
кону равенства действия и противодействия на ударяемую
часть конструкции передаётся такая же сила, но обратно
направленная (фиг. 596). Эти силы и вызывают напряжения в обоих телах.
Таким образом, в ударяемой части конструкции возникают такие
напряжения, как будто к ней была приложена сила инерции уда-
ударяющего тела; мы можем вычислить эти напряжения, рассматривая
(§ 215) силу инерции Рд как статическую нагрузку нашей конструк-
конструкции. Затруднение заключается в вычислении этой силы инерции.
Продолжительности удара, т. е. величины того промежутка времени,
в течение которого происходит падение скорости до нуля, мы не
знаем. Поэтому остаётся неизвестной величина ускорения а, а стало
быть, и силы Рд. Таким образом, хотя вычисление напряжений при
ударе представляет собой частный случай задачи учёта
сил инерции (§ 215), однако для вычисления силы Рд
и связанных с ней напряжений и деформаций здесь
приходится применять иной приём и пользоваться за-
законом сохранения энергии.
При ударе происходит очень быстрое превращение
одного вида энергии в другой: кинетическая энергия
ударяющего тела превращается в потенциальную энер-
энергию деформации. Выражая эту энергию в функции силы
Рд или напряжений, или деформаций (§ 125), мы по-
получаем возможность вычислить эти величины.
597.
§ 226. Общий приём вычисления напряжений
при ударе.
А. Предположим, что очень жёсткое тело Л весом
Q, деформацией которого можно пренебречь, падая
с некоторой высоты //, ударяет по другому телу В, опирающемуся
на упругую систему С (фиг. 597). В частном случае это может

702	НАПРЯЖЕНИЯ ПРИ УДАРЕ	[ГЛ. XXXVI
быть падение груза на конец призматического стержня, другой конец
которого закреплён (продольный удар), падение груза на балку,
лежащую на опорах (изгибающий удар), и т. п.
В течение очень короткого промежутка времени упругая система С
испытает некоторую деформацию. Обозначим через 8Д перемещение
тела В (местной деформацией которого пренебрежём) в направлении
удара. В упомянутых частных случаях при продольном ударе за пе-
перемещение 8Д соответственно нужно считать продольную деформа-
деформацию стержня А/д, при изгибающем ударе — прогиб балки /д в уда-
ударяемом сечении и т. и. В результате удара в системе С возникнут
напряжения рж (ад или тд — в зависимости от вида деформации).
Полагая, что кинетическая энергия Т ударяющего тела полностью
переходит в потенциальную энергию UA деформации упругой системы,
можем написать:
T=Ur	C6.1)
Так как к моменту окончания деформации ударяющее тело пройдёт
путь Н-\-Ъж, то его запас энергии будет измеряться произведённой
им работой Лд и будет равен:
Г = Лд = <?(Я-}-8д).	C6.2)
Вычислим теперь ?/д. При статической деформации потенциаль-
потенциальная энергия Uz численно равна половине произведения действующей
силы на соответствующую деформацию (§ 125):
4=4 <?5С.	C6.3)
Статическая деформация 8С в ударяемом сечении может быть вычи-
вычислена по закону Гука, который в общем виде можно записать так:
bc = Q:c или Q = cbc.
Здесь (см. § 222) с — некоторый коэффициент пропорциональности
(называемый иногда жёсткостью системы); он зависит от свойств
материала, формы и размеров тела, вида деформации и положения
ударяемого сечения. Так, при простом растяжении или сжатии 8С =
Ol	EF
= А/с=~рг и с = — ; при изгибе балки, шарнирно закреплённой
по концам, сосредоточенной силой Q посредине пролёта 8С =/с тах =
(?/3	48?/
= Ш7 и < = —г» Т- д'
Таким образом, формула C6.3) может быть переписана так:
В основу этой формулы положены две предпосылки: а) справедли-
справедливость закона Гука и б) постепенный — от нуля до окончательного
значения — рост силы Q, напряжений рс и пропорциональных им
деформаций 8С,

§ 226]	ОБЩИЙ ПРИЁМ ВЫЧИСЛЕНИЯ НАПРЯЖЕНИЙ ПРИ УДАРЕ	703
Опыты с определением модуля упругости по наблюдениям над
упругими колебаниями стержней показывают, что и при динами-
динамическом действии нагрузок закон Гука остаётся в силе, и модуль
упругости сохраняет свою величину. Что касается характера нара-
нарастания напряжений и деформаций, то и при ударе деформация про-
происходит, хотя и быстро, но не мгновенно; Ьж постепенно растёт
в течение очень короткого промежутка времени от нуля до оконча-
окончательного значения; параллельно росту деформаций возрастают и
напряжения /?д.
Реакция системы С на действие упавшего груза Q (назовём её Рл)
является следствием развития деформации &д; она растёт парал-
параллельно 8Д от нуля до окончательной, максимальной величины и, если
напряжения рж не превосходят предела пропорциональности мате-
материала, связана с ней законом Гука:
где с — упомянутый выше коэффициент пропорциональности, сохра-
сохраняющий своё значение и при ударе.
Таким образом, обе предпосылки для правильности формулы C6.3)
принимаются и при ударе. Поэтому можно считать, что вид формулы
для иж при ударе будет тот же, что и при статическом нагружении
системы С силой инерции Яд, т. е.
и*=тр&=тЪ=ъь*	C6-4)
(Здесь учтено, что по предыдущему c = Q:bc.) Подставляя значе-
значения Т и ?/д в уравнение C6.1), получаем:
<?(Я+8Д) = |-8Д	C6.5)
или
8Д_28С8Д — 2Я8с = 0.	C6.6)
Отсюда
или, удерживая перед радикалом для определения наибольшей вели-
величины деформации системы в направлении удара знак плюс, получаем:
C6.7)
Так как напряжения и усилия по закону Гука пропорциональны
деформации, то
[ A|]	C6.8)
C6.9)

704	НАПРЯЖЕНИЯ ПРИ УДАРЕ	[ГЛ. XXXVI
Из этих формул видно, что величина динамических деформаций,
напряжений и усилий зависит от величины статической деформации,
т. е. от жёсткости и продольных размеров ударяемого тела; ниже
это дополнительно будет показано на отдельных примерах. Величина
-1-~~	C6.10)
в данном случае представляет собой динамический коэффициент.
Заменяя в формуле C6.10) Н на -~—, где v — скорость ударяющего
тела в начальный момент удара, получаем:
Кроме того, так как
2Н _ QH _ То
где T$ = QH — энергия ударяющего тела к моменту начала удара,
то выражение для динамического коэффициента может быть пред-
представлено ещё и в таком виде:
1+^.	C6.12)
Б. Если мы в формулах C6.7) и C6.8) положим Н= 0, т. е.
просто сразу приложим груз Q, то 8Д = 28С и рЛ = 2рс; при внезап-
внезапном приложении силы Q деформации и напряжения вдвое больше,
чем при статическом действии той же силы.
Наоборот, если высота падения груза Н (или скорость v) вели-
велика по сравнению с деформацией 8С, то в подкоренном выражении
формул C6.7) — C6.11) можно пренебречь единицей по сравнению
с величиной отношения —. Тогда для 8Д и рл получаются следую-
следующие выражения:
2//
При очень большой величине отношения -г— можно пренебречь и еди-
единицей, стоящей перед корнем, т. е. написать:
Динамический коэффициент в этом случае определяется по формуле
-	<збл5)

§ 226]	ОБЩИЙ ПРИЁМ ВЫЧИСЛЕНИЯ НАПРЯЖЕНИЙ ПРИ УДАРЕ	705
Необходимо отметить, что в то время как пренебрежение единицей
9 г/
в подкоренном выражении допустимо уже при -^—^10 (неточность
приближённых формул будет не больше 5°/0), пренебрежение еди-
единицей, стоящей перед корнем, допустимо лишь при очень большой
ом
величине отношения -^-. Так, например, для того чтобы приближён-
приближённее
ные формулы C6.14) и C6.15) давали погрешность не более 10%»
отношение -i— должно быть больше НО.
Формулы ЪЛ = КЛЪС и рл = Клрс, в которых Кя выражается через
jj- C6.12), могут быть использованы также для решения задачи
о встречном ударе тел, двигающихся с некоторой скоростью, при
определении напряжений в цилиндре двигателя внутреннего сгора-
сгорания, вызванных резким повышением давления газа при вспышке горю-
горючей смеси и др. На этом основании их можно считать общими фор-
формулами для расчёта на удар.
Обобщая сказанное выше, можем наметить следующий общий
приём решения задач на определение напряжений при ударе. При-
Применяя закон сохранения энергии, надо:
1)	вычислить кинетическую энергию ударяющего тела Т;
2)	вычислить потенциальную энергию ?/д тел, воспринимающих
удар, под нагрузкой их силами инерции при ударе; потенциальная
энергия должна быть выражена через напряжение (ад, тд) в каком-
либо сечении, через деформацию (удлинение, прогиб) или через силу
инерции Рд ударяющего тела;
3)	приравнять величины UA и Т и из полученного уравнения
найти или непосредственно дийамическое напряжение, или деформа-
деформацию, а по ней, пользуясь законом Гука, напряжение или силу Рд и
соответствующие ей динамические напряжения и деформации.
Описанный общий приём расчёта на удар предполагает, что вся
кинетическая энергия ударяющего тела целиком переходит в потен-
потенциальную энергию деформации упругой системы. Это предположение
не точно. Кинетическая энергия падающего груза частично превра-
превращается в тепловую энергию и энергию неупругой деформации осно-
основания, на которое опирается система.
Вместе с тем при высоких скоростях удара деформация за вре-
время удара не успевает распространиться на весь объём ударяемого
тела и в месте удара возникают значительные местные напряжения,
иногда превосходящие предел текучести материала. Так, например,
при ударе свинцовым молотком по стальной балке большая часть
кинетической энергии превращается в энергию местных деформаций.
Подобное же явление может иметь место даже и в том случае, когда
скорость удара мала, но жёсткость или масса ударяемой конструкции
велика.
23 И. М. Беляев

706	НАПРЯЖЕНИЯ ПРИ УДАРЕ	[гл. XXXVI
Указанные случаи соответствуют большим величинам дроби -=г-«
Поэтому можно сказать, что описанный выше метод расчёта при-
меним, пока дробь -=— не превышает определённой величины. Более
"с
точные исследования показывают, что ошибка не превышает 10°/0>
если -?—^100. Так как эта дробь может быть представлена в виде
Т
отношения jj- (см. выше), то можно сказать, что изложенный ме-
метод применим, пока энергия удара превышает не более чем в 100 раз
потенциальную энергию деформации, соответствующую статиче-
статической нагрузке конструкции весом ударяющего груза. Учёт массы
ударяемого тела при ударе (см. § 231) позволяет несколько расши-
расширить пределы применимости этого метода в тех случаях, когда масса
ударяемого тела велика.
Более точная теория удара излагается в курсах теории упругости.
§ 227. Частные случаи вычисления напряжений
и проверки прочности при ударе.
А. Вид формул, выведенных в § 226, показывает, какие боль-
большие качественные различия ведёт за собой количественное измене-
изменение периода действия силы на тело.
Рассмотрим некоторые случаи удара при простейших деформа-
деформациях. При этом для нахождения коэффициента динамичности при-
применим основные формулы C6.10) и C6.12) и прибли-
r"]ff жённую формулу C6.15).
1~~	Для определения 8Д, рж и Рд используем зависимости:
a*ij:
В случае продольного растягивающего или сжимаю-
сжимающего удара (фиг. 598)
a a/ Ql	Q
Фиг. 598.	TJ —Sl — ^L- Al*EF
с 2EF~ 2E ~~ 21 *
Для вычисления динамического коэффициента Кл может быть выбрано
одно из следующих выражений:
C6Л6)
После этого без затруднений вычисляются Д/д, ад и Рд.

§ 227] ЧАСТНЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ НАПРЯЖЕНИЙ	707
Приближённая формула для вычисления напряжений в данном
частном случае получает такой вид:
1 — Г ОТ F	/'ОТ F
К* = Т\ПТ и ад = ас^д=]/^Г- C6.17)
Замечаем, что как при статической, так и при динамической на-
нагрузке напряжение в сжатом стержне зависит от величины сжимаю-
сжимающей силы и от площади поперечного сечения стержня.
Но при статическом действии груза Q передающаяся на стер-
стержень сила равна Q и не зависит от размеров и материала стержня,
при ударе же величина силы Рд, вызывающей напряжения в стержне,
зависит от ускорения, передающегося от ударяемого тела на ударя-
ударяющее, т. е. от величины промежутка времени, в течение которого
изменяется скорость ударяющего тела. В свою очередь этот проме-
промежуток времени зависит от величины динамической продольной де-
деформации А/д, от податливости стержня. Чем эта величина больше,
т. е. чем меньше модуль Е и чем больше длина стержня /, тем
больше продолжительность удара, меньше ускорение и меньше да-
давление Рж.
Таким образом, при равномерном распределении напряжений,
одинаковом во всех сечениях стержня, динамическое напряжение
будет уменьшаться с увеличением площади поперечного сечения
стержня и с увеличением его податливости (т. е. с увеличением длины
и уменьшением модуля упругости ?); именно поэтому смягчают удар
всякие рессоры и пружины, расположенные между ударяющимися
деталями. Всё это и отражают приведённые выше формулы. В ча-
частности, исходя из формул C6.17), с известным приближением мож-
можно считать, что при продольном ударе величина напряжений зависит
уже не от площади, а от объёма стержня.
Найдя по формулам C6.8) и C6.16) или C6.17) величину дина-
динамического напряжения, мы можем теперь написать условие прочно-
прочности в виде
°д<[°д]э	C6.18)
где [ад] — допускаемая величина нормальных напряжений при ударе,
равная для пластичного материала [а.] = ~. Величину коэффици-
«д
ента запаса &д можно было бы выбрать равной величине основного
коэффициента запаса kQ при статическом действии нагрузок (т, е.
1,5 -ь 1,6, § 17), так как динамичность нагрузки уже отражена в
формулах C6.16) и C6.17); однако, ввиду некоторой упрощённо-
упрощённости изложенного метода расчёта, этот коэффициент принимают не-
несколько повышенным — до 2. Кроме того, обычно в этих случаях
применяют материал более высокого качества (в отношении одно-
однородности и пластических свойств).
23*

708	напряжения при ударе	[гл. xxxvi
Б. При изгибе величина статической деформации 8С, представля-
представляющей собой статический прогиб балки /с в месте удара, зависит от
схемы нагружения и условий опирания балки.
Так например, для балки пролётом /, шарнирно закреплённой по
концам и испытывающей посредине пролёта удар от падающего с
высоты Н груза Q (фиг. 599, а),
|?|	получаем:
Т '	" * __, _ 9<3
Н '	°с —/с шах — 48?7 '
^"^	\ 	«^
/'с — Jc max —
_ Р/с max _
^с~~~ 2	96?У>
для консоли, испытывающей удар
от груза Q, падающего на свобод-
свободный конец консоли (фиг. 599, б):
'И I
L	°c—/с max — ~орУ'
¦H	/;c ^^ Jc max = y^
Фиг. 599.
Подставляя в формулу для коэффициента динамичности Кж значения
8с=/стах или Uc, находим Kv а затем и величину динамических
напряжений и деформаций. Так например, в случае балки на двух
опорах при вычислении динамического напряжения адтах имеем та-
такую формулу:
C6.19)
Условие прочности C6.18) в этом случае напишется так:
Приближённые формулы для вычисления /д ,пах и ад тах в случае
удара по балке на двух опорах (фиг. 599, а) получают такой вид:
с max |/ Щ — TggJ \ Q4* ~~ V 2\EJ
°дтах —

§ 227]	ЧАСТНЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ НАПРЯЖЕНИЙ	709
Аналогичные выражения для /дтах и адтах получаются и в слу-
случае удара по консоли (фиг. 599, б). Имея в виду, что
и
J	' Z	2 1
можем представить формулу C6.22) ещё и в таком виде:
^.	C6.23)
Из приближённой формулы C6.23) видно, что динамические напря-
напряжения при изгибе балки зависят от модуля упругости материала,
объёма балки, формы её поперечного сечения (отношение —r—j, a
также от схемы нагружения и условий опирания балки (в данном
случае в подкоренном выражении стоит 6Г0; для балок, иначе за-
загружённых и закреплённых, числовой коэффициент у Го будет дру-
другим). Таким образом, в балке прямоугольного сечения высотой к и
шириной by поставленной на ребро или положенной плашмя, наи-
наибольшие напряжения при ударе будут одинаковы и равны (по при-
приближённой формуле):
°д max ==:
так как в обоих случаях
L	А
2	2
1/
У
1
Ylbh V \2bh
_|/з"
Как известно, при одинаковой статической нагрузке наибольшие на-
напряжения в балке, положенной плашмя, будут в отношении -у
больше, чем напряжения в балке, поставленной на ребро. Сказан-
Сказанное выше, разумеется, справедливо лишь до тех пор, пока явление
удара происходит в пределах упругости.
Сопротивление балок ударным нагрузкам зависит и от момента
сопротивления и от жёсткости балки. Чем больше податливость,
деформируемость балки, тем большую живую силу удара она мо-
может принять при одних и тех же допускаемых напряжениях. Наи-
Наибольший прогиб балка даёт в том случае, когда во всех её сечениях
наибольшие напряжения будут одинаковыми, т. е. если это будет
балка равного сопротивления', такие балки при одном и том
же допускаемом напряжении дают большие прогибы, чем балки

710	НАПРЯЖЕНИЯ ПРИ УДАРЕ	[ГЛ. XXXVI
постоянного сечения, и значит, могут поглощать ббльшую энергию
удара. Поэтому рессоры обычно и делают в форме балок равного
сопротивления.
В. Рассмотрим теперь задачу определения напряжений при скру-
скручивающем ударе.
Если вращающийся вал внезапно останавливается торможением
одного из его концов, а на другом его конце на него передаётся
живая сила маховика Го, скручивающая вал, то напряжения также
могут быть определены указанным выше методом. Вал будет скру-
скручиваться двумя парами сил (силы инерции маховика и силы торможе-
торможения) с моментом М.
В данном случае
а 	 	Ml	_ 	М
°с — Тс — ~q]~ 9 Pz — тс max — деГ
Следовательно,
2GJp — 2/
,1ч	- 	#- - 	- l/^°
'А — хдтах — Ад^стах — ^стах I/ ~п~ —
так как
/ —HH-L w —— и -^й-—— — —
JP 2 ' Р 2	1^3 тхг2 F*
Имея в виду, что _ живая сила маховика То равна
где Jo — момент инерции массы маховика, а со — угловая скорость,
можем написать:
Замечаем, что и при скручивающем ударе наибольшие напряже-
напряжения зависят от модуля упругости и от объёма вала.
§ 228. Напряжения при продольном ударе стержня
о неподвижную плоскость.
На практике встречаются задачи определения величины напряжения в
самом ударяющем теле, например, при расчёте штока ковочного молота.
Наиболее опасным для прочности штока будет момент окончания ковки,
когда проковываемое изделие почти не деформируется и вся энергия удара
поглощается деформацией штока.

§ 228]
НАПРЯЖЕНИЯ ПРИ ПРОДОЛЬНОМ УДАРЕ СТЕРЖНЯ
711
Схематически этот случай соответствует удару призматического стержня
весом Q о неподвижную плоскость (фиг. 600). Высота падения стержня пусть
будет h, площадь поперечного сечения F, длина /, объёмный вес у. Кинети-
Кинетическая энергия стержня в момент удара равна Го = ^Flh = Qh. Мы считаем,
что эта энергия целиком переходит в потенциальную энергию деформации
стержня. В момент удара, как мы видели выше, между стержнем и непо-
неподвижной плоскостью возникают давления,
равные силе инерции ударяющего тела,	р
слагающейся из сил инерции отдельных его
частиц. Принимая, что в момент удара все
элементы стержня испытывают одно и то
же ускорение (направленное вверх), полу-
получаем, что напряжения в нашей системе
будут такими же, как будто ко всем части-
частицам падающего стержня были приложены
равномерно распределённые по объёму
силы инерции (фиг. 601).
Таким образом, динамическая нагрузка
стержня будет подобна статической на-
нагрузке его собственным весом. Поэтому
зависимость между его потенциальной энергией деформации при ударе UA
и наибольшим динамическим напряжением (в нижнем сечении) аДтах будет
такой же, как связь между ?/с и <*Стах при статической нагрузке собствен-
собственным весом стержня, опёртого нижним концом. В этом случае напряжения
по любому сечению, отстоящему на х от верхнего конца (фиг. 601), равны
(§ 29):
"Т
¦с:
г
7/ШШШ///ШШ
Фиг. 600.
Фиг. 601.
где <Jcmax=:K' — напряжение по нижнему сечению.
Энергия, накопленная в элементе длиной dx у сечения с абсциссой х,
равна:
Вся энергия Uc равна:
V
Г
J
x*dx— "c>m"f/
x ax- QE ti.
При ударе
Приравнивая величину UA кинетической энергии удара То — ^Flh = Qh, по-
получаем:
2
откуда

712
НАПРЯЖЕНИЯ ПРИ УДЛРЕ
[ГЛ. XXXVI
Так как /г = —, где v—скорость стержня в момент удара, то
д max '
Полученный результат можно сформулировать ещё иначе:
д max "
Fl
2EQh
Fl '
C6.27)
C6.28)
а) [Г б) \Т
Т"
„1т
т. е. напряжение в ударяющем стержне будет таким же, как будто он по-
получил удар от другого стержня с живой силой, в три раза большей.
§ 229. Напряжения в стержнях переменного сечения при ударе.
В § 227 показано, что для снижения напряжений при продольном
ударе следует увеличивать объём стержня. Однако надо помнить,
что это правильно лишь для того случая, когда площадь сечения
стержня по его длине не меняется,—
напряжения во всех сечениях одина-
одинаковы. Совершенно иначе может об-
обстоять дело, если разные участки длины
стержня будут иметь неодинаковую пло-
площадь поперечного сечения (фиг. 602).
Мы знаем (формулы C6.16) или
C6.17)), что динамическое напряжение
при продольном ударе зависит и от
площади поперечного сечения стержня
и от его податливости, деформируе-
деформируемости. Наибольшие напряжения в
стержне с выточкой (фиг. 602, а) бу-
будут, таким образом, определяться ве-
величиной наименьшей площади (в месте
выточки) и сжимаемостью стержня,
которая зависит от деформаций уже всего стержня, а не только
его ослабленной части.
Понижение напряжений в этом случае может быть достигнуто
двумя путями. Можно увеличить площадь в наиболее ослаблен-
ослабленном месте (если конструкция это позволяет) — вернуться к стержню
одного диаметра d\ (фиг. 602, б)\ в этом случае мы увеличиваем
площадь и в меньшей степени уменьшаем сжимаемость. Сила инер-
инерции немного возрастёт, но в большей степени возрастёт площадь
в ослабленном сечении, и напряжение понизится.
Однако обычно этот (первый) путь неприменим, ибо конструкция
может требовать сохранения выточки. Тогда для повышения прочности
стержня необходимо увеличить его податливость, уменьшая площадь
его сечения в утолщённой части. Если мы выполним весь стержень
диаметром d% (фиг. 602, в), то этим значительно увеличим сжимае-
сжимаемость стержня, уменьшим силу РА и динамическое напряжение. Таким
Фиг. 602.

§ 230] ПРАКТИЧЕСКИЕ ВЫВОДЫ ИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ 713
образом, снижение напряжений может быть достигнуто двумя путями,
ведущими к выравниванию напряжений, —увеличением объёма путём
уничтожения выточки и уменьшением объёма за счёт уменьшения
площади утолщённой части.
Эти выводы легко проверить расчётом; определим наибольшие
динамические напряжения, вызванные одним и тем же продольным
ударом с запасом энергии Го = QH для трёх стержней, показанных
на фиг. 602, а, б и в. Площадь утолщённой части стержня а назо-
вём Fl9 а тонкой /у, обозначим -~ = q и — = /;. Напряжения
в стержнях найдём по приближённым формулам C6.14) и C6.17).
Наибольшее динамическое напряжение в стержне а по формуле C6.14):
Так как
то
Напряжения в стержнях постоянного сечения б и в найдём по фор-
формуле C6.17):
"or F
У
так как
Так, если ^ = 0,8, а ~ = 0,1, то ^ = 0,64 и /?=0,1; в этом
случае вычисления дают: оа=1,52о^; ав==0у82са= 1,25а0-. Таким
образом, наличие выточки, уменьшающей диаметр на 20°/0 на одной
десятой длины стержня, вызывает повышение напряжений на 50°/0>
если теперь дать этому стержню минимальную площадь по всей
длине, то напряжения снизятся примерно на 20°/0-
Хотя эти подсчёты и сделаны по приближённым формулам, однако
найденные таким путём соотношения между оа, о^ и ав оказываются
достаточно близкими к тем, которые могут быть получены по более
точной формуле C6.8), если энергия удара Го не очень мала.
§ 230. Практические выводы из полученных результатов.
Результаты приведённых выше подсчётов имеют громадное практи-
практическое значение. Прежде всего они показывают, что характер сопро-
сопротивления стержней удару качественно резко отличается от сопро-
сопротивления их статической деформации. Утолщение одной половины

714
НАПРЯЖЕНИЯ ПРИ УДАРЕ
[ГЛ. XXXVI
стержня при статическом сжатии не вызывает изменения напряжений
в сечениях другой половины; при ударе же оно повышает их. Мест-
Местные уменьшения площади поперечного сечения на небольшой длине
стержня вызывают резкое повышение напряжений.
Для снижения напряжений надо стремиться, главным образом,
к увеличению податливости стержня путём увеличения его длины,
добавления буферной пружины, замены материала другим, с более
низким модулем упругости, выравнивания площадей поперечных се-
сечений. Наиболее эффективным может оказаться выравнивание пло-
площадей поперечных сечений по наименьшей.
Поэтому при конструировании стержней, работающих на удар,
надо добиваться постоянной площади сечения по всей длине стержня;
местные утолщения допустимы лишь на небольших участках длины;
местные же выточки небольшой протяжённости крайне нежелательны.
Если при таких условиях не удаётся сконструировать достаточно
прочный стержень, необходимо удлинение стержня или равномерное
увеличение площади.
В качестве примера можно привести болт, передающий от одной
части конструкции на другую растягивающий удар. Конструкция,
показанная на фиг. 603, а, будет плохо сопротивляться удару, так
Фиг. 603.
как участок болта с нарезкой, имеющий меньший диаметр, будет рабо-
работать как выточка. Большая часть энергии удара будет поглощаться
частью болта, имеющей нарезку. Обрыв весьма вероятен.
\\4\\\W\\XVC\\s
Фиг. 604.
Для улучшения конструкции надо заставить весь объём болта
более или менее равномерно поглощать энергию удара; для этого надо
сделать его площадь всюду (или почти всюду) равной площади по

§ 231] УЧЁТ МАССЫ УПРУГОЙ СИСТЕМЫ, ИСПЫТЫВАЮЩЕЙ УДАР	715
внутреннему диаметру нарезки. Этого можно достигнуть или обта-
обтачиванием тела болта (фиг. 603, б), или высверливанием в нём канала
(фиг. 603, в).
В качестве примера увеличения сопротивления болтов путём их
удлинения можно привести конструкцию, изображённую на
фиг. 604, а и б. Крышки цилиндра бурового инструмента иногда
испытывают сильные удары поршня. Короткие болты, прикрепляющие
крышку к цилиндру по варианту фиг. 604, а, давали обрыв. Выход
был найден путём удлинения болтов по варианту фиг. 604, б.
§ 231. Учёт массы упругой системы, испытывающей удар.
При вычислении напряжений при ударе мы считали, что вся энер-
энергия удара переходит в потенциальную энергию ударяемого тела.
В действительности часть её переходит в энергию местных деформа-
деформаций, происходящих около места удара. При более или менее значи-
значительной массе ударяемого тела эта поправка может оказаться суще-
существенной.
Исследуем, как отразится на величине расчётных напряжений
при ударе учёт массы ударяемого тела. В качестве примера рас-
рассмотрим случай удара при изгибе (фиг. 599, а). В момент удара груз
Q имел скорость -у, а балка была неподвижна. В течение очень ко-
короткого промежутка времени все элементы балки приобретут неко-
некоторую скорость, а груз несколько замедлит своё движение.
Можно считать, что в этот период удара балка практически
останется прямой, а уменьшение скорости груза будет происходить
за счёт местных деформаций как балки, так и самого груза. Этот
период окончится, когда скорости груза и балки в месте удара
сравняются между собой и достигнут некоторого общего значения vt;
после этого начнётся изгиб балки под действием груза Q, движу-
движущегося со скоростью vx вместе с получившим удар сечением, как
бы прикреплённым к грузу.
В этот второй период удара, когда имеют место деформации уже
всей балки, кинетическая энергия груза и движущейся балки пере-
переходит в потенциальную энергию изгиба. Для вычисления этой энергии
необходимо знать скорость груза vt и скорости остальных сече-
сечений балки.
В течение первого периода удара в основном происходит пре-
преобразование механического движения груза в механическое же дви-
движение груза и балки. Так как часть кинетической энергии падаю-
падающего груза переходит в энергию местных деформаций, то живая
сила груза и балки в конце первого периода удара меньше их живой
силы до удара.
Живая сила груза и балки до удара равна живой силе падаю-
щего груза ^— (балка неподвижна). В конце первого периода удара

716	НАПРЯЖЕНИЯ ПРИ УДАРЕ	[ГЛ. XXXVI
Qv*
живая сила груза равна —-1. Полагая, что при ударе балка гнётся
по той же кривой, что и при статической нагрузке силой инерции, прило-
приложенной посредине пролёта, для вычисления живой силы балки в конце
первого периода удара можем воспользоваться выводами § 223. По
формуле C5.32) живая сила балки равна половине произведения
приведённой массы балки на квадрат скорости, т. е. равна оз\? v\*
Таким образом, потерянная при ударе живая сила Т может быть
вычислена по формуле:
т Qv* (СМ
Потерянная скорость груза есть v — vi9 соответствующая ей жи-
живая сила равна ^- (v — v%)\ Живая сила всей балки, соответствующая
скорости Vi — 0, приобретённой получившим удар сечением балки,
равна живой силе балки в конце первого периода удара. Поэтому-
суммарная живая сила груза и балки Tl9 соответствующая потерян-
потерянным и приобретённым скоростям, может быть вычислена по формуле:
C6.30)
Приравнивая выражения для Т и Tt по формулам C6.29) и C6.30),
получаем:
откуда
Имея скорость vt движения груза и среднего сечения балки, вы-
вычислим теперь живую силу удара, переходящую в потенциальную
энергию изгиба балки. Эта живая сила складывается из кинетической
энергии груза ~^- и кинетической энергии балки, которая, как уже
было установлено выше, к концу первого периода удара равна ^ \у v\.
Таким образом, энергия удара Т равна:
	___ _	_	1 _ То
2g "T" 35 2g Vl 2gK
4 ^35 О 4^35Q
где
1 о — Чп — -^ .

§ 232]
ПРИМЕРЫ
717
Соответствующие наибольшие нормальные напряжения в балке должны
быть вычислены по формуле:
ид max •
j , 6Г0Е7	1 1
I™ J cmax i i 12lEi
1+35 Q\
Мы видим, что если отношение -J- не мало по сравнению с еди-
единицей, то энергия удара Т будет меньше величины Т^ = -—-у
т. е. учёт массы балки снижает расчётные напряжения при ударе.
Поступая аналогично вышеизложенному при исследовании явле-
явления удара с учётом массы ударяемого тела при деформации какого-
либо другого вида, получим для нахождения живой силы удара Т
и для вычисления динамических напряжений рж подобные же фор-
формулы. В эти формулы войдёт отношение приведённой массы ударяе-
Oi	О ъ*	Oy
мого тела — к массе ударяющего тела —.Обозначаяотношение ~4
g	8	Q
через р, в общем случае можем написать:
7 = -
C6.31)
C6.32) ,_
§ 232. Примеры.
Пример 137. Определим напряжения в канате подъём-
подъёмника при внезапном торможении опускающегося груза Q
(фиг. 605). Для смягчения удара между грузом и канатом
расположена буферная пружина. Длина каната в момент тор-
торможения пусть будет /, площадь его F, модуль упругости Я,
скорость груза в этот момент v, растяжимость пружины от
груза назовём а.
В момент удара живая сила груза То = -^— переходит в потенциальную
энергию деформации каната и пружины. При вычислении напряжений в ка-
канате выражение для динамического коэффициента C6.11) необходимо изме-
изменить на:
Фиг. 605.
единичного
1) Вывод этой формулы предлагается сделать самостоятельно (см. § 226),
учтя ту особенность, что груз Q не падает извне на упругую систему, а не-
неразрывно с ней связан.

718	напряжения при ударе	Ггл. xxxvi
Статическое удлинение каната и пружины от груза Q равно:
Отсюда
Из этого выражения ясна роль буферной пружины: чем она мягче, чем
её растяжимость а больше, тем динамическое напряжение меньше.
Возьмём числовой пример:
Е = 1,7 • 10° лгг/сж2 *), 1? = 1 м/сек, Q = 5 т,
F=6 см2, 1 = 20 м, а = 2,5
Выполняя вычисления, получаем:
5000 Г, , Г	1,7 • 10е • 6 • 10*
I1 Y
При отсутствии пружины а = 0 и ад = 3520 кг/см2.
Пример 138. Определить наибольшие допустимые энергии удара TL
и Г2 для двух балок, пролётом /, защемлённых одним концом. Первая балка
имеет постоянное прямоугольное сечение высотой h0 и шириной Ьо; вторая
представляет собой балку равного сопротивления изгибу с постоянной вы-
высотой h0 и переменной шириной dx = b0-j (§ 121). Удар наносится грузом,
падающим на свободный конец балок. Допускаемое напряжение равно [а].
В первой балке наибольшие нормальные напряжения будут в крайних
волокнах защемлённого сечения; во второй — нормальные напряжения одина-
одинаковы в крайних волокнах всех сечений, в том числе и опорного.
Размеры опорных сечений балок одинаковы; поэтому и наибольший
допускаемый изгибающий момент будет один и тот же для обеих балок;
его величины равны:
С другой стороны, этот момент равен:
где Рд — динамическое давление на конец балки; оно тоже должно быть
одинаково для обеих балок:
1РМ
Потенциальная энергия, накапливающаяся в балках при действии этой
силы, равна: для первой балки
1	1 /у3
д
1 /у
2 д/1 "~ 2 д 3EJ ~~
для второй балки
1
2 rv*— 2 гя 2EJQ
*) Для канатов модуль упругости значительно меньше, чем для мате-
материала проволок.

§ 232]
ПРИМЕРЫ
719
Здесь Jo — момент инерции сечения в защемлении, аЛ и /2 — прогибы от
действия силы Рд свободных концов первой и второй балок.
Допустимые величины энергии удара 7\ и Т2 должны соответственно
равняться Ui и U2. Следовательно,
	л 	 д
1 — Ul — -оЕГГ =
12?
Таким образом, вторая балка может выдержать энергию удара в 1,5 раза
болыие% чем первая. Балка равного сопротивления, несмотря на меньший
объём, лучше сопротивляется уда-
удару, чем
ния, за
балка постоянного сече-
счёт полного использо-
использования материала в крайних волок-
волокнах всех сечений.
Пример 139. В качестве
примера расчёта на удар сложной
конструкции разберём случай уда-
удара груза Q посредине пролёта
балки, опирающейся в Л на шар-
шарнирную неподвижную опору, а
в В— на шарнирную опору, по-
поставленную на вторую балку по-
посредине её пролёта (фиг. 606).
Пролёт первой балки равен 1и мо-
момент инерции Л, модуль упругости
Е; для второй балки соответствую-
соответствующие величины равны /2, Л, Б. Наибольшие динамические напряжения возник-
возникнут в крайних волокнах средних сечений балок: первой и второй. Найдём
эти напряжения.
Поставленную задачу решим, умножая статические напряжения от груза Q
в первой (АВ) и второй (CD) балках на динамический коэффициент
Фиг. 606.
,=1+|Л
2Я
'/с
Статический прогиб первой балки в ударяемом сечении определяется де-
деформацией всей конструкции и равен /0=/i +-К-/»» где /» и /* — соответ-
соответственно наибольшие статические прогибы первой балки от груза Q и вто-
второй— от груза Y» Так как
Q4
то
Ql\
48Я/»
Ql\ _
192?7S -
Qll
48Е7Г
I Л /МП
L + 4Л VT) J

720	напряжения при ударе	[гл. xxxvi
Наибольшие напряжения в первой и второй балках будут:
Так как количества потенциальной энергии, накапливающейся при
ударе в первой балке (?/Д1), во второй балке (?/Д2) и в обеих балках вместе
(?/д = ил + иж = Го) соответственно пропорциональны ?/Ci, UCfi и Uc (коэффи-
(коэффициентом пропорциональности служит квадрат динамического коэффициента), то
1=3=3=.
¦kQfi
.	/.
Л
гЛ
-=-ф- (а)
4<?/«
2
ис
_/о*
Л
(б)
Прогиб / является общей податливостью всей конструкции в точке,
где она испытывает удар; прогибы же /01 и /02 являются долями этой /ш-
датливости, зависящими от деформаций первой и второй балок в отдель-
отдельности. Из формул (а) и (б) следует, что
// 	-г /oi и /у .	г /оа
Д1"" °7о"	д* °/о *
Таким образом, энергия удара распределяется между балками пропор-
пропорционально их долям в общей податливости конструкции в месте удара.
Если размеры балок будут выбраны так, что/Oi =/02, то ?/Д1 = ?/Дз = у Го;
если бы вместо второй балки была жёсткая опора, то вся энергия удара
была бы целиком воспринята первой балкой; наличие второй балки смягчает
удар, приходящийся на первую.
Подобный же эффект получится, если вместо жёстких опор мы распо-
расположим по концам балки очень податливые опоры в виде резиновых про-
прокладок или винтовых пружин.
§ 233. Испытания на удар до разрушения. Ударная проба.
• Выше было указано, что динамическое действие нагрузок не
ограничивается тем, что напряжения (в пределах упругости) оказы-
оказываются иными, чем при ста-
статических нагрузках. Сам ма-
материал иначе реагирует на
динамическую нагрузку, чем
на медленно возрастающую.
Особенно это заметно при
ударе.
Опыты с ударным разры-
разрывом образцов показывают,
что диаграмма растяжения в этом случае имеет совершенно другой вид,
чем при статическом разрыве. На фиг. 607 изображены статическая и
9лшА1

§ 233J
ИСПЫТАНИЯ НА УДАР ДО РАЗРУШЕНИЯ
721
динамическая диаграммы растяжения образца мягкой стали; при ударе
характерным является резкое повышение предела текучести и смеще-
смещение положения наибольшего груза влево. Это показывает, что влияние
скорости при ударном действии нагрузки меняет и механические
характеристики материала. Бывают случаи, когда материал, отличаю-
отличающийся при статическом испытании прекрасными пластическими каче-
качествами, при ударном действии нагрузки оказывается хрупким *).
Поэтому при выборе материала для деталей, подвергающихся дина-
динамическим воздействиям, вводят так называемую ударную пробу. Эта
проба заключается в том, что образцы материала подвергают раз-
разрушению ударом при растяжении, а чаще при изгибе, и оценивают
количество энергии, затраченной на разрушение образца. Наиболее
распространена проба на удар при изгибе 2).
Если количество энергии, затраченной на излом образца, равно Т,
а площадь поперечного сечения образца в месте излома равна г, то,
деля Т на F, получаем так называемую величину ударной вязкости:
а _Т_ кгм,смч
к F '
Для того чтобы выявить свойства материала при ударной пробе,
образцу придают специальную фор^у — в том сечении, где наносится
удар, делают надрез. На практике встречаются различные формы
надрезов, изображённые на фиг. 608; наиболее распространённым
в настоящее время является
~1Ц
надрез типа б).
Смысл устройства над-
5
реза заключается в том,
что стараются поставить ма-
материал в наиболее тяжёлые
условия работы в отноше-
отношении ударных нагрузок. Над-
Надрез создаёт значительное
ослабление сечений посре-
посредине пролёта и, значит, рез-
резкое повышение напряжений
изгиба на протяжении не-
небольшой длины образца.
Мы уже видели (§ 229),
как сильно влияет на вели-
величину напряжений подобное местное ослабление сечения. Почти вся
энергия удара поглощается небольшим объёмом материала в зоне
местного ослабления, что и вызывает резкое повышение динамиче-
динамических напряжений. Кроме того, наличие надреза вызывает вблизи его
*) Причины этого явления объяснены в главе XXXVIII.
2) О писание см. Беляев Н. М, Лабораторные работы по сопротивле-
сопротивлению материалов, § 89, Гостехиздат, 1951.
Фиг. 608.

722
НАПРЯЖЕНИЯ ПРИ УДАРЕ
[ГЛ. XXXVI
Растяжение
150 100 50
Сжатие
50 100 кг/сМ1
дна ещё местные повышенные напряжения, подобные тем, которые
возникают около краёв отверстий (§ 16).
На фиг. 609 показано распределение напряжений в сечении
балки, ослабленном надрезом. Диаграмма а показывает эпюру на-
напряжений ot в сечении
без надреза; эпюра б даёт
нам распределение нор-
нормальных напряжений в
надрезанном сечении без
учёта местного повыше-
повышения; наконец, на эпюре
в показана полная кар-
картина нормальных напря-
t при изгибе.
ВИдим, что одно
уменьшение высоты се-
сежений
кг/см2 JO 0	32 57
Фиг. 609.
чения повышает напря-
напряжения в 2,25 раза; вместе же с местными напряжениями коэффи-
коэффициент концентрации достигает 5,22 по отношению к основной балке
и 2,32 по отношению к балке пониженной высоты.
Местные напряжения обычно представляют собой такую систему
напряжений, при которой материал находится в объёмном напряжён-
напряжённом состоянии; в этом случае затрудняются пластические дефор-
деформации, и материал вблизи дна надреза оказывается в хрупком со-
состоянии.
Так, в рассматриваемом примере помимо нормальных напряже-
напряжений ах по сечениям, перпендикулярным к оси образца, имеются ещё
растягивающие напряжения а2 по сечениям, параллельным оси. Их
эпюра показана тоже на фиг. 609. Кроме того, внутри образца имеет
место и третье главное напряжение а3, тоже растягивающее. Таким
образом, материал вблизи дна надреза подвергается всестороннему
растяжению, при котором затрудняются пластические деформации.
В самом деле, если предел текучести для материала при простом
растяжении равен ат, а напряжения с2 и о3 составляют некоторую
долю от ах, например 0,2 ох, то наступление текучести при сложном
напряжённом состоянии определится по третьей теории прочности
равенством
Таким образом, материал вблизи дна надреза получит пластические
деформации при значении напряжения ох, большем чем ст, а именно,
1,25 от. При таком затруднении пластических деформаций материал
может оказаться в хрупком состоянии. Это в свою очередь усили-
усиливает эффект ударной нагрузки.
Таким образом, наличие надреза в образце помогает резче раз-
разграничить материалы более чувствительные к неблагоприятному

§ 234]	ВЛИЯНИЕ НА РЕЗУЛЬТАТЫ УДАРНОЙ ПРОВЫ	723
действию удара от менее чувствительных. В этом отношении раз-
различные формы надреза влияют неодинаково: так, острый надрез
более обостряет действие удара, чем закруглённый надрез. Поэтому
величины ударной вязкости, получаемые при испытании различных
материалов, могут быть сравнимы лишь при условии однотипности
образцов.
Показанные на фиг. 608 формы образцов имеют тот недостаток,
что дно надреза попадает на растянутую сторону образца, где и на-
начинается разрушение; таким образом, сопротивление такого образца
в известной мере зависит от тщатель-
тщательности выполнения надреза, а с другой ^ J|-—	1+0
стороны, оказывается невозможным р^	г и	*^--р
испытание на удар образцов с сохра-	№
нением наружной поверхности изделия, |	'—'
что иногда имеет существенное зна- j-	55-
чение.
Г
Эти недостатки избегнуты в образце,	г=0,5
применявшемся нами в механической 	yk-p	Q_
лаборатории Ленинградского института	'
инженеров ж.-д. транспорта (фиг. 610).	Фиг. 610.
При изломе образца этого типа над-
надрез располагается параллельно направлению удара; при этом по-
прежнему почти вся энергия удара сосредоточивается в ослаб-
ослабленном месте, но картина разрушения оказывается более естест-
естественной.
Вид сломанных образцов этого типа пластичного и хрупкого
материала резко отличен; для материала, мало чувствительного
к ударам, в растянутой зоне наблюдается значительная пластическая
деформация; для материала же в хрупком состоянии разрушение
происходит почти без всяких остаточных деформаций.
§ 234. Влияние различных факторов на результаты
ударной пробы.
Как правило, испытание на удар производят при комнатной
температуре над партией однотипных образцов, количеством не
меньше четырёх. Такое число образцов необходимо потому, что
случайные обстоятельства изготовления и испытания образцов мо-
могут иногда очень сильно сказаться на величине их ударной вяз-
вязкости.
В качестве примера в таблице 36 приведены величины ударной
вязкости для ряда материалов при комнатной температуре; испыта-
испытания производились на образцах типа б) фиг. 608.
Однако оказывается, что на величине ударной вязкости сильно
отражается ряд обстоятельств, а именно: форма образцов, скорость
удара и особенно температура образца.

7 24	НАПРЯЖЕНИЯ ПРИ УДАРЕ
Таблица 36. Ударная вязкость для некоторых
[ГЛ. XXXVI
материалов.
Характеристика стали
и химический состав
Термическая обработка
закалка и отпуск
кг/мм2
кгм/см?
Углеродистые стали
С < 0,15 . .
С 0,15—0,20
С 0,20—0,30
С 0,30—0,40
С 0,40—0,50
С 0,50—0,60
" 0,60—0,70
> 0,7. . . ,
Специальные стали
Никелевая, С 0,20; Ni 3,0 . .
Хромоникелевая, С 0,3; Ni 2,5—3,0;
Сг 0,5—0,8
Хромоникелемолибденовая, С 0,25—
0,35; Ni 2,5-3,5; Сг 0,8-1,2; Мо 0,3—
0,5
35—45
40—50
50—60
60—70
70—80
80—90
85—95
>95
50-58
65—70
>25
>22
>20
>	16
>12
>Ю
>	8
>	6
25-20
>7
13
36—50
45—65
55—75
70—85
80—95
90—105
> 100
>105
70—80
75—90
95—100
>25
>20
>	8
>	5
>	3
>	2
24—18
>20
20—16
Ударная вязкость образцов одного и того же материала падает
по мере понижения температуры опыта. Для некоторых материалов
(мягкая сталь) это падение происходит очень резко; для сталей по-
повышенной твёрдости, а также для специальных сталей (хромонике-
(хромоникелевая) этот переход сглаживается. На фиг. 611, а, б, в показаны
диаграммы ударной вязкости, полученные в механической лаборато-
лаборатории Ленинградского института инженеров ж.-д. транспорта.
Перед испытанием образец доводится до заданной температуры
в ванне, или подогреваемой на электроплитке или охлаждаемой при
помощи жидкого воздуха. Изображённые на фиг. 611, а, б, в кри-
кривые показывают, что понижение температуры вызывает резкое умень-
уменьшение ударной вязкости и, таким образом, может вызвать хрупкое
разрушение частей конструкций. Это явление неоднократно наблюда-
наблюдалось на практике; так называемая хладноломкость рельсов, бандажей
и других деталей конструкций железнодорожного транспорта не-
неоднократно вызывала большие затруднения.
Наиболее существенно то обстоятельство, что для некоторых
материалов (фиг, 611, а) переход от пластичных изломов с большой
ударной вязкостью к хрупким происходит на протяжении весьма

§ 234]
ВЛИЯНИЕ НА РЕЗУЛЬТАТЫ УДАРНОЙ ПРОБЫ
725
небольшого интервала температур. Таким образом, материал, хоро-
хорошо сопротивляющийся удару при комнатной или близкой к ней
температуре, может дать хрупкий излом уже при сравнительно
небольшом понижении температуры. Поэтому результаты обычного
испытания на удар при
комнатной температуре
недостаточно характери-
характеризуют сопротивляемость
материала динамическим
воздействиям; следовало
бы получить полную кри-
кривую ударной вязкости в
зависимости от темпера-
температуры (фиг. 611, а, б, в).
Чем левее распола-
располагается так называемый
«критический» интервал
падения ударной вязко-
вязкости, тем материал менее
чувствителен к воздей-
воздействиям температуры при
ударных нагрузках, тем
более он надёжен в ра-
работе.
Изменением формы
образца можно в извест-
известной мере заменить испы-
испытание материала при раз-
разных температурах. Опыты показали, что переход к более широким
образцам сдвигает «критический» интервал температур вправо, т. е.
в сторону более высоких температур. Поэтому если обычная проба
на удар при комнатной температуре даёт удовлетворительный ре-
результат, то для проверки того, не находимся ли мы вблизи критиче-
критического интервала, можно произвести испытание на удар уширенных
образцов; если это испытание даёт хрупкий излом, то «критиче-
«критический» интервал расположен близко к температуре опыта.
Наконец, следует отметить, что на хрупкость материала могут
очень сильно влиять так называемые остаточные напряжения, кото-
которые могут получиться в материале при закалке, при холодной про-
прокатке или при недостаточной температуре горячей прокатки, когда
материал получает наклёп. Опытами на растяжение такие напряжения,
как правило, не могут быть выявлены. Остаточные напряжения
обычно связаны с возникновением объёмного напряжённого состоя-
состояния в материале; в связи с этим возможно хрупкое разрушение.
Такие случаи встречались при изготовлении мощных двутавровых
балок со сравнительно тонкими полками. В нашей практике был
Фиг. 61

726	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА [ГЛ. XXXVII
случай хрупкого разрушения двутавровой балки № 50 при сбрасы-
сбрасывании её на землю в морозный день. Результаты статических испы-
испытаний, химического и металлографического анализа показали, что
материал как будто вполне доброкачественный. Лишь ударные испы-
испытания при различных температурах обнаружили резкую хладнолом-
хладноломкость для образцов, вырезанных у края полки двутавра, — в наи-
наиболее наклёпанном месте. Что касается влияния на хрупкость хими-
химического состава сталей, то ударная вязкость понижается, как это
видно из таблицы 36, с увеличением количества углерода, т. е.
с повышением предела прочности и уменьшением пластических
свойств стали. Весьма неблагоприятно отражается на сопротивлении
удару, особенно при низких температурах, наличие фосфора. Поэтому
на практике при изготовлении материала для деталей, работающих
на удар, всячески ограничивают примесь этого элемента.
ГЛАВА XXXVII.
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ,
§ 235. Основные понятия о влиянии переменных напряжений
на прочность материала.
Сопротивление материалов действию нагрузок, систематически из-
изменяющих свою величину или величину и знак, существенно отли-
отличается от сопротивления тех же материалов статическому и ударно-
ударному действию нагрузок. Поэтому вопрос о проверке прочности мате-
материала при действии переменных нагрузок требует особого изучения.
Давно известно, что части машин, подвергающиеся усилиям, пе-
переменным по величине и повторяющимся большое число раз, иногда
ломаются внезапно, без наличия заметных остаточных деформаций,
при напряжениях, которым они сопротивляются при статических на-
нагрузках вполне надёжно. Внимание инженеров прежде всего
привлекло именно то обстоятельство, что элементы машины, изгото-
изготовленные из материалов, обладающих при обычных испытаниях пре-
прекрасными пластическими свойствами — достаточным удлинением,
сужением, ударной вязкостью, разрушаются без всяких видимых
остаточных деформаций, как будто бы они были выполнены из
хрупкого материала.
В ту эпоху, когда инженеры стали изучать подобные случаи
разрушения (первая половина XIX века), не было ясного представле-
представления о строении металлов; пластичные металлы считали обладающими
«волокнистой» структурой, а хрупкие — «кристаллической». Так как
изломы деталей происходили обычно не сразу, а спустя известный,
иногда довольно значительный, период времени работы машины, то
возникла гипотеза, что при действии переменных напряжений металл

§ 235] ВЛИЯНИЕ ПЕРЕМЕННЫХ НАПРЯЖЕНИЙ НА ПРОЧНОСТЬ МАТЕРИАЛА 727
«устаёт», изменяет свою структуру, из пластичного делается хруп-
хрупким, обладающим кристаллическим строением.
Сам вид поверхности излома, казалось, подтверждал такое пред-
предположение; эта поверхность, как правило, имела две зоны: одну —
гладкую, притёртую (поверхность постепенно развивающейся тре-
трещины), другую — грубозернистую
(поверхность окончательного изло-
излома в ослабленном трещиной сече-
сечении стержня). На фиг. 612 дана
фотография излома вагонной оси;
мы видим наружную, кольцеобраз-
кольцеобразную зону с гладкой поверхностью
и внутреннюю — зону хрупкого,
грубозернистого излома, действи-
действительно характерного для хруп-
хрупкого состояния материала.
Однако уже с начала XX сто-
столетия, после исследований струк-
структуры металлов при помощи микро-
микроскопа, стало ясно, что указанная
гипотеза неверна. Металлы и в пла-
пластичном состоянии оказались	Фиг. 612.
обладающими кристаллической
структурой; никаких принципиальных изменений ни в их строений,
наблюдаемом под микроскопом, ни в механических свойствах при дей-
действии переменных напряжений обнаружено не было. Материал штока
поршня паровой машины или вагонной оси сохраняет свою структуру
и свои пластические свойства, как бы долго он ни работал. Таким об-
образом, ни о каком «перерождении», перекристаллизации металла под
действием только переменных напряжений говорить не приходится.
Механизм разрушения от переменных нагрузок был раскрыт лишь
в начале текущего столетия. Многочисленные исследования показали,
что при действии переменных напряжений в металле возникает тре-
трещина, постепенно проникающая в глубь изделия. При переменных
деформациях края трещины то сближаются и нажимают друг на
друга, то расходятся; этим объясняется наличие гладкой, притёртой
зоны излома. По мере развития трещины усталости поперечное сече-
сечение ослабляется всё сильнее, и наконец, при случайном толчке или
ударе наступает окончательное разрушение, когда сопротивление
оставшейся части сечения оказывается недостаточным.
Трещина усталости является очень острым поперечным надрезом,
аналогичным надрезу в образцах для ударной пробы. У дна этой
трещины создаётся объёмное напряжённое состояние, обусловливаю-
обусловливающее хрупкий характер разрушения материала при ударе (см. § 233).
Этим и объясняется наличие в изломе грубозернистой зоны, соответ-
соответствующей хрупкому излому.

728	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА	[ГЛ. XXXVII
Таким образом, хрупкий характер окончательного излома при
переменных нагрузках объясняется не тем, что материал изменился,
переродился, стал хрупким, а тем, что он оказался благодаря на-
наличию трещины усталости в таком напряжённом состоянии, которое
обусловливает хрупкое, без остаточных деформаций, разрушение.
Разрушение при переменных нагрузках носит местный характер,
не затрагивающий всего материала конструкции в целом. Поэтому
при обнаружении развивающихся трещин при переменных нагрузках
во многих случаях нет необходимости ставить вопрос о смене всей
конструкции; достаточно заменить повреждённые части и уничтожить
причины, вызвавшие возникновение трещин.
Изложенная точка зрения является теперь общепринятой среди
инженеров; таким образом, само понятие «усталость» материала по-
потеряло свой физический смысл; описывая явление разрушения при
действии переменных нагрузок, надо говорить не о разрушении от
«усталости», а о разрушении путём постепенного развития трещины.
Однако благодаря краткости этого термина и широкому рас-
распространению его в технических кругах, выражение «усталость ма-
материалов» удержалось в литературе до настоящего времени, изменив
лишь свой смысл: под этим термином мы в дальнейшем и будем
подразумевать разрушение при постепенном развитии трещины.
Нашей задачей теперь будет установить обстоятельства, вызываю-
вызывающие появление трещин усталости, и дать такие правила конструирова-
конструирования элементов машин и сооружений и проверки их прочности, кото-
которые гарантировали бы их от разрушения при переменных нагрузках.
Эта задача является чрезвычайно важной, особенно для машино-
машиностроения, где мы чаще всего встречаемся с многократным повторе-
повторением переменных напряжений. Можно считать, что примерно 90°/о
всех поломок частей машин являются следствием развития трещин
усталости. Эти поломки чрезвычайно опасны и зачастую ведут
к очень тяжёлым катастрофам, так как обнаружить развивающуюся
волосную трещину усталости далеко не всегда удаётся. Изломы
вагонных и паровозных осей на железнодорожном транспорте обычно
вызываются подобными трещинами и сопровождаются почти неиз-
неизбежно сходом поезда с рельсов с крайне тяжёлыми последствиями.
Подобного же рода катастрофы известны и в авиации и в других
отраслях машиностроения.
§ 236. Составление условия прочности
при переменных напряжениях.
Опыты показывают, что постепенно развивающаяся трещина воз-
возникает только при переменных напряжениях, колеблющихся систе-
систематически между двумя крайними значениями. Изменение напряжений
от одной крайней величины до другой, и обратно, мы в дальнейшем
будем называть циклом напряжений.

§ 236] УСЛОВИЕ ПРОЧНОСТИ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ	729
С другой стороны, известно, что громадное количество элементов
машин и конструкций благополучно сопротивляется переменным на-
нагрузкам в течение весьма продолжительного срока, если напряжения
в них остаются в определённых границах. Таким образом, одной
переменности напряжений недостаточно; для образования трещины
усталости необходимо, чтобы действительная величина наибольшего
значения систематически колеблющегося напряжения превзошла
определённую границу, так называемый предел усталости, или предел
выносливости.
Пределом выносливости рк (ак, тк) мы будем называть наиболь-
наибольшую величину периодически меняющегося напряжения, которо.,
материал может противостоять практически неограниченно
долго без появления трещин усталости.
Таким образом, возможность разрушения путём постепенного
развития трещины обусловливается двумя обстоятельствами:
а)	периодическим колебанием напряжений между определёнными
крайними пределами;
б)	превышением наибольшими действительными напряжениями
в элементе конструкции предела выносливости материала.
Условие прочности в данном случае должно выражать, что наи-
наибольшие действительные напряжения р^ах должны быть с некото-
некоторым запасом меньше предела выносливости /?к:
»Д <&
/max ^ kK'
где kK — коэффициент запаса.
Для практического применения этого условия надо установить
методы определения предела выносливости и вычисления наиболь-
наибольших действительных напряжений.
В настоящее время определение предела выносливости материала
возможно лишь чисто экспериментальным путём. Величина этого
предела зависит в основном от:
а)	материала (сталь, чугун, цветные металлы),
б)	типа деформации (изгиб, кручение и т. д.),
в)	степени несимметрии цикла, т. е. соотношения между крайними
значениями меняющегося напряжения.
Некоторые дополнительные обстоятельства, влияющие на величину
предела выносливости (коррозия, размеры деталей), будут рассмотрено!
отдельно (§§ 239 и 240).
Что касается наибольшего значения действительных напряже-
напряжений /?5jax, то опыты показывают, что в противоположность разру-
разрушению от статической нагрузки появление трещин усталости не
только у хрупких, но и у пластичных материалов связано не с теми
расчётными наибольшими напряжениями /?тах, которые получаются для
чисто призматических стержней (например, при изгибе amax = ^rj,

730
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
а с так называемыми (§ 16) местными напряжениями, возника-
возникающими в местах нарушения призматической формы стержня (над-
(надрезы, выточки, отверстия, переход от тонкой к утолщённой
части и т. д.).
Эти местные напряжения /?м оказываются значительно выше наи-
наибольших общих напряжений /?гаах> вычисляемых для призматических
стержней, и могут быть представлены формулой
Рм — *кРтах>
где ак — так называемый коэффициент концентрации напряжений;
его величина зависит от характера нарушения призматической формы
стержня.
В дальнейших параграфах рассмотрено определение предела вы-
выносливости и коэффициентов концентрации напряжений.
§ 237. Определение предела выносливости
при симметричном цикле.
Как показывают опыты, величина предела выносливости мате-
материала в значительной степени зависит от соотношения между край-
крайними значениями ртлх и рт-т изменяющегося напряжения. Если эти
значения равны по величине ра и обратны по знаку (фиг. 613), то
мы имеем симметричный цикл, при котором предел выносливости
оказывается наименьшим.
Фиг. 613,
Если мы добавим к симметрично колеблющемуся в пределах -\-ра
и —ра напряжению ещё напряжение постоянной величины рт
(фиг. 614), то получим случай несимметричного цикла; в этом
случае предел выносливости оказывается выше, чем для симметрич-
симметричного цикла.
Крайние значения напряжения при несимметричном цикле /?тах
и Ршп будут (фиг. 614):
И Рт\п=Рт—Ра\
в свою очередь,
i + Pmin
Ятах

§ 237]	ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ВЫНОСЛИВОСТИ	731
Напряжение рт называют средним напряжением цикла, а ра—
амплитудой колебаний напряжения цикла. Отношение г = -^-
Pmzx
называется характеристикой цикла. При симметричном цикле
рт = 0, Pmin=—Ртах и г = —1; при постоянном статическом на-
напряжении /?а=0, Pmin—Pmax И Г — -\-1\ еСЛИ рт[п = О, ТО И Г=0.
Приведём несколько примеров несимметричных циклов:
a) /W = + 800 кг/см* \ рт = Ш кг/см2 \ г__п *
/?min = — 400 кг/см* } /?а = 600 кг/см* }	' '
б) Ртах = + 1000
= + 300
\ />т = 650 кг/см* \ _ , п ~
Удвоенная величина амплитуды колебаний напряжения ра
Ртах—Prnln ^^Pa
называется «размахом» цикла.
Значение предела выносливости для любого цикла переменных
напряжений будем обозначать через р, о или т со значком внизу,
указывающим на соответствующую характеристику цикла. Так, р_х —
предел выносливости при симметричном цикле с характеристикой
г=—1, /?0>2 — предел выносливости при несимметричном цикле
с характеристикой г = -{-0,2 и т. п.
Наибольший интерес представляет определение величины предела
выносливости при симметричном (рт = 0) цикле, как наименьшего.
Эта величина оказывается различной для случая деформации изгиба,
осевой деформации (растяжение и сжатие) и кручения.
Для определения предела выносливости при изгибе применяются
машины, в которых образец круглого поперечного сечения нагру-
нагружается через шарикоподшипники, или как консоль — силой на
конце, или как шарнирно-опёртая балка — симметрично расположен-
расположенными равными силами; образец вращается со скоростью около
2000—3000 об/мин. При каждом обороте материал образца в наи-
наиболее напряжённых местах испытывает симметричный цикл изменения
напряжений от наибольшего сжатия до такого же наибольшего
растяжения, и обратно. Число циклов, испытанных образцом, оп-
определяется числом его оборотов N, отмечаемым специальным
счётчикомх).
Образцам придаётся форма с весьма плавными очертаниями, исклю-
исключающими возможность появления местных напряжений. Опыт по
определению предела выносливости производится следующим об-
образом. Заготовляется партия образцов испытываемого материала в
количестве 6—10 штук; образцам даётся последовательная нуме-
нумерация: 1, 2, 3, ...
1) Описание см. Беляев Н. М., Лабораторные работы по сопротивлению
материалов, § 90.

732
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
Первый образец закладывается в машину и нагружается так,
чтобы получить определённую величину наибольшего нормального
напряжения а'; эту величину обычно берут равной 0,5—0,6 от пре-
предела прочности материала; затем машина пускается в ход, и образец
вращается, испытывая переменные напряжения от -j-a' Д° —°' Д°
тех пор, псхка произойдёт излом. В этот момент специальное при-
приспособление выключает мотор, машина останавливается, и счётчик
оборотов показывает число циклов Nlf необходимое для излома
образца при напряже-
напряжении af.
Тем же порядком
испытывают второй об-
образец при напряжении
о", меньшем of, тре-
третий — при напряжении
о"'<о", и т. д. Соот-
Соответственно возрастает
число циклов, необ-
необходимое для излома.
Уменьшая для каждого
нового образца рабо-
рабочее папряжение, мы, наконец, для какого-то из них не получаем
излома, даже при очень большом числе оборотов образца. Соответ-
сть^ ощее напряжение будет очень близко к пределу выносливости.
Опыты показали, что если стальной образец не разрушился после
10 • 10е циклов, то он может выдержать практически неограниченное
число циклов A00 • 106 — 200 • 106).
Поэтому при определении предела
выносливости для того или иного
сорта стали прекращают опыт, если
образец испытал 10 • 106 циклов и
не сломался. В ряде случаев при
испытаниях ограничиваются и мень-
меньшим предельным числом циклов,
однако, не меньше 5 • 10е.
Для цветных металлов подобной
зависимости нет, и чтобы обнару-
обнаружить, действительно ли при заданном
напряжении образец может выдер-
выдержать очень большое число перемен
знака, приходится давать до 200 • 106
и даже 500 • 106 циклов. В этом случае можно говорить об условном
пределе выносливости, соответствующем отсутствию излома при опре-
определённом числе перемен знака напряжений, — при 10 • 106, 30 • 106 и т. д.
Для нахождения числовой величины предела выносливости полу-
полученные результаты обрабатываются графически. На фиг. 615 и 616
/ИМ2
70
60
40
до
20
10
0
J_
Хромоникелебая сталЬ
GLf55 кг/мм*
I 2
д 4 5
Фиг. 616.
6 7
8Ж

§ 237]	ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ВЫНОСЛИВОСТИ	733
показаны два метода подобной обработки. На первой из них по
оси ординат откладываются величины ог, а", ... , а по оси абсцисс
Nl9 N% и т. д. Ордината горизонтальной касательной к полученной
кривой (асимптоты) и будет равна пределу выносливости с^г На
втором чертеже по оси абсцисс откладываются величины, равные
-Г7-. В этом случае предел выносливости определяется как отрезок,
отсекаемый на оси ординат продолжением полученной кривой,
так как начало координат соответствует N=co. В настоящее время
более употребительным является второй метод.
Подобным же образом определяется предел выносливости для
осевых усилий (растяжение и сжатие) и для кручения; для этой
цели также применяются специальные испытательные машины (пуль-
(пульсаторы и др.*).
В настоящее время получено громадное количество эксперимен-
экспериментальных результатов по определению предела выносливости различ-
различных материалов. Большая часть произведённых исследований отно-
относится к стали, как наиболее употребительному материалу в машино-
машиностроении. Результаты этих исследований показали, что предел
выносливости стали всех сортов связан более или менее опреде-
определённым соотношением лишь с величиной предела прочности при
растяжении ов. Для катаного и кованого материала предел выносли-
выносливости при симметричном цикле в случае изгиба составляет от 0,40
до 0,60 ов; для литья это соотношение заключается в пределах от
0,40 до 0,46.
Таким образом, в запас прочности с достаточной для целей
практики точностью можно принять для всех сортов стали
Если подвергать образец стали осевым усилиям при симметрич-
симметричном цикле (попеременному растяжению и сжатию), то соответствую-
соответствующий предел выносливости о^р как показывают опыты, будет ниже,
чем при изгибе; соотношение между этими пределами выносливости
может быть принято равным, как показывают опыты, 0,7, т. е.
о^1 = 0,7о.
Это снижение объясняется тем, что при растяжении и сжатии
всё сечение подвергается одинаковым напряжениям; при изгибе же
наибольшие напряжения имеют место лишь в крайних волокнах;
остальная часть материала работает слабее и, таким образом, не-
несколько затрудняет образование трещин усталости; кроме того,
на практике всегда имеет место некоторый эксцентриситет осевой
нагрузки.
Наконец, при кручении для симметричного цикла предел вынос-
выносливости по касательным напряжениям составляет в среднем 0,55 от
*) См. сноску на стр. 731.

734	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА [ГЛ. XXXVII
предела выносливости при изгибе. Таким образом, для стали при
симметричном цикле
]
оР1 = 0,7«1 =0,28ов,	C7.1)
J
Эти данные и могут быть положены в основу расчётных формул
при проверке прочности.
Для цветных металлов мы имеем менее устойчивое соотношение
между пределом выносливости и пределом прочности; опыты дают
о5 , = @,24 + 0,60) в..
При пользовании приведёнными выше соотношениями C7.1) надо
иметь в виду, что предел выносливости для данного материала
является характеристикой, зависящей от очень большого числа факто-
факторов (§ 239); данные C7.1) относятся к опытам с образцами сравни-
сравнительно малого диаметра G—10 мм) с полированной поверхностью
и отсутствием резких изменений формы поперечного сечения.
§ 238. Предел выносливости при несимметричном цикле.
Определение пределов выносливости при несимметричных циклах
требует значительно более сложного оборудования, чем при экспе-
экспериментах с симметричным циклом напряжений.
Применение простейших машин с изгибом вращающегося образца
требует добавления специальной пружины, растягивающей или сжимаю-
сжимающей образец; чаще приходится пользоваться ещё более сложными
машинами, осуществляющими осевую нагрузку образца (растяжение,
сжатие) при различных крайних значениях напряжений.
Однако в настоящее время мы имеем уже достаточное количество
опытных данных, чтобы иметь возможность представить графически
или аналитически зависимость предела выносливости металла от
характеристики цикла г, т. е. от соотношения JEL%
Ртах
Напомним принятые нами обозначения: рв— предел прочности
материала, рТ — предел текучести, рг — предел выносливости при
любом цикле напряжений с характеристикой г, р_х— предел вы-
выносливости при симметричном цикле, /?тах и /?min — верхняя и ниж-
нижняя границы цикла, рт — тах ? min	среднее напряжение цикла,
ра = ¦ тах . шш	амплитуда колебаний напряжения цикла, 2ра —
«размах» цикла, г = -^ — характеристика цикла.
Ртах

§ 238] ПРЕДЕЛ ВЫНОСЛИВОСТИ ПРИ НЕСИММЕТРИЧНОМ ЦИКЛЕ
735
Те значения напряжений ртах, рт\п, ра1 рт, при которых материал
будет работать на пределе выносливости, обозначим индексом г внизу:
наибольшее по абсолютной величине значение ргШах или ргт\п совпа-
совпадает с рг.
В частных случаях, когда речь идёт о нормальных или касатель-
касательных напряжениях, буква р заменяется соответственно через о или т;
для обозначения изгиба, кру-
кручения и осевых усилий до-
добавляются вверху индексы
«и», «к» и «о».
Изображая графически
или при помощи формул зави-
зависимость предела выносли-
выносливости от несимметрии цикла,
надо иметь в виду два край-
крайних случая: для симметрич-
симметричного ЦИКЛа (pmin=—pmax>
рт = 0 и г = — 1) эти зави-
зависимости должны давать нам
величину р_х\ для случая же
ПОСТОЯННОЙ НагруЗКИ (/7min =
= /?max> А* = 0 и Г = -|-1)
мы должны получить пре-
предел прочности материала рв.
Наиболее распростране-
распространены два вида диаграмм для
изображения зависимости
Фиг. 617.
Ртах]
диаграмма
,—рт и диаграмма ра—рт. На
диаграмме /?тах — рт (фиг. 617) напряжённое состояние мате-
материала при разной несимметрии цикла, характеризуемой отноше-
отношением -^- = г, изображается двумя точками с ординатами ртйх и
Ртах
Рт'т (например, точки / и 2 на фиг. 617); общей абсциссой этих
точек служит рт — среднее напряжение цикла. Получив из опыта
Ргтах — Рг—значение предела выносливости материала при известной
характеристике цикла г, вычисляем среднее напряжение цикла рт
(абсциссу) и наносим на диаграмму точки С и В с соответствую-
соответствующими ординатами ргтах и ргт{п. Поступая так для серии значений г и
соединяя полученные точки кривыми KF и MF, получаем диаграмму,
дающую зависимость ргтйх и ргт{п от среднего напряжения цикла рт.
(В некоторых случаях, в зависимости от рода материала, кривые KF
и MF могут обратиться в прямые линии.)

736
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
Кривые KF и MF сходятся в точке Fy абсцисса и ордината кото-
которой равны друг другу: ргтах = ргтт=РГт- Таким образом, для этой
точки рга = О и г = -|- 1; ордината её представляет собой разру-
разрушающее напряжение при статической нагрузке, т. е. предел проч-
прочности материала. Прямая, соединяющая точку F с началом коорди-
координат О, проходит под углом в 45° к осям рт и ртах (рт[П); ординаты
точек, расположенных на этой прямой, равны рт, а вертикальные
отрезки между нею и кривыми KF и MF (например, отрезки АС
и АВ) представляют собой опасные значения переменной составляю-
составляющей цикла (амплитуды колебаний напряжения) рга.
При симметричном цикле (рт[п = — /?тах, ра=ртах, рт = 0 и
г = — 1) предел выносливости/?^ изображается отрезками OD и ОЕ.
Точки К и М соответствуют случаю отрицательного рт (сжатие); пре-
предел выносливости изображается
величиной ординаты ргтт{НМ).
Диаграмма показывает, что при
заданной характеристике цикла г
разрушения не произойдёт, пока
амплитуда цикла ра будет меньше
отрезков АС и АВ, т. е. трещина
усталости не образуется, пока
точки / и 2 лежат между кри-
кривыми KF и MF.
На диаграмме ра-рт (фиг. 618)
напряжённое состояние материала
изображается одной точкой С с ординатой ра и абсциссой рт. Таким
образом, все циклы с одним и тем же отношением
ра
Рт ~
изображаются точками прямой ОЕ. Получив для выбранного отно-
отношения ^ величины рга и ргт, соответствующие пределу выносли-
Рт
вости материала, наносим на прямой ОЕ точку D с этими коорди-
координатами.
Ряд подобных точек, располагающихся на кривой ADB, изобра-
изображает напряжённое состояние материала на пределе выносливости
в^зависимости от характера цикла. Величина предела выносливости
при заданном отношении — определяется суммой координат точки
Рт
кривой ADB, т. е. рг = рга-\-ргт (при отрицательном ргт слагае-
слагаемое рга надо тоже брать со знаком минус, ибо в этом случае рг =
= ргтт)' Статической нагрузке соответствует точка В (пересечение
кривой ADB с осью абсцисс): ра = 0 w OB—pB; при симметричном
цикле (рт = 0) предел выносливости р_{ изображается отрезком ОД
на оси ординат.

§ 238]	ПРЕДЕЛ ВЫНОСЛИВОСТИ ПРИ НЕСИММЕТРИЧНОМ ЦИКЛЕ
737
Диаграмма ра-рт показывает, что все точки С, лежащие внутри
площади OADBy соответствуют циклам напряжений, безопасным
в отношении возможности обра-
образования трещины усталости.
Довольно много формул было
предложено для установления ана-
кг.шм2
30
20
10
-го чо о
_L
Фиг. 619.
10
Фиг. 620.
20 30 40
литической зависимости между пределом выносливости, пределом
прочности и характеристиками цикла. Из них заслуживает внимания
следующая формула:
„ Ргт У	/07 o\
кг/мР
«с?
W
1^36А/кг/
Коэффициенты щ и щ имеют
различные числовые значения в
зависимости от рода материала.
Для малоуглеродистой стали
лх = 0 и щ = 1 и зависимость
между рга и ргт имеет форму
параболы; для сталей с высоким
пределом прочности, наоборот,
nl=l, я2 = 0, и указанная зави-
зависимость имеет линейный вид.
Формула C7.2) может быть изо-
изображена графически в форме -20
любой из диаграмм.
На фиг. 619 изображена диа-
диаграмма amax-am, а на фиг. 620—диа-
620—диаграмма оа-от для обычной мало-
углеродистой стали; на фиг. 621
дана диаграмма от^-от для легированной хромоникелевой стали,
причём сплошной линией показана часть графика, полученная
24 Н. М. Беляев
60
40
20
0
-40
И//
//
40
60 80 кг/м*
Фиг. 621.

738
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
непосредственными экспериментами. Механические свойства этих
двух сталей таковы:
авкг/мм2 аткг/мм2 <*_i кг/мм2
Малоуглеродистая сталь @,13о/0 С)	 39,5	33,0	20,4
Легированная сталь @,3<у0С, 3,6o/o Ni, 0,6<>/0Cr) 80,0	55,5	36,4
0
7
7
А
27
/У
/0/10 20 дО
7
?
ю-
для второй
Фиг.
2д
622
ч
N
-30-
-20-
На фиг. 622 и 623
построены диаграммы
для серого чугуна;
механические свойства
этого материала та-
таковы: ой = 78 кг\мм\
19х'№ 30 40 30 20 10
Фиг. 623.
0 10 20 30
= 7,3 кг/мм* и о0 =
= 46 кг/мм* = 0,59cv,
а0 — предел выносли-
выносливости для односто-
одностороннего цикла (напря-
(напряжения меняются от
нуля в одну сторону,
г = 0) при сжатии.
Эти диаграммы сви-
свидетельствуют о том, что и при переменных нагрузках чугун на
сжатие работает значительно лучше, чем на растяжение.
§ 239. Местные напряжения.
Опыты показывают, что для образования трещины усталости имеет
значение величина так называемых местных напряжений, возникаю-
возникающих или в местах резкого изменения призматической формы стержня
(надрезы, выточки, переходы), или при повреждениях его поверх-
поверхности (царапины, риски), или в местах нарушения сплошности мате-
материала (пустоты, включения, трещины).
Все перечисленные факторы, вызывающие развитие местных на-
напряжений, «повышатели напряжений», мы в дальнейшем для кратко-
краткости будем обозначать термином «фактор (источник) концентрации»;

§239]
МЕСТНЫЕ НАПРЯЖЕНИЯ
739
в зависимости от степени резкости нарушения призматической фор-
формы стержня или сплошности материала мы будем говорить о «резком
или смягчённом характере» фактора концентрации.
Местные напряжения рм по своей величине обыкновенно значи-
значительно превышают те наибольшие напряжения /?тах, которые полу-
получаются при отсутствии факторов
концентраций, так называемые
общие напряжения: ры = а^щах,
ак ^> 1 — коэффициент концен-
концентрации напряжений. Величина
(ак—1) характеризует степень
превышения местных напряжений
над общими.
На фиг. 624, а показаны мест-
местные напряжения при изгибе, вы-
вызванные резким изменением раз-
размеров поперечного сечения стерж-
стержня; на фиг. 624, б для сравнения
показано распределение напря-
напряжений в случае плавного изме-
изменения диаметра стержня при от-
отсутствии местных напряжений.
На фиг. 625 изображены мест-
местные напряжения, вызванные на-
наличием отверстия в растянутом	Фиг. 624.
стержне. Из этих диаграмм видно,
что местные напряжения захватывают весьма небольшой объём и, быстро
затухая, падают до величины соответствующих общих напряжений.
Местные напряжения даже при линейном общем напряжённом
состоянии обычно образуют систему, соответствующую более слож-
сложному напряжённому состоянию. На фиг. 625 пока-
показано, что, помимо напряжений по сечениям, перпен-
перпендикулярным к оси стержня, у отверстия возникают
и добавочные меньшие нормальные напряжения по
площадкам, перпендикулярным к первым (о.2).
Величина коэффициента концентрации зависит,
главным образом, от степени резкости нарушения
призматической формы стержня. Если переход от
большего диаметра стержня к меньшему сделан
резким, под прямым углом, то мы получаем наи-
наибольшее значение ак; если же этот переход смягчён
галтелью того или иного радиуса, то величина
ак значительно снижается и может оказаться даже равной единице
(фиг. 624, а и б).
Для определения коэффициентов концентрации применяют сле-
следующие методы. В ряде случаев (например, растяжение и изгиб
ТГфТГ
Фиг. 625.

740	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА	[ГЛ. XXXVII
стержней с отверстиями и выточками) удаётся найти величину мест-
местных напряжений при помощи методов теории упругости. Затем
широкое распространение нашёл метод экспериментального опреде-
определения местных напряжений путём просвечивания поляризованным
светом плоской напряжённой модели из прозрачного материала
(стекло, целлулоид, бакелит); по получающейся при этом окраске
различных участков модели можно установить величину разности
главных напряжений в различных точках, а затем при помощи до-
дополнительных измерений и вычислений и сами величины главных
напряжений.
К числу экспериментальных методов относятся также исследова-
исследования местных напряжений с помощью лаковых покрытий *) или сеток2)
(из квадратов или окружностей малого диаметра), наносимых на
поверхности образцов испытуемого материала и исследования на
хрупких (гипсовых) моделях.
Определяя предел прочности материала путём испытания до раз-
разрушения двух моделей (фиг. 624, а и б), одной с местными напря-
напряжениями, а другой — без них, мы получаем для первой модели
меньшее значение ав, чем для второй (конечно, вводя в вычисления
один и тот же момент сопротивления сечения диаметром d); отно-
отношение этих величин ав и даёт искомый коэффициент концентрации ак.
Однако наиболее надёжным является способ получения ак путём
определения предела выносливости для образцов исследуемого мате-
материала с местными напряжениями и без них. Первые дают понижен-
пониженную (за счёт влияния местных напряжений) величину предела вы-
с"
носливости а'к по сравнению со вторыми а?, отношение -? и будет
равно ак. В результате применения всех указанных методов оказа-
оказалось, что величины коэффициентов концентрации напряжений, опре-
определённые разными методами для одного и того же типа фактора
концентрации, оказываются различными.
Первые два способа — применение теории упругости или опти-
оптического метода — дают близкие друг к другу величины ак; это по-
понятно, так как в обоих случаях результаты исследования относятся
к изотропному упругому материалу; между тем, величины ак, опре-
определённые при помощи испытаний на усталость, оказываются для неко-
некоторых сортов материала (хромоникелевая сталь, углеродистая сталь
высокого сопротивления) близкими к полученным первыми двумя мето-
методами, а для некоторых (малоуглеродистая сталь) значительно по-
пониженными. Оказалось, что коэффициент концентрации зависит
н-е только от формы детали, но и от материала образца. Он тем
ниже, чем материал пластичнее. Известное объяснение этому обстоя-
*) См., например, Прокофьев И. П., Методика изучения деформаций
при помощи лаковых покрытий, «Вестник металлопромышленности», 1936.
2) См., например, С м и р н о в - А л я е в Г. А., Сопротивление материалов
пластическим деформациям, 1949.

МЕСТНЫЕ НАПРЯЖЕНИЯ
741
§ 239]
тельству дано уже в § 17; пластические свойства материала обра-
образуют своеобразный буфер, смягчающий в той или иной степени
эффект местных напряжений.
Таким образом, можно рассматривать два коэффициента концен-
концентрации: первый — теоретический акт — учитывает лишь влияние формы
фактора концентрации и определяется, главным образом, при помощи
первых двух из указанных выше методов; второй же — действитель-
действительный коэффициент концентрации акд, — определяемый опытами на уста-
усталость, учитывает влияние не только формы, но и материала детали.
Так как это влияние сказывается только на превышении местных
напряжений над общими, т. е. на величинах (акт—1) и (акд—1),
то степень «чувствительности» материала к местным напряжениям
можно определить отношением этих двух величин, так называемым
«коэффициентом чувствительности»:
C7.3)
* —*кт-1-
Этот коэффициент зависит от характера материала: для высокока-
высококачественных, термически обработанных легированных сталей он дохо-
доходит до единицы, а для малоуглеродистых сталей падает до 0,5.
Крайне мало чувствительным к местным напряжениям оказывается
чугун; для него величина q близка к нулю и действительные коэф-
коэффициенты акд близки к единице. Это объясняется тем, что предел
выносливости чугуна весьма силь-
сильно зависит от наличия микроско-
микроскопических включений графита,
представляющих собою факти-
фактически очень острые трещины в
массе основного металла; влия-
влияние этих трещин, всегда имею-
имеющихся в чугуне, настолько велико,
что почти совершенно сглаживает
эффект других факторов концен-
концентрации напряжений.
Коэффициент чувствительно-
чувствительности не является, однако, только
характеристикой материала, он за-
зависит от геометрической конфигу-
конфигурации детали и от её абсолютных
размеров; с увеличением абсолют-
абсолютных размеров детали q растёт.
50 60 70 80
100 НО 120 150 14J
бу кг/мм2
Фиг. 626.
Приближённо (без учёта влия-
влияния абсолютных размеров детали)
величина коэффициента чувствительности q для стали может быть
определена из графиков на фиг. 626 в зависимости от предела проч-
прочности материала (в пределах от 40 до 130 /сг/лш2) и от теорети-

742
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
ческого коэффициента концентрации aKt (фиг. 627 и 628). Этот
график получен путём обработки экспериментальных данных по испы-
испытанию на усталость малых (диаметром 7—10 мм) образцов различных
марок стали при разных теоретических коэффициентах концентрации.
V
I*
1,0
0 0,1 0,2 0,2
0,5 0,6 0,7 0,8 0.9 n Ю
Фиг. 627.
Из него видно, что коэффициент чувствительности растёт с увели-
увеличением предела прочности материала и теоретического коэффициента
концентрации. Начиная со значения акт=1,8, дальнейшее увеличение акт
уже не влияет на величину коэффициента чувствительности. Для леги-
легированных сталей с высоким пределом
прочности A30 кг /мм*) можно счи-
считать коэффициент q равным единице
Для цветных металлов имеется
значительно меньше данных о ве-
величине коэффициента чувствитель-
чувствительности. Для электрона (сплав магния
с алюминием, цинком, марганцем)
в отливках этот коэффициент ра-
равен 0,15; в редких случаях он по-
повышается до 0,25. Для электрона
в тянутом или штампованном виде
коэффициент чувствительности по-
повышается и колеблется в пределах 0,35 — 0,50. Для алюминиевых
сплавов наблюдались несколько более низкие значения коэффициен-
коэффициентов чувствительности.
Для определения теоретического коэффициента концентрации
в наиболее распространённых случаях концентрации напряжений
(отверстия, выточки, галтели) могут быть использованы изображён-
41 0tZ 430,У Of 0,6 0,7 0,8 0,910
d
Фиг. 628.

§ 239]
МЕСТНЫЕ НАПРЯЖЕНИЯ
743
ные на фиг. 627 и 628 графики изменения величины акт в зависимости
от степени резкости нарушения формы детали при растяжении или
сжатии (фиг. 627) и чистом изгибе (фиг. 628). Эти коэффициенты
определены на плоских образцах с помощью оптического метода
измерения напряжений. Для круглых образцов с выточками и галте-
галтелями соответствующие значения акт оказываются несколько мень-
меньшими. Некоторые значения акт для круглых стержней приведены
в таблице 37.
Таблица 37. Коэффициенты концентрации.
Вид деформации и фактора концентрации напряжений
I. Изгиб и растяжение:
1.	Полукруглая выточка на валу; отношение радиуса
выточки к диаметру вала:
0,1
0,5
1,0
2,0
2.	Галтель
Отношение радиуса полной галтели к высоте сечения
(диаметру вала):
0,0625
0,125
0,25
0,5
3.	Переход под прямым углом
4.	Острая V-образная выточка
5.	Нарезка дюймовая
6.	Нарезка метрическая
7.	Отверстия при отношении диаметра отверстия к попе-
поперечному размеру сечения от 0,1 до 0,33	,
8.	Риски от резца на поверхности изделия
И. Кручение:
1.	Галтель при отношении радиуса галтели к наимень-
наименьшему диаметру вала:
0,02
0,10
0,20
2.	Шпоночные канавки
2,0
1,6
1,2
1Д
1,75
1,50
1,20
1,10
2,0
3,0
2,0
2,5
2,0
1,2-1,4
1,2
1,1
1,6—2,0
Следует подчеркнуть, что с помощью графиков фиг. 627 и 628
и таблицы 37 определяются теоретические, т. е. максимальные воз-
возможные значения коэффициентов концентрации; зная величину теоре-
теоретического коэффициента концентрации акт, величину действительного
коэффициента концентрации акд можно вычислить по формуле
«м=1-И(««-1).	C7.4)
вытекающей из соотношения C7.3). Однако если значение коэффи-
коэффициента чувствительности q> входящего в эту формулу, приближённо

744	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА	[гл. XXXVU
определять с помощью графиков фиг. 626, то искомая величина
действительного коэффициента концентрации акд окажется вычислен-
вычисленной тоже приближённо. Поэтому значения акд предпочтительнее
определять непосредственно из испытаний на усталость образцов
соответствующей формы. Значения коэффициентов концентрации
акт и акд для более широкого круга факторов концентрации приво-
приводятся в специальных курсах и справочных пособиях*).
Довольно простые приближённые эмпирические формулы были
предложены для вычисления действительных коэффициентов концен-
концентрации для стали в зависимости от предела прочности. В том случае,
когда деталь не имеет резких переходов, выточек, шпоночных кана-
канавок и обладает чисто обработанной резцом поверхностью (но не
полированной)
«„=1,2 + 0,2-2^.	C7.5)
В случае же, когда имеются резкие переходы, надрезы, выточки:
ам=1,5 + 1,5^=^.	C7.6)
Эти формулы годятся для стали с пределом прочности
40—130 кг\мм* и являются достаточными для практического при-
применения; ов выражается в кг/мм*.
Говоря о местных напряжениях, необходимо особенно подчерк-
подчеркнуть влияние всякого рода повреждений поверхности на величину
предела выносливости. Опыты показали, что кованые детали с по-
поверхностью, не подвергавшейся механической обработке, дают предел
выносливости, меньший, чем тот же материал после удаления по-
поверхностного слоя и полировки; разница достигает для малоуглеро-
малоуглеродистой стали 15—20%, для высококачественных сталей даже 50%.
Подобного же рода явление наблюдается при работе пружин,
изготовляемых из высокосортных легированных сталей, если поверх-
поверхность этих пружин после термической обработки (закалка и отпуск)
не подвергается уже механической обработке; наличие подобной
поверхности снижает предел выносливости в некоторых случаях
вдвое. Даже простые царапины и риски снижают предел выносли-
выносливости на 10—20%-
Очень важным фактором, вызывающим значительную концентра-
концентрацию напряжений, является плотная посадка с натягом одной детали
на другую, например ступиц шкивов, дисков и колёс на вал или
ось. Многочисленные опыты показали, что в этом случае действи-
действительный коэффициент концентрации доходит до 1,8—2,0. Конструк-
Конструктивными мерами (§ 245) можно понизить эту величину.
1) См., например, Серенсен СВ., Тетельбаум И. М., Пригоров-
ский Н. И., Динамическая прочность в машиностроении, 1946.

§ 240]	ВЛИЯНИЕ РАЗМЕРОВ ДЕТАЛИ	745
Специальный вид комбинированного влияния местных напряжений
и химического воздействия представляет собой резкое снижение
предела выносливости при коррозии. Опыты показывают, что если
производить испытания на усталость в воде или другой жидкости,
вызывающей коррозию металла, то предел выносливости значительно
снижается. Это влияние слабо сказывается на нержавеющей стали.
Наконец, за счёт своеобразных местных напряжений надо отнести
влияние на предел выносливости структуры стали. Так как металл
представляет собой конгломерат кристаллических зёрен различной
величины и различно ориентированных, то в действительности мы
всегда имеем в известной мере неравномерное распределение напря-
напряжений даже при простом растяжении. Эта степень неравномерности
увеличивается с неравномерностью величин отдельных зёрен. Поэтому
получение возможно более однородной мелкозернистой структуры
стали при помощи термической обработки повышает предел выно-
выносливости.
В заключение необходимо ещё раз подчеркнуть, что чем более
высокую прочность имеет сталь, тем она чувствительнее ко вся-
всякого рода надрезам и повреждениям поверхности, тем более
культурной обработки она требует.
Полученными данными о пределе выносливости и о коэффициен-
коэффициентах концентрации мы воспользуемся в дальнейшем, чтобы установить
правила для выбора допускаемых напряжений.
§ 240. Влияние размеров детали на величину
предела выносливости.
Приведённые выше данные о величине предела выносливости
получены, как правило, при испытании образцов малого диаметра,
от 7 до 10—12 мм. В последнее время начали определять предел
выносливости на образцах большого диаметра, до 40—50 мм. Суще-
Существуют машины для испытания на усталость осей подвижного состава
в натуральную величину, позволяющие испытывать оси диамет-
диаметром 150 и даже 300 мм.
Эти опыты показали, что, во-первых, результаты, получаемые для
отдельных образцов такого большого размера, дают очень значи-
значительный разброс точек при попытке определить предел выносливости
по методу, данному на фиг. 616, во-вторых, предел выносливости,
хотя и не очень точно определённый вследствие разброса данных
эксперимента, всё же оказывается для больших образцов ниже, и
иногда значительно ниже, чем для малых. Это снижение особенно
имеет место для легированных сталей; на предел выносливости угле-
углеродистых сталей влияние абсолютных размеров значительно слабее.
Экспериментально установленный факт снижения предела выно-
выносливости в изделиях по сравнению с величиной предела выносли-
выносливости в малых образцах, испытываемых обычно в лабораториях,

746	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА [гл. XXXVII
имеет очень большое значение, так как это обстоятельство идёт
не в запас прочности.
К сожалению, в настоящее время ещё не найдено более или менее
достоверное объяснение этому факту; по-видимому, указанное снижение
предела выносливости вызывается рядом обстоятельств, в частности:
а)	В больших образцах более вероятно наличие различных вну-
внутренних факторов концентрации напряжений (включения, пузыри
и т. д.); малые образцы оказываются в этом отношении обычно чище.
б)	При изготовлении образцов поверхностный слой получает
некоторый наклёп, который может оказаться относительно большим
в малых образцах; между тем опыты показывают, что наклёп в целом
ряде случаев может повышать предел выносливости.
в)	Наконец, при одной и той же величине наибольшего (в край-
крайнем волокне) напряжения в малых образцах падение напряжения при
переходе к более глубоко расположенным слоям металла происходит
интенсивнее, чем в больших; как говорят, градиент напряжений
в малых образцах больше, и отдельные кристаллические зёрна ока-
оказываются в лучших условиях.
Все эти соображения, однако, являются лишь некоторыми пред-
предположениями.
Эксперименты с определением действительных коэффициентов
концентрации на образцах разных размеров показали, что увеличение
абсолютных размеров образца в известной мере эквивалентно повы-
повышению коэффициента чувствительности материала. Например, испы-
испытание двух образцов с диаметрами 10 и 40 мм из углеродистой
стали с ов = 50 кг/мм* показало, что при ~ =0,025 для малого
образца акд = 1,5, в то время как для большого акд = 2,4, т. е. совпадает
с его теоретическим значением. Зато при увеличении -т коэффи-
коэффициент акд для больших образцов падает резче, чем для малых. Всё
это имеет большое практическое значение, так как показывает, что
факторы концентрации, вызывающие большие местные напряжения,
в действительности гораздо опаснее, чем это дают лабораторные
опыты с малыми образцами.
Таким образом, при проверке прочности материала влияние абсо-
абсолютных размеров детали на величину предела выносливости обяза-
обязательно должно быть учтено. Избежать необходимости такого учёта,
очевидно, можно было бы только, определяя величину предела
выносливости на моделях деталей, изготовленных в натуральную
величину. Последнее, однако, далеко не всегда возможно. Вместе
с тем в настоящее время уже имеется более или менее достаточное
количество данных по сравнительным испытаниям на усталость
малых лабораторных (диаметром 7—10 мм) и больших образцов
из одного и того же материала. Используя эти данные и оценивая
степень снижения предела выносливости за счёт увеличения размеров

§ 241]
ПРАКТИЧЕСКИЕ ПРИМЕРЫ РАЗРУШЕНИЯ
747
образца с помощью так называемого масштабного коэффициента
ам, представляющего собой отношение предела выносливости малого
образца рГ к пределу выносливости геометрически подобного боль-
большого образца или детали р*, можно по известному значению пре-
предела выносливости, полученному из испытаний малых образцов,
приближённо определить величину предела выносливости детали.
Так как <хм = —, то
м рж
р* = ^.	C7.7)
Величина масштабного коэффициента ам в зависимости от абсо-
абсолютных размеров образца или детали может быть определена по
графикам фиг. 629. При
этом снижение предела '&$
выносливости детали оп-
определяется по отноше-
отношению к пределу выносли-
выносливости, полученному из ис-
испытаний на усталость об-
V
/
/
/
/
/
/
у
/
/
/
/
/
Г
/
/
/
Г
1/
/
/
i
Г
10 15 20253035*0 50 60 80 100 150 200
Фиг. 629.
разцов диаметром 10 мм. /j
Величина ам зависит не
только от абсолютных .'
размеров детали, но и V
от материала детали и /^
фактора концентрации ..
напряжений. На фиг. 629 '
по кривой 1 определяются V
значения <хм для деталей
из углеродистых сталей
при отсутствии концен-
концентрации напряжений, по кривой 2 — для деталей из углеродистых сталей
при умеренной концентрации напряжений (акд <^ 2) и для деталей из
легированных сталей при отсутствии концентрации напряжений, по
кривой 3 — для деталей из легированных сталей при наличии кон-
концентрации напряжений. Графики фиг. 629 можно применять для глад-
гладких образцов только при изгибе и кручении, а для образцов с кон-
концентрацией напряжений — при всех видах напряжённого состояния.
§ 241. Практические примеры разрушения при переменных
нагрузках. Механизм появления и развития трещин усталости.
После того как установлены все обстоятельства, характеризую-
характеризующие явление разрушения при переменных нагрузках, следует рас-
рассмотреть некоторые практические случаи подобного вида поломок.
На фиг. 630 и 631 показан случай излома вагонной оси (изгиб
при вращении), вызванный резким переходом от утолщённой части

748
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[гл. xxxvu
к более тонкой; вместо плавного перехода галтелью дай ступенча-
ступенчатый переход с грубыми рисками от резца. Трещина усталости начи-
начинается с наружной поверхности и имеет кольцеобразную форму.
Фиг. 630.
Фиг. 631.
Материал оси вполне удовлетворителен; на это указывает и весьма
малая площадь зоны мгновенного излома.
На фиг. 632 показан излом оси, не вращавшейся, а лишь изгибав-
изгибавшейся в вертикальной плоскости. Материал — осевая сталь с преде-
Фиг. 632.
Фиг. 633.
лом прочности около 50 кг/мм*. Причиной развития трещины уста-
усталости явился резкий (под прямым углом) переход от квадратного
сечения оси к круглому.
На фиг. 633 показан продольный разрез другого конца этой же
оси, ещё не успевшего сломаться; ясно видны трещины усталости,

§241]
ПРАКТИЧЕСКИЕ ПРИМЕРЫ РАЗРУШЕНИЯ
749
Фиг. 634.
распространяющиеся от крайних волокон сечения в месте рез-
резкого перехода.
На фиг. 632 видны зоны этих трещин и зона окончательного
излома. Следует обратить внимание на ряд криволинейных полос и
линий на поверхности трещин усталости. Это — следы постепенного
развития трещины; разрушение идёт примерно по нормали к этим
линиям; таким образом,
изучая расположение этих
линий, мы всегда можем
найти исходный пункт,
откуда началось разви-
развитие трещины; как пра-
правило, там и следует
искать источник местных
напряжений, вызвавших
начало трещины. Рост
трещины объясняется тем,
что у её дна, в свою оче-
очередь, развиваются очень
высокие местные напряжения, которые и обусловливают дальнейшее
распространение трещины в глубь металла.
Интересно отметить, что оси, излом одной из которых изображён
на фиг. 632, не давали трещин усталости, когда они изготовлялись
из более мягкой стали (ов^40 кг[мм\ даже при той же конфи-
конфигурации. Здесь сказывается
различная чувствительность
этих сталей к местным на-
напряжениям.
На фиг. 634 показаны
трещины усталости, начав-
начавшие распространяться от от-
отверстия для смазки в шейке
коленчатого вала, работав-
работавшего на переменное (в раз-
разные стороны) кручение. Тре-
Трещины идут под углом 45°
к оси вала, перпендикулярно
к главным напряжениям.
На фиг. 635 показано
начало трещины усталости
на оси моторной дрезины, у места очень небольшого @,5 мм вы-
высотой), но очень резкого уступа. Мы видим, что трещина усталости
начинает развиваться в нескольких местах сразу и даже не строго в
одном сечении. Позднее все эти трещины сливаются в одну.
На фиг. 636 и 637 показаны очертания двух паровозных осей,
из которых одна, с плавными переходами, прослужила благополучно
Фиг. 635.

750
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
40 лет, вторая же, с резким надрезом, — всего один год. Материал
второй оси был лучше, чем первой.
Фиг. 636.
Фиг. 637,
Наконец, на фиг. 638 показан пример трещины усталости, на-
начавшейся от внутреннего фактора концентрации. Пустота или посто-
постороннее включение в головке рельса создали очаг местных напряже-
напряжений, вызвавший постепенное раз-*
витие трещины, ослабившей сече-ч
ние и приведшей к излому. На поверх-
поверхности излома трещина имеет вид
серебристого пятна.
Приведённых примеров доста-
достаточно, чтобы показать характерные
черты изломов усталости.
Опыт показывает, что главную
роль в образовании этих изломов
играет не качество материала (обычно
оно оказывалось вполне нормаль-
нормальным), а совершенно неправильная
обработка детали, вызывающая весь-
весьма значительные местные напряже-
напряжения. Гораздо реже могут быть случаи,
когда плохое качество материала
может обусловить появление тре-
трещины усталости при таком повре-
повреждении поверхности, которое при нормальном материале, может быть,
и не вызвало бы излома. Нам известен случай излома оси вследствие
наличия точки, выбитой острым керном на поверхности вагонной оси.
В заключение настоящего параграфа следует остановиться на том
физическом процессе, который вызывает и заставляет развиваться
трещину усталости.
Фиг. 638.

§ 241]	ПРАКТИЧЕСКИЕ ПРИМЕРЫ РАЗРУШЕНИЯ	751
При действии высоких местных напряжений, вызванных тем или
иным фактором концентрации и обычно значительно превышающих
предел текучести материала, в отдельных кристаллических зёрнах
начинаются сдвиги, аналогичные тем, которые имеют место и при
статическом растяжении. Разница заключается лишь в том, что при
растяжении образца пластические деформации и явления сдвига
в кристаллических зёрнах вызываются общими напряжениями, охва-
охватывают поэтому весь объём образца и растут в одном направлении;
при переменных нагрузках эти деформации происходят в пределах
очень малого объёма, подвергающегося местным напряжениям, и
происходят то в одном, то в противоположном направлениях. Поэтому
они не оказывают заметного влияния на прочность образца в целом,
но та часть материала, которая подвергается высоким местным
напряжениям, постепенно проходит все стадии пластической дефор-
деформации, которые испытывает материал всего образца, подвергающегося
простому растяжению.
При каждом цикле изменения нагрузок пластически деформиро-
деформированная часть материала, попавшая в зону высоких местных напря-
напряжений, испытывает сдвиги то в том, то в другом направлениях;
каждый новый сдвиг происходит в другой плоскости, чем предыдущий,
так как эти сдвиги сопровождаются упрочнением материала. По мере
упрочнения пластически деформированный объём всё более прибли-
приближается по своей жёсткости к упругому, окружающему его материалу,
и в связи с этим берёт на себя всё большую долю нагрузки. Это
вызывает непрерывный рост фактических максимальных напряжений
в рассматриваемом малом объёме материала при остающемся постоян-
постоянном среднем (измеряемом) напряжении. В то же время это разгру-
разгружает упругую зону, что влечёт за собой уменьшение её деформаций,
а значит, и деформаций пластической части материала, заключённей
внутри упругой зоны.
Таким образом, при переменных нагрузках происходит посте-
постепенный рост фактических наибольших напряжений перенапряжён-
перенапряжённого объёма материала, а в связи с этим постепенное затухание его
деформаций. Если это затухание успеет закончиться раньше, чем
фактические напряжения дойдут до величины разрушающего напря-
напряжения, материал не даст трещины; мы будем иметь случай работы
детали при напряжениях, лежащих ниже предела выносливости.
В противном случае, если эти напряжения успеют сделаться равными
разрушающему напряжению, возникает начальная трещина, у дна ко-
которой процесс повторяется и вызывает дальнейший рост трещины; де-
деталь работает при напряжениях, превышающих предел выносливости.
Физический процесс разрушения при переменных нагрузках по
существу не отличается в общих чертах от тех явлений, которые
имеют место при статическом растяжении. Это заключение подтвер-
подтверждается и современными исследованиями при помощи рентгеновских
лучей механизма разрушения в обоих случаях.

752
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
§ 242. Установление допускаемых напряжений.
Было установлено, что основную роль в образовании трещин
усталости и разрушении металла от повторно-переменных нагрузок
играют местные напряжения. Поэтому условие прочности при пере-
переменных напряжениях придётся Составлять так, чтобы именно местные
напряжения не превышали предела выносливости с коэффициентом
запаса &0, т. е.
или
Рг _|
°Якд
C7.8)
Величины рг и акд найдены; остаётся, выбрав основной коэффициент
запаса kOy найти допускаемые напряжения [рг]\ влияние динамич-
динамичности нагрузки следует учесть или при вычислении /?тах при помощи
динамического коэффициента (§ 216), или добавочным специальным
коэффициентом запаса kr Влияние размеров детали на величину
предела выносливости рг следует учесть введением масштабного
коэффициента <хм (см. § 240). Таким образом, для детали вместо
C7.8) будем иметь:
_ Рг _|
C7.9)
кд
Рассмотренные в § 238 диаграммы (фиг. 617 и 618) дают вели-
величины наибольших напряжений, при которых разрушение происходит
или путём развития трещины усталости, или (при ра = 0) путём
простого разрыва. Таким обра-
образом, из этих диаграмм можно
получить величины напряже-
напряжений, эквивалентных пределу
прочности материала.
Однако при применении
пластичных материалов нару-
нарушение нормальной работы кон-
Гт	/|' /§ /	о?	струкции обычно происходит
/ I /.[I /	уже при напряжениях, равных
пределу текучести /?т. По-
Поэтому, чтобы получить пол-
полный график разрушающих на-
напряжений, надо на диаграммах
pmiLX — pm и ра — рт нанести
| ? /	Фиг. 639.	линию, изображающую напря-
напряжённое состояние Ртм = Ръ-
На диаграмме РтцХ~~Рт эт0 сделать просто: достаточно провести пря-
прямую GK> параллельную оси абсцисс и имеющую ординатой/?т (фиг. 639).
с*1

§ 242]	УСТАНОВЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ	753
Тогда график «разрушающих», в практическом смысле слова, на-
напряжений изобразится линией DMTNE, заштрихованной на чертеже.
Этот график имеет достаточно сложный для практического приме-
применения вид. В запас прочности его можно заменить двумя прямыми,
соединив точку Т с D и Еу как показано на фиг. 639 пунктиром.
Таким образом, упрощённая диаграмма ртах—рт для разрушающих
напряжений имеет вид треугольника DTE с ординатами рТ (предел
текучести) в точке Т и р_х (предел выносливости при симметричном
цикле) в точках D и Е, Диаграмма легко может быть построена по
этим трём точкам.
Зная предел прочности ав, можно найти необходимую для построе-
построения графика величину р_г при любом виде деформации (растяжение
или сжатие, изгиб, кручение) и определить тем самым положение
точек D и Е.
Как мы видели выше (§ 237), величина предела выносливости
при симметричном цикле р_х связана с ав соотношением /?_1 = ркав,
где Рк — числовой коэффициент, соответствующий тому или иному
виду деформации. Мы имели:
растяжение и сжатие	а^_ х = 0,28ав,
изгиб .	о^_х =0,4ав,
кручение	TLj =0,22ав.
Подобным же образом можно связать предел текучести с пределом
прочности формулой рт = рт/?в. Результаты многочисленных опытов1)
дают следующие значения предела текучести:
Углеродистые стали
Растяжение или сжатие	а° = @,56 -ь 0,60) ав
Изгиб	a!j= 1,20 а° = @,67 4-0,72) <гв
Кручение	 т^ = 0,60 а° = @,34 -ь 0,36) зв
Специальные стали
Растяжение или сжатие	а° = @,75 -~ 0,8) ав
Изгиб	°; = 1,П °? = @,83 4- 0,89) jb
Кручение	< = 0,60 а°т = @,45 -Ь 0,48) зв
Здесь oj, a^ и т^ представляют собой значения предела текучести
при растяжении или сжатии, изгибе и кручении. Эти данные позво-
позволяют установить положение точки Т на диаграмме фиг. 639.
Разделив ординаты графика фиг. 639 на коэффициент запаса
и учитывая величину коэффициента концентрации акд, а также и
J) С е р е н с е н С. В., Тетельбаум И. М., П р и г о р о в с к и и Н. И.,
Динамическая прочность в машиностроении, 1946.

754
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
величину масштабного коэффициента ам, мы можем из этой диаграммы
получить график допускаемых напряжений для всех видов нагрузки
как переменной, так и постоянной.
Коэффициент запаса ?0, учитывающий влияние общих для всех
случаев работы материала обстоятельств, можно, как уже указано
(§ 17), принимать равным от 1,4 до 1,6. Так как величина коэф-
коэффициента концентрации акд отражается на прочности пластичных
материалов лишь при переменных напряжениях и почти не имеет
значения (§ 16) при дей-
действии постоянных нагру-
нагрузок, то полностью его
следует учесть лишь при
симметричном цикле; при
постоянной нагрузке его
можно не учитывать, а
при несимметричных цик-
циклах следует вводить по-
пониженные значения этого
коэффициента. Влияние
размеров детали сказы-
сказывается, главным образом,
также при переменных
напряжениях.
Таким образом, с из-
известным приближением
график допускаемых на-
напряжений [рг] может быть
получен таким путём
(фиг. 639): ординату точ-
точки Т делим на коэффи-
коэффициент запаса kQ, а ординаты точек D и Е — на ?оакдам; полученные
точки соединяем прямыми линиями (фиг. 640). При таком построе-
построеи ам постепенно падает от симметричного цикла к
640.
нии влияние а
случаю постоянной нагрузки. Ординаты прямой DT (фиг. 640) пред-
представляют собой величины допускаемых напряжений [рг] для раз-
различных случаев соотношений /?Шш и /?тах.
Для случая постоянной нагрузки допускаемое напряжение
[^+1] = ?i и изображается ординатой точки Т\ для случая симме-
тричного цикла допускаемое напряжение [p_t]= p~l изображается
#оаа
ординатой точки D\ наконец, при одностороннем цикле, когда напря-
напряжение меняется от нуля до определённой величины, величина допу-
допускаемого напряжения [р0] изображается ординатой точки N.
Чтобы получить графики разрушающих и допускаемых напряже-
напряжений из диаграммы ра—рт (фиг. 618), надо на этом чертеже нанести

§ 242]
УСТАНОВЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ
755
линию, изображающую условие /?max=/V> подставим вместо /?тах
его значение рт-\-Рф тогда на диаграмме ра — рт уравнение
изобразится прямой QMN (фиг. 641). Графиком разрушающих на-
напряжений будет линия AMN\ в запас прочности ей можно заменить
прямой AN.
Поступая так же, как при обра-
обработке предыдущей диаграммы, мы
получим график допускаемых на-
напряжений в виде, показанном на
фиг. 642. Сумма ординаты [ра]
и абсциссы [рт] каждой точки
прямой АВ представляет собой ве-
величину допускаемого напряжения
[рг] для того или иного цикла на-
напряжений
в
На
фиг.
и
Фиг. 641.
642 показаны и величины допускаемых напряжений
Чтобы при заданной характеристике цикла г найти при помощи
описанных диаграмм величину допускаемого напряжения [рг], надо
на диаграмме фиг. 640	i, .
провести луч ОС, на-	^ *'
клонённый к оси абс-
абсцисс под углом ^опре-
^определяемым условием
Рт
2/W
ордината точки С прямо
и даст нам величину	Фиг. 642.
допускаемого напря-
напряжения [рг]. На диаграмме фиг. 642 надо через начало координат
провести луч OD, наклонённый к оси абсцисс под углом рА, тан-
тангенс которого равен
ра Ртах Pmin I — Г
= — =	-г-	• = . . }
Рт Ятах + Pmin l "Г г
сумма абсциссы и ординаты точки D пересечения этого луча с пря-
прямой АВ и дает нам величину [рг].

756	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА [ГЛ. XXXVII
Легко получить и формулу, выражающую [рг] через [р+\], [p_i]
и характеристику цикла г. Используем, например, диаграмму ра—рт
(фиг. 642). Для заданной характеристики г отношение — = tg fa =
Рт
= у , ; допускаемое напряжение выражается суммой
[pr] = OK-\-KD = KD(l-\- ctg fa).
Величина KD определяется из подобия треугольников KDB и
ОАВ:
KD [p+l] -
_К]В Hm_
—ОВ ИЛИ
О A —OB	lP-i]~	Ip+i]
Отсюда
Подставляя значение ctg px = t , имеем:
\РЛ- A_r
После определения допускаемого напряжения можно составить
и условие прочности:
*?\Рг\-	C7.11)
Если переменные нагрузки меняются не плавно, а сопровождаются
резкими ударами, то допускаемое напряжение [рг] следует разделить
ещё на дополнительный коэффициент запаса kr Величина этого
коэффициента меняется в зависимости от несимметрии цикла. Чем
резче меняется напряжение, тем выше этот коэффициент; для по-
постоянной нагрузки он должен быть принят равным единице, для
симметричного цикла пусть его значение будет &д; для того чтобы
учесть влияние динамики при промежуточных типах нагрузок, можно
поступить так же, как и при учёте концентрации напряжений,
а именно, делить ординату р_г не на ?оакдам, а на ?оакдам&д; орди-
ординату же /?+1 делить только на kr Числовые значения коэффициента
kx обычно колеблются между 1 и 2.
Общий ход решения задачи установления допускаемых напряже-
напряжений описанным способом может быть представлен в виде следующей
схемы.
Дано: а) вид деформации; б) соотношение напряжений /?max w
ршт\ в) конфигурация детали; г) механические характеристики мате-
материала (ав). Требуется найти допускаемое напряжение [рг\.
Схема решения:
1. Вычислить
Ртах i ^min	Pmax ^rain
Р =И Р

§ 242]	УСТАНОВЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ	757
2. Найти
	Лпш
3. Определить предел выносливости для симметричного цикла при
данном виде деформации:
4.	По графикам фиг. 627 и 628 найти акт в зависимости от кон-
конфигурации детали.
5.	По графику фиг. 626 найти q.
6.	Вычислить действительный коэффициент концентрации:
Действительный коэффициент концентрации может быть вычислен и
по формулам (§ 239):
о jb — 40	1 - , 1 - сгв — 40
,2-^^, или ^=1,5 + 1,5-^щ-,
если известен лишь общий характер обработки детали.
7.	По графикам фиг. 629 в зависимости от размеров детали найти
величину масштабного коэффициента ам.
8.	Найти допускаемое напряжение для симметричного цикла
9. Найти предел текучести материала /;T = jJTaB.
10. Определить допускаемое напряжение при статической на-
нагрузке
11. Найти искомое значение допускаемого напряжения
Описанный выше метод установления допускавхмых напряжений
является в значительной мере приближённым за счёт спрямления
диаграмм и недостаточно точного учёта влияния коэффициента кон-
концентрации. При желании можно пользоваться более точным изо-
изображением графика разрушающих напряжений1), не прибегая к
спрямлению его пунктирными линиями, как это было показано на
фиг. 639 и 641. Уточнённый способ расчёта может дать значительное
г) См., например, Подзолов И. В., Расчёт допускаемых напряжений
для чёрных металлов, Оборонно, 1947.

758	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА [ГЛ. XXXVII
повышение расчётной величины допускаемого напряжения для циклов
с характеристикой г, близкой к г = 0, при значениях предела выно-
выносливости, близких к пределу текучести; в остальных случаях раз-
разница в результатах расчёта по спрямлённой и уточнённой диаграммам
будет сравнительно невелика.
§ 243. Примеры.
Пример 140. Проверить прочность штока поршня паровой машины
паровоза серии С. Давление пара в котле паровоза q = 10 am. Диаметр ци-
цилиндра D = 550 мм. Материал штока — углеродистая сталь с пределом
прочности <7в = 60 кг/мм*, диаметр штока с? ==90 мм.
Мы имеем дело с симметричным циклом; сила Р, растягивающая и сжи-
сжимающая шток, равна:
p = g^=	= 23760yg
4	4
Найдём допускаемое напряжение [рг]. Так как цикл напряжений симметричен,
то г = —1 и [Pr]==[/7-i]:=:[a-i]- Предел выносливости при симметричном
цикле (осевые усилия) равен р°__ t = a^_ i = 0,28aB = 0,28 • 6000 = 1700 кг/см2.
Поверхность штока обрабатывается чисто, переходы смягчаются достаточно
плавными галтелями; поэтому действительный коэффициент концентрации
равен:
«вд= 1,2+ 0,2-^^=1,24.
Дополнительный коэффициент запаса kA можно было бы принять, учи-
учитывая внезапное приложение нагрузки, равным 2; однако, в связи с некоторой
потерей давления пара при переходе в цилиндр и смягчением при этом удара,
его можно снизить и принять равным 1,6.
По графику фиг. 629 для детали диаметром 90 мм по кривой 2 (угле-
(углеродистая сталь при умеренной концентрации напряжений) находим величину
масштабного коэффициента ам=1,62. Основной коэффициент запаса k0 при-
принимаем 1,4. Допускаемое напряжение [s-i] = [<^_1] равно:
г> .	°1«	1700	1700 О7
1]	^	37
1°->] = Щ^= 1,4.1,6.1,24.1,62
Наибольшее действительное напряжение в штоке
Пример 141. Определить допускаемое напряжение на изгиб для пальца
кривошипа диаметром с? = 12 см, имеющего галтель радиусом г = 5 мм;
палец изготовлен из углеродистой стали с пределом прочности ав = 60 кг/мм2;
цикл напряжений симметричен.
В данном случае [рг] = [p_t] = [a^ t ]; предел выносливости для симме-
симметричного цикла при изгибе равен:
о^ 4 = 0,4ав = 0,4 . 6000 = 2400 кг/см2.
Отношение ¦х==Т20==0>042; П0 гРа*икУ Фиг- 628 нах°Дим акт ПРИ -^-=0,042:
«„ = 1,90.

§ 243]	примеры	759
По графику фиг. 626 находим коэффициент чувствительности q при
<хкт = 1,9 и ав = 60 кг!мм2:
? = 0,57.
Действительный коэффициент концентрации равен:
«кд= 1 +(«кт- 1)?= 1 +0,90- 1) . 0,57 = 1,51.
Надо заметить, что вычисленное значение акд близко к полученному прямым
опытом для этой стали.
По графику фиг. 629 для детали диаметром 120 мм по кривой 2 (угле-
(углеродистая сталь с умеренной концентрацией напряжений) находим величину
масштабного коэффициента ам=1,73. Основной коэффициент запаса с учётом
динамики принимаем равным ?<>'= 1,8, тогда допускаемое напряжение равно:
г ,	2400	2400
И = 1,8.1,5Ы,73 = W
Посмотрим, как изменится допускаемое напряжение, если палец сделать из
специальной стали с пределом прочности ав = 100 кг/мм2. Предел выносли-
выносливости при изгибе для симметричного цикла будет равен:
а^ = 0,4 ав == 0,4 • 10 000 = 4000 кг/см*.
Теоретический коэффициент концентрации останется прежним и равным 1,9;
коэффициент чувствительности будет равен (по графику фиг. 626) 0 = 0,82;
действительный коэффициент концентрации будет равен:
«кд = 1 + A,9 — I) 0,82 = 1,74.
Масштабный коэффициент, определённый по кривой 3 фиг. 629 (легированная
сталь при наличии концентрации напряжений), равен ам = 2. Допускаемое
напряжение равно:
Таким образом, хотя предел прочности материала увеличился более чем
на 65%, допускаемое напряжение повысилось всего лишь на 25%. Увеличим
теперь радиус галтели г до 10 мм, но оставим по-прежнему углеродистую
сталь с ав = 60 кг/мм2. Тогда
теоретический коэффициент концентрации акт=1,75; коэффициент чувстви-
чувствительности #«=0,56. Действительный коэффициент концентрации равен:
«ад =« 1+0,75-1). 0,56 =1,42.
Масштабный коэффициент равен ам = 1,73. Допускаемое напряжение
р
I
Пример 142. Определить допус-
допускаемую величину силы Р для вала,
изображённого на фиг. 643. Предел
прочности легированной стали, из ко- \*-мнАа в\**~БДп
торой изготовлен вал, равен <?в=х	' -	w"
= 90 кг/мм*. Сила Р состоит из двух	Фиг. 643.
частей: одна, величиной 0,25 Р, со-
сохраняет всё время своё направление; другая, 0,75 Р, меняет сво§ направление
на 2т. за один оборот вала. Коэффициент запаса равен 1,6.

760	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА [ГЛ. XXXVII
Выясним величину характеристики цикла; напряжения, вызванные силой
0,25 Р, будут постоянными; вызванные же силой 0,75 Р, будут изменяться
между крайними значениями, равными по величине, но обратными по знаку;
поэтому характеристика цикла равна:
г__Рт-Ра _ 0,25Р--0,75Р ___ -
Рт + Ра ~ 0,25 Р + 0,75 Р - и'°*
Опасными будут в первую очередь сечения Л и В, где могут возникнуть
значительные местные напряжения в связи с переходом от одного диаметра
к другому. Момент сопротивления для этих сечений равен:
W=^ = ^ = 9S см».
4	4
Изгибающий момент в сечении Л равен:
М(Л) = Р ,°>9>0>45 = 0,27 Р кгм = 27 Р кгсм
1,0
(Р—в килограммах). Наибольшее нормальное напряжение в сечении Л:
Аналогично для сечения В:
М(В) = РWj-W = о,24Р кгм = 24 Р кгсм;
ф
Найдём допускаемые напряжения [рг] = [а"] в этих сечениях:
[М A — г)
Величина [p+J] одинакова для обоих сечений; она равна [р+1] = [з] =
=-т—пределу текучести при изгибе, делённому на коэффициент запаса /г.
Предел текучести при изгибе для легированной стали (§ 242)
с? = 1,11 . 0,75ав = 1,11 - 0,75 • 90 = 75 кг/мм*
Для нахождения [рв1] = [а^] =—^- надо найти о^ и величину коэффи-
/гакд
циента концентрации акд: последняя будет иметь разное значение для сече-
сечений Л и В.
Величина a"j = 0,4aB = 0,4 • 90 = 36 кг/мм2. Для сечения Л радиус гал-
галтели равен ri = 2 см, а для сечения В г2 = 0,5 см. Диаметр вала tf== 10 см\
таким образом, для сечения А отношение — = 0,2 и теоретический коэффи-
коэффициент концентрации по графику II фиг. 628 равен <хкт= 1,48; коэффициент
чукствительности при ав = 90 кг/мм* по графику фиг. 626 равен ^ = 0,7;
таким образом,
«кд= 1+0^8- 1,0H,7= 1,34

§ 243]	примеры	761
Для сечения В
? = ^=0,05, «„ = 1,90, ? = 0,77;
«и=1 +0.9- 1,0H,77= 1,69.
Величина масштабного коэффициента одинакова для обоих сечений и
определяется по кривой 3 фиг. 629 (легированная сталь при наличии концен-
концентрации напряжений); для детали диаметром 100 мм ам = 2.
Допускаемое напряжение [<з\\ равно: для сечения А
для сечения В
г „ 1	3600	3600
Допускаемое напряжение [а"] равно: для сечения А
= 1055
о...
A+0,5) 4690+A-0,5) 655 = 845
Величина силы Р определяется из двух неравенств
0,276 Р^1055 кг/см2,
0,245 Р^845 кг/см2,
т. е.
- 0,5) 840
для сечения В
2 • 4690 . 655
Таким образом, сила Р должна быть не больше 3450 кг.
Пример 143. Полый вал диаметром а? = 80 мм из хромоникелевой
стали с ав = 110 кг/мм2 ослаблен кольцевой выточкой для смазки диаметром
2г = 8 мм; касательные напряжения при кручении вала меняются от — 1г
до -f г2; отношение — = —; найти допускаемое напряжение.
Находим характеристику цикла г = —^ =	 = — 0,25. Предел выно-
сливости при кручении для симметричного цикла равен:
т*! = 0,22 св = 0,22 -110 = 24,2 кг/мм2.
г 4
Отношение — = ^ = 0,05; теоретический коэффициент концентрации по
графику / фиг. 628 (принят как для изгиба) равен акт = 2,29; коэффици-
коэффициент чувствительности (фиг. 626) ^ = 0,89; действительный коэффициент кон-
концентрации акд = 1 -f B/29 — 1,0) X 0,89 = 2,15. Масштабный коэффициент
для детали диаметром 80 мм равен аи = 2 (кривая 3 фиг, 629;, Принимая

762	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА [ГЛ. XXXVII
основной коэффициент запаса (с учетом динамики) k = 2,0, получаем
для [x^J значение
Предел текучести для специальной стали при кручении равен (§ 242):
т? = 0,60 . 0,75 ав = 0,60 • 0,75 .110 = 49,5 кг/мм*.
Допускаемое напряжение [т+J равно:
[^1=^ = 2475 кг/сл».
Допускаемое напряжение [т*] равно:
КК1 Ь%1
-0,25) 280 =42
§ 244. Проверка прочности при переменных напряжениях
и сложном напряжённом состоянии.
Указанные выше приёмы проверки прочности материала при пере-
переменных напряжениях относятся к случаю простейших деформаций —
растяжения, сжатия, кручения и изгиба. Возникает вопрос, как
использовать полученные данные для случаев сложного напряжён-
напряжённого состояния.
Наибольшее значение для практики имеет случай совместного
действия изгиба и кручения. Как указано в § 167, проверке подлежит
элемент материала, испытывающий плоское напряжённое состояние;
по четырём его граням действует касательное напряжение т = ^и
по двум из них нормальное о = -^~, где W = ^	момент сопро-
сопротивления вала круглого поперечного сечения.
Для проверки прочности при постоянной нагрузке мы имели по
теории наибольших касательных напряжений (А) и по энергетической
теории (Б) такие условия:
А) У о* ~f- 4t2 ^ [о] и Б)
Обе эти формулы могут быть приведены к общему виду путём де-
деления обеих частей неравенства на [о]:
и Б)
иначе

§ 244] ПРОВЕРКА ПРОЧНОСТИ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ	763
где[т]=^ по теории наибольших касательных напряжений и
[t] = J-^L по энергетической теории.
Таким образом, проверка прочности как по той, так и по другой
теориям прочности приводит к одному и тому же уравнению:
iJ + FF^1-	C7Л2)
Так как появление трещины усталости обусловлено теми же
физическими процессами деформации материала, которые имеют место
и при статическом действии нагрузок, то условие C7.12) может быть
применено и к проверке прочности при переменных нагрузках. Вели-
Величины а и х могут быть разложены на составляющие от и аа> тт и та:
под [а] и [т] в этом случае надлежит понимать значения допускае-
допускаемых напряжений для изгиба и кручения [а?] и [тЦ], полученные из
спрямлённых диаграмм [рг] — [рт] или [ра] — [рт] (фиг. 640 и 642)
с учётом соответствующих каждому виду деформации коэффициен-
а .	т •
тов концентрации и характеристик цикла -^ и ——.
агаах ттах
Пример 144. Определить запас прочности в сечении вала диаметром
d=\QQ мм с галтелью радиусом г = 1 мм. Материал вала — углеродистая
сталь с пределом прочности ав = 60 кг/мм2.
Материал вала подвергается изгибу и кручению; нормальные и касатель-
касательные напряжения меняются от нуля до наибольшей величины
Механические характеристики материала равны:
о? = 1,20 • 0,6 ав = 1,2 • 0,6 • 60 = 43 кг/мм2;
т« = 0,6 • 0,6 • 60 == 22 кг/мм2;
oi1! = 0,4 . 60 = 24 кг/мм2; т*х = 0,22 • 60 = 13,2 кг/мм2..
Теоретический коэффициент концентрации при -t==:t7jq равен акт = 2,2;
коэффициент чувствительности ^ = 0,58; действительный коэффициент кон-
концентрации авд= 1+B,2—1H,58 = 1,64. Характеристика цикла г = 0. Мас-
Масштабный коэффициент для детали диаметром 100 мм> из углеродистой
стали равен <*„= 1,66 (кривая 2 фиг. 629).
Допускаемая величина напряжений:
для нормальных напряжений
г и л < 4300 у , Гй1 °"	2400	882
I * 1=т=тг кг1см2; WJ = ей;=гтщтщ = т
4300 . 882	1465
1 J

764	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА [гл. XXXVII
для касательных напряжений 1)
г к i_ *-i _
1320 490
. 1,64 . 1,66
Г к1 _ о 2200 . 490 __ 800
L"J Z 2200 , 490\ ~~ Т
Условие прочности принимает вид:
Ь2Л^ПП\8
Ш Ш2 ^~ A465J ^ (800)
откуда k = 1,45.
§ 245. Практические меры по борьбе с изломами усталости.
Результаты, изложенные в предыдущих параграфах, дают воз-
возможность установить те практические меры, которые позволяют
инженеру обеспечить прочность деталей машин и конструкций при
переменных напряжениях.
Эти меры могут быть разделены на две категории. С одной сто-
стороны, необходимо обеспечить изготовление элементов машин и кон-
конструкций из материала, который наилучшим образом сопротивлялся
бы действию переменных напряжений. Как мы видели, требования
к материалу в.этом отношении сводятся к двум положениям: во-пер-
во-первых, желательно применять металл с возможно более высоким
пределом прочности при достаточной пластичности, что обеспечит
высокое значение предела выносливости; во-вторых, материал должен
быть свободен от всяких внутренних «факторов концентрации»; это
требует возможно более однородной., мелкозернистой структуры,
отсутствия всяких остаточных напряжений (например, закалочных) или
нарушений сплошности материала в виде трещин, газовых пузырьков,
неметаллических включений.
Указанные требования к материалу объясняют, почему для ответ-
ответственных деталей, работающих на переменную нагрузку, применяют
так часто легированные (хромоникелевые, хромованадиевые) стали
с очень высоким пределом прочности, которым при помощи тщатель-
тщательной термической обработки (закалка с последующим отпуском) при-
придана мелкозернистая структура, свободная от внутренних напряжений.
Однако при применении таких сталей иногда приходится встре-
встречаться с наличием микроскопических трещин (особенно в хромо-
*) При кручении принят тот же коэффициент концентрации, что и при
изгибе. Пользуясь таблицей 37, можно подсчитать его точнее.

§ 245] ПРАКТИЧЕСКИЕ МЕРЫ ПО БОРЬБЕ С ИЗЛОМАМИ УСТАЛОСТИ
765
никелевых сталях), так называемых флокенов. Эти трещины, как и
включения, могут очень резко снизить предел выносливости стали,
обладающей в то же время высоким пределом прочности.
Таблица 38. Результаты испытаний хромоникелевой
№ марок
1
2
3
4
Предел проч-
прочности а^
кг/мм*
105,0
108,0
111,0
115,0
Предел про-
порционально-
порциональности а кг /мм2
100,0
100,0
106,0
Относитель-
Относительное удлинение
при разрыве
11,6
9,7
10,3
8,0
Относительное
сужение
59,0
60,3
61,6
59,0
стали.
Предел вы-
выносливости 1
кг/ММ'
30,5
45,0
50,0
54,0
В таблице 38 приведены результаты испытаний четырёх марок
хромоникелевой стали, из которых одна A) имела флокены; как
видно из таблицы, наличие этого порока могло вскрыть только испы-
испытание на усталость; все прочие характеристики (предел прочности
и т. д.), полученные гпри статических испытаниях для всех четырёх
марок, примерно одинаковы, а предел выносливости для первой марки
резко снижен.
Вторая категория мер, обеспечивающих прочность деталей при
переменной нагрузке, сводится к грамотной, культурной проекти-
проектировке внешних очертаний детали и тщательной обработке её
поверхности. Основная цель, которую должны ставить себе при этом
конструктор и технолог, сводится к возможному снижению коэффи-
коэффициентов концентрации напряжений, вызываемых всякого рода резкими
изменениями очертания детали и дефектами обработки поверхности.
Снижение местных напряжений достигается прежде всего возможно
более плавными очертаниями переходов, выемок, надрезов, галтелей.
Совершенно необходимо решительно не допускать переходов, вовсе
не смягчённых кривой хотя бы не очень большого радиуса; везде,
где возможно, следует применять радиус, достаточный для суще-
существенного снижения местных напряжений. Данные, позволяющие
соответствующим образом выбрать числовую величину этих радиусов,
приведены на фиг. 627 и 628. Надо заметить, что иногда даже не-
небольшое увеличение радиуса перехода избавляет деталь от опасности.
Известен случай большого количества изломов коленчатых валов
авиационных двигателей в английском воздушном флоте; эти изломы
происходили на галтели около места насадки пропеллера; стоило
увеличить радиус галтели всего на 1/8" я^З мм, и изломы пре-
прекратились.
Это объясняется тем, что при напряжениях, близких к пределу
выносливости, кривая зависимости разрушающего напряжения от

766
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
числа циклов идёт почти горизонтально (фиг. 615). Поэтому, если
действительное напряжение хотя бы немного превышает предел вы-
выносливости, излом неминуем, так как большинство деталей испыты-
испытывает достаточное число циклов напряжений, чтобы трещина уста-
усталости имела время образоваться. (В таблице 39 приведены ориенти-
ориентировочные данные о предельном числе циклов напряжений, испыты-
испытываемых различными деталями конструкций и машин во. время их
службы.)
Таблица 39. Число циклов напряжений в элементах конструкций.
Название частей конструкции или машины
Элементы главных ферм железнодорожных мостов ....
Балки проезжей части
Рельсы
Валы авиамоторов
Оси вагонов
Валы автомобильных двигателей
Штоки и шатуны паровых двигателей	I
Валы паровых турбин
Лопатки паровых турбин
Число циклов
2-106
40.10е
15-10°
18.10е
50.10е
120.10е
1000.106
15000.10е
250000.10е
С другой стороны, стоит смягчением коэффициента концентрации
снизить напряжение хотя бы немного ниже предела выносливости,
как трещина уже не может возникнуть. Коэффициент концентрации
напряжений тем больше, чем резче происходит изменение напряже-
напряжений, чем больше разница в жёсткости смежных частей стержня, чем
резче изменение очер-
очертаний детали. Поэтому
бороться с местными
повышениями напря-
напряжений можно не толь-
только путём установления
более плавных перехо-
переходов, но и путём сниже-
снижения разницы в жёст-
костях смежных частей
детали в тех местах,
где неизбежна концен-
концентрация напряжений.
Фиг. 644.	Так, в последнее вре-
время возникла идея «раз-
«разгружающих» надрезов. Например, при глухой посадке с натягом
ступицы колеса на ось или шкива на вал возникают очень значи-
значительные местные напряжения в материале вала (фиг. 644, а).

§ 245] ПРАКТИЧЕСКИЕ МЕРЫ ПО БОРЬБЕ С ИЗЛОМАМИ УСТАЛОСТИ 767
Коэффициент концентрации, отнесённый к нормальным напряже-
напряжениям от изгиба в сечении, перпендикулярном к оси вала, достигает
величины 1,8—2,0. На фиг. 644, а дан график величины нормальных
напряжений а в крайних волокнах изгибаемого вала, на который
насажена с натягом ступица шкива. Напряжения определены опти-
оптическим методом.
На чертеже видно, что около края ступицы напряжения о, осо-
особенно в сжатой зоне, дают резкое местное повышение.
Если в ступице около места посадки сделать вырез, смягчающий
жёсткость детали у её края, то местные напряжения падают и рас-
распределяются более равномерно (фиг. 644, б). Коэффициент концен-
концентрации падает с 2,0 до 1,4; если же, кроме окружной канавки, сде-
сделать подступичную часть вала несколько большего диаметра, как
показано на фиг. 645, то коэффициент концентрации удаётся сни-
Фиг. 645.
Фиг. 646.
зить до 1,0—1,05. Точно так же, если у места резкого перехода
(под прямым углом) сделать плавную выкружку в более толстой
части детали (фиг. 646, а и б), то местные напряжения резко
снизятся.
Во всех приведённых примерах изменения формы детали имеют
целью создать возможно более плавное изменение напряжений в месте
перехода.
Для сопротивления материала переменным нагрузкам не менее
важную роль, чем плавность очертаний, играет и чистота отделки
поверхности. Всякие царапины, риски от резца играют громадную
роль. Нам известен целый ряд случаев обрыва штоков паровой ма-
машины паровозов после того, как при ремонте изношенного кониче-
конического конца штока на него надевалась для утолщения коническая
втулка; перед посадкой втулки изношенная поверхность штока грубо
обтачивалась резцом и не подвергалась более чистой обработке. Тре-
Трещина усталости образовывалась под втулкой, начинаясь от места
концентрации напряжений, вызванной рисками от резца. Поэтому
чистота обработки поверхности изделия, применение никелировки или
лакировки для покрытия этой поверхности в случае возможности
коррозии являются не роскошью для деталей, работающих при

768
ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА
[ГЛ. XXXVII
переменных нагрузках, а во многих случаях совершенно необходи-
необходимой мерой для возможности благополучной работы конструкции.
Необходимо отметить, что вопросы о выборе материала и о пра-
правильном проектировании формы детали нельзя отрывать друг от
друга. Чем лучше материал, чем выше его предел прочности, тем
более тщательной обработки он требует. Применяя дорогостоящую
легированную сталь высокого качества и не обращая внимания на
снижение местных напряжений, мы рискуем свести на-нет все пре-
преимущества применения качественной стали. Коэффициент чувствитель-
чувствительности к местным напряжениям для такой стали будет значительно
выше, чем для более мягкой, простой углеродистой стали. На это
уже было указано в § 239.
Фиг. 647.
Фиг. 648.
На фиг. 647 и 648 показаны диаграммы ра — рт для всех сортов
материала: обыкновенной углеродистой стали и высококачественной
легированной стали. На этих диаграммах линии АМВ соответствуют
разрушению за счёт развития трещин усталости, линии же GN — за
счёт образования пластических деформаций при превышении напря-
напряжениями предела текучести.
Линии AMN, заштрихованные на чертеже, представляют диа-
диаграмму разрушающих напряжений (в широком смысле слова). Как мы
видим, для легированной стали возможность разрушения за счёт раз-
развития трещины усталости гораздо значительнее, чем для обычной
углеродистой стали. Смягчения местных напряжений за счёт пласти-
пластических деформаций в первом случае ждать гораздо труднее, чем
во втором. Этим в значительной степени и объясняется повышен-
повышенная чувствительность качественной стали к концентрации напря-
напряжений.
Резюмируя, можно сказать, что чем лучше применяемая нами
сталь как материал, тем более культурной и тщательной обра-
обработки она требует, чтобы все её преимущества могли быть
использованы в полной мере.

§ 246] СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ ДИНАМИЧЕСКИМ НАГРУЗКАМ	769
§ 246. Развитие вопроса о сопротивлении материалов
динамическим нагрузкам.
Вопросы сопротивления материалов действию динамических нагрузок
получили широкое развитие в связи с тем крупным переворотом, который
произошёл в экономическом фундаменте капиталистического общества
в конце XVIII и начале XIX столетий. В эти годы на месте старой мануфак-
мануфактурной промышленности с её узким ручным базисом начала создаваться
мощная фабричная индустрия, опирающаяся на мощную технику; широкое
применение нашла паровая машина, появились железные дороги с механиче-
механической паровой тягой и быстроходные пароходы.
В последующие десятилетия технические достижения были очень разно-
разнообразны и характеризовались в основном большими сдвигами в энергетиче-
энергетической промышленности, в области развития и усовершенствования всякого
рода двигателей — главным образом в отношении . увеличения их мощности и
быстроходности.
В связи с широким распространением машин, быстродвижущиеся элементы
которых подвергались воздействию динамических усилий и которые сами вызы-
вызывали подобные же усилия в поддерживающих их конструкциях, появилась
настоятельная необходимость в изучении сопротивления материалов действию
динамических нагрузок.
В прошлом столетии наша страна, значительно отстававшая в развитии
техники от крупных капиталистических стран, не имела, в сущности, своего
машиностроения и достаточно развитого железнодорожного и водного транс-
транспортов. В связи с этим и вопросы динамики в строительной механике в эту
эпоху не могли получить и не получили у нас надлежащего развития.
Экспериментальные и теоретические исследования в области динамики
широко развернулись у нас только после Великой Октябрьской социалисти-
социалистической революции — в особенности в годы выполнения Сталинских пяти-
пятилеток. Дело обороны нашей родины, грандиозное строительство новых фабрик
и заводов, молодое советское машиностроение, за короткий период добившееся
крупных успехов в различных областях техники, — выдвинули целый ряд
проблем, связанных с наиболее эффективным и рациональным конструирова-
конструированием новых типов машин и сооружений. В связи с этим перед отечествен-
отечественной наукой были поставлены многие важные задачи, относящиеся к области
динамического расчёта конструкций. В процессе решения этих задач работа
наших учёных за короткое время ознаменовалась целым рядом крупных
научных и технических достижений, значительно опередивших достижения
заграничной науки и техники.
В основу многих динамических расчётов в строительной механике поло-
положены данные теоретической и прикладной механики — главным образом
динамики материальной точки и системы. Поэтому развитие вопроса о со-
сопротивлении материалов действию динамических нагрузок должно быть
рассматриваемо в тесной связи с развитием смежных вопросов динамики
в механике.
Теория колебаний развилась из исследований Галилея о малых коле-
колебаниях маятника. Однако опыты Галилея, в сущности, лишь наметили
путь для дальнейшей работы в этой области. Возникновение учения о колеба-
колебаниях упругих тел в механике связано с именами академиков Петербургской
Академии наук—Д. Бернулли, Эрмана и Л. Эйлера. В 1716 г. Эрман нашёл
решение некоторых сложных задач о колебаниях маятника; в 1740 г. Эйлер
обобщил принцип Эрмана и применил его к исследованию колебаний струн
и тонких брусьев. В 1751 г. Эйлер и Бернулли впервые получили дифферен-
дифференциальные уравнения поперечных колебаний. Хотя общая теория колебаний
систем с конечным числом степеней свободы была дана в 1762—1765 гг.
в работах Лагранжа, но по его же собственному признанию эти работы
представляли собой «возврат к методу Эрмана и Эйлера».
25 Н. М. Беляев

770	ПРОВЕРКА ПРОЧНОСТИ МАТЕРИАЛА	[ГЛ. XXXVII
Однако пока не были открыты общие уравнения теории упругости,
разработанная Лагранжем теория колебаний ещё не могла быть эффективно
использована для расчётов в строительной механике. Это стало возможным
лишь в первой половине прошлого столетия, когда были выведены диффе-
дифференциальные условия равновесия и движения. В первой половине прошлого
столетия над вопросами механики твёрдого тела работал выдающийся русский
математик, новатор в области теоретической и прикладной механики, акаде-
академик М. В. Остроградский; его труды по математике и механике, и в част-
частности по теории колебательного движения, доставили ему мировую известность.
Широкое использование теории колебаний упругих тел в инженер-
инженерном деле началось, в сущности, только в текущем столетии; при этом в по-
построении и развитии общих методов динамического расчёта машин и со-
сооружений ведущая роль принадлежала и принадлежит нашим отечествен-
отечественным учёным.
Замечательные работы по теории колебаний были выполнены крупнейшим
учёным нашей страны академиком А. Н. Крыловым. Его классическая работа
о вынужденных поперечных колебаниях стержней и о влиянии резонанса,
теория вибрации корабля, изложенная в изящной математической форме,
разнообразные труды по динамике упругих систем, связанные с расчётом
быстро вращающихся валов, колеблющихся балок, нагружённых подвижными
грузами, и многие другие работы нашли широкое применение на практике
как в СССР, так и за границей.
Большую известность приобрели также работы В. 3. Власова (Колебания
тонкостенных стержней), Н. Е. Кочина (Крутильные колебания коленчатых
валов), П. Ф. Папковича (Теория вибрации корабля, поперечные колебания
трубчатых мостов), М. И. Яновского (Метод расчёта быстро вращающихся
дисков) и др.
Первые более или менее систематические исследования явления удара,
без обобщения и подведения под них какого-либо теоретического фундамента,
были выполнены известным художником и учёным средних веков (конец
XV столетия) Леонардо да Винчи. Первая теоретическая работа по этому
вопросу принадлежит Эйлеру («О распространении удара», 1748 г.).
В связи с тем, что сопротивление материалов динамическому (ударному)
действию нагрузок оказалось значительно отличающимся от сопротивления
их статическому действию сил, внимание исследователей было направлено,
главным образом, на экспериментальное изучение явления удара. В конце
прошлого столетия было обнаружено, что при ударном изломе надрезанных
образцов металл может обладать специфической хрупкостью, не проявляю-
проявляющейся ни при каких других видах испытаний. С тех пор такие испытания
металлов — так называемая ударная проба надрезанных образцов — широко
внедрились в заводскую и научно-исследовательскую практику.
Большое развитие подобные исследования получили у нас, и в особен-
особенности за последние 30 лет. Следует отметить многих русских учёных, занимав-
занимавшихся экспериментальным изучением явления удара вообще и вопросами
ударной пробы в частности — С. И. Дружинина и Н. М. Беляева (исследова-
(исследования рельсовой стали), А. Г. Гагарина (конструирование приборов, дающих
зависимость между деформациями и усилиями при ударе), А. Н. Динника,
И. А. Одинга, Б. Ф. Локшина, А. М. Драгомирова и др. Среди исследований
этих учёных особое место занимают систематические и глубоко проду-
продуманные опыты А. М. Драгомирова A917 г.), которые осветили ударную
пробу материала с самых разнообразных точек зрения; А. М. Драгомировым
были обстоятельно изучены многие факты, которые стали известны за гра-
границей только спустя целое десятилетие *).
Выдающиеся исследования явления удара как по охвату различных во-
вопросов, так и по обстоятельности и глубине их изучения принадлежат
1) Давиденков Н. Н., Динамические испытания металлов, 1936 г.

§ 246] СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ ДИНАМИЧЕСКИМ НАГРУЗКАМ	771
Н. Н. Давиденкову и его школе. Введённый им в практику исследований
новый метод испытания ненадрезанных образцов позволил изучить многие
явления, весьма существенные для теории удара (влияние состояния поверх-
поверхности, наклёпа, остаточных напряжений и т. п.). Вопрос об истинной природе
ударной хрупкости металлов, для разрешения которого различными исследо-
исследователями за границей был предложен ряд теорий, находившихся во взаимном
противоречии и оказавшихся не в состоянии дать строгое, основанное на
единой точке зрения, объяснение явлений в области ударных испытаний
получил правильное истолкование в результате работ Н. Н. Давиденкова и
его сотрудников.
Эти исследования значительно продвинули вперёд не только разрешение
вопроса о динамической прочности металлов в связи с их службой в деталях
машин и сооружений. Глубокое аналитическое изучение явления удара позво-
позволило Н. Н. Давиденкову построить новую общую теорию механизма разру-
разрушения материала (см. главу XXXVIII) и установить общие критерии прочности
материалов как при динамическом, так и при статическом действии сил.
Исследование вопроса о сопротивлении материалов действию перемен-
переменных нагрузок с самого же начала пошло чисто экспериментальным путём.
Наиболее тщательно поставленные опыты на специально сконструиро-
сконструированных для этой цели машинах были проведены в 1860—1870 гг. Вёлером.
Разработанная им методика длительного определения предела выносливости
металлов с небольшими изменениями сохранилась и до сих пор.
В начале текущего столетия получили широкое распространение эти
исследования и у нас. Пионерами по изучению явления усталости метал-
металлов в нашей стране были Воропаев и Симинский; серия опытов по усталости
мостового железа была осуществлена К. К. Симинским в 1920—1922 гг. в
Киевском политехническом институте. С 1925—1930 гг. исследования в этой
области получили дальнейшее развитие в работах Н. Н. Афанасьева, Н. Н. Да-
Давиденкова, И. А. Одинга, И. В. Подзолова, С. В. Серенсена и многих других.
В Ленинградском институте инженеров путей сообщения в течение ряда
лет, начиная с 1925 г., велись работы по борьбе с изломами от усталости
деталей подвижного состава железных дорог (главным образом вагонных и
паровозных осей). Многочисленные исследования, выполненные под руковод-
руководством Н. М. Беляева, позволили устранить основные причины этих изломов,
которые одно время являлись бичом железнодорожного транспорта. Не
менее практически важной была проведённая там же A925—1940 гг.) боль-
большая работа по изучению динамической (в основном — усталостной) прочно-
прочности рельсовой стали, результаты которой нашли отражение в наших техни-
технических условиях, обеспечивающих длительную и надёжную работу рельсов.
И. А. Одингу и «го сотрудникам принадлежит ряд работ по изучению
причин возникновения явления усталости и установлению критерия прочно-
прочности металлов при повторно-переменных напряжениях; эти исследования
привели к разработке ряда эффективных мероприятий по устранению разру-
разрушений деталей машин от усталости. В результате всестороннего изучения
вопроса о так называемой «циклической вязкости> (способности материала,
не разрушаясь, поглощать в необратимой форме за один цикл смены напря-
напряжений определённое количество энергии), как основной характеристики мате-
материала при повторно-переменных нагрузках, И. А. Одингом была выдвинута но-
новая теория усталостного разрушения металлов (теория гистерезисной энергии).
Внедрение результатов эксперимента в практику расчётов деталей
машин и сооружений при переменных напряжениях началось у нас примерно
с 1930 г. По методике расчётов на прочность в машиностроении широко
известны труды С. В. Серенсена и И. В. Подзолова. С. В. Серенсену при-
принадлежат работы, связанные с установлением критерия прочности и разви-
развитием методов определения запасов прочности деталей при повторно-перемен-
повторно-переменных нагрузках. И. В. Подзолову — работы по усовершенствованию методики
назначения допускаемых напряжений.
25»

772	прочность материалов	[гл. xxxviii
ГЛАВА XXXVIII.
ПРОЧНОСТЬ МАТЕРИАЛОВ.
§ 247. Основные понятия.
После того, как подробно рассмотрены разные случаи сопротивления
материалов действию всякого рода нагрузок при различных видах напря-
напряжённого состояния, целесообразно вновь вернуться к вопросу о том, чем
определяется прочность материала при различных обстоятельствах, и развить
более глубоко данные, приведённые в главе VIII.
Под прочностью материала или детали 'сооружения понимается их спо-
способность сопротивляться действию усилий, вызывающих ту или иную дефор-
деформацию. Деформация детали при достаточном её развитии приводит к разру-
разрушению — разделению детали на части. При этом в одних случаях разрушение
наступает после стадии малых деформаций, более или менее точно следую-
следующих закону Гука (хрупкое состояние материала); в других — между стадией
малых деформаций и окончательным разрушением материал проходит через
стадию значительных остаточных деформаций (вязкое или пластическое со-
состояние материала).
Для суждения о прочности материала, находящегося в хрупком состоя-
состоянии, требуется изучение только одного предельного (опасного) состояния —
перехода от упругой деформации к разрушению материала. Для суждения
о прочности материала, находящегося в пластичном состоянии, необходимо
изучение двух предельных состояний — перехода упругой деформации в пла-
пластическую и перехода от пластической деформации к разрушению материала;
очень важно при этом знать, как протекает деформация после достижения
предела текучести.
Известно (§ 27 и др.), что для пластичных материалов появление замет-
заметных остаточных деформаций и даже начало разрушения в отдельных наиболее
напряжённых местах детали во многих случаях ещё не приводит к потере
несущей способности или к разрушению этой детали в целом. Таким обра-
образом, знания предела текучести и сопротивления материала разрушению
может оказаться недостаточным для суждения о прочности детали. Здесь,
очевидно, необходимо изучение поведе-
поведения материала на протяжении всего про-
процесса пластического деформирования.
Таким образом, характеристиками,
качественно и количественно опреде-
определяющими упомянутые выше предельные
(опасные) состояния, являются: сопро-
сопротивление материала возникновению и
развитию значительных пластических де-
деформаций и сопротивление материала
разрушению.
Механизм пластической деформации
в кристаллической решётке твёрдых тел
изучен ещё недостаточно хорошо. Судя
по опытным данным, пластические дефор-
деформации развиваются за счёт сдвигов или
скольжений элементов кристаллической
решётки. Явление сдвига или скольжения
Фиг. 649.	заключается в параллельном смещении
одних частей кристалла по другим вдоль
кристаллографических плоскостей. Сдвиги в кристаллах часто происходят
вдоль очень большого числа плоскостей, причём число этих плоскостей
увеличивается с увеличением напряжений. Эти сдвиги бывают видны под

§ 248]	СОПРОТИВЛЕНИЕ ПЛАСТИЧЕСКИМ ДЕФОРхМАЦИЯМ	773
микроскопом на протравленных образцах деформированного металла в виде
системы параллельных линий, различно ориентированных в каждом кристал-
кристаллическом зерне. На фиг. 649 (рисунок с фото) показана подобная микро-
микрофотография (увеличение 250) образца мягкой стали. Линии сдвигов на
микрофотографии представляют собой изображение небольших ступенек, по-
получающихся при последовательных сдвигах в том или ином зерне (фиг. 650).
_ Плоскости сдвигов
По5ерхность
Пттщызфм
Шле деформации
Фиг. 650.
Микродеформации в отдельных зёрнах, суммируясь, дают полные де-
деформации тела в виде сдвига уже больших объёмов материала; так, при
простом растяжении эти сдвиги происходят по плоскостям, наклонённым
к направлению растяжения под углом в 45—50°.
Явление разрушения, несмотря на его большое практическое значение,
изучено пока меньше, чем процессы пластической и, тем более, упругий
деформации. Исследования показывают, что разрушение кристаллической ре-
решётки твёрдых тел может происходить как путём разъединения (отрыва),
атомов, при котором решётка сразу распадается на две части, так и путём
скольжения (сдвига) атомов, при котором решётка, постепенно деформи-
деформируясь, распадается только после значительного искажения. Явление разру-
разрушения кристаллического тела в целом оказывается более сложным. Фактор
ориентировки, играющий главную роль при разрушении отдельных кристалл
лов, теряет своё значение для кристаллического тела, представляющего собой,
совокупность различно ориентированных кристаллов.	¦
Разделение тела на части является следствием многих разрушений, про-
происходящих как внутри отдельных кристаллов, так и по поверхности раздела
между ними. Изучение явления разрушения в ряде случаев дополнительна
осложняется влиянием предшествующей пластической деформации, вызы-
вызывающей изменение напряжённого и деформированного состояния тела. Вслед-
Вследствие этого многие вопросы, связанные с явлением разрушения, несмотря
на длительное их изучение, и до сих пор ещё остаются неразрешёнными.
§ 248. Сопротивление пластическим деформациям.
Наиболее удобно, с точки зрения постановки эксперимента, изучать
характеристики" сопротивления материала нарушению прочности при простом
растяжении. Как уже было показано в § 13, характеристикой сопротивления
материала пластическим деформациям является так называемая истинная
диаграмма напряжений (фиг. 23). Ординаты её си(з) получаются делением
силы Р/, растягивающей в каждый момент времени t образец, на соответ-
соответствующую площадь поперечного сечения Ft. Абсциссы этой диаграммы
характеризуют степень пластической деформации. За эту характеристику
можно было бы взять или относительное удлинение образца е или относи-
относительное сужение й.
Как известно, при растяжении образцов пластичного материала можно
различать три стадии; в первой из них деформации упруги, следуют закону
Гука и одинаковы по всей длине образца. При этом поперечное сужение
может быть выражено через относительное удлинение с помощью коэффи-
коэффициента Пуассона \х (§ 9).

774
ПРОЧНОСТЬ МАТЕРИАЛОВ
[ГЛ. XXXVIII
Во второй стадии, которая продолжается до начала образования шейки,
практически соответствующего достижению грузом Pt наибольшего значения,
происходят значительные пластические деформации, одинаковые по всей
длине образца; эта стадия характеризуется наличием равномерного удлине-
удлинения. Связь между относительным удлинением и сужением здесь можно полу-
получить, принимая во внимание, что при пластических деформациях объём
образца практически не меняется.
Вторая стадия растяжения образца кончается достижением напряжениями
(отнесёнными к первоначальной площади) величины предела прочности
материала; в этот момент прекращается равномерное удлинение образца и
начинается образование шейки —третья стадия деформации.
В третьей стадии материал деформируется лишь около шейки. Относи-
Относительное удлинение в области шейки значительно меняется по длине дефор-
деформируемого участка и не может уже непосредственно служить характеристикой
степени пластической деформации; такой ха-
характеристикой является относительное су-
сужение в наиболее деформированном месте
образца.
Таким образом, наличие третьей стадии
растяжения образца заставляет выбрать за
характеристику степени пластической де-
деформации . именно относительное сужение,
которое однозначно определяет эту степень
деформации во всё время растяжения и
связано определённым образом с относи-
относительным удлинением в первой и второй
стадиях деформации.
На фиг. 651 изображена описываемая
диаграмма; точки Л, В и С разграничи-
разграничивают три стадии растяжения. Напряжение ai соответствует истинному
пределу текучести ат; напряжение а2 соответствует наибольшему грузу и
может быть названо истинным пределом прочности ав; наконец, о3 = ёр —
это напряжение в момент разрыва.
Величина й2, оценивающая равномерное сужение образца по всей длине,
характеризует способность материала к общей деформации; разность же
между полным сужением <Ь8 и равномерным й>2 оценивает способность мате-
материала к местным деформациям.
«Истинная> диаграмма показывает, как изменяется сопротивление мате-
материала пластической деформации в зависимости от величины этой дефор-
деформации — от степени наклёпа; по мере роста деформации растёт и это
сопротивление вплоть до момента разрыва, — материал упрочняется. Чем
круче идёт диаграмма, чем больше величина производной ~, тем больше
способность материала к упрочнению.
Так как при достижении напряжениями а величины ав процесс равномер-
равномерного растяжения образца теряет свою устойчивость, срывается, то эта величина
предела прочности, а равно и величина предела прочности св, по существу
является характеристикой сопротивления материала равномерному
растяжению.
Геометрические свойства истинной диаграммы описываются в специ-
специальных курсах *).
Фиг. 651.
1) См. например, Шапошников Н. А., Основы механических испы-
испытаний металлов, 1936; Марковец М. П., Диаграмма истинных напряже-
напряжений, 1943 и др.

§ 248]	СОПРОТИВЛЕНИЕ ПЛАСТИЧЕСКИМ ДЕФОРМАЦИЯМ	775
Форма истинной диаграммы напряжений, как характеристики сопроти-
сопротивления материала пластическим деформациям, и величина этого сопроти-
сопротивления— величина ординат — зависят от рода материала, температуры, ско-
скорости деформации и типа напряжённого состояния.
Влияние рода материала (сталь, алюминий, латунь и т. п.) сказывается
на абсолютной величине ординат и на крутизне диаграммы, т. е. на способ-
способности материала упрочняться.
Температура детали резко сказывается на величине сопротивления
пластическим деформациям; по мере понижения температуры это сопроти-
сопротивление возрастает.
Увеличение скорости деформации тоже увеличивает сопротивление
пластическим деформациям; это мы видели уже в § 233 при изучении дей-
действия ударов на материал. Если вести обычное растяжение образцов
с различными скоростями, то диаграммы растяжения располагаются тем
выше, чем больше скорость деформации.
Наконец, тип напряжённого состояния тоже отражается на сопротивле-
сопротивлении пластическим деформациям.
Так как эти деформации* связаны с наличием сдвигов, то все виды
напряжённого состояния, в которых касательные напряжения малы, будут
соответствовать высоким значениям сопротивления пластическим дефор-
деформациям. Так, всестороннее равномерное растяжение теоретически, а всесто-
всестороннее равномерное сжатие не только теоретически, но и экспериментально,
исключают возможность подобных деформаций; при напряжённых состоя-
состояниях, близких к этим двум, пластические деформации возникают лишь при
очень высоких значениях главных напряжений.
Наличие всякого рода резких переходов, изменений формы деталей,
надрезов, трещин создаёт, как показывают опыт и теоретические расчёты,
систему местных напряжений, характеризующуюся обычно тремя главными
напряжениями одного знака. Наличие такого напряжённого состояния
может в очень сильной степени повысить сопротивление материала пласти-
пластическим деформациям около надреза.
Описанные выше диаграммы истинных напряжений обладают некоторыми
существенными недостатками. Так, например, при вычислении относительного
удлинения или сужения образца при больших деформациях уже нельзя пре-
пренебречь тем, что начальные размеры образца, к которым обычно относят
приращение длины или изменение площади сечения, существенно изменились
в процессе деформации. Поэтому в качестве характеристик больших пласти-
пластических деформаций по аналогии с истинными напряжениями целесообразно
ввести так называемые истинные удлинения и сужения. Истинное удлине-
удлинение ё и истинное сужение <?, отнесённые соответственно к действительной
длине и площади сечения стержня в данный момент испытания, могут быть
вычислены по формулам:
Так как объём тела при пластической деформации можно считать постоян-
постоянным, т. е. V = Fl= const, то dV = ldF-\- Fdl = 0 и — = -— -у, откуда сле-
следует, что 6 = 1. Таким образом, две различные характеристики деформа-
деформации — истинное удлинение или истинное сужение — оказываются равными.
Метод изучения сопротивления пластической деформации по результа-
результатам испытаний на растяжение до сих пор является наиболее распростра-
распространённым. Однако полученные таким путём исходные данные о сопротивле-
сопротивлении пластической деформации делаются недостаточно точными, начиная

776	ПРОЧНОСТЬ МАТЕРИАЛОВ	[ГЛ. XXXVIII
с момента образования шейки. Распределение деформации и напряжений в
шейке становится очень неравномерным. Благодаря этому всякую характери-
характеристику деформации, в том числе и вычисленную по сужению шейки, в третьей
стадии растяжения образца только очень условно можно считать характе-
характеристикой, полученной при линейном напряжённом состоянии. Это в значи-
значительной мере снижает ценность результатов
испытаний на простое растяжение.
В последнее время делаются попытки по-
получения истинных диаграмм пластической де-
деформации по результатам испытаний на кру-
кручение. Так как при испытаниях на кручение
деформация даже очень пластичных материа-
материалов сохраняется достаточно равномерной но
всей длине образца (без образования шейки)
вплоть до момента разрушения, этот способ
получения истинных диаграмм обладает извест-
ными преимуществами перед вышеописанным.
Т
Углах Такие истинные диаграммы строятся в
координатах: истинное максимальное касатель-
Фиг. 652.	I _	1 _	_
ное напряжение ттах = —• (зтах—¦ smi]
максимальный сдвиг [ттах] (Фиг« 652). Так как при кручении етах = — и emin =
7	—	—
= —^-(§ 54), то Т = ?тах — ?min- Максимальный сдвиг связан с етах и emin
аналогичной формулой: Tmax==?max"~^min«
Однако и этот способ получения истинных диаграмм также не свободен
от некоторых недостатков. При кручении сплошных стержней трудно учесть
ълияние упруго деформирующейся центральной части стержня, при круче-
кручении же трубчатых образцов результаты испытания могут быть искажены
"благодаря потере устойчивости.
§ 249. Сопротивление разрушению. Отрыв и срез.
А. Сжимающие напряжения сами по себе не могут привести к разру-
разрушению материала; могут иметь значение, повидимому, вызванные ими каса-
"тельные напряжения или поперечные деформации удлинения.
В связи с этим уже давно возникло два различных представления
ч) разрушении материала: 1) как о явлении отрыва, обусловленном дефор-
деформациями удлинения или преимущественно действием нормальных растяги-
растягивающих напряжений, и 2) как о явлении среза или скалывания, обусловлен-
обусловленном преимущественно действием касательных напряжений. Исходя из этих
представлений, потребовалось различать и два вида сопротивления материа-
материалов разрушению: сопротивление отрыву и сопротивление срезу.
До последнего времени считалось, что каждый материал может обла-
обладать только одним каким-либо видом сопротивления разрушению — или
сопротивлением отрыву, или сопротивлением срезу. Однако такое односто-
одностороннее представление о явлении разрушения не позволило найти общее
решение вопроса о прочности материалов.
В противовес ему в самые последние годы у нас (см. §§ 250 и 252)
было выдвинуто иное, экспериментально обоснованное предположение, что
каждый материал в зависимости от того, в какие условия он будет поста-
поставлен, может разрушаться как путём отрыва, так и путём среза и может
поэтому обладать как тем, так и другим видом сопротивления разрушению.
Этот новый взгляд на вопросы разрушения способствовал разрешению

§ 249]	СОПРОТИВЛЕНИЕ РАЗРУШЕНИЮ. ОТРЫВ И СРЕЗ	777
целого ряда противоречий и неясностей, возникавших при рассмотрении
явления разрушения на основе прежних представлений. Поэтому именно
этот взгляд на современном этапе развития учения о прочности материалов
следует считать наиболее правильным.
Из сказанного ясно, что вопрос о двух типах разрушения материалов —
отрыве и срезе, требует подробного рассмотрения.
Теории разрушения материала от нормальных напряжений или вслед-
вследствие развития значительных деформаций удлинения являются наиболее
старыми теориями. Возможность разрушения материала путём отрыва, не-
неоднократно подтверждённая опытами, до сих пор не подвергалась каким-либо
сомнениям. Наоборот, в последнее время многие учёные были склонны
приписывать отрыву вообще все случаи разрушения материала.
Характер разрушения при отрыве зависит как от рода материала, так
равно и от вида напряжённого состояния; принципиально в одних случаях
возможен хрупкий отрыв — без остаточных деформаций, в других — вязкий
отрыв, сопровождающийся более или менее значительными пластическими
деформациями (см. ниже — § 252). Так, например, экспериментально устано-
установлено, что некоторые бронзы и алюминиевые сплавы способны разрушаться
путём отрыва даже при остаточной деформации около 20°/0.
Наиболее отчётливо характеристики сопротивления отрыву выявляются
при испытаниях хрупких неметаллических материалов. Так, при растяже-
растяжении образцов из хрупкого материала (стекла, пластмасс, бетона, камня)
разрушение их, как правило, происходит по площадкам, перпендикулярным
оси образца, т. е. как раз по тем, где действуют наибольшие нормальные
растягивающие напряжения. При кручении таких же образцов трещины
разрушения располагаются примерно под углом в 45° к оси образца, т. е.
опять-таки перпендикулярно к направлению наибольших растягивающих
напряжений. При сжатии призм из хрупкого материала разрушение начи-
начинается с появления трещин, параллельных направлению сжимающего
усилия, а следовательно, перпендикулярных к направлению деформации
растяжения (см. фиг. 32).
Получение характеристики сопротивления отрыву для пластичных мате-
материалов оказывается весьма затруднительным, так как при испытаниях, как
правило, не удаётся миновать стадии пластических деформаций, а следова-
следовательно, и значительных касательных напряжений. В связи с тем, что у
пластичных материалов сопротивление разрушению от касательных напря-
напряжений (срезу) значительно ниже сопротивления отрыву, при обычных испы-
испытаниях этих материалов не удаётся достигнуть сопротивления отрыву, так
как раньше происходит разрушение путём среза. Поэтому для определения
сопротивления отрыву необходимо такое изменение условий испы-
испытания (изменение вида напряжённого состояния, температуры, скорости
деформирования), которое, почти не изменяя характеристики сопротивле-
сопротивления отрыву, повлекло бы за собой значительное увеличение сопротивле-
сопротивления срезу.
При комнатной температуре и нормальной скорости испытания разру-
разрушение путём отрыва у большинства пластичных материалов могло бы
наблюдаться лишь при всестороннем равномерном растяжении; однако
такое напряжённое состояние до сих пор на опыте осуществлено не было.
При других напряжённых состояниях, близких к всестороннему равномер-
равномерному растяжению, величину сопротивления отрыву удалось определить
только у некоторых пластичных материалов, да и то лишь с помощью
динамических испытаний при низких температурах. Некоторые опытные
данные позволяют считать, что сопротивление отрыву сравнительно мало
зависит от изменения скорости деформирования и температуры испытания.
Отсюда следует, что в результате динамических испытаний при низких
температурах с известным приближением определяются и характеристики
сопротивления отрыву в нормальных условиях. Однако это обстоятельство

778	ПРОЧНОСТЬ МАТЕРИАЛОВ	[ГЛ. XXXVIII
может быть использовано при испытаниях лишь некоторых пластичных ме-
металлов (так называемые хладноломкие металлы). В связи с этим величина
сопротивления отрыву для очень многих пластичных материалов до сих пор
ещё не установлена.
Многие случаи разрушения путём отрыва на равных основаниях могут
быть приписаны как действию больших растягивающих напряжений, так и
развитию значительных деформаций удлинения. Таким образом, эти случаи
объясняются как с точки зрения теории наибольших нормальных напряже-
напряжений, так и на основе близкой к ней по своему физическому смыслу теории
наибольших удлинений.
Привлекая для объяснения явлений разрушения материала путём отрыва
теорию наибольших нормальных напряжений, следовало бы выражать истин-
истинное сопротивление отрыву через наибольшее растягивающее напряжение при
разрушении материала:	'
5. == тах ^разр. = 31 разр.
Привлекая для этой же цели теорию наибольших удлинений, следовало бы
выражать характеристику сопротивления отрыву через наибольшую дефор-
деформацию удлинения: max ipa3p. = eipa3p., что не вполне удобно. Используя за-
зависимости между напряжениями и деформациями (§ 40):
ei = y tJl ~~ ^ ^* + а*^ или Еч = Ч —
можно, как известно (§ 43), заменить алгебраическую сумму напряжений
в правой части последнего уравнения некоторым приведённым растягиваю-
растягивающим напряжением апр.
Следуя предложению Я. Б. Фридмана *), приведённое растягивающее на-
напряжение при разрушении материала можно, казалось бы, принять за истин-
истинное сопротивление отрыву аотр#:
5отр. =
Необходимо заметить, что вопрос о той или иной трактовке сопроти-
сопротивления отрыву, как характеристики материала, а равно и вопрос о методах
определения этой характеристики, в известной мере являются спорными2).
Некоторые опыты указывают на постоянство характеристики сопроти-
сопротивления отрыву при различных видах нагружения у хрупких материалов. Для
подобного же заключения в отношении пластичных материалов пока ещё
нет достаточных данных. По результатам некоторых опытов сопротивление
отрыву зависит от качества материала — с увеличением степени наклёпа оно
растёт. Изменение скорости деформации и температуры испытания, как уже
было сказано, сравнительно мало отражается на величине сопротивления
отрыву; однако достаточно надёжных данных о количественной стороне
этого явления пока нет.
Срез является более сложным видом разрушения, чем отрыв, так как
ему обычно предшествуют значительные пластические деформации, вызы-
вызывающие перераспределение напряжений и другие осложнения. На существо-
существование этого второго типа разрушения, обусловленного преимущественно
касательными напряжениями, указывает целый ряд опытных данных.
^Фридман Я. Б., Механические свойства металлов, Оборонгиз, 1946.
2) У ж и к Г. В., Сопротивление отрыву и прочность металлов, изд. АН
СССР, 1950.

§ 250]	теории прочности	779
Разрушение металлов при растяжении без шейки, при срезе, кручении
и изгибе обычно происходит по площадкам, очень близким к тем, на кото-
которых возникают наибольшие касательные напряжения. Хотя по углу излома
не всегда можно сделать окончательное заключение о характере разруше-
разрушения (отрыв или срез), однако в ряде случаев положение, а нередко и вид
поверхности разрушения могут в этом отношении иметь решающее значе-
значение. Так, например, если разрушение при кручении происходит по площад-
площадкам, перпендикулярным к оси стержня, то несомненно, что оно обусловлено
касательными напряжениями, так как по поверхности разрушения в этом
случае нормальных напряжений вообще нет.
Значительно более трудным становится проведение различия между
разрушением путём отрыва и среза при сложных напряжённых состояниях.
Всё же и здесь в ряде случаев удалось установить, что в образовании
некоторых из тех изломов, которые было принято считать наглядными при-
примерами разрушения путём отрыва, на самом деле главную роль играют
касательные напряжения.
Так как разрушение путём среза обусловлено касательными напряже-
напряжениями, играющими главную роль и при пластической деформации материала,
то у пластичных материалов без предшествующих, обычно довольно значи-
значительных, остаточных деформаций срез вряд ли возможен. По крайней мере,
практически такого разрушения у металлов до сих пор получить не удалось,
хотя некоторые из них (например, прессованный магний и сплавы на его
основе) разрушаются от среза при сравнительно небольших деформациях
E—15%) — имеет место так называемый «хрупкий срез».
В качестве характеристики сопротивления срезу можно принять истин-
истинное значение касательного напряжения в момент разрушения (тр). Опыт-
Опытные данные показывают, что для чистых металлов (медь, алюминий, железо)
и для некоторых сплавов сопротивление срезу (тр) практически не зависит
от вида напряжённого состояния. Вместе с тем установлено, что тр в зна-
значительно большей степени, чем сопротивление отрыву, зависит от скорости
деформирования и температуры опыта. При увеличении скорости и пони-
понижении температуры тр увеличивается.
Предположение об одновременном существовании у материалов двух
видов сопротивления разрушению наглядно подтверждается опытами над
разрушением хладноломких металлов и некоторых хрупких материалов.
Сопротивление отрыву и сопротивление срезу у одного и того же мате-
материала различны по величине; у пластичных материалов обычно тр < аотр,
у хрупких, наоборот, хр > 5отр. В зависимости от изменения состава,
а также термической и механической обработки тр и сотр могут меняться
по различным законам.
Описанные характеристики сопротивления материала разрушению могут
служить основой для расчётов на прочность при простом и сложном напря-
напряжённом состоянии; вопрос об использовании этих характеристик рассматри-
рассматривается в следующих параграфах.
§ 250. Теории прочности.
А. Изложенное в предыдущих параграфах является основой для решения
общей проблемы прочности материалов при сложном напряжённом состоя-
состоянии. Это решение, как мы уже видели (§ 42), невозможно без введения
некоторых экспериментально обоснованных гипотез, называемых теориями
прочности. Из сказанного ранее о сопротивлении пластическим деформа-
деформациям и о сопротивлении разрушению вытекает необходимость в прове-
проведении чёткого разграничения между теориями прочности, рассматривающи-
рассматривающими вопросы, связанные с наступлением текучести материала и развитием

780	ПРОЧНОСТЬ МАТЕРИАЛОВ	[ГЛ. XXXVIII
значительных остаточных деформаций (упрочнение) и теориями прочности,
рассматривающими вопросы, связанные с разрушением материала путём
отрыва или среза.
История развития взглядов на вопросы прочности материалов показы-
показывает, что с давних пор, на протяжении почти двухсот лет, шла борьба
представлений о разрушении, как о явлении отрыва и среза. В этом отно-
отношении старые теории прочности характерно разбиваются на две отдельные
группы. В первую входит теория наибольших нормальных напряжений
и теория наибольших удлинений, вторую группу образует теория наиболь-
наибольших касательных напряжений вместе с последующим её обобщением, изве-
известным под названием теории Мора (более подробно об этой теории см.
ниже — § 251). Представления, на которых основывались те или иные из
старых теорий, каждое в отдельности, как мы видели, не противоречат
и современным воззрениям на вопросы прочности материалов, признающим
существование двух форм разрушения и соответственно двух видов сопро-
сопротивления разрушению.
Однако старые теории прочности страдали односторонностью понима-
понимания явления; они ограничивались изучением или только действия отдель-
отдельных составляющих напряжения (нормальной или касательной), или только
влияния деформации, без учёта их взаимной связи. Они не проводили
чёткого разграничения между предельными (опасными) состояниями (пере-
(переходом за предел упругости и явлением разрушения материала). Вследствие
этого на основе той или иной из старых теорий общее решение вопроса
о прочности различных материалов в их хрупком и пластичном состоянии
оказалось невозможным.
Для лучшего приближения к данным опытов в эти теории приходилось
искусственно вводить не соответствующие их физическому смыслу допол-
дополнительные условия, к которым прежде всего следует отнести проверку по
наибольшим сжимающим напряжениям и соответственно по наибольшим
деформациям сжатия в теориях наибольших нормальных напряжений и
наибольших удлинений. Расчёты, сделанные на основе первых двух теорий,
достаточно хорошо сходились, как известно, лишь с результатами некото-
некоторых опытов над хрупкими материалами, а расчёты по теории наибольших
касательных напряжений оправдывали в известной степени опыты над пла-
пластичными материалами. Однако и применение этих теорий к объяснению
ограниченного круга явлений—1-й и 2-й теории прочности — только к слу-
случаям хрупкого, а 3-й теории — только к случаям пластичного разрушения, —
всё же не устраняло полностью возникающих противоречий.
Разрешение противоречий и неясностей в большой степени становится
возможным, главным образом, в результате исследований наших отечествен-
отечественных учёных и, в первую очередь, благодаря работам Н. Н. Давиденкова
и его школы. Опираясь на данные ряда опытов, Н. Н. Давиденков впервые 1)
указал на двойственный характер разрушения у металлов и, в связи с этим,
на существование у них одновременно двух различных как по величине, так
и по своей физической и механической природе сопротивлений разруше-
разрушению (сопротивления отрыву и сопротивления срезу).
Учение Н. Н. Давиденкова о двух различных механизмах разрушения
нашло дополнительное подтверждение в результатах многих поставленных
у нас опытов и с некоторыми изменениями было развито его сотрудниками
(Я. Б. Фридманом и др.) в применении к различным материалам и разным
видам напряжённого состояния. Этими исследованиями в вопрос о причинах
разрушения материала была внесена известная ясность, и развитие предста-
представлений о разрушении, как о явлении отрыва и среза, получило своё отра-
отражение в так называемой «объединённой теории прочности Давиденкова —
Фридмана» (§ 252).
1) Д а в и д е н к о в Н. Н.; Динамические испытания металлов, 1936.

§ 250]
ТЕОРИИ ПРОЧНОСТИ
781
л
Б. Переходим к анализу "сначала тех теорий прочности, которые основаны
на изучении сопротивления пластической деформации (§ 248).
Выше (§ 247) уже было отмечено, что наступление пластических дефор-
деформаций связано с образованием сдвигов в кристаллических зёрнах и даже
в целых слоях материала; поэтому условия для наступления текучести при
сложном напряжённом состоянии могут определяться либо теорией наиболь-
наибольших касательных напряжений, либо теорией энергии формоизменения. Эти
теории лежат в основе так называемых условий пластич.ности.
Обычно считают, что при оценке условий наступления текучести мате-
материала как при простом, так и при сложном напряжённом состояниях, лучшее
соответствие с результатами многочисленных опытов даёт энергетическая
теория, хотя уже неоднократно было отмечено
(Н. Н. Давиденков, И. А. Одинг и др.), что
мнение о неточности теории наибольших ка-
касательных напряжений в данном случае осно-
основано на недоразумении, связанном с непра-
неправильным определением предела текучести.
Как известно, энергетическая теория воз-
возникла на основе представления о постоянстве
удельной энергии изменения формы элемента
материала, как об условии наступления пласти-
пластических деформаций. Однако можно показать,
что эта теория, аналогично теории наиболь-
наибольших касательных напряжений, тоже требует
в качестве условия для наступления пластиче-
пластических деформаций постоянства касательного
напряжения, но не наибольшего, а действую-
действующего ио площадке, равнонаклонённой к на-
направлению главных напряжений в рассматри-
рассматриваемой точке.
Рассмотрим очень малый тетраэдр, образованный тремя плоскостями
главных напряжений и четвёртой плоскостью, равнонаклонённой к главным
осям (фиг. 653). Длину рёбер тетраэдра по главным осям возьмём равной
единице. Площадь каждой из боковых граней Fu F3 и Fa будет равна -н- • I3;
косинусы углов, составленных нормалью п к четвёртой грани с главными
осями 7, 2, 3, равны между собой и равны ——-. Площадь Fn четвёртой
грани, таким образом, равна
Фиг. 653.
F =
cos(l, п)
¦ = 4-^3 -I2.
Полное напряжение, действующее по наклонной грани тетраэдра, будет
равно геометрической сумме сил, приложенных к боковым граням, делён-
делённой на Fn. Обозначая это напряжение через рт а главные напряжения
через аи а2 и а3, получаем:
1
Напряжение рп можно разложить на нормальное ап и касательное т„. Нор-
Нормальное напряжение равно сумме проекций на нормаль сил, приложенных
к боковым граням, делённой на площадь Fn:
/Vi cos (/г, 1) + /%g2 cos (/г, 2) + /Va cos (n, 3) 1 . , . ,
Gn =	r	:	== T ^ ' °- *~Сз^
1 n	°

782	прочность материалов	[гл. xxxviii
касательное же напряжение по этой площадке тя равно:
= у У (*1 - а2J + (а2 - а3J + (*8 - *iJ-	C8.1)
При простом растяжении
х - У* а
Таким образом, если мы поставим условие, что наступление явления теку-
текучести соответствует достижению напряжением ^ величины предела теку-
текучести ат, то получим для простого растяжения
этой же величины должно достигать тл и при сложном напряжённом со-
состоянии, чтобы наступили пластические деформации:
C8.2)
Для того чтобы был обеспечен запас прочности k против наступления
явления текучести, надо, чтобы левая часть условия C8.2) после сокраще-
т/*2~
ния на -~— была не больше ~ = [с]; тогда мы приходим к условию проч-
прочности по энергетической теории, полученному нами иным путём в § 43.
Таким образом, энергетическая теория — это тоже теория постоянства каса-
касательных напряжений, но не наибольших, а действующих по указанной пло-
площадке. В этой теории учтены и физическая природа пластических дефор-
деформаций (сдвиг) и величина всех трёх главных напряжений. Равнонаклонённая
к главным осям площадка (октаэдрическая) является площадкой, в которой
происходит так называемый результирующий сдвиг.
Наибольшие касательные напряжения в плоскостях, параллельных каждой
из главных осей (§ 39), действуют по площадкам, делящим пополам углы
между соответствующими парами главных осей. Они равны соответственно
ti- § ; Т2~ 2 ; Тз~ 2 *
Таким образом, из C8.1) получаем:
*п = ^ 1/*т? + т! + т!.	C8.3)
По закону Гука этим напряжениям соответствуют сдвиги, лежащие
в тех же плоскостях:
Поэтому
¦zn = -|G Vll + il + tl = G1n,	C8.4)
9
где Тя = ~о~ К 7i + Ti + Ti — результирующий сдвиг.

§ 250]	теории прочности	783
Если мы условимся изображать каждый из сдвигов Yi, Ts и у3 вектором,
расположенным в соответствующей плоскости, то равнодействующий
сдвиг тЛ будет лежать в плоскости, равнонаклонённой к главным осям. Эта
площадка не случайно определяет условие прочности, она является пло-
плоскостью сдвига, который отражает на себе влияние всех трёх главных
напряжений.
Условие C8.2) относится к ненаклёпанному материалу; чтобы при помощи
его получить сопротивление пластическим деформациям для сложного на-
напряжённого состояния при постепенном росте пластических деформаций,
достаточно подставить в правую часть уравнения C8.2) вместо ат перемен-
переменную величину а, полученную в опытах при простом растяжении.
Таким путём мы можем получить полную механическую характеристику
сопротивления пластическим деформациям в самом общем случае. Если бы
мы попытались представить геометрически эту характеристику, то сделать
это так просто, как для случая линейного напряжённого состояния, не удастся.
Можно условиться изображать напряжённое состояние элемента материала
точкой трёхмерного пространства с координатами, равными главным напря-
напряжениям.
Уравнение типа C8.2) тогда окажется уравнением некоторой поверхности;
в случае использования энергетической теории это будет*) цилиндрическая
поверхность с осью, равнонаклонённой к главным осям напряжений, и радиу-
радиусом, равным:
Все точки, лежащие на поверхности цилиндра, изображают предельные на-
напряжённые состояния материала, соответствующие началу пластических де-
деформаций. Если мы воспользуемся теорией наибольших касательных напря-
напряжений, то предельной поверхностью будет шестигранная призма с той же
осью, что и цилиндр; длина стороны шестиугольного основания равна:
Вообще уравнение предельной поверхности имеет вид (для ненаклёпанного
материала):
ЛК °*> °; °т) = 0,	C8.5)
где /i — определённая функция главных напряжений и предела текучести; вид
этой функции зависит от принятой теории прочности. Учитывая влияние
упрочнения, мы должны постоянную величину ст заменить переменной о; с
наклёпом радиус нашего цилиндра (предельной поверхности) будет меняться.
В. Обратимся теперь к теориям прочности, основанным на изучении
явлений разрушения материала.
Как известно (§ 249), разрушение от среза практически невозможно без
предварительного прохождения через стадию более или менее значительных
пластических деформаций, обусловленных касательными напряжениями. По-
Поэтому в качестве теории разрушения путём среза при сложном напряжён-
напряжённом состоянии следует принять или, как более простую, теорию наиболь-
наибольших касательных напряжений, или энергетическую теорию. В первом случае
.за характеристику сопротивления срезу должна быть принята величина
*) См. проф. Дружинин С. И. и проф. Я г н Ю. И., Сопротивление
материалов, 1933.

784	прочность материалов	[гл. xxxvirt
максимального истинного касательного напряжения тр (§ 249), "во втором —
величина касательного напряжения тлр C8.2) на площадке результирующего
сдвига к моменту разрушения.
Что же касается теории сопротивления отрыву, то для этой цели, как
уже указывалось ранее (§ 249), следует выбрать или теорию наибольших
нормальных напряжений, или теорию наибольших удлинений. Какую бы из
этих теорий мы ни приняли, в общем виде условия для нарушения проч-
прочности путём среза и отрыва будут иметь вид, аналогичный уравнению C8.5):
Л К «„ «» тр) = 0 (срез)	C8.6)
и
/а (°i. *в, ?i °отр) = 0 (отрыв),	C8.7)
где тр — сопротивление срезу, а сотр — сопротивление отрыву (например,
приведённое растягивающее напряжение срРзр, подсчитанное на основе тео-
теории наибольших удлинений). Вид функций /2 и /3 зависит от принятой теории
прочности. Уравнения C8.6) и C8.7), в свою очередь, представляют собой
уравнение поверхностей, предельных по срезу и отрыву. Совокупность по-
поверхностей, заданных уравнениями C8.5), C8.6) и C8.7), выделяет в простран-
пространстве область, внутри которой точки изображают напряжённые состояния,
безопасные в отношении нарушения прочности. Точки же, попадающие на
ту или другую предельную поверхность, будут соответствовать напряжён-
напряжённым состояниям материала, при которых наступает то или иное нарушение
прочности.
§ 251. Обобщённая теория прочности Мора.
Допуская некоторые отступления от точного вида функций fly /2 и /3|
можно упростить вопрос о нахождении предельных поверхностей и све-
свести задачу к нахождению предельных кривых, расположенных в одной пло-
плоскости. Если исходить из теории наибольших касательных напряжений, то,
как известно (§ 43), условие прочности будет иметь такой вид:
Условие нарушения прочности за счёт появления пластических деформаций
напишется так:
где dj и а3 — наибольшее и наименьшее главные напряжения.
Можно рассматривать полученные формулы шире, чем интерпретацию
теории наибольших касательных напряжений; можно считать, что эти фор-
формулы выражают условие, что нарушение прочности зависит лишь от наи-
наибольшего и наименьшего главных напряжений. Мы знаем теперь, что это
предположение не вполне верно, что среднее по величине главное напряже-
напряжение о2 также влияет на прочность материала. Однако известно также, что это
влияние незначительно и погрешность от отбрасывания а2 не превысит
в крайних случаях 15%, а в большинстве случаев она будет значительно
меньше.
Если принять это упрощающее предположение, то вместо трёхмерного
пространства, координаты точек которого изображаются главными напряже-
напряжениями, мы получим плоскость с осями ах и а3; предельные поверхности /lt
/a и /8 обратятся в кривые, расположенные в этой плоскости.
Напряжённое состояние материала может быть изображено точкой с ко-
координатами ах н а,, а может быть с большей полнотой изображено кругом

§ 251]
ОБОБЩЁННАЯ ТЕОРИЯ ПРОЧНОСТИ МОРА
785
Фиг. 654.
Мора, построенным на главных напряжениях at и а3 в системе прямоугольных
координат а и х (§ 37). Этот способ изображения напряжённого состояния
более полон, потому что он характеризует напряжённое состояние мате-
материала в рассматриваемой точке не только величиной главных напряжений
at и а3, но и напряжениями сит, действующими по разным площадкам,
проходящим через рассматриваемую точку. Если напряжения ах и а3 дости-
достигают таких величин, что вызывают предельное напряжённое состояние, при
котором происходит нарушение проч-
прочности того или иного вида, то соответ-
соответствующий круг Мора будет называться
предельным. На фиг. 654 изображены
предельные круги 1 и 2 при простом
растяжении и сжатии для материала,
обладающего разной величиной предела
прочности при растяжении и сжатии
(чугун). Длина АО изображает предел
прочности при растяжении, а ОБ — при
сжатии. Если мы будем менять предель-
предельное напряжённое состояние от простого
растяжения до простого сжатия, умень-
уменьшая положительное at от О А до нуля
и увеличивая (по абсолютной вели-
величине) отрицательное а3 от нуля до ОВ, то предельный круг Мора 1 посте-
постепенно перейдёт в предельный круг 2.
Промежуточным предельным напряжённым состоянием будет соответ-
соответствовать непрерывный ряд предельных кругов Мора. При постепенном пе-
переходе круга 1 в круг 2 эта серия кругов даст нам некоторую кривую,
показанную на фиг. 654 пунктиром, являющуюся огибающей для семей-
семейства предельных кругов Мора. Эта огибающая и будет предельной кривой,
заменяющей совокупность кривых /2 и /8 или /t и /3; каждый круг Мора,
касательный (по свойству огибающей) к этой кривой, будет соответ-
соответствовать одному из предельных напряжённых состояний.
Огибающая пересечёт ось абсцисс в некоторой точке S, соответствую-
соответствующей всестороннему растяжению с предельным напряжением OS] действи-
действительно, в вершине огибаю-
огибающей круг Мора обратится
в точку, следовательно, на-
напряжения at и а8, а значит и а2,
будут равны между собой.
С противоположной сторо-
стороны предельная кривая остаёт-
остаётся незамкнутой, ибо невоз-
невозможно разрушить материал
путём всестороннего равно-
равномерного сжатия.
Если пределы прочности
при растяжении и сжатии
равны (сталь), то огибающая
идёт около начала коорди-	фиг, 655.
нат параллельно оси абсцисс
(фиг. 655).
Обычно построение огибающей упрощают; так как на практике чаще
приходится встречаться с напряжёнными состояниями, изображаемыми кру-
кругами Мора, расположенными между 1 и 2 (фиг. 654), то соответственную
часть огибающей заменяют просто прямой, касательной к этим кругам.
Уменьшая теперь масштаб чертежа в k раз, где k — коэффициент запаса, по-
получаем уже не предельные круги Мора, а круги, изображающие допускаемые

786
ПРОЧНОСТЬ МАТЕРИАЛОВ
[ГЛ. XXXVIII
напряжённые состояния. На фиг. 656 отрезок ОЛ изображает допускаемое
напряжение при простом растяжении [а+], а отрезок ОВ — допускаемое на-
напряжение при простом сжатии [а_].
Для некоторого промежуточного круга 3 с центром в О3, касающегося
линии ML (огибающей) в точке К и характеризующего напряжённое состояние
с главными напряжения-
напряжениями oj и а3, имеем:
или
NO-,
РО*
00
о,о3
• ГОТ
\-ool
или, заменяя отрезки ли-
линий значениями соответ-
соответствующих напряжений,
Фиг. 656.
Выполняя преобразования и вводя знак неравенства, получаем	условие проч-
прочности по теории Мора:
_ I +J „ ^.	г_ 1	/QQ С\
ON	г	г- ^8 ^^ l^-4-l»	luO.OI
которое при [а_] = [а+] обращается в условие прочности по теории наиболь-
наибольших касательных напряжений.	^
Это же уравнение можно вывести и без помощи кругов Морах), если
потребовать, чтобы на любой площадке было соблюдено условие безопас-
безопасности в отношении сдвига:
<спр == | т | +/с ^ С.	C8.9)
Здесь / играет роль коэффициента трения, С — предельное сопротивление
материала сдвигу, а тпр — некоторое приведённое касательное напряжение.
Положение площадок, на которых тпр достигает наибольшего значения,
определяется углом а по отношению к площадке с главным напряжением а2;
при этом tg2a = -^-. Плоскости сдвига проходят параллельно направлению
промежуточного главного напряжения о2. Можно показать ^, что
/== Ы-М и с^ VKU*-]
2 УМ К]	2
Из уравнения C8.9) следует, что в тех случаях, когда a > 0 (растягиваю-
(растягивающее напряжение), сдвиги начнутся при меньшей величине касательного на-
напряжения т, чем в тех случаях, когда а<0 (сжимающее напряжение). Та-
1) Проф. Дружинин СИ. и проф. Я г н Ю. И., Сопротивление мате-
материалов, 1933.

§ 252] ОБЪЕДИНЁННАЯ ТЕОРИЯ ПРОЧНОСТИ ДАВИДЕНКОВА—ФРИДМАНА 787
ким образом, уравнения C8.8) и C8.9) отражают то обстоятельство, что по
Мору на возникновение текучести, а равно и на разрушение материала,
кроме касательных напряжений, влияют также и нормальные напряжения,
возникающие на площадках скольжения (сдвига).
Теория Мора хорошо описывает явление пластической деформации
и разрушение материалов путём среза, но не даёт правильного освещения
явлению разрушения путём отрыва. Таким образом, хотя эта теория и пред-
представляет собой известный шаг вперёд по сравнению с другими старыми
теориями, всё же область её применения является ограниченной.
§252. Объединённая теория прочности Давиденкова—Фридмана1).
А. Взгляды Н. Н. Давиденкова, в дальнейшем с некоторыми изменениями
развитые Я. Б. Фридманом, легли в основу построенной ими новой объеди-
объединённой теории прочности материалов. Эта теория, описывающая как про-
процессы возникновения и развития пластических деформаций, так и явление
разрушения, повидимому, представляет более общее решение вопроса о проч-
прочности материала, получаемое путём синтеза двух ранее известных теорий —
теории наибольших касательных напряжений и теории наибольших удлинений.
Основные положения новой теории наиболее наглядно отражены в так
называемой диаграмме механического состояния материала, предложенной
Я. Б. Фридманом (фиг. 657). Эта диаграмма одновременно учитывает как вид
,7
6
I Сопротивление срезу т'р
1/1
Сопротивление срезу tD
Область пластической
деформации •
Предел текучест
Фиг. 657.
напряжённого состояния, так и свойства материала, оцениваемые пределом
текучести тт и сопротивлением срезу ъ^ определяемым на основе теории наи-
наибольших касательных напряжений, и сопротивлением отрыву %тр = ^зр (?Р*
определённым на основе теории наибольших удлинений.
На диаграмме по оси ординат откладывается наибольшее касательное
напряжение ^max, a
вающее напряжение + а]
по оси абсцисс — наибольшее приведённое растяги-
Найденные опытным путём значения предела
max*
J) Содержание § 252 представляет собой краткое изложение новой тео-
теории, составленное на основе работ Я. Б. Фридмана, в частности, его книги
«Механические свойства металлов», Оборонгиз, 1946.

788	прочность материалов	[гл. xxxviii
текучести тт и сопротивления срезу тр изображаются на диаграмме в виде
двух прямых горизонтальных линий; сопротивление же отрыву ajj изображается
вертикальной прямой, проведённой на соответствующем расстоянии от на-
начала координат. Прямолинейность линий, изображающих тт, тр и a|J вытекает
из определения тт и тр, сделанного на основе теории наибольших касатель-
касательных напряжений, а ар — на основе теории наибольших удлинений.
В качестве единой характеристики напряжённого состояния во всех
случаях принимается отношение наибольшего касательного напряжения
к наибольшему приведённому растягивающему напряжению в данной точке
тела т = —^—. Таким образом, прямые, проведённые из начала коорди-
~Г" атах
нат диаграммы под определённым углом к оси абсцисс, тангенс которого
равен /и, характеризуют то или иное напряжённое состояние, возникшее
в элементарном объёме тела в результате действия внешних усилий. На
фиг. 657 нанесено несколько таких прямых (лучи 1—7). Луч 7, соответствую-
соответствующий всестороннему равномерному растяжению, при котором ттах = 0 и
т = О, совпадает с осью абсцисс о?ах; луч 7, соответствующий различным
случаям всестороннего неравномерного сжатия, при которых а^ах равно
нулю (или меньше нуля) и, следовательно, т = со, совпадает с осью орди-
ординат ^тах. (Случаю всестороннего равномерного сжатия, когда, благодаря
отсутствию сдвигов и удлинений, ттах и а^ах равны нулю, отвечает начало
координат — точка О.)
Остальные лучи, характеризующие любые другие промежуточные виды
напряжённого состояния, располагаются между лучами 1 и 7. Так, например,
осевое растяжение р?ах = 2ттах; т = 0,5J изображается лучом 3; кручение
и сРез [°тах = 0 + f*) W т = Т+jTj ~~ ЛуЧ0М 4; 0СеВ0С СЖаТИе [5™х =
= 2(хттах; т = -к— — лучом 5. (Значения т для лучей 3> 4, 5 на фиг. 657
вычислены в предположении, что j* = 0,25.) Различным случаям растяже-
растяжения или изгиба надрезанных образцов (напряжённые состояния более или
менее близки к всестороннему равномерному растяжению) отвечает группа
лучей 2; случаям вдавливания или сжатия под боковым давлением — группа
лучей 6.
Диаграмма механического состояния даёт наглядное представление о фи-
физической природе нарушения прочности при различных обстоятельствах.
Прежде всего следует обратить внимание на взаимное расположение линий,
характеризующих свойства материала, и различные виды напряжённого со-
состояния. Если напряжённое состояние таково, что наклонный луч, его изо-
изображающий, пересекает сначала прямую тр (АВ), а потом уже прямую
Ср (а), например, луч 3 (осевое растяжение), то разрушение материала про-
произойдёт путём среза. В этом случае пластические свойства материала будут
использованы полностью. Если же изображающий луч пересекает пря-
прямую ар раньше, чем прямую тр (например, верхний луч группы 2), то мате-
материал разрушается путём отрыва, пластичность и вязкость его понижаются в тем
большей мере, чем ниже проходит изображающий луч, т. е. чем меньше
отношение т = —ш^х . Таким образом, можно условно различать отдельные
» атах

§ 252J ОБЪЕДИНЁННАЯ ТЕОРИЯ ПРОЧНОСТИ ДАВИДЕНКОВА—ФРИДМАНА 789
виды напряжённого состояния или способы нагружения по степени их
«жёсткости». «Жёстким» видам напряжённого состояния будут, очевидно,
соответствовать более пологие лучи У, 2 и 3, «мягким» — лучи 5, 6 и 7.
Отсюда следует, что положение линии сопротивления отрыву на диаграмме
механического состояния имеет очень большое значение. Различные вели-
величины сопротивления отрыву при одной и той же величине сопротивления
срезу изображены на фиг. 657 вертикальными линиями а, б, в и г. Нетрудно
заметить, что с перемещением линии сопротивления отрыву ближе к началу
координат опасность разрушения путём отрыва даже при «мягких» способах
нагружения значительно возрастает. Так, в положении а разрушение путём
отрыва не может быть получено ни при каких видах напряжённого состоя-
состояния, кроме очень близких к всестороннему равномерному растяжению (алю-
(алюминий, медь, аустенитные стали). В положении же г разрушение путём
отрыва может произойти даже и при осевом сжатии; только при вдавливании
и сжатии под боковым давлением разрушение происходит ещё путём среза
(мрамор, плексиглас). В положении б отрыв возможен при осевом растяже-
растяжении (закалённые и низкоотпущенные стали), в положении в отрыв происхо-
происходит уже при кручении (чугун и литые алюминиевые сплавы).
Таким образом, вид разрушения определяется отношением т = —™**
• атах
вместе с отношением -^р , характеризующим взаимное расположение линий
сопротивления отрыву и срезу; если первое отношение меньше второго,
имеет место отрыв, в обратном случае — срез. Если т = -р~ излом имеет
неустойчивый характер.
Отношение -~- вместе с отношением т позволяет установить наличие
или отсутствие пластической деформации перед разрушением путём отрыва;
если первое меньше второго, то отрыву будут предшествовать пластическая
деформация той или иной величины («вязкий» отрыв), в противном случае
излом будет хрупким. Так, например, при осевом растяжении материала,
для которого сопротивление отрыву определяется линией, близкой к ли-
линии (а), в образце при разрушении образуется шейка; если же сопротивление
отрыву определяется линией (б), то разрушение образца произойдёт без
образования шейки (некоторые бронзы). Материал во многих случаях (все-
(всестороннее, плоское и одноосное растяжения, сдвиг и кручение) будет разру-
разрушаться путём отрыва, обычно хрупкого, если тр будет значительно больше
а" (стёкла, . пластмассы, горные породы) и, наоборот, материал в большем
числе случаев будет разрушаться путём среза, если а" будет значительно
больше т-р (свинец, алюминий, медь, многие железные сплавы).
Переход от отрыва к срезу, а равно и от хрупкого разрушения к вяз-
вязкому, может быть осуществлён как изменением вида напряжённого состояния,
так и изменением свойств материала путём «внешних» (изменение темпера-
температуры, скорости деформирования) и «внутренних» (изменение состава и струк-
структуры) факторов. При «жёстких» способах нагружения более вероятным
является хрупкое разрушение путём отрыва, при «мягких» — разрушение
путём среза после довольно значительной пластической деформации. Этим,
в частности, объясняется склонность к хрупкому разрушению надрезанных
образцов даже сравнительно пластичных материалов и, наоборот, склонность

790	ПРОЧНОСТЬ МАТЕРИАЛОВ	[ГЛ. XXXVIII
к разрушению путём среза после довольно значительной деформации даже
таких хрупких материалов, как камень и бетон, подвергнутых сжатию под
боковым давлением. Заметим, однако, что материалы, у которых хр ^ тт
(например, стекло при 20° С), ни при каких способах нагружения не могут
быть переведены из хрупкого состояния в пластичное.
При каком-либо определённом виде напряжённого состояния все обстоя-
обстоятельства, которые могут увеличивать хт и ^р (т. е. перемещать вверх соот-
соответствующие горизонтальные прямые, например, из положения А В в поло-
положение i4i#i), при одной и той же величине сопротивления отрыву а? спо-
способны, очевидно, вызвать переход материала из пластического состояния
в хрупкое. Именно так следует объяснять хрупкость материала при пони-
пониженных температурах и при значительном повышении скорости деформа-
деформации,— например, при ударе. Таким образом, если при испытаниях нужно по-
поставить материал в наиболее тяжёлые условия работы, то необходимо принять
меры к увеличению жёсткости способа нагружения, а также к поднятию
сопротивления пластическим деформациям и сопротивления срезу, т. е.
испытывать надрезанный образец с большой скоростью, при низких темпера-
температурах.
Б. Описанная здесь диаграмма механического состояния относится,
собственно говоря, к случаям однократного статического и динамического
нагружения. Однако нет оснований предполагать, что и более сложные слу-
случаи разрушения при износе, резании, ползучести и усталости нельзя свести
к разрушению путём отрыва или среза и анализировать с помощью подоб-
подобной же диаграммы.
Следует отметить, что ряд положений, на которых основано построение
описанной выше диаграммы механического состояния, безусловно нуждается
в некоторых уточнениях и дополнениях. Так, например, линии, изображаю-
изображающие на фиг. 657 тт и тр, могут быть приняты за прямые только для чистых
металлов и некоторых сплавов, так как лишь для этих металлов величина
предела текучести и сопротивления срезу практически не зависит от вида
напряжённого состояния. Для ряда других металлов и сплавов предположение
о прямолинейности упомянутых линий может быть использовано лишь для
получения приближённого решения вопросов прочности. То обстоятельство,
что сопротивление отрыву, как показывают опыты, расчёт с увеличением
степени наклёпа, не позволяет, строго говоря, считать прямой и линию,
изображающую а?.
При построении диаграммы фиг. 657 принято допущение, что лучи,
характеризующие напряжённое состояние, остаются прямыми вплоть до
момента разрушения (т. е. предполагается, что напряжённое состояние
в процессе деформации не претерпевает изменения). Однако у пластичных
материалов возникновение больших пластических деформаций (т. е. переход
за линию, изображающую тт) в ряде случаев довольно существенно изменяет
картину. распределения напряжений внутри тела. Очевидно, что использова-
использование предположения о прямолинейности изображающих лучей в подобных
случаях может привести к ошибочным выводам.
Наконец, как уже было сказано ранее (§ 249), вопрос о привлечении той
или иной теории прочности (первой или второй) для объяснения явлений
разрушения материала путём отрыва, вообще говоря, является спорным, так
как одни случаи хрупкого разрушения могут быть более удовлетворительно
объяснены с помощью теории наибольших удлинений, другие — с помощью
теории наибольших нормальных напряжений.
Несмотря на всё это, нельзя не признать, что схема, изображённая на
фиг. 657, является удачной. В этой схеме наглядно отражены современные
воззрения на вопросы прочности материалов, признающие существование
двух форм разрушения (отрыв и срез) и предполагающие зависимость той

§ 252] ОБЪЕДИНЁННАЯ ТЕОРИЯ ПРОЧНОСТИ ДАВИДЕНКОВА—ФРИДМАНА 791
или иной из этих форм разрушения от вида напряжённого состояния. При
этом в ней используется единая система для измерения и сопоставления са-
самых разнообразных напряжённых состояний, характеризуемых одной величи-
величиной — углом наклона изображающей прямой, что во многих случаях позво-
позволяет правильно анализировать результаты опытов над сопротивлением мате-
материала тем или иным нарушениям прочности.
Диаграммы, подобные изображённой на фиг. 657, могут оказать помощь
при разрешении вопросов, связанных с процессами технологической обработки
металлов; для целого ряда употребляющихся в машиностроении материалов
они уже построены и используются в нашей промышленности.
Изложенные выше положения могут быть использованы и при проверке
прочности деталей машин и сооружений, работающих при напряжениях ниже
предела текучести материала. Для этого от предельных (опасных) напряже-
напряжений Ср и хр необходимо перейти к допускаемым напряжениям на отрыв и
срез [а+] и [т]. До уточнения вопроса о величине допускаемых напряжений
в качестве [а+] и [т] можно использовать допускаемые напряжения на растя-
растяжение и сдвиг по существующим нормам.
При этом проверку прочности в зависимости от условий работы детали
и характера напряжённого состояния следует производить по одной из двух
теорий: теории наибольших удлинений или теории наибольших касательных
напряжений. Если наклон луча, изображающего напряжённое состояние ма-
материала в упругой области, т. е. отношение
ашах
М
меньше отношения -г—у, то при увеличении напряжений разрушение путем
отрыва представляется более возможным, чем разрушение путём среза, и
в соответствии со сказанным выше следует применить теорию наибольших
удлинений; если же /я> -~4-, следует применить теорию наибольших каса-
[ч\
тельных напряжений.
Так, если уЦ- > -^ (хрупкие материалы), то отчасти при кручении
la+J *
!/и = ——>-о")» осевом сжатии (т = -к—>1) и других более «мягких»
!
V	+ (	/	\ W I
видах нагружения (т;>1) для проверки прочности следует использовать тео-
теорию наибольших касательных напряжений, так как m > J-т *). При осевом
LJ+i
растяжении и других более «жёстких» видах нагружения \т^~п') для про-
проверки прочности того же материала следует использовать теорию наиболь-
наибольших удлинений. Если же ¦ J = — (пластичные материалы), то проверку
[а+] 2
прочности почти во всех случаях необходимо производить по теории наи-
наибольших касательных напряжений; теорию наибольших удлинений придётся
использовать только при очень «жёстких» видах нагружения, когда т<.-к-
(всестороннее растяжение).
1) Следует заметить, что в этих случаях с результатами опытов лучше
согласуется не теория наибольших касательных напряжений, а теория Мора.

792	ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ	[ГЛ. XXXIX
ГЛАВА XXXIX
ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ.
§ 253. Влияние высоких температур на механические
свойства металлов.
В связи с быстрым развитием машиностроения в настоящее время всё
более важное значение приобретают расчёты на прочность деталей машин,
длительное время работающих при высоких температурах. К таким деталям
относятся, например, диски и лопатки паровых и газовых турбин, трубы и
другие детали паровых котлов, различные части двигателей внутреннего
сгорания, реактивных двигателей, химических установок и приборов и
многие другие.
На поведении материала таких деталей под нагрузкой сказывается как
абсолютная величина температуры, так, в особенности, и продолжитель-
продолжительность работы детали при этой температуре.
Под влиянием высокой температуры свойства металлов значительно из-
изменяются, так что знание характеристик прочности и пластичности металла
при нормальной (комнатной) температуре является уже далеко недостаточ-
недостаточным для расчёта детали из этого металла, работающей при повышенной
температуре. Вместе с тем, обычные методы кратковременных испытаний
оказываются пригодными для определения механических характеристик ме-
металлов только при сравнительно невысоких температурных (например, для
углеродистых сталей — до 300—350°, для легированных сталей — до 350—400°,
для цветных металлов — до 50—150°). При более высоких температурах
характеристики прочности и пластичности очень сильно зависят от продол-
продолжительности самого испытания. Вследствие этого при температурах выше 400°
для сталей и 150° для цветных металлов определение таких, например, ха-
характеристик металла, как предел пропорциональности и предел текучести,
является в значительной мере условным, а в некоторых случаях даже теряет
свой смысл.
С повышением температуры модуль упругости и предел пропорциональ-
пропорциональности металла снижаются сначала постепенно, а затем, начиная с указанных
выше температур, всё более резко. Так, значение модуля нормальной упру-
упругости стали при температуре 600° примерно на 25—30%, а при темпера-
температуре 800° примерно на 50% ниже его значения при комнатной температуре.
Понижение модуля упругости и предела пропорциональности у цветных ме-
металлов носит ещё более резко выраженный характер.
Величина коэффициента поперечной деформации у стали с повышением
температуры обычно несколько увеличивается.
Предел текучести углеродистой стали при повышении температуры
обычно сначала несколько повышается и при температуре около 200° дости-
достигает своей наибольшей величины. При дальнейшем увеличении температуры
величина предела текучести сильно уменьшается; так, при температуре 400°
предел текучести углеродистой стали составляет лишь от 60 до 70% его
величины при комнатной температуре. При этом длина площадки текучести
сокращается; у углеродистой стали примерно при 350—450° эта площадка
вовсе исчезает. У легированных сталей предел текучести с увеличением тем-
температуры, как правило, непрерывно понижается.
Величина отношения предела текучести к пределу прочности стали при повы-
повышении температуры обычно уменьшается, притом тем более, чем выше темпе-
температура; при температурах 300—350° величина этого отношения равна 0,35—0,4.
Пластические свойства стали (полное относительное удлинение и сужение
при разрыве) с повышением температуры от 20 до 200—300° несколько
снижаются; при дальнейшем повышении температуры пластичность стали,
как правило, снова возрастает (никелевые, хромоникелевые, хромокремни-

§ 253]
ВЛИЯНИЕ ВЫСОКИХ ТЕМПЕРАТУР
793
стые, хромовольфрамовые стали). У аустенитных хромоникелевых сталей
пластичность с повышением температуры понижается; у углеродистых сталей
снижение пластичности наблюдается при температурах 250—350° (так назы-
называемая синеломкость стали) и при температурах 900—1000° (красноломкость
стали). У одних цветных металлов (алюминий, магний) повышение темпера-
температуры вызывает непрерывное увеличение, а у других (медь, латунь, никель) —
наоборот, уменьшение относительного удлинения и сужения.
Предел прочности стали при повышении температуры, как правило, сна-
сначала повышается и при температуре 250—300° достигает своей наибольшей
величины, примерно на 20—25% превышающей величину предела проч-
прочности при комнатной температуре. При дальнейшем увеличении температуры
величина предела прочности резко уменьшается. Так, например, для мало-
малоуглеродистой стали при 600° величина предела прочности составляет только
около 40% величины предела прочности той же стали при комнатной тем-
температуре.
Добавка легирующих примесей (никеля, хрома, ванадия) замедляет сни-
снижение предела прочности стали с увеличением температуры. Предел проч-
прочности чугуна до 300° сохраняется почти неизменным; при дальнейшем повы-
повышении температуры он сильно уменьшается. У цветных ^металлов (алюминий,
медь, латунь, магний, олово, свинец, цинк, никель) и их сплавов предел проч-
прочности с повышением температуры непрерывно и сильно понижается. Так,
при 600° у этих металлов величина предела прочности составляет всего лишь
несколько процентов величины предела прочности при комнатной температуре.
Изменение предела выносливости стали с повышением температуры
более или менее соответствует изменению предела прочности, т. е. сначала пре-
предел выносливости несколько увеличивается, а затем непрерывно уменьшается.
25000
20000-
15000
10000
5000
п
тО.5
0,4
0,3
0,2
0,1
0
т50
30
20
10
¦>
л
—?—-\
\<5г
V
V
А
\^
\ \
\ 1
\ i
N
i
100
90
80
70
60
50
40
30
20
10
Т° 0
/
/ i
/ \
/ \
—)—,—,—.—,—^—t—I
0 100 200 300 400 500 600 700 800 0 W0 200 300 400 500 600 700 800
Фиг. 658.
В качестве примера на фиг. 658 приведены кривые изменения характе-
характеристик прочности и пластичности малоуглеродистой стали @,15% С) с повы-
повышением температуры до 800°.

794	основы расчётов на ползучесть	[гл. xxxix
§ 254. Явление ползучести и релаксации.
Описанное выше изменение характеристик прочности и пластичности
металлов с повышением температуры имеет весьма важное значение при
расчётах на прочность деталей машин и сооружений. Однако наиболее су-
существенным в поведении металлов при высоких температурах оказывается
явление так называемой ползучести или крипа.
Ползучестью называется непрерывно (хотя и сравнительно медленно)
растущая во времени деформация материала, происходящая под действием
постоянных по величине усилий (или напряжений) при повышенной темпера-
температуре. У ряда металлов (свинец, латунь, бронза, алюминий и некоторые другие
цветные металлы и сплавы) ползучесть может иметь место даже при ком-
комнатной температуре.
Чем выше температура, тем быстрее нарастает Деформация ползучести.
Иногда напряжения, меньшие не только предела прочности, но даже и пре-
предела пропорциональности материала при комнатной температуре, м'огут при
высокой температуре привести к разрушению детали в результате постепен-
постепенного нарастания деформации в течение достаточно большого промежутка
времени.
Таким образом, например, стальная труба, являющаяся паропроводом и
работающая при высоком давлении и температуре пара, будет непрерывно
увеличивать свой диаметр; в конце концов может произойти разрыв стенок
трубы (такие случаи иногда имели место на практике). В результате ползу-
ползучести диска и лопаток паровой турбины могут быть перекрыты зазоры,
имеющиеся между концами лопаток и корпусом турбины, что вызовет
поломку лопаток.
Деформация ползучести у металлов представляет собой необратимую
(пластическую) деформацию материала и может быть рассматриваема как
медленная текучесть металла. В результате развития пластических деформа-
деформаций за счёт ползучести в ряде случаев (особенно при сложном напряжённом
состоянии) происходит изменение величины напряжений и даж^ перераспре-
перераспределение их по объёму детали. Изменение величины напряжений будет осо-
особенно значительным тогда, когда вследствие тех или иных особенностей
работы детали полная деформация её с течением времени не сможет изме-
изменяться. В этом случае упругая деформация детали, полученная ею при на-
гружении, с течением времени будет уменьшаться; за счёт этого возникнет
и будет постепенно увеличиваться пластическая деформация. Вместе с тем,
напряжения в детали будут снижаться. Такое уменьшение напряжений в ре-
результате постепенного нарастания пластической деформации за счёт упругой
носит название релаксации напряжений.
Благодаря релаксации напряжений плотность соединения деталей, скре-
скреплённых при помощи упругого натяга, постепенно может быть настолько
ослаблена, что вызовет нарушение нормальной работы конструкции. Так,
например, ослабление плотности болтового соединения фланцев газопровода
или цилиндра высокого давления паровой турбины может, в конце концов,
привести к утечке газа или пара, если периодически не возобновлять затяжку
болтов соединения; ослабление плотности насадки диска турбины на вал
может привести к нарушению связи между диском и валом, к так называе-
называемому «сходу» диска.
Как уже было сказано, у некоторых цветных металлов и сплавов явление
ползучести может иметь место даже и при комнатной температуре. Однако
у стали, чугуна и ряда цветных металлов и сплавов ползучесть может воз-
возникнуть лишь при нагреве их выше некоторой, определённой для каждого
металла, температуры (углеродистые стали и чугун — выше 300—350°, леги-
легированные стали — выше 350—400°, лёгкие сплавы — выше 50—150° и т. п.).
При температурах ниже указанных явление ползучести у этих металлов не
наблюдается. Вместе с тем, при температуре, равной или превышающей ту,

§ 254]	ЯВЛЕНИЕ ПОЛЗУЧЕСТИ И РЕЛАКСАЦИИ	795
при которой в данном металле возможно явление ползучести, ползучесть
возникает лишь при напряжениях выше некоторой, определённой для каждого
металла, величины. Явление релаксации напряжений наблюдается примерно
при тех же температурах и напряжениях, что и явление ползучести.
Явление ползучести особенно резко выражено у металлов. Однако оно
имеет место и у ряда других материалов. Так, например, ползучесть при
комнатной температуре наблюдается у различных пластмасс (целлулоид,
бакелит, винипласт и др.), в бетоне и цементном растворе. В железобетонных
конструкциях ползучесть бетона влечёт за собой с течением времени пере-
перераспределение напряжений между бетоном и арматурой; последняя несколько
перегружается, а бетон начинает испытывать меньшие напряжения. Однако
на грузоподъёмности железобетонных сооружений ползучесть бетона и выз-
вызванное ею перераспределение напряжений почти не отражается. Пластиче-
Пластическое течение при комнатной температуре имеет место также и у дерева
при сжатии и, в особенности, при изгибе.
Опытные исследования явления ползучести начались сравнительно не-
недавно A910 г.). Более или менее широкое распространение эти исследования
получили только с начала 20-х годов текущего столетия, когда были опуб-
опубликованы результаты первых значительных экспериментальных работ.
Проведение испытаний на ползучесть даже при простом растяжении
представляет большие трудности. Такие испытания требуют применения
специальной аппаратуры для поддержания постоянной величины нагрузки и
температуры и для измерения деформаций образца. Для получения доста-
достаточно надёжных результатов испытания на ползучесть приходится проводить
с особенной тщательностью, продолжительность этих испытаний не должна
очень сильно отличаться от срока службы детали из испытуемого материала
и, таким образом, должна измеряться десятками тысяч часов. Всё это делает
испытания на ползучесть сложными, трудоёмкими и дорогостоящими.
Известна одна исключительная серия опытов на ползучесть, продол-
продолжавшихся несколько более 100 тысяч часов (с 27 марта 1931 г. по
8 октября 1942 г.). Продолжительность очень немногих испытаний превы-
превышала 10 тысяч часов (около 1 года), в большинстве же случаев эксперимен-
экспериментаторы ограничивались одной-двумя тысячами часов. Поэтому даже при
простом растяжении явление ползучести экспериментально изучено ещё да-
далеко недостаточно.
Опыты на ползучесть при сложном напряжённом состоянии ещё более
сложны и трудоёмки. Большинство таких опытов было проделано на тонко-
тонкостенных трубках, подвергнутых действию комбинации нагрузок: внутреннего
давления, крутящего момента и растягивающего усилия. Однако подобные
испытания пока ещё выполнены в очень небольшом количестве.
Попытки многих исследователей разработать те или иные методы уско-
ускоренных испытаний на ползучесть до сих пор не увенчались успехом. Это
объясняется тем, что надлежащая продолжительность испытания является
необходимым и наиболее существенным условием получения достаточно на-
надёжных результатов, на которых могли бы основываться расчёты деталей
машин на ползучесть. Результаты же ускоренных испытаний могут пока
служить лишь для приближённой качественной оценки поведения металлов
при высоких температурах.
В связи с быстрым развитием в СССР энергетического машиностроения
в годы первых сталинских пятилеток, а также и в настоящее время, вопросам
изучения явления ползучести у нас уделяется большое внимание. Экспери-
Экспериментальными и теоретическими исследованиями ползучести у нас занимались
и занимаются: Беляев Н. М., Губкин С. И., Ильюшин А. А., Качанов Л. М.,
Малинин Н. Н., Одинг И. А., Работнов Ю. Н., Серенсен С. В., Шапошни-
Шапошников Н. А. и многие другие. За границей наиболее известны исследования
явления ползучести, выполненные Бауманом, Бейли, Диккенсоном, Зодербер-
гом, Надаи, Тэпселом и др.

796
ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
[гл. xxxix
§ 255. Кривые ползучести и релаксации.
А. Выше уже было отмечено, что опытное изучение явления ползучести,
на результатах которого основываются расчёты деталей машин и сооруже-
сооружений, работающих при высоких температурах, производится преимущественно
на образцах из испытуемого материала, подвергнутых простому растяжению.
При этом в течение всего срока испытания обеспечивается как неизменяе-
неизменяемость температуры, так и постоянство величины растягивающей образец
нагрузки.
При таких испытаниях через некоторые определённые промежутки вре-
времени измеряется удлинение образца; по данным измерений в координатах —
ф	t
относительная деформация
€
р
г и время t
строится диаграмма испытания —
так называемая кривая ползучести
материала. Вид кривой ползучести
зависит как от рода материала,
так и от величины напряжения и
температуры. Одна из характер-
характерных кривых ползучести для ме-
металла схематически изображена на
фиг. 659 (кривая OABCD).
При нагружении образца, на-
нагретого до определённой темпе-
температуры Ту деформация его вначале
возрастает довольно быстро (в за-
зависимости от скорости нагруже-
ния) от нуля до некоторой вели-
величины OAi (предполагается, что
процесс нагружения заканчивается
в точке А диаграммы). Если при
наибольшем значении нагрузки на-
напряжение в образце не превосхо-
превосходит предела упругости материала при данной температуре Г, то деформация
OAi будет вполне упругой; в противном случае отрезок ОАХ будет включать
в себя не только упругую, но и остаточную (пластическую) деформацию.
Вслед за этим деформация полностью нагружённого образца постепенно
увеличивается во времени, материал образца «ползёт». Нарастание деформа-
деформации ползучести характеризуется кривой ABCD; ординаты точек этой кривой
(например, ордината точки К) представляют сумму величин относительной
упругой деформации sy = 6Mi и относительной деформации ползучести
Фиг.
е = еу + ?п-
Скорость деформации ползучести в любой точке кривой определяется вели-
величиной тангенса угла наклона касательной к кривой в этой точке к оси
абсцисс, т. е.
Весь процесс ползучести может быть разбит на три последовательные
стадии. В первой стадии, отвечающей участку АВ кривой ползучести, дефор-
деформация протекает с неравномерной, всё время уменьшающейся скоростью;
это — так называемая стадия неравномерной или неустановившейся ползу-
ползучести. Длительность первой стадии ползучести, в зависимости от рода мате-
материала и от величины температуры и напряжения, меняется от нескольких
десятков до нескольких сотен и даже (в исключительных случаях) тысяч
часов.

§ 255]
КРИВЫЕ ПОЛЗУЧЕСТИ И РЕЛАКСАЦИИ
797
Наиболее существенное влияние на характер протекания процесса пол-
ползучести в этой и последующей стадиях ползучести оказываются два основных
фактора: 1) упрочнение материала в результате наклёпа, связанного с уве-
увеличением остаточной (пластиче-
(пластической) деформации, и 2) устране-
устранение этого наклёпа или пониже-
понижение несущей способности мате-
риала под действием высокой
температуры. Явление ползу-
ползучести можно рассматривать, как
взаимодействие этих двух фак-
факторов, создающих в основном
картину «чистой» ползучести.
Эта картина, особенно на после-
последующих стадиях, может быть
осложнена влиянием различных
внутренних (например, струк-
структурные изменения и фазовые
превращения в металле) и внеш-
внешних причин (например, корро-
коррозия).
Когда влияние упрочнения
от наклёпа уравновешивается
1
vn-0
!А,,В,
ослабляющим материал влия- }[q
нием длительного действия вы-
высокой температуры, уменьше-
уменьшение скорости ползучести пре-
прекращается, наступает вторая
стадия ползучести (участок ВС
кривой) — стадия равномерной
или установившейся ползуче-
ползучести, на которой деформация
ползучести протекает с посто-
постоянной и притом минимальной
скоростью.
Эта скорость остаётся по-
постоянной до тех пор, пока на
образце не начинает образовы-
образовываться шейка (точка С кривой).
Если во время испытания не
меняется величина нагрузки,
то местное сужение площади
поперечного сечения образца
в третьей стадии ползучести
(участок CD кривой) сопрово-
сопровождается увеличением напряже-
напряжения, которое, в свою очередь,
вызывает увеличение скорости
ползучести. Вследствие этого
образец в конце концов разру-	Фиг. 661.
шается (точка D кривой).
При изменении температуры или величины напряжения вид кривых пол-
ползучести может значительно измениться. На фиг. 660 схематически изображены
кривые ползучести при одной и той же постоянной температуре 7, но при
различных постоянных напряжениях с,- (при этом ct < а3 < о3 <с <j4 < аБ), а на
фиг. 661 — кривые ползучести при одном и том же напряжении о, но при
различных постоянных температурах Г,- (при этом Тх <: Г2 <; Ть <; Г4 <: Тъ).

798
ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
[гл. xxxix
При относительно небольшом напряжении @ = 0^ или сравнительно не-
невысокой температуре (Г = 7\) деформация ползучести может вообще не
иметь места, т. е. после нагружения образца диаграмма е — t будет пред-
представлять собой прямую линию, проведённую из точки А± параллельно оси
абсцисс (см. фиг. 660 и 661). При несколько более высоком напряжении или
температуре (а = а2 или Т = Г2) после сравнительно короткой стадии неуста-
неустановившейся ползучести скорость ползучести может уменьшиться до нуля,
т. е. дальнейшее увеличение деформации образца прекратится. При ещё более
высоком напряжении или температуре (<j = <j3 или Г = Г3) может случиться,
что скорость установившейся ползучести хотя и не будет равна нулю, но ока-
окажется настолько малой, что приведёт к разрушению материала через очень
большой промежуток времени, значительно превышающий срок службы
детали из этого материала.
При напряжении а = с4 или температуре Т = Г4 получаем кривую пол-
ползучести, представленную на фиг. 659. При дальнейшем увеличении напряже-
напряжения или повышении температуры вид кривых ползучести ещё более изме-
изменяется: деформация ползучести протекает всё быстрее, прямолинейный уча-
участок— стадия установившейся ползучести — становится всё короче и,, нако-
наконец, превращается в точку (кривые 5 на фиг. 660 и 661), т. е. стадия неуста-
неустановившейся ползучести непосредственно переходит в стадию разрушения.
В этом случае участок установившейся ползучести существует в виде точки
перегиба кривой ABCD— точки В, совпадающей с точкой С.
Характер разрушения материала при ползучести в основном зависит от
свойств материала при данной температуре. Углеродистая сталь при темпе-
температурах не выше 550°, медь, свинец и некоторые лёгкие сплавы обычно раз-
разрушаются вязко, с образованием больших пластических деформаций и шейки.
Разрушение специальных жаропрочных сталей, хорошо сопротивляющихся
ползучести, сопровождается сравнительно небольшими деформациями и носит
хрупкий характер, начинаясь обычно в местах концентрации напряжений.
Б. Как уже было сказано, релаксацией называется постепенное сниже-
снижение напряжений в нагружённой детали, полная деформация которой не может
изменяться во времени и равна получен-
б	ной при нагружении упругой деформа-
ции. При этом снижение напряжений про-
происходит вследствие постепенного умень-
уменьшения упругой деформации и прираще-
приращения на ту же величину пластической
деформации по схеме
s = еу + еп = Const = е°
ИЛИ
dt "" dt
dt
Кривая релаксации схематически
изображена на фиг. 662. Процесс рела-
релаксации можно разделить на две стадии:
первую (участок АВ кривой релакса-
t ции), в течение которой снижение на-
напряжения в детали происходит весьма
быстро с резко уменьшающейся ско-
скоростью релаксации, и вторую (участок ВС
кривой), в течение которой снижение напряжения происходит значительно
медленнее с постепенно убывающей скоростью релаксации.
Длительность первой стадии релаксации в зависимости от рода материала,
а также величины температуры и начального напряжения, меняется от
Фиг. 662.

§ 255]	КРИВЫЕ ПОЛЗУЧЕСТИ И РЕЛАКСАЦИИ	799
нескольких десятков до нескольких сотен часов. Физическая сторона явле-
явления релаксации на первой и второй её стадиях освещена ещё недостаточно.
Имеется ещё очень мало тщательно поставленных опытов с релаксацией
напряжений, которые позволяли бы провести сопоставление полученных при
этом результатов с данными опытов на ползучесть. В большинстве машин,
применявшихся до сих пор при испытаниях на релаксацию, оказалось невоз-
невозможным получить явление релаксации в чистом виде.
Обычно принимают, что нарастание пластической деформации в процессе
релаксации подобно нарастанию её при ползучести и что поэтому скорость
релаксации можно вычислять по скорости ползучести. Исходя из этого пред-
предположения, казалось бы, не следовало заниматься специальным изучением
явления релаксации. Однако существует и мнение, что скорость релаксации
нельзя принимать за скорость ползучести, так как эти два процесса по суще-
существу не вполне тождественны, механизм возникновения и нарастания пласти-
пластической деформации при релаксации несколько иной, чем при ползучести.
При релаксации уменьшение напряжений в детали вызывается нараста-
нарастанием пластической деформации за счёт упругой деформации при неизмен-
неизменной длине детали, а при ползучести нарастание пластической деформации
происходит исключительно за счёт удлинения детали. При этом общая дефор-
деформация при ползучести значительно больше, чем при релаксации; величина
же деформации при высоких температурах может оказать существенное влия-
влияние на протекание ползучести, вызывая рекристаллизационные, диффузион-
диффузионные и другие процессы, отражающиеся на сопротивлении материала пласти-
пластической деформации.
В. При изучении явления ползучести весьма важной задачей является
установление функциональной зависимости между основными величинами,
характеризующими кривые ползучести: напряжением (а), температурой (Г),
временем (t) и деформацией ползучести (е или еп), или её скоростью (~ =0„) •
Различными исследователями был предложен целый ряд формул, связы-
связывающих указанные величины. Ббльшая часть этих формул получена чисто
эмпирическим путём и только некоторые из них построены, кроме того, ещё
и на приближённых физических представлениях о протекании процесса
ползучести. Поэтому ни одна из этих формул не отвечает достаточно хорошо
опытным данным на широком диапазоне изменения напряжений, температур
и времени. Большей частью расчёты по этим формулам удовлетворительно
совпадают с опытными данными только на отдельных участках кривой
ползучести — главным образом, на участке установившейся ползучести.
Представляющая значительный интерес с практической точки зрения
кривая 3 фиг. 660 или 661 может быть выражена приближённой формулой:
еп = Р (а, Т) О (*, Т) + tR (а, 7),	C9.1)
где Р(а, Т) и R(a, Т) — некоторые функции постоянного напряжения и тем-
температуры, a Q (/, Т) — функция температуры и времени. Первый член фор-
формулы характеризует главным образом явление неустановившейся ползучести;
им можно пренебречь во второй стадии ползучести. Он построен в предпо-
предположении, что на первой стадии ползучести кривые ползучести геометрически
подобны, т. е. при одной и той же температуре, но при различных напряже-
напряжениях, кривые ползучести могут быть получены из одной какой-либо кривой
путём умножения её ординат на некоторую функцию напряжений. Это пред-
предположение, вообще говоря, экспериментально не подтверждается. Второй член
формулы характеризует главным образом явление установившейся ползучести,
когда скорость деформации ползучести vn = R (a, T) постоянна; этим членом
можно пренебречь в первой стадии ползучести.
Так как опытное исследование стадии неустановившейся ползучести
представляет значительно большие трудности, чем исследование стадии

800
ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
[гл. xxxix
II
в) О
I I I I I I i I I I I I I I I I I I I I I I t ! I I
oooooooooooooooooooooooooo
1ОЮЮ
t^ CM CO CO Tf CM	CO ОО^ОГ^-ч^^-СО —<hi*-• l О CD ~-« О
_^<7S1__O] — ^CMCOCMCMLO^-—>'~*'-«'-«COCM~-«^-*CMCOCM'!tiO
ююою о о ю о юю о ю ю io ю	ю
СО СО "~^ 00 СО С75 Г*™ ^ СО lO '—* СО О5 О5 CM CO lO O5 ^ СО —* t*— <—'
со*4 со" со"* см"" со" со" •—«"
со а> Г*
*—< ^^ ^^ ^^ ^^ ^^ г—4 СО С^ ^^ ^"* ^^ ^^ ^^ »~^ СО ^^ ^^ СО С5 ^Э
*-«COiOOCOCOOOTfOCMCM'^t^tCOOC'—'OiOWO^OO
CMlQCMOi'—'CO'-^'—"—iTt»—"—*00ЮСМСМ'—•CM'—' *-'00CM>,
II I I I I I I I I I I I I I I I I I I I I I
i—iQOi-tOOCO'—'CO
It
I
a
о
¦в-
о
о
i
о
о
on
—1 cud
о со
n
c4
H
О
о
CJ
S
я
X
u
и
о
5;
ел
С
1
1
1
1
1
1
23
о
50
о
ю
о
1
8
о"
00
со
о
со
о
52
о
25
о
о
о
со
I—»
о
1
1
1
I
00
• о
см
50
о
42
о
45
о
_
<—>
о
1
1
1
1
1
о
см
1—1
52
о
см
со
о
49
о
00
о
ю
см
о»
ю
г^
г *
61
о
S?
о
СО
о
о
1
01
см
см
ю
__
ю
со
¦—'
57
о
00
о
1
см
ю
о
г—
о"
00
о
§
о
см
о
О)
о
is
2 u
Is
S
S «oo4
S aj 1
о со I
gS2
O5
CO

§ 255]
КРИВЫЕ ПОЛЗУЧЕСТИ И РЕЛАКСАЦИЙ
801
установившейся ползучести, то этот участок кривой ползучести изучен ещё
совершенно недостаточно. Поэтому надёжных данных о характере функций
Р (а, Т) и Q (t, T) до сих пор почти
нет. В связи с этим при расчётах
на ползучесть участком неустано-
неустановившейся ползучести нередко пре-
пренебрегают, продолжая прямую ВС
(фиг. 663) до пересечения её с осью
ординат в точке Вг и определяя ве-
величину полной деформации при пол-
ползучести (например, tk) по приближён-
приближённой формуле:
Ч =
= еу + h • tg« = ?y + tk
C9.2)
Значительно лучше эксперимен-
экспериментально изучена стадия установив-
установившейся ползучести. Из различных за-
зависимостей для ^(а, Г), предло-
предложенных разными исследователями, наиболее
являются следующие:
Фиг. 663.
проверенными экспериментально
C9.3)
В этих формулах k, и, а и Ь — некоторые коэффициенты, зависящие от
свойств материала и температуры испытания. Вторая зависимость лучше сов-
совпадает с данными эксперимента, чем первая, зато использование её при рас-
расчётах приводит к значительному усложнению вычислений. Вместе с тем дан-
данных о коэффициентах к и п в первой формуле получено значительно больше,
чем данных о коэффициентах а и Ъ во второй формуле. Поэтому в настоя-
настоящее время при расчётах на ползучесть чаще используют первую формулу.
В качестве примера в таблицах 40 и 41 приводятся данные о величине
коэффициентов, входящих в первую формулу, для сталей и некоторых других
материалов, испытанных на ползучесть при различных напряжениях и тем-
температурах.
Таблица 41. Коэффициенты к формуле C9.3).
Материал
1. Сталь с О,3о/О С
2. ъ > О,39о/о (кованая)
3. » > 0,45 С
4. » > 3,5о/о Ni
5. > > О,4о/о Мо
6. » > 12% Сг
7. > > 19о/о Ni; бо/о Сг; 1<>/о Si
8. i > 80/0 Ni; 18o/o Сг; 0,5<у0 Si
9. > > 2о/о Ni; О,8о/о Сг; О,4о/О Мо
10. > > О,3о/О С; 1,4% Мп
11. Чугун с 12% Сг; 3% W; 0,4% Мп
12. Свинец
Продол-
житель-
жительность
испыта-
испытания в
часах
400
400
400
400
700
Интервалы
напряжений
в кг/см2
200—490
245—460
1340—1900
1060—1440
56—107
Темпе-
Температура
400
400
540
540
450
455
540
540
460
450
550
40
п
6,9
8,6
5,9
7,2
3,2
4,4
13,1
14,8
3,0
4,7
1,9
5
кг час
1,5-101
5,4-108
1,2-Ю-
6 .10-»'
4,Ы0-2*
4,9-10-2з
1,8-108
2 -10-52
1,2-10'17
8,6-102
9,7-105
4,2-Ю-14
х/226 Н, М» Беляев

802
ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
§ 266. Основы расчётов на ползучесть.
[гл. xxxix
А. Первые исследователи явления ползучести пытались оценить способ-
способность металлов сопротивляться ползучести величиной так называемого пре-
предела ползучести сгс, понимая под этим то наибольшее напряжение в мате-
материале, при котором явление ползучести вовсе не наблюдается (кривая 1
фиг. 660 и 661). Несколько позже под пределом ползучести стали понимать
то наибольшее напряжение, при котором скорость ползучести, вызывая неко-
некоторую сравнительно небольшую остаточную деформацию в материале, в конце
концов становится равной нулю (кривая 2 фиг. 660 и 661).
Однако опытами вскоре было установлено, что определённые таким
путём пределы ползучести при температурах, при которых обычно работают
паропроводы, диски и лопатки турбин и другие детали машин, подвергаю-
подвергающиеся ползучести, представляют собой весьма небольшие напряжения, практи-
практически не интересующие машиностроителей, так как большинство даже самых
ответственных деталей машин в действительности работает при напряжениях,
превышающих эти пределы. При этом во многих машиностроительных дета-
деталях, находящихся в условиях высоких температур, допускаются небольшие
остаточные деформации, не превышающие некоторой определённой величины,
лишь бы они не вызывали нарушения нормальной работы конструкции
в течение срока её службы.
Вследствие этого в настоящее время при расчётах на ползучесть в боль-
большинстве случаев исходят из наибольшей допускаемой в течение срока
службы детали величины остаточной деформации ползучести или суммарной
деформации, складывающейся из упругой деформации при нагружении и оста-
остаточной деформации при ползучести. Соответствующее наибольшее напряже-
напряжение в материале, не вызывающее при данной температуре деформации детали,
превышающей допускаемую, может быть рассматриваемо как допускаемое
напряжение. Иногда это напряжение называют условным пределом ползучести
материала по допускаемой суммарной деформации ползучести (аСе). Вели-
Величина crcs, очевидно, является функцией температуры и допускаемой деформа-
деформации ползучести.
В качестве примера в таблице 42 приведены ориентировочные данные
о допускаемых величинах суммарной относительной деформации ползу-
ползучести [е] для некоторых деталей паровых котлов и турбин.
Таблица 42. Величины [е].
Детали
1. Трубки пароперегрева-
пароперегревателей
2. Паропроводы
3. Цилиндры паровых тур-
турбин
Срок службы
в тыс. часов
20
100
100
1 J см
0,02
0,003
0,001
При расчётах на ползучесть по суммарной деформации ползучести исход-
исходное расчётное уравнение при линейном напряжённом состоянии материала
может быть представлено в следующем виде (см. фиг. 663):
tA ^ [е], C9.4)

§ 256]	ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ	803
где ?у — упругая относительная деформация детали при её нагружении,
eni и ?п2 — относительные деформации детали в стадиях неустановившейся
и установившейся ползучести, е0 = ?у + ?ni» W — наибольшая допу-
допускаемая за время службы детали величина суммарной деформации ползу-
ползучести, tA — срок службы детали и vn=ksn — скорость установившейся пол-
ползучести.
Если пренебречь величиной ?п1 и считать, что
где Ет—модуль упругости материала при данной температуре Г, то вме-
вместо C9.4), получим:
или
# + *[']% = [«].	C9.5)
Из уравнения C9.5) можно определить величину допускаемого напряжения
[с] = сС?, соответствующего допускаемой величине суммарной деформации
ползучести [е]. Если допустимо пренебречь и величиной упругой деформа-
деформации ?у, то из C9.5) имеем:
j
j-\ •	C9.6)
В этом последнем случае условие прочности в напряжениях напишется так:
~1^д)
C9.7)
Следует, однако, заметить, что пренебрежение величиной упругой дефор-
деформации и деформации ползучести в стадии неустановившейся ползучести
может иногда привести при расчётах к большим погрешностям, особенно
в тех случаях, когда продолжительность стадии неустановившейся ползу-
ползучести не очень мала по сравнению со всем сроком службы детали.
Если же упругая деформация детали и её деформация в стадии неуста-
неустановившейся ползучести пренебрежимо малы по сравнению с деформацией
в стадии установившейся ползучести, то при расчётах на ползучесть можно
исходить из наибольшей допускаемой величины установившейся (мини-
(минимальной) скорости ползучести. Допускаемая величина скорости ползу-
ползучести, очевидно, должна быть определена опять-таки из условия, чтобы
деформация ползучести, нарастающая с этой постоянной скоростью, не
превзошла в течение срока службы детали некоторой допускаемой вели-
величины деформации, при которой не происходит нарушения нормальной работы
конструкции. Соответствующее наибольшее напряжение в материале, не
вызывающее при данной температуре скорости ползучести, превышающей
допускаемую, может быть рассматриваемо, как допускаемое напряжение.
Нередко это напряжение называют условным пределом ползучести мате-
материала по допускаемой минимальной или равномерной скорости деформа-
деформации (acv). Величина ccv, очевидно, является функцией температуры и допускае-
допускаемой минимальной скорости ползучести.

804
ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
ГЛ. XXXIX
В качестве примера в таблице 43 приведены ориентировочные данные
о допускаемых величинах минимальной относительной скорости ползучести
[vu] для некоторых деталей паровых котлов и турбин.
Таблица 43. Скорость ползучести.
Детали
1. Турбинные диски с тугой посад-
посадкой на вал
2. Болты, фланцы, цилиндры паро-
паровых турбин
3. Паропроводы, сварные швы ко-
котельных труб
4. Трубы пароперегревателей
[1>п] в час
ю-8
Ю-8
Ю-7
ю-*—ю-*
При расчётах на ползучесть по минимальной скорости ползучести исход-
исходное расчётное уравнение при линейном напряжённом состоянии материала
может быть написано в следующем
«ft/	Л	/ ВИД*
*	*п = Ло»^[*п]«Щ, C9.8)
так как
Из C9.8) следует, что
=ас„ = {^1}\ C9.9)
Условие прочности в напряжениях напи-
напишется так:
с^[а]==Ш1\ C9.10)
Б. Само собой разумеется, что при
расчётах на ползучесть по величине
допускаемой деформации или её ско-
скорости необходимо соблюдение условия,
данной температуре за время срока службы детали деформация
разрушению материала, но и был обеспе-
обеспечен некоторый запас прочности против возможности такого разрушения.
Таким образом, точки ku k2 и kb (фиг. 664) на различных кривых ползу-
ползучести 7, 2 и 3, отвечающие абсциссам *д1, *д2 и *д8 и ординаты [е]ь [е]2 и [е]3,
обязательно должны находиться на участках первой или второй стадии
ползучести.
Это обстоятельство должно быть проверено расчётом и поэтому требует
специального исследования. Расчёты по величине допускаемой деформации
ползучести или её скорости, как уже было показано, могут быть заменены
расчётами по соответствующим допускаемым напряжениям — пределам пол-
Фиг. 664.
чтобы при
ползучести не только не привела

§ 256]
ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
805
зучести асе или асх>. При этом необходимо убедиться, что величина <?с (jcs или ocv)
не превосходит величины допускаемого напряжения, представляющего неко-
некоторую долю предела прочности материала при данной температуре.
Известно (§ 253), что предел прочности материала при высоких темпе-
температурах очень сильно зависит от продолжительности испытания; сравни-
сравнительно небольшое увеличение длительности испытания вызывает значитель-
значительное уменьшение предела прочности. При некоторых температурах (например,
для малоуглеродистой стали при температурах выше 800°) испытуемый обра-
образец может быть разрушен нагрузкой, вызывающей напряжение ниже пре-
предела пропорциональности материала при комнатной температуре, если эта
нагрузка будет действовать достаточно продолжительное время. Поэтому
прочность металлов при высоких температурах в настоящее время харак-
характеризуют не величиной обычного предела прочности, определяемого путём
кратковременных испытаний, а величиной так называемого предела длитель-
длительной прочности (aBf). Этим термином обозначают такое напряжение при дан-
данной постоянной темпера-
температуре, при действии кото-
которого в течение заданного
промежутка времени в конце
этого промежутка произой-
произойдёт разрушение матери-
материала. В качестве примера на
фиг. 665 приведены графики
изменения величины пре-
предела длительной прочности
хромомолибденовой стали
@,1 о/о С; 1,55о/о Si; 4,88«/0
кг
см2-
3000
2500
2000
1500
1000
(, /о ; ,%
Сг; 0,51 о/о Мо) в зависи-
зависимости от времени при раз-
различных температурах.
Иногда высказывается
мнение о том, что нерав-
неравномерность распределения
напряжений в местах их
концентрации при ползу-
ползучести сглаживается и что
при расчётах на ползучесть
можно поэтому концентра-
концентрацию напряжений не учи-
учитывать. Следует заметить,
температурах, как правило,
500
300
200
100
50
g
Ю	100 W00 10000 (часов)
Фиг. 665.
что детали машин, работающие при высоких
изготовляются из специальных жаропрочных
сталей, обладающих сравнительно малой ползучестью; разрушение деталей из
таких сталей наступает обычно при небольших деформациях и носит хруп-
хрупкий характер. Поэтому в большинстве практически встречающихся случаеэ
выравнивание местных напряжений не успевает произойти и, таким образом,
при расчётах на ползучесть концентрацию напряжений необходимо прини-
принимать во внимание.
В связи с этим и при определении предела длительной прочности жаро-
жаропрочных сталей возможная в деталях концентрация напряжений должна
быть учтена, т. е. испытания по определению ав^ должны вестись на образ-
образцах соответствующей формы.
Для тех случаев, когда детали машин находятся в условиях совместного
действия двух факторов — усталости и ползучести, предел длительной проч-
прочности должен определяться из испытаний на усталость при соответствующей
температуре. Таким образом, при расчётах на прочность деталей машин и
сооружений, работающих при высоких температурах, необходимо различать
следующие основные случаи.
26 Н. М. Белаев

806
ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
[гл. xxxix
При температурах, не вызывающих в материале явления ползучести
(см. § 254), опасное состояние определяется пределом текучести или преде-
пределом прочности материала при данной температуре, полученными путём обыч-
обычных кратковременных испытаний. В этом случае условие прочности может
быть написано так:
eag[a] = ^.	C9.11)
Если при данной температуре ползучесть возможна (см. § 254), то необ-
необходимо прежде всего установить, какое из допускаемых напряжений при
заданном сроке службы детали *д является большим — допускаемое напря-
напряжение по суммарной деформации ползучести (aCe) или по минимальной её
скорости (асг>), или допускаемое напряжение, вычисленное по пределу дли-
дли^	— коэффициент запаса длительной
тельной прочности [ав^] = -~, где
прочности, который можно принимать приблизительно равным обычному
коэффициенту запаса прочности k (фиг. 666).
Если [а] = ас (асе, ccv) < [ов/] — область А на фиг. 666, то расчёт на пол-
ползучесть должен производиться по формулам C9.4), C9.7), C9.8) или C9.10).
Если же [а] = ас>[ав,] — область В на фиг. 666, то расчёт на ползучесть
должен, очевидно, производиться по
формуле:
°^[°B*] = 7f •	C9Л2)
В тех случаях, когда имеет место
явление релаксации напряжений, обычно
должно быть обращено внимание на то,
чтобы не произошло недопустимо боль-
большое ослабление соединения деталей,
скреплённых с помощью упругого на-
натяга; снизившееся благодаря релаксации
напряжение at не должно быть меньше
некоторой определённой минимальной
д величины напряжения, обеспечивающего
надлежащую плотность соединения:
а/ ^ amin-
Исходя из этого условия, могут быть установлены сроки, по истечении кото-
которых необходимо специальными мерами восстанавливать плотность соедине-
ния> _ например, подтягивать болты фланцев паро- или газопровода.
В заключение отметим, что в этом параграфе была рассмотрена мето-
методика расчётов на ползучесть в наиболее простых случаях (линейное напря-
напряжённое состояние), являющаяся основой для построения более сложных
расчётов. Методика расчётов на ползучесть при сложном напряжённом состоя-
состоянии рассматривается в специальных монографиях *).
§ 257. Примеры расчётов на ползучесть.
Пример 145. Стержень, изготовленный из хромомолибденовой стали
и имеющий площадь поперечного сечения F = 2 см2, растянут силой Р.
Определить наибольшую допускаемую величину силы Р в двух вариантах: при
Фиг. 666.
') Малинин Н. Н., Основы расчётов на ползучесть,
н о в Л. М., Некоторые вопросы теории ползучести, 1949.
1948; Кача-

§ 257]
ПРИМЕРЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
807
температурах 7\ = 480° и Т2 = 650°, если срок службы стержня ?д = 5000 часов.
Наибольшая величина равномерной относительной скорости ползучести не
должна превышать [г;п] = 6 • 10	. Коэффициент запаса прочности
час
по отношению к пределу длительной прочности принять равным fy=l,7.
Для материала стержня скорость установившейся ползучести может быть
вычислена по формуле vn = ?ал, а величина предела длительной прочности —
(KZ \ ва
	^ ) = -j-; значения коэффициентов k, я, а
¦ММ ) /
и b приведены в таблице 44.
Таблица 44. Значение коэффициентов.
Температура Т
480
650
п
8,35
3,25
k см2П
кгпчас
0,58 • Ю-30
0,17 . 102
а
4,2
2,3
ь
0,15
0,25
Решение. Допускаемое напряжение по допускаемой скорости устано-
установившейся ползучести определяем по формуле C9.9):
При температуре Тх = 480° имеем:
__
6 . Ю-7 I8'35
J
Г 6 . Ю-7 I8'35
= [o,58. Ш-зоJ =
а при температуре Г2 = 650°:
JL
6 • 10~7 I3'25
Допускаемое напряжение по пределу длительной прочности определяем
по формуле
При температуре Тх = 480° имеем:
KU =	=
= i>7 . з,588
а при температуре Г2 = 650°:
в2'3	9 974
1°«Ъ = 1,7. 50W» = IJT
= 10'93
26»

808	ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ	[ГЛ. XXXIX
Результаты вычисления показывают, что при температуре 7\ = 480э
[a]i "< [ав/]ь а ПРИ температуре Г2 = 650° [a]2 >> [sB^b- Следовательно, в нервом
случае допускаемое напряжение необходимо принять равным [а]х = 752 кг/см2,
а во втором случае — равным [св^]2 = 70 кг/см2.
Величина допускаемого усилия равна [Р] = F [a] = 2 [а]. При температуре
Тх = 480° [P]i = 2 • 752 ^ 1500 кг; а при температуре Т2 = 650° [Р]2 = 2 . 70 ==
= 140 кг.
Пример 146. Определить, как часто для предотвращения утечки пара
нужно возобновлять затяжку болтов фланцевого соединения паропровода,
если начальное упругое натяжение каждого болта, равное Р = 3000/сг, не
должно снижаться более, чем на 40%. Температура, при которой работают
болты, Г = 425°. Площадь поперечного сечения болта ^ = 3 см2; материал
болтов — углеродистая сталь с модулем упругости ЕГ= 1,77 • 10~6 кг/см2
(при Т = 425°), для которой скорость установившейся ползучести может быть
определена по формуле vn = kany причём при
Т = 425° k = 2,26 . Ю-25 см2п1кгпчас, а п = 6.
Задачу решить в предположении, что фланцы паропровода абсолютно не-
несжимаемы; при расчётах стадию неустановившейся ползучести во внимание
не принимать.
Решение. Если фланцы паропровода абсолютно несжимаемы, то полная
деформацггя болта, растянутого первоначально (при затяжке) на величину Д/о,
с течением времени не может измениться. При ползучести упругая деформа-
деформация болта А/у будет постепенно переходить в пластическую деформацию А/п;
за этот счёт напряжение в болте будет понижаться. При этом
А/у + А/п = А/о = const
или
I	a I	ao
где а0 — первоначальное упругое напряжение в болте, а — напряжение в нём
в момент времени t и Ет—модуль упругости материала при данной темпе-
температуре Т. Дифференцируя это уравнение по t, имеем
1 da dzn	 1 da		 1 da0 	-
T	T	T
Пренебрегая стадией неустановившейся ползучести и заменяя vn на kvny по-
получаем такое дифференциальное уравнение:
ИЛИ
Интегрируя это уравнение, находим
где С — постоянная интегрирования. Так как при t = 0 a = a0, i

§ 257]
ПРИМЕРЫ РАСЧЁТА НА ПОЛЗУЧЕСТЬ
809
Подставляя найденное значение С в уравнение (а), получаем формулу, связы-
связывающую а и t:
Используя числовые данные задачи, имеем:
3000
1000
\\ +F — 1) . 1,77 • 10е • 2,26 • 10-25 (^У * • tf l A +2 • Ю-3 • t) 5
L	\ *> / J
или
Таблица 45. Значения t
1 ¦/	1018\
^1A000--^).
Подсчитанные по последней формуле значения t} соответствующие раз-
различным значениям а, приведены в таблице 45 (столбец А). Если напряжение
в болтах не должно снижаться более чем на 40%, то дополнительную за-
затяжку болтов необходимо производить через каждые 5930 часов, или при-
примерно через 8,5 месяца.
Приведённое здесь решение задачи о релаксации напряжений в болтах
является весьма приближённым. Благодаря податливости фланцев паропро-
паропровода понижение напряжений в болтах бу-
будет происходить значительно быстрее.
Решение данной задачи с учётом подат-
податливости фланцев оказывается несколько
более сложным. Не рассматривая здесь
этого решения, ограничимся лишь тем,
что приведём его окончательные резуль-
результаты (см. таблицу 46, столбец В) для
того случая, когда упругая деформация
фланцев равна ?уф = 3 • 10~8 Р^, а ско-
скорость деформации ползучести их равна
яПф = 5 • 10~22Р| (здесь Pt кг— натяже-
натяжение одного болта в момент времени t).
Таким образом, исходя из резуль-
результатов более точного решения задачи,
дополнительную затяжку болтов необходимо производить не через 5930 часов,
а через 5000 часов, или 7 месяцев. Если же при решении задачи учесть и де-
деформацию ползучести в стадии неустановившейся ползучести, то последняя
цифра понизится ещё больше.
Пример 147. Круглый вал диаметром 24 мм, работающий при темпе-
температуре Т = 540°, скручивается постоянным моментом Мк = 20 кгм. Материал
вала — легированная сталь с модулем упругости G = 6 • 105 кг/см2 (при
Т = 540°). Скорость установившейся ползучести может быть вычислена по
формуле vn = kzn, причём при Т = 540° /с = 2,5 • 109 см2п/кгпнас и я = 5.
Найти распределение касательных напряжений в поперечном сечении
вала и его угол закручивания через 1000 часов после нагружения.
Решение. Предположим, что гипотеза плоских сечений при кручении
остаётся справедливой и в условиях ползучести материала (это предположе-
предположение довольно хорошо согласуется с опытными данными). В таком случае
(J
в кг/см%
1000
900
800
700
600
500
400
t (в \
А
0
347
1026
2475
5930
15500
48300
асах)
В
0
335
960
2230
5000
11900
31700

810	ОСНОВЫ РАСЧЁТОВ НЛ ПОЛЗУЧЕСТЬ	[ГЛ. XXXIX
два соседних поперечных сечения вала, расположенных на расстоянии dx
друг от друга, оставаясь плоскими, только повернутся одно относительно
другого на угол dy. Так как радиусы сечений не искривляются, то для отно-
относительного сдвига на расстоянии р от центра вала можем воспользоваться
известной (§ 57) формулой:
После нагружения вала деформации сдвига, вследствие ползучести мате-
материала, начнут постепенно увеличиваться; будет увеличиваться также и отно-
dy
сительный угол закручивания -j-. Полная деформация сдвига представится
п X
в виде суммы упругой деформации 7у и деформации ползучести -\и, т. е.
-v = fy + Тп- Скорость изменения полной относительной деформации сдвига
будет равна:
Для упрощения решения задачи относительно малой величиной скорости
упругой деформации пренебрежём по сравнению с большой величиной ско-
скорости деформации ползучести. Более точное решение этой задачи с учётом
того, что t/yi^O, представляет значительные трудности. Пренебрегая, кроме
того, стадией неустановившейся ползучести и полагая, что vn = k^ny получим:
откуда
"/Г _L J_
Lk dx - dt \
где
1^_
k dx-dt
(б)
Условие равенства друг другу моментов внешних сил (крутящего мо-
момента) и моментов внутренних сил упругости относительно оси вала запи-
запишется так:
Г	Г	\
2-Ь —
Л л ^Л
= f- z • ?dF= f 2яр тр dp = 2тсФ \
где г — радиус вала.
Обозначая
* , 1	~ Зл+1
можем написать
(в)
и, с учётом (а),
4

§ 257]
ПРИМЕРЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
811
Таким образом, распределение касательных напряжений по сечению вала при
ползучести уже не следует линейному закону.
Подставляя в выражение для Jрп значения г =1,2 см и п = 5, получаем:
Jpn =
9 o
1,2 5 = 1,964 • 1,2«* =3,52 см*'*.
Касательное напряжение на расстоянии р от оси вала равно:
4
4
„ — 200° Т
—- р " _- —— р :
В таблице 46 приведены значения т, соответствующие различным значе-
значениям р. В этой же таблице даны и значения х при упругой деформации
вала, вычисленные по формуле:
Мк ¦ р 2Л4кр 2-2000
Благодаря ползучести напряжения по поперечному сечению вала вырав-
выравниваются; у поверхности вала они несколько снижаются, а у оси его значи-
значительно увеличиваются (фиг. 667).
Таблица 46. Значения т.
р
мм
12
10
8
6
4
2
0
хупр0
кг /см*
737
614
492
369
246
123
0
полз
кг/см%
589
568
543
513
473
411
0
0 Ю0 200 300 400 500 600 700 600
Фиг. 667.
Определим угол закручивания вала на единицу длины. На основании
(б) и (в) можем написать:
dx dt
Интегрируя это уравнение по t, находим
P
P
Так как при t = 0 —¦ = \-г-) = г--т~»
~GJO

812	ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
Интегрируя и полагая х = 1 см, получаем:
ГЛ. XXXIX
GJn
\JPJ
При данных задачи
'fl = 6 • 105 • 3,14 • 1,24
2000- 2
/2000V
-1000 =
= 0,00102 + 0,01480 = 0,0158
рад
см
Замечаем, что угол закручивания вала при ползучести увеличился почти
в 16 раз по сравнению с углом закручивания при упругой деформации
(первый член последнего результата). Таким образом, значительное снижение
наибольшего касательного напряжения в вале отнюдь не свидетельствует
о том, что условия работы его при ползучести улучшаются.
Пример 148. Балка, имеющая длину 50 см, шарнирно опёртая по кон-
концам и нагружённая посредине пролёта сосредоточенной силой Р = 400 кг,
работает при температуре Т = 500°. Материал балки — углеродистая сталь
с модулем упругости ?"=1,6» 106 кг/см2 (при Т = 500fc). Скорость устано-
установившейся ползучести vn — kcn, причём при Т = 500°
час
=1,5. 10-» —)
\ кг }
t'-Змм
Пренебрегая стадией неустановившейся ползучести, найти распределение
нормальных напряжений в опасном сечении балки и определить наибольший
прогиб её через 10 000 часов после
нагружения. Исследовать два вари-
варианта поперечного сечения балки:
прямоугольное и двутавровое (см.
Ъг-3мм	\	А1>л_ фиг. 668).
Решение. При решении задачи
будем пренебрегать влиянием каса-
касательных напряжений и предполо-
предположим, что гипотеза плоских сечений
при изгибе остаётся справедливой
и при ползучести (это предположе-
•t
-е
	у
ЬшА
ч
i
-z
Фиг. 668.
ние довольно хорошо согласуется
с опытными данными). Считая, что
в растянутой и сжатой зоне балки
деформации волокон нарастают по одному и тому же закону, для от-
относительной деформации волокна, расположенного на расстоянии у
от нейтрального слоя, можем написать известное выражение (§ 78):
е = —, где р — радиус кривизны нейтрального слоя балки.
После нагружения балки деформации волокон её вследствие ползучести
материала начнут постепенно увеличиваться; кривизна нейтрального слоя
также будет увеличиваться. При этом полная деформация какого-либо во-
волокна представится суммой относительной упругой деформации и относи-
относительной деформации ползучести, т. е. е = еу -|- ?п. Скорость изменения пол-
полной деформации будет равна:
dt
'Ж
dev
dtn
' dt
Так же, как и в предыдущем примере, для упрощения решения пренебрежём
скоростью упругой деформации. (Более точное решение этой задачи с учётом

§ 257]	ПРИМЕРЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ	813
того, что vy -ф 0 см., например, М а л и н и н Н. Н., Основы расчётов на
ползучесть, 1948 г.)
Пренебрегая, кроме того, стадией неустановившейся ползучести и по-
полагая, что vn = kzn, получим
откуда
у п = фу п 9	(а)
где
1 л / 1 \ п
(б)
ф— . ,
k dt\p J
Условие равенства друг другу моментов внешних сил (изгибающего
момента) и внутренних сил упругости относительно нейтральной оси запи-
запишется так:
{'	I' i -и
М =
Вводя обозначение
получаем
Ф = -г-	(В)
Jzn
и, с учётом (а),
J zn
Замечаем, что распределение нормальных напряжений по высоте сечения-
балки при ползучести уже не следует линейному закону.
В случае прямоугольного сечения
л
~~ , , 1	,	2л+1
А/2 о	2 л
а в случае двутаврового сечения (фиг. 668):
2 »

814
ОСНОВЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
[гл. xxxix
Подставляя в формулы	для Jzu данные задачи, получаем для прямо-
прямоугольника
_ з	^щ ?.o.i *
J гп — ~5~i i	• 2 • 4 = -
3+1
2 3 B-3+1)
7 •
а для двутавра
3
2 • 3 + 1
2-3+1
10
3+1
2 3 B-3-
— X [2 • 5,6—з— — B,8—0,3) E,6—2 • 0,3) з ] = 8,34 см з #
Наибольший изгибающий момент равен:
..	Р/ 400 • 50
= 5000 К2СМ.
Нормальные напряжения в балке прямоугольного сечения должны быть
вычислены по формуле:
М ~ 5000 4-
л в балке двутаврового сечения — по формуле:
Вычисленные по этим формулам значения нормальных напряжений на раз-
различных расстояниях у от нейтрального слоя приведены в таблице 47. Для
сравнения в той же таблице помещены данные о распределении нормальных
^напряжений при упругой деформации.
Таблица 47. Нормальные напряжения.
\ кг
у мм N.
28
24
20
16
12
8
4
2
0
Прямоугольн. сечение
упругая
деформация
938
750
563
375
188
94
0
ползучесть
729
677
615
537
426
339
0
Двутавровое сечение
упругая
деформация
938
804
670
536
402
268
134
67
0
ползучесть
844
802
754
700
636
556
441
351
0

§ 257]
ПРИМЕРЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ
815
Благодаря ползучести нормальные напряжения по поперечному сечению
балки выравниваются; в наиболее удалённых от нейтрального слоя волокнах
они снижаются, а у нейтрального слоя увеличиваются (фиг. 699). При
этом в балке прямоугольного сечения снижение наибольших напряжений
заметнее, чем в балке двутаврового сечения, так как у последней вблизи
от нейтрального слоя расположено сравнительно немного материала.
Определим прогиб балки. Принимая для кривизны оси балки приближённое
выражение — = -
можем
^ rf2 Idy
р у =dx* \dx
Так как по (б) и (в):
написать -г-
dt
ТО
d*
В случае балки на двух
р
опорах (фиг. 670) М = -н- х и
d* !dy\
d*\Ttr
где
Фиг. 669.
kP"
Интегрируя уравнение (г) по дг, по-
получаем:
dt
2)
Фиг. 670.
CM*
где С и D — постоянные интегрирования. Так как при любых значениях t
у = 0 при х = 0 и ~z=zO при х = -^-, то и ~- = 0 при х = 0 и -
=?(f)==OnpHX==T-
Поэтому
(я + 1) 2Л+
и D = 0.
Наибольший прогиб балки будет в сечении, где х = -у; имеем:

816	ОСНОВЫ РАСЧЁТОВ НЛ ПОЛЗУЧЕСТЬ
Интегрируя по t, находим:
[гл. xxxix
где И — постоянная интегрирования. Так как при ? = 0
-^max v-^maxnnp "
РР
Таким образом, наибольший прогиб балки при ползучести равен:
4SEJ2
t.
Для некоторых балок, иначе нагружённых и закреплённых, формулы для
вычисления ( -j-) приведены на фиг. 671. Учащимся предлагается самим
\ (It /max
выполнить вывод этих формул (заметим,
что принцип независимости действия
сил в этом случае неприменим). Для
балки прямоугольного сечения
Схемы
балок
м„
о
Г
m гт
моп12
Monl2
8
Pnln
п+2
PnV
400 • 503
1ах' 48 . 1,6 • 10е • 10,67 п
1,5 • Ю~15 • 4003 . 503+2
+ 8,643C + 2) • 22C+1)
= 0,0611 + 0,3634 = 0,425 см.
Для балки двутаврового сечения
z~~	12
2 • 5,63 — 2,5 . 53
12
= 14,94 см*
400 ¦ 503
^"
'
— 48 . 1,6 • 106 • 14,94
1,5 • 10~15 ¦ 4003 ¦ 503+2 . 10 000 __
8,343 • C + 2) • 22C+1) ""
= 0,0436 + 0,4034 = 0,447 см.
Фиг. 671.
Замечаем, что прогиб двутавровой
балки при упругой деформации при-
примерно в полтора раза меньше, чем прогиб балки прямоугольного сечения;
при ползучести же он несколько больше прогиба балки прямоугольного
сечения. Таким образом, снижение наибольших нормальных напряжений в бал-
балках при ползучести отнюдь не означает, что условия работы балок улуч-

§ 257]	ПРИМЕРЫ РАСЧЁТОВ НА ПОЛЗУЧЕСТЬ	817
шаются. Наибольшая допускаемая нагрузка на балку при ползучести должна
определяться в зависимости от величины допускаемой деформации балки.
Если, например, наибольший прогиб балки прямоугольного сечения через
10 000 часов её работы не должен превышать ^. её длины, т. е. 0,1 см, то
наибольшая допускаемая нагрузка должна быть определена из условия:
Pi*
Подставляя числовые данные, имеем:
503 • ЗР , 1,5 • 10"
3.1,6.106^ 5-
или
Р + 0,2326Р3 • 10 ^ 40,96,
откуда
Р ^ 40,8 кг ^ 40 кг.

818
ПРИЛОЖЕНИЯ
те
5
К
Ш
а,
с
5
О
ее
Н
О
X
2
Q,
О
а
g
eg
а
О 2
С s
ихэо!ГAзах
ф % эинэжХэ
эончгзхиоонхо
30НЧ1ГЭХИЭ0НХ0
Р0\
%
Э0НЧ1ГЭХИЭ0НХ0
ихээьХнэх
ex
H
5
я
о
3
Я
U
CQ
:М§
го б
i i
Я Я 2
оосо —i
— см см
со см
см см
см
ю
см г-
4оосм
со сот
ю
UU
S
со ю~о c^fihTo г-^сГо г^"сГо сГсГо осГсГю	ю*
СМ-—'lOCMiOrOCMCOCOCOt^rOvOt— СО ^ Oi.c^.	^L
о'очочочо"о"о*о"о*о"о"очо"о"оч сГсГсГ	сГ
rf а> о емю см ооо смооюю оо ю ю , .оою	ю
сГсГо4	о*
а о 5
lit
СО ОС
со го
со
ОС О)
ЧАО
¦=* о

ПРИЛОЖЕНИЯ
819
си
3
аровоз
С
3
И-
ш о?
S 3
стали
автом
ас
к
ffl s
И
аз
О
3 5 -* s
а с з си
a EJ »=t
dKx3
>~> си - P»->
ые
трое
»*~> CD	i^~>
 а йй g с
3 о
орпус ко-
корабля
ные авто-
автокторные
али
пны
акт
ны
ак
ета
эуп
тра
дет
тр
де
~ —•	CM
Ю
Ю
CM
g s
00
s
S
CO 00
CM CM
о
см
CM Tf
CM CM
50—6
о
00
о
00
00 CO 00 rf
CM CM i—i CM
00
ю
см
Й
о
CO
S
	4
о ю о	сГо см
^^ II	СГ> ОС CM
<=><=> .11	ooo
r>CJr OO
r-zr- —'Юсмсооо^оооосооооо смосо
Г^ОЮЮ
оо о см г-
11й 111 | ТТТ!Т?1ТТ°Т Г\1.°\Щ 111J11
О Ю . *00 ОЮСМ ЧЛ ЮЮЮЮ^ЮОГ^ЮОГ*- ЮОГ^ООЮ I I . -Ю ONOiOiO
Ю »—' 00 Ю СО —« »—• О	О СМ у—• 00 »—< 00 Ю —^ Ю Ю *-^ ^н^^-^^Ю^ОО^СС^Ь—'t
U с^
ела
Нсо
О н
и
оо
О
о
см
20Г
СХЛ
X
о
20ХН
' о а
05 ^
S о
* .
II
!i
s
a
X
s
о
о
X

820
ПРИЛОЖЕНИЯ
к
я
о д о л ж е
ft
>?'
<ц
о?
Область
применени
—	чюонева
ж-гп
oiir9HHdg ou
Hxootfdgax oironh
ф % эинэжЛэ
ЭОНЧ1ГЭХИЭОНХО
% ЭИНЭНШГЯА
ЭОНЧ1ГЭХИЭОНХО
Р01 = 1
% эинэниьчгЛ
ЭОНЧ1ГЭХИЭОНХО
„ХООНЬо!^
ихээь^нэх irafadu
че-
I ХИМИ
состав
к*
О у
и
О
се
о.
о
Найме
и; -2
тветствен.
тали Kpyi
размеров
00
1
Ю
о
1
1
100
8
35—0,45;
25—1,75
6—0,9;
2—0,4
<^> »-^ со со
М II и ii
II II II II
<
X
X
о
моли
ль
ромонике
деновая
X
ысоконагр
са
S
о
100
о?
,20—0
6
жённые
i
м ii
II
*
25Х
i
СО
ft
§
са
ч
ромонике
X
и
z;
ленчатые
валы
1
> 00
II
A
II
II
1
я
S
ПРУ
пг
ремниста
ружинные
1—
о
СО
со
130
120
55;
45—0,
рессоры
—* у—
ОС
оо-
II <> <
II
•
ная . . .
И 1
Ее/
1=1
м О
ысокотвёр
детали
ысокоотве
венные аз
CQ
ю
1
о
1
1
155
130
1
S
со
1
1
100
00-^	ч* СО
8—0,1
8—1,1
9—1,2
38—0,
35—1,
ооооо—
1 II II 11 II II II
1 II
CJ
ЗОХ
.
ft "
со *
S «
О со
ремнехро
ганцовис
II II II II И
Q
38Х/
05
СО
зотируем
<
руемые
тали
..8
* 1
оо
II II
II II
<^
1 «>
г
ые стали.
я
о
&
s
грук
950
я
о
1
,урса]
ния,
S
и
со
Я
о
CQ
СО
го
НЛО
СО
н
О)
*
-я
ft СО
с
я
иал
спе
шия в
Осно
о"
я
0)
СО
id
S1-"
03
о
ж
проб
О
U 9Э1Г
Бо
о>
S
Я
со
3"
Приме
ггГ
СО
удцо
СО
сО
ft
ник под
о
за

ПРИЛОЖЕНИЯ
821
I
X
cd
26
нагруз
*
X
л\
0)
&
с
[ при
CCJ
н
X
3
X
1
о.
ICT
X
о
S
X
Б
1
а
ч
и
X
ристи
СО
а
Я
S
анич
и' "?
в»
* Н ^
К Н ^
3
отка'
>раб
о
о
Тер]
и
я
!Й COCTi
и
0)
к
к
X
2 s
Map*
стал
00
2—15
CM
i
2—42
CO
CM
00
аци
ЛИЗ
орма
X
^-. со
о4 сГ
о АГсоо
оооо
II II II II
о
00
>-^
С?
с
О)
CN
г-
S?
со
•S
см
см
аци
ЛИЗ
орма
X
ю t*** ю
см^оо^со^
00* СМ —• ^^ 00
ооооо
V/V/II II II
>5 л*л ^^ С/5 ^*"
8
СМ
СМ
, ,
с
см
с
см
8—60
со
со
см
аци
ЛИЗ
орма
X
оо со .-
ооооооо
IIV/V/II II II II
i ^^ ^"^ 1^ i
т" ^~г
75 СО
8
со
1
1
ю
9—25
со
Ю
СМ
ю
со
см
см
со
*
см
00
«
аци
ЛИЗ
орма
X
ю оо
п1
оооос
V/V/II II
*J* г^ ^^ СО
CM
o>
CM
о
s
CO
CO
00
Ю
i ^
^ Cft uQ
en
^00^ . > . _c
1 io r~* 1 ocT J
OfC-nOOOL
1 II II II II II
"^ "T"
en
40X
Ю
CO
CM
1
1
CM
CM
T
r-
CM
J>
CO
CM
Г—
4p
о
1
Wo
S CO
со10
о ad
о w
CO >~>
оо с
л и
N4 О
акал1
ле;
00
,37; |
ч о
D 1
1 V II
оо
2ХН
со

822
ПРИЛОЖЕНИЯ
я
*т*
s:
о
о
о
а,
о
1
05
0Q
85*
? о
U х
<
PQ
X
X
00
ел
со
X
X
is
X О
« 2
X
33»
CQ ? Kt
III
ей
s л
3 л I
X X.*
X S^
4tl^

ПРИЛОЖЕНИЯ
823
ПРИЛОЖЕНИЕ III.
Механические свойства отливок из углеродистой стали
и серого чугуна.
Наименование
отливок
Отливки фасон- J
ные из углеро- 1
диетой стали {
(ГОСТ 977-41) j
Отливки из се- i
рого чугуна >
(ГОСТ В-1412-42) 1
Марки отливок
15—4020
35—5015
СЧ-12-28
СЧ-15-32
СЧ-18-36
СЧ-21-40
Предел прочности
при растяжении
Предел прочности
при сжатии
Предел прочности
при изгибе
кг/мм2, не менее
40
50
12
15
18
21
—
50
60
67
75
—
28
32
36
40
Стрела проги-
прогиба стандарт-
стандартного образ-
образца при рас-
расстоянии
между
опорами
600 мм
300 мм
мм
—
6
7
8
8
—
2
2
2
2
Относительное
удлинение
образца
с 5-кратной
расчётной
длиной %,
не менее
20
15

ПРИЛОЖЕНИЕ IV.
Механические свойства сварных соединений и наплавленного металла.
Вид сварки
Ручная, тонко-
обмазанными
электродами
Ручная, толсто-
обмазанными
электродами и
автоматическая
под слоем
флюса
Сварное соединение встык
* о;
° к S
lie
о -
34
42
н
и
о
30
120
*8
о в
is
к <я"
8
Наплавленный металл
ч^1«
преде
ности
растя
кг/мм
ите.
ени
относ
удлин
не менее
30
42
6
18
Марка
электро-
электрода (по
ГОСТ
2523-44)
Э34
Э42

824
ПРИЛОЖЕНИЯ
и
о
о
с
м
о
«=;
Р5
2
а
о
а
х
X
s
н
о
s
аи
се
а
ее
х
ее
X
0)
к
Я
О)
Я
о
а
с
из
о
Обла
О 5 5 SNO
О н >»
»?§-¦!
НИ
химический
эстав
Г
м
Оснс
рка
о
25
я
CQ
И
О
1аимен
спл
дные
ОВОЛОК
сх
с
Гп
\о
>->
г>
ю
J,
X
00
1
23—30
II
с
N
.
X
ату
с?
3
1
00
сч
00
00
1
18—27;
1,75-2,5
II II
с *¦¦¦'
N
77-2
ЛА-
с;
пз
pa
<и
X
i
ч
сз
А
X
ату
3
н
и
S
рут
С
8
а
э
О
с
5
00
рут
С
о
00
0,5-
о
1
00
1
ю-
36—39;
1,0-2,0
36—39;
0,8-1,9
II II
с с
II II
NgNCu
00
«9
CQ *
О •
X *
apra
г .
сз w
2Q
к
СО
S
щ
S
нь ев
ату
о.
нная а
:тве
н
тве
О
о
ос
со
1
-90
9—11
II
с
ел
о
о
•
* 2
Ф н
^1
ЛОВ
о
03
гветст
о
03
Оч
ю
S
втулк
со >->
S Н
о
со
00
н q ir в х э о
с
г-
4—6
5—7;
5—7;
о л.
II
с
ел
Ц-8-4
О
Г1
IIIIIIII
спел
00
со
о
о,
•
пох
рни,
а
о
о
СО
1
9—11;
II
СГ
сл
Ф-10-
О
из
рдые
ёрдые
s :cj cq
itf CQ H
s н
= 2 §
s н н
Я X >~>
"-1 CJ О-
1 1
00~—«
СО Ю
1 1
II II II 1
Бр А-5
Бр АМц-9-2
3
CQ
S
S
лю»
<
трубы
S
рут
с
о
о
СО
А*
1 II II II
: г: «и с
ю
^7
со
о
)АЖМ
ел

ПРИЛОЖЕНИЯ
825
О
а.
I
к
X
о
ГС
а
о.
с
«а
н
тас
с
о . s = g
н ** с
К г; П X
Предел
проч-
прочности
Предел
теку-
текучести
кг/ммЗ
•К
?
о
Я*
аон
О
«в
Марк
I
ев
А
О
Я
<и
а
IS
¦0J
*q
5
с;
I
оо
в
1
а
о
с
к
(_
СП
я
о
паровоз
s ^
1
о
см
1
©
•о
см
1
пз—30НЧ1ГВ1ЭО
lii"
--
ю
«—1
АЖС-7
ш
а
а
си
В
ЛЮМ1
<5
Л
i и
ю
см
Бр ОС-
о;
ев
н
о
S
я
I
О
т
11
истая
ремн
it?ewc?
а
сплав
03
перессо
1ЛИ
100
50—
ем
см
15-
о
О
1
iv-
00 00 00
О
<©©
з rf ^ ckToo
со©©©©
IIIIIIIIII
й '
дура
ЛЬНЫЙ
орма
мин
X
профили
о
100
50-
00
22—42
10—24
— ЭОНЧ1ГВ!
юоооо
5—4,
4-0,
4-0,
00©©©©
IIII1111II
о*;
:
зуемый
мин. .
Sg
С
профили
VO
сх
Н
125
©
|
оо
18—50
5—38
	©
Ю© 1
СЛ СЛ Cft (>«Г(~-.
II II II II II
СО
X
<v
овыш
СТИ .
с о
II
27 Н. М. Беляев

82П
ПРИЛОЖЕНИЯ
с
Си
С
1
I о
а
', В,
с
л
ь
и
ГЗ
О
О
JL
О • ~ С-Р
с; СиН ^ *
Ы 'и О ^
уНЧОк
4- •" Л
S Q О
l33g*
О н >.
Преде/
проч-
прочности
ав
кг/мм-
_
Преде
теку-
текучести
кг/мм-
имическ
тав
*о
* S
о
я
0Q
О
в
о
О
се
И
О,
«ч
Е
а
се
i
я
SS
«
г 1
о >-•
S CU
ч с
а" а"
VO И
>-> О
р, S
н ^
О lO
со ю
ю о
ГС О
см см
1
со ю
ю см
с
0(
11—2
— 00
10—2
5—1
IV — эонч1ГВ1ЭО
| см ^-Г
М^ОЮЮ CMOOOOqq
о о см сГо о ^ о сГ^
11 II II II II II II II II II
II П II II II II II II II II
М «^ <? Cl СЭ ГТ'гг'чг'Гт^^
< <
« '. « '.
л • о
со . я •
s * й *
Алюмино-маг
сплав . . .
Алюмин.-мар!
сплав . . .
a s
Н н Н
>» CJ >-»
cu s a,
О 1 О
rf I CD
ю г- см
00 О 00
*—I СМСМ
i i
Sw — Э0НЧ1ГВЮ0
с
с
з сГ оо ^ с
5СМ00ОСМ
сГо сГ»-н irTo о о о
II II II II II II II II И
II II II II II и и 1> ¦•
о 52
а
со
cd
t?
С
Магниевые с
о,
IS
s-
О) Г
as
Я

ПРИЛОЖЕНИЯ
827
ПРИЛОЖЕНИЕ VI
Пределы прочности некоторых материалов (в кг/см2).
Материал
На растяжение
На сжатие
Чугун и
Чугун серый обыкновенный .
Чугун серый мелкозернистый
Чугун белый
Пластмассы
Бакелит
Целлулоид
Текстолит
Гетинакс
Бакелизованная фанера . . . .
Дерево
(при 15% влажности)
{вдоль волокон
поперёк волокон ....
вдоль волокон
поперёк волокон
вдоль волокон .......
поперёк волокон
1400-f- 1800
2100 4-2500
200 4- 300
500
850
1500
Сосна
Ель
Дуб{
1300
800
650
950
700
1000
1700
Естественные камни
(в среднем)
Гранит . .
Диабаз . .
Гнейс . . .
Кварцит .
Песчаник.
Известняк
Кирпич . .
Бетон . . .
30
50
20
Лёд
(в сред-
среднем)
при малых
скоростях
нагружения
при больших
скоростях
нагружения
= _12Ч-—15е
= —12Ч- —15е
10
6000 4- 10 000
до 14 000
до 17 500
800Ч-Ю00
1300-i-2500
1500 -4- 1800
1150
4Q0
50
350
40
500
150
1200 4-2600
1300-f-2100
1400-4-2400
1400 4- 2600
400 -Ь 1500
500-f-1500
74 4- 300
50 4- 350
104-20
57 4-70
5-4-10
154-48
27*

828
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ VII.
Модули упругости и коэффициент Пуассона.
Наименование
материала
Чугун серый, белый
Ковкий чугун
Углеродистые стали
Легированные стали
Стальное литьё
Медь прокатанная
Медь холоднотянутая....
Медь, литьё
Фосфористая бронза катан-
катанная
Латунь холоднотянутая . . .
Корабельная латунь катан-
катанная
Марганцовистая бронза ка-
катанная
Алюминий катанный
Алюминиевая проволока
тянутая
Алюминиевая бронза, литьё
Дуралюмин катанный ....
Цинк катанный
Свинец
Лёд
Стекло
Гранит 	 .
Известняк
Мрамор
Песчаник
Каменная кладка:
из гранита
известняка
кирпича
Бетон при пределе проч-
прочности
при 100 кг/см2
> 150 >
» 200 >
Дерево вдоль волокон . . .
> поперёк > ...
Каучук
Бакелит
Текстолит
Гетинакс
Модуль упругости Е
кг/см*
Модуль
упругости G
кг, см*
Коэффициент
Пуассона jj.
1,15 4 1,60. 10е
1,55. 10е
2,0 4-2,1 • 10е
2,1 . 10е
1,75. 10е
1,1 • 10е
1,3 • 10е
0,84 • 10е
1,15. 106
0,91 -ь 0,99» 10е
1.0	. 106
1.1	• 10е
0,69 • 10°
0,7 . 10е
1,05 • 10е
0,71 • 10е
0,84 • 10е
0,17 . 10е
0,1 . 10е
0,56 . 10е
0,49 • 10е
0,42 . 10е
0,56 • 10е
0,18 • 10е
0,09 4-'0,1 • 10е
0,06 • 10е
0,027 ч~0,030. 10е
0,196 4-0,146. 10е
0,214 4-0,164. 106
0,232 4-0,182- 10е
0,1 4-0,12 • 10е
0,005 4- 0,01 • 10е
0,00008 • 10е
0,02 4-0,03 • 10е
0,06 4-0,1 • 10е
0,1 4-0,17 • 10е
4,5 • 10»
8,1 • 10*
8,1 . 10"'
4,0 • 10*
4,9 • 105
4,2 • 10*
3,54-3,7-W
4,0 • 10»
2,64-2,7. 10*
4,2 • 106
2,7 . 10»
3,2 . 105
0,70 • 10б
0,284-0,3-10:
2,2 • 105
0,055 . 10*
0,23 4- 0,27
0,24 4- 0,28
0,25 4-0,30
0,314-0,34
0,32 4- 0,35
0,32 4-0,42
0,36
0,35
0,32 4-0,36
0,27
0,42
0,25
0,16 4-0,18
0,47

к4
с:
X
I
i
о
се
о
*к
4)
X
I
в
ваши
ала
о s
s °*
5 *
a ?
ОВ се
М ее
О К
к а.
к я
S 2*
к *
та Я
о Г Г
22
СО О О
.—> Г^ Ю
.' .!. .(.
... •]. .;.
ООО
. сз
ладь
и:
. 05 ¦
СЗ
' X О
.д S 0Q
га S О,
Н СЗ Oj
Кь
CM rf .
+ +§
ОО
t-O
Л * '
>~> # .
сз • •
«=: . .
s • •
Брон
Вето
Лёд
т т т
ООО
ю ю г—
lO Ю СО
...
. * .
S • •
АЛЮМИ!
Магний
Медь .
ПРИЛОЖЕНИЯ
829
ПРИ
CJ
О
о
X
тствн
ffl
57.
1
8510
57,
о
о
о
н
о
о.
Б
X
Двутаврь
га
Я
S
>о
га
Н
<
•S
о;
ДЛЯ
величины
фавочные
U
Размеры
1
1
~-
U
3
о
•с:
Вес
1 пог. м
кг
N* про-
профилей
1,22
1,38
1,55
оз см
со'оо"—г
ОЭ О5 О5
— см ^г
23,0
33,7
46,8
4,06
4,88
5,73
со ю оо
ООО СМ
О5 lO Г^~
O^l^rf
см со ю
ю -^со
юсо с^
ООО
о см ^
со
TJ^ Ю Г^
О5 »—^СО
осм ^г

830
ПРИЛОЖЕНИЯ
ooocMfcNjtotrortoo^ioo5a5iocvicc'i"Of^-rt< —-о
h-00-'OCOCMvOOOC?>iOOOCOC5t^OCO—' !М ^ 'X! h О О О
-? »-Г см' ci cn" ci см см см см~ cvf см~ см см" см~ со" со со со со :о со *? ^
о
о*
с
1—• -^ ^ cn (M со со
OO^rt 00^
Гт-Г aT^rfT-^cooooooooccMOiooooiiooooooo
1CMCM
5 t—i т^1 oo CM Ю Oi
У—I У—• T—I CM С
оо см -
OOOOOOOOC
¦ ОООЮОЬООС
COi" " "
OOOOOOO
оююооо^
f* СЧ »~H 'ЧФ Tt^ CO t 00
5lOO^С
00 CO <
5ООЮГООО
OOOOO
CDOOXOO
^-CNCSJ
OOOOOOC
>сооюо
) О О ОО
> ю о <
M О
ed Л со ее со d

ПРИЛОЖЕНИЯ
831
I
I
CO
a
CM
CO
«=:
3
и
ичи
Ч
Я
О)
3
К
о
а
а.
с
и
а,
м
|
V
со
. н
ц
*
н
Is
3 *
II
•с
Вес
09
ее
51
6»=
сх<и
СО
СХ)
о
см
со
ю
59
ю
см
о
О)
00
см
см
со
СО
о
S
84
ю
см
оо
о
00
СО
СО
о
00
о
о
о
ю
см
о
ю
со
00'
ю
см
S
S
ю
ю
со
со
ел
<—'
00
см
со
со
*—*
со
со
22
ел
00
00
о>
оо'
ю
S
S
00
со
со
со
8
о
см
а»
со
00
со
о
со
ю
со
100
59
00
о
ю
со
см
ю
00
см
со
СО
CD
см
00
Г4-
СО
S
со
со'
00
00
см
ю
120
о
см
со
о
о
ю
1
00
сГ
^*
со
ю
см
о
о
СО
15,
00
1
00
ю
140
со

832
ПРИЛОЖЕНИЯ
•к
осе
ее
я
5*
S
ные вел
У
ю
о.
О
«
ск
т
а
1
Н
1
н
о
С
и
CQ
в
«о
(
се
К
я
о
-V»
О
00
я
'—'
со
со
ю
ю
CD
CD
Ю
00
>О
ю
о
г-
00
см
CD
140
со
со
о
00
'-"¦'
00
1—'
00
со
^
со
со
CD
^,
ю
¦^
CD
s
00
00
о
ю
CD
160
см
14
CD
8
см
01
см
п*
CD
00
00
г-
СЕ>
ю
СЛ
"^
CD
§
СО
00
ю
2
о
о
ю
S
160
со
ю
2
04
см
о
~*
о
CD
00
00
СЕ>
CD
СМ
I"'
121
о
8
00
	.
ю
о
180
со
16
00
СО
СМ
00
см
о
о
см
105
_,
CD
<М
СО
132
S
см
см
см
со
а>
	.
О
180
ее
00
S
(М
20
см
vO
<м
со
00
00
о
00
152
о
\П
г—•
со
см
о
оэ
см
ю
CD
200
00
о
см
00
СМ
см
ю
(М
ТГ
С4}
со
ю
о
«—•
00
167
о
со
см
8
а>
см
ю
S
200
00
2
се
21
<м
СО
С4)
'О
,	1
ю
о
О)
00
00
192
о
СМ-
CD
см
ю
<м
00
220
о
см
й
CD
55
С4!
о
о
со
г-
00
см
О)
00
212
о
см
00
00
см
см
о
ю
00
220
CD
я
S3
см
см
S
см
CD
со
00
о
О1
О)
со
со
г-.
о
242
о
см
CD
8
о
о
CD
ю
S
240
о
a
см
67
см
00
см
см
со
см
,	,
00
сп>
265
о
00
со
а>
8
о
CD
ю
8
240
00
ю
см
см
47
<м
со
С4!
со
со
Г4!
CD
см
00
о
808
8
"**
см
35
ю
о
о
CD
270
^_
см
см
см
»о
(М
об
CJ
CD
СО
^
(М
со
¦^f
С4!
о
(М
387
о
ю
ю
о
ю
CD
100
300
00
со
с
СЛ
ю
00
,	г
ю
о
,	,
00
ел
»—•
со
484
о
ю
CD
о
•"-
105
330
ю
36
S
68
см
о
со
CD
со
iO
1^
Й
см
601
о
см
00
о
S?
CD
ю
о
098
а>
75
(М
со
С)
со
со
см
CD
ю
761
8
CM
ю
ю
CD
ю
со
о
00
115
400
СО
00
о

ПРИЛОЖЕНИЯ
833
*3
jL
xi
SSSSS&S^^
о
ш
а
о
со
S
к
ю
5
\
о
се
_
X
5*
S
CO
о
•я
*?
s
ев
С
О
N
1
!
***
*
о
н
1
ч
*
а
о
о
и
и;
о
и
лсак
о
Вес
1 пог. м
Го
Си
Раза
J2 OS
II
О О
•ч о,
<х
*|
ей
с
3
Г*
S3
оо
0,81
1,09
О5 00
го со
О О
ю со
г- г-
о о
сооо
СО Г-
оо
О5 00
оо
0,40
0,50
COCO
СО "^t1
о
см
см
го со
оо
ю ^
О5 00
оо
со ^
оо
ю со
О5 О5
оо
О) СМ
см со
,—. »-|
Ют*
оо
0,81
1,03
coco
rf OO
CM
2,5
s
о
2,20
в
о
00
о
о
S
Г-Н
о
1,16
1,27
1,62
со
00
см
2,8
оо
3,26
4,39
С0(М
сою
оо
оо
со —
(NCM
ООО
оою
ем со
t^CO
оо
1,77
2,26
1,86
2,43
СО TF
см
СО
со4

834
ПРИЛОЖЕНИЯ
Справочные величины для осей
№
н
I
н
Г
о
>\
Н
1
|'
а;
а
о
Вес
1 пог. м
Площадь
профиля
Размеры
Ч
**<
и
о
3
о
us
а
№
профилей
0,99
1,04
СО СМ
rf CD
о о
coco
СО 00
со со
осм
rf Ю
о со
со со
юсм
см со
юсо
о ю
00 rf
я
3,6
со со
СО Ю
СО 00
СО 00
оо
ю со
ю ю
со см
оо см
см см
юоо
ю ю
1,85
2,42
2,35
3,08
00 rf
о
см см оо
S-CO
— —
СО СО 00
00 ОС 00
о о о
CM rf СО
— г^ со
СМСМ СО
Ю rf CM
t— 1—• Г—
00
— ю г-
оо о" см"
со оо г-
00 00 00
00 00 00
— coo
Ю CD 00
00 00 Г*-
см" см" со"
ю оо со
CO^rf^CM^
«.*
ю
4,5
со ос см
rfCDCO
(М СО О
— — см
О СО 00
о со со
СО 00 СО
Ю rf CM
со со со
~~~
оо со оо
—1 rf Г-"
— СМСМ
см"со"оо"
2,96
3,89
4,80
00 rf ю
о
ю
ю
со со см
О СО СО
СМ СМСМ
см—. о
о —со
^гюсо
00 00 СО
СМСМ СМ
rf 00 rf
00 О Ю
— СМСМ
00 00 СМ
со —о
—Г со со"
00 rf ю
O^rfjr^
3,86
4,38
5,41
C0"rf Ю
со
ю
9'S
СО rf 00
ее г- t--
— ю о
СО—Г о"
ЮЮ rf
см см см
— см
ООЮСМ
Ю rf СО
rf rf rf
см"см"см"
со со со
со" со* см4
СМ 00 rf
со со со
со —•»—«
— см см
3,90
4,81
5,72
4,96
6,13
7,28
rf ЮСО
8
6,3
00 О rf СО СМ
ос со со со о
О Г- rf — СО
—ГСО 00 О"—*¦
Ю Ю CD 00 СО
СО СО 00 t^- h-"
СО СО СО 00 00
осм юооо
— — — — см
СМ СМ — СО ОО
Г- Г* Г^ СО CD
см"см"см"см"см
ON CO CM rf
со о" со" оо со"
rf ЮЮСО Г»
СО СОЮ rf 00
см см см см см
о сосоосм
СМ 00 00 rf rf
4,87
5,38
6,39
7,39
8,37
о со юсм
СМ 00 '—• rf l^-.
со" со" оо" аГ о"
rf"lO СО Г- 00
8

ПРИЛОЖЕНИЯ
835
К
a:
о
о*
с
(NCDOiOOO
см" см" см" см" см"
О5 СО Г^
— см см
" " " "
2,43
2,47
2,51
2,55
00 ^-н iO CO '—• СГ) СО
СО t^f- 00 О5 О5 О
см" см" см" см" см" см" со"
2,96
3,00
СО О СО
съсососъ г^
СО 00 Gi — CM
см см см со ^г ^ ю
С5 ОС 00 Г^. СО
О5 00 00 Г4-
iO Ю Ю Ю
5 00 00 СО Ю ^t **
осей
rf СО — 00 Ю
со'аГсм^^
^ —см см см
оо ю о со^
см см см со
О О ОС СО
СО СО Tf ^f
сГ -^ сГ rt^ со" с$ см
Ю Ю СО Г-00 О5 —
J
—^ о о г- со
О5 О5 00 00 00
см" см4 см4 см*4 с4?
со" со" со" со"
О О5 00 СО
со со со со
00 00 t^ Tf *-• 00 rf
оо^оо оо оо oq^^t^
со" со" со"со" со" со" со"
Н
СОС5СОО5
СМ^СО"-^ rf\O
СО t"» 00 050
СО тГ
CO"Of
ос оэо
О О 00 СО
со ю со оо
со г>» со п* —< ю со
О5 СО СО 00 СО Г*- *—*
^-^ см см см со со тр
со со см см см
см^смсмсмсм"
t>- t4- Ю ^
Т^ Tf Tf Tf
см"см"см"см"
§§ёё§8д
со" со" со" со" со" со" ci
39,5
46,6
53,3
59,8
66,1
СМ"'*"
ооа
СО 00
CM^t-O5O5^-
СМ СО Tf h* О CO
О CO С
Вес
пог.
6,78
7,36
8,51
9,65
со тр
СО СО О5 СМ
"""
— 00 CM ~* O5 СО СО
ddcfioVdco4
Площа
профи
39
,78
,1
,5
,8
7,
8,
0,
1,
2,
8,63
9,38
0,8
2,3
СО СО О5 СО
о см" со ю"
оо^оо^со^см оо^со t^-
см" со" ю" oi" см" со" аГ
^ —— г^СМСМСМ
СО
ю
СО
G5 00
см см
72,7
81,8
4,29
4,28
,40
,39
5,2
7,2
юсо г^оо о>
ю
Юсо г- оо
СО Г* 00 О)
со" г*- оо о см ^t со
S
00

836
ПРИЛОЖЕНИЯ
51
О ,^ у> ^сг
¦^f "*¦?* ic се се
-,-Г ,^-Г' ^-Г ^'Г --Г
со
ос"
ОС
О М О5 СМ ?
— ОС ^ СО '—
—' — см со
—| ОЗ h- iO
О5 —' -гГ Г-~
—< СМ СМ СМ
О ОС' Г— СО tO
(N005^0^
(NJC'sfNOM
— —I»— — CN СМ
Is- СО Tf !M 00 1С
00 СО 00 00 h- Г~-
- О—• О ч* 00
(М t4^ 1^» СО Ю
Г Ю Ю СО Г* СО
Г- СО Ю CNIO 00
00^ 00^ 00^ 00^00^ Г^
ее со со" ос" ос" со
тГГ О СМ СМ О)
о см со ез со оо
см ос оо ? ^ю
СТ) 00 '-О
!^ г- Г--
см см см"
<М — 00
О5 —- *
—« СМ С^1
О) **? Г-
00 -* Ю
г^- оо а>
СО СМ С4!
Tf iO СО
О5 00 Г^ СО -** ОС C^J
ос" ос" ос" ос" ос" ос" ос"
О5 00 СО <—' iO f~— CD
—< ^ Г- ОС ОС СО CO
ОС 00 00 ^Г ^ iO О
. Ю rf 00 О t^ 00 О
см см С4! см —^*-ч '—
со" со" со" ее" со" со" со
О1 *—О СМ СО — 00
CM rf Ю СО СО СО Г
СМ 00 тГ СО 00 О С
00 СО iO O5 О>
1 *—• Tf Is*» О —«
О5 О *-« CM Tf
О0 rf
СМ 'М
— СО
OJ СМ
О5 00
ос ос"
00 00
оо а
CDO
— см
5Ю
СО I—
СМ 00
^ ^- h- CM СО
ю~ г*-" аГеТ со" о
СМСМСМ
t С* * оо СО
см см см оо со*? ч*
оэ" см" т*<" оо" оо" t4^
г-СМ СМ СМ 00 00
Г- 00 iO
rfr^CM*4
см см оо
¦^Г vj «—» ^J ^T"
CO 00 00 Tf rf ЮСО
00 CM
oo'cm
00 ^
00 CT>O CM
O)OCM
О-> (M Tf CD 00 О
—«^-^^^—CM
о
00

ПРИЛОЖЕНИЯ
837
S
s
NMCDTfCOr
ГС чЗ* Tt* lO Г4*» 00 С
CM CM CM ^Ф i-O ГС <O
00	iC CM CD Ю ГС ГС
— rf Г-~ 01 ГС Г-~ —•
cc ее со ^r m fx> со
01	QC t^ 1O CO '—' O}
«Г го" со" co~ го" со" со"
,c со —• о — го *¦*
Г~ 00 O5 О — CM CO
Г O
rQ ГЧ 	1 ^ '
00 Tf О СО С
s
ю
О) Ю —• О О! 00 CO
Tf О CD Г- ОС ГС 00
h- 00 00 Oi — "* CD
Tf CO *-* 00 Ol ГО Ю
CO CO 00 t^ t^- CD Ю
О 00
сою
00 00
CD CD fO iO О "^f »—'
ОЭ »—• ГО Ю CD db iO
oo»-"' со г*"» io ^Ф со
CM CO CO CO ^J* iO CD
MONtMCOO
CM CM CM — — OrO
ciT ссГ с^Г ссГ ciT ссГ со
CO—«
00 00
Г
со—«г- со — coo
CM CO O5 «O t^- CO (>)
00CT> О СО 00 ¦«J'O
•—i ^ CM CM CM CO Tf
Й
00 —н
<M CO
C) OO О t^ h- О ffi
¦^ \.o t4- о oo a> oo
О —« CO iO 00 — CO
— !M CM CM OJ CO CO
00 Ю (>J O5 Tf O) CO
r r^ г^ со co ю ю
CM t^ О *— vC ^ vO
O5 CO CD CD CM "^* CO
Г*- 00 O5 O5 —• CM CM
CD CO •—' O5 Ю ¦—• O5
l^ t^ h CD CO CO Ю
Г Ю О CO Г Г
«-™1 ^ CO Г*- О *—• Г4-
О О5 OO^h* —< О СО
i^ o$ cS oo o~ ч^ к*
CO CO ^ Tf CD Г- 00
ю a» *-« co^
r-T OO~ ЮСб~^^
CD CO t— 00 O5 О *-^
If
^- O5 CD О iC ОС Ю
О ¦-* I4- "— О
oo f«r ccToT co'c^f
r- oo o> о —^ со -^
о
CM
CM
о
; CM
со ос о см ю oo о
«— — CM CM CJ CM CO

838
ПРИЛОЖЕНИЯ
I
о
X
0
се
а
I
О
с;
3
шые величи
о
са
п,
с
и
3
г
т
о.
a
|
1
~>
1
1
j
Вес
§1
с a
/ГОЛ
клон
и tg
So
8 '
*
I
^«
8 Я*
p cj Г»
Й =* ^
а о «
Расстояние
от центра
тяжести „Vo
H
H
1 пог. м
6?
OJQ,
•О
а,
•
*
u
u
5^
•4»
*
в
•s
с;
с
392
о
00
о
ГО
о
О)
о
со
о
0,86
со
о
S3
о
00
г—
о
о
о
0,91
со
00
СО
ю
со^
2,5/1
СМ ^
88S5
оо
00 00
оо
оо
осо
оо
<N(N
00 «—'
о^-Г
1,08
1,12
со оо
с^оо^
со ^
ю ю
со h»
оо
SS
,—1 ^-t
(N00
Ю О)
тг О)
1 1 г-Н
оо rj*
о
й
со
,385
,381
оо
оо
gpr
оо
О) СО
юсо
оо
оо io
ю*—
ЙЙ
t^-co
оо ю
СО 00
ОО)
l^co
о^о
о—г
t^-co
<N<N
»-Н г—t
co'co"
1,48
1,94
оо rf
00 rf
•я
С}

ПРИЛОЖЕНИЯ
839
о
о
о.
с
со
к
SS
Справочные величины для осей
а
1
1
н
1
н
1
н
н
Угол
наклона
оси tga
а
а-
а:
а
Расстояние
от центра
тяжести лг0
а
Расстояние
от центра
тяжести _Vq
.<
~»
~*
ч*
Вес
1 пог. м
Пло-
Площадь
профи-
профиля
Размеры
V)
СМ*
Ч
см*
о
см*
5
СМ*
i
см*
8
%
профилей
0,382
0,379
0,61
0,60
0,79
1,02
0,64
0,68
86*2
02*2
1,47
1,51
9,02
12,1
81*0
61*0
1,32
1,69
1,43
1,42
4,41
5,68
1,68
2,20
2,14
2,80
СО ч*
00
см
*
4,5/2,8
0,403
0,401
69*0
01*0
00 СМ
0,72
0,76
3,26
4,42
1,60
1,65
см" со"
0,91
0,90
1,99
2,56
1,60
1,59
6,17
7,98
1,90
2,49
2,42
3,17
СО ч*
8
8
5/3,2
0,407
0,406
0,404
СЛ 00 СО
1,95
2,19
2,66
0,82
0,84
0,88
5,43
6,25
7,91
осмео
00 00 00
20,3
23,2
29,2
1,02
1,02
1,01
3,30
3,70
4,48
О> 00 h*
t— r^ t^-
гНгНгН
O\-Ttff
00 *—• CO
cm"cm"co"
3,16
3,58
4,41
?-^ю
s
5,6/3,6
0,397
0,396
0,393
0,386
0,87
0,86
0,86
0,85
3,07
3,72
4,36
5,58
0,91
0,95
0,99
1,07
oo o~co i^-*4
CO 00 CM О
OO^CM
CM CM CM <M
CO^rfCO
CO CM f«O5
5,16
6,26
7,28
9,15
2,01
2,00
1,99
1,96
COJ3) COJO
со"аГсо"сэ"
3,17
3,91
4,63
6,03
^ooooo
О C> CiCO
т^Ю CO 00
о
s
6,3/4,0
0,407
0,406
0,98
0,98
4,88
5,34
1,03
1,05
13,6
15,2
82*2
92*2
-hCO"
ЮЮ
1,28
1,27
8,25
9,05
2,23
2,23
25,3
27,8
3,98
4,39
5,07
5,59
о
г-
1
0,436
0,435
0,430
ОЭ 00 Г>-
^ 00
см^о^
Г- — СТ>
'—СМ СМ
00 СМ СМ
см см со
О5 Tf СМ
со rt ю
см" см" см"
69,7
83,9
112
ж-
2,39
2,38
2,35
34,8
40,9
52,4
4,79
5,69
7,43
6,11
7,25
9,47
ЮСООО
S
7,5/5
0,387
0,386
1,09
1,08
7,58
8,88
со г-
20,8
25,2
2,6
2,65
84,6
102
2^6
2,55
41,6
49,0
4,99
5,92
SS
юсо
г
s
8/5

840
ПРИЛОЖЕНИЯ
s
а;
о
«=(
о
- 6 =
00 00 ОО
ОС ГС СС
ОО О
•я
си
3
о я н
u (LI U
а"8
СМ С4) 00
СМ«сГг-~
ос ос Tt
со сч *-. с^
О) а; ст. оо
СС ОС 00 00
о оо о"
<м,ос ^^
об" о" тс" эсГ
'—' CM CN СМ
О) Г- СО 00^
аГоо^г^ю"
'чГ Ю СО 00
СМ —
г-: со"
<СМСМ
ос со а>
ю'оо
ОС 00 (M О
см см ос тг
00 CM CO ОС
сг> ос- со oo
сос
со ос ос
O> 00 Ю
CO CO CO 00
000 h- rf
О r—i CM lO
iO '—* СО iO
of—гоГю*"
00
CO
8
rt* OC-l
h- 00 O5
1С uC CO
ее" ос" ос?
O5 ОС
йос
OCCMr-,
со со*4 со
00 rf
O5 COC5
O fO
о о о о
ТГ гг ^ ТГ
о" о" о" о4
^f ОС ТС uC
со оо* с. с:
О) г- ос о
1—' ОС Г"- •—|
*— iO "t CM
о о — см
CM 00 СГ>*—
Ю — ^ 00
СО СО С? I
t— ооо
^^ ОО Ю
О О^О^
rj^rf СО*4 СО**
r-cocMi
СМ Ю —'С
см см ос с
^о а
—« ^^ »—' CM
о
ОО
00
— о
do
ою
Г^- ОО
00 СО
юю
(NCM*4
ОСО
см ^
CM
00 (N4
CM

ПРИЛОЖЕНИЯ
841
о
*=c
о
a,
с:
»s
o>
о
S
3
3*
к
<u
тые в
Справо
еры
а
1
1
1
ее
i
1Л
Е О
%
1 ^S
О В и
й a S
а:
-Г
о к н
р 0) О
1 пог
I (Я
О. я
се
•о
1
с
1
5
—< О 00 Ю
О СЭ 00 00
се оо со со
оооо
О^ 00 СО
(>] — '— —
са с^4 jm см
О •—' "» С4!
— ^1 ^ГСС
ОС 00 СО ОС
СМ СМ ОС TF
сч см см см
О Ю Ю 1-
О ос О Г—
1221
1359
1634
1910
00 00 00 00
оГсчсмоГ
— СМ СМ СМ
юсе — оо
юю юю
СОГ- Ttr-
о со оо оэ
coco г*« оо
00 СО 00
1—•—¦ СМ СМ
оэсо г-
емю о ^
см см оооо
ОЭОСМ Tf
о
о
160
о
со
Ю rf
t^- г—
СО СО
о-о"
C^J О
см см
iO Tf
со оэ
^^
ТПО
см см
тг ю
00 Г-
00 ОЭ
юю
1933
2324
ОС СО
СО ч*
Г-СМ
см со
00 h-
юю
952
1123
CM Tf
см со
см см
оо г—
00 СО
см со
о см
о
180
оо
см см о оо
ОС Ш ОС ОС
оооо
ю ^ оо см
Tj< iQ f^- f^
CO 00 OJ CO
CM CM ОС ОС
оэ оо •—'Оэ
Г- 00 ОЭ ОЭ
см см см см
00 СО СМ —«
—' 00 СМ СО
со со со со
2920
3189
3726
4264
00 Г^ Tf СМ
ююю ю
сссососо
со см —¦ г—
rfOO Ю —
юсо^-оо
Tj* "^J* ^}* СО
1449
1568
1801
2026
rtr^Tt —
см см оо со
ОЭ ОЭ ОЭ 00
^**f-—"со сгГ
со со ^ ^
-см22
ю
см
200
2,5
см
о ос1^- ю
— ООО
оооо
^f О ОЭ 00
ос ос со со
rj< »—< СО ОЭ
О ОО СО Tf
ее t^ ос оэ
ОС ОЭ h- ю
LOCO Г- 00
ОС 00 00 СО
rt* О г— со
со о оо г^
СО CM TJ* Г-
^^ см см см
оэ — см ос
Коо"оо оо
6212
8308
9358
10410
СМ 00 СО 00
^^^^
1032
1333
1475
1613
г^смоэг^
СЭ *«—' О j ОЭ
3147
4091
4545
4987
ОЭ ОЭ 00 Г«-
It
coco —ю
оо со —"<хГ
TTCOt^t^
см со ооо
— —• — см
о
со
092
со

842
ПРИЛОЖЕНИЯ
Таблица 5. Секториальные геометрические характери-
характеристики прокатных двутавров (ОСТ 10016-39)
Номер
профиля
10
12
14
16
18
20а
b
22а
b
24а
b
21а
b
30а
b
с
33а
b
с
36а
b
с
40а
b
с
45а
Ъ
с
50а
b
с
55а
b
с
60а
b
с
векториальный
момент инер-
инерции /ш в см$
644,3
1353
2 560
4 879
8 219
13 121
13 857
22 773
23 930
33 799
35 426
52 987
55414
76 704
80114
83 612
107 160
111780
116 520
154 820
161210
167 760
228 900
237 950
247 210
376 630
390 770
405 220
611990
633 900
656 270
906 350
937 220
968 720
1349 900
1393 200
1 437 300
векториальная
площадь для
крайней точки
профиля
"max в см*
15,25
20,10
25,54
32,25
38,90
46,15
47,05
55,91
56,90
64,48
65,57
76,68
77,92
88,38
89,75
91,13
100,69
102,21
103,73
115,19
116,85
118,51
134,13
136,00
137,85
159,75
161,86
163,96
187,10
189,44
191,79
216,79
219,36
221,94
251,22
254,04
256,86
векториальный
момент сопро-
сопротивления
W^ в см*
42,26
67,33
100,23
151,30
211,28
284,31
294,50
407,33
420,55
524,15
540,25
690,99
711,21
867,93
892,60
917,50
1064,3
1 093,6
1 123,3
1344,0
1 379,6
1 415,6
1 706,6
1 749,6
1793,3
2357,6
2414,4
2 471,5
3 270,9
3346,2
3421,8
4 180,8
4 272,5
4 364,8
5373,4
5484,2
5595,7
Момент инер-
инерции при чи-
чистом кручении
/к в см*
2,873
4,243
5,911
8,406
11,37
14,81
17,85
20,32
24,08
25,57
30,12
31,93
37,60
38,83
45,78
55,23
46,19
54,49
65,74
56,85
66,72
79,99
68,75
80,68
96,55
95,31
111,3
131,8
131,2
150,3
174,9
159,9
182,7
211,5
195,5
221,9
255,3
Упругая изгибно-
крутильная харак-
характеристика
0,04122
0,03457
0,02966
0,02562
0,02295
0,02074
0,02215
0,01844
0,01958
0,01698
0,01800
0,01515
0,01608
0,01389
0,01475
0,01587
0,01281
0,01363
0,01466
0,01183
0,01256
0,01348
0,01070
0,01137
0,01220
0,009819
0,01041
0,01113
0,009038
0,009504
0,01007
0,008198
0,008617
0,009119
0,007427
0,007790
0,008226
Примечание.
: 2 100 000 кг/см2.
При вычислении а приняты G = 800 000 кг/сд3, ? =

ПРИЛОЖЕНИЯ
843
Таблица б. Секториальные геометри-
геометрические характеристики прокатных швел-
леров (ОСТ 10017-39).
Номер
про-
профиля
5
6,5
8
10
12
На
Ъ
16а
Ъ
18а
b
20а
b
22а
b
24а
b
с
21а
Ъ
с
30а
b
с
33а
b
с
36а
b
с
40а
b
с
VC
и
Координа
центра и
Хасм
1,08
1,15
1,22
1,34
1,48
1,58
1,39
1,68
1,48
1,83
1,57
1,94
1,73
2,07
1,86
2,10
1,88
1,67
2,14
1,91
1,70
2,26
2,03
1,80
2,25
2,02
1,80
2,47
2,24
2,02
2,43
2,21
2,00
•к 5
3 Я
х си
л о>
«=: к
2 s
§•!:*
о я s
a s **
«и о з
UK
24,91
64,88
141,8
354,8
768,3
1512
1711
2 760
3 099
4 745
5 292
7 698
8 560
11593
12 863
15326
17 007
18 640
24 337
26 883
29 355
36 645
40 436
44 104
52 630
57 844
62 890
92 189
100 430
108 420
148100
160 100
171 870
Секториальные
площади
2,70
3,86
5,15
7,19
9,54
12,03
11,46
14,74
14,03
17,68
16,83
21,27
20,24
24,84
23,63
27,48
26,10
24,91
31,85
30,23
28,82
37,21
35,23
33,59
41,39
39,27
37,44
49,50
47,30
45,36
55,78
53,51
51,51
О) 2 СМ2
4,26
6,36
8,75
12,71
17,31
22,63
23,85
28,63
30,09
35,32
37,02
42,46
44,45
49,60
51,88
55,21
57,75
60,09
66,46
69,39
72,10
76,54
79,98
83,06
88,54
92,27
95,69
104,55
108,51
112,18
121,67
125,86
129,80
Секториальные
моменты
сопротивления
СМ*
9,22
16,80
27,57
49,35
80,51
125,74
149,32
187,23
220,87
268,41
314,50
361,95
422,87
466,69
544,42
557,74
651,56
748,35
764,11
889,34
1018,6
984,87
1147,8
1313,0
1271,7
1473,2
1679,8
1862,2
2123,4
2390,2
2655,1
2991,7
3336,4
CMl
5,85
10,21
16,20
27,92
44,39
66,85
71,75
96,40
103,00
134,34
142,95
181,28
192,57
233,73
247,95
277,59
294,50
310,21
366,19
387,42
407,14
478,78
505,61
530,97
594,43
626,93
657,23
881,77
925,54
966,48
1217,2
1272,1
1324,0
рции
SS
S О т.
8 3 8*
2 cuo. a
5 с а*^
1,350
1,497
1,940
2,727
3,634
4,815
6,248
6,306
8,227
8,128
10,50
9,84
12,50
11,66
14,60
1321
16,47
21,31
16,25
20,34
26,34
20,39
25,01
31,75
24,29
29,92
38,04
38,91
46,56
57,18
59,74
70,78
85,72
? * Si и -
ORsh
S«HO
Упругая
крутильн
рактерис
i
$
0,1437
0,09375
0,07219
0,05411
0,04245
0,03483
0,03730
0,02950
0,03180
0,02555
0,02749
0,02207
0,02359
0,01958
0,02079
0,01812
0,01921
0,02087
0,01595
0,01698
0,01848
0,01456
0,01535
0,01656
0,01326
0,01404
0,01518
0,01268
0,01329
0,01417
0,01240
0,01298
0,01378
Примечание.
? = 2 100 000 кг/см2.
При вычислении а приняты G = 800 000 кг/см*,

УКАЗАТЕЛЬ ИМЁН.
Альперин И. Г. 482
Афанасьев Н. Н. 771
Бауман 795
Бейли 795
Белелюбский Н. А. 350
Беляев Н. М. 125, 153, 612, 621, 721,
731, 770, 771, 795
Бенардос Н. Н. 168
Бернулли Д. 769
Бернулли Я. 349
Блейх 532
Бубнов И. Г. 17, 419, 652, 672
Бычков Д. В. 528, 529, 537, 551, 554,
568
Вагнер 532
Вёлер 771
Верещагин А. К. 417, 425, 426, 437,
446, 522, 527, 566, 570
Власов В. 3. 17, 212, 350, 446, 528,
532, 563, 665, 666, 667, 672, 770
Вологдин 169
Воропаев 771
Гагарин А. Г. 768
Гадолин А. В. 598
Галеркин Б. Г. 16, 212, 350, 532, 672
Галилей Г. 16, 349, 769
Гвоздев А. А. 102
Герсеванов Н. М. 17, 481, 482
Голов А. Д. 644
Головин X. С. 16, 598
Голушкевич С. С. 482
Горбунов Б. Н. 529
Горбунов-Посадов М. И. 482
Губер 532
Губкин С. И. 795
Гук Р. 32, 34, 46, 50, 74, 83, 260, 261,
702
Давиденков Н. Н. 17, 150, 770, 771,
780, 781, 787
Джанелидзе Г. Ю. 528
Диккенсон 795
Динник А. Н. 17, 156, 212, 633, 671,
672, 673, 770
Драгомиров А. М. 770
Дружинин С. И. 770, 783, 786
Дутов Г. Д. 481, 482
Жемочкин Б. Н. 481, 482
Жирицкий Г. С. 686
Журавский Д. И. 16, 298, 304, 339,
350, 535, 555, 556
Завриев К. С. 482, 672
Задерберг 795
Знаменский П. М. 532
Ильюшин А. А. 673, 675
Канторович Л. В. 482
Каппус 532
Карман Т. 673
Кастильяно 405, 409, 416, 428, 521,
527
Качанов Л. М. 795, 806
Киселёв В. А. 482
Коренев Б. Г. 482
Корноухов И. В. 672
Коробов А. П. 482
Кочин Н. Е. 770
Кречмер В. В. 482
Крылов А. Н. 17, 481, 672, 770
Кулон 349
Лагранж 672, 769, 770
Лаплас 617
Лейбензон Л. С. 212, 532
Леонардо да Винчи 670, 770
Лойцянский Л. Г. 687
Локшин Б. Ф. 770
Лолейт 102, 349
Лурье А. И. 687
Максвелл 414, 416
Малинин Н. Н. 795, 806, 813

УКАЗАТЕЛЬ ИМЁН
845
Малкин Я. Ф. 686
Мариотт 349
Марковсц М. П. 774
Мачерег Я. А. 482
Мор О. 414, 416, 417, 424, 522, 780, 784
МрощинскиГг А. К. o2S, ,>3/, 551, 568
Мусхслишвплп II. И. 17, 212
Навье 349
Падай 795
Никитин 169
Николаи Е. Л. 672, 687
Одинг И. А. 770, 771, 781, 795, 800
Остроградскнй М. В. 770
Пановко Я. Г. 528
Папкович И. Ф. 482, 672, 770
Пастернак П. Л. 482
Патон Е. О. 169
Петров В. В. 168
Подзолов И. В. 757, 771
Попов Е. П. 672
Пратусевич Я. А. 482
Пригоровский Н. И. 744, 753
Прокофьев И. 11. 740
Проктор Г. Э. 482
Пуассон 39, 40, 137
Пузыревский Н. II. 17, 481, 482
Рабинович И. М. 672
Работнов Ю. Н. 795
Ренкин 668
Ржаницын А. Р. 528, 673
Сен-Венан 212, 350, 514, 515
Серенсен С. В. 744, 753, 771, 795
Симинскип К. К. 771
Синицкий А. К. 610
Славянов Н. Г.. 168
Смирнов-Аляев Г. А. 738
Снитко Н. К. 482, 672
Соколов А. 212
Стрельбицкаи А. И. 529
Тетельбаум И. М. 744, 753
Тетма-йер 670
Тимошенко С. II. 17, 649, 672, 673
Тэпсел 79о
Ужик Г. В. 778
У майский А. А. 481, 482, 528, 529
Филиппов А. П. 482
Филоненко-Бородич М. М. 482
Фридман Я. Б. 150, 778, 780, 787
Фусс Н. И. 473
Хренов 169
Шапошников Н. А. 774, 795
Шиманский Ю. А. 17
Штаерман И. Я. 112, 156, 672
Эйлер Л. 16, 622, 626, 630, 634, 667,
670, 672, 769, 770
Энгессер 673
Эрман 769
Ягн Ю. И. 783, 786
Яновский М. И. 686, 770
Ясинский Ф. С. 16, 627, 633, 671

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ.
Аварии вследствие потери устойчи-
устойчивости 644, 646, 671
¦	резонанса 687
¦	усталости 728, 747
Амортизатор 692
Амплитуда колебаний 686, 688
¦	вынужденных 670
—	напряжений цикла 73 \
Аналогия изгибного кручения и пло-
плоского изгиба 551
Арка как кривой стержень 580
Арматура железобетонных балок,
расположение 317, 345
Балка 221
—	бесконечно длинная 475
—	гибкая 355
—	двутавровая 294, 295, 328, 531
	, касательные напряжения 304
	, сортамент 836
—	двухпролётная 467
—	деревянная 342
	 составная 342
—, деформация 351, 490, 497, 517
—	железобетонная 317, 344
	, расчёт по нагрузкам 347
	, расчёт по напряжениям 344
—	защемлённая 355, 379, 383, 397,
405, 409, 419
—, изогнутая ось, см. Ось
—	клёпаная 328, 333
¦	, расчёт заклёпок 328
—	консольная 247, 381
—	круглого профиля 307
—	многопролётная 224, 377
—	на двух опорах 359, 379, 695
—	на упругом основании 473
•	бесконечно длинная 475
	конечной длины 479
—	неразрезная 448
	защемлённая концами 460
	, опорные реакции 456
•	с консолями 460
	, эпюры 456
Балка несимметричного сечения 285,
290
—	опёртая на разных уровнях 465
—, опорные реакций, см. Реакции
—	переменного сечения 388, 395
—, подбор сечений 323
—	подвесная 247, 373, 387
—, проверка прочности 267
—,	по главным напряжениям
337
—,	по касательным напряже-
напряжениям 336
—,	по нормальным напряже-
напряжениям 332
	сварной балки 340
—	прокатная, сортамент 829
—	пустотелая 307
—	равного сопротивления 388, 709
—	сварная 340
—	составная 328, 342
—	статически неопределимая 224, 400,
433, 467
—	статически определимая 224
—	трёхпролётная 470
—, учёт деформаций 497
—	фиктивная 375, 378, 384
—, эпюры моментов и сил 232, 240,
250, 253, 254, 382
—, — оси изогнутой 384
Балки сопряжённые 377
Бимомент изгибно-крутящий 536
Бипара 536
Болт под динамической нагрузкой
714
Бринелирование 53
Вал 391, 509, 524, 759
—	быстро вращающийся 681
—	коленчатый 510, 522
—	многопролётный 527
—	полый 204
—	прямой 509
—	трансмиссионный 186
—	трубчатый 195

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
847
Ванна сварочная 168
Верещагина способ 417, 425, 426, 437,
446, 566
Вес собственный 18
•	, учёт при растяжении, сжа-
сжатии 102
Взаимность перемещений 414
—	работ 413
Вибрации, см. Колебания
Виток пружины 206
Власова теория устойчивости тонко-
тонкостенных стержней 528
—	формула критической силы 667
Врубки 176, 344
—, допускаемые напряжения 177
Выносливость 66, 729, см. Предел
Выточка, влияние на напряжения 62,
712, 738
Вязкость ударная 721, 724
—	циклическая 771
Гагарина пресс 32
Гибкость балки 396
—	стержня 626, 633
Гипербола Эйлера 634
Гипотеза плоских сечений 212, 260
Гипотезы в теории изгиба 260
	 кручения 190
—	стеснённого кручения 532
Градиент напряжений 746
График допускаемых напряжений 754
—	разрушающих напряжений 752
Грузоподъёмность материала 324
—	расчётная 100
—	скручиваемого стержня 202
Гука закон 32, 34, 46, 50, 74, 83, 260,
261, 702
	для динамических нагрузок 703
	 для кручения тонкостенных
профилей 540
—	— для сдвига 185
Давиденкова — Фридмана теория проч-
прочности 150, 780, 787
Движение равномерно-ускоренное, на-
напряжения 676
Депланация 212, 529, 531
—	неравномерная 537
Деформация 20, 24, 118
—	балки 351, 490, 497, 517
—	изгиба 221, 351
	, аналитический метод 351
—	—, графический метод 384
	, графо-аналитический метод 375
—	кручения 186, 197
—	местная 638, 774
—	нити гибкой 113
Деформация объёмная 138
—	остаточная 20, 47, 51, 63, 142
—	пластическая 55, 97, 773, 794
—	ползучести 794
	 суммарная 802
—	поперечная 38
—	продольная 39, 120
—	простая 26
—	пружины 206
—	растяжения, сжатия 32
—	сдвига 120, 158, 183
—, скорость 775
—	сложная 26
—, совместность 73, 86, 434, 610,
682
—	состояния объёмного 136
	 плоского 136
—	статически неопределимых балок
447
—	стержня кривого 602
	под собственным весом 107
	 тонкостенного 537
—	упругая 20, 47
—, учёт кривизны стержня 604
—, учёт прогиба балки 497
—	цилиндра 610
Диаграмма механического состояния
787
—	напряжений 51
	 истинная 773
—	растяжения 45, 50
	для пластичных и хрупких ма-
материалов 55
	 истинная 54
—	сжатия 57, 58
Динамичность нагрузки 65
Диск вращающийся 681
—	равного сопротивления 685
Длина приведённая (свободная) стерж-
стержня 627, 671
—	расчётная 49
Жёсткость относительная 36
—	при изгибе 266
—	при кручении 198
—	при растяжении, сжатии 36
—	при сдвиге 418
—	системы 700
—	стержней в статически неопреде-
неопределимой системе 78
Журавского формула 298, 339, 535,
555, 556
Задача статически неопределимая 72,
192, 441
Заделка (защемление) балки 223» 251
Заклёпка 158

848
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Заклёпка двухсрезная 163
—	многосрезная 163
—	односрезная 162
—	поясная 338
	 расчёт в балке 338
—, расчёт на перерезывание 158
—, — на смятие 160
—, — на трение 165
—, шаг 332
Закон Гука, см. Гука закон
—	парности напряжений 127, 320
—	сохранения энергии 400
Запас прочности 23, 29, 733
¦	, выбор его 65
	излишний 182
	 на износ 68
	, коэффициент, см. Коэффициент
Защемление балки 223, 251
Звено цепи 41, 94, 507, 580
Зона пластичности 610
Изгиб 26, 221, 483, 495, 509
—, гипотезы 260
—, данные опыта 259
—, деформации 351
—, дифференциальные зависимости
374
—, история исследований 349
—	косой 483
—	плоский 260, 323, 351, 645
—, поворот сечения 351
—	под продольной и поперечной си-
силой 495
—	прогиб 351
—	продольный 621
—	с кручением 509
—	с растяжением, сжатием 495
—, устойчивость плоской формы 645
—	чистый 258, 323
—, энергия потенциальная 266, 400
Излом пластичный 724
—	усталостный 764
—	хрупкий 66, 725, 727
Износ 68
Интенсивность нагрузки 109, 221
	, связь с поперечной силой и
моментом 231
—	реакция основания 473
Интервал критический температур 725
Испытания конструкций 38
—	материала 25, 32
—	на изгиб 259
—	на кручение 190, 776
—	на растяжение 45
—	на сжатие 59
—	на удар 720
—	оптическим методом 740
Испытания покрытиями лаковыми 740
—	сетками 740
Канат подъёмный, расчёт 717
Кастильяно теорема 405, 409, 416,
425, 437, 521, 527
Колебания 674
—	вынужденные 686, 670
—, история вопроса 769
—-, определение модуля упругости 703
—, свободные 689
—	системы с большим числом степе-
степеней свободы 692
—	— с одной степенью свободы 687
Колонна железобетонная 83
—	трубчатая 37, 640
Кольцо вращающееся 677
—	круговое 606
Консоль 251, 253, 381
Конструкции тонкостенные 528
Концентрация напряжений, см. Коэф-
Коэффициент концентрации
Координата обобщённая 402, 542
—	секториальная 539, 557, 566
Коробление сечения 529, 638
Коррозия, влияние на выносливость
745
Коэффициент динамический 65, 677
—	динамичности при колебаниях 688,
690
—	длины 627
—	запаса (прочности) 23, 29, 65, 66,
729, 752
	длительной прочности 806
	дополнительный 756
	 основной 69, 70
	 устойчивости 635, 661
	 затухания колебаний 690
—	концентрации напряжений 62, 730,
739, 743
	действительный 741
.	теоретический 741
—	линейного расширения, таблица
829
—	масштабный 747
—	нарастания колебаний 690, 691
—	податливости основания 476
—	ползучести 799—80ft
—	поперечной деформации 38, 40,
799, см. Коэффициент Пуассона
—	поправочный при расчёте пружин
209
—	Пуассона 39, 40, 137, 138, 828
см. Коэффициент поперечной дефор-
деформации
—	уменьшения допускаемых напря-
напряжений 635

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
849
Коэффициент чувствительности 741
Кран консольный 498
Кривая верёвочная 256
—	ползучести 796
Кривизна начальная 658
Крип 794
Круг Мора 128, 282, 785
—	напряжений 128
Кручение 26, 158, 186
—, гипотезы 190, 532
—, грузоподъёмность предельная 202
—, деформация 186, 197
—	изгибное 530, 572
—, испытания 190, 776
—	рельса 218
—	с изгибом 509
—	свободное 212, 529
—	стеснённое 212, 529, 532, 548
—	стержней некруглого сечения 214
	f таблицы 214
	 прямоугольного сечения 212
—	— эллиптического сечения 212
	тонкостенных 217
	трубчатых 217
—, условие прочности 197
—, учёт ползучести 809
—	чистое 212, 534, 546
—, энергия потенциальная 201
Крюк грузоподъёмный 601
Лапласа уравнение для тонкостенных
сосудов 617
Линии Чернова 46
Линия грузовая 240
—	нейтральная (нулевая) 520
—	упругая балки, см. Ось изогнутая
Максвелла—Мора теорема 414,424,437
Масса неуравновешенная 698
—	приведённая балки 696
—	упругой системы, учёт при ко-
колебаниях 692
	, учёт при ударе 715
Материал аморфный 20
—	анизотропный 39, 60, 150
—	изотропный 39, 150
—	кристаллический 20
—	пластичный 45, 48, 49, 55, 61, 64,
69, 70, 147, 514, 675, 724
—, характеристики механические 23,
39, 45
—,	, таблицы 818
—, —, см. Характеристики
—	хрупкий 45, 55, 61, 64, 66, 70, 147,
675, 725
Материалы, механические характери-
характеристики 818
Метод аналитический определения
деформаций 351
—	Верещагина 417, 425, 437, 446, 566
—	графический определения дефор-
деформаций 384
	 моментов инерции 288
—¦ — построения изогнутой оси 384
—	графоаналитический определения
деформаций 375
—	оптический исследования местных
напряжений 740
—	сечений 21
Многоугольник верёвочный 254, 287,
385
Модуль объёмный деформации 138
—	упругости 35, 36, 57
	, определение в колебаниях 703
	переменный 673
	 сдвига 185
	, таблицы для материалов 828
Момент второго порядка 536
—	изгибающий 226
	добавочный от прогиба 497
	допускаемый 394
	¦, связь с нагрузкой и попереч-
поперечной силой 231
	кривого стержня 581
	при изгибе с кручением 509
	фиктивный 386
—	изгибно-крутящий 535
—	инерции 265, 279
	главный 280
	, графический метод 288
	 двутавра 273
	 круга 272
	несимметричного сечения 285
	осевой 265, 279
	относительно параллельной оси
275
	параллелограмма 272
	полярный 194, 279
	 круга 195
.	трубчатого сечения 196
	 при повороте осей 277
	 при кручении 213
•	, приближённый метод вычисле-
вычисления 288
	прямоугольника 271, 283
	секториальный 543, 564
	• сложного сечения 274
	 тавра 273
	• тонкостенного сечения 280
	• треугольника 273, 293
	центральный 276, 284
	центробежный 264
	экваториальный 265, 282
—	крутящий 186, 213

850
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Момент крутящий, эпюра 188
—	опорный 450
—	сопротивления осевой 268
¦	при кручении 194, 213
	 для круга 195
	трубчатого сечения 196
—	статический сечения 264
	относительно нейтральной оси
301
	секториальный 541, 564
	линейный 541, 564
—, теорема о трёх моментах 450
—	фиктивный 378
—	чистого кручения 534
Мора теория прочности обобщён-
обобщённая 784
Нагрузка внезапно приложенная 19
—	временная 18
—	гидростатическая 617
—	динамическая 19, 65, 644, 674
	, история вопроса 769
—	допускаемая 24, 95, 98
	, расчёт по ней 24, 95, 100, 204,
323, 347, 467
—	критическая 646
—	неравномерно распределённая 240
—	переменная 65, 70, 204, 727, 797,
822
—	повторно-переменная 19
—	постоянная 18
—	предельная 96, 98
—	разрушающая 48, 96, 620
—	распределённая 18, 222
	 по закону параболы 243
	 по закону треугольника 241
—	сосредоточенная 18, 222
—	сплошная 231
—	статическая 19, 65
—	ударная 19, 65, 70, 675
—	фиктивная 376
Надёжность конструкции 15
Надрез, влияние на напряжения 62,
721, 738
—	разгружающий 766
Наклёп 51, 746
Напряжение 20, 21, 22
—	главное 121, 127, 178
	 в балке 298, 309
	, направления 314
—, графическое определение 128, 132
—	динамическое 677
—	допускаемое 23, 25, 29, 45, 752
	 для врубок 176
	для динамических нагрузок 752
—	— для заклёпочных соединений 166
	для сварных швов 176
Напряжение допускаемое на растя-
растяжение 30
	 на устойчивость 71
	, таблицы 71
—	касательное 21, 119, 158, 179
	 в балке 298
	• дополнительное (вторичное) 535
	, закон распределения 193
	 кручения 322, 532
	 секториальное 535, 546
—	контактное 32, 122, 152
	наибольшее 154
—	косое 350
—	критическое 621, 630, 649
—	«ломающее» 633
—	местное 61, 66, 164, 598, 705, 722,
730, 738
—	на смятие 32
—	наибольшее 27, 121, 135, 143
—	наименьшее 121
—	начальное 80, 465, 613
—	нормальное 21, 28, 119, 127, 180
	наибольшее 143, 144
	при изгибе 258
—	— секториальное 541
—	общее 729
—	опасное 69 <
—	остаточное 725
—	переменное 675, 726, 762
—	по наклонным сечениям 118
—	при кручении по косым сече-
сечениям 199
•— при плоском напряжённом состоя-
состоянии 126
—	при разрыве 55
—	приведённое 145
—	растяжения, сжатия 26
—	расчётное 147, 156
—	сдвига 183
—	секториальное 535, 541, 546
—	смятия 160
—	среднее цикла 731
—	температурное 85
—	ударное 700
Натяжение нити 110
Начало возможных перемещений 401
Независимость действия сил 483
Нить гибкая 108
Нормы расчётные 29
Обод маховика 677
Оболочка 528
Объём, изменение при растяжении,
сжатии 40
Опора балки, влияние осадки 465
	защемлённая 223
	шарнирно-неподвижная 222

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
851
Опора балки шарнирно-подвижная
223
Осадка опор неравномерная 465
—	пружины 208, 210
Основание упругое балки 473
Ось изогнутая балки 352, 372
	, графическое построение 384
	, графо-аналитическое опре-
определение 375
—	, дифференциальное уравне-
уравнение 353
	,	приближённое 354,
427
	защемлённой 355
	 на двух опорах 359
	 на упругом основании 473
—	, представление тригономе-
тригонометрическим рядом 430
	с шарниром 370
	, состоящей из двух участ-
участков 361
¦	, состоящей из нескольких
участков 366
—	инерции главная 280
	центральная 275, 280, 284
—	нейтральная 259, 264, 487
	кривого стержня 585
	при внецентренном сжатии —
растяжении 502
	при косом изгибе 487
—	стержня 26
—	центральная 275, 536
Отрыв 120, 149, 773
Парность касательных напряжений
127, 320
Перекос при сдвиге 183
Перемещение обобщённое 536
Перерезывание 26
—заклёпок 158
—	пружины 209
Пластинка 350
Пластичность, см. Материал пластич-
пластичный, состояние пластичное
Плоскость главная балки 492
—	инерции главная 285
—	наибольшей жёсткости 490
—	нейтральная 491
Площадка главная 121
—	октаздрическая 780
—	текучести 56, 63, 324
Площадь грузовая 240
—	секториальная 539, 556
—	сечения брутто 164
	 нетто 164
Поворот сечения при изгибе 351
Поглотитель колебаний 691
Податливость конструкции 720
—	основания 476
—	стержня 707
Подбор сечений 29
¦	по допускаемым нагрузкам 24,
95, 100, 204, 323, 467
	по допускаемым напряжениям
24, 72, 100, 344
	 при косом изгибе 489
	с учётом собственного веса 102
Покрытия лаковые 740
Ползучесть 792, 794, 801
—	в железобетоне 795
—, кривая 796
—, расчёты 792
—, таблица коэффициентов 801
—	установившаяся 797
—, —' учёт при изгибе 812
—, — Уч^т ПРИ кручении 809
—, — учёт при растяжении 806
—	чистая 797
Полюс главный секториальный 558
Постоянная упругая 185
Потеря устойчивости 621
Предел выносливости 66, 729, 730,
732, 734
	, влияние коррозии 745
¦	влияние повреждений поверх-
поверхности 744
	, влияние размера 745
	при цикле несимметричном 734
	симметричном 730
	 стали 734
—	длительной прочности 805
—	ползучести условный 802
—	пропорциональности 34, 46, 47,
51, 633
—	прочности 22, 29, 30, 48, 57, 60,
347, 753
—	— при растяжении 60
	при сжатии 60
	истинный 55
—, таблицы для материалов 827
—	текучести 46, 51, 56, 164, 347, 633,
753
	 конструкции 98
—	упругости 23, 30, 47
—	усталости 66, 729
Пресс Гагарина 32
—	испытательный 32
Примеси легирующие, влияние на
прочность 793
Принцип независимости действия
сил 483
Проба ударная 720
Проверка на разрыв 160
—	на сдвиг 178

852
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Проверка на смятие заклёпок 160
—	на .устойчивость 619
—	при изгибе 221
—	при кручении 197
—	при сложном напряжённом состоя-
состоянии 142
—	при ударе 705
—	прочности но различным теориям
144
Провисание нити ПО, 114
Прогиб балки 351, 376
—	- , аналитический метод 351
	, графический метод 384
	, графо-аналитический метод 375
	, зависимость от нагрузки 372
	 от действия поперечной силы
419
—	—, приближённое вычисление 427
—	—, уравнение 354
—	—, учёт ползучести 812
Пролёт нити 108
Пропорциональность, предел 34, 46,
47, 51, 633
Профили прокатные, сортамент 829
—	тонкостенные 564
—	— открытые 665
Прочность 15, 22, 772
—	длительная 805
—	заклёпок 160
—, запас, см. Запас прочности, коэф-
коэффициент запаса
—	предел, см. Предел прочности
—	при изгибе 221
—	при кручении 197
—	при переменных напряжениях 726
—	при растяжении, сжатии 30
—	при сдвиге 178
—	при сложном напряжённом со-
состоянии 142
—	при ударе 706
—, теории, см. Теории прочности
Пружина винтовая 206, 211
—	клапанная 209, 210
—, колебания 688
—	коническая 210
—	цилиндрическая 206
Пуассона коэффициент 39, 40 137
138, 828	'
Пульсатор 733
Работа сил внешних 401, 402
	 внутренних 401
—	растяжения 50
—	удельная деформация 51
Равнопрочность 100
Радиус винтовой оси 206
—	инерции 286
Радиус инерции главный 286
¦— кривизны нейтрального слоя
590
¦— перехода контура в деталях 742,
743, 765
Размах колебаний 68Ь
—	цикла 731
Разрушение материала 45, 48, 57, 120,
142, 149, 727, 773, 776
—	отрыва 120
—	под переменной нагрузкой 747
—	пластичного материала 57, см.
Материал пластичный
—	ползучести 798
—	сдвига 120
—	удара 720
—	хрупкого материала 57, см. Мате-
Материал хрупкий
Рама 249, 445, 509, 600
Распределение напряжений по сече-
сечению 28
Расстояние полюсное 255
Растяжение, сжатие 26
	 внецентренное 499
—	— диаграмма 45, 50, 54
	, изменение объёма 40
	, сложные случаи 72
	 статическое 30
	стержней из разнородного ма-
материала 83
—, учёт ползучести 806
	, экспериментальное изучение
33, 45
Расчёт по допускаемым нагрузкам
24, 95, 100, 204, 323, 467
	напряжениям 24, 72, 100,
344
—	ползучести 800, 806
Реакция опорная 19
	 балки 222
—	— лишняя неизвестная 434, 437
	 неразрезной балки 456
	 фиктивная 386
Рёбра жёсткости 340
Резервуар толстостенный сфериче-
сферический 615
	цилиндрический 609
—	тонкостенный вращения 616
	 конический 617
	цилиндрический 122
Резонанс 675, 686, 691
Релаксация напряжений 744, 798
Рессора 208, 390
Решётка кристаллическая 20, 772
—	соединительная стержневая 638,
661
Ригель 249

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
853
Сварка 168
—, допускаемые напряжения 169
Сдвиг 120, 158
—	абсолютный 183
—	в кристаллах 772
—, закон Гука 185
—	относительный 183
—	при кручении тонкостенных про-
профилей 533
—	результирующий 782
—	чистый 158, 178
—, энергия 186
Сен-Венана формула 516
Сечение, метод 21, 22
-— несимметричное 269
¦— опасное балки 26, 226
—, подбор, см. Подбор сечений
—, роль формы 637
Сжатие 26
—	внецентренное 499
—, диаграмма 57, 58
—	осевое 666
—	центральное 666
Сила 17
—	активная 374
—	веса 18
—	взаимодействия 18
—	внешняя 18, 402
-г- внутренняя 20
—	возмущающая 687, 691
—	восстанавливающая 689
—	добавочная 411
—	инерции 674, 689, 701
—, классификация 17
—	критическая 620, 622, 628, 629, 633,
666, 668
—	— по Власову 667
	 экспериментальное определение
Ясинского 633
—	лишняя неизвестная 90, 437
	выбор её 439
—	обобщённая 402
—	объёмная 18
—	пассивная 374
—	перерезывающая 228
—	поперечная 226, 228
—	—, связь с нагрузкой и момен-
моментом 231
	фиктивная 378, 385
—	продольная в балке 497
—	распределения 18
—	сдвигающая 339
—	сопротивления среды 670
—	сосредоточенная 18
—г фиктивная 288
Система колеблющаяся 687
•— основная 91, 435
Система основная, выбор 439
—	с большим числом степеней сво-
свободы 692
—	с одной степенью свободы 687
—	статически неопределимая 24, 72,
76, 79, 400
	, расчёт по допускаемым
нагрузкам 95
—	-^ —, расчёт по допускаемым на-
напряжениям 72
—	статически определимая 95
—	стержневая 417
Скалывание дерева 176
Славянова метод сварки 168
Сложение действия сил 88, 253, 372
Слой нейтральной балки 259
—' — кривого стержня 590
—	—, приближённое определение 591
Смятие заклёпок 160
—	шпонок 343
Совместность деформаций 73, 86,
434, 610, 682
Соединения деревянных конструкций
176
—	металлических конструкций 158
	 болтовые 158
—	заклёпочные 158
	 внахлёстку 158
	, допускаемые напряжения 165
	 резервуаров 165
	, шаг 332
—	сварные 168
	 внахлёстку 171
	 встык 170
	, механические свойства 819
Сопротивление временное 22, 29, 48
	 истинное 55
—	материалов, задачи 22
	, история 16, 212, 304, 349, 481,
528, 670, 769
	, определение 15
—	отрыву 176, 787
—	переменной нагрузке 65
—	пластическим деформациям 55,
171
—	разрушению 776
—	растяжению равномерному 774
—	скалыванию 176
—	сложное 483
—	—, общий случай 517, 570
—	среды 690
—	срезу 787
—	удару 49, 675
Сортамент прокатной стали 829
Состояние механическое 787
—	напряжённое жёсткое 789
	линейное 63, 118, 121, 142

854
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Состояние напряжённое мягкое 789
	объёмное 63, 121, 135, 722,
725
	опасное 68, 142, 144, 772
	 плоское 121, 135, 311
	сложное 118, 762
—	пластичное 64, 70, 675, 724, 772
—.хрупкое 64, 70, 342, 725, 772
Сосуд толстостенный 609
—	— сферический 615
	цилиндрический 609
—	тонкостенный 616
	вращения 616
	 конический 617
Спарник, напряжения 678
Способ Верещагина 417, 425, 437, 446,
566, 570
—	сравнения деформаций 436
—	уравнивания моментов 469
Срез 776, 787
—	хрупкий 779
Сталь, характеристики механические
818
—, сортамент 829
Стенка подпорная 508
Степень несимметрии цикла 729
—	свободы 687
Стержень вращающийся 697
—, гибкость 626, 633
—	железобетонный 101
—	из разнородных материалов 83
—	кривой 580
	большой кривизны 598
	малой кривизны 598
—	некруглого сечения 212, 594
—	переменного сечения 87, 710
—, подбор материала 639
—	призматический 26, 692]
—	равного сопротивления 104
—	сжато-изогнутый 663
—	сжатый, устойчивость 617
—	составной 639
—	ступенчатый 105
—	тонкостенный 213, 528
	, неравномерная депланация 537
	открытого профиля 665
	, сложное сопротивление 570
	 трубчатый 638
—, устойчивость 619
—, целесообразная форма 103
Стойка рамы 249
—, расчёт 636, 643
Стрела провисания нити 110, 114
Сужение местное 55
	 истинное 775
—	остаточное относительное 49
—	полное 774
Сужение после разрыва
—	равномерное 55, 774
Твёрдость по Бринелю 53
—	по Роквеллу 53
Текучесть 46, 149, 794
—	бетона 101, 348
Температура, влияние на механиче-
механические характеристики 64, 792
—, — на модуль упругости 792
—, — на напряжения 85
—, — на предел выносливости 793
—, — на предел пропорциональности
792
—, — на предел прочности 793
Тензометр 32
Теорема Кастильяно 405, 409, 416,
425, 437, 521, 527
—	Максвелла—Мора 414, 424, 437
—	о взаимности перемещений 414
—	о взаимности работ 413
—	о трёх моментах 450
Теории прочности 142, 181, 513, 779
	, основанные на сопротивлении
пластическим деформациям 781
	, — на разрушении материала
783
Теория Власова устойчивости тон-
тонкостенных стержней 528
—	Мора 780, 784
—	наибольших касательных напряже-
напряжений 145
	нормальных напряжений 144
	 удлинений и укорочений 146
—	обобщённая Мора 784
—	объединённая Давиденкова—Фрид-
Давиденкова—Фридмана 150, 780, 787
—	энергетическая 781
—	энергии формоизменения 148
Точка нулевая 535
	 главная секториальная 558, 563
	 опасная 207
Траектория главных напряжений 315
Трение заклёпок 165
Трещины усталости 67, 69, 209, 326,
727, 747
Трос 108
Угол закручивания 194, 198, 213
	наибольший 198
—	— относительный 194
	при изгибе и кручении 548
—	поворота сечений балки 351, 354,
376
—	сдвига 183
Уголок жёсткости 332
Удар 675, 700

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
855
Удар балки 719
—	встречный 705
—	изгибающий 702
—	резкий 756
—	скручивающий 710
—	стержня переменного сечения 712
	продольный 702, 710
—, учёт массы 715
—, энергия 716
Удлинение абсолютное 34
—	истинное 775
—	наибольшее 143
—	остаточное 47
—	•— относительное 49, 56
—	относительное 34
—	полное 47
—	пружины 206
—	температурное нити 113
—	упругое 47
Узел жёсткий 249
Упрочнение 55, 780, 797
Упругость, модуль, см. Модуль
—, предел 23, 47
Уравнение изогнутой оси, см. Ось изо-
изогнутая
—	Лапласа для тонкостенных сосу-
сосудов 617
—	трёх моментов 450
Уравновешивание моментов 469
Усилие 21, 532
—	элементарное 22
Ускорение, влияние на напряжения 19,
400, 675
Усталость 66, 675
—, излом 764
—, предел 66, 729
—, трещины 67, 69, 209, 326, 727, 747
Устойчивость 619
—, история вопроса 670
—	неупругая 673
—	плит и оболочек 673
—	плоской формы изгибы 645
—	стенки балки 329
—	стержня сжатого 619
—	элементов конструкций 326, 619
Фактор концентрации 738, 764
—	силовой стеснённого кручения 548
552
Ферма многорешетчатая, устойчи-
устойчивость 645
Флокен 765
Форма провисания нити 112
—	стержня целесообразная 103
Формула Верещагина 522, 527, см.
Способ Верещагина
—	Власова для критической силы 667
Формула Журавского 298, 339, 535,
555, 556
—	Кастильяно 405, 409, 416, 425, 437,
521, 527
—	Максвелла—Мора 414, 424, 437
—	Сен-Венана 514
—	Эйлера 622, 626, 630, 631, 634
	, влияние способа закрепления
626
	, пределы применимости 630
—	эмпирическая критических напря-
напряжений 633
Характеристики геометрические сек-
ториальные 561, 563, 842
—	деформации 775
—- изгибно-крутильные 551
—	механические 23, 45, 48
	, влияние высоких температур
792
	пластических и хрупких мате-
материалов 61
	, таблицы 818
—	секториального сечения 541
—	сопротивления равномерному ра-
растяжению 774
—	цикла 731
Хладноломкость 724
Хрупкость, см. Материал хрупкий,
состояние хрупкое
Центр жёсткости 321
—	изгиба 318, 321, 536
—	кручения 536
—	скалывания 321
Цикл, амплитуда напряжения 731
—	несимметричный 729, 734, 756
—	симметричный 730, 756
—, число в элементах конструкции 766
Цилиндр составной 613
—	толстостенный 609
—	тонкостенный 616
Частота колебаний 689
Чернова линии 46
Число твёрдости 53
Чувствительности коэффициент 741
Шаг заклёпок 332, 335
Шарнир 222, 449
—	пластический 325
—	промежуточный 226
Шатун, напряжения 678
Шейка (вала) коренная 522
—	мотылёвая 522
—	(сужения) 47, 49
Шов (сварной) боковой 171, 172

856
Шов валиковый 171
~- косой 170
—	лобовой 171
—	прерывистый 341
-- прорезной 173
—	сплошной 341, 342
—	торцевой 171
—	фланговый 171, 172
Шпонка деревянная 342
—	сварная 341
Щека вала 522
Эйлера гипербола G34
—	формула 622
Экономичность в проектировании 15,
100, 182, 274
Эксцентриситет точки приложения си-
силы 499, 65S
Электросварка по методу Славянова
168
Эллипс инерции 286
—	— центральный 286
—	касания 154
—	контакта 153
—	напряжений 152
Энергия гистерезисная 771
—	деформации (потенциальная) 139,
400, 402, 420
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Энергия изгиба 261, 266, 402, 714
	¦ кручения 201
	 полная 140
	 пружины 209
—	— сдвига 186
	сложного напряжённого состоя-
состояния 139
	• удара 702, 716
_—	наибольшая 718
	 удельная 141
	 формоизменения 141
Эпюры главных секториальных пло-
площадей 558
—, графический метод построения 254
—	изгибающих моментов 230
—	крутящих моментов 188
—	напряжений бетонной балки 349
	 условная 321
—	неразрезных балок 456
—, преобразование 396, 399
—	секториальная 556
—	секториальных координат 566
¦	площадей 557
Ядро сечения 504
	 двутавра 507
Ясинского определение
силы 633, 671
критической

Н. М. БЕЛЯЕВ
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ИЗДАНИЕ ЧЕТЫРНАДЦАТОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов высших технических учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1965