Author: Сидоров Ю.В. Шабунин М.И. Болтянский В.Г.
Tags: математика
Text
В.Г.Болтянский, Ю.В.Сидоров, М.И.Шабунин
ЛЕКЦИИ И ЗАДАЧИ ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ
Книга содержит теоретический материал и задачи по курсу элементарной математики. Теоретический материал включает изложение наиболее трудных вопросов школьного курса алгебры и элементарных функций. Особое внимание обращено на те разделы курса, которые недостаточно полно освещены в учебной литературе.
Значительная часть задач, содержащихся в книге, предлагалась на вступительных экзаменах в МФТИ. Многие задачи специально составлены авторами для этой книги.
Книга предназначена для учителей математики, студентов педвузов, университетов и особенно для старшеклассников, готовящихся в вузы.
СОДЕРЖАНИЕ
Предисловие 7
Глава Е Необходимые и достаточные условия 9
§ Е Высказывания 9
§ 2. Отрицание 11
§ 3. Неопределенные высказывания 12
§ 4. Знаки общности и существования 14
§ 5. Необходимые и достаточные условия 22
§ 6. Обратная и противоположная теоремы 27
§ 7. Конъюнкция и дизъюнкция 30
§ 8. Некоторые приемы доказательства 33
Задачи к главе I 36
Глава II. Действительные числа 43
§ 1. Рациональные числа 43
§ 2. Свойства множества рациональных чисел 46
§ 3. Примеры применения свойств рациональных чисел 48
§ 4. Причины, заставляющие расширить множество рациональных чисел 51
§ 5. Предел монотонной ограниченной последовательности 56
§ 6. Свойства множества действительных чисел 59
§ 7. Абсолютная величина 63
§ 8. Числовая ось и координаты 65
§ 9. Некоторые числовые множества 68
Задачи к главе II 73
Глава III. Неравенства 76
§ 1. Определения 76
§ 2. Основные свойства неравенств 78
§ 3. Некоторые часто встречающиеся неравенства 82
§ 4. Примеры 85
§ 5. Два замечательных неравенства 89
Задачи к главе III 92
Глава IV. Комплексные числа 100
§1. Введение 100
§ 2. Определение комплексного числа 102
§ 3. Свойства действий 104
§ 4. Модуль комплексного числа. Комплексно сопряженные числа 108
§ 5. Геометрическая интерпретация комплексного числа 110
§ 6. Аргумент комплексного числа 112
§ 7. Тригонометрическая форма записи комплексного числа 113
Задачи к главе IV 118
Глава V. Квадратный трехчлен 122
§ 1. Квадратный трехчлен и его корни 122
§ 2. График квадратного трехчлена 127
§ 3. Исследование квадратного трехчлена 134
§ 4. Квадратные неравенства 139
§ 5. Наибольшее и наименьшее значение квадратного трехчлена 142
Задачи к главе V 143
Глава VI. Многочлены и алгебраические уравнения 148
§ 1. Многочлен и его значения 148
§ 2. Действия над многочленами 155
§ 3. Алгебраическое уравнение и его корни 163
Задачи к главе VI 172
Глава VII. Функции и графики 176
§ 1. Определение функции 176
§ 2. График функции 182
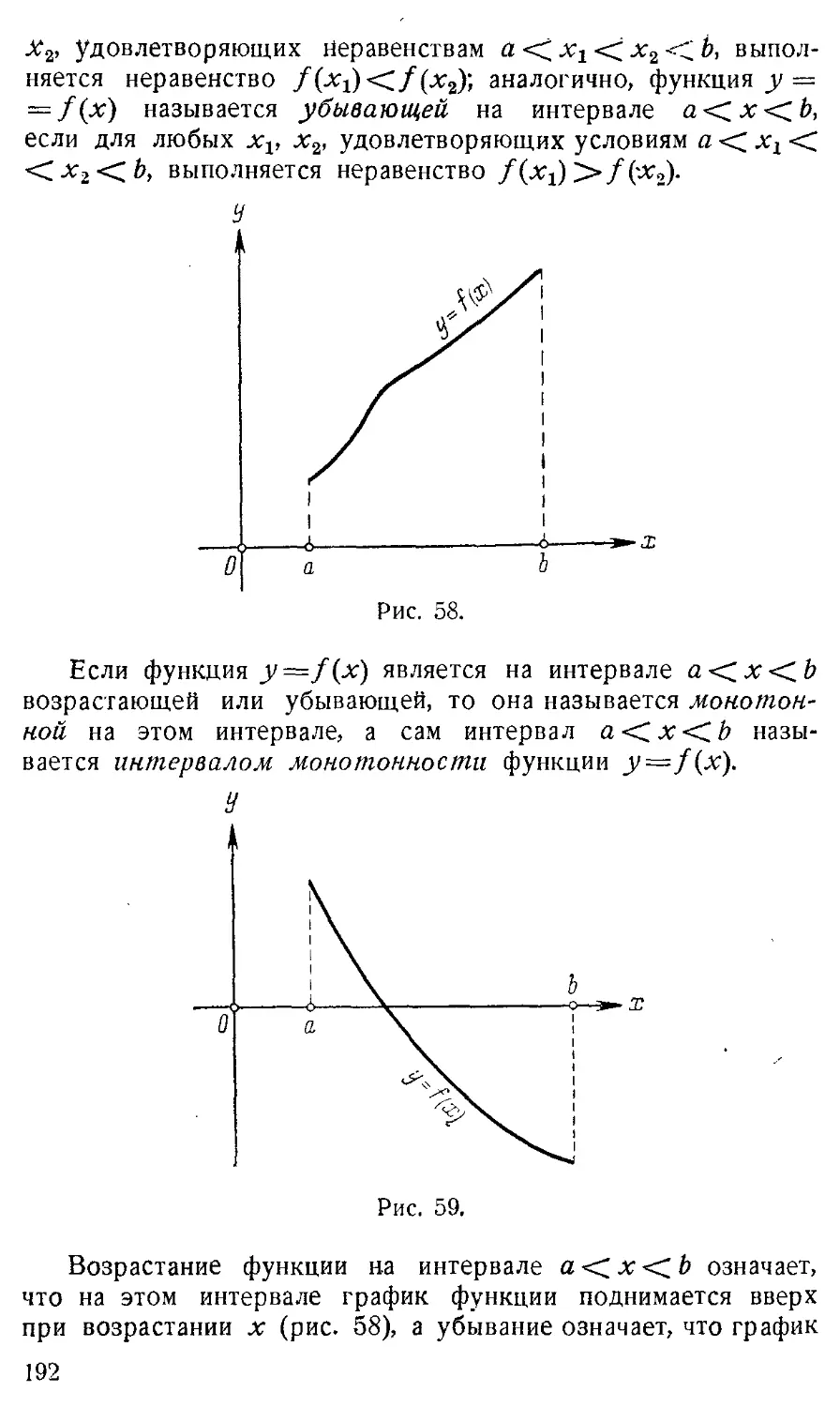
§ 3. Ограниченность, монотонность, четность, нечетность, 187
периодичность
§ 4. Композиция функций 205
§ 5. Обратная функция 209
§ 6. Обратные тригонометрические функции 218
§ 7. Линейные преобразования графика 222
§ 8. Применение функций и графиков к решению уравнений и 228
неравенств
Задачи к главе VII 236
Г лава VIII. Степенная, показательная и логарифмическая функции 242
§ 1. Степень с натуральным показателем 242
§ 2. Степенная функция с натуральным показателем 244
§ 3. Арифметический корень 247
§ 4. Степень с целым показателем 249
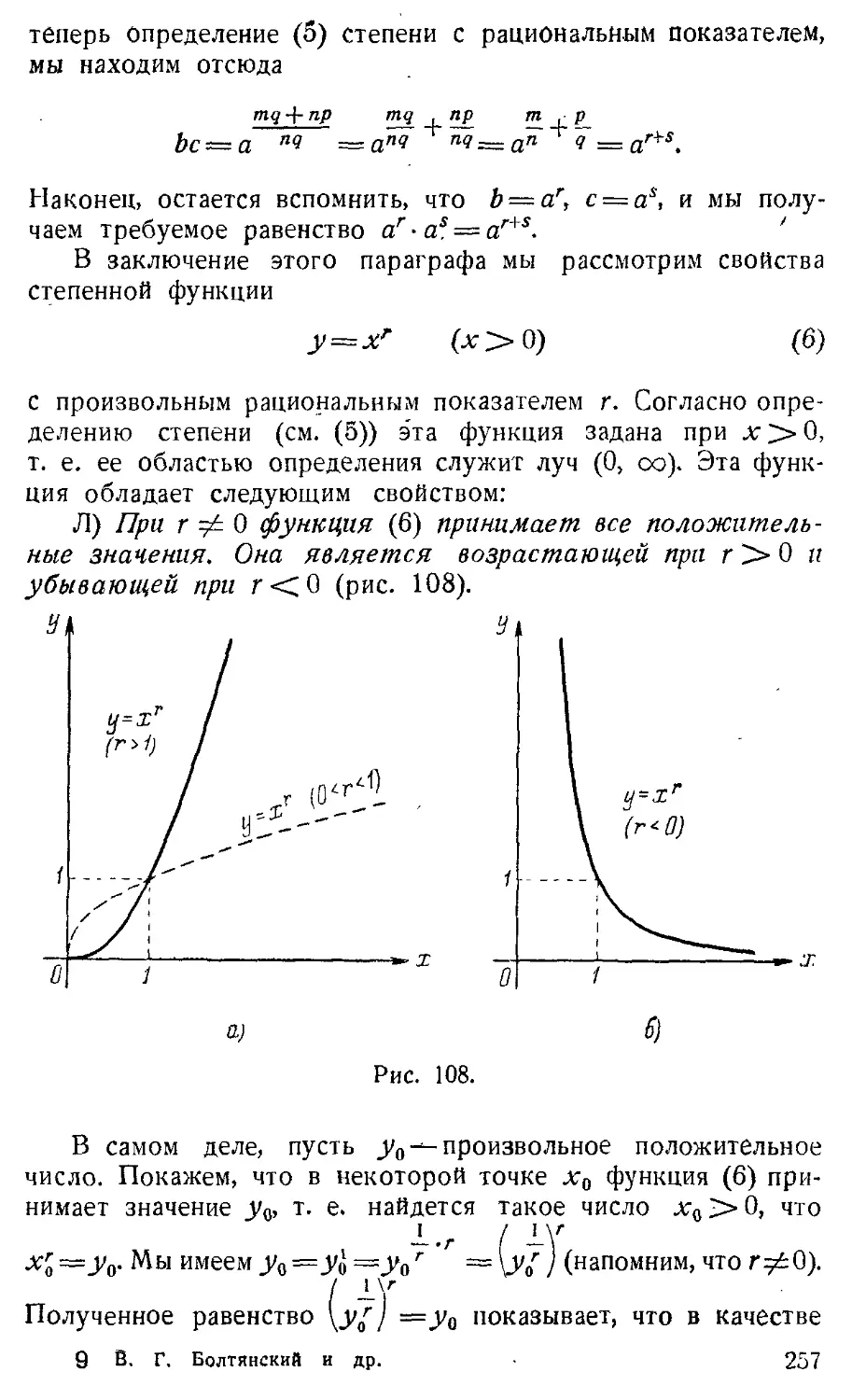
§ 5. Степень с рациональным показателем 253
§ 6. Степень с действительным показателем 258
§ 7. Показательная и логарифмическая функции 260
§ 8. Свойства логарифмов 263
Задачи к главе VIII 266
Глава IX. Уравнения 269
§ 1. Равенство, тождество, уравнение 269
§ 2. Потеря корней и появление посторонних корней при преобразовании 274
уравнений. Равносильные уравнения. Уравнение, являющееся следствием данного. Дизъюнкция уравнений
§ 3. Наиболее важные приемы преобразования и методы 281
§ 4. Простейшие иррациональные уравнения 292
§ 5. Логарифмические и показательные уравнения 296
Задачи к главе IX 305
Глава X. Системы уравнений 309
§ 1. Равносильные системы уравнений. Система, являющаяся следствием 309 данной
§ 2. Основные приемы и методы решения систем 312
§ 3. Однородные системы двух уравнений второй степени с двумя 320
неизвестными
§ 4. Системы симметрических алгебраических уравнений 323
Задачи к главе X 330
Глава XI. Тригонометрические уравнения и системы уравнений 349
§ 1. Простейшие тригонометрические уравнения 349
§ 2. Уравнения вида sinJ(x)=a,J(sin х)=0 и аналогичные им 352
§ 3. Уравнения, однородные относительно sin х и cos х 357
§ 4. Введение вспомогательного угла 362
§ 5. Метод замены неизвестного 363
§ 6. Метод разложения на множители 370
§ 7. Оценка левой и правой частей уравнения 374
§ 8. Системы тригонометрических уравнений 377
Задачи к главе XI 391
Глава XII. Задачи по планиметрии 400
§ 1. Прямоугольный треугольник 400
§ 2. Правильный треугольник 402
§ 3. Равнобедренный треугольник 403
§ 4. Произвольный треугольник 405
§ 5. Параллелограмм 407
§ 6. Трапеция 407
§ 7. Произвольный четырехугольник и многоугольник 409
§ 8. Окружность 410
Глава XIII. Задачи по стереометрии 412
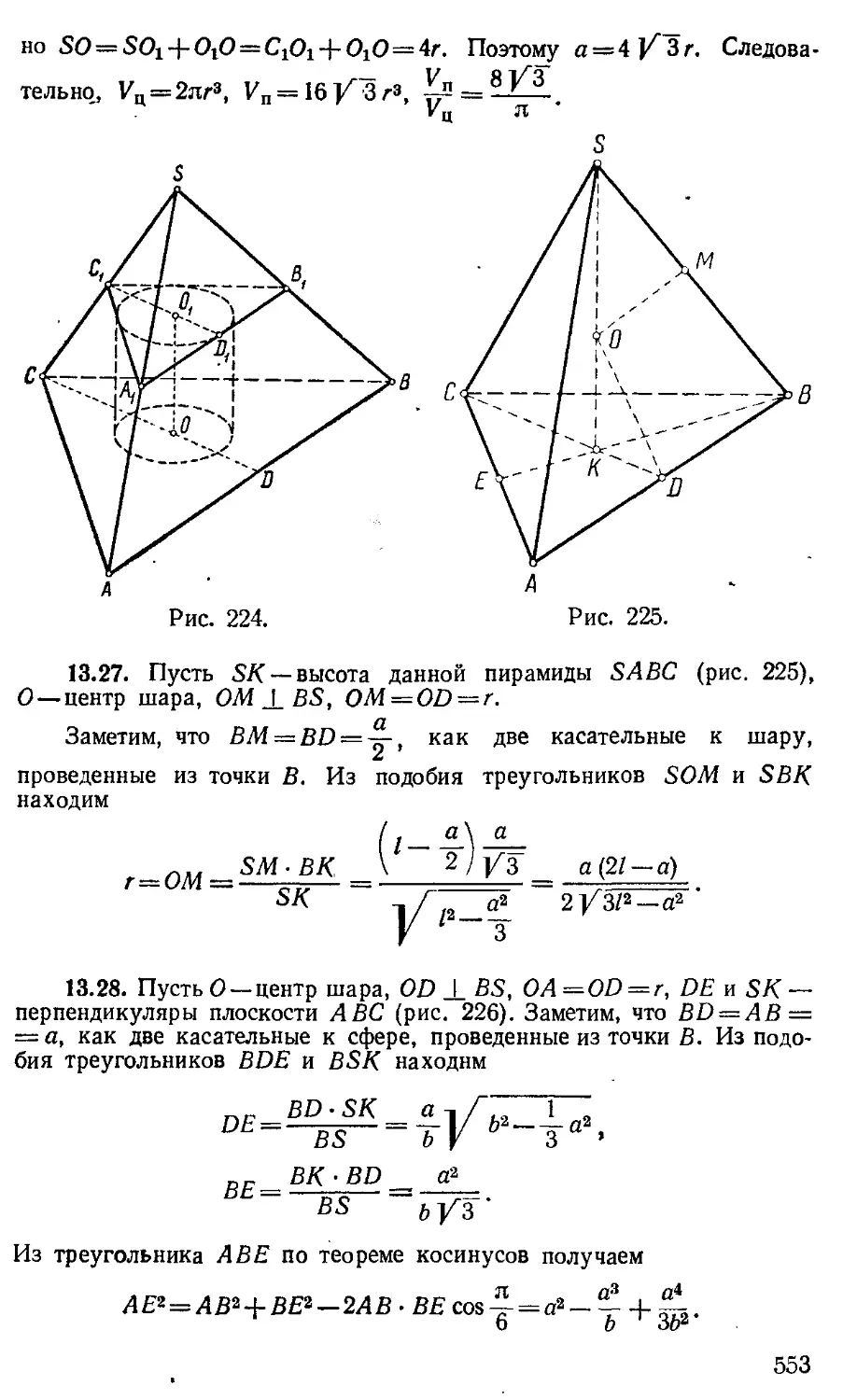
§ 1. Правильный тетраэдр 412
§ 2. Правильная треугольная пирамида 413
§ 3. Произвольная треугольная пирамида 415
§ 4. Правильная четырехугольная пирамида 417
§ 5. Произвольная четырехугольная пирамида и многоугольная пирамида 419 § 6. Усеченная пирамида 420
§ 7. Параллелепипед 421
§ 8. Призма 422
§ 9. Конус 423
§10. Усеченный конус, цилиндр и шар 424
Ответы к задачам главы I 426
Ответы к задачам главы II 429
Ответы к задачам главы IV 430
Ответы к задачам главы V 431
Ответы к задачам главы VI 433
Ответы к задачам главы VII 433
Ответы к задачам главы VIII 444
Ответы к задачам главы IX 448
Ответы к задачам главы X 449
Ответы к задачам главы XI 455
Ответы к задачам главы XII 464
Ответы к задачам главы XIII 466
Решения и указания к задачам главы II 469
Решения и указания к задачам главы III 470
Решения и указания к задачам главы V 477
Решения и указания к задачам главы VI 477
Решения и указания к задачам главы VII 479
Решения и указания к задачам главы IX 480
Решения и указания к задачам главы X 481
Решения и указания к задачам главы XI 505
Решения и указания к задачам главы XII 517
Решения и указания к задачам главы XIII 541
ПРЕДИСЛОВИЕ
Предлагаемая вниманию читателя книга предназначена для учащихся старших классов средней школы, для поступающих в вузы, для учителей и студентов пединститутов и университетов. Она содержит теоретический материал по некоторым разделам элементарной математики и задачи. Теоретический материал не охватывает всего школьного курса математики. Мы ограничились изложением некоторых разделов, которые недостаточно полно изложены в учебной литературе.
Некоторые разделы книги содержат теоретический материал, формально выходящий за рамки школьной программы по математике. Так, в гл. I рассказывается о простейших понятиях математической логики, в гл. II несколько полнее, чем это принято в школьных учебниках, излагается теория действительного числа, а в гл. VII, VIII глубже изучаются некоторые вопросы теории элементарных функций. Однако в действительности эти вопросы изучаются в школе (хотя, может быть, не так глубоко), и на приемных экзаменах в вузах требуется их ясное понимание. Например, учащиеся' обязаны знать, что такое условие и заключение теоремы, в чем сущность метода доказательства от противного, должны уметь правильно формулировать обратные и противоположные теоремы, уметь делать правильные логические выводы. Поэтому гл. I, в которой эти вопросы подробно рассматриваются, фактически полностью соответствует школьной программе. Во всяком случае, поступающие в вузы с повышенными математическими требованиями и претендующие на оценку «отлично», должны хорошо разбираться в этом. То же можно сказать и по поводу остальных глав книги. Вместе с тем теоретический
7
материал книги изложен достаточно подробно, с большим количеством примеров и потому будет доступен любому успевающему по математике старшекласснику.
Книга содержит свыше тысячи задач, значительная часть которых предлагалась на приемных экзаменах в МФТИ; другая же часть задач составлена авторами при написании книги. В конце книги приведены ответы к задачам, а также указания или решения для наиболее трудных из них.
Авторы
ГЛАВА I
НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
§ 1. Высказывания
В математике мы имеем дело с различными высказываниями. Вот некоторые примеры:
А = {число 100 делится на 4},
В = {число 17 делится на 8},
С = {три меньше пяти},
D = {число 2 является единственным корнем уравнения х3 —4 = 0}.
Сразу же видно, что в некоторых из этих высказываний утверждается нечто правильное; такие высказывания называются истинными. В других же из приведенных выше высказываний утверждается нечто неверное; такие высказывания называются ложными. В приводимой ниже таблице поставлена буква И под обозначением истинных высказываний и буква Л под обозначением ложных высказываний:
Высказывание А В С D
Его истинность И Л И Л
Указанные выше высказывания мы обозначали большими латинскими буквами. Так мы будем обозначать высказывания и в дальнейшем.
Всякое высказывание является предложением и может быть выражено словами. Однако при записи высказываний математики пользуются не только буквами, но и специальными математическими знаками. Каждый знак заменяет собой слово (или даже несколько слов). Используются знаки для сокращения записи. Например, высказывание С можно с помощью знаков записать следующим образом: 3 <; 5.
Мы уже говорили, что всякое высказывание является предложением. Однако далеко не каждое предложение является
9
высказыванием в математическом смысле. Вот несколько предложений, которые высказываниями не являются:
1) число 0,00000001 очень мало,
2) существует ли число, квадрат которого равен 2?
3) х> 2,
4) х 4-5 = 12.
Первое из этих предложений не является высказыванием потому, что оно не имеет точного смысла и мы не можем сказать, истинно оно или ложно. Один скажет, что число это в самом деле очень мало, другой же с этим не согласится. Второе предложение вообще ничего не утверждает, а содержит вопрос. Бессмысленно говорить, истинно оно или ложно.
Наконец, третье и четвертое предложения содержат букву х. При одних значениях х получается истинное высказывание, при других ложное. Значит, в таком виде (пока не сказано, чему равен х) мы не можем сказать, истину или ложь выражают эти предложения.
Заметим, что не о всяком высказывании можно сразу же, только услышав его, ответить, истинно оно или ложно. Речь идет о принципиальной возможности решить вопрос, истинно или ложно данное высказывание, хотя для ответа на этот вопрос, может быть, надо сделать столько действий, что и жизни человеческой не хватит. Вот два примера высказываний, вопрос об истинности которых принципиально может быть решен, но требует огромного количества вычислений:
Е = {число (1 2 63728 + 1515 876)°-387 4-
4-(11133 933— 1891183)4914 4 является простым},
О={в записи числа 1^2 в виде бесконечной десятичной дроби 1^2 = 1,41421... на 1 000 000-м месте после запятой стоит цифра 7}. Предложения Е и G мы также считаем высказываниями, поскольку принципиально возможно ответить на вопрос, истинны они или ложны.
Всякое высказывание является либо истинным, либо ложным (закон исключенного третьего).
Никакое высказывание не может быть одновременно истинным и ложным (закон противоречия).
Предложение, о котором невозможно однозначно решить вопрос, истинно оно или ложно, высказыванием не является.
10
§ 2. Отрицание
Из всякого высказывания А можно получить новое высказывание, отрицая его, т. е. утверждая, что высказывание А не имеет места, не выполняется. Отрицание высказывания А обозначается символом ”] А (или символом Л). Запись ”] А читается как «отрицание высказывания А» или, короче, «не А».
Отрицание высказывания можно получить, сказав: «утверждение А места не имеет» или «А не выполняется». Однако в ряде случаев отрицание можно получить еще проще. Если, например, высказывание А выражается простым предложением с одним сказуемым, то для получения его отрицания "1А нужно лишь добавить к сказуемому частицу «не». Приведем примеры высказываний и их отрицаний:
1) А ~ {число 23 делится на 7},
“]А = {число 23 не. делится на 7};
2) 7?={3>5} (т. е. три больше пяти),
ПВ={три не больше пяти} (т. е. 3sg5);
3) С = {5 + 3 = 8},
-]С^{5 + 3#8};
4) О = {30 (есть) простое число},
”]О = {30 не (есть) простое число}.
Рассмотрим теперь вопрос об истинности высказываний А и ”] А. Если высказывание А истинно (т. е. то, что утверждается в этом высказывании, действительно имеет место), то высказывание А, утверждающее, что А места не имеет, ложно. Итак, если А истинно, то "] А ложно. Наоборот, если А ложно, то высказывание "] А (как раз и утверждающее, что А места не имеет) истинно. Итак, если А ложно, то ~] А истинно.
Мы видим, что, каково бы ни было высказывание А, из двух высказываний А, “] А одно является истинным, а другое ложным.
Например, из высказываний, указанных выше, ”] А, В, С, “] D истинны, а А, В, “] С, D ложны.
Самый простой прием образования отрицания заключается, как мы отмечали, в том, что к сказуемому добавляется частица «не». Например:
А = {И делится на 3}, ~]А = {11 не делится на 3}.
11
Однако Этот простой прием будет неприменим, если само высказывание уже является отрицательным, т. е. уже содержит частицу «не» перед сказуемым. Рассмотрим, например, высказывание
В = {18 не делится на 5}.
Для образования отрицания ~|5 мы уже не можем добавить еще одно отрицание к сказуемому (т. е. не можем сказать: «18 не не делится на 5»). Поэтому отрицание приходится фор-мулироватьч так:
"] В = {высказывание «18 не делится на 5» места не имеет}. Но что означает это утверждение? Оно означает, что 18 делится на 5, т. е. отрицание "} В можно проще сформулировать так:
“]Д = {18 делится на 5}.
Таким образом, если в некотором высказывании В перед сказуемым уже стоит отрицательная частица «не», то для образования отрицания В достаточно выбросить частицу «не».
Пусть теперь А — произвольное высказывание. Его отрицание "] А также является высказыванием. Значит, можно рассматривать и его отрицание, т. е. высказывание "]"] А. Оно называется двойным отрицанием высказывания А. Его можно сформулировать словами так: утверждение о том, что высказывание А не выполняется, места не имеет. Но это по смыслу ничем не отличается от утверждения о справедливости самого высказывания А.
Более точно, двойное отрицание ~|"] А истинно в том и только в том случае, если истинно само высказывание А (т. е. если А истинно, то и "] А истинно, а если А ложно, то и "]"] А ложно).
Это правило называется законом отрицания отрицания.
§ 3. Неопределенные высказывания
Будем обозначать через N множество всех натуральных чисел. Через х условимся обозначать произвольное натуральное число, т. е. произвольный элемент множества N. Рассмотрим теперь следующие предложения:
Д(х) = {число х делится на 5}, 5(х)={х> 10}, С(х) = {х — простое число}, D(x)=={(x — б)2 < 10}.
12
Предложения А(х), В(х), С(х), D(x) высказываниями не являются. Действительно, об истинности, например, 'А(х) мы ничего не можем сказать, пока нам неизвестно число х. Однако, подставляя в А(х) вместо х различные натуральные числа, мы будем получать высказывания о натуральных числах— иногда истинные, иногда ложные. Подставляя в А(х) вместо х различные натуральные числа, мы получаем, например, следующие высказывания:
А (5) = {число 5 делится на 5} — истинное высказывание, А (13)= {число 13 делится на 5} — ложное высказывание
и т. д. Можно составить следующую таблицу истинности для этих высказываний: '
Л(1) А (2) Д(3) А (4) А (5) А (6) А(Т) А (8) А (9) А (Ю)
л Л л Л И Л Л Л Л И ...
Указанные выше предложения А(х), В(х), С(х), D(x),
содержащие переменное х, можно назвать неопределенными высказываниями (в математике их называют также предикатами). Каждое из них выражает некоторое свойство натурального числа х. Например, С (х) выражает свойство быть простым числом, А(х) — свойство делиться на 5 и т. п.
Если вместо х подставить любое получим обычное высказывание.
Неопределенное высказывание может быть задано на любом множестве, а не только на множестве натуральных чисел. Оно представляет собой высказывание о каком-то элементе х рассматриваемого множества. Для одних элементов эти высказывания истинны, для других — ложны.
Пример 1. На рис. 1 изображены точки, соединенные не-
натуральное число, то мы
сколькими отрезками. На множестве М, состоящем из точек а, Ь, с, d, е, f, g, задано неопределенное высказывание:
S(x)={k точке х в рассматриваемой фигуре примыкают три отрезка}.
13
Вот таблица истинности этого неопределенного высказы вания: *
5(a) S(b) S(c) S(d) ‘5(e) 5(7) S(g)
Л Л И И И Л л
Часто приходится рассматривать неопределенные высказывания, в которые входит не одно, а два или большее число переменных. Рассмотрим, например, следующие предложения, в которых под х и у понимаются произвольные натуральные числа:
А(х,_у) = {х<_у},
В (х,у) = {х У-у = 10}, С (х,у) = }х делится на у}, D(x,y)= {х -Уу — простое число}.
Мы нцчего не можем сказать об истинности или ложности этих утверждений, пока нам не указано, какие значения принимают х и у. Но если точно указано, чему равны х и у, каждое из сформулированных утверждений превращается в высказывание — для одних пар (х,_у) истинное, для других ложное. Вот примеры высказываний, получающихся из указанных предложений при конкретных значениях х и у.
А(1; 3)={1 < 3} — истинное высказывание,
А (2; 2) = {2 < 2} — ложное высказывание,
А (5; 4)= {5< 4} — ложное высказывание,
В (1; 3)= {1 -4- 3= 10} — ложное высказывание,
В (8; 2) = }8 4-2 = 10} — истинное высказывание и т. д.
§ 4. Знаки общности и существования
Отрицание представляет собой операцию над высказываниями (или над неопределенными высказываниями). При помощи этой операции из любого, например неопределенного, высказывания А (х) можно получить новое неопределенное высказывание ~|А(х)—его отрицание.
Большое затруднение у учащихся вызывает нахождение правильной формулировки отрицания 4 А в том случае, когда
14
высказывание А содержит слова «все», «каждый», «хотя бы один», «найдется», «существует» и т. п.
Пусть, например, высказывание А имеет вид
А = {каждое простое число нечетно}.
На вопрос о том, каково будет отрицание этого высказывания, многие отвечают, что отрицанием будет высказывание
В ~ {каждое простое число четно}.
Легко убедиться в том, что здесь ошибка, поскольку ни одно из этих высказываний не является истинным. Правильным будет следующий ответ:
“|Л = {не каждое, простое число нечетно}, иными словами,
1 А = {найдется (существует) простое число, которое четно}, или еще
“| А = {хотя бы одно простое число четно}.
Это высказывание истинно: существует (только одно!) четное простое число, а именно 2.
Сравним два только что рассмотренных высказывания:
А = {каждое простое число нечетно}, Л А = {хотя бы одно простое число четно}.
Мы видим, что если отбросить начальные слова в формулировках, то высказывание А будет иметь вид {.. .простое число нечетно}, а его отрицание “| А будет иметь вид {.. .простое число четно}, т. е. вторая часть высказывания просто заменится ее отрицанием. Но очень важно заметить, что при этом первое слово «каждое», стоявшее в высказывании А, заменится в высказывании П А словами «хотя бы одно» (или словом «найдется» или «существует»). Этот факт является общим, и его понимание может избавить от многих неприятных ошибок. Итак, если высказывание А начинается со слов «все», «каждый», «любой» и т. п., то для получения отрицания ~| А надо либо, ничего не меняя, поставить отрицание «не» перед этими словами, либо же поставить отрицание «не» после этих слов, но тогда эти слова непременно надо заменить на «хотя бы один», «найдется», «существует» и т. п. Разумеется верно и обратное: если в начале высказывания Стоят слова «хотя бы один», «найдется», «существует», то
15
при постановке отрицания «не» после этих слов они заменяются на «все», «каждый», «любой». Еще раз подчеркнем, что это происходит при постановке отрицания «не» после указанных слов. Если же отрицание «не» добавляется (или выбрасывается) перед указанными выше словами, то никакой замены слов не происходит.
Пример 2.
А = {каждое из чисел а, Ь, с делится на 7},
~]Л = {не каждое из чисел а, Ь, с делится на 7},
или иначе:
~|А^{хотя бы одно из чисел а, Ь, с не делится на 7}.
Пример 3.
А ~ {никакой ромб не может быть вписан в окружность}.
Это высказывание можно сформулировать иначе:
А = {не существует ромба, который может быть вписан в окружность}.
Поскольку здесь «не» стоит впереди, для получения отрицания можно просто отбросить это «не»:
“|Д = {существует ромб, который может быть вписан в окружность}.
Пример 4.
А = {во всяком треугольнике три медианы пересекаются в одной точке},
“| А = {не во всяком треугольнике три медианы пересекаются в одной точке}, или иначе:
1 А = {найдется треугольник, в котором три медианы не пересекаются в одной точке}.
Иногда используют специальные знаки V, В- Первый из них (знак общности V) заменяется в словесных формулировках словами всякий, каждый, любой, все. Второй знак В (знак существования) заменяется в словесных формулировках словами существует, найдется, какой-нибудь, хотя бы один.. Именно, если Р(х) — некоторое неопределенное высказывание, заданное на множестве М, то запись
(Vx)P(x)
16
означает: для любого элемента х (из множества М) имеет место Р(х). Эта запись уже представляет собой высказывание (а не неопределенное высказывание). Это высказывание истинно, когда Р(а) истинно для каждого элемента а множества М, и ложно в противном случае. Иными словами, чтобы убедиться в истинности высказывания (Vx) Р (х), нужно перебрать все элементы а, Ь, с,... множества М и убедиться, что все высказывания Р (а), Р (b), Р (с),... истинны (а если мы не можем или не хотим перебрать все элементы множества М, то должны доказать с помощью некоторого рассуждения, что для любого элемента а из М высказывание Р (а) истинно). Для того же, чтобы убедиться в ложности высказывания (Vx)P(x), достаточно найти лишь один элемент а множества М, для которого высказывание Р(а) ложно. Иначе говоря, для того чтобы убедиться в ложности некоторого общего высказывания (т. е. высказывания, содержащего знак общности V), достаточно найти один противоречащий пример.
Пример 5. Возьмем следующее неопределенное высказывание, заданное на множестве N всех натуральных чисел:
С(х) = {число 2(2*>1—простое}.
При х=1, 2, 3, 4 мы получаем следующие высказывания С(1)={число 2<21>-}-1 = 5 — простое}, С (2) = {число 2<22) 1 = 17 — простое},
С(3) = {число 2<23)-|- 1 = 257 — простое}, С (4) = {число 2(24> -|- 1 = 65537 — простое}.
Все эти высказывания истинны. Но можем ли мы из этого заключить, что истинно высказывание (Vx) С (х), т. е. что для любого натурального п число 2<2”) -{- 1 будет простым? Her, конечно, для такого заключения у нас нет оснований. Ведь мы же не перебрали все натуральные числа, да и не можем этого сделать, так как множество натуральных чисел бесконечно. Интересно, что известный французский математик Пьер Ферма был убежден в справедливости высказывания (Vx) С (х) и пытался найти общее доказательство этого факта. Однако другой известный математик, Леонард Эйлер, показал, что высказывание С (5) ложно (г. е. что число 2<25> 4* 1 = 2за + 1 не является простым: оно делится на 641). Таким образом, высказывание (Vx)C(x),
17
вопреки мнению Ферма, оказалось ложным. Этот пример показывает, что проверка истинности высказывания (Vx)P(x) для отдельных значений х не может заменить общего доказательства. Напротив, один противоречащий пример, найденный Эйлером, показывает ложность высказывания.
Пример 6. Рассмотрим высказывание (\x}D(x), где D(x) — следующее неопределенное высказывание, заданное на множестве N всех натуральных чисел:
D(x)~ {число х3-{-5х делится на 6}.
Легко проверить, что высказывания £7(1), 0(2), 0(3), 0(4), 0(5) истинны. Тот же результат будет получаться, если мы будем продолжать проверку дальше. Но мы уже знаем, что проверкой для отдельных значений х мы не можем установить истинность высказывания (Vx)O(x). Даже если мы испытаем миллион значений х, всегда остается опасность, что для миллион первого значения х утверждение О(х) окажется ложным. Доказательство истинности высказывания (Ух)О(х) можно провести, например, следующим образом. Мы имеем
х3 5х = л'3 — х 4~ 6х = х (х2 — 1) 4~ 6х =
= (х— 1)х(х-|- 1) + 6х.
Но из трех последовательных чисел х—1, х, х-{-1 обязательно одно делится на 3 и одно или два делятся на 2. Следовательно, произведение их делится на 6. Таким образом, и сумма (х—1)х(х-}~ 1)-{-6х = х8-j-5х при любом натуральном х делится на 6. Но это и означает истинность высказывания (Vx)O(x),
Перейдем теперь к знаку существования В. Если Р(х)— некоторое неопределенное высказывание, то запись
(Зх)Р(х)
означает: существует элемент х множества Л4, для которого имеет место Р (х) (или иначе: найдется хотя бы один элемент х, для которого имеет место Р (х)).
Запись (Зх)Р(х) не является неопределенным высказыванием, а представляет собой высказывание. Это высказывание истинно, если можно в множестве найти элемент а, для которого Р (а) истинно. В противном случае (т. е. если в 714 нет ни одного элемента а, для которого высказывание Р (а) истинно) высказывание (Зх)Р(х) ложно.
18
Пример 7. Рассмотрим следующее неопределенное высказывание, заданное на множестве М всех натуральных чисел:
С (xj= {х3 — 14х2 + 49х — 1 < 0}.
При х=1, 2, 3, 4 мы получаем следующие высказывания:
С(1)={13 — 14- I2 4-49- 1 — 1 <0(т. е. 35 < 0)},
С(2) = {23— 14-224-49-2—1 <0(т. е. 49< 0)}, С(3)= {З3 — 14.324-49.3 — 1 <0(т. е. 47 < 0)}, • С(4)={43 — 14.42-449-4— 1 <0(т. е. 35< 0)}.
Все эти высказывания ложны. Но можем ли мы из этого заключить, что ложно высказывание (Зх)С(х), т. е. что так и не найдется натурального п, для которого высказывание С (л) истинно? Нет, конечно, для такого заключения у нас нет оснований. Сколько бы мы чисел ни перебрали, всегда остается возможность, что где-то дальше найдется число п, для которого С (п) истинно.
Продолжим наши пробы дальше:
С(5)={53— 14.524-49.5— 1 <0(т. е. 19<0)},
С (6) = {63 — 14 • 62 49 6 — 1 < 0 (т. е. 5 <; 0)},
С(7) = {73— 14.72 4- 49.7— 1 <0(т. е. — 1 < 0)}.
Мы видим, что высказывания С (5) и С (6) ложны, а С (7) истинно. Итак, мы нашли такое п (а именно л = 7), для которого высказывание С (л) истинно. Следовательно, (Зх)С(х)— истинное высказывание.
Разумеется, метод проб является далеко не наилучшим для проверки истинности высказывания (Зх) Р (х) (где Р (х) — некоторое неопределенное высказывание). Ведь «благоприятное» значение п (для которого Р (п) истинно) может встретиться где-то очень далеко, и нахождение этого п методом проб будет мучительной работой. А может случиться, что высказывание Р (л) ложно для всех л, и тогда метод проб вообще ни к чему не приведет. Поэтому более предпочтительным является общее рассуждение. Например, в рассматриваемом случае можно было рассуждать так:
х3 — 14х2 -I- 49х — 1 = х (х2 — 14х 4- 49) — 1 = х (х — 7)2— 1.
Отсюда видно, что при х = 7 этот многочлен принимает значение — 1 (так как слагаемое х(х — 7)2 обращается в нуль). Итак, высказывание С (7) имеет вид —1 < 0, т. е. истинно, а потому истинно и высказывание (Зх)С(х).
19
Пример 8. Рассмотрим следующее неопределенное высказывание, заданное на множестве N всех натуральных чисел: •
5(х) = {число х2 4-2x4-3 делится на 7}.
С помощью него мы можем составить высказывание (Зх) В (х), т. е. в множестве N существует такой элемент х, что х2 4* 2X4-3 делится на 7. Посмотрим, истинно ли это высказывание. С этой целью рассмотрим высказывания 23(1), 5(2), 5(3), 5(4):
5(1)= {число I24-2-14-3 = 6 делится на 7}, 5(2)= {число 224~2 • 24~ 3= 11 делится на 7}, 5(3)={число 32 4-2 - 34-3= 18 делится на 7}, 5(4) = {число 42 4- 2 • 4 4- 3 = 27 делится на 7}.
Все эти высказывания ложны. Легко проверить таким же образом, что ложны и высказывания 5(5), 5(6), 5(7), В (8), 5(9), 5(10). Возникает гипотеза (т. е. предположение), что 5(л) ложно для любого п, т. е. что высказывание (Вх)5(х) ложно. Однако доказать это методом проб невозможно, это можно установить только с помощью общего рассуждения. Вот как можно провести это рассуждение.
Всякое натуральное число п можно записать в виде п — — 7k-\-q, где q принимает одно из значений 0, 1, 2, 3, 4, 5, 6. Здесь k — частное от деления числа я на 7, a q — остаток. Подставив это значение п в многочлен х2 4-2x4-3, мы получим
П24-2я4-3 = (7А4-9)24-2(7А4-?)4-3 =
= (49й24- Ий? 4- 14А)4-(924-294-3) =
= 7 (7 k2 + 2kq 4- 2k) 4- q2 4- 2q 4- 3.
Отсюда видно, что число w2-|-2«4-3 имеет тот же остаток от деления на 7, что и число g24-2g4~3 (так как их разность делится на 7). Значит, число я24-2«4-3 в том и только в том случае делится на 7, если на 7 делится число q2 -J- 2^4-3, где q остаток от деления числа п на 7. Но q может принимать лишь 7 значений: 0, 1, 2, 3, 4, 5, 6. Вычисляя значения многочлена ?24- 2^4-3 при этих значениях q, мы получаем числа 3, 6, 11, 18, 27, 38, 51. Ни одно из этих чисел не делится на 7. Значит, ни при каком натуральном п число л24-2п4-3 не делится на 7, т. е. при
20
любом натуральном п высказывание В (п) ложно. Тем самым доказано, что (Эх)В(х)— ложное высказывание.
Вернемся теперь к вопросу, который мы рассматривали в начале § 4, — вопросу об отрицании высказываний, содержащих слова «все», «каждый», «найдется», «существует» и т. д. Сказанное там можно теперь сформулировать следующим образом.
I. Пусть А(х)—некоторое неопределенное высказывание, заданное на множестве М. С помощью него мы можем образовать высказывание
(Vx)A (х),
т. е. для любого элемента х множества М имеет место А (х). Отрицание этого высказывания можно образовать двумя способами:
1) можно поставить знак отрицания перед всем высказыванием:
-]((Vx)A(x)),
т. е. не имеет места утверждение о том, что для любого х выполняется А(х);
2) можно поставить знак отрицания после. Vx, но тогда знак общности V обязательно нужно заменить знаком существования Н:
(Эх) (~|А (х)),
т. е. найдется в множестве М (хотя бы один) такой элемент х, для которого не выполняется А(х).
II. Рассмотрим далее высказывание
(Эх) А (х),
т. е. найдется элемент х в множестве М, для которого имеет место А (х). Отрицание этого высказывания можно образовать двумя способами:
1) можно поставить знак отрицания перед всем высказыванием:
-]((Зх)А(х));
2) можно поставить знак отрицания после Зх, но тогда знак существования 3 обязательно нужно заменить знаком общности V:
(Vx)(“]A(x)).
21
§ 5. Необходимые и достаточные условия
Рассмотрим какую-либо теорему. В большинстве случаев можно в ней выделить условие и заключение. При этом и условие и заключение теоремы являются некоторыми неопределенными высказываниями.
Возьмем, например, теорему Пифагора. Мы рассматриваем некоторый прямоугольный треугольник АВС', с — гипотенуза треугольника, а и b — его катеты. Теорема утверждает, что имеет место соотношение с2 = а2 -ф Ь2. Условие теоремы здесь можно записать в виде следующего неопределенного высказывания:
М = {в треугольнике АВС угол С — прямой}.
Заключение теоремы:
ЛГ=}с2 = а2 + &2}.
При таком обозначении условия и заключения теорема Пифагора может быть выражена краткой записью:
M-+N.
Эта запись означает, что из М следует (или вытекает) N. Иными словами, если для некоторого треугольника истинно высказывание М, то истинно и высказывание N. Разумеется, высказывание М не всегда истинно — не всякий треугольник является прямоугольным. Но если высказывание М истинно, если известно, дано, что треугольник АВС — прямоугольный (а его стороны обозначены, как указано выше), то высказывание М также истинно. Это и выражается словами «из М следует №.
Более четко условие и заключение теоремы Пифагора можно осмыслить так. Обозначим через Т множество всех треугольников, причем мы будем считать, что вершины каждого треугольника обозначены буквами А, В, С, а противолежащие им стороны обозначены соответственно буквами а, Ь, с. Тогда М и N представляют собой неопределенные высказывания, заданные на множестве Т, т. е. для всякого элемента А, взятого в множестве Т (иными словами, для всякого треугольника АВС), /И и У могут выполняться или не выполняться:
M(A) = {zC = |}.
N(A) = {c2 = a2 + b2}.
22
Теорема Пифагора в ее наиболее полной формулировке глат сит:
(УД) (Ж (Д)-+/У(Д)),
т. е. для любого треугольника Д, для которого истинно М (Д), истинно и N(A).
В качестве второго примера рассмотрим теорему: диагонали ромба взаимно перпендикулярны. Попробуем выделить условие и заключение теоремы. Условие здесь: четырехугольник ABCD есть ромб. Заключение: его диагонали взаимно перпендикулярны. Для удобства обозначим тот четырехугольник, о котором идет речь, через Q. Тогда условие и заключение теоремы можно будет выразить следующим образом:
Условие:
A(Q)= {четырехугольник Q — ромб,
т. е. AB = BC = CD = DA}. Заключение:
B(Q)~ {диагонали четырехугольника Q
взаимно перпендикулярны, т. е. AC | BD}, Сама теорема может быть выражена записью:
(VQ)(A(Q)^5(Q)),
т. е. для любого четырехугольника Q из А следует В. Иными словами, если для Q истинно высказывание A(Q), то истинно и высказывание B(Q). Разумеется, не всегда высказывание A (Q) истинно — не всякий четырехугольник Q является ромбом. Но если A (Q) истинно, если известно, дано что Q — ромб, то истинно и высказывание В (Q).
Нередко, однако, запись (УД), (VQ) и т. д. перед формулировкой теоремы опускают и записывают теорему просто в виде А —> В.
Итак, пусть справедлива теорема, в которой условием является высказывание1) А, а заключением В- Эту теорему:
если имеет место (т. е. истинно') высказывание А, то справедливо (истинно) и высказывание В,
кратко выражают в виде «если А, то В» или просто пишут А —> В или, в более полной записи, (Ул:) (А (х) -> В (х)).
Д В дальнейшем мы иногда вместо «неопределенное высказывание» будем говорить просто «высказывание», а вместо А (х), В (х) будем просто писать А, В.
23
На существуют и другие часто используемые способы выражения этой теоремы. Именно, теорему А -> В принято также выражать любой из следующих двух формулировок:
А 'является достаточным условием для В, В является необходимым условием для А.
В употреблении этих слов «необходимое условие», «достаточное условие» на приемных экзаменах в вузах приходится слышать огромное число ошибок.
Приведем точные определения. Пусть А — некоторое (неопределенное) высказывание.
Всякое высказывание, из которого А следует, называется достаточным условием для А. Всякое высказывание, которое вытекает из А, называется необходимым условием для А.
Ничего другого в этих терминах «необходимое условие»-, «достаточное условие» нет; ни в каком другом смысле они не употребляются. Фраза «А является достаточным условием для В» может также несколько видоизменяться, например: для справедливости высказывания В достаточно, чтобы имело место А. Смысл при этом остается тем же: из А следует В.
Итак, если справедлива теорема А -> В, то мы можем сказать, что А является достаточным условием для В (ведь из А следует В). Точно так же мы можем сказать, что В является необходимым условием для А (поскольку В следует из А).
Наконец, заметим, что слова «необходимое условие» часто заменяются словами «только в том случае», «только тогда», «требуется».
Таким образом, теорему А -> В можно выразить не только словами
В является необходимым условием для А,
но также следующим образом:
А может иметь место только в том случае, если справедливо В,
или
А может выполняться только тогда, когда имеет место В,
или
для выполнения А требуется справедливость условия В.
24
Пример 9. Рассмотрим высказывания:
А(х)= {число х делится на 4}, В (х)= {последняя цифра числа х четна}.
В этом случае имеет место теорема А -> В. Следовательно, В является необходимым условием для А, или, более подробно:
для делимости числа х на 4 необходимо, чтобы его последняя цифра была четной.
Иначе:
число х только в том случае может делиться на 4, если его последняя цифра — четная,
или еще:
для делимости числа на 4 требуется, чтобы его последняя цифра была четной.
Таким образом, необходимое условие В представляет собой то требование, которое непременно должно быть выполнено для справедливости высказывания А. Однако В не гарантирует справедливости высказывания А, не является достаточным для А: ведь из четности последней цифры не вытекает, что число х непременно делится на 4.
Далее, та же теорема А -> В означает, что А является достаточным условием для В, или, более подробно:
для четности последней цифры числа х достаточно, чтобы оно делилось на 4.
Таким образом, достаточное условие А содержит в данном случае больше требований, чем нужно для справедливости высказывания В (например, число 26 не делится на 4, но тем не менее его последняя цифра — четная).
Пример 10. Рассмотрим неопределенные высказывания:
А (а, Ь) = {каждое из целых чисел а, b делится на 3}, В (а, Ь) = {сумма а-±Ь делится на 3}.
Здесь имеет место заключение А —> В, т. е. А есть достаточное условие для В, г В есть необходимое условие для А. Иными словами,
для делимости суммы а-+-Ь на 3 достаточно, чтобы каждое из слагаемых а, b делилось на 3;
для того чтобы каждое из слагаемых делилось на 3, необходимо, чтобы сумма делилась на 3.
25
Заметим в заключение, что опускать запись (Ух) в формулировке теоремы (Ух) (А (х) -> В(х)) можно только в том случае, если о смысле и важности этой опущенной записи не забывают. В самом деле, рассмотрим такой пример: диагонали параллелограмма перпендикулярны. Каждый скажет, что эта теорема неверна. Но что это значит? Запишем сформулированную теорему в виде А —> В, для чего рассмотрим следующие неопределенные высказывания:
A (Q) = {четырехугольник Q — параллелограмм},
В(Q) ={диагонали четырехугольника Q перпендикулярны}.
Тогда сформулированная «теорема» принимает вид A(Q)->B(Q). В действительности же это вовсе еще не теорема, а лишь неопределенное высказывание (иногда верное, иногда — нет). Если мы добавим знак общности или существования, мы получим высказывание, о котором уже можно будет говорить, верно оно или нет. Так, добавляя знак существования, получаем высказывание
(3Q)(A(Q)->B(Q))
(т. е. существует параллелограмм с перпендикулярными диагоналями). В истинности этого высказывания никто не усомнится— такими параллелограммами являются ромбы. Однако знак общности дает высказывание
(VQ)(A(Q)->B(Q)), (1)
являющееся л о ж н ы м. Именно в этом смысле мы говорим о неверности теоремы «диагонали параллелограмма перпендикулярны». Иными словами, встречаются (существуют) параллелограммы с перпендикулярными диагоналями. Но сформулированную теорему неявно все воспринимают в форме: диагонали любого параллелограмма перпендикулярны, т. е. в форме (1). Эта теорема действительно неверна.
Еще пример: сумма корней приведенного квадратного уравнения равна свободному члену. Эта теорема неверна. Но неверна не в том смысле, что этого никогда не бывает: например, в уравнении х2— 8х-|~8 = 0 это именно так. Неверна теорема о том, что сумма корней любого приведенного квадратного уравнения равна свободному члену. Таким образом, пишем мы или не пишем (Vх) перед формулировкой теоремы, не следует забывать, что эта запись в формулировке присутствует (или подразумевается).
26
Сказанное, разумеется, не относится к так называемым теоремам существования, т. е. таким теоремам, где утверждается существование чего-либо. Примером может служить утверждение: существуют квадратные уравнения, не имеющие действительных корней. Это высказывание, конечно, истинно. Но в нем вовсе не утверждается, что любое квадратное уравнение не имеет действительных корней; иными словами, эта теорема не имеет вида
(Vx)(A(x)->B(x)).
§ 6. Обратная и противоположная теоремы
Разумеется, не всякое высказывание, записанное в виде А-+В (или, более подробно, (Vx) (Д (х)-> В(х))), является истинным, т. е. выражает верную теорему.
Пусть А и В — некоторые два (неопределенных) высказывания. Теоремы А—^В и В->А называются обратными друг другу. Иными словами, чтобы из теоремы А->В получить обратную, нужно поменять местами условие и заключение теоремы (т. е. то, что «дано», и то, что «требуется доказать»). Разумеется, из двух взаимно обратных теорем А -> В, В -> А каждая может оказаться верной или неверной.
Нередко одну из теорем А —> В, В —> А, скажем теорему А —> В, называют «прямой теоремой», а теорему В —> А—«обратной». В этой терминологии нет ничего предосудительного, однако следует ясно понимать, что любая из двух теорем А-+В, В —> А может быть принята за «прямую», и тогда другая будет обратной к ней.
Пример 11. Рассмотрим следующие неопределенные высказывания:
A (Q)= {четырехугольник Q — ромб},
В (Q) = {диагонали четырехугольника Q взаимно перпендикулярны}.
Теорема (VQ) (A (Q) —> В (Q)) имеет следующий вид:
если четырехугольник Q является ромбом, то его диагонали взаимно перпендикулярны:
Эта теорема верна. Обратная же теорема (VQ) (В (Q) -> A (Q)): если диагонали четырехугольника Q взаимно перпендикулярны, то он является ромбом,
неверна.
27
Пример 12. Рассмотрим следующие неопределенные высказывания:
А (а) = {натуральное число а >9 делится на 4}, В (а) = {двузначное число, выраженное последними двумя цифрами числа а, делится на 4}.
Теорема (Уа)(Д (а)-*В(а)) имеет следующую формулировку: если натуральное число а > 9 делится на 4, то двузначное число, выраженное последними двумя цифрами числа а, также делится на 4.
Она, очевидно, верна. Обратная теорема (Va) (В (а) -> А (а)) в этом случае также справедлива:
если двузначное число, выраженное последними двумя цифрами числа а > 9, делится на 4, то и само число а делится на 4.
Таким образом, иногда из двух взаимно обратных теорем справедлива только одна (как в примере И), иногда же, как в примере 12, — обе. (Приведите сами пример, иллюстрирующий тот неинтересный случай, когда обе взаимно обратные теоремы неверны.) Если справедливы обе теоремы А-*-В, В —> А (т. е. и «прямая» и «обратная»), то этот факт выражают сокращенной записью A^tB или же записью А<->В. Мы будем пользоваться последней записью.
Итак, пусть высказывания А и В таковы, что из каждого из них вытекает другое: А В. В этом случае говорят, что каждое из высказываний А, В является необходимым и достаточным условием для другого. Существуют и другие термины. Вот наиболее употребительные формулировки:
1) для справедливости А необходимо и достаточно, чтобы имело место В;
2) А имеет место в том и только в том случае, если выполняется В;
3) А справедливо тогда и только тогда, когда справедливо В.
Все эти формулировки выражают один и тот же факт А *-» В, ив каждой из них высказывания А и В можно поменять местами. Иными словами, если А есть необходимое и достаточное условие для Я, то и Я есть необходимое и достаточное условие для А.
Примеры необходимых и достаточных условий мы, по существу, уже имели выше. Например:
28
для делимости числа а > 9 на 4 необходимо и достаточно, чтобы делилось на 4 двузначное число, выраженное последними двумя цифрами числа а.
Заметим, что термин «условие» часто заменяют словом «признак». Так, вместо того чтобы сказать «достаточное условие», иногда говорят «достаточный признак» и т. п. При этом нередко вместо слов «необходимый признак», «достаточный признак», «необходимый и достаточный признак» говорят просто «признак», подразумевая, что должно быть ясно, какой именно признак имеется в виду. Так, сформулированное выше утверждение называется признаком делимости на 4 (этот признак является, таким образом, необходимым и достаточным условием).
Признаки равенства треугольников — это тоже признаки в этом смысле, причем эти признаки также являются необходимыми и достаточными. Например, возьмем третий признак. То, что для равенства двух треугольников необходимо равенство соответственных сторон, ясно из самого определения понятия равенства треугольников. Достаточность этого условия как раз и доказывается в рассматриваемой теореме. Иными словами, третий признак доказывается в школе как достаточное условие равенства треугольников, но необходимость этого условия также очевидна. Итак, третий признак есть необходимое и достаточное условие равенства треугольников.
Если в некоторой теореме А —► В заменить и условие и заключение их отрицаниями, то получится новая теорема Дкоторая называется противоположной к исходной.
Пример 13. Рассмотрим следующие высказывания:
А={многоугольник Q является четырехугольником}, В= {сумма внутренних углов многоугольника Q равна 2 тс}. Теорема А —В выглядит следующим образом: если многоугольник Q является четырехугольником, то сумма его внутренних углов равна 2 тс. Противоположная теорема
А -> В: если многоугольник Q не является четырехугольником, то сумма его внутренних углов не равна 2 тс. Здесь обе теоремы («прямая» и противоположная) справедливы.
Пример 14.
{Q— четырехугольник},
В= {сумма внешних углов многоугольника Q равна 2 тс}.
29
Теорема А—В имеет вид: если многоугольник Q является четырехугольником, то сумма его внешних углов равна 2 тс. Противоположная теорема А -> В', если многоугольник Q не является четырехугольником, то сумма его внешних углов не равна 2 тс. Здесь «прямая» теорема верна, а противоположная — нет.
Мы видим, что в случае истинной теоремы А —> В противоположная теорема Д—*-~\В может быть как истинной, так и ложной. Замечательным является тот факт, что теорема 3 В —> ~| А, противоположная обратной, истинна в том и только в том случае, если истинна «прямая» теорема Д —> В. Этот факт служит основой так называемого метода доказательства «от противного»: вместо нужной теоремы А—>В доказывают теорему ~]В—►"] Л противоположную обратной.
Метод доказательства от противного обычно применяют в следующей форме: для доказательства теоремы А—В предполагают истинным высказывание П В и пытаются вывести отсюда справедливость высказывания 3 А. Если это удается (т. е. если доказана теорема 3 В —> 3 А, противоположная обратной), то исходная теорема А —> В также считается доказанной. Примеры доказательства от противного в большом числе имеются в школьных учебниках геометрии.
§ 7. Конъюнкция и дизъюнкция
Мы познакомимся здесь с двумя операциями над высказываниями, которые из двух каких-либо высказываний позволяют получить новые высказывания. Первая из этих двух операций обозначается знаком V и называется дизъюнкцией (иногда ее называют «операцией или»).
Запись А \/ В означает: имеет место хотя бы одно из высказываний А, В. Высказывание A\J В называют дизъюнкцией высказываний А, В. Иногда запись A\JВ читают так: «А или В».
Если А истинно, то и высказывание А \/ В истинно (ведь, в самом деле, имеет место хотя бы одно из высказываний А, В — именно высказывание Д). Точно так же, если истинно В, то истинно и высказывание А \/ В. Если истинны оба высказывания А, В, то А \/ В также является истинным (действительно, хотя бы одно из высказываний А, В истинно—они истинны даже оба). Наконец, если оба высказывания А, В ложны, то ложно и высказывание А \/ В.
30
Итак, высказывание А \/ В ложно только в том случае, если ложны оба высказывания А, В. Заметим, что операция \J не вполне точно описывается связкой «или», употребляющейся в обычной речи. В обычной речи связка «или» чаще всего имеет разделительный оттенок, т. е. употребляется в смысле «либо — либо». Возьмем, например, фразу: «Я уезжаю, но за рукописью зайдет моя жена или сын». Здесь скорее всего имеется в виду, что зайдет либо жена, либо сын; возможность, что они зайдут оба вместе, не предусматривается. Так обстоит дело в обычной речи. В математической логике, напротив, операция \/ не имеет разделительного смысла, т. е. А \/ В означает, что либо имеет место А (но не В), либо имеет место В (но не А), либо же (и в этом отличие) имеют место А и В вместе. В устной речи операцию \J лучше называть дизъюнкцией, но можно также говорить «или», помня, однако, что это логическое «или» не имеет разделительного смысла.
Пример 15. Рассмотрим следующие неопределенные высказывания, заданные на множестве N всех натуральных чисел:
А (х) = {х — составное число}, В (х) = {х — нечетное число}.
С помощью дизъюнкции мы получаем неопределенное высказывание А (х) \/ В(х). Если а — четнре число, большее двух, то высказывание А (а) \/ В (а) истинно (поскольку а — составное число и, значит, А (а) истинно); если а — нечетное число, то высказывание Л (а) \/ В (а) также истинно. Наконец, высказывание А(2)\/В(2) ложно (2 не является ни составным, ни нечетным числом). Итак, высказывание А(х) \J В(х) истинно при и ложно при х = 2, т. е. оно равносильно высказыванию:
С (х)= {х=А= 2}.
Пример 16. Будем рассматривать всевозможные четырехугольники Q, причем будем считать, что в каждом четырехугольнике вершины обозначены последовательно буквами А, В, С, D. На множестве всех обозначенных таким образом четырехугольников рассмотрим следующие два неопределенных высказывания:
M{Q)=[AB || CD}, W(Q) = {AD [| ВС}.
31
Тогда высказывание Af(Q)\/N(Q) означает, что хотя бы одна пара противоположных сторон параллельна, т. е. это высказывание равносильно следующему:
Р (Q)= {четырехугольник Q — трапеция}.
Отметим, что поскольку связка «или» (т. е. \/) не имеет в математической логике разделительного смысла, то высказывание М (Q) \f N(Q) считается истинным и в том случае, если истинны оба высказывания M(Q), N(Q). Иными словами, параллелограмм рассматривается как частный случай трапеции.
Пример 17. Рассмотрим следующее хорошо известное утверждение: если произведение ab равно нулю, то хотя бы один из сомножителей а, b равен нулю. Чтобы записать эту теорему логическими знаками, рассмотрим следующие неопределенные высказывания:
М(а)={а — 0], N(a, b)= {ab—Q}.
Тогда сформулированная теорема может быть выражена следующим образом:
(Va, b) (N(a, Ь)->М(а)\/ М (Ь)).
Иначе говоря, для любых чисел а и b из того, что истинно высказывание ЛДа, Ь) (т. е. ab—0), вытекает, что справедливо хотя бы одно из двух высказываний М (а), М (Ь) (т. е. обращается в нуль хотя бы одно из чисел а, Ь).
Рассмотрим теперь еще одну операцию над высказываниями, обозначаемую знаком Д и называемую конъюнкцией (или, иначе, «операцией ;/»). Запись А Д В (словами читают: «А и В») означает, что одновременно имеют место и А и В. Высказывание А Д В истинно, если истинны оба высказывания А, В, и ложно во всех остальных случаях.
Пример 18. Рассмотрим снова неопределенные высказывания M(Q) и N(Q), указанные в примере 16. Тогда высказывание M(Q)/\N(Q) означает, что противоположные стороны четырехугольника Q попарно параллельны, т. е. это высказывание равносильно следующему:
L (Q)= {четырехугольник Q— параллелограмм}.
Пример 19. Рассмотрим следующие неопределенные высказывания о прямых линиях в пространстве:
А (I, т) = {прямые линии I, т лежат в одной плоскости}, В(1, т) = {прямые I, т имеют общую точку}.
32 .
Тогда высказывание Л(/, т) Д (~| В(1, т)) означает, что прямые Z, т лежат в одной плоскости и не имеют общих точек, т. е. это высказывание равносильно следующему:
С(1, т)={1\т\.
Иными словами, А Д ("] В) есть определение параллельности прямых в пространстве1).
Пример 20. Рассмотрим следующие неопределенные высказывания о прямых линиях в пространстве:
С (Z, т)~ {Z|| т],
D{1, tri) = {прямые I и т совпадают}.
Тогда запись
(С (Z, п) Д С (т, п)) (С (I, т) \j D (I, т))
выражает следующую теорему: две прямые I, т, каждая из которых параллельна третьей прямой п, либо параллельны между собой, либо совпадают. Эта формулировка является более четкой, чем та, которую обычно приходится слы- о
шать: две прямые, параллель- /\
ные третьей, параллельны / \
между собой. В самом деле, —------------Д------Ц---------—
если обозначить через п / \
основание АВ треугольника / \
АВС, через L и 7И — середи-----------А---------------------
ны его боковых сторон, А °
а через I и т — прямые, па- Рис. 2.
раллельные п и проходящие
соответственно через точки L и 7И (рис. 2), то мы имеем Z||/z, т || п, т. е. Z и т — две прямые, параллельные третьей. Но, как известно, I и т совпадают (т. е. не являются параллельными согласно принятому в школе определению).
§ 8. Некоторые приемы доказательства
Мы уже останавливались выше на некоторых правилах рассуждения, часто использующихся как приемы доказательства тех или иных теорем. Так на стр. 30 мы отмечали
!) Мы здесь придерживаемся принятого сейчас в школе определения параллельности, согласно которому две совпадающие прямые не считаются параллельными.
2 В. Г. Болтянский и др.. 33
метод доказательства от противного, заключающийся в равносильности теорем
(Vx)(A(x)^A?(x)) и (Vx)(f]B(x))-(-]A(x))).
На стр. 21 мы имели другие утверждения о равносильности (эквивалентности) высказываний:
“1 ((Vx) А (х)) равносильно (Эх) (“| А (х)),
“| ((Эх) А (х)) равносильно (Vx) ("| А (х)).
Вот еще важные примеры эквивалентностей:
Каковы бы ни были неопределенные высказывания 711 (х) и А'(х), заданные на некотором множестве, неопределенные высказывания
П(Л1(х) VN(x)) и (~] 7И(х)) Д (~| Л/(х)) (2)
эквивалентны. Точно так же эквивалентны высказывания
' -](7И(х)ДЛГ(х)) и С]/И(х)) VC]A/(x)). (3)
Пример 21. Пусть М и N имеют тот же смысл, что и в примере 16. Тогда высказывание 7H(Q)\/ N(Q) означает, что Q — трапеция, а потому высказывание (714 (Q) \/Al(Q)) означает, что Q—не трапеция. Но что означает «Q—не трапеция»? Это означает, что ни одно из высказываний М (Q), N(Q) места не имеет, т. е. справедливы оба высказывания ~|7H(Q) и N (Q). Значит, справедливо и высказывание (~| 7И (Q)) Д ("] N(Q)). Таким образом, высказывания
-](M(Q)VW(Q)) и (-|7И(<2))Д (W))
означают одно и то же. Это и дает интерпретацию эквивалентности высказываний (2). Аналогично можно получить интерпретацию для (3).
В заключение укажем один прием доказательства, часто оказывающийся полезным. Мы сформулируем его в виде следующей теоремы.
Теорема. Пусть Aj (х), А2 (х),..., Ап (х) и Вг (х), А’2(х),..., Вп(х) — неопределенные высказывания, заданные на некотором множестве 714 и обладающие следующими тремя свойствами:
а) всегда (т. е. для любого элемента х множества М) имеет место хотя бы одно из высказываний Ах(х), А2 (х),..., Ап (х),
б) справедливы теоремы Ах (х) -> Вх (х), As (х) -* Bs (х),... ..., Ап(х)->Вп(х);
34
в) высказывания В^х), В2(х),..., Вп(х) взаимно исключают друг друга, т. е. (для произвольно взятого элемента х) если одно из них истинно, то все остальные обязательно ложны.
Тогда все обратные теоремы Вг(х) Al(x), Z?2(x)-> ->Л2(х),..., Вп(х)Ап(х~) также справедливы.
В самом деле, пусть высказывание В1(х) истинно. Высказывание А2(х) при этом не может быть истинным, так как иначе в силу б) было бы истинным и В2(х), а это в силу в) невозможно. Так же показывается, что не могут быть истинными высказывания А3(х),..., А,г(х). Но если все высказывания А2(х),..., Ап(х) ложны, то в силу а) должно быть истинным высказывание А1(х). Итак, если истинно В1(х), то истинно и А1(х), т. е. имеет место теорема В1(х)->- At(x). Так же доказывается и справедливость теорем В2 (х') > А2 (х), ..., Вп (х) > Ап (х).
Заметим еще, что при указанных в теореме условиях всегда имеет место хотя бы одно из высказываний Вх (х), В2(х'),..., Вп(х), а высказывания Л^х), Л2(х),..., Ап(х) взаимно исключают друг друга.
Приведем два примера применения этой теоремы.
Пример 22. Рассмотрим следующие неопределенные высказывания (заданные на множестве Г всех треугольников):
Л1 = {угол А — острый}, Л2 = {угол А — прямой}, Ла={угол Л — тупой}, 51 = {а2<^2 + с2}, B.2=={a2 = b2 + c2}, В3 = {а2 > Ь2 + с2}.
Легко проверить, что условия а), б), в), указанные в приведенной выше теореме, выполняются. Следовательно, кроме теорем Лх-> Bv А2—>В2, А3—>В3 справедливы обратные теоремы £4—>ЛР Т!2—>-А2, В3->-А3. Например, первая из них гласит:
если квадрат некоторой стороны треугольника меньше суммы квадратов двух других сторон, то угол, лежащий против этой стороны, — острый.
Пример 23. Рассмотрим квадратное уравнение
ах2 + Ьх 4- с = 0, а 0, (4)
35
2
с действительными коэффициентами и обозначим через D его дискриминант: D — b2— 4ас. Рассмотрим, далее, следующие неопределенные высказывания (заданные на множестве всех уравнений вида (4)):
Д1 = {О>0},
Д2 = {О<0 , Д3={О = 0}, В1~ {корни уравнения (4) действительны и различны}, Z?2 = {уравнение (4) не имеет действительных корней}, В3~ {корни уравнения (4) совпадают}.
И здесь, как легко видеть, выполняются условия, указанные в приведенной выше теореме. Следовательно, верны не только прямые теоремы >Z?j, А2—>~В2, А3—>~В.Л, но и обратные: Bv —> Дх, В2 -* А2, В3—>Аэ. Например, первая из этих обратных теорем гласит: если корни уравнения (4) действительны и различны, то D > 0.
Задачи к главе I
1.1. Приведите примеры высказываний (истинных и ложных), которые можно записать одними только знаками, без слов.
1.2. Приведите примеры высказываний (истинных и ложных), которые одними только известными вам знаками записать невозможно.
1.3. Прочтите словами следующие высказывания, записанные знаками; какие из этих высказываний истинны, а какие ложны?
5<2, 114-3=18, 24-4=^10, 53= 125, 63=#216.
1.4. Сформулируйте отрицания следующих высказываний: М ={257 — четное число}, <2= (число ]/^2 рационально}, R= {число 7 положительно}, 5= {число 5 отрицательно}.
1.5. Для каждого из высказываний, сформулированных в задаче 1.4, укажите, что является истинным: само высказывание или его отрицание.
36
1.6. Рассмотрите следующие два высказывания:
А = {существуют четные простые числа}, {существуют нечетные простые числа}.
Определите их истинность. Является ли высказывание В отрицанием высказывания А? Составьте отрицания к обоим высказываниям.
1.7. Образуйте отрицания следующих высказываний:
С ={27 не делится на 2},
£)={не существует четных простых чисел}, Е={5-7=^35}.
Какие из этих высказываний и их отрицаний истинны?
1.8. Для каждого из следующих высказываний составьте отрицание, а затем двойное отрицание. Убедитесь, что двойное отрицание совпадает по смыслу с исходным высказыванием:
А={15 делится на 3}, В~{5— число положительное}, С={3<7}.
1.9. На множестве М, состоящем из чисел 1, 2, 3, 4, 5, 6, 7, задано неопределенное высказывание
А(л')={х — нечетное число}.
Заполните таблицу истинности:
Высказывание Л (1) А (2) Л (3) А (4) Л (5) А (6) Л (7)
Его истинность
1.10. На множестве М, состоящем из чисел 1, 2,..., 10, задано неопределенное высказывание
В(х)={х является делителем числа 60}.
Составьте таблицы истинности неопределенных высказываний В(х) и Tfi(x).
37
1.11. На множестве М, состоящем из чисел 3, 4, 5, 6, 7, 8, заданы два неопределенных высказывания:
К (х) = \х — простое число}, L(x) = {x— нечетное число}.
Составьте их таблицы истинности. Совпадают ли неопределенные высказывания К(х) и L (х) на множестве М? Совпадают ли они на множестве, состоящем из чисел 2, 3, 4, 5, 6, 7, 8?
1.12. На множестве М, состоящем из чисел
1, 2, 3, 4, 5, 6, 7, задано неопределенное высказывание
Е (х, _у) = {x-j-J принадлежит множеству Л4}.
Укажите все пары (а, Ь) элементов множества М, для которых высказывание Е(а, Ь) истинно.
1.13. На множестве N, состоящем из чисел
1, 2.. 10,
задано неопределенное высказывание
F (х, _у)= {число х является делителем числа _у}.
Укажите все пары (а, Ь) элементов множества N, для которых высказывание F(a, Ь) истинно. Имеются ли такие пары (а, Ь), для которых одно из высказываний F (a, b), F (Ь, а) истинно, а другое ложно? Имеются ли такие пары (а, Ь), для которых оба высказывания F(a, b), F(Ь, а) истинны? Имеются ли такие пары (а, Ь), для которых оба высказывания F (a, b), F (Ь, а) ложны?
В задачах 1.14—1.18 постройте отрицания высказываний и укажите в каждом случае, какое из высказываний А, Я А истинно.
1.14. 4 = {при каждом а>0 уравнение ха = а имеет действительный корень}.
1.15. 4 = {при любом действительном а уравнение х2 — а имеет действительный корень}.
1.16. 4 = {существует квадратное уравнение, не имеющее действительных корней}.
1.17. 4 = {каждые два треугольника подобны между собой}.
1.18. 4 = {хотя бы одно из произвольных двух чисел а, b делится на 3}.
38
1.19. Придумайте неопределенные высказывания, позволяющие с помощью знака общности V записать следующие высказывания:
1. Все простые числа нечетны.
2. Для любого целого х определено частное
3. Каждое натуральное число х удовлетворяет неравенству X2 > х.
4. Каждое действительное число выражается конечной десятичной дробью.
Убедитесь, что все эти высказывания ложны, и видоизмените их так, чтобы получить истинные высказывания.
1.20. Запишите с помощью знаков V, В следующие высказывания:
1. Не всякая простая дробь выражается конечной десятичной дробью.
2. Каково бы ни было натуральное число х, найдется такое натуральное число у, что х+У— простое число.
3. Каково бы ни было натуральное число х, можно подобрать такое натуральное у, что x2-f-_y2<; 100.
4. Каково бы ни было натуральное число у, среди натуральных чисел найдется такое число х,что х -|-_у— четное число.
5. Какова бы ни была точка х на прямой I, существует на этой прямой такая точка у, что расстояние между точками х и у равно трем единицам.
1.21. Запишите знаками следующие высказывания. Составьте (в двух формах) отрицания этих высказываний и прочтите их словами:
1. Любое натуральное число делится на 5.
2. Существуют четные простые числа.
3. Все натуральные числа четны.
4. Существует треугольник с тремя прямыми углами.
Выделите условие и заключение и запишите в виде А->В следующие теоремы (1.22—1.24):
1.22. Диагонали параллелограмма делятся в точке пересечения пополам.
1.23. Для любых положительных чисел а, b справедливо соотношение
lg(ai>) = lg а-ф lg b.
1.24. Всякое целое число, оканчивающееся двумя нулями, делится на 4.
39
В каждом из примеров 1.25—1.27 укажите, какое из двух утверждений вытекает из другого, и разными способами сформулируйте соответствующую теорему, используя термины «необходимоеусловие», «достаточноеусловие».
1.25. А = {число х равно нулю},
В = {произведение ху равно нулю}.
1.26. А = {прямые 4 и /2 расположены в одной плоскости}, 5= {прямые 4 и /3 параллельны},
1.27. А — {я2=Д=0}, В = {а > о}.
В каждом из примеров 1.28—1.30 сформулируйте теорему А—> В и обратную к ней теорему, укажите, в каких случаях обратная теорема верна.
1.28. А ~ {треугольник Д— равнобедренный},
5= {две медианы треугольника Д равны между собой}.
1.29. А == {четырехугольник Q является ромбом},
В = {диагонали четырехугольника Q делят его углы пополам}.
1.30. А = {натуральное число а делится на 9}, В~ {сумма цифр числа а делится на 3}.
1.31. Сформулируйте и докажите теорему, обратную теореме Пифагора.
Убедитесь в том, что в приводимых ниже случаях (1.32—1.34) справедливо соотношение А*->В, и сформулируйте соответствующие теоремы, используя слова «необходимо и достаточно» или «в том и только в том случае».
1.32. А~ ^функция постоянна в области своего определения^-, В~ ^ad — bc}.
1.33. А={из отрезков, длины которых равны а, Ь, с, можно составить треугольник}, В~ {положительные числа а, Ь, с связаны неравенствами аА-Ь>с, ЬА-с~у>а, а-усу>Ь}.
1.34. А = {многочлен Р (х) — аохп -{- аххп 1 -{-...
ап-гх 4- ап делится на х— а}» В=={Р (а) = 0}.
40
1.35. Докажите, что следующие утверждения равносильны:
А={двугранные углы при основании пирамиды равны}, Д ={высоты боковых граней пирамиды равны}, С={в основание пирамиды можно вписать окружность, а высота пирамиды проходит через центр этой окружности}, D= {высота пирамиды образует равные углы с боковыми гранями}.
1.36. Рассмотрите следующие неопределенные высказывания:
{все стороны основания пирамиды Р равны между собой}, Д={все боковые ребра пирамиды Р равны между собой}, С = {пирамида Р является правильной}.
Определите, верны ли теоремы:
А/\ ВС, С-> А Д В.
Сформулируйте теорему, пользуясь терминами «необходимое условие», «достаточное условие» (или «тогда и только тогда»).
1.37. Тот же вопрос (что и в задаче 1.36) относительно следующих трех высказываний:
/1 = {боковые грани пирамиды Р одинаково наклонены к плоскости основания}, Д={все плоские углы в основании пирамиды Р равны между собой},
С = {пирамида Р является правильной}.
1.38. Докажите, что пирамида является правильной в том и только в том случае, если в основании пирамиды лежит правильный многоугольник, а высота пирамиды проходит через центр этого многоугольника.
1.39. Какие из следующих теорем верны? Какие из них являются по отношению друг к другу обратными, противоположными?
1. Если каждое из слагаемых делится на И, то и сумма делится на 11.
2. Если ни одно из слагаемых не делится на 11, то и сумма не делится на И.
41
3. Если хотя бы одно слагаемое делится на 11, то и сумма делится на 11.
4. Если сумма делится на 11, то и каждое слагаемое делится на 11.
5. Если сумма не делится на 11, то ни одно слагаемое не делится на 11.
6. Если сумма не делится на 11, то хотя бы одно слагаемое не делится на И.
1.40. Рассмотрите следующие неопределенные высказывания, заданные на множестве N всех натуральных чисел:
А(х)={х делится на 5},
В (х) ~ {х — нечетное число}.
Укажите смысл неопределенного высказывания ~|(A(x) \/ В(х)), рассматривая последнюю цифру числа.
1.41. Рассмотрите следующие неопределенные высказывания, заданные на множестве N всех натуральных чисел:
А(х)={х делится на 2}, 5(х)={х делится на 3}.
Каков смысл неопределенного высказывания
(-|A(x))VC|5(x))?
ГЛАВА II
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
В школьном курсе математики теория действительного числа сколько-нибудь полно не излагается. И это неудивительно, так как доказательства, встречающиеся в этой теории, и даже само определение действительного числа весьма сложны и используют ряд идей, далеких от школьного курса. Между тем сам термин «действительное число» неизбежно появляется па уроках математики. В частности, школьникам говорят о рациональных и иррациональных числах (аккуратное определение которых также не приводится). Все это приводит к тому, что на вступительных экзаменах в вузах приходится слышать много ошибочных высказываний, связанных с действительными числами.
В этой главе собраны (как правило, без доказательств) свойства рациональных и действительных чисел. Эти свойства и дают (несмотря на отсутствие полной теории) четкое и математически правильное представление о множестве действительных чисел.
§ 1. Рациональные числа
К рациональным числам мы приходим, постепенно обобщая понятие числа. Самыми первыми числами, с которыми мы знакомимся еще в младших классах школы, являются натуральные числа: 1, 2, 3, ... Множество /V всех натуральных чисел бесконечно. В этом множестве М всегда выполнимы две операции: сложение и умножение. При этом сумма и произведение любых двух натуральных чисел снова являются натуральными числами. Что же касается обратных действий, вычитания и деления, то они выполняются в множестве натуральных чисел не всегда. Например, разность 5 — 9 и частное 2:3 невозможно вычислить, не выходя за пределы множества N всех натуральных чисел. Стремление сделать эти операции всегда выполнимыми приводит к введению
43
новых чисел, дробных и отрицательных. В результате мы и приходим к множеству R рациональных чисел.
Обычно дробные и отрицательные числа вводятся не одновременно. В школе сначала вводятся дробные числа (точнее, , 13 2 13 5
п о л о ж и т е л ь н ы е дробные числа: -у, v
£ 4 О ll) 4 tj
и т. п. ). В результате добавления этих новых чисел операция деления одного натурального числа на другое (или даже одного дробного числа на другое) оказывается всегда выполнимой. Затем вводятся нуль и отрицательные рациональные числа. В результате мы и получаем множество Я всех рациональных чисел. В этом множестве всегда выполнимы четыре арифметических действия (кроме деления на нуль). Иными словами, если а и b — рациональные числа, то определены их сумма а-}-Ь, разность а—Ь, произведение ab, а если b 0, то определено и частное -у.
Возможен и другой путь построения множества рациональных чисел Я- Именно, сначала к натуральным числам 1, 2, 3, ... присоединяют число 0 и отрицательные целые числа —1, —2, —3,... В результате мы получаем множество Z всех целых чисел:... —3, —2, — 1, 0, 1, 2, 3,... В этом множестве всегда выполнима операция вычитания- Однако деление выполнимо не всегда; например, частное (—2): 3 невозможно вычислить, не выходя за пределы множества Z всех целых чисел. Чтобы сделать операцию деления выполнимой, добавляют к целым числам дробные числа (как положительные, так и отрицательные), в результате чего мы и приходим к множеству Я всех рациональых чисел. Всякое рациональное число представляется в виде отношения двух целых чисел (например, —-~ = (—2):3, у = (—6):(—4), 0 = = 0:(—5)).
Разница между этими двумя путями построения множества Я состоит в том, что в первом случае мы сначала стремимся сделать выполнимой операцию деления, а потом обращаемся к вычитанию, а во втором случае мы сначала добиваемся выполнимости вычитания и лишь потом обращаемся к делению. Каждый из этих путей приводит к тому, что учащиеся быстро приобретают навыки выполнения действий с рациональными числами. При этом над вопросом «Что такое рациональное число?» обычно не задумываются. Когда же этот вопрос задают (например, на вступительных экзаменах в вузе), чаще
44
всего приходится слышать такой ответ (очевидно, связанный со вторым из намеченных выше путей построения множества рациональных чисел):
Рациональным называется всякое число, представляю-~ 'а , ,
щееся в виде частного некоторых двух целых чисел а, Ъ (где b =/= 0).
Обычно такой ответ признается правильным (за неимением другого). Однако он страдает существенными недостатками. В самом деле, что означает «всякое число»? По-видимому, предполагается известным, что такое «число» вообще, причем чисел имеется много и среди них этим определением выделяются те числа, которые считаются рациональными. Если так понимать это определение, то, видимо, естественнее всего считать, что речь идет о выделении рациональных чисел из всего множества действительных чисел. Иными словами, указанное выше определение следует понимать так: всякое дейст-вительное число, представляющееся в виде частного некоторых двух целых чисел а, b (где b 0), называется рациональным- В этой формулировке четко указано, каким свойством выделяются рациональные числа из множества всех действительных чисел, но все же за определение рациональных чисел ее принять нельзя. Ведь действительное число представляет собой более сложное понятие, чем рациональное число. Вводятся действительные числа после того, как уже стали известными рациональные числа. И потому пытаться определить рациональные числа через действительные— значит совершить порочный круг в рассуждениях.
Можно попытаться истолковать сформулированное выше «определение» рационального числа иначе: нам еще неизвестно, что такое рациональное (и тем более действительное) число; мы знаем лишь целые числа и хотим определить рациональное число как частное двух целых чисел. Но и эта точка зрения непоследовательна. Ведь если мы знаем лишь целые числа, то, например, частное 2 : 3 не существует (в множестве целых чисел); как же можно сказать, что это (не существующее!) частное называется рациональным числом?
Итак, хотя сформулированное выше «определение» обычно считается приемлемым, следует признать, что у нас в действительности нет корректного математического определения рациональных чисел.
45
§ 2. Свойства множества рациональных чисел
Как же все-таки можно точно математически описать множество К рациональных чисел? Положение вещей здесь несколько напоминает то, которое имеется в геометрии. В курсе геометрии мы также не находим точных определений таких основных понятий, как, например, точка или прямая. Говорится, что луч света дает представление о прямой линии, но это, конечно, лишь наглядное описание, а вовсе не математическое определение. Таким образом, строго говоря, понятия «точка» и «прямая» вводятся без определений. Однако основные свойства этих понятий указываются в аксиомах геометрии. Таковы, например, аксиомы: «Через две точки проходит одна и только одна прямая», «Через точку, лежащую вне данной прямой, проходит (в плоскости, содержащей эту точку и прямую) единственная прямая, не пересекающаяся с данной прямой» и др. Правда, полный список аксиом геометрии в школьном курсе не указывается, но существа дела это не меняет: первоначальные понятия (точка, прямая и др.) вводятся без определений, зато в аксиомах дается необходимый перечень их свойств (что, по существу, представляет собой «косвенное определение» точек, прямых и т. д.). С помощью этих свойств, указанных в аксиомах, выводятся все дальнейшие предложения (теоремы) геометрии.
Примерно так же обстоит дело с рациональными (или действительными) числами. Как мы видели, четкого определения рациональных чисел в школьном курсе нет. Однако остается другой (аксиоматический) путь построения множества рациональных чисел. В этом случае предполагается известным, что такое натуральное число; далее б е з определения вводится термин «рациональное число» и формулируются свойства рациональных чисел (т. е. аксиомы, дающие, по существу, «косвенное определение» множества рациональных чисел). Ниже дается перечисление основных свойств множества рациональных чисел.
Множество К всех рациональных чисел обладает следующими четырьмя группами свойств.
а) Для любых двух рациональных чисел а, b определена их сумма а-±-Ь. Операция взятия суммы (сложение) коммутативна и ассоциативна, т. е. для любых рациональных чисел а, Ь, с справедливы соотношения
а b — b -|-а, (а-\-Ь)-\-с —а-}-(Ь-\-с).
46
Имеется такое число 0 (нуль), что
а-\- 0 —а
для любого рационального числа а. Наконец, для любых двух рациональных чисел а, b найдется, и притом только одно, рациональное число, являющееся корнем уравнения
Ь-\-х = а;
это число называется разностью чисел а и b и обозначается через а — Ь, а операция взятия разности называется вычитанием. Разность 0 —а обозначают также просто через —а.
б) В множестве Я рациональных чисел содержатся все натуральные числа. Рациональные числа, представляющиеся в виде разности двух натуральных чисел, называются целыми числами. (Ниже, на стр. 50, будет доказано, что целыми являются числа 0, ±1, zt2, ±3, ... и только эти числа.)
в) Для любых двух рациональных чисел а, b определено их произведение ab. Умножение (операция взятия произведения) коммутативно, ассоциативно и дистрибутивно:
ab = Ьа,
(ab) с = а (Ьс), а (Ь 4- с) = ab Д- ас.
Для любого рационального числа а справедливо соотношение 1-а = а. Наконец, для любых двух рациональных чисел а, Ь, из которых b отлично от нуля, найдется, и притом только одно, рациональное число, являющееся решением уравнения Ьх = а\ это число называется частным чисел а н b и обозначается через у, а операция нахождения частного называется делением.
г) Любое рациональное число представляется в виде частного у некоторых двух целых чисел а, b (где &=Д=0).
Можно доказать (однако это выходит за рамки школьной программы), что эти четыре группы, свойств полностью характеризуют множество R всех рациональных чисел. Иными словами, выполнение этих свойств можно принять в качестве определения множества Я всех рациональных чисел (если свойства натуральных чисел считать известными). Отсюда, в частности, следует, что любое утверждение, касающееся рациональных чисел, может быть выведено из этих четырех групп свойств.
47
Итак, на вопрос о том, какие числа называются рациональными, правильнее всего ответить, что рациональными называются числа, обладающие указанными выше четырьмя группами свойств.
Как видите, ответ, обсуждавшийся в § 1 (стр. 45), является неполным: в нем учтена лишь последняя из перечисленных четырех групп свойств. Тем не менее такой краткий ответ обычно признают правильным, если, конечно, отвечающий понимает, что в множестве всех рациональных чисел выполнимы четыре арифметических действия, обладающие указанными выше свойствами а), б), в).
Наконец, напомним, что все рациональные числа распадаются на три типа чисел: положительные числа, число О и отрицательные чи-сла. Положительным называется рациональное число, которое можно представить в виде отношения двух натуральных чисел. Число 0 не является положительным. Все остальные числа (т. е. отличные от нуля и не являющиеся положительными) называются отрицательными. Часто встречаются также термины «неотрицательное число», «неположительное число». Число а называется неотрицательным, если оно либо равно нулю, либо положительно. Неположительным число а будет в том случае, если оно либо равно нулю, либо отрицательно.
§ 3. Примеры применения свойств рациональных чисел
Покажем в качестве примеров, как используются указанные выше четыре группы свойств для доказательства дальнейших свойств рациональных чисел.
Пример 1. Доказать, что 0-а = 0 (для любого рационального числа а).
Решение. Применяя свойства а) и в), мы находим
« = 1 • а = (1 -|-0) - 0=1 - a-4-0.<z = a-|-0,a-
Таким образом, число 0 • а является решением уравнения а = а-(-х. Но число 0 также является решением этого уравнения. Так как это уравнение имеет единственное решение (свойство а)), то 0-а = 0.
Пример 2. Доказать, что если произведение двух рациональных чисел равно нулю, то хотя бы одно из них равно нулю.
Решение. Пусть аб = О. Если 07=0, то мы можем рассмотреть частное — ^т. е. число, являющееся корнем уравнения а-х = 1 и, следовательно, удовлетворяющее соотношению Так’ как
ab = O, то, в силу результата примера 1, -~(ab) = -i- • 0 = 0 • ~~ = 0.
43
Но мы имеем —(ab) = [ — a}b = \a-— £>=!•& = Ь. Следователь-а \ а / \ а /
но, & = 0.
Пример 3. Доказать, что a-j-( — а) = 0.
Решение. По определению мы имеем —а = 0 — а, а это означает, в силу определения операции вычитания, что аД-( — а)=0.
Пример 4. Доказать, что (— 1) • (— 1) = 1.
Решение. Мы имеем (—1) (1 Д-(—1)) = (—1) • 0 = 0 (согласно примерам 1 и 3). Пользуясь дистрибутивностью умножения, мы можем переписать это равенство в виде ( —1) • 1+( —1) • (— 1)=0 или (—1) + (— 1) ’ (—0 = 0. Это означает, что число (—1)-(—1) является корнем уравнения (— l)-|-x = 0. Но число 1 также является корнем этого уравнения (ведь согласно примеру 3 мы имеем 1-|-(—1) = 0, а потому (—1)Д-1=0). Так как это уравнение имеет единственный корень, то (—!)•(—1) = 1.
Пример 5. Доказать соотношения: — а — (— 1) • а, — (— а) —а.
Решение. Мы имеем (1 + (— 1 ))а = 0 • а = 0, и потому 1 • а + + (— 1)а = 0, или аД-(— 1)а = 0. Это означает, что (— 1)а есть корень уравнения a-\-x = Q. Но число —а также является корнем этого уравнения (пример 3). Следовательно, —а = (—1) а.
Далее, — (—</) = (— 1) (—</) = (— 1) ((— 1) а) = ((— 1) (— 1))а = = 1 -а = а (в силу результата примера 4).
Пример 6. Доказать, что а — Ь=а-!г(—Ь).
Решение. Мы имеем
& + (« + (— *))=& + ((— 6) + <z) = (6 + (—£>))+а = 0+а = а, т. е. число аД-(— Ь) является решением уравнения 6+% = </. Но число а — Ь также является (по определению) корнем этого уравнения. Следовательно, а — Ь = д-р(—&).
Пример 7. Доказать, что сумма трех (или большего числа) рациональных чисел может быть вычислена в любом порядке, например:
(а + &)+с=& + (с-|-а) = а-|-(с+&) и т. д.
Решение. Это вытекает из коммутативности и ассоциативности сложения. Докажем, например, равенство (а-|-£>)-|-с = 6_|_(с-|_д). Имеем
(а + = (^ + я) + с = & -|- (а с) = & -|- (са).
Замечание. В силу доказанного можно писать просто а + &-)-с без указания порядка выполнения сложения, т. е. мы получаем возможность определить сумму трех (и более) рациональных чисел. Далее, учитывая результат примера 6, мы можем и в алгебраической сумме переставлять члены в любом порядке, например:
(а — &) +с = (« + (— &)) + с=а + (— Ь) -рс = с-|-а-р (— &) =
= (с + а) + (— Ь) = (с + а) — Ь. Поэтому алгебраическую сумму также можно писать без указания порядка выполнения сложения (т. е. без скобок), например:
а —£>Д-с = с+а — Ь и т. д.
Пример 8. Доказать соотношения: —(« + &) = — а — Ь, — (а — Ь) — Ь — а-
49
Решение. Имеем
-(« + &) = (-!)(« + £>) = (- 1)а + (-1)& = (- о) + (- &) =
= (— а) — b = — а — Ь. Далее,
- (а-&) = (- 1) = 1) (в + (_ &)) =
= (- 1) (a-j-(—1) 6) = (—1) а + (—1) ((—1) 6) =
= (— 1)а + ((—!)•(— !))& = (— а)+1 • & = (—а) + &= & + (—а)=&—а.
Замечание. Теперь мы получаем возможность обосновать правила сложения и вычитания многочленов. Например,
(а —& + <?) + (« —« + <7) = (а + (— &)4-с) + (« + (— «) + <?) =
= а + (— &) + с + т (— л)-|-7 = а — b -(-c-^-tn — n-^-q,
(а — Ь + с) — (т — п ф- q) = (а — b ф- с) ф- (— (т — п q)) =
= (« — &-J-C) +(— т-\-п~ q)~a~ b-^c— m-f-n — q.
Иными словами, для сложения и вычитания многочленов нужно лишь раскрыть скобки, пользуясь обычным правилом знаков.
Пример 9. Доказать, что а (Ь— c) = ab~ac.
Решение. Имеем
а(Ь — с) = «(& + (— с)) =«(& + (— 1)-с) =
= ab ф- а ((— 1) с) = ab ф- а (с (— 1)) = ab ф- (ас) (— 1) ==
= ab -|- (— 1) (ас) = ab ф- (— (ас)) — ab — ас.
Замечание. Вместе с равенством a (b-j-c) ~ab-\~ac (выражающим закон дистрибутивности) доказанное соотношение дает правило умножения одночлена на многочлен. Например,
а (т — п ф- р) = ат — ап-(-ар.
Дважды применяя это правило, мы получаем и обычное правило умножения многочлена на многочлен. Отсюда, в частности, вытекают все формулы сокращенного умножения.
Пример 10, Доказать, что всякое целое число, отличное от нуля, либо является натуральным, либо имеет вид —п, где л —натуральное число.
Решение. Пусть а —целое число, отличное от нуля. По определению a—k — l, где k и / — натуральные числа (свойство б)). При этом k ф I (нбо aj^O). Для двух различных натуральных чисел k, I имеет место одно из двух обстоятельств; k > I или k < I (свойства натуральных чисел нам известны). Если k > I, то a = k — I есть натуральное число. Пусть теперь k < I. Тогда —а = — (k — I) = I — k есть натуральное число; обозначим его через п, так что —а — п. Теперь имеем а — —(—а) = —п.
Пример 11. Вывести правило сложения дробей. „ас
Решение. Пусть р = —ид=—~два рациональных числа.
Здесь а, &, с,
d — целые
числа, причем b-ibO,
Запись
а Р-ь
означает, по определению, что а~Ьр; точно так же c = dq. Следовательно, ad=bp -d—bdp; далее, bc = b dq = bdq. Теперь мы находим
d yt 0.
50
ad-'-be ^bdp-'rbdq^bd (p-\-q). Так как bd^O (пример 2), то Из равенства ad-фbe — bd (р ф q) мы находим
Иначе говоря, а , с _ad-\-bc b 1 d — bd ’
а это и есть правило сложения дробей.
Аналогично устанавливаются и правила умножения и сокращения дробей.
Пример 12. Доказать, что сумма и произведение двух положительных рациональных чисел являются положительными числами.
Решение. Пусть р, q — положительные рациональные числа. „ а с , j
Тогда их можно представить в виде р = <7 = -g- где а, о, с, d —
натуральные числа. Имеем
В числителе и знаменателе этой дроби, очевидно, стоят натуральные числа. Значит, число p-\-q, являющееся отношением двух натуральных чисел, положительно. Аналогично доказывается, что pg —положительное число.
Разобранные примеры убедительно показывают, что, в самом деле, все свойства рациональных чисел могут быть выведены из указанных выше четырех групп свойств а), б), в), г).
§ 4. Причины, заставляющие расширить множество рациональных чисел
Множество R всех рациональных чисел обладает очень удачными свойствами и для целей арифметики является вполне достаточным. Возможность выполнения (в множестве рациональных чисел) четырех арифметических действий позволяет решать уравнения и системы уравнений первой степени и, следовательно, позволяет решать большое число задач.
И все-таки одними рациональными числами обойтись не удается. Кроме них приходится вводить еще новые числа, не являющиеся рациональными и называемые иррациональными. Вместе рациональные и иррациональные числа объединяют одним общим названием: действительные числа.
Прежде чем мы перейдем к описанию всего множества D действительных чисел, напомним те алгебраические и геометрические причины, которые заставляют вводить новые, иррациональные числа. Одна из основных алгебраических причин
51
заключается в тем, что квадратные уравнения и уравнения более высоких степеней с рациональными (и даже целыми) коэффициентами не всегда удается решить, оставаясь в множестве рациональных чисел. Даже такие простые уравнения, как №= а, х3 = а и т. д. (где а — положительное рациональное число), требуют для своего решения введения новых, иррациональных чисел, так как не из всякого положительного рационального числа удается извлекать корни (квадратные, кубические и т. д.). В школьных учебниках алгебры имеется доказательство того факта, что число ]/2 (т. е. положительный корень уравнения х® = 2) иррационально, или, точнее, что не [существует рационального числа, квадрат которого равен 2. Таким образом, уже извлечение корней (арифметических) требует введения иррациональных чисел.
Сказанное выше дает повод к одной весьма распространенной ошибке: нередко на вступительных экзаменах в вузах поступающие говорят, что «иррациональными называются числа вида ]/п , где п — натуральное число, не являющееся точным квадратом» . В чем здесь ошибка? Верно, что если натуральное число п не является точным квадратом, то число V п иррационально. Но далеко не все иррациональные числа имеют такой вид (или даже являются корнями алгебраических уравнений с рациональными коэффициентами). Для правильного ответа на указанный вопрос нужно сначала дать описание множества D всех действительных чисел, после чего иррациональные числа можно будет определить следующим образом: иррациональными называются действительные числа, не являющиеся рациональными, т. е. не представимые в виде отношения двух целых чисел.
Но прежде чем мы дадим описание множества D всех действительных чисел, мы укажем еще г е о м е т р и ч е с к и е причины введения иррациональных чисел. Одна из основных геометрических причин заключается в том, что рациональных чисел не хватает для измерения отрезков. Напомним, что результат измерения отрезка (длина отрезка) описывается следующим образом.
Пусть в качестве единицы измерения взят некоторый отрезок MN. Тогда каждому отрезку АВ можно приписать число | АВ | — его длину. При этом имеют место следующие свойства:
1) длина любого отрезка является положительным числом;
2) равные отрезки имеют равные длины;
52
3) если точка С лежит на отрезке АВ, то длина отрезка АВ равна сумме длин отрезков АС и ВС;
4) длина отрезка M~N равна 1.
Для нахождения длины данного отрезка АВ используется процесс измерения- Напомним, в чем он заключается. Сначала будем на отрезке АВ откладывать единицу длины MN(рис. 3).
Рис. 3.
Пусть, например, она уложилась на АВ три раза, после чего остался остаток AJ3, меньший MN. Тогда мы берем десятую часть TMjNj отрезка MN и этот отрезок начинаем откладывать на АгВ. Скажем, эта десятая часть единицы измерения уложится на А±В два раза, после чего остается остаток А2В, меньший (рис. 4). На этом отрезке
М, ^Л/,
Рис. 4.
АгВ мы будем откладывать сотую часть единицы измерения— пусть, например, она отложится 5 раз, — и т. д.
Теперь мы можем сказать, что на отрезке АВ уложилось 3 целых единицы измерения, да еще 2 десятых ее доли, да еще 5 сотых, ... В этом случае длину отрезка АВ принято записывать десятичной дробью 3,25... Вообще говоря, эта десятичная дробь будет бесконечной, поскольку после каждого откладывания может оставаться остаток, и процесс измерения за конечное число шагов не завершится. Итак, длина а отрезка АВ запишется в виде бесконечной десятичной дроби
а = 3,25
53
Вспомним теперь из курса арифметики, что всякое положительное рациональное число (т. е. отношение двух натуральных чисел) при записи (или, как говорят, «обращении его») в виде десятичной дроби дает либо конечную, либо бесконечную периодическую десятичную дробь. Значит, если бы длина любого отрезка выражалась рациональным числом, то у нас получались бы в результате измерения только конечные или бесконечные периодические десятичные дроби. Например, если отрезок АВ равен четверти единицы измерения MN, то его длина выражается конечной десятичной дробью 0,25, а если отрезок АВ равен третьей части единицы измерения MN, то его длина выражается бесконечной периодической десятичной дробью 0,3333... Но легко понять, что су-р шествуют и такие отрезки, длина которых
о. , не выражается конечной или бесконеч-
'к ной периодической десятичной дробью.
X. Пусть, например, NP— гипотенуза равно-
бедренного прямоугольного треугольника, 'х одним из катетов которого является единица __________\ измерения MN (рис. 5). Согласно теореме М_________N Пифагора, длина отрезка NP равна ]/2,
Рис. 5. и, следовательно, длина этого отрезка не выражается рациональным числом. Это означает, что при измерении отрезка NP мы получим десятичную дробь, которая не будет ни конечной, ни бесконечной периодической, т. е. мы получим бесконечную непериодическую десятичную дробь. Мы видим, что для геометрических целей (для измерения отрезков) рациональных чисел не хватает, и это также является одной из причин введения новых, иррациональных чисел. Еще одним хорошо известным примером иррационального числа является число л (иррациональность этого числа доказывается непросто, и мы здесь этого доказательства не приводим).
Сказанное выше является причиной возникновения хорошо известного «определения» иррационального числа — определения, которое внешне кажется простым и понятным, но в действительности математически корректным не является. Именно, мы знаем, что всякое рациональное число записывается в виде конечной или бесконечной периодической десятичной дроби и, обратно, каждая такая дробь изображает некоторое рациональное число. Поэтому число будет иррациональным в том и только в том случае, если оно записывается в виде бесконечной непериодической десятичной дроби. Это 54
свойство обычно и принимают за «определение» иррационального числа, т. е. говорят, что иррациональным называется число, записывающееся в виде бесконечной непериодической десятичной дроби.
В чем же некорректность такого определения? Прежде всего, в его неполноте, в том, что оно указывает лишь форму записи действительного числа, но ничего не говорит о действиях над такими числами. Ведь мало указать, как записываются действительные числа, надо еще определить сложение и умножение действительных чисел, а с этим в приведенном «определении» дело обстоит совсем не благополучно. Вспомните, каким трудоемким является умножение («в столбик») двух многозначных чисел, и вы легко сможете себе представить, насколько сложным окажется перемножение двух бесконечных (да еще непериодических) десятичных дробей. Во всяком случае, сложение и умножение действительных чисел должны быть четко определены, а этого в приведенной выше формулировке нет.
Надо сказать, что принципиально возможно дать определение действительного числа как бесконечной десятичной дроби, но в такое определение обязательно должно входить описание действий с бесконечными дробями. Такой путь построения теории действительного числа оказывается вовсе не простым, и в школе он подробно не рассматривается. Поэтому мы примем другой путь изложения: мы опишем множество действительных чисел с помощью его свойств (подобно тому как это было сделано для рациональных чисел) и лишь потом выясним, что означает запись действительного числа в виде бесконечной десятичной дроби.
В заключение этого параграфа разберем два примера.
Пример 13. Доказать, что число 0,123456789101112..., в котором после запятой выписаны подряд все натуральные числа, не является рациональным (т. е. что эта дробь — непериодическая).
Решение. Допустим, напротив, что эта дробь является периодической, и пусть ее период содержит k знаков, г. е., начиная с некоторого места, в этой дроби все время повторяется одна и та же последовательность из k цифр. Где-то дальше нам обязательно встретятся подряд k нулей (так как среди натуральных чисел имеются числа 10*, 10*4"1, 10*+2„..), а потому из периодичности дроби вытекало бы, что ее период состоит из одних нулей, т. е. что эта десятичная дробь является конечной. Нр это явно противоречит способу
55
образования этой дроби. Полученное противоречие и доказывает требуемое утверждение.
Пример 14. Доказать, что число /2-{-/3 иррационально.
Решение. Допустим, напротив, что ]/2-|-/з = г, где г — некоторое рациональное число. Заметим, что число г, очевидно, не равно нулю. Тогда ]/3 = г — /2, откуда, возводя в квадрат, находим 3 = г2 — 2г/2-|-2, или
/•2-1
2г
(напомним, что г =/= 0). Но стоящее в правой части число рационально (так как г рационально), и у нас получилось, что /2-—рациональное число. Полученное противоречие и доказывает наше утверждение.
§ 5. Предел монотонной ограниченной последовательности
Итак, мы пока еще не дали описания множества действительных чисел. Из геометрических соображений выяснилось, что числа, которые мы хотим определить (т. е. действительные числа), нужно уметь записывать в виде бесконечных десятичных дробей. Такая же запись используется и в алгебре. Например, мы пишем
/2 = 1,41421...
Какой смысл имеет эта запись? Чго означает бесконечное множество цифр после запятой? На этот вопрос отвечает последовательность чисел
а1=1,4; а2=1,41; а3= 1,414;
«*=1,4142; а5=1,41421; ...,
которые мы получим, если будем сохранять после запятой 1, 2 и т. д. цифр. Все эти числа av а2, а3>... рациональны. (они записываются в виде конечных десятичных дробей) и образуют неубывающую последовательность х):
*) Мы не можем сказать, что эта последовательность является возрастающей (хотя для первых членов имеют место строгие неравенства: аг < аг < а3 < а4 < ...). Ведь если на й-м месте после запятой нам встретится цифра 0, то мы будем иметь = щ, (а ueak^<ak).
56
Далее, эта последовательность ограничена: так как каждое из чисел ап (п=\, 2, 3, ...) имеет перед запятой цифру то 1<аи<2 (для любого п—1, 2, 3, ...).
Наконец, числа этой последовательности все более приближаются к числу 2 при возрастании п. Это означает, что, начиная с некоторого л, каждое из чисел ап будет отличаться от У~2 менее чем на (это, как легко понять, будет для всех п > 3), а если мы продвинемся дальше, то найдем такое п, начиная с которого ап будет отличаться от ]/~2 менее чем на -уроооббО’ и т’ д’ Вооб1це> какое бы положи-тельное число е мы ни взяли I , |o qqqOOO или любое другое j , найдется в последовательности av а2, а3, ... такое число а„0, начиная с которого каждое ап ______________
будет отличаться от ]/ 2 менее чем на е: д / ч. \\
— е<Ул2 — аи<е при п>п0 [ / (в данном случае можно было бы / даже написать 0</2-йл<8). /\
Это обстоятельство записывают V. ч. / ]
так; / I/
lim л—*оо ----------------------
и говорят, что У2 есть предел Рис- 6.
последовательности {аи}.
Другой пример возрастающей ограниченной последовательности известен из курса геометрии. Рассмотрим окружность радиуса 1 (рис. 6) и обозначим через р2 периметр вписанного в нее квадрата, через р3— периметр вписанного правильного восьмиугольника, ..., через рп — периметр вписанного правильного 2га-угольника, ... Мы получаем, таким образом, последовательность ра, р3, ..., рп, ... , причем эта последовательность будет возрастающей и ограниченной:
Рг<р3<....<Рп<.---> 0</>„<8
(последнее неравенство имеет место потому, что периметр любого вписанного многоугольника не превосходит периметра
57
описанного квадрата, рис. 6). И в этом случае рассматриваемая возрастающая ограниченная последовательность {рп} имеет предел: в данном случае пределом будет длина окружности, т. е.
lim р„ = 2л.
Можно построить и примеры невозрастающих ограниченных последовательностей. Например, рассмотрим приближения числа )'Л2 с избытком:
^=1,5; ^2=1,42; £3== 1,415; &4== 1,4143; £5== 1,41422; ...
Эта последовательность {Ьп} является невозрастающей и ограниченной:
b2 Ss b;> Г bt b& , 1<&и<2.
Ее пределом является число ] 2:
Um 6я=рЛ2. л->со
В качестве последнего примера рассмотрим последовательность чисел
с1==1,1; "с2 = 1,01; с3=1,001; с4== 1,0001; ...;
сп — 1 4- ]; • • •
Ясно, что эта последовательность является убывающей и ее предел равен 1:
Jim сп — 1. П->СО
Во всех четырех примерах числа, составляющие последовательность, являются рациональными (они записываются в виде конечных десятичных дробей). Но предел последовательности в первых трех случаях был иррациональным числом, а в последнем примере — рациональным.
Что бы мы сказали об этих последовательностях, если бы мы ограничились рассмотрением только рациональных чисел (не зная или не желая говорить о существовании иррациональных чисел)? Мы вынуждены были бы сказать, что первые три из этих последовательностей не имеют предела, в то время как четвертая имеет предел 1. В самом деле,
58
рационального числа, к которому приближались бы числа а2, а3, ..не существует (они приближаются к числу |/"2, но оно не является рациональным), т. е. в множестве одних только рациональных чисел первая последовательность не имеет предела.
Мы видим, что в множестве рациональных чисел не всякая монотонная (т. е. невозрастающая или неубывающая) ограниченная последовательность имеет предел. Если мы хотим, чтобы любая монотонная ограниченная последовательность имела предел, мы должны добавить к рациональным числам новые, иррациональные.
Это соображение и является тем последним звеном, которого нам не хватало для полного описания всех основных свойств множества действительных чисел.
Подчеркнем во избежание недоразумений, что этот параграф содержал лишь пояснения, необходимые для дальнейшего. Рассуждения носили лишь наводящий характер, и их никоим образом нельзя рассматривать как «доказательство» того факта, что любая ограниченная монотонная последовательность имеет предел (в множестве действительных чисел).
§ 6. Свойства множества действительных чисел
Теперь у нас есть все необходимое, чтобы дать полное описание множества действительных чисел. Как и в случае рациональных чисел, мы дадим «косвенное определение» множества действительных чисел, перечислив его основные свойства (аксиомы). Грубо говоря, с алгебраической точки зрения множество D всех действительных чисел устроено так же, как и множество R рациональных чисел. Однако действительных чисел больше — настолько больше, что любая монотонная ограниченная последовательность имеет в D предел. Более точно, множество D всех действительных чисел обладает следующими пятью группами свойств.
А) Множество D содержит все рациональные числа (а значит, и все целые числа, в частности числа 0 и 1).
Б) Для любых двух действительных чисел а, b определена их сумма а-\-Ь. Операция взятия суммы (сложение) коммутативна и ассоциативна, т. е. для любых действительных чисел а, Ь, с справедливы соотношения
a-]-b = b-]-a,
(а + &)4-с = а + (&4-с).
59
Далее, a-f-0 = а для любого действительного числа а. Наконец, для любых двух действительных чисел а, b найдется (и притом только одно) действительное число, являющееся решением уравнения Ь-)-х=а; это число называется разностью чисел а и b и обозначается через а — Ь, а операция взятия разности называется вычитанием. Разность 0 — 'а обозначают также просто через — а.
В) Для любых двух действительных чисел а, b определено их произведение ab. Умножение (операция взятия произведения) коммутативно, ассоциативно и дистрибутивно:
ab = Ьа, (ab) с = а (be), a (b с) = ab ас.
Для любого действительного числа а справедливо соотношение 1-а = а. Наконец, для любых двух действительных чисел а, b (где b ф 0) найдется (и притом только одно) действительное число, являющееся решением уравнения Ьх = а', это число называется частным чисел а и b и обознача-
а
ется через-у, а операция нахождения частного называется делением.
Г) Как и рациональные числа, все отличные от нуля действительные числа разбиты на положительные и отрицательные числа. При этом сумма и произведение положительных чисел снова являются положительными числами. Это дает возможность ввести в множестве D неравенства: по определению а^>Ь (или b<Za), если число а — b положительно. Далее, если а отрицательно, то —а положительно. Наконец, для любого положительного действительного числа а найдется такое положительное рациональное число г, что г < а.
Д) В множестве D каждая ограниченная монотонная последовательность имеет предел1).
х) Еще раз подчеркиваем, что здесь было дано лишь перечисление свойств множества действительных чисел. При выбранном здесь аксиоматическом описании множества действительных чисел было бы неправильно ставить вопрос о «доказательстве» этих свойств (в частности, свойства Д), утверждающего существование предела ограниченной монотонной последовательности). Более правильным было бы поставить вопрос: существует ли множество действительных чисел, т. е. чисел, обладающих всеми указанными свойствами? Математика дает утвердительный ответ на этот вопрос, но это уже далеко выходит за рамки школьного курса математики.
60
Этим и завершается описание свойств множества действительных чисел. Иными словами, выполнение свойств А), Б), В), Г), Д) можно принять в качестве определения множества D всех действительных чисел. Всякое утверждение, касающееся действительных чисел, может быть выведено из этих пяти групп свойств.
Так, из свойств Б) и В) вытекают (так же как и в случае рациональных чисел — см. примеры 1—9 на стр. 48 — 50) обычные правила действий над действительными числами: возможность в алгебраической сумме переставлять члены в любом порядке, правила сложения, вычитания, умножения многочленов, формулы сокращенного умножения и другие правила тождественных преобразований. Все эти правила вытекают только из свойств, сформулированных в Б) и В).
В математике принято называть числовым полем всякое множество чисел, которое обладает свойствами, указанными в Б) и В). Таким образом, множество D всех действительных чисел является полем. Его так и называют: поле действительных чисел. Другим примером поля может служить множество всех рациональных чисел (см. свойства а) и в) на стр. 46—47). Его называют поэтому полем рациональных чисел. Еще один пример поля — поле комплексных чисел — рассматривается в четвертой главе. Во всяком поле можно по обычным правилам производить тождественные преобразования (так как справедливость этих правил вытекает из аксиом — таких, как Б) и В),— которые имеют место, по определению, в любом поле).
Теперь мы можем вернуться к вопросу об изображении действительных чисел с помощью бесконечных десятичных дробей. Возьмем какую-либо бесконечную десятичную дробь, скажем дробь
0,123456789101112...,
рассмотренную в примере 13 на стр. 55. Попробуем понять, «изображает» ли эта дробь какое-нибудь действительное число и какое именно. С этой целью рассмотрим последовательность рациональных чисел
91 = 0,1; 92 = 0,12; 93 = 0,123;...; 913 = 0,123456789101 1;..., которые мы получим, если будем в написанной бесконечной дроби сохранять после запятой 1, 2 и т. д. цифр. Эти числа образуют, очевидно, ограниченную неубывающую последовательность. Согласно свойству Д) существует предел этой последовательности, который мы обозначим через а:
а= lim qn.
П-+СХ)
61
Об этом действительном числе а и говорят, что оно изображается взятой бесконечной десятичной дробью.
То же рассуждение применимо и к любой другой бесконечной десятичной дроби, т. е. любая бесконечная десятичная дробь изображает некоторое действительное число. (При этом любое действительное число может быть изобра-' жено бесконечной десятичной дробью.)
Теперь становится понятным, что, в самом деле, действительных чисел оказывается достаточно для измерения отрезков. Ведь, как мы видели на стр. 53, в процессе измерения отрезка получается бесконечная десятичная дробь, а каждая такая дробь изображает некоторое действительное число.
Пример 15. Вычислить несколько знаков бесконечной десятичной дроби, изображающей число |/"3.
Решение. Так как I3 <Z 3, а 23 > 3, то 1 <Tj3<C 2, т. е. |^3 = 1,... Рассмотрим теперь числа
1,0; 1,1; 1,2; ...; 1,9; 2,0
и будем возводить их в куб. Путем проб находим, что
1,4» = 2,744 < 3, 1,53 = 3,375 >3.
Таким образом, 1^3 = 1,4... Теперь испытаем числа
1,40; 1,41; 1,42; ...; 1,49; 1,50.
Возводя в куб, находим
1,44» = 2,985984 < 3, 1,45» = 3,048625 > 3.
Таким образом, |/'3=1,44... Аналогично можно находить последующие знаки. (Впрочем, существуют значительно более совершенные способы вычисления корней.)
Пример 16. Доказать, что между любыми двумя различными действительными числами имеется рациональное число.
Решение. Пусть а и р— два действительных числа, а=5^р. Будем для определенности считать, что числа а и р положительны, причем а<Р (другие случаи рассматриваются аналогично), т. е. а>0, р — а>0. Так как число положительно, то (в силу свойства Г)) найдется такое положи-тельное рациональное число г, что г < —. Точно так же
62
найдется такое положительное рациональное число rs, что
г"<;6—а. Мы можем написать г' = —, г" = —, где т, п, ' > п ’ q ’
р, q — натуральные числа. 1 огда — Сг, и потому—< — ,
т. е. a<Zn (мы здесь пользуемся обычными свойствами не-
равенств; подробно о неравенствах сказано в главе третьей).
Точно так же -- С Я п 1 2
перь числа 0, —, —, н q q
потому —а- Рассмотрим те-у =п. Первое из этих чисел меньше
и
г",
а, последнее больше а (т. е. 0<а, и>а). Значит, найдется такое натуральное k, что —— Из этого следует,
k , k k — 1 1 k ___OJA
что-----a=&~---------= — <p—а, и потому — < p. Итак,
q ' q q q r q
k о k
a<--<p, t. e. — — искомое рациональное число, заклю
ченное между аир.
§ 7. Абсолютная величина
Определение. Абсолютной величиной действительного числа а называется число а, если а положительно или равно нулю, и число — а, если а отрицательно.
Иначе говоря,
( а, если a О, | а ={
( — а, если а < 0.
Заметим, что если число а положительно, то (в силу свойства Г)) число —а отрицательно, т. е. —a<;0<;a. Таким образом, —а < а. В этом случае \а\ — а, т. е. \а\ совпадает с большим из двух чисел а, —а. Легко проверить, что и в случае, когда а отрицательно, число | а | совпадает с большим из чисел а, —а. Таким образом, можно дать и другое определение абсолютной величины:
Абсолютной величиной действительного числа а^О называется большее из двух чисел а, —а.
Из этого второго определения непосредственно следует, что | — a j = | а\. Точно так же из этого определения следует, что для любого действительного числа а справедливы неравенства
а 'С | а |, — а 'С | а
63
Умножая второе из этих неравенств на — 1 (при этом знак неравенства изменится на противоположный), мы получим следующие два неравенства:
а | а I, — | а |, справедливые для любого действительного числа а. Объединяя эти два неравенства в одну «цепочку», получаем
— | а ) а | а |.
Существует еще третье определение абсолютной величины (разумеется, эквивалентное предыдущим), которое в некоторых случаях бывает очень удобным. Именно, абсолютную величину можно определить формулой
| а I = ]/”а2, где в правой части берется арифметический корень (т. е. положительное значение корня).
Пример 17. Доказать, чго неравенство I а | С b эквивалентно соотношениям —bs^as^b.
Решение. Допустим, что имеет место неравенство \а\^Ь, т. е. |а| не превосходит Ь. Так как \а | — наибольшее из двух чисел а, —а, то каждое из них не превосходит Ь, т. е.
а Ь, — a-szb.
Умножая второе из этих неравенств на —1, получаем —Ь-^а. Объединяя полученные неравенства —&<«, в одну «цепочку», мы и получаем—b-^a-zb.
Обратно, пусть имеют место неравенства —b^Za^zb, т. е. — b-s'_a и as^b. Умножая первое из этих двух неравенств на — 1, перепишем их в виде— а sgi Ь, а?^Ь. Таким образом, каждое из чисел а, —а не превосходит Ь, а потому и наибольшее из них не превосходит Ь, т. е. | а | еД Ь.
Пример 18. Доказать, что для любых двух действительных чисел а, b справедливо неравенство
| а b | sj; | а | 1 b |.
Решение. Запишем для чисел а и b неравенства
— | а | а | а |,
— | b | | b |.
Сложив эти неравенства, получим
или
— | а ! — | b [ а b | а | -f- [ b |, — (| a | + j b а-^-Ь^, | а | 1 b |.
64
Таким образом, число с=|а|4-|/’| удовлетворяет неравенствам— с^а-^Ь^с, и потому (в силу предыдущего примера) | а b | с, т. е. | а b | | а 14-1 b |, что и требо-
валось.
Пример 19. Решить уравнение —1| = |х4"3|.
Решение. Используя третье определение абсолютной величины, мы можем переписать заданное уравнение в виде
(О
Возводя в квадрат обе части, получаем уравнение (х- 1)2 = (х4- 3)2. (2)
Раскрывая скобки и приводя подобные члены, мы получаем уравнение 8x48 = 0, из которого находим х =—1.
Заметим теперь, что переход от уравнения (1) к уравнению (2) совершался возведением в квадрат обеих честей уравнения. Такое преобразование уравнения никогда не приводит к потере корней, но может привести к появлению посторонних корней. Поэтому следует проверить, является ли найденное значение х =— 1 корнем исходного уравнения. Проверка показывает, что х =—1 удовлетворяет исходному уравнению.
Итак, данное уравнение имеет единственный корень х = — 1.
§ 8. Числовая ось и координаты
Пусть I — некоторая прямая. Отметим на ней произвольную точку О, которую будем называть началом отсчета (или просто началом). Точка О разбивает прямую I на два луча. Один из этих лучей условим- м N
ся считать положительным, а вто- 1---1
рой — отрицательным. На чертеже принято положительный луч отмечать стрелкой (рис. 7). Мы будем, _________।____________
кроме того, предполагать, что ука- р
зан отрезок MN, принимаемый за рис 7,
единицу измерения длин.
Итак, на прямой / отмечено начало отсчета О и указано, какой из двух лучей считается положительным; кроме того, выбрана единица измерения MN. При этих условиях каждой точке А прямой I сопоставляется некоторое действительное число х, называемое координатой точки А. Делается это
3 В. Г. Болтянский н др. 65
следующим образом: если точка А лежит на положительном луче,' то за х принимаем длину отрезка ОА (рис. 8); если А лежит на отрицательном луче, то за х принимаем отрицательное число, абсолютная величина которого равна длине отрезка ОА (рис. 9). Наконец, если точка А совпадает с О, то полагаем х=0. Короче,
| О А |, если А лежит на положительном луче;
— | ОА |, если А лежит на отрицательном луче; О, если А совпадает с О.
Итак, каждой точке
ное число — координата
прямой I сопоставляется действитель-этой точки. Весьма существенно, что
М
N н
М У
т =2 х = ~3
И-------г* -1------F
О А АО
Рис. 8. Рис. 9.
каждое действительное число является координатой некоторой (и притом только одной) точки на прямой I.
Этот факт (в школьном курсе алгебры не доказываемый) выражают следующими словами: установлено взаимно однозначное соответствие между всеми точками прямой I и всеми действительными числами. Вместо того чтобы сказать «точка А прямой I имеет координату х», говорят также «число х изображается точкой А». Для сокращения речи принято говорить «точка х» вместо «точка, изображающая число х». Иными словами, часто не различают число и изображающую его точку.
Прямая Z, на которой указанным способом изображаются действительные числа, называется числовой осью. Для наглядности указывают на числовой оси точки, имеющие целочисленные координаты ...—3,—2,—1, 0, 1, 2, 3, ..., и надписывают эти числа около соответствующих точек (рис. 10). В этом случае изображать на чертеже единицу измерения MN не обязательно (например, отрезок с концами в точках 0 и 1 равен единице измерения). Иногда указывают и более мелкие
66
деления (например, через каждую десятую часть единицы измерения).
Чаще всего числовую ось изображают горизонтально, причем положительным считают правый луч, а отрицательным— левый (как на рис. 10). В этом случае неравенства допускают очень простую геометрическую интерпретацию.
-4 -3 -2 -1 0 1 2 3
—----—I—--11।,--------------------»-
Рис. 10.
Именно, неравенство х1'>х2 означает, что точка хг расположена правее точки х2. Простую геометрическую интерпретацию допускает также факт, доказанный в примере 16 (стр. 62): между каждыми двумя точками числовой прямой найдется рациональная точка. Короче этот факт выражают так: множество рациональных чисел плотно на числовой прямой.
В заключение этого параграфа напомним следующую теорему, часто используемую при решении задач.
Теорема. Пусть Аг и Л2— две произвольные точки на числовой оси, хг и х2 — их координаты. Тогда расстояние между точками А! и А2 (т. е. длина отрезка Xt/12) равно | X! — х21.
Доказательство этой теоремы сводится к разбору различных случаев расположения точек Л1уи Л2 на числовой оси.
А., 0 А,
----------i-----------ч----».
Рис. 11.
Например, если точка лежит на положительном луче, а точка Л,— на отрицательном (рис. И), то хг =; ОА11, х2 =—| ОА21, и потому
Мт^21= ИгО] + 1 ОА2 ] = xi — х2.
Так как число хг— х2 в этом случае положительно (ибо хг > 0, х2 < 0), то j Хц — х2]—х1 — х2. Таким образом, |Л1Д21 = -х1— х21, т. ё. в рассматриваемом случае утверждение теоремы справедливо.
3*
67
Если же, скажем, обе точки Др А2 лежат на положительном луче, причем точка Ах расположена между О и Л2 (рис. 12), то хх = | ОА± |, х2 = |ОА2|, и потому
| АхДг I== I i°^i I== -^1== (-*1 ^-2)’
Так как число хх— х.г в этом случае отрицательно (ибо хх<х2), то | хх— х2) =— (xi— хг)- Таким образом, и в этом случае — х2 !•
О ----!------,------------,-----».
Рис. 12.
Аналогично рассматриваются другие возможные случаи расположения точек Av А2 на числовой оси.
В качестве иллюстрации мы решим «геометрически» уравнение примера 19.
Пример 20. Решить уравнение |х—1 I = | х 4- 3 |.
Решение. Число |х—1 [представляет собой, в силу сформулированной выше теоремы, расстояние между точками х и 1, а число [ х -J- 31 — расстояние между точками х и — 3. Таким образом, написанное уравнение геометрически
-3 -101
--1 --I---О----1 о-----1---о----1---1---Н»-
Рис. 13.
формулируется следующим образом: точка х находится на одинаковом расстоянии от точек 1 и —3. Иначе говоря, х — середина отрезка с концами в точках 1 и —3, т. е. х = — 1 (рис. 13).
Итак, написанное уравнение имеет единственный корень х — — 1.
§ 9. Некоторые числовые множества
Важную роль в математике играют различные множества. Например, мойгно говорить о множестве всех фигур, подобных данной, о множестве всех рациональных чисел и т. д. Мы здесь будем рассматривать только множества, составленные из чисел (их называют числовыми множествами). При-68
мерами могут служить множество всех целых чисел, множество всех рациональных чисел, множество всех корней данного уравнения и др.
Для того чтобы указать, что число х принадлежит множеству М (или, как говорят, является элементом множества М), пишут х М. Запись же х М означает, что число х не принадлежит множеству М. Например, если R означает множество всех рациональных чисел, то мы можем написать
2 (= R, -1 е У 2 R, л ^R.
Множество всех действительных чисел х, удовлетворяющих неравенствам
a'ss^x^b
(где а, b — действительные числа, причем a<Zb), называется числовым отрезком, или просто отрезком. Это множество обозначается символом [а, Ь]. Название «отрезок» объясняется
О а b
-----1-----> „ —,, —. -—и-----».
[ч.Ь]
Рис. 14.
тем, что на числовой оси это множество в самом деле изображается некоторым отрезком (жирная линия на рис. 14). Числа а, b (или изображающие их точки) называются концами отрезка [а, &]; остальные точки, принадлежащие этому отрезку, называются его внутренними точками. Например, 2 есть внутренняя точка отрезка [1, 6].
Множество всех действительных чисел х, удовлетворяющих неравенствам
a <Z х < b
(где a <. b), также изображается на числовой оси отрезком, к которому, однако, не причисляются его концевые точки. Это множество называется интервалом и обозначается символом (а, Ь).
Через [а, Ь) обозначается множество всех действительных чисел х, удовлетворяющих неравенствам asz х <^Ь, а через (а, Ь] — множество чисел, удовлетворяющих неравенствам а <; х sg: Ь. Эти множества называются полуинтервалами.
69
Они получаются из интервала добавлением лишь одной концевой точки.
Множество всех действительных чисел х, удовлетворяющих неравенству
х > а, обозначается символом (а, оо). Знак оо («бесконечность») не служит для обозначения какого-либо числа, а является лишь условным символом (оут как бы символизирует, что
О а.
--------।-----< — (С , Со)
Рис. 15.,
точки этого множества простираются вправо как угодно далеко, рис. 15). Иногда вместо неравенства a<Zx, определяющего множество (а, оо), пишут
х < оо.
Эта запись также лишь условная; обозначает она в точности то же самое, что и запись а < х.
Символами [а, оо), (— оо, а), (— оо, а] обозначаются множества, определяемые соответственно неравенствами
х^а, х <Z a, х«са.
Иногда эти неравенства (определяющие указанные множества)
записывают также в виде
а=Сх<оо, —co<2x<Za, —оо<х^а.
Множество D всех действительных чисел обозначается также символом (— оо, оо). По аналогии с рассмотренными выше случаями иногда говорят, что это множество описывается «неравенствами» —оо < х < оо.
В заключение укажем понятия объединения и пересечения множеств. Пусть М и N—два каких-либо (числовых) множества. Объединением этих двух множеств называется множество всех точек, принадлежащих хотя бы одному из множеств М, N. 'Объединение множеств М и N обозначается символом (J. Например,
(2,4) U (3,5) = (2,5)
70
(рис. 16). Далее, множество [1, 3] (J [4,5] «состоит» из двух отдельных отрезков (рис. 17), а множество [1, 3) (J (3,5] представляет собой отрезок [1, 5], из которого удалена («выколота») точка 3. Пользуясь знаком эквивалентности «->
О 2 Ь
С з . —
О 3 5
н-------------,-----» । >
(3,5)
О 2~ 5
------।-------с > I. >
(2,5)
Рис. 16.
О I 3
[1.3]
4 5
О ' / __________3 4 5
4 ' [1,3] U Ь~5]
Рис. 17.
и знаком дизъюнкции V (стр. 30), мы можем следующим образом записать определение объединения множеств:
(х е Л1 |J;V)«(.г е Л1) \/ (х е N).
Пересечением двух множеств М vi N называется множество всех тех точек, которые принадлежат обоим множествам М, N. Пересечение множеств М и 'N обозначается символом М (1N. Например,
(1,3]П[1,3)=(1,3), (О, оо) (—1, 3] =(0, 3].
С помощью знака конъюнкции Д можно следующим образом записать определение пересечения множеств:
(х €= М П N) «-> (х е М) Д (х е AZ).
71
Можно рассматривать также объединение (или пересечение) трех и большего числа множеств. Например, объединение A1UNIJP состоит из всех тех точек, которые принадлежат хотя бы одному из множеств М, N, Р.
Пример 21. Найти область определения функции
2х+5
•У ~ (x-f-1) (х—3) ’
Решение. Эта функция определена во всех точках, не являющихся корнями знаменателя. Иначе говоря, областью определения этой функции является множество всех действительных чисел, кроме х =—1 и х=3. Эту область определения можно записать в виде
(— оо, ^1) U (-1,3) U (3,оо).
Пример 22. Найти область определения функции j/ = ]/'2 — x-f-lgx.
Решение. Первое слагаемое в правой части представляет собой функцию, определенную при условии 2 — х^О, т. е. при х sj; 2. Иными словами, областью определения функции У"2 — х является множество (—оо, 2]. Второе слагаемое
о г
•..—"I "I" I I--------------1 1->—
(~ОО,2] -
О 2
---I---------» I I -Н I I >
(0,оо)
О 2
Рис. 18.
определено при х>0, т. е. областью определения функции 1g х является множество (0, оо). Наконец, заданная нам функция _у = ’|/'2— хЦ-lgx определена для всех тех х, для которых определено и первое, и второе слагаемое, т. е. для тех х, которые принадлежат как области определения функции J/2 — х, так и области определения функции 1g х. Иными 72
словами, область определения заданной функции представляет собой пересечение областей определения функций У2— х и Ig х. Таким образом, искомая область определения имеет вид (— со, 2] р (0, со) = (0, 2] (рис. 18).
Задачи к главе II
2.1. Вспомните правило обращения периодических десятичных дробей в обыкновенные и запишите дробь 1, 333... = =1,(3) в виде обыкновенной дроби.
2.2. Докажите, что У3 есть число иррациональное.
2.3. Докажите, что число У5—У2 иррационально.
2.4. Обладают ли операции вычитания и деления свойствами коммутативности и ассоциативности?
2.5. Может ли сумма рационального и иррационального чисел быть числом рациональным?
2.6. Может ли сумма двух иррациональных чисел быть рациональным числом?
2.7. Может ли произведение двух иррациональных чисел быть рациональным числом?
2.8. Выведите правило обращения бесконечной периодической десятичной дроби в обыкновенную.
2.9. Докажите, что любое рациональное число может быть представлено в виде бесконечной периодической десятичной дроби.
2.10. Докажите, что множество иррациональных чисел плотно на числовой прямой, т. е. что между любыми двумя неравными действительными числами имеется иррациональное число.
2.11. Докажите, чго число 0,101001000100001... (в котором после запятой записаны подряд числа 10,100,1000,...) является иррациональным.
2.12. Докажите, что число 0,1101000100000001... (в котором единицы стоят на 1-м, 2-м, 4-м, 8-м, ..., 2"-м, ... ... местах) иррационально.
2.13. Пусть п — любое целое число, удовлетворяющее
неравенствам 0<;п<;73. Запишем рациональное число ~
I о
в виде бесконечной десятичной дроби:
П п
73 = О, аха2а3 ...
Докажите, что в этой записи не содержится после запя той двух рядом стоящих одинаковых цифр.
73
Найдите {не используя таблиц) приближения с точностью до 0,1 следующих иррациональных чисел (2.14—2.17):
2.14. 2.15. /246. 2.16. /5. 2.17. V1.
4-/15
2.18. Найдите первые три цифры десятичного разложения числа
0,1234... 31
0,3130 ...21
(где в числителе стоят после запятой выписанные подряд числа 1, 2, 3, ..., 31, а в знаменателе — числа 31, 30,..., 2, 1).
2.19. Вычислите 200 знаков (после запятой) десятичного разложения числа
1
1,00...0 1
99 цифр
2.20. Вычислите 100 знаков (после запятой) десятичного разложения числа
у 0,99... 9.
100 цифр
2.21. В числе 0,1234567891011... 30 вычеркнуть после запятой 47 цифр так, чюбы полученное число было наименьшим.
2.22. Докажите, что неравенство | а | < b эквивалентно соотношениям —b<Za<zb.
2.23. Докажите, что для любых действительных чисел а, b справедливо неравенство
| а + b\ j | a j — I b 11.
2.24. Для каких действительных х справедлива формула 1g х2 = 2 1g х?
2.25. Для каких действительных х справедлива формула
lg х2 = 2 1g | х|?
Упростите следующие выражения (2.26—2.29):
2.26. У(1 — cos a cos |3)2— sin3 a sin2 (3.
2.27. ]/~а 2 ]/а— 1 а — 2 ’/а — 1 при а 1.
74
«ПО Vv2+l+Vx2-l V 1/ a2 + i2
. 2-28- при yc"’4T0 X==V ~^T
и ab > 0.
2.29.
/х2—1
при условии, ЧТО X —
М/т+]/'!)
и ab > 0.
Решите следующие уравнения (2.30—2.33): 2.30. I х I =,г. 2.31. | 2х - 1 | = 3.
2.32. । |х| 4- 3| = 3. 2.33. |х + 3| = !.г — 5 | J
Решите следующие неравенства (2.34 — 2.37):
2.34. |х— 1 |>|х + 3|. 2.35. |х|<1.
2.36. |х —3| ^2. 2.37. | х—1 12= 3.
ГЛАВА III
НЕРАВЕНСТВА
§ 1. Определения
Все действительные числа разбиваются на положительные числа, отрицательные числа и число нуль. Для того чтобы указать, что число а положительно, пользуются записью а >0.
Напомним (см. свойство Г) на стр. 60), что сумма и произведение положительных чисел также являются положительными числами. Далее, если число а отрицательно, то число — а положительно (и наоборот). Наконец, для любого положительного числа а найдется такое положительное рациональное число г, что г < а. Эти факты и лежат в основе теории неравенств.
По определению неравенство ау>Ь (или, что то же самое, b < а) имеет место в том и только в том случае, если а — b~y>Q, т. е. если число а — b положительно.
Рассмотрим, в частности, неравенство а <; 0. Что означает это неравенство? Согласно приведенному выше определению оно означает, что 0 — а>0, т. е. — а>0 или, иначе, что число — а положительно. Но это имеет место в том и только в том случае, если число а отрицательно. Итак, неравенство а < 0 означает, что число а отрицательно.
Часто используется также запись а>-.Ь (или, что то же самое, b а). Запись асмЬ, по определению, означает, что либо аУ>Ь, либо а = Ь. Если рассматривать запись ау~.Ь как высказывание, то в обозначениях гл. I (стр. 30) можно записать
(a Ss b) ++ [(а > b) V (а = #)].
В связи с употреблением знака учащиеся нередко допускают следующую ошибку. Дав правильное объяснение этого знака, они на вопрос: «Верны ли неравенства 5>И), 0с>0?» иногда отвечают так: «Нет, эти неравенства написаны неверно, а верными будут соотношения 5 > 0, 0 = 0».
76
Еще раз подчеркнем, что такой ответ является ошибочным. Неравенство аЭ=0, по определению, означает, что либо а>0 (т. е. а — число положительное), либо а — 0. В частности, соотношение 5 5а 0 надо понимать так, что имеет место одно из двух: либо 5 > 0, либо 5 = 0. В данном случае имеет место первая возможность (5 > 0), т. е. соотношение 5g>0 — верное. Аналогично обсуждается запись 0 5а0.
Неравенства вида а > b, a <Z b будем называть строгими, а неравенства вида a^b, а---Ь— нестрогими. Неравенства а^>Ь и c>d (или a<Zb и с<rf),будем называть неравенствами одинакового смысла, а неравенства a<Zb и c^>d — неравенствами противоположного смысла. Отметим, что эти два термина (неравенства одинакового и противоположного смысла) относятся лишь к форме записи неравенств, а не к самим фактам, выражаемым этими неравенстами. Так, по отношению к неравенству а < b неравенство c<Z.d является неравенством того же смысла, а в записи d^> с (означающей то же самое) — неравенством противоположного
смысла.
Наряду с неравенствами вида а^>Ь, а>-Ь употребляются так называемые двойные неравенства, т. е. неравенства вида a<Zc <ib, a^c<Zb, а <^с b, а аС сгС b. По определению
запись
а < с < b
(О
означает, что имеют место оба неравенства:
а < с и с < Ь.
Аналогичный смысл имеют неравенства а<:, с '^..Ь, а~<с <Cb, а<^с<_,Ь.
Двойное неравенство (1) в обозначениях гл. 1 можно
в эквивалентной форме записать так:
(а < с < Ь) «-> (а < с) Д (с < Ь),
а двойное неравенство as^cs^b можно записать в следующем виде:
(а с sg Ь) [(а < с) V (а = с)] Д [(с < Ь) \/ (с = £)].
Перейдем теперь к изложению основных свойств и правил действий над неравенствами.
77
§ 2. Основные свойства неравенств
Всюду в этом параграфе буквы а, Ь, с обозначают действительные числа,’ а п означает натуральное число.
1) Если а>Ь и Ьу> с, то а> с (транзитивность).
Доказате л ьс1 во. Так как по условию а > b и b > с, то числа а — b и b—с положительны, и, следовательно, число а — с = (а— й)-ф(/т— с), как сумма положительных чисел, также является положительным. Это означает, по определению, что а > с.
2) Если a Z>b, то при любом с имеет место неравенство а с у> b --- с.
Доказательство. Так как а)>Ь, то число а — b положительно. Следовательно, число (а-фс)— (£>-фс) = а— b также является положительным, т. е. a -ф с > b -ф с.
3) Если а-)-Ь^>с, то а^>с — Ь, т е. любое слагаемое можно перенести' из одной части неравенства в другую, изменив знак этого слагаемого на противоположный.
Доказательство вытекает из свойства 2) (достаточно к обеим частям неравенства а + Ь^>с прибавить число —Ь).
4) Если а~у>Ь и cy>d, то а-)- с >b d, т. е. при сложении двух неравенств одного и того же смысла получается неравенство того же смысла.
Доказательство. В силу определения неравенства достаточно показать, что разность (я-фс)— (b-)-d) положительна. Эту разность можно записать следующим образом:
(а -ф с) — (Ь -ф d) — (а — Ь) -ф (с — d).
Так как по условию числа а — b и с — d положительны, то (а-фс) — (b-\-d) также есть число положительное.
Следствие. Из правил 2) и 4) вытекает следующее правило вычитания неравенств: если ay>b, c~y>d, то а — d~y> У>Ь — с (для доказательства достаточно к обеим частям неравенства а-фс>й-ф<7 прибавить число —с — d).
5) Если а)>Ь, то при с > 0 имеем ас > Ьс, а при с < О имеем ас < Ьс.
Иначе говоря, при умножении обеих частей неравенства на положительное число знак неравенства сохраняется (т. е. получается неравенство того же смысла), а при умножении на отрицательное число знак неравенства меняется на противоположный (т. е. получается неравенство противоположного смысла).
78
Доказательство. Если a>b, то а—Ь есть число положительное. Следовательно, знак разности ас — Ьс — = с (а — Ь) совпадает со знаком числа с: если с — положительное число, то и разность ас — Ьс положительна и потому ас~>Ьс, а если с<0, то эта разность отрицательна и потому Ьс — ас положительно, т. е. ЬсУ>ас.
6) Если ау>Ь>0 а с > г/ > О, то ас > bd, т. е. если все члены двух неравенств одинакового смысла положительны, то при почленном умножении этих неравенств получается неравенство того же смысла.
Доказательство. Имеем ас — bd = ac — bc-\-bc — — bd = c(a — b)-]-b(c — d). Так как с>0, Ь>0, а — />>0, с — d^>0, то ас — bd^>0, г. е. ac>bd.
Замечание. Из доказательства видно, что условие d > 0 в формулировке свойства 6) несущественно: для справедливости этого свойства достаточно, чтобы были выполнены условия a^>by>Q, cy>d, с > 0. Если же (при выполнении неравенств a У>Ь, c~y>d) числа а, Ь, с не будут все положительными, то неравенство ас bd может не выполняться. Например, при а = 2, Ь=\, с ——2, d ——3 имеем а > b, cy>d, но неравенство ас > bd (г. е. — 4 > — 3) не выполнено. Таким образом, требование положительности чисел а, Ь,- с в формулировке свойства б) существенно.
7) Если aycb>Ci и с > <7 > 0, то (деление
7 а с v
неравенств).
Доказательство. Имеем
а b __ас — bd
de cd '
Числитель дроби, стоящей в правой части, положителен (см. свойства 5), б)), знаменатель также положителен. Следовательно, —^>0. Этим свойство 7) доказано.
Замечание. Отметим важный частный случай правила 7), получающийся при а — Ь=1: если cy>dy>0, то Таким образом, если члены неравенств положительны, то при переходе к обратным величинам получаем неравенство противоположного смысла. Предлагаем читателям проверить, что это правило сохраняется и в том случае, когда c<zO, d<zO. Таким образом, если с>(7 и cd>0, то
79
— <"-4 Если же c>(Z, но cd < 0 (т. е. с>0, (Z<"0), то с a v '
1->£ с d
Мы доказали выше несколько свойств неравенств, записанных с помощью знака > (больше). Однако все эти свойства можно было бы формулировать с помощью знака <; (меньше), так как неравенство b < а означает, по определению, то же самое, что и неравенство а > Ь. Кроме того, как это нетрудно проверить, доказанные выше свойства сохраняются и для нестрогих неравенств. Например, свойство 1) для нестрогих неравенств будет иметь следующий вид: если а -b и by. с, то а'угс.
Разумеется, сказанным выше не ограничиваются общие свойства неравенств. Существует еще целый ряд неравенств общего вида, связанных с рассмотрением степенной, показательной, логарифмической и тригонометрических функций. Общий подход для написания такого рода неравенств заключается в следующем. Если некоторая функция y=f(x) монотонно возрастает на отрезке [а, Ь], то при x1y>xi (где хг и х2 принадлежат этому отрезку) мы имеем /(xi)>/(х2)- Аналогично, если функция y=f(x) монотонно убывает на отрезке [a, b\, то при хх>хг (где xt и х2 принадлежат этому отрезку) мы имеем f(x1)<Zf(x2). Разумеется, сказанное не отличается от определения монотонности, но для запоминания и написания неравенств этот прием очень удобен.
Так, например, для любого натурального п функция у = = хп является монотонно возрастающей на луче [0, оо). Поэтому мы можем сформулировать следующее общее свойство неравенств:
8) Если аУ>Ьу^0, то ап~У>Ьп (где п — натуральное число).
Далее, функция у — х‘2п+х является (при любом натуральном п) возрастающей на всей числовой прямой. Иначе говоря, справедливо следующее свойство:
9) Если ау> Ь, то а2п+} (где п — натуральное
число).
Отметим один частный случай этого свойства, часто применяемый при доказательстве неравенств (он получается при п = 1): если а~у>Ь, то а3 > Ь3.
Наконец, заметим, что если некоторая функция является возрастающей, то и обратная ей функция является возрастаю-80
Л г— щей (подробнее см. ниже, стр. 213). Поэтому функция у=у х
_ 2/г-р I ,—
возрастает на луче [0, со), а функция _у = ух возрастает на всей чибловой прямой. Это позволяет сформулировать следующие свойства неравенств:
10) Если а^>Ь^0, то у а > у b (где п— натураль-ное число).
2п~]~ 1 г— 2п-\-1/~у~
11) Если а>Ь, то у а > уЬ (где п— натурам-ное число).
Следствие. Неравенство а2 > Ь2 имеет место в том и только в том случае, 'если | a j > I b i.
В самом деле, если а2^>Ь2, то мы можем написать а2> > Ь2 1?; 0, и потому, в силу свойства 10), имеем
т. е. । а I > I b j. Обратно, если ] a j > | b |, т. е. ]Ат2 > Уь2, то мы можем написать У а2 > У Ь2 0, и потому, в силу свойства 8), имеем (р^а2)2 > т. е. a2Z>b2.
Еще раз подчеркнем, что рассуждения о монотонности функций, с помощью которых мы написали здесь свойства 8)—11), не являются доказательствами этих свойств. Наоборот, лишь после того, как свойство 8) будет доказано, мы можем говорить о монотонности функции у = хп на луче [0, оо) (и аналогично для свойства 9)). О доказательстве свойств 8)—И) мы будем говорить в гл. VIII при рассмотрении свойств степенной функции.
Подобным образом можно написать и ряд других неравенств. Так, поскольку функция у = сх является при с>1 возрастающей на всей числовой прямой, то при с > 1 и а > b справедливо неравенство са >> сь. Если же 0 <; с < < 1, то при a Z> b справедливо неравенство (т. е. при
0 < с <Z 1 функция у = сх является убывающей). Об этих неравенствах мы также будем говорить в гл. VIII.
Еще один пример. Так как функция _y = sinx является [JT JT ]
— ”2’ Т монотонно возрастающей, то при а >
> Ь, где а и b принадлежат отрезку спра-
ведливо неравенство sin а > sin b.
В дальнейшей части этой главы мы при рассмотрении примеров не будем пользоваться показательными, логарифмическими и тригонометрическими неравенствами, а ограничимся использованием перечисленных выше свойств 1)—11). Для удобства приведем здесь сводку этих свойств (знак Д
§1
заменяет союз «и», а знак -> заменяет слово «следует», ср. стр. 30 и 22):
1) [(а>&)Л(&>О]-*(«>0;
2) (а > Ь) -> (а 4- с > b + с)-,
3) (а 4- b > с) -> (а > с — Ь);
4) [(а > ft) Д (с >(/)]-* (а + с > ft + </);
5) [(а > ft) Д (с > 0)] -> (ас 2> Ьс),
[(а > ft) Д (с < 0)] — (ас < Ьс);
6) [(а > ft > 0) Д (с > d > 0)] —► (ас > bd);
7) [(а^&>0)Д(С>с?>0Я->(|>|]:
8) (а > ft 2s 0) (ап > Ьп);
9) (а > ft) -> (а2”’'1 >. ft2ra + ’);
10) (а > ft 2г 0) -> (у a>Vb\ Пп+Л .------------- 2/1+1Л—X
11) (а > ft) -> \ а > ).
§ 3. Некоторые часто встречающиеся неравенства
1) Для любых действительных чисел а и b выполняется неравенство
а2 + Ь-^-2аЬ. (2)
Доказательство. В силу определения неравенства достаточно показать, что разность между левой и правой частями неравенства (2) есть неотрицательное число. Эта разность равна
а2 2аЬ -[-Ьъ = (а — ft)2.
Так как квадрат любого действительного числа есть число неотрицательное, то (а — Ь)21>=0, и неравенство (2) доказано. Из доказательства видно, что равенство в соотношении (2) имеет место в том и только в том случае, если а = Ь.
Замечание. Справедливо и более сильное неравенство
- a24-ft22s2|aft|. (3)
Неравенство (3) вытекает из следующего неравенства:
(| а | — | ft | )2 2г 0.
2) Если a it ft — действительные числа одного знака (т. е. аЬД>0), то 1
f + (4)
82
Доказательство. Умножив обе части неравенства (2) на положительное число получим, в силу свойства 5), неравенство (4). Как и в предыдущем примере, равенство в соотношении (4) имеет место в том и только в том случае, если а = Ь.
3) Если а As 0 и b 2s 0, то
О)
т. е. среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического.
Доказательство. Первый способ (алгебраическое доказательство). В силу правила умножения на положительное число (свойство 5)) неравенство (5) имеет место в том и только в том случае, когда
а + b — 2 ]/ab О,
или
(У а — У b)2ss0.
(6)
Так как в левой части (6) стоит квадрат действительного числа, то неравенство (6) справедливо, а следовательно, справедливо и неравенство (5).
Замечание. Из этого доказательства видно, что равен-
ство в (5) имеет место тогда и выполняется в (6), т. е. когда (У а—]/У)2 = 0, а это возможно лишь при а—Ь.
Второй способ (геометрическое доказательство). Если хотя бы одно из чисел а, b равно нулю, то неравенство (5) очевидно. Будем поэтому предполагать, что а > О, й>0. Пусть АВ и ВС — смежные
только тогда, когда оно
а
отрезки прямой, имеющие длины
соответственно а и b (рис. 19). На отрезке АС длины
как на диаметре построим окружность; центр этой окружности обозначим через О. Если D — точка пересечения окружности с перпендикуляром, восставленным к прямой АС в точке В, то (по известной теореме планиметрии) BD = У ab. Далее, OD~^A~ и, очевидно, BDszOD, т. е. У ab^a. Из
83
этого доказательства также видно, что равенство имеет место лишь при а = Ь.
4) Неравенство
\а\<Ь (7)
имеет место тогда и только тогда, когда выполняется следующее двойное неравенство-.
— Ь<^а<[Ь. (8)
Доказательство этого факта было приведено на стр. 64. Здесь мы дадим другое доказательство. Пусть имеет место неравенство (7). Если а^О, то |a| = a и неравенство (7) можно записать так: 0=Са</?. Так как by>0, ays О, то — ^<0sga. Следовательно, —b<Za<Zb, т. е. выполняется двойное неравенство (8). Аналогично рассматривается случай а < 0.
Обратно, пусть имеет место двойное неравенство (8). Если asgjO, то |а| = —а и неравенство (7), которое нам надо доказать, принимает вид — а < Ь. Но из (8) следует, что —Ь<^а, откуда и вытекает требуемое неравенство — а < Ь.
Случай а > 0 рассматривается аналогично.
Замечание. Полученный результат легко объяснить геометрически. Пусть имеет место двойное неравенство (8). Тогда -^-Ь<.Ь, т. е. &>0. Отметим на числовой оси точки b, — b и а (рис. 20). Так как b > 0, то точка b лежит на
ь
0 +
Рис. 20.
положительном луче, а точка — b лежит на отрицательном луче. Двойное неравенство — b <Z a <yb означает, что точка а находится на числовой оси между точками —b и Ь. Следовательно, расстояние от точки а до точки О (это расстояние, как известно, равно | а |) меньше Ь, т. е. | а | < Ь. Таким образом, из двойного неравенства (8) вытекает (7). Аналогично можно геометрически показать, что из (7) вытекает (8).
5) Для любых действительных чисел а и b выполняются неравенства-.
а) | а + b | | а | -f-1 b |, (9)
84
т. e. абсолютная величина суммы двух действительных чисел не превосходит суммы абсолютных величин этих чисел',
б) |а — — | b 11. (10)
Доказательство. Неравенство (9) было установлено ранее (стр. 64).
Докажем неравенство (10). Имеем
| а | =) (а — Ъ) 4- b j -1 а — b | 4-1 b |
(в силу (9)), откуда
| а — b | 2s | а | — | b |. (И)
Аналогично, из неравенства
\Ь | = | (Ь — а) 4- а | \Ь — а | 4~ | а | — ] а — /?|4_1а1
находим
[я — —I а I- (^2)
Из (И) и (12) следует:
— | а — b | -1 а | b | '' | а — Ь\,
откуда и вытекает неравенство (10).
Замечание. Методом математической индукции неравенство (9) можно доказать для любого числа слагаемых:
I «14- а2 + • • • + ап I ) ai j 4" | я214-... 4-1 ап |.
§ 4. Примеры
В этом параграфе мы рассмотрим решение нескольких типичных задач на доказательство неравенств. Заметим, что общего метода доказательства неравенств не существует. Иногда нужный результат можно получить, исходя из определения, т. е. из рассмотрения разности между левой и правой частями неравенства; иногда полезным оказывается использование некоторого известного неравенства или оценка левой и правой частей неравенства.
Отметим одну довольно распространенную ошибку, которую допускают учащиеся (и поступающие в вузы) при решении задач на доказательство неравенств. Учащийся пишет неравенство, которое нужно доказать, затем производит ряд преобразований и в конце концов приходит к известному неравенству (скажем, — 1 < 0 или я2 0); после всего этого
85
учащийся делает вывод: «Требуемое неравенство доказано». Это — грубая логическая ошибка.
Вот как, например, «доказывают» некоторые учащиеся справедливость для неотрицательных чисел а и b неравенства
(3)
«Возведем обе части неравенства (5) в квадрат. Получим (—g—I ab. J множив обе части полученного неравенства на 4, найдем (а~-Ь^ >:ЛаЬ. Теперь, перенося все члены в левую часть неравенства, получаем (а — Ь)22э0. Так как неравенство (а — Ь)2-:--0 верно, то верно и неравенство (5)».
Рассуждение, которое привел в этом случае учащийся, следует рассматривать лишь как поиск доказательства, как попытку найти путь доказательства. Если обозначить неопределенное высказывание, выражаемое неравенством (5), через А, а неравенства ^ab, (а+ /?)2 2s 4 а/?, (а — /?)22а0 обозначить соответственно как высказывания В, С, D, то рассмотренное выше рассуждение учащегося можно выразить в виде следующего соотношения:
Справедливость этих заключений вытекает из свойств 8), 5) и 3) неравенств (см. стр. 82). Таким образом, с помощью приведенного выше рассуждения установлено, что А -> D, т. е. что из неравенства (5) следует неравенство (а — /т)2>10.
Чтобы доказать справедливость неравенства (5), нужно провести все рассуждения в обратном порядке, т. е. доказать, что справедливы следующие заключения:
D -> С -> В -> А.
В рассматриваемом примере справедливость этих заключений нетрудно обосновать с помощью свойств 3), 5) и 10) неравенств.
Значит, проведя сведение доказываемого неравенства к некоторому известному неравенству, нужно затем обязательно проверить, проходят ли все рассуждения в обратно^ порядке. Впрочем, если при выполнении каждого преобразования мы каждый раз убеждались, что вновь полученное неравенство эквивалентно предыдущему, т. е. выполняется тогда и только тогда, когда выполняется предыдущее, то проводить рассуж-86
дения в обратном порядке не нужно. В данном примере это обстоятельство действительно имеет место, т. е.
A^B^C^D,
откуда следует, что неравенство (5) для неотрицательных чисел а и b выполняется в том и только в том случае, когда выполняется неравенство (а — &)2>;0. Так как (а — /?)25s0— верное неравенство, то неравенство (5) доказано.
Итак, если неравенство, которое нужно доказать, мы заменяем последовательно другими неравенствами, то либо на каждом шаге нужно проверять, что получаемое неравенство эквивалентно предыдущему (г. е. имеет место в том и только в том случае, когда справедливо предыдущее неравенство), либо же, если это не сделано, нужно обязательно проверить, проходят ли все рассуждения в обратном порядке.
Пример 1. Доказать, что для любых действительных чисел а и b имеет место неравенство а4 Д- М а3Ь 4- at?.
Решение. Разность между левой и правой частями неравенства можно записать так:
о4 + й4 — (а3/> + ab3) = а\а — Ь) — Ь3(а — Ь) =
= (а — Ь)(а3 — Ь3) — (а — Ь)2(а2 -{-аЬ-{- Ь2).
Эта разность неотрицательна, так как
(a — £)2SsO, a2-\-ab + b2 = (a 4-yf4--|z?2SsO.
Пример 2. Доказать, что при любом целом п > 1 выпол-1 , 1 । , 1 о
няется неравенство ——г4-----rs + ’-To—г-г<2.
г «+1 и+2 ' ' Зи4~1
Решение. В рассматриваемом примере достаточно грубо оценить левую часть . неравенства. Заметим, что сумма двух последних слагаемых левой части неравенства не превосхо-1 дит —, так как
±4__1_<±4.1 = 1
Зп ' Зи + 1 2п ' Чп п '
Каждое из оставшихся слагаемых левой части неравенства меньше —, а число этих слагаемых равно 2л—1. Следова
тельно,
«4-1 «4~ 2
+-...4-о-т-г< (2«—1)-4-~ = 2. 1 Зп 4-1 ' п 1 п
87
Пример 3. Доказать, что для любых действительных чисел а, Ь, с имеет место неравенство
а2 + Ь2 + с2 ab 4- Ьс + ас.
Решение. В силу неравенства (2) (стр. 82) мы можем написать следующие неравенства:
a2-j-b2>:2ab, b2 4- с2 2Ьс, с2 4- а2 2ас.
Сложив эти неравенства, а затем разделив обе части полученного неравенства на 2, приходим к- нужному неравенству.
Пример 4. Доказать, что если а, Ь, с — положительные числа, то
Ьс . ас , ab ,
а 1 Ь 1 с 1 1
Решение. На основании доказанного выше неравенства для среднего арифметического и среднего геометрического двух положительных чисел (неравенство (5) на стр. 83) мы можем написать
Аналогично
Складывая эти неравенства, получаем
Ьс .ас . ab.
а 4- b 4- с.
Пример 5. Доказать, что если а^эО, Ь'^0, с^О, то (а 4- Ь) (Ъ 4- с) (а 4- с) 8abc.
Решение. Снова воспользуемся неравенством для среднего арифметического и среднего геометрического двух чисел. Мы имеем
Перемножив эти неравенства (свойства 5) и б)), мы и получим требуемое неравенство.
Пример 6. Доказать, что если а, Ь, с— неотрицательные числа, то
а3 4- b3 4- с3 Заде.
Решение. Используя тождество
а3 4- Ь3 4- с3 — ЗаЬс = (а 4- b 4- с) (а2 4" Ь2 4- с2 — ab — Ьс — ас)
и неравенство примера 3, мы и получаем нужное неравенство.
Пример 7. Доказать, что для любых неотрицательных чисел ох, д2, а3, а4 имеет место неравенство
Решение. Снова воспользуемся неравенством (5) (стр. 83). Имеем
У + у а3а4 _ ]/ ---- -.г---- 4,------------
------у-1—2—I у а}а2- у а3а4 — у а1а2а3а4.
§ 5. Два замечательных неравенства
Неравенство для среднего арифметического и среднего геометрического «неотрицательных чисел (неравенство Коши). Если av а2, ..., ап— любые неотрицательные числа, то
^.±^±а^П/й1ц2...ця. (13)
Равенство имеет место лишь при а1 = а2 = .. . — ап.
Доказательство. При /г = 2 неравенство (13) справедливо (см. неравенство (5) на стр. 83). Пусть неравенство (13) верно при п = т; тогда оно будет верным и при п=2т. Действительно,
а14~а2 । аз4~а4 , , а2т-1 ~Уа2т
а1~Уа2~>г- ,.-![-а2т __ 2 2 2
2m т
-Г/ fll + fl2 аз + а4 а2тЛ~~а1т ~ 7,
I/ 9 к • • • 9 == У и}а2 ... а2т.
89
(Мы использовали неравенство (5).) Так как неравенство (13) имеет место при га = 2, то оно будет выполняться для га = 4, 8 и т. д., т. е., вообще, для всякого га = 2Р(р = 1, 2, ...).
Пусть теперь га —произвольное натуральное число. Если га^2Р, то найдем такое натуральное число s, что ra-[-s = 2P. Тогда для любых неотрицательных чисел alt а2, ..., a„+s, согласно доказанному, справедливо неравенство
ai + a2 + -- - + an + an-n + -- -+ ttn+s р + --ТГп------п
-------------,>_ s.-------------Г а1“2 • • • “п«я+1 • • “ra+s-
Положив в этом неравенстве
ai 4* °2 4“ • • 4~ ап an+i = ап+2 =... = a„+s =-------------,
получим
Й1 + а2 +... + ап +
ZZ Н- к
>Пл/~аа а Iа1 + «2 4- 4-«л7
Ss у а1аг...ап^ -J ,
-|~Я2 4" • • • ^Гап я
откуда, обозначив ----!—~Ап, найдем
П-Ьу------------;
Ап^ V аха2...ап Ап.
Возводя обе части последнего неравенства в степень (свойство 8)), найдем
откуда после умножения на (Лл)~5 (свойство 5)) получим (АпУ^а^ ...ап.
Наконец, извлекая корень га-й степени (свойство 10)), найдем
. я-------------tz, —йл -4-... —ац п ---------
Ап у О1«2 ••• ап, или -LJ—---------1—" у- Я1а2 ... ап.
Таким образом, неравенство (13) доказано для любого га.
Покажем, что в (13) равенство имеет место в том и только в том случае, если а1 = а2 = ... = ап.
Ясно, что если а1 = а2 = ... = ап, то соотношение (13) превращается в равенство. Докажем, что если хотя бы два из чисел аг, а2, , ап не равны между собой, то в (13) левая и правая части
не равны между собой. Пусть, например, Тогда
fli4~Q2 4~ • • 4~а« га
Q14~a2 I а14~П2 2 2
га
4-а34-
90
Но так как ахфа2, то — > V aja2 (см. замечание к неравен-
ству (5), стр. 83). Следовательно, если все числа а3, ..., ап положительны, то
п
a3...art>^a1a2...«rt
и потому
пГ'
(14)
...а,
бы одно из чисел
то
Если же хотя ство (14) также, очевидно, справедливо.
Неравенство Коши — Б у н я к о в ск о г о. Для любых действительных чисел аь а2..........ап, bv b2, ..., Ьп
выполняется неравенство
(aybi + а2Ь2 + • • • + anbn)2 «S
(ai 4- at 4- • • • 4" ап) (^i 4~ 4~ • • • 4~ 0 э)
Равенство в (15) имеет место тогда и только тогда, когда числа ak и bk пропорциональны, т. е. когда существуют такие числа а и (3, что а2О и для всех k=l, 2, п выполняется равенство
aafe4-pz?fe = 0.
Доказательство. Если — а2 = .. . = ап = 0, то в (15) имеет место равенство. Пусть теперь хотя бы одно из чисел alt а2...............ап
отлично от нуля, т. е. a24-а24~’••4~ая > 0. Рассмотрим выражение (clx + &1)2 + (a’2x + &2)2 + --- + (ortx4-&„)2. Это выражение можно записать так:
(<ЛЯ ~Ь ^i)2 + (а2х Ь2)- 4~ • • • ~Ь (апх + b Л2 — ox2 -j- 2bx у-с, (16)
где
a = aj’ +и.24--b — a1b1 -La2ft2-L... -\-anbn, с = b2 + Ь.2 4-• • 4* Ья
(17)
Левая часть равенства (16) при любом действительном значении х неотрицательна, так как она представляет собой сумму квадратов действительных чисел (числа сц, а2, ..., ап, Ьг, Ь2, ..., Ьп по условию действительны). Следовательно, и правая часть равенства (16) неотрицательна при любых действительных значениях х, т. е. квадратный трехчлен ах2у2Ьху-с принимает неотрицательное значение при любом х. Из этого вытекает, что дискриминант трехчлена ах2-\-2Ьху-с неположителен: 4Ь2 — 4лс;<0, откуда
Ь2^ас. (18)
91
Подставляя в (18) выражения для а, Ь, с из (17), получаем
+ а2&2 +... + anbn)2 (а2 + а* -]-+ ал) (fci + + • • + &«)•
Неравенство (15) доказано.
Выясним теперь, в каком случае в (15) имеет место знак равенства. Пусть в (18) имеет место случай равенства, т. е.
&2 = ас. (19)
Если а = 0, т. е. а1 = а2 = --- = ап = 01 то, положив а=1, (3 = 0 (так что а2 + |32>0), мы получим ocafeр&д. = 0 при k=l , 2, ..., п. Пусть теперь а^£0. Тогда дискриминант квадратного трехчлена ах2-\-2Ьх-^-с равен нулю, так что этот трехчлен имеет два совпадающих действительных корня: х1 = х2. Мы имеем
(aixi 4* ^i)3 4* (fl2xi 4* b2)2 +.. •4-(аяА:14-Ьл)3=ах( -\-2Ьх1-^-с = 0.
Но это возможно лишь в том случае, если все выражения, стоящие в скобках в левой части, обращаются в нуль:
a*xi + ^* = 0 (£=1, 2, ..., п).
Положив а = хх, (3 = 1, мы сможем записать эти равенства в виде oca* + pft* = 0 (£=1, 2, ..., п). (20)
При этом [1 ф 0, так что «2 — р2>0.
Итак, если в (15) имеет место знак равенства, то существуют такие числа ос и [3, хотя бы одно из которых отлично от нуля, что справедливы равенства (20). Легко проверить, проводя рассуждения в обратном порядке, что при выполнении равенств (20) соотношение (15) превращается в равенство.
Задачи к главе III
3.1. Докажите следующие утверждения:
1. [(а 2s Ь) Д (Ь > с)] -> (а > с).
2. [(а 2= Ъ) Д (Ь 2s с)] -> (а с).
3. {а Ь) —> (а с Ь 4- с).
4. [(а Ь) А (е 5== d)] -> (а 4- с b 4- d).
5. [(а 2s b) А (с > <01 (а 4~ с > b 4- d).
6. [(а Ь) А (с 0)] -> (ас Ьс).
7. [(а Ь) А (с sg 0)] -> (ас sg be).
8. [(а b 5s 0) A (cg-rf >б))| ->• (ас 5: bd).
9. [(а 5^ Ь > 0) А (с > d 5s 0)] -> (ас > bd).
10. (й 5^ 5s 0) (а" ::-Л-
11. (а 5= ^)-> (а2'!+! 5s^2" + 1)-
3.2. Докажите, что двойное неравенство a sg с <; b можно записать в виде
(agc<i)«[(a<c) V (a = c)J А (с <Ь).
92
3.3. Докажите неравенство ? 2 (где а — произ-
вольное действительное число).
3.4. Докажите, что для любых действительных чисел а, Ь, с имеют место неравенства:
1. а2 4- № -J- 1 За ab 4~ a 4- Ь.
2. 5а2 — 6аЬ4-5Ь2=>0.
3. (а24-Ь2)(а44-Ь4)^>(а34-Ь3)2.
3.5. Докажите, что если a b с ssz d и b-\-c — a-yd, то be ad.
3.6. Докажите, что если —2=g;asg2, то для любых действительных чисел а и Ь выполняется неравенство
а2 4- aab 4- Ь2 0.
3.7. Пусть а и Ь—произвольные положительные числа. Средним гармоническим этих чисел называется число —, _________________________________________ ~а+Т
Г а2 4- Ь3 п
а средним квадратическим — число I/ —~—. Докажите следующие неравенства, связывающие средние величины:
-j------р < V ab
~а+'~Ь
а 4- b _ -] Г а2 4- 62
—2-== у —
Покажите, что можно дать иллюстрацию этих неравенств
следующую геометрическую (рис. 21). Пусть ABCD —
трапеция, основания которой AD — a, ВС = Ь: О — точка пересечения диагоналей. Тогда:
а) Среднее арифметическое двух чисел а и b равно
длине средней линии трапеции KL.
93
б) Среднее геометрическое Уab этих чисел равно длине отрезка GH, который параллелен основаниям и обладает тем свойством, что трапеции BCHQ и QHDA подобны.
2
в) Среднее гармоническое q---р равно длине отрезка EF,
который параллелен основаниям и проходит через точку О.
г) Среднее квадратичное равно длине отрезка MN, который параллелен основаниям и разбивает трапецию ABCD на две равновеликие трапеции.
3.8. Докажите, что для любых положительных.чисел а и b выполняется неравенство
3.9. Докажите, что для любых неотрицательных чисел а и b выполняются неравенства:
1. ап Ьп (а Ь)п, где п — натуральное число.
п а3 А-Ь3 /а А-Ь\3
3. (1а 4- ]/р)8:э= 6АаЬ(а 4-£)2.
3.10. Пусть а и b—произвольные неотрицательные числа, w, k — натуральные числа, причем k-'Ап- Докажите, что имеет место неравенство ап 4- bn akbn~k 4- Ькап!г.
3.11. Докажите, что если а и b — неотрицательные числа, п—натуральное число, то (а 4-Ь)"^ 2"-1 (ап 4~Ь").
3.12. Докажите, что для любых действительных чисел а, Ь, с имеет место неравенство
]/а2 4~ Ь2 + с2 ! а । 4~ i j 4~ I с !•
3.13. Докажите, что для любых действительных чисел а, b справедливы неравенства:
1..' | а-b | | а | 4-\Ь\.
2. | а 4- b | [' | а | — | b )).
3.14. Пусть х, у, z— произвольные действительные числа. Докажите, что для чисел д^хА-уА-г, о2 = ху Д- xz A~yz, a3 = x_yz справедливы неравенства:
1. Зо2.
2. о^Зо1а3.
94
Докажите, далее, что если числа х, у, z положительны, то справедливы неравенства
3. 0^2 9ств. 5. о:> 27о:,.
4. ст} 27ст3. 6. ст} SOjOj.
Покажите, что равенство в соотношениях 1, 3—6 имеет место лишь при x=y — z.
3.15. Докажите, что для любых действительных чисел а,
Ь, с имеют место неравенства:
1. (a4-b + c)2s£3(a2 + b2 + c2).
2. (a-\-b — с)2 4- (Ь с — a)2 -j- (а с — Ь)2 ab 4- Ьс 4~ ас.
3.16. Докажите, что для любых неотрицательных чисел х, у, z выполняется неравенство
3.17. Докажите, что для любых неотрицательных чисел а, Ь, с, х, у, z справедливы следующие неравенства:
1. ab (а 4- b — 2с) 4~ Ьс (Ь Д- с — 2а) 4- ас (а 4- с — 2b)z> 0.
2. ab (а 4- b) 4- Ьс (Ь 4- с) 4- ас (а 4~ с) 5s 6 6abc.
3. (а 4- b 4- с)3 * — (а3 4" Ь3 4- с3) 2 (а 4- Ь) (Ь 4- с) (с 4-а)-
4. (а 4~ b 4- с) (а2 4~ Ь2 -4 е2) Ts 9abc.
5. (ху— z)(y + z—x)(z-]-x—y)xZxyZ.
6. ст} — 4cti<j2 4- 9<J3 Ss 0, где ct1 = x4-J'4-2,
CT2 = XV 4- xz-\- уZ, CT3 = xyz.
3.18. Докажите, что для любых положительных чисел а,
Ь, с, х, у, z имеют место следующие неравенства:
1 1 + 1 + 1>_и+Ц=4—L
а b с " уьс Уса УаЬ'
2 х3 + ^3 + г3 —- *+?/4-г
Х2 + г/2 + г2^ 3
3. (fl4-b + c)(-^ + y + 4-)ss9-
4. £4-±4-^5=.з.
о 1 с а '
5 2 | 2 , 2 9
/; + с + + а + ^4-с'
6 а I । с з
b-)-c‘ c-j-a' а-)-Ь' 2 ’
95
3.19. Докажите, что если а, Ь, с — произвольные неотрицательные числа, то выполняются неравенства:
1. 2 (а3 b3 Д- с3) ab (а Д- b) Д- Ьс (Ь Д- с) Д- ас (а Д- с).
2. 2 (а3 Д- Ь3 Д- с3) => а2 (Ъ Д- с) Д- Ь2 (с Д- а) Д- с2 (а Д- Ь).
3. 3 (а3 Д- Ь3 с3) {а Д- b Д- с) (ab Д- ас Д- Ьс).
4. 8 (а3 4- Ь3 4- с3) 5= 3 (а Д- Ь) (Ь Д- с) (с Д- а).
5. (а Д- Ь Д- с)3 -С 9 (а3 Д- Ь3 Д- с3).
6. а4-Д Ь4 Д-с4 abc(a-\-b-{-c).
3.20. Докажите, что для любых неотрицательных чисел а, Ь, с, d выполняется неравенство
У~(а Д- с) (Ь Д- d) ]/ ab Д- Vcd.
3.21. Докажите, что для любых действительных чисел а, Ь, с, d имеет место неравенство
а4 Д- Z>4 Д- с* Д- di ^abcd.
3.22. Докажите, что если |а|<; 1, то
I а Д- Ь | < | 1 Д- ab |.
3.23. Докажите, что если | b | < , то
I 1 1^2
| 'а — b I | а |
3.24. Докажите, что если а, Ь, с — произвольные действительные числа, удовлетворяющие условию а-\-Ь -\-с — 0, то
ab Д- Ьс Д- са 0.
3.25. Докажите, что если для действительных чисел а, Ь выполняется условие а2 4~^2=1, то | а-\-Ь\^]^2.
3.26. Докажите, что если действительные числа а, Ь, с удовлетворяют условию ас = 6, то
а2Д-^Д-с2^ 12.
3.27. Докажите, что если — у, Ь^—с^— и а -|- Z> Д’с — 1 > то
/гадТТ4-/2нТд-Угс+Т<4. .
96
3.28. Докажите, что если действительные числа а, Ь, с удовлетворяют условию a -f- b >: с, где с += О, то имеют место неравенства:
<2 М <8
1. я2+ Ь22. а* + Ь*^. 3. as + b^^.,
3.29. Докажите, что для любого натурального п справедливо неравенство
\ п] 2п) •
3.30. Докажите неравенство
2 ’ 4 '6'-”i00<'10'
3,31. Докажите неравенство
_ 1 , 1 । 1 , д_ 1 д_ 1 - 1
Sn 32+52 +-72 + •••+ (2n—l)2 "г (2ч + 1)2 < 4 ’
3.32. Докажите, что если д>1—натуральное число, то
1. (1 Д- а)п > 1 -j- ап при условии, что а>—1;
2. (1 +<z)"> 1 4-С*-а* при а>0 (k=\, 2, п).
3.33. Докажите, что для любого натурального 1 имеет, место неравенство
п +
3.34. Докажите, что для любого натурального п>2 справедливо неравенство
. / 1 \п
2< 1 +-) <3. \ п)
3.35. Пусть положительные числа alt а2, ..., ап образуют арифметическую прогрессию. Докажите, что
, И/- л _L (2
V агап у at а2 ... ап < —?—.
Получите отсюда, неравенства \п <^У"п\ <. для любого натурального п >2.
3.36. Докажите, что для любого натурального я>2 справедливо неравенство
У п > У п-\-1.
4 В. Г. Болтянский и др. 97
3.37. Докажите, что при любом натуральном п > 2 имеют место неравенства
3.38. Докажите, что для любого целого и>-2 выполняются неравенства
<1 +^ + 4= + --- + -7=<2/«-
' У 2 /3 Уп
3.39. Пусть т и п— целые числа, причем а>0. Докажите неравенство
ат + 4? 3= ап + -4 •
1 ат — 1 ап
3.40. Пусть а > 0, п — натуральное число. Докажите, что я(1 а2п)— ап^ а2п~] -ра2п~~2а2 у а.
3.41. Док а жите, что
где А — наименьшее, В — наибольшее из чисел
IM |а2|, ..., KI-
3.42. Пусть Ьр Ь.2, ..., Ьп — положительные числа, ар а2, ..., ап — произвольные действительные числа. Обозначим наибольшую из дробей ~, ..., через М, а наимень-01 о2 оп
шую — через т. Докажите, что
^1 + +
3.43. Докажите, что для любых действительных чисел ар а2, ..., ап имеет место неравенство
К + ач +... + ап)2 < я (а| 4- а| 4-... + а\).
3.44. Докажите неравенства
п п /--п----
т j г =5: У а, а2
__|--------—
Н1 «2 аП
„ а1 + я2 + -.- + йл
IX п - -
98
связывающие среднее гармоническое, среднее геометрическое, среднее арифметическое и среднее квадратическое положительных чисел ах, а2...ап.
3.45. Пусть действительные числа ах, а2, ап связаны равенством + + •.. + an==Q. Докажите, что
s = аха2-j-аха3. 4~ <zn-ian =С О
(в s входят всевозможные слагаемые вида а,а;-, I =4= /).
3.46. Докажите, что для произвольных действительных чисел
^2’ •' • • ’ ^2’ • • • ’
справедливы следующие неравенства:
1. aj 4- a-г 4~ • • • 4- ап 4- V 4~ + • • • 4~
==== V (ai 4~ ^i)2 4~ • • • 4~ (ап 4- М2-
2. | у/~а[ 4~ а->4- • • • 4- ап — Ь\ 4- Ь% 4- • • • 4- bn |
I ai b114-1 a2—^214-. • 4-1 bn |.
3.47. Пусть
1* , 2* , 3fe . , 100* , . _ „
mk — у4~у4~4~• • • 4~Доу, гДе £=1,2,3,...
Докажите, что sC тА+1/иА_х.
4*
Г Л А В A IV
КОМПЛЕКСНЫЕ ЧИСЛА
§ 1. Введение
Во второй главе говорилось о действительных числах. В множестве действительных чисел можно решать линейные уравнения, квадратные уравнения с неотрицательны® дискриминантом, уравнения вида хп = а при а;>0 и другие. Существуют, однако, такие алгебраические уравнения (и даже уравнения с целыми коэффициентами), которые не имеют действительных корней. Таковы, например, квадратные уравнения с отрицательным дискриминантом. Простейшее из них — уравнение х2 4-1=0. Естественно, возникает желание так расширить множество действительных чисел, добавив к нему новые числа, чтобы в этом расширенном числовом множестве имели корни квадратные уравнения с отрицательным дискриминантом и, в частности, уравнение №4-1=0. Такой прием нам уже знаком по второй главе: в связи- с невозможностью решать в множестве положительных чисел некоторые уравнения вида хмЬ--а вводились отрицательные числа; в связи с невозможностью решать в целых числах некоторые уравнения вида Ьх=-а вводились дробные числа п т. д.
Введем новое число I, которое будем считать корнем уравнения х2 4-1=0, т. е. будем считать, что для числа I выполнено равенство Z2 4-1=0. Далее, попытаемся расширить множество, действительных чисел так, чтобы в новом числовом множестве содержались все действительные числа и число I и чтобы в новом множестве были выполнимы операции сложения и умножения. Для этого нужно договориться, что мы будем понимать под суммой, произведением и равенством новых чисел. Ясно, что в.это множество новых чисел нужно включить произведение bi и сумму а-\-Ы для любых действительных чисел а и Ь. Выражения вида а-ч-Ы условимся называть комплексными числами.
100
Заметим, что мы вовсе. еще не дали определения комплексных чисел. Мы лишь представили себе, какой вид могут иметь новые числа. Эти рассуждения пока нестроги и не содержат еще определения множества комплексных чисел. Тем не менее сказанное дает повод для одной распространенной ошибки. Из равенства г24-1=0 делают «вывод», что / = ]/—1, в связи с чем на вопрос: «Что такое комплексное число?» часто можно услышать такой ответ: «Комплексное число — это выражение а-\-Ы, где г = ]/—1». Такой ответ является ошибочным. В множестве действительных чисел символ употребляется для обозначения арифметического корня из положительного числа и, значит, выражения ]/" — 1 не имеет смысла. Знак «4-» в выражении a-\-bi также не имеет прежнего смысла, означающего операцию сложения действительных чисел, так как число Ы не является действительным.
Это ошибочное определение можно попытаться «исправить» следующим образом: «Комплексные числа — это формальные выражения вида а-ГЫ, где а и b — действительные числа, а / — некоторый символ». В таком виде определение комплексного числа является неполным. Из него невозможно вывести правила. действий над комплексными числами и их свойства.
Чтобы получить полный ответ на поставленный вопрос, продолжим наши нестрогие рассмотрения, связанные с введением новых чисел. Посмотрим, как было бы желательно определить действия над этими числами. Попробуем определить сложение комплексных чисел таким образом, чтобы для них выполнялись все те законы действий, о которых говорилось в гл. II. Тогда сложение чисел а-\-Ы и с-)-di мы должны будем производить гак:
(а 4- bi) 4- (с 4- di) = а 4- Ы 4- с 4- di — (а 4- с) 4- (b -j- d) I.
Аналогично, вычитание мы должны выполнять следующим образом:
(а 4- Ы) — (с di) = (а — с) -\-(Ь — d) I.
Умножение тоже попробуем выполнять так, чтобы сохранились такие же законы действий, как и для действительных чисел. Тогда мы получим
(а 4- bi) (с -)-di) = ac-{- (ad4- be) 14- bd&.
101
Вспомнив, что /2-|-1=0, т. е. Р== — 1 (мы ведь хотим сохранить все свойства действий, а значит, и правила преобразования равенств), находим, что умножение комплексных чисел нужно определить следующим образом:
(а + Ы) (с + Л)=(ас — bd) Д- (ad -|- be) i.
Договоримся, наконец, какие комплексные числа следует считать равными. Начнем с равенства комплексного числа нулю. Из равенства а-^-Ы — 0 должно следовать, что Ь = 0: иначе оказалось бы, что = 1 = — т. е. i оказалось
бы действительным числом, что невозможно, так как никакое действительное число не является корнем уравнения №-4-1 = = 0. Итак, если a4-bi = 0, то Ь = 0. Тогда Ы--=(). и потому а = 0. Мы видим, что число а-\-Ы следует считать равным нулю лишь при а = Ь~0. Далее, если числа- а-\-Ы и с-т-di равны между собой, то (аКЫ)— (c-(-di) — 0, т. е. (а — с) Д--j- (Ь — d)i—0. Но тогда а — с = 0 и b — d — О, т. е. а —с и b — d. Таким образом, равенство комплексных чисел нужно определить так: a Д- bi = с Д- di, если а —с и b — d. 1
Итак, в определение комплексных чисел должны входить и соглашения относительно операций над ними. Мы выяснили, как это можно сделать, чтобы сохранить такие же правила действий, как и для действительных чисел. Еще раз подчеркнем, что наши рассуждения не являются «доказательством» правил действий над комплексными числами, — это только наводящие соображения к вопросу о том, как естественно вводить понятие комплексного числа.
Теперь перейдем к аккуратному определению комплексного числа.
§ 2. Определение комплексного числа
Определение. Комплексными числами называются выражения вида а-\-Ы (где а и b — действительные числа, a I— некоторый символ), если для этих выражений следующим образом определены понятие, равенства и операции сложения и умножения:
1. Два комплексных числа а-ybi и с-К di считаются равными тогда и только тогда, когда а —с и b = d.
2. Суммой двух комплексных чисел а-\-Ы и с-)-di называется комплексное число (a-]-c)-^(b-{-d)i.
3. Произведением двух комплексных чисела+Д/ и c-\-di называется комплексное число (ас — bd) Д- (ad Д- be) i.
102
Таково определение комплексного числа.
Комплексное число принято обозначать одной буквой (чаше всего буквой z). Равенство z = a-)-bi выражает тот факт, что комплексное число a-)-bi обозначено буквой z. Для обозначения " действий, над комплексными числами применяются те же знаки, что и для обозначения действий над действительными числами: запись z' —z" означает равенство двух комплексных чисел z' и z"\ далее, сумма чисел zx и z2 обозначается через zr Д- zz, а их произведение zj • z2 или ZiZv Таким образом, определение сложения и умножения двух комплексных чисел а-\-Ы и c-\-di можно записать так:
(а Д- bi) Д- (с Д- di) = (а Д- с) Д- (Ь Д- d) Z,
(а Д- bi) (с Д- di) = (ас — bd) Д- (ad Д- be) I.
Действительное число а называется дейс твительной частью комплексного числа z — a-^-bi и обозначается символом Re z. Таким образом, для комплексного числа z== а Д-&/ пишут: Rez = a или Re (а Д- Ы) = а. Число b называется мнимой частью комплексного числа z = a-)-bi и обозначается символом Im z. Таким образом, Im (a -)-bi) = b. Символ i называется мнимой единицей.
„Заметим, что в выражении a-(-bi знак «Д-» пока что не означает действия сложения, так же как и запись Ы еще чисто формальная. Однако запись a-(-bi не случайна. Она вытекает из следующих соглашений.
Рассмотрим комплексные числа вида аДОТ Формулы сложения и умножения для чисел такого вида (по определению сложения и умножения комплексных чисел) записываются следующим образом:
(ai 0 • О Д~ (а2 + ° • 0 “ (<ДД- и2) Д- 0 • I,
(а1 Д- 0 ’ 0 (аг 0 • /)д= (аха2) Д- 0 • Z.
Таким образом, при сложении и умножении чисел вида а Д-0-Z снова получаются числа того же вида. Если мы условимся писать аД-0-г' = а (т. е. условимся отождествлять число аД-O-Z с действительным числом а), то увидим, что операции над числами вида аД-O-Z проводятся так же, как над действительными числами. Это позволяет считать, что каждое действительное число а содержится в множестве комплексных чисел, а именно a = a-j-O-Z. В частности, число 0 = 0 Д-0-Z мы будем, как обычно, называть нулем, а число 1 = 1 Д-Д- 0-Z—единицей.
103
Числа вида O4-Z>z' называются мнимыми числами (или чисто мнимыми) и обозначаются следующим образом: О -|~ Ы = Ы. В частности, число 0 1 - z обозначается так:
О -j- 1 • i = i. Заметим, что, согласно этому определению, число 0 = 0 4- 0 -I также следует считать чисто мнимым. Число 0 — единственное комплексное число, которое является и действительным, и чисто мнимым.
Следуя этим обозначениям, каждое комплексное число можно записать в виде а -\-bi = (a 4~ 0 • I) 4- (Ь 4-0 • /) (0 -f-1 i). Значит, можно считать, что знак «-}-» в определении комплексного числа zz4~^z означает действие сложения чисел а и Ы, а запись Ы означает действие умножения чисел b и I.
Число г2 вычислим непосредственно, исходя из определения умножения комплексных чисел:
z2 = z-z = (04- 1 -г)(0 4-1 /) = — 1 4-0-z = — 1.
Итак, в любом промежуточном действии или в конечном результате число I2 можно заменять числом —1. Именно равенство /2 =— 1 послужило причиной того, что иногда пишут z = j/-~7. Выше уже отмечалось, что эта запись некорректна, так как символ ]/~ означает арифметический корень из положительного числа.
§ 3. Свойства действий
Теперь, когда мы имеем четкое определение комплексных чисел, можно изучать свойства действий над комплексными числами. Естественно ожидать, что действия сложение и умножение комплексных чисел обладают такими же свойствами, какими обладают сложение и умножение действительных чисел,— ведь именно так мы «подбирали» определение комплексных чисел. Более того, и свойства обратных операций (вычитания и деления) оказываются такими же, как и для действительных чисел. Более точно, справедливы нижеследующие теоремы 1 и 2.
Теорема 1. Сложение в множестве комплексных чисел обладает следующими свойствами-
1. zt 4- z2 — г2 4- zt для любых комплексных чисел zt и z2 (коммутативный закон сложения).
2. (zt 4- ^2) 4- z3 = 4- 4~ ^з) для любых комплексных
чисел zv z2, z3 (ассоциативный закон сложения).
3. z 4- 0 = z для любого комплексного числа z.
104
4. Для любых двух комплексных чисел гг и z2 существует, и притом только одно, число z, удовлетворяющее уравнению z-\-z2 = zr.
Доказательство. Докажем свойство 1. Пусть
21 = ^ + ^, z2 = a2-\-b2i.
По определению сложения комплексных чисел можно записать
zi + = (ai + ai) 4~ (^i + b2) I,
22 + Z1 — (а2 + а1) + (Ь2 + ^1) i-
Из свойств действительных чисел следует, что
а1 4~ а2 = а2 4~ а1' + Ь2 — Ь2 -f- blt
т. е. у чисел и 22 + zi Действительные части равны
и мнимые части равны. Значит, из определения равенства комплексных чисел следует, что zr + z2 = z2 zv что и требовалось доказать.
Свойства 2 и 3 доказываются аналогично. Рекомендуется в качестве упражнения доказать их самостоятельно. Заметим, что только после доказательства свойства 2 имеют смысл выражения z14-z2 + 2'3> zi 4" zz 4~ гз + zt и ДР-
Докажем свойство 4. Пусть z1 = a1-]-&Iz, z2 = a2-\-b2l, z.=x-\-yi, где действительные числа х и у неизвестны. По определению сложения
z + Zz — (x + аг) + (У +
Равенство z-}-z2 = z1, в силу определения равенства комплексных чисел, выполняется тогда и только тогда, когда
х-}-а2 = а1 и y-\-b2 = b1.
По правилам действий над действительными числами находим x = ai — a2, y==b1 — b2.
Таким образом, доказано, что равенство z-}-z2 = z1 выполняется тогда и только тогда, когда
z = («1 — а2) 4- (bi — b2)l.
Этим заканчивается доказательство теоремы 1.
Рассмотрим действие вычитания комплексных чисел. Вычитание определяется как действие, обратное сложению. Это
105
значит, что разностью двух комплексных чисел zr и д2 на-зывается такое число z, которое удовлетворяет уравнению д + д2 = д1; разность комплексных чисел zA и д2 обозначается через zt— z2. Другими словами, запись z = zr— z2 означает,,по определению, то же самое, что и запись z -{ z2 = zr. Из свойства 4 теоремы 1 следует, что разность комплексных чисел определяется однозначно с помощью формулы
(ai + ^10 — (а2 — (а1 — аг) + (^i — ^2)^
Отметим, что, как и для действительных чисел, разность 0 — z (для любого комплексного числа г) обозначается через — z, т. е. 0 — z=—z. Отсюда следует, что разность zr—z2 можно записать в виде zt— д2 = д'14-(— гг)-
Теорема 2. Умножение в множестве комплексных ‘ чисел обладает следующими свойствами:
1. z1z2 = z2z1 для любых комплексных чисел zr и z2 (коммутативный закон умножения).
2. (д^г) z3 = Zi (г2г3) для любых комплексных чисел zv z2, zs (ассоциативный закон умножения).
3. z1(z2 + z3) = z1z2 + z1z3 для любых комплексных чисел Д1, z2, z3 (дистрибутивный закон).
4. 1 • z = z для любого комплексного числа z,
5. Для любых двух комплексных чисеЛ гг и z2, где z2^0, существует, и притом только одно, число z, удовлетворяющее уравнению zz2 = z1.
Доказательство. Докажем свойство 5. Пусть
г1 = а1-|-&1г, г2 = а2 -\-b2i, z = x-\-yi,
где действительные числа х и у неизвестны. По определению умножения
z z2 = (ха2 — yb2) + (xb2 + уа2у.
Равенство zz2 — zlt в силу определения равенства комплексных чисел, выполняется тогда и только тогда, когда
ха2—уЬ2 = аг и' xb2 -j-ya2 — b1.
Мы получили линейную систему относительно х и у, определитель которой а2-|-^2#0, так как z2 0. Следовательно, эта система имеет единственное решение:
+ «А
al-f-bS. ’ у~ ’
106
Таким образом, доказано, что уравнение zz2 — z{ для любых комплексных чисел zr — ах -ф Ьг1, z2 == а2 -ф b2i (где z2 0) однозначно разрешимо и имеет следующее решение:
- а1д2~Ь Ф^2 | д2^1—° 1^2 ; /1\
+ *" al + Ь* >
Свойство 5 доказано.
Свойства 1—4 теоремы 2 легко доказываются так же, как и свойства 1—3 теоремы 1. Рекомендуется в качестве упражнения доказать их самостоятельно.
Заметим, что только после доказательства свойства 2 теоремы 2 имеют смысл выражения z{z2z3, z3 = zzz и др. . Рассмотрим действие деления комплексных чисел. Делением называется действие, обратное умножению. Это значит, что частным двух комплексных чисел Zj и z2, где z2 ф 0, называется такое число г, которое удовлетворяет уравнению zz2 = z^, частное двух комплексных чисел zi и z2 обозначается г, „ Zi
через г1:г2 или —. Другими словами, запись z =— озна-2^2 - ^2
чает, по определению, то же самое, что и запись — Из свойства 5 теоремы 2 следует, что для любых комплексных чисел z1 = a1-]-b1i, z2 = a2-{-b2i (где z2 ф 0) частное однозначно определено и имеет следующий вид:
Zi tZj bjj.
22 д2 -ф b2i
aia2 Ч- bib2 al+b%
a2b1 — a1b2 .
"Ф
Деление на нуль в множестве комплексных чисел, как и в множестве действительных чисел, не имеет смысла, т. е.
z частное ни при каком z не определено.
Замечание. Из определения комплексного числа следует, что формулы сложения и умножения комплексных чисел формально имеют такой же вид, как и формулы сложения и умножения алгебраических выражений вида a-{-bi, причем в любом промежуточном действии или в конечном результате число /2 можно заменять числом —1. В теоремах 1 и 2 доказано, что свойства действий сложения и умножения комплексных чисел и свойства обратных операций (вычитания и деления) такие же, как и для действительных
чисел. 3_________________________________________________2
Пример 1. Представить комплексное число t-j-t
* Т1
браической форме, т. е. в виде а -ф Ы.
в алге-
107
Решение. По формуле деления комплексных чисел находим
3—-2i 3 1-J-(—2) -1 , 1 • (—2) —3 -1 1 5.
Р4-Р + Р + Р 2 2 1'
Отметим, что в § 4 будет указан другой способ выполнения деления комплексных чисел.
Пример 2. Найти действительную и мнимую части комплексного числа (2 -фz)3.
Решение. По формуле куба суммы двух чисел находим
(2 + z)3 = 23 + 3 22. i 4- 3 • 2 z2 + i3.
Заменяя z2 числом — 1, получаем
(2 4- z)3 = 8 4- 12z — 6 — I = 2 4- 1U.
Следовательно, Re (2 4-z')3 = 2, Im (2 4-z')3= 11.
§ 4. Модуль комплексного числа. Комплексно сопряженные числа
Определение. Модулем | z | комплексного числа z—a-\-bi называется число фЛа24-^2:
j z | = | а 4- bi | = У а2 4- Ь2.
Следует помнить, что | z | всегда есть действительное неотрицательное число: j z | 0, причем |г| =
= 0 тогда и только тогда, когда z = 0.
Если z — действительное число, то | z | есть его абсолютная величина; поэтому модуль и обозначается так же, как и абсолютная величина.
Из определения модуля комплексного числа нетрудно вывести, что для любых комплексных чисел z, zx, z2 справедливы соотношения:
1. | = | М | • | z21.
2. ~ = Ы, если z2#0. г2 1 z2 1
3. zn = \z для любого целого числа п (причем при
п < 0 предполагается, что z 0).
Предлагаем читателю в качестве упражнения доказать соотношения 1—3.
108
О п р еде л ен и е. Комплексное число а—Ы называется комплексно сопряженным с числом z = a-\-bi\ число, комплексно сопряженное с z, обозначается через z:
2=а-]-Ы=а — bi.
Из этого определения нетрудно вывести, что для любых комплексных чисел z, zv z2 справедливы соотношения:
1. (+ ± z2) = zr ± г2.
2. (ггг2) = zp^.
3. 1—“'; = “-, если z2 0. ',Z2 , z2
4. (!) = <•
5. zz = \z\2.
6- И = 14
7. — если г2 # 0.
z2 | z2 р ’ 2 T-
B качестве упражнения предлагаем читателю доказать соотношения 1—7.
Замечание. Формулу 7 можно доказать следующим способом. Умножим числитель и знаменатель дроби — на z2 число z2, мы получим -’---Ц-. Воспользовавшись теперь со-^2 ^2<2
отношением z2Z2 = \ z2\2, находим
С помощью формулы (2) удобно выполнять деление комп-
лексных чисел. Решим
Умножая числитель и
таким способом пример 1
знаменатель дроби
3 — 21 1+i
(стр. 107).
на число
1 + г = 1 — z, получаем
3 — 2i__(3 — 20(1 — о 3 — 31 — 2;-|-2г2_3—5i — 2 _ 1 5.
1+г — (1+Q (1 —0 ~~ |1+г|2 ~ 12+12 “2 2 1'
Удобство использования формулы (2) для нахождения частного двух комплексных чисел заключается в том, что при этом не нужно помнить формулу (1) деления комплексных чисел (стр. 107).
109
Пример 3. Доказать, что для любых двух комплексных чисел и z2 выполняется соотношение
I I2 + I ^1 — ^2 I2 = 2 I *1 I2 + 2 I ^2 I2-
Решение. Применяя свойства 5 и 1 комплексно сопряженных чисел, получаем
|Z1+ ^2 Р+1 ^1—^2 ___
=(?i + г2) (zr + z2) + (z1 — z2)(z1 — z2) =
= (?i + *2) (21 + гг) + (?1 — ?2) (?! — z2) =
= 2гг zt 2z2z2 = 2 | zt |2 2 [ z2|2, что и требовалось доказать.
§ 5. Геометрическая интерпретация комплексного числа
Рассмотрим прямоугольную систему координат на плоскости. Условимся комплексное число а^-Ы изображать точкой плоскости с координатами (а, Ь) (рис. 22). Иначе говоря, на оси абсцисс будем откладывать действительные части комп-
лексных чисел, а на оси ординат— мнимые. При этом действительные числа будут изображаться точками оси абсцисс, которую называют поэтому действительной осью, а чисто мнимые числа— точками оси ординат, которую называют мнимой осью.
Обратно, каждой точке плоскости с координатами (а, Ь) поставлено в соответствие комплексное число а -\-Ы. Таким образом, соответствие между- множеством всех комплексных чисел и всех
точек плоскости взаимно однозначное. Поэтому в дальнейшем мы не будем различать понятия комплексного числа и точки плоскости и будем говорить, например, «точка z=l—z», «треугольник с вершинами в точках zlt z2, г3» и т. п.
Заметим, что каждой точке плоскости с координатами (а, Ь) соответствует один и только один вектор с началом в точке (0, 0) (начало координат). и концом в точке (а, Ь). Поэтому условимся также изображать комплексное число
110
а ~[-Ы вектором с началом в точке z — О и концом в точке z — a-]-bi (рис. 22).
Из данной выше геометрической интерпретации комплексного числа вытекают следующие свойства:
1. Длина вектора z равна | z |.
2. Точки z и z симметричны относительно действительной оси.
3. Точки z и — z симметричны относительно точки z=0.
4. Число zx-]-z3 геометрически изображается как вектор, построенный по правилу сложения векторов zr и z2 (рис. 23).
5. Расстояние между точками zr и z2 равно |zt— z2\.
Предлагаем читателю в качестве упражнения доказать свойства 1—4.
Докажем свойство 5. Построим вектор zr — z2 как сумму векторов zx и — z2 (рис. 24). Из равенства треугольников с вершинами в точках 0, zx, z2 и 0, zv zt — z2 следует, что длина вектора z1 — z2 равна расстоянию между точками zx и z2, что и требовалось доказать.
Пример 4. Множество точек z, удовлетворяющих уравнению |z— z0|=j=/?, есть окружность с центром в точке z0 и радиусом R, так как уравнение |z — zQ\ = R выражает тот факт, что расстояние от точки z до точки z0 равно R.
Пример 5. Множество точек z, удовлетворяющих уравнению |z — Zjl^jz — z21, есть прямая, перпендикулярная отрезку, соединяющему точки zr и z2, и проведенная через его середину. В самом деле, уравнению |z— z1\ — \z— z2| удовлетворяют все точки z, равноудаленные от точек zx и z2 (и только эти точки).
Ш
Пример 6. Множество точек z, удовлетворяющих неравенству 1т2>0, представляет собой верхнюю полуплоскость (т. е. множество точек, лежащих выше действительной оси). Это следует из того, что для точки z=x^-ly неравенство Im z > 0 имеет вид у > 0.
§ 6. Аргумент комплексного числа
Определение. Аргументом комплексного числа z^-0 называется угол между действительной осью и вектором z, отсчитываемый от положительного направления действительной оси. При этом, как обычно, если отсчет ведется против часовой стрелки, то величина угла считается положительной, если по часовой — о т р и ц а т е л ь н о й.
Для обозначения того факта, что число <р является аргументом комплексного числа z = aA-bi, пишут tp — argz или ф = arg (а + &/).
Для числа z = 0 аргумент не определяется. Поэтому во всех дальнейших рассуждениях, связанных с понятием аргумента, будем считать, что 2^0.
Заметим, что для фиксированного числа z 0 аргумент определяется не однозначно: если ф— некоторый аргумент числа г, то углы фН~2&л(/г = 0, ±1, ±2,...) тоже являются аргументами того же числа z (ср. рис. 22). Таким образом, для каждого числа z имеется бесконечное множество аргументов, каждые два из которых отличаются друг от друга на число, кратное 2л.
Из определения тригонометрических функций следует (ср. рис. 22), что если ф — arg (а -ф- bi), то имеют место равенства
Справедливо и обратное утверждение: если выполняются оба равенства (3), то ф = arg (а -f- bi). Таким образом, все значения аргумента можно находить, решая совместно уравнения (3). При этом полезно использовать геометрическую интерпретацию комплексного числа для определения той четверти, в которой находится точка z = a-ybi. Подчеркнем: для определения той четверти, в которой находится точка z—a-\-bi, нужно использовать оба соотношения (3) (или использовать геометрическую интерпретацию комплексного числа), а после того, как это сделано, можно для нахожде-112
ния аргумента воспользоваться одним (любым) из уравнений (3).
Пример 7. Найти аргумент числа z—1—I.
Решение. Так как Rez=l, Im г ——1, то точка z = = 1—I лежит в IV четверти. Поэтому достаточно найти такое решение одного из уравнений (3), которое является углом в IV четверти. Находим
1 7тт
cos ф = —, ф = —-|- 2kn „ (£ = 0, ±1, ± 2, ...).
У 2 4
Заметим, что если ф — arg (а -|- ЬГ), а^=0, то из (3) следует, что tgcp = -^-. Но обратное утверждение неверно: из равенства tg<p = -^- нельзя заключить, что ф = arg (а 4- bi).
Например, для числа —1—I значение <р = у является реше-, b .
нием уравнения tg(p==^-=l, но не является аргументом этого числа.
Но если сначала определить, используя геометрическую интерпретацию, в какой четверти находится точка а-\-Ы, и „ , b
затем найти такое решение уравнения tgcp = —, которое является углом в этой четверти, то получим аргумент числа а bi.
Пример 8. Найти аргумент числа —1—I.
Решение. Точка —1—i лежит в III четверги. Поэтому « х b
нужно найти такое решение уравнения tg<p = —, которое является углом в 111 четверти. Находим
tg(p = l, ф = ^4-2Лл (Л = 0, ±1, ±2, ...).
§ 7. Тригонометрическая форма записи комплексного числа
Пусть г — модуль, а ср — какой-либо из аргументов комплексного числа a-]-bi, т. е. г = | а -\-Ы = ]/а24- Ь2, ф = = arg (а 4- Ы). Тогда из формул (3) следует, что a = rcos<p, b = r sin ф, и, значит,
а 4- bi = г (cos ф 4* i sin ф).
ИЗ
Нетрудно доказать и обратное утверждение: если имеет место равенство = г (cos + z sin <р), где г>0, то г = | а -|- bl |, ф = arg (а -f- Ы).
Определение. Запись комплексного числа z в виде
z = г (cos ф + z sin ф), ...
где г > 0, называется тригонометрической формой комплексного числа.
Из сказанного выше следует, что любое комплексное число z =/= 0 можно записать в тригонометрической форме
z = r (cos фz sin ф), r^>0,
причем эти соотношения имеют место в том и только в том случае, если r = \z\, ф = агц г.
Необходимо усвоить, что не всякая запись комплексного числа через тригонометрические функции .является тригонометрической формой этого числа. Например, для числа 1 -ф I запись
1 4*z = ]/2 (.cos -J— Zsin 1 ' \ 4 1 4 /
есть тригонометрическая форма этого числа. Но запись в виде
11* т / л/ л . . . Зл \
1 +* = У 2 (^COS J 4-ZStn y j или
1 -|-z = — |Л2 (cos — + zsin^)
не является тригонометрической формой числа l-]-z.
Нетрудно доказать, что для двух комплексных чисел гх = ri (cos Ф1 + isin ф1)> ~2 = Г2 (cos ф-2 +1sin Фз)>
записанных в тригонометрической форме, равенство гх = гг имеет место тогда и только тогда, когда —г2 и фх = ф2 + 4- 2&л, где k — некоторое целое число.
Теорема 3. Пусть фх = ащг1, ф2 = аг§.г2. Тогда фх + ф2 = агё(гхг2).
Доказательство. Представим числа гх и z2 в тригонометрической форме: гх = rx (cos фх ~Н sin фх), ,г.> = = г2 (cos ф2 +1 sin ф2), где гх = | гх |, г2 = |г?|. Вычислим 114 ' .
теперь произведение чисел гг и z2.
гхг2 — Г], (cos фх + I sin фх) r2 (cos q>2 i sin <p2) =
= rxr2 [cos фх cos <p2 — sin <px sin <p2 +
1 (sin <px cos <p2 cos <px sin <p2)] —
= rxr2 [cos (<px + cp2) +1 sin (<px + <p2)].
Так как rxr2>0, то это есть тригонометрическая форма записи числа гхг2. Следовательно, <рх + Фг = arg (.zizi)’ что и требовалось доказать.
Заметим, _ что из приведенного рассуждения вытекает соотношение | гхг21 = гхг2 = | гх 11 z21; это дает новое доказательство свойства 1, сформулированного на стр. 108. Таким образом, модуль произведения двух комплексных чисел равен произведению модулей сомножителей, а сумма аргументов сомножителей является аргументом произведения. Заметим также, что формула
гхг2 = гх (cos <рх 1 sin фх) r2 (cos ф2 1 sin ф2) =
= rxr2 [ cos (фх + ф2) + i sin (фх + ф2)1, полученная при доказательстве теоремы 3, дает правило умножения комплексных чисел, записанных в тригонометрической форме.
Используя результат теоремы 3, нетрудно методом математической индукции доказать, что если фх, ф2, ..., ф„ — аргументы чисел гх, г2, ..., zn соответственно, то фх + ф2-г-.. •••+фп = аг§(гхг2...zn).
Теорема 4. Если фх — argzr и ф2 = argz2, то ф, — ф2 = Zi
-arg/.
г2
Эта теорема легко вытекает из теоремы 3. Из теоремы 4 следует, что формулу деления двух комплексных чисел и z2 (г2=/=0), представленных в тригонометрической форме
zi — ri (cos фх + isin Ф1)> — ri (cos фг +1sin фг),
можно записать в виде
г, г, (cos ср, -J-i sin ср,) г, г . , , . . ,
i = ^C0^+7-sEq>2)" = FT [cos (Ф1 - Ф*) +г sin (фХ - Ф2)1-
Другими словами, модуль частного двух комплексных чисел равен частному модулей делимого и делителя, а разность аргументов делимого и делителя является аргументом частного.
115
Теорема 5. Формулу возведения в целую степень it (л = 0, ±1, ±2, ...) комплексного числа г =# 0, представленного в тригонометрической форме z —г (cos <р ~Нsin ф)> можно записать в виде
гп = [г (cos ф -]-1 sin ф)]п = rn (cos «ф 4-1 sin /гф).
В частности, для любого числа ф и любого целого числа п выполняется соотношение
(cos ф 4- i sin ф)" — cos /7ф 4-1 sin «ф
(формула М у а в р а).
Теорема 5 легко доказывается методом математической индукции (с использованием теоремы 3 при п > 0 и теоремы 4 при /г<0).
Из сказанного выше ясно, что с помощью тригонометрической формы комплексного числа удобно выполнять умножение, деление комплексных чисел и возведение их в целую степень.
Пример 9. Представить комплексное число (1—/)8 в алгебраической форме, т. е. в виде а-\-Ы.
Решение. Модуль комплексного числа 1—/ равен ] 2, а аргумент равен Следовательно, по формуле возведения в целую степень имеем
(1 —z)8 = (]/2)8 (cos 14л 4- i sin 14л) = 16.
Тригонометрическую форму комплексного числа удобно также использовать при решении уравнений вида zn = zn, где z0 — заданное комплексное число, п — натуральное число.
Пример 10. Найти все решения уравнения г2 — /.
Решение. Представим число I в тригонометрической форме: z = cos4*sin у. Пусть z = г (cos ф 4-1 sin ф). Тогда уравнение г2 = / примет вид
г2 (cos 2ф 4- z sin 2ф) = cos 4~1 sin
Отсюда находим г=1, 2ф = у4-2£л, т. е. ф = -^4-Лл (k = 0, ±1, ±2, ...). Таким образом, все решения уравнения z2 — i представляются в виде
z — cos ^4-+ *sin (А"=о, ±1, ±2, ...).
116
Заметим, что для всех.четных k эта формула дает комплексное число
л ... л 1 . i
Zy = cos — + l Sin -Г = —r- 4- — , 1 4 т 4 /2 /2
а для всех нечетных k — комплексное число
5л , . ... 5л z, = cos — -4-1 sm -у-2 4 1 4
J____/
/2 /2’
Итак, уравнение z2 — i имеет два корня:
.. -4- / I___I____(_\
1,2 \/2 ' /2/
В общем случае решение уравнения z = г0, где п — на туральное число, описывается следующим образом. Пусть гп =
= г о (cos <р0 4-1 sin <р0) — тригонометрическая форма комплексного числа zc. Тогда все корни уравнения х'1 = г0 даются формулой
П / / Фо42^Л ;
z = / г о cos -------н
' и \ п 1
+ zsin Фо±2*л\
где k — 0, 1, 2, ..., п—1. Из этого нетрудно вывести, что точки, изображающие все корни уравнения zn = .<0,
Рве. 25.
являются вершинами пра-
вильного /г-уг.ольника (рис. 25), вписанного в окружность п г-------------------------------------------
с центром в точке г = 0 и радиусом / za |. Доказательство
этих утверждений мы предоставляем читателю.
В частности, при н=2 мы получаем следующее утверждение: уравнение г2 = г0, где c0 = r0(cos <p0-j-zsin<p0), имеет два корня:
Эти корни симметричны относительно начала координат, т. е. г2 = — zx (рис. 26). Заметим, что корни гх и г2
117
совершенно равноправны,т.е.у нас нет каких-либо объективных причин считать один из этих корней «первым» или «основным». Ведь наряду с <р0 аргументом числа zQ является также ф0 + 2л, а если вместо ф0 подставить в формулы (4) ф0-|-2л:, то и г2 .поменяются местами. Это пока-
зывает, что корни zi и г2 равноправны. Если мы условимся один (какой-нибудь) из этих корней обозначать через УzQ, то второй будет равен — Уz0. Сказанное делает ясным, что символ Уz0 не имеет в множестве комплексных чисел однозначного смысла, т. е. если мы хотим этот символ
применять, то каждый раз нужно указывать, какой из двух корней уравнения г2 = г0 обозначен через УzQ. В связи с этим знак квадратного корня в применении к Комплексным числам обычно не используется. Однако есть одно исключение: при решении квадратных уравнений с отрицательным дискриминантом пишут квадратный корень из отрицательного числа. К этому вопросу мы вернемся в следующей главе.
Задачи к главе IV
4.1. Представьте в алгебраической форме, т. е. в виде a-j-W, комплексные числа:
1. (1+2/)(2-z) + (1-2/)(2-H).
q 5 , 5 п 1 i । 1 -J- i
r+2z + T=T’ Г+7 “tT=T'
(1+0 (2 + Q (1—0(2 —0
2 — i 2 + <
4.2. Найдите действительную и мнимую части комплексных чисел:
1.(3 +2г)2. 2- (ШУ'
3. (2 + 3Z)2 — (2 — Зг)2. 4. (2 —г)3 *.
Q5+2 \2 (1+05
Vl8+i/ (1—г)3'
118
4.3. Докажите, что для любого комплексного -числа z выполняются соотношения
z 4- z = 2 Re z, z — z = 21 Im z.
4.4. Докажите, что если P (z)—многочлен с действительными коэффициентами, то Р (z) = Р (z).
4.5. Докажите, что для любых комплексных чисел гх и г2 выполняются соотношения:
1. I^A+l j2 + |^-Z„-SMKi2+l)(k2)2+l)-
2. |zxz2-l I2—|^x-z2|2 = (1z1|2-1)(|z2|2-1).
3. | гх + z2 }2 = (| z, \ + | z2 j)2 - 2 [| zA ! - Re (г^)].
4. [ Z14- z2 i2 = (j zx; — I z, I)2 + 2 [i zxz21 + Re (z-^)].
4. 6. Какой геометрический смысл имеет соотношение
I^i + ^2i2 + |^ — z212 = 2 j zx + 2 | z2 j2?
4. 7. Выясните геометрический смысл множества точек комплексной плоскости, удовлетворяющих соотношениям:
1. Rez>0. 2. ImzsCl.
3. О Re z 1-
5. |z|<l.
7. \z — z|> 1.
9- |z + z! = ^—1
4. | Im z | < 1.
6. | z-|-2z'| < 4.
8. 1 <|z — 1 ] < 2.
10. | l+z|<| l-z|.
4.8. Докажите, что для
люоого комплексного числа z
выполняются неравенства
Re z С j z I, Im z | z
4.9. Докажите (алгебраически и геометрически), что для любых комплексных чисел zx и z2 выполняются неравенства
I i I — I ^2 I I i Zi + z21 < I Zi i +1 z21.
4.10. Запишите в
, ные числа:
1. z.
3.-1+'^.
5.
7. (— 3 + 4Z)3
тригонометрической форме комплекс-
2. —2.
4. Z121+l.
г» JT . . . JT
D. -- COS -g- + I Sit! — .
8. (l+z)s(i-z/3)e.
119
4.11. Докажите равенство
/ 1 + i tg а у_1 4- Z tg па
' \ 1 — i tg а 1 — i tg па ’
где п — целое число, (Л’ = 0, ±1,
±2, ...). 2 2
4.12. Представляя комплексное число (cos a -фг sin а)3 в алгебраической форме по формуле куба суммы двух чисел и по формуле Муавра, докажите равенства
cos За = cos3 а — 3 cos а sin2 а, sin За = 3 cos2 а sin а— sin3 а.
4.13. Решите уравнения:
1. г2 = —z. 2. 23=1.
3. с6=64. 4. 4 = —1.
5. z8= 1-^-1. 6. г2 = 3 — 4г.
4.14. Докажите, что все решения уравнения z2 — a-[-bt, где а и Ъ — действительные числа, можно записать в виде
~. _4_ | 1 /"|/"а2 + &2 + а । . ] f 1 а2 + Ь- — а\
-1-2 — — 2 + г 2 ~Г
если & 0, и
ч,=± (_ I /ЁИ+pEZ), если b < 0.
4.15. Пусть z0, zx.znl— последовательные вершины
правильного и-угольника, вписанного в окружность с центром в точке z —0, причем нумерация вершин соответствует обходу окружности против часовой стрелки. Выразите г* через z0 (Л=1, 2, ..., п—1).
4.16. Найдите все корни уравнений:
1. 2 = с3.
2.
3- z +1 ~ + 1 ] + г = 0.
4. \z\*— 2г> + 2г = 0.
5. z | г J + 2г + г = 0.
- 4.17. Решите системы уравнений:
( \z — 21J — | z [ ! z“ 2^1 = 4,
1- а । ,! । 2. < |г +1 + < |
120
тогда и только тогда,
2— 1
4.18. Докажите, что число rqyy является действительным когда z — действительное
число,
4.19.
тогда и
4.20.
тогда и
мнимым
z2 и z3
п г~1
Докажите, что число ——г является чисто только тогда, когда | = 1, 2=4—1. Докажите, что три различные точки zlt
только тогда лежат на одной прямой,'когда отно-z, — г1 «
шение —----- является действительным числом.
г3~ 21
4.21. Пусть | zk | = 1 (k— 1, 2, 3). Докажите, что точки zx, z2, zs тогда и только тогда являются вершинами правильного треугольника, когда
ГЛАВА V
КВАДРАТНЫЙ ТРЕХЧЛЕН
§ 1. Квадратный трехчлен и его корни
Квадратным трехчленом относительно х называется выражение вида
ax2-{-bx-{-c, (1)
где а, Ь, с — некоторые числа, причем а ф 0. Числа а, Ь, с называются коэффицентами квадратного трехчлена. В дальнейшем будем предполагать, что а, Ь, с — действительные числа.
Значения х, при которых квадратный трехчлен (1) обращается в нуль, называются корнями трехчлена. Таким образом, для нахождения корней квадратного трехчлена нужно решить квадратное уравнение
ах2 + Ьх -|- с — 0. (2)
Напомним, каким образом находятся корни квадратного уравнения (2); при этом мы несколько уточним факты, обычно излагаемые в школьном курсе.
Для решения квадратного уравнения (2) пользуются приемом выделения полного квадрата в трехчлене (1), т. е. записывают его в виде (напомним, что а 0)
ах2 -[-Ьх-}-с = а [х2 + с = а [х2 -j-2 ~ x'jс—
Таким образом, уравнение (2) можно записать в виде
/ b \2 o' — 4ас п а х 4- s------------= 0 ,
\ 1 2а/ 4а ’
или (перенося дробь в правую часть и поделив на а) в виде
62 — 4ас 4а2
(3)
122
При этом уравнение (3) равносильно уравнению (2), т. е. имеет те же корни, что и уравнение (2). В самом деле, если некоторое число х удовлетворяет уравнению (2), то, как показывают проведенные выкладки, оно удовлетворяет и уравнению (3). Но эти выкладки можно провести и в обратном порядке, т. е. если число х удовлетворяет уравнению (3), то оно удовлетворяет и уравнению (2).
Иными словами, равенство (2) представляет собой неопределенное высказывание, которое для одних значений х (а именно для корней трехчлена) является истинным, а для других — ложным. Точно так же равенство (3) есть неопределенное высказывание. Эквивалентность уравнений (2) и (3) заключается в том, что эти два неопределенных высказывания одновременно истинны или ложны.
Итак, остается решить уравнение (3). Обычно число Ь2 — 4ас обозначают через D и называют дискриминантом квадратного трехчлена (1). Таким образом, уравнение (3) можно записать так:
+ где £ = й2~4«С. (4)
Теперь представляются три различных случая — в зависимости о г того, каким является число D.
а) Если число D положительно, то положительно и число D кт
Поэтому существуют два числа, квадрат каждого из
d л Yd Yd .
.которых равен это будут числа и —(где, как всегда, D— арифметический корень из положительного числа D). Но согласно (4) + как раз есть такое число,
D о
квадрат которого равен Значит, х удовлетворяет уравнению (4) в двух случаях:
, ь YD ( -b+YD\
1) если- х + о- = -о— и тогда х =-----;
7 1 2а 2а \ 2а /
от , b Yd I -b-YD\
2) если л’ + й- = — V- и тогда х —-------.
’ 1 2а 2а \ 2а ]
Итак, при Д > О уравнение (4), а значит и уравнение (2), имеет два корня:
хг~------—> х2 =-------о-*-—, гДе D = b2 — 4ас. (5)
1 2а 2 2а ’
123
Заметим, что в этом причем х1=^х2 (т. корня).
б) Если число D мает вид
случае оба корня xv х2 действительны, е. уравнение в самом деле имеет два
равно нулю, то уравнение (4) прини-
Но квадрат числа равен нулю -только в том случае, если само число равно нулю, и потому мы отсюда получаем
b „ b
x + = = 0, или х =— '2а 2а
Итак, при 0 = 0 уравнение (4), а значит и уравнение' (2), b
имеет только один корень х — — т. е. существует
только одно тело 1а именно —g-j, удовлетворяющее этому уравнению. Однако в целях единообразия считают, что и в этом случае уравнение (2) имеет два корня, только они оба совпадают. Иными словами, условно считают, что и при 0 = 0 уравнение (2) имеет два корня:
b х. = = — =.
12 2а
Заметим, что - то же получается и из формул (5), поскольку 0 = 0. Таким образом, если мы условимся при 0 = 0 счи-& .
тать корень х =—два раза (или, как еще говорят, уславливаемся считать его двукратным корнем), то формулы (5) для корней сохраняют силу и в этом случае. Мы увидим, что и во многих дальнейших случаях это соглашение (считать при 0 = 0 корень двукратным) оказывается очень удобным: иначе во многих теоремах приходилось бы делать специальные оговорки, относящиеся к этому случаю. Поэтому в математике всегда принято считать, что при 0 = 0 уравнение (2) имеет два совпадающих корня. Однако читатель должен отдавать себе ясный отчет в том, что это лишь условное соглашение', при 0=0 из всех действительных ! ь\
чисел только одно ^а именно —удовлетворяет уравнению (2).
в) Осталось рассмотреть случай, когда число О отрицательно. В этом случае и число отрицательно. А так как
124
квадрат действительного числа не может быть отрицательным, то, значит, в этом случае уравнение (2) не имеет действительных корней. Как мы знаем, существует два комплексных числа, квадрат каждого из которых равен отрицательному числу D (см. стр. 117). Эти числа являются чисто мнимыми и притом сопряженными. Если мы условимся одно из них (безразлично, какое) обозначать через ~\УD, то другое будет равно —]/£). Тогда числами, квадрат каждого из которых равен отрицательному числу будут чисто /О Кб .
мнимые числа и (а других таких чисел не существует). Но согласно (4) -v + Jj есть число, квадрат кото-
D г-
рого равен Следовательно, х удовлетворяет уравнению (4), а значит и уравнению (2), в двух случаях:
1) если * + ^ = -2^ ^и тогда х =----------у ;
... , ь УБ / — Ь — УВ\
2) если х--о =-------=— и тогда х = ——=------------ .
7 1 2а 2а \ 2а ]
Таким образом, и в этом случае (т. е. при £)<0) уравнение (2) имеет два корня, вычисляемые по формулам (5) и являющиеся комплексно сопряженными числами. Еще раз подчеркнем, что это утверждение имеет лишь условный смысл — если мы уславливаемся через У D обозначать какое-либо одно из комплексных чисел, квадрат которого равен отрицательному числу D. Эго, в самом деле, лишь условное соглашение, так как знак используется, по определению, для обозначения арифметического корня из положительного действительного числа, а в комплексной области этот знак однозначного смысла не имеет. Тем не менее уславливаются при решении квадратных уравнений с отрицательным дискриминантом всегда считать, что \D обозначает одно из двух чисел, квадрат которого равен D. Тогда формулы (5) для корней сохраняют смысл и при D < 0.
Итак, при указанных выше соглашениях (и только при условии принятия этих соглашений!) справедлива следующая
Теорема 1. Квадратный трехчлен ах2 Л-Ьх-ус с действительными коэффициентами а, Ь, с, где а=£0, всегда имеет два корня, определяемых по формулам (5). Эти корни
125
а) действительны и различны, если О > 0;
б) действительны и совпадают, если D — 0-,
в) не являются действительными (и будут комплексно сопряженными) при D < 0.
Следствие. Складывая и перемножая корни Х{, х2 квадратного трехчлена (1) (см. формулы (5)), получаем
, Ь с
xi + x2 = —^, ххх2 = —. (6)
Формулы (6) называются формулами Виета.
С помощью формул Виета можно получить разложение квадратного трехчлена ах2 4-^x4-с на множители:
ах2 4- Ьх 4- с = а (х— хх)(х— х2). (7)
Более подробно, имеет место следующая
Теорема 2. Пусть xt и х2— корни квадратного трехчлена ах2 -\-Ьх 4- с. Тогда для любого значения х справедлива формула (7).
Доказательство. Из формул (6) следует, что
Ь = — a (xt 4- х2), с = ахус2.
Поэтому для любого (действительного или комплексного) значения х мы имеем
ах2 4- Ьх 4- с = ах2 — а (х{ 4- х2) х 4- аххх2 =
= ах (х — хД — ах2 (х — хх) = а (х — xj) (х — х2).
Пример 1. Пусть Xi и х2 — корни квадратного уравнения ах2 4- Ьх 4- с = 0, где а ф 0. Не решая этого уравнения, выразить через его коэффициенты сумму xf-}-x2.
Реше и и е. Имеем xj 4- хъ = (x‘i — ххх3 4- х2) =
= (Xj 4- х2) [(Xj 4- х2)г — Зххх2]. Используя формулы Виета, получаем
Пример 2. Доказать, что корни хг и х2 квадратного трехчлена x2-[-px-{-q действительны и положительны тогда . и только тогда, когда выполняются условия
D=p2 — 4<?>г0, p<ZO, <?>0. (8)
Доказательство. Необходимость. Пусть корни трехчлена положительны:
хг > 0, х2 > 0. (9)
126
Покажем, что выполняются условия (8). Из неравенств (0) следует, что Xj Ц- х2 > О и хх х2 > 0, и потому, в силу формул Виета (6), мы имеем р <; 0, q > 0. Кроме того, D — р2 — 4q 0 (ибо при D <2 0 корни не были бы действительными).
Достаточность. Пусть выполнены неравенства (8). Покажем, что корни трехчлена x2-}-px-1(-q положительны, г. е. имеют место неравенства (9). Так как D>^0, то в силу теоремы 1 корни трехчлена действительны. По формулам Виета
— Р = Х1 + х2 ><? = х1х2>0. (Ю)
Из второго неравенства (10) вытекает, что действительные числа хх и х2 имеют одинаковый знак (т. е. либо оба положительны, либо оба отрицательны), а из первого неравенства (10) вытекает, что эти числа положительны. Итак, Xj > 0, х2 > 0.
Замечание. Требование О;:>0 в условии этого примера существенно: корни квадратного трехчлена х2 — 2хф-2 .равны х1=1 -|-г, х2=1—I. Неравенства (10) для них имеют место, тогда как условия (9) не выполняются.
§ 2. График квадратного трехчлена
Функцию
у — ах2- -ф Ьх 4- с, (11)
где а, Ь, с — действительные числа, причем а-^ 0, будем называть квадратичной функцией. Хотя значение у по формуле (11) может быть вычислено для любых комплексных значений х, мы будем в дальнейшем рассматривать эту функцию лишь для действительных значений аргумента х. В формуле (11) х может принимать л юб о е действительное значение. Иными словами, область определения, квадратичной функции (И) есть все множество действительных чисел.
Для изучения функции (11) и построения ее графика снова применим к выражению ах2-|- Ьх 4- с прием выделения полного квадрата:
У=а(х + 4^~^- (12>
Для сокращения записи введем следующие обозначения:
Ь
4а
(13)
2а ’
127
Тогда формула (12) примет вид у = а(х — т)2 +1. (14)
Ниже будет показано, как получить график функции (11). Именно, мы сначала рассмотрим график более простой функции
у —ах2, (15)
а потом покажем, что график функции (И) может быть получен сдвигом графика функции (15).
График функцииу = х2. Рассмотрим сначала функцию (15) при а = 1, т. е. функцию
у — х2. (16)
Эта функция при всех действительных значениях х принимает неотрицательные значения. При х = 0 она имеет наименьшее значение, равное нулю.
Кроме того, при х>0 функция у — х2 является возрастающей (большему значению аргумента х соответствует большее значение функции). В самом деле, если 0<xx<;x2, то л'2 — х1>0, л'о 4-.vt > 0, и потому число (х2 — хх)(х2 + хх), как произведение положительных чисел, положительно, т. е. Х.2 — Х;>0, или Х,<^Х).
Наконец, каждой паре значений аргумента, равных по абсолютной величине и противоположных по знаку, соот-ветствуют равные значения функции у = л*2, так как (— хп)2 — х2,. Иначе говоря, функция у =№ является чет-V/ ной. Эго означает, что график ее
/ симметричен относительно оси
___________М ординат. Поэтому для построения
V/ графика функции у—х2 достаточно
/'=ж2 построить ту часы, графика, кото-
/' рая соответствует положительным
7 значениям х, а затем эту часть гра-
[i *~х фика симметрично отразить относи-
тельно оси ординат.
Рис. 27. На рис. 27 изображен график
функции у — х2 (точка А' симметрична точке А относительно оси Оу). Этот график носит название параболы. Ось ординат является осью симметрии параболы. Точка пересечения параболы с ее осью симметрии называется вершиной параболы. Таким образом, точка О (начало координат) — вершина параболы у — х2.
128
График функции у —ах2. Рассмотрим теперь способ получения графика функции у = ах2 при произвольном а ф 0. При этом мы отдельно исследуем случаи а>1, 0 •< а •< 1, а < 0.
а) Случай а> 1. При одном и том же значении х значение функции у —ах2 в а раз больше, чем значение функции у=хг. Следовательно, точка графика функции у —ах2 получается из соответствующей точки графика функции у = х2
растяжением ординаты в а раз и, следовательно, расположена выше, чем соответствующая точка графика функции у = х2. Такум образом, график функции у —ах2 при а>1 получается растяжением всех ординат графика функции у = х2 в а раз и потому расположен выше графика функции у — х2 (имея с ним единственную общую точку—начало координат). Можно сказать, что парабола у —ах2 при а>1 является «более узкой», чем парабола у — х2 (см. график функции У — 2х2 на рис. 28).
б) Случай 0<а<1. В этом случае точки графика функции у— ах2 получаются из соответствующих точек графика функции у — х2 сжатием ординат в раз. Так как ^>1, то точки графика функции у —ах2 при 0<а-<1 расположены ниже соответствующих точек графика функции
5 В. Г. Болтянский н др.
129
у — х4, так что парабола у — ах3 при 0 < а < 1 является «более
широкой», чем парабола у = х3 fcM. график функции у = ~х3
на рис.
28^ J
. На рис. 28 изображены графики функций
у = х3, у = -^-х3 и у — 2х3.
При этом (для любой точки М оси абсцисс)
1ММ2, ММ3 = 2ММ2.
в) Случай a<0. В этом случае —а>0, и потому график функции у=—ах3 мы уже строить умеем. Сравнивая
У
Рис. 29.
графики функций у —ах3 и у = —ах3 при одном и том же значении х, мы видим, что их ординаты равны по абсолютной величине и противоположны по знаку. Следовательно, график функции у = ах2 симметричен графику функции у = — ах3 относительно оси Ох (рис. 29). На рис. 29 ММ2=М.М1 (для любой точки М оси абсцисс).
Сравнивая все разобранные выше случаи, мы приходим к выводу, что знак коэффициента а определяет направление ветвей параболы у = ах3: при а>0' ветви параболы у —ах3 направлены вверх, при a<0 — вниз.
График функции у = а(х— т)3. Для большей наглядности рассмотрим сначала пример у — 2 (х -ф 2)2. Сравним функцию _у=2(х4-2)2 с функцией у — 2х3. При х = х0 функция _у = 2х2 принимает значение 2х„. Такое же значение функция д/ = 2(х-|-2)2 примет при х = х0 — 2. Значит, для получения одинаковых значений функций у = 2х3 и у = = 2 (х 2)2 нужно придать аргументу функции у = 2(х-у2)3
значение на две единицы меньшее, чем аргументу функции у — 2х3. Следовательно, график функции у = 2(х-\-2)3 можно
130
получить из графика функции у — 2х2 сдвигом графика функции у = 2х2 на две единицы влево вдоль оси Ох (рис. 30). ' Вершина Ах параболы _у = 2(хЦ-2)2 находится на оси Ох и имеет абсциссу, равную —2.
Аналогично, график функции _у=2(х — 2)2 графика функции у = 2х2 сдвигом (рис. 31), так что имеет координаты В общем случае строения графика у = а (х — т)2 нужно нести график функции у = ах2 вдоль оси абсцисс вправо на т единиц, если т > 0, и влево на | т | единиц, если т < 0. При этом вершина А параболы у = а(х— т)2 имеет координаты А(т, 0).
График функции у = = а(х— /w)2-|-Z. Сравним значения функций у = = а (х — т)2 4-1 и у = а (х — т)2. одном и том же х значение функции на I единиц больше, чем значение функции у = а(х— т)2. При /<; 0 функция у = а(х— т)2-\-1 принимает при одном и том же х значение на 111 единиц меньшее, чем функция
вершина
Лг(2, 0).
для по-
функции пере-
получается из вправо на две единицы параболы у=‘2(х— 2)2
Если
Z>0, то при у = а (х — т)2 ф-1
5*
131
у = а(х—т)2. Следовательно, для получения графика функции у = а(х— от)2 4-^ нужно сдвинуть график функции у = а(х — от)2 вдоль оси ординат на I единиц вверх при
/>0 и на |/| единиц вниз при Z<0.
На рис. 32 в качестве примера приведены графики функций
у = 2 (х + 1 )2, j = 2(x+ 1)24-3
и j=2(x+ 1)2-3.
Вершины соответствующих парабол имеют координаты
Д(-СО), А(—1,3), а2(- 1,-з).
Подведем итоги. На основе изложенного выше можно утверждать, что
1) функцию у —ах2 А-Ьх А-с можно записать в виде у = — а (х~ т)2 +1, где
b , ft3 D
т = — Х-; I —с — ~ ;
2а ’ 4а 4а'
2) для построения графика функции у — а (х— т)2А-1 надо сдвинуть график функции у — ах2 вдоль оси абсцисс на отрезок от, а затем сдви
нуть вдоль оси ординат на отрезок Z; следовательно, графиком функции у = ах2 4- Ьх 4- с является такая же парабола, как у = ах2, но сдвинутая так, чю ее вершина находится в точке А (от, Z), где от = —
3) коэффициент а влияет на форму графика у —ах2'. чем больше | а |, тем «уже» парабола; знак числа а определяет направление ветвей параболы.
Результаты этого параграфа мы сформулируем в виде следующей теоремы.
Теорема 3. Точка а(—где D — b2 — 4ас, к \ 2а’ 4aj'
принадлежит графику квадратичной функции у = ах2-\~ 4~Ьл'4-с; она называется вершиной параболы, служащей
132
графиком этой функции. Указанный график получается из графика функции у—ах2 сдвигом вершины 0(0, 0) в точку А (т. е. сдвигом графика функции у —ах2 на т — — вдоль оси абсцисс и на 1= — вдоль оси ординат). Прямая, проходящая через вершину А параллельно оси ординат, является осью симметрии параболы у— ах24-+ Ьх + с. Наконец, если q — прямая, проходящая через вершину А параллельно оси абсцисс, то при а > 0 весь график функции у = ах2 Ц- Ьх 4- с {кроме вершины) лежит выше прямой q, а при а < 0 — ниже этой прямой.
Для получения графика функции у — ах2 -ф- Ьх 4- с можно действовать по следующему плану.
а) Преобразовать квадратичную функцию у = ах2 4- Ьх 4- с к виду у—а(х— т)2-\-1 и найти отсюда координаты (т, I) вершины А (формулы (13), но которым определяются координаты вершины А, запоминать нет необходимости).
б) Найти точки пересечения параболы с координатными осями. Ясно, что парабола у = ах2 4- Ьх 4- с пересекает ось Оу в точке 5(0, с). Ось Ох парабола пересекает в тех точках, в которых квадратный трехчлен ах2 A-Ьх -'^с обращается в нуль; эти точки существуют лишь в случае, когда корни уравнения ах2 A-bx-f-с = 0 действительны, т. е. при выполнении условия D = b2 — 4ас^г0 (теорема 1). Итак, если то, определив корни хг и х2 уравнения ах2 4- Ьх 4- с = 0, найдем две точки Aj(хР 0) и Аг(х2, 0) пересечения параболы с осью Ох (при 5 = 0 эти точки совпадают).
в) Зная вершину А (т, Z) параболы у —ах24-^x4* с и точки пересечения параболы с осями координат, а также учитывая, что знак коэффициента а определяет направление ветвей (вверх при й>0, вниз при а < 0), можно нарисовать эскиз графика. Для более точного изображения графика можно наметить еще несколько принадлежащих ему точек.
Замечание. Координаты (т, I) вершины А можно искать и иначе, не приводя квадратный трехчлен ах2 А~Ьх А- с к виду а(х— т)2А~1. Именно, сравнивая формулы (6ф и (13), мы замечаем, что т = ?~~—. Таким образом, для нахождения вершины нужно вычислить корни квадратного уравнения ах2 4- Ьх с = 0, затем найти абсциссу вершины параболы по
формуле — и, наконец, определить ординату I вер-
шины как значение квадратичной функции у — ах2 4- Ьх 4- с 133
при х = т. Такой, метод иногда является более предпочтительным, поскольку корни квадратного трехчлена ах2 -ф bx -ф с понадобятся не только для нахождения вершины, но и для определения точек пересечения графика с осью абсцисс.
Пример 3. Построить график функции у= 2х2 -ф 4х -ф 3.
Решение. Имеем_у=2(х2-ф 2х-ф1)+ 1 = 2 (х-ф 1)2-ф 1.
Отсюда видно, что вершиной является точка А(— 1,1). Так как д = 2>0, то ветви направлены вверх и, значит, с осью
абсцисс график пересекаться не будет. Далее, точка пересечения графика с осью Оу имеет вид 5(0,3). График функции _у=2х2-ф 4x4-3 изображен на рис. 33.
Пример 4. Построить график функции у — х (4— х).
Решение. Корнями уравнения х(4 — х)=0 являются числа хх = 0, х2 = 4. Это дает точки пересечения графика с осью абсцисс. Кроме того, абсцисса вершины (согласно замечанию на 0 + 4
предыдущей странице) равна т — —= 2 . Ордината I вершины равна значению функции при х=т = 2, т. е. эта ордината равна /=2(4 — 2) = 4. Ветви направлены вниз, так как а —— 1 <; 0.
График функции у — х(4— х) изображен на рис. 34.
§ 3. Исследование квадратного трехчлена
Геометрическое исследование. Цель проводимого ниже исследования — выяснить, как располагается парабола у = = ах2 + Ьх 4- с относительно оси абсцисс в зависимости от знака дискриминанта D — b2— 4ас. (Напомним еще раз: мы 134
всегда предполагаем, что а, Ь, с—действительные числа.) Рассмотрим три возможных случая: D<Z.O, D = 0, D>0.
а) Случай Так как 1=^^-, то при D < 0 числитель — D положителен, и потому знак ординаты вершины совпадает со знаком числа а. Пусть сначала а>0. Тогда (поскольку D < 0) I > 0, т. е. вершина параболы лежит выше оси абсцисс. Но при а > 0 ветвц параболы направлены вверх. Значит, при и а>0 вся парабола лежит выше оси
абсцисс. Точно так же, если D<0 и а<0, то парабола располагается целиком ниже оси абсцисс. Итак, если D < 0, то парабола _у=ах24Т,х-|-с не пересекает оси абсцисс, причем при а>0 она лежит выше этой оси (рис. 35), а при а<0 — ниже ее (рис. 36).
б) Случай D = 0. В этом случае 7=0, т. е. вершина параболы _у = ахг + £x-f- с лежит на оси абсцисс. Расположение параболы относительно оси абсцисс в зависимости от знака числа а показано на рис. 37 и 38.
в) Случай £)>0. Знак числа I— — в этом случае противоположен знаку числа а. Если а>0, то I<0, т. е. вершина расположена ниже оси абсцисс, а ветви параболы направлены вверх (так как а>0). Таким образом, если и а>0, то парабола пересечет ось абсцисс в двух точках Ах и А2 (рис. 39).
Случай а < 0 рассматривается аналогично (рис. 40).
Замечание. При £)>0 осью симметрии параболы является прямая, проходящая через середину Ао отрезка А±А2 параллельно оси ординат.
Алгебраическое исследование. Рассмотрим снова три случая: D<0, D — Q, D^>0.
Теорема 4. Если D < 0, то при всех действительных значениях х знак квадратного трехчлена у = ах2-\-bx~t с совпадает со знаком числа а.
Доказательство. Воспользуемся формулой (12):
о . l । / . b \2 D
у = ах2А-ЬхА-с = а х+х- —т~ -г 11 \ 1 2а 4а
Вынося в правой части последнего равенства число а за скобку, получаем
^=ах« + &х + с = о[(х+^У+4^]. (17)
135
У
Рис. 35.
Рис. 37.
Рис. 36.
Выражение, стоящее в квадратных скобках в формуле (17), / b \2 положительно при любом значении х, так как I -v+gj)
0, — D > 0, а2 > 0. Следовательно, при D < 0 знак квадратного трехчлена совпадает (при любом х) со знаком числа а (ср. рис. 35, 36).
Теорема 5. Если D = 0, то при всех действительных значениях х, кроме х — — знак квадратного трехчлена у — ах2-\-Ьх-фс совпадает со знаком числа а\ при х = — трехчлен обращается в нуль.
Доказательство. Если 0 = 0, то (см. формулу (17)) получаем
/ 6'2
У = а\Х + Та)- (18)
Ь 1
Из формулы (18) следует, что при х = —квадратный л р z b / .6 п
трехчлен обращается в нуль. Если х ?£—=, то х-фу- >0, , ь
и потому при х#~2а знак тРехчлена совпадает со знаком числа а (ср. рис. 37, 38).
Теорема 6. Если D~y>Q, то знак квадратного трехчлена у = ах2-\-Ьх-\-с совпадает со знаком числа а для всех х, лежащих вне отрезка [х1( х2], где xY и х2 — корни уравнения ах2 + Ьх -фс = 0; далее, знак квадратного трехчлена противоположен знаку числа а для всех х, лежащих внутри этого отрезка (т. е. для всех х, заключенных между корнями трехчлена’. хх < х < х.-); наконец, при х = хх и х — х2 трехчлен обращается в нуль.
Доказательство. Используем разложение (7) квадратного трехчлена на множители:
_у = ах2-ф/>х-фс = а(х— хх)(х— х2). (19)
Так как О>0, то корни хг и х2 действительны и различны (теорема 1). Пусть для определенности х, <х2. Если х<хР то подавно х<х2, и потому х — хг < 0, х — х2<0; следовательно, (х — хх)(х — х2)>0. Из формулы (19) вытекает тогда, что при х<хх знак трехчлена совпадает со знаком числа а. Аналогично устанавливается, что при х>х2 знак трехчлена также совпадает со знаком числа а. Далее, если -Kj<x<x2, то х — Х|>0, а х — х?<0, откуда получаем,
137
что (х—хх)(х— х2)<0. Следовательно, если хх<х <х2, то знак квадратного трехчлена противоположен знаку числа а. Наконец, при х — хх и х=х2 имеем у = 0.
Результат исследования квадратного трехчлена можно сформулировать в следующем удобном для запоминания виде: трехчлен ах2йх-фс при всех х сохраняет знак коэффициента а, за исключением лишь случая, когда его корни хх и х2 действительны (DS&O) и число х удовлетворяет неравенствам хх«Сх«Сх2.
Замечание. Пусть D > 0. Отметим на числовой оси корни хх и х2 квадратного трехчлена (пусть для определенности хх <; х2). Для всех х из бесконечного интервала (—оо, хх) (отмеченного на рис. 41 цифрой 7) разность х — xt отрицательна, а для всех х, больших хх, эта разность положительна. Таким образом, разность х — хх в точке хх меняет знак. Точно так же разность х— х2 меняет знак в точке х2.
1 Л Ш
Xi х2
Рис. 41.
Значит, при движении по числовой оси слева направо — от меньших значений к большим — произведение (х — хх)(х —х2) меняет знак в точках хх и х2, и только в этих точках. Следовательно, знаки произведения (х — хх)(х — х2) на интервалах 7, II, III (рис. 41) чередуются. Так как квадратный трехчлен отличается от произведения (х — хх)(х— х2) лишь постоянным отличным от нуля множителем а (см. (19)), то и знаки, которые принимает трехчлен на отмеченных интервалах, чередуются. Достаточно поэтому определить знак трехчлена на каком-либо одном из интервалов 7, 77, III.
Пример 5. Доказать, что квадратный трехчлен у ~ — ах2Ьхс принимает положительные значения при всех действительных значениях х тогда и только тогда, когда D <; О и а > 0.
Доказательство. Достаточность следует из теоремы 4. В самом деле, если D <0, то, по теореме 4, знак квадратного трехчлена совпадает со знаком числа а, и, следовательно, при а>0 трехчлен принимает положительные значения при всех действительных значениях х.
Докажем необходимость, т. е. покажем, что если трехчлен принимает при всех действительных х положительные 13§
значения, то О<0 и а>0. Допустим, что условие О<0 не выполняется, т. е. Тогда, по теореме 1, трехчлен
имеет действительные корни хх и х2 (возможно, совпадающие) и, следовательно, обращается в нуль при х—х1 и х — х2, что противоречит условию его положительности. Итак, £)<0. Согласно теореме 4 находим теперь, что а > 0.
§ 4. Квадратные неравенства
Неравенство вида ax24-fcx + c>0, (20)
где а, Ь, с — действительные числа, а 0, будем называть квадратным неравенством.
Если вместо х в левую часть неравенства (20) подставить некоторое действительное число х0, то получим числовое неравенство ах„ 4- Ьх0 -]- с > 0, которое при одних значениях хь может оказаться верным, а при других — неверным.
Иначе говоря, неравенство (20) можно рассматривать как неопределенное высказывание, которое для одних значений х является истинным, а для других — ложным. Число х0 назовем решением неравенства (20), если при подстановке вместо х числа х0 получается верное числовое неравенство axjj 4~
4~ с > 0, т. е. если квадратный трехчлен ах2 -}-Ъх при х = х0 принимает положительное значение.
Решить неравенство (20) — значит найти все решения этого неравенства.
Если использовать график функции у = ах2 -f- Ьх -|- с, то решение неравенства (20) сводится к отысканию всех тех значений х, для которых точки графика функции y = ax2-j-у-Ьх-I-с лежат выше оси абсцисс.
Наряду с неравенствами вида (20) можно рассматривать, например, такие неравенства:
ах2 4- Ьх 4- с < :о, (21)
ах2 4- Ьх 4- с S = 0, (22)
ах2 4- Ьх 4- с ;о, (23)
(24)
ахх2 4- Ьгх 4" а2х2 4~ Ь2х 4~ с2.
Эти неравенства мы также будем называть квадратными (если в (24) Я1 = а2, то это неравенство становится линейным).
Введем следующее определение. Два квадратных неравенства будем называть равносильными, если эти неравенства
139
MMetoT оДни й те же решения, т. ё. если всякое решение первого неравенства является решением второго и, обратно, всякое решение второго неравенства является решением первого.
Из этого определения следует, что
а) неравенство ах2 -J-Ьх 4- с <; 0 равносильно неравенству — ах2 — Ьх — с > 0;
б) неравенство а2х2 -J- Ь2х 4- > а2х2 + Ь2х 4~ с2 равносильно неравенству (аг — a2)x24-(bi— Ь2)х-\-с1— с2>0(при любых действительных av а2, Ь2, Ь2, сх, с2).
Докажем, например, первое из этих утверждений.
Пусть х0 — решение неравенства ах2 -f- Ьх 4- с <; 0; тогда ах„ 4- Ьх0 4- с < 0 — верное числовое неравенство. Умножив обе части этого неравенства на — 1, в силу свойств неравенств получаем — ахд — Ьх0 — с>0, откуда видно, что х0—решение неравенства —ах2 — Ьх—с> 0.
Обратно, если х2 — решение неравенства —ах2 — Ьх — — с > 0, то—ах\—Ьх2—с >• 0 — верное числовое неравенство, откуда находим ах[ 4~ Ьх2 4- с <; 0, т. е. х2 — решение неравенства ах2 4- Ьх 4- с <; 0.
Перейдем к нахождению решений квадратных неравенств. Мы ограничимся рассмотрением строгих неравенств, т. е. неравенств, содержащих знаки > или <. Такими являются неравенства (20), (21), (24). В отличие от строгих неравенства вида (22), (23) называют нестрогими.
Заметим, что всякое строгое квадратное неравенство можно привести к одному из следующих видов:
а) ах2 4-4~ с > 0 при а > 0; (25)
б) ах2 4- Ьх 4- с < 0 при а > 0. (26)
Действительно, если а < 0, то неравенство ах2 4-Ьх 4- с>0, но доказанному выше, равносильно неравенству ахх2 4~ 61-^4-+ <д < 0, где aj = —а, Ь2 — —Ь, с2 — —с, причем аг > 0 (г. е. равносильно неравенству вида (26)). Аналогично, при а<0 неравенство ах2 4- Ьх 4- с <; 0 умножением на —1 сводится к равносильному неравенству вида (25).
Итак, рассмотрим неравенства (25) и (26), в которых а>0.
Проведенное в § 3 исследование квадратного трехчлена позволяет утверждать, что
1) если £><0, то неравенство (25) имеет место при всех действительных х, а неравенство (26) не имеет решений (см. рис. 35, 36);
140
при всех решений
39) вы-отрезка С х2— корни трехчлена), а неравенство при хх<;х<;х2 (т. е. на интервале
О выпол-х< х2, а О имеет место лишь
его корни: хх = 2, х2=3. Так имеет место при х < 2 в х> 3.
42) точ-рас-при
2) если D = 0, то неравенство (25) имеет место х, кроме х = — а неравенство (26) не имеет (см. рис. 37, 38);
3) если О>0, то неравенство (25) (см. рис. полняется при х<хх и х>х2 (т. е. вне х2], где хх (26) выполняется
х2У).
Итак, при а > О неравенство ах2foe-)-с няется всегда, кроме случая, когда О 4== О и хх неравенство ах2 -|- Ьх -ф с <; 0 при а тогда, когда D > 0 и х2 < х < х2.
Пример 6. Решить неравенство х2—5х4-6>0.
Решение. Имеем О=52— 6-4=1 >0. Решив уравнение х2 — 5x4-6 = 0, находим ' ~ ~
как а = 1 > 0, то неравенство Этот же результат можно получить, используя замечание к теореме 6, из разложения х2 — 5x4-6 = = (х — 2) (х—3).
Наконец, решение неравенства можно найти графически: график функции _у = х2— 5х-|-6 (рис. пересекает ось Ох в ках хх — 2 и х2 = 3 и положен выше оси Ох х < 2 и х > 3.
Пример 7. Решить неравенство 6х—9<х2.
Решение. Неравенство
— 6х4-Э>0 или (х—З)2>0; оно выполняется при всех х, кроме х=3.
Пример 8. Решить неравенство 2х2 4~ 4х 4~ 3 < 0.
Решение. Так как 0=16 — 24<0 и а = 2>0, то данное неравенство не имеет решений.
Пример 9. Решить неравенство x2sg;4x — 4.
Решение. Неравенство равносильно следующему: х2— — 4x4- 4 «4 0 или (х — 2)2 «С 0; оно имеет место лишь при
141
§ 5. Наибольшее и наименьшее значение квадратного трехчлена
Теорема 7. Если а > 0, то квадратный трехчлен у — ах2 -(-Ьх 4* с при х — — имеет наименьшее значение, равное (где D = b2— 4ас). Если а<0, то квадратный трехчлен имеет при х = —наибольшее значение, D равное — .
Доказательство. Пусть сначала а > 0. Тогда в фор-муле (12) первое слагаемое неотрицательно, т. е. a =S;0.
Поэтому при любом действительном х значение у не может быть меньшим, чем —При х = — функция (12) при-D нимает значение _ут1п = — которое является наименьшим среди значений, принимаемых функцией на всей числовой оси.
Этот факт можно также объяснить, используя график функции у = ах2 -ф Ьх 4* с. При д>0 ветви параболы направлены вверх, самая нижняя точка графика — ее вершина (рис. 35, 37, 39). Очевидно, ордината вершины и есть наи-, D меньшее значение квадратного трехчлена, т. е. I——=_ymin,
Ь и это значение трехчлен принимает при х = т — —
Заметим, что при а>0 квадратный трехчлен не имеет наибольшего значения.
Пусть теперь а < 0. Рассуждая аналогично, найдем, что при а<0 квадратный трехчлен имеет наибольшее значе-, D
ние _уП1ах = / =— и это значение он принимает при х = = -£ (рис. 36, 38, 40).
Пример 10. Данное положительное число М представить в виде суммы двух слагаемых так, чтобы их произведение было наибольшим.
Решение. Обозначим одно из слагаемых через х; тогда другое слагаемое равно М— х.
Нам нужно найти наибольшее значение произведения х(М— х). Рассмотрим квадратный трехчлен у = х(М — х)— =—х24~Л4х. Коэффициент при х2 этого трехчлена отрица-142
телен (равен —1); следовательно, при х — — =
= у трехчлен принимает наибольшее значение (теорема 7). Так как х = -^, то М — х = у. Итак, произведение двух чисел, сумма которых равна данному положительному числу, является наибольшим, если эти числа равны между собой.
Задачи к главе V
5.1. Квадратный трехчлен ах2 -f- bx -f- с при х=1; 2; 3 принимает значения, соответственно равные 0; 1; 4. Найдите значение этого трехчлена при х=11.
В задачах 5.2—5.4 коэффициенты р и q могут быть как действительными, так и комплексными.
5.2. Корни квадратного уравнения х2 -f-рх -f-q = 0 не являются действительными и не являются комплексно сопряженными. Что можно сказать о коэффициентах этого уравнения?
5.3. Может ли один из корней уравнения х2 -{-рх -f- q = 0 быть действительным, а другой — не действительным (т. е. комплексным числом с отличной от нуля мнимой частью)?
5.4. Один из корней уравнения х2 + рх -f- q = 0 равен 1-f-i. Что можно сказать о другом корне этого уравнения?
5.5. Докажите, что если один из корней квадратного трехчлена (с действительными коэффициентами) является действительным числом, то и второй корень трехчлена действителен и при этом выполняется неравенство D 0.
5.6. Докажите, что если один из корней квадратного трехчлена (с действительными коэффициентами) не является действительным числом, то и второй корень не является действительным и при этом D < 0.
5.7. Может ли уравнение x2--f-рх -f-q = 0, где р и q — рациональные числа, иметь следующие корни:
1. Х1 = Г2, х2=±?
2. х^К'2+1, х2=1— У~2?
5.8. Известно, что сумма корней квадратного трехчлена является действительным числом. Можно ли отсюда заключить, что все коэффициенты трехчлена действительны?
143
5.9. Известно, что сумма и произведение корней квадратного трехчлена являются действительными числами. Можно ли отсюда заключить, что все коэффициенты трехчлена действительны?
5.10. Известно, что сумма корней квадратного трехчлена и произведение его корней являются действительными числами и, кроме того, один из коэффициентов трехчлена действителен. Вытекает ли отсюда, что и два других коэффициента трехчлена действительны?
5.11. Докажите, что первое основное утверждение теоремы 1 о корнях квадратного трехчлена можно высказать в виде теоремы А «-> В \J С, где А, В, С — следующие неопределенные высказывания: А = [ах2~уЬхА- с = 0}, В~{х — х1}, С={х=х2}, а числа хг, х2 определяются формулами (5).
5.12. Корни уравнения х2— 4rx-f-7r2 = 0 таковы, что xf + Хг = 2. Найдите г.
5.13. Пусть Xj и х2— корни уравнения ах2 4~ bx -f- с = О, а =/= 0. Не решая этого уравнения, выразите через а, Ь и с следующие суммы:
1. xf-f-Xfr
2. х! + х1.
5.14. Пусть х, и х2— корни уравнения X2 +//х<7 = О-Найдите р и q, если известно, что хг-f-1 и x2-f-l являются корнями уравнения х2—p2x-\-pq = Q. -
5.15. Не находя корней хг и х2 уравнения Зх2 — 5x-f--|-6 = 0, вычислите сумму х’хг + хгх2.
5.16. Составьте квадратное уравнение, имеющее корни хГ3 и Х23, где хг и х2 — корни уравнения х2 — 8х-{-2 = 0.
5.17. Постройте графики следующих функций:
а) у — 4 — х2; в) у = — х2 -f- 2х — 1;
б) у = х2 — 3x4*2; г) у = х2 — 2х-{-2.
5.18. Определите знаки чисел а, Ь, с, исходя из расположения параболы у=ах2-{-Ьх-{-с относительно координатных осей в каждом из случаев, показанных на рис. 43.
5.19. Докажите, что если а>0, то функция у = ах2 4* -(-Z’X-}-c является возрастающей при х> — Иначе говоря, для любых Xj и х2, удовлетворяющих условию
Ь . . о . , .
— 2^г<х1<х2, имеет место неравенство ах\ Ьхх 4- с <; < axi -f- bx2 с.
144
5.20. Даны три различные точки А, В, С: две из них лежат на оси абсцисс, третья — на оси ординат, причем ни одна из точек не совпадает с началом координат. Существует ли квадратный трехчлен, график которого проходит через эти три точки? Единственный ли такой трехчлен можно подобрать?
Решите задачу в следующих случаях:
1. А (—1,0), 5(2,0), С(0,—4).
2. А (3,0), 5(1,0), С (0,3).
3. А (—5,0), 5 (—1,0), С (0,—5).
5.21. Даны две точки А и 5, причем отрезок АВ не параллелен ни одной из осей координат. Существует ли квадратный трехчлен, график которого имеет вершину в точке А и проходит через точку 5? Единственный ли такой трехчлен можно подобрать? Решите задачу в следующих случаях:
1. А (0, 1), 5(1,3).
2. А (3,1), 5(5,—3).
3- А (2, 4), 5(0,0).
145
5.22. Решите следующие неравенства:
1. х(4 —х)<0. 4. x2sg2x—1.
2. х2<х—1. 5. 4х2>4х—1.
3. х2-{-Зх — 4<0.
5.23. Решите следующие неравенства:
. 4х—х2 „ 9 х2 —3x4-4
*• Х2_Х4-1^и- 1 - х2 -^>и-
5.24. При каких г сумма квадратов корней уравнения х2—rx-j-r — 3 = 0 является наименьшей?
5.25. Квадратный трехчлен y = ax2-ybxJrc при х=1 принимает наибольшее значение, равное 3, а при х = — 1 обращается в нуль. Какое значение он примет при х=5?
5.26. Пусть a, b, с, d — действительные числа, а24-с2у=0. При каком значении х функция у = (ах 4- Ь)2 4-(сх 4- d~)2 принимает наименьшее значение? Найдите это наименьшее значение.
5.27. При каких значениях г уравнение х2 4- (4 -f- 2г) х 4-4~54-4г=0 имеет: 1) равные корни? 2) корни, равные по абсолютной величине, но противоположные по знаку?
5.28. Найдите необходимое и достаточное условие того, что корни квадратного трехчлена ах24-Ьх4-с (а, Ь, с действительны, ау=0) действительны и имеют: 1) одинаковые знаки; 2) противоположные знаки.
5.29. Найдите все действительные значения г, при которых корни уравнения х2 — 2(г — 1)х-|~2г + 1 =0 действительны, и исследуйте их знаки в зависимости от г.
5.30. Докажите, что квадратный трехчлен ах2 -\-bx-\-c имеет один и тот же знак при всех действительных х тогда и только тогда, когда D = b2 — 4ас<^0.
5.31. Докажите, что квадратный трехчлен ах2 -[-Ьх-\- с отрицателен при всех действительных х в том и только в том случае, если D < 0, а < 0.
5.32. Найдите все значения г, при которых квадратный трехчлен х24-2гх4-1 положителен при всех действительных значениях х.
5.33. Докажите, что корни уравнения х2 4-Дх: 4-<7 = О (р и q — действительные числа) действительны и отрицательны тогда и только тогда, когда р1— 4q~^Q, р>0, q>0-
5.34. Найдите все значения г, при которых корни уравнения (г — 1)х2—- 2гх-{-г-{-3 = 0 действительны и положительны.
146
5.35. Найдите все действительные значения г, при которых функция у = (г2—1)х2-ф2(г—1)хф2 принимает положительные значения при всех действительных х.
5.36. Найдите все действительные значения, г, при которых квадратный трехчлен у = гх2 ф 2 (r-ф 2)х-ф 2г-ф4 принимает отрицательные значения при всех действительных х.
5.37. Найдите необходимое и достаточное условие того, что корни X! и х2 уравнения х2фрх + <7 = 0 действительны и удовлетворяют неравенствам а<Сх2<р.
5.38. Найдите все действительные значения г, при которых корни уравнения 2гх2— (r-ф 1)х-ф 1 =0 действительны и оба по абсолютной величине меньше единицы.
5.39. Пусть коэффициенты уравнений х2 фprx -фq1 — О и х2 -фр2х ф q2 = 0 действительны и связаны соотношением р1р2 = 2(71-ф72)- Докажите, что по крайней мере одно из этих уравнений имеет действительные корни.
5.40. Найдите наибольшее и наименьшее значения функции
у = , если — 1 С 1.
х2фхф1’
5.41. Найдите наибольшее и наименьшее значения функции
у = х4 ф Зх2 -ф 2, если —2sgxsg3.
5.42. Найдите наибольшее и наименьшее значения функции у = sin2 х ф sin х-ф 1.
ГЛАВА VI
МНОГОЧЛЕНЫ И АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
§ 1. Многочлен и его значения
Многочленом от X называется выражение вида
айхп + агхп 1 + а2х" 2 4-.. .-|-а„-2х24-й„.1х + ап. (1)
Здесь щ., alt..., ап — некоторые числа, называемые коэффициентами многочлена, а х — символ, вместо которого мы можем подставить любое числовое значение.
Можно рассматривать многочлены как с действительными, так и с комплексными коэффициентами. Но мы в дальнейшем будем рассматривать только многочлены с действительными коэффициентами (а чаще всего коэффициентами будут целые или рациональные числа). Напротив, вместо х мы будем часто подставлять не только действительные, но и комплексные числовые значения.
Пусть с — некоторое число (действительное или комплексное). Значением многочлена (1) при х = с называется число, которое получится, если в (1) вместо х подставить число с и произвести указанные действия. Например, многочлен
л3 - 2л-2 4- Зл - 5 (2)
принимает при х = 2 значение
23 — 2-22 4-3-2 — 5= 1;
значение многочлена (2) при л—1—У'2. равно
(1 _/2)3 —2(1 — /2)24-3(1 — /2) — 5 = — 1—4/2,
а его значение при х = 2-Н равно
(2 4-г)3 - 2(24-/)24-3(24-/)—5 = —34-6/.
148
Часто для сокращения Записи используют функциональную символику для обозначения многочленов. Условимся, например, обозначать многочлен (1) символом f(x}.
f(x) — аохп 4~ 1 'г an-ix 4* ап.
Тогда значение этого многочлена при х — с обозначается через f(c):
f(c) — аосп Ц- агсп 1 -ф-... -ф- ап-гс -ф- ап.
Так, если через <р(х) обозначить многочлен (2), т. е. <р(х) = = х3 — 2х2 4- Зх — 5, то
<р(2)= 1, ф(1—=—1—4]/2, ф(24-/) = —34-6/.
Коэффициент ап в выражении (1) называется свободным членом этого многочлена. Очевидно, что при х = 0 многочлен (1) принимает значение ап. Таким образом, значение произвольного многочлена при х = О равно свободному члену этого многочлена.
Далее, при х= 1 многочлен (1) принимает значение ап + ai 4- • • + ап 14-Яп- Таким образом, значение произвольного многочлена при х= 1 равно сумме всех коэффициентов этого многочлена.
Эти два простые замечания часто используются при решении задач.
Обычно «многочленами» называют не только выражения вида (1), но и выражения, приводимые к этому виду с помощью тождественных преобразований: раскрытия скобок, приведения подобных членов, перестановки слагаемых. В частности, если какой-либо из коэффициентов в (1) обращается в нуль, то соответствующее слагаемое в записи многочлена просто пропускают. Например, многочлен
О х4 4- 2х3 4 0 х2 -J- -V + 5 записывают просто в виде
2х34-х4-5. (3)
Далее, в записи многочлена (1) все слагаемые расположены по убывающим степеням буквы х. Однако, если слагаемые расположены в ином порядке, мы тоже называем их сумму многочленом. Например,
х4- 1 —х3 — х* (4)
149
есть многочлен: переставляя слагаемые, мы можем записать это выражение в виде (1):
(—1)х*+(— 1)х3 + 0.х2-Н -х+1.
Наконец, в тех случаях, когда для приведения к виду (1) нужно в выражении раскрыть скобки и произвести приведение подобных членов, мы также называем это выражение «многочленом». Например,
l+(x2-f-2)(x2 — х+ 1) (5)
есть многочлен: раскрывая скобки и производя приведение подобных членов, мы легко приведем его к виду
х4 - ха + Зх2 — 2х -f- 3.
Таким образом, называя ‘ выражения (3), (4), (5) и аналогичные им «многочленами», мы подразумеваем, что их можно, пользуясь законами сложения и умножения (стр. 46— 47), привести к виду (1). Такого расширенного понимания термина '«многочлен» мы и будем придерживаться в дальнейшем.
Если в многочлене, записанном в виде (1), коэффициент при х" отличен от нуля, то слагаемое аохп называется старшим членом, коэффициент ай называется старшим коэффициентом, а сам многочлен называется многочленом п-й степени. Если же ао = О, то слагаемое айхп можно отбросить, и многочлен запишется в виде o^x"-1-f-... .. .-j- cin-iXan. Если теперь =/= 0, то рассматриваемый многочлен имеет степень п—1. Если же и al — Q, то слагаемое «|ХЛ 1 также можно отбросить и т. д. Таким образом, мы всегда можем считать (отбросив стоящие в начале нулевые слагаемые, если они есть), что в записи (1) коэффициент ап отличен от нуля. Исключение составляет лишь случай, когда все коэффициенты многочлена (1) обращаются в нуль. В этом случае многочлен называется нулевым многочленом (или нулем) и обозначается символом 0.
Итак, всякий отличный от нуля многочлен можно записать в виде (1), где ао=/=О, а п — некоторое неотрицательное целое число. Такую запись называют канонической записью1) многочлена /г-й степени.
!) Канон — закон; поэтому «каноническая запись» означает: узаконенная, общепринятая запись.
150
Пример 1. Найти сумму коэффициентов многочлена, получающегося из многочлена
1 + № — 6x4-5) (х5 + Зх4 — 2Х3 4-х2 — х — 7)34-
4- (х2 — Зх + 1 )25 (х3 4- 5х 4- 7) приведением к каноническому виду.
Решение. Обозначим данный многочлен через /(х). Для того чтобы определить сумму коэффициентов этого многочлена, вовсе не нужно приводить его к каноническому виду, т. е. раскрывать скобки, приводить подобные члены и складывать коэффициенты получающегося многочлена. В самом деле, искомая сумма коэффициентов равна /(1). Полагая х = 1, легко находим
/(1)= 14-0.(...) + (— I)25- 13=1—13 = — 12.
Таким образом, искомая сумма коэффициентов равна — 12.
Два многочлена считаются равными, если их каноническая запись одинакова, т. е. коэффициенты этих многочленов соответственно равны. Иными словами, если
Р (х) = аохп 4- aix" 1 4-... ani
Q(x)^boxm + b1xm^ + ... + bm '
— два многочлена в канонической записи, то, по определению, равенство P.(x)=Q(x) имеет место в том и только в том случае, если т—п и коэффициенты многочленов соответственно равны, т. е. a0 = b0, a^^bi и т. д.
Из этого определения вытекает, что если Р (х) и Q (х) — равные многочлены (т. е. многочлены, имеющие одинаковую каноническую запись), то для любого числа с значения этих многочленов при х = с совпадают.
Теорема, обратная этой (а также противоположная теорема и теорема, противоположная обратной), также справедлива. Таким образом, имеют место следующие четыре теоремы:
Теорема 1. Если P(x) = Q(x), то для любого числа с справедливо равенство P(c) — Q(c).
Теорема 2. Если для любого числа с справедливо равенство Р (c)=Q(c), то Р (x) = Q(x).
Теорема 3. Если Р (х) =/= Q (х), то существует такое число с, что Р(с)=£ Q(c).
Теорема 4. Если существует такое число с, что Р (с)=/= Q (с), то Р (х) =4= Q (х).
151
Теорема 1 (а значит, и эквивалентная ей теорема 4) очевидна: если два многочлена равны (т. е. тождественными преобразованиями приводятся к одному и тому же каноническому виду), то при подстановке х = с они принимают одинаковые числовые значения. Напротив, теорема 2 (и эквивалентная ей теорема 3) вовсе не очевидна: в ней утверждается, что если два многочлена Р(х) и Q(x) принимают при любом с одинаковые значения (т. е. Р (c) = Q(c)), то (при приведении к каноническому виду) эти многочлены имеют одинаковые коэффициенты. Доказательство теоремы 2 будет приведено в конце главы.
Рассмотрим пример. Ученик произвел умножение многочленов и получил следующий результат:
(х5 — х4 + х2 — х -j- 1) (х 1) = х6 Ц- 1.
Чтобы проверить, правильно ли выполнено умножение, обозначим многочлен, стоящий в левой части, через Р (х), а многочлен, стоящий справа, через Q(x) и придадим аргументу х несколько числовых значений. Подставляя х = 0, легко находим Р(0) = 1, Q(0)=l, т. е. P(0) = Q(0). Аналогичный результат мы получаем и при х=1: Р(1) = 2, (2(1) = 2, т. е. P(1) = Q(1). Можем ли мы на основании этого сделать вывод, что P(x) = Q(x), т. е. что умножение выполнено правильно? Ни одна из приведенных выше четырех теорем не позволяет сделать такого вывода. Наиболее подходящей является вторая из этих теорем. Однако, чтобы ее применить, мы должны знать, что равенство Р (c) = Q(c) имеет место для любого с, а нам это вовсе не известно. Но продолжим нашу проверку дальше: подставим х——1. Мы легко находим Р(—1) = 0, Q(—1) = 2, т. е. Р(—1)=4=
—1). Теперь четвертая теорема позволяет нам сделать вывод, что Р (х) Q (х), т. е. умножение выполнено неверно.
Мы видим, что совпадение значений двух многочленов Р(х) и Q(x) в одной-двух точках еще не гарантирует выполнения равенства P(x) = Q(x). Тем не менее, сделав достаточно большое число проб, можно установить равенство двух многочленов по совпадению их значений в отдельных точках. Именно, справедлива следующая теорема, существенно усиливающая утверждение теоремы 2.
Теорема 5. Пусть Р(х) и Q(x)— два многочлена, степень каждого из которых не превосходит п. Тогда, если значения многочленов Р(х) и Q(x) совпадают в n-f-l точках, то P(x) = Q(x).
152
Иначе говоря, если Р (cj) = Q (сх), P(c2) = Q(c2),... ..., Р (с„+1) = Q (с„+1) (где cv с2, ..., сл+1 —различные числа), то Р(х) — Q(x). Ясно, что теорема 2 вытекает из теоремы 5. Доказательство теоремы 5 мы приведем ниже (в конце главы).
Смысл теорем 1, 2 и 5 можно пояснить следующим образом. Каждый многочлен Р(х) можно рассматривать как функцию аргумента х. Теорема 1 утверждает, что если Р(х) и Q(x) совпадают как многочлены (г. е. имеют при приведении к каноническому виду одинаковые коэффициенты), то они совпадают и как функции (т. е. при любом значении аргумента они принимают одинаковые значения). Теорема 2 утверждает обратное: если Р(х) и Q(x) совпадают как функции, то они совпадают и как многочлены. Наконец, теорема 5 усиливает теорему 2: если степень каждого из многочленов Р(х), Q(x) не превосходит п и если значения функций Р (х) и Q (х) совпадают в п -ф 1 точках, то Р (х) и Q(x) совпадают как многочлены.
Пример 2. Подобрать числа а, b и с таким образом, чтобы выполнялось равенство
* + 5 __ а । b с
(х — 1) (х — 2) (х— 3) х-1+х-2 + х-3‘
Первое решение. Приводя дроби в правой части к общему знаменателю, перепишем требуемое равенство в виде
x-f-5 _ _а(х — 2)(х —3) + Ь(х— 1)(х —3)4~с(х — 1)(х — 2)
(х - 1) (х - 2) (х - 3) ~ (х- 1)(х- 2)(х- 3) •
Таким образом, задача заключается в том, чтобы подобрать числа а, b и с, для которых выполняется равенство
х ~у5 = а(х—2)(х — 3)-\-Ь(х— 1)(х — 3)-фс(х— 1)(х — 2). (6) Раскрывая скобки и приводя подобные члены, перепишем это равенство в виде
х-ф5 = (а-ф5-ф с)х2 — (5а -ф 45 -ф Зс)х -ф (6а -ф 35 -ф 2с).
Теперь, согласно определению равенства многочленов, справа должен стоять многочлен первой степени с теми же коэффициентами, что и у многочлена, стоящего слева. Иначе говоря, должны выполняться соотношения
а -ф 5 -ф с = О, 5а -ф 45 -ф Зс = — 1, 6а -ф 35 -ф 2с = 5.
153
Рассматривая эти соотношения как систему уравнений относительно а, b и с и решая эту систему, находим требуемые значения:
а = 3, Z>=—7, с = 4.
Второе решение. Как и при первом решении, находим, что задача заключается в отыскании чисел а, b и с, для которых выполняется равенство (6). Но согласно теореме 1 (стр. 151) из равенства двух многочленов вытекает совпадение их значений для любого х. Иными словами, если бы задача была уже решена (т. е. числа а, Ь, с подобраны), то в равенство (6) мы могли бы вместо х подставлять любое числовое значение. Подставим в это равенство х—1, затем х = 2 и, наконец, х = 3. Мы получим
6 = 2а, 7= — Ь, 8 = 2с.
Таким образом, если равенство (6) выполняется, то числа а, Ь, с-должны иметь следующие значения: а = 3, Ь = —7, с = 4. Но действительно ли при этих значениях а, b и с имеет место равенство (6)? Утвердительный ответ на этот вопрос вытекает из теоремы 5. В самом деле, мы подобрали значения а, b и с так, чтобы при х=\, х~2 и х — 3 левая и правая части соотношения (6) принимали одинаковые значения. Но так как слева и справа стоят многочлены не выше второй степени и так как значения этих многочленов совпадают в трех точках, то, по теореме 5, слева и справа стоят равные многочлены.
Пример 3 (задача-шутка). Пусть а, b и с —три различных числа. Рассмотрим уравнение
(х —а)(х — 6) , (х —6)(х —с) (х —с)(х —а)_ .
(с— а) (с— Ь) (а — Ь) (а — с) (Ь— с) (Ь—а) ‘ '
Так как в знаменателе каждой дроби стоит число, а в числителе— многочлен второй степени, то мы имеем квадратное уравнение. Непосредственная проверка показывает, что числа а, b и с удовлетворяют этому уравнению. Таким образом, написанное квадратное уравнение имеет три различных корня. Чем это объясняется?
Решение. Слева и справа в равенстве (7) стоят многочлены не выше второй степени. Так как значения этих многочленов совпадают в трех точках, то многочлены, стоящие слева и справа, равны (по теореме 5). Значит, при приведении левой части к каноническому виду получится 1, т. е.
154
коэффициенты при х1 и при х обратятся в нуль, и мы получим тождество 1 = 1, а не квадратное уравнение. В этом можно убедиться и непосредственно (произведя сложение дробей в левой части).
Заметим, что до того, как многочлен приведен к каноническому виду, определить его степень иногда бывает трудно. Например, в многочлене
(х5 + х* + х3 + х2 + х+ 1)(х — 1) — х2(х2+ 1)(х2—1)
в такой записи имеется, например, пятая степень буквы х. Однако, раскрывая скобки и приводя подобные члены, мы запишем этот многочлен в виде jc2—1, так что в действительности это — многочлен второй степени. То же мы видели при решении примера 3: левая часть соотношения (7) равна 1„ т. е. является многочленом нулевой степени, хотя по внешнему виду она похожа на многочлен второй степени.
§ 2. Действия над многочленами
Сумма, разность и произведение двух многочленов также являются многочленами.
Это утверждение справедливо именно, в силу принятого в предыдущем параграфе расширенного понимания термина «многочлен». В самом деле, если
Р(х) = аохп 4- а^1 + ап,
Q(x) = boxm + Ь,хт^ +... + Ьт
— два многочлена, то выражения
P(x)+Q(x) =
= (апхп а1хп 14- ••• 4_ ап) + (Ьохт 4- Ь1хт 1 4- • 4_ Ьт), P(x)-Q(x) =
= (аихп 4- ауС1 14-... 4- ап) — (Ьохт 4- ftjx'”-14- • • 4* bm), P(x)-Q (х) =
— (аох” 4" Qi.xn 14- • • • 4~ и„) (Ьохт 4- Ьгхт 14- • • 4- Ьт)
легко приводятся к виду (1) (раскрытием скобок и приведением подобных членов), т. е. являются многочленами.
Следующие легко доказываемые теоремы часто оказываются полезными при решении ряда задач.
Теорема 6. Пусть Р (х) и Q(x) — два отличных от нуля многочлена. Тогда степень многочлена Р (x)Q (х) равна
155
сумме степеней многочленов Р (х) и Q (х), а старший коэффициент многочлена Р (х) Q(x) равен произведению старших коэффициентов многочленов Р (х) и Q(x).
Теорема 7. Степень многочлена Р (х) 4- Q (х) (или Р (х)-— Q (х)) не превосходит наибольшей из степеней многочленов Р (х), Q (х).
Заметим, что степень многочлена P(x)±Q(x) может оказаться меньше степени каждого из многочленов Р (х), Q(x). Например, если
' Р (х) = х3 — х2 Зх 5,
Q (х) = — х3 4- х2 — х — 3,
то сумма этих двух многочленов третьей степени будет многочленом первой степени:
P(x)4-Q(x) = 2x + 2.
Напомним следующие формулы умножения многочленов, часто применяемые при решении задач (в этих формулах т, п — произвольные натуральные числа):
(хп + ахп^ > + а2хл 2 + ... + ап-2х2 + ап^х + ап)(х-а)= .
= xn+1 —a”+I, (8)
(х2я — ах2'" -1 4- а2х2т'2 —... 4- а2'" ~ 2х2 — а2т1х 4- а2"1) X
X (х4-а) = х2т + 1 4-а2'п + 1. (9)
В частности, при а = 1 имеем
(хл4-хл-,4-...4-х24-х+ 1)(х— l) = x,l+1 — 1, (10)
(x2m — х2т ~14- х2т ~2 —... 4- х2 — х 4-1) (х 4-1) = х2"1 +14-1 •
(И)
Доказательство этих формул непосредственно получается раскрытием скобок и приведением подобных членов.
Пример 4. Доказать, что не существует многочлена, квадрат которого был бы равен многочлену
х1000-|_х9»в + ...+ х+ 1.
Решение. Допустим, напротив, что
xiuoo + xe#» + ... + x+ 1 = [Р(х)]2, (12)
где Р (х) —некоторый многочлен. Полагая х==1, находим отсюда [Р (1)]2= 1001, так что сумма коэффициентов многочлена Р (х) равна У 1001 или —}Л1001. Значит, сумма коэффициентов многочлена Р (х) 156
является иррациональным числом, и потому среди его коэффициентов имеется хотя бы один иррациональный.
Запишем многочлен Р (х) в каноническом виде:
Р (x)=ao*n + «i*n_1 + --- + «n (где а07^0).
Тогда старший член многочлена (Р (х))2 = Р(х) • Р (х) равен аохп • аохп — = а';1х2п, и потому должно быть а‘;х2л = х,00°. Из этого следует, что п = 500 и <т§ = 1, т. е. а0= ± 1. Так как Р (0) — ап = а^т, то из (12) мы получаем 1=(й5ОТ)2, т. е. а-м—± 1.
Итак, старший коэффициент а0 есть рациональное число, но среди последующих коэффициентов alt a4ss многочлена Р (х) имеется хотя бы один иррациональный. Обозначим через m наименьшее целое число, для которого коэффициент ат иррационален (здесь т<500). Тогда мы имеем
Р (х) = йох500 +... + ат _ jxboo-fm -1 > + атх™пт 4-... 4- амо =
= (я0х500 +... + ат _ jxboo- -1 >) + (атХмо -т _|_... _|_ а^} = q (х} _|_ (х)>
где Q (х) = йох500 - + ат 1х600 ~'т'"1! —многочлен, все коэффициенты которого рациональны, a R (х) = afflx600~m 4-• •. 4~ — многочлен с
иррациональным старшим коэффициентом. Возводя в квадрат, находим
[Р (х)]2 = [Q (х) + R (х)]2 = [Q (X)]2 + 2Q (х) • Р (х) + [Р (х)]2.
Многочлен [Q (х)]2 имеет рациональные коэффициенты. Старший член многочлена 2Q (х) Р (х) равен 2о0х600 • ятх600“ m = 2о0ятх1000’т. Коэффициент 2аеат этого члена иррационален. Наконец, многочлен [Р (х)]3 имеет степень 1000—2m, т. е. степень меньшую, чем 1000—т (ибо т > 0). Поэтому многочлен [Р (х)]2 не содержит xiooo -т
Таким образом, коэффициент при xiono'm в многочлене [Р (х)]2 равен fem + 2fl(/zm, где Ьт — коэффициент при уккю- т в многочлене [(?(х)]2. Но мы видели, что Ьт — рациональное число, а 2аоат — иррациональное, так что сумма fem + 2a0flm также является иррациональным числом.
Итак, коэффициент при х1000~ т в многочлене [Р (х)]2 есть иррациональное число. Но это противоречит равенству (12), так как в левой части этого равенства стоит многочлен с рациональными коэффициентами.
Перейдем теперь к рассмотрению деления многочленов. Пусть f(x) и g(x)— два многочлена, причем многочлен g(x) отличен от нуля. Если существует такой многочлен q(x), что f(x) = g(x) q (х), то говорят, что многочлен f(x) делите я на g(x) (или что g(x) является делителем многочлена /(х)), а многочлен q (х) называют частным от деления f(x) на g(x).
Например, равенство (10) показывает, что при любом натуральном k многочлен хк—1 делится на х—1 (и частное равно хк~1 4-х*’24-...4-х 4- 1).
Простые примеры показывают, что один многочлен делится на другой не всегда. Например, многочлен х2-|-1 не
157
делится на х—1. В самом деле, если бы многочлен х24-1 делился на х—1, мы имели бы (х2Ц-1) = (х—\)q(x), где q(x)— некоторый многочлен. Но при х— 1 левая часть принимает^ значение 2, а правая — значение 0. Следовательно, написанное равенство не может иметь места ни при каком q(x) (теорема 4 на стр. 152), т. е. х2 +1 не делится на х— 1.
Итак, в множестве многочленов деление осуществимо не всегда. Однако имеется более общая операция, называемая делением с остатком и осуществимая в множестве многочленов всегда (за исключением случая, когда делитель равен нулю). Напомним определение этой операции.
Пусть f(x) и g(x)— два многочлена, причем многочлен g(x) отличен от нуля. Разделить многочлен f(x) на многочлен g(x) с остатком означает (по определению) записать многочлен /(х) в виде
+ (13)
где q(x) и г(х)—некоторые многочлены, причем г (х) либо равен нулю, либо имеет меньшую степень, чем многочлен g(x). Многочлен q(x) называется частным, а многочлен г(х)— остатком от деления многочлена /(х) на g(x).
Следующая теорема показывает, что деление с остатком является однозначной всегда выполнимой операцией.
Теорема 8. Пусть f(x) и g(x) — два произвольных многочлена, причем многочлен g(x) отличен от нуля. Тогда существуют такие многочлены q(x) и г(х), что выполнено равенство (13) и многочлен г(х) либо равен нулю, либо имеет меньшую степень, чем многочлен g(x). Указанными условиями многочлены q (х) и г (х) определяются однозначно.
Доказательство. Прежде всего установим существование требуемых многочленов q(x) и г (х). Если /(х) = 0, то равенству (13) удовлетворяют многочлены q(x) — 0, г (х) = = 0, т. е. в этом случае искомые многочлены q(x) и г(х) существуют. Пусть теперь /(х) 0, и пусть
/(х) = аохп + а,хп~14-... + ап,
g (х) = Ьохт + /71хш^'1 +... + Ьт
— каноническая запись многочленов /(х) и g(x), так что т и п — неотрицательные целые числа и ао^0, 0. Если
п<т, то многочлены q(x) — Q, г(х)=/(х) удовлетворяют
158
Поставленным условиям. Поэтому остается рассмотреть слу-
чай, когда п^пг. Рассмотрим многочлен
\°0 /
Старший член этого многочлена равен ух" т • Ьохт= аохт (см. теорему 6 на стр. 155), т. е. совпадает со старшим чле-
уЛ-т
Ь0Х
ном многочлена /(х). Поэтому многочлен f(x)—
•g(x)
(если он не равен нулю) имеет степень, меньшую чем п. Мы
можем теперь написать следующее очевидное тождество:
f(x^xn-mg(x) + ^f(x)-a^xn-mg(x)). (14)
Обозначим многочлен ^-х" т Ьо
через д* (х), а второе слагае
мое в правой части равенства (14) через /* (х); тогда равенство (14) перепишется в виде
/(х) = д* (х) g (х) +/* (х),
причем многочлен f*(х) либо равен нулю, либо имеет меньшую степень, чем /(х). Если многочлен /*(х) 'равен нулю или имеет степень, меньшую чем т, то наша цель достигнута: требуемым условиям удовлетворяют многочлены д(х) — = д* (х) и Если же /* (х) все еще имеет сте-
пень, большую или равную т, то наша цель еще не достигнута. Но все же мы несколько приблизились к цели, так как многочлен /* (х) имеет меньшую степень, чем /(х). Мы можем, далее, точно так же поступить с многочленом /* (х), т. е. записать этот многочлен в виде
. /*(x) = 9**(x)g(x) + /**(x),
где /** (х) имеет еще меньшую степень. Теперь мы можем написать
fix) = д* (х) g (х) 4- (д* * (х) g (х) + f* * (х)) =
=(?* (х) + д** (x))g(x) +/** (•*)•
Если многочлен /** (х) равен нулю или имеет степень, меньшую чем т, то наша цель достигнута: требуемым условиям удовлетворяют многочлены д (х) = д* (х)4-<?** (х) и г(х) — = /** (х). Если же /** (х) все еще имеет степень, большую или равную т, то мы точно так же поступим с многочленом /** (х), в результате чего придем к многочлену еще меньшей степени, и т. д. Так как степени многочленов /(х), /*(х), /**(х),... все время уменьшаются, то после конечного
159
ЧиСла шагов мы обязательно придём к мйОгбчлёну либо равному нулю, либо имеющему меньшую степень, чем т. В результате мы и получим требуемые многочлены q(x) и г (х).
Итак, деление с остатком всегда осуществимо. Докажем теперь единственность. Пусть многочлен f(x) двумя способами представлен в виде (13):
f{x) = qx (х)^(х) + Г1 (х), (15)
/W = <72WgrW + ''2(x), (16)
причем многочлен (х) либо равен нулю, либо имеет степень, меньшую чем т, и то же справедливо для многочлена г2(х). Иными словами, двумя способами произведено деление с остатком многочлена /(х) на g(x). Докажем, что равенства (15) и (16) совпадают (т. е. <71 (х) = у2 (х) и гг(х) = = г2(х)), чем и будет установлена единственность. Вычитая равенство (16) из (15), получим
(.Я 2 (х) — (х)) g (х) = г! (х) — г2 (х).
Справа стоит многочлен, имеющий степень, меньшую чем т (или равный нулю). Значит, тем же свойством обладает и равный ему многочлен, стоящий в левой части равенства. Но если бы многочлен у2(х) — <?х(х) был отличен от нуля, то, по теореме 6 (стр. 155), левая часть имела бы степень, не меньшую чем т (ибо степень многочлена g(x) равна т), чего быть не может. Следовательно, q2(x) — <?1(х) = 0, и потому гг(х)— г2(х) = 0. Но это и означает, что у1(х) = = </2(х) и ri (х) = г2 (х). Этим и завершается доказательство теоремы 8.
Проведенное доказательство позволяет получить простой способ выполнения деления с остатком, называемый способом «деления в столбик». Он основан на рассмотрении равенства (14). Именно, многочлены, участвующие в равенстве (14), располагаются следующим образом:
_ f(x) | g(x)
%Xn-mg(x) а^хп-т ~ f^x) °
причем, как мы знаем, многочлен /*(х)=/(х)— т_х"'тр(х) И)
либо равен нулю, либо его степень меньше, чем степень многочлена /(х). Заметим еще, что стоящее под уголком 160
(знаком деления) выражение у хп т
получается делением
старшего члена многочлена f(x) на старший член многочлена g(x)- Если теперь степень многочлена /* (х) все еще
больше или равна т, то мы так же поступаем с многочленом /* (х), приписывая под уголком еще одно слагаемое. Например, если /* (х) = спхр с1хр~1 . ,4-ср (где п>р^ т), то процесс деления продолжается следующим образом:
_ f(x) \g(x)__________
^xn-mg(x) ^.хп-т + ^хР_т
£»__________ b0 Ьо
£xp-mg(x) °0__________
Степень многочлена /** (х) (если он не равен нулю) стала еще меньше, и т. д. Процесс деления с остатком оканчивается, когда после очередного вычитания мы получаем многочлен либо равный нулю, либо имеющий степень, меньшую чем т. Этот многочлен и представляет собой остаток от деления /(х) на g(x), а под уголком мы получаем частное, т. е. мы получаем в конце концов следующую запись:
_ /(*) | g(x)
^xm~ng(x) Рр__________
_/*(х)
^x^g(x)
r(x)
Еще раз подчеркнем, что результат деления с остатком записывается следующим образом:
f(x) = q(x)g(x) + r(x).
Если г(х) = 0, то многочлен /(х) делится на g(x) (или, как еще говорят, «делится без остатка»); если же остаток г(х) отличен от нуля, то /(х) не делится на g(x).
Пример 5. Произвести деление с остатком многочлена х4 — Зх32х2х — 5 на х24-2х—3.
6 В. Г. Болтянский и др.
161
Решение.
х4 —- Зх3-|- 2х2 4- х —5
— х44-2х3 —Зх2
__— 5х3 + 5х2 + х — 5 — 5х3 — 10х2+15х
15х2 — 14х — 5
15х24-30х— 45 — 44x4-40
I х2 4- 2^ — 3 х2 — 5х-{-15
Мы видим, что частное равно х2—5x4-15, а остаток равен — 44x4-40. Таким образом,
х4 — Зх3 -{- 2х2 4-х — 5 =
= (х24-2х — 3)(х2 — 5х-|-15) 4-(—44x4-40)
делитель частное остаток
В заключение отметим следующие две теоремы, нередко бывающие полезными при решении задач.
Теорема 9. Если /(х) и g(x)— многочлены с целыми коэффициентами, причем старший коэффициент многочлена g(x) равен 1 или —1, то и частное q(x) и остаток г (х), получающиеся при делении f(x) на g(x), также являются многочленами с целыми коэффициентами.
Теорема 10. Если делимое и делитель — многочлены с рациональными коэффициентами, то частное и ос
таток также являются многочленами с рациональными коэффициент ами.
В самом деле, если /(х) и g(x) имеют целые коэффициенты, причем старший коэффициент Ьо многочлена g(x)
равен 1 или —1, то старший коэффициент частного также ^0
является целым числом, а многочлен /*(х) = /(х)—
— ^х" mg(x) (см. (14)) имеет целые коэффициенты. Таким И)
же образом мы получаем, что следующий коэффициент частного также является целым числом, а многочлен /** (х) имеет целые коэффициенты, и т. д. Из этого и вытекает справедливость теоремы 9. Теорема 10 доказывается аналогично.
Пример 6. Пусть х2 и х2 — корни квадратного уравнения х2 -J- ах 4-/> = 0 с целыми коэффициентами а и Ь. Пусть, далее, /(х) — произвольный многочлен с целыми коэффициентами. Доказать, что /(хх) 4-/(хг) — целое число.
162
Решение. Разделим многочлен /(х) на многочлен g(x) — x2-{-ax-{-b. Мы получим
/(х) = (х24-ах4-&)7(х)4-г(х), (17)
причем остаток г (х) (если он не равен нулю) является многочленом не выше первой степени. Согласно теореме 9 и частное q(x) и остаток г(х) являются многочленами спелыми коэффициентами. В частности, отсюда следует, что г (х) = сх -yd,
где с и d — некоторые целые числа.
Подставляя в (17) значение х = хг и замечая, что xj4- ах{ + 4- b = 0, получаем
/(Х1) = 0-7 (xr) + г (хх) = г (хх) = схх + d.
Аналогично f(x2) = cx2-]-d. Следовательно,
/(•*1) = (cxr + d) + (сх2 + d) = с (хх + х2) + 2d.
Но по формулам Виета х1-)-х2= — а, так что
/(Х1) +/(х2) = — ас + 2d.
Теперь ясно, что /(хх)+/(х2) — целое число (так как а, с и d — целые числа).
§ 3. Алгебраическое уравнение и его корни
Число с называется корнем многочлена /(х), если /’(с) = 0. Задачу «найти все корни данного многочлена /(х)>> принято также формулировать следующим образом: «решить уравнение /(х) = 0>. Иными словами, когда идет речь об уравнении /(х) = 0, то мы вовсе не хотим этим сказать, что запись /(х) = 0 означает равенство многочленов (т. е. что все коэффициенты многочлена /(х) равны нулю). Мы лишь хотим сказать, что рассматривается задача о нахождении корней многочлена /(х), т. е. тех точек, в которых значение многочлена /(х) равно нулю. Например, говоря о квадратном уравнении
х2 4- рх 4- q — 0, (18)
мы тем самым ставим задачу найти корни квадратного трехчлена x2-ypx-yq, а вовсе не хотим понимать соотношение (18) как равенство многочленов. Отметим еще, что корни многочлена /(х) называются также корнями уравнения
6‘ 163
/(х) = 0. Поэтому задачу «решить уравнение /(х)=0» формулируют также как задачу «найти корни уравнения/(х) —О». Еще раз подчеркнем, что решить уравнение — значит найти все его корни.
В школьном курсе рассматриваются различные уравнёния: иррациональные, логарифмические, показательные, тригонометрические и др. Алгебраическим уравнением называется уравнение /(х)=0, где /(х)—некоторый многочлен. Если У(х) — многочлен n-й степени, то уравнение /(х) = 0 называется алгебраическим уравнением п-й степени.
При решении алгебраических уравнений полезна следующая теорема (называемая теоремой Безу).
Теорема И. Остаток от деления многочлена f(x) на х—а равен f (а) (т. е. равен значению этого многочлена при х — а).
В самом деле, произведем деление с остатком многочлена /(х) на х — а:
f О) = (* — a) q (х) + г (х),
где остаток г (х), если он неравен нулю, является многочленом, степень которого меньше степени делителя х — а, т. е. равна нулю. Поэтому г(х) = г является числом:
У(х) = (х — a)q(x) + r.
Чтобы найти число г, положим в этом равенстве х = а. Мы получим f(a) — r, что и доказывает теорему.
Непосредственным следствием этой теоремы является следующее утверждение:
Теорема 12. Если а — корень многочлена f(x), то этот многочлен делится на х — а.
Заметим, что в теоремах И и 12 число а и коэффициенты рассматриваемого многочлена могут быть как действительными, так и комплексными.
На стр. 48 мы указали, что произведение двух чисел в том и только в том случае обращается в нуль, если равно нулю хотя бы одно из этих чисел. Отсюда непосредственно вытекает следующая теорема, играющая важную роль при решении алгебраических уравнений:
Теорема 13. Пусть f(x) и g(x) — два произвольных многочлена. Число а в том и только в том случае является корнем уравнения f(x)g(x) — Q, если оно является корнем хотя бы одного из уравнений /(х) = 0, g(x) = 0.
164
Иными словами, чтобы получить все корни уравнения /(х)^(х) = 0, нужно взять корни уравнения /(х)=0 и добавить к ним корни уравнения -g(x) = 0.
Из этой теоремы вытекает важное следствие. Пусть /(х) = 0—алгебраическое уравнение n-й степени (т. е. f(x)— многочлен степени п). Предположим, что нам известен один корень х = а этого уравнения. Тогда, по теореме 12, многочлен f(x) делится на х — а, т. е. /(х)==(х— a)g(x'). Согласно теореме 6 многочлен g(x) имеет степень и—1. Применяя теорему 13, мы находим, что для получения всех корней уравнения f(x) — 0 нужно взять корни уравнения х — а = 0 и добавить к ним корни уравнения g(x)=0. Но уравнение х — а —О имеет единственный корень х — а, который нам был известен с самого начала. Значит, для получения всех корней уравнения f(x)==0 нужно, кроме корня х = а, взять все корни уравнения g(x) = 0.. Заметим теперь, что уравнение g(x)=Q проще исходного уравнения в том смысле, что оно имеет степень п—1, т. е. меньшую степень, чем исходное уравнение.
Итак, если нам известен один корень х = а алгебраического уравнения/(х) = 0, то f(x) = (x— a)g(x) и нахождение остальных корней этого уравнения сводится к решению уравнения g(x)~0, имеющего на единицу меньшую степень, чем исходное уравнение. Короче, знание одного корня позволяет снизить степень уравнения на единицу.
В ряде случаев нахождение корней алгебраических уравнений облегчается следующей теоремой:
Теорема 14. Если все коэффициенты многочлена
f (х) = аохп + а^1 +... + ап_гх Ц- ап являются целыми числами, то всякий целый корень этого многочлена является делителем свободного члена ап.
В самом деле, пусть с — целый корень многочлена /(х), т. е.
f (с) = аосп 4- +... + ап_гс -ф ап = 0>.
Тогда
ап = ~ с (аос'г1 + age«-2 +... + а„_л).
Так как число, стоящее в скобках, является целым (ибо^все коэффициенты <г0, ..., апЛ, так же как и число с,— це-
лые), то ап делится на с.
Доказанная теорема значительно облегчает отыскание целых корней многочленов с целыми коэффициентами. Именно, 165
надо взять свободный член многочлена и выписать все его делители (как положительные, так и отрицательные). После этого надо проверить, какие из них являются корнями данного многочлена. Если же окажется, что ни один делитель свободного члена не обращает многочлен в нуль, то этот многочлен целых корней не имеет.
Пример 7. Решить уравнение х4— 4Х3— 13х24-28хЦ-+ 12 = 0.
Решение. Возьмем свободный член 12 и выпишем его делители:
1; — 1; 2; —2; 3; —3; 4; —4; 6; —6; 12; —12.
Теперь, подставляя эти числа в многочлен /(х) = х4— 4х3— — 13х24-28хЦ- 12, проверим, нет ли среди них корней этого многочлена. Мы находим:
/(1) = 24 (т. е. 1 не является корнем);
/(—1) = —24 (т. е. —1 также не является корнем);
/(2) = 0 (т. е. 2 есть корень многочлена /(х)).
Итак, один корень найден: х = 2. По теореме 12 многочлен f(x) делится на х — 2. Производя деление («в столбик»), находим
/(х) = (х— 2)(х3 — 2х2 — 17х — 6).
Таким образом, для нахождения остальных корней нужно решить уравнение х3 — 2х2—17х —6 = 0. Опять выписываем делители свободного члена 6:
1; —1; 2; —2; 3; —3; 6; —6.
Числа 1 и —1 не могут быть корнями написанного кубического уравнения (так как мы уже видели, что они не являются корнями исходного уравнения). Испытаем дальнейшие делители, подставляя их один за другим в многочлен g (х) = = х3 — 2х2—17х — 6. Мы находим:
g(2) =—40 (т. е. 2 не является корнем);
g (—2) = 12 (т. е. —2 не является корнем);
g(3) =—48 (т. е. 3 не является корнем);
g(—3) = 0 (т. е. —3 есть корень многочлена g(x)).
Итак, найден еще один корень: х = —3. По теореме 12 многочлен g (х) делится на х + 3. Производя деление, находим
Xs — 2х2— 17х—6 = (х4-3)(х2—5х —2).
166
Значит, для нахождения оставшихся корней нужно решить квадратное уравнение х2—5х — 2 = 0. Это дает еще два корня: -|-±ypA33. Таким образом, исходное уравнение четвертой степени имеет четыре корня:
Х1 = 2-, -х2 = —3; х3 = 4 + 1]/33; х4 = |-|]/33.
В заключение мы рассмотрим вопрос о разложении многочлена на множители первой степени и связанный с ним вопрос о числе корней алгебраического уравнения. Основной здесь является следующая теорема:
Теорема 15. Любой многочлен п-й степени
f (х) = аох” + а^1 + ... 4-ая (19)
(где а0 у= 0 и и > 0) может быть представлен в виде произведения
/(х) = а0 (х — с4) (х — с2)... (х — сп).
Это разложение единственно с точностью до порядка сомножителей.
В этой теореме коэффициенты а0, av .ап и числа с1( с2, ..., сп могут быть как действительными, так и комплексными.
Доказательство теоремы 15 основано на следующей теореме, которую называют основной теоремой алгебры:
Теорема 16. Любой многочлен f(x), степень которого отлична от нуля, имеет по крайней мере один корень.
В этой теореме коэффициенты многочлена и его корни также могут быть действительными или комплексными числами.
Хотя по своей формулировке теорема 16 имеет чисто алгебраический характер, по методам доказательства она является неалгебраической теоремой. Все известные доказательства основной теоремы алгебры неэлементарны (эти доказательства можно найти в учебниках высшей алгебры). Поэтому мы примем здесь теорему 16 без доказательства, а на ее основе проведем полное доказательство теоремы 15.
167
Доказательство теоремы 15. Мы применим метод математической индукции. Любой многочлен первой степени имеет внд
/(х) = аох + а1 (ао=^О), и потому
/(х) = а0 (х + у). \ “о/
Единственность разложения в этом случае очевидна. Таким образом, для многочленов первой степени теорема доказана.
Предположим теперь, что эта теорема доказана для всех многочленов, имеющих степень, меньшую чем п. Возьмем произвольный многочлен (19) степени п. Согласно теореме 16 он имеет хотя бы один корень с1. Но тогда, по теореме 12, многочлен /(х) делится на х — сг, т. е.
/(х) = (х — cr)g(x),
где g(x) — некоторый многочлен степени п — 1. Согласно теореме 6 старший член многочлена g(x) равен аох”-1. Но по предположению индукции многочлен g(x) можно следующим образом разложить на множители:
g(x) = a0(x — c2)...{x — cn)
(где сг, ..., сп — некоторые числа, действительные или комплексные). Следовательно,
f (х) = (х — q) g (х) = аа (х — сх) (х — с2)... (х — с„).
Мы доказали, что многочлен /(х) разлагается на множители первой степени. Осталось доказать, что это разложение единственно (с точностью до перестановки множителей).
Предположим, что
а0 (х—сх) (х — с2)... (х — сп) = Ь0 (х — dj) (х —d2)... (х — dn).
(20)
Сравнивая коэффициенты при х” слева и справа, убеждаемся, что а0 — Ь0. Далее, заметим, что при х = сх левая часть равенства (20) обращается в нуль. Следовательно, должна обращаться в нуль и правая часть этого равенства. Но тогда хотя бы одно из чисел dlt d2, ..., dn должно быть равно сг: в противном случае в правой части мы имели бы произведение п отличных от нуля разностей сх— с/х, сх — d2, ... .... ci — d„.
168
Пусть, например, d1 = c1. Тогда равенство (20) можно переписать в виде
аа (х — сi) (х — с2)... (х — сп) —
— а0 (x — Cj) (x — d2)...(x — dn) = 0 или, иначе,
а0 (х — сх) [(х — с2)... (х — с„) — (x — d2)...(x — d„)] = 0. (21)
Если бы многочлен, стоящий в квадратных скобках, был отличен от нуля, то и вся левая часть в (21) была бы отличным от нуля многочленом (например, по теореме 6 старший коэффициент в левой части был бы отличен от нуля). Но это означало бы, что равенство (21) места не имеет. Следовательно, в квадратных скобках стоит нулевой многочлен, т. е.
(x—c2)...(x—c„)=(x—d2)...(x—d„).
Обе части этого равенства являются многочленами степени и— 1, и по предположению индукции множители первой степени слева и справа могут отличаться лишь порядком следования. Значит, и в равенстве (20) множители справа и слева могут отличаться лишь порядком следования. Теорема доказана.
Следующее утверждение является почти очевидным следствием теоремы 15:
Теорема 17. Пусть
/(х) = а0(х —Cj)(x —с2)...(х —с„) (22)
— разложение многочлена п-й степени на множители первой степени. Тогда числа cv с2, ... , сп являются корнями многочлена f (х) и других корней этот многочлен не имеет.
В самом деле, если в (22) подставить х — ст (где т — одно из чисел 1,2, ..., и), то мы, очевидно, получим /(ст) = 0, т. е. каждое из чисел ст является корнем многочлена /(х). Если же вместо х подставить любое число с, не совпадающее ни с одним из чисел с1, с2, ..., сп, то ни один множитель в правой части (22) не обратится в нуль, т. е. будет f(c) у= 0.
Теперь мы имеем возможность дать точное определение термина «множество всех корней многочлена /(х)»: по Определению под множеством всех корней мы уславли-
J69
ваемся понимать числа cv с2, ..., сп, участвующие в разложении (22). Если среди этих чисел имеются совпадающие, то мы говорим, что у многочлена есть кратные корни. Именно, если среди чисел ср с2, ..., сп встречается k раз число с, а все остальные из этих чисел отличны от с, то с называется k-кратным корнем многочлена f(x). Такое понимание, при котором каждый корень считается столько раз, какова его кратность, позволяет утверждать, что справедлива следующая теорема, значительно уточняющая основную теорему алгебры:
Теорема 18. Каждое алгебраическое уравнение п-й степени имеет ровно п корней.
Пример 8. Доказать, что не существует многочлена, квадрат которого был бы равен многочлену хп 4- х”-1 4-... ...Ц-x4-1 (где //—-натуральное число).
Решение. Допустим, напротив, что
хп4_хл-14-...4- 1=[Р(х) ]2,
где Р(х) — некоторый многочлен, и пусть
Р (х) — а0(х—cj (х — с2)... (х — ст)
— разложение этого многочлена на множители первой степени. Тогда
хл4-хя^14-. ..4- 1 — ао(х — с1')2(х — с2)2...(х — ст)2,
откуда видно, что каждый корень многочлена хп 4- х”^14- • 4* 1 является кратным (т. е. имеет кратность, не меньшую 2)'. Умножив теперь многочлен хп х"14-... 1 нах—1, мы
найдем, что многочлен
хл+1 — 1 = (х — 1) (хл 4- х”"14-... 4-1)
имеет корень х=1, а все остальные его корни являются кратными. Однако это неверно: согласно сказанному на стр. 177 корни многочлена хя+1—1 имеют вид
Xb = COS——r-P/sin——г (k— 1, 2, ... , «4- О
й «4-1 1 «4-1 4 ’ ’ 1 ’
и все эти корни различны (т. е. кратными не являются). Полученное противоречие и доказывает утверждение задачи.
Заметим, что при п = 1000 мы уже рассматривали эту задачу на стр. 156 (пример 4). Приведенное там решение при-170
годно лишь для тех и, для которых п-|-1 не является точным квадратом. Решение, изложенное здесь, пригодно для л ю-б ы х п-
Пример 9. Найти остаток от деления многочлена х100— — 2х51 4-1 на х2 — 1.
Решение. Остаток является многочленом степени не выше первой. Иначе говоря, деление с остатком многочлена х100 — 2х51 4-1 на х2—1 приводит к следующему результату:
xioo_2x=14-! ==(х2—1)(7(х)4-(ах4-&), (23)
где <?(х) — частное, а г(х) = ах-\-Ь — остаток. Наша задача заключается в том, чтобы определить числа а и Ь. При х=1 мы из равенства (23) находим
О = а 4- Ь,
а при х = —1 получаем
4 = — а-\-Ь.
Таким образом, для
систему уравнений
определения чисел а и b мы получили
b 4- а — О, b—а = 4.
Решив ее, находим: Ь — 2, а — — 2. Следовательно, искомый остаток равен —2x4-2.
В заключение этой главы мы приведем доказательство теоремы 5, сформулированной на стр. 152. Итак, пусть Р (х) и Q(x)—два многочлена, степень каждого из которых не превосходит п, и пусть выполнены соотношения
Р (сх) = Q (сх), Р (с2) = Q (с2),..., Р (сп^ = Q (сп^),
где Cj, с2,..., сп+[ — различные числа. Тогда многочлен /(х) = Р(х)—Q(x) обращается в нуль в n-j-l точках сп с2,..., с„+р т. е. имеет не меньше «4-1 корней. Заметим теперь, что степень многочлена/(х) не превосходит п. Если бы этот многочлен был отличен от нуля и имел степень k, то уравнение /(х) = 0 имело бы ровно k корней (считая их кратности), т. е. имело бы не больше п корней. Но это противоречит сказанному ранее. Следовательно, многочлен f (х) = Р (х) — Q(x) равен нулю, т. е. Р (x)=Q(x).
171
Задачи к главе VI
6.1. Найдите сумму коэффициентов многочлена (1 -ф 2х — 4х2)248 (1 — 7х + 5х2)345.
6.2. Пусть /(х)— многочлен с целыми коэффициентами. Докажите, что при любых целых а и Ь число f {a -j-Уь) -ф -ф f(a— Vb) — целое.
6.3. Делится ли многочлен х100— 3x4-2 на х2—1?
6.4. Некоторый многочлен при делении на х—1 дает остаток 3, а при делении на х — 2 дает остаток 4. Чему равен остаток от деления этого многочлена на (х—1)(х— 2)?
6.5. Некоторый многочлен при делении на х4~Ъ х — 2, х—3 дает в остатке соответственно 3, 1, —1. Чему равен остаток от деления этого многочлена на (х-ф 1)(х — 2)(х — 3)?
6.6. Докажите, что многочлен х44 -ф х33 + х’22 -ф х11 4- 1 делится на х4 -ф х3 -ф х2 -ф х -ф 1. Найдите частное.
6.7. Найдите а и Ь, если известно, что многочлен ах4 -ф -ф^х3-ф1 делится на (х—I)2.
6.8. Число 1 -ф ]/3 является корнем уравнения
х4 -ф ах3 4- Ьх2 -ф 6х 4- 2 = 0.
Найдите остальные корни этого уравнения, если известно, что а и b — рациональные числа.
6.9. Число 14- /2 является корнем уравнения
х5 -ф ах3 4- Ьх2 4- 5х 4- 2 = 0.
Найдите остальные корни этого уравнения, если известно, что а и b—рациональные числа.
6.10. Найдите общие корни уравнений:
Xе 4- -V5 4~ 2х4 4- х3 4- 2х2 -ф х -ф 1 = о,
Xе — х5 4- 2х4 — х3 -ф Зх2 — 2х 4- 2 = 0.
6.11. Найдите общие корни уравнений:
х6 4-2х5-ф Зх4 4-2х3-ф Зх2 4-2х 4-2 = 0, х4 -ф Зх3 -ф 6х2 -ф 6х -ф 4 = 0.
6.12. Докажите, что при любых целых неотрицательных т, п, р многочлен х3"1 -ф х3я+1 -ф х3р+2 делится на х24- х 4-1.
172
6.13. Докажите, что если хх, X'.,, Х3— корни уравнения х3 -ф ах2 -ф Ьх ф с = О,
то имеют место следующие формулы:
Л"1 -ф х2 + х3 = — а,
ххх2 -ф х3х3 -ф х.2х3 ~ Ь,
х3х,х3 = — с
(формулы Виета для кубического уравнения).
6.14. Уравнение 2а;3 ф- тх2 -ф пх -ф 12 = 0 имеет корни хх=1, х2 =—2,- Найдите третий корень этого уравнения.
6.15. Вычислите сумму х^-ф^, если х0 — корень уравнения х2 + х -ф 1 = 0.
6.16. Докажите, что при а ф 0 многочлен хп -фа” делится на х-]-а в том и только в том случае, если п — нечетное число.
6.17. Пусть х3, х2, х3 — корни уравнения х3+рх4-<7 = 0. Докажите, что х\ -ф х2 -ф х| = Зххх2х3.
6.18. Докажите, что при Ьх^О, сХ>:0 многочлен х3— — ах2 — Ьх — с не может иметь двух положительных корней.
6.19. При каком условии уравнение х3 -\-рх = 0 имеет
два равных корня?
6.20. Пусть хх, х2, ... , хп— корни многочлена
Р(х) — аохп -ф ахх” 1 -ф.... -ф a-n-jX + ап,
где аа уХ 0, ап ф 0. Какие корни имеют многочлены
А (х) = аохп — а^х” 1 + а2хп~2 —... -ф (— 1)" ап и
В (х) = апхп -ф а.п1хп 1-ф • • -ф ахх -ф а0?
6.21. Пусть Р (х) = А (х) В (х), причем многочлен £>(х) дает при делении на С'(х) остаток 7?(х). Докажите, что остаток от деления многочлена Р (х) на Д(х)(?(х) равен Д(х)/?(х).
6.22. Найдите остаток от деления многочлена х1971 — 1 на (х24-1)(х2фх+1).
6.23. Докажите, что многочлен
/ (х) — х” -ф а2хп 1 -ф а2х” 2 -ф... -ф ап
173
в том и только в том случае делится на (х— Ь)*, если
Ьп -ф -ф а2Ьп~2 -ф... -ф ап = О и
пй"'1 + aY(n— 1)bn2 -ф а2(п — 2) bn~s +.. • + ая4 = 0.
6.24. Докажите, что при и произвольном действительном b уравнение х3ахb = О имеет только один действительный корень.
6.25. Докажите, что при любом действительном с уравнение х3— х2 -ф х Ц- с = 0 имеет только один действительный корень.
6.26. Докажите, что если х = с — целый корень многочлена
f (х) = хп -ф ajX””1 -ф...-ф х + ап
с целыми коэффициентами, то для любого целого числа т число /(/и) делится на с — т.
6.27. Пусть многочлен А(х) может быть представлен в виде суммы квадратов двух многочленов с действительными коэффициентами и тем же свойством обладает многочлен В (х). Докажите, что тогда и многочлен А (х) В (х) обладает этим свойством.
6.28. Докажите, что если многочлен с действительными коэффициентами имеет комплексный корень а -ф Ы, то он делится на многочлен (х—а)2-\-Ь2.
6.29. Докажите, что всякий многочлен с действительными коэффициентами делится на какой-либо многочлен первой или второй степени с действительными коэффициентами.
6.30. Докажите, что всякий многочлен нечетной степени с действительными коэффициентами имеет хотя бы один действительный корень.
6.31. Докажите, что если многочлен /(х) с действительными коэффициентами принимает при всех действительных х положительные значения, то он представляется в виде суммы квадратов двух многочленов с действительными коэффициентами.
6.32. Все коэффициенты многочлена
х" fljX” 1 -ф... -ф ап_лх -ф ап
— целые числа. Докажите, что любой рациональный корень этого многочлена является целым числом.
174
6.33. Докажите, что всякий рациональный корень многочлена л-й степени
аох” + а^-1 +... + ап
с целыми коэффициентами а0, av ..., ап представляется
в виде несократимой дроби
£.
Я ’
где р — некоторый делитель
свободного члена ап, a q — некоторый делитель старшего
коэффициента а0.
6.34. Пусть xv х2, х3— корни кубического уравнения Xsах2Ьхс = О с целыми коэффициентами а, Ь, с. Пусть, далее, f(x)— произвольный многочлен с целыми коэффициентами. Докажите, что f (х±) +/(х2) +/(х3) — целое
число.
6.35. Пусть q, с2, ..., сп, cnj\-—попарно различные действительные числа. Существует ли многочлен степени п, имеющий корни cv с2, сп и принимающий значение 1 в точке c„+i?
6.36. Пусть ci, с2, ..., сп, cn+i и d2, dn, dn^
— действительные числа, причем числа cv с2.........сп, сп1
попарно различны. Докажите, что существует один и только один многочлен степени не выше п, принимающий. в точках cv с2,... , с„+1 соответственно значения dv d2, ... , dn+1.
ГЛАВА VII
ФУНКЦИИ И ГРАФИКИ
§ 1. Определение функции
Понятие функции часто встречается в школьном курсе математики и хорошо знакомо учащимся. Тем не менее на приемных экзаменах в вузах поступающие допускают много ошибок при использовании этого понятия. Объясняется это различными причинами, но в первую очередь тем, что слово «функция» используется в математике в нескольких смыслах, а в школьных учебниках это обстоятельство не разъяснено. Поэтому мы прежде всего обратимся к определению функции и другим относящимся сюда понятиям и подробно остановимся на тех различных пониманиях слова «функция», которые встречаются в школьном курсе математики.
Самым общим (и, безусловно, основным) является в математике следующее определение понятия функции. Говорят, что определена некоторая функция, если, во-первых, задано некоторое множество, называемое областью определения функции, во-вторых, задано некоторое множество, называемое областью значений функции, и, в-третьих, указано определенное правило, с помощью которого каждому элементу, взятому из области определения, ставится в соответствие некоторый элемент из области значений.
Приведем несколько примеров, иллюстрирующих это общее определение.
Пример 1. Обозначим через А множество всех треугольников на плоскости, а через В — множество всех окружностей, взятых на этой же плоскости. Множество А будем считать областью определения, а множество В — областью значений (той функции, которую мы определяем). Наконец, каждому треугольнику поставим в соответствие окружность, вписанную в этот треугольник. Это есть вполне определенное правило, которое каждому элементу, взятому из 176
области определения (т. е. треугольнику), ставит в соответствие некоторый элемент из области значений (т. е. окружность).
Пример 2. Сохраним те же самые множества А и В, что и в примере 1, т. е. по-прежнему будем считать областью определения множество всех треугольников на плоскости, а областью значений — множество всех окружностей. Далее, каждому треугольнику поставим в соответствие его описанную окружность. Мы получаем функцию с той же областью определения А и той же областью значений В. Но это уже другая функция, так как окружность сопоставляется треугольнику с помощью другого правила.
Пример 3. Обозначим через К множество всех кругов на плоскости, а через D — множество всех действительных чисел. Далее, выберем единицу измерения площадей и каждому элементу множества К (т. е. кругу) поставим в соответствие число, равное площади этого круга. Мы получаем функцию с областью определения К и областью значений D.
Пример 4. Обозначим через N множество всех натуральных чисел, а через D — множество всех действительных чисел. Далее, выберем два действительных числа ах и г и каждому натуральному числу п поставим в соответствие действительное число, равное д-му члену арифметической прогрессии с первым членом а± и разностью г (т. е. натуральному числу п поставим в соответствие действительное число а1 + (я—О г). Мы получаем функцию с областью определения и областью значений D.
Пример 5. Теперь мы примем и в качестве области определения, и в качестве области значений множество D всех действительных чисел. Далее, выберем два действительных числа ах и г и каждому действительному числу х поставим в соответствие число ax4-(x—1)г. Мы получаем функцию с областью определения D и областью значений D.
Заметим, что в примерах 4 и 5 одинакова область значений D и одинаково правило соответствия: формулы ах-|-(я—1)г и + —1)г показывают, что в обоих случаях надо над выбранным числом (п или х) проделать одни и те же действия, чтобы узнать, какое число поставлено ему в соответствие. Однако области определения этих двух функций различны, и потому мы имеем в примерах 4 и 5 разные функции. Таким образом, для задания функции мало указать правило соответствия, а надо еще обязательно указать область определения и область значений.
177
Для обозначения функций обычно пользуются буквами. Одна буква (чаще всего х) используется для обозначения произвольного элемента, взятого из области определения функции. Эта буква называется аргументом. Таким образом, если сказано, что х — аргумент некоторой функции, то вместо х мы можем подставить любой элемент, принадлежащий области определения этой функции. Далее, другая буква (чаще всего _у) используется для обозначения произвольного элемента, взятого из области значений. Эта буква называется функцией (и это — второе значение слова «функция»). Наконец, третья буква (чаще всего /) используется для обозначения правила соответствия. Это значит, что если а — произвольное значение аргумента (т. е. произвольный элемент, взятый из области определения функции), то элемент, поставленный ему в соответствие, обозначается через /(а). Элемент _у=/(а) называется значением рассматриваемой функции при х — а.
Все три буквы х, у, f объединяются одной записью:
ф=/(х)
(1)
(«игрек равен эф от икс»), которая и означает, что х — аргумент, у — функция, a f— правило соответствия. Иногда букву f или выражение /(х) также называют функцией (и это — уже третье значение .слова «функция»).
Пример 6. Обратимся снова к функции, рассмотренной в примере 4. Аргумент обозначим через п, функцию — через у, а правило соответствия — через f. Таким образом, мы запишем эту функцию в виде у =f(n). Вот несколько значений этой функции:
/(l) = ai, /(2) = а2 = ах + г, /(З) = а3 = а1-\-‘2г и т. д.
Пример 7. Рассмотрим функцию у = <р (х), у . которой областью определения и областью значений является множество D всех действительных чисел, а правило соответствия имеет следующий вид:
О, если х=сО, х, если х > 0.
Вот несколько значений этой функции:
<р(—5) = 0, <р(— л) = 0, <р(—1) = 0, ф (0) = 0, ф(1)==1, ф(З) —3, ф(л) = л, ф(100)= 100, .,,
178
Разумеется, вместо букв х, у, f можно использовать и другие буквы. Например, запись х = <р(7) означает, что s есть функция аргумента t (или короче: s есть функция от f), причем правило соответствия обозначается буквой <р.
Следует подчеркнуть, что область значений функции представляет собой множество элементов (или чисел), среди которых обязательно содержатся все значенйя рассматриваемой функции. Однако в области значений могут содержаться и «лишние» элементы, не являющиеся значениями функции. Иными словами, множество значений функции обязательно содержится в области значений, но не обязательно совпадает с ней. Так, в примере 3 значениями функции являются лишь положительные числа, тогда как область значений есть множество всех действительных чисел. Несовпадение множества значений функции и области значений можно видеть также в примерах 4 и 7.
В заключение рассмотрим еще одно (четвертое!) понимание слово «функция», являющееся для школьного курса математики наиболее важным. Именно, функцией называют произвольное выражение, содержащее аргумент х, а также знаки действий и числа. Например, функциями (в этом смысле) являются
У = .г2т1, (2)
Т = (3)
_у = |х—1|, (4)
х — 5
У=^’ (0)
1 +*, (6)
у/ = ]/-(х-2)2(х+1)2(х + 5)2. (7)
Почему же такие формулы называют «функциями» и не
противоречит ли это понимание функции сказанному выше? Связь со сказанным выше устанавливается следующим соглашением, которого мы всюду в дальнейшем будем придерживаться:
Если функция задана в виде равенства, в левой части которого стоит у (или другая буква, обозначающая функцию), а в правой части стоит некоторое выражение, содержащее аргумент х, а также знаки действия и числа (причем область определения не указана), то принято считать, что
179
1) за область значений принимается все множество Ь действительных чисел;
2) за область определения принимается множество всех тех действительных чисел, при подстановке которых вместо х выполнимы (в множестве действительных чисел) все действия, указанные в правой части;
3) если число а принадлежит области определения, то значение функции при х=а равно числу, получающемуся, если в правую часть подставить х = а и произвести указанные действия.
Итак, задание функции формулой содержит в себе и указание области определения, и задание правила соответствия.
Пример 8. Найти область определения функций (2) и (3); определить, совпадают ли эти функции.
Решение. Действия, указанные в правой части равенства (2), выполнимы при любом действительном значении х, т. е. областью определения функции (2) является все множество D действительных чисел (или, иначе, бесконечный интервал —со < х < оо). Функция (3) определена для всех действительных чисел х, кроме х— 0, т. е. область определения этой функции получается выбрасыванием (или, как еще говорят, «выкалыванием») из множества D точки х = 0. Можно описать область определения функции (3) и иначе: она представляет собой объединение двух бесконечных интервалов (— со, 0) и (0, со).
Заметим, что при любом х 0 значения функций (2) и (3) совпадают. Тем не менее (2) и (3) — различные функции, так как их области определения не совпадают.
Пример 9. Найти области определения функций (5), (6), (7).
Решение. Функция (5) определена для всех значений аргумента, кроме х= —2. Таким образом, область определения этой функции получается выкалыванием из числовой оси точки х = —2; иначе говоря, эта область определения является объединением двух бесконечных интервалов (— оо, — 2) и (— 2, оо).
Область определения функции (6) состоит из всех точек, для которых подкоренное выражение неотрицательно, т. е. эта область определения задается неравенством 1 -ф х 2= 0, или х — 1. Иначе говоря, область определения функции (6) представляет собой бесконечный полуинтервал [— 1, оо). Концевая точка х = —1 этого полуинтервала принадлежит области определения.
180
Наконец, область определения функции (7) состоит из всех значений х, для которых подкоренное выражение в правой части равенства (7) неотрицательно. Но если это подкоренное выражение отлично от нуля, то оно непременно отрицательно. Значит, область определения функции (7) состоит лишь из тех точек х, для которых подкоренное выражение обращается в нуль. Это будет при х = —5, х =—1 и х = 2. Таким образом, область определения функции (7) состоит лишь из трех точек: — 5, — 1 и 2.
Пример 10. Найти область определения функции т=Ж)+£(*), глеи Ж) = /б —х2.
Решение. Первое слагаемое /(х) определено при выполнении двух условий: 1) подкоренное выражение неотрицательно, 2) знаменатель не обращается в нуль. Первое условие
__________________। [- - .Область опреЗеления п у 2........................функции f(x)
___Обметь опреЗеления
-фу о V5 функции д(х)
________________। । ) с| Область опреЗеления о ; 2 VS_функции f(x)+g(x)
Рис. 44.
означает, что хт> 1; второе условие означает, что х=/= 2. Таким образом, область определения функции /(х) представляет собой объединение полуинтервала [1, 2) и бесконечного интервала (2, оо). Далее, второе слагаемое g(x) определено при 5 — х2т>0, т. е. при —]/~5бх5 . Иначе говоря, областью определения функции g (х) является отрезок 1—1Л5-, +]ЛГ].
Но для того, чтобы некоторая точка х=а принадлежала области определения функции у=f(x) -фg (х), необходимо и достаточно, чтобы при х = а была определена и функция /(х), и функция g(x). Иными словами, область определения Функции _у =/(х)-ф£(х) представляет собой пересечение
181
областей определения функций f{x) и g(x). Следовательно (рис. 44), область определения функции y=f(x')-\-g(x) представляет собой объединение полуинтервалов [1, 2) и (2, Г5"к
§ 2. График функции
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х, а на оси ординат — значения функции y=f(x). Графиком функции _у=/(х) называется множество всех точек, у которых абсциссы принадлежат об-
ласти определения функции, а ординаты равны соответствующим значениям функции
у = /(х).
Другими словами, график функции у =/(х) — это множество всех точек плоскости, координаты х,у ко!брых удовлетворяют соотношению у —f(x).
На рис. 45 и 46 приведены графики функций _у = 2х-|-1 и у = х2 — 2х.
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его куска, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график»,, а не «эскиз графика».
182
С помощью графика можно находить значение функции в точке. Именно, если точка х~а принадлежит области определения функции _у=/(х), то для нахождения числа /(а) (т. е. значения функции в точке х — а) следует поступить так. Нужно через точку с абсциссой х=а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y=f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(a) (рис. 47). Например, для функции f(x) = x2— 2х с помощью графика (рис. 46) находим/(—1) = 3, /(0) = 0, /(1)=— 1, /(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у — хг— 2х принимает положительные значения при х<0 и при х>2, отрицательные — при 0 < х < 2; наименьшее значение функция у = х2— 2х принимает при х=1.
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х, у которых удовлетворяют уравнению y=f(x). В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, xv ..., xh — и составляют' таблицу, в которую входят выбранные значения аргумента и соответствующие значения функции. Таблица выглядит следующим образом:
X Х1 х2 Xk
У fM /W f(Xk)
183
Составив такую таблицу, мы можем наметить несколько точек графика функции y=f(x). Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y=f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле, поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 11. Для построения графика функции y=f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48. На осно вании расположения этих точек он сделал вывод, что гра
фик функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным?
Рис. 48.
Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. Простой пример иллюстрирует сказанное. Рассмотрим функцию
184
Вычисления показывают, что значения этой функции в точках — 2, —1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x-j- 1 -j-sinnx; ее значения тоже описываются приведенной выше таблицей.
Этот пример показывает, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции, как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим в следующем параграфе, а сейчас раз-бере,м некоторые часто применяемые способы построения графиков.
График функции у = |/(х) |. Нередко приходится строить график функции у = |/(х) |, где fix')— заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
( f(x), если /(зф^О,
( —fix), если /(х)<0.
Это значит, что график функции _у = |/(х)| можно получить из графика функции у— f(x) следующим образом: все тонки графика функции y — flx), у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y—f(x), имеющих отрицательные координаты, следует построить соответствующие точки графика функции у——f(x) (т. е. часть графика функции y=f(x), которая лежит ниже оси х, следует симметрично отразить относительно оси х).
Пример 12. Построить график функции у — | х
Решение. Берем график, функции у — х (рис. 50, а) и часть этого графика при х<0 (лежащую под осью х) симметрично отражаем относительно оси х. В результате мы и получаем график функции _у = |х| (рис. 50, б).
185
Пример 13. На рис. 51 построен график функции = = | х2— 2х\ исходя из графика функции у = х2— 2х (см. рис. 46). Для этого часть графика функции у = х2 — 2х при О < х <Z 2 симметрично отражена относительно оси х.
Рис. 50.
График функции у=Л (х)-|-/2 (х). Рассмотрим задачу построения графика функции —/1 (х)-ф/2 (х), если заданы графики функций _У=/1(х) и _у=/2(х).
Заметим, что областью определения функции _у=/1(х)-|-
+ А (х) является множество всех тех значений х, для кото-
Рис. 51.
причем любая точка
рых определены обе функции у =fx (х) и у =f2 (х), т. е. . эта область определения представляет собой пересечение областей определения функций А (х) и /2 (х).
Пусть точки (х0,ух) и (х0,_у2) соответственно принадлежат графикам функций J=/1(x) и >=/2(х), т. е. Л=А(х0)> уг — f% (Хо)- Т огда точка
(х0, _У1+_У2) принадлежит графику функцииy=fx (х) +/2 (х) (ибо Л (х0) 4-А (х0)=Ух + у2), графика функции y—fx (х) + /2 (х)
может быть получена таким образом. Следовательно, график
функции у —fx (х) Д-/2(х) можно получить из графиков функций у=Л(х) и y=f2(x) заменой каждой точки (х0, yt) графика
186
функции y=fi (х) точкой (х0, >! + _у2), где _у2 =/2 (х0). т. е. сдвигом каждой точки (х0, _ух) графика функции _y=/i(x) вдоль оси у на величину y2—f2(x0). При этом рассматриваются только такие точки х0, для которых определены обе функции y=f1(x) и j=/2(x).
Такой метод построения графика функции у (х) 4- /2(х)
называется сложением графиков функций y=J\ (х) и_у=/2(х).
Пример 14. На рис. 52 методом сложения графиков построен график функции
_y = x-|-sinx.
(Предполагается, что читатель знаком со свойствами тригонометрических функций sin х, cos х, tgx, ctgx и с их графиками.
§ 3. Ограниченность, монотонность, четность, нечетность, периодичность
1. Ограниченность. Функция /(х) называется ограниченной снизу, если существует такое число а, что для любого значения х (взятого из области определения функции) справедливо неравенство /(х)>а.
187
Функция f(x) называется ограниченной сверху, если существует такое число Ь, что для любого значения х (взятого из области определения функции) справедливо неравенство f{x)<_b.
Функция f(x) называется ограниченной, если она одновременно является и ограниченной снизу, и ограниченной сверху.
Ограниченность функции (сверху или снизу) весьма существенно влияет на вид и расположение ее графика. Если
функция _у=/(_х) ограничена снизу, т. е. f (х)~у>а для любого х из области определения функции, то все точки графика расположены выше прямой у = а (рис. 53). Если функция _у=/(х) ограничена сверху, т. е. f(x)<Zb для любого х из области определения функции, то все точки
графика расположены ниже прямой у — Ь (рис. 54). Наконец, если функция y=f(x) ограничена, т. е. a<_f(,х)<.Ь для любого ‘х из области определения функции, то все точки графика расположены в полосе между прямыми у = а и у — b (рис. 55).
188
Пример 15. Построить график функции /(х) = -у-г 2 .
Решение- Область определения функции f(x) совпадает со всей числовой прямой —оо<;х<;оо. Далее, так
как числитель и знаменатель дроби положительны (при любом х), то /(х)>0 для любого х. Таким образом, функция f(x) ограничена снизу. Наконец, так как 1 х2 1, то /(x)s-C 1 для любого х, т. е. функция /(х) ограничена сверху. Следовательно, график функции _у=/(х') целиком расположен в полосе между прямыми j = 0 и у~1.
Легко заметить еще одно свойство функции /(х) = j-j— когда х принимает большое по абсолютной величине значение (положительное или отрицательное), соответствующее
189
значение / (х) близко к нулю. Иначе говоря, при перемещении далеко вправо (или далеко влево) график функции _у=/(х) «прижимается» к прямой _у = 0. Положив х = 0, находим /(0)=1, так что график функции проходит через точку (0; 1). Учитывая все сказанное, легко прикинуть эскиз графика (рис. 56). Находя затем еще несколько точек графика (полагая, скажем, х=±у, х = ± 1, х — ± 2, х=±3), мы сможем вычертить этот график более точно (рис. 57).
является ограниченной сверху.
Решение. Нужно доказать, что для любого числа b существует (хотя бы одно) значение х из области определения функции, для которого f(x)^b, т. е. Xg? Ь.
Область определения функции представляет собой
объединение двух бесконечных интервалов (—оо, 1) и (1, со). Очевидно, что если Ь^О, то неравенство полняется, например, при х = 0. Если же венство 5г о в области определения
ВЫ’ b > 0, то нера-Функции -(х11)5; равносильно неравенству \х—1 которое выполняется,
например, при х— что и требовалось доказать.
Замечание. Определение ограниченной сверху функции (см. стр. 188), применяя обозначения гл. I, можно записать следующим образом. Обозначим через А (х, Ь) неопре-
деленное высказывание
А(х, b) = {f(x)<b},
190
заданное на множестве всех значений х, которые входят в область определения функции f(x), и всех действительных значений Ь. Тогда неопределенное высказывание
В(Ь) = ^х)А{х, Ь)
задано на множестве всех действительных значений Ь. Это неопределенное высказывание читается так: для любого х из области определения функции f(x) выполнено неравенство f (х) <z b. Оно является именно неопределенным высказыванием: при одних значениях b оно, возможно, истинно, при других — ложно.
Запись (Зй) Ь’(й) уже представляет собой высказывание (а не неопределенное высказывание). Обозначим это высказывание через С:
С = (3b) В (b) == (3b) (Vx) А (х, Ь),
г. е. существует такое действительное число Ь, что для любого х из области определения функции /(х) выполнено неравенство f(x)<zb. Теперь определение можно сформулировать так: функция /(х) называется ограниченной сверху, если высказывание С истинно.
В противном случае, т. е. если высказывание С ложно, функция /(х) не является ограниченной сверху. Но если высказывание С ложно, то высказывание ~] С (не С) истинно. Применяя правила о равносильности высказываний, сформулированные на стр. 21, можно записать:
] С = -] (36) В (b) == (V6) (-] В (6)) = (V6) -] (Vx) А (х, Ь) =
==(V&)(3xH4(x, b).
Итак, функция /(х) не является ограниченной сверху, если для любого действительного числа b существует (хотя бы одно) значение х из области определения функции, для. которого f(x)^b. Это определение и приведено в начале решения примера 16.
2. Монотонность. Функция называется возрастающей на некотором интервале. (целиком содержащемся в области определения этой функции), если при увеличении аргумента (на этом интервале) увеличивается значение функции; функция называется убывающей на некотором интервале, если при увеличении аргумента значение функции уменьшается.
Другими словами, функция y=f(x) называется возрастающей на интервале a<x<6 (целиком содержащемся в области определения этой функции), если для любых xv
191
Х2, удовлетворяющих Неравенствам а < х2 < х2 < Ь, выполняется неравенство f(x1)<^f(x2)', аналогично, функция у = = /(х) называется убывающей на интервале а<^х<^Ь, если для любых xv х2, удовлетворяющих условиям a <Z х2 < <Zx2<zb, выполняется неравенство /(Xj)
Если функция y=f(x) является на интервале a<zx<Z.b возрастающей или убывающей, то она называется монотонной на этом интервале, а сам интервал а<б.х<б.Ь называется интервалом монотонности функции y=f(x).
Возрастание функции на интервале а<б.х<б.Ь означает, что на этом интервале график функции поднимается вверх при возрастании х (рис. 58), а убывание означает, что график 192
опускается вниз при возрастании х (рис. 59). Функция у ~ =х3— Зх, график которой изображен на рис. 60, не является ни возрастающей, ни убывающей на всей числовой прямой. Однако точками х=— 1 и х=1 вся числовая ось разбивается на три интервала: (—оо, —1), (—1, 1), (1, со), каждый из которых является интервалом монотонности этой функции.
Рис. 60 иллюстрирует тот факт, что на интервалах (— со, — 1) и (1, оо) эта функция возрастает, а на интервале (— 1, 1) убывает. Аналогичным свойством обладают все функции, встречающиеся в курсе математики средней школы: область определения каждой из них может быть разбита на интервалы монотонности.
Пример 17: Функция '_у = 2х +1 (рис. 45) возрастает на интервале (— оо, оо), т. е. на всей оси х. Функция у = =х3—2х (рис. 46) не является возрастающей или убывающей на всей числовой оси. Однако точка х=1 разбивает числовую ось на два интервала (—со, 1) и (1, со), каждый из которых является интервалом монотонности этой функции: на интервале (—оо, 1) функция у = х2— 2х убывает, а на интервале (1, оо) возрастает.
2х
Пример 18. Доказать, что функция /(х) = д_^Х2' во3' растает на интервале (0, 1) и убывает на интервале (1, оо).
7 В. Г. Болтянский и др.
193
Решение. Согласно определению нужно доказать, что: 1) при 0<хх<х2<;1 выполняется неравенство /(хД-С </(х2), т. е.
2*1 2х3
1 Д-Xj 1 +х| ’
и 2) при 1<;х1<х2 выполняется неравенство /(хД> >/(х2), т. е.
2xj 2х2
l+x?-'* 1+хГ
Рассмотрим разность
/(Л) — /(х2) =
__ 2хг 2х, 2 (xt Д-xixj — ха — х;х2) 2 (х2—x1)J(x1xa — 1)
1+х; 1 + хз . (1 Д-xj) (1 Д-Хз) (1 Д-xj) (1 Д-хз)
Отсюда видно, что если x2>Xi, то знак рдзности /(хД— — /(х2) совпадает со знаком выражения хгх2—1.
Если 0 <xr <х2 < 1, то xrx2 <Z 1, XiX2— 1 <0 и потому /(хД—/(х2)<0, т. е./(хД</(х2). Если же 1<х1<х2, то XjXgS-l, хгх2—1>0 и потому /(xj) — /(х2)>0, т. е. /(хД>/(х2), что и требовалось доказать.
Пример 19. Доказать, что функция/(х) = х4— х2 не является монотонно возрастающей на интервале (— 2, 2).
Доказательство. Согласно определению нужно доказать, что существуют хх и х2, удовлетворяющие условиям — 2<xf<x2<2 и /(хД^/(х2).
Замечая, что в точках хх = 0 и х2=1 функция /(х) = = х4 — х2 обращается в нуль, получаем равенство /(хД = = /(х2) = 0, которое и доказывает требуемое утверждение.
3. Четность и нечетность. Функция y=f(x) называется четной, если она обладает следующими двумя свойствами: 1) область - определения этой функции симметрична относительно точки О (т. е. если точка а принадлежит области определения, то точка —а также принадлежит области определения); 2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство /(х)=/(—X).
Функция _у=/(х) называется нечетной, если: 1) область определения этой функции симметрична относительно точки О; 2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство /(х) =—/(—х).
Без труда проверяется, что функция _у = |х| является четной. Точно так же функция у = х2л четна, а функция
194
_y = x2n+1 нечетна* (при любом целом п). Без труда проверяется также, что сумма, разность, произведение и частное двух четных функций снова являются четными функциями. Далее, сумма и разность двух нечетных функций являются нечетными функциями. Наконец, произведение и частное двух нечетных функций являются четными функциями, а произведение и частное четной и нечетной функций являются нечетными функциями. Доказательство всех этих утверждений мы предоставляем читателю.
Из сказанного следует, например, что многочлен, у которого все показатели четны, является четной функцией, а многочлен, у которого все показатели нечетны, является нечетной функцией. Так, функция _у = х44-2хг—1 четна, а функция Xs — х5 нечетна. В качестве других примеров четных функций можно взять следующие:
1 И + 1
-У —Г»+Г У~ 1 +х2+|Х | ’
у = ]/'х4 — jx|(xe— 2х44-Зх24-5) и т. п„
а в качестве примеров нечетных функций можно взять
- „ о , _ х54-Зх3 , х5 — х
y = xs— 2хл-4-7х, у =------------, у = х7----- и т. п.
х4+2х2 + 3 К|х| + *2
Не следует думать, что всякая функция непременно является или четной или нечетной: существуют функции, не являющиеся ни четными, ни нечетными.
Пример 20. Доказать, что функция /(х) = 2x4-1 не является ни четной, ни нечетной.
Решение. Областью определения этой функции является вся числовая ось, т. е. условие 1) в определении четной и нечетной функций выполнено. Чтобы доказать, что функция f (х) не является четной, мы должны поэтому доказать, что условие 2) в определении четной функции не выполнено, т. е. что существует (хотя бы Одно) значение х, для которого /(х)#/(—х). Возьмем х— 1. Тогда/(1) = 3,/(—1)— = — 1, т. е. /'(1)т£:/(—1). Таким образом, функция /(х) не является четной. Аналогично, так как /(1) —/(—1), то функция /(х) = 2x4-1 не является нечетной.
Замечание. Разобранный пример показывает, что высказывание «функция /(х)' нечетна» не является отрицанием высказывания «функция /(х) четна». Иначе говоря, высказывания «функция /(х) нечетна» и «функция /(х) не является четной» означают не одно и то же. Чтобы выяснить
7*
195
логическую структуру этих утверждений, предположим, что дана некоторая функция/(х), и рассмотрим следующие высказывания:
А = {область определения функции f(x) симметрична относительно точки О};
В (X) == \f(x) = f(- X)}, С (X) = {/(х) = -/(- х)}
(переменные высказывания В(х) и С (х) рассматриваются для тех х, для которых обе точки х, —х принадлежат области определения функции /(х)). Далее, через Р обозначим высказывание {функция /(х) четна}, а через N— высказывание {функция /(х) нечетна}. Тогда определения четности и нечетности могут быть записаны следующим образом:
Р = АД((Ух)В(х)), /У= А Д ((Vx)C(x)).
Высказывание "] Р = {функция /(х) не является четной}, согласно правилам на стр. 34, может быть записано следующим образом:
1 Р = -| (А Л ((Vx) В (X))) = (-] А) V 1 (Vx) В (х) =
= (-] A) V((3x)-]B(x)).
Итак, высказывание «функция /(х) не является четной» означает, что либо область определения функции /(х) несимметрична, либо же существует такое х, что f(x)^f(—х). Именно эта форма высказывания "] Р и была использована в примере 20 при доказательстве того, что функция /(х) = = 2x4-1 не является четной.
Четность или нечетность функции весьма существенно сказывается на форме графика этой функции. Именно, имеют место следующие две теоремы:
Теорема 1. График четной функции симметричен относительно оси у.
Доказательство. Пусть точка (х0;_у0) принадлежит графику четной функции _у=/(х), т. е. ^0=/(х0). Точка, симметричная с точкой y=f(x) относительно оси у, имеет координаты (—_у0). Надо доказать, что точка (—х0; _у0) принадлежит графику функции у =/(х), т. е. доказать, что У'о=/(—Но это следует из определения четной функции: /(—х0)=/(х0)=у/„.
196
В качестве упражнения предлагается аналогичными рассуждениями доказать следующую теорему.
Теорема 2. График нечетной функции симметричен относительно начала координат (0; 0).
Замечание. Из этих теорем следует, что для построения графика четной функции достаточно построить часть графика этой функции для х 0, а затем построенную часть графика симметрично отразить относительно оси у, т. е. для каждой точки графика с абсциссой х>0 построить точку, симметричную ей относительно оси у. В частности,
У
таким способом можно построить график функции у =/([ х |), так как функция /(| х|) является четной. Для построения графика нечетной функции достаточно построить часть графика этой функции для хДь-0, а затем построенную часть графика симметрично отразить относительно точки (0; 0), т, е. для каждой точки графика с абсциссой х>0 построить точку, симметричную ей относительно начала координат. (Заметим, что для осуществления симметрии некоторой кривой относительно начала координат можно поступить следующим образом: сначала данную кривую Асимметрично отразить относительно оси ординат, а затем полученную кривую А симметрично отразить относительно оси абсцисс, рис. 61.) Пример 21. Построить график функции у = х2 — 2 | х |. Решение. Заметив, что эта функция четная, сначала построим часть ее графика при При этих значениях
197
х мы имеем у — х2— 2|х’| = х2— 2х, и потому искомая часть графика — это часть параболы рис. 46 при хОэО. Затем построенную часть графика симметрично отражаем относительно оси у (рис. 62).
Пример 22. Построить график функции у=~ •
Решение. Функция у = -i- обладает следующими свойствами:
1. Выражение имеет смысл для любого х^О, т. е.
„ д. 1
областью определения функции У=— является множество всех действительных чисел, кроме точки х = 0, или, иначе говоря, объединение двух бесконечных интервалов (— оо; 0) и (0; оо).
2. Функция у— у нечетна. Поэтому все дальнейшие свойства будем рассматривать только для х > 0.
3. При любом значении х>0 функция _у = у принимает положительные значения, т. е. часть графика функции у = = — при х > 0 расположена выше оси х.
4. Если 0 < Xj <Z х2, то выполняется неравенство — >— , , I Xl 4г
т. е. функция У = ~ монотонно убывает на интервале (0; -фоо).
198
5. Если значения аргумента х неограниченно увеличи-ваются, то значения функции у—— все более приближаются к нулю. Если значения х приближаются к нулю, то значе-, 1
ния функции У—~ неограниченно увеличиваются.
6. Вычисляя значения функции = получаем таблицу
графика симметрично отражаем относительно начала координат (рис. 63, б).
Рис. 63.
Заметим, что свойства 1—6 нельзя выводить из рассмотрения графика (рис. 63, а), так как график строился на основании этих свойств. Но из графика можно выводить некоторые двойства функции У — ~ Для х<0. Например, из
199
рассмотрения графика (рис. 63, б) ясно, что функция У — ~ монотонно убывает на интервале (— оо; 0); далее, ясно, что при х<0 функция У = ~^ принимает отрицательные значения; легко обобщается для значений х <Z 0 и сформулированное выше свойство 5.
4. Периодичность. Функция _у=/(х) называется периодической, если существует такое число Т > 0, что для каждого значения х из области определения этой функции значения x-fT и х — Т также принадлежат области определения и выполняется равенство /(х+ T)—f(x). При этом число Т называется периодом функции y=f(x).
Из этого определения следует, что
f(x + 2Т)=/[(х + Г) + Т\ =f(x + 7) =/(х), fix + 37’) =/[(х + 20 + 7’] =/(х + 27’)=/(х), /(О=/[(х-О+^=/(х-О
и т. д. Отсюда, используя метод математической индукции, получаем, что для любого н = 0, ±1, ±2, ... выполняется равенство f{x-fnT)=f{x). Таким образом, каждое из чисел пТ (zi=l, 2, 3, ...) также является периодом функции fix').
Мы предполагаем, что читатель хорошо знаком с периодическими функциями sin X, COS X и tgx.
Пример 23. Доказать, что функция /(х) = 5— яв-
ляется периодической с периодом 2л.
Решение. Область определения рассматриваемой функции получается выбрасыванием из числовой оси тех точек, в которых знаменатель обращается в нуль, т. е. точек — — целое). Отсюда видно, что если точка х при-
надлежит области определения рассматриваемой функции /(х), то точки х-(-2л и х—2л также принадлежат этой области определения. Остается проверить, что выполнено равенство /(х4-2л)=/(х). Мы имеем
1 olll (Л 1 bill X
Пример 24. Доказать, что функция /(x)=|sinx| является периодической с периодом л.
Решение. Областью определения функции /(х) является вся числовая ось. Поэтому для любого х точки х-фл и 200
х—л принадлежат этой области определения. Остается проверить, что выполнено равенство /(хф л)=/(х). Мы имеем
f(x л) = | sin (х 4- л) | = |—sin х | = | sin х | = /(х).
Пример 25. Найти наименьший период функции
/(х) = 3 sin х 4- sin 2х.
Решение. Пусть Т — период данной функции, т. е. для всех х имеет место равенство
3 sin (х 4- Т) 4- sin 2 (х 4- 7 ) = 3 sin х 4- sin 2х.
В частности, отсюда при х — 0 имеем
3 sin Г 4~ sin 27' = 0, или sin Т (3 4- 2 cos Т) — 0.
Так как 3-f-2 cos 7 =4= 0, то sin 7' = 0. Таким образом, периодом данной функции может быть только такое число Т, которое удовлетворяет условию sin Т = 0, т. е. период нужно искать лишь среди чисел 7' = Ал (А= 1, 2, 3, ...).
Непосредственной проверкой убеждаемся, что число л не является периодом данной функции. Например, при х = у имеем
/(х 4- л) =/ (у 4- л^ = 3 sin ^у 4- 4- sin 2 4~ = — 3,
/(х) =/{= 3 sin f 4- sin 2 | = 3,
т. e. /(x4-л) =4=/(x). Число 2л является периодом данной функции, так как для любого х имеем
3 sin (х 4- 2л) 4- sin 2 (х 4- 2л) = 3 sin х 4- sin 2х.
Итак, Т = 2л — наименьший период функции
/(х) = 3 sin х 4- sin 2х.
Нередко поступающие в вузы допускают ошибки при решении задач вида: доказать, что некоторая функция н е является периодической. В связи с этим полезно разобрать логическую структуру определения периодичности. Пусть дана некоторая функция /(х). Область ее определения обозначим через А. Рассмотрим следующие неопределенные высказывания, в которых х может принимать любое значение,
201
принадлежащее множеству А, а Т — произвольное положительное число:
В(х, 7^ = {точка х-\-Т принадлежит множеству Л}, С(х, Т) = {точка х—Т принадлежит множеству А}, D(x, T)^{f(x~pT)=f(x)}.
Согласно определению функция /(х) называется периодической, если существует такое положительное число Т, что для любого х (из множества А) справедливы высказывания В(х, Т), С (х, Г) и D(x, Т). Иначе говоря, высказывание
Р ~ {функция f(x) является периодической} может быть записано в следующем виде:
Р==(ЭТ)(Ух)(В(х, Т)/\С(х, T)/\D(x, Г)).
Каким же образом убедиться в том, что функция f(x) не является периодической, т. е. что истинно высказывание "] Р? Согласно правилам на стр. 34 высказывание Р можно записать следующим образом:
1 Р = 1 (ЗП (Vx) (В (х, 7’) Л С (х, 7') Л D (х, Т)) ~
= (V7") "] (Vx)(B(x, 7')ДС(х, T)/\D(x, Г)) =
(V Г) (Зх) 1 (В (х, Т) Д С (х, Т) Д D (х, 7')) ==
= (V7-) (Зх) ((1 В (х, Г)) V (1 С (х, Т)) V ("I D (х, 7'))).
Иначе говоря, для того чтобы убедиться, что функция /(х) не является периодической, нужно установить следующее: для любого Т > 0 найдется такое х (из области определения функции /(х)), что не будет выполнено хотя бы одно из указанных выше условий В (х, Г), С(х, Т), D(x, Г).
Пример 26. Доказать, что функция' /(х)=8Шуне является периодической.
Решение. Область определения получается выкалыванием из числовой оси точки х = 0. Пусть Т — произвольное положительное число. Так как —7'у=0, то точка х0 = —Т принадлежит области определения функции. В то же время точка х04-7’ = (—7')+ Т= 0 не принадлежит области определения. Итак, для любого 7'>0 существует такое х=х0 (из области определения функции /(х)), что точка х-}- Т не 202
принадлежит области определения. Следовательно, функция /(x) = sin-^- не является периодической.
Пример 27. Доказать, что функция /(х) = х3 не является периодической.
Решен и е. Областью определения является вся числовая прямая. Поэтому для любого Т точки х-\-Т и х — Т принадлежат области определения. Значит, у нас есть единственная возможность установить, что функция /(х) не является периодической: нужно доказать, что для любого Т > О существует (хотя бы одно) значение х, для которого f{x-\-T)^=f{x). Легко видеть, что в качестве такого х можно взять, например, х = 0. Тогда /(х)=/(0) = 0, f(x-\-T) = = /(Г)=Р>0, т. е. /(х + 7-)^=/(х).
Рассмотрим теперь вопрос о построении графика периодической функции. Пусть функция y — f(x)— периодическая с периодом Т. Если точка (хп, _у0) принадлежит графику этой функции, т. е. _у0=/(х0), то точки (х0-\-пТ', у0)
(я=±1, ±2, ...) также принадлежат этому графику, так как /(х0 + /17')=/(х0)=_у0. Значит, для построения графика периодической функции достаточно построить часть ее графика, расположенную над каким-нибудь отрезком а х sC а Т, и тогда весь график получается сдвигом построенной части вдоль оси х на отрезки ± Т, ± ЧТ,... (рис. 64).
Пример 28. Построить график функции
Решение. Рассматриваемая функция определена на бесконечном числе полуинтервалов kn х -у + kn (k = 0,
203
±1, ±2, ...). Поэтому, если х принадлежит области определение, то точки хул и х —31 также принадлежат области определения. Далее, для любого значения х, принадлежащего области определения этой функции, выполняется соотношение Ktg (х + л) = У tg х. Таким образом, функция _y = P^tgx— периодическая с периодом л. Поэтому все дальнейшие свойства достаточно рассматривать только на полуинтервале Osgx<;y.
Ясно, что функция T=y"tgx при х = 0 принимает значение 0 и монотонно возрастает на полуинтервале 0 х<-^-.
При этом, если значения х приближаются к у, оставаясь меньше у, то значения функции = tgx неограниченно увеличиваются. Воспользовавшись для большей точности следующей таблицей:
мы теперь легко можем начертить часть графика функции _y = ]/tgXHa полуинтервале О^х(рис. 65). Затем
204
сдвигом вдоль оси х на Ал (А = ± 1, ±2, ...) мы получим весь график рассматриваемой функции.
Итак, для построения графика функции рекомендуется, по возможности, изучить следующие ее свойства:
1) область определения;
2) множество значений (в частности, ограниченность);
3) четность или нечетность;
4) периодичность;
5) монотонность;
6) поведение функции при приближении аргумента к граничным точкам области определения функции;
7) интервалы, на которых функция положительна или отрицательна.
Для большей точности построения следует вычислить значения функции в нескольких точках (при этом желательно найти точки пересечения графика с осями координат).
При решении конкретных задач приведенный выше рецепт для построения графика не всегда является самым рациональным. В следующих параграфах рассматриваются некоторые случаи, когда график функции может быть построен преобразованием ранее известного графика. При этом нередко удается выводить некоторые свойства функции из ее графика.
§ 4. Композиция функций
Рассмотрим некоторую функцию y—f(x\ областью определения которой является множество А. Разумеется, вовсе не обязательно обозначать аргумент этой функции именно буквой х, а саму функцию именно буквой у. Например, запись будет означать, что рассматривается та же
функция f (с той же областью определения А), но только ее аргумент обозначается буквой t, а сама функция — буквой х. Нередко под знак функции подставляется вместо аргумента не только другая буква, но какое-либо более сложное выражение. Например, если задана некоторая функция у = = f(x), то запись f[tA. ) означает, что надо проделать
те действия, которые предусматриваются правилом соответ-
ствия /, но только эти действия надо проделать не над аргу-
t
ментом х, а над выражением ~2 .
4 -f- 1
Пример 29. Пусть /(х) = ^-у; найти /[руру
205
Решение. Нам нужно в обе части равенства f(x) = х2 - t
q-p вместо х подставить выражение Мы получаем
/ t \2 ‘ ft
ft t \ _ V2+J = (*2 + 1)2
7 У2+О / t, \ £±£i±l
V2+l^ /2+1
Так как t2-j-1^0, то мы можем умножить числитель и знаменатель последней дроби на (/2-|-1)2, после чего получим
J\ft+ll (?2 + ? + 1)(/2 + 1)-
В разобранном примере под знак функции f вместо аргумента х была подставлена функция нового аргумента t, а именно х = . В общем случае такую подстановку
можно описать следующим образом. Пусть f и g— две функции. Подставив под знак функции y=f(x) вместо аргумента х функцию x = g(f), мы получаем новую функцию у — f(g(t)), в которой аргументом является t. Функция у — = f(g(t)) называется композицией (а иногда также суперпозицией) функций f и g.
Пример 30. Объем конуса постоянной высоты Н является функцией от площади основания конуса: _у=/(х) = = В свою очередь площадь основания конуса есть функция от радиуса основания: x = g(f)~nt2. Значит, композиция этих функций flaef зависимость объема конуса от радиуса основания:
y=f(g(t))=± aHt2.
Весьма важным является вопрос о том, какова область определения функции y—f(g(t)), являющейся композицией двух данных функций f и g. Ясно, что если t не принадлежит области определения функции g, то выражение f(g(f)) не определено: ведь чтобы вычислить это выражение, мы должны сначала найти g(t). Однако, даже если t принадлежит области определения функции g(f), выражение f(g(t)) может все же не иметь смысла: это будет тогда, когда значение x = g(t) не принадлежит области определения функции /(х). Итак, область определения функции y=f(g(fj) 206
содержится в области определения функции g(f), но может не -совпадать с ней.
Пример 31. Пусть _у=/(х) = ^^, x=g(f)=^4-l.
Найти вид и область определения функции y=f(g (/)).
Решение. Областью определения функции g{t) является все множество D действительных чисел. Мы имеем
.. _£(0 + 1_ Д2+0+1 ^24-2_ /2 + 2
У— J g(t)-2 (/2+1)-2 /2-1 (t— 1)(;+ 1)•
Из этого выражения видно, что область определения функции y—f(g(t)) получается выкалыванием из множества D двух точек I ——1 и t—\. Таким образом, область определения функции /(§(/)) не совпадает с областью определения функции g(t).
Нередко при решении задач используются выражения такого вида: «в функции /(х) заменим х на g(x)» или «в функции /(х) вместо х подставим g(x)». Смысл этих выражений заключается в том, что рассматривается функция _y=/(g(x)). Иными словами, рассматривается композиция функций _у = /(х) и x = g(t), т. е. функция у— f(g(tj), и'в этой функции аргумент обозначается не через t, а снова через х; в результате- мы и получаем новую функцию _y=/(g(x)). Для сокращения речи не говорят «рассмотрим функцию y=f(g(t)) и обозначим ее аргумент не через f, а через х», а применяют указанные выше более короткие фразы. Разумеется, при рассмотрении композиции _y=/(g(x)) надо всегда внимательно следитй за областью определения этой функции.
х 2 ’
Пример 32. В функции f(x) = ~y[ вместо х подставить
х
х—Г
Решение. Мы должны рассмотреть функцию f
Имеем
^гт+2
Зх —2 х — 1
1 х—1
Область определения этой функции получается из множества D всех действительных чисел выкалыванием точки х= 1, т. е. эта область определения является объединением двух
207
бесконечных интервалов (— оо, 1) и (1, оо). Если х принадлежит этой области определения, т. е. х ф 1, то х—1 ф О и потому можно умножить числитель и знаменатель дроби на х— 1:
Зх — 2
/ х \ х—1 Зх —2
\х=л/~ Г~~~ i “
X— 1
Итак, функция не определена в точке х = 1; во всех
остальных точках она совпадает с функцией у = 3х— 2. Более коротко это можно записать формулой:
х \ (Зх — 2) (х—1)
' \х^Г)= х^П •
Пример 33. Определить вид функции f(x), если известно, что ''.—хгЗг2х (при х ф 1).
2х I" 1
Решение. .Обозначим (при х ф 1) t Тогда
2x3r\=t(x—1) и потому х=рЦ. Следовательно, если
/л 1 t=£2, то, полагая x = -£g
и проводя вычисления в обрат-
„ j 2х -р 1 ..
ном порядке, мы найдем ( = . Заменяя
нам равенстве /I = х2-(-2х аргумент возможно при любом t 96 2), мы получим
7+1?_Ц9 1^+Ц— 3
t-2) +Z\t-2j~~ (/-2)2
теперь в данном /+1 ,
X на f32 (чт0
(( ф 2).
Обозначая t через х, получаем
(ПРИ х^2)- (8)
Замечание. Поставленное в скобки указание «при х 2» является в формуле (8) существенным. В самом деле, функция, стоящая в правой части равенства (8), в точке х = 2 не определена, т. е. ее область определения получается выкалыванием точки х — 2 из множества D. Что же касается функции /(х), то о ее поведении при х = 2 мы ничего не знаем. Мы лишь установили, что при х=р=2 функция /(х) 208
совпадает с правой частью (8). Определена ли функция /(х) при х = 2 (и если определена, то чему равна), условия задачи узнать не позволяют. Поэтому написать просто
/(х)
3x2 — 3 (х-2)2
(без указания «при х^=2») у нас нет никаких оснований. Решение примера 33 можно изложить и иначе (хотя до этого второго решения труднее догадаться). Ведь в приве-f-f-l
денном выше решении мы заменяли х на p-g, а затем в конце заменяли t на х. Значит, можно было просто заменить х на Тогда решение будет выглядеть следующим образом.
Заменим в данном равенстве х на . Мы получим
/чх+1 , , \
I х — 2 'j / х-|- Г-2 „ х-р 1
i хф! \х —2/ + х—2‘
\ х—2 /
Если х '=/= 2, то числитель и знаменатель дроби, стоящей под знаком функции /, можно умножить на х — 2, и мы получим г/2(х-р1)-|-х — 2\ /х-р1\2 , лХр! /_
f I Т~Т" -----НТ- I = I —6 + 2 —Ч; (при X =7^ 2).
J \ х+1-(х-2) j \х — 2/ 1 х —2 ' f ’
Отсюда непосредственно получается равенство (8).
§ 5. Обратная функция
Пусть /(х)— некоторая функция, заданная на отрезке [а, Ь]. Если эта функция не является монотонной, то может случиться, что двум различньпм значениям аргумента соответствует одно и то же значение функции. Рис. 66 дает графическую иллюстрацию этого утверждения: /(xj) =/(х3) =_у0. Разумеется, для функции, график которой изображен на рис. 66, мы, как и для любой другой функции, можем, зная значение аргумента, однозначно определить соответствующее значение функции. Однако обратный переход (от значения функции к значению аргумента) здесь не является однозначным. Например, значение у0 функция принимает в двух точках хр х2.
Для того чтобы обратный переход (от значения функции к соответствующему значению аргумента) был однозначным,
209
Рис. 68.
ограничиваются рассмотрением монотонных функций. Пусть, например, на отрезке [а, Z?] задана монотонно возрастающая функция f(x), причем когда х пробегает весь отрезок а^х^Ь, значения функции /(х) пробегают некоторый отрезок csgj/sgS (рис. 67). В этом случае каждому значению функции, взятому из отрезка c^y^cd, соответствует в точности одно значение аргумента, т._ е. обратный переход
(от значения функции к соответствующему значению аргумента) однозначен. То же самое будет, если рассматриваемая функция монотонно убывает (рис. 68) или если монотонная функция задана не на отрезке, а на интервале (рис. 69), полуинтервале (рис. 70), луче (рис. 71) или на всей числовой прямой (рис. 72).
Рассмотрение обратного перехода (от значения функции к соответствующему значению аргумента) и позволяет по исходной функции y — f(x) построить некоторую новую функцию,
называемую обратной к исходной функции. Для определен-
ности будем по-прежнему считать, что исходная функция _у=/(х) возрастает, определена на отрезке [а, &], а ее значениями служат все точки отрезка [с, d] (см. рис. 67). По опре
делению обратная функция сопоставляет каждой точке у0 отрезка c^ye=:d ту точку х0 отрезка a sg х гС Ь, в которой исходная функция /(х) принимает значение _у0. Если мы условимся обратную функцию обозначать через g, то мржно ее определение сформулировать следующим образом: равен-
ство х0 = £(_у0), по определению, означает, что в точке х0 исходная функция принимает значение Д'о, т. е. yo=f(Xo):
{x0-=g(y0)} {Л = /(^о)}-
(9)
Можно сказать и иначе: через g(y0) обозначается та точка х0 отрезка а^-х^Ь, в которой функция /(х) принимает значение _у0, т. е.
g(y() есть корень уравнения f(x)—yQ. (10)
211
У
Рис. 70.
Рис. 72.
А мы уже знаем, что для монотонной функции этот корень — единственный.
Из сказанного вытекают все основные свойства обратных функций и способ их отыскания.
Прежде всего заметим, что утверждение (10) можно записать следующим образом: чтобы найти g (у0), надо решить уравнение f(x)=y0 относительно х. Заменим здесь буквы: вместо х поставим у, а затем вместо _у0 поставим х (ведь аргумент и функцию можно обозначать любыми буквами). Мы получим: чтобы найти g(x), надо решить уравнение f(y) = x относительно у. Это и дает способ нахождения обратной функции:
А. Чтобы найти функцию, обратную монотонной функции y=f(x), нужно поменять местами буквы х и у, т. е. написать x=f(y), и из полученного равенства, как из уравнения, найти у. Это и даст обратную функцию y = g(x).
Теперь рассмотрим основные свойства обратных функций.
Б. Если f(x) — монотонная функция, a g(x)— обратная ей функция, то функция g(x) также монотонна, причем если f—возрастающая функция, то и g— возрастающая, а если f—убывающая, то и g—убывающая функция.
В самом деле, пусть f—возрастающая функция, т. е. при х0<.х'й числа _у0=/(х0) и То==/(хо) связаны неравенством То<То- Так как обратный переход однозначен, то отсюда следует, что и, наоборот, еслиу0<^у'й, то х0<^х^. Поскольку хй = £ (То). х'»=ё(.Уо) (см. (9)), мы получаем: если ^0<Л> то S (ТоХ S (То)- Таким образом, обратная функция g также является возрастающей. Аналогично рассматривается случай убывающей функции.
В. При переходе от функции к обратной ей функции область определения и множество значений меняются местами.
Например, если монотонная функция /(х) определена на отрезке [а, Ь], а значения этой функции заполняют отрезок [с, d], то обратная функция g (х) определена на отрезке [с, d] и ее значения заполняют отрезок [а, Ь].
Это непосредственно вытекает из определения обратной функции.
Г. Графики взаимно обратных функций f(x) и g(x) симметричны друг другу относительно биссектрисы первого и третьего координатных углов (рис. 73).
213
Действительно, пусть точка (х0; _у0) принадлежит графику функции _у ==/(%), т. е. _уо=/(*о)- Тогда x0=g(_y0) (см. (9)), т. е. когда аргумент принимает значение уй, обратная функция g принимает значение х0. Но это означает, что точка (_у0; х0) принадлежит графику обратной функции. Заметим теперь, что точки (х0; _у0) и (_у0; х0) симметричны относительно указанной в формулировке биссектрисы (рис. 74). Таким образом, если неко
торая точка принадлежит графику функции y—f(x),
то симметричная ей точка принадлежит графику обратной функции y — g(x). Аналогично доказывается и обратное: если точка принадлежит графику функции y — g(x), то симметричная ей точка принадлежит графику функции y — f(x).
Д. Для любого х, принадлежащего области определения функции f(x), справедливо соотношение g(f(x)) = x; точно так же для любого х, принадлежащего области определения обратной функции g(x), справедливо соотношение f(g(xy) — x.
В самом деле, пусть х0 — точка, принадлежащая области определения функции y=f(x), а _у0—соответствующее значение функции, т. е. у0=/(х0). Тогда x0 = g-(j0) (см. (9)). Подставив в последнее равенство вместо _у0 его значение /(х0), получаем x0=>g(y0) — g(/(х0)). Таким образом, для любой точки х0 из области определения функции f(x) справедливо равенство x0 = g(f(x0J). Аналогично доказывается равенство f(g(x)) = x.
Пример 34. Для функции у — Зх— 5 найти обратную функцию.
214
Решение. Данная функция /(х) = 3х— 5 является возрастающей и определена на всей числовой прямой. Для нахождения обратной функции y = g(x) надо, согласно А, поменять в равенстве у = Ъх—5 буквы х и у местами, т. е. написать х — Ъу—5, и решить это уравнение относительно у. Решая, легко находим у~ . Таким образом, обратной □
, г , х 5
является функция g(x) = ~—. о
На этом примере легко проследить выполнение свойств ' х4-5
Б—Д. Обратная функция у — —является возрастающей, □
как и исходная функция /(х) '(ср. Б). Свойство В в данном
случае тривиально: обе функции /(х) и g(x) определены на всей числовой прямой и принимают все действительные значения. Рис. 75 дает иллюстрацию свойства Г. Наконец, легко проверяется и свойство Д:
/ (g (•*)) = 3 • g (х) — 5 = 3 • х-~ — 5 = X.
Пример 35. Найти обратную функцию для _у —]/х.
Решение. Функция/(х) = фЛх (арифметический корень) определена при х>;0 и принимает неотрицательные значения, т. е. и областью ее определения и множеством значений служит бесконечный полуинтервал [0, оо). Для нахождения
215
обратной функции y~g(x) надо, согласно А, поменять в равенстве у — Ух буквы х и у местами, т. е. написать х = У~ у, и решить это. уравнение относительно у. Решая, находим у = х2', при этом следует помнить, что функцию у = х2 мы должны рассматривать лишь при х2э0, так’как множеством значений исходной функции y—f(x) был полуинтервал [0, оо). Итак, обратной для функ-
ции у=ух является функция у — х2, рассматриваемая лишь при х2>0 (рис. 76).
Пример 36. Рассмотрим теперь функцию у = х2 при Т-СО. Какая функция является обратной к ней?
Решение. Исходной
является функция f(x) = x2 при х =С 0. Ее областью определения является бесконечный полуинтервал (—оо, 0], а множеством значений — бесконечный полуинтервал [0, оо). Значит, согласно свойству В, обрат
ная функция y = g(x) будет определена на полуинтервале [0, оо) и будет принимать значения на полуинтервале (— оо, 0]. Найдем теперь эту обратную функцию. Для этого, согласно А, надо в равенстве у~х2 поменять местами буквы х и у, т. е. написать х=у2, и решить это уравнение относительно у. Решая, находим два корня: у=± Ух. Однако, вспоминая, что обратная функция должна принимать
значения на полуинтервале
(—оо, 0], мы должны оставите лишь значение у — — У~х. Итак, обратной для рассматриваемой функции является функция g(x) = — Ух (рис. 77).
216
Этот и предыдущий примеры весьма поучительны: они показывают, что при рассмотрении обратных функций надо всегда помнить об области определения и множестве значений. Мы еще встретимся с этим ниже, при рассмотрении обратных тригонометрических функций.
В заключение заметим, что монотонность исходной функции _у = /(х) в действительности не является необходимым условием для возможности рассмотрения обратной функции. Для возможности определения обратной функции необходимо и достаточно, чтобы обратный переход (от значений функции к значениям аргумента) был однозначным, т. е. чтобы каждому значению функции соответствовало лишь одно значение аргумента. Монотонность является достаточным условием для этого, т. е. для монотонной функции обратный переход всегда однозначен. Но существуют и другие функции (не являющиеся монотонными), для которых обратный переход однозначен и для которых,, следовательно, можно найти обратную функцию.
Пример 37. Найти обратную функцию для у — - —у
Решение. Исходная стве области определения
функция /(х) = ^у имеет в каче-множество D с выколотой точкой
х = — 1, т. е. объединение двух бесконечных интервалов (—оо, —1) и (—1, оо). Эта функция не является монотонной. Например, /(—2)>/^—(так что функция f не является возрастающей) и в то же время —у^</(0 (так что функция f не является и убывающей). Однако обратный переход здесь однозначен. В самом деле, освобождаясь в соотно-
х
шении у= . от знаменателя, мы получим уравнение пер-
вой степени относительно х; значит, для любого у
найдется не более чем одно соответствующее значе-
ние х.
Для нахождения обратной функции y = g(x) надо, согласно А, поменять в равенстве _y=yqL_ буквы х и у местами, и
и решить это уравнение относи
т. е. написать
тельно^. Освобождаясь от знаменателя, находим-х(_у + 1)—_у, откуда y = YZ~;- Итак, обратной для /(х) является функция
217
X
g (,v) =-j—. Ee область определения получается выкалыванием точки х=1 из множества D- На рис. 78 показан
график функции /(х) (сплошная линия) и обратной функции g(x) (пунктир).
§ 6. Обратные тригонометрические функции
Рассмотрим функцию у — sin х. Эта функция, рассматриваемая ' на всей числовой прямой —оо<х<;оо, не является монотонной. Поэтому, чтобы говорить об обратной функции, мы прежде всего должны выделить участок монотонности функции _y = sinx. Одним из участков монотонности этой функции является отрезок —этом 0ТР'езке мы и будем рассматривать функцию _y=sinx, т. е. в качестве исходной функции у —f(x) мы возьмем функцию у = sin х, рассматриваемую на отрезке —Обратная ей 218
функция обозначается через arcsin х. Таким образом, из А — Д вытекают следующие свойства функции arcsin х.
Соотношение а = arcsin а означает, что выполнены соотношения — у -2-, sina = a: .
{a=arcsina}<-»|—Д {sin а = а}.
Функция arcsin х определена на отрезке —Isgx^l и
является монотонно возрастающей, ее значения заполняют
отрезок —График функции _y = arcsin х пока-
зан на рис. 79. Наконец, для любого х, принадлежащего отрезку — ls=;x-Cl, справедливо соотношение sin(arcsinx) = = х, а для любого х, принадле-л _ л жащего отрезку —
справедливо соотношение arcsin (sinx) = x.
Это и дает полный перечень основных свойств функции arcsin х. Все эти свойства вытекают из общего определения обратной функции (см.свойства
А — Д на стр. 213—214).
Пример 38. Найти значение выражения arcsin (sin 3). Решение. При решении примеров подобного типа школь-
ники и поступающие в вузы нередко допускают стандартную ошибку: пишут arcsin (sin 3)= 3. Причина этой ошибки — использование соотношения arcsin (sin х) = х без учета того факта, что оно имеет место лишь при —-|-sgx-Cy. Так как число 3 не принадлежит указанному отрезку, то ясно, что ответ ошибочен.
Для правильного решения нужно, пользуясь формулами приведения, заменить sin 3 синусом другого угла х, удовлетворяющего неравенствам —у=Сх«^-^-- Мы имеем (на основании формулы sina = sin(n—a))
и потому
sin 3 = sin (ат— 3)
arcsin (sin 3) — arcsin (sin (л — 3)).
219
В то же время число л—3 0,14 удовлетворяет неравен-
ствам —g eg л— так что
arcsin (sin (л — 3)) = л — 3.
Таким образом, arcsin (sin 3) = л — 3.
/ 2 \
Пример 39. Найти значение выражения tg(arcsin.
\ •J /
2
Решение. Обозначим arcsin — = а. Эта запись означает, л л , 2 ...
что —у=с а и sin а=-у. 1ак как в четвертой четверти синус отрицателен, то а—угол, заключенный в первой четверти, т. е. 0<ga<gy. Теперь имеем
I cos<х | = —sin2a = l/" 1 — =^-Х,
у \ О / □
а так как в первой четверти косинус положителен, то ]'5 „ , sin а 2 ]'5 2 ,г
cosa = -4r-- Отсюда находим tga —------= -5-: —=- = -7=.Та-
3 ь cos a 3 3 у 5
ким образом, окончательно
/ 2 \ 2
tg arcsin — = tg a = -7=.
\ 3 / b /5
Аналогичным образом определяются остальные обратные тригонометрические функции. Функция _y = cosx не является монотонной. Одним из участков ее монотонности является отрезок 0 eg х eg л. Принимая за исходную функцию у=/(х) функцию cos х, рассматриваемую на этом отрезке, мы сможем построить обратную к ней функцию. Эта обратная функция и обозначается через arccos х. Из свойств А — Д (стр. 213—214) вытекают следующие свойства этой функции.
Соотношение a = arccos а эквивалентно следующим двум соотношениям: O-gagn, cos а = а, или в другой записи:
{a = arccos а} «-> {0 ’ a =g л] Д (cos а = а}.
Функция arccos х определена на отрезке — 1 -sg х -sg 1 и является монотонно убывающей; ее значения заполняют отрезок Ogg'ga. График функции у= arccos х показан на рис. 80. Наконец, для любого х, принадлежащего отрезку — Igxg 1, справедливо соотношение cos (arccos х) — х, 220
а для любого х, принадлежащего отрезку спра-
ведливо соотношение arccos (cos х) — х.
Отметим еще одно соотношение, связывающее функции arcsin х и arccos х. Пусть х — произвольное число, удовлетворяющее неравенствам —IsAx^l, жит области определения каждой из функций arcsin х, arccos х. Положим
а = arcsin х, Р = arccos х.
Тогда выполнены соотношения
(ЬСр-г'л, sina = x, cosP = x.
Первое и третье из этих соотноше-ний означают, что —а-С л и cos^y—<zj = sina = x. Следовательно,
у—a = arccosx = p, т. е. а+Р = у. Итак, для любого х, удовлетворяющего неравенствам —Isgx-C!, справедливо соотношение
так что х принадле-
, л
arcsin х + arccos х = у.
Далее, функция у = tg х не является монотонной. Одним л л
из участков ее монотонности является интервал — — <х <Z -% • Принимая за исходную функцию y=f(x') функцию tg х, рассматриваемую на этом интервале, мы сможем построить обратную к ней функцию. Эта обратная функция обозначается через arctgx.
Соотношение a = arctgn означает следующее:
{a = arctga} «->{- <а<у| A {tga = a}.
Функция arctgx определена на всей числовой прямой и является монотонно возрастающей; ее значения заполняют интервал — График функции _y = arctgx пока-
зан на рис. 81. Наконец, для любого действительного х ' 221
справедливо соотношение tg (arctg х)=х, а для любого х, принадлежащего интервалу — у<х<у, справедливо со-
Таковы основные свойства функции arctg х. Аналогично определяется функция _y=arcctgx. Мы лишь отметим, что функция arcctgx определена на всей числовой прямой и связана с функцией arctg х соотношением
arctg х ф- arcctg х — у.
§ 7. Линейные преобразования графика
В этом параграфе рассматривается вопрос о построении графика функции у = Af(ax -ф Ь) -ф В, если известен график функции _v=/(x).
1°. y=f(x-\-c). Рассмотрим задачу построения графика функции y—f(x-\-c), если задан график функции Т = /(х). ‘ .
Пусть точка (х0; _у0) принадлежит графику функции у=f(x), т. е. _у0=/(х0). Тогда точка (х0— с; у0) принадлежит графику функции y—f(x-]~cy, действительно, Д(х0— с)-фс] = = f(x0) —у0. Обратно, если точка (х0— с; То) принадлежит графику функции y=f(x-yc)> то точка (х0; То) принадлежит графику функции y=f(x). Таким образом, график функции y—f(x-]-c) можно получить из графика функции y=f(x) сдвигом каждой точки (х0; _Уо)> принадлежащей графику функции y=f(x), в точку (х0— с; То)> т- е- сдвигом всего рра-222
фика функции у —f(x) вдоль оси х на (—с) единиц. Сдвиг на (— с) единиц означает: сдвиг на с единиц влево, если с > 0, и сдвиг на | с | вправо, если с <z 0.
Пример 40. На рис. 82 построены графики функций у — ^х—2| и _у==|х4-1|. Они получаются сдвигом графика функции _у==|х| (см. рис. 50, б) вдоль оси х соответственно на две единицы вправо и на единицу влево.
2°. ys=f{ax). Рассмотрим задачу построения графика функции y—f(ax), где а =4=0, если задан график функции >=/(*)•
Пусть точка (х0; у0) принадлежит графику функции y — f(x), т. е. у0==/(х0). Тогда точка принадлежит
графику функции у=/(ах); действительно, =
= f(xg) —уд. Обратно, если точка принадлежит гра-
фику функции y—f(ax), то точка (х0; у0) принадлежит графику функции y~f(x)- Таким образом, график функции y=f(ax) можно получить из графика функции y=f(x) заменой каждой точки (х0; _у0), принадлежащей графику функции y—f{x), точкой у^. Эта замена означает: 1) сжатие графика вдоль оси х к оси у в а раз, если а> 1; 2) растяжение (тоже вдоль оси х) в ± раз, если 0<а<; 1; 3) симметрию относительно оси у, если а ——1; 4) симметрию относительно оси у, сопровождаемую сжатием в | а | раз, если a <_—1; 5) симметрию относительно оси у, сопровождаемую растяжением в раз, если —1<а<0.
223
Пример 41. График функции у= \/~—х получается из графика функции симметрией относительно оси у
(рис. 83).
Заметим, что свойств функции х<0, принимает вающей.
Пример 42.
из этого графика можно получить ряд _у = ]/—х: эта функция определена при неотрицательные значения и является убы-
г
На рис. 84 из графика функции у — arcsin х (см. рис. 79) получены: график функции у — arcsin 2х (сжатием графика функции_у = arcsin х вдоль оси х к оси у в два раза) и график функции у= arcsin у (растяжением
графика функции = arcsin х в два раза).
3°. y=f(ax-}-b). Рассмотрим задачу построения графика функции у = = f(ax 4- b) (где а Ф 0), если задан график функции .У = /(•*)•
Пусть точка (хп;_уп) принадлежит графику функции
_у=/(х), т.е. j/0=/(x0). Тогда графику функцииу — f(axЬ) принадлежит такая точка (ху,у0), для которой -)-b = x0, т. е.
xa — b ха b
1 а а а
(И)
Обратно, если точка (xlt у0) принадлежит графику функции y—f(ax-\-b) (где определяется равенствами (11)), то точка (х0; _у0) принадлежит графику функции _у=/(х). Ра-
224
венства (11) означают, что точка хг может быть получена, из точки х0 любым из следующих двух способов: 1) сначала сдвиг на (—Ь) единиц, затем «сжатие» в а раз; 2) сначала
I ь\
«сжатие» в а раз, а затем сдвиг на —) единиц.
Таким образом, график функции y=f(ax-\-b) можно построить из графика функции у — f(x) любым из следующих двух способов:
1) Сначала из графика функции y=f(x) сдвигом вдоль оси х на (— Ь) единиц получаем график функции y—f(x-\-b)~ = g(x), затем из полученного графика функции y=g(x) получаем график функции y=g(ax)=f(ax-}-b), как в 2°.
2) Сначала из графика функции y = f(x) получаем график функции y—f(ax) (см. 2°), затем из полученного графика функции у—f(ax) получаем график функции y=f\a[x-\-~ 4 = = J(ax-\-b) сдвигом графика функции у — f(ax) вдоль оси х на единиц (см. 1°).
Для определенности всюду в дальнейшем применяется второй способ.
Пример 43. Построить график функции у= { 2хД- 3 |.
Решение. Сначала из графика функции _у = {х! (см. рис. 50, б) сжатием в два раза вдоль оси х к оси у строим
график функции _у=|2х | (рис. 85). Затем из полученного графика функции _у = |2х| сдвигом влево вдоль оси х на 3 I / 3 \ I
у получаем график функции у— j 2 -j-yj |= 12-^ + 3 | (рис. 86).
4°. .у = /(*) +С. Рассмотрим задачу построения графика функции _y = /(x)4-C, если задан график функции y—f(x).
8 В. Г. Болтянский и др.
225
Пусть точка (х0; у0) принадлежит графику функции у~ — f(x), т. е. _Уо=/(-ко)- Тогда точка (хп; _у04~С) принадлежит графику функции _у=/(х)-фС; действительно,/(х0)-|-+С=_у04-С. Обратно, если точка (х0; _у0-фС) принадлежит графику функции у/=/(х)4-С, то точка (х0; _у0) принадлежит графику функции y=f(x). Таким образом, график функции _у==/(х)4-С можно получить из графика функции у= =/(х) заменой каждой точки (_v0; _у0), принадлежащей графику функции _у=/(х), точкой (х0; _y0-f-C), т. е. сдвигом всего графика функции _у=/(х) вдоль оси у на С единиц. Сдвиг на С единиц означает: сдвиг на С единиц вверх, если С > О, и сдвиг на | С | единиц вниз, если С < 0.
Пример 44. На рис. 87 из графика функции _у = |х| (см. рис. 50, б) получены: график функции у == | х 14- 1 (сдвигом вдоль оси у на единицу вверх) и график функции у = | х | — 2 (сдвигом на две единицы вниз).
5°. _у = Л/(х). Рассмотрим задачу построения графика функции y = Af(x), где Л =4= 0, если задан график функции y=f(x).
Пусть точка (х0, _уи) принадлежит графику функции у = >гда точка (х0; Лу0) принадлежит ), так как Af(x0)=Ay0. Обратно,
если точка (л'о; Ау0) принадлежит графику функции у = = Af(x), то точка (х0; у0) принадлежит графику функции y—f(x). Таким образом, график функции y = Af(x) можно получить из графика функции y—f(x) заменой каждой точки (х0-, у0), принадлежащей графику функции y=f(x), точкой (л*0; Ау0). Эта замена означает: 1) растяжение графика вдоль оси у от оси х в А раз, если А > 1; 2) сжатие в i раз, если 0<А<1; 3) симметрию относительно оси х,
= /(*), графику
Т- е. y0=f(x0). Т функции у —А/(л
если А ——1; 4) симметрию относительно оси х, сопровождаемую растяжением в | А | раз, если А<—1; 5) симмет
рию относительно оси х, сопровождаемую сжатием раз, если — 1 < A <Z 0.
1
Ml
226
Пример 45. На рис. 88 из графика функции _y = cosx получены: график функции _y = 3cosx (растяжением графика функции _y = cosx вдоль оси у от оси х в три раза) и график функции у = — у cos х (симметрией относительно оси х и сжатием в два раза).
6°. j = 4/(x) + B. График функции y=Af(x)-\- В, где А Ф 0, можно получить из графика функции J'=/(х) следующим образом: сначала из графика функции _у=/(х) получаем график функции д/ = Д/(х) (см. 5°), а затем из построенного графика функции y — Af(x) получаем график функции y = Af(x)~yB сдвигом графика функции y~Af(x) вдоль оси у на В единиц (см. 4е).
Пример 46. Построить график функции
л 1
у =у —2~ arcsin х.
Решение. Сначала из графика функции у— arcsinх (см. рис. 79) симметрией относительно оси х строим график функции у ——arcsin х (рис. 89). Затем из построенного графика функции _у =— arcsin х сжатием вдоль оси у к оси х в два раза строим график функции у —------~ arcsin х. И, на-
. . 1
конец, сдвигом графика функции у = — arcsin х вдоль
8*
227
оси у вверх на у получаем график функции У — —% arcs,njv (рис. 90).
Сопоставляя все сказанное в этом параграфе, мы приходим к следующему общему выводу. График функции
у = В можно получить из графика функции
у = f(x) следующим образом: сначала из графика функции y=f(x) построить график функции у —f(ax -f- b) (см. 3°), а затем из полученного графика функции y=f(ax-\-b) построить график функции у = А/(ах-\-Ь)-\-В (см. 6°). Описанный выше способ построения графика функции _у = = Af(ax ф- b)-\- В из графика функции y=f(x) называется линейным преобразованием графика функции y=f(x)-
§ 8. Применение функций и графиков к решению уравнений и неравенств
1°. Рассмотрим вопрос о решении уравнения А (х)~/2(х) с помощью графиков функций _у=А(х) и у=/^(х).
Если х0 — решение этого уравнения, то это означает, по определению, что точка х0 принадлежит области определения каждой из функций А (-О’ /2(-0 и выполнено равенство А (л'о) =/2 (х0). Обозначим число A(-Vo) через у0, так что Л=А(-*Т)==А(*о)- Так как Л>=Л (*о)> то точка (х0; Уо) принадлежит графику функции у =fr (х). Так как, кроме того, _Уо=А(хо)>10 точка. (х0; у0) принадлежит также
228
графику функции y—fzfx). Таким образом, (х0; _у0) есть точка пересечения графиков функций _у=/х(х) и y=f2(x). Обратно, пусть графики функций _у = /х(х) и _У=Л(Х) пересекаются в точке (х0; _у0), т. е.
To=/i(^»)==/2(xo)-
Это означает, что число х0 является решением уравнения /1(-г)=/2(*)-
Таким образом, для нахождения решений уравнения /Х(х)=/2(х) нужно определить абсциссы точек пересечения графиков функций y=f\(x) и у—-фЛх)- Такой способ решения уравнений называется графическим. Как правило, он не дает точного решения уравнения (по-
скольку практически мы всегда имеем дело не с графиком
а лишь с эскизом графика), но часто позволяет установить число решений данного уравнения и оценить погрешность найденных решений.
Пример 47. Из рассмотрения рис. 91, на котором построены графики функций у = /х (х) = 2 Y х и у - /2 (х) = х2 — х — 2, ясно, что уравнение 2У х = = х2 — х—2 имеет только один корень х0 № 2,9.
Замечание. Графиче-
ским способом можно решать
также уравнение вида /(х) = 0, которое является частным случаем уравнения /1(х)=/2(х) при /, (х)е=0.
2°. В примерах 48, 49 рассматривается решение нера-
венств с помощью графиков функций. Пример 48. Решить неравенство
I X | > X2 — X.
Решение. Построим графики функций y=fi (х)= | х | и _у=/2(х) = х2— х (рис. 92).
Решениями неравенства /Х(х)>/2(х) являются действительные числа х, для которых график функции .у = /х (х) расположен выше графика функции y = fi(x).
229
Из рассмотрения рис. 92 следует, что решениями неравенства |х|>х2— х являются все числа х из интервала 0<х<2.
Пример 49. Решить неравенство (х2 — 2х — 3) (/х—1 — 1) < 0.
Решение. Построим графики функций _У = /1(х) = — х2 — 2х—3 и у=/2(х)=/х—1 — 1 (рис. 93).
Решениями неравенства (х)(х) < 0 являются действительные числа х, для которых значения функций ft(x) 230
и /2(х) имеют разные знаки (или 4(х)<0 и f2(x)>Q, или /1(х)>0 и /2(х)<0). Это означает, что' нужно найти такие числа х, для которых точки графиков функций y — f1(x) и y=f2(x) расположены по разные стороны от оси х. Из рассмотрения рис. 93 следует, что решениями неравенства (х2— 2х— 3) (]/ х—1 — 1) «появляются все числа х из интервала 2<х<3.
3°. Бывают случаи, когда никакие алгебраические преобразования не помогают решить уравнение или неравенство (или решение получается очень громоздким), а ключом к решению служит изучение области определения функций, входящих в это уравнение или неравенство, или их м н о-жества значений. Ниже приведены два таких примера.
Пример 50. Решить неравенство ]Л‘2 -ф- х — х2 > х3—9. Решение. Переписав неравенство в виде
—(х— 2)(х-ф 1)>х3— 9,
мы найдем, что областью определения функции, стоящей в левой части этого неравенства, служит отрезок — 1 х-<2,
причем во всех точках своей области определения эта функция неотрицательна (так как каждое ее значение представляет собой арифметический корень из неотрицательного числа). Но при —1Сх<2 правая часть отрицательна, и потому написанное неравенство имеет место при всех х из отрезка —Таким образом, решениями неравенства являются все числа отрезка [— 1, 2].
Пример 51. Решить уравнение
х4 —2х24- 2= 1 — Ух3 — \х\.
Решение. Рассмотрим функции
А (*) = — 2х2 ф-2, f2 (х) = 1 — Ух3 — | х I,
так что данное уравнение записывается в виде /1(х)=/2(х). Мы имеем /1(х) = х4—2х24-2 = (х2—1)24-1, откуда видно, что /х(х)^=1 при всех х, причем значение 1 функция Л(х) принимает лишь при х = ± 1. Для функции же /2(х) имеет место (при любом х из области ее определения) неравенство /2(ус)^Л, так как значение арифметического квадратного корня всегда неотрицательно. Следовательно, равенство /1(х)=/2(х) возможно лишь при А(х)= = /2(х)=1, т. е. лишь при х = ± 1. Проверкой убеждаемся, что х = — 1 корнем исходного уравнения не является,
231
a x=-f-l является корнем. Таким образом, данное уравнение имеет лишь один корень х — 1.
4°. В заключение опишем один часто применяемый способ
решения неравенств, называемый методом интервалов.
Прежде всего заметим, что если монотонная функция
обращается в нуль при х—а, то она сохраняет посто-
янный знак при х <^а и про тивоположный знак при ху>а. Более точно, если возрастающая функция f(x) обращается в нуль при х — а, то /(л')<0 при х<а и /(х)>0 при х> а (рис. 94), а если убывающая функция /(х) обращается в нуль при х — а, то f(x) > 0 при х < а и f(x) <0 при х > а (рис. 95).
Метод интервалов теперь можно описать следующим образом. Пусть /1(х), А(4 ..., А(х) и ^(х), g2(x), ..., gi(x)— монотонные функции, определенные на всей числовой прямой и обращающиеся в нуль в различных точках. Занумеруем точки, в которых эти функции обращаются в нуль, в порядке возрастания: аг, а2, ..., ak+i (т. е.
в каждой из этих точек одна из функций, (х) или gj(x), обращается в нуль и при этом аг < а2 < ... <; ak^). Эти
точки разбивают числовую прямую на A-f-Z-f-l интервалов:
(—оо, aj), (at, а2), (а2, а8), ..., (ak^v akU), (ak+l, со). Тогда функция
F(x) =
/1(х)/2(х) (х)
gl (х) g2 (х)
сохраняет постоянный знак а при переходе от каждого знак на противоположный.
на каждом из этих интервалов, интервала к следующему меняет Это утверждение (составляющее
232
основу метода интервалов) без труда доказывается и часто применяется при решении неравенств.
Замечание. Иногда приходится рассматривать более сложную функцию, имеющую вид
F (МХУ)Р° -(fk(x))Pk '
1 (gi (*))’ (*))’’ (gi (xyfi’
где pi, р2, Pk, 7i> 7г> •••> 4i— натуральные числа. Исследование знака такой функции также не представляет труда. Именно, если число рг четно, то функция (/i(x))ri положительна (всюду, кроме точки, где она обращается в нуль) и потому может не учитываться при определении знака функции Fj(x). Если же число рг нечетно, то функция (^(х))'’1 имеет тот же знак, что и (х). Аналогичное замечание относится и к остальным множителям в числителе и знаменателе. Поэтому при определении знака функции Fj (х) нужно учитывать лишь множители, имеющие нечетные показатели.
Пример 52. Решить неравенство х5ф-х4 — 5х3 ф-ф- Зха —4х—12>0.
Решение. Непосредственной проверкой (ср. стр. 165) находим, что числа —3, —1 и 2 являются корнями многочлена, стоящего в левой части неравенства. Следовательно (см. теорему 12 на стр. 164), многочлен этот делится на х-]-3, на х-]-1 и на х — 2. Произведя деление, найдем
х5 ф- х4 — 5х3 -ф- Зх2 — 4х — 12 =
= (х-ф-3)(хф- 1)(х —2)(х2—хф- 2).
Поэтому данное неравенство переписывается в виде
(х ф- 3) (х ф- 1) (х—2) (х2 — х ф- 2) > 0.
Но квадратный трехчлен х2 — хф-2 положителен при всех х (его корни комплексны). Поэтому рассматриваемое неравенство равносильно следующему:
(хф-3)(хф- 1)(х — 2)>0.
Каждая из функций хф-3, хф-1, х — 2 монотонна, и мы можем применить метод интервалов. Эти функции обращаются в нуль соответственно в точках —3, —1, 2, которые делят числовую прямую на четыре интервала: (—оо, — 3), (—3,— 1), (—1,2), (2,оо). На последнем (четвертом) из этих интервалов все три функции х-]-3, х-]-1, х — 2 положительны, и потому функция
F(x)=(x + 3)(x+l)(x-2)
233
на этом интервале положительна. Следовательно, на третьем интервале она отрицательна, на втором положительна и на первом опять отрицательна (рис. 96). Таким образом, неравенство F(x) > 0 имеет место на интервале (— 3, — 1), а
Рис. 96.
также на интервале (2, оо), т. е. решениями исходного неравенства служат все числа, удовлетворяющие неравенствам — 3<х<— 1, а также все числа, удовлетворяющие неравенству х>2.
Пример 53. Решить неравенство
(х + 7)з(х+4)2 (х-1)
(% + 5) (х 2)5
Решение. Мы должны исследовать знак функции
(х+7)з(х + 4Р(х-1)
(х + 5) (х—2у
При этом мы можем не обращать внимания на множитель (х-)-4)2, имеющий четный показатель (помня, однако, что при х =—4 этот множитель обращается в нуль). Остальные множители в числителе и знаменателе представляют собой монотонные функции, обращающиеся в нуль соответственно в
IV V
Рис. 97.
точках —7, —5, 1, 2. Эти точки разбивают числовую прямую на пять интервалов:
(—оо, — 7), (-7,-5), (—5,1), (1,2), (2,оо),
причем на последнем из них Fr (х) > 0 (все множители в числителе и знаменателе положительны). Поэтому (рис. 97) на. первом, третьем и пятом из этих интервалов F1(x)>0, а на втором и четвертом рх (х) < 0 (только надо помнить, что при х =—4 функция Fi(x) обращается в нуль). Следовательно, решения строгого неравенства Fi(x)<0 запол-
234
няют два интервала: (—7, —5) и (1, 2). Сюда надо добавить еще точки, в которых F1(x)~ О, т. е. точки х —— 7, х — —4,
полуинтервала [—7, —5), а также все точки полуинтервала [1,2) и, кроме того, точка х ——4.
Пример 54. Решить неравенство
(х + 3) (2х + | х | — 9) „
(х —2) (х-|-2 I х Ц-1)
Решение. Функция х + 2 | х | + 1 положительна при всех х (ее график показан на рис. 98), и потому ее можно не учитывать, т. е. мы должны решить неравенство
FW_(« + 3)(2,+2M-9>>t,.
Функции Л' + З и х — 2, очевидно, монотонны. Функция 2х + | х | — 9 (график которой показан на рис. 99) также
+
О
‘ Рис. 100.
монотонна. Таким образом, в числителе и знаменателе дроби F (х) мы имеем три монотонные функции, обращающиеся
235
в нуль соответственно в точках —3, 2, 3. Эти три точки разбивают числовую прямую на четыре интервала:
(—сю, —3), (—3, 2) (2, 3), (3, оо),
на последнем из которых F (х) > 0. Следовательно (рис. 100), неравенство F (х) > 0 имеет место при —3<х<2, а также при 3<х<оо.
Задачи к главе VII
В задачах 7.1 — 7.5 требуется найти области опреде-' ления заданных функций и вычислить значения этих функций в указанных точках.
7.1. /(x) = ^J~-^2; х1 = 0, х2 = 1, х3 = —3.
7.2. f(x) = ]х3— 4х; хг — —1, х2 = 2, х3 = 3.
7.3. /(Х)=^=^; х1==0, х2=1, х3 = —2.
7.4. /(х)
cos 2х sin х ’
Л /л
A’i= "J" > х2 = •
7.5. /(х) = —-—; х, = 0, х2 = — 1, Хо = 100.
4 1 cos л.х 1 - d
Постройте графики функций (7.6—7.14):
7.6. у = Зх— 1.
7.7. _у = х2 + 2х— 1.
7.8. jU b е“И
( (х — 1 )2, если х > 0.
7.9. 7===/ l*i’ если |х |^1,
\ 2 — х2, если | х । > 1.
_ ( 1, если —1<х<'0,
7.10. у = {
( х2, если 0 «£ х < 1.
1, если — 2 ' х 3 — 1,
7.11. у = . — х, если — 1 < :х=с 0,
1, если о< х < 1.
3, если - — 2 X s= —1
7.12. у=< — Зх, если - - 1 < X ^0,
| Зх, если 0 < X Sg 1,
1 3, если 1 <х = =g4.
236
7.13. _v = |x4-l |--|x —1|.
7.14. j = l 1 — |x|| — |x|+ 1.
7.15. Докажите, что функция f(x) ограничена (см. определение на стр. 187—188) тогда и только тогда, когда существует такое число 0, что для любого значения х (взятого из
области определения функции) справедливо неравенство \f(x)\<c.
7.16. Приведите пример функции, определенной на отрезке OCx-s'l и неограниченной на этом отрезке.
7.17. Пусть функции j\(x), f2(x) и /3(х) определены на отрезке [а, Ь], причем функции fi(x) и /2(х) ограничены, а функция fs(x) не ограничена. Что можно сказать об ограниченности функций Л (х)-j-/2 (х), /1(х)+/3(х), Л(х)/2(х), /1(х)/з(х), frr~; Г7Д?
1 f3(x)
Найдите интервалы 7.23): монотонности функций (7.18 —
7.18. >=1—2х. 7.19. j/ = x3.
7.20. у = 3 — 2х — х2. 7.21. J = -J-r. J х+1
7.22. у — cos х. 7.23. y = lgx.
Найдите наибольшее и наименьшее значения функций (7.24—7.27):
7.24. _y=3sinx—4 cos х.
7.25. у = 3 sin2 х-|- 4 sin х • cos х + cos2 x.
7.26. у — sinG x 4- cos'1 x.
7.27. y = sin4 x -t~ cos1 .v.
Найдите наибольшее значение функций (7.28—7.29):
7.28. у =
7.29.
J 1 + х + х-
7.30. Найдите наименьшее значение функции х2 —3 ,
У=г¥~, х> —1.
-z 1 —L Г ’
237
Выясните, является ли заданная функция четной или нечетной или не является ни четной, ни нечетной (7.31—7.36):
7.31. j = ДД. 7.32. _у = х34-2х.
7.33. y = Vx— 1,
7.35. у — х + tg х.
7.34. у = | х j 4- cos x.
7.36. y = x2 + sin x.
7.37. Пусть функция f(x)—четная, а функция g(x) — нечетная. Докажите, что функции \f(x) J, ] g(x) j и f (— x) + g(! x j) — четные, а функции g(—x), xf (x) -ф x-g (x) и g(x|x|)— нечетные.
7.38. Пусть область определения функции f(x) симметрична относительно точки х = 0. Докажите, что функция fi(x) = = у [/(*) + /(— х)] —четная, а /2 (х) = у [f(x) — / (— х)] — нечетная. Таким образом, функцию /(х) можно представить в виде /(х) =/i (х)-ф/2 (х), где функция Д(х)— четная, а функция /2 (х)— нечетная.
Найдите наименьший период каждой из следующих функций (7.39—7.44):
7.39. sin х • sin Зх. 7.40. sin x4-sin 2x.
7.41. sin2 х. 7.42. sin x
1 + COS X
7.43. tg х -ф sin 2x. 7.44. 2tg|-3tg|.
7.45. Докажите, что функция sinx4“sin^x не является
периодической.
Определите, какие из следующих функций являются периодическими (7.46—7.48):
7.46. >== Vsin х. 7.47. у — sin Ух. 7.48. у— | sin [ х} |-
Постройте графики ф = х3.
7.51. y = xi — 2х2.
7.53. у = Д.
|х|
функций (7.49—7.71):
7.50. у = [ х |3.
7.52. ,у = х2 —3) х| + 2-
_ _ . 2х
7.54. У = 7-7—7.
1 -Jf-X2
7.56. у = | sin х |.
238
7.57. у = sin | X 7.58. У = *+±-
7.59. у = X 4- cos X. 7.60. у = х3 — 2х24-^-
7.61. у = — х5 4- 2Х3 — х. 7 «2 v — 2
ло/- > xa-2x + 3-
7.63. у = У х 4- 1 — ]/ х. 7.64. у= |/ х4-1— У |х|.
7.65. № —1 7.66. =
у х44-П
7.67. 1 -Л"2 7 йо v — 1
у х2у-х^- /.оо. У х^ + 2х~3-
7.69. л’2 — 4х 4- 3 7 70 v — *
У х2 — ‘2х /•/«• У х1^4хза_4х2-
7.71. __ 1*! У !*+И
7.72. Пусть /(х) = Ух, = Найдите/(g (0).
7.73. Пусть f(x) = }^-, = ’ НайДите
f(g (0)-
7.74. Пусть /(*)== Найдите f(^Y
7.75. Пусть f(x)~yx3 — 1. Найдите /(Уx2/-l).
7.76. Пусть f(x) — _. Найдите /(tgx).
7.77. Пусть /f3x ПРИ -v# —2; 1. Найдите /(x).
\ X j 2. 1 X L
7.78. Пусть /fl 4--^ = x2—1 при x 0. Найдите f(x~).
7.79. Пусть f(x) = ax2 /- bx + с. Докажите, что
f(x + 3) - 3/(x + 2) + 3f(x + 1)-/(x) = 0.
В задачах 7.80—7.86 требуется найти функции f(x) и g(x), удовлетворяющие заданной системе уравнений.
Г 7(2x4-l)4-g(x—l) = x,
I /(2x4-l)-2g(x-l)^2x2.
7.81.
' /(2x4- l) + 2g(2x 4- 1) = 2х, Д х \ . I х \ /[^Т} + 8[^ = Х-
239
( f(x+ l) + xg(x+ l) = 2x, 7.82.
( J \x — — 1/
Г /(2x+2) + 2^(4x + 7) = x-l,
I /(x-l) + ^(2x+l)=2x,
7 84 f A4x + 3) + -^(6x+4) = 2’ 84’l /(2x+1) + £(3x+1) = x+1.
f /(3x-l)4-g(6x-l)=3x, •85‘ I f(x + 1) + x3g (2л- + 3) = 2x2 + x.
[ /(2x-l) + g(l-x) = x+l,
В задачах 7.87—7.90 требуется найти функцию f(x), удовлетворяющую заданному уравнению.
7.87. /(х) + 2/(1) = х.
7.88. (х-1)/(х) 4-/(1)==^
7.89. /(х) + х/(^л) = 2.
7.90. 2f I— 3f = 913* 742
J \x — 1/ \2x+l/ 2x — 3x2
Найдите функции, обратные no отношению к заданным (7.91 — 7.94):
7.91. у = х3. 7.92. у = 1 4-1.
_ ах-\-Ь 4/—
7.93. у = ——, 7.94. у х.
J сх — а
Линейными преобразованиями графика функции _у = |х| (см. рис. 50, б) постройте графики функций (7.95—7.97):
7.95. у=\х4-41. 7.96. >==2|х —1 |4-1.
7.97. _у = ] 3x4-1 !•
Линейными преобразованиями графика функции у = хъ (см. задачу 7.49) постройте графики функций (7.98, 7.99):
7.98. у = (х — 1 )3. 7.99. > = 1 — х3.
240
Линейными преобразованиями графика функции у = 1^х постройте графики функций (7.100, 7.101):
7.100. j==]/'2x + 3. 7.101. j = 1 — 2 V~x.
Линейными преобразованиями графиков тригонометрических функций _y = sinx и ^ = tgx постройте графики функций (7.102—7.104):
7.102. j/ = sin^• — lj. 7.103. j = 3sin2x—1.
7.104. j=l-|tgx.
Линейными преобразованиями графиков обратных тригонометрических функций постройте графики функций (7.105—7.107):
7.105. у — arcsin (2х 4).
7.106. У — ~2 arccos х—4".
7.107. _у = 2 arctg 2х.
Определите число действительных решений уравнений (7.108—7.111):
7.108. 1 4-х —х2 = |х|3. 7.109. х(х + l)(,v+2) = 0,01.
7.110. x = tgx. 7.111. x=100sinx.
Решите уравнения (7.112—7.114):
7.112. 44-Зх—x2 = j 1 4- х I.
7.113. |х2 — 2х — 31 = *+ 1-
7.114. 6х— 1 = 2 cos пх.
Решите приближенно (с ошибкой не больше 0,125) уравнения (7.115, 7.116):
' 7.115. х2 —х —2 = 2]/х? 7.116. х2—2х = ]/£
Решите неравенства (7.116—7.120):
7.117. х2 —2|xj<3. 7.118. 2 — х2 > ' х | 4-- 2 'л:— 1 |.
ГЛАВА VIII
СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
§ 1. Степень с натуральным показателем
Первоначально степень определяется для случая, когда показатель является натуральным числом, большим единицы; основание степени может в этом случае быть любым действительным (или даже комплексным) числом. Именно, если п — натуральное число, большее единицы, и а — произвольное действительное (или комплексное) число, то под ап понимают произведение п сомножителей, каждый из которых равен а: ап=а-а...а. (1)
п раз
Случай, когда /1=1, под это определение не подпадает, так как «произведение одного сомножителя» не имеет смысла. Уславливаются, однако, считать, что (для любого а) число а1, по определению, равно а. В результате мы получаем определение степени с натуральным показателем: число ап считается равным а при л=1 и определяется формулой (1) при п > 1.
Из этого определения легко выводится целый ряд свойств степени. Мы разобьем эти свойства на две группы:
I. Свойства, выражающиеся равенствами:
а) ат~- ап—ат п для любого а и любых натуральных т, л; б) (ат)п — атп для любого а и любых натуральных т, п; в) (ab)n = апЬп для любых а, b и любого натурального л;
62^ *
г) — = ап~т для любого а^О и любых натуральных т, л, удовлетворяющих условию пу> т;
/ а\п
д) — ] =ттт для любого а, любого и любого
' \Ь и1 натурального п\
е) 0^ = 0, 1"= 1 для любого натурального л;
ж) | ап | = | а ]” для любого а и любого натурального п-
242
П. Свойства, выражающиеся неравенствами: з) если 0-xCa<Zb, то ап <^Ьп для любого натурального п\
и) если ау>\, то ат~у>ап при ту>п\
к) если 0<а<1, то ат<^ап при т'у>п\
л) если а < 0, то ап'у>0 при четном п и ап < 0 при нечетном п.
Заметим, что свойства а) — ж), выражающиеся равенствами, имеют место для любых комплексных чисел а, Ь; свойства же з) — л), выражающиеся неравенствами, справедливы для любых действительных чисел а, Ь. В дальнейшем мы везде ограничиваемся случаем, когда основание степени — действительное число.
Доказательство перечисленных выше свойств несложно. Мы приведем для примера доказательство свойства з) (ср. стр. 80).
Нам нужно доказать, что Ьп— а”>0. Согласно формуле (8) на стр. 156 мы имеем
bn — ап = (b - a) (bnl + bn~2a + bn' sa2 +... + ban~2 + a"1).
Так как то первая скобка в правой части положительна. Вторая скобка также положительна, поскольку а Тз 0, b > 0. Таким образом, правая часть положительна, и, следовательно, Ьп — anZ>Q-
Пример 1. Решить уравнение sin10.v-t-cos10x = 1.
Решение. Прежде всего заметим, что если x—k^, где k — целое число, то одна из функций sin х, cosx принимает значение 0, а другая — значение zt 1. Поэтому все числа у (где k = 0, ±1, ±2,...) являются корнями заданного уравнения.
Пусть теперь х отлично от чисел вида . Тогда каждая из функций sin х, cosx принимает значение, отличное от 0 и ± 1, и потому 0 < sin2x < 1, 0<cos2x<l. В силу свойства к) мы имеем поэтому (sin2x)3 < (sin2^)1, т. е. согласно свойству б) sin10x < sin2x. Аналогично cos10x < <cos2x. Таким образом, sin10x -(- cos10x< sin2x -(- cos2x= 1, и, следовательно, sin10x-(-cos10x 1. Это означает, что x не является корнем заданного уравнения.
Итак, корнями заданного уравнения являются числа (где k = 0, ±1, ±2,...), и только эти числа.
243
Пример 2. Доказать, что если 0<а<;1, то, каково бы ни было положительное число е, найдется такое натуральное п, что ап < е.
Решение. .Выберем такое натуральное число k, что (см. свойство Г) на стр. 60). Тогда Требуе-
мое неравенство ап <е будет установлено, если мы покажем, 1,1- л
что -й>~. Значит, если мы сумеем подобрать такое п, что то мы получим k > ~, что и требуется. Таким образом, достаточно подобрать такое я, чтобы В силу
1 1" /1
свойств д) и е) мы имеем — == —= '^—। . Итак, задача све-/ уп' лась к нахождению такого //, что (— | > k.
\ я /'
Так как 0<а<1, то — >1, т. е. число------------1 положи-
fl а
тельно. Поэтому найдется такое натуральное число q, что -1- < -— 1, т. е. — > 1 4- —. Согласно свойству з) мы имеем q a a q J 1
( \ \П / ] \п
I ~ j > 1 4- — j . Поэтому нам достаточно подобрать такое л, чтобы Д-— j Z> k. Но (1Д-—> 1 + у (это неравенство без труда доказывается методом математической индукции). Поэтому нам достаточно подобрать такое п, чтобы 1 -j- у > k. Но это последнее неравенство равносильно неравенству
п q
>k — 1
например,
а значит, неравенству ny>q(k—1). Достаточно, взять n~q(k—1)4-1, и мы получаем требуемое
значение п.
§ 2. Степенная функция с натуральным показателем
Рассмотрим теперь функцию
у~хп,
где п — натуральное число. Согласно сказанному в предыдущем параграфе областью определения этой функции является вся действительная прямая, т. е. степень хп определена при любом действительном х. Далее, в силу свойств е) и з) функция у = хп принимает значение 0 при х — 0, принимает зна-244
чение 1 при х—1 и монотонно возрастет на луче х^О (рис. 101).'Наконец, поведение этой функции при х<0 зависит от четности или нечетности числа п. Именно,
.П
(— х)п = (— 1 -х)п = (— 1)пхп = 1
при четном п, при нечетном п.
Следовательно, если п четно, то функция у = хп является четной; значит, ее график симметричен относительно оси ординат, и потому на луче х<:0 эта функция - убывает (рис. 102). Если же п нечетно, то функция у = хп является нечетной; значит, ее график симметричен относительно
начала координат, и потому функция является возрастающей на всей числовой прямой (рис. 103).
Теперь мы сформулируем и докажем еще одно важное свойство функции у — хп-.
м) Функция у — хп, рассматриваемая на луче х>0, принимает все положительные значения- Иными словами, каково бы ни было положительное число у0, найдется такое число хо>0, что (х0)п—у0. (Эта теорема в школьных учебниках не доказывается.)
Доказательство. При и=1 свойство м) очевидно, и мы будем считать, что ит>2. Обозначим через q целое число, большее чем у0. Так как q 1, то (в силу
свойств з) и е)). Перемножив неравенства qn' 1 и qZ>y0, получим qn>y0- Таким образом, 0” <_у0 < qn.
Согласно свойству з) имеем
0"< 1Л< 2Л<...<(^—1)Л<9Л.
245
А так как у0 заключено между 0” и qn, то найдется такое неотрицательное целое число k (меньшее q), что kn <^уп-^ sg(&4~l)" Это число k мы обозначим через а0, а число k 4-1—через Ьо. Итак, причем Ьо—а0=1.
Далее, согласно свойству з) имеем
А так как а" <2Уо^^, то найдется такое число Z' (=0, 1,...
/ /' \п ! /' . I р п у
• ••> 9), что 1^о+ уо] • Число а04-^мы
бого натурального k
обозначим через аг, а число а° 10 1—чеРез Таким образом, а” < у0sg b-, причем
и Ь]_ — ^ = 10-
Совершенно так же мы найдем такое число I" (=0, 1,...,9), что / V \п I /"4-1 \" \О1 + Т00/ <3'о=еЦа1 + 100 / • г
Число «14-100 обозначим через
Г +1
а2, а число ai + "]^o--через Ь2.
Таким образом, а? < у0 Ь", причем aosg а2 <^b2^~ b1^b0
. 1
И «2 °2-- 1Q0 •
Продолжая таким образом, мы получим две последователь
ности чисел а0, av а2, as, ... и Z>0, bv b2, b3,..., причем для лю-
п <П
выполнены соотношения а^<СУо^Ь^
a6^ji}<ay^...^ai<bil^bk-}<s...--yi>1^blj и bk~ ________I
ak— lOft.
Заметим, что для любых натуральных чисел k и I справедливо неравенство ак <g bt. В самом деле, если т — натуральное число, большее каждого из чисел k, I, то мы имеем ak ат> ат <; bm, bm sg; bv откуда и вытекает, что ak <g bt.
Так как последовательность а0, av а2,... является неубывающей (т. е. а0 aj sg а2 г£':... sg -g ...) и ограниченной (поскольку ak < Ъй при любом k), то она имеет предел.
246
Этот предел мы обозначим через х0. Так как последовательность а0, av а2,... является неубывающей, то x(lyzak при любом k. Далее, так как каждое из чисел а0, av а2> меньше bt, то xl)-<zbl (при любом I). Итак, а^^Хд^Ь^ Из этого, в силу свойства з), вытекает, что ак^х"^Ь". В частности, ак^х"^Ьк. А так как, кроме того, апк < <_У0=С&а, то (при любом k) справедливо неравенство
]у0 — х^\^Ьк—ак.
(2)
Теперь уже нетрудно доказать, что х^=_у,,. Допустим противное. Тогда число а = | yti— х” | положительно. Далее, разность Ьк — ак можно оценить следующим образом:
— ak — (Ьк — ак)(Ьк + bk 4-.•. + Ькак “Д-а* )
— l~t~bk 2afe-}- .. bkdk !) <
Таким образом, из (2) мы получаем неравенство
0 < а <
10s
справедливое для любого натурального k, т. е.
П* 10/
(А = 1>2,...).
Но это противоречит утверждению, доказанному в примере 2 на стр. 244.
Полученное противоречие доказывает, что х”—у0, т. е. свойство м) справедливо.
§ 3. Арифметический корень
Итак, функция у — хп, рассматриваемая на луче О^СхС < оо, является (при любом натуральном п) возрастающей, причем множеством ее значений является, в силу свойства м), весь луч [0, оо). Это позволяет рассматривать обратную к ней функцию. Эта обратная функция обозначается симво-лом у = у х и называется арифметическим корнем п-и п ,----------------------------------------------------
степени. Согласно сказанному на стр. 213 функция _у = у х
247
определена на всем луче [0, оо) и множеством ее значений также является весь этот луч (свойство В на стр. 213).
п t—'
Далее, функция у = у х является возрастающей (свойство Б
п /—
на стр. 213). Графики функций у=у х показаны на рис. 104
(ср. свойство Г на1 стр. 213). Подчеркнем, что из л ю-б о г о неотрицательного числа у0 может быть извлечен арифметический корень л-й степени.УУо (так как областью определения функ-п /—
ции у = у' х служит весь луч 0 sg х < оо). Далее, соотношение лг0 = уЗф означает (согласно свойству А на стр. 213), что уо^О, хоДэО и выполнено соот-
ношение у0 — х^. Наконец, отметим, что, в силу свойства Д на стр. 214, для любого положительного числа а справедливы
! П y—\ П /‘—2.
соотношения \у а) = а, у а =а.
Замечание. При нечетном п функция у — хп является, как мы видели, возрастающей на всей прямой (— оо, оо), а не только на луче [0, оо). Множество значений этой функции также совпадает со всей числовой прямой (—оо, оо). Это позволяет рассматривать (при нечетном п) обратную
п
функцию у = у х на всей прямой —сю < х < оо, а не только на луче [0, оо). Обычно эта функция обозначается тем же символом у х. 1 ак, например, у х, у х, у х можно рассматривать при любом х (а не только при х^зО).
Функция у х, определенная при нечетном п на всей числовой прямой, совпадает при х>:0 с рассмотренным выше арифметическим корнем, а при х<0 принимает отрицательные значения. Из того, что функция у = хп является при п .— n=2k—1 нечетной, вытекает, что и функция у = у х явля-
ется нечетной, т. е. у—х — — у х (при нечетном п). Рис. 105 иллюстрирует сказанное. В дальнейшей части этой главы мы, однако, будем рассматривать лишь арифметические корни, т. е. даже при нечетном п будем рассматри-
248
вать функцию y — l/'x лишь для х^О. Причины этого
выяснятся в § 5.
Пример 3. Доказать, что если 0<а<; 1, то, каково бы ни было положительное число е<1, найдется такое п,
п i—
что у а >1 —е.
Решение. Так как оба числа j а и 1 —е положительны, П г — /Пу--\п
то неравенство у а > 1 —е равносильно неравенству ij/ а) > >(1—е)" (так как функция у^=хп— возрастающая), т. е. неравенству а>(1—е)”. Иначе говоря, нужно доказать, что найдется натуральное п, для которого (1—е)п<а. Но это непосредственно вытекает из примера 2 на стр. 244 (так как О < 1 — е < 1).
§ 4. Степень с целым показателем
После того как определена степень с натуральным показателем, следующим этапом является распространение понятия степени на случай любых целых показателей. Иными словами, речь идет об определении выражений а0, а*1, а-2, ... Причем определить смысл этих выражений нужно так, чтобы сохранились основные свойства степени. Прежде всего потребуем, чтобы сохранилось свойство а), указанное на стр. 242. Оказывается, этого уже достаточно, чтобы определить, каков должен быть смысл выражений а0, а-1, а'2 и т. д. В самом деле, пусть а — произвольное отличное от нуля действительное число. Тогда, в силу свойства а), мы имеем
ат • а° — ат+° = ат, и потому а° = ^;=1;
249
далее,
а~п • ап = а^п'>+п = а°— 1, и потому а~п = ^. Итак,
а°=1, а'"==^ (при а^О). (3)
Приведенные рассуждения не являются, конечно, доказательством формул (3), поскольку мы еще не определили, что следует понимать под а0 и а'”. Однако эти рассуждения доказывают следующее: если мы хотим определить степени с произвольными целыми показателями так, чтобы сохранилось свойство а), то это неизбежно приводит к формулам (3).
Поэтому формулы (3) принимают за определение степеней с нулевым и отрицательными показателями. Более точно, при а = 0 степени а° и ап (где п — натуральное), не определяются', при а О эти степени определяются формулами (3).
Приняв это определение степеней с нулевым и отрицательными показателями, мы можем теперь поставить вопрос о том, сохраняются ли при таком понимании степени указанные выше свойства. Оказывается, что все свойства сохраняются, кроме свойства 0"==0, которое для нулевого и отрич цательных показателей теряет смысл. Таким образом, степени с целыми показателями обладают следующими свойствами, в формулировке которых везде предполагается, что а Ф О, 6^0.
I. Свойства, выражающиеся равенствами:
а) ат • ап = ат+п для любых целых т, п;
б) (ат)п — атп для любых целых т, п\
в) (ab)n = anbn для любого целого п;
г) ~=а”~т для любых целых т, л;
/ а \ п
д) (-j-l = Г-)ЛЯ любого целого л;
е) 1Л=1 для любого целого л;
ж) | ап | — | а | " для любого целого п.
II. Свойства, выражающиеся неравенствами:
з) если 0<Za<Zb, то ап < Ьп при целом л > 0 и ап~у> Ьп при целом л < 0;
и) если л>1, то атУ>ап при целых т~у>п',
к) если 0<л<1, то am<ian при целых т~>п\
л) если a<z0, то ап^>0 при четном п и ап <0 при нечетном л.
250
Для примера докажем свойство а).
Если оба целых числа т, п положительны, то мы имеем дело с натуральными показателями, для которых, как мы знаем, свойство а) справедливо.
Если хотя бы один из показателей т, п равен нулю— скажем, т = 0, — то мы имеем
ат ап = а° • ап= 1 • ап = ап = а° + п = ат+п,
т. е. свойство а) справедливо.
Если оба показателя т, п отрицательны, т. е. т = = —k, п——I, где k и I—натуральные числа, то мы имеем
ак aL akal ak+l
= = а(-*)Н-0 =
т. e. свойство а) справедливо.
Остается рассмотреть случай, когда один из показателей положителен, а другой — скажем, т— отрицателен, т. е. т — = —k, где k и л —натуральные числа. Здесь могут представиться три случая:
при k < п имеем
ат ап = а~к ап = — ап = ~ = ап-к = а^1,^п = ат+я-, ak а1г
при k = n, т. е. т= —п, имеем *
ат • ап = ап ап = 4 • ап = = 1 = а» = an~n = = ат+п'
ап ап ’
при k > п имеем
ak ak an ak n ak n =zcr^-n)==a(-k^n = amirn.
Итак, во всех случаях свойство а) имеет место. Так как рассмотрены все возможности, то свойство а) доказано для любых целых показателей т, п.
Аналогично (рассмотрением всех возможных случаев) доказываются остальные свойства.
В заключение этого параграфа рассмотрим кратко свойства функции у = хп с целым показателем л. При натуральном л свойства этой функции были рассмотрены в § 2. При л = 0 получаем функцию у = х°. Эта функция определена при х О
251
Рис. 107.
и всюду в области определения принимает значение 1. Наконец, рассмотрим функцию у = хп при целом отрицательном п, т. е. функцию
y = x~k = — (4)
xk
где k — натуральное число. Областью определения этой функции является числовая прямая с выколотой точкой 0. При х>0 функция (4) является убывающей (так как х!<— возрастающая функция при х > 0). При х < 0 функция (4) также монотонна: она является на луче (— оо, 0) возрастающей при четном k и убывающей при нечетном (рис. 106, 107). В целом же (т. е. во всей своей области определения) функция (4) ни при каком натуральном k монотонной не является.
§ 5. Степень с рациональным показателем
Дальнейшим этапом является распространение понятия степени на случай рациональных показателей. Как и в § 4, мы должны определить смысл степени аг при рациональном г. Попытаемся прежде всего понять, каким образом эта степень может быть определена. При этом, как и в § 4, мы будем исходить из того, что для целых показателей степень уже определена, и попробуем определить смысл степени аг с рациональным показателем так, чтобы сохранилось свойство б) (стр. 242 или 250). Таким образом, мы рассмотрим наводящие соображения, которые помогут нам выбрать разумное определение.
Прежде всего заметим, что число аг должно быть положительным. В самом деле, так как число г рационально, то у также рационально, и мы имеем, в силу свойства б), г > [ г\2 ar=a 2 =\а21 ’
откуда видно, что число аг неотрицательно. Далее, так как число — г рационально, то должна быть определена и степень аг. При этом
а-г=аг- '-В = (аг)-1>
откуда видно, что аг 0. Итак, если мы хотим, чтобы число аг было определено для любого рационального показателя
253
г и при этом выполнялось свойство б), то должно быть выполнено неравенство аг>0.
Далее, если рациональное число г отлично от нуля, то определено число — (также являющееся рациональным). Сог-2 ласно сказанному выше число аг положительно и число (агу 2 1
также положительно. Но мы имеем (аг)г =а г—а1 = а; таким образом, число а должно быть положительным. Итак, если мы хотим, чтобы число аг было определено для любого рационального показателя г и при этом выполнялось свойство б), то основание степени а должно быть (при г у 0) положительным и сама степень аг также должна быть положительным числом. На основании этих наводящих соображений мы всюду в дальнейшем принимаем, что степень аг определяется только при положительном основании а и сама степень аг также является положительным числом (при этом показатель г может быть любым рациональным числом).
Сказанное задает лишь те ограничения, которые обязательно нужно ввести при определении степени с рациональным показателем. Но как получить само определение степени? Нетрудно понять на основании свойства б), каким должно быть это определение. Пусть г — произвольное рациональное число; т
его можно записать в виде г = -, где w — некоторое целое число, ап — натуральное число. Мы имеем (при любом положительном а)
/ т\п т {У)п=\ап} = а*'П=ат.
Так как оба числа аг, ат положительны, то из соотношения (аг}п = ат вытекает (но определению арифметического корня и-й степени), что аг=]/ат. Этот вывод сделан только на основании свойства б). Таким образом, степень аг с рациональным показателем следует определить формулой
а — у а (где г = -п, причем т—целое число и
п—натуральное). (5)
Итак, если мы хотим, чтобы степень с рациональным показателем удовлетворяла свойству б), то мы неизбежно приходим к формуле (5). Поэтому формулу (5) принимают за 254
определение Степеней с рациональными показателями. Еще раз подчеркнем, что основание степени а всегда предполагается положительным.
Однако принятое определение (5) страдает одним недостатком. Возьмем, например, рациональное число г = у. Это рациональное число можно бесконечно многими способами представить в виде —. Например, мы можем написать г =
3 5 (
= 4-, t = и т. д. Поэтому степень аг\т. е. а'1) на осно-вании формулы (5) может быть записана бесконечно многими способами:
з _____ а ______
ar = а^ = с?, аг — а,й = у^ а5 и т. д.
К счастью, этот недостаток определения (5) в действительности является несущественным. Более точно, если рациональное число г двумя способами представлено в виде дроби т р , , .
(где т, р — целые, а п, q — натуральные числа), п п/— ч /—
то имеет место равенство у ат = у ар. Это равенство (которое мы сейчас докажем) показывает, что определение (5) математически корректно, т. е. равенством(5)задается одно и то же, вполне определенное число, независимо от того, как записано рациональное число г в виде дроби —.
п/—т ч/—п -г т Р
Итак, докажем равенство у а =у ар. 1ак как — =у, то мы имеем mq — np. Обозначим число ат через Ь, т. е. п ,-------------
напишем Ь = у ат. Число Ь, по определению, положительно; число а (основание степени) также положительно. Равенство Ь = у^ат означает, по определению корня, что Ьп = ат. Возведя обе части этого равенства в степень q, мы получим (Ьп)4 = (ат)4, или Ьпч = атч. Но mq — np, и потому bnq — anp. Это равенство на основании свойства б) (для целых показателей, как мы знаем, оно справедливо) можно переписать в виде (bq)n = (ар)п. А так как оба числа Ьч и ар положительны, то отсюда следует, что Ьч = ар (ибо функция при х > 0 монотонна). Наконец, поскольку b > 0, мы можем равенство Ь9 = ар переписать в виде Ь = у/Гар. Таким образом, Ь = угат, Ь = ]/'ар, откуда и вытекает, что ат — у'"ар.
255
Тем самым корректность определения (5) установлена. Итак, мы принимаем соотношение (5) за определение степени с рациональным показателем, причем основание степени а всегда считаем положительным. Теперь мы можем поставить вопрос, сохраняются ли при таком понимании степени рассматривавшиеся ранее свойства (стр. 250). Оказывается, что все свойства, кроме л), сохраняются; кроме того, свойство ж) становится тривиальным. Иначе говоря, степени с рациональными показателями обладают следующими свойствами, в формулировке которых везде предполагается, что а > 0, &>0, аги х — произвольные рациональные числа.
I. Свойства, выражающиеся равенствами:
A) ar-as~ar~s\
Б) (ar)s = a";
В) (ab)r—arbr-, аГ г-S / as >
Д) / -X = — •
\ ь; Ы •
Е) lr= 1, а°=1.
Добавим к этим свойствам еще следующее свойство, непосредственно вытекающее из формулируемых ниже свойств И), К) и часто применяемое при решении задач:
Ж) если ar~as а а 1, то r = s.
II. Свойства, выражающиеся неравенствами: 3) если а<_Ь, то аг <_ЬГ при г > 0 zz ar>br при г-<0; И) если а^>1, то ar'>as при г > s;
К) если 0<Za<Z 1, то ar <Zas при r~>s.
Для примера докажем свойство А). Пусть r = ^, где т, р — целые, а п, q — натуральные числа. Число аг обозначим через Ь, а число as — через с. Таким образом, Ь = аг= = Гу^ат, c — as = j/'ар. Оба числа Ь, с положительны. При этом, по определению корня, Ьп=ат, сч = ар. Возведем первое из этих равенств в степень q, а второе — в степень п. Мы получим (bn)g = (am)g, (сд)п = (ар)п, или, иначе, b”g = amg, спд — апр. Перемножив два последних равенства, получаем Ьпд спд = атд апр. Применяя свойства в) и а) (для целых показателей, как <мы знаем, они справедливы), перепишем это равенство в виде (&с)”9 = am?+rep. Из этого следует, по определению арифметического корня, что Ьс = "угатд+пр. Вспоминая
256
теперь Определение (5) степени с рациональным показателем, мы находим отсюда
тд пр т ,р~
nq —а"ч nq = an~i~V = a'+s.
mq + пР Ьс~ а
Наконец, остается вспомнить, что b — ar, c = as, и мы получаем требуемое равенство ar-as = ar+s. '
В заключение этого параграфа мы рассмотрим свойства степенной функции
у = хг (х>0)
(6)
с произвольным рациональным показателем г. Согласно определению степени (см. (5)) эта функция задана при х > О, т. е. ее областью определения служит луч (0, оо). Эта функция обладает следующим свойством:
Л) При г 0 функция (6) принимает все положительные значения. Она является возрастающей при г>0 и
В самом деле, пусть _у0 —произвольное положительное число. Покажем, что в некоторой точке х0 функция (6) принимает значение _уа, т. е. найдется такое число ха>0, что хо-Уо- Мы имеем уй=у1> —уог Г — {уог) (напомним, что г^О). Полученное равенство \j/or) =у0 показывает, что в качестве
9 В. Г. Болтянский и др. 257
искомого числа х0 можно взять x0=_yur, и мы получим Jo-
Тем самым доказано, что функция (6) принимает все положительные значения. Из свойства 3) непосредственно вытекает, что эта функция является возрастающей при г > 0 и убывающей при г < 0.
§ 6. Степень с действительным показателем
Теперь мы подходим к заключительному этапу обобщения— к распространению понятия степени на случай любых действительных, показателей. Как и в случае рациональных показателей, мы должны ограничиться случаем, когда основание степени положительно. Мы должны так определить степень с действительным показателем, чтобы в случае рациональных показателей степень имела тот же смысл, как и в § 5, и чтобы для степеней с действительными показателями сохранились все свойства, указанные в предыдущем параграфе. На этот раз, чтобы понять, как следует определить степень с действительным показателем, мы воспользуемся свойствами Е), И), К).
Пусть а — произвольное действительное число. Рассмотрим неубывающую последовательность рациональных чисел r1( г2, т3, ..., имеющую число а своим пределом. Таким образом,
Г1 r2 sS г3 ==£... sS а, (7)
причем разность а — rk неограниченно уменьшается с ростом k. Например, в качестве rlt г2, г3, ... можно взять последовательность все более точных десятичных приближений числа а с недостатком (ср. стр. 61). Предположим сначала, что а>1. Если мы хотим, чтобы степени с действительными показателями обладали свойством И), то, в силу (7), должны написать
аЛ| si С... С аа.
Таким образом, последовательность чисел аг', аг^, аг\ ... является неубывающей. А так как числа гг, г2, г3, ... все более приближаются к числу а, то естественно предположить, что числа аг‘, аЧ аГз, ... будут все более приближаться к числу а\ т. е. что аа есть предел последовательности аг', аг‘, аг*, ... (Можно было бы доказать, что из выполнения свойства И) с необходимостью вытекает, что а" есть предел этой после-258
довательности, но мы этого доказывать не будем, так как речь идет здесь о наводящих соображениях, которые позволят найти определение степени с действительным показателем.) В случае, если а<1, из1 (7) вытекает на основании свойства К), что
аг' аГз > аГл ^... ^а1,
т. е. последовательность ar‘, аЧ аГз, ... является невозрастающей, и снова естественно предположить, что ал есть предел этой последовательности. Наконец, при а=1 каждое из чисел аг‘, аг*, аг?, ... и а* равно 1 (свойство Е)), и в этом случае ах также есть предел последовательности аг‘, аГг, аг-1, ... В результате мы приходим к мысли о том, что степень а* в любом случае (а>1, а<1, а=1) можно определить как предел последовательности ar>, аЧ аг’, ... Это определение мы и примем.
Итак, пусть a — произвольное действительное число и ri> г2> гз’ ••• — неубывающая (или невозрастающая) последовательность рациональных чисел, имеющая число а своим пределом (г. е. lim гп = а). Тогда, по определению, п -* со
aa = lim а’’1. (8)
/г —> со
Чтобы убедиться в математической корректности этого определения, необходимо проверить два факта. Во-первых, надо убедиться, что неубывающая (или невозрастающая) последовательность чисел аг', аГз, аГз, ... является ограниченной и, следовательно, можно говорить о ее пределе. Во-вторых, надо убедиться, что предел (8) не изменится, если последовательность rv г2, г3, ... заменить другой неубывающей (или невозрастающей) последовательностью рациональных чисел, также имеющей число а своим пределом. Оба факта доказываются сравнительно несложно, но мы здесь этих доказательств не приводим, поскольку в школьном курсе эти факты не доказываются (и обычно даже не формулируются). Тем не менее обсуждение этих фактов нам кажется важным, так как поступающие в вузы (особенно с повышенными математическими требованиями) должны ясно представлять себе, какие факты лежат в основе определения понятия степени, какие из этих фактов доказаны в школьном курсе, а какие — нет.
Итак, формула (8) дает определение степени с действительным показателем. Оказывается при этом, что все
9»
259
свойства степеней, рассмотренные в предыдущем параграфе для Случая рациональных показателей степени, сохраняются и для действительных показателей. Иначе говоря, все свойства А) —К) (стр. 256) остаются в силе при а > 0, и любых действительных г, s. Свойство Л) (стр. 257) также сохраняется. Иными словами, функция
У — х“,
где а — произвольное действительное число, определена на луче (0, оо) и при 0 принимаеа все положительные значения. Она является возрастающей при а>0 и убывающей при а<0. В частности, аа>0 при любом а>0 и любом действительном а. Доказательства этих свойств мы не приводим.
§ 7. Показательная и логарифмическая функции
Функция у — ах называется показательной функцией.
Число а (основание) всегда предполагается положитель-
н ы м. Согласно определению понятия степени (§ 6) показа-
тельная функция у = ах определена на всей числовой прямой —оо < <х<оо. Из сказанного в предыдущем параграфе непосредственно вытекают следующие свойства показательной функции (см. свойства И) и К)).
Показательная функция у — ах принимает только положительные значения. При а > 1
она является возрастающей, а при а < 1—убывающей (рис. 109). При а~1 имеем ах= 1.
Имеется еще одно важное свойство показательной функции: М) При а 1 показательная функция у = ах прини-
мает все положительные значения, т. е. множество значений этой функции представляет собой луч (0, оо).
Доказательство этого свойства основано примерно на тех же идеях, что и доказательство свойства Л) на стр. 257.
260
•Рднако это доказательство выходит за рамки курса математики средней школы, и мы его здесь не приводим.
Итак, для любого положительного числа а, отличного от единицы, функция у — ах определена на всей числовой прямой — оо<х<;оо, монотонна (возрастает при а>1 и убывает при 1) и значения этой функции заполняют бесконечный интервал 0<у/<;оо. Следовательно, можно рассматривать обратную к ней функцию (см. § 5 гл. VII), которая обозначается символом y = \ogax и называется логарифмической функцией. Подчеркнем еще раз, что функция_y = logax определена только при а > 0, а 1.
Из свойств обратной функции, доказанных в § 5 гл. VII, вытекают следующие свойства логарифмической функции.
1. Функция _y = logax (согласно свойству В на стр. 213) определена на бесконечном интервале 0 < х < оо (и только на этом интервале), а множеством значений этой функции является вся числовая прямая — оо<_у < оо.
2. Функция y = \ogax является возрастающей при а > 1 и убывающей при 0<а< 1 (свойство Б на стр. 213).
3. График функции y — \ogax симметричен графику функции у=ах относительно биссектрисы первого и третьего координатных углов (свойство Г на стр. 213). Графики различных функций j/ = logax показаны на рис. НО и 111.
4. Соотношение -v0 = loga_y0 означает (согласно свойству А на стр. 213), что у0 > 0 и выполняется соотношение j/0 = = ах°:
{x0=loga_y0} {Jo>O} л {Уъ=ах°}-
(9)
261
5. Для любого а >0, 1 (согласно свойству Д на
стр. 214) выполняются соотношения
aioeax = x (х>0), (10)
log„aJC = x. (11)
Указанные выше свойства, в частности свойства, задаваемые формулами (9), (10), (11), являются основными свойствами логарифмов (соотношение (9) обычно принимается за определение логарифма в курсе математики средней школы). Из этих соотношений вытекает ряд дальнейших свойств логарифмов, которые мы рассмотрим в следующем параграфе.
Пример 4. Найти loga 9, log, 4, log4 2.
Решение. Обозначим loga 9 через х. Соотношение х= = loga согласно свойству 4, равносильно соотношению 3* = 9, которое выполняется при х — 2 и только при этом значении х, так как функция 3* монотонна. Следовательно, loga9 = 2 (произносится: логарифм девяти по основанию три равен двум).
Аналогично находим
I 1 \*2 log, 4 =— 2, так как (у) = 4; з ' !
1 L
log4 2=2’, так как 4s = 2.
Пример 5. Доказать, что для любого а>0, а 1, выполняются соотношения
loga а =1, 10ga 1=0.
Решение. Указанные соотношения получаются из соотношения (11) при х=1 и х = 0, так как для любого a > 0 имеем а°=1 (см. формулу (3) на стр. 250).
Замечание. Из соотношения loga 1 = 0 и монотонности функции y = logax (см. свойство 2, стр. 261) следует, что если а > 1, то
loga х > 0 при Х>1, loga х < 0 при 0<Х-<1, а если а < 1, то
loga х < 0 при х>1, logax>0 при 0<х<1
(ср. рис. 110, 111).
262 •
Эти неравенства часто используются при решении задач. Их легко запомнить следующим образом: если числа а и х лежат на числовой прямой по одну сторону от единицы, то l°ga-r>0, а если числа а и х лежат по разные стороны от единицы, то loga х < 0.
§ 8. Свойства логарифмов
1°. Логарифм произведения двух положительных чисел по данному основанию равен сумме логарифмов этих чисел по тому же основанию, т. е. для любых чисел а > 0, а У- 1, Xj > 0, х2>0 выполняется соотношение
logo (Xjx2) = loga Xi + logo x2. (12)
Доказательство. Обозначим логарифмы log0 xy и 10go x2 через yi и y2:
lOgoXj^^j, 10gox2=j/2. (13)
Тогда согласно свойству 4 (стр. 261)
Xi — аУ>, х2 = аУ‘,
откуда получаем (в силу свойства А) на стр. 256)
х2х2 = а'-’< = й-’т + х?.
Применяя снова свойство 4 (стр. 261), находим отсюда 10go(x1x2)=j»I+^2. (14)
Из формул (13) и (14) вытекает равенство (12).
2°. Логарифм частного двух положительных чисел по данному основанию равен разности логарифмов делимого и делителя по тому же основанию, т. е. для любых чисел о > 0, a 1, jqX), х2>0 выполняется соотношение
logo ~ = logo Xi — logo Х2. (15)
*2
Это свойство доказывается так же, как предыдущее.
3°. Для любых чисел a > 0, а#1, х>0 и любого действительного числа а выполняется соотношение
logo хл = a logo х. (16)
Доказательство. Обозначим logax через у:
y = \ogax. (17)
263
Тогда согласно свойству 4 (стр. 261)
Возводя обе части этого равенства в степень а, находим (в силу свойства Б) на стр. 256)
ха = (а>)а=аа>’.
Применяя снова свойство 4 (стр. 261), находим отсюда
logax’ = ay. (18)
Из формул (17) и (18) вытекает равенство (16).
4°. Для любых чисел а>0, а ф 1, £>Д>0, by 1, х>0 выполняется соотношение
io^x=hb’log6x- (19)
Доказательство. Обозначим logaх через у.
у=\о%ах. (20)
Соотношение (20) согласно свойству 4 (стр. 261) равносильно соотношению
а'1 — х, из которого получаем
log6a-v = logft х.
На основании свойства 3° это равенство можно записать в виде
_ylog6 a = log„x. (21)
Из формул (20) и (21) получаем равенство (19).
Замечание. По формуле (19) можно находить логарифмы
чисел по любому основанию а, если известны логарифмы
чисел по некоторому заданному основанию Ь.
„ 1
Число т—— logfitz
в формуле (19) называется модулем перехода от логарифмов по основанию а к логарифмам по основанию Ь. В частности,
при £=10 формула (19) имеет вид
logax==
1g х
Iga '
По этой формуле можно находить логарифмы чисел по любому основанию с помощью таблиц десятичных логарифмов.
Сформулируем дальнейшие свойства логарифмов.
264
5°. Для любых чисел <z>0, a^l, _г>0, а 0 вы-
полняется соотношение
10gaaX = -^-10g;X.
(22)
6°. Для любых чисел a>0, a 1, t>0, b \ выпол
няется соотношение
\ogab-\ogba=\.
(23)
7°. Если основание и число, стоящее под знаком логарифма, возвести в одну и ту же степень, отличную от нуля, то логарифм не изменится, т. е. для любых чисел a>0, а 1, х>0, а ф О выполняется соотношение
logo" x“==log0x.
(24)
Доказательство свойств 5°—7°, которые легко можно получить как следствия свойств 1°—4°, мы предоставляем читателю.
Пример 6. Доказать, что для любых чисел а>0, а^Ы, а Ф 0 и любого действительного числа р выполняется соотношение
log0“(a₽) = -|.
(25)
Доказательство. Обозначим logoCI(a₽) через у:
J/==10gaa(<Z₽). (26)
Соотношение (26) согласно свойству 4 на стр. 261 равносильно соотношению
(ау> = а?. (27)
Из соотношения (27) по свойствам степени находим
а7у=а‘', ау = $, _У = -|.
Наконец, подставляя найденное значение для у в формулу (26), мы и получаем соотношение (25).
Заметим, что соотношение (25) можно получить и другим способом, например применяя последовательно формулы (16), (22) и реаультат примера 5.
265
В заключение приведем общую сводку формул для действий над логарифмами, полученных в этом параграфе:
10go (XiX2) = 10go Xi + loga х2, (12)
loga^r = 10gaX! — 10go X2, (15)
logax“ = alogax, (16)
loga-v==hi^ ’ log*x’ O9)
loga«x = ~-\ogax, (22)
loga & • logb a= 1, (23)
loga«xa = logax. (24)
ОтметИхМ еще раз, что все эти соотношения выполняются тогда и только тогда, когда все выражения, стоящие в этих соотношениях, имеют смысл, т. е. 1) основание логарифма должно быть положительным числом, отличным от единицы, 2) выражение, стоящее под знаком логарифма, должно быть положительным числом.
Задачи к главе VIII
8.1. Найдите числовые значения выражений:
1. log2 4. 4. log5^.
2. log i 2. 5. log27 9.
4
3. log i 6. log8 16.
3 y
8.2. Найдите числовые значения выражений (считая, что а > 0, а 1 ):
1. loga3 а. 3. log 1 а7.
а
1 _
2. loga4a3. 4. log/5]/a.
8.3. Решите уравнения:
1. logo.i х — —2. 3. log^ 7 = — 1.
2. log81x = -~. 4. log^-8 = 3.
266
8.4. Найдите числовые значения выражений:
1о£23 1см? 2
1.4 . 3. 9 .
2. 271о®«2. 4. 41ог>27.
8.5. Найдите числовые значения выражений (считая, что а > 0, а 1):
log 2 log I
1. а “ . 3. (2а) .
log 4 4 log 5
2. а ^а. 4. а а .
8.6. Выясните, какие из указанных ниже логарифмов положительны, какие отрицательны.
1. log25. 3. logo,2 0,8.
2. log6 2. 4. log^]/?.
5
8.7. Выясните, какое из указанных чисел больше другого.
1. log3 4 или log4 у.
2. logo.i ]/2 или logo,2 0,34.
•2 3
3. Iog3y ИЛИ log^-j. 4 2
4. 2l°s>3 или 3log“2-
8.8. Докажите, что для любых чисел а > 0, а 1, хг < 0, х2 < 0 выполняются соотношения
10ga (х3Х2) = 10go 1^1+ logo I Х2 !>
logo ~ = logo I *1 I — logo I X2 |.
Л2
8.9. Докажите, что для любых чисел а> 0, а 1, х3 > 0, х., > 0, ..., xk > 0 выполняется соотношение
logo (Х3Х2 ...Xk) = logo Х3 + logo Х2 + . . . + logo Xk.
8.10. Докажите, что для любых чисел a > 0, а 1, х # 0 и любого целого четного числа п выполняется соотношение
logo = » logo |х|.
8.11. Найдите log48 32, если log214 = a.
8.12. Найдите log15 49, если log79 = a и log7 45 = Z>.
267
В задачах $.13 — 8.17 требуется доказать равенства, предполагая, что указанные выражения имеют смысл.
8.13. logox (Ьх) = 1Og,alt'OgaX. . > l + logaX
8.14. = loga b.
log,, X sa
8.15. -^ = log X1.
loga *2 2 1
8.16. _j— +L_ 4-... _1_ __L_ =
loga X loga2.*' leg kx
a
*(* + 1)
2 loga X •
8.17. 10ga,a2 ...ak x — j----------j--------------j---
10gO1 * + l°ga2 * +' ‘ ‘+ l°gafe x
Постройте графики функций (8.18 — 8.32):
8.18. y = 2l*'.
8.20. у = | log2 x |.
8.22. y — 2x — 2x.
8.24. у = 2 log., x.
8.26. j = |log2(x- 1)|.
8.28. у = | log21 x - 1 11.
8.30. у = 2*«a.
8.32. y = lg tgx.
8.19. y=2~W.
8.21. у = | x31 + 2~x.
8.23. _у = 21оЯ2\
8.25. у = log2 x2.
8.27. _y = log2lx— 1
8.29. _y=2c°3-T.
8.31. у = 1g sin x.
ГЛАВА IX
УРАВНЕНИЯ
§ 1. Равенство, тождество, уравнение
Знак равенства используется в математике очень часто, и смысл, который придается этому знаку, далеко не всегда один и тот же. Так, часто мы соединяем знаком равенства два числа, например:
651 = 2^7 (1)
257 257’ .
1236 = 22.3. 103, (2)
(]/Г + 1)2 = 3 4-2/Г, (3)
l°g^-(4)S=10- (4)
Каждая такая запись представляет собой некоторое высказы-
вание, которое может быть истинным или ложным. Среди приведенных выше четырех высказываний такого рода первые три являются истинными, а четвертое — ложным.
Для того чтобы убедиться в истинности (или ложности) такого высказывания, нередко бывает нужно произвести те или иные действия: сложение дробей, разложение на множители, возведение суммы двух чисел в квадрат и т. п. Однако смысл знака равенства во всех этих случаях один и тог же: истинность такого высказывания означает, что слева и справа от знака равенства стоит одно и то же число (только, может быть, записанное по-разному).
Высказывания такого вида мы будем называть числовыми равенствами. Если некоторое числовое равенство представляет собой истинное высказывание, то для краткости говорят: «это — верное равенство». Так, равенство (1) — верное. Если же некоторое числовое равенство представляет собой ложное высказывание, то для краткости говорят: «это — неверное равенство». Так, (4) — неверное равенство.
269
В ином смысле применяется знак =, когда идет речь о равенстве функций. Напомним, что две функции /(х) и g(x) считаются равными (г. е. совпадающими), если, во-первых, области определения этих двух функций совпадают и, во-вторых, для любого числа х0, принадлежащего общей области определения этих функций, значения функций в точке х0 совпадают, т. е. верно числовое равенство f(x0) = g(х0). Равенство функций /(х) и g(x) обычно выражают записью /(x) = g(x). Например, мы пишем
(х2+ 1)3 = х64-3х4 + 3х2+ 1,
выражая этой записью тот факт, что слева и справа от знака = стоят равные функции (т. е. слева и справа стоит одна и та же функция, только, может быть, записанная по-разному).
В записи, выражающей равенство (т. е. совпадение) двух функций, вместо знака = часто используют знак =, называемый знаком тождественного равенства. Запись/(x) = g(x) означает совпадение функций /(х) и g(x). Запись равенства двух функций (г. е. соотношение /(x)=g(x) или f (х) = g(x)) называют также тождеством. Подчеркнем еще раз: когда мы говорим, что /(x) = g(x) есть тождество, то это означает, что области определения функций /(х) и g(x) совпадают и при этом для любого х0, принадлежащего этой области определения, справедливо числовое равенство /(х0) = g (х0). Примерами тождеств могут служить соотношения (х+1)2 = х2 + 2х+1,
log2 2* = х,
I___ИГ+1
Ух — 1 х — 1
sin2 X = 1 —COS2X
И др.
Иногда при рассмотрении тождеств приходится ограничивать области определения функций. Именно, будем говорить, что равенство f(x) = g(x) является тождеством на множестве 7И, если, во-первых, множество М содержится в области определения каждой из функций /(х), g(x) и, во-вторых, для любого числа х0, принадлежащего множеству М, справедливо числовое равенство f (х0) = g (х0). В этом случае пишут:
/(x) = g(x) на множестве Л7 или
/(x) = g(x) при хе/И.
270
Пример 1. Равенство ]/х2=х является тождеством на множестве неотрицательных чисел, т. е.
]/х2=х при х^О.
Заметим, что обе функции Ух2 и х определены на множестве всех действительных чисел, но значения их совпадают лишь на множестве неотрицательных чисел. На множестве всех действительных чисел соотношение ]/х2 = х тождеством не является.
Пример 2. Рассмотрим равенство
arcsin (sin х) = Ух2.
Обе функции (стоящие в левой и правой частях равенства) определены на множестве всех действительных чисел. Однако написанное равенство является тождеством лишь на отрезке ^0, yj, т.е. arcsin (sin х) = /х2 при Осх •
Разумеется, при написании тождеств вовсе не обязательно обозначать аргумент функций буквой х. Можно аргумент обозначить буквой z, буквой а или любым другим символом. Так, соотношения
(z-4- 1)г = 224-2г4- 1,
(а — 1) (а2 4- а -j- 1) = а3 — 1
являются тождествами на множестве всех действительных чисел (или даже на множестве всех комплексных чисел).
Можно также рассматривать функции, зависящие от двух или большего числа аргументов, и писать тождества для таких функций. Конечно, и в этом случае надо указывать, при каких значениях аргументов написанное равенство является тождеством. Например, равенство
log2 aft = 61og2a
является тождеством при а > 0 и любом действительном Ь\
равенство
tg (х + J')
tgx + tgy
1 — tg х • tg г/
является тождеством при х^ -^-ф^л, .У =5^ у 4-«л, х4-_У=# где k, п, т — любые целые числа, и т. д.
271
Мы рассмотрели два случая использования знака = в алгебре: для записи числовых равенств и для записи тождеств (в последнем случае он иногда заменяется знаком = ). В совершенно ином смысле используется знак = при рассмотрении уравнений. Уравнение с одним неизвестным х в общем случае записывается в виде
/(*)=£(*)> (5)
где /(х) и g(x) — произвольные функции. Таким образом, по внешнему виду уравнение выглядит так же, как и тождество: две функции, соединенные знаком равенства. Но когда мы говорим, что соотношение (5) есть уравнение, то это показывает наше отношение к этому равенству. Именно, когда мы говорим, что (5) есть уравнение, то это означает, что равенство (5) рассматривается как неопределенное высказывание (при одних значениях х истинное, при других — ложное), и мы интересуемся нахождением корней этого уравнения, т. е. таких значений х, при подстановке которых это неопределенное высказывание становится истинным. Более подробно, корнем (или решением) уравнения называется всякое число, при подстановке которого вместо неизвестного в обе части уравнения получается справедливое (верное) числовое равенство. Но что значит «получается справедливое числовое равенство»? Это означает, во-первых, что при подстановке этого числа вместо неизвестного все действия, обозначенные в левой и правой частях уравнения, оказываются выполнимыми и, во-вторых, в результате выполнения этих действий в левой и правой частях получается одно и то же число. Иначе говоря, число а называется корнем уравнения (5), если, во-первых, это число принадлежит как области определения функции /(х), так и области определения функции g(x) и, во-вторых, значения этих функций в точке а совпадают, т. е. /(a) = g(a).
Итак, если сказано, что равенство (5) рассматривается как уравнение, то это означает, что мы интересуемся нахождением корней этого уравнения, т. е. тех значений х, которые обращают соотношение (5) в верное числовое равенство.
Пример 3. Для уравнения (х—1)2 = х2— 2x4-1 любое комплексное число является корнем, так как равенство (х0—1)3 = Хд — 2х04~ 1 имеет место для любого комплексного числа х0-
Пример 4. Если рассматривать уравнение |х| = х на множестве всех действительных чисел, то всякое неотрица-272
тельное число является корнем этого уравнения (других корней нет).
Пример 5. Уравнение lgx = lg(—х) не имеет решений, так как левая часть этого уравнения определена при положительных значениях х, а правая — при отрицательных, т. е. области определения левой и правой частей не имеют общих точек.
Пример 6. Уравнение cosx = 2 не имеет решений на множестве действительных чисел, так как | cos х01 1
для любого действительного числа х0.
Пример 7. Уравнение х2 =—1 не имеет решений на множестве действительных чисел и имеет два решения, x1 = z и х2 = — z, на множестве комплексных чисел.
Если найдена некоторая совокупность значений х, каждое из которых является корнем уравнения /(х) = g(x), то это еще не значит, что мы решили уравнение.
Решить уравнение — значит найти все его решения (или доказать, что уравнение не имеет решений).
Отметим, что бессмысленно ставить вопрос, «является ли равенство f(x)=g(x) тождеством или уравнением». Одно и то же равенство f(x) — g(x) в различных условиях может рассматриваться и как тождество, и как уравнение. Если мы говорим, что «/(x)=g (х) есть т о ж д е с т в о», то непременно надо указывать, на каком множестве это равенство является тождеством. Фраза «/(x) = g(x) есть тождество на множестве Л1» есть некоторое утверждение, некоторое высказывание. Если же мы говорим, что рассматриваем уравнение f(x) = g(x), то мы, по существу, имеем дело с вопросительным предложением: мы ставим вопрос, каковы корни этого уравнения, т. е. каковы те значения х, которые обращают соотношение /(x)=g(x) в верное числовое равенство.
Пример 8. Равенство j/x2 = x можно рассматривать и как тождество, и как уравнение. Если мы относимся к этому равенству как к тождеству, то наиболее полной формулировкой будет следующая: равенство ]/х2 = х является тождеством при х^дгО. Если же мы относимся к этому равенству как к уравнению, то это означает, что мы рассматриваем задачу: решить уравнение ]Аг2 = х, т. е. ставим вопрос о том, каковы корни этого уравнения. Ответ будет таков: корнями уравнения ]/х2 = х являются все неотрицательные числа и только они.
273
Пример 9. Бессмысленно ставить вопрос, является ли соотношение 0-хЦ-5 = 5 тождеством или уравнением. Мы можем сказать, что оно является тождеством на множестве всех действительных чисел. Но мы можем также рассматривать это соотношение как уравнение и тогда скажем, что корнями этого уравнения являются все действительные числа.
Замеча ние. Кроме рассмотренных выше случаев использования знака = в математике встречаются и другие. Так, выражение вида «рассмотрим функцию f(x) = x3— Зх2-j-4- 5х— 7» часто используется в качестве определения. В этом случае знак = имеет тот смысл, что всюду в проводимом рассуждении /(х) будет обозначать именно эту функцию. Встречаются и иные случаи использования знака = в математике, на чем мы, однако, не останавливаемся.
§ 2. Потеря корней и появление посторонних корней при преобразовании уравнений. Равносильные уравнения.
Уравнение, являющееся следствием данного.
Дизъюнкция уравнений
В процессе решения уравнения мы обычно производим некоторые преобразования, т. е. последовательно заменяем данное уравнение другими уравнениями, все более простыми, пока наконец не получим уравнение, которое мы умеем решать. Трудно перечислить все виды преобразований, которые мы выполняем при решении уравнений: их очень много. Еще труднее дать полный список рекомендаций, в каких случаях следует выполнять те или иные преобразования. Но есть одно непреложное правило, которое никогда не следует забывать: нельзя выполнять преобразования, которые могут привести к потере корней. Ведь мы говорили уже, что решить уравнение — значит найти все его корни, так что потеря корней в процессе решения недопустима.
Есть и другая опасность, которая может подстерегать нас при решении уравнений, правда, опасность, значительно меньшая, чем потеря корней. Заключается она в том, что при некоторых преобразованиях могут появиться новые корни, г. е. может оказаться, что новое уравнение (к которому мы приходим в результате преобразования) имеет больше корней, чем первоначальное. Иными словами, в новом уравнении, кроме корней первоначального уравнения, могут появиться лишние, посторонние корни. С этим обстоятельством связана необхо-274
димость проверки корней. Именно, если хоть один раз в процессе решения применялось преобразование, которое может привести к появлению посторонних корней, то после окончания процесса решения обязательно нужно проверить, какие из найденных корней удовлетворяют исходному уравнению, а какие ему не удовлетворяют, т. е. являются посторонними и, следовательно, должны быть отброшены. Проверку можно не производить только в том случае, если ни одно из примененных преобразований не приводит к появлению посторонних корней.
Уточним смысл терминов «потеря корней», «посторонний корень».
Пусть f(x) = g(x)— заданное уравнение, а А(^) = = gi(x)— некоторое новое уравнение, которое мы хотим рассматривать вместо первоначального уравнения (например, уравнение, полученное в результате «преобразования»). Мы говорим, что при переходе от уравнения f(x) — g(x) к уравнению = происходит потеря корней, если существует число х0 (хотя бы одно), являющееся корнем уравнения /(x) = g(x) и не являющееся корнем уравнения fi(x) = gi{x). Далее, число xL называется посторонним корнем, получающимся при переходе от уравнения f(x)=g(x) к уравнению А (х) = g± (х), если это число является корнем уравнения fi(x)=g1(x) и не является корнем первоначального уравнения f(x) = g(x).
Заметим, что при выполнении таких преобразований, как приведение в уравнении подобных членов, сокращение обеих частей уравнения на общий множитель, отбрасывание общего множителя числителя и знаменателя дроби, могуг быть потеряны корни или появятся посторонние корни. Рассмотрим несколько простых примеров.
Пример 10. Если в уравнении
ха + 6 + -Ц=5хН------Ц.
1 1 х—2 1 х—2
привести подобные члены, то получится уравнение х2— 5х -J-4-6 = 0, имеющее корни х1 = 2, х2 = 3. Однако число хх = 2 не входит в область определения левой и правой частей исходного уравнения и не является его корнем, так как выражение “yg теРяет смысл при х~2. Приведение подобных членов в рассматриваемом примере привело к расширению области определения функций, стоящих в левой и правой
275
частях исходного уравнения, и к появлению корня х=2, который для исходного уравнения является посторонним.
Пример 11. Если разделить обе части уравнения х3 = х на х, то получим уравнение х2=1, имеющее корни х1=1, хг = — 1, в то время как исходное уравнение х3 — х, кроме корней х1=1, Л'а = —1, имеет корень х = 0. Значит, сокращая обе части уравнения на х, мы потеряли корень х==0.
Пример 12. Рассмотрим уравнение
sin х sin 2х Q sinx
Если разделить числитель и знаменатель левой части уравнения на sin х, то получится уравнение sin2x = 0, имеющее корни х = ™ (п — 0, ± 1,±2,...). Однако исходному уравнению удовлетворяют только те корни уравнения sin 2х==0, которые удовлетворяют условию sin х 0 k — целое).
Таким образом, сокращение числителя и знаменателя левой (или правой) части уравнения на общий множитель- может привести к появлению посторонних корней.
Пример 13. Рассмотрим уравнение
cos х cos Зх
sin х sin х
Отбрасывая знаменатели дробей, приходим к уравнению cosx = cos3x или
2 sin х-sin 2х = 0. (6)
Так как корни уравнения sinx = 0 удовлетворяют уравнению sin2x = 0, то уравнение (6) имеет те же корни, что и уравнение sin2x = 0, т. е.
х = ™ (п — целое). (7)
Однако исходному уравнению удовлетворяют лишь значения х, получаемые из формулы (7) при нечетном п, т. е. х — ==| (2Л+ 1), k — целое.
Если же в (7) п—четное (д = 2Л), то x = nk, sinx = 0; но. такие х не входят в область определения левой и правой частей уравнения. Таким образом, отбрасывание знаменателя дроби привело к появлению посторонних корней.
Разобранные примеры убеждают в необходимости рассмотрения общей теории уравнений, уяснения влияния тех 276
йлй иных преобразований на уравнения. Нам потребуется ввести для уравнений понятия равносильности, следствия, дизъюнкции.
Определение. Два уравнения
f{x) = g(x) (8)
и
(9)
называются равносильными (эквивалентными) на некотором множестве М, если они имеют в этом множестве одни и те же решения, т. е. каждый корень уравнения (8), принадлежащий множеству М, является корнем уравнения (9) и, наоборот, каждый корень уравнения (9), принадлежащий множеству М, является корнем уравнения (8).
Для сокращения записи равносильные уравнения будем соединять знаком «->. Иначе говоря, запись
{/(*) = § (*)} ** {fi = gi (х)}
ИЛИ
(8)^(9)
будет означать, что уравнения (8) и (9) равносильны.
Замечание. В дальнейшем, если не оговорено противное, под множеством М мы будем понимать множество всех действительных чисел и вместо слов «уравнения равносильны на множестве действительных чисел» будем употреблять слова «уравнения равносильны», т. е. указание на множество М будем опускать.
Рассмотрим несколько простых примеров, иллюстрирующих определение равносильности.
Пример 14. |х-}-4 = Зх} {х—2 = 0}.
Пример 15.
{2 cos2x = 1 + cos 2х} -м- {х2— 2х = (х— I)2— 1}.
Любое действительное число является корнем каждого из этих уравнений.
Пример 16. {lgx=lg(—р—x + j-Lj =1+
J } • Обэ уравнения не имеют корней (множество корней каждого из этих уравнений является пустым множеством).
277
Пример 17. {х Ч-1 =0} «-> {(хЧ~ 1)3 = 0}.
Число х =—1 является корнем (простым) первого уравнения и корнем кратности 3 второго уравнения (определение кратности корня дано на стр. 170). Однако понятие кратности корня определяется лишь для алгебраических уравнений, а для уравнений общего вида, рассматриваемых в этой главе, оно не определяется. Поэтому всюду в этой главе кратность корня не учитывается и два уравнения, имеющие одни и те же корни (без учета кратности), считаются равносильными.
КТ 1 О 17 9 Ч~ 1 % Ч~ 1
Пример 18. Уравнения хг = х и —— не равносильны: число х=0 является корнем первого уравнения, но не удовлетворяет второму уравнению, так как при х = 0 левая и правая части второго уравнения не определены.
Пример 19. Уравнения х = 0 и х(х2Ч-1) = 0 равносильны на множестве действительных чисел (оба имеют единственный корень х = 0) и не равносильны на множестве комплексных чисел, где второе уравнение, кроме корня х1=0, имеет еще два корня: x2 = i, х3 — —I.
Заметим, что если при решении некоторого уравнения мы заменяем его другим, равносильным уравнением, то, находя корни второго уравнения, мы тем самым найдем корни первоначального уравнения.
Однако далеко не всегда удается заменить данное уравнение равносильным. Довольно часто, применяя к данному уравнению некоторое преобразование, мы получаем новое уравнение, корнями которого являются все корни данного уравнения и, быть может, некоторые другие числа, не являющиеся корнями данного уравнения. Иными словами, речь идет о преобразованиях, при которых не происходит потери корней; в таких случаях от посторонних корней можно избавиться с помощью проверки.
Определение. Пусть дано некоторое уравнение
f(x)=g(x). (10)
Уравнение
Л (*) = &(•*) О1)
называется с л е д с т в и е м уравнения (10), если при переходе от уравнения (10) к уравнению (11) не происходит потери корней, т. е. если все корни уравнения (10) являются корнями уравнения (11).
278
Иногда вместо фразы «уравнение (11) является следствием уравнения (10)» используют выражение «уравнение (11) является выводным из уравнения (10)».
Из приведенного определения следует, что уравнения (10) и (11) равносильны в том и только в том случае, когда каждое из этих уравнений является следствием другого. Из определения вытекает также, что уравнение (И), являющееся следствием уравнения (10), может иметь более широкое множество решений, чем множество решений уравнения (10).
В целях сокращения записи будем использовать знак -> для обозначения того факта, что второе уравнение (записанное справа от этого знака) является следствием первого. Иначе говоря, запись
{/(*) = §(*)}-> {Л (х) = gl (х)} или
(10)->(11)
означает, что уравнение (11) есть следствие уравнения (10).
Пример 20. {х= 1} —> {х2= 1}. Число х=1 является единственным корнем первого уравнения, и вместе с тем это число является корнем второго уравнения.
Пример 21. {Зх = 2х-ф 1}-> {sin3x=sin(2x-{-1)}. Второе уравнение является следствием первого (обратное неверно, т. е. второе уравнение имеет более широкое множество решений).
В заключение этого параграфа рассмотрим понятие дизъюнкции уравнений.
Определение. Будем говорить, что уравнение
/(x) = g(x) (12)
равносильно дизъюнкции уравнений
/1(*) = &(*)> fdx) = g2(x), ..., /„(x) = g„(x), (13)
если выполнены следующие условия:
1) каждый корень уравнения (12) является корнем по крайней мере одного из уравнений (13);
2) любой корень любого из уравнений (13) является корнем уравнения (12).
Из этого определения следует, что если уравнение (12) равносильно дизъюнкции уравнений (13) и если М — множество корней уравнения (12), а Alj, Л1г,..., Мп — множества
279
корней соответственно уравнений A (x)=g1 (х), АС*) — = & (*)> • > A W=g> (*), то
2И=м1иД!и...имл.
Иначе говоря, в этом случае вместо того, чтобы решать уравнение (12), можно решить каждое из уравнений (13) и множества корней всех этих уравнений объединить, Это объединение и будет представлять собой множество всех корней уравнения (12).
Тот факт, что уравнение (12) равносильно дизъюнкции уравнений (13), будем записывать следующим образом:
{/(•*) = gC*)}~
{[/1 (*) = gi (-*)] V [A (*)=& (*)] V • • • V [Л (*) = gn (•*)]}•
(Впрочем, можно было бы условиться опускать в этой записи фигурные и квадратные скобки.)
Пример 22. {х2— 5х6 = 0} *->
«->{[х—2 = 0] V [х—3 = 0]}.
Пример 23. {sin2 х= cos4 х} «->
«-> {[sin х = cos2 х] у [sinx-f- cos2x = 0J}.
Переход от данного уравнения к дизъюнкции более простых уравнений широко применяется при решении уравнений. Как правило, процесс решения уравнения заключается в следующем. Имея уравнение /(x) = g(x), мы (один или несколько раз) применяем переход к новому уравнению или дизъюнкции уравнений, т. е. каждый переход имеет вид
{/(•*) = £(*)} —
** {[A (-*) = & (•*)] V [А (*) = g2 (•*)] V • • • V [A (*) = §» (•*)]}•
При этом обязательным является соблюдение следующих правил:
1) При указанном переходе не происходит потери корней, т. е. если число х0 есть корень уравнения /(x) = g(x), то число х0 должно являться корнем хотя бы одного из уравнений
fi (х) = & (х), А (х) = g2 (х).fn (х) = gn (х).
2) Для решения исходного уравнения /(x) = g(x) нужно решить все уравнения А (*) = gi (*)> A (x) = gz (*)> ..., fn(x) = gn(x) и взять объединение множества корней первого из этих уравнений, множества корней второго из этих уравнений и т. д.
28Q
3) Если нет уверенности в том, что не появилось посторонних корней, то каждое число, входящее в это объединенное множество, должно быть проверено — является оно корнем исходного уравнения или нет.
В результате мы и получаем множество всех корней уравнения f (x) = g(x). Если какое-либо из уравнений/* (х) = = gk(x) (А=1, 2, ..., п) не решается непосредственно, то к нему применяется тот же прием. Почти все дальнейшее содержание главы (и рассматриваемые ниже примеры) дает иллюстрацию этого правила решения уравнений.
§ 3. Наиболее важные приемы преобразования и методы решения уравнений
1°. Перенос слагаемых из одной части уравнения в другую, т. е. переход от уравнения
/(х)-=ф(х)/«(х) (14)
к уравнению
/(х) —ф(х) = §(х). (15)
Указанный переход всегда приводит к равносильному уравнению, т. е., каковы бы ни были функции /(х), ф(х), g(x), мы имеем (14) «->(15). В самом деле, пусть х0 — корень уравнения (14), т. е. соотношение
/(x0) = cp(x0) + g(x0) (16)
представляет собой верное числовое равенство. Это означает, что 1) точка х0 принадлежит области определения каждой из функций /(х), ф(х), g(x), т. е. определены числа /(х0), ф (х0), g(x0), и 2) эти числа связаны соотношением (16). Прибавляя к обеим частям равенства (16) число — ф (х0), получаем
/(х0)—ф (х0) = ф (х0) — ф (х0) +g(x0), ИЛИ
/(х0) —ф(х0) = §(х0) (17)
(поскольку для любого числа а, в частности для а = ф(х0), мы имеем а — а = 0). Таким образом, (17) есть верное числовое равенство. Но это означает, что х0 есть корень уравнения (15). Итак, каждый корень уравнения (14) является также корнем уравнения (15), т. е. (14)—>(15). Аналогично доказывается, что (15)->-(14).
281
Итак, мы доказали, что при переносе любого слагаемого из одной части уравнения в другую с противоположным знаком получается равносильное уравнение.
В частности, мы можем, если нужно, перенести все слагаемые в одну часть уравнения. Иначе говоря,
{/(х) = ср (х)} +-> {/(х) — ф (х) = 0}
что является частным случаем эквивалентности (14) «->(15) при g(x) = 0). Мы видим, что любое уравнение с одним неизвестным может быть заменено эквивалентным уравнением вида /г(х) = 0, т. е. уравнением, в левой части которого стоит некоторая функция, а правая часть равна нулю.
Указанное преобразование (перенос членов из одной части уравнения в другую) применяется при решении уравнений чрезвычайно часто. Например, при решении иррациональных уравнений применяется «уединение радикала», т. е. перенос всех членов, кроме одного, имеющего вид /(х), в другую часть уравнения.
Подчеркнем, что в этом пункте шла речь только о перенесении членов из одной части уравнения в другую без последующего приведения подобных членов (если таковые имеются). Приведение подобных членов является новым преобразованием (которое, как показывает пример 10, может вызвать появление посторонних корней). К рассмотрению этого преобразования мы и переходим.
2°. Приведение подобных членов, т. е. переход от уравнения
/(х) + ф (х)—ср (x)=g(x) (18)
к уравнению
f<x)=g{x). (19)
Прежде чем рассматривать переход от уравнения (18) к уравнению (19), сделаем следующее замечание. Согласно сказанному в предыдущем пункте уравнение (18) равносильно уравнению
/(х) + ф (х) = §-(х) + ф (х). (20)
Поэтому переход от уравнения (18) к уравнению (19) означает то же самое, что и переход от уравнения (20) к уравнению (19), т. е. во всех рассуждениях уравнение (18) можно заменять равносильным ему уравнением (20). Таким образом, 282
сказанное в этом пункте будет относиться не только к приведению подобных членов в одной части уравнения, но и к вычеркиванию (взаимному уничтожению) одинаковых слагаемых в левой и правой частях.
Прежде чем сформулировать общее утверждение, относящееся к переходу от уравнения (18) к уравнению (19) или, что то же самое, от уравнения (20) к уравнению (19), рассмотрим следующие примеры.
Пример 24. {.V1— хф2 = х2 — хф- 2} «-» {х4 = х2}.
При вычеркивании в обеих частях уравнения xi— хф2 = = х2— Х---2 слагаемого q>(x) = x — 2 получается равносильное уравнение х4 = х3.
Пример 25. {х2 ф 1g х = х ф- 1g х] -> {х2 = х}.
Уравнение х2 = х имеет два корня xt= 1, х2 = 0, тогда как уравнение x34-lg х~ хф-lgx имеет единственный корень х=1 (число x — G не является корнем уравнения х2 ф- 1g х = х ф- 1g х, так при х = 0 левая и правая части этого уравнения не определены).
Таким образом, уравнение х2 = х не равносильно уравнению х2 ф 1g х — хф- 1g х, а лишь является следствием этого уравнения.
Появление постороннего корня х = 0 при переходе ог уравнения х2ф- 1g х = хф 1g х к уравнению х2 = х связано с тем, что при этом переходе расширяются множества, на которых были определены функции, стоящие в левой и правой частях первого уравнения: в уравнении х2ф lgx = x4-ф- 1g х левая и правая^ части определены при х>0, а в уравнении х2 = х — при всех х.
Очевидно, обратный переход, т. е. переход от уравнения х3 = х к уравнению х2 ф- 1g х = х ф- 1g х недопустим, так как этот переход ведет к потере корня х — 0.
Теперь мы сформулируем общее утверждение. Каковы бы ни были функции f(x), g(x), ф(х), уравнение (19) является следствием уравнения (18) (или иначе: уравнение (19) является следствием уравнения (20)). Таким образом, при переходе от уравнения (18) к уравнению (19) (или от уравнения (20) к уравнению (19)) потери корней не происходит, но, как показывают примеры 10 и 25, могут появиться посторонние корни. Доказательство этого утверждения аналогично рассуждению на стр. 281; мы предлагаем читателю провести это доказательство.
Из сказанного ясно, что при применении рассматриваемого преобразования (перехода от уравнения (18) или (20)
283
к уравнению (19)) необходимо после решения производить проверку корней, так как могут появляться посторонние корни.
Естественно возникает вопрос: в каких случаях рассматриваемое преобразование приводит к равносильному уравнению (как это было в примере 24) и, следовательно, применение этого преобразования не требует последующей проверки корней? Ответ на этот вопрос дает следующее утверждение х). Обозначим через М множество, на котором определены функции f(x) и g(x)> стоящие в левой и правой частях уравнения (19) (/и. е. пересечение областей определения функций f(x) и g(x)). Тогда, если множество 44 содержится в области определения функции ср(х), то уравнение (18) равносильно уравнению (19) (п также уравнение (20) равносильно уравнению (19)).
В самом деле, если х0 — корень уравнения (19), то точка х0 принадлежит области определения каждой из функций f(x), g(x) (т. е. принадлежит множеству 44) и числовое равенство /(x0) = g(x0)— верное. Но так как х0 принадлежит множеству 44, то, по предположению, х0 принадлежит и области определения функции гр(х), т. е. определено число <р(х0). Прибавляя к обеим частям равенства /(x0) = g(x0) число гр(х0), получаем верное числовое равенство f (х0) -]~ гр(х()) = = g(x0) ф- ср (х0), показывающее, что х0 есть корень уравнения (20). Таким образом, (19) ->(20). Обратное (т. е. (20) —> (19)), как мы знаем, имеет место всегда. Следовательно, (19)» (20) (а потому и (18)» (19)).
Итак, мы пришли к следующим выводам:
1) (18)->(19);
2) если пересечение областей определения функций f(x) и g(x) содержится в области определения функции гр(х), то (18)» (19);
3) если нет уверенности в равносильности уравнений (18) и (19), то переход от уравнения (19) к уравнению (18) недопустим: он может привести к потере корней.
В этих утверждениях уравнение (18) везде можно заменить уравнением (20).
!) Заметим, что это утверждение дает лишь достаточное условие равносильности уравнений (18) и (19). Иначе говоря, даже если это условие не выполнено, то в некоторых случаях может оказаться, что (18) —(19). Пример: {х2 — 5х + 6lg х — lgx=0} — {ха —5х-|-6 = 0}.
284
3°. Умножение обеих частей уравнения на одно и то же выражение, т. е. переход от уравнения
f(x)=g(x) (21)
к уравнению
f(x)q(x)==g(x)q(x). (22)
По поводу этого перехода можно высказать следующие утверждения:
1) Если в каждой точке, где определены обе функции /(х), g(x), определена также и функция (р(х) (иначе говоря, если пересечение областей определения функций /(х) и g (х) содержится в области определения функции ср (х)), то уравнение (22) является следствием уравнения (21), т. е. (21)—>(22).
2) Если при выполнении условия 1) функция ср(х) отлична от нуля на пересечении областей определения функций /(х) и g(x), то уравнения (21) и (22) равносильны, т. е. (21)» (22).
Доказательство утверждений 1) и 2) предоставляем читателю. Заметим, что в общем случае переход от уравнения (22) к уравнению (21) может привести как к появлению посторонних корней, так и к потере корней.
Пример 26. Рассмотрим уравнение
х2 — х = 0.
хг х 1
Умножив обе части этого уравнения на мы получим уравнение
х
которое не является следствием исходного.
В самом деле, исходное уравнение имеет корни xt = 0, j^2 _______________%
х2= 1, а уравнение —-— = 0 — лишь корень х=1. Потеря корня связана с тем, что функция у не определена при х = 0, а как раз это значение х является корнем заданного уравнения.
4°. Переход от уравнения
/1(х)/2(х).../„(х)==0 (23)
к дизъюнкции уравнений
Л(х) = 0, /2(х) = 0,...,/„(х) = 0. (24)
285
Такой переход применяется довольно часто при решении уравнений. Естественно, возникает вопрос: можно ли утверждать, что уравнение (23) равносильно дизъюнкции уравнений (24)? Иными словами, можно ли получить множество всех корней уравнения (23), решив все уравнения (24) и объединив их корни? Ответ на этот вопрос дает следующая теорема.
Теорема 1. Если все функции А (х), А (х), ..., fn(x) определены на множестве М (т. е. если множество М содержится в области определения каждой из функций /1 (*)> А (*)> • • ’ fn (*))> то на этом множестве уравнение (23) равносильно дизъюнкции уравнений (24).
Доказательство. Пусть х0 £ 7И, и пусть х — х0 — корень одного из уравнений (24). Не теряя общности, будем считать, что х = х0— корень уравнения f1(x) — 0. Тогда функция А(х) определена при х = х0 и /1(хо)=0. Так как х0 £ М, то функции f2(x), .... fn(x) также определены при х = х0 и
/i(^o)A(^o)---A(^o) = O
(первый множитель в левой части равен нулю).
Итак, любой (содержащийся в множестве Л1) корень каждого из уравнений
/1(х) = 0, /3(х) = 0,...,/„(х) = 0
является корнем уравнения (23).
Обратно, пусть х — а — такой корень уравнения (23), что а £ М. Тогда все функции А(х), f2(x), ..., fn(x) определены при х = а и
А(а)А(«)---А(а) = 0-
Из этого следует, что равно нулю хотя бы одно из чисел /1(а), /2 (a),..., fn (а).
А это означает, что х = а является корнем по крайней мере одного из уравнений
/1(х) = 0, /2(х) = 0,...,/п(х)=0.
Доказанная теорема лежит в основе часто применяемого метода разложения уравнения на множители.
286
Пример 27. Легко проверить, что xe + Зх5— х4— Зх3 = = х3(х2—1)(х + 3), поэтому уравнение х6+3х5 — х4— — Зх3 = 0 равносильно дизъюнкции уравнений
х3 = 0, х2—1=0, х4-3 = 0
и имеет следующие корни 4): = 0, х2 — 1, х3 = — 1, х4 = — 3.
Следующий пример показывает, что в общем случае уравнение
А(х)/г(х).../я(х) = 0
не равносильно дизъюнкции уравнений
А(х) = 0, /2(х) = 0,...,/„(х) = 0.
Пример 28. Пусть Д(х) = х2— 1, A W — х 2_ f - Тогда уравнение f2(x) = 0 не имеет корней, уравнение Л(х) = 0 имеет два корня х1=1, х2 = — 1, а уравнение (х) А (х) = 0 имеет только один корень х1 — —1, так как при х=1 левая часть этого уравнения не определена.
Теорема 2. Каждый корень уравнения (23) является корнем одного из уравнений (24).
Иначе говоря, дизъюнкция уравнений (24) есть следствие уравнения (23):
{AWAW--A(x)=0}->
v IAW=0] V... V [AW=0]}.
Доказательство предоставляем читателю. Из этой теоремы вытекает, что если мы найдем все корни уравнений (24), то среди этих корней будут содержаться все корни уравнения (23) и, быть может, некоторые числа, не являющиеся корнями уравнения (23). Посторонними для уравнения (23) будут те значения х, полученные при решении уравнений (24), для которых хотя бы одна из функций А(х), f2(x), ..., fn(x) не определена.
Замечание. Выше было отмечено, что переход or уравнения
f(x)<p(x)=g(x)<p(x) (25)
к уравнению
в общем случае недопустим.
!) Еще раз напоминаем, что кратность корней мы в этой главе не учитываем.
287
/При решении уравнения (25) обычно поступают так. Вместо уравнения (25) рассматривают уравнение
(/(*)—£(*)] Ф (х) = °- (26)
которое эквивалентно уравнению (25). В свою очередь дизъюнкция уравнений
/(x)-g(x)=0, <р(х) = 0 (27)
является следствием уравнения (26).
Таким образом, если мы решим уравнения (27), объединим их корни, а затем проверкой (подстановкой в уравнение (25)) отсеем лишние корни, то тем самым мы найдем все корни уравнения (25).
Пример 29. Решить уравнение
sin х ctg 2х arcsin (х— !)• 1g (х— 1) = 0.
Решение. Рассмотрим уравнения sin х — 0, ctg 2 х — О, arcsin (х—1) = 0, 1g (х—1) = 0. Они имеют соответственно корни
х — лп, + (л = 0, ±1, ±2, ...), х=1, х = 2.
Те из этих корней, которые принадлежат области определения левой части исходного уравнения, являются корнями исходного уравнения.
Обозначим эту область определения через М. Множество М состоит из всех тех значений х, при которых определена каждая из функций sin х, ctg 2х, arcsin (х—1), 1g (х—1). Но функция sinx определена при всех х, а области определения остальных трех функций задаются соответственно следующими условиями:
х у (Л = 0, ± 1, ± 2, ...), О sg х 2, х > 1.
Таким образом, множество М состоит из тех значений х, которые удовлетворяют неравенству 1<;х=С2 и условию х^ (6 = 0, ±1, ±2, ...),
т. е. это множество получается выбрасыванием точки ~ из полуинтервала 1<7х=С2. Числа х = лп(п=0, ± 1, ±2, ...), являющиеся корнями уравнения sin х — 0, не принадлежат множеству М и являются для исходного уравнения посторонними. Число х=1, являющееся корнем уравнения arcsin(х—1) = 0,
288
также не принадлежит множеству Ai и является посторонним корнем.. Далее, число х = 2, являющееся корнем уравнения 1g (х—1) = 0, принадлежит множеству М и является корнем исходного уравнения.
Наконец, ни одно из чисел вида х = ” + (н = 0, ± 1, ±2, ...), удовлетворяющих уравнению ctg2x = 0, не удовлетворяет неравенству 1 < х sC 2 и потому не принадлежит множеству Л1.
Таким образом, корнем исходного уравнения является только одно число х1 = 2.
5°. Переход от уравнения f(x) = g(x) к уравнению [f(x)]” = ,£ (х)!"• Такой переход нередко используется при решении уравнений, особенно при решении иррациональных уравнений.
Пусть функции f(x) и g(x) определены на множестве М (т. е. множество М содержится в области определения каждой из функций f(x), g(x)) и п—произвольное натуральное число. Будем предполагать, что М — некоторое множество действительных чисел и что на этом множестве функции /(х) и g(x) принимают действительные значения.
Мы можем утверждать следующее:
1) при любом натуральном п уравнение
[/(*)]" = [£(-ОГ (28)
является следствием уравнения
/(x) = g(x); (29)
2) если п — нечетное число (/г = 2АЦ-1), то уравнение (28) равносильно уравнению (29) на множестве М\
3) если п — четное число, то уравнение (28) равносильно на множестве М уравнению
l/WI = |g(x)|, (30)
которое в свою очередь равносильно дизъюнкции уравнений /(*) = g (х) и /(х) = — g (х)
на множестве М. Если при этом окажется, что второе из этих уравнений не имеет решений (например, если обе функции /(х), g(x) принимают на М только положительные значения), то уравнение (28) оказывается равносильным уравнению (29). В общем же случае переход от уравнения (28) к уравнению
10 В. Г. Болтянский и др. 289
(29) при четном п недопустим, так как такой переход может привести к потере корней.
Пример 30. Решить уравнение
/2х24-5х—3=х4-1. (31)
Решение. Возводя обе части уравнения (31) в квадрат, получим уравнение
2х2 4- 5х— 3 = х2 4- 2х 4-1, являющееся следствием уравнения (31). Полученное уравнение равносильно уравнению
х2 4~ Зх — 4 = 0,
корнями которого являются числа хг = — 4, х2=1. Проверка показывает, что корень xt— — 4 является посторонним для уравнения (31), а корень х2=1 удовлетворяет уравнению (31).
Таким образом, уравнение (31) имеет единственный корень х = 1.
Более общим, чем рассмотренный в 5°, является переход от уравнения
/(x) = g(x) (32)
к уравнению
Ф L/C*)] = ф [£(*)]> (33)
где cp(Q— некоторая заданная функция.
Заметим сразу, что в общем случае такой переход недопустим. В самом деле, пусть Et и Е2— множества значений соответственно функций /(х) и g(x) и Е— общая часть (т. е. пересечение) множеств Ех и В2. Если функция ср (t) не определена на множестве Е, то уравнение (33) не имеет решений, в то время как исходное уравнение (32) могло иметь решения. Если же множество Е содержится в области определения функции гр(/), то, как легко доказать, (32)—>(33). Если же, кроме того, функция гр(1) монотонна, то (32) «-> (33).
Пример 31. Уравнение —х2 = — х4 имеет корни хх = 0, х2=1, х3 = —1, а уравнение lg(—x2) = lg(—х4) не имеет решений. Произошло это потому, что обе функции /(х)= = —х2, g(x)~ — х4 принимают значения, принадлежащие множеству Е = (—оо, 0], а на этом множестве функция 1g х не определена.
Мы рассмотрели лишь некоторые преобразования уравнений. Разумеется, этими преобразованиями не исчерпываются 290
все те разнообразные преобразования, которые приходится применять при решении уравнений. В частности, мы пока не рассматривали преобразования, связанные со свойствами логарифмической и показательной функций. Но об этом будет сказано ниже (см. § 5). Мы закончим этот параграф рассмотрением одного важного метода решения уравнений.
6°. Метод замены неизвестного. Метод замены неизвестного применяется при решении уравнений вида
/(g(x)) = 0. (34)
Он основывается на следующей теореме.
Теорема 3. Рассмотрим уравнение
= (35)
где t — вспомогательное неизвестное, и пусть /), I.,- ... ..., tk — все корни уравнения (35). Тогда для решения уравнения (34) достаточно найти все корни каждого из уравнений
g{x)=tm (т= 1,2,. .., k) (36)
и объединить множества корней этих уравнений. Иначе говоря,
УШ=0} - {[g (х)=V [g (х)=t2] V- • • V [g (х)=tk\}.
Доказательство. Пусть t = tm — один из корней уравнения (35), а х = х0 — корень уравнения g(x) = tm. Тогда /(М = о, g(x0) = tm и потому /(g(xo)) = O, т. е. х0 — корень уравнения (34). Обратно, пусть х = хп— корень уравнения (34), т. е. /(g(xu)) = 0. Тогда ясно, что х0 принадлежит области определения функции g(x). Положим g(x0) = 10. Из равенства f (g(xo)) = O мы теперь получаем /(^о) = О, т. е. t0 — один из корней уравнения (35), скажем t0 = tm. Теперь ясно, что х0 — корень уравнения g(x) = tm.
Доказанная теорема позволяет свести решение уравнения вида (34) к решению нескольких более простых уравнений (35), (36).
Обычно эта теорема применяется следующим образом. Дано некоторое уравнение F(x) = 0. Задача заключается в том, чтобы умело подобрать функцию g(x), позволяющую ввести новое неизвестное t = g(x), и затем в ы р а з и т ь функцию F (х) через t, т. е. представить ее в виде F (х) =/(g (х)). В результате данное уравнение запишется в виде (34), и для его решения можно будет применить доказанную теорему, ‘ 10* 291
Такой прием решения уравнений и называется методом замены неизвестного (поскольку вначале решается уравнение (35), в котором неизвестное х заменено новым, вспомогательным неизвестным £).
'Пример 32. Решить уравнение
4 9
х2+ ~^—х-----4-4.
1 хг х '
2
Решение. Введем новое неизвестное t = x— Тогда
заданное уравнение примет вид
Z2 —Z = 0.
Уравнение t2 —t = 0 имеет корни ^ = 0, Следова-
тельно,
( 4 21(Г9ТГ9 11
л-2 4-4 = х— -4-4 ~ х — - = 0 V х — ~ = 1 .
( Л2 X 1 J X J V I X JJ
2 2
Решив теперь уравнения х — = и X— х~^’ найдем все корни исходного уравнения:
^ = 1/2, х2=—V%, х3 = 2, х4=— 1. I
§ 4. Простейшие иррациональные уравнения
Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо эквивалентно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.
При решении иррациональных уравнений необходимо учитывать следующее:
1) если показатель радикала — четное число, то подкоренное выражение должно быть неотрицательно; при этом значение радикала также является неотрицательным (ср. стр. 248);
2) если показатель радикала -— нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак радикала совпадает со знаком подкоренного выражения.
292
Пример 33. Решить уравнение /х-^-о + /20 —х = 7.
Решение. Возведем обе части уравнения в квадрат (п. 5° § 3) и произведем приведение подобных членов (п. 2° § 3), перенос слагаемых из одной части равенства в другую (п. 1° § 3) и умножение обеих частей на ~ (п. 3° § 3). В ре-зультате мы получим уравнение
]/х + 5 • /20 —х = 12, (37)
являющееся следствием исходного. Снова возведем обе части уравнения в квадрат. Получим уравнение
(х4-5)(20 —х)= 144,
которое (в силу сказанного в пп. 1° и 2° § 3) приводится к виду
х2 — 15х + 44 = 0.
Эго уравнение (также являющееся следствием исходного) имеет корни Xj = 4, х2=11. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Отв. х1 = 4, х2=11.
'Пример 34. Решить уравнение
/2x4-1 4- /JF=^3 = 4.
Решение. Возводим обе части уравнения в квадрат:
2x4-1 4-х—34-2)/2x4-1 .J/x—3=16, откуда переносом слагаемых в другую часть равенства и приведением подобных членов получаем уравнение
2/2x4- 1 -]/х—3 = 3(6 —х). (38)
Снова возводим обе части получившегося уравнения в квадрат:
8х2 —20х — 12 = 324— 108х4-9х2, и после приведения подобных членов приходим к уравнению х2 —88x4-336 = 0.
Это' уравнение является следствием исходного и имеет корни х2 = 4, х2=84. Корень х2 = 4 удовлетворяет исход
293
ному уравнению, а корень х2 = 84 является для исходного уравнения посторонним.
Отв. х = 4.
Замечание. При возведении уравнений в квадрат учащиеся нередко в уравнениях типа (37), (38) производят перемножение подкоренных выражений, т. е. вместо этих уравнений пишут уравнения
. /(х-)-5)(20 —х)=12, (37')
2/(2х+1)(х—3) = 3 (6 — х). (38')
Это не приводит к ошибкам, поскольку уравнения (37'), (38f) являются следствиями уравнений (37), (38):
(37)->(37')> (38)->(38')-
Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения. Это можно видеть на примере уравнений ]/х—1 -Ух— 4 = 2 и У(х—1)(х— 4) = 2: число х — 0 является корнем второго уравнения и не является корнем первого уравнения. Общий факт можно сформулировать следующим образом:
{/7(х) • Vg(x) = а} -> {K/(x)g(x) = а}.
Здесь именно односторонняя стрелка (а не равносильность), т. е. обратный переход от уравнения Уf (х) g (х) = а к уравнению //(x)Vs(x)=a недопустим: он может привести к потере корней. Правильный переход осуществляется так:
{]//(x)g(x) = а}
★+ {I//(*) /g(-v) = а] vI/—/'(*) V— g (X) = а]}.
В рассмотренных выше примерах можно было сначала перенести один из радикалов в правую часть уравнения. Тогда в левой части уравнения останется один радикал и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональная функция.
Такой прием (уединение радикала) довольно часто применяется при решении иррациональных уравнений.
Пример 35. Решить уравнение
]/х2 + 5х4-2 — /х2—Зх + З = 3.
294
Решение. Уединив первый радикал, получаем уравнение /х2 4-5x4-2 = V х2 —3x4-3 4- 3, равносильное исходному (п. 1° § 3).
Возводя обе части этого уравнения в квадрат, получаем уравнение
х2 4- 5х 4- 2 = 9 4- х2 — Зх-рЗ-р 6)/ х2 — Зх 4- 3, равносильное уравнению
4х — 5 = 3/х2 —3x4-3. (39)
Уравнение (39) является следствием исходного уравнения. Возводя обе части уравнения (39) в квадрат, приходим к уравнению 16х2 — 40х 4- 25 = 9 (х2 — Зх 4- 3), или
7х2 — 13х —2 = 0.
Это уравнение является следствием уравнения (39) (а значит, и исходного уравнения) и имеет корни
хх = 2, х2=— у.
Первый корень удовлетворяет исходному уравнению, а второй — не удовлетворяет.
Отв. х = 2.
Заметим, что если бы мы сразу, не уединив один из радикалов, возводили обе части исходного уравнения в квадрат, то нам пришлось бы выполнять громоздкие преобразования.
При решении иррациональных уравнений, кроме метода уединения радикала, применяются, с учетом вида уравнения, и другие методы. Рассмотрим пример использования метода замены неизвестного при решении иррационального уравнения.
Пример 36. Решить уравнение
У х-1 у 12-2х 2 •
Решение. Положим
у х — 1
Тогда уравнение примет вид
295
откуда получаем следствие!
2u2 — 5и + 2 = 0.
Решая это квадратное уравнение, находим два корня:
„ 1 — 2, и2 — 2 •
Задача сводится теперь к решению следующих двух уравнений:
^/1|^2х = 2, (40)
3/12 —2х 1
у-^г=-2- ei)
Возводя обе части уравнения (40) в куб, получаем
12 —2х о
1 - б,
X — 1
откуда = 2.
97
Аналогично, решив (41), находим х2=у.
Оба найденных корня удовлетворяют исходному уравнению, так как в процессе решения мы использовали (кроме замены неизвестного) только преобразование вида
[/W = g(x)] -* { [f (X) ]3= [g(x) ]3},
а при таком преобразовании, как было отмечено выше (стр. 289), получается равносильное уравнение.
„97
Отв. х, — 2, х<, — tv .
§ 5. Логарифмические и показательные уравнения
Рассмотрим преобразования, которые чаще всего применяются при решении логарифмических и показательных уравнений.
1°. Потенцирование. Так называется преобразование, заключающееся в переходе от уравнения
log«,(x)f(-v)=,log?wg(x) (42)
к уравнению
f(x) = g(x). (43)
296
Как видно, здесь рассматривается общий случай, когда неизвестное х входит и в основание логарифмов, и в выражения, стоящие под знаком логарифма. Потенцирование является допустимой операцией, т. е. при этом преобразовании потери корней не происходит. Однако могут появиться посторонние корни. В самом деле, если некоторое число х0 является корнем уравнения (42), то (на основании свойств логарифмов) это означает, что выполняются следующие условия:
1) <р(х0)— положительное число, отличное or 1;
2) оба числа /(х0) и g(x0) положительны;
3) f (х0)=^(хп).
Но последнее как раз означает, что х0 есть корень уравнения (43). Итак, каждый корень уравнения (42) является и корнем уравнения (43), т. е. уравнение (43) является с л е д-ствием уравнения (42), и потери корней не происходит. В то же время уравнение (43) может иметь такие корни, для которых первое или второе условие не имеет места, т. е. может иметь корни, не удовлетворяющие уравнению (42).
Пример 37. Решить уравнение
log2x = log2(6 — х2).
Решение. Потенцируя, получаем уравнение х — 6 — х2,
имеющее корни xL = 2 и х.> = — 3.
Проверка показывает, что корень Xj = 2 удовлетворяет исходному уравнению (при подстановке получаем log22 = = log22, т. е. 1 = 1)- Второй же корень является посторонним: при подстановке его в исходное уравнение под знаком логарифма получается отрицательное число. Итак, исходное уравнение имеет только один корень х — 2; число же х=—3 корнем исходного уравнения не является. Как видим, в результате потенцирования появился посторонний корень, так что проверка была необходима.
2°. Логарифмирование. Логарифмирование и потенцирование — взаимно обратные преобразования, т. е. если потенцирование заключалось в переходе от уравнения (42) к уравнению (43), то, напротив, логарифмирование означает переход от уравнения (43) к уравнению (42). Иными словами, мы берем от обеих частей уравнения (43) логарифмы при основании ф(х). Сразу же ясно, что логарифмирование является, вообще говоря, недопустимой операцией. Ведь если при
297
переходе от уравнения (42) к уравнению (43) могут появиться посторонние корни, то это означает, что при переходе от уравнения (43) к уравнению (42) часть корней уравнения (43) может быть утеряна.
Пример 38. Решить уравнение
(1 + х2)1 + ^х = (1 4- х2) 2 + ^х.
Если взять от обеих частей логарифм при основании 1 4-х2, то мы получим уравнение
1 + У"х = 2 4* Ух,
не имеющее корней. Между тем исходное уравнение, как легко проверить, имело корень х=0.
Таким образом, в результате логарифмирования произошла потеря корней. Значит, логарифмирование было в данном случае недопустимым преобразованием.
В каких же случаях все же можно применять логарифмирование? На этот вопрос легко ответить, вспомнив сказанное ранее.
Если х0 является корнем уравнения (43), т. е. для него имеет место третье из упоминавшихся выше условий, то число х0 будет корнем уравнения (42) лишь тогда, когда выполнены и первые два условия. Иными словами, переход от уравнения (43) к уравнению (42) допустим лишь в том случае, если мы уверены, что для каждого из корней уравнения (43) выполнены первые два условия. Например, если хотя бы одна из функций /(х), g(x) принимает лишь положительные значения, а функция <р (х) — лишь положительные и отличные от 1 значения, то логарифмирование (т. е. переход от уравнения (43)к уравнению (42)) допустимо, причем при этих условиях (43) (42).
В частности, если а—-положительное число, отличное от 1, и хотя бы одна из функций /(х), g(x) принимает лишь положительные значения, то от уравнения (43) можно перейти к уравнению 4
log0/(x) = log0g(x), (44)
причем в данном случае не происходит ни потери корней, ни появления новых корней, т. е. уравнение (44) равносильно уравнению (43). Например, уравнение
(45)
298
где Л — положительное число, отличное От 1, равносильно уравнению
/(x)=g(x).
Пример 39. Решить уравнение
2^2-3x_J_
Решение. Обе части этого уравнения положительны при всех х.
Беря от обеих частей логарифм при основании 2, получаем х2 —Зх = — 2,
откуда находим корни ^=1, х2 = 2. Проверку можно не производить. Исходное уравнение имеет два корня: х1=1, х2 — 2.
3°. Применение основного логарифмического тождества. Это преобразование заключается в переходе от уравнения
y(x)log?W/w = /i(x) к уравнению
/(х) = /г(х).
Такое преобразование всегда допустимо, т. е. потери корней при этом преобразовании не происходит. Но могут появиться посторонние корни (по тем же причинам, что и при потенцировании).
Пример 40. Решить уравнение
(№ + з) _ 4
Применяя основное логарифмическое тождество, получаем уравнение х2-|-3 = 4, откуда легко находим х2 = I, х2 = —1. Но ни одно из чисел 1 и —1 .не является корнем исходного уравнения, так как ни 1, ни — 1 не может служить основанием логарифма.
Таким образом, применение основного логарифмического тождества привело к появлению посторонних корней. Значит, при применении этого преобразования проверка необходима.
4°. Переход к новому основанию логарифмов. Рассмотрим уравнение
Iog¥ (л) f О) = logp (х) g{x). (46)
Если в уравнении (46) перейти к логарифмам по основанию /г(х), то получится уравнение
logftw/(x) = log/z<x>g(x) /47ч
iogA<x>q>(«) iogA1JPp(x)’ v ’
299
Пусть Эо— корень уравнения (46). Это означает, Что выполняются следующие условия:
1) функции ср (х), f (х),р (х), g (х) определены прих = х0;
2) ф(х0)>/ (х0),р (х0), g(x0)— положительные чис-ла, причем ф(*о)^1, Р(х0)^\;
3) log?(X0) f(x0)= logp(*o)g(x0).
Если функция h(x) определена при х = х0 и удовлетворяет условиям /г (х0) > 0 и /i(x0)^l, то выражения IOgA(xo)f(-^o)> logft(xl)) Ф(*о), logA(je|))g(Xo) И 10gA(Jfo)^ (Хо) имеют смысл, причем
IOgA(x0) ® (хо) # о, log*<jro) р (х0) # 0.
В этом случае имеет место равенство (см. стр. 264)
lOg/K-VQ./fa) = lOghiXp, g(x0) 10gA<^OI ф М logA(x0) р(х0) ’
т. е. число х0 является корнем уравнения (47).
Таким образом,- если функция h(x) определена и принимает положительные значения, отличные от I, в точках, где определены левая и правая части уравнения (46), то при переходе к логарифмам по основанию h(x) потери корней не происходит. Ясно, что в этом случае переход от уравнения (47) к уравнению (46) также не приведет к потере корней, т. е. уравнения (46) и (47) равносильны.
Однако, если переход к новому основанию h(x) совершается формально, без учета требования о том, чтобы h(x) была положительной функцией и не принимала значение 1, можно потерять корни.
Пример 41. Если в уравнении log2* х= log х перейти к логарифмам по основанию х, то получится уравнение log** __ log** log,. 2* , х ’
S log*-2-
левая и правая части которого при х—1 не определены. Но число х==1—корень исходного уравнения. Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня х—1, надо указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай х—1.
300
5°. Применение свойств логарифмов. Остановимся лишь на применении формулы логарифма произведения. Это преобразование заключается в переходе от уравнения
bg¥(x) f(x) -р logT(.v) g(x) = h (x) (48)
к уравнению
log^, [/(x)g(x)] = /i(x). (49)
Это преобразование допустимо, т. е. не приводит к потере корней. Однако оно может привести к появлению посторонних корней. В самом деле, если некоторое число х0 является корнем уравнения (48), то это означает, что выполняются следующие условия:
1) <р(х0)— положительное число, отличное от 1;
2) оба числа /(х0), g(x0) положительны;
3) число х0 удовлетворяет уравнению (48).
Отсюда на основании свойств логарифмов вытекает, что logi(xo) f(Xo) + Iog¥(xo) £(*о)= logyfxo) [/(х0)^(х0) ], так что х0 удовлетворяет и уравнению (49). Итак, каждый корень уравнения (48) является и корнем уравнения (49), т. е. уравнение (49) является следствием уравнения (48), и потери корней не происходит. В то же время уравнение (49) может иметь такие корни, для которых условие 2) не выполняется (хотя по-прежнему f(x0)g(x0) > 0), г. е. корни, для которых выполнено условие:
2') оба числа /(х0), g(x0) отрицательны.
Этим и объясняется возможность появления посторонних корней при переходе от уравнения (48) к уравнению (49).
Пример 42. Решить уравнение
log6 (х — 1) + logo (5х + 3) = 2.
Решение. Применяя указанное преобразование, мы приходим к уравнению
log6 (х— 1) (5x4-3)= 2, а от него (потенцированием) — к уравнению
(х — 1) (5х 4- 3) = 36,
имеющему два корня: Xj = 3, х2 =—у. Проверка показывает, что Xj — корень исходного уравнения, а х2 является посторонним корнем. Заметим, что появление постороннего
301
корня произошло именно в результате применения формулы логарифма произведения, а не в результате потенцирования (так как х2 является корнем промежуточного уравнения).
Следует заметить, что обратное преобразование (т. е. переход от уравнения (49) к уравнению (48)) является, вообще говоря, недопустимой операцией, т. е. при переходе от уравнения (49) к уравнению (48) может произойти потеря корней. Чтобы этого не произошло, нужно в случае необходимости переходить от уравнения (49) не к одному уравнению (48), а к дизъюнкции двух уравнений:
log¥(.v) f (х) 4- log.^ g (х) = h (х), (50)
log^x) [ — f{x) ] + log^-v) I — g (x) ] = h (x). (51)
Такое преобразование не приведет ни к потере корней, ни к появлению посторонних корней, т. е. (49) «-» {(50) \/ (51)}. Иначе говоря, объединяя вместе все корни уравнений (50), (51), мы получим все корни уравнения (49).
В заключение параграфа рассмотрим некоторые типы простейших показательных и логарифмических уравнений.
А. Показательные уравнения. 1. Пусть дано уравнение вида
a₽(.v) = ^ ' (52)
где а > 0, <2^1, £>0, Р(х) — заданный многочлен (с действительными коэффициентами).
Так как левая и правая части уравнения (52) положительны, то, логарифмируя обе части уравнения (52) по основанию a (а>0, a# 1), получим уравнение
- P(x)=log61fe,
равносильное (см. 2°) уравнению (52).
Заметим, что при Ь<_0 (<2>0, а#1) уравнение (52) решений не имеет.
Пример 43. Решить уравнение
Решение. Имеем {4*"+0,“л: = 8 }<-»{№-]-0,5x=log4 8}, откуда находим: хх=1, х2=—1,5.
2. Аналогично решаются уравнения более общего вида:
af*(4 up^...apnn^=b,
(53)
302
где Др аг,..., ап, b — заданные положительные числа, Рг{х), Р.2 (х),Р„(х) — заданные многочлены. Логарифмируя обе части уравнения (53) по некоторому основанию а (а > О, ау_ 1), получим уравнение
Pi (X) log^i + Р2 (х) logaa2 +... + Ря(х) logaan = logab,
равносильное уравнению (53).
Пример 44. Решить уравнение
2л'Зх'15*+2 = 4.
Решение. Логарифмируя данное уравнение по основанию 2, получаем равносильное уравнение
х + (х— 1) log2 3-ф- (х-{-2) log25 = 2, откуда
2 + log23-21oga5 .
1 +log23 + log25
3. Рассмотрим показательное уравнение вида
P(V) = 0, (54)
где а — заданное положительное число, а 1, Р (t)—заданный многочлен.
Заменив неизвестное по формуле
t = ax, получим уравнение
Р(/) = 0. (55)
Пусть tlt t2,..., tn — все положительные корни уравнения (55). Так как уравнение
ах = Ь (а 0, a# 1)
имеет решение в том и только в том случае, когда Ь^>0, то корнями исходного уравнения будут все корни уравнений вида ax=tm, т. е. числа x = logatm (т= 1, ..., п).
Пример 45. Решить уравнение
8Г — 2-9л — 3 = 0.
Решение. Полагая / = 9A, получаем уравнение
/2 —2/ —3 = 0,
имеющее единственный положительный корень ^ = 3.
303
Решив уравнение 9* = 3, находим х = Следователь-
„ 1 но, данное уравнение имеет единственный корень х — -^. Проверка не нужна.
Б. Логарифмические уравнения. I. Пусть дано уравнение вида
logaP(x) = &, (56)
где а, b — заданные числа, д)>0, a^l, Р (х)—заданный многочлен.
Уравнение (56), как было отмечено выше (стр. 302), равносильно. уравнению
Р(х) = аь. (57)
Все корни уравнения (57) и только они являются корнями уравнения (56).
Пример 46. Решить уравнение logj (2х'~— 2х—1)=— •
9
1 /1 \ — 2
Решение. Уравнение 2х2—2х—1 = (д-1 , равно-
сильное заданному уравнению, имеет два корня: хг= — 1, х2 = 2.
Отв. х± = — 1, х2 — 2.
2. Рассмотрим уравнение более общего вида:
«iIogaP1(x) + n2IogaP2(x)+ ... +»* logaP*(%) = &, (58)
где а и b — заданные числа, а)>0, a # 1; nlt пг,..., Пь— заданные целые числа; Р1(х), Р2(х), ..., Р*(х)— заданные многочлены.
Потенцированием перейдем от уравнения (58) к уравнению [Pi(x)]n4^Win2--[^(-v)]^ = a6. (59)
Уравнение (59), как было отмечено на стр. 296—297 и 301, является следствием уравнения (58).
Решениями уравнения (58) будут те и только те корни уравнения (59), для которых каждый из многочленов Рх(х), Р2(х),..., Pk(x) принимает положительное значение.
Пример 47. Решить уравнение
2 Iog8 (х — 2) — 1 og3 'х2 — 4х + yj = 2, (60)
304
Р е ш-е н и е. уравнение
Потенцированием уравнения (60) получаем
(61)
2 . , 28 ’
х2-4х+^-
имеющее корни х1=1, х2 = 3.
Корнями уравнения (60) будут те из найденных корней,
ДЛЯ которых одновременно выполняются неравенства [х — 2>0, ) 2 Л | 28 \О (62) X2 4х + 0> 0.
Из чисел Xj = l, х2=3 неравенствам (62) удовлетворяет только число х.2 = 3.
Отв. х=3.
3. Рассмотрим уравнение
logP(JC) N=n, (63)
где N —заданное положительное число, п — заданное целое число, Р (х)— заданный многочлен.
Следует отметить, что левая часть уравнения (63) имеет смысл только для таких значений х, при которых /•’(х)'>0 и Р(х)у±1. Потенцированием переходим от уравнения (63) к уравнению
1Р(х)]л = М (64)
которое является следствием уравнения (63).
Корнями уравнения (63) будут те и только те корни уравнения (64), которые удовлетворяют условиям Р(х)^>0, Р(Х) # 1.
Пример 48. Решить уравнение logv х 9 = 2.
Решение. Решая уравнение (х — 1)2 = 9, находим xt = 4, х.2 =—2. Условиям х—1^>0, х—1 1 удовлетворяет
только корень х1 — 4.
Отв. х = 4.
Задачи к главе IX
9.1. Можно ли утверждать, что верное числовое равенство переходит в верное равенство, если применяются следующие преобразования:
а) прибавление одного и того же числа к обеим частям равенства;
б) умножение обеих частей равенства на одно и то же число;
305
в) возведение обеих частей равенства в одну и ту же степень п (п — натуральное число)?
9.2. Можно ли утверждать, что при применении преобразований, указанных в предыдущей задаче, неверные числовые равенства переходят в неверные?
9.3. Можно ли утверждать, что если = — неверное равенство7 то а — b также является неверным равенством?
9.4. Покажите, что . понятие равносильности уравнений обладает свойством транзитивности: если уравнение А равносильно уравнению В, а уравнение В равносильно уравнению С, то Л и С — равносильные уравнения, т. . е. если А<-*В, В <->С, то А-^-С.
9.5. Покажите, что введенное для уравнений понятие следствия обладает свойством транзитивности: если для уравнений А, В и С имеют место соотношения А-+В, В-+С, то А —> С.
9.6. Покажите, что если для уравнений А, В и С имеют место соотношения А^В. В^-С, то А -> С.
9.7. Покажите, что на множестве всех действительных чисел уравнения х2 = 2х—1 и х2 (х4 1) = (2х—1)(jc4—|—1)
равносильны.
9.8. Пусть функции f(x), g(x), /j (х), gj (х) и <р (х) определены на множестве М действительных чисел. Проверьте, равносильны ли на этом множестве указанные ниже пары уравнений. Какое из двух уравнений каждой пары является следствием другого?
a) /W = g(x) и ~=~;
б) /(x)-g(x) и /?W = /i(x);
B)/(x) = g(x) и sin/(x) = sing(x);
г) f(x) = g(x) и arcsin/(х) = arcsin g(x);
Д) gW = gTW и /(х) й (х)=Л (х) 8 (х);
е) У7(Х)У^(Х) =ф(х) и K/(x)g(x) = tp(x).
9.9. Пусть функции /(х) и g (х) определены на множестве М действительных чисел и принимают на этом множестве действительные значения одного знака. Докажите, что на множестве М {/(x) = g(x)}<-»{[/(x)]2 = [g(x)]2}.
9.10. Покажите, что уравнение [/(x)]2 = [g(x)]2 может иметь корни, отличные от корней уравнения /(x)=g(x), 306
й Что эти корни, если они есть, удовлетворяют уравнению /(x)4-g(x)=0.
9.11. Пусть функции /(х) и g(x) определены на множестве М, и пусть Et и Е2 — множества значений соответственно функций /(х) и g(x). Докажите, что если функция ср (7) определена на множестве Е — Е1(]Е2, то на множестве М уравнение <р [ f(x)] = ср [ g (х)] является следствием уравнения /(x)=g(x).
9.12. Используя метод замены неизвестного, решите уравнения:
а) (х2 — 2х)2 — 2х2-ф4х— 3 = 0;
б) (х-ф 1)(х-ф 2)(х-ф 3)(х -ф 4)= 3.
Решите иррациональные уравнения (9.13 — 9.22):
9.13. ]/х + 7+/х^2 = 9. 9.14./х 4-17 —]/х —7 = 4.
9.15. /2х— 15 — ]/х4- 16 = — 1.
9.16. /2х24-3x4-2 — /2х24-3х —5 = 1.
9.17. 2/х2 —2x4-4 — |/'х2 —2x4-9 = 1.
g । g 1^3 -[- х 4~ У$ — х_2
(734-х — УЗ — х
9.19. у 5-фх — 2pz5— х=у^25 — х2.
9.20. Ух4-У'х+1 4-/х + 2 = 0.
9.21. ]/х4-6 —4/х4-2 4-]/И 4-х— 6]/х4-2 = 1.
9.22. V784-х4-1/259 —х = 7.
Решите показательные уравнения (9.23 — 9.41):
9.23. З^+^'Э3*-1. 9.24. 4Л'2~*+1 = 8*.
1 - 1
9.25. 2 (23+^)2<-* = 16^7-'-
9.26. 2-За+3 4-7-3*-2 = 493.
9.27. б2-*-1 —5*= 100. 9.28. 33-2-*-1 — 4*+1 = 2.
9.29. ЗЛ*-1-)--^- 9*+1 = 6 • 22А — у-32<
9.30. 22* • 9* — 2 • 63* ~14- 42*~1 • З4* -2 == 0.
9.31. 23х-3х—2ЗА’-1 • 3*+1-}-288 = 0.
9.32. 3 • 4х-|-2 • 9*= 5 6А'. <
307
9.33. 5I+— 7 -10 * 4-2-4 х =0.
9.34. 4-1/8Т —12 у 36 4-9^16 =0.
9.35. (V3 - /8 У 4- (У 3 4- J/8 У = 6.
9.36. 52* — 3х — 15-25*4-15-Зх=0.
9.37. 53л4-53<1-*’4-15(5х4-51-*) = 216.
9.38. 8-v+14- 8 • (0,5)3х 4- 3 • 2*+з = 125 — 24. (0,5)х. П л ______ /
9.39. у Xх = х? х (п— натуральное число).
9.40. хх = У хх (/г —натуральное число). п----------------
9.41. (хх)п = х? х (п— натуральное число).
Решите логарифмические уравнения (9.42 — 9.47).
9.42. log4[logs(log2x)] = -i-.
9.43. 1g (х24- 19) —lg (х — 8) = 2.
9.44. У 5 log2 (— х) = log2 V х2.
9.45. log^S-log.v 34-logx 3 = 0.
3 81
9.46. loglexx34-logx}/x=2.
9.47. loga (ax) • 1g д; (ax) = logU2 У, a>0, a^l.
ровно один корень?'
9.49. При каких значениях а уравнение ^а— имеет хотя бы одно решение? Найдите все решения.
Решите уравнения (9.50 — 9.55):
9.50. 1g (х2— х — 6) 4-х = 1g (х 4- 2)-|-4.
9.51. 2х — lg(52x4-x — 2) = lg4x.
9.52. log3(4-3x — 1) = 2x4-1-
9.53. log2 (2*4- 1) • log2 (2X+14- 2) = 2.
9.54. 90-3logj;4 — (дУ°г* 8 = 81‘°г*2
9.55. 0,1 -x'g*-' =10.
ГЛАВА X
СИСТЕМЫ УРАВНЕНИЙ
§ 1. Равносильные системы уравнений.
Система, являющаяся следствием данной
В этой главе мы для простоты изложения будем рассматривать системы уравнений с двумя неизвестными. Однако все основные результаты остаются в силе и для систем с большим числом неизвестных.
Систему двух уравнений с двумя неизвестными будем записывать в следующем виде:
y) = g^x, у), /2(х, y) = g,(x, у).
Решением системы. (1) называется пара чисел (х0, у0), при подстановке которых соответственно вместо хну каждое уравнение системы (1) становится верным числовым равенством, т. е.
fi(xw Уо)~ gi(.xo> А'о)> Уо) = ёз(хо’ У а)-
Решить систему — значит найти в с е ее решения.
Заметим, что фигурная скобка в записи системы уравнений (см. (1)) заменяет собой знак конъюнкции. В самом деле, при решении системы мы ищем такие пары чисел (х0, у0), при подстановке которых в систему и первое и второе уравнения превращаются в верные числовые равенства.
Две системы уравнений
fi(x> У) = ёАх, У),
А(х, y)=g2(x> у) и
/з(х> У) = ёз(х> У)< 3
А(х, y)=gi(.x, у)
309
называются равносильными (эквивале нт ним и), если они имеют одни и те же решения, т. е. всякое решение системы (2) является решением системы (3) и, наоборот, всякое решение системы (3) является решением системы (2).
Понятие равносильности систем зависит от того, на каком множестве мы ищем решения. Так, система
Г (х2+У+ l)(x+j) = 0,
х—_у = 0
равносильна системе
( х4-у = 0,
I х—_у = 0,
если мы ищем только действительные решения, и не равносильна, если допускаются комплексные решения.
Из определения равносильности систем вытекает, что любые две системы, не имеющие решений (несовместные системы), равносильны.
Из определения равносильности систем следует также, что если в системе уравнений заменить любое из уравнений равносильным ему уравнением, то получим систему, равносильную исходной. В частности, система (1) равносильна следующей системе:
( fax, уУ—g^x, _у) = 0,
I fax, у') —fax, у) = 0.
Таким образом, любая система двух уравнений с двумя неизвестными может быть записана в виде
| Fi(x, j) = 0,
I F2(x, т) = 0.
Систему уравнений
( fax, y)=g6(x, у), I fax, У)=ёв(х, у)
назовем следствием системы (1), если каждое решение системы (1) является решением системы (4). Аналогично, уравнение
F(x, y) = G(x, у) (5)
310
есть следствие системы (1), если каждое решение системы (1) удовлетворяет уравнению (5).
Из определения равносильности и следствия непосредственно вытекает, что к системе можно присоединить любое уравнение, являющееся ее следствием, и при этом множество решений системы не изменится. Иными словами, если уравнение (5) есть следствие системы (1), то система (1) равносильна системе трех уравнений (1), (5).
Пример 1. Найти действительные решения системы уравнений
xj + 24=^-,
ху — 6 = •
Решение. Перемножая уравнения, получаем
(ху 4- 24)(ху — 6) = х2у2, откуда находим
ху = 8. (6)
Уравнение (6) является следствием исходной системы. Поэтому, присоединив к исходной системе уравнение (6), получим систему
1ху = 8,
ху + 24 = ^-,
о ху — 6 = ,
которая равносильна исходной системе. Используя первое уравнение этой системы, мы легко упростим второе и третье уравнения и придем к системе
/ ху — 8,
I
I —— = 32,
< У
£- = 2. х
Если теперь почленно перемножить первое и второе уравнения этой системы, то мы получим уравнение
311
х4 = 8 • 32 = 28, являющееся следствием этой системы. Точно так же, перемножив первое и третье уравнения, мы получим уравнение >4 = 16 = 24. Таким образом, мы приходим к системе | х4 = 28, I У = 24,
являющейся следствием данной системы.
Так как мы ищем действительные решения, то из этой системы находим
х — ±4, у=±2.
Используя уравнение (6), получаем два действительных решения: (— 4; —2) и (4; 2). Проверка показывает, что оба решения удовлетворяют исходной системе.
§ 2. Основные приемы и методы решения систем
При решении систем уравнений применяются различные приемы и методы: метод линейного преобразования системы, метод приведения системы к дизъюнкции более простых систем, метод подстановки, метод исключения неизвестных, метод замены неизвестных и т. д.
Применяя эти методы (при определенных условиях), мы заменяем исходную систему равносильной ей более простой системой, а затем решаем эту более простую систему (или совокупность более простых систем).
Перейдем к изложению перечисленных выше методов решения систем уравнений.
1°. Метод линейного преобразования системы. Пусть дана система уравнений
(А(х,у) = 0,
\f2(x,y)<=0. U
Будем говорить, что система уравнений
f aJi (х, у) + а2/2 (х, у) = О,
I bifi О У) + b2f2 (х, у) = О
получена из системы (7) с помощью линейного преобразования (av а2, blt b2— заданные числа), а число
Д =
Я1
bi
а2
^2
= агЬ2 — а2Ьх
312
будем называть определителем этого линейного преобразования.
Такие преобразования применяются довольно часто при решении систем. Рассмотрим в качестве примера систему уравнений
fi(x, У)+/г(х, _у) = 0,
fi(x, У) — АО- у) = 0,
полученную из системы (7) сложением и вычитанием уравнений системы (7). Нетрудно проверить, что эта система равносильна системе (7).
Естественно выяснить вопрос: в каком случае система (8), получающаяся из системы (7) линейным преобразованием, равносильна системе (7)? Ответ на этот вопрос дает следующая теорема.
Теорема 1. Если
то система (8) равносильна системе (7).
Доказательство. Пусть (х9, у0)— решение системы (7). Тогда имеют место числовые равенства
fi Оо- То) = О, А Оо- у0) = 0.
Отсюда следует, что при любых av а2, blt b2 справедливы числовые равенства
aifi Оо- _у0) + а2/2 Оо- у0) = 0, bifi Оо- То) + b2f2 Оо- То) = 0-
т. е. Оо-То) — решение системы (8).
Докажем теперь, что если выполнено условие (9), то всякое решение системы (8) является решением и для системы (7). Пусть OpTi) — решение системы (8). Тогда имеют место числовые равенства
( aifi Oi- Ti) + Or- Ti) = 0>
I bifl О1- Ti) + b2f2 (xt, у J == 0.
Для сокращения записи введем обозначения
ti =A (х» У1), t2 =f2 (x1; у J.
313
Тогда система равенств (10) примет вид f ci-tti —I— cintu —— 0, I 1112- (Ц)
1 Vi + ^2=o. ’
Докажем, что если Д 0, то из (11) вытекают равенства ^i =/i (xv _У1) = 0> —fi (xi> У1) = 0. (12)
Рассмотрим систему двух уравнений ( а,и 4-a2v — 0,
. L. п (13)
( bpi + b2v — О
с двумя неизвестными и и v. Заметим, что, в силу равенств (И), пара чисел (tv t2) образует решение системы (13). Пара чисел (0, 0) также, очевидно, является решением этой системы. Но так как определитель Д = а1&2—йха2 системы (13) отличен от нуля (условие (9)), то система (13) имеет только одно решение. Значит, ^ = 0, £2 = 0.
Итак, мы доказали справедливость равенств (12). Следовательно, (хх; _ух) — решение системы (7).
Теорема 1 доказана.
2°. Метод приведения системы к дизъюнкции более -простых систем. Будем говорить, что система уравнений
( A(x,j) = 0,
равносильна дизъюнкции систем
( gi(-v, Т) = 0,
I §2(*>-У)=° и
( Ф1(х, _У) = 0,
I <Р2(*> ^) = 0>
(14)
(15)
(16)
если каждое решение системы (14) является решением хотя бы одной из систем (15), (16) и всякое решение каждой из систем (15), (16) является решением системы (14).
Вместо слов «система (14) равносильна дизъюнкции систем (15) и (16)» употребляют также слова «система (14) распадается на две системы (15) и (16)» или «система (14) равносильна совокупности систем (15) и (16)».
314
Разумеется, можно говорить о равносильности системы уравнений (14) дизъюнкции трех и более систем уравнений.
Пример 2. Система уравнений
| х2—_у2 = 0, ( ху —1 = 0
равносильна дизъюнкции систем
( х — у = 0, ( x-j-y = 0,
< и <
( ху — 1=0 ( ху — 1=0.
Теорема 2. Если функции /j (х, у), f, (х, у),..., fk (х, у), g(x, у) определены на некотором множестве М, то на этом множестве система уравнений
( fi(x, y)f2(x, у) ... fh(x, у) = 0,
I. g(x, _у) = 0
равносильна дизъюнкции систем
( /1(-К, т) = °> ( Л(*> т) = о, / Л(*>т) = °>
I g(x, _у) = 0, ( g(x, т) = 0, ” ( g(x, y) = 0.
Доказательство. Пусть (x0; y0) e M, и пусть (x0; _y(l) — решение системы (17). Тогда все функции, стоящие в левых частях системы (17), определены при х = х0, у=уо и справедливы числовые равенства
J fi (хо> y^f2 (-’“О' То) • • • fk (-*ч)> То)== О Я)
I g(x& То) = О. (20)
Из (19) следует, что хотя бы одно из чисел /р(х0, _у0) (р=1, 2, ..., k) равно нулю. Пусть, например,
Л(^о>То) = О. - (21)
Из (20) и (21) следует, . что (х0; _у0) — решение одной из систем (18), а именно системы
( fi(x, _у) = 0,
I £(-*> Т)=°
(причем (х0, у0) е М). Обратно, пусть (х0; _у0) — решение системы
(fPO> т) = о,
I g(x, т) = 0
315
(здесь р — одно из чисел 1, 2, k), причем (х0, _у(|) е М.
Тогда fp(x0, _уР) = 0, g(x0, уо) = О, причем в точке (х0, _у0) все функции /1 (х, _у), ...,/* (х, _у) определены, откуда следует, что пара чисел (х0, _у0) удовлетворяет и системе (17). Теорема доказана.
Замечание. Всякое решение системы (17) есть решение одной из системы (18). Обратное, вообще говоря, неверно. Это связано с тем, что одна из систем (18) (например, система /х(х, _у) = 0, g(x,y)=Q) может иметь такое решение (х0; _у0), которое не входит в область определения какой-либо из функций /2 (х, j), ..., fk (х, _у), а значит, не является решением системы (17).
Поэтому обычно при решении систем вида (17) поступают так. Находят все решения всех систем (18), а затем подстановкой в систему (17) отсеивают те из найденных решений, которые не удовлетворяют системе (17) (не входят в область определения левой части первого уравнения (17)).
Предоставляем читателю доказать, что имеет место следующая более общая теорема.
Теорема 3. Если функции fp (х, _у) и gm (х, _у) (р = 1 ,... ..., Л; т=1, ..., п) определены на множестве М, то на этом множестве система уравнений
( /1 (х, У)/г (х, у) ...fk (х, у) = О,
I gl(*> У)§2 (X, У) • • • gn (X, у) = О равносильна дизъюнкции kn систем
)/р(х, Т) = 0, j 2, ..., k\ т~\, 2, ..., и).
lgm(-V,T) = °> 7
3°. Метод подстановки. Этот метод позволяет сводить решение системы уравнений с двумя неизвестными к реше-ihjio одного уравнения с одним неизвестным. Обоснованием метода подстановки служит следующая теорема.
Теорема 4. Система уравнений
( -к = ф(т)>
i F(x, j-) = 0
(22)
(23)
равносильна системе уравнений
х==ф(Т)>
/ЧфСу), tJ = o.
316
Доказательство. Пусть (х0; _у0) — решение системы (2-2). Тогда справедливы числовые равенства
-4) = фСУо)> (24)
F(xo,yo) = O. (25)
Из (24) и (25) следует, что
F[<POo)> То] = О. ' (26)
Равенства (24) и (26) показывают, что (xQ; _у0) — решение системы (23).
Обратно, пусть (х(|; _у(|) — решение системы (23). Тогда справедливы числовые равенства (24) и (26), откуда следует равенство (25). Из равенств (24) и (25) заключаем, что (х0; д'о) — решение системы (22). Теорема доказана.
Пример 3. Решить систему уравнений
J х~у2 + 1, t ху = у2+у3.
Решение. Исходная система, согласно теореме 4, равносильна системе уравнений
( х =у2 4- 1, { Х = у2 4~ 1,
1 (>24- 1)т=У+т3> Т' е’ I т = у2-
Последняя система распадается на две системы:
[ х =_у24~1, f х=_у24~1>
< и <
I J’ = ° I
Отв. (1; 0), (2; 1).
4°. Метод исключения неизвестного. Пусть дана система уравнений
( F\ (х, у) = 0,
I 7 (27)
\ F2(x, у)=0,
и пусть одно из уравнений этой системы, например первое, можно разрешить относительно х (или у). Точнее, пусть уравнение /4 (х, у)=0 равносильно уравнению х = <р(у). Тогда, в силу теоремы 4, система (27) равносильна системе { х — <р(у), (28)
I Рг [<Р СУ), Т1 = 0, (29)
т. е. справедлива следующая теорема.
311
Теорема 5. Если уравнение (х, у) = 0 равносильно уравнению x = tp (у), то система уравнений (27) равносильна системе (28)—(29).
Заметим, что решение системы (28) — (29) сводится к нахождению корней уравнения F2 [ср (у), у] = 0. Таким образом, мы исключили неизвестное х из системы и вместо системы должны решать уравнение с одним неизвестным. Поэтому такой прием решения и называется методом исключения неизвестного.
Если мы умеем находить все корни yv у2.......ут урав-
нения (29), то можно сразу написать все решения системы (27). Эти решения таковы:
(ф О1)> Л)> (Ф Ог)’ Уг)> •••> (ф (Ут), Ут)-
Пример 4. Найти действительные решения системы уравнений
| х + 4 =_у3, | х2— _у6 = 8.
Из первого уравнения находим х = у3— 4 и, подставляя во второе, получаем _у3= 1.
Уравнение _у3=1 имеет один действительный корень у=1.
Отв. (— 3; 1).
5°. Метод замены неизвестных (введение новых неизвестных). Поясним вначале метод замены неизвестных на следующем примере.
Пример 5. Решить систему уравнений
L-l 1 = А
У + у 6 ’ .
2 _ 1 =_5
х2 у2 ~ 36'
Решение. Введем новые неизвестные п== —, г = —. х у Тогда система примет вид
( । 5
» + ^==1Р
I и2 — =
I об
318
Эта система уравнений равносильна системе
. 5
н + г’= У’
1
И — 1» = с",
6
„ 1 1 г
имеющей единственное решение н = у, V — у. Следовательно, исходная система имеет одно решение (2; 3).
Отв. (2; 3).
В общем случае метод замены неизвестных (для системы двух уравнений с двумя неизвестными) состоит в следующем.
Пусть дана система уравнений
, ( F, (х, у) = О,
I IV (30)
I F2(x, _у) = 0,
и пусть функции Fj (х, у) и F2 (х, у) можно представить в виде
( FJx, >»)=/;[ф1 (аг, у), (р2(х,у)],
I F2 (*> у) =/2 [Ф1 (х, у), <р2 (х, _у)].
Положим
Ф1 (х> У) = «> ф2 У) = (32)
Тогда в силу (31) система (30) преобразуется к виду
( Л (и, v) = 0,
I ’ (33)
I /г(и> v)=0.
Предположим, что мы умеем решать систему (33), и пусть vk) (Л=1, 2, ..., я)— все решения системы (33). Тогда, решив п систем уравнений
Ф1(*> =
ф2(х, y) = vk
(Л=1, 2, ..., и)
(34)
и объединив решения систем (34), мы найдем все решения системы (30).
* *
*
Все рассмотренные методы имеют одну общую особенность: они позволяют заменить данную систему другой системой (или совокупностью систем), равносильной данной системе.
319
§ 3. Однородные системы двук уравнений второй степени с двумя неизвестными
Однородными системами двух уравнений второй степени с двумя неизвестными будем называть системы вида
( a1x2-^-b1xy-^-c1y2 — d1, (35)
( а2х2 + bycy с2у2 = d2. (36)
Предположим сначала, что ни одно из чисел dv d2 не равно нулю. Умножая уравнение (35) на d2, а уравнение (36) на — t/j и складывая' полученные уравнения, мы придем к уравнению вида
Ах2Вху-\-Су2— О, (37)
являющемуся следствием системы (35) — (36). Из теоремы 1 (стр. 313) следует, что исходная система (35) — (36) равносильна системе (35), (37). Таким образом, описанный метод «уничтожения» свободных членов позволяет свести систему (35) — (36) с отличными от нуля правыми частями к системе того же вида, у которой, однако, одно из чисел dv d2 равно нулю.
Итак, пусть мы имеем систему (35), (37) (где возможны оба случая: dx О, <Z1 = 0). Рассмотрим нахождение тех решений этой системы, для которых у 0 (отыскание решений, для которых у — 0, если они есть, не представляет труда). При у 0 уравнение (37) равносильно уравнению
д(у)2 + ^(у) + С = °. (38)
Для решения системы (35), (38) нужно решить уравнение (38) как квадратное относительно ~. После этого, подставляя най-
денные значения — в уравнение (35), мы найдем решения системы (35), (38).
Пример 6. Решить систему уравнений
( х2 4~ Зху2_у2 = 3, (39)
| 5х2 — Чху— _у2 = 5. (40)
Решение. Умножая первое уравнение на 5, а второе на 3, получаем после вычитания
13_у2 4-21ху— 10х2 = 0. (41)
320
Таким образом, МЫ должны решить Систему (39), (41), равносильную исходной. При _у = 0 мы из (41) получаем х = 0, а пара (0; 0) не удовлетворяет уравнению (39). Следовательно, у 0, и потому уравнение (41) можно заменить уравнением
Ю f—У—21 {—— 13 = 0, \у) \У/
(42)
из которого получаем
_х\____1_ _13
2’ \yj~5’
(43)
Таким образом, система (39), (42), равносильная исходной, равносильна в силу (43) дизъюнкции следующих двух систем (распадается на две системы):
х2 + Зху / 2_у2 = 3, у = — 2х
х2 + 3ху + 2у2 = 3,
Решив эти системы, найдем четыре решения исходной системы:
(1; -2), (-1; 2),
/ 13 5 \ / 13
\/Г38’ /138/ ’ /138’
Подобный способ применим и для решения систем вида ( f(x, _у) = 0, (44)
|g/,j) = 0, (45)
где хотя бы одна из функций f (х, у) или g(x, у), например f(x, у), является однородным многочленом относительно х и у, т. е.
/(х, j)=апхп 4- +... + + апуп. (46)
Как и для системы (35), (37), при рассмотрении системы (44), (45) (где функция f(x, _у) имеет вид (46)) отдельно ищутся решения, для которых _у = 0, и решения, для которых у 0.
Решения, для которых _у = 0 (если они существуют), находятся следующим образом. Если а0 0, то из (44), (46) находим при _у = 0, что аох” = О, т. е. х = 0, и остается проверить, удовлетворяет ли пара (0; 0) уравнению (45). Если
11 В. Г. Болтянский н др. 321
ао==О, то при у = 0 уравнение (44) удовлетворяется (в силу (46)) при любом х, и потому остается найти корни уравнения g(x, 0) = 0 (т. е. уравнения, получающегося из (45) при _у = 0).
При нахождении решений, для которых у 0, можно разделить обе части уравнения (44) на уп- Мы получим уравнение
/ X \п , / X \ ”~1 , . / X \ , п
a°\V/ + +• • •+—о,
левая часть которого представляет собой многочлен относительно t=-~. Если tv t2, ..., tn — корни этого многочлена, то задача сводится к дизъюнкции систем
( х —t
< у (А=1, 2, и),
I g(x, _у) = 0
т. е. к рассмотрению п уравнений (с одним неизвестным у) вида
§(hy, У) = 0 (А=1, 2, ..., и).
Пример 7. Решить систему уравнений
( Xs 4- 2х2у — ху2 — 2у3 — О,
I х2 + у2 = 8.
Решение. Из первого уравнения при j> = 0 получаем х=0, но пара чисел (0; 0) не удовлетворяет второму уравнению, т. е. не является решением системы. Значит, для любого решения мы будем иметь у 0. Разделим первое уравнение на _у3 и положим ~ = Получим уравнение I3 -|--|-2/2—t — 2 = 0, имеющее корни t1=l, — 1, t3 =—2.
Теперь задача сводится к нахождению решений следующих трех систем:
( х=_у, ( х——у, ( х ——2у,
| х2+У = 8, j х2+у2 = 8, | х2+у2 = 8.
Отв. (2; 2), ( — 2; -2), ( — 2; ’2), (2; —2),
/4/2. 2 /Т\ / 4/2 . 2/2\
\ Кб’ Кб/’ \ Кб' Кб/
322
§ 4. Системы симметрических алгебраических уравнений
1°. Симметрические системы с двумя неизвестными. Пусть система
( fi(x, _у) = 0, I fi(x, у) = Ъ
такова, что (х, у) и /2 (*> У) являются симметрическими многочленами от х и у, т. е. j\ (х, у) и /2 (х, У) не меняются при замене х на у, а у на х.
Простейшей системой указанного типа является система уравнений
| х4-_у = а, (47)
| ху = Ь, (48)
прием решения которой описывается следующей теоремой. , Теорема 6. Система уравнений (47), (48) и квадратное уравнение
t2—at-\-b = 0 (49)
связаны следующим образом: если и t.,— корни квадратного уравнения (49), то система (47), (48) имеет два решения: (ff, t2) и (t2, С)— и не имеет других решений. Обратно, если (х0; _у0)—решение системы (47), (48), то числа х0 и у0 являются корнями уравнения (49).
Доказательство. Пусть 1г, t2 — корни уравнения (49). По формулам Виета имеем
~^2 ===::
Ц2 = Ь,
т. е. пары чисел (/х; ^2) и (t2, ^) являются решениями системы (47), (48).
Покажем, что других решений система (47), (48) не имеет. Пусть (х0; у0) — какое-либо решение системы (47), (48). Тогда х0+_у0 = а, хоуо — Ь, и потому многочлен t2— at-\-b можно записать следующим образом:
t2 — at + b=t2 — (x0 + j0) t + xoyo=(t—x0) (t —y0).
Отсюда мы заключаем, что числа х0 и у0 являются корнями квадратного уравнения (49). Теорема 6 доказана.
11* 323
Пример 8. Решить систему уравнений
x+j=1, ху= — 2.
Решение. Уравнение (49) для данной системы имеет вид t2— t — 2 = 0. Его корни £t = 2, t2= — 1. Следовательно, данная система имеет решения (2; —1) и (—1; 2).
В теореме 6 были использованы простейшие симметрические многочлены от двух переменных:
-х + у и ху.
Введем для этих многочленов следующие обозначения:
x+j' = o1, ху — а2. (50)
Можно показать, что любой симметрический многочлен /(х, у) может быть выражен через симметрические многочлены <т1 = х4~_у и O2 = XJ4
Поэтому при решении симметрических систем алгебраических уравнений рекомендуется вводить новые неизвестные о., по формулам (50). Выгода такой замены неизвестных заключается в том, что степени многочленов в результате замены, как правило, уменьшаются и система сводится к более простой.
Пример 9. Найти действительные решения системы уравнений
( ху(х-\-у) = &,
| х3+у3 = 9.
Решение. Мы имеем
xy(x+j') = a1a2> х3 + у3 — (х+у) (х2—ху+у2) =
= (х+У) 1(х+у)2—Зху] = ot (а? — Зст2), и потому в результате замены (50) система примет вид
0iO2 = 6,
°i — Зо1оа = 9.
324
Отсюда находим of = Зс^Оз 4-9 — 27. Так как мы ищем только действительные решения, то о1 = 3, и тогда а2 = 2. Решив систему
-Г-|-_у=3,
ху—2,
найдем два решения: (1;2) и (2; 1).
Отв. (1;2), (2; 1).
В общем случае решение симметрической системы
[ А(^т) = о, I А(х,у) = 0
можно проводить по следующей схеме. Нужно ввести новые неизвестные ах, <j2 (можно их обозначать через и, v или как-либо иначе) по формулам (50). Мы получим новую систему относительно неизвестных olt о2. Предположим, что эту новую систему мы сумели решить, и пусть
(<hl а2), (bi, b2), (li, 12)
— все ее решения. Тогда исходная симметрическая система равносильна дизъюнкции систем
( x-\-y — ai, ( x-\-y—bv ( x-]-y=li,
( ху—а2, | xy = b2, ’ ( xy—l2.
При использовании этого приема приходится выражать симметрические многочлены от х, у через Oj и о2. На практике достаточно уметь выражать через о2 симметрические многочлены вида
Sn = xn + yn,
называемые степенными суммами.
Степенные суммы Si, Si, Si, S4, S5 выражаются через о1==х4-у и a2 — xy следующим образом:
S) — х + у — cTi, (51)
S2 = x2 + >2 = (x+j')2 — 2x_y==oj— 2cr2, (52)
Si = x3+у3 = (x 4-y) [(x 4-y)2 — 3xy] = crl — Зо^, (53)
Si = xi +У1 = (x2 4- y2)2 — 2x2y2 — (a'i — 2a2)2 — 2o4 =
= aj—4a^a24-2a|, (54)
Si = x® 4- J*5 = (x2 4- y2) (x3+y3) — x2y2 (x 4- y) —
= S2S3—GjOi = (of — 2a2) (o4 — SctjG.,) аха|=
= ~ 5afa3 4- OGjoi- (55)
325
2°. Решение некоторых иррациональных уравнений путем сведения к решению систем симметрических уравнений. Рассмотрим уравнение вида
. Va-f{x) + Vb+f(x)^c. (56)
Для его решения введем вспомогательные неизвестные и и v, полагая
У a—f(x)=u, Vb+f(x)=v. (57)
Из (56) и (57) для определения и и v получаем симметрическую систему алгебраических уравнений
Пусть х = х0 — решение уравнения (56). Тогда пара чисел («0; г»0), где
zz0 = /a —f(Xo), v0=Vb+f(x0),
является решением системы (58), причем оба числа и0, т0 неотрицательны. Обратно, пусть (zz0; т>0)—произвольное неотрицательное решение системы (58) (т. е. и0 Эг О, ц(| 0).
Докажем, что всякое решение уравнения
u0 = Va—f(x) (59)
(или уравнения т»0 = Vb+f(x)) удовлетворяет уравнению (56).
В самом деле, если x = xt— корень уравнения (59), то
«o=V a—f(x1').
Тогда из системы (58) находим
= (а + Ь) — и"й = b+/(х^,
и так как то^О, то v,, — ]/b 4- f (Xj). Первое уравнение системы (58) дает теперь
/«-/(ХО + Г^ + /(хх) = с,
т. е. х = хх— корень уравнения (56).'
Таким образом, для решения уравнения (56) нужно прежде всего решить систему (58). Если (ult (и2, т2) — решения 326
системы (58), то уравнение (56) равносильно дизъюнкции уравнений (см. (59)):
[]/a—/(x)=hJ V [Ка—/(-^) = «21-
Пример 10. Решить уравнение
Ух+ 5 4- /20 —х = 7.
Решение. Система (58) для данного уравнения имеет вид
и 4- -v = 7, Z?2 4-7?2==25.
Эта система имеет два решения: (3; 4) и (4; 3). Если и = 3, то из уравнения/х 4~ 5 = 3 (или из уравнения/20— х = 4) находим х = 4. Аналогично, при и = 4 получаем х=И.
Отв. х1 = 4, х2=11.
Замечание. При решении уравнений вида /«4-/(x)4-/^4-/(-v) = f (с#=0)
удобно, положив и —Уа 4- f (х), и =/ь 4-/(х), перейти к системе
J и 4- v — с, ( и2 — v2 = a— b,
которая, как легко видеть, при с ф 0 эквивалентна системе
3°. Симметрические системы с тремя неизвестными. Обратимся теперь к системам трех уравнений (с тремя неизвестными), левые части которых симметрично зависят от неизвестных х, у, z.
Пусть система
’ А(х, у, г)=0, /2(х, у, г) —0, /8(х, у, г) = 0
такова, что /2, /3 являются многочленами, симметричными относительно х, у, z, т. е. каждый из этих многочленов
327
не меняется, если поменять местами любую пару из трех чисел х, у, z.
В этом случае удобно ввести новые неизвестные
x-j-y-j-z = u, xy-j-xz-j-yz = v, xyz — w.
Такая замена, как правило, ведет к упрощению исходной системы. Простейшей системой рассматриваемого типа является следующая система:
•г+т + г==а’ (60)
ху + zx = Ь, (61)
xyz = с, (62)
прием решения которой описывается следующей теоремой.
Теорема 7. Система уравнений (60) — (62) и кубическое уравнение
t8-at2-\-bt — c = Q (63)
связаны друг с другом следующим образом. Если tx, t2, t3 — корни уравнения (63), то система уравнений (60) — (62) имеет следующие шесть решений: (^; t2, t3), (tf, t3, t2), (t2, ty, t3), (f3; ^i)> (^ ^i)> (ми решения получаются
всевозможными перестановками трех чисел t2, t3) и не имеет других решений. Обратно, если (х0; у0; z0) — решение системы (60) — (62), то числа х0, у0, z0 — корни уравнения (63).
Доказательство. Пусть tx, t2, t3 — корни уравнения (63). Воспользуемся формулами Виета для корней кубического уравнения:
^1 + G + ^3 = а’
^1 ^2 ^2^3 4* =
Ti t213 — с.
Эти равенства показывают, что набор чисел (^; f2; t3) образует решение системы (60) — (62). Другие пять решений получаются перестановками чисел tb t2, ts. Покажем, что этими шестью решениями исчерпываются все решения системы (60) — (62). Пусть (x0',y0;z0)— какое-нибудь решение системы (60) — (62). Тогда справедливы числовые равенства
хо + Уо 4~ го = а’
хоУо + У о? о + гохо ~
хоУо2о ~
328
Следовательно, многочлен t3— at2-\-bt— с можно записать следующим образом:
t3 — at2-\-bt — с =
= t3 — (х0 + + z0) t2 + (XOJ/O + JVo + zoxo) t—x(ly(lz(l =
= (^ — x0)(t— — Zo).
Из последнего равенства заключаем, что числа х0, _у0, z0 являются корнями уравнения (63). Теорема 7 доказана.
Пример 11. Решить систему уравнений
хуz = 2, xy+yz + zx= —1, xyz = —2.
Решение. Составляем кубическое уравнение f3 —2f2 —^+2 = 0.
Находим корни этого уравнения: t1—l, f2== — 1, ^а = 2. Согласно теореме 7' данная система имеет следующие решения: (1;—1;2), (—1; 1;2), (— 1;2; 1), (2;—1; 1), (2; 1;—1),(1; 2;—1).
Замечание. К системе вида (60) — (62) сводятся следующие системы:
х ~)~у 4~ z = x2+y2 + z2 = b, xyz — с,
x+y-\-z = a, х2 +у2 + ~2 — Ь, х3 4-У3 + z3 — с,
х2 +_Уа + z2 = а, ху + xz-\-yz = b, xyz = с, х2 + у2 + z2 = а, xy + xz+yz — b, х3 -J-j/3 4- z3 = c.
При сведении этих систем к системе (60) — (62) можно использовать следующие тождества:
х2 _1__у2 = (х _|__у г)2 — 2 (xy-j-yz + xz),
(x+y + z)3 =
= № +.У3 + Z3 + 3 (x 4- z) (xy-\-yz 4- xz) — 3xyz, (x-j-y-j-z) (x2 4~T2 + Z2 — xy — xz —yz) =
= x3 4->3 + z3 — Sxyz.
329
Задачи к главе X
10.1. Докажите, что система уравнений fi(x, _у) = 0, f2(x, у) = $ равносильна каждой из следующих систем:
а ( Л(*>-У)+А(*- J)=0;
б) f Л(х,у)=0,
' I fi(x, у)—/2(х,» = 0;
в) Г /j(-v, У) = 0,
j а/j (х, j/) + ₽А(^ J')=0 (₽ 0, а —любое).
10.2. Докажите, что система уравнений х3 —д,з _ a —уу хл +.У3 — Ь(х + у)
равносильна дизъюнкции следующих четырех систем:
а)
в)
X—у = Ъ, х 4-_у = 0;
х—у— О, х2— хуУ-у2 — Ь = 0;
б)
г)
х+_у = 0, х2 4- ху -|- у2 — a = 0:
х2 + ху +_у2 — a = 0; х2 — ху+у2 — b==G.
10.3. Рассмотрим систему уравнений
( Л(х, >) = а,
I f2{x,y) = b, где ab =# 0.
а) Докажите, что система уравнений
(64)
/1(-г, y)f2(x, y) = ab, Л (.х, У) a
fi (х, у) b
является следствием системы (64).
б) Докажите, что при ab^ 0 система (64) равносильна системе
( /1 (х, у) а
J f2 (х, у) b ' ( Л(х,у) = а.
330
10.4. Докажите, что система уравнений ( [Л (х, у/)]2 = [ft (х, У)]2, I f2(x,y) = 0
является следствием системы
I f2(x,y)=0.
10.5. Докажите, что если функция ф(х, у) определена при всех значениях неизвестных, для которых определены левые части системы
/ А(*>_У) = 0,
I А(Х,у) = 0,
(65)
то система
/1 (х, у) + <р (х, у) • f2 (х, у) = О, /2(х,у/) = 0
равносильна системе (65).
10.6. Пусть функции А(х, у), gk(x>y) (k=l, 2) определены на множестве М. Докажите, что на этом множестве а) каждое из уравнений
flgl~ f2gi> flg2~fiSl
есть следствие системы
fi — f>’
gi g2>
(66)
б) каждая из систем
| Л=А>
I figi ~fzg&
fi=f»
figi —figi
равносильна системе (66) на множестве М, если хотя бы одна из функций fv f2 не обращается в нуль на множестве М.
10.7. Докажите, что система уравнений
Л(х,^, г) = 0, f2(x,y, z) = 0, f3(x,y, z) = 0
331
равносильна каждой из следующих систем (неизвестные для краткости записи опущены):
а) /1 = 0> /1+/2 = 0> Л4’А+Л:=®5
б) /1 = 0, /2 = 0, Л-/3=0;
В)/1 = 0, А+/3 = 0, Л-/3 = 0;
г) fi + /2 ~ 0, '/1+/з = 0, /г + /з = О;
Д) /2 + /3 — /1 — 0, /з—/г + /1 = 0, /1+/2 — /з = 0;
е)/2 = 0> /з = 0> fi + “/2 +'₽/з == 0 (а, 0 — любые числа).
10.8. Докажите, что если abc =/= 0, то система уравнений
' fi(x, у, z)=a,
f2(x, у, z)=b, f3(x, у, z) — c
равносильна системе уравнений
' /1(х, у, z) — a, fs(x, у, г) = h fi (х, у,. г) а ’ /з(*. У, г) _ с_ fi (х, у, г) а'
Решите системы уравнений (10.9—10.17):
10.9. | х2 —_у2 = 5, х+_у = 5. 10.10. ( х—у = 3, | х24-_у2 = 5.
10.11. [ х2+у=13, | ху = 6. 10.12. < f X2— у2 = 3, ( х2-^-ху+у2 = 7.
10.13. 1 х2 + Зху = 54, | 4j/24-xj=115. 10.14. 1 ' хз + ху=10) 1 j'34-xaj’=5.
10.15. ( х4-_у + х_у = 5, | х2+у2 + ху=7. 10.16. | { (х~у)(у~ 1)=з, 1 (х+2) (.у+ 2) =24.
|-(х2 + х+1)(У+у/+1)=3, ( (1-х)(1-J)=6.
332
Решите симметрические системы (10.18, 10.19) с помощью замены неизвестных по формулам (50):
10.18.
х 4-4=1, xs+y=19.
[ л-4 4- у4 = 82, 10.19.
( ху — 3.
10.20. Решите уравнение
/ х + 3 + Y 94—х = 5
методом сведения к системе симметрических уравнений.
10.21. Докажите формулы (обозначения см. на стр. 325):
1) = О'г'-’л-г (я > 2);
2) S6 = o| ——2о4
Решите системы уравнений (10.22—10.29):
10.22. Зх34 2уЗ= 26, 1 - -- = 4, 10.23. { х У 6
10.24. Xs—у3 = 61 (х—у), (^4-1)(j+1)=12.
10.25. < х3 4- х3У3 + У3 = 17, ху 4-х4~у = 5. Х1 4- у1 — 2 у "i* х — 2 ’ ( x-j-y=3,
10.26. i+i=2 =зз. X у 2 ’
10.28. •! х4+У= 17 (х 4-у)3, ху = 2(х+у). ' х2 4- у2 = х 4- у,
10.29. < X4 4-y = l(X4.J7)2.
10.30. Найдите действительные решения системы уравнений
(ха+У)(х-у)=13, ху (х—у) — 6.
333
Решите системы уравнений (10.31—10.37):
( х2(1+у+у2+у3)=160, 0,3 ’ ( х2(1—j'+y2—У) = —80. •
( (х+Жх—_у)2= 125,
( (х—_у)3 (х + у)2 = 25.
( х2 = Зх -4- 4у, ( х3 = 1 Ох + у,
10.33. { 2 . ' 10.34. { , , 1Л
( у2 = 4х + Зу ( у3 = х 1Оу.
( 2х2у2 — 3_у2 + 5ху — 6 — 0,
10,35‘ 1 Зх2>2 — 4у2 у Зх_у — 2 = 0.
( Зх2у2 + х2 — Зху — 7 = 0, Ю-Зб. j Юх2>2 + 3х2 —20xjr —3 = 0.
( 4 (х3 + У3) = 9 х2у2,
10 47 J
’ . ' | 4(х2+_у2) = 9х2^2 — 8ху.
10.38. Найдите действительные решения системы уравнений
( (х-^)(х2-У)=7,
I (x+j)(x2+/)= 175.
Решите системы уравнений (10.39, 10.40):
10.39.
10.40.
' xs^ + xy = ^(x + y)2, xtv + xy4 =у (x+j)3. х(У2+1) . 3 х2 + у2 5 ’
t/(x2-l) = 4_ х2-уу2 5 ’
Найдите действительные решения систем уравнений (10.41, 10.42):
( х3 + 4у—у3 -|- 16х,
10.41. { 1+г/2_5
( 1+х2
( х3+у3 + х2у + ху2 = 5, 10 42 <
| х*у2 + х2у* = 20.
334
' Решите системы уравнений (10.43, 10.44):
10.43.
10.44.
ху । х + 2у о
х-у2у + ху ’
ху , х—2у _ 4 '
X — 2у -г ху
х2 + ху + -1^ у2 — х — ^-у=2, ~ х2 — ху +у2 + 2у — х = 3.
10.45. Найдите действительные значения а, при которых система уравнений
х2 — у'2 — 1,
у — ax-yb
при любом действительном значении b имеет действительные решения. •
Найдите действительные решения систем уравнений (т, п — целые положительные) (10.46, 10.47)?
( х2-|-у2=1,
10,46’ I х2т+у2п=1.
Г x2+j,2==1)
10.47. S 2л+1 I 1 _v2zi+l I 1
( Л I у1т~ 1 I х2т+1 •
Решите системы уравнений с тремя неизвестными (10.48—10.64):
ху — §,
2
10.48.
10.50.
yz = 3, Ю.49.
zx—2.
ч 1 Х3== д У2, y3 = ^zx, 10.51.
з 8
z3 = ^xy.
3 2-v=2 У’ ху = 6z.
' x(y-J!-z) = 27, у (x + z) — 32, z(x-j-y) = 35.
335
10.52.
10.53.
10.54.
10.55.
*
10.57.
10.58.
10.59.
10.60.
10.61.
' x(x+j + ^) = 7, y(x+y + z)=14, z (x + У + ~) — 26.
’ (^+^)(^+^ + 2)=18, (j4-z)(x+_y + £) = 30,
. (x + z)(x+y + z) = ‘24. x2-\-xy-\-xz— x = 2, y2 + xy+yz—y= — 2, Z2 -|- XZ -f-yz — z = 6.
y3 + z3 = 7л-3, y + z — 3x = 0, 10.56.
z — x=y — 2.
, 1 3
J' + y-- 4 .
, * 9
Z "T" " === "o" •
1 x 2
1+1+1 *
x 1 у 1 г 6 x-yy = z, у —|— z —— — 2/Х»
2x + -W15, \г у /
Мт + тЬ20’
6z(- + ~] = 13.
\У X /
27л-3— v3— 13 —= О, г
Зх2г — 4ху + у = О, 3xz—yz= 1.
' (x+y)2 — z2 = 4, (y-^z)2 — x2=2, (z + x)2 — y2 = 3.
x-yy + z = l, • xy -\-yz 4- zx = — 4.
X3 4~_y3 + 23=1.
336
x-}-y-}-z = 2,
10.62. X2 -\-у2 + z2 = 6, xs_|_j,3_|_2s_ 8. x+j + ^ = 4,
10.63. x2+y2 + z2=l4, xy + xz—yz = 5. 5ху=6(х-]-у),
10.64. 3yz = 2(y + z), 4zx = 3 (z -|- x).
10.65. I Зайдите действительные решения системы ху + xz + yz — И, х2+у2-j-z2 = 14, xyz — 6.
10.66. 1ри каких значениях а система уравнений хи хг цг „ = а, —— = а, — = а2 х + г у + г
имеет хотя бы одно решение? Найдите эти решения.
Решите системы уравнений с тремя неизвестными (10.67—10.71):
10.67. ху-\- х-\-у — 1, yz -|-у z = — 3, zx -j- z 4~ х = — 5. 24 (х-[-у — z) — xyz,
10.68. 24 y(j'4-2 — x) = xyz,
10.69. - 8 (х 4- z —у) = xyz. х+у = 1_ хуг 12’ У + г = _5 хуг 12 ’ гу-х _ 1 хуг ~ Т-
337
10.70.
10.71.
х2 + 5уг + 4г2 4- 4ху 4- 4yz — 125, х2 4- 3_у2 — 4г2 4- 4х_у — 4yz =±=75, х 4-.У 4--г —8-
х—2у 4" Зг = 9, х2 4* 4_у2 4* 9^2= ! 89, 3x2 = 4_у2.
10.72. Найдите все действительные решения системы уравнений
х2 4- 4х_у 4- бу2=з, х2 — 4x^4- 12г2 = 2, .
у24- Ъуг 4- 2г2 == 0.
Решите системы уравнений с тремя неизвестными (10.73—10.75):
10.73. ' X-j-y — 2=1, x24-v2—22=—з, xs+ys — z3 = —29.
10.74. x+y + ? = 0, x2-{-y2 — 23 — 20, x4-j-y4 — 24 = 560.
10.75. to |io CO 4 O1 |co II II n Im a, ~ 4" ~ 4— 4 1 x ч + + + -^ | X | St — | *>
10.76. Найдите действительные решения системы уравнений 3(х4-^) = 2,
• 3(x24-j2)=52,
3 (х3 4- У3) = 7г.
10.77. Найдите все решения системы уравнений 1 x+y = z, J у2 4- z2 = 1 Зх2, ( 2(x34-^3)=7y3'
338
Решите системы уравнений с тремя неизвестными (10.78—10.82):
(х4-у/)(х4-2,)=х, (х + 2у) (х + 2г) — х,
(y + z)(y + x)=y, 10.79.- (j + 2x)(j + 22)=j', (z + x)(z+y)=z.
' ху — х-\-у — z, xz = 2(x— y + z), Ю.81. yz — 3 (_y - - x + z).
10.78.
10.80.
10.82.
xyz 4- xz2 = 2, ху 4- ‘Zxz — —z, x2yz — —15.
10.83.
уравнений
. (z + 2х) (z + 2у) = z. ' {xy-y)(x-^z) = x,
. U 4~Л')(~ +j)— %z.
Найдите все действительные решения системы
x2 + xy 4- ^xz — 4г2 = 0, у2 + ху + ^yz — 8г2 = 0, xyz — 8.
10.84. Пусть (х; у, z) — решение системы уравнений (х — а) (у — a) (z — a) — d, (х—Ь)(у— b) (z — b) = d, (х — с) (у — с) (z — c) = d,
а, b, с нет равных.
причем известно, что среди чисел - Найдите x3-[-ys-]-z3.
Решите системы уравнений с тремя неизвестными (10.85—10.90):
10.85.
2(x2-\-y2) = xyz, \0{y2 + z2) = 2Qxyz, 5 (г2 -|- х2) = 13xyz.
10.86.
6х (у2 4- z2) 13yz, 3y(x2 + z2) = 5xz, 6z (х2 4- У2) — 5ху.
10.87.
4^ = 22.
х2у2
339
10.88.
2 (x2y2 -\-y2z2 -J- z2x2) Qxyz = 0, 2_y (x2 — z2) + 3xz — 0, ‘2z(x2—y2) + 3xy = 0.
22 _ 3_ ху ~ г ’ + м |<е + X | N II 1 ьз] СО
10.89. уг-\-гг~х2 = 2 10.90. Z/Z х ’ * + Ч: | м + м 5 х II ьг| со
г/2 —х2 —г2 _ 2[ xz ~ у ' ху + yz 4-zx = — з.
10.91. Найдите все действительные решения системы уравнений
х3-{уа— za— xyz——4,
ха — у3 z3 — xyz = 8,
—x3-j-J'3 + ^3 — xyz — —2.
10.92. Решите систему уравнений
2х2 +_у2 + z2 = 9 +_уг, x2 + 2y + z2=6+.V2, х2 -|~_у2 -|- 2г2 = 3 -|- ху.
10.93. Найдите действительные решения системы уравнений
х2 -|- 2yz = 1, у2 4-2гх = 2, z2 4- 2ху=1.
Решите системы уравнений с тремя неизвестными (10.94—10.96):
х2 -{-yz = 42, ' х2— _у.г = 3,
10.94. _у24-хг = 42, 10.95. J,2 —хг = 5,
z2 4- ху = 50. " х2 4- ху +j'2 = 7, Z2—ху — — 1.
10.96. у2 +уг 4- z2 = 3, Z2 4- XZ 4- х2 — 1.
340
xz -\-yt=.2, xz2 -\-уР — 5, хг34-vi3= 14.
Решите системы уравнений с четырьмя неизвестными (10.97, 10.98):
ху + xz -\-yz — 27, yz + ty-{-tz—0, zx-\-tz-{-tx=O, xy + tx 4- ty = 0.
10.98.
10.97.
10.99. Решите систему уравнений ’ х2 + х3 + ... + х„^+х„=1, , хх -j- х3 • • + xn_i хп = 2,
. *1 + *г + *з + -•• + *«-! ==»•
10.100. Найдите все решения системы уравнений Зх^х2 == Х-^ 4~ х% 4- 2, Зх2х3 = х24-х34-2,
3xn_jхп=хл_] 4- хп 4- 2, 3xnX] — хп 4~ X} 4- 2.
Решите системы уравнений (10.101—10.144):
10.101.
|<х4-улу = 3, х2 4~72 = 65.
10.102.
l/x24-y + /2xj» = 2V2,
Vx-^Vy^-
10.103.
l у ly x + y 2 ’ x24-j2 = 226.
10.104.
10.105.
5-21/х2-14-у2 = 3, У
3 (X -У) 4- Т7=-+ ЗУ = 0.
У х2 — 1 — х
^4-2]/^Т14-У = з)
341
10.106.
/25—х® — /25—/ = у 8,
/ 25- л'2 + /25—^2 = /16+ (х'+уУ
ЗА- । 2^+1 = 5, (3х —22>’=65,
10.107.'! Ю.108. ,
I • (З2—2J' = 5.
( 272*+ 27^ =12, [ ху =9,
10.t0S.| 27„,= 3,/3. '0.110.
10.111. I /> + 7у = 3,
I (2х+ 14_у)2А = 72.
( х2у +16 = 3уху + 2 у2,
Ю.112+1 ^4 + ЗхЛ
10.113. / 10.114
( уху =хв.
гг = _у3,
2
,г — х\
2 /х + 2 У у = 9г.
( х-9У~Х-}-2у 3~х~у = 8 3 2х+У,
10,115, | Зх < 32-v+A'+2_у • 32х"'5’+1 = 72 •
1 х-2х~у+1 + Зу-22хЬ' = 2,
1 °’116’ I 2х • 22х+У + Зу • 8 V+V = 1.
,п I lg2x + lg2J/=5,
10-117. ,
I 'g* — lg>=l-
1П ИЯ I Ig(x2+j2)=l+21g2,
I lg(x+j)-lg(x-y) = lg2.
( 101 + >?(* +y) = 2,5,-
;2^>2=4 + 2_y.
10.119.
i) В этом примере (и последующих) мы придерживаемся следующего соглашения: если в уравнении содержится выражение, представляющее собой степень, в основание и показатель которой входят неизвестные, то ищутся лишь такйё решения, при подстановке которых основание степени положительно. Например, так как в системе 11.112 содержится выражение хУ, то берутся лишь те решения системы, для которых х>0.
342
10.125.
10.128.
10.129.
(5—logt(x—» 9 2 =81,
log2 (x 4-_y) 4- log2 (x —y) = 3.
( (Хг__у2уогнх~л =8, 10Л21‘\ (x+j,)10^<*2~'’’) = 64.
( (x—4)^<л' + ’'5)==0,2, 10Л22. J (0,l)ig(*-j0 = 2x4-3.
j y^-3x-4__ J I 321OS’<4>’S-*> = 1
10.123. { , ’ ------
I log2x=>.
2 1 1 1 10
x3_V3 4-x3^3 =y,
. 21og3x4-log3> = 3.
!1 2
л3 +>3 = 13, logex4-21og6j/ = 3.
in 197 / !og2 (iv) + 2 iog, (x — _y) = ^ — log4 32, х2+У = 20.
y2 n2
±_4-«~== 12, z/ x
log. — 1
2-iog>^_(_5 ^=2.,
22log2x 4-3210^3) =8, 21og j x 21og
2 2 4-3 3 =|.
10.124. < -y-.v v-v
[ 2 2 —2 4 =2.
Ю.130. M°g2^ + log4 7 = 3, I x24-16p2=17.
10 131 J log8(,og2*) + lo£l^oglJ^ = l, ( Л-2_/=16.
10.132. ( ^‘-2'“-’-.11,
10.133 J 1оё2—4—=1,
I 31Og3xlOg3y2=:4.
• 343
10.134. f log3O —x) = log8(3_y—5х), I x24-_y2 = 5.
10.135. [ 5(logj,x4-logx>) = 26, [ xy = 64.
10.136. ( 5 1 10gJ,x4-10gx> = y,
[ log12(x2+>2)= 1.
10.137. f xy2 2x — x2 — 2xy = 0, I 21og.v>4-logJ,x = 3,
10.138. ' 20-х|огз>4-7-_у!°8зЛ=81 f3, [ xy = 9 9.
10.139. | [ log2x.logx(x—3y)=2, [ X • _у'°ел> =y2 •
10.140. I 3 10gxa4-10gaZ> = 2, ( a'og/«-v=y,
tz tz 1.
10.141. 1 ' logttx- log6> = loga&, >0, >0, a =4= 1,
10.142. j [ logax + loga2y=l, 1 b'°s^y + x2 = 2a, a > >0, >0, a =7^ I, 1.
Г logax4-loga2> = c,
10.143. i - log ] у >0, a =7^ 1.
. x2 4- a a = 2ac,
10.144. { ' (ax)'za =(&y)!gft, >0, tz =4 1,
/,1g (ax) _ a^g(by)> >0, b=£ 1.
Задачи на составление уравнений1)
10.145. Кусок материи стоит 35 рублей. Если бы в куске было на 4 м материи больше, а каждый метр стоил на 1 рубль дешевле, то стоимость куска материи осталась бы прежней. Сколько метров материи было в куске?
Некоторые из предлагаемых задач можно решить непосредственно, не составляя уравнений.
344
10.146. бассейн можёт наполняться водой из Двух краНбв. Если первый кран будет открыт в течение 10 мин, а второй — в течение 20 мин, то бассейн будет наполнен. Если первый кран будет открыт в течение 5 мин, а второй — в те-
3
чение 15 мин, то заполнится -у бассейна. Определить, сколько времени нужно для наполнения бассейна каждым краном в отдельности.
10.147. Лодка должна проплыть по реке из пункта А в пункт В и обратно. Расстояние между А и В равно а; скорость течения реки равна v. Какова должна быть скорость лодки, чтобы время движения было меньше t?
10.148. Из пункта А, расположенного на кольцевой дороге, выезжают одновременно в одном и том же направлении велосипедист и мотоциклист. Пока велосипедист прошел один круг, мотоциклист прошел несколько больше трех полных кругов и оказался в том пункте В, где он в первый раз обогнал велосипедиста. Во сколько раз скорость мотоциклиста больше скорости велосипедиста?
10.149. Пассажирский поезд обгоняет товарный, идущий по параллельному пути. Мимо машиниста товарного поезда пассажирский проходит за 10 сек, а мимо машиниста пассажирского поезда товарный проходит за 40 сек. Если бы эти поезда двигались с теми же скоростями навстречу друг другу, то полное время встречи (от встречи локомотивов до расставания хвостовых вагонов) было бы равно 16 2/3 сек. Во сколько раз скорость пассажирского поезда больше скорости товарного?
10.150. Пловец плывет против течения реки и встречает по пути плывущую по течению пустую лодку. Он продолжает плыть еще т мин после момента встречи против течения, а затем поворачивает назад и догоняет лодку в s м от места встречи. Найти скорость течения реки.
10.151. Два велосипедиста выехали одновременно: один из А в В, а другой из В в А. Каждый ехал с постоянной скоростью и, приехав в конечный пункт, тут же поворачивал обратно. Первый раз они встретились в р км от В, а второй раз — после того как оба повернули обратно — в q км от А. Найти расстояние АВ.
10.152. Из пункта А в пункт В одновременно отправляются пешеход и велосипедист. Доехав до В, велосипедист поворачивает обратно и встречает пешехода через 1 час после выезда из пункта А. После встречи пешеход продолжает
345
идти в В, а велосипедист поворачивает и тоже едет в В. Доехав до В, велосипедист снова поворачивает обратно и встречает пешехода через 40 мин после первой встречи. Определить, за какое время пешеход пройдет расстояние от А до В.
10.153. Один вкладчик положил в сберкассу некоторую сумму денег, а второй вкладчик — вдвое большую сумму. Сумма первого вкладчика через т лет стала р рублей, а сумма второго через п (п т) лет стала q рублей. Определить, какова первоначальная сумма денег каждого вкладчика и сколько процентов (в год) выплачивает сберкасса.
10.154. Пароход отправляется из пункта А вниз по течению реки. Через час за ним отправляется катер и догоняет пароход в 60 км от А. Если бы с момента отправле-ния катера пароход увеличил скорость на 5 км/час, то катер, двигаясь с прежней скоростью, догнал бы пароход в 120 км от А. Определить, на сколько км/час скорость катера больше скорости парохода.
10.155. Катер с постоянной скоростью, в k раз большей скорости парохода, отправляется одновременно с пароходом из одного пункта вниз по течению реки. Через сколько времени после отправления парохода они встретятся, если через t мин катер повернул назад и уменьшил скорость в два раза?
10.156. Из одного пункта в одном направлении через -каждые полчаса выезжает велосипедист. Первый едет со скоростью 10 км/час, второй — со скоростью 8 км/час. Найти скорость третьего велосипедиста, если известно, что он обогнал первого велосипедиста на 4 часа позже, чем второго.
10.157. Бригада рабочих строит мост за 14 дней. Если бы в бригаде было на 4 человека больше и каждый работал бы на один час в день больше, то та ж'е работа была бы выполнена в 10 дней. При увеличении же бригады еще на 6 человек и рабочего дня еще на один час вся работа была бы выполнена в 7 дней. Сколько человек было в бригаде и сколько часов в день они работали?
10.158. Из сосуда с кислотой отлили 1 л кислоты и добавили 1 л воды, затем отлили 1 л смеси и добавили 1 л воды и т. д. п раз, после чего отношение объема кислоты к объему воды в смеси оказалось равным k. Сколько кислоты первоначально было в сосуде?
10.159. Расстояние между городами А и В равно 60 км. Два поезда выходят одновременно: один из А в В, другой 346
из В в А. Поезд, идущий из А в В, пройдя 20 км, стойт полчаса, затем отправляется дальше и через 4 мин встречает поезд, идущий из В в А. Оба поезда прибывают к месту назначения одновременно. Определить скорости поездов.
10.160. Из пункта А в пункт В отправляется автобус, а из пункта В в пункт А — поезд. Если поезд отправится на 3 часа позже автобуса, то они встретятся на середине пути. А если поезд отправится на 1 час 12 мин позже автобуса, то до их встречи автобус успеет пройти 2/5 всего расстояния от А до В. Определить, через какое время они встретятся, если отправятся одновременно.
10.161. Из пункта А в пункт В против течения реки отправляется пароход. Одновременно из В в А отправляется лодка и, пройдя 1/3 расстояния от В до А, встречает пароход. В пункте В пароход сразу же поворачивает обратно, обгоняет лодку и прибывает в А в момент, когда лодка находится на расстоянии 20 км от А. Если бы скорость лодки относительно воды была в три раза больше, то первая встреча произошла бы на середине пути между А и В. Определить расстояние между пунктами А и В.
10.162. Из пункта А в пункт В против течения реки отправляется пароход. Одновременно из В в А отправляется лодка и, пройдя 3/8 всего расстояния от В до А, встречается с пароходом. В пункте В пароход сразу же поворачивает обратно и прибывает в А одновременно с лодкой. Если бы скорость лодки относительно воды была в два раза больше, то в пункт А она прибыла бы на 1 час 10 мин раньше парохода. Определить, через какое время после отправления пароход возвратился в пункт А.
10.163. Три велосипедиста выехали одновременно: первый и второй из пункта А, двигаясь с различными скоростями, а третий — навстречу им из пункта В. Через 1,5 часа после начала движения первый велосипедист был на равном расстоянии от двух других, а через 2 часа после начала движения третий велосипедист был на равном расстоянии от первого и второго. Через сколько часов после начала движения второй велосипедист находился на равном расстоянии от первого и третьего?
10.164. На берегу реки по ее течению расположены два пункта А и В, а на полпути между ними в реку впадает приток, в устье которого находится пункт С. Лодка на путь из В в А затрачивает 3,5 часа, а на обратный путь — 1 час 25 мин. Путь из В в С и затем вверх по притоку
347
на такое же расстояние до пункта D она проходит за 4 часа. За какое время лодка проплывет из D в В, если этот путь в стоячей воде занял бы у нее 2 часа? (Скорость течения реки после впадения притока уменьшается.)
10.165. Русло реки разветвляется на два потока с разными скоростями течения. На развилке расположен пункт А. Лодка на путь по первому потоку из пункта А в пункт В затрачивает на 21 мин меньше, чем на путь по второму потоку из пункта А в пункт С. Известно, что расстояние от Л до В равно расстоянию от А до С. На обратный путь из В в Л лодка затрачивает на 1 час 10 мин больше, чем на путь из С в Л. Если бы скорость лодки в стоячей воде была в 2 раза больше, то на путь из В в Л она затратила бы на 12 мин больше, чем на путь из С в Л. За какое время лодка пройдет в стоячей воде путь, равный расстоянию от Л до В?
10.166. Моторная лодка отправилась вниз по течению реки из пункта Л в пункт В. Когда она прошла 3/4 пути, кончилось горючее, и оставшийся путь пришлось идти на веслах. Весь путь из Л в В занял 1 час 50 мин. Если бы горючего хватило лишь на 1/1 пути и оставшийся путь надо было идти на веслах, то весь путь занял бы 3,5 часа. За какое время лодка проходит путь из В в Л на веслах, если путь из Л в В и обратно с включенным мотором занимает 2 часа 5 мин?
10.167. Из пункта А в пункт В вдоль берега реки по ее течению идет тропа. Охотник вышел из А на 3/7 часа позже рыбака, отправившегося из Л в В на лодке. В пункт В они прибыли одновременно, а спустя 4 часа мимо них проплыла ветка, брошенная охотником в реку при выходе из А. В обратный путь охотник вышел на 2 часа 20 мин позже рыбака, однако догнал его лодку в пункте А. За какое время рыбак вернулся из В в Л?
10.168. Катер и пароход, отправляясь одновременно из пункта А в пункт В по направлению течения реки, осуществляют безостановочное движение между Л и В. За один рабочий день катер делает 5 рейсов, а пароход — 9 рейсов (рейс — движение от А в В и обратно). Через 20 мин после начала движения, когда катер прошел 5/6 всего расстояния от А до В, происходит их первая встреча. Определить продолжительность рабочего дня.
ГЛАВА XI
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
§ 1. Простейшие тригонометрические уравнения
В этой главе мы рассмотрим некоторые виды уравнений и систем, в которых неизвестные содержатся под знаком тригонометрических функций. Такие уравнения будем называть тригонометрическими уравнениями.
Решение тригонометрических уравнений сводится в конечном итоге (с помощью различных преобразований) к решению простейших тригонометрических уравнений:
sinx = a, cosx = a, tgx = a, ctg.r==a. (1)
Поэтому мы прежде всего напомним, при каких значениях а уравнения вида (1) разрешимы (имеют решения) и как правильно находить все решения таких уравнений.
Г. Уравнение
sin х = а.
(2)
Так как значения функции у = sinx заполняют отрезок [— 1, 1], то уравнение (2) разрешимо в том и только в том случае, когда
| а | -С 1. (3)
Если условие (3) выполнено, то все решения уравнения (2), как известно, содержатся в формуле
х — {—1)" arcsin а + пп, (4)
где п принимает произвольные целые значения, т, е. л = 0, ± 1, ±2, ... (по поводу смысла записи arcsinа см. стр. 219).
Если же условие (3) не выполняется, т. е. | а | > 1, то Уравнение (2) не имеет (действительных) решений. Это последнее обстоятельство следует хорошо помнить, так как, забывая об этом, учащиеся и поступающие в вузы нередко допускают
349
ошибки. Например, при решении уравнения sinx=-g некото-л /5
рые учащиеся, не обращая внимания на то, что 1, вы-
1/5
писывают «ответ» х=(—1)"arcsin~ + лп, который не имеет никакого смысла, так как функция arcsinх не опре-/5 ,
делена в точке х — -% (т. е. эта точка не принадлежит области определения функции arcsin х).
Замечание. Всюду в дальнейшем при решении тригонометрических уравнений и систем мы для сокращения записи не будем писать в ответах, что п, k, m — Q, ±1, ±2, ... (хотя забывать об этом нельзя).
Пример 1. Решить уравнение sinЛ'= g .
1 JT
Решение. х = (— 1)"arcsing-/- ля = (—
I/ з
Пример 2. Решить уравнение sinx =--------g- .
Решение. х = (— 1)"arcsin^— — 1)"(—
4-ля=(— 1)”+I +
тт о в /Тб^-1
Пример 3. Решить уравнение sinx = %—.
Решение. Эго уравнение не имеет решений, так как 1/ГЛ^ о /ТО-к .
у 10 >3 и, значит, '—%—> 1.
2°. Уравнение
cos х — а. (5)
Это уравнение также имеет решения тогда и только тогда, когда
!а|<1. (6)
Если условие (6) выполнено, то все решения уравнения (5) записываются формулой
х = ± arccos а 4- 2лл. (7)
Если | а | > 1, то уравнение (5) не имеет решений.
Пример 4. Решить уравнение cosx = y.
350
1 rt
Решение. x=±arccos-^-y 2ли = ± -5-4-2л//.
2 О
ГТ к п Из
Пример 5. Решить уравнение cosx = —
Решение. х — ± arccos (—О) У 2ли = Эз | л У 2лп.
Пример 6. Решить уравнение cosx=l—У 5.
Решение. Это уравнение не имеет решений, так как I —/5<_1.
3°. Уравнение
tgx^a. (8)
Это уравнение разрешимо при любом а. Все решения уравнения (8) содержатся в формуле
х — arctg а у ли. (9)
Пример 7. Решить уравнение tgx —13.
Решение. х = arctg у"3 у ли = у У ли.
Пример 8. Решить уравнение tgx =—1.
Р е ш е н и е. x = arctg (—1)улн = — ~у ли.
4°. Уравнение
ctgx = a. (10)
Это уравнение разрешимо при любом а. Все решения уравнения (10) содержатся в формуле
х = arcctg а У ли. (И)
Пример 9. Решить уравнение ctgx=y 3.
Решение. х = arcctg у"3 у ли = У ли.
Пример 10. Решить уравнение ctgx =—
В заключение выпишем решения для некоторых часто встречающихся частных случаев простейших тригонометрических уравнений:
a) sinx = 0, х = лн;
б) sinx = l, х = уУ2ли;
351
в) sinx = — 1,
г) COS X = О, д) cosx=l, е) cos х=— 1,
х= — у + 2ля;
ft , х = у + ли;
х — 2лн;
Х — Т1 (2нф- 1).
§ 2. Уравнения вида sin/(x) = a, /(sinx) = 0 и аналогичные им
В этом параграфе мы рассмотрим решение уравнений вида sin/(x) — a, cos/(x) = a, tg/(x) = a, ctg/(x) = «, (12) а также уравнений вида
/(sinx) = 0, /(cosx) = 0, /(tgx) = 0, /(ctgx) = 0. (13)
Все эти уравнения легко сводятся к простейшим тригонометрическим уравнениям, рассмотренным в предыдущем параграфе.
Уравнения (12) введением вспомогательного неизвестного f=/(x) сводятся к простейшим тригонометрическим уравнениям и уравнениям вида f(x) — b. Так, уравнение sin/(x) = a указанной заменой приводится к системе
( /(*)=Л I sin t = а.
Второе уравнение имеет (при | а | sc 1) решение t — (— l)"arcsina4-nn,
подставляя которое в первое уравнение, получаем уравнение /(х) = (—l)”arcsin а-ф ли, (14)
которое проще исходного уравнения (и равносильно ему). При | а | > 1 исходное уравнение sin f(x) — a не имеет решений. Аналогично, уравнение cos f(x) — a при | а | 1 равно-
сильно уравнению
/(х) = ± arccos а + 2 ли. (15)
Таким же приемом решаются и последние два уравнения (12). Пример 11. Решить уравнение
sin(3x—1) = у.
352
Решение. Данное уравнение равносильно (см. (14)) уравнению Зх — 1=(—l)"arcsinулп, из которого находим х=у 4- —(—1) arcsm-y 4--3-.
Пример 12. Найти действительные решения уравнения cos(x2 — 2) = у.
Решение. Данное уравнение равносильно (см. (15)) уравнению х2— 2=±у4-2лга, т. е. равносильно уравнению х2 = 2 ± у +
Так как значения х должны быть действительными, то должно выполняться условие 2±у-+-2лл^0; поэтому п может принимать только значения 0, 1, 2, ...
Отв. х = лк|/2_Ту-(-2п/г, где и = 0, 1, 2, ...
Замечание. Нередко при решении уравнений вида (12) учащиеся и поступающие в вузы допускают одну типичную ошибку, связанную с неправильным истолкованием периодичности тригонометрических функций. Например, при решении о 1
уравнения cos 2х =—некоторые учащиеся рассуждают так: «Найдем какое-нибудь значение х0, удовлетворяющее урав-нению; например, можно взять х0 = -к-. 1огда все решения можно записать так: х = ± ~ -}-2пп». Ошибка здесь заключается в том, что функция cos 2х имеет период л, а не 2л, что в этом решении не учтено. Для правильного решения следует воспользоваться формулой (15), согласно которой 2х = ± 2лл, откуда х = ±у + лп. Вот другой пример. Найти действи тельные решения уравнения cos (х2 - 4)=1. При решении этого уравнения некоторые учащиеся рассуждают так: «Очевидно, что х = ±2 удовлетворяют уравнению; поэтому все решения можно записать так: х = 4: 2 4-2лл». Здесь допущена еще более грубая ошибка: ведь функция cos (х2— 4) не является периодической. Правильное решение этого уравнения получается на основе уравнения (15): х2 — 4 = 2пя, откуда находим х = ±рЛ4 4-2ля (и —0, 1, 2, ...). Таким образом, использование указанного выше
12 В. Г. Болтянский и др. 353
способа решения (основанного на формулах (14), (13)) гарантирует от ошибок.
Перейдем теперь к рассмотрению уравнений (13). При решении этих уравнений введение вспомогательного неизвестного t по формуле f==sinx (или соответственно f = cosx, Z = tgx, f = ctgx) приводит к уравнению f(t) = 3, решив которое мы приходим к рассмотрению простейших тригонометрических уравнений. Разберем более подробно первое из указанных уравнений: /(sinx) = 0. Замена неизвестного Z=sinx приводит нас к системе уравнений
t — sin х, f(t)=O.
Если второе уравнение этой системы имеет корни tv tt,..tn, то исходное уравнение /(sinx) = 0 равносильно дизъюнкции простейших тригонометрических уравнений
sinx = ^, sinx = ^2, ..., sinx==fn.
Возьмем в качестве примера уравнение вида asinsx-|-Z>sinx-}-c = O, а 0. (16)
Это уравнение имеет вид /(sinx) = 0. Положим sinx=t Тогда уравнение (16) примет вид
/(0=а^ + ^ + с=0, (17)
откуда
С — b -J- V Ь3 — 4 ас 2а (18)
с — ь—V 2а — 4ас (19)
Следовательно, уравнение (16) равносильно дизъюнкции уравнений
sinx — tv sinx~t2.
Отсюда вытекает, что уравнение (16) имеет решения в том и только в том случае, когда корни и t2 уравнения (17) действительны (т. е. D — b2 — 4асЗг0) и по крайней мере один из этих корней по абсолютной величине не превосходит единицы.
354
При этом: 1) если | | > 1, то уравнение (16)
не имеет решений; 2) если |^|^1, то уравнение
имеет одну серию решений:
х = {—1)" arcsin -ф ли, (20)
где определяется формулой (18) (аналогично при 1t2 | 1,
| | > 1); 3) если | ф | -s; 1, 1121 eC 1, то уравнение (16) имеет, кроме серии (20), еще одну серию решений:
х = (— 1)" arcsin t2 -ф ли,
где t2 определяется формулой (19).
Пример 13. Решить уравнение sin2 хф- 3 sin х + 5 = 0.
Решение. Так как уравнение t2-ф3>t-ф5 — 0 не имеет действительных решений (О = 32— 5 • 4<;0), то исходное уравнение не имеет решений.
Пример 14. Решить уравнение 2sin2x4~sinx—1=0.
Решение. Уравнение 2£2ф-£—1=0 имеет корни
——Ъ ^2—^2-
Следовательно, исходное уравнение имеет две серии решений:
' х =— ~ + 2лл, х = (—1)"-|--флл.
Пример 15. Решить уравнение 3sin2x—5sinx — 2 = 0. Решение. Уравнение 3£2— 5t — 2 = 0 имеет корни
= д-, = 2.
Исходное уравнение имеет одну серию решений:
х = (—l)n+1 arcsin 4- ф ля. О
К уравнению вида (16) легко сводится уравнение
A cos2x ф В sinx -фС = 0. (21)
В самом деле, cos2x=l—sin2x, и поэтому уравнение (21) можно записать в виде Л(1—sin2x)-f-Ssinx-|-C = 0, или (— Л) sin2 х -ф В sin х -ф (С -ф Л) = 0.
Пример 16. Решить уравнение cos2x— sinx—1=0.
Решение. Данное уравнение перепишем в виде sin2 х-ф + sinx = 0, или sinx(sinх-ф 1) = 0. Отсюда видно, что
12* 355
исходное уравнение равносильно дизъюнкции уравнений sin х = 0, sin х = — 1.
Отв. х = лп, х== — у-|-2лл.
Более общим, чем (16), является уравнение
а0 sin" х аг sin”'1 х 4* • • • + а,. г sin х 4~ ап = 0. (22)
Заменой ^ = sinx оно сводится к алгебраическому уравнению aotn 4- 4- • • • + an-J + = 0. (23)
Согласно сказанному выше уравнение (22) равносильно дизъюнкции уравнений
sinx = /1, sinx = f3, ..., sin x = £„,
где tv t2, tn — корни уравнения (23). Из этого следует, что уравнение (22) имеет решения в том и только в том случае, если уравнение (23) имеет действительные корни и по крайней мере один из этих корней по абсолютной величине не превосходит единицы.
Уравнение вида а0 sin2,1+1 х 4- cos211 х 4- a2sin2,l lx 4~ 4-а3 cos 2’г-2х4-. • .4-a2'!sinx 4“а2>г л = 0 также сводится к алгебраическому уравнению относительно ^ = sinx, так как cos2*x —(1 —sin2 х)* = (1 —£2)*.
Все, что было сказано об уравнениях, сводящихся к алгебраическим относительно / = sinx, очевидным образом переносится на уравнения, содержащие только cosx.
В частности, уравнение
a cos2 x-\-b cos х4~ с = 0 (24)
заменой ^ = cosx приводится к квадратному уравнению at2 4- bt с = 0.
К уравнению вида (24) приводится уравнение
a sin2 х 4- b cos х 4~ с = 0, если заменить sin2x на 1—cos2x.
Предоставляем читателю самостоятельно сформулировать необходимые и достаточные условия разрешимости уравнения (24) и решить вопрос о том, в каких случаях это уравнение имеет две серии решений, одну серию решений или не имеет решений.
356
Рассмотрим уравнения, сводящиеся к алгебраическим уравнениям относительно функций tg х и сtg х\
а0 tg” х + aj tg””1 х +... + ап_г tg х + ап = 0, (25)
bg ctg” х 4- Ъг ctg"1 х 4-... 4- bnl ctg х 4- bn-= 0. (26)
Уравнение (25) подстановкой tgx = t сводится к алгебраическому уравнению
14~ • • • Ч" + <2га = 0. (27)
Согласно сказанному выше уравнение (25) равносильно дизъюнкции уравнений
tgx = ^, tgx = t2, ..., tgx = ^,
где tv t2, ..., tn— корни уравнения (27). Из этого следует, что уравнение (25) разрешимо в том и только в том случае, когда по крайней мере один из корней уравнения (27) является действительным. Аналогично обсуждается вопрос о разрешимости уравнения (26).
Пример 17. Решить уравнение tg3 x- !-2 tg2x4~ 3 tgx= 0. । Решение. Полагая tg х = t, получаем уравнение t34~2t24-
4- 3^ = 0, или t (t2 -j- 2t 4- 3) = 0. Это уравнение имеет только один действительный корень t — О. Следовательно, исходное уравнение равносильно уравнению tgx = 0.
Отв. х = пп.
Пример 18. Уравнение ctg2 х 3 ctgx-f- 5 = 0 не имеет решений, так как уравнение гга 4~ Згг 4-5 = О не. имеет действительных корней.
§ 3. Уравнения, однородные относительно sinx и cosx
Рассмотрим уравнение вида
ад sin” х 4- «j sin”*’1 х cos х 4- а2 sin п 2 х cos2 х 4-...
... 4- o-n-isi!! х cos ” 1 х 4~ ап cos" х = 0, (28)
где а0, alt ..., ап — действительные числа. В каждом слагаемом левой части уравнения (28) сумма степеней синуса и косинуса одна и та же и равна п. Такое уравнение называется однородным относительно sin х и cos х, а число п называется
показателем однородности.
Ясно, что если ао = О, то все корни уравнения cosx = 0 (г. е. числа у 4~nnj удовлетворяют уравнению (28). Если же
357
а0 =/: 0, то эти числа не являются корнями уравнения (28). Действительно, при х = у пп мы имеем cos х = 0, sinx=±l, и потому левая часть уравнения (28) принимает значение Hz а0 0. Итак, вопрос о том, являются ли числа у-|~ля корнями уравнения (28), решается непосредственно.
Будем теперь искать корни уравнения (28); отличные от этих чисел, т. е. при + ял. Для этих значений х мы имеем cos х =/; 0, и потому обе части уравнения (28) можно разделить на cos"x. В результате мы получим уравнение
«о tg71 x+«itg'l~1x + ... + ara_1tgx + a„ = O, (29)
которое мы уже умеем решать (см. уравнение (25)). Заметим, что при аи =£ 0 уравнение (29) равносильно уравнению (28).
Изучим более подробно однородные уравнения с показателями однородности. 1 и 2. При п— 1 имеем уравнение
a sin х Ц- b cos х — 0.
Если а 0, то это уравнение равносильно уравнению a tg х-|-+ b = 0, или tg х — —откуда х — —arctgy + лл.
Пример 19. Решить уравнение 2sinx—3cosx = 0.
Решение. Данное уравнение равносильно простейшему , 3
тригонометрическому уравнению tgx= 2 -
з
Отв. х = arctg -% пп.
При «=2 имеем однородное уравнение вида
о sin2 X + & sin х cos x-j-c cos2x = 0. (30)
Если а =т^= 0, то уравнение (30) равносильно уравнению
a tg2 x-\-b tg x-]-c = Q. (31)
Уравнение (31) подстановкой tgx = t сводится к квадратному уравнению
at2 + bt + с = 0. (32)
Если Ьг — 4ac2s0, то уравнение (32) имеет действительные корни
, — b + VЬ2 — 4ас , — b — V Ь2 — 4ас
h - 2S > 4 ~-----------------25------
358
и, следовательно, уравнение (31) имеет две серии решений:
х — arctg Д -f- лп, х — arctg t2 Д- лп.
Если b2— 4ас<0, то уравнение (31) не имеет решений.
Пример 20. Решить уравнение 2 sin2 х Д- 3 sin х cos хД-Д- cos2 х = 0.
Решение. Данное уравнение равносильно уравнению 2 tgax-}-3 tg х Д- 1 =0, которое подстановкой tgx = i сводится к квадратному уравнению 2t2 Д- 3Z Д- 1 — 0. Корни квадратного уравнения: t± — — 1, t2 ——у. Отсюда находим две серии решений исходного уравнения.
Отв. X—— х—— arctg |~Д-лп.
Пример 2'1. Решить уравнение sin2 х Д- 5 sin х cos х Д-Д- 8 cos2x = 0.
Решение. Данное уравнение равносильно уравнению
tg2 х 5 tg х Д- 8 = 0.
Так как соответствующее квадратное уравнение t24- 5^Д- 8 = 0 не имеет действительных корней, то заданное уравнение не имеет решений.
К уравнению вида (28) сводится уравнение
а0 sin2" х Д- «j sin2"1 х cos х Д-. •.
.. .Д-а2П-1 sin х cos2"-1 х-\-агп cos2n x = q.
Для этого достаточно воспользоваться тождеством
q = q (sin2 х 4- cos2 х)п.
В частности, уравнение
a sin2 х Д-ft sin х cos x-j-c cos2x = d (33)
сводится таким способом к уравнению вида (30). Действительно, так как t/t/(sin2 х Д- cos2x), то уравнение (33) равносильно уравнению
(а — d) sin2 х Д- b sin х cos х Д-(с — d) cos2 х = 0.
Пример 22. Решить уравнение 2 sin х cos хД-5 cos2 х — 4.
359
Решение.
4 sin2 х — 2 sin xcosx — cos2 x = 0,
4 tg2 x—2 tg x— 1 = 0,
4/2 —2/—1=0,
t _J+/5 t .1-/5
I 4 ’ 2 4
1 _L ]/5~ y'l./’g'_ /
Отв. x = arctg—-------(-ля, x = — arctg i——!-|~ля.
Для сведения уравнения (33) к уравнению (30) мы использовали основное тригонометрическое тождество:
sin2x-f- cos2x = 1. (34)
Это тождество не только позволяет сводить некоторые уравнения к уравнениям вида (28), но и в некоторых случаях дает возможность найти более простые решения таких уравнений. Для этой цели используются некоторые тождества, получаемые с помощью соотношения (34). Мы имеем
1 — (sin2 x-f- cos2 x)2 = sin4x-|- 2 sin2 х cos2 х Ц- cos4x, откуда находим
sin4x-|- cos4x = 1—ysin2 2x. (35)
Далее,
sin6 x-|-cosex = (sin2x4-cos2x)(sin’x - cos4x — sin2x cos2x) =
= 1----sin2 2x—j- sin2 2x.
2 4
Итак,
sin6 x Д-cos6 x= 1—|-sin2 2x. (36)
Преобразуем теперь сумму sin8x-|- cos8x, используя формулу (35). Мы имеем
sin8 х + cos§ х = (sin4 x 4- cos4 x)2 — 2 sin4 x cos4 x =
= j 1--sin2 2x j —sin4 2x =
\ 2 / °
= 1 — sin2 2x 4- 4 sin4 2x--sin4 2x.
'4 8
Отсюда находим
sin8 x + cos8 x= cos2 2x sin4 2x. (37)
360
Формулы (35)—(37) нередко используются при решении тригонометрических уравнений.
Пример 23. Решить уравнение
sin4x-(- cos4x = g-sin2 2х.
Реше н и е. Можно было бы представить правую часть в виде 2 sin2 х cos2 х и затем решить полученное уравнение как однородное относительно sin х и cos х (т. е. как уравнение вида (28)). Мы приведем другое решение.
Используя формулу (35), преобразуем уравнение к виду sin22x=l, или cos22x = 0. Остается решить уравнение cos 2х = 0.
Отв. х = + g .
Пример 24. Решить уравнение
sin6 х + cos6 х =
Решение. Данное уравнение также может быть сделано однородным относительно sin х и cos х: нужно умножить правую часть на (sin2 х -) cos2 х)3. Но решение с помощью формулы (36) проще. В силу формулы (36) получаем последовательно:
- =1 — j sin3 2х, sin2 2х — 1, cos2 2х = 0.
л . лм
Отв. х= 4~ + -2-.
Пример 25. Решить уравнение
sin8 х + cos8 х = cos2 2х.
Решение. И эго уравнение легко приводится к виду (28), для чего нужно представить правую часть в виде (cos2x— sin2 х)2, а затем умножить ее на (cos2 х + sin2 х)2. Проделав это и произведя упрощения, мы приведем данное уравнение к виду 2 sin4xcos4x = 0, или sin42x = 0. Но еще проще получить это уравнение с помощью формулы (37).
361
§ 4. Введение вспомогательного угла
В этом параграфе мы рассмотрим решение уравнений вида a cos х 4- b sin х — с. (38)
Наиболее простой способ решения уравнения (38) основан на введении вспомогательного угла.
Заметим, что если с —О, то уравнение (38) является однородным (см. § 3).
Пусть с 0 и, кроме того, о2-}-ft2# О, т. е. по крайней мере одно из чисел а, b не равно нулю (если одно из чисел а, b равно нулю, например, а = 0, но b # 0, то получаем простейшее тригонометрическое уравнение ft sin х = с, или с \ sin х — -г- .
& j
Разделив обе части уравнения (38) на |/а2 + Ь2, получаем уравнение
равносильное уравнению (38). Так как
/ а У , ! b
\fa2 + b^/ ~Г\Уа'> + Ь^
то существует такой угол <р, что
а Ь
= Sill ф, 77=== = cos ф. (39)
(s2 + l’a |/п2-]_&2 V V )
Отсюда следует, что уравнение (38) можно переписать в виде
с
COS X Sin ф + Sin X COS ф — ,-= ,
|г 1 )Лиа + &а
или
Sin(x + <p)=~== (40)
Уравнение (40), а вместе с ним и уравнение (38), разрешимо в том и только в том случае, если
или c2=Ca2 + ft2. (41)
362
Если это условие выполнено, то уравнение (38) имеет следующие решения:
х = - Ф + (- !)" arcsinp^== + лп,
где ф определяется из формул (39).
Если условие (41) не выполнено, т. е.
== ! > 1, или с2 > а3 4- Ь2, аг-\-Ь~\ г
то уравнение (38) не имеет решений.
Пример 26. Решить уравнение 3sinx-|-4cosx=5.
3 4
Решение. Запишем уравнение в виде-.- sin х + cos х — 1 <3 э
к 3 4
и введем вспомогательный угол: у == cos ф, у=sin ф.
Так как з1пф>0, созф>0, то в качестве ф можно взять • 4 п
угол ф = arcsin. Получаем уравнение □
sin („Гф) = 1.
Отв. х——arcsin2л«.
О Z
Пример 27. Решить уравнение 2 sin x-f- 3 cos х = 4.
Решение. Так как 22 З2 •< 42, то данное уравнение решений не имеет.
§ 5. Метод замены неизвестного
В гл. IX мы рассмотрели метод замены неизвестного при решении уравнений (см. стр. 291). Здесь мы отметим три наиболее употребительных приема введения нового неизвестного при решении тригометрических уравнений.
1°. Замена Z = sinx-f-cosx. Пусть дано некоторое тригонометрическое уравнение F (х) = 0. Обозначим через g(x) функцию sinx-|-cosx и введем новое неизвестное f = g(x)~ = sin х + cos х. Если нам удастся выразить функцию F(x) через t, т. е. представить ее в виде F (х) =/(§ (х)), то решение уравнения F (х) = 0 будет сведено к решению уравнения /'(£) = 0 (см. теорему 3 на стр. 291). Разумеется, не всегда левую часть F (х) удается достаточно просто выразить через ^ = sinx-]-cosx. Мы рассмотрим один случай, когда это удается просто сделать.
363
Итак, введем (в некотором тригонометрическом уравнении) новое неизвестное t = sin х -1- cos х. Применяя тождество (sin х cos х)г = 1 4- sin 2х, находим sin2x=42—1.
Ясно поэтому, что если левая часть тригонометрического уравнения F(x) = 0 выражается через sin x-f-cosx и sin 2х, т. е. F(x) = cp (sin хcos .г, sin 2х), то мы легко можем выразить F (х) через t. Итак, если левая часть тригонометрического уравнения F(x) = 0 может быть выражена через sinx-Fcosx и sin 2х. то целесообразно применить замену неизвестного по формулам
sin х + cos x = t,
sin 2x = F— 1.
Рассмотрим, например, уравнение вида
a (sin x-|-cos х) 4- b sin 2x4- с = 0 (42)
и произведем в нем указанную замену неизвестного. Тогда уравнение (42) сведется к квадратному уравнению относительно t: -
at + b(P— 1)4-с = 0, или
bt2 + at + (c — b) = 0. (43)
Если 4 и /2 — корни этого квадратного уравнения, то, согласно теореме 3 на стр. 291, уравнение (42) равносильно дизъюнкции уравнений
Sin X 4-COS X = 4> Sinx4-COSX = 4
(которые принадлежат к типу, рассмотренному в предыдущем параграфе).
П р и м е р 28. Решить уравнение 2 (sin х 4- cos х) 4- sin 2х-\--4-1=0.
Решение. Полагая sin х 4* cos х =/, получаем квадратное уравнение 2^4-(^2—1) + 1 = 0, или F 4- 2£ = 0. Отсюда находим t1 = 0, t2 ——2, так что данное уравнение равносильно дизъюнкции уравнений sinx4*cosx = 0 и sinx + -|-cosx=—2. Первое из этих уравнений равносильно уравнению tgx= — 1 и имеет решения х——Второе уравнение решений не имеет.
Отв. х——~ 4- ли.
364
Замечание. Уравнение (42) имеет решения в том и только в том случае, когда дискриминант уравнения (43) неотрицателен и по крайней мере один из корней уравнения (43) удовлетворяет условию j^==sp2, так как | sin х + cos х i | sin [x + | sC У 2.
Аналогично решаются уравнения вида
a (sin х— cos х) 4- b sin 2х-|- с = 0.
Здесь удобно положить / = sin х — cosx (и тогда sin 2х = = 1 — Г2).
2°. Замена Z = cos2x. При такой замене через t легко выражаются sin-cv и cos2x:
. , 1 — cos 2х > 1 — t
sin2 X =-------= —— ,
о 1 —|- cos 2x 1 4~1
cos-x==----—
Таким образом, если левая часть тригонометрического уравнения F (х) = О выражается через cos 2х, sin2 х и cos2 х, то целесообразно применить замену неизвестного по формулам
' cos 2х = t,
sin2X=l^> (44)
9 1-Н
cos2 х=~- .
Рассмотрим, например, уравнение a cos 2х 4* 2b cos2 х = с. (45)
Это уравнение приводится к однородному относительно sinx и cos х (см. § 3). Однако проще его решить с помощью замены cos2x = i. С помощью этой замены уравнение (45) сводится к уравнению at 4- 2&-^1 = с, нли (ау-Ь)1--с— b. Иначе говоря, уравнение (45) сводится к следующему уравнению относительно cos 2х:
(а b) cos 2х = с — b
^что, впрочем, можно получить непосредственно, заменив в / , - о' 14” cos 2х\
(45) cos2 х через —.
365
Аналогично можно решать уравнения вида a cos 2х 4- 2b sin2 х = с.
Пример 29. Решить уравнение
cos 2хф-4 sin4 х— 8 cos® х.
Решение. Применяя замену (44), получаем уравнение (4-(1 — ()2 = (1 1)3, т. е. /34~2/24~4( = 0, или, наконец,
t(t2 4- 2t 4- 4) = 0. Это уравнение имеет единственный действительный корень ( = 0, и потому исходное уравнение равносильно уравнению cos2x = 0.
у--] Л . Л11
Отв. х = -4--2.
Пример 30. Решить уравнение sinex-|-cos6x = 4 .
Решение. Мы уже рассматривали это уравнение (см. пример 24). Здесь мы его решим с помощью замены (44).
Применяя эту замену, сведем данное уравнение к следующему:
\ 2 / Л 2 / 4 ’
или, после упрощений, = 0, т. е. cos22x —0.
Отв. х=4-4-у.
Таким же приемом может быть решено и уравнение примера 25.
Рассматриваемая в этом пункте замена (44) основана на формулах
• , 1 — cos 2х , l-f-cos2x
sm2x — , cos2x =—L-g---------. (46)
Иногда бывает удобнее применять непосредственно формулы (46), а не замену (44) (мы это видели при рассмотрении уравнения (45)). Так, с помощью формул (46) уравнения вида
a sin 2х 4- 2b sin2x = с, a sin 2х 4- 2b cos2x = с
приводятся к уравнениям вида A sin2x-|-5cos2x = C, изученным в § 4.
Рассмотрим еще несколько примеров, в которых полезными оказываются формулы (46).
366
Пример 31. Решить уравнение
2cos2 4х 4- sin 1 Ох — 1.
Решение. Так как 2cos24х—l=cos8x, то уравнение можно записать так:
sin 1 Ох 4-cos 8х —О, или sin 1 Ох 4- sin —8xj = 0.
Отсюда находим
2 sin [х 4- cos f 9х — = 0.
— л. । л, л/г
Отв. х— — -г 4-пп, х = ТЙ4-~н~.
4 1 12 1 9
Пример 32. Решить уравнение
sin2x 4- cos2 2х = sin2 Зх 4- cos2 4х.
Решение. Используя формулы (46), получаем
1 — cos2.v. 1 4-cos4х_1 — cos6х . 1 4*cos8х
2 " ' 2 — 2 1 2 ’
или
cos 4х — cos 2х = cos 8х — cos 6х.
Преобразуя разности косинусов, находим
2 sin х sin Зх = 2 sin 7х sin х, sinx(sin7x— sin 3x) = 0, sinxsin2x cos 5x = 0.
Отв. x=~, х = ~й4--£ (A ^=5/4-2).
Формулы (46) можно также использовать при решении уравнений следующего вида:
cos2 ах 4- cos2 Ьх = cos2 сх 4- cos2 dx, .
sin2 ах 4- sin2 bx — sin2 ex 4- sin2 dx,
если числа a, b, c, d удовлетворяют одному из условий: аb — сd, а — b = с — d.
367
3°. Замена f = tg^. При такой замене через t несложно выражаются sinx и cosx:
о . х х о. х
2 sin 2 cos g- 2 tg 2-
sin х = sin3 g +cos2*- ’ + ^2 1 + Р
cos2 g - - sin2 i-tg2* I-/3
COS X — -------------=----------= q-——,
. „Х , „X X 1+^2
sin2 2 q-COS- l+tg2 -
Таким образом, мы получаем следующую замену:
' tg2V=/,
< sinx^—, (47)
1 — « COSX = j-т-^.
Замена (47), в частности, может быть применена, если рассматривается тригонометрическое уравнение F(x) = 0, левая часть которого является рациональной функцией о г sinx и Р
cosx, г. е. представляется в виде , где Р и Q— некоторые многочлены от sinx и cosx. Примерами могут служить уравнения
sin3 х + 2 cos х_1
3cos2 х q- sin x 2 ’
sin ox + cos x n cos 3x + sin 2x
(второе уравнение является рациональным относительно sin х и cosx, так как sin 5х, cos3x, sin2x—многочлены от sinx и
cosx).'Если к уравнению рассматриваемого типа применить
замену (47), то, как легко понять, мы получим (после упро-
. м (о
щения) уравнение видау
О, где Л1 н N — некоторые мно-
гочлены, т. е. получим алгебраическое уравнение34(f) = О
относительно t = tg *
Следует, однако, отметить, что исполь-
зование подстановки tg л = t при решении тригонометричес-4*
3(?8
ких уравнений нередко приводит к трудной задаче нахождения корней многочлена. Поэтому эту подстановку, как правило, применяют при решении тригонометрических уравнений лишь в том случае, когда нет других путей решения.
Замечание. Формулы (47) теряют смысл, если
cos 2= 0, т. е. если х = л (2п -{- 1 )•
Поэтому при решении уравнений с помощью подстановки tg| = t нужно проверить, не являются ли значения х — = л (2п+ 1) корнями исходного уравнения.
Пример 33. Решить уравнение
sin X-{-ctg * = 2.
Решение. Заметим, что значения л- = (2д1) л не являются корнями исходного уравнения и потому можно приме
нить замену (47). Тогда уравнение примет вид I поскольку
, X 1 \ \
cts2=d
+ ! =2, 2/2+1+(2 = 2(3 + 2(, 1 1“ I
2/3 _ 3/2 + 2/ — 1 = О,
2 ((3 — г2) -• (/2 — () -{- ((— 1) = О, (/ — 1)(2/2—— /+1) = 0.
Так как уравнение 2/2— /-{-1=0 не имеет действительных корней, то исходное уравнение сводится к уравнению t = 1, или tg 2 = 1, откуда
х — + 2л/г.
Отв. х = ?- -)-2ля.
Рассмотрим еще два примера применения метода замены неизвестного.
Пример 34. Решить уравнение
. „ , 1 . 17
sin2x-4- . „ -—sin х-г—-4-
1 sm2x sin л-т 4
369
Решение. Положим sin х-----— = t, тогда 72 — sin2 х 4-
sin х 1
и данное уравнение можно записать так: 72-(-2 =
, 7 /, 1 \2 л . 1
— i-f-, или II — =0, откуда 7 = 2 . Итак, получаем
1 1 О • , . о п 1 + /17
sin х---.— = <-. , 2 sin2 х — sin х —2 = 0, sinx=—-
sin x 2 4
Отв. x = (— 1)”+1 arcsin —- -\- un.
Пример 35. Решить уравнение
Решение. Положим ~ ~ —t. Тогда 3~ 4 х =
и 2 о
/л х\
= л— 2 (д- — 2/Я— 21 и уравнение примет вид sin (л — 27) = 2 sin t, или 2 sin t — 2 sin t, 2 sin 7 (cos 7— l) = 0. Мы пришли к дизъюнкции уравнений sin 7 = 0, cos 7=1. Но так как при cos 7=1 непременно будет sin7=0, то достаточно рассмотреть только одно уравнение sin 7 = 0. Итак, 7 = ля,
л или Д- — о
Оте.
х
2=ЯП-
х = у (1—-5и).
§ 6. Метод разложения на множители
Одним из наиболее употребительных методов решения тригонометрических уравнений является метод разложения на множители.
Обшие вопросы, касающиеся этого метода, рассмотрены в гл. IX, § 3, и. 4° (стр. 285).
Здесь мы ограничимся решением нескольких простых тригонометрических уравнений методом разложения на множители.
Пример 36. Решить уравнение
2sinxcos2x—l-|-2cos2x— sinx = 0.
Решение. Вынося общий множитель первого и третьего слагаемых, запишем уравнение в таком виде:
2cos 2x(sinx-|- 1) — (sinx-(-1) = 0, или
(2 cos 2х — 1)(sin х-(-1) = 0,
370
Так как левая часть этого уравнения определена при всех х, то исходное уравнение распадается на следующие два уравнения:
2 cos 2х — 1 = 0, (48)
sin х + 1 = 0 (49)
(или: исходное уравнение равносильно дизъюнкции уравнений (48) и (49)).
Уравнения (48) и (49) имеют следующие решения:
X = ± g- + лп, х = — ^4-2л£.
В этих формулах содержатся все решения исходного уравнения.
Пример 37. Решить уравнение
cos Зх cos 5х sin 2х sin 2х '
cos Зх—cos5x „
Решение. J равнение можно записать так:-----4444---=
или, используя формулу для разности косинусов, в виде
2 sin 4х sin х q
sin 2х
Задача свелась к нахождению корней уравнений
sin4x = 0, (50)
sinx —0. (51)
Исходному уравнению - будут удовлетворять те корни уравнений (50) и (51), для которых sin 2x^0. Но если sinx = = 0, то sin2x = 0, и поэтому корни уравнения (51) не являются корнями исходного уравнения. Если sin4x = 0, то либо cos2x = 0, либо sin2x=0. Таким образом, исходное уравнение равносильно уравнению cos2x = 0.
у--] П .
Отв. х = Т- + -П-’
4 1 2
Пример 38. Решить-уравнение
cos3x sin3x = cos 2х.
371
Решение. Исходное уравнение преобразуется к виду (cos х sin х) (cos2 х — cos х sin х sin2 х) = cos2 х — sin2 х, или
(cos х sin х) [ 1 — cos х sin х — (cos х — sin х)] = О,
и потому распадается на два уравнения: cosx4-sin х = 0,
1 —(cosx— sinx) — cosxsinx=0.
Первое уравнение имеет решение х =—Второе за-1-так что cos х sin х =—g-
— —у— = 0, или (2 — 2( -J- 1=0. От-
/ JT \
находим (=1,или cosx — sinx=l, т. е. cos х-|~т) =
меной cosx — sinx
дится
к уравнению 1—t
сво-
сюда
1
г Следовательно, х-|-’-’-=± 4-2ля.
2 1 4 4 1
Отв. х=—4- пп, х = 2лп, х ——~-^-2лп.
Методом разложения на множители можно решать уравнения следующих видов:
1) sin (ахa) = sin {Ьх -ф |3), (52)
2) cos (ах -ф а) = cos (bx -ф|3), (53)
3) sin(ax + a) = cos(Z>x + P) ' (54)
при любых значениях а, Ь, а, р.
Рассмотрим, например, уравнение (52). По формуле разности синусов это уравнение можно записать в виде
2 sin + cos = о. (55)
Будем предполагать, что а =4 Ь и а ф—Ь. Тогда из (55) находим
(a + &)x+a+P л । _ ____л (2я ф ]) —(а ф 0)
2 — 2- Т ля, х —
372
Аналогично можно найти решение уравнения (53). Уравнение (54) сводится к уравнению вида (52), так как
cos (Ьх + ₽) = sin — Ьх — .
Пример 39. Решить уравнение
cos Зх sin 5х = 0.
Решение.
cos Зх cos — 5х j = О,
/ Л \ [ . л \ р.
cos ---х cos 4х— г ) = 0,
\4 ) \ 4 /
Иногда, прежде чем применять метод разложения на множители, приходится использовать другие преобразования, например преобразование произведения тригонометрических функций в сумму.
Пример 40. Решить уравнение
sin х cos 5x = sin 9х cos Зх. (56)
Решение. Преобразуя произведение тригонометрических функций в сумму, запишем уравнение в виде
I / \ 1 / \
~ sin 6х — sin 4х ^sin 12х 4- sin 6х ).
Отсюда получаем
sin 12x4-sin 4х = 0.
Теперь можно применить метод разложения на множители:
2sin 8xcos4x = 0.
/-Х Л/t
Отв. x = -g~.
Нам удалось легко решить уравнение (56) с помощью приема, основанного на переходе от произведения тригонометрических функций к сумме, потому, что после преобразования в левой и правой частях уравнения оказались одина
373
ковые члены ^sin6x^. Этим же способом можно решать уравнения вида
sin ах co.s Ьх — sin ex cos dx, sin ах sin bx = cos ex cos dx, sin ax sin bx — sin ex sin dx, cos ax cos bx = cos ex cos dx,
если, например, выполнено условие а — b — c — d.
§ 7. Оценка левой и правой частей уравнения
Предварительная оценка левой или правой частей уравнения иногда помогает решить уравнение или убедиться в том, что уравнение не имеет решений. Рассмотрим несколько примеров.
Пример 41. Решить уравнение 2sins х 4- 3cos8 х = 5.
Решение. В данном случае достаточно грубой оценки левой части уравнения. Так как isin.r; sgjl, Icosxj^b го
I 2sin3 х 4- 3coss х) 2 j sin3 x 4- 3cos* x 5,
причем это неравенство могло бы стать равенством лишь в случае, когда sinx=l и icosx|=l, что невозможно (так как sin2 х 4- cos2 х = 1). Следовательно, данное уравнение не имеет решений.
Пример 42. Доказать, что уравнение sin4 х 4- cos6 х= а не имеет решений при а>1.
Доказательство. Здесь грубая оценка isinxjsgl, । cos х । 1 не проходит. Воспользуемся неравенствами
sin4 х sin2 х, cos6 x sg cos2 x.
Сложив эти неравенства, получаем
sin'1 х 4-cos6 Л'•<. sin2 x + cos2= !•
Итак, sitilx4-cos6XiC 1. Отсюда следует, что исходное уравнение при а > 1 не имеет решений.
Пример 43. Решить уравнение
sin 2х 4- sin Зх 4- sin 4х = 3.
374
Решение. Левая часть уравнения может равняться трем лишь в этом случае, когда одновременно имеют место три равенства:
sin2x=l, sin3x=l, sin4x = l.
Но если sin 2х = 1, то х = ~ 4- пп и sin Зх=sin 4- Зля)
. 4 1 \4 1 /
1. Следовательно, уравнение не имеет решений.
Пример 44. Решить уравнение
(cos 2х — cos 4х)2 = 4 + cos2 Зх.
Решение. Имеем
| cos 2х — cos 4х! -С 2,
(57)
причем в этом неравенстве знак равенства имеет место лишь в следующих двух случаях:
a) cos2x=l и cos4x=—1; (58)
б) cos2x== — 1 и cos4x=l. (59)
Из (57) следует, что левая часть уравнения не превосходит 4 и равна 4 лишь в случае, когда одновременно выполняются либо равенства (58), либо равенства (59).
Для правой части уравнения имеем 4 Д- cos23x Дэ 4, причем равенство здесь имеет место лишь в случае, когда cos Зх=0.
Таким образом, исходное уравнение может иметь решения в двух случаях (при одновременном выполнении трех равенств):
a) cos2x=l, cos4x= — 1, cos3x = 0;
б) cos 2х'=— 1, cos4x=l, cos3x = 0.
Рассмотрим первый случай.
Пусть cos2x=l, так что х — лк. Но тогда cos4x = = cos4n6=l. Следовательно, в первом случае решений нет. Пусть теперь cos2x= — 1; тогда х = л [k 4- |У Эти значения х удовлетворяют каждому из уравнений cos4x=l, cos3x = 0.
Отв. х=л fk Ц- .
375
Если тригонометрическое уравнение имеет вид +/:(*)+••+/"(*) =^° (6°) или приводится к виду (60), то решения уравнения (60), если они существуют, могут быть найдены как решения системы уравнений
/1W-0, /2(х) = 0,..., Л(х)=0 (61)
с одним неизвестным.
В самом деле, так как функции fk(x) (k—\, 2,..., ri) предполагаются действительными, то при каждом х (из облает определения левой части уравнения (60)) левая часть уравнения (60) неотрицательна и принимает значение нуль лишь в случае, когда Д(х) —0 для всех k— 1, 2,..., п.
Таким образом, уравнение (60) равносильно системе уравнений (61).
Пример 45. Решить уравнение
sin2 2„v + 1 = cos2 Зх.
Решение. Уравнение можно записать в виде sin2 2х -ф sin2 Зх = 0.
Отсюда следует, что исходному уравнению будут удовлетворять те и только те значения х, которые являются корнями каждого из уравнений sin 2х == 0, sin3x = 0. Уравнение sin 2х = 0 имеет две серии решений:
х = nk, х = g- -ф лп.
Числа x = nk являются решениями уравнения sin3x = 0, а значения х= ^фл» не удовлетворяют уравнению sin Зх = 0. Отв. х = л!г.
Пример 46. Решить уравнение
cos2 2х -ф sin2 4х -ф 1 = sin 4х cos 2х -ф sin2 х.
Решение. Данное уравнение запишем в виде
cos2 2х — sin 4xcos 2хф | sin2 4х-фсо82 х = 0, или
^cos 2х— sin4x^24-cos2x = 0.
376
Последнее уравнение равносильно системе
cos 2х = ~ sin 4х, cos х~ 0.
Уравнение cosx —0 имеет решения х=^--\-пп, однако эти значения х не удовлетворяют уравнению cos2x = g sin 4х. Таким образом, исходное уравнение не имеет решений.
§ 8. Системы тригонометрических уравнений
Мы ограничимся рассмотрением тригонометрических систем лишь немногих типов и укажем наиболее употребительные методы их решения, основываясь на общей теории систем уравнений (см. гл. X).
1°. Системы вида
sinxsiny — а,
(62)
COS X cos у = Ь-
Складывая и вычитая уравнения системы (62), получаем равносильную систему
/ cos (х-у) =<? + />, ( cos(x4-y) = £— а.
Система (63), а значит и система (62), имеет решение в том и только в том случае, когда выполняются условия
1, \b — a[s^l.
Если эти условия выполнены, то
х—у = ± arccos (а ф- Ь) ф- 2л&, х-\-у ~± arccos (Ь— а)-\-2лп.
В формулах (64) k и п—любые целые числа, а знаки выбираются произвольно. Таким образом, формулы (64) определяют в общем случае четыре серии решений. Полагая
arccos (а ф- Ь)= а, arccos (b—а) = Р,
377
получаем из (64)
х—y — a.-\-‘2nk, х 4- у — Р + 2пп, х —у — — а -f- 2лЛ, х4~.У = Р4-2л/г, х—у — а-\- 2л&, х 4- у = — Р + ^лп, х—у = — а 4~ 2 х-{-у — —Р4-2ля, откуда находим четыре серии решений:
x = ^-(a + f>) + n(k + n), ^ = |(Р — «) + л (п — k),
х = (Р -- а) 4- л (й 4- п), у = (а 4- Р) 4- л (п — k),
х = ~ (а — р) 4- л (k 4- п),
J = —-1-(а4-р)4-л (п —А),
х = — I (а 4- Р) + л (k 4- п), У = [ (« —Р) + л (я —й)-Аналогично можно получить решение системы вида sin х cosy— а, cos х sin y = b.
Пример 47. Решить систему уравнений
1
sin х cosy — — 2 , 1 COS X Sin .у = 2".
378
(65)
Решение. Система
( sin х cos _у-}-cosx sin_y = sin(x4-_y) = 0, | cosx sin у — sinxcos_y = sin(j> — x) = l равносильна исходной системе. Отсюда получаем х-1гу = пп,
у — х = ^- -{-2л&.
Отв. x = nQ — k — +
Замечание. Следует обратить внимание читателей на одну типичную ошибку, которую часто допускают учащиеся
(и поступающие в вузы) при решении тригонометрических систем. Рассмотрим для простоты изложения систему уравнений
( sinnx = 0,
{ • п (66)
( зшлу = 0. ' '
Очень часто записывают решение в таком виде:
х = п, у — п> где п~0, ±1, ±2,... (67)
379
Легко понять, что в формулах (67) содержатся не все решения системы (66).
Для большей наглядности каждой паре чисел (х0; _у0), образующей решение системы (66), поставим в соответствие точку /И (х0; _у0) плоскости хОу. Тогда в формулах (67) содержатся лишь такие решения системы (66), которым соответствуют точки (0, 0), (1, 1), (—1, —1) и т. д., т. е. точки с целыми координатами, лежащие на прямой у — х (рис. 112). Однако исходной системе удовлетворяют всевозможные пары целых чисел, которые соответствуют точкам пересечения координатных линий х = 0, х=1, х = = — 1,... и у=0, у=1, у — — 1,...
Таким образом, решение системы (66) следует записывать так:
х = п, y = k, где п = 0, ± 1, ±2,..., k = 0, ± 1, ± 2,..., т. е. п и k «пробегают» (независимо друг от друга) все целые значения.
Системы вида
( (68)
( tg х tg у — b, ab 0, а также системы вида
{sin _rsin_y = a, ctg х ctg_y = b,
сводятся к системам вида (62). Например, система (68), в силу условия ab =£= 0, равносильна системе
(sin xsiny = a,
cos x cos у =-г-, ab^O.
К системам вида (65) сводятся системы
( sin х cos у = а,
( tg х ctg_y = b, ab 0.
2°. Системы вида
| sin x 4- sin у = a, [ sin2 x 4- sin2у = b
380
сводятся заменой неизвестных rz = sin х, x> = sin_y к алгебраической системе
и2 -\-v2 = b.
(70)
Система (70) равносильна системе
и 4- v = а,
и имеет решения (tr, t2), (t2, где
a + /2& —_a —/гй-а2 — 2 ’ 12 ~~ 2
Так как » = sinx, T>==sinv, то система (69) имеет решения в том и только в том случае, если выполняются условия: а2
а) »=Ц-;
б) i^!< 1-
Если эти условия выполнены, то решению (tv t2) системы (70) соответствуют уравнения sinx = /1, sin_y = /2, откуда
х = (—1)" arcsin С 4- ля, 1
4, } (72)
у = (—1 )* arcsin t2 Ц- л/г, J
где и t2 определяются формулами (71).
Аналогично, решению (/а, 4) системы (70) соответствует следующая серия решений исходной системы (69):
х = (—1)" arcsin t2 4- ля, у — (—1)* arcsin 1Л 4“
(73)
(если /1 = г‘а и j 4 J 1, г. е. а2 — 2Ь и ! а | 2, то серии
решений (72) и (73) совпадают).
К системам вида (69) сводятся системы
sin л-4- sin_y = а, cos2 х 4- cos2 у = b.
381
Действительно, если во втором уравнении заменить cos3x и cos2_y соответственно на 1—sin3 х и 1 — sin2_y, то получим равносильную систему
( sinx4-sin_y = a,
| sin3 х -f-sin2j/ = 2—b.
Аналогично можно получить решения следующих систем:
cos x + cosj’ = a,
cos х 4- cos у — a,
( cos2 x 4- cos2_y = b, ( sin2 x 4- sin2у = b.
Еще проще найти решения систем вида
{sinx 4-sin_y = a, sin2x — sin2 y=-b
и других подобных систем. Действительно, если a=j^0, то эта система равносильна системе
sinx4~sin_y = a,
Ь sin х—sin у — —
из которой легко найти sinx и sin_y. Система вида
( a, tgx4-£j tgy = Cp ( a3ctgx4-fe2ctg_y = c2
сводится к алгебраической системе
a^i 4- b}i> = сР
Я, , Ь2
— 4- — = с«
и ’ v 3
заменой w = tgx, x>=tgj.
3°. Системы вида
sin x4~sin_y = a, x4-_y = a.
(74)
Используя формулу для суммы синусов, запишем первое уравнение системы (74) в виде
о . х+и х — и
2 sin cos —~ = а.
382
Так как х-|-_у = а, то исходная система равносильна системе
о . а х—у
2 sin -g- cos = а, х +у = а.
(75)
Рассмотрим два возможных случая:
a) sin = 0 (т, е. а = 2лт).
Тогда _у = 2л»г—х (т — некоторое целое число), и из первого уравнения системы (74) получаем
sinx—sinx —а, т. е. а — 0.
Итак, если sin~ = 0, то система разрешима лишь при а = 0 и сводится к одному уравнению х-Уу—а.
б) sin у ф 0.
Тогда система (75) равносильна системе
(76)
х-Уу — а.
Если выполнено условие
2 81П у
то из (76) получим
х — у = ± 2arccos / —-—\4-4лл, о '7-
\2smT)
х+_у = а,
откуда
а , / а \ , „
х = ± arccos /--------\ 4- 2лл,
2 о “
\2sin¥/
а / а \ п
у — = гр arccos /-----— 2ли.
2 И, а
\2 sin ¥ /
(77)
Если условие (77) не выполняется, т. е. система (74) решений не имеет.
а
п а
2smy
> 1, то
383
Аналогично решаются системы вида
sin х — sin у = а, ( cos х ± cos у = а, х±у = а, i х±у — а. К системе вида (74) сводится система sin х + cos _у = а, х + у = а.
Действительно, полагая ~—y = t, получаем систему sin х + siiH = а, , л х — t = a —% .
Аналогично можно решать системы вида ( sinx±cosy = a,
Пример 48. Решить систему уравнений . 2 , , I
Sin45 X + cos- у = у ,
л > — 4 .
Решение. Система равносильна каждой из следующих систем:
1 — cos 2х , 1 + cos 2у 2 2
1
2 ’
х +> — 4 >
cos 2_у — cos 2х = — 1,
[ Х + У=уу,
2sin (х + J') sin (х—>) = — 1, . Л
-+J=4-,
1
л
4“-
sin (х — у) =
384
Отсюда находим
х— у = (—l)n+i -^- + лп, х+У—4>
и потому
-v=~[i+(-ir+i] + ^, у = |[1 +(-1)я]
4°. Системы вида
( sinxsiny = a, ( х + у = а.
Эту систему заменим следующей равносильной
( cos(x—у) — cos (х+_у) = 2а,
I х+_у = а,
или
( cos(x—у) — 2а + cos а,
I х+_у = а.
Если | 2а + cos а [ ^1, то система (79), а вместе с стема (78), имеет решения, причем
х — у ± у arccos (2а + cos а) + лп, у — у zp ~ arccos (2а + cos а) — лп.
Аналогично можно найти решения систем
( cosxsin_y = a, Г cos х cos у = а, ( xzt_v = a, ( x±y = a.
Пример 49. Решить систему уравнений
• 1
cosx sin у = —
/2
3
Д х + у=уЛ.
13 В- Г. Болтянский и др.
т
~2‘
(78) системой:
(79)
ней и си-
385
Решение. Исходная система равносильна каждой из следующих систем:
sin(x-f-j') — sin(.v—у) —У 2, . 3
Х+У=^п>
sin Су—.v)=-— ,
У 2 , 3
х + У = 4 Л,
откуда
У + х = 4‘ л;
x = + у = |[3 + (-1)”] + ™.
Рассмотренный в и. 4° метод можно использовать и при решении систем следующих типов:
( tgx±tgy = a, | ctg х ± ctg у = а,
I х±у~а, [ х ± у —а,
J tgxtgy = a, С ctgxctgy = a, ( х± у— а, | х± у— а.
Рассмотрим, например, систему
f tgx-\-tgy — a,
( х-{-у = а.
Имеем
. . , 2 sin (х + w) 2 sin а
tg х 4- tg v = —:—г2,——;-ч -----:------•, = а,
& । cos (x + </)+ cos (х — у) cos а + cos (х — у)
откуда можно найти cos (л—у), а затем х—у. (Полного исследования системы мы не проводим.)
При решении систем вида
( tgxtgy = a,
| х±у~а
386
можно использовать следующую формулу:
te X ta V = cos(x-j/)-cos(x + y)
ё ё У COS (X + у) 4- cos (х — у) ’
5°. Системы вида
( sin х cosy = а,
I (80)
у cos х cos у — b, Ь =т^= 0.
Разделив первое уравнение системы (80) на второе, получаем
tgx = |. (81)
Уравнение (81) вместе со вторым (или первым) уравнением системы (80) образуют систему, равносильную исходной.
Из (81) находим х = arctg-~ -{- лп, и, подставляя во второе уравнение системы (80), получаем
b cos у —----------------г—.
cos I arctg-y 4-лп1
Обозначим arctgy = <p. Так как —~ < ср < у, то cos ср > >0. Пусть для определенности Ь>0. Тогда cos ср = — cos I arctg —'}== b — и cosy — (—1)” У а2 + Ь2. Если
\ 0/ уа2^_у2
a2-f-b2^l, то у = ± arccos [(—1)” Угг2 4- ft2| + 2nk. Итак, если Ь=^0 и а2~гЬг---:~ 1, то система (80) имеет следующие решения (Ь > 0):
г а , х — arctg -у 4- ля,
у — ± arccos [(— 1)" У а2 4- У| 4-2 nk.
Метод решения системы (80) можно применить и к системе вида
sin х cosy — а, sin xsiny==b.
13*
387
к системам вида (80) сводятся следующие системы: sin х 4- sin у = а,
(82)
cosx 4- cos _у = Ь, sin х — sin_y = a, cos x± cosy = b, sin x4~ cos y — a,
, . h (83)
COS X-f-Sin_y = P.
Будем предполагать, что ab 0.
Рассмотрим систему (82). Эта система равносильна следующей:
. x-i-у х — у а
sincos-^=у, х 4- и х —у b
COS -у^ COS -g-4 = g-.
Полагая x^lJ = u, ^-^=v, получим систему вида (80):
а
SIH It COST = y , b cos и cos v = у .
Аналогично рассматривается система (83). Пример 50. Решить систему уравнений
, . 1
Sinx — Sinj = y, . • j/T
COS X 4- cos у = -g- ..
Решение. Имеем
1
Sinn COS И = у ,
/3
COS U COS V = -г-
где
x 4- У х — у v=^--
388
Отсюда находим
s Fr о-1-""’
sitw = (— 1)”^> COSH = ( 1)В|, г/_________________nnq
и — ± arccos 12nk.
Рассмотрим два случая: а) п — четное, б) п — нечетное.
^=4 +2л/.,
а)
-Р = ±3 + 2л^,
х = J(1 ± 2) + 2л/, у=~(- 1 ± 2) + 2пр (84)
(/, р — произвольные целые числа).
б)
£1^=^ + п(2от + 1)’ ^ = гЬу+2л/г,
х=^(1±4) + л(2/+1), _у = ^(-1±4) + л(2р+1).
(85)
Нетрудно проверить, что совокупность решений, определяемых формулами (85), совпадает с набором решений (84).
Отв. х = ~+2л/, у = ” 4- 2лр;
х — —6 4~ 2nZ, У — — 2'4_2лр.
6°. Системы вида
ar sin х 4- bi sin у = q, а2 cos х 4- b2 cos у = с2
(86)
являются более общими, чем системы (82). Изложенный в п. 5° метод решения систем (82) непригоден в общем случае для решения систем (86).
389
Заметим сначала, что система легко решается, если какое-либо из чисел av bv а2, b2 равно нулю. Пусть, например, аг = 0. Тогда из первого уравнения находим
а затем из второго определяем cosx.
Пусть теперь aibJa.2b2 # 0. Систему (86) естественно решать методом исключения одного из неизвестных, например х. С этой целью заменим систему (86) следующей равносильной системой:
sinx = ~ —— siny, «1 а,
с, Ьп
cos X = ----------- cos у.
а2 а2 '
(87)
Возводя уравнения системы (87) в квадрат и складывая, получаем уравнение вида
a cos у -|~ b siny + с sin2 у = d. (88)
Уравнение (88) подстановкой tg-| = Z сводится к уравнению вида
а0/4 + а^3 + a2t2 Ц- a3t + — 0.
Таким образом, в общем случае нахождение решений системы (86), несмотря на кажущуюся простоту этой системы, является весьма трудной задачей.
Если же одно из чисел с1, с2 равно нулю, то в уравнении (88) либо а —0, либо Ь — 0, и, следовательно, уравнение (88) сводится к квадратному относительно siny или cosy.
Находя sin у (или cosy) и подставляя найденное значение в систему (87), мы определим из этой системы sinx или cos х.
Заметим, что уравнение (88) вместе с одним из уравнений системы (87) образуют систёму, являющуюся следствием исходной системы. Поэтому возможно появление посторонних корней, которые выявляются проверкой (подстановкой в исходную систему (86)).
Пример 51. Решить систему уравнений
siny = 5sinx, - (89)
3cosx-|- cosy = 2. (90)
390
Решение. Исключим из системы у. С этой целью второе уравнение запишем в виде
cos у = 2— 3 cos х, (91)
а затем, возведя уравнения (89) и (91) в квадрат и складывая, получаем
1=25 sin2 х + 4 —12 cos х -р 9 cos2 х,
16 cos2 х + 12 cos х — 28 = 0, (92)
7
откуда cos х = 1, х=2пп; cosx =— (нет корней). Из (90) находим cosy =—1, у = (2А1) л. Итак, система (90), (92), являющаяся следствием исходной системы, имеет следующие решения:
х = 2лл, у = п(2/г4~1).
Эти решения удовлетворяют и исходной системе (89), (90). Отв. х — 2л.п, у = л (2&-j-1).
Задачи к главе XI
Решите уравнения (11.1—11.30):
11.1. 2 sinx+3 cos х = 0.
11.2. sin2 2х — -^.
11.3. sin2 Зх = cos2 Зх.
11.4. sin + cos x = 1.
11.5. 2 cos * = 1 4- cos x.
11.6. 2 sin2 2x= 3 cos 2x.
11.7. S^=0. 11.8. -^ = 0. sin X cos 3x
11.9. 2 sin = 3 sin fx—
11.10. sin (x + 5 j + cos (x-f-z-'j + cos x— 1.
11.11. sin 2x+cos 5x = 0.
11.12. cos2x— sinx2 = 0.
11.13. 3 sin1 x-J-4 cos9 x= 7.
11.14. 8cos65x—3sinx-|-4=0.
391
11.15. 2 sinx — sin5x = 0.
11.16. sin 2x sin 3x4-cos 5x = 0.
11.17. cos x = cos 3x cos 2x.
11.18. sin2 x 4-2 sin2 2xcos2x = 1.
11.19. sin2 x-|-sin2 2x-|-sin2 3x = 0.
11.20. 3 sin x — 4cosx = 5.
11.21. 2 sin 7х4-У 3 cos 3x4-sin 3x==0.
11.22. 3 sinx4-4 cosx4-5sin 3x = 0.
11.23. cos5 2x4-2 sin2 x= 1.
11.24. 2 sin2 x-f- -j- cos3 2x — 1.
11.25. 1—sin 10x = 2 sin218 x.
11.26. 2 cos2 3x-|-sin 5x= 1.
11.27. (sin 7x 4~ cos 7x)2 = 2 sin21 lx.
11.28. tgx=9 tg3*-.
11.29. sin 2x — 5sinx5cosx5 = 0.
11.30. sinxcosx= 6(sinx — cosx—1).
11.31. Найдите наименьший положительный корень уравнения
sec х = 10 sin х — 8 cos х.
Решите уравнения (11.32—11.52):
11.32. cos2 4х — 4 cos2 2х 4-2 = 0.
11 оо 3 V 3 cos 2«4-3 sin 2х . 1
11.33. — -=------—-------= 4 cos х-------.
У 3 cos х 4- sin х cos х
11.34. sin хcos х = У 2 sin 7 x.
11.35. sinx4~sin 2x4~sin 3x = 0.
11.36. sinx — sin3x = sin4x — sin 2x.
11.37. sin6 x cos x cos6 x sin x = sin 2x.
11.38. sin7 x cos3 x—cos7 x sin3 x — cos 2x.
11.39. sin8x — cos8x — cos2x = 0.
11.40. sin 4x= 6 cos2 2x — 4.
11.41. (sin 3x-|-sin 5x)2 = (cos 3x 4-cos 5x)2.
11.42. cos2 x 4-cos2 2x-(-cos2 3x = |.
11.43. cos 7x -j-sin2 2x=cos2 2x—cosx.
392
11.44. cos2 x 4- cos2 2x = cos2 3x 4- cos2 4x.
11.45. cos2 2x 4- cos2 3x 4-cos2 4x 4- cos2 5x = 2.
11.46. sin2 x 4- sin2 2x — sin2 3x4-sin2 4x.
11.47. 2sin32x— 4 cos 4x = sin 4x.
11.48. sin 2x cos 4x — sin 6x cos 8x.
11.49. cos 7x cos 13 x = cos x cos 19x.
что уравнение
11.50. sin xsin 5x = sin 2x sin 4x.
11.51. cos x cos 3x = -i-.
11.52. sin x sin 3x =
11.53. Докажите, не имеет решений.
11.54. Докажите, то уравнение
sin 5xsin 7х— 1
а
что если -я есть число иррациональное,
sin ах sin [Зх = 1
не имеет решений.
Решите уравнения (11.55 — 11.112):
11.55. 2 (sin 2х 4- cos 2х) = tg х 4- ctg х.
11.56. (1 4- ctg х) sin2 х = sin х 4- cos х.
11.57. (1 — ctgx)(l 4-sin 2х)= 1 4- ctg х.
11.58. sin3x(l 4-ctgx)4-cos3x(l 4- tg x) = cos 2x.
11.59. 3- W--* = 2cos2x—1.
1 —tg*
11.60. tg^x—~^==1 — sin 2x.
11.61. sin (,x4~-~H == “7=^(1—sin x cos x).
\ 4 J /2
11.62. sinx4-cosx=T=^2F.
11.63. tg2x4~cos4x = 0.
11.64. tg2 x 4- 8 cos 2x ctg 2x = ctg2 x.
11.65. tgx + ctgx = sin^x4--^.
11.66. ctgx—2cos2x=l.
393
11.67. sin3 x 4-cos3 x 4-sin (-r4“^j = 0-
11.68. cos2x = cos3x—sin3x.
, sin2 .v—“Sinx4-i-
11.69. (tg x) 2 2 = 1.
11.70. cos x (tg x 4- tg 3x) = 4 sin 3x sin 4x.
11.71. tg 3x— tg 2x— tgx = 0.
11.72. 2 + ctg 4x = ctg 2x.
11.73. 3 tg 3x— ctg2x = 4tgx.
11.74. ctg x 4- ctg 3x = tg 2x.
11.75. tgx— ctg 3x 4- ctg 4x = 0.
11.77. sin2x —cos2x = 2]/2cos2(x —]Z2-\ о -•
11.78. sin x 4- sin 2x4-sin 3x4- sin-4x4-sin 5x = 0.
11.79. sin x 4- sin 2x 4- sin 3x = 1 4- cos x 4- cos 2x.
11.80. sin3x4-1 = cos2x4-sinx.
11.81. 2 sin 3x4-2 sin 2x4-sin x = 0.
11.82. sin 3x4-sin3 x = sin 2x.
11.83. sin 4x — sin 3x— 2 sin 2x4-3 sin x = 0.
11.84. sin3 X 4- sin4 X = C0S3 X 4- COS4 X.
11.85. у (sin4 x4-cos4 x) = sin2 x cos2 x 4- sin x cosx.
11.86. 4cosx — 2cos2x — cos4x=l.
11.87. 2 4-4cos4x = tgx4-ctgx.
11.88. 2 4- cos 4x = 5 cos 2x 4- 8 sin6 x.
11.89. 4 4-cos 2x 4-3 cos 4x= 8 cos6 x.
11.90. 35 4-3 cos 4x— 12 sin2 2x — 32 cos2 x= 32 sin6 x.
11.91. sin6 x -j- cos6 x — sin 2x.
11.92. sin9 x cos x — cos9 x sin x = sin 4x.
11.93. tg3x = tgx tg (44-*k
j I 94 1-|-lg Л-Ч-ctg л:_________ctg x________ J
sector g-tg x cosec2 л-4-tg2 x — ctg2 x
11.95. tgx — tg 3x4- tgx tg 2x tg 3x = 0.
11.96. 4 tg 4x — 4 tg 3x — tg 2x = tg 2x tg 3x tg 4x.
11.97. tg x = tg2 ctj tg2 ^x-|-^ 4- 2ctgx —2 ctg 2x.
394
11.98. tgx — tg2^x—— tg2G + ^-^ + ctgx—2 tg 2x.
, < пл s’n2 5x cos2 5x o n
11.99. ------------x— = 8 cos2x.
Sin2 X COS2 X
11.100. sin x 4- sin2 x 4- sin3 x = cos x 4- cos2 x 4- cos3 x.
11.101. 1 4- 2 cos x (1 4- sin 2x) = sin 2x— cos 2x.
11.102. 4 sin x cos2 x = cosec x — sin x — cos x.
11.103. 5 cos 3x + 3 cos x — 3 sin ix.
11.104. sin3 x 4- cos3 x 4- sin 2xsin \ x 4- ~'j =
= cos л'4-sin 3x.
11.105. sin 2x-|-sin 6x = sin 4x4-cos 4x4-2 sin2 x.
11.106. 2 cos2 {x— y) + cos 4x4-sin 6x = cos 2x4-sin
11.107. sinx4-sin 2x4- 2 sinx sin 2x = 2 cosx4-cos 2x.
11.108. 2 sin x4-3 cos x4-2 cos xsin2x=2 4-cos2x4-3sin2x.
11.109. tg 2x4--^— = ctg x4--Др-.
& 1 sin x b 1 sin 5x
11.110. ctg 2x4-3tg 3x = 2 tgx4-^?_.
11.111. 14- sin 2x 4- 2 V 2 cos 3x sin ' 4- =
— 2 sin x 4- 2 cos 3x 4- cos 2x.
11.112. sin 4x j 2 4- ctg x 4* ctg —Д| =
= 2)^2 (1 4~ sin 2x4-cos 2x).
11.113. Определите все значения а, при которых уравнение (а2 4- 2) sin2 х 4- 4а sin х cos х = а2 4~ 3
имеет решения. Найдите эти решения.
11.114. Определите все значения а, при которых уравнение cos214- 6 sin t = 4a2 — 2
имеет решения. Найдите эти решения.
11.115. Определите все значения В, при которых уравнение sin 2х—2В |/2(sin х 4- cos х) 4-1 — ()№==0
имеет решения. Найдите эти решения.
395
11.116. При каких значениях В уравнение sin 2х 4- 2В ]/2 (sin х— cos х) 4-1 — 42? = О
имеет решения? Найдите эти решения.
11.117. При каких значениях а уравнение
sin4 хч-cos4 х=а
имеет решения? Найдите эти решения.
11.118. При каких значениях В уравнение
cos2 х cos 2x4- В (cos4x— sin4 х) = (2В 4-1)2
имеет решения? Найдите эти решения.
11.119. Определите, при каких значениях а уравнение
2а (sin4 х — cos4 х) — 1 4- cos2 2х
разрешимо, и решите это уравнение.
11.120. Покажите, что если а, Ь, с действительны и а2 4-С2 =4 О, то по крайней мере одно из двух уравнений
a sin х 4- b cos х 4- с — О, a tg х 4- b ctg х 4- 2с = О
имеет решения.
11.121. Решите уравнение
tg (х 4- a) tg (х 4- 2а) tg (х 4- За) = 1.
Сколько решений имеет это уравнение в зависимости от а?
Решите уравнения (11.122—11.133):
11.122. sin 2x4- ctg х— 2.
11.123. cos2 2х -4---= cos 2x-----4- 4.
1 cos2 2x cos 2x 1 .
11 .124. sin3 [x = У2 sinx.
11. 125. cosx = cos2~x.
4
11 iл• /1। тг \ г» . !3jt x\
1 1.126. sin f у 4- = 3 sin (-jq-—yj.
it шт * 2x 4x I
1L I 27. cos cos cos — .
ODDO
11.128. sin 3x sin3 x-j-cos 3xcos3x —
о
396
11.129. sin — x\ sin — 2x\ sin — Зх') -f-
У o j \ о / \ 3 у
4-sin)^4-x') sin (-5- 4- 2x^ sin (^4- 3x^ = 0.
'. о у \ о у у о У
11.130. 2tg6x4~4tg 12x4-8 ctg 24x4~ tg 3x = tg 2х.
11.131. cos2 Зх 4- 4- cos3 х = cos Зх cos1 x.
1 4
11.132. sin2 4x 4~ cos2 x = 2 sin 4x cos1 x.
11.133. sin5 x 4- cos3x 4~ 3 sin fx 4- y) =
11.134. Решите уравнение
sin2"1 x 4- cos2" x = 1
(m, n — натуральные числа, хотя бы одно из которых больше единицы).
11.135. Решите уравнение
Sin2" + 1 X 4-«т+Г' = COS2" +1 х 4- 2m+i
1 cos2m+1 х 1 sm2'"1 х
(т, п — целые положительные).
Решите системы уравнений (11.136—11.143):
11.136. . 1 ( . /3 sin XCOS_y=-H-, 1 sinxsin у — ——, х 11.137. 4_ siny/ cos x = -g. [ COSX cos у = -!^-.
11.138. . 3 sinxsin У =-r, . tgxtgj = 3.
11.139. 14-/2 COS X COS у = , ctg x ctg у — 3 4- 2 ]/2.
11.140. < sin2 x = cosxcosy, cos2 x = sin xsin_y.
11.141. . . 3 . 1 sin X 4- Sin у = -S- , COS X 4- cos V = -A- , 11.142. cosx 4- cos y — ~. sin2 x 4- sin2 у 397
11.143. ( sin у = 3 sin X, \ 2 cos x-f- cosj/= 1.
11.144. Решите, систему уравнений f х-]-у — а, [ sinxcos у~а.
При каких 11.145. условиях система имеет решения? Решите систему уравнений ( tg х4~ ctg_y = а, 1 ctg х + tg у = 2.
При каких 11.146. а задача имеет решения? Решите систему уравнений ( cos2 х cos2 у — а, 1 x+_V = a.
Найдите условие разрешимости системы.
11.147. Найдите все значения а, при которых система
уравнений ( sin 2х cos j'= а2 1, 1 cos 2х sin_y = 5а
имеет решения, и решите эту систему.
Решите системы уравнений (11.148— 11.166):
11.148. cos2_v + 3 sin х sin_v = 0, 21cos2x— cos2j/=10. ' cos (x —y) — 2 cos (x +_y),
11.149. . 3 COSXCOS_y = y . ЛГ-1-М X—I! 1
11.150. COS —~ COS —= у , 1 COS X COS у = у . tgxtgy=l,
11.151. . , , 1 Sin X COS у 4- ctg X tg J/ —у .
398
11.152. ' sin x 4- sin у — sin3 x 4- sin3y, j sin2 x 4-sin2_y = sin4x4-sin4>.
sin2 x = sin y, . 11.154. cos4 X = cos y. cos x 3
11.153. sin (x+y) 2 ’ cos у 3
sin (ху-y) 4‘
11.155. cos x -4 3 sin x = 2 cosy, cos_y4-3sinj/ = 2 cosx.
11.156. ctg x 4- sin 2y = sin 2x, 2 sin_v sin (x 4-_v) = cos x.
11.157. 4 tg 3x= 3 tg 2y, 2 sin x cos (x—j/) = sin_v.
4cosxtgv—2 cos 2x— sec2_y=l,
11.158. . (4 x + ctgy) (2 sin x + tgy') =1 •
J cos2j/ 4-cos x sin 2y = 1, 11.159. у (tgX_|_ctgy)(2sinx — tgy)4-cos2x = 0. ,
11.160. sin x-\-a cosj = -j^-(l +a)>
cos x 4- a sin у — G +«)•
11.161. 11.162. a cos (2x 4-_y) = cos_y, a cos (x 4~ 2y) = cos x, где 4 sin (3x 4- 2y) 4- sin x = 0, 4 sin (2x4- 3_y)4-sinj =0. я>1.
11.163. 3 cos2 x 4- 4 sin (x 4-j)4- 3 cos2j/ = —1, sin x 4- sin_y 4- 2 (cos x 4- cos j') = 1.
11.164. 4 sin2 x— 3 sin (x 4-.V) 4- 4 sin2_y= 1,
3(sinx4-sinj) —cosx—c os_y = 2.
11.165. < cos x cos 2_v4-sin V cos 2x4-2 cos x= 1,
cos 2x4-3 cos 2y 4- 8 sin_y = 84-4 sinxcosj/.
sin x cos 2_y + sin_y cos 2x 4- sin_y= 1,
2 cos 2x -f- 8 cos x cos у 7 = 4 siny.
399
ГЛАВА XII
ЗАДАЧИ ПО ПЛАНИМЕТРИИ
§ 1. Прямоугольный треугольник
12.1 . Сумма катетов прямоугольного треугольника равна I, а высота, опущенная из вершины прямого угла, равна /г. Найти площадь этого треугольника.
12.2 . Высота прямоугольного треугольника, опущенная из вершины прямого угла, равна /г, разность между проекциями катетов на гипотенузу также равна h. Найти гипотенузу этого треугольника.
12.3 . Высота прямоугольного треугольника, опущенная из вершины прямого угла, равна h, разность между проекциями катетов на гипотенузу равна I. Найти площадь этого
треугольника.
12.4 . В прямоугольном треугольнике АВС из вершины прямого угла С опущена высота CD. Проекция отрезка BD на катет ВС равна I, а проекция отрезка AD на катет АС равна т. Найти длину гипотенузы АВ.
12.5 . Катеты прямоугольного треугольника равны b и с. Найти длину биссектрисы прямого угла этого треугольника.
12.6 . Один из катетов прямоугольного треугольника равен Ь, а радиус описанной около этого треугольника окружности равен R. Найти длину биссектрисы угла, заключенного между данным катетом и гипотенузой.
12.7 . В прямоугольном треугольнике гипотенуза равна с,
а биссектриса одного из острых углов равна ^=. Найти
катеты этого треугольника.
12.8 . В прямоугольном треугольнике известны отрезки а и Ь, на которые точка касания вписанного в треугольник круга делит гипотенузу. Найти площадь этого треугольника.
12.9 . Доказать, что в прямоугольном треугольнике сумма катетов равна сумме диаметров вписанной и описанной окружностей.
400
12.10 . Из вершины прямого угла С прямоугольного треугольника АВС опущена высота CD. Доказать, что длина CD равна сумме радиусов окружностей, вписанных в треугольники ABC, ACD и BCD.
12.11 . В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота CD. Известно, что радиусы окружностей, вписанных в треугольники ACD и BCD, равны р и г. Найти радиус окружности, вписанной в треугольник АВС.
12.12 . Центр окружности, вписанной в прямоугольный треугольник, находится на расстоянии Уб см и ]/"10 см от концов гипотенузы. Найти катеты этого треугольника.
12.13 . Найти острые углы прямоугольного треугольника, если известно, что отношение радиуса описанной около этого треугольника окружности к радиусу вписанной в него окружности равно l-f-pz3.
12.14 . Найти катеты прямоугольного треугольника, если известно, что радиус описанной около этого треугольника окружности равен R, а радиус вписанной в него окружности равен г.
12.15 . В прямоугольном треугольнике один из острых углов равен а, гипотенуза равна с. Найти расстояние между центрами вписанной и описанной окружностей.
12.16 . В прямоугольном треугольнике высота, опущенная из вершины прямого угла, равна h, а проекция одного из катетов на гипотенузу равна I. Найти радиус окружности, касающейся катетов, если центр этой окружности лежит на гипотенузе.
12.17 . В прямоугольном треугольнике АВС гипотенуза АВ —с, А_ А = а. Найги радиус окружности, касающейся катета АС, гипотенузы АВ и окружности, описанной около треугольника АВС.
12.18 . Прямоугольный треугольник с острым углом а расположен внутри окружности радиуса R так, что гипотенуза треугольника является хордой окружности, а вершина прямого угла треугольника лежит на диаметре, параллельном гипотенузе. Найти площадь этого треугольника.
12.19 . Острый угол прямоугольного треугольника равен а, а радиус окружности, касающейся гипотенузы и продолжений двух катетов, равен R. Найти гипотенузу этого треугольника.
2
12.20 . Площадь прямоугольного треугольника равна уГ2, где г — радиус окружности, касающейся одного катета и
401
продолжений другого катета и гипотенузы. Найти стороны этого треугольника.
12.21 . В острые углы прямоугольного треугольника вписаны два равных касающихся друг друга круга. Сумма площадей этих кругов равна площади круга, вписанного в треугольник. Найти острые углы этого треугольника.
12.22 . На сторонах прямоугольного треугольника с катетами a w b построены квадраты, лежащие вне треугольника. Найти площадь треугольника с вершинами в центрах квадратов.
12.23 . Катеты прямоугольного треугольника равны 6 см и 8 см. На всех его сторонах как на диаметрах построены полуокружности, лежащие вне треугольника. Найти радиус окружности, касающейся построенных полуокружностей.
12.24 . В прямоугольном треугольнике АВС катет АВ — 3 см, катет ЛС = 6 см. Центры окружностей радиусов 1 см, 2 см и 3 см находятся соответственно в точках А, В а С. Найти радиус окружности, касающейся каждой из трех данных окружностей внешним образом.
§ 2. Правильный треугольник
12.25 . На стороне ВС правильного треугольника АВС расположена точка £); угол CAD равен а. Найти отношение площади треугольника ACD к площади треугольника АВС
12.26 . В правильном треугольнике АВС со стороной а проведена средняя линия MN параллельно АС. Через точку А и середину MN проведена прямая до пересечения с ВС в точке D. Найти длину AD.
12.27 . В правильном треугольнике АВС сторона равна а. На стороне ВС лежит точка D, а на стороне АВ — точка Е так, что BD — -^, AE = DE. Найти длину СЕ.
12.28 . Все вершины правильного треугольника лежат на сторонах прямоугольного треугольника. Одна из сторон правильного треугольника параллельна гипотенузе, и длина ее в три раза меньше длины гипотенузы. Найти углы прямоуголного треугольника.
12.29 . Диаметр окружности радиуса г является основанием правильного треугольника. Найти площадь той части треугольника, которая лежит вне круга.
12.30 . На высоте правильного треугольника, длина сторо- • ны которого равна Ь, как на диаметре построена окружность.
402
Найти площадь той части треугольника, которая лежит внутри окружности.
12.31 . Вершины правильного треугольника расположены на трех параллельных прямых. Расстояния от средней прямой до двух крайних равны а и Ь. Найти сторону треугольника.
12.32 . Даны две концентрические окружности радиусов г и R, причем г< R. Определить сторону правильного треугольника, у которого одна вершина лежит на окружности радиуса г, а две другие — на окружности радиуса R.
12.33 . Окружности радиусов г и R касаются друг друга внутренним образом. Найти сторону правильного треугольника, у которого одна вершина находится в точке касания данных окружностей, а две другие лежат на разных данных окружностях.
§ 3. Равнобедренный треугольник
12.34 . В равнобедренном треугольнике АВС боковая сторона равна Ь, а угол между боковыми сторонами АВ и АС равен а. Через вершину В и центр окружности, описанной около треугольника АВС, проведена прямая до пересечения со стороной АС в точке D. Найти длину BD.
12.35 . Определить площадь равнобедренного треугольника, если длина его основания равна Ь, а высота, опущенная на боковую сторону, равна Л.
12.36 . В равнобедренном треугольнике боковая сторона равна 20 см, а основание равно 24 см. Найти расстояние между точкой пересечения медиан и точкой пересечения биссектрис этого треугольника.
12.37 . В равнобедренном треугольнике высота, опущенная на основание, равна h, а радиус вписанной окружности равен г. Найти радиус окружности, описанной около этого треугольника.
12.38 . В равнобедренном треугольнике угол при основании равен а, а разность между радиусами описанной окружности и вписанной окружности равна Ь. Найти длину основания этого треугольника.
12.39 . В равнобедренном треугольнике АВС угол между боковыми сторонами АВ и ВС равен а, где а<у. На продолжении высоты BD расположена точка Л1 так, что прямая МС касается окружности, описанной около треугольника АВС. Найти отношение площади треугольника CDM к площади треугольника АВС.
403
12.40 . Равнобедренный треугольник рассечен биссектрисой угла при основании на два треугольника; площадь первого из них (прилежащего к основанию) равна уу с.и , площадь
60 „ „ ,
второго— уу см. Определить стороны равнобедренного треугольника.
12.41 . В равнобедренном треугольнике длина боковой стороны равна а, длина основания равна Ь. Вписанная в этот треугольник окружность касается его сторон в точках М, N и К. Определить площадь треугольника MNK.
12.42 . В равнобедренном треугольнике АВС угол при основании АС равен а. Окружность, вписанная в этот треугольник, касается его сторон в точках М, N и К. Найти отношение площади треугольника MNK к площади треугольника АВС.
12.43 . В равнобедренном треугольнике АВС, у которого АВ = ВС и угол В равен -2-, опущен перпендикуляр AD на сторону ВС. В треугольники ABD и ACD вписаны полукруги так, что их диаметры лежат соответственно на BD и AD. Определить отношение площадей построенных полукругов.
12.44 . На основании АС равнобедренного треугольника АВС расположена точка D так, что AD = a, CD — b. Окружности, вписанные в треугольники ABD и BCD, касаются прямой BD соответственно в точках М и М Найти длину MN.
12.45 . В равнобедренном треугольнике АВС параллельно основанию АС проведена средняя линия MN. Радиус окруж-ности, описанной около трапеции ACMN, в раз больше радиуса окружности, описанной около треугольника АВС. Найти углы треугольника АВС.
12.46 . Угол при основании равнобедренного треугольника равен 2 arcctg 2. Внутри треугольника расположены три окружности так, что каждая из них касается двух других окружностей и двух сторон треугольника. Найти отношение радиусов этих окружностей.
12.47 . В равнобедренном треугольнике с углом 120° радиус вписанной окружности равен R. Внутри треугольника лежат два равных касающихся друг друга круга, каждый из которых касается одной боковой стороны треугольника и вписанной в треугольник окружности. Определить радиусы этих кругов.
404
12.48 . Определить углы равнобедренного треугольника, зная, что точка пересечения его высот лежит на вписанной окружности.
12.49 . На боковых сторонах АВ и ВС равнобедренного треугольника АВС расположены соответственно точки М и N AM CN ...»
так, что дду = //г> -£ду = «- Прямая MN пересекает высоту BD в точке О. Найти отношение
§ 4. Произвольный треугольник
12.50 . В треугольнике АВС угол при вершине А в два раза больше угла при вершине В, АВ —с, АС — b. Определить ВС.
12.51 . В треугольнике АВС дано; ВС —а, АС — b, АВ = с. На ВС выбрана точка D таким образом, что окружности, вписанные в треугольники ABD н ACD, касаются друг друга. Найти BD.
12.52 . В треугольнике АВС угол А равен 2а, АВ = с, АС — b. Найти длину биссектрисы угла А.
12.53 . Две стороны треугольника равны соответственно 6 см и 8 см. Медианы, проведенные к серединам этих сторон, пересекаются под прямым углом. Найти третью сторону этого треугольника.
12.54 . В треугольнике АВС угол А равен 60°, АВ: АС — = 3:2. На сторонах АВ и АС расположены соответственно точки М и N так, что BM — MN—NC. Найти отношение площади треугольника AMN к площади треугольника АВС.
12.55 . Основание треугольника равно Ь, а высота, опущенная на основание, равна Л. В треугольник вписан квадрат, одна из сторон которого лежит на основании треугольника, а две вершины — на боковых сторонах. Найти отношение площади квадрата к площади треугольника.
12.56 . В треугольнике известны отрезки т и п, на которые точка касания вписанной окружности делит одну из сторон треугольника, а противолежащий этой стороне угол равен 60°. Найти площадь треугольника.
12.57 . В треугольнике АВС дано: АС — b, АВ = с, а биссектриса угла А равна I. Найти ВС.
12.58 . В треугольнике АВС дано: АВ —2 см, АС —5 см, ВС =6 см. Найти расстояние от вершины В до точки пересечения высот треугольника АВС.
405
12.59 . В треугольнике АВС проведены биссектрисы AM и CN. Известно, что ЛС=6 см, AN—2 см, СМ — 3 см. Найти длину MN.
12.60 . В треугольнике АВС биссектриса AD делит сторону ВС в отношении BD:CD — 2:1. В каком отношении медиана СЕ делит эту биссектрису?
12.61 . На сторонах АС и ВС треугольника АВС распо-.. лл AN
ложены соответственно точки N и М так, что ^-=«,
= Прямые AM и BN пересекаются в точке О. Найти
АО ВО
ОМ и ON
12.62 . Биссектрисы AM и BN треугольника АВС пересекаются в точке О. Известно, что АО = У'3-МО, NO = = (V3 — 1). ВО. Найти углы треугольника АВС.
12.63 . Найти плошадь треугольника, медианы которого равны 12, 15 и 21 см.
12.64 . В углы В и С треугольника АВС вписаны окружности радиусов 2 см и 3 см, касающейся биссектрисы угла А. Найти длину этой биссектрисы, если расстояние между точками, в которых окружности касаются ВС, равно 7 см.
12.65 . В остроугольном треугольнике две высоты равны соответственно 3 см и 2]/ 2 см, а их точка пересечения делит третью высоту в отношении 5:1, считая от вершины треугольника. Найти площадь треугольника.
/ 12.66. Около окружности описан треугольник АВС, и в эгу же окружность вписан треугольник Л1Й1С1, подобный треугольнику АВС. Отношение плошадей треугольников равно 4 (1 + ]/2)2. Найти углы этих треугольников, если угол ВАС равен 60°.
12.67. В треугольнике АВС проведены медиана AD, биссектриса АЕ и высота AF. Площадь треугольника AED равна площади треугольника АВС, а площадь треугольника AFD 7
равна -gg площади треугольника АВС. Найти углы треугольника АВС.
12.68. В окружность вписан треугольник АВС. Расстояния от точек Л и С до прямой, касающейся окружности в точке В, соответственно равны а и с. Найти высоту треугольника АВС, проведенную из вершины В.
406-
§ 5. Параллелограмм
12.69. Окружность радиуса R касается сторон АВ и AD квадрата ABCD, пересекает сторону ВС в точке М и проходит через точку С. Найти длину отрезка ВМ.
12.70. Внутри окружности с центром в точке О радиуса R расположен квадрат ABCD так, что вершины В и С лежат на окружности, а сторона AD проходит через точку О. Найти радиус окружности, вписанной в треугольник ВОС.
12.71. В параллелограмме ABCD одна диагональ в ]Лз раз больше другой, а периметр равен 4 см. Известно, что точка Av симметричная с точкой А относительно точки С, симметрична с точкой В относительно прямой CD. Найти площадь параллелограмма ABCD.
12.72. Одна из диагоналей параллелограмма равна Ь, а другая образует со смежными сторонами параллелограмма углы, равные а и [}. Найти стороны параллелограмма.
12.73. Найти площадь параллелограмма, если его большая диагональ равна 5 см, а высоты — 2 см и 3 см.
12.74. Стороны параллелограмма равны а и Ь, а острый угол между диагоналями равен а. Найти площадь параллелограмма.
12.75. Стороны параллелограмма равны 3 см и 2 см, 5 ' „
а угол между ними равен arccos jg. Две перпендикулярные прямые делят параллелограмм на четыре равновеликие части. Найти длины отрезков, на которые эти прямые делят стороны параллелограмма.
12.76. В параллелограмме отношение сторон и отношение диагоналей одинаковы и равны 2. Из вершины тупого угла А опущена высота АЕ на большую сторону CD. Найти отношение длины отрезка DE к длине отрезка СЕ.
12.77. Радиус окружности, вписанной в ромб ABCD, равен г, угол АВС равен [}. На сторонах АВ и ВС расположены соответственно точки Е и F так, что прямая ' EF касается окружности, вписанной в ромб. Найти произведение AE-CF.
§ 6. Трапеция
12.78. Основания трапеции равны 10 см и 24 см, а боковые стороны —13 см и 15 см. Найти площадь трапеции.
12.79. В трапеции основания равны 84 см и 42 см, а боковые стороны — 39 см и 45 см. Через точку пересечения
407
диагоналей параллельно основаниям проведена прямая. Определить площади получившихся трапеций.
12.80. Основания равнобочной трапеции равны а и Ь, боковая сторона I. Найти радиус окружности, описанной около этой трапеции.
12.81. Около окружности описана трапеция с боковыми сторонами, равными а и Ь. Найти сумму квадратов расстояний о г центра окружности до вершин трапеции.
12.82. Около окружности радиуса R описана равнобочная трапеция, площадь которой равна S. Найти основания этой трапеции.
12.83. Около окружности описана равнобочная трапеция, у которой одно основание в три раза больше другого. Найти отношение радиуса окружности, описанной около трапеции, к радиусу окружности, вписанной в трапецию.
12.84. Сумма высоты и средней линии равнобочной трапеции равна с, а площадь трапеции равна S. Найти угол между диагоналями трапеции.
12.85. Основания равнобочной трапеции равны а и Ь, причем <з > Ь. Прямые, соединяющие середину большего основания с концами меньшего основания, пересекают диагонали трапеции в точках М и N. Найти длину отрезка MN.
12.86. Равнобочная трапеция, у которой угол при основании равен описана около окружности. В каком отноше-О
нии прямая, соединяющая точки касания окружности с боковыми сторонами, делит площадь трапеции?
12.87. В трапеции средняя линия равна 7 см, высота — 15/3
—— см, а угол между диагоналями против основания равен 120°. Найти диагонали этой трапеции.
12.88. Длины оснований трапеции равны а и Ь. Точки М и X лежат на боковых сторонах так, что прямая MN параллельна основаниям и делит трапецию на две равновеликие части. Найти длину отрезка MN.
12.89. В трапеции основания равны а и Ь, диагонали перпендикулярны, а угол между боковыми сторонами равен а. Найти площадь трапеции.
12.90. В равнобочной трапеции ABCD основания AD и ВС связаны равенством АД = (1 Д- У \5)ВС. Окружность 2
с центром в точке С радиуса ,~ВС высекает на основании О
408
Vi
AD хорду EF длины -Ат— ВС. В каком отношении эта О
окружность делит сторону CD?
12.91. Основания равнобочной трапеции относятся, как 3 : 2. На большем основании как на диаметре построена окружность, высекающая на верхнем основании отрезок, равный половине верхнего основания. В каком отношении эта окружность делит боковые стороны трапеции?
12.92. Около окружности описана равнобочная трапеция. Площадь четырехугольника с вершинами в точках касания составляет 4- площади трапеции. Найти отношение оснований О
трапеции.
12.93. Около окружности описана равнобочная трапеция. Радиус этой окружности в ]/"6 раз меньше радиуса окружности, описанной около трапеции. Найти угол при большем основании трапеции.
§ 7. Произвольный четырехугольник и многоугольник
12.94. В окружность вписан четырехугольник, три последовательные стороны которого равны соответственно 2]/"5 см, 2)^5 см, 6 см, а четвертая сторона является диаметром окружности. Найти радиус окружности.
12.95. Дан четырехугольник ABCD. Известно, что АВ2 -j- CD2 — АС2 -|- BD2. Найти угол между сторонами AD и ВС.
12.96. Найти отношения сторон выпуклого четырехуголь-л
ника, имеющего угол -тр если этот четырехугольник описан около окружности и имеет равные и взаимно перпендикулярные диагонали.
12.97. В окружность вписаны три правильных многоугольника таких, что число сторон каждого последующего вдвое больше, чем у предыдущего. Площади первых двух многоугольников соответственно равны и 52. Найти площадь третьего.
12.98. Два правильных многоугольника с периметрами а и b описаны около окружности, а третий правильный многоугольник вписан в эту окружность. Второй и третий многоугольники имеют вдвое больше сторон, чем первый. Найти периметр третьего многоугольника.
409
§ 8. Окружность
12.99. Круг вписан в круговой сектор с углом 2а. Найти отношение площади сектора к площади круга.
12.100. Окружности радиусов г и R\r<Z^Rj имеют внутреннее касание в точке А. Через центр большей окружности проведен диаметр ВС, касающийся меньшей окружности. Найти площадь треугольника АВС.
12.101. Две равные окружности радиуса R касаются друг друга внешним образом. Найти радиус окружности, касающейся двух данных окружностей и их общей внешней касательной.
12.102. Две окружности радиусов г и Зг касаются внешним образом. Найти площадь фигуры, заключенной между окружностями и их общей внешней касательной.
12.103. В окружности радиуса R проведена хорда. Сумма ее длины и расстояния от центра круга до хорды равна а. Найти длину хорды. При каких условиях задача имеет решение?
12.104. Длина внешней касательной окружностей радиусов г и R в два раза больше длины внутренней касательной. Найти расстояние между центрами этих окружностей.
12.105. Две окружности радиусов /\ и г2 касаются окружности радиуса R внешним образом в точках, расстояние между которыми равно а. Найти длину общей внешней касательной к первым двум окружностям.
12.106. Угол между внешними касательными двух непе-ресекающихся окружностей равен а, а угол между их внутренними касательными равен Р (в обоих случаях рассматриваются углы, для которых линия центров является биссектрисой). Найти острый угол между касательными, проведенными из центра большей окружности ко второй окружности.
12.107. На отрезке длины 2R как на диаметре построена полуокружность. В получившуюся фигуру вписана окружность радиуса Найти радиус окружности, касающейся построенных .окружности, полуокружности и данного отрезка.
12.108. На отрезке длины 2R как на диаметре построена полуокружность. В получившуюся фигуру вписана окружность R
радиуса Д. Найти радиус окружности, касающейся построенных окружности, полуокружности и данного отрезка.
410
12.109. Окружности радиусов R и г (R>r) касаются внутренним образом. Найти радиус третьей окружности, касающейся первых двух и их линии центров.
12.110. Найти радиус окружности, внутри которой расположены две окружности радиуса г и одна окружность радиуса R так, что каждая окружность касается трех других.
12.111. На отрезке АВ и двух его частях АС и ВС как на диаметрах построены полуокружности, лежащие по одну сторону от отрезка. Найти радиус окружности, касающейся трех построенных полуокружностей, если АС = 2а, ВС — 2Ь.
12.112. Внутри четверти круга АОВ радиуса R лежит 3
окружность радиуса -&R, касающаяся дуги АВ и отрезка ОВ. Найти радиус окружности, касающейся внешним образом данной окружности, дуги АВ и отрезка АО.
12.113. На окружности расположены точки А, В и М. Расстояния от точки М до прямых, касающихся окружности в точках А и В, соответственно равны а и Ь. Найги расстояние от точки М до прямой АВ.
ГЛАВА XIII
ЗАДАЧИ ПО СТЕРЕОМЕТРИИ
§ 1. Правильный тетраэдр
13.1 . Ребро правильного тетраэдра равно а. Найти радиус сферы, касающейся боковых граней тетраэдра, если центр этой сферы лежит на основании тетраэдра.
13.2 . Ребро правильного тетраэдра ABCD равно Ь. Найти радиус шара, вписанного в трехгранный угол, образованный гранями тетраэдра с вершиной в точке А, и касающегося плоскости, проведенной через середины ребер АВ, AD и ВС.
13.3 . Внутри правильного тетраэдра с ребром а лежат четыре равных шара так, что каждый шар касается трех других шаров и трех граней тетраэдра. Определить радиус этих шаров.
13.4 . Через середину ребра AD правильного тетраэдра ABCD параллельно ребру ВС проведена плоскость, пересекающая грань АВС под углом Найти площадь сечения, если ребро тетраэдра равно а.
13.5 . Диаметр шара является высотой правильного тетраэдра с ребром а. Найти площадь поверхности тетраэдра, лежащей внутри шара.
13.6 . В трехгранный угол, образованный гранями правильного тетраэдра с вершиной в точке А, вписан шар радиуса R. Найти расстояние от точки А до центра шара.
13.7 . Ребро правильного тетраэдра ABCD равно а. На ребре АВ как на диаметре построен шар. Найти радиус шара, вписанного в трехгранный угол тетраэдра с вершиной в точке А и касающегося первого шара.
13.8 . Внутри правильного тетраэдра ABCD расположены два шара радиусов 2R и 3/?, касающиеся друг друга внеш-ним образом, причем один шар вписан в трехгранный угол тетраэдра с вершиной в точке А, а другой — в трехгранный угол с вершиной в точке В. Найти длину ребра этого тетраэдра. 412
13.9 . Ребро правильного тетраэдра ABCD равно а. На ребре BD расположена точка М так, что 3£М4 = а. Прямой круговой конус расположен так, что его вершина находится на середине ребра АС, а окружность основания проходит через точку М и пересекает ребра АВ и ВС. Найти радиус основания этого конуса.
13.10 . Ребро правильного тетраэдра SABC равно а. Через вершину А параллельно ребру ВС проведена плоскость так, зт что угол между прямой АВ и этой плоскостью равен Найти площадь сечения.
13.11 . Ребро правильного тетраэдра равно а. Найти расстояние между скрещивающимися высотами граней тетраэдра. (Найти все решения.)
13.12 . Даны две концентрические сферы радиусов г и R, причем r<CR- Три вершины основания правильного тетраэдра лежат на сфере большего радиуса, а боковые грани касаются сферы меньшего радиуса. Определить ребро этого тетраэдра.
§ 2. Правильная треугольная пирамида
13.13 . В правильной треугольной пирамиде высота, опущенная на основание, равна h, а расстояние от центра основания до боковой грани равно Ь. Определить радиус вписанного в пирамиду шара.
13.14 . В правильной треугольной пирамиде площадь боковой поверхности равна S, а угол между боковой гранью и основанием равен а. Найти высоту пирамиды, опущенную на основание.
13.15 . Полная поверхность правильной треугольной пирамиды равна S, а угол между боковыми ребрами равен а. Найти высоту пирамиды, опущенную на основание.
13.16 . В правильной треугольной пирамиде высота, опущенная на основание, равна h, а угол между боковыми ребрами равен а. Найти расстояние от центра основания до боковой грани.
13.17 . В правильной треугольной пирамиде сторона основания равна а, а двугранный угол между боковыми гранями равен а. Найти высоту пирамиды, опущенную на основание.
13.18 . В правильной треугольной пирамиде сторона основания равна а, а двугранный угол между боковыми гранями равен а. Вычислить объем и боковую поверхность этой пирамиды.
413
13.19 . В правильной треугольной пирамиде сторона основания равна Ь, а боковое ребро равно 2Ь. Через середину бокового ребра перпендикулярно к нему проведена плоскость. Найти площадь сечения.
13.20 . В правильной треугольной пирамиде высота, опу-' щенная на основание, равна h, а сторона основания равна а. Через одну из вершин основания параллельно противоположной стороне основания проведена плоскость так, что угол между этой плоскостью и плоскостью основания равен а. Найти площадь сечения.
13.21 . В правильной треугольной пирамиде высота, опущенная на основание, равна h, а расстояние от центра основания до бокового ребра равно Ь. Определить радиус вписанного в пирамиду шара.
13.22 . Радиус шара, описанного около правильной треугольной пирамиды, равен R, а двугранный угол между боковыми гранями равен а. Найти сторону основания этой пирамиды.
13.23 . В правильной треугольной пирамиде двугранный угол между основанием и боковой гранью равен . Найти О
отношение радиуса описанного около пирамиды шара к радиусу вписанного в нее шара.
13.24 . В правильной треугольной пирамиде расстояния от середины высоты, опущенной на основание, до бокового ребра и до боковой грани соответственно равны hub. Найти объем пирамиды.
13.25 . Найти двугранный угол между основанием и боковой гранью правильной треугольной пирамиды, если двугранный угол между боковыми гранями этой пирамиды равен а.
13.26 . В правильной треугольной пирамиде угол между боковым ребром и основанием равен —. В пирамиду вписан прямой круговой цилиндр так, что одно основание цилиндра лежит на основании пирамиды, а окружность другого основания касается боковых граней пирамиды. Высота цилиндра равна диаметру его основания. Найти отношение объема пирамиды к объему цилиндра.
13.27 . Сторона основания правильной треугольной пирамиды равна а, а боковое ребро равно /. Найти радиус шара, касающегося всех ребер пирамиды.
13.28 . В правильной треугольной пирамиде SABC сторона основания АВС равна а, боковое ребро равно Ь, причем а <.Ь. 414
Найти радиус сферы, касающейся ребра ВС и плоскости АВС в точке А.
13.29 . В правильной треугольной пирамиде SABC сторона основания равна а, высота пирамиды равна а]/3- Точки М, N и К являются серединами соответственно боковых ребер HS, BS и CS. Найти радиус шара, касающегося основания пирамиды и прямых АК, CN и ВМ.
§ 3. Произвольная треугольная пирамида
13.30 . В треугольной пирамиде все боковые ребра и две стороны основания равны Ь. Угол между равными сторонами основания равен а. Вычислить объем пирамиды.
13.31 . Доказать, что если в треугольной пирамиде все грани имеют равные периметры, то все грани равны.
13.32 . Треугольная пирамида рассечена плоскостью на два многогранника. Найти отношение объемов этих многогранников, если известно, что секущая плоскость делит три боковые ребра, сходящиеся в одной вершине, в отношениях 1 :2, 1:2 и 2:1, считая от этой вершины.
13.33 . В треугольной пирамиде три грани взаимно перпендикулярны и их площади равны S2 и Найти площадь четвертой грани.
13.34 . В треугольной пирамиде боковые ребра, равные а, Ь, с, взаимно перпендикулярны. Высота, опущенная на основание, равна h. Доказать, что
±=±+±+± /г2 а2 ' Ь2 ' с2 '
13.35 . Все плоские углы при вершине S треугольной пирамиды SABC прямые; AS=a, BS=b, CS=c. Найти радиус сферы, описанной около этой пирамиды.
13.36 . В основании треугольной пирамиды лежит прямоугольный треугольник, гипотенуза которого равна Ь. Каждое боковое ребро пирамиды образует с плоскостью основания угол р. Найти радиус сферы, описанной около этой пирамиды.
13.37 . В основании треугольной пирамиды лежит прямоугольный треугольник, острый угол которого равен а. Каждое боковое ребро пирамиды образует с плоскостью основания угол р. Найти отношение объема пирамиды к объему описанного около пирамиды шара.
13.38 . В треугольной пирамиде боковые ребра равны, а в основании лежит прямоугольный треугольник, высота которого,
415
опущенная из вершины прямого угла, равна /?. Двугранные углы, образуемые гранями пирамиды, пересекающимися по катетам основания, равны аир. Найти объем пирамиды.
13.39 . В основании треугольной пирамиды SABC лежит прямоугольный треугольник АВС, ребро SB перпендикулярно плоскости основания. Дано: АВ = ВС —a, SB = h. Найти радиус вписанного в пирамиду шара.
13.40 . В треугольной пирамиде периметр основания рарен 2р, радиус вписанного шара равен R, а боковые грани образуют с основанием равные углы а. Найти объем пирамиды.
13.41 . В треугольной пирамиде SABC ребро ВС равно а, АВ —АС, ребро £4 перпендикулярно основанию АВС, двугранный угол при ребре £4 равен а, а при ребре ВС равен {3. Найти радиус шара, описанного около пирамиды.
13.42 . В треугольной пирамиде SABC грань SBC перпендикулярна грани АВС, все плоские углы при вершине S равны у, £B = SC=1 см. Найти объем этой пирамиды.
13.43 . В основании треугольной пирамиды лежит равнобедренный прямоугольный треугольник, гипотенуза которого равна I. Боковые грани образуют с плоскостью основания двугранные углы, соответственно равные а, 0 и у (у соответствует гипотенузе). Найти радиус шара, вписанного в эту пирамиду.
13.44 . В треугольной пирамиде ABCD ребро АВ равно 6 см, CD = 8 см, остальные ребра равны У74 см. Найти радиус шара, описанного около этой пирамиды.
13.45 . В треугольной пирамиде SABC высота SK равна h, АВ = АС, SB — SC, ВС = а, двугранный угол между гранями АВС и SBC равен у. Найти радиус шара, описанного около этой пирамиды, если известно, что центр шара лежит в плоскости АВС.
13.46 . В треугольной пирамиде SABC все плоские углы при вершине S прямые, АС = ВС, ребро SC наклонено к плоскости АВС под углом На ребре АВ как на диаметре построена сфера радиуса R. Найти радиус сферы, вписанной в трехгранный угол при вершине С и касающейся'данной сферы. (Найти все решения.)
13.47 . В треугольной пирамиде ABCD ребро АВ равно а, высота СЕ грани АВС равна b (точка Е лежит между А и В), высота DF пирамиды равна с (точка F лежит внутри тре-
416
угольника АВС). В пирамиду вписан куб так,
что грань PQMN куба лежит на грани АВС, ребро лежит на грани ABD, а вершины Мг и лежат на гранях ACD и BCD соответственно. Найти ребро куба.
13.48 . В 1реугольной пирамиде ABCD ребра АВ и CD взаимно перпендикулярны и' соответственно равны а и Ь. Общий перпендикуляр к этим ребрам пересекает ребро АВ в точке М и ребро СО в точке N, MN=c. В пирамиду вписан куб так, что четыре ребра куба параллельны MN и на каждой грани пирамиды лежат ровно две вершины куба. Найти ребро куба.
§ 4. Правильная четырехугольная пирамида
13.49 . В правильной четырехугольной пирамиде двугран-ный - угол между основанием и боковой гранью равен у. Найти отношение объема пирамиды к объему вписанного в нее шара.
13.50 . В правильной четырехугольной пирамиде сторона основания равна Ь, а двугранный угол между основанием и боковой гранью равен а. Определить радиус описанного около пирамиды шара.
13.51 . Сторона основания правильной четырехугольной пирамиды равна а, а двугранный угол между основанием и боковой гранью равен а. Найти расстояние между центром шара, вписанного в пирамиду, и центром шара, описанного около пирамиды.
13.52 . Сторона основания правильной четырехугольной пирамиды равна а, высота пирамиды равна h. Через сторону основания пирамиды и середину скрещивающегося с ней бокового ребра проведено сечение. Найти расстояние от вершины пирамиды, противолежащей основанию, до плоскости сечения.
13.53 . Расстояние от центра основания правильной четырехугольной пирамиды до бокового ребра равно h, а до боковой грани равно Ь. Найти объем пирамиды.
13.54 . Угол между соседними боковыми ребрами правильной четырехугольной пирамиды равен а, радиус описанной около пирамиды сферы равен R. Найти длину бокового ребра пирамиды.
13.55 . Найти наибольшую величину боковой поверхности правильной четырехугольной пирамиды, вписанной в шар радиуса R.
14 В. Г. Болтянский и др.
417
13.56 . В правильную четырехугольную пирамиду вписан куб так, что одно ребро куба лежит на средней линии основания пирамиды, вершины куба, не принадлежащие этому ребру, лежат на боковой поверхности пирамиды, центр куба лежит на высоте пирамиды. Найти отношение объема пирамиды к объему куба.
13.57 . Центр шара, описанного около правильной четырехугольной пирамиды, находится на расстоянии а от боковой грани и на расстоянии b от бокового ребра. Найти радиус шара.
13.58 . Центр шара, вписанного в правильную четырехугольную пирамиду, находится на расстоянии ]/"2 см от бокового ребра и на расстоянии ]/5 см от стороны основания. Найти радиус шара.
13.59 . Плоскость пересекает боковые ребра &4, SB, SC и SD правильной четырехугольной пирамиды SABCD соответственно в точках М, N, К и L так, что
AM
SM ~т’
BN
SN ~~П’
ск
SK ~Р’
Найти отношение
13.60 . В правильной четырехугольной пирамиде апофема равна стороне основания. Внутри пирамиды расположены два шара: шар радиуса г касается всех боковых граней, шар радиуса 2г касается основания и двух смежных боковых граней, оба шара касаются друг друга внешним образом. Найти апофему этой пирамиды.
13.61 . В правильной четырехугольной пирамиде SABCD сторона основания ABCD равна а, высота SO равна 2]/"2а. Через вершину А параллельно диагонали основания пирамиды BD проведена плоскость так, что угол между прямой АВ и этой плоскостью равен Найти площадь сечения.
13.62 . В правильной четырехугольной пирамиде SABCD сторона основания равна Ь, угол между боковым ребром и плоскостью основания равен arccos -у. Плоскость, параллельная диагонали основания АС и боковому ребру BS, пересекает пирамиду так, что в сечение можно вписать окружность. Определить радиус этой окружности. (Найти все решения.) 418
13.63 . В правильной четырехугольной пирамиде SABCD высота равна диагонали основания ABCD- Через вершину А параллельно прямой BD проведена плоскость, касающаяся вписанного в пирамиду шара. Найти отношение площади сечения к площади основания пирамиды.
§ 5. Произвольная четырехугольная пирамида и многоугольная пирамида
13.64 . В основании четырехугольной пирамиды лежит квадрат со стороной а, одно боковое ребро перпендикулярно плоскости основания, а большее боковое ребро наклонено к плоскости основания под углом р. Найти радиус шара, вписанного в эту пирамиду.
13.65 . В основании четырехугольной пирамиды SABCD лежит квадрат ABCD со стороной а. Ребро SD—h перпендикулярно плоскости основания. Внутри пирамиды расположен прямой круговой цилиндр так, что окружность одного его основания вписана в треугольник SCD, а окружность другого основания касается грани SAB. Найти высоту цилиндра.
13.66 . В основании четырехугольной пирамиды SABCD лежит квадрат со стороной а. Ребро S/1 перпендикулярно плоскости основания и равно h. Через вершину А параллельно диагонали основания BD проведено сечение, которое делит ребро SC в отношении 2:1, считая от вершины S. Найти площадь сечения.
13.67 . Основанием четырехугольной пирамиды SABCD является ромб с диагоналями АС = а, BD=b- Боковое ребро перпендикулярно плоскости основания и равно h. Через точку А и середину ребра SC проведена плоскость, параллельная диагонали основания BD. Найти площадь сечения.
13.68 . В правильной шестиугольной пирамиде через центр основания проведено сечение параллельно боковой грани. Найти отношение площади сечения к площади боковой грани.
13.69 . Два боковых ребра пирамиды, длины которых равны а и Ь, образуют угол у. Угол между проекциями этих ребер на плоскость основания равен . Найти высоту пирамиды.
13.70 . В пирамиде SABC... К проекция вершины S на основание лежит внутри угла АВС, угол АВС равен О
14*
419
углы SAB и SCB прямые, АВ = а, BC — b, SC = l- Найти высоту этой пирамиды.
13.71 . В правильной шестиугольной пирамиде вписанная сфера проходит через центр описанной. Во сколько раз радиус описанной сферы больше радиуса вписанной? (Найти все решения.)
§ 6. Усеченная пирамида
13.72 . Около шара описана правильная треугольная усеченная пирамида, боковая грань которой наклонена к плоскости основания под углом а. Найти отношение объема шара к объему усеченной пирамиды.
13.73 . В правильной треугольной усеченной пирамиде ABCAiBiCi сторона большего основания АВС равна Ь. Расстояние от точки А до. плоскости треугольника AiBCi равно т, а расстояние от точки В\ до той же плоскости равно п. Найти высоту этой усеченной пирамиды.
13.74 . В правильную треугольную усеченную пирамиду с боковым ребром I можно поместить шар, касающийся всех граней, и шар, касающийся всех ребер пирамиды. Найти стороны оснований пирамиды.
13.75 . В правильной четырехугольной усеченной пирамиде ABCDA^BiCiDi проведено два сечения: Л41С1С и ABC\Di. Первое сечение имеет площадь Si, второе —площадь Sa-Найти площадь сечения, проходящего через середину высоты пирамиды параллельно основаниям.
13.76 . В правильной четырехугольной усеченной пирамиде проведено сечение через диагонали оснований и сечение, проходящее через сторону нижнего основания и противолежащую сторону верхнего основания. Острый угол между этими секущими плоскостями равен а. Найти отношение площадей сечений.
13.77 . Разность периметров нижнего и верхнего оснований правильной четырехугольной усеченной пирамиды равна 4а, высота пирамиды равна h. Расстояние от центра описанного около пирамиды шара до плоскости боковой грани в У 2 раз меньше радиуса этого шара, Найти стороны оснований пирамиды.
13.78 . Стороны оснований правильной шестиугольной усеченной пирамиды равны а и За. Через два параллельных ребра пирамиды, лежащих на разных основаниях и разных.. боковых гранях, проведено сечение. Угол между сечением и основанием пирамиды равен а. Найти площадь сечения.
420
§ 7. Параллелепипед
13.79 . Ребро куба равно а. Найти радиус сферы, проходящей через вершины нижнего основания куба и касающейся ребер верхнего основания.
13.80 . Ребро куба равно Ь. Найти объем прямого кругового конуса, вершина которого совпадает с вершиной куба А, а окружность основания проходит через центры граней куба, не проходящих через вершину А.
13.81 . Ребро куба равно а. Через диагональ АС грани ABCD проведена плоскость так, что в сечении получилась трапеция, острый угол которой равен arccos . Найти расстояние от вершины В до секущей плоскости.
13.82 . В основании прямоугольного параллелепипеда лежит квадрат со стороной Ь, а высота параллелепипеда 5Ь
равна Найти радиус сферы, проходящей через концы стороны основания АВ и касающейся граней параллелепипеда, параллельных АВ.
13.83 . Ребро куба ABCDAtBiCiDi равно а. Найти радиус сферы, проходящей через середины ребер AAlt ВВ{ и через вершины А и Ci-
13.84 . В прямоугольном параллелепипеде ABCDAiBiC\D\ ребра АВ, AD и A At соответственно равны а, b и с. Найти угол между плоскостями ABrDi и AiCiD.
13.85 . На ребре ВВу куба ABCDAiBiCiDi расположена точка М так, что BM = ^BBi. Черев точки А, М и центр куба проведена плоскость. Найти угол между этой плоскостью и плоскостью грани ABCD.
13.86 . В основании прямоугольного параллелепипеда ABCDAiB^CiDi лежит квадрат со стороной 5 см. Высота параллелепипеда равна 4 см. В трехгранные углы при вершинах А и Ci вписаны равные касающиеся друг друга шары. Третий шар касается двух первых шаров и бокового ребра BBi в его середине. Найти радиус третьего шара.
13.87 . В основании прямоугольного параллелепипеда ABCDAiBiCiDi лежит квадрат ABCD со стороной а. Через диагональ АС грани ABCD проведена плоскости, пересекающая грань A\BiC\Di. В трехгранные углы В и Di вписаны
421
шары, касающиеся этой плоскости и имеющие радиусы, соот-ветственно равные $ и р Найти высоту параллелепипеда.
13.88 . В прямоугольном параллелепипеде ABCDAiBiCiDi ребра АВ, AD и AAi соответственно равны 3 см, 2 см и 1 см. Найти радиус шара, вписанного в трехгранный угол при вершине А и касающегося диагонали BDy.
§ 8. Призма
13.89 . Все ребра правильной треугольной призмы равны а. Найти площадь сечения, проведенного через сторону основания под углом р к плоскости основания.
\ ч /
13.90 . В шар радиуса R вписана правильная треугольная призма, площадь боковой грани которой равна S. Найти ребра призмы.
13.91 . В основании прямой треугольной призмы ABCAiBiCi лежит равнобедренный треугольник (АВ = ВС), высота которого, опущенная из вершины В, равна см. На ребре BBi расположена точка Р так, что угол А^РС равен AiP — = 2]/2с.и и PC— о см. Найти объем призмы.
13.92 . Сторона основания правильной треугольной призмы ABCAtBiC равна Ь, а высота призмы равна h. Через вершины A, Bi и точку Р на ребре CCi проведено сечение так, 2л
что угол APBi равен -у . Найти площадь этого сечения.
13.93 . В основании прямой треугольной призмы лежит прямоугольный треугольник, катеты которого равны а и Ь. Некоторая плоскость пересекает все боковые ребра призмы так, что в сечении получается правильный треугольник. Определить сторону этого треугольника.
13.94 . В основании треугольной призмы лежит правильный треугольник со стороной а. Прямая, соединяющая одну из вершин верхнего основания с центром нижнего основания, перпендикулярна плоскостям оснований. Известно, что внутрь этой призмы можно поместить шар, касающийся всех граней призмы. Найти боковое ребро призмы.
13.95 . В треугольной призме ABCAiBiCi боковое ребро равно /. В основании призмы лежит правильный треугольник со стороной Ь, а прямая, проходящая через вершину В\ и центр основания АВС, перпендикулярна основаниям. Найти 422
площадь сечения, проходящего через ребро ВС и середину ребра AAt.
13.96 . В основании прямой треугольной призмы лежит равнобедренный прямоугольный треугольник, гипотенуза которого равна с. Через гипотенузу нижнего основания проведена плоскость так, что в сечении призмы получился правильный треугольник. Известно, что можно вписать шар, касающийся боковых граней призмы, верхнего основания и сечения. Найти объем призмы.
13.97 . В треугольной призме ABCAiBtCi проведены два сечения. Первое сечение проходит через ребро АВ и середину ребра AiCi, а второе — через ребро AtBi и середину ребра СС1- Найти отношение длины заключенного в призме отрезка линии пересечения этих сечений к длине ребра АВ.
13.98 . Сторона основания правильной треугольной призмы ABCAiBiCi равна Ь, а высота призмы равна 2. Через вершины А, Ву и середину ребра CCi проведено сечение. Второе сечение проведено через вершину В, середину ребра АС и середину ребра ByCi- Найти длину отрезка, по которому пересекаются эти сечения.
§ 9. Конус
13.99 . Прямой круговой конус вписан в шар. Найти отношение объема конуса к объему шара, если образующая конуса наклонена к его основанию под углом а.
13.100 . В прямой круговой конус вписаны два шара: первый шар касается боковой поверхности конуса и его основания, второй — боковой поверхности конуса и первого шара. Отношение объемов этих шаров равно 27. Найти угол при вершине конуса.
13.101 . Найти объем тела, полученного вращением равнобедренного треугольника около оси, лежащей в его плоскости и проходящей через вершину угла при основании параллельно противоположной боковой стороне. Известно, что боковая сторона треугольника равна а, а угол при основании равен а.
13.102 . На основании полусферы радиуса R построен прямой круговой конус, боковая поверхность которого пересекает эту полусферу в точках, отстоящих от основания на расстоянии, равном высоты конуса. Найти объем конуса.
13.103 . В сферу радиуса 7? вписаны два прямых круговых конуса с общим основанием. Объем одного из них в четыре
423
раза превосходит объем другого. Найти боковую поверхность каждого из конусов.
13.104 . Высота прямого кругового конуса, равная /г, является диаметром сферы, которая делит боковую поверхность конуса в отношении т: п. Найти радиус основания конуса.
13.105 . В прямой круговой конус с высотой h. и радиусом основания 2/г вписан шар. Найти площадь сечения этого шара плоскостью, проходящей через вершину конуса под углом л -г к его оси.
4
13.106 . В прямой круговой конус вписана сфера. В эту сферу вписан прямой круговой конус, объем которого в а раз меньше объема первого конуса, а угол при вершине равен углу при вершине первого конуса. Найти этот угол.
13.107 . Дан прямой круговой конус с радиусом основания 7? и высотой Н. Определить радиус основания и высоту цилиндра, вписанного в этот конус, если боковая поверхность цилиндра имеет наибольшее значение.
13.108 . Отношение радиуса основания прямого кругового конуса к радиусу вписанного в конус шара равно Ь. Найти отношение объема конуса к объему шара.
13.109 . Шар радиуса 7? вписан в прямой круговой конус. Внутри конуса дан шар радиуса г, касающийся боковой поверхности конуса и первого шара. Найти объем конуса и показать, что он не меньше, чем удвоенный объем первого шара.
13.110 . Внутри прямого кругового конуса расположен куб так, что одно ребро куба лежит на диаметре основания конуса, а вершины куба, не принадлежащие этому ребру, лежат на боковой поверхности конуса. Найти отношение объема конуса к объему куба.
13.111 . Около прямого кругового конуса с высотой 2 см описана правильная треугольная пирамида, сторона основания которой равна Зф^Зсж. Найти радиус шара, вписанного в трехгранный угол при основании пирамиды и касающегося боковой поверхности конуса внешним образом.
§ 10. Усеченный конус, цилиндр и шар
13.112 . Образующая прямого кругового усеченного конуса, равная гф<2, наклонена к плоскости основания под углом а радиус верхнего основания равен г. Найти радиус шара, описанного около этого конуса.
424
13.113 . Около шара описан прямой круговой усеченный конус. Отношение объема усеченного конуса к объему шара 13
равно -у. Найти угол между образующей конуса и его основанием.
13.114 . Прямой круговой усеченный конус описан около шара. Радиус этого шара в ]/30 раз меньше радиуса сферы, описанной около усеченного конуса. Найти угол между образующей конуса й его основанием.
13.115 . Внутри прямого кругового цилиндра лежат два
5
шара радиуса г и один шар радиуса -^- г так, что каждый шар касается двух других, одного и того же основания цилиндра и его боковой поверхности.. Найти радиус основания цилиндра.
13.116 . Внутри прямого кругового цилиндра, высота которого равна Зг, лежат три равных шара радиуса г так, что каждый шар касается двух других шаров и боковой поверхности цилиндра, причем два шара касаются нижнего основания цилиндра, а третий шар касается верхнего основания цилиндра. Найти радиус основания цилиндра.
13.117 . Два шара радиуса г и два одинаковых шара неизвестного радиуса расположены так, что каждый шар касается трех других и данной плоскости. Найти радиусы двух последних шаров.
13.118 . В полусферу радиуса /? вписаны три равных шара так, что каждый шар касается двух других шаров, полусферы и ее основания. Найти радиус этих шаров.
13.119 . В двугранный угол а вписаны два щара радиуса г, касающиеся друг друга. Найти радиус шара, касающегося граней угла и данных шаров.
ОТВЕТЫ
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ I
1.3. Высказывания {2 + 4г^10}, {53 = 125} истинны, а высказывания {5 <2}, {11 +3= 18}, {63т^216} ложны.
1.4. М = {257 — нечетное число},
1Q= {число К 2 не является рациональным},
1 R = {число 7 неположительно},
“| S = {число 5 неотрицательно}.
1.5. Истинны высказывания П-И, ~IQ> IS-
1.6. Оба высказывания А, В истинны. Высказывание В не является отрицанием высказывания А.
“]/!—(все четные числа составные},
~]В^{все нечетные числа составные}.
1.7. “jC^{27 делится на 2),
. “j D = {существует (хотя бы одно) четное простое число}, 1 £ = {5-7 = 35}.
Истинны высказывания С, D, “j Е.
1.8. ~]А = {15 не делится на 3},
П В = {5 —число неположительное}, |Cs{3>7}.
1.9. Высказывания А (1), А (3), А (5), А (7) истинны, а высказывания А (2), А (4), А (6) ложны.
1.10. Истинными являются высказывания В (1), В (2), В (3), В (4), В (5), В (6), В (7), "] В (8), 1 В (9), В (10); остальные высказывания ложны.
1.11. Высказывания К (3), L (3), К (5), L (5), К (7), L (7) истинны, а высказывания К (4), L (4), К (6), L (6), К (8), L (8) ложны; неопределенные высказывания К (х) и L (х) совпадают на множестве М, но не совпадают на множестве, состоящем из чисел 2, 3, 4, 5, 6, 7, 8.
1.12. (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2, 4), (2, 5), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (6, 1).
1.13. Истинными являются высказывания F (а, Ь), где а=1, b — любое число из множества N; также истинны высказывания F (а, Ь), если а = Ь, и, кроме того, истинны высказывания В (2, 4), F (2, 6), F (2, 8), F (2, 10), F (3, 6), F (3, 9), F (4, 8) и F (5, 10). Пары (а, Ь), для которых одно из высказываний F (a, b), F (Ь, а) истинно, а другое ложно, имеются; например, высказывание F (1, 2) истинно, а высказывание 426
F (2, 1) ложно. Высказывания .F (а, b) и F (b, а) являются одновременно истинными тогда и только тогда, когда а = Ь. Высказывания F (2, 5) и F (5, 2) ложны.
1.14. 1 А ~ {существует (хотя бы одно) а>0, при котором уравнение х2 = а не имеет действительных корней}; А истинно, ”| А ложно.
1.15. 1 А = {существует действительное число а, для которого уравнение х2 = а не имеет действительных корней}; А ложно, ”] А истинно.
1.16. {корни любого квадратного уравнения действительны}; А истинно, А ложно.
1.17. “| А = {существуют два треугольника, которые не являются подобными между собой}; А ложно, “| А истинно.
1.18. “i А = {существуют два числа а, Ь, ни одно из которых не делится на 3}; А ложно, А истинно.
1.19. 1. Если на множестве М, состоящем из всех простых чисел, задано неопределенное высказывание (х) = {число х нечетно}, то (Vx) ^i(x)^{Bce простые числа нечетны}.
2. Если на множестве К, состоящем из всех целых чисел, задано неопределенное высказывание Д2(х)=^число — определено^-, то (Vx) Д2(х)^|для любого целого х определено частное —|.
3. Если на множестве N, состящем из всех натуральных чисел, задано неопределенное высказывание А3(х)={х2>х}, то (Vx) А3(х) = == {каждое натуральное число х удовлетворяет неравенству х2>х}.
4. Если на множестве D, состоящем из всех действительных чисел, задано неопределенное высказывание Л4(.г)—: {число х выражается конечной десятичной дробью}, то (Vx) Д4 (х) = {каждое действительное число выражается конечной десятичной дробью}.
Высказывания (Vx)A„(x) (п = \, 2, 3, 4) ложны, а высказывания ~]((Vx) Ап (х)) = (Зх) (1 Ап (х)) (п = 1, 2, 3, 4) истинны.
1. 20. 1. Если на множестве, состоящем из всех простых дробей, задано неопределенное высказывание Вг (х) ss {число х выражается конечной десятичной дробью}, то высказывание ((Vx) В4(х)) = — (Зх) (“| Bi (х)) означает: не всякая простая дробь выражается конечной десятичной дробью, т.е. существует простая дробь, которая не выражается конечной десятичной дробью.
2 — 4. Пусть на множестве V, состоящем из всех натуральных чисел, заданы следующие неопределенные высказывания:
Е2 (х, у) = {ху — простое число},
Е3 (х, У) = {х2 + £/2 < ЮО}, Et (х, у) = {х-}-г/ — четное число}.
Тогда высказывания 2 — 4 можно записать в виде:
2. (Vx) (Зг/) £2 (х, у),
3. (Vx) (3//) Е3 (х, у),
4. (Vу) (Зх) Et (х, у).
5. Если на множестве, состоящем из всех точек прямой I, задано неопределенное высказывание
Е6 (х, у) = {расстояние между точками х и у равно трем единицам},
427
то высказывание (V х) (Эу) Е-а (х, у) означает: какова бы ни была точка х на прямой I, существует на этой прямой такая точка у, что расстояние между точками х и у равно трем единицам.
1.21. 1. Если на множестве N, состоящем из всех натуральных чисел, задано неопределенное высказывание Аг (х) = {число х делится на 5}, то (Ух) А[ (х) дд {любое натуральное число делится на 5}; высказывание 1 ((Ух) At (х)) = (3х) ("| А4(х)) означает: не любое натуральное число делится на 5, т. е. существует натуральное число х, которое не делится на 5.
2. Если на множестве, состоящем из всех четных чисел, задано неопределенное высказывание А2 (х) = {х— простое число}, то (Зх) Аг (х) = {существуют четные простые числа}; высказывание ((Зх) А2 (х)) = (Ух) (1 Аг (х)) означает: не существует четных простых чисел, т. е. все четные числа составные.
3. Если на множестве N, состоящем из всех натуральных чисел, задано неопределенное высказывание А;| (х) де { число х четное}, то (Ух) А3 (х) = {все натуральные числа четны}; высказывание ((Ух) А3 (х)) = (Зх) (~| А3 (х)) означает: не все натуральные числа четны, т. е. существует нечетное натуральное число.
4. Если на множестве, состоящем из всех треугольников, задано неопределенное высказывание А4 (х) = {у треугольника х три прямых угла}, то (Зх) А 4 (х) = {существует треугольник стремя прямыми углами}; высказывание ((Зх) А4 (х)) е= (Ух) (”| А4 (х)) означает: не существует треугольника с тремя прямыми углами, т. е. в каждом треугольнике хотя бы один угол не прямой.
1.22. А (х) = {четырехугольник х—параллелограмм},
В (х) ~ {диагонали четырехугольника х в точке пересечения делятся пополам}.
1.23. А (х, у) = {числа х и у положительны},
В (х, у) = {для чисел х и у справедливо соотношение 1g (ху) = = 1g х+ 1g у].
1.24. А (х) еен {целое число х оканчивается двумя нулями}, В (х) = {целое число х делится на 4}.
1.25. А — В. (Для того чтобы произведение ху было равно нулю, достаточно, чтобы число х было равно нулю. Иначе: для того чтобы число х было равно нулю, необходимо, чтобы произведение ху было равно нулю.)
1.26. В — А. (Для параллельности прямых /4 и /2 необходимо, чтобы они лежали в одной плоскости. Иначе: для того чтобы прямые /j и /2 были расположены в одной плоскости, достаточно, чтобы они были параллельны.)
1..2 7. В—>Д. (Для выполнения соотношения а-дАО достаточно, чтобы было а>0. Иначе: для справедливости неравенства а>0 необходимо, чтобы было выполнено условие а2^Е0.)
1.28. (А — В) до (в равнобедренном треугольнике две медианы равны между собой}: (В —• А) {если две медианы треугольника равны между собой, то этот треугольник равнобедренный}; обратная теорема верна, т. е. высказывание (В —» А) истинно.
1.29. (А — В) = {диагонали ромба делят его углы пополам}; (В —- А) = {если диагонали четырехугольника делят его углы пополам, то этот четырехугольник является ромбом}; обратная теорема верна, т. е. высказывание (В-»А) истинно.
428
1.30. (Л —»В) = {если натуральное число а делится иа 9, то сумма цифр числа а делится на 3}; (В —»А) = {если сумма цифр натурального числа а делится иа 3, то число а делится на 9}; обрат-
ная теорема неверна, т. е. высказывание (В —* А) ложно.
. Л ах-}-6
1.32. Функция сх_^_^ постоянна в том и только в том случае,
, , . ах-Ab
если ad —ос (предполагается, что функция имеет смысл, т. е. хотя бы одно из чисел с, d отлично от нуля).
1.33. Для того чтобы из отрезков, длины которых равны а, Ь, с, можно было составить треугольник, необходимо и достаточно, чтобы числа а, Ь, с были связаны неравенствами а-|-&>с, 6-{-с>а, а-рс > Ь.
1.34. Многочлен Р (х) =а0 хпА-а1хп~1-А...А-ап_1хА~ап тогда и только тогда делится на х — а, когда Р(а) = 0.
1.36. Обе теоремы верны, т. е. верна теорема: для того чтобы пирамида Р была правильной, необходимо и достаточно, чтобы все стороны основания этой пирамиды были равны между собой и все боковые ребра этой пирамиды были равны между собой.
1.37. Верна теорема Д ДВ —С, т. е. пирамида Р является правильной тогда и только тогда, когда все плоские углы в основании пирамиды равны и все боковые грани одинаково наклонены к плоскости основания этой пирамиды.
1.39. Теоремы 1 и 6 верны, а теоремы 2, 3, 4 и 5 неверны. Теорема 1 и 4 обратны друг другу, теоремы 2 и 5 обратны друг другу. Теоремы 2 и 3 противоположны друг другу, теоремы 4 и 6 противоположны друг другу.
1.40. “| (Д{х) V В (х)) = (1 А (х)) Д (~| В (х)) = {последняя цифра числа х четна и отлична от нуля}.
1.41. ( | А (х)) V (”| В (х)) = (А (х) Д В (х))е{х не делится на 6}.
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ 11
2.4. Нет. 2.5. Нет. 2.6. Да. Например, {Аз +(5 — ^3 ) = 5. 2.7. Да. Например, ({/2 ) ({^8 ) = 4. 2.14. 7,9 (с избытком). 2.15. 15,7 (с избытком). 2.16. 1,7 (с .недостатком). 2.17. 1,5 (с избытком). 2.18. 0,394. 2.19. 0,99 ... 9 00 ...0 ... 2.20. 0,99 ... 9 ... 2.21. 0,0010.
100 цифр 100 цифр 100^ цифр
2.24. х > 0. 2.25. х^О. 2.26. |cosa — cos Р |.
2.27. + + Уа-^Уа^Т=
( 2, если 1 a •< 2,
I 2 У а — 1> если a > 2.
a2 62
2-28- г>~, если । а | сэ | b если | а | < | Ь |.
62 ’ ' ' ' cP Illi
2.29. , если -I a I I b 1; -к— > если I а I < I b I.
26 1 ' ' 2a ’ 11 11
2.30. х=г0. 2.31. xt = 2, х2 = —1. 2.32. х=0. 2.33. х=1.
2.34. х<—1. 2.35. -1 <х< 1. 2.36. 1 х 5. 2.37. xs= -2, x^4.
429
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ IV
'* 14
4. 1. 1. 8. 2. З-z. 3. 0. 4.
5
4. 2.1.5,12. 2.0,1. 3.0,24. 4. 2, -11. 5. -2, у. 6.2,0.
4. 6. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
4. 7. 1. Множество всех точек, лежащих правее мнимой оси.
2. Множество всех точек, лежащих на прямой у=\ и ниже ее.
3. Множество всех точек, лежащих на прямых х = 0, х=1 и между этими прямыми.
4. Множество всех точек, лежащих между прямыми у — — 1 и 7/=1.
5. Круг с центром в точке 0 радиуса 1, включая точки окружности.
6. Круг с центром в точке — 2г радиуса 4, исключая точки окружности.
7. Множество всех точек, лежащих вне окружности с центром в точке i радиуса 1.
8. Кольцо между двумя окружностями, радиусов 1 и 2, с общим центром в точке 1, исключая точки окружностей.
9. Прямая, перпендикулярная отрезку, соединяющему точки — г и 1, проходящая через его середину.
10. Множество всех точек, лежащих левее мнимой оси.
4.10. 1. cos +1 sin у. 2. 2 (cos л +г sin л). 3. cos у + г sin -у .
. . /"гт ( л ... л \ _ Зя . . Зл _ 8л . . 8л
4. У 2 ( cos -т- +1 sin -j- . 5. cos + г sin . 6. cos +1 sin -z- .
\ 4 4 / 2 2 9 9
4
7. 125 (cos 3<p-j-7 sin 3<p), где <p — л — arctg . 8. 1024 (cosO-f-г sinO).
3. г = 2 ^cos у-j-г sin yj (fe = 0, 1, ..., 5).
. (2&+1)л , . . (2^+1)л ,, „ .
4. г—cos-—y-i—psin-----у - (k — 0, 1 .... 6).
к ie<o L (8fe4-l)n . . (8k -p- 1) л ]
5. 2= /2 [cos'- + ? sin-^—32---]
(fe=0, 1. 7).
6. г — :± (2 — г).
4.15. = zQ ^cos4-г sin \ (fe=l, 2....n— 1).
3
4.16. 1. ct = 0, г2.3=±1, г^-а—± i- 2. г = у — 2i. 3. г — — 1— i.
4. г=1 —i. 5. г=(1-К2)ь
4.17. 1. г=14-г. 2. г=+(1— i).
430
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ V
5.1. 100.
5.2. По крайней мере одно из чисел р, q не является действительным.
5.3. Может. Пример: ха —гх = О. Если же известно, что р и q действительны, то это невозможно.
5.4. Если р и q—действительные числа, то другой корень равен 1—г; если же не требовать, чтобы р и q были действительными, то другой корень может быть любым.
5.7. 1. Нет. 2. Да. 5.8. Нет.
5.9. Нет. Пример: ix1 2-3ix^-2i. Если же известно, что коэффициент при х2 действителен, то (при выполнении условия задачи) и два других коэффициента действительны.
5.10. Нет. Пример: гх2-(-0х — г. Если же действительный коэффициент отличен от нуля, то (при выполнении условий задачи) и два другихкоэффициента действительны.
5.12. н= 1, r2 = — 1.
5.13. 1. ^(Ы-4аЬ2с+2а2с2).
2. (b2 — 2ас) (bl — 4аЬ2с + а2с2).
5.14. р = —2, q ——1; р— 1, q — любое. 5.15.
5.16. х2 — 58x4-4 — 0.
О
100
243'
5.17. См. рис. 113.
5.18. а) а<0, b < 0, с>0;
б) а > 0, b <4 0, с>0;
в) а>0, &>0, с = 0;
г) а < 0, b > 0, с < 0.
5.20. В условиях задачи всегда существует, и притом единственный, квадратный трехчлен, график которого проходит через точки А, В, С.
При указанных в задаче наборах точек А, В, С находим: 1. у = = 2х2 — 2х — 4. 2. у = х2 — 4%4-3. 3. у = —х2 — 6х — 5.
5.21. В условиях задачи всегда существует, и притом единственный, квадратный трехчлен, график которого имеет вершину в точке А и проходит через точку В.
Для указанных в задаче точек А, В находим: 1. г/ = 2ха4~1. 2. у ——ха + 6х—8. 3. у — — х2А-4х.
5.22. 1. х < 0 и х > 4. 2. Нет решений. 3. — 4 < х < 1. 4. х = 1.
5. х^у. 5.23. 1. 0sgxs=4. 2. —1<х<1. 5.24. г = \.
5.25. —9.
__ ab + cd. _ (ad — be)2 Х— — а2 + с2 - ^min а2_|_с2 •
5.26.
5.27.
5.28.
1. г=1, г =— 1. 2. г —— 2.
1. D = b2 — 4ас4х0, ас> 0.
2. D 4г 0, ас < 0.
431
5.29. Оба корня положительны при г 2= 4; .оба корня отрицательны при — 2~<г «:0; корни имеют противоположные знаки при
У
Рис. 113.
1
г < — ; один из корней равен
1
Г-----2
нулю, а другой отрицателен при
о
5.32. — 1 < г < 1, 5.34. г < - 3 и 1 < г <
*
432
5.35. r< —3 и r^l. 5.36. r< —2.
5.37. p2 —4^3:0, — 2{J<p< —2a, a24-ap-|-?>0, P2 + f}p4* + q > 0. 5.38. r< — у и <=>34-2/2.
4 /
5.40. Наибольшее значение функции равно достигается при
1 \ 1,
х =—yl, наименьшее значение равно у (достигается при х=1).
5.41. Наибольшее значение функции равно НО (достигается при х = 3), наименьшее значение равно 2 (достигается при х = 0).
5.42. Наибольшее, значение равно 3, наименьшее значение рав-3
но 4-.
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ VI
6.1. —1. 6.3. Нет. 6.4. х±2. 6.5. — ух2— уХ-]-3.
6.6. X40 — X38 + X36 — X34 + X3» — X28 + X25 — X23 + X20 — X17 + X15 —
— Х12+ X10 — Xе 4-х6 — X 4- 1 •
6.7. а = 3, Ь= — 4. 6.8. х2=1 —/3, х3= 1 4-/2, х4=1 —/2.
6.9. х2 = 1 — /2, х3 = 1, х4 = — 1, х8 = — 2.
610 ’+‘V3 х 1-//3
о. ш. Xj — —- , х2 —-----g---
6.11. Xj = — I +«, х2 =— 1 — г. 6.14. х3 = 3. 6.15. —1.
6.19. 4р34- 27р2 = 0.
6.20. Корнями многочлена Д(х) являются числа —Xj, — х2, ...
...,—хп, а корнями многочлена В(х) — числа —, —, ... , —.
Xj %2 %П
6.22. х3—!. 6.35. Существует.
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ VII
7.1. Область определения: ( — со, — 2) (J (— 2, — I) U (—1> + =с). т. е. х^-1 и х^-2; /(0)=-1, f(l) = 0, /(-3) = -2.
7.2. Область определения: [ — 2, 0] (J [2, 4-00), т- е- — 2:<:xsg0 или xSs2; )(-1)=/з, /(2)=0, / (3) = /15.
7.3. Область определения.. [ — 3, — 1)U( —1,3], т. е. |х| 3 и
х^-1; f(0) = 3, Н1) = /2, Н-2) = -/5.
7.4. Область определения: x^kn (k = 0, ±1, ±2,...);
'Ш-’-'С?)"1-
7.5. Область определении: x^~-^k (fe=0, ±1, ±2,...); f (0) =0, f (-1) = 1, f (1'00) = 100.
433
7.6.
У
7.10.
434
7.12.
У
7.17. Функции A(*) + AW и Л W A W ограничены, функция A W + A W не ограничена, а про функции (х) (3 (х), -4^ и 4~ /2 W Гз W ничего определенного сказать нельзя.
7.18. Убывает на всей оси х.
7.19. Возрастает на всей оси х.
7.20. Возрастает на интервале (— оо, — 1), убывает на интервале (— 1, +оо).
7.21. Убывает на интервалах ( — со, —1) и (—1, -(-со).
7.22. Возрастает на интервалах (л + 26л, 2л-|-2йл), убывает на интервалах (26л, л-|-2йл) (6 = 0, ±1, ±2, ...).
7.23. Возрастает на интервалах —5--|-6л, (6 = 0,
±1, ±2,
/ 4
7.24. Наибольшее значение равно 5 достигается при х = arctg -f-5Т \ \ О-
-g-4-2л6 (6 = 0, +1, ±2, ...)!, наименьшее значение равно—5 (4л \
Достигается при х = arctg -5------=-4-2л6 (6 = 0, ±1, +2, ...)).
«3 Л j
435
7.25. Наибольшее значение равно 2 + КЗ ^достигается при х =
1 1 л> \
= -уarctg-y + у4-nfe (k = Q, ±1, ±2, ...)), наименьшее значе-— / 11л
ние равно 2—^5 (достигается при х— -yarctg -------------{k = Q,
± 1. ±2. ...)
7.26. Наибольшее значение равно 1 ^достигается при х —
(6 = 0, ±1, ±2, наименьшее значение равно -±- ^достигается
ЗТ . 2Т& /1. г\ 1 л \\
при х = у + -у- (6 = 0, ±1, ±2,
7.27. Наибольшее значение равно 1 ^достигается при х=-^~ (6 = 0, ± 1, 12, наименьшее значение равно -у ^дости-гается при х=у|—— (6 = 0, ±1, ±2,
7.28. Наибольшее значение равно у (достигается при х=1).
7.29. Наибольшее значение равно (достигается при х=1).
7.30. Наименьшее значение равно 2 (достигается при х=1).
7.31. Четная. 7.32. Нечетная. 7.33. Не является ни четной, ни нечетной.
7.34. Четная. 7.35. Нечетная. 7.36. Не является ни четной, ни нечетной. 7.39. л. 7.40. 2л. 7.41. л. 7.42. 2л. 7.43. л. 7.44. 6л. 7.46. Периодическая с периодом 2л. 7.47. Не является периодической. 7.48. Периодическая с периодом л.
436
437
7.55.
Рис. 130.
438
439
440
7Л0. у
Рис. 144. Рис. 145.
7 72 111 7 73 __111—LL— i1
7 УГ-i' 7‘73’ 2t^-2t+l ’
_ 1—№ , п _ „ . , sin2x
7.74. ——- х=£0. 7.75. х . 7.76. --------г.
1 +х2 ’ г 11 I COSX I
7-77. /(х) = 3±£ Прих^4,3.
7.78. /(х)=^ при х^1.
7.80. /(x) = -L(x2-1), g (х) =- 1- (2х2 + 3х+ 1).
, . х2 —4x4-1 х2 — Зх-J-l ,,
7.81. f(x) =-j—, g (x) = _-T- , x 1
7.82. /(x) = —2, gW=^, x^l,2.
7.83. f(x) = ~(7x+12), g(x) = -^-(3x + 7).
7.84. f(x)= ^x-7)-19 ^=Т(£Т- ^10-
7.85. /(x)===x—1, x^O, 2; g(x) = 2, х^ Г, 5.
7.86. /(x) = x, x^l; g(x)=14-x, x^O.
7.87. f(x) = ^=p-3 при x^O.
7.88. f(x) = y-l^ при x^O, 1.
7.89. /(x) = -y^p при L
7.90. /(«)= v nP“ Xz£— 2> °> л <5
7.91. у = Ух. 7.92. g = —1-. я r я x~ 1
7.93. g = 7.94. g = x* при xSsO.
a ex—a s f
441
7.98.
У
7.99. у
442
7.102.
У
7.104. у
Рис. 155.
443
7.107.
У
7.108. Два.
7.109. Три.
7.110. Уравнение имеет бесконечно много решений.
7.111. Шестьдесят три.
7.112. Xj=—1, х2 = 3.
7.113. xl =—1, х2 = 2, х3 = 4. 7.114. х =
7.115. х«=2,875. 7.116. х1==0, х2 «а 2,625.
7.117. — 3 < х < 3. 7.118. 0<х<1.
7.119. 1<х<2 и 3<х<4.
7.120. х< —2, — 1<х<0их>1.
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ VIII
1 2 4
8.1. 1.2; 2.—---; 3.2; 4.-2; 5.4; 6.4.
2 О О
1 1 2
8.2. 1. -5-; 2. 3.-7; 4.
О о
8.3. 1. 100; 2. 9; 3. 4. 4.
8.4. 1. 9; 2. 2/2; 3. 16; 4. 9.
8.5. 1. 2; 2. 16; 3. 1; 4. 25.
8.6. I. log2 5>0; 2. log62>0; 3. logo.20,8>0; 4. logt /7<0.
К
8.7. 1. log3 4 > log4; 2. log011/2 < log0,2 0,34; 3. log3-|->
>logA|; 4. 210gl 3 > 1 > з'°г’.
2
444
8.18.
8.20.
8.21. у 8.22. у
445
446
8.29.
У
8.31. У
447
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ IX
9. 1. Да.
9. 2. а) Да.
б) При умножении обеих частей неверного равенства на число, отличное от нуля, получается неверное равенство. Если же обе части неверного равенства умножить на нуль;' те получится верное равенство.
в) Если п —нечетное число, то при возведении обеих частей неверного равенства в степень п получится неверное равенство. Если п —четное число, то из неверного равенства вида а — —а (уле ajtO) получается верное равенство, а из любого другого неверного равенства получается снова неверное равенство. (Предполагается, что в обеих частях равенства стоят действительные числа.)
9. 3. Да.
9. 8. а) Уравнения f(x)—g(x) и Цх}=^~^ в °бщем случае неравносильны, первое уравнение есть следствие второго. Если хотя бы одна из функций f (x), g(x) отлична от нуля на множестве М, то на этом множестве уравнения равносильны.
б) Уравнения f(x)=g(x) и У f (x) = /g(x) в общем случае неравносильны, первое уравнение является следствием второго. Если хотя бы одна из функций f(x), g (х) принимает неотрицательные значения на множестве М, то на этом множестве уравнения равносильны.
в) Уравнения /(х) =g(x) и sin f (х) = sin g (х) неравносильны, второе уравнение есть следствие первого.
г) Уравнения f (x)=g(x) и arcsin f(x) = arcsin g(x) неравносильны, первое уравнение есть следствие второго. Если хотя бы одна из функций /(x)ng(x) такова, что все ее значения на множестве М принадлежат отрезку [ — 1, 1], то на множестве М уравнения равносильны; — ...
д) Уравнения = и f (х) gt (х) = (х) g (х) в общем случае неравносильны, второе уравнение есть следствие первого. Если на множестве М функции g (х) и g, (х) отличны от нуля, то на этом множестве уравнения равносильны.
е) Уравнения У f (х) У g(x) = <p(x) и У f (х) g (х) = ф (х) в общем случае неравносильны, второе уравнение является следствием первого. Если функции f (х) и g(x) принимают неотрицательные значения на множестве М, то на этом множестве уравнения равносильны.
9.12. а) х,= 1, х2 = 3, х3 = —1. б) X] =——, х2 = -5-/13 -5 + ;/з __5_(-/з
------2 ’ Хз~ 2 ’ 4 2 •
9.13. х=18. 9.14. х = 8. 9.15. х = 20. 9.16. х,=2, х2 = — у.
9.17. хх = 0, х2 = 2. 9.18. х= '_2 . 9.19. х = -^-. 9.20. х=-1.
9.21. 2^х,==7. 9.22. X! = 3, х2 = 178. 9.23. х= — 1.
448
9.24. хх = 2, х2 = -^-_ 9.25. х = 9. 9.26. х = 2. 9.27. х=2. 9.28. х1 = 2, х2 = —3. 9.29. х = у. 9.30. х=1. 9.31. х = 2. 9.32. xt = 0, х2=1. 9.33. х = —1. 9.34. х = 2. 9.35. хх = 3, х2 = — 3. 9.36. х = 0.
9.37. х1=0, х2—1. 9.38. хх=1, х2 =—1.
п
9.39. Х!=1, х2 = пп~1 при п > 1; х — любое положительное число при п= 1.
1
9.40. хх = 1, х2 = п' —” при п> 1; х —любое положительное число при п= 1.
п
9.41. хх=1, х2 = п|-,г при п>1; х —любое положительное число при п=1.
9.42. х = 512. 9.43. Xj = 9, х2 = 91.
9.44. хх = —1, х2 = —32. 9.45. хх = 9, х2 = -^-.
9.46. xt —4, х2 = 4/4.
9.47. Ху ———, Х2=—.
У а ’ а
9.48. 6=4, а также любое k < 0.
9.49. При а = 0 и а = —1 уравнение не имеет решений. При a <Z—1 одно решение: х = а2, при а>0 одно решение: х = (а + I)2, при а — — у одно решение: x = — t при — I<a<v,a^:— два решения: Ху = а2 и х2 = (а-|-1)2.
9.50. х = 4. 9.51. х = 2. 9.52. Xj = 0, х2 = —1.
9.53. х = 0. 9.54. х = 2. 9.55. хх = 100, х2 = 0,1.
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ X
10.9. (3; 2). 10.10. (2; -1), (1; -2).
10.11. (2; 3), (3; 2), (—2; -3), (— 3;-2).
10.12. (2; 1), ( — 2; -1), \ Уз’узУ \/з’ /з/-
10.13. (3; 5), ( — 3; —5), (зб; (~36; f
10.14. (2; 1), (- 1 +1 УЗ; (- 1 - i /3; ~ •
10.15. (1; 2), (2; 1), (-2 + 1/5; -2-1/5),
(-2 — 1/5; —2 + 1/5).
10.16. (4; 2), (2; 4).
10.17. ; (—1; -2), (—2; —1), (—1+1/2; -1-1/2),
(-1-1/2; -1+1/2).
10.18. (—2; 3), (3; —2).
15 В. Г, Болтянский и др. 449
10.19. (1; 3), (—1; -3), (i;-3i), (-i; 3i), (3; 1), (-3; -1), (3z; — i), ( — 31; i).
10.20. xx=13, x2 = 78.
10.22. (2; 1), (-l + « /3; ~ 1 - i /3; ~*+1^ ,
(// 2/B
10.23. (2; 3), (—3;—2), (.l..+ ‘^|. -'+>'Г^
/1 — i/23. — 1 - i /23\
\ 2 ’ 2 j'
10.24. (-4;-5), (-5; -4), (- 1 + 2 У~3;- 1 +2 /з),
(-1-2/3; -1-2/3), (4 + /13; 4-/13), (4-/13; 4 +/13).’
10.25. (2; 1), (1; 2), (l+i/2; l-Z/2), (1-i /2; 1 + Z/2).
10.27. (1: 2). <2; ;»=^>»), +/” .
10.28. (0; 0), (6; 3), (3; 6), (—2; 1), (1; -2),
10.29. (0; 0), (1; 1).
10.30. (3; 2), ( — 2; -3).
10.31. (2; 3), ( — 2; 3).
in „„ Г/ 2kn . . 2kn\ f 2kn. , . . 26л\1 „
10.32. 3 cos +1 sin ; 2 cos-=-+1 sm-=-) (k = 0, 1, 2, L \ э э у \ Ь / |
3, 4).
10.33. (0; 0), (7; 7),
/—l-Z/15 — 1+Z/I5\
\ 2 2 _ /• _ _
10.34. (0; 0), (/11; /П), (-/11; -/11), (3; -3),
(-3; 3), (/2 + /3; /2-/3), (_/2 + /3; -/2-/3),
(/2 —/3; /2 + /3), (-/2-/3; -/2 + /3).
>0.32. (2 2). (-U-2). (JL. /67), -ГТ7).
10.36. (1; 2), (—l;-2), fi/209; --^=\ (—1^209; -Д-У
\ /209/’ \ /209/
450
10.37. (0; 0), (1; 2), (2; 1), [L 3-fг A.15.
/_3_t-/15 _3 + ij/15\
6 ’ 6 /
10.38. (4; 3), (3; 4). 10.39. (0; 0), (2; 1), (-2; -1), (1; 2), (-1; —2).
10.40. (3; 1), A ; -1^. 10.41. (0; 2), (0; -2), (1; -3), (— 1; 3).
10.42. (2; -1), (-1; 2).
10.43. ^24-2/3; 1+-Д]; [2-2/3; 1-pA).
10.44.
\ 5 ’ 5/’\5 5 / \5 5 j ’ \ 5 5/
10.45. — 1 <a< 1.
10.46. При m — n=l решения имеют вид x = cosa, z/=sina, где a —любое действительное число. В остальных случаях четыре решения: (1; 0), (0; 1), (-1; 0), (0; -1).
/_/ _L\ / /_______________
10.47. (у2; /2/’ \ /2’ /2/’
10.48. (2; 3; 1), (-2; -3; -1).
10.49. (0; 0; 0), (3; 2; 1), (-3; -2; 1), (3; -2; -1), (-3; 2; — 1).
10.50. (0;0;0), (1; 3; 2), (l;-3;-2), (1; 3Z;—2Z), (1;—3i;2Z), (i;3;-2i), (i;3Z;—2), (Z;—3; 2i), (Z; —3£; 2), (—1; 3; —2), (— 1; 3Z;2t), (—1; —3;2), (—1; —3t;—2Z), ( —Z; 3;2Z), ( —Z; 3Z; 2), ( —Z;—3; —2Z), ( —Z; — 3Z; — 2).
10.51. (3; 4; 5), ( —3; —4;—5). 10.52. (1;2;4), ( —1;—2;—4).
10.53. (1; 2; 3), (- 1; -2; -3). /22 \
10.54. (1; — 1; 3), v; -2 .
У O <J у
10.55. (0;1;-1), (3; 4; 5), 2^ .
10.56. -y), (2; ~1;4). 10.57. (-2; 3; 1).
10.58. (3; 2; 1), ( — 3; — 2; 1); (3; — 2; — 1), ( — 3; 2; — 1). /15 15 4\ / 37 37 12 \
10.59. [ 8 ; 8 , -15 ),( уз ; 8 ’ 37 / '
10.60. (1; 1; I), (-7.-1;
\ 6 о / \ 6 6/
10.61. (1;2;—2), (2;l;-2), (-2; 1;2), (1;—2;2), (2;-2;l), ( —2;2;1).
10.62. (1;2;-1), (1; — 1; 2), (- 1; 1;2), (—1; 2; 1), (2; 1; - 1), (2; - 1; 1).
10.63. (3; 2; - 1), (3; - 1; 2), (1; ,
/ 3-/17 3+/17\
V; 2’2 /•
10.64. (0; 0; 0), (3; 2; 1).
10.65. (1; 2; 3), (2; 1; 3), (3; 1; 2), (3; 2; 1), (1; 3; 2), (2; 3; 1).
15* 451
10.66. При а = 0 и а = ~2 система не имеет решений, а при
I 2а2 \
прочих значениях а имеет единственное решение j J %a2’ 2o2).
10.67. (-5; -3; 0), (3; 1; —2).
10.68. (0; 0; 0), (2; 3; 4), (— 2; — 3; - 4).
10.69. (3; 4; 1), ( -3; -4; - 1). /32 1 7 \
10.70. (4; 3; 1), -v; ,
\ О u u j
52. __4£. 13
3 ’ 3’3
10.71. (3; 3; 4), (12; 3; 1).
10.72. [ — 1;
/ 32 31 23 \
3 ’ 3’3/
3’ 6/’ V: 3’ 6/’ V: ’ 2
(3; 2; 4).
2/
10.73. (2; 3; 4),
10.74. (2; - 5; 3), (- 2; 5; - 3), (5; - 2; - 3), ( - 5; 2; 3).
10.75. (1;2; 3). 10.76. (0; 0; 0), (2; — 1; 3), ( — 1; 2; 3).
10.77. (a; 2a; 3a), где a — любое число.
10.78. (0; 0; 0), (0;0; 1), (l;0;0), (0; 1; 0), 1; 1).
10.79. (0; 0; 0), (0; 0; 1), (0; 1; 0), (1; 0; 0), (1; 1; B).
\ У У У j
5 5 4 \ / 5 4 . 5 \ / 4 5. 5 \
9 ’ 9 ’ 9 / * \ 9’9’ 9/’ \9 ’ 9 ’ 9/'
/75 \
10.80. (0; 0; 0), (2; 2; 0), (4; 0; 4), (0; 6; 6), -5-; 4; -1 . \ о 2 j
10.81. (0; 0;„0), (0; 0; 3), (0;2;0), (1; 0; 0),
10.82. (-3; - ОЛ-ЗЛ; -D.f-A; - B^;2j/2), О О \ * U j
4’5 /
10.83. ( — 2; - 4; 1), (у >/9; ;|/9; J .
10.84. 3d + a3'+&2 + c3.
10.85. (0; 0; 0), (1; 2; 5), (1;—2; — 5), ( — 1; 2; — 5), ( — 1;— 2; 5).
10.86. 1. (a; 0; 0), (0; b; 0), (0; 0; с), где a, b, с — любые числа.
2 fl. 1. В f-1- -1. В fl- _B -Д
В ’ 2 ’ 3/B ’ 2 ’ 3/’ \ 2 ’ 3/’
-1;B_B
1 2 ’ 3/’
10.87. (L+!; l±i; -2 (1 +0) ;
_i±]-. 2(i+0\ fLJ. LB. 2(£_i)\
10.88. 1. (a; 0; 0), (0; &; 0), (0; 0; с), где a, b, с — любые числа.
2. (2;1;-1), (2;-l;l), (— 2; 1; 1), (-2;-l;-l).
452
10.89. (1; 3; 1), (-1;-3; 1), (— 1; 3; — 1), (1;-3;-1).
10.90. (1; 1; — 2), (-1; -1; 2), (1; —2; 1), (-1; 2; — 1), (—2; 1; 1), (2; — 1; — 1). _ _
10.91. (2; /3; /9),(^;
10.92. (2; 1;0), (-2; — 1; 0). /1 4 1\ / 1 4 1\
10.93. (1;0; 1), (—1;0; —1), (у у, (-у
10.94. (7; 7; -1), (-7; -7; 1), (3/2; 3/2; 4/2),
(-3/2;-3/2; -4/2),
'/46 +/30, /46-/30 _ //46-/30. /46 +/30
2 2 / \ 2 2 у *
^-/46 + /30. -/46-/30.
/-/46-/30. -/46+/30.
10.95. (1; 2; — 1), (— 1; —2; 1).
10.96. (1; 2; -1), (-1; -2; 1),
\/7
/___/._______5_ _1_\
\ /7 ’ /Г’ /7/’
10.97. (Ь!;!. з), (1; / 1). / ч \ / Ч \
10.98. (3; 3; 3; — у), (—3; — 3; — 3;
10.99. xA = 2(n~i)~k (fc = 1’ 2 * * * * * *.")•
5_______1_\
/7’ /7/
10.100. Если п — нечетное, то х1 — х2 = ... — хп
1 ± /7 3
Если п — четное, то х1=ха — ... = хп_1=а, х2 = Хц = ... = хп= а+2 , 1
~ За ' Г ’ ГДе а — лю°ое число> не равное у.
10.101. (8; 1), (1; 8). 10.102. (1; 1).
10.103. (15; 1), (—15;—1), (— 15а; 16а), (15а; — 16а), где
1/226
а~У 48Г
10.104. [A; -9%F1T) , (4: 9-Р1-) - Ю.105. (0; - 1). \ о о J \ о и j
10.106. (—2/2 +/з; —2/ 2 — /3), (2/2-/3 J 2/2 + /3 ), 5/2 7/2\ / 5/2 7/2\
2 : 2 / ’ \ 2 ’ 2 )'
10.107. (0; 1). 10.108. (4; 2). 10.109. (vl тИ. (vl vb
10.110. (3; 2). 10.111. (2; 1). 10.112. (2; 2), —в).
\/2 /
453
10.115. (2; 1). 10.116. (Г, — 1). 10.117. (100; 10). JU. \ 1U 1 w у
10.118. (6; 2). 10.119. — 1^. 10.120. (3; 1). 10.121. (3; 1),
/_3 __П \8 ’ 8/’
/7 17\ / 7 Ч9\
10.122. 4; АД —4:—^. 10.123. (2; 1), (4; 2). \ 2 5 / \ о 5/
10.124. (3;'— 1), 10.125. (27; 1).
10.126. (8; /27); (27; /8).
10.J27. (4; 2/ (—2; —4), (2 + /6J — 2 + /б),
(2-/6; -2-/6).
10.128. (6; 6). 10.129. (2; 2). 10.130. ^4; J-). 10.131. U; J-j.
10.132. (81; 16). 10.133. (2; 4), (/2; 16).
10.134. (1; 2), (—/^5; 0), (-±=; -jLV \/2 /2/
10.135. (2; 32), (32; 2). 10.136. (3; / 3), (/ 3J 3).
10.137. (2; 2). 10.138. (9;/9), (/9; 9). 10.139. (16; 4).
10.140. (а?-, а), (а6; аз), ю.141. (b; b), (J-; 10.142. (/а; а).
[ с_ \
10.143. \а2; ас/'
10.144. При а — Ь решение имеет вид (с, с), где о 0 —любое. При ab = 1 решение имеет вид (с; J-^ , где с > 0 — любое. Приа^й и ab -ф 1 имеется единственное решение .
10.145. 10 м. 10.146. 50/3 мин и 50 мин.
10.147. х > a + . 10.148. В 2 + /2 раза.
10.149. В 2 раза. 10.150. м/мин.
10.151. Зр — q. 10.152. 3 часа. т т г 1
10.153. р (— )л—m и 2р( —100 — 1
\ <7 / \ <7 / ’ 1\ <7 /
10.154. На 10 км/час. 10.155. 2’^./г мин-
10.156. 12 км/час. 10.157. 20 человек; 6 часов в день.
10.158. I 1 — у литров.
10.159. 60 км/час, 40 км/час. 10.160. Через 4 часа.
10.161. 120 км. 10.162. 3 ч 10 мин.
%-
454
10.163. Три решения: 3 часа, -2- часа—\ час 48 мин и 1 час. ь
10.164. 11/8 часа. 10.165. 7 часов. 10.166. 6,5 часа.
10.167. 10/3 часа. 10.168. 6 часов.
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ XI
з
11.1. х = —arctg —4~ля.
11.2.
л , ля _ „ л , ля
±12 + Т’ 11,3'
11.4. х = 2ля, х = (— 1)* ~ 4-2л£.
11.5. х = (2п4-1)л, х = 4лй.
11.6. х— ±"б+лл. 11.7. х = —, пфЗт.
11.8. Уравнение не имеет решений.
, < п г 3Уз~4- 2 /2 ,
11.9. x = arctg — -1—----к ля.
3 — 2]/ 2
11.10. х = ± arccos -----|-2ля.
]Лз-н
,, ,, л , 2 3,2.
11.11. х =-g-4-у ля, х=]^л4-улй.
11.12. Уравнение не имеет решений.
11.13. Уравнение не имеет решений.
11.14. Уравнение не имеет решений.
., л , ля л ak
11.15. х = ля. 11.16. х = у + > х="’б^~’ТГ'
ля ak
11.17. х — 'у, x = 4j'-
11.18. х = 4-ля, х = — 4- у. 11.19. х = ля. 4 "I
11.20. x=arctg - -j- 4-2ля.
., л л/г л ak
Н.2!. х = -зб+у, ^ = 'з +Т-
11.22. х = —|-4-^т, ^== -'^~-Я Ч-л^, <р = arctg у.
11.23. х = 11.24. x = -J + ^.
л ля л ля
11.25. х- 52+13, а-92 + 23'
11.26. х = у 4-2ля, х= |,| + ур
11.27.
л ля
Гб+ т-
л ля
24 + 18-
11.28.
х = 2ля, x=±2arctg у4-2лА, х = ± 4- 2ляг.
455
11.29. х = л(2л+1), х=(4й-|-1).
11.30. х = л ^2л +х=л (2А+1).
11.31. л .. л . ял х = т. 11.32. х=у + т.
л
11.33. х = лп, х=—-f-nk. О
11.34. л , л л Зл , nfe Х=й + т- *=32+Т-
11.35. х=±^+2*л.
11.36. л , 2 , „ „ лп х = лп, х~-=- + -=-nk. 11.37. х = -?г. оо 2
11.38. Л , ЯП лл л , лп х — ^ + '2' П'39’ Х~ 4' + Т’
11.40. 1 . 1 , лл л , nfe x = -arctgy + _, Х = __ + _.
11.41. л л лЬ х = т + лл, X = jg + T.
11.42. Л ЛЛ л , ^=8- + т- *=±у + ^.
11.43. л , лл л . 2 . Х = ¥ + Т- х=±-9+ТяА-
11.44. лл л/г Х=Т’ х=т-
11.45. л , лл л , nk Х=П + Т- х=т + т-
11.46. лл лй х~т-
11.47. л лл 1 , 2 , nfe Х = -8+Т> Х = " 2 arCtgT+T‘
11.48. ЛЛ Л life Х==Т’ Х = 20 + Т0'
11.49. лл ,, лл x = -jg. 11.50. х = -^-.
11.51. 1 /17-1 , к х = ± —- arccos'—1 Ь nk. ' 2 4
11.52. л , лл я , , *=Т+-2-> *=±T+llA-
11.55. Л Л fl л . л^ Х=т + т- Х==-8+~2-
11.56. х — —х=—4~2л&.
11.57. л , л . . ——+лп, х = ~2 + л«.
11.58. х=— -^--j-лп. 11.59. х=—-^-4-лп.
л / 1 \
11.60. Х = ^-4-ЯП, \л.
л
11.61. х = 2лп, x = y + 2nfe.
11.62. х =—-^4-ли, х — 2лк, х — ^--]-2лт.
11.63. 1 У"5 — 1 , . л , лп х=± у arccos—g \-лк, х==—. л , лп л лк
11.64. *=т+т- %==^+т-
11.65. Уравнение не имеет решений, л , л лк
11.66. % = т + лл, х=8- + т.
11.67. л , х =— 4~ + ЗХп-
11.68. л , л , , х = + лл, х = + 2лй, х = 2л/п.
11.69. Л . Л . Q , х = -;—|-лп, х~ — 4-2л&. 4 о
11.70. Х=Т> ^(-^Зб + тг-лп
11.71.
11.72. x=-|arctg (2 ±^3)4—.
11.73. х=± arcsin4-лп. л , лп 1 / 1 \
11.74. Х=-£- + п5-, X=±-~- arccos п-)+л/П. 0 о Л \ о /
11.75. л . лк л . л п / 1 । п * = -g +-4~, * =-g- + -у, 1+%гп.
11.76. л х=2ли, х —-у4-л^, л / 1 \ х==—~4-(— l)m arcsin 1 — 4-лпг. 4 \ /2/
11.77. 5л , х=+ jg+лп- лп 2л&
11.78. %-Т’ Х~5~-
11.79. х=±^г4-2лп, х = 44-лй, х = (—1)т-S-4-лпг. о Z 0
11.80. л 2 х = лп, x = -g-4--д лт.
11.81. 1 4- х = лп, х= ± arccos =——.4-2лй.
457
11.82. х==~2~, х = ± arccos ~ 4~ 2 лк.
11.83. х = лп, х = ± -^-±-2лк.
О
11.84. х — ~ + лп, х= —у-|-2л£, х = л(2т+1).
,, о, , ... I . Кб — 1 , л/г
11.85. х = (— 1)” у arcsin -----------.
11.86. х = (2n+1) у, х = 2лй.
11.87. x=g + ™.
1 1 ОО Л I ЛН Л . t
11.88. ^f + y, х = у + л&.
11.89. х=лп, х = -? + ^. 4 1 2
Л , ЛП п
11.90. х==^-+~2, х=+у + лА.
11.91. х = (—1)лу arcsin у +
11.93. , л Л , х = ли, х = лк — -у , х = — лт.
11.94. Уравнение не имеет решений. 11.95. х — лп.
11.96. , 1 , , х = лп, х— ± arctg —rr- 4- лк. 1/9
11.97. г z Уравнение не имеет решений.
11.98. 1 . . лл х= —у arctg4 + -4- .
л лп л , лк „ „л л
11.99. х = '4 +“2 > х= 8+ Т- И-ЮО. х = у+лп.
11.101. х-~-]-лп, х = л (2^+1).
11.102. х — у4-лп, х = —-^--}-лк, х — у -|—у.
11.103. х = ~ + лп, х = (— 1)* 4 + я&>
2 х — (— l)m + 1arcsin у
л лк
11.104. х = лп, Х = у + у-.
11.105. л , л лк л , л/п Х=±_ + л„, Х=(_1)Аг2+т1 Х = у+у-.
11.106. л , лп л , , , л , лт Х = т + Т’ х=± б+я/г’ х =+l 12 +
458
.. Я , 2лп 2л , _ ,
11.107. x=-g-4--у-, х=±-у4-2л&.
11.108. х = 2лп, х— ± ^--,-2.т./г, х = (—1)тлт. •э о,
11.109. х=Л + -™, х=|. + 2р. (2fe+1^9m).
11.110. х = ± 4- arccos '--4^4-.тп.
2 \ 4 /
.. ... <, л — , л Зл . л1
11.111. х — 2лп, х = ---4-2лд, х—-~4-лт, х=-й- + тг. ’ 2 4 1 8 2
11.112. х=у+лп, х=—” +л&, х=|+ли.
11.113. Если I а \ 1, то уравнение имеет следующие решения:
х = arctg (2а ± За2 —3)4-ля. Если |а| < 1, то решений нет.
11.114. Если | a I sg |/2 , то уравнение имеет следующие решения: х = (—1)” arcsin (3 — 2^3 — а2- )4-лл. Если j а | > 1/^2 , то уравнение не имеет решений.
11.115. Если IВ | > 1, то уравнение не имеет решений. Если | В j 1, то уравнение имеет решения. При этом, если | В | ,
то уравнение имеет следующие две серии решений:
х = — у — ( — 1)" arcs'n В + лп, х = — -^ + (— 1.)* arcsin ЗВ 4-л/г.
Если же ~<|В!гС1, то имеется одна серия решений х =
= — ~ — arcsin В 4- лп.
11.116. Уравнение при любых значениях В имеет серию решений вида
3
х = -л 4- 2лп. (*)
Если OsgBsgl, то, кроме серии решений (*), уравнение имеет еще одну серию решений
х= -у4-(—О* arcsin (2В — 1)4-л#.
11.117. Уравнение разрешимо в том и только в том случае, когда — ттсаттс 1, и имеет решения вида х = ± — arccos (4а — 3) 4-.
11.118. Уравнение имеет решения тогда и только тогда, когда | а | 1, где а= 2В4-1, т. е- пРи — 1 В sg 0. При этом, если | а | sg
1 3 _ 1
sg — т т. е. — sg В — -у ,то уравнение имеет две серии решении: х = ± ~ arccos а4-яп и x = ±i- arccos (— 2а)4-лА. Если же 2 ~
459
7Г<|а|^1, т. е. — isc.B<z—г или —О, то имеется 2 1 1 4 4
одна серия решений х = ±-g- arccos а 4- лп.
11.119. Уравнение разрешимо тогда и только тогда, когда | а | 1.
При рассматриваемое уравнение имеет серию решений вида х — ± arccos( — а 4- Иа2— 1)4-лп, а при asg—1—серию решений
вида х = ± у arccos ( — а — Vаг — 1 ) + nk.
11.121. При любых действительных значениях а, кроме а = УРавнение разрешимо и имеет серию решений вида
Л х 2ct л п.
Если | cos a j < (г. е. если при некотором целом m выполняются
л 3 \
неравенства л/п < а С-^-л + л/п!, то, кроме серии (*), уравнение имеет еще одну серию решений: (—1 )k+1 arcsin (2 cos2 а) 4-
4-~—2а. Если а — то уравнение не имеет решений.
11.122. х = -^-4-лп.
4 1
11.123. х= ±arccos (1—И2 ) + лп, х= ±у arccosi^—- + 4- nk.
11.124. х=^-}-лп. 11.125. х = 4лл, х=±у4-2л&.
Зл
11.126. х==-^ + 2лл. о
11.127. х = {n^lk, k — целое), 5 10
х = -д-л 4*-д’~т (т Ф 9/4*4, / — целое).
11.128. х= ±4-4-лп.
о
4 4 4 Л I ЛЛ Л .
11.129. %~1 х~
11.130. х = ^; + ~. 11.131. х = 4-4-лп. 1U D 2,
11.132. х = ~-]-лп. 11.133. х = — ~-{-лп.
11.134. х = ~. 11.135. х = ^ + лп.
460
11.136. х = л (п+ y + > у = я\п — у + ^-
11.138. х = л(/^Ч-п+4-\ у = л [k— п+44
\ 3 J \ 3 /
Х=л — y=n(k—n—±-\
\ з j \ з /
_ Л ЛМ Л . ЛЛ _ t
11.140. x = "j'+'2", У =-4-+ + 2л&.
11.141. х = ^--j-2nk , у — ~4-2жп;
х = + 2nfe, у = ~ 4- 2лт.
11.142. х = л (2п ± Jr-\ /
Х = л +
y = ^k+
11.143. х = 2лп, у = л (2k-\-i).
11.144. Система разрешима в том и только в том случае, когда | 2а — sin а | sg 1, и имеет следующие решения:
О* । 1 , , \П . . лп
x= 2- + ’2‘( —i) arcsin (2а — sin а) 4--ту,
ОС . 1 , (‘.„J-l * in • \ ЛП
(/=-g-4--2 (—1)и+1 arcsin (2а —sin а) —-g-.
11.145. Система разрешима, если а<0 или а 5:2, и имеет следующие решения:
, а + Ка2 —2а , , , а±}^а? — 2а ,
х — arctg-----g---------J- nk, у = arctg----------1- лп.
С Л \
а=лт), то система разрешима
лишь при а=1 и имеет решения вида х = Ь, у = а — Ь, где Ь — любое
461
действительное число. Если cos а ф 0, то система разрешима тогда 1 а — 1 I
и только тогда, когда -------- sg 1, и имеет следующие две серии
I COS OS I
решений:
а , 1 а — 1 ,
х = тт + л- arccos-----Р лй,
2 2 cos а
а 1 а—1 ,
и—-п —=- arccos---------nk;
я 2 2 cos а
а 1 а— 1 ,
х = — — arccos----------k nk,
2 2 cos а
а , 1 а— 1 ,
{/=-«- +тт arccos-----nk.
я 2 1 2 cos а
11.147. Система разрешима лишь при а = 0 и имеет решения x = ---y = (k-n)n.
11.148. х=(—1)« ^-Н-яп, х=(—1)*+1 j + лй,
11.149. х = у + л (k-j-n), Л
Х= — у + Л / + «),
11.150. х = + 2лп, У
* = “ + 2лл, у
_ ... п , пп 5л
11.151. х = 7+т, у = -т
11.152.
пп nk
Х = Т’ у==~т
£,==(-1)*+! ^ + nk; у==(—\)п у+лп.
у= у+л (£-«);
л , .
У = — g- + л (k — n).
± + 2лй;
± + 2лй.
пп , о ,
+ 2nfe.
11.153. х = пп, y = 2nk; х = ~ + пт, у = ^ + 2л/.
1 i 43
11.154. х = (—lf+i arcsin—|-лп, у = (— 1)” arccin^-p-n(n-j-2m).
11.155. х = -^--{-п (n-)~2k), у—-----^--f-nn;
x = arcsin ;L^A-nl4-2nm, y — arcsin 4-nl.
J/10 /10
462
11 4 Е£» I L. ЛЛ
11.156. х = -^-\-пк, у = л . , Л ,
х = -д-+яй, у= — —-[-лп;
О о
л , , Л .
х=— д- + лй, г/=-о- + лл; V О
11.157. х = лп, y = nk.
11.158. х = лп, у — (—1)" arctg 2-f-nk.
11.159. х = у+лп, (/=(—l)ra arctg/2'-|-л^
х — лт, У = (—l)m arctg 2-к л/.
11.160. При а=0 х— ^-(-2лп, у — любое;
при а ——1 y—~ — x-\-2nk, х —любое’
при ат^О и аф—1 х = ~-[-2лт, у — -^-]-2л1.
11.161. х=^-|-лп, y = g+nk;
1 я -к 1 . 1 а-к 1 . .
х = =• arccos —7;-к ля, у = =- arccos —4-к л1;
2 2а ' v 2 2а
1 а-к1 , 1 а 4-1 , ,
х= — arccos —4--------к ли, и = — - arccos —4----к лк
2 2а 1 * 3 2 2а 1
11.162. х = яп, y — nk;
1 1 , 1 1 , . х = — arccos -к лп, у= arccos -(- як;
1 I 3\ , 1 ! 3\ , ,
х— ~ arccos I — j-1 + лп, у = arccos I — -jl-клй;
1 1 , 1 1 , ь
х=—arccos 4-лп, у=—arccos 7 -к ля;
2 4 3 2 4 1
1 / 3\ , 1 / 3\ , ,
х = — =г arccos — у- + лп, у = — — arccos — т -к ля.
2 \ 4) v 2 \ 4/ 1
11.163. х = ^ + 2лп, y = 2ztk;
13 1
Х= (— 1)т arcsin Jg + пт, у = (~ l)m+1 arccos yg -к 2л/;
Зл х ~ 2лп, у = + 2л&;
1 1 ч
х = (— l)m+1 arccos R-к2л/, у — (— l)m arcsin т^+л/п.
*0 1э
463
11.164. х = 2ля, y = ~ -f-2nk;
+2лт, y~2nl;
/ ’ 19\ 7
x = (— 1)” arccos (— 20) + 2лй, у = (— 1 )я arcsin + лп;
7 I 19\
x = (— l)m arcsin ^Q-f-лт, y = (—l)marccosf — ^}-[-2л1.
11.165. х = ~ + 2лп, y=^-i-2nk;
«rt rt Л л t
х~—^-~]-2лп, y= -^4-2л^.
11.166. x=(-1)т^ + шя, (/ = (—l)m+i g+л(2/+1) + пот.
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ XII
12.1. ^(|/'F+T2-/i). 12.2. й/5. 12.3. | П2 + 4Ь2 .
12.4Д«Ч/3К 12.5. 12.6. j^=. 12.7. |иф-.
12.8. ab. 12.11. /р2+А 12.12. 3 см и 4 см. 12.13. £ и
о о
12.14. r-\-R + YR2 — r2~2rR. 12.15. ~ ]/~3 — 2 (cos a + sin a.).
12.16.
12.19.
л/л2 + /2 h-\-l 2R
12.23.
R2 sin 2a
1 +sin2 2a '
—--------—-----. 12.20. г, ^-гн|г. 12.21. J. 12.22. ^ + &)2
1 +cos a + sin a 3 3 4
144 юо« 8K11 —19 sin a
-HK- cm. 12.24.---=----cm. 12.25.--------
^*0 / . I ,
sin a-k
12.17. c-tg
12.18.
4
12.26. ДД О
12.27. ^. 12.28Д и 12.29. r2 12.30. (2л + 3 /3)-
10 oO \ X О j
12.31.
12.33.
12.37.
2 /3
У a2 + ab + b2
rR УЗ yr2-rR + R2'
У-г)2
2(/i-2r)J2,38,
12.34.
. 3a s,nT 2b sin 2a
i . „ . a‘ 1 — sin 2a tgQ
&
12.32. ’ Q/4/?2-r2 ± r /3).
b2ft о
’2-35- 12.36.
12.39. 1 tg a tg . 12.40. Ocho-z z
464
вание равно 6 см, боковая сторона 5см. 12.41. у^-(2а — Ь)/4а2 — b2.
12.42. 2 sin2 %, cos а. 12.43. ctg2^. 12.44. . 12.45. ~ и ~
2 1о 2 24
12.46. q(3+J/"5)- 12.47. | R и (1 — R- 12.48. Угол при основа-У □ \ о /
2 1 г________ 1
нии равен arccos 12.49. 12.50. р Ь2 + &с. 12.51. % (а—Ь-[-с).
,2.52. ,2.53. 2/5 12.51.1 12.55.
12.56. тп /З- 12.57. (b + c)^ 1 - ~. 12.58. ^== см. 12.59. j/ ~ см. ,2.50. М. 12.61. l"-™(l + l). 12.02. X4.J,
Z в = ^ и z С = ” . 12.63. 48/6 см2. 12.64. 16 см. 12.65. 6 см2.
12.66. ~ и 12.67.”, arcsin | и arcsing. 12.68. Vac
12.69. И1------Ц 12.70. 12.71. cm2.
\ /2/’ 10 2
1
12.72. b sin a ' [sin2 a sin2 p — 2 sin a sin p cos (a -|- P)] 2
и b sin p [sin2 a sin2 p — 2 sin a sin p cos (a + P)J 2 ’ R 1
12.73. 4(3/21 — 8) см2. 12.74. -/a2 —b2|tga. 12.75. 2 см и 1 см, o z
2 4 CM И CM. о 0 12.76. 3:5. 12.77. f~• >2.78. 204 см2. \cos4/
12.79. 588 см2 и 1680 см2. 12.80. 1|/Iz2Y^YY)2- ,2’81- a2 + b2'
12.82. 4=(S + /S2- 16Z?4). 12.83. 2^. 12.84. 2arctgC |Z/—— = 2a 3 c,p c2-- 4.S
= + arctg—7^= 12.85. 12.86. 5: 27.
6 C/C2_4S- a + 2b
12.87. 6 см и 10 см. 12.88. 1/"° 12.89. tg a.
Г 2 21 a — b |
12.90. 1:2. 12.91. 1 : 2. 12.92.3. 12.93. ~.
4
12.94. 5см. 12.95. ~. 12.96. 1 : 1 : J/2-/3 :/2-/3.
12.97. S2l/~ 2_f2 . 12.98. bl/"—12.99. “ (11 ”” a)2 .
У 5х+52 У 2a — b л sin2 a
12.100. 12.101. 4- 12.102. f4/3-^V2-
R.—r 4 \ 6 /
465
12.103. Задача имеет решение, если А’<а«£7?/5, причем при _ 2
/?<а<27? и при a = RV§ есть одно решение: — (2а — /5+ — а2), О
а при 2R а < R /5 — два решения: ~ (2а + V'bR- — а2). О
12.104. ]//?2 + r2 + jRr. 12.105. a]Z(1 + j) f1 + j)
12.106. 2 arcsin R [sin—sin . 12.107. . 12.108. и —.
12.109. -^|^R 12.110. (r + 2/? + 2 + 2r/?); решение
существует лишь при г <Z 4R.
12.111. 12.112. 22~?R-?. R . 12.113. /а&.
а2 + ао + &2 75
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ XIII
13.1.
а /2 „ &(/3 - 1)
3 У 3 4 У 2
а
2(1+Кб)'
13.4. glQ+L—. 13.5. ~(2л + 3/з)- 13.6. 3R. 13.7. ~ (Уб ± 1).
6 К3 27 8
13.8. (5/6+/22) Л. 13.9. 13°L . 13.10. 3 12 а-.
_ 6/51 25
13.11. -RR- и 13.12. г Уб +//?2-3+ 13.13.
/10 /35 b + h
13.14. sinal/ —------. 13.15. 1/ — fctga-RR.
Г 3 /3 cos а Г 3 \ УЗ)
13,16. — tg —. 13.17. __ ? . о а a3 cos - - 13.18. И
/3 2 ]/ 9 tg2|-3 12 / 1—2 cos а
За2_______ 1Д 1Д 2&3 /11 ]3 20 За3/г (/г /3 cos а — a sin а)
4 /1 — 2 cos а 49 (a sin а + 2/г /з cos а)2
3'21' Й+/4+— 3&2' ,3'22- 2/?ctgy j/^l--у ctg2 -2-. 13.23. у.
18Z>3/?3 . / 2 а\ 81/3
,3-24- (h2 — b2)V4b2 — h2 13.25. arcsin i --rz cos — 1. \/3 2/ 13.26. Л,
13 27 ° ~~а) 13.28. а (2b — а) 13.29. а
2/3/2-а2 2]Z62-ya2 2/3
466
h'3 (у r ........... ,. О ___________
13.30. -J.-sin —/1+2 cos a- 13.32. 13.33. /Sf + Si + Sj-
6 2 2o ’ 1 _ 3
13.35. /a2 + &2 + <?2. 13.36. U 65 . 13.37. ~ sin 2 a tg В sin3 2B.
2 ' 2sin2p 4л
13.38. yf. ctg a ctg P (tg2 a + tg2 р/, 13.39. --------ah ..........
a + 2h 4- }z a2 + 2/z2
13.40. 1 pR2 tg a ctg2 . 13.41. 1/lytg^cosU
3 2 2 sin a У r 2
13.42. ~ см». 13.43. ----------------i-------------3-
2 ctg у +/2 'ctg у + ct§ y)
z \ 2 2 >
13.44. 5 cm. 13.45. ^/о4 + 64/г4. 13.46. (3 ) л2у 1 j. ]/10 —6 | 2)
и | (з/2-1 ± /10-6 | 2 ). 13.47. UML
Jz \ CL U C
/ 1 1 1 \~1 9 b
13.48. (y + y+yj . 13.49. 13.50. y(tg ay2 ctg a).
13.51. ° I 2ctga —2tg %- — tg a I. 13.52. -7~^ah —
4 I 2 I /4Л2 у 9a2'
9h3/,3 ,____ 191-2
13.53. —.... .......... 13.54. 27?/cosa. 13.55. 4/?2. 13.56. — ----1.
3(/г2—&2)/ 2b2—H2 _ 6
ab 1/ 5 2r _____ __
13.57. ^7=== 13.58. ~cM. 13.59. m—n+p. 13.60.-j (8J 3+/37).
13.61. ЦД- a2. 13.62. и r = ^3-. 13.63. 3-
5 6 4 3
13.64. 4(1,+ 1/2 tg P —У 1+2 tg2 p). 13.65. ^-(Уа2 + /12-a). 2 !1 13.66. ||]/'16й2 + 2/г2. 13.67. -|уо2 + Л2- 13.68.
13.69. ^ab-a2-b2. IQ 71 II л/~ 7 13.72. 13.70. у Z2-y(a2-aZ> + &2) . 2л. b (n+2m)
‘ 1 Y 3 •_ 3]/ 3 (3 + 4 ctg2 a) |'9&2—12n2
13.74. Ц1 ± ]/ yj. 13.75. |/Si-lsj. 13.76. 2 cos a.
13.77. 7j/2"I+VIiT' 13.78. -PU a2. 13.79. 2 cos a 8
13.80. -4=&3- 13-81- 9/3 3 13.82. —. 13.83. «У^у.
13.84. 13.87. 2 arctg &^a2+c-. 13.85. ac ly 13.88. g±-LU. 14 (2/14/ 1/к 25 arcts - 13.86. - см. 8 3 2 (5/2 + 3) 13.89. — fl --Lctgp'j sin p ( /3 j'
467
13.90. Сторона основания равна ]/"З/?2 + У 9/?4 — 3S2, боко-
вое ребро равно "j/” у /^З/?2 Т /9/?4— 3S2-
13.92.—^(2&//+4^-&2). 13.93.1/” 1(а2 + &2 + /а4 + &4_а2&2).
4 у 3 У 3
13.94. ^=(/5-1)- 13.95. уК15&2 + 4/2. 13.96. ^ (1 +/6 -/3).
13.97. /. 13.98. 13.99. 2sin4acos2a.
5 Зо
13.101. 4- ла3 sin2 2a. 13.102. 4- nR3 /7- 13.103.-^—/?2
3 _______ 3 5/5
а,04. »j///i.
13.106. 2 arcsin [77 (1 ± 1
13.91. 3/3 см3.'
13.100. у.
‘ и -l^L £2. 5/5
Зл/г2
2(9 + 4/5~)’
9 \ I 1 1
1-^ . 13.107. г = 4-R, у а / J 2
bi 13 109 2зг7?5 13П0 л/2
2(&2-1)‘ 13-109- 3r(R-r)- ,ЗЛ1°- 48
/с.и. 13.112. г/5- 13.113. у. 13.114. arcctg 2.
3+ г. 13.117. (2 + /3)г. 13.118.
2/2
— (3 — cos а + /7 — 8 cos а 4- cos2a).
1 + cos а ’ 1 7
13.105.
13.108.
13.111.
13.116.
13.119.
(53 —7/3 )• 13.115.!^. у (/2Т-3).
РЕШЕНИЯ И УКАЗАНИЯ
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ II
2.4. Некоторая операция а* b считается коммутативной, если для любых чисел а, b выполнено соотношение a * 'b = b * а. В частности, коммутативность вычитания означала бы соотношение а — Ь~ = Ь — а (получающееся заменой знака * знаком —). Но для любых чисел а, Ь это неверно (при а -ф Ь указанное равенство не выполняется). Аналогично разбирается случай деления.
Ассоциативность некоторой операции а* b означает, что для любых чисел а, Ь, с справедливо соотношение (а * Ь) * с = а * (Ь * с). В частности, ассоциативность деления означала бы, что (а:&):с = = а : (& : с). Но для любых а, Ь, с это неверно. Аналогично разбирается случай вычитания.
2.9. Сначала докажите равенство
0,00...01 =0,00...00999 ... k нулей нулей
2.10. Пусть а и р — два действительных числа, а<^. Выберем такое рациональное число а, что а<а<Р (см. пример 16 на стр. 62). Затем выберем такое рациональное число &, что а<6<(3. Пока-
, Ь — а
жите далее, что число с = а-|--— иррационально и удовлетворяет
1^2
неравенству а < с < р.
2.11 и 2.12. Доказательство аналогично рассуждениям, приведенным при решении примера 13 на стр. 55.
2.13. Сначала докажите, что а,:у1:с/.2. Чтобы доказать, что a*~i ф ^6 ак+2 2, ...), умножьте равенство ~ = 0,а1а2а3 ... на 10* и запишите результат в виде
я-10* —73-а1а2 ... а* п
— — 0,а*+1ай+2 ...
2.19. Воспользуйтесь равенством
1 _ 1
1,00 ... 01 ~___________1
99 цифр 10100
1 , 1 1 1Q100 + 1Q200 1Q300
469
Другое решение:
1
1,00 ... 01
99 цифр
1 100 цифр
* 1 ~ TW
1 + Ю100 1 10200
юо юо
цифр цифр
О,9Э“7Т7^бО~Т?—0
0,99 ... 9
0,999 ... 9
200 цифр
100 100
цифр цифр
0, (^.Тэбб^То) =
200 цифр
100 цифр 100 100 100 ...
= 0, ^ПоТ^ОкГГэбо'ГоЭ
2.20. Покажите, что если 0 <_а< 1, то
а < У а < 1.
2.27. Воспользоваться следующим преобразованием:
“Г =У(а- 1)4-2 fa- 1 + 1 =
= /(|4Г=1+1)2 = I + 1 | = f^l + 1
(и аналогично для второго корня).
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ III
Предварительное замечание. Пусть требуется доказать, что для любого положительного числа а выполняется неравенство
а + ~ + 2. (*)
Неравенство (*), в силу условия а>0 и правил действий с неравенствами, имеет место тогда и только тогда, когда выполняется неравенство (а—!)- : 0. Если неравенство (?) обозначить буквой А, то можно записать, -что
А — [(а- I)2 0].
Условимся о том, что запись
А - [В]
означает, что рассматриваемое в задаче неравенство А выполняется в том и только в том случае, когда имеет место неравенство В. Такие записи мы будем употреблять в данной главе в качестве указаний к решениям задач.
3.4. 1. А-Ч(а—&)2 + (а—l)2 + (&-l)2+:0].
/ 3 \2 16
2. 5а2 —6а* + 5&2 = 5 а—-+& + ~Ь*.
\ 5 / 5
3. А--[а+2(а —Ь)2 + 0].
470
3.5. be — ad = be — acф-ас — ad = c (b— a) — a(d — c) =
= (b—a) (c — a).
3.6. Л~ a + -=-bj + 1 -^-)Ь2Э=0 .
3.8. Л — [(/^-/r)2(|/H" + /b3>:0].
3.9. 1. Разложить (а-\-Ь)п по формуле бинома (или применить метод математической индукции).
а3ф-Ь3 /аф-Ь\3 3
2. —Л-----= у (а~гЬ)(.а-by.
3. Л ~ [(а + Ь--|-2ИяЬ)3 3; 8 К^Ь (а-|-Ь)] «
-» [(аф-Ь)2ф- 4 /ab (a + b) -f-4ab >, 8 УаЬ (а ф-Ь)] -*
~ [(а + Ь - 2|/db)2 0].
3. 10. Разность между левой и правой частями неравенства равна (а* — bfi) (а" к — bn~k\, рассмотреть два возможных случая: a sg b, а > Ь.
3. 11. Использовать неравенства задачи 3.10 при Ь = 0, 1,...,п и формулу J] С* =2".
k=-.o
3. 12. Возвести в квадрат.
3. 14. 1. А —» [(.V — г/)2 + («/ — г)2ф-(г —х)2Зс01; см. неравенство примера 3, стр. 88.
2. Задача сводится к предыдущей, если положить
№/ = ?!, xz^ylt уг=хг.
3. Перемножить неравенства
O'i 5г Зо2, о] Эг ScFjOg
(см. задачи 3.14, 1 и 2).
4. Перемножить неравенства oj Зд Зо2 (задача 3.14,1) и
9о3 (задача 3.14,3).
5. Перемножить неравенства о 5 >: Зо^Оз (задача 3.14,2) и (gogc-5=9o3 (задача 3.14,3).
6. Умножить обе части неравенства о; Зо2 (см. 3.14,1) на о, Д-?0.
3.1 5.1 и 2. Л ~ [(а —b)2 + (b —с)2ф-(с—а)25г0].
3.16 . 1-й способ. Обозначить х = а3, у — Ь3, z-е? и использовать неравенство а3 Ь3 ~-с3 Дд ЗаЬс (см. пример 6, стр. 89).
2-й способ. См. неравенство Коши (13) при я = 3 (стр. 89). 3.17.1. Л[(а-rb-J-c) (ab-( Ьсас) тд 9а/;с] (см. задачу 3.14,3). 2. 1-й способ. Л «— [а (Ь — с)24-Ь (с — а)2 + с (а — Ь)2 5г0].
2-й способ. Раскрыть скобки в левой части неравенства и трижды использовать неравенство вида х2у -|-г2г/ у • 2хг, у^О, которое следует из неравенства (2) стр. 82.
3-й способ. Пример 3.17,2 —лишь другая запись примера 3.17,1.
3. (а-|-Ь-|-с)3 — (о3 + Ь3 + с3) = 3 (а Ь) (Ь с) (сф-а).
4. Л «-» [(аф-Ьф-с)3 2 (а + & + с) (ab-j-bc-|-ca) + 9abc]; сложить
неравенства, доказанные в задачах 3.14,6 и 3.
471
5. 1-й способ. Положить
l/ + z-x п x + z~y_h У + х-г
2 ' 2 ’ 2 ~С
и для случая аЭ:0, & Э=0, сДдО использовать неравенство примера 5 (стр. 88).
Если хотя бы одно из чисел а, Ь, с отрицательно, например, а<0, то х~>г-\-у, откуда х^г, х^у, и поэтому сУьО.
Но тогда и неравенство хуг^8аЬс очевидно.
2-й способ. Можно считать, что числа а, Ь, с (см. 1-й способ) неотрицательны, так как в противном - случае, как показано выше, неравенство выполняется. Для доказательства в случае ЯЭ=О, 6^0, сД-ьО достаточно перемножить очевидные неравенства
х2Э=х2— (у—г)2, у2 у2 — (z — х)2, z2y-z2 — (х — у)2,
а затем извлечь корень из обеих частей неравенства.
6. Записать неравенство, доказанное в задаче 3.17,5, в следующем виде: Оз (Oi —2х) (Oj —2//) (Oj—2z), или
Оз of — of (2х + 2у -|- 2z) -|- ох (Аху -|- 4xz + 4//z) — 8xyz,
И т. д.
3.18. 1. Положить х = —7=-. ц = ——, z = —и использовать
У<1 Vb' Z Ус
неравенство х2у2z2 хухгуг (см. пример 3, стр. 88).
2. 1-й способ. Л--[2о{ — 7О1О2-'-9о,з У--0];
для получения неравенства, указанного в скобках, использовать тождества
х3 + У3 + г3 = о’ — 3O]O2j- Зо3, х2 + у2 + z2 = of — 2оа.
2-й способ. Трижды использовать неравенство вида
a3-\-b3^a2b-\-ab2 (аУ-ьО, 6удО)
(см. задачу 3.10).
3. 1-й способ. Применить неравенство
2-й способ. А «— [(-?• -|- —] + + тй + + —-'j ----- б],
[ \ b ' а) \с b ] ' \а ' с I J ’ см. (4), стр. 82.
3-й способ. Использовать неравенство Коши — Буняковского (Стр. 91):
Я1 = Ха, а2=угЬ, а3 — Ус, Ь1=—Ь2 = —г=, Ь3 — ——=..
У а У b Ус
4. Использовать неравенство задачи 3.16.
5. Обозначить
b -4- с , d 4- с d —I— Ь
и использовать неравенство задачи 3.18,3.
472
6. 1-й с по с о б.
A ~[(a + b) (a-b)2 + (b + c) (Ь-с)2 + (с4-а) (с-о)2=э0].
2-й способ. Левую часть неравенства можно записать так:
<«+»+«) (уру + -3 =
-I №+«>+(«+»)+<»+»>1 + pip + - 3.
Далее использовать неравенство задачи 3.18,3.
3.19. 1. А — [(о3 — а2Ь— ab2-\- b3) -j- (а3 — а'-с — ас2 + с3) -j- (b3— Ь2с— — be2 -J- с3) 2s 0] — [(о — b)2 (a -J- 6) + (о — с)2 (а±с) + (Ь~ с)2 (Ь + с) =э 0].
3. Сложить неравенство задачи 3.19.1 с неравенством примера 6 на стр. 89.
4. Сложить утроенное неравенство задачи 3.19,1 с удвоенным неравенством примера 6 на стр. 89.
5. Задача сводится к предыдущей.
6. l-й с п о с о б.
а4 + Ss 2а2&2, b3-\-ci:^2b2t2, с4-|-а42-' 2а2с2,
затем использовать неравенства вида (2), стр. 82.
2-й способ.
Л —4о?о2 + 2ог2-|-Зо1Оз2?0],
к неравенству задачи 3.17, 6, умноженному на ох, прибавить 2оз 2s 6i7|O3 (см. задачу 3.14,2).
3.20. Возвести в квадрат; А^~ [bc-i-ad>:2 Уabed]; далее использовать (5), стр. 83.
3.21. а4 + &42a2b2, ci-{-di ^2c2d2; далее использовать (5), стр. 83. Можно также использовать неравенство (13), стр. 89.
3.22. Возвести в квадрат;
А — [(a2-l)(l-Z>2)<0].
3.24. Л ~[а&-(а + ^)2^0]~ [a2 + a& + &22s0].
3.25. 1-й способ. Положить a = cosqp, 6 = sin<p; тогда
а b — У 2 sin ^<jp + .
2-й с п о с о б.
|а + b | = У(а±Ь)2 = У2 (a2-f-Ь2) — (а — Ь)2 У2 (а2 + Ь2) = /2.
3.26. Использовать неравенство а2 + Ь2 + с2 5= -у (а + 6+с)2 (см. за-
дачу 3.15, 1). _____ _____________ ____________
3.27. Положить У2а-1-1 = и, y2b-f-l — v, j/2c-j-l=a>; тогда «2 + о2-|-а’2 = 5; далее использовать неравенство задачи 3.15, 1.
473
3.28. 1. fl2 + 62 = l(fl + b)2+l(fl-&)2Ss^(a + &)2. z z z
(a-J-&)2 > c2.
2. Применить к неравенству a2b2 с2 прием, указанный в решении задачи 3.28, 1.
3. См. 3.28, 1 и 2.
3.29. Возвести в степень п неравенство
/ 1 \2 1
3.30. Перемножить неравенства
_1 2 А 4 99 100
2 < 3‘ ’ 4 < 5 ’ ”' ’ 100 < 101 ’
1
получим где а —произведение, стоящее в левой части
доказываемого неравенства; отсюда
1 1 a <Z •. <С —.
jZioi ю
3.31. Сложить неравенства вида
1 " 1 1 / 1 1 \ „
(2/г+ 1)2<2й(2/г-)-2) ~'2\2k~ 2k+2l ~1, 2’"" П’'
Тогда
„ 1 ' 1 1,1 1 , ,1 1,1 1 \ Sn< 2 \ 2 4'4 6 г2п- 2 2п ' 2п 2п±2'
_ 1 : 1 1 \ 1
”2\2 2nJr2ll<'4‘
3.32. 1. Применить метод математической индукции. Если имеет место неравенство (l-j-a)*> l-t-ak, то, умножив это неравенство на 1-|-а>0, получим
(1 +a)*+i > (1 4-afe) (1 -J-a) = 1 + (&+ 1) a +k а2 > 1 Ц-а (k +1).
2. В разложении бинома (1+а)" все слагаемые положительны, если а > 0.
3.33. 1 + 1 + 1- + ... + 1<1+1 + 1 + ... +
<l+-2+22+”- + 2« + ---=2.
474
3.34. По формуле бинома Ньютона
Л, 1 \"_i > ] > «(«-О 1 ,п(п-1)(п-2) 1
\1 + ^/ -1 + 1 + -Пу--7Г2 +-----П2Тз------^ + -
п (п— 1)... (п — k-\-1) 1 , , п (п~ 1)... 2 • 1 1
1 2 ... k ' nk + + 1 2 ... п ' hn~
о , 1 Л 1' , , 1 Л 1 \ Л k-\, ,
- 2+Ь2 I1 “7Г/+ '+Ь2ТМ И
_____1________L'M2.i и И
п i \ п) п /'
f 1 \«
Отсюда >2 и, кроме того,
/ 1 \« 11 1
(1+М <2 + 2Т + зГ + -"М! <3
(см. задачу 3.33). 3.35. В силу неравенства Коши (13), стр. 89,
'1/~7Гй п~ < а1 ~г а2 4~ + а/г а1 + ап п 2
Далее, akan~k+1 <han (для fe=l, 2, ..., п) (см. задачу 3.5). Поэтому (а1аз... ая)2 = (axa„) (а2а„^) ... (а„ах) =э (а1ап)п,
или у аха2...ап >: Кахая.
3.36.
при /I;;; 3 (см. задачу 3.33).
3.37. При « Уд 2 имеем рЛ«>уЛ1 =1 (свойство 10, стр. 81). п,— 2
Неравенство у п <1+—_ сводится к следующему:
Использовать 3.32,2: a = ——t k — 2\ имеем
И п
Нд_ 2 YM 1 д-"(«-О 4 л(п-1) 2
V+M 2 ’ п 2 п
3.38. -4= >-~= при k = l, 2, .... п— 1, отсюда ММ
1 -|—+ ... Н—у=. 3> п .
у2 У п У п
475
Проверить, что
(fe = 2, 3.п).
3.39. 11 1 — ат~п
ат+-^-ап---------- = a«(a^-n-l) + L—±— =
1 ат \ ап ат
_(ат~п— l)(am+« — 1) ~ о™ ’
рассмотреть два случая: а>: 1 и 0 <а < 1.
3.40.
д «Гпр+ 4) &2 + р-Ч-^Ц + р-2 + ^! + ... L \ I» > \ I* / \ Lt
...-|-1а2-|—-''j -j- fa-| ;
\ а2 ] \ 1 a /J
далее использовать неравенство предыдущей задачи.
3.41. Д2=^а|==^В2 (£=1, 2, п).
3.42. (k— 1, 2, ..., п), откуда (^>0)
mbk^ak^Mbk< т £ bk-g: J] ak^M J] bk. k=\ *=i *=i
3.43. 1-й способ. Воспользоваться неравенством Коши — Бу-няковского (стр. 91).
2-й способ. Рассмотреть неравенство -g-(flk~az)s^0 (суммирование производится по всем k и / от 1 до п и таким, что k^l). Сложить это неравенство с равенством
(П \ 2 П
2а*) = S S akai-
*=1 / fe=l kizl
3.44. Левое неравенство доказывается с помощью неравенства Коши (стр. 89) для чисел
± 1 X.
ai ’ а2 ’ ’ а„’
среднее неравенство доказано (формула (13), стр. 89); правое можно доказать на основе неравенства предыдущей задачи.
3.45. Рассмотреть тождество (П \ 2 п
S а* = S а*+ S akOi-k=i / ft=l k^l
3.46. 1. Возведением в квадрат свести к неравенству Коши —Бу-няковского ((15), стр. 91).
476
2. Возведением в квадрат свести к неравенству
/’л п п
2 J] akbk,
k= 1 й= 1 к= 1
которое, вытекает из неравенства Коши.— Буняковского (если | а | >2 :>(&!, то | а | > Ь),
3.47. Показать, что выражение
mkJ,1x2-2mkx-\-mk_i принимает неотрицательные значения при всех действительных значениях х..
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ V
с=Уо-
5.20. Если A (xlt 0), В (х2, 0), С (0, у0) — заданные точки, то трехчлен должен иметь вид а (х—хг) (х — х2). Поскольку график должен проходить через С, имеем axxx2 = z/0. Коэффициенты искомого трехчлена ах2А~Ьх-[-с определяются формулами
а __ Уо ь =______Уо (-И Ч~ xi)
ххх2’ xtx2
5.21. Если А (хх, Ух), В (х2, у2) — заданные точки (х2^Хх), то искомый трехчлен должен иметь вид
ах2А-Ьх-\-с=а (х— х^А-Ут,-
Так как график должен проходить через точку В, то а(х2— хх)2 4-+ У1 = Уъ откуда
_ У2 — У1 h__ ^Х1(У2 — У1) ,Х'1(У2 — У1)
(^-И)2’ (х2-хх)2 ’ У1Г (х2-Х1)2 '
Заметим, что а^О, так как Ух~/-У2-
5.34. См. пример 2 на стр. 126.
5.37. Положить Ух = хх — а, р2 = х2 —а и использовать пример 2 на стр. 126; положить zx = xx —р, z2 = x2— Р и использовать задачу 5.33.
5.38. См. задачу 5.37.
5.39. Предположение о противном приводит к противоречивому неравенству (рх — р2)2 < 0.
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ VI
6.2. 1-й способ. С помощью бинома Ньютона или методом математической индукции доказать, что если а и Ь — целые числа, то для любого п = 0, 1, 2,... число (а + ]/б )"+(а— I'b )”— целое.
2-й способ. Числа a-f-J^b и а — \b являются корнями квадратного уравнения х2 — 2ах->-(а2— Ь) = 0 с целыми коэффициентами. Далее применить результат примера 6 на стр. 162.
6.3. Доказать, что если многочлен f(x) делится (без остатка) на многочлен А(х), то корни многочлена А(х) являются корнями многочлена f(x).
477
6.4. См. пример 9 на стр. 171.
6.8. Сначала доказать, что число 1—]/з является корнем данного уравнения.
6.9. Сначала доказать, что число 1 —]/2 является корнем данного уравнения.
6.10. Пусть при делении многочлена f (х) на многочлен <р (х) меньшей степени получается частное (х) и остаток Rx (х), т. е.
/(х) = Дх (х)ф («)+/?! (х).
Из этой формулы следует, что если у многочленов f (х) и <р (х) есть общий корень, то он является корнем многочлена Rt (х), степень которого меньше степени многочлена <р (х).
Поделив <р (х) на (х), получаем
<р (х) = Д2 (х) Ri (x)-irR2 (х),
где степень многочлена R% (х) меньше степени многочлена R1 (х), причем общий корень многочленов ср (х) и Rt (х) (а значит, и / (х)) является корнем многочлена Д2(х). Продолжая такой процесс, получим в данной задаче многочлен R, (х) второй степени. Отыскав корни многочлена (х), нужно проверить, какие из них являются общими корнями многочленов f (х) и <р (х).
6.11. См. указание к задаче 6.10.
6.12. 1-й способ. Показать, что если хх —корень многочлена х2 + х4- 1, то х{= 1.
2-й способ. хзт + x3/z+1 -J- х3₽+2 = хзт — 1 + х (хзге — 1) + 4-х2(х3₽—l)-j-x2-|-x-f-1 Далее воспользуйтесь тем, что x3ft—1 (k — натуральное) делится на х3—1 (а значит, и на х24-х-|-1).
6.15. См. первое указание к задаче 6.12.
6.17. Докажите сначала, что хх-j-х2-J-х3 = 0, и воспользуйтесь тем, что а3 4- Ь3 + с3 — ЗаЬс делится на а 4-^4-с-
6.18. Пусть хх, х2 —два положительных корня, х3 — третий корень. Тогда (х— хх) (х— х2) (х— х3) = х3 — ах2 — Ьх—с, откуда с = ххх2х3, и потому х3Э;0. Но тогда Ь — —(ххх2 4~ ххх3 4~ х2х3) < 0, что противоречит условию.
6.25. Так как /(с) = 0, то
f (m) — f (т) — f (с) — (mn —с")4~ах (тп~1 — с""1)4-...-|-ал_1 (т — с).
Далее воспользуйтесь тем, что целое число rrfl— сЧ делится на целое число т—с при любом натуральном q.
6.27. Воспользоваться равенством
(а24-Ь2) (c24-d2) = (ac4-^^)2 + (a^ — be)2.
6.31. Используя результат задачи 6.28, покажите, что многочлен /(х) можно представить в виде
f (х) = аа [(х-ах)2 4- Ь2] [(х- а2)24- Н] • [(х- ал)24- Ь*п].
Остается применить результат задачи 6.27.
6.34. Методом математической индукции доказать, что х" х % + — целое число для любого п=1, 2, 3,...
478
6.35. Если C!,c2, ..., сп — попарно различные корни многочлена f(x) степени п, то f (х) — а0(х — сх) (х — с2)... (х — сп). Из условия f (cn+i) — 1 находим
___________________1_______________ (сл+1 с1) fcn+l С2) • (<4г+1 сп)
6.36. 1-й способ. Заметим, что если многочлен Р (х) степени п—1 принимает в точках с2, с3,...,сп+1 соответственно значения —---------th-Ё”+1---------то многочлен f (х) = dx -I- (х — сх) Р(х)
с2 —сх’с3 —сх’ 'сп.г — сх
удовлетворяет условиям задачи. С помощью этого замечания методом математической индукции легко доказать существование многочлена, удовлетворяющего условиям задачи. Единственность следует из теоремы 5 на стр. 152.
2-й способ. Пусть Pk{x) (где /г — любое из чисел 1, 2,... ... , п 1) — многочлен степени п, принимающий во всех точках сх, с2, ..., сп, кроме Ch, значение 0, а в точке q --значение 1 (см. задачу 6.35). Тогда dxPx (х) -|- d2P2 (х) -j- ... -]-dn+1Pn+1 (х) — искомый многочлен.
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ VII
7.13. Данную функцию представить в виде
г/=
— 2, если х — 1, 2х, если —l-<№gl, 2, если х>- 1.
7.14. Данную функцию представить в виде
(2x-j-2, если — 1-ух^О, — 2x-j-2, если 0 1,
О, если | х | >- 1.
7.81. Полагая в первом уравнении 2х-|-1 =t, получаем f(/) + + 2g (0 =t — 1, т. е.
f{x) + 2g (х)=х- 1. (1)
X Z
Из второго уравнения заменой------[ = г полУчаем f (z)-J-g (г) =--
г 1, т. е.
+ = ПРИ (2)
Решая систему уравнений (1) — (2), находим
. х2 —4x4-1 х2 —3x4-1
l-х"’ -x~Z2-r~’ х^1-
479
7.83. Полагая в первом уравнении 2х2 — t ~ 1, получаем t_____ч
х =—%—, 4x-j-7 = 2/-J-l,
f V - 1) + 2§(2/+1) = Ц^ - 1, т. e.
Hx-l) + 2g(2x+l) = ^T5.
Решая совместно это уравнение со вторым уравнением исходной системы, находим
И*) =4 (7*+12), g(x) = -l(3x+7).
7.84. В первом уравнении сделать замену 4л'->-3 = 2t + 1.
7.85. В первом уравнении сделать замену Зх — 1 =/+1.
7.86. Во втором уравнении сделать замену
-^-j = 2t - 1.
7.87. Полагая х = —
при получаем
т. е.
'(7)+2'«>=Z,’
Решая совместно это уравнение с исходным уравнением, 2____________х2
дим /(х)=~з^— ПРИ xz£0.
7.88. Сделать замену х~у.
нахо-
X
7.89. Сделать замену 2Х _ 1
7.90. Сделать
Зх — 2 t замену +
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ IX
9.16. Ввести новое неизвестное / = 2х2 + 3х.
9.17. Ввести новое неизвестное t = x2— 2х + 4.
9.19. Заменив неизвестное по формуле i= -»У 5 + х
2 ' 5 х
уравнение / —— =1.
получить
480
9.20. Записать уравнение в следующем виде-. х 1 =
= —х4-2, затем возвести обе части полученного уравнения в куб. Получится уравнение 1) (% + 2) =х-|-1) являющееся след-
ствием заданного.
9.21. Записать уравнение в виде
| 2— УТ+2 | +1 3 - /^+2 | = 1.
9.22. Заменить уравнение системой с двумя неизвестными и = у'’78-)-*, о = |Л259 — х (ср. стр. 326 — 327). Получится система
J u-\-v = 7, |Ц4_|_а4 = 337.
При решении системы ввести неизвестные w = u-\-v, t — uv и воспользоваться равенством u4-f-vi=wi — 4w2/2z"“.
9.35. Использовать равенство 3 — У8 = д у g •
9.37. Записать уравнение в виде (5-¥-J-б1-4*)3 = 63.
/5 \3
9.38. Записать уравнение в виде (2-*-J-2 •v)3 = !x-
9.50. 1-й способ. Заданное уравнение равносильно уравнению 10ГЛ‘ = л- — 3. Последнее имеет единственное решение х = 4, так как при х>4 выполняются неравенства I04 Л' < 1 < х— 3, а при х <. 4 — неравенства 104--* > 1 > х— 3.
2-й способ. Заменой z — x—3 уравнение приводится к виду z4-lgz = l. Так как обе функции г, 1g г (а значит, и их сумма) являются возрастающими, то это уравнение может иметь не более одного корня. Очевидно, что этим корнем является z=l, т. е. х = 4.
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ X
10.24. Исходная система распадается на две системы: ( х — у = 0, ( х2 -|- г/2 4- ху = 61,
1(*+ О(« + 1) = 12 И l(* + 1) {У + 1) = 12.
10.25. Ввести сначала неизвестные и — х -|- у, v = xy, а затем неизвестные и -f- v = w, uv = t.
10.27. Ввести неизвестные х -|- у = и, ху = v и использовать формулу х5 -j- z/6 = и6 — 5Л> -j- 5(w2 (см. стр. 325, формула (55)).
10.28. Ввести неизвестные и = х 4- у, v — ху и, исключив v, получить уравнение и4 — 8и3 — 9и2 = 0.
10.29. 1-й способ. Возводя в квадрат первое уравнение и вычитая (из полученного уравнения) удвоенное второе уравнение, приходим к уравнению (х2— у2)2 — 0. Это уравнение является следствием исходной системы; из него получаем, что либо х = у, либо х = — у.
2-й способ. Введем новые неизвестные х-|-у —u, xy — v. Тогда система примет вид
и2 — 2v — м, (1)
и4 — 4и2о -ф- 2v2 — и2 • (2)
16 В. г. Болтянскцй и др.
481
Возводя уравнение (1) в квадрат и используя (2), приходим к уравнению и2 = 4о2, откуда и = ± 2v, и т. д.
10.32. Положить х у ==и, х —- y = v, а затем почленно разделить уравнения (или из первого уравнения вычесть второе, умноженное на 5). Тогда получим и = 5v и г6 = 1. '
10.33. Из первого уравнения вычесть второе; в результате получается уравнение (х — у) (х-|- у 4- 1) = 0.
10.34. Складывая и вычитая уравнения системы, получить систему (х — у) (х2 + ху + Z/2 — 9) = 0, (х + у) (х2 — ху 4- у2 — 11) = 0, равносильную исходной.
10.35. Из данной системы исключить члены, содержащие у2, а затем решить уравнение (ху}2 — И.п/4- 18 = 0.
10.37. Положить х-\-у = и, ху — v. Второе уравнение преобразуется к виду 4u- = 9t»2.
10.38. Положить (х — у)2 = и, х-(-у = и и исключить и из системы. Получится уравнение о3 = 73.
10.39. Положить и — х 4- у, v = ху. Тогда система запишется в виде V (и2 — 2v) = 15 Ц2, (1)
UV (и2 — 3v) = ~ и3.
Если и = 0, то из (1) получаем о = 0. Если же и -ф 0, то, вычитая из уравнения (1) уравнение (2), поделенное на и, получаем 4
V2 = д- и2, И Т. д.
10.40. Возводя оба уравнения в квадрат и складывая, получим после упрощений (х2 — 1) (у2 — 1) = 0. Но х2 -ф. 1 в силу второго из данных уравнений. Поэтому у2 = 1, и т. д.
10.41. Запишем систему в виде
х (х2 — 16)=z/(z/2 — 4), (!)
5х2 = у2— 4. (2)
Возможны два случая: х-~~0 и х = 0. а) Если х^0, то, разделив (1) на (2), получаем
Подставив у из (3) в (2), приходим к уравнению 31х4 ЗЗх2 — 64 = 0, 64
откуда х2 — 1, х2 = — зу (в этом случае исходная система не имеет действительных решений), б) Если х = 0, то у2 = 4.
10.42. Ввести новые неизвестные и = х-]-у, v — ху и преобразовать систему к виду
и (и2 — 2v) = 5,
v2 (и2 — 2v) = 20,
откуда получить соотношение
482
10.43. Ввести новые неизвестные
i±^ = u, = ху ху
1 2
а затем решить две линейные относительно — и — системы, у X
10.44. Ввести новые неизвестные
। У к
Х + 2 = “’ 2~y = V-
Получится система
J и2 — и — 2 = О, V2 _ 2о — 3 = О-
10.45. Подставляя у = ах-\-Ь в уравнение х2 —р2=1, получаем
х2(1-а2) - 2а&х-(1 +&2) =0. (1)
Исходная система будет иметь при любом действительном значении b действительные решения в том н только в том случае, когда уравнение (1) будет иметь действительные корни (так как уравнение (1) вместе со вторым из данных уравнений образует систему, равносильную исходной). Дискриминант уравнения (1) D = 1 -|-&2 — а2.
Если — 1 < а < 1, то D = Ь2 + (1 — а2) > Ь2 >:0, и потому уравнение (1) имеет действительные корни при любом действительном Ь. Если |а| = 1, то при & = 0 уравнение (1) не имеет решений.
Если |а|> 1, то при &=0 имеем D <0. Поэтому в случае | а | >= 1 найдется b (именно Ь = 0), для которого исходная система не имеет действительных корней.
10.46. Очевидно, пары чисел (1; 0), (0; 1), ( — 1; 0), (0; —- 1) образуют решения данной системы уравнений.
Покажем, что если хотя бы одно из натуральных чисел т, п отлично от единицы, то других действительных решений система не имеет.
Пусть (х0; г/0) — действительное решение системы, отличное от указанных выше четырех решений. Тогда 0<|хо|<1,0<[уо|<1и
I хй !2+|(/о I2 = x2 + y2= 1. (])
Используя свойства степени с натуральным показателем (см. стр. 242), можем записать, что
I хо !2 = %2 Х2т, (2)
Ш2 = Й^С- (3)
причем хотя бы в одном случае неравенство — строгое. Складывая (2) и (3) и учитывая (1), получаем
*-m + C<L (4)
Но данная пара чисел (х0; по предположению, образует решение системы и, следовательно, должна удовлетворять второму уравнению системы, т. е.
%о2т + С=1> (5)
что противоречит условию (4).
16* 483
Полученное противоречие и доказывает, что данная система ие имеет никаких действительных решений, кроме решений (1; 0), (0; 1), (-1;0), (0; -1).
10.47. Рассмотрим два случая: х — у и х^у. В первом случае система имеет следующие два решения:
/ 1 1 \ / 1 1 \
\/2 ’ У2/ И \ /2 ’ ~~У2/
Покажем, что если х-by, то решений нет.
Из второго уравнения системы заключаем, что
хУО, У У 0, (1)
а из первого уравнения, в силу (1), находим
1*|<1, |У|<1. (2)
Так как имеет место (1) (да/^О), то либо ху < 0 (х и у имеет разные знаки), либо ху > 0 (х и у — числа одного знака).
а) Предположим сначала, что ху < 0. Тогда либо х>0, у <0, либо х<0, р>0. Пусть, например,
х > 0, у < 0. (3)
Записав второе уравнение системы в виде j __________________x2im+n+it j ___y2im+n+i>
y2m+l > (4)
в силу (2) и (3) получаем, что левая часть (4) положительна, а правая — отрицательна и, следовательно, второе уравнение не удовлетворяется. Аналогично рассматривается случай х <Z 0, у > 0.
б) Пусть теперь ху > 0. (5)
Условие (5) с учетом того, что х^£у, может выполняться только в следующих случаях:
х<г/<0, (6)
У< х<0, (7)
0 < хсу, (8)
0<у<х. Пусть имеет место (6). Тогда (9)
(Ю)
1 1 у2т+1 <~ х2М+1 • (П)
Сложив (10) и (11), получаем
v2«+l I 1 ,,2Л+1 д_ *
х Г у2т+1^~У ' х2т+1 >
т. е. второе уравнение системы не удовлетворяется.
Аналогично можно показать, что и в случаях (7), (8), (9) второе уравнение не удовлетворяется.
484
10.48. Перемножить уравнения.
10.51. Сложить уравнения и найти ху, xz, уг.
10.54. Сложить уравнения и найти x-(-y-(-z из уравнения (х + у + г)2 - (х 4- у 4- г) = 6.
. 10.55. Выразить из второго и третьего уравнений у и г через х и подставить в первое.
10.56. Из первых двух уравнений выразить х и г через у и подставить в третье уравнение.
10.57. Из второго и третьего уравнений выразить х и у через z и подставить в первое уравнение.
10.58. Записать систему в следущем виде: ху , хг 15
7 + V = T’
х ' г 3 ’ xz yz_____13
У х — 6
„ ху хг уг
и решить ее как линейную относительно ~ , — , —.
10.59. Первое и третье уравнения системы запишем в таком
виде:
(Зх — у) (9х2 зХу _п у2) = 1 з ,
Зх-У = ±-- 0)
X
Отсюда находим 9х2— 10ху+у2 = 0 и, следовательно, —=1 или
х 1
— —-Q-. Если х=у, то из (1) следует, что
У У
(2)
Подставляя выражения для х и у через г из (2) во второе уравне-„ 4 д
ние исходной системы, получаем г = у=. Аналогично рассматривается
10
случай у = 9х.
10.60. Разлагая левые части уравнений на множители, а затем складывая, находим (х-|-у 4~г)2 = 9> и т. д.
10.61. Из тождества
(x+(/4-z)3 = x4-l/3+z3 + 3 (x + y+z)(xy + xz-(-yz) — 3xyz найти xyz = —4, затем решить кубическое уравнение /3 — /2 — 4< 4-+ 4 = 0 (см. замечание на стр. 329).
10.63. Положить y-{-z = u, yz = v, а затем исключить из системы х. Получится система
и2 — 4и — о 4* 1 =0,
и2 — 4и + у4-5=0,
из которой находим о — —2, а затем их = 1, и2 = 3.
485
10.64. Если одно, из неизвестных равно нулю, то равны нулю и два других неизвестных. Если хугуЬО, то система равносильна следующей системе:
= А ±4.1 = 1 14-1 = 1
х + у 6’ У ' г 2 ’ г ' х 3’
И т. д.
10.65. Введем новые неизвестные
x + y+z=a, x(/ + xz + yz = P, xyz = w.
Тогда мы получим систему относительно a, v, w, имеющую следующие два решения: (6; 11; 6) и (—6; 11; 6). Таким образом, исходная система распадается на две системы:
x+p4-z = 6, г x + y+z = —6,
xy-\-xz-{-yz — И, J xy-j-xz-l-yz=ll, (1)
xyz = 6, I xyz = 6.
В силу теоремы 7 на стр. 328 первая из них имеет шесть решений: (1; 2; 3), (1; 3; 2), (2; 1; 3), (2; 3; 1), (3; 1; 2), (3; 2; 1).
Для решения второй нужно, согласно той же теореме, рассмотреть кубическое уравнение I3 -|- 6^2 +111 — 6 = 0. Покажем, что это уравнение имеет только один действительный корень и потому вторая система (1) не имеет действительных решений. В самом деле, квадратный трехчлен ^4-6^4-11 положителен при всех t, и потому при < < 0 имеем & + 6/24-11t—6 = < (/24-6/4-11)— 6 < 0. На полупрямой же 1^0 функция <34~6<24- Ш — 6, очевидно, монотонно возрастает и, потому многочлен <34-6/24- 1И — 6 имеет ровно один действительный корень. Легко проверить, что этот корень не является кратным (так что два других корня не действительны).
10.66. Легко проверить, что при а = 0 система не имеет решений.
Пусть а ф 0, тогда хуг ф 0, и поэтому исходную систему можно записать так:
7Г-± + ± = ±, z х а ’ 1+1=1 у ' г а2'
Из этой системы находим — = —, и т. д. х 2а2 ’
10.67. Прибавить к обеим частям каждого из уравнений по единице. Далее систему записать в следующем виде:
(%4-1)(р4-1) = 8, (r/4-l)(z4-l) = -2, (z4-1) (х4-1) =— 4t
а затем перемножить уравнения.
486
10.68. Приравнивая левые части уравнений, выразить у и г через 3
х. Подставляя г = 2х, у = —х в первое уравнение, получить уравнение 4х = х3.
10.69. Записать систему в виде
1 + 1 = 1
уг хг 12’
- + - = -
j хг ху 12 ’
1 + 1 = 1
( ху ' уг 3
и найти отсюда — , — , — . ху ’ хг ’ уг
10.70. Система
(х + 2р)2 = 100, (р 4-2г)2 = 25, х-(-«/+г = 8,
первые два уравнения которой получены сложением и вычитанием первых двух уравнений исходной системы, равносильна исходной системе. Эта система распадается на четыре линейных системы.
10.71. Возводя первое уравнение в квадрат и вычитая полученное уравнение из второго уравнения, находим
2ху — Зхг -J- брг == 54,
откуда, в силу третьего уравнения,
ху — 2у- -J- Зрг = 27.
(1)
Умножив далее первое уравнение на у и вычитая полученный результат из уравнения (1), находим 27 — 9р = 0, р = 3. Остается решить систему
у = 3, х — 2р4~3г = 9, Зхг = 4z/2,
которая является следствием исходной системы, и произвести проверку.
10.72. Решая третье уравнение как квадратное относительно у, находим у = — г и у —— 2г, и т. д.
10.73. Положим х-\-у = и, xy — v. Тогда систему можно записать в следующем виде:
г и— 1=г, (1)
J и2 —2о4~3 = г2, (2)
• ' I и3 — Зии29 = г3. (3)
Из (1) и (2) находим (и— 1)2 = и2 — 2о4-3, откуда получаем
v = u-j- 1.
(4)
487
Исключим из системы г. Для" этого умножим (1) на (2) и, учитывая (3), получим
(и— 1) (и2 —2о+3) = и3 — 3ut>4~29. (5)
Из (5), в силу (4), находим и = 5. Остается решить систему
х + (/ = 5, ху = 6.
10.74. Ввести неизвестные х-^-у — и, xy=v. Исключала из системы
«4-2 = 0, и2 — 2о — г2 = 20, и4 — 4u2u-i-2u2~ z4 = 560,
найти из этой системы v=—10, а затем «х = 3 или «2 =—3, 10.75. Запишем систему в следующем виде (хуг^О): и т. д.
5 ху4-х2=-у(х4-г/4-г), (1)
4 ху4-г/г = у (х4-у4-г), (2)
3 zx4-zy = у (x4-t/4-z). (3)
Складывая уравнения (1) и (2) и вычитая (3), получаем
ху= у (х4-(/4-г). (4)
Аналогично находим
уг = х4-у4-г, (5)
2х = -?Г (* + </ +г). • (6)
Разделив (4) и (6) на (5), получаем
г = 3х, у — 2х. (7)
Остается подставить г и у из (7) в одно из уравнений исходной
системы.
10.76. Полагая x-j-y = u, xy = v и исключая г из системы, получаем
« = 1(«2-2о), (1)
О
« = у(«з—Зио). (2)
Из (2) следует, что либо « = 0 (и тогда 0 = 0), либо
и2 — 7
v=—3~- , (3)
Подставляя (3) в (1), получаем уравнение
и2—15«4~ 14 = 0,
и т. д.
488
10.77. Если (х0, у0, z0) — решение данной системы, то при любом t набор чисел (fx^, ty^, tz0) также образует решение этой системы. Пусть х = 0; тогда из системы находим, что y = z = 0. Если х^О, то, положив = J7 = v’ из пеРвого и второго уравнений найдем, что 1 + w — V, и34-о2=13, откуда
«1^ = 2, Oj = 3, (1)
u2 = —3, i>2 = —2. (2)
Из третьего уравнения следует, что
2 (1 4-у3) = 7и3. (3)
Остается лишь заметить, что набор чисел (1) удовлетворяет уравнению (3), а набор чисел (2) не удовлетворяет этому уравнению.
10.78. Раскрывая скобки в левых частях уравнений и вычитая из первого уравнения сначала второе, а затем третье, получаем
J (x-t/)(x+y-l) = 0, (1)
I (х — z) (% + ?— 1) = 0. (2)
Уравнения (1), (2) вместе с любым из уравнений исходной системы образуют систему, равносильную исходной системе. Исходная система распадается на следующие четыре системы:
1) г х — у = 0, J х — г = 0,
L (* + */) (х + г) = х;
2) г х — у —0, < x-f-z—1—0, I (х+у) (%4-г) = х;
3) । х + у—1=0; 4)
J X — 2 = 0,
( (х + р) (% + г) = х;
x-f-r/— 1 =0,
%4-г — 1 =0, (х + р) (х + г) = х.
10.79. Раскрывая скобки в левых частях уравнений и вычитая из первого уравнения второе, а затем из второго третье, получаем
Г(х — у)(х + у — 2г—1) = 0, (1)
I (У— 2)(У + 2 — 2х— 1) = 0. (2)
Система (1) —(2) вместе с первым уравнением исходной системы образует систему, равносильную исходной.
10.80. Запишем систему в следующем виде:
ху = х + у — Z,
хг
—- = х — i/4-z,
: 2 (1)
г/г
I з=г/-х+г-
Сложив все уравнения, получаем
, хг , yz
х + У + г = ху + ~ -Ьу. (2)
489
Подставляя (2) в систему (1), находим
2г = ^ + ^ 2'3’
2t/ = x(/ + ^, О
о , Хг
2х=хг/ + у.
(3)
Систему (3), равносильную исходной системе, можно записать так:
' г(4+|-2) = 0, у[х+^-2} = 0,
( z \
х [у + ^-2 =о. \ /
10.81. Рассмотрим два случая: хуг=0, xyzz£0. В первом случае хотя бы одно из чисел х, у, г равно нулю.
Из системы следует, что если одно из чисел х, у, г равно нулю, то по крайней мере одно из оставшихся чисел также равно нулю. Если х=р = 0, то г2 = 3г; если х = г = 0, то у2 —2у; наконец, если г/ = г = О, то х-~х.
Пусть теперь xyz ф 0. Из системы видно, что ни одно из чисел х~ЬУ, « + ?, z/ + z не равно пулю. Разделив сначала второе уравне-у г пие на первое, а затем третье на первое и положив -^- = u, ~ =v<
получим
= 2и,
- = 3о,
откуда находим u = -=-v, а затем и = — —
О 7
Подставляя
К X
найденные значения у =-----=- и г —---=- в первое уравнение исход-
о I
нон системы, найдем х, а затем у и г.
10.82. Умножая второе уравнение на г н вычитая из полученного первое уравнение, находим хга = — 2 — za, откуда
2-f-z2 х~ Г- •
Из третьего уравнения имеем
15
~ х2г ’
(1)
(2)
а из второго уравнения, в силу (2), находим
15 , п
-------t-2xz = — z.
1
(3)
490
Подставляя х из (1) в (3), после преобразований получаем уравнение z4 —9z2 4-8 = 0. Находим корни этого уравнения, а затем из (1) и (2) определяем х и у.
10.83. Умножая первое уравнение на у, второе иа х и вычитая полученные уравнения, находим
8z2x —4z2p = 0. (1)
Так как в силу третьего уравнения г^О, то из (1) следует, что z/ = 2x. (2)
Исключая с помощью (2) у иг из первого и третьего уравнений, получим уравнение
Зхв+16х3 —64 = 0. (3)
Уравнение (3) имеет два действительных корня: xt = — 2 и х2 = 2
= Остается найти соответствующие значения у и z из уравнений У 3
у=2х, хуг = 8.
10.84. Обозначим
u = x-f-p + z, v — xy-\-xz-[-yz, w = xyz.
Тогда данную систему уравнений можно записать в следующем виде:
(а2и — av-^-w — ct‘ = d, (1)
b2u — bv-\-w — b3 = d, (2)
c2u— cv-<!-w—c3 = d. (3)
Если мы найдем и, v, w из системы (1)—(3), то искомую сумму можно вычислить, используя равенство
’с3+?/3 + г3 = 3® + и (и2 —Зо). (4)
Решим систему (1)—(3) относительно и, v, w. Вычитая из уравнения (1) уравнение (2), а затем из уравнения (1) уравнение (3), получаем (после сокращения на отличные от нуля множители b — а, с — а)
( V — (а+&) u-\-a2-\-ab-\-b2 — 0, (5)
( V — (а + с) u4-a24-ac4-c2 = 0. (6)
Из (5)—(6) находим
и = а-\-Ь-\-с, v = ab-'rbc4-ac. (7)
Подставляя найденные значения и и v из (7) в (1), получаем to = d4* -}- abc, а затем из (4) определяем x34-y34-z3.
10.85. Запишем систему в следующем виде:
x2 + y2 = -l- Хуг,
29
</2 + г2=10«/г,
13
22 х2 — хг/Z.
о
491
Складывая первые два уравнения и вычитая третье, получаем
2
у2 = уХ(/г. (1)
Аналогично находим
5
г2 = ^хуг, (2)
х2 = -^хуг. (3)
Перемножив (1)—(3), находим
откуда xyz = 0 или хуг =10, и т. д.
10.86. Рассмотрим два случая: хуг = 0 и хуг^О.
В первом случае хотя бы одно из . чисел х, у, г равно нулю. Пусть, например, х = 0. Тогда из системы следует, что уг = 0, т. е. хотя бы одно из чисел у, г равно нулю. Если х = у = 0, то система удовлетворяется при любом г. Итак, система имеет решение вида (0; 0; с), где с — любое число. Точно так же установим, что тройки чисел (а; 0; 0), (0; Ь; 0), где а, Ь— любые числа, образуют решение системы.
Пусть xyzz£0. Тогда, умножая первое уравнение на х, второе на у и третье на г, заменим исходную систему следующей равносильной системой:
( 13
I х2у2 + х2г2 = -g- хуг,
I 5
х2у2 4- у2г2 = хуг,
О
5 х2г2+у2& = -g- хуг.
Складывая первые два уравнения и вычитая третье, получаем
ч
Х2у2 = уХуг. (1)
Аналогично находим
2 х2г2 = -у хуг, (2)
у2г2=~хуг. (3)
Перемножив все уравнения (1) —(3), находим хуг, и т. д.
10.87. Из рассмотрения системы следует, что хуг ф 0. Умножая первое уравнение на ху2г2, а второе на ух2г2 и вычитая одно из другого, получим
4г(х —у) = 0. (1)
Так как г^0, то из (1) следует, что у = х, и т. д.
492
10.88. Умножим второе уравнение на у, третье на г, первое оставим в прежнем виде, а затем решим полученную систему относительно х2!/2, у2г2, z2x2. Будем иметь систему
у2?2 = — у хуг, г2х2-=—2хуг, х2#2 — — 2хуг.
Эта система является следствием исходной системы. Перемножая уравнения системы (1), получаем хуг —О или хуг — —2, и т. д.
10.89. Из вида системы заключаем, что хуг zjb. 0. Напишем систему в следующем виде:
Сложив первое и второе третье и, наконец, второе уравнения системы (1), затем первое и и третье, получим систему 21,2 = '1х!/ + 3-уг у г ~ х ' 2х2 = ^—— (2) г у ' ^ = 3yz 21*г
Эта система равносильна к следующему виду: х у ' исходной системе. Система (2) приводится 2хуг = Зх2 + 3z2, 2хуг = 3у2 — 21г2, (3) 2хуг = 3у2--21х2.
Система (3) равносильна системе (2), если xyz^tO. Из второго и третьего уравнений системы (3) находим
г2 = х2, (4)
а затем, используя (4), из первых двух уравнений системы (3) получаем
у2 - . 9х2, и т. д.
10.90. Из системы видно, что xyz^O. Умножая первое уравнение на х, второе на у и вычитая одно из другого, получаем
откуда
(х—у) ^2+у ху+у2)=0.
493
Из этого уравнения находим, что либо у = х, либо у —— 2х, либо X
У = ~^, и т. д.
10.91. Перенося во всех уравнениях хуг в правую часть и решая систему относительно х3, у3, г3, получаем ' х3 = хуг-'-2,
у3 = Хуг—3, (1)
г3 = хуг^3.
Перемножая уравнения системы (1) и полагая xyz = t, находим Z3 = (Z-|-2) (t— 3) (/4-3), или 2/2 —9/—18 = 0, откуда/1==6, 4 — —g. Далее из (1) находим х, у, г.
10.92. Вычитая из первого уравнения второе, а затем из второго уравнения третье, получаем
(х У) (* + У + 2) = 3, (У — z) (% + !/ + г) = 3, откуда следует, что х = 2у— г, и т. д.
10.93. Вычитая из первого уравнения заданной системы третье уравнение, получаем х2 — г2 = 2у (х — г), откуда
x = z, (1)
или x4~z — 2у = 0. (2)
Сложив все уравнения исходной системы, находим
(х + !/4-г)2 = 4.
Исходная система распадается на следующие четыре системы: (х = г ( x~z,
х + у+? = 2, J х + г/ + г = — 2, х2 4- 2yz = 1, ( х2 2уг — 1,
(x-f-z — 2у = 0, ( x-\-z — 2y = 0,
x+y+z = 2, J х4-у4-г = —2, х2 4- 2уг = 1, ( х2 4- 2yz = 1.
10.94. Вычитая из первого уравнения системы второе уравнение, получаем
(x-(/)(x4-j/-z) = 0.
Исходная система распадается на две системы: Г у24-хг = 42, Г у24-хг = 42,
< г2 4-ху = 50, (1) j г24-ху = 50, (2)
I Х=У, I г = х+у.
Обратимся к системе (1). Эта система равносильна системе ( у2 4- уг = 42, (3)
J г2 4- у2 = 50, (4)
I Х = У-
494
Решая систему (3) — (4) как однородную, находим у = — г или у = — — 7г, а затем из (3) определяем г1 = 4рЛ2, г2= — 4 рЛ2, г3 = 1, г4 = — 1, и т. д.
10.95. Умножая уравнения заданной системы соответственно на у, г, х и складывая, получаем
Зу + 5г —х=0. (1)
Если умножим уравнения исходной системы соответственно на г, х, у и сложим, то найдем
Зг5х — у = 0. (2)
Система (1) —(2) дает у — —2г, х = — z. (3)
Подставляя у и х из (3) в одно из уравнений исходной системы, получаем г2=1, и т. д.
10.96. Умножая уравнения заданной системы соответственно на (х —у), (у —г), (г —х) и складывая, получаем
г = 3х—2у. (1)
Уравнение (1) является следствием исходной системы. Подставляя (1) в исходную систему, получаем однородную систему
( х2 + хг/ + г/2 = 7,
I Зх2—3xyJry2=l, и т. д.
10.97. Заметим, что г ф t, так как в противном случае мы имели бы
1 ~ t ~ t2 ~ t3 °)>
что невозможно.
Учитывая, что гф1, выразим из первых двух уравнений х и у через г и 1:
а затем подставим найденные значения х и у в третье и четвертое уравнения. После сокращения на г —Z, получаем систему
1 2(г + 0~г< = 5,
1 2(г2+г/ + /2)-г/(г + /)=14.
Полагая в системе (1) z-\-t=v, zt = w и решая систему, находим v — 4, w = 3.
Далее из системы z-[-t — 4, zt = 3 определяем zt = l, ti — 3; г2 = 3, <2 = 1, и т. д.
10.98. Составляя разности второго и третьего уравнений, а также второго и четвертого, находим
(У — х) (г + <)=0, (г— х) (у +<)=0, В Т. Д.
495
10.99. Складывая все уравнения, получаем
(п — 1) (х4 + *2+. .. + *«) = 1 +2-J-... +л=—2^" \ откуда
*1 + ха+ • • + = 2 it 1) П)
Подставляя (1) в k-e уравнение исходной системы (Jfe=l, 2,..., п), получаем
10.100. Вычитая из первого уравнения второе, получаем
Зх2 (.Vi — л.-3) = х1 — х3,
1
откуда следует, что лиоо х2 = —, лиоо Xj = x3.
„ 1 .7
Пусть гс2 — -.3 , тогда из первого уравнения находим ,
3 3
что невозможно. Итак, х1 = х3.
Аналогично, рассматривая второе и третье уравнения, находим х2 = х4, и т. д.
Итак, если система имеет решения, то должны выполняться условия
х4 = х3 = х5 = х7 =..., (1)
х2 = х4 = х6 = л-8 = ... (2)
Вычитая из предпоследнего уравнения последнее, получаем
х1 = хп~1- (3)
Рассмотрим два возможных случая:
1) п — нечетное число. В этом случае из (1), (2) и (3) находим х1 = х2 = х3 = ... = х„ = 4;. (4)
Взяв любое из уравнений системы и используя (4), будем иметь Зх1 2 — 2х2, откуда
1 ± |/7 х- 3 .
2) п — четное число. В этом случае имеем
Х1 = Х3 = ...= Х„_1 = Х, х2 = х4 = ... = х„ = г/.
Исходная система сводится к одному уравнению
Зху = % +(/+2
и имеет бесконечно много решений.
496
Если х = а, то
о+2 / , 1 \
У~За-1
10.101. Положить Ух — и, Уy = v. Получится система и + о = 3, и6+^ = 65. При решении системы положить u-j-v = w, uv = t и воспользоваться равенством
и6 ое _ _|_ 9ai2/2 _ 2^з.
10.102. Записав первое уравнение в виде
Ух^Уу2 = 2 /2—У2ху,
, после возведения в квадрат получаем
х2 + у2 = 8 — 8 Уху + 2ху. (1)
С другой стороны,
х2 + у- = (х-\-у)2 — 2ху. (2)
Возводя второе уравнение исходной системы в квадрат, находим
х-\-у = Ь — 2У~ху
и после возведения в квадрат получаем
(* + у)2= 16— 16 1ЛЙ/ + 4-ЧЛ (3)
Из (1), (2) и (3) следует, что Уху — 1, и т. д.
10.103. Положить
тогда первое из данных уравнений приводится к виду
2/2 —5/+ 2 = 0.
10.104. Записав заданную систему в следующем виде:
' (у + yf-2(К^+Г+х) = 3,
3 _ 2 (Ух^Т + х) = 3,
и решив систему
j и2 — ч = 3,
I За — о = 3, где
и = ~ + у, o = 2(j/x2 — 1 +«),
получим
иг — 0, Vj = — 3; а8 = 3, v2 = 6.
497
к виду
Если и —— 3, то, преобразуя уравнение 2(/^Т+х) = —3 2]/х2^1=—2х~3,
(1)
13 -
— 12 . Этот ко-
а затем возводя обе части (1) в квадрат, находим рень является посторонним для уравнения (1).
_______ 5
Если v = 6, то из уравнения ух2— 1 = 3 —х получаем x=-^-t
О
5
а затем, решив уравнение ^ + (/ = 3, находим
_9 + /21 9-/21
У1---§ ' ---6—•
10.105. Записать систему в следующем виде: +2(/х2Н~1—х) = 3,
(у + !/) + (К^+Т-*) = 0.
10.106. Возводя уравнения системы в квадрат и складывая, получаем
76-2(x2 + y2) = (x + y)2. (1)
Перемножая уравнения исходной системы, находим
У2 — х2 = У 8 [16 + (% + у)2], откуда после возведения в квадрат будем иметь
(х-у)2(х + у)2 = 8[16+(х + у)2]. (2)
Система (1)—(2) является следствием исходной системы.
Полагая (x-j-y)2 = u, (x — y)2 = v, запишем систему (1), (2) в следующем виде:
( 76 = 2и4-у,
< (3)
I uv = 8 (16-f-u).
Система (3) имеет два решения:
и, = 32, о, = 12; «2 = 2, ц2 = 72.
Задача сводится к решению систем вида (х-)-у)2 — а, (х — у)2 = Ь и проверке найденных решений.
10.115. Вычитая из первого уравнения второе, умноженное на З"1-3-*, находим х = 3у — 1. Подставляя это значение для х в первое уравнение, получаем уравнение 8-31~>'=11у—3, которое имеет только один корень у = 1, так как функция г = 8 • 31-У — убывающая, а функция z=lly —3— возрастающая.
10.116. Решение аналогично решению задачи 10.115-
498
10.161. Пусть vlt V2, t) — соответственно скорости парохода, лодки, течения реки (в км/час), s — расстояние между пунктами А и В (в км).
Условия задачи позволяют написать следующую систему уравнений:
2s _____ s
3(^1’ у) 3(У2~Ь0 *
s s _ s — 20 vt~v Oi+f — t's + c ’
____s______s
2 (Pj — v) ~ 2 (3o2 + v) ‘
Из первого уравнения находим у1 = 2у2-|-Зу> а из третьего получаем о1 = Зу2 + 2у, откуда v2 = v, Vi~5v. Подставляя найденные выражения для v2 и гд во второе уравнение, определяем з —120 км.
10.163. Пусть vlt v2, v3 — соответственно скорости 1-го, 2-го и 3-го велосипедистов (в км/час), s — расстояние от А до В (в км), /—искомое время.
Первое условие задачи может быть выполнено в двух случаях: а) второй и третий велосипедисты находятся через полтора часа по разные стороны от первого велосипедиста; б) через полтора часа второй и третий велосипедисты встретились. Этим случаям соответствуют следующие уравнения:
3 3
3t>1 = y o24-s— у v3, (la)
ч ч
= (16)
Второе условие задачи дает уравнение
s—2v3=vlA-o2- (2)
Требование задачи выполняется также в двух случаях: а) второй велосипедист через t часов оказался между первым и третьим; б) через t часов первый и третий велосипедисты встретились. Этим случаям соответствуют следующие уравнения:
2tv2 — s— /Vg-j-^Vn (За)
tox -|- tv3 = s. (36)
Система (la), (2), (За) дает решение / = 3 (часа). Система (1а), g
(2), (36) дает решение t — (часа). Система (16), (2), (За) дает ре-
шение /=1 (час). Наконец, система (16), (2), (36) снова дает решение / = 3 (часа).
10.164. Пусть vt, v2, и3 — скорости течения реки соответственно на участках СВ, AC, DC, а —скорость лодки в стоячей воде,
499
s —расстояние от А до С. Используя условия задачи, составляем си-
стему уравнений (s — u):
1 К + и u — v2 7 ~ 2 ’
U ‘ д_ и = - О) 12’ = 4.
«+«1 и и — vr г + CZ ^2 и u~v3
Из этой системы нужно определить величину
и 1й
И Уд И
Обозначим
Тогда система (1) примет вид
I 1____1____7_
1 — Хх 1 — х2 — 2 ’
11 17
j 1 + *1 1 + ~ 12 ’
I т-^—+ = 4.
I 1 Х1 1 хз
(2)
Первые два уравнения системы (2) можно записать так:
7
2 — (*i + хг) = "2" [* — (xi + ХА + х1хг ] >
17
2 + (Х1 + *2) = Jr; 11 + (-И + ха) + Х1Х2 )•
Решая систему (3) как линейную относительно х2 и г2 = х2х2,
находим
, 5
Х1 + Х2 — "g" ,
1 (4)
*Л=0-.
Так как по условию Vj < v2, то х1<х2. Учитывая это, из (4) полу-1 1
чаем x1 = -g-i х2 = -^, а затем из третьего уравнения системы (2) на-3
ходим Хз=т. о
Следовательно,
1,1 11
х=т—;---г — = -5- часа.
1 + х3 l+xj 8
500
10.165. Пусть и — скорость лодки в стоячей воде, щ и v2— скорости течения соответственно в 1-м и 2-м протоке (в км/мин), s — расстояние (в км) от Д до В.
Тогда
S S 21,
и + п2 «+»1
S S 70,
и — и — о2
S S 12.
(. 2u — v1 2и — v2
(1)
г> £ « S гт 5 ^1 ^2
В задаче требуется наити —. Полагая — = х. — = г/, — =z, и и и и
запишем систему (1) в виде
______L_-21
1+г 1+у ’
Освобождаясь от знаменателей в системе (2), получаем
’ х(у — z) = 21 (l+y + z-f-yz),
• *(У~ z) = 70 (1 — у — z-\-yz), (3)
. х(у — г) = 12 (4 — 2у — 2г + уг).
Из системы (3) получаем
Г 21 [1+(!/ + z) + !/z] = 70[1-(!/ + z) + !/z](
I 21 [1 + (г/+г)4-г/2] = 12 [4 — 2 (у-|-г)+//г].
Решая систему (4) как линейную относительно у-\-г и yz, получаем , 7 1
y + z~12’ уг 12’
откуда следует, что 1 1
= г=Т.
Наконец, из (3) находим
х= — =420 мин = 7 часов, и
10.166. Пусть s —расстояние от А до В, V—скорость течения, fx — собственная скорость лодки с мотором (в стоячей воде), — скорость движения на веслах (в стоячей воде).
501
Тогда
Требуется найти Обозначим Тогда система (1) п 3s s И
4 (У1 + у) 4 (о24-о) ~ 6 ’ S 4- 3S - 7 (П
Э1 4(^+0 1 4(у2 + о) 2’ U7 s s _ 25 + У1~ v — 12 * S v2 — v Vt V2 v ~=х, —=у, — — г. s s S мет вид 3 1 11
Решая систему (2 получаем откуда Подставляя (5) в (4), откуда 4(х+г) 1 4(f/-J-z) 6- W 1 + 3 7 (3)
4(.т4-г) 4(у + г) 2 ’ 17 _1_ + -2_=25 (4) х+г 1 х — z 12’ 17 )—(3) как линейную относительно —J— и ' , X -(-Z у Z 1 1 _ 13 x-\-z у -j-z 3 ’ X -|- 2 — 1, (5) ^+2=13' находим 1 _ 13 х-г 12’ 12 х~г~Гз- (7)
Из системы (5)—(7) определяем У = 2§, г==26 > а затем находим искомую величину:
—•— — —J— — 1? — 6i/2 (часа) .
v2 — v y—z 2 11 ' '
502
10.167. Пусть v — скорость течения, Oj—скорость лодки в сто-
ячей воде, о2 —скорость охотника, s —расстояние от А до В. По условиям -задачи составляем систему уравнений;
s s 3 о» - 7 ’ ±-± = 4, V v2 (1)
| s s __ 7 ' vt— v v2 — 3 n , s „ V V, В задаче требуется наити . Пусть — — х, ~ = ~-У. — = г.
Тогда система (1) примет Vi — V s s вид i L_ A x + y г ~ 7 ’ 1 1 Л x z S (2)
Исключим из системы (2) i L-Z. у — X Z 3 • x и у. С этой целью запишем систему (2)
в виде , 7г Х + У 74-Зг’ г х=, - . . , 1 -г 4г ’ Зг (3) 0) ла
Вычитая из уравнения (3) уравнение (5), находим
2х = 7г Зг 3 + 7г (6)
7 + Зг
Из (4) и (6). следует, что
7г Зг 2г П\
74-3z 3 + 7г 1-|-4г'
Уравнение (7) можно преобразовать к виду
откуда
59г2 — 38г — 21=0,
19 ± 40 г~ 59 •
Так как г>0, то г=1, и тогда из (5)
s 1 Ю , .
Мая величина ------— =-------= (часа).
ох — v у —х 3
3 „ получаем у — х*=-^. Иско-
503
10.168. Пусть Ci—скорость парохода в стоячей воде, v2 — скорость катера, у —скорость течения реки, « — расстояние от А до В, t — продолжительность рабочего дня.
Обозначим .
S = х, V (1)
S (2)
S (3)
V-2 — V
S (4)
v2 + v
Тогда t — 9 (* + у) = 5 (? + «). (5)
По условиям задачи , х _ 1 6 3 ’ (6)
5 1 б“_з- (7)
Из (5), (6) и (7) находим
2
5 >
, t
х-{-6у = 2,
(8)
(9)
(Ю)
Мы получили систему трех уравнений (8)—(10) с четырьмя неизвестными х, у, z, i. Не хватает еще одного уравнения. Это уравнение мы получим из (1)—(4). Дело в том, что неизвестные х, у, г, и не являются независимыми. Они связаны в силу (1)—(4) уравнением
1_1-
у х и г ’
( 2 \ или (если учесть, что и — ^\
(id
у х 2 z .
Исключая нз системы (8)—(11) х, у, г, получаем
45 15 _ 5 5 ..р-,
18 —~ 2(/-3)- У- Г^2‘ ' '
504
Уравнение (12) можно преобразовать к виду
/з_4/2_12/ = 0, откуда
/1=0, /2 = — 2, /3 = 6.
Так как / > 0, то t = 6.
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ XI
11.33. Уравнение приводится к виду
2 sin? х + 2]^ 3 sin 2 x cos x — 3 sin x = 0.
11.37. sin x cos x (sin5 x+cos5 x — 2) = 0.
Уравнение sin5 x+cos5 x = 2 не имеет решений.
11.38. i-sin32x(—cos 2x) = cos 2x. О
11.39. cos2x(cos4x-|-sin4x-|-1) =0.
11.40. 2tg22x + tg2x—1=0.
11.41. cos2 x cos 8x = 0.
11.42. cos2x-|-cos6x+cos4x = 0.
11.47. (sin 2x — cos 2x) (3 sin 2x -f- 2 cos 2x) = 0.
11.51. cos 4x-|-cos 2x= 1, 2 cos2 2x + cos 2x — 2 = 0.
11.55. sin 2x cos 2x=cos2 2x.
11.58. (cos x+sin x) (cosx — sin x—l) = 0, x^^.
sinx4~cosx = i, P-\-2t — 3 = 0.
cos2x = t, /3-|-/2 —1 — 0.
cos 2x (sin 4x— 11 = 0.
sin 2x sin I x+v ) = 2. \ 4 /
(cos x — sin x) (cos 2x — sin 2x) = 0.
11.67. (sinx+cosx) sin'2x — 2 ( 1 4-Yl = 0.
I \ /2/1
11.68. (cosx—sinx) 14-sinxcosx—(sinx+cosx)]=0.
3 1
11.69. Два случая: a)tgx=l; 6)tgx>0, sin2 x—sin x + ~ =0.
11.70. sin 4x (2 sin 6x—l) = 0.
11.73. 3 (tg 3xctg 2x) = 4 (tgx + ctg2x),
3 4
—=- =-------, 4 (cos3x—cosx) + cosx = 0,
cos3x cosx’ v ' 1
cos x sin2 x —
11.61.
11.63.
11.64.
11.65.
11.66;
cos х -ф. 0.
cos3x sin 2х cosx cos3x
11 74. “—5--п------- — — . п j
sin Зх cos 2х sin х sin х cos 2х ’
a) cos Зх = 0;
б) sin Зх+sin xcos2x = 0, sin х (3 —4 sin2 х+1 —2 sin2 х)=0,
. , 2 1
sm2x= —, cos2x = —5-.
505
,, __ sin x sin x „ sin x cos 4x cos 3x .
11.75.--------; 5 ; — 0, --------; — = 0.
cos x sin 3x sin 4x cos x sin 3x sin 4x
1176 * ~ cos * /1 4- cos x 1 4-cos x 4-cos2 x\ _q
1 — sin x \ 1 4- sin x 1 4- sinx 4- sin2 x J ’
(cos x — 1) (sin x —cos x) (sin x 4-cos x 4-sin xcos x) = 0.
11.77. sin 2x — cos2x = j/2 cos ^2x — -5-j 4- j/3,
sin2x— cos 2x = cos 2x4-sin 2x4-j/3 , cos2x= —
11.78. Умножить уравнение на sin А и преобразовать произведения синусов в алгебраическую сумму.
11.79. sin 2х (1 4-2 cos x) = cos х (1 4-2 cos х).
11.80. 1 —cos 2х = sin х — sin Зх, 2 sin2 х4-2 sin xcos 2x = 0.
11.81. Выразить sin Зх и sin 2x через sinx и cosx.
11.82. Использовать формулу sin Зх = 3 cos2 x sin x—sin3 x.
11.83. Использовать формулы
sin 4x = 2 sin 2x (1 — 2 sin2 x),
sin 3 x=3 sin x—4 sin3 x.
11.84. (sin x —cos x) (1 4-sin x cos x4-sin x-|-cos x) =0.
t2
11.85. sin2x = t, sin4 x4-cos4 x= 1— —( /24~/—1=0.
11.86. 2 cos x = cos2x (1 4-cos 2x), cos x (cosx cos 2x— l) = 0.
9
11.87. 24-4(1—2sin22x) = -—— 3sin2x — 4sin32x= 1, sin6x = l. sin 2x ’
/1 _ f\3
11.88. Положить cos 2x = t. Тогда cos 4x=2^2 — 1, sin6 x= (—g—j , /з_/2_2/ = о.
11.89. cos2x = Z, t2 — 3/2-|-2Z = 0.
11.90. cos2x = t, 4/34-6/2 — 4/= 0.
11.91. Положить sin2x = t и использовать формулу
3 sin6 x4-cos6 x= 1 — — sin2 2x (см. стр. 360).
11.93. Использовать формулу
tg3x = tgxtg — xHg I3-4-X).
., „.' , , , , 1 4-cos х sin х
11.94. 14-tg x-(-ctg x=—1-----;----
cosx sin x ’
, , , 1 4-COS X sin X „ , , „ 1
sec2x-|-tgx = ——5-----------, cosec2x4-tg2x — ctg2 x = —5—.
1 b COS2 X ’ 1 b COS2 X
11.95. Использовать формулу
tgx-|-tg2x — tg 3x = — tgx tg 2x tg 3x.
506
11.96. Используя формулу tg4x—tg3x = tgx(1 -J-tg3xtg4x), привести уравнение к виду
(1 4-tg 3xtg 4x) (4 tg x — tg2x)=0.
11.97. Использовать формулу tg x+= — ctg x — ^имею-
JI \
щую место при xф kn 1; выразить ctg х и ctg2x через tg х.
11.98. Использовать формулу
tg2(x-^)tS2(x + ^) = 1
и привести уравнение к виду tg4x = —4.
,. „„ 4 sin 4х sin 6х _ / sin 6х \
11.99.-- --—--------= 8cos2x, cos2x -г-д------1=0.
sin22x \sin2x j
11.100. (sin x—cosx) (24- sin x-|-cos x-f-sin xcos x) = 0.
11.101. cos x(cos x—sin x4-2 sin xcos x4- l) = 0.
11.102. (sin 2x—cos 2x) (cos 2x-j- sin 2x-|- 1) = 0.
11.103. Используя формулы
cos 3x = 4 cos3 x— 3cosx = cosx(l —4 sin2 x), sin 4x=4 sin xcos x (1 —2 sin2 x),
привести уравнение к виду cos x(sin х—1) (6 sin2 x-f-sin х —2) = 0.
11.104. Использовать формулы
sin3 х4-cos3 х = (sin х 4-cos х) (1 — sin x cos x),
—— sin 2x sin ]/2
(x+4j
sin xcos x(sin x4-cos x).
11.105. 2sin 4xcos 2x— sin 4x = 2 cos2 2x—cos 2x, cos2x(2 cos2x—1) (2 sin 2x— l)=0.
11.106. sin 2x4-sin 6x+ 1 4-cos 4x = cos 2x4-sin 4x.
2 sin 4x cos 2x4-2 cos2 2x = cos 2x4- sin 4x, cos 2x (2 cos 2x— 1) (1 4-2 sin 2x) = 0.
11.107. sin x-t-2 sin xcos x4-4 sin2 xcos x = 2 cos x-|-cos2 x —sin2 x, (2 cos x-|- 1) (2 sin2 x-|-sin x— 1) =0.
11.108. 4 sinxcos2 x4-2 sin x-|-3 cos x= 1 4-2 cos2 x-t-6 sin xcos x,
2 sin x (1 4-2 cos2 x — 3cos x)= 1 4-2 cos2 x—3 cos x.
cos x cos 2x — sin x sin 2x __ sin 5x — sin x sin x cos 2x sin x sin 5x ’
cos 3x 2 sin 2x cos 3x
cos2x— sin 5x
< cos 3x (sin 5x — sin 4x) = 0;
при проверке учесть, что cos 2x^:0, sin5xr^0.
507
11.110. Используя формулы
M = tg2<+ctg2x( tg2x = r2t|±.>
tg3x=tgxfef&+-
привести уравнение к виду
tgx(3 tg4 х— 2tg2x — 5) = 0.
11.111. 1 —cos 2x -j- sin 2x+2 cos 3x (sin x+cos x) — 2 sin x—
— 2 cos 3x=0,
sin2 x+ sin xcos x— sin x+cos 3x (cos x + sin x— 1) = 0, (cos x+ sin x— 1) (cos 3x+ sin x) = 0.
. л
sin ~r
4
11.112. Имеем ctg x + ctg I ~ — x'j =
' sin x sin
2
У 2 cos I 2x —
1 + sin 2x+cos 2x = 1 + У 2 cos
Уравнение примет вид 2 sin 4x 1 4
___________[
/2 cos I2x
2—
sin 4x cos (2x — ~ | = 2 cos2 (2x—~ ] — 1 =cos \ 4x—^4 = sin 4x \ 4 / \ 4 \ 2)
sin 4x [cos ^2x— — l^j = 0,
11.113. tgx=+ /2 — 4o/+tz2 + 3 — 0.
11.114. Полагая sinx=Z, получаем уравнение & — 6^ + 4a2 — 3 = 0, имеющее корни
Z1 = 3-2/3-a2, f2 = 3 + 2/3—a2-
Если | a | < /3 , то корни действительны, причем уравнение имеет решения, если | | < 1, т. е.
/2 > 1. Исходное
-1 <3-2/+=++ < 1.
11.115. Положив sin х + cos х = t, получим уравнение fl — 2BV2t — 6Ss=0, откуда /1 = ЗВУ2. /2 = — S/Г, т. е. sin [х + -—^ = ЗВ, sin [х + = — В.
11.116. Положить sinx—cosx=Z.
508
11.117. 1—^-sin22x = a, cos4x = 4a —3.
11.118. cos2x = /, ^ + (2S + 1)/ —2(264-1)2=0.
11.119. cos2x=/, /2-|-2а/4-1 =0.
11.120. Уравнение a cos x-\-b sin x-|-c = 0 имеет решения, если c2 sg а2 &2; уравнение a tg x-)-b ctg х-|-2с = 0 имеет решения, если а = 0, а также если ахО и квадратное уравнение а/24-2с/-[-й=0 имеет действительные решения, т. е. если с2 ^ab.
Если первое из рассматриваемых в задаче уравнений не имеет решений, то с2>а24-62. Но тогда заведомо выполняется условие с2 > ab (так как a2-\-b2^: ab), откуда следует, что второе уравнение имеет решения.
11.121. Преобразовать произведения sin (х-|-а) sin (x-J-3a), cos (х4-a) cos (х4-За) в сумму. Получится уравнение
[ sin (х -j- 2а) — cos (х 4- 2а)] cos 2а =
= [sin (х 4-2а) 4-cos (х-|-2а)] cos (2x4-4а). Используя формулу cos (2x4-4а) = cos2 (х4-2а) — sin2 (х4-2а), записать это уравнение в виде
[sin (х4-2а) — cos (х-|-2а)] [cos 2а4-1 4- sin (2x4-4а)] =0.
11.122. 1-й способ. 1 — sin 2x = ctg х — 1,
(cos х— sin x)2 =---, (cos x— sin x) (cos x sin x—sin2 x— I)=0.
2-й способ. Выразить sin 2x и ctg x через tg x. Получится уравнение 2 tg3 x —3 tg2 x-|-2 tg x—1 =0, имеющее корень tgx=l.
11.123. Положить cos2x------^- = /, /2 — t— 2 = 0.
cos 2x
11.124. Полагая x4r— = t, получаем
sin3 t = sin t — cost, sin t cos21 —cost = 0.
3
11.125. Выразить cosx и cos2 ~^x через
< = cos-|-, 4/3 — 4/2 — 3/4-3=0, (4Za — 3) (/-l)=0.
11.126. Пусть — у = 1/, тогда Зу = л — , sin(n—3,y)=
= 3siny. Далее использовать формулу sin Зу = 3 sin у — 4 sin3 у.
11.127. Умножив обе части уравнения на 8sin^-, получаем 5
. 8х . х sin -=- = SH1 .
5 5
Исходному уравнению будут удовлетворять те и только те корни . х этого уравнения, которые не являются корнями уравнения sin —0. о
509
11.128. Использовать формулы
. „ 3 sinx—sin Зх . cos 3x4-3 cosx
sin3 x=---------------, cos3 x =--------L-------
4 ’ 4
Получится уравнение 3 cos 2x-|-cos 6х = -^-1 которое, в силу написанной выше формулы для cos32x, сводится к уравнению cos32x = -^-. 8
11.129. Преобразуя произведения sin (
и
\ . / Л , „ \
x sin + Зх в суммы, запишем уравнение в виде
/ \ *5 I
sin — 2х cos 2х — cos (-х-
V о /I V о
+ sin
cos 2x — cos
„ . /л о \ /2л
Выражая, далее, произведения sin -5— 2х cos -я- —
\ О / \ о
. /я , Л \ /2л , . \
sin — 4-2x1 cos ( “з“ + 4* ! через суммы, получаем уравнение
и
cos 2x sin I — 2x
+ sin (л — 6х) | +
1 Г • / о п\ , • -g- sin I — 2х —yl-f-sin
Так как
sin
( Л л\| ♦ f , С. \
__2xH-sm v4-2x =
у <5 / \ о /
2 sin 4 cos2x=]/3 cos2x,
sin (л + 6x) sin (л — 6x) = 0,
sin
2x—-5-)-|-sin( — 2x—w) = — /3 cos 2x, □ / \ о /
то уравнение можно представить в виде cos 2х ^cos 2х -|- = 0.
11.130. Применяя формулу 2ctg2a4-tga = ctga имеем
8 ctg 24x-j-4 tg 12 x = 4 ctg 12x,
4 ctg 12x-j-2 tg 6x = 2 ctg 6x, 2 ctg 6x 4- tg 3x=ctg 3x.
Таким образом, приходим к уравнению ctg3x = tg2x, или cos 5х _
sin Зх cos 2х —’
510
11.131. Решая данное уравнение как квадратное относительно cos Зх, находим ____________
„ cos4 х + V cos8 х — cos2 х .
cos 3 х =---------------------. (1)
Если cosx = 0, то из (1) получаем cos3x = 0. Если |cosx| = l, то из (1) получаем cos3x=-g-, что, однако, противоречит равенству | cos х | = 1. Наконец, если 0 < | cos х | < 1, то cos8 х < cos2 х и уравнение (1) не имеет решений.
Таким образом, решения исходного уравнения обязаны удовлетво-л
рять сразу двум уравнениям: cosx = 0, cos3x = 0, откуда х= --|-л/г.
„ л
Проверка показывает, что значения х — -^4~лп удовлетворяют исходному уравнению.
11.132. Задача аналогична предыдущей.
11.133. Уравнение можно записать в виде
(sin x-j-cos х) £sin4 х— sin? х cos x-|-sin2 х cos2 х—
— sin х cos3 x cos4x -j-
Выражение, стоящее в квадратных скобках, равно (sin2 х 4- cos2 х)а — sin2 х cos2 х — sin х cos х
= 1 — sin2 х cos2 х — sin х cos x-i—.
V2
T ак как | sin x cos x | eg i, to
. . » 2 i 3 3
I Sin2 X COS2 X 4- Sin X COS X — < 1-4-Z .
уч
Следовательно, выражение в 'квадратных скобках ни при каком х в нуль не обращается. Поэтому исходное уравнение равносильно уравнению
sin x-|-cos х = 0.
11.134. Обозначим sin2x = u, cos2x = n. Тогда задача о нахождении решений уравнения
sin2m x-|-cos2" х= 1
сводится к задаче о нахождении действительных решений системы уравнений
u24-n2 = l, u2m_|_y2«=l.
Такая система (см. задачу 10.46) имеет действительные решения (0, 1), (0, — 1), (1, 0), (— 1, 0). Следовательно, исходное уравнение
511
удовлетворяется лишь в том случае, когда либо |sinx| = l, либо lit пп
I cos х | = 1, т. е. x = -g-.
11.135. Обозначив sinx = u, cosx = n, получаем систему уравнений
и8-|-р» = 1, ,,2n+l I V,—f.an+i । *
U Г" у2ОТ4-1 и г usm+1'
Эта система (см. задачу 10.47) имеет два действительных решения:
1 1
И = О = ——, U = v =--------=.
/2 Jz2
Итак, получаем sinx = cosx, x=-^--)-nn.
11.147. Так как | sin 2х cos у j s: 1, то система может иметь решения лишь при а=0.
11.148. Из первого уравнения находим sinx =
(sint/^O,
так как в противном случае sin у = cos у = 0) и, подставляя во второе уравнение, после преобразований получаем 2 cos2 2г/-f-25 cos 2у — 13 = = 0, откуда cos2(/ = -g-. Тогда из второго уравнения получаем
cos 2х = -g-. Система
cos2r/==-g-, о 1
cos 2х = -g-
является следствием исходной системы.
11.149. Преобразовать произведение cos xcosу в сумму.
11.150. Система равносильна следующей:
cosx-|-cos у — 1,
1
COS X COS У — -г-.
4
11.151. Из первого уравнения находим
cos (x4-z/)=0, х4-г/ = у + лй; и т. д.
11.152. Второе уравнение преобразуется к виду
sin2 2х 4- sin2 2z/ = 0, откуда
Всякая пара чисел х, у вида (*) удовлетворяет первому уравнению. 512
11.153. Возводя уравнения в квадрат и складывая, получаем уравнение
sin4 x + cos8 х— 1,
являющееся следствием исходной системы и имеющее решения
(см. задачу 11.134).
Если х = л/?, то из исходной системы получаем sin у —О, cosj/=l, откуда у — 2лт.
Если х = -?~4тлй, то cos// = 0, siny=l, откуда
/у = у + 2лт.
11.154. Разделив первое уравнение на второе, находим
cos х = 2 cos у. (1)
Подставляя (1) в первое уравнение, получаем после сокращения на cosследующее уравнение:
3 sin х + 6 sin у — 4. (2)
Система (1) —(2), равносильная исходной системе, аналогична рассмотренной в примере на стр. 390.
11.155. Сложив уравнения и преобразовав суммы синусов и косинусов в произведения, получаем уравнение
х — у /„ . « + </ х-}-у\ п ,,,
cos —— (3 sin —~~—COS—?pj=O. (1)
Уравнение (1) вместе с первым уравнением исходной системы образует систему, равносильную исходной.
Уравнение (1) распадается на два уравнения:
а) cos Л = 0, х — у = л (2&+ 1); (2)
б) , х + у 1 tg 2 — 3 , X + у — 2 arctg -l-f-2n/z. О (3)
Остается выразить из (2) уравнение исходной системы, а и (3) у через х, подставить в затем решить уравнения вида первое
a sin х b cos х = 0.
11.156. Второе уравнение можно записать в виде cosx — cos (x-f-2у) — cosx, или cos (х+2г/)==0, откуда
*=у — 2г/ + лл. (1)
17 В. Г. Болтянский и др.
513
Подставляя х из (1) в первое уравнение системы, находим tg 2у + sin 2у = sin 4i/, sin 2у (1 + cos 2у — 2 cos3 2у) = О, и т. д.
11.157. Второе уравнение можно записать так: sin (2х—у) + sin у = sin у, или sin (2х — у) = 0, откуда
у = 2х— nk. 1 (1)
Подставляя у из (1) в первое уравнение системы, получим уравнение 4 tg Зх = 3 tg 4х.
Выразив tg 3 х и tg 4х через tg х, после преобразований приходим к уравнению
tg3 х (tg4 х+7) = 0, откуда tgx = O, х=лл.
11.158. Первое уравнение записать в виде (2 cosx—tgi/)3 = 0, а затем подставить tgу = 2 cosx во второе уравнение.
После преобразований получится уравнение sin х (sin x+cos х+ 1) = 0.
11.159. Первое уравнение запишем в виде
2 cos х sin у cos у= sin3 у. (1)
Из второго уравнения следует, что sin у cosy 0. Поэтому уравнение (1) можно записать так:
tg у = 2 cos х. (2)
Подставляя (2) во второе уравнение исходной системы, получаем после преобразований
(sin х — cos х) (2 sin х + 1 — sin х cos х — cos2 х) = О, или
(sin х —cos х) sin х (sin х— cos х + 2) = 0, и т. д.
11.160. Возведя уравнения данной системы в квадрат и складывая, получаем уравнение
2а sin (х + г/) = 2а, (1)
являющееся следствием исходной системы.
Возможны два случая: а — 0, aj^O.
Если а = 0, то исходная система примет вид
1 1 smx=—. cosx=——, V 2 V 2
Л
откуда x = ~-f~2nk, а у может принимать любые значения. Если а 0, то из (1) получаем sin (х-^у) = 1, откуда
г/ = -~- + 2л& —х. (2)
514
Подставляя у из (2) в исходную систему, находим
(1= (l+a)cosx=^-. (3)
Из (3) видно, что нужно отдельно рассмотреть случай а = —1. При а-— 1 исходная система имеет вид
{sin x = cos у, cos х = sin у,
откуда следует, что х~^у^=~^--{-2пп.
л
Если —1, то из (3) получаем х = —~4~2лт, а затем из (2)
Л
определяем 'у = ~-\-2л1. Полученные решения удовлетворяют исходной системе.
11.161. Уравнение
a cos (2ху) cos х — a cos (х-\-2у) cos у, полученное перемножением уравнений исходной системы, является следствием исходной системы. Это уравнение запишем в виде
2 [cos (Зх + у) + cos (х-(-у)] =2 [cos(х 4- Зу) + cos (x-f-у)], или
cos (Зх у) = cos (х + Зу),
откуда либо
x — y = nk, (1)
либо
х+у = ^-. (2)
Если имеет место (1), то из первого уравнения системы находим acos3i/ = cosy, откуда, используя формулу
cos Зу = 4 cos3 у — 3 cos у,
получаем cos у (За -[- 1 — 4а cos2 у) = 0,
или cos у (а4~ 1 — 2а cos 2у) = 0.
Следовательно,
а) л . У = ~2+^ (3)
б) 1 а-$-1 у — ± -х- arccos -х к л/л, а 2 2а 1 (4)
Если имеет место cos у = 0. равенство (2), то из первого уравнения получаем
17* 515
Легко проверить, что каждая пара чисел (х, у), определяемая как формулами (1), (3), так и формулами (1), (4), удовлетворяет и второму уравнению исходной системы.
11.162. Запишем систему в виде
J 4 sin (Зх-\-2у)~—sin х,
I sin у = — 4 sin (2х ф- Зу)
и, перемножив уравнения системы (1), получим уравнение
sin (Зх ф- 2у) sin у = sin (2х ф- Зу) sin х, (2)
являющееся следствием исходной системы.
Преобразовав произведения тригонометрических функций в левой и правой частях уравнения (2) в сумму, получим уравнение
cos (Зх ф- у) = cos (х ф- Зу), откуда
х — у = лп (3)
либо
2х 2у = xk. (4)
Если имеет место (3), то из первого уравнения исходной системы получаем после простых преобразований
sin у (16 cos2 2у -|- 8 cos 2у — 3) = 0.
Если выполняется равенство (4), то sin у = 0.
11.163. Запишем систему в следующем виде:
| (sin х ф- 2 cos у)2 ф- (sin у ф- 2 cos х)2 = 1,
I (sin х ф- 2 cos у) ф- (sin у ф- 2 cos х) = 1.
Тогда исходная система распадается на две системы:
( sin х ф- 2 cos у = 1, ( sin х ф- 2 cos у — 0, ( sin у 2 cos х = 0, (. sin г/4~ 2 cos х= 1.
Каждая из этих систем является системой того же вида, что и система, рассмотренная в примере на стр. 390.
11.164. Представить систему в виде
| (3 sin х — cos у)2 4~ (3 sin у — cos х)2 = 4,
I (3 sin х — cosy) ф- (3 sin у — cos х) = 2.
11.165. Решая второе уравнение как квадратное относительно sin х, получаем
sin х = — cos у + V — (1 — 2 sin у)3. (1)
Подкоренное выражение в (1) неотрицательно лишь при 1—2 sin у = 0, т. е. при
siny = y. (2)
516
Из (1) тогда находим
sin х = — cos у. (3)
Из (2) и (3) следует, что
cos 2y = ~t cos 2х = —. (4)
Используя равенства (4), из первого уравнения исходной системы получаем
с05.
откуда
х = ± -^--{-2л£,
а из (2) находим
'/ = (—!)“ у +л«;
учитывая еще соотношение (3),
получаем
х=±~ + 2л/г, О
г/— ± -у + 2“ + 2лт.
11.166.
находим
Задача аналогична
предыдущей. Из второго уравнения
cos x =s — cos у з V — (1 — 2 sin y)3,
откуда
1 1 о 1
smy^-y, cosx = —cos у, co?, 2y = -^-t cos2x = -g-.
Тогда из первого уравнения имеем
1 smx=j.
Заметим, что к этому же результату можно прийти несколько иным путем. Представим второе уравнение в виде
4 (cos х + cos г/)3 -ф (2 sin у — I)3=О, откуда
cos х -ф cos у — 0, 2 sin у — 1=0, и т. д.
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ XII
В приводимых ниже указаниях и кратких решениях часто формулируются без обоснования те или иные утверждения (например, подобие треугольников, параллельность прямых, отбрасывание из геометрических соображений одного из корней квадратного уравнения и т. n.j. Следует иметь в виду, что для получения полного решения такие утверждения должны быть обоснованы.
517
12.21. Пусть Ох, О2 —центры равных касающихся друг друга кругов, вписанных в острые углы прямоугольного треугольника АВС (рис. 174), £, F — точки касания этих кругов с гипотенузой АВ, О —
тельно, с2 = a2 -j- &2 —
центр вписанного в треугольник круга, К —точка касания этого круга с гипотенузой.
Введем следующие обозначения: ВС —а, АС = Ь, АВ=с, OK = r, O1E = OiF = x.
По условию задачи яг2 = = 2ях2, т. е. г — хУ2.
Из подобия треугольников ОАВ и OO1O2 находим
с _ г
2х — г — х
ci Ч-получаем с———. Следова-/2
, (а— &)2 = 0, а = Ь.
с(|/2 -1) 2
л
Значит, каждый из острых углов треугольника равен .
12.22. Пусть Л1, N, К — центры квадратов, построенных на сторонах прямоугольного треугольника АВС (рис. 175), О —середина гипотенузы АВ, АВ = с, L ВАС = а. Тогда £КОМ=^л — а, LM0N=^, LK0M = ^+a,
„ , „ , о 1с а-4-& . ,1с а+&
$MNK SK0N + SK0M + SMON = у T “Fsm “ + T T ~~2~ cos а + . 1 /й4-&\2 b ,,,, a , , M , 1 , /a+b\2
— “g" (e + ^) + _g‘ (a + ^) + “g~ (a + ^)2— 2 у ’
518
12.23. Пусть М, N, К — середины сторон данного прямоугольного треугольника АВС (рис. 176), О —центр окружности, -касающейся данных полуокружностей, R — ее радиус. Проведем ОЕ I MN и OF_l_RM. Обозначим ОЕ = х, OF = y. Тогда OK--R — 3, ON = R— 4, ОЛ4 = 7?-5, NE = 3—y, KF^4 — x.
Из прямоугольных треугольников OEN, OEM и OFK получаем
/ (fl-4)2 = X2+(3-J/)2,
J (R-5)2^x2 + y2,
I (£ —3)2 = г/2+(4_х)2.
144
Решая эту систему уравнений, находим R = см.
12.24. Пусть О —центр окружности, касающейся трех данных окружностей, х—ее радиус, X ОАС—а (рис. 177). Тогда
ЛО = х+1, ВО = % + 2, СО = % + 3.
Из треугольников АОС и АОВ по теореме косинусов получаем
( (х + 3)2 = (х+1)2 + 36— 12 (x+l)cosa, ( (х 4- 2)2 = (х + 1 )2 + 9 — 6 (х 1) sin а.
Решая эту систему уравнений, находим
8/11-19 ч =----у--И).
Рис. 178.
12.31. Через вершину В правильного треугольника АВС (рис. 178) проведем перпендикуляр BE к данным параллельным прямым. Пусть АВ — АС = ВС—х, £CBD = a.. Из прямоугольных треугольников BCD и АВЕ получаем
(л -г—a О
Решая эту систему уравнений, находим
х— /а2 + ab + Ь2.
519
12.32. 1-е решение. Возможны два случая, указанные на рис. 179. Пусть О — центр данных окружностей,
АВ = АС=ВС=х, А31 — ЛС1 = В]С1 = 1/.
Из прямоугольных треугольников COD и СХОЕ получаем
Решая эти уравнения, находим
х = 1(1/'4^-7з+гКз’)-
у = у(К4^=Т^-гИз).
2-е решение. Заметим, что Af = rlz3, как сторона правиль-Г пого треугольника, вписанного в окружность радиуса г; OG = ,
CSJ=2CG = 2j/' R2—r-~— — ABi^^-(CBi-AF) =
= y(/4/?2--r2-r/3), ЛС = СВ1-ЛВ1 = у(И' 4/?2-г2 +г/3).
12.33. Пусть Oj и О2 — центры данных окружностей, А—точка касания, AD — диаметр большей окружности, АВС — правильный треугольник (рис. 180). Обозначим
АВ = АС--ВС — х, £ BAD = u.
520
Из прямоугольного треугольника ABD и равнобедренного треугольника АОгС получаем
(Л \
"з— 1'
Решая эту систему уравнений, находим
|Л2-гР+7?2 '
12.45. Пусть AB = BC — l, L ВАС = а, R — радиус окружности, описанной около треугольника АВС, ОМ = ОС = г — радиус окружности, описанной около трапеции ACMN (рис. 181).
Из треугольника АВС по теореме синусов находим
---•
2. sin а.
3
Проведем OL.LBC. Тогда BL=— I. Из треугольников BOL и OML получаем
3/
OL = BL • tg Z ОВС= ctg а,
г = ОМ = /О£2 + Л4£2 = 11/ l+9ctgaa.
/5
По условию задачи г^-у-Р, т. е.
J-/l + 9ctg2a = ^L.
4 & 4 sm a
г-. л
Решая это уравнение, находим а —
521
12.46. Пусть 01( 02, 03 — центры данных кругов (рис. 182), О1М=г и O3N = O2E = O2L = радиусы этих кругов, OiK\\MN.
Рис. 182.
Так как ВО2—биссектриса угла АВС, то
BN - BL = R ctg (arcctg 2) = 2R.
Из прямоугольного треугольника BCD находим
CD = BD = 3/? ’ 2 cfg (arcctg 2) ctg (2 arcctg 2) ctg2 (arcctg 2) — 1 ’
BC = VBD^ + CD^ = 5R.
Из треугольника ОгО2К имеем
MW = O,W = K(W + r)2-(/?-r)2==2 VW.
Из треугольника CQ^M находим
СМ г
ctg (2 arcctg 2) “ У •
Из соотношения ВС = BN-\-MN-\-СМ получаем 5W = 2R~-2 г.
Отсюда
3Т-2/т—Т=0’
Так как 1/^—>0, то — =~(3 + К5)-у г ГУ
12.47. Возможны два случая. Первый случай: равные касающиеся друг друга круги (с центрами в точках Ot и О2) касаются внутренним образом окружности, вписанной в данный треугольник АВС (рис. 183).
522
В этом случае треугольник ОО^ — правильный. Обозначим OtAi = = 02<V = x. Тогда OOi = /? —х, OjO2=2x. Отсюда /? — х — 2х, x=~R. О
Второй случай; равные круги касаются внешним образом окружности, вписанной в треугольник АВС (рис. 184). Введем обозначения
OJN = O1E = y. Тогда из рассмотрения треугольников AOjE, 001Е и АОМ находим длины трех отрезков АЕ, ОЕ, АО:
AE=OtE ctg^ = y/3,
ОЕ = VbO‘i~EOj = VR^ + 2Ry,
Ао=.°™-=^. . л i/з ЯП 3
523
Из соотношения АО-АЕ^-ОЕ получаем
г °
/ 2 1/2\
Решая это уравнение, находим t/=(l±—-—|/?. Так как y<R, \ о )
то 4/=^1---g— )R.
12.48. Пусть г —радиус окружности, вписанной в данный треугольник АВС (рис. 185), AB = BC—l, L АСВ — а, AD 1 ВС. Тогда
BE AC /sinacosa _ / sin 2a
----------- Д'! г = 2т —-------
1 4- cos a ’ 1 + cos a ’
BDM находим
АС + 2АВ
Из треугольников ABD и
BD — А В • cos z
вм=
АВС = I cos (л — 2а) = — / cos 2а,
BD _ I cos 2а :os Z. MBD ~ sin а '
Из соотношения ВЕ = ВМ-\-МЕ получаем
, . I sin 2а I cos 2а
I sin а = -г—------—;------.
1 + cos а sm а
2 2
Решая это уравнение, находим cos а — , а = arccos
о 3
12.49. Обозначим угол ABD через а (рис. 186). Из соотношения SB4i.v = 5волт + 5вол' получаем
у ВМ • BN • sin 2a = ~ ВМ • ВО sin a + у BN • ВО • sin a.
Отсюда
cos a _ 1 /_J______1_'\
~BO^ “ "2 + Ж/ •
524
Теперь находим
DO _ BD — ВО _5C-cos« ВС ! 1 Ц
ВО ~ ВО ~ ВО 1 ~ 2 \ВМ + AV 1
1 ,'AM + BM CN + BN\
2 < BM + BN y
, 1 / , 4
1 = у (mA-п).
12.61. Проведем MK || BN (рис. BCN и СКМ находим
.187). Из подобия треугольников
СМ
С7<=СЛ"ВС=СТ-СЛ1ТЖ
СМ
= CN
Отсюда
KN = CN - СК = CN 11 - -г-4—'': = CN -г^— ; 1 т: 1 ~~т
Из подобия треугольников
AON и АМК получаем
АО ЛЛ? ЛЛ' \А~т п
OM~KN~CN‘ т '~т
Аналогично находим
12.62. Обозначим АВ = х, ВС = у, АС —г. Из треугольников АВМ и ABN (рис. 188) по свойству биссектрисы внутреннего угла треугольника получаем
ВМ _ ОМ _ 1 ' AN _ ON _ ,
АВ ~ АО ~~ /3 ’ АВ ~ ВО ~ b
Отсюда
5Л1 = -рбр AN = х (/Т - 1).
525
Из треугольника АВС имеем
AN _ АВ ' ВМ _ АВ CN ~ ВС ' СМ~ АС ’
т. е.
х (КЗ — 1) _ х
z - х (/3 - 1) ~ У ’
X X
Из этой системы уравнений находим у = х рЛ3 , г = 2х. Отсюда следует, что х2 -f- у2 = г2, и по теореме, обратной теореме Пифагора, /.АВС — j, Следовательно,
/ВАС = arcsin У- = =
z 3 о
12.63. 1-й способ. Прежде всего надо доказать, что в треугольнике со сторонами а, Ь, с медиана тс, проведенная к стороне с, определяется формулой
2а24-262 = с24-(2тс)2.
Пусть теперь х, у, г — длины сторон данного треугольника. Тогда
2х2 4- 2у2 = z2 4- 242, 2у2 4- 2z2 = х2 4- 302, 2х2 4- 2z2 = у2 + 422.
Решая эту систему уравнений, находим х = 2^105, у — 2 КЗЗ , z = 2 И132, 5Д = 48 Кб И2).
2-й способ. Пусть О — точка пересечения медиан данного треугольника АВС. Продолжим медиану BN на отрезок NK = ON. Тогда А ЛON = ДМСК, и потому 5Д0СА- = 5ДЛ0С — ^s^abc Но стороны треугольника ОСК равны двум третям соответствующих медиан треугольника АВС, т. е. /ОС К имеет стороны 8, 10 и 14 (с.м). Следовательно, S&OCK — 16 1^6 (см2), 5ддвс = 48 Кб (см2).
12.64. Пусть Oj и О2 — центры данных окружностей, AD — биссектриса угла ВАС (рис. 189). По условию задачи О]М = OrF = 2, OtN = ОгЕ = 3, EF = 1.
Из подобия треугольников OjAM и O2AN получаем
а
AN = ~AM. (1)
Отсюда вытекает, что точка N находится ближе к точке D, чем точ-526
ка М, т. е. DN<zDM. Но DM — DF и DN = DE. Следовательно, DM + DN = DE + DF = EF = 7. (2)
Заметим, что OtD 1 О2О, как биссектрисы углов ADB и ADC, составляющих в сумме л. Следовательно, углы O-JDM и DO2N
ED ЕВ
Рис. 189.
равны, как углы с соответственно перпендикулярными сторонами, и прямоугольные треугольники О-рМ и O.2DN подобны. Отсюда
DN DM = 6.
Решая систему уравнений (2), находим DN = 1, DM = 6. MN = = DM — DN = 5.
Из соотношения (1) получаем
•5
AM + MN = g AM, AM = 10.
Теперь находим AD = AM -|-4- DM = 16 (cm).
12.65. По условию задачи BD = = 3 см, AF — 2 \/ 2 см, СО : ОЕ = = 5:1 (рис. 190).
Обозначим ОЕ=х, OF = y, OD = г. Тогда ОС = 5х.
Из подобия треугольников AOD и BFO и треугольников OCD и ВОЕ получаем OD -ОВ — АО
г (3 — г) = у (2
(3) и учитывая, что DN <iDM,
OF — OC-OE, г. е.
— у) = 5х*. (1)
Площадь треугольника АВС запишем в виде
sabc = Зл--ЛД = |/2 -ВС = ЛС = * (Х. АВ ру ВС + г- ДС).
Отсюда
ВС=~- АВ, /2
6х • АВ — х АВ + у
АС = 2х-АВ,
Зх
• АВ + г 2х • АВ.
/2
527
Разделив обе части этого равенства на х-АВ, получаем
Зу + 2 z = 5 К2 .
Решая систему уравнений (1) —(2), находим х^, у = 2=1,
F5
а затем из прямоугольников AOD и COD получаем AD — 1, CD—3. Следовательно,
$Авс~ (СЛ*2)-
(2)
12.66. Пусть О —центр данной окружности, г —ее радиус, ODJ_BC, В. ОВС — х, — ОС В —у (рис. 191). Тогда из треугольника АВС нахо
Рис. 191.
дим х+у=~. Из треугольника А1В1С1 по теореме синусов находим
51C1=2rsin Z ВАС = г^З.
Так как отношение площадей подобных треугольников равно квадрату отношения сходственных сторон, то ВС = 2(1 + |2~) ВгС1 =
= 2r/3 (1+/2 ).
Из прямоугольных треугольников BOD и COD получаем
ВС — BD + CD = r(ctgx + ctgi/) =
= 2r/3'(l-i-/2')-
Отсюда
sin (х+у) _
cos (x —- у)— cos (x + y)
= ГЗ (1 +/2“).
Подставляя в это уравнение л
хнаходим О
, , 1 л
cos(x-y)=—, х~у = —,
Z ЛВС = 2х = ^-, С.АСВ=О1у=^.
12.67. Обозначим ВС —а, АС = Ь, АВ—с (рис. 192). Так как 1 7
SAED = 14 SABC’ SAFD ~ §0 S АВС
и высоты этих треугольников равны, то
ED = — FD- —
L 14’ SO-
528
Отсюда
B£ = BD + D£ = ^, С£ = ~, CF=CD-£D = ^, BF^~.
/ / zO ztj
По свойству биссектрисы внутреннего угла треугольника получаем
АС_С/? ±__3
АВ BE’ с ~ 4 ' (1)
Из треугольников АСЕ и АВЕ получаем
/0'2 1 R's
^-ЙЗ~Ыа3 = СЗ-\25Га' <2>
Из системы уравнений (1) —(2) находим
Ь = ^а, с—^ а, сР = Ь*-4-&,
5 5 1
ZA=~, £ В = arcsin , АС = arcsin
ZOO
ABM
J2.68. Проведем AM и CN перпендикулярно прямой, касающейся окружности в точке В, и BD I АС (рис. 193). По условию задачи АМ=а, CN--—с. Заметим, что углы АСВ и АВМ равны, как углы, измеряющиеся половиной одной и той же дуги АВ. Следовательно, прямоугольные треугольники BCD и подобны и
AM-ВС BD-----~АВ~'
Аналогично из подобия треугольников ABD и BCN получаем dL>
(1)
(2)
Перемножая соотношения (1) и (2), находим BD'i = AM-CN—ac, BD^Vac-
529
12.71. Доказать, что АС = ВС — АВ.
12.72. Обозначая стороны параллелограмма через х и у, получить систему уравнений
х у sin a sinf> ’
й2 = х2—у- — 2ху cos (а -|- Р).
12.73. Пусть х и у —стороны параллелограмма. Тогда площадь параллелограмма
S = 2x=3p. (1)
По теореме о квадрате стороны, лежащей против тупого угла треугольника, получаем
25 = x2+p2-f-2x)/p2^4. (2)
Решая систему уравнений (1)-—(2), найти S.
12.74. Пусть а>Ь, 2х и 2у — диагонали параллелограмма. По теореме косинусов имеем
а2 = х2 -j-у2 -j- 2ху cos а, = х2 -j- у2 — 2ху cos а. Отсюда
. cfi — b2
а1 — o- = 4xwcos«, ху — -----.
4 cos а
Теперь находим площадь параллелограмма:
S = 2ху sin а = —• (а2 — й2) tg а.
12.75. Всякая прямая, делящая параллелограмм на две равновеликие части, проходит через центр симметрии параллелограмма.
Поэтому данные прямые ЛЖ и NL пересекаются в центре симметрии параллелограмма ABCD (рис. 194). Четырехугольник MNK.L — ромб, так как его диагонали взаимно перпендикулярны и в точке пересечения делятся пополам.
530
По условию задачи АВ = 3, AD—2, Z А — arccos yg и площади четырехугольников AMOL и OKDL равны. Треугольники OML и OKL равны, так как MNKL — ромб. Значит,
SAML ~ SKDL-
Обозначим АМ=х, AL = y. Тогда
KD—3 — х, DL — 2 — у, SAMl ху sin Z A,
SKDL = ~(3—x)(2 — y) sin Z D = y (3 — x) (2 — y) sin Z A. Отсюда
(3 — x) (2 — y) = xy. (1)
Из треугольников AML и KDL по теореме косинусов находим
ML* = x*+y*-2xy^,
К
КЛ2==(3_х)2 + (2_р)2 + 2 (3-х) (2-у) 1g.
Приравнивая ML? и KL?, получаем
Л'2т~'/2— | -Р/ = (3 —х)2 —(2—у)2~г- (3 —х) (2 — у). (2)
о о
Решая систему уравнений (1) —(2), находим
ЛЛ4 = х = 2 (см), ВМ = 1 (см),
2 4
AL = y = v (см), DL = -%- (см).
О □
12.76. По условию задачи в данном параллелограмме ABCD (рис. 195) AB = 2AD, BD = 2AC. Так как в параллелограмме сумма
квадратоа диагоналей равна сумме квадратов всех его сторон, то
5- ЛС2 = 10. AD\ АС=\С2 -AD.
Из треугольника ACD по теореме о квадрате стороны, лежащей против острого угла, имеем
АС2 = AD* + CD* - 2CD • DE,
2АD2 = AD* 4- 44D2 - 4AD • DE.
531
Отсюда
DE — ^-AD, EC = CD—DE — 2AD—^-AD = ~ AD, 4 4 4 CE 5
12.77. Пусть О—центр ромба, ОМ I ВС, ON |_ Л В, ОКА. ЕЕ (рис. 196). Заметим, что из равенства соответствующих треугольников вытекает равенство углов, обозначенных на рис. 196 одинаковыми буквами. Следовательно, «+ 2+v==2‘ И
ZCOB = a + | = ^-V=£ NEO.
12.86. Дополнить трапецию
Кроме того, /_OCF=A.OAE. Поэтому треугольники COF и АОЕ подобны, откуда находим
/ f \ 2
АЕ CF ~ АО • СО —-g-\ .
V0S2./
12.81. Доказать, что угол между прямыми, соединяющими центр окружности с концами боко-л вой стороны, равен .
до треугольника, продолжив боко
вые стороны.
12.87. По условию задачи в данной трапеции ABCD (рис. 197)
AB~)-CD = 14, L АОВ = Дгь высота И = —.
О /
А
Рис. 197.
Через вершину С проведем прямую, параллельную диагонали BD, до пересечения с продолжением стороны АВ в точке М. Тогда AM = = ЛД-j-CD = 14, Z.4CM=^. Обозначим АС = х, CM — BD=y. Из треугольника АСМ по теореме косинусов получаем
142 = Д= + гЛ4-л/.
(1)
532
Площадь треугольника АСМ равна
1 1 2л
4 AM • Н = 4 АС • СМ • sin 4- .
z 2. о
Отсюда
30 Г 3 =1л7/]/'3.
(2)
Решая систему уравнений (1) —(2), находим
х=10 (сл|), г/ = 6 (см).
12.88. Пусть Л1.¥ = х, hi — высота трапеции ДВУЛ1, h2 — высота трапеции MNCD (рис. 198). По условию задачи АВ = а, CD—b. Площадь трапеции ABCD равна
J- (а + Ь) (^ + /?2) = (а + х) /гг = (Ь + х) /г2.
Отсюда, обозначая ?— = //, получаем
«1
(а + b) (1 + у) = 2 (а + х) = 2 (Ь + х) у.
12.89. В данной трапеции ABCD проведем DM || ВС (рис. 199) Тогда АМ—\а— Л|, L ADM=c/,. Пусть Н— высота трапеции, AD — x, DM — ВС =у. Так как по условию задачи диагонали трапеции перпендикулярны, то
л-2 + У2 = ЛО2 + ВО2 + СО2 = а2 + Ь-.
Из треугольника A DM по теореме косинусов получаем
(а — Ь)2 = х2 4- у2 — 2ху cos а = а2 + Ь2 — 2ху cos а, откуда
ab
ху —-----.
cos а
533
Площадь треугольника ADM равна
yW -|а — d| = yA#sina = ya6tga.
Отсюда
„ об tg а Н-^=Г1-
с 1 . м a&(a + &)tga
SABCD = у Н а + = 2ja —6| '
- 12.90. Пусть L—точка пересечения данной окружности со стороной (.7) (рис. 200), CMJ.AD, ВС = Ь. По условию задачи ЛО = = (1+Г15)&,
2 1 VT
CE = CF = CL^~b, MF = ~EF=D^-b.
о zb
Из прямоугольного треугольника CMF находим
СМ = /СЛ-Л1Р = у.
Так как трапеция равнобочна, то
DM = у (AD - ВС) =
Из прямоугольного треугольника CMD находим
CD = V С M^ + DM^ = 2b.
Отсюда DL=CD-CL = ~- b, CL:LD = \ : 2.
Рис. 200.
12.91. Пусть О —середина стороны АВ, АВ = Зи (рис. 201). Проведем OK, LF и CN перпендикулярно АВ. Тогда
CD = 2a, OF=KL = ~, BN = ~ (АВ-CD) = ~ .
Следовательно, OBCL — равнобочная трапеция, откуда
BC=OL = BO = ^.
534
По свойству секущих CL СЕ = СМ ВС, т. е. -g- • ~ = СМ , откуда
СМ = ~, ВМ = ВС-СМ = а.
Следовательно, искомое отношение СМ : ВМ = 1:2.
12.92. Пусть О —центр окружности, вписанной в данную трапецию ABCD (рис. 202), М, N, К, L — точки касания. Обозначим ОМ — = ON = 0K=R, £МВ0 = а. Тогда
1 4R1 2
BM = Rctga, KC = Rtga, SABCD = ^ КМ (AB + CD) = -^~. £ olli ZCA
Заметим, что углы NOE и АВС равны, как углы с соответственно перпендикулярными сторонами, т. е. £ N0E = 2a. Из треугольника NOE находим EN = R sin 2а. Отсюда
1 1 3 л
SMNU = ~RM.LN = 2R*sm2a, = -sin22a = - a=-w ,
z ‘-'ABCD z О о
ЛВ_2Я ctg а
CD ~ 2R tg а “ д’
12.93. Пусть О —центр окружности, вписанной в данную трапецию ABCD (рис. 203), М — центр окружности, описанной около этой трапеции. Обозначим OK = OL = r, 2. BAD = а. Из треугольников АОК и DOL находим 71R = rctg-^-, DL = rtg^-,
По условию задачи СМ = ВМ = г |6 . Из треугольников CML и ВКМ находим
LM = r j/~6 — tg2y, КМ = г '|/'б — ctg2 ~ .
Из соотношения KL = LM±KM получаем
2=]/6-tga ± ]/б-ctg2 -J.
535
(знак плюс соответствует случаю, когда точка М лежит внутри трапеции, минус —когда точка М вне трапеции). Возведя обе части этого уравнения в квадрат и замечая, что
, 2 а , 3 а _ 1 — cos ос 1 + cos а _ 4
g 2 + с 8 2 — 1 + cos а -г 1 — cos ос — sin2 а ’
после упрощении получаем
2____
sin3 а
24 49-^-. sin2 а
Решая это уравнение и учитывая, что 0<ос<-^-, находим а = -^-.
12.94. Показать, что в данную окружность можно вписать равнобочную трапецию, у которой боковая сторона равна 2 у 5 см, одно основание равно 6 см, а другое основание является диаметром окружности и найти радиус окружности, описанной около этой трапеции.
12.95. Продолжим стороны AD и ВС до их пересечения в точке М (рис. 204). Обозначим AD=a, BC = b, DM = x, СМ=у, L AMB = cl. Из треугольников ABM, CDM, АСМ и BDM по теореме косинусов находим
ЛВ2 = (а + х)3 + (& + 1/)2 —2 (а-ух) (b-\-y) cos а,
СО3 = х2 4- у2 — 2ху cos ос,
Л С2 = (а + х)2 + у2 — 2 (а + х) у cos а,
BD2 = х2 + (Ь + у)2 — 2х (Ь + у) cos а.
536
Подставляя найденные выражения в заданное соотношение
А В2 + CD2 = АС2 + BD2,
после упрощений получаем aicosa = 0. Так кака^О, Ь^О, то cos а = 0, а = g-.
12.96. Пусть в данном четырехугольнике ABCD (рис. 205) ДВ=а, BC = b, CD~x, AD = y. Так как четырехугольник описан около окружности и его диагонали взаимно перпендикулярны, то
( хА-а = уА-Ь,
I х2А-а2 = у2 + Ь2.
Из этой системы получаем: или х = Ь, у —а, или х — у, а~Ь. Не теряя общности, будем считать, что х—Ь, у —а. Тогда треугольник BCD — равнобедренный и BM = DM.
По условию задачи один из углов q
четырехугольника равен
Докажем,
что угол АВС не может быть Обозначим ^.ABM — a, Z. Тогда
равен —, СВМ = р.
, , , „ AM , СМ _ tg «4-tg Р- вм + вм — 2;
, , А я дт • с /и ,
далее, так как tgatgp = ——< 1,
Рис. 205.
то
tg (а + ₽)
_ tga + tgp l-tgatgp^2’
Отсюда а -р Р S-- ' arctg 2 > . Следовательно, не теряя общности, можно
считать, что угол BAD равен у, Тогда треугольник ABD — правильный и AB — BD — AC. Из равнобедренного треугольника АВС, Л
у которого Z. ВАС = —, находим
Окончательно
BA : AD : CD : СВ = 1 : 1 : ^2-/З : ]Z2-/3 .
12.103. Длина хорды х определяется из уравнения Я2 = J- + (а — х)2, причем должны выполняться неравенства Осх^а.
537
12.105. Обозначая угол между прямыми, соединяющими центр окружности радиуса А? с центрами двух других окружностей, через а, расстояние между центрами окружностей радиусов гг и гг через у и искомую длину внешней касательной через х, получить систему уравнений
' а2 = 2R2 — 2R2 cos а,
!/2 = (^ + о)2 + (^ + о)2 —2(/? + rj) (Я + г2) cos а,
. *2 = */2 — (О — г2)2.
12.106. Обозначая расстояние между центрами данных окружностей через /, а искомый угол через х, получить соотношения
R — r a. R-[-r .В . х г = sm~2> -r~=smi> Sltl2=7’
I
откуда
. х 1 / . Р .
sinT = THinT-sinTl-
12.107. Пусть х— искомый радиус окружности, Л—точка касания этой окружности с данным отрезком, О — середина данного отрезка. Тогда х находится из уравнения
7? \2 /Р \2
+ = (R-x)2-x2.
12.108. Дано CD = 2R, ЛЛ1 = ~- (рис. 206). Обозначим BN через х. Имеем
г r \2 / R \2
AB2==MN2—(BN~AM)2=[~ + xj — — х) =
= (АО±ВОУ =[]Z(я-у)2 - •
о R R
Решая это уравнение, находим x=-g- и Л: = Т8’
538
12.109. Дано
OD = R, AD=r
(рис. 207). Обозначим ВС через х. Имеем
А В2 = (г + xf = ВС2 +АС2 =
= х2 + (АО ± V ВО2 —ВС2)2 = tf + tR-r± У (R — x)2 — x2]2.
Решая это уравнение, находим
4г/?(/?-г) (R + ry ’
12.110. Дано
AD = R, ВС=г
(рис. 207). Обозначая OD через х, так же как и в задаче 12.109, получаем уравнение
(/? + гу = г2 + [х — R ± /(х —г)2 —г2]2.
Решая это уравнение, находим
12.111. Дано АМ = а, BN =Ь (рис. 208). Обозначим
KL = x, £NMK = a.
Выражая RN2 из треугольника MNR и ОК2 из треугольника ОМК по теореме косинусов, получаем
( (6-f-х)2 = (а + х)2 + (а + 6)2 — 2 (а-f-x) (а-|-&) cos а,
t (а + b — х)2 = (а + х)2 + Ь2 — 2 (а + х) b cos а.
Решая эту систему уравнений, находим
ab (а + Ь)
X~a2 + abyb2 '
539
з
12.112. Дано OB = R, NE — R (рис. 209). Из треугольника ONE о
находим
О£=1/=
Г \ о / \ о / *
Обозначим FM через х. Тогда
KN=OE — FM=—- — x,
OF=\' ОМ2 - FM2 = JMR — x)2 — x2, KM = OF — NE = YR*-2Rx - 4 R. О
Из соотношения M\'2 = KN2A-KM2 получаем
\8
xf + |Уяз - 2Rx - A rJ .
2 R
' -\2
Решая эго уравнение, находим
22-2 /21
75---R-
шимся окружности в точках
12.113. Проведем МС и MD перпендикулярно прямым, касаю-А и В соответственно, и ME F АВ (рис. 210). По условию задачи
Рис. 209.
МС = а, MD = b. Заметим, что углы АВМ и САМ равны, как углы, измеряющиеся поло
Рис. 210.
виной одной и той же дуги AM. Следовательно, прямоугольные треугольники ВМЕ и АСМ подобны и
МЕ =
МС-ВМ AM
О)
540
Аналогично из подобия треугольников АМЕ и BDM получаем
DM-AM ВМ
(2)
Перемножая соотношения (1) и (2), находим
ME^ — MC-DM—ab, ME_=]rab.
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ ГЛАВЫ XIII
В приводимых ниже указаниях и кратких решениях часто формулируются без обоснования те или иные утверждения (например, параллельность или перпендикулярность прямых и плоскостей, касание шара с прямой или плоскостью и т. п.). Следует иметь в виду, что
для получения полного решения такие утверждения должны быть обоснованы.
13.2. Искомый шар касается трех плоскостей: ABC, ACD и
данной секущей плоскости, которые образуют боковую поверх-
ность треугольной призмы. Поэтому большая окружность шара вписана в перпендикулярное сечение этой призмы. Следовательно, радиус г шара равен радиусу окружности, вписанной в треугольник MNK (рис. 211), где М — середина ребра АС. Имеем
,.,, ,,,. и7 з , -,, b
MN = КМ=-17— , KN = тг.
4 ’ 2
Следовательно,
23 ww Н/3~-1)
~ KN + 2MN~ 4/2
13.3. Пусть М, N, К, L — центры данных шаров радиуса х. Легко видеть, что MNKL —
правильный тетраэдр, у которого ребро равно 2х, а грани параллельны граням данного тетраэдра ABCD.
Обозначим через О центр шара, вписанного в тетраэдр ABCD.
Радиус этого шара г = ^ _. Заметим, что точка О удалена от граней тетраэдра MNRL на расстояние, равное г — х, и, следовательно, является центром шара, вписанного в тетраэдр MNKL. Радиус этого
шара равен х Г—Х=—^. /6
Отсюда __
_ г |7б _ а Х~1 + /б ~2(1+/Г)’
541
13.4. Пусть DO —высота тетраэдра ABCD, L OAD = a, MNK — данное сечение (рис. 212). Так как прямая ВС параллельна плоскости MNK, то линия пересечения' плоскостей АВС и MNK параллельна
ВС, т. е. MN ВС. По условию задачи К А = у, Z ALK = -j- (как линейный угол двугранного угла между плоскостями КЛ1Л' и АВС).
Из треугольника AOD находим
АО 1 cos а = — = ——, sin а =
AD /3
Из треугольника AKL по теореме синусов получаем
. К А • sin а а
/\ L —
. л 1/3 ’
sin т У 6
' / ЭТ \
АК • sin а + -г- /
\ 4 / а . л , .л
AL =----------5-------- — —= sm а cos -г- 4- cos а sin ~-г
. л 1/9 \ 4 4
Sin
4
«(1 +/2)
2/3
Из подобия треугольников AMN и АВС находим
ВС-AL _а(1+/2Э
АЕ 3
542
Следовательно,
5 — 1 мм тгг _ e20+V^)
Smnk-^MN-KL-----
13.5. Внутри шара лежит часть грани ACD (рис. 213), которая заключена между отрезками DK, DM и дугой MNR окружности с
центром в точке Oi радиуса r = O1D — O1M — OiN, где О —центр шара, 001 ± DE. Таким образом, искомая площадь
S = 6 (501Л1О + S012MJV).
Из подобия треугольников OO^D и DEE находим
Л n 0D • DF 2а
r—01D=------------- ——
DE 3 1-3
Так как треугольник 0]MD равнобедренный (0iM = 0iD) и ^.0iDM=-^< то ZA'1O1D = “™ и zA40!N = -^-. Следовательно,
S = 6 '2 sin v + 4- ягА = (2л + 3 /3 ).
\ X о О I I
13.6. Проведем к шару касательную плоскость, параллельную грани BCD тетраэдра (причем так, чтобы шар и точка А располагались по одну сторону от этой плоскости). Эта плоскость отсечет от трехгранного угла с вершиной А правильный тетраэдр, для которого радиус вписанного шара равен R. Расстояние от центра О шара до точки А равно радиусу шара, описанного около полученного тетраэдра, т. е. равно 3R.
543
Замечание. Опустим из точки О перпендикуляры ОК и OL на плоскость АВС и прямую АС (рис. 214). Тогда из соотношений ОК = R, О А = 3R легко получаем
АК=2К)~2, KB^RA'2, OL = R/T, AL = Rf&.
Эти соотношения удобно использовать при решении следующих задач.
13.7. Пусть О — центр искомого шара, Л' — его проекция на грань ABC, OMj.AB, L —середина АВ (рис. 215). Обозначим ON через г. Тогда (см. замечание к решению задачи 13.6) A4N = r]‘ 2, AM = = г V 6, ОМ = т 3. Очевидно, что ML = j AL —AM ) = — r}6 ,
544
0L = -^ ± г, где знак плюс соответствует внешнему касанию шаров, знак минус —внутреннему. Но OL2 = OM2+ML2, т. е.
(у ±г)2 = 3г2+^_г/б)2.
Решая это уравнение, находим г = ~(]^6 ± 1).
О
13.8. Пусть 0lt 02—центры данных шаров, О3, 04 —их проекции на грань ABC, OtMJ-AB, O2N I АВ (рис. 216). Тогда
ЛМ = 2Я/б, В# = ЗЯ/б, О3М = 2Я/2, О4Л/ = ЗЯ /2 (см. замечание к решению задачи 13.6).
Из трапеций О]О2О4О3 и 0304ЯЛ1 находим
О3О* = (3/? + 2Я)2 - (37? - 2Я)2 = 2Ж
MN = УО3О1-(О^-О3М)2 = R /22.
Следовательно,
ЛВ = ЛЛ1 + Л1Я + ВЯ = (5/б'+ /22) Я.
13.9. Пусть S—середина AC, SK = SM = SW—образующие конуса (рис. 217). Радиус основания конуса является радиусом окружности, описанной около треугольника M.NK. Найдем стороны этого треугольника.
Из равнобедренного треугольника BDS (BS*=DS) находим
cos 4 BDS —
2DS / з
18 В. Г. Болтянский и др.
545
Из треугольника DSM по теореме косинусов находим
19а2
SM2 = SD2 + DM2-2SD -DM - cos Z BDS=~.
Так как SK = SN, то KN || AC и, значит, треугольник BKN — правильный. Следовательно,
ВЕ = УЗ NE, SE = ^^--V3NE.
Из треугольника SNE получаем S№ = NE2-]- SE2, т. е.
^ = ME2+[j-^-V3Ne\ .
г, а (9 ± 7) „ _ а
Решая это уравнение, находим NE—— % , Но зна-
чит, NE — ^%, KN = BN = (Заметим, что знак плюс соответствует
конусу, пересекающему не сами ребра АВ, ВС, а их продолжения за точки А, С.) Из треугольника BMN по теореме косинусов находим
51 13^2
MN2 = ВМ2 + BN2 - 2ВМ BN • cos ~,
3 оо
т. е. MN — KNl—^^-. о
Радиус г. окружности, описанной около треугольника MNK, находим по формуле
W MN2 13а
2 sin Z MKN ~ 2МЕ ~ 6 1/51
546
13.10. Так как прямая ВС параллельна секущей плоскости и принадлежит плоскости грани BCS, то линия пересечения секущей плоскости и плоскости грани BCS параллельна ВС. Отсюда следует, что в сечении получится равнобедренный треугольник где
MN\\BC, AN — AM (рнс. 218). Пусть D — середина ВС, DO н BE — перпендикуляры на секущую плоскость. Так как прямая ВС
Рис. 218.
параллельна секущей плоскости, то DO = BE. Угол ВАЕ является углом между прямой АВ и секущей плоскостью, т. е. Z ВАЕ — ^-.
о
Из прямоугольного треугольника ВАЕ находим
РО = В£' = у.
Для определения площади треугольника AMN найдем АК и MN. Обозначим Z/</4D = a, z KDA = [i. Из треугольника AKD по теореме синусов получаем
АР sin Р _________АР_______
sin (а + Р) sin а ctg £ -f- cos а '
Из прямоугольного треугольника AOD находим
OD 1 1 /’2'
S1" а~ AD ~ /з’ С08а-У У-
Из равнобедренного треугольника находим ctg Р = <“‘ле"
3aV2 ..
довательно, АК = —|—. Из треугольника AK.D по теореме косинусов получаем
KD = УЛ№ + АР*-2АК AD cos a = .
18*
547
Из подобия треугольников SMN и SBC следует, что
BC-SK _a(SD — KD) 2а
SD SD ~ 5 •
Окончательно с 1 л ь- лллг 3]^2а2
$AMN 2 25
Замечание. При решении этой задачи на вступительных экзаменах в МФТИ некоторые абитуриенты допускали ошибки при построении точки Е. Заметим, что точка Е лежит на пересечении прямых BE и ОЕ, где BE || DO и ОЕ || ВС.
13.11. Возможны два различных случая: 1) найти расстояние между высотой SD грани SBC и высотой ВК грани ВЛВ (рис. 219);
2) найти расстояние между высотой SD грани SBC и высотой AN грани ВЛВ (рис. 220).
Первый случай. Проведем Л’Л1 |! ВО (см. рис. 219). Так как прямая SD параллельна плоскости ВЛ1д,то искомое расстояние х равно высоте пирамиды BDK.M, проведенной нз вершины D.
Будем находить х из уравнения
V = -g xSBKA1 = у hSBDM, где V —объем пирамиды BDK.M., Л—расстояние от точки К до плоскости BDM. Так как К — середина ЛВ, то Л = Н, где Я —высота тетраэдра ВЛВС, т. е.
548
Далее, так как К.М. [| SD, то М — середина AD, и, следовательно,
Sbdm^^BD.DM = ^-.
Для нахождения площади треугольника ВК.М вычислим длины его сторон. Имеем: ВК=^~3 , KM=~SD = ?^-I ВМ = = УBD2A-DM2= а . По формуле Герона находим
с а2/5
г>ВКЛ1= 16- •
Следовательно, ^вом а x = ~q------------------------=
SBKM V10
Второй случ'ай. Проведем NL || SD (см. рис. 220). Так как прямая SD параллельна плоскости ANL, то искомое расстояние у равно высоте пирамиды ADNL, проведенной из вершины D.
Будем находить у из уравнения
1/1 ~'3' USANL = ~3 /lSADL> где Vi — объем пирамиды ADNL,
Л = тУ4- Sadl = ~AD.DL=^-
(4 —середина BD, так как NL || SD).
549
Для нахождения площади треугольника ANL вычислим длины его сторон. Имеем: Л^=?p| NL = SD =а , AL — = A D2 -j-DL2 = , По формуле Герона находим
о а2 /35
^ANL = ~32 •
Следовательно,
,lSADL = а/2
SANL V35 ’
13.12. Пусть О —центр данных сфер. Так как точка О равноудалена от вершин А, В, С тетраэдра SABC (рис. 221), то она расположена на высоте S7< тетраэдра или на ее продолжении. Из точки О
опустим перпендикуляр ОМ на грань SAB. Этот перпендикуляр лежит в плоскости треугольника SCD, где D — середина АВ. Дано: OM=r, OC = R.
Из подобия прямоугольных треугольников ЗОЛ1 и SKD с общим острым углом KSD находим
SO _SD
МО RD ’
т. е. SO = 3r.
Обозначим АВ через х. Тогда КС = ~=
= \SK-SO[= хЛ/ --Зг . Но КО2 + КС2 = ОС2, т. е.
вд=
550
Решая это уравнение, находим
х = гУб ±]/>2 —ЗА
(1)
Теперь нужно определить, какой знак следует выбирать в формуле (1) в зависимости от соотношения между R и г. Во-первых, выражение (1) должно быть действительным. Значит, должно выполняться неравенство
R2 — 3r2=s0, т. е. /?Ssr]/"3.
Далее, заметим, что по уеловию задачи сфера радиуса г должна касаться боковых граней тетраэдра, т. е. должно выполняться нера-х 3
вепство SM s^SD. Но SD = ——, а из прямоугольного треугольника
SOM следует, что ЗМ = 2гУ2. Таким образом, должно выполняться неравенство
(г У 6 ± //?2-Зг2) А 2г У 2,
т. е.
2 У2
Значит, в формуле (1) следует выбрать знак плюс. Итак,
х = гУ1+У R2 — 3r2.
13.24. Пусть К — середина высоты SO правильной треугольной пирамиды SABC (рнс. 222), КМ LAS, KN \_DS. Дано KM=h, KN = b. Обозначим
Рис. 222.
OD = x, OS —у. Из подобия треугольников SNK и SOD получаем
ху 4- У2 — № =by. (1)
Из подобия треугольников SMK и S/IO имеем
2х']/'-^у2-Л2 = /и/. (2)
Решая систему уравнений (1) —(2), находим
ЬЬУ'З 2ЬЬУЗ
/г2 — 62’ У~ /462 —Л2‘
Следовательно, .. 1 , о а. i/Г 1863Л3
5ДВС= з АВС х (№ — Ь2)У4Ь2—Ь2
551
13.25. Пусть АВ = а— сторона основания пирамиды SABC (рис. 223), SO —высота пирамиды, плоскость АСМ перпендикулярна ребру BS, £BDS = x. Тогда £АМС=а,
АМ =-----,
„ . а ’ 2яп-2
00 = -/-, SD = —^--
2/3’ 2/3 cosx
AS—Л/ а2 I а2
6 V 4 + 12 cos2/
Площадь треугольника ABS равна
4- AM BS = ±-AC-SD,
2
т. е.
1
. а sm-
1 __ 2
3cos2x j/з cosx
Решая это уравнение, находим
. / 2 а \
х= arcsin / —— cos — ,
\/3 2 /
2 а
sin х=cos , следовательно, уз *
13.26 . Окружность верхнего основания цилиндра вписана в треугольник ДтВхСу, который получается в сечении данной пирамиды SABC плоскостью верхнего основания цилиндра (рис. 224). Пусть SO—высота пирамиды, АВ = а, OiD^r. Тогда
ОО) =2г, S0 = C0 = -4=,
/3
552
но SO — SOf]-O1O = C1O1 + O1O=4r. Поэтому а = 4/3г. Следова-
тельно, Уц = 2лгЗ, Уп = 16/3/3, =
Vu л '
13.27 . Пусть SK — высота данной пирамиды SABC (рис. 225), О—центр шара, ОМ I BS, OM = OD—r.
Заметим, что ВМ — BD = , как две касательные к шару, проведенные из точки В. Из подобия треугольников SOM и SBK находим
/ а\ а
f~0M~SM.BK \ S'W а(2/-а)
SK
13.28 . Пусть О—центр шара, OD I BS, OA=OD = r, DE и SK— перпендикуляры плоскости АВС (рис. 226). Заметим, что BD = AB — = а, как две касательные к сфере, проведенные из точки В. Из подобия треугольников BDE и BSK находим
ВК • BD _ а2
be=-bs~—^-
Из треугольника АВЕ по теореме косинусов получаем
Л£2=4В2 + ВВ2—24В • BE cos 4 = а2 - -4- ~.
6 6 Зо2
553
В трапеции AODE углы при вершинах А н Е прямые. Следовательно, ОР2 = Д£'2 + (ДО-£>£)2, т. е.
Рис. 226.
Решая это уравнение, находим
г_ а(2Ь-а)
2 j/" *2- у «2
13.29 . Легко доказать, что центр шара О лежит на высоте SD пирамиды SABC (рис. 227). Проведем OL X ВМ. Обозначим OL — — OD = r. Заметим, что BL = BD=-^~ как две касательные к ша-/3
ру, проведенные из точки В. Медиану ВМ найдем из соотношения (2В/И)2 +Д52 = 2ДВ24-2В52.
Из прямоугольного треугольника ASD находим
/3
554
Тогда
BM=~t ML = BM-BL = — /з’ у у
Из прямоугольного треугольника MOL находим MO2 = r2+ 1 а2.
Из треугольника MOS по теореме косинусов получаем
MO2 = MS2-\-OS'2 —
— 2MS OS cos / MSO.
Ho SO = SD — OD — аУЗ—г, а из треугольника ASD находим
cos Z /WSO = ?f =-4^.
Следовательно,
~ , 1 , 10a2 i <— \2
r24--a3 =------Ma]/ 3 — r) —
3 12
2/3 /10
Решая это уравнение, находим
_ а
Г~2УЗ'
13.34. Показать, что abc = 2hS, где
S = у /а2&2+а2с2 + ЬЧ2
— площадь основания данной пирамиды (см. результат задачи 13.33).
13.35. Показать, что сфера, описанная около данной пирамиды,
описана около прямоугольного параллелепипеда с ребрами BS и CS.
13.36. Пусть ABS— боковая грань данной пирамиды, где АВ — гипотенуза основания. Доказать, что 2.SAB = Z.SBA =|3 и что радиус сферы, описанной около данной пирамиды, равен радиусу окружности, описанной около треугольника ABS.
13.37. Воспользоваться результатом задачи 13.36 и доказать, что в данной пирамиде высота, опущенная на основание, совпадает с высотой SD треугольника ABS (см. указание к задаче 13.36).
13.38. Доказать, что в данной пирамиде боковые ребра образуют с основанием равные углы, и воспользоваться указанием к задаче 13.37.
655
13.41. Показать, что центр шара, описанного около данной пирамиды, лежит в точке пересечения плоскости, перпендикулярной к ребру 8Д, проведенной через его середину, и перпендикуляра к плоскости АВС, проведенного через центр окружности, описанной около треугольника АВС.
13.42. Пусть О —середина ВС. Тогда ДО —высота данной пира-
1 Уз
миды. Обозначим AD через х. Имеем BD = —, SD = ^-g-, Д8 =
= у Из треугольников ABD и ДВ8 (по теореме косину-
сов) получаем
ДВ2 = ;С2 + 1=1+^+|\_у\2+|.
i/"3~
Решая это уравнение, находим х = 2_—. Следовательно, /2
1 У2
VSABC~ У xSBCS = ~g~ (СЛ|3)-
13.43. Пусть О—центр шара, вписанного в данную пирамиду ABCD (рис. 228), ОК —г — его радиус, АВ — гипотенуза основания ABC, OL X АВ, ОМ X ВС, ON j_AC.
Так как центр шара, вписанного в пирамиду, лежит на пересечении биссекторных плоскостей двугранных углов, образованных
556
гранями пирамиды, то Z.OMK = ~, Z.ONK = ^, AOLK=^. Сле-довательно,
/GW = rctg-^-, KN —г ctg A KZ, = rctg-£.
Площадь треугольника АВС равна
у /2 = у (ВС • КМ + АС • KN + А В • KL) =
=i (й '”** I+ЙI+*'cls i)1 откуда
г_____________I____________
2 ctg -|- + /2^ctgy 4-ctg -j-j
13.44. Пусть CM J. AB, MN J_ CD (рис. 229), К —центр окружности, описанной около треугольника АВС, КО ± СМ. Легко
видеть, что точка О—центр шара, описанного около данной пирамиды, ОС — радиус этого шара. Имеем
DM = СМ = УДС^—АМ*=/65,
М N = /СЛ42 - С № = 7.
, г. abc „„ 37
По формуле К=— находим КС = ——, откуда
4S у 65
'MK=CM-KC = -^L.
/65
557
Из подобия треугольников МОК и MCN получаем
16
W /§5'
Следовательно,
ОС = /0№+/СС2 = 5 (см).
13.45. Пусть О —середина ВС, О —центр шара, описанного около данной пирамиды (легко доказывается, что он лежит на прямой AD),
0.4= ОС —его радиус, ОМ I DS (рис. 230). Тогда Л! —центр окружности, описанной около треугольника BCS. Из треугольников KDS ^по условию задачи угол KDS равен и SCD находим
SD = hVr2, SC^J/^^+^a2.
Из треугольника MCS получаем
5Л] sC . п2 + 8/г'2
2 cos Z DSC 2SD 8h /2 ’ откуда
яьа — Q2
DM = SD-SM = “
8ft/2
Из треугольника OMD находим
___ 8A2__a2
Sh
Следовательно,
ОС = /OD2 + CD2 = ~ /a4 + 64/i4 .
558
13.46. Пусть D — середина АВ (рис. 231). Из условий задачи следует, что SCD — равнобедренный прямоугольный треугольник, SD = = AD — R, SCD —биссекторная плоскость двугранного угла SC, центр О сферы, вписанной в трехгранный угол С, лежит в плоскости SCD.
Проведем OK I CD, OF | SD, FM I AS, KL _L CS. Обозначим OK = FM=x. Имеем LE = SF — FM /2 = x/2, EE-==zy^ 0K~ = x, Зх
= Z-/f=L£' + £'K==yy’ Ctf = C/C/2=3x, CD = SD/2 =
— R /2. Очевидно, что DK = | CD — CK | = | R /2 — Зх | (точка К может лежать на продолжении CD), 0D = |7?±x|, где знак плюс
А В
Рис. 231. Рис. 232.
соответствует внешнему касанию сфер, знак минус —внутреннему. Из прямоугольного треугольника KOD получаем OD2 = O№4-7<D2, т. е. (7? ± х)2 = х2 + (Т? У2—Зх)2. Решая это уравнение, находим х= (з /2 +1 ±У 10 + 6/2) и х = £ (3/2‘-1±'/10-б/1).
У У '
13.47. Проведем сечение А1В1С1 пирамиды ABCD плоскостью PiQi^iNi (рис. 232). Это сечение параллельно грани АВС. Проведем CiDj X А^. Обозначим ребро куба через х. Тогда высота пирамиды AjBjCjD, проведенная из вершины D, равна с—х. По теореме о параллельных сечениях пирамиды получаем
А1В1 _С1Е1 _с—х
~АВ~ СЕ ~"
~ Л D а (с— х) Ь(с — х)
Отсюда находим Л1В1=—---, С1Е1 = —------Из подобия
559
а (с—х)_ b (с—х)
сх b (с—х)—сх
,, АТ ^1^1 Cl/?!
и М^С1 получаем = ^-1-1-, т. е.
Решая это уравнение, находим
13.48. Прежде всего следует доказать, что четыре ребра куба параллельны АВ и четыре ребра куба параллельны CD (рис. 233).
Обозначим через К и L точки пересечения прямой MN с плоскостями граней куба, KL = x, КМ—у, NL—г. Тогда х-\-у-\-г—с. Плоскость ABN параллельна некоторой грани куба, так как MN и АВ параллельны некоторым ребрам куба. Следовательно, прямые AN и BN пересекают ребра куба соответственно в таких точках Е и F, что ЕЕ=х и EF || АВ. Из подобия треугольников EFN и ABN находим EF LN х г сх
___ ____ Т Р -— 7
АВ MN’ а с ’ а"
Аналогичными рассуждениями из треугольника CDM (ои на рисунке СХ
не указан) находим у=. Подставляя найденные выражения для у
и г в уравнение х-\-у-\-г—с, получаем 0ТКУда
13.56. Пусть О—центр куба, а—ребро куба, SC=h — высота пирамиды, х—сторона основания пирамиды (рис. 234). Так как по условию задачи нижнее ребро куба лежит на CD, а центр куба — на 560
высоте пирамиды, то верхнее ребро куба параллельно CD и лежите плоскости SCD. При этохМ верхнее ребро куба пересекается с высотой пирамиды SC в точке М, которая является серединой верхнего
ребра куба. Имеем
MN = ~a, СМ=аУ2,
SM = h~a)'2, ВО = ОС =
Из подобия треугольников SBO и Sx4C получаем
ВО _ SO АС ~ SC ’ т. е.
а 1'<2 „ h I2 — а ,п х h Г 2 ’
Рис. 234.
Из подобия треугольников SMN и SCD получаем ==—— , т. е.
а /1-аУ2
х Л 1 '
Из системы уравнений (1) —(2) находим значения х = а(2| 2— 1), , ° /о , Q ‘и x2h 19 У2 .
h — -^- (2 + 3 J/2). Следовательно, =—--------I.
“ ’К 'dCI О
Рис. 235.
13.57. Пусть О — центр шара, описанного около пирамиды SABCD (рис. 235), OS = О A =R — радиус этого шара, SK—высота
19 В. Г. Болтянский и др.
561
пирамиды. Проведем SE j_ ВС, ОМ 1 SE, ON 1 4S. По условию задачи ОМ=а, ON — b. Из подобия соответствующих треугольников a KE b АК V2KE „
получаем = SK ~ ~SK~' СлеДОВательио,
b а У 2 п ab
>___ . - ~ ----- . откуда R = .
)/А’а--/>- Т'/?2-а2 /За2-*2
13.58. Пусть О —центр шара, вписанного в пирамиду SABCD (см. рис. 235), £/< — высота пирамиды. Проведем SE J_ ВС, ОМ X SE, ON 1 /45. По условию задачи ОК = У2, ОЕ = ]/5. Обозначим ОМ —
— OK = r, OS—x. Тогда /<£ = ]Л5— г'2, АК =]/2]/5 — г2. Из подобия треугольников SOM и SKE получаем
x-j-r _ Ух-—г'2 УУ^У ~ г
Из подобия треугольников SON и SAK получаем
(2)
Задача свелась к решению системы (1) —(2). Из уравнения (1) возведением в квадрат находим
х2 (5 — 2г2) — 2хг3 — 5г2 = О,
г2 + (г2 —5)
х — т —„ а-.,--.
о — 2г2
Так как х > 0, то х=?—Вычитая из уравнения (1) уравнение
(2), получаем г Ух'2 —2 —У х2 —г2, откуда х =
. Следовагедь-
5 . 1
н°, 5—Ий ~ Решая это
<J I/ yi —. j
13.59. Прежде всего отметим, что точка пересечения диагоналей четырехугольника SAC, т. е. лежит гольников получаем
У 5 уравнение, находим г= ~ (см).
в плоскости SBD и в плоскости
SAC и
KLMN лежит на высоте SO пирамиды. Из равнобедренных треу-SBD (рис. 236), применяя результат задачи 12.49,
ОР _ SP
откуда
СК \ _ 1 fBN SK1~~ 2 \SN
DL ^т-п+р.
13.60. Пусть О! и О2 — центры данных шаров (рис. 237). Так как пирамида правильная, то точки О, и О2 лежат в плоскости треугольника S4C, причем точка Ot лежит на высоте SK пирамиды,
562
а точка 02 —в биссекторной плоскости двугранного угла АВ. Проведем SD 1 ВС, ОХЕ 1 SD, О2Ь\\АС, О2М 1 AC, O2N 1 АВ. Тогда по теореме о трех перпендикулярах MN J. АВ и угол O2NM. равен
половине двугранного угла между основанием и боковой гранью пирамиды, т. е. / O2jVA1 = ~ Z /\DS-
Обозначим SD через х. Из условия задачи следует, что KD — = ~ х и = Значит, /.О3УУЛ1 = ~-. Из треугольника
O2NM получаем
MN—О2М ctg-g- =2гКз,
19*
563
а из треугольника AMN имеем
АМ = ММУ2 = 2г /б.
Следовательно,
O2L = MK ~АК — AM — ~^= — 2л/6. /2
/ Лг \
Из треугольника SOjE ^Z OjSE = jy находим
O1S = 2OlE = 2r.
Следовательно,
О У =SK- SOt— K.L = - Ar.
Ho OxOs^OiP + OaL3, T. e.
9r2 = (£p_4ry + ^ _2r j/б'у. \ 2 / \/2 /
Решая это уравнение, получаем
х = ~(8 УЗ ± /37). О
По условию задачи шары лежат внутри пирамиды. Значит, должно выполняться неравенство т. е. Из найден-
ных значений для х этому неравенству удовлетворяет только
х = ~(8УЗ + У37).
13.61. В сечении данной пирамиды получается четырехугольник АМК-У (рис. 238), диагонали которого перпендикулярны. Его площадь равна
$сеч = 4 ЛК-MW-
Опустим перпендикуляр ВР на плоскость сечения. Тогда угол ВАР является углом между прямой АВ и плоскостью сечения. По
Л 11
условию задачи z ВАР=~. Значит, ВР--= --- АВ= ~^-а. Из центра основания пирамиды опустим перпендикуляр OL на секущую плоскость. Так как прямая BD параллельна секущей плоскости, то OL =
= ВР , Из прямоугольного треугольника AOL находим
. , , л Е 1 г , л
sin Z LAO = - - = ---, Z LAO = ,
АО у 2 4
откуда
ЕО = АО = ~, SE = SO-EO = ~~. УУ У2
564
Из подобия треугольников SMN н SBD находим
BD-SE _ За/2 SO 4
Обозначим угол АСК через а. Так как угол КАС равен — ( то из треугольника АКС по теореме синусов получаем
AC sin а _ ]''2ЛС
~~ ! , л \ — 1 + ctg а ’ sm । а + 1
\ 4/
ОС 1
Из треугольника SOC находим ctga=^ = —, Следовательно, о С/ 4
о _3/2 2
АК , ^сеч— й
13.62. 1) Рассмотрим случай, когда сечение проходит через диагональ основания АС (рис. 239). В этом случае в сечении получается равнобедренный треугольник ALC. Найдем радиус г, окружности, вписанной в этот треугольник. Из прямоугольного треугольника SPB, где Р — центр основания пирамиды, находим
DC РВ
cos L SBP~
__ РВ 3b
{ 2 \ ~ 21/2'
cos (arccos у I z Г -
Так как PL || BS, то PL — средняя линия в треугольнике SBD. Следовательно,
PL = ^BS^~=, 2 4/2
AC-PL _6/2 ri~AC + 2AL ~-
2) Если секущая плоскость пересекает диагональ основания BD в точке, лежащей между точками Р и D, то в сечении получится треугольник, подобный треугольнику ALC, причем стороны этого
565
треугольника соответственно меньше сторон треугольника ALC. Радиус окружности, вписанной в такой треугольник, меньше г\ и может быть любым числом между нулем и /д. Таким образом, любое число г, удовлетворяющее неравенству
о<^ф, о
является решением задачи.
3) Рассмотрим случай, когда секущая плоскость пересекает диагональ BD в точке Q, лежащей между точками В и Р. Тогда в сечении получится такой пятиугольник EFMNK, что в него можно вписать окружность. Пусть О —центр этой окружности, г — ее радиус.
Докажем, что MN — ON. Проведем OG 1 MN и ОН Д MF. Прямоугольные треугольники OMG и ОМИ с общей гипотенузой ОМ равны, так как OG — ОН — г. Значит, L МОН=А MOG- откуда
Z NOM = Z NOH-L МОН = ~ - L MOG.
А из прямоугольного треугольника OMG следует, что
Z OMG - L MOG = Z NOM,
t. e. треугольник OMN равнобедренный н MN —ON.
Из подобия треугольников DNQ и BDS, учитывая, что BQ — = QF = г, находим
DU 4
566
откуда
ON = QN - OQ = у (3& /2 - 7r).
Из подобия треугольников MNK и ALC находим (см. случай 1))
/1 С. 4
Ь 12
Из равенства MN = 0N получаем теперь r = —j—•.
13.63. Обозначим высоту SF
Тогда AB = ~^h,
пирамиды через Л (рис. 240).
3Осн=4Ла’
2ТЛ2 h
(Q —середина ВС),
SQ = У+ = _JL h.
2)2
Радиус шара, вписанного в данную пирамиду, является радиусом окружности, вписанной в треугольник SPQ, где Р —середина AD (этот треугольник на рисунке не указан), т. е.
. . PQ-SF 1 PQ+2SQ “ 4п'
В искомом сечении данной пирамиды получается четырехугольник AMNK., диагонали которого перпендикулярны. Его площадь
567
равна
Sce4 = ~KM-AN.
Пусть О — центр шара, вписанного в данную пирамиду, ОЕ 1 ЛУУ. Прямоугольные треугольники АОЕ и AOF равны, так как они имеют общую гипотенузу АО и OE = OF = r = ~/i. Значит, Z ОАЕ =
= Z OAF. Обозначим Z NAC — a, Z ЛСУУ = р. Тогда Z OAF—
Из треугольника A OF находим
9 t а
a OF 1 2tgT 4 4 3
tg 2~AF 2’ tga- а ~ 3 ’ Sln а “ 5 ’ C0S 5 ’
l-tgsy
Из треугольника ALF получаем
LA-ЛА tga-y h\ значит,
SL = SF-LF = y h.
Из подобия треугольников SKM и SBD находим
KM^
BD-SL SF
Из треугольника HCW по теореме синусов получаем
AN =
AC sin р _____ h
sin (а + fi) — sin а ctg р -f-cos а '
Из
FC 1 треугольника SFC находим ctg р = . Следовательно,
1 14 1
ДУ=Л, Sce4^i-KM AN= ^h\ 1^ = 4-.
Z О ^осн
13.65. Из условия задачи следует, что цилиндр касается грани SAD по образующей EF, где Е — точка касания ребра SD с окружностью основания цилиндра (рис. 241). Плоскость другого основания цилиндра пересекает грани SAD и SAB по прямым MN и 7И/С соответственно. Эта плоскость параллельна прямым SD и АВ. Следовательно,
МЛ'сЗО, Л1КЦДВ и МЛ'=2гг
где г —радиус окружности основания цилиндра.
568
Из прямоугольного треугольника SCD находим
г = L (а + h _ + M
Обозначим EF — DN = x. Из подобия треугольников AMN и ASD получаем
2г _ а — х h ~ а ’
откуда
х = а (1 — ~ ~ (Ка2 + Л2 — а)-
\ h I п.
S
Л В
Рис. 241.
13.66. В сечении данной пирамиды получается четырехугольник AM.NK (рис. 242), площадь которого S = ~MK-AN. Проведем NE [ АС. Так как SN:NC — 2:1, то из подобия треугольников CNE и СЛЗ находим
NE = ~h, ДЕ=~ АС = И^1.
Следовательно,
AN = /Д£2+^2= у
Проведем OL Л AN. Так как О —середина ДС, то L — середина CN, откуда
NL=~NC = ~- SC, 2 6
S№ SL = Т sc : f-f--SC + 4-SC') = 4 : 5.
О \ О 6 /
569
Из подобия треугольников SPN и SOL получаем SP: SO = SN:SL = = 4:5, а из подобия треугольников SMK и SBD находим
О D
Следовательно,
$=1 МК AN
/16аа + 2Л3.
13.67. Решение эюй задачи аналогично решению задачи 13.66.
13.68. Пусть а —сторона основания данной пирамиды, li — апофема пирамиды. Показать, что в сечении получается равнобочная трапеция, у которой основания равны 2« и а, а высота равна ~-h.
Тогда плошадь боковой грани S = -~ah, площадь сечения
е 5 , S, 5
Sx- 8 ah, s _.-4 .
13.69. Пусть SO —высота пирамиды, .4S н &S —данные боковые ребра, SO = x. Тогда АО — Уа2 — х-, ВО~Уьг — х2- Из треугольников ABS и АВО по теореме косинусов получаем
АВ- = <Р + 63 - ab = (а3 - х3) + (&2—л'2) К(а3-х3) (ZP-x3).
Решая это уравнение, находим
х — -1 У4аЬ — а2 — Ь2.
УЗ
13.70. Пусть SO —высота данной пирамиды. Из условия задачи по теореме о трех перпендикулярах следует, что углы ОАВ и ОСВ 570
прямые, а
SO = ]rBS2 — ВО2 = У" I'2 — вог.
Рассмотрим четырехугольник АВСО (рис. 243). Проведем АЛ4 J_ ВС, ON I ДЛ1. Имеем
ВМ ~ А В cos у = ~ а,
NO — MC — BC — BM — b—-^-a,
АО sin ~ I 3
ВО2 = А В2 + А О- = ± („2 _ ah j_ щ _
Следовательно,
13.71. 1) Рассмотрим случай, когда центр описанной сферы (точка Oj лежит в центре основания пирамиды (рис. 244). Пусть О — центр сферы, вписанной в пирамиду. Проведем апофемы пирамиды 5Л4, SN и OR I S34. Обозначим OiS = OiB = /?, ОО1 = ОД' = г. Из правильного треугольника АВОХ находим
MO^’—BO^—R.
Из треугольника SAlOi находим
М S = /AfOj’ + SOI = тг Я.
571
Площадь треугольника SMN равна
-i Л4Л/ • SOx = у г (MN + 2MS),
т. е.
/?2/з = г(/?)/з + /?|<7)1
Отсюда
2) Рассмотрим случай, когда
Рис. 245.
Из подобия треугольников SOK и
центр описанной сферы лежит в точке О2 на высоте пирамиды SOX, так что ООХ = ОО2, где О — центр вписанной сферы. Обозначим OsS = O,B = R, OOl -OK — = r. Из треугольника ВО/К
находим BOt--
= |ZP2—4r2- Тогда
l/З r_______
Л4Ох = ~Ч<Р2-4г2.
Из треугольника S/<0 находим
S/< = ] 'SO2 - KO^\'R- + 2rR.
SMOt получаем
Л1О1 SOt
KO ~ SK’
t. e.
ГЗ| - I;2 R0-2r
2r ~
K#4-2r
l-'R
Сокращая это уравнение на ]/~R + 2г, после возведения в квадрат и упрощений получаем
-6 — -4 = 0,
и так как
13.73.
R „ К ,, -1/ 7
— >0, то —=1+ I/ —, г г у 3
Рассмотрим сечение данной усеченной пирамиды плоскостью, проходящей через ребро ВВХ н точки D и Оъ которые являются серединами ребер АС и Л/Л соответственно (рис. 245). Пусть О и 01 — центры оснований пирамиды, DM BDlt В^К I BD1 и DtK I BD. По условию задачи
= DM = m, BiN = n.
572
Из подобия прямоугольных треугольников B1D1W и BDM, У которых углы Bj^DjN и L)Blvi равны, как накрест лежащие при параллельных прямых BD и BjOj, находим
п г, — BD ' Biyv bn /3
2 1
Так как ВО~~х- BD, 01£>1 = —- ВгГ)ъ то о о
В7< = ВО + OjDx = -4 {1 + ~ V
>3\ 2'«
Обозначим ООг через Н. Площадь треугольника BDD1 равна
± BD-Drf^ — BD^DM,
откуда
Но BDj^D^ + BK2, т. е.
3&2№ _ !А ’ п_\2
4/п2 ~ 1 3 2т/
Отсюда b (n-t~2in)
77 ==У’962 - 12/г2‘
Рис. 246.
13.74. Пусть 0 и О1~ центры оснований данной усеченной пирамиды, DD, —ее апофема (рис. 246). Обозначим АВ = х, Л1В1 = !/. Из трапеции ЛЛ1О1О находим
DD‘i = AAi- (AD- A.D^ = Z2 - | (х-у^.
573
Шар, вписанный в пирамиду, Касается оснований пирамиды В точках О, 01 и касается апофемы L)Z)h. Следовательно,
OOj-OO+OiO^ii^.
2J<3
Отсюда
(!)
Грань ВВ^СуС пересекает шар, касающийся всех ребер пирамиды, так, что в сечении получается окружность, вписанная в трапецию BBjCfi. Значит,
BC-L-BiC^BBi-i-CCt, х+у = 21. (2)
Решая систему уравнений (1)—(2), находим
! I Г~2\
13.75. Пусть /г—высота данной усеченной пирамиды, I — средняя линия боковой грани. Показать, что
h - , S-2) 'НЧ = 1/ В +1 Sf.
I | 2 r z
Тогда искомая площадь
s = ^=j/s?-lsf.
Рис. 247.
13.76. Данные секущие плоскости d/ljCjC и BA^Dfi пересекаются по прямой Л]С (рис. 247). Пусть О— центр основания пира
574
миды. Так как пирамида правильная, то ВО —перпендикуляр к плоскости A.4hChC. Проведем ОК ± АХС. Тогда по теореме о трех перпендикулярах ВК J_ AjC, т. е. угол ОКБ равен углу между секущими плоскостями, и по условию задачи £ ОКБ = Из прямоугольного треугольника ОКБ получаем ОК = ВК -cos а. Проведем AM _L AjC. Так как О —середина АС, то ОК является средней линией треугольника АМС, т. е. AM = 2ОК = 2ВК cos а. Отсюда
с = 1 .4ХС АМ = • ВК • cos а == SABC • 2 cos а.
Аналогичными рассуждениями доказывается, что
Следовательно,
SjjCC, -~$Д1СОХ ’ 2 cos а.
^лл,с1с=='5д1о1св ’ 2 cos а,
т. е. отношение площадей данных сечений равно 2 cos а.
13.77. Пусть К и Ki — центры оснований усеченной пирамиды ABCDAjBtCjP!, О —центр описанного шара (рис. 248). Так как
пирамида правильная, то точка О лежит на прямой КК1- Пусть точка 0 находится вне пирамиды. Обозначим АВ = х, AiB1 = y (х>у), OA=OA1 = R. Опустим перпендикуляр ОР на плоскость ABBjAj. Легко видеть, что точка Р является центром окружности, описанной около трапеции АВВ1А1, и лежит на прямой EEt, соединяющей середины АВ и А1В1. По условию задачи
х—у=а, KKi=h, ОР=^=°-А,
У 2 у 2
Следовательно, А1Т’=АР = —= (из прямоугольного треугольии-У *
ка ОАР).
51Ь
Так как АК.= ~^= = Л~, ОА = ОА,=Я, то из равенства
/2 ’ У 2
OKi — OK = K.Ki получаем
Ф-^у*~У R*-^x2=h. (1)
Из трапеции КЕЕУКЛ находим
£Е1 = |/ Л2
'^;' = ]/АЗ + Та2
Из равенства EtP-J-РЕ = ЕЕг получаем
У ~ У“ + ]/^R2~ j х2 = уГ 2h2 -F 1 а2
(2)
(предполагается, что точка Р
В Рпс. 249.
находится внутри трапеции АВВ^).
Умножив (1) на (2), получаем
x2-y2 = 2h jA/P-j-la2 . (3) Решая систему, состоящую из уравнения (3) и уравнения х— У —а, находим
+ + ±а,
У = у |/Г2/Р- + у а2 - а.
Замечание. Если предположить, что точка О находится внутри пирамиды, то в левой части уравнения (1) получится сумма корней вместо разности, и тогда из (1) и (2) Л= |/ 2/г2а2, что невоз-
Т 1 2
можно. Аналогично показывается, что точка Р не может находиться вне трапеции ABBjAj.
13.78. В сечении данной усеченной пирамиды получается шестиугольник BCMLQN (рис. 249), площадь которого S = S1-|-S2, где Sj —площадь трапеции BCMN, a S2~площадь трапеции MLQN. Пусть Ри Р} — центры оснований пирамиды, К и f(i — середины сторон ВС и QL. Так как пирамида правильная, то прямые ММ, РРг и
MKi пересекаются в одной точке О-
576
По условию задачи L ОКР = OKiPi = a, QL — a, ВС = За.
Следовательно, р% =-а^ -, ОК1 =
= — . Из подобия треугольников ОКР и OKjPi получаем
Л COS ОС
0Л„Л/<1= 1 ор рк з •
Проведем DtF J. AD. Обозначим через Е точку пересечения прямых
MN и D1F. Из подобия треугольников Г\ЕМ и DXFD получаем
ЕМ DXE OPt _ 1
FD ~ DyF ~ OPl + OP' 4 '
Но FD = PD — Следовательно,
EM=a-t OM^P^+EM^,
1Л3
MN = 3a—BC, S^OK BC- ^-P~l 2 cos a ’
S2=yOK1(.'W1V+QZ.)=^1 Z. Lvb C4
13.83. Так как сфера проходит через середины ребер ААг и ВВ±, то центр этой сферы (точка О) лежит в плоскости EEi/\F, перпендикулярной ребру АВ и проходящей через его середину (рис. 250).
577
Кроме того, точка О лежит в плоскости Р, перпендикулярной отрезку ЛС\ и проходящей через его середину К (плоскость Р на рисунке не указана). Заметим, что точки Ех и F принадлежат плоскости Р, так как каждая из этих точек равноудалена от концов отрезка Следовательно, прямая E{F является линией пересечения плоскости Р с плоскостью EEjF^F и точка О принадлежит прямой EtF. И наконец, так как сфера проходит через точку А и середину ребра BBlt то точка О находится на прямой MN, проведенной
= = -^а. Проведем KL J_ MN. Имеем
KL = ~a, OL — KL = ~a, 4 4
Радиус сферы АО находим из прямоугольного треугольника АОК
/а X
13.84. Плоскости AEFJ)^ и A-fi^D пересекаются по прямой MN, где /И — центр грани ADD^A^, а А? —центр грани (рис. 251).
D
Рис. 251.
Из середины К ребра AtD^ проведем KL 1 MN. Легко видеть, что угол A^LDx является линейным углом искомого двугранного угла и Z. Д1Д£>1 = 2 д KLD^ Имеем
K(V=|, км=Л, «о1=4. i it
578
Из прямоугольного треугольника KMN Находим
KM-K.N
KL ~ MN
ас
ТУа^с*'
Следовательно,
ig^KLD^-^
b \а- + с3 ас
AJ.Dj = 2 arctg
b |'rcsH-c4
ас
13.85. Пусть О —центр куба. Продолжим прямую O.W до пересечения с продолжением диагонали DB в точке Л’. Так как точки А и .V принадлежат секущей плоскости и плоскости ABCD (рис. 252),
Рис. 252.
то прямая AN является линией пересечения этих плоскостей. Проведем OL J AN и OK J_BD. Тогда по теореме о трех перпендикулярах KL ± ЛЛ', т. е. угол OLK является линейным углом искомого двугранного угла.
Обозначим ребро куба через а. Имеем
<ж=4. вк=-^=.
2 ’ 3 р 2
Из подобия треугольников BMN и NON получаем
BN _ BN + BK вм ~ ок
откуда
BN=a]'r2, KN^BK + BN = -^=, AN = /Л№ + О2 = a /5 .
579
Из подобия треугольников KLN и AKN находим
AK-KN За
AN 2 Кб '
Следовательно,
ОК Кб
Z OLK = arctg ~ = arctg Ц—. '
1\L о
13.86. Пусть Olt О2 и О3 —центры шаров, г — радиус первых двух шаров, R — радиус третьего шара (рис. 253). Точки Ot и 0.2
лежат в плоскости /I/IjCjC, так как ABCD — квадрат. OiM ± AC, O2N ± AC, ME ± АВ. Тогда
Проведем
MO1 = ME = r,
AM=CN = rV2, O.JV=4—r, О1Р2 = 2г, MN = yOiOS-lOtN-OrMy- = 4 Кг — I •
Подставляя найденные значения величин AM, MN, CN в соотношение AC = AM + MN + CN,- получаем 5 |/Z2 = 2r К2 -j-4 \Ar — I, откуда I 3
r = -y (7 * 4). Так как OtM < т. e. г < 4, то r = y.
Из условий задачи вытекает, что точка О3 лежит на перпендикуляре к прямой ВВГ, проведенном в плоскости через сере-
дин}' К отрезка ВВг. Проведем O3L ± BD. Тогда
BL — 03К—O3L — -g- В Bi — 2, О2О3-—К zL г
580
(знак плюс соответствует внешнему касанию шаров, минус — внутреннему). Из трапеции MO]O3L находим
Л4^ = О1О5-(ОзД-О1М)2 = ^± у) -т,
а из треугольника MFl(MF MN = V2j
! Ч \8
MLa-=MFa-+LF2 = 2 + [^=-R\
\/2 /
Отсюда
Q \ 2 1
__1 = 2+
2 4 1
\V2 У
Решая это уравнение,
получаем
R = . 25 - .....< (см).
2 (5/2 ±3)
13.87. Рассмотрим плоскость (рис. 254). Эта плоскость
пересекается с данной секущей плоскостью по прямой KL, где К — середина BD. Центры данных шаров О, и О2 лежат в плоскости
BB^D так, что О1Е = О1М = -|, = O2F= О2К - °-,
-> 12
DjF='——. Обозначим Z LRB^= Z KLD2 — a. Тогда LO.2LF —
= £ OtKE = а. Из треугольника КО2Е находим
_ Ох£ /2
ё 2 ВК — ВЕ 3 ’
581
Из треугольника FLO^ получаем
F!
fg“ 4/2’ ё 2
откуда
O1L = O1F + FL=-^, K'L^L-DK^-^
4 } 2 4 I' 2
(/Ct — середина BjPj). Из треугольника КВК{ находим
КК1
14’
13.88. Пусть О-центр шара, г—его радиус (рис. 255). Проведем ОК перпендикулярно плоскости ABD, ОЕ I BDlt OF ji KD, КM I АВ, KN J_ AD. Тогда
К.И = КЛ' = О/(=О£ = г, ВО2 = ЛВ2 + .4О2=13, BDj = Vbd^dd^ = J "И.
Из треугольников ВК.\! и К!.>•.' находим
В К - = КМ - + ВМ2 =-г- -у (3 — г)2, DK2 — К N - -j- DN- = г- + (2 - г)-.
Заметим, что
BE — ВК = Yrs + (3 — г)2, как две касательные к шару,
из одной точки В. Из треугольников FODt и EOD-,
проведенные нахотпм
ODi = DK-- + (О£>! - DFY =-- г- + (2 - г)2 + (1 - г)2, I 'ODi- ОЕ2 = /(2-r)2 + (l --г/
Подставляя найденные выражения в соотношение BDr = BE-\~DtE, получаем
/14 = /? + (3- г)2 + /(2-г)2 + (1-г)2.
582
Решая это уравнение, находим
_ 3 , 3
Г~ 2 - /И’
Найденные значения для г удовлетворяют всем условиям задачи. При этом знак минус соответствует случаю, когда точка К лежит внутри треугольника 4BD, а знак плюс —случаю, когда точка К — вне треугольника ABD.
13.91. Для нахождения ВС — х и получить систему
уравнений
—х3 +К8 —Xs , z/2= 13 —4 (х2 —3).
13.92. Для нахождения АР~х и BjP=y получить систему уравнений
( х2А-у2-гХу — Ь2А~^2>
t Ух2 — Ь2А-]^У2 — b2 — h.
треугольник, получающийся А ВС- сечение, параллельное
13.93. Пусть CMN — правильный в сечении данной призмы (рис. 256),
основанию призмы, где угол АСВ прямой, АС=а, ВС = Ь. Обозначим сторону треугольника CMN через х. Тогда
А М = Ух2—a2, BN = Ух2 — Ь2.
Из трапеции A MN В получаем
МN1 = А В2 + (BN - А М)2, т. е.
х2 = а- + b- + _ Ух2 —а2)2
(В z
(предполагается, что точки М и N лежат по одну сторону от плоскости АВС). Решая уравнение (1), находим
х — _____________,_____________
Г 2 i ,_____________. Рис. 256.
= J/ у (а3 + Ь3 + У а* + fr* - а2Ь2).
Замечание. Точки М и N не могут лежать по разные стороны от плоскости АВС, так как тогда вместо уравнения (1) получилось бы уравнение, которое не имеет решений. Это ясно и геометрически: тогда было бы MN > ЛМ > NC (так как ЛВ>ВС), т. е. MN =£ NC, что противоречит условию.
13.94. Пусть О —центр основания призмы (рис. 257), R — радиус шара, вписанного в призму, ААг = х. Из условий задачи следует, что Д1О = 2Р. Объем призмы равен
О
583
где S —полная поверхность призмы. Подставляя в это выражение Afi = 2R, получаем соотношение
S = eSABC- (О
Покажем, что ВВ^С — прямоугольник. В плоскости АВС проведем AM 1 АО. Тогда по теореме о трех перпендикулярах AtA ВАМ.
Рис. 257.
Но ВС || AM и BBi II AAt. Следовательно, ВВХ J. ВС. Имеем
SBB1C1C = ax> $АВС = ^4" °2-
Проведем OD 1 АВ. Тогда по теореме о трех перпендикулярах А]Р ± АВ. Отсюда
= = j/ х2——а- ,
^ЛЛ1В1В = ^^ ' ^1Р = а х~ 4 °2 •
Подставляя найденные выражения в соотношение (1), получаем
Решая это уравнение, находим
х=-^-(Г5-1).
ГЗ
13.95. Пусть О—центр основания АВС, /И —середина ААГ (рис. 258). Из условий задачи следует, что АА^С — прямоугольник 584
(см. решение задачи 13.94). Следовательно,
СМ = У АС'- + AM'- = |/"&2 + -1 /а .
Обозначим угол ВАМ через а. Из треугольника ВАМ по теореме косинусов получаем
ВМ- = Ь2 4-Д-1' — bl cos а.
1 4
Проведем OD 1 ВС. Тогда по теореме о трех перпендикулярах
B±D J_ ВС. Из треугольника BDBr находим
cos Z ABBt — cos Z ОВВ1 = со5 (л — а) = — cos а = -^- = ,
DDi 21
По трем сторонам находим площадь треугольника ВСМ-.
SbCM=^V™ + W.
13.96. Пусть О —центр шара (рис. 259), г —его радиус, АВ — гипотенуза треугольника А ВС, М — середина А В, N — середина A.Bi, ab=ad=bd.
Из условий задачи следует, что точка О находится в плоскости ССгММ. Проведем ОК 1 МЫ, ОЕ ± С±Ы, OL J. DM. Тогда OL = = OK — OE — r. Так как призма прямая и шар касается всех боковых граней, то радиус шара равен радиусу окружности, вписанной
585
в треугольник АВС. Отсюда
г = |(Г2-1).
Обозначим угол KML через а. Из треугольника CDM получаем cos Z CMD = cos I — — а''; = sin а = ,
> 2 ! DM У 3
К 2 , ос -j Г1 -f- cos ос 1К7Г , iZ?r
cosa = —— ctg ту — I/ -j— ----—У3 +У2 .
уз ’ 2 У 1 — cosa 1 ’
Рис. 259.
Из треугольника КМО находим
КМ=ОК ctg ~ = г (УЗ +У2), откуда
MiV=Of-w=r (1 + К2 +/з) = у (i+vT-KT),
V = 4- А В • СМ • МЛГ=^ (1 + Кб - уз). 2 о
13.97. Пусть К — середина О —середина CCj (рис. 260).
Так как основания призмы параллельны, то первое сечение пересекает плоскость Лгй1Сг по прямой KL, параллельной прямой АВ. Следовательно, первое сечение является трапецией ABLE.. Второе сечение является треугольником Л1В1О, MN — линия пересечения данных сечений. Проведем DE || ВС. Тогда
EF^By^B^,
DF=By\~EF = ~ Вуг^Ву.
586
Из подобия треугольников BtLN и DFN находим
DF 3
DN =~В$: BlN^ i (BlD — DN), откуда
DN 3
BtD (Г'
Прямая AB лежит в плоскости первого сечения и параллельна прямой .4^!, лежащей в плоскости второго сечения. Следовательно, линия пересечения MN этих плоскостей параллельна AJK- Из подобия треугольников DMN и A^D находим
MN DN _ 3
AtBt ~ BXD ~ 5 ‘
Рис. 261.
Рис. 260.
13.98. Пусть К —середина CCt, £ —середина BjC\ и /. — середина АС (рис. 261). В сечении данной призмы первой плоскостью получается треугольник ЛВ^К. Вторая плоскость пересекает основание призмы по прямой EF, параллельной прямой BL, так как
плоскости оснований призмы параллельны. Следовательно, в сечении призмы второй плоскостью получается трапеция BEFL. Данные сечения пересекаются по отрезку MN, длину которого нужно найти.
Из прямоугольных треугольников АВВ1 и АСК находим я
АВ'[ = ЗЬ’, Вх/е = ДК-==у&3, откуда
АВ'^В^ + АК*.
587
Далее, по теореме, обратной теореме Пифагора, следует, что угол
AKBt прямой. Значит, MN = ]/КМ'2 . Найдем КМ и KN.
Проведем KD || ВС. Тогда РО= *-В1£ = ~Ь, KP=KD — PD= 3 3
= -j- b = --; В±Е. Из подобия треугольников МКР и В}ЕМ получаем
= ^Л1В1 = |дВ1К-О1) = |7ь|/ км], откуда
—3-Т-
Из подобия треугольников ЕЕС\_ и BCL с соответственно параллельными сторонами находим
„ „ CL СХЕ b
РС1^-вс~ = ^-
Проведем КН || АС. Тогда
/<Д=1(С/, + ГС1) = 4&. Z о
Из подобия треугольников NKH и А К L получаем
kn кн\
/\L, т: т: у £ ]
3 -| Г 3 , .. । / Г/ m—;—,, 3&КГ11
откуда КК = у1/ b и МК = у КМ- -J- KN- =—.
13.110. Прежде всего следует доказать, что центр куба лежит на высоте конуса. Пусть О —центр куба, SK — высота конуса, АВ—
ребро куба, лежащее на основании конуса. Проведем плоскость через точку О и прямую АВ (рис. 262, а) и плоскость через точку О
588
СЕ = DE =
Из подобия
параллельно основанию конуса (рис. 262, б). Обозначим АВ=а, SK = h, 1{М = г — радиус основания конуса. Тогда
ВК = ОЕ=~а, CE=DE^=~, 2 у2
ON = 0D= VOERDE* = .
треугольников K.SM, BCM и ECN получаем
KS “ ВС ~ СЕ'
т. е.
1 г г~ 2а h~ а ]А2
а Уз а ~2 ~2
Отсюда
/2
Vкон лЛг~
UKy6 За3
л£1(53_7|/з).
Пусть прямая MN параллельна стороне основания пирамиды ABCD и касается окружности основания конуса в точке К
13.111.
(рис. 263). Тогда искомый шар вписан в треугольную пирамиду 3 V
MNBD. Радиус этого шара г будем находить по формуле r = -g , где V и S — объем и полная поверхность пирамиды MNBD.
По условию задачи DO = 2, АВ = зУз. Значит,
М N = 4- А В = /3'= BN = ВМ, О
DK=yD0s + 0K2 = ~.
589
Высота треугольника BDM, проведенная из вершины D, является апофемой пирамиды и образующей конуса, т. е. равна DK- Следовательно,
О ОО , О __9^3 [/ = _22_(.д4Л/ч2 1^3 Г = —(СМ).
S = 3Soaw + SBjUjV=—2~, г 4 |/з (MN)“=—, Л 3 1 1
13.114. Рассмотреть осевое сечение данного усеченного конуса (см. решение задачи 12.93).
13.115. Пусть 01, 0>, Од — центры данных шаров, А, В, С — соответственно их проекции на основание цилиндра, О —центр основания цилиндра (рис. 264). Из трапеции ВСО3О2 (она на рисунке не указана) находим
ВС* = 020д - (СО3 - ВО^ = [ А г + /3 - ’ А г - г * = 1(И.
Из треугольника BCD находим CD — I'' ВС- - BDl = 3r. Обозначим радиус основания цилиндра через х. Тогда
ОС = х-~г, ОВ — х—г, OD = V ВО3 —BD3=Vx3-2xr.
Из соотношения CD — CO-^OD получаем
К _________
Зг — х —- г + К х3 — 2хг.
п 121
Решая это уравнение, находим х=—г.
13.116. Пусть О2, 03 — центры данных шаров, А, В, С—соответственно их проекции на нижнее основание цилиндра, О — центр основания цилиндра (рис. 265). Так как высота цилиндра равна Зг и третий шар касается верхнего основания цилиндра, то СОз — 2г. Из 590
трапеции ВС030., (она на рисунке не указана) находим ВС2 = О3О3- - (О3С - О2В)2 = (2г)2 - (2г - г)2 = Зг2.
Из треугольника BCD находим CD = JBC2 — ВО'2 = г К1Г.
Обозначим радиус основания цилиндра через х. Тогда
OC = x — r, OB — x — r, OD = ]'OB2-BD2 = jCr2-2.rr.
Из соотношения СО = Решая это уравнение, находим
CO-[-OD получаем г ]' 2 — х—г-}~Ух2—2хг-
13.117. Пусть А и В —проекции центров шаров радиуса г на данную плоскость, а Л1 и /V — проекции центров шаров искомого радиуса х на ту же плоскость (рис. 266). Тогда ОЛ = 4/<=г, OjM =
= .Ш\’ = .V, ООг = г -) х.
Из трапеции АООгМ получаем АМ2 — ОО^~(АО — О1М)г = 4гх, а из треугольника ЛМК имеем АМг=А-]-А. Следовательно,
г2+Х2 = 4rV( х = (2-± УЗ ) г.
13.118. Пусть О —центр данной полусферы, А, В, С —проекции центров шаров искомого радиуса х на основание полусферы,
Oj —центр одного из шаров радиуса х (рис. 267, а и б). Тогда АВС— правильный треугольник со стороной 2х, О —центр этого
591
Треугольника,
OK = OM = R, АО1 = х,
OOt=R-x, A0 = V00i-A0i==VR*-2Rx .
Из треугольника ABC имеем
2 АВ^З 2х
ЛО--.—— _ —
Следовательно,
-Л^ = /Р2-2Рх, х = ^(|Л2Т -3).
I 3
13.119, Пусть Ох и 0.2 — центры данных шаров радиуса г, О — центр шара искомого радиуса х, OtB, 03А и ОС —перпендикуляры на ребро данного двугранного угла, —точка пересечения прямых OtO2 и ОС (рис. 268). Так как шары вписаны в двугранный угол, то центры шаров лежат в биссекторной плоскости этого двугранного угла (эта плоскость указана на рис. 268) и OjB = ОгА = —-—, sin
ОС _ —f—. yj3 треугольника 002К sin у
получаем OK2 — (x-j-r)2 — r2 = x2A~2xr. С I г___________ X (
другой стороны, ОК = ; CR — СО | = ------1 (точка О может лежать
sin-J
на продолжении отрезка СК)- Следовательно,
9 а 8Ш 2
Решая это уравнение, находим
х = г— (3 — cos а ± ]/7 — 8 cos а 4- cos2 а) , 1 Н-cos а ’
где знак плюс соответствует случаю, когда точка О лежит на продолжении отрезка СК, а минус —случаю, когда точка О лежит между точками С и К-