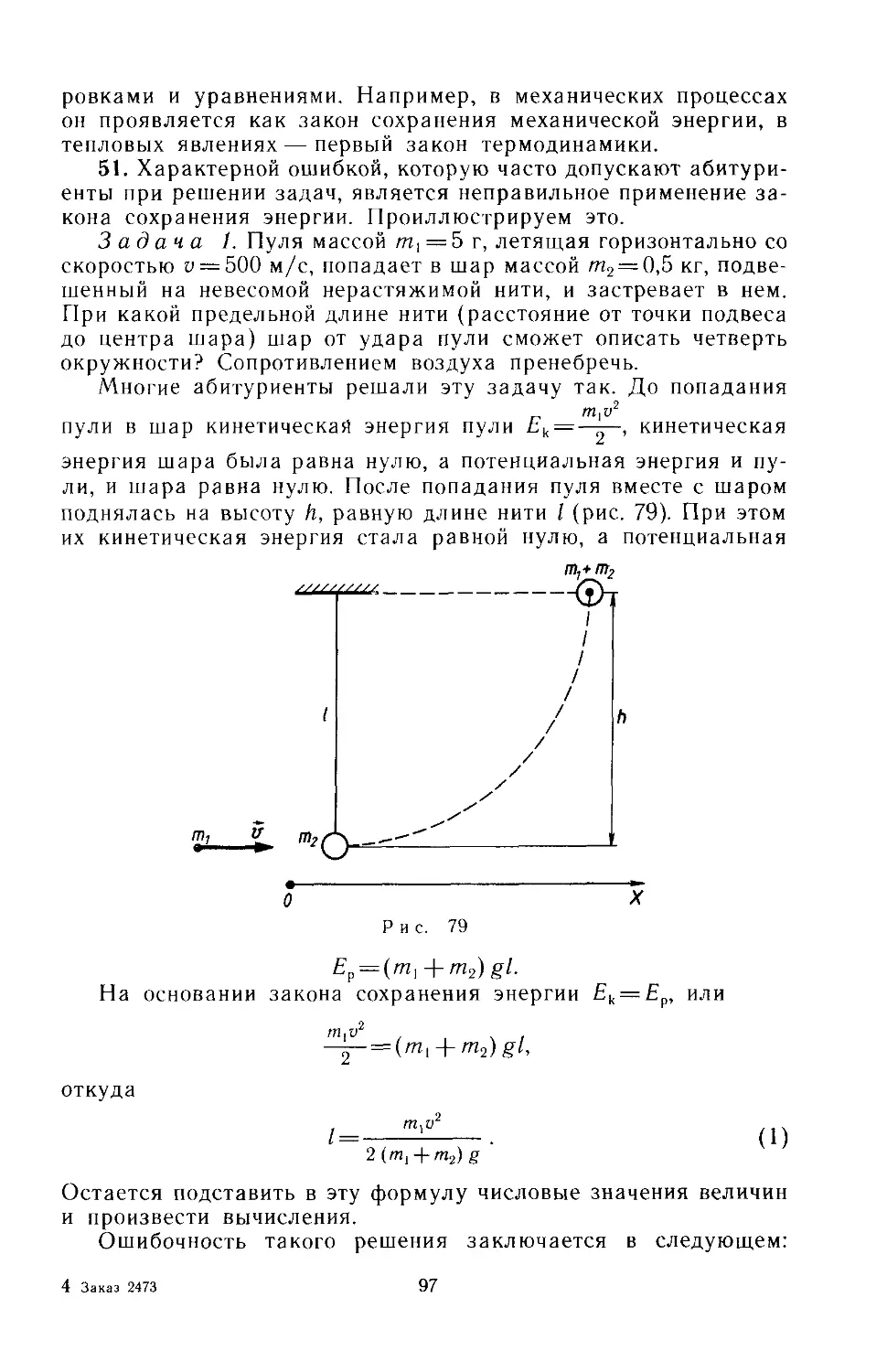
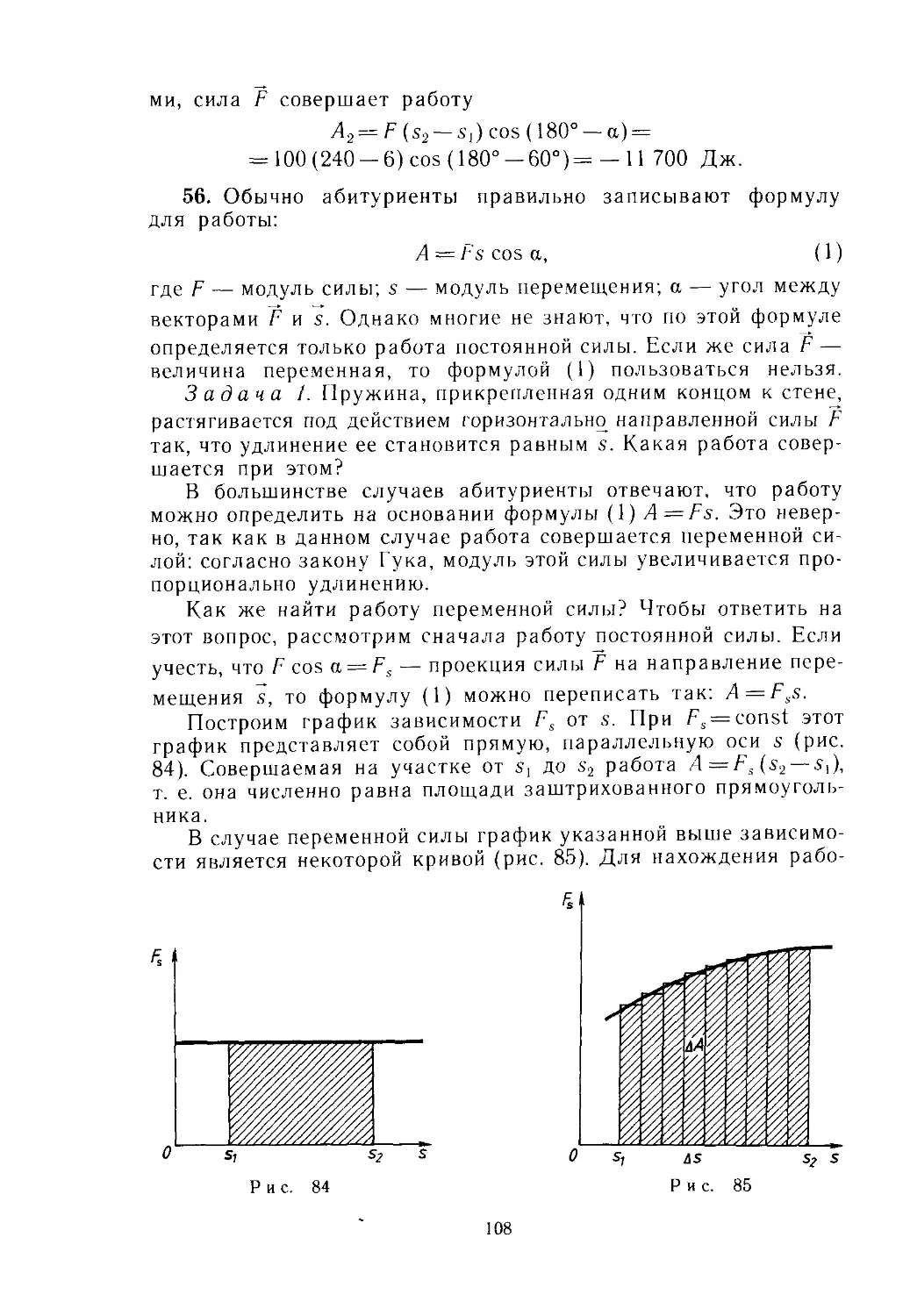
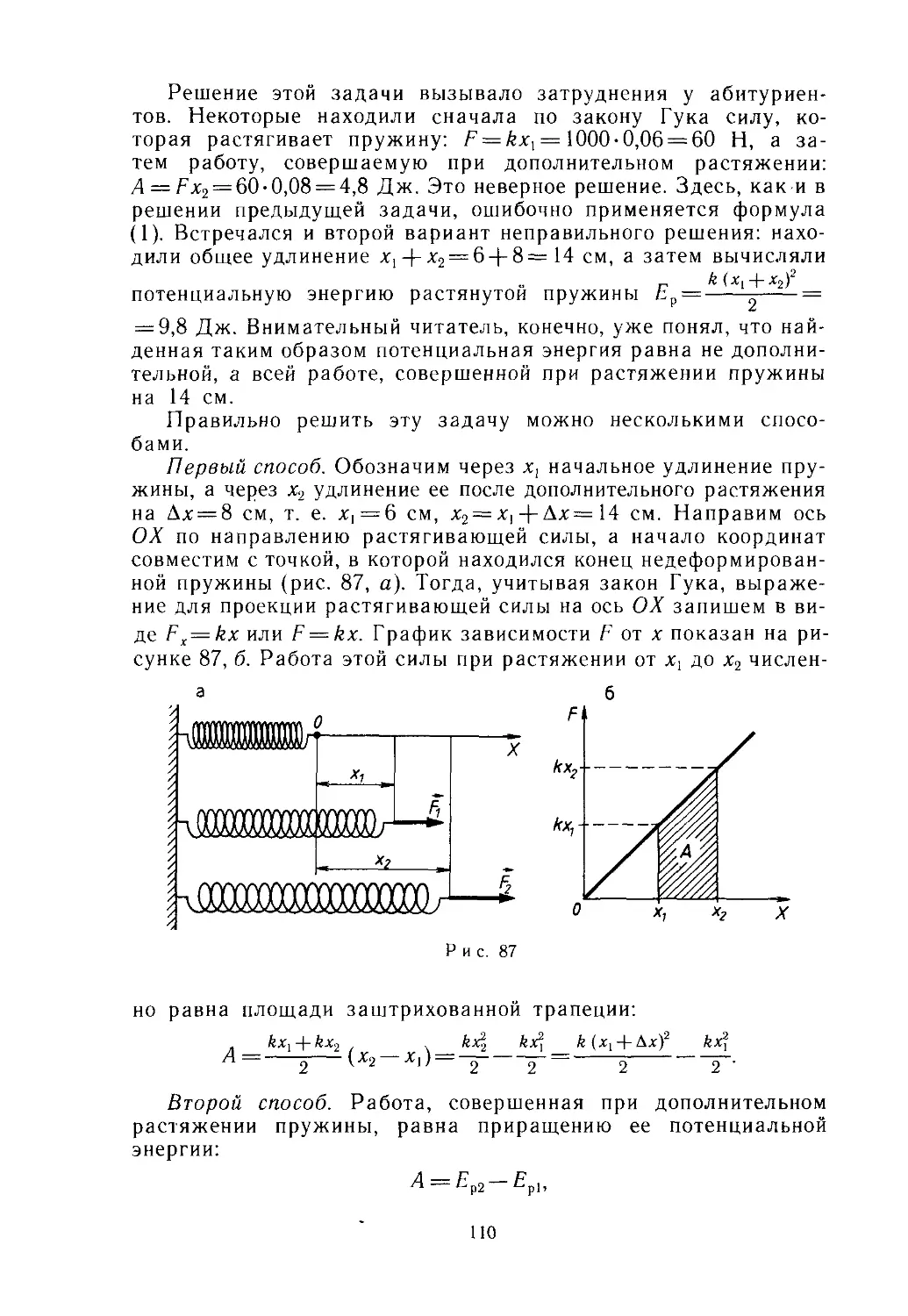
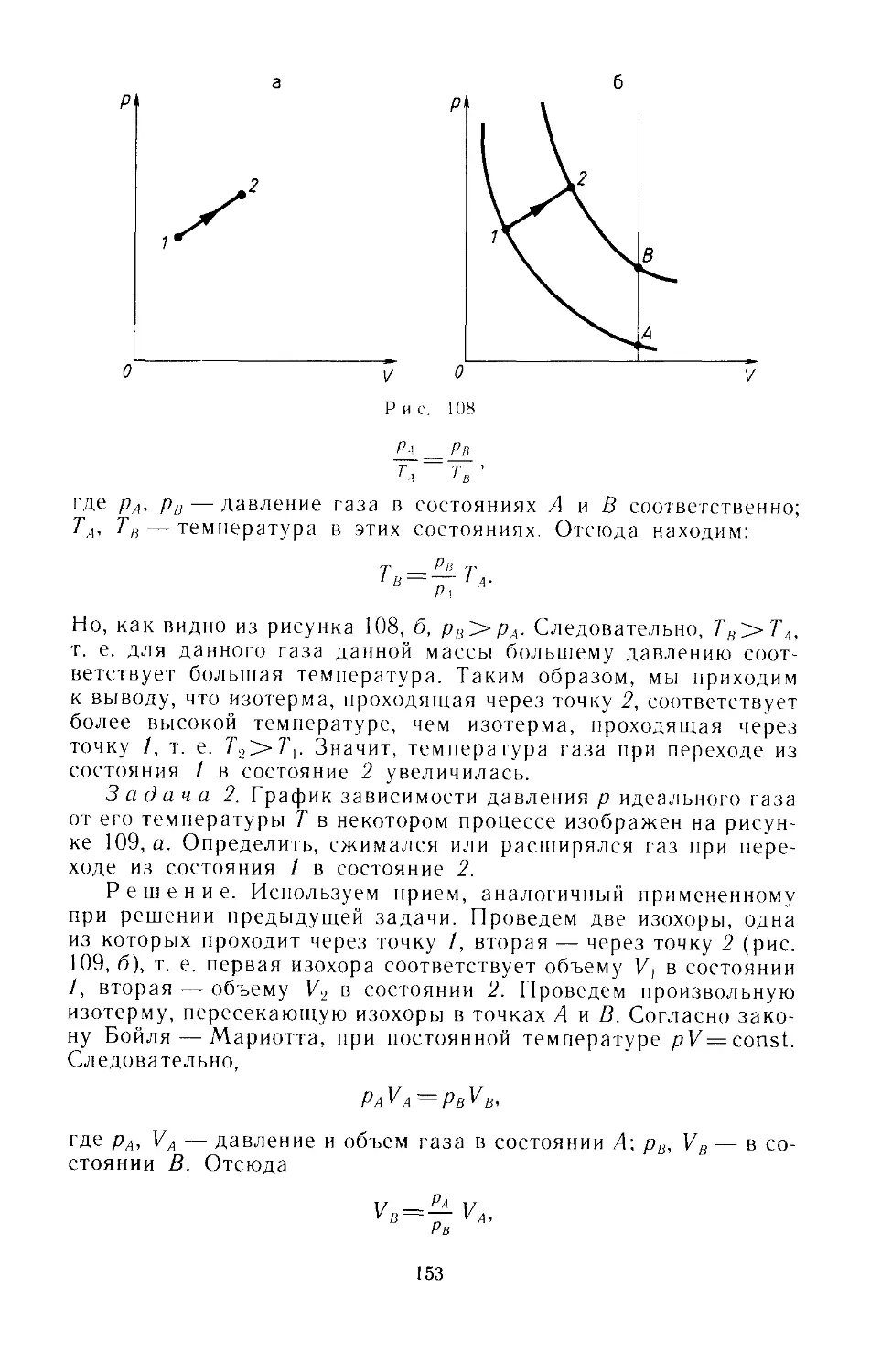
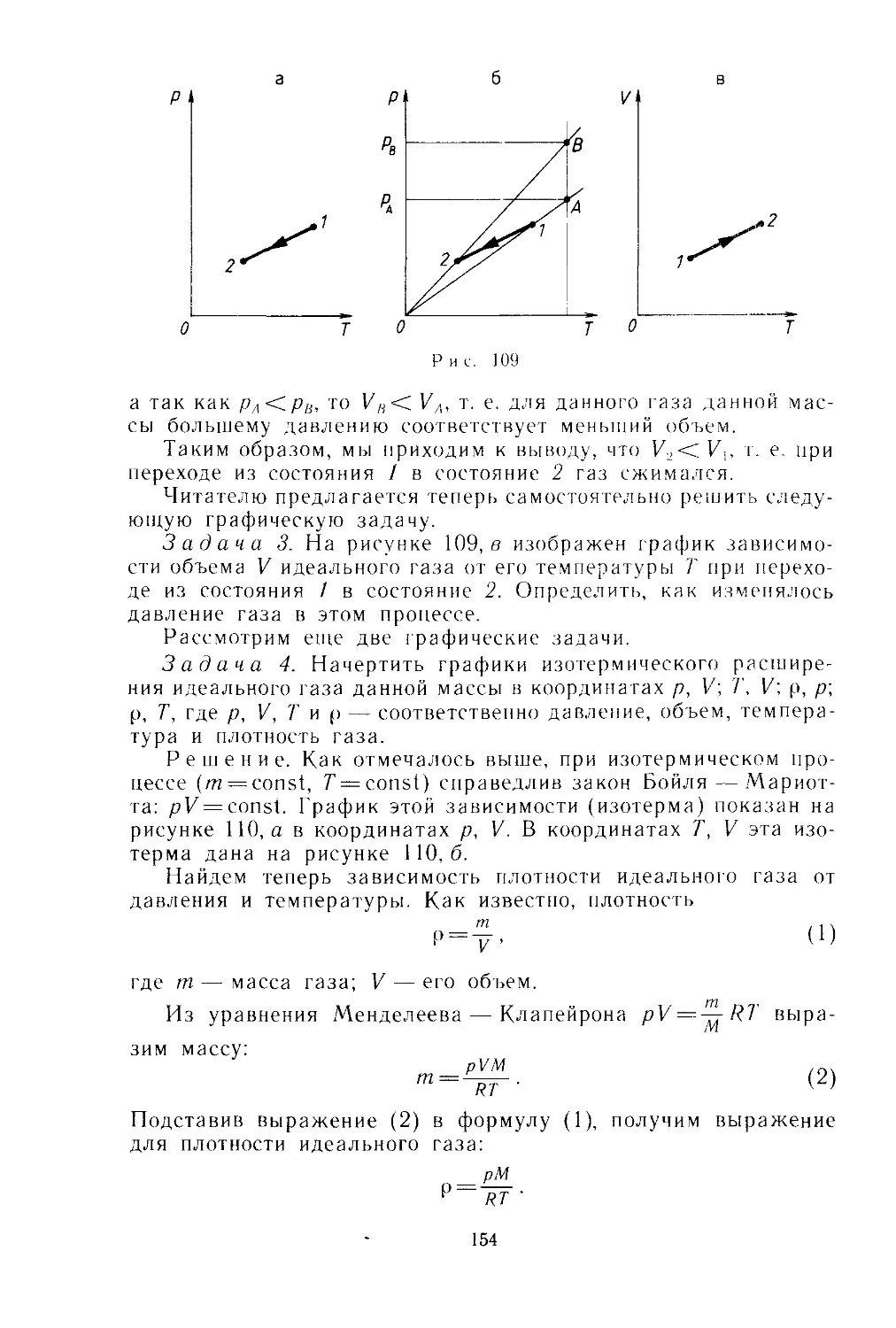
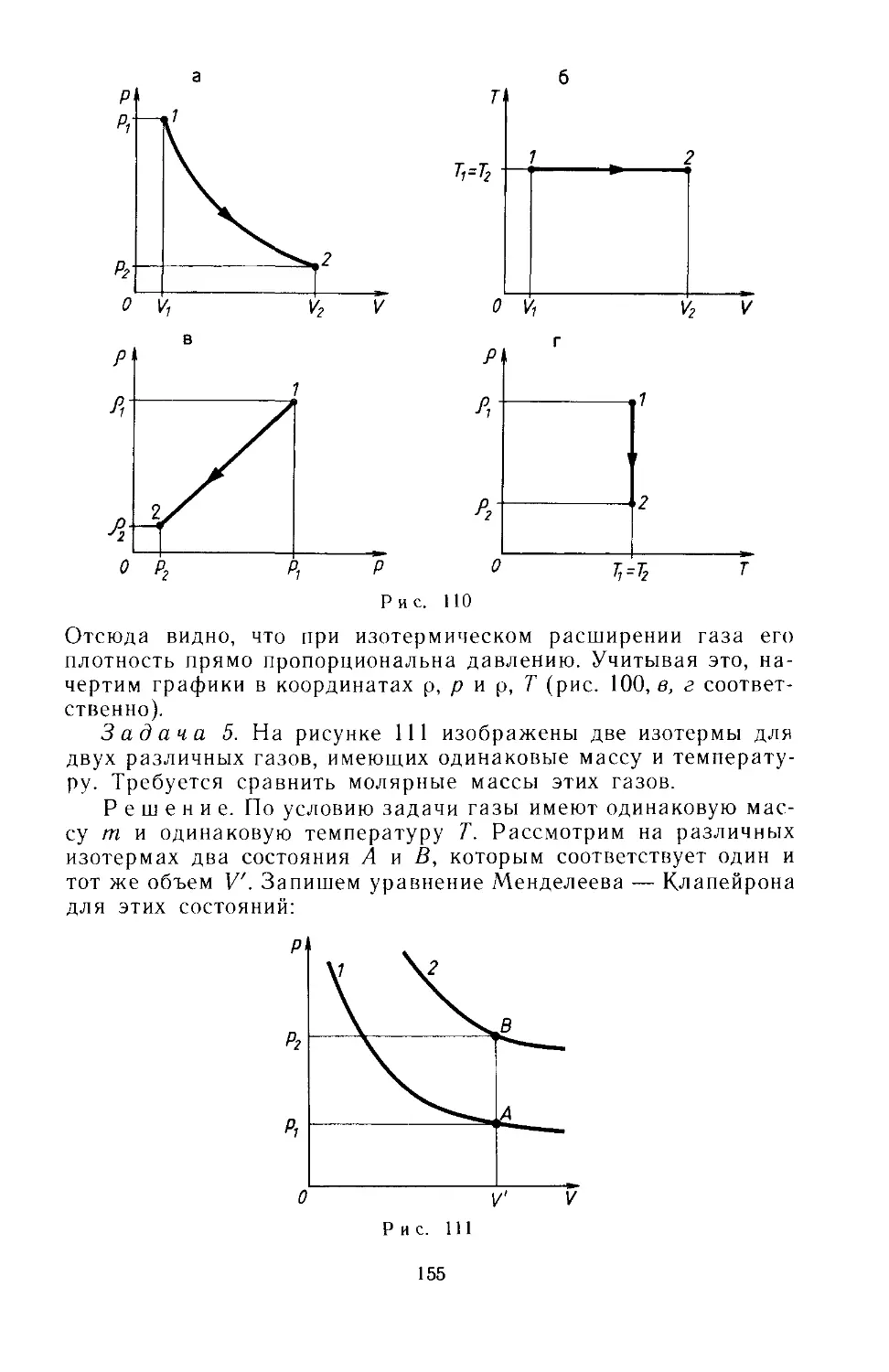
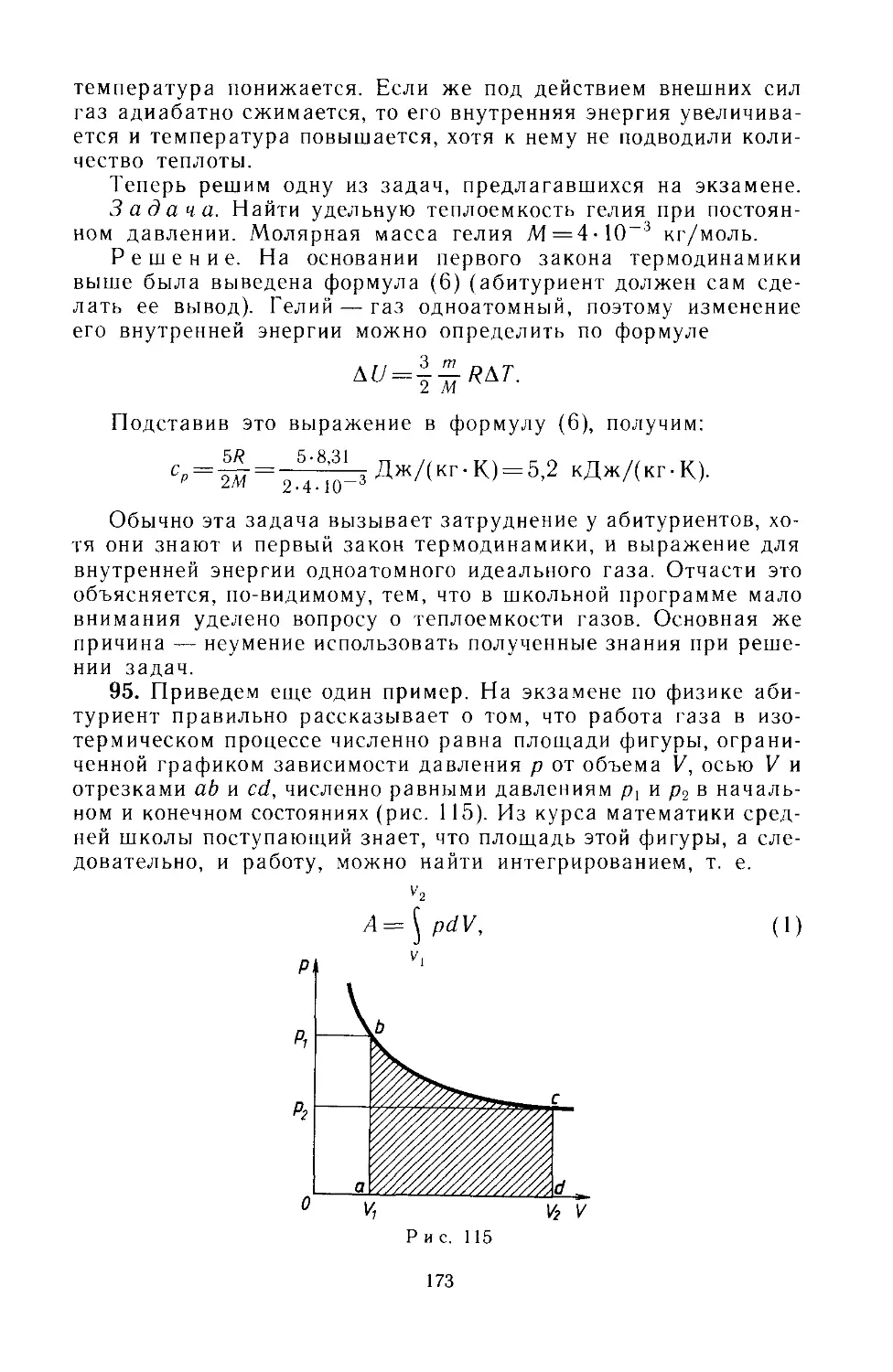
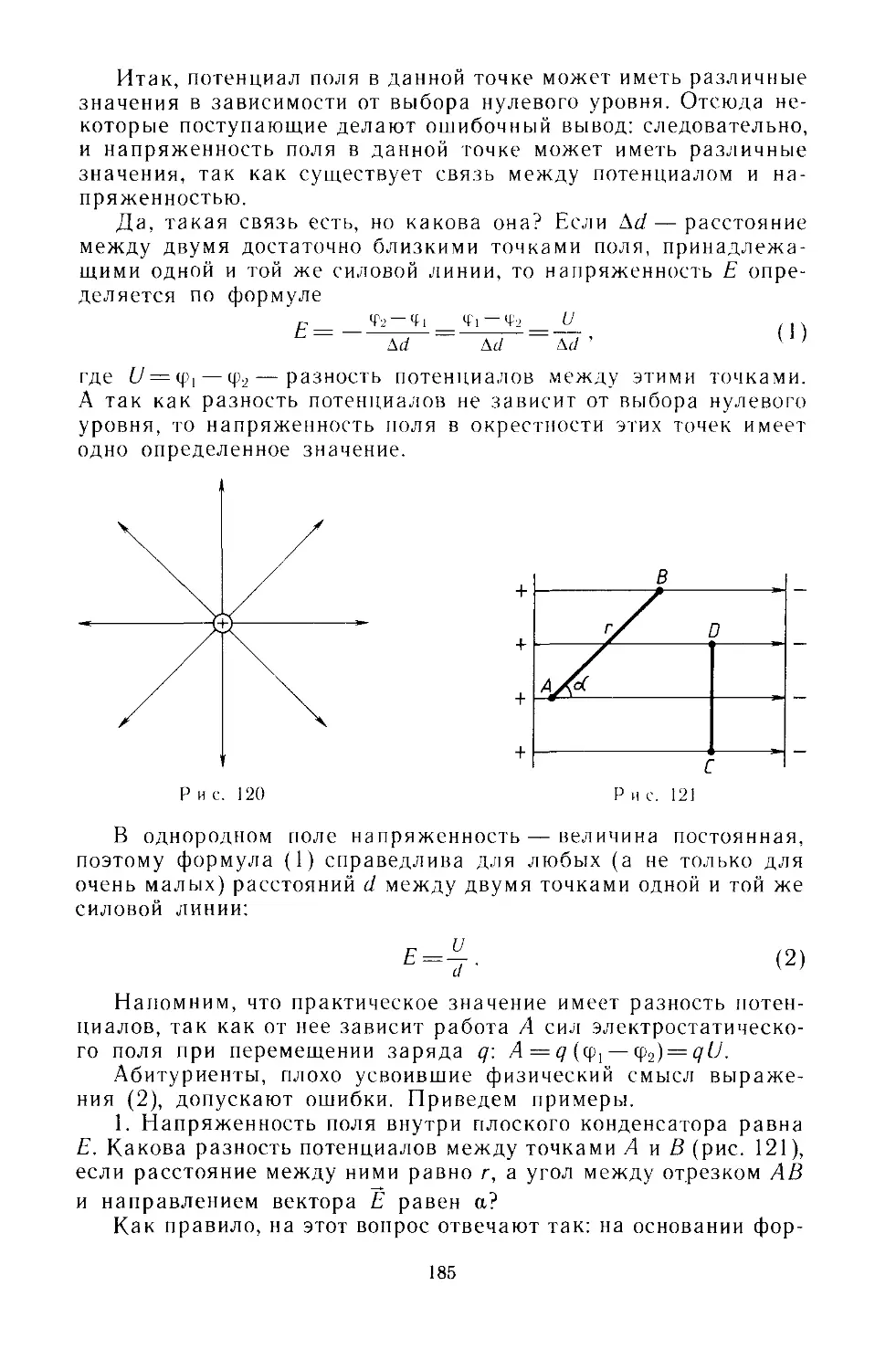
Text
Н.Е. Савченко
ЗАДАЧИ ПО ФИЗИКЕ С АНАЛИЗОМ ИХ РЕШЕНИЯ
В книге дана методика решения задач но физике с анализом типичных
ошибок, допускаемых абитуриентами на вступительных экзаменах.
Сборник рекомендуется поступающим в вузы, учащимся старших классов,
техникумов, слушателям подготовительных отделений и курсов, учителям
физики.
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ 3
МЕХАНИКА 5
Кинематика _
Основы динамики 36
Законы сохранения в механике 95
Жидкости и газы 118
МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ 145
Основы молекулярно-кинетической теории. Газовые законы
Тепловые явления 162
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 176
Электростатика —
Законы постоянного тока 194
Магнитное поле. Электромагнитная индукция 213
КОЛЕБАНИЯ И ВОЛНЫ 233
ОПТИКА 249
Квантовая физика 264
Советы абитуриентам 275
ПРИЛОЖЕНИЯ 278
1. Образцы билетов устного экзамена по физике —
2. Задачи устного экзамена по физике 279
3. Варианты заданий письменного экзамена по физике 290
4. Основные формулы элементарной физики 300
ОТВЕТЫ 308
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 317
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Авогадро постоянная 147 Влажность абсолютная 168
Активность радиоактивного —относительная 168
вещества 273 Волна 242
Ампер на килограмм 273—274 Вольт-амперная характеристика 194
Архимеда закон 126 Вольт на метр 186
Архимедова сила 122 Газ идеальный 150
Атомная единица массы 147 — реальный 150
Бойля — Мариотта закон 151 Гей-Люссака закон 152
Бэр 274 Генри 231
Вебер 227 Герц 234
Вес тела 54 Гидростатический парадокс 121
Гравитационная постоянная 54
График скорости 25
Грэй 274
Гука закон 71—72
Давление 118—119
— нормальное атмосферное 140
— парциальное 160
Дальтона закон 160
Де Бройля волна 264—265
Джоуля — Ленца закон 202—203
Дисперсия света 254
Диссипация энергии 112
Диссоциация электролитическая 212
Дифракция света 249
Длина волны 243
Доза излучения поглощенная 274
эквивалентная 274
экспозиционная 273
Единица СИ дополнительная 89
основная 88
производная 88
— физической величины 87
внесистемная 90
дольная 90
кратная 90
основная 88
производная 88
Закон всемирного тяготения 54
— сохранения электрического заряда
177
энергии 96, 238, 262, 267
в механике 96
— электромагнитной индукции 224
— термодинамики первый 170
Законы внешнего фотоэффекта 266
Зиверт 274
Значение физической величины 88
числовое 88
Изобара 152
Изопроцесс 151 —152
Изотерма 151
Изохора 152
Индуктивность 231
Индукция магнитная 218—219
— электромагнитная 219
Кипение 169
Кирхгофа правила 206
Колебания 241—242
— гармонические 241—242
— непериодические 241
— периодические 241
Количество теплоты удельное 163
Конденсатор воздушный 188
Контур 206
Коэффициент качества 274
Кулон на килограмм 273
Кулона закон 177—178
Кюри 273
Ленца правило 222
Линия магнитной индукции 214
— магнитного поля силовая см.
Линия магнитной индукции
Лоренца сила 228
Масса молярная 147
— относительная молекулярная 146
Международная система единиц (СИ)
88
Менделеева — Клапейрона
уравнение 151
Микрорентген 273
Миллиметр ртутного столба 140
Миллирентген 273—274
Моль 147
Мощность экспозиционной дозы 273
Наклонение магнитное 217
Напряженность электрического поля
179
Нуль температуры абсолютный
149—150
Ньютон 89
Ньютона законы 38—39
Ом 196
Ома закон для замкнутой цепи 204
участка цепи 194
цепи переменного тока 247
Падение напряжения 206
Пар насыщенный 166
Паскаля закон 119
Перемещение 5
Плечо силы 76
Показатель размерности физической
величины 91
Поле магнитное 213—214
— однородное 184
—электрическое 214
— электромагнитное 213
Полюс магнитный 216
Потенциал электростатического поля
184
Поток магнитный 220
Проекция вектора 6—7
Процесс изобарный 152
— изотермический 151
— изохорный 152
Путь 5—6
Рад 274
Размер физической величины 87
Размерность физической величины
90—91
Рассеяние энергии см. Диссипация
энергии Рентген 273
Рентген в секунду 274
Самоиндукция 230
Секунда в минус первой степени 234
Сила диссипативная см. Сила
неконсервативная
—консервативная 96, 111
—неконсервативная 112
— потенциальная см. Сила
консервативная
— трения 47
— тяготения 54, 65
— упругости 71
— тяжести 54, 66
— центростремительная 57
Силы взаимодействия 39
Система единиц физических величин
88
— электрически изолированная 177
— отсчета инерциальная 37
неинерциальная 57, 243
— физических величин 88
Склонение магнитное 217
Скорость первая космическая 70
— средняя 14—15
— — прохождения пути см..
Скорость средняя
путевая см. Скорость средняя
Соединение конденсаторов
параллельное 191
последовательное 191
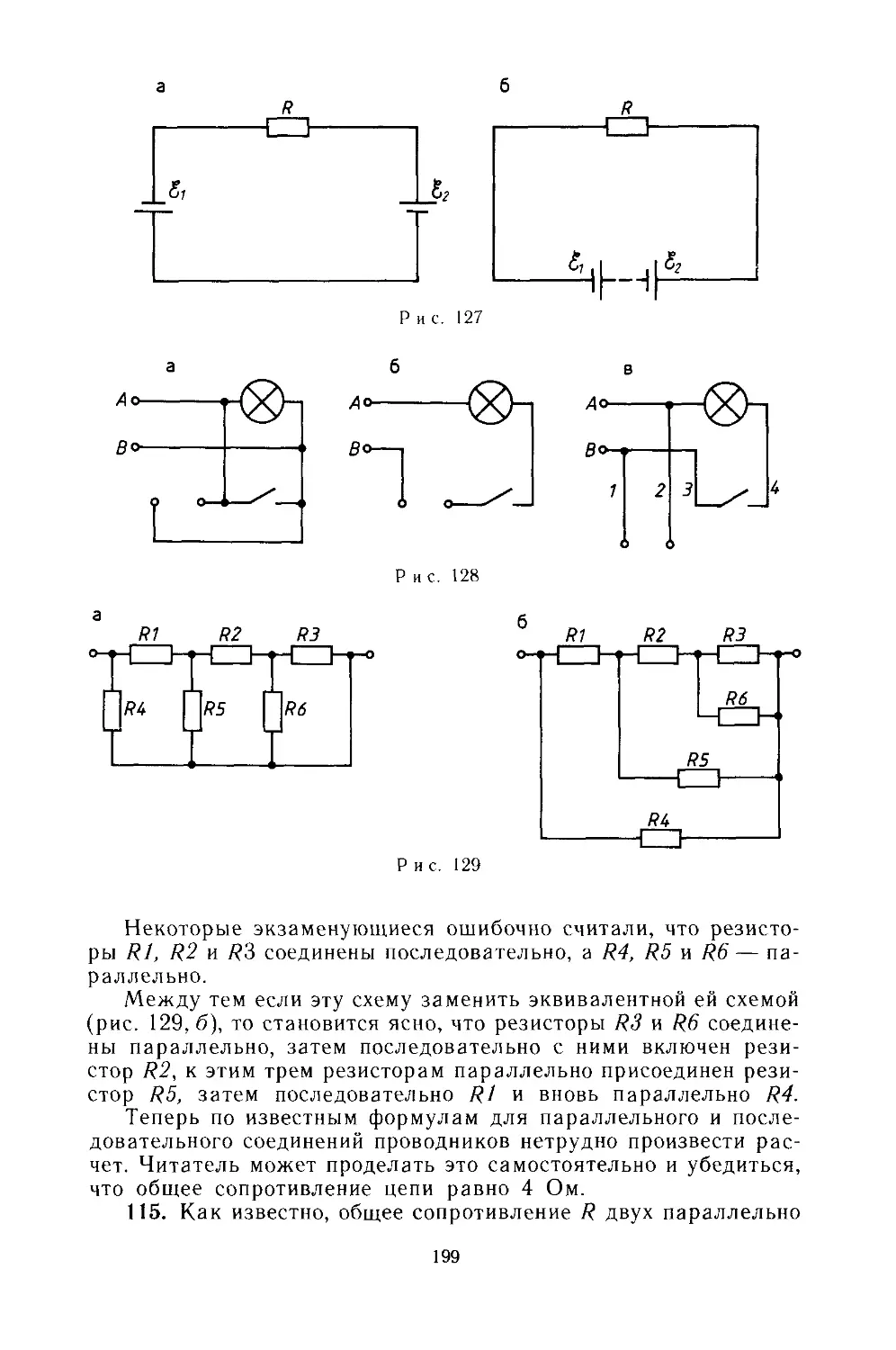
— проводников параллельное 199—
200
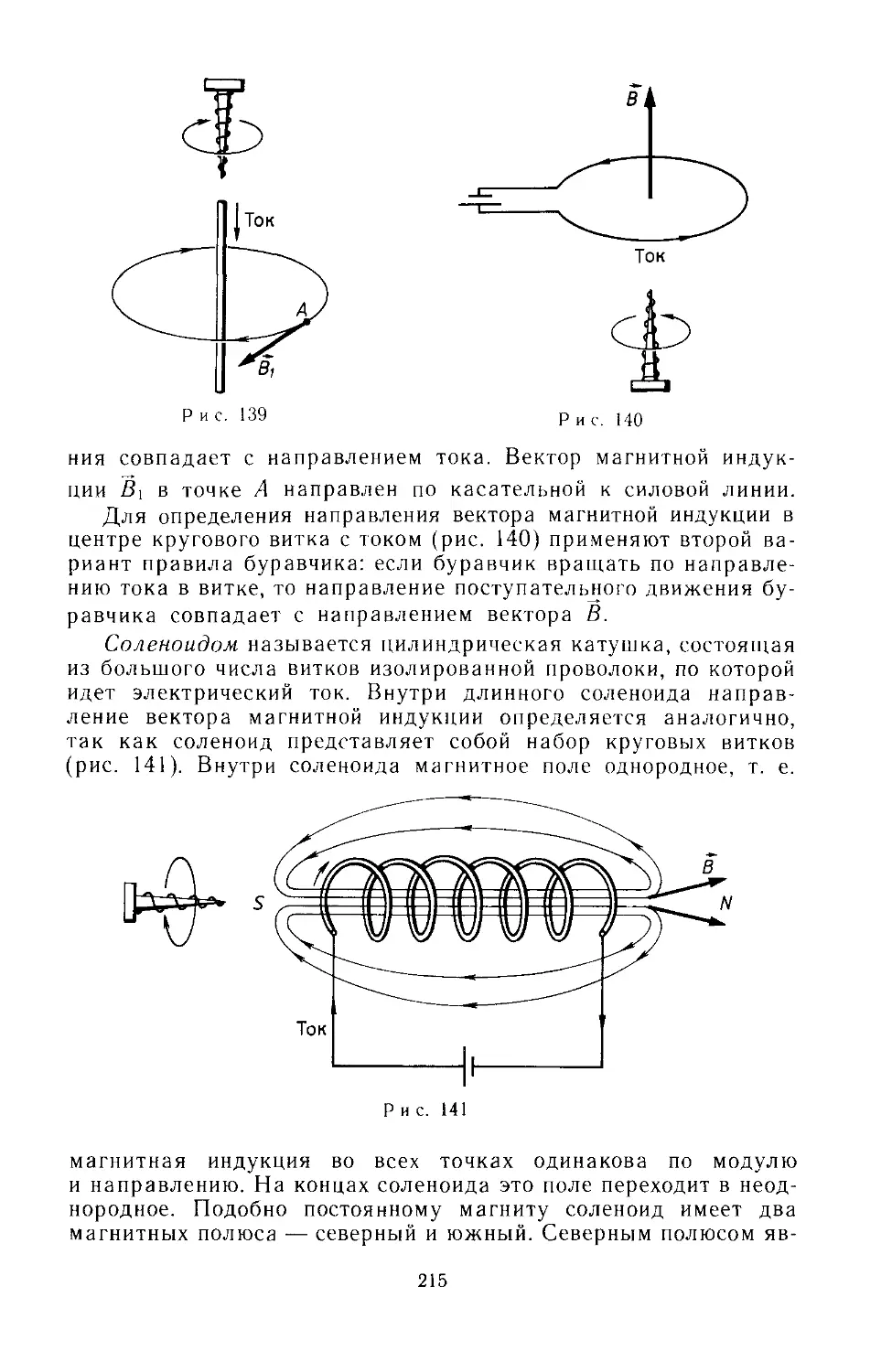
Соленоид 215
Сопротивление проводника 107
— цепи переменного тока полное 247
Составляющая вектора 7
Температура абсолютная 149
Теплоемкость тела 163
— удельная 163
Теплота плавления удельная 162
— сгорания удельная 162—163
Ток насыщения 266
Томсона формула 240
Точка росы 167
Угол полного отражения предельный
250
Удар абсолютно неупругий 100
упругий 100
— центральный 100 Узел
206
Уравнение молекулярно-кинетиче-
ской теории газов основное 151
— состояния идеального газа см..
Менделеева — Клапейрона
уравнение
— теплового баланса 164
Ускорение 17—18
— касательное 19
— мгновенное 18
— нормальное см. Ускорение
центростремительное
— полное 58
— среднее 17
— тангенциальное см. Ускорение
касательное
— центростремительное 19, 22
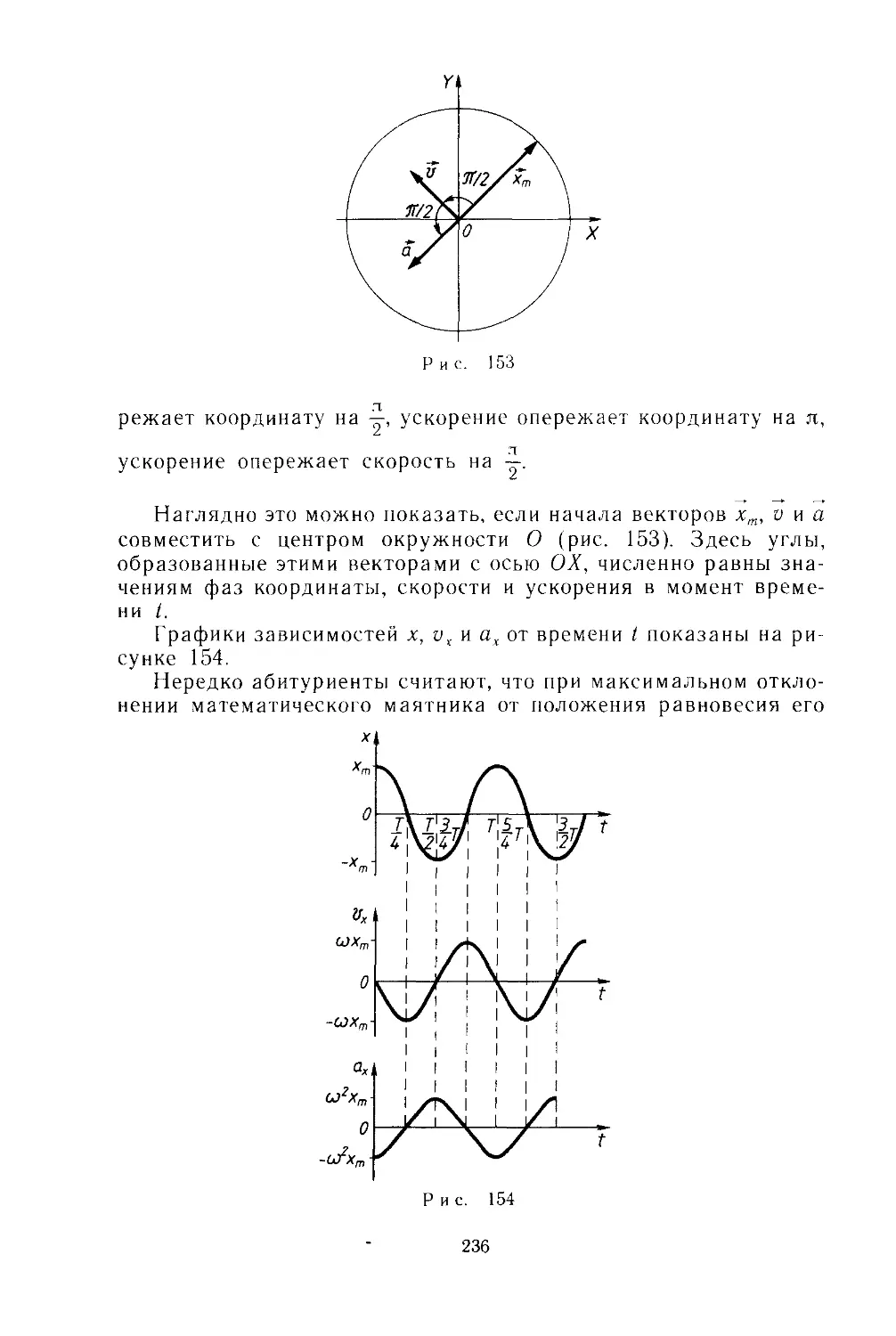
Фаза колебаний 233
Фарадея закон для электролиза 197
— постоянная 198
Физическая величина 87—88
безразмерная 91
основная 88
производная 88
размерная 92
Формула линзы 261
Цена деления 201
Частота круговая 233
— угловая см.. Частота круговая
— циклическая см. Частота круговая
Шарля закон 152
ЭДС индукции 224
— самоиндукции 230
Эйнштейна уравнение для
фотоэффекта 266—267
Электрическая емкость 187
— проводимость 194—195
Электрический заряд 176
отрицательный 176
положительный 176
элементарный 177
Электролиз 213
Электронвольт 268
Эталон единицы физической
величины 90
ПРЕДИСЛОВИЕ
Необходимой базой для обучения физике в вузе являются
знания, полученные в средней школе. Основная цель вступитель-
ных экзаменов — отобрать людей, знания и способности которых
позволят им успешно заниматься в высшем учебном заведении,
стать специалистами и в дальнейшем использовать новейшие до-
стижения науки и техники в своей практической деятельности.
На вступительных экзаменах по физике к абитуриентам
предъявляются требования, определяемые программой для по-
ступающих в вузы, которая ежегодно утверждается Министерством
общего и профессионального образования Российской Федерации.
Она соответствует типовой программе средней общеобразователь-
ной школы. Согласно этим требованиям, при проведении экзаменов
по физике основное внимание должно быть обращено на понима-
ние экзаменующимися сущности физических явлений и законов,
на умение истолковывать смысл физических величин и понятий,
а также на умение решать физические задачи по разделам про-
граммы. Абитуриент должен знать и уметь пользоваться при
расчетах Международной системой единиц (СИ), указанных в
программе, проявить осведомленность в вопросах, связанных с
историей важнейших открытий в области физики.
Опыт вступительных экзаменов показывает, что, к сожале-
нию, не все ответы абитуриентов соответствуют этим требова-
ниям. Среди недостатков общего характера наиболее распро-
страненным является неумение решать задачи. Часто встречают-
ся абитуриенты, которые правильно формулируют физические
законы, но не могут использовать их в конкретных условиях при
решении задач или применяют ошибочно. В этом проявляется
один из серьезнейших недостатков в подготовке выпускников
средних школ — формализм знаний. К другим общим недостат-
кам можно отнести следующие: неверные определения физиче-
ских понятий и величин; нечеткое понимание основных физиче-
ских законов; неумение применять при решении физических за-
дач знания, полученные при изучении математики; неумение
объяснить применение физических законов в технике; некритиче-
ское отношение к результатам, полученным при решении задач;
неумение применять знание одних разделов курса физики к ре-
шению задач из других разделов; слабое знание единиц физиче-
ских величин.
В данной книге приводятся систематизированные сведения
об ошибках, допускаемых абитуриентами на вступительных эк-
заменах по физике в ответах на вопросы и при решении задач.
Книга предназначена для поступающих в вузы, а также для уча-
щихся старших классов. Как гласит народная мудрость, на
ошибках учатся. Лучше, конечно, учиться не на своих ошибках,
а на чужих, на тех, которые делали другие абитуриенты. Поэто-
му важное значение имеет обобщение опыта вступительных эк-
заменов прошлых лет. «О сколько нам открытий чудных готовят
просвещенья дух и опыт — сын ошибок трудных...» Эти слова
A. С. Пушкина не утратили со временем своей актуальности.
В книге обобщены результаты вступительных экзаменов мно-
гих лет.
Предполагается, что готовящийся к поступлению в вуз выпу-
скник средней школы будет читать эту книгу внимательно, не
торопясь, с карандашом в руке, с остановками, пытаясь всякий
раз сначала самостоятельно ответить на вопрос, найти ошибку
или правильное решение задачи, а потом двигаться дальше.
В книге приведено несколько образцов билетов устного экза-
мена по физике и вариантов заданий письменного экзамена,
предлагавшихся в различных технических и других вузах. Озна-
комление с этими материалами и решение содержащихся в них
задач создаст у абитуриента определенное представление об
уровне требований, предъявляемых на экзамене по физике, по-
может лучше подготовиться к вступительному экзамену.
Автор выражает благодарность рецензентам рукописи
B. А. Орлову и А. Н. Тарасовой за ряд полезных советов и заме-
чаний, способствовавших улучшению книги.
Все отзывы и пожелания просьба направлять по адресу:
129846, Москва, 3-й проезд Марьиной рощи, 41, издательство
«Просвещение».
АВТОР
МЕХАНИКА
КИНЕМАТИКА
1. Многие абитуриенты ошибаются, давая такое определение
равномерного прямолинейного движения: «Равномерным прямо-
линейным движением называется движение, при котором тело за
равные промежутки времени совершает одинаковые перемеще-
ния». Ошибка заключается в том, что перед словом «равные»
пропущено слово «любые». Чтобы убедиться в этом, достаточно
рассмотреть такой пример: автобус дальнего следования за каж-
дые 2 ч (равные промежутки времени) проходит 120 км (совер-
шает одинаковые перемещения), двигаясь прямолинейно в одном
направлении, но при этом скорость его на разных участках шос-
се различна. Например, за первый час он прошел 57 км, а за
второй — 63 км. Поэтому движение его является неравно-
мерным. Движение автобуса было бы равномерным в том слу-
чае, если бы он совершал одинаковые перемещения за любые
равные промежутки времени, например за каждую минуту, каж-
дую секунду, а не только за каждые 2 ч.
Рассмотренная ошибка указывает на то, что при ответе на
экзамене надо обращать внимание на точность формулировок
определений, законов, понятий. Это, конечно, не означает, что их
надо формально заучивать по учебнику. Важно правильно пони-
мать физический смысл и четко выражать его своими словами.
Например, можно дать такое определение: «Равномерным пря-
молинейным движением называется движение, при котором мо-
дуль и направление вектора скорости остаются постоянными».
2. Некоторые абитуриенты плохо усвоили такие важные по-
нятия кинематики, как перемещение и путь. Об этом свидетель-
ствует, например, такой ответ: «Перемещение — это кратчайшее
расстояние между точками / и 2 траектории тела (рис. 1)».
Напомним, что перемещением называется вектор, начало ко-
торого совпадает с начальным положением движущейся матери-
альной точки, а конец — с конечным. На рисунке 1 перемеще-
ние — это вектор s.
Путь — это длина траектории от начального положения мате-
риальной точки до конечного. Путь — величина скалярная. На
рисунке 1 путь равен длине траектории от точки / до точки 2.
Р и с. 1
При прямолинейном движении в одном направлении модуль
перемещения равен пути (рис. 2).
Рис. 2
3. На вопрос «Что называется скоростью равномерного пря-
молинейного движения?» некоторые экзаменуемые отвечали, что
скорость
о = 7, A)
где s — путь, пройденный телом за время t. Отсюда следовало,
что скорость — скалярная величина, так как путь s и время t —
величины скалярные.
Нужно помнить, что скорость равномерного прямолинейного
движения — это векторная величина:
где s — перемещение тела за промежуток времени t. Направле-
ние скорости совпадает с направлением перемещения.
По формуле A) находим модуль скорости равномерного пря-
молинейного движения, так как при таком движении (без изме-
нения направления), как отмечалось выше, путь равен модулю
перемещения.
4. Нередко абитуриенты смешивают понятия проекции векто-
ра на ось и составляющей этого вектора по оси. Напомним эти
понятия применительно к декартовой прямоугольной системе ко-
ординат.
Проекцией вектора а на ось ОХ называется скалярная ве-
личина
ах — а cos a,
где а — угол, отсчитываемый от положительного направления
оси ОХ против часовой стрелки до направления вектора. Если
угол а острый, то ах~>§, если а— тупой угол, то ах<0, если
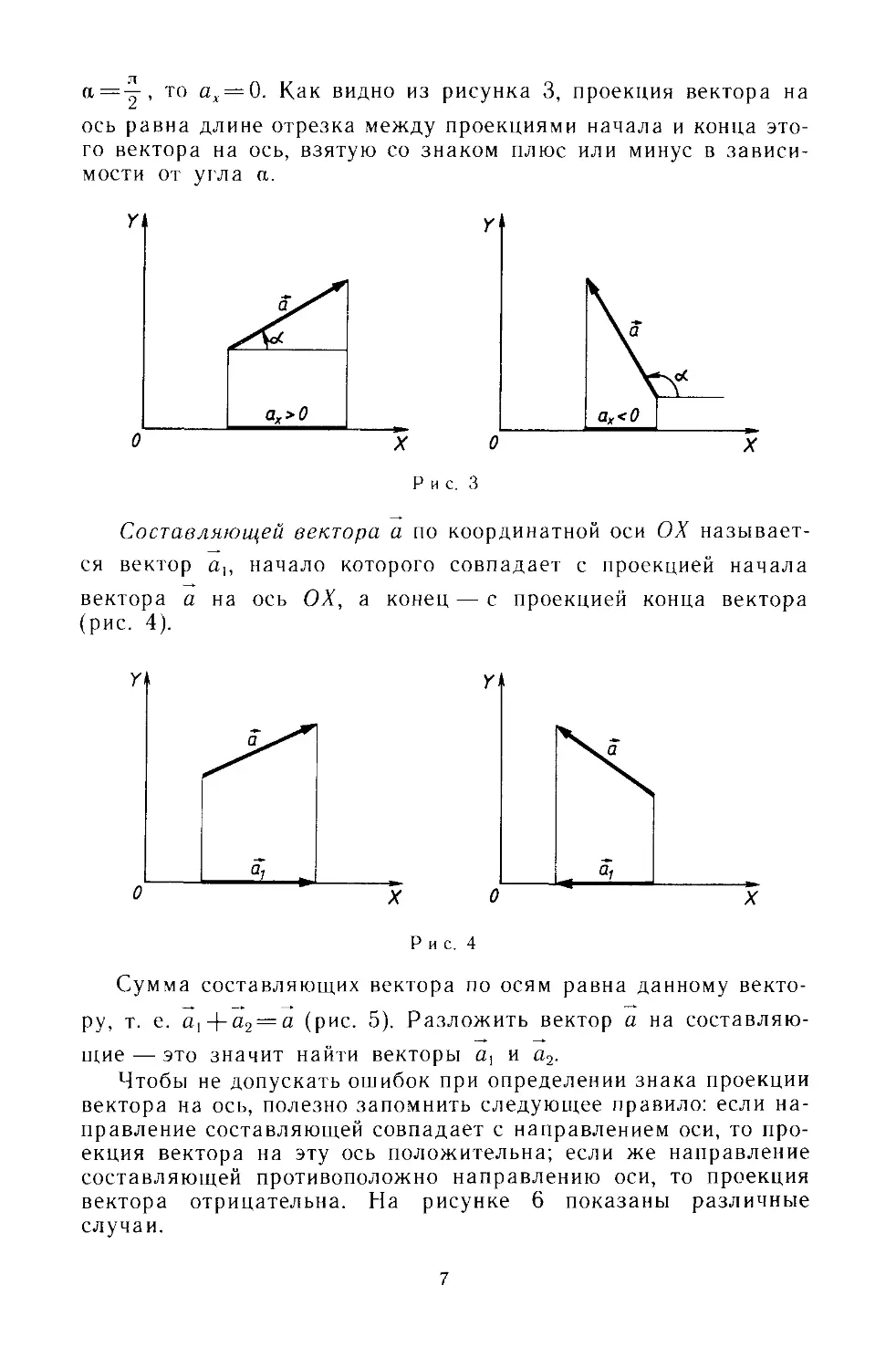
а=у, то a^ = 0. Как видно из рисунка 3, проекция вектора на
ось равна длине отрезка между проекциями начала и конца это-
го вектора на ось, взятую со знаком плюс или минус в зависи-
мости от угла а.
ах>0
Р и с. 3
Составляющей вектора а по координатной оси ОХ называет-
ся вектор аи начало которого совпадает с проекцией начала
вектора а на ось ОХ, а конец — с проекцией конца вектора
(рис. 4).
Y
Р и с. 4
Сумма составляющих вектора по осям равна данному векто-
ру, т. е. al-\-a2 = а (рис. 5). Разложить вектор а на составляю-
щие— это значит найти векторы а{ и а2.
Чтобы не допускать ошибок при определении знака проекции
вектора на ось, полезно запомнить следующее правило: если на-
правление составляющей совпадает с направлением оси, то про-
екция вектора на эту ось положительна; если же направление
составляющей противоположно направлению оси, то проекция
вектора отрицательна. На рисунке 6 показаны различные
случаи.
Рис. 5
X
~ b
bx=b
с
c
--0 dx
d
\
-1
e
ex=-
e
P и с. 6
Зная проекции вектора на координатные оси, можно найти
модуль этого вектора:
Рассмотрим некоторые задачи по кинематике, вызвавшие
затруднения у абитуриентов.
Задача 1. Движение материальной точки описывается следу-
ющими уравнениями: лс = 2-|-3/, г/=1-|-4/, в которых координа-
ты х и г/, а также время t заданы в единицах СИ. Найти ско-
рость точки.
Решение. Сравнивая заданные уравнения с уравнениями
зависимости координат от времени при равномерном прямоли-
нейном движении:
vx = 3 м/с,
находим проекции скорости на оси ОХ и OY:
vy = \ м/с. Следовательно, модуль скорости
Эту задачу абитуриент ошибочно решал и пояснял решение
так: скорость численно равна перемещению, совершаемому точ-
кой за 1 с, поэтому, подставив в заданные уравнения t=\ с, по-
лучим: лс, = 5 м, #i = 5 м; потом найдем перемещение за 1 с:
Следовательно, и = 5 у2 м. Это неверно. Подставляя t=\ с в
кинематические уравнения, абитуриент находил координаты точ-
ки в момент времени t=l с. Результат получился бы правиль-
ный, если бы были найдены изменения координат за единицу
времени, т. е. х, — xQ = 5 — 2 = 3 м, (/, — уо = 5— 1 = 4 м, которые,
как известно, численно равны проекциям скорости на соответст-
вующие координаты оси.
Обратим внимание на то, что данную задачу можно решить
другим способом. При любом движении (как равномерном, так
и неравномерном) проекция скорости точки на координатную ось
равна производной соответствующей координаты по времени:
их=х', vy = y'.
Учитывая это, по заданным уравнениям находим: vx~x' = 3 м/с,
vy = у' = 4 м/с. Затем находим модуль скорости:
Задача 2. Для материальной точки, движущейся по оси
ОХ, зависимость координаты от времени выражается урав-
нением
x = 6 — 4t + t2, A)
в котором все величины заданы в единицах СИ. Определить че-
рез ?,=5 с после начала движения координату точки, ее ско-
рость и пройденный путь.
Решение. В случае движения с постоянным ускорением
уравнение для координаты имеет вид
x = xo + vOxt + -^-; B)
а для проекции скорости
Vx=vOx+axt. C)
Сравнивая уравнения A) и B), находим: хо = 6 м, vQx —
= —4 м/с, ах = 2 м/с2. Затем, согласно уравнению C), имеем:
vx=-4 + 2t. D)
Найдем координату точки и ее скорость в момент времени
^i = 5 с, подставив это значение времени в уравнения A) и D):
лг, = 6 —4^ + ^=11 м, vlx=— 4 + 2-5 = 6 м/с.
Мы видим, что иОх<.О, а ии>0. Следовательно, точка снача-
ла двигалась в направлении, противоположном направлению
оси ОХ, а затем с некоторого момента времени t2 стала двигать-
ся в обратную сторону. В этот момент проекция скорости на ось
ОХ равна нулю. Согласно уравнению D), получим 0=—4
откуда t2 = 2 с. Координата точки в этот момент времени
x2 = 6 — 4t2 + t22 = 2 м.
Как видно из рисунка 7, путь
s= \х2 — хо
, — х2\ = 13 м.
Многие абитуриенты, решая эту задачу, не учитывали изме-
нение направления скорости и поэтому путь находили как раз-
ность лс, — х0.
х, X
Р и с. 7
Задача 3. Над ямой глубиной h бросают вертикально
вверх камень с начальной скоростью v0. Через какое время ка-
мень упадет на дно ямы? Сопротивление воздуха не учитывать.
Решение. Абитуриенты часто начинали решение с того, что
находили сначала время /,, за которое камень поднимается до
верхней точки траектории, затем высоту Н (рис. 8), после чего
определяли время t2, за которое камень упадет с высоты H-\-h.
Тогда искомое время равно tx-\-t2. Такое решение длинное и не-
рациональное.
Будем решать задачу координатным методом. Начало коор-
динат расположим на уровне земли, ось OY направим верти-
кально вверх (рис. 8).
Обратим внимание на тот факт, что
ускорение камня равно ускорению сво-
¦ бодного падения g, модуль и направ-
ление которого постоянны в течение
всего времени движения камня. Следо-
вательно, независимо от того, движет-
ся ли камень вверх или вниз, его коор-
дината в момент времени t
у/////////.
7'
X
Р и с. 8
Так как yo = O, vOy=vo, gy= —g, то
y = v0t-gt2/2.
В момент t=tn падения камня на
дно ямы его координата у=—h. По-
этому
10
Решим это уравнение относительно /„:
Значение t',=——— отбрасываем, так как /',<0, что не
имеет смысла.
Итак, окончательный ответ:
Разумеется, можно было бы систему координат выбрать ина-
че, расположив, например, начало координат на уровне дна ямы.
Тогда уравнение будет иметь другой вид:
В момент падения камня на дно ямы его координата (/ = 0,
t = tn. Подставив эти значения в последнее уравнение и решив
его, читатель убедится, что для /„ получается то же значение,
что и в первом случае.
Абитуриенты ошибочно считали, что кинематические уравне-
ния, описывающие движение камня вверх и вниз, будут различ-
ными, потому что меняется направление движения.
Задача 4. По наклонной плоскости из точки О толкнули
снизу вверх небольшой шарик. Точку А, находящуюся на некото-
ром расстоянии / от точки О, шарик проходит с промежутком
времени т между моментами прохождения. Найти начальную
скорость шарика и время, за которое он вернется в точку О. Уско-
рение шарика считать постоянным и равным а.
Решение. Начало координат совместим с точкой О, в кото-
рой шарик находился в начальный момент времени /0 = 0, ось ОХ
направим вдоль наклонной плоскости снизу вверх (рис. 9). Тогда
координата х шарика в момент времени / определяется урав-
нением
, at'2
X=V0t — ,
где и0 — начальная скорость.
Решив это квадратное уравнение, получим два значения t:
11
Р и с. 9
Разность t2 — tx этих значений равна промежутку времени между
моментами прохождения шариком точки с координатой х:
2Л]и1-2ах
At = t2 — /j, А/ =
При х=1, А^ = т получим:
Отсюда найдем начальную скорость:
1 -\ / 9 9
! = тг Л/а т2-
-8а/.
Если в выражение для А/ подставим х=0 (координата на-
чальной точки О), то получим время, за которое шарик вернется
в точку О:
Подставив в эту формулу выражение для v0, получим:
5. При нахождении пути, пройденного телом, абитуриенты
иногда ошибочно считают, что если начало координат совпадает
с начальной точкой траектории прямолинейно движущегося те-
ла, а направление оси ОХ совпадает с направлением начальной
скорости, то координата х тела равна пути /. Это неверно в об-
щем случае. Например, в задаче 3 (п. 4) в момент падения камня
на дно ямы его координата у= —h, а путь, пройденный камнем
за время полета, равен суммарной длине отрезков траектории,
т. е. l = 2H-\-h. Если же начало координат находится на дне
ямы, то в момент падения камня его координата у = 0, а путь,
пройденный камнем, / = 2Я + /г.
6. Иногда поступающие забывают о том, что все кинематиче-
ские величины и характеристики движения тела (координаты,
скорость, ускорение, путь, траектория) зависят от выбора систе-
мы отсчета.
Задача. С самолета, летящего горизонтально с постоянной
скоростью ио= 125 м/с на высоте h— 1960 м, сброшен небольшой
12
предмет. На каком расстоянии от самолета будет находиться
предмет: через rf, = 10 с после выбрасывания; через /2 = 25 с? Со-
противление воздуха не учитывать.
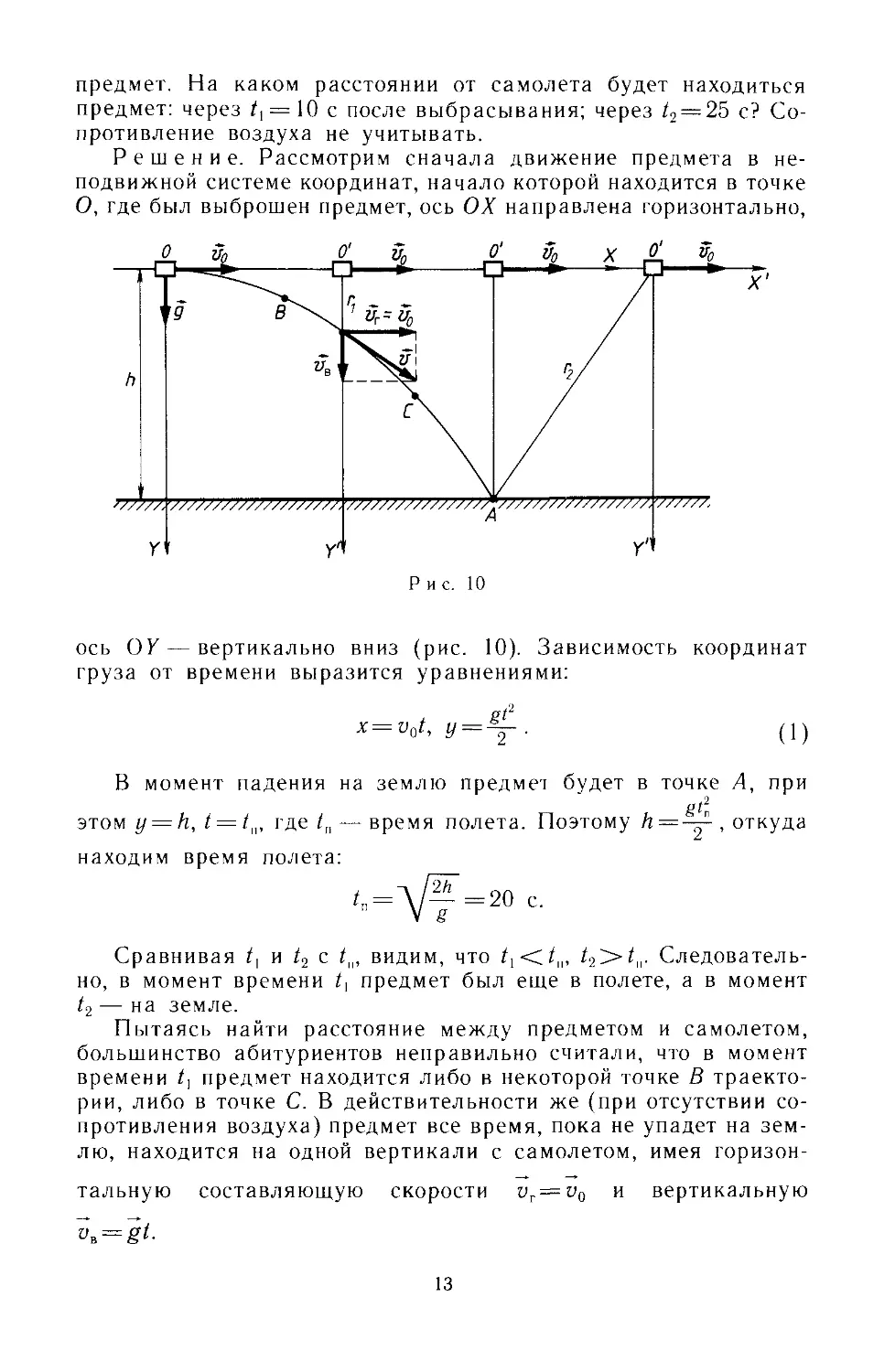
Решение. Рассмотрим сначала движение предмета в не-
подвижной системе координат, начало которой находится в точке
О, где был выброшен предмет, ось ОХ направлена горизонтально,
Рис. 10
ось OK — вертикально вниз (рис. 10). Зависимость координат
груза от времени выразится уравнениями:
1 gt
x=vot, У = \- ¦
A)
В момент падения на землю предмет будет в точке А, при
этом y = h, t = ttl, где tn — время полета. Поэтому h=—^-, откуда
находим время полета:
гтгг
= 20 с.
Сравнивая (, и (, с tu, видим, что t\<itu, t.2>tu. Следователь-
но, в момент времени t{ предмет был еще в полете, а в момент
t2 — на земле.
Пытаясь найти расстояние между предметом и самолетом,
большинство абитуриентов неправильно считали, что в момент
времени *, предмет находится либо в некоторой точке В траекто-
рии, либо в точке С. В действительности же (при отсутствии со-
противления воздуха) предмет все время, пока не упадет на зем-
лю, находится на одной вертикали с самолетом, имея горизон-
тальную составляющую скорости vr=uQ и вертикальную
13
Как известно из курса математики, расстояние между двумя
точками (*,, «/,) и (х2, у2) находится по формуле
г = У(х2-х1J + (у2-у,J. B)
Из сказанного выше ясно, что в момент времени tx координа-
ты х самолета и предмета одинаковы и равны xl = voti, а коорди-
ната у предмета в этот момент yi=gt\/2. Следовательно, пред-
мет находится от самолета на расстоянии гг=уи т. е.
л, ==^- = 490 м.
В момент времени г2 = 25 с координаты самолета были
x2=v0t2, г/9 = 0. Предмет был на земле. Определим его коорди-
наты:
/2/Г
По формуле B) находим расстояние между предметом и са-
молетом:
Г — \ /I 71 / 71 \ \ J- h1 ~ 9ГК7 1U rf">
Г2— Y^U0'2— ^g ,/ +ft ~^D/ M. (J)
В системе координат XOY траектория предмета представляет
собой параболу. В этом легко убедиться, если найти уравнение
траектории y = f(x). Используя уравнения A), находим:
t=±, У = -^х>.
Рассмотрим теперь движение предмета в системе координат
X'O'Y', связанной с самолетом. В этой системе координаты пред-
мета jt' = O, y' — gt'i/2. Отсюда видно, что траектория пред-
мета — прямая линия. В момент времени /, расстояние между
предметом и самолетом
В момент падения на землю t = tn, y' = h. Поэтому, как и в си-
стеме XOY, получим время полета:
2/Г
В момент времени t2 в системе X'O'Y' координаты предме-
та — vo(t2 — tn) и /г, а самолета 0 и 0. Подставив эти значения ко-
ординат в формулу B), получим тот же результат C).
7. Нередко абитуриенты допускают ошибки при решении за-
дач, связанных с нахождением средней скорости.
Имеются два понятия средней скорости. Первое: средняя ско-
рость — это векторная величина, равная отношению перемеще-
14
ния ко времени, за которое было совершено это перемещение,
т. е.
Второе: средняя скорость — скалярная величина, равная от-
ношению пути ко времени, за которое пройден этот путь, т. е.
Ее называют также средней скоростью прохождения пути или
средней путевой скоростью, чтобы отличить от первого понятия
средней скорости.
В задачах, связанных с движением транспорта, чаще исполь-
зуют понятие средней скорости прохождения пути, чтобы учесть
расход топлива, степень износа машин и т. п.
При прямолинейном движении с постоянным ускорением
средняя скорость равна полусумме начальной и конечной скоро-
стей:
vt-\-v2
Рассмотрим решение двух задач.
Задача 1. Первую половину пути автомобиль двигался со
скоростью и, =50 км/ч, а вторую — со скоростью о2 = 80 км/ч.
Найти среднюю скорость автомобиля на всем пути.
Решение. Обозначим через / весь путь, пройденный авто-
мобилем. Тогда средняя путевая скорость Уср = -, где t — время,
за которое пройден путь /. Первую половину пути автомобиль
прошел за время tl= ——, вторую — за время t.2 = -—. Следова-
тельно,
а средняя скорость
/ 2vxv2 2-50-80 , С1 _ ,
V,p — - = ———= 50-4-80 км/4 Л* 61,5 км/ч.
Некоторые поступающие решали эту задачу так:
+ ^2 50 + 80 , сс ,
иср =—-— = —-— км/ч=о5 км/ч.
Это неверно. Как уже отмечалось, по последней формуле можно
находить иср только при равноускоренном движении.
Задача 2. Тело падает без начальной скорости с высоты
h. Найти среднюю скорость на нижней половине пути. Сопротив-
ление воздуха не учитывать.
15
л
\
\
2
Y
д
9
h/2
д
Решение. Свободное падение —
это равноускоренное движение, поэто-
му средняя скорость на нижней поло-
вине пути
i
A)
Рис. 11
ср 2 '
где v{, v2 — скорости тела в точках / и 2
соответственно (рис. 11). Найдем эти ско-
рости. Совместим начало координат с
точкой О, в которой тело находилось в
начальный момент времени /0 = 0, и на-
правим ось OY вертикально вниз. Тогда
движение тела будет описываться ки-
нематическими уравнениями:
y = ML, Vy = gt< B)
где у — координата тела в момент времени /; vy — проекция ско-
рости на ось OY. В точке / #,=— v[f/ = vh / = /,. На основании
уравнений B) находим:
Отсюда ti=~\J—, f|=
В точке 2 y2 = h, v2!l=v2, t = t2. Следовательно,
—.
откуда
Подставив найденные значения и, и v2 в формулу A),
получим:
Кстати, значения и, и v2 можно найти другим способом, ис-
пользуя закон сохранения энергии. Будем считать, что в точке
2 потенциальная энергия тела Ер2 — 0. Тогда в точке О она равна
Ер0 = mgh, а в точке / — Epi =-^|— . Кинетическая энергия тела в
точке О Ek0 = 0, в точке / — Еи =—^-, в точке 2 — Ek2 — —-?-. На
16
основе закона сохранения энергии Ек1)-\-ЕрП = Ек]-{-Е1,1, Em-\-Ep() =
= Ек2 + Ер2, или
mv\
—
Отсюда найдем: vl=\gh, v2=y'2gh .
8. Допускались ошибки при указании направления ускоре-
ния: некоторые абитуриенты утверждали, что это направление
всегда совпадает с направлением скорости, другие говорили, что
при прямолинейном движении с уменьшающейся скоростью уско-
рение направлено противоположно скорости, но доказать это не
могли.
Вспомним, что такое ускорение. Ускорение — это векторная
величина, характеризующая быстроту изменения скорости. При
прямолинейном движении с постоянным ускорением вектор ско-
рости за любые равные промежутки времени изменяется на рав-
ные величины. Поэтому для любого промежутка времени отно-
шение изменения скорости тела к промежутку времени будет од-
ним и тем же, т. е. ускорение
о = -
Аи
Вектор а совпадает по направлению с вектором Ли.
Р и с. 12
d=b-c
d = г - b
Р и с. 13
Как известно, разность двух векторов находится так: нужно
совместить начала этих векторов и соединить их концы векто-
ром, направленным от вычитаемого к уменьшаемому (рис. 12, 13).
Пользуясь этим правилом, найдем изменение скорости
До в случае увеличения ее модуля (рис. 14) и в случае уменьше-
ния его (рис. 15). Мы видим, что в первом случае Аи, а следова-
тельно, и а направлены так же, как и скорость тела, а во вто-
ром — противоположно скорости.
Если скорость прямолинейно движущегося тела изменяется
неравномерно (т. е. аФconst), то различают среднее ускорение
17
аср=—— и мгновенное ускорение а— величину, равную пределу
отношения изменения скорости Аи к промежутку времени At, в
течение которого произошло это изменение, при условии, что
этот промежуток времени стремится к нулю:
.. Аи
hm
Мгновенное ускорение называют также ускорением тела в
данный момент времени или просто ускорением. Ясно, что при
движении с постоянным ускорением a =a = const.
A2T
P и с. 14
ли
Рис. 15
При криволинейном движении, как и при прямолинейном,
ускорение а направлено так, как направлен вектор Аи при стрем-
лении At к нулю. На рисунке 16 показан вектор Av = v2 — vu
где v, и2 — скорости тела в точках / и 2 соответственно. При
А/-»-0 направление вектора Аи будет совпадать с направлением
ускорения а.
2
Рис. 16
Заметим, что ускорение определяется не значением скорости
в данный момент времени, а изменением скорости. Проекция
ускорения на координатную ось равна производной проекции
скорости по времени, т. е. второй производной координаты по
времени:
9. Слабое усвоение понятия ускорения приводит поступаю-
щих к затруднениям при попытке ответить на такой вопрос: «По-
чему мы говорим о наличии ускорения у точки, которая равно-
18
мерно движется по окружности, ведь ускорение характеризует
изменение скорости, а при равномерном движении скорость не
изменяется?»
Из сказанного выше ясно (см. рис. 16), что изменение вектора
скорости, который в каждой точке криволинейной траектории
направлен по касательной к ней, обусловлено, в общем случае,
двумя причинами: 1)изменением направления скорости; 2) изме-
нением модуля скорости. Когда говорят о равномерном движе-
нии точки по окружности, то имеют в виду движение, при кото-
ром модуль скорости остается постоянным. Направление же ско-
рости в различных точках окружности различно. Например,
в положениях / и 2 (рис. 17) векторы vt и v2 по модулю равны
(и, = у2=у), а по направлению не совпадают. Разность этих вех-
торов Av^=v.2—v[ в пределе при стремлении к нулю промежутка
времени At, по прошествии которого точка переходит из положе-
ния / в положение 2, направлена к центру окружности по норма-
ли к скорости. Такое же направление имеет и ускорение, поэтому
оно называется центростремительным (или нормальным) ускоре-
нием. Модуль этого ускорения
где v — модуль скорости точки; R — радиус окружности.
LJ,
Рис. 17
Рис. 18
Оставаясь постоянным по модулю, центростремительное
ускорение непрерывно изменяется по направлению при движе-
нии точки по окружности, так как оно всегда направлено по ра-
диусу к центру окружности.
Если материальная точка движется по окружности неравно-
мерно, то вектор ускорения можно представить в виде суммы
двух составляющих. Одна из них — это центростремительное
ускорение ап, характеризующее изменение вектора скорости по
направлению, вторая—касательное (или тангенциальное)
ускорение ах, которое характеризует изменение модуля скорости
19
и направлено по касательной к траектории (рис. 18). В этом слу-
чае полное ускорение точки
Модуль полного ускорения определим по теореме Пифагора:
При равномерном движении по окружности касательное
ускорение отсутствует, поэтому а = ап.
10. Среди задач по кинематике, предлагавшихся на вступи-
тельных экзаменах, трудными для абитуриентов оказались зада-
чи, связанные с законом сложения скоростей.
Задача. Капли дождя, падающие отвесно, образуют на ок-
не движущегося трамвая полосы под углом а = 30° к вертикали.
Скорость трамвая vl=5 м/с. Какова скорость капель относи-
тельно земли?
Решение. Чтобы найти скорость капель относительно зем-
ли, воспользуемся законом сложения скоростей: скорость тела
относительно неподвижной системы отсчета равна векторной
сумме скорости этого тела относительно подвижной системы от-
счета и скорости подвижной системы относительно неподвижной.
Неподвижную систему координат XOY свяжем с землей, по-
движную Х'0'Y' — с трамваем. Обозначим через v2 скорость
капли в системе XOY, v'2— скорость капли в системе Х'0'Y'. По
закону сложения скоростей v2—v'2-\-v[.
Сложение векторов v'2 и v{ показано на рисунке 19. Получен-
ный треугольник прямоугольный, поэтому
м/с?к
tg а tg 30°
м/с.
При решении этой задачи некоторые абитуриенты ошибочно
строили чертеж так, как показано на рис. 20. Такое построение
У
V2
О1
X'
Рис. 19
Рис. 20
20
противоречит закону сложения скоростей и повседневному опы-
ту: получается, что капли на окне движущегося трамвая откло-
няются по направлению движения. Хотя формально из этого тре-
угольника получится тот же результат, что и выше, но решение
неверное.
11. Часть абитуриентов считала, что закон сложения скоро-
стей справедлив только для равномерных и прямолинейных дви-
жений. В действительности же этот закон справедлив для любых
движений. Если движение тела или системы отсчета (или того
и другого) не является равномерным и прямолинейным, то закон
сложения можно применять для мгновенных скоростей. В связи
с этой ошибкой рассмотрим следующую задачу.
Задача. Обруч катится по горизонтальной плоскости со
скоростью v без проскальзывания. Определить мгновенные ско-
рости нижней и верхней точек обруча.
Решение. Неподвижную систему координат XOY выберем
так, что ось ОХ лежит в плоскости, по которой катится обруч.
Подвижная система Х'О'У движется поступательно вместе с
осью обруча со скоростью v (рис. 21). Скорости v'B и v'c точек В и
С обода в подвижной системе одинаковы по модулю и направле-
ны по касательной к ободу. Согласно закону сложения скоро-
стей, скорость любой точки обруча относительно неподвижной
системы координат равна векторной сумме скоростей v и v .
Y,
Y'
ff
A
4
УЧ
> ¦ <1» -
UA A V
Рис. 21
X
Пусть vA — скорость точки А относительно плоскости. Тогда
vA = v'AJrV. При отсутствии проскальзывания нижняя точка А об-
руча, касаясь плоскости, неподвижна относительно ее, поэтому
vA = 0, т. е. 0 = vA-\-v. Для проекций скоростей на ось ОХ
получим:
0 = v'Ax+vx, 0=-v'A + v.
Отсюда v'A = v. Следовательно, относительно системы Х'О'У ско-
рость любой точки по модулю равна v. Относительно системы
21
XOY точка В имеет скорость vB = v'B-\-v. Спроектировав эти ско-
рости на ось ОХ, получим:
vBx=v'Bx + vx, vB = v'B-\-v.
Но v'B = v. Следовательно, vB = 2v.
Теперь читатель может легко найти, что скорости точек С и
D обруча, удаленных от плоскости на расстояние, равное радиусу
обруча, равны по модулю:
ис=ьп = л]2 v.
12. Многие поступающие не могут объяснить зависимость
центростремительного ускорения а„ от радиуса R окружности, по
которой движется тело (материальная точка). Рассматривая
формулы а„ = -~ и а„ = оJ/<? (где со — угловая скорость), они дела-
ют противоречивый вывод: центростремительное ускорение одно-
временно обратно пропорционально радиусу и прямо пропорцио-
нально ему.
Приведенные формулы не противоречат друг другу. Вторая
следует из первой, так как v = a>R. Первая формула отражает
тот факт, что из двух тел, движущихся с одинаковыми линейны-
ми скоростями по окружностям различных радиусов, большее
центростремительное ускорение имеет тело, движущееся по
окружности меньшего радиуса. Иначе говоря, при постоянной
линейной скорости центростремительное ускорение обратно про-
порционально радиусу.
Вторая формула показывает, что при постоянной угловой
скорости (о центростремительное ускорение прямо пропорцио-
нально радиусу, т. е. если два тела движутся с одинаковыми уг-
ловыми скоростями по окружностям различных радиусов, то
центростремительное ускорение больше там, где больше радиус.
13. Распространенным источником ошибок при решении за-
дач является неумение правильно применять кинематические
уравнения:
vx=vOx-\-axt, x=KQ+voxt + ^-, A)
позволяющие найти проекцию скорости тела и его координату
в момент времени t. Например, при решении задач на движение
тела, брошенного под углом к горизонту, абитуриенты нередко
рассматривают отдельные этапы этого движения, отдельные
«кусочки» траектории: сначала поднимается, затем падает и т. д.
Нужно твердо помнить, что при движении тела с постоянным
по модулю и направлению ускорением уравнения A) справедли-
вы для всего времени движения независимо от того, в каком на-
правлении движется тело — поднимается или падает.
Задача. С башни высотой Н брошен камень с начальной
22
скоростью v0, направленной под углом а к горизонту. Пренебре-
гая сопротивлением воздуха, определить дальность полета кам-
ня по горизонтальному направлению и скорость его в момент па-
дения на землю.
Решение. Выберем систему координат так, чтобы век-
торы vQ w g лежали в плоскости XOY, начало координат совпа-
дало с точкой башни, откуда брошен камень, ось ОХ была на-
правлена горизонтально, ось OY— вертикально вверх (рис. 22).
Камень движется с постоянным ускорением g, поэтому, согласно
уравнениям A), в момент времени t он имеет координаты:
х = vQt cos a, B)
= vQt sin а — ^-.
C)
Н
Г9
. Vox
Vny
Рис. 22
Искомая дальность полета s равна координате х в момент па-
дения, т. е. s — x,, при t = tu, где tn — время полета камня. Со-
гласно уравнению B),
s = votn cos a. D)
Учитывая, что в момент падения у— —Н, t = tn, на основании
уравнения C) получим:
— H = Vf)tn sm а —~ или ^—votns\na~H = O.
Решив это квадратное уравнение, найдем:
v0 sin art~\Jvl sin2 a-j-2gH
t=-
Так как время полета не может быть отрицательно, то берем
значение
23
va sin
sin2 a + 2gH
E)
Подставив это значение tn в формулу D), найдем горизонталь-
ную дальность полета:
(v0 sin a-j-ytijj sin2 a-\-2gH ) v0 cos a
В момент падения модуль скорости
v = ^vl + v2ag, F)
где vnx, у — проекции вектора скорости vn на оси ОХ и OY со-
ответственно. Согласно уравнениям A), в момент времени t про-
екции скорости камня выражаются так:
Dj=u0cosa, vy=v0 sin a — gt.
Значит, в момент падения
un;c=D0cosa, vny=vosin a —gtn.
Подставив в последнюю формулу вместо tn выражение E),
получим:
Теперь на основании формулы F) находим, что в момент па-
дения камня на землю модуль его скорости
Решая эту задачу, некоторые абитуриенты сначала рассмат-
ривают движение камня до точки А как движение тела, брошен-
ного под углом к горизонту, а затем движение из точки А, оши-
бочно считая его движением тела, брошенного горизонтально с
высоты И.
Остановимся теперь на ошибках, допускаемых абитуриента-
ми при чтении и построении графиков.
0 t, ft. ft ti t 0 t, t, t, t tO
ъ ь n t
14. Часто поступающие не учитывают существенных призна-
ков графиков и поэтому делают неправильные выводы. Напри-
мер, по графикам зависимости проекций скорости от времени
(для краткости такие графики называются графиками скорости),
показанным на рис. 23, поступающие заключали, что скорость
второго тела больше скорости первого.
15. Затруднения у некоторых абитуриентов вызывало такое
упражнение: по графикам (рис. 24) описать характер движения
тел А, В, С, D, Е, F и объяснить, что означают точки пересечения
графиков между собой и с осью времени, если известно, что все
эти тела движутся вдоль оси ОХ.
Внимательное рассмотрение графиков позволяет сделать сле-
дующие выводы. В промежутке времени 0 — t] тело А двигалось
равномерно, о телах В, D и F ничего не известно, тело С двига-
лось равноускоренно, т. е. с постоянным ускорением, при кото-
ром модуль скорости увеличивался, тело Е двигалось с перемен-
ным ускорением, модуль которого возрастал со временем. В про-
межутке t{ — t2 тело А покоилось, В и С двигались равномерно,
D и Е — равноускоренно, F — с возрастающим ускорением. В про-
межутке t2 — t4 тело А двигалось равномерно в направлении,
противоположном направлению оси ОХ, тело С — равнозамед-
ленно, т. е. с постоянным ускорением, при котором модуль скоро-
сти уменьшался, тело Е двигалось с переменным ускорением,
модуль которого уменьшался, тело В — равномерно, D — равно-
ускоренно, F — с возрастающим ускорением.
Точки /, 2 и 3 пересечения графиков между собой означают
соответственно, что в момент времени t3: 1) координаты тел А и
В были одинаковы, т. е. эти тела встретились; 2) тела С и D имели
одинаковую скорость; 3) тела Е и F имели одинаковое ускорение.
Точки пересечения графиков с осью времени означают, что
в начальный момент времени (/0 = 0) тело А находилось в начале
координат, тело С не имело начальной скорости, тело Е не имело
начального ускорения, тело В находилось в начале координат в
момент времени /,, в этот же момент скорость тела D и ускоре-
ние тела F были равны нулю. В момент времени ti координата
тела Л, скорость тела С и ускорение тела Е стали равными нулю.
Ошибки абитуриентов при решении этого упражнения весьма
разнообразны. Отвечали, например, что в промежутку tx —12
25
тело В двигалось равноускоренно, а А — равномерно; что в проме-
жутке /2—/4 тела А и Е двигались равнозамедленно; что тела
В и D двигались все время с одинаковой скоростью.
Чтобы не допускать ошибок при чтении графиков, нужно не
только обращать внимание на вид графиков, но и учитывать фи-
зический смысл величин, зависимость которых изображена, а
также направления координатных осей. Только что рассмотрен-
ные графики имеют одинаковый вид, а отражают зависимости
разных величин при различных движениях тел.
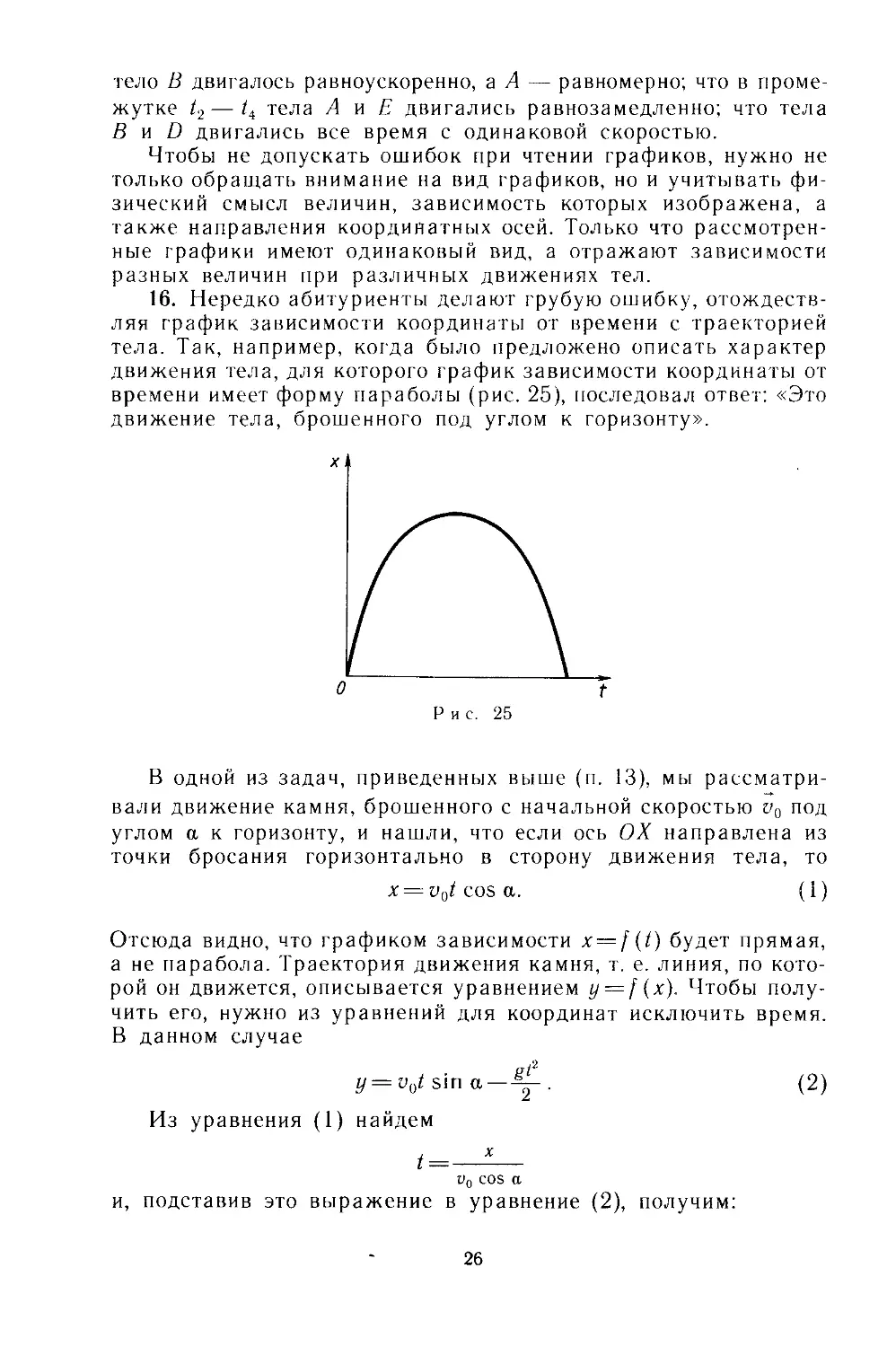
16. Нередко абитуриенты делают грубую ошибку, отождеств-
ляя график зависимости координаты от времени с траекторией
тела. Так, например, когда было предложено описать характер
движения тела, для которого график зависимости координаты от
времени имеет форму параболы (рис. 25), последовал ответ: «Это
движение тела, брошенного под углом к горизонту».
Рис. 25
В одной из задач, приведенных выше (п. 13), мы рассматри-
вали движение камня, брошенного с начальной скоростью и0 под
углом а к горизонту, и нашли, что если ось ОХ направлена из
точки бросания горизонтально в сторону движения тела, то
x=vot cos a. A)
Отсюда видно, что графиком зависимости x = f(t) будет прямая,
а не парабола. Траектория движения камня, т. е. линия, по кото-
рой он движется, описывается уравнением y = f(x). Чтобы полу-
чить его, нужно из уравнений для координат исключить время.
В данном случае
y = votsin a — Ц-. B)
Из уравнения A) найдем
v0 cos a
и, подставив это выражение в уравнение B), получим:
26
va cos a
Это уравнение параболы. Она обращена ветвями вниз, так как
коэффициент при х2 отрицателен.
Показанный на рис. 25 график отражает зависимость коорди-
наты х от времени t для случая, когда тело движется с началь-
ной скоростью v0 и постоянным ускорением а, направленным
противоположно v0. При этом ось ОХ начинается в начальной
точке траектории и сонаправлена с v0. Действительно, в этом
случае уравнение для координаты имеет вид:
, at2 а о , 1
X=Vot — ИЛИ Х=— —t +VQt,
т. е. имеем уравнение параболы, обращенной ветвями вниз. При-
ведем пример такого движения. Тело брошено вертикально
вверх с начальной скоростью v0 (ось ОХ направлена тоже верти-
кально вверх). В этом случае зависимость координаты х от вре-
мени t имеет вид x=vot — -^-. Графиком этой зависимости являет-
ся парабола, а траектория движения тела — отрезок прямой г/ = 0.
Аналогичным является движение тела по наклонной плоско-
сти с постоянным ускорением (см. п. 4, задача 4).
Рассмотрим еще один пример, наглядно иллюстрирующий
различие между траекторией движения и графиком зависимости
координаты от времени (графиком движения).
Пусть точка А равномерно движется по окружности радиу-
сом хт (рис. 26). При этом радиус, соединяющий точку А с цент-
Рис. 26
ром окружности, за время t поворачивается на угол ф = ш^, где
со — угловая скорость. Пусть в начальный момент времени (^0 = 0)
точка находилась в положении Ао. За начало отсчета координат
выберем центр окружности, ось ОХ направим от О к Ао. Угол
Ф будем отсчитывать от оси ОХ против часовой стрелки. Тогда в
момент времени / точка А имеет координаты:
27
л:= хт cos со/, г/ = хт sin w^.
Следовательно, график зависимости координаты х от време-
ни t представляет собой косинусоиду (рис. 27), а координаты
г/ — синусоиду (рис. 28), в то время как траектория движения точ-
ки — окружность.
Рис. 27
Р и с. 28
17. Среди экзаменационных задач встречаются задачи, кото-
рые требуется решить графически. При решении таких задач
распространенными являются ошибки, связанные с выбором си-
стемы отсчета и неумением правильно построить соответствую-
щие графики.
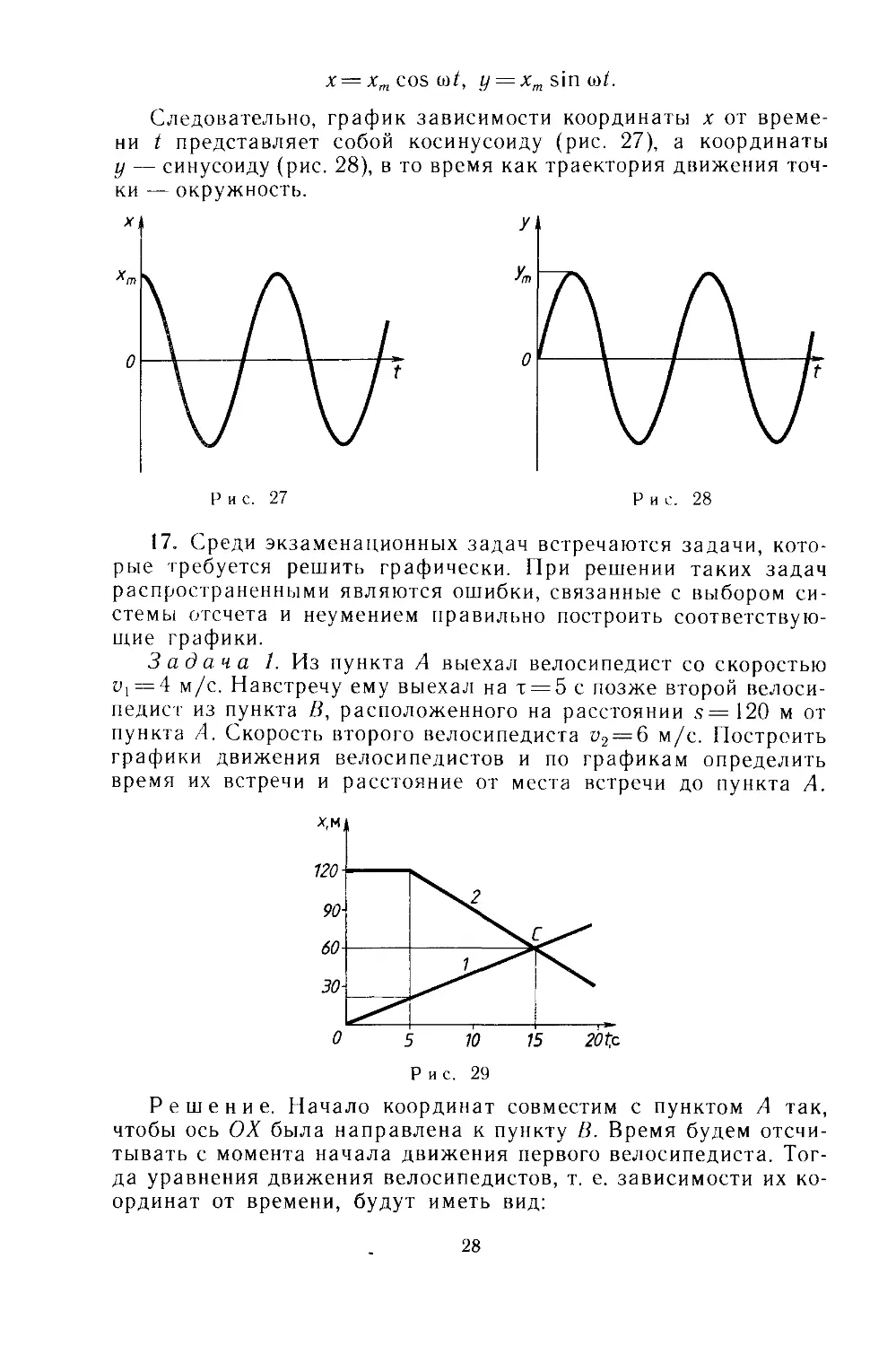
Задача 1. Из пункта А выехал велосипедист со скоростью
U[ = 4 м/с. Навстречу ему выехал на т = 5 с позже второй велоси-
педист из пункта В, расположенного на расстоянии s = 120 м от
пункта А. Скорость второго велосипедиста v2 = 6 м/с. Построить
графики движения велосипедистов и по графикам определить
время их встречи и расстояние от места встречи до пункта А.
20fc
Решение. Начало координат совместим с пунктом А так,
чтобы ось ОХ была направлена к пункту В. Время будем отсчи-
тывать с момента начала движения первого велосипедиста. Тог-
да уравнения движения велосипедистов, т. е. зависимости их ко-
ординат от времени, будут иметь вид:
28
Xl = Vi(, X2 — S — U2{/ — T).
Построим графики согласно этим уравнениям (рис. 29). Гра-
фики пересекаются в точке С. Это означает, что велосипедисты
встретились. Из рисунка видно, что встреча произошла через
15 с после выезда первого велосипедиста на расстоянии 60 м от
пункта А.
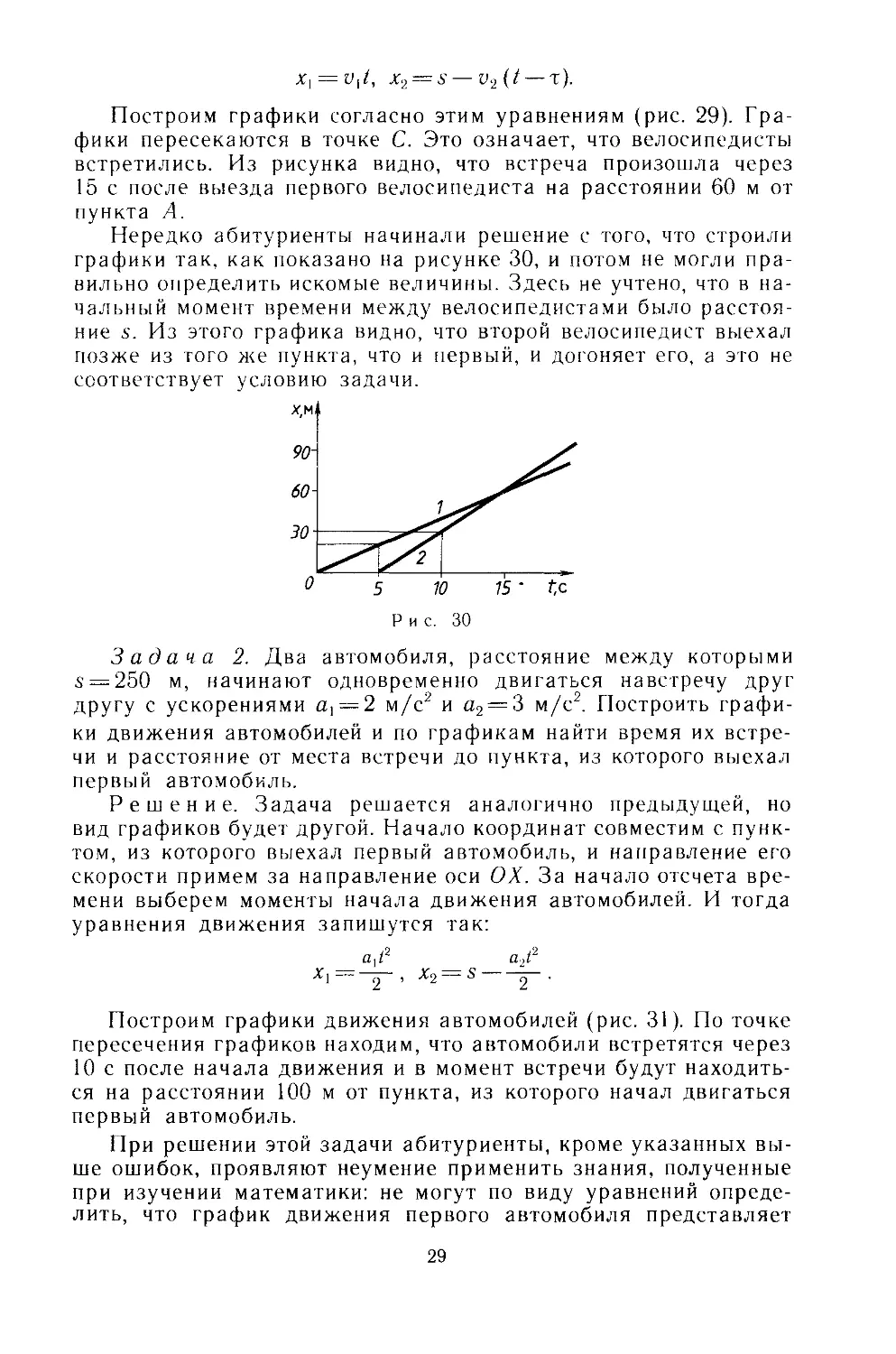
Нередко абитуриенты начинали решение с того, что строили
графики так, как показано на рисунке 30, и потом не могли пра-
вильно определить искомые величины. Здесь не учтено, что в на-
чальный момент времени между велосипедистами было расстоя-
ние s. Из этого графика видно, что второй велосипедист выехал
позже из того же пункта, что и первый, и догоняет его, а это не
соответствует условию задачи.
Задача 2. Два автомобиля, расстояние между которыми
s = 250 м, начинают одновременно двигаться навстречу друг
другу с ускорениями а, = 2 м/с2 и а2 = 3 м/с2. Построить графи-
ки движения автомобилей и по графикам найти время их встре-
чи и расстояние от места встречи до пункта, из которого выехал
первый автомобиль.
Решение. Задача решается аналогично предыдущей, но
вид графиков будет другой. Начало координат совместим с пунк-
том, из которого выехал первый автомобиль, и направление его
скорости примем за направление оси ОХ. За начало отсчета вре-
мени выберем моменты начала движения автомобилей. И тогда
уравнения движения запишутся так:
а/г а,/
Построим графики движения автомобилей (рис. 31). По точке
пересечения графиков находим, что автомобили встретятся через
10 с после начала движения и в момент встречи будут находить-
ся на расстоянии 100 м от пункта, из которого начал двигаться
первый автомобиль.
При решении этой задачи абитуриенты, кроме указанных вы-
ше ошибок, проявляют неумение применить знания, полученные
при изучении математики: не могут по виду уравнений опреде-
лить, что график движения первого автомобиля представляет
29
О 2 4 6 8 10 t,c
Рис. 31
собой параболу, ветви которой направлены вверх, потому что в
первом уравнении коэффициент при f положительный, а график
движения второго автомобиля — парабола, обращенная ветвями
вниз, так. как во втором уравнении коэффициент при t2 отрица-
тельный. (Заметим, что мы рассматриваем только ветви пара-
бол, соответствующие положительным значениям /, так как
/<0 в данной задаче смысла не имеет.)
Вместе с тем на вопрос преподавателя: «Что представляет
собой график функции у — ах2-\-Ьх-\-с?» — нередко следует пра-
вильный ответ, поясняющий, при каком условии ветви параболы
направлены вверх или вниз, при каком условии парабола смеще-
на вправо или влево, вверх или вниз. Получается, что знания по
математике существуют сами по себе, причем в каком-то застыв-
шем виде: стоит только обозначить величины другими буквами,
как абитуриент эту функцию уже не распознает.
Задача 3. На рисунке 32, а изображен график зависимости
координаты некоторого тела, движущегося прямолинейно вдоль
оси ОХ, от времени. Криволинейные участки графика являются
частями парабол. Построить графики зависимости скорости и
ускорения от времени.
Решение. Чтобы построить графики скорости и ускорения,
установим по данному графику характер движения тела в раз-
ные промежутки времени.
В промежутке 0 — tl график координаты представляет собой
часть параболы, ветви которой направлены вверх. Следователь-
но, в уравнении
а/
выражающем в общем виде зависимость координаты х от време-
ни t, коэффициент перед t2 положительный, т. е. ах>0. А так как
парабола смещена вправо, то это означает, что vQx<0, т. е. тело
имело начальную скорость, направленную противоположно на-
правлению оси ОХ. В течение промежутка 0 — t} скорость тела
30
X
0
0
U2
щ
OX:
0
a
M
6
/
/
в
1
1
t,
\
\
t?
t3
tB
\
n
n
i ts
tst
t
Рис. 32
сначала уменьшилась до нуля, а затем, изменив направление на
противоположное начальному, увеличилась до некоторого значе-
ния и,. График скорости на этом участке — отрезок прямой, про-
ходящей под некоторым углом к оси t (рис. 32, б), а график уско-
рения — отрезок прямой, лежащей выше оси времени (рис. 32, в).
В промежутке tx —12 тело двигалось равномерно со ско-
ростью и,. В промежутке времени t2 — /3 график координаты —
часть параболы, ветви которой направлены вниз. Следовательно,
здесь ах<0, скорость тела убывает до нуля к моменту времени
/3, а в промежутке t3— ti тело покоится. Затем в течение проме-
жутка <4 — ^5 тело движется равномерно со скоростью v2 в обрат-
ную сторону. В момент времени t5 оно достигает точки начала
отсчета координат и останавливается.
Учитывая характер движения тела, построим соответствую-
щие графики скорости «и ускорения (рис. 32,6, в).
При решении этой и аналогичных задач поступающие испы-
тывают большие трудности при выяснении характера движения
тела и при построении графиков.
18. Многие абитуриенты допускают ошибки при построении
графика скорости и нахождении по этому графику перемещения
тела и пройденного пути. Так, например, для тела, брошенного
вертикально вверх, график зависимости проекции скорости на
31
ось OY, направленную вверх из точки бросания, один из экзаме-
нуемых изобразил так, как показано на рисунке 33.
Рис. 33
Р и с. 34
Правильно этот график показан на рис. 34. Здесь учтено, что
в верхней точке траектории (в момент времени tx) скорость тела
равна нулю, а затем увеличивается, направлена противополож-
но оси OY, изменившись по направлению, и в момент падения
равна по модулю начальной скорости v0. График является отрез-
ком прямой vy=v0 — gt.
Как по графику скорости найти перемещение и пройденный
путь? При равномерном прямолинейном движении проекция пе-
ремещения s на ось ОХ:
Отсюда следует, что sx численно равна (с учетом соответствую-
щего масштаба) площади прямоугольника, ограниченного осью
времени, отрезками прямых t = tu t = t2 и графиком скорости:
сверху, если vx>0 (рис. 35, а), и снизу, если vx<.0 (рис. 35, б). При
их>0 проекция перемещения sx положительна, при
отрицательна.
Рис. 35
32
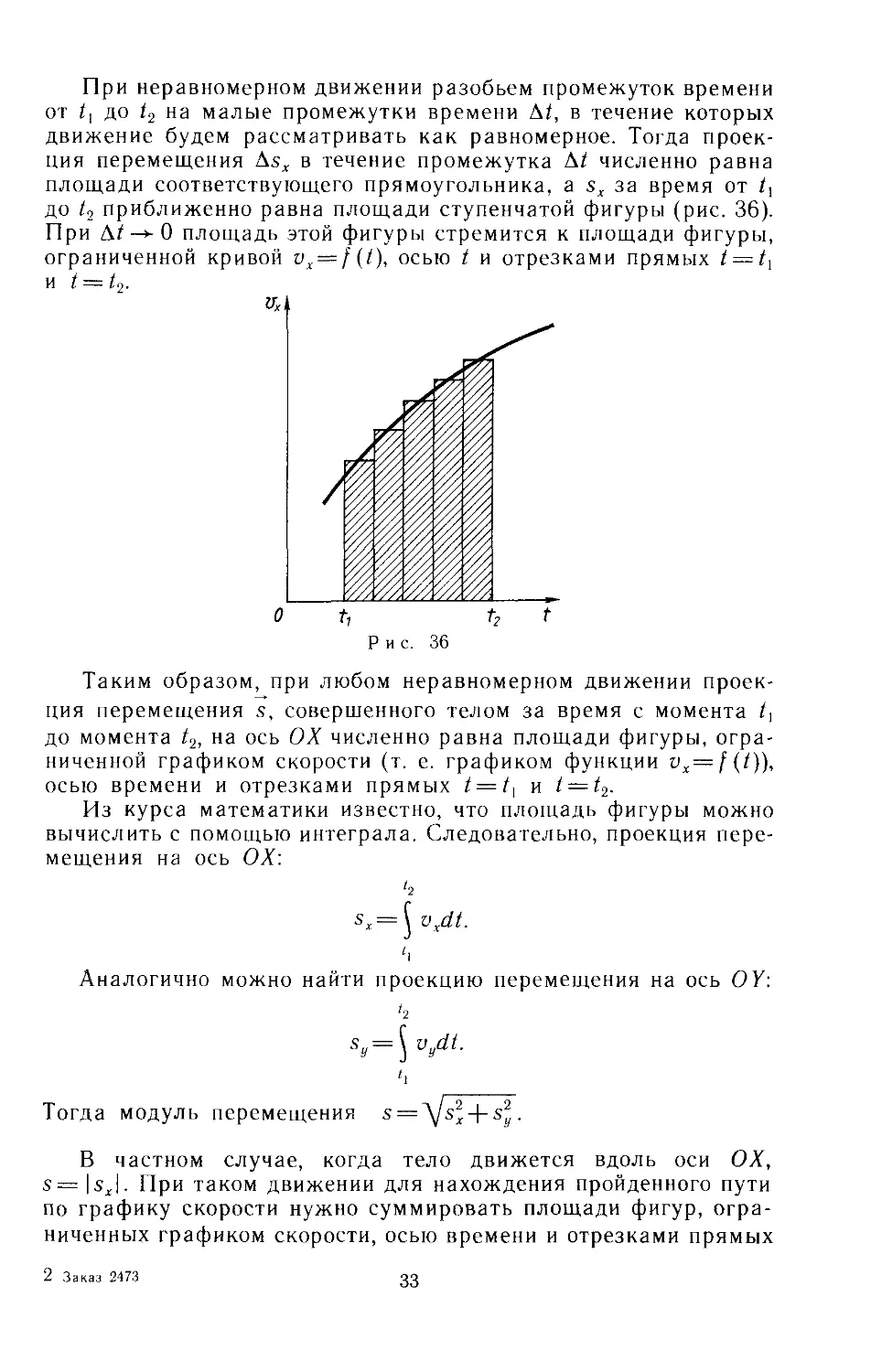
При неравномерном движении разобьем промежуток времени
от tx до t2 на малые промежутки времени At, в течение которых
движение будем рассматривать как равномерное. Тогда проек-
ция перемещения As, в течение промежутка А^ численно равна
площади соответствующего прямоугольника, a sx за время от tf,
до t2 приближенно равна площади ступенчатой фигуры (рис. 36).
При Л^ —*- 0 площадь этой фигуры стремится к площади фигуры,
ограниченной кривой vx — f(t), осью t и отрезками прямых t = tx
и t = U.
Рис. 36
Таким образом, при любом неравномерном движении проек-
ция перемещения s, совершенного телом за время с момента /,
до момента t2, на ось ОХ численно равна площади фигуры, огра-
ниченной графиком скорости (т. е. графиком функции dx = /(/)),
осью времени и отрезками прямых t=tx и t = t2.
Из курса математики известно, что площадь фигуры можно
вычислить с помощью интеграла. Следовательно, проекция пере-
мещения на ось ОХ:
s*=)vxdt.
Аналогично можно найти проекцию перемещения на ось OY:
sy=\vudt.
h
Тогда модуль перемещения s = ~\Jsx-\-s2!/.
В частном случае, когда тело движется вдоль оси ОХ,
5=15,1. При таком движении для нахождения пройденного пути
по графику скорости нужно суммировать площади фигур, огра-
ниченных графиком скорости, осью времени и отрезками прямых
2 Заказ 2473
33
t = t{ и t = t2, считая значения этих площадей величинами поло-
жительными независимо от того, находится ли фигура выше или
ниже оси времени.
Вернемся к графику, изображенному на рис. 34. Проекция
перемещения на ось OY за время от to = O до tt положительна и
численно равна площади треугольника АОВ, т. е.
_ 1
а за время от момента tt до момента t2 — отрицательна и равна
площади треугольника BCD:
— ' М
В момент времени t{ проекция скорости vy = Q. На основании
этого находим /,:
0=v0 — gth <i=y-
В момент времени t2 координата у = 0. Учитывая это, на-
ходим:
„ , gl\ , / вк\ п 1 2ио
(Второе значение ^2 = 0 соответствует моменту бросания, так как
тогда тоже было г/ = 0.)
Находим проекцию перемещения, совершенного телом за вре-
мя от начального момента ^0 = 0 Д° момента t2:
_ _ 1 1 , ._
Геометрически это отображается тем, что треугольники АОВ и
BCD имеют одинаковые площади.
Чтобы найти путь, пройденный телом за время полета, сло-
жим площади этих треугольников, считая их положительными:
Задача 1. Тело, имеющее начальную скорость do = 2O м/с,
двигалось прямолинейно с постоянным ускорением и через х=10 с
остановилось. Построить график скорости тела и, используя этот
график, найти перемещение и путь, пройденный телом.
Решение. За начало координат примем начальную точку
траектории и направим ось ОХ по направлению вектора ско-
рости v0. Тогда для момента времени t проекция скорости тела
на ось ОХ выразится так: vx=vQ-\-aJ,
34
где ах—проекция ускорения. Так как конечная скорость равна
нулю, то
0-v0x 0-v0 2
ах = = =—2 м/с.
XX
Следовательно, зависимость vx от t имеет вид:
i»x = 20 — 2t.
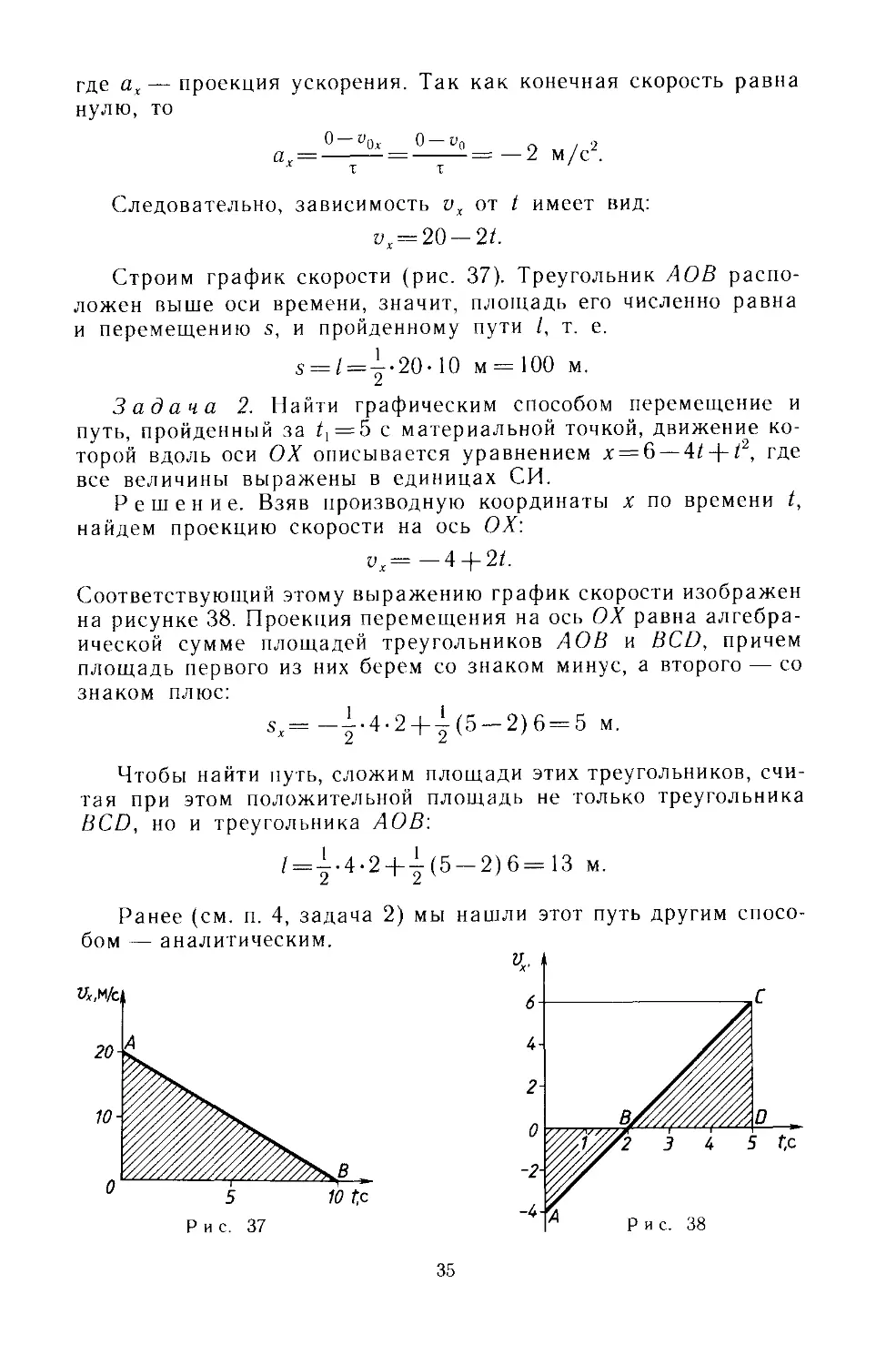
Строим график скорости (рис. 37). Треугольник АОВ распо-
ложен выше оси времени, значит, площадь его численно равна
и перемещению s, и пройденному пути /, т. е.
s==/ = i.20-10 м = 100 м.
Задача 2. Найти графическим способом перемещение и
путь, пройденный за /, = 5 с материальной точкой, движение ко-
торой вдоль оси ОХ описывается уравнением х = 6 — At-\-t2, где
все величины выражены в единицах СИ.
Решение. Взяв производную координаты х по времени t,
найдем проекцию скорости на ось ОХ:
их = —4 + 2/.
Соответствующий этому выражению график скорости изображен
на рисунке 38. Проекция перемещения на ось ОХ равна алгебра-
ической сумме площадей треугольников АОВ и BCD, причем
площадь первого из них берем со знаком минус, а второго — со
знаком плюс:
sx=-{-4-2 + 1E-2N = 5 м.
Чтобы найти путь, сложим площади этих треугольников, счи-
тая при этом положительной площадь не только треугольника
BCD, но и треугольника АОВ:
= {¦4
1E-2N=13 м.
Ранее (см. п. 4, задача 2) мы нашли этот путь другим спосо-
бом — аналитическим.
К.
10 fcc
Рис. 38
35
19. При решении задач по кинематике, кроме перечислен-
ных выше ошибок, абитуриенты нередко допускают следующие
ошибки и недочеты: не делают схематический рисунок, поясняю-
щий описанную в задаче ситуацию, либо делают его, но небреж-
но, невнимательно, так что он получается не соответствующим
условию задачи; смешивают виды движения — равномерное и
равноускоренное, что является грубой ошибкой, но, к сожале-
нию, еще встречается; вместо внимательного анализа задачи пы-
таются просто подобрать «подходящую» формулу и подставить
в нее значения заданных величин (одна из распространенных
ошибок); вместо того чтобы решать задачу в общем виде, т. е. в
буквенных обозначениях, делают промежуточные вычисления;
опасаются использовать формулы, содержащие величины, кото-
рые не даны в задаче; не учитывают векторный характер пере-
мещения, скорости, ускорения. Приведем ориентировочный план
решения задач по кинематике.
1. Внимательно прочитать задачу, проанализировать усло-
вие, выяснить характер движения.
2. Выписать числовые значения заданных величин.
3. Сделать схематический чертеж, отображающий описанное
в задаче движение. Изобразить на нем траекторию движения,
векторы скорости, ускорения, перемещения.
4. Выбрать систему координат, при этом координатные оси
направить так, чтобы проекции векторов на них выражались
возможно более простым образом.
5. Составить для данного движения уравнения, отражающие
математическую связь между проекциями векторов на оси коор-
динат. Число уравнений должно быть равно числу неизвестных
величин.
6. Решить составленную систему относительно искомых вели-
чин, т. е. получить расчетные формулы.
7. Подставить в расчетные формулы вместо обозначений фи-
зических величин обозначения их единиц СИ, произвести преоб-
разования и убедиться, получаются ли в результате единицы ис-
комых величин.
8. Подставить в расчетные формулы числовые значения фи-
зических величин и произвести вычисления. Оценить реальность
полученного результата.
ОСНОВЫ ДИНАМИКИ
20. Анализ ответов показывает, что абитуриенты не всегда
правильно понимают и истолковывают законы Ньютона, хотя и
приводят правильные формулировки этих законов. Формальное
их усвоение обнаруживается при ответе на вопросы, требующие
правильного применения изученного теоретического материала.
Так, например, некоторые абитуриенты считают, что движу-
36
щийся с некоторой скоростью автомобиль после выключения
двигателя «сохраняет свое движение», «движется по инерции со-
гласно первому закону Ньютона». Это неверно. После выключе-
ния двигателя на автомобиль действуют только силы трения, и
под действием этих сил изменяется (уменьшается) его скорость,
т. е., согласно второму закону Ньютона, автомобиль движется
с ускорением. Инерция здесь проявляется в том, что скорость ав-
томобиля изменяется не мгновенно, а в течение некоторого про-
межутка времени.
Согласно первому закону Ньютона, автомобиль, имевший не-
которую скорость, после выключения двигателя сохранял бы эту
скорость постоянной, т. е. двигался бы равномерно и прямоли-
нейно, только в том случае, если бы на него не действовали ни-
какие силы. В реальных условиях избавиться полностью от
внешних воздействий на автомобиль (и, разумеется, не только на
него) невозможно.
При изучении законов Ньютона важно помнить, что, во-пер-
вых, эти законы выполняются только в инерциальных системах
отсчета; во-вторых, в них рассматривается только движение ма-
териальных точек или поступательное движение абсолютно твер-
дых тел (так как последнее, как известно, сводится к движению
центра масс, т. е. к движению материальной точки).
Напомним, что инерциальной системой отсчета является си-
стема отсчета, которая покоится или движется равномерно и
прямолинейно относительно некоторой другой инерциальной си-
стемы. Инерциальными, например, можно приближенно считать
системы отсчета, покоящиеся или движущиеся равномерно и
прямолинейно относительно Земли (приближенно потому, что
Земля вращается вокруг своей оси и движется вокруг Солнца).
В механике, основанной на законах Ньютона, считается, что,
во-первых, течение времени во всех инерциальных системах от-
счета происходит одинаково; во-вторых, масса тела — величина
постоянная; в-третьих, ускорение тела и силы взаимодействия
между телами не зависят от скорости движения инерциальной
системы отсчета.
В любых инерциальных системах отсчета все механические
явления протекают одинаково при одних и тех же условиях
(принцип относительности Галилея).
21. Часто экзаменуемые проявляют неполное усвоение второ-
го закона Ньютона, записывая такое уравнение: F = ma и пояс-
няя при этом, что сила, действующая на тело, равна произведе-
нию массы этого тела на его ускорение.
Во-первых, здесь упущено, что сила и ускорение — величи-
ны векторные и что ускорение а имеет такое же направление,
как и сила F, действующая на тело, т. е. следует записывать
уравнение так:
F = ma. A)
37
Во-вторых, некоторые абитуриенты делают из этого уравне-
ния ошибочный вывод: сила зависит от массы тела и ускорения.
В действительности же второй закон Ньютона показывает, что
под действием силы F тело массой т движется с ускорением а,
прямо пропорциональным силе и обратно пропорциональным
F -
массе, т. е. а = —. Сила является причиной, а ускорение — след-
ствием. Уравнение A) отражает связь между силой, массой тела
и ускорением.
В-третьих, если на тело действует несколько сил, то модуль
и направление ускорения определяются равнодействующей этих
сил, т. е. их векторной суммой:
Каждая сила действует на тело так, как если бы других сил
не было (принцип независимости действия сил). Результирующее
ускорение а такое, как если бы на тело действовала одна сила,
равная равнодействующей. Следовательно, второй закон Ньюто-
на— основной закон динамики — математически выражается
векторным уравнением
?!+?2 + -+^ = ™. B)
При решении задач нужно выяснить, какие силы действуют
на каждое тело, обозначить эти силы на схематическом рисунке,
выбрать систему координат и, спроектировав все силы на оси ко-
ординат, перейти от векторного уравнения B) к скалярным урав-
нениям для проекций сил и ускорения на оси ОХ и OY:
22. Приведем пример грубой ошибки. Второй закон Ньютона
абитуриент сформулировал правильно, но тем не менее вскоре
после этого утверждал, что под действием постоянной силы тело
движется равномерно. По-видимому, эта ошибка вызвана тем,
что в реальных условиях тело движется с постоянной скоростью
в том случае, если на него действует сила, равная по модулю и
противоположная по направлению силе трения, т. е. действия
этих сил скомпенсированы.
Согласно второму закону Ньютона, под действием постоян-
ной силы тело движется с постоянным ускорением.
23. Еще одна ошибка, связанная с применением второго зако-
на Ньютона: поступающий уверен, что если на тело, имеющее
большую массу, действует малая сила, то она не может сооб-
щить ему ускорения. Свой ответ он «аргументирует» так: «Чем
38
больше масса тела, тем сильнее тело будет противоборствовать
силе, а если к тому же сила малая, то...»
В действительности это не так. Полезно напомнить, что вто-
рой закон Ньютона имеет и другую формулировку: изменение
импульса тела равно импульсу силы, действующей на него. Ма-
тематически это утверждение выражается уравнением
Fkt = mv2 — mvv
где F — сила, действующая в течение промежутка времени А^ на
тело массой т\ и,, и2 — скорости тела соответственно в начале и в
конце промежутка А/. Из этого уравнения видно, что изменение
импульса тела Ap = mv2 — mvx можно получить в результате дей-
ствия на тело малой силы в течение большого промежутка вре-
мени. Например, один человек может сдвинуть с места легковой
автомобиль, стоящий на шоссе. Заметим также, что это уравне-
ние показывает, что изменение импульса тела Ар имеет такое же
направление, как и сила F, действующая на это тело.
24. Многие абитуриенты не понимают, какая связь существу-
ет между законами Ньютона. Приходилось слышать даже такие
ответы, в которых говорилось, что будто бы первый закон Нью-
тона является следствием второго закона Ньютона. Это неверно.
Первый закон Ньютона (закон инерции) — важный и само-
стоятельный закон. Он утверждает, что если на тело не действу-
ют другие тела, то оно находится в состоянии покоя или равно-
мерного прямолинейного движения относительно инерциальной
системы отсчета. Из этого закона следует, что причиной измене-
ния скорости является сила. На вопрос о том, как движется тело
под действием силы, отвечает второй закон Ньютона, устанавли-
вающий количественное соотношение между ускорением и силой.
В первом и втором законах рассматривается только одно тело.
Третий же закон Ньютона отражает тот факт, что если одно тело
действует с некоторой силой на другое тело, то на него со сторо-
ны другого тела также действует сила, равная по модулю и про-
тивоположная по направлению первой. Таким образом, силы
всегда действуют парами: каждой силе F{ соответствует сила F2,
равная ей по модулю и противоположная по направлению,
т. е. F] = —F2. Эти силы называют силами взаимодействия. Они
направлены вдоль одной прямой и приложены к различным те-
лам. Таким образом, между законами Ньютона существует вза-
имная связь и их нельзя рассматривать в отрыве друг от друга.
25. Абитуриенты, формально усвоившие третий закон Ньюто-
на, не могли правильно объяснить ряд вопросов, которые мы
сейчас рассмотрим.
1. Человек передвигает по полу шкаф, толкая его вперед, в
результате чего человек и шкаф движутся с некоторым ускоре-
39
нием. Но, согласно третьему закону Ньютона, с какой силой че-
ловек действует на шкаф, с такой же силой, но направленной
противоположно, шкаф действует на человека. Почему же они
движутся вперед?
Здесь имеются три взаимодействия: человек — шкаф, чело-
век — пол и шкаф — пол. Взаимодействие человека и шкафа ха-
рактеризуют силы F1 и —Т7,, человека и пола — силы F2 и —F2,
шкафа и пола — силы F3 и —^з (рис. 39) (точнее говоря, это го-
ризонтальные составляющие сил взаимодействия). Системе че-
ловек — шкаф ускорение сообщает результирующая сила Fu
— F,, F2 и Fy По отношению к этой системе силы F, и —F, взаимно
уравновешиваются, поэтому результирующая сила F = F2-\-F3, a
ее модуль, как видно из рисунка, F = F2 — F3. Сила F2 возникает
вследствие того, что человек упирается ногами в пол. Если бы
сила трения покоя между ступнями человека и полом оказалась
меньше силы трения покоя между шкафом и полом, то человек
не смог бы сдвинуть шкаф с места. Так что в данном случае си-
ла трения, препятствуя проскальзыванию ступней, делает воз-
можным движение человека со шкафом.
Таким образом, если тела рассматривать как части одной и
той же системы, то силы взаимодействия этих тел взаимно урав-
новешиваются и поэтому не могут сообщить ускорение системе
в целом. Чтобы система двигалась с ускорением, необходимо,
чтобы на нее действовали другие тела, не входящие в эту сис-
тему.
Абитуриенты обычно твердо уверены, что силы взаимодейст-
вия не могут уравновешивать друг друга.
2. Как объяснить движение тепловоза? Работающий двига-
тель приводит во вращение ведущие колеса, которые действуют
на рельсы с некоторой силой. По третьему закону Ньютона,
рельсы действуют на колеса с такой же, но противоположно на-
правленной силой. Взаимодействие колес с рельсами осуществ-
ляется благодаря трению, причем сила трения действует в на-
правлении поступательного движения тепловоза, т. е. толкает
его вперед. Если бы трение отсутствовало, то при работающем
двигателе колеса вращались бы, но тепловоз не сдвинулся бы
40
с места. Машинист для увеличения силы трения между колеса-
ми и рельсами на некоторых участках пути (например, на подъ-
емах) включает специальное устройство, с помощью которого
рельсы посыпаются песком.
3. Если движутся два тела, связанных между собой нитью, то
каков физический смысл условий невесомости и нерастяжимо-
сти этой нити? Чтобы выяснить этот вопрос, рассмотрим задачу.
Задача 1. Два тела, массы которых тх и ть связаны неве-
сомой нерастяжимой нитью и лежат на горизонтальной плоско-
сти. С каким ускорением будут двигаться эти тела, если к телу
массой т, приложить горизонтально направленную силу F{?
Трением между телом и плоскостью пренебречь.
Y
1
<
"г
I2 i §
т2д
F
Х
Рис. 40
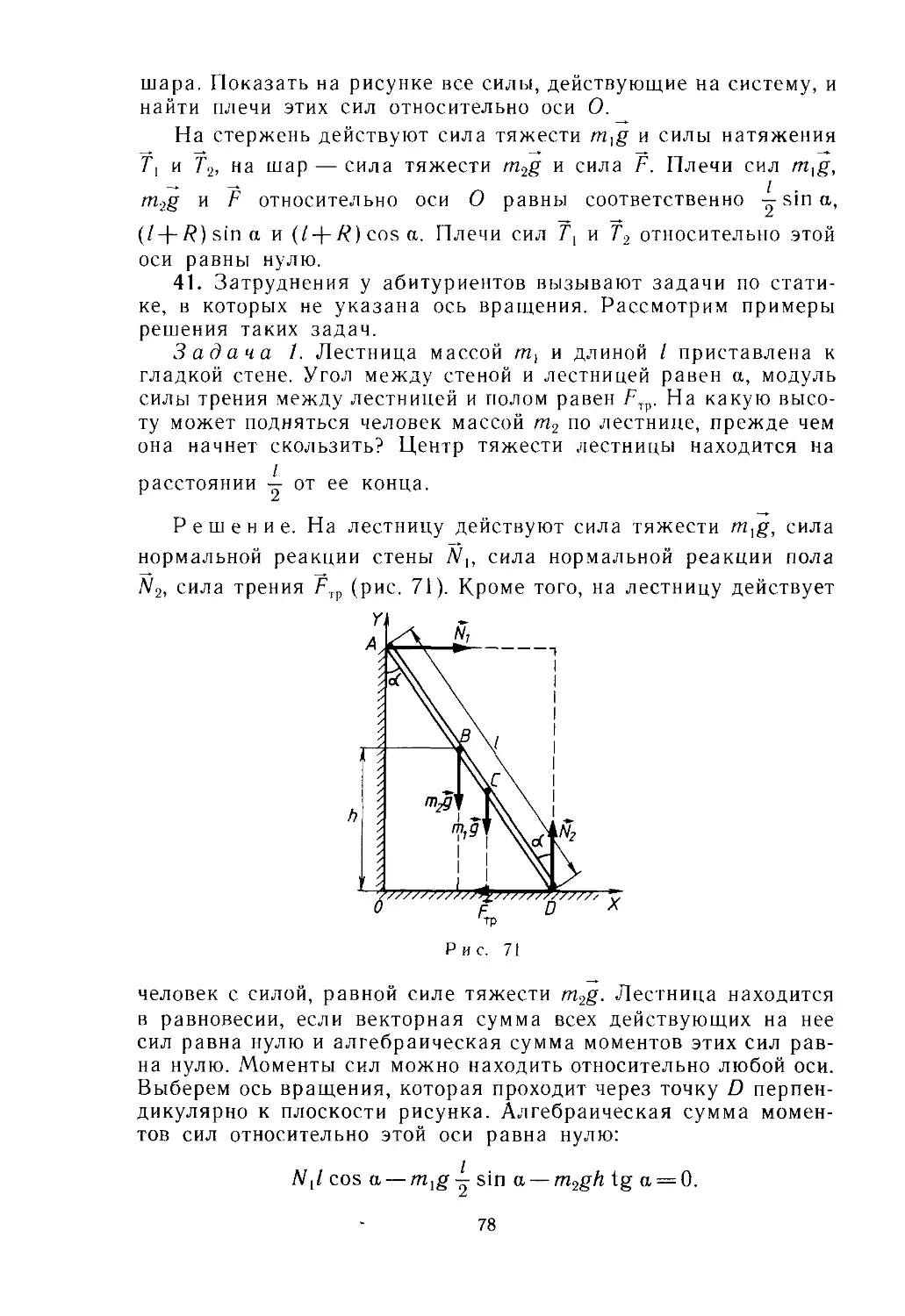
Решение. На первое тело (рис. 40) действуют сила F, сила
тяжести m,g, сила реакции плоскости JV, и сила натяжения нити
f[. На второе тело действуют сила тяжести m2g, сила реакции
плоскости N2 и сила натяжения нити Т2. Выберем систему коор-
динат так, чтобы ось ОХ была направлена так же, как и сила F.
Нерастяжимость нити означает постоянство ее длины. По-
скольку грузы перемещаются только вправо, то разность их ко-
ординат, равная длине нити, остается постоянной, т. е.
х{ — x2 = const. Тогда, взяв производную по времени левой и пра-
вой частей этого равенства, получим: х\ — .4 = 0 или х\^=х'<1. Возь-
мем еще раз производную по времени, получим: х'{ = х",
т. е. аи = а2х, где а1х и а2х— проекции ускорений тел на ось ОХ.
Следовательно, условие нерастяжимости нити позволяет сделать
вывод: ускорения связанных тел и всех точек нити одинаковы,
т. е. alx = a2x = ax.
На нить со стороны первого тела действует сила Fu со сторо-
ны второго — сила F2. Согласно второму закону Ньютона, соста-
вим уравнение движения нити:
F\-\- F2 = tna,
41
где а — ускорение; т — масса нити. Поскольку нить невесома,
то т~0. Тогда Fl-\-F2 = 0. Следовательно, ?,= — F2.
Согласно третьему закону Ньютона, с какой силой тело дей-
ствует на нить, с такой же по модулю, но направленной противо-
положно силой действует нить на тело. Поэтому Г, = —Fu
Т2 =—F2. Если учесть теперь, что F{ =—F2, то получим:
7\=-Г2.
Таким образом, из условия невесомости нити следует, что та-
кая нить действует на связанные тела с силами, равными по мо-
дулю и противоположными по направлению.
Абитуриенты, как правило, утверждали, что Г, = —Т2, со-
гласно третьему закону Ньютона. Это неправильно. Третий за-
кон Ньютона рассматривает силы, с которыми два тела действу-
ют друг на друга. Здесь же речь идет о силах взаимодействия
третьего тела — нити — с двумя другими телами.
Продолжим решение задачи. Учитывая, что, как показано
выше, Тх = Т2 = Т, составим для каждого тела уравнение на осно-
вании второго закона Ньютона, спроектировав все силы на
ось О*:
F— Т = тха,
Т = т2а.
Решив эту систему уравнений, получим:
_
Задача 2. На пружине, длина которой в недеформирован-
ном состоянии равна /0, подвешен неподвижный блок. Через него
перекинута нить, к концам которой прикреплены грузы массами
т{ и т2>тх. Пренебрегая трением и считая нить невесомой и не-
растяжимой, а блок невесомым, определить ускорение, с кото-
рым будут двигаться грузы, силу натяжения нити, а также дли-
ну пружины, если известно, что ее жесткость равна k.
Решение. Обозначим силы, действующие на каждое тело
и на блок. На первое тело действуют сила тяжести mxg и сила
натяжения нити Г,, на второе — m2g и Т2 (рис. 41). На блок дей-
ствуют силы натяжения нити Т\ и Т'ъ а также сила реакции
N оси.
Согласно третьему закону Ньютона, сила N, с которой ось
действует на блок, равна по модулю и противоположна по на-
правлению силе F, с которой блок действует на ось и, следова-
тельно, на пружину. Согласно закону Гука, удлинение Д/ пружи-
ны пропорционально действующей силе: F = kAl. Отсюда удли-
нение Д/=—. Значит, длина пружины после того, как к ней
42
прикрепили блок, станет равной 1 = 10-\—.
Но F = N, поэтому
Из условия невесомости нити следует
(см. решение предыдущей задачи), что
Т1 = Т\ и Т2 = Т'2. Силы Т'2 и Т\, вообще гово-
ря, не равны между собой, и их результи-
рующая сообщает ускорение нити. Нить
не проскальзывает по блоку, поэтому
блок вращается под действием результи-
рующей сил Т\ и Т2, модуль которой ра-
вен Т2—Т[. Если считать блок невесомым
(его массу принять равной нулю), то по-
лучим, что Т2=Т\=Т.
Систему координат выберем так, что-
бы ось OY была направлена вертикально
вверх. Из условия равновесия блока следует, что сумма проек-
ций на ось OY всех сил, действующих на блок, равна нулю,
т. е. Tly-\-T2y-\-Ny = 0 или Т-\-Т — /V = 0. Отсюда N = 2T. Подста-
вив это значение в выражение A), получим:
l = h + ~- B)
Из условия нерастяжимости нити заключаем, что грузы дви-
жутся с одинаковым по модулю ускорением, поэтому, учитывая
направление ускорений, можем записать: а]у = а, а2у =—а.
Спроектировав на ось OY все векторы сил и ускорений, со-
ставим, согласно второму закону Ньютона, уравнения движения
грузов:
Т — m,e = m,a.
Рис. 41.
Т — tn-2g= —m2a.
Решив эту систему уравнений, найдем, что грузы движутся с
ускорением
(с таким же ускорением движутся все точки нити). Сила натяже-
ния нити
2m,m«
т=-
Подставив это выражение для Т в формулу B), найдем, что
при движении грузов пружина будет иметь длину
Еще раз обращаем внимание на связь между законами Нью-
43
тона, которую мы использовали, в частности, при решении этих
задач. Второй закон Ньютона применяется к каждому телу в от-
дельности. Чтобы применить его, надо установить все силы, дей-
ствующие на данное тело, а для этого надо применить третий за-
кон Ньютона, так как силы взаимодействия существуют попарно.
26. При решении задач по динамике абитуриенты часто не
могут правильно указать силы, действующие на тело. Часто,
кроме реальных сил, придумывают всякие другие: сила движе-
ния, ускоряющая сила, сила толчка, броска, инерции и т. п. Так,
например, говорят, что на тело, которое равноускоренно движет-
ся в горизонтальном направлении, кроме приложенной силы,
действуют сила тяжести, сила реакции опоры, сила трения, сила
тяги и «ускоряющая» сила. На самом деле реально существуют
только первые четыре силы.
Приведем еще один пример. Абитуриент считал, что на тело,
которое скользит вниз по наклонной плоскости, действуют сила
тяжести FT, сила трения F и скатывающая сила FCK (рис. 42).
lip
Рис. 42
Как уже отмечалось выше, чтобы правильно указать действу-
ющие на данное тело силы, надо установить, с какими другими
телами оно взаимодействует. Тело, скользящее по наклонной
плоскости, взаимодействует с плоскостью и Землей. Со стороны
Земли на тело действует сила тяжести FT, со стороны плоско-
сти — сила нормальной реакции опоры N и сила трения Fip (точ-
нее говоря, это составляющие силы, с которой плоскость действу-
ет на тело, причем сила N направлена перпендикулярно плос-
кости, а /\р — параллельно ей). Других сил нет. Ошибки абиту-
риента заключаются в том, что он не указал силу N и, кроме
того, указал две силы: FT и FCK. В действительности так называе-
мая скатывающая сила является составляющей силы тяжести
по направлению вдоль плоскости. На рисунке 43 показано раз-
ложение силы тяжести по двум направлениям — вдоль наклон-
ной плоскости и перпендикулярной к ней: FT = FCK-\-TH.
Сила FK— это сила, с которой тело действует на плоскость в
перпендикулярном ей направлении. По третьему закону Нью-
тона, N= —FH.
Значит, если указана действующая на тело сила тяжести, то
44
скатывающую силу указывать не надо. Таким образом, на тело,
скользящее по наклонной плоскости,.действуют силы Fr, Frp и N
(рис. 44).
Рис. 43
Рис. 44
Решим две задачи, в которых рассматривается движение те-
ла по наклонной плоскости.
Задача 1. По наклонной плоскости, составляющей с гори-
зонтом угол а, движется вверх груз массой т, к которому прило-
жена сила F, направленная под углом р к наклонной плоскости.
Коэффициент трения скольжения равен д.. Найти ускорение
тела.
Решение. Кроме силы F, на тело действуют сила тяжести
FT = mg, сила трения /\р и сила реакции опоры N (рис. 45). Коор-
динатную ось ОХ направим вверх вдоль плоскости, OY—вверх
перпендикулярно плоскости. В векторной форме уравнение, со-
ставленное на основании второго закона Ньютона, имеет вид:
F + FTp 4- N
= та.
Спроектировав все векторы на оси ОХ и OY, получим два
уравнения:
fcosf} — fTp — mg sin a == ma, A)
Fsin p — mgcos a = 0. B)
Из второго уравнения находим:
N = mg cos a — Fsin p.
Так как Frf = \iN, то Fr? = [i (mgcos a — Fsin p). Подставив это
выражение для fTp в уравнение A), после очевидных преобразо-
ваний получим:
а = — (cosP4"HSin р) — g (sin a 4-
a).
При решении этой задачи абитуриенты допускали различные
ошибки. Некоторые, например, указывали, кроме сил, обозна-
ченных на рисунке 45, еще силу скатывающую FCK и наряду с
45
Рис. 45
проекцией силы тяжести находили проекцию силы /\.к, а следо-
вательно, составленное уравнение было неправильным. Другие
ошибочно считали, что Frp = \img.
Задача 2. Тело начинает скользить с верхней точки на-
клонной плоскости, высота которой равна /г, а угол с горизонтом
а. Найти скорость тела в конце плоскости, если коэффициент тре-
ния равен |л, начальная скорость тела равна нулю.
Решение. Начало координат совместим с начальной точкой
траектории движения тела, ось ОХ направим вниз вдоль наклон-
ной плоскости, ось OY — перпендикулярно ей (рис. 46). Время
Рис. 46
будем отсчитывать с момента, когда тело начало двигаться.
Начальная скорость ио = О, поэтому кинематические уравнения
движения тела имеют вид:
где х—координата тела в момент времени t; vx, ax—проекции
соответственно скорости и ускорения на ось ОХ в этот же мо-
мент. В нижней точке А наклонной плоскости координата
х, = ОА =—— , t = tu vx=vu где v, — модуль искомой скорости.
sin a
Подставив эти значения в кинематические уравнения, получим:
sin a 2
46
Отсюда находим:
ах sin a
Остается найти ах—проекцию ускорения. На тело во время
движения действуют сила тяжести FT = mg, сила нормальной ре-
акции опоры N и сила трения FTp. Согласно второму закону Нью-
тона, составим уравнение, спроектировав все силы на ось ОХ:
mg sin a — Fтр = тах.
Сумма проекций всех сил на ось OY равна нулю, т. е.
N — mg cos a = 0. Отсюда N = mg cos а. Тогда Fтр = \iN = \kmg cos a,
rag sin а — \irng cos a = max, откуда
a^ = g(sin a — ц, cos a).
Следовательно,
и, =Д / g (sina — |л cos a) =^j2gh (I — ц, ctg a).
у sin a
27. Остановимся на одной из распространенных ошибок. При
нахождении модуля силы трения считают, что всегда FTp=iimg,
где |л — коэффициент трения; га—масса тела, g — ускорение
свободного падения. Но это неправильно. Выражение FJf=\img
справедливо только в частном случае, когда тело движется по
горизонтальной поверхности (или покоится на ней, если рассмат-
ривается сила трения покоя), и при этом на тело в вертикальном
направлении никакие силы, кроме силы тяжести mg и силы нор-
мальной реакции опоры N, на действуют (рис. 47). В этом слу-
чае, спроектировав на ось OY действующие на тело силы, полу-
чим: N — rag = 0 или N = mg. Следовательно, сила трения
Необходимо твердо помнить, что модуль силы трения пропор-
ционален силе нормальной реакции опоры: FTp = \iN, и именно
это выражение надо использовать при нахождении силы трения.
Чтобы найти N, нужно обозначить все силы, действующие на те-
ло. При этом надо учитывать, что сила нормальной реакции
опоры N всегда направлена вдоль прямой, перпендикулярной к
Y
Ft,
N
тд
Рис. 47
47
поверхности в точке соприкосновения тела с поверхностью. За-
тем необходимо составить уравнение: сумма проекций всех сил
на ось, направленную параллельно вектору JV, равна нулю (так
как ускорение вдоль этой оси равно нулю), и из этого уравнения
найти N.
Таким способом, например, мы находили N в двух предыду-
щих задачах. В последней из них, в частности, показано, что при
скольжении тела массой т по наклонной плоскости, составляю-
щей с горизонтом угол а, модуль силы трения
/\р = \y-tng cos а.
Абитуриенты нередко допускали ошибку, считая, что и в этом
случае Fip =
Рассмотрим одну простую задачу, при решении которой по-
ступающие часто допускали эту же ошибку, считая /7Tp = |a.mg.
Задача. Тело массой т скользит по горизонтальной плоско-
сти под действием силы F, направленной под углом а к горизон-
ту. Найти ускорение тела, если коэффициент трения равен jx.
Решение. Ось ОХ направим вдоль плоскости, ось OY —
перпендикулярно к ней (рис. 48). Найдем проекции всех сил на
оси OX, OY и составим, согласно второму закону Ньютона, урав-
нения:
f cos а — FTp = max, N-\-F s\n a — mg = 0.
Из второго уравнения находим N = mg— F sin а. Следовательно,
FTp = iiN = \i(mg — f sin a)
(т. е. Fjp=?\img\). Подставим значение fTp в первое уравнение:
f cos а — \i (tng — F sin a) = max.
Отсюда найдем:
F cos a — \i (mg — F sin a)
a = .
m
Так как тело движется вдоль оси ОХ, то модуль ускорения
а=\ах\.
48
При решении этой задачи, кроме указанной ошибки, слабо
подготовленные абитуриенты иногда допускали такие ляпсусы:
1) не делая рисунка, сразу же писали такие уравнения:
F — Fjp = ma, FTp = \},mg и из них находили а; 2) за-
писывали: FTp — piN, что, конечно, неверно, так как силы fTp и N
имеют различные направления.
28. При решении задач, в которых рассматривается взаимо-
действие нескольких тел или одно тело, к которому приложено
несколько различных сил, не всегда ясно заранее, в каком на-
правлении будет двигаться тело или система тел, если началь-
ная скорость равна нулю. А это направление надо знать, чтобы
правильно указать направление силы трения скольжения (эта
сила всегда направлена противоположно скорости). В таком слу-
чае задачу можно решать двумя способами.
Первый способ. Выбираем произвольно направление движе-
ния, изображаем на рисунке все силы, действующие на каждое
тело, в том числе и силу трения. Выбираем прямоугольную си-
стему координат так, чтобы направление оси ОХ совпадало с на-
правлением движения. Проектируя на оси ОХ и OY все силы,
для каждого тела составляем уравнения движения на основании
второго закона Ньютона. Решив полученную систему, найдем
проекцию ускорения ах. Если при этом значение ах получится по-
ложительным, то приходим к выводу, что направление движения
указано правильно. Если же значение ах получится отрицатель-
ным, то это означает, что направление движения выбрано непра-
вильно. В таком случае нужно изменить направление оси ОХ и
силы трения на противоположное, снова составить систему урав-
нений и решить ее.
Многие абитуриенты допускают здесь такую ошибку: они
считают, что если получилось ах<.0, то в действительности си-
стема движется в противоположном направлении с таким же по
модулю ускорением. В неправильности этого заключения легко
убедиться на примере решения следующей задачи.
Задача 1. К телу массой т=10 кг, покоящемуся на гори-
зонтальной плоскости, приложены сила /71 = 10 Н, составляющая
с плоскостью угол а = 60° и сила /72 = 20 H, направленная гори-
зонтально. Определить ускорение, с которым тело начнет дви-
гаться, если известно, что коэффициент трения скольжения
0
Рис. 49
Y
0
x
mq
49
Решение. Предположим, что под действием сил тело нач-
нет равноускоренно двигаться вправо, и направим ось ОХ по на-
правлению ускорения, т. е. тоже вправо (рис. 49). Тогда сила
трения /\р будет направлена влево. На тело действуют также
силы f|, F2, сила тяжести FT — mg и сила нормальной реакции
опоры N. Найдем проекции всех сил на оси ОХ и OY и составим
уравнения согласно второму закону Ньютона:
F[ cos а — F,2 — F.ip = max, A)
N-\-Fl sin а — mg = Q.
Отсюда находим N = mg— Z7, sina. Тогда /7,p = [iN = \l (mg —
— Fx sin a). Подставим последнее выражение в уравнение A) и най-
дем ах:
F{ cos a — F2— |i. (mg — Ft sin <x) = max,
ax =— (Fi (cos a + ixsina) — F2— \nmg).
После подстановки числовых значений величин и вычислений по-
лучим ах= — 2,5 м/с2. Найденное значение проекции ускорения
отрицательное, а это означает, что ускорение направлено проти-
воположно оси ОХ, т. е. влево, что противоречит сделанному на-
ми предположению. Следовательно, ускорение найдено неверно,
движение вправо невозможно.
Направим теперь ось ОХ влево, а силу трения вправо (на ри-
сунке это не показано). Уравнения для проекций на оси теперь
будут иметь вид:
F2 — Fl cos a — FTp = max,
iV-ff, sin a — mg = 0.
Как показано выше, сила трения Frp = [i(mg — f, sin a). Най-
дем ax:
F2— F{ cos a — |x (mg — F, sin a) = max,
ax = — (F2 — F, (cos a — ц, sin a)— \img).
Вычисления дают ax = 0,5 м/с2. Следовательно, тело движется
влево с ускорением а = 0,5 м/с2.
Теперь естественно возникает вопрос: а если бы и во втором
случае значение ах получилось отрицательным, то что из этого
следовало бы? Это означало бы, что и движение влево тоже не-
возможно, так как тело удерживается силой трения покоя. Так,
например, при коэффициенте трения ц, = 0,2 в результате вычис-
лений по последней формуле получим ах=—0,3 м/с2. Следова-
тельно, движение влево невозможно. А поскольку вправо тело
тоже не может двигаться (это показано выше), то, следователь-
но, оно находится в состоянии покоя и поэтому а = 0 при ц, = 0,2.
Второй способ. Этот способ основан на том, что сила трения,
возникающая при движении тела, не может изменить направле-
50
ние его скорости. Предположив, что трение отсутствует, найдем
равнодействующую всех сил, приложенных к системе тел (или
к одному телу) и по направлению этой равнодействующей опре-
делим направление движения системы (или тела): направление
движения совпадает с направлением равнодействующей. А по-
скольку сила трения не может изменить направление скорости,
то и при наличии трения система тел (или тело) будет двигаться
в том же направлении, что и при отсутствии трения.
Так, например, если бы на тело, рассматриваемое в предыду-
щей задаче, не действовала сила трения, то вдоль оси ОХ на
тело действовали бы только сила f2 = 20 H, направ-
ленная влево, и составляющая силы /•",, равная f,cosa =
= 10cos60° = 5 H, направленная вправо. Равнодействующая
этих сил по модулю равна F2— f, =20 —5=15 Н и направлена
влево. Следовательно, при наличии трения тело будет двигаться
влево, а сила трения, возникающая при движении, направлена
вправо. С учетом этого ускорение находится затем на основании
второго закона Ньютона. При этом выбор направления оси
ОХ—влево или вправо—не имеет значения. Результат всегда
получится правильным, только в первом случае будет ах>0, а
во втором — аЛ.<0.
Задача 2. К грузу массой т1 = 20 кг, находящемуся на на-
клонной плоскости, привязана нить, перекинутая через блок.
К другому концу нити подвешен груз массой га2 = 4 кг. С каким
ускорением будут двигаться грузы, если угол наклона плоскости
а = 30°? Нить считать невесомой и нерастяжимой. Коэффициент
трения |л = 0,2.
Решение. Как было показано ранее, из условия нерастяжи-
мости нити следует, что грузы движутся с одинаковым по моду-
лю ускорением. Будем считать, что грузы образуют единую си-
стему. Определим направление движения первого груза. Пред-
положим, что трение отсутствует. Тогда ускорение определяется
равнодействующей сил m,g, m2g, N, /', и 7'2 (рис. 50). Поскольку
нить невесома, то Г, = — Т2. Значит, по отношению к системе эти
силы являются взаимно уравновешивающимися, их равнодейст-
вующая равна нулю. Составляющая силы нормальной реакции
'N
опоры N по оси ОХ, направленной вдоль наклонной плоскости,
равна нулю. Составляющая силы тяжести mlg по этой оси равна
mxg sin а. Таким образом, ускорение системы определяется равно-
действующей двух сил: ni\g sin а и m2g. Найдем и сравним моду-
ли этих сил:
ra,g sin a = 20-9,8 sin 30° = 98 H,
m2g = 4 -9,8 = 39,2 Н.
Так как mxg sin a>ra2g, то груз массой га, будет двигаться по
наклонной плоскости вниз. Следовательно, и при наличии трения
направление движения будет таким же, а сила трения fTp будет
направлена противоположно.
Теперь направим ось ОХ вниз вдоль наклонной плоскости, а
ось OY— перпендикулярно к ней, как показано на рис. 50. Пер-
вый груз движется вдоль оси ОХ с ускорением а, поэтому проек-
ция ускорения на эту ось ах = а. С таким же по модулю ускоре-
нием второй груз движется вверх. Согласно второму закону
Ньютона, составим уравнения в проекциях на оси ОХ и OY для
первого груза, учитывая при этом, что Т] = Т2—Т. Получим:
ra,g sin a — FTp—T = mxa, A)
N — niyg cos a = 0. B)
Спроектировав силы T2 и m2g на направление ускорения вто-
рого груза, т. е. вверх, составим уравнение движения:
Т — ra2g = ra2a. C)
Сложив левые и правые части уравнений A) и C), получим:
ra,gsin a — fTp — m2g = (m,-\-m2) a. D)
Из уравнения B) следует, что N = m{g cos a. А так как /\гр =
= \iN, то
fTp = |xra[g cos a.
Подставив это выражение в уравнение D), получим:
ra,g(sin a —p, cos a) —ra2g = (ra, + ra2) a.
Отсюда
(m, (sin a — |i cosa) —m2) g
mx-\-m2
После подстановки числовых значений и вычислений получим
а= 1,1 м/с2.
При решении этой задачи мы воспользовались описанным
выше вторым способом, чтобы определить направление движе-
ния системы. Покажем теперь, как можно было найти это на-
правление первым способом.
52
Предположим, что груз массой тх скользит вниз по наклон-
ной плоскости. Обозначим все силы, действующие на тело
(см. рис. 50). Направим ось ОХ по направлению ускорения этого
тела, т. е. вниз вдоль плоскости. Далее решаем так же, как и вы-
ше: составляем уравнения A) — D) и вычисляем а. Получаем
а = ах= 1,1 м/с2>0. Следовательно, мы правильно угадали на-
правление движения. А если бы мы считали, что груз массой т,
движется вверх по плоскости, то нужно было бы ось ОХ напра-
вить тоже вверх, а силу трения, разумеется, противоположно.
После этого надо было составить уравнения для каждого груза
на основании второго закона Ньютона и найти проекцию ускоре-
ния ах. Читатель может сделать это самостоятельно и убедиться,
что в этом случае получится ах<С0. Из этого следует, что в вы-
бранном направлении движение невозможно. Значит, надо изме-
нить направление оси ОХ и Fгр на противоположные, составить
уравнения заново и найти ах.
29. Правильно формулируя тот или иной закон, абитуриенты
не всегда могут указать условия, при которых он справедлив.
В своих ответах многие не подчеркивают, например, что закон
Гука верен только при упругих деформациях, что законы Ньюто-
на выполняются только в инерциальных системах отсчета при
движении тел со скоростями, малыми по сравнению со скоро-
стью света, и т. п.
30. Приведем еще один пример неполного понимания закона.
На экзамене абитуриенты формулируют закон всемирного тяго-
тения так: «Все тела притягиваются друг к другу с силой,
модуль которой прямо пропорционален произведению их
масс и обратно пропорционален квадрату расстояния между
ними».
Здесь имеются неточности. Во-первых, надо говорить не о
всех телах, а о любых двух телах. Во-вторых, если закон форму-
лировать таким образом, то надо, чтобы обязательно выполня-
лось условие: размеры тел пренебрежимо малы по сравнению
с расстояниями между ними, т. е. тела можно считать матери-
альными точками. Непонимание этого важного условия приво-
дит к ошибкам в ответах на такой вопрос: «Как найти силу вза-
имного притяжения двух огромных камней, лежащих на неболь-
шом расстоянии друг от друга?» Обычно отвечают, что эту силу
можно найти по закону всемирного тяготения:
F = G^p-, A)
где Ш|ИШ2 — массы камней; г — расстояние между ними. А ког-
да экзаменуемого просят уточнить, какое же расстояние он име-
ет в виду, то следуют различные ответы: часто говорят, что г —
это расстояние между центрами масс камней, иногда — кратчай-
шее расстояние, иногда — какое-то среднее расстояние, затруд-
няясь объяснить, что это такое.
53
Напомним правильную формулировку закона всемирного тя-
готения: две любые материальные точки притягиваются друг к
другу с силой, прямо пропорциональной произведению масс этих
точек и обратно пропорциональной квадрату расстояния между
ними. Эта сила направлена по прямой, соединяющей точки. Ко-
эффициент пропорциональности G в формуле A) называется
гравитационной постоянной:
0 = 6,67-10-" Н-м2/кг2.
Итак, еще раз подчеркнем: закон всемирного тяготения
справедлив только для материальных точек. Чтобы найти силу
взаимного притяжения двух тел, имеющих определенную форму
и размеры (например, двух камней, о которых говорилось выше),
нужно мысленно разбить эти тела на такие маленькие части,
чтобы каждую из них можно было считать материальной точкой.
Затем найти силы взаимодействия этих частей следующим обра-
зом: сначала находим силы взаимодействия первой части перво-
го тела с каждой частью второго тела, затем — второй части
первого тела с каждой частью второго тела и так далее, пока не
переберем все части первого тела. Получим большое количество
векторов сил, приложенных к первому телу («ежик» сил, если
изобразить их на рисунке). Сложив эти силы по правилу сложе-
ния векторов, получим их результирующую. Это и будет сила,
с которой первое тело притягивается ко второму. С такой же
по модулю силой, направленной противоположно, притягивается
второе тело к первому.
Этот пример показывает, что в общем случае задача нахож-
дения силы тяготения между протяженными телами является
довольно сложной. Но строго доказано, что силу тяготения меж-
ду двумя телами можно находить по формуле A) в следующих
случаях: 1) если оба тела являются однородными шарами; тогда
тх и т2 — их массы, г — расстояние между центрами шаров;
2) одно из тел является однородным шаром, второе — матери-
альной точкой; тогда т1 и пг2 — их массы, г— расстояние от ма-
териальной точки до центра шара.
31. Абитуриенты нередко считают, что вес тела всегда равен
силе тяжести, и ссылаются при этом на формулу
P = mg, A)
где Р — вес тела, т — его масса, g — ускорение свободного па-
дения.
Но равенство A) справедливо в том случае, когда горизон-
тальная опора, на которой находится тело, или нить, на которой
оно подвешено, покоится или движется равномерно и прямоли-
нейно относительно Земли.
Вес тела и сила тяжести — различные силы. Вес тела — это
сила, с которой тело действует на горизонтальную опору или
растягивает нить, на которой оно подвешено. Сила тяжести —
54
это сила притяжения тела Землей (точнее — отвесная составля-
ющая этой силы). Вес тела приложен к опоре или подвесу (нити),
сила тяжести — к телу. Именно сила тяжести сообщает телу
массой т ускорение свободного падения g. Согласно второму за-
кону Ньютона, FT = mg.
Что же отражает формула A)? Чтобы ответить на этот во-
прос, вспомним, что на тело, которое покоится на горизонталь-
ной опоре, действуют две силы: сила тяжести FT — mg и сила
нормальной реакции опоры N (рис. 51). Почему тело находится
в равновесии (покоится)? Некоторые поступающие утверждали,
что тело покоится потому, что, согласно третьему закону Ньюто-
на, сила реакции опоры N равна по модулю и противоположна
по направлению силе тяжести FT. Такое объяснение ошибочно.
В действительности же на основании второго закона Ньютона
N + mg = та, а так как тело покоится, то его ускорение а = 6.
Следовательно, N = mg = 0, N = —mg. Значит, модули этих сил
равны: N = mg.
Кроме того, согласно третьему закону Ньютона, сила реакции
опоры равна по модулю и противоположна по направлению си-
ле, с которой тело действует на опору, т. е. весу тела: N= —Р.
Следовательно, P = N, а так как N = mg, то P = mg.
Таким образом, формула A) отражает тот факт, что вес тела
численно равен силе тяжести, если оно находится на покоящейся
относительно Земли опоре или подвешено на нити, неподвижной
относительно Земли. Если же опора или подвес вместе с телом
будут ускоренно двигаться вверх или вниз, то вес тела будет от-
личаться от силы тяжести, т. е. P=^=mg.
Yi в
г
,N
"|
' тд
Рис. 51
Рис. 52
Задача. С какой силой будет давить на дно лифта груз мас-
сой т, если лифт движется: с ускорением а, направленным
55
вверх; с ускорением а, направленным вниз; свободно падает?
Решение. На груз действуют две силы: сила тяжести
FT = mg и сила реакции опоры N (рис. 52). Координатную ось OY
направим вертикально вверх и, спроектировав на нее силы FT
и N, составим, согласно второму закону Ньютона, уравнение
N — mg = тау,
где ау—проекция ускорения на ось OY. Отсюда
Согласно третьему закону Ньютона, с такой же по модулю
силой тело давит на дно лифта, т. е. вес тела равен силе реакции
опоры: P = N. Следовательно, в ускоренно движущемся лифте
тело имеет вес
y). A)
Если ускорение направлено вверх, то ау = а и, согласно фор-
муле A),
Таким образом, в этом случае вес тела больше силы тяжести.
Если ускорение направлено вниз, то ау=—а и
P2 = m(g-a), C)
т. е. вес тела меньше силы тяжести.
Обратим внимание на то, что как видно из формулы A), вес
тела зависит от направления ускорения а, направление же дви-
жения лифта при этом не имеет значения. Так, например, вес те-
ла в лифте будет выражаться формулой B) в двух случаях:
1) если лифт движется вверх равноускоренно (т. е. скорость его
увеличивается); 2) если лифт движется вниз равнозамедленно
(т. е. скорость его уменьшается). В обоих этих случаях ускорение
а направлено вверх, ау>0. Формула C) справедлива тоже в двух
случаях: 1) если лифт движется равноускоренно вниз; 2) если
лифт движется равнозамедленно вверх. В этих случаях ускоре-
ние а направлено вниз,
При a = g (лифт свободно падает) по формуле C) получим
Р3 = 0, т. е. груз не давит на дно лифта, находится в состоянии не-
весомости.
Если а = 0, т. е. лифт движется равномерно прямолинейно, то
P = mg. Система отсчета, связанная лифтом, который движется
равномерно и прямолинейно относительно Земли, является инер-
циальной системой. Отсюда следует, что вес равен силе тяжести
во всех инерциальных системах отсчета.
Система отсчета, движущаяся с ускорением относительно ка-
56
кой-либо инерциальной системы отсчета, называется неинерци-
альной. В инерциальных системах отсчета P^mg, т. е. вес отли-
чается по модулю от силы тяжести.
32. Рассматривая конкретные примеры движения тел по
окружности, абитуриенты иногда утверждают, что центростре-
мительное ускорение сообщается телу особой силой, которая на-
зывается центростремительной. Считают, например, что на ша-
рик, который прикреплен к нити и движется по окружности, дей-
ствуют сила тяжести нити и центростремительная сила.
В самом деле, термин «центростремительная сила» применя-
ется в некоторых учебных пособиях. Но надо иметь в виду, что
так называемая центростремительная сила не является какой-то
силой особой природы. На тело, равномерно движущееся по
окружности, обычно действуют какие-либо силы, рассматривае-
мые в механике: силы упругости, силы тяготения или силы тре-
ния. Векторная сумма всех действующих на тело сил, т. е. их
равнодействующая F = f, + ~F2-j-...-\-~Fn, перпендикулярна к век-
тору скорости тела и направлена к центру окружности. Эту
равнодействующую иногда называют центростремительной си-
лой, а поступающие считают ее некой самостоятельной силой.
В действительности никаких особых центростремительных сил,
не связанных с взаимодействием тел, нет.
Равнодействующая F сообщает телу центростремительное
(нормальное) ускорение ап. Значит, согласно второму закону
Ньютона, для равномерного движения тела по окружности спра-
ведливо уравнение
Чтобы перейти к скалярному уравнению, нужно спроектиро-
вать все векторы на ось ОХ, направленную по радиусу к центру
окружности (т. е. по направлению ускорения о„), и сумму проек-
ций всех сил приравнять произведению массы тела на модуль
центростремительного ускорения:
2
Заметим, что при указанном выборе оси ОХ а„х = ап = — . Ес-
ли же взять направление оси ОХ противоположное, то нужно
учесть, что при этом проекция вектора а„ будет отрицатель-
ной: апх= —ап= — —.
Если тело движется неравномерно, то скорость его изменяет-
ся не только по направлению, но и по модулю. В этом случае
центростремительное ускорение ап сообщают составляющие при-
ложенных к телу сил, действующие вдоль радиуса, а составляю-
щие, действующие вдоль касательной, сообщают телу касатель-
57
ное (тангенциальное) ускорение. Полное ускорение равно век-
торной сумме центростремительного и касательного ускоре-
ний: а = а„-\-ах.
Равнодействующая всех приложенных к телу сил при нерав-
номерном движении по окружности составляет с радиусом неко-
торый отличный от нуля угол, т. е. она направлена не к центру
окружности. Согласно второму закону Ньютона,
F = ma или Fl + F2 + ... + Fn = m(an + ax).
Чтобы найти а„ и ах, нужно координатную ось ОХ направить
вдоль радиуса к центру окружности, а ось OY — по касательной.
Тогда в проекциях на эти оси получим два скалярных
уравнения:
Решив эту систему уравнений, найдем апх и аху. При указанном
выборе осей координат апх=ап, поэтому всегда должно полу-
чаться anx>Q. Значение аху будет положительным, если направ-
ления ах и оси OY совпадают, и отрицательным, если они проти-
воположны.
Векторы ап и ах взаимно перпендикулярны, поэтому модуль
полного ускорения
В элементарном курсе физики, как правило, не рассматрива-
ются задачи, связанные с нахождением тангенциального и пол-
ного ускорений, но понятие о них желательно иметь для того,
чтобы отчетливо представлять себе динамику движения тела по
окружности. В противном случае возникают затруднения при ре-
шении ряда задач, абитуриенты нередко допускают ошибки. На-
пример, считают, что тело имеет центростремительное ускорение
только при равномерном движении по окружности. На самом же
деле, как показано выше, центростремительное ускорение ап —
одна из составляющих (радиальная) полного ускорения, вторая
составляющая (касательная) — тангенциальное ускорение ат.
При равномерном движении по окружности ат = 0, поэтому
- - v1
а = ап и а = ап = —.
Задача 1. Шарик массой т=100 г подвешен на невесомой
и нерастяжимой нити. В натянутом состоянии нить расположили
горизонтально и отпустили шарик. Какова сила натяжения нити
в момент, когда она образует с вертикальным направлением
угол а = 60°?
58
Рис. 53
Решение. На шарик действуют сила тяжести FT = mg и си-
ла натяжения нити Т (рис. S3). Он движется по дуге окружно-
сти, радиус R которой равен длине нити /. Это движение нерав-
номерное, так как вектор скорости шарика изменяется не только
по направлению, но и по модулю. В рассматриваемый момент
времени шарик находится в точке О. Направим координатную
ось ОХ из этой точки к центру окружности (т. е. к точке А, в ко-
торой закреплен конец нити), а ось OY — по касательной, прове-
денной к траектории в точке О.
Найдем проекции сил на ось ОХ и на основании второго зако-
на Ньютона составим уравнение
Обозначим через v скорость шарика в точке О. Так как
то уравнение A) примет вид: Т — mg cos a = mv2/l. Отсюда
= m(
g cos
B)
Чтобы найти скорость шарика в точке О, воспользуемся зако-
ном сохранения механической энергии. Потенциальную энергию
будем отсчитывать от горизонтального уровня СО, проходящего
через точку О. Согласно закону сохранения энергии,
Екв + Ерв = Ею + Еро, C)
где EkB, ЕрВ — соответственно кинетическая и потенциальная
энергия шарика в точке В; Ek0, Ер0 — его кинетическая и потен-
циальная энергия в точке О:
Из рис. 53 видно, что h = l cos а. Поэтому ЕрВ = mgl cos а. На
59
основании уравнения C) получим: mgl cos a = ——- . Отсюда най-
дем v'2 = 2gl cos а и, подставив это выражение в формулу B), по-
лучим: T = 3mg cos a, 7"= 1,5 Н.
Некоторые абитуриенты решали эту задачу так: проектиро-
вали силы Т и FT на ось ОХ, направленную вдоль нити, и счи-
тали, что поскольку шарик вдоль нити не движется, то сумма
этих проекций равна нулю: Т — mg cos а = 0. Отсюда T = mg cos a,
что, конечно, неверно.
Аналогичная ошибка встречалась в ответах, разъясняющих
динамику движения математического маятника. Разложив силу
тяжести FT на две составляющие: Z7,, направленную вдоль нити,
и F2, направленную по касательной к траектории (рис. 54), аби-
туриент утверждал, что сила F2 уравновешивается силой натя-
жения нити Т. В действительности же отличная от нуля резуль-
тирующая сил Т и F2 сообщает шарику центростремительное
ускорение.
На примере решения приведенной выше задачи можно пояс-
нить, как найти касательное (тангенциальное) ускорение. Для
этого проектируем на ось OY действующие на шарик силы Т и
FT и составляем уравнение:
— FT sin a = maTy,
где ач — проекция касательного ускорения а% на ось OY,
направленную по касательной к траектории. Отсюда
ату=—g sin а. Эта проекция характеризует скорость изменения
модуля скорости шарика, а центростремительное ускорение ха-
рактеризует скорость изменения направления вектора скорости
шарика.
Решим еще одну задачу, вызывавшую затруднения у абиту-
риентов.
Рис. 54
Рис. 55
60
Задача 2. Шарик массой т, прикрепленный к нити, дви-
жется равномерно по окружности в горизонтальной плоскости
(конический маятник). Расстояние от точки подвеса до горизон-
тальной плоскости равно h. Найти угловую скорость шарика.
Решение. Пусть а — угол, составляемый нитью с вер-
тикалью (рис. 55). На шарик действуют две силы: сила натяже-
ния нити 7" и сила тяжести FT = mg. Направим ось ОХ вдоль ра-
диуса к центру окружности О,, а ось OY — вертикально вверх.
Спроектировав силы Fr и 7" на ось ОХ, составим на основании
второго закона Ньютона уравнение:
Т sin a = man или Т sin а = ты2/?, A)
где (о — угловая скорость шарика; /? — радиус окружности.
Вдоль оси OY ускорения нет, поэтому сумма проекций на эту
ось равна нулю:
7" cos a — mg = 0 или Т cos а = mg. B)
Разделив почленно равенство A) и B), получим: tga — .
п
С другой стороны, как видно из рисунка 55, tga — —. Следова-
тельно, /?/Л = . Отсюда находим угловую скорость шари-
б
ка: ы=Л ~ .
V ^
В отличие от предыдущей задачи здесь шарик движется с по-
стоянной по модулю скоростью, касательное ускорение ат = 0,
силы 7" и Fr сообщают телу только постоянное по модулю цент-
ростремительное ускорение а„. А в задаче 1 как а„, так и ат — ве-
личины переменные.
При решении задачи 2 абитуриенты нередко не могли пра-
вильно составить уравнения, ссылаясь при этом на то, что якобы
не хватает данных. Вводить же обозначения некоторых величин,
не заданных в условии, абитуриенты, как правило, опасаются.
Этот недостаток встречается часто и при решении задач из дру-
гих разделов курса физики средней школы.
Второй недостаток — неумение правильно выявить все силы,
под действием которых тело, движущееся по окружности, приоб-
ретает центростремительное ускорение. Некоторые поступаю-
щие, например, указывали на рисунке, что на шарик действуют
не две, а три силы (сила тяжести, сила натяжения нити и цент-
ростремительная сила).
Предупреждая подобные ошибки, рассмотрим несколько при-
меров, иллюстрирующих применение второго закона Ньютона к
движению тела по окружности.
1. Тело массой m скользит без трения по поверхности сферы,
радиус которой /? (рис. 56). На тело действуют сила тяжести FT
61
и сила нормальной реакции опоры N. Ось ОХ направим к цент-
ру сферы. Моменту, когда эта ось составляет с вертикалью угол
а, соответствует, согласно второму закону Ньютона, уравнение
FTX-\-Nx = manx или mg cos a — N = -
R '
где v — скорость тела в этот момент времени.
2. Тело массой т скользит по внутренней поверхности сферы,
радиус которой R (рис. 57). На тело действуют три силы: сила
тяжести /•',, сила трения FTp и сила нормальной реакции опоры
N. Спроектировав эти силы на ось ОХ, направленную к центру
сферы, составим на основании второго закона Ньютона урав-
нение
Flx-\- Fipx-\- N х = tnanx или N — mg cos a=-
R
где a — угол между осью ОХ и вертикалью; и — скорость тела.
Y/
N
Рис. 56
Рис. 57
3. Луна движется вокруг Земли по орбите, которую можно
приближенно считать окружностью (рис. 58). Сила тяготения F
Земли сообщает Луне центростремительное ускорение. Согласно
второму закону Ньютона,
г, „ Mm mv2
t =та„г или О—г- = ,
R2 R
где М, т — массы Земли и Луны соответственно; R — радиус ор-
биты Луны.
Такой же вид имеет и уравнение движения искусственного
спутника Земли, масса которого т. В этом случае R — расстоя-
ние от спутника до центра Земли. (Рассматривая движение Лу-
ны вокруг Земли, мы считаем их материальными точками, так
как их размеры малы по сравнению с расстоянием от оси Земли
до Луны, равным приблизительно 3,8-105 км.)
4. Плоская шайба массой т лежит на горизонтальном круге,
62
Рис. 58
который равномерно вращается с угловой скоростью со. Коэффи-
циент трения шайбы о круг ц. Расстояние от шайбы до оси вра-
щения равно R. Направим ось ОХ к центру О, окружности, по
которой движется шайба, а ось OY — вертикально вверх (рис. 59).
На шайбу действуют сила тяжести FT = mg, сила нормальной
реакции опоры N и сила трения FTp. Спроектировав эти силы на
оси ОХ и OY, составим, согласно второму закону Ньютона, два
уравнения:
Отсюда N — mg. Так как F —\aN, то F
\img = man или \img = nwJR.
5. В верхней точке петли Нестерова
на летчика действуют в вертикальном
направлении сила тяжести FT = mg и
сила нормальной реакции опоры N
(рис. 60). На основании второго закона
Ньютона составим уравнение в проек-
циях на ось ОХ, направленную верти-
кально вниз:
= \img. Следовательно,
6. Чтобы двигаться по окружности
радиусом R со скоростью и, велосипе-
дист, повернув руль, должен накло-
ниться в сторону поворота. Найти угол наклона велосипедиста к
плоскости дороги. __
Когда велосипед наклонен, сила реакции дороги Q направле-
на под углом а к поверхности дороги (рис. 61). Эта сила являет-
ся равнодействующей двух сил — силы нормальной реакции
дороги N и силы трения Frp. Последняя всегда принимает такое
значение, что сила Q проходит через центр тяжести системы
63
Рис. 60
Рис. 61
тел, состоящей из велосипедиста и велосипеда. На систему дей-
ствует, кроме силы Q, сила тяжести FT = mg, направленная вер-
тикально вниз.
Систему координат выберем так, чтобы ось ОХ была направ-
лена к центру окружности, а ось OY — вертикально вверх.
В проекциях на эти оси составим уравнения на основании второ-
го закона Ньютона:
или
„ mv ,-. .
Qcosa = -—, Qsina = mg.
A;
Разделив почленно последнее уравнение на предпоследнее, полу-
чим
a = -2y. Следовательно, угол наклона велосипедиста
V
а = arctg ^—.
V
33. Значительные затруднения вызывает у абитуриентов во-
прос об ускорении свободного падения. Большинство считает,
что это постоянная величина, и только немногие указывают на
то, что ускорение свободного падения уменьшается с увеличени-
ем высоты над Землей, потому что при этом уменьшается сила
притяжения тел Землей.
В действительности ускорение свободного падения g одинако-
во для всех тел в данном месте Земли, но оно зависит, во-пер-
вых, от высоты над уровнем моря и, во-вторых, от географиче-
ской широты места.
Ускорение свободного падения обусловлено действующей на
тело силой тяжести FT:
64
Если не учитывать суточное вращение Земли, то можно счи-
тать, что сила тяжести равна силе, с которой тело притягивается
Землей согласно закону всемирного тяготения, т. е. силе тяго-
тения
F = GmM
где G — гравитационная постоянная; т — масса тела; М — мас-
са Земли; R — радиус Земли. Тогда модуль ускорения свободно-
го падения
Р =— = — ИЛИ Р=6—г.
& т т & ft2
Из последней формулы следует, что ускорение свободного па-
дения не зависит от массы т тела, оно одинаково для всех тел.
Применяя здесь закон всемирного тяготения, мы считаем те-
ло материальной точкой, а Землю — однородным шаром. Поэто-
му расстояние от тела, находящегося вблизи поверхности Земли,
до ее центра приблизительно равно радиусу R Земли. Если же
тело находится на высоте h над уровнем моря, то расстояние до
центра Земли равно R-\-h и ускорение свободного падения
G
Сравнив две последние формулы, приходим к выводу, что
, T- е- с подъемом над поверхностью Земли ускорение сво-
бодного падения уменьшается:
Из этого соотношения следует, что на высотах, которые на-
много меньше радиуса Земли, изменение ускорения свободного
падения мало. Так, например, если вблизи поверхности Земли
g- = 9,8 м/с2, то на высоте h = 25 км
** = 9'8( 6370 + 25 )~9'7 М/С'
т. е. ускорение свободного падения уменьшается на 0,1 м/с2. Та-
ким малым изменением можно пренебречь и во многих практиче-
ских расчетах считать ускорение свободного падения величиной
постоянной.
Если учитывать суточное вращение Земли, то надо прини-
мать во внимание, что сила тяготения и сила тяжести для одного
и того же тела, находящегося на поверхности Земли, отличаются
друг от друга по модулю и по направлению. Сила тяготения F
всегда направлена по радиусу к центру Земли, сила тяжести
3 Заказ 2473 65
i
/V. '
\
Nn
I
Рис. 62
FT — по линии отвеса в данном месте Земли (рис. 62). Сила тя-
жести зависит от географической широты ф. Причина этой зави-
симости заключается в том, что любое тело, покоящееся относи-
тельно Земли, участвует в ее суточном вращении и, следователь-
но, движется вокруг земной оси по окружности, радиус которой
r = R cos ф. На тело действуют сила тяготения F и сила реакции
опоры N, направленная под некоторым углом к F. Равнодейству-
ющая этих сил Fr сообщает телу центростремительное ускоре-
ние, модуль которого
ап = со2г = со2/? cos ф,
где со — угловая скорость суточного вращения Земли. Это уско-
рение направлено так же, как и сила Fn т. е. вдоль радиуса г по
направлению к центру окружности О{.
Следовательно, сила реакции опоры N уравновешивает не си-
лу тяготения F, а ее составляющую FT, которая называется
силой тяжести. Второй составляющей силы тяготения является
сила Fr. Из рисунка 62 видно, что сила тяжести всюду, кроме
полюсов и экватора, направлена не к центру Земли, а под неко-
торым углом а к ее радиусу.
Сила тяжести зависит от широты места, поэтому и ускорение
свободного падения имеет различные значения в разных местах.
Максимальное значение сила тяжести и, следовательно, ускоре-
ние свободного падения имеют на полюсах Земли, так как там
г —0 и центростремительное ускорение равно нулю. На полюсах
сила тяжести равна силе тяготения. Минимальные значения си-
ла тяжести и ускорение свободного падения имеют на экваторе.
В одном и том же месте Земли угол а между векторами F
66
и FT очень мал, поэтому различие между силой тяготения и си-
лой тяжести незначительно и им можно пренебречь, т. е. считать,
что модули этих сил равны и ускорение свободного падения
вблизи поверхности Земли везде одинаково и равно 9,8 м/с2.
Другой причиной зависимости силы тяжести от географиче-
ской широты является то, что земной шар немного сплюснут: его
полярный радиус меньше экваториального приблизительно на
21,5 км. Однако эта причина менее существенна, чем суточное
вращение Земли. Расчеты показывают, что из-за сплюснутости
Земли значение ускорения свободного падения на экваторе
меньше его значения на полюсе на 0,18%, а из-за суточного вра-
щения — на 0,34%.
Как отмечалось выше (п. 31), вес тела, покоящегося или дви-
жущегося равномерно прямолинейно относительно Земли, чис-
ленно равен силе тяжести: P = mg. Следовательно, вес тела тоже
зависит от широты местности: он максимален на полюсах и ми-
нимален на экваторе.
Задача. Определить вес тела массой т = 1000 кг и ускоре-
ние свободного падения на полюсе, на экваторе и на широте
Ф = 60°, если известно, что средний радиус Земли /? = 6,37-106 м,
масса Земли М = 5,98-10 кг, гравитационная постоянная
G = 6,67-10~" Н-м2/кг2. Тело покоится относительно Земли.
Решение. На полюсе на тело действуют две силы: сила
тяготения F и сила реакции опоры Л/п (см. рис. 62). По третьему
закону Ньютона вес тела, т. е. сила, с которой тело действует на
опору, равен по модулю силе реакции опоры: Pn = Nn. Тело нахо-
дится в равновесии, поэтому NU = F. Следовательно, вес покоя-
щегося тела на полюсе численно равен силе тяготения: Pn = F.
По закону всемирного тяготения
F=GmM
R2 '
Подставив в эту формулу значения заданных величин, получим:
/? = 6,67-10-"-1000'5>98'1°24 Н = 9,83-103 Н.
F,37-106J
Следовательно, на полюсе тело имеет вес Я„ = 9,83 ¦ 103 Н.
Сила тяжести на полюсе равна силе тяготения: FT = F. Следо-
вательно, F = mgu, откуда ускорение свободного падения на
полюсе
F 9,83-Ю3 „ п оо ,2
?? н 983м/с
На экваторе на тело действуют сила тяготения F и сила ре-
акции опоры Л/э, при этом тело, участвуя в суточном вращении
Земли, движется по окружности радиусом R. Составим уравне-
ние на основании второго закона Ньютона:
67
F— /V3 ^,
где со— угловая скорость: ю=-^; Т — период вращения Земли
вокруг своей оси: Т = 24 ч = 86 400 с. Тогда F — Л?, = m (-=-) /?,
откуда
Л? = F
Э
По третьему закону Ньютона вес тела на экваторе Р, = ЫЭ.
Вычислим
Р3 = 9,83-103-4-3-14М000-6-37-|0бН^9,78-103 Н.
86 4002
Как отмечено выше, вес покоящегося тела численно равен си-
ле тяжести: P^ = mg3. Отсюда находим ускорение свободного па-
дения на экваторе:
Ра 9,78- 103 /2 то /2
^ = м/с978м/с
На широте ф тело движется по окружности радиусом
г = ^соэф (см. рис. 62). Составляющая Fr силы тяготения, на-
правленная вдоль радиуса г к центру окружности О,, сообщает
телу центростремительное ускорение, модуль которого равен
(x>2r=tt>2R cos ф. По второму закону Ньютона Fr — mu>2R cos ф. При-
менив теорему косинусов, найдем модуль силы тяжести на широ-
те ф:
где F — модуль силы тяготения, которая для данного тела оди-
накова в любой точке земной поверхности, т. е. не зависит от ши-
роты места. Как показано выше, для тела массой щ== 1000 кг си-
ла тяготения Z7 = 9,83 -103 Н. Вычислим теперь Fr:
г 2 г> 4л2тЯ
rr= пш R cos ф = — cos ф,
4.3,14М000.6,37.10*
86 4002
Затем в выражение для FT подставим значения F и Fr и вычис-
лим модуль силы тяжести:
3-103J+ 16,832 — 2-9,83-103-16,83-0,5 Н = 9,82-103Н.
Вес покоящегося тела численно равен силе тяжести. Следова-
тельно, на широте ф = 60° тело массой т=1000 кг имеет вес
Я = 9,82-103 Н.
Найдем ускорение свободного падения на этой широте:
68
9,82-103 . 2 r, or, /2
м/с=9'82 м/с-
Приблизительно такое значение имеет ускорение свободного
падения на широте Санкт-Петербурга (ср = 59,57°).
Результаты сделанных при решении этой задачи расчетов по-
казывают, что ускорение свободного падения незначительно за-
висит от широты места. На практике во многих случаях этой за-
висимостью пренебрегают, т. е. не учитывают суточное вращение
Земли.
34. Выяснив, что сила тяжести и, следовательно, вес тела за-
висят от широты места, рассмотрим такой вопрос: «С помощью
рычажных весов взвесим 10 кг апельсинов на экваторе. Изме-
нится ли результат взвешивания, если те же апельсины с по-
мощью тех же весов взвесить на полюсе? Считать, что условия
взвешивания (температура, плотность воздуха и др.) одинако-
вые». Нередко приходилось слышать неправильный ответ: «Из-
менится, так как вес тела на полюсе больше, чем на экваторе».
Между тем нетрудно понять, что результат взвешивания бу-
дет тот же, потому что изменится не только вес тела, но и вес
гирь, и весы останутся в равновесии. Другое дело, если бы взве-
шивали с помощью пружинных весов. В этом случае под дейст-
вием силы тяжести пружина растянулась бы на полюсе больше,
чем на экваторе, результат взвешивания был бы больше.
Таким образом, зависимость веса тела от широты места мож-
но обнаружить с помощью пружинных весов, а с помощью ры-
чажных — нельзя. Когда рычажные весы уравновешены, можно
только утверждать, что вес тела равен весу гирь и что масса те-
ла равна массе гирь.
35. Не все абитуриенты, правильно формулировавшие закон
всемирного тяготения, могли объяснить, почему вследствие при-
тяжения Луна не падает на Землю, почему планеты не падают
на Солнце. Некоторые пытались объяснить это наличием сил
притяжения со стороны других планет, другие утверждали, что
есть какая-то сила, уравновешивающая силу тяготения. Оба от-
вета неправильные.
Если бы сила тяготения уравновешивалась какой-либо дру-
гой силой, то Луна, например, двигалась бы прямолинейно, а не
по круговой орбите. То же можно сказать и о движении планет
(заметим, что мы приближенно считаем орбиты круговыми, а не
эллиптическими). Каждая планета потому и движется по орбите,
что на нее действует сила притяжения к Солнцу. Если бы этой
силы не было, планета двигалась бы с большой скоростью рав-
номерно и прямолинейно (согласно первому закону Ньютона).
Сила тяготения изменяет направление этой скорости, сообщая
планете центростремительное ускорение.
Луна движется вокруг Земли под действием силы тяготения
между Луной и Землей. Надо сказать, что сама постановка во-
проса (почему Луна не падает на Землю?) не совсем корректна.
69
В действительности Луна именно падает на Землю, т. е. движет-
ся с ускорением свободного падения под действием силы тяготе-
ния, и одновременно с этим движется равномерно прямолинейно
по инерции. В результате сложения этих движений Луна непре-
рывно падает, но к центру Земли не приближается и от него не
удаляется, т. е. движется вокруг Земли, или, как отвечал один
экзаменуемый, «падает к Земле, но никак не попадет на нее».
Аналогично объясняется движение искусственного спутника
Земли. Чтобы тело стало искусственным спутником Земли, дви-
жущимся на расстоянии h от нее, нужно поднять это тело на вы-
соту h и там сообщить ему в направлении, перпендикулярном к
вертикали, такую скорость v, чтобы, согласно второму закону
Ньютона, выполнялось условие
с т1>2
= R + h '
где F — сила тяготения; т — масса тела; R — радиус Земли
(считаем ее шаром). Тогда
р тМ mv2
где G — гравитационная постоянная; М — масса Земли. Отсюда
Если спутник запускается вблизи поверхности Земли (/г = 0),
ему необходимо сообщить по касательной к поверхности Земли
скорость
_-. Гам~
Это первая космическая скорость — скорость, при которой тело,
находящееся у поверхности Земли, при отсутствии сопротивле-
ния воздуха становится искусственным спутником Земли. Если
бы не было силы тяготения, то это тело полетело бы по касатель-
ной к поверхности Земли.
При скорости, меньшей первой космической, тело под дейст-
вием силы тяготения упадет на Землю.
36. Рассмотрим еще один вопрос, вызывавший у абитуриен-
тов значительные затруднения. Предположим, что искусствен-
ный спутник Земли, движущийся на расстоянии h{ от ее поверх-
ности со скоростью и, по круговой орбите, нужно перевести на
более низкую орбиту. Для этого включается установленный на
спутнике тормозной ракетный двигатель. При этом газ из сопла
двигателя вылетает в ту же сторону, куда направлен вектор
скорости У[. За время работы двигателя скорость спутника
уменьшается, и он приближается к Земле. После прекращения
70
работы тормозного двигателя спутник движется вокруг Земли
на расстоянии h2<Ch[ от нее со скоростью v2. Сравнить скорости
и, и и2.
Обычно поступающие утверждают, что v2<Lv{. Это не-
правильно. Из формулы
следует, что скорость спутника v увеличится, если уменьшить /г,
т. е. перевести его на более низкую орбиту. Ошибка абитуриен-
тов вызвана, по-видимому, их «земным» представлением о том,
что всякое торможение приводит к уменьшению скорости.
37. В ответах абитуриентов довольно часто встречаются не-
точные формулировки физических законов, что свидетельствует
о неправильном понимании их, а отсюда следует неумение при-
менять эти законы при решении задач. Третий закон Ньютона,
например, некоторые экзаменуемые формулируют так: «Все тела
взаимодействуют с силами, равными по модулю и противопо-
ложными по направлению». В действительности же в этом зако-
не рассматриваются не все тела, а любые два тела, взаимодей-
ствующие между собой, и утверждается, что сила, с которой пер-
вое тело действует на второе, равна по модулю и противопо-
ложна по направлению силе, с которой второе тело действует на
первое: Fl2= — F2[.
Математическое выражение закона Гука абитуриенты запи-
сывают либо в виде F= —kx, либо F = kx, где k — жесткость те-
ла. При этом они не могут объяснить различный физический
смысл этих формул. Поясним это различие на примере упругой
деформации стержня, один конец которого закреплен, а к друго-
му приложена сила F, растягивающая стержень. Под действи-
ем этой силы стержень деформируется до тех пор, пока возника-
ющая в нем сила упругости Fy не станет равной по модулю при-
ложенной силе (рис. 63).
Рис. 63
Y
\
А Г
Л
F
X
71
После этого стержень находится в равновесии. Обозначим через
Л/ вектор удлинения стержня, т. е. перемещение свободного кон-
ца стержня при деформации. Согласно закону Гука, сила упру-
гости пропорциональна удлинению и направлена в противопо-
ложную сторону: _
где k — жесткость стержня.
Направим координатную ось ОХ параллельно стержню, а за
начало отсчета примем точку О, определяющую положение сво-
бодного конца недеформированного стержня. В проекциях на эту
ось уравнение A) имеет вид FyK = —k(Al)x. Но (А1)х = х, поэтому
Fgx=-kx. B)
Кроме того, из условия равновесия получим:
Fyx+Fx = 0 или Fx=-Fyt.
Следовательно,
Fx = kx. C)
Таким образом, если абитуриент записал выражение закона
Гука в виде F= — kx, то он должен понимать, что здесь F — это
проекция силы упругости на ось ОХ, ах— модуль вектора удли-
нения. Если же записано F = kx, то здесь F — проекция прило-
женной силы на ту же ось. Чтобы не смешивать эти понятия,
лучше применять математическое выражение закона Гука для
рассматриваемого здесь случая в векторной форме A), либо в
скалярной B) или C).
Отметим еще одну ошибку, допускаемую иногда при приме-
нении закона Гука. Спроектировав силы F и Fy на ось ОХ
(см. рис. 63), поступающий записывал условие равнове-
сия стержня так: F — Fy = 0, а затем в это уравнение подставлял
вместо Fy ее значение в виде Fg=—kx и получал выражение
F-\- kx = 0, которое, конечно, является неправильным.
Встречались на экзаменах и такие высказывания: «Я пони-
маю закон, но сформулировать его не могу»- Это, конечно, не-
правильное рассуждение. Тот, кто хорошо понял закон, может
сформулировать его. Обратное утверждение, вообще говоря, не-
верно: можно выучить дословно формулировку закона, не пони-
мая его сути. Но это непонимание проявляется сразу же, как
только нужно применить этот закон в какой-либо конкретной си-
туации, например при решении задачи.
38. При решении задач по динамике поступающие нередко
допускают ошибки, не учитывая векторный характер физических
величин. Покажем это на примере применения второго закона
Ньютона. Как известно, одна из формулировок этого закона та-
кова: изменение импульса тела равно импульсу силы, действую-
щей на него, т. е.
72
mv2— mvl = FAt или Ap = FAt.
Абитуриенты не всегда правильно применяют это уравнение, до-
пускают ошибки. Рассмотрим следующую задачу, которая сама
по себе проста, но аналогичная ей составная часть может вхо-
дить в другие задачи.
Задача 1. Мяч массой т подлетает к вертикальной стенке
со скоростью vb направленной перпендикулярно стенке, ударя-
ется о нее и отскакивает с такой же по модулю скоростью. Опре-
делить среднюю силу удара мяча о стенку, если продолжитель-
ность удара равна t.
Встречалось такое ошибочное решение: поскольку v2=vx — v,
то Ft = mv — mv = Q, откуда следует, что F = Q.
После напоминания экзаменатора о том, что удар мяча, на-
пример, в спину, достаточно ощутим (F=?0), абитуриенты пони-
мали, что в решении допущена ошибка, но, к сожалению, не все-
гда могли ее исправить. А ошибка эта довольно грубая: не учте-
но, что импульс силы и импульс тела — величины векторные.
ту,
ту2
N
X
тиг
Рис. 64
Nt
Рис. 65
Решение. Первый способ. Координатную ось ОХ направим
перпендикулярно к стенке, а ось OY—вдоль стенки (рис. 64).
В момент удара на мяч со стороны стенки действует сила нор-
мальной реакции N, импульс которой равен Nt. Согласно второ-
му закону Ньютона, Nt = mv2 — mvx. В проекциях на ось ОХ это
уравнение имеет вид Nt = mv2x — mvlx. Учитывая, что v2x—v,
vu= —v, получим Nt = 2mv, откуда N = 2mv/t. Согласно третье-
му закону Ньютона, мяч во время удара действовал на стенку
с такой же по модулю, но противоположно направленной силой
(на рисунке не показана).
Второй способ. Найдем построением векторную разность
mv2 — my,. Она представляет собой вектор, начало которого совпа-
дает с концом вектора mvb а конец — с концом вектора mv2. Со-
гласно второму закону Ньютона, полученный вектор равен им-
пульсу силы Nt (рис. 65). Из рисунка видно, что модуль импуль-
са силы равен сумме модулей импульсов мяча до и после удара:
Nt = mvi -\- mv2. Отсюда
73
,, 2mv
а так как vl = v2, то N =—-—.
Согласно третьему закону Ньютона, такая же по модулю, но
противоположная по направлению сила действовала на стенку.
Задача 2. Шарик массой т, движущийся со скоростью и,
направленной под углом а к гладкой стенке, абсолютно упруго
ударяется о нее и отскакивает. Продолжительность удара равна
/. Определить среднюю силу, с которой шарик действует на стен-
ку при ударе.
Решение. При абсолютно упругом ударе кинетическая
энергия сохраняется, поэтому шарик отскакивает с такой же по
модулю скоростью, т. е. vl = v.2=v. Поскольку стенка гладкая, то
вдоль нее на шарик не действует сила трения. Направление ско-
рости шарика изменяется в результате действия силы нормаль-
ной реакции опоры N. Согласно второму закону Ньютона,
Nt = mv2 — mvu
где vh v2 — скорость шарика до и после удара соответственно.
Как указывалось выше, согласно третьему закону Ньютона,
средняя сила, с которой шарик действует на стенку во время
удара, равна по модулю силе N и противоположна ей по направ-
лению. Поэтому мы ответим на поставленный в задаче вопрос,
если найдем N. Сделать это можно двумя способами.
Yk
X
Рис. 66
Первый способ. Направим ось ОХ перпендикулярно стенке,
а ось OY — вертикально вверх вдоль стенки (рис. 66). Пусть р —
угол между стенкой и импульсом шарика ти2 после удара.
Спроектировав импульсы на оси ОХ и OY, составим два урав-
нения:
Nt = mv2 sin
v2 sin p + mo sin a,
= m»2 cos p — mv cos a.
A)
B)
74
/77 Ц
Рис. 67
Ho v2=v, поэтому из второго уравнения следует, что р = а. Та-
ким образом, при упругом соударении с гладкой стенкой шарик
отскакивает от нее под таким же углом, под каким надает. Те-
перь, учитывая это, на основании уравнения A) получим:
,. 2ти sin a
Второй способ. Построим разность векторов mv2 — mvl = Ap
(рис. 67). По второму закону Ньютона этот вектор равен
импульсу силы Nt. Так как стенка гладкая, на шарик действует
только сила нормальной реакции опоры N, поэтому вектор Nt,
а следовательно, и вектор Ар направ-
лены перпендикулярно стенке. Учиты-
вая это, а также равенство о2=о, = и,
приходим к выводу, что а = |3. Теперь
из построенного треугольника нахо-
дим: Д/? = 2/гш sin а. А так как
Ap — Nt, то
2mu sin a
~~ t
Пытаясь решить эту задачу, неко-
торые абитуриенты строили паралле-
лограмм, складывая векторы скоростей шарика до и после уда-
ра, а потом не могли найти правильное решение.
Может возникнуть вопрос: почему, рассматривая упругий
удар шарика о стенку, мы говорим о средней силе взаимодейст-
вия? Дело в том, что при соударении эта сила за короткое время
взаимодействия сначала увеличивается до максимального значе-
ния, а затем уменьшается до нуля. Аналогичная картина наблю-
дается, например, если пружину быстро сжать и отпустить: сила
упругости при этом сначала возрастает до некоторого наиболь-
шего значения, а потом падает до нуля. Поэтому импульс силы
мы находим как произведение среднего значения силы на время
ее действия.
39. Приведем еще один пример ошибочного применения вто-
рого закона Ньютона. Для пояснения этого закона абитуриент
рассказывал о таком эксперименте: тело массой тх скользит без
трения по горизонтальной плоскости под действием груза массой
тъ связанного с телом нерастяжимой и невесомой нитью, которая
перекинута через неподвижный блок (рис. 68). Если вместо этого
груза подвесить другой груз, масса которого больше т2 в 2 раза,
то сила тяжести тоже будет в 2 раза больше, а так как, согласно
второму закону Ньютона, ускорение пропорционально силе, то
оно увеличивается в 2 раза.
Ошибочность такого рассуждения станет ясной, если пра-
вильно применить второй закон Ньютона. На тело действуют си-
ла тяжести mxg, сила нормальной реакции опоры Nx и сила
75
л/,
т,д
Рис.
X
\т2д
натяжения нити Ти на груз — сила тяжести m2g и сила натяжения
нити 7\>. Из условия невесомости и нерастяжимости нити следу-
ет, что ТХ — Т2~Т и что груз и тело движутся с одинаковым
ускорением а. Ось ОХ направим слева направо вдоль горизон-
тальной плоскости, а ось OY — вертикально вверх. Затем, со-
гласно второму закону Ньютона, составим уравнения в проекци-
ях на оси ОХ и OY для тела и для груза в отдельности:
Т = гп{а, Т —
Решив эту систему двух уравнений, найдем модуль ускорения:
a = -
Отсюда видно, что если вместо груза массой т2 подвесить груз
массой 2т2, то тело и груз будут двигаться с ускорением
2т,
а' =
ml-\-2m2
B)
Сравнение формул A) и B) показывает, что а''ф2а.
Поставим теперь такой вопрос: груз какой массой т3 надо
подвесить, чтобы ускорение стало равным 2а? Для ответа на не-
го решим уравнение
m, + m3
В результате получим:
»3 —"
40. При решении задач на равновесие тела абитуриенты ча-
сто ошибочно считают, что плечом силы является расстояние от
оси вращения до точки приложения силы.
Напомним, что плечом силы относительно оси называется
длина перпендикуляра, проведенного от оси вращения на линию
действия силы. Рассмотрим примеры, в которых абитуриенты не
всегда могли правильно найти плечи сил.
76
1. Силы Fu F2, F3, действующие на тело (рис. 69), лежат в
плоскости рисунка. Ось вращения проходит перпендикулярно к
Рис. 69
этой плоскости через точку О. Нередко поступающие говорили,
что плечом силы F{ относительно указанной оси является длина
отрезка ОА{, плечами сил F2 и F3 — длины отрезков ОА2 и ОА3
соответственно. В действительности же плечом силы Ft относи-
тельно этой оси является длина /, перпендикуляра, проведенного
из точки О на линию действия силы F{. Аналогично находим пле-
чо /2 силы F2. Плечо силы F3 равно нулю, так как линия ее дей-
ствия проходит через ось вращения.
Т"
L
Рис. 70
2. Стержень длиной / и массой га, скреплен одним концом с
однородным шаром, масса которого равна т2, а радиус R. Дру-
гой конец стержня шарнирно связан с осью, проходящей через
точку О перпендикулярно к плоскости рисунка (рис. 70). Систе-
ма отклонена на угол а от вертикали горизонтально направлен-
ной силой F, линия действия которой проходит через центр
77
шара. Показать на рисунке все силы, действующие на систему, и
найти плечи этих сил относительно оси О.
На стержень действуют сила тяжести mxg и силы натяжения
Тх и Т2, на шар — сила тяжести m2g и сила F. Плечи сил msg,
m2§ и Р относительно оси О равны соответственно —sin а,
(/ + ?!) sin а и (l-^-R) cos а. Плечи сил 7", и Т2 относительно этой
оси равны нулю.
41. Затруднения у абитуриентов вызывают задачи по стати-
ке, в которых не указана ось вращения. Рассмотрим примеры
решения таких задач.
Задача 1. Лестница массой пг1 и длиной / приставлена к
гладкой стене. Угол между стеной и лестницей равен а, модуль
силы трения между лестницей и полом равен FTp. На какую высо-
ту может подняться человек массой гп2 по лестнице, прежде чем
она начнет скользить? Центр тяжести лестницы находится на
расстоянии — от ее конца.
Решение. На лестницу действуют сила тяжести mlg, сила
нормальной реакции стены Nu сила нормальной реакции пола
N2, сила трения /\р (рис. 71). Кроме того, на лестницу действует
Y
Рис. 71
человек с силой, равной силе тяжести m2g. Лестница находится
в равновесии, если векторная сумма всех действующих на нее
сил равна нулю и алгебраическая сумма моментов этих сил рав-
на нулю. Моменты сил можно находить относительно любой оси.
Выберем ось вращения, которая проходит через точку D перпен-
дикулярно к плоскости рисунка. Алгебраическая сумма момен-
тов сил относительно этой оси равна нулю:
Л/[/ cos а — mlg — sin а — m2gh tg а = 0.
78
Сумма проекций всех сил на ось ОХ равна нулю: Nt — FTp = 0.
Отсюда Nl = FTp. Учитывая это, решим уравнение для моментов
и получим выражение для высоты h, на которую может поднять-
ся человек:
/ BFTp cos a —m,g sin а)
2m2g tg а
При решении этой и аналогичных задач некоторые поступаю-
щие не могли правильно определить, какие силы вызывают вра-
щение тела по часовой стрелке и какие — против часовой стрел-
ки, хотя сделать это очень просто: надо представить себе, что
действует только интересующая нас сила, тогда можно легко
установить направление вращения тела, вызываемого этой
силой.
Задача 2. Центр тяжести системы, состоящей из однород-
ного массивного стержня с укрепленными на его концах грузами
/л, =5,5 кг и т2 = 1 кг, находится на расстоянии 1/5 длины стерж-
ня от более тяжелого груза. Найти массу стержня.
1/5
АЛ/
/7?, д
1/2
1 тд
'т2д
Рис. 72
Решение. Если в центре тяжести поставить опору (или
укрепить подвес), то система будет находиться в равновесии.
Сделаем схематический рисунок и покажем действующие на си-
стему силы: силу реакции опоры N, силы тяжести грузов и
стержня mtg, m2g и mg, учитывая, что последняя приложена в
середине стержня (рис. 72). Алгебраическая сумма моментов
всех сил относительно оси, проходящей через центр тяжести С,
равна нулю:
Решив это уравнение, найдем:
т = Bт]— 8от2)/3=1 кг.
При решении этой задачи некоторые абитуриенты составляли
уравнение для моментов в таком виде:
79
При этом силу тяжести mg на рисунке они не показывали, пояс-
няя, что учли ее при составлении уравнения: «пятая часть этой
силы — слева от точки С, четыре пятых — справа». Можно было
бы, конечно, и так рассуждать, но при составлении уравнения
1
1 /
1 1 /
учитывать, что сила — mg приложена на расстоянии — — слева от
JL О
/-4 14,
точки С, а сила - mg — на расстоянии - - / справа от этой точ-
0 /О
ки. А последнее уравнение ошибочно составлено так, как если
бы эти силы были приложены к концам стержня.
42. Встречаются и такие абитуриенты, которые дают без-
упречно правильные формулировки условий равновесия тел и
вместе с тем не могут правильно ответить на вопросы, требую-
щие применения этих знаний в конкретной ситуации. Так, напри-
мер, многие поступающие правильно объясняли, что действие
рычажных весов основано на правиле моментов сил, т. е. весы
находятся в равновесии, если Я1/1 = Я2/2, где Я,, Р2 — вес груза
и гирь соответственно; /,, /2 — плечи этих сил; если весы равноплеч-
ные (/| = /2), то Я] = Я2- Но они не могли объяснить, почему коро-
мысло рычажных весов имеет положение устойчивого равновесия.
На первый взгляд кажется, что если уравновесить весы, а за-
тем вывести из горизонтального положения коромысло, накло-
нив его на некоторый угол а (рис. 73), то и в этом случае плечи
будут одинаковыми, равными / cos а, и поэтому равновесие не
нарушится, коромысло останется в наклонном положении.
Таким образом, мы приходим к выводу, что уравновешенные
рычажные весы находятся в состоянии безразличного равнове-
сия. Но из опыта хорошо известно, что коромысло рычажных ве-
сов имеет положение устойчивого равновесия: если наклонить
коромысло и отпустить его, то оно возвращается в горизонталь-
ное положение. Почему?
Рис. 73
80
Дело в том, что конструкция весов такова, что центр тяжести
коромысла находится ниже точки опоры О, через которую прохо-
дит ось вращения (рис. 74, а). При наклоне коромысла его центр
тяжести поднимается на высоту h (рис. 74, б), вследствие чего
момент силы тяжести mg коромысла становится отличным от
нуля:
M = mg-OD = mgL sin a,
где т — масса коромысла; L — расстояние от его центра тяже-
сти С до точки опоры О. Этот момент силы возвращает коромыс-
Р и с. 74
ло в положение равновесия. Из последней формулы, в частности,
видно, что если бы точки О и С совпадали, то было бы М = 0 и
коромысло поэтому находилось бы в безразличном равновесии.
Кроме того, эта формула показывает, что момент силы М тем
больше, чем больше L. Конструкция ряда рычажных весов по-
зволяет изменять расстояние L: передвигая специальный грузик
Р (см. рис. 74, а) вверх или вниз, можно менять положение центра
тяжести коромысла, а следовательно, и расстояние L. При этом
изменяется чувствительность весов.
43. Рассказывая о принципе устройства и действия рычаж-
ных весов, экзаменуемые нередко утверждают, что с помощью
этих весов можно сравнивать только массы тел, а веса тел нель-
зя. Ошибочность этого утверждения легко видеть. Как сказано
выше, если равноплечные весы уравновешены, то вес груза ра-
вен весу гирь: РУ = Р2. С другой стороны, вес покоящегося на го-
ризонтальной поверхности чаши весов тела равен его силе тяже-
сти (об этом говорилось выше): Р\ = т^, Pi = mie- При равнове-
сии выполняется условие mxgl = m2gl, откуда следует, что
От|=от2. Таким образом, с помощью рычажных весов можно срав-
нивать и веса тел, и их массы.
Другая сторона этого вопроса состоит в том, что с помощью
рычажных весов нельзя обнаружить изменение веса тела, напри-
мер при его ускоренном движении или при изменении географи-
ческой широты места. Можно только утверждать, что при равно-
81
весии вес тела равен весу гирь. Масса же тела всегда остается
постоянной, поэтому на гирях указываются их массы, и при взве-
шивании на рычажных весах мы определяем массу тела.
44. Некоторые экзаменуемые ошибочно считают, что центр
тяжести тела не может находиться за пределами этого тела. На
самом же деле может. Достаточно рассмотреть, например, квад-
рат, сделанный из проволоки, кольцо, полый шар и др.
45. В затруднительное положение часто ставят абитуриентов
задачи на нахождение центра тяжести тела. Рассмотрим приме-
ры таких задач, предлагаемых на вступительных экзаменах.
Задача 1. Два однородных шара, имеющих массы /п, и тъ
а радиусы — соответственно Л?, и R2, соединены однородным
стержнем, масса которого т3, длина /. Центры шаров лежат на
продолжении оси стержня. Найти центр тяжести этой системы.
Решение. Первый способ. На первый и второй шары дей-
ствуют силы тяжести mtg и m2g соответственно, приложенные
в центрах О, и О2 шаров. Сила тяжести m3g, действующая на
стержень, приложена в его центре тяжести О3, находящемся на
расстоянии 1/2 от конца стержня.
Предположим, что искомый центр тяжести С находится на
расстоянии х от поверхности второго шара (рис. 75). Если в этой
точке поставим опору, то система будет находиться в равновесии
и поэтому сумма моментов всех действующих на систему сил от-
носительно оси, проходящей через точку С перпендикулярно к
плоскости рисунка, будет равна нулю:
Отсюда после несложных преобразований найдем, что
При составлении приведенного выше уравнения мы учли, что
момент силы реакции опоры N относительно указанной оси ра-
вен нулю.
Второй способ. Поскольку система находится в равновесии,
то сумма проекций всех сил на ось OY равна нулю:
jV —/w,g—m2g —/n3g = 0, откуда
N = mxg + m2g-\-mzg. A)
Кроме того, алгебраическая сумма моментов всех сил относи-
тельно любой оси равна нулю. На основании этого составим
уравнение для моментов сил относительно оси, проходящей через
точку О, перпендикулярно к плоскости рисунка:
+ B)
82
Рис. 75
Подставив в уравнение B) вместо N выражение A) и решив
его относительно х, получим такое же значение х, как и при пер-
вом способе решения.
Читатель самостоятельно может убедиться в том, что такой
же результат получится, если составить уравнение для моментов
сил относительно оси, проходящей через какую-либо другую точ-
ку (например, точку О2), и решить его, используя выражение A).
Многие поступающие не знают, что уравнение для моментов
сил можно составить, выбрав любую точку и ось, проходящую
через эту точку перпендикулярно к плоскости, если в этой плос-
кости лежат все силы, приложенные к находящемуся в равнове-
сии телу.
Задача 2. Определить положение центра тяжести однород-
ной круглой пластинки радиусом R, в которой вырезано квад-
ратное отверстие так, как показано на рис. 76.
Решение. Расположим пластинку так, чтобы ось симмет-
рии была горизонтальна, и предположим, что вырезанный квад-
рат помещен на прежнее место. Тогда на пластинку действует
сила тяжести
где mxg — сила тяжести, приложенная в
центре О] квадрата, m2g — сила тяжести,
действующая на пластинку с отверстием
и приложенная в искомом центре тяже-
сти С. При вставленном квадрате центр
тяжести пластинки совпадает с центром
ее симметрии О. Если в этой точке поста-
вить опору, то пластинка будет находить-
ся в равновесии и сумма моментов всех
сил относительно оси, проходящей через
точку О, равна нулю:
R =0.
83
Отсюда следует, что х = -—.
4/л2
Пусть h — толщина пластинки, р — плотность материала, из
которого она изготовлена. Тогда
X2. pR2h
) h
r>2, pRh pRh i. . ч
m.2 = m — m{ = рл/? h — ^~==4— Dл — 1 )¦
Подставив в выражение для х значения т, и от2, получим:
___ R
4Dл-1) '
46. Говоря о возможности переноса в твердом теле, находя-
щемся в равновесии, точек приложения внешних сил, не все аби-
туриенты могли это обосновать.
Действительно, в твердом теле точку приложения внешней
силы можно переносить только вдоль линии действия этой силы.
Такой перенос не изменяет плечо силы, а следовательно, остает-
ся постоянным ее момент относительно любой оси вращения, по-
этому алгебраическая сумма моментов всех сил по-прежнему бу-
дет равна нулю. Неизменной останется при таком переносе и
векторная сумма всех сил, действующих на тело. Следовательно,
равновесие тела не нарушится.
47. Некоторые абитуриенты при решении задач на равнове-
сие тел делали разложение сил на составляющие, а затем допу-
скали такую ошибку: при нахождении проекций сил на оси коор-
динат проектировали и силы, и их составляющие.
Встречаются и другие ошибки при нахождении действующих
на тело сил. Покажем это на примере решения следующей за-
дачи.
Задача. К вершине вертикальной мачты прикреплена ан-
тенна, действующая на нее в горизонтальном направлении с си-
лой /71 = 500 Н, и оттяжка, которая действует на мачту с силой
/72=1000 Н. Считая мачту невесомым твердым телом, найти угол
между оттяжкой и вертикалью и силу, с которой мачта давит на
землю.
Решение. Кроме сил F] и F2, приложенных к вершине мач-
ты, на ее основание действует Земля с силой N, направленной
вертикально вверх (рис. 77, а). Согласно третьему закону Ньюто-
на, мачта действует на Землю с такой же по модулю и противо-
положной по направлению силой, т. е. F3 = —./V. Следовательно,
определив N, мы ответим на один из вопросов, так как F3 = N.
Выберем систему координат так, чтобы ось ОХ была направ-
лена горизонтально, а ось OY— вертикально вверх. Мачта нахо-
84
дится в равновесии, поэтому суммы проекций всех сил на оси ОХ
и OY равны нулю:
F{ — F2 sin a = 0, N — /72cosa = 0.
Из первого уравнения найдем: sina = -7^-. Вычислим:
sin°530°
Из второго уравнения получим: N = F2cosa. Следовательно,
N= 1000 cos 30° ж 866 Н.
С такой же по модулю силой действует мачта на Землю.
А теперь приведем пример ошибочных рассуждений абитури-
ентов при решении этой задачи. Сложив силы Fx и F2 по правилу
а
X
N
Рис. 77
параллелограмма (рис. 77,6), получим силу F, с которой мачта
давит на Землю. Как видно из рисунка,
sina = —i-, F = F2cosa,
l~2
т. е. получается такой же результат, как и в приведенном выше
решении с помощью метода проекций. Ошибка заключается в
том, что полученная сила F приложена не к Земле, а к вершине
мачты.
Можно эту задачу решить, не прибегая к нахождению проек-
ций сил, если рассуждать так: поскольку мачта находится в рав-
новесии, то векторная сумма приложенных к ней сил Fu F2 v\ N
равна нулю, т. е.
85
= 0 или F, + F2=— N.
Построенная на рисунке 77,6 сила F=FX -\- F2. Поэтому F =
= —N. Но по третьему закону Ньютона мачта действует на
Землю с силой F3 = —N. Следовательно, F = F3, и, найдя модуль
силы Р, мы тем самым найдем модуль силы Р3, т. е.
/73= F = F2 cos a.
Пытаясь решить эту задачу, экзаменуемые иногда делали
графическую ошибку: складывая геометрически силы F, и F2,
они получали, что равнодействующая F этих сил направлена под
некоторым углом к мачте. При этом упускалось из виду, что по-
скольку мачта находится в вертикальном положении, то равно-
действующая сил F{ и F2 направлена вдоль нее, и поэтому па-
раллелограмм, сторонами которого являются векторы F{ и F2,
нужно строить так, чтобы его диагональ была направлена вдоль
мачты.
Такая графическая ошибка исключена при решении этой за-
дачи методом проекций сил, как показано выше, поэтому приме-
нение этого метода предпочтительнее.
Хотелось бы подчеркнуть, что при решении физической зада-
чи нужно всегда делать такой рисунок (чертеж), который пра-
вильно иллюстрирует ее содержание и отражает в выбранном
масштабе близкие к реальным соотношения между векторами,
углами и т. п. Это значительно облегчает поиск путей решения
задачи, уменьшает вероятность возникновения ошибок.
48. Много ошибок связано с плохим усвоением единиц физи-
ческих величин. Причина, по-видимому, заключается в том, что
в школе учащиеся знакомятся с единицами физических величин
постепенно, по мере изучения соответствующего раздела курса
физики, и поэтому у многих из них складывается неправильное
представление, будто бы для измерения величин единицы вво-
дятся совершенно произвольно. Большинство абитуриентов, упо-
требляя термины «физическая величина», «числовое значение
физической величины», «система единиц физических величин»,
«размерность», не могут объяснить содержание этих понятий.
Перечислим еще несколько характерных ошибок. На вопрос:
«Какие единицы СИ являются основными?» поступающие часто
отвечают так: «К основным единицам относятся: килограмм, се-
кунда, ньютон, вольт, джоуль, метр, ватт и другие». По-видимо-
му, они считают, что основными являются наиболее часто упо-
требляемые единицы, что, конечно, неверно.
Определение единиц физических величин многие поступаю-
щие дают неточно, а то и совсем неправильно. Например, отвеча-
ют так: «Ньютон — это сила, которая телу массой 1 кг сообщает
ускорение 1 м/с2» или так: «Ньютон равен килограмму, умно-
86
женному на метр и деленному на секунду в квадрате».
Понятия «единица физической величины» и «размерность фи-
зической величины» большинство абитуриентов отождествляют,
т. е. ошибочно считают, что это одно и то же. Встречалось, на-
пример, такое утверждение: «Ньютон — это размерность силы»,
и даже такое: «F — это размерность силы».
Еще одна ошибка: отождествляют единицу физической вели-
чины с эталоном. Например, на вопрос: «Какова единица длины
в СИ?» — последовал ответ: «Это метр — определенный эталон».
В ответах экзаменуемые часто неправильно используют тер-
мины, применяя такие сочетания: «величина ускорения», «сила
по величине и направлению», «величина давления» и т. п. Слово
«величина» в этих сочетаниях лишнее, так как ускорение, сила,
давление сами являются величинами, и поэтому получается «ве-
личина величины».
Чтобы избежать указанных выше ошибок, необходимо при
подготовке к вступительному экзамену систематизировать и
обобщить свои знания, чтобы иметь четкое представление о том,
что такое физическая величина, ее единица, что такое система
единиц и какова ее структура. Рассмотрим коротко основные по-
нятия, а также построение Международной системы единиц
(СИ).
Физическая величина* — это характеристика одного из
свойств физического объекта (физической системы, явления или
процесса), общая в качественном отношении многим физическим
объектам, но в количественном отношении индивидуальная для
каждого объекта.
Например, тела, скорости которых с течением времени изме-
няются, движутся с ускорением. В качественном отношении
ускорения всех тел одинаковы: они характеризуют быстроту из-
менения вектора скорости со временем. Но в количественном от-
ношении ускорения разных движущихся тел могут быть различ-
ными. Например, ускорение взлетающего самолета больше уско-
рения трогающегося с места поезда. Приведем еще один пример:
расстояние от Земли до Луны и длина комариного носа одинако-
вы в качественном отношении, но в количественном отношении
различны.
Размер физической величины — это количественное содержа-
ние в данном объекте определенной физической величины. Этот
термин можно применять ко всем физическим величинам, поэто-
му можно говорить «размер скорости» (а не «величина скоро-
сти»), «размер давления», «размер силы электрического тока»
и т. п.
Единица физической величины — это физическая величина,
* Вместо термина «физическая величина» допускается применение его крат-
кой формы «величина» в том случае, когда из контекста ясно, что речь идет
именно о физической величине, а не о математической.
87
фиксированная по размеру и принятая в качестве основы для
количественной оценки конкретных физических величин.
Значение физической величины — это количественное содер-
жание в объекте конкретной физической величины, выраженное
в виде некоторого числа принятых для нее единиц.
Значение X конкретной физической величины можно предста-
вить в виде
где {X} — отвлеченное число, называемое числовым значением
величины; [X] — единица этой величины. Например, 2 м — значе-
ние длины некоторого стержня, 2 — числовое значение этой дли-
ны, м — единица длины (точнее, обозначение единицы длины —
метра).
Системой физических величин называется совокупность взаи-
мосвязанных физических величин. Система физических величин
состоит из основных и производных величин.
Основная физическая величина — это физическая величина,
принятая за независимую и используемая для определения дру-
гих величин.
Производная физическая величина — это физическая величи-
на, определяемая через основные величины системы с помощью
уравнений, выражающих связь между величинами.
Системой единиц физических величин называется совокуп-
ность единиц физических величин, образованная в соответствии
с принятыми принципами для некоторой системы физических ве-
личин. Система единиц состоит из основных и производных
единиц.
Основными называются единицы, выбранные произвольно
при построении системы и являющиеся единицами основных фи-
зических величин.
Производными называются единицы, которые образуются по
определяющим их уравнениям из других единиц системы и явля-
ются единицами производных физических величин.
Международная система единиц имеет сокращенное наимено-
вание SI, что означает «Sistem International» — «международ-
ная система», или в русской транскрипции — СИ, что означает
«система интернациональная», т. е. «международная». СИ при
чтении произносится раздельно: «эс-и», а не слитно «си». При
использовании этого сокращенного наименования следует гово-
рить и писать: «единица СИ», а не «единица системы СИ», так
как слово «система» уже входит в виде буквы «С» в это наиме-
нование. СИ состоит из основных, дополнительных и производ-
ных единиц.
Основными единицами СИ являются следующие семь единиц:
единица длины — метр (м), единица массы — килограмм (кг),
единица времени — секунда (с), единица силы электрического
тока — ампер (А), единица термодинамической температуры —
кельвин (К), единица силы света — кандела (кд) и единица коли-
чества вещества — моль (моль).
Дополнительными единицами СИ являются две единицы, еди-
ница плоского угла — радиан (рад) и единица телесного угла —
стерадиан (ср).
Производные единицы СИ — единицы всех остальных физи-
ческих величин. Они образуются с помощью определяющих
уравнений из основных и дополнительных единиц, а также ранее
образованных производных единиц.
Так, например, единица силы — ньютон — производная еди-
ница. Она образована из одной основной единицы (килограмм)
и одной производной (метр на секунду в квадрате) с помощью
определяющего уравнения
F = ma. A)
Подставив в это уравнение единицы СИ [т]=1 кг и
[а|= 1 м/с2, получим единицу силы — ньютон:
= \m\\a\ =
кг-
м/с2=1 кг-м/с2=1 Н.
Надо иметь в виду, что при применении этого уравнения учи-
тывается такая ситуация: к телу массой пг=\ кг приложена си-
ла F= 1 Н, в результате чего оно движется без трения с ускоре-
нием а=\ м/с2 в направлении действия силы (рис. 78, а). Дей-
ствительно, согласно второму закону Ньютона, F = ma. Найдя
проекции сил N, F и mg на ось ОХ, сонаправленную с F, полу-
чим скалярное уравнение Fx=max. Но FX=F, ax = a, поэтому
приходим к уравнению A), в соответствии с которым дается сле-
дующее определение: ньютон равен силе, сообщающей телу мас-
сой 1 кг ускорение 1 м/с2 в направлении действия силы.
Если в этом определении выбросить слова «в направлении
действия силы» (что нередко встречалось в ответах на экзаме-
нах), то оно будет неправильным. Поясним это на следующем
примере.
Пусть по горизонтальной плоскости движется без трения тело
массой т=\ кг под действием силы F = 2 H, направленной под
углом <х = 60° к плоскости (рис. 78,6). Легко видеть, что в этом
случае ах = а, FX = F cos а, поэтому
89
F cos a 2 cos 60° . 9 ,
g M/c =1
т. е., в соответствии с неправильным определением, сила равна
1 Н, что неверно, так как в действительности значение этой силы
равно 2 Н.
Эталоном единицы физической величины называется сред-
ство измерений, обеспечивающее воспроизведение и хранение
единицы с целью передачи ее размера нижестоящим по повероч-
ной схеме средствам измерений, выполненное по особой специ-
фикации и официально утвержденное в установленном порядке
в качестве образца. Например, эталон килограмма представляет
собой специально изготовленную платино-иридиевую гирю, кото-
рая хранится в Международном бюро мер и весов во Франции.
В других странах имеются точные копии этого эталона, по кото-
рым устанавливаются массы применяемых гирь.
Внесистемными единицами физических величин называются
единицы, не входящие ни в одну из общепринятых систем
единиц. Примерами внесистемных единиц являются едини-
ца времени — час A ч = 3600 с), единица вместимости—литр
A л = 10~3 м3), единица массы — тонна A т=103 кг), единица
площади — гектар A га = 104 м2) и др.
Кратной называется единица, которая в целое число раз
больше системной или внесистемной единицы. Например,
километр A км = 103 м), минута A мин = 60 с), киловатт
A кВт=103 Вт).
Дольной называется единица, которая в целое число раз
меньше системной или внесистемной единицы. Например, мил-
лиметр A мм=10~3 м), микроампер A мкА=10^6 А).
Кратные и дольные единицы от единиц СИ не являются еди-
ницами СИ.
Десятичные кратные и дольные единицы и их наименования
образуются с помощью следующих приставок (в скобках дано
русское обозначение приставки): экса (Э) соответствует множи-
телю 1018, пета (П)— 1015, тера (Т) — 1012, гига (Г)— 109, мега
(М)~ 106, кило (к)— 103, гекто (г)— 102, дека (да)— 10', деци
(д)—10 ', санти (с)— 10~2, милли (м)—10~3, микро (мк) —
1(Г6, нано (н)~ \0~\ пико (п)— КГ'\ фемто (ф) — КГ, атто
(а)— 108. Например, 1 МГц=106 Гц, 1 пФ = 1(Г12 Ф,
1 нм = 1(Г9 м.
Размерностью физической величины называется выражение,
отражающее связь данной величины с основными величинами
системы единиц, в котором коэффициент пропорциональности
принят равным единице. В СИ для основных единиц условно
приняты следующие размерности: размерность длины — L, мас-
сы— М, времени — Т, силы электрического тока — I, термоди-
намической температуры — в, количества вещества — N и силы
света — J. Размерность производной величины выражается про-
$0
изведением размерностей основных величин, возведенных в соот-
ветствующие степени.
Показателем размерности физической величины называется
показатель степени, в которую возведена размерность основной
величины, входящая в размерность производной величины. Над
размерностями величин можно производить действия умноже-
ния, деления, возведения в степень и извлечения корня.
Размерность величины X обозначается так: dim X. Здесь
dim — сокращение от английского слова dimension, что в пере-
воде на русский язык означает «размерность».
В качестве примера рассмотрим размерность силы. На осно-
вании определяющего уравнения A) можно записать:
dim f = dim m-dim а. B)
Размерность массы равна М, т. е. dim от = М. Найдем раз-
мерность ускорения. Его определяющее уравнение имеет вид:
где а — модуль ускорения точки, движущейся прямолинейно и
равноускоренно с возрастающей скоростью; v0, v — модули ско-
рости этой точки в начальный момент времени (/0 = 0) и в момент
времени t. Следовательно,
.. dim Av dim Av
dim a = = —=— .
dim t T
Размерность скорости выразим на основании ее определяю-
щего уравнения v = s/t, где v — модуль скорости равномерно и
прямолинейно движущейся точки; s — модуль перемещения, ко-
торый равен пройденному пути; t — время движения точки. По-
лучим:
Тогда
,. dim s L , ~_
dim v— = — =LT
dim t T
,. dim Av dim v LT , -r,
dima = —-— = —^— = —j—=L1
Подставив размерности массы и ускорения в выражение B),
получим:
2. C)
Безразмерной физической величиной называется величина, в
размерности которой все показатели размерности равны нулю.
Например, относительное удлинение е = А/// — безразмерная
величина, так как
.. dim Д/ L ,
dim е = = —= 1.
dim / L
91
Размерной физической величиной называется величина, в
размерности которой хотя бы один из показателей размерности
не равен нулю. Например, сила — размерная величина, это вид-
но из выражения C), в котором показатели размерностей L и М
равны единице, а показатель размерности Т равен —2.
Из изложенного выше ясно, что размерность физической ве-
личины и единица физической величины — это не одно и то
же. Например, размерность силы равна LMT~2, а единицей си-
лы является ньютон. Абитуриенты нередко допускают ошибку,
называя единицу физической величины ее размерностью.
Пользуясь размерностями физических величин, можно обна-
ружить ошибки при решении задач по физике. Обычно задача
решается в общем виде, в результате чего получается расчетная
формула, выражающая искомую величину через заданные вели-
чины. Прежде чем производить вычисления, нужно обязательно
проверить, совпадают ли размерности левой и правой частей
этой формулы. Если они не совпадают, то это свидетельствует о
том, что в решении задачи допущены ошибки.
Пусть, например, для кинетической энергии рассматриваемо-
го в задаче тела получена расчетная формула такого вида:
Проверим, имеет ли правая часть этого выражения такую же
размерность, как и левая. Размерность кинетической энергии
(в этом легко убедиться на основании формулы ?ft=—— Y Най-
дем размерность правой части расчетной формулы:
Следовательно, размерность левой и правой частей совпадают.
При решении физических задач в школе и на вступительных
экзаменах все величины выражают в единицах СИ, поэтому пра-
вильность расчетной формулы рекомендуется проверять следую-
щим образом: в правую часть формулы нужно вместо буквенных
обозначений физических величин подставить обозначения еди-
ниц этих величин и произвести с ними необходимые действия; в
результате должно получиться обозначение единицы искомой ве-
личины. Если оно не получилось, то это означает, что задача ре-
шена неверно.
Проделаем такую проверку приведенной выше расчетной
формулы для кинетической энергии. Посмотрим, получится ли
в результате произведенных действий единица энергии —
джоуль.
92
. м = Н • м = Дж.
Если в правой части расчетной формулы имеется алгебраиче-
ская сумма, то нужно сначала проверить, одинаково ли выража-
ются через обозначения единиц слагаемые. Если одинаково, то
соответствующее выражение надо подставить в формулу вместо
суммы, а затем производить возведение в степень, умножение и
деление. Поясним это на примере.
В результате решения задачи получена следующая расчет-
ная формула:
где V — объем; р — плотность; g — ускорение свободного паде-
ния; т — масса; R — универсальная газовая постоянная; AT —
изменение температуры; М — молярная масса; h — высота; р —
давление; S — площадь. Проверим сначала каждое слагаемое:
Дж
[mRATl моль-К Дж Н-м „
Mh J кг мм'
• м
Слагаемые выражаются одинаково. Следовательно,
КГ-М 2 2
- ' н нУ-с2,-!2-"" :лз_
Получили обозначение единицы объема, соответствующее ис-
комой величине, обозначение которой стоит в левой части фор-
мулы.
Здесь уместно отметить, что при такой проверке рационально
применять в обозначениях единиц только горизонтальную черту,
так как это облегчает правильное выполнение необходимых дей-
ствий. Это, конечно, не означает, что косую черту применять не-
льзя. Действующим стандартом допускается при написании
дробных производных единиц применять косую или горизонталь-
ную черту, например: м/с или —. При применении косой черты
обозначения в числителе и знаменателе должны быть помещены
в одну строку. Если в знаменателе стоит произведение, то оно
обязательно заключается в скобки, например: Дж/(кг-К).
В ответах абитуриентов встречаются ошибки, связанные с
применением косой черты. Пишут, например, единицу удельной
теплоемкости так: 1 Дж/кг-К- Это неверно. Напомним, что эта
единица определяется на основании уравнения
93
°~ mAT'
где с — удельная теплоемкость вещества; Q — количество тепло-
ты, подводимое к телу или отводимое от него; т — масса тела;
AT— изменение температуры тела при подводе (или отводе) ко-
личества теплоты. Единица удельной теплоемкости
1 ' [т\[АТ\ 1 кг-1 К КГ-К /V ;
Если же запись (ошибочную!) 1 Дж/кг-К. переписать матема-
тически правильно, с применением горизонтальной черты, то
получим 1 К, что не соответствует приведенному выше опре-
деляющему уравнению.
49. Кроме перечисленных выше ошибок и недостатков при ре-
шении задач по динамике и статике, встречаются следующие:
абитуриенты, не проанализировав условие задачи, не сделав
чертеж, начинают просто подбирать «подходящие» формулы,
чтобы затем подставить в них значения известных величин; при-
меняя второй закон Ньютона, а также записывая условия равно-
весия тел, неправильно делают переход от векторных уравнений
к скалярным; не решают задачу в общем виде, т. е. в буквенных
обозначениях, а делают промежуточные вычисления; не могут
правильно построить свою логику рассуждений, чтобы найти
подход к решению задачи и составить общий план решения.
Чтобы избежать подобных ошибок, рекомендуется соблюдать
следующий план решения задач по динамике.
1. Выяснить, каким законам подчиняется описываемый в за-
даче физический процесс, какие силы действуют на интересую-
щие нас тела. Выписать значения заданных величин.
2. Сделать схематический чертеж и указать все силы, дейст-
вующие на каждое тело, а также ускорения и скорости.
3. Выбрать прямоугольную систему координат. При этом в
случае прямолинейного (равноускоренного или равномерного)
движения за положительное направление оси ОХ обычно прини-
мается направление движения тела; при движении тела по
окружности положительное направление оси ОХ совпадает с на-
правлением центростремительного ускорения, т. е. вдоль радиу-
са к центру окружности. Указать начало координат и начало от-
счета времени.
4. Для каждого тела найти проекции всех сил на оси ОХ и
OY и на основании второго закона Ньютона составить
уравнения:
где а„ ау — проекции ускорения тела массой m на оси ОХ и О У.
94
Если тело движется по окружности радиусом R равномерно, то
ax=v2/R, ay = 0. Если тело движется равномерно прямолинейно,
то ах = 0, ау = 0. Если вдоль оси OY тело не движется, то выпол-
няется условие равновесия: сумма проекций всех действующих
на это тело сил на ось OY равна нулю. Соответствующее уравне-
ние дает возможность найти силу нормальной реакции опоры
(или силу натяжения нити, если тело подвешено).
5. Если число неизвестных больше числа записанных уравне-
ний, то нужно составить еще и кинематические уравнения.
6. Решить полученную систему уравнений относительно иско-
мых величин.
Решение задач по статике выполняется по следующему
плану.
1. Сделать чертеж и указать все силы, действующие на тело,
которое находится в равновесии. (Обычно в учебных задачах
рассматриваются только случаи, когда все силы лежат в одной
плоскости.)
2. Выбрать прямоугольную систему координат, найти суммы
проекций всех действующих на тело сил на оси ОХ и OY и при-
равнять эти суммы нулю:
3. Найти сумму моментов сил относительно оси вращения и
приравнять эту сумму нулю:
Это уравнение для моментов сил можно составлять не только от-
носительно оси вращения, явно указанной в задаче, но и относи-
тельно любой оси, проходящей через произвольно выбранную
точку перпендикулярно к плоскости, в которой лежат все силы.
4. Решить полученную систему уравнений относительно иско-
мых величин.
Решение задач на нахождение центра тяжести тела сводится
в основном к составлению уравнения для моментов сил. Если в
центре тяжести тела приложить силу, направленную вертикаль-
но вверх и равную по модулю силе тяжести, то тело будет нахо-
диться в равновесии и, следовательно, сумма моментов всех сил
относительно оси, проходящей через центр тяжести (или через
любую другую точку), будет равна нулю.
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
50. Закон сохранения механической энергии многие поступа-
ющие формулируют так: «Энергия не возникает и не исчезает,
а только превращается из кинетической в потенциальную и об-
95
ратно». Такое утверждение, вообще говоря, неверно, так как в
нем не указываются те условия, при которых оно выполняется:
во-первых, система тел должна быть замкнутой, т. е. эти тела не
взаимодействуют ни с какими другими телами, не входящими в
данную систему (отсутствие взаимодействия равнозначно отсут-
ствию сил или равенству нулю равнодействующей внешних сил);
во-вторых, между собой тела этой системы взаимодействуют
только силами упругости и тяготения.
Правильная формулировка закона сохранения энергии в ме-
ханике такова: полная механическая энергия замкнутой системы
тел, взаимодействующих силами упругости и тяготения, остается
постоянной:
?k + ?p = const.
На основании этого закона можно для любых двух состояний
замкнутой системы тел составить уравнение
где Ек1, Ер1 — соответственно кинетическая и потенциальная
энергия тел в состоянии 1; Ек2, Ер2 — в состоянии 2.
Отметим, что этот закон может быть выражен другими сло-
вами. Дело в том, что работа силы тяжести и силы упругости не
зависит от формы траектории тела и определяется только на-
чальным и конечным положениями тела. При перемещении по
замкнутой траектории работа этих сил равна нулю. Силы, обла-
дающие такими свойствами, называются консервативными (от
лат. conservare — сохранять). Учитывая это, закон сохранения
энергии в механике можно сформулировать короче: полная меха-
ническая энергия замкнутой системы тел, между которыми дей-
ствуют только консервативные силы, остается постоянной.
Закон сохранения механической энергии является частным
случаем закона сохранения энергии — одного из фундаменталь-
ных законов природы, согласно которому энергия любой замкну-
той системы при всех процессах, происходящих в системе, оста-
ется постоянной. В замкнутой системе энергия может только пе-
реходить из одной формы в другую и перераспределяться между
частями системы, но сумма всех видов энергии остается постоян-
ной. Если же система не является замкнутой, то ее энергия мо-
жет изменяться — уменьшаться или увеличиваться при одновре-
менном увеличении или уменьшении энергии взаимодействую-
щих с ней тел.
Встречается в ответах абитуриентов также ошибочное утвер-
ждение, будто бы единственным выражением закона сохранения
энергии как общего закона природы является постоянство сум-
мы потенциальной и кинетической энергий. Это указывает на от-
сутствие у них четкого представления о том, что существует один
всеобщий закон сохранения энергии, а в различных процессах
и явлениях он выражается различными конкретными формули-
96
ровками и уравнениями. Например, в механических процессах
он проявляется как закон сохранения механической энергии, в
тепловых явлениях—первый закон термодинамики.
51. Характерной ошибкой, которую часто допускают абитури-
енты при решении задач, является неправильное применение за-
кона сохранения энергии. Проиллюстрируем это.
Задача 1. Пуля массой тх = 5 г, летящая горизонтально со
скоростью о = 500 м/с, попадает в шар массой от2 = 0,5 кг, подве-
шенный на невесомой нерастяжимой нити, и застревает в нем.
При какой предельной длине нити (расстояние от точки подвеса
до центра шара) шар от удара пули сможет описать четверть
окружности? Сопротивлением воздуха пренебречь.
Многие абитуриенты решали эту задачу так. До попадания
пули в шар кинетическая энергия пули ?к = ——-, кинетическая
энергия шара была равна нулю, а потенциальная энергия и пу-
ли, и шара равна нулю. После попадания пуля вместе с шаром
поднялась на высоту h, равную длине нити / (рис. 79). При этом
их кинетическая энергия стала равной нулю, а потенциальная
?
Рис. 79
p (l+2)g
На основании закона сохранения энергии Ек = Е или
откуда
2(m, + m2) g
A)
Остается подставить в эту формулу числовые значения величин
и произвести вычисления.
Ошибочность такого решения заключается в следующем:
4 Заказ 2473
97
здесь не учтено, что при неупругом ударе суммарная кинетиче-
ская энергия соударяющихся тел уменьшается, при этом их
внутренняя энергия возрастает на величину Д1/, равную убыли
кинетической энергии. Согласно закону сохранения энергии, сум-
ма всех видов энергии остается постоянной: Ек = Ер-+-AU.
Приводим правильное решение этой задачи. Сразу же после
удара шар с застрявшей в нем пулей приобретает скорость и, в
результате чего поднимается на высоту h = l относительно нуле-
вого уровня потенциальной энергии, на котором находились пуля
и шар в момент удара. Согласно закону сохранения энергии, со-
ставим уравнение Ек — Ер, или
Отсюда
Чтобы найти скорость и, воспользуемся законом сохранения
импульса. До удара импульс пули был равен /л,и, импульс ша-
ра — нулю, а сразу же после удара импульс шара с застряв-
шей в нем пулей равен (тх-\-т2) и. Спроектировав эти импульсы
на горизонтальную ось ОХ, составим уравнение: сумма проекций
импульсов пули и шара на эту ось до удара равна сумме проек-
ций импульсов этих тел после удара, т. е.
от,о =(т1 -\- т2) и.
Отсюда находим:
m,-|-m2'
Подставив это выражение в формулу B), получим:
Вычисления по формуле C) дают /= 1,25 м, а по формуле A),
выведенной при неправильном решении, получается /=126, 3 м.
Такая длинная нить понадобилась бы в том случае, если бы
вся кинетическая энергия перешла бы в потенциальную. В дей-
ствительности же часть кинетической энергии расходовалась на
увеличение внутренней энергии пули и шара. Нетрудно рассчи-
тать, какую долю от начальной кинетической энергии пули со-
ставляет эта часть, т. е.
_ 2 @,005 + 0,5) -9,8 -1,25
0,005 -5002 ~ '
98
Таким образом, 99% кинетической энергии пули затрачено
на нагревание шара и пули и только 1% — на подъем их на вы-
соту h = I.
Задача 2. Найти количество теплоты, которое выделяется
при центральном абсолютно неупругом ударе двух шаров мас-
сами тх и т2, движущихся навстречу друг другу со скоростями
у, и v2.
Сославшись на закон сохранения энергии, многие абитуриен-
ты ошибочно составляли такое уравнение:
A)
т. е. они считали, что вся кинетическая энергия соударяющихся
шаров идет на увеличение их внутренней энергии, а это, вообще
говоря, неверно. После абсолютно неупругого удара слипшиеся
шары движутся как одно целое с некоторой скоростью и и, сле-
довательно, имеют кинетическую энергию
u2
Согласно закону сохранения импульса, составляем уравнение
для проекций импульсов на ось ОХ (рис. 80) до и после удара:
mxvx — m2v2 = (mx -j- т2) ux.
Отсюда
m,o, — m2v2
U ^
Учитывая, что в данном случае и2 = и2х, по формуле B) нахо-
дим кинетическую энергию шаров после удара:
_ (m^i — m2v2f
2(т, + т2)
Теперь на основании закона сохранения энергии находим вы-
делившееся при ударе количество теплоты как убыль суммарной
кинетической энергии шаров:
_т^\ m2v\ (mlui~m2v2J
У~~Л 2 2(m, + m2) '
Таков правильный ответ на поставленный в задаче вопрос. Не-
трудно понять, что уравнение A) было бы правильным, если бы
///??/// *, р и с
99
после абсолютно неупругого удара шары остановились, т. е.
их = 0. А это произошло бы, как видно из формулы C), только при
условии, что myvx = m2v2, т. е. в следующих частных случаях:
1) массы шаров одинаковы (ml = m2) и модули их скоростей оди-
наковы (vl = v2); 2) скорости шаров обратно пропорциональны их
/ щ тЛ
массам — = —).
При решении этой и аналогичных задач выявлялось непра-
вильное усвоение абитуриентами используемых понятий, связан-
ных с ударами тел. В связи с этим приведем следующие опреде-
ления таких понятий.
Абсолютно упругим ударом называется такой удар, при кото-
ром сумма кинетических энергий соударяющихся тел сохраняет-
ся, абсолютно неупругим — такой удар, после которого соударя-
ющиеся тела движутся с одинаковой скоростью, образуя одно
целое тело. При абсолютно неупругом ударе суммарная кинети-
ческая энергия уменьшается. Сумма импульсов тел сохраняется
как при абсоютно упругом, так и при абсолютно неупругом
ударе.
Удар называется центральным, если скорости шаров направ-
лены по линии, соединяющей их центры.
52. Рассмотрим теперь задачи, связанные с применением за-
конов сохранения энергии и импульса к абсолютно упругому
удару. Обычно абитуриенты испытывают серьезные затруднения
при решении таких задач.
Задача I. Происходит абсолютно упругий центральный
удар двух шаров, массы которых ml и пг2, а скорости v{ и v2.
Найти скорости шаров после удара.
Решение. Обозначим скорости шаров после удара через
М] и и2. На основании закона сохранения импульса m^v^-\- m2v2 =
= mlul-\-m2u2. Составим уравнение для проекций импульсов на ось
ОХ (см. рис. 80):
mivu + m2v2x = miulx+m2u2x. A)
Второе уравнение составим согласно закону сохранения
энергии:
m.{u\ m2vlr гп^и] m^ul
2 2 2 2 ' '
В этих уравнениях мы будем оставлять обозначения vlx и v2x
проекций скоростей шаров на ось ОХ до удара, чтобы получить
результат не только для ситуации, показанной на рис. 80, когда
шары движутся навстречу друг другу, но и для других слу-
чаев, когда, например, один шар догоняет другой либо один из
шаров покоится. Кроме того, в уравнении B) учтено, что
v\x=v\, v\x=v\, u\x = u\, u\x = u\, так как скорости шаров до и по-
сле удара направлены вдоль оси ОХ.
100
Итак, имеем систему двух уравнений A) и B) с двумя неизве-
стными ии и и2х. Как видно, для составления этих уравнений
нужно четко знать, какие законы выполняются при абсолютно
упругом ударе. К сожалению, даже те поступающие, которые
верно записывали эти уравнения, в подавляющем большинстве
случаев не справлялись с решением системы. Здесь опять про-
является один из распространенных недостатков в знаниях вы-
пускников средних школ: неумение применять знания, получен-
ные при изучении математики, к решению физических задач.
Чтобы найти и1х и и2х, перепишем систему в таком виде.
mx{vu — uu) = m2(u2x~v2x\ C)
mi(vu — u2lx) = m2(u22x—v22x). D)
Разделив почленно уравнение D) на уравнение C), получим:
Vu + ulx = u2x+v2x. E)
Умножим левую и правую части уравнения E) на т2 и из по-
лученного уравнения вычтем почленно равенство C). В результа-
те будем иметь:
откуда
Для нахождения и2х умножим обе части уравнения E) на ть
а затем сложим почленно с равенством C). Будем иметь:
2mivlx = u2x(ml + т2) + v2x {mx — т2),
откуда следует:
_2mlvlx + (m2-ml)v2x
*- ^Тщ ' ( '
Рассмотрим следующие частные случаи.
1. Если массы шаров одинаковы (ml = m2), то из формул F) и
G) получим: ulx==v2x, u2x=v{x, т. е. шары в результате упругого
удара обмениваются скоростями. В частности, если второй шар
до удара покоится (v2x = 0), то после удара ulx = 0, u2x = vlx,
т. е. первый шар остановится, а второй начнет двигаться с такой
же скоростью, какую имел до соударения первый.
2. Если массы шаров различны {тх=^т2) и второй шар до
удара покоится, то из формул F) и G) следует:
(m1 — m2)vlx 2miuu
и\х = 1 . и2х = ; • (о)
ml-{-m2 x т1-\-т2
Выражения (8) показывают, что при тх>т2 первый шар по-
сле удара будет двигаться в том же направлении, что и до уда-
ра, а при m{<Lm2 — в противоположном направлении. Второй
шар в обоих случаях будет двигаться в том направлении, в кото-
ром двигался первый шар до удара.
101
При решении этой и других задач, аналогичных рассмотрен-
ным выше, многие абитуриенты не могли обосновать возмож-
ность применения закона сохранения импульса. В самом деле,
на каждый из соударяющихся шаров действуют сила тяжести
и сила нормальной реакции опоры (силой трения пренебрегаем),
значит, эта система не замкнута. Но сумма проекций этих сил
(и, следовательно, их импульсов) на горизонтальное направление
равна нулю. Поэтому остается постоянной сумма проекций им-
пульсов шаров на это направление, т. е. для этого направления
выполняется закон сохранения импульса.
В задаче 1 из п. 51 система пуля — шар тоже не замкнута,
так как на пулю во время полета действует направленная верти-
кально вниз сила тяжести, а на подвешенный шар действуют си-
ла тяжести и сила упругости нити. Но в горизонтальном направ-
лении закон сохранения импульса выполняется.
Закон сохранения импульса можно применять также к систе-
мам, в которых время взаимодействия настолько мало, что воз-
никающие в системе силы во много раз превосходят внешние си-
лы, и поэтому действием внешних сил можно пренебречь (напри-
мер, силами, возникающими при выстреле, взрыве, ударе и др.)
Задача 2. Пуля массой /rz, = 10 г, летящая горизонтально,
абсолютно упруго соударяется с шаром массой /тг2 = 6 кг, подве-
шенным на легком стержне длиной /=1 м, и отскакивает в про-
тивоположном направлении. В результате удара шар отклоняет-
ся от вертикали на угол а = 40°. Найти скорость пули до и после
удара. Массой стержня пренебречь.
Решение. В горизонтальном направлении на пулю и шар
внешние силы не действуют, поэтому сумма проекций импульсов
пули и шара на ось ОХ (рис. 81, а) остается постоянной:
mivl=—mlu] -\-т2и2, A)
где «1, м2 — модули скоростей соответственно пули и шара после
удара.
т,
Рис. 81
102
Поскольку удар абсолютно упругий, то суммарная механиче-
ская энергия пули и шара сохраняется:
ту\ ти\ ти1
2 ~ 2 + 2 '
На основании закона сохранения энергии имеем:
где h — высота, на которую поднялся шар. Как видно из
рис. 81, б, h = l — I cos a = / A —cos а). Подставив это выражение
в последнее уравнение, получим:
u\ = 2gl{\ — cos a). C)
Нами получена система трех уравнений с тремя неизвестны-
ми у,, И], и2. Для решения этой системы удобно переписать урав-
нения A) и B) так:
ml(vl+ul) = m2u2, D)
Разделив теперь почленно уравнение E) на уравнение D), по-
лучим:
и, —ы, = м2. F)
Умножив обе части этого уравнения на т[ и после этого сложив
его почленно с уравнением A), получим: 2mlvl = u2(rnx-\-m2),
откуда
тх -\-т2
или, учитывая выражение C),
1—cosa). G)
1 2m,
На основании уравнений C), F) и G) получим:
и] =—^ ^2gl A — cos a). (8)
Подставив в формулы G) и (8) числовые значения величин и
произведя вычисления, получим: у, = 631 м/с, м, = 629 м/с.
53. Обратим внимание еще на одну ошибку, часто допускае-
мую абитуриентами при применении закона сохранения импуль-
са. Для этого покажем, как решалась (неправильно) следующая
типичная задача. Предлагаем читателю сначала самому обнару-
жить ошибку, а потом рассмотреть правильное решение.
Задача. Лодка стоит неподвижно в стоячей воде. Человек,
находящийся в лодке, переходит с носа на корму. На какое рас-
стояние переместится лодка, если масса человека /тг, =60 кг,
103
масса лодки /тг2= 120 кг, длина лодки / = 3 м? Сопротивление во-
ды не учитывать.
Абитуриенты часто решают эту задачу так: по закону сохра-
нения импульса mlvl = m2v2, где и,, v2— скорости человека и
лодки соответственно. Отсюда находим скорость лодки:
Скорость человека v{=-, где / — время, за которое человек
перешел с носа на корму. За это время лодка переместится на
расстояние
m,u, m,/
; = vt = ? = t = -
m., m,,t
S==-
60-3
м = 1,5 м.
Здесь допущена грубая ошибка: скорости человека и лодки
найдены относительно различных систем отсчета.
При составлении уравнений на основании закона сохранения
импульса необходимо руководствоваться следующим правилом:
скорости всех тел, входящих в рассматриваемую систему, дол-
жны находиться относительно одной и той же системы отсчета.
Приводим правильное решение этой задачи. Система чело-
век — лодка не замкнута, так как на тела этой системы действу-
ют внешние силы: на человека — сила тяжести, на лодку — сила
тяжести и архимедова сила. Но эти силы направлены по верти-
кали, а по горизонтальному направлению внешних сил нет, поэ-
тому сумма проекций импульсов человека и лодки на ось ОХ
(рис. 82), направленную горизонтально, остается постоянной и
равной нулю, так как вначале лодка и человек покоились. Систе-
му координат XOY свяжем с водой. Пусть v{ — скорость челове-
ка относительно воды, v2—скорость лодки относительно воды.
Тогда, согласно закону сохранения импульса,
msvlx + m2v2x = 0. A)
Yi
2^
1
s
5.
J
Рис. 82
104
Отсюда v2x = -v]x. Так как тх>0, т2>0, то на основании
т2
последней формулы делаем вывод, что v2x и vlx имеют различные
знаки, а это значит, что скорость лодки v2 направлена противо-
положно скорости человека а,. Учитывая это, имеем vlx—vx,
v2x=—v2. Уравнение A) теперь запишется так:
m,y, — m2v2 = 0. B)
Обозначим через / время, за которое человек перешел с носа
на корму, через v\ — скорость человека относительно лодки.
Тогда v\ = -, v2 = -j, где s — расстояние, на которое переместится
лодка за время /.
На основании закона сложения скоростей vl = v/i-\-v<i. В про-
екциях на ось ОХ это уравнение будет иметь вид vu=v\x-\-v2x,
. I S 1 — S „
или vi = v\ — v2, или vl= — —-^—-—. Подставив выражения для
у, и v2 в уравнение B), получим:
Отсюда находим:
60+120
Отметим, что встречалось, кроме приведенного выше, и дру-
гое неправильное решение. Экзаменуемый рассуждал так: чело-
l
век движется со скоростью i>,=-, а в то же время лодка с чело-
веком движется в противоположном направлении со скоростью
v2. На основании закона сохранения импульса составляем уравне-
ние mxV\ = {rri\ -\-m2) v2 или
m, - = (/?Zi -f- m2) v2.
Отсюда
Следовательно, лодка переместится на расстояние s = v2t или
Получена такая же формула, как и при правильном решении,
но это случайное совпадение. В рассуждениях допущена та же
ошибка: скорости тел отсчитаны относительно различных систем
отсчета.
54. Встречались абитуриенты, допускавшие грубую ошибку
105
при объяснении принципа действия реактивного двигателя. Они
утверждали, что движение реактивного самолета обусловлено
взаимодействием выбрасываемых газов и воздуха: самолет дей-
ствует на воздух, а воздух, согласно третьему закону Ньютона,—
на самолет, в результате чего он движется. Это, конечно, невер-
но. Действительной причиной движения реактивного самолета
является взаимодействие истекающих из сопла газов, которые
образуются при сгорании топлива. За счет большого давления
в камере сгорания эти газы приобретают некоторый импульс,
поэтому,согласно закону сохранения импульса, самолет получа-
ет такой же по модулю, но противоположный по направлению
импульс. Так что самолет не отталкивается от воздуха. Напро-
тив, атмосферный воздух является лишь помехой движению са-
молета, создает сопротивление этому движению. Следует, одна-
ко, иметь в виду, что на самолетах применяются воздушно-реак-
тивные двигатели, в которых для горения топлива используется
кислород атмосферного воздуха, т. е. воздух, являясь помехой
движению, в то же время нужен как источник окислителя, необ-
ходимого для горения топлива.
В ракетных двигателях имеется не только топливо (жидкое
или твердое), но и окислитель, поэтому ракета может двигаться
в безвоздушном пространстве. С помощью ракет запускаются
искусственные спутники Земли, космические корабли. Это один
из важнейших примеров практического применения закона со-
хранения импульса.
55. Не все поступающие в вуз знают, что механическая энер-
гия и работа — величины относительные. В лучшем случае в от-
ветах указывается на относительный характер потенциальной
энергии.
Действительно, значение потенциальной энергии зависит от
выбора ее нулевого уровня. Если, например, потенциальную
энергию тела, находящегося на поверхности Земли, считать рав-
ной нулю, то потенциальная энергия тела массой т, поднятого
над Землей на высоту hu Epl = mghu а если оно находится на дне
ямы глубиной Л2, то имеет потенциальную энергию Яр2 = —rngh2-
Если же за нулевой уровень принять уровень дна этой ямы, то
?р2 = 0, а ?р1 = mg (ht + /г2). Отметим, что мы лишь для краткости
говорим о потенциальной энергии тела, имея в виду потенциаль-
ную энергию системы тело — Земля. Потенциальная энергия —
энергия взаимодействия. Если бы Земля и тело не притягива-
лись друг к другу, то не было бы и потенциальной энергии.
Относительность кинетической энергии Ек следует непосред-
ственно из ее определяющей формулы
где т — масса тела; v — его скорость.
Скорость — величина относительная, ее значение различно в
106
разных системах отсчета. Следовательно, и кинетическая энер-
гия— величина относительная. Проиллюстрируем это следую-
щим примером. Если по шоссе равномерно движутся в противо-
положных направлениях два автомобиля со скоростями и, и v2,
то относительно системы отсчета, связанной с Землей, кинетиче-
ская энергия первого автомобиля Ekl = mv2l/2, второго ?к2 = —~.
А относительно системы отсчета, связанной с первым автомоби-
лем, второй движется со скоростью v = vl-\-v2. Следовательно,
его кинетическая энергия
Кинетическая энергия первого автомобиля в этой системе отсче-
та равна нулю.
Механическая работа также является величиной относитель-
ной. Это видно из формулы работы А = Fs cos а, где F, s — моду-
ли силы и перемещения соответственно; а — угол между векто-
рами F и s. Значение силы взаимодействия одних и тех же тел
одинаково во всех инерциальных системах отсчета, а значение
перемещения зависит от выбора системы отсчета. Следователь-
но, и значение работы различно в различных системах отсчета.
В качестве примера рассмотрим следующую задачу.
Задача. Поезд движется равномерно по прямолинейному
горизонтальному участку железнодорожного пути. В одном из
вагонов перетаскивают по полу груз на расстояние Sj = 6 м в на-
правлении, противоположном направлению движения поезда,
приложив силу F= 100 Н под углом а = 60° к перемещению гру-
за. За время движения груза поезд проходит расстояние
s2 = 240 м. Найти работу, которую совершает сила F относительно
вагона; относительно Земли.
Г) О
о о
Рис. 83
Решение. Относительно вагона совершаемая работа
Al = Fsl cos a= 100-6 cos 60° = 300 Дж.
Относительно системы отсчета, связанной с рельсами, груз
совершает перемещение s = S! + s2 (рис. 83), которое составляет
с вектором F угол 180° —а. Модуль перемещения s = s2 — s,. Сле-
довательно, в неподвижной системе отсчета, связанной с рельса-
107
ми, сила F совершает работу
A2 = F(s2 — s,) cos A80° — a) =
= 100B40 — 6) cos A80° — 60°)= — 11 700 Дж.
56. Обычно абитуриенты правильно записывают формулу
для работы:
А = Fs cos a, A)
где F — модуль силы; s — модуль перемещения; а — угол между
векторами F и s. Однако многие не знают, что по этой формуле
определяется только работа постоянной силы. Если же сила F —
величина переменная, то формулой A) пользоваться нельзя.
Задача 1. Пружина, прикрепленная одним концом к стене,
растягивается под действием горизонтально направленной силы F
так, что удлинение ее становится равным s. Какая работа совер-
шается при этом?
В большинстве случаев абитуриенты отвечают, что работу
можно определить на основании формулы A) A = Fs. Это невер-
но, так как в данном случае работа совершается переменной си-
лой: согласно закону Гука, модуль этой силы увеличивается про-
порционально удлинению.
Как же найти работу переменной силы? Чтобы ответить на
этот вопрос, рассмотрим сначала работу постоянной силы. Если
учесть, что F cos a = Fs — проекция силы F на направление пере-
мещения s, то формулу A) можно переписать так: A = Fss.
Построим график зависимости Fs от s. При Fs = const этот
график представляет собой прямую, параллельную оси s (рис.
84). Совершаемая на участке от s, до s2 работа А = Fs(s,2 — s,),
т. е. она численно равна площади заштрихованного прямоуголь-
ника.
В случае переменной силы график указанной выше зависимо-
сти является некоторой кривой (рис. 85). Для нахождения рабо-
s? s
108
ты на участке от s, до s2 разделим его на несколько малых участ-
ков. На каждом малом участке As будем считать силу прибли-
зительно постоянной, тогда элементарная работа АЛ на этом
участке численно равна площади прямоугольной полоски шири-
ной As, а вся работа на участке от s, до s2 — приблизительно
равна площади заштрихованной ступенчатой фигуры. Если
уменьшать As, т. е. производить разбиение на большее число
элементарных участков, то в пределе (при As->-0) работа числен-
но равна площади фигуры, ограниченной графиком Fs, осью s и
вертикальными прямыми s = s{ и s = s2- Из курса математики
известно, что эта площадь вычисляется с помощью интеграла.
Поэтому работа переменной силы находится по формуле
A = \Fsds. B)
Вернемся теперь к задаче 1 и найдем работу, совершенную
при растяжении пружины. Согласно закону Гука, F = ks, где
k — жесткость пружины. В данном случае FS = F и график зависи-
Рис. 86
мости силы от перемещения имеет вид, показанный на рис.
86. Совершенная работа численно равна площади заштрихован-
ного треугольника:
Этот же результат можно получить, воспользовавшись форму-
лой B):
А = \
= -^- = — Fs.
Задача 2. Пружина жесткостью й = 1000 Н/м растянута
на 6 см. Какую работу нужно совершить, чтобы растянуть эту
пружину дополнительно еще на 8 см?
109
Решение этой задачи вызывало затруднения у абитуриен-
тов. Некоторые находили сначала по закону Гука силу, ко-
торая растягивает пружину: F = kxx = 1000-0,06 = 60 Н, а за-
тем работу, совершаемую при дополнительном растяжении:
A = Fx2 = 60-0,08 = 4,8 Дж. Это неверное решение. Здесь, как и в
решении предыдущей задачи, ошибочно применяется формула
A). Встречался и второй вариант неправильного решения: нахо-
дили общее удлинение х] —f- л:2 = 6-f- 8 = 14 см, а затем вычисляли
f
потенциальную энергию растянутой пружины
?р =
= 9,8 Дж. Внимательный читатель, конечно, уже понял, что най-
денная таким образом потенциальная энергия равна не дополни-
тельной, а всей работе, совершенной при растяжении пружины
на 14 см.
Правильно решить эту задачу можно несколькими спосо-
бами.
Первый способ. Обозначим через х, начальное удлинение пру-
жины, а через х2 удлинение ее после дополнительного растяжения
на Дл; = 8 см, т. е. л;, = 6 см, х2 = х, + Ах= 14 см. Направим ось
ОХ по направлению растягивающей силы, а начало координат
совместим с точкой, в которой находился конец недеформирован-
ной пружины (рис. 87, а). Тогда, учитывая закон Гука, выраже-
ние для проекции растягивающей силы на ось ОХ запишем в ви-
де Fx = kx или F = kx. График зависимости F от х показан на ри-
сунке 87, б. Работа этой силы при растяжении от ху до х2 числен-
а б
Рис. 87
но равна площади заштрихованной трапеции:
А=-
Х2 xi)—^- ~Y г Г-
Второй способ. Работа, совершенная при дополнительном
растяжении пружины, равна приращению ее потенциальной
энергии:
ПО
где fpl, EP2 — потенциальная энергия пружины при растяжении
ее на х] и х2 = х1-\-Ах соответственно. Следовательно
/1_
Третий способ. Воспользовавшись формулой B), найдем ра-
боту, совершаемую силой F = kx при растяжении пружины от хх
до х2:
Х2 2 Л
A = \kxdx = — - — = -.
х\
Как видно, результат получается один и тот же при решении
каждым из рассмотренных способов. Подставив числовые значе-
ния заданных величин, получим:
1000 F-10 + 8-10~2J 1000 F-10~2J _ _
А= 2 2 = 8 ДЖ-
57. Обычно большинство экзаменуемых дают правильное
определение потенциальной энергии как энергии взаимодейст-
вия, но почему-то считают, что эту энергию можно вычислить
только по формуле Ep = mgh.
Следует обратить внимание на то, что для различных видов
взаимодействия потенциальная энергия находится по разным
формулам.
Так, например, по формуле Ev = mgh вычисляется потенци-
альная энергия тела массой ш, поднятого на высоту h над уров-
нем, на котором ?р = 0 (точнее, это потенциальная энергия систе-
мы тело — Земля). Этой формулой можно пользоваться только
при условии, что высота h мала по сравнению с радиусом Земли.
Потенциальная энергия упруго деформированного тела (на-
пример, пружины) зависит от взаимного расположения частиц
тела и вычисляется по формуле
р ,*?.
Ер 2 '
где k — жесткость; х—модуль вектора удлинения или сжатия.
Потенциальная энергия заряда q, помещенного в электроста-
тическом поле, равна произведению этого заряда на потенциал
Ф поля в точке, где находится этот заряд:
Понятие «потенциальная энергия» имеет место только для
таких систем, в которых действуют консервативные (потенциаль-
ные) силы, т. е. силы, работа которых не зависит от траектории,
а определяется лишь начальным и конечным состоянием систе-
мы. Работа консервативной силы по произвольной замкнутой
ill
траектории равна нулю. Консервативными являются силы упру-
гости, силы тяготения, силы электростатического поля.
Отметим здесь, что существуют также и неконсервативные
(диссипативные, от лат. dissipatio — рассеяние) силы, работа ко-
торых зависит от траектории. К диссипативным силам относит-
ся, например, сила трения. Работа этой силы при любой траек-
тории отлична от нуля. Полная механическая энергия системы,
в которой действуют силы трения, при движении убывает, пере-
ходя во внутреннюю энергию. Этот процесс называется диссипа-
цией (рассеянием) энергии.
58. Нередко задача может быть решена разными способами.
Поэтому, приступая к решению, нужно сначала внимательно
проанализировать задачу, выявить сущность описанного в ней
явления или процесса, вспомнить, какие физические законы ле-
жат в основе этого явления или процесса, а затем наметить план
решения. Если окажется, что искомую величину можно опреде-
лить различными способами, то надо выбрать более рациональ-
ный. К сожалению, многие абитуриенты часто поступают иначе:
вместо обоснованных рассуждений и целенаправленных дейст-
вий они либо начинают подбирать «подходящую» формулу, в ко-
торую входит искомая величина, либо пытаются обязательно
применить определяющую формулу этой величины. Так, напри-
мер, если в задаче требуется найти работу, то многие, не заду-
мываясь, пишут определяющую формулу работы А = Fs cos a,
затем начинают искать F, s, а, хотя не всегда можно это сделать.
Между тем в ряде задач работу удобно находить как меру изме-
нения механической энергии:
где ?,, Е2 — энергия системы соответственно в начальном и ко-
нечном состояниях.
Если внешние силы совершают над телом или системой рабо-
ту, то f2>f[. Если же тело или система совершает работу над
внешними телами, то ?12<f1.
Задача 1. Столб длиной / и массой т, имеющий цилиндри-
ческую форму, лежит на земле. Какую минимальную работу
нужно совершить, чтобы поставить этот столб в вертикальное
положение?
Решение. При повороте столба вокруг точки О (рис. 88)
внешние силы совершают работу, в результате чего увеличива-
ется потенциальная энергия столба (точнее, системы столб —
Земля). Совершаемая минимальная работа равна изменению по-
тенциальной энергии:
A = Ev2-Evl, A)
где ?pi — потенциальная энергия столба, лежащего на земле;
?р2 — потенциальная энергия, соответствующая положению, когда
высота центра тяжести С столба над поверхностью Земли имеет
112
Рис.
наибольшее значение, т. е. когда отрезок ОС занимает
вертикальное положение. После этого столб переводится в вер-
тикальное положение за счет работы силы тяжести, центр тяже-
сти С при этом опускается несколько ниже.
Когда столб лежит на земле, его потенциальная энергия
где D — диаметр столба.
При максимальной высоте Л2 центра тяжести столба потенци-
альная энергия
Е 2 = mgh2 =
Подставив эти значения потенциальной энергии в формулу A),
получим выражение для минимальной работы, совершаемой при
повороте столба:
B)
Из полученной формулы B) следует, что если диаметр D мал
по сравнению с длиной /, т. е. столб тонкий, то Л да mgl/2.
Ряд задач более рационально решать, применяя закон сохра-
нения энергии, а также теорему об изменении кинетической
энергии. Однако абитуриенты, как правило, редко демонстриру-
ют умение решать задачи энергетическим методом. Рассмотрим
несколько примеров решения задач, которые предлагались на
вступительных экзаменах в вузах и вызывали затруднения у
абитуриентов.
Задача 2. Тело свободно падает без начальной скорости с
высоты Н. На какой высоте его кинетическая энергия будет
вдвое больше потенциальной? За нулевой уровень потенциаль-
ной энергии принять поверхность Земли. Сопротивление воздуха
не учитывать.
Решение. Воспользуемся законом сохранения энергии. Си-
стема тело — Земля замкнута, и в ней действуют только силы
тяготения, поэтому сумма кинетической и потенциальной энер-
гии остается постоянной:
ИЗ
1
где Ekl, Epl — соответственно кинетическая и потенциальная
энергия тела, когда оно находилось на высоте Н; EW2, Ер2— кине-
тическая и потенциальная энергия тела на искомой высоте h
(рис. 89). Обозначим массу тела через т. Тогда ?к| = 0,
= rngH, Ev2 = mgh. Учитывая условие Ек
2Е
р2,
имеем:
Ek2 = 2mgh. Подставив эти значения в уравнение A), получим:
0 + mgH = 2mgh-\-nigh, откуда h=—.
Абитуриенты обычно начинают искать скорость v тела на вы-
соте Л, используя для этого кинематические уравнения. Затем
, ~ mv2
определяют кинетическую энергию по формуле кк2 = —^- и потен-
циальную энергию Ep2 = mgh, а после этого составляют уравне-
ние на основании закона сохранения энергии. Решив таким пу-
тем эту задачу самостоятельно, читатель может легко убедиться
в том, что приведенное выше решение более рационально.
Отметим далее, что эту задачу можно решить и другим спо-
собом, используя теорему об изменении кинетической энергии:
изменение кинетической энергии тела равно работе всех сил,
действующих на это тело. Эти силы могут быть как внутренни-
ми, так и внешними. В данном случае на тело действует только
1
Рис. 89
сила тяжести. На участке от точки / до точки 2 эта сила совер-
шает работу A = mg(H — h). Так как ?kl = 0, Ek2 = 2Ep2 = 2mgh,
то изменение кинетической энергии A?k = ?k2 — Ekl = 2mgh. Сле-
rr
довательно, 2mgh — mg (H — h), откуда h = —.
О
Задача 3. Тело брошено под углом а к горизонту со скоро-
стью v0. He учитывая сопротивления воздуха, определить ско-
рость тела в тот момент, когда оно находится на высоте h над го-
ризонтом.
Решение. В системе тело — Земля механическая энергия
114
сохраняется потому, что, во-первых, эта система является зам-
кнутой и, во-вторых, внутри нее действуют силы тяготения. Сле-
довательно, для любых двух состояний выполняется равенство
?kl + ?pl = ?k2 + ?p2. A)
Потенциальную энергию будем отсчитывать от поверхности
Земли. Тогда в момент бросания тела его потенциальная энергия
?Р1 =0, а кинетическая Еы =—^-, где т — масса тела. Когда тело
находится на высоте h (рис. 90), его потенциальная энергия
„ , с mv2 ,-,
tp2 = mgh, а кинетическая ck2 = ——, где v — скорость тела. Под-
ставив эти выражения в формулу A), получим:
откуда v=yvl —
Из полученного результата следует, что задавать угол а в
условии задачи не обязательно, так как найденная скорость от
него не зависит. Такая же по модулю скорость была бы на высо-
те h, если бы тело было брошено, например, вертикально вверх.
Р и с. 90
Большинство абитуриентов обычно при решении подобных
задач применяют уравнения кинематики, что очень усложняет
решение.
Насколько проще и короче решение энергетическим методом,
хорошо видно и на примере задачи, приведенной в п. 13, где она
решена с помощью кинематических уравнений. Скорость тела в
момент падения легко найти, используя закон сохранения энер-
гии. Здесь такая же система тел, как и в рассмотренной выше
задаче 3, поэтому сумма кинетической и потенциальной энергии
остается постоянной. В момент бросания кинетическая энергия
г- mvl г I
тела Ьк]=——, потенциальная bpi = mgn, а в момент падения на
землю ?к2 = —у-, ?р2 = 0. На основании уравнения A)
l mv\
Отсюда vn=
115
59. Некоторые абитуриенты ошибочно считают, что энергети-
ческий метод решения задач нельзя применять, если в системе
действуют силы трения.
Если в системе действуют силы трения, то они совершают,
как правило, отрицательную работу, в результате чего полная
механическая энергия системы уменьшается. Поэтому при нали-
чии сил трения работа Атр этих сил равна изменению механиче-
ской энергии:
р р — л
В этом случае механическая энергия не исчезает, а превращает-
ся во внутреннюю энергию (трущиеся тела нагреваются). При
этом выполняется общий закон сохранения энергии: в замкнутой
системе сумма всех видов энергии остается постоянной.
Решим энергетическим методом задачу 2 из п. 26. Выберем
за нулевой уровень отсчета потенциальной энергии основание
наклонной плоскости. Тогда в верхней точке наклонной плоско-
сти потенциальная энергия тела Ер] = mgh, где m — масса тела,
а кинетическая ?к|=0, так как начальная скорость равна нулю.
Обозначим через v скорость тела в конце плоскости. Тогда кине-
тическая энергия тела в конце плоскости Ек2-—^-, а потенци-
альная ?р2 = 0. Изменение механической энергии тела равно ра-
боте силы трения:
или
--К- (!)
Но /lTp = FTp/cos 180°=—FTp/, так как угол между силой трения
и перемещением равен 180°. Здесь Frp — модуль силы трения,
/ — длина наклонной плоскости. Как видно из рис. 46, / = .
sin a
Сумма проекций всех сил на ось OY равна нулю, т. е.
N — mg cos а = 0. Отсюда N = mg cos а. Следовательно, FTp =
\xN = fxmg cos а (здесь jx — коэффициент трения). Тогда-
л , cos a
Л TD = — umgn = — amgh ctg а.
sin а
Подставив это выражение в уравнение A), получим:
mv2 . , ,
— mgh = — \xmgh ctg a.
Отсюда находим скорость тела в конце наклонной плоскости:
116
60. Многие абитуриенты не могут дать полный и правильный
ответ на вопрос: в каких случаях можно применять законы со-
хранения импульса и энергии? Полезно запомнить следующие
критерии применимости этих законов.
1. Закон сохранения импульса можно применять в следую-
щих случаях:
а) система тел замкнута, т. е. на тела этой системы не дейст-
вуют внешние силы;
б) на тела системы действуют внешние силы, но их векторная
сумма равна нулю;
в) система не замкнута, но сумма проекций всех внешних сил
на какую-либо координатную ось равна нулю; тогда остается по-
стоянной и сумма проекций импульсов всех тел системы на
эту ось;
г) время взаимодействия тел мало (например, время удара,
выстрела, взрыва); в этом случае импульсом внешних сил можно
пренебречь и рассматривать систему как замкнутую.
2. Сумма кинетической и потенциальной энергии системы тел
остается постоянной в следующих случаях:
а) система замкнута и ее тела взаимодействуют между собой
силами тяготения и упругости (консервативными силами);
б) система не замкнута, но алгебраическая сумма работ всех
внешних сил, действующих на тела данной системы, равна нулю.
61. Применяя законы сохранения при решении задач, абиту-
риенты допускают, кроме указанных выше, и другие ошибки и
недочеты: не учитывают, что импульс — величина векторная, и
поэтому не различают векторные и скалярные уравнения, непра-
вильно составляют их; не всегда делают анализ условия задачи
и чертеж (рисунок, схему); многие задачи, которые можно легко
решить с помощью законов сохранения, решают нерациональны-
ми способами и зачастую неверно; не знают общего плана реше-
ния задач данного типа.
Чтобы избежать подобных ошибок, целесообразно при реше-
нии задач с применением закона сохранения импульса руковод-
ствоваться следующим планом.
1. Выяснить возможность применения этого закона (см.
п. 60, 1).
2. Сделать схематический чертеж и изобразить на нем векто-
ры скоростей тел до и после взаимодействия.
3. Выбрать прямоугольную систему координат так, чтобы
проекции скоростей на координатные оси выражались по воз-
можности проще.
4. Составить уравнения на основании того, что сумма проек-
ций импульсов всех тел системы на координатную ось до взаимо-
действия равна сумме проекций импульсов этих тел на ту же ось
после взаимодействия. Если число неизвестных больше числа со-
ставленных уравнений, то нужно добавить к ним уравнения, свя-
зывающие кинематические величины.
117
5. Решить полученную систему уравнений.
Задачи на применение закона сохранения энергии в механике
решаются по следующему плану.
1. Выяснить возможность применения этого закона (см.
п. 60, 2).
2. Сделать схематический чертеж.
3. Выбрать нулевой уровень потенциальной энергии.
4. Изобразить на чертеже силы, действующие на тела, скоро-
сти тел и высоты тел над нулевым уровнем потенциальной энер-
гии в начальном и конечном состояниях.
5. Если система замкнута, то составить равенство
^kl Г Ср) =Ск2-)-Ср2,
где ?ki, ?р| — соответственно кинетическая и потенциальная
энергия системы в начальном состоянии; Ек2, Ер2 — кинетическая
и потенциальная энергия системы в конечном состоянии.
Если при переходе системы из начального состояния в конеч-
ное на тела действовали внешние силы, а в системе — силы тре-
ния, то составить равенство
где А — работа внешних сил; Атр — работа сил трения.
Если количество неизвестных величин больше числа состав-
ленных уравнений, то к ним следует добавить либо уравнения,
составленные на основании второго закона Ньютона и закона со-
хранения импульса, либо кинематические уравнения.
6. Решить систему уравнений относительно искомых величин.
ЖИДКОСТИ И ГАЗЫ
62. Нередко абитуриенты ошибочно считают, что давление —
векторная величина, что свидетельствует о слабом усвоении это-
го важного физического понятия.
Напомним, что давлением, называется скалярная физическая
величина, равная отношению модуля силы F, действующей пер-
пендикулярно к участку поверхности и равномерно распределен-
ной вдоль него, к площади S этого участка:
Если сила F, направлена так, что угол между ней и нормалью
к поверхности равен а, то давление
F, cos a
"=—s—•
Если внутри покоящейся жидкости расположить в окрестно-
сти некоторой точки А небольшую площадку площадью AS, то на
118
нее со стороны жидкости будет действовать сила AF; при этом
давление р=-— не зависит от ориентации площадки. Именно
До
это имеют в виду, когда говорят, что давление в жидкости одина-
ково по всем направлениям. В пределе, при стремлении AS к ну-
лю, говорят о давлении в данной точке жидкости. Давление яв-
ляется характеристикой состояния жидкости в данном месте и не
зависит от площади AS и ориентации площадки.
63. Грубые ошибки встречаются при выяснении содержания
закона Паскаля. Многие экзаменуемые формулируют его так:
«Давление в жидкостях и газах везде одинаково». В действите-
льности же закон Паскаля не отвечает на вопрос о том, каково
давление в той или иной точке жидкости или газа. Этот закон от-
вечает на вопрос о том, как передается давление, производимое
на жидкость или газ. Правильная формулировка закона Паска-
ля такова: давление, производимое внешними силами на жид-
кость или газ, передается без изменения по всем направлениям
в каждую точку жидкости или газа.
Пусть, например, в открытом сосуде находится жидкость.
Давление на ее поверхность, производимое атмосферным возду-
хом, передается, согласно закону Паскаля, во все точки жидко-
сти. На глубине Л, в этой жидкости давление равно сумме атмо-
сферного давления р0 и давления, создаваемого весом столба
жидкости высотой Л, (гидростатического давления):
где р — плотность жидкости; g — ускорение свободного падения.
На глубине /г2>/г, давление
Ясно, что Р2>Р\ и что утверждение абитуриентов «давление
в жидкости везде одинаково» неверно. Одинаковым будет давле-
ние на одном и том. же уровне (hl = h2), т. е. горизонтальные
плоскости представляют собой поверхности равного давления.
Чем глубже в жидкости находится такая плоскость, тем больше
давление.
Рассмотрим несложную задачу, при решении которой абиту-
риенты допускают ошибку.
Задача. На какой глубине в озере давление в 3 раза боль-
ше атмосферного давления /о0=105 Па? Плотность воды р =
ЫО3 кг/м3.
Решение. Как показано выше, на глубине h давление
p = po-\-pgh. Используя условие р = 3ро, получаем: 3po = po-|-pg/z.
Отсюда находим:
и 2р« 2'1(M on л
п = — = : м = 20,4 м.
pg Ы03-9,8
Поступающие решали так: 3pQ = pgh, h = 3pQ/(pg), т. е. не
учитывали, что в соответствии с законом Паскаля атмосферное
119
давление передается без изменения во все точки жидкости.
64. Используя для нахождения давления жидкости формулу
p = pgh, экзаменуемые иногда ошибочно считают, что h — это
высота столба жидкости, расположенного непосредственно над
тем местом, где надо найти давление. Пусть, например, имеется
сосуд сложной формы и нужно найти давление в точке А
(рис. 91). Некоторые поступающие находили так: PA~pgh[- Это
неверно.
h
D
|
351
C—__—
Рис. 91
Возьмем на поверхности жидкости точку D и соединим ее с
точкой А с помощью ломаной линии ABCD, последовательно
расположенные звенья которой вертикальны и горизонтальны, и
ломаная линия целиком лежит в жидкости. Тогда pA = pB-{-pgh2-
Но рв = Рс, так как точки В и С находятся на одном уровне.
В свою очередь рс = р0-\-pgha (р0—атмосферное давление). Из
этих равенств следует, что
Pa — Ро~Ьр?Г'?з~Ь Pgh2 — Po~\~ Pg (^з~Ь^2)==/°о ~\~Pgh,
где /г — глубина точки А под свободной поверхностью жидкости.
Таким образом, распределение давления по глубине не зависит
от формы сосуда.
65. Объясняя устройство гидравлического пресса, абитуриен-
ты нередко допускают грубые ошибки. Так, например, в некото-
рых ответах встречалось утверждение, что гидравлический пресс
дает выигрыш не только в силе, но и в работе. Нетрудно выяс-
нить ошибочность этого ответа, если вспомнить принцип устрой-
ства гидравлического пресса.
Гидравлический пресс состоит из двух сообщающихся цилин-
дров разного диаметра с поршнями, под которыми находится
жидкость (рис. 92). Если на малый поршень действует сила Fb
F,
то она создает давление р=—, которое в соответствии с зако-
ном Паскаля передается во все точки жидкости. Вследствие это-
го на большой поршень со стороны жидкости будет действо-
вать сила
F — nS — F Sa
120
s,
л,
—
Рис. 92
где S2—площадь большого поршня. Отсюда видно, что F2>F{
s2
в — раз, т. е. гидравлический пресс дает выигрыш в силе во
столько раз, во сколько раз площадь большого поршня больше
площади малого поршня. Между тем некоторые абитуриенты,
слабо знающие принцип работы пресса, говорят так: «С какой
силой мы действуем на малый поршень, с такой же силой жид-
кость действует на большой поршень, только эта сила направле-
на противоположно приложенной. Это, конечно же, грубая ошибка.
Найдем теперь работу Л,, совершаемую силой F,, и работу
А2, совершаемую силой F2. Если малый поршень опустится вниз
на расстояние /г,, то большой поднимется на расстояние И2. Тог-
да Al = F\hl, A2=F2h2. Если учесть, что объем жидкости, вытес-
ненной из первого цилиндра, равен объему жидкости, поступив-
шей во второй цилиндр, т. е. S]h] = S2h2, то получим: /z2 = /z,—^-,
2
и поэтому
Таким образом, гидравлический пресс выигрыша в работе не
дает. Здесь, так же, как и при работе других простых машин
(блока, рычага, ворота и др.), обнаруживается справедливость
так называемого «золотого правила механики»: «во сколько раз
выигрывается в силе, во столько раз теряется в расстоянии».
66. Очень немногие абитуриенты могли объяснить, почему
сила, с которой жидкость действует на дно сосуда, может быть
в зависимости от формы сосуда больше или меньше веса нали-
той в сосуд жидкости (это явление называется гидростатическим
парадоксом).
Если в сосуды, форма которых различна, а площади дна оди-
наковы, налить до одинакового уровня жидкость (рис. 93) плот-
ностью р, то сила, с которой жидкость действует на дно, одинако-
ва во всех сосудах. Действительно, эта сила F = pS, где р — дав-
121
ление на глубине h; S — площадь дна. Но давление покоящейся
жидкости, как было показано выше (п. 64), не зависит от формы
сосуда, оно зависит только от глубины h и плотности жидкости р:
Р = Pgh-
Следовательно, во всех сосудах жидкость действует на дно с
одинаковой силой F = pghS, в то время как вес жидкости в раз-
ных сосудах разный.
Гидростатический парадокс объясняется следующим об-
разом. Сила Гж, с которой жидкость действует на стенку сосуда,
направлена перпендикулярно стенке. Согласно третьему закону
Ньютона, стенка действует на жидкость с такой же по модулю
и противоположной по направлению силой Fc. Разложим эту си-
лу на две составляющие — вертикальную F, и горизонтальную
F2. Мы видим, что в суживающемся кверху сосуде (рис. 93, а)
сила Z7, направлена вниз, поэтому жидкость давит на дно
с силой, большей веса жидкости. В расширяющемся кверху сосу-
де (рис. 93, б), наоборот, сила Ft направлена вверх, поэтому
жидкость давит на дно с силой, меньшей веса жидкости. В сосу-
де с вертикальными стенками (рис. 93, в) F,=0 и жидкость дей-
ствует на дно с силой, равной весу жидкости.
~—~л F ~-~z.
_ (с
-—-— S -~-~
Рис. 93
67. Перейдем теперь к рассмотрению ошибок, связанных с
понятием архимедовой силы. Надо сказать, что ошибки эти
встречаются довольно часто, и одной из причин, на наш взгляд,
является то, что этот материал не изучается в старших классах
средней школы, а при изучении его в младших классах решают-
ся лишь очень простые задачи. На вступительных же экзаменах
часто предлагаются комбинированные задачи, для решения ко-
торых нужно применить знания не только по данному разделу,
но и по другим разделам курса физики. Сказывается, конечно,
и забывание того, что изучалось давно и применялось редко.
В ответах абитуриентов нередко встречаются такие, напри-
мер, неправильные формулировки: «На тело, погруженное в
жидкость, действует выталкивающая сила, равная объему вы-
122
Рис. 94
тесненной жидкости», «Тело, погруженное в жидкость или газ,
вытесняет такой объем жидкости или газа, какой объем имеет
это тело», «Тело вытесняет объем жидкости, вес которого равен
весу тела» и др. Многие поступающие ошибочно утверждают,
что архимедова (выталкивающая) сила всегда приложена в цен-
тре тяжести погруженного в жидкость или газ тела. Эта и дру-
гие ошибки порождены непониманием природы архимедовой си-
лы или, говоря иначе, неумением объяснить, вследствие чего воз-
никает эта сила при погружении тела в жидкость или газ. Рас-
смотрим этот вопрос на следующем примере.
Пусть сосуд с жидкостью неподвижен в некоторой инерци-
альной системе отсчета. Погрузим в эту жидкость вертикально
расположенный прямоугольный параллелепипед (рис. 94). Силы,
с которыми жидкость действует на противоположные боковые
грани, уравновешиваются. На верхнюю грань действует направ-
ленная вниз сила Fu модуль которой Fl = piS (р,—давление
жидкости на глубине hu где находится эта грань; S — площадь
грани). На нижнюю грань действует направленная вверх сила
F2, модуль которой F2 = p2S, где р2 — давление жидкости на глу-
бине /г2; S — площадь грани. Пусть плотность жидкости р,
тогда pl = pghl, p2 = pgh2 и, следовательно, F{ = pghxS, F2 =
= 9gh1S.
Результирующая сила FA = Fl-\-F2, а ее модуль FA — F2—Fy,
так как /72>^i вследствие того, что /z2>'/z,. Таким образом, при-
ходим к выводу: на параллелепипед со стороны жидкости дейст-
вует направленная вертикально вверх выталкивающая сила:
FA = F2 — Fl = pgh2S ~ pgh{S = pg(h2 — hl)S = pghS,
где h — высота параллелепипеда. Но hS = V — это объем парал-
лелепипеда, поэтому выталкивающая (архимедова) сила
?A = PgV. A)
Итак, причиной возникновения выталкивающей (архимедо-
вой) силы является зависимость давления в жидкости от глуби-
ны, вследствие чего на нижнюю часть тела со стороны жидкости
123
действует большая сила, чем на верхнюю. Архимедова сила яв-
ляется равнодействующей (векторной суммой) всех сил, с кото-
рыми жидкость давит на погруженное в нее тело.
Если тело погружено в жидкость не полностью, то выталки-
вающая сила также находится по формуле A), при этом V —
объем погруженной части тела.
Если учесть, что pV=m — это масса вытесненной жидкости,
то формулу A) можно переписать так: FA = mg, т. е. архимедова
сила в данном случае равна по модулю силе тяжести, действую-
щей на вытесненную жидкость. Но, как отмечалось выше
(см. п. 31), вес неподвижной относительно инерциальной системы
отсчета жидкости по модулю равен силе тяжести. Поэтому вы-
талкивающая сила равна по модулю и противоположна по на-
правлению весу вытесненной жидкости.
К выводу о существовании выталкивающей силы можно
прийти также путем следующих рассуждений. Внутри покоящей-
ся жидкости выделим мысленно некоторый объем (рис. 95) и
предположим, что жидкость в нем затвердела без изменения
плотности. Этот объем покоится. Следовательно, равнодействую-
щая всех сил, действующих на него со стороны окружающей
жидкости, равна по модулю и противоположна по направлению
силе, с которой этот выделенный объем действует на жидкость,
т. е. весу этого объема жидкости. Если теперь мысленно заме-
нить выделенную жидкость твердым телом, занимающим точно
такой же объем, то на это тело окружающая жидкость будет
действовать с такой же силой. Таким образом, на тело, погру-
женное в жидкость, действует выталкивающая сила, по модулю
равная весу вытесненной жидкости (другими словами: равная
весу жидкости в объеме тела).
Приведенные рассуждения справедливы также и в том слу-
чае, если тело погружено в газ.
Yk
Рис. 95
Обратим внимание на то, что архимедова сила, вообще гово-
ря, равна не силе тяжести, действующей на вытесненную жид-
кость, а весу этой жидкости. В этом можно убедиться, если пред-
124
ставить, что рассмотренный выше сосуд с жидкостью находится
в лифте, который движется с постоянным ускорением а, направ-
ленным вверх. На выделенный объем жидкости действуют две
силы — сила тяжести FT=mg и архимедова сила FA. Спроекти-
ровав эти силы на вертикальную ось OY, составим, согласно вто-
рому закону Ньютона, уравнение FA— mg = ma. Отсюда F к =
= m(g-\-a). Если р — плотность жидкости, а V — выделенный
объем ее, то масса m = pV. Следовательно,
FA = p(g + a)V. B)
Согласно третьему закону Ньютона, выделенный объем дей-
ствует на окружающую жидкость с такой же по модулю силой,
направленной противоположно. А эта сила и есть вес выделенно-
го нами объема жидкости.
Сравнивая формулы A) и B), видим, что при равноускорен-
ном движении сосуда с жидкостью архимедова сила, равная ве-
су вытесненной жидкости, отлична от силы тяжести, действую-
щей на вытесненную жидкость. Эта сила тяжести остается по-
стоянной независимо от того, движется сосуд или покоится.
Нетрудно показать, что если сосуд с жидкостью находится
в лифте, движущемся с постоянным ускорением а, которое на-
правлено вниз, то архимедова сила
FA = p(g-a)V. C)
Из формулы C) видно, что при a = g /гд=0, т. е. если сосуд
с жидкостью свободно падает, то на погруженное в эту жидкость
тело архимедова сила не действует. Жидкость при этом находит-
ся в состоянии невесомости.
В частности, в космическом корабле, движущемся на орбите
с выключенными двигателями, жидкость также находится в со-
стоянии невесомости, гидростатическое давление отсутствует и
на погруженные в жидкость тела архимедова сила не действует:
любое тело в жидкости находится в состоянии безразличного
равновесия. Между тем закон Паскаля в условиях невесомости
действует: если на поверхность жидкости создавать внешнее
давление, например, с помощью вставленного в сосуд поршня, то
это давление будет передаваться во все точки жидкости.
Выталкивающая сила всегда приложена в центре тяжести
вытесняемого объема жидкости или газа, а не в центре тяжести
погруженного тела, как часто считают экзаменуемые. В частных
случаях, конечно, эти точки могут совпадать. Например, для по-
груженного в жидкость или газ однородного сплошного шара
точкой приложения выталкивающей силы является его центр тя-
жести, так как он совпадает с центром тяжести вытесняемого
объема жидкости или газа. Но если, например, неоднородный
шар, часть А которого изготовлена из свинца, а часть В — из де-
рева, погрузить в жидкость так, как показано на рисунке 96, а, то
125
сила тяжести ~FT будет, как и до погружения, приложена в цент-
ре тяжести С, шара, а выталкивающая сила FA — в точке С2, яв-
ляющейся геометрическим центром шара. Под действием этих
сил шар повернется и займет положение, показанное на рисунке
96, б. Дальнейшее поведение шара будет зависеть от соотноше-
ния между FA и FT: если FT>FA, то шар будет тонуть; если
FT = .FA, то он будет находиться внутри жидкости в состоянии без-
различного равновесия; если FT<FA, то шар будет всплывать до
тех нор, пока выталкивающая сила F'A, действующая на часть
Рис. 96
шара, оставшуюся под поверхностью жидкости, не уравновесит
силу тяжести, т. е. будет выполняться равенство F'A = Fr, и шар
будет плавать. Некоторые абитуриенты ошибочно считают, что
тело плавает, если архимедова сила больше силы тяжести.
Итак, учитывая сказанное выше, мы можем сформулировать
следующее утверждение (закон Архимеда): на тело, погружен-
ное в жидкость или газ, действует выталкивающая сила, числен-
но равная весу жидкости или газа, вытесненных телом, направ-
ленная вертикально вверх и приложенная в центре тяжести вы-
тесненного объема жидкости или газа.
68. Абитуриенты, усвоившие закон Паскаля и понятие архи-
медовой силы слабо и чисто формально, допускают ошибки при
решении задач.
Задача 1. Гладкую нижнюю грань площадью S = 36 см2
квадратной березовой пластинки толщиной /г = 2 см натерли па-
рафином, приставили ко дну сосуда и осторожно заполнили со-
суд водой до высоты Я=12 см. Пластинка осталась лежать на
дне. Какую наименьшую силу, направленную вертикально вверх,
нужно приложить к середине одного из верхних ребер пластин-
ки, чтобы она всплыла на поверхность воды? Плотность воды
р, = 1-103 кг/м3, плотность березы р2 = 0,65-103 кг/м3, атмосфер-
ное давление ро=Ю5 Па. Считать, что ускорение свободного па-
дения g= 10 м/с2.
Решение. Деревянная пластинка сначала лежит на дне в
126
—_ _
•F,
I
H
Рис. 97
сосуде с водой и не всплывает потому, что плотно прилегает ко
дну сосуда и вода не проникает между ее нижней гранью и дном.
Силы, с которыми вода давит на боковые грани пластинки, вза-
имно компенсируются. Сила F, (рис. 97), действующая со сторо-
ны воды на верхнюю грань пластинки, не выталкивает, а, наобо-
рот, прижимает ее ко дну. Таким образом, выталкивающая (ар-
химедова) сила здесь отсутствует, чего не учитывали многие
абитуриенты: при решении этой задачи они считали, что на пла-
стинку, плотно прилегающую ко дну, действует архимедова си-
ла. Кроме того, они не учитывали, что атмосферное давление, в
соответствии с законом Паскаля, передается во все точки жидко-
сти по всем направлениям и что поэтому полное давление на
уровне верхней грани пластинки равно сумме гидростатического
и атмосферного давлений:
Pi=Pig (Н — h)-\-p0, A)
где р, — плотность воды.
Как только под действием силы F2, направленной вертикаль-
но вверх и приложенной к середине одного из ребер, пластинка
приподнимется, под нее проникнет вода и вследствие этого снизу
на пластинку будет действовать со стороны воды сила большая,
чем сверху, так как нижняя грань находится глубже. На уровне
нижней грани давление р2 — Р\ёН ~\~ Ро- Так как р2>Р\, то воз-
никнет выталкивающая (архимедова) сила /7А = (р2 — р,) S.
Проделанный анализ задачи приводит к следующему реше-
нию. Чтобы пластинка всплыла, нужно приподнять ее, а для это-
го необходимо приложить такую минимальную силу F2, чтобы
выполнялось условие равновесия: алгебраическая сумма момен-
тов всех сил относительно оси О, совпадающей с нижним ребром
пластинки, должна быть равна нулю. Кроме сил Fx и F2, на пла-
стинку действует сила тяжести FT, а также сила реакции опоры
N. Пусть / — длина пластинки, тогда плечи сил ~Ри ~РЪ Рт и N
127
равны соответственно —, /, — и 0. Составим уравнение для мо-
ментов этих сил:
Отсюда
B)
S. C)
D)
Подставив выражения C) и D) в формулу B), получим:
Учитывая выражение A), имеем:
Сила тяжести
= 1-36-10-4A03-10A2-2)-1СГ2+105
Х103-10-2-10)Н = 182 H.
Задача 2. Однородный сплошной стальной цилиндр плава-
ет в ртути, при этом его основания горизонтальны. Поверх ртути
наливают такой слой воды, что весь цилиндр находится в жидко-
сти. Плотность воды р,, плотность ртути р2, плотность стали р3.
Какая часть объема цилиндра находится в ртути?
Решение. В горизонтальном направлении на цилиндр со
всех сторон действуют силы, обусловленные давлением жидко-
стей. Эти силы уравновешиваются. В вертикальном направлении
на цилиндр действуют три силы (рис. 98): сила тяжести FT, силы
Г, и F2, с которыми жидкость давит на верхнее и нижнее основа-
X
Рис. 98
128
ния цилиндра соответственно. Поскольку цилиндр плавает,
т. е. находится в равновесии, сумма проекций этих сил на ось OY
равна нулю:
или
-Гт-Г, + Г2 = 0. A)
Выразим модули этих сил. Модуль силы тяжести
, B)
где т — масса цилиндра; V — его объем; А,, h2 — высоты частей
цилиндра, находящихся в воде и ртути соответственно.
Модуль силы Z7,
F\ = U\gh + Po)S, C)
где h — толщина слоя воды над верхним основанием цилиндра;
р() — атмосферное давление.
Модуль силы F2
где р2 — давление на уровне, где находится нижнее основание.
Здесь, кроме давления, создаваемого столбом ртути высотой /г2,
необходимо учитывать давление, создаваемое столбом воды
высотой /г + /гь и атмосферное давление р0, которые по закону
Паскаля передаются во все точки ртути по всем направлениям.
Поэтому
S. D)
Подставив выражения B) — D) в уравнение A), получим по-
сле преобразований:
МРз —Pi) = Mp2 —р3),
откуда
h-2 Pi —P,
Найдем, какая часть объема цилиндра находится в ртути:
Vj_ Sh2 _ 1 1 р3 —Pi
V S (Л, + /г2) h\ Рг —Рз . P2~Pi '
— -+- l 1- 1
PS"Pi
При решении этой задачи многие абитуриенты неправильно
определяли силы, действующие на цилиндр. Они считали, что
вода прижимает цилиндр к ртути, а ртуть, наоборот, выталкива-
ет его, т. е. не учитывали, что в соответствии с законом Паскаля
5 Заказ 2473 129
создаваемое водой давление передается и на нижнее основание,
поэтому и вода вносит свой вклад в создание выталкивающей
силы. В самом деле, на цилиндр действует выталкивающая (ар-
химедова) сила, модуль которой FA = F2 — Fx. Учитывая выраже-
ния C) и D), получаем:
Y
= ihghtS + p2gh2S = pxgVx + p2gV2 = FAX + FA2,
где FAX, FA2 — модули выталкивающих сил, создаваемых водой
и ртутью соответственно. Мы видим, что вода не прижимает, а,
наоборот, выталкивает цилиндр из ртути.
69. Некоторые экзаменуемые говорили, что если тело погру-
зить в жидкость, то уменьшится сила тяжести, так как на тело
будет действовать архимедова сила. В действительности же сила
тяжести не изменяется, а уменьшается вес тела.
Предположим, что тело подвешено на нити в жидкости
(рис. 99). На него действуют три силы: сила тяжести FT, сила на-
тяжения нити Тх и архимедова сила
FA. Тело находится в равновесии, следо-
вательно, сумма проекций этих сил на
вертикально направленную ось OY
равна нулю: Тх -\- FA — FT = 0. Отсюда
T, = FT-FA. A)
Согласно третьему закону Ньюто-
на, тело действует на нить с такой же
по модулю силой, т. е. вес тела РХ = ТХ.
Если это тело подвесить на нити в ва-
кууме, то в этом случае FA = 0, поэто-
му сила натяжения
v X
Рис. 99 T2=Fr, B)
следовательно, вес тела Р2=Т2= FT.
Сравнивая выражения A) и B), находим, что уменьшение ве-
са в жидкости равно по модулю архимедовой силе:
"¦i^y...
Задача. Вес тела, погруженного в жидкость плотностью рь
равен Ph а погруженного в жидкость плотностью р2—Р2. Найти
плотность тела.
Решение. На основании формулы Т{ = FT — FA запишем вы-
ражение для веса тела массой m в жидкости, плотность которой
равна р,:
где р — плотность тела; V — его объем.
130
Аналогично выразим вес этого тела в жидкости плотно-
стью р2:
Разделив почленно первое выражение на второе, получим:
Р| p~Pl m
Отсюда найдем плотность тела:
р= р _р . B)
Таким образом, плотность тела можно найти путем взвеши-
вания его в двух различных жидкостях с известными плотно-
стями.
Практически с незначительной погрешностью можно опреде-
лить плотность тела, взвесив его сначала в воздухе, а потом в
жидкости с известной плотностью. При этом выталкивающей си-
лой, действующей на тело в воздухе, пренебречь, т. е. считать
плотность воздуха р,=0. Тогда, согласно формуле B), плот-
ность тела
Р.Р2
Р=-р Б".
t 1 —г 2
где Ри Р2 — вес тела в воздухе и жидкости соответственно; р2 —
плотность жидкости. Так можно определить плотность тела, име-
ющего сложную геометрическую форму.
Согласно преданию, древнегреческий царь Гиерон заподо-
зрил, что при изготовлении для него золотой короны часть золо-
та была заменена серебром, и попросил знаменитого ученого Ар-
химеда B87—212 гг. до н. э.) выяснить это, не разрушая корону.
Архимед догадался, как это сделать, когда купался в ванне, и
голый побежал по улицам города Сиракузы с криком «Эврика»
(«Нашел!»). Взвесив корону в воздухе и в воде, Архимед смог
найти плотность вещества, из которого была сделана корона.
Эта плотность оказалась меньше плотности золота. Следователь-
но, корона была изготовлена с добавлением более легкого ме-
талла.
Обратим внимание на то, что плотность жидкости тоже мож-
но определить аналогичным способом. Если известна плотность
р тела, его вес Pi в жидкости плотностью р, и вес Р2 в жидкости,
плотность р2 которой неизвестна, то, используя выведенную вы-
ше формулу A), найдем:
131
70. Рассказывая о плавании тел, поступающие нередко гово-
рят, что тело плавает, если его плотность меньше плотности
жидкости, и при этом не все могут объяснить, почему же не то-
нет, например, металлическая лодка, ведь плотность металла
больше плотности воды.
Необходимо хорошо знать условия плавания тел. На тело
массой т, погруженное в жидкость, действуют две силы: сила
тяжести FT = mg, направленная вертикально вниз, и архимедова
сила FA, направленная вертикально вверх. Если /7Т>/7Д, то тело
тонет. Если FT=FA, то тело находится в положении безразлично-
го равновесия на любой глубине внутри жидкости. Если FT<CFA,
то тело всплывает до тех пор, пока архимедова сила по модулю
не станет равной силе тяжести, т. е. FT = FA, и потом плавает.
Но выталкивающая (архимедова) сила зависит, как об этом
уже говорилось выше, от объема V вытесненной телом жидкости,
а этот объем в свою очередь зависит от формы тела. Поэтому,
в частности, металлический лист тонет, а лодка, сделанная из
такого металла, плавает.
Только для однородного сплошного (без полостей) тела мож-
но, сравнивая плотности тела и жидкости, приходить к правиль-
ному выводу о том, будет ли это тело плавать в данной жидкости
или тонуть. В самом деле, тело будет всплывать, если FT<iFA.
Выразим модули силы тяжести и архимедовой силы:
Fr=mg = prVg, FA = pxgV,
где рт, рж — плотность тела и жидкости соответственно; V —
объем тела. Тогда условие, при котором сплошное тело всплыва-
ет, запишется так: pTVg-<p1K gV. Отсюда рт<рж.
71. При решении некоторых задач приходится искать силу,
с которой жидкость давит на вертикальную стенку сосуда, и это
вызывает затруднения у абитуриентов. Они иногда находят эту
силу по формуле F = pghS, где р — плотность жидкости;
h — глубина сосуда; S — площадь его стенки. Это грубая ошибка.
По данной формуле можно найти силу, с которой жидкость дей-
ствует на дно сосуда, т. е. вес жидкости, если S — площадь дна.
Кроме того, на дно действует сила, обусловленная атмосферным
давлением, которое, согласно закону Паскаля, передается во все
точки жидкости. Таким образом, на дно сосуда действует сила,
модуль которой
где ра — атмосферное давление. Здесь мы имели в виду, что на
уровне дна давление одинаковое. При нахождении силы, дейст-
вующей со стороны жидкости на стенку сосуда, необходимо учи-
тывать, что давление возрастает с увеличением глубины. Рас-
смотрим это на конкретном примере.
Пусть в сосуд, имеющий форму прямоугольного параллеле-
132
AX
h X
пипеда, налита до высоты h жидкость плотностью р. Найдем си-
лу, действующую на стенку этого сосуда длиной /. Внешнее дав-
ление равно р0.
Выделим мысленно на стенке узкую горизонтальную полоску
в виде прямоугольника со сторонами / и Ах (рис. 100, а). Вслед-
ствие малости Ах будем считать, что давление жидкости на эту
полоску одинаково во всех точках и равно полному давлению на
глубине х. Выразим модуль силы, действующей на эту полоску:
Fi = (po + pgx) ASi = {p0 + pgx) lAx = (pQl-\-pglx) Ах,
где S, — площадь полоски.
Выражение, стоящее в скобках перед Ах, обозначим через ух:
Ух=Ро1 + Рё1х- A)
Тогда
F, = yxAx. B)
Построим график зависимости ух от х согласно формуле A).
Поскольку эта зависимость линейная, то график представляет
собой прямую (рис. 100, б). На оси ОХ отрезок от нуля до h разо-
бьем на несколько равных частей длиной Ах. На каждом из от-
резков построим прямоугольники, высоты которых равны г/0, уи
..., ун. Тогда в соответствии с выражением B) площади этих пря-
моугольников равны модулям силы, с которыми жидкость давит
на соответствующие полоски, выделенные на стенке и находящи-
еся на различных глубинах. Все эти силы направлены горизон-
тально, поэтому их равнодействующая тоже направлена гори-
зонтально, а ее модуль равен сумме модулей сил, действующих
на все полоски: F = F0-\-Fl -j-... -\-Fh. Нетрудно видеть, что
эта сумма численно равна площади ступенчатой фигуры на
рис. 100, б. Если уменьшать Ах, то площадь этой фигуры будет
все больше приближаться к площади трапеции, ограниченной
133
графиком t/^ = /(x), осями OX, OY и прямой x = /z. В пределе,
т. е. когда интервалы Ах будут становиться бесконечно малы-
ми (Дх-кО), площадь этой фигуры станет равной площади
трапеции.
Следовательно, модуль силы, действующей со стороны жид-
кости на стенку сосуда, численно равен площади этой трапеции:
F (
Учитывая, что, согласно формуле A), yo = pQt, yh =
получаем:
Но lh = S — площадь соприкосновения стенки с жидкостью,
поэтому
( f. C)
В формуле C) р0— внешнее давление, которое, согласно за-
кону Паскаля, без изменения передается во все точки жидкости.
Второе слагаемое выражения в скобках представляет собой обу-
словленное весом жидкости среднее давление (среднее гидроста-
тическое давление)
Р = ^- D)
которое можно взять вместо переменного давления, считая, что
это среднее давление одинаково во всех точках стенки на разной
глубине. На основании этого формулу C) можно переписать в
таком виде:
F = (Ро + РсР) 5 = p0S -f pcpS = Fx + F2.
Здесь F{ — модуль силы, действующей со стороны жидкости на
стенку сосуда вследствие наличия внешнего давления. Если со-
суд открыт, то внешним является атмосферное давление,
т. е. ро = ра. Второе слагаемое F2— модуль силы, с которой жид-
кость давит на стенку, т. е. силы, обусловленной гидростатиче-
ским давлением.
Обычно очень немногие абитуриенты используют формулу
D), но к тому же не могут объяснить, почему именно это давле-
ние берется как среднее давление.
Задача. В аквариум, имеющий форму куба с ребром дли-
ной а = 40 см, налита вода до высоты /г = 30 см. Найти, какая
сила действует на дно и какая — на одну боковую стенку аква-
риума. Атмосферное давление ро=\О5 Па. Плотность воды
р=Ы03 кг/м*
Решение. На дно аквариума действует сила, модуль кото-
рой Fl = pS], где р — давление на уровне дна; S{ = a2 — площадь
134
дна. Давление pt равно сумме гидростатического и атмосферно-
го давлений: /?, = pgh-\-р0. Следовательно,
po)^. A)
Модуль силы, действующей на одну стенку сосуда, F2 = p2S2,
где р2 — давление, равное сумме среднего гидростатического
давления и атмосферного давления:
Р-2 = Рср + Ро =
Площадь соприкосновения стенки с водой S2 = ah. Учитывая
это, находим:
(^ )h. B)
Подставив в формулы A) и B) числовые значения и произве-
дя вычисления, получим: /7, = 16,5 кН, /72=12,2 кН.
При выводе формул A) и B) мы учитывали, что в соответст-
вии с законом Паскаля атмосферное давление передается во все
точки жидкости. Следует отметить, что снаружи на дно и на
стенку также действуют силы, обусловленные давлением атмо-
сферы и направленные вовнутрь аквариума.
Найдем силы Flr и F2n с которыми вода давит на дно и одну
стенку вследствие наличия гидростатического давления (давле-
ние атмосферы при этом не учитываем):
Fir = pgha2, F2r = -pgah2.
После подстановки в эти выражения числовых значений и вычис-
лений получим: Flr = 464 H, F2r= 176 Н. Сравнивая эти резуль-
таты с найденными выше значениями сил Z7, и F2, нетрудно ви-
деть, какая большая часть этих сил обусловлена атмосферным
давлением.
72. Рассматривая движение тела в жидкости, многие абиту-
риенты допускают ошибки при применении закона сохранения
энергии.
Задача 1. Однородный металлический шар, масса которого
т=\ кг, а плотность р, = 2-103 кг/м3, погрузили в воду и отпу-
стили. Найти кинетическую энергию шара в момент времени,
когда он погрузился на глубину /г = 10 м, а также архимедову
силу, действующую на шар. Силой трения пренебречь. Плот-
ность воды р2 = 1 -103 кг/м .
Решение. Обычно большинство поступающих решают эту
задачу так: начальная скорость, а следовательно, и начальная
кинетическая энергия шара равны нулю; в результате опускания
шара на глубину h его потенциальная энергия уменьшится на
mgh, а кинетическая на столько же увеличится, поэтому
Ek = mgh= 1-9,8-10 Дж = 98 Дж.
Архимедова -сила FA = p2gV, где V — объем шара:
135
V——. Следовательно, r« =
Pi Pi
Здесь архимедова сила найдена правильно, а при нахожде-
нии кинетической энергии шара допущена ошибка: не учтено из-
менение потенциальной энергии воды.
При опускании шара вниз на глубину h вытесненная им вода
поднимается на такое же расстояние вверх и займет место, осво-
божденное шаром (рис. 101). Уровень 00{ примем за нулевой
уровень потенциальной энергии. Обозначим через т2 массу воды
в объеме, равном объему шара.
В начальный момент времени, когда шар отпустили, он нахо-
дился на высоте h над уровнем 00, и, следовательно, его потен-
циальная энергия была равна mtgh, а кинетическая равна нулю,
так как шар начинал двигаться без начальной скорости. В этот
же момент вода массой т2 находилась на уровне OOt и ее потен-
циальная и кинетическая энергия были равны нулю.
В тот момент, когда вода и шар поменялись местами, потен-
циальная энергия воды массой т2 стала равной m2gh, а потенци-
альная энергия шара — нулю. Кинетическую энергию шара в
этот момент обозначим через Ек. Согласно закону сохранения
энергии, m]gh = Ek-\-m,2gh. Отсюда
rn2g)h. A)
Учитывая, что m., = p2V=p2—, получаем:
Pi
Pi
B)
= 49 Дж.
Теперь полезно обратить внимание на то, что в приведенном
здесь решении мы не применяли понятие архимедовой силы. Бо-
лее того, на основании закона сохране-
ния энергии можно прийти к выводу о
существовании этой силы.
В самом деле, так как начальная
кинетическая энергия шара была рав-
на нулю, а на уровне OOt стала равна
Ек, то изменение кинетической энергии
АЕк = Ек~0 = Ек. Поэтому формулу A)
можно переписать так:
m2g)/z. C)
Рис- 101
Нетрудно видеть, что и в этом слу-
чае, если бы шар имел начальную ско-
рость и, следовательно, некоторую на-
чальную кинетическую энергию Ек0,
мы пришли бы к выражению C). Дей-
136
ствительно, на основе закона сохранения энергии в этом случае
можно составить уравнение
к0 = Ек + m2gh,
откуда
Ек — Ek0 = (mtg — m2g)h,
а так как Ек— Ем = АЕк, то получаем выражение C). Итак, это
выражение справедливо и при наличии у шара начальной
скорости.
Теперь вспомним теорему об изменении кинетической энер-
гии. Изменение кинетической энергии тела равно работе всех
сил, действующих на него. Следовательно, правая часть форму-
лы C) представляет собой работу действующих на шар сил:
A=(mlg — m2g)h = mlgli + ( — m2g)h. D)
Учитывая, что вектор перемещения шара направлен, как и си-
ла тяжести, вниз, мы на основании формулы D) приходим к
выводу, что в воде на шар действуют две силы: сила тяжести
Fr — mg и сила, проекция которой на направление пере-
мещения равна —w2g, т. е. сила, направленная вертикально
вверх и равная —гп^ё- А это и есть архимедова (выталкиваю-
щая) сила:
FA=—m2g=— p2Vg.
Модуль этой силы равен весу жидкости, вытесненной телом:
Таким образом, закон Архимеда можно рассматривать как след-
ствие закона сохранения энергии.
Решим эту задачу другим способом. На шар в воде действу-
ют сила тяжести F,, направленная вертикально вниз, и архиме-
дова сила FA, направленная вертикально вверх. При опускании
шара вниз на глубину h эти силы совершают работу
А = FTh + FAh cos 180° = (FT —FA) h.
Согласно теореме об изменении кинетической энергии,
АЕк = А, т. е. AEk = (Fr — FA) h, а так как начальная скорость шара
равна нулю, то Д?к = ?'к, где Ек — кинетическая энергия шара на
глубине h. Следовательно,
Сравнивая последнее выражение с формулой B), видим, что
пришли к тому же результату.
137
Задача 2. Тело массой т и плотностью р, равномерно дви-
жется вертикально вниз в жидкости, плотность которой р2. Какое
количество теплоты выделяется при прохождении телом пути
длиной Л?
Решение. В отличие от предыдущей задачи здесь необходи-
мо учитывать силу трения. Решим эту задачу двумя способами.
Первый способ. На тело, опускающееся в жидкости, действу-
ют следующие силы: сила тяжести FT = mg, направленная верти-
кально вниз, сила трения Frp и архимедова сила FA, которые на-
правлены вертикально вверх. Из условия равномерности движе-
ния тела следует, что сумма проекций этих сил на вертикальное
направление равна нулю: mg— Fk — /7тр = 0. Отсюда
FTV = mg-FA. A)
Количество теплоты, выделившееся при прохождении рассто-
яния /г, равно работе против силы трения: Q=A. Работа против
силы трения равна взятой со знаком «—» работе силы трения,
т. е. А — — Лтр. Учитывая, что сила трения направлена противо-
положно вектору перемещения, получаем:
ATp = FTfh cos 180°=-V-
Следовательно,
Q = A = -Al? = Fiph. B)
Модуль архимедовой силы FA = c>2gV, где V — объем тела.
Выразим его, зная массу т тела и его плотность р,: V=m/p{.
Тогда
г, т
Подставив это выражение в формулу A), получим:
На основании выражений B) и C) приходим к выводу, что выде-
лившееся количество теплоты
Второй способ. Решим теперь эту задачу энергетическим ме-
тодом. В результате равномерного опускания тела на расстояние
h кинетическая энергия его не изменяется, а потенциальная
уменьшается на mgh. В то же время жидкость в объеме, рав-
ном объему тела, поднимается вверх на высоту h (см. рис.
101), поэтому ее потенциальная энергия увеличивается на m2gh,
где т2 — масса поднявшейся жидкости:
m
p2— .
138
Таким образом, убыль потенциальной энергии равна
mgh— m2gh и, согласно закону сохранения энергии, выделившее-
ся количество теплоты
Q = mgh — m2gh.
Подставив в эту формулу значение т2, получим:
Такой же результат был получен и при решении первым
способом.
Абитуриенты часто решали эту задачу так: кинетическая
энергия тела не изменяется, поэтому выделившееся количество
теплоты равно убыли потенциальной энергии: Q = mgh. Ошибоч-
ность этого результата видна после рассмотрения приведенного
выше правильного решения.
73. В ответах экзаменуемых часто встречается неправильное
понятие об опыте Э. Торричелли. Напомним кратко суть этого
важного опыта, а затем отметим допускаемые абитуриентами
ошибки.
Стеклянную трубку длиной около 1 м, запаянную с одного
конца, наполняют ртутью. Затем отверстие трубки закрывают,
чтобы ртуть не вылилась, переворачивают трубку запаянным
концом вверх и опускают ее в вертикальном положении отвер-
стием вниз в открытый сосуд с ртутью. После этого открывают
отверстие трубки, в результате чего уровень ртути в ней пони-
зится и над поверхностью ртути в трубке образуется пустота
(так называемая «торричеллиева пустота»). Почему ртуть не вы-
текает полностью из трубки, а устанавливается на некоторой вы-
соте (рис. 102)? Это явление впервые в 1643 г. объяснил италь-
янский ученый Э. Торричелли. Давление атмосферы, действую-
щее на поверхность ртути в сосуде (точка Л), равно давлению
столба ртути внутри трубки на уровне поверхности ртути в сосу-
де (точка В), т. е. рА = рв.
Таким образом, опытом Торричелли было доказано существо-
вание атмосферного давления и, кроме того, показана возмож-
ность измерять это давление высотой ртутного столба. Эта высо-
та /г«760 мм.
Некоторые абитуриенты не понимают, почему атмосферное
давление равно давлению столба ртути в трубке Торричелли,
ведь и атмосфера, и этот столб давят вниз. Объясняется это так.
Атмосферное давление, действующее на поверхность ртути в со-
суде, передается, в соответствии с законом Паскаля, без измене-
ния во все точки ртути и по всем направлениям, в том числе и на
нижнее основание ртутного столба через нижний открытый ко-
нец трубки. В результате этого на нижнее основание ртутного
столба действует сила F1=/?,VS, где S — площадь поперечного
сечения столба. Сверху на это основание столб ртути действует
с силой /?2 = pS/?gr, где р — плотность ртути. Эти силы уравнове-
шиваются: F]=F2 или pAS=pShg, поэтому P\ = pgh, т. е. атмо-
сферное давление равно давлению столба ртути в трубке. Отсю-
да следует, что
т. е. высота столба ртути прямо пропорциональна атмосферному
давлению, и, следовательно, высотой ртутного столба можно из-
мерять атмосферное давление. На практике используется внеси-
стемная единица давления — миллиметр ртутного столба (мм
рт. ст.). Миллиметр ртутного столба равен давлению, создавае-
мому столбом ртути высотой 1 мм. Переведем 1 мм рт. ст. в еди-
ницы СИ, т. е. в паскали. Для этого в формулу pA = pgh подста-
вим значения плотности ртути р= 13,6-10 кг/м3, ускорения сво-
бодного падения g = 9,8 м/с2 и высоты h=\ мм = 10 м. После
умножения получим 1 мм рт. ст.» 133 Па.
Нормальным атмосферным давлением называется давление
/?0=101325 Па = 760 мм рт. ст.
Формула A) показывает, что высота столба ртути в трубке не
зависит от площади ее поперечного сечения S. Абитуриенты же
иногда ошибочно утверждают, что при одном и том же атмо-
сферном давлении в трубке меньшего диаметра уровень ртути
будет выше, чем в трубке большего диаметра.
Такое утверждение, возможно, связано с явлением капилляр-
ности. Но, во-первых, в опыте Торричелли не использовалась ка-
пиллярная трубка, а во-вторых, ртуть в стеклянном капилляре
не поднимается, а опускается и тем ниже, чем меньше его диа-
метр.
Поверхностное усвоение понятия атмосферного давления при-
водит к затруднениям при решении задач. Рассмотрим в каче-
стве примеров две несложные задачи.
Задача 1. Трубку в опыте Торричелли наклонили так, что
она составляет с горизонтом угол а = 70°. Какова длина столба
140
ртути в трубке, если атмосферное давление нормальное?
Решение. При наклоне трубки уровень ртути остается на
одной и той же высоте h (рис. 103). Если атмосферное давление
нормальное, то /г = 760 мм. При этом столб ртути в наклонной
трубке имеет длину
760
sin 70°
мм»809 мм.
Задача 2. Какой длины трубку нужно было бы взять для из-
мерения атмосферного давления в опыте Торричелли, если бы
в ней и в сосуде была не ртуть, а вода? Атмосферное давление
нормальное.
Решение. В этом случае давление столба воды высотой h
должно быть равно атмосферному давлению: Ра = Рв (см- РИС-
102) или PA = Pgh, где р — плотность воды. Следовательно,
Рё
Подставив в эту формулу значения р = 1 -103 кг/м3, g = 9,8 м/с2,
рл = 760-133 Па и произведя вычисления, получим /г=10,3 м.
Рис. 103
Таким образом, если бы в опыте Торричелли применялась не
ртуть, а вода, то нужно было бы брать трубку длиной не менее
10,3 м. А если трубка будет иметь меньшую длину, то нисколько
воды из нее не выльется.
74. Грубую ошибку допускают некоторые абитуриенты, счи-
тающие, что однородная жидкость в сообщающихся сосудах раз-
личной формы устанавливается на разных уровнях: в более уз-
ком сосуде, например, жидкость находится выше, чем в
широком.
Напомним, что однородная жидкость в сообщающихся сосу-
дах, т. е. в сосудах, соединенных между собой в нижней части,
всегда устанавливается на одном уровне независимо от формы
сосудов и площади их поперечного сечения. Объясняется это
141
тем, что на свободных поверхностях жидкости в сосудах давле-
ние одно и то же, оно равно атмосферному давлению. Но, как из-
вестно, в покоящейся однородной жидкости давление одинаково
во всех точках, находящихся на одном уровне. Следовательно,
все свободные поверхности находятся на одном и том же уровне
(рис. 104).
Если в сообщающиеся сосуды налиты различные несмешива-
ющиеся жидкости, то они устанавливаются на разных уровнях.
При этом высоты столбов жидкостей (считая от уровня их разде-
ла) обратно пропорциональны плотностям жидкостей. Поясним
это на примере решения следующей задачи.
Рис. 104
Задача. В сообщающиеся сосуды налили сначала ртуть, а
затем в один из сосудов — масло, в результате чего уровень рту-
ти во втором сосуде стал выше на /г, = 2 см, чем в первом. Высо-
та столба масла /г2 = 30 см. Плотность ртути р, = 13,6-103 кг/м3.
Определить плотность р2 масла.
Решение. Выберем в качестве поверхности одного уровня
горизонтальную плоскость ООи проходящую по границе раздела
масла и ртути (рис. 105). Давление в точках А и В этой поверх-
ности одинаковое: рА = рв. Учитывая, что
где рг — атмосферное давление, получаем:
откуда следует, что
h2 р, '
т. е. высоты столбов масла и ртути обратно пропорциональны их
плотностям. Отсюда находим плотность масла:
p2 = p,|i, р2=13,6-103~ кг/м3 = 0,9-103 кг/м3.
Таким способом практически можно определить плотность
жидкости, если известна плотность второй жидкости.
142
В ответах абитуриентов встречаются ссылки на формулу A),
но не у всех есть четкое представление, как располагаются в со-
общающихся сосудах жидкости, имеющие различные плотности:
более плотная жидкость занимает нижние части сосудов. Абиту-
Р и с. 105
риенты же иногда делают такие рисунки: в одном из сосудов на-
ходится одна жидкость, в другом — другая.
При решении задач не учитывают, что если в сообщающихся
сосудах имеются различные жидкости, то для расчета давления
рационально выбирать такой уровень на границе раздела жид-
костей, что ниже его располагается только какая-либо одна жид-
кость. Легко видеть, что если бы, например, при решении преды-
дущей задачи мы выбрали уровень, находящийся ниже уровня
00, на h, то как в выражение для рА, так и для рв вошло бы до-
полнительное слагаемое p{gh, а в результате преобразования
уравнения Ра=:Рн мы все равно получили бы формулу (i).
75. При решении задач этого раздела программы ошибки
возникают в основном из-за неумения правильно установить си-
лы, действующие на тело. Иногда абитуриенты забывают, что
сила, с которой верхний слой жидкости давит на погруженное
в нее тело, уже учтена в выталкивающей (архимедовой) силе;
отождествляют вес тела в жидкости с силой тяжести, действую-
щей на это тело, и др. Учитывая это, изложим кратко порядок
решения таких задач.
Задачи, в которых рассматривается плавание тел, решаются
по такому же общему плану, как и задачи на динамику и равно-
весие тел, только необходимо при этом учитывать архимедову
силу. Обозначаются все действующие на тело силы и составля-
ется либо уравнение в соответствии со вторым законом Ньютона,
либо уравнение, выражающее условие равновесия тела.
Если в задаче говорится о весе тела в жидкости, то удобно
изобразить тело подвешенным на нити в жидкости; при этом си-
ла натяжения нити равна весу тела.
В задачах, связанных с определением давления жидкости,
143
используются закон Паскаля и следствия из него. Сделав схемати-
ческий чертеж, изображают на нем уровни, занимаемые жидко-
стью согласно условию задачи. Поверхность нулевого уровня вы-
бирают так, чтобы она проходила по самой нижней границе
раздела сред. Затем на основании следствия из закона Паскаля
составляют уравнение равновесия жидкости
Рл = Рв, A)
где рА, рв — полные давления в точках А и В, расположенных на
поверхности одного уровня в покоящейся жидкости.
Если по условию задачи происходит переливание жидкости
из одной части сосуда в другую, то к составленному уравнению
A) можно добавить условие несжимаемости жидкости:
Л1/,=Л1/2, где AV,, AV2 — соответственно уменьшение объема
жидкости в одной части сосуда и увеличение его в другой части.
Затем составленную систему уравнений решают относительно
искомой величины.
МОЛЕКУЛЯРНАЯ ФИЗИКА.
ТЕПЛОВЫЕ ЯВЛЕНИЯ
ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ.
ГАЗОВЫЕ ЗАКОНЫ
76. На вопрос об основных положениях молекулярно-кинети-
ческой теории абитуриенты, как правило, дают неполный ответ,
ограничиваясь лишь информацией о том, что этих положений
три: вещество состоит из частиц; эти частицы хаотически дви-
жутся; частицы взаимодействуют между собой.
Отвечая на этот вопрос, нужно рассказать о взаимодействии
частиц— атомов и молекул, качественно описать это взаимодей-
ствие, обратив внимание на то, что между атомами и молекула-
ми одновременно действуют силы притяжения и силы отталкива-
ния. На малых расстояниях (меньших некоторого расстояния г0,
характерного для данного типа молекул) преобладают силы от-
талкивания, но с увеличением расстояния эти силы убывают бы-
стрее, чем силы притяжения, поэтому на больших расстояниях
(превышающих г0) преобладают силы притяжения. На расстоя-
нии г0 модули сил притяжения и отталкивания равны. На рисун-
ке 106 показаны зависимости от расстояния проекций сил оттал-
кивания Fи, притяжения F2r и результирующей силы взаимодей-
ствия F г.
Не все абитуриенты правильно объясняют различие в харак-
тере хаотического (теплового) движения молекул в газах, жидко-
стях и твердых телах.
В газах молекулы находятся на достаточно больших расстоя-
ниях друг от друга, поэтому силы притяжения пренебрежимо
малы, вследствие чего газы могут неограниченно расширяться.
Молекулы газа хаотически движутся, соударяясь, подобно ша-
рикам, друг с другом и со стенками сосуда.
В жидкостях молекулы расположены практически вплотную
друг к другу. Они колеблются около некоторого положения рав-
новесия, как бы «топчутся на месте», а также перескакивают из
одного положения равновесия в другое.
В твердых телах молекулы и атомы располагаются в опреде-
ленных местах и образуют кристаллическую решетку. Они ко-
леблются около некоторых средних положений равновесия, на-
зываемых узлами кристаллической решетки.
77. Встречалось в ответах абитуриентов утверждение, что
броуновское движение — это движение молекул, которое впер-
145
Рис. 106
вые наблюдал в микроскоп английский ученый Р. Броун. Это
грубая ошибка.
Суть броуновского движения состоит в том, что достаточно
мелкие твердые частицы, взвешенные в жидкости, совершают
беспорядочное движение. Броун в 1827 г. впервые наблюдал в
микроскоп движение этих частиц, а не молекул, невидимых в
микроскоп. Броуновское движение может наблюдаться и в газе.
Броуновское движение можно объяснить только на основе мо-
лекулярно-кинетической теории. Молекулы жидкости или газа,
беспорядочно двигаясь, сталкиваются с твердой частицей, пере-
давая ей некоторый результирующий импульс. Направление это-
го импульса, а следовательно, и скорости частицы беспорядочно
изменяются вследствие хаотичности движения соударяющихся с
частицей молекул: в какой-то момент времени преобладает дей-
ствие молекул с какой-нибудь стороны, и частица движется в од-
ном направлении, через некоторое время будут преобладать уда-
ры с другой стороны, и частица изменит направление движения
и т. д. Таким образом, броуновское движение является следстви-
ем хаотического движения молекул жидкости или газа. Броунов-
ское движение явилось одним из важнейших обоснований моле-
кулярно-кинетической теории.
78. Многие экзаменующиеся демонстрировали поверхностное
усвоение таких важных физических понятий, как относительная
атомная масса, относительная молекулярная масса, единица ко-
личества вещества — моль, молярная масса, постоянная Авогад-
ро. Об этом свидетельствуют ошибки, допускавшиеся в ответах
и в решениях задач. Так, например, некоторые говорили, что от-
носительная молекулярная масса — это масса одной молекулы
данного вещества, что, конечно, неверно. Поясним это на следу-
ющем примере.
Относительная молекулярная масса азота Мг = 28. Обратим
внимание на то, что это величина безразмерная. Напомним, что
относительной молекулярной массой Мг называется отношение
массы m молекулы данного вещества к 1/12 массы атома
углерода
12С:
146
Масса, равная 1/12 массы атома углерода |2С, называется
атомной единицей массы (а. е. м.); 1 а. е. м. = 1,66057-10~27 кг.
омной единицей массы (
Масса молекулы азота
ш0 = -jL Отосуиг =1.66057-10^27-28 кг = 4,65-10~26 кг.
Моль — единица количества вещества СИ. Моль равен коли-
честву вещества, в котором содержится столько же молекул или
атомов, сколько содержится атомов в 0,012 кг углерода |2С.
Молярной массой М называется масса вещества, взятого в
количестве 1 моль.
Постоянной Авогадро NA называется величина, равная числу
молекул или атомов, содержащихся в одном моле вещества. За-
метим, что здесь речь идет о любом веществе — твердом, жид-
ком или газообразном. Абитуриенты иногда ошибочно считают,
что постоянная Авогадро относится только к газам. Постоянная
Авогадро ЛА^ = 6,02 ¦ 10 моль.
Из приведенных выше определений следует важный практи-
ческий вывод: молярная масса, выраженная в граммах на моль,
численно равна относительной молекулярной массе. Так, напри-
мер, относительная молекулярная масса азота Мг = 28, моляр-
ная масса азота М = 28 г/моль = 28-10~3 кг/моль. Теперь мы мо-
жем найти массу молекулы азота, разделив его молярную массу
на постоянную Авогадро:
М 28-10~3 . сс ,А_26
- = 4,65-10 кг.
na 6,02-1023
Такой же результат получится, конечно, если учесть приведенное ,
выше соотношение между атомной единицей массы и кило-
граммом:
то = 28-1,66057-10™27 кг = 4,65-Ю6 кг.
79. Многие абитуриенты не имеют четкого наглядного пред-
ставления о массе и размерах молекул, не могут произвести
оценку этих величин. В приведенном выше примере показано,
как найти массу молекул азота. Чтобы представить себе, на-
сколько малы молекулы и насколько велико их число, рассмот-
рим следующие два примера.
1. Произведем приближенный расчет объема молекулы воды.
Можно считать, что в жидкости молекулы расположены вплот-
ную друг к другу, поэтому объем одной молекулы воды найдем,
разделив объем моля воды на число молекул в одном моле,
т. е. на постоянную Авогадро:
V = ?- A)
147
Относительная молекулярная масса воды М,= 18. Следова-
тельно, ее молярная масса М=18 г/моль= 18-10 кг/моль.
Разделив молярную массу на плотность р = 1-103 кг/м , найдем
объем моля воды:
К = — =18-10 6 м3/моль.
р
Теперь по формуле A) найдем объем одной молекулы воды:
к=18-10-6мУмоль 3.10-»мз.
6.02- 10 моль"
Оценим приблизительно линейные размеры молекулы воды:
гж^З-К)-29 м3 «0,3-10~9 м = 0,3 нм.
Размеры такого же порядка имеют молекулы других веществ.
2. Рассмотрим такой мысленный эксперимент. Нальем в ста-
кан т= 100 г воды и предположим, что каждую секунду из него
вылетает п=\ млрд. = 109 молекул воды. Через сколько време-
ни из стакана вылетят все молекулы воды?
Если предложить учащимся хотя бы очень приблизительно
оценить без расчетов это время, то, как правило, называют зна-
чения, очень далекие от действительного. (Читатель может здесь
остановиться и для самопроверки попробовать без расчетов оце-
нить это время, а затем читать дальше.)
Вычислим время t, за которое вылетят из стакана все моле-
кулы воды. Очевидно, что t = N/n, где N — число молекул воды,
масса которой т: N = —NA; M — молярная масса воды; NA —
постоянная Авогадро. Таким образом,
,_т /Уд _ ЮР-10~3.6.02-1023 _оо iq15
М п 18-10 -109
Учитывая, что 1 год содержит 365 сут = 365-24-3600 с =
= 31 536 000 с, получаем:
, 3,3 -10 . , ~й . ~r.
t = лет=1-Ш лет=100 млн лет.
31 536 000
Столько времени пришлось бы ждать, пока вылетят все молеку-
лы из 100 г воды. Даже если бы был всего 1 г воды, и то понадо-
билось бы на это миллион лет.
Обычно абитуриенты называют несколько часов или суток,
очень редко несколько недель; при этом они обосновывают ответ
известным из практики фактом: если оставить открытым стакан
с водой, то она через несколько дней испарится. Но, во-первых,
в задаче говорится не об испарении, а во-вторых, сопоставив
опытный факт с приведенным выше расчетом, можно сделать
148
вывод, что при испарении каждую секунду вылетает не 109 моле-
кул, а во много раз больше.
80. Абитуриенты, не имеющие четких представлений о моле-
кулярно-кинетической теории строения вещества, не могли объ-
яснить физический смысл понятия «температура», несмотря на
то что этот вопрос подробно изложен в учебнике для средней
школы. Встречался такой ответ: «Температура — это степень на-
гретости тела». При этом подразумевалось ощущение, возникаю-
щее при прикосновении к предмету, т. е. физический смысл поня-
тия «температура» ошибочно сводился к субъективному физио-
логическому понятию «степень нагретости».
Как известно, температура — это физическая величина,
т. е. измеряемая характеристика физических объектов. Приведем
следующее определение. Абсолютная температура — это скаляр-
ная физическая величина, характеризующая интенсивность хао-
тического движения молекул (или атомов), образующих систему.
и пропорциональная средней кинетической энергии одной моле-
кулы (или атома).
Напомним, что системой в молекулярной физике называется
как отдельное макроскопическое тело, так и совокупность та-
ких тел.
Температура является мерой средней кинетической энергии
хаотически движущихся частиц. Чем больше их средняя ско-
рость, тем выше температура системы, и наоборот, чем меньше
эта скорость, тем ниже температура. В принципе можно было бы
измерять температуру в единицах энергии—джоулях, но, во-
первых, непосредственно измерить кинетическую энергию моле-
кул трудно и, во-вторых, это очень малая величина. Поэтому для
измерения температуры используют зависимость от нее какой-
нибудь физической величины. Например, в устройстве ртутного
термометра используется увеличение объема ртути при нагрева-
нии. Если ртутный термометр привести в тепловой контакт с ка-
ким-нибудь телом, то с течением времени между ними устано-
вится состояние теплового равновесия, т. е. средние кинетиче-
ские энергии хаотического движения молекул ртути и тела ста-
нут одинаковыми. Это состояние характеризуется одинаковостью
температур.
Температура характеризует состояние тела независимо от его
массы и химического состава, поэтому температура является па-
раметром состояния.
По шкале Цельсия за нулевую температуру принята темпе-
ратура тающего льда, а за 100 градусов — температура кипя-
щей воды при нормальном атмосферном давлении. По абсолют-
ной шкале температур (шкале Кельвина) за нулевую температу-
ру принят абсолютный нуль температуры, т. е. температура, при
которой давление идеального газа при постоянном объеме дол-
жно быть равно нулю. По размеру один кельвин и один градус
Цельсия равны: 1°С=1 К.
149
Абсолютный нуль температуры соответствует — 273 °С (бо-
лее точно,— 273,15°С). Таким образом, абсолютная шкала и
шкала Цельсия смещены относительно друг друга: если по шка-
ле Цельсия значение температуры равно t, то по абсолютной
шкале ему соответствует температура 7" = ^4-273.
Обратим внимание на то, что при приближении температуры
к абсолютному нулю средняя скорость хаотического движения
молекул также стремится к нулю, а при температуре, равной аб-
солютному нулю, тепловое движение молекул прекращается.
Часто в ответах абитуриентов встречается утверждение, что
при абсолютном нуле прекращается всякое движение частиц.
Это неверно. При 7^ = 0 К прекращается только тепловое (хаоти-
ческое) движение молекул и атомов, но не прекращается движе-
ние частиц, образующих молекулы и атомы (например, движе-
ние электронов вокруг ядер атомов), движение электронов в ме-
таллах и некоторые другие виды движения.
В термодинамике доказано, что достичь абсолютного нуля
температуры невозможно, но приближаться к нему можно сколь
угодно близко (достигнуты температуры в миллионные доли
кельвина).
81. Не всегда правильно объясняют экзаменуемые различие
между идеальными и реальными газами. Были, например, такие
ответы: «Идеальный газ — это реальный газ без примесей»,
«Идеальный газ — это реальный газ при низкой температуре»
и т. п.
Слово «идеальный» означает «воображаемый, реально не су-
ществующий». Идеальный газ — это теоретическая модель газа:
хаотически движущиеся молекулы между собой не взаимодейст-
вуют на расстоянии; собственный суммарный объем молекул ни-
чтожно мал по сравнению с объемом сосуда, в котором находит-
ся газ; соударения молекул друг с другом и со стенками сосуда
являются абсолютно упругими, т. е. молекулы при столкновении
ведут себя подобно маленьким твердым шарикам.
Идеальный газ подчиняется уравнению Менделеева — Кла-
пейрона, а также газовым законам (законам Бойля — Мариотта,
Гей-Люссака и Шарля). Реальный газ отличается от идеального
наличием взаимодействия молекул. При малых плотностях в нем
преобладают силы притяжения, что приводит к появлению до-
полнительного давления: газ как бы сжимает сам себя. При
больших плотностях действуют силы отталкивания, вследствие
чего молекула не допускает проникновения других молекул в за-
нимаемый ею объем. Пренебрегать собственным объемом моле-
кул реального газа нельзя.
При не слишком высоком давлении (например, при атмо-
сферном) и не слишком низкой температуре (например, при ком-
натной) реальный газ с достаточной степенью точности подчиня-
ется законам идеального газа.
82. Экзаменуемые довольно часто на вопрос: «Какой вид име-
150
ет основное уравнение молекулярно-кинетической теории га-
зов?»— дают такой ответ:
pV = %RT. A)
Это ошибочный ответ. Напомним, что уравнение A) представля-
ет собой уравнение состояния идеального газа (уравнение Мен-
делеева — Клапейрона). Оно связывает макроскопические пара-
метры — давление р, объем V и температуру Т данной массы m
газа, молярная масса которого равна М. Здесь R — универсаль-
ная (молярная) газовая постоянная.
Основное уравнение молекулярно-кинетической теории газов
имеет вид:
p = ~nmo(v2), B)
где р — давление; п — концентрация молекул, т. е. число моле-
кул в единице объема; пг0 — масса одной молекулы; (v2) —
средний квадрат скорости молекул. Это уравнение связывает
макроскопический параметр — давление — с микроскопически-
ми величинами, характеризующими молекулы газа.
Уравнение Менделеева — Клапейрона A) является следстви-
ем основного уравнения молекулярно-кинетической теории га-
зов B).
83. Многие абитуриенты не могут правильно изобразить в
различных системах координат графики, выражающие связь
между параметрами состояния идеального газа в изопроцессах,
затрудняются сделать переход от графика в координатах р, V к
графикам в координатах р, Т и V, Т. Рассмотрим этот вопрос и
проиллюстрируем несколькими примерами.
Изопроцессами называются процессы, протекающие при по-
стоянной массе газа и неизменном значении одного из парамет-
ров: р, V или Т. Эти процессы подчиняются газовым законам, ко-
торые являются частными случаями уравнения Менделеева —
Клапейрона
PV = ^RT. A)
При m = const и 7 = const (изотермический процесс) на осно-
вании уравнения A) получаем зависимость
pl/ = const,
выражающую закон Бойля — Мариотта: для газа данной массы
при постоянной температуре произведение давления газа на его
объем остается постоянным.
График этой зависимости называется изотермой. В координа-
тах р, V (рис. 107, а) изотерма / представляет собой гиперболу
(обратная пропорциональная зависимость), в координатах р,
Т (рис. 107,6) и V, Т (рис. 107, в) изотерма / — прямая.
151
2
V 0
T 0
Рис. 107
При m = const и /? = const (изобарный процесс) из уравнения
A) следует:
_ = const.
Эта зависимость называется законом Гей-Люссака: для газа
данной массы при постоянном давлении отношение объема газа
к его температуре остается постоянным.
График этой зависимости называется изобарой. В координа-
тах р, V, а также р, Т и V, Т изобара 2 (рис. 107, а — в соответст-
венно) — прямая.
При m = const и J/ = const (изохорный процесс), из уравнения
A) имеем зависимость
-^• = const,
которая называется законом Шарля: для газа данной массы при
постоянном объеме отношение давления газа к его температуре
остается постоянным.
График этой зависимости называется изохорой. В координа-
тах р, V, а также р, Т и V, Т изохора 3 (рис. 107, а — в соответст-
венно) — прямая.
Рассмотрим примеры решения графических задач, которые
вызывали затруднения у многих экзаменуемых.
Задача /.В координатах р, V (рис. 108, а) изображен гра-
фик зависимости давления р от объема V при переходе идеаль-
ного газа из состояния / в состояние 2. Как изменялась темпера-
тура в этом процессе?
Решение. Проведем две изотермы так, что одна из них
пройдет через точку /, а вторая — через точку 2 (рис. 108,6).
Обозначим через 7, температуру, соответствующую первой изо-
терме, Т2 — второй изотерме. Чтобы выяснить, какая из этих
температур выше, проведем произвольную изохору, пересекаю-
щую изотермы в точках А и В. При постоянном объеме, согласно
закону Шарля, у = const. Следовательно,
152
т.
где рА, рв — давление газа в состояниях А и В соответственно;
Тл, Тн — температура в этих состояниях. Отсюда находим:
т _ Р» г
'в-—'а-
Но, как видно из рисунка 108, б, рв~>рА. Следовательно, ТН^>ТА,
т. е. для данного газа данной массы большему давлению соот-
ветствует большая температура. Таким образом, мы приходим
к выводу, что изотерма, проходящая через точку 2, соответствует
более высокой температуре, чем изотерма, проходящая через
точку /, т. е. Г2>7',. Значит, температура газа при переходе из
состояния / в состояние 2 увеличилась.
Задача 2. График зависимости давления р идеального газа
от его температуры Т в некотором процессе изображен на рисун-
ке 109, а. Определить, сжимался или расширялся газ при пере-
ходе из состояния / в состояние 2.
Решение. Используем прием, аналогичный примененному
при решении предыдущей задачи. Проведем две изохоры, одна
из которых проходит через точку /, вторая — через точку 2 (рис.
109, б), т. е. первая изохора соответствует объему V, в состоянии
/, вторая — объему V2 в состоянии 2. Проведем произвольную
изотерму, пересекающую изохоры в точках А и В. Согласно зако-
ну Бойля — Мариотта, при постоянной температуре /?K=const.
Следовательно,
где рА, VA — давление и объем газа в состоянии А; рв, Vв — в со-
стоянии В. Отсюда
Рв
153
p \
Рис. 109
а так как рл<СРв, то VH<C Vл, т. е. для данного газа данной мас-
сы большему давлению соответствует меньший объем.
Таким образом, мы приходим к выводу, что V2<zVu т. е. при
переходе из состояния / в состояние 2 газ сжимался.
Читателю предлагается теперь самостоятельно решить следу-
ющую графическую задачу.
Задача 3. На рисунке 109, в изображен график зависимо-
сти объема V идеального газа от его температуры Т при перехо-
де из состояния / в состояние 2. Определить, как изменялось
давление газа в этом процессе.
Рассмотрим еще две графические задачи.
Задача 4. Начертить графики изотермического расшире-
ния идеального газа данной массы в координатах р, V; 7', V; р, р\
р, Т, где р, V, Т и р — соответственно давление, объем, темпера-
тура и плотность газа.
Решение. Как отмечалось выше, при изотермическом про-
цессе (m = const, r = const) справедлив закон Бойля—Мариот-
та: pV = const. График этой зависимости (изотерма) показан на
рисунке 110, а в координатах р, V. В координатах Т, V эта изо-
терма дана на рисунке 110,6.
Найдем теперь зависимость плотности идеального газа от
давления и температуры. Как известно, плотность
Р = у. A)
где m — масса газа; V — его объем.
Из уравнения Менделеева — Клапейрона pV = —RT выра-
зим массу:
m =
pVM
RT
Подставив выражение B) в формулу A
для плотности идеального газа:
рМ
B)
получим выражение
Р =
RT
154
О V,
p
JJi
л-
в
/
О А
Отсюда видно, что при изотермическом расширении газа его
плотность прямо пропорциональна давлению. Учитывая это, на-
чертим графики в координатах р, р и р, Т (рис. 100, в, г соответ-
ственно).
Задача 5. На рисунке 111 изображены две изотермы для
двух различных газов, имеющих одинаковые массу и температу-
ру. Требуется сравнить молярные массы этих газов.
Решение. По условию задачи газы имеют одинаковую мас-
су m и одинаковую температуру Т. Рассмотрим на различных
изотермах два состояния А и В, которым соответствует один и
тот же объем V. Запишем уравнение Менделеева — Клапейрона
для этих состояний:
155
где Мь М2 — молярная масса первого и второго газов соответст-
венно. Разделив почленно первое уравнение на второе, получим:
_ = _, откуда
Учитывая, что /7, <С/72, приходим к выводу, что Af2<CM|,
т. е. изотерма 2 соответствует газу, имеющему меньшую моляр-
ную массу, чем газ, которому соответствует изотерма /.
Абитуриенты, формально усвоившие закон Бойля — Мариот-
та, эту задачу не могли решить. Некоторые из них вспоминали,
что различным температурам соответствуют различные изотер-
мы, но не знали, что это справедливо только для данного газа
данной массы. Как показано при решении этой задачи, изотер-
мы, соответствующие одной и той же температуре, но различным
газам, могут не совпадать вследствие различия масс и молярных
масс газов, так как от этих величин зависит константа, входя-
щая в математическое выражение закона Бойля — Мариотта
pV = const. В самом деле, это выражение, как отмечалось выше,
является частным случаем уравнения Менделеева — Клапейро-
на. Поэтому
const = — RT.
м
Отсюда видно, что константа имеет различные значения при
различных т, М и Т. Чем больше числовое значение этой кон-
станты, тем дальше от начала координат р, V будет распо-
лагаться соответствующая изотерма.
84. Затруднения у абитуриентов вызывают, как правило, за-
дачи, связанные с нахождением давления газа. Рассмотрим одну
из них.
Задача. Закрытая с одного конца пробкой стеклянная
трубка погружена вертикально открытым концом в сосуд с во-
дой, при этом вода в трубке поднялась на высоту h (рис. 112).
Каково атмосферное давление, если длина трубки от пробки до
открытого конца равна /, а глубина погружения трубки //?
Плотность воды равна р. (Искривлением поверхности воды в
трубке пренебречь.)
Решая эту задачу, абитуриенты чаще всего обращают внима-
ние на трубку и воду, упуская из виду самое главное — воздух,
заполняющий трубку. Поэтому они не учитывают, что уровень
воды в трубке зависит от давления находящегося в ней воздуха.
Ниже приводится правильное решение этой задачи.
Решение. Температура и масса воздуха в трубке остаются
постоянными, поэтому выполняется закон Бойля — Мариотта:
156
P]Vl-=p2V2. A)
где ри V\ — соответственно давление и объем воздуха в трубке
до погружения ее в воду; р2, V2 — после погружения.
h
1
В
*
\
>r-j-i-z-z-r-r-:
Рис. 112
До погружения давление /?, в открытой трубке равно атмо-
сферному давлению /?а, а объем У, = /5, где 5 — площадь попе-
речного сечения трубки. После погружения трубки в воду воздух
стал занимать объем V2 = (l — h)S. Найдем давление воздуха р2
в этом состоянии. Давления в точках А и В одинаковы, так как
эти точки находятся на одном уровне. Выразим эти давления:
где р — плотность воды; Н, h — высоты столбов воды в сосуде
и трубке соответственно.
С учетом равенства рд = Рв получим:
Подставив теперь выражения для pu Vh p2 и V2 в уравнение
A), получим:
nJS = (Ps + 9g(H-h))(l-h)S,
откуда найдем атмосферное давление:
85. Рассматривая переход идеального газа из одного состоя-
ния в другое, абитуриенты при решении задач нередко ошибочно
применяют уравнение Клапейрона там, где этого делать нельзя.
Напомним, что уравнение Клапейрона (объединенный газо-
вый закон) связывает давление, объем и температуру идеально-
го газа в двух любых состояниях, если при переходе из одного
состояния в другое масса газа остается постоянной. Это уравне-
ние имеет вид:
157
^± = ?±.2 или i^_ = const при m = const. A)
Если же масса газа изменяется, то приведенное соотношение
между параметрами р, V и Т не выполняется.
Задача 1. В баллоне содержится сжатый газ при темпера-
туре /, = 27°С и давлении /7, = 4 МПа. Каково будет давление,
если из баллона выпустить п = 0,4 массы газа, а температуру
понизить до /2=17°С?
При решении этой задачи некоторые из экзаменующихся до-
пускали такие ошибки: применяли уравнение Клапейрона; под-
ставляли в формулу A) при вычислениях значение температуры
в градусах Цельсия, ошибочно считая, что это можно делать, так
как в уравнение A) температура входит в качестве делителя в
левую и правую части.
Решение. Рассмотрим два состояния газа: до разрежения
и после, когда осталось 1 — п массы m газа. Параметры каждого
из этих состояний связаны уравнением Менделеева — Клапей-
рона:
(' ~п) m ПТ
где /?,, Ти р2, Т2 — соответственно давление и температура газа
до и после выпуска; пг — масса газа; М — молярная масса; V —
объем.
Разделив почленно первое равенство на второе, получим:
Pi (\—п)Т2 '
откуда
(\~п)РхТ2
Рч — 7 • \z)
• i
Выразим заданные значения в единицах СИ: Pi = 4 МПА =
= 4-106 Па, 7м = 27+ 273 = 300 К, Т2= 17 + 273 = 290 К. После
подстановки этих значений в формулу B) и вычислений по-
лучим: р2 = 2,3-106 Па = 2,3 МПа.
Задача 2. В вертикальном цилиндрическом сосуде, пло-
щадь дна которого S= 100 см2, содержится воздух при темпера-
туре ^i = 12°C. На высоте /г, = 60 см от дна находится поршень.
На какой высоте от дна расположится поршень, если на него по-
ставить груз массой пг= 100 кг, а затем воздух в сосуде нагреть
до температуры /2 = 27°С? Атмосферное давление pa = l05 Па.
Поршень считать невесомым и трением его о стенки сосуда
пренебречь.
Решение. В отличие от предыдущей задачи здесь можно
воспользоваться уравнением Клапейрона, потому что масса газа
в сосуде остается постоянной. Абитуриенты не всегда учитывали
158
это и поэтому испытывали затруднения при решении.
В первом состоянии, когда на поршне груза не было, давле-
ние воздуха в сосуде равно атмосферному давлению: Р\ = ря (что,
кстати сказать, не всегда замечали поступающие), объем
Vх = Sh{, абсолютная температура Г, = 12 + 273 = 285 К. После то-
го как на поршень положили груз и подогрели воздух, он пере-
шел во второе состояние с температурой Т2 = 27-)-273 = 300 К и
объемом V2 = Sh2. В этом состоянии воздух в сосуде находился
под давлением, равным сумме атмосферного давления и давле-
ния, производимого весом груза, лежащего на поршне:
В соответствии с уравнением Клапейрона
_ ™
n2 — -
получим:
Отсюда
Подставив в эту формулу числовые значения величин и произве-
дя вычисления, получим Л2 = 0,32 м = 32 см.
86. Говоря об ошибках и затруднениях абитуриентов при ре-
шении задач, нельзя обойти задачи, связанные с давлением сме-
си газов. Дело в том, что в школьном учебнике физики вопрос
о смеси газов лишь кратко рассматривается при изучении влаж-
ности воздуха. Там говорится, что атмосферный воздух пред-
ставляет собой смесь различных газов и водяного пара и что
каждый из газов вносит свой вклад в суммарное давление, про-
изводимое воздухом на находящиеся в нем тела. Вводится поня-
тие парциального давления водяного пара как давления, которое
производил бы водяной пар, если бы все остальные газы отсут-
ствовали.
У многих поступающих сложилось представление, будто по-
нятие парциального давления относится только к водяному
пару, что неверно. По-видимому, вследствие этого они не могут
установить связь между давлением смеси газов и их парциаль-
ным давлением. Покажем эту связь.
Пусть в сосуде находится смесь N различных газов при тем-
пературе Т и давлении р. Как и для любого идеального газа, для
159
смеси газов зависимость давления от температуры выражается
формулой
P = nkT, A)
где п — концентрация молекул, т. е. число молекул в единице
объема; k — постоянная Больцмана.
Парциальным давлением называется давление газа, входя-
щего в состав газовой смеси, которое он производил бы, если бы
он один занимал весь объем смеси и находился при температуре
смеси. (Парциальный (от лат. pars — часть) — частичный, от-
дельный.)
На основании этого определения и формулы A) выразим пар-
циальные давления составляющих смесь газов:
pi = n[kT, p2 = n2kT, ..., pN = nNkT.
Сложив почленно эти уравнения, получим:
Учитывая, что сумма концентраций газов, входящих в смесь,
равна концентрации этой смеси, т. е. nt-\-n2-\- ...-\-nN = n, имеем:
B)
Из уравнений A) и B) следует:
Это уравнение выражает закон Дальтона: давление смеси газов,
химически не взаимодействующих между собой, равно сумме их
парциальных давлений.
Задача. Найти плотность смеси кислорода массой /п, =64 г
и азота массой т2 = 56 г при температуре t = 27°C и давлении
р=\05 Па. Молярная масса кислорода Af]=32-10~3 кг/м3, азо-
та М2 = 28-10 кг/м3.
Решение. Плотность любого идеального газа, согласно
определению, равна отношению массы газа к его объему:
m ...
Р = у- A)
Из уравнения Менделеева — Клапейрона
рУ~ЯТ B)
следует:
y_mRT
рМ '
Подставив это выражение в формулу A), получим:
где р — давление; М — молярная масса газа; R — универсаль-
ная газовая постоянная; Т — температура.
160
Формула C) применима, разумеется, и к смеси, так как смесь
идеальных газов тоже представляет собой идеальный газ.
Найдем теперь молярную массу смеси газов. Пусть рх и р2 —
парциальные давления кислорода и азота соответственно, V —
объем смеси, Т — ее температура. Тогда, согласно уравнению
Менделеева — Клапейрона, имеем:
Сложив почленно эти уравнения, получим:
Учитывая, что, согласно закону Дальтона, /?i+/?2 = /?, будем
иметь:
Так как для смеси газов справедливо уравнение B), где
т = ш, + тг — масса смеси; М — ее молярная масса, то на осно-
вании уравнений B) и D) получим:
га, ~\- га2 га, т2
М Мх М2 '
откуда молярная масса смеси газов
М=-
Подставив это выражение в формулу C), найдем плотность
смеси:
p(m + m)
Выразим значения заданных величин в единицах СИ:
т, = 64 - 10~3 кг, /п2 = 56-Ю-3 кг, Г = 27+ 273 = 300 К,
/? = 8,31 Дж/(моль-К). Подставив в формулу E) числовые значе-
ния и произведя вычисления, получим р = 1,2 кг/м3.
Нетрудно показать, что в случае смеси iV различных газов
молярная масса смеси
87. При решении задач по молекулярной физике и газовым
законам абитуриенты допускают, кроме отмеченных выше, и
6 Заказ 2473 161
другие ошибки. Обнаруживаются пробелы в знаниях, а довольно
часто — и неумение применить знания для анализа конкретной
физической задачи.
Задачи на газовые законы можно решать по следующему
плану.
Если в задаче рассматривается одно состояние газа и требу-
ется найти какой-либо параметр этого состояния, нужно вос-
пользоваться уравнением Менделеева — Клапейрона. Если зна-
чения давления и объема явно не заданы, их нужно выразить че-
рез заданные величины, подставить в записанное уравнение и,
решив его, найти неизвестный параметр.
В том случае, когда в задаче рассматриваются два различ-
ных состояния газа, нужно установить, изменяется ли масса газа
при переходе из одного состояния в другое. Если масса остается
постоянной, можно применить уравнение Клапейрона. Если же
при постоянной массе в данном процессе не изменяется какой-
либо из параметров (р, V или Т), применяют уравнение соответст-
вующего закона (Гей-Люссака, Шарля или Бойля — Мариотта).
Если в двух состояниях масса газа разная, то для каждого
состояния записывают уравнение Менделеева — Клапейрона.
Затем систему уравнений решают относительно искомой вели-
чины.
ТЕПЛОВЫЕ ЯВЛЕНИЯ
88. Довольно часто абитуриенты дают неправильные опреде-
ления таких понятий, как удельная теплота плавления, удельная
теплота парообразования, удельная теплота сгорания топлива.
Приходилось слышать, например, такой ответ: «Удельная тепло-
та плавления — это количество теплоты, необходимое для пере-
хода 1 кг вещества из твердого состояния в жидкое». Здесь допу-
щена, во-первых, грубая ошибка: не указано, что вещество дол-
жно быть взято при температуре плавления. Во-вторых, удель-
ная теплота плавления и количество теплоты — это различные
величины. Единицей удельной теплоты плавления является джо-
уль на килограмм (Дж/кг), единицей количества теплоты —
джоуль (Дж). Напомним правильное определение: удельной теп-
лотой плавления называется величина, равная количеству тепло-
ты, которое необходимо для превращения одного килограмма
кристаллического вещества при температуре плавления в жид-
кость той же температуры.
Приведем еще один пример грубой ошибки. Экзаменующийся
давал такое определение: «Удельная теплота сгорания — это ко-
личество теплоты, необходимое для сгорания 1 кг топлива». Как
известно, при сгорании топлива количество теплоты не поглоща-
ется, а выделяется.
Удельной теплотой сгорания называется величина, равная
Г62
количеству теплоты, которое выделяется при полном сгорании
1 кг топлива.
Обратим внимание на то, что используемые при изучении
тепловых явлений понятия удельная теплота плавления X, удель-
ная теплота парообразования г, удельная теплота сгорания q яв-
ляются частными случаями понятия удельного количества теп-
лоты.
Удельным количеством теплоты q называется величина, рав-
ная отношению количества теплоты Q, полученного (или пере-
данного) системой, к массе системы:
Поэтому единицы величин k, r и q одинаковые:
W = [r} = [q}= 1 Дж/кг.
Вообще, прилагательное «удельный» дополнительно применя-
ется для величин, представляющих собой отношение какой-либо
физической величины к массе тела. Например, удельным объе-
мом называют величину, равную отношению объема V тела к его
массе m:v=V/m. Единица удельного объема [р]=1 м3/кг.
89. Некоторые из поступающих не различают понятия тепло-
емкости тела и удельной теплоемкости. Ниже приводятся пра-
вильные определения.
Теплоемкостью С тела (или системы тел) называется величи-
на, равная отношению количества теплоты Q, подводимого к те-
лу (или отводимого от него), к изменению температуры AT при
подводе (или отводе) теплоты:
где АТ=Т2—Т1.
Удельной теплоемкостью с вещества называется величина,
равная отношению теплоемкости однородного тела к его массе:
m mAT'
Единицы этих величин: [С]=1 Дж/К, [с]=1 Дж/(кг-К).
Иначе говоря, теплоемкость тела численно равна количеству
теплоты, которое получает или отдает тело при изменении его
температуры на 1 К, а удельная теплоемкость — количеству теп-
лоты, которое получает или отдает 1 кг вещества при изменении
его температуры на 1 К-
90. При решении задач, связанных с нахождением количества
теплоты, абитуриенты часто не учитывают количества теплоты,
которое выделяется или поглощается при переходе вещества из
одного агрегатного состояния в другое.
Многие забывают, что при кристаллизации (затвердевании)
выделяется такое же количество теплоты, какое поглощается
163
при плавлении; при конденсации выделяется такое же количе-
ство теплоты, какое поглощается при испарении.
Задача I. Какое количество теплоты необходимо затра-
тить, чтобы кусок льда массой т = 20 г, взятый при температуре
*i= —15 °С, превратить в пар при температуре /2=100°С?
Удельная теплоемкость льда c, = 2,M0d Дж/(кг-К), воды
с2 = 4,19-10л Дж/(кг-К), удельная теплота плавления льда
^ = 3,3-105 Дж/кг, удельная теплота парообразования воды
л = 22,6-105 Дж/кг.
Решение. Для превращения льда в пар необходимо коли-
чество теплоты
где Q, — количество теплоты, необходимое для нагревания льда
до температуры плавления (/,1Л = 0°С):
Q1 = c1m{^1 —/,); B)
Q2 — количество теплоты, необходимое для превращения льда в
воду, т. е. теплота плавления льда:
Qi = Xm; C)
Q3 — количество теплоты, необходимое для нагревания образовав-
шейся воды до температуры t2:
Qz = c2m(t2-tlul); D)
Q4— количество теплоты, необходимое для превращения воды в
пар, т. е. теплота парообразования воды:
Qi = rm. E)
Подставив значения B) — E) в формулу A), получим:
После подстановки числовых значений величин и вычислений по-
лучим Q=60,81 кДж.
В некоторых решениях этой задачи поступающие не учитыва-
ли либо Q,, либо Q2.
Задача 2. Расплавленный металл массой /и, при темпера-
туре плавления /, вливают в сосуд с водой, масса которой т2,
температура t2- Какая температура установится в сосуде, если
его теплоемкость С? Испарение воды не учитывать.
Решение. Составим уравнение теплового баланса: количе-
ство теплоты, отданное металлом, равно количеству теплоты, по-
лученному водой и сосудом, т. е. Q0T= Qnojr Пусть / — температу-
ра, установившаяся после охлаждения металла. Тогда
где первое слагаемое — это количество теплоты, выделившееся
при затвердевании металла, второе — при охлаждении затвер-
164
девшего металла от температуры плавления tx до установившей-
ся температуры t; X — удельная теплота плавления металла;
с, — его удельная теплоемкость.
Полученное количество теплоты
где первое слагаемое—это количество теплоты, полученное во-
дой, второе — сосудом; с2— удельная теплоемкость воды.
Составим уравнение
Хтх + с{ту (/, — t) = c2m2 (t — t2) + C(t — t2), A)
решив которое получим:
mi (X-\-Cft^-^ t2 (C-\-c2m2)
С-\-с^тх-\-с2т2
При решении этой задачи абитуриенты, как правило, не учи-
тывали количество теплоты, выделившееся при затвердевании
(кристаллизации) металла.
В приведеном выше решении при составлении уравнения теп-
лового баланса мы везде из большего значения температуры вы-
читали меньшее, поэтому значения количеств теплоты всегда по-
лучались положительными. Возможен и другой подход к состав-
лению этого уравнения.
Количество теплоты, получаемое телом, будем считать поло-
жительным, а количество теплоты, отдаваемое телом,— отрица-
тельным. Тогда при теплообмене между телами замкнутой (изо-
лированной) системы алгебраическая сумма количеств теплоты,
полученных или отданных телами, равна нулю:
Это и есть уравнение теплового баланса. Составляя его, нужно
в формуле для подсчета количества теплоты
Q = cm (t2 — ?,)
всегда вычитать из конечной температуры t2 начальную /,. Тогда
в случае нагревания тела получим Q>0, а при охлаждении —
Q<0. Кроме того, нужно брать с минусом количество тепло-
ты, выделяемое при конденсации пара, т. е.
Qk = — гт,
где г—удельная теплота парообразования; т—масса пара.
Отрицательным следует считать также и количество теплоты,
выделяемое при кристаллизации:
где X—удельная теплота плавления; т—масса вещества.
Используя такой подход, решим приведенную выше задачу
другим способом. Составим уравнение теплового баланса:
165
(t-t2) = 0. C)
Легко видеть, что уравнение C) равносильно уравнению A),
т. е. в результате решения его мы получим такое же значение t.
Иногда абитуриенты при составлении уравнения B) допуска-
ют ошибки: при нахождении количества теплоты, отдаваемого
телом, вычитают из начальной температуры конечную.
91. В затруднительное положение ставили абитуриентов за-
дачи на составление уравнения теплового баланса, в которых ко-
нечное состояние системы не очевидно. Рассмотрим одну из та-
ких задач.
Задача. Смешивают /п,=300 г воды при температуре
/i = 10°C и /п9 = 400 г льда при температуре t2=—20 °С.
Определить установившуюся температуру 6 смеси. Удельная
теплоемкость воды С|=4,19-103 Дж/(кг-К), льда с2 = 2,1-10'3
Дж/(кг-К), удельная теплота плавления льда Я = 330• 103 Дж/кг.
Решение. Так как конечное состояние не очевидно, будем
решать задачу поэтапно. Подсчитаем сначала количество тепло-
ты, необходимое для нагревания льда до температуры плавле-
ния *пл = 0°С:
Дж.
Теперь найдем количество теплоты, которое отдает вода, ох-
лаждаясь до 0 °С:
<?, = c,mt(tl-iajl) = 12 570 Дж.
Мы видим, что для того, чтобы нагреть весь лед до 0 °С, недо-
стает Q2—Q]=4230 Дж. Такое количество теплоты выделится
при превращении в лед некоторой массы воды пг3:
откуда
пг3= Q'2~Ql = 12,8 г.
Таким образом, в конечном состоянии в сосуде будет
т2-\- т3 = 4\2,8 г льда и /п, — /п3 = 287,2 г воды при температуре
6 = 0°С
92. Многие поступающие слабо знают свойства паров. В ка-
честве примера грубой ошибки приведем один из ответов: «На-
сыщенный пар — это пар, в котором молекулы уже не возвраща-
ются обратно в жидкость». В действительности же насыщенным
называется пар, находящийся в динамическом равновесии со
своей жидкостью. Это означает, во-первых, что число молекул,
вылетающих из жидкости, равно в среднем числу молекул, воз-
вращающихся из пара в жидкость за то же время и, во-вторых,
что насыщенный пар — это пар, имеющий наибольшую плот-
ность при данной температуре.
166
Абитуриенты дают в лучшем случае приблизительно верное
качественное описание процессов, что же касается количест-
венных соотношений между параметрами пара, то здесь нередко
допускаются ошибки. Так, при решении задач применяют газо-
вые законы (Бойля — Мариотта, Гей-Люссака, Шарля), в то
время как насыщенный пар этим законам не подчиняется, пото-
му что при переходе из одного состояния в другое масса насы-
щенного пара изменяется. Указанным законам подчиняется не-
насыщенный пар, если его масса остается постоянной. Эти зако-
ны можно применять и к процессам перехода насыщенного пара
в ненасыщенный и наоборот, если при этом масса пара не изме-
няется.
В каждом состоянии насыщенного пара его параметры связа-
ны между собой уравнением Менделеева — Клапейрона.
Абитуриенты иногда ошибочно утверждают, что давление на-
сыщенного пара прямо пропорционально температуре.
Прямо пропорционально температуре растет давление идеаль-
ного газа, как это видно из формулы
р = nkT,
где п — концентрация молекул газа; k — постоянная Больцмана,
Т — температура.
Давление же насыщенного пара с ростом температуры рас-
тет быстрее, чем давление идеального газа, так как при этом не
только увеличивается скорость молекул, но и возрастает их кон-
центрация, потому что продолжается испарение жидкости, нахо-
дящейся в том же сосуде, что и пар.
При решении задач можно использовать справочные табли-
цы, в которых приводятся давление и плотность насыщенного
пара при данной температуре.
Некоторые экзаменующиеся затруднялись ответить на такой
вопрос: «Как можно превратить ненасыщенный водяной пар, на-
ходящийся в сосуде, в насыщенный?» Напомним, что такое пре-
вращение можно осуществить, во-первых, путем сжатия газа,
вставив в сосуд поршень и опуская его. Второй способ — охла-
дить пар. В процессе охлаждения при некоторой температуре на
стенках сосуда появятся капельки воды вследствие конденсации.
Это означает, что пар стал насыщенным.
Абитуриенты должны понимать, что ненасыщенный пар, от-
деленный от жидкости, переходит в насыщенный, если его изо-
термически сжимать или изохорно охлаждать. Температура, при
которой ненасыщенный пар превращается в насыщенный в ре-
зультате охлаждения, называется точкой росы.
Насыщенный пар можно превратить в ненасыщенный путем
изотермического расширения или изохорного нагревания.
При решении задач, связанных с влажностью воздуха, ошиб-
ки возникают в основном по двум причинам. Первая причина —
плохое знание определения понятия «относительная влажность».
167
Так, например, не могут ответить на вопрос: «Какова относитель-
ная влажность насыщенного пара?»
Правильный ответ— 100%. Это очевидно, если вспомнить
определение: относительной влажностью ср называется отноше-
ние парциального давления р водяного пара, содержащегося в
воздухе при данной температуре, к давлению р0 насыщенного
водяного пара при той же температуре, выраженное в про-
центах:
Ф = ^-.100%. A)
В некоторых задачах нужно находить либо массу водяного
пара, содержащегося в заданном объеме воздуха, либо массу во-
ды, которую нужно испарить, чтобы довести влажность до неко-
торого требуемого значения. Такие задачи, как правило, приво-
дят абитуриентов к затруднениям и ошибкам. В связи с этим от-
метим, что относительную влажность можно определить, исполь-
зуя понятие абсолютной влажности.
Абсолютной влажностью р называется величина, равная мас-
се водяного пара, содержащегося в 1 м3 воздуха. Иначе говоря,
абсолютная влажность — это плотность водяного пара, находя-
щегося в воздухе.
Относительную влажность можно определить как отношение
абсолютной влажности р к плотности р0 насыщенного водяного
пара при данной температуре, выраженное в процентах,
ф %. B)
Ро
Оба определения эквивалентны, потому что отношение давле-
ний равно отношению плотностей. Это легко показать. Выше
(п. 86) мы, используя уравнение Менделеева — Клапейрона,
выразили плотность идеального газа при давлении р и темпера-
туре 7":
¦¦=#¦ <3>
Считая, что водяной пар ведет себя подобно идеальному газу, на
основании этой формулы получим:
_р_ = _р_
Ро Ро'
Поэтому при расчетах можно использовать как выражение A),
так и B). Другое дело, что практически легче измерить давле-
ние, чем плотность пара, находящегося в воздухе, поэтому отно-
сительную влажность определяют через давление.
Конечно, при решении задач можно, зная давление, найти
плотность, используя формулу C). Но нередко решение получа-
ется более наглядным и понятным, если применять определяю-
щее выражение B).
Задача. Вечером температура воздуха была /, = 15°С, от-
168
носительная влажность ф = 80%. Ночью температура воздуха
понизилась до /2 = 8°С. Была ли роса? При температуре 15 °С
плотность насыщенного водяного пара рш=12,8 г/м3, а при
8°С — рО2 = 8,3 г/м3.
Решение. Насыщенный пар — это пар, имеющий макси-
мальную плотность при данной температуре. Поэтому, чтобы уз-
нать, была ли роса, найдем плотность р, водяного пара при тем-
пературе /, и сравним ее с плотностью р02 насыщенного водяного
пара при температуре t2. Если р, -< р02, пар конденсироваться не
будет (не будет росы). Если же pi>pO2> то роса будет, причем из
каждого 1 м3 влажного воздуха сконденсируется масса пара,
численно равная разности р,—р02.
Так как относительная влажность <p = Pi/Poi, то pi = <ppoi =
= 0,8-12,8 г/м3?» 10,2 г/м3. Сравнивая это значение с рО2 =
= 8,3 г/м3, делаем вывод: роса была, причем из каждого 1 м3
воздуха сконденсировалось 1,9 г пара.
93. Многие экзаменующиеся неверно объясняют процесс ки-
пения, зависимость температуры кипения от давления. Некото-
рые, например, говорят, что кипение — это интенсивный процесс
отрыва молекул от поверхности сильно нагретой жидкости, что
с понижением атмосферного давления молекулам легче вырвать-
ся из жидкости, и поэтому температура кипения понижается.
Встречались и такие ответы: «Кипение — это вытеснение воз-
душных пузырьков из жидкости».
В действительности кипение — это процесс перехода жидко-
сти в пар, происходящий с образованием в объеме жидкости пу-
зырьков пара. Эти пузырьки пара возникают вследствие испаре-
ния жидкости внутрь мельчайших пузырьков газа, имеющихся
на дне и стенках сосуда. Пузырьки газа наполняются насыщен-
ным паром, давление которого с повышением температуры уве-
личивается. Когда давление внутри пузырька становится немно-
го больше внешнего давления, которое равно сумме атмосферно-
го и гидростатического давлений, пузырек всплывает на поверх-
ность и лопается.
Давление насыщенного пара зависит от температуры. Поэто-
му температура кипения зависит от внешнего давления. С умень-
шением внешнего давления температура кипения понижается, с
увеличением — повышается. Температуры кипения различных
жидкостей неодинаковы, так как давления насыщенных паров
этих жидкостей при одной и той же температуре отли-
чаются друг от друга.
Почему при неизменном внешнем давлении температура ки-
пящей жидкости не повышается, хотя мы и подводим к ней неко-
торое количество теплоты? На этот вопрос абитуриенты редко
дают правильный ответ.
Дело в том, что энергия, подводимая к кипящей жидкости из-
вне, расходуется на увеличение потенциальной энергии взаимо-
действия молекул. Пар, вылетающий из лопающегося на поверх-
169
ности кипящей жидкости пузырька, расширяется и, следователь-
но, охлаждается, поэтому от жидкости отнимается некоторое
количество теплоты. Чем больше количество теплоты подводим
к жидкости, тем большее количество теплоты отнимается от нее,
так как возрастает число лопающихся пузырьков. Поэтому тем-
пература кипения остается постоянной.
94. Формализм знаний теоретического материала, неумение
применить его в заданной ситуации обнаруживает значительная
часть абитуриентов в ответах на вопросы и в решениях задач,
связанных с первым законом термодинамики. Например, очень
редко можно услышать правильный и обоснованный ответ на во-
прос экзаменатора: «От чего зависит удельная теплоемкость
идеального газа?»
Чтобы ответить на этот вопрос, надо вспомнить первый закон
термодинамики: количество теплоты, сообщенное системе, расхо-
дуется на изменение ее внутренней энергии и на совершение сис-
темой работы над внешними телами, т. е.
. A)
Пусть, например, в цилиндре, закрытом подвижным порш-
нем, находится газ (рис. 113). Если газ нагревать, то при этом
будет повышаться его температура, т. е. увеличиваться внутрен-
няя энергия, и, кроме того, будет отодвигаться поршень, совер-
шая некоторую работу против внешних сил.
Вспомним теперь, что удельная теплоемкость газа
'--if- <2>
где Q — количество теплоты, подводимое к газу массой m для
повышения его температуры на А7'.
Теплоемкость зависит от условий, при которых происходит
нагревание газа.
На основании выражений A) и B) имеем:
AU . А ._.
с = —— -\ — C)
где А — работа, совершаемая газом при переходе из одного состо-
яния в другое. Но такой переход может быть осуществлен раз-
личными способами, и совершаемая при этом работа будет раз-
личной. Поясним это на примере. Из состояния а (рис. 114) в со-
стояние b газ переводится двумя способами: / и 2. Изменение
At/ внутренней энергии газа в первом и во втором процессах од-
но и то же. В первом процессе газ совершает работу Аь числен-
но равную площади фигуры Vxa]bV2, а во втором —А2, численно
равную площади фигуры V,a2bV2. Ясно, что Л,>Л2, а из уравне-
ния A) следует, что Q, > Q2, т. е. в первом процессе к газу подве-
дено большее количество теплоты, чем во втором. Поэтому на
основании формулы C) приходим к выводу: удельная теплоем-
кость газа в первом процессе больше, чем во втором.
170
¦ ¦'.¦ли'-':.
Q
I
//>
//
A
1
i
i
I
l
i
Vi
V? V
Рис. 113
Рис. 114
Существует много способов перехода газа из одного состоя-
ния в другое, и каждому из них соответствуют различные значе-
ния совершаемой газом работы и, следовательно, различные
значения теплоемкости. Поэтому можно говорить о какой-то
определенной удельной теплоемкости только применительно к
какому-то определенному процессу.
Сравним, например, удельную теплоемкость ср идеального га-
за при постоянном давлении с удельной теплоемкостью cv этого
газа при постоянном объеме. В первом случае происходит изо-
барный процесс, поршень отходит вправо (см. рис. 113), при этом
совершается работа
Эту работу можно выразить и другой формулой, которую, как
правило, многие абитуриенты не знают:
Л=^ггЛ!А7\ E)
где m — масса газа; М — его молярная масса; ЛГ= 7— Tt — из-
менение температуры.
Вывод формулы E) очень простой. Запишем уравнение Мен-
делеева — Клапейрона для двух состояний газа — до изобарного
расширения и после него:
Вычитая почленно первое уравнение из второго, получаем выра-
жение:
левая часть которого, согласно формуле D), и есть работа газа
при изобарном расширении. Следовательно, эта работа может
быть выражена формулой E).
Подставив значение работы E) в формулу C), получим:
171
Л (У . R
+ лГ- F)
При изохорном нагревании объем газа остается постоянным,
поршень закреплен, неподвижен, работа газом не совершается:
Л=0. Следовательно, согласно формуле C), при постоянном
объеме удельная теплоемкость идеального газа
AU
Сравнив выражения F) и G), получим:
^ = ^ + 1- (8)
Таким образом, cp^>cv. Практически это означает, что для
повышения температуры газа на одну и ту же величину Л7' при
постоянном давлении к газу нужно подвести большее количество
теплоты, чем при постоянном объеме.
Попутно обратим внимание, что на основании формулы E)
можно пояснить физический смысл универсальной газовой по-
стоянной R. Если — — v= 1 моль и AT = 1 К, то А = R, т. е. уни-
версальная газовая постоянная R численно равна рабо-
те, которую совершает в изобарном процессе 1 моль идеаль-
ного газа при повышении его температуры на 1 К: /? =
= 8,31 Дж/(моль-/().
А какова удельная теплоемкость газа в изотермическом про-
цессе? В этом процессе внутренняя энергия газа не изменяется
(Л?/ = 0), температура остается постоянной, т. е. А7 = 0, поэтому
удельная теплоемкость
Ст = ——= оо.
Согласно первому закону термодинамики, в изотермическом
процессе Q = A, т. е. все переданное газу количество теплоты
Q затрачивается на работу А, совершаемую газом против внеш-
них сил.
На примере этого процесса отметим, что, применяя термин
«нагревание», надо точно указывать, что имеется в виду — под-
вод некоторого количества теплоты или повышение температу-
ры, так как не всякий подвод количества теплоты сопровожда-
ется повышением температуры. Например, в изотермическом
процессе температура не изменяется, какое бы количество теп-
лоты мы ни сообщали системе.
В адиабатном процессе теплообмен отсутствует (Q = 0),
поэтому удельная теплоемкость газа сад = 0. В этом процессе,
согласно первому закону термодинамики, 0 = AU-\-А или А =
= —At/, т. е. при адиабатном расширении газ совершает рабо-
ту за счет убыли его внутренней энергии. Вследствие этого его
172
температура понижается. Если же под действием внешних сил
газ адиабатно сжимается, то его внутренняя энергия увеличива-
ется и температура повышается, хотя к нему не подводили коли-
чество теплоты.
Теперь решим одну из задач, предлагавшихся на экзамене.
Задача. Найти удельную теплоемкость гелия при постоян-
ном давлении. Молярная масса гелия М=4-10~3 кг/моль.
Решение. На основании первого закона термодинамики
выше была выведена формула F) (абитуриент должен сам сде-
лать ее вывод). Гелий — газ одноатомный, поэтому изменение
его внутренней энергии можно определить по формуле
Подставив это выражение в формулу F), получим:
_ 5R _ 5-8,31
-1-3
Дж/(кг-К) = 5,2 кДж/(кг-К).
2-4-10"
Обычно эта задача вызывает затруднение у абитуриентов, хо-
тя они знают и первый закон термодинамики, и выражение для
внутренней энергии одноатомного идеального газа. Отчасти это
объясняется, по-видимому, тем, что в школьной программе мало
внимания уделено вопросу о теплоемкости газов. Основная же
причина — неумение использовать полученные знания при реше-
нии задач.
95. Приведем еще один пример. На экзамене по физике аби-
туриент правильно рассказывает о том, что работа газа в изо-
термическом процессе численно равна площади фигуры, ограни-
ченной графиком зависимости давления р от объема V, осью V и
отрезками ab и cd, численно равными давлениям рх и р2 в началь-
ном и конечном состояниях (рис. 115). Из курса математики сред-
ней школы поступающий знает, что площадь этой фигуры, а сле-
довательно, и работу, можно найти интегрированием, т. е.
А= J pdV,
A)
v2 v
но сделать это не может, хотя это совсем несложно.
Из уравнения Менделеева — Клапейрона находим зависи-
мость давления от объема:
_ mRT
р-~ш-
Подставив это выражение в предыдущую формулу, найдем ра-
боту газа в изотермическом процессе:
I', V2
Обратим внимание, что по формуле A) находится работа га-
за в различных процессах. Так, например, при изобарном про-
цессе (/? = const) работу можно найти:
=\i pdV =
96. При решении задач на тепловые явления абитуриенты до-
пускают, кроме перечисленных выше, и другие ошибки. Редко
поступающие оценивают реальность полученного результата.
Например, получив после вычислений значение коэффициента
полезного действия (КПД), большее 100%, не задумываются о
возможности существования такого КПД (явно ошибочного!).
Еще примеры: смешивают понятия КПД нагревателя и КПД теп-
лового двигателя; разность Л/ температур, заданную в градусах
Цельсия, переводят в кельвины так: Д7" = Д/ + 273, что неверно,
так как 1 °С равен 1 К, и, следовательно, Л/ = А7". Чаще всего
ошибки обусловлены либо слабыми теоретическими знаниями,
либо поверхностным анализом описанной в задаче ситуации, ли-
бо неумением логически правильно составить план решения и
найти пути реализации этого плана. Учитывая это, приведем ни-
же общие указания к решению задач на тепловые явления.
Если в задаче рассматривается только теплообмен, то нужно
на основании закона сохранения энергии составить уравнение
теплового баланса:
где Q,,T—количество теплоты, отданное одними телами; Qn0JI —
количество теплоты, полученное другими телами. Если задан
КПД теплообмена, то t]Qot= Q,,0.v
Если внутренняя энергия 0 системы изменяется вследствие
совершения системой механической работы /1, над внешними те-
лами, то составляется уравнение
174
где т] — КПД процесса. (В таких задачах теплообмен между те-
лами обычно не учитывается).
Если внутренняя энергия системы увеличивается в результа-
те того, что внешние тела совершают над ней механическую ра-
боту Аъ то Д?/ = т|у42.
Записав затем выражения Qm, Q,,0JI, ISU, Л, и А2, подстав-
ляют их в приведенные выше уравнения и решают относительно
искомой величины.
Применяя первый закон термодинакими, надо учитывать, что
в его уравнении Q = lsU-\-A каждая из величин может быть ли-
бо положительной, либо отрицательной, либо равной нулю в за-
висимости от характера процесса. Если система получает коли-
чество теплоты Q, то Q>0, если отдает, то Q<CO, если теплооб-
мена нет, Q = 0; AU>0, если внутренняя энергия системы уве-
личивается, А(/<0, если уменьшается, А(/ = 0 при неизменной
внутренней энергии; /1>0, если система совершает работу над
внешними телами; А<С0, если внешние тела совершают работу
над системой, /1 = 0, если работа не совершается.
При изобарном процессе Q^=0, АфО, А11ф0.
При изотермическом процессе k.U = Q, Q=A, т. е. все пере-
данное системе количество теплоты идет на совершение работы
над внешними телами.
При изохорном процессе /1=0, Q = AU, т. е. все сообщенное
газу количество теплоты идет на увеличение его внутренней
энергии.
При адиабатном процессе Q = 0, /1 = — /Sil, т. е. газ совер-
шает работу за счет убыли его внутренней энергии.
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
ЭЛЕКТРОСТАТИКА
97. Как показывает опыт вступительных экзаменов, выпуск-
никами средних школ слабо усвоено одно из основных понятий
электродинамики — понятие электрического заряда. Большин-
ство экзаменующихся знают только, что существуют положи-
тельные и отрицательные заряды и что одноименные заряды от-
талкиваются, а разноименные притягиваются. Среди характер-
ных ошибок и недостатков в ответах абитуриентов отметим
следующие: 1) отождествление заряда с частицей («Электриче-
ский заряд—это частицы, которые могут вступать в электро-
магнитное взаимодействие». «Электрический заряд имеет массу,
меньшую массы электрона»); 2) представление об электрическом
заряде как потоке электронов («Заряд — это направленное дви-
жение электронов»); 3) отождествление электрического заряда с
единицей количества электричества («Заряд — это один кулон»);
4) некорректные выражения («Электрическим зарядом обладают
частицы, которые взаимодействуют с силами, превышающими
силы всемирного тяготения», «Электрический заряд сообщается
телу при трении»).
Понятие электрического заряда должно быть сформировано
у абитуриентов на основе следующих знаний.
1. Электрический заряд — это скалярная физическая величи-
на, характеризующая взаимодействие элементарных частиц и
тел с внешним электромагнитным полем, а также взаимосвязь
с собственным электромагнитным полем.
2. Различают два вида электрических зарядов, условно на-
званных положительными и отрицательными.
3. Не существует электрического заряда без частиц, но суще-
ствуют частицы без электрического заряда.
4. Электрический заряд макроскопического тела равен алгеб-
раической сумме электрических зарядов всех частиц тела.
5. Одноименно заряженные частицы (тела) отталкиваются
друг от друга, а заряженные разноименно — притягиваются.
6. Взаимодействие неподвижных заряженных частиц (тел)
осуществляется посредством электростатического поля. Движу-
щиеся заряженные частицы (тела) взаимосвязаны с магнитным
полем и взаимодействуют посредством магнитного поля.
176
7. Существует минимальная порция электрического заряда,
называемая элементарным электрическим зарядом. Модуль эле-
ментарного электрического заряда е=1,6-10~19 Кл.
8. Система тел или частиц называется электрически изолиро-
ванной, если между ней и внешними телами нет обмена электри-
чески заряженными частицами. В электрически изолированной
системе выполняется один из фундаментальных законов физи-
ки— закон сохранения электрического заряда: алгебраическая
сумма электрических зарядов тел или частиц, образующих элек-
трически изолированную систему, остается неизменной при лю-
бых процессах, происходящих в этой системе.
9. Только для краткости говорят об электрических зарядах
как о чем-то самостоятельном. На самом же деле имеются в ви-
ду заряженные частицы (тела), так как заряд неотделим от ча-
стицы.
98. Некоторые абитуриенты не могут раскрыть полностью фи-
зический смысл закона Кулона. В частности, не указывают, что
сила взаимодействия двух точечных зарядов направлена вдоль
прямой, соединяющей эти заряды, при этом одноименные заря-
ды взаимно отталкиваются, а разноименные притягиваются.
Нередко забывают, что этот закон относится только к взаимо-
действию точечных зарядов, т. е. таких заряженных тел, разме-
рами которых можно пренебречь (заряженных материальных то-
чек). Это приводит к ошибкам в решениях задач.
Задача. Точечный заряд q{ находится вблизи большой
квадратной равномерно заряженной пластины напротив ее цент-
ра. Расстояние г от заряда до пластины мало по сравнению со
стороной а квадрата. Поверхностная плотность заряда на пла-
стине равна а, диэлектрическая проницаемость окружающей
среды равна е. Найти силу, действующую на заряд.
Многие ошибочно находили эту силу по закону Кулона:
где q2 = oS = aa2— заряд пластины; е0— электрическая посто-
янная. Приведем правильное решение.
Решение. Электрическое поле вблизи большой плоской
пластины можно считать однородным. Напряженность это-
го поля
На заряд q, находящийся в этом поле, действует сила
\q\\a\
F=\q\E=-
2б0е ¦
Из последнего выражения видно, что эта сила не зависит от рас-
стояния.
177
Следует обратить внимание на то, что в тех случаях, когда
размеры заряженных тел велики, для нахождения их силы взаи-
модействия нужно мысленно разбить эти тела на такие малые
заряженные элементы, чтобы их можно было считать точечными
зарядами, затем найти по закону Кулона силы взаимодействия
каждой пары этих зарядов и произвести векторное сложение
этих сил.
Закон Кулона можно применять для нахождения силы взаи-
модействия двух равномерно заряженных сфер, при этом в фор-
муле A) <7i и Я-2 — заряды этих сфер, г — расстояние между их
центрами, т. е. сила взаимодействия в этом случае такова, как
если бы заряды были сосредоточены в центрах сфер.
По формуле A) можно также вычислить силу взаимодействия
двух зарядов, один из которых точечный, а второй равномерно
распределен по поверхности сферы. В этом случае г — расстоя-
ние от точечного заряда до центра сферы.
99. Раскрывая физический смысл понятия напряженности
электрического поля, абитуриенты правильно указывают на то,
что силовое действие поля можно обнаружить с помощью заря-
да, вносимого в это поле (пробного заряда), но не все могут объ-
яснить, почему пробный заряд должен быть достаточно малым.
Дело в том, что большой пробный заряд может внести изме-
нения в исследуемое поле. Например, если заряды, создающие
исследуемое поле, расположены на проводнике, то может слу-
читься, что под воздействием электрического поля пробного за-
ряда заряды проводника переместятся, что приведет к измене-
нию их поля.
Редко, но встречается такая грубая ошибка: считают, что в
формуле Ь=—, определяющей напряженность поля с, q — это
заряд, создающий поле. В действительности же q — это пробный
заряд, т. е. заряд, внесенный в ту точку электрического поля, в
которой напряженность равна Е, a F — сила, действующая со
стороны поля на заряд q.
100. Некоторые абитуриенты затрудняются ответить на во-
прос, почему сила взаимодействия зарядов, находящихся в ди-
электрике (например, в воде), меньше, чем в вакууме.
Отвечая на этот вопрос, нужно пояснить, что вследствие по-
ляризации диэлектрика в нем возникает электрическое поле свя-
занных зарядов, напряженность которого направлена противопо-
ложно напряженности внешнего поля, поэтому в диэлектрике
напряженность электрического поля уменьшается в е раз, где
е — диэлектрическая проницаемость среды. Соответственно в е
раз уменьшается и сила взаимодействия точечных зарядов в од-
нородном диэлектрике (в воде, например, в 81 раз).
101. Много ошибок допускают абитуриенты в ответах на во-
просы и при решении задач, связанных с понятием напряженно-
178
сти электрического поля. Само понятие электрического поля
многие усвоили неверно, о чем свидетельствуют, например, такие
ошибки: отрицание материальности поля («Электрическое по-
ле — это абстракция»); отождествление пространства и поля
(«Электрическое поле — это пространство, окружающее заряд»);
существование напряженности в некоторой точке поля связыва-
ется с наличием в этом поле пробного заряда («Если в эту точку
не вносим пробный заряд, то там нет напряженности»).
Поступающие плохо различают формулу, являющуюся опре-
делением напряженности поля:
Е=|, A)
и формулы, устанавливающие связь напряженности с другими
величинами. Дают, например, такое определение: напряженно-
стью называется величина
Е = -
\ч\
4ле„ег
B)
где q — точечный заряд; г — расстояние от данной точки до это-
го заряда. Но ведь формула B) не является определяющей, по
ней вычисляется напряженность поля точечного заряда. Опреде-
ляющей является формула A), согласно которой дается следую-
щее определение: напряженность электрического поля — это
векторная физическая величина, характеризующая силовое дей-
ствие электрического поля на вносимые в него электрические за-
ряды, равная отношению силы, с которой поле действует на по-
ложительный точечный заряд, помещенный в данную точку, к
этому заряду.
Обратим внимание на то, что, во-первых, согласно этому
определению, вектор Е направлен так же, как и сила F, действу-
ющая на положительный заряд; во-вторых, напряженность ха-
рактеризует любую точку поля, независимо от того, внесен в нее
пробный заряд или нет.
Неумение применить принцип суперпозиции полей при рас-
смотрении конкретных систем зарядов приводит к ошибкам.
Задача 1. На одной прямой расположены три точечных за-
ряда: — qu +<72 и —<7з- Определить напряженность поля в точ-
ках А и В (расстояния указаны на рисунке 116). Система нахо-
дится в вакууме (е=1).
—
^ „
4—v;—'
0
А
Е3 с
+
Ь
« о
в ъ
—
X
Рис. 116
179
Решая эту несложную задачу, поступающие делают такую
ошибку: считают, что в точке А поле создается зарядами —qx
и -\-q2, а заряд — q3 «заслоняется» зарядом +<?2> поэтому его не
учитывают при определении напряженности в точке А. Опреде-
ляя напряженность в точке В, не учитывают заряд —<?,.
Решение. Напомним, что, согласно принципу супер-
позиции, заряды действуют независимо друг от друга и напря-
женность электрического поля в любой точке равна векторной
сумме напряженностей полей, создаваемых в этой точке каждым
зарядом:
Учитывая это, выразим значение напряженности в точке А:
Направим ось ОХ вправо вдоль прямой, на которой располо-
жены заряды, и запишем уравнение для проекций векторов на-
пряженности на эту ось:
ЕАх = Еи + Е2х + Е,х = _?,-?,+ Е3, A)
где ?ь Е2, Е3 — модули векторов ?,, ?2 и Ез соответственно:
F l<?|1 F |<?2' р __ \Чз\ г9ч
С j = г , С, = , С3 7, ¦ \^ )
4леоег, " 4ке0ег$ 4ле0е (г2 + г3 + г4)
Подставив значения B) в формулу A), найдем ЕАх. Значение
ЕДх зависит от значений модулей зарядов \q{\, \q2\, и 1<?з1 и от
расстояний до точки А. Если в результате вычислений получится
, то это будет означать, что напряженность Ел в точке А на-
правлена вправо вдоль оси ОХ; если же получится ЕАх<С.О, — то
влево.
Напряженность в точке В находится аналогично (рекоменду-
ется читателю сделать это самостоятельно).
Задача 2. Два точечных заряда <?]>0 и q2-<0 расположе-
ны в воздухе на расстоянии г друг от друга. Найти напряжен-
ность поля, создаваемого этими зарядами в точке А, находящей-
ся на расстоянии гх от положительного заряда и г2 от от-
рицательного. Точка А не лежит на прямой, соединяющей заря-
ды, r<.rx-\-r2.
Обычно ряд абитуриентов допускают здесь такие ошибки:
1) неправильно изображают на рисунке векторы напряженно-
стей, совмещая начала этих векторов с зарядами (рис. 117, а);
2) неверно указывают направления векторов напряженностей
(рис. 117,6); 3) не используют соотношения между сторонами и
углами треугольника, известные им из курса математики. При-
ведем правильное решение.
180
Решение. Согласно принципу суперпозиции, в точке А на-
пряженность
ЬА = с, -\-Еъ
где ?ь ?2— напряженности полей, создаваемых в этой точке за-
рядами <7, и q2 соответственно. Вектор ЕА является диагональю
параллелограмма со сторонами ?, и ?2 (рис. 117, в). Воспользо-
вавшись теоремой косинусов, найдем:
A
где ЕА, ?,, Е2 — модули векторов ЕА, Et и Е,2 соответственно:
B)
4ле0ел, 4яеоег$
Применив теорему косинусов к треугольнику со сторонами г,
гь и г2, получим: r'2 — r]-\-rl — 2л,л2 cos а, откуда
cos a = -
C)
Подставив выражения B) и C) в формулу A), найдем ЕА.
Задача 3. Электрическое поле создано двумя бесконечны-
ми параллельными заряженными плоскостями с поверхностны-
ми плотностями заряда а,^0,5 мкКл/м2 и а2=—0,3 мкКл/м2.
Определить напряженность поля между плоскостями, а также
слева от плоскости А и справа от плоскости В (рис. 118). Плоско-
сти находятся в воздухе (е=1).
Решение. Каждая плоскость создает свое электрическое
поле: плоскость А создает справа от себя однородное поле на-
пряженностью ?,, слева Е\, плоскость В — справа от себя одно-
181
Рис. 118
родное поле напряженностью Е2, слева Е'2. Направления этих
векторов показаны на рисунке 118. Найдем модули этих
векторов:
р —р>— |а'! р —Р'— |02'
Согласно принципу суперпозиции, напряженность поля слева
от плоскости А Е]=Е\-\-ЕB, между плоскостями Еи^=Е1-\-Е/2,
справа от плоскости В Еп[ = ?\+ Е,2. В проекциях на ось ОХ бу-
дем иметь:
= Е2 — ?,=
G,1),
Ь[[|. tL г Lo
2е0е
(i)
Подставив значения величин в эти формулы и произведя вы-
числения, найдем:
?„=-
1
—- @,3- 10-ь — 0,5-10-") В/м =
2-8,85-10"
= — 11,3 кВ/м,
?„, = 42,2 кВ/м, ?,„,= 11,3 кВ/м.
Из того, что ?|х<0, ?,,,>>0 и ?,„,>>0, следует, что слева от
плоскости А направление вектора напряженности противо-
положно направлению оси ОХ, а между плоскостями и справа от
плоскости В совпадает с направлением оси ОХ.
Довольно распространенная ошибка: абитуриенты считают,
что плоскостью А «экранируется» плоскость В и поэтому слева
от плоскости А поле плоскости В отсутствует.
182
Полезно сделать анализ полученных в результате решения
формул A). Из него вытекают следующие частные случаи.
1. Если поверхностная плотность заряда плоскостей одинако-
ва (|а,| = j ст21 = | сг |), а знаки зарядов противоположные, то
Е1х=ЕШх = 0, т. е. поле справа и слева от плоскостей отсутствует,
а ""между плоскостями имеется однородное электрическое поле
напряженностью Е, равное:
?==М. B)
еое
В частности, такова напряженность поля между пластинами
(обкладками) плоского конденсатора.
2. Если |tr,| = |cx2l = tсг 1, а знаки зарядов одинаковы, то на-
пряженность поля между плоскостями равна нулю, а слева и
справа от них выражается формулой B).
102. Искаженное, неверное представление о силовых линиях
электрического поля (линиях напряженности) обнаруживают
абитуриенты, дающие такое (ошибочное!) определение: «Силовой
линией называется линия, вдоль которой действуют электриче-
ские силы».
Напомним правильное определение: силовой линией называ-
ется линия, касательная к которой в каждой точке совпадает с
вектором напряженности поля в этой точке. На рисунке 119, а
показаны векторы напряженности ?,, Еъ ?3, в точках /, 2, 3.
С помощью силовых линий можно изобразить поле графиче-
ски. Силовые линии обладают следующими свойствами: 1) сило-
вые линии непрерывны, они начинаются на положительных за-
рядах и заканчиваются на отрицательных; 2) силовые линии
между собой не пересекаются, так как если бы они пере-
секались, то точке пересечения соответствовали бы два различ-
ных направления вектора напряженности.
Рис. 119
183
Из определения силовых линий ясно, что сила, с которой поле
действует на внесенный в него положительный заряд, направле-
на по касательной к силовой линии. Только в частном случае,
когда силовая линия представляет собой прямую, вектор напря-
женности и, следовательно, сила, действующая на положитель-
ный заряд, направлены вдоль этой линии.
При графическом изображении электрического поля силовые
линии проводят гуще там, где больше напряженность; при этом
число силовых линий, проходящих через единичную площадку,
перпендикулярную к силовым линиям, равно напряженности
электрического поля в том месте, где расположена эта
площадка.
Однородное поле, т. е. поле, напряженность которого во всех
точках одинакова по направлению и по модулю, графически
изображается параллельными силовыми линиями одинаковой
густоты. Однородным является, например, поле между пласти-
нами плоского конденсатора вдали от их краев (рис. 119,6).
Здесь уместно отметить одну грубую ошибку, встречающуюся
иногда в ответах абитуриентов: в качестве примера однородного
электрического поля приводят поле уединенного точечного заря-
да. Но ведь достаточно посмотреть на графическое изображение
этого поля (рис. 120), чтобы убедиться, что это поле не является
однородным, так как силовые линии имеют различные направле-
ния. Кроме того, как известно, модуль вектора напряженности
точечного заряда убывает обратно пропорционально квадрату
расстояния от точки до заряда.
103. Остановимся теперь на ошибках, связанных с понятием
потенциала. Значительная часть экзаменующихся считают, что
потенциал проводника — это свойство заряженного проводника,
а это неверно. Потенциал характеризует электростатическое по-
ле вблизи поверхности проводника.
У многих абитуриентов отсутствует правильное представле-
ние о том, что значение потенциала зависит от выбора нулевого
уровня (начала отсчета) потенциала.
Потенциал электростатического поля — это скалярная физи-
ческая величина, характеризующая энергетическое состояние
поля в данной точке и равная отношению потенциальной энер-
гии, которой обладает электрический заряд, помещенный в дан-
ную точку, к этому заряду:
_ w
ф~~ ч
Так как значение потенциальной энергии W зависит от выбо-
ра ее нулевого уровня, то и значение ф может быть определено
лишь по отношению к нулевому уровню, выбранному произволь-
но. Нулевой уровень может быть выбран, например, на поверх-
ности Земли или на бесконечно большом расстоянии от рассмат-
риваемого проводника.
184
Итак, потенциал поля в данной точке может иметь различные
значения в зависимости от выбора нулевого уровня. Отсюда не-
которые поступающие делают ошибочный вывод: следовательно,
и напряженность поля в данной точке может иметь различные
значения, так как существует связь между потенциалом и на-
пряженностью.
Да, такая связь есть, но какова она? Если Ad — расстояние
между двумя достаточно близкими точками поля, принадлежа-
щими одной и той же силовой линии, то напряженность Е опре-
деляется по формуле
Е = — 'f2. 'h = **'. Ф~ =-т-т, A)
Ad
Ad
Ad
где ?/ = ipi — ф2 — разность потенциалов между этими точками.
А так как разность потенциалов не зависит от выбора нулевого
уровня, то напряженность поля в окрестности этих точек имеет
одно определенное значение.
г/ D
а/*
Рис. 120
Р и с. 121
В однородном поле напряженность — величина постоянная,
поэтому формула A) справедлива для любых (а не только для
очень малых) расстояний d между двумя точками одной и той же
силовой линии:
? = у- B)
Напомним, что практическое значение имеет разность потен-
циалов, так как от нее зависит работа А сил электростатическо-
го поля при перемещении заряда q: Л = <7 (ф, — <p2)=qU.
Абитуриенты, плохо усвоившие физический смысл выраже-
ния B), допускают ошибки. Приведем примеры.
1. Напряженность поля внутри плоского конденсатора равна
Е. Какова разность потенциалов между точками А и В (рис. 121),
если расстояние между ними равно г, а угол между отрезком АВ
и направлением вектора Е равен а?
Как правило, на этот вопрос отвечают так: на основании фор-
185
мулы B) имеем ц>А — фв = ?г при любом а. Это неверно. Как уже
отмечалось выше, расстояние d, входящее в формулу B), отсчи-
тывается вдоль силовой линии. В данном случае d = r cos а, по-
этому (fA — ips = ?Vcosa.
Если а = 90°, то разность потенциалов между точками (на-
пример, С и D) равна нулю независимо or расстояния между
ними.
2. Многие абитуриенты не могут
дать правильное определение еди-
ницы напряженности электрическо-
го поля — вольт на метр. Эта едини-
ца определяется правильно на осно-
ве формулы B) так: вольт на метр
равен напряженности однородного
электрического поля, при которой
между двумя точками, находящими-
ся одна от другой на расстоянии 1 м
вдоль линии напряженности поля,
создается разность потенциалов 1 В.
104. Еще одна ошибка, связан-
ная с понятием потенциала: мно-
гие уверены, что поскольку напряженность электростатиче-
ского поля внутри заряженного проводника равна нулю, то и по-
тенциал в любой точке внутри этого проводника равен нулю.
Пусть имеется равномерно заряженный проводящий шар
(рис. 122). Напряженность электрического поля внутри шара
равна нулю. Для любых двух точек А и В, расстояние между ко-
торыми равно d, имеем:
Рис. 122
ь, =
Чм — Ч'в
а так как ? = 0, то Фл = Фд- Если одна из произвольно выбранных
точек С и D лежит на поверхности шара, а вторая внутри, то по-
лучим фс — фо = 0 или фс = ф;>
Таким образом, внутри заряженного проводника потенциал
во всех точках одинаков и равен потенциалу на поверхности это-
го проводника.
Во всех точках поверхности заряженного проводника потен-
циал одинаков, т. е. это эквипотенциальная поверхность. Следо-
вательно, силовые линии поля перпендикулярны к этой поверх-
ности. При графическом изображении поля это необходимо учи-
тывать, что не всегда делают абитуриенты.
При рассмотрении электрического поля системы точечных за-
рядов многие абитуриенты также считают, что если в какой-либо
точке напряженность поля равна нулю, то и потенциал в этой
точке равен нулю, и наоборот: если потенциал равен нулю, то и
напряженность равна нулю. В ошибочности этого легко убедить-
ся на примере решения следующей задачи.
186
fi
fr f
Рис. 123
Задача. Найти напряженность и потенциал электрического
поля в точке А (рис. 123, а), расположенной посередине отрезка,
соединяющего одинаковые одноименные заряды q. Как изменит-
ся результат, если заряды будут иметь противоположные знаки?
Решение. Согласно принципу суперпозиции, напряжен-
ность в точке А равна векторной сумме напряженностей ?, и Еъ
создаваемых каждым зарядом в отдельности: ЕА^Е^-\-Е2. Моду-
ли векторов ?, и Е2 одинаковы:
F —F - ^
1 г 42
а направления противоположны. Следовательно, напряженность
в точке А равна нулю (ЕА = 0).
Потенциал поля в этой точке равен алгебраической сумме по-
тенциалов, создаваемых каждым зарядом в отдельности:
4яе0ег 4я80ег 2ле0ег
Таким образом, срл=И=О, а ЕА = 0.
Если заряды будут иметь противоположные знаки (рис. 123,
б), то
f __l?i_ —п
?л~2лЁ0ег2' Фл~и'
105. Пример грубой ошибки: давая определение потенциала
электростатического поля, абитуриент говорит, что в формуле
W /Т-,
Ф = — q — это заряд, создающий поле. (Правильный ответ
см. в п. 103.)
106. Не все абитуриенты овладели понятием электрической
емкости. В ответах встречаются расплывчатые, а иногда и не
имеющие смысла формулировки: «Электроемкость — способ-
ность проводника накапливать заряд», «Конденсатор набирает
излишки тока», «Когда конденсатор перенасыщается зарядом,
он разряжается» и т. п.
Напомним правильное определение. Электрической емкостью
двух проводников называется скалярная физическая величина,
равная отношению заряда одного из проводников к разности по-
тенциалов между этими проводниками:
С = -
A)
187
(Для краткости вместо «электрическая емкость» говорят «элект-
роемкость» или просто «емкость».)
Электроемкость уединенного проводника — величина, равная
отношению заряда проводника к его потенциалу: С = —.
Нередко на вопрос: «От чего зависит емкость проводника?»
поступающие отвечают, ссылаясь на формулу A), что емкость
С зависит от заряда q и напряжения U. Чем больше q, тем больше
С; чем больше U, тем меньше С. Это неверно.
Электроемкость двух проводников зависит от их формы, вза-
имного расположения, размеров, диэлектрической проницаемо-
сти окружающей среды и от расположения тел, окружающих
данные проводники. Электроемкость не зависит от заряда и на-
пряжения. Так, если одному и тому же конденсатору, ранее не
заряженному, сообщить заряд qh то разность потенциалов меж-
ду его пластинами будет ?/,, а если сообщить заряд q2, то Иъ
но отношение заряда к разности потенциалов будет одинаковым:
Другое дело, что формула A) позволяет сравнивать емкости
различных систем проводников, например конденсаторов. Если
на первом и втором конденсаторах заряды q одинаковые, а на-
пряжения ?/, и 02 на них при этом различные, то отсюда следу-
ет, что емкости этих конденсаторов различные: если U{>U2, то
С,<ГС2; если Ul<ZU2, то С1^>С2- Читателю предлагается самосто-
ятельно сравнить емкости двух конденсаторов, напряжения на
которых одинаковы, а заряды различны.
107. Рассмотрим теперь характерные ошибки абитуриентов
при решении задач, связанных с понятием электроемкости.
Задача 1. Плоский воздушный конденсатор, площадь каж-
дой пластины которого равна S, а расстояние между ними db за-
рядили с помощью источника напряжения U, отключили от ис-
точника напряжения, а затем увеличили расстояние между пла-
стинами до d2. Как изменится при этом энергия конденсатора?
(Воздушным называют конденсатор, между пластинами которого
находится воздух, е=1.)
Абитуриент, решая эту задачу, рассуждал так: энергия кон-
денсатора емкостью С, заряженного до напряжения U, равна:
Г!!2
ш=Щ-. A)
Из формулы емкости плоского конденсатора
С = ^Г B)
следует, что с увеличением расстояния d между пластинами ем-
кость С конденсатора уменьшается. Следовательно, в соответст-
188
вии с формулой A) энергия его тоже уменьшается. А это невер-
но. Даже рассуждая на качественном уровне, без использования
формул, легко убедиться, что в данном случае энергия конденса-
тора увеличится. В самом деле, раздвигая пластины, мы совер-
шаем работу против сил их взаимного притяжения, следователь-
но, энергия конденсатора увеличится.
Какую же ошибку допустил абитуриент? Он считал, что по-
сле раздвигания пластин напряжение на конденсаторе останется
неизменным, а в действительности оно изменится. Если конден-
сатор отключен от источника напряжения, то его заряд q не бу-
дет изменяться при раздвигании пластин. В то же время
емкость, как это следует из формулы B), будет уменьшаться.
Поэтому напряжение, согласно формуле
?/=¦§. C)
увеличится.
Решение. Воспользуемся формулой, которая выражает
энергию заряженного конденсатора через его заряд и емкость:
Так как заряд q остается неизменным, а емкость конденсато-
ра, согласно формуле B), в результате увеличения расстояния
между пластинами от dx до d2 уменьшилась, то энергия конденса-
тора увеличилась на
atw ш щ/ ц2 ц1 __ ц i i i_\
где С,, С2 — емкости конденсатора в начальном и конечном со-
стояниях соответственно.
Используя соотношение C), найдем заряд конденсатора
q = ClU и, подставив это значение в предыдущую формулу,
получим:
Учитывая, что, согласно формуле B),
_ ee0S ee,0S
будем иметь:
Задача 2. Плоский воздушный конденсатор, площадь каж-
дой пластины которого S, а расстояние между ними d\, зарядили
с помощью источника постоянного напряжения U. Как изменит-
189
ся энергия конденсатора, если, не отключая его от источника,
увеличить расстояние между пластинами до d2?
Решение. В отличие от ситуации, рассмотренной в преды-
дущей задаче, здесь при раздвигании пластин напряжение на
конденсаторе остается постоянным, так как он подключен к ис-
точнику, а электроемкость, как и в задаче 1, уменьшается.
На основании формулы № = —т—, выражающей энергию
W конденсатора через емкость С и напряжение U, приходим к вы-
воду, что в этом случае энергия конденсатора уменьшится.
Найдем изменение энергии конденсатора:
2
PF0S^2
2
1 1
Так как d2>d{, то AW<C0, т. е. энергия конденсатора умень-
шится.
Задача 3. Конденсатор емкостью С, = 4 мкФ, заряженный
до разности потенциалов /У, = 100 В, соединили одноименно за-
ряженными обкладками с конденсатором емкостью С2 = 6 мкФ,
заряженным до разности потенциалов ?/2=150 В. Найти раз-
ность потенциалов между обкладками конденсаторов после их
соединения.
U,
4
и2
Г, С,
с
и
Рис. 124
Решение. Изобразим ситуацию до соединения (рис. 124, а)
и после него (рис. 124,6). Используя определение емкости кон-
денсатора, найдем заряды конденсаторов до их соединения:
<7, = С1?/1, <72=C2t72. Согласно закону сохранения электрического
заряда, общий заряд конденсаторов после их соединения равен
сумме зарядов конденсаторов до соединения: q = ql-lrq2. Кроме
того, при соединении одноименно заряженных обкладок конден-
саторов их общий заряд равен сумме зарядов каждого конденса-
тора после соединения: q = q[-\-q'2. Следовательно,
= q'i + qf2- A)
190
Ho q\ = CKU, q'2=C2U, где U— разность потенциалов между об-
кладками конденсаторов после их соединения. Подставив зна-
чения qu q2, q\ и q'2 в выражение A), получим:
CiUi + C2U2 = ClU + C2U. B)
Отсюда
U = ^±^l. C)
После подстановки числовых значений заданных величин и
вычислений получим {/=130 В.
Отметим, что соединение конденсаторов, при котором соеди-
няются одноименно заряженные обкладки, называется парал-
лельным. При параллельном соединении разность потенциалов
между обкладками конденсаторов одинакова, общий заряд бата-
реи равен сумме зарядов конденсаторов, а их общая емкость
С = С1 + С2 + ... + Сп. D)
При решении данной задачи мы не использовали соотноше-
ние D), но фактически пришли к нему. В самом деле, общий за-
ряд q связан с общей емкостью С и напряжением U: q=CU.
С другой стороны, q=C]Ul-\-C2U2. На основании этих выраже-
ний и равенства B) получим: CU = CXU-\- C2U, откуда
С=С\-\-С2, т. е. общая емкость конденсаторов, соединенных па-
раллельно, равна сумме емкостей отдельных конденсаторов, что
соответствует формуле D).
Абитуриент, которому известна формула D), мог бы, восполь-
зовавшись ей, решать задачу так: общий заряд конденсаторов
после их соединения
q = <7, + q2 = С, {/, + C2U2.
а их общая емкость C = Ct-\-C2. Так как q = CU = (Cx-\-C2) U, то
Отсюда получаем выражение C).
Попутно отметим, что последовательным соединением кон-
денсаторов называется такое соединение, при котором отрица-
тельно заряженная обкладка первого конденсатора соединяется
с положительно заряженной обкладкой второго конденсатора и
т. д. (рис. 124,в). При последовательном соединении заряды на
всех конденсаторах равны между собой и равны заряду батареи,
а общая емкость С находится из формулы
С С, т С2~'"^ С„ '
где С,, С2, ..., Сп — емкости отдельных конденсаторов.
Напряжение на всей батарее равно сумме напряжений на от-
дельных конденсаторах.
191
108. Встречаются ошибки при решении задач, связанных с
движением заряженных частиц в электрическом поле. Одну из
характерных ошибок рассмотрим на примере решения следую-
щей задачи.
Задача. Два точечных положительных заряда qx и q2 нахо-
дятся в воздухе на расстоянии л, друг от друга. Какую работу
надо совершить, чтобы сблизить эти заряды до расстояния г2
(рис. 125)?
Рис. 125
Абитуриент, получивший эту задачу, решал ее так. Согласно
закону Кулона, заряды отталкиваются друг от друга с силой
F-^. A)
4aerf
Оставляя заряд qx неподвижным, нужно передвинуть заряд
q2 на расстояние гх— г2, для чего надо совершить против сил от-
талкивания работу A = F(rx—г2). Подставив сюда значение си-
лы A), найдем работу.
Это неверно. Абитуриент упустил из виду тот факт, что сила
взаимодействия зарядов — величина переменная, зависящая от
расстояния между ними, и ошибочно применил формулу для ра-
боты постоянной силы. Решим эту задачу двумя способами.
Решение. Первый способ. Для уменьшения расстояния
между зарядами нужно совершить работу А против сил поля:
А = —А', где А' — работа сил электростатического поля заряда
<7, при перемещении заряда q2 из точки / в точку 2 (заряд qi при
этом остается неподвижным). Электростатическое поле потенци-
ально, поэтому его работа равна убыли потенциальной энергии
заряда q2:
где Wp2, Wpl — потенциальная энергия заряда q2 в точках 2 и
У соответственно. Следовательно,
А=—А'= Wp2 — WpX = q2q2 ~ Wi = Яч (фг — <Pi).
где ф2, ф! — потенциалы электростатического поля заряда в точ-
ках 2 и 1 соответственно. Учитывая, что
4ле0л2
получим:
192
Второй способ. Как и в предыдущем случае, считаем, что за-
ряд qx неподвижен, а заряд q2 приближаем к нему. При этом бу-
дет совершаться работа А против сил поля: А=—А', где Л' —
работа сил поля. Так как кулоновская сила изменяется с растоя-
нием, то
2
А=—А'=-\
4яеп
4лг„
Г2 / _ j_\ _ Wh_ /J 1_\
гД г) 4лг0 ^л2 л1у) '
Получили, естественно, тот же результат, что и в первом
случае.
109. Далеко не все поступающие понимают условия равнове-
сия зарядов на проводниках. Рассмотрим качественную задачу.
Задача. На двух металлических шарах имеются одинако-
вые положительные заряды. Соединим эти шары проволокой.
Изменятся ли заряды шаров?
Давались различные неправильные ответы на этот вопрос.
Одни сразу же утверждали, что переход заряда с одного шара
на другой невозможен, потому что заряды всегда переходят с
проводника с большим зарядом на проводник с меньшим заря-
дом. Другие говорили, что перехода не будет потому, что одно-
именные заряды отталкиваются. Третьи считали, что переход
возможен только в том случае, если поверхностная плотность за-
ряда одного шара больше поверхностной плотности заряда дру-
гого шара.
Что же происходит в действительности? Если соединить про-
волокой два проводящих заряженных шара, то они вместе с про-
волокой образуют единый проводник. Если до соединения потен-
циалы шаров были различными, то после него возникнет кратко-
временный ток, проходящий до тех пор, пока заряды перераспре-
делятся так, что потенциалы обоих шаров и проволоки станут
одинаковыми.
Таким образом, заряды шаров изменятся только в том слу-
чае, если до соединения их потенциалы были различными.
110. Решая задачи по электростатике, абитуриенты допуска-
ют, кроме перечисленных выше, и другие ошибки: не всегда учи-
тывают, что напряженность электрического поля — величина
векторная; забывают, что знак потенциала такой же, как и знак
заряда, создающего поле, что потенциал системы точечных заря-
дов равен алгебраической сумме потенциалов, создаваемых в
данной точке поля каждым зарядом в отдельности; не учитыва-
ют, что положительные заряды в электрическом поле движутся
в направлении уменьшения потенциала, а отрицательные — на-
оборот; не используют закон сохранения заряда и закон сохране-
7 Заказ 2473 193
ния энергии, вследствие чего не могут решить ряд задач.
Можно рекомендовать следующий порядок решения задач по
электростатике.
В задачах, где рассматриваются точечные заряды, нужно
сделать чертеж и обозначить все силы, действующие на заряд.
Если по условию задачи заряд находится в покое, то записывают
условие равновесия заряда (так же, как и для равновесия тела
в механике). Если заряженная частица движется, то нужно со-
ставить уравнение ее движения (так же, как и в задачах по ме-
ханике). К, этому уравнению добавляют уравнения, составленные
на основе закона сохранения электрического заряда, если про-
исходит перераспределение зарядов, и на основе закона сохране-
ния энергии, если рассматривается работа сил поля при переме-
щении заряда. Затем выражают силы электрического взаимо-
действия через заряды и напряженность поля, работу сил по-
ля — через заряды и разность потенциалов, подставляют их
в основные уравнения и решают полученную систему уравнений.
Следует отметить, что изложенный выше план решения задач
по электростатике дает лишь общее направление, решение же
каждой конкретной задачи имеет свои особенности, связанные
с ее условием.
ЗАКОНЫ ПОСТОЯННОГО ТОКА
111. Согласно закону Ома для участка цепи, сила тока / пря-
мо пропорциональна приложенному напряжению U и обратно
пропорциональна сопротивлению R проводника:
'-¦jf. (.)
Выразив отсюда сопротивление R=—, некоторые абитуриен-
ты делают ошибочный вывод, что сопротивление проводника за-
висит от напряжения и силы тока. Эта ошибка свидетельствует
о формальном усвоении закона Ома и непонимании его физиче-
ской сущности.
Напряжение и сила тока не определяют сопротивление. Фор-
мула A) отражает тот факт, что для данного проводника
(/? = const) сила тока тем больше, чем больше напряжение. Гра-
фик этой зависимости представляет собой прямую линию
(рис. 126) и называется вольт-амперной характеристикой про-
водника. Угол наклона ср этой прямой зависит от сопротивления
, /, 1
проводника: tg(p = —= —-.
Величина, обратная сопротивлению проводника, т. е. G=—,
называется электрической проводимостью проводника. В СИ
единицей этой величины является сименс (См). Сименс равен
194
/i
Рис. 126
электрической проводимости проводника сопротивлением 1 Ом:
1 См = 1 Ом.
Кроме того, согласно формуле A), при заданном напряжении
(?/ = const) сила тока будет больше в том проводнике, сопротив-
ление которого меньше.
Для данного проводника при различных напряжениях сила
тока будет иметь различные значения, но отношение напряже-
ния к силе тока (при постоянной температуре) будет одинаковым
и равным сопротивлению этого проводника.
Сопротивление R зависит только от материала проводника,
его длины /, площади поперечного сечения S и температуры t:
где р — удельное сопротивление. Зависимость от температуры
выражается соотношением
R = R0(l+nt), p = po(l+af), B)
где R, р — соответственно сопротивление и удельное сопротивле-
ние проводника при температуре /; Ro, р0 — при О °С; a — темпе-
ратурный коэффициент сопротивления.
В связи с соотношениями B) отметим две ошибки, которые
иногда встречаются в ответах экзаменующихся: 1) считают, что
/?о и р0 — это начальные значения сопротивления и удельного со-
противления соответственно; 2) объясняют, что причиной увели-
чения сопротивления проводника с ростом его температуры яв-
ляется изменение размеров проводника вследствие его теплового
расширения.
В действительности изменения размеров проводника, обу-
словленные тепловым расширением, незначительны. С ростом
температуры проводника увеличивается амплитуда колебаний
ионов кристаллической решетки, свободные электроны при
своем движении чаще соударяются с ионами, увеличивается си-
ла трения при упорядоченном движении электронов по провод-
нику.
В ответах абитуриентов встречаются некорректные утвержде-
195
ния, свидетельствующие о поверхностном усвоении понятия со-
противления. Вот два примера: «Сопротивление 1 Ом образуется
при силе тока 1 А и напряжении 1 В», «Сопротивление провод-
ника возникает, когда по нему идет ток».
Как уже отмечено выше, сопротивление — это величина, ха-
рактеризующая электрические свойства проводника. Она не воз-
никает и не образуется. Приведенные выше утверждения по
своему характеру аналогичны такому: «Волосы на голове возни-
кают, когда человек снимает шляпу». Но, понятно, волосы су-
ществуют и под шляпой (если, конечно, человек не совсем
лысый).
112. Как известно, внутри заряженного проводника (напри-
мер, внутри металлического шара, сферы) напряженность элект-
рического поля равна нулю. Отсюда поступающие иногда дела-
ют неверное заключение, что и внутри проводника, но которому
идет ток, электрическое поле отсутствует. Это грубая ошибка.
Электрическое поле внутри проводника с током существует, и
именно оно является причиной, благодаря которой свободные
электроны совершают упорядоченное движение вдоль про-
водника.
113. Поступающие нередко дают неправильные определения
единиц электрических величин. Отвечают, например, так: «Ом —
это вольт, деленный на ампер; вольт — это ампер, умноженный
на ом; ампер — это вольт, деленный на ом». Получается замкну-
тый круг, в котором говорится лишь о том, как одни единицы вы-
ражаются через другие.
Напомним, что определения единиц физических величин да-
ются на основе определяющих формул (уравнений), имеющих
конкретный физический смысл. Например, для единицы элект-
рического сопротивления определяющей является следующая из
закона Ома формула R=-r, согласно которой,
Определение этой единицы такое: ом равен электрическому со-
противлению проводника, в котором при напряжении между
концами 1 В сила тока равна 1 А.
Некоторые поступающие уверены, что установленные в квар-
тирах счетчики учитывают потребляемую мощность. В действи-
тельности же в киловатт-часах измеряется не мощность, а энер-
гия (работа) электрического тока. Если током мощностью Р за
время t совершается работа Л, то Л = Pt. При Р=\ кВт и t=\ ч
работа Л = 1 кВт-ч, т. е. киловатт-час равен работе, совершае-
мой током мощностью 1 кВт за время 1 ч. Следовательно,
1 кВт-ч=1 кВт-1 ч= 103 Вт-3600 с = 3,6-10б Дж.
Нередко поступающие, правильно записав формулу, не могут
196
объяснить физический смысл входящих в нее величин. Напри-
мер, смысл величины р в формуле
* = Р^. 0)
выражающей зависимость сопротивления R проводника от его
длины / и площади поперечного сечения S.
Физический смысл величины р станет ясен, если положим
/=1 единицы длины, S=\ единицы площади. Тогда р численно
равно R, т. е. удельное сопротивление р вещества численно равно
сопротивлению изготовленного из данного вещества провода с
постоянной площадью поперечного сечения, равной единице пло-
щади, и длиной, равной единице длины. Значения удельного со-
противления р различных веществ даются в справочных таб-
лицах.
Из формулы A) следует выражение
R
являющееся определяющим для единицы удельного сопротив-
ления:
Ом-метр равен удельному электрическому сопротивлению ве-
щества, при котором изготовленный из этого вещества провод-
ник длиной 1 м и площадью поперечного сечения 1 м2 имеет со-
противление 1 Ом.
Наглядно такой проводник можно представить в форме куба
с ребром, равным 1 м. Возьмем, например, такой медный куб и
измерим его сопротивление, если ток направлен вдоль нормали
к двум противоположным граням. Полученное значение числен-
но равно удельному сопротивлению меди. Проделав то же самое
с золотым кубом, получим значение удельного сопротивления зо-
лота и т. д. На практике, конечно, используются проводники с
меньшей площадью поперечного сечения, но при расчетах надо
все величины выражать в единицах СИ.
Разумеется, вовсе не обязательно брать куб, как это утверж-
дают некоторые абитуриенты. Важно, чтобы было S=l м2,
/= 1 м. Можно взять, например, проводник в форме прямой тре-
угольной призмы высотой 1 м, основанием которой является рав-
нобедренный треугольник с высотой 2 м и основанием 1 м; при
этом ток пропускать вдоль нормали к основаниям призмы. Полу-
чим тот же результат, что и с кубом.
Постоянная Фарадея (/*"== 9,65• 104 Кл/моль) часто приводит-
ся в экзаменационных задачах, но абитуриенты не всегда пра-
вильно объясняют физический смысл этой величины.
Согласно закону Фарадея, за время / при прохождении элек-
197
трического тока через раствор электролита на электроде выде-
ляется вещество массой
т = — — It,
F п
где М — молярная масса вещества; п — его валентность; / — си-
ла тока. Отсюда
F = ±*-q, B)
где It = q — заряд, прошедший через электролит за время t.
Пусть л=1, тогда из формулы A) следует, что F = q, если
т = М. Таким образом, постоянная Фарадея численно равна
электрическому заряду, при прохождении которого через элект-
ролит на электроде выделяется 1 моль одновалентного вещества.
114. Довольно часто встречаются абитуриенты, которые пра-
вильно отвечают на теоретические вопросы, и вместе с тем не мо-
гут применить эти знания в конкретной ситуации. Они не могут,
например, разобраться в схемах несложных электрических це-
пей. Приведем примеры из практики вступительных экзаменов.
1. Посмотрев на схему, приведенную на рисунке 127, а, не-
редко поступающие говорят, что источники с ЭДС W{ и W2 сое-
динены параллельно, хотя в действительности они соединены по-
следовательно, как это видно из рисунка 127, б, на котором изоб-
ражена схема, эквивалентная первой.
2. Абитуриенту предлагается такая задача практического ха-
рактера: «Требуется установить в комнате в определенных местах
электрическую лампочку, выключатель и розетку; изобразите
схематически, как вы будете делать электропроводку, если под
напряжением находятся точки А и В».
Примеры неправильных ответов показаны на рисунке 128,
а, 6. Ошибки в этих схемах читатель легко обнаружит, срав-
нив их с правильной схемой (рис. 128, в).
3. Абитуриенту задается такой вопрос: «В комнате установ-
лены электрическая лампочка, розетка и выключатель. Возмож-
но ли короткое замыкание, если провода, подведенные к выклю-
чателю, освобождать от изоляции (зачищать) ножом с изолирую-
щей ручкой?»
Часто следует ответ: «Конечно возможно, так как при этом
нож может замкнуть эти провода». На самом деле короткого за-
мыкания не будет. Если нож соединит провода 3 и 4 (рис. 128, в),
то лампочка загорится, если перед этим она не горела, а если го-
рела, то будет продолжать гореть. А если соединить ножом про-
вода / и 2, подходящие к розетке, то короткое замыкание прои-
зойдет.
4. Не все могли определить общее сопротивление цепи, изоб-
раженной на рисунке 129, а, где резисторы R1 и R2 имеют оди-
наковые сопротивления, равные 4 Ом, а резисторы R3, R4, R5 и
R6 — одинаковые сопротивления, равные 8 Ом.
198
ft
s1
R
Рис. 127
So-1
Рис. 128
R1 R2 R3
R1 R2
R3
R5
Рис. 129
Некоторые экзаменующиеся ошибочно считали, что резисто-
ры Rl, R2 и RS соединены последовательно, a R4, R5 и R6 — па-
раллельно.
Между тем если эту схему заменить эквивалентной ей схемой
(рис. 129, б), то становится ясно, что резисторы R3 и R6 соедине-
ны параллельно, затем последовательно с ними включен рези-
стор R2, к этим трем резисторам параллельно присоединен рези-
стор R5, затем последовательно R1 и вновь параллельно R4.
Теперь по известным формулам для параллельного и после-
довательного соединений проводников нетрудно произвести рас-
чет. Читатель может проделать это самостоятельно и убедиться,
что общее сопротивление цепи равно 4 Ом.
115. Как известно, общее сопротивление R двух параллельно
199
соединенных проводников с сопротивлениями /?, и R2 определя-
ется из формулы
R R, R2'
п р
откуда /?= ' д . Иногда абитуриенты считают, что для трех
параллельно соединенных проводников общее сопротивление на-
ходится по аналогичной формуле, т. е. R = ' 2 3 . Это, ко-
нечно, грубая ошибка, и читатель может легко найти правильное
значение R, выразив его из формулы
R Rt R2 R3
116. Формализм в знаниях абитуриентов проявляется в не-
умении применить знание законов постоянного тока при реше-
нии конкретных задач. Так, например, большинство поступаю-
щих знают закон Ома для участка цепи, правильно рассказыва-
ют о последовательном и параллельном соединениях проводни-
ков, но вместе с тем не могут произвести расчет сопротивления
шунта к амперметру и добавочного резистора к вольтметру, не
могут объяснить, как зашунтированный амперметр и вольтметр
с добавочным резистором включаются в цепь для измерения си-
лы тока и напряжения.
Задача 1. Амперметр предназначен для измерения силы
тока до /а = 2 А и имеет сопротивление /?а = 0,2 Ом. Найти со-
противление Rm шунта, который надо подключить к этому ампер-
метру, чтобы можно было измерить силу тока до /=10 А. Как
изменится при этом цена деления амперметра?
Решение. Шунт — это резистор, подключенный параллель-
но амперметру. Для измерения силы тока / в проводнике ам-
перметр включается последовательно с этим проводником
(рис. 130). При этом ток, идущий в проводнике, частично ответв-
ляется в шунт, поэтому / = /а-)-/ш, где /а, /ш — силы токов, прохо-
дящих через амперметр и шунт соответственно. Пусть / больше
/а в п раз, т. е. / = л/а, тогда
Так как амперметр и шунт соединены параллельно, то паде-
ние напряжения на них одинаковое и, согласно закону Ома,
равно /ап\ = /ш/?ш. На основании двух последних формул полу-
чим:
D
А,,, =
л—1 "
200
h
Рис. 130
где л = — Подставив в эту формулу числовые значения, найдем:
/?„, = ¦
0,2
12.
2 "
Ом = 0,05 Ом.
Цена деления амперметра при этом увеличится в 10 раз. Напом-
ним, что ценой деления прибора называется величина, равная
значению измеряемой физической величины, соответствующему
отклонению стрелки на одно деление.
Задача 2. Вольтметр, рассчитанный на измерения напря-
жений до UB = 2 В, имеет сопротивление RB = 3 кОм. Найти со-
противление Ra добавочного резистора, который надо подклю-
чить к вольтметру, чтобы можно было измерять напряжение до
U = 22 В.
Решение. Добавочный резистор соединяется последова-
тельно с вольтметром, а вольтметр с этим резистором подключа-
ется параллельно к тому участку цепи, на котором надо изме-
рить напряжение (рис. 131). Измеряемое напряжение равно сум-
R
пз
и
Рис. 131
ме напряжений на вольтметре UB и на добавочном резисторе
и=ив+ил. Пусть U = nUR, тогда
201
Сила тока, проходящего через вольтметр и добавочный рези-
стор, одинакова и, согласно закону Ома, равна
R. Л, ¦
Отсюда /?д = /?в(л— 1), где п = — .
Подставив числовые значения величин, найдем:
— Л кОм = 30 кОм.
Отметим, что один и тот же электроизмерительный прибор,
предназначенный для измерения силы токов и напряжений
(например, гальванометр), может быть использован как в каче-
стве амперметра, так и в качестве вольтметра. В первом случае
его нужно зашунтировать, во втором — последовательно с ним
включить добавочный резистор.
Существенное различие между амперметром и вольтметром
заключается в том, что внутреннее сопротивление амперметра
должно быть по возможности очень малым, чтобы меньше вли-
ять на силу измеряемого тока, а сопротивление вольтметра дол-
жно быть как можно больше, чтобы сила тока, идущего через не-
го, была как можно меньшей. Не все абитуриенты это усвоили,
некоторые видят различие только в том, что амперметром изме-
ряют силу тока, а вольтметром — напряжение.
117. Правильно сформулировав закон Джоуля — Ленца,
многие абитуриенты допускают ошибки, применяя этот закон в
конкретной ситуации. Приведем несколько примеров таких
ошибок.
1. Как изменится количество теплоты, выделяемое электро-
плиткой за определенное время, если ее спираль укоротить?
Абитуриенты часто отвечают, что количество теплоты
Q уменьшится, и обосновывают свой ответ так: согласно закону
Джоуля — Ленца, при прохождении тока силой / по проводнику
с сопротивлением R в течение времени t в нем выделяется коли-
чество теплоты
Q = I2Rt. A)
С уменьшением длины спирали уменьшится ее сопротивле-
ние, следовательно, уменьшится и количество теплоты Q. Ответ
ошибочен.
И формула A) верна, и верно, что, если спираль укоротить, ее
сопротивление уменьшится. Но не надо забывать, что при этом
увеличится сила тока /, так как, согласно закону Ома, / = -r-, a
R
напряжение в сети осталось прежним. Подставив это значение / в
формулу A), получим:
202
откуда видно, что с уменьшением сопротивления R количество
теплоты Q увеличивается. Если сделать очень короткую спираль,
то она перегорит.
2. Соединим параллельно два проводника, сопротивления ко-
торых равны /?, и R2, и подключим их к источнику тока. В каком
из проводников выделится большее количество теплоты за одно
и то же время, если известно, что R{>R2?
Некоторые поступающие утверждают, что большее количе-
ство теплоты выделится в том проводнике, сопротивление кото-
рого больше, и что это видно из формулы A). Это неверно, так
как сила тока в проводниках различная.
При параллельном соединении напряжения на проводниках
одинаковые, поэтому, воспользовавшись формулой B), приходим
к правильному ответу: большее количество теплоты выделится
в проводнике, сопротивление которого меньше.
Если те же проводники соединить последовательно, то сила
тока в них будет одинаковой, и, согласно формуле A), большее
количество теплоты выделится в том проводнике, сопротивление
которого больше.
3. Две электрические лампочки, рассчитанные на напряже-
ние ^ = 220 В и мощности /3,=60 Вт и Р2—Ю0 Вт соответст-
венно, соединили последовательно и включили в сеть с напряже-
нием 220 В. Требуется сравнить яркости этих лампочек.
По мнению ряда абитуриентов, ярче будет гореть лампочка
мощностью 100 В, другие считали, что яркость их будет одинако-
вой, потому что при последовательном соединении сила тока в
лампочках одинакова.
Каков же правильный ответ? Ярче будет гореть та лампочка,
нить которой выделяет большее количество теплоты. При после-
довательном соединении лампочек сила тока / в них одинакова.
За время t, согласно закону Джоуля — Ленца, количество тепло-
ты, выделяемое нитью первой лампочки, Qi=I2R]t, второй —
Q2=/2/?2^, где /?,и^ — сопротивления первой и второй нитей со-
ответственно. Отсюда видно, что ярче будет гореть та лампочка,
сопротивление нити которой больше.
Чтобы сравнить сопротивления /?, и R2, воспользуемся соот-
ношением P=U2/R, где Р —мощность лампочки; U—напря-
жение, на которое она рассчитана; R — сопротивление нити. Тог-
да
Так как Р, = 60 Вт, Р2=100 Вт, т. е. РХ<Р2, то RX>R2. Следо-
вательно, 60-ваттная лампочка будет гореть ярче, чем 100-ваттная.
4. Электродвигатель постоянного тока имеет обмотку, сопро-
тивление которой равно R. Если двигатель работает от сети с на-
203
пряжением U, то по обмотке идет ток силой /. Найти работу, со-
вершаемую двигателем за время t, и количество теплоты, выде-
ляемое обмоткой за это время.
Большинство абитуриентов допускают здесь ошибки. Некото-
рые считают, что электродвигатель совершает работу A=IUt,
а выделяемое количество теплоты Q——t; другие утверждают,
н
что и количество теплоты, и искомая работа могут быть опреде-
лены по одним и тем же формулам:
Q = A=f2Rt=~t = lUt. A)
н
Следует обратить внимание на то, что если единственным ре-
зультатом прохождения электрического тока по проводнику яв-
ляется только нагревание проводника, то работа электрического
тока равна количеству теплоты, выделяемому проводником,
т. е. справедливы соотношения A).
Если же на участке цепи часть электрической энергии пре-
вращается в механическую, то количество теплоты нужно нахо-
дить по формуле Q = I2Rt. Поэтому в рассматриваемом примере
обмоткой электродвигателя выделяется количество теплоты
Q = I2Rt. Потребляемая электродвигателем энергия W=IUt, a
совершаемая им механическая работа
118. На вопрос экзаменатора: «Что покажет вольтметр, под-
ключенный к зажимам источника тока (рис. 132)?» — абитури-
енты отвечают, что он покажет значение ЭДС этого источника.
Это неверно.
Вольтметр покажет напряжение на нем самом, т. е. U = fRB,
где / — сила тока; RB — сопротивление вольтметра. По закону
Ома для замкнутой цепи найдем силу тока:
где ?— ЭДС источника тока; г — его внутреннее сопротивление.
Отсюда получим: IRB= f—Ir. Следовательно, вольтметр пока-
жет напряжение
U=$—Ir. B)
Задача. Вольтметр, сопротивление которого /?в=150 Ом,
присоединили к зажимам источника тока, внутреннее сопротив-
ление которого л = 0,2 Ом. Какая относительная погрешность бу-
дет допущена, если показание вольтметра считать равным зна-
чению ЭДС?
Решение. Используя приведенные выше формулы B) и A),
найдем:
204
Относительная погрешность
б=-Ц^-юо%=-
100%,
C)
6=-
0,2
100% =0,13%.
150 + 0,2
Из выражения C) следует, что относительная погрешность
будет меньше, если взять вольтметр с большим сопротивлением.
Так, например, если RE= 15 кОм, то расчет по формуле C) при-
водит к результату 6 = 0,001%.
6. г &.г
Рис. 132
Рис. 133
119. Серьезные трудности возникают у абитуриентов при ре-
шении задач, в которых требуется найти силы токов в цепях, со-
держащих несколько источников тока. В связи с этим полезно
обратить внимание на следующие случаи.
1. Если замкнутая цепь содержит п последовательно соеди-
ненных одинаковых источников тока с ЭДС $ и внутренним со-
противлением г (рис. 133), то сила тока в этой цепи
/ =
R + nr '
где R — сопротивление внешнего участка цепи.
Если ЭДС ?,, ?2> —>$п и внутреннее сопротивления г,, г2, ...,г„
источников тока, соединенных последовательно, различны, то си-
ла тока
2. Если замкнутая цепь содержит п параллельно соединен-
ных одинаковых источников тока с ЭДС f и внутренним сопро-
тивлением г (рис. 134), то во внешнем участке цепи, сопротивле-
ние которого R, сила тока
/ = ——
3. Если в разветвленной электрической цепи имеется не-
сколько различных источников тока с известными значениями
205
ЭДС и внутренних сопротивлений, а также несколько резисто-
ров, сопротивления которых известны, то для нахождения сил
токов во всех участках такой цепи удобно пользоваться правила-
ми Кирхгофа*:
1) алгебраическая сумма сил токов, сходящихся в узле, рав-
на нулю:
/, + /2+... + /„ = 0; A)
2) в любом замкнутом контуре алгебраическая сумма паде-
ний напряжений на всех его участках равна алгебраической
сумме ЭДС источников тока, имеющихся в этом контуре:
Л/?!+ /2#2 +••• + /„#„= У.+ % + -+?„• B)
Узел — это точка разветвления, в которой сходится не менее
трех проводников. Контур — это любая замкнутая часть схемы
электрической цепи. Падением напряжения на участке на-
зывается произведение силы тока на сопротивление этого
участка.
При использовании правил Кирхгофа нужно действовать в
такой последовательности:
1) произвольно обозначить на схеме стрелками направления
токов во всех участках цепи;
2) произвольно выбрать направление обхода контуров (по ча-
совой стрелке или против);
3) на основании первого и второго правил Кирхгофа соста-
вить систему уравнений, соблюдая при этом правило знаков:
а) при составлении уравнения A) силы токов, входящих в узел,
считаются положительными, выходящих из узла — отрицатель-
ными; б) при составлении уравнения B) падение напряжения бе-
рется со знаком « + », если направление тока на данном участке
совпадает с направлением обхода контура, и со знаком «—», ес-
ли не совпадает; ЭДС берется со знаком «4-», если при обходе
контура приходится идти внутри источника от отрицательного
полюса к положительному, в противном случае — со зна-
ком «—»;
4) контуры надо каждый раз выбирать так, чтобы они содер-
жали хотя бы одну цепь, не входящую в уже использованные
контуры;
5) в полученные уравнения подставить числовые значения
всех известных величин и решить систему уравнений; если при
этом значения некоторых сил токов получатся со знаком «—», то
это указывает на то, что действительные направления этих токов
противоположны тем направлениям, которые мы произвольно
указали на схеме.
* В школьном учебнике эти правила не рассматриваются, но они изучались
выпускниками школ с углубленным изучением физики, а также ряда техникумов
и профессионально-технических училищ.
206
Рис. 134
Рис. 135
Задача 1. Два элемента с ЭДС ?,= 1,25 В и f2 = 1,5 В,
имеющие одинаковые внутренние сопротивления г1 = г2 = 0,4 Ом,
соединены параллельно и замкнуты резистором, сопротивление
которого /?=10 Ом. Найти силы токов в резисторе и в каждом
элементе.
Решение. Обозначим направления токов и выберем на-
правление обхода контуров так, как показано на рисунке 135.
По первому правилу Кирхгофа составим уравнение для уз-
ла А:
По второму правилу Кирхгофа составим уравнение для кон-
туров A^BRA и Л^В^А соответственно:
Подставив числовые значения ЭДС и сопротивлений, полу-
чим систему уравнений:
/-/,—/2=0,
0,4/, +10/= 1,25,
0,4/, - 0,4/2 =—0,25. J
Решив эту систему, получим: /«0,135 А, /,«—0,245 А,
/2«0,38 А. Значение силы тока /, получилось отрицательным,
это указывает на то, что действительное направление данного то-
ка противоположно обозначенному.
207
Задача 2. Аккумулятор, разряженный до <f=6 В, подклю-
чен для зарядки к выпрямителю с напряжением 11 = 10 В.
Внутреннее сопротивление аккумулятора г == 1,5 Ом, сопротив-
ление подводящих проводов /? = 0,5 Ом. Какова сила тока при
зарядке?
R
czi
Т
Рис. 136
Решение. При зарядке аккумулятора его положительный
полюс соединяют с положительным полюсом выпрямителя, а от-
рицательный— с отрицательным (рис. 136). Обходя контур по
часовой стрелке, составляем по второму правилу Кирхгофа
уравнение
где / — сила зарядного тока. Отсюда
-те- <»
Подставив числовые значения величин и произведя вычисле-
ния, получим / = 2Л.
К формуле A) можно прийти и без применения второго пра-
вила Кирхгофа, воспользовавшись только законом Ома для зам-
кнутой цепи, учитывая, что направления сторонних сил в акку-
муляторе и выпрямителе противоположны.
Абитуриенты, решая эту задачу, ошибочно вычисляют силу
тока по формуле
,_и+г
R + r ¦
120. Слабо усвоено многими абитуриентами понятие коэффи-
циента полезного действия (КПД) источника тока. Рассмотрим
задачу, которую многие не смогли решить.
Задача. Два потребителя подключаются к источнику тока
один раз последовательно, другой раз параллельно. Сравнить
КПД источника в обоих случаях.
Ответы поступающих были различные: одни утверждали, что
КПД больше во втором случае, так как общее сопротивление
двух потребителей при параллельном соединении меньше, чем
при последовательном, и сила тока будет больше; другие счита-
208
ли, что для данного источника тока КПД является величиной по-
стоянной. Оба ответа ошибочны.
Решение. КПД источника тока равен отношению мощности
Ри выделяемой внешним участком электрической цепи (полезной
мощности), к полной мощности Р, развиваемой источником:
л-—•
Если R — сопротивление внешнего участка цепи, г — внут-
реннее сопротивление источника, '{— его ЭДС, / — сила тока, то
Тогда КПД источника
_I^R___ IR
Согласно закону Ома для замкнутой цепи, / = —— . Следо-
R-\-r
вательно,
_ № _ R
11 "¦"¦(/? + /-)?" R + r ' С)
Таким образом, КПД источника тока зависит от значений со-
противления R внешнего участка цепи и внутреннего сопротив-
ления г источника. Один и тот же источник тока в различных це-
пях работает с различными КПД, поэтому иногда говорят не о
КПД источника, а о КПД цепи.
Вернемся теперь к задаче. Разделив в выражении A) числи-
тель и знаменатель на R, получим:
Отсюда следует, что с увеличением R увеличивается и КПД
источника. Следовательно, в первом случае КПД источника
больше, чем во втором, так как при последовательном соедине-
нии потребителей сопротивление внешнего участка цепи больше,
чем при параллельном.
Встречались также и такие ответы абитуриентов: «В этой за-
даче не хватает данных». В связи с этим обращает на себя вни-
мание общий недостаток в подготовке выпускников средних
школ: учащиеся приучены к тому, что в задачах обязательно
должны быть заданы все необходимые величины, не должно
быть недостающих и лишних. Но ведь в жизни, на практике за-
дачи встречаются чаще всего не в таком готовом виде, как учеб-
ные. При решении их приходится искать дополнительную инфор-
мацию, отбрасывать лишние, несущественные данные. Более то-
го, в конкретной производственной ситуации нужно уметь уви-
деть задачу, сформулировать ее.
209
121. При решении задач на постоянный ток часто обнаружи-
вается, что абитуриенты не могут применить математические
знания. В качестве иллюстрации рассмотрим следующую зада-
чу, которая, как правило, вызывала затруднения у многих уча-
щихся.
Задача. Источник тока с ЭДС $и внутренним сопротивле-
нием г подключен к реостату, с помощью которого можно изме-
нять силу тока в цепи. Выразить зависимость мощности Ри вы-
деляемой внешним участком цепи (полезной мощности), от силы
тока /, построить график этой зависимости и определить, при ка-
ком условии полезная мощность будет максимальной.
Решение. Мощность, развиваемая источником, Р=0.
Часть ее выделяется на внешнем участке цепи — это полезная
мощность Рх. Остальная мощность /з2 = /2г выделяется внутри
источника. Следовательно, Pt = P — Р2 или
Р,= Г/ — /V. A)
Уравнение A) выражает искомую зависимость полезной мощ-
ности Р, от силы тока /.
Из курса математики известно, что графиком функции
у = ахг-\-Ьх-\-с является парабола. Легко видеть, что выражение
A) — частный случай такой функции, поэтому график зависимо-
сти Р{ от / — парабола, обращенная выпуклостью вверх (рис.
137), так как перед членом, содержащим /2, стоит минус.
Найдем точки пересечения параболы с осью /. Уравнение
этой оси
Л = 0 B)
Решив совместно уравнения A) и B), получим /,=0, /2 = —.
Учитывая симметричность параболы, находим, что вершина ее
имеет абсциссу
_/, + /2_ г
°~~ 2 ~~ 2г ¦
Таким образом, полезная мощность максимальна при силе
тока
7о=27- C)
Согласно закону Ома для замкнутой цепи,
Из уравнений C) и D) следует, что R = r, т. е. полезная мощ-
ность будет максимальной в том случае, когда сопротивление
внешнего участка цепи равно внутреннему сопротивлению источ-
ника.
Построенный график позволяет сделать также следующие
210
выводы: 1) каждому значению полезной мощности Рь кроме
максимального, соответствуют два значения силы тока; 2) при
силе тока ?2=— полезная мощность равна нулю.
Напомним, что при коротком замыкании (/? = 0) сила тока,
согласно закону Ома, равна —. Поэтому второй вывод можно
сформулировать так: при коротком замыкании полезная мощ-
ность равна нулю.
Условие, при котором мощность Рх максимальна, можно най-
ти и другим способом. Выразим зависимость Pt от R:
2 ¦ E)
Исследуем эту функцию на экстремум. Для этого возьмем про-
изводную Р\ этой функции по R и приравняем ее нулю:
rf — (R + rf ~
Так как (R-\-rf^0, f?=0, то г — R = 0 или R = r. Исследуем
знак производной слева и справа от точек R = r. Если R<ir, то
Р\~>§, если же R>r, то Р\<С.Ь. Следовательно, в этой точке функ-
ция имеет максимум.
Таким образом, при R = r полезная мощность Р] имеет мак-
симальное значение. Из выражения E) следует, что это значение
я2
р, = —
При таком режиме работы источника его КПД т| = 50%.
Рис. 137
Рис. 138
122. В решениях задач абитуриенты иногда допускают такую
грубую ошибку: рассматривая разветвленные цепи постоянного
тока, содержащие на некоторых участках конденсаторы, они счи-
тают, что ток проходит и через эти участки.
Наличие конденсатора в цепи постоянного тока равносильно
разрыву цепи, так как обкладки конденсатора разделены ди-
211
электриком. В разветвленной электрической цепи постоянной ток
проходит только по тем участкам, которые не содержат конден-
саторов. Рассмотрим следующую задачу.
Задача. В цепи, схема которой показана на рис. 138, ем-
кость конденсатора С = 3 мкФ, ЭДС источника тока f=6 В, его
внутреннее сопротивление г = 2 Ом, сопротивления резисторов
RI и R2— соответственно /?)=4 Ом, /?2 = 5 Ом. Определить за-
ряд конденсатора.
Решение. В этой цепи ток идет только через резистор
R\. Через конденсатор и, следовательно, через резистор R2 ток
не проходит. Разность потенциалов между обкладками конден-
сатора равна падению напряжения на резисторе R\:
U = IRh
где / — сила тока.
Заряд конденсатора q = CU= С/Л?,. Согласно закону Ома,
Следовательно, заряд конденсатора
сж.
После подстановок числовых значений и вычислений получим
q=\2 мкКл. Из последней формулы видно, что заряд конденса-
тора не зависит от значения сопротивления R2. Резистор
R2 влияет на процесс зарядки конденсатора после замыкания
цепи: чем больше сопротивление R2, тем медленнее будет заря-
жаться конденсатор.
При решении этой задачи некоторые учащиеся ошибочно счи-
тали, что ток расходится в точке / по двум ветвям, а затем схо-
дится в точке 2, утверждали, что резисторы соединены парал-
лельно.
В отличие от постоянного тока переменный ток идет через
конденсатор: под действием переменного напряжения происхо-
дит периодическая зарядка и разрядка конденсатора.
123. Рассказывая об электролизе, некоторые абитуриенты
объясняют механизм проводимости растворов электролитов так:
«Под действием электрического тока соль начинает диссоцииро-
вать, т. е. молекулы ее распадаются на ионы». Это неверно.
При растворении в воде молекулы некоторых веществ, назы-
ваемых электролитами, под влиянием электрического поля по-
лярных молекул воды распадаются на отдельные положительно
и отрицательно заряженные ионы. Этот процесс называется
электролитической диссоциацией. Если присоединить к источни-
ку тока два электрода и опустить их в раствор электролита, то
имеющиеся в нем отрицательные ионы начнут двигаться к элект-
роду, соединенному с положительным полюсом источника (ано-
212
ду), а положительные — к электроду, соединенному с от-
рицательным полюсом (катоду). Вследствие этого в цепи будет
проходить электрический ток. Таким образом, проводимость рас-
творов электролитов обусловлена наличием в них ионов, т. е. это
ионная проводимость. При прохождении тока через раствор про-
исходит перенос вещества. В результате окислительно-восстано-
вительных реакций на электродах происходит выделение
веществ, входящих в состав электролитов. Этот процесс называ-
ется электролизом.
124. Выше сказано о ряде ошибок, встречающихся при реше-
нии задач, связанных с расчетом цепей постоянного тока. Кроме
того, можно отметить следующие ошибки и недостатки при ре-
шении таких задач: 1) неумение разобраться в условии задачи и,
как следствие этого, замена сознательного решения механиче-
ским подбором формул, часто таких, которые неприменимы в за-
данной ситуации; 2) небрежные, а порой и безграмотные постро-
ения схем электрических цепей; 3) неумение заменить заданную
схему другой, эквивалентной ей, но более простой или более на-
глядной, удобной для решения задачи; 4) неправильное примене-
ние закона сохранения энергии в задачах, где рассматривается
превращение электрической энергии во внутреннюю и механиче-
скую энергию.
Задачи по разделу «Законы постоянного тока» разнообразны.
На экзаменах часто предлагаются комбинированные задачи,
требующие применения формул из других разделов. Поэтому
трудно наметить общий план решения таких задач. Однако по-
лезно обратить внимание на ряд важных моментов. Нужно на-
чертить схему электрической цепи и внимательно проанализиро-
вать ее, установить тип соединения проводников (последователь-
ное или параллельное); иногда полезно заданную схему начер-
тить иначе, чтобы тип соединения был очевиден. В задачах на
работу, мощность и тепловое действие тока нужно установить,
какие превращения энергии происходят, и составить уравнение
на основе закона сохранения энергии. Задачи по электролизу ре-
шаются путем составления уравнения на основе закона Фа-
радея.
МАГНИТНОЕ ПОЛЕ.
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
125. Встречались абитуриенты, которые ошибочно считали,
что магнитное поле существует совершенно самостоятельно и ни-
как не связано с электрическими зарядами, с электрическим
полем.
В действительности же существует особая форма материи,
единое целое — электромагнитное поле. Магнитное поле — одна
из форм проявления электромагнитного поля (другой формой яв-
213
ляетея электрическое поле). Магнитное поле действует только
на движущиеся заряженные частицы или тела, на проводники
с током и намагниченные тела (например, на магнитную
стрелку).
Магнитное поле существует в пространстве, окружающем
проводники с током, намагниченные тела, а также движущиеся
электрически заряженные тела. Природа магнитного поля во
всех этих случаях едина: магнитное поле возникает в результате
движения заряженных микрочастиц (электронов, протонов,
ионов), а также благодаря наличию у микрочастиц собственных
магнитных свойств.
Переменное магнитное поле возникает также там, где есть
изменяющееся во времени электрическое поле. В свою очередь
при изменении во времени магнитного поля возникает электри-
ческое поле. Магнитное и электрическое поля взаимосвязаны и
не существуют отдельно друг от друга.
126. Нередки случаи, когда абитуриенты не могут опреде-
лить направление силовых линий и векторы магнитной индукции
полей прямолинейного проводника с током, кругового витка с то-
ком, соленоида. Не все учащиеся правильно усвоили понятие си-
ловых линий (линий магнитной индукции), о чем свидетельству-
ют такие, например, выражения в их ответах: «Если буравчик
вывинчивать, то силовые линии будут направлены против часо-
вой стрелки», «Чем сильнее магнитное поле, тем сильнее притя-
гиваются силовые линии и поэтому становятся гуще», «Силовая
линия направлена так, как направлены магнитные силы» и т. п.
Напомним, что линия магнитной индукции (силовая линия
магнитного поля) — это линия, касательная к которой в каждой
точке совпадает с направлением вектора магнитной индукции В.
Это воображаемые линии, они не могут между собой ни притяги-
ваться, ни отталкиваться. С помощью силовых линий графически
изображают магнитные поля, при этом проводят линии гуще в
тех местах, где больше магнитная индукция.
В отличие от силовых линий электростатического поля, кото-
рые всегда не замкнуты, силовые линии магнитного поля всегда
замкнуты, т. е. магнитное поле является вихревым. Картину рас-
положения этих линий можно наблюдать экспериментально:
железные опилки, помещенные в магнитное поле, выстраивают-
ся вдоль линий магнитной индукции.
Чтобы определить направление вектора магнитной индукции
В в какой-либо точке магнитного поля прямолинейного проводни-
ка с током, например, в точке А (рис. 139), нужно провести через
эту точку силовую линию. Она представляет собой окружность,
лежащую в плоскости, перпендикулярной к проводнику. Центр
этой окружности находится на оси проводника. Направление си-
ловой линии совпадает с направлением вращения буравчика
(правого винта), если направление его поступательного движе-
214
Ток
Рис. 139
Рис. 140
ния совпадает с направлением тока. Вектор магнитной индук-
ции Si в точке А направлен по касательной к силовой линии.
Для определения направления вектора магнитной индукции в
центре кругового витка с током (рис. 140) применяют второй ва-
риант правила буравчика: если буравчик вращать по направле-
нию тока в витке, то направление поступательного движения бу-
равчика совпадает с направлением вектора В.
Соленоидом называется цилиндрическая катушка, состоящая
из большого числа витков изолированной проволоки, по которой
идет электрический ток. Внутри длинного соленоида направ-
ление вектора магнитной индукции определяется аналогично,
так как соленоид представляет собой набор круговых витков
(рис. 141). Внутри соленоида магнитное поле однородное, т. е.
Ток
Рис. 141
магнитная индукция во всех точках одинакова по модулю
и направлению. На концах соленоида это поле переходит в неод-
нородное. Подобно постоянному магниту соленоид имеет два
магнитных полюса — северный и южный. Северным полюсом яв-
215
ляется тот конец соленоида, из которого выходят линии магнит-
ной индукции, а южным — тот, в который они входят.
127. Затруднения испытывают многие абитуриенты, когда
требуется определить направление вектора магнитной индукции
поля, создаваемого несколькими проводниками.
Рассмотрим простой пример. По двум длинным прямолиней-
ным параллельным проводникам, расположенным друг от друга
на расстоянии г, проходят в противоположных направлениях то-
ки. Каково направление магнитной индукции поля в точке А,
удаленной на расстояние г, от первого проводника и г2 от второ-
го (рис. 142, а)? Сечения проводов обозначены кружочками. Ток,
направленный к читателю, условно обозначен точкой (мы как бы
видим острие стрелы, движущейся к нам), а ток, идущий от чи-
тателя, обозначен крестиком (виден хвост стрелы, движущейся
от нас).
В точке А магнитное поле создается двумя проводниками с
током. Согласно принципу суперпозиции магнитных полей, маг-
Рис. 142
нитная индукция В результирующего поля равна векторной сум-
ме магнитных индукций полей, создаваемых каждым проводни-
ком с током в отдельности: S = Si + S2.
Проведем через точку А линии магнитной индукции полей
первого и второго проводников с током (рис. 142, б), по правилу
буравчика определим направление этих линий, изобразим векто-
ры В\ и Вч и, сложив их геометрически, найдем вектор В.
128. Абитуриенты не всегда правильно понимают физический
смысл встречающихся в некоторых задачах понятий, связанных
с магнитным полем Земли. Учитывая это, приведем важнейшие
из них.
Земля окружена магнитным полем. Точки Земли, в которых
вектор магнитной индукции имеет вертикальное направление,
называются магнитными полюсами. Магнитных полюсов Земли
два: Северный, где линии магнитной индукции выходят верти-
216
кально из Земли, и Южный, где они вертикально входят в Зем-
лю. Северный магнитный полюс Земли находится вблизи Южно-
го географического полюса, а Южный магнитный — вблизи Се-
верного географического. Так как магнитные и географические
полюсы Земли не совпадают, то магнитная стрелка указывает
направление на север приблизительно. Угол между направлени-
ями магнитного и географического меридианов называется маг-
нитным склонением.
Угол а, которой составляет с плоскостью горизонта вектор
магнитной индукции поля Земли, называется магнитным накло-
нением. Магнитная стрелка, которая может свободно вращаться
вокруг горизонтальной оси, устанавливается под углом а к гори-
зонту (рис. 143).
Рис. 143
Вектор магнитной индукции ноля Земли можно разложить на
две составляющие — вертикальную Вл и горизонтальную Вг:
Модули этих составляющих:
Ва = В sin а, В, = В cos а,
где а — магнитное наклонение.
Магнитная стрелка компаса указывает направление горизон-
тальной составляющей магнитной индукции поля Земли.
Магнитное наклонение и магнитное склонение полностью
определяют направление вектора магнитной индукции земного
магнитного поля в данном месте.
129. Записав правильно выражение для модуля силы Лорен-
ца, учащиеся допускают ошибки при определении направления
этой силы. Например, применяя правило левой руки, нередко за-
бывают, что если в магнитном поле движется отрицательно за-
ряженная частица, то четыре пальца должны быть направлены
навстречу вектору скорости движения, а если заряд частицы по-
ложительный, то эти пальцы располагаются по направлению
скорости. В обоих случаях в ладонь должна входить составляю-
щая магнитной индукции В, перпендикулярная к скорости час-
тицы, тогда отклоненный на 90° большой палец покажет направ-
ление силы Лоренца. Абитуриенты часто и при отрицательном
217
заряде частицы направляют четыре пальца по направлению
скорости.
130. Рассказывая о взаимодействии параллельных токов, не-
которые абитуриенты делают такую ошибку: считают, что если
токи в параллельных длинных проводниках идут в противопо-
ложных направлениях, то проводники притягиваются, а если в
одном направлении, то отталкиваются (по-видимому, поступаю-
щие усматривают кажущуюся аналогию с взаимодействием за-
рядов: разноименные притягиваются, одноименные отталкивают-
ся). В действительности, наоборот, параллельные проводники от-
талкиваются, если токи в них проходят в противоположных
направлениях, и притягиваются, если токи направлены одинако-
во. Это нетрудно показать с помощью правила буравчика и пра-
вила левой руки.
На рисунке 144 показаны сечения проводов / и 2. В первом
проводе ток идет от нас, во втором — к нам. Определим направ-
ление силы, действующей на второй провод. Для этого сначала
определим по правилу буравчика направление вектора магнит-
ной индукции В\ поля, создаваемого первым проводом в том ме-
сте, где находится второй провод. Затем по правилу левой руки
определим направление силы F,2i, действующей во второй про-
вод. Аналогично определим направление силы f]2, действующей
на первый провод в магнитном поле, создаваемом вторым прово-
дом. В результате мы видим, что силы взаимодействия направ-
лены противоположно, т. е. проводники отталкиваются.
Рис. 144
Аналогично можно показать, что параллельные проводники,
в которых направления токов одинаковы, притягиваются. Уча-
щимся рекомендуется сделать это самостоятельно.
131. Нередки случаи, когда абитуриенты смешивают понятие
магнитной индукции с понятием электромагнитной индукции.
Это грубая ошибка: физическую величину не отличают от яв-
ления.
Магнитная индукция — это векторная физическая величина,
являющаяся силовой характеристикой магнитного поля. Модуль
вектора магнитной индукции равен отношению модуля макси-
218
мальной силы Fwa^, действующей со стороны магнитного поля на
участок проводника с током, к произведению силы тока / на дли-
ну / этого участка:
max
ii
Аналогично тому, как напряженность Е электростатического
поля характеризует силовое действие поля на вносимый в него
заряд, магнитная индукция характеризует силовое действие маг-
нитногс поля на электрический ток, т. е. на движущиеся
электрические заряды.
Электромагнитная индукция — это явление возникновения
электрического тока в проводящем контуре при изменении маг-
нитного потока через поверхность, ограниченную этим контуром.
132. Многие абитуриенты не имеют четкого представления о
явлении электромагнитной индукции, о процессе возникновения
ЭДС индукции в проводнике. На вопрос, что такое электромаг-
нитная индукция, встречались, например, такие ответы: «Это яв-
ление, заключающееся в том, что в проводящей катушке возни-
кает электрический ток, если вставить в нее магнит», «Это явле-
ние возникновения электрического тока в проводящем контуре
при прохождении через него магнитного потока», «Это явление
отклонения стрелки гальванометра, соединенного с катушкой, в
которую вставляют магнит» и т. п.
Расплывчатость, неопределенность этих формулировок оче-
видна. Скажем, из первого ответа не ясно даже, когда возникает
ток в катушке: при движении магнита или когда он покоится в
катушке; во втором ответе не понятно, о каком магнитном потоке
идет речь: о постоянном или изменяющемся; в третьем не ясно,
обязательно ли наличие гальванометра, будет ли ток в катушке
без него и т. д.
Выше (п. 131) уже отмечалось, в чем заключается явление
электромагнитной индукции. Электрический ток в контуре (ин-
дукционный ток) обусловлен возникновением ЭДС индукции в
этом контуре, а это означает, что на заряды в проводнике дейст-
вуют сторонние силы.
Если неподвижный проводник находится в изменяющемся
магнитном поле, то сторонними силами являются силы вихрево-
го электрического поля, которое возникает там, где есть изме-
няющееся магнитное поле. В явлении электромагнитной индук-
ции обнаруживается важный, фундаментальный факт: при вся-
ком изменении со временем магнитного поля в пространстве,
окружающем изменяющееся магнитное поле, возникает электри-
ческое поле. Электрическое вихревое поле образуется независи-
мо от того, имеется ли в магнитном поле проводящий контур или
нет. Поместив контур в изменяющееся магнитное поле, мы мо-
жем только обнаружить вихревое электрическое поле по вызван-
ному им индукционному току. Как только магнитное поле пере-
219
станет изменяться, вихревое электрическое поле исчезнет и ин-
дукционный ток прекратится.
В случае, когда проводник движется в постоянном магнитном
поле, сторонними силами, действующими на свободные заряды
проводника, являются силы Лоренца. Под действием этих сил
происходит разделение зарядов, в результате чего между конца-
ми проводника возникает разность потенциалов.
133. Значительное число абитуриентов считает, что индукци-
онный ток в проводящем контуре возникает всегда при движе-
нии этого контура в однородном магнитном поле. Такое мнение
ошибочно.
Необходимым и достаточным условием возникновения индук-
ционного тока в контуре является изменение магнитного потока
через поверхность, ограниченную контуром.
Магнитным потоком через поверхность называется скаляр-
ная физическая величина
Ф = .85 cos a,
где В — модуль вектора магнитной индукции; S — площадь по-
верхности; а — угол между вектором В и нормалью к поверхно-
сти.
Из этого определения следует, что в однородном магнитном
поле (8 = const) магнитный поток изменяется при изменении
площади S или угла а. Если площадь контура остается постоян-
ной, то индукционный ток в контуре возникает только при таком
движении, при котором изменяется угол а. Например, если кон-
тур вращается в однородном магнитном поле вокруг оси, лежа-
щей в плоскости контура и перпендикулярной к вектору магнит-
ной индукции (рис. 145, а), то в нем возникает индукционный
ток, потому что при вращении изменяется угол а между векто-
ром В и нормалью п к плоскости контура.
Индукционный ток возникает и в том случае, если при неиз-
менном угле а изменяется площадь S контура, например он де-
формируется (рис. 145, б).
Приведем теперь два примера движения контура в однород-
ном магнитном поле, при которых индукционный ток не возника-
ет, так как магнитный поток через поверхность, ограниченную
контуром, не изменяется: 1) контур вращается вокруг оси, лежа-
щей в плоскости контура и направленной вдоль вектора магнит-
ной индукции (рис. 145, в); 2) контур движется поступательно
(рис. 145, г). В обоих приведенных случаях остаются постоянны-
ми В, S и а и, следовательно, Ф = const.
Последние примеры показывают, что ошибаются те абитури-
енты, которые считают, что всегда при пересечении контуром ли-
ний магнитной индукции в нем возникает индукционный ток.
Здесь такое пересечение есть, однако тока нет, потому что не из-
меняется магнитный поток.
220
о
U
134. Слабо усвоено экзаменующимися понятие магнитного
потока. Записав приведенную выше определяющую формулу
Ф = Б5 cos а, они не подчеркивают, что она справедлива для од-
нородного поля и плоской поверхности. В случае любой (не плос-
кой) поверхности и неоднородного поля расчет магнитного пото-
ка усложняется: нужно разбить поверхность на такие малые
участки, чтобы их можно было считать плоскими, а поле в окре-
стности каждой из них — однородным. Элементарный поток че-
рез такую площадку АФ = ВА5 cos a, a поток через всю данную
поверхность равен пределу суммы этих элементарных потоков
при AS^>-0, и находится он путем интегрирования.
Рассмотрим в качестве примера вопрос, отвечая на который
абитуриенты, как правило, допускают ошибку. Проводящее
кольцо площадью 5 расположено в однородном магнитном поле
так, что вектор магнитной индукции В перпендикулярен к плос-
кости кольца. Каково будет изменение магнитного потока через
поверхность, ограниченную кольцом, если его повернуть на 180°?
Часто отвечают так: АФ = 0, так как Ф, = Ф2 = В5. Ошибоч-
ность такого ответа становится очевидной, если рассмотреть ри-
сунок 146. При первом расположении кольца (рис. 146, а) маг-
нитный поток Ф, = В5, так как угол а, между нормалью п и
вектором В равен нулю и cosa,= l; после поворота кольца на
180° векторы п и В направлены противоположно (рис. 146, б),
а2 = л, cos а2= — 1, магнитный поток Ф2= —BS. Следовательно,
изменение магнитного потока
= ф2 — ф,= — 2BS.
221
a
к
\
\
/
ч». _ _ ^v
п о
fr<2=Jr\
1 1
_
» •-
X
X
(
X
X
1
X
1
X
X
,F
X
mi}
X
Рис. 147
Рис. 146
135. Зная формулировку правила Ленца, абитуриенты часто
обнаруживают неумение применить его для определения направ-
ления индукционного тока. Поясним это на примерах.
1. По двум вертикальным параллельным
металлическим шинам, верхние концы кото-
рых замкнуты, скользит без трения, не те-
ряя контакта, проводящий стержень (рис.
147). Система находится в однородном маг-
нитном поле, вектор магнитной индукции В
которого перпендикулярен к плоскости чер-
тежа и направлен от читателя, что условно
обозначено крестиками. Определить на-
правление индукционного тока.
Почему в контуре, образованном шина-
ми и стержнем, возникает ток? При сколь-
жении стержня увеличивается площадь по-
верхности, ограниченной этим контуром, и,
следовательно, за счет этого увеличивается магнитный поток че-
рез эту поверхность. Согласно закону электромагнитной индук-
ции, в контуре возникает при этом индукционный ток.
Чтобы определить направление этого тока, воспользуемся
правилом Ленца: индукционный ток всегда имеет такое направ-
ление, при котором создаваемое им магнитное поле противодей-
ствует изменению магнитного потока, вызывающего этот ток.
В данном случае магнитное поле индукционного тока будет пре-
пятствовать увеличению магнитного потока, которым он вызван.
Следовательно, вектор индукции магнитного поля индукционно-
го тока будет направлен противоположно вектору В, т. е. из-за
плоскости чертежа к читателю. Теперь применим правило бурав-
чика: будем вращать буравчик так, чтобы его поступательное
движение тоже имело направление из-за плоскости чертежа к
нам. Очевидно, для этого нужно вращать буравчик против часо-
вой стрелки. Такое же направление имеет индукционный ток в
контуре. В частности, в стержне этот ток идет слева направо.
К этому же выводу можно прийти, рассуждая несколько ина-
че. Согласно правилу Ленца, индукционный ток будет иметь та-
кое направление, чтобы своим магнитным полем препятствовать
причине, которой он обусловлен, т. е. противодействовать со-
222
скальзыванию стержня. Значит, на стержень с индукционным
током будет действовать, согласно закону Ампера, сила F, на-
правленная противоположно силе тяжести mg. Теперь применим
правило левой руки: расположим ее так, чтобы вектор В входил
в ладонь, а отогнутый на 90° большой палец был направлен так
же, как и сила F, тогда четыре вытянутых пальца покажут на-
правление тока в стержне — слева направо.
2. К замкнутому проводящему кольцу приближается север-
ный полюс постоянного магнита, при этом ось магнита остается
перпендикулярной к плоскости кольца (рис. 148). Каково направ-
ление индукционного тока в кольце?
Рис. 148
При движении магнита магнитный поток через ограниченную
кольцом поверхность увеличивается. Следовательно, согласно
правилу Ленца, индукционный ток в кольце будет иметь такое
направление, что создаваемое им магнитное поле будет противо-
действовать этому увеличению. Значит, вектор магнитной
индукции В2 поля тока направлен противоположно вектору В1
поля постоянного магнита. Теперь, применяя правило буравчи-
ка, нетрудно найти, что индукционный ток в кольце направлен
против часовой стрелки, если смотреть по направлению вектора
скорости v магнита.
136. Анализ ответов экзаменующихся показывает, что вопро-
сы по электромагнетизму вызывают у них большие затруднения
потому, что основные понятия и законы многими либо не усвое-
ны, либо усвоены чисто формально и слабо.
Рассмотрим следующий пример. Магнитный поток, пронизы-
вающий контур, равномерно возрастает от Ф,=2 Вб до
Ф2 = 6 Вб за время А^= 1 с. Определить значение ЭДС индукции,
возникающей в контуре.
Обычно абитуриенты правильно находят это значение на
основании закона электромагнитной индукции:
?_ АФ_ Ф2-Ф,= 6-2в_ 1В
Но они не могут объяснить, каков физический смысл знака «—»
в полученном результате.
223
В уравнении
АФ
выражающем закон электромагнитной индукции, знак «—»
соответствует правилу Ленца. ЭДС индукции % всегда имеет
знак, противоположный знаку АФ.
По определению ЭДС индукции — скалярная физическая ве-
личина, равная работе, совершаемой вихревым электрическим
полем при перемещении единичного положительного заряда по
замкнутому контуру. Знак ЭДС связан с произвольно выбран-
ным положительным направлением нормали п к плоскости кон-
тура. Выбрав направление нормали п, мы тем самым задаем по-
ложительное направление тока в контуре, так как оба этих на-
правления должны быть связаны между собой правилом бу-
равчика (правого винта). ЭДС индукции «Г, положительна, если
направление индукционного тока совпадает с заданным положи-
тельным направлением тока в контуре, и отрицательна в против-
ном случае. Определив знак %, мы определим также направле-
ние линий напряженности вихревого электрического поля,
т. е. направление силы, действующей со стороны этого поля на
единичный положительный заряд.
Проиллюстрируем сказанное следующим примером. Пусть к
замкнутому проводящему контуру приближается северный по-
люс постоянного магнита, при этом ось магнита остается перпен-
дикулярной к плоскости контура (рис. 149, а). Выберем (произ-
вольно) положительное направление нормали п слева направо,
тогда положительное направление тока в контуре должно совпа-
дать с направлением вращения буравчика при его поступатель-
ном движении слева направо (на рисунке обозначено штриховы-
ми стрелками). При таком выборе нормали магнитный поток,
пронизывающий контур, Ф>0. Приближение магнита равно-
сильно увеличению магнитного потока, т. е. АФ>0. Из
формулы fj= — следует, что ^<0. Это означает, что индук-
ционный ток будет идти в направлении, противоположном вы-
бранному положительному направлению, т. е. так, как показано
на рисунке сплошными стрелками.
Конечно, может возникнуть вопрос: какой был бы результат,
если бы мы выбрали положительное направление нормали п
справо налево? При таком выборе (рис. 149, б) будет Ф<0,
АФ<С0, f,>0. Следовательно, индукционный ток будет идти в
направлении, совпадающем с положительным направлением то-
ка, что и показано на рисунке: сплошные стрелки направлены
так же, как и штриховые. Мы видим, что направление индукци-
онного тока такое же, как и в первом случае, чего и следовало
ожидать, ибо этот ток зависит только от того, в каком направле-
нии движется магнит.
Возвращаясь теперь к полученному выше значению f,= —4 В,
легко видеть, что описанная в примере ситуация аналогична
той, которая показана на рисунке 149, а.
Читателю предлагается самостоятельно найти, какими были
бы знаки $ и направление индукционного тока, сели бы магнит
удалялся от контура.
137. Рассмотрим некоторые задачи, вызывающие серьезные
затруднения у абитуриентов.
Задача 1. Металлический стержень равномерно вращает-
ся вокруг одного из его концов в однородном магнитном поле в
плоскости, перпендикулярной к силовым линиям поля (рис. 150).
Угловая скорость стержня ы = 75 рад/с, его длина / = 0,4 м, Mar-
в
хххххххх
X X X^--5f
х / х
Л
v
\
X \ X
\
X X
X
/
X X Х^^Х___Х,^Х X X
ххххх ххх
Рис. 150
Заказ 2473
225
нитная индукция поля В = 0,1 Тл. Найти ЭДС индукции в
стержне.
Экзаменующиеся, как правило, решают эту задачу так:
!, = Blv, A)
где v — скорость стержня: у = со/. Следовательно, f, = (o.6/2.
Это неверно. Формула A) справедлива при поступательном
движении проводника перпендикулярно к силовым линиям. Кро-
ме того, у = со/ — это линейная скорость вращающегося конца
стержня, а не всего стержня.
Решение. При вращении в стержне возникает ЭДС индук-
ции, модуль которой
_ ДФ __ BAS
1~~КГ ~ м •
где AS — площадь, которую прочерчивает стержень за время
At. За один оборот стержень описывает площадь л/2, за время
At — площадь AS = Nnl'2, где N — число оборотов: N =^-— . Сле-
довательно,
AS = ^, с==^!=0,6 В.
Задача 2. Плоский проводящий контур площадью S =
60 см2 находится в однородном магнитном поле с индукцией
.8 = 0,4 Тл. Какой заряд пройдет по контуру, если его повернуть
на угол: 90°; 180°? Сопротивление контура R = 2 Ом.
Решение. При повороте контура изменяется пронизываю-
щий его магнитный поток, поэтому возникает ЭДС индукции и в
контуре идет индукционный ток. За время А/ по контуру пройдет
заряд
где / — сила тока. Согласно закону Ома для замкнутой цепи,
где f, — ЭДС индукции:
/==— B)
ДФ _ Ф2-Ф,
Ф,, Ф2 — магнитный поток, пронизывающий контур, до и после по-
ворота его соответственно.
На основании выражений A) — C) имеем:
*=-х- D)
Если повернуть контур на угол 90°, то Ф2 = 0. Учитывая, что
Ф, = В5, найдем АФ = 0 — BS= —BS. Подставив это выражение
в формулу D), получим:
226
BS ...
9.=x- E)
Если контур повернуть на угол 180°, то, как показано выше
(см. рис. 146), ЛФ=—2BS. Следовательно, по контуру пройдет
заряд
2BS /с.
**=-*-¦ F)
Подставив числовые значения в формулы E) и F) и произве-
дя вычисления, получим: (/,= 1,2 мК,л, </2 = 2,4 мК,л.
Определения величин и законы, применяемые при решении
этой задачи, абитуриентам известны, но использовать их они,
как правило, не могут. Одни, например, записав формулу A),
этим ограничиваются, так как время At не дано. Другие ошибоч-
но считают, что здесь нельзя применять закон Ома B), потому
что нет источника тока. Некоторые ошибаются при нахождении
ЛФ (об этом говорилось выше), считая, что при повороте на 180°
АФ = 0.
Из приведенного решения следует, что если измерить заряд,
прошедший по контуру при его повороте в магнитном поле, мож-
но найти значение магнитной индукции поля:
Для измерения заряда контур подключается к гальваномет-
ру. При этом результат не зависит от времени А/, за которое по-
ворачивается контур. Полезно заметить также, что на основании
формулы D) дается определение единицы магнитного потока
СИ — вебера:
[ДФ] = [<7][/?]=1 к.л-1 Ом=1 Кл-Ом = 1 Вт.
Вебер равен магнитному потоку, при убывании которого до
нуля в сцепленной с ним электрической цени сопротивлением
1 Ом через поперечное сечение проводника проходит электриче-
ский заряд 1 Кл. Нетрудно показать, что 1 Вб = 1 Кл-Ом =
= 1 В-с=1 Тл-м2. Эти равенства можно использовать при про-
верке правильности размерностей расчетных формул, получае-
мых при решении задач.
Задача 3. Прямоугольная проводящая рамка площадью S,
содержащая N витков, равномерно вращается с угловой скоро-
стью со в однородном магнитном поле, вектор магнитной индук-
ции В которого направлен по вертикали (см. рис. 145, а). В на-
чальный момент времени угол а между нормалью п к плоскости
рамки и вектором В равен нулю. Найти ЭДС индукции в момент
времени t.
Решение. Поскольку при равномерном вращении рамки
227
угол а = со/, то магнитный поток, пронизывающий все витки, за-
висит от времени:
Ф = NBS cos a = NBS cos со/.
Согласно закону электромагнитной индукции, ЭДС индукции
в рамке равна взятой со знаком «—» скорости изменения маг-
нитного потока, т. е. Щ является взятой со знаком « — » производ-
ной магнитного потока по времени:
?,= — Ф'@= —(NBS cos ti)t)/ = NBS<i} sin со/ =
= '4т sin со/,
где $m = NBSw — максимальное (амплитудное) значение ЭДС.
Таким образом, в рамке возникает переменная ЭДС, изменя-
ющаяся по закону синуса. Такую вращающуюся в магнитном по-
ле рамку можно рассматривать как простейшую модель генера-
тора переменного тока.
Одной из причин, вызывающих затруднения у абитуриентов
при решении этой задачи, является то, что они, как правило,
применяют закон электромагнитной индукции только в виде
$1= —АФ/At, а более строгая математическая запись этого зако-
на f,= — Ф'@ остается за пределами их внимания.
138. На вопрос, как движется заряженная частица в однород-
ном магнитном поле, абитуриенты, как правило, отвечают, что
она движется по окружности. Это, вообще говоря, неверно.
Если частица с зарядом q и массой т, имеющая скорость v,
попадает в магнитное поле, то ее траектория зависит от угла а
между вектором магнитной индукции В и скоростью v. Для
определенности будем считать заряд q положительным и рас-
смотрим несколько случаев.
1. Векторы v и В направлены одинаково (рис. 151, а),
т. е. а = 0.
Сила Лоренца
Fn = qvB sin a.
Отсюда видно, что в этом случае Fn = 0, так как sina = 0;
магнитное поле не влияет на движение частицы.
2. Векторы v и В направлены противоположно (рис. 151, б).
В этом случае a =180°, sin a = 0, /7л==0; магнитное поле также
не влияет на движение частицы.
3. Частица влетает в однородное магнитное поле со ско-
ростью v, направленной перпендикулярно вектору В (рис. 151, в),
а = 90°. Сила Лоренца Fл = qvB, направленная всегда перпенди-
кулярно к скорости, сообщает частице центростремительное
2
ускорение а=—. Согласно второму закону Ньютона, Fn = ma
или
228
/
X / X
х В
X
X \ X Л
х \ х
\
¦ /С
X / X
х
Рис. 151
qvB=-
R '
где /? — радиус окружности, по которой движется частица в маг-
нитном поле. Отсюда
Период обращения частицы по окружности
„ 2nR 2лт
~~ v qB '
A)
B)
Последняя формула показывает, что период Т не зависит от ско-
рости V.
4. Частица влетает в однородное магнитное поле так, что век-
тор скорости v составляет с вектором магнитной индукции В
угол 0<а<90° (рис. 151, г).
Разложим вектор скорости v частицы на две составля-
ющие: у,, направленную вдоль линий магнитной индукции, и v2,
перпендикулярную этим линиям. Модули этих составляющих
равны соответственно:
На частицу действует сила Лоренца, обусловленная состав-
ляющей v2. Вследствие этого, как показано выше, частица дви-
жется со скоростью v2 по окружности в плоскости, перпендику-
лярной линиям индукции. Согласно формуле A), радиус этой
окружности,
229
tnv sin a
K=~q~F= q~B '
Одновременно частица будет равномерно двигаться вдоль ли-
ний индукции со скоростью у,, так как эта скорость не вызывает
появления силы Лоренца. В результате одновременного движе-
ния по окружности и по прямой частица будет двигаться по вин-
товой линии, «навиваясь» на линии магнитной индукции. Шаг
этой винтовой линии
и = V| / , (о)
где Т — период обращения частицы по окружности.
На основании формул B) и C) получим:
2лти cos a
= qB '
Имея четкое представление о рассмотренных выше случаях,
абитуриенты могли бы справиться с предлагаемыми на экзаме-
нах задачами, в которых рассматривается движение заряжен-
ных частиц в магнитном поле.
139. Плохо усвоено многими абитуриентами явление самоин-
дукции. Некоторые путают его с другими явлениями и даже ве-
личинами (ЭДС индукции, индуктивность, индуктивное со-
противление и др.).
Самоиндукция — это частный случай явления электромагнит-
ной индукции. Явление самоиндукции заключается в возникно-
вении ЭДС индукции в проводящем контуре при изменении силы
тока в нем или индуктивности контура.
Электрический ток, идущий в контуре, создает собственный
магнитный поток через поверхность, ограниченную контуром.
Этот поток Ф пропорционален силе тока / в контуре:
Ф = и, A)
где L — индуктивность контура.
При изменении собственного магнитного потока в контуре,
согласно закону электромагнитной индукции, возникает ЭДС са-
моиндукции
?s At ¦
Из формулы A) видно, что собственный магнитный поток
Ф изменяется, если изменяется сила тока. / или индуктивность
L. Если L = const, а изменяется только сила тока, то ЭДС самоин-
дукции
* / А/ <9\
*L B)
А/
где ——скорость изменения силы тока.
230
Если же / = const, a L изменяется, то
где скорость изменения индуктивности.
В общем случае ЭДС самоиндукции
Знак « —» указывает на то, что при увеличении силы тока
(или индуктивности) вихревое электрическое поле препятствует
этому увеличению, а при уменьшении препятствует этому умень-
шению.
140. Довольно часто экзаменующиеся ошибочно считают,
что индуктивность контура зависит от ЭДС самоиндукции fs и от
скорости изменения силы тока, ссылаясь при этом на вытекаю-
щее из формулы B) выражение
В действительности индуктивность контура зависит от его
геометрической формы и размеров, а также от магнитных
свойств среды, в которой находится контур (от магнитной прони-
цаемости среды).
Формулируя определение единицы индуктивности, некоторые
абитуриенты говорят: «Генри — это индуктивность, которая воз-
никает...» и т. д. Это неправильное выражение. Индуктивность
не возникает, она имеется, это скалярная физическая величина,
характеризующая магнитные свойства электрической цепи. Дру-
гими словами, индуктивность — это количественная характери-
стика связи между силой тока / в цепи и магнитным потоком Ф,
создаваемым этим током.
Из формулы Ф = И следует выражение L=—, согласно ко-
торому дается определение единицы индуктивности СИ — генри:
Генри равен индуктивности электрической цепи, с которой
при силе постоянного тока в ней 1 А сцепляется магнитный по-
ток 1 Вб.
141. Задачи по электромагнетизму вызывают большие за-
труднения у абитуриентов. Учитывая это, приведем ориентиро-
вочный план решения таких задач.
Сделать схематический чертеж, указать на нем направление
тока, направления вектора магнитной индукции и сил, действую-
231
тих на проводник или контур. Если по условию задачи провод-
ник (контур) находится в равновесии, то, как и при решении за-
дач по статике, записывают условия равновесия.
Задачи на движение заряженных частиц в магнитном и элек-
трическом полях решают в большинстве случаев путем составле-
ния уравнения движения материальной точки с учетом всех сил,
действующих на частицу со стороны магнитного и электрическо-
го полей.
Если требуется найти ЭДС индукции, необходимо установить,
изменением какой величины — вектора магнитной индукции В,
площади поверхности S, ограниченной контуром, или угла а
между вектором В и нормалью к поверхности — вызывается из-
менение АФ магнитного потока, а затем составить уравнение на
основе закона электромагнитной индукции и решить его.
КОЛЕБАНИЯ И ВОЛНЫ
142. Часто абитуриенты не могут правильно объяснить физи-
ческий смысл величин, входящих в уравнение
x = xmcos(a>t + <p0), A)
описывающее гармонические колебания. Напомним, что это
уравнение выражает зависимость от времени координаты х точ-
ки, совершающей гармонические колебания вдоль оси ОХ; при
этом начало координат совпадает с положением равновесия ко-
леблющейся точки, т. е. х — это отклонение (смещение) колеблю-
щейся точки от ее положения равновесия. Здесь хт — амплитуда
колебаний (максимальное отклонение от положения равновесия),
/ — время, со— круговая частота (ее также называют угловой
или циклической частотой). Величина а>г-\-щ, стоящая под зна-
ком косинуса, называется фазой колебаний; ср0—начальная
фаза.
Понятие фазы колебаний многими поступающими усвоено
слабо, о чем свидетельствуют ошибки в ответах на экзаменах.
Так, например, рассматривая колебания математического маят-
ника, абитуриенты нередко называют фазой угол отклонения ни-
ти от вертикали, что неверно. В самом деле, если представлять
себе фазу как угол, то о каком угле может идти речь, например,
при колебании груза, прикрепленного к пружине? Более того,
уравнение A) описывает, как известно, не только механические
гармонические колебания, но и периодические изменения любой
физической величины х, происходящие по закону косинуса. Из
этого уравнения видно, что если известны амплитуда хт, круго-
вая частота со и начальная фаза ф„, то значение величины х в
любой момент времени / однозначно определяется величиной
a>tf + ip0. Поэтому можно сказать, что фаза колебаний — это ска-
лярная физическая величина со/ + фо, являющаяся аргументом
косинуса в уравнении гармонических колебаний и характеризу-
ющая состояние колебательного процесса в каждый момент вре-
мени t. Начальная фаза ф0 определяет значение колеблющейся
величины х в начальный момент времени (/0 = 0).
Являясь аргументом тригонометрической функции, фаза вы-
ражается в угловых единицах — радианах.
233
Учитывая, что u>=-jr, где Т — период колебаний, фазу мож-
но представить в виде:
Отсюда видно, что любому значению времени, выраженному в
долях периода, соответствует определенное значение фазы, вы-
раженное в угловых единицах. Так, например, при фо = О момен-
ту времени t\=~r соответствует фаза ф,=у, моменту t2 = -~ —
фаза ф2 = л, моменту ^з = т Г — фаза ср3 = Зл/2, моменту t4= T —
фаза ф4 = 2л.
Циклическая частота со равна числу колебаний, совершаемых
за 2л с.
Отметим, что уравнение движения для одних и тех же гармо-
нических колебаний может быть записано как в виде A), т. е. с
использованием косинуса, так и с помощью синуса:
x=xm sin (со/
Встречались в ответах абитуриентов и такие грубые ошибки:
смещение точки от положения равновесия путали с амплитудой,
циклическую частоту со — с частотой v. Напомним, что цикличе-
ская частота связана с частотой соотношением co = 2jtv. Едини-
цей циклической частоты СИ является секунда в минус первой
степени (с~'), единицей частоты — герц (Гц).
143. Рассказывая о колебательных движениях, многие абиту-
риенты не могут объяснить, как изменяются скорость и ускоре-
ние гармонически колеблющейся точки. В лучшем случае они го-
ворят, что скорость есть производная координаты по времени,
а ускорение — производная скорости по времени или вторая
производная координаты по времени, но при этом затрудняются
указать различия между равноускоренным и колебательным
движениями.
Рассмотрим вопрос о скорости и ускорении колеблющейся
точки и покажем, что уравнение, выражающее зависимость ко-
ординаты гармонически колеблющейся точки от времени, можно
получить более простым и наглядным способом, чем с использо-
ванием понятия производной.
Пусть точка А (рис. 152) движется равномерно со скоростью
v по окружности радиусом хт. Тогда вектор хт, проведенный из
центра О окружности к точке А, будет равномерно вращаться
вокруг точки О с постоянной угловой скоростью со. Для простоты
будем считать, что в момент начала отсчета времени точка
А совпадает с точкой Ао, т. е. вектор хт образует с осью ОХ угол
фо = О при to = 0. Тогда в момент времени t угол между хт и осью
234
JT/2
X
Рис. 152
OX будет равен at, а проекция вектора хт на ось ОХ выразит-
ся так:
= хш cos со/,
A)
т. е. с течением времени она изменяется по закону косинуса. По
такому же закону изменяется координата точки В, являющейся
проекцией точки А.
Таким образом, проекция равномерно вращающейся по
окружности точки совершает гармонические колебания согласно
уравнению A), в котором хт — амплитуда колебаний, со — цик-
лическая частота, равная угловой скорости вращения вектора
хт. Спроектировав на ось ОХ скорость и ускорение точки А, най-
дем проекции на эту ось скорости и ускорения колеблющейся
точки В:
v=v cos
х = а cos
Подставив в эти формулы значения линейной скорости v = (oxm
точки А и центростремительного ускорения а = (й'2хт, получим:
B)
C)
ах = ю2хт cos (со/ + я).
Выражения B) и C) показывают, что скорость и ускорение
гармонически колеблющейся точки изменяются по гармониче-
скому закону. В отличие от равномерного прямолинейного дви-
жения скорость колеблющейся точки изменяется, в отличие от
равноускоренного движения ускорение колеблющейся точки то-
же изменяется по модулю и по направлению.
Сопоставляя выражения A)—C), приходим к выводу, что
имеется сдвиг фаз (разность фаз) между координатой, скоростью
и ускорением гармонически колеблющейся точки: скорость опе-
235
Рис. 153
режает координату на —, ускорение опережает координату на л,
ускорение опережает скорость на
2'
Наглядно это можно показать, если начала векторов хт, v и а
совместить с центром окружности О (рис. 153). Здесь углы,
образованные этими векторами с осью ОХ, численно равны зна-
чениям фаз координаты, скорости и ускорения в момент време-
ни /.
Графики зависимостей х, vx и ах от времени / показаны на ри-
сунке 154.
Нередко абитуриенты считают, что при максимальном откло-
нении математического маятника от положения равновесия его
ускорение равно нулю. Ошибочность такого ответа становится
очевидной, если сопоставить графики зависимостей х и ах от t:
при х = хт ускорение имеет максимальное значение \ах\ =ю2хт.
Наконец, отметим, что взяв производную по времени коорди-
наты, заданной уравнением A), мы получим x' = vx или
vx =—ыхт sin at. D)
Взяв теперь производную скорости по времени, найдем уско-
рение:
а^= — co2xm cos (о/. E)
Так как, согласно известным формулам приведения,
cos (mt-\-^-)= —sin bit, cos (u>t-\-n) = —cos со/,
то, следовательно, выражения B) и C) тождественны выражени-
ям D) и E) соответственно.
В общем случае, когда начальная фаза сро=^=О, в аргументах
косинуса и синуса выражений A)—E) добавится слагаемое ф0.
144. Нередко абитуриенты испытывают большие затруднения
при решении задач с применением уравнения, описывающего ко-
лебания. Рассмотрим две такие задачи, предлагавшиеся на эк-
заменах.
Задача I. Материальная точка совершает колебания, при
которых ее координата х изменяется со временем t по закону
х = 0,06 cos 50nt, A)
где все величины выражены в единицах СИ. Найти амплитуду,
циклическую частоту, частоту, период и начальную фазу колеба-
ний. Вычислить смещение точки при фазе л/3 рад и максималь-
ное значение скорости колеблющейся точки.
Решение. Запишем уравнение движения в общем виде:
о/ + ф0). B)
Сопоставляя уравнения A) и B), находим: амплитуда хт = 0,06 м,
циклическая частота со=50я с, начальная фаза фо = О. Теперь
найдем частоту v и период Т колебаний:
v=— =—— Гц = 25 Гц, Т = - =—с = 0,04 с.
2л 2л v 25
При фазе ф)=— рад смещение хх =0,06 cos ^- м= 0,03 м.
О О
Взяв производную координаты B) по времени, получим выра-
жение для скорости:
Максимальное (амплитудное) значение скорости \v ___ \=а>хт.
Вычислим:
237
\v I = 50л-0,06 м/с = 9,42 м/с.
х max
Задача 2. Написать законы изменения напряжения и и
силы тока i со временем / для электроплитки с сопротивлением
А? = 50 Ом, включенной в сеть переменного тока с частотой
v = 50 Гц и напряжением (/ = 220 В.
Решение. Напряжение изменяется по гармоническому за-
кону:
м= Uт cos со/, A)
где и — напряжение в момент времени /; Um — амплитудное
(максимальное) значение напряжения; со — циклическая часто-
та: со = 2jiv = 110я с~'. Зная действующее значение напряжения
U, находим U'т.
Um = ^2 и= 1,41 -220 В = 310 В.
Подставив значения Um и со в уравнение A), получим:
u = 310 cos 100л/.
Электроплитка имеет только активное сопротивление, поэто-
му колебания силы тока в ней совпадают по фазе с колебаниями
напряжения. Следовательно, закон изменения силы тока i име-
ет вид:
i = /mcos 100л/,
где /т — амплитудное значение силы тока. По закону Ома
Таким образом, i = 6,2 cos 100л/.
145. Слабо усвоен рядом экзаменующихся процесс превраще-
ния энергии при гармонических колебаниях. Так, например, не
все могли сформулировать закон сохранения энергии примени-
тельно к колебательным системам. Этот закон заключается в
следующем: полная энергия изолированной колебательной сис-
темы с течением времени не изменяется.
При колебаниях происходит превращение энергии из одного
вида в другой и обратно, благодаря чему наблюдается характер-
ная для колебаний повторяемость процесса. Так, в механических
колебательных системах происходит превращение потенциаль-
ной энергии в кинетическую и обратно, в колебательном конту-
ре — энергии электрического поля в энергию магнитного поля
и обратно. Если система изолирована, то в первом случае сумма
потенциальной и кинетической энергии остается постоянной, а во
втором случае остается постоянной сумма энергии электрическо-
го и магнитного полей.
В тот момент времени, когда энергия одного из видов дости-
гает максимального значения, энергия другого вида равна нулю.
238
Следовательно, при механических колебаниях полная механиче-
ская энергия равна максимальному значению кинетической
энергии колеблющейся точки либо максимальному значению по-
тенциальной энергии:
mv2m ггш?у?т k>?m
где т — масса точки; vm — ее максимальная скорость; со — цик-
лическая частота; хт — амплитуда колебаний; k — коэффициент
возвращающей силы, т. е. силы вида Fx= —kx (в частности, для
пружинного маятника k — это жесткость пружины).
Полная энергия колебательного контура равна максимально-
му значению энергии электрического поля конденсатора либо
максимальному значению энергии магнитного поля катушки ин-
дуктивности:
2С =^~'
где qm — амплитудное значение заряда конденсатора; С — ем-
кость конденсатора; L — индуктивность катушки; 1т—ампли-
тудное значение силы тока в контуре.
Задача /.На горизонтальной поверхности лежит шарик
массой т, прикрепленный к стенке с помощью пружины, жест-
кость которой равна k. Шарик сместили из положения равнове-
сия на расстояние х0 и толкнули влево, сообщив ему начальную
скорость v0 (рис. 155). Найти амплитуду колебаний. Массой пру-
жины и трением пренебречь.
Рис. 155
Решение. Рассмотрим два состояния системы: первое, ког-
да пружина была растянута и шарику сообщили скорость v0, и
второе, когда шарик максимально сместился влево, пружина
сжата. В первом состоянии полная энергия системы складыва-
ется из потенциальной энергии растянутой пружины и кинетиче-
ской энергии шарика:
_ М> I mvl
l 2 ' 2~
239
Во втором состоянии полная энергия системы равна потенци-
альной энергии сжатой пружины:
где хт — амплитуда колебаний.
Согласно закону сохранения энергии, Е{ = Е2 или
Отсюда найдем:
V, mvl
Из полученного результата следует частный случай: при
vo = O имеем хт = х0, т. е. если бы шарик отпустили без начальной
скорости, то амплитуда колебаний была бы равна х0.
Задача 2. В колебательном контуре происходят свободные
незатухающие электромагнитные колебания, период которых
7 = 0,2 мс. Найти амплитуду колебаний заряда, если известно,
что амплитуда колебаний силы тока /т = 31,4 мА.
Решение. Согласно закону сохранения энергии,
1С 2 '
откуда
где qm — амплитуда колебаний заряда; L — индуктивность ка-
тушки, С — емкость конденсатора. Из формулы Томсона
Т = 2n\jLC следует:
т
Подставив это выражение в формулу A), получим:
Подставив числовые значения, найдем qm=\ мкКл.
146. Как правило, большинство абитуриентов знают, что в го-
ризонтальном направлении шарик под действием силы упруго-
сти пружины (см. рис. 155) совершает гармонические колебания,
период которых
Т_9ттЛ №-
V я
где m — масса шарика; k — жесткость пружины. Но они не мо-
гут обосновать, почему по этой же формуле находится период
240
вертикальных колебаний шарика, под-
вешенного с помощью пружины. Пока-
жем это.
После того как подвесили шарик,
пружина удлинится на х, и будет нахо-
диться в равновесии под действием си-
лы упругости F\ и силы тяжести mg
(рис. 156, а). Координатную ось ОХ на-
правим вертикально вниз, совместив
ее начало с положением равновесия.
В положении равновесия сумма про-
екций сил F, и mg на ось ОХ равна
нулю:
mg — /глг,=О. A)
Рис. 156
Если шарик сместить от положения равновесия на х и отпу-
стить, не сообщая начальной скорости, то под действием силы
упругости F2 и силы тяжести mg шарик начнет двигаться с
ускорением, проекция которого на ось ОХ ах—х", где х" — вто-
рая производная координаты х по времени. Согласно второму
закону Ньютона, составим уравнение движения:
mg-k(Xl + x) = mx". B)
Выразив из уравнения A
в уравнение B), получим:
= kxt и подставив это значение
X" = X.
т
^ = i?L= 2л
А это и есть уравнение гармонических колебаний, циклическая
частота которых
а период
О слабом знании раздела «Колебания и волны» свидетельст-
вуют встречающиеся иногда грубые ошибки. Вот одна из них: не-
которые абитуриенты не видят различия между колебаниями и
гармоническими колебаниями, между колебаниями и волнами.
Напомним, что колебания — это движения или изменения со-
стояния, характеризующиеся той или иной степенью повторяемо-
сти во времени. Колебания делятся на периодические и неперио-
дические. Простейшими периодическими колебаниями являются
гармонические колебания. Гармоническими колебаниями назы-
241
ваются периодические изменения физической величины со вре-
менем, происходящие по закону синуса или косинуса. Различные
периодические процессы могут быть представлены как резуль-
тат сложения нескольких гармонических колебаний.
Волны — это изменения состояния среды (возмущения), рас-
пространяющиеся в пространстве с конечной скоростью. Колеба-
ния, возникшие в некоторой точке упругой среды, передаются со-
седним точкам, которые также начинают колебаться. Частицы
среды, в которой распространяется волна, не переносятся вместе
с волной, а лишь совершают колебания около своего положения
равновесия. В поперечной волне они колеблются в направлении,
перпендикулярном к направлению распространения волны, а в
продольной—вдоль направления распространения волны. Рас-
пространяясь в среде, волна переносит энергию от источника ко-
лебаний.
Механические поперечные волны могут возникать только в
твердой среде. Возникновение продольных волн возможно в
твердых телах, жидкостях и газах.
Колебания электромагнитного поля порождают электромаг-
нитную волну.
147. Большие затруднения вызывал у абитуриентов следую-
щий вопрос. На рисунке 157, а изображен график зависимости
координаты от времени при гармонических колебаниях, а на ри-
сунке 157, б—поперечная волна. Обе кривые — косинусоиды.
Какой физический смысл имеет каждая из них? Правильный от-
вет приходилось слышать очень редко.
Первая косинусоида показывает, каковы координаты одной
и той же колеблющейся точки в различные моменты времени.
Вторая кривая изображает смещения от положения равновесия
различных точек среды в один и тот же момент времени, причем
эти точки находятся на различных расстояниях s от источника
колебаний.
Рис. 157
242
148. В качестве примеров грубых ошибок приведем такие
(неправильные!) определения, встречавшиеся в ответах абитури-
ентов: «Продольной называется волна, которая распространяет-
ся горизонтально, а поперечной — волна, распространяющаяся
вертикально», «Длиной волны называется длина косинусоиды от
начальной до конечной точки».
Напомним, что длиной волны называется расстояние между
двумя ближайшими точками, разность фаз колебаний которых
равна 2л радиан.
Рассмотрим задачу, вызывавшую затруднения у абитури-
ентов.
Задача. Вдоль натянутого шнура распространяется попе-
речная волна. Разность фаз колебаний двух точек шнура, отстоя-
щих друг от друга на расстоянии / = 0,2 м, равна Лф = — рад.
Найти скорость волны, если известно, что частота колебаний
v = 5 Гц.
Решение. Скорость волны
v = Xv, A)
где X — длина волны; v — частота.
Найдем длину волны. Разность фаз колебаний двух точек
шнура, отстоящих друг от друга на расстоянии, равном длине
волны, равна 2л рад. Если же расстояние между точками равно
/, то разность фаз Дф их колебаний связана с длиной волны соот-
ношением
/ Дф
откуда
—
Дф
Подставив это выражение в формулу A), получим:
_ 2n/v
Дф
Подставив числовые значения, получим v=\0 м/с.
149. Подавляющее большинство абитуриентов не могли спра-
виться с задачами, в которых нужно определить период колеба-
ний математического маятника, находящегося в системе, движу-
щейся с ускорением (например, в лифте, ракете, вагоне и др.).
В некоторых вузах такие задачи предлагаются абитуриентам,
несмотря на то что в курсе физики средней школы рассматрива-
ются только колебания маятников в инерциальных системах от-
счета. Учитывая это, мы ознакомим читателя со способом реше-
ния таких задач.
Если математический маятник находится в неинерциальной
системе отсчета, т. е. в системе отсчета, которая движется отно-
243
сительно инерциальной системы отсчета с некоторым ускорени-
ем а, то период колебаний его
гг
A)
= 2я\—,
где g, —ускорение свободного падения в неинерциальной систе-
ме отсчета. Это ускорение можно найти из векторного уравнения
?,=? + (-а), B)
где g — ускорение свободного падения в инерциальной системе
отсчета. Проиллюстрируем это примерами.
1. В кабине лифта, движущегося с ускорением а, направлен-
ным вверх, ускорение свободного падения gi=gJr(—а). Так как
векторы g и —а сонаправлены, то модуль вектора gt равен
g\—g-\-Q- Следовательно, согласно формуле A), период колеба-
ний математического маятника длиной / в этом лифте
7\=2я
Рассуждая аналогично, можно показать, что в случае движе-
ния лифта с ускорением а, направленным вниз, период колеба-
ний маятника
В обоих случаях направление скорости лифта не влияет на
период колебаний маятника.
2. Математический маятник длиной / подвешен в вагоне, дви-
жущемся горизонтально с ускорением а. Найти период колеба-
ний этого маятника.
Построим gx
рисунка 158,
согласно уравнению B). Как видно из
Рис. 158
244
Направление вектора gi определяет направление нити, когда
маятник находится в положении равновесия. Если вывести его
из этого положения и отпустить, то он будет совершать колеба-
ния с периодом
7" = 2л
Задача. Математический маятник длиной / = 0,8 м подве-
шен в кабине самолета, взлетающего с аэродрома под углом
а = 30° к горизонту с ускорением а = 5 м/с2. Найти период коле-
баний маятника.
Решение. Сложив векторы g и — а, найдем ускорение сво-
бодного падения в самолете g{ (рис. 159). Найдем модуль этого
ускорения. По теореме косинусов имеем:
ё\ = а2 + g2-2ag cos (90° + а) = a2 + g2 + 2ag sin а.
Следовательно,
ina. A)
Период колебаний маятника
Т = 2пЛр-. B)
После вычислений по формулам A) и B) получим 7"= 1,6 с.
а
Рис. 159
150. Рассказывая о звуковых волнах, некоторые абитуриенты
ошибочно считают, что это особые волны, отличающиеся от меха-
нических волн. В действительности же это распространяющиеся
в упругой среде механические колебания. Человеческое ухо вос-
принимает звуковые волны, частота которых лежит в пределах от
16 Гц до 20 000 Гц.
Следует различать объективные и субъективные характери-
стики звука. Объективными характеристиками звуковой волны
являются частота, амплитуда колебаний, спектральный состав
волны. При восприятии органами слуха впечатление о звуке опи-
245
сывают субъективные характеристики: высота (чем больше ча-
стота, тем выше звук), громкость (чем больше амплитуда коле-
баний, тем больше громкость звука), тембр (качественная оцен-
ка звука, характеризующая его определенный оттенок, завися-
щая от спектрального состава звука).
151. Слабо усвоено абитуриентами понятие действующего
значения силы переменного тока. Некоторые понимают его как
значение силы тока в данный момент времени, т. е. смешивают
это понятие с понятием мгновенного значения силы тока. Как из-
вестно, действующее значение силы переменного тока равно си-
ле постоянного тока, который выделяет в проводнике такое коли-
чество теплоты, что и переменный ток за то же время.
Действующее значение силы переменного тока / связано с
его амплитудным значением 1т соотношением
1т
/
Нередко абитуриенты ошибочно утверждают, что амперметр
и вольтметр, включенные в цепь переменного тока, показывают
амплитудные значения силы тока и напряжения. На самом же
деле амперметром и вольтметром мы измеряем действующие
значения силы тока и напряжения.
152. Абитуриенты знают, что если участок цепи постоянного
тока состоит из нескольких проводников, соединенных последо-
вательно, то напряжение между концами этого участка равно
сумме напряжений на всех отдельных проводниках этого участ-
ка. Исходя из этого, некоторые абитуриенты считают, что анало-
гичное соотношение справедливо и для цепи переменного тока,
т. е. что в цепи переменного тока, состоящей из последовательно
соединенных резистора с активным сопротивлением, катушки
индуктивности и конденсатора, амплитудное значение напряже-
ния на участке равно алгебраической сумме амплитудных значе-
ний напряжений на резисторе, катушке и конденсаторе:
Um=UmR+UmL+UmC.
Это грубая ошибка. В действительности напряжения на этих
участках — величины переменные, гармонически колеблющиеся,
причем их фазы колебаний не совпадают. Можно доказать, что
указанные выше амплитудные значения напряжений связаны
соотношением
Um = ^UlR + (UmL-~UmCf. A)
Отметим, далее, что отсюда легко получить формулу, выра-
жающую связь между силой тока, напряжением и сопротивлени-
ем в цепи переменного тока. Если амплитудное значение силы
тока равно /ш, то
246
где R — активное сопротивление; L — индуктивность; со — цик-
лическая частота; С — емкость. Подставив эти значения в фор-
мулу A) и сделав несложные преобразования, получим:
'¦= , "" . ... B)
Выражение B) называется законом Ома для цепи переменно-
го тока, а величина
называется полным сопротивлением цепи переменного тока.
153. Рассказывая о назначении, устройстве и работе транс-
форматора, некоторые экзаменующиеся допускают грубые
ошибки. Об этом свидетельствуют, например, встречавшиеся в
ответах такие утверждения: «Трансформатор служит для преоб-
разования тока высокой частоты в ток низкой частоты», «Транс-
форматор вырабатывает ток», «Первичная обмотка трансформа-
тора подключается к источнику постоянного тока, а вторич-
ная — к потребителю».
Напомним, что трансформатор предназначен для преобразо-
вания переменного тока одного напряжения в переменный ток
другого напряжения при неизменной частоте. Принцип работы
трансформатора основан на явлении электромагнитной индук-
ции. Переменный электрический ток, проходящий по первичной
обмотке трансформатора, создает переменный магнитный поток,
который возбуждает ЭДС индукции в каждой обмотке. Отноше-
ние ЭДС индукции е, в первичной обмотке к ЭДС индукции е2 во
вторичной обмотке равно отношению числа витков /V, в первич-
ной обмотке к числу витков N2 во вторичной обмотке:
е2 N2 ¦
154. Не все абитуриенты правильно понимают, каковы усло-
вия возникновения электромагнитных волн.
Напомним, что источником электромагнитных волн являются
электрические заряды, движущиеся с ускорением. Лишь в том
случае, когда заряд движется с ускорением, переменное элект-
рическое поле будет порождать переменное магнитное поле, а
переменное магнитное поле в свою очередь вызовет появление
переменного электрического поля.
Условиями излучения контуром электромагнитных волн до-
статочной интенсивности являются высокая частота колебаний
и открытая форма колебательного контура.
155. Некоторые абитуриенты не могли объяснить, какие ве-
личины изменяются с течением времени в электромагнитной
волне.
247
В бегущей электромагнитной волне колеблются векторы на-
пряженности электрического поля Е и магнитной индукции В
магнитного поля. Эти векторы в каждой точке пространства в
данный момент времени взаимно перпендикулярны и каждый из
них перпендикулярен направлению скорости волны v. Взаимная
Bj
Рис. 160
ориентация векторов Е, В и v определяется правилом буравчи-
ка: если буравчик вращать так, чтобы направление его поступа-
тельного движения совпадало с направлением вектора и, то вра-
щательное движение буравчика будет соответствовать повороту
вектора Е к вектору В в сторону наименьшего угла (рис. 160).
ОПТИКА
156. Некоторые абитуриенты имеют ошибочное представле-
ние о процессе распространения света от источников конечных
размеров при его прохождении через отверстия и при образова-
нии теней от предметов. Они считают, например, что свет, иду-
щий от источника через круглое отверстие, должен давать на эк-
ране резко ограниченный светлый кружок на темном фоне, а ес-
ли вместо отверстия поставить на пути пучка света круглый
непрозрачный диск, то на экране должна быть видна резкая
тень в форме темного кружка. Но это не всегда так. Опыт пока-
зывает, что если размеры отверстия или диска во много раз
меньше, чем расстояние от них до экрана, то на экране наблюда-
ется система чередующихся темных и светлых колец. Более того,
вопреки законам геометрической оптики, в центре тени от непро-
зрачного диска всегда наблюдается светлое пятно. Здесь обна-
руживается отклонение света от прямолинейного распростране-
ния, огибание им краев препятствий. Это явление, называемое
дифракцией света, обусловлено волновой природой света.
Встречалась в ответах и грубая ошибка: поток света от точеч-
ного источника рассматривался как совокупность параллельных
лучей, а не лучей, расходящихся по всем направлениям.
В ответах и решениях задач, связанных с применением зако-
на отражения света, ошибки были обусловлены либо нечетким
знанием этого закона (пример ответа: «Луч света как упал, так и
отразился»), либо тем, что экзаменующиеся путали угол падения
(угол между нормалью и падающим лучом) с углом скольжения
(угол между падающим лучом и границей раздела двух сред).
Еще пример неправильного ответа: считают, что если светя-
щаяся точка расположена не напротив плоского зеркала (рис.
161, а), то изображения ее в зеркале не будет. Однако изображе-
ние будет наблюдаться, если смотреть под некоторым углом к
плоскости зеркала (рис. 161, б). Напомним, для построения изоб-
ражения точки S надо построить ход двух лучей, исходящих из
этой точки. После отражения они попадают в глаз наблюдателя,
и ему будет казаться, что лучи выходят из точки S:, которая яв-
ляется изображением точки S в плоском зеркале. Нетрудно до-
казать, что S/4=/4S,.
249
Зеркало
Зеркало
Р и с. 161
157. Многие абитуриенты чувствуют себя крайне неуверенно,
когда приходится рассматривать вопрос о полном отражении
света, допускают ошибки при решении задач. Например, для
определения предельного угла полного отражения а0 они во всех
случаях используют формулу
sinao = -, A)
приведенную в школьном учебнике, что, вообще говоря, неверно,
и вот почему.
В чем заключается явление полного отражения? Если свет
идет из оптически более плотной среды в оптически менее плот-
ную, то из закона преломления
sin а п2
следует, что угол преломления
п =
1, sin В=
sin
B)
"i
больше угла падения а, так как
sin а. При падении на гра-
ницу раздела двух сред свет частично проходит во вторую среду,
преломляясь при этом, и частично отражается. Если увеличи-
вать угол падения, преломленный луч будет приближаться к
границе раздела сред и становиться менее ярким, а яркость от-
раженного луча растет. При некотором угле падения а0, который
называется предельным углом полного отражения, преломлен-
ный луч идет по границе раздела, т. е. угол преломления р = 90°,
а отраженный луч имеет почти такую же яркость, как и падаю-
щий. При этом, согласно формуле B), учитывая, что sin 90° = l,
имеем:
sin ao = — = п,
C)
где щ, «2 — абсолютные показатели преломления соответственно
первой и второй среды; п — относительный показатель прелом-
ления.
250
В частности, если вторая среда — вакуум (п2=\) или воздух
(л2«1), то sin ao= l/«i-
Таким образом, формула A) является частным случаем вы-
ражения C) при условии, что под п понимают показатель пре-
ломления первой среды (л = л,). Четкого представления об этом
у поступающих, как правило, нет.
Чтобы не допускать путаницы, целесообразно в ответах на
вопросы и особенно в решениях задач обозначать относительный
показатель преломления буквой п с двумя индексами: п2] — по-
казатель преломления второй среды относительно первой. Тогда
s\nao = ^- = n2i. D)
Задача. Световой пучок идет из алмаза, показатель пре-
ломления которого Я! = 2,4, в стекло с показателем преломления
л2=1,5. Найти угол, на который отклонится пучок от перво-
начального направления на границе раздела этих сред, если
угол падения: а, = 50°; а2 = 30°. Определить скорость света в
стекле, если известно, что в алмазе скорость света
и, = 1,25-108 м/с.
Один из абитуриентов решал эту задачу так: из закона пре-
ломления B) следует, что в первом случае синус угла прелом-
ления
. и, sin a, 2,4 sin 50°
sin 8= = — = 1,23.
r n.2 1,5
Но синус угла не может быть больше единицы. Вспомнив это,
абитуриент остановился, сказав, что тут что-то не так. Последо-
вал вопрос экзаменатора: «Всегда ли световой пучок перейдет из
алмаза в стекло, т. е. из среды, оптически более плотной, в сре-
ду, оптически менее плотную?» Экзаменующийся, вспомнив о яв-
лении полного отражения, ответил правильно: «Нет, не всегда,
а только в том случае, когда угол падения меньше предельного
угла полного отражения а0. Теперь ход решения ясен: сначала
найдем а0». А искал он его так:
1 «1 2,4 , с
sin ao = —= —= -г-=-= 1,6.
и п п2 1,5
Получив опять синус больше единицы, абитуриент сказал: «За-
дача простая, но решить не смог».
Читатель, конечно же, заметил, что абитуриент допустил
ошибку, о которой сказано выше. Каково же правильное реше-
ние этой задачи?
Решение. Найдем предельный угол полного отражения, ис-
пользуя формулу D):
ao = 38,68°
251
В первом случае угол падения а, больше предельного угла а0>
поэтому световой пучок полностью отражается (рис. 162, а), от-
клоняясь при этом от первоначального направления на угол
Ф, = 180° — 2а, = 80°. Во втором случае а2<а0, свет переходит из
алмаза в стекло. Найдем угол преломления:
sin B9 = — sin a, = -
P и с. 162
2,4 sin 30°
Гб
= 0,8;
Как видно из рис. 162, б, световой пучок при этом отклонится
от первоначального направления на угол Ф2 = Р2 — а2 = 23°.
Чтобы найти скорость света в стекле, воспользуемся соотно-
шением
где и,,
Отсюда
скорости света в алмазе и стекле соответственно.
2,4-1,25-108
Us
м/с = 2-108 м/с.
158. Правильно формулируя закон преломления света, неко-
торые экзаменующиеся не могли применить его в конкретной фи-
зической ситуации. Они не могли, например, объяснить, где ви-
дит наблюдатель камешек, лежащий на дне водоема, если он
смотрит почти вертикально вниз. Пытаясь ответить на этот во-
прос, абитуриент изображал на рисунке какой-то луч, исходя-
щий из глаза и попадающий на камешек (рис. 163, а), но этим
ничего не объяснялось. На самом же деле лучи идут не из глаза,
а от камешка и попадают в глаз человека. Проведем луч SA,
перпендикулярный к поверхности воды, и луч SB, составляющий
с перпендикуляром малый угол (рис. 163, б). Первый луч не пре-
ломляется, второй преломляется. Когда они попадают в глаз, че-
ловек видит изображение камешка в точке S,, в которой пересе-
каются продолжения расходящихся лучей. Поэтому и кажущая-
ся глубина водоема h меньше его истинной глубины Н. Из ри-
сунка 163, б видно, что utgp = #tga. Для малых углов
252
и
-h
=?!-
A
<
Щ
f
7
/в
1
1
i'Ii
Рис. 163
tga«sina, поэтому можно записать: h sin р = Я sin a, откуда
где п„ п2 — абсолютные показатели преломления воды и воздуха
соответственно. Так как л,=—, п2=1, то h = —H.
3 4
159. Абитуриенты обычно правильно объясняют общий ха-
рактер хода луча, падающего из воздуха на прозрачную тре-
угольную призму: преломляясь на двух гранях, луч всегда откло-
няется к основанию призмы (рис. 164). Но многие из них не мо-
гут вычислить угол 8 отклонения луча призмой, если известны
угол падения а, преломляющий угол призмы ф и показатель пре-
ломления материала призмы п. Здесь опять обнаруживается
уже отмечавшийся выше недостаток в подготовке выпускников
средней школы — неумение применять при решении физических
задач знания, полученные при изучении математики.
Покажем, как найти угол отклонения луча призмой.
Этот угол
-о1) A)
как внешний угол треугольника ABC. Кроме того,
ZLAEB= /LBDK как углы со взаимно перпендикулярными сторо-
нами. Угол BDK является внешним углом треугольника ABD,
поэтому
Ф = Р + а,. B)
На основании закона преломления света можем записать:
sin a .„.
—— = п, C)
sin р
sina,i_
sin р, п
Дальнейший ход вычислений таков: находим из выражения
C) р, затем из формулы B) а,, потом из формулы D) C, и, нако-
нец, подставив найденные значения углов в выражение A), нахо-
дим 6.
Обратим внимание на два важных момента.
1. Угол отклонения луча, как видно из формул A) — D), зави-
сит от показателя преломления материала призмы. А показа-
тель преломления в свою очередь зависит от длины световой
волны (эта зависимость называется дисперсией света). Поэтому
если на пути узкого луча белого света поставить прозрачную
призму, то на экране, расположенном за ней, будет виден непре-
рывный спектр — радужная полоска, содержащая семь основ-
ных цветов, которые следуют в таком порядке: красный, оранже-
вый, желтый, зеленый, голубой, синий, фиолетовый. Наименьший
показатель преломления и наибольшая длина волны (Лк = 760
нм) соответствуют красному свету, наибольший показатель пре-
ломления и наименьшая длина волны (Лф = 400 нм) — фиолето-
вому.
Абитуриенты нередко дисперсией ошибочно называют разло-
жение белого света на монохроматические лучи.
2. Если треугольная призма находится в среде, оптически бо-
лее плотной, чем материал призмы (иначе говоря, абсолютный
показатель преломления среды больше абсолютного показателя
преломления материала призмы), то при прохождении через
призму луч света отклоняется не к основанию, а от него (рис.
165). Этот факт почему-то остается за пределами внимания мно-
гих абитуриентов, и поэтому они, например, твердо уверены, что
двояковыпуклая линза всегда является собирающей, что, вообще
говоря, неверно.
Двояковыпуклую линзу можно схематично представить как
совокупность призм (рис. 166). Если среда, окружающая такую
линзу, оптически более плотная, чем материал линзы, то линза
будет рассеивающей, так как световые лучи отклоняются от
оснований призм.
Рассуждая аналогично, читатель легко придет к выводу, что
двояковогнутая линза не всегда является рассеивающей. Если,
например, в стекле имеется двояковыпуклая воздушная полость,
254
Р и с. 165 Рис. 166
то она играет роль рассеивающей линзы. Если же воздушная по-
лость двояковогнутая, то она действует как собирающая линза.
160. Опыт вступительных экзаменов показывает, что абиту-
риенты испытывают большие трудности при построении изобра-
жений в линзах. Как правило, они знают только один или два
простейших примера, а в других случаях допускают ошибки. На
рисунке 167, а приведено сделанное абитуриентом неправильное
построение изображения предмета АВ.
б
Рис. 167.
Напомним, что для построения изображения предмета в лин-
зе нужно построить сначала изображение нескольких точек это-
го предмета, а затем по ним построить изображение предмета.
Для построения изображения точки нужно взять два луча, ход
которых легче всего построить. Такими лучами являются: 1) луч,
падающий на линзу параллельно главной оптической оси; 2) луч,
проходящий через оптический центр линзы; 3) луч, проходящий
через главный фокус.
На рисунке 167,6 показано правильное построение изобра-
жения А\ВХ предмета АВ. Сначала построено изображение точки
А, затем — точки В. Изображение предмета в данном случае
мнимое, прямое и увеличенное. Из рисунка также видно, что
если плоский предмет АВ расположен перпендикулярно к глав-
ной оптической оси, то его изображение АХВХ перпендикулярно
к этой оси.
255
Задача. Плоский предмет АВ установлен перпендикуляр-
но к главной оптической оси собирающей линзы. Построить изоб-
ражение этого предмета в линзе при различных расстояниях d
от предмета до линзы. Положения фокусов линзы и ее главной
оптической оси заданы.
Решение. На рисунке 168—172 построено изображение
Л|В, предмета АВ для пяти различных случаев.
1. Если d<CF, где F — фокусное расстояние, т. е. предмет на-
ходится между фокусом и линзой, то изображение мнимое, уве-
личенное и прямое (рис. 168).
Рис. 168
2. Если d = F, т. е. предмет находится на расстоянии, равном
фокусному расстоянию, то изображение находится на бесконеч-
ности (рис. 169).
3. Если F <.d<2F, т. е. предмет находится между фокусами
и точкой, отстоящей от линзы на расстоянии, равном двойному
фокусному расстоянию, то изображение действительное, увели-
ченное и перевернутое (рис. 170).
2F
A
I
F
В
\
0
\
N
2F
\
Рис. 169
4. Если d = 2F, т. е. предмет находится от линзы на расстоя-
нии, равном двойному фокусному расстоянию, то изображение
действительное, такое же по размеру, как и сам предмет, и пере-
вернутое (рис. 171).
5. Если rf>2F, т. е. предмет находится от линзы на расстоя-
нии, превышающем двойное фокусное расстояние, то изображе-
ние действительное, уменьшенное и перевернутое (рис. 172).
256
л
2F\
' В
Г4
/
\
0
\
\
\
2F В,
Рис. 172
Чаще всего абитуриенты допускают ошибки при построении
изображений в первом и втором случаях, а также в случае если
линза рассеивающая.
Полезно обратить внимание на то, что в случае рассеиваю-
щей линзы изображение А{ВХ предмета АВ всегда мнимое,
уменьшенное и прямое (рис. 173) независимо от расстояния d
между предметом и линзой. При построении изображения в рас-
сеивающей линзе мы воспользовались двумя лучами: лучом, иду-
щим параллельно главной оптической оси, и лучом, проходящим
через оптический центр линзы. Первый луч после преломления
линзой идет так, что его продолжение проходит через главный
фокус, а второй луч, как и в случае собирающей линзы, не изме-
няет своего первоначального направления.
161. Многие абитуриенты не могли правильно построить ход
луча, падающего под углом к главной оптической оси собираю-
9 Заказ 2473
257
щей или рассеивающей линзы. В лучшем случае они делали ри-
сунки, лишь качественно пояснявшие ход такого луча: собираю-
щая линза отклоняет его в сторону главной оптической оси (рис.
174, а), а рассеивающая — от этой оси (рис. 174, б).
Для правильного построения этого луча надо провести побоч-
ную оптическую ось, параллельную лучу, и построить фокальную
плоскость. Точка пересечения побочной оси и фокальной плоско-
сти является побочным фокусом /*",. В случае собирающей линзы
луч после линзы пройдет через точку /•", (рис. 175, а), а в случае
рассеивающей луч после линзы идет так, что его продолжение
проходит через побочный фокус Ft (рис. 175, б).
6 w
Рис. 174
Рис. 175
258
162. Неумение использовать побочные оптические оси приво-
дит к затруднениям при построении изображения в линзах све-
тящейся точки, особенно если эта точка лежит на главной опти-
ческой оси линзы.
Задача 1. Построить изображение светящейся точки, ле-
жащей на главной оптической оси собирающей линзы на рассто-
янии от нее, большем фокусного расстояния. Сделать такое по-
строение для рассеивающей линзы. Положения фокусов линзы
заданы.
Решение. Для собирающей линзы (рис. 176) построим ход
двух лучей: луча SFOSb идущего вдоль главной оптической оси,
и произвольно выбранного луча SA. После преломления линзой
первый луч не изменит своего направления, а второй пройдет че-
рез побочный фокус Fu т. е. через точку пересечения побочной
оси, параллельной лучу SA, с фокальной плоскостью. Изображе-
нием точки S является точка S,, в которой пересекаются эти лу-
чи после прохождения линзы.
Предлагаем читателю самостоятельно построить изображе-
ние светящейся точки, лежащей на главной оптической оси соби-
рающей линзы между фокусом и линзой, и убедиться, что в этом
случае изображение точки будет мнимым.
Для случая рассеивающей линзы построение изображения S,
точки S показано на рисунке 177. В отличие от собирающей лин-
зы здесь через побочный фокус F{ проходит продолжение луча
SA, преломленного линзой.
Задача 2. Построить изображение светящейся точки S,
расположенной перед рассеивающей линзой (рис. 178).
Решение. Выбираем два луча: луч SO, идущий через опти-
ческий центр линзы, и луч SA, направленный под некоторым уг-
лом к главной оптической оси. Построив, как показано выше, ход
этих лучей после преломления линзой, найдем точку S[ — изоб-
ражение точки S.
Здесь абитуриентов затрудняло то, что луч, параллельный
главной оптической оси, не попадал на линзу.
Задача 3. Известен ход луча ABC до собирающей линзы
и после нее (рис. 179, а). Найти построением положение главных
фокусов этой линзы.
259
V/
Л
Рис. 177
Рис. 179
Решение. Проведем побочную оптическую ось, параллель-
ную лучу АВ (рис. 179, б). Точка пересечения луча ВС с этой
осью совпадает с побочным фокусом Z7,. Построим фокальную
плоскость, тогда точка пересечения с главной оптической осью
и есть главный фокус линзы. Второй главный фокус расположен
по другую сторону линзы на таком же расстоянии от нее.
Задача 4. Построить изображение в собирающей линзе
плоского предмета АВ, наклоненного к главной оптической оси
(рис. 180, а).
Решение. Сначала строим изображение Л, точки А, взяв
два луча, исходящих из этой точки: луч АС, идущий парал-
лельно оптической оси, и луч АО, идущий через оптический
центр (рис. 180, б). После преломления линзой эти лучи пересе-
каются в точке Аи являющейся изображением точки А. За-
тем строим ход двух исходящих из точки В лучей: ВО, идущего
вдоль главной оптической оси, и BD, направленного под некото-
рым углом к ней. Полученное изображение В{ точки В соединяем
с точкой /4,.
Решая эту задачу, абитуриенты правильно находили изобра-
жение Л, точки А, но затем проводили из этой точки отрезок
А,ВЬ параллельный АВ, что неверно.
260
163. Как отмечалось выше, для построения изображения в
линзе точки достаточно выбрать два исходящих из нее луча и,
построив ход этих лучей после преломления линзой, найти точку
пересечения их или их продолжений. Отсюда некоторые абиту-
риенты делают ошибочный вывод, что изображение точки созда-
б
\
В F О
\/
Рис. 180
ется только двумя лучами, и поэтому считают, например, что ес-
ли на пути двух лучей, с помощью которых построено изображе-
ние светящейся точки S, поставить непрозрачный экран, то
изображения S, не будет (рис. 181, а).
Изображение будет наблюдаться и при наличии этого экра-
на, так как оно создается бесконечно большим числом лучей
(рис. 181, б).
164. Применяя формулу тонкой линзы, не все экзаменующие-
ся правильно учитывают знаки (плюс или минус) перед величи-
нами, входящими в эту формулу.
В общем виде формулу линзы можно записать так:
где F — фокусное расстояние линзы; d — расстояние от предме-
та до линзы; / — расстояние от линзы до изображения. При та-
кой записи величины F, d и f считаются положительными, а пра-
вило расстановки знаков следующее: если фокус, предмет или
изображение являются действительными, то перед соответствую-
щим членом формулы A) ставится плюс, если мнимыми,— то ми-
б
N
F
Рис. 181
261
нус. Если знаки в формуле расставлены правильно, то в ответе
должно получиться положительное число.
Например, в рассеивающей линзе изображение всегда мни-
мое, фокус ее тоже мнимый, поэтому для нее формула A) име-
ет вид:
1 _ 1 _ I
~~ т -"у
1
если предмет действительный, а если мнимый, то и перед — надо
ставить минус.
Предмет является действительным, если на линзу падает
расходящийся пучок лучей. Мнимым предмет считают в том
случае, если на линзу падает сходящийся пучок лучей, что быва-
ет, когда до данной линзы лучи проходят через другую линзу.
165. Абитуриенты правильно объясняют, что явление интер-
ференции подтверждает волновую природу света, но многие не
могут четко сформулировать условия, при которых наблюдаются
интерференционные максимумы (усиление света) и интерферен-
ционные минимумы (ослабление света).
Напомним, что при интерференции двух монохроматических
световых волн максимумы наблюдаются в точках, для которых
разность хода волн Л/ равна четному числу полуволн, или, что то
же самое, целому числу длин волн:
Д/ = 2А-| =kX (k = 0, I, 2, 3, ...).
Интерференционные минимумы наблюдаются в точках, для
которых разность хода равна нечетному числу полуволн:
M = {2k+\)\.
Схематично это показано на рисунке 182.
Отметим, что при интерференции света перераспределяются
энергии двух когерентных световых волн в пространстве, где
происходит их сложение. При этом выполняется закон сохране-
ния энергии: суммарная энергия световых волн остается неиз-
менной.
262
166. Рассматривая дифракцию света, нередко абитуриенты
не видят связи между образованием дифракционной картины и
явлением интерференции света.
Согласно принципу Гюйгенса — Френеля, каждая точка по-
верхности, которой достигла световая волна, является точечным
источником когерентных вторичных волн. Результирующее вол-
новое возмущение в данной точке пространства можно рассмат-
ривать как следствие интерференции вторичных волн. Если на
пути волн поставить непрозрачный экран с малым отверстием,
то отверстие станет источником света, вторичные волны от кото-
рого падают также и в область тени, т. е. происходит огибание
световыми волнами препятствий.
167. Некоторые абитуриенты ошибочно считают, что при пе-
реходе света из одной среды в другую изменяется его частота.
В действительности на границе раздела прозрачных сред изме*
няется скорость световой волны, а в связи с этим — длина вол-
ны. Частота света и его цвет при переходе из одной среды в дру-
гую не изменяются.
Задача. Вода освещена зеленым светом, длина волны кото-
рого в воздухе Я) = 540 нм. Определить длину волны и частоту
этого света в воде. Какой цвет увидит человек, открывший гла-
за под водой? Показатель преломления воздуха /г,= 1, воды
/г2 = —. Скорость света в вакууме с = 3-108 м/с.
О
у
Решение. Длина световой волны в воздухе Xt=—, в воде
А,2= — , где vh v2 — скорости распространения волны в воздухе
и в воде соответственно; v — частота световых колебаний, кото-
рая не изменяется при переходе света из воздуха в воду. Разде-
X, v, v, п2
лив почленно эти уравнения, получим: — =—. Но — =—, где
/г,, п2— абсолютные показатели преломления воздуха и воды со-
ответственно. Следовательно, — =—, откуда
Х п
Подставив числовые значения величин и произведя вычисления,
получим А,2 = 405 нм.
Найдем частоту:
v, с 3-Ю8
v ==-
540-10"
= 5,6-1014 Гц.
Человек под водой увидит свет зеленого цвета, так как цвет
не изменится при переходе из воздуха в воду.
263
КВАНТОВАЯ ФИЗИКА
168. Понятие корпускулярно-волнового дуализма слабо усво-
ено многими абитуриентами. Они, как правило, понимают под
корпускулярно-волновым дуализмом только двойственность
свойств света.
В действительности же одновременное сочетание корпуску-
лярных и волновых свойств присуще не только свету, но и части-
цам. Так, например, пучок электронов, падающих на кристалл,
дает дифракционную картину, которую можно объяснить лишь
на основе волновых представлений: с движущимся электроном
связана так называемая волна де Бройля, длина которой
где h — постоянная Планка; p = mv— импульс электрона; т —
масса электрона; v — его скорость.
Французский физик Луи де Бройль в 1924 г. высказал гипо-
тезу о том, что корпускулярно-волновой дуализм присущ всем
частицам, при этом формула A), связывающая длину волны с
импульсом частицы, аналогична соотношению, выражающему
длину световой волны через импульс фотона. Найдем это соотно-
шение.
В теории относительности выражения для модуля импульса
р частицы и ее энергии Е имеют вид:
Р=
где т — масса частицы; v — ее скорость; с — скорость света в
вакууме.
Возведем обе части каждого равенства в квадрат, а затем
первое умножим на с2:
2 2_
Р ь
Теперь вычтем из второго равенства первое:
2
Мы получили связь между энергией и импульсом частицы:
264
Согласно этой формуле, фотон как частица, имеющая массу
т = 0 и скорость с, обладает энергией
Е = рс. B)
Но энергия фотона
E = hv, C)
где h — постоянная Планка; v — частота света.
На основании выражений B) и C) имеем:
_ __hv _h
С А
где X— длина световой волны. Отсюда
Формула де Бройля A) аналогична формуле D). В 1927 г. ги-
потеза де Бройля получила экспериментальное подтверждение
в опытах по дифракции электронов.
Согласно формуле A), длина волны де Бройля тем меньше,
чем больше масса частицы. Для макроскопических тел длины
волн де Бройля очень малы, поэтому волновые свойства этих тел
несущественны. Микрочастицы одновременно обладают и волно-
выми, и корпускулярными свойствами, которые дополняют друг
друга.
Корпускулярно-волновой дуализм является универсальным
свойством материального мира: электромагнитные волны обна-
руживают сходство с потоком частиц—фотонов, и наоборот,
микрочастицы вещества обладают волновыми свойствами.
169. Не все экзаменующиеся могли объяснить, в чем причи-
на нелинейности вольт-амперной характеристики фотоэлемента.
Эту характеристику, т. е. зависимость силы фототока / от на-
пряжения U (рис. 183) при одной и той же освещенности катода
фотоэлемента, можно найти, изменяя с помощью потенциометра
U3 0 и
Рис. 183
R напряжение, подаваемое на фотоэлемент Ф (рис. 184). Две ба-
тареи Б1 и Б2 включены «навстречу друг другу» и позволяют
265
т
Б1
\Б2
Рис. 184
изменять с помощью потенциометра не только абсолютное значе-
ние, но и знак напряжения U.
С повышением напряжения сила фототока увеличивается,
так как при этом увеличивается число электронов, достигающих
анода. Начиная с некоторого напряжения, сила тока остается
постоянной, так как все вылетевшие из катода электроны дости-
гают анода. Максимальное значение /н силы фототока называ-
ется током насыщения.
Из рисунка 183 видно, что существует некоторый фототок и в
области отрицательных напряжений от 0 до U3. Это означает,
что фотоэлектроны, выбитые светом из катода, имеют некоторую
кинетическую энергию. Это позволяет им совершить работу про-
тив сил задерживающего электрического поля и достигнуть ано-
да. При задерживающем напряжении ?/3 сила фототока стано-
вится равной нулю, потому что все электроны, включая и те, ко-
торые имели при вылете из катода максимальную скорость и, не
достигают анода. В этом случае максимальное значение кинети-
ческой энергии фотоэлектронов равно работе тормозящего элект-
рического поля:
ту2
где m — масса электрона; е — его заряд.
Таким образом, измерив задерживающее напряжение U3,
можно найти максимальное значение кинетической энергии фо-
тоэлектронов.
170. Рассказывая о фотоэффекте, нередко абитуриенты огра-
ничиваются описанием лишь некоторых экспериментальных фак-
тов и не могут четко сформулировать его основные законы.
Напомним, что опытным путем установлены следующие
основные законы внешнего фотоэффекта: 1) количество электро-
нов, вырываемых светом в единицу времени, пропорционально
интенсивности света; 2) максимальная кинетическая энергия фо-
тоэлектронов линейно возрастает с частотой света и не зависит
266
от его интенсивности; 3) для каждого вещества существует крас-
ная граница фотоэффекта, т. е. минимальная (граничная) часто-
та vmin света, при которой еще возможен фотоэффект.
Отметим, что минимальной частоте vmin для данного вещества
соответствует максимальная длина волны
mm
где с — скорость света в вакууме.
Термин «красная граница» объясняется тем, что она (грани-
ца) соответствует частоте или длине световой волны, ограничен-
ной со стороны длинноволнового участка спектра. Красная гра-
ница лежит не обязательно в красном участке спектра, как ино-
гда утверждают абитуриенты. Например, для калия красной
границе фотоэффекта соответствует длина волны Я1Пах = 550 нм
(зеленый свет), для серебра А,тах = 260 нм (ультрафиолетовое из-
лучение).
Из приведенных выше законов фотоэффекта второй и третий
нельзя объяснить на основе представлений классической элект-
родинамики. Согласно этим представлениям, энергия фотоэлект-
ронов должна определяться только интенсивностью света и не
зависеть от частоты. Кроме того, фотоэффект должен был на-
блюдаться при любой частоте света. С точки зрения электромаг-
нитной теории считалось, что световая волна, падая на вещество,
«раскачивает» его электроны и они рано или поздно отрываются
от вещества. Но, как показали опыты, на самом деле этого не
происходит.
А. Эйнштейн показал, что все законы внешнего фотоэффекта
можно объяснить на основе представлений о свете как потоке
фотонов. Каждый единичный акт взаимодействия фотона и элек-
трона подчиняется закону сохранения энергии. Пусть А — рабо-
та выхода (наименьшая работа, которую надо совершить, чтобы
освободить электрон из металла), ftv— энергия фотона, —
максимальная кинетическая энергия фотоэлектрона. Тогда, со-
гласно закону сохранения энергии,
Это и есть уравнение Эйнштейна для фотоэффекта. Оно объяс-
няет все три закона фотоэффекта.
171. Применяя уравнение Эйнштейна для фотоэффекта при
решении задач, абитуриенты нередко испытывают затруднения
и допускают ошибки.
Задача 1. При каком наименьшем напряжении полностью
задерживаются электроны, вырванные из вольфрамовой пластин-
ки ультрафиолетовым излучением с длиной волны Я= 100 нм? Для
вольфрама работа выхода /4=4,5 эВ.
267
Решение. Электроны перестанут вылетать из пластинки,
когда работа eU3 тормозящего электрического поля станет рав-
ной максимальной кинетической энергии электрона:
eU3 = ^f. A)
Согласно уравнению Эйнштейна для фотоэффекта,
— =h\ — A, B)
где h\ — энергия фотона; А—работа выхода. Из уравнений
A) и B) получим:
Так как частота v = ^-, где с — скорость света в вакууме; К —
длина волны, то
Выразим все величины в единицах СИ: е = 1,6-10 19 Кл,
/г = 6,63-10 34 Дж-с, с = 3-108 м/с; А, = 100-10~9 м;
А =4,5* 1,6-10~19 Дж. Подставив эти значения в формулу C) и
произведя вычисления, получим U3~7,9 В.
При решении этой задачи некоторые абитуриенты писали:
h\ = A—eU, что неверно. Эта грубая ошибка является, по-види-
мому, следствием простого запоминания уравнения Эйнштейна,
без должного понимания его физического смысла.
Многие не могли правильно выразить в джоулях работу вы-
хода, так как не знали, что такое электронвольт.
Электронвольт (эВ)—единица энергии, равная энергии, ко-
торую приобретает частица, обладающая зарядом, равным заря-
ду электрона, проходя разность потенциалов 1 В.
Определяющей формулой для электронвольта является фор-
мула, по которой находится работа Л, совершаемая электриче-
ским полем при перемещении заряда q из одной точки в другую:
где ф, — ф2 — разность потенциалов этих точек. Подставив в эту
формулу q = e = 1,6-10~19 Кл, ф, —ф2=1 В, получим /4 = 1 эВ,
т. е.
1 эВ = 1,6-10 19 Кл-1 В== 1,6-10~19 Дж.
Задача 2. Объяснить, что представляет собой график за-
висимости максимальной кинетической энергии фотоэлектронов
от частоты света, падающего на фотоэлемент. Как опытным пу-
тем построить график и какие величины можно определить с по-
мощью этого графика?
268
Решение. Из уравнения Эйнштейна для фотоэффекта сле-
дует, что кинетическая энергия фотоэлектрона
Так как для данного вещества работа выхода А — величина
постоянная, то, как видно из формулы A), кинетическая энергия
фотоэлектрона является линейной функцией частоты v. График
этой функции представляет собой прямую (рис. 185), пересекаю-
щую ось частот v в точке В, которая соответствует красной гра-
нице vmin фотоэффекта для данного вещества. В этой точке
?к = 0. С осью кинетической энергии Ек график пересекается в
точке М, соответствующей работе выхода. В этой точке ?к= —А.
Рис. 185
Для построения такого графика опытным путем можно ис-
пользовать электрическую цепь, схема которой показана на ри-
сунке 186. Катод фотоэлемента Ф нужно освещать, пропуская
свет от электрической лампы через светофильтр. Меняя свето-
фильтр, мы тем самым изменяем частоту падающего на катод
света. Для каждой частоты v находим задерживающее напряже-
ние ?/3, изменяя с помощью потенциометра R напряжение так,
чтобы прекратился фототок, т. е. когда миллиамперметр будет
показывать, что сила тока равна нулю, показание вольтметра
равно U3.
Теперь для каждого значения частоты вычислим кинетиче-
скую энергию фотоэлектрона по формуле Ек = е11л, где е — заряд
электрона, и по точкам построим график.
Продолжив график до пересечения с осями частот v и кинети-
ческой энергии Ек, найдем красную границу vmin фотоэффекта и
работу выхода А для материала катода. Кроме того, с помощью
этого графика можно определить постоянную Планка.
д
Так как граничная частота vmin = -T-, то работа выхода
/l=/zvmin и уравнение Эйнштейна можно записать в виде
hv = hvmm-\-Ek. Отсюда
h=~^~- B)
269
Для некоторых значений v, и ?к1, соответствующих точке С гра-
фика, получим:
и ?*l CD +
htg
Таким образом, тангенс угла наклона графика к оси частот
численно равен постоянной Планка. Отсюда следует, что для
различных веществ угол а будет одинаков, а так как vmin для них
различна, то для различных веществ графики зависимости кине-
тической энергии фотоэлектронов от частоты света будут пред-
ставлять собой параллельные прямые.
К сожалению, у большинства абитуриентов отсутствует уме-
ние строить графики и «читать» их, т. е. находить значения физи-
ческих величин по заданному графику. Поэтому они не справля-
ются с приведенной выше задачей и другими графическими за-
дачами. Здесь еще раз отметим очень существенный недостаток
в подготовке выпускников средних школ: неумение применять
знания, полученные при обучении математике, к решению задач
по физике. Наглядная тому иллюстрация: абитуриент не мог по-
строить график, соответствующий уравнению A), но когда ему
предложили построить график функции у = ах—Ь, он быстро это
сделал. А ведь эти функции различаются только обозначениями
величин, и это уже вызвало затруднения.
172. При решении задач, связанных с постулатами Бора, аби-
туриенты довольно часто допускают ошибки, большинство из ко-
торых обусловлено неумением применять известные законы ме-
ханики и электростатики.
Задача. Используя модель атома водорода по теории Бора,
найти энергию фотона, испускаемого при переходе электрона в
атоме водорода со второй орбиты, радиус которой г2, на первую,
радиус которой rt.
Абитуриент решал эту задачу так. При переходе электрона
со второй орбиты на первую испускается фотон, поэтому энергия
электрона уменьшилась на величину, равную энергии фотона ?ф,
т. е.
^ф — ^кг ?kl. A)
где ?к2, Ек[ — кинетическая энергия электрона на второй и пер-
вой орбитах соответственно.
Кинетическая энергия электрона на л-й орбите
Е —^ B\
где т — масса электрона; vn — его скорость на этой орбите.
Согласно теории Бора, движение электрона подчиняется за-
конам классической механики. По второму закону Ньютона
270
где F — сила взаимодействия электриче-
ских зарядов ядра и электрона (рис. 186);
т — масса электрона; ап — центростреми-
тельное ускорение; гп — радиус п-й ор-
биты.
По закону Кулона
-в
г
п,
+е
где е — заряд электрона; е0 — электриче-
ская постоянная.
Следовательно,
Р и с. 186
то,
г„
Из формул B) и C) находим:
C)
D)
Согласно формулам A) и D), энергия фотона
F —
8ле,
Л" ~У
Но так как г.2>гь то из последней формулы следует, что
?ф<0> а это не имеет смысла. Где допущена ошибка? Советуем
читателю попытаться найти ее и только после этого читать
дальше.
Ошибка заключается в том, что не учтена потенциальная
энергия электрона. Приведем правильное решение.
Решение. Энергия фотона равна убыли полной энергии
электрона:
?ф = (?..2 + ?р2)-(?к1 + ?р,), E)
где ?р2, ?Р1 — потенциальная энергия электрона на второй и пер-
вой орбитах соответственно.
Кинетическая энергия электрона на п-й орбите найдена выше
правильно. Согласно формуле D),
F —
F)
Найдем потенциальную энергию электрона (точнее говоря,
потенциальную энергию системы двух разноименно заряженных
частиц — электрона и протона) на второй и первой орбитах:
G)
4ле0г,
Подставив выражения F) и G) в формулу E) и выполнив не-
обходимые преобразования, получим:
271
Теперь ?ф>0, что соответствует действительности.
Многие абитуриенты не понимают, почему полная энергия
электрона в атоме водорода отрицательна. Дело в том, что когда
электрон находится на бесконечно большом расстоянии от прото-
на, его потенциальная энергия принимается равной нулю, а на
расстоянии г от протона потенциальная энергия электрона
Е=- е'2
4ле</ ¦
Сравнивая выражения F) и G), приходим к выводу, что по-
тенциальная энергия взаимодействия электрона и ядра по моду-
лю в два раза больше кинетической энергии электрона. А так
как ?р<с0, то полная энергия, равная сумме потенциальной и
кинетической энергии, отрицательна.
173. Обычно абитуриенты правильно отвечают, что спект-
ральный анализ — это метод определения химического состава
вещества по его спектру, что каждый химический элемент имеет
характерный для него линейчатый спектр. Но вот экзаменатор
задает вопрос: «Имеется образец некоторого твердого вещества,
например стали. Как получить линейчатый спектр для определе-
ния химического состава этой стали?» Экзаменующиеся часто
отвечают так: «Нужно этот образец сильно нагреть, раскалить
добела, чтобы он светился, а затем через спектроскоп рассмат-
ривать его спектр и сравнивать с известными спектрами».
Такой ответ ошибочен, потому что нагретые тела дают не ли-
нейчатый, а сплошной спектр. Линейчатый спектр дают вещест-
ва в газообразном атомарном состоянии. Для получения линей-
чатого спектра твердого вещества нужно это вещество перевести
в газообразное (парообразное) состояние и заставить этот газ
испускать свет. Обычно с этой целью используется дуговой раз-
ряд. Проба исследуемого вещества в измельченном виде, поме-
щенная в плазму дуги, превращается в пар, происходит возбуж-
дение и ионизация атомов.
174. Рассказывая о явлении радиоактивности, некоторые аби-
туриенты ошибочно утверждают, что |3-лучи, представляющие
собой поток электронов, испускаются не ядрами атомов, а элект-
ронными оболочками, так как внутри ядер электронов нет.
Напомним, что все виды радиоактивного излучения испуска-
ются ядрами атомов. Ядра всех атомов состоят из протонов и
нейтронов. Откуда же при |3-распаде появляется электрон, если
его в ядре нет? Дело в том, что в ядре при определенных услови-
ях происходит превращение нейтрона в протон с одновременным
образованием электрона, который при этом вылетает из ядра
(покидает ядро и еще одна частица — антинейтрино).
175. Вопрос о биологическом действии радиоактивных излу-
272
чений стал особенно актуален в связи с аварией на Чернобыль-
ской АЭС. Выпускники средних школ, естественно, как и многие
люди, особенно те, которые находятся на загрязненных радионук-
лидами территориях, часто слышат такие слова, как «рентген»,
«бэр», «кюри» и др., но физического смысла большинства этих
терминов многие не понимают. Учитывая это, дадим краткие
сведения о важнейших величинах в области ионизирующих излу-
чений и единицах этих величин.
Активностью радиоактивного вещества называется величина,
равная числу распадов, происходящих за единицу времени.
В СИ единицей активности является беккерель (Бк). Беккерель
равен активности радионуклида, при которой за 1 с происходит
один акт распада.
В настоящее время используется еще и внесистемная едини-
ца активности — кюри (Ки); 1 Ки =3,7- 10ю Бк, т. е. при активнос-
ти 1 Ки происходит 3,7-Ю10 распадов в секунду. Применя-
ются также дольные единицы — милликюри, микрокюри
A мКи=10~3 Ки, 1 мкКи=1(Г6 Ки).
В опубликованных картах загрязнения территории Беларуси
цезием-137 и стронцием-90 уровень радиоактивности указан
в кюри на квадратный километр (Ки/км2). Например, если ак-
тивность равна 40 Ки/км2, то что это означает? Переведем в еди-
ницы СИ:
лп v / 2 40 Ки 40-3,7-Ю10 Бк 4 2
40 Ки/км = — = — =148-10 Бк/м .
1 км Ю м
Это означает, что на площади 1 м2 содержатся радионуклиды,
148-104 из которых распадается каждую секунду.
Экспозиционной дозой гамма- и рентгеновского излучений
называется величина, равная отношению суммы электрических
зарядов всех ионов одного знака, возникающих в сухом атмо-
сферном воздухе, когда все освобожденные в результате облуче-
ния электроны и позитроны полностью остановились, к массе
этого воздуха.
В СИ единицей экспозиционной дозы является кулон на ки-
лограмм (Кл/кг). Кулон на килограмм равен экспозиционной до-
зе гамма- и рентгеновского излучений, при которой в 1 кг сухого
атмосферного воздуха образуются ионы, несущие электрический
заряд каждого знака, равный 1 Кл.
Внесистемной единицей экспозиционной дозы является рент-
ген (Р); 1 Р = 2,58-10 4 Кл/кг. Применяются дольные едини-
цы — миллирентген A мР=10~3 Р), микрорентген A мкР=10~6 Р).
Мощностью экспозиционной дозы гамма- и рентгеновского
излучений называется величина, равная отношению экспозици-
онной дозы излучения ко времени, за которое получена эта доза.
В СИ единицей мощности экспозиционной дозы является ам-
пер на килограмм (А/кг). Ампер на килограмм равен мощности
экспозиционной дозы, при которой за 1 с сухому атмосферному
273
воздуху передается экспозиционная доза излучения 1 Кл/кг.
На практике еще применяется внесистемная единица мощно-
сти экспозиционной дозы излучения — рентген в секунду (Р/с);
1 Р/с = 2,58-10 А/кг. Применяются также единицы, дольные
и кратные от этой единицы. Например, некоторые дозиметры да-
ют показания в миллирентгенах в час (мР/ч).
Поглощенной дозой излучения называется величина, равная
отношению энергии ионизирующего излучения, переданной облу-
ченному веществу, к массе облученного вещества.
В СИ единицей поглощенной дозы излучения является грэй
(Гр). Грэй равен поглощенной дозе излучения, при которой облу-
ченному веществу массой 1 кг передается энергия ионизирующе-
го излучения 1 Дж.
Внесистемной единицей поглощенной дозы является рад;
(rad — сокр. от англ. radiation absorbed dose — поглощенная до-
за излучения); 1 рад=10~2 Гр.
Разные виды излучения обладают различными ионизацион-
ными свойствами, поэтому даже при одной и той же поглощен-
ной дозе они оказывают не одинаковое поражающее действие на
организм. Гамма- и бета-излучения поражают органическую
ткань почти одинаково, а альфа-частицы — в 20 раз сильнее.
Для каждого вида излучения можно установить их относитель-
ную биологическую эффективность и приписать каждому излуче-
нию коэффициент качества. С учетом этого для определения сте-
пени воздействия излучения на организм человека введено поня-
тие эквивалентной дозы излучения.
Эквивалентной дозой излучения называется величина, рав-
ная поглощенной дозе излучения, умноженной на безразмерный
коэффициент, учитывающий неблагоприятные биологические по-
следствия облучения человека в малых дозах.
В СИ единицей эквивалентной дозы является зиверт (Зв). Зи-
верт равен эквивалентной дозе излучения, при которой погло-
щенная доза равна 1 Гр и коэффициент качества равен единице.
Внесистемной единицей эквивалентной дозы излучения явля-
ется бэр (биологический эквивалент рентгена); 1 бэр = 10~2 Зв.
СОВЕТЫ АБИТУРИЕНТАМ
1. Готовиться к вступительному экзамену надо начинать как
можно раньше, по заранее обдуманному плану, составленному
на основе программы, и твердо придерживаться этого плана.
Подготовка к экзамену — своеобразный этап в обучении, когда
выпускник школы должен осмыслить содержание предмета в це-
лом, выделить в нем главное, основное, понять связь между от-
дельными разделами, упорядочить и обобщить свои знания.
2. Нужно готовить себя к тому, чтобы на экзамене давать ло-
гически построенные и исчерпывающие ответы на вопросы.
С этой целью настоятельно рекомендуем руководствоваться
обобщенными планами*, которые выражают требования к изу-
чению основных элементов знаний по физике. Эти планы называ-
ются обобщенными потому, что могут использоваться при изуче-
нии не только физики, но и других учебных предметов естествен-
ного цикла.
Ниже приводятся обобщенные планы по изучению явлений,
величин, законов и теорий.
Что надо знать о явлении
1. Внешние признаки явления (признаки, по которым обнару-
живается явление).
2. Условия, при которых протекает явление.
3. Сущность явления (объяснение явления на основе совре-
менных научных теорий).
4. Связь данного явления с другими.
5. Величины, характеризующие явление.
6. Примеры использования явления на практике.
7. Способы предупреждения вредных действий явления на
технические установки, созданные человеком, и окружающую
среду.
Что надо знать о величине
1. Какие свойства (качества) тел (или явлений) характеризует
данная величина.
2. Какая это величина (скалярная или векторная).
3. Формула, определяющая связь данной величины с другими
величинами (определяющая формула).
4. Определение величины.
5. Единица величины в СИ (наименование единицы и ее опре-
деление).
6. Способы измерения величины.
* Усова А. В., Завьялов В. В. Воспитание учащихся в процессе обучения фи-
зике — М.: Просвещение, 1984.— С. 37.
275
Что надо знать о законе
1. Связь между какими явлениями (или величинами) выра-
жает закон.
2. Формулировка закона.
3. Математическое выражение закона.
4. Каким образом был открыт закон: на основе анализа опыт-
ных данных или как следствие из теории.
5. Опытные факты, на основе анализа которых был сформу-
лирован закон.
6. Опыты, подтверждающие справедливость закона, сформу-
лированного как следствие из теории.
7. Примеры использования и учета закона на практике.
8. Границы применимости закона.
Что надо знать о теории
1. Опытные факты, послужившие основанием для разработки
теории.
2. Основные понятия теории.
3. Основные положения (принципы) теории.
4. Математический аппарат теории (основные уравнения).
5. Опыты и наблюдения, подтверждающие справедливость
положений теории.
6. Следствия из теории: а) явления и свойства тел, объясни-
мые теорией; б) явления и свойства тел, предсказываемые тео-
рией.
Знание и применение обобщенных планов помогает более ор-
ганизованно работать при повторении учебного материала, а на
экзамене строить свои ответы так, чтобы они были исчерпываю-
щими, логичными и краткими.
3. Повторение теоретического материала обязательно должно
сочетаться с решением задач. Прежде чем приступать к реше-
нию задач, необходимо повторить материал данного раздела
курса физики по школьным учебникам и другим учебным посо-
биям, ознакомиться с типичными ошибками, систематизирован-
ными в данной книге.
При решении задач, как и при повторении теории, очень важ-
но руководствоваться общим планом. Ниже следует его краткое
изложение.
Внимательно прочитав текст задачи, надо проанализировать
ее, чтобы четко представить описанное в ней явление или про-
цесс, разобраться, как он протекает, какие закономерности ле-
жат в его основе. Следует выяснить, каковы начальное и конеч-
ное состояния процесса, какими параметрами они описываются,
что дано, что требуется найти. Надо сделать соответствующий
рисунок, указать на нем все векторные величины.
После выяснений физической сущности задачи надо соста-
276
вить систему уравнений, число которых равно числу неизвестных
величин. От векторных уравнений нужно перейти к скалярным
уравнениям, для чего выбирается система координат и находят-
ся проекции векторов на оси координат. Затем система решается
в общем виде, в результате чего для искомой величины получа-
ется расчетная формула.
После этого надо проверить правильность расчетной форму-
лы следующим образом: вместо обозначений физических величин
подставить в формулу обозначения их единиц СИ и затем одина-
ковые единицы в числителе и знаменателе сократить. В резуль-
тате должно получиться обозначение единицы искомой величи-
ны. Затем в расчетную формулу надо подставить числовые зна-
чения физических величин и произвести вычисления. После этого
следует оценить реальность полученного результата, а также по-
пытаться решить задачу другим способом.
4. При подготовке к экзамену полезно решать задачи, ранее
предлагавшиеся на вступительных экзаменах в различных ву-
зах. Ряд таких задач приведен в этой книге.
5. Нужно учесть, что только регулярные систематические за-
нятия, глубокое изучение всех вопросов программы и решение
задач обеспечат успешную сдачу экзамена.
ПРИЛОЖЕНИЯ
1. ОБРАЗЦЫ БИЛЕТОВ УСТНОГО ЭКЗАМЕНА
ПО ФИЗИКЕ
Билет № 1
1. Механическое движение. Относительность движения. Система от-
счета. Материальная точка. Траектория. Путь и перемещение.
2. Действие магнитного поля на движущийся заряд. Сила Лоренца.
3. Задача.
Билет № 2
1. Графики зависимости кинематических величин от времени в равно-
мерном и равноускоренном движении.
2. Принцип действия тепловых двигателей. КПД теплового двигателя
и его максимальное значение. Тепловые двигатели и охрана природы.
3. Задача.
Билет № 3
1. Давление. Закон Паскаля для жидкостей и газов. Принцип устрой-
ства гидравлического пресса.
2. Деление ядер урана. Ядерный реактор. Биологическое действие ра-
диоактивных излучений.
3. Задача.
Билет № 4
1. Сопротивление проводников. Последовательное и параллельное сое-
динение проводников.
2. Математический маятник. Период колебаний математического ма-
ятника.
3. Задача.
Билет № 5
1. Идеальный газ. Основное уравнение молекулярно-кинетической тео-
рии идеального газа.
2. Кинетическая и потенциальная энергия. Закон сохранения энергии
в механике.
3. Задача.
Билет № 6
1. Явление самоиндукции. Индуктивность. Энергия магнитного поля.
2. Распространение колебаний в упругих средах. Поперечные и про-
278
дольные волны. Длина волны. Связь длины волны со скоростью ее распро-
странения.
3. Задача.
Билет № 7
1. Масса. Сила. Второй закон Ньютона.
2. Фотоэффект и его законы. Кванты света. Уравнение Эйнштейна для
фотоэффекта. Постоянная Планка. Применение фотоэффекта в технике.
3. Задача.
Билет № 8
1. Взаимодействие заряженных тел. Закон Кулона. Закон сохранения
электрического заряда.
2. Когерентность. Интерференция света и ее применение в технике.
3. Задача.
2. ЗАДАЧИ УСТНОГО ЭКЗАМЕНА
ПО ФИЗИКЕ
Кинематика
1. Гребец сообщает лодке скорость а, = 2 м/с относительно воды. Под
каким углом к течению должен он направлять лодку, чтобы плыть точно
поперек реки (перпендикулярно течению), если скорость течения У2 =
= 1 м/с? Сколько времени потребуется гребцу, чтобы пересечь реку, если ее
ширина / = 20 м?
2. Дан график скорости некоторого движения (рис. 187). Определить
характер этого движения и написать уравнение зависимости координаты
от времени. Что происходит с движущимся телом в момент времени, соот-
ветствующий точке А графика? Как движется тело после этого момента?
Начальная координата равна нулю.
3. На какой высоте была сброшена бомба с самолета, летевшего гори-
зонтально со скоростью у0, если она попала в вершину горы высотой h на
расстоянии s по горизонтали от точки бросания?
4. На рисунке 188 дан график зависимости ускорения от времени при
прямолинейном движении материальной точки. Построить график зависи-
мости скорости точки от времени. Определить путь, пройденный точкой за
время движения. Начальная скорость точки равна нулю.
5. Камень, падающий свободно без начальной скорости, пролетел вто-
рую половину мути за t = 1 с. С какой высоты он падал?
6. Тело начало двигаться прямолинейно равноускоренно и в течение
пятой секунды от начала движения прошло путь / = 45 м. С каким ускоре-
нием оно двигалось?
7. Тело массой т = 0,5 кг брошено со скоростью ио = 2О м/с под углом
а —30° к горизонту. Определить наибольшую высоту подъема тела, даль-
ность полета и изменение импульса тела за время полета. Сопротивлением
воздуха пренебречь.
8. Два тела одновременно брошены из одной точки. Начальная ско-
рость первого тела и, = 10 м/с и направлена вертикально вверх, второго
у2 = 20 м/с и направлена под углом а = 30° к горизонту.
279
о
-1-
8 t,c
Рис. 187
Рис. 188
Определить расстояние между телами через /=1 с после броска. Сопро-
тивлением воздуха пренебречь.
9. Линейная скорость точек обода вращающегося диска Uj=6 м/с,
а точек, находящихся на / = 20 см ближе к оси вращения, U2 = 4 м/с. Най-
ти радиус диска и угловую скорость вращения.
10. Из шланга, лежащего на земле, бьет под углом а = 30° к горизонту
струя воды с начальной скоростью Uo = 10 м/с. Площадь поперечного се-
чения отверстия шланга S = 5 см2. Определить массу воды, находящейся
в воздухе. Плотность воды р=Ь103 кг/м3.
Основы динамики
1. На тело массой т, расположенное на горизонтальной плоскости,
действует сила F, направленная вниз под углом а к горизонту. Коэффици-
ент трения тела о плоскость равен ц. Найти ускорение тела.
2. Две гири массами т, = 7 кг и т2=11 кг висят на концах нити,
которая перекинута через блок. Гири вначале находятся на одной высоте.
Через какое время после начала движения более легкая гиря окажется на
Л = 20 см выше тяжелой? Массой блока и нити, а также трением в блоке
пренебречь, считать нить невесомой и нерастяжимой, а ускорение свободно-
го падения g=10 м/с2.
3. К потолку вагона подвешен на нити шарик. При движении вагона
по окружности со скоростью у=108 км/ч нить отклонилась от вертикали
на угол а = 30°. Найти радиус окружности.
4. Вагон массой т=16т, движущийся с начальной скоростью
уо = 36 км/ч, останавливается, пройдя на горизонтальном участке железно-
дорожного пути расстояние / = 0,5 км. Вычислить силу сопротивления дви-
жению.
5. Груз массой т = 200 кг, лежащий на полу кабины опускающегося
лифта, давит на пол с силой F = 2060 H. Найти модуль и направление
ускорения лифта.
6. При каком ускорении разорвется трос, прочность которого на раз-
рыв Т= 15 кН, при вертикальном подъеме груза массой т = 500 кг?
7. Найти первую космическую скорость для планеты, масса которой
в Я|=3 раза больше массы Земли. Радиус планеты больше земного в
п2 = 1 раза. Принять первую космическую скорость для Земли равной
у = 8 км/с.
8. Спутник называется синхронным или геостационарным, если при
движении по круговой экваториальной орбите он остается над одной и той
же точкой Земли. Найти радиус орбиты такого спутника. Радиус Земли
считать равным /?3 = 6400 км.
9. По выпуклому мосту, имеющему радиус кривизны /? = 40 м, дви-
жется автобус массой т = 2-103 кг со скоростью и = 36 км/ч. Определить
ускорение автобуса и силу, с которой он давит иа мост в верхней точке
моста.
280
10. Математический маятник массой т отклонили от вертикали на
угол а. Какова сила натяжения нити при прохождении маятником положе-
ния равновесия?
Законы сохранения в механике
1. Граната, брошенная под углом а к горизонту со скоростью v0, раз-
рывается в некоторой точке траектории на два осколка одинаковой массы,
один из которых начинает двигаться по вертикали, а другой — под углом
Р к горизонту. С какой скоростью начинает двигаться второй осколок? Со-
противление воздуха не учитывать.
2. Человек массой т = 70 кг находится на корме лодки, покоящейся на
поверхности озера. Длина лодки / = 5 м, ее масса Ai=280 кг. Человек
переходит на нос лодки. Пренебрегая сопротивлением воды, найти, на ка-
кое расстояние переместится человек относительно воды.
3. Пуля, летящая горизонтально, попадает в ящик с песком, подве-
шенный на нити длиной 1 = 2 м, и застревает в нем. При ударе ящик откло-
нился на угол а=14°. Масса пули /и, = 10 г, масса ящика с песком т2 =
= 2 кг. Найти скорость пули.
4. Определить работу, совершенную при подъеме тела массой
т=\00 кг на высоту /z = 4 м, если скорость его при этом увеличилась от
нуля до и = 2 м/с. Трением пренебречь.
5. Тело массой т=\ кг брошено горизонтально со скоростью
уо = 6 м/с с высоты Н = 5 м. Найти кинетическую энергию тела при паде-
нии на землю. Сопротивление воздуха не учитывать.
6. Движущаяся частица, кинетическая энергия которой равна Ео,
сталкивается абсолютно упруго с такой же неподвижной частицей и откло-
няется от первоначального направления на угол а = 60°. Определить кине-
тическую энергию каждой частицы после соударения.
7. Два шарика массой /и = 0,2 кг каждый, имеющие скорости
у, = 4 м/с и и2 = 3 м/с, налетают друг на друга под углом 90°. Происходит
абсолютно неупругий удар. Определить кинетическую энергию шаров по-
сле соударения.
8. Какую работу совершит сила F = 20 H, подняв по наклонной плос-
кости груз массой /и = 2 кг на высоту Л = 2,5 м с ускорением а = 5 м/с2?
Сила действует параллельно наклонной плоскости. Трением пренебречь.
9. Гладкий легкий горизонтальный стержень АВ может вращаться без
трения вокруг вертикальной оси, проходящей через конец А. На стержне
находится небольшая муфточка массой т, соединенная с концом А невесо-
мой пружиной длиной 10 . Жесткость пружины равна k. Муфточка может
без трения скользить по стержню. Какую работу надо совершить, чтобы
эту систему медленно раскрутить до угловой скорости «? Массой стержня
пренебречь.
10. Пуля массой /и =10 г, летящая горизонтально со скоростью
ц = 200 м/с, попадает в покоящийся ящик с песком массой М = 2 кг, лежа-
щий на гладком горизонтальном столе, и застревает в нем. К противопо-
ложной стороне ящика прикреплена пружина жесткостью k — 2 Н/см
(рис. 189), второй конец которой соединен со стеной. Скорость пули на-
правлена вдоль оси пружины. Определить амплитуду колебаний ящика.
т
Рис. 189
281
Элементы статики. Жидкости и газы
1. Деревянный брусок находится на наклонной плоскости. С какой
наименьшей силой нужно прижать брусок к наклонной плоскости, чтобы
он остался на ней в покое? Масса бруска т = 0,2 кг, длина наклонной
плоскости /=1 м, высота h = 0,5 м, коэффициент трения бруска о наклон-
ную плоскость (i = 0,4.
2. Однородный брус массой т = 50 кг одним концом опирается о гори-
зонтальную плоскость. Другой его конец удерживается веревкой так, что
веревка и брус образуют прямой угол, а брус и горизонтальная плос-
кость— угол а = 60°. Найти силу натяжения веревки.
3. К правому концу стержня длиной / = 30 см прикреплен шар радиу-
сом /? = 6 см так, что центр шара лежит на продолжении оси стержня.
Масса шара в два раза больше массы стержня. Где находится центр тяже-
сти этой системы?
4. Однородное бревно длиной / и массой m = 100 кг лежит на двух опо-
рах горизонтально. Расстояние от правого конца бревна до ближайшей
1 I п „ „ Л
опоры равно — , от левого . С какой силой давит бревно на каждую
о 4
опору?
5. Цилиндрическая труба малого диаметра, имеющая массу т =
= 2-103 кг, лежит на земле. Какую наименьшую силу надо приложить,
чтобы приподнять трубу за один из ее концов?
6. На малый поршень гидравлического пресса действует сила
F = 50 H. Поршень медленно опускается на ht = 15 см. При этом большой
поршень поднимается на h,2 = 3 мм. Определить массу груза, лежащего на
большом поршне.
7. В сообщающиеся сосуды с ртутью добавили: в один сосуд столб
масла высотой ht = 30 см, в другой столб воды высотой Л2 = 20 см. Опреде-
лить разность уровней ртути в сосудах. Плотность масла р, = 0,9Х
X 103 кг/м3, воды р2 = 1-10 кг/м3, ртути р3 = 13,6- 103 кг/м3.
8. Тело массой т, утонувшее в жидкости плотностью р,, давит на дно
с силой Ft. Какая часть тела будет погружена в жидкость плотностью р2,
на поверхности которой оно плавает?
9. Полый цилиндр плавает в керосине. Чтобы цилиндр плавал с такой
же глубиной погружения в воде, в него требуется поместить груз массой
/7г=100 кг. Определить массу цилиндра. Плотность керосина р| = 0,8Х
Х103 кг/м3, воды р2=Ы03 кг/м3.
10. На сколько плотность некоторого тела больше плотности воды,
если вес этого тела в воде в я = 9 раз меньше, чем в воздухе? Плотность воды
рв= 1 - I03 кг/м3.
Основы молекулярно-кинетической теории.
Газовые законы
\. Какова максимальная разность масс воздуха, заполняющего ком-
нату вместимостью V=100 м3 зимой и летом при атмосферном дав-
лении р=105 Па, если летом температура в комнате повышается до
^, = 30 °С, а зимой падает до /2=10°С? Молярная масса воздуха
М = 29-10~ кг/моль, универсальная газовая постоянная R —
= 8,31 Дж/(моль-К).
2. Во сколько раз возрастет число молекул идеального газа в единице
объема, если в процессе изотермического сжатия давление увеличивается
в я = 2,5 раза?
3. В озере на глубине Л = 50 м при температуре < = 5°С находится в
равновесии тонкостенный резиновый шар, наполненный воздухом. Масса
резины т=100 г. Найти массу воздуха внутри шара, если атмосферное
давление ра = 99,7 кПа. Молярная масса воздуха Л1 = 29'10~ кг/моль,
282
универсальная газовая постоянная /? = 8,31 Дж/(моль-К), плотность воды
р=Ы03 кг/м3.
4. Средняя квадратичная скорость молекул газа и = 400 м/с. Опреде-
лить объем, который занимает т=1 кг газа при давлении р = 10 Па.
5. Определить плотность идеального газа при температуре i=100°C
и давлении р=105 Па, а также массу одной молекулы этого газа, если из-
вестно, что его молярная масса Af = 32-10~ кг/моль. Постоянная Авогад-
ро Л/А = 6,02-1023 моль.
6. В вертикально расположенном цилиндре под невесомым подвиж
ным поршнем находится воздух. На поршень помещают гирю массой
т= 10 кг. На сколько опустится поршень, если температура воздуха в ци-
линдре поддерживается постоянной? Атмосферное давление ра— 105 Па,
площадь поршня 5=100 см2, расстояние от ненагруженного поршня до
дна цилиндра /i0=100 см.
7. Два сосуда одинаковой вместимостью содержат воздух: один при
температуре 7", и давлении рь другой при температуре Т2 и давлении р2.
Сосуды соединяют, и после выравнивания давлений и температур воздух
оказывается нагретым до температуры Т3. Какое давление устанавлива-
ется при этом?
8. В результате изохорного охлаждения давление газа уменьшилось
на Лр= 100 кПа, а абсолютная температура — в я= 1,5 раза. Определить
начальное давление.
9. Смешали V, = 1 м3 воздуха влажностью <р,=20% и V2 = 2 м3 возду-
ха влажностью ср2 = 30%. При этом обе порции были взяты при одинако-
вых температурах. Определить относительную влажность смеси.
10. На дне цилиндра, заполненного газом, лежит шар. До какого дав-
ления надо сжать газ, чтобы шар поднялся наверх? Считать, что газ при
больших давлениях подчиняется уравнению Менделеева — Клапейрона.
Температура газа постоянна и равна i = 20°C, молярная масса газа
Л1 = 29-10~3 кг/моль, плотность шара р== 7,8-103 кг/м3.
Тепловые явления
1. Кусок льда массой /и, = 20 кг при температуре tt = —20 °С опусти-
ли в сосуд с водой, масса которой т2 = 20 кг, а температура <2 = 70°С. Что
будет в сосуде после того, как установится тепловое равновесие? Удельная
теплоемкость льда с, = 2,1 -10 Дж/(кг-К), воды с2 = 4,2-103 Дж/(кг-К),
удельная теплота плавления льда Х. = 3,36-105 Дж/кг.
2. Нагретое до температуры i[ = 100oC тело опустили в сосуд с водой,
и при этом температура воды повысилась от <2 = 20 °С до /3 = 30 "С. Какой
стала бы температура воды, если бы в нее одновременно с первым опус-
тить еще одно такое же тело, нагретое до ^4 = 50°С?
3. Для приближенного определения удельной теплоты парообразова-
ния воды был проделан следующий опыт. На электроплитке нагрели воду,
причем оказалось, что на нагревание ее от <i = 10°C до /2=100°С потре-
бовалось т, = 18 мин, а для обращения & = 0,2 ее массы в пар — т.2 =
= 23 мин. Какова удельная теплота парообразования воды по данным
опыта? Удельная теплоемкость воды с = 4,2 кДж/(кг-К).
4. С какой высоты упал без начальной скорости свинцовый шар, если
при падении температура его повысилась на Д7"=10 К? Считать,
т| = 0,8 энергии шара пошло на его нагревание. Сопротивлением воздуха
пренебречь. Удельная теплоемкость свинца с = 130 Дж/(кг-К).
5. Для изобарного нагревания v = 800 моль газа на Л7' = 500 К ему со-
общили количество теплоты Q = 9,4 МДж. Определить работу газа и при-
ращение его внутренней энергии. Универсальная газовая постоянная
/? = 8,31 Дж/(моль-К).
6. В изотермическом процессе газ совершил работу А = 1000 Дж. На
сколько увеличится внутренняя энергия этого газа, если ему сообщить ко-
283
личество теплоты в я = 2 раза большее, чем в первом случае, а процесс
проводить изохорно?
7. При адиабатном расширении v=l моль идеального одноатомного
газа он совершил работу А = 1,25 кДж. Найти изменение температуры га-
за. Универсальная газовая постоянная /? = 8,31 Дж/(моль-К).
8. В процессе изобарного нагревания гелия к нему было подведено ко-
личество теплоты Q = 300 Дж. Определить работу, совершенную газом.
9. На электроплитке мощностью N=1 кВт кипит чайник с водой. Вы-
числить скорость истечения пара из его носика, если площадь поперечного
сечения носика S=l см2, давление на выходе из носика равно атмосфер-
ному давлению ро= Ю5 Па, все количество теплоты, выделяемое плит-
кой, передается воде без потерь. Удельная теплота парообразования
воды г = 2,26 МДж/кг, универсальная газовая постоянная /? = 8,31
Дж/(моль-К), молярная масса воды А1 = 18-10~3 кг/моль.
10. Идеальная тепловая машина Карно имеет КПД г| = 60%. Во
сколько раз количество теплоты, полученное от нагревателя, больше коли-
чества теплоты, отданного холодильнику?
Электростатика
1. В вершинах квадрата со стороной а= 10 см расположены три отри-
цательных и один положительный заряды, модули которых одинаковы и
равны <? = 7-10~8 Кл. Заряды находятся в воздухе. Определить напряжен-
ность электрического поля в центре квадрата. Электрическая постоянная
ео = 8,85-1О-'2 Ф/м.
2. Найти наименьшее расстояние, на которое может приблизить-
ся электрон, движущийся из бесконечности с начальной скоростью
ио=105 м/с, к неподвижному отрицательному иону, заряд которого
</ = 3,2-10~'' Кл. Заряд электрона е=1,6-10~19 Кл, масса электрона
т = 9,Ы0~'' кг, электрическая постоянная ео = 8,85-10~12 Ф/м.
3. Два положительных точечных заряда q^ = q и q2 = 4q находятся на
расстоянии л = 3 м один от другого. На каком расстоянии от заряда qt на-
ходится точка, напряженность электрического поля в которой равна нулю?
4. Электрическое поле переместило частицу с зарядом ^ = 0,2 Кл из
точки А с потенциалом <рд = 600 В в точку В, потенциал которой неизве-
стен. При этом кинетическая энергия частицы изменилась на Д№ =
— 1H Дж. Определить потенциал точки В.
5. Между горизонтальными обкладками плоского конденсатора нахо-
дится в равновесии пылинка массой /и = 3-10~ г. Каков заряд пылинки,
если разность потенциалов между обкладками С = 450 В, а расстояние
между ними d=\,5 см?
6. Электрон влетает в плоский конденсатор длиной / = 5 см под углом
а=--30° к поверхности пластин, расположенных горизонтально, а вылетает
из него параллельно пластинам. Определить начальную энергию электро-
на, если внутри конденсатора напряженность электрического поля
? = 600 В/см. Заряд электрона е= 1,6-10~ Кл. Силой тяжести, действу-
ющей на электрон, можно пренебречь по сравнению с силой электрическо-
го поля.
7. Шарик, имеющий массу т = 0,4 г и заряд ^ = 4,9- 10 7 Кл, подве-
шен на нити в однородном электрическом поле, силовые линии которого
горизонтальны, а напряженность ? = 8-103 В/м. Найти угол, на который
отклонена нить от вертикали.
8. Конденсатор емкостью С, заряженный до разности потенциалов
и, =40 В, соединяется одноименно заряженными обкладками с конденсато-
ром емкостью 2С, заряженным до разности потенциалов U2 = 400 В. Опре-
делить напряжение на конденсаторах после соединения.
9. Расстояние г между двумя точечными зарядами ^1 = 64-10~9 Кл
284
и q2=—48-10 Кл равно 10 см. Найти напряженность электрического
поля в точке, удаленной на Г|=8 см от первого заряда и на г2 = 6 см
от второго. Заряды находятся в воздухе. Электрическая постоянная
ко = 8,85-1О~12 Ф/м.
10. Плоский конденсатор с площадью пластин S=10~ м2 и расстоя-
нием между ними d= 1 мм имеет заряд (/= 10~ Кл. Пространство между
пластинами конденсатора заполнено диэлектриком с диэлектрической про-
ницаемостью е=10. Определить напряженность и энергию электрического
поля конденсатора. Электрическая постоянная ео = 8,85- 10~ |2 Ф/м.
Законы постоянного тока
1. Какой заряд протекает за время t = 5 с через поперечное сечение
проводника, если за это время сила тока равномерно возрастает от
/, = 0 до /2=12 А?
2. Три одинаковых резистора, соединенных последовательно, имеют
общее сопротивление Rt = 9 Ом. Чему будет равно сопротивление, если эти
же резисторы соединить параллельно?
3. Схема электрической цепи и ее параметры показаны на рисунке
190. Найти заряд на конденсаторе и определить показание вольтметра,
считая его идеальным.
R1\
R2\
Рис. 190
4. Рассчитать длину никелиновой проволоки кипятильника, с помощью
которого можно в течение т= 1 ч довести до кипения /и= 10 кг воды, взя-
той при температуре 2=10 "С, если его КПД т] = 84%, напряжение в сети
?/= 120 В, площадь поперечного сечения проволоки S = 5-10 м2. Удель-
ное сопротивление никелина р = 0,4-10 Ом-м, удельная теплоемкость
воды с = 4190 Дж/(кг-К).
5. Источник тока с внутренним сопротивлением г = 1,5 Ом замкнут на
реостат, сопротивление которого изменяется от /^, = 3 Ом до /?2 = 7,5 Ом.
Во сколько раз изменяется при этом мощность, выделяемая на реостате?
6. Два проводника, сопротивления которых /?,=7 Ом и R2 = 5 Ом, со-
единили параллельно и подключили к источнику тока. В первом проводни-
ке за некоторое время выделилось количество теплоты Q, = 300 Дж. Какое
количество теплоты выделится во втором проводнике за то же время?
7. К источнику тока с ЭДС 8Г = 10 В и внутренним сопротивлением
г=\ Ом подключена система из четырех резисторов сопротивлением
/?=1 Ом каждый. Как нужно соединить эти резисторы, чтобы в них выде-
лилась максимальная мощность?
8. Батарея, имеющая ЭДС W = 60 В и внутреннее сопротивле-
ние л = 4 Ом, замкнута на внешнюю цепь, потребляющую мощность
Р = 200 Вт. Определить силу тока в цепи, падение напряжения на внешней
цепи, сопротивление внешней цепи.
9. Обмотка электродвигателя постоянного тока сделана из проволоки
285
общим сопротивлением /? = 2 Ом. По обмотке работающего двигателя,
включенного в сеть с напряжением С=110 В, проходит ток силой
/=ц Д. Определить КПД двигателя.
10. Деталь надо покрыть слоем хрома толщиной d = 50 мкм. Сколько
времени потребуется для покрытия, если при хромировании норма плотно-
сти тока (отношение силы тока к площади поперечного сечения проводни-
ка) / = 2 кА/м2? Плотность хрома р = 7,2-103 кг/м3, его электрохимический
эквивалент ? = 0,18-10~6 кг/Кл.
Магнитное поле. Электромагнитная индукция
1. Определить удельный заряд частицы, т. е. отношение ее заряда к
массе, если в магнитном поле с индукцией В=10~ Тл она движется по
окружности радиусом /? = 23 см с постоянной скоростью у = 4-107 м/с.
2. Под действием однородного магнитного поля в нем движется с уско-
рением а = 2 м/с2 прямолинейный проводник с током силой /=1 А, пер-
пендикулярный линиям магнитной индукции. Плотность материала про-
водника р = 2,5-103 кг/м3, площадь его поперечного сечения S=l мм2.
Определить магнитную индукцию поля.
3. Электрон, имеющий скорость и = 2-10б м/с, влетел в однородное
магнитное поле с индукцией й = 0,03 Тл под углом а = 60° к направлению
силовых линий поля. Определить радиус и шаг винтовой линии, по которой
будет двигаться электрон. Масса электрона т = 9,1 • 10~31 кг, заряд элект-
рона е=1,6-10~19 Кл.
4. Пройдя ускоряющую разность потенциалов С = 3520 В, электрон
попал в однородное магнитное поле с индукцией В = 0,002 Тл, перпендику-
лярной скорости электрона. Найти радиус окружности, по которой бу-
дет двигаться электрон. Отношение заряда электрона к его массе
е/т = 1,76-1011 Кл/кг.
5. Проволочный виток площадью S и сопротивлением R находится во
внешнем магнитном поле, магнитная индукция В которого изменяется со
временем по закону В = В0 cos int. Определить максимальное значение си-
лы тока и тепловую мощность, выделяемую в витке. Линии магнитной ин-
дукции поля перпендикулярны плоскости витка. Значения Во и «
известны.
6. Из куска провода длиной / = 8 м, замкнув его концы, сделали квад-
рат и поместили его в однородное магнитное поле с индукцией й = 0,2 Тл.
Плоскость квадрата перпендикулярна силовым линиям поля. Затем растя-
нули квадрат так, что получился сложенный вдвое провод. Какой заряд
прошел по проводу, если его площадь поперечного сечения S = 0,l мм , а
удельное сопротивление материала провода р = 0,2 мкОм-м?
7. Самолет, размах крыльев которого / = 20 м, летит горизонтально со
скоростью и = 500 км/ч. Вертикальная составляющая магнитной индукции
поля Земли Вв = 5-10~ Тл. Определить разность потенциалов, возникаю-
щую между концами крыльев самолета. Что покажет вольтметр, соединен-
ный с концами крыльев?
8. Плоский проволочный виток, площадь которого S= 103 см2, а сопро-
тивление R = 2 Ом, расположен в однородном магнитном поле с индукцией
В = 0,1 Тл таким образом, что его плоскость перпендикулярна линиям маг-
нитной индукции. Виток замкнут на гальванометр. При повороте витка че-
рез гальванометр протек заряд ^ = 2,5-10 ~3 Кл. На какой угол повернули
виток?
9. На горизонтальных проводящих стержнях, расположенных на од-
ном уровне (рис. 191), лежит проводящая перемычка массой т. Коэффици-
ент трения между стержнями и перемычкой равен \i. Стержни замкнуты
на резистор сопротивлением R. Сопротивления стержней и перемычки пре-
небрежимо малы. Система находится в магнитном поле, индукция которо-
286
%
i
h
//
,1
V
/
i
Рис. 191
го направлена вертикально вверх и равномерно изменяется с течением
времени по закону B = At, где Л — постоянная положительная величина,
выраженная в Тл/с. Определить направление индукционного тока. Найти
ЭДС индукции в моменты времени, когда перемычка покоилась. В какой
момент времени перемычка начнет двигаться по стержням? Указанные на
рисунке размеры I и h известны.
10. Катушка диаметром rf = 0,4 м находится в переменном магнитном
поле. При изменении магнитной индукции поля на ДВ = 127,4 Тл в течение
Д^ = 2 с в катушке возбуждается ЭДС индукции Wt = 200 В. Сколько вит-
ков имеет катушка?
Колебания и волны
Т. На какую высоту над Землей следует поднять математический ма-
ятник, чтобы его период колебаний увеличился на 1%? Радиус Земли
/? = 6370 км.
2. Точка совершает гармонические колебания согласно уравнению
х = 2 cos ф, где все величины выражены в единицах СИ; ф — фаза колеба-
ний. Начальная фаза (ро=15°. Найти смещение точки от положения рав-
новесия к моменту времени t{=—7", где Т—период колебаний.
3. Два математических маятника с периодами колебаний 7", =6 с и
7 = 5 с соответственно одновременно начинают колебания в одинаковых
фазах. Через какой наименьший промежуток времени фазы их колебаний
снова будут одинаковыми?
4. Груз массой т = 400 г, прикрепленный к пружине, жесткость кото-
рой ? = 250 Н/м, совершает колебания с амплитудой хп=\5 см. Найти
максимальное значение скорости груза.
5. В неподвижном лифте математический маятник совершает колеба-
ния, период которых Т = 2 с. Чему будет равен период колебаний этого ма-
ятника, если лифт начнет опускаться с ускорением а = 2 м/с2?
6. Определить резонансную частоту контура, если максимальный за-
ряд конденсатора qm=\ мкКл, а максимальная сила тока в контуре
/„=10 А.
7. Колебательный контур состоит из катушки, индуктивность которой
/_=10~ Гн, и конденсатора емкостью С= 10 Ф. Конденсатор заряжен
до максимального напряжения Сш=100 В. Определить максимальную си-
лу тока в контуре при свободных колебаниях в ием.
8. Если в катушке индуктивности сила тока изменяется на Д/=1 А за
время Д^ = 0,6 с, то в ней возникает ЭДС самоиндукции Ws = 0,2 мВ. Ка-
кую длину будет иметь радиоволна, излучаемая генератором, колебатель-
287
ный контур которого состоит из этой катушки и конденсатора емкостью
С = 14,1 нФ? Скорость света в вакууме с = 3-108 м/с.
9. Скорость звука в воде и=1450 м/с. Найти расстояние между бли-
жайшими точками, совершающими колебания в противоположных фазах,
если частота колебаний v = 725 Гц.
10. При какой скорости поезда математический маятник длиной
/=Н см, подвешенный в вагоне, особенно сильно раскачивается, если дли-
на рельсов L=12,5 м?
Оптика
1. На рисунке 192 показано, как проходит луч ABC через тонкую соби-
рающую линзу. Найти построением фокусное расстояние линзы.
А
В
Рис. 192
2. Луч света, направленный горизонтально, попадает на вертикальный
экран. На пути луча поместили небольшое плоское зеркало. Световое пят-
но на экране при этом сместилось вверх на л = 8 см. Определить угол па-
дения луча на зеркало, если расстояние от зеркала до экрана / = 80 см.
3. Луч света падает из воздуха на плоскую стеклянную пластину под
углом а = 30°. На сколько сместится этот луч в результате прохождения
через пластину, если толщина ее d = 20 мм, а показатель преломления
стекла п= 1,5?
4. Луч света, распространяясь в воздухе, падает на плоскую стеклян-
ную пластинку с показателем преломления л =1,5. Определить угол паде-
ния луча, если известно, что отраженный от пластинки луч перпендикуля-
рен преломленному лучу.
5. На дне сосуда, наполненного водой до высоты я,, находится точеч-
ный источник света. На поверхность воды налит слой масла толщиной я2
и опущен непрозрачный диск, который располагается на поверхности мас-
ла так, что его центр находится точно над источником света. При каком
наименьшем радиусе диска наблюдатель, который смотрит сверху, не смо-
жет увидеть свет от источника? Показатель преломления воды я( меньше
показателя преломления масла я2.
6. На какой высоте находится воздушный шар, если с холма высотой
я = 200 м он виден под углом а = 30° к горизонту, а его отражение в озере
видно с этого холма под углом fj = 60° вниз от горизонтали?
7. Построить изображение светящейся точки, расположенной на глав-
ной оптической оси тонкой рассеивающей линзы в одном из ее фокусов.
8. Плоское зеркало установлено перпендикулярно главной оптиче-
ской оси тонкой собирающей линзы на расстоянии от нее, равном ее фокус-
ному расстоянию /7 = 30 см. С другой стороны линзы на расстоянии
d = 45 см от нее находится плоский предмет, установленный перпендику-
лярно главной оптической оси. Где и какое получится изображение пред-
мета?
9. Найти показатель преломления стекла, если на пути /=10 мкм в
стекле укладывается N = 40 длин волн монохроматического света, имею-
288
щего в вакууме длину волны Я, = 0,4 мкм. Частота света в стекле и в вакуу-
ме одинакова.
10. Дифракционная решетка освещена нормально падающим монохро-
матическим светом. В дифракционной картине максимум второго порядка
наблюдается под углом ф=14°. Под каким углом виден максимум третье-
го порядка?
Квантовая физика
1. Определить энергию фотона света с длиной волны Л. == 6-10 7 м.
Найти частоту колебаний напряженности электрического поля световой
волны. Скорость света в вакууме с = 3• 108 м/с, постоянная Планка
/1 = 6,63-10~34 Дж-с.
2. Во сколько раз импульс рх фотона, соответствующего инфракрасно-
му излучению с длиной волны А. = 800 нм, меньше импульса р2 фотона, со-
ответствующего ультрафиолетовому излучению с частотой v= 1,5- 10 Гц?
Скорость света в вакууме с = 3-108 м/с.
3. Определить длину волны излучения, фотоны которого имеют такую
же энергию, как и электрон, ускоренный разностью потенциалов
(/ = 4,1 В. Скорость света в вакууме с = 3-108 м/с, постоянная Планка
Л = 6,63-10~34 Дж-с, заряд электрона е=1,6-10~19 Кл.
4. При освещении пластинки, изготовленной из некоторого металла,
светом с частотой v,=8-1014 Гц, а затем v2 = 6-10' Гц обнаружили, что
максимальная кинетическая энергия фотоэлектронов изменилась в
я = 3 раза. Определить работу выхода электрона из этого металла. По-
стоянная Планка Л = 6,63-10 4 Дж-с.
5. Красная граница фотоэффекта для некоторого металла соответст-
вует длине волны Я.тах = 2,75-10~7 м. Найти работу выхода электрона из
этого металла и максимальную скорость электронов, вырываемых из этого
металла светом с длиной волны >.= 1,8-10~ м. Постоянная Планка
/j = 6,63-10~34 Дж-с, скорость света в вакууме с = 3-108 м/с. Масса элек-
трона mf = 9,l-10~ кг.
6. На плоский алюминиевый электрод падает ультрафиолетовое
излучение с длиной волны Х = 83 нм. На какое максимальное расстоя-
ние от поверхности электрода может удалиться фотоэлектрон, если вне
электрода имеется задерживающее электрическое поле напряжен-
ностью Я = 7,5 В/см? Красная граница фотоэффекта для алюминия
соответствует длине волны ^тах = 332 нм- Постоянная Планка
Л = 6,63-Ю4 Дж-с, заряд электрона е=1,6-109 Кл, скорость света
в вакууме с = 3-108 м/с.
7. Определить период полураспада радона, если известно, что за вре-
мя t=\ сут из первоначального количества No= 10е атомов распадается
N, = 175-103 атомов.
8. Удельная энергия связи ядра гелия Е =7 МэВ/нуклон. Найти
минимальную энергию гамма-кванта, способного разделить это ядро 2Не
на свободные нуклоны.
9. В ядерной реакции в ядро попадает ускоренный протон и вылетает
альфа-частица. На сколько единиц уменьшается массовое число ядра-
мишени?
10. Ядерный реактор приводит в действие турбогенератор мощностью
/> = 2-108 Вт. Определить КПД турбогенератора, если в течение t=\ сут
расход урана g2U составляет т = 0,54 кг, а при делении одного ядра этого
элемента выделяется энергия, равная в среднем ?0 = 3,2-10~" Дж. По-
стоянная Авогадро Л/А = 6,02-1023 моль.
Заказ 2473 289
3. ВАРИАНТЫ ЗАДАНИЙ ПИСЬМЕННОГО
ЭКЗАМЕНА ПО ФИЗИКЕ
Вариант 1
1. Определить среднюю плотность планеты, продолжительность суток
на которой Т = 6 ч. На экваторе этой планеты пружинные весы показыва-
ют на k = 0,\ меньший вес, чем на полюсе. Гравитационная постоянная
0 = 6,67-К)"" м3/(кг-с2).
2. Сможет ли воздушный шар, наполненный гелием, поднять груз мас-
сой /и, = 100 кг, если объем шара У = 150 м3, а масса оболочки т2 = 8 кг?
Гелий внутри шара и воздух снаружи имеют одинаковое давление
р == 105 Па, температура гелия и воздуха также одинаковая, / = 15°С. Мо-
лярная масса гелия Мг = 4 г/моль, воздуха Л!в = 29 г/моль. Универсальная
газовая постоянная /? = 8,31 Дж/(моль-К).
3. Элемент атомной батареи (источника тока) представляет собой пло-
ский конденсатор, на одну из обкладок которого равномерно нанесен ра-
диоактивный препарат, испускающий альфа-частицы со скоростью
и=1,2-106 м/с. Определить ЭДС такого элемента, если отношение заряда
альфа-частицы к ее массе -у == 4,8-107 Кл/кг.
4. Определить массу меди, выделившейся из раствора за т=100 с, ес-
ли сила тока, прошедшего через электролитическую ванну, изменялась по
закону I (t) = E — 0,020 А, где t — время в секундах. Постоянная Фарадея
F = 9,65-104 Кл/моль, валентность меди п = 2, молярная масса меди
/И = 63,5 г/моль.
5. В дно водоема глубиной Н = 2 м вертикально вбита свая, выступаю-
щая из воды на /i = 0,5 м. Найти длину тени от сваи на дне водоема, если
высота Солнца над горизонтом <р = 60°. Показатель преломления воды
л = 4/3.
6. Период полураспада одного из радиоактивных изотопов йода
7" = 8 сут. Через какое время число атомов этого вещества окажется в
я=100 раз меньше по сравнению с их начальным числом?
Вариант 2
1. Закон сохранения энергии в тепловых процессах (первый закон тер-
модинамики). Применение этого закона к изопроцессам.
2. Окраска небольших предметов разбрызгиванием краски становится
выгодной и безвредной для работающего, если приложить высокое напря-
жение к струе краски и заземлить окрашиваемый предмет. Дайте объяс-
нение.
3. Из резисторов с сопротивлениями /?= 12 Ом и г = 6 Ом спаяна цепь,
изображенная на рисунке 193. Определить сопротивление между точками
А и В цепи.
R
Рис. 193
290
4. Первый раскат грома дошел до наблюдателя через t = 25 с после
вспышки молнии. На каком расстоянии от наблюдателя возникла молния?
Скорость звука в воздухе ияй340 м/с.
5. Коэффициент полезного действия теплового двигателя т] = 20%. Ка-
кова должна быть температура нагревателя 7",, если температура холо-
дильника 7 = 300 К?
Вариант 3
1. Тонкая однородная палочка шарнирно укреплена за верхний конец,
а нижний ее конец погружен в воду. При этом равновесие достигается,
когда палочка расположена наклонно к поверхности воды и в воде нахо-
дится половина палочки. Какова плотность материала палочки? Плотность
воды рв= 103 кг/м3.
2. Какое количество теплоты необходимо сообщить гелию массой
т = 40 г, содержащемуся в баллоне, для нагревания его на АТ = 20 К?
Чему равна удельная теплоемкость гелия в этом процессе? Молярная
масса гелия Л1 = 4-10~' кг/моль. Универсальная газовая постоянная
Я = 8,31 Дж/(кг-К).
3. Два протона, находящиеся на достаточно большом расстоянии друг
от друга, начинают двигаться навстречу друг другу с одинаковыми по мо-
дулю начальными скоростями. Определить начальную скорость сближения
протонов, если минимальное расстояние, до которого они могут сблизить-
ся, равно г.
4. Плоский воздушный конденсатор после зарядки отключают от ис-
точника и погружают в керосин с диэлектрической проницаемостью г. Как
изменится энергия конденсатора?
5. Как нужно расположить две собирающие линзы, чтобы пучок па-
раллельных лучей, пройдя через обе линзы, снова стал параллельным?
Главные оптические оси линз при этом должны не совпадать друг с
другом.
Вариант 4
1. На рисунке 194, а показан график скорости первого тела, на рисун-
ке 194,6 — график движения второго тела. Каков характер движения
каждого тела? Для второго тела изобразить график скорости.
Рис. 194
2. Два шара одинакового объема — деревянный и свинцовый — дви-
жутся с одинаковыми скоростями. Какой из них имеет больший импульс
и почему?
3. Сформулировать словами и записать в виде формулы закон электро-
магнитной индукции.
291
4. В идеальном тепловом двигателе абсолютная температура нагрева-
теля в п = 4 раза выше, чем температура холодильника. Определить КПД
двигателя.
5. С какой скоростью нужно бросить вертикально вниз мяч, чтобы он
подпрыгнул на Л = 10 м выше того уровня, с какого он был брошен? Удар
мяча о землю считать абсолютно упругим. Сопротивление воздуха не учи-
тывать.
6. Определить, возникнет ли фотоэффект в оксиде бария под действи-
ем излучения, имеющего частоту v = 3-10 Гц. Работа выхода для оксида
бария Л=4,6-10~19 Дж. Постоянная Планка Л = 6,63• 10~34 Дж-с.
7. В точке А (рис. 195) напряженность поля точечного заряда
?1 = 36 В/м, а в точке В ?2 = 9 В/м. Найти напряженность в точке С, лежа-
щей посередине между точками А и В. Заряд находится в воздухе.
Рис. !95
Вариант 5
1. Показатель преломления стекла относительно воздуха П| = 1,50.
Определитель показатель преломления воды относительно стекла, если по-
казатель преломления воды относительно воздуха /г2 = 1,32.
2. Найти амплитудное значение напряжения в сети переменного тока,
если на спираль нагревателя мощностью Р = 600 Вт израсходовано
1=1,2 м проволоки, изготовленной из электротехнического сплава, удель-
ное сопротивление которого р = 4- 10~ь Ом • м. Площадь поперечного сече-
ния проволоки S = 0,2 мм2.
3. Электрическая цепь состоит из источника с ЭДС ^" = 100 В и
внутренним сопротивлением г = 5 Ом и резистора с сопротивлением
/?, == 100 Ом. Параллельно резистору подключили конденсатор с последо-
вательно соединенным с ним другим резистором, сопротивление кото-
рого R2 = 200 Ом. При этом заряд на конденсаторе оказался равным
q=\0~ Кл. Определить емкость конденсатора.
4. Два математических маятника в одном и том же месте Земли за
одинаковое время совершают первый я, =20, а второй я2 —40 колебаний.
Разность длин маятников Д/ = 0,06 м. Какова длина первого маятника?
5. В закрытый сосуд, на дне которого лежит твердый шар, нагнетают
воздух при температуре ^ = 27 °С. Когда давление р в сосуде стало равным
2-10 Па, шар начал подниматься вверх. Найти массу шара, если извест-
но, что его радиус г = 5 см и что при нормальных условиях (ро=1О5 Па,
/0 = 0°С) плотность воздуха ро=1,29 кг/м3.
6. За какое время тело, не имеющее начальной скорости, соскользнет
с наклонной плоскости высотой h и углом наклона р, если по наклонной
плоскости с углом наклона а<{5 оно скользит вниз равномерно? В обоих
случаях коэффициент трения имеет одно и то же значение.
Вариант 6
1. Свободно падающий камень пролетел последние три четверти пути
за т= 1 с. С какой высоты падал камень, если его начальная скорость рав-
292
на нулю? Сопротивление воздуха не учитывать.
2. Тело массой т = 30 г, брошенное с поверхности Земли вертикально
вверх, достигло максимальной высоты // = 20 м. Найти модуль импульса
силы, действовавшей иа тело в процессе бросания. Сопротивлением возду-
ха пренебречь.
3. При торможении тела массой т = 2 кг скорость его уменьшилась
от у, = 3 м/с до У2 = 2 м/с. Определить работу тормозящей силы.
4. Два шара, имеющих одинаковый диаметр, связаны нитью и опуска-
ются в жидкости вертикально один за другим с малой постоянной ско-
ростью. Определить силу натяжения нити, если массы шаров /и, = 2,2 кг
и /п2=1,4 кг соответственно.
5. В запаянной с обоих концов горизонтальной трубке газ разделен ка-
пелькой масла на два объема по 1/== 70 см3 каждый при температуре
7", = 400 К. На сколько уменьшится объем газа справа от капельки, если ох-
ладить этот газ до Г2 = 300 К?
6. Какую долю составляет разность температур нагревателя и холо-
дильника от температуры нагревателя, если максимальный коэффициент
полезного действия машины т]тах=17%?
7. Расстояние между пластинами заряженного и отключенного от це-
пи плоского конденсатора увеличивается в я = 2 раза. Во сколько раз воз-
растет при этом энергия электрического поля в конденсаторе?
9. Сколько цепей с различными сопротивлениями может получить экс-
периментатор, имея в своем распоряжении три резистора с сопротивлени-
ем R = 5 Ом каждый?
9. Во сколько раз уменьшится энергия магнитного поля катушки, если
силу тока уменьшить на 50%?
10. При включении конденсатора в цепь переменного тока с цикличе-
ской частотой w = 200 рад/с его емкостное сопротивление Хс = 50 Ом.
Определить емкость конденсатора.
11. Луч света падает на границу раздела двух прозрачных сред под
углом полного внутреннего отражения. Определить угол между прелом-
ленным лучом и нормалью к границе раздела.
12. Электрическая мощность атомной электростанции Р=109 Вт, а
КПД т] = 25%. Найти число ядер, распадающихся в реакторе за /= 1 с, ес-
ли в одном акте деления высвобождается энергия W = 250 МэВ.
Вариант 7
1. С высоты /i = 20 м начало свободно падать тело. Одновременно с
поверхности Земли бросили вертикально вверх другое тело со скоростью
ио = 20 м/с. На какой высоте эти тела встретятся? Сопротивление воздуха
не учитывать.
2. Две гири массами т] = 0,5 кг и т2=1,5 кг соединены невесомой и
нерастяжимой нитью, перекинутой через блок. С каким ускорением дви-
жутся гири? Массой блока и трением его об ось пренебречь.
3. Определить силу, действующую на тело, если при перемещении его
на расстояние s = 20 см совершена работа Л =500 Дж, а сила направлена
под углом а = 60° к направлению перемещения.
4. Из орудия, стоящего на покоящейся платформе, произвели выстрел
в горизонтальном направлении. Масса снаряда т=100 кг, его скорость
v = 400 м/с. Масса платформы с орудием /И = 20 т. Определить расстоя-
ние, на которое откатилась платформа после выстрела, если коэффициент
сопротивления ее движению ц == 0,1. Ускорение свободного падения при-
нять равным g=10 м/с2.
5. Какой объем занимают v = 3 кмоль газа при давлении р= 1 МПа и тем-
пературе /= 100 °С? Универсальная газовая постоянная /? = 8,31 Дж/(моль-К).
6. Для расплавления т=1т латуни используется электропечь мощно-
стью /)=105 Вт. Сколько времени длится плавка, если до начала плавле-
ния слиток нагрели на Д/ = 900°С? Удельная теплоемкость латуни
293
с = 386 Дж/(кг-К), ее удельная теплота плавления Х = 2-105 Дж/кг. Энер-
гетические потери отсутствуют.
7. Батарея гальванических элементов с ЭДС W = 15 В и внутренним
сопротивлением г = Ъ Ом замкнута проводником, имеющим сопротивление
/?=10 Ом. К зажимам батареи подключен конденсатор емкостью
С=1 мкФ. Определить заряд конденсатора.
8. Найти силу взаимодействия двух зарядов по q=\ Кл каждый, рас-
положенных на расстоянии г=1 км друг от друга в воздухе. Электриче-
ская постоянная ео = 8,85- 10~12 Ф/м.
9. Два иона, имеющих одинаковые заряды и одинаковые кинетические
энергии, влетели в однородное магнитное поле. Первый ион описал окруж-
ность радиусом /?! = 3 см, а второй — R2=l,5 см. Определить отношение
массы первого иона к массе второго.
10. Найти абсолютный показатель преломления среды, в которой свет
с энергией фотона Я = 3-10~19 Дж имеет длину волны Я. == 0,44-10 м.
Скорость света в вакууме с = 3 - 108 м/с. Постоянная Планка
/1 = 6,63-104 Дж-с.
Вариант 8
1. Мотоциклист, двигаясь прямолинейно, за первые /, = 5 мин проехал
путь s, = 3 км, за последующие /2 = 8 мик — s2 = 9,6 км и за последние
<3 = 6 мин — s3 = 5,4 км. Определить среднюю скорость за все время дви-
жения.
2. С каким ускорением падает тело массой т = Ъ кг, если при этом си-
ла сопротивления /7с = 20 Н?
3. Молот массой /и = 5 кг падает на деталь с высоты /j = 80 см. На-
сколько увеличится внутренняя энергия детали, если на ее нагревание
идет т] = 0,25 количества теплоты, выделившегося при ударе?
4. Найти период свободных колебаний математического маятника
длиной / = 39,2 см.
5. Найти среднюю квадратичную скорость молекул кислорода при
температуре / = 48 "С. Молярная масса кислорода Л1 = 32-10~ кг/моль.
Универсальная газовая постоянная /? = 8,31 Дж/(моль-К).
6. Гелий массой т = 8 г был нагрет на АГ=100 К при постоянном
давлении. Какое количество теплоты было передано этому газу? Молярная
масса гелия Af = 4-10~ кг/моль. Универсальная газовая постоянная
Я = 8,31 Дж/(моль-К).
7. Два одинаковых металлических шарика, имеющих заряды
</, = —8-10 8 Кл и ^2 = 28-10 8 Кл, привели в соприкосновение, а затем
раздвинули на расстояние г= 10 см. Определить силу взаимодействия ша-
риков. Шарики находятся в воздухе (е=1). Электрическая постоянная
ео = 8,85-1О-'2 Ф/м.
8. Электрическая лампочка мощностью /> = 60 Вт рассчитана на на-
пряжение U, = 120 В. Найти сопротивление резистора, который нужно
включить последовательно с лампочкой, чтобы она нормально горела при
включении в сеть с напряжением t/2 = 220 В.
9. Какова индукция магнитного поля, в котором на проводник длиной
/ = 20 см действует сила F = 0,l Н при силе тока в проводнике / = 20 А?
Направление тока перпендикулярно линиям индукции.
10. Во сколько раз энергия фотона с длиной волны Я, = 0,66 мкм мень-
ше энергии покоя электрона? Масса электрона /ие = 9,1 • 10~31 кг. Ско-
рость света в вакууме с = 3-108 м/с. Постоянная Планка /i = 6,63X
ХЮ4 Дж-с.
294
Вариант 9
1. С какой высоты падает без начальной скорости тело, если путь,
пройденный им за последнюю секунду движения, в п = 7 раз больше
пути, пройденного за первую секунду? Ускорение свободного падения
g = 10 м/с2.
2. Тело массой т = 2 кг брошено с поверхности Земли со скоростью
уо= 6 м/с под углом а = 30° к горизонту. На сколько увеличится потенци-
альная энергия тела, когда оно достигнет высшей точки подъема?
3. Маленький шарик массой т = 0,3 кг привязан к концу вертикаль-
ной нерастяжимой нити, другой конец которой закреплен. Шарик с нитью
переводят в горизонтальное положение и отпускают без начальной скоро-
сти. Найти силу натяжения нити в тот момент, когда она составит угол
а = 60° с вертикалью. Ускорение свободного падения g=10 м/с2.
4. Прямой конус плавает в жидкости так, что его ось вертикальна и
вершина обращена вверх. Плотность материала конуса составляет
я = 7/8 плотности жидкости. Во сколько раз высота подводной части кону-
са меньше всей его высоты?
5. До какой температуры следует нагреть изобарно газ, чтобы его
плотность уменьшилась в п = 2 раза по сравнению с его плотностью при
7'0 = 273 К?
6. Определить начальную температуру азота массой /и = 0,56 кг,
если при изобарном нагревании до 7" = 370 К газ совершил работу
/1 = 16,6 кДж. Молярная масса азота Л1 = 28-10~ кг/моль, универ-
сальная газовая постоянная R = 8,31 Дж/(моль-К).
7. На точечный заряд, находящийся внутри плоского конденсатора ем-
костью С=100 мкФ, действует некоторая сила. Напряжение на конденса-
торе U=\Q кВ. Во сколько раз увеличится сила, действующая на заряд,
если конденсатор в течение / = 2 мин подзаряжать током силой / = 0,1 А?
8. В однородном магнитном поле с индукцией В = 0,1 Тл находится ви-
ток площадью S= 10 см2, расположенный перпендикулярно линиям индук-
ции. Сопротивление витка R = 2 Ом. Какой заряд протечет по витку при
выключении ноля?
9. Амплитуда незатухающих колебаний точки струны хт= 1 мм, часто-
та v=l кГц. Какой путь пройдет точка за время /=1,2 с?
10. В цепочке радиоактивных превращений элемента с порядковым
номером 2 = 92 и атомной массой Л,=235 в элемент с Z = 82 и Л2 = 207
(урана в свинец) содержится несколько альфа- и бета-распадов. Сколько
всего распадов в этой цепочке?
Вариант 10
1. Явление самоиндукции. Индуктивность. Энергия магнитного поля.
2. Вагон шириной / = 3 м, движущийся равномерно прямолинейно со
скоростью а, = 15 м/с, пробивает пуля, летящая горизонтально в направ-
лении, перпендикулярном направлению скорости вагона. Определить ско-
рость пули, если известно, что отверстия, пробитые пулей, смещены отно-
сительно друг друга на s = 9 см вдоль вагона.
3. В вертикальном цилиндре вместимостью V = 200 см3 под тяжелым
поршнем находится газ при температуре Г = 300 К. Масса поршня
т = 50 кг, его площадь S = 50 см2. Для повышения температуры газа на
ДГ = 100 К ему было сообщено количество теплоты Q = 46,5 Дж. Найти из-
менение внутренней энергии газа. Атмосферное давление ро=105 Па. Тре-
ние при движении поршня не учитывать.
4. Воздушный плоский конденсатор заряжен до разности потенциалов
U =100 В. Расстояние между пластинами конденсатора d=\ см, площадь
каждой пластины S = 200 см . Найти энергию электрического поля конден-
сатора. Электрическая постоянная ео = 8,85-10~ Ф/м.
295
Вариант 11
1. С крыши дома высотой // = 28 м брошен вертикально вверх камень
с начальной скоростью ио = 8 м/с. Определить скорость камня в момент
падения его на землю. Сопротивлением воздуха пренебречь.
2. Какая сила требуется для того, чтобы бруску массой т = 1 кг, ле-
жащему на горизонтальной поверхности, сообщить ускорение а = 2 м/с2?
Коэффициент трения между бруском и поверхностью ц = 0,02.
3. Два сосуда вместимостью V,=3 л и 1/2 = 5 л наполнены воздухом
под давлением р, =8-10° Па и p2 = 6-10° Па соответственно. Сосуды сое-
диняют трубкой, вместимостью которой можно пренебречь. Найти устано-
вившееся в сосудах давление, если температура воздуха в них была одина-
кова и после установления равновесия не изменилась.
4. Определить потенциал шара, если известно, что на расстоянии
/ = 0,9 м от него потенциал электрического поля ф, =20 В. Радиус шара
/? = 0,1 м.
5. При замыкании источника постоянного тока резистором с сопротив-
лением /?| = 5 Ом в цепи идет ток силой /, = 5 А, а при замыкании резисто-
ром с сопротивлением R2 = 2 Ом —ток силой /2 = 8 А. Найти ЭДС источ-
ника и его внутреннее сопротивление.
6. Проволочный виток, площадь которого S = 2 см2, расположен пер-
пендикулярно силовым линиям однородного магнитного поля. Чему равна
индуцированная в витке ЭДС, если за время Л/ = 0,05 с магнитная индук-
ция равномерно убывает от В, = 0,5 Тл до Й2 = О,1 Тл?
7. На конденсаторе емкостью С=10 пФ, включенном в колебательный
контур, эффективное напряжение С=100 В. Определить максимальные
значения энергии электрического поля и энергии магнитного поля в этом
контуре. Рассеянием энергии пренебречь.
8. На поверхность лития падает монохроматический свет, длина волны
которого Х = 310 нм. Определить работу выхода электрона из лития, если
известно, что фотоэлектроны полностью задерживаются напряжением
С=1,7 В. Заряд электрона е = 1,6- 10 Кл, скорость света в вакууме
с = 3'108 м/с, постоянная Планка /г = 6,63-10"' Дж-с.
Вариант 12
1. Танк массой /и = 5-10! кг проходит по выпуклому мосту со скоро-
стью ц = 72 км/ч. С какой силой давит он на середину моста, если радиус
кривизны моста R = 50 м?
2. На неподвижной железнодорожной платформе массой m=10 t укреп-
лено орудие, ствол которого направлен вдоль полотна железной дороги
и поднят на угол а = 60°. С какой скоростью начнет двигаться платфор-
ма, если орудие выпустит снаряд массой /и2 = 50 кг со скоростью ц = 500 м/с?
Изменение массы платформы после вылета снаряда не учитывать.
3. Проволока длиной /=10 м и площадью поперечного сечения
S = 0,5 мм2 при растяжении силой /-" = 100 Н удлинилась на Д/=1 см.
Каков модуль упругости вещества проволоки?
4. Найти напряженность электрического поля точечного заряда
,7 = 4,4-10~5 Кл на расстоянии г=1 м от него. Электрическая постоянная
12
0~12 Ф/м.
5. Определить массу голого медного провода, имеющего сопротивле-
ние /? = 3,4 Ом и длину /=1 км. Удельное сопротивление меди
р=1,7-10~8 Ом-м, ее плотность ?> = 8,9-103 кг/м3.
6. Площадь каждой пластины плоского воздушного конденсатора
S=100 см2, расстояние между ними d = 0,4 см. До какой разности потен-
циалов был заряжен конденсатор, если при его разрядке выделилась энер-
гия № = 4,5-10~~7 Дж? Электрическая постоянная ео = 8,85-1О~ Ф/м.
296
7. В проводнике длиной / = 0,3 м, движущемся со скоростью у = 5 м/с,
направленной перпендикулярно линиям индукции однородного магнитного
поля, возникает ЭДС индукции У1==2,4 В. Определить магнитную индук-
цию поля.
8. Проводник длиной / = 40 см расположен перпендикулярно к сило-
вым линиям однородного магнитного поля, индукция которого В = 0,8 Тл.
Когда по проводнику пропустили ток силой / = 5 А, проводник пришел в дви-
жение. Определить работу магнитного поля, если проводник переместился
на расстояние 5 = 2 м.
9. Найти показатель преломления вещества, если скорость света в нем
а=187 500 км/с. Скорость света в вакууме с = 3-108 м/с.
10. Работа выхода электрона из цинка Л=6,6'10~ Дж. Какой дли-
не волны соответствует красная граница фотоэффекта для цинка? По-
стоянная Планка Л = 6,63 -10 Дж-с. Скорость света в вакууме
г = 3-108 м/с.
Вариант 13
1. Поезд начинает двигаться из состояния покоя и равномерно увели-
чивает свою скорость. На первом километре она возросла на Аи, = 10 м/с.
На сколько она возрастает на втором километре?
2. Определить, с какой силой давит автомобиль массой m = 3 t на вер-
шину выпуклого моста радиусом Л! = 50 м при движении со скоростью
о = 10 м/с.
3. Двигатель насоса, развивая мощность Л/ = 25-103 Вт, поднимает
1/= 100 м3 нефти на высоту Л = 6 м за время ^ = 8 мин. Найти коэффици-
ент полезного действия установки.
4. Кусок медного купороса весит в воздухе />, = 0,11 H, а в керосине
Р2 = 0,07 Н. Опречелить плотность медного купороса. Плотность керосина
р, = 0,8-103 кг/м3.
5. Какой из графиков (рис. 196) правильно показывает зависимость
плотности р идеального газа от абсолютной температуры Т при изобарном
процессе?
6. Во сколько раз уменьшится сила взаимодействия двух точечных
электрических зарядов, если их из вакуума перенести в глицерин, а рас-
стояние между ними увеличить в я = 2 раза? Диэлектрическая проницае-
мость глицерина е = 39.
7. Генератор питает я = 50 ламп, включенных параллельно, сопротив-
лением R,=300 Ом каждая. Напряжение на зажимах генератора С =
= 128 В, а сопротивление подводящей линии /?2 = 0,4 Ом. Найти силу тока
в линии.
8. При силе тока / = 0,5 А на резисторе выделяется мощность
Р==6 Вт. Найти сопротивление резистора.
9. Найти индуктивность проводника, в котором при равномерном изме-
297
нении силы тока на Д/ = 2 А в течение Д/ = 0,25 с возникает ЭДС самоин-
дукции rs = 20 мВ.
10. На дифракционную решетку нормально падает красный свет с
длиной волны А, = 700 нм, при этом для спектра, порядок которого &i = 3,
угол отклонения лучей (р, = 24°48'. Если же на эту решетку падает зеленый
свет, то для спектра второго порядка (&2 = 2) угол отклонения ср2=12°12'.
Какова длина волны зеленого света?
Вариант 14
1. На рисунке 197 даны графики зависимости модуля импульса от
скорости для двух тел. У какого из них масса больше?
2. Три одинаковых груза связаны нерастяжимой нитью, которая пере-
кинута через неподвижный блок (рис. 198). С каким ускорением движутся
грузы? Силы сопротивления не учитывать, массой нити и блока прене-
бречь.
3. Температура нагревателя идеальной тепловой машины tt = \27 °С,
а холодильника /2 = 27 °С. За время т= 1 с машина получает от нагревате-
ля количество теплоты Q = 60 кДж. Вычислить мощность машины.
4. Между пластинами плоского воздушного конденсатора, располо-
женными горизонтально, находится заряженная капелька масла, масса
О
Рис. 197
Рис. 198
которой т = 10 кг, а заряд q = \0 . Кл. При разности потенциалов
между пластинами U = 600 В и начальной скорости Уо = 0 капелька прохо-
дит некоторое расстояние вл = 2 раза быстрее, чем при отсутствии элект-
рического поля. Найти расстояние между пластинами.
5. Как изменится показатель вольтметра (рис. 199), если с помощью
реостата уменьшить сопротивление цепи?
Рис. 199
298
6. Один из математических маятников за некоторое время совершил
/V, = 40 колебаний, другой за то же время —/V2=10 колебаний. Разность
длин этих маятников Д/ = 0,9 м. Найти длину каждого маятника.
7. Найти импульс частицы, движущейся со скоростью и = 0,6 с, где
с = 3- 108 м/с — скорость света в вакууме. Масса частицы т= 1 ¦ Ю~ кг.
8. Определить число нейтронов в ядре 27С0.
Вариант 15
1. Два тела брошены вертикально вверх с одинаковыми начальными
скоростями с интервалом времени т. С какой скоростью будет двигаться
второе тело относительно первого?
2. Точка находится на расстоянии rf = 50 см от плоскости линзы, а ее
мнимое изображение — на расстоянии вдвое меньшем. Найти фокусное
расстояние линзы.
3. Два сосуда, наполненные воздухом под давлениями р, = 8-105 Па
и р2 = 6-105 Па, имеют вместимости V{ = 3 л и V2 = 5 л соответственно. Со-
суды соединяют трубкой. Найти установившееся давление в сосудах, если
температура в них постоянна и одинакова до и после соединения.
4. Определить расстояние г, между двумя одинаковыми точечными
электрическими зарядами, находящимися в масле, если сила взаимодей-
ствия их такая же, как и в воздухе на расстоянии г2 = 30 см. Диэлектриче-
ская проницаемость масла ё] = 3, воздуха — г2=\.
5. Вольтметр, соединенный последовательно с резистором, сопротивле-
ние которого /?! = 10 кОм, при включении в сеть напряжением ?/ = 220 В
показывает ?/, = 70 В, а соединенный последовательно с другим резисто-
ром и включенный в ту же сеть, показывает ?/2 = 20 В. Найти сопротивле-
ние этого резистора.
Указатель распределения приведенных выше задач
письменного экзамена по физике
по основным разделам программы для поступающих в вузы
Раздел
Кинематика
Основы динамики
Законы сохранения
в механике
Элементы статики.
Жидкости и газы
Основы молекулярно-
кинетической теории.
Газовые законы
Тепловые явления
Электростатика
Законы постоянного
тока
Магнитное поле.
Электромагнитная ин-
дукция
Колебания и волны
Оптика
Квантовая физика
1
1
2
3
4
5
6
2
5
2
3
4
3
1
2
со"
4
1
2
5
4
7
3
6
5
6
5
2,3
4
1
и
..мера
задач
Зариант задания
6
1
2
3
4
5
6
7
8
9
10
11
12
7
1
2
3,4
5
6
8
7
9
10
8
1
2
3
5
6
7
8
9
4
10
9
1
3
2
4
5
6
7
8
9
10
10
2
3
4
11
1
2
3
4
5
6
7
8
12
1
2
3
4,6
4
7,8
9
10
13
1
2
3
4
5
6
7,1
9
10
14
1,2
3
4
5
6
7
8
15
1
3
4
5
2
299
4. ОСНОВНЫЕ ФОРМУЛЫ ЭЛЕМЕНТАРНОЙ
ФИЗИКИ
Механика
Равномерное прямолинейное движение. Координата х тела (матери
альной точки) в любой момент времени / определяется уравнением
где х0 — начальная координата; vx—проекция скорости на ось ОХ.
Равноускоренное прямолинейное движение. Координата х тела в лю-
бой момент времени t определяется уравнением
а/
х — хо + v(af Л—2~i
где ха — начальная координата; о0х — проекция начальной скорости на ось
ОХ; ах—проекция ускорения.
Проекция скорости на ось OX vx= vOx-\-aJ.
Равномерное движение по окружности. Линейная скорость
где R — радиус окружности; Т — период вращения; п — частота вра-
щения.
Угловая скорость ю = vj R = 2n/T = 2лп.
Центростремительное (нормальное) ускорение a = v2/R — (o2R.
Второй закон Ньютона: F — ma, где F = F, + F2 + ¦¦¦ + Fn — векторная
сумма всех сил, действующих на тело; m — масса тела; а — ускорение.
Закон всемирного тяготения:
m,m2
F — О
г2 '
где F — модуль силы взаимного притяжения материальных точек; G —
гравитационная постоянная; m,, m2 — массы точек; г — расстояние между
ними.
Сила тяжести F = mg, где m — масса тела; g — ускорение свободного
падения.
Сила трения скольжения F\ =\iN, где ц — коэффициент трения; N —
сила нормальной реакции опоры.
Закон Гука: сила упругости
- = 44' или сг= |е|
где k — коэффициент упругости (жесткость); А/ — вектор удлинения (сжа-
тия); F — модуль приложенной силы; /0 — начальная длина тела; S — пло-
щадь его поперечного сечения; Е — модуль упругости (модуль Юнга);
F М
(Т = ——механическое напряжение; е = — относительное удлинение.
S /0
Момент силы относительно оси M = Fl, где F — модуль силы, / — ее
плечо, т. е. расстояние от оси до линии действия силы.
Импульс силы 7t = mv2 — mvl, где F — сила; t — время ее действия;
mv2 — начальный и конечный импульсы тела.
300
Закон сохранения импульса: векторная сумма импульсов всех тел зам-
кнутой системы остается постоянной, т. е.
o2 -[-... + и„в, = const.
Работа постоянной силы F
А = Fs cos a,
где s — модуль перемещения; а — угол между векторами F и s.
Мощность Р = —, где А — работа, совершаемая за время t.
Кинетическая энергия тела массой гп, движущегося со скоростью и,
Теорема об изменении кинетической энергии: ?к2 — Eki =А, где А — ра-
бота равнодействующей всех сил, приложенных к телу.
Потенциальная энергия: 1) тела массой /га, поднятого в поле тяжести
Земли на высоту h над уровнем с нулевой потенциальной энергией,
Ep = mgh, где g — ускорение свободного падения; 2) упруго деформирован-
ного тела (сжатой или растянутой пружины) Ер = —
Закон сохранения энергии в механике: ?k + ?p = const, если система
замкнута и ее тела взаимодействуют между собой силами упругости и си-
лами тяготения.
Давление р =—, где F — модуль силы; S — площадь поверхности, пер-
о
пендикулярно которой действует эта сила.
Гидростатическое давление внутри жидкости на глубине h p = pg/z, где
р — плотность жидкости; g — ускорение свободного падения.
Архимедова сила FA = pxgVT, где рж— плотность жидкости; g— уско-
рение свободного падения; VT — объем погруженной части тела.
Молекулярная физика. Тепловые явления
Основное уравнение молекулярно-кинетической теории идеального
газа:
где р — давление газа; т0 — масса молекулы; п — концентрация мо-
лекул; (о ) —средний квадрат скорости молекул.
Зависимость давления газа от концентрации его молекул и температу-
ры: p = nkT, где k — постоянная Больцмана; Т — абсолютная температура:
7" = ( + 273; ( — температура но шкале Цельсия.
Средняя кинетическая энергия поступательного движения молекул
газа {E)=—kT.
Уравнение состояния идеального газа (уравнение Менделеева — Кла-
пейрона).
где р — давление; V — объем; m—масса газа, М — его мо-
лярная масса; R — универсальная газовая постоянная; Т — абсолютная
температура газа.
301
Внутренняя энергия одноатомного идеального газа
Работа совершаемая газом при изобарном расширении, A=p(V2 —
Количество теплоты, необходимое для нагревания тела массой m от
температуры Г, до температуры Т2 (? = cm (Т2 — Г,), где с — удельная
теплоемкость вещества.
Количество теплоты, необходимое для плавления тела массой ш,
Qnll = Xmt где Я — удельная теплота плавления.
Количество теплоты, необходимое для превращения в пар жидкости
массой m, Qn3n*=rm, где г — удельная теплота парообразования.
Относительная влажность воздуха
ф %
Ро Ро
где р — парциальное давление водяного пара, содержащегося в воздухе
при данной температуре; ра— давление насыщенного водяного пара при
той же температуре; р— плотность водяного пара, содержащегося в воз-
духе при данной температуре (абсолютная влажность); р0— плотность на-
сыщенного водяного пара при той же температуре.
Первый закон термодинамики: Q = AU-{-А, где Q — количество тепло-
ты, переданное системе; AU—изменение внутренней энергии системы;
А — работа, совершенная системой над внешними телами.
Коэффициент полезного действия (КПД) теплового двигателя:
где А — работа, совершаемая двигателем; Ql — количество теплоты, полу-
ченное двигателем от нагревателя; Q2 — количество теплоты, отданное хо-
лодильнику. КПД идеальной тепловой машины Карно:
Imax
где Tj—температура нагревателя; Т2 — температура холодильника.
Основы электродинамики
Закон Кулона:
4ле0ег2
где F — модуль силы взаимодействия двух неподвижных точечных зарядов
</, и q2, е0 — электрическая постоянная; s — диэлектрическая проницае-
мость среды; г — расстояние между зарядами.
Напряженность электрического поля в данной точке Е = —, где F —
сила, с которой поле действует на положительный точечный заряд </0, по-
мещенный в эту точку.
Напряженность электрического поля точечного заряда q на расстоя-
нии г от него
302
Е \я\
4ле0ег2
Потенциал электростатического поля в данной точке <p=W?/q, где
Wp — потенциальная энергия заряда </, помещенного в эту точку.
Работа, совершаемая электростатическим полем при перемещении за-
ряда q из точки с потенциалом ф, в точку с потенциалом ф2, A = q (ф, — ф2).
Связь между напряженностью однородного электростатического поля
и разностью потенциалов: Е = , где ф,— ф2 — разность потенциалов
между точками, находящимися одна от другой на расстоянии d вдоль ли-
нии напряженности поля.
Электроемкость плоского конденсатора, площадь каждой пластины
которого 5, а расстояние между ними d, C = Et0S/d, где s — диэлектриче-
ская проницаемость диэлектрика, заполняющего пространство между пла-
стинами.
Энергия электростатического поля заряженного конденсатора емко-
стью С
w-qU- ql cu2
2 2С 2 '
2С
Сила постоянного электрического тока / = —, где q — заряд, переноси-
мый через поперечное сечение проводника за время I.
Закон Ома для участка цепи, 1 = —, где / — сила тока; U— напряже-
R
ние; R — сопротивление.
Сопротивление проводника длиной I с постоянной площадью попереч-
ного сечения S:
-4
где р — удельное сопротивление.
Общее сопротивление при последовательном соединении проводников
Общее сопротивление при параллельном соединении проводников на-
ходится по формуле — = — + — + ...+—-.
Закон Ома для замкнутой цепи: 1= , где / — сила тока в цепи;
/? + /¦
Г— ЭДС источника; R — сопротивление внешнего участка цепи; г — внут-
реннее сопротивление источника.
Работа постоянного электрического тока на участке цепи:
A = Wt = I2Rt=— t = qU,
R
где / — сила тока; U — напряжение; t — время прохождения тока; R — со-
противление участка; q — заряд, прошедший по проводнику.
Мощность постоянного тока
Закон Джоуля — Ленца: Q = I2Rt, где Q — количество теплоты, выде-
ляемое проводником сопротивлением R с током силой /; t — время про-
хождения тока.
303
1 M
Закон Фарадея для электролиза: m = kq = klt или т= — — //, где
m — масса вещества, выделившегося на электроде; k — электрохимический
эквивалент вещества; / — сила тока; / — время прохождения тока; F —
постоянная Фарадея: F = Л^е = 9,65- 104 Кл/моль; NA — постоянная Аво-
i адро; е — элементарный заряд; М — молярная масса вещества; п — ва-
лентность.
Закон Ампера: F=IBl sina, где F — модуль силы, действующей на
проводник длиной I с током силой /, помещенный в магнитное поле с ин-
дукцией В, а — угол между направлением тока и вектором магнитной ин-
дукции.
Сила Лоренца Fn= \q\ vB sin a, где Fr — модуль силы, действующей
на заряженную частицу, движущуюся в магнитном поле; q — заряд части-
цы; v — ее скорость; В — магнитная индукция; a — угол между векторами
скорости частицы и магнитной индукции.
Магнитный поток через поверхность площадью S
Q) = BS cosa,
где В — модуль вектора магнитной индукции; a — угол между вектором В
и нормалью п к поверхности.
ДФ
Закон электромагнитной индукции: 8S= , где щ — ЭДС индукции;
ДФ — изменение магнитного потока за время \t.
ЭДС самоиндукции $\=—L—, где L — индуктивность проводника;
Д/ — изменение силы тока за время At.
LI2
Энергия магнитного поля W = , где L — индуктивность проводни-
ка; / — сила тока в нем.
Колебания и волны
Механические колебания и волны. Гармонические колебания тела опи-
сываются уравнением х = xm cos (w/-(- ср0), где х—координата тела (сме-
щение его от положения равновесия) в момент времени t\ xm — амплитуда
колебаний (модуль наибольшего смещения от положения равновесия); со —
угловая (циклическая) частота; о)^ + ф0 — фаза колебаний в момент време-
ни t\ ф0 — начальная фаза.
Частота колебаний v=—, где Т—период колебаний.
Угловая (циклическая) частота колебаний со = 2яд> = —- , где v — час-
тота; Т — период.
Полная механическая энергия гармонически колеблющейся точки мас-
сой m
Период колебаний математического маятника Г = 2лД/—, где / —
V в
длина маятника; g — ускорение свободного падения.
Период колебаний пружинного маятника Т = 2л \ /—, где m — масса
груза, прикрепленного к пружине; k — жесткость (коэффициент упругости)
пружины.
304
Связь между длиной волны X, скоростью волны v и периодом колеба-
ний Т (или частотой v): v = — = Xv.
Электромагнитные колебания. Переменный ток. Формула Томсона:
где Т — период свободных электромагнитных колебаний в колебательном
контуре, состоящем из конденсатора емкостью С и катушки с индуктивно-
стью L.
Индуктивное сопротивление катушки с индуктивностью L XL — hiL, где
to—угловая (циклическая) частота переменного тока.
Емкостное сопротивление конденсатора емкостью С Хс = .
Действующие значения силы переменного тока, напряжения и ЭДС:
Уг" У2"' У2~'
где /m, Um, lfm — амплитудные значения.
л, {/,
Коэффициент трансформации k = — = ~ТГ' г^е пъ пг — число витков
п2 и2
первичной и вторичной обмоток трансформатора; Ub U2 — напряжения на
первичной и вторичной обмотках.
Оптика
Закон преломления света:
sin а Щ
sin Р л,
где а — угол падения; р — угол преломления; л21 — относительный пока-
затель преломления второй среды относительно первой; л,, л2 — абсолют-
с с
ные показатели преломления этих сред: л, =— ; л2 = — ; с — скорость све-
Vl V2
та в вакууме; vlt v2 — скорости света в первой и второй средах.
Предельный угол полного отражения определяется из соотношения
л2
sin ао = —.
л,
Формула тонкой линзы: ± —= ± — ±—, где F — фокусное расстояние
линзы; d — расстояние от предмета до линзы; / — расстояние от линзы до
изображения. Если фокус, предмет или изображение являются действи-
тельными, то перед соответствующим членом этой формулы ставится
плюс, если мнимыми — минус.
Оптическая сила линзы ?) = —.
Условие максимумов интенсивности света при интерференции:
где Д = L2 — L| — оптическая разность хода двух световых волн; X — длина
световой волны.
Условие минимумов интенсивности света при интерференции:
| ,.=..,, .....
305
Дифракционная решетка. Максимум (усиление света) наблюдается в
том случае, если выполняется условие
d sin ц> = k\,
где (/ — период решетки; ср — угол между нормалью к поверхности решет-
ки и направлением дифрагированных волн; & = 0, 1, 2, 3, ...; X — длина плос-
кой монохроматической волны, падающей нормально на поверхность ре-
шетки.
Элементы теории относительности
Релятивистский импульс тела:
Р = -
где m — масса тела; и — его скорость; с — скорость света в вакууме.
Энергия покоя тела:
Е0 = пгс2.
Полная энергия тела:
9
Е=-
Закон взаимосвязи массы и энергии:
где Д?о—изменение энергии покоя тела, Am— изменение его массы.
Квантовая физика
Энергия фотона E = hv, где h — постоянная Планка; v — частота
света.
2
Уравнение Эйнштейна для фотоэффекта: hv = A -| —, где ftv — энер-
гия фотона; А — работа выхода электрона; — максимальная кинети-
ческая энергия вылетающего электрона.
Правило квантования по теории Бора:
где me — масса электрона; vn — его скорость на п-й орбите; г„ — радиус
л-й орбиты: л=1, 2, 3, ...; h — постоянная Планка.
Энергия фотона по теории Бора: h\mn~Em — Е„, где h — постоянная
Плаика; vmn—частота колебаний, соответствующая испускаемому (или
поглощаемому) кванту излучения; m, n — номера стационарных состояний;
Ет, Еп — энергия атома в стационарных состояниях.
306
Энергия связи атомного ядра
где Z — число протонов в ядре (зарядовое число); тр — масса протона;
А — массовое число; та — масса нейтрона; тя — масса ядра; с — скорость
света в вакууме.
Закон радиоактивного распада: /V = iV0-2 ' , где N—число нерас-
павшихся атомов в момент времени t, No— начальное число радиоактив-
ных атомов в момент времени, с которого начинается наблюдение (/ = 0);
Т— период полураспада (время, в течение которого распадается половина
исходного числа атомов).
ОТВЕТЫ
К ЗАДАЧАМ УСТНОГО ЭКЗАМЕНА
ПО ФИЗИКЕ
Кинематика
1. cosa=——; а=120°; t= = 11,5
v, v, sin a
2. До момента времени ib соответствующего гочке А на рисунке 187, тело
двигалось равнозамедлеино, при t = (l остановилось, а после этого дви-
галось равноускоренно; х = 81 — 0,4/2.
vt
3. hQ = h + gs2/Bv20). 4. См. рисунок 200; / = — =16 м.
5. Л=
;233 м.
21
=10 м/с2 (здесь /2 = 5 с, /, = 4 с).
1. h = -
- = 5 м; / =
?>„ sin 2a
= 34 м; t\p = 2mv0 sin a= 10 кг-м/с.
(f2cos aJ =17,3 м.
lo,
9. R = — = 0,6 m; a>= — =10 рад/с.
10. m = -
-^5 кг.
Основы динамики
F (cos a —ц sin a) .
1. o = - — fig, если F cos a> I». (mg-\-F sin a); o = 0, если
F cos a<Jn (mg-\- F sin a).
12 =0,3 с 3. R =
308
gtga
=159 м.
4. /\ ———— = 1,6 кН. 5. a — F/m— g = 0,5 м/с; ускорение направлено
вверх.
6. а = Т/т — g = 20 м/с2. 7. и = Л — а, = 9,8 км/с.
3
¦л I/RJY
8. /?= \/g I —— I =42 400 км (здесь 7" = 24 ч — период вращения Зем-
ли вокруг собственной оси).
9. a = v2/R = 2,5 м/с2; F = m (g— v2/R)= 14,6 кЫ.
10. Т = mg('i — 2 cos a).
Законы сохранения в механике
2v0 cos а /И/
1. v., = . 2. s = = 4 м.
cos p m-\-M
m, + /га, /
3. t>=———- V2g/A— cos а).
m,
4. yi = m(gft + ti2/2) = 4,12 кДж. 5. ?k = m (gH + ц2/2) = 68 Дж.
6. ?, = ?0/4; ?2 = 3?0/4. 7. ?k —m (ц?+ц|)/4= 1,25 Дж.
= 100 Дж. 9. А=-
10. г„= , т" - = 01 м.
V*(M )
2A— ты2/кJ
Элементы статики. Жидкости и газы
~ I \М. / ~ 2 ~
3. На расстоянии х = B,5/ + 2/?)/3 = 29 см от левого конца стержня.
5. F = mg/2 = 9,8- 103 Н. 6. m = Fft1/(gft2) = 255 кг.
р^! p2ft2
7. А/г3 = = 0,51 см (уровень ртути ниже там где находится
Рз
масло).
V2 Pimg mo,
8. -f = —J-L-S-—. 9. УИ= — = 400 кг.
V р2 (mg — ?,) р2 —Pi
10. Др = —?^= 125 кг/м3.
Основы молекулярно-кинетическои теории.
Газовые законы
1' 2
3. m, = m//,,/lJ, ,-П = 34 г.
,-«/(-
309
4. V = m/(p)
5. р = ^-=1,03 кг/м3; то = А = 5,4
RT NA
„ , Kmg I /p, р2\
6. /г = = 9 см. 7. р, = — ( I 7\.
S + g ^3 2^7- 7-/ 3
_ пАр „пп Ф1^1 + Ф2^2 ov0/
8. о — ^— = 300 кПа. 9. ф = ;—«27%.
п—\ V\+V2
10. p>p/?77Af = 6,55-108 Па.
Тепловые явления
1. Вода массой т\ = т[-\ =35 кг (здесь
в~0°С) и лед массой т'2 = Ь кг.
Xо ( X | —г- I л ) to ( М ~Т~ '4 )
i. i^ — — s^j OA,A \^ ,
3. Я=С 2 =2,4-106 Дж/кг. 4. А = -^-=166 м.
5. /1 = W?A7" = 3,3 МДж; AU = Q — A = 6,1 МДж.
6. Д?/ = /гЛ=2000 Дж. 7. Д7"= — 2A/(^Rv)= — 100 К.
8. А =0,4^=120 Дж.
9. ц= = 7,6 м/с (здесь Г^ЗУЗ К — температура кипения воды).
pSMr
Электростатика
1. ?=—^— = 2,5-105 В/м. 2. г = *?——.= 10Ы0~9 м
2f
леоеа
3. х = /-/3=1 м. 4. 4>B = (fA — AW/q=l00 В.
_ mgrf_ m-14 к 6 W — eE1 —55 1
" ?~ U ~ ' ' ' °~ sin 2а ~ '
оЕ U. + 2U2
7. a = arctg-^— = 45°. 8. U = —±— ^ = 280 В.
mg 3
9. ? = - '
4лё0
10. ? = —2—«1,13-Ю5 В/м; Ц7 = -1-^- = 5,65-10~7 Дж.
Законы постоянного тока
310
5. ^ = ^1^+^=0,625. 6. Q,= «!*l = 420 Дж.
7. В две параллельные ветви, каждая из которых состоит из двух после-
довательно соединенных резисторов.
8. Возможны два случая: 1) /, = 10 А, {/, = 20 В, Л, = 2 Ом; 2) /2==5 А,
?/2 = 40 В, «2 = 8 Ом.
9. т) = Л-—I00% = 80%. 10. / = -^=16,7 мин.
\ и / ft/
Магнитное поле. Электромагнитная индукция
1. ^. = _iL==i,74-1011 Кл/кг. 2. S=-^- = 5-10-3 Тл.
3. fi=wosina=3,3-10-4 м; A=
еВ
3,310 м; A
еВ еВ
4 к_л1пЩм_0Л м. 5. /m=
6. q = = 0,05 Кл. 7. U = BJv = 0,l4 В; Uv = 0.
lop
Q „
О. ft —-~.~.w~, . no
DO
9. Индукционный ток направлен по часовой стрелке; ЗГi = Ahl\ т= ,—
10. /V =—^— = 25.
Колебания и волны
3. t= ' 2 =30 с. 4. vm = xm^k/m =3,75 м/с.
5- Г = ГVg/(g-а) =2,24 с. 6. m = /m/?m=107
с
7. !т=иЛ ^-=[0 А. 8. Я = 2лсЛ/-1—^^- =2,45-103 м.
9. / = _ =1 м. 10. „ = ^.\/4«18.8 м/с.
Опгыка
1. См. рисунок 201. 2. а = 90° —-iarctgy»;87o6'.
о ,/ . cos а \
о. s — а I 1 :^==^^^^^ I sin а = 3,8 мм.
311
4. a = arctgn«56°20'. 5. R =
tgp-tga
7. Изображение S[ точки S находится на главной оптической осн посере-
дине между точкой S и линзой (рис. 202).
Л
Рис. 202
Рис. 203
8. Изображение получится между предметом и линзой на расстоянии
15 см от нее; изображение действительное, перевернутое, таких же раз-
меров, как и предмет (рис. 203).
9. и = -^=1,6. 10. <p' = arcsin (— sin ф\ = 2Г12'.
Квантовая физика
Дж; v = c/X = 0,5-1015 Гц.
2. Zi = ^ = 4. 3. Я = ^ = 3.
р2 с ell
л—1
5. A =-
6
: 1,5- 10~^ M.
312
7. т = Т"ё;^3,8 сут.
8. Е =4? =28 МэВ.
у min св. уд
9. На 3 единицы. 10. т) = РШ 100% =39%.
?/Vm
К ЗАДАЧАМ ПИСЬМЕННОГО ЭКЗАМЕНА
ПО ФИЗИКЕ
Вариант 1
»3-10Ш кг/м3. 2
&G7"
1. р = ^—»3-10Ш кг/м3. 2. Сможет. 3. & = v2/By)= 15 кВ.
&G7"
4. т =
5. 1 = 1— 1 ===== j cos ф» 1,1 м. 6. < = 7"log2n«53 сут.
Вариант 2
2. В возникающем электрическом поле заряженные капли краски движут-
ся по направлению к окрашинаемому предмету. В результате уменьша-
ются потери краски и степень загрязнения воздуха.
3. RAB = 5 Ом. 4. l=vt = 8500 м = 8,5 км.
Вариант 3
1. р = ^рв. 2. <? = |-^-«Л7' = 2,5-103 Дж;
с = Н = 3,Ы03 Дж/(кг-К).
2 Л/
„ е
3. v=— , где е — заряд протона; т — его масса; е0 — электриче-
екая постоянная.
4. Уменьшится в е, раз.
5. Линзы надо расположить так, чтобы точка пересечения лучей после
прохождения первой линзы совпадала с передним для второй линзы и
задним для первой побочными фокусами.
Вариант 4
1. Первое тело движется равноускоренно, второе — равномерно. Для вто-
рого тела график скорости показан на рисунке 204.
2. Больший импульс имеет свинцовый шар, так как его масса больше.
4. п = A — \/п) 100% = 75%. 5. vo = ^2gh =14 м/с. 6. Нет.
313
VA
7. ?, = -
О
Рис. 204
• = 16 В/м.
I. ra21= —= 0,88. 2. Um =
Вариант 5
= 170 В.
3. C=q l~j~ =105 мкФ. 4. /,= — - = 0,08 м.
5. т = 1л:3Г7'0 =0.012 кг.
2ft cos a
g sin p cos (P — а)
Вариант 6
1. ft = 2gx2=19,6 м. 2. Ft = m^J2gH =0,6 м.
3. A=^-(v\—v\)= —Ъ Дж. 4. F = (ml — m.2)g/2 = 4 H.
Г,) V , 7\ — Г, 1
5- AV =
=1° см •
Тоо%
=0'17-
7.
, = « = 2. 8. 7. 9.
.0. С=1/(Ш*с>=10-« Ф. 11. 90°. .2. Af-
> а р и а н т 7
а/г
, = Л—sAr=15,l м. 2. o = -
22
= 4,9 м/с2.
3. F =
s cos а
= 50 Н. 4. /=
5. 1/ = —= 9,3 м3. 6. т = -
Р
= 5474 с.
7. а=^1^=10 мкФ. 8. F = —1—^9-Ю3 Н.
/? + г 4яе0г
т, \ /?, / ЕХ
314
Вариант 8
1. <»>=-
3. \U = i\mgh = $fi Дж. 4. 7" =
5- <цкв>
7. f=
= 9-10~ Н. 8. /? =
16ле0г2
F Е„ т.сХ
9. fi = —= 0,025 Тл. 10. — = —-— = 27-104.
// Eh
L = 200 Ом.
1. A_
Вариант 9
= 80 „ (здесь Д^= 1с).
mv\ sin2 a
2. А?„= — = 9 Дж. 3. F = 3mgcosa = 4,5 H.
4. x = -
^ 2
1
- = 2. 5. 7" = я7"„ = 546 К.
1
V
iL
6. 7"O=7"- — = 270 К. 7. n=l+-iL=13. 8. ?= — = 50 мкКл
/И С С/
/Ид
С С/
А
9. / = 4A:mvi = 480 см. 10. n = ——! - —(Z, —Z2)= 11.
Вариант 10
2. v2 = — - = 500 м/с. 3. MJ=Q — (po + ^-)
4. W = ~-— = 8,85-10~8 Дж.
Вариант 11
^«33 Дж.
3-
6. «г,= —
= 24,8 м/с. 2. F =
р,у,+Р2у2 cvc ^^
) = 40 В; г = -
R
- = 3 Ом.
,4 Н.
= 200 В.
7.
8.
1-7
Дж.
= ^_еу = 3,7.10-19 Дж.
315
Вариант 12
nuu cos a
= 1,25 м.
F = m g =9-10J H. 2. u =
= -^- = 2-10" Па. 4. ?=—Ч-— = 39,6-104 В/м.
5Д/
5. m =
7. В = — =1,6 Тл. 8. A = lBls = \2 Дж.
9. n = c/v = lfi. 10. A,max = йс/Д = 300 нм.
Вариант 13
— 1)Ди,=4,1 м/с (здесь sl = s2=l км).
T1=?^..100% = 39%.
= m(g-— ) = 23,4-103 Н. 3.
iVi
-/?,
= 2,2-
кг/м'.
График 3. 6. Ft/F2 = n2e= 156.
/у р
/= = 20 А. 8. R= — = 24 Ом.
9. L =
Д/
4
= 2,5 мГн. 10. X2 =
sin tp2
k2 sin ф[
Вариант 14
У первого тела. 2. a = g/3 = 3,3 м/с2.
^ ' 2 =15 кВт. 4. rf= 2 ? = 2 см.
л/?д/
—г = 0,3 м; /2 = /, + Д/=1,2 м.
тТ,
Увеличится. 6. ^ =
тч
р=-
= 2,25-10"^ кг-м/с. 8. 33.
Вариант 15
= d = 50 см; линза рассеивающая.
V
P,Vl+p2V2
= 6,75-105 Па.
4. г, =
= 17,3 см.
=46.7 кОм.
316
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Авогадро постоянная 147
Активность радиоактивного веще-
ства 273
Ампер на килограмм 273—274
Архимеда закон 126
Архимедова сила 122
Атомная единица массы 147
Бойля — Мариотта закон 151
Бэр 274
Де Бройля волна 264—265
Джоуля — Ленца закон 202—203
Дисперсия света 254
Диссипация энергии 112
Диссоциация электролитическая 212
Дифракция света 249
Длина волны 243
Доза излучения поглощенная 274
эквивалентная 274
экспозиционная 273
Вебер 227
Вес тела 54
Влажность абсолютная 168
— относительная 168
Волна 242
Вольт-амперная характеристика 194
Вольт на метр 186
Газ идеальный 150
— реальный 150
Гей-Люссака закон 152
Генри 231
Герц 234
Гидростатический парадокс 121
Гравитационная постоянная 54
График скорости 25
Грэй 274
Гука закон 71—72
Давление 118—119
— нормальное атмосферное 140
— парциальное 160
Дальтона закон 160
Единица СИ дополнительная
основная 88
производная 88
— физической величины 87
внесистемная 90
дольная 90
кратная 90
основная 88
производная 88
Закон всемирного тяготения 54
— сохранения электрического заря-
да 177
энергии 96, 238, 262, 267
в механике 96
— электромагнитной индукции 224
— термодинамики первый 170
Законы внешнего фотоэффекта 266
Зиверт 274
Значение физической величины 88
числовое 88
317
Изобара 152
Изопроцесс 151 —152
Изотерма 151
Изохора 152
Индуктивность 231
Индукция магнитная 218—219
— электромагнитная 219
Кипение 169
Кирхгофа правила 206
Колебания 241—242
— гармонические 241—242
— непериодические 241
— периодические 241
Количество теплоты удельное 163
Конденсатор воздушный 188
Контур 206
Коэффициент качества 274
Кулон на килограмм 273
Кулона закон 177—178
Кюри 273
Ленца правило 222
Линия магнитной индукции 214
— магнитного поля силовая см.
Линия магнитной индукции
Лоренца сила 228
Масса молярная 147
— относительная молекулярная 146
Международная система единиц
(СИ) 88
Менделеева — Клапейрона уравне-
ние 151
Микрорентген 273
Миллиметр ртутного столба 140
Миллирентген 273—274
Моль 147
Мощность экспозиционной дозы 273
Наклонение магнитное 217
Напряженность электрического по-
ля 179
Нуль температуры абсолютный
149—150
Ньютон 89
Ньютона законы 38—39
Ом 196
Ома закон для замкнутой цепи 204
участка цепи 194
— цепи переменного тока 247
Падение напряжения 206
Пар насыщенный 166
Паскаля закон 119
Перемещение 5
Плечо силы 76
Показатель размерности физической
величины 91
Поле магнитное 213—214
— однородное 184
— электрическое 214
— электромагнитное 213
Полюс магнитный 216
Потенциал электростатического по-
ля 184
Поток магнитный 220
Проекция вектора 6—7
Процесс изобарный 152
— изотермический 151
— изохорный 152
Путь 5—6
Рад 274
Размер физической величины 87
Размерность физической величины
90—91
Рассеяние энергии см. Диссипация
энергии
Рентген 273
Рентген в секунду 274
Самоиндукция 230
Секунда в минус первой степени
234
Сила диссипативная см. Сила не-
консервативная
—консервативная 96, 111
—неконсервативная 112
— потенциальная см. Сила консер-
вативная
— трения 47
— тяготения 54, 65
— упругости 71
— тяжести 54, 66
318
— центростремительная 57
Силы взаимодействия 39
Система единиц физических вели-
чин 88
— электрически изолированная 177
— отсчета инерциальная 37
неинерциальная 57, 243
— физических величин 88
Склонение магнитное 217
Скорость первая космическая 70
— средняя 14—15
прохождения пути см. Ско-
рость средняя
путевая см. Скорость средняя
Соединение конденсаторов парал-
лельное 191
последовательное 191
— проводников параллельное 199—
200
Соленоид 215
Сопротивление проводника 107
— цепи переменного тока полное
247
Составляющая вектора 7
Температура абсолютная 149
Теплоемкость тела 163
— удельная 163
Теплота плавления удельная 162
— сгорания удельная 162—163
Ток насыщения 266
Томсона формула 240
Точка росы 167
Угол полного отражения предель-
ный 250
Удар абсолютно неупругий 100
упругий 100
— центральный 100
Узел 206
Уравнение молекулярно-кинетиче-
ской теории газов основное 151
— состояния идеального газа см.
Менделеева — Клапейрона урав-
нение
— теплового баланса 164
Ускорение 17—18
— касательное 19
— мгновенное 18
— нормальное см. Ускорение центро-
стремительное
— полное 58
— среднее 17
— тангенциальное см. Ускорение
касательное
— центростремительное 19, 22
Фаза колебаний 233
Фарадея закон для электролиза 197
— постоянная 198
Физическая величина 87—88
безразмерная 91
основная 88
производная 88
размерная 92
Формула линзы 261
Цена деления 201
Частота круговая 233
— угловая см. Частота круговая
— циклическая см. Частота круго-
вая
Шарля закон 152
ЭДС индукции 224
— самоиндукции 230
Эйнштейна уравнение для фотоэф-
фекта 266—267
Электрическая емкость 187
— проводимость 194—195
Электрический заряд 176
отрицательный 176
положительный 176
элементарный 177
Электролиз 213
Электронвольт 268
Эталон единицы физической вели-
чины 90
319
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ
МЕХАНИКА
Кинематика —
Основы динамики ., 36
Законы сохранения в механике 95
Жидкости и газы 118
МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ .... 145
Основы молекулярно-кинетической теории. Газовые законы —
Тепловые явления 162
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 176
Электростатика —
Законы постоянного тока 194
Магнитное поле. Электромагнитная индукция 213
КОЛЕБАНИЯ И ВОЛНЫ 233
ОПТИКА 249
Квантовая физика 264
Советы абитуриентам 275
ПРИЛОЖЕНИЯ 278
1. Образцы билетов устного экзамена по физике .... —
2. Задачи устного экзамена по физике 279
3. Варианты заданий письменного экзамена по физике . 290
4. Основные формулы элементарной физики 300
ОТВЕТЫ 308
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 317