■ J
ных генк
Арифметическая
разминка
Учимся решать необычные

•# V
Азбука пажи*
ьдл
г'*
Н. Аменицкий,
И. Сахаров, С. Тромгольт
Арифметическая
разминка
Учимся решать необычные
Москва
Ц6НТРПОЯИГРАФ

УДК 51
ББК 22.1я92
А81
Охраняется законодательством РФ
о защите интеллектуальных прав.
Воспроизведение всей книги или любой ее части
воспрещается без письменного разрешения издателя.
Любые попытки нарушения закона
будут преследоваться в судебном порядке.
Художественное оформление
ИЛ. Озерова
Иллюстрации А. С. Никулиной
Аменицкий Н., Сахаров И., Тромгольт С.
А81 Арифметическая разминка. Учимся решать
необычные задачки/ Н. Аменицкий, И. Сахаров,
С. Тромгольт. — М.: Центрполиграф, 2011. — 220,
[4] с. — (Азбука науки для юных гениев).
ISBN 978-5-9524-4956-5
Вы не знаете, как привить вашему ребенку любовь к математике? На
помощь вам придет эта увлекательная книга, написанная опытными
педагогами-математиками!
Магические квадраты и волшебные таблицы, задачи-шутки и задачи на
разрезание, перестановки и перемещения, рассказы о старинных мерах
длины и массы, любопытные древние легенды и истории, так или иначе
связанные с математикой, а также игры и забавы со спичками, фокусы и конечно же
конструирование! Все это поможет ребенку с удовольствием и интересом
погрузиться в изучение школьной математики, развить в себе способности к
неординарному и оригинальному мышлению, поможет ему научиться
нестандартно мыслить!
УДК 51
ББК 22.1я92
ISBN 978-5-9524-4956-5

ПРЕДИСЛОВИЕ ИЗДАТЕЛЬСТВА
Как легко и увлекательно изучить
математику? Конечно же стоит начать с азов —
изучения арифметики! И знакомство с ней будет
более полноценным и интересным, если вы
начнете не со штудирования школьных
учебников, а с решения забавных и
оригинальных задач. Наша книга, составленная из двух
книг — «Забавной арифметики» Николая Аме-
ницкого и Ивана Сахарова и «Игр со
спичками» Софуса Тромгольта, — не только поможет
вам в изучении арифметики, но и даст идеи
новых необычных игр, научит проводить
неожиданные фокусы и конструировать
объемные фигуры из спичек.
Готовя к выпуску эту книгу, мы
постарались, насколько это было возможно, дать
такой материал, который бы пришелся по вкусу
детям совершенно разных возрастов и сумел
бы развить в них способность к
математическому мышлению, дал возможность проявить
природную смекалку и сообразительность.

Арифметические задачи, написанные
Николаем Аменицким и Иваном Сахаровым,
разделены на три группы по разной степени
сложности. Нами сохранен авторский вариант
деления — для юных читателей, только
начинающих знакомиться с основами арифметики,
для детей среднего возраста, у которых знания
по предмету более глубоки, и для детей
старшего возраста, которых уже можно знакомить
с такими понятиями, как арифметическая и
геометрическая прогрессия.
В последующих разделах, написанных Со-
фусом Тромгольтом, вы найдете игры, фокусы,
забавы и примеры конструирования, которые
можно провести, пользуясь только самыми
обыкновенными спичками!
Авторы этой книги — опытные педагоги
и математики, книги которых не единожды
переиздавались.

Николай Аменицкий
Иван Сахаров
Забавная
арифметика

Аля детей
младшего возраста

L Задачи-шутки
1. Три мальчика, Коля, Петя и Ваня,
отправились в магазин. По дороге у скамейки они
нашли 3 рубля. Сколько бы денег нашел Баня,
если бы он один отправился в магазин?
2. По дороге в Москву
женщина встретила троих мужчин.
Каждый из них нес по
мешку, в каждом мешке по коту.
Сколько существ
направлялось в Москву?
3. Длина бревна 5 метров. В одну минуту от
этого бревна отпиливают по одному метру. Во
сколько минут будет распилено все бревно?
4. В комнате 4 угла. В
каждом углу сидит кошка. Напротив
каждой кошки сидят по 3
кошки. Сколько кошек всего в
комнате?

5. Летела стая гусей: один гусь впереди, а
два позади; один позади и два впереди; один
между двумя и три в ряд. Сколько было всех
гусей?
6. Мальчик, придя в магазин, попросил
себе грушу. Ему предложили на выбор две
груши: одну за 5 рублей, а другую за — 10.
Мальчик выбрал более дешевую грушу,
заплатил торговцу 5 рублей и побежал домой.
Только что он собрался
приняться за еду, как ему в
голову пришла следующая
мысль: «Ведь я уже
заплатил продавцу 5 рублей, да
у меня еще есть груша,
которая стоит тоже 5 рублей.
Значит, если я отдам
теперь эту грушу торговцу, то он получит от
меня всего 10 рублей. Тогда я могу взять из
магазина ту лучшую грушу, которая стоит
10 рублей!» И мальчик побежал обратно в
магазин... Сбылись ли его мечты о более
дорогой груше?
7. Какие числа при чтении не изменяются
от их переворачивания?
8. В таверну пришли 11 человек и
попросили подать им рыбы. К сожалению, у повара
оказалось всего три небольшие рыбы. Тем
10

не менее он не желал
упустить посетителей. Имея в
своем распоряжении три
рыбы, он обещал гостям
подать на стол одиннадцать. Те
заинтересовались этим и даже согласились уплатить
деньги вперед. Как повар исполнил свое
обещание?
И. Забавные исчезновения.
Остроумный дележ. Затруднительные
положения
9. У одного человека был золотой крест,
украшенный бриллиантами. Он никогда не
интересовался тем, сколько всего бриллиантов
вставлено в крест, но знал лишь одно: если
начать считать с одного из боковых концов
или с верхнего конца вниз до основания
креста, то всегда окажется 6 бриллиантов.
Однажды этот крест был отдан в починку золотых
дел мастеру. Мастер поте-
рял два бриллианта и, не
вставляя на их место дру- О
гих, вернул крест почи- Г^ О О О О
ненным, лишь расположив 12321
бриллианты по-другому.
Владелец пересчитал брил- Q
лианты «по-своему» и
ничего не заметил.
11

Как мастер ухитрился расположить
бриллианты в золотом кресте?
10. Один человек встретил во время
прогулки знакомую семью, состоящую из деда, отца
и сына. Поздоровавшись со всеми, он спросил
их в шутку, сколько им лет. «Нам всем вместе
100 лет», — ответил за всех дед и важно
зашагал вперед. Тогда же, продолжая
интересоваться их возрастом, друг спросил отца: «Ну,
скажите же, сколько вам лет?» — «Мне вместе
с сыном 45 лет, — отвечал отец, — а сын на
25 лет моложе меня». Так любопытному и не
пришлось узнать, сколько лет каждому из них.
Не сообразите ли вы?
11. Два мальчика, Коля и Петя, стали
расставлять вдоль стен беспорядочно стоящие
стулья. Вскоре Коля остановился и сказал Пете:
«Стой, а расставь-ка ты все эти 12 стульев
тремя рядами так, чтобы в каждом ряду было по
5 стульев». Петя сначала
не сумел этого сделать, но
потом все же расставил
стулья так, как просил его
Коля. После этого он
сказал Коле: «А не расставишь
ли ты теперь эти 12 стульев
у 4 стен так, чтобы у
каждой стены было по 4 стула».
Коля два раза ошибался
12

при расстановке стульев, но в конце концов
сумел это сделать.
Как расставлял стулья Петя? Как расставлял
стулья Коля?
12. Торговка, сидя на
рынке, соображала: «Если
бы к моим яблокам
прибавить половину их да еще
десяток, то у меня была
бы целая сотня!» Сколько
яблок у нее было?
13. Брат и сестра получили на двоих 90
рублей. Если сестра отдаст брату из своей доли
10 рублей, то у брата окажется вдвое больше
денег, чем у сестры. Сколько денег у брата и
сколько у сестры?
14. У отца есть сын, который вдвое моложе
отца. Сын родился тогда, когда отцу было
24 года. Сколько теперь лет сыну?
15. Маленький Коля пришел из школы
домой и сказал папе: «А меня сегодня учитель
похвалил за решение задач». Услышала это его
сестра Шура (тоже школьница) и сказала Коле:
«За что тебя хвалят, не знаю, а вот я — лучшая
ученица по математике». Отец, послушав их,
сказал: «Вот что, ребятки, хвастать может
каждый, было бы чем. Раз вы такие знатоки мате-
13

матики, решите-ка мне по задачке». И отец
передал детям по записке.
Коля прочитал следующее: «Если к моим
деньгам прибавить их половину, то получится
81 рубль. Сколько у меня денег?»
А Шура прочитала вот что: «Если мама
положит в свой кошелек еще треть денег,
находящихся в нем, то в кошельке станет 68
рублей. Сколько денег в кошельке?»
Так как дети не отличались хорошими
знаниями в математике и в школе их никто не
хвалил (папу они обманули), то задачи они не
решили, и им было очень стыдно перед папой.
Не поможете ли вы им в их затруднительном
положении?
16. Петя, Коля и Шура прибежали из лесу
и радостно сообщили маме, что нашли 6
белых грибов. «Я нашла, —
сказала Шура, — три гриба,
Петя — один, а Коля —
два». Мать поцеловала
детей и, передавая им 18
грецких орехов, сказала: «Вот
вам, мои милые, орехи в
награду. Разделите их так, чтобы каждый из
вас получил по заслугам». По сколько орехов
должно достаться каждому из детей?
17. Жила в реке большая прожорливая щука.
Все рыбы боялись ее. В особенности не было
от нее житья маленьким рыбкам. Только они
14

превратятся из икринок в рыбок, а пасть
зубастой щуки тут как тут. Трудно уберечься в
одиночку маленьким рыбкам, вот и плавают
они целыми стаями — не заметит врага одна
рыбка, усмотрит его другая. Еще издали
увидит в прозрачной воде хищную щуку какая-
нибудь из рыбок и закружится около подруг.
Все тогда поймут, что враг близко, разбегутся
во все стороны и сию же минуту спрячутся.
Так щуке никто и не попадется в пасть.
Раз стая в 55 рыбок — плотва, окуньки и
пескари — плавала в зарослях осоки. Щука
издалека увидела этих
рыбок и решила ими
полакомиться. Взмахнула хвостом
и стрелой бросилась к
осоке. Но сорвалось: рыбки
все-таки заметили ее и
успели уплыть. Так никто
и не попал к ней на обед.
Задумалась хищница. Ведь этак и с голоду
погибнешь. Всю ночь она продумала, на какую
бы ей хитрость пуститься, и додумалась. Рано
утром она опять заметила в зарослях осоки ту
же стаю и злорадно подумала: «Ну, погодите,
вертушки, попадетесь сейчас!» Хитрая щука
стала тихонько мутить хвостом воду на дне, и
вода сделалась мутной. Мутит она воду, а сама
незаметно подплывает к рыбкам. Глупые
рыбки лишь тогда заметили ее, когда хищница
стремглав бросилась на стаю. Через некоторое
15

время испуганные рыбки снова собрались в
стаю и увидели, что их осталось всего лишь
42 рыбки, причем пескарей осталось вдвое
меньше, чем окуньков, а плотвы вдвое
больше, чем окуньков. Рыбки заметили также, что
они лишились только одной плотвы, тогда
как окуньков погибло в 8 раз больше, чем
плотвы.
Помогите рыбкам разобраться, сколько у
них погибло и сколько осталось в целости
плотвы, пескарей и окуньков?
III. Игры со спичками
Параллельные прямые
5
Угол
Горизонтальная прямая
Квадрат
18. Как сделать из двух спичек десять, не
ломая их?
19. Нельзя ли из трех спичек сделать шесть,
не ломая их?
20. Нельзя ли из четырех спичек сделать
семь?
16

21. К разложенным на столе
пяти спичкам приложите еще
пять спичек так, чтобы
получилось три.
22. От разложенных на
столе 30 спичек (их расположение ПИ CD П1
показано на рисунке) поста- '—I—' ' ' ' '
райтесь отнять 13 спичек и
получить три.
23. К разложенным на столе
четырем спичкам прибавьте еще
пять спичек так, чтобы
получилось сто.
24. От данных 5 квадратиков из
спичек отнять 3 спички так, чтобы
осталось три таких же квадратика.
25. Семнадцать спичек
составляют 6 одинаковых (в 2 ряда), .
прилегающих друг к другу квадра- |
тиков. Снимите 5 спичек так,
чтобы после этого осталось 3 таких
же квадратика.
26. Из 18 спичек, составляющих
6 данных квадратиков, отнимите
2 спички так, чтобы осталось 4
таких же квадратика.
17

27. Девять квадратиков составле- Г
ны из 24 спичек. Отнимите от них Г
8 спичек так, чтобы осталось 2 квад- г
рата различной величины.
28. От 7 квадратиков, которые
составлены из 22 спичек и
образуют крест, отнимите 6 спичек так,
чтобы осталось 4 таких же
одинаковых квадратика.
п
а
29. От данных 24 спичек, расположенных
указанным образом, отнять 8 спичек так,
чтобы осталось шесть.
ш в о ш в
30. Переложите 2 спички так, 1
чтобы образовалось 5 равных квад- j ь
ратов.
31. а) Переложите 2 спички так,
чтобы получилось 7 одинаковых
квадратов, б) Из полученной
фигуры отнимите 2 спички так, чтобы
осталось 5 квадратов.
32. Отнимите 8 спичек так, чтобы Г
из оставшихся образовалось 4 оди- Г
наковых квадрата (2 способа ре- г
шения).
18
=1

33. Отнимите 4 спички так,
чтобы образовалось 5 квадратов,
причем не обязательно
одинаковых по величине (2 способа
решения).
OLD
34. Отнять 6 спичек так, чтобы |
из оставшихся образовалось 4 раз- | |
личных по величине квадрата. | j J
35. Три спички лежат на столе.
Как удалить среднюю спичку из
середины, не трогая ее?
36. Переложить 4 спички так,
чтобы образовалось 3 одинаковых
квадрата. А теперь переложите 3 спички
так, чтобы образовалось 3 квадрата.
37. Этот дом составлен из 10
спичек. Требуется повернуть его к нам
другой стороной, переложив только
2 спички.
{
11
38. У меня три спички. Если я к
ним прибавлю еще две, то получу
восемь. Как это может случиться?
39. Убрать 2 спички и
получить 4 квадрата.
19

40. Переложить 6 спичек так, \ / \ /
чтобы из 2 бокалов получился дом, t ?
изображенный на рисунке в за- —L JL
даче 37.
41. Отнять 4 спички так,
чтобы оставшиеся спички
образовали 5 квадратов, причем квадраты
могут быть и не одинаковой
величины.
42. Отнять 3 спички так, чтобы оставшиеся
спички образовали 5 одинаковых квадратов.
шг
LD
43. Как при помощи спичек посадить утку
в клетку?
44. Люба и Шура играли в спички. Шура
спросила Любу: «Как доказать на спичках, что
если отнять пять от восьми, то ничего не
останется?»
20

Люба сначала не сообразила, но, взглянув
на стенные часы, улыбнулась и решила задачу.
Потом она, в свою очередь, задала Шуре
задачу: «Как двумя спичками, не кладя одну
поперек другой, изобразить крест?»
Шура решила эту задачу только на
следующий день, но зато она предложила Любе
подобную задачку-шутку: «Как образовать
треугольник одной спичкой, не расщепляя и не
ломая ее?»
Люба не сумела решить эту задачу, и Шура
была очень довольна.
Дайте решение всех этих задач.
1
2
3
1
2
3
1
2
3
IV. Волшебные квадраты и волшебная
таблица
45. Расставьте цифры,
помещенные в квадратиках, так, чтобы
суммы чисел по любой горизонтали,
вертикали и диагонали (из угла в
угол большого квадрата) были
одинаковы.
46. Переместите цифры,
помещенные в квадратиках,
так, чтобы суммы чисел по
любой горизонтали,
вертикали и диагонали большого ква-
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
21

драта были одинаковы, но притом на каждой
из названных прямых не встречались две
одинаковые цифры.
47. Числа 1, 2, 3, 4, 5, 6, 7, 8 и 9
требуется разместить в 9 клетках
нарисованного здесь квадрата, и
притом так, чтобы суммы чисел по любой
его горизонтали, вертикали и диагонали были
одинаковы и составляли каждый раз число 15.
48. Числа 2, 3, 4, 5, 6, 7, 8, 9 и 10
требуется разместить в 9 клетках
нарисованного здесь квадрата, и
притом так, чтобы суммы чисел по
любой его горизонтали, вертикали и диагонали
были одинаковы и составляли каждый раз
число 18.
49. В 36 клетках поставьте
по нулю, а затем зачеркните
6 нулей так, чтобы в каждой
из четырех сторон осталось
по 4 нуля.
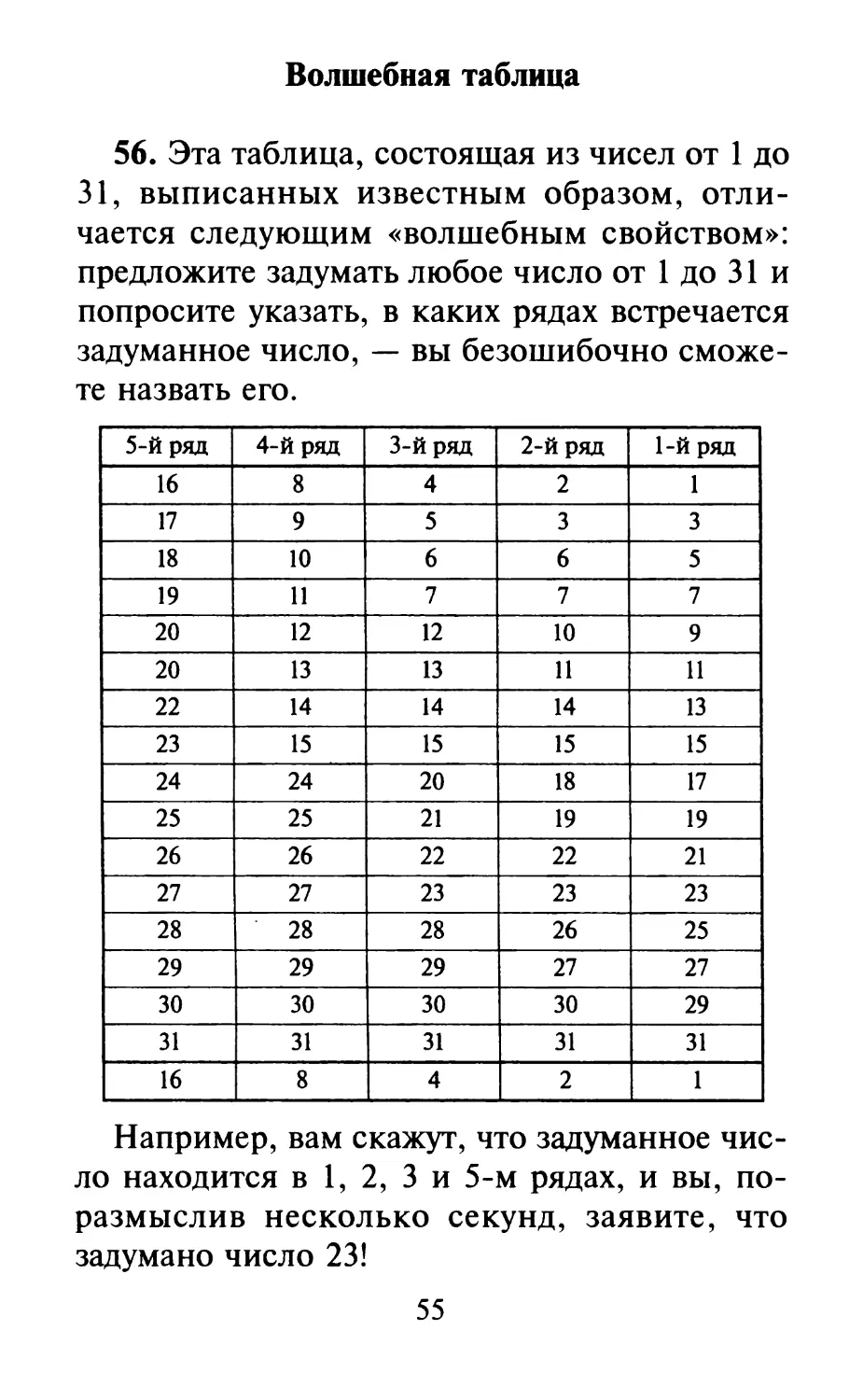
Волшебная таблица
Эта таблица, состоящая из чисел от 1 до 31,
выписанных определенным образом,
отличается следующим «волшебным свойством»: пред-
22

ложите задумать любое число от 1 до 31, и пусть
вам только укажут, в каких столбцах
встречается задуманное число, и тогда вы имеете
возможность безошибочно назвать его.
Например, вам скажут, что задуманное
число находится в 1, 3, 4 и 5-м рядах. Подумав
несколько секунд, вы заявляете, что задумано
число 23.
Чтобы угадать задуманное число, которое
находится, как вам сказали, в 1, 3, 4 и 5-м
рядах, сложите числа, стоящие в этих рядах
внизу, то есть 1 + 2 + 4 + 16 = 23. Таким же
образом можно указать любое другое число.
Такую же волшебную таблицу вы можете
составить, заменив числа от 1 до 31 столькими
же именами (мужскими или женскими).
1-й ряд
16
17
18
19
20
20
22
23
24
25
26
27
28
29
30
31
16
2-й ряд
8
9
10
11
12
13
14
15
24
25
26
27
28
29
30
31
8
3-й ряд
4
5
6
7
12
13
14
15
20
21
22
23
28
29
30
31
4
4-й ряд
2
3
6
7
10
11
14
15
18
19
22
23
26
27
30
31
2
5-й ряд
1
3
5
7
9
И
13
15
17
19
21
23
25
27
29
31
1
23

V. В часы досуга
1. Угадывание числа
Предложите кому-нибудь из товарищей
написать (не показывая вам) любое двузначное
число, состоящее из различных цифр, а затем
попросите переставить цифры этого числа и
из большего числа вычесть меньшее. Цифры
полученной разности предложите опять
переставить и, наконец, сложить полученное число
с этой разностью.
После всех этих действий вы можете смело
заявить, что ваш товарищ получил число 99.
Поясним это на примере.
Пусть задумано число 72.
Число, написанное теми же цифрами, но
в обратном порядке, есть 27. Из 72
вычитаем 27.
72 — 27 = 45 (разность). Складываем эту
разность с 54 (то есть с числом,
изображенным цифрами 4 и 5, но в обратном порядке):
45 + 54 = 99.
2. Игра в извозчика
Эта игра для двоих. Написав числа,
например, от 1 до 9 или до 12 и т. д., игрок-седок
приказывает игроку-извозчику ехать к какому-
нибудь номеру. Извозчик обозначает свой путь
чертой. Своего пути (начерченной линии) он
24

не должен пересекать.
Разумеется, седок старается
делать такие концы, чтобы
извозчику необходимо
было пересечь дорогу.
Например, если извозчик
поедет из 4-го пункта в 3-й,
потом в 8-й, затем снова в
4-й и, наконец, в 5-й, то,
понятно, он не попадет уже в пункты 1-й, 7-й
и т. д., не нарушив условия (не пересекать свой
путь). В таком случае он проигрывает, уступая
свое место седоку.
3. Забавы маленького художника
Петя нарисовал свинку. Его брат Коля
увидел рисунок Пети и говорит: «Твоя свинка
грустная, а ты посмотри, какой веселой она
станет на моем рисунке». И Коля нарисовал
веселую свинку.
А
А
25

VI. Решения и ответы
1. Ваня нашел бы те же 3 копейки.
2. В Москву шла только женщина.
3. В первую минуту отпиливается 1-й метр,
во вторую минуту отпиливается 2-й метр, в
третью минуту отпиливается 3-й метр, в
четвертую минуту отпиливается 4-й метр, и
5-й метр остается. Следовательно, для
распилки бревна потребуется четыре минуты.
4. Очевидно, только те 4 кошки, которые
сидят в углах.
6. Конечно нет! Если мальчик возвратит
торговцу грушу, то получит обратно 5 рублей.
Чтобы получить 10-рублевую грушу, мальчик
должен прибавить к этим 5 рублям еще 5
рублей.
7. 8, 69, 88 и др.
8. Хозяин подал гостям
свои три рыбы, сложенные
так, как показано на рисунке
справа.
26

,о
АО,о
9. 3 10. Деду 55 лет, то есть
4О (100 - 45), отцу 35 лет, а
его сыну 10 лет, то есть
(45 - 25) : 2.
11. Первое расположение стульев:
о
о о
о о
о о
о о о о о
Второе расположение стульев:
о о о о
о о
о о
о о о о
12. Эту задачу надо решать с конца: отнимем
излишек в 10 яблок, тогда останется 90 яблок;
в это количество входят 3 части (торговка
сказала: «Если бы к моим яблокам прибавить
половину их»). Следовательно, в числе 90
заключаются 2 части да еще та часть (половина всех
яблок), которую старуха желает вновь
прибавить. Разделив 90 на 3, мы узнаем, что
половина всех яблок равна 30 яблокам. Значит, у
торговки было 30 х 2, то есть 60 яблок.
27

13. Эта задача похожа на предыдущую: в
ней также деление на части. Когда брат
окажется вдвое богаче сестры, то количество
денег брата будет равно 2 частям, а сестры —
1 части. Разделив 90 на 3 части, мы узнаем,
что у сестры тогда будет 30 рублей, а у брата
(он имеет вдвое больше денег) 60 рублей. Но
ведь у брата потому стало 60 рублей, что
сестра из своих денег дала ему 10 рублей.
Значит, у брата прежде было 50 рублей, а у сестры
40 рублей.
14. Теперь сын вдвое моложе отца (2
части + 1 часть = 3 части). Когда же родился
сын, отцу было 24 года, то есть, когда сыну
будет 24 года, а отцу 48 лет, отец будет вдвое
старше сына. Следовательно, теперь сыну
24 года.
15. Задача, данная Коле, решается так: в
числе 81 заключены 3 части (2 половины
да еще 1 половина). Узнаем, чему равняется
1 часть: 81 : 3 = 27. Две части (или 2
половины) по 27, то есть 54 копейки, и составляют
сумму бывших у отца денег.
Задача, данная Шуре, решается так: в
числе 68 заключается 4 части (3 трети да еще
1 треть); узнаем, чему равна 1 часть: 68 : 4 =
= 17. Три части (или 3 трети) 28 по 17, то есть
51 копейка, и составляют сумму бывших у
мамы в кошельке денег.
28

16. Восемнадцать орехов нужно разделить
на следующие части: 1 часть Пете, 2 части
Коле и 3 части Шуре (всего 6 частей).
Разделив 18 на 6, мы узнаем, что 1 часть Пети
равна 3 орехам, которые он получил. Коля
получил вдвое больше Пети, то есть 2x3 = 6
орехов, а Шура втрое больше Пети, то есть
3x3 = 9 орехов.
17. Прежде всего узнаем, сколько рыбок
погибло: их было 55, а осталось после
нападения щуки 42, значит, погибло 13 рыбок. Из
этих 13 рыбок погибли: 1 плотва, 8 окуньков
и 13 — 9 = 4 пескаря. Осталось 42 рыбки. Из
них приходится на долю пескарей 1 часть, на
долю окуньков (их вдвое больше, чем
пескарей) 2 части и на долю плотвы (ее вдвое
больше, чем окуньков) 4 части. Всего 7
частей. Разделив 42 на 7, мы узнаем, что
пескарей осталось 6 штук, окуньков (вдвое больше)
12 штук, а плотвы (ее вдвое больше, чем
окуньков) 24 штуки.
18. Спички следует сложить так: X (римская
цифра, изображающая число 10).
19. Сложите спички в виде римской цифры
VI (шесть).
20. Сложите спички в виде римской цифры
VII (семь).
29

2i. T D И
22. (Отнятые спички показаны
пунктирными линиями.)
L1 СП I/. J
23.
! IJ
24.
25.
27.
или
■
28.
щ::ш »-шест
30.
DID
30

31. а)
Г~Г~~~
1J
QLJ
D
р::р пл::
32. 1)
2)!
-BIB
34.
I - - -1- - - -
Duqp
LJUD
35. Одну из крайних
спичек кладут рядом
с другой крайней.
36- _сР d~b 37-d
38.
V
41.
П
Г
гг
31

К КЛЕТКЕ
44. Задача, данная Шурой Любе, решается
очень просто: от числа 8, изображенного
спичками римской цифрой, отнимите 5 спичек, и,
разумеется, тогда ничего не останется.
Задача, данная Любой Шуре, решается так:
одну из двух спичек немного обжигают на
огне и обугленной стороной прикладывают к
бумаге, а на полученный оттиск кладут
поперек его другую, необугленную спичку.
Другая задача, предложенная Шурой Любе,
решается так: кладут спичку на угол стола так,
чтобы края стола образовали две другие
стороны треугольника.
45.
47.
3
1
2
1
2
3
2
3
1
2
9
4
7
5
3
6
1
8
46.
48.
3
4
1
5
2
2
1
3
4
5
4
2
5
1
3
5
3
4
2
1
5
4
9
10
6
2
3
8
7
1
5
2
3
4
49.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Аля детей
среднего возраста

I. Задачи-шутки
1. В корзине 4 яблока.
Разделите их между
четырьмя людьми так, чтобы
каждый получил по яблоку
и одно яблоко осталось бы
в корзине.
2. Два отца и два сына
съели за завтраком 3 яйца,
причем каждому из них
досталось по целому яйцу.
Как это могло случиться?
3. Две старушки
отправились из Москвы в Тро-
ице-Сергиеву лавру. Обе
они прошли 60 верст.
Сколько верст прошла
каждая, если шли они с
одинаковой скоростью?
35

40
32 1
8
8
8
41
4. Сколько концов у 4 палок? У 5 палок?
А у 5 с половиной палок?
5. От 20 отнять 88 так, чтобы осталось 22.
6. При решении задачи мальчику
пришлось делить 40 на 8. Он
расположил ход действия так, как
показано справа. 0
Когда его сестра, увидав такое
неправильное решение, заметила ему об этом, то он стал
проверять деление, умножая
делитель на частное, и, про- Проверка:
изводя проверку, как показа- А, ...делитель
^ * J x41 ... частное
но слева, получил делимое — —g"
число 40. + 32
Укажите неправильность в 40 ... делимое
ходе действий мальчика.
7. Какие числа (свыше ста) при чтении
не изменяются при перевертывании их?
8. Число 66 моментально увеличьте на
половину этого числа.
9. Число 666 увеличьте моментально в
полтора раза.
10. Разделите на бумаге число 12 на две
равные части так, чтобы половина этого числа
была семь.
36

11. Как разделить 188 на две равные части,
чтобы в каждой из них получилось сто?
12. Четыре брата владели сообща одним
ослом: каждому брату принадлежала одна нога
этого животного.
Случилось, что осел поранил ногу,
принадлежавшую одному из братьев. Нога
разболелась, и осел не мог более работать. Так как от
этого страдали и три других брата, то все
четверо братьев решили лечить осла сообща, для
чего вздумали приложить к больной ноге
паклю и поджечь ее. Когда они это сделали, осел,
испугавшись огня и почувствовав боль,
вырвался и бросился бежать куда глаза глядят.
Вскоре он очутился во владении одного
помещика, где были сложены снопы хлеба. От
горевшей пакли солома моментально
вспыхнула, и весь сложенный хлеб сгорел. Помещик
потребовал от братьев возмещения
понесенных им убытков в размере 300 рублей.
Кто из братьев и в каком размере должен
уплатить эту сумму?
П. Забавные исчезновения
и остроумный дележ
13. У одного вельможи был крест,
украшенный крупными бриллиантами. Он никогда
не интересовался тем, сколько бриллиантов
вставлено в крест.
37

,О Вельможа знал лишь
2О одно: если он начинал счи-
3О тать с одного из боковых
,О 2О3О4О3О2О ,О концов или с верхнего кон-
5О s ца вниз до основания кре-
6О * ста, то всегда насчитывал
7О 9 бриллиантов. Как-то раз
8О понадобилось отдать крест
9О в починку. Вельможа
позвал мастера и, отдавая ему
крест, сказал: «Прошу вас, чтобы все
бриллианты были в целости. Давайте вместе проверим
их». И вельможа стал вслух «по-своему»
считать бриллианты. Мастер заметил это и, так как
он не отличался особой честностью, при
починке вынул два камня и возвратил крест
вельможе, не подменив, однако, настоящих камней
фальшивыми. Тот пересчитал камни и нашел,
что они все целы. Как мастер ухитрился
провести вельможу?
14. Шел бедный крестьянин по мосту,
присел у перил и тяжко-тяжко вздохнул. Шел
мимо цыган и спросил его: «О чем, приятель,
38

вздыхаешь?» — «Эх, брат, — ответил
крестьянин, — нужда заела. Нужно сейчас долг
платить, а я и половины его не имею в кармане.
И как это у других легко копейка к копейке
прибавляется? Смотришь, сейчас пятак, через
пять минут вдвое, а еще через пять минут —
вчетверо». — «Есть о чем вздыхать, — сказал
цыган, — я знаю секрет, как удваивать деньги.
Хочешь, научу?» — «Научи, пожалуйста,
сделай милость!» — взмолился крестьянин. «Так
и быть, услужу, — согласился цыган, — но и
ты меня не забудь. Ну а теперь делай так, как
скажу. Ступай через мост, потом обратно, а я
за тобой пойду. Перейдешь мост, положишь
свои деньги в шапку, и будет у тебя денег
вдвое больше, чем было. И каждый раз, как
будешь переходить мост, денег у тебя будет
ровно вдвое, чем было до этого». — «Да что
ты!» — воскликнул крестьянин. «Ну вот еще,
божиться, что ль, тебе? — самоуверенно
сказал цыган. — Однако по рукам, приятель, а за
мою услугу ты каждый раз, как перейдешь
мост, должен отдавать мне 8 копеек, иначе
ничего не выйдет». — «Ну что же! Ежели
деньги будут удваиваться, то изволь, буду каждый
раз отдавать тебе 8 копеек». Когда они
уговорились, крестьянин перешел мост и высыпал
деньги в шапку. Цыган встряхнул их — и
денег стало в шапке вдвое больше! «Вот так
диво!» — воскликнул мужик и отсчитал
цыгану 8 копеек. Перешел он мост второй раз —
39

и денег в его шапке снова стало вдвое больше,
чем было перед этим. Мужик отдал цыгану
8 копеек и перешел мост в третий раз. Денег
стало опять вдвое больше, чем было перед
этим. Но — странное дело! — их оказалось
ровно 8 копеек, которые цыган и потребовал
по уговору. Мужик, ошеломленный таким
исходом, отдал цыгану 8 копеек и остался без
денег. Пока он разводил руками, цыгана и
след простыл.
Сколько денег было у крестьянина до
встречи с цыганом?
15. У помещика в погребе был шкаф,
похожий по форме на квадрат, разделенный на
9 ящиков (клеток). В среднем ящике была
сложена пустая посуда, а в остальных ящиках
были расставлены 32 бутылки
вина так, что в каждом
угловом ящике было по 1 бутылке,
а в каждом из средних ящиков
по 7 бутылок. Словом, на
каждой стороне квадрата было по
9 бутылок.
Лакей помещика заметил, что скупой
хозяин, проверяя число бутылок, считает только
бутылки по сторонам квадрата. Для помещика
важно лишь, чтобы на каждой стороне
квадрата было по 9 бутылок. На следующий день
лакей унес 4 бутылки, а остальные расставил так,
чтобы на каждой стороне квадрата шкафа по-
40
1
7
1
7
7
1
7
1

лучилось по 9 бутылок. Помещик вскоре
пересчитал бутылки по-своему и не догадался, что
4 из них украдены. Лакей был рад этому и на
следующей неделе снова унес 4 бутылки, а
остальные расставил так, что на каждой
стороне шкафа было опять по 9 бутылок. Помещик
и тут не заметил пропажи. Тогда лакей и в
третий раз украл бутылки, а остальные расставил
так, что на каждой стороне квадратного шкафа
по-прежнему оставалось по 9 бутылок. Как
лакей расставлял бутылки после каждой кражи?1
16. Разделите 7 яблок между 6 мальчиками
поровну.
17. Разделите 7 яблок между 10 мальчиками,
а затем 9 яблок между теми же мальчиками.
18. Двум братьям отец
принес несколько груш.
Когда они разделили эти
груши между собой (не
поровну), старший брат
сказал другому: «Дай мне еще
одну грушу, я ведь старше тебя. Тогда у меня
будет груш вдвое больше, чем у тебя!» — «Ну
нет, — ответил младший, — хотя ты и старше
меня, но я так же, как и ты, люблю груши.
1 Решение этой задачи основано на использовании
магических квадратов.
41

Дай лучше ты мне одну грушу, и тогда у нас
будет груш поровну и никому из нас не будет
завидно». Сколько груш было взято сначала
каждым мальчиком?
19. Старший брат сказал младшему: «Дай
мне 8 рублей, и тогда у меня денег будет вдвое
больше, чем у тебя». А младший возразил:
«Дай лучше ты мне 8 рублей, тогда у нас будет
денег поровну».
Сколько денег у каждого из братьев?
20. Дед, отец и сын во время прогулки
встретили знакомого, который спросил их,
сколько им лет. «Нам 121 год», — ответил за
всех дед и важно зашагал вперед. Тогда
знакомый, продолжая интересоваться возрастом,
спросил отца: «Ну, скажите же, сколько вам
лет?» — «Мне вместе с сыном 44 года, —
отвечал отец, — а сын на 28 лет моложе меня».
Так знакомому и не пришлось узнать, сколько
лет каждому из них. Не сообразите ли вы?
21. Канат длиной 11 аршин рабочие
разрезали на две части так, что в одной из них
оказалось столько вершков, сколько в другой
дюймов. Какой длины каждый кусок?
22. Девочки принесли лавочнику
землянику. Лавочник дал им за это несколько
одинаковых медных монет. Девочки поблагода-
42

рили лавочника и ушли.
Дорогой они стали делить
монеты. Оказалось, что
если девочки возьмут себе
по одной монете, то
одной из девочек не хватит
монеты, а если разделить
монеты так, что любым
двум девочкам достанется по одной монете,
то одна монета останется лишней. Сколько
было девочек и сколько монет дал им
лавочник?
23. Летели галки,
видят — березы. Стали
рассаживаться. Попробовали
сесть по одной на
дерево — четырем галкам не
хватило деревьев. Стали
садиться по две на
березу — одна береза осталась
незанятой. Сколько было
галок и сколько берез?
24. Петя и Коля играли
в шашки. Петя задумался
над своим ходом, а Коля
от скуки сосчитал, что на
доске (состоящей, как
известно, из 64 клеток)
пустых клеток втрое больше,
43

чем занятых, и что у него на две шашки
больше, чем у Пети. Сколько шашек было у
каждого из них в этот момент?
25. Два крестьянина расположились у
лесной опушки перекусить. В это время к ним
подошел путник и попросил поделиться
завтраком, пообещав уплатить, что следует. Те
согласились и достали свой скудный завтрак:
у одного крестьянина было 2 хлебца, а у
другого такой же один. Все втроем закусили,
причем ели поровну. Уходя, путник заплатил за
свою долю 5 копеек. Как крестьяне должны
разделить эти деньги между собой?
26. Два работника сели обедать. У одного
было 4 лепешки, у другого только 3 лепешки.
Стоимость лепешек была одинаковой.
Подошел к ним прохожий и попросил у них
поесть, причем обещал уплатить деньгами за
ту часть лепешек, которая придется на его
долю. Работники согласились. После обеда, за
которым все ели поровну, прохожий отдал
обоим работникам 7 копеек. Не поможете ли
вы разделить эти деньги работникам между
собой?
27. Две женщины варили кашу. Одна дала
2 фунта крупы, другая — 3 фунта. Только
сварилась каша, как пришли еще две работницы.
Все четыре женщины сели за стол и съели
44

всю кашу. По окончании
еды каждая из пришедших
женщин уплатила по 5
копеек.
Как должны женщины разделить
полученные деньги, если все ели поровну?
III. Затруднительные положения
28. На реке во время половодья оторвало от
берега и унесло большую лодку, на которой
перевозили через реку окрестных жителей.
У перевозчика осталась лишь одна маленькая
лодка, на которой можно переправить либо
одного взрослого, либо двух мальчиков,
которые всегда помогали перевозчику
переправлять народ. В это время к реке подошла партия
землекопов. Поразмыслив немного, все
землекопы ухитрились переправиться через реку
именно на этой лодке.
Как им удалось это сделать?
29. Мужичку надо переправить через реку
волка, козу и капусту, да вот беда: лодка так
мала, что в ней может поместиться только
мужичок, а с ним либо волк, либо коза, либо
капуста. Дело усложняется еще тем, что при
переправе волка нельзя оставить с козой,
так как он ее съест. Капусту также нельзя
оставить с козой: коза съест капусту. Мужи-
45

чок думал-думал, но все-таки перевез всех
на другую сторону. Как ему удалось это
сделать?
30. В одной из комнат было 12 табуреток.
Два мальчика, Петя и Ваня, стали расставлять
вдоль стен беспорядочно раскиданные
табуретки. Вскоре Петя остановился и сказал Ване:
«Постой, расставь-ка, брат, все эти 12
табуреток тремя рядами так, чтобы 2 ряда содержали
по 4 табуретки, а один ряд — 6 табуреток».
Ваня не сумел сначала этого сделать, но потом
расставил табуретки так, как просил его Петя.
«А не расставишь ли ты теперь эти 12
табуреток у четырех стен так, чтобы у каждой стены
было по 4 табуретки?» — спросил Ваня Петю.
Петя дважды ошибался при расстановке
табуреток. В это время в комнату вошел отец и
стал наблюдать за детьми. Наконец Пете все
же удалось расставить табуретки. Тогда отец
сказал детям: «Эка невидаль! Дайте-ка мне две
табуретки, я сяду на них посреди комнаты, а
остальные вы расставьте у четырех стен так,
чтобы у каждой стены их оказалось поровну».
Долго пришлось ждать отцу, но в конце
концов дети расставили табуретки так, как он
хотел.
Как Ваня расставил табуретки в первый раз?
Как Петя расставил табуретки во второй раз?
Как они оба расставили табуретки в
последний раз?
46

31. Однажды лесничий поймал
крестьянина, рубившего деревья в чужом лесу, и, чтобы
тот не убежал, пока он пойдет с докладом к
помещику, лесничий привязал его вот так:
кисти рук он связал одной веревкой, а другую
веревку продел сквозь связанные руки и
прикрепил обоими концами к стене своего дома.
Но мужичок был хитер! Когда лесничий ушел,
он тотчас же освободился, причем обе веревки
и узлы, завязанные лесничим, остались
нетронутыми.
Как он это сделал?
Примечание. Решить задачу будет
легче, если вы попросите кого-нибудь связать
вам руки, как показано на рисунке.
IV. Задачи, требующие большей
сообразительности и более сложных
вычислений
32. Ваня купил себе игрушку, Петя — книгу
с картинками, а Коля приобрел столярный
станок. Оказалось, что каждый из них истра-
47

тил впятеро больше, чем предыдущий, а все
вместе израсходовали 2 рубля 48 копеек.
Сколько стоит каждая из покупок?
33. Помещик, рассчитав, что корова стоит
вчетверо дороже собаки, а лошадь
вчетверо дороже коровы, захватил с собой в город
200 рублей и на все эти деньги купил собаку,
две коровы и лошадь.
Сколько стоит каждое из купленных
животных?
34. Из двух деревень шагают навстречу друг
другу два работника. От нечего делать они
считают свои шаги (в аршин каждый). Один
насчитал в минуту 133 шага, другой — 167
шагов. Через 5 минут они встретились. Узнайте
расстояние между деревнями.
35. Два родных брата, Карп и Поликарп,
получили в наследство 240 рублей. Карп и
говорит Поликарпу: «Дай мне из свой доли
25 рублей, и я стану вдвое богаче тебя». —
«Нашел простачка», — подумал,
усмехнувшись, Поликарп и, разумеется, не дал брату
25 рублей.
Сколько денег досталось каждому из
братьев?
36. Одного человека спросили, сколько у
него денег. Он ответил: «Мой брат втрое бога-
48

че меня, отец втрое богаче брата, дед втрое
богаче отца, а у всех нас ровно 1000 рублей.
Вот и узнайте, сколько у меня денег».
37. Мальчик добежал от
деревни до школы за 15
секунд, пробегая в секунду
по 1 сажени 2 аршина.
За какое время
проползет это расстояние
червячок, если в минуту он
может продвинуться лишь на
1 фут?
38. «Дедушка, сколько тебе лет?» — спросил
деда внук. «А вот прибавь к каждому полному
десятку моих лет по 2 года, и получишь 84
года», — отвечал старик. Внук едва сообразил,
сколько лет дедушке. Так сколько лет деду?
39. Жили-были два
брата-близнеца. Один из них
ежедневно спал !/3 суток, а
другой 1/4 суток. Дожили
они так до 72-летнего
возраста. Сколько лет за это
время проспал каждый из
них?
40. Сын втрое моложе отца. Когда отцу
было 37 лет, сыну было только три года.
Сколько лет теперь каждому из них?
49

41. Дети играли в лото на орехи. Ване очень
не везло: он сыграл 4 партии и, проиграв их
все, отдал 255 орехов, при этом каждый раз
вчетверо больше, чем в предыдущий.
Сколько орехов проиграл Ваня в
последнюю партию?
42. Деду 56 лет, а внуку — 14.
Когда дедушка будет вдвое старше своего
внука?
43. Коле так надоели мухи, что он решил их
всех переловить. За 4 дня он наловил 216 мух,
причем каждый день ловил столько мух,
сколько за все предыдущие.
Сколько мух Ваня ловил в каждый из
четырех дней?
44. Часы отстают каждый день на 6 минут.
Через сколько дней они будут показывать
опять верное время?
45. Отец роздал орехи
поровну пятерым
сыновьям. Трое сыновей съели
по 5 орехов и увидели,
что у них осталось
столько орехов, сколько дано
двум другим сыновьям.
Сколько орехов роздал
отец?
50

46. У 35-летнего отца 4 сына. Каждый
моложе другого на два года, причем старшему
8 лет.
Когда всем детям вместе будет столько же
лет, сколько и отцу?
47. Один работник
получал в день столько
копеек, сколько дней он
работал, а другой получал в
день на копейку больше
первого, но работал днем меньше. Кто из
работников заработал больше денег?
48. Между школой и библиотекой 33
сажени. Из библиотеки в школу ползет паук, а
навстречу ему из школы двигается червячок.
Пока червяк проползает один дюйм, паук
успевает продвинуться на целый вершок. На
каком расстоянии от библиотеки они
встретятся?
49. Когда Ваню спросили, сколько ему лет,
он подумал и сказал: «Я втрое моложе папы,
51

но зато втрое старше Сережи». Тут подбежал
маленький Сережа и сообщил, что папа
старше его на 40 лет. Сколько лет Ване?
50. Во время прогулки я и товарищ решили
измерить длину бульвара шагами. Начав
измерение от ближайшей липы, мы пошли от
нее в противоположные стороны. Я насчитал
до конца бульвара 108 шагов, а мой товарищ
только 69. Кроме того, идя вдоль бульвара, мы
считали липы, мимо которых проходили. Я
насчитал 37, а он 23 дерева. И я, и товарищ
начали считать деревья с той липы, от которой
пошли. Через сколько шагов друг от друга
посажены липы?
51. Племянник спросил дядю, сколько тому
лет. Дядя ответил: «Если к половине моих лет
прибавить 7, то узнаешь мой возраст 13 лет
тому назад». Сколько лет дяде?
52. Однажды со мной
произошел такой случай. Проснувшись
утром, я увидел, что мои
стенные часы стоят. Других часов у
меня не было, и я, чтобы узнать,
который час, отправился к
приятелю, живущему на другой
улице. Придя к нему, я немедленно
справился о времени моего
прихода и, посидев с ним немного,
52

ушел домой, предварительно взглянув на его
часы. Придя домой, я правильно поставил
часы.
Каким образом мне удалось это сделать,
если допустить, что на дорогу к приятелю и от
него к себе домой я потратил одинаковое
количество времени?
53. Из двух городов, Нижнего Новгорода
и Вязников1, расстояние между которыми
300 верст, в один и тот же день, час и в одну
и ту же минуту выезжают два велосипедиста
и мчатся навстречу друг другу со скоростью
50 км/ч каждый. С велосипедистом,
выехавшим из Вязников, в момент его
отправления вылетает муха и летит тоже навстречу
нижегородскому велосипедисту со скоростью
'Вязники- город во Владимирской области.
(Примеч. ред.)
53

100 км/ч. Встретив велосипедиста, она тотчас
поворачивает назад и летит навстречу
первому. Повстречав того, муха все с той же
скоростью летит обратно, пока не встретит
снова второго велосипедиста. Так муха летала от
одного велосипедиста к другому до тех пор,
пока они не встретились. Тогда она
успокоилась и села на спину одного из них. Сколько
верст пришлось пролететь мухе до встречи
велосипедистов?
Волшебные квадраты
54. Расположите все
цифры, помещенные в данной
фигуре, по клеткам
заштрихованного квадрата так,
чтобы суммы чисел по любой
его горизонтали, вертикали
и диагонали были
одинаковы и каждая из них была
равна 13.
55. Расставьте в шести
(из всех данных) квадратах
по кресту так, чтобы число
пустых квадратов как по
любой вертикали, так и на
любой горизонтали было
четное.
54

Волшебная таблица
56. Эта таблица, состоящая из чисел от 1 до
31, выписанных известным образом,
отличается следующим «волшебным свойством»:
предложите задумать любое число от 1 до 31 и
попросите указать, в каких рядах встречается
задуманное число, — вы безошибочно
сможете назвать его.
5-й ряд
16
17
18
19
20
20
22
23
24
25
26
27
28
29
30
31
16
4-й ряд
8
9
10
11
12
13
14
15
24
25
26
27
28
29
30
31
8
3-й ряд
4
5
6
7
12
13
14
15
20
21
22
23
28
29
30
31
4
2-й ряд
2
3
6
7
10
11
14
15
18
19
22
23
26
27
30
31
2
1-й ряд
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
1
Например, вам скажут, что задуманное
число находится в 1, 2, 3 и 5-м рядах, и вы,
поразмыслив несколько секунд, заявите, что
задумано число 23!
55

Попробуйте догадаться, как находится это
число (или любое другое). Если это вам не
удастся, то загляните в раздел «Решения и
ответы».
V. Ряды чисел, суммы которых
можно получать, не производя
сложения этих чисел
Пояснение. Если вы вздумаете узнать,
чему равна сумма чисел 1, 2, 3, 4, 5, 6, 7, 8, то
вы легко можете найти ее, не складывая самих
чисел.
Возьмите 8 карточек и нарисуйте на
одной из них 1 кружок, на другой 2 кружка, на
третьей 3 кружка и т. д. Затем разложите
эти карточки в ряд по порядку, начиная с
той, на которой нарисован 1 кружок. Сделав
еще 8 таких же карточек, разложите их под
первым рядом в обратном порядке (то есть
под карточкой с 8 кружками положите
новую карточку с 1 кружком, под карточкой с
7 кружками — новую карточку с 2 кружками
и т. д.).
Нетрудно видеть, что наши два ряда
образовали 8 столбиков по 2 карточки в каждом.
Сосчитайте, сколько кружков в каждом
таком столбике. Оказывается, что, какой бы
столбик мы ни выбрали, в нем всегда 9
кружков. Число 9 есть сумма кружков на первой
56

и последней карточках в верхнем (первом)
ряду.
Наши два ряда состоят из 8 столбиков, и в
каждом столбике на двух карточках в сумме
5 кружков. Значит, повторив 9 кружков 8 раз,
вы узнаете, сколько всего кружков в обоих
рядах: 9 х 8 = 72 кружка, или (1 + 8) х 8 =
= 72 кружка.
Теперь уже совсем нетрудно узнать, сколько
кружков в одном ряду (первом или втором —
безразлично). Для этого стоит лишь разделить
72 кружка на 2 части:
72 : 2 = 36 кружков.
Следовательно,
1+2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 36.
Посмотрим, что нам пришлось сделать для
того, чтобы получить сумму:
1) 8 + 1 = 9, то есть сложить первое и
последнее числа нашего ряда;
2) 9 х 8 = 72, то есть полученную сумму
умножить на столько, сколько чисел в ряду;
3) 72 : 2 = 36, то есть произведение
разделить пополам.
57

Рассмотрим еще один пример.
Предположим, что вам надо поскорее
сложить числа 2, 5, 8, 11, 14, 17 и 20.
Этот ряд отличается от первого тем, что
здесь каждое число больше предыдущего на
3 единицы, а не на одну, как было в первом
примере.
Не смущайтесь: и в этом случае можно
воспользоваться уже известным вам приемом.
1) Сложите последнее число с первым: 2 +
+ 20 = 22.
2) Умножьте эту сумму на 7 (в новом ряду
семь чисел): 22 х 7 = 154.
3) Разделите полученное произведение
на 2: 154 : 2 = 77.
Попробуйте теперь проверить полученный
ответ, сложив все числа нашего ряда, и вы
убедитесь, что решили задачу правильно.
Ниже вы найдете несколько задач, для
решения которых можете употребить новый
прием, с которым только что
познакомились.
57. Сколько ударов в сутки делают часы с
боем?
Примечание: предполагается, что часы
бьют только тогда, когда показывают целое
число часов.
58. Журавли обыкновенно летают стаями
так, что образуют треугольник: впереди один
58

журавль (вожак), за ним два, потом три
журавля и т. д. Сколько летело в стае журавлей, если
в последнем ряду их было 15?
VI. Игры со спичками
Прежде чем вы приметесь играть со
спичками, не мешает познакомиться: 1) с
положением линий, которые они могут иметь одна по
отношению к другой; 2) с формой некоторых
фигур и углов и, наконец, 3) с очертаниями
простейших геометрических тел.
Линии, которые вы видите на рисунке,
сколько бы вы их ни продолжали в обе
стороны, никогда не пересекутся. Они называются
параллельными.
Линии, которые
изображены на том же
рисунке ниже, если их
продолжить вправо,
непременно пересекутся
и образуют то, что
называется углом.
59
Параллельные прямые
Угол
Горизонтальная прямая

Прямоугольник
А вот перечень наиболее часто
встречающихся геометрических фигур.
Четырехугольник, у которого
все стороны одинаковы и все
углы равны, называется
квадратом. Такие углы, как у
квадрата, называются прямыми.
У этого четырехугольника
все стороны тоже одинаковы,
но углы, как видите, разные.
Он называется ромбом.
А у этой фигуры, наоборот,
все углы одинаковые, а
стороны (верхняя и боковая) имеют
разную длину. Стороны,
находящиеся друг против друга, равны. Такой
четырехугольник называется прямоугольником.
Этот четырехугольник
называется
параллелограммом. У него углы разные, а
стороны одинаковы
только те, которые лежат друг
против друга.
Такой четырехугольник,
у которого две
противоположных стороны
параллельны, а две другие — нет,
называется трапецией.
Если в каком-нибудь из этих
четырехугольников проведете из одного угла в другой прямую
линию, то она будет называться диагональю.
60
: Параллелограмм >
Трапеция

А вот некоторые из объемных
геометрических тел.
Кубом называется тело, у
которого длина, ширина и высота
одинаковы. Ребра куба образуют
между собой прямые углы.
Куб
Если основанием пирамиды служит
треугольник, то она называется треугольной.
Если же в основании пирамиды лежит
четырехугольник, то она называется
четырехугольной пирамидой.
Пирамиды
Призма
Это геометрическое тело называется
призмой.
Основания призмы находятся в одной
плоскости.
59. Расположите 6 спичек так, чтобы
каждая соприкасалась с четырьмя другими.
60. Из 12 спичек получите ноль.
61. Доказать «на спичках», что 9 без 3 равно
четырем, а 11 без 3 равно шести.
61

62. Переложить 5 спичек так, чтобы
получилось два квадрата.
D
Fb
63. При помощи двух спичек, не ломая и
не разрезая их, построить квадрат.
64. Из 9 целых спичек составить 6
квадратов.
65. Из 16 спичек составлено 4 квадрата. Как
из тех же 16 спичек составить 5 таких же
квадратов?
О D D D
66. Переложить 3 спички так, чтобы
получилось 3 квадрата.
62

67. На этих весах, составленных из спичек,
требуется переложить 5 спичек так, чтобы
весы оказались в равновесии.
л
68. Был скучный осенний вечер. Дедушка
собрал вокруг себя внуков и сказал: «А не
рассказать ли вам, ребятки, сказочку о пастухах
и разбойниках?» — «Расскажи, милый
дедушка, расскажи!» — запрыгали i о ^ 4 S
дети. «Ну, слушайте». — При
этих словах дедушка взял 5
спичек и положил их на стол так.
В каждую руку он взял еще по одной
спичке и начал: «Пять овец (дедушка показал на
5 спичек) паслись на лугу, а в лесу находились
два разбойника (он показал две спички в
руках). Разбойники украли овец одну за другой
(с этими словами дедушка взял 1 -ю спичку
левой рукой, 5-ю правой, 2-ю левой, 4-ю правой
и 3-ю левой). В это время пришел пастух, и
разбойники отпустили овец обратно (дедушка
выложил 1 спичку из правой руки, спичку из
левой, 1 спичку из правой, 1 — из левой, 1 —
из правой). Пастух удалился, и разбойники
опять забрали одну за другой всех овец (и
дедушка начал брать спички, как и прежде,
сначала левой рукой). Но в это время пришли
63

солдаты, и разбойники убежали, оставив овец
в лесу». Дедушка открыл руки, и в самом деле:
в одной руке у него было 5 овец, в другой
2 разбойника. Как это случилось?
69. Отнимите от 7 спичек 5 спичек так,
чтобы осталось пять.
70. Спички лежат в двух кучках. Если из
первой кучки переложить 2 спички во вторую,
то во второй спичек будет в 5 раз больше, чем
в первой. Если же из второй кучки переложить
в первую 5 спичек, то в первой будет в три
раза больше, чем во второй. Сколько спичек в
каждой кучке?
VII. Игры и забавы
71. Однажды дядя сказал детям: «Хотите,
покажу вам, как в турецкую войну наши
матросы взорвали турецкий мост и турецкую
башню?» Дети обрадовались и немедленно
согласились. Дядя составил («сплел») из спичек1
мост (А) и две башни (Б и В) и, переплетя их,
положил на пепельницу. Затем он поджег
сначала мост, а потом и башни возле того места,
где пересекались концы спичек (д, е). Как
1 Спички для описываемого опыта удобнее брать
плоские, а не обычные, которые могут легко
сломаться.
64

только пламя достигло
точки пересечения, все
спички взлетели вверх.
Детям эта забава очень
понравилась, и они
хотели попробовать зажигать спички сами, но дядя
им сказал: «Милые детки, пусть вам эту
забаву показывают взрослые, но сами вы
никогда не играйте со спичками, так как может
случиться пожар, а вы знаете, какое это
великое бедствие для всех». Умные дети
послушались дядю и никогда не баловались со
спичками.
72. Два мальчика придумали такую игру.
Они поочередно произносили произвольные
числа (не больше 10). Эти числа складывались,
и победителем считался тот, кто первым
произносил число 100.
Поставьте себя на место одного из
мальчиков. Как сделать так, чтобы всегда оставаться
победителем?
73. Мальчик, сидя за столом перед
зеркалом, вздумал начертить на бумаге фигуру,
изображенную на рисунке слева.
При этом он мог видеть в
зеркале только отражение листа
бумаги со своим рисунком, так как
пишущая рука была загорожена
от глаз мальчика картонной пап-
3 Н. Аменицкий и др. £^

кой. К великому изумлению мальчика, эта,
казалось бы, легкая затея удалась не сразу: он
долго не мог начертить желаемую фигуру.
Попробуйте, и вы сами убедитесь в трудности
затеи.
74. Вырезать из этой фигуры
такую часть, чтобы, приложив ее к
оставшейся части, вы получили бы
внутри фигуры полный квадрат.
75. Как зайцы нашли свои уши. Однажды
неведомо как зайки ушки потеряли. Как же
быть без ушек серым? Делать что в такой
печали?
Тотчас зайки побежали, только лапки
засверкали, по проталинкам, по кочкам... Вдруг
под низеньким кусточком часть пропажи
отыскалась! Трое ушек перед ними, перед
зайками моими. Впрочем, зайки не тужили, трое
ушек разделили и с ушами снова стали: с
парой ушек каждый зайка!
Как зайки разделили ушки? Не нарисуете
ли вы трех заек так, чтобы у каждого зайки
было по два уха, а у всех трех вместе только
три уха?
66

76. Как собаки испугались
На лугу лежали две собаки. В тот момент,
когда они, играя, приняли положение,
изображенное на рисунке, раздался свист. Собаки
моментально приняли другое положение и
бросились бежать.
Изобразите бегущих
собак, дополнив
несколькими линиями рисунок и
стерев некоторые из уже
имеющихся.
VIII. Решения и ответы
1. Это легко сделать, если один человек
возьмет свое яблоко вместе с корзиной.
2. Дело в том, что завтракали только трое:
дед, его сын и внук, то есть два отца и два
сына.
3. Каждая старушка прошла 60 верст.
4. У 4 палок 8 концов, у 5 палок 10 концов,
у 5 палок с половиной 12 концов, так как у
половины палки два конца.
5. Напишите римскими цифрами XX
20 (XX), под ними — арабскими циф- —88
рами 88 и произведите вычитание: 22
67

6. Ошибка в делении: неверно взята
цифра частного — вместо 4 надо было взять 5,
так как остаток делится на 8; ошибка в
проверке деления, то есть в умножении:
цифра, показывающая число десятков (32),
написана под цифрой, выражающей число
единиц (8).
7. 111, 619, 689, 818, 888, 986 и др.
8. Переверните данное вам число, и вы
получите 99 — число, равное сумме прежнего
числа 66 и его половины 33.
9. См. предыдущее решение.
10. Изобразив число 12 римскими цифрами
(XII) и «разрезав» его пополам
горизонтальной черточкой по возможности на две равные
части, вы получите в верхней половине запись
числа 7 римскими цифрами (VII).
11. Задача решается так же, как и задача 10:
разделите число 188 пополам горизонтальной
черточкой.
12. Сумму 300 рублей должны заплатить
помещику те три брата, которым принадлежали
три здоровых ноги осла, потому что осел
бежал только на здоровых ногах.
68

13. Мастер взял два
крайних камня от поперечной
перекладины креста и, кро-
ме того, переставил вниз
верхний камень (№ 1).
Ъ'
«о
,о
.о
,о
,о
14. Эту задачу надо
решать с конца. После
третьего перехода у мужичка было
8 копеек, а до третьего
перехода 4 копейки (8:2 = 4).
Но перед этим он отдал
цыгану 8 копеек. Следовательно, после второго
перехода через мост у крестьянина было 12
копеек (4 + 8 = 12), а до второго перехода —
6 копеек (12 : 2 = 6). Перейдя мост в первый
раз, крестьянин отдал цыгану 8 копеек.
Следовательно, после первого перехода через мост
у него было 14 копеек (6 + 8 = 14), а до
первого перехода (то есть первоначально) — 14 :
: 2 = 7 копеек.
15. После 1, 2 и 3-й краж лакей расставлял
бутылки так, как показано на рисунке.
69

16. Дайте каждому мальчику по яблоку, а
одно яблоко разрежьте на 6 равных частей и
дайте каждому мальчику по одной дольке
разрезанного яблока.
17. Пять яблок замените 10 половинками,
а каждое из 2 остальных яблок разрежьте на
5 равных частей. Таких частей получится
всего 10. Каждый мальчик получает по
половинке и по 4 яблока.
18. У старшего брата на две груши больше,
чем у младшего, так как в задаче сказано, что
если старший отдаст 1 грушу младшему, то у
обоих братьев груш станет поровну. Если же
младший брат отдаст из своей доли 1 грушу
старшему брату, то у старшего брата будет
на 4 груши больше (у него было на 2 груши
больше, да еще 1 грушу дал ему младший, но
у младшего стало на 1 грушу меньше, стало
быть, разница будет 2+1 + 1=4), чем у
младшего. Но известно, что в этом случае у
одного из братьев груш окажется вдвое
больше, чем у другого. Следовательно, эти 4
груши и есть одна из половин груш старшего
брата, или !/3 всех груш. Значит, у старшего
брата стало 8 груш, а у младшего — 4 груши.
Но последний отдал 1 грушу своему брату.
Следовательно, прежде у младшего брата было
4+1=5 груш, а у старшего брата 5 + 2 =
= 7 груш.
70

19. Младший брат просит у старшего брата
8 рублей, утверждая, что тогда денег у них
будет поровну. Следовательно, у младшего брата
на 2 х 8 = 16 рублей меньше, чем у старшего
брата. Если же младший брат не только не
получит 8 рублей от старшего брата (чтобы у них
было поровну), но еще отдаст 8 рублей
старшему брату, то у последнего денег станет вдвое
больше, то есть уже не на 16, а на 32 рубля.
Следовательно, одна половина денег старшего
брата нам известна. Значит, у старшего брата
было 56 рублей, а у младшего 40.
20. Деду 121 — 44 = 77 лет. Так как отец на
28 лет старше сына, то сыну (44 — 28) : 2 =
= 8 лет. Следовательно, отцу 44 — 8 = 36 лет.
21. Напомним, что 1 аршин = 16 вершков =
= 28 дюймов. Выразив длину бревна, равную
11 аршинам, в вершках (16x11 = 176 вершков)
и разделив эти 176 вершков на общее число
вершков и дюймов в 1 аршине (16 + 28 = 44),
получим, что меньшая часть бревна равняется
4 аршинам.
22. Четыре девочки и 3 монеты.
23. Десять галок и 6 берез.
24. Занятых клеток было втрое больше, чем
незанятых. Узнаем, сколько у Коли и Пети
было шашек на доске, для чего делим 64 на
71

4 (части). Полученное число 16 и есть
общее количество шашек. У Коли было на две
шашки больше, чем у Пети. Следовательно,
если бы не эти 2 шашки, то шашек у
мальчиков было бы поровну (16 — 2 = 14, 14 : 2 =
= 7) — по 7 шашек. Но у Коли на 2 шашки
больше, то есть у него 7 + 2 = 9 шашек, а у
Пети 7.
25. Трое съели 3 хлебца. Следовательно,
каждый съел по 1 хлебцу. Поэтому тот
крестьянин, у которого был 1 хлебец, не получает
ничего, а все 5 копеек должны достаться
другому крестьянину, у которого было 2 хлебца.
26. Весь запас лепешек, съеденный двумя
работниками и прохожим, стоит 7x3 = 21
копейку. Значит, каждая лепешка стоит 21:7 =
= 3 копейки. Работник, у которого было 4
лепешки, израсходовал 3x4=12 копеек, из них
7 копеек на себя, а остальные 5 копеек он
должен получить из уплаченных прохожим денег.
Другой работник, у которого было 3 лепешки,
израсходовал 3x3 = 9 копеек, из них 7
копеек на себя, а остальные 2 копейки он должен
получить с прохожего.
27. Десять копеек следует разделить так же,
как в предыдущей задаче. Одна женщина
должна получить 3 копейки, а другая — 7
копеек.
72

28. Сначала переправились через реку оба
мальчика. Один из них остался на том берегу,
а другой пригнал лодку назад. Затем
переправился через реку 1 землекоп, а бывший на том
берегу мальчик пригнал лодку обратно, взял
другого мальчика, и они оба переправились
через реку. Обратно вернулся только один
мальчик и вышел на берег, а через реку
переправился второй землекоп.
Так переправа продолжалась до тех пор, пока
все землекопы не оказались на другом берегу.
29. Переправа совершается так:
1) туда — мужик и коза, обратно — один
мужик;
2) туда — мужик и волк, обратно — мужик
и коза;
3) туда — мужик и капуста, обратно — один
мужик;
4) туда — мужик и коза.
30. Вот как расставил в первый раз
табуретки Ваня:
о о о о о о
о о
о о
о о
Вот как расставил табуретки во второй раз
Петя: о о о о
о о
о о
о о о о
73

А вот как они расставили табуретки в
последний раз:
о о о о
о
о
• о
о •
о
о
о о о о
31. Если нижнюю руку
продеть сквозь петлю А,
то тогда, потянув руки
назад, можно освободиться
от веревки,
прикрепленной к стене.
32. Покупка Вани заключает в себе 1 часть,
покупка Пети 5 частей, а покупка Коли 25
частей. Всего получается 31 часть. Узнаем, чему
равна 1 часть (Вани). Для этого разделим
2 рубля 48 копеек на 31. Полученное число
(8 копеек) и есть стоимость покупки Вани.
Петина покупка стоит 8 х 5 = 40 копеек, а Ко-
лина — 40 х 5 = 200 копеек = 2 рубля.
33. Если стоимость собаки принять за
1 часть, то стоимость коровы надлежит
принять за 4 части, стоимость 2 коров — за 8
частей, а стоимость лошади — за 16 частей.
Узнаем, чему равна 1 часть. Для этого
разделим 200 рублей на (1 + 8 + 16) = 25 частей.
Полученное число (8 рублей) и есть сумма,
затраченная на покупку собаки. На покупку
коровы было затрачено вчетверо больше, то есть
74

8 х 4 = 32 рубля, а на покупку лошади
вчетверо больше, чем на покупку коровы, то есть
32 х 4= 128 рублей.
34. 1 верста.
35. 105 рублей и 135 рублей.
36. 25 рублей.
37. За 2 часа 55 минут.
38. В числе 84 заключается столько же
полных десятков, сколько и двоек (по одной
двойке на каждый десяток). Поэтому для того,
чтобы узнать, сколько лет деду, надо 84
разделить на 10 + 2 = 12. Полученное число 7
означает 7 частей (то есть 7 десятков и 7 двоек), или
70+14 лет. Значит, деду 70 лет.
39. Один спал !/3 суток, или !/3 года, то есть
проспал треть своей жизни: 72 : 3 = 24 года.
Другой спал У4 суток, или У4 года, то есть
проспал четверть своей жизни: 72 : 4 = 18 лет.
40. В момент рождения сына отцу было
34 года. Теперь отец втрое старше сына, то
есть число лет сына составляют 1 часть, а
число лет отца 3 части, то есть 34 года составляют
2 части, одна же часть составляет 17 лет.
Следовательно, отец только тогда станет втрое
старше сына, когда ему исполнится 17x3 =
= 51 год, а сыну — 17 лет.
75

41. Узнаем, скольким частям равняется
проигрыш в каждой партии. В первой партии
проигрыш равен 1 части, во второй — 4 частям, в
третьей — 16 частям и в четвертой — 64 частям
(всего 1 + 4 + 16 + 64 = 85 частей).
Выясним теперь, чему равна 1 часть
проигрыша. Для этого разделим 255 на 85.
Полученное число (3 ореха) и есть проигрыш
в первой партии. Узнать проигрыш в
остальных партиях не составляет труда.
42. В момент рождения внука деду было
42 года. Вдвое старше своего внука дед будет
тогда, когда число его лет удвоится, то есть
когда деду исполнится 42 х 2 = 84 года, а
внуку 42 года. Теперь внуку 14 лет, и до 42 лет
ему не достает 28 лет. Значит, дед будет вдвое
старше внука через 28 лет.
43. В первый день Коля поймал 1 часть мух,
во второй тоже 1 часть, в третий день 2 части
и в четвертый день — 4 части. Разделив 216 на
1 + 1 + 2 + 4 = 8 частей, мы узнаем, что в
первый день Коля поймал 27 мух.
44. Часовая стрелка станет на старое
(правильное) место, когда отстанет на 12 часов (на
циферблате 12 часовых делений). В одном часе
60 минут, в 12 часах — 720 минут.
Следовательно, сколько раз 6 частей содержится в 720,
через столько дней часовая стрелка вернется
на старое место, то есть 720 : 5 = 120 дней.
76

45. Все сыновья получили орехов поровну.
После того как три сына съели вместе 15
орехов, оставшееся у них количество орехов стало
равно всему количеству орехов у двух
остальных сыновей. Следовательно, съеденная часть
(15 орехов) равнялась числу орехов,
предназначенных одному сыну. Значит, у пяти
сыновей было всего 75 орехов (15 х 5).
46. Старшему сыну 8 лет, второму сыну 6 лет,
третьему 4 года и четвертому 2 года, а всем
вместе — 20 лет. Через каждый год количество лет,
прожитых отцом, увеличивается только на
1 год, а количество лет, прожитых четырьмя
детьми, на 4 года. Нетрудно подсчитать, что
через 5 лет отцу исполнится 40 лет, а всем детям
вместе — столько же.
47. Возьмите произвольное число,
обозначающее количество дней, отработанных
первым работником, и решайте далее в
соответствии со сказанным в задаче, и у вас всегда
будет получаться в ответе, что первый
работник заработал 1 копейкой больше
второго.
48. В то время как червячок проползет
28 дюймов (или 16 вершков), паук пробежит
28 вершков, вдвоем же они пройдут
одновременно 28 + 16 = 44 вершка. Разделив 33
сажени, или 1584 вершка, на 44, мы узнаем,
77

что червячок проползет до момента встречи
36 аршин (12 саженей) и до бани он не
доползет 21 сажень.
49. Возраст Сережи (в годах) содержит
1 часть, возраст Вани — 3 части, а возраст
папы — 9 частей. Значит, возраст папы на
8 частей больше возраста Сережи. В задаче
сказано, что папа на 40 лет старше Сережи.
Разделив 40 на 8, узнаем, что Сереже было
5 лет, Ване 15 лет, а папе 45 лет.
50. Длина бульвара равна 108 + 69 = 177
шагам. Число насчитанных деревьев равно 37 +
+ 23 =60. Число деревьев на расстоянии 177
шагов составляет 60 — 1 = 59 (одну и ту же липу,
от которой начали отсчет, мы сосчитали
дважды). Следовательно, расстояние между двумя
соседними липами равно 177 : 59 = 3 шагам.
51. Двадцать лет назад (13 + 7) дядя был
вдвое моложе, чем теперь. Следовательно,
теперь дяде 40 лет.
52. Уходя из дому, я завел свои стенные часы
и пустил их. Благодаря этому я смог узнать,
сколько времени был в отсутствии. Если из
этого времени вычесть то время, которое я
пробыл у товарища (а оно известно), то получится
время, потраченное на ходьбу в оба конца.
Разделив его пополам, я узнаю, сколько времени
мне понадобилось, чтобы добраться от товари-
78

ща до своего дома. После этого остается только
прибавить это время к тому, когда я вышел от
приятеля.
53. Каждый час велосипедисты сближались
на 100 верст. Следовательно, они встретились
через 3 часа (300 : 100 = 3). Так как муха
вылетела одновременно с велосипедистами и
летала, пока они не встретились, ясно, что она
летала в продолжение 3 часов, пролетая
каждый час по 100 верст. Всего она пролетела
300 верст.
54.
2
9
4
7
5
3
6
1
8
55.
X
X
X
X
X
X
56. Чтобы «угадать» задуманное число,
которое находится, как вам сообщили, в 1, 2, 3
и 5-м рядах, сложите числа, набранные под
каждым из этих рядов, то есть 1 + 2 + 4+16 =
= 23. Таким же образом можно угадать любое
другое задуманное число. Вы можете
составить «волшебную таблицу», заменив числа от
1 до 31 различными (мужскими или
женскими) именами.
57. Сумма ударов часов равняется удвоенной
сумме чисел ряда 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и
12. Вычисляем эту сумму по выведенному пра-
79

вилу: 1 + 12 = 13, 13 х 12 = 156. Делить эту
сумму на 2 в этой задаче не следует, так как
результат все равно пришлось бы удвоить. Таким
образом, за сутки часы пробьют 156 раз.
58. Число журавлей в стае равно сумме чисел
ряда 1,2, 3,4,5,6,7,8,9, 10, 11, 12, 13, 14 и 15.
Эта сумма равна (1 + 15) х 15) : 2 = 120.
59. Шесть спичек следует располо- /\ t
жить следующим образом: сначала из у у
3 спичек построить треугольник, за- \\ /»
тем из 3 других спичек сложить дру- ™
гой треугольник и наложить второй
треугольник на первый так, чтобы получилась фигура в
форме шестиугольной звезды.
«••Н IIIЛ к
61.
IV IV VI VI
1Л Л1
62.
63. Две спички следует положить на угол
стола так, чтобы края стола были двумя
сторонами квадрата.
80

64. EED 65-
pi—|
67. д д
68. После того как дедушка выложит 1
спичку из правой руки, 1 из левой, 1 из правой, 1
из левой и 1 из правой (разбойники отпустили
овец), зрители полагают, что в каждой руке у
него находится по одной спичке. На самом
деле в этот момент у дедушки в левой руке
находятся 2 спички. В этом и заключается весь
фокус задачи.
«да
7 спичек
70. 4 и 8 (см. решение задачи № 19).
72. Вы выиграете, если, называя очередное
число, постараетесь сделать так, чтобы назвать
число 89 выпало вам. А для этого вам
необходимо постараться устроить так, чтобы вы, а не
ваш соперник называли числа 12, 23, 34, 45, 56,
67, 78 и, наконец, 89. В этом случае, какое бы
число (не больше 10) ни прибавил ваш товарищ
к 89, вы будете иметь возможность закончить
игру торжествующим возгласом: «Сто!»
81

73. Если ваша попытка нарисовать фигуру,
изображенную на рисунке, с соблюдением всех
условий не увенчается успехом, то
воспользуйтесь следующим советом: рисуя фигуру,
старайтесь запоминать направление проведенных
вами линий и, глядя в зеркало, не
руководствуйтесь тем, что оно вам показывает.
74. Из фигуры А вырезается часть а и
прикладывается к оставшейся части так, что
получается квадрат Б (с квадратной дырой
посередине).
А.
г

Аля детей
старшего возраста

I. Задачи-шутки
1. Сколько концов у 5 палок? У 5 с
половиной палок? У 6 с четвертью палок?
2. а) Разделите полсотни на {/г б)
Разделите рубль на У3.
3. На лугу близ рощи паслись в течение 1
часа 2 одинаковые по своим достоинствам
лошади с совершенно одинаковым аппетитом.
Отличались они друг от друга только тем, что
у одной из них хвост был вдвое короче, чем
у другой.
Какая из лошадей съела больше травы, если
они начали и закончили есть одновременно?
85

4. Захватив с собой несколько орехов,
встаньте посреди комнаты и очертите вокруг себя
мелом круг лишь такой величины, чтобы вы
могли в нем поместиться, а затем попробуйте
положить в каждый из углов комнаты по ореху,
не выходя из начерченного вами круга.
5. Три брата жили в одной комнате.
Каждый из них имел свой висячий замок и ключ,
подходивший только к этому замку.
Как братья должны были запирать дверь
своей комнаты, чтобы каждый из них мог войти
к себе в комнату, имея только свой ключ?
6. Как можно получить 4, отняв от девяти
половину девяти?
7. Как разделить 1888 на две равные части,
чтобы в каждой из них получилась тысяча?
8. Богач, умирая, завещал все свое состояние
тому монастырю, который возьмется отслужить
по нему столько заупокойных обеден, чтобы
86

число их составляло половину числа лет,
которые остались монастырю существовать после
смерти завещателя. Один монастырь взялся
исполнить волю умершего. Как он это сделал?
9. Из гавани французского города Гавра
ежедневно ровно в полдень отправляется в
Нью-Йорк почтовый пароход. Из Нью-Йорка
ежедневно и тоже ровно в полдень в Гавр
отправляется такой же почтовый пароход. На
переход через Атлантический океан как в
одну, так и в другую сторону требуется ровно
7 суток.
Сколько пароходов встретит на своем пути
пароход, отплывший из Гавра в понедельник
7 июля строго по расписанию, ровно в
полдень?
10. а) Изобразите число 31 шестью (или
пятью) тройками, б) Изобразите число 100
четырьмя одинаковыми цифрами.
11. На лесопильном заводе машина
отпиливает каждую минуту от бревна кусок длиной
в 710 метра.
87

За сколько минут такая машина распилит
бревно длиной в 1 метр?
12. Двум чудакам американцам надоело
играть на бегах, и они вздумали держать друг с
другом следующее пари: их прекрасные
скакуны должны пробежать от дома 2 километра до
берега реки, но выигрывает пари тот, чья
лошадь придет к реке не первой, а последней.
Приготовившись, владельцы сели на своих
лошадей, но никто из них не решался
тронуться с места из боязни проиграть. Долго
стояли они так, не зная, как выйти из этого
затруднительного положения.
Видя их беспомощность, один из стоявших
поблизости зрителей подошел к ним и что-то
шепнул каждому из них. Владельцы слезли с
лошадей, потом снова сели в седла и во весь
дух помчались к реке. После этого один из
них выиграл пари.
Что посоветовал владельцам лошадей
зритель и как могло быть выиграно пари при
соблюдении изложенных выше условий?
П. Забавные исчезновения
и остроумный дележ
13. Однажды хитрый цыган предложил
бедному мужичку легкий способ быстро
разбогатеть. Мужичок поверил цыгану и поплатился
88

за это: он не только не разбогател, но и
лишился даже тех денег, которые у него были.
Спустя некоторое время наш мужичок
случайно встретил около того же моста цыгана и
задумал перехитрить его.
— Знаешь, — сказал мужик, — я хочу еще
раз попытать счастья, только теперь давай
условимся иначе: каждый раз, когда я
перейду мост, я буду отдавать тебе только 4
копейки.
— Ладно, — согласился цыган, — но тогда
и твои деньги будут увеличиваться не вдвое,
как прежде, а лишь в полтора раза.
Мужик согласился и пошел через мост, а
цыган стал его дожидаться. Каждый раз, когда
он возвращался к цыгану, его деньги
увеличивались в полтора раза, и мужичок аккуратно
уплачивал цыгану обещанные 4 копейки.
Перейдя мост в пятый раз и отдав
цыгану 4 копейки, он решил посмотреть, сколько
денег у него стало. Подсчитав наличность,
мужичок увидал, что у него на 4 копейки
больше половины того, что было
первоначально.
Сколько денег было у мужика вначале?
Получил ли он на этот раз прибыль или остался
в убытке?
14. Две торговки принесли на базар
яблоки и решили, сложив их вместе, торговать
сообща. У каждой из них было по 30 яблок. Пер-
89

вая собиралась продавать за копейку пару
яблок, вторая — за копейку 3 яблока. Первая
рассчитывала выручить от продажи 15 копеек,
вторая — 10 копеек, а обе вместе — 25 копеек.
Сложив яблоки в одну корзину, они решили
продавать 5 яблок за две копейки, рассуждая,
что если одна продаст на копейку 2 яблока,
а другая на копейку 3 яблока, то это все равно
что продать за две копейки 5 яблок.
Распродав яблоки по две копейки за пяток, торговки
стали подсчитывать выручку. Они очень
удивились, когда насчитали всего 24 копейки.
Торговки стали проверять яблоки по пяткам и
насчитали 12 пятков (то есть 5 х 2 = 60 яблок,
как и было), сосчитали 12 раз по две
копейки. «Куда же девалась копейка?» — думали
они.
Помогите найти недостающую копейку.
15. Три торговца, не желая переманить друг
у друга покупателей, решили продавать свои
апельсины по одинаковой цене. У одного
торговца было 50 апельсинов, у другого 30, у
третьего только 10. Торговцы условились, что
цену можно изменять, лишь бы продажа
одновременно производилась у всех трех торговцев
по одной и той же цене. Когда весь товар был
распродан, то оказалось, что каждый из
торговцев выручил за свои апельсины 50 копеек.
Как и по какой цене они должны были
продавать апельсины?
90

16. Как разделить поровну 5 яблок между
шестью мальчиками, не разрезая ни одного
яблока на 6 и более равных частей?
17. Дед, отец и сын встретили во время
прогулки знакомого, который спросил, сколько
каждому из них лет. «Нам 131 год и 10
месяцев», — ответил за всех дед и важно зашагал
вперед. Тогда их знакомый, продолжая
интересоваться их возрастом, спросил отца: «Ну,
скажите же, сколько вам лет?» — «Мне вместе
с сыном 57 лет и 2 месяца, — отвечал отец, —
а сын на 19 лет и 10 месяцев моложе меня».
Так знакомому и не пришлось узнать, сколько
лет каждому из них.
Сколько лет деду, отцу и сыну?
18. Охотник, проголодавшись на охоте,
обратился к двум пастухам с просьбой покормить
его. Посоветовавшись, пастухи приняли его
обедать. Один пастух имел
три кушанья, а другой —
два. По окончании обеда,
во время которого все ели
поровну, охотник
поблагодарил пастухов дал им
50 копеек и ушел. Пастухи
стали было делить
полученные деньги, но у них
ничего не вышло.
Пришлось вернуть охотника,
91

который, узнав, в чем дело, разделил между
пастухами 50 копеек так, что каждый из них
получил ту долю, которая ему причиталась.
Как охотник произвел дележ?
19. Однажды двое арабов сидели под
пальмой и собирались обедать. К ним подошел
третий араб и предложил присоединить к
обеду свои припасы. Всю провизию разделили
поровну на троих. У первого араба был
кувшин молока, у второго — один хлеб и у
третьего — 6 фиников. По окончании трапезы
третий араб сказал: «Так как каждый из вас
внес больше меня, вот вам 20 одинаковых
медных монет, разделите их между собой».
Как арабы разделят полученные деньги,
если известно, что 4 кувшина молока стоят
столько же, сколько 3 хлеба, а один кувшин
молока ценится так же, как 36 фиников?
20. Ехали два крестьянина и нашли 3
бочонка: один восьмиведерный с вином, другой —
пятиведерный — пустой и третий — трехве-
92

дерный — тоже пустой. Крестьяне задумали
поделить вино поровну тут же, на месте, с
помощью этих трех бочонков, не прибегая к иной
посуде.
Как они разделили вино?
21. Сельский виноторговец призвал трех
своих сыновей и велел поделить им поровну
между собой 7 полных бочонков с вином, 7 таких
же бочонков, наполненных вином наполовину,
и 7 таких же бочонков, но пустых.
Как сыновья могут поделить вино и
бочонки, чтобы каждому досталось и одинаковое
количество вина, и одинаковое число
бочонков, если переливать вино из одного бочонка
в другой нельзя?
22. На скотном дворе гуляли гуси и
поросята. Хозяин двора и его сын вышли на двор.
Сын и спрашивает: «Папа, сколько у нас гусей
93

и сколько поросят?» — «Если считать по
головам, то на дворе 25 голов, а если по ногам, то
70 ног».
Сколько было гусей и сколько поросят?
23. Хозяйка накопила два горшка масла:
один в 8 фунтов, другой в 3 фунта, а третий
горшок в 5 фунтов остался у нее пустым.
Перед праздником хозяйке понадобилось
одолжить 6 фунтов масла соседке.
Как она это сделала, если меркой могли
служить только те же три горшка?
24. Помещик нанял две партии крестьян и
обещал по окончании работы дать каждой
партии по 5 мер овса. Когда работа была
окончена, помещик велел отдать в распоряжение
работавших 3 мешка: один мешок с 10
мерами овса, а два других, вместимостью 7 мер и
3 меры, пустые. Других мешков или других
емкостей у крестьян не было, однако они
разделили овес так, что каждая партия унесла по
5 мер овса.
Как крестьяне произвели этот дележ?
25. В школе учится столько мальчиков,
сколько и девочек. Однажды учитель принес
в класс 234 ореха и разделил их: каждому
мальчику досталось по 5 орехов, а каждой
девочке — по 4 ореха. Но так как девочки оби-
94

делись на такую несправедливость, учителю
пришлось еще раз принести с собой орехи
и разделить их так, чтобы в конце концов
всем досталось поровну, а именно по 6
орехов. Сколько орехов принес учитель во
второй раз?
III. Задачи, требующие большей
сообразительности и более сложных
вычислений
А) Целые числа
26. В школе учатся 13 детей. У мальчиков
столько зубов, сколько у девочек пальцев на
руках и на ногах1. Сколько в школе мальчиков
и сколько девочек?
27. Колокольня высотой
в 40 аршин состоит из двух
ярусов. В нижнем ярусе
столько аршин, сколько в
верхнем футов. Какова
высота каждого яруса?
28. Дорога длиной 2
версты от лесной сторожки до
1 Предполагается, что у каждого мальчика и каждой
девочки по 32 зуба (как у взрослых людей).
95

сельской церкви шла сначала лесом, а потом
открытым полем. Два сына лесника, Сергей и
Николай, вздумали измерить длину этой
дороги с разных концов. Сергей шел от
сторожки и мерил палкой длиной в 1 сажень, а
Николай шел от церкви и мерил палкой
длиной в 1 фут. На опушке леса они встретились
и, к своему удивлению, обнаружили, что у
каждого из них палка уложилась одинаковое
число раз. На каком расстоянии дорога
тянется лесом?
29. К Володе на день рождения собрались
гости — все его друзья, и каждый из них
пришел со своей сестрой. Если бы три девочки
остались дома, то мальчиков (не считая
самого Володи) было бы вдвое больше, чем
девочек. А если бы трое товарищей не пришли
в гости, то было бы наоборот.
Сколько гостей собралось у Володи?
30. У мальчика столько сестер, сколько и
братьев, а у его сестры сестер вдвое меньше,
чем братьев.
Сколько всего братьев и сколько всего
сестер в этой семье?
31. В один прекрасный воскресный день,
ровно в 6 часов утра, гусеница вздумала
взобраться с земли на вершину дерева высотой
96

12 футов. За день она успевала подняться
на 4 фута, а ночью во сне сползала вниз на
3 фута.
Когда гусеница достигнет вершины дерева?
32. Найти двузначное число, которое в 7 раз
больше, чем число его единиц.
33. Два массивных колеса, большое и
маленькое, наглухо скреплены между собой и
надеты на одну ось. Оба колеса поставлены на
особый двойной рельс. Известно, что, когда
колесо совершает один оборот, оно проходит
расстояние, равное длине окружности самого
колеса.
Большое колесо После одного оборота
.Малое колесо
А В
Большое колесо, катясь по своему рельсу,
совершило один оборот и, стало быть, прошло
расстояние от А до Б. Маленькое колесо,
наглухо скрепленное с большим, также должно
4 Н. Аменицкий и др.
97

Jn
совершить только один оборот и
пройти за это время расстояние от
В до Г. Эти расстояния, как видно
из прилагаемого справа чертежа,
совершенно одинаковы. Но
расстояние АБ — длина окружности
большого колеса, а ВГ — длина
окружности маленького колеса! Выходит, что
большая длина равна меньшей?!
Где ошибка в наших рассуждениях?
Б) Дробные числа
34. Племянник спросил дядю, сколько тому
лет. Дядя ответил: «Если к половине
прожитых мной лет прибавить еще 10 лет, то
получится число, которое составит 3/4 моего
возраста».
Сколько лет дяде?
35. Отец привел сына на приемные
экзамены в школу. Тот успешно справился с
вопросами по всем предметам. Осталась одна
арифметика. Учитель спросил: «Можешь ли
ты сказать, сколько учеников будет в твоем
классе? Известно, что, если к числу учеников
прибавить еще столько, да еще полстолько, да
четверть столько, да тебя самого, получится
100 учеников».
Сколько учеников в классе?
98

36. Рассказывают, что некто при встрече с
греческим философом и математиком
Пифагором спросил того: «Который час?» Пифагор
ответил: «До конца суток осталось дважды две
пятых того, что уже прошло от начала».
Спрашивавший не сразу сообразил, в котором часу
произошла встреча. Который был час?
37. Торговка продавала цыплят. Одна
кухарка купила у нее половину всех цыплят и
еще полцыпленка. Другая кухарка купила
половину всех оставшихся цыплят и еще
полцыпленка. Наконец, третья кухарка купила
половину всех оставшихся цыплят и еще
полцыпленка, после чего у торговки не осталось
ни одного цыпленка.
Сколько у нее было цыплят, если все
купленные кухарками цыплята были живыми?
38. Во время прогулки по бульвару я и мой
товарищ решили измерить длину бульвара
шагами, условившись считать наш шаг за аршин.
Начав измерение от ближайшей липы, мы
пошли от нее в противоположные стороны.
99

Я намерил до конца бульвара 51 аршин, а мой
товарищ — 48 аршин. Кроме того, идя по
бульвару, мы считали липы, мимо которых
проходили. Я насчитал 35 лип, а мой
товарищ — 33 липы. И он, и я начали считать с
той липы, от которой пошли.
На каком расстоянии друг от друга
посажены липы?
39. Два крестьянина, Петр и Иван, пришли
покупать избу, за которую хозяин просил
38 рублей. Ни у того ни у другого таких денег
не было. Тогда Петр шутя
сказал Ивану: «Если бы ты
дал 2/3 своих денег, то я
смог купить избу». Иван
возразил на это: «Лучше
ты, Петр, дай мне 3/4
твоих денег, тогда я смогу
сделать эту покупку».
Сколько денег было у
каждого из крестьян?
40. Араб, чувствуя близкую свою кончину,
призвал трех своих сыновей и сказал им:
«Когда я умру, разделите между собой мое стадо
верблюдов. Пусть старший из вас возьмет {/2
всего стада, средний 1/4, а младший !/5». Когда
араб умер, сыновья хотели разделить стадо,
как завещал отец, но у них ничего не вышло,
так как в отцовском стаде оказалось 19 вер-
100

блюдов. На их счастье, мимо проходил мулла,
слывший за умного человека. Узнав, в чем
дело, он предложил сыновьям занять у соседа
на короткое время одного верблюда. Когда
этот верблюд был приведен, мулла спросил:
«Сколько у вас теперь верблюдов?» —
«Двадцать», — отвечали сыновья. Тогда мулла
приказал старшему сыну взять половину стада,
то есть 10 верблюдов, среднему — четвертую
часть, то есть 5 верблюдов, а младшему —
пятую часть, то есть 4 верблюда. «Сколько
верблюдов вы разобрали?» — спросил мулла.
Братья сосчитали и ответили: «Девятнадцать».
«Ну а оставшегося верблюда верните
соседу», — сказал мулла.
Все ли участники дележа рассуждали
правильно и не заблуждался ли кто-нибудь из них?
41. Три брата пришли на постоялый двор и
спросили себе картошки. В ожидании, пока
поспеет ужин, братья заснули. Первым про-
101

снулся старший брат и, увидав
на столе блюдо с картошкой,
съел свою долю и опять лег
спать. Немного спустя
проснулся средний брат и, не
подозревая, что старший уже
поужинал, а думая, что он
начинает есть первым, съел свою
долю и тоже лег спать.
Наконец, проснулся младший брат
и, рассуждая так же, как и второй, отсчитал
свою долю, съел ее и лег спать. После него на
блюде осталось еще 24 картофелины.
Сколько всего было сварено картошки и
каким образом должны разделить братья
оставшиеся картофелины?
42. В Нью-Йорке каждые два
часа происходит несчастный
случай со смертельным исходом
и через каждую У20 часа кого-
нибудь арестовывают.
Определите число несчастных случаев в
Нью-Йорке за год и число
арестованных за сутки.
43. Когда о ком-нибудь хотят сказать, что
он мало ест, говорят: «Он ест как птичка». Но
такое сравнение весьма неудачно. В этом
можно убедиться на таком примере. Птичка
(малиновка), которая весит 21 золотник, в те-
102

чение дня способна съесть такое количество
земляных червей (каждый из которых длиной
в 1 дюйм, весит У4 золотника), что все они,
будучи разложены на земле, вытянулись бы
на 2 сажени.
Каков вес червей, съедаемых птичкой за
день? Сравните его с весом самой птички.
44. Борода у человека растет, удлиняясь в
неделю на !/5 дюйма.
Предположим, что борода растет с
постоянной скоростью на протяжении всей жизни
человека.
Какой длины достигла бы борода у
мужчины, который не брился в течение 30 лет?
45. Сына спросили, сколько ему лет. Он
ответил: «Когда отцу было 28 лет, то мне
исполнилось лишь У4 того числа лет, которые я
прожил теперь, когда стал вдвое моложе отца».
Сколько лет сыну теперь?
46. Ягодное решето весит 13/5 фунта и стоит
16 копеек.
Почем за фунт следует заплатить за ягоды,
чтобы не потерпеть убытка, принимая решето
103

в общий вес с ягодами, то есть платить за
решето не дороже, чем за ягоды?
47. Три брата разделили между собой 24
яблока так, что каждый из них получил столько
яблок, сколько ему лет. Младший брат,
которому досталось меньше всех яблок, остался
недоволен и предложил братьям следующее: «Я
оставлю себе только половину своих яблок, а
остальные разделю между вами поровну, а
затем пусть сначала средний, а потом и старший
братья поступят так же, как и я». Братья, не
подумав, согласились... и прогадали: яблок у всех
в результате оказалось поровну.
Сколько лет было каждому из братьев?
48. Ученик при решении задачи должен был
умножить некоторое число на 0,5 и к
полученному произведению прибавить 3. Вместо этого
ученик по ошибке разделил число на 0,5 и от
полученного частного отнял 3. Несмотря на
такие ошибки, он получил правильный ответ.
Какое число встретилось ученику в задаче?
49. Даны два числа: 2 и 3. Какой знак
следует поставить между ними, чтобы получить
число больше двух, но меньше трех?
50. В понедельник в час дня от берегов
Камчатки к берегам Аляски отправился
пароход, делающий по 25 верст в час. В 7 часов
104

вечера того же дня вслед за ним отошел
парусник, развивавший среднюю скорость на !/5
меньше скорости парохода. На полпути на
пароходе случилась поломка в машине.
Простояв 2 часа без движения, он двинулся дальше,
но уже вдвое медленнее.
В какой день и час парусник догнал
пароход, если весь путь до Аляски и обратно
пароход с исправной машиной мог бы пройти за
32 часа?
51. Из двух городов, Нижнего Новгорода
и Вязников, расстояние между которыми
330,66 версты, в один и тот же момент
выезжают два велосипедиста и мчатся навстречу
друг другу: один со скоростью 50,7 версты в
час, другой — 49,5 версты в час. С
велосипедистом, выехавшим из Вязников, в момент его
отправления вылетает муха и летит тоже
навстречу нижегородскому велосипедисту со
скоростью 100 верст в час. Встретив
велосипедиста, муха тотчас поворачивает назад и летит
навстречу первому. Повстречав того, она (все
с той же скоростью) летит обратно, пока не
встретит снова второго велосипедиста. И так
муха летает от одного велосипедиста к другому
до тех пор, пока велосипедисты не
встречаются. Тогда муха преспокойно садится на спину
одному из них.
Сколько верст успела пролететь муха до
встречи велосипедистов?
105

52. Из деревни, расположенной у
шоссейной дороги, выехал в город крестьянин,
проезжавший в час 6У2 версты. Одновременно с
ним в том же направлении из другой деревни,
отстоящей от первой на 9 верст, вышел его
брат, который проходил за час 4!/4 версты.
У одного из братьев была собака, которая
начала бегать от одного брата к другому со
скоростью 15 верст в час и продолжала так бегать
до тех пор, пока ехавший крестьянин не
догнал брата.
Сколько верст успела пробежать собака?
Зависит ли это расстояние от того, кому из
двух братьев (едущему или пешеходу)
принадлежала собака?
53. Во время охоты собака погналась за
зайцем, который находился от нее на расстоянии
100 саженей. Зайцу удалось спастись от
преследования. Во время завтрака на открытом
воздухе охотники разговорились, и один из
них заявил, что ничуть не жалеет об убежав-
106

шем зайце, так как, по его соображениям,
собака все равно никогда не догнала бы зайца,
даже если бы бежала в 10 раз быстрее его. «Как
так? — воскликнули в один голос его
собеседники. — Этого не может быть!» — «Нет, все
обстоит именно так, как я сказал, — возразил
охотник. — Судите сами. Собаку отделяло от
зайца расстояние в 100 саженей. Когда собака
пробежит это расстояние, заяц, который
бежит в 10 раз медленнее собаки, успеет
пробежать 10 саженей. Когда собака пробежит и
эти 10 саженей, заяц успеет продвинуться еще
на 1 сажень. Когда собака пробежит эту
сажень, заяц успеет пробежать !/10 сажени и,
стало быть, опять окажется впереди собаки на
!/10 сажени. Рассуждая далее таким же
образом, вы убедитесь в том, что заяц всегда, хотя
бы на очень небольшое расстояние, будет
находиться впереди собаки!»
Слушавшие охотники были поражены
явной несообразностью, и у них начался
оживленный спор по этому поводу.
Правильно ли рассуждал охотник и если
нет, то почему?
107

IV. Затруднительные положения
54. Дело было в Америке. Как-то раз
подошли к реке англичанин, негр и индеец,
каждый со своей женой. Всем нужно было
переправиться на другой берег. В их распоряжении
была только одна лодка, да и то без гребца,
способная вместить лишь
двоих. Договорившись
между собой, мужчины
решили было приступить
к переправе, как вдруг
выяснилось, что ни одна
из жен не желает
переправляться в лодке с
чужим мужем или
оставаться на берегу в мужском
обществе без своего мужа. Мужья
призадумались, но все же сумели догадаться, как
выполнить желание своих жен.
Как они сумели переправиться через реку?
55. Товарный поезд из 26 вагонов
приближается к станции железной дороги. Его
нагоняет по тому же пути пассажирский поезд
из 14 вагонов, который необходимо
пропустить вперед. На станции в сторону от
главного пути отходит боковая ветка (тупик),
который может вместить только 13 вагонов.
Хотя тупик и не вмещал целиком товарный
108

поезд, начальник станции сумел пропустить
пассажирский поезд.
Как он это сделал?
А
Разъезд
■ •
Б
Примечание. Поезда могут давать и
задний ход.
56. По одноколейной железной дороге идут
навстречу друг другу поезда. В каждом из них
по 18 вагонов. Разъезд, около которого они
встретились, может вместить только 9 вагонов
и паровоз. Вследствие такого затруднения у
разъезда поезда остановились, так как
машинисты сначала не знали, как им быть. Но
потом, маневрируя, сумели разъехаться
благополучно. Как им это удалось?
57. По бурному морю мчится парусное
судно. На нем несколько пассажиров, среди
которых два скотопромышленника — грек и
турок. Скотопромышленники везут с собой по
15 быков каждый; грек везет быков бурой
масти, а турок — черной. Вдруг поднимается
буря. Волны захлестывают судно и грозят
потопить его. Значительную часть груза
необходимо срочно сбросить в море. Пассажиры
решают выкинуть за борт половину своего
имущества. Каждому скотопромышленнику
109

необходимо расстаться с половиной быков.
Переговорив между собой, они решают
предоставить выбор случаю: поставить всех
быков в ряд и, отсчитывая по порядку от 1 до 9,
бросать в воду каждого девятого быка до тех
пор, пока на корабле не останется только
15 быков. Скотопромышленник-грек
исхитряется и расставляет быков так, что за бортом
оказываются все 15 быков черной масти, а
15 быков бурой масти (то есть его
собственных) остаются на судне.
Как были расставлены быки?
58. На полотне железной дороги стоят
паровоз и два вагона А и Б в таком порядке, как
это показано на рисунке. Требуется
переформировать этот короткий состав так, чтобы
вагоны поменялись местами (то есть чтобы вагон
А оказался справа, а вагон Б — слева). Для
этого имеется запасной путь. Но дело в том,
что через запасной путь перекинут неудачно
построенный мост, под которым вагоны
проходят свободно, а паровоз пройти не может
из-за трубы, которая не снимается и не
наклоняется.
Мост
Запасной путь
Паровоз Б Главный путь
по

59. Железнодорожные ветки расположены
так, что образуют с главным путем
треугольник. В одном из углов этого треугольника
имеется тупик, в котором может поместиться
один вагон (начальное расположение
паровоза и двух вагонов А и Б показано на
рисунке).
Требуется сцепить два вагона с
паровозом так, чтобы они стояли на главном пути в
следующем порядке: вагон Б — паровоз —
вагон А.
60. По шоссейной дороге ехали вместе
домой два велосипедиста, каждый со скоростью
15 верст в час. Когда им оставалось проехать
всего 40 верст, у одного из них сломался
велосипед, и он вынужден был отдать его в
починку. Не желая прерывать своего путешествия,
они решили выйти из затруднительного
положения следующим образом: отправиться даль-
111

ше — один на велосипеде, другой пешком.
Спустя некоторое время велосипедист
остановится, спрячет велосипед у шоссе и, оставив
условную метку, отправится дальше пешком.
Его товарищ, дойдя до того места, где спрятан
велосипед, продолжит свой путь на
велосипеде и догонит пешехода, тут они снова
поменяются ролями и, продолжая в том же духе,
закончат свой путь. Каждый путешественник
способен проходить пешком по 5 верст в час.
Где следует оставить велосипед в последний
раз, чтобы оба путешественника добрались до
дома одновременно? Дает ли описанный
способ выигрыш во времени (если да, то какой)
по сравнению с передвижением пешком?
Когда путешественники доберутся до дома, если
после поломки велосипеда они отправились в
путь ровно в полдень?
У. Любопытные особенности
некоторых чисел и действий с ними
61. Возьмите число 123 456 789 (которое,
как видите, запомнить совсем не трудно) и
попробуйте умножить его а) сначала на 9;
б) потом его же на 18; в) на 27; г) на 36; д) на
45; е) на 54; ж) на 63; з) на 72 и, наконец,
и) на 81. Умножив 123 456 789 на
приведенные выше девять чисел, вы получите девять
произведений, которые отличаются тем, что
112

1) легко запоминаются; 2) каждое из них
получается из первого произведения другим,
более простым способом, чем непосредственное
умножение.
В чем состоит этот более легкий способ?
62. Умножив одно и то же число 142 857 на
2, 3, 4, 5 и 6, вы получите произведения, в
которых легко заметите одну интересную
особенность1.
В чем состоит эта особенность?
63. Число 2519 обладает любопытным
свойством, которое вы легко обнаружите, разделив
это число на 2, 3, 4, 5, 6, 7, 8 и 9.
64. Напишите число, изображаемое
первыми девятью цифрами, начиная с 9 и до 1, и
вычтите из него число, написанное теми же
цифрами, но в обратном порядке.
Полученная разность обладает таким же свойством,
как уменьшаемое и вычитаемое.
В чем заключается это свойство?
65. Напишите любое трехзначное число
(первая и последняя цифры которого должны
быть различными). Подпишите под ним
число, изображенное теми же цифрами, но в об-
1 При умножении на 7 получается произведение,
не обладающее этой особенностью, но тоже весьма
любопытное.
113

ратном порядке. Вычтите из большего числа
меньшее. Полученная разность обладает
такими свойствами, которые дают возможность
угадать ее, не только не зная первого числа,
но и не глядя на самый ход действий: стоит
узнать лишь последнюю цифру этой
разности. Поупражняйтесь на нескольких
примерах и постарайтесь подметить
вышеупомянутые свойства получающихся разностей.
Пояснение. 1) Возьмем, например,
число 652. Число, изображаемое теми же
числами, но в обратном порядке, есть 256.
Вычитаем из большего числа меньшее: 652 — 256 =
= 396. Зная последнюю цифру 6 (которую вы
можете спросить у того, кто задумал число и
производил с ним действия), но не зная
самого числа 652, вы должны угадать полученную
разность, то есть 396.
2) Возьмем еще одно число, например 580.
Вычитать из него придется число 085 : 580 -
- 85 = 495. Каким образом, зная только
цифру 5, узнать всю разность 495?
66. Напишите любое трехзначное число
(первая и последняя цифры которого должны
быть различными). Переставьте цифры этого
числа в обратном порядке и из большего
числа вычтите меньшее. После этого переставьте
цифры в обратном порядке в полученной
разности и сложите разность и ее «зеркальное
отражение».
114

Проделав несколько таких упражнений,
постарайтесь подметить любопытную
особенность суммы, получаемой от таких действий
с любым трехзначным числом.
67. Произведите указанные действия:
12 х 9 + 3 =
123 х 9 + 4 =
1234 х 9 + 5 =
12 345 х 9 + 6 =
и т. д.
Результат, который вы получите в каждом
из этих случаев, отличается особенностью,
которая бросается в глаза.
68. Близкую (хотя и не совсем такую же)
особенность вы обнаружите, выполнив
следующие действия:
9x9+7=
98 х 9 + 6 =
987 х 9 + 5 =
9876 х 9 + 4 =
и т. д.
69. В старинных итальянских рукописях
встречается любопытный способ умножения
многозначных чисел, который известен под
названием мусульманского (или индусского)
метода. Предположим, что нам надо
перемножить числа 9347 и 258. Для этого начертите на
клетчатой бумаге три ряда по четыре клетки в
115

\ 2
7 \
\ 5
4 \
\ 8
1 \
\ 4
2 \
\ 5
1 \
\ 6
\ 2
з\
\ 0
2\
\ 8
\ 6
5\
\ 5
3 \
\ 4
1 \
каждом. Наверху
напишите слева направо цифры
множимого 9, 3, 4 и 7, а
слева снизу вверх цифры
множителя 2, 5 и 8.
Проведя диагонали, как
показано на рисунке, можете
начинать умножение с любой цифры
множимого на любую цифру множителя.
Получающееся произведение (двузначное
число) следует вписывать в
соответствующий квадрат так, чтобы цифра десятков
стояла в левом отделении квадратика, а цифра
единиц — в правом. Когда все клетки
окажутся заполненными, остается произвести
сложение по направлению диагоналей. В нашем
примере получается произведение 2 411 526
(читай слева направо и вверх).
В настоящее время для школьников этот
метод представляет интерес как экскурс в
прошлое.
VI. Ряды чисел, суммы которых
можно получать, не производя
сложения этих чисел
Пояснение. Если вы вздумаете узнать,
чему равна сумма чисел, стоящих в ряду 1,2,
3, 4, 5, 6, 7, 8, то вы легко можете найти ее,
не складывая самих чисел.
116

Возьмите 8 карточек и нарисуйте на
одной из них 1 кружок, на другой 2 кружка, на
третьей 3 кружка и т. д. Затем разложите эти
карточки в ряд по порядку, начиная с той,
на которой нарисован 1 кружок. Сделав еще
8 таких же карточек, разложите их под первым
рядом в обратном порядке (то есть под
карточкой с 8 кружками положите новую
карточку с 1 кружком, под карточкой с 7
кружками — новую карточку с 2 кружками и т. д.).
Нетрудно видеть, что наши два ряда
образовали 8 столбиков по две карточки в каждом.
Сосчитайте, сколько кружков в каждом таком
столбике. Оказывается, что, какой бы столбик
мы ни выбрали, в нем всегда 9 кружков.
Число 9 есть сумма кружков на первой и
последней карточках в ряду.
Наши два ряда состоят из 8 столбиков, и в
каждом столбике на двух карточках в сумме
9 кружков. Значит, повторив 9 кружков 8 раз,
вы узнаете, сколько всего кружков в обоих
рядах:
9 х 8 = 72 кружка, или (1 + 8) х 8 =
= 72 кружка.
117

Теперь уже совсем нетрудно узнать, сколько
кружков в одном ряду (первом или втором,
безразлично). Для этого стоит лишь разделить
72 кружка на две части:
72 : 2 = 36 кружков.
Следовательно,
1+2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 36.
Посмотрим, что нам пришлось сделать для
того, чтобы получить сумму:
1)8+ 1 = 9, то есть сложить первое и
последнее числа нашего ряда;
2) 9 х 8 = 72, то есть полученную сумму
умножить на столько, сколько чисел в ряду,
3) 72 : 2 = 36, то есть произведение
разделить пополам.
А
Б
Все, что сейчас было сказано о
складывании чисел такого ряда, как 1, 2, 3, 4, 5, 6 и 7,
можно легко представить себе наглядно, если
воспользоваться клетчатой бумагой. Возьмите
на такой бумаге 7 рядов по 8 клеток в каждом
и разделите такой прямоугольник на две
(совершенно одинаковые) части А и Б так, как
показано на рисунке, жирной линией. Посмо-
118

трите повнимательнее сначала только на часть
А, и вы увидите, что в ней в верхнем ряду
находится 1 квадратик, во втором ряду — 2
квадратика, в следующем ряду — 3 квадратика и
т. д., а в последнем (нижнем) ряду — 7
квадратиков. Таким образом, в части А содержится
всего 1+2 + 3 + 4 + 5 + 6 + 7 квадратиков,
то есть как раз сумма чисел нашего ряда. Чтобы
узнать, чему равна эта сумма, можно,
конечно, сложить все эти числа, и тогда мы
получим 28. Но сделать это не всегда бывает легко,
и вот почему.
Представьте себе, что в нашем ряду
находились бы числа от 1 до 500. Тогда пришлось бы
складывать 500 чисел, а это, разумеется, и
долго, и скучно. Вместо этого проще поступить так:
на нашем чертеже имеется 7 рядов по 8 клеток,
то есть 7 х 8 = 56 клеток. В части А клеток вдвое
меньше (так как части А и Б совершенно
одинаковы), то есть 56 : 2 = 28 клеток.
Точно таким же образом можно узнать и
сумму чисел от 1 до 500. Для этого надо
только выполнить следующие действия:
(500 х 501) : 2 = 25 250.
Это, конечно, гораздо короче, чем
выполнять сложение.
Рассмотрим еще один пример.
Предположим, что вам надо поскорее
сложить числа 2, 5, 8, 11, 14, 17 и 20.
Этот ряд отличается от первого тем, что
здесь каждое число больше предыдущего на
119

3 единицы, а не на одну, как было в первом
примере.
Не смущайтесь: и в этом случае можно
воспользоваться уже известным вам приемом.
1) Сложите последнее число с первым: 2 +
+ 20 = 22. 154 |_2_
2) Умножьте эту сумму на 7 (в _14 \тГ
новом ряду 7 чисел): 22 х 7 = 154. и
3) Разделите полученное произ- -14
ведение на 2. 0
Попробуйте теперь проверить полученный
ответ, сложив все числа нашего ряда, и вы
убедитесь, что решили задачу правильно и
притом достаточно быстро.
Решим теперь другую задачу.
Возьмем опять ряд чисел: 2, 5, 8, 11, 14, 17,
20, 23 и т. д.
В этом ряду числа идут, увеличиваясь на
3 единицы:
2-е число 5 = 2 + 3,
3-е число 8 = 2 + 3 + 3,
4-е число 11 = 2 + 3 + 3 + 3,
5-е число 14 = 2 + 3 + 3 + 3 + Зит. д.
Отсюда видно, что любое число нашего ряда
можно составить из первого числа и одной,
двух, трех и т. д. троек.
При этом заметьте следующее.
Чтобы получить, например, третье число,
надо к первому числу прибавить 2 тройки.
Чтобы получить четвертое число, надо к
первому числу прибавить 3 тройки. Чтобы по-
120

лучить пятое число, надо к первому числу
прибавить 4 тройки. Одним словом, чтобы
получить какое-нибудь число из нашего ряда,
надо к первому числу прибавить столько
троек, сколько чисел находится в ряду перед этим
числом.
Например, узнаем тринадцатое число в
нашем ряду. Для этого к первому числу, то есть
к 2, прибавим 12 троек, то есть 36:
13-е число 2 + 36 = 38.
Или 24-е число:
24-е число 2 + 23 х 3 = 2 + 69 = 71.
Ниже вы найдете несколько задач, для
решения которых можете употребить новый
прием, с которым только что
познакомились.
70. Узнайте сумму всех целых чисел от 1
до 20.
71. Узнайте сумму всех целых чисел от 1
до 100.
72. Узнайте сумму всех целых чисел от 4
до 50.
73. Узнайте сумму всех целых чисел от 10
до 70.
74. Найдите сумму чисел 3, 5, 7, 9, 11, 13,
15, 17 и 19.
121

75. Найдите сумму чисел 7, 10, 13, 16, 19,
22, 25, 28 и 31.
76. Сколько ударов делают часы с боем с
часу дня до 12 часов ночи?
77. Наводнение продолжалось ровно сутки.
В первый час вода в реке поднялась на 1 дюйм,
во второй — на 2 дюйма, в третий — на 3
дюйма и т. д.
На сколько прибыла вода в реке за сутки?
78. Пароход, отойдя от пристани, прошел за
первый час 25 верст. Но так как ветер был
попутный, пароход ускорял свой ход каждый час
на версту. На восьмом часу пути он шел уже
со скоростью 32 версты в час.
Какое расстояние прошел пароход за 8
часов?
79. Номера домов, находящихся на левой
стороне, все нечетные (то есть 1, 3, 5-й и т. д.),
а номера домов на правой стороне — четные
(то есть 2, 4, 6-й и т. д.).
Какова будет сумма номеров домов по
левой стороне и сумма номеров по правой
стороне улицы, если всего домов на этой улице
200? (Номера домов начинаются с 1-го.)
80. Однажды умный бедняк попросил у
скупого богача приюта на две недели, причем
сказал: «За это я тебе в первый день заплачу
122

1 рубль, во второй день — 2 рубля, в третий
день — 3 рубля и т. д. Словом, каждый день я
буду прибавлять тебе по одному рублю, так
что за один четырнадцатый (последний) день
я заплачу тебе 14 рублей. Ты же будешь мне
подавать милостыню: в первый день 1
копейку, во второй — 2 копейки, в третий день —
4 копейки и т. д., увеличивая каждый день
свою милостыню вдвое». Богач с радостью
согласился на такие условия, которые ему
показались выгодными.
Сколько прибыли принесла эта сделка
богачу?
Примечание. Сумму, которую должен
заплатить богач, вы вычислите, сложив
милостыню, подаваемую за все дни (см. также
рассказ «Богач и бедняк» в разделе X).
81. Найдите двадцать пятое число в таком
ряду, который начинается с 3, а каждое
последующее число в нем на 1 больше
предыдущего.
82. Найдите двадцать первое число в таком
ряду, который начинается с 5, а каждое
последующее число в нем на 2 больше
предыдущего.
83. У меня в комнате окно было отворено
с 2 часов дня. Я заметил, что за первый час
в комнату влетело 3 комара, за второй час —
123

5 комаров, за третий час — 7 комаров и т. д.
В 9 часов вечера я закрыл окно и хотел уснуть,
но комаров в комнате оказалось так много и
кусались они так больно, что это оказалось
невозможным.
Сколько комаров налетело в мою комнату?
VII. Волшебные квадраты
84. В помещенном справа квадрате
расставьте цифры (по одной в каждой клетке)
0, 1, 2, 3, 4, 5, 6, 7 и 8 так, чтобы
суммы чисел по любой
горизонтали, вертикали и диагонали были
одинаковы и чтобы каждая из этих
сумм равнялась 12.
85. В помещенном здесь квадрате
расставьте числа (по одному в каждой клетке) 0, 1,2,
3 и т. д. до 24 включительно так, чтобы суммы
чисел по любой горизонтали, вертикали и
диагонали были одинаковы и каждая из этих
сумм равнялась 60.
124

VIII. Игры со спичками
86. Положите в ряд 10 спичек на
одинаковом расстоянии друг от друга. Требуется в пять
приемов переложить спички в кучки из 2
скрещенных спичек, наподобие римской цифры X,
перенося всякий раз очередную спичку через
две спички (уже перекрещенные спички
считаются за две).
123456789 10
IMMIIMI
87. Пятнадцать спичек разложены в ряд.
Требуется собрать их в 5 групп по 3 спички в
каждой, причем, перекладывая по одной
спичке, каждый раз переносить очередную спичку
через 3 спички.
123456789 101112131415
IIIIIIIIIMIIII
88. Переложите эти 12 спичек так, чтобы
вдоль каждой стороны четырехугольника их
лежало не четыре, как сейчас, а пять штук.
мм
125

89. Изображенные на рисунке двенадцать
спичек требуется переложить так, чтобы вдоль
каждой стороны их было а) по 5; б) по 6 штук.
I I
90. Составьте из 6 спичек 4 одинаковых
равносторонних треугольника.
91. Составьте из 9 спичек 3 полностью
замкнутых равных четырехугольника.
92. Составьте из 12 спичек 3 равных
четырехугольника и два равных треугольника.
93. Составьте из 20 спичек два квадрата так,
как показано на рисунке. Затем с помощью
10 спичек разделите внутренность большого
квадрата (незаштрихованную часть) на 5
частей, одинаковых по форме и величине.
94. Сосчитайте 22 спички, разложенные так,
как показано на рисунке слева, выбрасывая
каждую седьмую спичку. Начинать счет нужно
126

с такой спички, чтобы выброшенными
оказались все спички, кроме той, которая лежит
отдельно.
— 1 I 21 —
•— 2 22 20
3 19
4 18
• 5 17
6 16 •
' 78 9 1011 121314 15 '
IIIIIII
95. Сложите из спичек фигуру,
изображенную на рисунке, и отнимите 5 спичек так,
чтобы осталось 5 треугольников.
л
АЛ
АЛЛ
96. Разложите в ряд 8 спичек и,
перекладывая одну спичку через две, составьте в 4
приема 4 группы по 2 спички в каждой.
12 3 4 5 6 7 8
МШИ!
97. В звезде, изображенной на рисунке,
переложите 6 спичек так, чтобы получилось
3 равных и одинаково расположенных
четырехугольника.
\~ "7
/_ \
\/
127

98. В коробке находится несколько
спичек. Если раскладывать их по 3 спички в ряд,
то останется 1 спичка. Если раскладывать по
4 спички в ряд, то останется 2 спички. Если
раскладывать по 5 спичек в ряд, то
останется 3 спички. Наконец, если раскладывать по
6 спичек в ряд, то останется 4 спички.
Сколько спичек в коробке?
99. Поднимите 3 спички с помощью одной,
не прикасаясь к поднимаемым спичкам.
100. В фигуре, составленной из 12 спичек
(см. рисунок), требуется переложить 5 спичек
так, чтобы получилось 3 квадрата.
i
! I
101. Переложите 6 спичек так, чтобы
получилось 6 равных, симметрично
расположенных четырехугольников.
V V
_
V
128

102. В спирали на рисунке, составленной из
35 спичек, переложите 4 спички так, чтобы
получилось 3 (неравных) квадрата.
П=П1
103. Изображенная на рисунке
зигзагообразная фигура состоит из 24 спичек. Переложите
8 спичек так, чтобы получилось 2 неравных
квадрата.
I П П
I I I I I
Mill
U LI
IX. Разрезание и перекладывание
фигур
104. Кусок картона (или бумаги), имеющий
форму прямоугольника длиной 9 вершков и
шириной 4 вершка, разрежьте на 2 равные
части так, чтобы из них можно было сложить
квадрат.
105. Кусок картона (или бумаги),
имеющий форму прямоугольника длиной 1 аршин
5 Н. Аменицкий и др. 129

и шириной 9 вершков, разрежьте на 2 равные
части так, чтобы из них можно было сложить
квадрат.
106. Разрезать данный треугольник на 3
неравные части, из которых можно было бы
составить 2 равных квадрата.
107. Из данного квадрата сделайте два
меньших, равных по величине квадрата. Решите
обратную задачу.
108. Разрежьте квадрат на 4 части так,
чтобы каждая часть прикасалась к 3 остальным
частям.
109. Четыре брата после смерти отца
получили в наследство сад, имеющий форму
квадрата. Посреди сада росли 4 дерева (Д), у
каждой из 4 сторон ограды было выстроено по
оранжерее, а в каждом из углов сада возведено
по беседке (Б). Братья разделили свой сад на
130

4 равные (по форме и величине) части так, что
в каждой из них оказались и дерево, и
оранжерея, и беседка. Как братья провели в саду
границы владений?
f
I Оранжерея |
Д.# #Д.
д. • #д.
I Оранжерея I
I
110, Вырежьте из бумаги или
картона 4 такие одинаковые
фигуры и сложите из них крест.
111. Разрежьте данный квадрат
на 5 частей — 4 равных
треугольника и 1 квадрат — и сложите их
так, чтобы всего получилось три
квадрата.
112. Двор персидского шаха имел форму
квадрата и был вымощен плитами в 1
квадратную сажень1 каждая. Сторона двора
составляет 8 саженей.
'Квадратная сажень — квадрат со
стороной в 1 сажень.
131

Однажды придворный звездочет сообщил
шаху, что тот проживет на свете всего столько
лет, сколько плит пошло на замощение его
двора. Шах тотчас же послал приближенных
сосчитать, сколько плит на его дворе.
Разумеется, оказалось, что двор имеет 64 квадратные
сажени (8x8), то есть покрыт 64 плитами. А
шаху шел уже 64-й год! Не желая скоро
умирать, шах объявил по всему государству, что
выдаст огромную награду тому, кто возьмется
перемостить его двор, не прибавляя и не
убавляя плит, но так, чтобы площадь двора (то
есть число квадратных саженей) стала больше.
Все математики персидского государства
принялись за работу, и вот через день к шаху
является один перс и просит позволения
перемостить двор, обещая выполнить поставленные
условия.
5 саженей 3 сажени
А
Б
о
и
•О
•ч,
s
X
*
о
{
\
\
в
V
\
г
V
И он сделал это следующим образом:
разделил двор шаха на 4 части — две одинаковые
трапеции А и Б и два одинаковых
треугольника В и Г. Затем рабочие по его указаниям
переместили эти части так, как показано на
нижнем рисунке, и двор принял форму пря-
132

моугольника длиной 8 + 5 = 13 саженей и
шириной 5 саженей. Площадь перемощенного
двора стала равна 13 х 5 = 65 саженей.
5 саженей 8 саженей
Б
ин
*
г
в
о
X
S
*^
А
Благодаря изобретательности перса шах
получил возможность прожить не 64 года, а
65 лет! Но одна и та же площадь не может
быть равна то 64, то 65 квадратным саженям.
Следовательно, в перемощении двора что-то
не так. Что именно?
X. Огромные числа
В разделе VI этого выпуска вы
познакомились с такими рядами чисел, в которых каждое
следующее число больше предыдущего на одно
и то же число. Взгляните теперь на такой ряд
чисел: 3, 6, 12, 24, 48, 96, 192, 384, 768 и т. д.
Этот ряд совершенно другого рода и
замечателен тем, что в нем каждое следующее число
вдвое больше предыдущего.
Если вы сравните два таких ряда:
1-й ряд: 3, 5, 7, 9, И, 13, 15, 17, 19 (каждое
следующее число на 2 единицы больше
предыдущего);
133

2-й ряд: 3, 6, 12, 24, 48, 96, 192, 384, 768
(каждое следующее число вдвое больше
предыдущего), то заметите, что во 2-м ряду числа
растут гораздо быстрее, чем в 1-м. Например,
восьмое число 2-го ряда равно 384, а восьмое
число 1-го ряда равно только 17.
При помощи таких рядов, как 2-й, иногда
приходится решать интересные задачи. При
этом результаты нередко получаются довольно
неожиданные.
Ниже вы найдете несколько любопытных
рассказов, в которых вам встретятся такие
большие числа, что вы и назвать-то их не
сумеете. Но это не беда!
1. Догадливый индус
Одной из трудных, но вместе с тем
увлекательных игр издавна считается игра в
шахматы. Трудно сказать, кто изобрел эту игру,
так как существует она уже
не одну тысячу лет. По этому
поводу у индусов есть
старинная легенда.
Когда-то очень давно жил
на свете индийский царь. Все
ему в жизни удавалось, всего у него было
вдоволь, народ его жил счастливо, но странное
дело: с некоторых пор придворные стали
замечать, что их государь тоскует. Чтобы раз-
134

влечь царя, каждый из них старался придумать
какое-нибудь средство, но ничто не помогало.
Царь скучал и тосковал по-прежнему.
Однажды пришел к царю индус и
попросил позволения показать новую
придуманную им игру. Царь нехотя согласился. Но
игра оказалась настолько интересной и так
понравилась государю, что он в восторге
воскликнул:
— Если твоя голова могла придумать такую
игру, то она заслуживает величайшей награды!
Проси у меня чего хочешь!
— Великий государь, — отвечал индус, —
я много не прошу. Повели твоим царедворцам
положить 1 зерно пшеницы на первую клетку
моей шахматной доски, 2 зерна на вторую,
4 зерна на третью и т. д., увеличивая число
зерен вдвое до тех пор, пока не дойдут до
последней, шестьдесят четвертой клетки.
— Немного же ты просишь, — сказал царь,
усмехнувшись при мысли, как прост и наивен
бедный индус.
Но всемогущий повелитель индусов не был
силен в математике!
Когда приближенные по приказанию царя
приступили к выплате награды, они скоро
убедились, что это невыполнимая задача.
Дело в том, что число зерен, которое
попросил индус, есть сумма 64 чисел, стоящих в
ряду: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024,
2048, 4096, 8192 и т. д.
135

Мы выписали здесь только 14 чисел, сумма
которых равна количеству зерен, которое
должно быть положено на первые 14 клеток
шахматной доски. Остальные 50 клеток еще предстоит
заполнить! Стоит лишь посмотреть, как быстро
растут эти числа, и вы поймете, с какими
огромными числами пришлось бы иметь тут дело.
Легенда гласит, что придворные математики
занялись подсчетом того числа зерен пшеницы,
которое пришлось бы выдать изобретателю
шахмат. Оказалось, что если бы возможно было
засеять пшеницей всю поверхность земного
шара и собирать урожай от такого посева
ежегодно в течение 8 лет, то и тогда не хватило бы
пшеницы, чтобы выплатить индусу «скромное»
вознаграждение.
Вот это число зерен: 18 446 744 070 709 551 615.
В нем 20 цифр!
Рассказывая такие легенды, индусы, как
большие любители математики, по-видимому,
пытались возбудить такую же любовь к этой
науке и в других людях и для этого придавали
своему рассказу такую занимательную форму.
2. Богач и бедняк
В огромном красивом доме жил очень
богатый человек. Кругом себя он видел много
бедных людей, но не считал нужным облегчить их
жалкое существование.
136

Проведал про того богача один умный
бедняк, который, должно быть, знал легенду об
изобретателе шахмат, и решил попытать
счастья.
Он отправился в дом богача и объяснил
слуге, что пришел к хозяину по очень
важному делу. Бедняка повели в роскошные покои,
где он встретил и самого хозяина.
— Что угодно? — сухо спросил тот,
подозрительно оглядывая бедного человека.
— Я слышал, — отвечал бедняк, — что вам
нужен конторщик. Я хорошо знаю эту
работу и согласился бы выполнять ее за дешевую
плату.
— А сколько вы желаете? — спросил
богач.
— Сущие пустяки. Заплатите мне за первый
день работы !/4 копейки, за второй день —
!/2 копейки, за третий день 1 копейку, и, так
как я уверен, что вы останетесь довольны моей
работой, пусть плата за каждый день идет,
увеличиваясь вдвое до тех пор, пока не прЪй-
дет месяц.
Богач, известный своей скупостью, был
очень удивлен скромными требованиями
молодого человека и решил, что иметь такого
служащего — дело весьма выгодное.
— Хорошо, я согласен. С завтрашнего дня
вы можете приниматься за работу. Ступайте
в контору и подпишите контракт на тех
условиях, которые вы предложили, а я принял.
137

Прошла неделя. Хозяин только руки
потирает от удовольствия. Еще бы! Новый
конторщик работает чуть ли не целый день, а платить
ему приходится какие-то гроши. Например,
последний раз (за седьмой день работы) он
получил с хозяина всего 16 копеек!
Но не долго пришлось так торжествовать
богачу. Скоро кошелек его стал пустеть
быстрее, чем он ожидал: ведь по условию плата
конторщику с каждым днем должна была
увеличиваться вдвое. И вот по прошествии двух
недель, на пятнадцатый день службы, богач
убедился, что за один только этот день
конторщику придется уплатить 40 рублей 96
копеек!
С каждым днем хозяин убеждался, что
бедняк его перехитрил, но платить
приходилось столько, сколько следовало по
контракту.
Когда прошел месяц и контррщик
подсчитал, сколько он заработал, то оказалось, что
его месячное жалованье составило солидную
сумму в 2 684 354 рубля 55 3/4 копейки!
Когда этот счет представили хозяину,
последний был страшно поражен, а
торжествующий конторщик сказал ему:
— С вас, хозяин, причитается 2 684 354
рубля 55 3/4 копейки, но я с удовольствием
уступлю вам для круглого счета 553/4 копейки и
довольствуюсь остальной суммой.
138

3. Превращения копейки
Чтобы понять то, о чем пойдет здесь речь,
надо иметь в виду следующее.
Известно, что банк за помещенный в него
капитал платит владельцу капитала проценты
(%), то есть прибыль на этот капитал. Если
капитал в 5000 рублей положен в банк под 5%,
то это значит, что на каждую сотню рублей
по прошествии года нарастает 5 рублей
прибыли.
Следовательно, на весь капитал в 5000
рублей (в котором 50 сотен) получится (5 х 50) =
= 250 рублей прибыли.
В нашем примере каждые 100 рублей через
год превращаются в 105 рублей. Если эту
годовую прибыль (5 рублей) не брать из банка,
то в течение следующего года прибыль будет
насчитываться уже не на каждую сотню, а на
каждые 105 рублей. В таком случае проценты
называются сложными.
Интересно, что когда число лет
значительно, то прирост капитала, отданного под
сложные проценты, делается невероятно
большим.
Представьте себе такой случай.
Мы живем теперь в XXI веке. Если бы кто-
нибудь из самых далеких наших предков,
живших ровно 1000 лет тому назад, вздумал бы
положить в банк одну копейку под 5% (слож-
139

ных), то оказалось бы, что теперь эта копейка
превратилась бы в огромный капитал. Чтобы
судить о величине этой суммы, представьте
себе миллиард шаров из чистого золота,
каждый величиной с земной шар. Стоимость их
и есть эта сумма.
Возьмем другой, более вероятный случай.
Если бы во времена Ивана Грозного,
например в 1532 году, кто-нибудь догадался
поместить в банк (если бы таковой существовал!)
1 копейку под 5%, то через 378 лет
наследник стал бы обладателем целого миллиона
рублей.
Из этих примеров видно, как невероятно
сильно может увеличиться капитал,
положенный под сложные проценты.
4. Китайские церемонии
Дело происходило в одном из китайских
городов.
Богатый местный сановник устроил званый
обед, на который были приглашены не только
знатнейшие мандарины, но и некоторые из
европейцев, проживавших в этом городе.
Стол был накрыт на 12 персон (по числу
приглашенных) и обильно уставлен
всевозможными изысканными китайскими кушаньями.
Когда хозяин пригласил гостей садиться за
стол, произошло некоторое замешательство.
140

Дело в том, что нигде не придается столь
большого значения различным церемониям и
размещению гостей за столом, как у китайцев.
Среди присутствующих начался вежливый
спор о том, где кому сидеть, и, так как никто
из китайских сановников не желал уступить
другому в вежливости и знакомстве с
правилами приличия, эти пререкания грозили
затянуться надолго, что никак не устраивало
изрядно проголодавшихся европейцев.
Желая положить конец спорам,
гостеприимный хозяин предложил:
— Господа, я предлагаю попробовать
разместиться за столом несколько раз
различными способами, и, когда мы испытаем все
возможные способы размещения, нам будет
легче выбрать из них какой-нибудь один.
Предложение было принято, и гости стали
рассаживаться за столом и меняться друг с
другом местами.
Получилась невообразимая толчея и
путаница, а время все уходило!
Среди приглашенных на обед европейцев
находился один, который особенно выказывал
нетерпение и недовольство по поводу
происходившего. Это был профессор математики
одного из французских университетов.
Так как пересаживания с места на место все
продолжались и гости находили все новые и
новые способы размещения, профессор,
наконец, не выдержал и сказал:
141

— Милейший и гостеприимнейший хозяин
и вы, мои добрые друзья! Последуйте моему
искреннему совету, который осмеливаюсь вам
дать только потому, что обладаю некоторыми
математическими познаниями. Сядем за стол
как придется и прежде всего удовлетворим
настоятельные требования наших желудков, а
тем временем я постараюсь доказать вам, что
выполнить предложение нашего любезного
хозяина, не садясь за обед, — дело весьма
рискованное для каждого из нас!
Присутствующие согласились, и обед
начался при большом оживлении, которое
объяснялось, с одной стороны, хорошим
аппетитом всех гостей, а с другой — обещанием
профессора.
Когда обед подходил к концу и подали
десерт, профессор обратился к присутствующим
с вопросом:
— Не может ли кто-нибудь из вас, господа,
сказать мне хотя бы приблизительно, сколько
времени понадобилось бы нам, чтобы
совершить все пересаживания, даже если бы мы на
каждое наше перемещение тратили только
одну секунду!
Общество было удивлено вопросом и
молчало.
— Если бы мы, — продолжал профессор, —
твердо решили довести это занятие до конца
и занимались пересаживанием непрерывно
день и ночь, то все эти прекрасные и вкусные
142

кушанья, которые мы видели на столе, не
только остыли бы и засохли, но и успели бы
совершенно истлеть, а мы давно погибли бы
от голода и истощения. Дело в том, что мы
могли бы размещаться за столом 479 001 600
способами, и каждое из этих размещений чем-
нибудь отличалось бы от другого. Поймите,
господа, что мы были бы обречены на это
занятие в течение 479 001 600 секунд, а это
составляет не более и не менее как 15 лет и 2
месяца с лишком.
Профессор умолк, а присутствовавшие,
пораженные таким сообщением, недоверчиво
молчали.
— Как же так? — спросил, наконец,
хозяин. — На днях обедали у меня трое моих
друзей, и мы с успехом и очень быстро проделали
все возможные пересаживания.
— В том-то и дело, — отвечал профессор, —
что четверо могут разместиться лишь 24
различными способами, и, следовательно, на это
потребуется меньше полминуты. Если же вы
хотите узнать, каким образом я узнал это, то
потрудитесь перемножить все
последовательные1 числа от 1 до числа, равного числу
человек, сидящих за столом. Если бы нас было
четверо, то число пересаживаний было бы
1 х 2 х 3 х 4 = 24.
'Последовательными называются числа,
которые идут, увеличиваясь на единицу, например 5, 6,
7, 8, 9 и т. д.
143

Если бы обедало семь человек, то им
пришлось бы пересаживаться
1x2x3x4x5x6x7 = 5040 раз.
Вы видите, господа, как неимоверно быстро
растет число пересаживаний по мере
увеличения числа гостей.
Гости поняли, в чем дело, и были весьма
благодарны профессору за разъяснение,
которое, как они потом шутили, спасло их от
голодной смерти.
Составьте таблицу числа всех возможных
перемещений для случая, когда за столом
сидят 2, 3, 4, 5 и т. д. до 12 лиц.
XI. Решения и ответы
1. У пяти палок 10 концов, у пяти с
половиной палок 12 концов, у шести с четвертью
палок 14 концов.
2. а) 100; б) 3 рубля.
3. Лошадь с длинным хвостом съела
больше, так как имела возможность отгонять мух
и оводов, мешающих лошадям утолять голод.
4. Очертите мелом круг прямо по себе,
тогда исполнить требуемое будет легко, так как
вы получите возможность передвигаться, куда
вам угодно, оставаясь внутри очерченного
вами круга.
144

6. Изобразив число 9 римскими цифрами
(IX) и разделив пополам горизонтальной
чертой, вы получите в верхней части запись
числа 4 римскими цифрами (IV).
7. Разделив изображение числа 1888
горизонтальной чертой, проходящей через точки
самопересечения восьмерок, вы получите то,
что требовалось.
8. Для исполнения воли завещателя
монастырь должен служить обедни через год: в
первый год по смерти богача не служить
вовсе, во второй год отслужить одну обедню, в
третий год опять не служить обедни, в
четвертый год снова отслужить одну обедню и т. д.
Тогда число обеден, отслуженных
монастырем, будет вдвое меньше числа лет, которое
суждено просуществовать монастырю.
Возможно, что число обеден окажется на 1
больше или меньше половины этого числа лет.
При каком условии это может случиться?
9. Задача с первого взгляда может
показаться вам совершенно простой и понятной, и вы,
быть может, решили ее так: если пароход на-
145

ходится в пути 7 дней, а навстречу ему каждый
день отплывает по одному пароходу, то
очевидно, что наш пароход встретит на своем
пути 7 пароходов. Но если вы так думаете, то
жестоко ошибаетесь! Дело в том, что вы
учитываете только те пароходы, которые отплыли
из Нью-Йорка за то время, когда гаврский
пароход был в пути, но совершенно
забываете о тех пароходах, которые уже плыли в
Европу, пока наш пароход еще не вышел из
Гавра. Например, вы забыли о пароходах,
отправившихся из Нью-Йорка в воскресенье
6 июля, в субботу 5 июля, в пятницу 4 июля и
т. д. Все они также попадутся навстречу тому
пароходу, который вышел из Гавра в
понедельник 7 июля. Примите во внимание это
обстоятельство, и вы увидите, что всех встреч
будет не 7, а 14 (считая тот пароход, который
отправляется из Нью-Йорка в момент
прибытия туда гаврского парохода).
10. а) 3 х 3 х 3 + 3 + 3/3; 33 - 3 + 73; 33 -
-<э + эуз)1в
б) 99 + 9/9.
11. За 9 минут, так как работа
заканчивается после того, как отпилен девятый кусок.
1 С введением в арифметику понятия о степени
число решений для этой задачи увеличивается и
становится практически неограниченным.
146

12. Совет, данный каждому из американцев,
состоял в следующем: «Поменяйтесь лошадью
с вашим приятелем». Ясно, что, последовав
такому совету, каждый из наездников гнал изо
всех сил чужую лошадь (на которой он ехал),
чтобы его собственная лошадь (на которой
ехал его соперник) отстала как можно больше.
Так одна из лошадей и выиграла это странное
пари.
13. У крестьянина первоначально было
8 копеек. После пятого перехода через мост у
него должно оказаться также 8 копеек, то есть
от заключенной сделки он не выиграл и не
проиграл. При решении этой задачи следует
помнить, что увеличить какое-нибудь число в
полтора раза все равно что прибавить к этому
числу его половину.
14. Дело в том, что торговки упустили из
виду одно обстоятельство: сложив яблоки,
предназначавшиеся к продаже по двум разным
ценам и продавая их сообща, они продавали
яблоки уже по другой цене, чем прежде. В
самом деле, каждое яблоко первой торговки
стоило 72 копейки, а каждое яблоко второй
торговки — !/3 копейки. Когда же они стали
продавать яблоки сообща (5 яблок за 2
копейки), то каждое яблоко шло за 2/5 копейки, а не
за '/2 и не за У3 копейки. Из-за этого торговки
и не выручили последней копейки.
147

15. Сначала торговцы решили продавать
свои апельсины по 5 копеек за каждые
7 штук.
Первый торговец продал 7 х 7 = 49
апельсинов и выручил 35 копеек.
Второй торговец продал 7 х 4 = 28
апельсинов и выручил 20 копеек. Третий торговец
продал 7x1 = 7 апельсинов и выручил 5
копеек.
После этого у первого торговца остался
1 апельсин, у второго — 2 апельсина, у
третьего — 3 апельсина. Оставшиеся апельсины
торговцы решили продать по 15 копеек за
штуку.
Первый торговец выручил 15 копеек, а
всего 15 + 35 = 50 копеек.
Второй торговец выручил 30 копеек, а всего
20 + 30 = 50 копеек.
Третий торговец выручил 45 копеек, а всего
45 + 5 = 50 копеек.
16. Три яблока надо разрезать на
половинки. Получится 6 половинок. Каждое из
остальных двух яблок разрезать на три равные части.
Таких частей (третей яблока) будет тоже 6.
Следовательно, каждый мальчик должен
получить по половинке и еще по одной трети
яблока.
17. Деду — 74 года и 8 месяцев, отцу — 38 лет
и 6 месяцев, сыну — 18 лет и 8 месяцев.
148

18. Так как охотник съел третью часть всего
обеда и уплатил за это 50 копеек, то весь обед,
то есть все 5 кушаний, стоят 1 рубль 50
копеек (50 х 3). Следовательно, одно кушанье
стоит 30 копеек (1 рубль 50 копеек : 5). Пастух, у
которого было 3 кушанья, стоившие 90
копеек, сам съел на 50 копеек, а 40 копеек должен
получить с охотника. Пастух, у которого было
2 кушанья, стоившие 60 копеек, сам съел
на 50 копеек, а 10 копеек должен получить с
охотника.
19. Кувшин молока, имевшийся у одного
из арабов, можно заменить 36 финиками, а
один хлеб другого араба — 48 финиками (так
как 4 кувшина молока или 144 финика стоят
столько же, сколько 3 хлеба). Прибавив к
этому 6 фиников третьего араба, мы видим, что
у всех как будто было 90 фиников, то есть на
долю каждого приходится как бы по 30
фиников. Стало быть, первый араб должен
дополучить за 36 — 30 = 6 фиников, а второй —
за 48 — 30 = 18 фиников. Иначе говоря,
второй араб должен получить втрое (18 : 6 =
= 3) больше, чем первый. Следовательно,
первый араб должен взять себе 5 монет, а
второй — 15 монет.
20. Крестьяне поделили вино с помощью
2 пустых бочонков в результате 7
переливаний, получив по четыре ведра вина каждый.
149

(Существует и другой способ переливания в
7 приемов.)
До переливания
После 1-го переливания
После 2-го переливания
После 3-го переливания
После 4-го переливания
После 5-го переливания
После 6-го переливания
После 7-го переливания
8-
5-
3-
ведерный
8
3
3
6
6
1
1
4
0
5
2
2
0
5
4
4
0
0
3
0
2
2
3
0
21. Каждый из сыновей должен получить по
7 бочонков. Все же вино можно представить
себе так:
7 полных бочонков равны 14 полным
наполовину бочонкам плюс 7 полных наполовину
бочонков, то есть всего 21 полный наполовину
бочонок. Следовательно, каждый из сыновей
должен получить по 7 полных наполовину
бочонков вина. Это можно сделать, не переливая
вина из одного бочонка в другой, следующим
образом:
Первый сын
Второй сын
Третий сын
Полных
бочонков
2
2
3
Полных
наполовину бочонков
3
3
1
Пустых
бочонков
2
2
3
150

22. Так как голов 25, всех гусей и поросят
25 штук. Если бы на дворе гуляли только одни
гуси (то есть 25 гусей), то у них было бы 50 ног.
На самом же деле ног у всех обитателей
скотного двора 70. Следовательно, «лишние» 20 ног
принадлежат гулявшим на дворе поросятам,
у каждого из которых на 2 ноги больше, чем
у гуся. Значит, поросят было 20 : 2 = 10, а гусей
25 - 10 = 5.
23. Хозяйка поступила так
Первоначально
После 1-го перекладывания
После 2-го перекладывания
8-
3-
5-
фунтовый горшок
8
8
6
3
0
0
0
3
5
(то есть в 5-фунтовый горшок хозяйка
доложила масла из 8-фунтового горшка, в котором
осталось такое количество масла, которое
требовалось).
24. Чтобы добиться желаемого, крестьяне
должны пересыпать овес (с помощью
имеющихся у них мешков) за 7 приемов следующим
образом:
Первоначально
После 1-го пересыпания
Мешок в
10
7
3
меры
10
7
0
0
0
3
151

После 2-го пересыпания
После 3-го пересыпания
После 4-го пересыпания
После 5-го пересыпания
После 6-го пересыпания
После 7-го пересыпания
После 8-го пересыпания
После 9-го пересыпания
После 10-го пересыпания
Мешок в
10
7
3
меры
7
4
4
1
1
8
8
5
5
3
3
6
6
7
0
2
2
5
0
3
0
3
2
2
0
3
0
После 10-го пересыпания в двух мешках
окажется по 5 мер овса.
25. Первый раз каждый мальчик и каждая
девочка получили от учителя вместе по 9
орехов. Следовательно, как мальчиков, так и
девочек в школе было по 234 : 9 = 26 человек, а
общее число учащихся 26 х 2 = 52 человека.
Поэтому всего учитель должен был принести
6 х 52 = 312 орехов. Следовательно, во второй
раз учитель принес 312 — 234 = 78 орехов.
26. Мальчиков 5, а девочек 8.
27. Высота нижнего яруса 28 аршин, а
высота верхнего — 12 аршин.
28. Дорога тянется лесом на расстоянии
875 саженей.
152

29. Всех гостей было 12 человек.
30. 4 брата и 3 сестры.
31. К концу первых суток гусеница
подвинется на 1 фут, к концу вторых суток — еще на
1 фут, то есть всего на 2 фута. К концу третьих
суток она окажется на высоте 3 футов, к концу
четвертых суток — на высоте 4 футов и т. д.,
к концу восьмых — на высоте 8 футов. Далее,
с 6 часов утра до 6 часов вечера (на девятые
сутки) гусеница взберется еще на 4 фута, то есть
окажется на высоте 8 + 4 = 12 футов, и
достигнет вершины дерева. Стало быть, это
произойдет на девятые сутки, то есть в понедельник на
следующей неделе в 6 часов вечера.
32. Искомое число 35.
33. Дело в том, что, когда большое колесо
сделает один оборот, маленькое колесо
действительно должно пройти расстояние ВГ,
равное расстоянию АБ (см. рисунок), но
расстояние ВГ не равно длине окружности
малого колеса потому, что, достигнув точки Г,
малое колесо вынуждено было не только
катиться по рельсу, но и скользить по нему и,
следовательно, за один оборот прошло путь
больший, чем длина окружности малого
колеса.
34. 40 лет.
153

35. Так как в целом классе 4/4 ученика, в
половине класса 2/4 ученика, смысл сказанного
учителем сводится к следующему: (4/4 + V4 +
+ 2/4 + У4) общего числа учеников в классе
составляют 100 — 1 = 99 учеников.
Следовательно, V/4 искомого числа есть 99 учеников,
отсюда 74 составляет 9 учеников, а 4/4 - 9 х
х 4 = 36 учеников.
36. Встреча произошла в 1 час 20 минут
пополудни.
37. У торговки всего было семь цыплят.
Первая кухарка купила 3!/2 + 1/2 = 4 цыпленка.
Осталось 3 цыпленка. Вторая кухарка купила
V/2 + У2 = 2 цыпленка. Остался 1 цыпленок.
Третья кухарка купила {/2 + !/2 = 1 цыпленка
(последнего). Все кухарки покупали целое
число цыплят.
38. Длина бульвара составляет 51 + 48 =
= 99 аршин. Число сосчитанных деревьев
равно 35 + 33 = 68. Поскольку самую первую
липу сосчитали дважды, на расстоянии 99
аршин посажено 67 лип, а число промежутков
между ними равно 66. Следовательно,
расстояние между соседними липами равно 99 : 66 =
= V/2 аршина.
39. У Ивана было 19 рублей, у Петра
25У3 рубля.
154

40. Заблуждался сам завещатель: отказывая
в своем завещании сыновьям У2, х/4 и !/5 всего
стада, он упустил из виду, что эти доли не
составляют в сумме единицу, то есть всего стада.
Действительно, !/2, или 10/20, всего стада
должен получить первый брат; '/4, или 5/20,
получит второй брат и !/5, или 4/20> всего стада
достанется третьему брату. Следовательно, все
три брата получат 10/20 + 5/20 + 720 = 19/20 стаДа:
720, как мы видим, не хватает. Это и понял
мулла и приказал добавить к стаду одного
верблюда, то есть недостающую часть стада.
41. Всего была сварена 81 картофелина. Из
оставшихся картофелин старшему брату не
причитается ничего, средний брат должен
получить 9 картофелин, а младший — 15.
42. 4380 несчастных случаев в год, 480
арестов за сутки.
43. Вес червяков, съедаемых птичкой за
день, составляет 42 золотника, что вдвое
больше, чем вес самой птички.
44. 3 сажени и 5 футов.
45. Сыну 21 год, отцу 42 года.
46. Ягоды должны быть не дешевле 10
копеек за фунт.
155

47. Младшему 4 года, среднему 7 лет,
старшему 13 лет.
48. Число 4.
49. Поставив между данными числами
запятую, вы получите число 2,3 (две целых и 3
десятых), которое меньше 3, но больше 2.
50. Путь от Камчатки до Аляски пароход
покрывает за 16 часов. Следовательно, за 1 час
он проходит */16 расстояния от Камчатки до
Аляски. Скорость же парусника составляет
4/5 скорости парохода, то есть за 1 час
парусник проходит У16 х 4/5 = 720 того же
расстояния. До остановки, продолжавшейся 2 часа,
пароход шел в течение 8 часов. Стало быть,
пароход возобновил свое движение по
прошествии 10 часов, а парусник вышел в море на
6 часов позднее.
Поэтому, когда пароход, преодолевший
У2 всего расстояния, снова двинулся в путь,
парусник успел пройти У20 х 4 = У5 всего
расстояния. Следовательно, их отделяет У2 — У5 =
= 3/10 всего пути. При новой скорости
парохода (У32 расстояния в час) парусник с каждым
часом приближается к пароходу на У20 - У32 =
= 3/160 всего расстояния. Следовательно, он
догонит пароход через 3/10: У32 = 16 часов. За эти
16 часов пароход пройдет У32 х 16 = У2 пути,
то есть прибудет в порт на Аляске, где и про-
156

изойдет встреча (через 10 + 16 = 26 часов
после отплытия парохода из порта на Камчатке).
Иными словами, эта встреча произойдет во
вторник в 3 часа дня.
Примечание. Скорость парохода
(25 верст в час), приведенная в условии
задачи, как нетрудно видеть, — условие
совершенно излишнее и умышленно введено
только для усложнения задачи. Более того, эта
величина (25 верст в час) несообразна с
действительностью, так как при такой скорости
расстояние от Камчатки до Аляски было бы
равно 25 х 16 = 400 верстам. На самом же
деле оно гораздо больше. В действительности
скорость парохода в этой задаче не играет
роли, и с изменением ее ответ и решение
никак не изменятся.
51. Задача решается гораздо проще, чем
может показаться с первого взгляда. Каждый
час велосипедисты приближаются друг к
другу на расстояние 50,7 + 49,5 = 100,2 версты.
Следовательно, их встреча произойдет через
330,66 : 100,2 = 3,3 часа. Так как муха
вылетела одновременно с велосипедистами и
летала до их встречи, она летала в продолжение
3,3 часа, пролетая каждый час по 100 верст.
Всего она пролетела 100 х 3,3 = 330 верст.
52. Крестьянин в течение часа может
приблизиться к идущему впереди брату на 6У2 —
157

— 4!/4 = 2!/4 версты. Следовательно, встреча
братьев произойдет через 9 х 2!/4 = 4 часа
после отправления. Собака пробежит за эти
4 часа 15 х 4 = 60 верст, и это расстояние,
очевидно, совершенно не зависит от того,
кому из братьев принадлежит собака, то есть
от кого она начнет свое путешествие.
53. Охотник, безусловно, заблуждался.
Попробуем сложить пути, пробегаемые зайцем,
то есть 10 саженей, 1 сажень, !/10 сажени,
У100 сажени, У|000 сажени и т. д., и в результате
такого сложения мы получим 11,1111..., то
есть 11У9 сажени1. Разумеется, собака,
пробежав это расстояние, поравняется с зайцем,
а затем и оставит его позади себя.
54. Чтобы выйти из такого
затруднительного положения, надо переправляться на тот
берег так (А — англичанин, а — его жена, И —
индеец, и — его жена, Н — негр, н — его
жена):
1)
«Этот берег»
А
пи1 н
и 1 н ,
«Тот берег»
н
Периодическая дробь 11,1111..., или 11,(1),
обращается в простую по следующему правилу: числителем
ставят период, то есть 1, а знаменателем цифру 9,
записанную столько раз, сколько цифр в периоде, то есть
один раз.
158

2)
А
а
и
—
Н
—
-
и
н
3) Негритянка возвращается и берет
англичанку:
И
Н
и
н
4) Негритянка (или другая женщина)
возвращается и остается со своим мужем:
L
Н
н
И
и
5) Англичанин возвращается с женой, а
обратно переправляется с негром:
"1"
н
Л
и
-нн
6) Жена индейца возвращается и берет
англичанку:
н
'AJ_H
Ца_1_и_
Н
7) Негр едет за своей женой:
I
и
1 | 1__а_ , и | н j
Н
55. Путевое хозяйство в районе станции
имеет вид, показанный на рисунке.
По главному пути в направлении,
указанном стрелкой, идет товарный поезд, а за ним
159

Пассажирский поезд Товарный поезд
Главный путь
следует пассажирский поезд, который
требуется пропустить вперед, используя для этого
запасную ветку, вмещающую лишь 13 вагонов.
Нагнав товарный поезд, пассажирский поезд
останавливается. Товарный поезд идет по
главному пути и проходит весь за начало
запасной ветки. Затем он останавливается и
задним ходом заходит на боковую ветку, где
останавливает 13 вагонов и отцепляет их, а сам
проходит вперед. Затем пассажирский поезд
проходит вперед за начало ветки, к
последнему своему вагону прицепляет оставшиеся в
тупике 13 товарных вагонов поезда и уводит
их на главный путь вправо. Затем
пассажирский поезд подают задним ходом по главному
пути за начало ветки и оставляют там 13
товарных вагонов. Другая половина товарного
поезда вместе со своим паровозом идет задним
ходом и заходит на запасную ветку, открывая
свободный путь пассажирскому поезду. После
того как тот уходит, товарный поезд (13
вагонов и паровоз) выходит на главный путь и,
прицепив 13 оставшихся сзади товарных
вагонов, следует за пассажирским поездом.
56. Поезда разъезжаются так: один из них,
например идущий справа, дает задний ход и
отходит на такое расстояние, чтобы между
160

ним и разъездом свободно мог поместиться
другой поезд. После этого он отцепляет 9
задних вагонов, а с остальными входит на ветку
А разъезда. Поезд, идущий слева, проходит
разъезд по ветке Б и останавливается справа
от разъезда. Паровоз и 9 вагонов, стоящих на
ветке А, проходят разъезд и останавливаются
на таком расстоянии слева от него, чтобы
между ними и разъездом хватило места для
другого поезда.
После этого поезд, шедший слева и
стоящий теперь справа от разъезда, дает задний
ход и возвращается .на то место, где стоял
сначала. Паровоз отцепляет свои вагоны, идет за
оставшимися справа от разъезда 9 вагонами и
ставит их на любую из веток А или Б. Затем,
прицепив свои вагоны, уходит по свободной
ветке и главному пути по назначению.
Паровоз с 9 вагонами, стоящий слева от переезда,
дает задний ход, прицепляет остальные 9
вагонов, оставленных на разъезде, а затем
продолжает свой путь (налево).
57. Быков следует расставить так («б» —
бурая масть, «ч» — черная масть): бббб-ччччч-бб-
ч-ббб-ч-б-чч-бб-ччч-б-чч-бб-ч. Чтобы
запомнить это решение, рекомендуется следующее:
1) выучите наизусть фразу «От бурь есть
защита, спасенье, избавленье нам!»; 2)
запомните гласные русской азбуки А, Е, И, О, У. Пусть
А означает 1, Е— 2, И— 3, О — 4 и У— 5.
6 Н. Аменицкий и др. 161

Поставьте теперь на место гласных букв в
приведенной выше фразе соответствующие им
числа, и вы получите ответ в виде ряда чисел,
указывающих, в каком количестве и порядке
надо ставить быков той или другой масти,
начиная с бурой (б).
58. Первое положение: А + П + Б.
(5) Б+П
(1)А+П+Б (4)П+Б+А
Сцепка А + П + Б (положение 1) подходит
к мосту слева, и вагон А проталкивается под
мост (положение 2), а паровоз с вагоном Б
подъезжает к А с другой стороны (положение
3). В комбинации П + Б + А состав
переезжает в положение 4 и оставляет вагон А справа
от запасного пути, а оставшийся короткий
состав Б + П подходит к мосту справа и
проталкивает вагон Б налево от моста (положение
5). Затем паровоз подходит к вагону Б с
другой стороны и в сцепке П + Б возвращается в
положение 1, в котором теперь вагоны
поменялись местами, и состав будет Б + П + А.
59. Паровоз (П) в сцепке с вагоном Б
(положение 1) отправляется по главному пути и
останавливается у въезда на запасной путь в
162

положении (2). Здесь к вагону Б прицепляют
вагон А, и паровоз оставляет сцепку вагонов
Б—А в положении (3), а сам, отцепив вагоны,
подходит к ним с другой стороны (положение
4) и двигает оба вагона в положение (2), где
оставляет вагон Б, а сам отправляется вместе
с вагоном А на запасной путь в положение (5).
Отцепив вагон А в положении (1), паровоз
возвращается к вагону Б и ставит его на
требуемое место. В результате вагоны А и Б
меняются местами, и паровоз может занять свое
место между ними.
60. Так как путешественники передвигаются
как на велосипеде, так и пешком, оба с
одинаковой скоростью и должны добраться до дома
одновременно, каждый из них должен
половину пути (20 верст) проехать на велосипеде, а
другую половину пути пройти пешком.
Следовательно, простейшее из решений — оставить
велосипед на полдороге, то есть в 20 верстах от
места отправления. Действительно, велосипед
преодолеет 20 верст за 1 час 20 минут, а
остальные 20 верст он пройдет пешком за 4 часа.
Следовательно, он прибудет домой в 5 часов
20 минут. Его спутник сначала идет пешком
163

в течение 4 часов, а потом 1 час 20 минут едет
на велосипеде, то есть прибудет домой
одновременно с путешественником.
Так как путь в 40 верст проделан за 5
часов 20 минут, скорость такого передвижения
(7У2 версты в час) больше скорости пешехода
(5 верст в час).
Эта задача имеет и другие решения, причем
следует заметить, что скорость такого
передвижения увеличивается по мере того, как
число пересадок становится больше.
61. Первое произведение равно 1 111 111 101.
Из него легко получается второе произведение
(2 222 222 202) с помощью умножения на 2 (ибо
18 = 9x2). Третье произведение (3 333 333 303)
получается при умножении первого
произведения на 3 (ибо 27 = 9 х 3) и т. д.
62. Особенность произведений, получаемых
от этого умножения, состоит в том, что они
все изображаются одними и теми же цифрами
(1, 4, 2, 8, 5 и 7), располагающимися в
различном порядке. Кроме того, если «разрезать»
данное число 142 857 посередине, то сумма
двух трехзначных чисел 142 и 857 окажется
равной 999. Тот же самый результат
получится, если разрезать таким же образом и любое
из пяти полученных произведений.
63. Остаток от каждого из делений
получается на единицу меньше делителя.
164

64. Сумма цифр как каждого из двух
данных чисел, так и их разности равна 45 : 1 + 2 +
+ 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45.
65. Поупражнявшись на нескольких
примерах такого рода, вы, вероятно, заметите, что
средняя цифра получаемой разности всегда 9.
Последнюю цифру вы знаете. Первую же
цифру вы получите, если из средней цифры
отнимете последнюю. В приведенных примерах
имеем: 9 — 6 = 3,9 — 5 = 4.
66. Сумма, получаемая от указанных
действий, всегда равна 1089. Вы можете
воспользоваться этим любопытным свойством,
например, следующим образом. Напишите заранее
на бумажке число 1089 и положите ее в
конверт, который для большего эффекта можете
запечатать. Затем, отдав этот конверт своему
приятелю, попросите его задумать любое
трехзначное число и проделать с ним указанные
действия. Когда он исполнит вашу просьбу,
попросите вскрыть ваш конверт. Каково же
будет изумление вашего товарища, когда он
прочтет там то самое число, которое только
что получил.
67. Числа, получающиеся от указанных
действий, состоят только из повторяющейся
цифры 1.
165

68. Числа, получающиеся от указанных
действий, состоят только из повторяющейся
цифры 8.
69. Преимущества следующие: 1) не надо
запоминать или записывать «на стороне» (то
есть держать в уме) цифру десятков каждого
отдельного произведения; 2) умножение
можно производить в каком угодно порядке,
заботясь лишь о том, чтобы клетки были
заполнены все и надлежащим образом. Недостаток
того же метода состоит в том, что много
времени тратится на подготовительную работу
(черчение квадратиков и проведение
диагоналей), хотя при некотором навыке и наличии
готовой клетчатой бумаги «мусульманский
метод» может оправдать свое название «способа
молнии», как его называли индусы.
70. Сумма первого и последнего чисел
равна 21, сумма всех чисел равна 20.
Следовательно, искомая сумма равна (21 х 20) : 2 =
= 210.
71. (1 + 100) х 100 = 10 100; 10 100 : 2 =
= 5050.
72. 4 + 50 = 54, так как всех чисел 46,
искомая сумма равна (54 х 46) : 2 = 1242.
73. (80 х 60) : 2 = 2400.
166

74. 99.
75. 171.
76. 78 ударов.
77. На 300 дюймов, или на 3 сажени 4 фута.
78. 228 верст.
79. Для нечетных номеров: (1 + 199) х 100 =
= 20 000; 20 000 : 2 = 10 000. Для четных
номеров: (2 + 200) х 100 = 20 200; 20 200 : 2 =
= 10 100.
80. Бедняк заплатит богачу: [(1 + 14) х 14] :
: 2 = 105 рублей, а богач бедняку — 163 рубля
83 копейки. Следовательно, богач не только
не получил прибыли, но и сам вынужден был
доплатить бедняку 58 рублей 83 копейки.
81. Двадцать пятое число равно 3 + (24 х
х 1) = 27.
82. Двадцать первое число равно 5 + (20 х
х 2) = 45.
83. Окно было открыто 7 часов. В
последний (седьмой) час в окно влетело 3 + (6 х 2) =
= 15 комаров. Следовательно, всего влетело
[(3 + 15) х 7] : 2 = 63 комара.
167

84.
3
2
7
8
4
0
1
6
5
85.
0
23
16
14
7
19
12
5
3
21
8
1
24
17
10
22
15
13
6
4
11
9
2
20
18
86. Спички надо перекладывать в порядке,
указанном стрелками с номерами (рисунок
внизу).
4 2
87. Спички надо перекладывать так:
2 на 6
1 на 6
8 на 12
7 на 12
II
Ч I
II I II
II I II I
89.
II I II
168

90. Расположите 6 спичек так, чтобы они
образовали треугольную пирамиду, причем
основание-треугольник должен лежать на
столе, а остальные треугольники — в воздухе,
сходясь в верхней вершине.
91. Два четырехугольника (б и в) стоят под
прямыми углами друг к другу и к
четырехугольнику я, лежащему на столе, образуя угол
как пол и две стены, сходящиеся в углу
комнаты.
г
LJ I
94. Счет следует начать с 16-й спички
сначала вниз, а потом налево (то есть 16, 15, 14-я
и т. д.).
169

95. Задачу можно решить двумя способами:
д SL
Л_ ААА
АА ~ ~
96. Перекладывать спички следует так:
5-ю ко 2-й 4-ю к 1-й
3-ю к 7-й 6-ю к 8-й.
л
97. \/
98. 58 спичек.
99. Одна из спичек расщепляется на конце,
и в расщелину вставляется другая спичка. Обе
спички подпираются третьей так, чтобы все
три стояли на столе в виде пирамиды.
Четвертую спичку надо просунуть между третьей и
первыми двумя и двинуть их так, чтобы
верхний конец третьей попал под соединение
первых двух.
D 101 ~\Г7
id
D
100.
170

i паi
102.1 I I I
I I I I
103.
LI
П
I
104. Прямоугольник, разрезанный на две
равные части.
1
1
105. Квадрат, составленный из двух равных
частей.
IT
171

106. К данному треугольнику вдоль
гипотенузы приложите такой же треугольник и
обрисуйте его пунктиром, а затем разделите
полученный квадрат на четыре равных
квадратика. После этого отбросьте пристроенный
(пунктирный) треугольник, и вы увидите, что
исходный треугольник разделен на 3 неравные
части, одна из которых квадрат, а две другие —
половинки квадрата. Приложив одну
половинку квадрата к другой, вы получите решение
задачи.
j\fc квадрата
1
1
'
•
•
\й квадрата
107. Данный квадрат разделите на четыре
равные части диагоналями, а затем приложите
часть а к части А, а затем часть б — к части Б
вдоль гипотенузы.
172

108.
l
ш
и
IV
109.
Треугольник/
^Треугольник
Треугольник4
Треугольник
111. Соединив середины сторон квадрата
линиями, вы получите четыре равных
треугольника и один квадрат. Из полученных четырех
треугольников легко составить два квадрата
(каждый из двух треугольников). Площадь этих
двух квадратов (взятых вместе) равна площади
полученного квадрата.
Треугольник/ ^Треугольник
Треугольник
Треугольник
173

112. Разрезав картонный квадрат,
изображающий двор шаха, и приложив одну фигуру
к другой, как это сделал перс, мы увидим, что
приложенные стороны этих фигур не будут
образовывать прямых линий (они лишь
кажутся прямыми, а в действительности имеют
излом), между ними после перемещения
образуется просвет, на долю которого и
придется 1 «лишняя» квадратная сажень.

Софус Тромгольт
Игры
со спичками

Игры
6 8 10 12 14
29 27 25 23 21 19 17
15

Игра «Ступеньки»
Два участника игры обозначают свои места
монетами, пуговицами и т. п. Выигрывает тот,
кто, начав с 1-й ступеньки, первым доходит до
7-й. Лестницу можно, конечно, продолжать в
обе стороны, как угодно. При 1, 2 и 3 очках
(игральной кости) следует передвинуться на
столько же ступенек вперед; при четырех
очках оставаться на месте; при 5 очках
передвинуться на 1 ступеньку назад; при 6 очках
опуститься под черту и затем передвигаться
влево, пока не достигнете 4
1-й, 2-й ступеньки, откуда 3 I—I 5
продолжать движение к 2| |6
7-й ступеньке. Для нахо- jj |7
дящегося под чертой очки
кости имеют то же значение, что и раньше;
только при 6 очках можно опять перескочить
поверх той ступеньки, под которой находится
играющий.
179

Игра «Лесенка»
Участники игры, число которых
безразлично, отмечают свои места на лестнице
монетами, пуговицами и т. п. Начинают с 1-го места,
и выигрывает тот, кто первый дойдет до 12 и
1|2|3|4|5|6|7|8|9|1О|И|12
затем обратно от 12 до 1. Движение
участников определяется бросанием кости: 1, 2, 3 очка
означают 1, 2, 3 ступеньки вперед; 4 очка —
оставаться на месте; 5 очков — одну
ступеньку назад; 6 очков — 2 ступеньки назад. Если
кому-нибудь придется попасть позади другого,
то он может перескочить через него и занять
следующее свободное место. А если «судьба»
(кость) посылает в занятое уже кем-нибудь
место, то нужно вернуться и пройти
назначенное число ступеней в обратном направлении.
Ниже 1-го места спускаться нельзя.
Игры «Скачки»
Каждый из двух участников играет со своей
собственной лошадью. Последнюю изображает
спичка, надломанная в двух местах и
расщепленная на обоих концах пополам,
расщепленные концы изобразят ноги (расщепив
концы на три части, можно получить также шею
180

13
14
15
16
12
11
10
9
5
6
7
8
4
3
2
1
с головой и хвост).
Лошади должны проскакать
весь путь от 1-го до 16-го
номера.Выигрывает тот,
кто первый достигает
16-го номера. Движение
каждой лошади
определяется бросанием игральной
кости. При 1, 3, 5 очках данная лошадь
остается на месте, а при 2, 4, 6 очках передвигается
вперед на половинное (то есть 1, 2, 3) число
мест. Если 2 лошади станут друг около друга в
косом направлении (в местах,
соприкасающихся углами), то нагоняющая лошадь может
ударить другую; лошадь, получившая удар, должна
тогда начинать сначала, а ударившая
становится на ее место.
Игра «Зигзаги»
В этой игре нужно пройти вдоль сторон
зигзагообразной линии из 14 спичек через все
места, помеченные на рисунке номерами от 1-го
до 29-го. Число мест, на которое каждый
участник передвигается вперед, определяется
игральной костью; 1, 2, 5 очков обозначают такое же
число мастей; при 6 очках, находясь над
линией, играющий переходит в соответствующее
место под ней (например, с 8-го на 22-е) и
обратно, находясь под линией, переходит в соот-
181

ветствующее место над ней (так с 22-го на 8-е).
Положения участников игры обозначаются
монетами или пуговицами. Последним ходом
нужно попасть как раз на 29; кто бросит
больше очков, чем ему требуется, тот передвигается
назад на столько мест, сколько у него лишних
очков. Выигрывает тот, кто первый достигает
29-го места.
Игра «Висюльки»
Число играющих произвольно. Каждый
играющий берет 8 спичек между большим
пальцем и четырьмя остальными так, чтобы в
большой палец упирались 8 головок, а во все
остальные пальцы по два свободных конца спичек.
Затем руку держат так, чтобы спички стояли
головками вниз приблизительно вертикально,
слегка зажимают пальцы и отпускают большой
палец (все играющие совершают это
одновременно), причем рука находится в покое. Часть
спичек тут же упадет, а некоторые останутся
висеть и будут отпадать по очереди. Тот, у кого
останется последняя спичка, выиграл.

Забавы

«Летающий генерал»
Как один генерал при осаде города взлетал
на воздух, можно легко увидеть на следующем
опыте. По бокам коробки вставляют
вертикально две спички, как показано на рисунке;
между их концами помещают третью
горизонтальную и на нее кладут надломленную
половинку спички, которая изобразит нам
генерала. Горизонтальную спичку зажигают между
одним из ее концов и генералом; последняя
тотчас же взлетает на воздух.
Если вставить горизонтальную
спичку так, чтобы ее головка
касалась головки вертикальной, и
затем зажечь обе головки сразу,
то горизонтальная спичка
полетит далеко вверх в ту сторону,
куда направишь ее головку.
Спичку, вставленную
последним способом, зажги посредине
185

и задай вопрос присутствующим, какой конец
загорится раньше. Этого никто не угадает:
спичка раньше полетит вверх.
Если по сторонам коробки вставить по 2 или
по 3 спички, а спичку с генералом вставить
между 2 спичками, лежащими горизонтально,
то действие будет значительно сильнее.
«Спичечная артиллерия»
Спички можно использовать для
импровизированного артиллерийского обстрела.
Спичка с одного конца расщепляется на 3 части
и ставится вертикально на стол, например на
1 метр от края (см. рис.). На краю стола
параллельно ему кладется вторая спичка,
поперек нее третья; конец последней пусть слегка
выдается за край стола. Теперь нужно ударить
щелчком последнюю спичку так, чтобы она
попала в первую и опрокинула ее. Если по-
186

ставить подобным образом несколько спичек,
то можно бомбардировать полки.
Вообще эту игру можно значительно
преобразить и тем еще больше заинтересовывать
присутствующих. Некоторые спички могут
быть отмечены маленькими бумажками в
качестве генералов, государей и т. п.,
батареи можно поставить с четырех сторон стола
и т. д. Есть и еще лучший способ стрельбы.
Внутренняя часть коробки выдвигается на
2 сантиметра, между ней и внешней стенкой
вставляют спичку, которая выдается на 2
сантиметра над внутренней частью. Приделанная
таким образом спичка очень хорошо
пружинит. Коробку кладут на стол, придерживают
187

левой рукой, правой оттягивают спичку и
затем отпускают ее так, чтобы она ударила в
спичку, лежащую перед ней. (Если вторую
спичку надломить в нескольких местах так,
чтобы она образовала дугу, то при выстреле
она завертится на столе.)
Для стрельбы вверх может служить
следующий прием: вставляют 2 спички в отверстия,
проделанные в длинных сторонах внутренней
части коробки так, чтобы одна спичка была
ближе ко дну и к короткой стороне коробки,
чем другая. Между ними вставляют конец
стреляющей спички. Если поставить коробку на
короткую сторону, можно стрелять
вертикально вверх, а если поставить ее на длинную
сторону так, чтобы вделанные в коробку спички
были вертикальны, то стрельба будет
происходить в горизонтальном направлении.
Можно также сделать из бумаги узкую
трубочку и выдувать из нее спички.
За цель принимают, конечно, не только
упомянутые предметы; можно, например, взять
188

наперсток, висящий на трех спичках. Для
защиты спичечных солдат можно сделать из
коробок валы, рвы и т. п.
Забавы с надломанными спичками
Четыре надломанные в середине спички
кладут на стол, тарелку и т. п., располагая их
так, как указано на рисунке слева. В середину
этой звезды пускают каплю воды, после чего
спички начинают двигаться, образуя сначала
крест, а затем фигуру, представленную на
рисунке справа.
Если расположить таким образом 6, 8 или
более спичек вокруг одной точки, то
получится более быстрое движение в стороны.
На этом свойстве надломанных спичек
основан следующий опыт. Кладут спичку,
надломанную в середине и согнутую под острым
углом, на горлышко бутылки, помещая на ней
маленькую монетку. Если пустить теперь в
место излома каплю воды, то стороны угла,
несмотря на тяжесть монеты, удаляются друг от
189

друга, и монета падает в бутылку. Как здесь,
так и в подобных опытах следует отделившиеся
в местах излома волокна срезать ножом или
ножницами. Наиболее пригодны здесь большие
спички, не пропитанные парафином.
Надламывают спичку вблизи конца,
получают острый угол и зажимают короткий конец
спички в спичечной коробке, поставленной
вертикально; длинный конец спички может
свободно двигаться. К этому длинному концу
спички привязывают на ниточке другую
спичку так, что она лишь слегка касается стола.
Стоит теперь пустить каплю воды на место
излома спички, чтобы она выпрямилась и под-
190

няла другую. Слегка видоизменив последний
опыт, мы получим «спичку-рыбака». На конец
нитки помещают вместо спички, например,
маленькую металлическую петельку; затем ее
опускают в стакан с водой, притом так, чтобы
она находилась у самой поверхности воды.
Если теперь смочить место излома, то спичка,
поднимаясь, выудит вместе с тем и петельку.
Надламывают спичку у самого конца без
головки и короткий конец прикрепляют
булавкой к верхней поверхности пробки,
находящейся в горлышке бутылки, так, чтобы длинный
191

конец спички мог свободно двигаться в
горизонтальном направлении. Затем около бутылки
ставят зажженную свечу так, чтобы спичка при
своем движении могла головкой коснуться
пламени. Теперь стоит пустить в место излома
каплю воды — и спичка, выпрямляясь и попадая
в пламя, зажигается сама.
Последнего можно также достигнуть,
прикрепив спичку к самой свечке так, чтобы она,
поднимаясь вверх, попала бы в пламя.
Расщепляют конец спички натрое и
надламывают остальную часть, образуя острый угол.
Теперь эта спичка может стоять на столе.
Капля воды на место излома заставит свободный
конец спички выпрямиться.
кл При помощи тех же приемов
JJ можно провести еще несколько
jy опытов. Надламывают спичку у
f самого конца и короткий конец
прикрепляют булавкой к короб-
Кке так, что длинный конец мо-
/жет свободно двигаться в го-
- ризонтальной плоскости; затем,
192

расщепив конец другой спички, помещают
последнюю на конце первой в вертикальном
положении. Если теперь надломленная спичка
придет в движение, то она увлечет с собой и
другую, находящуюся на ней. Надломанная и
закрепленная таким образом спичка при
своем движении может опрокинуть спичку,
расщепленную внизу натрое и поставленную на
ее пути.
Надламывают и прикрепляют спичку
вышеописанным способом. Затем расщепляют
конец второй спички и защемляют в ней
первую, так что получается прямая
(горизонтальная) линия. Так поступают с третьей спичкой
и даже, пожалуй, с четвертой. Если теперь
пустить на место излома каплю воды, то вместе
с первой спичкой двинется вся система, и
конец последней спички может описать доволь-
7 Н. Аменицкий и др.
193

но большую дугу — сантиметров пятнадцать
или даже больше. Если на дороге поставить
зажженную свечу, то спичка, конечно, сама
зажжется о нее.
На длинный конец таким же образом
прикрепленной спички накладывают другую
надломленную спичку так, чтобы ее длинный
конец, смоченный чернилами, слегка касался
стола; он оставит на столе след своего
движения: у вас будет самопишущая спичка.
К концу таким же образом прикрепленной
спички привязывают нитку, другим концом
которой обвязаны 3, 4 или более спичек. При
движении надломленной спички она потянет
за собой и все остальные: спичка-ломовик.
194

Надломанная у одного из концов спичка
прикрепляется булавкой к внутренней стороне
коробочки, поставленной отверстием вверх
так, чтобы длинный конец, двигаясь,
поднимался вверх. Поперек коробочки кладут
другую спичку, которую первая при своем
движении поднимет либо сбросит.
Наконец, мы применяем это свойство
надломанных спичек для изготовления
движущихся фигур людей и животных. Сперва следует
вырезать из плотной бумаги корпус и отдельные
его части, которые будут двигаться; на
обратной стороне фигуры (лицевую сторону можно
разрисовать и раскрасить) прикрепляют
посредством надломанных спичек части тела
соответственно их спокойному положению. Одни
концы спичек прикрепляются сургучом к
корпусу фигуры, а другие к подвижным членам.
Если поместить готовую фигуру задней
стороной в тарелку, покрытую тонким слоем воды,
то спички начинают свою деятельность,
вызывающую в фигурах жизнь. Высушив фигуру,
195

можно пользоваться ею снова. Кроме
изображенных здесь в очень уменьшенном масштабе
трех фигур (клоун, танцовщица, петух), можно,
конечно, сделать массу других фигур.
Следует заметить, что нагревание места
излома производит в надломанной спичке то же
действие, что и капля воды. Для игры в
лестницу понадобится игральная кость и лестница
из спичек, которую можно взять длиннее или
короче по желанию.

Фокусы

Фокус с осью вращения
Посередине двух спичек проводят
поперечную черту. Большим и указательным пальцами
правой руки берут спички так, чтобы обе черты
были видны сверху; затем теми же пальцами
левой руки поворачивают эти спички на
полоборота вокруг их короткой оси (то есть
принимая черту за ось вращения) так, что пальцы
правой руки будут уже касаться
противоположных концов спичек. Теперь спрашивают:
«Черточки — сверху или снизу?» Всякий ответит:
«Снизу», и ошибется, если ты, поворачивая
спички вокруг их короткой оси, в то же время
незаметно повернешь их в пальцах левой руки
вокруг длинной оси (то есть параллельной
длине спичек).
199

Как поднять три спички
при помощи одной?
Одной спичкой можно поднять три
следующим образом. Одна из спичек на конце
расщепляется, конец другой всовывают в расщелину,
и обе спички подпираются третьей так, чтобы
все три спички стояли на столе в виде
пирамиды. Теперь четвертой спичкой легко поднять
их; стоит только просунуть ее между третьей и
первыми двумя и, отклонив слегка конец пары,
постараться, чтобы верхний конец третьей
попал под соединение первых двух.
Как поднять 15 спичек
при помощи одной?
Решить трудную на первый взгляд задачу,
а именно поднять одной спичкой 15 спичек,
можно очень легко. Поперек спички, лежащей
на столе (обозначим ее буквой А), кладут
вплотную одну около другой, попеременно вправо и
влево, 14 спичек, и именно так, чтобы их
головки выдавались на 1 — 1,5 сантиметра над А,
в то время как концы без головок опирались бы
200

на стол. Сверху, в углубление, образуемое
верхними частями спичек, кладут затем 16-ю
спичку параллельно А. Если поднять теперь
последнюю за конец, то, к нашему удивлению, вместе
с ней поднимутся и остальные 15 спичек. Для
этого опыта удобнее брать большие, толстые
четырехугольные спички.
Шуточный вариант: как поднять 1 спичкой
50 или более спичек? Берут коробку спичек,
содержащую 50 или более спичек, и
всовывают между внешней и внутренней частью
коробки спичку, за которую и поднимают всю
коробку.
Спички-перевертыши
Кладут 14 спичек в круг, головками внутрь;
начиная с какой-нибудь спички,
переворачивают каждую седьмую (так, чтобы головка
была наружу) до тех пор, пока все спички не
будут головками наружу. Перевернутые
спички продолжают считать, но каждая седьмая, к
которой мы последовательно приходим, долж-
201

на быть еще неперевернутой. Как разрешить
эту задачу? Замечают какую-нибудь спичку, от
которой начинают счет, седьмую
переворачивают. Начиная затем с этой последней,
считают до 7 и переворачивают, следовательно,
13-ю. Так продолжают до тех пор, пока не
будет перевернута спичка, с которой начался
счет. После этого меняют начало счета, а
именно: в этот раз начинают счет не с
последней перевернутой спички, а следующей; затем
продолжают считать так, как и раньше. Этой
уловкой, которую нужно сделать незаметно, и
решается задача. Иначе говоря, спички
переворачивают в следующем порядке: 7, 13, 5, 11,
3, 9, 1, 8, 14, 6,12, 4, 10, 2.
Ту же шутку можно сделать с 10, 18, 22,
26... спичками, если соответственно
отсчитывать по 5, 9, 11, 13... спичек.
Равновесие на спичках
Из опытов сохранения равновесия, которые
можно проделать со спичками, мы отобрали
наиболее интересные. Ниткой туго
обвязывают верхнюю часть горлышка бутылки, кладут
конец спички горизонтально на пробку и,
придерживая спичку пальцем, туго завязывают
над ней концы нитки. (Вынув спичку, можно
удостовериться, что бутылка не привязана.)
Если поставить эту систему на край стола, то
202

оказывается, что бутылка, которая может быть
довольно велика и тяжела, висит на спичке.
Конец не совсем открытого перочинного
ножа втыкают в бок спички так, чтобы черенок
ножа был внизу; тогда спичка, поставленная на
кончик пальца, на сторону или конец другой
спички, на угол или ребро коробки от спичек,
на острие, головку или бок булавки и т. п.,
будет оставаться в равновесии, заняв
вертикальное, наклонное или горизонтальное положение
(в зависимости от положения ножа).
Можно поставить спичку с ножом в
вертикальном положении на конец другой спички,
держа ее горизонтально. Под конец
последней подложить конец еще одной
горизонтальной спички и, отпустив первую, держать за
вторую — эта система будет в равновесии,
хотя части ее не будут связаны друг с другом.
Под конец второй спички можно подложить
третью и т. д.
203

Уравновесив спичку с ножом на конце
горизонтальной спички, можно на первую
поставить вторую спичку с приделанным
подобным же образом (лучше немного меньшим)
ножом. И даже на конец этой второй,
балансирующей спички можно поместить еще
третью спичку с ножом.
Конец спички втыкают в пробку, которая
поддерживается вилкой и ножом так, чтобы их
ручки свешивались немного вниз;
поставленная вертикально на какую угодно точку, эта
система сохранит равновесие.
Спичечную коробку дважды обвязывают
ниткой поперек. Нитку туго завязывают на
ребре между дном и боковой стороной.
Посредине коробки между нитками вставляют спичку и
поворачивают ее несколько раз около оси,
образованной нитками, пока спичка, отпущенная
у одного края коробки, вследствие упругости
натянутых и скрученных
ниток, не будет с силой
ударяться своим длинным концом
о противоположный край
коробки. Теперь приводят ее
204

в положение наибольшего напряжения и
параллельно ей вставляют между дном коробки и
ниткой другую спичку так, чтобы обе спички
одинаково выдавались над краем коробки.
Затем обе спички соединяют кусочком бумаги,
так что первая спичка,
оставаясь в напряженном
состоянии, может отскочить назад.
Приготовив таким образом
коробку, кладут ее на тарелку
или т. п. дном вверх и зажигают бумагу; как
только пламя достигает одного из отверстий на
бумаге, вся система мгновенно летит вверх и,
перевернувшись несколько раз в воздухе,
падает дном на пол. Шутку можно повторить
несколько раз, нужно только каждый раз менять
бумажку.
Расщепляют конец одной спички и в
расщелину вставляют под возможно более
острым углом заостренный конец другой спички.
Этого наездника сажают на острие столового
ножа (см. рисунок) и держат нож в руке, ни
на что ею не опираясь, так, чтобы головки
спичек слегка касались гладкой
горизонтальной поверхности. Задача состоит в том, чтобы
наездник в указанном положении оставался
неподвижным. Это почти невозможно; в боль-
205

шинстве случаев наездник будет отодвигаться
в сторону, противоположную от руки. Чтобы
сделать опыт более эффектным, можно
надломить в середине каждую из двух спичек,
тогда получим как бы ноги наездника, и затем
прикрепить в месте соединения спичек
корпус, вырезанный из бумаги.
Фокус с крестами
Между указательным и большим пальцами
каждой руки я держу по спичке, спичку в
левой руке горизонтально, в правой —
вертикально; я приближаю руки друг к другу так,
чтобы спички скрестились. Теперь я делаю
быстрое движение руками... и спички опять
образуют крест, но теперь горизонтальная
спичка находится по другую сторону вертикальной.
Снова делаю движение руками, и спички
снова находятся в первоначальном положении.
Можно повторить этот фокус несколько раз,
но никто не может понять, как это делается.
Этот хорошенький фокус, который требует
небольшого упражнения, производится
следующим образом. Вертикальная спичка поме-
206

щается головкой вниз, так
что последняя покоится
на большом пальце, в то
время как указательный
палец опирается о другой
ее конец. При небольшом
сдавливании этих пальцев спичка пристает к
указательному пальцу. Теперь стоит только
слегка раздвинуть пальцы, и спичка
удерживается одним указательным пальцем — как бы
висит на нем. Через полученное таким
образом маленькое отверстие между спичкой и
большим пальцем я быстро и незаметно для
других ввожу и вывожу горизонтальную
спичку, всякий раз тотчас же закрывая отверстие.
Фокус «Мельница»
Пять спичек лежат на столе. Попробуй
поднять сперва № 1 двумя большими пальцами,
затем № 2 указательными, № 3 средними, № 4
безымянными и № 5 мизинцами так, чтобы все
5 спичек находились каждая между двумя
соответствующими пальцами.
Если это, после
больших усилий, тебе удастся,
то попробуй точно так же
двумя соответствующими
пальцами поднять по 2,
по 3 спички.
207

Фокус «Магнитная спичка»
Осторожно раскалывают спичку по длине
на 2 части; во внутренней части каждой
половины делают желобок для швейной иглы, в
желобок вкладывают намагниченную иглу,
половинки соединяют и склеивают. (Пока клей
сохнет, спичку можно обмотать ниткой.)
Когда клей высохнет, то, при аккуратной работе,
спичка наша с виду ничем не будет
отличаться от других; если же ее пустить в воду, то с
ней можно производить такие же опыты, как
и с магнитной иглой.

Конструирование
го спичек

Объемные фигуры
Если вы обладаете достаточным терпением
и ловкостью, вы можете научиться складывать
из спичек различные объемные фигуры.
1. 2 спички кладут на расстоянии друг от
друга немного меньше длины спички. На их
концы кладут 2 другие спички так, что
получается квадрат. На этом квадрате, как на
фундаменте, строят такой же второй, и, продолжая
дальше в том же порядке вертикально вверх,
получают четырехугольную призму.
2, Если, начав с квадрата, строить вверх и
класть каждую спичку ближе к середине на ее
толщину, нежели соответствующая лежащая
ниже, то получается четырехугольная
пирамида.
211

Строя пирамиду на призме, получают дом
или башню.
3. Кладут 4 спички, а на их концы 4 другие
спички так, что получается восьмиугольник.
На этот фундамент дальнейшие спички
постепенно кладут немного ближе к середине, пока
не получится квадрат. Рисунок дает вид
такого основания сверху.
о
4. Начав с восьмиугольника и дойдя до
квадрата, как указано, продолжать постройку,
сначала кладя спички ближе друг к другу, как
212

для пирамиды, а затем опять располагая их
дальше одну от другой. В постройке башни
получится перехват.
Можно также строить в обратном порядке:
начав с квадрата, привести его к
восьмиугольнику. Тогда получается постройка в
опрокинутом виде. И здесь можно сначала построить
узкий фундамент, так что получится
основание в виде чаши.
Л
4о
На том и на другом основании можно
построить пирамиду, острую или закругленную,
так что получится купол. Купол, построенный
на призме, дает башню.
5. Здания большего размера воздвигаются
на более сложных фундаментах. План церкви,
общий вид которой изображен на рисунке.
Над средней частью строится большой купол,
а на четырех пристройках 4 малых.
213

6. Начав с правильного многостороннего
основания, можно, при достаточном терпении
и осторожности, сделать постройку вокруг
любого круглого предмета, например стакана,
чашки. В последнем случае получится как бы
корзина, внутри которой будет находиться сам
предмет. Если начинать строить, имея в
основании количество спичек, равное степени 2
(то есть 2, 4, 8, 16 и т. д.), то всегда можно
прийти к квадрату; если же число спичек иное,
то нужно во время постройки постепенно
подгонять конструкцию к этому случаю.
7. Для прочности этих построек можно
смазать концы спичек рыбьим клеем1. Работа
требует тогда больше времени, но зато можно
1 Получают размачиванием в теплой воде
внутренней оболочки плавательного пузыря рыб. Рыбий клей
применяют в кулинарии для осветления мутных
жидкостей, делая их прозрачными. В текстильной
промышленности им пропитывают нити для повышения
износоустойчивости, при его помощи изготавливают
абразивные круги и наждачные шкурки.
214

делать более сложные вещи, переворачивая
готовую высохшую постройку и продолжая
строить на ее основании.
8. Если работать с клеем, то можно
построить ветряную мельницу, положив 4 (или 8)
спички, как указано на рисунке, в виде креста
так, чтобы между ними осталось отверстие в
толщину спички; в это отверстие
вкладывается смазанная клеем спичка, после чего
готовые крылья остается только приделать к самой
мельнице. (Если начать строить с
восьмиугольника по схеме, суживая кверху, то
получается корпус большой мельницы, на который
нужно поместить еще крышу с крыльями.)
9. Пользуясь клеем, можно также построить
Эйфелеву башню. Сперва строят 4 косые и
несколько согнутые четырехугольные призмы,
которые кверху постепенно сближаются;
сойдясь, они образуют большую квадратную
площадку, на которой можно легко продолжать
постройку вверх, после того как клей
высохнет.
10. Так как может возникнуть желание
зажечь такого рода постройку, то мы
предупреждаем, что такой фейерверк не представляет
ни малейшего интереса, а только опасность
пожара, так как сразу зажигается большое
количество спичек.
215

Одной из самых
красивых лежащих фигур
является сердце. На одну
спичку кладется другая так, что
головкой она опирается на
первую спичку, а другим
концом на стол; вторая и
третья кладутся точно так же, пока не
получится половина сердца, после чего строится
другая половина, симметрично первой.
11. Чтобы образовать крест ордена,
начинают с основания, подобного мельничным
крыльям, но без отверстия посредине. Затем по обе
стороны каждого из концов
креста прикладывается по
нескольку спичек, до
желаемой толщины; после этого
углы между концами креста
заполняются спичками
(лучше меньшими по величине)
так, что каждая спичка делит угол, в который
она вкладывается, пополам.
12, Для Рождественской звезды кладут
спички под углом в 120° друг к другу
головками в середину. Затем в получившиеся углы
кладут спички, делящие эти углы пополам,
до тех пор, пока не будет заполнено все
пространство или пока звезда не достигнет
желаемой величины. Все спички кладутся голов-
216

ками к центру, так что
получаются концентрические
круги. Для того чтобы
сохранить такую звезду, а
также орден, достаточно
наложить на них лист бумаги,
покрытый гуммиарабиком1,
и затем высушить или же можно наклеивать
спички прямо на бумагу во время самой
постройки.
13, Как в постройках, так и в лежащих
фигурах надо следить за тем, чтобы головки
спичек располагались симметрично.
Можно получать красивые
сочетания, выбирая спички
с головками разных цветов,
разноцветные спички или,
наконец, спички разной
величины. Можно также
сочетать описания формы одни с
другими, так, например, на Рождественской
звезде (с желтыми головками), как на фоне,
можно изобразить сердце (из маленьких
красных спичек) и над последним уже построить
\
'Гуммиарабик- твердая прозрачная масса,
выделяемая различными видами акаций. Ранее широко
применяли во многих отраслях промышленности как
клеящее вещество. В кулинарии гуммиарабик
позволяет предотвратить засахаривание, не сильно меняя вкус
продукта.
217

какое-нибудь здание (из спичек с черными
головками). Вообще эти работы, изложенные
здесь только в общих чертах, могут дать очень
богатый материал как для развлечения, так и
для развития художественного вкуса.
При помощи спичек и картона
Для развлечения маленьких детей можно
сделать из спичек и картона (или карт) массу
различных предметов. Чтобы изготовить стул,
вырезают из картона бока согласно рис. (а); в
местах, обозначенных точками, проделывают
отверстия, в которые вставляют спички так,
чтобы только концы их выглядывали
наружу, — и стул готов (б). Подобным же образом
можно соорудить люльку (в), кровать (г),
скамью (д и е), качалку (ж), сани (з), носилки
(и), лестницу (к), двойную лестницу (л), дом
(мин), башню (о), повозку (п) (колеса делают
из четырех кружков картона; можно также
сделать повозку из ящичка спичечной короб-
218

ки, вставив непосредственно у дна поперек
2 спички, на которые надевают 4 колеса),
тачку (рис). Стол можно сделать, взяв
четырехугольный кусок бумаги, загнув его, как
показано на рисунке (т), и вставив в загнутые
вниз края 4 спички. Корзина делается из
круглого или четырехугольного обода и нижнего,
немного меньшего, кружка или
четырехугольника (у и ф).
п
ж
А
тпг
А
WT* Т1
а
ф

Приложение
Старинные меры, встречающиеся
в этой книге
Единицы массы
1 золотник = 4,266 г
1 фунт = 96 золотникам = 0,4095 кг
1 пуд = 40 фунтам = 16,38 кг
Единицы измерения сыпучих и жидких тел
1 пуд = 40 фунтам
1 мера (четверик) = 26,24 л
Единицы длины
1 аршин = 16 вершкам = 71,12 см
1 верста = 500 саженям = 1,0668 км
1 вершок = 7/4 дюйма = 4,445 см
1 дюйм = У12 фута = 2,54 см
1 сажень = 3 аршинам = 7 футам = 48
вершкам = 2,1336 м
1 фут =12 дюймам = У7 сажени = 30,48 см
1 миля = 7 верстам = 7,4676 км
770

Содержание
Предисловие издательства 3
Николай Аменицкий, Иван Сахаров
ЗАБАВНАЯ АРИФМЕТИКА
Задачи для детей младшего возраста
I. Задачи-шутки 9
II. Забавные исчезновения. Остроумный дележ.
Затруднительные положения 11
III. Игры со спичками 16
IV. Волшебные квадраты и волшебная таблица... 21
Волшебная таблица 22
V. В часы досуга 24
VI. Решения и ответы 26
Задачи для детей среднего возраста
I. Задачи-шутки 35
II. Забавные исчезновения и остроумный
дележ 37
221

III. Затруднительные положения 45
IV. Задачи, требующие большей
сообразительности и более сложных вычислений .... 47
Волшебные квадраты 54
Волшебная таблица 55
V. Ряды чисел, суммы которых можно получать,
не производя сложения этих чисел 56
VI. Игры со спичками 59
VII. Игры и забавы 64
VIII. Решения и ответы 67
Задачи для детей старшего возраста
I. Задачи-шутки 85
II. Забавные исчезновения и остроумный
дележ 88
III. Задачи, требующие большей
сообразительности и более сложных вычислений 95
А) Целые числа 95
Б) Дробные числа 98
IV. Затруднительные положения 108
V. Любопытные особенности некоторых
чисел и действий с ними 112
VI. Ряды чисел, суммы которых можно
получать, не производя сложения этих чисел... 116
VII. Волшебные квадраты 124
VIII. Игры со спичками 125
IX. Разрезание и перекладывание фигур 129
X. Огромные числа 133
1. Догадливый индус 134
2. Богач и бедняк 136
3. Превращения копейки 139
4. Китайские церемонии 140
XI. Решения и ответы 144
222

Софус Тромгольт
ИГРЫ СО СПИЧКАМИ
Игры
Игра «Ступеньки» 179
Игра «Лесенка» 180
Игры «Скачки» 180
Игра «Зигзаги» 181
Игра «Висюльки» 182
Забавы
«Летающий генерал» 185
«Спичечная артиллерия» 186
Забавы с надломанными спичками 189
Фокусы
Фокус с осью вращения 199
Как поднять три спички при помощи одной?... 200
Как поднять 15 спичек при помощи одной? . .. 200
Спички-перевертыши 201
Равновесие на спичках 202
Фокус с крестами 206
Фокус «Мельница» 207
Фокус «Магнитная спичка» 208
Конструирование из спичек
Объемные фигуры 211
При помощи спичек и картона 218
Приложение
Старинные меры, встречающиеся в этой книге... 220

Научно-популярное издание
Азбука науки для юных гениев
Для семейного чтения
Н. Аменицкий, И. Сахаров, С. Тромгольт
АРИФМЕТИЧЕСКАЯ РАЗМИНКА
Учимся решать необычные задачки
Ответственные редакторы А. В. Бутурова, А.С. Никулина
Технический редактор Н.Н. Должикова
Корректор О.А. Левина
Компьютерная верстка М. С. Исакова
Подписано в печать 21.07.2011.
Формат 84xl08'/jr Бумага офсетная. Гарнитура «Ньюгон».
Печать офсетная. Уел печ. л. 11,76. Уч.-изд. л. 7,36.
Тираж 3 000 экз. Заказ JSfe 5998.
ЗАО «Центр пол и граф»
121471, Москва, Можайское ш., 29/2
Редакция приглашает к сотрудничеству авторов и переводчиков
E-mail редакции: glavred@CHpol.ru
Отпечатано с готовых файлов заказчика
в «УЛЬЯНОВСКОМ ДОМЕ ПЕЧАТИ»,
филиале ОАО «Первая Образцовая типография»
432980, г. Ульяновск, ул. Гончарова, 14

для юных гени
разминка
1имся решать необычные
ь своему ребенку в изучении матема
ки? Сухие школьные параграфы совершенно неин
ресны, а примеры однотипны и скучны? Совсем
по-другому заиграет эта наука в свете занимательных и
наглядных задач!
С помощью нашей книги вы сможете развить в своем
ребенке способности к неординарному и оригинальн
му мышлению, помочь ему научиться нестандарт
мыслить!
Магические квадраты и волшебные таблицы, задачи-
шутки и задачи на разрезание, перестановки и
перемещения, рассказы о старинных мерах длины и массы,
любопытные древние легенды и истории, так или иначе
связанные с математикой, а также игры и забавы со
спичками, фокусы и конечно же конструирование! Все
это поможет ребенку с удовольствием и интересом
погрузиться в изучение школьной математики.
Хотите сложить из спичек колодец или движущуюся
фигурку? А может быть, решить вечную задачу о
шахматной доске и пшеничных зернышках? Тогда эта книга
опытных математиков-педагогов - для вас!
ISBN 978-.r-. 4-4956-5I
7859r
11€НТРПОЛИГРЙЯР*