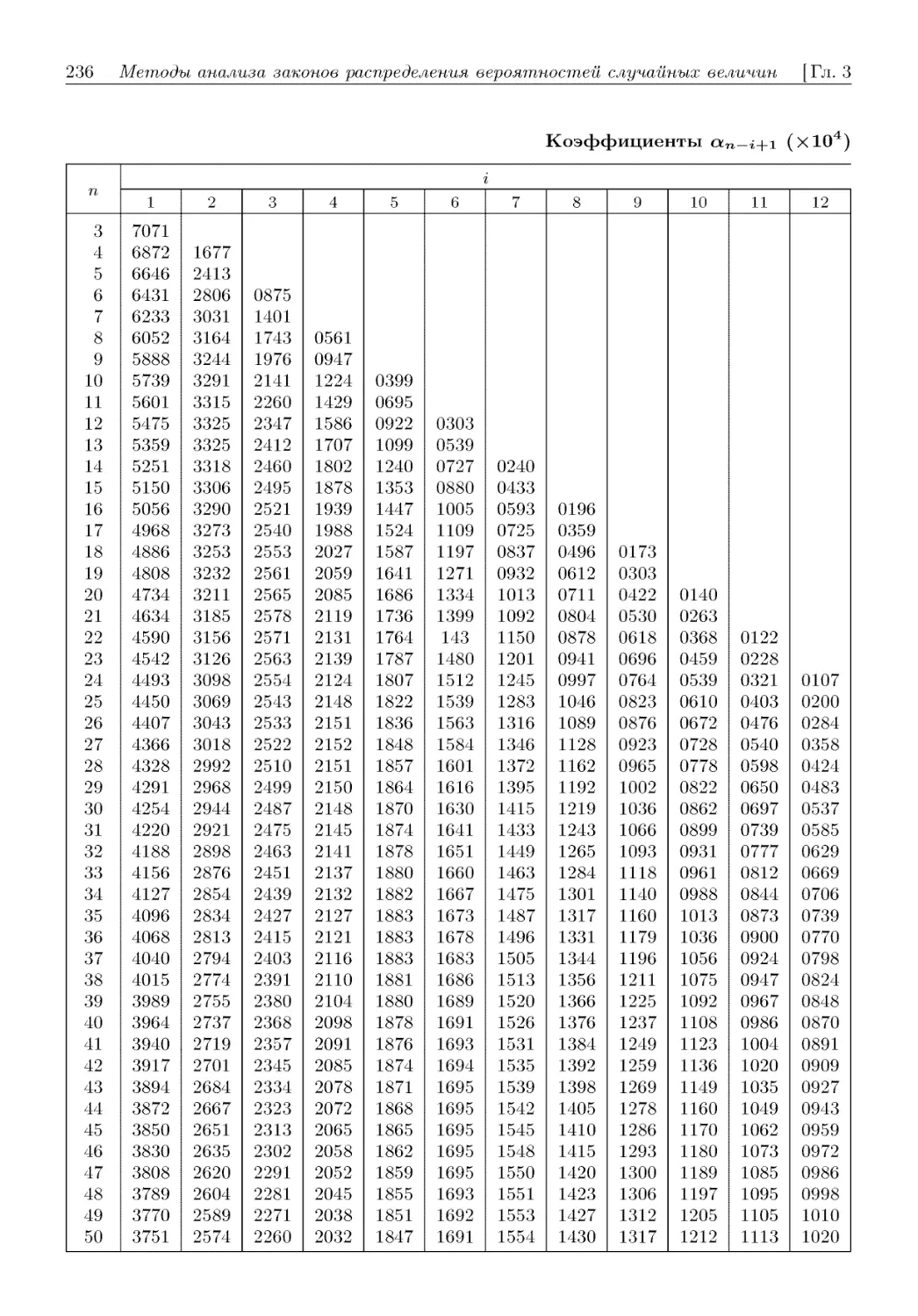
Author: Кобзарь А.И.
Tags: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов
ISBN: 5-9221-0707-0
Year: 2006
Text
УДК 519.22
ББК 22.172
К 55
Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных
работников. - М.: ФИЗМАТЛИТ, 2006. - 816 с. - ISBN 5-9221-0707-0.
В книге рассматриваются способы анализа наблюдений методами математической ста-
статистики. Последовательно на языке, доступном специалисту — не математику, излагаются
современные методы анализа распределений вероятностей, оценки параметров распределений,
проверки статистических гипотез, оценки связей между случайными величинами, плани-
планирования статистического эксперимента. Основное внимание уделено пояснению примеров
применения методов современной математической статистики.
Книга предназначена для инженеров, исследователей, экономистов, медиков, аспирантов
и студентов, желающих быстро, экономично и на высоком профессиональном уровне исполь-
использовать весь арсенал современной математической статистики для решения своих прикладных
задач.
© ФИЗМАТЛИТ, 2006
ISBN 5-9221-0707-0 © А. И. Кобзарь, 2006
Посвящаю моей жене,
терпению которой
обязана эта книга
СОДЕРЖАНИЕ
О математической статистике и об этой книге ........................... 13
Глава 1. Распределения вероятностей случайных величин ........... 23
1.1. Непрерывные распределения ................................... 24
1.1.1. Нормальное распределение B4). 1.1.2. Равномерное распределение C4).
1.1.3. Логарифмически нормальное распределение C5). 1.1.4. Экспоненциаль-
Экспоненциальное распределение C6). 1.1.5. Распределение Вейбулла C7). 1.1.6. Гамма-
распределение C8). 1.1.7. Бета-распределение C9). 1.1.8. Распределение х2
(распределение Пирсона) D4). 1.1.9. Распределение Стьюдента (?-распределе-
ние) E1). 1.1.10. Распределение Фишера (F-распределение) E6). 1.1.11. Усе™
ченное нормальное распределение F1). 1.1.12. Распределение модуля слу-
случайной величины, распределенной нормально F2). 1.1.13. Распределение,
порождаемое нормальной плотностью с линейным дрейфом среднего F4).
1.1.14. Распределение, порождаемое нормальной плотностью с линейным дрей-
дрейфом среднеквадратического отклонения F5). 1.1.15. Распределение Рэлея F8).
1.1.16. Распределение Максвелла F8). 1.1.17. Распределение экстремального
значения G0). 1.1.18. Треугольное распределение (распределение Оимпсо-
на) G1). 1.1.19. Распределение Коши G2). 1.1.20. Логистическое распреде-
распределение G3). 1.1.21. Распределение Парето G3). 1.1.22. Композиции законов
распределения вероятностей случайных величин, возникающие при расчете на-
надежности по схеме „нагрузка-напряжение" G4). 1.1.23. Нецентральное распре-
распределение Стьюдента (нецентральное ^-распределение) G9). 1.1.24. Нецентраль-
Нецентральное распределение Пирсона (нецентральное распределение хи-квадрат) (80).
1.1.25. Нецентральное распределение Фишера (нецентральное ^-распределе-
^-распределение) (81).
1.2. Дискретные распределения .................................... 84
1.2.1. Биномиальное распределение (распределение Бернулли) (84). 1.2.2. Рас-
Распределение Пуассона (88). 1.2.3. Отрицательное биномиальное распределе-
распределение (90). 1.2.4. Распределение Паскаля (91). 1.2.5. Геометрическое распре-
распределение (распределение Фарри) (92). 1.2.6. Гипергеометрическое распределе-
распределение (92).
Глава 2. Оценка параметров распределений вероятностей ........... 96
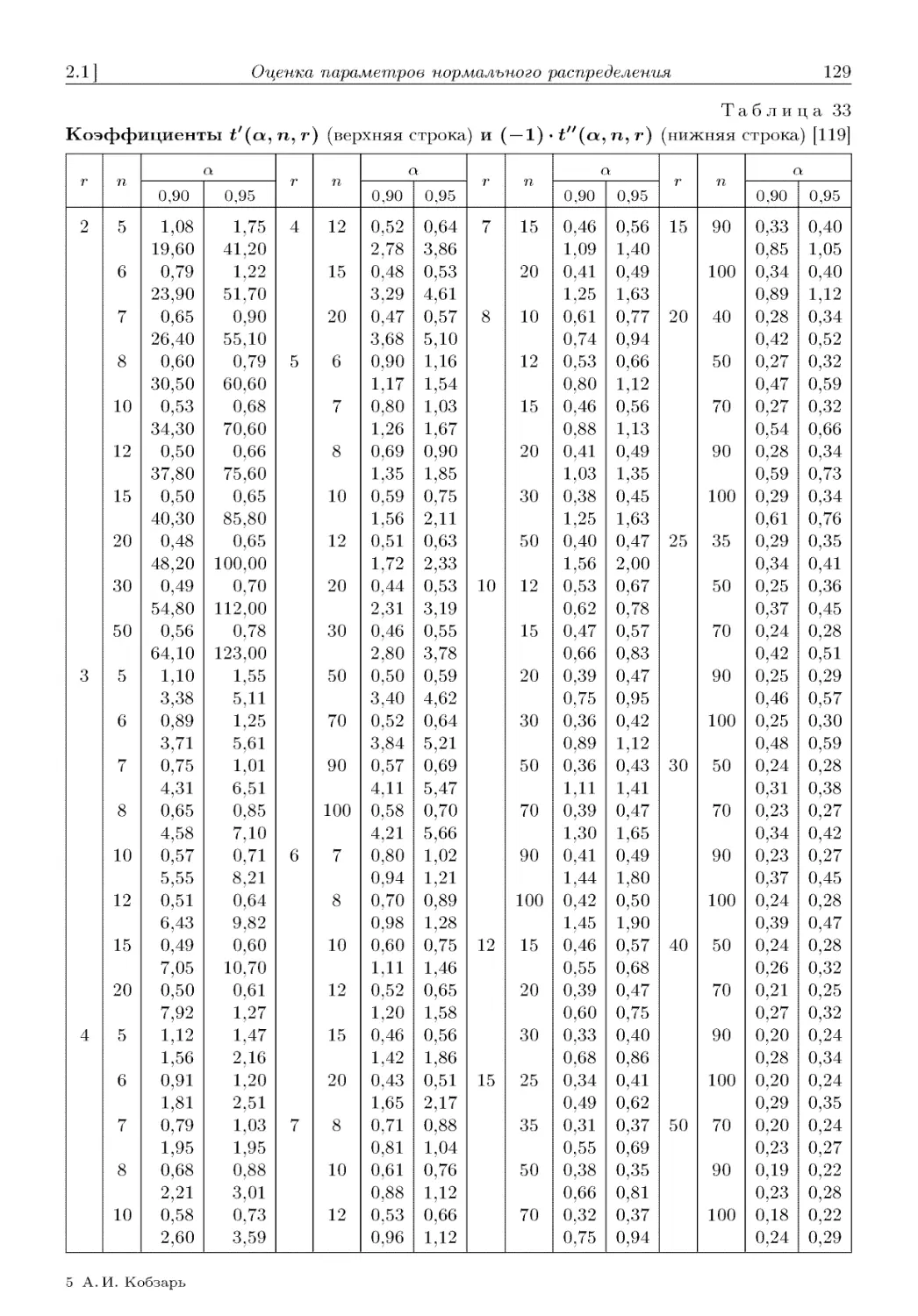
2.1. Оценка параметров нормального распределения ..................... 98
2.1.1. Оценка среднего значения (/л) (98). 2.1.1.1. Точечные оценки (98).
2.1.1.1.1. Оценка максимального правдоподобия (98). 2.1.1.1.2. Оценка с помо-
помощью медианы (98). 2.1.1.1.3. Оценки с помощью порядковых статистик (98).
2.1.1.1.3.1. Простые оценки Диксона A00). 2.1.1.1.3.2. Оценка Огавы A01).
2.1.1.1.3.3. Оценка Пирсона-Тьюки A01). 2.1.1.1.3.4. Быстрые оценки Ке-
нуя A01). 2.1.1.1.3.5. Оптимальные комплексные оценки, использующие об-
общий набор порядковых статистик A02). 2.1.1.1.3.6. Устойчивая (робастная)
оценка Ходжеса^Демана по средним Уолша A03). 2.1.1.1.4. Упрощенная оцен-
оценка по шаблону A03). 2.1.1.2. Интервальные оценки A05). 2.1.1.2.1. Оценка /i
при известной дисперсии а A05). 2.1.1.2.2. Оценка /х при неизвестной диспер-
дисперсии A06). 2.1.1.2.3. Оценка по выборочному размаху A06). 2.1.1.2.4. Оценка
Содержание
по интерквартильной широте A07). 2.1.1.2.5. Оценка по среднему абсолют-
абсолютному отклонению A07). 2.1.1.2.6. Оценка 50%-го доверительного интервала
по вероятному отклонению A08). 2.1.1.2.7. Интервальная оценка для меди-
медианы A08). 2.1.2. Оценка дисперсии а и стандартного отклонения а A11).
2.1.2.1. Точечные оценки A11). 2.1.2.1.1. Оценка максимального правдо-
правдоподобия A11). 2.1.2.1.2. Оценка а по выборочной дисперсии s A11).
2.1.2.1.3. Оценка сг по среднему абсолютному отклонению A12). 2.1.2.1.4. Оцен-
Оценка а по выборочному размаху A12). 2.1.2.1.5. Упрощенная оценка а по
шаблону A12). 2.1.2.1.6. Оценка с помощью порядковых статистик A13).
2.1.2.1.6.1. Оптимальная линейная оценка A13). 2.1.2.1.6.2. Оценка Ога-
вы A14). 2.1.2.1.6.3. Линейная оценка Даутона A15). 2.1.2.1.6.4. Оценка по
сумме подразмахов (оценка Диксона) A15). 2.1.2.1.6.5. Оценка Джини A15).
2.1.2.1.6.6. Оптимальные комплексные оценки, использующие общий набор по-
порядковых статистик A16). 2.1.2.2. Интервальные оценки A18). 2.1.2.2.1. Ин-
Интервальные оценки дисперсии а2 A18). 2.1.2.2.2. Интервальная оценка а по
размаху A18). 2.1.2.2.3. Оценка по среднему абсолютному отклонению A18).
2.1.2.2.4. Интервальная оценка <т, основанная на ее точечной оценке s A19).
2.1.3. Оценки в усеченных и цензурированных выборках A23). 2.1.3.1. Оценки
максимального правдоподобия A23). 2.1.3.1.1. Оценки в усеченных выбор-
выборках A23). 2.1.3.1.2. Оценки в неполностью определенных выборках A24).
2.1.3.1.3. Оценки в цензурированных выборках A26). 2.1.3.1.3.1. Оценка мак-
максимального правдоподобия A26). 2.1.3.1.3.2. Оценки с помощью порядковых
статистик A28).
2.2. Оценка параметров экспоненциального распределения ................. 134
2.2.1. Точечные оценки A34). 2.2.1.1. Оценка максимального правдоподо-
правдоподобия A34). 2.2.1.2. Уточненная двухстадийная оценка A35). 2.2.1.3. Оценки,
основанные на порядковых статистиках A35). 2.2.1.3.1. Оптимальная линей-
линейная оценка A35). 2.2.1.3.2. Оценка по одной порядковой статистике A36).
2.2.1.3.3. Оценка Эпштейна A36). 2.2.1.3.4. Оценка Огавы A37). 2.2.2. Ин-
Интервальные оценки A41).
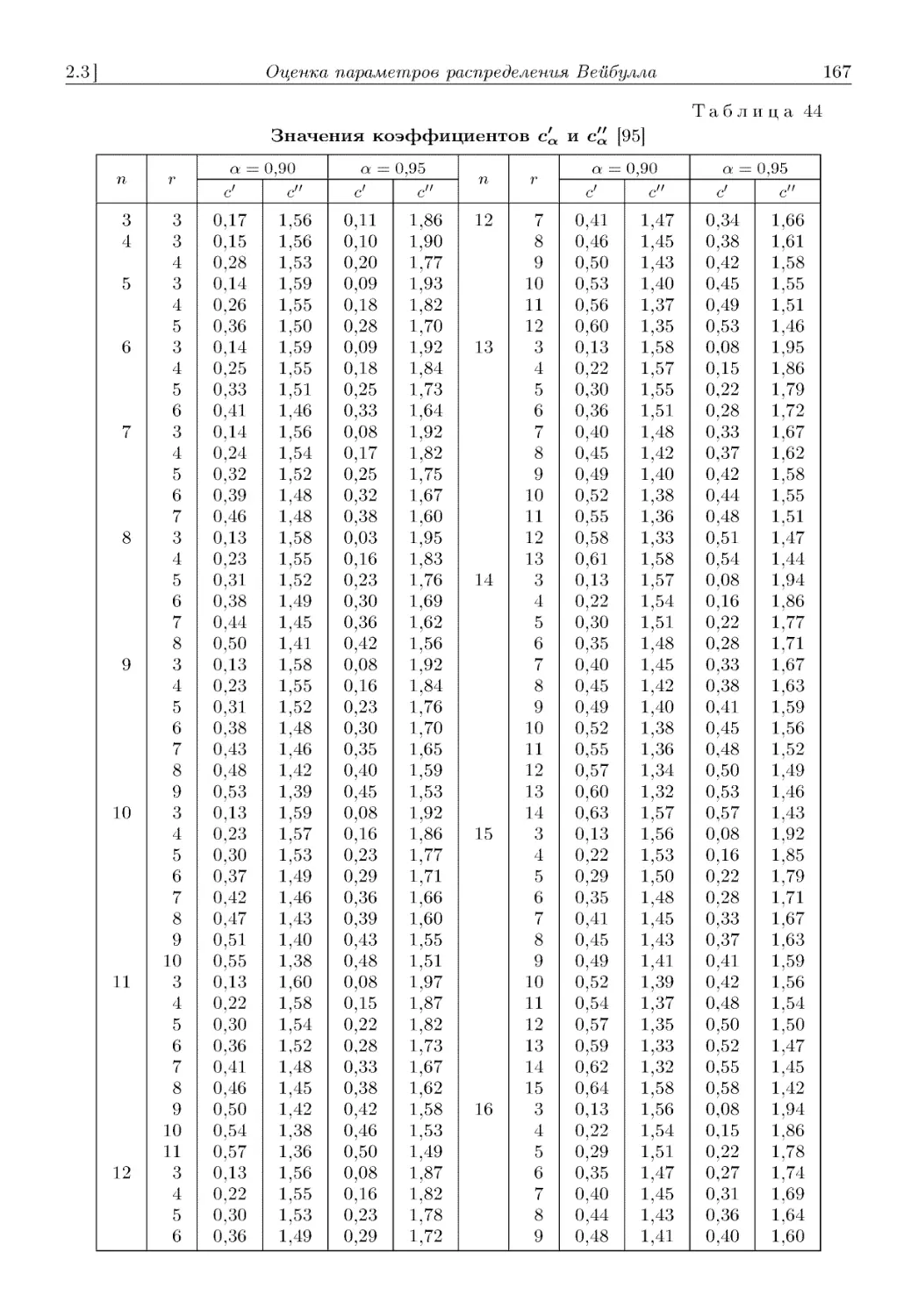
2.3. Оценка параметров распределения Вейбулла. ....................... 146
2.3.1. Точечные оценки A46). 2.3.1.1. Оценка максимального правдоподо-
правдоподобия A46). 2.3.1.2. Метод моментов A47). 2.3.1.3. Метод наименьших ква-
квадратов A50). 2.3.1.4. Оценка с помощью квантилей A51). 2.3.1.5. Оцен-
Оценки, основанные на порядковых статистиках A52). 2.3.1.6. Оценка парамет-
параметров распределения Рэлея (частный случай распределения Вейбулла) A52).
2.3.2. Интервальные оценки A65). 2.3.2.1. Оценка а при известном /3 A65).
2.3.2.2. Совместная интервальная оценка параметров а и C A66).
2.4. Оценка параметров гамма-распределения .......................... 179
2.4.1. Точечные оценки A79). 2.4.1.1. Оценка /3 при известном а A79).
2.4.1.2. Совместная оценка параметров A79). 2.4.1.2.1. Оценка максималь-
максимального правдоподобия A79). 2.4.1.2.2. Несмещенная оценка для малых выбо-
выборок A80). 2.4.1.2.3. Оценка методом моментов A80). 2.4.2. Интервальная
оценка параметра /3 A80).
2.5. Оценка параметров биномиального распределения. ................... 182
2.5.1. Точечная оценка A82). 2.5.2. Интервальные оценки A82). 2.5.2.1. Ап-
Аппроксимация бета-распределением A82). 2.5.2.2. Аппроксимация F-pacnpe-
делением A82). 2.5.2.3. Аппроксимация распределением Пуассона A82).
2.5.2.4. Аппроксимация биномиальной суммы распределением хи-квад-
хи-квадрат A83). 2.5.2.5. Аппроксимация нормальным распределением A84).
2.5.2.6. Аппроксимация Титенко A86).
2.6. Оценка параметров гипергеометрического распределения ............... 191
2.7. Оценки при неизвестном законе распределения вероятностей ............ 192
2.7.1. Оценки для центра распределения A92). 2.7.1.1. Неравенства чебышев-
ского типа A92). 2.7.1.1.1. Неравенство Чебышева A92). 2.7.1.1.2. Неравен-
Содержание
ство Кантелли A92). 2.7.1.1.3. Неравенство Мейделя A92). 2.7.1.2. Оценка
Нётера A93). 2.7.2. Оценка рассеяния распределения A94).
2.8. Некоторые специальные практические задачи ....................... 195
2.8.1. Оценка интенсивности отказов с периодом приработки A95). 2.8.2. Про-
Прогнозирование для экспоненциальных выборок A95).
2.9. Планирование экспериментов для оценки параметров распределений ...... 197
2.9.1. Нормальное распределение A97). 2.9.1.1. Оценка среднего при известной
дисперсии A97). 2.9.1.2. Оценка среднего при неизвестной дисперсии A97).
2.9.2. Распределение Вейбулла A98). 2.9.3. Биномиальное распределение A99).
2.9.4. Экспоненциальное распределение B00). 2.9.5. Гамма-распределе-
Гамма-распределение B01).
Глава 3. Методы анализа законов распределения вероятностей случай-
случайных величин ................................................. 202
3.1. Общие критерии согласия ..................................... 204
3.1.1. Критерии, основанные на сравнении теоретической плотности распреде-
распределения и эмпирической гистограммы B04). 3.1.1.1. Критерий согласия % B04).
3.1.1.2. Критерий числа пустых интервалов B09). 3.1.1.3. Квартальный кри-
критерий Барнетта-Эйеена B11). 3.1.2. Критерии, основанные на сравнении
теоретической и эмпирической функций распределения вероятностей B13).
3.1.2.1. Критерий Колмогорова—Смирнова B14). 3.1.2.2. Критерий Смирнова—
Крамера-фон Мизеса B16). 3.1.2.3. Критерий Реньи (J?-критерий) B18).
3.1.2.4. Критерий Андерсона-Дарлинга (критерий nQ2) B20). 3.1.2.5. Крите-
Критерий Ватсона B22). 3.1.2.6. Критерий Купера B23). 3.1.2.7. Критерий согла-
согласия Дарбина B24). 3.1.2.7.1. Модифицированный медианный критерий B25).
3.1.2.7.2. Модифицированный критерий Колмогорова-Смирнова B25).
3.1.2.7.3. Модифицированный вероятностный критерий B26). 3.1.2.8. Двух-
выборочные критерии согласия B27). 3.1.2.8.1. Двухвыборочный критерий
Колмогорова—Смирнова B27). 3.1.2.8.2. Критерий Катценбайссера—Хак-
ля B28). 3.1.2.8.3. Двухвыборочный критерий Андерсона B29).
3.2. Критерии нормальности распределения ........................... 231
3.2.1. Общие критерии согласия, модифицированные для проверки нормаль™
ности распределения B31). 3.2.1.1. Модифицированный критерий %2 B31).
3.2.1.2. Критерии типа Колмогорова-Смирнова B33). 3.2.1.3. Критерий Фро-
цини B35). 3.2.2. Специальные критерии нормальности B35). 3.2.2.1. Кри-
Критерий Шапиро—Уилка B38). 3.2.2.2. Энтропийный критерий нормальности
(критерий Васичека) B41). 3.2.2.3. Критерий Хегази-Грина B43).
3.2.2.4. Критерий Али—Чёрго-Ревеса B44). 3.2.2.5. Корреляционный крите-
критерий Филлибена B45). 3.2.2.6. Регрессионный критерий нормальности Ла Бре-
ка B48). 3.2.2.7. Критерий нормальности Локка—Спурье B52). 3.2.2.8. Крите-
Критерий нормальности Оя B54). 3.2.2.9. Критерий среднего абсолютного отклоне-
отклонения (критерий Гири) B57). 3.2.2.10. Критерий Дэвида-Хартли-Пирсона B58).
3.2.2.11. Комбинированный критерий Шпигельхальтера B60). 3.2.2.12. Крите-
Критерий нормальности Саркади B61). 3.2.2.13. Критерий нормальности
Лина-Мудхолкара B63). 3.2.2.14. Критерий нормальности Мартинеса-Игле-
вича B65). 3.2.2.15. Критерий нормальности Д'Агостино B66). 3.2.2.16. Кри-
Критерии асимметрии и эксцесса B68). 3.2.2.17. Критерий характеристической
функции (критерий Муроты-Такеучи) B72). 3.2.2.18. Критерии проверки
нормальности распределения по совокупности независимых выборок малого
объема B73). 3.2.2.18.1. Применение критерия Шапиро-Уилка B74).
3.2.2.18.2. Применение критерия Саркади B74). 3.2.2.18.3. Критерий Смир-
Смирнова B75). 3.2.2.19. Сравнительная мощность различных критериев нормаль-
нормальности B77).
Содержание
3.3. Критерии проверки экспоненциальное™ распределения ................ 279
3.3.1. Критерий Шапиро-Уилка B79). 3.3.2. Критерии типа Колмогорова™
Смирнова B82). 3.3.3. Критерии типа Смирнова-Крамера-фон Мизеса для
цензурированных данных B86). 3.3.4. Критерий Фроцини B88). 3.3.5. Корре-
ляционный критерий экспоненциальности B88). 3.3.6. Регрессионный
критерий Брейна—Шапиро B90). 3.3.7. Критерий Кимбера—Мичела B92).
3.3.8. Критерий Фишера B93). 3.3.9. Критерий Бартлетта-Морана B94).
3.3.10. Критерий Климко-Антла-Радемакера^Рокетта B94). 3.3.11. Критерий
Холлендера-Прошана B95). 3.3.12. Критерий Кочара B98). 3.3.13. Кри-
терий Эппса-Палли-Чёрго-Уэлча B99). 3.3.14. Критерий Бергмана C01).
3.3.15. Критерий Шермана C03). 3.3.16. Критерий наибольшего интерва-
ла C04). 3.3.17. Критерий Хартли C05). 3.3.18. Критерий показательных
меток C05). 3.3.19. Ранговый критерий независимости интервалов C06).
3.3.20. Критерии, основанные на трансформации экспоненциального распре™
деления в равномерное C08). 3.3.20.1. Критерий U C08). 3.3.20.2. Крите-
рий U C09). 3.3.20.3. Критерий Гринвуда C09). 3.3.21. Критерий Манн^
Фертига-Шуера для распределения Вейбулла C11). 3.3.22. Критерий Дешпан-
де C16). 3.3.23. Критерий Лоулесса C17).
3.4. Критерии согласия для равномерного распределения .................. 319
3.4.1. Критерий Шермана C19). 3.4.2. Критерий Морана C20). 3.4.3. Крите-
Критерий Ченга—Спиринга C22). 3.4.4. Критерий Саркади—Косика C23). 3.4.5. Эн-
Энтропийный критерий Дудевича-ван дер Мюлена C24). 3.4.6. Критерий Хе-
гази-Грина C26). 3.4.7. Критерий Янга C28). 3.4.8. Критерии типа Кол-
Колмогорова—Смирнова C30). 3.4.9. Критерий Фроцини C31). 3.4.10. Крите-
Критерий Гринвуда-Кэсенберри-Миллера C32). 3.4.11. „Сглаженный" критерий
Неймана-Бартона C33).
3.5. Критерии симметрии ........................................ 336
3.5.1. „Быстрый" критерий Кенуя C36). 3.5.2. Критерий симметрии Смир-
Смирнова C37). 3.5.3. Знаковый критерий симметрии C37). 3.5.4. Одновыбо-
рочный критерий Вилкоксона C39). 3.5.5. Критерий Антилла—Керстинга—
Цуккини C40). 3.5.6. Критерий Бхатачарья-Гаствирта-Райта (модифициро-
(модифицированный критерий Вилкоксона) C42). 3.5.7. Критерий Финча C44). 3.5.8. Кри-
Критерий Бооса C45). 3.5.9. Критерий Гупты C48). 3.5.10. Критерий Фрезе-
Фрезера C50).
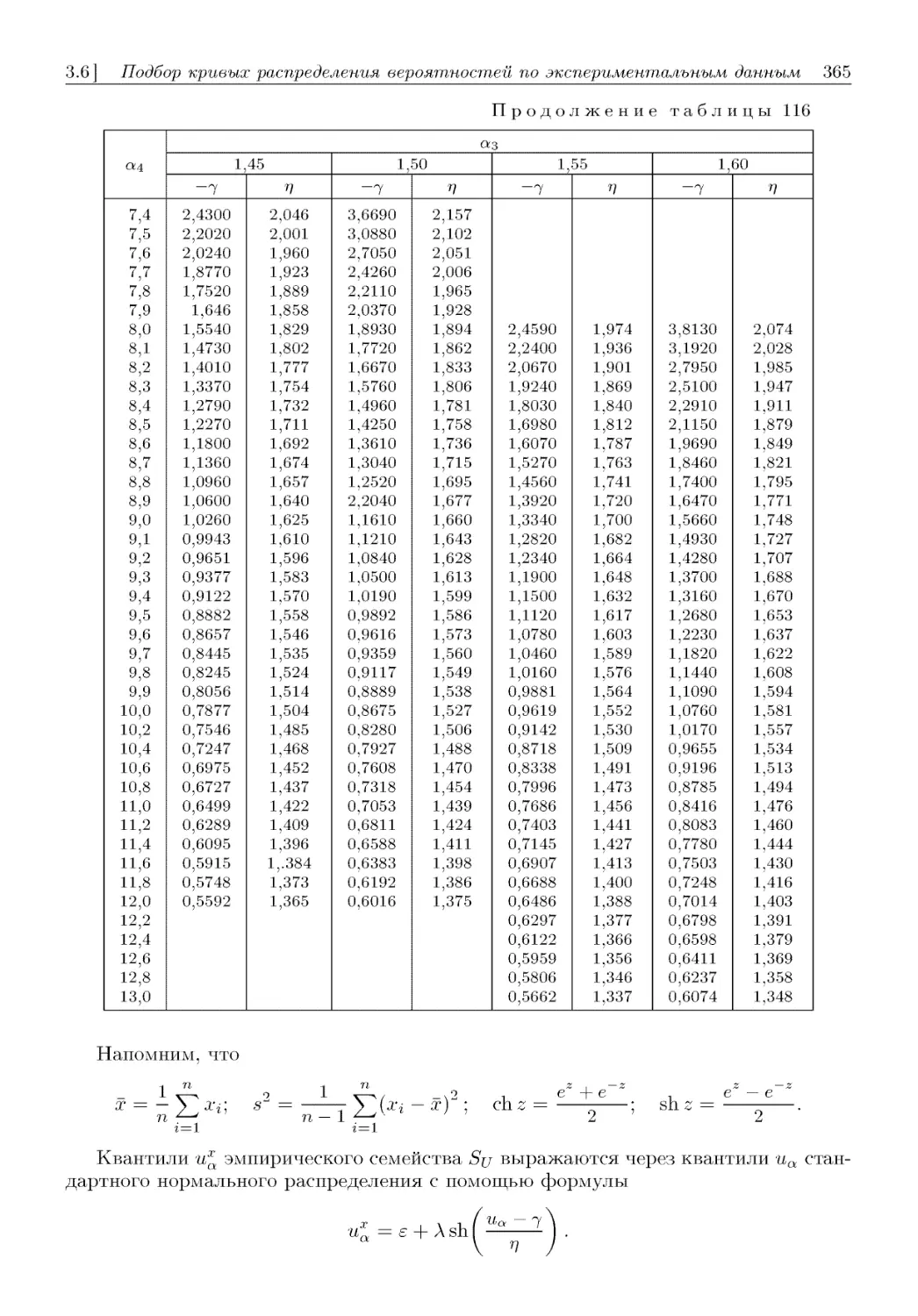
3.6. Подбор кривых распределения вероятностей по экспериментальным данным . 352
3.6.1. Кривые распределения Джонсона C52). 3.6.1.1. Семейство распреде-
распределений Sl Джонсона C53). 3.6.1.2. Семейство распределений Sb Джонсо-
Джонсона C55). 3.6.1.3. Семейство распределений Su Джонсона C57). 3.6.2. Кри-
Кривые распределений Пирсона C68). 3.6.2.1. Кривые Пирсона типа I C69).
3.6.2.2. Кривые Пирсона типа II C75). 3.6.2.3. Кривые Пирсона типа III C77).
3.6.2.4. Кривые Пирсона типа IV C78). 3.6.2.5. Кривые Пирсона типа V C80).
3.6.2.6. Кривые Пирсона типа VI C81). 3.6.2.7. Кривые Пирсона типа VII C82).
3.6.3. Разложение теоретических распределений C84). 3.6.4. Метод вкла-
вкладов C85).
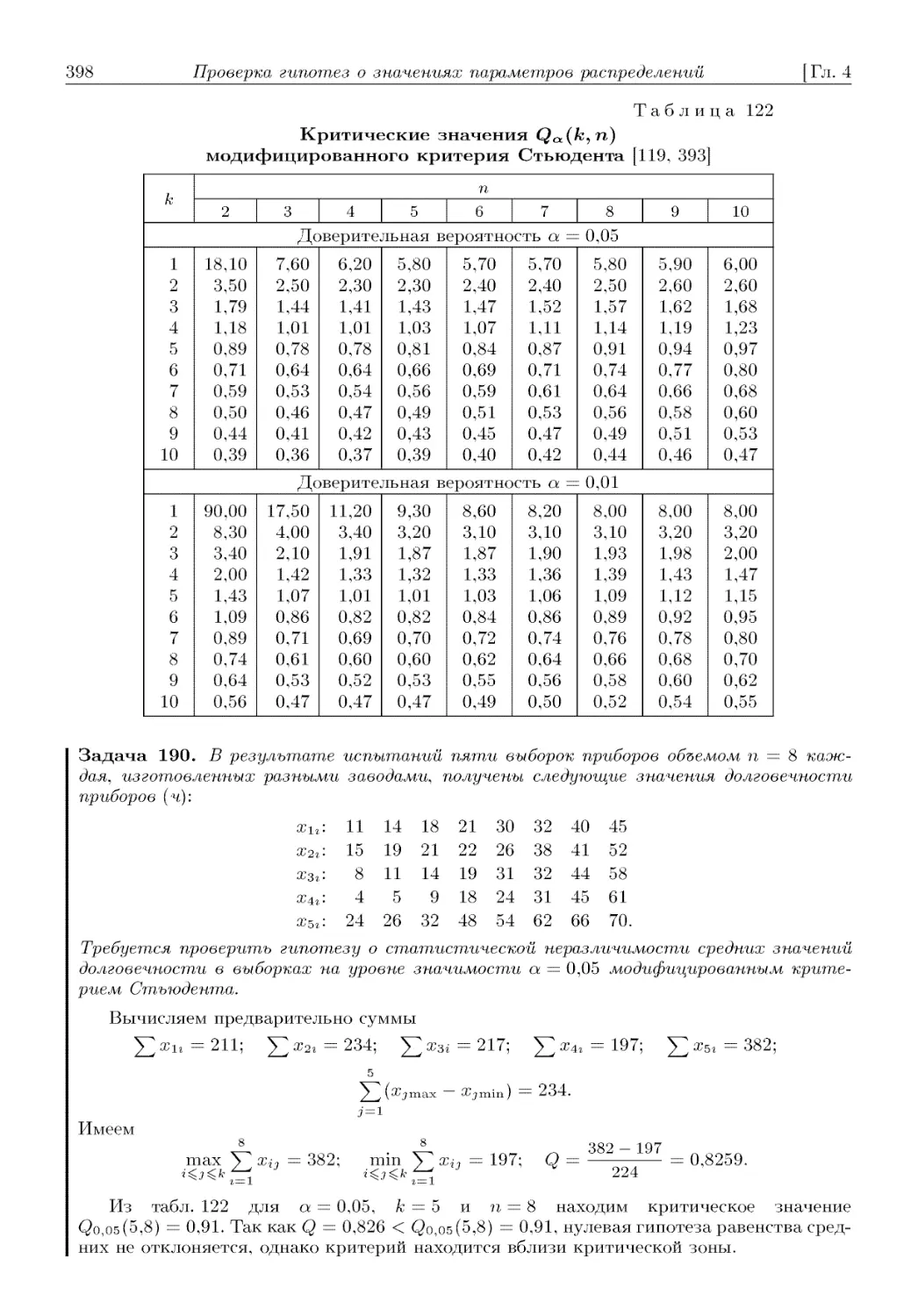
Глава 4. Проверка гипотез о значениях параметров распределений. . . . 388
4.1. Сравнение параметров распределений ............................ 389
4.1.1. Сравнение параметров нормальных распределений C89). 4.1.1.1. Срав-
Сравнение двух средних значений C89). 4.1.1.1.1. Сравнение при известных дис-
дисперсиях а\ и <j\ C89). 4.1.1.1.2. Сравнение при неизвестных равных диспер-
дисперсиях C90). 4.1.1.1.3. Сравнение при неизвестных неравных дисперсиях C91).
4.1.1.1.3.1. Критерий Кохрана-Кокса C91). 4.1.1.1.3.2. Критерий Сатервай-
та C91). 4.1.1.1.3.3. Критерий Уэлча C92). 4.1.1.1.4. Модифицированный
критерий Стыодента C92). 4.1.1.1.5. Парный t-критерий сравнения сред-
средних C93). 4.1.1.1.6. Критерий Уолша, основанный на порядковых статисти-
Содержание
ках C94). 4.1.1.1.7. Двухступенчатый двухвыборочный медианный критерий
Волфа C95). 4.1.1.1.8. F-критерий для сравнения двух средних с одинаковы-
одинаковыми дисперсиями C96). 4.1.1.2. Сравнение нескольких (к > 2) средних C97).
4.1.1.2.1. Модифицированный критерий Стьюдента C97). 4.1.1.2.2. Крите-
Критерий „стьюдентизированного" размаха C99). 4.1.1.2.3. Дисперсионный кри-
критерий C99). 4.1.1.2.4. Критерий Полсона D02). 4.1.1.2.5. Метод прямого
сравнения (критерий Тыоки) D03). 4.1.1.2.6. Критерий „стьюдентизирован-
ного" максимума (обобщенный критерий Тыоки) D05). 4.1.1.2.7. Критерий
Шеффе D06). 4.1.1.2.8. Критерий Стьюдента-Ньюмена-Кейлса D07).
4.1.1.2.9. Критерий Дункана D08). 4.1.1.2.10. Критерий Линка—Уоллеса D08).
4.1.1.3. Сравнение двух дисперсий D12). 4.1.1.3.1. Критерий Фишера D12).
4.1.1.3.2. Критерий Романовского D13). 4.1.1.3.3. Критерий отношения раз™
махов D14). 4.1.1.3.4. Критерий „стьюдентизированного" размаха D15).
4.1.1.3.5. Критерий Аризоно-Охты D15). 4.1.1.4. Сравнение нескольких (к > 2)
дисперсий D16). 4.1.1.4.1. Критерий Бартлетта D17). 4.1.1.4.2. Критерий
Кохрана D18). 4.1.1.4.3. Критерий Неймана—Пирсона (критерий отношения
правдоподобия) D19). 4.1.1.4.4. Критерий Блисса-Кохрана—Тыоки D21).
4.1.1.4.5. Критерий Хартли D21). 4.1.1.4.6. Критерий Кэдуэлла-Десли-Бра-
уна D22). 4.1.1.4.7. Критерий Самиуддина D23). 4.1.2. Сравнение парамет-
параметров экспоненциальных распределений D24). 4.1.2.1. Сравнение двух парамет-
параметров D24). 4.1.2.1.1. Критерий Фишера D24). 4.1.2.1.2. Критерий Фишера
при сравнении интенсивностей отказов (А) D25). 4.1.2.1.3. Двухвыборочный
пуассоновский критерий D26). 4.1.2.1.4. Сравнение значения параметра с
заданным D26). 4.1.2.2. Сравнение нескольких (к ^ 2) параметров D29).
4.1.2.2.1. Критерий Дэвида D29). 4.1.2.2.2. Критерий максимального прав-
правдоподобия D30). 4.1.2.2.3. Критерий отношения правдоподобия (критерий
Нагарсенкера) D31). 4.1.2.2.4. Критерий Чена для двухпараметрических экс-
экспоненциальных распределений D32). 4.1.2.2.5. Комбинированный критерий
Сингха D33). 4.1.3. Сравнение параметров биномиальных распределе-
распределений D35). 4.1.3.1. Сравнение двух параметров D35). 4.1.3.2. Сравнение зна-
значения параметра с заданным D36). 4.1.3.3. Сравнение нескольких парамет-
параметров (к ^ 2) D37). 4.1.4. Последовательные методы проверки гипотез о зна-
значениях параметров распределений (последовательный анализ Вальда) D38).
4.1.4.1. Проверка гипотез о параметрах нормального распределения D39).
4.1.4.1.1. Проверка гипотезы о значении среднего D39). 4.1.4.1.2. Проверка
гипотезы о значении дисперсии D46). 4.1.4.2. Проверка гипотезы о параметре
экспоненциального распределения D47). 4.1.4.3. Проверка гипотезы о пара-
параметре биномиального распределения D49).
4.2. Непараметрические (свободные от распределения) критерии однородности ста-
статистических данных ......................................... 451
4.2.1. Непараметрические критерии сдвига D52). 4.2.1.1. Сравнение парамет-
параметров сдвига двух совокупностей D52). 4.2.1.1.1. Быстрый (грубый) критерий
Кенуя D52). 4.2.1.1.2. Ранговые критерии сдвига D53). 4.2.1.1.2.1. Быстрый
(грубый) ранговый критерий D53). 4.2.1.1.2.2. Критерий Манна—Уитни—Вил-
коксона D54). 4.2.1.1.2.3. Критерий Фишера-Йэйтса-Терри-Гёфдинга D59).
4.2.1.1.2.4. Критерий Ван дер Вардена D60). 4.2.1.1.2.5. Медианный кри-
критерий D62). 4.2.1.1.2.6. Критерий Мостеллера D64). 4.2.1.1.2.7. Критерий
Розенбаума D64). 4.2.1.1.2.8. Критерий Хаги D64). 4.2.1.1.2.9. ^-крите-
^-критерий D65). 4.2.1.2. Сравнение параметров сдвига нескольких (к > 2) совокупно-
совокупностей D66). 4.2.1.2.1. Критерий Крускала-Уоллиса D66). 4.2.1.2.2. Критерий
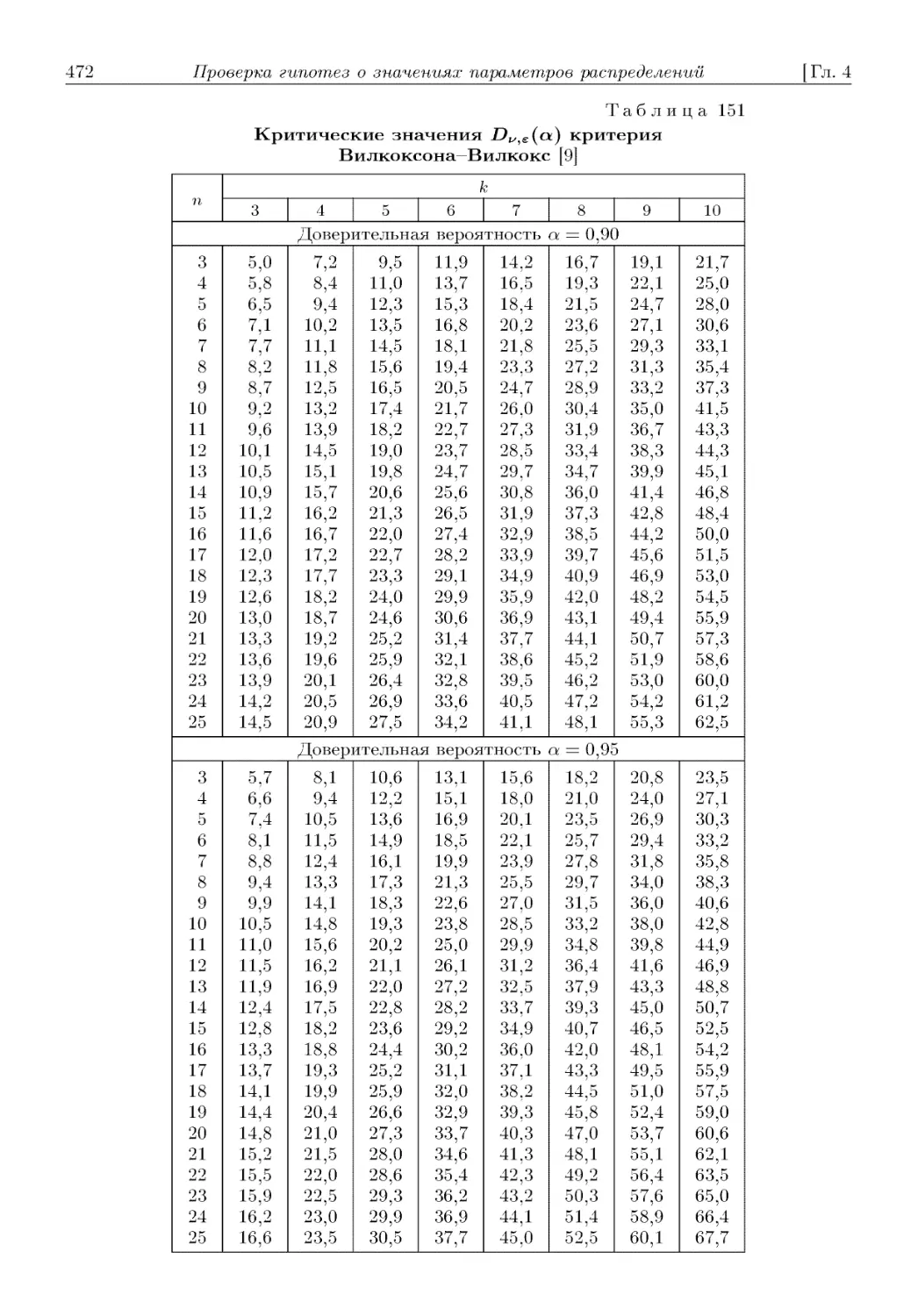
Неменьи D69). 4.2.1.2.3. Критерий Вилкоксона-Вилкокс D71). 4.2.1.2.4. „Бы-
„Быстрый" критерий Кенуя D73). 4.2.1.2.5. Критерий Фишера-Терри-Йэйтса-
Гёфдинга D73). 4.2.1.2.6. Критерий Ван дер Вардена D75). 4.2.1.2.7. Ме-
Медианный критерий D75). 4.2.1.2.8. Критерий Хеттманспергера D76).
4.2.1.2.9. Критерий Терпстры-Джонкхира D77). 4.2.1.2.10. Критерий Мое-
10 Содержание
теллера D79). 4.2.1.2.11. Критерий Левиса D79). 4.2.1.2.12. L-критерий,
основанный на 17-статистиках D80). 4.2.1.2.13. Критерий Краузе D81).
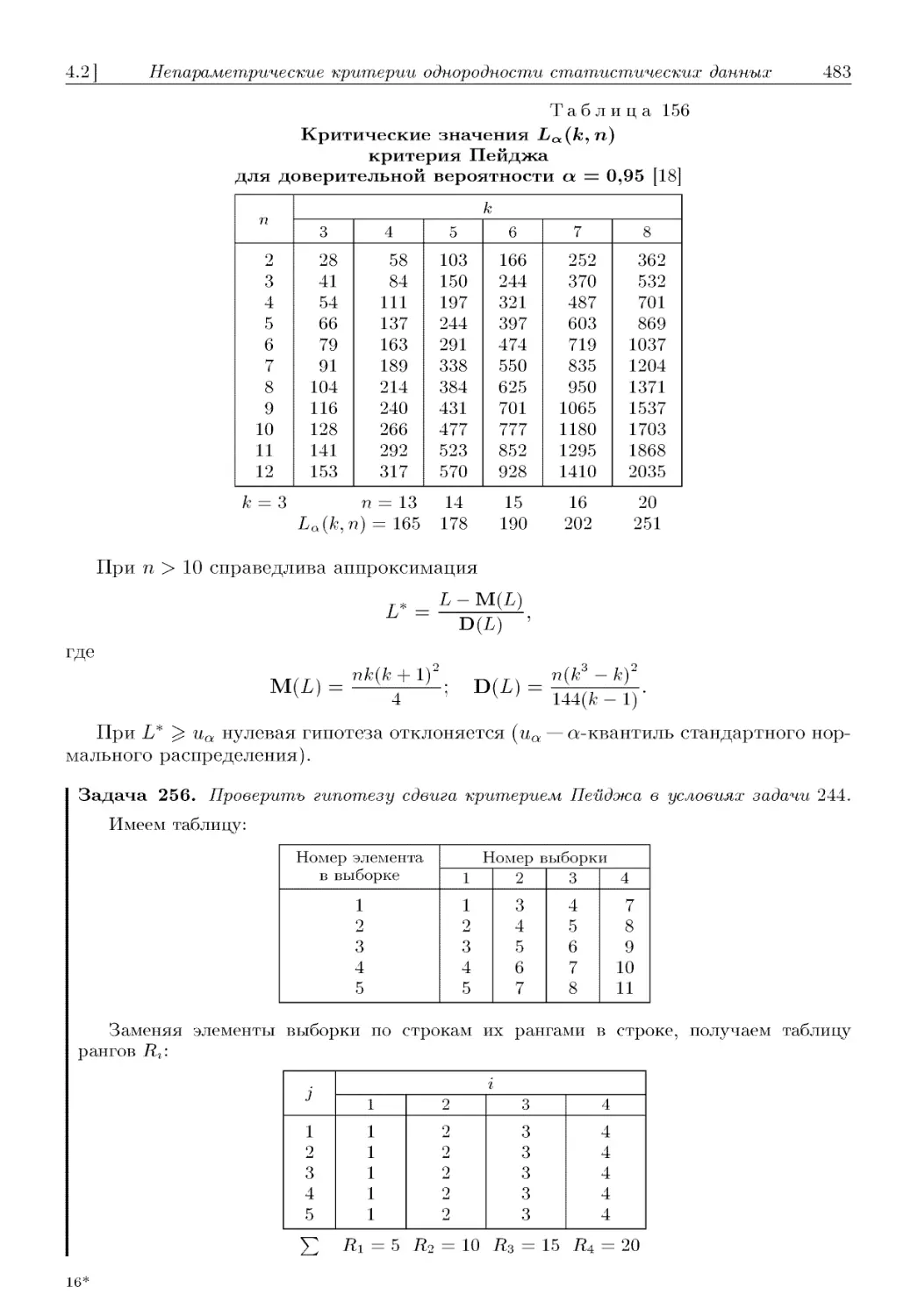
4.2.1.2.14. Критерий Пейджа D82). 4.2.1.2.15. Критерий Фридмена—Кендалла—
Бэбингтона Смита D84). 4.2.1.2.16. Критерий Андерсона-Каннемана-
Шэча D86). 4.2.1.2.17. Критерий со взвешенными ранжировками Даны
Квейд D87). 4.2.1.2.18. Критерий Кендалла-Эренберга D89). 4.2.1.2.19. Кри-
Критерий Ходжеса—Лемана—Сена D90). 4.2.2. Непараметрические критерии мас-
масштаба D92). 4.2.2.1. Сравнение параметров масштаба двух совокупнос-
совокупностей D92). 4.2.2.1.1. Критерий Ансари-Бредли D92). 4.2.2.1.2. Критерий
Сижела-Тыоки D95). 4.2.2.1.3. Критерий Кейпена D96). 4.2.2.1.4. Критерий
Клотца D99). 4.2.2.1.5. Квартальный критерий E01). 4.2.2.1.6. Критерий
Сэвиджа E02). 4.2.2.1.7. Критерий Муда E04). 4.2.2.1.8. Критерий Сукхат-
ме E05). 4.2.2.1.9. Критерий Сэндвика-Олссона E07). 4.2.2.1.10. Критерий
Краута-Динерта E08). 4.2.2.1.11. Критерий Камата E09). 4.2.2.1.12. Комби-
Комбинированный критерий Буша—Винда E11). 4.2.2.2. Сравнение параметров мае™
штаба нескольких (к > 2) совокупностей критерием Бхапкара-Дешпанде E14).
4.3. Критерии тренда и случайности ................................ 517
4.3.1. Критерий Аббе—Линника E17). 4.3.2. Критерий Фостера-Стюарта E19).
4.3.3. Критерий Кокс-Стюарта E20). 4.3.4. Критерий обнаружения сдвига
дисперсии в неизвестной точке (критерий Хсу) E22). 4.3.5. Ранговый крите-
критерий обнаружения сдвига дисперсии в неизвестной точке E24). 4.3.6. Сериаль-
Сериальный критерий случайности E26). 4.3.6.1. Критерий Вальда-Волфовитца E26).
4.3.6.2. Критерий Рамачандрана-Ранганатана E30). 4.3.6.3. Сериальный кри-
критерий Шахнесси E30). 4.3.6.4. Критерий Олмстеда E32). 4.3.6.5. Критерий
числа серий знаков первых разностей E33). 4.3.7. Критерий инверсий E35).
4.3.8. Критерий автокорреляции E36). 4.3.9. Критерии ранговой корреля-
корреляции E39). 4.3.9.1. Критерий Вальда-Волфовитца E39). 4.3.9.2. Критерий
Бартелса E40). 4.3.10. Критерий кумулятивной суммы E41). 4.3.11. Знаково-
ранговый критерий Холлина E42). 4.3.12. Критерии обнаружения выбро-
выбросов E43). 4.3.12.1. Критерии выбросов в случае нормального распределе-
распределения E44). 4.3.12.1.1. Критерий Шовене E44). 4.3.12.1.2. Критерий Ирви-
на E44). 4.3.12.1.3. Критерий Груббса E45). 4.3.12.1.4. Критерий наиболь-
наибольшего абсолютного отклонения E47). 4.3.12.1.5. Критерий Дэвида E47).
4.3.12.1.6. Критерии Диксона E48). 4.3.12.1.7. Критерий Хоглина-Иглеви-
ча E50). 4.3.12.1.8. Критерий Титьена—Мура для обнаружения нескольких
выбросов E53). 4.3.12.1.9. Критерий Роснера для обнаружения нескольких
выбросов E57). 4.3.12.2. Критерии выбросов для экспоненциального рас-
распределения и распределения Вейбулла E59). 4.3.12.2.1. Критерии выбросов
для экспоненциального распределения E59). 4.3.12.2.1.1. Критерий Смоляка—
Титаренко E59). 4.3.12.2.1.2. Критерий Бродского-Быцаня-Власенко E59).
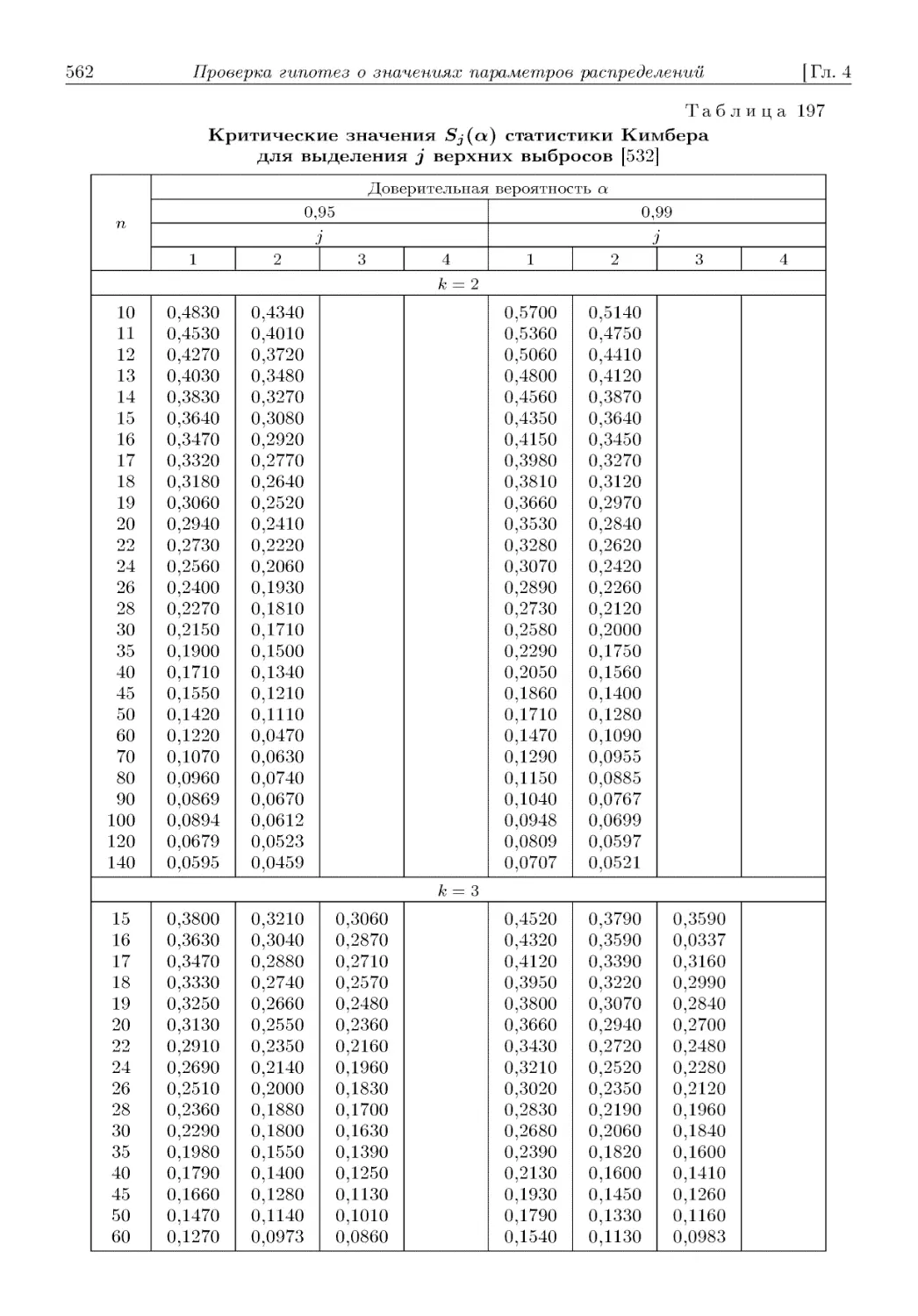
4.3.12.2.1.3. Критерий Кимбера для нескольких выбросов E61). 4.3.12.2.2. Кри-
Критерии выбросов для распределения Вейбулла E64). 4.3.12.3. Критерий выбро-
выбросов для любого непрерывного распределения (критерий Дарлинга) E65).
4.4. Толерантные пределы ........................................ 569
4.4.1. Толерантные пределы в случае нормального распределения E69).
4.4.1.1. Толерантные пределы при известных параметрах распределения
(/i, мо") E69). 4.4.1.2. Толерантные пределы при неизвестных параметрах рас-
распределения E69). 4.4.1.2.1. Среднее/i неизвестно, дисперсия сг2 известна E69).
4.4.1.2.2. Среднее /j, известно, дисперсия а2 неизвестна E72). 4.4.1.2.3. Сред-
Среднее II и дисперсия а2 неизвестны E73). 4.4.1.2.4. Толерантные пределы, осно-
основанные на выборочном размахе E77). 4.4.1.2.5. Толерантные пределы для
выборочных дисперсий E79). 4.4.2. Непараметрические толерантные преде-
пределы E80). 4.4.3. Толерантные пределы для будущих наблюдений и прогнозиро-
прогнозирование E83). 4.4.3.1. Прогнозные интервалы Холла—Прейри E83). 4.4.3.2. Про-
Прогнозные интервалы в задачах испытаний на надежность E87).
Содержание 11
Глава 5. Методы исследования связей между случайными величинами 590
5.1. Дисперсионный анализ ....................................... 590
5.1.1. Классический дисперсионный анализ нормально распределенных слу-
случайных величин E91). 5.1.1.1. Однофакторный дисперсионный анализ E91).
5.1.1.2. Двухфакторный дисперсионный анализ E94). 5.1.2. Дисперсионный
анализ с использованием размахов E96). 5.1.3. Непараметрический диспер-
дисперсионный анализ E98). 5.1.3.1. Двухфакторный непараметрический диспер-
дисперсионный анализ для неполных данных E98). 5.1.3.1.1. Критерий Принти-
са E98). 5.1.3.1.2. Критерий Мака^Скиллингса F01). 5.1.3.1.3. Критерий
Лемаыа-Мака F03).
5.2. Корреляционный анализ ...................................... 606
5.2.1. Классический корреляционный анализ нормально распределенных слу-
случайных величин F06). 5.2.1.1. Оценка коэффициента корреляции F06).
5.2.1.2. Оценка корреляционного отношения F09). 5.2.1.3. Частная и мно-
множественная корреляции F11). 5.2.2. Непараметрический корреляционный
анализ F14). 5.2.2.1. Оценивание корреляции с помощью порядковых
статистик F14). 5.2.2.1.1. Оценка корреляции с помощью тренда F14).
5.2.2.1.1.1. Критерий Кенуя F14). 5.2.2.1.1.2. Критерий Кокс^Стюарта F15).
5.2.2.1.2. Знаковый корреляционный критерий Нелсона F16). 5.2.2.1.3. Ква-
Квадрантный критерий F17). 5.2.2.1.4. "Угловой критерий Олмстеда—Тьюки F20).
5.2.2.1.5. Приближенный критерий Шахани F21). 5.2.2.1.6. Сериальный
критерий Шведа—Эйзенхарта F21). 5.2.2.1.7. Критерий автокорреляции
Кенуя F22). 5.2.2.1.8. Критерий Блума-Кифера-Розенблатта F23).
5.2.2.2. Ранговая корреляция F24). 5.2.2.2.1. Коэффициент ранговой корре-
корреляции т Кендалла F24). 5.2.2.2.2. Коэффициент корреляции р Спир-
мена F26). 5.2.2.2.3. Критерий Гёфдинга F28). 5.2.2.2.4. Критерий
Ширахатэ F30). 5.2.2.2.5. Критерий корреляции Фишера-Йэйтса F32).
5.2.2.2.6. Коэффициент корреляции Ван дер Вардена F33). 5.2.2.2.7. Коэф-
Коэффициент конкордации Кендалла-Бэбингтона Смита F34). 5.2.2.2.8. Коэф-
Коэффициент конкордации Шукеыи-Фроли F36). 5.2.2.3. Точечыо-биеериальная
корреляция F38). 5.2.2.4. Статистическая оценка связи между качественными
признаками (таблицы сопряженности признаков) F39). 5.2.2.4.1. Оценка свя-
связи признаков в таблицах сопряженности 2x2 F39). 5.2.2.4.1.1. Меры связи
в таблицах сопряженности 2x2 F40). 5.2.2.4.1.1.1. Коэффициент ассоциа-
ассоциации F40). 5.2.2.4.1.1.2. Коэффициент коллигации Юла F40). 5.2.2.4.1.1.3. Ко-
Коэффициент контингенции (сходства) F41). 5.2.2.4.1.1.4. Точный критерий
Фишера F41). 5.2.2.4.1.1.5. Быстрые критерии оценки связи в таблицах сопря-
сопряженности 2x2 F42). 5.2.2.4.1.1.6. Модифицированный критерий знаков Мак-
Нимара F43). 5.2.2.4.1.1.7. G-критерий Вулфа F44). 5.2.2.4.1.1.8. Критерий
Ле Роя для сравнения двух таблиц сопряженности 2x2 F45). 5.2.2.4.1.1.9. Вы-
Выбор числа наблюдений для анализа таблиц сопряженности 2x2 F45).
5.2.2.4.2. Оценка связи признаков в многоклеточных таблицах сопряженности
г х с F46).
5.3. Регрессионный анализ ....................................... 648
5.3.1. Линейный регрессионный анализ F49). 5.3.1.1. Оценка коэффициентов
регрессии F49). 5.3.1.1.1. Оценка наименьших квадратов F49). 5.3.1.1.2. Про-
Простейшие оценки коэффициентов регрессии F52). 5.3.1.1.2.1. Метод Бартлетта—
Кенуя F52). 5.3.1.1.2.2. Метод Керрича F52). 5.3.1.1.3. Робастные методы
оценки параметров регрессии F53). 5.3.1.1.3.1. Медианный критерий Брауна™
Муда F53). 5.3.1.1.3.2. Оценка Тейла F54). 5.3.1.2. Статистическое оценива-
оценивание регрессии F55). 5.3.1.2.1. Статистический анализ коэффициентов регрес-
регрессии F55). 5.3.1.2.1.1. Оценки наименьших квадратов F55). 5.3.1.2.1.2. Ро-
Робастные оценки Тейла F57). 5.3.1.2.2. Статистический анализ уравнения
регрессии F58). 5.3.1.2.2.1. Оценка адекватности регрессии F58).
5.3.1.2.2.2. Анализ регрессионных остатков F58). 5.3.1.2.2.3. Оценка выбросов
12 Содержание
в регрессии F60). 5.3.1.2.2.3.1. Критерий Эктона F61). 5.3.1.2.2.3.2. Кри-
Критерий Титьена—Мура—Бекмана F62). 5.3.1.2.2.3.3. Критерий Прескотта—
Лунда F63). 5.3.1.2.3. Доверительные области и толерантные границы ре-
регрессии F65). 5.3.1.2.3.1. Доверительная область простой линейной регрес-
регрессии F65). 5.3.1.2.3.2. Оценка обращенного уравнения регрессии F69).
5.3.1.2.3.3. Толерантные интервалы для линейной регрессии F70).
5.3.1.3. Сравнение линейных регрессий F72). 5.3.1.4. Некоторые специаль-
специальные задачи линейного регрессионного анализа F74). 5.3.1.4.1. Оценка вер-
вершины кусочно-ломаной линии регрессии F74). 5.3.1.4.2. Определение объ-
объема испытаний для получения заданной точности оценки коэффициента ре-
регрессии F78). 5.3.2. Множественная линейная регрессия F80). 5.3.3. Нели-
Нелинейный регрессионный анализ F81). 5.3.3.1. Линеаризация нелинейной мо-
модели заменой переменных F81). 5.3.3.2. Полиномиальная нелинейная ре-
регрессия (полиномы Чебышева) F82). 5.3.4. Выбор наилучшей регрессион-
регрессионной модели по Вильямсу—Клуту F87). 5.3.5. Прогнозирование по регрес-
регрессии F89). 5.3.6. Специальные методы сглаживания экспериментальных дан-
данных F91). 5.3.6.1. Метод наименьших модулей F92). 5.3.6.2. Метод послед-
последней точки F94). 5.3.6.3. Метод однозначной аппроксимации F94). 5.3.6.4. Ме-
Метод обратных разделенных разностей F96). 5.3.6.5. Метод условно-относи-
условно-относительных разностей F96).
5.4. Контрольные карты ......................................... 697
5.4.1. Контрольные карты Шухарта F97). 5.4.1.1. х- и 1?-карты F98).
5.4.1.2. s-карта F99). 5.4.1.3. х- и s-карты для выборок неравного объема G00).
5.4.1.4. Контрольная карта для доли дефектных изделий (р-карта) G01).
5.4.1.5. Контрольная граница числа дефектов (с-карта) G03). 5.4.1.6. Карты
индивидуальных значений и скользящего размаха G03). 5.4.2. Контроль-
Контрольные карты накопленных сумм (ККНС) G04). 5.4.2.1. ККНС для среднего
значения G05). 5.4.2.2. ККНС выборочных размахов G07). 5.4.2.3. ККНС
для выборочных дисперсий G09). 5.4.2.4. ККНС для доли дефектных изде-
изделий G10). 5.4.2.5. ККНС для числа дефектных изделий, основанная на рас-
распределении Пуассона G11). 5.4.3. Относительная эффективность контроль-
контрольных карт G12). 5.4.4. Контроль без использования контрольных карт G13).
5.5. Математико-статистические методы планирования эксперимента ......... 715
5.5.1. Планирование регрессионных экспериментов при изучении механизма
явления (статистическое моделирование) G15). 5.5.1.1. Линейные ортогональ-
ортогональные планы (планирование первого порядка) G16). 5.5.1.1.1. Полный фактор-
факторный эксперимент G16). 5.5.1.1.2. Дробный факторный эксперимент G20).
5.5.1.2. Нелинейные планы второго порядка G22). 5.5.1.2.1. Симметричные
планы второго порядка G22). 5.5.1.2.2. Ортогональные симметричные пла-
планы G24). 5.5.1.2.3. Ротатабельные планы G27). 5.5.1.2.4./^-оптимальные пла-
планы G28). 5.5.1.2.5. Несимметричные планы второго порядка G29). 5.5.2. Пла-
Планирование экспериментов по поиску оптимума G32). 5.5.2.1. Метод крутого
восхождения G32). 5.5.2.2. Симплексное планирование G34).
Очень короткое послесловие ....................................... 736
Список литературы ............................................. 737
Сокращенные названия использованных журналов ....................... 760
Перечень демонстрационных задач .................................. 761
Перечень математико-статистических таблиц ........................... 789
Предметный указатель ........................................... 806
Именной указатель .............................................. 811
Всякая вещь есть форма проявления
беспредельного разнообразия.
Многие вещи нам непонятны
не потому^ что наши понятия слабы;
но потому, что сии вещи не входят
в круг наших понятий.
Козьма Прутков
О математической статистике и об этой книге
(обращение к читателю)
"Что такое математическая статистика и зачем она нам?
Здравствуй, уважаемый читатель! Кто бы ты ни был — инженер, медик, эконо-
экономист, агроном, биолог, психолог или географ, каждый день и каждый час ты имеешь
дело с потоком данных, обрушивающихся на тебя. С их помощью окружающий нас
мир пытается поведать о себе. Результатами испытаний прибора сообщить инжене™
ру о том, что он создал; сведениями о заболеваниях рассказать медику о результатах
его работы; информацией о работе промышленности заставить экономиста еще раз
проверить эффективность экономической системы. Так или иначе, каждый из нас,
оглядываясь в прошлое или заглядывая в будущее, не уйдет от необходимости
получать информацию и извлекать из нее ответы на свои многочисленные вопросы.
Казалось бы, чего проще — взглянул инженер на результаты испытаний прибора
и выявил все свои недоработки, медик получил результаты анализов и безошибочно
поставил правильный диагноз. Однако горький опыт подсказывает, что это далеко
не всегда так. Оказывается, что, наблюдая одно и то же явление, мы будем полу™
чать все время разные результаты. Это — проявление могущества Его Величества
Случая. Слово случай, такое прозрачное для статистика-профессионала, остается
для большинства инженеров промышленности, медиков, биологов и экономистов
символом вмешательства темных, не поддающихся контролю сил. Отчасти это
является интуитивной реакцией „здравого смысла" на двойственность и взаимо™
обусловленность понятийной пары „случайность — детерминированность".
Любое событие (или цепь событий) наблюдатель справедливо считает проявле-
проявлением реальности. С точки зрения теории вероятностей любое наблюдаемое событие
уникально, неповторимо и, стало быть, формально невероятно, ибо для математи-
математической случайности нет нулевой и единичной вероятностей. Однако версия матема-
математической случайности предполагает, что наблюдаемая последовательность событий
является частью более общей последовательности громадного периода, в которой
наблюдаемая последовательность содержится много раз. Так детерминированность
здравого смысла соприкасается со случайностью математической абстракции.
Возможности человека, слава Богу, будут всегда ограничены. Он не сможет
повторить один и тот же опыт бесконечное число раз, а поэтому он никогда не
узнает все обо всем, и ему всегда придется, принимая решение, исходить из своего
нелегкого опыта. Однако надежды его не так уж беспочвенны, ибо еще гениальный
В. Шекспир отметил, что „непременно за шалой случайностью, радуясь своей
странноватой склонности, как свинья в грязи бескрайности, прикорнула наглейшая
определенность".
14 О математической статистике и об этой книге
Как поймать за хвост эту „наглейшую определенность", как увидеть что-то
осмысленное в обрушивающейся на нас лавине информации, чем защититься от
потока досаждающих случайностей?
Такой инструмент человек нашел более 300 лет тому назад: это математическая
статистика — теория познания мира через опыт. Ее приемы и правила позволяют,
располагая противоречивыми результатами наблюдений, выбрать из всех гипотез
наиболее правдоподобную.
Один из основателей и корифеев математики случайностей Влез Паскаль
определил ее как „учение, объединяющее точность математических доказательств
с неопределенностью случая и примиряющее эти, казалось бы, противоречивые эле-
элементы". Однако у неискушенного в премудростях науки современника статистика
ассоциируется скорее с метким афоризмом Дизраэли — „есть ложь, большая ложь
и статистика", чем с изящным инструментом, крайне необходимым ему в работе.
В Англии конца 18-го века описательная статистика получила знаменательное
название „политическая арифметика". Вот такой „политической арифметикой", спо-
способной на потребу политикам „гармонизировать" любые данные, и осталась для
многих статистика. Подобно „доброму человеку из Сезуана" Б. Брехта, мы привык™
ли к тому, что „дурной конец заранее отброшен, он должен, должен, должен быть
хорошим".
Ясно, что такие призывы никак не могут быть питательной средой математиче-
математической статистики. Ее питательной средой и ресурсной базой являются эксперимен-
экспериментальные и прикладные науки, практическая деятельность человека, рассматрива-
рассматривающая повторяющиеся опыты как единое целое.
Мы познаём окружающий нас мир, выдвигая и проверяя по результатам экспе-
римента гипотезы о его свойствах. Получающиеся при этом выводы и заключения,
никогда не обладая абсолютной достоверностью, тем не менее способны обострить
интуицию исследователя, привести его от предварительных гипотез к более общим
и строгим теориям. Другими словами, методы математической статистики — это
мощный (а иногда, и единственный) многофункциональный инструмент в руках
инженера и исследователя, медика и биолога, психолога и географа, студента и про-
профессора.
Более ста лет тому назад человек, к своему изумлению, выяснил, что если бы
случайность отсутствовала, ее нужно было бы изобрести, ибо, оказывается, в слу-
случайности заключены не только растерянность неопределенности, но и созидающая
сила многовариантности. Как ни парадоксально, но поиск оптимальных условий
протекания процесса наиболее эффективен, когда он реализуется в форме слу-
чайного поиска. Контроль качества изделий в производстве наиболее эффективен
при обеспечении случайного отбора изделий из контролируемой партии. В конце
концов, происхождению жизни, а, следовательно, и нашему существованию, мы
обязаны случаю. Все мы помним пушкинскую строку „ ... гений, парадоксов друг".
Но, если внимательно дочитать поэта, то вслед за этой чудесной строкой следует
не менее замечательная „...и случай, Бог — изобретатель". Поэтому не следует
считать математическую статистику только инструментом устранения досадного
влияния случая. Нет, вместе с созидающим случаем математическая статистика
является языком, на котором „Бог — изобретатель" разговаривает с нами. И знать
этот язык обязан каждый инженер, исследователь, каждый специалист. Если „перед
ошибками захлопываем дверь, в смятеньи истина: „Как я войду теперь?" — справед-
ливо подметил Р. Тагор.
Практически любое решение, которое приходится принимать инженеру, руко-
руководителю производства, так или иначе требует применения методов обработки ре-
результатов наблюдений. Приведет ли внедренное новшество к повышению качества
продукции? зависит ли наблюдаемый процесс от заданного фактора? существует
О математической статистике и об этой книге 15
ли связь между исследуемыми величинами? сколь она сильна? — это типовые зада™
чи математической статистики. Сколь долго можно ожидать безотказной работы
прибора? как спланировать его заводские испытания? — это тоже задачи математи-
математической статистики. Перечисление таких примеров можно продолжать бесконечно,
столь бесконечны и сложны взаимосвязи нашего разума с вечно меняющимся,
бесконечным по форме и бездонным по содержанию миром, нас окружающим.
Однако вместе с разумом человек обрел не только гордость бесконечности, но
и привычку довольствоваться достаточным.
Почему появилась эта книга? Чем она отличается от других?
Можно надеяться, что, вняв изложенным аргументам, инженер или исследо-
исследователь пожелает незамедлительно обострить свою интуицию, раздобыть чудодей-
чудодейственный инструмент решения своих повседневных задач.
Казалось бы, возможности прикладной математической статистики неоспори™
мы. Почему же тогда инженеры и ученые, мастера и рабочие остаются в неведении
относительно этих возможностей? Имея многолетний опыт подготовки студентов
старших курсов вузов, могу утверждать, что и сегодняшние выпускники имеют
весьма смутное представление о современных методах математической статистики,
чаще всего не способны применять их на практике. Преподавание этого курса
в вузах находится далеко не на должном уровне. Практические навыки выпуск-
выпускников ограничиваются туманными воспоминаниями о различных определениях
вероятности, иссушающими душу нудными задачами из теории вероятностей, заста-
заставляющими вычислять вероятности появления событий методами комбинаторики.
Относительно математической статистики молодой специалист знает только одно —
дело это темное и „лучшая из парадигм — это правило трех сигм".
Для аспирантов и соискателей ученых степеней математическая статистика
является чаще всего красивой рамкой или упаковкой для диссертации. Присутствуя
на защитах диссертаций и оппонируя их, автор часто разочарованно убеждался, что
соискатель не владеет основами обработки результатов наблюдений, а соответству-
соответствующие разделы диссертации не более чем подарок коллеги-профессионала.
Так почему же инженеров и ученых промышленности не увлекают прелести при-
прикладной статистики? Оставив в стороне мотивации, способные склонить их к этому,
отметим, что они неизбежно столкнутся, прежде всего, с серьезнейшей проблемой —
неимоверным количеством монографий, книг, статей, таблиц и справочников.
По данным российского исследователя А. И. Орлова, шестая часть публика-
публикаций в математике относится к теории вероятностей, математической статистике
и их применениям в различных прикладных областях. Ежегодно появляются более
5 000 статей и книг по этой тематике (читатель вправе заметить: ну вот, еще одна
появилась, но об этом позже). К настоящему времени известно более миллиона (!)
работ по статистическим методам, причем только по прикладной статистике сохра-
сохраняют актуальность более 100 000 статей и книг. В мире издаются более 400 журналов
и периодических изданий по проблемам математической статистики.
Можно назвать десятки зарубежных журналов математической статистики для
инженеров и исследователей: „Annals of the Institute of Statistical Mathematics",
„The Annals of Mathematical Statistics" (AMS), „Journal of the Royal Statistical
Society" (JRSS), „Biometrics", „Biometrika", „Communication In Statistics", „Journal of
the American Statistical Association" (JASA), „Technometrics", „Statistica Neerlandica",
„Sunkhya", „The American Statistical", в то время как у нас в стране можно отметить
лишь раздел „Математические методы испытаний" в журнале „Заводская лаборато-
лаборатория", журнал „Надежность и контроль качества" (в 1991 году в нем выделено место
для выпусков „Статистические методы") и отчасти журнал „Теория вероятностей
16 О математической статистике и об этой книге
и ее применения" (большинство материалов которого не только начинающему, но
и мне не по зубам).
Простая „лоция" по океану публикаций в области математической статистики не
поможет инженеру или исследователю, лишенному профессиональной подготовки
в теоретических вопросах математической статистики. Да и вряд ли ему будут до™
ступно большинство заокеанских книг и журналов — „материков и островов" этого
океана, о существовании которого подавляющая часть инженеров и исследователей
и не догадывается.
Вряд ли еще в каких-нибудь дисциплинах можно встретить книги, содержащие
такое огромное количество литературных ссылок (например, в книге Л. Закса „Ста-
„Статистическое оценивание"—около 1500 ссылок, в книге М. Холлендера и Л. Вулфа
„Непараметрические методы статистики"—около 800). Даже разнобой в термино-
терминологии может привести неискушенного читателя в замешательство. Вряд ли он сразу
сообразит, что „итерационный" и „сериальный" критерии, „фазочастотный" и „зна™
ковый сериальный" критерии — это различные названия одного и того же критерия.
А от такого, например, оборота лихого статистика-профессионала, как „проверив
предварительно нормальность распределения критерием Лина^Мудхолкара, допол-
дополненным комбинированным критерием Шпигельхальтера, можно приступить к срав-
нению средних нескольких выборок, например, с помощью критерия Стьюдента™
Ньюмена^Кейльса", любой нормальный инженер неизбежно должен впасть в тихую
грусть и навсегда потерять желание заглядывать в этот раздел науки.
Как же быть? Как сделать достоянием практикующих инженеров и исследовате-
исследователей сокровищницу наработанных мировой наукой эффективных методов статисти-
статистического анализа результатов наблюдений? Эти методы адаптируются к реальным
потребностям практиков и включаются в пособия, ориентированные на специали™
стов-нематематиков, как правило, через 10—15 лет после их появления.
Такой попыткой является предлагаемая книга. Математическая статистика —
наука, устроенная довольно своеобразно, и ее применение — искусство, требующее
не только знаний, но и практики, опыта, чутья и интуиции. Сделать такую практику
достоянием инженеров и исследователей — цель автора книги. Автор стремился
прежде всего отобразить богатую палитру методологических подходов прикладной
математической статистики. Он исходил из того, что инженеров и научных работ-
работников нужно знакомить с новыми методами и удачными приемами, если даже их
приходится излагать на эвристическом уровне. Цель книги — научить пользоваться
прикладными методами математической статистики, не требуя владения ее теоре-
теоретическими основами. Недостаток понимания основ восполняется подробными реко-
рекомендациями и предостережениями, а также обширнейшей библиографией. Древние
греки справедливо заметили, что „способности чахнут и теряют естественность при
соприкосновении с иссушающими природу учеными наставлениями". Поэтому автор
стремился елико возможно избегать таковых и, следуя мудрости Ньютона — „при
изучении наук примеры полезнее правил", обратился к наиболее эффективному для
пользователя методу изложения материала — в форме демонстрационных примеров
и задач. Изложение техники и последовательности расчетных процедур заменены,
там, где это не в ущерб истине, пояснением конкретных примеров. При этом ав-
автор исходил из того, что заинтересованный только приложениями математической
статистики инженер-практик не будет читать все подряд, а попытается разыскать
пример, похожий на тот, что его интересует. И он будет прав, ибо прикладная
математическая статистика не является наукой, которая может быть изучена только
путем чтения. Умение и своеобразное чутье выбрать правильный метод приходит
только в процессе решения практических задач. Следуя мудрецу Дейлу Карнеги,
признаем, что „в сущности, всё, в конечном счете, сводится к одному — нужно
О математической статистике и об этой книге 17
практиковаться, практиковаться и практиковаться". Компьютер поможет выпол-
выполнить расчеты, но не заменит ни процесс формирования гипотезы, ни творчество,
проистекающее из воображения.
В книге предлагаются около 400 статистических приемов решения всевозмож-
ных практических задач. То, что автор приводит такое изобилие различных совре™
менных методов, многие из которых известны пока не каждому профессионалу, не
является следствием его неразборчивости, а делается им осмысленно.
Причин тому несколько:
— современные компьютеры сделали доступными ранее недоступные в вычис-
вычислительном отношении методы;
— не следует исключать стремление читателя к разнообразию, проистекающее
от природного любопытства;
— демонстрация различных подходов к одной и той же задаче помогает глубже
ее осмыслить.
Автор на себе опробовал этот путь, именно так начав знакомство с приклад™
ной математической статистикой, будучи молодым специалистом™электронщиком.
Конечный итог даже только знакомства со всем разнообразием методов — путь
к пониманию математической статистики, к овладению практическими навыками
пользования ее методами. Ведь каждый метод — это демонстрация тех или иных
положений статистики.
Обилие различных критериев и оценок в статистике не должно пугать — это
следствие множественности ситуаций, возникающих в реальной жизни. Знаком™
ство с массой различных приемов статистической обработки данных способству-
способствует демонстрации самого механизма, способа мышления, методологии прикладной
статистики, помогает глубокому усвоению как ее методов, так и философии. Поль™
зователя не должна смущать эквивалентность некоторых методов, как не пугает
его возможность решать одну и ту же жизненную коллизию разными способами.
Знакомство с множеством практических приемов позволяет пользователю почув-
ствовать „воздух" математической статистики, на уровне подсознания уяснить ее
методологию, внутреннюю логику, разнообразие и остроумие подходов. Это способ
учиться статистике, да и необходимость выбора подходящего приема из большой
совокупности возможных — неплохой тренинг на долгом пути знакомства с мате-
математической статистикой для любого инженера или исследователя. Так или иначе,
пользователю предлагается совокупность методов и приемов прикладной матема-
математической статистики, которая никогда еще не собиралась в одной книге.
Изложение материала в книге преследует цель дать по каждому методу на™
бор стандартной информации, включающий в себя: логическое обоснование, связь
с другими методами, назначение, авторство, методику расчетов, необходимые та-
таблицы и аппроксимации, указания по особенностям применения и статистическим
характеристикам, набор демонстрационных задач. Располагая такой исчерпыва-
исчерпывающей информацией, пользователь может решать свои практические задачи, не
обращаясь ни к каким другим дополнительным источникам.
Исчерпывающий характер предлагаемой информации дает пользователю уни-
уникальный шанс приобрести в компактной форме весь мировой опыт прикладной
математической статистики, в десятки раз сократить время поиска необходимых
методов в океане публикаций, в сотни раз повысить эффективность своей работы
за счет принятия оптимальных решений в море возможных, сокращения объема
испытаний и экспериментальных работ, повышения качества продукции. Эта книга
полезна для аспирантов и ученых, желающих (и обязанных) на современном уровне
проводить эксперименты и обрабатывать их результаты. Она может быть исполь-
использована студентами вузов как универсальное справочное пособие.
18 О математической статистике и об этой книге
"Что есть в книге и немного теоретических основ статистики
Предлагаемая книга включает в себя пять глав. Все главы связаны между собой
единой логикой методологического подхода и посвящены отдельным важнейшим,
имеющим самостоятельное практическое значение задачам прикладной математи-
математической статистики.
Состав и тематика отдельных глав последовательно отражают логику развития
самой теории вероятностей и математической статистики. Мы уже говорили о том,
что потребность каким-то образом справиться с потоком информации у человека
возникла давно, сразу после того, как он стал понимать, что это информация. Есте-
Естественно, первое, что отметит каждый из нас — это наличие в потоке информации
определенных закономерностей. Источником такой закономерности является нечто
объективное, содержащееся в природе наблюдаемого процесса или явления. Прояв-
Проявлением этого „нечто" является частота появления определенных событий (величин).
Мы отмечаем, что одни события встречаются чаще (или реже), чем другие. Это
наблюдение потребовало найти „нечто", которое, говоря словами Гете, „единичное
искусно обобщает, объединяя все в торжественный аккорд", и это „нечто" было
названо вероятностью. Обращу внимание читателя на одну любопытную деталь.
Хорошо известны такие журналы по прикладной математической статистике, как
„Технометрикс", „Биометрика", „Эконометрика", „Психометрика". Казалось бы, они
являются журналами для специалистов разных профессий, но все они — журналы
прикладной математической статистики, и именно она — математическая статисти-
статистика — является той „метрикой", которая объединяет все прикладные науки, имеющие
дело с потоком числовых данных, ибо, как тонко заметил Валлювар, „что, в сущ-
сущности, буква и цифра? Не глаза ли два, которым открыта вся суть естества?"
Вернемся к вероятности. Понимая под ней частоту появления отдельных собы-
событий в наблюдаемом потоке, человек, естественно, попытался связать вероятность
появления случайного события с ее количественным значением. Такая связь может
быть описана как функция распределения вероятностей или плотность распреде-
распределения вероятностей, являющаяся производной от функции распределения. Опи-
Описанию распределений вероятностей посвящена первая глава книги.
У читателя может возникнуть вопрос: а зачем, собственно, специально описы-
описывать какие-то функции, и откуда они вообще взялись? В конце концов, существуют
достаточно хорошо разработанные в математическом анализе приемы исследова-
исследования функций, изучаемые еще в школе. Можно, конечно, воспользоваться этими
приемами, но мы все-таки имеем дело не просто с математическим соотношением,
а с вероятностной моделью. Поэтому для описания функций распределения веро-
вероятностей используются специальные меры (параметры), называемые моментами.
Отдельные моменты и их комбинации характеризуют такие важные в практическом
отношении характеристики распределения вероятностей, как центр группирования
данных, степень их рассеяния относительно центра, поведение случайных величин
в районе центра группирования, симметричность распределения вероятностей.
Среди известных законов распределения вероятностей каждый наверняка назо-
назовет нормальный закон. Но немногие спросят: а почему он называется нормальным?
Уж не потому ли, что другие распределения ненормальны? Вопрос не так наивен,
как кажется. Ничего нормального, судя по математической функции плотности
распределения вероятностей
/(*) =
в нем нет, если не считать, что она содержит достаточно полный набор символов,
обычно употребляемых в математике.
О математической статистике и об этой книге 19
Дело в том, что если наблюдаемый процесс зависит от совокупности болыно™
го числа взаимонезависимых (или слабозависимых) факторов, вклад каждого из
которых в процесс мал, то, поверь мне, читатель, на слово (это доказали весьма
ученые мужи), мы неизбежно придем к нормальному распределению вероятностей.
Наверное, оттого, что описанная ситуация представляется нам нормальной, назван
нормальным и закон, отражающий влияние случайных факторов на результирую-
результирующий процесс.
Большинство используемых в прикладной математической статистике распре-
распределений вероятностей, так или иначе связано с нормальным законом или сводится
к нему. В первой главе книги „Распределения вероятностей случайных ве-
величин" приведены подробные сведения более чем о 30 непрерывных и дискретных
распределениях вероятностей, исчерпывающих большинство мыслимых практиче-
практических ситуаций. Описаны области их применения, методы расчета вероятностей
и необходимые аппроксимации.
Во второй главе книги „Оценка параметров распределений вероятностей"
рассмотрены методы оценки параметров различных распределений вероятностей.
Математическое понятие параметр распределения в практике инженера представ™
лен такими знакомыми категориями, как средняя наработка на отказ, интенсив-
интенсивность отказов, точность показаний измерительного прибора и т. п. Поэтому ме-
методы оценки параметров распределений для инженера и исследователя являются
методами извлечения из результатов наблюдений, испытаний и экспериментов ин-
информации, позволяющей оценить качество изделий, уровень принятых технических
решений.
Рассмотрены точечные и интервальные оценки всех наиболее распространен™
ных распределений. Большое внимание уделено „быстрым" упрощенным оценкам,
а также непараметрическим (свободным от распределения) и так называемым
робастным (robust) оценкам, устойчивым к засорению выборок посторонними
наблюдениями.
Для практического применения методов математической статистики чрезвычай-
чрезвычайно важно знание закона распределения вероятностей. По существу, сама изучаемая
величина представлена для исследователя только законом распределения вероят-
вероятностей реализации ее значений.
Попытка применить методы анализа результатов наблюдений, разработанные
для конкретных законов распределения вероятностей, в условиях, когда реальное
распределение отличается от гипотетического, является самой распространенной
ошибкой, приводящей к неверным выводам и, в конечном итоге, к существенным
материальным потерям и затратам времени. Именно поэтому любая обработка
результатов наблюдений должна неизменно начинаться с ответа на главный вопрос:
каким законом описывается распределение вероятностей совокупности, из которой
извлечена обрабатываемая выборка случайных величин? На практике обычно эта
проблема формулируется следующим образом. Выдвигается гипотеза, утверждаю-
утверждающая, что наблюдаемое распределение случайных величин описывается конкретным
законом (нормальным, экспоненциальным, равномерным, Вейбулла и т.д.). Задача
первичного анализа — принять или отклонить выдвинутую гипотезу. Если ни одна
из гипотез относительно формы закона распределения не принимается, то может
быть сформулирована более мягкая гипотеза, например — „наблюдаемое распреде-
распределение вероятностей симметрично относительно определенной точки". Установление
даже этого факта дает в руки исследователя более эффективные методы анализа
наблюдений, чем при полном незнании закона распределения вероятностей. И, на-
наконец, если исследователь не получил достаточных оснований для выбора типа рас-
распределения, то возникает задача подбора кривой распределения непосредственно по
экспериментальным данным.
20 О математической статистике и об этой книге
Критерии проверки гипотез о законе распределения вероятностей принято на™
зывать критериями согласия, подразделяя их на две группы — общие и специаль-
специальные критерии согласия. Общие критерии согласия применимы к формулировке
гипотезы о согласии наблюдаемых результатов с любым априорно предполагаемым
распределением. Специальными критериями проверяются специальные гипоте-
зы, формулирующие согласие с конкретной формой распределения — нормальной,
экспоненциальной и т. п. Такие критерии носят соответствующие названия — кри-
критерии нормальности, критерии экспоненциально сти^ критерии равномерности.
Естественно, что при формулировании специфичных требований общие критерии
согласия могут быть трансформированы в специальные критерии.
Следует отметить, что многообразие возможных альтернатив, противостоящих
выдвинутой гипотезе, порождает и чрезвычайное многообразие статистических
критериев, имеющих различную мощность по отношению к различным альтернати-
альтернативам. В третьей главе „Методы анализа законов распределения вероятностей
случайных величин" представлена широкая гамма критериев согласия (более 80),
впервые собранная в одной книге.
В четвертой главе „Проверка гипотез о значениях параметров распреде-
распределений вероятностей" рассматриваются методы проверки предположений о значени-
значениях параметров распределений. Формулирование гипотез о свойствах окружающего
нас мира и проверка их непосредственно наблюдениями или с помощью целенаправ-
ленного экспериментирования составляет основу того, что мы называем наукой или
научной деятельностью.
Проверка гипотез применительно к потребностям ежедневной практики ин-
женера или исследователя приобретает вполне конкретный смысл, зависящий от
специфики наблюдаемых реалий, особенностей возникающих коллизий, потреб-
потребностей практики, стимулировавших сам процесс зарождения и формулирования
гипотезы. Например, часто встречающаяся задача — соответствуют ли параметры
разработанного изделия предъявляемым требованиям — в математико-статистиче-
ской формулировке может звучать так: „необходимо проверить гипотезу о том, что
параметр ? распределения случайной величины X превосходит заданную контроль-
контрольную величину ?0"-
Сколь разнообразен и сложен окружающий нас мир, столь велико и разнообраз-
разнообразно семейство возможных гипотез о его свойствах. Поэтому четвертая глава является
самым объемным разделом книги.
Автор надеется, что знакомство с многочисленными примерами решения задач
является лучшим способом узнавания палитры методов прикладной статисти-
статистики. Впрочем, в случае нежелания наблюдать палитру прагматик, располагая этой
книгой, получает инструмент решения своих практических задач без необходимости
вникать в глубину захватывающего мира обработки результатов наблюдений. Сле-
Следует всегда помнить об антагонистическом противоречии между категоричностью
и надежностью высказывания по гипотезе: надежное высказывание некатегорично,
категоричное высказывание ненадежно. Мы выдвигаем гипотезу и отвергаем ее
тогда, когда получаем результат, маловероятный при истинности выдвинутой гипо-
гипотезы. Принятая граница маловероятности называется уровнем значимости. Если
мы наблюдаем событие, вероятность появления которого не превышает уровень
значимости, мы называем его значимым, используя этот термин в качестве анто-
антонима термину случайность. Такой метод принятия решений в статистике получил
название принципа значимости.
При проверке гипотез возможны ошибки двух типов — неправильное отклонение
верной гипотезы (ошибка первого рода) и неправильное принятие ложной гипо-
гипотезы (ошибка второго рода). Следует помнить, что уровень значимости должен
устанавливаться перед получением данных. Это требование для практи-
О математической статистике и об этой книге 21
ка вообще является некоторой головоломкой, но, уважаемый читатель, поверь,
что это очень важно. Ты можешь задать естественный вопрос: а какой уровень
значимости или достоверности следует выбирать? Увы, но это твоя проблема,
читатель, а не математической статистики. Достоверность, с которой ты бы хотел
получить ответ на поставленный вопрос, должна определяться тобой исходя из
практической ситуации. Желание повысить достоверность заключения по гипотезе
связано с увеличением затрат, стремление снизить затраты на проверку гипотезы
неизбежно приводит к повышенному риску принять ложное решение. Всё должны
определять конкретная ситуация и цена риска. Например, проектируя атомный
реактор или переходя дорогу перед транспортом, мы стремимся свести к нулю
риск даже повышением затрат, ибо цена высока. Одним из методов сохранения
достоверности выводов при снижении затрат на проверку гипотезы является выбор
эффективного статистического приема обработки результатов наблюдений. В этом
поможет предлагаемая книга.
Обычно на практике применяются уровни значимости 0,01; 0,05; 0,1. Важно
неукоснительно выполнять основное требование — гипотезы должны быть выдви™
нуты перед статистическим анализом, а сам числовой материал не должен
быть использован для выдвижения гипотезы. Гипотезы, выдвинутые на основе
анализа полученного материала, могут быть полезны только в качестве новых
гипотез для последующих проверок. Перефразируя Томаса Гексли, укажем на вели™
кую трагедию математической статистики как науки — „она способна уничтожить
прекрасную гипотезу одним безобразным фактом".
В первых четырех главах книги рассмотрены методы и приемы математиче-
математической статистики, позволяющие оценить параметры статистических совокупностей,
сравнить их между собой. При этом, как правило, предполагалась взаимная неза-
независимость сравниваемых совокупностей. В последней, пятой главе „Методы
исследования связей между случайными величинами" рассмотрены вопросы оценки
связей между статистическими совокупностями. В ней последовательно излагаются
методы и приемы дисперсионного, корреляционного и регрессионного анализов,
являющихся последовательными ступенями при изучении характера и особенностей
связей между случайными величинами.
Методами дисперсионного анализа устанавливается влияние заданного фактора
на процесс, отображаемый наблюдаемой статистической совокупностью данных.
Корреляционный анализ позволяет оценить силу (степень) такой связи, а методами
регрессионного анализа можно установить конкретную математическую модель,
адекватно отражающую установленную связь.
Стоит ли иметь эту книгу? Подумай!
Здесь будет немного рекламы. Но кто без нее сегодня обойдется? Если ты при™
обретешь эту книгу, ты станешь обладателем системы знаний в области обработки
и анализа результатов наблюдений.
У читателя может возникнуть вопрос: а не проще ли воспользоваться одним из
пакетов статистического программного обеспечения и поручить ему обработку ре™
зультатов наблюдений, оставив за собой роль беспечного наблюдателя? Несомненно,
такой пакет является изящным и мощным инструментом в руках профессионала,
которому знаком язык математической статистики, но он вряд ли поможет ин™
женеру или исследователю, далекому от мира формальной математики и от тер™
минологического языка математической статистики, творчески осмыслить систему
решения тех или иных задач, логику изучения процессов методами статистики.
Предлагаемая книга может с успехом обеспечить начальный тренинг неподготов-
неподготовленному пользователю, подготовив тем самым ему плацдарм для штурма высот
современного программного статистического обеспечения.
22 О математической статистике и об этой книге
В книге содержится подробное описание около 400 задач, иллюстрирующих
решение практически любой проблемы обработки результатов наблюдений. Пере-
Перевод методов математической статистики, иногда довольно сложно описываемых
языком формальной математики, на язык последовательности выполнения эле-
элементарных вычислительных операций делает их доступными неподготовленному
пользователю, позволяет ему успешно справляться с возникающими затруднениями
на высоком уровне профессионала, не требуя его квалификации и подготовки.
Более 200 математико-статистических таблиц являются мощной „базой данных",
они предоставляют в распоряжение читателя практически весь арсенал известных
таблиц, большая часть которых пока содержится только в специализированных
научных журналах, мало известных большинству инженеров^практиков. В распо™
ряжение читателя, который пожелает углубиться в основания прикладной матема-
математической статистики, предлагается обширный перечень литературы, содержащий
около 700 наименований.
Прикладная статистика становится таковой тогда, когда ее методы широко
применяются на практике. Наша цель — сделать ее таковой, доведя методы матема-
математической статистики до тех, кто, пасуя перед ее высокой математизацией, не вникал
в достаточно простой смысл математических символов.
Некоторое представление об объеме сведений, содержащихся в книге, и ее базе
данных дают содержание глав и перечень основных использованных информацион-
информационных источников. Весьма полезен также прилагаемый перечень задач, являющийся
ориентиром при выборе задачи, похожей на ту, которую предстоит решить пользо-
пользователю.
С уважением,
Доктор технических наук,
профессор
А. И. Кобзарь
ГЛАВА 1
РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН
Общие положения. Распределение значений случайной величины по вероят-
ности их появления характеризуется интегральной функцией распределения (зако-
(законом распределения) и плотностью вероятностей.
Интегральная функция (закон) распределения случайной величины X обозна-
обозначается через F(x) ж определяется как
где Р[Х ^ х]—вероятность того, что значение случайной величины X не превы-
превысит X.
Плотность вероятности выражается формулой
Свойства функций F(x) и f{x) определяются соотношениями:
F{x)= | f(x)dx,
(^oo) = lim F(x) = 0, f f(x) dx = 1,
F(+oo) = lim F{x) = 1, ?[хг < x ^ x2] = F(x2) - F(x{),
^(^г) ^ F(xi), если Х2 ^ x\.
Если известен закон распределения вероятностей случайной величины, то можно
решать многие практические задачи, возникающие при статистическом анализе экс-
экспериментальных данных. Например, вычисление вероятности попадания случайной
величины в заданный интервал, вероятности превышения случайной величиной
заданного значения и т. п. Определенное представление о функции распределения
дают его квантили. По определению а • 100 %-я квантиль (а-квантиль) распреде-
распределения, обозначаемая ха, соответствует условию
Р(Х < ха) = F(xa) = a.
Для описания функций распределения пользуются специальными мерами, по-
позволяющими охарактеризовать положение, форму и другие их особенности.
Центр распределения характеризуется средним значением /i, медианой Me,
модой Мо. Среднее значение ц равно первому начальному моменту, медиана явля-
является 50%-й квантилью распределения, мода соответствует значению х случайной
величины, для которого f(x) = max.
Рассеяние случайных величин вокруг центра группирования оценивается дис-
дисперсией (математическое ожидание квадрата отклонения случайной величины от
24 Распределения вероятностей случайных величин [Гл. 1
среднего значения), стандартным отклонением (квадратный корень из диспер™
сии), коэффициентом вариации (отношение стандартного отклонения к математи™
ческому ожиданию случайной величины), размахом w = жшах — хш1п.
Симметричность распределения характеризуется коэффициентом асиммет-
асимметрии аз, особенности поведения случайной величины в области максимума ее плот-
плотности описываются коэффициентом эксцесса «4-
Подробно с теоретическими основами теории вероятностей и функциями рас™
пределения можно ознакомиться, обратившись к монографиям [1-22]. Исходя из
природы возникновения случайных величин, различают распределения непрерыв-
непрерывных и дискретных случайных величин.
1.1. Непрерывные распределения
1.1.1. Нормальное распределение
Описание, применение. Наиболее широко применяемое распределение. В са-
самом названии распределения отражена идея его универсальности. Нормальное рас™
пределение подробно исследовано в работах Муавра, Лапласа, Гаусса, Чебышева,
Ляпунова, Бернштейна. Теоретической основой нормального закона распределения
вероятностей является центральная предельная теорема Ляпунова, утверждающая,
что распределение суммы независимых случайных величин с любым исходным рас-
распределением будет нормальным, если число слагаемых достаточно велико, а вклад
каждого в сумму мал.
Нормальное распределение является краеугольным камнем математической ста™
тистики в силу ряда причин:
— схема его возникновения соответствует многим реальным физическим про™
цессам, порождающим результаты обрабатываемых наблюдений;
— при возрастании объема выборки предельное распределение для большин-
большинства распределений является нормальным и с успехом может использоваться для
аппроксимации последних;
— нормальное распределение обладает рядом благоприятных математико-ста-
тистических свойств (легко нормируется и аппроксимируется, обладает свойством
аддитивности).
В теории надежности нормальное распределение обычно используется для опи-
описания износовых отказов, интенсивность которых со временем возрастает.
Свойства
Обозначение -^"(м?а)
Параметры /х, а
ТТ ?( X 1 I I X - U
Плотность j(x;/i,(j) = —-j= ехр < — I
X ,
Функция распределения F(x;u1a) = —-= ехр < —-
— оо ^
(^оо < х < +оо)
Среднее М(ж) = ц
Дисперсия D(x) = a2
Стандартное отклонение а
Коэффициент вариации v = —
1.1] Непрерывные распределения 25
Коэффициент асимметрии аз = О
Коэффициент эксцесса «4 = 3
Мода Мо = и
Медиана Me = /i
Распределение симметрично относительно точки х = /i и имеет два параметра
/л и сг, совпадающих со средним значением и стандартным отклонением.
Для удобства в практических приложениях применяется нормированная слу™
чайная величина z = (х — /i)/c", распределение которой называется стандартным
нормальным с нулевым средним и единичной дисперсией: 7V@,1).
В большинстве пособий по теории вероятностей и математической статистике
приводятся таблицы функции
или связанной с ней функции (интеграла) Лапласа
Очевидно, что
F(-*) = 1 - F(z) и P(a^z^b) = F(b)-F(a).
п
Сумма у = ^Р а^ж^ нормально распределенных случайных величин N(/j,i]ai) рас™
г=1
преде лена нормально, р-квантиль нормально распределенной случайной величины
i?(/i, а) связан с квантилью ис случайной величины, имеющей стандартное нор-
нормальное распределение 7V@,1), соотношением
Up = /JL + UpCT.
В силу симметричности нормального распределения и^ = ^и\_р.
Обширные таблицы нормального распределения приведены в [23—29]. Часть их
воспроизведена в табл. 1. Так как таблицы всегда ограничены, приведем известные
аппроксимации, достаточно легко реализуемые применением существующих массо-
массовых микрокалькуляторов или персональных ЭВМ.
Аппроксимация 1 [30]:
где А = A + bzy1; Ь = 0,33267; аг = 0,4361836; а2 = ^0,1201676; а3 = 0,937298.
Абсолютная погрешность ^ 1 • 10~5.
Аппроксимация 2 [30]:
F(z) = 1 - (V2^2/2) ~X J2 ^\
где А = A + bzy1; Ь = 0,2316419; аг = 0,31938153; а2 = -0,35656378; а3 = 1,7814779;
а4 = -1,821256; а5 = 1,3302744.
Абсолютная погрешность ^ 1 • 10~ .
26
Распределения вероятностей случайных величин
[Гл. 1
Таблица 1
Квантили стандартного нормального распределения
р
0,50
0,52
0,54
0,56
0,58
0,60
0,62
0,64
0,66
0,68
0,70
0,72
0,74
0,76
0,78
0,80
0,00000
0,05015
0,10043
0,15097
0,20189
0,25335
0,30548
0,35846
0,41246
0,46770
0,52440
0,58284
0,64334
0,70630
0,77219
0,84162
Р
0,820
0,840
0,860
0,880
0,900
0,910
0,920
0,930
0,940
0,950
0,960
0,970
0,980
0,990
0,992
0,994
ир
0,91536
0,99446
1,08032
1,17499
1,28155
1,34075
1,40507
1,47579
1,55477
1,64485
1,75069
1,88079
2,05375
2,32635
2,40891
2,51214
Р
0,995000
0,996000
0,997000
0,998000
0,999000
0,999200
0,999400
0,999500
0,999600
0,999700
0,999800
0,999900
0,999950
0,999990
0,999995
0,999999
Up
2,57583
2,65207
2,74778
2,87816
3,09023
3,15591
3,23888
3,29053
3,35279
3,43161
3,54008
3,71902
3,89059
4,26489
4,41717
4,75342
Аппроксимация 3 [31-33]:
(c5 + z(c4 + z(c3 + z(c2
где a = 5,383; c2 = 48,891; c3 = 38,004; c4 = 3277,626; c5 = 21141,006; c6 = 49867,347.
Абсолютная погрешность ^ 5 • 10 .
Аппроксимация 4 [32, 34]:
Относительная погрешность ^ 0,3%.
Аппроксимация 5 [32]:
= <1^ехр И , 0<z^l,96; 0 ^ #(z) ^ 0,95.
Абсолютная погрешность ^ 0,114.
Аппроксимация 6 [32]:
= il-
0 < z ^ 5,327; 0 ^ #(z)
где k = 0,1253.
Относительная погрешность ^ 1%.
Аппроксимация 7 [35]:
ехР Г - *Ч (-
1-7
4
Z
¦°4Т
где ai = 0,278393; a2 = 0,230389; a3 = 0,0000972; a4 = 0,078108.
1.1] Непрерывные распределения 27
Аппроксимация 8 [36]:
{(i±ifpJ'34}, г>0;
при z < 0 F(-z) = 1 - F(z).
Абсолютная погрешность ^ 0,0002.
Аппроксимация 9 [37]:
[] ^ , Р ^ 0,01.
Аппроксимация 10 [38]:
где с0 = 2,515517; а = 0,802853; с2 = 0,010328; 4 = 1,432788; d2 = 0,189269;
d3 = 0,001308.
Абсолютная погрешность ^ 0,00045.
Аппроксимация 11 [37]:
[()] У , Р ^ 0,05.
Аппроксимация 12 [32]:
= --1пA -р2) , р<0,99.
Относительная погрешность ^ 3,7%.
Аппроксимация 13 [32]:
2
где к = 1,898.
Относительная погрешность
Аппроксимация 14 [32]:
0 < р ^ 1 - 1 • 10,
Относительная погрешность ^ 0,3%.
Аппроксимация 15 [39]:
Относительная погрешность ^ 0,3%.
Аппроксимация 16 [36]:
/ X 0,4274
и = 2,0637 In 0,16 - 1,5774, 0,5 ^ р ^ 0,999.
V г~Р J
Абсолютная погрешность ^ 0,0008.
28 Распределения вероятностей случайных величин [Гл. 1
Аппроксимация 17 [33]:
- -lnl-pU -Ьл/2 1-р
0,0455 > 1 - р > 1,244 • 10
Относительная погрешность ^ 0,6%.
Аппроксимация 18 [40]:
где 5 = -0,717; а = -0,416.
Аппроксимация 19 [40]:
~5;
0,
^ (-6 - Л/Ь2+4а1пA-р)), р > 0,5,
где Ь = -0,717; а = -0,416.
Относительная погрешность ^ 0,5%.
Аппроксимация 20 [114]:
F(z) = {1 + exp[^0,0725zB2 + z1'96)] }~\ z ^ 0;
при z < 0 F(z) = l-F(-2).
Точность при трех знаках абсолютная, в четвертом знаке максимальная погрень
ность 0,02%. Это одна из наиболее простых и весьма точных аппроксимаций.
Аппроксимация 21 [114]:
124 + 085Ж0;657
р ^ 0,5,
о,ооож3 + ^р'
где К = — In ( — — 1
\Р
Относительная погрешность 0,3%.
Для многих приложений требуется знание математического ожидания г-й поряд™
ковой статистики в выборке объема п из стандартного нормального распределения,
т. е. математического ожидания г-го по номеру члена выборки, упорядоченной по
возрастанию.
Известно, что математическое ожидание г-го по величине члена выборки из стан-
стандартного нормального распределения М(^) равно квантили ир>, где р' = -^- [40].
Таким образом, аппроксимации для квантилей могут быть использованы и для
аппроксимации математических ожиданий порядковых статистик, что позволяет
отказаться от применения громоздких таблиц.
Поясним применение предложенных аппроксимаций при решении практических
задач.
Задача 1. Вычислить значение функции распределения вероятностей в точке
х = 200, если случайная величина распределена нормально со средним ц = 100 и дис-
дисперсией а = 2500.
Значение нормированной переменной определим по формуле
_ х - fj, _ 200 - 100 _
Z ~~ a ~ 50 ~
Таким образом, смысл задачи состоит в нахождении значения F(z) = P(z ^ 2).
1.1] Непрерывные распределения 29
Для вычисления FB) воспользуемся приведенными ранее аппроксимациями. Для
контроля будем иметь в виду, что точное табличное значение FB) = 0,97725.
Аппроксимация 1. Вычисляем Л = = 0,60047798.
F щ 1 + 0,332567-2
Далее имеем (л/2тге~2~) = B, 506628275е2)~1 = 0,053990966.
з
Находим ]Г а»Л* = 0,436836 • 0,60047798 - 0,1201676 • @560047798J + ... = 0,421529962.
г=1
Вычисляем FB) = 1 - 0,053990966 • 0,421529962 = 0,97724119.
_ . 0,97725-0,97724119 _
Относительная погрешность о = = 0,0009%.
Аппроксимация 2. Вычисляем
Л = = 0,683394431 и л/2тгехр — = 0,053990966.
1 + 0,2316419-2 \ \2 J J
5
Вычисляем ]Г а{ • А* = 0, 31938153 • 0,683394431 - 0,35656378 • @,683394431J + ... =
= 0,421367913.
Находим FB) = 1 - 0,053990966 • 0,421367913 = 0,977249939.
0 97725 — 0 9772499
Относительная погрешность S = — = 0,000006%.
F 0,97725
Аппроксимация 3. Последовательно вычисляем 5,383 • 2 + 48,891 = 59,657; 59,657 • 2 +
+ 38,004 = 157,318; 157,318 • 2 + 3277,626 = 3592,262; 3592,262 • 2 + 21141,006 = 28325,53;
28325,5 • 2 + 49867,347 = 1065518,407; A + 10~6 • 2 • 1065518,407)~16 = 0,45500513.
Находим ФB) = 1 - 0,45500513 = 0,954499486 и окончательно
,_,, ч 1 + ФB) 1 + 0,954499486
FB) = — = - = 0,'
К J 2 2
Относительная погрешность S = 0,00003%.
Аппроксимация 4. Вычисляем
v^ {-lf'Z2i _ 22 24 -z-
^ 2* .г! • Ai + Л\ ~ ~ 2^ 22 • 2! • Б ~ 23 • .4! • 7
2*-г!-Bг + 1) 2-3 22 • 2! • 5 23 • 3! • 7 24 • 4! • 9
и находим
ФB) = \ - • 2 • 0,616931216 = 0,984479744; FB) = 1 + Ф^ = 0,992239892.
V тг 2
Относительная погрешность S = 1,5% велика.
2 • 2"
Аппроксимация 5. Вычисляем ФB) = Wl —ехр( 1 = у/1 — е™2'546479089 =
V v ж )
= 0,960022359.
Имеем FB) = 1 + Ф^ = 0,98011179.
Относительная погрешность S = 0,28% велика, так как аппроксимация применена
для z > 1,96; Ф(^) > 0,95, т.е. за пределами допустимого диапазона.
Аппроксимация 6. Вычисляем последовательно 1+0Д253-22 = 1,5012; ( 0,1253 1 х
х 22 = 2,045279089; е'045279089 = 0,129344086; 1 - °?129344086 = 0,913839537.
Далее имеем ФB) = ^0,913839537 = 0,955949547 и окончательно
= 0,977974773.
т
к J 2
Относительная погрешность S = 0,07%.
30 Распределения вероятностей случайных величин [Гл. 1
2
Аппроксимация 7. Вычисляем последовательно 0,27893 • —^ = 0,393707156; 0,23089 х
V2
4 23 24
х ~~ = 0,460778; 0,000972 . —= = 2,7492311 • 10~3; 0,078108 • — = 0,312432.
2 ' ' ' 2лД ' ' 4
Окончательно вычисляем
FB) = 1 - 0,5A + 0,393707156 + 0,460778 + 2,7492311 • 10~3 + 0,312432) =
= 1 - 0,5 • 2,169666387^4 = 0,977436931.
Относительная погрешность 8 = 0,02%.
+ :
^0637
2 + 1 5774 \ '
Аппроксимация 8. Вычисляем ( ;^ОУу ) = 3,623055577 и е-з,б23055577 =
= 0,026700965.
Окончательно находим FB) = 1 - 0,852 • 0,026706965 = 0,977250777.
Относительная погрешность 8 = 0,00007%.
Аппроксимация 18. Вычисляем ^0,717 • 2 - 0,416 • 22 = ^3,098; е'098 = 0,04513939.
Находим F{2) = 1 - 0,5 • 0,04513939 = 0,97743005.
Относительная погрешность 8 = 0,018%.
Аппроксимация 20. Вычисляем FB) = {l + exp [^0,0725 • 2 • B2 + 21'96)] j =
= 0,977115384.
Относительная погрешность S = 0,014%. Это одна из наиболее простых и точных
аппроксимаций.
Задача 2. Для случайной величины, имеющей стандартное нормальное распределение,
найти значение, вероятность превышения которого равна 0,05.
Другими словами, требуется найти значение ир: Р (х ^ ир) = 0,95, или Р (ж > ир) =
= 0,05. По определению ир —верхняя 95%-я квантиль случайной величины. Воспользуем-
Воспользуемся аппроксимациями для стандартного нормального распределения. Табличное значение
его квантили гхо,95 = 1,64485363.
Аппроксимация 9. Так как эта аппроксимация применима только для значений
р ^ 0,01, воспользуемся соотношением ир = ^и\^р и будем искать квантиль и\-р = 1^0,95,
ИМеЯ В ВИДУ, ЧТО 1l.o,95 = — ^0,05 •
Вычисляем
1 г
tio,o5 =-[-21п(у2тг-0,05)] 2 = - [-2 In0,125331413] 2 =-2,038035201.
Следовательно, ио,95 = 2,038035201.
Относительная погрешность 8 = 23,95% очень велика. Это объясняется тем, что
аппроксимация применена вне допустимых пределов (должно быть р ^ 0,01).
I 2
Аппроксимация 10. Вычисляем t = [-2 In A - 0,95)] 2 = 2,447746831 и ]Г а? =
i=0
= 2,515517 + 0,802853 • 2,447746831 + 0,010328 • 2,4477468312 = 4,542577732.
з
Далее J2 dit% = 1,432788-2,447746831+0,189269-2,4477468312+0,001308-2,4477468313 =
= 4,66028338.
Вычисляем —1 = 0,80253539 и окончательно и0 95 = 2,447746831 ~~
1 + 4,66028338 '
- 0,80253539 = 1,64521144.
Относительная погрешность 8 = 0,02%.
Аппроксимация 11. Вычисляем последовательно л/2жр = л/2ж • 0,05 = 0,125331413;
^/0,125331413 = 0,35402177; -2 In 0,35402177 = 2,07679374; лДж • 0,05 • 2,076679374 =
= 0,260287495; -2 • In 0,260287495 = 2,69193701; ^0,05 = -^2,69193701 = -1,64071235.
Следовательно, г^о,э5 = — tto,o5 = 1,64071235.
Относительная погрешность 8 = 0,25%.
1.1] Непрерывные распределения 31
Аппроксимация 12. В нашем случае = 0,95, откуда р = 0,9 и г^о,95 =
= J-- 1пA - 0,92) = 1,615137313.
Относительная погрешность S = 1,8%.
Аппроксимация 13. Имеем по аналогии = 0,95 и р = 0,9. Далее вычисля-
1
ем -In A - 0,91>898) = 1,707888074; 1,707888074^эв = 1,325793782. Окончательно имеем
^о,95 = у - ' 1,325793782 = 1,66163609.
Относительная погрешность 6=1%.
1 -\- р
Аппроксимация 14. По аналогии = 0,95 и р = 0,9. Далее вычисляем
- 1пA - 0,94) = 1,067404362; A,067404362I = 1,102791627; - In y/l - 0,92 = 0,830365603;
7т( — • 1,102791627 + 0,830365603 J = 2,693171017.
Окончательно имеем ио,95 = ^25693171017 = 1,641088363.
Относительная погрешность 6 = 0,2%.
Аппроксимация 15. Вычисляем 0,950'14 = 0,9922844661; A - 0,95H'14 = 0,65743951.
Следовательно, ио,95 = 4,91@,992844661 - 0,65743951) = 1,646839291.
Относительная погрешность 5 = 0,12%.
Аппроксимация 16. Вычисляем In 0,16 = 2,835732274; 2,8357322740'4274 =
1-0,95
= 1,561238015.
Окончательно имеем ио,95 = 2,0637 • 1,561238015 ~~ 1,5774 = 1,644526892.
Относительная погрешность 6 = 0,02%.
Аппроксимация 17. Вычисляем -1пA - 0,95L = 3,744665342; -1п-\/2A - 0,95) =
= 1,151292546; 3^744665342 + 1Д51292546 = 1,314104083.
/———————————————————
Окончательно вычисляем гхо,95 = V71" * 1,314104083 = 2,031841464.
Относительная погрешность S = 23,5% велика, так как значение р = 0,05 находится
вне области применения этой аппроксимации.
Аппроксимация 19. В нашем случае = 0,95 и р = 0,9.
Вычисляем 4- (-0,416) • 1пA - 0,9) = 3,831501595 и ^0,7172 + 3,831501595 = 2,084608019.
^ 0,717^2,084608019 „.__„
Окончательно имеем uq 95 = = 1,643759638.
—2 • 0,416
Относительная погрешность S = 0,066%.
Аппроксимация 21. Вычисляем i^ = — In f 1 1 = 2,944438979. Далее имеем
1,24 + 0,85 • 2,Э44438Э7Э
0'657
1 + 0,0001 • 2,9444389793 -\ :
' 2,944438979
Относительная погрешность S = 0,35%.
Задача 3. Найти математические ожидания 3-й, 7-й и 9-й порядковых статистик
в выборке объема п = 15 из стандартного нормального распределения.
Вычислим необходимые вероятности
о о /о
— для третьей порядковой статистики (г = 3) рз = т~ = 0,172131148;
у о /о
— для седьмой порядковой статистики (г = 7) р7 = у- = 0,434426230;
32 Распределения вероятностей случайных величин [Гл. 1
9 — 3/8
— для девятой порядковой статистики (г = 9) рд = у- = 0,565573770.
15 -f- 1/4
Далее воспользуемся простыми, но достаточно точными аппроксимациями 15 и 16.
В соответствии с аппроксимацией 15 находим
z3 = 4,91[0,1721311480'14 - A - 0Д72131147H'14] = -0,9438796;
z7 = 4,9l[0,4344262300'14 - A - 0,434426230H'14] = -0,1643847;
z9 = 4,9l[0,5655737700'14 - A - 0,565573770H'14] = 0,1643847.
При использовании аппроксимации 16 получаем (для z3 и z7 используем соответственно
формулы для р = 1 — рз и р = 1 — ру с заменой знака перед ир, так как ир = 1 — и\-р):
/ \ 0,4274
Z3 = 1X0,172131148 = -2,06371 In ni>7Oiqi1>ia - 0,16 1 + 1,5774 = -0,94508893;
\ 0,lizloll4o /
/ \ 0,4274
z7 = tto,43442623o = -2,0637 f In 0,16 J + 1,5774 = -0,16577582;
/ \ 0,4274
Z9 = tto,56557377o = 2,0637 ( In r-rrrrzrzzr - 0,16 ) - 1,5774 = 0,16577582.
Задача 4. Долговечность прибора подчиняется нормальному распределению со сред-
средним /i = 100 ч и стандартным отклонением а = 50 ч. Вычислить вероятность то-
го, что долговечность прибора будет больше 200 ч; меньше 50 ч; будет находиться
в интервале от 70 ч до 120 ч. Вычислить значение долговечности прибора, вероят-
вероятность превышения которого равна 0,01; 0,95. Вычислить математическое ожидание
2-й и П-й порядковых статистик в выборке из 20 испытываемых приборов.
х — 100
Переходим к нормированной переменной z = . При х = 200 ч имеем
ои
200 100
z = = 2. Вероятность того, что долговечность прибора будет превышать 200 ч,
50
равна (по определению)
Р(ж > 200) = 1 - Р(ж ^ 200) = 1 - F{z) = 1 - F{2).
Используя полученное в задаче 1 значение F{2) = 0,97725, получаем 1 — FB) = 0,02275.
Следовательно, вероятность того, что долговечность прибора превысит 200 ч, равна
0,02275.
При х = 50 имеем z = = — 1. Вероятность того, что долговечность прибора
5U
не превысит 50 ч, равна Р(ж < 50) = F(z) = F(—1) = 1 — ^A)- Используя простую ап™
проксимацию 18, вычисляем
F(l) = 1 - - ехр (-0,714 • 1 - 0,416 • 1) = 0,838967;
Р (х < 50) = 1 - 0,838967 = 0,16103.
Следовательно, вероятность того, что долговечность прибора будет меньше 50 ч, равна
0,16103.
Для вычисления вероятности попадания долговечности прибора в интервал G0; 120] ч
70 - 100 120 - 100
определим z\ = = —0,6 и Z2 = = 0,4.
50 50
Имеем РG0 < х ^ 120) = F@,4) - F(-0,6) = F@,4) + F@,6) - 1.
Воспользуемся аппроксимацией 8:
F@,6) = 1 - 0,852 ехр - (^Ж^) ' = 0,725795209;
1.1] Непрерывные распределения 33
Г /0 4 + 15774\2'341
F@,4) = 1 - 0,852 ехр - ( ? ; ] = 0,655128697.
|_ V / j
Находим
РG0 < х ^ 120) = 0,725795209 + 0,655286976 - 1 = 0,321082197.
Следовательно, вероятность того, что долговечность прибора будет находиться в ин-
интервале G0; 120] ч, равна 0,381.
Найдем теперь значение долговечности прибора, вероятность превышения которого
равна 0,01. Это значение равно квантили распределения при р = 0,99. Воспользуемся
аппроксимацией 16. При р = 0,01 имеем
/ г 4 0,4274
и0 99 = 2,0637 In 0,16 - 1,5774 = 2,3269978.
V 1 - 0,99 'у
Это квантиль стандартного (нормированного) нормального распределения, а искомая ве-
величина является квантилью исходного ненормированного распределения. Переход к нему
осуществляется по формуле
г^дэ = М + ио,99(т = ЮО + 50 • 2,3266997 = 216,35.
Следовательно, с вероятностью 0,01 можно утверждать, что долговечность прибора
превысит 216,35 ч.
Долговечность прибора, вероятность превышения которой 0,95, соответствует кван-
квантилю ио,о5 = ^^о,95- В соответствии с аппроксимацией 16 получим
/ \ 0,4247
и0 95 = 2,0637 [ In 0,16 ) - 1,5774 = 1,644527.
V 1 - 0,95 'у
В нашем случае искомая стандартизованная величина квантили есть tio,o5 = —1,644527,
или для исходного ненормированного распределения
^о)О5 = /л + и0}05а = 100 - 50 • 1,644527 = 17,77.
Таким образом, с вероятностью 0,95 долговечность прибора будет больше 17,8 ч.
Вычислим теперь математическое ожидание 2-й и 11-й порядковых статистик в вы-
выборке испытываемых приборов численностью п = 20. Имеем
3 3
2^8 И^8
для г = 2 р2 = у = °5°802469; Для i = И Ри = J" = 0,52469138.
20 + - 20 + -
4 4
Тогда с помощью аппроксимации 16 имеем
/ 4 0,4274
«2 = ио,о8О24б9 = -2,0637 I In 0,16 ] + 1,5774 = -1,402743931,
или для исходного распределения
жB) = 100 - 50 • 1,402743931 = 29,86 ч.
По аналогии для z\\ имеем
0,4274
211 = «0,52469136 = 2,0637 Ь -— - 0,16 - 1,5774 = -0,062226575,
у I — O,5z4oyi«3o J
или для исходного распределения
Ж(ц) = 100 - 50 • 0,062226575 = 96,89 ч.
Таким образом, при испытании 20 приборов с заданным распределением долговеч-
долговечности математические ожидания долговечности 2-го и 11-го приборов, ранжированных
в порядке возрастания долговечности, будут равны соответственно 29,9 ч и 96,9 ч.
2 А. И. Кобзарь
34 Распределения вероятностей случайных величин [Гл. 1
1.1.2. Равномерное распределение
Описание, применение. Находит широкое применение в непараметриче-
непараметрической статистике. Равномерному распределению подчиняются случайные величины,
имеющие одинаковую вероятность появления (например, погрешность измерений
с округлением).
Свойства
Обозначение .R(a, Ь)
Параметры а, Ь
Плотность /(ж; а, 6) = <
I 0, х < а; х > b
х ^ а;
Функция распределения F(x; а, Ь) = ^ , а < х < Ь;
Среднее М(ж) = ' ™
Дисперсия 13 (ж) = —
12
Коэффициент вариации г; = —=-
лДЬ + а
Коэффициент асимметрии «з = О
Коэффициент эксцесса «4 = 1,8
Ъ + а
Медиана Me = ^-^ = ЪА(х)
2
Мода не определена
Сумма п независимых равномерно распределенных случайных величин описы-
описывается нормальным распределением уже при п ^ 5. Функция распределения любой
случайной величины у — F(y) сама распределена равномерно на отрезке [0,1].
Задача 5. Погрешность измерения прибора распределена равномерно на интервале
[5; 10]. Найти вероятность того, что погрешность прибора не превышает 7 ед. Вычис-
Вычислить погрешность измерения, вероятность превышения которой равна 0,95. Вычис-
Вычислить вероятность того, что погрешность измерения будет находиться в интервале
6 -г- 8 ед.
Имеем равномерно распределенную случайную величину с параметрами распределен
ния а = 5 и Ъ = 10.
Вероятность того, что погрешность не превысит х = 7 единиц, равна FG) = =
Хи — о
= 0,4. Значение случайной величины, вероятность превышения которого равна 0,95, на-
находим из условия F(x) = = 1 — 0,95 = 0,05, откуда xq 95 = (Ю — 5) • 0,05 + 5 = 5,25.
о — а '
Вероятность того, что погрешность измерения будет находиться в интервале [6; 8], нахо™
дим из условия
РF ^ х < 8) = F(8) - FF) = ^- - ?=4- = 0,4.
1.1] Непрерывные распределения 35
1.1.3. Логарифмически нормальное распределение
Описание, применение. Если случайная величина Y распределена нормаль-
нормально, то случайная величина х = In У подчинена логарифмически нормальному (или
логнормальному) закону распределения. Часто используется для описания изно-
совых отказов. У многих невосстанавливаемых электронных приборов (некоторые
типы электронных ламп, полупроводниковые приборы) наработка на отказ распре-
распределена логарифмически нормально.
Свойства
Обозначение LN(/i, a)
Параметры /i, a
1 ( (] \21
Плотность f(x'j /^ а) = 1= ехР л — 2— м ж, сг > О
хау2тт [ 2а J
X
Функция распределения F(x; /i, a) = —-= ехр < — - ^— > dt; x > О
<ту2тг J [ 2а J
о
Среднее М(ж) = ехр< /z И—сг2 >
Дисперсия О(ж) = exp{2jti, + сг2}(е<7 — l)
Коэффициент вариации v = (еа — l) ^
2 ^ 2
Коэффициент асимметрии «з = (e<J ~~ l) 2 (е<т + 2)
Коэффициент эксцесса «4 = 3+ (е*7 — l) (е3<т + Зе2ст + б)
Мода Мо = ехр(/х — ст2)
Медиана Me =
Распределение имеет положительную асимметрию. Произведение независимых
случайных величин, подчиняющихся логарифмически нормальному распределе-
распределению, также распределено логарифмически нормально.
Логарифмически нормальное распределение иногда ошибочно принимается за
экспоненциальное [47]. При вычислениях, связанных с логарифмически нормаль™
ным распределением, пользуются приемами для нормального распределения, за™
меняя при этом значение случайной величины ее логарифмом. Подробный анализ
этого распределения приведен в [42].
Укажем приблизительные критерии проверки логнормальности распределе-
распределения [43]. Распределение случайной величины близко к логнормальному, если
—^ У\Ых-Ых\ = \ -= 0,79788
па\пх ^—^ у ^
или
lgMe = ln#, где In ж = - )• In ж^ и аых = 7 У.{^пх{ ~ 1пз^) .
71 П — 1
i=l
Задача 6. Предполоэюим, что время безотказной работы элемента прибора — случай-
случайная величина, подчиняющаяся логарифмически нормальному закону распределения ве-
вероятностей с медианой, равной 1000 ч, и модой, равной 400 ч. Вычислить вероятность
того, что элемент будет работать меньше 2000 ч.
Имеем Me = ем = 1000, или fi = In 1000 = 6,908; Mo = exp(/i - a2) = 400, или
fi-a2 = In400 = 5,991 ж a2 = 8,908 - 5,991 = 0,917 (a = 0,958).
36 Распределения вероятностей случайных величин [Гл. 1
Воспользуемся нормированной случайной величиной z = и для х = 2000
а
In 2000- 8,908 п _
имеем z = = 0,723. Применяя аппроксимацию 8 для нормального распре-
распределения, получим
Р(ж < 2000) = Viz < 0,723) = Fiz) = 1 - 0,852 exp \ - ( °'723 + 1>;
I у 2,063 <
5774\2'34
I \ 2,0637 )
= 1 - 0,852 ехрA - 1,289278973) = 0,76553.
1.1.4. Экспоненциальное распределение
Описание, применение. Одно из наиболее часто встречающихся распределе-
распределений в теории надежности и в теории массового обслуживания. Используется для
описания внезапных отказов, когда износом изделия можно пренебречь. Наработка
на отказ многих невосстанавливаемых изделий и наработка между соседними отка-
зами у восстанавливаемых изделий в случае простейшего потока отказов подчинены
экспоненциальному распределению. Наработка на отказ большой многокомпонент-
многокомпонентной системы может быть описана экспоненциальным распределением при любом
распределении наработки на отказ компонентов системы.
Свойства
Параметр Ь
1 / х \
Плотность f(x; b) = - expf — — 1, х ^ 0
Функция распределения F(x1b) = 1 — ехр( — — J, х ^ 0
Среднее М(ж) = b
Дисперсия 1}(х) = Ь2
Коэффициент вариации v = 1
Коэффициент асимметрии аз = 2
Коэффициент эксцесса «4 = 9
Мода Мо = 0
Медиана Me = bin 2 = 056931Ь
Экспоненциальное распределение является частным случаем гамма-распределе-
гамма-распределения (см. раздел 1.1.6) и распределения Вейбулла (см. раздел 1.1.5). Отличитель-
Отличительная особенность экспоненциального распределения — постоянство интенсивности
отказов 1/b = const — в теории надежности интерпретируется как независимость
вероятности отказа от наработки, что эквивалентно отсутствию износа.
Задача 7. Наработка на отказ прибора распределена экспоненциально с интенсивно-
интенсивностью отказов А = 1СР51 ч^1. Вычислить вероятность того^ что наработка на отказ
превысит 1000 ч. Найти вероятность того, что наработка на отказ будет находиться
в интервале от 1200 до 1500 ч. Вычислить значение наработки^ вероятность превы-
превышения которой 0,8. Определить^ как изменится наработка прибора при уменьшении
интенсивности отказов до X = 0,5 • 10~ ч~ .
Вероятность того, что наработка на отказ превысит 1000 ч, равна
Р(ж > 1000) = 1 - FA000) = 1 - 1 + е^1000'10™5 = е^10™2 = 0,99.
1.1]
Непрерывные распределения
37
Вероятность того, что наработка будет находиться в интервале от 1200 ч до 1500 ч,
определяем по формуле
РA200 < х < 1500) = FA500) - FA200) = 1 - е^1500-10™5 _ \ + e^i2oo-io™5 =
= е^0'012 - е^0'015 = 0,988071712 - 0,985111939 = 0,0029598.
БСаработку у, вероятность превышения которой равна 0,8, находим из соотношения
Р(ж >у) = 1- F(y) = 0,8. Отсюда имеем 1 - 1 + е^у'10^ = 0,8, или уЛ0~5 = 0,22314355.
Окончательно у = 2,23 • 104 ч.
При снижении интенсивности отказов до Л = 0,5-10™5 имеем у-0,5• 10" = 0,22314355,
или у = 4,46 • 104 ч.
1.1.5. Распределение Вейбулла
Описание, применение. Этому распределению подчиняется наработка на
отказ многих невосстанавливаемых электронных приборов (электроннвге лампы,
полупроводниковые приборы, некоторые приборы СВЧ). Характеризуется разно™
образием форм кривых распределения.
Свойства
Обозначение
Параметры
Плотность
Функция распределения
Среднее
Дисперсия
Коэффициент вариации
Коэффициент асимметрии
М(ж) = аГA + ^
' х\@
= 1-ехр|-(-
х ^ 0, а,/3>0
х ^ 0, а,/3>0
ш
v =
~~ 1
Коэффициент эксцесса
Мода
38 Распределения вероятностей случайных величин [Гл. 1
При /3 = 1 распределение Вейбулла переходит в экспоненциальное (см. раз™
дел 1.1.4) с параметром а, а при /3 = 2 — в распределение Рэлея (см. раздел 1.1.15).
Вычисление моментов распределения Вейбулла производится по таблицам гамма-
функции. Таблицы функции и моментов распределения Вейбулла приведены в [44].
Задача 8. Наработка прибора подчиняется распределению Вейбулла с параметрами
а = 2 и /3 = 3. Вычислить моду распределения и вероятность нахождения наработки
прибора в интервале между 5 и 6.
Находим моду распределения Мо = а( 1 — — 1 = 2A J = 1,74716.
Далее
РE ^ х ^ 6) = FF) - FE) = 1 - exp I - ( - ) ? - 1 + expi - f -
' ^exp<J^(") [> = 1,6373771 • 1(Г7 - 1,8795288 -1(Г12 = 1,637-10"
1.1.6. Гамма-распределение
Описание, применение. Широко используется в теории надежности и в тео™
рии массового обслуживания. Наработка между несмежными отказами подчиняет-
подчиняется гамма-распределению. Этому распределению (с параметром а = г — 1) подчиня-
подчиняется сумма г независимых случайных величин, каждая из которых имеет экспонен-
экспоненциальное распределение. Если наработка на отказ невосстанавливаемого прибора
распределена экспоненциально, то, при испытаниях на безотказность с заменой
отказавших приборов, момент г-го отказа подчиняется гамма-распределению с па-
параметром а = г — 1. Гамма-распределение с целочисленным значением параметра
называется также распределением Эрланга.
Свойства
Обозначение j(a^C)
Параметры а, /3
Плотность
/(ж;а,/3) = хтж" ехр( —— J, ж>0, /3>0, а>1
Функция распределения
г=0
где Т^(а + 1) —неполная гамма-функция, значения которой приведены, например,
в [45-47]
Среднее М(х) = /3(а + 1)
Дисперсия D(x) = /32(а + 1)
Коэффициент вариации v = (а + 1)~2
Коэффициент асимметрии аз = 2(а + 1)~^
Коэффициент эксцесса «4 = 3 + 6(а + I)™1
Мода Мо = а/3
1.1] Непрерывные распределения 39
При а = 0 гамма-распределение переходит в экспоненциальное (см. раздел 1.1.4).
При использовании в теории надежности интенсивность отказов убывает при а < О,
постоянна при а = 0 и возрастает при а > 0, что позволяет использовать гамма-
распределение при моделировании различных ситуаций, возникающих в процессе
анализа надежности изделий.
Гамма-распределение обладает свойством аддитивности, т. е. сумма независи-
независимых величин, подчиняющихся гамма-распределению с параметрами C и о^, имеет
также гамма-распределение с параметрами /3 и ]Р щ. Подробно гамма-распределе-
гамма-распределение исследовано в [48, 49].
При (а + 1) полуцелом (т. е. когда 2(а + 1) —целое число) гамма-распределение
можно рассматривать как частный случай распределения %2 (см. раздел 1.1.8)
с 2(а + 1) степенями свободы. Поэтому для расчетов, связанных с гамма-распре-
гамма-распределением, могут быть использованы таблицы и аппроксимации распределения %2.
Распределению х2 с / = 2(а + 1) степенями свободы подчинена случайная вели-
2х „ „
чина 7 = "~тг? т-е- квантиль случайной величины 7 может быть вычислена как
7р = 77Хр [2(« + 1)] > гДе Хр [2(а + 1)] ^р™квантиль %2-распределения с / = 2(а + 1)
степенями свободы.
Задача 9. Испытывающем четыре прибора, интенсивность отказов которых извест-
известна и равна X = 1CF5 ч~г. Вычислить вероятность того, что суммарная наработка
приборов не превысит 300 000 ч.
В нашем случае имеет место гамма-распределение с параметрами а = 4 — 1 = 3
и /3 = — = 105. Тогда искомая вероятность равна
А
Р(ж < 300 000) = FC00 000) = 1 - e~d 1 + 3 + 3 • - + 3 • - = 0,352768.
V 2 6/
1.1.7. Бета-распределение
Описание, применение. Часто используется в математической статистике,
так как через бета^распределение могут быть выражены практически все приме™
няемые распределения вероятностей, в том числе и дискретные. Доля дефектных
изделий в партии подчиняется бета-распределению. Особенно велико значение бета-
распределения в непараметрической статистике (т. е. при решении задач, не требу-
требующих знания закона распределения вероятностей случайной величины).
Свойства
Обозначение В(а,/3)
Параметры а, C
Плотность
Функция распределения
х
где Вж(а + 1,/3 + 1) = жаA — x)^dx — неполная бета-функция
40 Распределения вероятностей случайных величин [Гл. 1
Среднее М(х) = _ а Q , о
Дисперсия О(ж)
Коэффициент вариации v = <
v л,л, 2(/3-а) [ а
Коэффициент асимметрии «з =
(а + /3 + 2J(а + ^ + 3)
/5 + 1 1 ^
« + д + 4 [(« + 1)(/3 + 1)
Коэффициент эксцесса
+ 2)(-а + 2/3
« + /3 + 5 « + /3 + 2
Мода Мо =
и, т /J
Наиболее компактно функция бета-распределения может быть записана с ис-
использованием бета-функции Эйлера
Тогда
Распределение симметрично при а = /3 , «з > 0 ПРИ « < /5 и «з < 0 при а > /3.
Широкое применение бета-распределения вызвано чрезвычайным разнообразием
кривых распределения, порождаемых функцией бета-распределения при различ™
ных сочетаниях его параметров. При а = /3 = 0 бета™распределение превращается
в равномерное, а при а = /3 = —1/2 — в распределение арксинуса.Через бета-распре-
бета-распределение могут быть выражены функция распределения Фишера (i^-распределение,
см. раздел 1.1.10)
* \Х, /Ь J2) = J- fix
/2+/1
и функция биномиального распределения (см. раздел 1.2.1)
J2 С1пРгA -Р)п-1 = 1 - 1р(к,п-к + 1).
г=0
Из приведенных соотношений следует связь между бета™ и ^-распределениями:
Следовательно, случайная величина B(/i, /2) = -7 ^ j?f -р—FT имеет бета-расп-
бета-распределение, или (что эквивалентно) величина
FB/1J/2) = -
1.1]
Непрерывные распределения
41
имеет ^распределение с 2/i и 2/2 степенями свободы. Отметим также, что
1х(а,0) = 1 - (l-
г=0
Для расчетов используются таблицы неполной бета-функции [50]; таблицы функ-
функции и квантили бета-распределения приведены в [51].
Если х\ и Х2—случайные величины, подчиненные гамма-распределению (см.
раздел 1.1.6) с f\ и /2 степенями свободы, то случайная величина В = х\/{х\ + Х2)
имеет бета-распределение с параметрами f\ и /2. Поскольку /ж(а,/3) = \—I\—x(Ji, a),
таблицы бета-распределения составлены для 0 < а ^ C. Однако разнообразие задач
прикладного математико-статистического анализа в настоящее время не удовле-
удовлетворяется существующими таблицами бета-распределения. Поэтому на практике
применяются различные приближения, позволяющие вычислить бета-распределе-
бета-распределение с помощью таблиц или аппроксимаций нормального распределения. Приведем
некоторые аппроксимации.
Аппроксимация Кэдуэлла [52] (при а = C)
2(а- 1)Bа + 1
Dа - IL
где у — решение уравнения
и F(y)—функция стандартного нормального распределения.
Более удобна эквивалентная формула
У=<
\4a-
т)
где ир—р™квантиль стандартного нормального распределения (см. раздел 1.1.1) и
х-2
1
2
Наиболее употребляемые значения функции (р(у) приведены в табл. 2 [50].
Таблица 2
Значения
У
0
1
2
3
0
0,000
0,339
0,367
0,125
0,1
0,040
0,360
0,348
0,105
0,2
0,079
0,377
0,326
0,087
0,3
0,118
0,391
0,302
0,071
0,4
0,156
0,400
0,272
0,057
0,5
0,191
0,406
0,249
0,046
0,6
0,226
0,406
0,222
0,036
0,7
0,258
0,403
0,196
0,028
0,8
0,288
0,395
0,171
0,022
0,9
0,315
0,383
0,147
0,017
При а ^ 5 погрешность не более 1-10 5, при а ^ 4 /ж(а, а) = F(y) дает погреш-
погрешность не более 0,00045.
Приведем еще одну полезную формулу:
1х(а,а) = 21х.(а,а), где х' = | [l - A - х)Ц .
42 Распределения вероятностей случайных величин [Гл. 1
Аппроксимация Уайза [43]. При а ^ /3 позволяет выразить бета^распределение
через х2~РаспРеДеление:
¦-1)
А—-
\24TV'
где TV = a+ ——-; y = —Nlnx и х^ имеет х2тРаспРеДеление с 2C степенями
свободы (см. раздел 1.1.18).
Еще одна аппроксимация Уайза [54]
если
1 2г|^-°>5Iп^г^т + (а-°'5Iп
! ТЬ\ 1 X I
\Р-0,5-пA-Х/1 , 1 + ^_
6п
где п = а + /3 — 1.
Приведем эквивалентную формулу
а-0,5^ 2
где di = )8 - 0,5 + ^ - (n + i) A - ж) и g(x) =
о V о /
1 -х2 + 2ж1пж
(l^f
Лучший результат дает аппроксимация для Z2, получаемая заменой в формуле
для z\ параметра d\ на d2; где
50 [ /3 а а + /
Погрешность этой аппроксимации < 0,001 при а,/3 ^ 2,0 и < 0,1 при а,/3 ^ 1,0.
Аппроксимация Кемпа-Полсона [55]. Случайная величина у имеет стандартное
нормальное распределение TV(O; 1), если
где ж — случайная величина, имеющая бета-распределение с параметрами а и E.
1.1] Непрерывные распределения 43
Задача 10. Вычислить значение функции бета-распределения с параметрами а = 4
и /3 = 3 в точке х = 0,6.
Используем формулу для прямого точного вычисления
= l -1A - св)^4-1 >: ci+3_t (т^-\г = 1 - о,4 y: <
' / г=О
= 1 - 4,096 • 103 (Се + С\ • 1,5 + Cl • 2,25 + Cf • 3,75) = 0,54432.
Рассмотрим случай а = /3 = 3 и используем аппроксимацию Кэдуэлла. Будем искать
т / \ тт 0,6-0,5
1о,бC,3). Находим р = — —(-
утг/3
проксимацию 16 из раздела 1.1.1
/о,бC,3). Находим р = -^— —(-0,5 = 0,5977205. Для вычисления ир используем ап™
/тг/3
г„ = 2,0637 ( In 0,16 - 1,5574 = 0,26816878.
р \ 1 - 0,5977205 /
1
Тогда у = ир = 0,513504118.
Для вычисления F(y) воспользуемся аппроксимацией 18 из раздела 1.1.1
F{y) = 1 - i exp(-0,717|/ ~~ 0,416t/2) = 0,68995.
Из табл. 2 имеем ip(y) « 0,192.
Окончательно получаем
/о,бC,3) = 0,68995 + 2-C~1)-B-3 + 1) . 0д92 = 0;б903>
Задача 11. Вычислить значение /о,бE,4) с помощью аппроксимации Уайза.
Имеем х = 0,6; а = 5; C = 4. Находим п = 5 + 4—1 = 8.
Далее имеем а = 4 — 0,5 Н A4— 1 • 0,4 = - и
6 у Зу 3
= 1,09375; 2_ = ^^ = 0,9375.
п • ^i — х) о • и,4 " ~
1 _ 1 ПОЧТЕ;2 _L О . 1 flQQ
g(l,09375) =
п-A-ж) 8-0,4 ' ' п-х 8-0,6
Далее имеем
- 1.093752 + 2 ¦ 1,09375 In 1,09375
A- 1,09375J
= A - 1,19628906 + 0,196026597) • 113,7777 = -0,029862726;
= 1-0,9375^ + 2.0,93751n0,9375 =
61 ' ; A09375J
Вычисляем
1
1 [1 + 0,6 • (^0,029862726) + 0,4 • 0,021509854] 2
*1 = о '
+ - ) -0,4-0,6
6
Окончательно имеем
F(z) = 1-- ехр(^0,717 • 0,169274 - 0,416 • 0Д592742) = 0,562.
44 Распределения вероятностей случайных величин [Гл. 1
Точное значение /о,бE,4) = 0,6. Точность аппроксимации может быть повышена приме-
применением более точных аппроксимаций входящих величин (функции и квантилей стандарт-
стандартного нормального распределения).
Задача 12. Вычислить 1о,бE,4) с помощью аппроксимации Кемпа-Полсона.
Вычисляем
D . 0,6I • (l - -М - E ¦ 0,4M • (l -
( (
у = 3 ^ ^-±1 i !L_V = 0,239151678.
Используя аппроксимацию 15 (см. раздел 1.1.1) для ир, имеем
ир = -4,91 • [0,23Э151678ОД4 - A - 0,239151678H'14] = 0,7068,
что не очень близко к точному значению /о,вE,4).
1.1.8. Распределение %2 (распределение Пирсона)
Описание, применение. Распределение открыто и изучено Пирсоном в 1900 г.
Если #i, ..., х f—независимые случайные величины, имеющие стандартное нор-
нормальное распределение, то сумма их квадратов ^ ж2 подчиняется % -распреде-
-распределению. Распределение хи-квадрат широко используется в прикладных задачах
математической статистики. С его помощью проверяются гипотезы относительно
значений дисперсий, проверяется согласие экспериментальных данных с теорети-
теоретическими законами распределения. Распределение хи-квадрат широко применяется
в непараметрической статистике, являясь предельным для многих выборочных
статистик.
Свойства
Обозначение X2(f)
Параметр /
1 Lzl Г Y2 ]
Плотность (р(х2; f) = ——77V ЬB) 2 ехР1 —тг > , X2 ^ 0
Функция распределения ^f(x) = -Р{х2(/)?ж} = ~—/ г\ У^"~ ехр< — — > dy.
х > 0
Среднее М[Х2(/)] =/
Дисперсия Е»[х2(/)] = 2/
[2
Коэффициент вариации v = I —
2
Коэффициент асимметрии аз = 2 ( —
1.1]
Непрерывные распределения
45
Коэффициент эксцесса
Мода
Мо = /-
Распределение имеет один параметр / — число степеней свободы, определяемый
количеством независимых случайных величин, сумма квадратов которых соста-
составляет х2- Плотность распределения х2 асимметрична, унимодальна (т.е. имеет
единственную моду) и с ростом числа степеней свободы / становится более пологой
и симметричной.
X2-распределение обладает свойством аддитивности, т. е. сумма двух независи-
независимых величин x2(/i) и Х2(/2) имеет распределение x2(/i + /2)-
Таблицы х2™РаспРеДеления имеются во многих руководствах и сборниках та™
блиц [23-25, 29, 44, 56, 57]. Предложены номограммы для расчетов х2™распределе™
ния [58].
Большинство аппроксимаций квантилей х2™РаспРеДеления основано на преоб-
преобразовании исходной случайной величины в величину, имеющую распределение,
близкое к стандартному нормальному 7V@,1).
Рассмотрим известные аппроксимации. Везде будем рассматривать верхнюю
р-квантиль, т. е. величину х»? удовлетворяющую соотношению р = 1 — Р(х2 < Хр)-
Напомним, что ир — верхняя р™квантиль стандартного нормального распределе-
распределения (т. е. р = 1 — Р(ж < ир)).
Аппроксимация 1. При / > 200 Х«(/) = / + V^f'ир-
1
Аппроксимация 2 (Фишера) [59, 60]. При / > 100 xl(f) = «(
Аппроксимация 3 (Вчлсона-Хчлфертч) [61]:
1-
9/
30.
Аппроксимация 4 [62—64]. В [62] показано, что величина (х2L близка к нор-
нормальному распределению со средним /л = (/ — 1/2L и дисперсией а2 = (8/). По
сравнению с аппроксимацией 3, эта аппроксимация предпочтительнее для малых
значений / и уступает ей при больших значениях /.
В [63, 64] показано, что для
личных / и равно:
оптимальное значение А различно для раз-
раз/
А
1
0,2084
2
0,2654
3
0,2887
4
0,3006
6
0,3124
Аппроксимация 5 (Голдштейна) [65]:
2 4ж4 + 16ж2 - 28 ^ 8ж6
'9/+ ^^
720ж4 - 3216ж2 + 2904
1215/2 229635/3
;) Зж5 + 40ж3 + 45ж 301ж7 - 1519ж5 - 3269ж3 - 79349ж\
J) \ 162/
или в форме
xlU) = f
5832/2
Р ~П п^Ъ I
7873200/3
i=0
46
Распределения вероятностей случайных величин
[Гл. 1
где х = ир и
а0 = 1,0000886;
аг = 0,4713941;
а2 = 0,0001348028;
а3 = -0,008553069;
а4 = 0,00312558;
а5 = -0,0008426812;
а6 = 0,00009780499;
Ъо = -0,2237368;
Ьг = 0,02607083;
Ь2 = 0,01128186;
Ь3 = -0,01153761;
Ь4 = 0,005169654;
Ь5 = 0,00253001;
Ь6 = -0,001450117;
Аппроксимация 6 [66]. При / > 10
с0 = -0,01513904;
ci = -0,008986007;
с2 = 0,02277679;
с3 = -0,01323293;
с4 = -0,006950356;
с5 = 0,001060438;
с6 = 0,001565326.
1 3
9/
где
или в модифицированной форме
f
(9/ + 16)(ж3 - Зх) - 24(ж2 - l)y/2f
о •
486/2
Аппроксимация 7 (Хэлдена) [67]
4(f) = п
6 1-
18/
12/
Аппроксимация 8 (Корниша-Фишера) [68]. Упрощенная (ж = кр):
где
= У2х; С2(ж) = ^(Ж2-1); G3(x) =
6ж4 + 14ж2 - 32
9ж5 + 256ж3 - 433ж
Некоторые значения Gi(x) приведены в табл. 3.
Аппроксимация 9 (Гилберта) [69]. При / > 30
где п{—коэффициенты, приведенные в [69].
In /,
1.1]
Непрерывные распределения
47
Таблица 3
Значения функции Gi(x)
р
0,999
0,995
0,990
0,975
0,950
0,900
0,750
0,500
0,250
0,100
0,050
0,025
0,010
0,005
0,001
ир
-3,090232
-2,575829
-2,326347
-1,959964
-1,644854
-1,281551
-0,674490
0,000000
0,674490
1,281551
1,644854
1,959964
2,326347
2,575829
3,090232
Сг(х)
-4,370248
-3,642772
-3,289952
-2,771807
-2,326174
-1,812387
-0,953873
0,000000
0,953873
1,812387
2,326174
2,771807
3,289952
3,642772
4,370248
G2(x)
5,699689
3,756595
2,941261
1,894305
1,137029
0,428249
-0,363376
-0,666667
-0,353376
0,428249
1,137029
1,894305
2,941261
3,756595
5,699688
G3(x)
-0,619005
0,073889
0,290267
0,486317
0,554981
0,539450
0,346842
0,000000
-0,346842
-0,539450
-0,554981
-0,486317
-0,290267
-0,073889
0,619005
G4(x)
-1,602111
-0,802517
-0,541970
-0,272398
-0,122957
-0,017722
0,060220
0,079012
0,060220
-0,017722
-0,122957
-0,272398
-0,541970
-0,802517
-1,602111
G5(x)
-1,273497
-0,622767
-0,411565
-0,194832
-0,077898
-0,002186
0,030881
0,000000
-0,030881
0,002186
0,077898
0,194832
0,411565
0,622767
1,273497
Аппроксимация 10 (Хозяина) [70]. При р > 0,05 (/ ^ 30)
x2p(f) = |l,00991v7+l,9518[-lg(l-p)]^
Bp(f) = jl,06807v7 + 2,13161 lg(l - p)h - 0,04589v7[^
- 1,37266
При p sS 0,05 (/ ^ 30)
Xlif) = {l,14309v7 - 0,9459(- \gp)l -
xl(f) = {0,97657^ - l,46049(-
- 0,06198
} ;
0,5902б
} ;
Отличительной чертой этих аппроксимаций является то, что они не требуют знания
квантилей стандартного нормального распределения. Квантили Хр аппроксимиру-
аппроксимируются непосредственно по значениям / и р.
Аппроксимация 11 (Арояна) [71]
где Ъ\ и &2 — коэффициенты, приведенные в [71].
Аппроксимация 12 (Пейзера-Пратта) [72-74]
d\(f - 1) In
L
( 1г-
\xl(f),
- (/ - 1)
где d = xlif) ~ f + I ~ ^p X%f) Ф f ~ I-
48 Распределения вероятностей случайных величин [Гл. 1
Аппроксимация 13 [36]. Для р = 0,95 имеет место
Д95(/) = И2,6- ^о A47,4 -/J.
При 5 ^ / ^ 30 погрешность ^ 1%.
Аппроксимация 14 [114]. Является уточнением аппроксимации 3 (Вилсона™
Хилферти)
где tp(f)—р-квантиль распределения Стьюдента (см. раздел 1.1.9) и
_ (о,4(р - ОД) Для 0,7 ^ р ^ 0,825,
^ [0,3@,99 -р) для р> 0,825.
Из приведенных аппроксимаций наиболее точны аппроксимации 5, 6 и 8 (уже при
/ > 3 погрешность не превышает 0,05%) [75].
Отметим (ранее мы уже об этом говорили), что через функцию распределе-
распределения х2 могут быть выражены функции многих других распределений: гамма-
распределения (см. раздел 1.1.6), распределения Эрланга, экспоненциального рас™
пределения (см. раздел 1.1.4), распределения Вейбулла (см. раздел 1.1.5), рас-
распределения Пуассона (см. раздел 1.2.2), распределения Рэлея (см. раздел 1.1.15),
распределения Паскаля (см. раздел 1.2.4).
Задача 13. Вычислить различные аппроксимации квантилей Xp(f) пРи Р — 0,05 и
0,95 и f = 10 и оценить ошибку аппроксимации (табличные значения Хо,об(Ю) = 3,9403
и Xo,9sA0) = 18,307). Для вычислений понадобятся значения гхо,о5 = ™ 1,644854 и
и0?95 = 1,644854 (их можно аппроксимировать, пользуясь аппроксимациями для нор-
нормального распределения — см. раздел 1.1.1).
Аппроксимация 1. Имеем
Xo,osA0) = 10 + л/2-10 • (-1,644854) = 2,643989 (S = 32,8%);
Хо,9бA0) = 10 + л/2-10 • A,644854) = 17,356 E = 5,1%).
Большая погрешность объясняется тем, что аппроксимация 1 дает удовлетворительный
результат только при / > 200.
Аппроксимация 2:
Хо,об(Ю) = - • (-1,644854 + V20 - IJ = 3,683 (8 = 6,5%);
Хо,95(Ю) = \ • A,644854 + ^20^ТJ = 18,022 (S = 1,6%).
ЕСогрешность аппроксимации остается значительной, так как аппроксимация 2 удовле-
удовлетворительна только при / > 100.
Аппроксимация 3:
з
Хо,9б(Ю) = 10 11 - — + 1,644854А/ 7Г-^ | = 18,29178 (S = 0,08%).
Аппроксимация 4. Имеем
1.1] Непрерывные распределения 49
Тогда
A0 - 0,5) i - 1,644854 J—j= = A,755621543 - 0,327026059L = 4,16521;
Хо,95(Ю) = A,755621543 + 0,327026059L = 18,81322 (S = 2,7%).
Аппроксимация 5. Для р = 0,05 и х = г^о,5 = — 1, 644854 имеем
2 (т\ шГшпппяяй °-2237368 Q.Q1513904
Хо,обA0) = Ю 1,0000886 — — h
1 , ч / 0,02607083 0,08986007\
+ ^=(-1,644854) @,4713941 + -^— - -^55—J +
A,644854) @,0001348028 + °'°1128186 + °'°2277679
101 ' ; \ ' 10 100
1 ч3/ 0,01153761
{1M48Mf (-0,008553069 - ^— -
(-0,0
{1
(-1,644854)^0,00312558+ °-
^(
M,644854f( ^0,0008426812 +2,002^001
^(-1,644854)» @,00004780499 + °-^^1 + Ш^^ = 3,940420741
+ ^( (
(E = 0,003%).
При р = 0,95 и г^о,95 = 1,1644854 имеем
Хо,95(Ю) = @,977563529 + 0,52014855 • 0,473911322 + 0,27554468 • 1,4907559 • 1Q~3 -
- 0,40728579 • 9,8391593 • 10^3 +0,07319972 • 3,5730418 • 10^3 - 0,038074725 • 5,7907562 • 10^4 -
- 0,01980451 • 3,155345 • 10^5K = 18,30737 (S = 0,002%).
Аппроксимация 6. Для р = 0,05 имеем
= _J_ /2^A,644854^-1) _ (-1,644854K-3(-l>644854)\ = _2 s
27-10 V Зл/lO 4 )
Xo,osA0) = 10 3J^^
1 — + (-1,644854 + 2,8697122417 • 10^3)J^^ = 3,93481
\3 " _L\J У JLU I
(E = 0,047%).
Для Xo,9sA0) имеем
hw = ^7,4074074 • 10^3@,508495179 + 0,121084002) = ^4,6635494 • 10™3
и
Г f^l3
Xo 9sA0) = 10 0,977777+ A,644854 + 4,6635494- 10^3W = 18,3229961
L V 9 • 10 j
F = 0,087%).
В модифицированной форме для р = 0,05
. (9 ¦ 10)(-1,644854K ~~ 3(-1,644854) - 24A,6448542 ~~ 1)^20 п ^3
плп = о = —2,7102602 • 10 ;
486 • 102
50 Распределения вероятностей случайных величин [Гл. 1
г /—I3
Xo,osA0) = 10 1 - — + (-1,644854 + 2,7102602 • Ю^3)у — = 3,93802 (S = 0,058%).
I yu Y уи I
Для р = 0,95 получаем
, -51,33961699-183,0582646
Лю = ^^ = ^4,8230016,
Хо,95(Ю) = 10@,977777 + 0,24448138K = 18,25954 (S = 0,29%).
Аппроксимация 7:
12 • 10
Х5,О5(Ю) =
5(-1,644854) 5 / 7
48-10
18- 10/
+ 10
13
18
120(-0,308212739 + 1 - 0,02818287) 5 + 1Q
= 3,94758 (E = 0,18%);
±о
18
., 19fVf1 ЧПЯ9197ЗД О- 1 _ П П9«18987'| К _L 1 П
Хо,95(Ю) =
13
18
2 /1гЛ ±zu^u,ouoz±z/oy-|-1 - 0,02818287) 5 +10
13 ~~
Аппроксимация 8. Упрощенная формула:
Хо osA0) = Ю+ (-1,644854)^2 • 10+ -A,6448542 - 1) +
' 3
Н ^A,64485422 - 7- (-1,644854)) = 4,134 (S = 4,9%);
х§?95A0) = 10 + 7,356010714 + 1,137029788 + 0,353286881 = 18,846327 (S = 2,9%).
Точная формула (р = 0,05 и ир = —1,644854):
Gi(x) = -2,326174; G2(x) = 1,137029; С3(ж) = 0,554981;
G4(x) = -0,122957; G5(x) = -0,002186.
Хо,о5(Ю) = 10 - 2,326174^10 + 1,137029 + -^= 0,554981 ^= 0,002186 = 3,9441565
vlO lOvlO
(E = 0,01%).
При р = 0, 95 и ир = 1, 644854 имеем
Gi(z?) = 2,326174; С2(ж) = 1,137029; G3(x) = -0,554981;
G4(x) = -0,122957; G5(aj) = 0,077898
и
Xo,9sA0) = 10 + 2,326174^10 + 1,137029 ^0,554981 - ^0,122957 +
vlO 10
1 0,077898 = 18,30770 (S = 0,004%).
10л/Ш
Аппроксимация 10. Для р = 0,05
Хо
Г i— 1 , 1 I2
,обA0)= l,14309>/l0-0,9459(-lg0,05J - 0,13138>/l0(- lg0,05) 2 -0,06198 =
= 3,9999 (E=1,5%);
Г ^- I ]2
,osA0)= 0,9765V10-l,46049(-lg0,05J +0,59025 =4,04951 (E = 2,8%);
Г 1 2
Xo\o5A0)=K/l0-l,5(-lg0,05J =4,20798 (E = 6,8%).
Xo,(
1.1] Непрерывные распределения 51
Для р = 0,95
1,0099л/10 + 1,9518 [-lg10 A-0,95)] 5 I =29,37488 (? = 60%);
Хо,95@) = {l,06807>/l0 + 2,13161[-lglo(l-0,95)]5 -
- 0,0458Э7Т0[- lglo(l - 0,95]i - 1,97266 j2 = 21,06223;
Г 1 71 2
Xo,9sA0) = b0 + 2[-lglo(l-0,95)]2 --1 =21,435 E = 1,5%).
I 6J
Эти аппроксимации явно неточны для малого количества степеней свободы (их рекомен-
рекомендуется применять при / > 30).
Аппроксимация 12. Здесь, располагая точными значениями Хр(/)? можно проверить
их нормальную аппроксимацию.
Для р = 0,05 и / = 10 имеем
" 10 + f " ^f = -5,4010333;
/9
- 5,4010333 9 In \- 3,9403 - 9
\ 39403
и0 05 = — \ 3'9403| i- = -1,644725.
|3,9403 - 9|
Для р = 0,95 имеем
d = 18,307 - 10 + - - — = 8,965666;
о Хи
1
/9 \ 2
8,965666 ( 9 In h 18,307 - 9 1
^0,95 = V 188307^9 ^- = 1,6454169 (J = 0,02%).
Аппроксимация 13
xS,98A0) = П2,6 - {U7A2~0 10J = 18,2062 (S = 0,5%).
Аппроксимация 14. Будем использовать результаты, полученные при применении
аппроксимации 3, а именно Хо,об(Ю) = 3,93152 и Хо,9б(Ю) = 18,29178.
Вычислим корректирующий множитель для р = 0,95:
МЛ = гоМЩ = 1т =
Up Wo,95 1,645
ft fio)\0'012
и для (р = 0,3@,99 - 0,95) = 0,012 имеем I 0;951 j I = 1,00116.
V м0,95 /
Тогда
Хо,95(Ю) = 18,29178 • 1,100116 = 18,313,
что соответствует ошибке E = 0,03%, т.е. ошибка по сравнению с аппроксимацией
Вилсона—Хилферти снижается более чем в 2 раза.
1.1.9. Распределение Стьюдента (t-распределение)
Описание, применение. Впервые предложено английским статистиком Госсе-
Госсетом (псевдоним Стьюдент) в 1908 г. Если у — нормалвно распределенная случайная
величина с нулевым средним и единичной дисперсией, а независимая от нее слу™
чайная величина %2 имеет распределение хи-квадрат (см. раздел 1.1.8) с / степе-
_i
нями свободы, то случайная величина t = |/(х2//) 2 подчиняется распределению
Стьюдента с / степенями свободы. Распределение Стьюдента широко применяется
52
Распределения вероятностей случайных величин
[Гл. 1
в задачах обработки экспериментальных данных (например, при построении дове™
рительных интервалов и проверке гипотез относительно среднего при неизвестной
дисперсии). С помощью распределения Стьюдента описываются распределения
коэффициентов корреляции и регрессии.
Обозначение
Параметр
Плотность
Функция распределения
Среднее
Дисперсия
Коэффициент вариации
Коэффициент асимметрии
Коэффициент эксцесса
Медиана
Мода
Свойства
/ — число степеней свободы
ш
?>(*;/) =
F(t;f)=P[t(f)<t] =
M(t) = О
f+i
2
^ОО < t < ОО
1 — 2'
v = 0
Мо = 0
При / —>> оо t-распределение совпадает со стандартным нормальным (хорошая
аппроксимация достигается уже при / > 30). Таблицы распределения Стьюдента
можно найти во многих руководствах по математической статистике [7, 23, 24, 25,
56, 57]. График плотности ^-распределения напоминает по форме плотность нор™
мального распределения, но значительнее медленнее приближается к оси абсцисс.
Приведем аппроксимации для расчетов, связанных с ^-распределением.
Аппроксимация 1
tp(f) =up
при / > 30 (ир — квантиль стандартного нормального распределения).
Аппроксимация 2 (Корниша-Фишера) [76]
16и2р
15
4/
96/2
384f
При / ^ 5 погрешность ^10 3.
Аппроксимация 3 (Кёхлера) [77, 78]
0,81
_. , = I -0,0953 - ^ + "'"х + 0,076DРл//O
При / ^ 8 погрешность < 1,4%, при / ^ 50 погрешность < 0,6% для диапазона
0,00001 <р< 0,2.
Аппроксимация 4 (Нельсона) [79, 80]. Очень простая аппроксимация дляр = 0,95
: 2, или (что эквивалентно) ?0,975 (/) = ^
1.1]
Непрерывные распределения
53
Аппроксимация 5 [36]
Аппроксимация 6 [81]
^0,975 ~ 1,96 +
2,5
/-1,8"
г=0
, где а =
з=о
-, t^o,
аю = 0,09979441; а20 = 0,04431742; а30 = 0,009694901; а40 = -0,0000918228;
аи = -0,58121; a2i = -0,2206018; а31 = -0,1408854; а41 = 0,03789901;
а12 = 1,390993; а22 = 0,03317253; а32 = 1,88993; а42 = -1,280346;
а13 = -1,222452; а23 = 5,679969; а3з = -12,75532; а43 = 9,249528;
ам = 2,151185; а34 = -12,96519; а34 = 25,77532; а44 = -19,08115;
а50 = 0,000579602; Ъг1 = -5,537409; 532 = 14,3963;
аЪ1 = -0,02763334; Ь12 = 11,42343; Ь41 = -2,777816;
а52 = 0,4517029; Ъ2г = -5,166733; 542 = 16,461132;
«53 = -2,657967; Ь22 = 13,49862; Ъ51 = -0,5657187;
а54 = 5,127212; 631 = ^4,233736; ЬЪ2 = 21,83269.
При / ^ 5 погрешность ^ 10^4.
Аппроксимация 7 (Пейзера-Пратта) [72, 73]
== I / — — \
In 1 +
/
Аппроксимация 8 (Уоллиса) [74]
.. _8/ + 1
п 1 +
Аппроксимация 9 (Морана) [82, 84]
при / ^ 5.
4/
-1
При / ^ 5 погрешность не более 10~3.
Аппроксимация 10 (Даусона) [83]
= -0,5059 - l,261gBp) - 0,1093[lgBp)]2 + exp
При 0,005 ^ р ^ 0,1 и
1,994-2,7497lgBp)l
погрешность равна ±8%.
Аппроксимация 11 (Вонга) [85, 86]
/ I'
погрешность составляет ±5%, при 0,001 ^ р ^ 0,2
ехр
v 0,9975/~ 0,445
При р « 0,025 и 8 ^ / ^ 18 погрешность ^ 0,005.
- 1
54 Распределения вероятностей случайных величин [Гл. 1
Аппроксимация 12 (Локтева) [114]
{1 + In p(l - р) + 0,004 ^рЧ
1 - @,325 - 0,022In/) L J J
При / ^ 3 максимальная ошибка 0,3 для величины
Задача 14. Вычислить tp(f) и оценить ошибку аппроксимации при р = 0,05, / = 5
wp = 0,95, / = 10.
Точные табличные величины to,osE) = -—2,0150 и to,9sA0) = 1,8125. Вспомним, что
^0,95 :=: 1,644854 = —ti.o,o5-
Аппроксимация 2:
/ia\ 1 г л лохл \л 156448542 + 1 5- 1,6448544 + 16 • 1,6448542 + 3
to 05 (Ю) — —1,544854 • < 1 + Ь о Н~
[ 4-5 96 • 52
3 • 1,6448546 + 19 • 1,6448544 + 17 • 1,6448542 + 15 1 _АО с0/х
+ 5 / ^ —2,1I5о08 (о = 0,015 /о);
384- 53 J V ' ;'
*о,95(Ю) = 1,644854 • {1 + 0,092638617 + 8,6342265 • 10^3 + 6,757481 • 10^4} = 1,8125445
(8 = 0,0024%).
Аппроксимация 3:
Г 0 631 ! ! 1 ^1
to osE) = \ -0,0953™ +0,81- [- lnD • 0,05 • 0,95I" а + 0,076 • D • 0,5 • лД) 5 I =
I 6 J
= 2,0293 (E = 0,7%);
*o,9sA0) = I ^0,0953 - ^i + 0,81 • [- lnD • 0,95 • 0,5)]" 2 + 0,076 • D • 0,95 • л/W)To I =
= 1,761817 (8 = 2,8%)
Аппроксимация 4:
*o,9sA0) = 2- J у = 2,236.
Табличное значение to,975A0) — 2,228.
Аппроксимация 5:
*о,975(Ю) = 1,96 + 1п2;Б1 о = 2,2649.
10 — 1,8
Аппроксимация 6. Пусть ?рE) = 2,015. Требуется отыскать значение р, соответствую-
соответствующее этой квантили. Вычисляем
1 /1\2 /1\3 /1\4
0,09879441 - 0,58121 • - + 1,390993 • ( - ) - 1,222452 • ( ~ ) + 2,151185 ¦ ( - 1
1 - 5,537409 • - + 11,42343 • ( - )
5 \5/
По аналогии находим
с2 = 0, 0465169; с3 = -0, 00505661; с4 = -0, 000348176; с5 = 0, 00003584898.
Окончательно получаем
р=-A + 0,0936657 • 2,015 + 0,045169 • 2,0152 - 0,005661 • 2,0153 - 0,000348176 • 2,0154 +
+ 0,0000358489 • 2,0155) = 0,05055.
Точное значение р = 0,05.
1.1] Непрерывные распределения 55
Аппроксимация 7:
2,015^
2\ I \ 5
^0,05 =
R2\ \ 2
E--W—^ 5 ~\ =^1,6367697 (E = 0,5%);
^ 3/1 _ — — I
2,015^ ^ 2
In 1+-^—
1_
1,81252^ ^ 2
In 1 +
=,644324 E = 0,03%);
2\ | \ 10
^0,95 —
10~б
B \ I \ 1и / I
Ю--К — 5 \ =1,64300 (с5 = 0Д%);
In 1
1,8125* \ ^ 2
10
= A0 - ^ + —) I —^ 5 } = 1.64476 (S = 0,0056%).
ю- ю/ lcrg
Аппроксимация 8:
о с _|_ I Г / 2П1112\1'2
гбоо5 = 5In( 1 + ) = -1,6438427 (/ = 5; S = 0,06%);
8-5 + 3 [ у 5 /J
1
ио^95 = 8'1Q + 1 10In( 1+ 1?1825 ) 2 = 1,64480229 (/ =10; 6 = 0,003%).
8 • 10 —|— 3 I у 10 / I
Аппроксимация 9:
-1
to,O5E) = -1,644854 1 - 7 ^ = -2,0189125 (S = 0,2%);
У 4-5 /
to,95A0) = -1,644854 М- 1;644854 + г J = 1,812788 (E = 0,01%).
Аппроксимация 10:
*о,9бE) = -0,5059 - 1,26 lgB • 0,05) - 0,1093[lgB • 0,05)]2 +
' 1,1994- 2,7479 lgB ¦ 0,05)"
-г ехр'
Аппроксимация 11:
г
to osE) =J5|"exPf 1?6448542 ^ -l]}2 =-2,01758 E = 0,12%);
' W \ [ Fy0,9975-5-0,445/ J/ ' V ' ;'
l
to 95A0) =< 10 exp 7 -1 = 1,81189675 (E = 0,03%).
' V ; \ [ У 0,9975- 10-0,445/ J/ V > У
Аппроксимация 12:
/ 5-5
1 + In 0,95 • 0,05 + 0,004 •
*о,о5E) = -1,644854 I 1 - @,325 - 0,022 • In5) ^ —- } = -2,058;
56 Распределения вероятностей случайных величин [Гл. 1
1 + In @,95 ¦ 0,05 + 0,004 • ^^
= 1,644854 { 1 - @,325 - 0,022 • In 10) ^ —'- } = 1,8308.
Из рассмотренного примера видно, что наиболее просты и достаточно точны аппрокси-
аппроксимации 3, 4, 5, 7, 8, 9 и 11.
1.1.10. Распределение Фишера (.F-распределение)
Описание, применение. Если две независимые случайные величины %f и х|
распределены по закону хи-квадрат соответственно с Д и /2 степенями свободы,
то случайная величина F = —|— имеет распределение Фишера, .F-распределение
широко применяется при обработке данных (при сравнении дисперсий, анализе кор-
корреляций). С помощью ^распределения можно вычислять некоторые дискретные
распределения, например, биномиальное.
Свойства
Обозначение -^(/ъ/г)
Параметры Д, /2
Плотность
f(x;hj2)= x " f l Jlx
х 2
Функция распределения
S(x) = P{F<x}= A,2,LfhP K"" ¦ ""^
i г т
Среднее M[F(f1,f2)] = 1^, /2 > 2
h- *
Дисперсия D[F(/i,/2)l = 2f^h+2h~2) , /2 > 4
i_
Коэффициент вариации v = J~,.—2 , /2 > 4
L h (/2 - 4) J
v .л. 2/x + /2 - 2 [ 8(/2 - 4) ] *
Коэффициент асимметрии а3 = — —^- , /2 > о
/2-0 [/i +/2 - 2J
Мода Mo = ^"gj
В большинстве руководств по математической статистике, например, [24, 29, 87],
приводятся квантили .F-распределения. Для .F-распределения справедливо соот-
соотношение -Fp(/i,/2) = "^ 77—t\i что позволяет ограничиться только таблицами
для р < 0,5 или р > 0,5. При Д = 1 и /2 = оо или Д = оо и /2 = 1 распределение
1.1] Непрерывные распределения 57
совпадает с нормальным, а при /i = 1, /2 = 00 или /2 = 1, Д = оо — с распредели
нием квадрата случайной величины, имеющей t-распределение Стьюдента с /2 (Д)
степенями свободы. При /2 —» оо ^распределение совпадает с %2™распределением
при /i степенях свободы.
flFp(fi, f2) r / 1 1 ^7\
Величина — i^ подчиняется бета-распределению (см. раздел 1.1.7),
/2 + Jl^p(jl,/2J
поэтому функция ^-распределения может быть выражена через функцию бета-
распределения
В общем случае случайную величину i^ (/i, /2) ? подчиняющуюся распределению
- /271
Фишера, можно интерпретировать как отношение ——, где 71 и 72 — независи™
/172
мые случайные величины, подчиняющиеся гамма-распределению (см. раздел 1.1.6)
с параметрами /i/2 и /2/2. В связи с широким использованием ^-распределения
применяются различные его аппроксимации и нормализующие преобразования.
Аппроксимация 1
Аппроксимация 2 (при Д, Д > 30) [26]
где
ClB) = -7= ~ г;? = 2,1213203 -
V2 V3/iB) /1B)
Аппроксимация 3 [32]
Аппроксимация 4 (Полсона) [88]
2 j. 2 phf f
9K + W2 p{flj2
Отсюда следует, что
^ [(9Д - 2)(9/2 - 2) + Зир{2/г{9/2 - 2J -
(9/2 - 2J -
58
Распределения вероятностей случайных величин
[Гл. 1
Аппроксимация 5 (Пейзера-Пратта) [72, 73]
¦Qg
Up = di
fp
-Pg
fq
/+6 )РЯ
/2/5
;p =
2 '
-x) -2.
2 \2 2
+
JlpiJl, J2J + /2
При /i, /2 ^4 погрешность ^ 0,001.
Аппроксимация 6 (Воглера-Нортона)
,/2) =
Аппроксимация эффективна для /i, /2 ^ 30, если p — не на „хвосте" распределения.
Эта аппроксимация следует из нормализующего преобразования Полсона (аппрок-
(аппроксимация 4).
Аппроксимация 7 (Хейнса) [89]. Основана на аппроксимации Вилеона^Хилфер-
ти для х2 (см- раздел 1.1.8, аппроксимация 3) и аппроксимации Гастингса для
нормального распределения (см. раздел 1.1.1)
- 2аЬ - [Babf - Ц2х20с - a2)Bx20d - Ъ2)] "'
2Bжос - d
где
а3 , E-R
+ ;
«2
п1 = 0,278393; а2 = 0,230389; а3 = 0,000972; а4 = 0,078108;
, 1
= 51,21114354
1
3] 2
1
= -| - [(у)' + (у)'] 2
^A -р)]4
- 54,06887755;
с2 = -100,70032831|A -рI 4 +86,13944869.
Аппроксимация слишком сложена и применяется редко.
1.1]
Непрерывные распределения
59
Аппроксимация 8 (Картера) [90]
1
1
/i-l
2) = expBz), где
5 , 1/1
1,
/2-1 /l - 1
При /ь /2 ^ 30 и р ^ 0,0001 погрешность ^ 10^3.
Аппроксимация 9 [9, 91, 92]
lg ^р(/ъ/2) = a(h-b)~ 2 - eg, где /г =
Коэффициенты а, Ь и с приведены в таблице:
2Л/2
/l + /2 '
р
а
Ь
с
0,50
0
0,290
0,75
0,5859
0,58
0,355
0,90
1,1131
0,77
0,527
0,95
1,4287
0,95
0,681
0,975
1,7023
1,14
0,846
0,99
2,0206
1,40
1,073
0,995
2,2373
1,61
1,250
0,999
2,6841
2,09
1,672
0,9995
2,8580
2,30
1,857
Задача 15. Вычислить^ пользуясь аппроксимациями^ значение .Ро,э(Ю, 12).
Для справки — точное значение i<o,9 A0,12) = 2,1878.
Аппроксимация 6. Имеем табличное значение гхо,э = 1,281551.
2 2 2 2
Вычисляем 1 = 1 = 0,9777 и 1 = 1 = 9,98148. Окончательно
9/i 90 ' 9/2 108
находим
Fo,9A0,12) =
0,9777- 0,98148 + 1,28155 0,02222 • 0,981482 + 0,0185185 • 0,97772 -
81-10- 12
1,281155^
I 3
2
0,98148^ - 0,0185185 ¦ 1,281552
1,21140198 V
0,932891651/
= 2,189632439 (8 = 0,03%).
Аппроксимация 8. Имеем С/о,9 :=: 1,281551 и
9
h =
¦ +
-— = 9,9; Л = -A,2815512 - 3) = -0,226271172;
10-1
1,281551(9,9 - 0,226271172)^
9,9
— + -]-- 0,226271172 - - ( — + - ) =0,511656907;
11 9/ L6 3 V11 9/J
Fo,9A0,12) = expB • 0,511656907) = 2,782399.
Погрешность S = 27% велика, так как малы степени свободы Д и Д.
Аппроксимация 9. Имеем а = 1,1131; Ь = 0,77 и с = 0,527. Далее находим h =
2 *
10
12 + 10
= 10,90909 и g =
12- 10
= 0,016666. Тогда
lgjPo,9A0,12) = 1,1131A,90909 - 0,77)" 2 _ 0,527 • 0,016666 = 0,340787085
F0,9A0,12) = 2,19173 (8 = 0,18%).
60 Распределения вероятностей случайных величин [Гл. 1
Задача 16. Вычислить нормализующее преобразование для .Ро,э(Ю, 12) и оценить точ-
точность нормализации.
Для р = 0,9 имеем гло,э = 1,2811551.
Аппроксимация 2. Имеем .Ро,э(Ю,12) = 2,1878 и находим
а = 2,1213203 - °^471404521 = 2,074179848, с2 = 2,1213203 - °?47140452 = 2,08203659,
1
-2,074179848 + 2,08203659-2,1878 3 /г ^ч
d = up= — y2 = 1,28212 (ё = 0,01%);
11 \ 2
1 ¦ 2,18783
10 12
d' = 1,28212 ( 1 + 0,8- — • 1,2821224 ) = 1,282282 (S = 0,06%).
Аппроксимация 3:
ио,9 = — 1 = 1,259744 (S = 0,04%).
10 \ 2
Ц • 2,187^
Аппроксимация 4:
2,18783 [ 1 — ) - [ 1 —\
у 9-12У V 9-10У 9Й9199 /е пПЛо/л
1iO,9 = 1 = I,2o212z (О = U,U47o).
2 2
Н • 2,18783
ч9-10 9-12
Оценим квантиль .Ро,э(Ю, 12), пользуясь этой аппроксимацией. Имеем
(9/i - 2)(9/2 - 2) = (9 • 10 - 2)(9 • 12 - 2) = 9328;
[2/i(9/2 - 2J + 2/2(9/i - 2J - 36/2Мр] 2 = 635,2015025;
(9/2 - 2J - 18/2tXp - (9 • 12 - 2J - 18 • 12 • 1,2815512 = 10881,24744;
F ПП19^ [1,2(9328 + 3 • 1,281551 • 635,2015025I 3
^0,9A0,12) = ^ 10881,24744 J = 2'187013
Аппроксимация 5. Вычисляем
= °>354212173; в = 1 - Р = 0,645787826; 5 = ^-^ = 5,5;
Z А
10-2,1878 + 12 ' 7 " r 7 ' 2
10 — 1 10 4- 12 — 2 S T
T = = 4,5; / = — = 1; — = 1,552741557; — = 0,69682329;
2 2 fp fq
g(l,55271667) = -0,145733931; g@,69682329) = 0,119889378;
0,645787826 0,354212173 0,645787826 \ _
12 10 10 + 12 у ~~
= 2,007475058;
l
n лл^^глго # - '" 0,645787826(^0,145733931 + 0,3542121173 • 0,119988937)
uoy9 = 2,007475058 \ -p —, >
1 + - j • 0,354212173 • 0,645787826 I
Относительная погрешность S = 0,03%.
1.1] Непрерывные распределения 61
1.1.11. Усеченное нормальное распределение
Описание, применение. Если из генеральной совокупности, имеющей нор-
нормальное распределение iV(/x, <т), изъять все элементы, меньшие или большие опреде-
определенных граничных значений а\ и u2, to образуется совокупность, подчиненная усе-
усеченному нормальному распределению. Граничные значения называются точками
усечения. На практике могут возникнуть случаи двустороннего и одностороннего
усечения. Часто это распределение используется при анализе точности производ-
производства [93].
Свойства
Двустороннее усечение
Обозначение N1 (/х, а, а\, а 2)
Параметры /х, а, а\, п2
Плотность Lp'f(x) =
a J \ а
где (f(x) — плотность вероятностей стандартного нормального распределения iV@,1);
х п
1 г *_
Ф(ж) = —= е~ 2 dt — функция Лапласа; /i, a — параметры исходного нормального
V 2тг J
о
распределения; а\ < п2—точки усечения
Среднее М(ж) = /х — (А2 — Ai)cr,
Г^е Л1 - фЩтщ; Л2 - фF)фF); 6 - -^-; 6 - —г-
Дисперсия В(ж) = A + Ai^i - А26 - А2 + Ai)V2
В случае симметричного усечения, т.е. когда а\ — /i = п2 — \х = ^
имеет место
г 1
х е [ц — а\ < х < fji + а2\
1 I
Функция распределения F'(х) = — —-р—™ —, а\ < х <
Среднее (мода, медиана) М(ж) = Me = Mo =
Дисперсия Щх) = A - 2^AW2, где С = —; А =
2Ф —
Одностороннее усечение (а2 = оо)
Обозначение N/f (/i, сг, ai)
Параметры /i, сг, ai
Среднее М(х) = // - 7о-, где 7 = 0 5^
Дисперсия О(ж) = сг2A — ^7 ~ 72)
62 Распределения вероятностей случайных величин [Гл. 1
Вид кривых распределения разнообразен в зависимости от соотношения пара™
метров ад, ai, а^ и <т, но во многих случаях кривые будут образованы отрезками
нормальной кривой с соответственно увеличенными координатами. Кривые сим-
симметричны при а\ = —п2 и несимметричны в иных случаях.
Доля усечения определяется формулами — слева: 0,5 —Ф(?х) и справа: 0,5 — Ф(?г)•
Если заданы не границы, а доли усечения, то такие выборки называются не
полностью определенными (расчеты для них аналогичны).
Задача 17. Из нормальной выборки с параметрами /х = 100 и а = 30 изъяты члены
с х < 70 и х > 160 (а\ = 70, «22 = 160). Как изменятся параметры полученного распре-
распределения по сравнению с исходным нормальным?
Вспомним, что функция Лапласа Ф(ж) связана с функцией F(x) соотношением
Ф(х) 1
= F(x) (см. раздел 1.1.1). Для расчетов Ф(ж) воспользуемся аппроксимацией 5
из раздела 1.1.1, в соответствии с которой
Находим
Ф(х) = i|l-exp( -^
/160 - 100\ = = 1 Г / 8Л1 t =
V 30 / Ч \ *)\
ФB) - Ф(-1) = ФB) + ФA) = 0,48 + 0,3431 = 0,8231.
Вычисляем среднее:
A ^(Ci) д Ч>{&) * =70^Ю0= = 160 - 100 =
1 фF)фF)' 2 фF)-фF)' зо ' ^2 зо
Имеем
ФF) = ФB) = 0,48; ФF) = Ф(-1) = -0,3431; Ф(?2) - ФF) = 0,823118.
1 Г ж2 1
Вспомним, что (р(х) = exPi г5 в нашем случае
V2tt [ 2 J
<р(-1) = 0,398942ехрМ - - ) = 0,24197; <^B) = 0,398942expf -- J = 0,05399;
= 0,24197 = ^ = 0^5399 =
0,8231 0,8231
Итак,
М(ж) = // - (Л2 - Ai)a = 100 - @,06559 - 0,29396) • 30 = 106,851,
и
Щх) = A + AiCi - А26 - А2 + AiJ(j2 =
= A + 0,29396 • (-1) - 0,06559 • 2 - 0,06559 + 0,2939J • ЗО2 = 580,652; л/Щх) = 24,0967.
1.1.12. Распределение модуля случайной величины, распределенной нормально
Описание, применение. Если случайная величина х распределена нормально
7V(^, сг), то случайная величина у = \х\ будет иметь распределение модуля. Приме™
няется при анализе допусков на изготовление деталей машино- и приборостроения.
1.1] Непрерывные распределения 63
Свойства
Обозначение |7V|(//, сг)
Параметры /i, a
Плотность гЬ(у;и,,а) = - \<р(У~*1) + <р(У I , 2/ > О,
<7 [ \ <Т / V СГ / J
где <?>(ж)—плотность стандартного нормального распределения
Функция распределения F(y: /i, ст) = Ф ( 1 + Ф ( ), у > О,
\ a J \ a J
t 9
где Ф(?) = —= e~~ 2 с?ж — функция Лапласа
V 2тг J
о
Среднее МЫ = 2 \иФ(- ) +ст<р(-
(при /х = 0 М(з/) = J^a^ 0,7979(j)
Дисперсия D(y) = а2 + fi2 — [М(у)]2
(при /i = 0 D(y) = ^у^ а2 « 0,3634(т2)
Коэффициент асимметрии а3 = —^== ^ 0,99527
(тг — 2) • v тг — 2
Коэффициент эксцесса «4 = ^^ 2 ^ 0,8691772
(тг - 2)
Вид распределения определяется соотношением между параметрами исходного
распределения /л и а. При \х ^> а распределения N и \N\ практически совпадают.
Задача 18. Случайная величина х распределена нормально с параметрами ц = 10
и а = 5. Найти вероятность того, что модуль случайной величины х не превысит 3,
т. е. Р{|ж| < 3}. Вычислить параметры распределения случайной величины у = \х\.
1 Г / 2ж2\1 2
Воспользуемся аппроксимацией 5 — Ф(х) = - 1 — ехр( 1 (раздел 1.1.1) для
2 L V ж /J
вычисления Ф(ж) = ^(ж) — 0,5.
Имеем
Далее вычисляем
I
/З^МА =ф^_х^ = _фA?4) = ^iri^expf^^^I 2 = ^0,422154;
V 5 2L V J
= фB>в) = I [х _ ехр(_^!)] h = 0,496608;
Р(|ж < 3|) = -0,422154 + 0,496608 = 0,074454.
Находим
<рB) = -^= е~% = 0,053991; М(|ж|) = 2 • A0 • 0,48 + 5 • 0,053991) = 10,13991;
л/2тг
В(|ж|) = 102 + 52 - 10Д39912 = 22,18223; уЩ\х\) = 4,7098.
64 Распределения вероятностей случайных величин [Гл. 1
1.1.13. Распределение, порождаемое нормальной плотностью
с линейным дрейфом среднего
Описание, применение. Такое распределение возникает при смещении центра
группирования мгновенного нормального распределения и является композицией
нормального и равномерного распределений, описывая распределение вероятностей
за весь период наблюдения. Применяется при изучении износа режущего инстру™
мента, дрейфа параметров электронных приборов.
Свойства
Пусть дрейф среднего во времени описывается формулой
fi(t) = /jl0 + 2Acr0t,
где jLto, cfq — параметры исходного распределения (при t = 0):
A = B(j)^1[/i(t)max^/i(t)min]e
Параметры /х, и, t
Плотность <p(z, А) = — [Ф(гш + А) — Ф(гш — А)],
х - М(х)
где z = — , , — нормированное значение переменной;
ш = I 1 Н ] ; Ф(у) = e^^dt — функция Лапласа
v 7 о
Функция распределения
F(z, A) = ||l+ ^[(^ + А)Ф(^ш + АЬ(^ - A)#(zcj - А) + фш + А) - ^
где (р(у)—плотность стандартного нормального распределения
Среднее М(ж) = /xq + Actq
Дисперсия D(x) = а^ш2
Коэффициент вариации v = -
Коэффициент асимметрии «з = О
Коэффициент эксцесса «4 = —А4C + А2)^2
5
При <то —У 0 распределение стремится к равномерному (см. раздел 1.1.2), при
А —} 0 — к нормальному (см. раздел 1.1.1). Таблицы плотности <p(z,\) и функции
F(z,X) для А = 3, 6, 10 и 25 приведены в [93].
Задача 19. Начальное напряжение зажигания газоразрядного прибора распределено
нормально с параметрами /хо = 1000 В и сто = 150 В. В течение срока службы среднее
значение напряэюения зажигания увеличивается до 1500 В. Определить вероятность
того, что напряжение зажигания в течение срока службы будет находиться в ин-
интервале 900 -^ 1100 В.
Имеем 15оо - 1000
/i(t)max = 1500; /x(t)min = ЮОО; А = = 1,666;
.2 • 1<5и
/ А2\ 2
о; = 1 + — = 1,387; М(х) = ц0 + Ха0 = 1000 + 1,666 • 150 = 1249,9;
V 3 /
2 = 43284,802; у/Щх) = 208,05.
1.1] Непрерывные распределения 65
900 - 1249,9 1100 - 1249,9
208,5 = -1'6825 ?2 = 208,5 = ^^
Для вычисления значения Ф(ж) воспользуемся аппроксимацией из раздела 1.1.1
Л [
Ф(х) = i { 1 1
2 1 + 0Д253ж2
Имеем для z\ = —1,682
Ф(-1,682 • 1,387 + 1,666) = Ф(~0,666334) = -1\-
1
'2 \] \ 2
ехр|( 0Д253(~0,б66334J
2 | 1 +0,1253-0,6663342
= -0,247536883;
Ф(-1,682 • 1,387 ~~ 1,666) = Ф(-3,998934) = -0,4999766;
(^(-0,666334) = 0,3135136; (^(-3,998934) = 1,344 • 10^4.
Для ^2 = —0,72 имеем
Ф(-0,72 • 1,387 + 1,666) = Ф@,66796) = 0,248057;
Ф(-0,72 • 1,387 - 1,666) = Ф(-2,66524) = -0,41313076;
«^@,66796) = 0,3191724; (^(-2,66524) = 0,0114394.
Находим
F(zuX) = -\l-\ ^@,666334 • 0,247536283 + 3,998934 • 0,49997666 + ...) i = 0,0453049;
v ' ; 2\ l,666l ' ' ' ' /
F(z2,X) = -|l + ^^@,66796-0,248057-2,66524-0,41313076 + 0,
V ' ; 2\ 1,666V ' ' '
= 0,311692225.
Окончательно
P(-l,682 < z < -0,72) = F(-0,72) - F(-l,682) = 0,311692225 - 0,0453049 = 0,2663873.
Следовательно, при таком дрейфе вероятность того, что напряжение зажигания нахо-
находится в интервале 900 + 1000 В, равна р « 0,266.
Для сравнения найдем вероятность попадания в этот интервал напряжения зажига-
зажигания при отсутствии дрейфа, т. е. когда Л = 0.
900-1000 Л_ 1100-1000 Л^
В этом случае z\ = = —0,667: z2 = = 0,667,
J 150 ' 150 '
Р(-0,667 < z < 0,667) = 2F@,667) - 1.
Находим с помощью аппроксимации 18 из раздела 1.1.1
F@,667) = 1 - - ехр(-0,717 • 0,667 - 0,416 • 0,6672) = 0,7423.
Таким образом, Р(—0,667 < z < 0,667) = 0,4846. Следовательно, отсутствие дрейфа су-
существенно (почти в 2 раза) увеличивает вероятность нахождения напряжения зажигания
в интервале 900 + 1100 В.
1.1.14. Распределение, порождаемое нормальной плотностью
с линейным дрейфом среднеквадратического отклоненим
Описание, применение. Распределения такого типа встречаются при авто-
автоматическом изготовлении деталей, когда за время изготовления партии деталей
изменяется рассеяние начального нормального распределения (например, при за-
3 А. И. Кобзарь
66 Распределения вероятностей случайных величин [Гл. 1
туплении режущего инструмента, при изменении механических свойств заготовок).
Распределение погрешностей при измерениях близко к рассматриваемому, если
за время проведения измерений имеет место систематическое смещение точности
процесса измерения.
Свойства
Пусть дрейф среднеквадратического отклонения описывается формулой
a(i) = о"оA + 2At);
где а® — параметр исходного распределения (t = 0); А = ^а®)^1 [cr(t)max — cr(i)min].
Г / 2 2 \ / 22
Плотность (p(z: A) = —; < Е» ( — | — ЕЛ — -
б ; г\ 6(i +2A)
х - М{х) „ Г е"
где z = — —нормированное значение переменной; bi{z) = —сш — инте-
\/Т}(т,') I ^
тральная функция (табулирована); ш = C + 6А + 4А )
Функция распределения
0
Среднее М(ж) = /ig
Дисперсия О(ж) = -?- ш2
о
Здесь /jlq и сг0 — параметры исходного нормального распределения.
Коэффициент вариации v =
Коэффициент асимметрии а% = 0
Коэффициент эксцесса «4 = 12А2
Значения cp(z; X) и i^(z; А) табулированы в [93] для значений параметра А = 1,
3, 6 и 9. Значения F(z; А) для различных z и А приведены в табл. 4.
Задача 20. Начальная погрешность измерения подчинена нормальному распределению
с параметрами цо = 100 ед. и о~о = 20 ед. В процессе проведения измерений о~о линейно
увеличивается до 60 ед. Найти вероятность того, что при проведении измерений
погрешность не превысит 40 ед.
Имеем
А = ^t^. = i; ш= C + 6-1 + 4- I2)i = 3,60555; М(х) = ц0 = 100;
2 2\
/ 2
лУЩх) = \ — - 3,605552 = 41,6333; z = 4° ~ 10° = -1,44115.
v v ; V 3 41,6333
Необходимо найти Р(ж < 40) = F(-l,44; 1) = 1 - F(l,44; 1). По табл.4 для А = 1
и z = —1,44 находим, что 1^A,44; 1) та 0,93 и, следовательно, искомая вероятность равна
Р(ж < 40) = 1 - 0,93 = 0,07.
Если бы дрейфа стандартного отклонения не было, то Р(ж < 40) = Fl I =
= F(—3) = 1 — i^C). Здесь F(x) — функция стандартного нормального распределения.
Так как FC) = 0,9977, то Р(х < 40) = 1 - 0,9977 = 0,0023.
1.1]
Непрерывные распределения
67
Таблица 4
Z
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
2,00
2,05
2,10
2,15
2,20
2,25
2,30
2,35
2,40
2,45
Значения функции
Л
1
0,5000
0,5225
0,5453
0,5678
0,5900
0,6118
0,6332
0,6540
0,6742
0,6938
0,7126
0,7307
0,7481
0,7646
0,7803
0,7953
0,8094
0,8228
0,8354
0,8472
0,8583
0,8687
0,8784
0,8875
0,8960
0,9039
0,9113
0,9182
0,9246
0,9305
0,9360
0,9411
0,9459
0,9503
0,9543
0,9581
0,9616
0,9648
0,9678
0,9705
0,9730
0,9754
0,9775
0,9795
0,9813
0,9830
0,9845
0,9859
0,9872
0,9884
3
0,5000
0,5281
0,5560
0,5831
0,6094
0,6346
0,6585
0,6810
0,7022
0,7220
0,7405
0,7578
0,7739
0,7889
0,8029
0,8160
0,8282
0,8394
0,8503
0,8603
0,8697
0,8784
0,8866
0,8943
0,9015
0,9082
0,9145
0,9204
0,9259
0,9311
0,9359
0,9405
0,9447
0,9486
0,9528
0,9558
0,9590
0,9620
0,9648
0,9674
0,9699
0,9721
0,9743
0,9762
0,9781
0,9798
0,9813
0,9828
0,9842
0,9854
6
0,5000
0,5234
0,5653
0,5969
0,9624
0,7505
0,6745
0,6965
0,7168
0,7355
0,7527
0,7688
0,7837
0,7977
0,8107
0,8228
0,8342
0,8448
0,8548
0,8642
0,8729
0,8812
0,9889
0,8961
0,9029
0,9093
0,9153
0,9203
0,9262
0,9311
0,9358
0,9401
0,9442
0,9480
0,9516
0,9550
0,9581
0,9611
0,9638
0,9664
0,9668
0,9710
0,9713
0,9751
0,9769
0,9785
0,9802
0,9817
0,9831
0,9844
9
0,5000
0,5264
0,5711
0,6030
0,6317
0,6576
0,6810
0,7025
0,7221
0,7403
0,7571
0,7726
0,7872
0,8007
0,8134
0,8252
0,8363
0,8466
0,8564
0,8655
0,8741
0,8821
0,8897
0,8968
0,9034
0,9097
0,9156
0,9211
0,9263
0,9311
0,9357
0,9400
0,9400
0,9478
0,9514
0,9547
0,9578
0,9607
0,9635
0,9660
0,9684
0,9707
0,9727
0,9747
0,9765
0,9782
0,9798
0,9813
0,9827
0,9840
z
2,50
2,55
2,60
2,65
2,70
2,75
2,80
2,85
2,90
2,95
3,00
3,05
3,10
3,15
3,20
3,25
3,30
3,35
3,40
3,45
3,50
3,55
3,60
3,65
3,70
3,75
3,80
3,85
3,90
3,95
4,00
4,05
4,10
4,15
4,20
4,25
4,30
4,35
4,40
4,45
4,50
4,55
4,60
4,65
4,70
4,75
4,80
4,85
4,90
4,95
F(z;X)
X
1
0,9894
0,9904
0,9913
0,9922
0,9929
0,9936
0,9942
0,9948
0,9953
0,9958
0,9962
0,9966
0,9969
0,9972
0,9975
0,9978
0,9980
0,9982
0,9984
0,9986
0,9987
0,9989
0,9990
0,9991
0,9992
0,9993
0,9994
0,9994
0,9995
0,9996
0,9996
0,9997
0,9997
0,9997
0,9998
0.9998
0,9998
0,9998
0,9999
3
0,9866
0,9877
0,9887
0,9896
0,9905
0,9913
0,9920
0,9927
0,9933
0,9939
0,9944
0,9949
0,9953
0,9958
0,9961
0,9965
0,9965
0,9971
0,9974
0,9976
0,9978
0,9980
0,9982
0,9984
0,9985
0,9987
0,9988
0,9989
0,9990
0,9991
0,9992
0,9993
0,9994
0,9994
0,9995
0,9996
0,9996
0,9996
0,9996
0,9997
0,9997
0,9998
0,9998
0,9998
0,9998
0,9998
0,9999
6
0,9856
0,9867
0,9877
0,9887
0,9896
0,9904
0,9912
0,9919
0,9925
0,9932
0,9937
0,9942
0,9947
0,9952
0,9956
0,9959
0,9963
0,9966
0,9969
0,9972
0,9974
0,9977
0,9979
0,9981
0,9981
0,9984
0,9985
0,9987
0,9988
0,9989
0,9990
0,9991
0,9992
0,9993
0,9993
0,9994
0,9995
0,9995
0,9996
0,9996
0,9997
0,9997
0,9997
0,9998
0,9998
0,9998
0,9998
0,9998
0,9998
0,9999
9
0,9852
0,9864
0,9874
0,9884
0,9893
0,9901
0,9909
0,9916
0,9923
0,9929
0,9935
0,9940
0,9945
0,9949
0,9954
0,9957
0,9961
0,9964
0,9967
0,9970
0,9973
0,9975
0,9977
0,9979
0,9981
0,9983
0,9984
0,9986
0,9987
0,9989
0,9989
0,9990
0,9991
0,9992
0,9993
0,9994
0,9994
0,9995
0,9995
0,9996
0,9996
0,9996
0,9997
0,9997
0,9997
0,9998
0,9998
0,9998
0,9998
0,9998
68 Распределения вероятностей случайных величин [Гл. 1
1.1.15. Распределение Рэлея
Описание, применение. Применяется для описания распределения неотри-
неотрицательных случайных величин, являющихся векторной суммой двух нормальных
случайных величин с равными дисперсиями. Ему подчиняются погрешности гео-
геометрической формы (овальность, конусообразность), ошибки взаимного расположе-
расположения поверхностей (эксцентриситет, разностенность). Распределение Рэлея широко
применяется в радиолокации при оценке погрешности обнаружения объектов.
Свойства
Обозначение
Параметр
Плотность
Функция распределения
Среднее
Дисперсия
Коэффициент вариации
Коэффициент асимметрии
Коэффициент эксцесса
Мода
Медиана
Ща)
а
/(*;<
F(x;
М(х
D(x)
v=\
а3-
МО:
Me:
ч X (
a) = — exp 1 -
a V
a) = 1 — exp |
) = Vl0Ssl
¦=B-5).
< 4 V-l
V4-7T/
2^тг(тг - 3)
л/D - тгK
V \ /
24тг - 16тг2 -
(А J
= а
= aB1n2)i =
2 \
X \
^ 2 \
,253a
= 0,429a2
913
= 0,631
16 П 9d^
1,177a
Для удобства табуляции на практике применяется нормирование случайной ве-
величины z = х/а. Векторная сумма двух нормальных случайных величин с нулевым
средним и одинаковым стандартным отклонением а имеет распределение Рэлея
с параметром а.
Задача 21. Случайная величина распределена по закону Рэлея с параметром а = 4.
Вычислить вероятность того, что случайная величина не превысит значения х = 3,
и вычислить 95%-ю квантиль распределения.
Имеем Р(ж < 3) = 1 — expj ^ 1 =0,24516. Для вычисления 95%-й квантили
/ \ г\ г\г- л ( Ж0,95 \ 1 гл глг- Ж0,Э5
(жо,9б) используем равенство 0,95 = 1 — ехр ¦— 1; 1п0,05 = ¦—, и окончательно
у 2 • 16 J 2-16
г
имеем жо,95 = (—2 • 16 • In 0,05) 2 = 9,790987, т. е. с вероятностью 0,95 случайная величина
не превысит значение 9,971.
1.1.16. Распределение Максвелла
Свойства, применение. Векторная сумма трех нормально распределенных
случайных величин с нулевыми средними и равными дисперсиями имеет распре™
деление Максвелла. Распределением Максвелла описывается абсолютная величина
скорости движения молекул.
1.1]
Непрерывные распределения
69
Обозначение
Параметр
Плотность
Функция распределения
где (p(z) =
Среднее
Дисперсия
О,
Свойства
М(х,а)
а
х2 B \ 2 Г х2 ]
/(*;a) = ?(-j expj-^j, * > О
F(x;a)=2[*(H)-?v(?)l,
v 7 [ \а/ а \а/J
>(z) = -p= e 2 dt
о
i
M(x) = 2аГ-^ 2 = 1,596a
В(ж) = а2 (з - ^1 = 0,454a2
i
2
Коэффициент вариации v = 21 о 1 = 2,369
\О7Г — 8/
Коэффициент асимметрии аз = — = 0,486
Коэффициент эксцесса
Медиана
Мода
1607Г - 12тг2 - 384
«4 = о = 0,108
9тг2 - 48тг + 64
Me = 1,538а
Мо = лДа = 1,414а
Обычно распределение Максвелла используется в нормированной форме
{z = x/a).
Задача 22. Вычислить вероятность того, что значение случайной величины, имею-
имеющей распределение Максвелла с параметром а = 10, превысит х = 11.
Имеем
Р(ж > 11) = 1 - F(ll; 10) = 1 - 2[ФA,1) - 1,1 • <рA,1)].
Для вычисления Ф(ж) воспользуемся аппроксимацией 6 из раздела 1.1.1, в соответствии
с которой
Г / Г) \
0Д253)(-ж2)
^ + 0,1253ж2
Тогда
Н^ =фA ,l) = ±<Jl
10у v ; 2 |
-0,1253- 1,1
i,i2
= 0,364784;
10/ —-' ЛИГ =°'217852-
Окончательно имеем Р(ж > 11) = 1 — 2 • @,364784 - 1,1 • 0,217852) = 0,749707.
70 Распределения вероятностей случайных величин [Гл. 1
1.1.17. Распределение экстремального значения
Описание, применение. Рассмотрим распределение вероятностей экстре-
экстремальных выборочных значений случайной величины х: у\ = min(#i, х^-, . ..,жп)
и уп = max(#i, X2, ..., хп). Различают распределения экстремальных значений по™
следовательности независимых случайных величин двух типов, когда распределе-
распределение самих случайных величин сосредоточено на конечном и бесконечном интер-
интервалах. Если распределение исходных случайных величин ограничено некоторым
интервалом [а, 6], то для экстремальных значений имеет место так называемое
распределение типа III с функцией
— для минимального значения
Г (Ха\\
, = 1-ехр -1—^—1 , х > а;
для максимального значения
Г /b-x\P]
Fm,n = ехр -(^—^—J > x<b.
Очевидно, что распределения этого типа совпадают с распределением Вейбулла
(см. раздел 1.1.5).
Наибольшее практическое применение находит закон распределения экстре-
экстремальных значений для выборки случайных величин, распределенных на беско-
бесконечном интервале. Этот закон принято называть двойным показательным, или
распределением типа I [12, 94]. Рассмотрим распределение минимального значения
(распределение максимального значения следует из него заменой знака перед х).
Свойства
тт ж( тл 1 (х-а\ Г (х-а
Плотность j(x; а, о) = - ехр{ —-— )ехр< — ехр
Функция распределения F(x;a,h) = 1 — ехр< — expf —^
Среднее М(х) = а- 0,577Ь
2
Дисперсия В(х) = —, Ь2 = 1,645Ь2
Коэффициент вариации v = «— = 0,608-^ ;—
1,64562 б2 Ь
Коэффициент асимметрии «з = —1,14
Коэффициент эксцесса а4 = 2,4
Мода Mo = a
Медиана Me = а + Ып1п2 = а^ 0,3666
Распределение неограничен© и несимметрично. Если случайная величина х име-
имеет распределение Вейбулла, то случайная величина у = In x имеет распределение
минимального значения. Поэтому необходимые расчеты и оценки, связанные с рас-
распределением экстремальных значений, могут быть получены из расчетов и оценок
распределения Вейбулла.
Если имеется последовательность п независимых случайных величин, имеющих
распределение минимального значения с параметрами а и 6, то наименьшая из них
имеет такое же распределение с параметрами а-61ппи 6.
1.1]
Непрерывные распределения
71
Задача 23. Известно, что распределение минимальной наработки электронного при-
прибора имеет среднее значение, равное 1000 ч, и стандартное отклонение, равное 750 ч.
Найти вероятность того, что значение наработки превысит 1500 ч, и вычислить
95%-ю квантиль распределения минимальной наработки.
Имеем а = 0,5776 = 1000 и л/1Щ)Ъ = 750.
Отсюда а = 1000 + 0,577 • 584,76 = 1337,41 и Ь =
750
/1,645
= 584,76.
Далее Р(ж > 1500) = 1 - Р(ж < 1500) =
р-квантиль находим из условия р = ]_ — ехр< —
I
/1500- 1337,41
ехр(^
584,76
= 0,266989.
( (хр~а\\
< — ехр( J >,
I V 6 /J
где
хр = а + Ь ln[- ln(l - р)] = 1337,41 + 584,76 ln(- In 0,05) = 1979,
т.е. вероятность того, что наработка превысит 1979 ч, равна 0,05.
1.1.18. Треугольное распределение (распределение Симпсона)
Описание, применение. Сумма двух независимых равномерно распределен™
ных случайных величин имеет треугольное распределение.
Свойства
Параметры
Плотность
а, Ъ
f(x;a,b) =
0,
4(ж - а)
(Ъ - аJ '
х ^ а;
а < х <
х > а.
Функция распределения F(x;a,b) =
о,
(Ъ-а? '
1 — ------------------
х ^ щ
а < х
U,
2
х > Ъ.
< х < Ь;
Среднее М(ж) =
Дисперсия О(ж) =
Коэффициент вариации г; =
а + i
24
Коэффициент асимметрии аз = 0
Коэффициент эксцесса а4 = 2,4
Мода
Медиана
Мо =
Ме =
2
Распределение применяется редко, чаще всего в демонстрационных целях.
72 Распределения вероятностей случайных величин [Гл. 1
Задача 24. Случайная величина х имеет треугольное распределение с дисперсией
ТУ(х) = 24 и со средним М(ж) = 8. Найти вероятность того, что значение случайной
величины будет находиться в интервале [0,5].
Имеем М(ж) = ^^ = 8 и D{x) = l^H^L = 24, отсюда 6 - а = 24 и b = 20, а = -4.
2 24
Далее Р@ < ж < 5) = FE) - F@) = 2 " E + 4\ - 2 ' (° + 4)9 = 0,22569.
V ; W V ; B0 + 4J B0+ 4J
1.1.19. Распределение Коши
Описание, применение. Описывает распределение отношения двух незави-
независимых нормально распределенных случайных величин. В прикладной статистике
используется редко.
Свойства
Параметры a, b
Плотность f(x; а, Ъ) = — ехр(—=—) +1
7ГО [ \ О / J
1 1 ( х —- а\
Функция распределения F{x\a,b) = —I— arctgf —-— J
Мода Mo = а
Медиана Me = b
У распределения Коши не существует ни среднего, ни дисперсии. Отношение двух
независимых случайных величин, имеющих стандартное нормальное распределение,
имеет распределение Коши с параметрами а = 0 и Ъ = 1. Распределение Коши сов™
падает с ^-распределением Стьюдента (см. раздел 1.1.9) при / = 1 степени свободы.
Сумма п независимых случайных величин, имеющих распределение Коши с па-
параметрами щ и bi, также имеет распределение Коши с параметрами ]Р щ и ]Р Ъ{.
Если случайная величина х имеет распределение Коши с параметрами а и Ь, то
обратная ей случайная величина у = 1/х будет иметь распределение Коши с пара-
параметрами а1 = а /(а2 + Ь2) и Ъ' = Ь/(а2 + Ь2).
Задача 25. Отношение энергии разряда W газоразрядного прибора к его предельной
энергии Wnp называется фактором нагрузки к. Известно^ что предельная энергия
прибора распределена нормально со средним 1000 Дэт и стандартным отклонением
150 Дою. Также нормально со средним 500 Дтс и стандартным отклонением 60 Дтс
распределена энергия разряда прибора во время работы. Необходимо вычислить веро-
вероятность того, что при энергии разряда 600 Дмс фактор нагрузки не превысит 0,7.
Вычислить вероятность того, что значение к будет лежать в интервале 0,4^0,5.
Запишем отношение двух нормированных нормально распределенных случайных
величин
600 - 500 600 - 500
У =
w пр — ±\j\jkj kjuxj
150 _к_
150
Очевидно, что требование fc^057 и 054^ifc^0,5 эквивалентно условиям у ^ —7/4 и
0,5 ^ у ^ 1,25. Случайная величина у имеет распределение Коши с параметрами а = 0,
Ь= 1, и
О -j) =1-P{y^ -j) =l-F(a;O,l) = l-i-iaxctg(-j) =0,83475.
Далее
Р@,5 ^ у ^ 1,25) = F(l,25) - F@,5) = - + - arctg 1,25 — i — — arctg0,5 = 0,137639.
2 7Г 2 7Г
60
Wnp - 1000
150
600
к
60
- 1000
5
4
3
к
-5k
1.1] Непрерывные распределения 73
1.1.20. Логистическое распределение
Описание, применение. Чаще всего используется в описательной статистике.
Может быть использовано как простейшая модель для приближения распределения
нормальной случайной величины.
Свойства
Параметры а, Ъ
Гтг(ж — а)
expl—-7
Плотность f(x:a,b) = —7= ¦
+ ехр -
_ 7-!/ I \ I -I К(Х ~ t
Функция распределения г (ж; а, о) = \ 1 + ехр |
Среднее М(ж) = а
Дисперсия О(ж) = Ь2
Коэффициент вариации v = —
Коэффициент асимметрии а3 = 0
Коэффициент эксцесса «4 = 4,2
Мода Mo = a
Медиана Me = a
Задача 26. Случайная величина имеет логистическое распределение со средним а = 15
и коэффициентом вариации v = 3,3. Вычислить вероятность того, что значение слу-
случайной величины не превысит 10. Найти 15%-ю квантиль распределения.
Имеем Ь=- = — = 4,2857 и
v 3,5
{г 1 ^ ~1
1 + ехр - 710 ~ 1Б^ I = 0,1075.
Далее из условия
1С V3-4,2857 0,85
= т 1 г\п имеем г^о is = 15In
Г 7Г(«О15 - 15I '
1 + е
niK г 1С V34,2857 0,85
0,15 = = т 1 г\п имеем г^о is = 15 In = 10,9.
Г 7Г(«О15 15I ' 7Г 015
2857 J
=т1 г\п имеем г^о is = 15In
Г 7Г(«О,15 - 15I ' 7Г 0,15
ехр —
L VS- 4,28
1.1.21. Распределение Парето
Описание, применение. Применяется в основном в описательной статисти-
статистике. Впервые рассмотрено при изучении распределения доходов населения. Иногда
используется как простейшая математическая модель изменения интенсивности
отказов приборов на этапе приработки.
Свойства
Параметр с
Плотность f(%]c) = сх~^с+1\ 1 ^ х ^ о©
Функция распределения F(x;c) = 1 — ж^с, 1^ж^оо
Среднее М(ж) = -, с > 1
74 Распределения вероятностей случайных величин [Гл. 1
с / с \ ^
Дисперсия D(x) = — ( ) , с > 2
С z! \ С I/
Коэффициент вариации v = 1 , с > 2
\ с J
Если случайная величина х распределена равномерно на интервале [0,1], то
случайная величина A/ж)с имеет распределение Парето с параметром с.
Задача 27. Случайная величина х имеет распределение Парето с параметром с = 2,4.
Вычислить вероятность того, что х ^ 5, и 95%-ю квантиль распределения.
Имеем Р(ж ^ 5) = FE; 2,4) = 1 - 5~2'4 = 0,979. Из условия 0,95 = 1 - щ2^ получаем
^о,95 =0505~2^ =3,484.
1.1.22. Композиции законов распределения вероятностей случайных величин,
возникающие при расчете надежности по схеме „нагрузка-напряжение"
Если х — прочность объекта испытаний, а у— действующая на него нагрузка, то
вероятность безотказной работы объекта испытаний равна
Л = Р(ж> у) = Р(х - у > 0).
В общем случае х ж у являются случайными величинами с плотностями распре™
деления вероятностей f(x) и f(y) соответственно. Легко видеть, что вероятность
безотказной работы равна Р(ж — у > 0) = 1 — F(x — г/), где F(x — у) — функция
распределения разности случайных величин х и у.
Рассмотрим соотношения для вероятности безотказной работы R при различных
законах распределения вероятностей значений прочности и напряжения.
Случай 1. Прочность и напряжение распределены нормально (см. раздел 1.1.1)
; f(y) =
аху~ш [ ^ v ux / j
Тогда
V2tt J
где F(z) — функция стандартного нормального распределения.
Случай 2. Прочность и напряжение распределены логарифмически нормально
(см. раздел 1.1.3):
(Ых ~
. 2a*
1 Г i
/Ы = -
где (i\n х, (i\n у, а\п х, <Jin у — параметры нормальных распределений величин In x
и \пу.
Случай 3. Прочность и напряжение распределены по экспоненциальному закону
(см. раздел 1.1.4)
f(x) = Хх ехр(^Ажж); f(y) = Ху ехр(-Ауу); R = -—^—.
1.1] Непрерывные распределения 75
Случай 4. Прочность распределена нормально (экспоненциально), а напряже™
ние экспоненциально (нормально):
X — Цх
Тогда [93]
При
f{x) = Ххещ>{-\хх}; f(y) = -±= ещ>[-\(у—>
ауу2ж { 1 V (Ту
Случай 5. Прочность и напряжение имеют гамма-распределение (см. раздел 1.1.6)
Вероятность безотказной работы имеет вид:
при ах ф 0 и ау ф О
р _ Г(аж + ау - 2) , _ ,
где Г(...) — гамма-функция, В7(а, Ь) —неполная бета-функция иг = -^;
Рх
при аж = ау = 0 (х и г/ имеют экспоненциальное распределение)
при аж = 0, ау т^ 0 (прочность распределена экспоненциально, а напряжение имеет
гамма-распределение)
при ах ф 0, о^ = 0 (прочность имеет гамма-распределение, а напряжение распре-
распределено экспоненциально)
R= 1-
Случай 6. Напряжение распределено нормально, а прочность по закону Вей™
булла (см. раздел 1.1.5):
1 Ру в -
-ihyv
Вероятность отказа равна
2тг ^ж
о
Таблицы значений интеграла приведены в [95] и в табл. 5.
76
Распределения вероятностей случайных величин
[Гл. 1
Таблица 5
А
Значения A -
- А), умноженные на
1СГ (А
= -Цх/сгх, С = <
С
10
20
30
40
50
60
70
80
90
100
/Зу = 1
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
-1,4
-1,8
-2,2
-2,6
-3,0
-3,4
-3,8
-4,2
-4,6
-5,0
-5,5
-6,0
-6,5
-7,0
-8,0
-9,0
-10,0
0001
0003
0004
0005
0008
ООН
0016
0022
0030
0041
0069
0111
0169
0247
0349
0475
0630
0815
1031
1279
1634
2037
2485
2973
4039
5265
6269
0000
0000
0000
0001
0001
0001
0002
0003
0005
0005
0009
0014
0022
0032
0045
0062
0082
0108
0138
0173
0255
0287
0360
0443
0645
0897
1202
0000
0000
0000
0000
0000
0000
0001
0001
0002
0002
0003
0004
0006
0009
0013
0018
0024
0032
0041
0052
0067
0086
0108
0134
0196
0276
0374
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0003
0004
0006
0008
0010
0014
0017
0022
0029
0036
0046
0057
0083
0117
0160
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0003
0004
0005
0007
0009
ООН
0015
0019
0023
0029
0043
0050
0082
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0002
0003
0004
0005
0006
0008
ООН
0014
0017
0025
0035
0048
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0001
0002
0003
0003
0004
0005
0007
0009
ООН
0016
0022
0030
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0002
0003
0004
0005
0006
0007
0010
0015
0020
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0002
0003
0003
0004
0005
0007
0010
0014
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0001
0002
0002
0003
0004
0005
0008
0010
Pv = 2
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
-1,4
-1,8
—2 2
-2^6
-3,0
-3,4
-3,8
-4,2
-4,6
ООН
0017
0025
0035
0049
0067
0089
0116
0149
0188
0284
0407
0557
0733
0935
1159
1406
1671
1954
0003
0004
0007
0009
0012
0017
0023
0030
0038
0048
0073
0105
0144
0191
0246
0308
0377
0453
0536
0001
0002
0003
0004
0006
0008
0010
0013
0017
0021
0032
0047
0065
0086
ОНО
0138
0170
0205
0243
0001
0001
0002
0002
0003
0004
0006
0007
0010
0012
0018
0026
0036
0048
0062
0078
0096
0116
0137
0000
0001
0001
0001
0002
0003
0004
0005
0006
0008
0012
0017
0023
0031
0040
0050
0062
0074
0088
0000
0000
0001
0001
0001
0002
0003
0003
0004
0005
0008
0012
0016
0022
0028
0035
0043
0052
0061
0000
0000
0001
0001
0001
0001
0002
0002
0003
0004
0006
0009
0012
0016
0020
0026
0031
0038
0045
0000
0000
0000
0001
0001
0001
0001
0002
0002
0003
0005
0007
0009
0012
0016
0020
0024
0029
0035
0000
0000
0000
0000
0001
0001
0001
0001
0002
0002
0004
0005
0007
0010
0012
0015
0019
0023
0027
0000
0000
0000
0000
0001
0001
0001
0001
0002
0002
0003
0004
0006
0008
0010
0013
0015
0019
0022
1.1]
Непрерывные распределения
77
А
п
р о д о л
жени
е та б л
ицы 5
С
10
20
30
40
50
60
70
80
90
100
f3y = 2
-5,0
-5,5
-6,0
-6,5
-7,0
-8,0
-9,0
-10,0
2251
2640
3043
3457
3876
4713
5525
6285
0626
0748
0879
1020
1170
1493
1845
2222
0284
0341
0402
0468
0539
0695
0969
1059
0161
0193
0228
0266
0307
0398
0499
0611
0103
0124
0147
0171
0198
0256
0322
0396
0072
0086
0102
0119
0138
0179
0225
0277
0053
0064
0076
0088
0101
0132
0166
0204
0041
0049
0058
0067
0078
0101
0127
0157
0032
0038
0046
0053
0062
0080
0101
0124
0026
0031
0037
0043
0050
0065
0082
0100
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
-1,4
-1,8
-2,2
-2,6
-3,0
-3,4
-3,8
-4,2
-4,6
-5,0
-5,5
-6,0
-6,5
-7,0
-8,0
-9,0
-10,0
0001
0003
0004
0005
0008
ООН
0016
0022
0030
0041
0069
0111
0169
0247
0349
0475
0630
0815
1031
1279
1634
2037
2485
2973
4039
5265
6269
0000
0000
0000
0001
0001
0001
0002
0003
0005
0005
0009
0014
0022
0032
0045
0062
0082
0108
0138
0173
0255
0287
0360
0443
0645
0897
1202
0000
0000
0000
0000
0000
0000
0001
0001
0002
0002
0003
0004
0006
0009
0013
0018
0024
0032
0041
0052
0067
0086
0108
0134
0196
0276
0374
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0003
0004
0006
0008
0010
0014
0017
0022
0029
0036
0046
0057
0083
0117
0160
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0003
0004
0005
0007
0009
ООН
0015
0019
0023
0029
0043
0050
0082
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0002
0003
0004
0005
0006
0008
ООН
0014
0017
0025
0035
0048
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0001
0002
0003
0003
0004
0005
0007
0009
ООН
0016
0022
0030
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0002
0003
0004
0005
0006
0007
0010
0015
0020
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0002
0003
0003
0004
0005
0007
0010
0014
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0001
0002
0002
0003
0004
0005
0008
0010
/Зу=4
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
0000
0000
0001
0001
0001
0002
0003
0005
0007
0010
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
78
Распределения вероятностей случайных величин
[Гл. 1
А
Окончани
е та б л
ицы 5
С
10
20
30
40
50
60
70
80
90
100
-1,4
-1,8
— 2 2
-2,6
-3,0
-3,4
-3,8
-4,2
-4,6
-5,0
-5,5
-6,0
-6,5
-7,0
-8,0
-9,0
-10,0
0018
0033
0055
0088
0136
0201
0289
0404
0501
0732
1015
1366
1788
2282
3466
4838
6252
0001
0002
0003
0006
0009
0013
0019
0026
0036
0048
0068
0094
0126
0167
0275
0429
0638
0000
0000
0001
0001
0002
0003
0004
0005
0007
0010
0014
0019
0025
0033
0055
0087
0130
0000
0000
0000
0000
0001
0001
0001
0002
0002
0003
0004
0006
0008
ООН
0017
0027
0041
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0002
0003
0004
0007
ООН
0017
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0002
0003
0005
0008
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
0002
0003
0004
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0002
0003
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0002
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0000
0001
0001
0001
Задача 28. Прочность элемента конструкции распределена нормально с парамет-
параметрами fix = 100 и ах = 50. Нагрузка^ действующая на элемент^ такэже распределена
нормально с параметрами \ху = 50 и ау = 25. Вычислить вероятность безотказной
работы элемента.
Имеем z= ^ 2 = — 0,89442. Далее, используя аппроксимацию 8 (см. раз-
раздел 1.1.1), получаем
2,34"
F(-0,89442) = l-F@,89442) = 1-0,852 expi - f °^89442 + 1>5774 ) К =0,185337;
I у 2,0637 J I
R = 1 - F(-0,89442) = F@,89442) = 0,814662.
Задача 29. Прочность элемента конструкции распределена логарифмически нормаль-
нормально с медианой 1000 ед. и модой 60 ед., а нагрузка распределена логарифмически нор-
нормально с медианой 80 ед. и модой 40 ед. Вычислить вероятность безотказной работы
элемента.
Имеем
exp(/iinJC) = 100; ехр(^1ПЖ - а?пх) = 60; ехр((цпу) = 80; exp(/iin2/ - (Тыу) = 40.
Тогда
jtxinx = 4,605; /Лпу = 4,382; afnx = fi\nx - In60 = 0,511; afny = fnny - In40 = 0,693.
Далее
^605 - 4,382
= _ 18521 Д= l^F(-0,18521) = 1-1 +F@,18521) =F@,18521).
0,511 + 0,693
Применив аппроксимацию из задачи 28, находим
R = F@,18521) = 1 - 0,
2,0637
= 0,573257.
1.1] Непрерывные распределения 79
Задача 30. Прочность элемента конструкции распределена экспоненциально
с Хх = 1CF3, а нагрузка также имеет экспоненциальное распределение с Ху = 1CF4.
Вычислить вероятность отказа элемента.
Вероятность отказа элемента равна
1 _ Л = 1 *»_ = _*?_ = 0,909.
«^Ж I Лу Л.х \ ^у
Задача 31. Прочность элемента конструкции распределена нормально с парамет-
параметрами fix = 200 и ах = 30, а нагрузка распределена экспоненциально с параметром
Ху = 10~2. Вычислить вероятность безотказной работы элемента.
Имеем
= 1 ~~ F(-6,6667) - ехр(-1,955){A - F(-6,6667)} = FF,6666) - 0,14156 • FF,6667).
Очевидно, что ,РF,6667) « 1, и окончательно получаем R = 1 — 0,14156 = 0,858. Легко
видеть, что если поменять местами прочность и нагрузку, то R = 0,142.
Задача 32. Прочность элемента конструкции имеет гамма-распределение с пара-
параметрами ах = 3 и j3x = 10^3, а нагрузка распределена экспоненциально с параметром
/Зу = 10~3. Вычислить вероятность безотказной работы элемента.
Имеем R=l- ( —^— ) = 0,75.
Задача 33. Прочность элемента конструкции распределена по закону Вейбулла с па-
параметрами ау = 800 и /Зу = 3, а нагрузка распределена нормально с параметрами
цх = 400 и ох =80. Вычислить вероятность безотказной работы элемента.
Имеем А = ^— = ^— = ^5; С = — = 10. Из табл. 5 для /3 = 3, А = ^5 и С = 10
<7Х 80 80
имеем 1 - Д = 0,1279 ий = 0,8721.
1.1.23. Нецентральное распределение Стьюдента
(нецентральное t-распределенме)
Описание, применение. Если случайная величина х имеет нормальное расп-
распределение со средним S и единичной дисперсией, а независимая от нее случайная
величина %2 имеет распределение хи-квадрат с / степенями свободы, то случайная
величина tf = х/х имеет нецентральное t-распределение с / степенями свободы
и параметром нецентральности S.
При S = 0 нецентральное i-раепределение совпадает с центральным (см. раз™
дел 1.1.9). Пусть 5(/,tg,p) — значение параметра нецентральности, при котором
случайная величина t7, имеющая нецентральное t-распределение с параметрами /
и <5, превышает значение to с вероятностью р, т. е. P{t;(/, S) > to} = p.
Очевидно, что
S(f,to,p) = -S(f,-to,p).
Таблицы, необходимые для расчетов в случае нецентрального ^распределения,
приведены в [24, 29, 96, 97].
80 Распределения вероятностей случайных величин [Гл. 1
При / > 30 применимо приближение
где U\—v—р-квантиль стандартного нормального распределения.
В [97] приведена достаточно простая аппроксимация, основанная на том, то
Arsh tW— имеет нормальное распределение
L V j J
где Arsh(x) = In (ж + л/х2 + l) —гиперболический арксинус, a t — случайная вели-
величина, имеющая распределение Стьюдента.
Нецентральное t-распределение используется при планировании эксперимента
и оценке мощности критериев проверки гипотез с помощью статистик, основанных
на ^критерии.
Задача 34. Вычислить значение параметра нецентральности 5, при котором слу-
случайная величина, имеющая нецентральное t-распределение с / = 10 степенями свободы,
превысит величину to = 2 с вероятностью р = 0,9.
Используя нормальную аппроксимацию, имеем
/ 22 \
5A0; 2; 0,9) = 2 - uo,i I 1 Н ) = 2 - uOjl • 1,095445.
Пользуясь аппроксимацией 15 из раздела 1.1.1, имеем
г*0,1 = 4,91 • (ОД0'14 - 0,90'14) = -1,2812615 и E = 2 + 1,2812615 • 1,095445 = 3,40356.
1.1.24. Нецентральное распределение Пирсона
(нецентральное распределение хи-квадрат)
Описание, применение. Сумма квадратов п независимых нормально распре™
деленных случайных величин с единичной дисперсией, среди которых по крайней
мере одна имеет ненулевое математическое ожидание, подчиняется нецентральному
Х! -распределению.
Нецентральному %' -распределению подчинена сумма
/v / j \ 1
где Х{ — независимые нормально распределенные величины с нулевым средним
^ п ^ п
и общей дисперсией а2 ; 7г — постоянные со средним j = ^^7i иж= — У^ Xj.
п f—' n
г=1 г=1
Величина \' подчиняется нецентральному х -распределению с / = п степенями
П 1
свободы и параметром нецентральности а = V^ ^"Gг — О7J-
Таблицы нецентрального х' ^распределения приведены в [24].
2а)
1.1] Непрерывные распределения 81
Пирсон предложил преобразование, позволяющее вычислить нецентральное
X2-распределение через центральное [98]:
а2
(п _i_ 2аK
где Х2(/;)—центральное х2тРасг[РеДеление с /' = 2 степенями свободы.
(п + За)
При а —> О Х2(/0 отличается от функции точного распределения хи-квадрат на
величину порядка а2, а при а —>¦ оо на величину порядка —.
а
Более простое, но менее точное преобразование предложено Патнайком [99]:
х" (/;/) = X2(fi а)ч гДе /;/ = . Полезно следующее преобразование [97]:
/ + 2а j + 2а
обычная величина сх2(/;) имеет то же распределение, что и нецентральная х' (/? а)?
/ + 2а , / + а2
если с = --—— и /' = - , о .
/ + а / + 2а
Нецентральное х2~РаспРеДеление применяется при планировании эксперимента
для проверки гипотез, когда используются статистики, основанные на случайных
величинах х2-
Задача 35. Вычислить 95%-ю квантиль случайной величины^ имеющей нецентраль-
нецентральное х2 -распределение с / = 30 степенями свободы и параметром нецентральности
а= 10.
Из соотношения
/ + За [
/ + За
2/ л ч 2//^/\/ +
апедует Х (/,а) = х (/ )уТ^ - jj^, или
'00,10) = /(Л ¦ ^^ - ^^ = 1,2х2(Л - 1,6667
v ' ; л u ; 30 + 20 30 + 30 v '
( f -4- *}п\^ ^П^
= 34,722.
(/ + ЗаJ 602
Найдем теперь верхнюю 95%-ю квантиль обычного х2~РаспРеДеления с / — 34,722 сте-
степенями свободы. Воспользуемся аппроксимацией 10 (Хоглина) из раздела 1.1.8:
Хр = \ 1,06807у? + 2,13161 [- lg(l - р)] 2 - 0,04589^/ • [- lg(l - р)] 2 - 1,37266 \ =
= < 1,06807^/34,722+ 2,13161-1,140627-0,04589^34,722-1,140627-1,37266^ =49,6168.
1.1.25. Нецентральное распределение Фишера
(нецентральное .F-распределенме)
Описание, применение. Если xi —случайная величина, имеющая нецен™
тральное распределение хи-квадрат с Д степенями свободы и параметром нецен-
нецентральности а, а х! —независимая от нее случайная величина, подчиняющаяся рас™
fry "V-,
пределению хи-квадрат с /2 степенями свободы, то случайная величина F* = j-
/1X2
имеет нецентральное ^-распределение.
82 Распределения вероятностей случайных величин [Гл. 1
Для проведения расчетов, связанных с нецентральным ^-распределением, могут
быть использованы графики, приведенные в [29, 100]. Нецентральное .F-распреде-
ление используется при планировании эксперимента и оценки мощности критериев
проверки гипотез, основанных на применении ^-распределения.
Табулирование нецентрального ^-распределения затруднено из-за большого ко-
количества независимых переменных (Д, /2, а), поэтому разработаны его аппроксима-
аппроксимации обычным (центральным) .F-распределением [101, 102]. Наиболее проста и точ-
F* + с
на аппроксимация М. Тику [101], в соответствии с которой величина F = —-—
имеет центральное ^-распределение с параметром Ъ и /2 степенями свободы, где
Ь 1 Н „ Н2
г^2К^ ^^К3'
= (/i+«J + (/2^2)(/! + 2a);
а)(/2^2) + (/1+За)(/2^2J.
В [97] предложена упрощенная формула для нецентрального ^-распределения.
Случайная величина F^ j2(«), имеющая нецентральное F-распределение со степе-
степенями свободы /i и /2 и параметром нецентральности а, распределена как величина
1 + т~ j-^X/i ?/2)? где /* = -Ц — и F{у 1,1/2)—обычная ^-величина с \/\ и щ
/1 / Ji + 2а
степенями свободы.
Более точные аппроксимации можно найти в [115].
Задача 36. Вычислить верхнюю 10%-ю точку нецентрального F1'-распределения с па-
параметрами /i = 10, /2 = 12 и а = 2.
Используем аппроксимацию Тику. Имеем
Н = 2 • A0 + 2K + 3 • A0 + 2) • A0 + 4) • A2 - 2) + A0 + 6) • A2 - 2J = 10096;
2
К = A0 + 2J + A2 - 2) • A0 + 4) = 284; Е = =- = 4,4498325;
284
h = ^^ I г™* = 1,212314;
10 2-10,72558 + 12-2 284 '
Ъ = ^—^ . [ /4-4498325 - 1 ) = 10,72558; с = ^^ • ( 1,212314 - ^^ ) = 0,0147768.
1 I V 0,4498325 / ' ' 12-2 \ ' 10 ' '
F* + с
Исходя из того, что случайная величина F = имеет центральное jF-распределение,
находим искомую величину, где F — обычная F-величина с Ь = 10,725933 и /2 = 12 сте-
степенями свободы. Для ее вычисления воспользуемся аппроксимацией 9 из раздела 1.1.10.
Для р = 0,9 (верхняя 10%-я точка; не путать h и Ь в этих обозначениях с обозначениями,
ранее применяемыми) имеем
о = 1,1131; 6 = 0,77; с = 0,527;
h=2HK = 2-10,72558.12 = = 12-10,72558 = . 3
fi + /2 10,72558 + 12 ' ' Б 10,72558 ¦ 12
Тогда
lgF0,9A0,72558; 12) = 1,1131 • A1,32705612 - 0,77) 2 - 0,527 • 9,901791 • 10^3 = 0,3373623
и Fo,9@,72558; 12) = 2,1745; F0*9 = 1,2123267 • 2,1745 - 0,014792021 = 2,621412.
1.1] Непрерывные распределения 83
A0 + 2J
Используем теперь второе приближение. Находим fl = = 10,285714 и вы-
вычисляем /о,э(Ю, 285714; 12) по аналогии (а = 1,1131; Ь = 0,77; с = 0,527)
2-10,285714.12 = 12 - 10,285714 =
10,285714+12 ' ' & 10,285714-12
lg10 Fo,9A0,285714; 12) = 1,1131 • A1,0769229 - 0,77) 2 - 0,527 • 0,01388889 = 0,339393;
Fo,9A0,285714; 12) = 2,184707 и F0*9A0; 12; 2) = ( Ц 1 • 2,184707 = 2,621648.
Видно, что погрешность аппроксимации вторым способом удовлетворительна, а сам
способ много проще в вычислительном отношении.
84 Распределения вероятностей случайных величин [Гл. 1
1.2. Дискретные распределения
1.2.1. Биномиальное распределение (распределение Бернулли)
Свойства, применение. Если событие осуществляется в единичном испытании
с некоторой постоянной вероятностью, то число появлений события в последо-
последовательности независимых испытаний подчинено распределению Бернулли. При
испытаниях невосстанавливаемых изделий на фиксированную наработку число
отказов подчиняется биномиальному распределению. Оно широко применяется при
выборочном приемном контроле качества продукции и статистическом предупреди-
предупредительном контроле технологических процессов в производстве.
Свойства
Распределение вероятностей
— вероятность появления события ровно х раз в серии из п испытаний, при условии,
что в единичном испытании вероятность его появления равна р.
Функция распределения
г=0
— вероятность появления событий ^ х раз в серии из п испытаний.
Среднее М(ж) = пр
Дисперсия D(x) = прA — р)
Коэффициент вариации v =
пр
Коэффициент асимметрии аз = A — 2р)[прA — р)] 2
Коэффициент эксцесса а^ = 3 \-
п прA — р)
Таблицы вероятностей биномиального распределения приведены в [16, 23, 29, 44].
Однако появление современных компактных и весьма мощных микрокалькулято-
микрокалькуляторов позволяют достаточно быстро производить расчеты без применения таблиц [30,
31, 33].
При п —>• оо, р —>¦ 0 и пр = const биномиальное распределение сводится к распре-
распределению Пуассона (см. раздел 1.2.2) с параметром А = пр (приближение приемлемо
при п>10ир<0,1). В силу взаимосвязи распределения Пуассона с распределе-
распределением хи-квадрат (см. раздел 1.1.8) функция биномиального распределения может
быть выражена через интеграл вероятностей % -распределения:
F(x; n,p) = Y^ ^r e~np = PX2Bnp, 2x + 2),
i=0
где РХ2 (г/, и) = 1 — Fx^{x) — интеграл вероятностей ^-распределения с v степенями
свободы, FX2 (ж) — функция распределения jq с у степенями свободы.
При п —^ оо биномиальное распределение стремится к нормальному со средним
/J, = пр и дисперсией а2 = прA — р). Сходимость удовлетворительна при
прA — р) > Б и 0,1 $С р ^ 0,9 или при прA — р) > 25 и любом р. Наилучшая схо-
сходимость обеспечивается при р = 0,5 и ухудшается при р < ир> -.
1.2] Дискретные распределения 85
Таким образом, в указанных диапазонах имеет место
1
- пр + -
F(x;n,p) = Ф
л/прA - р) 1
где Ф(...) —функция стандартного нормального распределения.
Биномиальное распределение может быть выражено через функцию бета™рас™
преде ления (см. раздел 1.1.7)
F(x;n,p) = 1 — /р(ж1,п — х) = Ii-P(n - х,х + 1),
где 1р(а,Ъ)—неполная бета-функция, и через функцию F-раепределения (см. раз™
дел 1.1.10)
F(x;n,p) = с\^^^;2(п - х),2(х + 1I ,
I fh Ju tj I
где G(y; fi, /2) — функция ^распределения относительно переменной у с Д и /2
степенями свободы.
Приведенные соотношения позволяют использовать таблицы и аппроксимации
бета™ и ^распределений для расчетов при биномиальном распределении.
Пуассоновские и нормальные приближения, рассмотренные выше, относительно
грубы. Поэтому был предложен ряд точных приближений, например, в [104]:
где при у = у* = — погрешность ^ —~ при р < 0,2 и п ^ 300 [17], а при
2 — р п
y = y**=y*{l + [x(x + 2) + xy*-2y*]2l6Bn-x2)~1]y1 погрешность ^\ (при
р ^ 0,12 и п ^ 300 [17]).
Моленаром [55] предложены весьма точные аппроксимации биномиального рас-
распределения нормальным:
— для „хвостов" распределения @,005 ^ р ^ 0,05 и 0,93 ^ р ^ 0,995)
F(x;n,p) =
— для распределения между „хвостами"
ж + 2,5)A ^р)з - [Dп - 4ж -
при этом должны выполняться приблизительно следующие соотношения между
пир:
п = 3; 0,25 ^р^ 0,75;
п = 30; 0,40 ^ р ^ 0,60;
п = 300; 0,46 ^ р ^ 0,54.
Для более точной аппроксимации используется формула [105]
F(x; п,р) = ф[[А(х, А)] а - [А{п - х - 1, -А)] 2 } ,
\\ 15 + 12Л + 5Л2 , C + 6Л + 7Л2)Bж + 1+пЛ)
A)+А = 1-
где
Л2 C + 6Л + 7Л2
_
86 Распределения вероятностей случайных величин [Гл. 1
При табулировании биномиального распределения возникают трудности из™за
того, что его параметр р одновременно входит в выражения для среднего и для
дисперсии. Специальные преобразования исходной биномиально распределенной
случайной величины позволяют устранить эти трудности. В [106] показано, что
случайная величина z = 2 aresin у/х/п, где х — биномиально распределенная слу-
случайная величина, имеет при п > 50 нормальное распределение с математическим
ожиданием /л = 2arcslnv/p и дисперсией а2 = 1/п. При умеренных п (п < 50) Ан™
скомбом [107] предложено уточненное преобразование
z* = aresin
\
аппроксимирующееся
2 1
иг = -.
X
n
3
+ 8
3'
+ 4
нормальным
удовлетворительно аппроксимирующееся нормальным распределением
/л = aresin
3
I 2 !
. 2"
4n
Характеристическим свойством биномиального распределения — дисперсия
меньше среднего — можно руководствоваться при выборе между ним и отрица-
отрицательно-биномиальным (см. раздел 1.2.3), для которого дисперсия больше среднего,
и распределением Пуассона (см. раздел 1.2.2), у которого дисперсия равна среднему.
Задача 37. Вероятность появления дефектного изделия в производстве равна ОД.
Вычислить вероятность появления в партии из 60 изделий не более 10 дефектных.
Имеем р = ОД; п = 60; ж = 10 и пр = 6. Необходимо вычислить величину
FA0] 0,1; 60). Непосредственный расчет (точное решение) дает
ю
; ОД; 60) = ]Г Сг60 • 0,1* • 0,960~* = Cq0 • 0,960 + С\о • ОД • 0,959 + Cq0 • ОД2 • 0,958 =
г=0
= О630 • ОД3 • 0,957 + О640 • ОД4 • 0,956 + О650 • ОД5 • 0,955 + О660 • ОД6 • 0,954 + О670 • ОД7 • 0,953 +
+ Оео • ОД8 • 0,952 + Оео ' ОД9 • 0,951 + С&? • ОД10 • 0,950 = 0,96570865.
Аппроксимация с помощью распределения Пуассона:
ю i
FA0; 60; ОД) = ]Г — • е = 2,478752 • 10 х
г=0 %
( 36 216 1296 7776 46656 279936 1679616 10077696 60466176"
X 1 + 6 Ч 1 1 1 1 1 1 1 1
\ 2 6 24 120 720 5040 40320 362880 3628800
= 0,9573799 (E = 0,87%).
Если воспользоваться соотношением между распределением Пуассона и х2™распреде™
10 gi
лением ^ — е^6 = Р%2 B • 6; 20 + 2) = РХ2 A2,22) и применить аппроксимацию 3 (см. раз™
г=0 1'
дел 1.1.8), то получим из соотношения Xp = /(l \-ир\ — 1 , имея в виду, что
\ 9/ V 9/ /
2 ( 2 Г^\3
Хз :=: 12 и / = 22, уравнение 12 = 221 1 Ь ир\ 1 , решением которого явля-
является величина нормальной квантили ир = 1,719747.
1.2]
Дискретные распределения
87
Используем аппроксимацию 8 из раздела 1.1.1:
2,0637
= 0,957302.
Полученное значение вероятности РХ2 A2,22) = 1 — F(x2 < 12) « 0,957302 очень близко
к точной величине 0,95778.
Используем теперь нормальное приближение
F(x;n,p) = Ф
- пр + -
= Ф
10-6 + 0,5
л/6 • 0,9
= ФA,93649).
С помощью аппроксимации 18 из раздела 1.1.1 получаем
ФA,93649) = 1-- ехр(-0,717 • 1,93649 - 0,416 • 1,936492) = 0,97378 (S = 0,
С помощью приближения бета-распределением имеем
F(x;n,p) = в(^ • ^; 100,22^ = G(l,98; 100,22).
Применим аппроксимацию 4 (см. раздел 1.1.10):
I / 2
1,983 • 1 -
9-22
-(г-
9- 100 )
= 1,820406.
v9-100 9-22
Далее, используя аппроксимацию 8 из раздела 1.1.1, получаем:
FK) = ^A,820406) = 1 - 0,852еХр [- {^Щ^)^
что очень близко к точному значению 0,96579.
Рассмотрим нормализующие преобразования
= 0,96567,
z = 2 aresin ( — ) = 0,84106867; и = 2 arcsin ^ОД = 0,643501;
а = I- = 0,1290994; ир = "^^867-0,643501 =
60 р 0,1290994
Далее
F(up) = 1 - 0,852 exp -
1,5303518 + 1,5774
2,0637
= 0,9371266.
Для уточненного преобразования имеем
= 0,426028; // = arcsin
z = arcsin
60+ -
0,1-
1 +
4
3
^¦60
3
¦60
/4-60 + 2
^0,0642824; ир =
0,0642824
Окончательно
F(l,49551) = 1-0,852 exp
1,49551 + 1,5774
2,0637
44-
= 0,3298829;
= 1,49551.
= 0,93271.
'8 Распределения вероятностей случайных величин [Гл. 1
Задача 38. Имеем р = 0,5 и п = Ъ. Вычислить FC; 0, 5, 5), используя аппроксимацию
Моленара.
Имеем Ах + 2,5 = 1545; An - Ах - 1 = 20 - 12 - 1 = 7 и
FC; О55, 5) = Ф{^14,5-О55- у/7 • 0,5} = Ф@,8217537) = 0,793382.
Для сравнения найдем точное значение:
з
FC; 0,5, 5) = J2 С5 * °^ * О?5^ = °^5 • A + 5 + 10 + 10) = 0,8125 (S = 2,3%).
г=0
1.2.2. Распределение Пуассона
Описание, применение. Если вероятность появления независимых событий
в малом промежутке времени At пропорциональна At, то число их появлений имеет
распределение Пуассона. Распределение Пуассона широко применяется в теории
массового обслуживания. Часто оно используется для аппроксимации биномиаль-
биномиального, так как легче табулируется (имеет только один параметр). Распределению
Пуассона подчинено число отказов невосстанавливаемых электронных приборов
в течение периода приработки. Если наработка на отказ изделия является случай-
случайной величиной, распределенной экспоненциально с параметром А, то число отказов
в интервале времени t подчиняется распределению Пуассона с параметром tX.
Свойства
Распределение вероятностей
/(ж; А) = —¦ , х = 0,1, 2, ...; А > 0;
/(ж; A) = max при х = [А] (наибольшее целое число ^ А)
Функция распределения F(x; X) = 2_^ .f
г=0
Среднее М(ж) = А
Дисперсия D(x) = A
Коэффициент вариации v = A~2
1
Коэффициент асимметрии аз = А~ 2
Коэффициент эксцесса а^ = 3 + -т-
А
При А > 9 распределение Пуассона можно аппроксимировать нормальным
/ 1
I X ~т~ — /\ (
с ц = А и а = уА, т.е. Ф I ™= = F(x] А) A/2 — поправка Йэтса на непре-
1 v A
рывность).
Распределение Пуассона является предельной формой биномиального распре-
распределения (см. раздел 1.2.1), т.е.
lim ^2 ^пРг(^ — Р)П^г = ~J e^X-
пр—*\ г=0
1.2]
Дискретные распределения
89
Функция распределения Пуассона может быть выражена через функцию %2™
пределения
г=0
где -РBА, 2х + 2)—функция ^-распределения относительно переменной 2Л
с/ = 2(ж + 1) степенями свободы.
По аналогии с биномиальным распределением Анскомб [107] показал, что
случайная величина 2л/х при Л —>> оо распределена асимптотически нормально
с /х = 2уЛ и сг = 1.
С учетом поправки на непрерывность можно для прикидочных расчетов исполь-
использовать формулы
Аге
ж + 1 — 2А) —на „хвостах" распределения;
+ 0,75 — 2А) —между „хвостами" распределения.
Высокой точностью обладает аппроксимация
г=0
9
36
где 7 = [x =
(здесь Ф(...)—функция стандартного нормального распределения, обозначенная
в разделе 1.1.1 как F(z)).
Учитывая связь ме^ду распределением Пуассона и х2™распределением, для его
аппроксимации можно использовать аппроксимации для распределения хи™квадрат.
Сумма случайных величин, распределенных по закону Пуассона, также будет
иметь распределение Пуассона с параметром, равным сумме параметров слагаемых.
Существуют обширные таблицы распределения Пуассона, например, в [23-25, 57].
Характеристической особенностью распределения Пуассона является равенство
среднего и дисперсии.
Задача 39. Случайная величина имеет распределение Пуассона с параметром А = 5.
Вычислить вероятность того^ что случайная величина не превысит значение 3.
Прямой расчет по формуле распределения:
FC; 5) =
A + 5 + 12,5 + 20,833) = 0,265023669.
Грубая нормальная аппроксимация (см. аппроксимацию для Ф(ж) в разделе 1.1.1):
3+5
= 1^0,852 ехр| -
Нормальная аппроксимация между „хвостами":
FC; 5) = Ф{2^3 + 0,75 - 2^5} = Ф(-0,5991526) =
= 0,26367.
= 1 - 0,852 ехр< -
1
2,0637
90 Распределения вероятностей случайных величин [Гл. 1
Уточненная нормальная аппроксимация:
X±i J ( Х^ ]
7 = — = 0,67222; х + ^— = 1,8759359; Л + = 2,19008;
5 \ 9 / \ 36 /
Далее
FC; 5) = ФB • 1,8759359 - 2 • 2,19008) = Ф(^0,6282882) =
= 1 - 0,852еХр|-(-°'628228086з7+1'5774J'34} = °'27573 <* = 3'8%)-
Погрешность аппроксимации достаточно высока, даже с учетом примененной простой
аппроксимации для стандартного нормального распределения.
1.2.3. Отрицательное биномиальное распределение
Описание, применение. Если р — вероятность появления события в единич-
единичном испытании, то случайное число х неудачных испытаний до появления га-го
успеха подчиняется отрицательному биномиальному распределению. Распределе-
Распределение используется при планировании запуска изделий в производство для получения
требуемого количества годных изделий при известном проценте выхода годных, при
планировании объема испытаний до получения заданного числа отказов.
Свойства
Распределение вероятностей
f(x;m,P) = C™+m_lPm(l-p)x, m = 0,1,2,...; х = 0,1,2,...
т
-рУ
Функция распределения
Среднее
Дисперсия
Коэффициент
Коэффициент
Коэффициент
вариации
асимметрии
эксцесса
F(x;
М(х
Т>(х)
V
а3 =
т,р) =
) —
тA
г
1
\/тA-
г=1
1 -р)
Р
-Р)
2
7
B-p)[m(l-
з+ 6
т
4- Р
mil
р)]-5
2
-р)
В отличие от биномиального (см. раздел 1.2.1), при отрицательном биномиаль-
биномиальном распределении множество возможных значений случайной величины не ограни-
ограничено сверху. Функция распределения отрицательного биномиального распределе™
ния может быть вычислена с помощью таблиц для биномиального распределе-
распределения [108].
Известны аппроксимации отрицательного биномиального распределения поло-
положительным биномиальным [109] и гамма-распределением [110]. Характеристиче-
Характеристической особенностью отрицательного биномиального распределения является то, что
его дисперсия больше среднего (у обычного биномиального — наоборот).
1.2] Дискретные распределения 91
Задача 40. Вероятность получения дефектного изделия равна 0,1. Вычислить веро-
вероятность того, что будут произведены 50 годных изделий до появления 10-го дефектного
изделия (т = 10; р = 0,1; х = 50). Вычислить вероятность того, что до появления 2-го
дефектного изделия будут произведены не менее 5 годных изделий.
Вычисляем /(ж; т,р) = С50+10-1 • ОД10 • 0,950 = Cl9 • ОД10 • 0,950 = 0,03238 ^такова
вероятность того, что потребуется произвести 50 изделий до появления 10-го дефектного
изделия.
Вероятность того, что до появления 2-го дефектного изделия будет произведено не
более 5 годных изделий, равна
F(x;m,p) = E^2+»-i • ОД2 • 0,9* =
г=1
= ОД2 • {Cl • 0,9 + Cl • 0,92 + ... + <?!• 0,94 + Cq • 0,95) = 0,13969.
1.2.4. Распределение Паскаля
Описание, применение. Если в схеме, рассмотренной выше (см. раздел 1.2.3)
для отрицательного биномиального распределения, в качестве случайной величины
принять число удачных испытаний до появления т-го успеха (включая и этот
успех), то она будет подчинена распределению Паскаля.
Свойства
Распределение вероятностей
/(ж; m,p) = C™-fpm(l - p)*~m, х = т, m + 1, ...
— это вероятность того,что в х испытаниях наблюдаемое событие произойдет рав-
равно т раз, если вероятность появления его в каждом испытании равна р.
Функция распределения
— это вероятность появления т успехов не более, чем за х испытаний.
Среднее М(ж) = —
Дисперсия U(x) =
Р
1
Коэффициент вариации v =
Задача 41. Если вероятность отказа изделия в одном испытании равна ОД, то какова
вероятность того, что понадобятся 50 испытаний до появления 5 отказов (р = ОД;
т = 5; х = 50)? Вычислить вероятность того, что не более, чем за 8 испытаний,
будут зафиксированы 2 отказа (ж = 50; т = 2; р = ОД).
Вероятность того, что понадобятся 50 испытаний до появления 5 отказов:
/(ж; 5; ОД) = С% • ОД5 • 0,945 = 211876 • 10~5 • 8,72796 • 10~3 = 0,01849.
Вероятность того, что не более, чем за 8 испытаний, будут зафиксированы 2 отказа,
равна
8 8
F(x; т,р) = J2 Ci-iP^1 ~ рУ^2 = J2 С^ ' °'9^ ' °^2 = 0,011224.
г=2 г=2
92 Распределения вероятностей случайных величин [Гл. 1
1.2.5. Геометрическое распределение (распределение Фарри)
Описание, применение. Если р— вероятность появления события в одном
испытании, то число испытаний до появления события подчинено геометрическому
распределению, с помощью которого можно определить объем выборки, необходи-
необходимой для получения одного отказа по заданной вероятности отказа одного прибора.
Свойства
Распределение вероятностей f(x;p) = рA — р)х^г, ж = 1, 2, ...; O^p^l
ж
Функция распределения F(x;p) = ^рA — р)г~г = 1 — A — р)х
Среднее
Дисперсия
Коэффициент вариации
Коэффициент асимметрии
Коэффициент эксцесса щ = ~ ¦
1 -р
Очевидно, что геометрическое распределение следует из распределения Паскаля
(см. раздел 1.2.4) при т = 1. При р —> 0 геометрическое распределение переходит
в экспоненциальное (см. раздел 1.1.4).
Задача 42. Вероятность безотказной работы изделия равна 0,95. Вычислить вероят-
вероятность того, что для получения одного отказа необходимо испытать выборку изделий
из 10 приборов (х = 10; р = 0,05). Вычислить вероятность тогоу что для получения
первого отказа понадобится испытать не более 5 приборов.
Вероятность того, что для получения одного отказа необходимо испытать 10 прибо-
приборов, равна f(x; 0,05) = 0,05 • 0,959 = 0,031.
Вероятность того, что для получения первого отказа понадобится испытать не более
5 приборов, равна F(x; 0,05) = 1 - A - 0,05)9 = 0,3697.
1.2.6. Гипергеометрическое распределение
Описание, применение. Если в партии из N изделий находится D дефектных,
то вероятноств появления х дефектных изделий в выборке объема п изделий
без возвращения будет подчинена гипергеометрическому распределению. Гипергео-
Гипергеометрическое распределение широко применяется в задачах выборочного контроля
качества продукции.
Свойства
Распределение вероятностей /(ж;7?, n,D) =
X i
Функция распределения F(x; JV, n, D) = Л, —
Среднее М(ж) = ^г^
тт r^f \ nD (л D^ (N ^п
Дисперсия Б(ж) = — I 1 - —
1.2] Дискретные распределения 93
Коэффициент вариации v =
nD N ~~
1
I / N — 1 \ 2 7V — 2п
Коэффициент асимметрии а3 = GV — 2D)[nD(N — D)]~2 I vr ) —г;—тг
Коэффициент эксцесса
f 7V(TV + 1) - 6N(N - n) 3n(TV-n)(TV + 6) \
~n) \ D(N~D) + Jp J
Таблицы гипергеометрического распределения приведены в [23-25]. Наиболее
полные таблицы опубликованы в [111, 112].
При расчетах полезны следующие рекуррентные формулы
l;N,D,n) = f(x;N,D,n)[ п ~
f(x;N,D,n) = f(x;N,n,D) = f(D - x;N,D,N - п) = f(n- x;N,N - D,n) =
= /(TV - n - D + x; TV, TV - D, TV - n);
F(x; TV, Д n) = F(x; TV, n, D) = 1 - F(n - x - 1; TV, TV - Д n) =
= 1 - F(D - я - 1; TV, Д TV - n) = F(TV - n - D + x; TV, TV - D, TV - n).
Поскольку таблицы гипергеометрического распределения громоздки, а при боль-
больших значениях параметров TV, n и D они отсутствуют, применяются различные
аппроксимации этого распределения.
п Г)
При ^-чоои D(z) > 9 [52]
F(x;N,n,D) =
где Ф(...) —функция стандартного нормального распределения.
При п < ОДЛГ и D < 0,17V [51] гипергеометрическое распределение аппрокси™
nD
мируется распределением Пуассона (см. раздел 1.2.2) с параметром Л = ——. При
п < 0,17V, TV —^ оо и фиксированном — гипергеометрическое распределение аппрок-
аппроксимируется биномиальным (см. раздел 1.2.1) с параметрами п ж р = —. Указанные
аппроксимации действуют в различных диапазонах изменения параметров и не
заменяют друг друга.
В [25] приведена аппроксимация с помощью бета-распределения (см. раздел 1.1.7),
удовлетворительная при всех 7V ^ 25 (независимо от D и 7V),
F{x;N,n,D) = Ii-X*(nr - ж + с,ж - с+ 1),
где /1_ж(а, Ь)—функция бета-распределения;
, _ N(n + D - 1) - 2nD _ _ nD(D - Щп - 1)
п =
N(N -2) ' (TV ¦
(TV - 2J nD(N - n)(N - D)
N - 1 [(TV - D)(N -n) + nD^ N][N{n + D - 1) - 2тШ]#
94
Распределения вероятностей случайных величин
[Гл. 1
2п — х
Укажем более точные приближения:
— биномиальным распределением с параметрами D, p = 9rJ'" П^ или (для
более точной аппроксимации)
р =
2п - х
BD-x)Bn-x)
— распределением Пуассона с параметром А = , =™ ^
2BN-D-n
при
D n
- нормальным распределением
2
Ф
Ф<
/N-1
- D
при 0,005 ^ р ^ 0,05 и 0,95 ^ р ^ 0,995;
"ж4 rj4
при 0,05 ^ р ^ 0,95.
Сравнительная точность различных аппроксимаций гипергеометрического рас™
пределения изучена в [113].
Задача 43. Дано: N = 20, ж = 3, D = 10 и п = 10. Вычислить значение F(x]N,n,D).
Точное значение:
FC; 20,10,10) = V Cl°C11n° = —-—A + 100 + 2025 + 14400) = 0,0894477.
Биномиальное приближение:
FC; 20,10,10) = J2 °
Ошибка велика, так как при р = 0,5 биномиальная аппроксимация наименее удачна.
Более точное биномиальное приближение:
FC;20,10,10) =
A^/
20-3
40-10 +
1-
20-3
40-10 + 1
= 0,10387.
Ошибка еще велика, несмотря на уточнение.
Еще более точное приближение:
Р =
2-10-3
2-20-10 +
/1 10
2 ¦ 10- ЗН 10- —
V 2 20
3- B-20- 10 + IJ
= 0,53798117;
FC; 20,10,10) = J2 Clo ' 0,53798117* • 0,46201882710^г = 0,1166096.
г=0
Точность недостаточна, так как диапазон аппроксимации не подходит для биномиального
распределения.
1.2] Дискретные распределения 95
Пуассоновское приближение:
10-10
Л = = 5 и
20
FC; 20,10,10) = Ve-- = 6,737947 • 10^3 -|1 + 5+^ + — ) = 0,265025.
Ы il V 2 6 /
Приближение очень грубо.
Так как — = — > 0,1, применим уточненную аппроксимацию:
10-10 1 /10- 10 Л / 1Л 10•10-10
Л + Л3J010+
FC; 20,10,10) = ]Г е^7 • ^ = е^7 Yl + 7 + у + — \ = 0,0817654 (S = 8,6%).
г=0 г- V /
Это уже достаточно близко к точному значению.
Нормальное приближение:
FC; 20,10,10) = Ф 2 = Ф(-1,307) =
= 1 - 0,852 • ехр [- ( -М07-1,5774\ 2
Р \ 2,0637 /
Более точное нормальное приблилсение:
FC;20,10,10) = Ф< -^= .
10 - 3 - -Д 10 - 3 - -J >= Ф(-1,3416) = 0,090 (S = 1,1%).
/ V / J J
Бета-прибл ижение:
, _ 20A0 + 10^1)^2-10-10 _ _ 10 • 10 • 9 • 9
Х ~ 20^15 " ' ; С " 19.A0.10 + 100-20) " ' ;
/ = 18^ 10 • 10 • B0 - 10) ¦ B0 - 10) = 2бз>
19 * [B0 - 10) • B0 - 10) = 10 • 10 - 20] • [20 ¦ A0 + 10 - 1) - 2 • 10 ¦ 10] ' '
FC; 20,10,10) = /о,5E,263 - 3 + 2,368; 3 - 2,368 + 1) = /0,5D,631; 1,632) = 0,0938
ГЛАВА 2
ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ ВЕРОЯТНОСТЕЙ
Общие положения. В первой главе, посвященной анализу различных распре™
делений вероятностей случайных величин, мы рассмотрели множество примеров
применения математической статистики к решению практических задач. Однако
в реальной жизни практически никогда не бывает так, чтобы исследователь распо-
располагал точным знанием закона распределения вероятностей наблюдаемых случай™
ных величин. Ему в общем случае неизвестны как сам закон распределения вероят-
вероятностей, так и его параметры. В распоряжении исследователя имеется лишь совокуп™
ность результатов наблюдений, и, основываясь только на них, он должен сделать
выводы о параметрах распределения, если вид закона распределения вероятностей
ему известен. Если же нет, то и сам закон распределения вероятностей ему придется
выбирать на основании выборочных результатов наблюдений. В настоящей главе
мы рассмотрим методы оценки параметров различных, заранее определенных по
форме, распределений вероятностей случайных величин.
Различают два вида оценок параметров — точечные и интервальные. Предпо-
Предположим, оценке подлежит параметр j некоторого распределения вероятностей по
выборочным данным #i,#2? • • • > хп некоторой случайной величины X. Точечной
оценкой параметра 7 по выборочным данным является некоторый функционал
jn = <??(#!, #2, • • •; %п)ч позволяющий получить наилучшую оценку в принятых кри-
критериях.
В качестве критериев, характеризующих пригодность оценки параметра распре-
распределения, используются такие ее свойства, как состоятельность, несмещенность,
эффективность и достаточность.
Оценка jn параметра j является:
— состоятельной, если при п -^ оо 7п ~^ 7?
— несмещенной, если М (jn) = 7 (т- е- математическое ожидание оценки совпа™
дает с ее истинным значением);
— достаточной, если оценка jn извлекает максимальную информацию из выборки;
— эффективной, если D (jn) = min (т.е. когда дисперсия оценки минимальна).
Под интервальной оценкой параметра 7 понимается интервал, границы кото-
которого 7п (°0 и 7п (а) являются функционалами от выборочных значений случайной
величины, и который с заданной вероятностью а содержит оцениваемый параметр:
Р{7^(«) < 7 < 1п(а)} = а- Вероятность а называется доверительной вероятно-
вероятностью, а оценки 7п(а) и 7п(а) — соответственно нижней и верхней доверительными
границами. Интервал [j^(a), j^(a)] называется доверительным интервалом. Если
длина доверительного интервала 1(а) = 7п(°0 ~~ 7п(°0 = const, то для состоятель-
состоятельных и несмещенных оценок а —>• 1 при п —>• оо. При фиксированном объеме выборки
п, а будет тем больше, чем больше I.
Различают два вида интервальных оценок: одно- и двусторонние. При двусто-
двусторонней оценке задаются обе границы доверительного интервала, так что
= а и Л7<7 а =«; г 7 > 1"[а = а'
Оценка параметров распределений вероятностей 97
1 — а
где а1' + а/; = 1 —а. Если а; = а" = —-—, то двусторонний доверительный интервал
называется симметричным. Для него справедливы соотношения
При односторонних доверительных интервалах границы интервалов задаются
так, чтобы
7п(«)} = « или
Величина A — а) —дополнение доверительной вероятности до единицы — назы-
называется уровнем значимости. Этим термином обозначается вероятность появления
события, которую исследователь связывает с неслучайным (значимым) событием.
Очевидно, что двусторонний интервал для симметричных распределений аналоги™
чен одностороннему при удвоенном уровне значимости.
Перед изложением конкретных методов оценки приведем ряд практических
соображений. Наиболее существенной характеристикой оценки параметра распре-
распределения является ее эффективность. Именно эта характеристика обычно исполь-
используется для сравнения методов оценки параметров распределения между собой. Как
правило, эффективность оценки сравнивается с эффективностью оценки параметра
распределения методом максимального правдоподобия (т. е. с наиболее эффектив™
ной оценкой). Легко видеть, что применение менее эффективных оценок (требу-
(требующих, как правило, меньшего объема вычислений) может быть скомпенсировано
соответствующим увеличением объема выборки.
И, наконец, поясним практический смысл процедуры оценки параметров распре-
распределения вероятностей. Так как само распределение наблюдаемых случайных вели™
чин является для исследователя той совокупностью данных, которой он располагает
относительно наблюдаемого процесса, то и параметры распределения позволяют
судить об основных чертах этого процесса. Например, когда мы спрашиваем, какова
долговечность прибора, мы, по сути, ставим задачу оценки среднего значения (или
математического ожидания) наблюдаемого распределения показателей долговеч-
долговечности. Если нас интересует, насколько стабилен наблюдаемый технологический
процесс, то ответ на этот вопрос требует оценки разброса (рассеяния) наблюдаемых
случайных величин, характеризующих качество технологического процесса.
4 А. И. Кобзарь
98 Оценка параметров распределений вероятностей [Гл. 2
2.1. Оценжа параметров нормального распределения
Напомним, что плотность вероятностей нормально распределенной случайной
величины описывается формулой
2az
где /j, и а — параметры распределения, совпадающие со средним значением и сред-
неквадратическим отклонением.
2.1.1. Оценка среднего значения (/х)
2.1.1.1. Точечные оценки
2.1.1.1.1. Оценка максимального правдоподобия
Вычисляется по формуле ж=—^а^. Оценка — состоятельная, несмещенная,
п *=i
эффективная, достаточная и распределена как случайная величина также нормаль™
но со средним М (ж) = /л и дисперсией D (х) = —. Оценка максимального правдо-
правдоподобия для случая выборок малого объема (п ^ 10) может быть модифицирована
в форме [116]
п _ п
X / J п ~ 5 гДе di / j \xj ~ хг) •
1 \—"^ ¦ 1
Эта форма позволяет несколько стабилизировать оценку в области центра груп™
пирования данных.
2.1.1.1.2. Оценка с помощью медианы
В качестве оценки /л может быть использована выборочная медиана
" 1 / \ п
если — —целое;
-целое,
где хщ — к-я порядковая статистика, равная k-му по величине значению выборочно™
го ряда х\ ^ Х2 ^ ... ^ жп, ранжированного по возрастанию (будьте внимательны
к тексту! — иногда квадратные скобки опускаются и х^ обозначает к~ю порядковую
статистику).
Эффективность этой оценки при п —Ь- оо равна 2/тг = 0,637, т. е. для того, чтобы
эта оценка не уступала оценке максимального правдоподобия (см. раздел 2.1.1.1.1),
необходим в тг/2 ~ 1,6 раза больший объем выборки.
2.1.1.1.3. Оценки с помощью порядковых статистик
Поясним сначала смысл понятия „порядковая статистика". Как только лю-
любому члену наблюдаемого выборочного ряда ставится в соответствие его номер
в упорядоченном по возрастанию ряду выборочных значений — этот член выборки
становится порядковой статистикой. Для полного координирования порядковой
статистики необходимо указать объем выборки и номер статистики. Впредь для
того, чтобы отличить просто член выборки х от порядковой статистики, будем при-
2.1] Оценка параметров нормального распределения 99
менять для ее обозначения символ Ж[^п] —т. е. г-я порядковая статистика в выборке
объема п.
Теперь рассмотрим оценки среднего значения с помощью порядковых статистик.
Предельным случаем такой оценки является оценка максимального правдоподо-
правдоподобия (см. раздел 2.1.1.1.1), когда в оценке участвуют все члены выборки. Вторым
предельным случаем является оценка с помощью медианы (см. раздел 2.1.1.1.2),
т. е. с помощью только одной порядковой статистики. Естественно, что в этот
диапазон эффективности возможных оценок (от 1 до 0,637) будут укладываться
все остальные возможные оценки, использующие порядковые статистики.
Эти оценки будут уступать по эффективности оценке максимального правдо™
подобия. Однако в большинстве случаев соответствующим увеличением объема
выборки, а также подбором порядковых статистик, используемых для оценки, и их
весового вклада в общую оценку можно обеспечить достаточно высокую эффек-
эффективность таких оценок. При этом сохраняются основные достоинства оценок по
порядковым статистикам — простота, легкость вычислений, возможность получения
оценок при отсутствии некоторых выборочных значений и, что особенно важно,
устойчивость таких оценок к отклонению от нормальности распределения, от засо-
засорения выборки аномальными наблюдениями.
Среди широко применяемых порядковых статистик напомним хщ, Ж[п] —экстре™
мальные значения; ш = хщ — хщ —выборочный размах; х — медиана; выборочные
квантили (ж[пд]_|_1—выборочная А-квантиль).
Предварительно рассмотрим способы вычисления математических ожиданий
порядковых статистик из стандартного нормального распределения.
.Ьсли р = , то р-квантиль стандартного нормального распределения бу-
п + 0,250
дет аппроксимировать математическое ожидание г-й порядковой статистики в вы™
борке объема п из JV@,1), т.е. М(хщ) = и г~о,з75 . Поэтому необходимые аппрок-
п+0,250
симации могут быть получены из соответствующих аппроксимаций для квантилей
стандартного нормального распределения.
Приведем некоторые полезные аппроксимации, полученные из аппроксимаций
нормальных квантилей.
Из аппроксимации 5 раздела 1.1.1 [32]
1
2
1 — ехр — ^^
имеем
= {-2,177586 + 3,14159 In (n + 0,25) - l,570796[ln (n + 0,625 - г) + In (г - 0,375)]}
при ^-^ ^ г ^ 0,Э75в + 0,68175.
Погрешность аппроксимации не более 0,114.
Из аппроксимации 15 раздела 1.1.1 [39] получаем
из чего следует
М{хщ) = 4,91(п + 0,25H'14 Г(г - 0,375H'14 + (п - г + 0,625H'14
100
Оценка параметров распределений вероятностей
[Гл. 2
Из аппроксимации 16 раздела 1.1.1 [36] имеем
0,4274
- 0,16 \ - 1,5774.
М(Х[г]) = 2,0637 ( In
- % + 0,625
Ошибка этой аппроксимации не более 0,0008 при г
И, наконец, из аппроксимации 19 раздела 1.1.1 [40]
ир = ^- \-Ь - \/Ь2 - Аас\ , где а = ^0,416; Ь = -0,717; с = - In Bр)
ACL L J
получаем
М(х[{]) = -0,86178 + 1,2019 2 + 1,664In
п - г + 0,625
Отметим, что во всех случаях при г <
п + 0,250
абсолютное значение
сохра-
няется (изменяется только знак).
Всегда
М{хщ) = 0 при г =
л) > 0 при
(п — нечетное) и г = — (п — четное);
А
П + 1 / Пч щ ж/ ч _ . П -
г > —-— (или -); М(хщ) < 0 при г < —;
(или ^)-
2 v 2J -
Рассмотрим теперь разные оценки среднего нормального распределения с помо-
помощью порядковых статистик.
2.1.1.1.3.1. Простые оценки Диксона [117]
Диксон предложил две простые оценки:
— среднее из двух наилучших наблюдений
1
+ хи]);
— среднее из всех наблюдений, кроме двух крайних
В табл. 6 приведены рекомендуемые номера оптимальных статистик (г и j) для
га= 1AJ0.
Таблица 6
Оптимальные порядковые статистики Диксона [117]
п
г
Э
п
г
3
2
1
2
12
4
9
3
1
3
13
4
10
4
2
3
14
4
11
5
2
4
15
4
12
6
2
5
16
5
12
7
2
6
17
5
13
8
3
6
18
5
14
9
3
7
19
6
14
10
3
8
20
6
15
11
3
9
оо
0,27п
0,73п
Относительная эффективность первой оценки стремится к 0,81 при п —>¦ оо,
вторая практически не уступает оценке максимального правдоподобия (> 0,99).
2.1]
Оценка параметров нормального распределения
101
2.1.1.1.3.2. Оценка Огавы [118, 119]
Вычисляется по формуле
хо = ]Гж[пЛ.+1],
г=1
где т — число наблюдений (га < п), по которым проводится оценка /i; [n\i + 1] —
целое число, ближайшее справа к (п\ + 1) (определяет номера порядковых стати-
статистик, используемых для оценки); А^, Л^ —числовые коэффициенты, табулированные
в [119] (приведены в табл. 7).
Таблица 7
Значения коэффициентов оценки Огавы
для различного числа оптимально расположенных порядковых статистик
(Лг—верхняя строка; ki—нижняя строка)
т
2
3
4
5
6
7
8
9
10
1
0,270
0,500
0,163
0,297
0,107
0,197
0,074
0,133
0,055
0,099
0,040
0,071
0,031
0,049
0,024
0,044
0,020
0,036
2
0,730
0,500
0,500
0,407
0,351
0,308
0,255
0,233
0,195
0,181
0,147
0,140
0,115
0,111
0,092
0,091
0,076
0,075
3
0,837
0,297
0,649
0,308
0,500
0,269
0,395
0,220
0,308
0,186
0,247
0,155
0,202
0,130
0,167
0,109
4
0,893
0,197
0,745
0,233
0,605
0,220
0,500
0,203
0,412
0,178
0,343
0,155
0,288
0,133
5
0,926
0,133
0,805
0,181
0,692
0,186
0,588
0,178
0,500
0,163
0,427
0,147
6
0,945
0,099
0,853
0,140
0,753
0,155
0,657
0,155
0,573
0,147
7
0,960
0,071
0,885
0,111
0,798
0,130
0,712
0,133
8
0,969
0,049
0,908
0,091
0,833
0,109
9
0,976
0,044
0,924
0,175
10
0,980
0,136
Оценка Огавы используется для нахождения /л по выборке большого объема
с помощью нескольких (га < п), оптимальным образом отобранных порядковых
статистик. При п ^ 5 эффективность оценки не уступает оценке х.
2.1.1.1.3.3. Оценка Пирсона-Тьюки
В [120] предложены упрощенные оценки, основанные на расстоянии между
процентными точками частотных кривых распределений. Отметим, что р™точка
кривой равна порядковой статистике хуп\/\, где Л^ = р.
Для /I Пирсоном и Тьюки [120], в частности, предложена оценка
А = ff[0,5n] + 0Д85Д, где А = x[0j95n] + ж[о,о5п] - 2ж[0}5п]-
2.1.1.1.3.4. Быстрые оценки Кенум [121]
Среднеквартильный размах
102
Оценка параметров распределений вероятностей
[Гл. 2
Эффективность оценки « 1,21/п, предельная эффективность равна 0,64. Метод
достаточно груб и может рекомендоваться как быстрый приближенный способ.
Быстрая оценка по трем квантилям
X = О,2ЖГЛ] + OfiXfn] + 0,2жП5п1 •
L i6 j L 2 J [T^J
Эффективность оценки « 83%, метод достаточно устойчив к отклонениям от нор™
мальности.
Быстрая оценка по пяти квантилям
X = -\X\ni +X\ni + 2х\пл + Хгзп] + ЖГ15п"
6 L L16 J L 4 J L 2 J [Т\ [Т^
Эффективность оценки « 0,93, метод нечувствителен к отклонениям от нормаль-
нормальности.
2.1.1.1.3.5. Оптимальные комплексные оценки,
использующие общий набор порядковых статистик
По набору порядковых статистик может быть проведена оценка и стандартного
отклонения (а). Однако для этого требуется иной, отличный от используемого
при оценке /л, набор порядковых статистик. Представляется полезным рассмотреть
вопрос об использовании общего набора порядковых статистик для совместной
оценки /л и а. При этом должен быть удовлетворен некий комплексный критерий
оптимальности такого набора. Такие оценки рассмотрены в [122, 123].
Укажем оценку по двум порядковым статистикам (напомним, одинаковым
при оценке и /л и сг), которая минимизирует линейную комбинацию дисперсий
D(/i) + cD(a) (см. табл. 8). Оценка имеет вид
\Л = гС(Ж[ап] + Х[рп]).
Аналогичная оценка по четырем порядковым статистикам имеет вид
Она минимизирует сумму дисперсий D(/jl) + D{a). Необходимые константы оценок
приведены в табл. 9.
Таблица 8
Оценка /л по двум статистикам [122]
с
1
2
3
к
0,5
0,5
0,5
а
0,1525
0,1274
0,1174
Ь
0,8475
0,8726
0,8853
Эффективность
0,729
0,683
0,594
Таблица 9
Вариант
оценки
1
2
0
0
Оценка
кг
,1414
,1097
0
0
/х по четырем
к2
,3586
,4029
а
0,0688
0,0389
совместным квантилям
0
0
а'
,2912
,2160
0
0
Р
9332
9611
Cf
0,7088
0,7840
[122]
Эффективность
0,9080
0,8570
2.1] Оценка параметров нормального распределения 103
2.1.1.1.3.6. Устойчивая (робастнам) оценка Ходжеса-Лемана по средним Уолша
гл с- г п(п + !) Xi + хз
Определим в выборке х\, ...,хп набор из — средних вида Zij = -
(г ^ j), называемых средними Уолша [124].
Оценка Ходжеса^Лемана [124] определяется как медиана средних Уолша, т. е.
медиана ряда Z\ ^ Z2 ^ ... ^ zn(n+i) • Следует отметить высокую устойчивость этой
2
оценки к отклонениям от нормальности распределения и засоренности выборки
аномальными наблюдениями.
2.1.1.1.4. Упрощенная оценка по шаблону [125]
Произвольно, но симметрично относительно предполагаемого среднего значе-
значения, выберем два числа а и Ь, определяющих размер шаблона (а < Ь). Подсчитаем
количество значений т, для которых х ^ а, и количество значений I, для которых
ж О-
Для величин pi = — и »2 ~ " находим по табл. 10 значение коэффициента
п п
k(pi1p2)- Искомая оценка определяется по формуле
х = а — (Ь — a)k(pi,p2).
Задача 44. В результате испытаний 30 приборов получены следующие значения ре-
ресурсной наработки:
Xi = 721, 741, 752, 761, 763, 780, 794, 840, 890, 911, 944, 960, 961, 967, 1010, 1011,
1012, 040, 1090, 1096, 1111, 1120, 1240, 1340, 1341, 1390, 1411, 1420, 1445, 1512.
Вычислить различными методами среднее значение ресурсной наработки.
Оценка максимального правдоподобия
г п г зо
x=-"pxi = ^y"xi = 1045,8.
п 4-Г 30 Аг
г=1 г=1
Оценка с помощью медианы
»=15;П±2=16 и .= «[1
2 ' 2
Простые оценки Диксона B.1.1.1.3.1)
Имеем 0,27п = 8,1 и 0,73?г = 21,9. Следовательно, оценку будем проводить по 9-й
и 22-й порядковым статистикам, т. е.
_ ж[9]+ж[22] 890 + 1120 _ 1 ^ типтк
^1 = 1005 и х = > ж^ = 1040,75.
те 2 ^
х 1005 и х
2 2 те - 2 ^
Оценки Огавы B.1.1.1.3.2)
— по двум статистикам:
[nAi + 1] = [30 • 0,27 + 1] = Ю; [п\2 + 1] = [30 • 0,73 + 1] = 23;
хо = 0,5(ж[ю] + Ж[2з]) = = 1075,5;
— по трем статистикам:
[п • Ai + 1] = [30 • 0,163 + 1] = 9; [п • А2 + 1] = [30 • 0,50 + 1] = 16;
[п • Аз + 1] = [30 • 0,837 + 1] = 27;
хо = 0,297 • (х[9] + х[27]) + 0,407 • х[Щ = 0,297 • (890 + 1411) + 0,407 • 1011 = 1094,874;
104 Оценка параметров распределений вероятностей [Гл. 2
— по десяти статистикам:
[п • Ai + 1] = [30 • 0,020 + 1] = 2; [п • Л6 + 1] = [30 • 0,573 + 1] = 19;
[п • А2 + 1] = [30 • 0,076 + 1] = 4; [гс • Л7 + 1] = [30 • 0,712 + 1] = 23;
[п • Аз + 1] = [30 • 0,167 + 1] = 7; [п • А8 + 1] = [30 • 0,833 = 1] = 26;
[п • А4 + 1] = [30 • 0,288 + 1] = 10; [п • А9 + 1] = [30 • 0,924 + 1] = 29;
[п • А5 + 1] = [30 • 0,427 + 1] = 14; [п • Х10 + 1] = [30 • 0,98 + 1] = 30.
Воспользовавшись коэффициентами из табл. 7, вычисляем
хо = 0,03б(ж2 + ж30) + 0,075(ж4 + ж29) + 0,109(ж7 + ж26) + 0,133(жю + ж23) +
+ 0,147(ж14 + х19) = 0,036 • G41 + 1512) + 0,075 • G61 + 1445) + 0,109 • G94 + 1390) +
+ 0,133 • (911 + 1240) + 0,147 • (967 + 1090) = 1073,076.
Оценка Пирсона-Тьюки B.1.1.1.3.3)
Имеем [0,5гс] = [0,5 • 30] = 15.
Далее А = ж[28] + х{2] - 2 • х[15] = 1420 + 741 - 2 • 1010 = 141.
Окончательно имеем jl = х[15] + 0,185 • 141 = 1010 + 0,185 • 141 = 1036,085.
Быстрые оценки Кенуя B.1.1.1.3.4)
— оценка по двум квантилям:
[0,25 • п] = [0,25 • 30] = 8; [0,75 • п] = [0,75 • 30] = 23;
z х8 + ж23 840 + 1240
2
- оценка по трем квантилям:
= 1040;
жгл.1 — жгзсп — ж2; ж го 5-ni — Ж155 Жг15-п] — ж29;
L16J [Те] L"™T6™~J
I = 0,2 • 741 + 0,6 • 1010 + 0,2 • 1445 = 1043,2;
— оценка по пяти квантилям:
5 = - • (х2 + х8 + 2 • х15 + ж23 + ж29) = ^ • G41 + 840 + 2 • 1010 + 1240 + 1445) = 1047,67.
6 6
Оптимальные комплексные оценки B.1.1.1.3.5)
— оценка по двум статистикам (с = 1):
[0,1525 • п] = [0,1525 • 30] = 5; [0,8475 • п] = [0,8475 • 30] = 26;
Д = 0,5 • (х5 + ж26) = 0,5 • G63 + 1390) = 1076,5;
— оценка по четырем статистикам (с = 1):
(вариант 1)
[0,0668 • п] = [0,0668 • 30] = 2; [0,9332 • п] = [0,9332 • 30] = 28;
[0,2912 • п] = [0,2912 • 30] = 9; [0,7088 • п] = [0,7088 • 30] = 22;
/х = 0,1414 • (х2 + ж28) + 0,3586 • (х9 + ж22) =
= 0,1414 • G4 + 1420) + 0,3586 • (890 + 1120) = 1026,35;
(вариант 2)
[0,0389 • п] = [0,0389 • 30] = 2; [0,9611 • п] = [0,9611 • 30] = 29;
[0,2160 • п] = [0,2160 • 30] = 7; [0,784 • п] = [0,784 • 30] = 24;
А = 0,0971 • [х2 + ж29) + 0,4029 • (х7 + ж24) =
= 0,0971 • G41 + 1445) + 0,4929 • G94 + 1340) = 1072,049.
2.1]
Оценка параметров нормального распределения
105
Оценка Ходжеса-Лемана B.1.1.1.3.5)
Продемонстрируем вычисление оценки на примере пяти выборочных значений (пол-
п(п + 1) 30 ¦ 29
ная оценка должна быть получена по
= 435 средним Уолша). Выберем
2 2
для примера пять выборочных значений (вблизи среднего): х%: 1012, 1040, 1090, 1096,
(ft _|_ ~\\ К . А
= = 10 средних Уолша:
1111. Вычислим
Zi = 1026; 1051; 1054; 1061,5; 1065; 1068; 1075,5; 1093; 1100,5; 1103,5.
Далее вычисляем медиану значений z%
z5+z6 1065 + 1068
р, =
= 1066,5.
к tf 2 2
Упрощенная оценка по шаблону
Выбираем границы шаблона а = 785 и Ь = 1115. Имеем т = 6 и I = 21, откуда
pi = — = 0,2 и р2 = — = 0,7.
F 30 F 30
Из табл. 10 находим fc@,2;0,7) = -0,62.
Следовательно, х = 785 - A115 - 785) • (-0,62) = 989,6.
Для уточнения оценки попытаемся применить более узкий шаблон а = 960,5;
Ъ = 1060.
Тогда т = 12 (Рг = 0,4); I = 18 (Р2 = 0,6) и fc@,4; 0,6) = -0,50.
Окончательно имеем х = 960,5 - A060 - 960,5) • (-0,50) = 1010,25.
Таблица 10
Значения коэффициентов
Р1
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,10
4,33
1,91
1,10
0,68
0,44
0,24
0,11
0,00
-0,09
-0,16
-0,23
-0,28
-0,34
-0,40
-0,45
-0,50
0,15
-5,33
—
4,20
1,81
1,00
0,60
0,32
0,14
0,00
-0,11
-0,19
-0,27
-0,33
-0,39
-0,45
-0,50
-0,55
0,20
-2,91
-5,20
—
3,94
1,62
0,87
0,42
0,18
0,00
-0,13
-0,23
-0,32
-0,38
-0,44
-0,50
-0,55
-0,60
0,25
-2,10
-2,81
-4,94
—
3,46
1,39
0,60
0,24
0,00
-0,16
-0,27
-0,37
-0,44
-0,50
-0,56
-0,61
-0,66
0,30
-1,68
-2,00
-2,62
-4,47
—
3,00
0,93
0,33
0,00
-0,20
-0,32
-0,43
-0,50
-0,56
-0,62
-0,67
-0,71
0,35
-1,44
-1,60
-1,87
-2,39
-4,00
—
1,79
0,50
0,00
-0,25
-0,39
-0,50
-0,57
-0,63
-0,68
-0,73
-0,77
0,40
-1,24
-1,32
-1,42
-1,60
-1,92
-2,79
—
1,08
0,00
-0,34
-0,50
-0,61
-0,68
-0,73
-0,77
-0,81
-0,84
0,45
-1,11
-1,14
-1,18
-1,24
-1,33
-1,00
-2,08
—
0,00
-0,50
-0,66
-0,75
-0,80
-0,84
-0,87
-0,89
-0,91
0,50
-1,00
-1,00
-1,00
-1,00
-1,00
-1,00
-1,00
-1,00
—
-1,00
-1,00
-1,00
-1,00
-1,00
-1,00
-1,00
-1,00
Примечание. Для определения значений коэффициентов за пределами табличных
значений р\ и pi следует пользоваться соотношением fc(pi,p2) + k(p2jPi) = — 1.
2.1.1.2. Интервальные оценки
2.1.1.2.1. Оценка /х при известной дисперсии <т2
Интервальная оценка с доверительной вероятностью а:
= х-
= х
106
Оценка параметров распределений вероятностей
[Гл. 2
где и7 — 7"квантиль стандартного нормального распределения;
сторонней оценки, j = а для односторонней оценки.
2.1.1.2.2. Оценка /л при неизвестной дисперсии
для дву-
где try — 7™квантиль распределения Стьюдента с / = п — 1 степенями свободы;
¦л П -л П -I,
2 1 v^/ -\2 - 1^ 1 + О
s = 2^(ж^ — х) ; ж = — 2^ я^; 7 = —«— Для двусторонней оценки, j = а для
i=l г=1
односторонней оценки.
Для квантилей стандартного нормального распределения и распределения Стью-
Стьюдента рекомендуется использовать аппроксимации, приведенные в разделе 1.1.9:
/ - ч 0,4274
и7 = 4,91[70'14 - A - 7)°'14]; % = 2,0637f In - - 0,16 j - 1,5774;
_ 0,717 - [0,7172 - 40,8116 In 2A -7)]^ _
Uj ~ -20,416 ~
= -0,8617788 + l,20192[0,846758 - 1,664 In 2A - 7)] 2 ;
1
4/
2,5
r; ^0,975 = 2
0,9975/ - 0,445
7
-1
2.1.1.2.3. Оценка по выборочному размаху
/4 (а) = х- G7u; цъп (а) = х + C7w,
где ш = жтах — xmin — выборочный размах; G7 — 7~квантиль распределения разма-
размаха; 7 = Для двусторонней И7 = а для односторонней оценки. Значения G1
табулированы, например, в [24, 119]. Оценку рекомендуется применять при п ^ 20
(при дальнейшем росте объема выборки эффективность оценки резко падает).
Некоторые критические значения G1 приведены в табл. 11.
Критические значения Gy [119]
Таблица 11
п
2
3
4
5
6
7
8
9
10
11
7
0,95
3,157
0,885
0,529
0,388
0,312
0,263
0,230
0,205
0,186
0,170
0,975
6,353
1,304
0,717
0,507
0,399
0,333
0,288
0,255
0,230
0,210
0,99
15,910
2,111
1,023
0,685
0,523
0,429
0,366
0,322
0,288
0,263
0,995
31,000
8,800
1,316
0,843
0,628
0,507
0,429
0,374
0,333
0,302
п
12
13
14
15
16
17
18
19
20
7
0,95
0,158
0,147
0,138
0,131
0,124
0,118
0,113
0,108
0,104
0,975
0,194
0,181
0,170
0,160
0,151
0,144
0,137
0,131
0,126
0,99
0,241
0,224
0,209
0,197
0,186
0,177
0,168
0,161
0,154
0,995
0,277
0,256
0,239
0,224
0,212
0,201
0,191
0,182
0,175
2.1]
Оценка параметров нормального распределения
107
2.1.1.2.4. Оценка по интерквартильной широте
Дэвид и Джонсон [119] предложили интервальную оценку /х, основанную на
выборочной медиане х (см раздел 2.1.1.1.2) и интерквартильной широте I, равной
разности между верхним и нижним выборочными квартилями, которые для выбо™
рок объема п = 3 + 41с определяются порядковыми статистиками с номерами
И Хп+1
—Х
Оценка имеет вид
где I — интерквартильная широта; 1г7—7™квантиль распределения I; 7= для
двусторонней оценки, 7 = а Для односторонней оценки. Значения Щ приведены
в табл. 12.
Таблица 12
Значения
[119]
п
11
15
19
23
27
31
7
0,95
0,470
0,400
0,354
0,321
0,296
0,276
0,975
0,623
0,514
0,448
0,402
0,367
0,341
0,99
0,876
0,676
0,573
0,506
0,458
0,422
п
35
39
43
47
51
7
0,95
0,260
0,246
0,234
0,224
0,215
0,975
0,319
0,301
0,286
0,273
0,261
0,99
0,393
0,369
0,349
0,332
0,317
2.1.1.2.5. Оценка по среднему абсолютному отклонению
Если С = - У
г=1
—среднее абсолютное отклонение, то интервальная оцен™
ка для среднего может быть определена, как
где К^ — 7~квантиль распределения С (табулирована в [9, 127, 128]). Значения
для 7 = 0,975 приведены в табл. 13.
Таблица 13
Значения
п
2
3
4
5
6
7
8
^0,975
12,71
3,45
2,16
1,66
1,40
1,21
1,09
п
9
10
11
12
13
14
^0,975
1,00
0,93
0,87
0,82
0,78
0,75
п
20
25
30
40
60
120
^0,975
0,71
0,60
0,48
0,41
0,33
0,23
108
Оценка параметров распределений вероятностей
[Гл. 2
2.1.1.2.6. Оценка 50%-го доверительного интервала по вероятному отклонению
1
_ 1
г=1
= х- 0,84535
-lAf1 *
<@,5) = ж+ 0,84535
Используется при п ^ 7 [129].
2.1.1.2.7. Интервальная оценка длм медианы
При п > 50 доверительный интервал для медианы ж определяется порядковыми
статистиками
где
Хк ^ X
fe = -(n - 1,64л/п - 1) при а = 0,9;
к = hn - l,96>/n - 1) при а = 0,95;
fc = i(n - 2,58л/п - 1) при a = 0,99.
Для значений п ^ 50 номера порядковых статистик, заключающих в себе
медиану, при а = 0,95 и а = 0,99 (двусторонние интервалы) приведены в табл. 14,
заимствованной из [9].
Таблица 14
Доверительный интервал для медианы
(номера порядковых статистик) [9]
п
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
а
0,95
0
1
1
1
2
2
2
3
3
3
4
4
5
5
5
6
5
5
6
7
7
8
9
9
10
11
11
12
12
13
14
14
0
0
0
0
1
1
1
1
2
2
2
3
3
3
4
4
4
,99
5
6
7
7
8
9
10
10
11
12
12
12
14
14
14
16
п
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
0
6
6
7
7
8
8
8
9
9
10
10
10
11
11
12
а
,95
15
16
16
17
17
18
19
19
20
20
21
22
22
23
23
0
5
5
5
6
6
7
7
7
8
8
8
9
9
10
10
,99
16
17
18
18
19
19
20
21
21
22
23
23
24
24
25
п
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
0
12
13
13
13
14
14
15
15
16
16
16
17
17
18
18
а
,95
24
24
25
26
26
27
27
28
28
29
30
30
31
31
32
0,99
1
11
11
12
12
12
13
13
14
14
14
15
15
16
16
26
26
27
27
28
29
29
30
30
31
32
32
33
33
34
При симметричном непрерывном распределении, каковым является нормальное,
справедливы предложенные в [119] формулы односторонних доверительных интер™
валов для медианы:
2.1] Оценка параметров нормального распределения 109
fe-i
2
— при доверительной вероятности а = 1 :
2 71
1/ \ ~ 1/
х < -{хп + xn+i^fe); х > -{x
— при доверительной вероятности а = 1 — —:
ATI
~ ^ \ Жп+Жп + i^fc] ,. .Г
ж < max\хп-г, ; х > mm ж2,
— при доверительной вероятности а = 1 (к > 1):
^ [жп1+Жп2 Жп+Жп + ifc] ^ .
< max ; ; х > mm
1 +
— при доверительной вероятности а = 1
2 ' 2
j
1
:-3)
~ ^ [ Жп+Жп + i^fc] ^^ .Г
х < max жп_4; ^ ; х > mm ж5;
— при доверительной вероятности
, (fc-!)(&-2)
\ 6 + 120
а = 1
2п
х < max жп^5 5
ж > mm
— при доверительной вероятности а = 1
2n
x < max I ' """•* ^ ""Т1"л I ; x > min I ' '*
i+ 2
— при доверительной вероятности а = 1 —
2
fe(fe-l)
х < max I Жз; ; х > mm
2п
хп
5
3n
Оценки эффективны при к ^ — в случае нормального распределения (при
п < 20).
Задача 45. В результате наблюдений был получен следующий ряд данных:
хц 2,4; 3,2; 4,1; 4,2; 4,8; 5,1; 6,2; 7,0; 9,0; 9,6 (га = 10).
Найти двустороннюю интервальную оценку среднего при доверительной вероятности
а = 0,95.
Оценка при неизвестной дисперсии
1
1 п \ 1 п „]2 1+«
Находим х = — У^ Х{ = 5,56 и s = УЧжг ~~ жJ = 2,3796. Далее j = =
°79Б = 0,975; / = га-1 = 10-1 = 9; to,975 « 2i/^ = 2,267.
110 Оценка параметров распределений вероятностей [Гл. 2
Окончательно имеем
2 3796
/4(а) = /iiO@,95) = 5,56 - 2,267 • ' = 3,854;
v 10
2 3796
fj,l(a) = /xiO@,95) = 5,56 + 2,267 • -?-=- = 7,266.
vlO
Таким образом, с вероятностью 0,95 значение параметра (среднего значения) нахо-
находится в интервале 3,854 ^ \х ^ 7,266.
Если бы интервалы были односторонними G = а = 0,95), то следовало бы использо-
использовать to,95 ВМеСТО to,975 И, ИМСЯ В ВИДУ, ЧТО Но,95 = 1,645,
^95 = ^0,95 ( 1 - "^ 1 = !'834'
Тогда получаем
/?@,95) = 5,56 - 1'834^!796 = 3,938; д* @,95) = 5,56 + "'"*"рГ" = 6,94.
vlO л/Ю
С вероятностью 0,95 имеем односторонние интервалы /л ^ 6,94 или \х ^ 3,938.
Оценка по выборочному размаху B.1.1.2.3)
Вычисляем размах выборки ш = жтах — Жтт = 9,6 — 2,4 = 7,2.
Для 7 = ^-^ = 0,975 и п = 10 находим из табл. 11 G0,975A0) = 0,23. Тогда
V* (а) = х - G1 • ш = 5,56 - 0,23 • 7,2 = 3,904;
(j,l (а) = х + G1 • ш = 5,56 + 0,23 • 7,2 = 7,216.
Следовательно, с вероятностью 0,95 имеем 3,904 ^ \х ^ 7,216.
Оценка по интерквартилъной широте B.1.1.2.4)
Для удобства демонстрации добавим еще один член выборки жц=10,0.
3-(п + 1) 3-12 п + 1 11 + 1
Имеем —v ; = = 9; —— = —— = 3; I = х9 - х3 = 9 - 4,1 = 4,9;
4 4 4 4
Медиана равна xn+i = xq = 5,1. Для 7 :=: 0,975 (а = 0,95) из табл. 12 находим
#0,975A1) =0,623.
Окончательно получаем
jtC (а) = 5,1 ~~ 0,623 • 4,9 = 2,047; /г* (а) = 5,1 + 0,623 • 4,9 = 8,153;
2,047 ^ [л ^ 8,153.
Оценка по среднему абсолютному отклонению B.1.1.2.5)
Находим
г ю
C=I5-E|xi-x| =
= — • C,16 + 2,36 + 1,46 + 1,36 + 0,76 + 0,46 + 0,64 + 1,44 + 3,44 + 4,04) = 1,912.
Из табл. 13 для п = 10 имеем JiTo,975A0) = 0,93 и далее
fin(a) = 5,56 - 0,93 • 1,912 = 3,782; /?(а) = 5,56 + 0,93 • 1,912 = 7,338.
Следовательно, доверительный интервал равен 3,782 ^ /i ^ 7,338.
Оценка 50%™го доверительного интервала B.1.1.2.6)
тг
Имеем ^2 \хг — х\ = 19,12 и
г=1
*( \ кка 0?84535 • 19,12 Ъ( , к ^ , 0,84535 • 19,12
fjbn{a) = 5,56 ^ = 5,021; /in(a) — 5,56 -\ -= = 6,0987.
10 • у 9 10 • v 9
2.1] Оценка параметров нормального распределения 111
Интервальная оценка для медианы B.1.1.2.7)
Из табл. 14 для п = 10 (а = 0,95) находим, что медиана лежит между 2-й и 8-й
порядковыми статистиками, т. е. между Х2 = 3,2 и xs = 7,0. Следовательно, 3,2 ^ х ^ 7,0.
Для приближенного подсчета имеем
п-1,96-л/п-1 10-1,96-V10-1
А; = = = 1,4.
2 2
Следовательно, [fc] = 2; [гг — к + 1] = 10, т.е. необходимо использовать статистики хч
и жю, что приводит к результату 3,2 ^ х ^ 9,6.
Приведем примеры вычисления односторонних приближенных оценок для медианы:
к = 1 (а=1- — = 0,95)
х < хю = 9,6; х > хг = 2,4;
fc = 2 (а=1- — = 0,9)
1 2n ' ;
[ж9+ж8 ж9+жю] [9 + 7 9,6 + 9]
ж < max ; = max —; —-— = 9,3;
~ . [ж2+жз хг+х2} . [3,2 + 4,1 3,2 + 2,4]
ж > mm ; = mm ; = 2,,
2.1.2. Оценка дисперсии о*2 и стандартного отклонения а
2.1.2.1. Точечные оценки
2.1.2.1.1. Оценка максимального правдоподобия
I n 1
Подсчитывается по формуле s2 = —
Для расчетов удобна формула s2 = — J^ х2 — ж2, из которой следует, что оценка
ъ=1
максимального правдоподобия а2 является разностью между среднеарифметиче™
ским квадратом результатов наблюдений и квадратом среднего арифметического.
Оценка — состоятельная, достаточная, эффективная, но при малых п не являю-
являющаяся несмещенной. При п < 30 рекомендуется использовать несмещенную оценку
s2 =
n_l ^ v-* ~> tv
%=1 \ъ=1
Если вместо оценки х используется параметр /л (когда он известен заранее), то
во всех случаях используется оценка с п в знаменателе.
2.1.2.1.2. Оценка <т по выборочной дисперсии s
2
Оценка s = vs^, где s2 — оценка максимального правдоподобия для дисперсии
(см. раздел 2.1.2.1.1), является смещенной. Несмещенной оценкой для а являет™
ся [25]
V
s = ^? гДе ^=\ —о /^—V^' ^( • • •)—гамма-функция.
2
При п > 30 Л « 1 — -. Значения Л при n ^ 45 приведены в табл. 15.
112
Оценка параметров распределений вероятностей
[Гл. 2
Таблица 15
Значения Л [25]
п
1
2
3
4
5
Л
0,7979
0,8862
0,9213
0,9400
0,9515
п
6
7
8
9
10
Л
0,9594
0,9650
0,9693
0,9727
0,9753
п
11
12
13
14
15
Л
0,9776
0,9794
0,9810
0,9823
0,9835
п
16
17
18
19
20
Л
0,9845
0,9540
0,9862
0,9869
0,9876
п
25
30
35
40
45
Л
0,9900
0,9917
0,9929
0,9938
0,9945
2.1.2.1.3. Оценка <т по среднему абсолютному отклонению
Вычисляется по формуле
= -?
Xi - Х\
При п ¦
ОО С :
тг V 2га - 1
где
з 0,79788 •
20.
c-\l
7Г
X
. В силу невысокой эффектив™
ности оценка используется при п
2.1.2.1.4. Оценка о* по выборочному размаху
Подсчитывается по формуле sp = —, где ш = жтах — хш-1П — размах выборки; d —
коэффициент, зависящий от п (его значения табулированы в [25]), фрагмент этой
таблицы содержится в табл. 16.
Таблица 16
Значения 1/cf
п
2
3
4
5
6
1/d
0,8862
0,5908
0,4857
0,4299
0,3946
п
7
8
9
10
11
1/d
0,3698
0,3562
0,3367
0,3249
0,3152
п
12
13
14
15
16
1/d
0,3069
0,2998
0,2935
0,2880
0,2831
п
17
18
19
20
1/d
0,2787
0,2747
0,2711
0,2677
При п < 20 эффективность оценки sp практически не отличается от эффектив™
ности оценки s (см. раздел 2.1.2.1.2), поэтому эта оценка предпочтительнее при
малых выборках.
С помощью размаха можно быстро оценить верхнюю границу стандартного отк-
отклонения: а ^ — [130]. При п ^ 200 в качестве грубой оценки а можно использовать
оценку 5 = -.
2.1.2.1.5. Упрощенная оценка а по шаблону
По аналогии с оценкой ц для быстрой, но грубой оценки а можно исполь-
использовать метод шаблонов [125]. При этом оценка имеет вид лш = (б?2 — ^i)/(pi,P2M
где U2 > d\—размеры шаблона; pi, P2—доля ж, меньших d\ и d^ соответственно;
Pz) —коэффициент, зависящий от р\ и р2 (табулирован в табл. 17).
2.1]
Оценка параметров нормального распределения
113
Таблица 17
Значения коэффициента
рг
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
рг
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,10
—
-4,16
-2,27
-1,64
-1,32
-1,12
-0,97
-0,87
-0,78
-0,71
-0,65
-0,60
-0,56
-0,51
-0,47
-0,43
-0,39
0,15
4,17
—
-5,00
-2,70
-1,92
-1,54
-1,26
-1,10
-0,96
-0,85
-0,78
-0,70
-0,64
-0,58
-0,53
-0,48
-0,43
0,20
2,27
5,00
—
-5,88
-3,12
-2,22
-1,69
-1,41
-1,19
-1,03
-0,92
-0,81
-0,74
-0,66
-0,60
-0,53
-0,47
0,25
1,64
2,70
5,08
—
-5,67
-3,57
-2,38
-1,85
-1,49
-1,25
-1,09
-0,94
-0,84
-0,75
-0,66
-0,58
-0,51
0,30
1,32
1,92
3,12
6,67
—
-7,69
-3,70
-2,56
-1,92
-1,54
-1,30
-1,10
-0,96
-0,84
-0,75
-0,64
-0,56
0,35
1,12
1,54
2,22
3,57
7,70
—
-7,14
-3,85
-2,56
-1,92
-1,56
-1,28
-1,10
-0,94
-0,81
-0,70
-0,60
0,40
0,97
1,27
1,68
2,38
3,70
7,14
—
-8,33
-4,00
-2,63
-2,00
-1,56
-1,30
-1,09
-0,92
-0,73
-0,65
0,45
0,87
1,10
1,41
1,85
2,56
3,85
8,33
—
-7,69
-3,85
-2,63
-1,92
-1,54
-1,25
-1,03
-0,85
-0,71
0,50
0,78
0,96
1,19
1,49
1,92
2,56
4,00
7,69
—
-7,69
-4,00
-2,56
-1,92
-1,49
-1,19
-0,96
-0,78
0,55
0,71
0,85
1,03
1,25
1,53
1,92
2,63
3,85
7,69
—
-8,33
-3,85
-2,56
-1,85
-1,41
-1,10
-0,87
0,60
0,65
0,78
0,92
1,09
1,30
1,56
2,00
2,63
4,00
8,33
—
-7,14
-3,70
-2,38
-1,69
-1,27
-0,97
0,65
0,60
0,70
0,81
0,94
1,10
1,28
1,56
1,92
2,56
3,85
7,14
—
-7,69
-3,57
-2,22
-1,54
-1,12
0,70
0,56
0,64
0,74
0,84
0,96
1,10
1,30
1,54
1,92
2,56
3,70
7,69
—
-6,67
-3,12
-1,92
-1,32
0,75
0,51
0,58
0,66
0,75
0,84
0,94
1,09
1,25
1,49
1,85
2,38
3,57
6,67
—
-5,88
-2,70
-1,32
0,80
0,47
0,53
0,60
0,66
0,74
0,81
0,92
1,03
1,19
1,41
1,69
2,22
3,12
5,88
—
-5,00
-2,20
0,90
0,39
0,43
0,47
0,51
0,56
0,60
0,65
0,71
0,78
0,87
0,97
1,12
1,32
1,64
2,27
4,17
—
2.1.2.1.6. Оценка с помощью порядковых статистик
2.1.2.1.6.1. Оптимальная линейная оценка [24, 25, 118, 119]
Находится по формуле <т =
где
г-я порядковая статистика;
г=1
коэффициенты оценки (табулированы в [24, 118, 119]).
Значения коэффициентов ki приведены в табл. 18. Учитвгоая, что kn+i = 0,
2
ki = — kn^i^i, в таблице приведены значения для членов выборки от 1 до в/2 (п —
четное) или (п — нечетное).
114
Оценка параметров распределений вероятностей
[Гл. 2
Значения
Таблица 18
для оптимальной линейной оценки и [119]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
кг
8862
5908
4539
3724
3175
2778
2476
2237
2044
1883
1748
1632
1532
1444
1366
1297
1235
1178
1128
к2
0
1102
1352
1386
1352
1294
1233
1172
1115
1061
1013
0968
0927
0899
0854
0822
0792
0765
к3
0
0432
0625
0713
0751
0763
0760
0749
0735
0717
0699
0681
0663
0645
0628
0611
к4
0
0230
0360
0436
0481
0506
0520
0526
0526
0524
0519
0512
0525
0497
0
0142
0234
0294
0335
0362
0379
0391
0398
0401
0402
0402
к6
0
0087
0164
0212
0247
0272
0290
0302
0312
0318
к7
0
0070
0122
0160
0189
0211
0228
0241
к8
0
0530
0094
0125
0150
0169
kg
0
0041
0074
0101
кю
0
0033
Эффективность оценки практически не уступает оценке максимального правдо-
правдоподобия (см. раздел 2.1.2.1.2).
2.1.2.1.6.2. Оценка Огавы [118, 119]
Аналогична оптимальной линейной оценке, но вычисляется по га < п порядко-
порядковым статистикам, выбранным исходя из получения максимальной эффективности
оценок в больших выборках без увеличения объема вычислений.
Вычисляется по формуле а =
ь ГДе т — число выборочных поряд™
г=1
ковых статистик, по которым производится оценка; Л^ — коэффициенты, определя-
определяющие номера порядковых статистик, участвующих в оценке; @i —весовые коэффи-
коэффициенты оценки.
Коэффициенты Л^ и /% табулированы в [118, 119] и приведены в табл. 19 {\n\j\ —
целое число, ближайшее справа к пЛ^, и [n\i] + 1 — порядковый номер наблюдения).
Таблица 19
Значения Лг (верхняя строка) и /Зг (нижняя строка)
для оценки Огавы [119]
т
2
4
6
1
0,069
-0,674
0,023
-0,115
0,011
-0,056
2
0,931
0,674
0,127
-0,237
0,056
-0,126
г
3
0,873
0,237
0,171
-0,181
4
0,977
0,115
0,829
0,181
5
0,944
0,126
6
0,990
0,056
2.1]
Оценка параметров нормального распределения
115
2.1.2.1.6.3. Линейная оценка Даутона
Даутон [131] предложил простую, но весьма эффективную оценку для а в виде
1,77245 " о. 1Х
а =
п(п - 1)
При п ^ 10 эффективность оценки равна 0,94 по сравнению с оценкой максималь™
ного правдоподобия.
2.1.2.1.6.4. Оценка по сумме подразмахов (оценка Диксона) [117]
Вычисляется по формуле
г
где Ui = xn+i—i — xi —г-й подразмах; kn — коэффициент оценки. Значения кп и но-
номера используемых в оценке подразмахов табулированы в [118, 119] и приведены
в табл. 20 (очевидно, что ш\ = ш — обычный размах). Там же приведены коэффи-
коэффициенты к оценки а по размаху {а = кш, см. табл. 16).
Таблица 20
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
к
(по размаху)
0,886
0,591
0,486
0,430
0,395
0,370
0,351
0,337
0,325
0,315
0,307
0,300
0,294
0,288
0,283
0,279
0,275
0,271
0,268
Оценки &
Эффективность
оценки
по размаху
1,000
0,992
0,975
0,955
0,933
0,911
0,890
0,869
0,850
0,831
0,814
0,797
0,781
0,766
0,751
0,738
0,725
0,712
0,700
по подразмахам
Оценка по сумме
подразмахов
(оценка Диксона)
0,8862ш
0,5908а;
0,4857а;
0,4299ш
0,2916(а; + а;2)
0,2370(ш + ш2)
0,2197(ш + ш2)
0,2068(а; + а;2)
0,1968(ш + а;2)
О,16О8(С47 + Ш2 +О74)
0,1524(а; + а;2 + О74)
0,1456(ш + ш2 +ш4)
0,1399(а; + а;2 + ш4)
0,1352(а; + а;2 + ш4)
О,1311(Ш + Ш2 +Ш4)
0,1050(а; + а;2 + а;3 + а;5)
0,1020(ш + ш2 + ш3 + ш5)
0,0993(ш + ш2 + ш3 + ш5)
0,10446(ш + ш2 + ш4 + ш6)
Эффективность
оценки
по подразмахам
1,000
0,992
0,975
0,955
0,957
0,967
0,970
0,968
0,964
0,967
0,972
0,975
0,977
0,977
0,975
0,978
0,978
0,979
0,980
2.1.2.1.6.5. Оценка Джини [122]
Используется как быстрая оценка для а и подсчитывается по формуле
. п — 2г -
г=1
п(п — 1)
где Ш{ — г-й подразмах.
Оценка не уступает оценке Даутона (см. 2.1.2.1.6.3).
116
Оценка параметров распределений вероятностей
[Гл. 2
2.1.2.1.6.6. Оптимальные комплексные оценки, использующие общий набор
порядковых статистик
Подробнее о сути оценки ем. в разделе 2.1.1.1.3.5. Укажем оценку по двум поряд-
порядковым статистикам (напомним, одинаковым при оценке /л и а), минимизирующую
линейную комбинацию дисперсий D(/i) + cD(a) (табл. 21):
о- = к(х[ап] -Х[рп]).
Аналогичные оценки по четырем порядковым статистикам имеют вид (с = 1)
~ х[0,0668п]) + 0>2051(Ж[0,7088п] ~~ ж[0,2Э12п])
Эффективности оценок равны соответственно 0,735 и 0,792.
Таблица 21
с
1
2
3
Оценка
к
0,4875
0,4391
0,4160
(Т по двум статистикам [117]
а
0,8475
0,8726
0,8853
Р
0,1525
0,1274
0,1174
Эффективность
0,552
0,594
0,614
Задача 46. Имеется набор результатов измерений
хц 1,4; 2,1; 2,9; 3,1; 3,8; 4,1; 4,3; 4,6; 5,1; 6,1.
Необходимо вычислить оценку дисперсии и среднеквадратического отклонения различ-
различными способами.
Оценка максимального правдоподобия B.1.2.1.1)
s2 = -
{ - xf = -
n
= — • 158,51 - C,75J = 1,7885
10
или s2 =
ixi ~~
= 1,9872 (с использованием поправки на смещение).
Следует помнить, что при малых п смещение оценки может быть значительным.
Оценка по среднему абсолютному отклонению B.1.2.1.3)
1 "
\Xi-x\, где с= \ -
. = 0,75694.
10/
Имеем
= 11 и s* =
1
¦ 11 = 1,4181.
10 • 0,75694
Оценка по выборочному размаху B.1.2.1.4)
Имеем со = жтах — xmin = 6,1 — 1,4 = 4,7. Для п = 10 из табл. 16 получаем - = 0,3249
и sp = 4,7 • 0,3249 = 1,529.
Упрощенная оценка по шаблону B.1.2.1.5)
Выбираем d,2 = 4,5 и d\ = 2,5, тогда pi = 0,2 и pi = 0,8. Из табл. 17 имеем /@,2; 0,8) =
= 0,60 и 5Ш = D,5 - 2,5) • 0,6 = 1,20.
2.1] Оценка параметров нормального распределения 117
Оптимальная линейная оценка B.1.2.1.6.1)
Находим с помощью табл. 18
a = J2ki' Щг] = 0,2044 • F,1 - 1,4) + 0,1172 • E,1 - 2,1) + 0,0763 • D,6 - 2,9) +
г=1
+ 0,0436 • D,3 - 3,1) + 0,0142 • D,1 ~~ 3,8) = 1,49857.
Оценка Огавы B.1.2.1.6.2)
Выполним оценку по четырем порядковым статистикам. В соответствии с табл. 19 их
номера будут
[п • Ai] + 1 = [10 • 0,023] + 1 = 1; [п • Л2] + 1 = [10 • 0,127] + 1 = 2;
[п • Аз] + 1 = [10 • 0,873] + 1 = 9; [п • А4] + 1 = [10 • 0,977] + 1 = 10.
Тогда имеем, используя коэффициенты из табл. 19,
а = -0,115 • хг - 0,237 • х2 + 0,237 • х9 + 0,115 • х10 =
= 0,115 • F,1 - 1,4) + 0,237 • E,1 - 2,1) = 1,2515.
Линейная оценка Даутона B.1.2.1.6.3)
1,77245
а =
• ]Р Bг - п - 1) • хг = 0,01Э694-(-9 • 1,4 - 7 • 2,1 ~~ 5 • 2,9 - 3 • 3,1 ~~
-(Ю-1) ^
- 1 • 3,8 + 1 • 4,1 + 3 • 4,3 + 5 • 4,6 + 7 • 5,1 + 9 • 6,1) = 1,49083.
Оценка по сумме подразмахов B.1.2.1.6.4)
Из табл. 20 (для п = 10) следует, что
а = 0,1968 • (ш + ш2) = 0,1968 • (жю - ал + ж9 - х2) =
= 0,1968 • F,1 - 1,4 + 5,1 - 2,1) = 1,51536.
Оценка Джини B.1.2.1.6.5)
Имеем
Г-1
п L2 J
J2 \хг - хА = 1С (п ~~2i + *) • ^ = (п -1)'Ш1 + (w -3) •Ш2 + (п -5) • Шз+
i,j = l г=1
+ (п - 7) • ш4 + (п - 9) • ш5 = 75,7 и <т = • 75,7 = 0,842.
Из результата видно, что оценка очень груба.
Оценки, использующие общий набор порядковых статистик B.1.2.1.6.6)
Имеем для двух статистик (пусть с = 1)
а = 0,4875 • (ж[0,8475.ю] - ^0,1525.10]) = 0,4875 • (х8 ~~ хг) = 0,4875 • D,6 - 1,4) = 1,56;
оценка по четырем статистикам:
вариант 1
а = 0,2581 • (X[O;9332-1O] — Ж[0,0688-10]) + 0,2051 • (Ж[О,7О88-Ю] — Ж[о, 2912-10]) =
= 0,2581 • (х9 - хг) + 0,2051 • (х7 - х3) = 0,2581 • E,1 - 1,4) + 0,2051 • D,3 - 2,9) = 1,2421.
вариант 2
«7 = 0,1787 • (#[0,9611.10] ~~ Ж[0,0389-10]) + 0,2353 • (Ж[О,784О-1О] — #[0,2160-10]) =
= 0,1787 • (жю - хг) + 0,2353 • (ж8 - х2) = 0,1787 • F,1 - 1,4) + 0,2353 • D,6 - 2,1) = 1,428.
118
Оценка параметров распределений вероятностей
[Гл. 2
2.1.2.2. Интервальные оценки
2.1.2.2.1. Интервальные оценки дисперсии и2
Интервальные оценки при доверительной вероятности а равны
1 п 1
_ V (т- — тJ- (^2)в —
тJ
где x^f —7™квантиль распределения %2 с / = в—1 степенями свободы (если параметр
/л известен, то / = n); jf =
¦ для двусторонней оценки wjf = a для односто™
ронней оценки; jf/ =
оценки.
1-а
для двусторонней оценки иУ' = 1 — « для односторонней
Для аппроксимации Xj рекомендуется использовать формулу Вилсона—Хил™
ферти [61]
xW =
где и7 — 7™квантиль стандартного нормального распределения.
Для практически применяемых уровней достоверности а = 0,9; 0,95 и 0,99 зна™
чения и^ приведены в табл. 22.
Таблица 22
Значения
а
0,90
0,95
0,99
Односторонние границы
У
0,90
0,95
0,99
1"
0,10
0,05
0,01
*v
1,28255
1,64485
2,32635
-1,28255
-1,64485
-2,32635
Двусторонние границы
У
0,950
0,975
0,995
1"
0,050
0,025
0,005
wy
1,64485
1,95996
2,57582
ну'
-1,64485
-1,95996
-2,57582
2.1.2.2.2. Интервальная оценка а по размаху
Оценка находится по формулам
где а; G)—7™квантиль распределения размаха выборки объема п из стандартного
нормального распределения (табулированы в [25, 29]); jf = —-— для двусторонней
ш jf = а для односторонней оценки; jf/ =
1-а
для двусторонней, j/f = 1 — а для
односторонней оценки. Оценка применяется при п ^ 20. Для обычно применяемых
величин а = 0,90; 0,95 и 0,99 необходимые значения о;G) для п = 1AJ0 приведены
в табл. 23.
2.1.2.2.3. Оценка по среднему абсолютному отклонению
Вычисляется по формулам
1
Xi — х ;
1
2.1]
Оценка параметров нормального распределения
119
Таблица 23
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Значения
квантилей распределения размаха из("у) [25]
Односторонние оценки
а =
1
0,90
2,90
3,24
3,48
3,66
3,81
3,93
4,04
4,13
4,21
4,29
4,35
4,41
4,47
4,52
4,57
4,61
4,65
4,69
0,90
1"
0,10
0,62
0,98
1,26
1,49
1,68
1,83
1,97
2,09
2,20
2,30
2,39
2,47
2,54
2,61
2,67
2,73
2,79
2,84
а =
V
0,95
3,31
3,63
3,86
4,03
4,17
4,29
4,39
4,47
4,55
4,62
4,68
4,74
4,80
4,85
4,89
4,93
4,97
5,01
0,95
V
0,05
0,43
0,76
1,03
1,25
1,44
1,60
1,74
1,86
1,97
2,07
2,16
2,24
2'32
2,39
2,45
2,51
2,57
2,62
а =
i
0,99
4,12
4,40
4,60
4,76
4,88
4,99
5,08
5,16
5,23
5,29
5,35
5,40
5,45
5,49
5,54
5,57
5,61
5,65
0,99
l"
0,01
0,19
0,43
0,66
0,87
1,05
1,20
1,34
1,47
1,58
1,68
1,77
1,86
1,93
2,01
2,07
2,14
2,20
2,25
Двусторонние оценки
а =
i
0,95
3,31
3,63
3,86
4,03
4,17
4,29
4,39
4,47
4,55
4,62
4,68
4,74
4,80
4,85
4,89
4,93
4,97
5,01
0,90
i1
0,05
0,43
0,76
1,03
1,25
1,44
1,60
1,74
1,86
1,97
2,07
2,16
2,24
2,32
2,39
2,45
2,51
2,57
2,62
а = 0,95
V
0,975
3,68
3,98
4,20
4,36
4,49
4,61
4,70
4,79
4,86
4,92
4,99
5,04
5,09
5,14
5,18
5,22
5,26
5,30
0,025
0,30
0,59
0,85
1,06
1,25
1,41
1,55
1,67
1,78
1,88
1,97
2,06
2,14
2,21
2,27
2,34
2,39
2,45
а =
V
0,995
4,42
4,69
4,89
5,03
5,15
5,26
5,34
5,42
5,49
5,54
5,60
5,65
5,70
5,74
5,78
5,82
5,85
5,89
0,99
l"
0,005
0,13
0,34
0,55
0,75
0,92
1,08
1,21
1,33
1,45
1,55
1,64
1,72
1,80
1,88
1,94
2,01
2,07
2,12
Таблица 24
Значения квантилей распределения среднего абсолютного отклонения m(j) [25]
2
3
4
5
6
7
8
9
10
Односторонние оценки
а =
7
0,90
1,163
1,117
1,089
1,069
1,052
1,038
1,026
1,016
1,007
0,90
1"
0,10
0,088
0,238
0,328
0,386
0,428
0,459
0,484
0,504
0,521
а =
i
0,95
1,386
1,276
1,224
1,187
1,158
1,135
1,116
1,100
1,086
0,95
i'
0,05
0,044
0,166
0,254
0,315
0,360
0,394
0,422
0,445
0,464
а =
i
0,99
1,821
1,586
1,489
1,419
1,366
1,325
1,292
1,264
1,240
0,99
7"
0,01
0,009
0,073
0,145
0,203
0,250
0,287
0,318
0,344
0,366
Двусторонние оценки
а =
i
0,95
1,386
1,276
1,224
1,187
1,158
1,135
1,116
1,100
1,086
0,90
l"
0,05
0,044
0,166
0,254
0,305
0,360
0,394
0,422
0,445
0,464
а =
У
0,975
1,585
1,417
1,344
1,292
1,253
1,222
1,196
1,175
1,156
0,95
i1
0,025
0,022
0,116
0,199
0,260
0,306
0,342
0,372
0,396
0,417
а =
У
0,995
1,985
1,703
1,59
1,507
1,445
1,397
1,358
1,326
1,299
0,99
7;/
0,005
0,004
0,073
0,145
0,203
0,25
0,287
0,318
0,344
0,366
где m(j) — 7~квантиль распределения среднего абсолютного отклонения; jf= A + ol)/2,
г)" = A + а)/2 Для двусторонней оценки и jf = a, jff = 1 — а для односторонней
оценки.
Для п = 1AI00 и а = 0,90; 0,95 и 0,99 значения 772G) приведены в табл. 24.
2.1.2.2.4. Интервальная оценка и, основанная на ее точечной оценке s
Оценка вычисляется по формулам
120
Оценка параметров распределений вероятностей
[Гл. 2
где s =
7™квантиль распределения
с / = п — 1 сте™
1 + о
пенями свободы; 7/= {l' = °0 Для двусторонней (односторонней) оценки;
7//= —-— (jff = 1 — а) для двусторонней (односторонней) оценки. Значения w——
2 V Х7
табулированы в [25, 46] и приведены в табл. 25.
В [36] для а = 0,95 приведены достаточно простые и точные эмпирические
формулы:
Значения
Таблица 25
для интервальной (двусторонней) оценки и
ft 1
П I
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
22
24
26
28
30
35
40
45
50
55
60
70
80
90
100
а =
i = 0,95
0,578
0,620
0,649
0,672
0,690
0,705
0,718
0,729
0,739
0,748
0,755
0,762
0,769
0,775
0,780
0,785
0,790
0,794
0,798
0,805
0,812
0,818
0,823
0,828
0,838
0,847
0,854
0,861
0,866
0,871
0,879
0,886
0,892
0,897
0,90
7/; = 0,05
4,42
2,92
2,37
2,09
1,92
1,80
1,71
1,65
1,59
1,55
1,52
1,49
1,46
1,44
1,42
1,40
1,39
1,37
1,36
1,34
1,32
1,30
1,29
1,27
1,25
1,23
1,21
1,20
1,19
1,18
1,16
1,15
1,14
1,13
а =
У = 0,975
0,521
0,566
0,599
0,624
0,644
0,661
0,675
0,688
0,699
0,708
0,717
0,725
0,732
0,739
0,745
0,750
0,756
0,760
0,765
0,773
0,781
0,788
0,794
0,799
0,811
0,821
0,829
0,837
0,843
0,849
0,858
0,866
0,873
0,879
0,95
7/; = 0,025
6,28
3,73
2,87
2,45
2,20
2,04
1,92
1,83
1,75
1,70
1,65
1,61
1,58
1,55
1,52
1,50
1,48
1,46
1,44
1,42
1,39
1,37
1,35
1,34
1,30
1,28
1,26
1,24
1,23
1,22
1,20
1,18
1,17
1,16
а =
У = 0,995
0,434
0,483
0,519
0,546
0,569
0,588
0,604
0,618
0,630
0,641
0,651
0,660
0,669
0,676
0,683
0,690
0,696
0,702
0,707
0,717
0,726
0,734
0,741
0,748
0,762
0,774
0,784
0,793
0,801
0,808
0,820
0,829
0,838
0,845
0,99
7;/ = 0,005
14,12
6,47
4,40
3,48
2,98
2,66
2,44
2,28
2,15
2,06
1,98
1,91
1,85
1,81
1,76
1,73
1,70
1,67
1,64
1,60
1,56
1,53
1,50
1,48
1,43
1,39
1,36
1,34
1,32
1,30
1,27
1,25
1,23
1,22
2.1]
Оценка параметров нормального распределения
121
— для нижней границы
— для верхней границы
1п-1
- 1,74
1 < 96 + \/2п - 2 '
11,54(п-3,61J + 1,Э8; 2
х/2п - 0,47
4;
п > 5.
/2п - 0,8 - 1,96
Оценки улучшаются, если вместо s использовать несмещенную оценку s* = fcs,
где к = 1 + ^^ [36].
Отметим, что в нашем случае рассматриваются симметричные квантили jf = 0,95
и 7;/ = 0,05, 7; = 0,975 и г)!1 = 0,025. Интервалы такого типа называются централь™
ными [132]. Однако они не являются кратчайшими при одной и той же дове™
рительной вероятности. Более того, в силу несимметричности распределения s,
центральные интервалы не могут быть кратчайшими [133].
В табл. 26 приведены кратчайшие доверительные интервалы для <т, равные
zis ^ 0" ^ Z2S Для заданных доверительных вероятностей. При п ^ 70 разница меж-
между кратчайшими и центральными интервалами становится менее 1%, поэтому
кратчайшими интервалами рекомендуется пользоваться при п ^ 70. Полное срав™
нительное исследование оценок дисперсии и стандартного отклонения нормального
распределения приведено в [134].
Задача 47. Для данных задачи 46 (ж«: 1,4; 2,1; 2,9; 3,1; 3,8; 4,1; 4,3; 4,6; 5,1; 6,1) найти
двустороннюю интервальную оценку для стандартного отклонения при доверительной
вероятности а = 0,95.
Интервальная оценка дисперсии B.1.2.2.1)
I ю ю
Находим S2 = J2(xi ~ xf = 1,9872, или J^(xi - xf = 17,885.
Для а = 0,95 (двусторонние границы) из табл. 22 имеем tio,975 = 1,95996 и tio,o25 =
= -1,95996.
Отсюда при / = п — 1 = 9
Х0,975 = 9 '
Х0,025 —
1 -
1-
9- 10
2
+ 1,95996 •
- 1,95996 •
Далее
• 17,885 = 0,97025;
= 18,4333;
= 2,9004.
• 17,885 = 6,1664.
18,4333
Следовательно, с вероятностью 0,95 имеем 0,97025 ^ о ^ 6,1664.
Интервальная оценка а по размаху B.1.2.2.2)
Имеем жтах — xmin = 6,1 — 1,4 = 4,7. Из табл. 23 для п = 10 и а = 0,95 имеем
ало @,975) = 4,79 и ало @,025) = 1,67. Следовательно,
si = — = 0,9457; si = — = 2,8144,
4,97 1,67
и с вероятностью 0,95 имеем 0,9457 ^ а ^ 2,8144.
122
Оценка параметров распределений вероятностей
[Гл. 2
Таблица 26
Коэффициенты z\ и z^ кратчайших
доверительных интервалов [133]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
35
40
45
50
60
70
а =
21
0,272
0,400
0,478
0,531
0,571
0,601
0,627
0,647
0,664
0,679
0,692
0,704
0,714
0,724
0,732
0,740
0,747
0,753
0,759
0,765
0,770
0,775
0,779
0,783
0,788
0,791
0,795
0,798
0,802
0,816
0,827
0,837
0,844
0,857
0,868
0,90
Z2
7,944
3,112
2,304
1,980
1,805
1,693
1,616
1,558
1,512
1,476
1,447
1,421
1,400
1,381
1,365
1,350
1,337
1,326
1,315
1,306
1,297
1,288
1,281
1,274
1,267
1,261
1,256
1,250
1,245
1,224
1,207
1,193
1,182
1,164
1,151
а =
z\
0,246
0,364
0,439
0,491
0,531
0,562
0,587
0,609
0,627
0,642
0,656
0,668
0,679
0,689
0,698
0,706
0,714
0,721
0,727
0,733
0,739
0,744
0,749
0,754
0,758
0,762
0,766
0,770
0,773
0,789
0,801
0,812
0,821
0,835
0,847
0,95
16,004
4,434
2,949
2,405
2,124
1,950
1,832
1,746
1,680
1,628
1,585
1,550
1,520
1,494
1,461
1,451
1,433
1,417
1,402
1,389
1,377
1,366
1,356
1,347
1,338
1,330
1,322
1,315
1,308
1,280
1,258
1,241
1,226
1,203
1,186
а =
z\
0,220
0,310
0,378
0,428
0,467
0,497
0,523
0,544
0,563
0,580
0,594
0,607
0,619
0,629
0,639
0,648
0,656
0,664
0,671
0,678
0,684
0,690
0,695
0,701
0,705
0,710
0,715
0,719
0,723
0,741
0,755
0,767
0,778
0,795
0,808
0,99
Z2
80,062
9,990
5,131
3,691
3,027
2,647
2,402
2,229
2,101
2,002
1,982
1,858
1,804
1,758
1,718
1,683
1,653
1,625
1,601
1,579
1,559
1,541
1,525
1,509
1,495
1,482
1,470
1,458
1,448
1,403
1,369
1,342
1,320
1,285
1,260
Оценка а по среднему абсолютному отклонению B.1.2.2.3)
ю ю
Находим ]Р \х% — х\ = ]Р \xi ~ ^-^Щ = 11- Из табл. 24 для а = 0,95 и п = 10 имеем
г=1 г=1
,975 = 1Д56 и то,025 = 0,47, тогда
1 = 2,3404.
s" = 1^мй •n = °'9515; s"
Окончательно имеем 0,9515 ^ а ^ 2,3404.
10 • 0,47
Интервальная оценка а, основанная на ее точечной оценке B.1.2.2.4)
J1 ю
~ 2 (Xi ~ хJ = 1,40969. Из табл. 25 для а = 0,95 ип-1 = 9 имеем
2.1]
Оценка параметров нормального распределения
123
= 0,688;
= 1,83.
Тогда
si = 0,688 • 1,40969 = 0,96986; si = 1,83 • 1,40969 = 2,57973.
Если воспользоваться аппроксимациями, то
Хо,975 1,96 + V20 - 2
что очень близко к табличным значениям.
Теперь воспользуемся кратчайшим доверительным интервалом. Из табл. 26 имеем
для а = 0,95 и п = 10: z\ = 0,642 и Z2 = 1,628, откуда
S* = 0,642 • 1,40969 = 0,90502 и s* = 1,628 • 1,40969 = 2,29497,
0,90502 <С а <: 2,29497.
Видим, что в этом случае длина доверительного интервала равна 2,29497^ 0,90502 =
= 1,38995 по сравнению с 2,57973 — 0,969986 = 1,60974 в случае центрального интервала
(т.е. меньше на « 14%).
2.1.3. Оценки в усеченных и цензурированных выборках
На практике встречаются ситуации, когда некоторые выборочные значения слу-
случайной величины отсутствуют. Например, при испытаниях электронных приборов
на гарантийную наработку для части приборов фиксируются значения наработки,
а для остальных известно только, что их наработка не меньше некоторой таранти™
руемой величины.
Выборки, в которых отсутствуют значения случайной величины, большие (или
меньшие) некоторого граничного значения, называются усеченными. Если степень
усечения известна заранее, то имеет место так называемая не полностью опре-
определенная выборка. Выборки, в которых часть членов отбрасывается, называются
цензурированными (например, при измерениях отбрасываются крайние значения,
как наиболее грубые).
2.1.3.1. Оценки максимального правдоподобия
2.1.3.1.1. Оценки в усеченных выборках
Оценка параметров усеченного нормального распределения производится по
формулам
где z = f(y) — функция аргумента у =
Е2
(z) — функция аргумента
табулированы в [29], часть этих таблиц
Значения функций z = f(y) и
воспроизведена в табл. 27 и 28.
Сначала по выборочным данным подсчитывается у, затем по табл. 27 и 28 — z
и g(z) (при необходимости используется интерполяция). В приведенных формулах
предполагается, что точка усечения ху известна и равна 0 (если ху ф 0, то формулы
справедливы для переменной х* = xi — ху).
124
Оценка параметров распределений вероятностей
[Гл. 2
Таблица 27
Значения функции z = f{y) [29]
У
0,550
0,555
0,560
0,565
0,570
0,575
0,580
0,585
0,590
0,595
0,600
0,605
0,610
0,615
0,620
0,625
0,630
0,635
0,640
0,645
0,650
0,655
0,660
0,665
z
-3,145
-2,990
-2,851
-2,777
-2,613
-2,508
-2,410
-2,319
-2,232
-2,151
-2,073
-1,999
-1,928
-1,859
-1,792
-1,728
-1,665
-1,604
-1,545
-1,486
-1,429
-1,373
-1,318
-1,263
У
0,670
0,675
0,680
0,685
0,690
0,695
0,700
0,705
0,710
0,715
0,720
0,725
0,730
0,735
0,740
0,745
0,750
0,755
0,760
0,765
0,770
0,775
0,780
0,785
-1,209
-1,158
-1,103
-1,051
-0,999
-0,947
-0,896
-0,845
-0,894
-0,743
-0,692
-0,641
-0,589
-0,538
0,487
-0,435
-0,383
-0,330
-0,277
-0,224
-0,170
-0,116
-0,060
-0,040
У
0,790
0,795
0,800
0,805
0,810
0,815
0,820
0,825
0,830
0,835
0,840
0,845
0,850
0,855
0,860
0,865
0,870
0,875
0,880
0,885
0,890
0,895
0,900
0,905
z
0,052
0,110
0,168
0,228
0,289
0,351
0,414
0,479
0,545
0,613
0,683
0,754
0,829
0,905
0,984
1,066
1,151
1,240
1,332
1,428
1,530
1,636
1,749
1,868
Таблица 28
Значения функции g(z) [29]
2
-3,0
-2,9
-2,8
-2,7
-2,6
-2,5
-2,4
-2,3
-2,2
-2,1
-2,0
-1,9
s(z)
0,3328
0,3341
0,3561
0,3689
0,3826
0,3977
0,4128
0,4294
0,4472
0,4662
0,4866
0,5082
z
-1,8
-1,7
-1,6
-1,5
-1,4
-1,3
-1,2
-1,1
-1,0
-0,9
-0,8
-0,7
g{z)
0,5314
0,5560
0,5823
0,6102
0,6398
0,6713
0,7045
0,7396
0,7766
0,8156
0,8565
0,8993
z
-0,6
-0,5
-0,4
-0,3
-0,2
-0,1
0,0
0,1
0,2
0,3
0,4
0,5
0,9442
0,9909
1,0396
1,0902
1,1428
1,1917
1,2533
1,3113
1,4323
1,4953
1,5599
1,6259
z
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
g(z)
1,6935
1,7624
1,8327
1,9043
1,9771
2,0511
2,2024
2,2796
2,3578
2,4369
2,5169
2,5978
2.1.3.1.2. Оценки в неполностью определенных выборках
Неполностью определенная выборка имеет место, когда о части членов выборки
известно только, что они не больше (не меньше) некоторого граничного значения.
Предположим, что имеется выборка объема п из нормального распределения.
Для (п — По) членов выборки известны точные значения Xi {х\1Х21х% ... ,жп^По).
2.1]
Оценка параметров нормального распределения
125
Таблица 29
У
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,62
0,64
0,66
0,68
0,70
0,72
0,74
0,76
0,78
0,80
0,85
0,90
0,95
1,00
1,30
1,50
У
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,62
0,64
0,66
0,68
0,70
0,72
0,74
0,76
0,78
0,80
0,90
1,00
1,30
1,50
Значения функции ,
* = /О,!
/) Р9]
h
0,05
-2,786
-2,562
-2,384
-2,239
-2,117
-2,013
-1,923
-1,844
-1,710
-1,602
-1,512
-1,435
-1,369
-1,311
-1,260
-1,214
-1,173
-1,135
-1,055
-0,989
-0,934
-0,887
-0,702
-0,626
0,10
-2,680
-2,445
-2,263
-2,115
-1,992
-1,889
-1,800
-1,722
-1,653
-1,591
-1,536
-1,441
-1,360
-1,292
-1,233
-1,180
-1,134
-1,092
-1,055
-1,021
-0,990
-0,922
-0,866
-0,819
-0,778
-0,613
-0,545
0,15
-0,985
-1,862
-1,759
-1,671
-1,595
-1,528
-1,468
-1,415
-1,366
-1,322
-1,282
-1,211
-1,150
-1,097
-1,050
-1,009
-0,971
-0,937
-0,906
-0,878
-0,852
-0,795
-0,747
-0,706
-0,671
-0,525
-0,463
0,20
-1,537
-1,463
-1,398
-1,340
-1,289
-1,242
-1,200
-1,162
-1,127
-1,094
-1,064
-1,010
-0,963
-0,921
-0,884
-0,850
-0,819
-0,792
-0,766
-0,742
-0,721
-0,673
-0,631
-0,596
-0,565
-0,436
-0,381
0,25
-1,207
-1,158
-1,114
-1,074
-1,037
-1,004
-0,973
-0,945
-0,919
-0,894
-0,871
-0,829
-0,792
-0,759
-0,729
-0,702
-0,677
-0,654
-0,632
-0,613
-0,594
-0,553
-0,518
-0,488
-0,461
-0,347
-0,297
0,30
-0,943
-0,909
-0,877
-0,849
-0,822
-0,797
-0,774
-0,753
-0,733
-0,714
-0,696
-0,663
-0,634
-0,607
-0,583
-0,561
-0,540
-0,521
-0,503
-0,487
-0,471
-0,437
-0,407
-0,380
-0,357
-0,257
-0,212
0,35
-0,720
-0,695
-0,672
-0,651
-0,631
-0,612
-0,595
-0,579
-0,563
-0,548
-0,534
-0,508
-0,485
-0,463
-0,444
-0,425
-0,408
-0,393
-0,378
-0,364
-0,351
-0,322
-0,296
-0,273
-0,253
-0,165
-0,125
0,40
-0,523
-0,505
-0,488
-0,472
-0,457
-0,443
-0,429
-0,416
-0,404
-0,393
-0,382
-0,361
-0,343
-0,325
-0,309
0,294
-0,280
-0,267
-0,255
-0,243
-0,232
-0,207
-0,186
-0,166
-0,149
-0,072
-0,036
h
0,45
-0,345
-0,331
-0,318
-0,306
-0,295
-0,284
-0,273
-0,263
-0,254
-0,245
-0,236
-0,220
-0,204
-0,190
-0,177
-0,166
-0,154
-0,143
-0,133
-0,123
-0,114
-0,074
-0,043
0,025
0,056
0,50
-0,178
-0,168
-0,158
-0,149
-0,140
-0,132
-0,124
-0,116
-0,108
-0,101
-0,094
-0,081
-0,069
-0,058
-0,047
-0,037
-0,027
-0,019
-0,010
-0,002
0,006
0,039
0,066
0,124
0,151
0,55
-0,019
-0,017
-0,004
0,003
0,010
0,016
0,023
0,029
0,035
0,040
0,046
0,056
0,066
0,075
0,084
0,092
0,100
0,107
0,114
0,121
0,127
0,154
0,177
0,237
0,251
0,60
0,136
0,142
0,147
0,153
0,158
0,163
0,168
0,173
0,177
0,182
0,186
0,194
0,202
0,210
0,216
0,223
0,229
0,235
0,241
0,246
0,252
0,275
0,294
0,336
0,357
0,65
0,291
0,295
0,300
0,304
0,308
0,312
0,315
0,319
0,323
0,326
0,330
0,336
0,342
0,348
0,353
0,359
0,364
0,368
0,373
0,377
0,382
0,401
0,416
0,452
0,470
0,70
0,449
0,453
0,456
0,459
0,462
0,465
0,468
0,471
0,473
0,476
0,479
0,484
0,488
0,493
0,497
0,501
0,505
0,509
0,513
0,516
0,520
0,535
0,548
0,578
0,593
0,75
0,616
0,619
0,621
0,623
0,625
0,628
0,630
0,632
0,634
0,636
0,638
0,642
0,645
0,649
0,652
0,655
0,658
0,661
0,664
0,667
0,670
0,681
0,692
0,716
0,728
0,80
0,797
0,799
0,801
0,802
0,804
0,806
0,807
0,809
0,810
0,812
0,813
0,816
0,818
0,821
0,823
0,826
0,828
0,830
0,833
0,835
0,837
0,846
0,854
0,873
0,883
126
Оценка параметров распределений вероятностей
[Гл. 2
Оценки параметров /л и а тогда подсчитываются по формулам [29]
n-no
1 v^
x = — zs: s = У Х{
п — п0
г=1
где /г = —; z = /(/i, y) —функция аргументов /г и у = (п — '
п—по
v—л
г=1 о
значения табулированы в [29]; i/j(z)— функция аргумента z (значения приведены
в [29]).
Таблица 30
z
-3,0
-2,9
-2,8
-2,7
-2,6
-2,5
-2,4
-2,3
-2,2
-2,1
2,0
-1,9
-1,8
-1Д
-1,6
-1,5
-1,4
Значения функции ф
tjj(z)
3,2831
3,1903
3,0979
3,0058
2,9141
1,8227
2,7318
2,6414
2,5515
2,4621
2,3732
2,2849
2,1973
2,1103
2,0241
1,9387
1,8541
z
— 1,3
-1,2
-1,1
-1,0
-0,9
-0,8
-0,7
-0,6
-0,5
-0,4
-0,3
-0,2
-0,1
0,0
0,1
0,2
0,3
1,7704
1,6876
1,6058
1,5251
1,4456
1,3674
1,2905
1,2150
1,1411
1,0688
0,9982
0,9294
0,8626
0,7979
0,7353
0,6751
0,6172
[z) [29]
z
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
0,5619
0,5092
0,4591
0,4119
0,3676
0,3251
0,2876
0,2520
0,2194
0,1897
0,1629
0,1388
0,1173
0,0984
0,0819
0,0676
0,0552
Значения функций z = /(/г, у) и ip(z) воспроизведены в табл. 29 и 30. Сначала по
выборочным значениям Х{ вычисляются у и /г, затем по табл. 29 и 30 определяются
соответствующие им значения z = f(h,y) и tp(z).
2.1.3.1.3. Оценки в цензурированных выборках
2.1.3.1.3.1. Оценка максимального правдоподобия
Наиболее полно оценки такого типа рассмотрены в [135, 136]. Пусть из выборки
объема п известны только г первых членов. Это, кстати, классическая ситуация,
возникающая при проведении испытаний приборов на долговечность, когда из
п испытываемых приборов наблюдаются г отказов.
Итак, наблюдаются значения х\ ^ Х2 ^ . •. ^ хГ1 а для всех оставшихся (п — г)
приборов примем одно значение жд, равное хг.
Для первых г членов выборки имеем
x = -
,2 = i
-*)¦
г=1
Th V
Далее находим параметры h = ^^^ и 7 =
— x)
2.1]
Оценка параметров нормального распределения
127
Оценки для /л и а будут иметь вид [136]
где Aj(/i,7)—коэффициенты, приведенные в табл. 31.
Таблица 31
7
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
Значения
k(h,j) [
136]
h
ОД
0,1102
0,1180
0,1247
0,1306
0,1386
0,1409
0,1455
0,1499
0,1540
0,1579
0,1617
0,1932
0,2182
0,2395
0,2585
0,2757
0,2916
0,3065
0,3205
0,3337
0,2
0,2426
0,2574
0,2703
0,2819
0,2926
0,3025
0,3118
0,3207
0,3290
0,3370
0,3447
0,4093
0,4609
0,5052
0,5450
0,5803
0,6134
0,6442
0,6733
0,7009
0,3
0,4021
0,4233
0,4422
0,4595
0,4755
0,4904
0,5045
0,5180
0,5308
0,5340
0,5548
0,6547
0,7349
0,8038
0,8653
0,8912
0,9729
1,0210
1,0670
1,1100
0,4
0,5961
0,6234
0,6483
0,6713
0,6927
057129
0,7320
0,7502
057676
0,7844
0,8005
0,9382
1,0490
1,1460
1,2310
1,3090
1,3820
1,4400
1,5130
1,5730
0,5
0,8368
0,8703
0,9012
0,9300
0,9570
0,9826
1,0070
1,0300
1,0530
1,0740
1,0950
1,2740
1,4200
1,5460
1,6590
1,7620
1,8570
1,9460
2,0310
2,1100
0,6
1,1450
1,1850
1,2220
1,2570
1,2900
1,3210
1,3510
1,3800
1,4080
1,4350
1,4610
1,6860
1,8700
2,0310
2,1750
2,3070
2,4280
2,5430
2,6500
2,7530
0,7
1,5610
1,6080
1,6510
1,6930
1,7320
1,7700
1,8060
1,8410
1,8750
1,9080
1,9400
2,2170
2,4470
2,6490
2,8290
2,9950
3,1490
3,2930
3,4300
3,5590
0,8
2,1760
2,2290
2,2800
2,3290
2,3760
2,4210
2,4650
2,5070
2,5480
2,5880
2,6260
2,9680
3,2550
3,5080
3,7360
3,9450
4,1400
4,3220
4,4950
4,6600
0,9
3,2830
3,3450
3,4050
3,4640
3,5200
3,5750
3,6280
3,6790
3,7300
3,7790
3,8270
4,2580
4,6250
4,9520
5,2490
5,5220
5,7880
6,0180
6,2450
4,4620
Двусторонние доверительные интервалы с доверительной вероятностью а нахо-
находятся по формулам [136]
(а, п, г);
, п, г),
где %'(«, п, г), х/;(а, п, г)—коэффициенты, приведенные в табл. 32. При г = п (от-
(отсутствие цензурирования) оценки превращаются в обычные.
Двусторонний доверительный интервал для /л имеет вид [136]
, n, г)а; ?° (а) = А - t/;(
, n,
где tf(a,n,r), t"{a,n,r) — коэффициенты, приведенные в табл. 33.
Отметим основные особенности рассмотренных оценок:
— точная длина доверительного интервала в большей степени зависит от г
п — г
и в меньшей степени от п = :
п
— при фиксированном значении г длина доверительного интервала для /л оста-
остается практически постоянной при 0 ^ /i ^ 0,7 и увеличивается при h > 0,7;
— при г = const доверительный интервал для а медленно увеличивается с ро-
ростом п (или h);
— при п = const длина доверительного интервала уменьшается с ростом г.
128
Оценка параметров распределений вероятностей
[Гл. 2
Коэффициенты %'{
(верхняя строка) и
Таблица 32
, то, г) (нижняя строка) [119]
г
2
3
4
5
6
п
4,5
10
50
4
5
20
5
10
20
6
10
20
50
100
7
а = 0,90
0,7187
27,7780
0,7143
31,2500
0,7092
34,4830
0,7042
5,8820
0,7042
6,2500
0,6849
7,1430
0,7092
3,5710
0,6993
4,1660
0,6896
4,1660
0,7194
2,7780
0,7092
3,0300
0,7042
3,1250
0,6896
3,2260
0,6803
3,3330
0,7299
2,3810
а = 0,95
0,6097
58,8230
0,6024
66,1670
0,5952
66,1670
0,6329
8,3330
0,6211
9,0900
0,6060
10,0000
0,6452
4,5450
0,6289
5,2630
0,6173
5,5550
0,6622
3,4480
0,6452
3,7100
0,6329
4,0000
0,6250
4,0000
0,6135
4,1660
0,6803
2,7780
г
6
7
8
10
12
п
10
20
8
10
20
9
10
20
50
12
20
50
100
15
20
50
а = 0,90
0,7194
2,5190
0,7143
2,6310
0,7407
2,1280
0,7299
2,2220
0,7246
2,3250
0,7519
1,9610
0,7463
2,0410
0,7353
2,1280
0,7194
2,2220
0,7633
1,7860
0,7519
1,8520
0,7407
1,9230
0,7799
2,0000
0,7752
1,6660
0,7692
1,6950
0,7519
1,7540
а = 0,95
0,6622
2,9250
0,6536
3,1250
0,6896
2,4390
0,6803
2,6310
0,6667
2,7030
0,7042
2,2220
0,6944
2,3250
0,6944
3,4390
0,6666
2,5640
0,7143
2,0000
0,7042
2,0830
0,6896
2,1740
0,6803
2,2220
0,7299
1,8180
0,7246
1,8870
0,7042
1,9610
г
15
20
25
30
50
70
90
п
20
50
100
30
50
100
30
50
100
50
100
70
100
100
100
а = 0,90
0,7874
1,5620
0,7752
1,6130
0,7575
1,6670
0,8064
1,3500
0,8000
1,4920
0,7874
1,5150
0,8196
1,3510
0,8130
1,3890
0,8064
1,4280
0,8624
1,3330
0,8817
1,3700
0,8620
1,2340
0,8547
1,2500
0,8771
1,1900
0,8928
1,1490
а = 0,95
0,7463
1,6950
0,7299
1,7540
0,7143
1,8180
0,7633
1,5850
0,7576
1,6130
0,7463
1,6390
0,7936
1,4490
0,7752
1,4700
0,7692
1,5150
0,7692
1,4080
0,7874
1,4490
0,8333
1,2820
0,8264
1,2990
0,8547
1,2190
0,8772
1,1760
2.1.3.1.3.2. Оценки с помощью порядковых статистик
Предположим, что цензурирование заключается в отбрасывании из выбор-
выборки ri наименьших и г2 наибольших членов, а параметры /л и а оцениваются по
оставшимся (п — Г\ — г^) наблюдениям.
Наиболее просты в вычислительном отношении оптимальные линейные оцен-
оценки [118, 119]. Они находятся по формулам
где Xi — г~я порядковая статистика в выборке, упорядоченной по убыванию
(х\ ^ Х2 ^ • • • ^ хп); hi, k[ — коэффициенты оценки, табулированные в [118, 119].
Коэффициенты ki и к[ для выборки объема п = 10 приведены в табл. 34.
Очевидно, что таблицы для ki и к[ при различных сочетаниях п, 7*1 (гг) очень
громоздки и практически неприменимы. Поэтому рекомендуется использовать так
2.1]
Оценка параметров нормального распределения
129
Таблица 33
Коэффициенты 4#(о:, тг, г) (верхняя строка) и (— 1) • 4/#(о:, то, г) (нижняя строка) [119]
г
2
3
4
п
5
6
7
8
10
12
15
20
30
50
5
6
7
8
10
12
15
20
5
6
7
8
10
а
0,90
1,08
19,60
0,79
23,90
0,65
26,40
0,60
30,50
0,53
34,30
0,50
37,80
0,50
40,30
0,48
48,20
0,49
54,80
0,56
64,10
1,10
3,38
0,89
3,71
0,75
4,31
0,65
4,58
0,57
5,55
0,51
6,43
0,49
7,05
0,50
7,92
1,12
1,56
0,91
1,81
0,79
1,95
0,68
2,21
0,58
2,60
0,95
1,75
41,20
1,22
51,70
0,90
55,10
0,79
60,60
0,68
70,60
0,66
75,60
0,65
85,80
0,65
100,00
0,70
112,00
0,78
123,00
1,55
5,11
1,25
5,61
1,01
6,51
0,85
7,10
0,71
8,21
0,64
9,82
0,60
10,70
0,61
1,27
1,47
2,16
1,20
2,51
1,03
1,95
0,88
3,01
0,73
3,59
г
4
5
6
7
п
12
15
20
6
7
8
10
12
20
30
50
70
90
100
7
8
10
12
15
20
8
10
12
а
0,90
0,52
2,78
0,48
3,29
0,47
3,68
0,90
1,17
0,80
1,26
0,69
1,35
0,59
1,56
0,51
1,72
0544
2,31
0,46
2,80
0,50
3,40
0,52
3,84
0,57
4,11
0558
4,21
0,80
0,94
0570
0,98
0,60
1,11
0,52
1,20
0,46
1,42
0,43
1,65
0,71
0,81
0,61
0,88
0,53
0,96
0,95
0,64
3,86
0,53
4,61
0,57
5,10
1,16
1,54
1,03
1,67
0,90
1,85
0,75
2,11
0,63
2,33
0,53
3,19
0,55
3,78
0,59
4,62
0,64
5,21
0,69
5,47
0,70
5,66
1,02
1,21
0,89
1,28
0,75
1,46
0,65
1,58
0,56
1,86
0,51
2,17
0,88
1,04
0,76
1,12
0,66
1,12
г
7
8
10
12
15
п
15
20
10
12
15
20
30
50
12
15
20
30
50
70
90
100
15
20
30
25
35
50
70
а
0,90
0,46
1,09
0,41
1,25
0,61
0,74
0,53
0,80
0,46
0,88
0,41
1,03
0,38
1,25
0,40
1,56
0,53
0,62
0,47
0,66
0,39
0,75
0,36
0,89
0,36
1,11
0,39
1,30
0,41
1,44
0,42
1,45
0,46
0,55
0,39
0,60
0,33
0,68
0,34
0,49
0,31
0,55
0,38
0,66
0,32
0,75
0,95
0,56
1,40
0,49
1,63
0,77
0,94
0,66
1,12
0,56
1,13
0,49
1,35
0,45
1,63
0,47
2,00
0,67
0,78
0,57
0,83
0,47
0,95
0,42
1,12
0,43
1,41
0,47
1,65
0,49
1,80
0,50
1,90
0,57
0,68
0,47
0,75
0,40
0,86
0,41
0,62
0,37
0,69
0,35
0,81
0,37
0,94
г
15
20
25
30
40
50
п
90
100
40
50
70
90
100
35
50
70
90
100
50
70
90
100
50
70
90
100
70
90
100
а
0,90
0,33
0,85
0,34
0,89
0,28
0,42
0,27
0,47
0,27
0,54
0,28
0,59
0,29
0,61
0,29
0,34
0,25
0,37
0,24
0,42
0,25
0,46
0,25
0,48
0,24
0,31
0,23
0,34
0,23
0,37
0,24
0,39
0,24
0,26
0,21
0,27
0,20
0,28
0,20
0,29
0,20
0,23
0,19
0,23
0,18
0,24
0,95
0,40
1,05
0,40
1,12
0,34
0,52
0,32
0,59
0,32
0,66
0,34
0,73
0,34
0,76
0,35
0,41
0,36
0,45
0,28
0,51
0,29
0,57
0,30
0,59
0,28
0,38
0,27
0,42
0,27
0,45
0,28
0,47
0,28
0,32
0,25
0,32
0,24
0,34
0,24
0,35
0,24
0,27
0,22
0,28
0,22
0,29
5 А. И. Кобзарь
130
Оценка параметров распределений вероятностей
[Гл. 2
Таблица 34
Коэффициенты ki (верхняя строка) и к[ (нижняя строка) для п = 10
7*1
' 1
0
1
2
3
4
0
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
2
3
4
5
6
3
4
5
4
i
1
0,1000
-0,2044
0,0843
-0,2364
0,0605
-0,2753
0,0244
-0,3252
-0,0316
-0,3930
-0,1240
-0,4919
-0,2923
-0,6520
-0,6598
-0,9625
-1,8634
-1,8608
-0,5877
-1,4678
-1,9000
-2,8960
2
0,1000
-0,1172
0,0921
-0,1314
0,0804
-0,1523
0,0636
-0,1758
0,0383
-0,2063
-0,0016
-0,2491
-0,0709
-0,3150
-0,2138
-0,4357
2,8634
1,8608
0,1884
-0,4034
0,7525
-0,4803
0,0942
-0,5842
-0,0043
-0,7959
-0,1866
-1,0120
-0,2918
2,9000
2,8960
3
0,1000
-0,0763
0,0957
-0,0851
0,0898
-0,0947
0,0818
-0,1058
0,0707
-0,1192
0,0549
-0,1362
0,0305
-0,1593
1,8734
1,3981
0,1036
-0,1074
0,0961
-0,1235
0,0846
-0,1440
0,0665
-0,1719
0,0351
-0,2145
1,6166
1,7595
0,2798
-0,7021
0,2050
-0,8898
0,0706
-1,1952
-0,2648
-1,7947
-1,3406
-3,5677
4
0,1000
-0,0436
0,0986
-0,0465
0,0972
-0,0488
0,0962
-0,0502
0,0962
-0,0501
0,0990
-0,0472
1,3327
1,1263
0,1040
-0,0616
0,1013
-0,0674
0,0979
-0,0734
0,0938
-0,0797
0,0892
-0,0859
0,1099
-0,0947
0,1038
-0,1101
0,0935
-0,1318
0,0735
-0,1688
2,3406
3,5677
0,3807
-1,2832
0,1871
-1,9791
-0,4747
-3,9511
5
0,1000
-0,0142
0,1011
-0,0110
0,1037
-0,0077
0,1089
-0,0006
0,1185
0,0111
0,9718
0,9243
0,1041
-0,0201
0,1057
-0,0166
0,1095
-0,0097
0,1179
0,0031
1,0623
1,2835
0,1103
-0,0310
0,1122
-0,0262
0,1178
-0,0144
1,1914
1,9635
0,1193
-0,0589
0,1198
0,0553
1,4847
3,9511
0,5000
-4,0761
6
0,1000
0,0142
0,1036
0,0215
0,1099
0,0319
0,1207
0,0469
0,7078
0,7576
0,1041
0,0201
0,1098
0,0325
0,1204
0,0514
0,7261
0,9844
0,1103
0,0310
0,1198
0,0549
0,7281
1,3415
0,1193
0,0559
0,6930
2,0344
0,5000
4,0761
7
0,1000
0,0436
0,1060
0,0559
0,1161
0,0722
0,5045
0,6107
0,1040
0,0616
0,1138
0,0827
0,4933
0,7599
0,1099
0,0947
0,4592
0,9711
0,3807
1,2832
8
0,1000
0,0763
0,1085
0,0937
0,3424
0,4746
0,1036
0,1074
0,3209
0,0572
0,2798
0,7021
9
0,1000
0,1172
0,2101
0,3423
0,1884
0,4034
10
0,1000
0,2044
2.1] Оценка параметров нормального распределения 131
называемые альтернативные оценки Гупты [137, 138], вычисляемые по формулам
где щ и bi —весовые коэффициенты, вычисляемые по формулам
_ ! &(ui -U) _ Ui-U
J2 (Ui - uf J2 (Ui - uf
Щ — математическое ожидание г-й порядковой статистики из стандартного нор-
нормального распределения;
Эффективность этой оценки составляет 0,96 -т- 0,98 от оптимальной линейной
при п > 10. Напомним, что для Щ может быть использована полезная аппроксима™
ция
Щ = 4,91(п + 0,25)^0'14 [(г - 0,375H'14 - (п - г + 0,625H'14].
В заключение приведем простую оценку для /i, предложенную Диксоном [139]:
"*П Г /V -I- IVt i 1 -I- т ^
^r -t- ij^r+i +жп^г;
i=2
где г = max(ri,r2).
Эффективность этой оценки не уступает эффективности оптимальной линейной
оценки.
Задача 48. Испытаны 15 приборов. При этом значения параметра — критерия годно-
годности зафиксированы у 10 приборов:
Xi: 1,1; 2,1; 2,4; 3,1; 3,5; 3,7; 4,2; 4,8; 5,9; 6,3,
а для остальных известно, что их наработка имеет большее значение. Необходимо
вычислить оценки максимального правдоподобия для /i и а.
ю ю
10 162 11
Находим Yxi = 37,1; Y xi = 162,11 иу= ^ и 0,59.
г^ ^1 2 - C7,1J
Для г/ = 0,59 из табл. 27 имеем z = —2?232, а из табл. 28 (интерполируя) имеем
g(z) ~ 0,439. Окончательно оценки равны
ю 10
s = 5^ ~ ' S(z) = ^^ * J2 Xi = 0^0439 * 37,1 = 1,628; х = 2,232 • 1,628 = 3,635.
Задача 49. Решить задачу 48, исходя из того, что степень усечения известна (пред-
полоэюим, она равна оценке h = по/п).
Пользуемся формулами для неполностью определенной выборки (см. раз™
10
10 J2 ж?
дел 2.1.3.1.2). Имеем у = — ^ = °'59-
132 Оценка параметров распределений вероятностей [Гл. 2
Оценку нормированной точки усечения z = f{h^y) находим из табл.29 (h = 0,333
и у = 0,59): z = /@,333; 0,59) = -0,631.
Далее из табл. 30 имеем ф(г) = 0,4355 и находим
l~h 1333 =1,17918.
h • ф(г) - A - /i) ¦ z 0,333 • 0,4355 + 0,6666 • 0,631
Окончательно, s = — • 37,1 • 1,17918 = 4,374; x = 0,631 • 4,374 = 2,756.
Разница в оценках является следствием отклонения истинной степени усечения от ее
оценки, полученной по малой выборке.
Задача 50. Для данных задачи 48 найти оценки /х и ст, исходя из того, что в выборке
объема п = 10 два наибольших наблюдения цензурированы.
Из условия задачи следует, что известны 8 значений:
Xi: 1,1; 2,1; 2,4; 3,1;; 3,53,7; 4,2; 4,8,
а два наибольших члена выборки E,9 и 6,3) из нее исключены (цензурированы).
Оценка максимального правдоподобия B.1.3.1.3.1)
1 8 24 5 1 8
Имеем п = 10, г = 8 и х = - • ]Г хг = —^- = 3,0625; s2 = - • ]Г(з^ - xf = 1,3523.
г=1 i=l
Далее h = ^—^ = 0,2 и 7 = о = ^^^ о = 0,4479.
10 ' ' (Жо _ жJ D,8 - 3,0625J
Из табл. 31 для 7 « 0,45 и /i = 0,2 имеем ifc@,2; 0,45) « 0,2872.
Тогда окончательно
Д = 3,0625 + D,8 - 3,0625) • 0,2875 = 0,5615;
а = [1,3523 + D,8 - 3,0625J • 0,2872] \ = 1,4897.
Найдем теперь двусторонний доверительный интервал при а = 0,95 для ц и а. Из табл. 32
находим значения х;@,95; 10,8) = 0,6944 и х/;@,95; 10,8) = 2,325 и далее вычисляем:
<т* = а • х = 1,4897 • 0,6944 = 1,0344; <т? = а • х" = 1,4897 • 2,325 = 3,4635,
т.е. 1,0344 ^ <т ^ 3,4635 с доверительной вероятностью 0,95.
Теперь из табл. 33 имеем ?;@,95; 10,8) = 0,77 и ?;/@,95; 10,8) = 0,94.
Следовательно,
(а1 = 3,5615 - 0,77 • 1,4897 = 2,414; /^ = 3,5615 + 0,94 • 1,4897 = 4,962,
и доверительный интервал равен 2,414 ^ /j, ^ 4,692 с вероятностью а, = 0,95.
Оценка с помощью порядковых статистик B.1.3.1.3.2)
В нашем случае Гг = 0;г2 = 2ип = 10. Из табл. 34 находим
кг = 0,0605; к2 = 0,0804; к3 = 0,0898; к4 = 0,0972;
к5 = 0,1037; к6 = 0,1099; к7 = 0,1161; к8 = 0,3224;
к'г = -0,2753; к'2 = ^0,1523; к'3 = -0,0947; к'А = -0,0488;
к'Б = -0,0077; к'6 = 0,0319; к'7 = 0,0722; к8 = 0,4746.
Далее имеем
8
fin = J2ki'Xi = °5°605 ' 1Д + 0,0804 • 2,1 + 0,0898 • 2,4 + 0,0972 • 3,1 + 0,1037 • 3,5 +
i=1 + 0,1099 • 3,7 + 0,1161 • 4,2 + 0,3424 • 4,8 = 3,6529;
(тп = -0,2753 • 1,1 - 0,1523 • 2,1 - 0,0947 • 2,4 - 0,0488 • 3,1 - 0,0077 • 3,5 +
+ 0,0319 • 3,7 + 0,0722 • 4,2 + 0,4746 • 4,8 = 1,671.
2.1] Оценка параметров нормального распределения 133
Рассмотрим простую оценку Диксона для /i (r = 2)
В заключение рассмотрим вычисление необходимых оценок с помощью оценок Гупты.
Предварительно вычислим математические ожидания необходимых порядковых стати-
статистик:
11г = 4,91 • A0,25H'14 • [A - 0,375H'14 - (п - 1 + 0,625H'14] =
= 3,5447-[A - 0,375H'14 - A0 - 1 + 0,625H'14] = 355447-@,6250'14 - 9,6250'14) = -1,54797;
U2 = -0,99874; U3 = -0,65329; U4 = -0,37392; U5 = 0,122032;
UQ = 0,122033; U7 = 0,37392; Us = 0,65329.
Далее вычисляем:
8
U = ^0,3833875; J2 (Ui ~ ^f = 29,967746.
i=l
Вычисляем коэффициенты оценки:
1 (-0,31833875) • (-1,54797 + 0,31833875) ПЛЛЛЛА
ai = 8 ^^S = °'1П94;
a2 = 0,11772293; a3 = 0,1214419; a4 = 0,1244092; a5 = 0,127085;
a6 = 0,1296779; a7 = 0,1323536; a8 = 0,1353213.
Таким образом, оценка равна
fin = 0,11194 • 1,1 + 0,11777 • 2,1 + 0,12144 • 2,4 + 0,124409 • 3,1 + 0,127085 • 3,5 +
+ 0,12968 • 3,7 + 0,132354 • 4,2 + 0,13532 • 4,8 = 3,17746.
134 Оценка параметров распределений вероятностей [Гл. 2
2.2. Оценка параметров экспоненциального распределения
Напомним, что плотность экспоненциального распределения вероятностей слу-
случайной величины описывается формулой
1 / х\
f(x;u) = -exp^--J, x ^ О,
где v — параметр распределения.
Экспоненциальное распределение широко применяется при анализе надежности
технических устройств. Поэтому представляет интерес оценка параметра экспо-
экспоненциального распределения применительно к различным планам испытаний на
надежность. В качестве оцениваемого параметра в этом случае рассматривается,
Л 1
как принято в теории наделености, интенсивность отказов А = —.
Для обозначения планов испытаний применяется 3-позиционный код, предло-
предложенный авторами работы [140]. Первая позиция кода обозначает число испытывав™
мых изделий (объем выборки). Вторая позиция — буква, указывающая, заменяются
ли при испытаниях отказавшие приборы или нет (В — заменяются; Б — не заменя-
заменяются). Третья позиция кодирует условия проведения испытаний (Т — испытания
ведутся в течение заданного времени Т; г — испытания ведутся до получения г
отказов). Например, код [15, Б, 2] означает, что оценка Л проводится по результатам
испытаний 15 приборов, без замены отказавших в процессе испытаний, до получения
двух отказов. Иногда используются смешанные планы. Например, [7V, В,(г,Т)] —
план, при котором N приборов испытываются с заменой отказавших до появления г
отказов, но не более времени Т.
2.2.1. Точечные оценки
2.2.1.1. Оценка максимального правдоподобия
Обозначим через d число изделий, отказавших за время проведения испыта-
испытаний Т. Тогда оценки параметра Л находятся по формулам [140]:
1 d л г-1 d
—, если tr > Т;
где tr — время наступления г~го отказа; t{ — наработка г-ro прибора до отказа.
Справедливы аппроксимации
при — ^ 0,1 и d ^ 10;
при 0,2 <^ 0,8.
Оценка параметров экспоненциального распределения
135
Далее
А
М,з,(г7Т)
если tr > T:
r-1
если tr
T.
-r)tr
2.2.1.2. Уточненная двухстадийная оценка
В [141] предлагается эффективная оценка параметра z/, основанная на двух-
стадийной процедуре. Оценка исходит из того факта, что величина
2пх
имеет
распределение х2 с / = 2п степенями свободы (п — объем выборки, х = —
г=1
Суть процедуры оценки заключается в следующем. На первой стадии рассма-
рассматривается предполагаемое значение щ. Далее, устанавливая приемлемый уровень
достоверности а, проверяем справедливость неравенства
X
2
2пх
<Х
где Х2(Р) ~~ /^^квантиль распределения %2 с / = 2п степенями свободы.
Если неравенство не отклоняется, то принимаются более точные оценки
2пх
Эффективность первой оценки в 2 + 2,5 раз выше обычной, второй — в 2 + 3,5 раз
(обычная оценка v = х).
2.2.1.3. Оценкм, основанные на порядковых статистиках
2.2.1.3.1. Оптимальная линейная оценка
Предположим, что имеет место двустороннее цензурирование, т. е. неизвестны
значения г\ наименьших и г2 наибольших членов выборки объема п. При г\ = г2 = О
будем иметь случай полной (нецензурированной) выборки.
Оптимальная линейная оценка находится по формуле [119]
жГ1+1+г2жп_Г2 +
где
n - ri - r2 - 1; m=
г=1
г=1
_ • ¦ i •
136
Оценка параметров распределений вероятностей
[Гл. 2
Здесь Xi—г-я порядковая статистика выборки (г-й по величине член выборки,
ранжированной по возрастанию х\ ^ х^ ^ . •. ^ хп); 7*1,7*2 —количества цензуриро™
к
ванных соответственно наименьших и наибольших наблюдений в выборке; ^ сц —
г=1
математическое ожидание к-й порядковой статистики в выборке объема п из нор-
нормированного экспоненциального распределения.
При п = Г2 = 0 оценка щ совпадает с оценкой максимального правдоподобия
г=1
При ri = 0 имеем щ =
+
, что совпадает с оценкой для
V )
плана испытаний [7V, Б, г] (при r^ = ^V — г, см. раздел 2.1.1). Иногда в выборке от-
отсутствует (цензурирована) часть центральных (средних по величине) выборочных
значений. Если известны только s наименьших и г наибольших членов выборки, то
оценка для v имеет вид [119]
щ =
где
/
s-l
г=1
п-г+1
\
n-r+l
i=s+l
ui
— г ¦
Е
г=1
г-г+1+г
n-r+l
Е-
i=s + l
л- - ¦ • - ¦ n-r+l
i=s+l
2.2.1.3.2. Оценка по одной порядковой статистике
Хартер [142] и Эпштейн [119] предложили оценку г/, основанную на одной
порядковой статистике хг (т.е. на одном r-м по величине наблюдении). Оценка
находится по формуле
Хг
Эпштейн показал, что эффективность этой оценки по сравнению с оценкой щ
г 2 г 1
больше 0,96 при — ^ - и 0,98 при — ^ -.
2.2.1.3.3. Оценка Эпштейна [119]
Если в выборке цензурированы (s — 1) наименьших членов, то оценка находится
по формуле
\
1
V = —
п
- s — п
L \ г=1
i=s+l
Оценка параметров экспоненциального распределения
137
При цензурировании (s — 1) наименьших и (г — 1) наибольших по величине
наблюдений оценка Эпштейна имеет вид
\
п — г + 1
1
+ s — п
+ У2 Xi + хп^г+\
2.2.1.3.4. Оценка Огавы [119]
Оценка Огавы позволяет произвести оценку параметра Л = 1/и экспоненциала
ного распределения по ограниченному числу порядковых статистик. Оценки рас™
к
смотрены в [142-151] и имеют вид i/0 = ]Р 6^Ж[пе.]+1, где к— количество порядковых
статистик, по которым производится оценка ([...]—целая часть числа); bi,ei —
коэффициенты оценки, приведенные в табл. 35.
Двумя наилучшими наблюдениями, по которым при к = 2 следует находить
оценку z/°, являются:
xn—i,xn при 4
п^45 ^п ПРИ 15 ^
п ^ 2; хп^2^хп при 7 ^ п ^ 5; жп^з5жп ПРИ 11 ^ тг ^ 8;
^ 12; xn^Q^ xn^i при 18 ^ п ^ 16; жп„7? хп-1 ПРИ 21 ^ n ^ 19.
Задача 51. Партия изделий объема N = 100 испытана на надежность с заме-
ной отказавших приборов в течение времени Т = 1000 ч, при этом наблюдались
d = 10 отказов. Найти оценку интенсивности отказов X.
Для плана испытаний [100, Л, Т = 1000] имеем
_ d _ 10
Aiv,B,T = ^^ = 100.1000
Задача 52. Найти оценку интенсивности отказов в условиях задачи 51, приняв, что
100 ч — это момент отказа 10-го изделия.
Имеем г = 10, tr = 1000 ч. Для плана [100, В, г = 10] получаем
у, ^
N -U
10-
100 • 1000
=9-10
Задача 53. Партия изделий объема N = 10 шт. была испытана на надежность в те-
течение 1000 ч без замены отказавших изделий. При этом были зафиксированы 5 отказов
в моменты времени (ч)
ti = 120, t2 = 170, t3 = 210, U = 250, t5 = 600.
Вычислить оценку интенсивности отказов.
Имеем план [10, Б, Т = 1000] и d = 5. Для него получаем
5
A20 + 170 + 210 + 250 + 600) + A0 - 5) • 1000
= 7,874-
Задача 54. Найти оценку интенсивности отказов в условиях задачи 53, если испы-
испытания приборов были завершены после получения Б-го отказа.
Находим
Xn б г = т ^—^ ч ; ч = 9,195 • 10^4 ч.
' ' A20 +170 + 210 + 250 + 600) + A0-5)-600
138
Оценка параметров распределений вероятностей
[Гл. 2
Я"
н
VD
Е-"
я
со
ю
со
см
о
оо
t>
СО
ю
со
см
т-Н
о
т-Н
г-
о
00
о
00
т—1
о
СМ
О)
т-Н
о
Is-
ю
о
СМ
о
г-
о
см
см
о
т-Н
Of)
СО
СМ
о
00
00
ю
СМ
о
Is-
см
00
СМ
о
Т-Ч
СМ
т-Н
СО
О
СЮ
Is-
СО
О
т—I
СО
СЛ
0О
О
т—I
ю
о
СО
О)
см
ю
о
со
00
СО
ю
о
on
СО
СЛ
Is-
о
т—1
СО
т-Ч
СО
т-Ч
О
СО
О
Is-
т-Ч
О
Is-
о
00
1—1
о
СО
СМ
СЪ
т—1
О
СО
Ю
О
СМ
О
ч—|
О
см
см
о
ю
Is-
СО
см
о
ел
Is-
ю
см
о
СЛ
т-Ч
Of)
см
о
00
о
т-Ч
СО
о
СО
CD
СО
О
Is-
о
СЛ
СО
О
I4-
Is-
О
см
00
см
ю
о
ю
Is-
см
СО
о
00
о
СМ
СО
о
00
СО
СО
О
ю
Of)
Ю
СО
О
О
1—1
0Г")
СО
О
со
СО
О
О
со
со
о
о
СО
т-Н
ю
ю
о
со
со
о
ю
о
СО
1—1
ю
Ю
о
см
о
со
о
о
ь-
со
СО
о
СЛ
т-Ч
t-
о
о
о
СО
00
о
со
со
см
СЛ
о
см
см
т-Ч
т-Ч
о
О)
Is-
т-Ч
о
т—1
ю
ю
т-Ч
о
Is-
см
СО
т-Ч
о
т-Ч
т-Ч
Is-
т—1
о
О)
о
о
см
о
СЛ
т-Ч
т-Ч
см
о
СЛ
о
о
см
о
СЛ
т-Ч
т-Ч
см
о
00
см
см
см
о
о
см
СО
см
о
т-Ч
со
СО
см
о
со
со
см
см
о
о
СЛ
Is-
т—1
о
Ю ^ СО
т—1 CM Tt
Ю (М СО
^ т-Ч Ю
о о о
Ю GO Ю
\ff CD О
t- СМ СЛ
^ т-Ч Ю
о о о
т-Ч СМ т-Ч
О т-Ч О)
О СО т-Ч
Ю т-Н СО
о о о
^ СО СМ
00 Ю О
СМ СО Ю
Ю т-Ч СО
о о о
СО (М т-Ч
О) О ^
Ю ^ 00
Ю т-Ч СО
о о о
СО СО СМ
^ ^ т-Ч
О) ^ СМ
Ю т-Ч Ь-
о о о
О СО СО
^ GO H
СО ^ CD
со т-ч ь-
о о о
СМ т-Ч СО
00 т-Ч т-Ч
ь- ю со
сонь
о о о
Ь Q Ь-
t- т-Ч ""ЧН
см ю о
Ь- т-ч оо
о о о
00 СМ 00
CM CJ Ь-
оо ^ as
Ь н оо
о о о
^ см ^
СО О СО
"чН ^ ^
00 т-Ч Си
о о о
ь- ю о
СО СЛ т-Ч
О т-Ч 00
ОН©
о о о
ю ю
ю ь-
СО Ь-
СЛ О
о о
СО Tf
т-Ч
ю
о
о
СО
Is-
о
т-Ч
о
СО
СЪ
о
т-Ч
о
т_н
т-Ч
т-Ч
т-Ч
о
см
т-Ч
т-Н
о
Is-
см
т-Ч
тН
о
ю
т-Ч
т-Ч
о
CD
т-Ч
т-Ч
т-Ч
о
см
Of)
о
т-Ч
о
см
о
О)
о
о
О)
о
Is-
о
о
О5
о
3
о
ю
о
СО
со
о
о
Of)
Of)
со
о
ю
т—1
It-
CD
т-Ч
О)
о
см
00
t-
о
т-Ч
Of)
т-Ч
00
о
т-Ч
ю
ю
00
о
00
см
ел
00
о
ь-
см
ел
о
т—1
со
со
ел
о
ю
00
Of)
О)
о
ю
О)
00
оо
о
о
ю
О)
00
о
о
со
СЪ
00
о
о
т-Ч
О)
0Г")
о
о
ю
Is-
00
о
о
Is-
00
о
о
ел
О)
Is-
о
о
ю
см
1^-
о
о
ю
т-Ч
со
о
о
со
ю
о
о
СО
см
о
о
СО
т-Ч
t-
о
CD
Of)
CD
t-
o
Is-
Oi
t-
o
Is-
CM
GO
о
CO
00
Ю
00
о
CD
Q)
00
GO
О
Ю
о
CM
о
CD
О)
О
CD
Is-
O5
О
Ю
CM
Oi
O5
о
CD
т-Ч
Is-
О
о
CO
CO
Is-
o
о
00
т-Ч
Is-
o
о
О)
CO
О
о
СЪ
ю
со
о
о
Is-
о
СО
о
о
со
СО
ю
о
о
00
СО
о
о
т-Ч
т-Ч
СО
О
о
со
ю
т-Ч
о
о
т-Ч
00
о
00
О
о
СО
00
О
СО
О
СО
00
о
Is-
(X)
00
О
о
т—|
CD
о
ев
ОО
О5
О
со
см
со
о
о
00
тН
00
о»
о
00
СИ
ел
о
1>
Is-
о
СО
о
о
Is-
00
ю
о
о
о
СО
ю
о
о
см
см
ю
о
о
см
Is-
о
о
Is-
о
о
о
см
СО
о
о
см
см
см
о
о
Is-
о
т-Ч
о
о
см
со
00
о
00
ю
00
00
о
т—1
СЪ
о
ел
о
Is-
1—1
со
О)
о
оо
см
ю
О)
о
ю
т-Ч
Is-
о
ю
со
00
О)
о
СО
со
О)
О)
о
00
со
00
о
о
00
ю
о
о
т—1
см
о
о
со
о
о
СО
т-Ч
СО
О
О
СО
см
о
о
со
т-Ч
о
о
со
Is-
о
о
о
СО
ю
о
ел
о
LO
ю
см
Oi
о
00
ел
о
ю
см
СО
ел
о
оо
Is-
Is-
О5
о
Is-
сл
00
ел
о
СО
г-
сл
ел
о
О)
о
00
со
о
о
СО
о
о
т-Ч
о
00
о
о
о
ю
см
о
о
т-Ч
О)
т-Ч
о
о
см
т-Ч
о
о
ю
ю
о
о
о
СО
00
со
ел
о
00
^t*
ю
CD
о
Is-
съ
со
ел
о
см
Of)
О)
о
о
см
(Л
ел
о
ел
Is-
сл
О)
о
о
ю
00
см
о
о
Is-
см
о
о
см
о
см
о
о
т-Ч
ю
1—1
о
о
Is-
сл
о
о
о
см
о
о
о
ю
см
СО
ел
о
см
ю
Is-
сл
о
00
ю
00
C7i
о
со
СО
СЪ
ел
о
сю
ел
ел
о
т-Ч
о
см
о
о
ю
со
т-Н
о
о
см
см
т-Ч
о
о
Is-
Is-
о
о
о
со
СО
о
о
о
ел
Is-
О)
о
ОО
Of)
00
ел
о
ел
ел
ел
о
Is-
00
СЪ
ел
о
см
ел
00
т-Ч
о
о
о
о
т-Ч
о
о
см
СО
о
о
о
со
см
о
о
о
СО
о
СЪ
ел
о
00
ю
ел
CD
о
о
СЪ
ел
ел
о
СО
СО
00
о
о
о
т—1
ю
о
о
о
т—|
см
о
о
о
ю
СО
СЪ
ел
о
т-Ч
ел
О)
ел
о
см
о
о
о
Is-
т—1
о
о
о
СО "^
ел т-ч
ел о
ел о
о о
ю
2.2] Оценка параметров экспоненциального распределения 139
Задача 55. Получена выборка значений экспоненциально распределенных величин xf.
10,1; 10,6; 11,2; 12,6; 13,4; 14,8; 15,9; 17,1; 19,1. Необходимо найти уточненную двухста-
дийную оценку параметра v = 1/Л (см. раздел 2.2.1.2).
Пусть предполагаемым значением и является щ = 15. Выбираем уровень достовер-
достоверности а = 0,95. Находим по табл. 55 или с помощью апппроксимаций (см. 1.1.8) при
/ = 2 • 10 = 20: х2 ( г ~ °?95 ) = Х2@,025) = 9,59 и Х2@,Э75) = 34,2.
Далее вычисляем
х=±±х> = 13,66 и ^ = 2013'66 = 18,2133.
Убеждаемся, что 9,59 < = 18,2133 < 34,2. Так как неравенство выполняется, вы™
числяем уточненные оценки:
Задача 56. Используя данные задачи 55, найти оценки параметра экспоненциального
распределения с помощью порядковых статистик.
Оптимальная линейная оценка B.2.1.3.2)
Рассматриваем вариант отсутствия цензурирования, т. е. когда п = г2 = 0. В этом
случае вычисляем:
1 1 2 1 /1
тп = а,\ = = —; I = п\ = —7?; с = I —
71 — 1 + 1 71 П \П
Следовательно,
1 Г/^2 \ п 1 1 п
xi + V хА = - • У" Xi = 13,66,
i^l \ n i^l
т. е. оценка совпадает с обычной оценкой максимального правдоподобия.
Предположим, что п = 2 первых и Г2 = 1 последних членов выборки цензурированы.
В этом случае имеем
™ = 2>; ' = ?«?; ^ = = ;
г=1 г=1
Тогда
Предположим теперь, что цензурированы (исключены из выборки) центральные ее
члены — известны только s = 3 первых члена и г = 4 наибольших члена. Для вычисления
оценки в этом случае найдем
,-r+l
?4 (?«*
У^ а2
140
Оценка параметров распределений вероятностей
[Гл. 2
Последовательно вычисляя, получаем
11 11
а4 =
п-4+ 1 7'
2
a4 =0,576876; ]Г а* = 0,1506859;
г=4 / г=4
0,576876
= 0,759523;
0,1506859
= 9,82833343
и окончательно
1
щ =
0,82833343
2
г=1
0,75952
= 20546177.
Оценка по одной порядковой статистике B.2.1.3.2)
Предположим, что оценка производится по 7-й порядковой статистике Х7.
Имеем
Ещ = V = — + - + ... + - = 1,09563492; i/7 = — = 13,508149.
^ n ~ i + 1 10 9 4 ' ' 1,09563492
г=1 г=1
Оценка Эпштейна B.2.1.3.3)
Предполож:им, что в выборке цензурированы 2 наименьших наблюдения (s — 1 = 2;
s = 3). Тогда получаем
X
3-10
= 0,1 х
111
. 10 + 9 + 8
- 7 • 11,2 + 11,8 + 12,6 + 13,4 + 14,8 + 15,9 + 17,1 + 19,1
= 12,626694.
Предположим, что в выборке цензурировано s — 1 = 2 наименьших и г — 1 = 2 наи-
наибольших наблюдений. Тогда оценка будет равна
п- 2
\
3- 10
¦Е--
г=4
• жз + 2^ жг + 3 •
= 15,120867.
Оценка Огавы B.2.1.3.4)
Будем искать оценку по четырем, оптимальным образом выбранным, порядковым
статистикам. Из табл. 35 для к = 4 находим:
?1 = 0,4514; е2 = 0,7419; е3 = 0,9067; е4 = 0,9810;
bi = 053907; Ь2 = 0,2361; Ь3 = 0,1195; Ь4 = 0, 0409.
Тогда для оценки отбираем порядковые статистики с номерами
[п • 0,4514] + 1 = 5; [п • 0,7419] + 1 = 7; [п • 0,9067] + 1 = 9; [п • 0,9810] + 1 = 10.
Оценка параметров экспоненциального распределения
141
Вычисляем оценку
и0 = 0,3907 • х5 + 0,2361 • х7 + 0,1195 • х9 + 0,0409 • х10 =
= 0,3907 • 12,6 + 0,2361 • 14,8 + 0,1195 • 17,1 + 0,0409 • 19,1 = 11,2417.
Если бы мы хотели произвести оценку по двум оптимально выбранным порядковым
статистикам, то ими должны быть х7 и %, для которых Ь\ = 0,5232 и 62 = 0,1790.
Тогда оценка равна и0 = 0,5232 • 14,8 + 0,1790 • 19,1 = 11,16226.
2.2.2. Интервальные оценки
Интервальная оценка параметра v (средняя наработка между отказами) при
доверительной вероятности а подсчитывается по формулам
2
Ху
2
ХУ
где х^—7™квантиль распределения хи^квадрат с f = 2п степенями свободы;
для двусторонней оценки и jf = a, jff = 1 — а для односто™
7 =
1 + а
-, 7 =
1-а
2 ' ' 2
ронней оценки.
На практике интервальные оценки записываются в форме
2пх
2пх
Xj/f
_
где ж =
1
Обычно используются табулированные коэффициенты оценок
2пх
Значения коэффициентов кш и кв для двусторонней интервальной оценки при
а = 0,90 и а = 0,95 приведены в табл. 36, заимствованной из [16].
Таблица 36
п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
а =
К
0,333
0,422
0,476
0,515
0,546
0,568
0,592
0,610
0,625
0,637
0,650
0,660
0,662
0,675
0,685
Значения коэффициентов кш ш
0,90
19,20
5,62
3,68
2,92
2,54
2,30
2,13
2,01
1,92
1,84
1,78
1,73
1,69
1,65
1,62
а =
К
0,270
0,360
0,420
0,455
0,480
0,515
0,535
0,555
0,575
0,585
0,598
0,610
0,620
0,630
0,640
0,95
К
28,60
9,20
4,80
3,70
3,00
2,73
2,50
2,32
2,19
2,09
2,00
1,93
1,88
1,82
1,79
п
16
17
18
19
20
25
30
40
50
70
100
200
300
500
а =
К
0,690
0,700
0,710
0,715
0,719
0,740
0,756
0,787
0,806
0,830
0,852
0,890
0,910
0,930
кш [16]
0,90
К
1,59
1,57
1,54
1,52
1,51
1,44
1,39
1,31
1,28
1,23
1,19
1,13
1,10
1,08
а =
К
0,645
0,655
0,660
0,665
0,675
0,700
0,720
0,750
0,770
0,800
0,830
0,870
0,895
0,915
0,95
К
1,75
1,71
1,69
1,66
1,64
1,55
1,48
1,40
1,35
1,28
1,23
1,16
1,12
1,09
142
Оценка параметров распределений вероятностей
[Гл. 2
По аналогии с точечными оценками интенсивности отказов (А = l/i/) для раз™
личных планов испытаний на надежность (см. раздел 2.2.1.1), приведем формулы
для интервальных оценок.
план[ЛМ?,Т]: AJ = Щ^; К = Ш>
NT
NT
где cfaJ c'^—коэффициенты, выражающиеся через квантили распределения Пуас-
Пуассона.
Значения коэффициентов cfa{d) и
Таблица 37
для « = 0,90 [140]
d
0
1
2
3
4
5
cf
0,05129
0535536
0,81769
1536632
1,87015
2,61301
с"
2,99573
4,74386
6,29579
7,75366
9,15352
10,51300
d
6
7
8
9
10
11
с'
3,28532
3,98082
4,69523
5,42541
6,16901
6,92421
с"
11,84240
13,14810
14,43460
15,70520
16,99220
18,20750
d
12
13
14
15
16
с1
7,68958
8,46394
9,24633
10,03590
10,83210
с"
19,44260
20,66860
21,88650
23,09710
24,30120
Значения коэффициентов cfa(d) и cf^(d) для доверительной вероятности а = 0,90
в зависимости от числа отказов d приведены в табл. 37, заимствованной из [140].
, г]:
А» = Щ
Значения коэффициентов с'а{г — 1) и с'^{г — 1) для а = 0,90 находятся по табл. 37
при d = г — 1.
[N,E,r]: XI = -г-^
"> Лп — Т
са(г-1)
где bfa(d) и bf^(d)—коэффициенты оценки, приведенные в табл.38 для а = 0,95
и различных N.
Для плана [N^ В^ (г^Т)] интервальные оценки А аналогичны оценкам плана
[N.B.T], если tr > Т, и плана [N,B,r], если tr < Т.
план [Ж, Б, (г, Т)]: А^ = ^^; А^ = ^^, tr > Т,
где bfa(d) и 6^(d)—коэффициенты, тождественные коэффициентам для плана
[N,B,T\.
При ^- < ОД планы [N,B,(r,T)] и [Ж, Б, (г, Г)], [N,B,r] и [TV, Б, г] практически
совпадают [140]. При < ОД практически совпадают планы [JV, Б, Т] и [7V, Б, Т].
В указанных условиях мо^но использовать одинаковые оценки для таких планов.
Для оценок, основанных на порядковых статистиках, укажем один результат —
величина Irv имеет распределение %2 с / = 2г степенями свободы. Если в выборке
объема п известны г младших наблюдений, а (п — г) старших наблюдений цензу™
Оценка параметров экспоненциального распределения
143
Таблица 38
Значения коэффициентов bfa{d) (нижняя строка)
и ba(d) (верхняя строка) для ос = 0,95 [140]
d
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
N
50
0,0733
0,0000
0,1126
0,0005
0,1475
0,0049
0,1809
0,0126
0,2136
0,0225
0,2461
0,0338
0,2785
0,0464
0,3111
0,0599
0,3441
0,0744
0,3774
0,0896
0,4130
0,1057
0,4457
0,1225
0,4808
0,1399
0,5166
0,1582
0,5532
0,1771
0,5907
0,1968
0,6292
0,2172
0,6687
0,1383
0,7094
0,2603
0,7513
0,2830
60
0,0615
0,0000
0,0936
0,0004
0,1225
0,0041
0,1499
0,0105
0,1767
0,0186
0,2032
0,0280
0,2295
0,0383
0,2558
0,0494
0,2823
0,0612
0,3089
0,0736
0,3358
0,0866
0,3630
0,1001
0,3905
0,1141
0,4185
0,1286
0,4469
0,1437
0,4758
0,1592
0,5052
0,1752
0,5352
0,1918
0,5658
0,2088
0,5970
0,2264
80
0,0461
0,0000
0,0701
0,0003
0,0915
0,0031
0,1117
0,0078
0,1314
0,0139
0,1507
0,0208
0,1697
0,0284
0,1887
0,0366
0,2077
0,0452
0,2267
0,0542
0,2458
0,0636
0,2649
0,0733
0,2842
0,0834
0,3036
0,0937
0,3232
0,1044
0,3429
0,1153
0,3629
0,1265
0,3831
0,1380
0,4036
0,1498
0,4243
0,1619
100
0,0369
0,0000
0,0560
0,0003
0,0730
0,0024
0,0890
0,0063
0,1045
0,0111
0,1197
0,0166
0,1347
0,0226
0,1496
0,0290
0,1643
0,0358
0,1791
0,0429
0,1938
0,0502
0,2085
0,0578
0,2234
0,0657
0,2383
0,0737
0,2536
0,0820
0,2683
0,0904
0,2834
0,0991
0,2986
0,1079
0,3140
0,1169
0,3295
0,1261
150
0,0246
0,0000
0,0373
0,0002
0,0485
0,0016
0,0590
0,0041
0,0692
0,0073
0,0791
0,0110
0,0889
0,0149
0,0985
0,0191
0,1080
0,0236
0,1175
0,0282
0,1269
0,0330
0,1361
0,0379
0,1457
0,0429
0,1551
0,0481
0,1644
0,0534
0,1738
0,0587
0,1832
0,0642
0,1927
0,0698
0,2021
0,0755
0,2116
0,0812
200
0,0184
0,0000
0,0279
0,0001
0,0363
0,0012
0,0422
0,0031
0,0517
0,0055
0,0591
0,0082
0,0663
0,0111
0,0734
0,0143
0,0804
0,0176
0,0874
0,0210
0,0943
0,0245
0,1012
0,0282
0,1081
0,0319
0,1149
0,0357
0,1218
0,0396
0,1286
0,0435
0,1354
0,0475
0,1423
0,0516
0,1491
0,0557
0,1559
0,0599
рированы, то оптимальная линейная оценка (см. раздел 2.2.1.3.1) имеет вид
\Xi + (n-r) хг
1
г/ = —
г
г=1
а интервальные оценки равны 0% = кш • г); i/^ = кв • ?, где кш и fcB — коэффициенты,
приведенные в табл. 36 (здесь вместо п в таблицу следует входить со значением г).
144 Оценка параметров распределений вероятностей [Гл. 2
Задача 57. Имеются результаты наблюдений над экспоненциально распределенной
величиной Xii 12,13,16,17,21,24,29,31,42,45,54 (п=11). Необходимо найти двусто-
двусторонний доверительный интервал для параметра v при доверительной вероятности
а = 0,95.
•^ п
Имеем х = - • J2 хг = 27,63636. В табл. 36 для п = 11 и а = 0,95 находим fcH = 0,598
и ks = 2,00. Тогда
ul = 0,598 • 27,63636 = 16,526; ifn = 2,00 • 27,63636 = 55,2727.
Следовательно, 95%-й доверительный интервал для параметра v равен
16,526 ^ v ^ 55,2727.
Задача 58. Партия электронных приборов объемом N = 100 шт. была испытана на
надежность с заменой отказавших приборов в течение 200 ч. При этом наблюдалось
d = 5 отказов. Необходимо найти двустороннюю 90%-ю оценку для интенсивности
отказов приборов.
Имеем план [100, .В, Т = 200]. По таблице 37 находим
c(d - 1) = с D) = 1,97015 и c'(d) = с/;E) = 10,5130.
Окончательно имеем
1,97015 5 10,51303 4
Л^ = = 9,8507 • 1и ; Л„ = = o.zooo • ill
100 -200 100 • 200
Следовательно, 90%-й доверительный интервал для интенсивности отказов равен
9,8507 • 10^5 ^ Л ^ 5,2565 • 10^4 ч^1.
Задача 59. Испытаны на надеэюность 100 приборов с заменой отказавших приборов.
При этом наблюдались 5 отказов и момент наступления последнего отказа равен
212 ч. Найти 90%-г! доверительный интервал для интенсивности отказов приборов.
Имеем план [100, В, г = 5] при tr = 212. Из табл. 37 получаем
с (г- 1) = с'D) = 1,97015 и с"(г- 1) = с'{А) = 9,15352.
Тогда
= 2,9701! = 16 . . = ^1535^ = 4
100-212 ' ' п 100-212
Следовательно, 9,29316 • 10^5 ^ А ^ 4,13698 • 10^4.
Задача 60. Решить задачу 59 при условии, что испытания проводились без заме-
замены отказавших приборов и моменты наступления отказов были (ч): t\ = 50, ?2 = 80,
t3 = НО, ?4 = 190 и U = 212.
Имеем из табл. 37 с {г - 1) = с D) = 1,97015 и с"(г - 1) = с"(А) = 9,15352.
Тогда
5
J2 U = 50 + 80 + 110 + 190 + 212 = 642;
= 9,4800 • КГ"; К = ^^ = 4,4045 ¦
' ' 642 + A00 5) 212 '
^9,4800 КГ; К ^^
642 + A00 - 5) ¦ 212 ' ' 642 + A00 - 5) ¦ 212
9,4800 ^ Л^ 4,4045 •
2.2] Оценка параметров экспоненциального распределения 145
Задача 61. Решить задачу 59 при условии, что испытания проводились без замены
отказавших приборов.
Находим для d = 5 и N = 100 из табл. 38: Ь'E) = 0,0166 и Ь" (Ъ) = 0,1197. Тогда
¦л-4
^ = 8,3.10-; Л- 2^1 = 5,985.10
8,3-10 ^ А ^ 5,985 • 10~4.
Задача 62. Были проведены испытания на безотказность десяти приборов. В ре-
результате были получены 7 отказов в моменты времени t%\ 10, 11, 13, 16, 18, 21, 29.
Необходимо найти 95%-й доверительный интервал для наработки на отказ.
1 \г 1
Имеем г = 7, п = 10 и ?> = - • ]Г ж» + A0 - 7) • 29 = 26,71428.
|_г= J
Далее из табл. 36 для п = г = 7 имеем fcH = 0,592 и fcB = 2,13.
Тогда
ul = 0,592 • 26,71428 = 15,8148; i/* = 2,13 • 26,71428 = 56,9014;
15,8148 <: и <С 56,9014.
146 Оценка параметров распределений вероятностей [Гл. 2
2.3. Оценка параметров распределения Вейбулла
Напомним основные формы распределения Вейбулла. Закон распределения слу-
случайной величины запиевшается либо в двухпараметрической форме
либо в трехпараметрической
Fix) = 1-ехр< - -
Оценке подлежат либо два параметра: а — параметр масштаба и /3 — параметр
формы, либо три, включая /i — параметр сдвига.
Известно, что случайная величина у = \пх имеет распределение наименьших
значений с функцией
F(y) = 1 — ехр < — ехр
Оценки параметров й и Ъ связаны с оценками а и /3 соотношениями /3 = —
Ъ
Поэтому на практике часто используется следующий прием. Обработкой ряда
величин \nxi оцениваются параметры й и Ь, а затем переходят к оценкам а и /3.
Особенность распределения Вейбулла — чрезвычайно богатое разнообразие форм
кривых распределения — обуславливает его широкое распространение в практике,
поэтому совершенствование методов оценки его параметров актуально. Обширный
обзор методов оценки параметров распределения Вейбулла приведен в [152].
2.3.1. Точечные оценки
2.3.1.1. Оценка максимального правдоподобия
При известном параметре формы /3 оценка для а имеет вид
Легко видеть, что при /3 = 1 имеем оценку a = —^2xii T-e- оценка совпадает
с оценкой для параметра экспоненциального распределения, что следует из факта
перехода распределения Вейбулла в экспоненциальное при /3 = 1 (см. раздел 1.1.5).
При неизвестном /3 совместные оценки максимального правдоподобия парамет-
параметров а и /3 являются решением системы уравнений
п
пар — 2_^ xi = О?
г=1
п ~| п
~о ~1~ 5^ "^П Xi ~~ ^0 5Z i ^П Xi = ^*
^ г=1 ° г=1
2.8]
Оценка параметров распределения Вейбулла
147
В общем случае эта система решается методом последовательных приближений.
Интересный метод ускоренного решения приведенной системы уравнений предло-
предложен в [153]. Система сводится к
Р п *
= 0.
г=1
Существование и единственность решения этой системы уравнений показаны в [152].
Система решается методом символических операторов [154] с начальным прибли™
жением /30, исходя из зависимости коэффициента вариации v от C. Точная завися™
мость f (/3), определяемая формулой
v =
±
- 1
достаточно просто аппроксимируется соотношением v = /3 °'93 или Cg = v 1'075 [155]
(при 1 ^ /3 ^ 50 ошибка менее 3%, при 1 ^ /3 ^ 25 — не более 0,4%).
В работе [153] предлагается оценка
где
г=1
^ - ± ) А - 1
г=1
г=1
г=1
г=1
По оценке p вычисляется оценка параметра а: а = — > a:^ .
2.3.1.2. Метод моментов
Метод моментов основан на приравнивании эмпирических моментов статисти-
статистического ряда их теоретическим значениям, являющимся функциями параметров
распределения. Зависимость моментов распределения Вейбулла от его параметров
очень сложна (включает в себя комбинацию гамма-функций). Поэтому чаще всего
пользуются заранее подготовленными таблицами. Одна из них воспроизведена
в табл. 39.
Порядок вычисления оценок а и /3 включает в себя последовательное вычисле™
1
ние x,s,v,/3 = v
- „-1,075
148
Оценка параметров распределений вероятностей
[Гл. 2
Таблица 39
Зависимость параметра /3 распределеним Вейбулла
от коэффициента вариации v = s/x [44, 46]
V
3,14
2,93
2,75
2,57
2,40
2,24
2,08
1,94
Р
0,400
0,417
0,435
0,455
0,476
0,500
0,526
0,556
V
1,80
1,67
1,55
1,43
1,32
1,21
1,10
1,00
Р
0,588
0,625
0,667
0,714
0,769
0,833
0,909
1,000
V
0,910
0,837
0,775
0,723
0,681
0,640
0,605
0,575
1,10
1,20
1,30
1,40
1,50
1,60
1,70
1,80
V
0,547
0,523
0,496
0,480
0,461
0,444
0,428
0,365
1,90
2,00
2,10
2,20
2,30
2,40
2,50
3,00
Для трехпараметрического распределения оценка параметров а, /5 и ц методом
моментов рассмотрена в [156]. Авторами рассматривается система трех уравнений,
связывающих моменты распределения (аз — коэффициент асимметрии, s— средне™
квадратическое отклонение и х— среднее значение) с параметрами а, /3 и \х этого
распределения. Система имеет вид
«з =
¦ = a|l
Исполвзуются оценки
a = —-
n
S =
x = - T
Из зависимости а3 = f{f3) и можно найти оценку а3 и вычислить оценку J3. Распо™
лагая зависимостью s = /(а,/?) и зная /3, находим оценку а. Располагая значения-
значениями а и s, находим оценку /i. Значения необходимых для расчета величин «з? Р,
Ь и с приведены в табл. 40. Схема ввшислений включает в себя вычисление «з
по выборочным данным и определение по табл. 40 соответствующей оценки /3,
а также коэффициентов Ъ и с. Параметрвх аи \i оцениваются по формулам а = s • Ь;
/J, = X — SC.
Однако этот метод применим только при значительном объеме выборки, так
как при п ^ 30 точность выборочной оценки коэффициента вариации v мала, что
приводит к большим погрешностям при оценке параметров распределения. Более
точную оценку можно получить, воспользовавшись характеристической порядко-
порядковой статистикой, как методом моментного сравнения. Очевидно, что для х = ц:
F(x) = 1--= 0,632.
2.8]
Оценка параметров распределения Вейбулла
149
Таблица 40
Значения «з? /3, I/ и с, используемые при оценке параметров
распределения Вейбулла [156]
«3
-1,0
-0,9
^0,8
-0,7
-0,6
-0,5
-0,4
-0,3
-0,2
-ОД
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
Р
40,818
22,922
15,626
11,664
9,185
7,493
6,271
5,350
4,634
4,064
3,602
3,222
2,905
2,637
2,410
2,216
2,048
1,802
1,774
1,662
1,564
1,477
1,399
1,329
Ь1
32,827
18,858
13,153
10,046
8,094
6,755
5,780
5,039
4,456
3,986
3,599
3,274
2,997
2,759
2,551
2,368
2,206
2,060
1,929
1,811
1,703
1,605
1,515
1,432
с
32,381
18,417
12,717
9,617
7,672
6,341
5,375
4,464
4,073
3,616
3,243
2,933
2,673
2,452
2,262
2,097
1,954
1,828
1,717
1,618
1,530
1,452
1,381
1,316
«3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
1,267
1,211
1,160
1,115
1,073
1,035
1,000
0,968
0,939
0,911
0,886
0,863
0,841
0,821
0,803
0,785
0,769
0,753
0,739
0,725
0,712
0,700
0,688
0,677
У
1,355
1,284
1,219
1,158
1,102
1,049
1,000
0,954
0,911
0,871
0,833
0,798
0,765
0,734
0,704
0,677
0,650
0,626
0,603
0,581
0,559
0,540
0,521
0,503
с
1,258
1,205
1,157
1,113
1,072
1,035
1,000
0,968
0,938
0,911
0,884
0,860
0,837
0,816
0,796
0,787
0,759
0,743
0,727
0,712
0,697
0,684
0,671
0,658
Пусть Жо,б32п —порядковая статистика и г1 = 0,632(в + 1).
Тогда xr =
где г < г'. Рассмотрим систему
xR = а + /х,
откуда, приравнивая
G =
Xr- X
находим оценку /3, а затем а. = sbf и /х = хц — а.
Необходимые значения G, /5, b и Ь' приведены в табл. 41, заимствованной из ра™
боты [156]. Вычисляя выборочное значение G, находим по табл. 41 соответствующие
ему значения C и Ь;, затем вычисляем оценки а = sb' и /х = xr — а. Такая оценка
вдвое точнее, чем рассмотренная ранее.
150
Оценка параметров распределений вероятностей
[Гл. 2
Таблица 41
Значения G, /3 и Ь' длм оценки параметров распределении Вейбулла [156]
G
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
1,000
1,024
1,049
1,074
1,101
1,127
1,155
1,184
1,214
1,245
1,278
Ъ'
1,000
1,034
1,068
1,103
1,139
1,175
1,212
1,250
1,288
1,328
1,368
G
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,20
0,21
Р
1,311
1,347
1,384
1,422
1,463
1,506
1,551
1,599
1,649
1,703
1,760
Ъ1
1,410
1,453
1,497
1,542
1,589
1,638
1,689
1,741
1,797
1,854
1,915
G
0,22
0,23
0,24
0,25
0,26
0,27
0,28
0,29
0,30
0,31
0,32
Р
1,821
1,887
1,958
2,034
2,117
2,208
2,307
2,417
2,539
2,675
2,829
У
1,978
2,045
2,117
2,193
2,274
2,361
2,455
2,557
2,669
2,793
2,931
G
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
3,005
3,207
3,445
3,728
4,072
4,502
5,057
5,808
6,895
8,636
11,966
Ъ'
3,085
3,262
3,365
3,705
3,992
4,347
4,801
5,409
6,279
7,660
10,283
2.3.1.3. Метод наименьших квадратов
Метод рассмотрен в [157]. Идея метода заключается в следующем. Если два ра-
раза прологарифмировать плотность распределения Вейбулла f(i) = ехр
то получим линейную зависимость вида у = с + Ъх. Оценки плотности вероятно-
вероятностей f(ti) получаются из выборочной гистограммы
где wij —частоты разрядов гистограммы; N — объем выборки.
Для рассматриваемого случая имеют место соотношения
j/ = lg[-lg/(*<)> x = kt; с =-0,3622-biga.
Число таких уравнений равно числу разбиений выборочной гистограммы (предпо-
(предположим, в нашем случае оно равно п). Для отыскания параметров с и b методом
наименьших квадратов необходимо решить систему уравнений
г=1
г=1
г=1
Искомые оценки определяются по формулам
г=1 i=l
г=1
г=1 г=1
Этот метод позволяет находить параметры распределения Вейбулла непосред-
непосредственно по статистической гистограмме, не затрачивая время на вычисление его
параметров по выборке. Отметим, что можно использовать и графические мето™
2.3] Оценка параметров распределения Вейбулла 151
ды, идея которых — графическая линеаризация функции распределения Вейбулла
путем введения логарифмической шкалв! аргумента и двойной логарифмической
шкалы функции:
lnx, -/ЗЫа, где F(xt) = ——-.
F(Xi)
Угловой коэффициент такой прямой является оценкой /3. Однако графический ме-
метод требует точных графических построений (особенно для значений /3 = 0,2 ^ 1,5).
Для устранения таких трудностей в [158] предложен графоаналитический метод,
однако и он может использоваться только для грубой оценки параметров распре-
распределения.
В [36] предложена еще одна простая, но достаточно эффективная оценка пара™
метров распределения Вейбулла. Как и ранее, имеем оценки коэффициента асим™
1
л п -п. 2
метрии и стандартного отклонения «з = —з /С (xi ~ •
~3 " ч " ' ' п
Оценки основанв! на аппроксимации
1=1
G = ГМ + -И « 1 - 0,427(/3 - l)^'9.
При /3^1 ошибка аппроксимации ^ 0,2%.
Оценки вв1числяются по формулам
/3 « 4,8(а3 + 1.23)-1-4; /3 = |; Д = ж - «5; <5 « fo,5 + 0,784/3 - 2^) s.
При 1,5 ^ /3 ^ 20 ошибка аппроксимации ^ 0,7% для /3 и < 0,2% для 5.
Для двухпараметрического распределения Вейбулла (когда заранее известно,
что /i = 0) оценки параметров /3 и а имеют вид
f 0,465^ + 1,282- - 0,7^ ; а = ^.
Р « f 0,465 + 1,282 0,7^ ; а = ^
Ошибка аппроксимации /5 в этом случае ^ 0,25% для /3 ^ 1,5.
2.3.1.4. Оценка с помощью квантилей
Обозначим через хр и xq соответственно р- и g-квантили распределения Вейбул™
ла (т. е. F(xp) = p и F(xq) = g). Тогда оценки параметров распределения Вейбулла
имеют вид [159]
^1?i a exp<
iHXp — iflXq I ill ttp — III Uq
где dp = — ln(l -р)ис!д=:- ln(l — g).
В [159] показано, что наиболвшая эффективноств оценки а достигается при
р = 0,398 и q = 0,821 (dp = 0,5074 ш dq = 1,7203), а /З^при р = 0,167 и q = 0,974
(dp = 0,1827 и dg = 3,6496).
Рекомендуется для совместной оценки параметров а и /3 использовать квантили
уровней р = 0,2 и 0,95 (в этом случае эффективность оценок не менее 60% по сравне-
сравнению с оценками максимального правдоподобия (см. раздел 2.3.1.1) при всех оси. р).
152 Оценка параметров распределений вероятностей [Гл. 2
Окончательно рекомендуемые оценки имеют вид
/3 = -2,5973In ^^; а = ехр@,42241пж0 95).
Жо,2 '
Квантиль жо,95 оценивается порядковой статистикой Ж[о,о5п]+ь а жо,2 — соответ-
соответственно Ж[0;8п]+ъ гДе [• • •] —целая часть числа, заключенного в скобках.
2.3.1.5. Оценки, основанные на порядковых статистиках
Такие оценки наиболее эффективны в обычной практике оценки надежности
изделий по данным о наработке первых г отказавших приборов из общего числа п
испытываемых. В прикладной математической статистике такая задача формули-
формулируется как задача оценки параметров распределения вероятностей по цензуриро-
ванной сверху выборке (при оценке не учитываются (п — г) наибольших по величине
членов выборки).
Оценки для цензурированных выборок, основанные на линейной комбинации
порядковых статистик (простые линейные оценки), рассмотрены в [160—164]. В [165]
рассмотрена задача оценки параметров распределения Вейбулла при прогрессив™
ном цензурировании, когда часть изделий снимается с испытаний после каждого
отказа.
Мы рассмотрим наиболее простые для практического применения и достаточно
эффективные наилучшие линейные оценки.
Напомним, что если случайная величина х имеет двухпараметрическое распре™
деление Вейбулла с функцией F(x) = 1 — ехр< — | — J >, то случайная величина
у = In х будет иметь распределение наименьших значений с функцией
Суть метода заключается в поиске параметров распределения величины In х (й и Ъ)
в форме
с последующим переходом к оценке параметров распределения исходной величи-
величины х (не следует забывать, что оценка проводится по первым г наблюдениям из
выборки объема п).
Оценки й и Ь являются смещенными, и для исключения смещения используются
поправки, с учетом которых несмещенные оценки равны
u*=u + b*fci; S* = ^—.
1
Значения коэффициентов a,i,Ci,ki и &2 приведены в табл. 42 и 43, заимствованных
из [95].
2.3.1.6. Оценка параметров распределения Рэлем
(частный случай распределения Вейбулла)
Распределение Рэлея (см. раздел 1.1.15) является частным случаем распределе-
распределения Вейбулла при /3 = 2. Значение /3 = 2 является граничным между регулярным
и нерегулярным случаями распределения Вейбулла и заслуживает отдельного рас™
смотрения. Достаточно полно это сделано в [166].
2.3]
Оценка параметров распределения Вейбулла
153
Таблица 42
п
2
3
3
4
4
4
5
5
5
5
6
6
6
6
6
7
г
2
2
3
2
3
4
2
3
4
5
2
3
4
5
6
2
i
1
2
1
2
1
2
3
1
2
1
2
3
1
2
3
4
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
Значения коэффициентов
щ
0,110731
0,889269
-0,166001
1,166001
0,081063
0,251001
0,667936
-0,346974
1,346974
-0,044975
0,088057
0,956918
0,064336
0,147340
0,261510
0,526813
-0,481434
1,481434
-0,137958
-0,025510
1,164680
-0,006983
0,059652
0,156664
0,790668
0,052975
0,103531
0,163808
0,246092
0,433593
-0,588298
1,588298
-0,211474
-0,112994
1,324468
-0,063569
-0,006726
0,079882
0,990412
0,007521
0,048328
0,101608
0,172859
0,669685
0,048826
0,079377
0,117541
0,163591
0,226486
0,368179
-0,676874
1,676874
Ci
-0,421383
0,421383
-0,452110
0,452110
-0,278666
-0,190239
0,468904
-0,465455
0,465455
-0,297651
-0,234054
0,531705
-0,203052
-0,182749
-0,070109
0,455910
-0,472962
0,472962
-0,306562
-0,257087
0,563650
-0,217766
-0,199351
-0,118927
0,536044
-0,158131
-0,155707
-0,111820
-0,005600
0,431259
-0,477782
0,477782
-0,311847
-0,271381
0,583229
-0,225141
-0,209083
-0,146386
0,580610
-0,169920
-0,166319
-0,129510
-0,054453
0,520201
-0,128810
-0,132102
-0,111951
-0,064666
0,031796
0,405733
-0,481140
0,481140
п
7
7
7
7
7
8
8
8
8
8
8
г
3
4
5
6
7
2
3
4
5
6
7
ai и
г
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
Ci [95]
щ
-0,272195
-0,184061
1,456255
-0,110274
-0,060226
0,018671
1,151829
-0,030368
0,004333
0,052957
0,117599
0,855480
0,013524
0,041588
0,075499
0,117461
0,172092
0,579835
0,038743
0,064086
0,090785
0,120971
0,157657
0,207825
0,319934
-0,752513
1,752513
-0,323875
-0,243808
1,566830
-0,149973
-0,105015
-0,032257
1,287245
-0,062656
-0,032248
0,012767
0,072446
1,009691
-0,013509
0,010292
0,041357
0,080475
0,130327
0,751058
0,015973
0,036729
0,060439
0,088239
0,122062
0,165529
0,511030
Ci
-0,315369
-0,281139
0,596507
-0,229691
-0,215611
-0,164168
0,609472
-0,176203
-0,172398
-0,141218
-0,082820
0,572640
-0,138436
-0,140342
-0,121821
-0,082994
-0,015394
0,498931
-0,108323
-0,113479
-0,103569
-0,078748
-0,032632
0,054727
0,382022
-0,483616
0,483616
-0,317890
-0,288231
0,606120
-0,232805
-0,220324
-0,176675
0,629805
-0,180231
-0,176510
-0,149566
-0,101642
0,607948
-0,143834
-0,145006
-0,128393
-0,095696
-0,043280
0,556209
-0,116317
-0,120331
-0,110582
-0,088450
-0,050995
0,009700
0,476975
154
Оценка параметров распределений вероятностей
[Гл. 2
Продолжение таблицы 42
п
8
9
9
9
9
9
9
9
9
'Г
8
2
3
4
5
6
7
8
9
г
1
2
3
4
5
6
7
8
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
0,034052
0,053552
0,073452
0,095062
0,119768
0,149934
0,191236
0,282943
-0,818444
1,818444
-0,368833
-0,296280
1,664113
-0,184461
-0,143505
-0,075815
1,403781
-0,907260
-0,063541
-0,021495
0,034259
1,141604
-0,037118
-0,016377
0,012499
0,049305
0,095614
0,896078
-0,004220
0,013386
0,035068
0,061198
0,093013
0,153879
0,647676
0,016797
0,032919
0,050582
0,070497
0,093635
0,121560
0,157175
0,456836
0,030338
0,048720
0,061368
0,077742
0,095769
0,116517
0,141932
0,176764
0,253697
-0,093270
-0,098886
-0,093994
0,079752
-0,053918
-0,010179
0,069325
0,360675
-0,485517
0,485517
-0,319786
-0,293621
0,613407
-0,235080
-0,223891
-0,185970
0,644941
-0,183061
-0,179515
-0,155825
-0,115133
0,633534
-0,147411
-0,148150
-0,133219
-0,105060
-0,062073
0,595913
-0,120988
-0,124245
-0,115091
-0,095508
-0,064162
-0,038125
0,558119
-0,100011
-0,104750
-0,099608
-0,086226
-0,063541
-0,028346
0,026525
0,455956
-0,081777
-0,087308
-0,085084
-0,076470
-0,060667
-0,035136
0,006001
0,078828
0,341614
п
10
10
10
10
10
10
10
10
10
г
2
3
4
5
6
7
8
9
10
г
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
щ
-0,876869
1,876869
-0,408602
-0,340443
1,749045
-0,214930
-0,177223
-0,113820
1,505973
0,115524
-0,090868
-0,511341
0,000925
1,256809
-0,058017
-0,039595
-0,012513
0,022314
0,065750
1,022062
-0,022198
-0,006900
0,013224
0,037994
0,068153
0,105164
0,804572
0,001179
0,014889
0,030998
0,049734
0,071745
0,096114
0,130649
0,602692
0,016841
0,029807
0,043570
0,058640
0,075576
0,095169
0,118707
0,148575
0,413116
0,027331
0,040034
0,052496
0,065408
0,079263
0,094638
0,112414
0,134239
Ci
-0,487022
0,487022
-0,321265
-0,297858
0,619124
-0,236817
-0,226688
-0,193159
0,656663
-0,185169
-0,181821
-0,160698
-0,125311
0,652997
-0,149985
-0,150451
-0,136941
-0,112224
-0,075721
0,625321
-0,124170
-0,126894
-0,118392
-0,100924
-0,073988
-0,035501
0,579868
-0,104082
-0,108163
-0,103119
-0,090835
-0,070902
-0,041560
-0,000799
0,517864
-0,087358
-0,092405
-0,089839
-0,081428
-0,066855
-0,044670
-0,011816
0,038159
0,436394
-0,072734
-0,077971
-0,077242
-0,071876
-0,061652
-0,045420
-0,020698
0,017927
2.3]
Оценка параметров распределения Вейбулла
155
г?
10
11
11
11
11
11
11
11
11
11
г
10
2
3
4
5
6
7
8
9
10
7
9
10
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
а2
0,164178
0,230001
-0,929310
1,920310
-0,444245
-0,380642
1,824887
-0,242206
-0,207204
-0,147490
1,596900
-0,137718
-0,115110
-0,077762
-0,028411
1,359000
-0,076739
-0,060142
-0,034581
-0,001490
0,039518
1,133434
-0,038349
-0,024842
-0,005964
0,017632
0,046354
0,081182
0,923987
-0,012943
-0,001050
0,013869
0,031661
0,052723
0,077815
0,108161
0,729765
0,004425
0,015498
0,028023
0,042178
0,058340
0,077093
0,099349
0,126592
0,548502
0,016502
0,027205
0,038291
0,050160
0,063170
0,077772
с?
0,085070
0,324597
-0,488243
0,488243
-0,322452
-0,301277
0,623620
-0,238188
-0,228941
-0,198888
0,666017
-0,186803
-0,183651
-0,164597
-0,133278
0,668329
-0,151936
-0,152221
-0,139907
-0,117886
-0,086131
0,648081
-0,126507
-0,128838
-0,120951
-0,105219
-0,081602
-0,048929
0,612047
-0,106922
-0,110498
-0,105662
-0,094405
-0,076693
-0,051525
-0,016860
0,562564
-0,091115
-0,095437
-0,092780
-0,084833
-0,071581
-0,052182
-0,024880
0,013606
0,499202
-0,077717
-0,082449
-0,081388
-0,075977
-0,066222
-0,051429
п
11
11
12
12
12
12
12
12
12
12
П]
г
10
11
2
3
4
5
6
7
8
9
зодолжение таблицы 42
г
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
1
2
0,094625
0,114811
0,140333
0,377130
0,024850
0,035456
0,045727
0,056215
0,067261
0,079220
0,092560
0,108034
0,127068
0,153197
0,210412
-0,976872
1,976872
-0,476530
-0,416836
1,893367
-0,266888
-0,234180
-0,177681
1,678749
-0,157792
-0,136684
-0,101445
-0,054640
1,450761
-0,093679
-0,078561
-0,054320
-0,022769
0,016136
1,233193
-0,052987
-0,040893
-0,023072
-0,000515
0,026930
0,059918
1,030620
-0,025785
-0,015312
-0,001353
0,015634
0,035853
0,059835
0,088444
0,842684
-0,006944
0,002669
-0,030120
0,000537
0,044638
0,418384
-0,065444
-0,070318
-0,070456
-0,067076
-0,060207
-0,049300
-0,033156
-0,009427
0,026879
0,089148
0,309357
-0,489254
0,489254
-0,323426
-0,304093
0,617519
-0,239300
-0,230796
-0,203562
0,673657
-0,188109
-0,185012
-0,167790
-0,136930
0,680734
-0,053471
-0,153632
-0,142329
-0,122474
-0,094355
0,666261
-0,128308
-0,130339
-0,123007
-0,108712
-0,087681
-0,059256
0,637304
-0,109045
-0,112224
-0,107627
-0,097276
-0,081361
-0,059315
-0,029900
0,596748
-0,093658
-0,097540
156
Оценка параметров распределений вероятностей
[Гл. 2
т?
12
12
12
12
13
13
13
13
г
9
10
11
12
2
3
4
5
7
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
12
1
2
1
2
3
1
2
3
4
1
2
3
0,014239
0,027669
0,043189
0,061225
0,082441
0,107856
0,667655
0,006411
0,015598
0,025675
0,036799
0,049211
0,063256
0,079438
0,098522
0,121752
0,503338
0,015982
0,024997
0,034156
0,043790
0,054149
0,065515
0,078264
0,092958
0,110521
0,132666
0,347003
0,022771
0,031776
0,040408
0,049122
0,058175
0,067800
0,078281
0,090017
0,103664
0,120475
0,143566
0,193947
-1,020378
2,020378
-0,506031
-0,449735
1,955765
-0,289420
-0,258687
-0,205024
1,753131
-0,176109
-0,156637
-0,122893
с?
-0,094893
-0,087448
-0,075374
-0,058180
-0,034802
-0,003342
0,545234
-0,080881
-0,085171
-0,083952
-0,078714
-0,067610
-0,056237
-0,037675
-0,012272
0,022956
0,481555
-0,069798
-0,074285
-0,074131
-0,070617
-0,063891
-0,053621
-0,039034
-0,018715
0,009948
0,052280
0,401864
-0,059449
-0,063952
-0,064601
-0,062489
-0,037754
-0,050137
-0,039010
-0,023199
-0,000505
0,033696
0,091751
0,295648
-0,490105
0,490105
-0,324239
-0,306454
0,630694
-0,240219
-0,232349
-0,207450
0,630018
-0,189177
-0,186381
-0,170454
п
13
13
13
13
13
13
13
П]
г
5
6
7
8
9
10
11
зодолжение таблицы 42
г
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
-0,078337
1,533976
-0,109187
-0,092014
-0,076615
-0,041997
-0,004940
1,323488
-0,066358
-0,055414
-0,038503
-0,016879
0,009416
0,040810
1,126930
-0,037540
-0,028206
-0,015049
-0,001123
0,020686
0,043677
0,070830
0,944372
-0,017389
-0,008934
0,001863
0,014684
0,029637
0,047027
0,067346
0,091328
0,774437
-0,002927
0,005067
0,014356
0,024891
0,036816
0,050389
0,065995
0,084201
0,105863
0,615348
0,007628
0,015408
0,023732
0,032743
0,042611
0,053556
0,065876
0,080005
0,096594
0,116703
-0,144971
0,690983
-0,172412
-0,168148
-0,144215
-0,101104
-0,001512
0,711124
-0,129743
-0,131538
-0,124701
-0,111609
-0,092649
-0,067475
0,657714
-0,110704
-0,113563
-0,109206
-0,099644
-0,085204
-0,065581
-0,039995
0,623896
-0,095590
-0,099109
-0,096521
-0,089554
-0,078490
-0,063068
-0,046607
-0,015928
0,580865
-0,083170
-0,087085
-0,085792
-0,080789
-0,072325
-0,060181
-0,043768
-0,022048
0,006715
0,528441
-0,072617
-0,076746
-0,076418
-0,072938
-0,066531
-0,057014
-0,043886
-0,026244
-0,002552
0,029910
2.3]
Оценка параметров распределения Вейбулла
157
п
13
13
13
14
14
14
14
14
14
г
11
12
13
2
3
4
5
6
7
г
11
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
щ
0,465143
0,015382
0,023100
0,030818
0,038824
0,047302
0,056444
0,066482
0,077739
0,090699
0,106166
0,125627
0,321416
0,021005
0,028757
0,036127
0,043501
0,051078
0,059028
0,067533
0,076831
0,087274
0,099441
0,114446
0,135068
0,179913
-1,060461
2,060461
-0,533185
-0,479874
2,013059
-0,310144
-0,281132
-0,229990
1,821266
-0,192947
-0,174709
-0,142478
-0,099930
1,610065
-0,123352
-0,110490
-0,088443
-0,059523
-0,024111
1,405919
-0,078656
-0,068666
-0,052554
-0,031776
-0,006522
0,023467
0,465037
-0,063288
-0,067492
-0,067892
-0,065622
-0,060887
-0,053540
-0,043158
-0,028970
-0,009644
0,017233
0,056547
0,386713
-0,054436
-0,058585
-0,059535
-0,058259
-0,054942
-0,049472
-0,041504
-0,030980
-0,015037
0,006644
0,038943
0,093324
0,283257
-0,490831
0,490831
-0,324929
-0,308462
0,633391
-0,240982
-0,233670
-0,210735
0,685397
-0,190068
-0,187427
-0,172710
-0,149393
0,699598
-0,155736
-0,155747
-0,146054
-0,120460
-0,106556
0,693553
-0,130915
-0,132521
-0,126123
-0,114051
-0,096788
-0,074184
п
14
14
14
14
14
14
14
П
г
7
8
9
10
11
12
13
родолжение таблицы 42
г
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
12
1
ai
1,214708
-0,048365
-0,039964
-0,027495
-0,011849
0,006905
0,029002
0,054897
1,036868
-0,027030
-0,019516
-0,009363
0,002928
0,017368
0,034165
0,053685
0,076476
0,871287
-0,011580
-0,004548
-0,004548
0,014100
0,025647
0,038794
0,053879
0,071335
0,091783
0,716445
-0,000170
0,006622
0,014283
0,022800
0,032273
0,042866
0,054817
0,068463
0,084290
0,103025
0,570731
0,008361
0,015058
0,022076
0,029552
0,037615
0,046411
0,056132
0,067039
0,079506
0,094096
0,111723
0,432431
0,014760
Ci
0,674581
-0,112041
-0,114637
-0,110509
-0,101635
-0,088422
-0,088422
-0,048074
0,640520
-0,097117
-0,100334
-0,097827
-0,091298
-0,081103
-0,067124
-0,048921
-0,025720
0,609445
-0,084931
-0,088528
-0,087207
-0,082451
-0,074573
-0,063473
^0,048768
-0,029776
-0,005398
0,565101
-0,074686
-0,078499
-0,078064
-0,074680
-0,068624
-0,059816
-0,047926
-0,032355
-0,012126
0,014349
0,512429
-0,065816
-0,069728
-0,099620
-0,067659
-0,063070
-0,056130
-0,046558
-0,033834
-0,017101
0,005064
0,035156
0,449638
-0,057849
158
Оценка параметров распределений вероятностей
[Гл. 2
т?
14
14
16
16
16
16
16
16
г
13
14
2
3
4
5
6
7
7
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
а2
0,021453
0,028054
0,034842
0,041933
0,049474
0,057619
0,066569
0,076605
0,088151
0,101914
0,119200
0,299416
0,019487
0,026238
0,032614
0,038941
0,045399
0,052097
0,059168
0,066767
0,075102
0,084482
0,095428
0,108942
0,127523
0,167807
-1,123243
2,132243
-0,581757
-0,533457
2,115214
-0,347172
-0,321026
-0,274186
1,942384
-0,223015
-0,206788
-0,177158
-0,138048
1,745009
-0,148725
-0,137508
-0,117232
-0,090481
-0,057883
1,551828
-0,100621
-0,092121
-0,077354
-0,058057
-0,034624
-0,007020
с?
-0,061764
-0,062506
-0,061704
-0,057693
-0,052317
-0,044707
-0,034420
-0,020713
-0,002338
0,022943
0,059643
0,372795
-0,050186
-0,054008
-0,055130
-0,054419
-0,052075
-0,048606
-0,042197
-0,034099
-0,022315
-0,008285
0,012430
0,043015
0,094166
0,272004
-0,492005
0,492005
-0,326035
-0,311694
0,637730
-0,242220
-0,235794
-0,215984
0,693998
-0,191470
-0,189099
-0,176323
-0,156390
0,713282
-0,157331
-0,157263
-0,148785
-0,134532
-0,115196
0,713108
-0,132718
-0,134040
-0,128381
-0,117942
-0,103296
-0,084506
п
16
16
16
16
16
16
16
П
г
7
8
9
10
11
12
13
родолжение таблицы 42
г
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
12
1
1,369798
-0,067719
-0,060754
-0,049415
-0,034868
-0,011736
0,003178
0,026973
1,199963
-0,044303
-0,038218
-0,029094
-0,017697
-0,004166
0,011570
0,028712
0,050576
1,041619
-0,027135
-0,021550
-0,013895
-0,004646
0,006132
0,018515
0,032675
0,048869
0,067459
0,893576
-0,014263
-0,008950
-0,002286
-0,002286
0,005469
0,014703
0,024296
0,035593
0,048404
0,063020
0,079847
-0,004450
0,000732
0,006721
0,013424
0,020868
0,029314
0,038344
0,048668
0,060342
0,073692
0,089173
0,623351
0,003118
0,700883
-0,114069
-0,116260
-0,112545
-0,104798
-0,093508
-0,078726
-0,060251
0,680158
-0,099396
-0,102138
-0,099811
-0,094037
-0,085242
^0,073467
-0,058535
^0,040084
0,652711
-0,087496
-0,090585
-0,089277
-0,084992
-0,078105
-0,068653
-0,056482
-0,041268
-0,022503
0,619360
-0,077597
-0,080895
-0,080349
-0,077313
-0,071820
-0,064207
-0,054237
-0,041635
-0,025917
-0,006432
0,580293
-0,069172
-0,072584
-0,072615
-0,070383
-0,066184
-0,060054
-0,051876
-0,041398
-0,028216
-0,011716
-0,009035
0,535164
-0,061843
2.3]
Оценка параметров распределения Вейбулла
159
п
16
16
16
16
г
13
14
15
16
г
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
щ
0,008356
0,013789
0,019747
0,026189
0,033196
0,040872
0,049357
0,058836
0,069568
0,081920
0,096438
0,498713
0,008992
0,014141
0,019370
0,024804
0,030525
0,036615
0,043164
0,050284
0,058124
0,066884
0,076854
0,088469
0,102433
0,379341
0,013547
0,018743
0,023778
0,028849
0,034060
0,039489
0,045218
0,051338
0,057965
0,065253
0,074425
0,082818
0,093994
0,107995
0,263528
0,017016
0,022284
0,027208
0,032046
0,036918
0,041887
0,047042
0,052455
0,058216
0,064444
0,071304
Ci
-0,065297
-0,065770
-0,064259
-0,061031
-0,056120
-0,049427
-0,040731
-0,029675
-0,015710
0,002010
0,024833
0,483018
-0,055309
-0,058750
-0,059563
-0,058635
-0,056208
-0,052317
-0,046867
-0,039699
-0,030467
-0,018695
-0,003625
-0,015969
0,042224
0,421953
-0,049291
-0,052670
-0,053739
-0,053290
-0,051538
-0,048520
-0,044164
-0,038307
-0,030678
-0,020850
-0,008156
0,008503
0,031075
0,063476
0,348149
-0,043375
-0,046633
-0,047890
-0,047839
-0,046675
-0,044432
-0,041053
-0,036402
-0,030249
-0,022230
-0,011772
п
16
18
18
18
18
18
18
18
18
18
П]
г
16
2
3
4
5
6
7
8
9
10
зодолжение таблицы 42
г
12
13
14
15
16
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
1
2
3
щ
0,079051
0,088111
0,099315
0,114733
0,147977
-1,195128
2,195128
-0,624252
-0,580008
2,204260
-0,379529
-0,355679
-0,312382
2,047590
-0,249266
-0,234618
-0,207148
-0,170883
1,861914
-0,170868
-0,160910
-0,142100
-0,117175
-0,086906
1,677960
-0,119793
-0,112406
-0,098738
-0,080698
-0,058807
-0,033165
1,503605
-0,084626
-0,078711
-0,068272
-0,054656
-0,038217
-0,019006
0,003084
1,340405
-0,059414
-0,054359
-0,046030
-0,035375
-0,022631
-0,007819
0,009161
0,028495
1,187973
-0,040776
-0,036223
-0,029314
Ci
0,002079
0,021044
0,048675
0,094419
0,252333
-0,492912
0,492912
-0,326884
-0,314183
0,641066
-0,243153
-0,237429
-0,219992
0,700574
-0,192523
-0,190376
-0,179091
-0,161679
0,723670
-0,158516
-0,158405
-0,150876
-0,138383
-0,121647
0,727829
-0,134044
-0,135163
-0,130098
-0,120904
-0,108183
-0,092095
0,720486
-0,115541
-0,117434
-0,114068
-0,107202
-0,097349
-0,084645
-0,069301
0,705270
-0,101022
-0,103411
-0,101260
-0,096099
-0,088374
-0,078203
-0,065532
-0,050186
0,684087
-0,089291
-0,091997
-0,090739
160
Оценка параметров распределений вероятностей
[Гл. 2
п
18
18
18
18
18
г
10
11
12
13
14
г
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
-0,020701
-0,010540
-0,001172
0,014523
0,029671
0,046841
1,045347
-0,026669
-0,022402
-0,016466
-0,009294
-0,000979
0,008496
0,019212
0,031300
0,044847
0,060404
0,911490
-0,015793
-0,011677
-0,006416
-0,000278
0,006695
0,014529
0,023297
0,033110
0,044122
0,056540
0,070367
0,785235
-0,007289
-0,003238
0,001550
0,006940
0,012925
0,019540
0,026851
0,034951
0,043969
0,054072
0,065486
0,078516
0,665728
0,000568
0,003471
0,007930
0,012775
0,018027
0,023730
0,029942
0,036744
0,044239
Ci
-0,086863
-0,080764
-0,072544
-0,062157
-0,049445
-0,034147
0,657947
-0,079582
-0,082484
-0,081896
-0,079012
-0,074183
-0,067503
-0,058930
-0,048324
-0,035451
-0,019962
0,627325
-0,071378
-0,074393
-0,074315
-0,072211
-0,068395
-0,062952
-0,055848
-0,046959
-0,036073
-0,022877
-0,006924
0,592326
-0,064317
-0,067387
-0,067701
0,066218
-0,063222
-0,058792
-0,052898
-0,045430
-0,036200
-0,024926
-0,011201
0,005561
0,552731
-0,058133
-0,061213
-0,061830
-0,060849
-0,058527
-0,054936
-0,050053
-0,043781
-0,035952
п
18
18
18
18
Продол
г
14
15
16
17
г
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
жение таблицы 42
ai
0,052564
0,061904
0,072509
0,084730
0,552004
0,004780
0,008843
0,013074
0,017522
0,022232
0,027249
0,032630
0,038443
0,044772
0,051728
0,059460
0,068169
0,078145
0,089813
0,443142
0,009048
0,013157
0,017235
0,021396
0,025706
0,030212
0,034966
0,040027
0,045465
0,051368
0,057855
0,065087
0,073294
0,082827
0,094248
0,338109
0,012444
0,016611
0,020593
0,024555
0,028573
0,032702
0,036990
0,041487
0,046252
0,051355
0,056889
0,062980
0,069810
0,077655
0,086979
0,098636
Ci
-0,026314
-0,014497
0,000034
0,018080
0,507970
-0,052617
-0,055674
-0,056526
-0,055995
-0,054191
-0,051331
-0,047281
-0,042029
-0,035403
-0,027176
-0,017018
-0,004442
-0,011289
0,031340
0,456986
-0,047594
-0,050597
-0,051629
-0,051393
-0,050102
-0,047820
-0,044532
-0,040165
-0,034587
-0,027599
-0,028906
-0,008069
0,005581
0,023119
0,046408
0,397887
-0,042879
-0,045800
-0,046965
-0,047008
-0,046121
-0,044362
-0,041722
-0,038137
-0,033494
-0,027618
-0,020248
-0,010994
-0,000742
0,015937
0,036313
0,065331
2.3]
Оценка параметров распределения Вейбулла
161
п
18
18
20
20
20
20
20
20
20
г
17
18
2
3
4
5
6
7
8
г
17
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
3
4
5
6
щ
0,235490
0,015092
0,019328
0,023258
0,027089
0,030909
0,034773
0,038728
0,042820
0,047095
0,051612
0,056443
0,061685
0,067477
0,074032
0,081713
0,091221
0,109314
0,132411
-1,251068
2,251068
-0,662014
-0,621129
2,283144
-0,408252
-0,386289
-0,345972
2,140513
-0,272551
-0,259179
-0,233536
-0,199675
1,964941
-0,190502
-0,181539
-0,163969
-0,140605
-0,112303
1,788917
-0,136790
-0,130201
-0,117518
-0,100561
-0,079995
-0,056007
1,621135
-0,099621
-0,094504
-0,084808
-0,071993
-0,056488
-0,038416
0,327023
-0,098116
-0,038165
-0,042221
-0,042947
-0,041963
^0,040676
-0,038627
-0,035765
-0,031992
-0,027160
-0,021041
-0,013300
-0,003410
-0,009488
0,026940
0,052132
0,093529
0,235693
-0,493634
0,493634
-0,327555
-0,316157
0,643712
-0,243885
-0,238726
-0,223155
0,705766
-0,193344
-0,191335
-0,181278
-0,165821
0,731828
-0,159435
-0,159298
-0,152528
-0,141408
-0,126651
0,739321
-0,135060
-0,136029
-0,131448
-0,123236
-0,111990
-0,097918
0,735681
-0,116659
-0,118326
-0,115235
-0,109093
-0,100352
-0,089210
п
20
20
20
20
20
20
П
г
8
9
10
11
12
13
родолжение таблицы 42
г
7
8
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
ai
-0,017755
1,463585
-0,072826
-0,068644
-0,060858
-0,050834
-0,038781
-0,024779
-0,008798
0,009270
1,316151
-0,052900
-0,049115
-0,042792
-0,034710
-0,025087
-0,013973
-0,001335
0,012921
0,028939
1,178052
-0,037716
-0,034222
-0,028845
-0,022146
-0,014276
-0,005262
0,004930
0,016382
0,029216
0,043593
1,048347
-0,025922
-0,022589
-0,017879
-0,012183
-0,005600
0,001858
0,010227
0,019578
0,030012
0,041668
0,054724
0,926107
-0,016619
-0,013364
-0,009129
-0,004170
0,001453
0,007742
0,014732
0,022485
Ci
-0,075681
0,724575
-0,102246
-0,104362
-0,102371
-0,097711
-0,090828
-0,081874
-0,070863
-0,057714
0,707969
-0,090626
-0,093031
-0,091837
-0,088309
-0,082842
-0,075573
-0,077511
-0,055584
-0,042651
0,686964
-0,081036
-0,083625
-0,083028
-0,076014
-0,076014
-0,070070
-0,062554
-0,053398
-0,042476
-0,029594
0,662168
-0,072964
-0,075662
-0,075522
-0,073554
-0,070076
-0,065197
-0,058928
-0,051211
-0,041931
-0,030912
-0,017911
0,633868
-0,066052
-0,068809
-0,069021
-0,067601
-0,064335
-0,060825
-0,055581
-0,049051
6 А. И. Кобзарь
162
Оценка параметров распределений вероятностей
[Гл. 2
п
20
20
20
20
20
г
13
14
15
16
17
г
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
о*
0,031087
0,040654
0,051333
0,063321
0,810474
-0,009191
-0,005961
-0,002065
0,002348
0,007248
0,012649
0,018585
0,025109
0,032297
0,040241
0,049069
0,058941
0,070007
0,700660
-0,003203
0,000035
0,003690
0,007695
0,012048
0,016769
0,021892
0,027467
0,033552
0,040230
0,047602
0,055804
0,065012
0,075467
0,595940
0,001656
0,004926
0,008410
0,012111
0,016046
0,020247
0,024742
0,029575
0,034801
0,040482
0,046707
0,053585
0,061262
0,069938
0,079893
0,495616
0,005617
0,008931
Ci
-0,041132
-0,031666
-0,020429
-0,007116
0,602120
-0,060043
-0,062821
-0,063307
-0,062329
-0,060148
-0,056856
-0,052465
-0,046929
-0,040154
-0,031999
-0,022261
-0,011999
-0,003196
0,566775
-0,054744
-0,575130
-0,058213
-0,057596
-0,055899
-0,053209
-0,049537
-0,044884
-0,039043
-0,032010
-0,023560
-0,013436
-0,001280
0,013416
0,527466
-0,050002
-0,052742
-0,053608
-0,053287
-0,051997
-0,049816
-0,046757
-0,042785
-0,037825
-0,031763
-0,024342
-0,015601
-0,004939
-0,008023
0,023984
0,483548
-0,045695
-0,048385
п
20
20
20
Продол
г
17
18
19
г
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
жение таблицы 42
ai
0,012297
0,015773
0,019394
0,023192
0,027201
0,031459
0,036010
0,040910
0,046228
0,052055
0,058509
0,065756
0,074029
0,089671
0,398968
0,008847
0,012215
0,015502
0,018813
0,022197
0,025690
0,029324
0,033136
0,037162
0,041450
0,046055
0,051050
0,056532
0,062634
0,069547
0,077558
0,087131
0,305157
0,011469
0,014895
0,018135
0,021329
0,024554
0,027802
0,031153
0,034624
0,038247
0,042061
0,046112
0,050458
0,055176
0,060372
0,066198
0,072887
0,080830
0,090746
0,212971
Ci
-0,049380
-0,049304
-0,048357
-0,046613
-0,044083
-0,040736
-0,036510
-0,031298
-0,024954
-0,017265
-0,007934
0,003474
0,017606
0,035486
0,433947
-0,041706
-0,044331
-0,045422
^0,045550
-0,044896
-0,043529
-0,041460
-0,038666
-0,035086
-0,030632
-0,025168
-0,018506
-0,010374
-0,000381
0,012071
0,027938
0,048871
0,376826
-0,037905
-0,040446
-0,041607
-0,041903
-0,041503
-0,040467
-0,038810
-0,036509
-0,033514
-0,029746
-0,025085
-0,019364
-0,012340
-0,003660
0,007217
0,021167
0,039737
0,066024
0,308714
2.3]
Оценка параметров распределения Вейбулла
163
Окончание таблицы 42
п
20
г
20
г
1
2
3
4
5
6
7
8
9
10
щ
0,013555
0,017039
0,020257
0,023370
0,026464
0,029565
0,032711
0,035932
0,039258
0,042720
Ci
-0,034055
-0,036484
-0,037686
-0,098123
-0,037945
-0,037211
-0,035932
-0,034091
-0,031016
-0,028527
п
20
г
20
г
11
12
13
14
15
16
17
18
19
20
щ
0,046357
0,050215
0,054354
0,058856
0,063842
0,069496
0,076128
0,084346
0,095669
0,119862
Сг
-0,024632
-0,019814
-0,013860
-0,006460
0,002866
0,014902
0,031052
0,054203
0,092028
0,221415
Таблица 43
п
2
3
4
5
6
7
8
9
г
2
2
3
2
3
4
2
3
4
5
2
3
4
5
6
2
3
4
5
6
7
2
3
4
5
6
7
8
2
3
4
5
6
7
8
9
Значения коэффициентов к
кг
0,037574
0,257509
-0,018421
0,413509
0,084775
-0,028312
0,533791
0,166129
0,030763
-0,029135
0,631490
0,232697
0,080351
0,008881
-0,027716
0,713665
0,288854
0,122608
0,042126
-0,001300
-0,025789
0,784533
0,337341
0,159281
0,071292
0,022472
-0,006413
-0,023866
0,846604
0,379959
0,191609
0,097153
0,043783
0,011395
-0,009069
-0,022094
к2
0,415839
0,450055
0,256346
0,464388
0,281729
0,183862
0,472308
0,294192
0,202419
0,142830
0,477340
0,301732
0,212422
0,156905
0,116577
0,480082
0,306813
0,218847
0,164973
0,127606
0,098365
0,483377
0,310476
0,223358
0,170378
0,134224
0,107264
0,025017
0,485329
0,313246
0,226712
0,174294
0,138801
0,112788
0,092365
0,074824
п
10
11
12
13
г
2
3
4
5
6
7
СХ)
9
10
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
1 и к2 [95]
кг
0,902322
0,417951
0,229478
0,120330
0,062998
0,027627
0,004749
-0,010438
-0,020508
0,952399
0,452207
0,246536
0,141299
0,080450
0,042460
0,017512
0,000584
-0,011097
-0,019101
0,997998
0,483387
0,270268
0,160246
0,096410
0,056079
0,029301
0,010873
-0,002107
-0,011349
-0,017385
1,039851
0,511988
0,292046
0,177997
0,111099
0,068047
к2
0,486871
0,315415
0,229309
0,177275
0,142198
0,116706
0,097048
0,081004
0,066792
0,488120
0,317159
0,231380
0,179627
0,144834
0,116760
0,100437
0,085031
0,060304
0,060304
0,489151
0,318593
0,233072
0,181531
0,146945
0,122006
0,103043
0,087994
0,075575
0,064873
0,054954
0,490018
0,319794
0,234480
0,183107
0,148677
0,123901
164
Оценка параметров распределений вероятностей
[Гл. 2
Окончание таблицы 43
п
13
14
16
18
г
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
кг
0,040225
0,020463
0,006357
-0,003882
-0,011361
-0,016749
1,078521
0,538401
0,312161
0,194239
0,124694
0,080302
0,050382
0,029469
0,014307
0,003200
-0,005064
-0,011233
-0,015764
1,480153
0,585828
0,348282
0,223426
0,149158
0,101317
0,068748
0,045666
0,028811
0,016221
0,006658
-0,000690
-0,006373
-0,010762
-0,014090
1,209127
к2
0,105124
0,090302
0,078188
0,067951
0,058952
0,050470
0,490757
0,320813
0,235672
0,184433
0,150126
0,025473
0,106830
0,092166
0,080248
0,070275
0,061682
0,053001
0,046657
0,491948
0,322450
0,237577
0,186541
0,152413
0,127935
0,109474
0,095010
0,083327
0,073645
0,065435
0,058318
0,051997
0,046198
0,040524
0,492867
п
18
20
г
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
кг
0,627488
0,308007
0,249075
0,170681
0,119838
0,084973
0,060068
0,041720
0,027876
0,017236
0,008940
0,002403
-0,002784
-0,006912
-0,010185
-0,012727
1,263654
0,664622
0,408277
0,271937
0,189878
0,136375
0,099482
0,072972
0,053316
0,038380
0,026809
0,017704
0,010451
0,004619
-0,000103
-0,003943
-0,007067
-0,009596
-0,011599
к2
0,323709
0,239034
0,188145
0,154141
0,129778
0,111433
0,097092
0,085544
0,076015
0,067989
0,061101
0,055086
0,049739
0,044879
0,040334
0,035808
0,493598
0,324060
0,240184
0,189405
0,155492
0,131212
0,112948
0,098688
0,087226
0,077792
0,069871
0,063107
0,057241
0,052208
0,047471
0,043295
0,039437
0,035771
0,032070
Запишем функцию распределения Рэлея в двухпараметрической форме:
x\il) = 1 -ехр
Оценки параметров \х и а методом моментов имеют вид
Их дисперсии равны:
D{aM) =
D + 2тг-тг2)
4пD-тг) ;
= к2 + j
а2D-тг)
2.3] Оценка параметров распределения Вейбулла 165
Оптимальные квантильные оценки имеют вид [166]
л Хр-, ^vo ^ О1\Хр~ СХ2Хр-,
ак = ; II к =
где xPi—выборочные квантили уровня pi\ щ = — 1пA — pi), г = 1,2; pi = 0,93
и р2 = 0,07.
Дисперсии таких оценок равны
2 2
?>(йк) = 0,7681^; D(p,K) = 1,7506 — .
Эффективность моментных и квантильных оценок по сравнению с оценками мак™
симального правдоподобия равны « 0,45 для ам и « 0,33 для а^.
2.3.2. Интервальные оценки
2.3.2.1. Оценка а при известном /3
Интервальные оценки имеют вид
где х^ — 7"квантиль распределения хи-квадрат с / = 2п (п — объем выборки) степе-
г г 1 -\- а П 1 — a f и л
нями свободы; 7 = ? 7 = Для двусторонних оценок 17 =ft, 7 = 1 — а
для односторонних оценок (а — доверительная вероятность, которую не следует
путать с а — параметром распределения).
Для нахождения этих оценок можно использовать результаты, полученные ра™
нее для оценки параметра экспоненциального распределения (см. раздел 2.2). По
аналогии искомые оценки можно записать в форме
где кн и кв — коэффициенты оценок, табулированные в табл. 36;
х = - V хр- .
п ^^ %
В [36] предложены достаточно точные и простые аппроксимации для нахожде-
нахождения интервальных оценок параметров распределения Вейбулла при доверительной
вероятности а = 0,95:
— ^ р ^ pA:n; agi ^ a ^ ag2?
где /3, а — точечные оценки соответственно параметров /3 и а,
2 05
fen = 1 + ? 0;55 (при n ^ 6 ошибка не более 0,2%);
1 1
И 1,659 /з 3,01 /з
= I1 ~ , , ^0,4675 5 «2= U+7 ч ^40,5623 (ошибка МСНЬШС 1 %).
(п + 3) ' J [ (w ~ ЗД5) ' J
166 Оценка параметров распределений вероятностей [Гл. 2
2.3.2.2. Совместная интервальная оценка параметров о и /3
Манн и Фертиг [95, 162, 167] предложили оценки для а и /3, основанные на
их точечных линейных оценках по цензурированием сверху выборкам (см. раз™
дел 2.3.1.5). Оценки имеют вид
/QH _ / о. ОВ _ Пп
где /3 — точечная линейная оценка параметра /3, а с'а и с^ —коэффициенты оценки;
а — доверительная вероятность.
Значения коэффициентов cfa и ё'а для различных доверительных вероятностей а
приведены в табл. 44.
Интервальные оценки для параметра а находятся по формулам
&l = exp(U - ScQ; o? = exp(U - Sd?),
где й, Ь — оценки параметров распределения наименьших значений (напомним,
п п
что й = ^ а^ 1нж^, Ь = ^ Ci Inxi с коэффициентами оц и С{ из табл. 42); d'a, d!^ —
коэффициенты оценок, а — доверительная вероятность. Значения коэффициентов
d'a и d'^ приведены в табл. 45.
Для распределения Вейбулла представляют интерес оценки, связанные с его
широким применением при исследовании надежности технических компонентов
и систем. Например, в практике часто возникает задача, которую можно сфор-
сформулировать следующим образом: найти значение наработки t? компонента (или
системы), при котором вероятность безотказной работы компонента (или системы)
равна заданной величине е.
1
Точечная оценка подсчитывается по формуле t? = — a(lne)^, где d, J3 — точеч-
точечные оценки параметров распределения.
Интервальная оценка находится по формуле ехр[й — bkf(?^a)] ^ t? ^
г г
^ ехр [й — bkrf(e, а)], где й = ^ а^ In t^, b = ^ Ci In t^ — линейные оценки параметров
i=l г=1
гх и Ь с коэффициентами а^ и q из табл.42; fc;(e,a) и fc/;(e,a)—коэффициенты
оценки и а — доверительная вероятность. Значения коэффициентов fc;(e,a)
и fc;/(e, а) приведены в табл. 46.
Учитывая чрезвычайно широкое применение распределения Вейбулла и его
частного случая — экспоненциального распределения — при планировании и оценке
результатов испытаний на надежность, в заключение попытаемся ответить еще на
один интересный в практическом отношении вопрос: зачем ставить на испытания
п > г изделий, если оценка параметров производится по результатам первых г
отказов? Ответ прост (хотя и не тривиален)—для экономии времени. Не вдаваясь
в математические тонкости (о них желающий может узнать из [95]), приведем
известные результаты расчетов показателя ц = —. ™, где t\r,n) — ожидаемая про™
t(r,r)
должительность испытаний п изделий до появления г™го отказа и t(r^r)—ожи-
t(r^r)—ожидаемая продолжительность испытаний, когда на испытания ставятся г изделий
и испытания проводятся до отказа всех изделий.
Значения 7] для разных г шп приведены в табл. 47 для случая экспоненциального
распределения (таблица заимствована из [95]). Табл. 47 применима и при оценках,
связанных с распределением Вейбулла (при известном заранее параметре /3). В этом
i_
случае следует найденную по табл. 47 величину rj заменить величиной г/ = г]@ .
2.3]
Оценка параметров распределения Вейбулла
167
Таблица 44
п
3
4
5
6
7
8
9
10
11
12
Т
3
3
4
3
4
5
3
4
5
6
3
4
5
6
7
3
4
5
6
7
8
3
4
5
6
7
8
9
3
4
5
6
7
8
9
10
3
4
5
6
7
8
9
10
11
3
4
5
6
а =
с'
0,17
0,15
0,28
0,14
0,26
0,36
0,14
0,25
0,33
0,41
0,14
0,24
0,32
0,39
0,46
0,13
0,23
0,31
0,38
0,44
0,50
0,13
0,23
0,31
0,38
0,43
0,48
0,53
0,13
0,23
0,30
0,37
0,42
0,47
0,51
0,55
0,13
0,22
0,30
0,36
0,41
0,46
0,50
0,54
0,57
0,13
0,22
0,30
0,36
Значения коэффициентов cfa
0,90
с"
1,56
1,56
1,53
1,59
1,55
1,50
1,59
1,55
1,51
1,46
1,56
1,54
1,52
1,48
1,48
1,58
1,55
1,52
1,49
1,45
1,41
1,58
1,55
1,52
1,48
1,46
1,42
1,39
1,59
1,57
1,53
1,49
1,46
1,43
1,40
1,38
1,60
1,58
1,54
1,52
1,48
1,45
1,42
1,38
1,36
1,56
1,55
1,53
1,49
а =
с1
0,11
0,10
0,20
0,09
0,18
0,28
0,09
0,18
0,25
0,33
0,08
0,17
0,25
0,32
0,38
0,03
0,16
0,23
0,30
0,36
0,42
0,08
0,16
0,23
0,30
0,35
0,40
0,45
0,08
0,16
0,23
0,29
0,36
0,39
0,43
0,48
0,08
0,15
0,22
0,28
0,33
0,38
0,42
0,46
0,50
0,08
0,16
0,23
0,29
0,95
с"
1,86
1,90
1,77
1,93
1,82
1,70
1,92
1,84
1,73
1,64
1,92
1,82
1,75
1,67
1,60
1,95
1,83
1,76
1,69
1,62
1,56
1,92
1,84
1,76
1,70
1,65
1,59
1,53
1,92
1,86
1,77
1,71
1,66
1,60
1,55
1,51
1,97
1,87
1,82
1,73
1,67
1,62
1,58
1,53
1,49
1,87
1,82
1,78
1,72
п
12
13
14
15
16
т
7
8
9
10
11
12
3
4
5
6
7
8
9
10
11
12
13
3
4
5
6
7
8
9
10
11
12
13
14
3
4
5
6
7
8
9
10
11
12
13
14
15
3
4
5
6
7
8
9
и с« [95]
а = 0,90
с'
0,41
0,46
0,50
0,53
0,56
0,60
0,13
0,22
0,30
0,36
0,40
0,45
0,49
0,52
0,55
0,58
0,61
0,13
0,22
0,30
0,35
0,40
0,45
0,49
0,52
0,55
0,57
0,60
0,63
0,13
0,22
0,29
0,35
0,41
0,45
0,49
0,52
0,54
0,57
0,59
0,62
0,64
0,13
0,22
0,29
0,35
0,40
0,44
0,48
с"
1,47
1,45
1,43
1,40
1,37
1,35
1,58
1,57
1,55
1,51
1,48
1,42
1,40
1,38
1,36
1,33
1,58
1,57
1,54
1,51
1,48
1,45
1,42
1,40
1,38
1,36
1,34
1,32
1,57
1,56
1,53
1,50
1,48
1,45
1,43
1,41
1,39
1,37
1,35
1,33
1,32
1,58
1,56
1,54
1,51
1,47
1,45
1,43
1,41
а =
с'
0,34
0,38
0,42
0,45
0,49
0,53
0,08
0,15
0,22
0,28
0,33
0,37
0,42
0,44
0,48
0,51
0,54
0,08
0,16
0,22
0,28
0,33
0,38
0,41
0,45
0,48
0,50
0,53
0,57
0,08
0,16
0,22
0,28
0,33
0,37
0,41
0,42
0,48
0,50
0,52
0,55
0,58
0,08
0,15
0,22
0,27
0,31
0,36
0,40
0,95
с"
1,66
1,61
1,58
1,55
1,51
1,46
1,95
1,86
1,79
1,72
1,67
1,62
1,58
1,55
1,51
1,47
1,44
1,94
1,86
1,77
1,71
1,67
1,63
1,59
1,56
1,52
1,49
1,46
1,43
1,92
1,85
1,79
1,71
1,67
1,63
1,59
1,56
1,54
1,50
1,47
1,45
1,42
1,94
1,86
1,78
1,74
1,69
1,64
1,60
168
Оценка параметров распределений вероятностей
[Гл. 2
ТЬ
16
18
10
11
12
13
14
15
16
3
4
5
6
7
8
9
10
11
12
13
14
15
16
а =
с'
0,51
0,53
0,56
0,59
0,61
0,63
0,65
0,12
0,22
0,29
0,35
0,40
0,44
0,47
0,51
0,53
0,56
0,58
0,60
0,62
0,64
0,90
с11
1,39
1,38
1,36
1,34
1,34
1,32
1,29
1,59
1,58
1,54
1,51
1,48
1,46
1,43
1,41
1,39
1,38
1,36
1,35
1,33
1,31
а =
с'
0,43
0,46
0,49
0,51
0,54
0,56
0,59
0,07
0,15
0,22
0,27
0,33
0,37
0,40
0,43
0,46
0,49
0,51
0,54
0,56
0,57
0,95
с"
1,57
1,54
1,50
1,48
1,46
1,43
1,40
1,93
1,87
1,79
1,73
1,68
1,63
1,59
1,56
1,54
1,52
1,48
1,46
1,44
1,42
ть
18
20
О
17
18
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ко н ч
а =
с'
0,65
0,67
0,12
0,22
0,29
0,35
0,40
0,43
0,47
0,50
0,53
0,55
0,57
0,60
0,61
0,63
0,65
0,66
0,68
0,70
ание
0,90
с"
1,30
1,28
1,60
1,57
1,55
1,52
1,49
1,46
1,44
1,42
1,40
1,38
1,36
1,35
1,34
1,33
1,31
1,30
1,28
1,27
та б л \
[цы 44
а = 0,95
с1
0,59
0,61
0,07
0,15
0,22
0,27
0,32
0,35
0,39
0,43
0,45
0,48
0,50
0,52
0,54
0,56
0,58
0,60
0,62
0,64
с"
1,39
1,37
1,97
1,89
1,81
1,75
1,70
1,65
1,61
1,58
1,54
1,52
1,50
1,48
1,46
1,44
1,42
1,40
1,37
1,36
Таблица 45
п
3
4
5
6
7
8
9
V
3
3
4
3
4
5
3
4
5
6
3
4
5
6
7
3
4
5
6
7
8
3
а =
d'
2,12
1,55
1,49
1,20
1,22
1,20
1,02
1,03
1,04
1,04
0,90
0,89
0,89
0,90
0,90
0,88
0,83
0,82
0,82
0,82
0,82
0,86
Значеним коэффициентов dfa и d^
:0,90
d"
-2,54
-3,85
-1,50
-5,22
-1,94
-1,08
-6,12
-2,39
-1,36
-0,91
-7,39
-2,95
-1,59
-1,04
-0,79
-8,15
-3,30
-1,86
-1,20
-0,88
-0,70
-9,12
а = 0,95
в!
3,39
2,43
2,15
1,76
1,74
1,64
1,39
1,42
1,41
1,39
1,20
1,20
1,21
1,20
1,18
1,72
1,07
1,07
1,08
1,08
1,07
1,06
d"
-4,47
-6,92
-2,37
-9,35
-3,13
-1,63
-10,54
-3,69
-2,05
-1,29
-13,00
-4,67
-2,48
-1,54
-1,09
-14,26
-5,34
-2,78
-1,81
-1,28
-0,97
-15,68
ть
9
10
11
т
4
5
6
7
8
9
3
4
5
6
7
8
9
10
3
4
5
6
7
8
9
10
а -
в!
0,79
0,76
0,76
0,76
0,76
0,76
0,87
0,77
0,72
0,71
0,70
0,71
0,71
0,71
0,87
0,75
0,69
0,66
0,65
0,65
0,65
0,65
[95]
= 0,90
d"
-3,78
-2,10
-1,38
-0,99
-0,76
-0,64
-9,98
-4,17
-2,37
-1,51
-1,08
-0,86
-0,70
-0,60
-10,68
-4,57
-2,58
-1,67
-1,21
-0,92
-0,76
-0,63
а -
d'
1,00
0,98
0,99
0,99
0,99
0,98
1,07
0,96
0,93
0,92
0,93
0,93
0,93
0,92
1,07
0,92
0,88
0,85
0,86
0,86
0,86
0,86
= 0,95
d"
-6,31
-3,19
-2,01
-1,43
-1,08
-0,87
-17,45
-6,54
-3,56
-2,21
-1,56
-1,20
-0,97
-0,80
-18,52
-7,26
-4,00
-2,45
-1,70
-1,30
-1,06
-0,87
2.3]
Оценка параметров распределения Вейбулла
169
п
11
12
13
14
15
16
г
11
3
4
5
6
7
8
9
10
11
12
3
4
5
6
7
8
9
10
11
12
13
3
4
5
6
7
8
9
10
11
12
13
14
3
4
5
6
7
8
9
10
11
12
13
14
15
3
4
5
а -
d!
0,65
0,88
0,75
0,68
0,64
0,62
0,62
0,62
0,62
0,62
0,62
0,88
0,76
0,68
0,64
0,61
0,59
0,58
0,58
0,58
0,59
0,59
0,90
0,77
0,69
0,63
0,60
0,58
0,56
0,56
0,56
0,56
0,56
0,56
0,89
0,78
0,70
0,64
0,59
0,57
0,56
0,55
0,54
0,54
0,54
0,54
0,54
0,92
0,79
0,70
= 0,90
d"
-0,55
-11,23
-4,81
-2,72
-1,83
-1,32
-1,00
-0,80
-0,67
-0,58
-0,53
-11,66
-5,21
-2,95
-1,94
-1,40
-1,06
-0,86
-0,72
-0,63
-0,56
-0,51
-12,49
-5,38
-3,13
-2,10
-1,50
-1,15
-0,93
-0,76
-0,65
-0,57
-0,51
-0,47
-13,14
-5,55
-3,35
-2,21
-1,56
-1,20
-0,96
-0,82
-0,70
-0,62
-0,55
-0,50
-0,46
-13,55
-5,89
-3,45
а -
d1
0,85
1,10
0,92
0,84
0,81
0,80
0,79
0,80
0,80
0,80
0,79
1,09
0,93
0,84
0,79
0,77
0,75
0,74
0,74
0,75
0,75
0,75
1,11
0,94
0,84
0,79
0,75
0,73
0,72
0,72
0,72
0,72
0,72
0,72
1,12
0,95
0,85
0,78
0,74
0,71
0,69
0,68
0,68
0,68
0,68
0,68
0,68
1,13
0,97
0,85
= 0,95
d"
-0,75
-19,08
-7,44
-4,17
-2,63
-1,91
-1,41
-1,15
-0,91
-0,78
-0,69
-19,77
-8,22
-4,44
-2,86
-2,04
-1,52
-1,18
-1,00
-0,85
-0,74
-0,67
-21,43
-8,30
-4,72
-3,07
-2,16
-1,67
-1,30
-1,07
-0,89
-0,76
-0,68
-0,63
-23,14
-8,79
-4,88
-3,21
-2,29
-1,72
-1,35
-1,10
-0,96
-0,83
-0,73
-0,66
-0,59
-22,72
-9,38
-5,17
п
16
18
20
г
6
7
8
9
10
11
12
13
14
15
16
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Оке
а -
d!
0,63
0,59
0,56
0,54
0,53
0,52
0,52
0,52
0,52
0,52
0,52
0,97
0,83
0,72
0,65
0,60
0,55
0,52
0,50
0,49
0,48
0,48
0,48
0,48
0,48
0,48
0,48
0,99
0,83
0,73
0,65
0,59
0,55
0,52
0,49
0,47
0,46
0,45
0,45
0,45
0,45
0,45
0,45
0,45
0,45
>нчани(
= 0,90
d"
-2,34
-1,68
-1,30
-1,05
-0,86
-0,72
-0,64
-0,56
-0,51
-0,46
-0,44
-14,29
-6,23
-3,74
-2,56
-1,87
-1,42
-1,16
-0,95
-0,81
-0,69
-0,61
-0,55
-0,50
-0,46
-0,44
-0,41
-15,33
-6,64
-4,00
-2,73
-2,04
-1,55
-1,26
-1,03
-0,88
-0,76
-0,67
-0,59
-0,53
-0,49
-0,46
-0,43
-0,41
-0,40
э таблицы 45
а = 0,95
d1
0,77
0,73
0,70
0,68
0,67
0,66
0,66
0,66
0,66
0,66
0,66
1,21
1,00
0,87
0,78
0,72
0,68
0,65
0,63
0,62
0,61
0,61
0,60
0,61
0,60
0,61
0,61
1,25
1,02
0,89
0,79
0,72
0,68
0,63
0,60
0,59
0,59
0,58
0,57
0,57
0,57
0,57
0,57
0,57
0,57
d"
-3,34
-2,42
-1,81
-1,44
-1,18
-1,00
-0,87
-0,76
-0,68
-0,61
-0,56
-25,90
-9,67
-5,55
-3,67
-2,64
-2,02
-1,62
-1,33
-1,13
-0,95
-0,84
-0,74
-0,67
-0,61
-0,57
-0,54
-26,67
-10,49
-5,99
-3,95
-2,91
-2,20
-1,72
-1,42
-1,19
-1,02
-0,89
-0,80
-0,70
-0,65
-0,60
-0,56
-0,53
-0,53
170
Оценка параметров распределений вероятностей
[Гл. 2
Таблица 46
п
т
а = (
к1
Коэффициенты fc'i
3,90
к"
а =
к'
0,95
к"
и к"(е,а) [95]
т
а = 0,90
к1
к"
а =
к'
0,95
к"
е = 0,90
3
4
5
6
7
8
9
10
11
12
3
3
4
3
4
5
3
4
5
6
3
4
5
6
7
3
4
5
6
7
8
3
4
5
6
7
8
9
3
4
5
6
7
8
9
10
3
4
5
6
7
8
9
10
11
3
4
5
13,16
13,07
8,39
12,58
8,48
6,73
11,74
8,18
6,73
5,83
11,12
7,89
6,68
5,82
5,25
10,67
7,79
6,50
5,83
5,31
4,90
10,21
7,39
6,34
5,67
5,28
4,95
4,66
9,36
7,17
6,13
5,59
5,18
4,91
4,63
4,41
9,11
7,04
6,07
5,52
4,96
4,87
4,63
4,44
4,26
8,40
6,60
5,79
1,10
1,16
1,16
1,18
1,23
1,23
1,18
1,28
1,29
1,27
1,18
1,31
1,33
1,32
1,32
1,13
1,33
1,36
1,36
1,36
1,36
1,12
1,36
1,41
1,41
1,41
1,40
1,40
0,99
1,34
1,42
1,43
1,43
1,43
1,42
1,42
0,90
1,35
1,43
1,45
1,45
1,45
1,44
1,44
1,45
0,75
1,34
1,11
20,93
20,93
11,66
20,38
11,73
8,66
18,65
11,39
8,89
7,31
17,54
10,90
8,44
7,23
6,37
16,36
10,76
8,62
7,18
6,40
5,84
15,61
10,26
8,13
7,06
6,46
5,94
5,50
14,88
9,60
8,02
6,99
6,29
5,83
5,51
5,16
14,47
9,98
7,83
6,96
6,34
5,82
5,54
5,23
4,94
12,96
9,07
7,35
0,75
0,75
0,87
0,78
0,97
0,97
0,73
1,00
1,02
1,02
0,64
1,04
1,08
1,08
1,08
0,49
1,04
1,11
1,13
1,12
1,12
0,42
1,06
1,17
1,19
1,19
1,19
1,19
0,09
0,99
1,17
1,20
1,21
1,21
1,21
1,21
-0,09
0,97
1,18
1,24
1,25
1,25
1,25
1,25
1,25
-0,38
0,95
1,20
12
13
14
15
16
6
7
8
9
10
11
12
3
4
5
6
7
8
9
10
11
12
13
3
4
5
6
7
8
9
10
11
12
13
14
3
4
5
6
7
8
9
10
11
12
13
14
15
3
4
5
6
7
5,31
4,98
4,75
4,53
4,37
4,23
4,07
8,16
6,45
5,75
5,30
4,96
4,73
4,55
4,37
4,23
4,09
3,96
7,69
6,17
5,54
5,12
4,82
4,61
4,45
4,30
4,20
4,09
3,98
3,85
7,23
5,95
5,36
4,97
4,72
4,57
4,40
4,26
4,15
4,08
3,98
3,89
3,77
7,07
5,90
5,33
4,98
4,74
1,46
1,47
1,47
1,46
1,47
1,46
1,47
0,72
1,31
1,45
1,48
1,49
1,49
1,49
1,49
1,49
1,49
1,49
0,57
1,29
1,46
1,51
1,52
1,52
1,52
1,51
1,51
1,51
1,51
1,51
0,43
1,26
1,44
1,50
1,52
1,52
1,52
1,52
1,52
1,52
1,52
1,51
1,52
0,25
1,23
1,45
1,52
1,53
6,61
6,09
5,71
5,40
5,11
4,88
4,68
12,45
8,82
7,32
6,49
6,02
5,63
5,32
5,11
4,90
4,73
4,51
11,56
8,28
6,96
6,27
5,75
5,47
5,18
4,94
4,79
4,67
4,51
4,36
10,78
7,94
6,85
6,19
5,77
5,40
5,16
4,95
4,76
4,62
4,51
4,39
4,23
10,49
7,94
6,73
6,18
5,81
1,26
1,28
1,28
1,27
1,27
1,27
1,28
-0,45
0,88
1,20
1,27
1,30
1,30
1,30
1,30
1,30
1,30
1,30
-0,81
0,83
1,18
1,28
1,32
1,33
1,33
1,33
1,33
1,33
1,33
1,33
-1,05
0,77
1,15
1,29
1,33
1,34
1,35
1,35
1,35
1,34
1,35
1,35
1,35
-1,38
0,74
1,17
1,30
1,35
2.3]
Оценка параметров распределения Вейбулла
171
а = (
к'
3,90
к"
а =
к1
0,95
к"
Продолжени
а = 0,90
к1
к11
е та б л
а =
к1
и ц ы 46
0,95
к"
е = 0,90
16
18
8
9
10
11
12
13
14
15
16
3
4
5
6
7
8
9
10
11
12
13
14
15
4,56
4,38
4,24
4,13
4,05
3,94
3,87
3,79
3,71
6,43
5,52
5,04
4,73
4,55
4,39
4,25
4,14
4,05
3,97
3,91
3,84
3,75
1,54
1,54
1,54
1,54
1,54
1,54
1,54
1,54
1,54
0,11
1,19
1,45
1,53
1,56
1,57
1,58
1,58
1,58
1,58
1,57
1,57
1,57
5,38
5,17
4,97
4,79
4,65
4,49
4,38
4,26
4,16
9,64
7,38
6,40
5,79
5,41
5,15
4,99
4,80
4,63
4,51
4,40
4,30
4,21
1,37
1,37
1,37
1,37
1,37
1,37
1,37
1,37
1,37
-1,61
0,66
1,10
1,30
1,37
1,40
1,41
1,41
1,41
1,41
1,41
1,41
1,41
18
20
16
17
18
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
3,71
3,66
3,59
6,04
5,24
4,82
4,55
4,41
4,29
4,15
4,05
3,97
3,92
3,84
3,77
3,72
3,67
3,61
3,57
3,52
3,47
1,57
1,58
1,58
-0,19
1,10
1,42
1,54
1,58
1,59
1,60
1,60
1,60
1,60
1,60
1,60
1,60
1,60
1,60
1,60
1,60
1,60
4,14
4,04
3,97
9,01
7,00
6,16
5,68
5,33
5,06
4,85
4,71
4,57
4,46
4,39
4,29
4,20
4,12
4,04
3,97
3,92
3,84
1,41
1,41
1,42
-2,27
0,46
1,07
1,30
1,38
1,42
1,43
1,44
1,44
1,44
1,44
1,44
1,44
1,44
1,44
1,44
1,44
1,44
е = 0,95
3
4
5
6
7
8
9
3
3
4
3
4
5
3
4
5
6
3
4
5
6
7
3
4
5
6
7
8
3
4
5
6
17,21
17,55
10,88
17,36
11,14
8,68
16,66
10,95
8,82
7,53
16,07
10,80
8,84
7,61
6,73
15,76
10,74
8,78
7,67
6,91
6,29
15,33
10,40
8,59
7,51
1,64
1,73
1,69
1,79
1,76
1,74
1,83
1,83
1,81
1,80
1,87
1,88
1,86
1,84
1,85
1,90
1,91
1,90
1,89
1,89
1,89
1,93
1,96
1,95
1,95
27,32
27,54
15,06
28,30
15,51
11,14
26,85
15,32
11,58
9,39
25,31
14,80
11,18
9,40
8,19
24,57
15,22
11,57
9,43
8,38
7,50
23,80
14,41
11,05
9,46
1,26
1,38
1,36
1,44
1,45
1,44
1,48
1,52
1,51
1,50
1,52
1,59
1,59
1,57
1,58
1,53
1,63
1,63
1,62
1,62
1,62
1,55
1,67
1,69
1,68
9
10
11
12
7
8
9
3
4
5
6
7
8
9
10
3
4
5
6
7
8
9
10
11
3
4
5
6
7
6,91
6,39
6,00
14,50
10,12
8,39
7,50
6,83
6,40
6,01
5,67
14,11
10,03
8,34
7,42
6,83
6,38
6,04
5,75
5,49
13,40
9,56
8,08
7,22
6,66
1,94
1,94
1,95
1,91
1,98
1,97
1,97
1,96
1,96
1,96
1,96
1,93
2,01
2,01
2,00
1,99
1,99
1,98
2,00
2,00
1,91
2,02
2,03
2,02
2,02
8,40
7,73
7,09
23,00
13,69
11,00
9,42
8,29
7,61
7,12
6,65
22,60
14,44
10,39
9,39
8,42
7,65
7,23
6,73
6,35
21,39
13,27
10,40
9,00
8,08
1,67
1,68
1,69
1,51
1,70
1,72
1,71
1,71
1,70
1,71
1,72
1,48
1,73
1,75
1,75
1,75
1,75
1,75
1,76
1,77
1,42
1,74
1,79
1,79
1,79
172
Оценка параметров распределений вероятностей
[Гл. 2
п
Т
а = (
к'
3,90
к"
а = (
У
3,95
к"
п
т
Окон
а = (
к'
чание
3,90
к"
таблицы 46
а = 0,95
к'
к"
е = 0,95
12
13
14
15
16
8
9
10
11
12
3
4
5
6
7
8
9
10
11
12
13
3
4
5
6
7
8
9
10
11
12
13
14
3
4
5
6
7
8
9
10
11
12
13
14
15
3
4
5
6
7
8
9
10
6,27
5,95
5,67
5,47
5,26
13,11
9,47
8,04
7,24
6,68
6,29
6,00
5,70
5,50
5,30
5,12
12,73
9,10
7,82
7,07
6,53
6,16
5,88
5,65
5,48
5,31
5,14
4,97
12,22
8,90
7,64
6,91
6,41
6,10
5,81
5,61
5,43
5,31
5,17
5,02
4,88
11,98
8,88
7,67
6,92
6,47
6,12
5,84
5,60
2,01
2,00
2,01
2,01
2,02
1,92
2,05
2,06
2,05
2,05
2,04
2,04
2,04
2,04
2,04
2,05
1,92
2,06
2,08
2,08
2,07
2,07
2,07
2,06
2,07
2,07
2,07
2,08
1,88
2,06
2,09
2,09
2,08
2,08
2,07
2,07
2,07
2,07
2,07
2,07
2,08
1,85
2,06
2,11
2,11
2,11
2,10
2,10
2,09
7,49
7,06
6,63
6,29
6,00
20,76
13,09
10,25
8,89
8,10
7,43
7,83
6,99
6,66
6,36
5,80
19,14
12,45
9,93
8,71
7,78
7,30
6,92
6,49
6,26
6,06
5,80
5,60
18,38
11,93
9,79
8,55
7,90
7,26
6,87
6,50
6,22
6,00
5,88
5,66
5,46
18,76
12,30
9,72
8,63
7,98
7,27
6,92
6,60
1,79
1,78
1,77
1,78
1,80
1,44
1,78
1,82
1,82
1,82
1,81
1,81
1,81
1,81
1,81
1,83
1,39
1,77
1,84
1,85
1,85
1,85
1,84
1,85
1,85
1,85
1,85
1,85
1,24
1,77
1,84
1,87
1,87
1,86
1,86
1,85
1,85
1,86
1,87
1,87
1,89
1,13
1,77
1,87
1,89
1,89
1,89
1,88
1,88
16
18
20
11
12
13
14
15
16
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
5,44
5,30
5,14
5,02
4,91
4,80
11,18
8,46
7,32
6,61
6,23
5,95
5,72
5,51
5,35
5,23
5,12
5,01
4,88
4,83
4,74
4,65
10,78
8,16
7,09
6,49
6,11
5,88
5,62
5,43
5,29
5,18
5,07
4,96
4,86
4,78
4,70
4,64
4,57
4,49
2,09
2,09
2,09
2,10
2,11
2,12
1,83
2,09
2,14
2,14
2,14
2,14
2,14
2,13
2,13
2,14
2,14
2,13
2,14
2,14
2,15
2,17
1,75
2,09
2,15
2,17
2,17
2,17
2,16
2,16
2,16
2,16
2,16
2,16
2,16
2,16
2,17
2,18
2,18
2,19
6,30
6,06
5,87
5,68
5,53
5,35
17,89
11,66
9,43
8,27
7,45
6,97
6,71
6,38
6,15
5,96
5,75
5,60
5,46
5,36
5,22
5,11
16,96
11,03
9,12
8,11
7,42
6,97
6,56
6,30
6,09
5,92
5,79
5,63
5,49
5,37
5,23
5,14
5,06
4,95
1,89
1,88
1,89
1,90
1,90
1,92
1,11
1,81
1,90
1,93
1,94
1,94
1,94
1,93
1,93
1,93
1,92
1,93
1,94
1,94
1,95
1,97
0,94
1,79
1,92
1,94
1,95
1,96
1,96
1,95
1,95
1,95
1,96
1,96
1,96
1,97
1,98
1,98
1,99
2,00
2.3]
Оценка параметров распределения Вейбулла
173
Таблица 47
г
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
г
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Значения г\
= t(r,n)/t(r,r)
к
1
1,000
0,500
0,333
0,250
0,200
0,167
0,143
0,125
0,111
0,100
0,091
0,083
0,077
0,071
0,067
2
1,000
0,556
0,389
0,300
0,244
0,206
0,179
0,157
0,141
0,127
0,116
0,107
0,099
0,092
3
1,000
0,590
0,427
0,336
0,278
0,237
0,207
0,183
0,165
0,150
0,137
0,126
0,117
4
1,
0,
о,
о,
о5
0,
о,
0,
о,
о,
о,
о,
000
616
450
365
365
262
230
205
185
169
155
143
5
1,000
0,635
0,479
0,387
0,327
0,283
0,250
0,224
0,202
0,185
0,170
6
1,000
0,650
0,497
0,406
0,345
0,301
0,267
0,240
0,218
0,200
7
1,000
0,663
0,513
0,423
0,361
0,316
0,282
0,254
0,232
8
1,000
0,673
0,526
0,437
0,375
0,330
0,295
0,267
к
9
1,000
0,682
0,537
0,449
0,388
0,342
0,307
10
1,000
0,690
0,547
0,460
0,399
0,353
11
1,000
0,696
0,536
0,470
0,409
12
1,000
0,703
0,564
0,479
13
1,000
0,708
0,572
14
;
(
1,000
3,713
15
1,000
Задача 63. Получена выборка из распределения Вейбулла с параметром f3 = 3,1:
Xi\ 0,74; 0,78; 0,94; 1,26; 1,39; 2,17; 2,19; 3,18; 5,16; 6,12.
Необходимо найти оценку максимального правдоподобия параметра а.
Имеем
а= \ -
п •
_1_
/3 Г -,
10 V
зд
0,78
зд
¦6Д23'1'
1
зд
= 3,53601.
Задача 64. Найти совместные точечные оценки параметров распределения Вейбулла
по выборке данных задачи 63.
Используем метод ускоренного решения системы уравнений максимального правдо-
правдоподобия. Вычислим оценки среднего и стандартного отклонения
•=-4yXi = 2,393;
п *-—'
174 Оценка параметров распределений вероятностей [Гл. 2
s =
1
= 1,88539
g
и найдем оценку коэффициента вариации и = — = 0,78777.
ж
Из соотношения /Зо ~ i/~1?075 находим приближение
/Зо = @,787877)^l!075 = 1,292.
Далее вычисляем
ю
si = ]Г х1г2Ш = 0Д41'292 + • • • + 6Д21'292 = 33,85538;
ю
S2 = J2lnXi = Ы °'74 + • • • + Ь 6,12 = 6,11698;
г=1
10
= Y, х\'292 •ln Xi = 0,741>292 • In 0,74 + ... + 6Д21'292 • In 6,12 = 42,26807;
г=1
tf = 0,74х'292 • AпО,74J + ... + 6Д21'292 • Aп6Д2J = 66,16118.
Вычисляем оценки:
- [42,26807 611698 ^ ОЛО 42,268072 - 33,85538 • 66,16118
в = { — Ь 1,292 • —' ъ х
[33,85538 10 33,855382
х \(*Ш!. tbll^) . 1>292 - ll Г= 1,37481;
LV 33,85538 10 ) J/
1
1 10 \ 1,37481
: = I — J2 ^'3?481 I = 2,58882.
Задача 65. Имеется выборка из распределения Вейбулла:
хц 12, 14, 21, 38, 42, 44, 46, 59, 61, 72.
Вычислить оценки параметров а и C методом моментов.
Воспользуемся простейшим методом (оценка по коэффициенту вариации). Вычисля-
Вычисляем последовательно
1
»ffc~rf =19,208; |/=з =0,4708.
n ,ti J *
Имеем /3 = 0,4708^l!°75 = 2,247 или из табл. 39 /3 « 2,19.
Оценку а ищем в форме
1
/in \ 2,247
а= ^Еж?'247 =46,0656.
Воспользовавшись близостью /3^2, продемонстрируем оценку параметров распределе-
распределения Рэлея (см. раздел 2.3.1.6). В нашем случае s = 19,208 и х = 40,8.
Тогда имеем
2^= = 41,46; Ам = 40,8 - 19f!^ = 4,05.
4 — тг V 4 — тг
«1 • X\
X9 ~
«1 -
- a2
- x\
- OL2
¦ X2
= 10,626.
2.3] Оценка параметров распределения Вейбулла 175
Дисперсии этих оценок приближенно равны (hi = 20,745; k2 = 36,8886; fe = 11,6404):
D(aM) = J^fci = 96,478 (y/D(aM) = 9,82);
D(jim) = k2 H fci ^^= = 88,829
4 — 7Г V4 — 7Г
Полагая (весьма условно — только для демонстрации техники вычислений), что
L == жо,93-ю ~ жд и хР2 = Жо,07-ю ~ #1, имеем для квантильных оценок
l = - ln(l ~~ pi) = 2,659; а2 = - 1пA - р2) = 0,0725):
61^ 12 = 18,94;
2,659 - 0,0725
12 • 2,659 - 61 • 0,0725
«1 • а2 2,659 • 0,0725
Дисперсии их равны:
D(ak) = 0,7681 • ^ = 27,55
D(uk) = 1,7506 • ^ = 62,79 (х/В(ак) = 7,92).
те
Не следует приходить в отчаяние от несовпадения оценок ам и а&. Это является след-
следствием того, что квантильные оценки применимы при п > 50 (у нас, вспомните, речь
шла только о демонстрации техники вычислений).
Рассмотрим теперь оценку параметров распределения Вейбулла с помощью коэф-
коэффициента асимметрии. Отметим сразу, что достаточно точные оценки коэффициента
асимметрии требуют объема выборки п > 100. Мы преследуем цель продемонстрировать
только технику вычислений, поэтому следует помнить, что приведенный пример позво-
позволит понять суть метода, но для получения точных оценок с его помощью необходимо
располагать значительно большим объемом данных. Имеем
аз = —^ ' У" (хг - xf = ч * К12 - 40,81K + ... + G2 - 4,81K1 = -0,0707.
10 ¦ s3 fr[ V ; 10 ¦ 19,2083 LV ; V ; J
Примечание. Отличие в оценках от предыдущего метода не должно вводить в за-
заблуждение. Ведь когда мы говорим, что имеем выборку из распределения Вейбулла —
это не более, чем гипотеза (мы не знаем даже, сколько в нем значимых параметров). Как
узнать, каково же истинное распределение — это самостоятельная задача, рассматрива-
рассматриваемая в главе 3 настоящей книги.
Задача 66. Для данных задачи 65 найти оценки параметров по одной характеристи-
характеристической порядковой статистике.
Имеем г1 = 0,632 • (п + 10) = 0,632 • 11 = 6,252; xR = ^x6 • х7 = л/М • 46 = 44,989.
Вычисляем G = XR^X = —1— . D4,9889 - 40,8) = 0,218086.
s 19,208 v ;
Из табл. 41 имеем /3 ~ 1,821 и Ь1 = 1,978, и окончательно
а = s • У = 19,208 • 1,978 = 37,993; Д = xR - а = 44,989 - 37,993 = 6,996.
Задача 67. Имеется гистограмма выборочных данных по наработке приборов
U: 0^5 5^10 10-=-15 15^20 20^25 25^30 30^35 35^40
тц 21 24 12 10 5 13 9 6
(wii — количество данных, попавших в г-й интервал, JV=100). Найти оценку пара-
метров распределения наработки приборов методом наименьших квадратов {см. раз-
дел 2.3.1.3).
176
Оценка параметров распределений вероятностей
[Гл. 2
Вычисления сведем в таблицу (здесь т* = — I ]P rriij — 0,5 ]):
и
0-5
5-10
10-15
15-20
20-25
25-30
30-35
35-40
mi
21
24
12
10
5
13
9
6
mi
0,205
0,445
0,565
0,665
0,715
0,845
0,935
0,995
Рс
0,795
0,555
0,435
0,335
0,285
0,155
0,065
0,005
^igPc
0,0996
0,2557
0,3615
0,4749
0,5451
0,8097
1,1871
2,3010
У
-1,0016
-0,5922
-0,4419
-0,3233
-0,2635
-0,0917
0,0745
0,3619
X
0,6990
1,0000
1,1761
1,3010
1,3979
1,4771
1,5441
1,6020
х2
0,4886
1,0000
1,3832
1,6927
1,9541
2,1819
2,3841
2,5666
ху
-0,70010
-0,59220
-0,51970
-0,42060
-0,36847
-0,13540
0,11503
0,57980
100
-2,2778 10,1972 13,6512 -2,04154
Находим (п = 8 — число интервалов гистограммы):
¦О2^
Xil =8-13,6512-10,1972=5,2267;
t
Dc = J2 У*' Л xi ~ J2 Xi' 12 Xi ' Vi = (~ 252778) • 13,6512 - 10,1972 • (- 2,04154) = - 1,2767;
n n n
Db = n • J2 xi ' Vi ~ JZ xi • Y, Vi = 8 * (^2,04154) - 10,1972 • (-2,2778) = 6,89486;
D* 10,2767 Db 6,89486
с = — = = —1,9661; b = — = = 1,3192.
Do 5,2267 ' ' Do 5,2267
Параметр b является искомой оценкой /3 = b = 1,3192. Параметр а является искомой
оценкой а. Находим ее из условия с = 0,3622blga, откуда имеем
lga = -
с+ 0,3622
- 1,9661 + 0,3622
1,3192
= 1,215813 и & = 16,4366.
Задача 68. В условиях задачи 65 найти оценку параметров распределения методом
аппроксимации (см. [36]).
Имеем а3 = -0,0707 и оценку $ и 48 • (-0,0707 + 1,23)~м = 3,9027.
Далее
1 - 0,427 • C,9027 - 1) • 3,9027~1>9 = 0,6824;
¦ = 8 • 0,5 + 0,784 • /3 - ^^ = 19,208 ¦ 0,5 + 0,784 . 3,9027 - ^^
1 J3 ) \ 3,9027
= 66,874.
Окончательно получаем
= 97,998; Д = 40,8 - 66,874 = -26,074.
5 5^' ? ^
a
0,6824
Если принять в качестве исходного двухпараметрическое распределение Вейбулла,
то оценки будут равны
10
о,465 •
40,8
1,282 •
19,208
= 2,0178; а =
0,6824
= 59,79.
Напомним, что мы решаем задачу, исходя из того, что закон распределения вероят-
вероятностей случайной величины нам известен заранее.
2.3] Оценка параметров распределения Вейбулла 177
Задача 69. В условиях задачи 67 найти оценки параметров с помощью квантилей.
Нам потребуются квантили жо,95 и жо,2-
Имеем Жо,95 = Ж[0?05-100] + 1 = #5i; Ж[о,8О-1ОО] + 1 = #81-
В нашем Р^ДУ данных xsi ~ 27 и хы ~ 11, и окончательно получаем
а = ехр@,4224 • In 27 + 0,5776 • In 11) = 16,073.
Задача 70. Но данным задачи 65 найти оценки с помощью порядковых статистик
(см. раздел 2.3.1.5), если а) цензурированы 5 больших членов выборки; б) выборка не
цензурирована.
Для варианта а) имеем п = 10, г = 5 и из табл. 42 находим
oi = -0,115524; а2 = -0,090668; а3 = -0,051341; а4 = 0,000925; а5 = 1,256809;
а = -0,185169; с2 = -0,181821; с3 = -0,160697; с4 = -0,125311; с5 = 0,625997.
Из табл. 43 находим к\ = 0,120330 и къ = 0,177275. Далее оценки находятся по фор-
формулам
й= ]Гщ >yi = -0,115524-In 12...+ 1,256809-In 42 = 4,01772;
г=1
Ь = J2 ci ' Vi = ^0185169 • In 12 ... + 0,652997 • In 42 = 0,555648.
г=1
л 1
Искомые оценки равны /3 = - = 1,800; а = ехрD,01772) = 55,574 или (с учетом смеще»
b
ния)
U Ь 0,555648 п^гЛ а 1 , AQa
Ь = = = 0,6754: /3 = ^ = 1,480;
1-к2 1 - 0,177275 ' Ь*
и* = и + S* • кг = 4,01772 + 0,6754 • 0,12033 = 4,099; а* = ехр D,099) = 60,279.
Для случая б) по аналогии с помощью табл. 42 и 43 имеем
и = 0,02331 • In 12 + ... 0,230001 • In 72 = 3,8619;
b = ^0,072734 • In 12 - ... + 0,324597 • In 72 = 0,446372.
Из табл. 43 имеем кг = -0,020508 и к2 = 0,06692. Тогда
Ы °?446372
1 - 0,06692
Окончательно получаем
= 0,4784; й* = 3,8619 + 0,4784 • (-0,020508) = 3,852.
= 2,090; а = ехр(й*) = ехрC,8520) = 47,087.
5* 0,4784
Задача 71. Имеется выборка данных из распределения Вейбулла с параметром
P = 2,l-Xi\ 4,2; 5,2; 6,1; 8,9; 10,1; 12,4; 13,9; 16,1; 17,2; 21,0.
Найти интервальную оценку параметра а при доверительной вероятности а = 0,90
(Не путать! Разный смысл вкладывается в а — это и параметр распределения и дове-
доверительная вероятность. Необходимо следить за указаниями в тексте).
Имеем из табл. 36 для а = 0,90 и п = 10: кн = 0,637 и кв = 1,84.
Далее х = - jr xf = — • D,22Д + 5,22Д + ... + 212'1) = 210,64941.
Окончательно
_L_ JL- 1 1
al = @,637) 2Д • B10,64941) 2,1 = 10,30338; авп = A,84) 2Д • B10,64941) 2Д = 17,08287.
Следовательно, с вероятностью 0,90 значение параметра а находится в диапазоне
10,30838 ^ а ^ 17,08287.
178 Оценка параметров распределений вероятностей [Гл. 2
Задача 72. В условиях задачи 65 с учетом точечных оценок параметров, полученных
в задаче 70, найти интервальные оценки параметров а и /3 при доверительной вероят-
вероятности а = 0,90.
Точечные оценки: /3 = 1,800, а = 455,574 при п = 10 и г = 5 (т. е. когда оценка выпол-
выполняется по пяти порядковым статистикам) и /3 = 2,090, /3 = 47,087, если оценка ведется
по всем п = г наблюдениям. Ищем оценки при г = 5ип = 10(а = 0,90). Из табл. 44
находим с = 0,30 и с" = 1,53. Тогда /3^ = 0,30 • 1,8 = 0,54; /3^ = 1,53 • 1,8 = 2,54.
Следовательно, 0,54 ^ /3 ^ 2,754.
Для вычисления интервальной оценки а воспользуемся результатами решения зада-
задачи 70, из которых следуют оценки й* = 4,099 и Ь* = 0,6754. Из табл. 45 для г = 5, п = 10
и а = 0,90 находим d! = 0,72 и d" = -2,37.
Тогда
а? = ехр D,099 - 0,6754 • 0,72) = 37,066; а? = ехр D,099 - 0,6754 • (-2,37)) = 298,777
и 37,066 ^ а ^ 298,777.
По аналогии для случая г = п имеем
/3 = 2,090; а = 0,71; с' = 0,55; с' = 1,38; и* = 3,8520; S* = 0,4784;
d1 = 0,71; d/; = -0,60.
Тогда
PI = 0,55 • 2,090 = 1,149; J3l = 1,38 • 2,090 = 2,884;
сС = ехрC,852 - 0,4784 • 0,71) = 33,526; сТп = ехрC,852 - 0,4784 • (-0,60)) = 62,742.
Легко видеть,что увеличение количества наблюдений, участвующих в оценке, повьь
шает ее точность.
Задача 73. В условиях задачи 65 с учетом точечных оценок, полученных в задаче 70,
найти интервальную оценку 95%-й квантили случайной вейбулловской величины х при
доверительной вероятности а = 0,90 для случая г = 5, п = 10.
Для случая г = 5, п = 10 точечные оценки й* = 4,099, Ь* = 0,6754.
Из табл. 46 находим к1 @,95; 0,90) = 8,39 и fc/;@,95; 0,90) = 1,97.
Тогда имеем
ехрD,099 - 0,6754 • 8,39) ^ жО)95 ^ ехрD,099 - 0,6754 • 1,97); 0,208 ^ жо,95 ^ 15,934.
Задача 74. Решить задачу 73 d/ш случая г = п = 10.
Для случая г = гг = 10 имеем
Ь* = 0,4784; й* = 3,852; А;'@,95; 0,90) = 5,67; fc;/@,95; 0,90) = 1,96.
Тогда
ехрC,852 - 0,4784 • 5,67) ^ жо,95 ^ ехрD,099 - 0,4784 • 1,96);
3,125 ^ жо,95 ^ 18,436.
Задача 75. Оценить для г = 3,5 ti 7 при п = 10 ожидаемую экономию в продолжи-
тельности испытаний изделий, если распределение контролируемого параметра подчи-
подчиняется а) экспоненциальному распределению, б) распределению Вейбулла с параметром
/3 = 3,8.
Из табл. 47 для случая а) имеем rj = 0,183 (г = 3); rj = 0,283 (г = 5) и rj = 0,423 (г = 7).
Таким образом, ожидаемая продолжительность испытаний составит соответственно
18,3%, 28,3% и 42,3% от времени, необходимого при испытаниях в варианте г = п. Для
1 1
случая б) эти величины будут равны ц = 0,1833'8 = 0,639(г = 3), ц = 0,2833'8 = 0,717
(г = 5); 7]1 = 0,4233^ = 0,797 (г = 7).
2.4]
Оценка параметров гамма-распределения
179
2.4. Оценка параметров гамма-распределения
Плотность гамма-распределения имеет вид (см. раздел 1.1.6)
-^р х,/3>0, а>1,
где а и /3 — параметры распределения, подлежащие оценке по выборочным данным.
2.4.1. Точечные оценки
2.4.1.1. Оценка /3 при известном а
» * _ 1 "
1 — — Г ЯР Т — — > Т •
Р-а, где х-п^хг.
г=1
2.4.1.2. Совместная оценка параметров
2.4.1.2.1. Оценка максимального правдоподобия
Оценки максимального правдоподобия а и C по выборке объема п являются
решением системы уравнений
1 с?[1пГ(аI "
—птв — п ~ + >
= О,
^
+
= 0.
Система мож:ет быть решена методом последовательных прибли^кений. Когда а
не слишком мало, можно использовать приближение [16]
Интересный метод решения системы уравнений максимального правдоподобия
предложен в [168—170]. Запишем систему уравнений максимального правдоподобия
в виде
i ~ nf3a = 0,
где ф(а) — логарифм производной гамма™функции.
Предлагается решение системы с помощью параметра
п
п | ||ж,
основанное на аппроксимации зависимости а от А [171].
180 Оценка параметров распределений вероятностей [Гл. 2
Из системы уравнений следует Ыа — ф(а) = А. В диапазоне значений
0,025 ^ А ^ 8,2 (что соответствует 0,10 ^ а ^ 20) применима аппроксимация
0,9885
ехр[^0,187(С - А)}, А < С;
а =
где С = 0,5772 — постоянная Эйлера (относительная погрешность аппроксимации
не превышает 0,8%).
1 п
Параметр /3 оценивается, как и ранее, по формуле /3 = ~™г ^ Х{.
i=i
Оценка для а может быть упрощена:
Л _ |о,521143А^'09885 ехр @Д87А) при А < 0,5772;
\о,61998А^0'8699 при А ^ 0,5772.
Еще одна оценка, основанная на аппроксимации гамма-функции, рассмотрена
в [172]. Предлагается разложение гамма-функции по формуле Стирлинга
Г(а) = е^ааа^
+ + Ц
12а 288а2
При использовании первых трех членов разложения приходим к оценке
— = —3 + \/9 + 12 (lnsi — s2), где si = -^^, 52-^г
г=1 г=1
Оценка для /5 в этом случае, как и ранее, определяется по формуле /3 = ^т = ^т-
2.4.1.2.2. Несмещенная оценка для малых выборок
В [173] предложена оценка
1 1 1
в = — \^ Х4 \ПХ4 \^ Х4 - — \^ In Xi.
%=1 %=1 %=1
Ее точность, несмотря на простоту вычислений, вполне удовлетворительна.
2.4.1.2.3. Оценка методом моментов
Метод применим при п ^ 50. Оценки имеют вид
2
; ^ = ?' где x=n^Xl" s =п
2.4.2. Интервальная оценка параметра /3
При известном параметре а интервальная оценка для /3 имеет вид
кшх ^ /3 ^ квх,
где кШ1 кв — коэффициенты, которые могут быть взяты из табл. 36 с заменой п
на па.
2.4] Оценка параметров гамма-распределения 181
Задача 76. Имеется ряд выборочных значений случайной величины, имеющей гамма-
распределение
Xi: 144, 216, 816, 71,1147, 2120, 912,150, 50,1450, 3500,189, 21, 914,1500,1700,300, 650.
Необходимо найти оценки параметров а и /3.
Оценка /3 при известном а B.4.1.1)
Пусть а = 0,8. Тогда оценка равна
J3 =- = — • V" xi = — • 15850 = 1100,69.
а п ^ 18
Оценка максимального правдоподобия (ускоренный метод) B.4.1.2.1)
Имеем
±.?> = 880,555; А = In 88°'555 = 0,71217.
г=1 \г=1 / П 1=1 431,9807
Так как А > 0?5772, то п
а = 0,61998 • 0,71217^0'8699 = 0,8329; /3 = ^— = 1057,163.
п • а
Оценка с разложением по формуле Стирлинга B.4.1.2.1)
Имеем 8-1 = - -Y\xi- 880,555; s2 = - . УЧпж* = 6,06838.
П г=1 П г=1
Далее вычисляем
= 0,84118; J3 = 880?Б55 = 1046,809.
-3 + i/9 + 12 ¦ (In 880,555 - 6,06838) 0,84118
Несмещенная оценка B.4.1.2.2)
Имеем
-•irxi-\nxi = 6392,798; - • Y" Xi = 880,555; - • Y In Xi = 6,06838.
г=1 г=1 г=1
Тогда
P = 6392,798 - 880,555 • 6,06838 = 1049,225; a = % = S80'555 = 0,8392.
P '
Оценка методом моментов B.4.1.2.3)
Имеем
х = - • У" Xi - 880,555; s2 = - • Y (xi ~ xf = 795821,914; s = 892,0885.
n f—f n f—'
Находим
^551] =0,974; p =
892,0885/ 880,555
= 9о3,77з,
Отметим, что полученные оценки грубы (существенно отличаются от полученных
ранее), так как мал объем выборки (а оценки методом моментов применимы при п > 50).
Интервальная оценка /3 при известном а
Примем, что а = 0,8 и доверительная вероятность равна 0,95. Имеем х = 880,555,
и из табл. 36 для п • а = 18 • 0,8 = 4,4, интерполируя, получаем кш « 0,635 и кв рз 1,805;
окончательно
0,635 • 880,555 ^ /3 ^ 1,805 • 880,555, или 559,152 <С /3 ^ 1589,393.
182 Оценка параметров распределений вероятностей [Гл. 2
2.5. Оценка параметров биномиального распределения
2.5.1. Точечная оценка
Если имеется реализация из п испытаний, в которых событие наблюдалось т
раз, то несмещенной точечной оценкой максимального правдоподобия параметра р
является величина рп = —. Напомним, что плотность вероятностей биномиального
п
распределения имеет вид
Распределение имеет единственный параметр р.
2.5.2. Интервальные оценки
Интервальные оценки параметра р с доверительной вероятностью а являются
решениями уравнений Клоппера-Пирсона [174]
JT C*pl{l-pHy-x = Ц^{1 - а); ? ЩA -рв)п-* = f (а).
х=т х=0
В скобках приведены вероятности, соответствующие границам рн и рв одно™
сторонних доверительных интервалов. Значения рш и рв, соответствующие различ™
ным п и а, приведены в [16, 24, 25, 29].
Известно (см. раздел 1.2.1), что биномиальное распределение может быть ап™
проксимировано с помощью бета™ и i^-распределений, нормального распределения
и распределения Пуассона. Поэтому значения рн и рв для двусторонней интерваль-
интервальной оценки можно выразить через квантили этих распределений.
2.5.2.1. Аппроксимация бета-распределением
где B(j^kJ) —7™квантиль бета-распределения с параметрами к и I.
2.5.2.2. Аппроксимация .F-распределением
Рн (п - х + l)Fi±a [2(га - ж + 1), 2х]' Рв гс - х + (ж + l)Fi+a [2(ж + 1); 2(п - ж)]'
2 2
где F*f(k,l) —7"квантиль ^-распределения с /i = Aj и /2 = I степенями свободы.
2.5.2.3. Аппроксимация распределением Пуассона
В данном случае используется связь между распределением Пуассона и распре™
делением хи-квадрат.
1 о 1 о
-1- Z (ел \ zl ГО/' I I M
2П 2 ^^ 2
где х^—7"квантиль распределения хи~квадрат с / = к степенями свободы.
2.5]
Оценка параметров биномиального распределения
183
Более точные результаты дает приближение
Ры =
Рв =
2п - х + 1 + -х i+a ± 2ж
1 2
При ж = 0 имеем р = 0 и рв = 1 - \
Значения ж ( 2п — ж + 1 + ™Х
V 2
пХ
х [ 2в — ж + ™
V 2
Для разных п, ж и
табулированы в [46]. Точностные характеристики этих аппроксимаций исследованы
в [175], где показано, что при 1 ^ п — ж ^ 40, п ^ 40, при 25 ^ п — х ^ 40, х ^ 25 или
при п — ж ^ 40 (х — любое) относительная погрешность не превышает 0,01.
2.5.2.4. Аппроксимация биномиальной суммы распределением хи-квадрат
В [182] предлагается численное решение задачи аппроксимации доверительных
границ параметра биномиального распределения, основанное на аппроксимации
биномиальной суммы
J2 Clnq\\ - q)n-% « 1 - Р2х [2%), Цп, х)},
г=0
где P2d(x) —значение функции ^-распределения с 2d степенями свободы в точке ж;
k(q) = In ^—; k(n, ж) = ^^——
У —
Отсюда следует
Рн =
Рв =
1 — ехр —
ехр
1 -ехр{ -
ехр<
ж ^ 0,5п;
, ж > 0,5п;
, ж ^ 0,5в;
ж > 0,5п.
Это наиболее точная аппроксимация из известных. Если п и ж достаточно
велики, можно использовать приближение
I
, / ч А л (п — х +1
^(п,ж) ^ _ ? где
Погрешность этого приближения равна 0,1% при п = 10 и ж = 5; 0,12% при п = 20
и ж = 10; 0,06% при п = 40 и ж = 20.
184
Оценка параметров распределений вероятностей
[Гл. 2
2.5.2.5. Аппроксимация нормальным распределением
Для упрощения записи впредь вместо ui+a , , будем использовать обозначе-
2 \а)
^квантиль (для двустороннего интервала)
или а-квантиль (для односторонних интервалов) стандартного нормального рас-
распределения (напомним, что а — это доверительная вероятность, с которой опреде-
определяются интервалы оценки параметра р).
Аппроксимация 1:
ние и, т.е. помнить, что и — это
Рн =
1 2 /Ж , 1 .
ж + -и — аду — (п — ж) + -ад2
ж + -ад2 + аду — (п — ж) + -и2
I У п 4
п + ад п + ад
Эта аппроксимация рекомендуется [2] при ж^4ип-жL.
Аппроксимация 2 (arcsln):
если биномиальное распределение нормализуется с помощью преобразования
arcsln, то
= Sin2
arcsin \ -=и
; рв = sin
arcsln \ —
V
Аппроксимация 3 [176]:
Рн =
х ^0,5 и х ^0,5 / х ^0,
1 1
/п \ п
х + 0,5 и х + 0,5 Л ж+ 0,5
Рв = + -^W I 1 -
/П П
Аппроксимация 4 [176]:
Рн =
Рв =
ж
ж
-
+
о,
о,
54
,5 4
~ 2U
+ и\
п -
х 4
-0,5-
¦f и2
-0,5-
п
1
п
-0.
+ 0
,5)М
,5JН
-ад2
п + и
Аппроксимация 5 (при р « 0,5) [175]:
ж-0,5 ад /ж-0,5 / ж-0,5
Рн= — , 4/ I 1-
ж + 0,5 ад /ж+ 0,5 Л ж+ 0,5
Рв = ^^+ ; А/ I 1-
Аппроксимация 6 (Холла):
Рн =
ж/-| ж \
г* + 0,5 / ^ 2ж
ж , и /ж / ж\ ад +0,5 / ж
V^ у п \ п) Зп I п
2.5]
Оценка параметров биномиального распределения
185
Более точная аппроксимация с поправкой 0,5 на непрерывность:
_ж-0,5 и /ж-0,5 / ж-0,5\ ti +0,5
Рш ~ ""га" 7^\ ^^ \ п"
.ж-0,5
Рв =
0,5
гг х/п \ п
ж+ 0,5 / ж + 0,5\ , nz+0,5
Аппроксимация 7 (Моленара):
Рш =
Згг / 3
2 + ^
Рв =
1-и\ 2 + w
+
7-ti2
) 18п
2 +и
Большей точностью обладает аппроксимация
18n
Рв =
1 — гх \ 2 + и 1 - '
18n
1)-
18n
Аппроксимация 8
Рн =
2 + г?
ж 1 I 3
— гг
[(-
7 2 N
п +
-ж +
7 2
18
1-
7-^2\1
18 )
1
2
2 + ii
П + 2--5--1
Рв =
Ж + 1 -
18
7-'
18
п + 11.^-4
186
Оценка параметров распределений вероятностей
[Гл. 2
Аппроксимация 9 (Полсона-Кэмпа-Пратта)
Полсон [178], используя преобразование Вилсона—Хилферти [61] для распреде-
распределения хи-квадрат, показал, что
9/х
2 2
' 3 + 9/х
где .F — квантиль распределения Фишера с Д = /л и /2 = ^ степенями свободы
(см. раздел 1.1.10).
Кэмп [179] использовал этот факт для аппроксимации биномиального распреде-
распределения, а Пратт [180] применил для получения доверительных интервалов параметра
биномиального распределения
Рв =
81 (ж + 1)(га - ж) - 9п - 8 -
+ 1)(гс - х)(9п + 5 - и2) + п +
У
-1
81 (ж + IJ - 9(ж + 1)(?г - х){2 + и2) + 1
При замене ж + 1 на ж и и на -и получаем выражение для рн.
2.5.2.6. Аппроксимация Титенко [181]
В [181] сделана попытка найти более точные, чем нормальные, аппроксимации
где р =
(l-dp2)J/'
1 = (n-x)(n + l)r f =
(х + 1) (х + 2) ' J
Cl
или более точно:
где
н = P* = +
4A-dp2J :
(п - xf{x + 1) + (Зп - х + 4)(ж + IJ
Используя упрощенную запись, получим
Ч> W
¦ + т 2\~ г 5 гДе ^ = 1 + р
Аналогично для рв
Iff 7i; о; = —.
п
V
<?_
A-/3,7
2\2
2.5] Оценка параметров биномиального распределения 187
где
/3 =
п-х + Г
lgrc; а; = -.
Эти результаты следуют непосредственно из решения уравнения Клоппера—
Пирсона.
Достаточно подробный обзор и анализ интервальных оценок параметра би-
биномиального распределения приведены в [176]. Различные методы графического
решения аппроксимационных задач приведены в [2, 126].
Задача 77. При п = 20 испытаниях имели место 6 событий. Найти 95%-й двусто-
двусторонний доверительный интервал для вероятности появления события в серии незави-
независимых испытаний.
Точечная оценка вероятности равна т = — = 0,3. Имеем а = 0,95, или = 0,025;
= 0,975. Точные табличные значения искомых вероятностей равны рн = 0,119
и рв = 0,543 (приводятся для последующего сравнения с аппроксимациями).
Рн =
Аппроксимация F-распределением B.5.2.2)
6 6
B0 - 6 + 1) • F0,975[2 ¦ B0 - 6 + 1); 2 ¦ 6] 15 • F0,975C0,12)"
Из таблиц или аппроксимаций (см. раздел 1.1.10) находим Fo,97sC0,12) = 2,963.
Тогда
* = 15^963 = 0Д35'
.F0,975[2-F + l);B0-6)] _ 7-^0,975A4,28)
20 - 6 + F + 1) • Fo,975[2 • F + 1); B0 -6)] 14 + 7 • Fo,9y5A4,28)'
7-23
Имеем (из таблиц или аппроксимаций) -Fo,975 = 2,3 и рв = = 0,535.
Окончательно получаем 0,135 ^J p ^ 0,535.
Аппроксимация распределением Пуассона B.5.2.3)
Имеем табличные значения Хо,э7бB • 6 = 12) = 4,4 и Хо,о2бB • 7 = 14) = 26,1.
Тогда
4,4 = 0,11; рв = — = 0,652;
40
*- 2-20 ' ' ' * 40
0,11 ^р^ 0,652.
Более точная аппроксимация:
= 0,118; рв = ^Ц = 0,555;
2 • 20 - 6 + - • 4,4+1 2 • 20 - 6 + - • 26,1
2 2
0,118 ^р^ 0,555.
Аппроксимация биномиальной суммы распределением хи~квадрат B.5.2.4)
1
/ 20 ¦— б 4- 1 \ 6 Л
Имеем А = — = 0,9454647; ifcB0,6) = = 17,336747; Ш0,7) = 16,762.
Находим из таблиц Хо97бA2) = 4,4 и Xo,o2sA4) = 26,1.
188 Оценка параметров распределений вероятностей [Гл. 2
Окончательно получаем
/ 4,4
{ 2 • 17,3
= 1 - exp <J — 1 = 0,119; рв = 1 - exp J —— } = 0,541;
1 ° ^,336] [ 2-16,762/
0,119 ^р ^ 0,541.
Аппроксимация нормальным распределением B.5.2.5)
Аппроксимация 1:
Имеем C/i+a = С/0,975 = 1,96.
2
Тогда
6 + 0,5 • 1,Э62 - 1,96 • у ^ • B0 - 6) + \ ¦ 1,96* ^ _ 6 +1,9208 +1,96-уЧ2 +0,9604.
~ 20 + 1,962 ' Рв ~~ 23,8416 '
0,145 ^р ^ 0,519.
Аппроксимация 2 (arcsin):
1г I—
= 0,124: рв = sin2 arcsin\ 1 ¦== • 1,96 I =0,513:
V 20 2.V20 '
0,124 ^р^ 0,513.
Аппроксимация 3:
6-0,5 1,96 / 6 - 0,5 Л 6 - 0,5
0,5 1,96 /6 + 0,5 / 6 + 0,5 \ пк._
+ ^ ' ( " ^^ ' = °'530;
р- ^ + 15
0,079 ^ р ^ 0,530.
Аппроксимация 4:
6 - 0,5 + - • 1,962 - 1,96 ¦ W6 - 0,5 - — ¦ F - 0,5J + ^ - 1,962
20 + 1,962
6 + 0,5 + 1,9208 - 1,96 • 1/6,5 • 6,52 + 0,9604
рв = ¦ ^ ^^ ¦ = 0,543;
23,8416
0,128 ^ р ^ 0,543.
Аппроксимация 5:
20 ^20 - 1,962 У 20 ^ 20
_
6,5 1,96 /6,5 Л 6,5.
рв = ^ + . J _!_ . ( 1 !_ = 0,533;
20 ^/20 - 1,962 V 20 \ 20/
0,057 ^ р <: 0,533.
Аппроксимация 6 (Холла):
6 1,96 /6 Л б\ 1,962+0,5 Л 2-6
рв = 0,3 + 0,43827 • 0?45826 + 0,07236 • 0,4 = 0,530;
0,128 ^р^ 0,530.
2.5]
Оценка параметров биномиального распределения
189
Более точная аппроксимация:
20 V20
6-0,5 1,96 /6-0,5 / 6 - 0,5
Рн = —-г 1= • 4 / ._ -(I-
20
20
3-20
i_2.?zM)=0>ii2
20 f
М
= М + 0,43827 М/М . ( 1 _ М ) + 0,07236 • A - 2 • М) = 0,555;
20 \/ 20 V 20 / V 20 / ' '
0,112 ^р ^ 0,555.
Аппроксимация 7 (Моленара):
5- 1
Рн =
3-20
¦ 1,96J
- 1,96 ¦
6- 15
20
¦• 1
7- 1,962
18- 20
-21 •
7- 1,96^
18-20
20 +
2 + 1,96"
2
= 0,1194;
/7 • 14
6 • 0,95264 + 1,9472 + 1,96 • \l • 1,00877 - 0,18424
Pb ~~ 21,9472
0,119 ^p ^ 0,544.
Или более точная аппроксимация:
= 0,544;
5-
1-1,962\ 2 + 1,962 1-1,962
3- 20
6- 20
6- 15
20
¦ A
7-1,96^
18-20
-21-
7-1,962
18-20
20+ ¦
6 • 0,95264 + 1,9472 - 0,02368 + 1,96 •
2 + 1,96'
2
= 0,1183;
1,00877 - 0,18477 - 0,18424
21,9472
0,1183 ^ р ^ 0,5429.
Аппроксимация 8 (Закса):
6-1-
1,962
- 1,96-
Рн =
6-
7 - 1,962
18
15-
7- 1,9
18
20 + ц.IZ^__4
2 + 1,96^
20 + 2 • ¦ 1
= 0,5429;
= 0,116:
6 + 1,9472 + 1,96-
Рв =
6,82453 • 13,8253
17,93013
22,8944
0,116 ^р^ 0,5435.
Аппроксимация 9 (Полсона-Кэмпа-Пратта):
= 0,5435;
Рв =
81-7-14
- 9 • 20 - 8 - 3 • 1,96 ¦ ^/9 • 7 • 13 • A80 + 5 + 1,96J + 21
81-72 -9-7- B + 1,962)
= 0,5428;
190 Оценка параметров распределений вероятностей [Гл. 2
рн = 1 + 0,16 • I 102 + Б?88'383;0918 I = 0,1185; 0,1185 ^ р ^ 0,5428.
L ^ ' J J
Аппроксимация Титенко B.5.2.6)
Имеем
' 1 - 0,95 \ б
On = С20 = 38760; / = I 2 = 0,092707; d = Ш^ = 5,25;
20 ' J ' 38760 I ' ' 7-8
р = °'°92707 = 0,113809;
1 - - ¦ 0,092707
pi = 0,113809 • 11 + - • 5,25 • 0Д138092 • 1 + ^ 1 = 0,118.
[ 4 L (^5,25-0,1138092JJ J
Более точные оценки равны:
"=2,6; рн= 0,118+ 5,26-2,6.0,113809* =
7-10-21 ^ 4- A-5,25 -0Д138092)
В случае упрощенной формы записи имеем
/i _1_ 0 3\ 1>3
ш=-= 0,3; <р = 1 + 0,113809 • [ ' | • lg 20 = 1,40457;
n ^ 2 • 0,3 у
1 - 0,95 \ 14
2 = 0,37960; ^ = 6 ' 21 = 0,525; <т = 0;37960 = 0,44756;
38760 I 15'16 1-^-0,37960
^ = 1 + 0,44756 • A + 0,3) • [1,8 + A - 2,2 • 0,3) • lg 0,3] • lg 20 = 2,48535.
Окончательно получаем
рш = 0,113809 -{1 + -- 5,25 • 0Д138092 • 1 + ->--¦ i i = 0Ц887;
1 4 [ A~5,25-0Д1380Э242 ' '
рв = 1 - 0,44756 • ^ 1 + - • 0,525 • 0,447562 • Ц ^48535 . . =
1 4 ' ' [ A-0,525-0,447562JJ f
0,1189 ^р^ 0,504.
2.6] Оценка параметров гипергеометрического распределения 191
2.6. Оценка параметров гипергеометрического распределения
Случайной величиной ж, имеющей гипергеометрическое распределение, являет™
ся число дефектных изделий в выборке объема п из партии изделий объема JV,
содержащей D дефектных изделий. Практический интерес представляет оценка по
выборочному контролю числа дефектных изделий в партии.
Доверительный «-интервал для D определяется границами DH и DB, являющи-
являющимися целочисленными решениями неравенств
Р(х - 1, ?>н, п) ^ а; ?(х - 1, Д* + 1, п) < а;
Р(ж, DB; п) ^ 1 - а; Р(ж, Ds-l,n)>l-a.
где Р(ж, .D,n)— вероятность появления в выборке объема п ровно х дефектных
изделий, если в партии изделий их количество равно D.
Так как Р(ж, DB, п) = 1 — Р(в — ж — 1, iV — DB, n), то N — DB является нижним
доверительным пределом для N — D, построенным по случайной величине п — ж,
и тогда достаточно иметь решение неравенств для DH при различных a, iV, n и ж.
Таблицы таких решений для различных о;, n, iV - п и ж приведены в [25]. Они
составлены для в, удовлетворяющих неравенству 2п ^ N. При 2п < N таблицей
молено пользоваться со следующей заменой переменных:
п = N — щ N — щ Z)H — х = п — х.
Для заданных h,N — n по таблицам [25] находится значение, соответствующее
значению Z)H — х = п — ж, а затем и сама оценка Dn = xJrN — п — х.
Верхний а • 100%™й доверительный интервал для D по выборке объема п из
партии изделий объема N при х = О
где [у] —целая часть числа у.
Задача 78. В выборке объема п = 10 из партии объема N = 200 изделий не обнару-
обнаружено дефектных изделий (ж = 0). Найти верхнюю доверительную границу количества
дефектных изделий в партии (D) при доверительной вероятности а = 0,95.
Имеем
D ^ jl- A-0,95)То I . 200- i^—Ч =0,258865-195 = 50.
192 Оценка параметров распределений вероятностей [Гл. 2
2.7. Оценки при неизвестном законе
распределения вероятностей
2.7.1. Оценки для центра распределения
В качестве первичных (достаточно грубых) оценок центра группирования значе-
значений случайных величин при неизвестном законе распределения вероятностей могут
быть использованы различные предельные неравенства.
2.7.1.1. Неравенства чебышевского типа
2.7.1.1.1. Неравенство Чебышева
Неравенство Чебышева имеет вид
^ к2'
где \х и а — соответственно среднее значение и стандартное отклонение.
Из неравенства Чебышева следует, что
X — , ^ /JL ^ X + , ,
V 1 — OL V 1 — OL
где а — доверительная вероятность.
Если вместо значения случайной величины х используется выборочное среднее
х = — \^ Х{. то имеет место неравенство
х —
/пA - а) у/п{1 - а)
Если известно, что распределение симметрично относительно центра /i, то до-
доверительный интервал равен
» ^ х + о п— или х - „ / ,. ^ М
3V^(l-«)
Отсюда легко видеть, что только знание того факта, что распределение случай™
ной величины симметрично, уже позволяет построить более узкий доверительный
интервал для центра распределения.
2.7.1.1.2. Неравенство Кантелли
P(x^fi^X)^ / 2, А^О.
Отсюда следует /j, ^ х — а
2.7.1.1.3. Неравенство Мейделя
Если распределение х имеет единственный максимум в точке /io, причем
т = а2 + (/i — /jLq) , s = -, то имеет место неравенство
P(\x-w,\
2.7] Оценки при неизвестном законе распределения вероятностей 193
откуда
3 3
ИЛИ Ж — -OLT ^ /X ^ X + Г «Г.
2.7.1.2. Оценка Нётера
Нётер [183] показал, что с коэффициентом доверия
доверительный интервал для центра симметричного распределения определяется
неравенствами
1 1
где Х{ — i-я порядковая статистика.
Значения а для различных g и h табулированы в [183].
При g + h > 12 имеет место аппроксимация
а « 1 — 2Ф
где Ф(ж) — функция стандартного нормального распределения.
Для распределений нормального типа оптимальная величина g ~ 0,27тг.
Задача 79. Имеются результаты наблюдений над случайной величиной с неизвест-
неизвестным законом распределения вероятностей (известна только дисперсия а2 = 75):
хц 1,2; 3,4; 6,1; 8,3; 12,1; 13,1; 14,8; 16,7; 21,9; 23,7; 24,5; 28,4.
Найти доверительный интервал для центра распределения при а = 0,95.
Неравенство Чебышева B.7.1.1.1)
Имеем
х = 14,516; 14,516 . ^ /i ^ 14,516 +
/12 A 095)
^ /i ^ 14,516 + . =;
A - 0,95) ^/12 • A - 0,95)
3,336 ^ fi ^ 25,696.
Если бы мы располагали информацией о том, что распределение вероятностей слу-
случайной величины х симметрично, то имело бы место
14,516 ^ II <С 14,516 + ; 7,062 ^ д ^ 21,96,
3 • v/12 • 0,05 3- ^12-0,05
т. е. доверительный интервал длины 25,696 — 3,336 = 22,36 уменьшался бы в 1,5 раза до
21,96 - 7,062 = 14,898.
Оценка Нётера B.7.1.2)
Находим g ^0,27- 12 = 3. Будем использовать для оценки величины g = 3 и h = 5.
Тогда центр распределения находится в интервале
I - (х3 + х8) < fji < I • (х5 + жю); \ • F,1 + 14,8) < // < i • A2,1 + 23,7);
10,45 < -—- < 17,9.
7 А. И. Кобзарь
194 Оценка параметров распределений вероятностей [Гл. 2
Вероятность попадания /х в этот интервал равна
• A + 7 + 21) ^0,55.
\ А I
2.7.2. Оценка рассеяним распределения
Некоторое представление о степени рассеяния непрерывного распределения
дают его выборочные квантили. В общем случае доверительный интервал для
р-квантили ограничен элементами упорядоченной по возрастанию выборки с но-
номерами г и s, так как доверительная вероятность равна [5]
s-1
i=r
где /р(а, Ь) — функция бета-распределения с параметрами а жЬ.
п — г
Если s = п — г + 1 (случай симметричного интервала), то а = ^ СгпргA — р)п~г.
Значения г и s при р = 0,25 и р = 0,75 (т. е. для 25%- и 75%-х квантилей — кварти-
квартилей) для различных п и а приведены в [46].
Разность между Жо,75 и жо,257 называемая интерквартильной широтой, является
характеристикой степени рассеяния распределения относительно его центра.
Задача 80. В условиях задачи 79 найти доверительный интервал для 25%-й квантили
распределения.
Предположим, что г = 3 и s = п ~ г + 1 = 10. Тогда доверительная вероятность
того, что в интервале [жз — жю] находится 25%-я квантиль (р = 0,25), равна
9
а = ]Г С{2 - 0,25* • A - 0,25I2^ = 0,5521664.
2.8] Некоторые специальные практические задачи 195
2.8. Некоторые специальные практические задачи
В этом разделе мы рассмотрим ряд задач, встречающихся в практике оценки
надежности технических систем. Эти задачи носят специфический характер и не
рассматриваются в широко распространенных учебных и рекомендательных посо-
биях.
2.8.1. Оценка интенсивности отказов с периодом приработки
Известно, что в классическом варианте экспоненциального распределения
f(x) = Аехр(^Аж) его параметр А = const. На практике обычно интенсивность
отказов А не является постоянной. Начальный этап работы изделия, характери-
зующийся увеличением интенсивности отказов, называется периодом приработки.
Будем анализировать следующую модель изменения интенсивности отказов во
времени:
Если время приработки мало (а это обычная практическая ситуация), т.е. когда
7o?7i ^ а? то Для случая, когда п изделий испытываются в течении времени tn,
оценки параметров a, 7i и 7© имеют вид [184]
1 , г 1 - г2 л 1 ГгГз — rl л (п — г2K
а = — т ; 7о = т г 5 7i = а
i r r t щг 2г + г)
ti г2^г3' /u tin(n-2r2+r3)' ' n(n -2r2+r3J '
где ti = —?n; r^ — количество отказов изделия в промежутки времени t\ = i^ =
1
- *з - з*п-
Эффективность таких оценок по отношению к оценкам максимального правдо™
подобия « 0,90 для 7о « 0,95, 71 ~ 0,90 -г- 0,95 и а « 0,90 -г- 0,99.
Задача 81. 20 изделий были испытаны в течение 900 ч. При этом в первые 300 ч
получены 4 отказа^ во вторые 300 ч — 1 отказ^ в последние 300 ч отказов не было.
Найти оценку интенсивности отказов с учетом ее изменения во времени.
Имеем tn = 900; ?i = ?2 = ^з = 300; п = 4; г2 = 1; гз = 0. Вычислим оценки а = х
300
х In -^—^ = 3,662 • 10^3; 7о = — • 4°°^г— = 1 66 • 10; 71 = 9 = 6,75.
1-0 300 4-2-1 + 0 D-2 + 0J
Имеем A(t) = 1,666 • 10~3 + 6,75 • е^3'662-10™3^ = 15б66 • 10~3 + 6,75 • @,0134)*.
2.8.2. Прогнозирование для экспоненциальных выборок
Для практики представляет интерес следующая задача. Имеются данные по
моментам отказов т изделий. Необходимо найти нижний доверительный предел
с вероятностью а для среднего времени наработки до отказа для к будущих выборок
объема п.
-I m
Предположим, что ti, ^2, ..., tm — наблюдаемые моменты отказа и i = — У^ tj.
Отберем к выборок объема п. Тогда а • 100%-я доверительная нижняя граница для
средних наработок до отказа будущих к выборок есть
, 2n, 2m, 1 — a),
где ш{к^ 2n, 2m, 1 — a) —коэффициенты оценки.
196
Оценка параметров распределений вероятностей
[Гл. 2
В [185] для коэффициентов ш(...) предложена аппроксимация
FBm,2n;ak)
Значения коэффициентов V = FBm, 2щ afc) приведенв! в табл. 48.
Таблица 48
п
3
5
10
20
Значения /' =
п = 2
к
2
0,8
0,5
0,2
0,1
3
1,1
0,7
0,4
0,2
5
1,4
0,9
0,4
0,2
8
1,5
0,8
0,4
0,3
12
1,7
0,9
0,5
0,2
= F{2
m,2r
ца*)
для
а =
п = Ъ
к
2
1,9
1,1
0,5
0,3
3
2,8
1,6
0,8
0,4
5
3,6
2,1
1,0
0,5
8
4,0
2,5
1,1
0,5
12
4,7
2,7
1,3
0,6
0,95
185]
п = 10
к
2
3,3
2,0
1,0
0,5
3
4,9
3,0
1,5
0,7
5
6,5
4,1
2,0
0,9
8
7,9
4,9
2,3
1,0
12
9,0
5,6
2,6
1,2
а • 100%~ая нижняя граница наработки на отказ к будущих выборок объема п
по данным i и т равна [186]
111111 kFBm, 2щ а)'
где FBm^ 2щ а) — «-квантиль i^-раепределения с Д = 2т и /2 = 2п степенями сво-
свободы.
Задача 82. В результате испытаний получены отказы изделий в моменты време-
времени (ч): t\ = 26, ?2 = 38, ?3 = НО, ?4 = 250, ?5 = 300. Необходимо найти нижнюю 95%-ю
границу средних наработок на отказ в пяти будущих выборках изделий объема п = 10
каждая.
1 5
Имеем t = - • ]Р U = 144,8. Из табл. 48 для fc = 5, п=10ит = 5 находим I1 = 4,1.
5 i=i
Следовательно, искомая величина равна tmin =
144,8
4,1
= 35,31 ч.
Для нижней 95%-й границы наработки на отказ имеем (!*о,95A0,20) = 2,35):
t 144,8
5 -^0,95A0,20) 5- 2,35
= 12,32 ч.
2.9] Планирование экспериментов для оценки параметров распределений 197
2.9. Планирование экспериментов
для оценки параметров распределений
2.9.1. Нормальное распределение
2.9.1.1. Оценка среднего при известной дисперсии
Объем выборки, необходимый для оценки среднего /л с заданной предельной аб-
абсолютной ошибкой е и доверительной вероятностью а при известной дисперсии а2,
определяется соотношением
( иао~
Можно использовать аппроксимацию иа « 4,91 [а0'14 — A — аH'14].
Тогда имеем
га = 24,1081 I- L°'14 ^ -Л°'14
Задача 83. Напряжение зажигания газоразрядного прибора распределено нормально
со стандартным отклонением а = 50 В. Найти объем выборки, позволяющий оце-
оценить среднее значение напряжения зажигания с предельной абсолютной ошибкой
е = 20 В при доверительной вероятности а = 0,95.
Имеем
п = 24,1081 • |~ [0,950'14 - A - 0,95H'14] V = 17.
Следовательно, желаемая точность оценки с вероятностью ^ 0,95 достигается при
объеме выборки п ^ 17.
2.9.1.2. Оценка среднего при неизвестной дисперсии
Необходимый объем выборки определяется из соотношения
я — ? — ta s
X л/пХ^
где ta — а-квантиль распределения Стьюдента при / = п степенях свободы; s и х —
выборочные оценки соответственно стандартного отклонения и среднего значения.
Необходимые значения приведены в табл. 49.
Определение объема выборки происходит в следующей последовательности.
Сначала по заданным величинам 5 = — и а и предполагаемому значению коэффи-
s r Л(Л ta(n)
циента вариации v = — по табл. 49 находим значение —)=+ и по нему определяем
х у/п
искомое значение п.
Если для найденного объема выборки п выборочное значение окажется больше
предполагавшегося, то эксперимент должен быть продолжен.
Укажем один частный случай, основанный на чрезвычайно простой аппрокси™
мации ta(n) для а = 0,975:
= 2 / ^ (Ц)
В этом случае по заданной абсолютной ошибке е и предполагаемому стандарт™
ному отклонению s может быть непосредственно определен объем необходимой
198
Оценка параметров распределений вероятностей
[Гл. 2
Таблица 49
ть
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
а
0,90
0,899
0,739
0,715
0,657
0,611
0,574
0,541
0,515
0,491
0,471
0,453
0,436
0,422
0,410
0,396
0,386
0,376
0,366
0,357
0,349
0,95
1,150
1,000
0,890
0,816
0,754
0,706
0,663
0,630
0,598
0,572
0,550
0,530
0,512
0,495
0,479
0,466
0,454
0,442
0,431
0,421
0,99
1,800
1,510
1,320
1,190
1,080
1,000
0,936
0,881
0,833
0,797
0,762
0,730
0,704
0,679
0,655
0,637
0,618
0,601
0,585
0,571
Значение
ть
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
[ ta(n)f
а
0,90
0,342
0,334
0,328
0,322
0,316
0,310
0,304
0,295
0,290
0,288
0,286
0,282
0,278
0,274
0,270
0,266
0,264
0,260
0,256
0,253
0,95
0,412
0,403
0,394
0,387
0,380
0,372
0,366
0,354
0,349
0,347
0,346
0,344
0,333
0,329
0,324
0,320
0,316
0,312
0,308
0,304
0,99
0,558
0,545
0,532
0,521
0,513
0,502
0,492
0,475
0,468
0,463
0,461
0,459
0,447
0,441
0,434
0,428
0,422
0,417
0,411
0,406
ть
45
46
47
48
49
50
55
60
65
70
75
80
90
100
120
150
200
250
300
400
а
0,90
0,250
0,248
0,245
0,242
0,240
0,237
0,226
0,216
0,207
0,199
0,192
0,186
0,175
0,166
0,151
0,135
0,117
0,104
0,095
0,082
0,95
0,300
0,297
0,294
0,290
0,287
0,284
0,270
0,258
0,248
0,238
0,230
0,222
0,209
0,198
0,181
0,161
0,139
0,124
0,114
0,098
0,99
0,401
0,396
0,392
0,388
0,383
0,379
0,360
0,343
0,329
0,316
0,305
0,295
0,277
0,263
0,239
0,213
0,184
0,164
0,150
0,129
выборки п. Как и ранее, если значение s в эксперименте окажется больше пред™
полагавшегося, то эксперимент должен быть продолжен.
Задача 84. Определить необходимый объем выборки для оценки среднего значения
с предельной относительной ошибкой S = 0,4 при доверительной вероятности а = 0,95,
если предполагаемое значение коэффициента вариации равно v = 0,1.
Имеем —'—=— = 5 = 0,4. Тогда из табл. 49 для а = 0,95 непосредственно находим
Необходимый объем выборки для оценки среднего значения с относительной точно-
точностью - = 0,4 при а = 0,975 равен п = [ 2 • — ) + 2 = 27.
з V 0,4/
2.9.2. Распределение Вейбулла
Значения необходимых объемов выборок для оценки среднего значения случай™
ной величины, имеющей распределение Вейбулла с известным параметром /3, при
S S
различных значениях 6 = —,аиу= — приведены в табл. 50, заимствованной из [44].
Зависимость /3 от v приведена в табл. 39, из которой по заданному значе-
значению /3 может быть оценено v. Может быть также использована аппроксимация
Задача 85. Определить для распределения Вейбулла с параметром /3 = 1,8 объем
выборки, необходимый для оценки среднего значения с относительной погрешностью
S = 0,15 при а = 0,95.
Имеем и w 1,8~ ' = 0,58. Из табл. 50 интерполяцией находим п = 52. Следователь-
Следовательно, необходимо испытать 52 прибора.
2.9]
Планирование экспериментов для оценки параметров распределений
199
Таблица 50
V
0,40
0?45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
Значеним п
для распределения Вейбулла
а = 0,95
S
0,05
175
225
250
300
400
500
600
600
800
800
800
1000
0,10
45
60
75
90
113
138
150
175
200
225
250
250
0,15
25
30
37
45
54
60
75
80
100
113
125
138
0,20
15
19
23
28
33
38
45
50
57
65
75
80
0,25
10
13
17
20
23
27
32
36
38
45
50
54
Q
= 0,975
S
0,05
250
300
400
450
500
600
800
800
1000
1000
1000
1000
0,10
64
87
110
130
150
200
225
250
275
300
400
400
0,15
33
42
53
64
76
87
110
120
140
150
175
200
0,20
20
26
32
39
46
55
64
72
80
94
110
120
0,25
14
19
23
28
32
38
44
50
55
64
72
76
2.9.3. Биномиальное распределение
Предположим, что задано некоторое значение параметра биномиального рас-
распределения— ро. Тогда наименьший объем ьыборки, необходимый для того, чтобы
подтвердить с вероятностью а, что р ^ ро, равен
п =
1пA - а)
ln(l-po)'
Если среди п испытанных приборов не будет ни одного отказа, то с вероятно-
вероятностью а можно утверждать, что р ^ ро-
Рассмотрим еще одну практическую задачу. Имеем совокупность из N приборов
с г дефектными приборами (доля дефектных приборов равна ро). Необходимо для
предполагаемой величины доли дефектных приборов ро найти объем выборки п, ко-
который с заданной достоверностью а обеспечивает заданную длину доверительного
интервала I для оценки ро- Необходимый объем выборки п в этом случае равен [187]
-1
п =
ui+app(l — ро)
Для квантили нормального распределения можно использовать аппроксимацию
uj+a = 24,1081
2
0,14
1 - а
0,14'
Приведем еще один результат. Если необходимо найти такой объем выборки п,
для которого, при числе дефектных изделий в ней х = 0, с вероятностью а можно
утверждать, что в партии размера N число дефектных изделий будет не более к,
то можно использовать неравенство
" к-1
где [... ] — целая часть числа в скобках.
200
Оценка параметров распределений вероятностей
[Гл. 2
Задача 86. Найти объем выборки, позволяющий с достоверностью а = 0,90 уста-
установить, что доля дефектных изделий в партии не превышает заданную величину
Ро = 0,05.
ln(l -a) _ In0,1
Имеем п =
ln(l-po) In 0,95
i 45.
Задача 87. Необходимо найти объем выборки, при котором для заданной доли дефект-
дефектных приборов Ро = 0,1 в партии из N = 200 приборов будет с вероятностью а = 0,95
получен доверительный интервал для оценки Ро длиной I = 0,2.
Имеем
I °5°4
a = Uq 975 = 1,96 И П = < 5
2^ [1,962-0,1-0,9
1
200
^ «9.
Задача 88. Найти объем выборки п, для которого, при отсутствии в выборке дефект-
дефектных приборов, с достоверностью а = 0,95 можно утверждать, что в партии N = 1000
приборов будет не более 100 дефектных приборов.
Имеем га = 1 - A - 0,95) ioo • 1000 =28.
100
2.9.4. Экспоненциальное распределение
Предположим, что в течение некоторого времени tm испытывается п приборов
и при испытаниях обнаруживается г отказов. Необходимо определить значения п
и г, обеспечивающие оценку интенсивности отказов Л с заданной относительной
предельной ошибкой 8 при доверительной вероятности а.
При испытаниях невосстанавливаемых приборов требуемый объем выборки ра-
равен
П =
где Ад — предполагаемое значение интенсивности отказов; а — коэффициент, зави™
сящий от г и а.
Значения коэффициента а^г^а) приведены в табл. 51. Значения г находятся из
соотношения A + <5) х = Ь, где Ь — коэффициент, зависящий от г и а (его значения
приведены в табл. 52). По заданным значениям а и 8 сначала определяется Ь,
затем по заданному значению а и вычисленному Ь из табл. 52 находится г. Далее
Таблица 51
Значения о (г, а)
1
2
3
4
5
6
8
10
15
а
0,90
0,43
0,51
0,57
0,60
0,62
0,65
0,68
0,70
0,74
0,95
0,33
0,42
0,48
0,52
0,55
0,57
0,61
0,64
0,68
0,99
0,22
0,30
0,36
0,40
0,43
0,46
0,50
0,53
0,59
20
25
30
40
50
60
80
100
150
а
0,90
0,77
0,79
0,80
0,83
0,84
0,86
0,87
0,88
0,90
0,95
0,72
0,74
0,76
0,78
0,80
0,82
0,84
0,86
0,88
0,99
0,63
0,66
0,68
0,71
0,74
0,76
0,78
0,80
0,84
200
250
300
400
500
600
800
1000
а
0,90
0,92
0,92
0,93
0,94
0,94
0,95
0,96
0,96
0,95
0,89
0,90
0,91
0,92
0,93
0,94
0,94
0,95
0,99
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
2.9]
Планирование экспериментов для оценки параметров распределений
201
Таблица 52
Значения Ь(г, ск)
1
2
3
4
5
6
7
8
9
10
а
0,90
0,26
0,38
0,45
0,50
0,54
0,57
0,59
0,62
0,63
0,65
0,95
0,21
0,32
0,39
0,44
0,48
0,51
0,53
0,55
0,57
0,59
0,99
0,15
0,24
0,30
0,35
0,38
0,40
0,44
0,46
0,48
0,50
11
12
13
14
15
20
25
30
40
50
а
0,90
0,66
0,67
0,68
0,69
0,70
0,74
0,76
0,78
0,81
0,83
0,95
0,60
0,62
0,63
0,64
0,65
0,69
0,72
0,74
0,77
0,79
0,99
0,51
0,53
0,54
0,55
0,56
0,60
0,64
0,66
0,70
0,73
60
80
100
150
200
250
300
400
500
600
а
0,90
0,84
0,86
0,88
0,90
0,91
0,92
0,93
0,94
0,94
0,95
0,95
0,81
0,83
0,85
0,87
0,89
0,90
0,91
0,92
0,93
0,94
0,99
0,75
0,78
0,80
0,83
0,85
0,86
0,88
0,89
0,90
0,91
для найденного значения г и заданного а по табл. 51 находится значение а(г,а),
и по заданному im и предполагаемому значению Aq вычисляется требуемый объем
выборки п. В случае испытаний восстанавливаемых приборов может быть получена
оценка необходимого времени испытаний
То,
а(г,а)
где Tq — ожидаемое время наработки на отказ.
Задача 89. Найти требуемый объем испытаний для оценки интенсивности отка-
отказов невосстанавливаемого прибора^ если заданы время испытаний tu = 1000 ч, предель-
предельная относительная ошибка S = 0,2, предполагаемое значение интенсивности отказов
Ло = Ю™3, доверительная вероятность а = 0,95.
Находим
1
= 0,833. Из табл. 52 для Ь(г, а) = 0,833 и а = 0,95 находим
5 1 + 0,2
г = 80. Из табл. 51 для г = 80 и а = 0,95 находим а(г^а) = 0,84. Тогда искомый объем
выборки п = 5 =95.
10~3 • 1000 • 0,84
2.9.5. Гамма-распределение
Для оценки среднего значения случайной величины, имеющей гамма-распреде-
гамма-распределение с параметром а1 с предельной относительной ошибкой S при доверительной
вероятности 7? объем выборки должен быть не менее
где
""" (а + 1)^'
- 7-квантиль стандартного нормального распределения.
Задача 90. Определить объем выборки^ позволяющей найти с предельной относи-
относительной ошибкой S = 0,05 при доверительной вероятности 7 = 0,95 среднее значение
случайной величины, имеющей гамма-распределение с параметром а = 2.
Имеем искомый объем выборки
«0,95 1,6452 1Q
п = г = = 18.
B + 1)-0,05 0,15
ГЛАВА 3
МЕТОДЫ АНАЛИЗА ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН
Общие положения. Для практического применения методов теории вероят-
ностей и математической статистики знание закона распределения вероятностей
чрезвычайно важно. По существу, сама изучаемая случайная величина для иссле-
исследователя представлена только законом распределения вероятностей реализации ее
значений.
Зная закон распределения вероятностей наблюдаемой случайной величины, ис-
исследователь или инженер в состоянии решать многие практические задачи, свя-
связанные с планированием производства, обеспечением качества продукции, оценкой
эффективности и стабильности производства.
Попытка применить методы анализа результатов наблюдений, разработанные
для конкретных законов распределения вероятностей, в условиях, когда реальное
распределение отличается от гипотетического, является самой распространенной
на практике ошибкой, приводящей к неверным выводам и, в конечном итоге,
к существенным материальным потерям и затратам времени.
Именно поэтому любая обработка результатов наблюдений должна неизменно
начинаться с ответа на главный вопрос: каково распределение вероятностей обраба-
обрабатываемого ряда случайных величин? На практике эта проблема обычно формули-
формулируется следующим образом. Выдвигается гипотеза — „наблюдаемое распределение
случайных величин описывается некоторым конкретным законом (нормальным,
экспоненциальным, Вейбулла, ...)". Задача первичного исследования — принять
или отклонить выдвинутую гипотезу.
Если ни одна из гипотез, связанных с формой закона распределения вероятно-
вероятностей, не принимается, то может быть сформулирована более мягкая гипотеза — на-
например, „наблюдаемое распределение симметрично относительно какой-то точки".
Даже установление только этого факта дает в руки исследователя более эффек-
эффективные методы анализа наблюдений, чем полное незнание закона распределения
вероятностей. И, наконец, если исследователь не получил достаточных оснований
для выбора вида распределения, то возникает задача подбора формы распреде-
распределения непосредственно по экспериментальным данным. При этом распределение
вероятностей должно быть подобрано так, чтобы оно удовлетворительно описывало
имеющийся экспериментальный материал.
Мы встречаемся здесь с понятием статистической гипотезы. Статистической
гипотезой называется предположение, выдвигаемое относительно особенностей
распределения вероятностей случайной величины, которое проверяется по резуль-
результатам наблюдений над ней.
Проверка любой статистической гипотезы сводится к следующему. По выбороч-
выборочным значениям случайной величины подсчитывается некоторая величина — стати-
статистический критерий (статистика критерия). При допущении, что распределение
вероятностей используемой статистики критерия в условиях справедливости про-
проверяемой гипотезы известно, определяется вероятность появления вычисленного
Методы анализа законов распределения вероятностей случайных величин 203
значения статистики. На основе так называемого принципа значимости устанав-
устанавливается уровень значимости — наибольшее значение вероятности, несовместимое
с признанием случайности экспериментально вычисленного значения статистики
критерия. Событие называется значимым (а не случайным), если теоретическая
вероятность его случайного появления меньше, чем принятый уровень значимости.
Уровнем значимости определяется критическое значение статистики критерия. Как
правило, если значение статистики критерия, вычисленное по экспериментальным
данным, больше критического, то гипотеза отклоняется на выбранном уровне
значимости. В противном случае она признается не противоречащей результатам
наблюдений. Дополнение до единицы уровня значимости называется уровнем до-
достоверности (достоверностью).
Поскольку статистика критерия для проверки гипотезы вычисляется по вы-
выборочным реализациям случайной величины, то и сама она является случайной
величиной. Поэтому суждения по гипотезе на основе статистики критерия могут
носить только вероятностный характер. При этом различают ошибки первого рода,
заключающиеся в отклонении верной гипотезы, и ошибки второго рода^ заключа-
заключающиеся в принятии ложной гипотезы. Вероятность ошибки первого рода совпадает
(по крайней мере не выше) с уровнем значимости и обозначается в литературе через
а. Ошибка второго рода обозначается через C. Эффективность статистического
критерия проверки гипотезы оценивается его мощностью 1 — /3, равной вероятности
отклонения ложной гипотезы.
Выбор значений а и /3 определяется условиями эксперимента и требованиями,
предъявляемыми к достоверности суждения по проверяемой гипотезе. Обычно на
практике используются значения а, /3, равные ОД; 0,05; 0,01.
Проверяемая гипотеза называется нулевой и обозначается символом Но. Напри™
мер, запись Но '• F(x) = G(x) означает, что проверяется нулевая гипотеза о совпаде-
совпадении функций распределения F(x) и G(x). Подробно теория статистических гипотез
изложена в [1, 132, 188-192].
В классификации статистических критериев проверки гипотез о законе рас-
распределения вероятностей принята определенная терминология. Такие критерии
подразделяются на два класса — общие критерии согласия и специальные критерии
согласия. Общие критерии согласия применимы к самой общей формулировке
гипотезы, как гипотезы о согласии наблюдаемых результатов с любым априорно
предполагаемым распределением вероятностей. Специальные критерии согласия
предполагают специальные нулевые гипотезы, формулирующие согласие с опре-
определенной формой распределения вероятностей — нормальной, экспоненциальной,
Вейбулла и т. д. Такие критерии носят соответствующие названия — критерии нор-
нормальности, критерии экспоненциальности и т. п.
Естественно, что при формулировании специфических требований общие крите-
критерии согласия могут быть трансформированы в специальные критерии. Следует от-
отметить, что многообразие возможных альтернатив, противостоящих нулевой гипо-
гипотезе, порождает и чрезвычайное многообразие статистических критериев, имеющих
различную мощность по отношению к различным альтернативам. Поэтому далее
приведена весьма большая гамма известных статистических критериев, впервые
собранная в одной книге.
204 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.1. Общие критерии согласия
Нулевая гипотеза при применении общих критериев согласия записывается
в форме
Но: Fn(x) = F(x),
где Fn(x)—эмпирическая функция распределения вероятностей; F{x)—гипотети-
F{x)—гипотетическая функция распределения вероятностей.
Все известные общие критерии согласия можно разбить на три основные группы:
— критерии, основанные на изучении разницы между теоретической плотностью
распределения и эмпирической гистограммой;
— критерии, основанные на расстоянии между теоретической и эмпирической
функциями распределения вероятностей;
— корреляционно™регрессионные критерии, основанные на изучении корреляци™
онных и регрессионных связей между эмпирическими и теоретическими порядко-
порядковыми статистиками.
Кроме критериев, входящих в перечисленные группы, известен ряд критериев,
использующих специфичные характеристические свойства различных распределе-
распределений, и они будут представлены в книге в разделах, посвященных специальным
критериям согласия, ориентированным на фиксированные нулевые гипотезы.
3.1.1. Критерии, основанные на сравнении теоретической плотности
распределения и эмпирической гистограммы
3.1.1.1. Критерий согласим %2
Критерий основан на сравнении эмпирической гистограммы распределения слу-
случайной величины с ее теоретической плотностью. Диапазон изменения эксперимен-
экспериментальных данных разбивается на к интервалов, и подсчитывается статистика
2
х ~
2^, nPi
i=t
где щ — количество значений случайной величины, попавших в г-й интервал;
к
п = ^2,пг — объем выборки; F{x) — гипотетический теоретический закон распре™
деления вероятностей случайной величины; щ = F{xi+\) — F{xi)—теоретическая
вероятность попадания случайной величины в г-й интервал.
Дисперсия статистики критерия х2 равна [193]
к
Если 2_^ — < п и fe < п, то D(%2) = 2(к — 1), т. е. совпадает с дисперсией случай™
г=1
ной величины, имеющей %2™распределение. На этой основе принято считать, что
статистика %2 имеет распределение, близкое к распределению хи-квадрат (см. раз-
раздел 1.1.8).
На мощность статистического критерия %2 сильное влияние оказывает чис™
ло интервалов разбиения гистограммы (к) и порядок ее разбиения (т. е. выбор
длин интервалов внутри диапазона изменения значений случайной величины). На
практике принято считать, что статистику х2 можно использовать, когда npi ^ 5.
3.1] Общие критерии согласия 205
В [194, 195] показано, что такое приближение допустимо и тогда, когда не бо™
лее, чем в 20% интервалов имеет место 1 ^ npi ^ 5 (для гладких унимодальных
альтернатив). В [196, 197] рекомендуется при в ^ 200 выбирать к из условия
I 2
к = 4 {0,75(в ^ IJ}5 ~ 3,78(в ^ 1) 5. Можно рекомендовать еще одно простое пра-
правило— нужно выбирать как можно большее Aj, но не превышающее в/5. Исчер-
Исчерпывающие рекомендации по методологии выбора числа к приведены в проекте
методических рекомендаций „Прикладная статистика. Правила проверки согласия
опытного распределения с теоретическим. Часть 1. Критерии типа %2. Госстандарт
России, 2000 г.", разработанном Лемешко Б.Ю., Денисовым В. И. и Постовало-
вым С. Н. из Новосибиского государственного технического университета. Границы
интервалов рекомендуется выбирать случайно, исходя из условия pi = — = const.
Однако в [198] показано, что мощность критерия х2 с увеличением числа классов
разбиения снижается, и оптимальная мощность соответствует к ~ 10.
Укажем также на следующие правила выбора к:
Jfe = 1+ 3,32lgn [314]; k = b{^n~1)V [11],
где а, /3 — ошибки первого и второго рода; Ь — коэффициент из диапазона 2^4 (для
простой гипотезы и /3 ~ 0,05 рекомендуется Ь = 4 [194]); и7 —7гаКвантиль стандарт-
стандартного нормального распределения.
Так или иначе, статистика %2 имеет распределение хи™квадрат с / = п — 1 сте™
пенями свободы в том случае, когда проверяется простая нулевая гипотеза .Hq,
т.е., когда гипотетическое распределение, на соответствие которому проверяется
эмпирический ряд данных, известно с точностью до значения своих параметров.
Если гипотеза сложная и параметры гипотетического распределения оцениваются
по самой выборке, то число степеней свободы уменьшается на число оцениваемых
параметров т и равно f = к — 1 — т.
Правило проверки гипотезы просто: если
^^ npi
г=1
то на уровне значимости а, т. е. с достоверностью A — а) гипотеза Hq отклоняется.
Вопрос о выборе к с учетом частных альтернатив рассмотрен в [196, 199-201].
Например, в [196] показано, что против альтернативных распределений с „тяжелы-
„тяжелыми хвостами" необходимо выбирать к сравнительно большим. В [202] рассмотрена
частная задача построения х2-критерия со случайными интервалами разбиения для
проверки нормальности распределения, когда параметры распределения оценива-
1 п ( 1 п V
ются не по группированной выборке (х = — V^ xi\ s = < — У^(ж^ — хJ > ). Подроб-
Пг=1 [Пг=1 J
но такой подход рассмотрен в разделе 3.2, посвященном критериям нормальности
распределения.
Аппроксимация статистики %2 для малых значений pi и ее поведение изучались
в [203, 204] в сравнении с двумя другими критериями максимального правдоподобия
к ш к
Y2 = 2У^пЛп—L; Т2 = У^(лАг7+ \/щ+1 — \/4гш* + 1).
r-J npi -л
г=1 г=1
(в этом случае разница будет ощущаться на „хвостах" распределений).
206 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Показано, что критерий %2 предпочтительнее указанных критериев. Для случая
малых pi в [205] предложено правило: если k ^ 3 и число попаданий (ожидаемых)
г < 5, то можно использовать соотношение (пр{)ш-ш = 5™.
к
Если — N — велико (р{ мало), то дисперсия D(X2) > D(x2), т. е. в этом случае
П ^~i Pi
г=1
разница будет ощущаться на „хвостах" распределения. Поэтому в [203] предложена
аппроксимация х2-критерия с помощью двухпараметрического логарифмически
нормального распределения (см. раздел 1.1.3), как это предложено в [206]. Ап-
Аппроксимация имеет вид Р(х > z) « Р(^ > z), где z — логнормальная случайная
величина с параметрами распределения вероятностей /л и а:
Если иа — а-квантиль стандартного нормального распределения, то
Х^ = ехр(/х + aua). Мощность %2™критерия снижается в связи с тем, что он не
учитывает знака разностей (щ — npi)- Эту информацию использует критерий
серий. Его статистикой является число подряд следующих групп „плюсовых"
и „минусовых" значений (щ — npi). Например, для последовательности знаков
разностей (щ — пр^ „ ... + Н 1 Ы 1— ..." число плюсовых серий равно
М = 4, а число минусовых серий N = 4, общее число серий равно R = М + N = 8.
Известно, что
c\f~lX — 1 s~iX — 1 fiX — 2 s~iX — 1 i^ flX — 1 s~iX — 2
= 2x)= Cm-JCn-1; Р(Д = 2x - 1) = Cm-i0n_1+ Cu_xCn_1 ;
2MN . nrm 2MiVBMiV -M-N)
Случайная величина — распределена приблизительно нормально. Хотя
этот критерий имеет мощность меньше, чем %2-критерий, но он от него не зависит
и поэтому их можно использовать совместно.
Следует помнить, что при сложной гипотезе (т.е., когда параметры гипотети-
гипотетического распределения оцениваются по имеющейся единственной выборке) кри-
критерий х2 еЩе асимптотически независим от критерия серий, но в этом случае
распределение х2 известно лишь приближенно, а распределение критерия серий
совсем неизвестно. Таким образом, критерий, комбинирующий критерии %2 и се-
серий, применим только для полностью определенного (с точностью до параметров)
гипотетического распределения.
Если ol\ — уровень значимости для х -критерия, а а,2 — уровень значимости для
критерия серий, то уровень значимости комбинированного критерия будет равен
а = а1а2A - 1пага2).
Следует иметь в виду, что величина a = ^lnai«2 имеет распределение х2
с / = 4 степенями свободы, что и является, по существу, основанием для построения
комбинированного критерия.
3.1] Общие критерии согласия 207
В заключение приведем простые (хотя и не менее чувствительные) правила
проверки нулевой гипотезы (приближенные критерии):
— если х2 > /, то Hq отклоняется;
I 2 f I
— если R = -— ^ 3, то Hq отклоняется (критерий Романовского [207]).
V2/
Задача 91. Имеем ряд выборочных значений случайной величины (п = 100):
43
54
56
57
61
64
67
73
74
76
76
77
77
78
78
79
79
82
82
83
84
84
85
85
86
87
87
87
88
89
91
91
91
91
92
92
93
93
93
95
95
96
96
96
97
97
98
98
99
101
101
101
101
103
103
104
104
104
104
105
105
106
107
107
107
108
111
112
113
114
114
114
115
116
116
116
117
118
118
119
122
122
122
123
124
124
125
125
125
126
129
132
134
136
136
138
143
143
145
150
Необходимо проверить критерием %2 гипотезу о том^ что распределение случайной
величины не противоречит нормальному закону с параметрами /i=101 и а = 16 на
уровне значимости а = 0,1.
Сначала примем решение, на какое количество классов следует разбить гистограмму
эмпирического распределения. Различные рекомендации дают следующие результаты
(примем а = 0,1 и /3 = 0,2):
1 1
к = 4- [0,75- (?г-1J]5 =4- @,75 • 0,992) 5 =24; к = 1 + 3,321п?г = 1 + 3,32 In 100 = 8.
Учитывая, что первая рекомендация эффективна при п ^ 200, и исходя из огра-
ограничения к ^ — = 20, примем к = 8. Продемонстрируем теперь технику вычисления
5
теоретических вероятностей pi. Пусть х% и Жг+i—границы г-ro класса разбиения.
Тогда теоретическая вероятность попадания случайной величины в этот интервал
равна F ( —^ ) — F I — ) = pi, где F(x) —функция стандартного нормального
распределения.
Для нахождения F(x) можно использовать либо таблицы, либо аппроксимации.
Приведем одну аппроксимацию [36]
При х < 0 используется соотношение F(—x) = 1 —- F(x).
Вероятность попадания случайной величины в интервал Xi < х ^ жг+i, где хг = 90
и Жг+i = 100, равна
16 ) \ 16 ) \ 16 у V 16
Выберем границы классов разбиения из условия равномерного разбиения диапазона
изменения случайной величины на 8 классов, с условием попадания в крайние классы не
менее 5 наблюдений. Результаты сведем в таблицу:
208 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
i
1
2
3
4
5
6
7
8
Xi
< 70
70-80
80-90
90-100
100-110
110-120
120-130
> 130
щ
7
10
13
18
17
14
12
9
F(xi+1)
0,0263
0,0945
0,2458
0,4751
0,7131
0,8827
0,9650
1,0000
F(xi)
0,0000
0,0263
0,0945
0,2458
0,0475
0,7131
0,8827
0,9650
Pi
0,0263
0,0682
0,1513
0,2293
0,2380
0,1696
0,0824
0,0350
npi
2,6300
6,8200
15,1300
22,9300
23,8000
16,9600
8,2400
3,5000
(щ npiJ
19,0969
10,1124
4,5369
24,3049
46,2400
8,7616
14,1317
30,2500
{rii - npiJ
npi
7,2610
1,4830
0,2998
1,0600
1,9428
0,5166
1,7157
8,6428
100
1,0 10,1972 13,6512
= 22,9217
Итак, мы получили значение статистики критерия %2 = 22,9217. Теперь необходимо
найти критическое значение статистики, равное Xi_a (f = k — 1).
В нашем случае число степеней свободы равно / = ,fc — 1 = 8 — 1 = 7. Используем для
вычисления критического значения аппроксимацию Вилсона-Хилферти
где и а. — а-квантиль стандартного нормального распределения. В нашем случае для
1 — а = 1 — 0,1 = 0,9 имеем
Так как % = 22,92 > 11,98, нулевая гипотеза отклоняется, т.е. утверждение о том,
что исследуемая выборка взята из нормального распределения с параметрами ц = 101
и а = 16, не подтверждается.
Проверим возможность использования логнормальной аппроксимации для %2- Нахо-
Находим
1 = 114,4613; M = 21n7-llnG2-l+114'4613-7 ~2 7 + 2j> = 1,95068.
Pi ' ' ^ 2 I 100 ' '
Далее
2 , I.. Л
сг = In 149 - Ц
114,4613-49-14
¦
- 2 In 7 < 0.
Видим, что аппроксимация в нашем случае неприменима, так как > — & п.
i=lPi
Теперь применим комбинированный критерий знаков разности (щ — npi) с учетом
критерия серий. Последовательность знаков разности (jii —- npi) в нашем случае имеет
вид + + ++.
Таким образом, всего имеется R = 3 серии знаков, в том числе положительных М = 2
и отрицательных N = 1. Тогда имеем
М(Д) = 1+^ = 2,33; В(Д)=2?.-1;5Г!8:1:2:1) =0,222;
R-M(R) 302,33
B + 1J-(^
= 1,415.
Находим F(l,415) = 1 - 0,852 • ехр ( -
2,0637
Следовательно, уровень значимости ol\ = 1 — 0,9216 = 0,0784.
1,415 + 1,5774
2,34
= 0,9216.
3.1]
Общие критерии согласия
209
Для критерия Х2G) уровень значимости равен «2 ~ 0,0005 и а = ^2 In 0,0784 х
х 0,0005 = 20,29, что также отклоняет нулевую гипотезу, так как Хо,9бD) = 9,49 < 20,29.
Теперь приведем другой вариант решения задачи, чтобы продемонстрировать техни-
технику применения критерия %2- Предположим, что параметры распределения неизвестны
и определяются по выборке. Примем то же самое число классов разбиения — 8, од-
однако границы классов разбиения будем определять из условия щ = - = 0,125 = const.
к
Тогда, например, для первого класса должно быть F
= 0,125; — = wo,i2s;
s
х\ = х + s - и 1 . Для второго класса ж 2 = х + s • ito,255 и в общем виде х% = х + s • и i .
~k ' fc
Оценки параметров распределения по выборке равны
ж = -
п
= 100,77; s =
хг -х)\ = 21,691.
Для иа будем использовать аппроксимацию
л rki f 0,14 /-, \0,14l
иа Ра 4,91 • {а ' — A — а) ' ) .
Результаты расчетов сведены в таблицу:
г
1
2
3
4
5
6
7
8
< 75,84
75,84^86,18
86,18^99,37
99,37^100,77
100,77^102,17
102,17-103,74
103,74^105,85
> 105,85
щ
9
16
24
0
4
2
6
39
Pi
0,125
0,125
0,125
0,125
0,125
0,125
0,125
0,125
npi
12,5
12,5
12,5
12,5
12,5
12,5
12,5
12,5
(щ npiJ
12,25
12,25
132,25
156,25
72,25
110,25
42,25
702,25
(Пг - npiJ
npi
1,00
1,00
10,58
12,50
5,78
8,82
3,38
56,18
100 1,0
X
2 = 99,24
22 9217 — 7
Со всей очевидностью критерий отклоняет гипотезу нормальности распределения,
что видно по совершенно неестественному для нормального распределения правому
„хвосту" эмпирического распределения, делающего его явно несимметричным. Кри-
Критическое значение статистики в этом случае при / = ^^1^2 = 8^1^2 = 5 равно
/ I \ 3
/ 2 / 2 \
Xoj9 = 5-1 Ь 1,28 • 4/ = 9,2. Явное неравенство х2 = 99,24 > Хо,эE) = 9,2
отклоняет нулевую гипотезу.
Применение упрощенного критерия Романовского R =
отклоняет гипотезу.
3.1.1.2. Критерий числа пустых интервалов
Этот не очень мощный, но простой для применения критерий рассмотрен в [11].
Имеем выборку a?i, ..., хП1 разделенную на к интервалов в соответствии с гипотети™
ческим распределением. Обозначим через ад число оставшихся пустыми интервалов
(щ = 0). Тогда имеет место
= 4,25 > 3 также
= 7) = -гп
г=0
где
= с, с + 1, ..., к — 1; с = тах@, к — п).
210 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Математическое ожидание и стандартное отклонение числа пустых интервалов
равны соответственно
ТЬ
При 1с,в ^ ос, р = — >0 распределение ag асимптотически нормально с пара-
параметрами
М(а0) = fee"*, D(a0) = k [е~р - е~2рA + р)] .
Рекомендуется выбирать р = 1,255 или Aj « 0,8в (наилучшая сходимость к нор-
нормальному распределению). Тогда можно утверждать, что величина
и ао - ке~р
имеет стандартное нормальное распределение и, следовательно, критическое зна-
значение статистики равно
ао(а) = 0,285^ + ^«
Если эмпирическое значение числа пустых интервалов превысит ао(ск) {pt —
уровень достоверности), то с вероятностью а можно утверждать, что нулевая
гипотеза отклоняется.
Возможна модификация этого критерия для проверки совпадения двух эмпири-
эмпирических распределений, т. е. для проверки гипотезы Но: Fn(x) = Gn{x). Рассмотрим
выборку х\ ^ Х2 ^ ... ^ хП1 упорядоченную по возрастанию. На этой совокупности
определим интервалы 1\ —>• (—оо, Жх), /2 —>- (жх, Жг)? • • • > 4+i(^n) °°)- Предположим,
что имеется вторая выборка данных объема га, из которой г^ членов попадает
в 7^-й интервал разбиения первой выборки. Обозначим через uq число оставшихся
пустыми ячеек. Тогда
РD = а) = °прпСт^\ где а = с,с+1, ...,п; с = max@, n + 1 - га).
В пределе
а/г/ /\ гг + 1 —., ,ч (гг + 1I2 т
M(ao) = ^TT; D(ao) = ^T]^; / = -
, п+1
Следовательно, критическая величина af0(a) равна
где wa — a-квантиль стандартного нормального распределения.
3.1] Общие критерии согласия 211
Задача 92. Имеются выборки данных:
xf. 1, 3, 5, 7, 9, 11, 13, 18, 21, 23, 25, 30, 32, 34, 35, 37
уп -8, -7, 4, 5, 6, 7, 8, 12, 14, 15, 18, 19, 20, 21, 23, 25
Необходимо проверить критерием числа пустых интервалов при достоверности
а = 0,90 гипотезу о том, что случайная величина х подчиняется экспоненциальному
распределению с параметром — = 20. Проверить гипотезу о совпадении распределений
А
случайных величин х и у.
х
Имеем теоретическое распределение F(x) = 1 — е"~ 20 .
Находим fc^0,8-n = 0,8-16=12. Примем для упрощения расчетов к = 10
и pi = 0,1 в каждом интервале. Тогда для границ интервалов имеем уравнение
-20-1п[0,1- (г- 1)] =Xi.
Например, для Х2 имеем Х2 = ^20 • 1п[1 — 0,1 • B — 1)] = 2,1.
Получаем 10 интервалов:
0-=-2,1; 2,1^4,46; 4,46^7,13; 7,13-=-10,2; 0,2^13,86;
0,86^18,3; 18,3-=-24,1; 24,1^32,19; 32,19^46,05; 46,05 -=- оо.
Очевидно, что пустым остался один последний интервал, т.е. ао = 1.
Вычисляем
\ 16
- - — ) = 1,85;
D(a0) = 10 • 9 • I 1 1 + 10 • I 1 1-100
Следовательно, и = — 7 = —0,87. Критическое значение статистики при а = 0,90
(^о,эо = 1,28) равно
ао@,9) = 1,85 + 1,28 • ^0,952 = 3,1.
Так как ао = 1 < ао@,9) = 3,1, нулевая гипотеза отклоняется.
Теперь разобьем элементы первой выборки на 16 интервалов и проверим попадание
в них элементов второй выборки. Видим, что незаполненными остаются 7 интервалов,
. е. ад = 7. Тогда при I = — = 1 имеем
п
а{,@,9) = — + ! 28 . — . А/^±1 = ю,366.
ov , ; 1 + 1т ' 1 + 1 V 1 + 1
Так как ад @,90) = 10,366 > а0 = 7, нулевая гипотеза не отклоняется.
3.1.1.3. Квартильный критерий Барнетта-Эйсена
В [208] предложен простой непараметрический критерий проверки согласия
двух эмпирических распределений. Если разница в эмпирических распределениях
является следствием разницы в параметрах положения и дисперсиях, то квартиль™
ный критерий может быть более эффективным, чем другие известные критерии.
Предположим, имеются две выборки х\, ..., хш и t/i, ..., уп и (га + п) делит™
ся на 4. Объединим обе выборки в одну объема (га + п). Обозначим через сц
(г = 1,2,3,4) — число членов выборки х в г-й квартили объединенной выборки. Если
обе выборки принадлежат одному распределению, то щ имеет гипергеометрическое
распределение и
Р(«. = ^) = ^; М(аг) = -; D(a<)= ; Q = —.
212 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Введем обозначения
si = «1 + а4; d0 = а4 - «i; di = аз — а2.
Тогда имеют место соотношения:
M()
v f 4(m~
Введем обозначения
s =
В качестве критерия согласия предлагается статистика
имеющая при т, п —>• оо распределение хи-квадрат с / = 3 степенями свободы. Если
D > Ха(^)? то гипотеза Н® отклоняется.
Задача 93. Имеются две выборки объема га = п = 16 каждая:
Xii 1, 3, 5, 7, 9, 11, 13, 18, 21, 23, 25, 30, 32, 34, 35, 37
уц -8, -7, 4, 5, 6, 7, 8, 12, 14, 15, 18, 19, 20, 21, 23, 25
Необходимо проверить гипотезу о согласии эмпирических распределений в выборках
критерием Барнетта-Эйсена.
Составим объединенную выборку, отмечая в ней элементы обеих выборок с их по-
порядковыми номерами
^8 ^7 1 3 4 5 5 6 7 7 8 9 11 12 13 14
2/1 2/2 х\ х2 2/з хз 2/4 2/5 ж4 2/6 2/7 ж5 ж6 2/8 ж7 2/9
15 18 18 19 20 21 21 23 23 25 25 30 32 34 35 37
2/10 2/И Х8 2/12 2/13 2/14 Ж9 2/15 Ж10 Жц 2/16 #12 Ж13 #14 #15 #16
Имеем Q = = 8. В первой квартили (первых 8 членах объединенной выборки)
находятся а\ = 3 элемента выборки ж, во второй п2 = 4; далее «з = 2 и а4 = 7.
Имеем
5 = ai + 04 = 10; do = «4 — а = 4; d = аз — а = —2;
M(s) = - = 8; M(d0) = M(di) = 0; D(s) = ^^ = 2,0645 (\/D(s) = 1,4368);
D(d0) =
10 — 8 9 4 9
S = 1.39198 (S2 = 1,9376); d0 = —- = 1,9686 (d02 = 3,875);
= -0,9842 {di = 0,9687); D = s + dS + d? = 6,7813.
Для a = 0,90 и / = 3 имеем %о,эоC) = 6,251.
Так как D = 6,7813 > Хо,эоC)? нулевая гипотеза отклоняется.
3.1] Общие критерии согласия 213
3.1.2. Критерии, основанные на сравнении теоретической
и эмпирической функций распределения вероятностей
Обозначим через F{x) (х^ < Жг+i) эмпирическую функцию распределения вероят-
вероятностей, а через Ф(х) — теоретическую функцию распределения (xi = Ф™1 ( — )).
\ ТЬ /
Расстояние между эмпирической и теоретической функциями распределения
вероятностей является весьма эффективной статистикой для проверки гипотез
о виде закона распределения вероятностей случайной величины.
Среди известных критериев согласия такого типа отметим серию критериев,
использующих различные варианты анализа расстояния между F{x) и Ф(ж):
— критерий Джини A941 г.)
7(х)-Ф(х)\с1х;
— критерий Крамера-фон Мизеса A928 г.)
f г , ч , „9
I | Л. I JU I jbr I du I j Ll/Ju «
— критерий Колмогорова—Смирнова A933 г.)
sup \F\X] — Ф(ж) *
— оо<ж<оо
— критерий Смирнова-Крамера-фон Мизеса A936 г.)
{F(x) - Ф(х)}2
— критерий Андерсона-Дарлинга A952 г.)
Ф(х){1 - Ф(х)}
— критерий Купера A960 г.)
sup {F(x) - Ф(х)} + sup {Ф(х) -
— оо<ж<схэ —оо<ж<оо
— критерий Ватсона A961 г.)
[ {F(x) - Ф(х) - I [F(x) -
— критерий Фроцини A978 г.)
\F(x) -Ф(х)\AФ(х).
Из приведенного перечня видно, что исследователи весьма изобретательны,
конструируя мыслимые и немыслимые варианты критериев. Однако не только из
любви к собственно математической статистике они делают это. Разные критерии
имеют различную мощность по отношению к различным альтернативам, т. е. пред-
пол ожениям, противостоящим выдвинутой (нулевой) гипотезе. Для того, чтобы
наилучшим способом противостоять наиболее „опасной" альтернативе, необходим
достаточно широкий арсенал статистических инструментов. Проблема выдвижения
альтернатив и оценка их „нежелательности" не является задачей математической
статистики, это проблема иных наук, занимающих исследователя.
214 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Еще несколько важных замечаний, после чего приступим к изложению и иллю-
страции основных практических критериев.
Если случайная величина имеет функцию распределения Ф(ж), определенную
с точностью до параметров, то случайная величина Ф(а^) распределена равно-
равномерно на интервале [0,1]. Таким образом, критерий согласия трансформируется
в критерий проверки равномерности распределения случайной величины Ф(а^) на
интервале [0,1]. В этом смысле все критерии согласия являются также критериями
проверки равномерности распределения.
Следует избегать основной ошибки, совершаемой, к сожалению, подавляющей
массой исследователей и инженеров. Общие критерии согласия, которые мы будем
рассматривать далее, предполагают знание теоретического закона распределения
с точностью до параметров. Так как это бывает редко в реальных ситуациях,
исследователь мгновенно разрешает возникшую проблему простейшим способом —
он проводит оценку параметров по самой выборке. Этого делать нельзя, так как
достоверность полученных таким образом статистических выводов может быть
сильно искажена [209]. Возможные варианты разрешения проблем, возникающих
в случае отсутствия надежной информации о параметрах распределения, приведе-
приведены в разделах, посвященных специальным критериям нормальности и экспонен™
циальности распределения. Поэтому, если вам необходимо проверить, нормально
ли распределение полученных выборочных данных, а параметры гипотетического
нормального распределения вы собираетесь также оценивать по выборке, не спеши™
те воспользоваться общим критерием согласия из раздела 3.2.1. Пропустите этот
раздел и обратитесь к разделу 3.2.2, в котором вы найдете квалифицированные
рекомендации для такой ситуации.
3.1.2.1. Критерий Колмогорова-Смирнова
Пусть Fn(x) — эмпирическая функция распределения случайной величины ж,
представленной выборкой х\ ^ х^ ^ . • • ^ хп:
0, х < х\\
Fn(x) = { - Xi ^ х < жг+ь 1 < г ^ га - 1;
1 п
1, X ^ Хп.
Для проверки нулевой гипотезы Hq: Fn(x) = Ф(ж), где Ф(ж)—полностью опреде-
определенная (с точностью до параметров) теоретическая функция распределения, рас™
сматривается расстояние между эмпирической и теоретической функциями распре-
распределения
?>„ = sup \Fn(x) - Ф{х)\- D+^ sup (Fn(x) - Ф(х));
|ж|<оо |ж|<оо
d- = - inf сад-Ф(ж)).
(ж|<оо
Здесь sup, Inf — точные верхняя и нижняя границы соответствующих разностей.
Для практического применения используются формулы
D+ = max (j- - ФОг)) ; D~ = ш (ф(я) - l-^j ; Dn = (+ )
Колмогоров [210] нашел предельное распределение статистики л/пПп (при п -^ ос).
Смирнов [211] развил результаты Колмогорова на случай статистик D^ , D~. Точ-
Точные распределения статистик D^ D~, Dn приведены в [24, 25, 29, 57].
3.1]
Общие критерии согласия
215
Между критическими значениями Dn и D+(Dn) существует соотношение
D+ (a)(D~ (a)) = DnBa) (а— уровень значимости).
В качестве первого приближения можно использовать соотношение
Если Dn > Dn(a), гипотеза согласия (Но) отклоняется на уровне значимости а.
При п ^ 20 полезна аппроксимация [25]
распределение которой удовлетворительно описывается распределением хи^ква™
драт с / = 2 степенями свободы.
При п ^ 10 необходимо использовать более точное приближение
2п
у ¦
2у -— 4у -—
18га
где у = ^lna для Dn и у = —\п(а/2) для Dn, при 0,01 ^ а ^ 0,2 и 0,005 ^ а.
Наиболее просты в приложениях результаты Стефенса [212], который предложил
преобразования статистик Dn , Dn, устраняющие зависимость их процентных
точек Dn, Dn от объема выборки п:
0,275 -
0,04
-0,12-
0,11
-0,12-
0,11
Первые две аппроксимации используются соответственно для нижних и верхних
процентных точек. Критические значения статистик Стефенса приведены в табл. 53.
Таблица 53
Процентные точки статистик Dn и
D
[215]
а
Dt(^
0,150
0,973
1,138
0,100
1,073
1,224
0,050
1,224
1,358
0,025
1,358
1,480
0,010
1,518
1,628
Модифицированные статистики критерия Колмогорова^Смирнова, позволяю™
щие применять их в некоторых частных случаях и для ситуаций с неизвестными
параметрами гипотетических распределений, рассмотрены в [209, 213] и будут
подробно проанализированы нами ниже в разделах, посвященных специальным
критериям согласия. Ситуация, когда выборка усечена или цензурирована, рассмо-
рассмотрена в [214], в которой приведены и процентные точки критерия Колмогорова^
Смирнова для разных степеней цензурирования.
Задача 94. Проверить на уровне значимости а = 0,10 нормальность распределения
выборки х%: 4, 7, 8, 12, 18, 19, 21, 25, 30 при условии что Ф(х) = АГA0; 5) (т. е. гипоте-
гипотетическим распределением является нормальное распределение с параметрами /i = 10
и а = 5).
Задача является демонстрационной — на практике критерий Колмогорова—Смирнова
применяется при п ^ 50. Для вычисления значений функции нормального распреде-
216 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
ления Ф(ж) можно использовать либо таблицы, либо аппроксимации (см. раздел 1.1.1).
Необходимо выбирать аппроксимации повышенной точности, что позволит избежать
накопления погрешностей аппроксимации. Результаты расчетов сведем в таблицу; на-
напомним, ЧТО Ф( — Zi) = 1 —- Ф(^г).
г
1
2
3
4
5
6
7
8
9
10
Xi
4
7
8
9
12
18
19
21
25
30
z%
-1,20
-0,60
-0,40
-0,20
0,40
1,60
1,80
2,20
3,00
4,00
Ф(**)
0,1151
0,2743
0,3446
0,4207
0,6554
0,9452
0,9641
0,9866
0,9986
0,9996
г
п
0,10
0,12
0,30
0,40
0,50
0,60
0,70
0,80
0,90
1,00
i - 1
п
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
-0,0151
-0,0743
-0,0446
-0,0207
-0,1554
-0,3452
-0,2641
-0,1866
-0,0986
0,00005
ФЫ ^
0,11510
0,17430
0,14460
0,12070
0,25540
0,44520
0,36410
0,18660
0,19860
0,09996
г- 1
= 0,4452;
Из таблицы следует, что
-+- fi , Л
DT0 = max ФЫ) = 0,0005: D10 = max
\п J
Dw = max(Di,D^0) = 0,4452.
Критическое значение равно Dio@,l) = J • In — = 0,1998.
у 2L " Wj U.У
Так как D\o = 0,4452 > Dig (о) =::: 0,1998, гипотеза нормальности отклоняется
на уровне значимости =0,1. Более точное приближение вычисляется по формуле
A0 - 0,4453 + 1J=8536,
9-10
Критическое значение х2A ~~ а) ПРИ / — 2 степенях свободы равно 1,8856.
Так как %2 = 8,536 > %2A — а) = %2@,90) = 1,8856, гипотеза Но отклоняется. Рассмо-
Рассмотрим более точную аппроксимацию
= -100,1 = 2,302;
' = ,/^. B,302-
%1 20 \
18-10
1
6- 10
= 0,3224.
Так как Dn = 0,4453 > Dn(a) = 0,3224, Но отклоняется. Далее находим статисти-
статистику Dn = 0,4453 ( л/10 + 0,12 '-= ) = 1,477. Ее критическое значение равно 1,224 (см.
табл. 53 при а = 0,1). Так как D~ = 0,4453 > D~(a) = 1,224, гипотеза Но отклоняется.
3.1.2.2. Критерий Смирнова-Крамера-фон Мизеса
Статистика критерия имеет вид [216-218]
1
2
Yin
г=1
Fixi
\
2п
где F{xi)—теоретическая функция распределения.
Необходимо помнить, что теоретическая функция распределения должна быть
известна с точностью до параметров. Распространенная ошибка — использование
в качестве F{x) функции распределения с параметрами, оцениваемыми по выбор™
3.1]
Общие критерии согласия
217
ке [209]—приводит к уменьшению величины критического значения статистики,
т. е. к увеличению количества ошибок второго рода.
При объеме выборки п > 40 можно использовать приведенные в табл. 54 кван-
квантили распределения во;2, которые следуют из его предельного распределения [218]
(а — уровень значимости, принятый для проверки Hq).
Таблица 54
а
ш2(
а)
Квантили распределения
0,900
0,3473
0,950
0,4614
0,990
0,7435
пш
0
0,
' I218J
,995
8694
0
1,
,999
1679
При п < 40 таблицей можно пользоваться [215, 218] с заменой пш2
(по;2)' =
на
п п ) \ п /
Известна аппроксимация распределения пш^ с помощью х2™РаспРеДеления [220]
пш\ = а + Ь%2, где х2—случайная величина, имеющая распределение хи^квадрат
с / степенями свободы;
ЗЗбп - 959тг + 609
210C2п2 -61п + 30)'
ь =
32п - 61га + 30
84ггDтг - 3) '
пDп - ЗK
5 {Шп -
Исследования авторов работы [221] позволяют сделать вывод о том, что на
уровне значимости а > 0,01 квантили точной и предельной функций распреде-
распределения пш2 практически неразличимы уже при объеме выборки п ^ 4. При таких
(пш2)
вместо пш не дает
уровнях значимости использование преобразования
существенных преимуществ.
Необходимо отметить, что и критерий пш2 и критерий Колмогорова—Смирнова
(см. раздел 3.1.2.1) подсчитываются по негруппированным выборкам (в отличие от
критерия х2 —см- раздел 3.1.1.1). В [226] приведен анализ модификаций критериев
типа пш2 для группированных данных и показано, что группировка приводит
к потере мощности критерия на 5-15%.
Задача 95. В условиях задачи 94 проверить нулевую гипотезу нормальности распре-
распределения случайных величин критерием пш .
Вычисления сводим в таблицу:
г
1
2
3
4
5
6
7
8
9
10
Xi
4
7
8
9
12
18
19
21
25
30
Zi
-1,2
^0,6
~054
-0,2
0,4
1,6
1,8
2,2
3,0
4,0
0,1151
0,2743
0,3446
0,4207
0,6554
0,9452
0,9641
0,9866
0,9986
0,9996
2г - 1
п
ОД
0,3
0,5
0,7
0,9
1,1
1,3
1,5
1,7
1,9
г(-) 2%~х
1 Ы
0,0151
^0,0257
-0,1554
-0,2793
-0,2446
-0,1548
-0,3359
-0,5134
-0,7014
-0,9000
\rW п J
2,28-10
6,60 • 10~4
0,02415
0,0780
0,0598
0,0240
0,1183
0,2636
0,4919
0,8100
1,8706
218 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Имеем пш2 = \- 1,8706 = 1,8789. При а = 0?9 критическое значение равно
пш2 @,9) = 0,3473. Так как пш2@,Э) = 0,3473 < 1,8789, гипотеза нормальности отклоня-
отклоняется. Вычислим более точный критерий
(пс2)' = A,8789 - ^ + MV A + ±-) = 2,029.
1 ; V ю юо/ \ 10/
Видим, что результат тот же— Но отклоняется,
айдем %2™ аппроксимацию критерия
336-100^959-10 + 609 ааАЛ^Л , 32 ¦ 100 - 61 • 10 + 30
°°4474 Ь
Теперь найдем %2™ аппроксимацию критерия пш2 и оценим ее точность. Вычисляем
210 ¦ C2 ¦ 100 -61-10 + 30) ' ' 84 ¦ 10 ¦ D - 10 - 3)
QQ in (Л in q\3
/ = — • { j 2 = 1,446; пш2 @,9) = 0,04474 + 0,0843 • Xl 9 A,446).
5 C2 • 100 - 61 • 10 + 30J '
Из таблиц имеем
Xo,9A,446) « 3,65 и пш2@,9) = 0,04474 + 0,0843 • 3,65 = 0,352.
Видим, что это значение близко к предельной квантили пш2@,Э) = 0,3473, т.е. аппрок-
аппроксимация удовлетворительна.
Небольшое отступление: для удобства приведем квантили распределения %
(табл. 55).
3.1.2.3. Критерий Реньи (М-критерий)
Отклонения на правом конце эмпирического распределения являются суммой
многих отклонений, в том числе и расположенных на левом конце. Поэтому воз-
возможно, что эти отклонения будут принимать большие значения. Реньи [220] пред-
предложил критерий согласия, основанный на взвешивании статистики Колмогорова-
Смирнова (см. раздел 3.1.2.1) обратным значением гипотетической теоретической
функции распределения вероятностей F(x). Статистики критерия Реньи имеют вид
%
о+ Fn(x)-F(x) n~F^
i —- 1
D_ . - Fn{x)~F(x) F(Xi) ~ ^T
Rn = - inf EV ч = maX t?( ч
F(x)^a F(x) F(Xi)^a F(Xi)
Rn = sup J ' , , = max
Для больших n (n —> oo) [220]
" -Д+ < x } = 2Ф(ж) - 1,
где Ф(ж) — функция распределения iV@,1) (см. раздел 1.1.1), т.е.
+ (а) =
п v 7
3.1]
Общие критерии согласия
219
Таблица 55
Квантили распределения %2 (/ — число степеней свободы) [25]
/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
а
0,01
0,0001
0,0201
0,1150
0,2970
0,5540
0,8720
1,2390
1,6460
2,0880
2,5580
3,0530
3,5710
4,1070
4,6600
5,2290
5,8120
6,4080
7,0150
7,6330
8,2600
8,8970
9,5420
10,1960
10,8560
11,5240
12,1980
12,8790
13,5650
14,2560
14,9530
0,025
0,0010
0,0506
0,2160
0,4840
0,8310
1,2370
1,6900
2,1800
2,7000
3,2470
3,8160
4,4040
5,0090
5,6290
6,2620
6,9080
7,5640
8,2310
8,9070
9,5910
10,2830
10,9820
11,6880
12,4010
13,1200
13,8440
14,5730
15,3080
16,0470
16,7910
0,05
0,0039
0,1030
0,3520
0,7110
1,1450
1,6350
2,1670
2,7330
3,3250
3,9400
4,5750
5,2260
5,8920
6,5710
7,2610
7,9620
8,6720
9,3900
10,1170
10,8510
11,5910
12,3380
13,0910
13,8480
14,6110
15,3790
16,1510
16,9280
17,7080
18,4930
0,10
0,0158
0,2110
0,5840
1,0640
1,6100
2,2040
2,8330
3,4900
4,1680
4,8650
5,5780
6,3040
7,0420
7,7900
8,5470
9,3120
10,0850
10,8650
11,6510
12,4430
13,2400
14,0410
14,8480
15,6590
16,4730
17,2920
18,1140
18,9390
19,7680
20,5990
0,90
2,706
4,605
6,251
7,779
9,236
10,645
12,017
13,362
14,684
15,987
17,275
18,549
19,812
21,064
22,307
23,542
24,769
25,989
27,204
28,412
29,615
30,813
32,007
33,196
34,382
35,563
36,741
37,916
39,087
40,256
0,95
3,841
5,991
7,815
9,488
11,070
12,592
14,067
15,507
16,919
18,307
19,675
21,026
22,362
23,685
24,996
26,296
27,587
28,869
30,144
31,410
32,671
33,924
35,172
36,415
37,652
38,885
40,113
41,337
42,557
43,773
0,975
5,024
7,378
9,348
11,143
12,832
14,449
16,013
17,535
19,023
20,483
21,920
23,336
24,736
26,119
27,488
28,845
30,191
31,526
32,852
34,170
35,479
36,781
38,076
39,364
40,646
41,923
43,194
44,461
45,722
46,979
0,99
6,6350
9,210
11,345
13,277
15,086
16,812
18,475
20,090
21,666
23,209
24,725
26,217
27,688
29,141
30,578
32,000
33,409
34,805
36,191
37,566
38,232
40,289
41,638
42,980
44,314
45,642
46,963
48,278
49,588
50,892
Отметим, что R^(a) = RnBa). При малых п имеет место соотношение [222]
г —1
г=0
г
1 + .Г
где х > 0, к = п — [паA + х)} — 1; [... ] — целая часть числа.
При а = 0 имеем P(-R:[" ^ х) = z •
4 п 7 1 + х
Задача 96. В условиях задачи 94 проверить нулевую гипотезу нормальности распре-
распределения критерием Реньи.
Вычисления сводим в таблицу.
Положим, что а = 0,5. Тогда из таблицы следует: R% = 0,0005; R~ = 0,4710
ш Rn = 0,4710. Далее ^^_
^ - ^^ 0,4710 = 1,489;
220 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
г
1
2
3
4
5
6
7
8
9
10
4
7
8
9
12
18
19
21
25
30
Zi
-1,2
-0,6
-0,4
-0,2
0,4
1,6
1,8
2,2
3,0
4,0
*«>
0,11510
0,27430
0,34460
0,42070
0,65540
0,94520
0,96410
0,98660
0,99860
0,99996
i
п
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
п
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
п
-0,0151
-0,0743
-0,0446
-0,0270
-0,1554
-0,3452
-0,2641
-0,2866
-0,0986
0,0005
-0,1312
-0,2709
-0,1294
-0,0642
-0,2371
-0,3652
-0,2739
-0,2905
-0,0969
0,0005
F, ч *~1
п
0,11510
0,17430
0,14460
0,12070
0,25540
0,44520
0,36410
0,28660
0,19860
0,09996
п
1,00000
0,63540
0,41960
0,28690
-0,38970
0,47100
0,37760
0,29050
0,19890
0,09996
R~ < 1,4897 = 2A,4897) - 1 = 0,864;
R~ > 1,4897 = 1 - 0,864 = 0,136;
O,95 = 0,521.
Rn (a = 0,1) = \ -иЛ_а = -1=
У na 2 VI0
Так как
• Rn = 1,489 > 0,521, нулевая гипотеза отклоняется.
3.1.2.4. Критерий Андерсона-Дарлинга (критерий пО2)
По аналогии с критерием Реньи (см. раздел 3.1.2.3) Андерсон и Дарлинг [223]
предложили критерий, использующий нормирование статистики критерия пш2
(см. раздел 3.1.2.2) обратным значением теоретической функции распределения.
Статистика Андерсона—Дарлинга имеет вид
пп2 = -п-2
г=1
i- 1){ЫР(хг)
Предельное распределение статистики пО2 (при п -^ оо) табулировано в
[25, 218, 224]. В табл 56 приведены некоторые квантили предельного распределения
nft2 (приближение приемлемо при п > 50).
Таблица 56
Квантили предельного распределения
статистики nft2
а
nU2(a)
0,90
1,94
0,95
2,50
0,975
3,08
0,99
3,88
Сходимость к предельному распределению становится лучше, если использовать
вместо статистики пп2 ее модифицированную форму [226]
/ О2\; п (п^ ) + п + 1
(nil 1 = 9
V 7 п2 + п + 1
3.1]
Общие критерии согласия
221
В [227] предложена модификация статистики Андерсона-Дарлинга в форме
U2 = nU2(U)^nU2(LI
где пО2(С7) — версия критерия вО2 для правого (верхнего) „хвоста"; nQ2(L) — версия
критерия nQ2 для левого (нижнего) „хвоста".
Значения вП2(С/) и nQ2(L) вычисляются по формулам
г=1
= -^+2
- ± 53 Bг - 1) lnF(Xl).
г=1
г=1
Распределение величины nO2(t/) может быть вычислено по формуле [227]
где п02(С/)оо—предельное распределение, для которого справедлива аппроксима-
аппроксимация
где
(а) = 0,1170 - 0,03791?/ + 0,06318z + 0,09878t/z + 0,009184|/2z - 0,0000742/z;
у = ln
1-а'
z= 1
0,3
-l
Значения nO2(L) могут быть вычислены из условия симметрии. Модифициро-
Модифицированный критерий Андерсона—Дарлинга более чувствителен к поведению функции
распределения вероятностей на ее хвостах.
Задача 97. В условиях задачи 94 проверить нулевую гипотезу нормальности распре-
распределения вероятностей критерием Андерсона-Дарлинга.
Вычисления сведем в таблицу (используем обозначение ф = Bг —
[()]})
г
1
2
3
4
5
6
7
8
9
10
Xi
4
7
8
9
12
18
19
21
25
30
Zi
-1,2
-0,6
-0,4
-0,2
0,4
1,6
1,8
2,2
з'о
4,0
0,1151
0,2743
0,3446
0,4207
0,6554
0,9452
0,9641
0,9866
0,9986
0,9999
Хп-г+1
30
25
21
19
18
12
9
8
7
4
Zn-i+l
4,0
3,0
2,2
1,8
1,6
0,4
-0,2
-0,4
-0,6
-1,2
F{zn^i+1)
0,9999
0,9986
0,9866
0,9641
0,9452
0,6554
0,4207
0,3446
0,2743
0,1151
lnF(Zi)
-2,1619
-1,2935
-1,0653
-0,0658
-0,4225
-0,0563
-0,0366
-0,0135
-0,0014
-4-10^5
ln[l-F(*n_i+i)]
-10,1266
-6,5713
-4,3125
-3,3210
-2,9041
-1,0653
-0,5459
-0,4225
-0,3206
-0,1223
#
-12,2885
-27,9716
-26,8890
-29,9394
-29,9394
-12,3376
-7,5725
-6,5400
-5,4740
-2,3245
-161,2765
На основании данных таблицы имеем
пп2 = -10 - — • (-161,2765) = 6,127; (пп2)' =
6,127- 100 + 10 + 1
100 + 10 + 1
= 5,619.
222 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Из табл. 56 имеем nl^2@,9) = 1,94.
Так как (nQ2)f = 5?619 > nQ2@,9) = 1,94, нулевая гипотеза нормальности распреде-
распределения Но отклоняется.
3.1.2.5. Критерий Ватсона
Так как у^ = F(xi) имеет равномерное распределение на единичном интервале
[0,1], то проверка гипотезы равномерности распределения yi равносильна проверке
нулевой гипотезы о подчинении выборочных данных распределению F(x). Поэтому
предложенный Ватсоном [225] критерий для проверки таких гипотез в литературе
чаще всего представлен как критерий равномерности распределения. Статистика
критерия Ватсона имеет вид
U2n=n
Fn(x) - F(x) - | [Fn(y) - F(y)} dF(y) I dF(x),
или в форме, удобной для расчетов:
г=1
Необходимо помнить, что yi = F{xi).
Приведем эквивалентную форму
г=1
г=1
Между критерием пш Смирнова—Крамера—фон Мизеса (см. раздел 3.1.2.2)
и критерием Ватсона существует простое соотношение
Ul = гш2 - ¦
Для практических расчетов рекомендуется формула
п 2 n п
n~tiVi ny nhi%Vl+ n+ у+12'
Статистика
при п ^ 10 имеет предельное распределение, критические нижние точки кото™
рого приведены в табл. 57 (а — уровень значимости).
Таблица 57
Нижние критические точки
статистики Ватсона U^ [228]
а
{UIY
0,10
0,152
0,05
0,187
0,025
0,221
0,01
0,267
Нулевая гипотеза отклоняется, если
)f <
3.1] Общие критерии согласия 223
Процентные точки и полную функцию распределения U% можно найти в [218].
Там лее, как и для распределения пш2 (см. раздел 3.1.2.2), для U% предложена
аппроксимация с помощью х2~распределения [219]
где
21п-56 , 1 / з\ , 49п(п-1)
а = ; Ь=(п); / =
Задача 98. Проверить гипотезу нормальности распределения вероятностей в усло-
условиях задачи 94 критерием Ватсона.
Имеем
(^^) F(-l,2) = 0,1151;
2/2 = F(x2) = ^(-0,6) = 0,2743; у3 = F(x3) = F(-0,4) = 0,3446;
2/4 = F(x4) = F(-0,2) = 0,4207; y5 = FE) = F@,4) = 0,6554;
2/6 = ^(ж6) = ^A,6) = 0,9452; y7 = F{x7) = F(l,8) = 0,9641;
2/8 = F(x8) = FB,2) = 0,9866; y9 = F(x9) = FC,0) = 0,9986;
yi0 = F(xio) = FD,0) = 0,99996.
Тогда у = 0,670456 и
Уг - ^—^ - 0,670456 + 0,5 ) + — = 0,1290.
n ) 120
Вычисляем модифицированную форму критерия
№)' = f0,129 - М + ^liV f! + MU 0,1296.
1 n; \ ' io iooy \ io/
Из табл. 57 при а = 0,1 находим 17^@,1) = 0,152.
Так как {U^)' = 0,1296 < (L^@,l)); = 0,152, гипотеза нормальности распределения
случайных величин отклоняется.
Воспользуемся теперь х2™аппроксимацией:
21-10-56 = = _J_ / _ 3\ =
4210 V 2^
= =
мо.(ю-|) 42'10
49 Ю-9
20
Из табл. 55 находим Хо,эC) = 6,251 и вычисляем
С/п@Д) = 0,02157 + 0,02029 • 6,251 = 0,148,
что очень близко к табличной величине f/n@,l) = 0,152.
3.1.2.6. Критерий Купера
Купер [229] предложил расширенную статистику критерия типа Колмогорова-
Смирнова (см. раздел 3.1.2.1)
Vn= sup {Fn(x) - F{x)} - inf {Fn{x)-F(x)}, или Vn
оо<ж<оо
224 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
где
Г A I Г А _ 1
D+ = тах^ - - Fix) \ и D^ = тах^ F(a) - -—-
n [n V 7J П [ V 7 П
— статистики Колмогорова-Смирнова.
Верхние квантили предельного распределения Vn приведены в [230].
fi \ ( г-1\
Если А = тах| у^ I, _В = max! у^ ), где у^ = F(xi), to расчетная фор-
мула может быть записана в простейшей форме
Vn = A + B.
К предельному распределению быстро сходится модифицированная форма ста-
статистики критерия
— для верхних процентных точек VI = [ х/п + 0,155 -\—"*-= 1 Vn:
\ VnJ
— для нижних процентных точек У' = ( л/п + 0,41 "*-=¦ 1 Vn.
Критические значения для верхних процентных точек приведены в табл. 58.
Таблица 58
Критические значения V^(a)
для верхних процентных точек
статистики Купера [212]
а
0,10
1,62
0,05
1,747
0,025
1,862
0,01
2,001
Если V^ < V^(a), то нулевая гипотеза принимается. Подробно применение кри™
терия Купера и расширенные таблицы его квантилей приведены в [231]. Применение
критерия Купера в частном случае проверки соответствия эмпирического распре-
распределения распределению Вейбулла рассмотрено в [212].
Задача 99. В условиях задачи 94 проверить гипотезу нормальности распределения
критерием Купера.
При решении задачи 94 было получено D^ = 0,00005 и D™ = 0,4452, откуда
Уп = ?)+ + Вп = 0,44525, или в модифицированной форме
V^ = 0,44525 • ( л/10 + 0,155 - ^ ) = 1,443.
V V10/
Из табл. 58 имеем К @,1) = 1,62. Так как К = 1,443 < К @,1) = 1,62, нулевая гипоте-
гипотеза нормальности исходного распределения случайных величин не отклоняется (делать из
этого вывода трагедию не стоит — критерий Купера хорошо работает только при п ^ 20).
3.1.2.7. Критерий согласим Дарбина
Наиболее известный критерий согласия — критерий %2 (см. раздел 3.1.1.1) ги-
гибок, легко используется, но имеет элемент произвола в выборе границ группи-
группирования экспериментальных данных. Критерий Колмогорова-Смирнова (см. раз-
раздел 3.1.2.1) [232] свободен от этих недостатков и имеет хорошую асимптотическую
мощность по сравнению с альтернативами, определенными в терминах расстояния
между функциями распределения. Однако исследования показывают [233], что
на практике для выборок среднего объема он часто непригоден, в отличие от
критерия х2 •
3.1] Общие критерии согласия 225
Критерии типа Колмогорова-Смирнова хороши, когда альтернативное распре™
деление таково, что разница между ним и исходным (например, разница в сред-
средних) велика. Однако если разница между средними и дисперсиями невелика, но
две частотные функции заметно отличаются формой, то критерий Колмогорова—
Смирнова не будет мощным критерием.
В [233] предлагаются новые критерии, свободные от распределения, более могц™
ные, чем критерий Колмогорова—Смирнова.
Пусть F{x) — гипотетическая теоретическая функция распределения вероятно™
стей, определенная с точностью до параметров. Обозначим Uj = F(xj), j = 1, ..., п.
При справедливости гипотезы Щ величина Uj должна быть распределена равно-
равномерно на единичном интервале [0,1].
Пусть U\ ^ U2 ^ • • • ^ Un — порядковые статистики ряда Uj. Сформируем но-
новую последовательность
d = U- С, = Uj - Uj-!, (j = 2, ..., n); Cn+1 = 1 - Un;
где C(j) —порядковая статистика ряда Cj, т.е. j-e по величине значение Cj в упо-
упорядоченном по возрастанию ряду значений Cj.
n+l
Введем переменную шг = J^ gj. Очевидно, что
n+l n+l
^2ej = Yl c(j) = 1; Vj = C(i) + • • • + c{j-i) + (n + 2 - j) . C(j),j = 1, ..., щ
C(l) ^ CB) ^ . . . ^ C(n+1).
Сутью предлагаемых критериев является проверка равномерности распределе-
распределения ujj на интервале [0,1].
Рассмотрим различные варианты критериев проверки равномерности распреде-
распределения o;j, предложенные в [233].
3.1.2.7.1. Модифицированный медианный критерий
Статистика критерия
п + 1 — г шг
п +1 / \ п ( \
где г = (в— нечетное] иг=- (п — четное).
При справедливости нулевой гипотезы статистика Мг распределена как
F2(n+i^rM2r5 т-е- как случайная величина, имеющая ^-распределение Фишера
с Д = 2(в + 1 — г) и /2 = 2г степенями свободы.
Гипотеза f/o отклоняется с достоверностью а, если Мг > F(a), где F(a) —
критическое значение i^-распределения.
3.1.2.7.2. Модифицированный критерий Колмогорова-Смирнова
Статистика критерия
Кт = max ш7
г=1, ...,п\П
Нулевая гипотеза отклоняется, если Кт превышает критическое значение стати-
статистики Колмогорова—Смирнова (см. раздел 3.1.2.2).
8 А. И. Кобзарь
226 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.1.2.7.3. Модифицированный вероятностный критерий
п ( 1 \
В [234] показано, что \\ Uj —> expf ~-\2 ) ? гДе X2 —хи~квадрат~распределенная
случайная величина с / = 2п степенями свободы (см. раздел 1.1.8). Тогда случайная
величина
п
рт = ^2 In Л ujj
i=i
имеет ^-распределение с / = 2п степенями свободы.
Если рт > %2Bп), то гипотеза Hq отклоняется с достоверностью а.
Мощность этого критерия исследована в [235], где показано, что этот критерий
может иметь большую мощность для широкого класса альтернатив. Однако сле-
следует помнить, что статистика рт сильно зависит от ошибок округления величин
C/i, ..., Un и расчеты следует вести с максимально возможной точностью.
Сравнительный анализ рассмотренных критериев показывает, что:
— критерий Колмогорова—Смирнова уступает критерию % ;
— критерий Мг лучше критерия Колмогорова-Смирнова, но хуже критерия %2;
— критерий Кт мощнее, чем критерий Колмогорова—Смирнова, и не уступает
критерию х2-
Задача 100. В условиях задачи 94 проверить гипотезу нормальности распределения
случайной величины критерием Дарбина.
Имеем
иг = Ф(-1,2) = 0,1151; U6 = ФA,6) = 0,9452;
U2 = Ф(-0,6) = 0,2743; U7 = ФA,8) = 0,9641;
U3 = Ф(-0,4) = 0,3446; U8 = ФB,2) = 0,9866;
U4 = Ф(-0,2) = 0,4207; U9 = ФC,0) = 0,9986;
U5 = Ф@,4) = 0,6554; U10 = D,0) = 0,99996.
Сформируем новую последовательность
C1 = U1 = 0,1151; C2 = U2 — t/i = 0,1592; С7 = U7 - U6 = 0,0189;
С3 = U3 - U2 = 0,0703; С8 = U8 - U7 = 0,0255; С4 = U4 - U3 = 0,0761;
С9 = U9 - U8 = 0,0120; C5 = U5 - U4 = 0,2347; do = U10 - U9 = 0,00136;
C6 = U6-U5= 0,2898; Сц = 1 - Uw = 0,00004.
Ранжируем ряд Cj по возрастанию величины:
C(i) = 0,00004; CB) = 0,00136; CC) = 0,0120; CD) = 0,0189;
GE) = 0,0225; CF) = 0,0703; CG) = 0,0761; C(8) = 0,1151;
C(9) = 0,1592; G(ю) = 0,2347; C{11) = 0,2898.
Формируем ряд значений gj:
gi = (n + 2 - 1) • (C(i) - 0) = 0,00044;
g2 = 10 • (CB) - CA)) = 0,0132; g3 = 9 • (CC) - CB)) = 0,09576;
g4 = 8 • (CD) - CC)) = 0,0552; g5 = 7 • (CE) - CD)) = 0,0252;
g6 = 6 - (CF) - CE)) = 0,2868; g7 = 5 - (CG) - CF)) = 0,0290;
g8 = 4 - (C(8) - CG)) = 0,1560; g9 = 3 - (C(9) - C(8)) = 0,1323;
gio = 2 • (C(io) - C(9)) = 0,1510; gu = 1 • (CA1) - Cm) = 0,0591.
3.1] Общие критерии согласия 227
Окончательно имеем ряд значений шг:
ал = g = 0,00044;
ш2 = 0,00044 + 0,09576 = 0,01324; ш3 = 0,01324 + 0,09576 = 0,10890;
ш4 = 0,1090 + 0,0552 = 0,1652; ш5 = 0,1642 + 0,0252 = 0,1894;
ш6 = 0,1894 + 0,2868 = 0,4762; ш7 = 0,4762 + 0,0290 = 0,5052;
ш8 = 0,5052 + 0,1560 = 0,6612; ш9 = 0,6612 + 0,1323 = 0,7935;
ало = 0,7935 + 0,1510 = 0,9445; ал = 0,9445 + 0,0551 = 0,9996.
Модифицированный медианный критерий
ш 10 к пж 5 1-W5 5 1-0,1894
Имеем г = — = 5, М = • = - • = 3,5665.
2 ' 10+1-5 ш5 6 0,1894
Для степеней свободы Д = 2 • (п + 1 — г) = 12 и /г = 10 (а = 0,90) имеем из таблиц
^-распределения (или аппроксимаций из раздела 1.1.10) i<i2,io@,9) = 2,284.
Так как Ms = 3,5665 > .?12,10@,9) = 2,284, нулевая гипотеза отклоняется.
Модифицированный критерий Колмогорова-Смирнова
Имеем разности
ол = 0,09956; ш2 = 0,1868; о;3 = 0,1910; ш4 = 0,2358;
71 71 71 71
- - ш5 = 0,3106; - - о;6 = 0,1238; - - ш7 = 0,1948; - - о;8 = 0,1388;
п п тг п
9 10
ш9 = 0,1065; ало = 0,0555.
п п
Отсюда Кт = 0,3106 и из раздела 3.1.2.1 находим критическое значение статистики
Колмогорова—Смирнова (при а = 0,10). Оно равно для модифицированной статистики
1)п@,1) = 1,073. Тогда имеем
Кт = Кт (у/й + 0,275 - ^ ) = 1,0715.
Значение Кт = 1,0715 очень близко к критическому .К"ш@,1) = 1,073, поэтому гипо-
гипотезу нормальности следует отклонить.
Модифицированный вероятностный критерий
п + 1
рт = ^2 In Yl ujj = 39,633.
3=1
Из табл. 55 для / = 2п = 20 имеем Х2о@?Э) — 28,412 (а = 0,90, т. е. берется верхняя 10%-я
точка распределения).
Так как рт = 39,693 > Х2о@?Э) — 28,412, нулевая гипотеза отклоняется.
3.1.2.8. Двухвыборочные критерии согласим
3.1.2.8.1. Двухвыборочный критерий Колмогорова-Смирнова
Рассматриваются выборки случайных величин
х: хг,х2, .. .,Хщ и У' У1,У2, • • • ,Уп2-
Перед исследователем стоит вопрос: обе выборки извлечены из совокупности с од™
ним и тем же законом распределения вероятностей? Говоря языком математиче™
ской статистики, ему необходимо проверить нулевую гипотезу Hq : Fni (x) = Fn2 (у)
о совпадении функций распределения вероятностей в двух выборках. Статистики
228 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
критерия имеют вид [211]
Dn = max \Fni(x) - Fn2(y)\; D*n = max[Fni(z) - Fn2(y)]
и определяются разностью двух эмпирических функций распределения вероятностей.
Распределение статистик Dn и D* приведено в [25, 29]. Предельное распределен
ние (п*\_,П2 —Ь оо) табулировано в [29]. Критерием рекомендуется пользоваться для
выборок объема п ^ 100. В этом случае справедливо соотношение
max[Fni (х) - Fn2 (у)} < z ) « 1 - e^2z".
Задача 101. В результате сравнения двух выборок случайных величин X uY, объемом
Гц = 100 и П2 = 300 соответственно, получено максимальное расхождение их функций
распределения вероятностей, равное 0,252. На уровне значимости а = 0,1 проверить
гипотезу о неразличимости функций распределения вероятностей в обеих выборках.
Находим вероятность
— • max [Fioo (x) - F300 (y)] < 0,252 = 1 - exp (-2 • 0,2522) = 0,119.
Так как полученная величина 0,119 превышает а = 0,1, нулевая гипотеза отклоняется.
3.1.2.8.2. Критерий Катценбайссера-Хакля
В [236] предложен новый критерий, основанный на сравнении эмпирических
функций распределения вероятностей, более мощный, чем критерий Колмогорова—
Смирнова. Статистика критерия (Т) определяется числом точек, в которых эмпи™
рические функции распределения совпадают. Рассмотрим две выборки случайных
величин равного объема х: х\, Х2, • • •, хп и у: t/i, t/2 5 • • • •> Уп •
Составляем из них новую, упорядоченную по bosj астан-по, выборку {zi} объема
N = 2п. Определим сравниваемые эмпирические фун ц распределения следую-
следующим образом: Fn(zi) = (Gn(zi) = ), где пх(г) (пу(г)) — количество ж™ов
(у-ов), меньших или равных Z{.
В [236] показано, что
Математическое ожидание и дисперсия числа совпадающих точек равны
Для больших выборок (п —>- оо)
М(Т) = лДп2 + -л/^П^2 + _^П^2;
ЩТ) = D - тг) п - V^J + ^2 - | V ^
е 4
где М = —-— и х =
3.1]
Общие критерии согласия
229
Приближение удовлетворительно, когда п ^ 5. Если для полученного значе™
ния Т вероятность Р(Т ^ t) будет меньше уровня значимости а, то нулевая ги-
гипотеза отклоняется и функции распределения не признаются совпадающими.
Задача 102. Даны две выборки случайных величин:
хц 10 12 14 14 18 21 27 28 35 36
уц 1 8 10 14 26 27 28 30 31 40
Проверить совпадение законов распределения вероятностей двухвыборочным кри-
критерием Катценбайссера-Хакля на уровне значимости а = 0,1.
Имеем ряд:
z(i): 1(г/), 8(j/), 10B;), 10B/), 12(х), 14(х), 14(х), 14B/), 18(х), 21(х),
26B/), 27(ж), 27B/), 28(х), 28(у), 30(у), 31(у), 35(х), 36(х), 40(у).
В скобках указана принадлежность значения первоначальным выборкам х и у. Вы-
Вычисляем выборочное распределение. Результаты вычислений приведены в таблице:
г
1
2
3
4
5
6
7
*Vi (*(*))
0,0
0,0
0,1
0,1
0,2
0,4
0,4
0,1
0,2
0,3
0,3
0,3
0,4
0,4
г
8
9
10
11
12
13
14
Fn(z{t))
0,4
0,5
0,6
0,6
0,7
0,7
0,8
0,4
0,4
0,4
0,5
0,6
0,6
0,7
i
15
16
17
18
19
20
Fn[z{%))
0,8
0,8
0,8
0,9
1,0
1,0
Gn(z(l))
0,7
0,8
0,8
0,9
0,9
1,0
Из табл. видим, что функции распределения вероятностей совпадают в точках 0,4
(г = 6, 7, 8); 0,8 (г = 16); 0,9 (г = 18) и 1,0 (г = 20), т. е. Г = 5.
Вычисляем
м(г) = V5^+o-V-
, — • \- = 5,605 + 0,0700 + 4,379 • 1G~4 = 5,675;
п 128п V п
В(Т) = D-.).п-^+B-^-^.1-^^ =
= 8,584 - 5,605 + 1,2146 - 0,0700 - 0,0098 = 4,1138 (-/D(T) = 2,028).
Видим, что значение Г близко к М(Т). Следовательно, можно ожидать принятия
нулевой гипотезы. Вычисляем
Р(Г > 5) = J— • 1 — • A,46064 - 12 • 1,46062 + 12)
1 ; V 7,5 [ 96-7,5 V ' ' J
7,5
12I х
1
80
\ _
-1-е
1,46062
= 0,6938.
128-100/
Отсюда Р(Т ^ 4) = 1 — 0,6938 « 0,3, что существенно превышает уровень значимости
а = 0,1. Следовательно, нулевая гипотеза (совпадение эмпирических функций распреде-
распределения вероятностей) не отклоняется.
3.1.2.8.3. Двухвыборочный критерий Андерсона
Поступим по аналогии с рассмотренным выше критерием (имеем выборку х
объема п и выборку у объема га). Составим объединенную выборку и упорядочим
ее по возрастанию. Обозначим через RXi и Ry.—ранги элементов выборки х и у
230 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
в общем упорядоченном ряду (ранг — номер элемента, полученный им в упорядо™
ченном ряду).
Статистика Андерсона имеет вид [237]
Т =
1
mn(m + п)
г=1
4тпп — 1
6(т + п)'
При n, m —> оо и — = const статистика Т распределена как статистика Смирно™
п
ва-Крамера-фон Мизеса (см. раздел 3.1.2.2).
Напомним, что можно использовать критические точки из табл. 54.
Задача 103. В условиях задачи 102 проверить нулевую гипотезу критерием Андерсо-
Андерсона.
Находим ранги RXi и Ryi в общей выборке
Rx\ = 3,5; RX2 :=: 5; RX3 = 7; RX4 = 7; RX5 = 9; RX6 = 10; RX7 = 12,5;
RXg = 14,5; RXq = 18; Rx10 = 19; Ryi = 1; i?y2 = 2; It^ = 3,5; i?y4 = 7;
#y5 = ii; Rve = 12& Ry7 = u& Rvs = 16; RV9 = 17; Rvm =20-
Если значения ж-ов и у-ов совпадают, им присваиваются средние ранги. Например,
значениям хз = Ж4 = 2/4 = 14 присваивается одинаковый средний ранг
Дс3 — Rx4 ^ Ry4 — —
По аналогии определяются все остальные ранги.
Вычисляем статистику критерия
Т =
= 7.
10-10- A0 + 10)
4-10-10-1
6- A0 + 10)
= 0,0675.
Из табл. 54 находим критическое значение (для а = 0,90) па;2 (а) = 0,3473. Так как
Т = 0,0675 < 0,3473, нулевая гипотеза не отклоняется.
3.21
Критерии нормальности распределения
231
3.2. Критерии нормальности распределения
Нормальный закон распределения вероятностей получил наибольшее распро-
распространение в практических задачах обработки экспериментальных данных. Боль™
шинство прикладных методов математической статистики исходит из предположе-
предположения нормальности распределения вероятностей изучаемых случайных величин.
Широкое распространение этого распределения вызвало необходимость разра-
разработки специальных критериев согласия эмпирических распределений с нормаль™
3.2.1. Общие критерии согласия, модифицированные для проверки
нормальности распределения
3.2.1.1. Модифицированный критерий %2
В [199] предложена и исследована форма критерия согласия %2, модифициро™
ванная применительно к проверке нормальности распределения, когда параметры
распределения оцениваются по негруппированной выборке. После оценки парамет™
ров распределения совокупность выборочных данных разбивается на к равнове-
равновероятных интервалов (pi = - = const) и статистика критерия подсчитывается по
к
формуле
2
X = -
2
Ш7- — П,
%
г=1
где п — объем выборки; mi — количество членов выборки, попавшее в г-й интервал.
Границы интервалов определяются как
+ CiSi (г = 0, ...,&), где х =
1 ,
х = —
п
s = < -
~xf
г=1
Значения коэффициентов С{ приведены в табл. 59. Следует помнить, что Cq = ^
и Ck = оо. Так как С{ симметричны относительно нуля, то недостающие значения
Таблица 59
Значения коэффициентов Ci модифицированного %2-критерия
нормальности для к = 3 -?- 15 [199]
к
3
4
5
6
7
8
9
10
11
12
13
14
15
с\
-0,4307
^0,6745
-0,8416
-0,9674
-1,0676
-1,1503
-1,2206
-1,2816
-1,3352
-1,3830
-1,4261
-1,4652
-1,5011
0
-0,2533
-0,4307
-0,5659
-0,6745
-0,7647
-0,8416
-0,9085
-0,9674
-1,0201
-1,0676
-1,1108
сз
0
-0,1800
-053186
-0,4307
-055244
-0,6046
-0,6745
-0,7363
-0,7916
-0,8416
0
-0,1397
-0,2533
-0,3488
-0,4307
-0,5024
-0,5660
-0,6229
0
-0,1142
-0,2194
-0,2934
-0,3661
-0,4307
се
0
-0,0966
-0,1800
-0,2533
0
-0,0837
232 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
можно найти из соотношений
(¦ 1 к-Л и
с\ п лЛ . = —ci п л, . I г = 1, ..., —-— —для нечетных /с;
тт (к — 1)+г оЧ"' — J-/ — * \ 2 1
Z Z \ /
= —ci.
• 1
г = 1, ...,
—для четных к.
Если %2 > dfc(a), ГДе ^fc(a) — критическое значение статистики критерия на
уровне значимости а, то гипотеза нормальности отклоняется. Критические зна-
значения dk(ct) приведены в табл. 60.
Таблица 60
Критические значения dk(ct)
модифицированного х2-критерия нормальности
к
3
4
5
6
7
8
9
а
0,10
25371
3,928
5,442
6,905
8,322
9,703
11,055
0,05
3,248
5,107
6,844
8,479
10,038
11,543
13,007
0,01
5,418
7,917
10,075
12,021
13,837
15,567
17,234
к
10
11
12
13
14
15
а
0,10
12,384
13,694
14,988
16,267
17,535
18,792
0,05
14,438
15,843
17,226
19,589
19,937
21,270
0,01
18,852
20,431
21,977
23,495
24,990
26,464
Задача 104. Для данных задачи 91 проверить модифицированным критерием %2 на
уровне значимости а = 0,1 гипотезу нормальности распределения при оценке его пара-
параметров по негруппированным данным.
1
[
Имеем х = — • ? ^ = Ю0,77; s = I — • ^ (хг ^ хJ \ = 21,5827.
[ J
—
г=1 ^ """ г=1
Из табл. 59 находим коэффициенты разбиения (принимаем к = 10):
d = -1,2816; с4 = ^0,2533; с7 = 0,5244;
с2 = -0,8416; с5 =0; с8 = 0,8416;
сз = ^0,5244; с6 = 0,2533; с9 = 1,2816.
Результаты расчетов сведем в таблицу:
i
1
2
3
4
5
6
7
8
9
10
Границы интервалов
^оо -
72,79-
82,40-
89,32-
95,24-
100,77-
106,30-
112,22-
119,14-
128,40-
-72,79
-82,40
-89,32
-95,24
-100,77
-106,30
-112,22
-119,14
-128,40
- сю
гщ
7
12
11
11
8
13
6
12
10
10
о
49
144
121
121
64
169
36
144
100
100
100 1048
3.21
Критерии нормальности распределения
233
Статистика критерия равна
9 10
1? - п = • 1048 - 100 = 4,8.
100
Из табл. 60 находим критическое значение статистики для к = 10 и а = 0,1: ^ю(ОД) =
= 12,384. Так как %2 = 4,8 < dio@,l) = 12,384, гипотеза нормальности исходного распре-
распределения вероятностей не отклоняется.
3.2.1.2. Критерии типа Колмогорова-Смирнова
Применение критерия согласия пи (см. раздел 1.2.2) для задачи проверки ги-
гипотезы нормальности распределения вероятностей случайных величин рассмотрено
в [218]. Алгоритм вычисления статистики критерия в этом случае не меняется — меня-
меняются только критические значения статистики проверки гипотезы. Для различных си-
ситуаций, когда параметры гипотетического распределения оцениваются непосредствен-
непосредственно по самой выборке, критические значения статистики пш2 приведены в табл. 61.
По аналогии в [209, 215] рассмотрено применение критерия Колмогорова-Смир-
Колмогорова-Смирнова (см. раздел 3.1.2.1) для проверки нормальности распределения в ситуации,
когда оба его параметра оцениваются по выборке. Алгоритм проверки нулевой гипо-
гипотезы Н® и для этого случая сохраняется, меняются только критические значения —
используется модифицированная статистика
: = a
критические значения которой
(a — уровень значимости) приведены в табл. 62.
Таблица 61
Критические значения статистики пш2 для проверки
нормальности распределения A — а — уровень значимости) [218]
Исходные условия
Параметры (/i и а) известны заранее
Параметр а известен, а параметр /j,
оценивается по выборке
Параметр \х известен, а параметр а
оценивается по выборке
Параметры ц и о оцениваются по вы-
выборке
а
0,90
0,3473
0,1344
0,2370
0,1035
0,95
0,4614
0,1653
0,4418
0,1260
0,99
0,7435
0,2380
0,7245
0,1788
0,995
0,8694
0,2698
0,8506
0,2018
0,999
1,1679
0,3443
1,1490
0,2559
Таблица 62
Критические значения статистики
Колмогорова^Смирнова, модифицированной
для проверки нормальности распределения [209]
а
0,15
0,775
0,10
0,819
0,05
0,895
0,03
0,955
0,01
1,035
234 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Задача 105. Для данных задачи 94 проверить гипотезу нормальности распределения
случайных величин критерием типа Колмогорова-Смирнова с оценкой параметров
распределения по выборке.
1
Находим х = —
п
I I
Xi = 15,3; s = < — •
\n
— хJ
= 8,149.
Имеем Zi =
i ~ 15'3
8,149
Критерий Колмогорова-Смирнова
. Результаты расчетов сведем в таблицу:
г
1
2
3
4
5
6
7
8
9
10
х-
4
7
8
9
12
18
19
21
25
30
zi
-1,386
-1,018
-0,896
-0,773
-0,405
0,331
0,454
0,699
1,190
1,804
0,0823
0,1535
0,1841
0,2207
0,3446
0,6293
0,6753
0,7580
0,8830
0,9640
i
п
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
i - 1
п
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
- - ф(*0
п
0,0179
0,0465
0,1159
0,1793
0,1554
0,0293
0,0247
0,0420
0,0170
0,0360
ф(*0 - —
п
0,0823
0,0535
-0,0159
-0,0793
-0,0554
-0,1293
-0,1293
-0,0420
-0,0170
-0,0360
Из таблицы следует, что
= max [ - - Ф(гЛ J = 0,1793;
\п J
г - 1
= 0,1293;
Dn =
= 0,1793.
Далее DI = 0,1793 - [ у/п - 0,01 + -у= = 0,613. Из табл. 62 имеем D*(a) = 0,819. Так
V vlO,
как DI = 0,613 < DI
= 0,819, гипотеза нормальности распределения не отклоняется.
Критерий пш2
Результаты работы сведены в таблицу:
г
1
2
3
4
5
6
7
8
9
10
21
7
8
9
12
18
19
21
25
30
z%
-1,386
-1,018
-0,896
-0,773
-0,405
0,331
0,454
0,699
1,190
1,804
F(*i)
0,0823
0,1535
0,1841
0,2207
0,3446
0,6293
0,6753
0,7580
0,8830
0,9640
F(z-) 2г~г
-0,0177
-0,1465
-0,3159
-0,4793
-0,5554
-0,4707
-0,6247
-0,7420
-0,8170
-0,9360
h(z-) *-Ч2
Г^ и )
3,13-Ю^4
0,0214
0,0998
0,2297
0,3085
0,2215
0,3902
0,5506
0,6675
0,8761
Находим пш2 =
- 3,3656 = 3,374.
12 • 10
Так как пш2 = 3,374 > пш2@,1) = 0,1035 (см. табл. 61 при 1 - а = 1 - 0,1 = 0,9), ну-
нулевая гипотеза нормальности распределения отклоняется.
3.21
Критерии нормальности распределения
235
3.2.1.3. Критерий Фроцини
В [238, 239] Фроцини предложил простой, но достаточно мощный критерий
нормальности с параметрами, оцениваемыми по выборке, основанный на статистике
/ \ г-0,5
Xi-X _ 1 ,
где 2* = ;я=-
~ Функция распределения 7V@,l).
г=1
Критические значения статистики Вп приведены в табл. 63.
Таблица 63
Критические значения статистики Фроцини Вп
для проверки нормальности распределения
(а — уровень значимости) [239]
п
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
сю
а
0,80
0,2115
0,2132
0,2143
0,2175
0,2186
0,2179
0,2191
0,2212
0,2207
0,2204
0,2226
0,2226
0,2228
0,2233
0,2232
0,2257
0,2250
0,85
0,2245
0,2265
0,2276
0,2303
0,2314
0,2304
0,2332
0,2335
0,2336
0,2335
0,2354
0,2356
0,2362
0,2363
0,2367
0,2385
0,2390
0,90
0,2422
0,2434
0,2448
0,2477
0,2491
0,2485
0,2500
0,2508
0,2525
0,2518
0,2530
0,2519
0,2551
0,2536
0,2533
0,2556
0,2560
0,95
0,2666
0,2698
0,2702
0,2756
0,2753
0,2789
0,2774
0,2795
0,2784
0,2791
0,2820
0,2804
0,2812
0,2822
0,2830
0,2839
0,2840
0,99
0,3120
0,3148
0,3224
0,3286
0,3331
0,3332
0,3317
0,3356
0,3385
0,3367
0,3370
0,3376
0,3376
0,3374
0,3413
0,3363
0,3410
Задача 106. В условиях задачи 94 проверить гипотезу нормальности распределения
случайных величин критерием Фроцини.
Воспользуемся данными из таблицы расчета критерия Колмогорова—Смирнова и по-
получим
1
Вп =
/10
• @,0323 + 0,0035 + 0,0659 -
+ 0,1293 + 0,1054 + 0,0793 + 0,0253 + 0,008 + 0,033 + 0,014) = 0,1558.
Из табл. 63 находим критическое значение Вп(а = 0,1) = 0,2485.
Так как Вп = 0,1568 < Вп@,1) = 0,2485, гипотеза нормальности распределения слу-
случайных величин не отклоняется.
3.2.2. Специальные критерии нормальности
Учитывая чрезвычайно широкое распространение нормалвного распределения,
предложено множество критериев проверки нормалвности, использующих раз™
личные характеризации нормального распределения и направленные на защиту
236 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Коэффициенты an—i-\-i
п
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
1
7071
6872
6646
6431
6233
6052
5888
5739
5601
5475
5359
5251
5150
5056
4968
4886
4808
4734
4634
4590
4542
4493
4450
4407
4366
4328
4291
4254
4220
4188
4156
4127
4096
4068
4040
4015
3989
3964
3940
3917
3894
3872
3850
3830
3808
3789
3770
3751
2
1677
2413
2806
3031
3164
3244
3291
3315
3325
3325
3318
3306
3290
3273
3253
3232
3211
3185
3156
3126
3098
3069
3043
3018
2992
2968
2944
2921
2898
2876
2854
2834
2813
2794
2774
2755
2737
2719
2701
2684
2667
2651
2635
2620
2604
2589
2574
3
0875
1401
1743
1976
2141
2260
2347
2412
2460
2495
2521
2540
2553
2561
2565
2578
2571
2563
2554
2543
2533
2522
2510
2499
2487
2475
2463
2451
2439
2427
2415
2403
2391
2380
2368
2357
2345
2334
2323
2313
2302
2291
2281
2271
2260
4
0561
0947
1224
1429
1586
1707
1802
1878
1939
1988
2027
2059
2085
2119
2131
2139
2124
2148
2151
2152
2151
2150
2148
2145
2141
2137
2132
2127
2121
2116
2110
2104
2098
2091
2085
2078
2072
2065
2058
2052
2045
2038
2032
5
0399
0695
0922
1099
1240
1353
1447
1524
1587
1641
1686
1736
1764
1787
1807
1822
1836
1848
1857
1864
1870
1874
1878
1880
1882
1883
1883
1883
1881
1880
1878
1876
1874
1871
1868
1865
1862
1859
1855
1851
1847
6
0303
0539
0727
0880
1005
1109
1197
1271
1334
1399
143
1480
1512
1539
1563
1584
1601
1616
1630
1641
1651
1660
1667
1673
1678
1683
1686
1689
1691
1693
1694
1695
1695
1695
1695
1695
1693
1692
1691
7
0240
0433
0593
0725
0837
0932
1013
1092
1150
1201
1245
1283
1316
1346
1372
1395
1415
1433
1449
1463
1475
1487
1496
1505
1513
1520
1526
1531
1535
1539
1542
1545
1548
1550
1551
1553
1554
8
0196
0359
0496
0612
0711
0804
0878
0941
0997
1046
1089
1128
1162
1192
1219
1243
1265
1284
1301
1317
1331
1344
1356
1366
1376
1384
1392
1398
1405
1410
1415
1420
1423
1427
1430
9
0173
0303
0422
0530
0618
0696
0764
0823
0876
0923
0965
1002
1036
1066
1093
1118
1140
1160
1179
1196
1211
1225
1237
1249
1259
1269
1278
1286
1293
1300
1306
1312
1317
10
0140
0263
0368
0459
0539
0610
0672
0728
0778
0822
0862
0899
0931
0961
0988
1013
1036
1056
1075
1092
1108
1123
1136
1149
1160
1170
1180
1189
1197
1205
1212
11
0122
0228
0321
0403
0476
0540
0598
0650
0697
0739
0777
0812
0844
0873
0900
0924
0947
0967
0986
1004
1020
1035
1049
1062
1073
1085
1095
1105
1113
12
0107
0200
0284
0358
0424
0483
0537
0585
0629
0669
0706
0739
0770
0798
0824
0848
0870
0891
0909
0927
0943
0959
0972
0986
0998
1010
1020
3.21
Критерии нормальности распределения
237
Таблица 64
критерия Шапиро^Уилка [13,
240]
г
13
0094
0178
0253
0320
0381
0435
0485
0530
0572
0610
0645
0677
0706
0733
0759
0782
0804
0824
0842
0860
0876
0892
0906
0919
0932
14
0084
0159
0227
0289
0344
0395
0441
0484
0523
0559
0592
0622
0651
0677
0701
0724
0745
0765
0783
0801
0817
0832
0846
15
0076
0144
0206
0262
0314
0361
0404
0444
0481
0515
0546
0575
0602
0628
0651
0673
0694
0713
0731
0748
0764
16
0068
0131
0187
0239
0287
0331
0372
0409
0444
0476
0506
0534
0560
0584
0607
0628
0648
0667
0685
17
0062
0119
0172
0220
0264
0305
0343
0379
0411
0442
0471
0497
0522
0546
0568
0588
0608
18
0057
ОНО
0158
0203
0244
0283
0318
0352
0383
0412
0439
0465
0489
0511
0532
19
0053
0101
0146
0188
0227
0263
0296
0328
0357
0385
0411
0436
0459
20
0049
0094
0136
0175
0211
0245
0277
0307
0335
0361
0386
21
0045
0087
0126
0163
0197
0229
0259
0288
0314
22
0042
0081
0118
0153
0185
0215
0244
23
0039
0076
0111
0143
0174
24
0037
0071
0104
25
0035
238 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
нулевой гипотезы нормальности распределения от всевозможных альтернатив. Мы
попытались (насколько это возможно) сгруппировать эти критерии в относительно
однородные группы.
3.2.2.1. Критерий Шапиро—Ушжа
Критерий Шапиро-Уилка [240] основан на отношении оптимальной линейной
несмещенной оценки дисперсии (см. раздел 2.1.2.1.6.6) к ее обычной оценке методом
максимального правдоподобия (см. раздел 2.1.2.1.1). Статистика критерия имеет
вид
к п -1 п
2 ^^ / »х2 _ I
/ \ G>n-i+l\xn-i+l — xi
г=1
где s" =y [Xi-x) ; х = -
п
Числитель является квадратом оценки среднеквадратического отклонения Ллой-
да [241].
Коэффициенты an—i+i приведены в табл. 64, заимствованной из [13, 240]. Крити™
ческие значения статистики FF(a) приведены в табл. 66, заимствованной из [13, 240].
Если W < W(a)^ то нулевая гипотеза нормальности распределения отклоняется
на уровне значимости а. Приближенную вероятность получения эмпирического
значения W при Hq можно вычислить по формуле [242]
где 7? V и Е — коэффициенты, приведенные в табл. 65.
Изучение мощности критерия Шапиро^Уилка [243] показало, что это — один из
наиболее эффективных критериев проверки нормальности распределения случай-
случайных величин. Для больших п таблицы коэффициентов an^+i становятся неудобны-
неудобными, поэтому была предложена модификация критерия Шапиро-Уилка — критерий
Шапиро—Франчиа [244].
Его статистика имеет вид
1 2
к
г=1
где
и mi1n —математическое ожидание г-й порядковой статистики из стандартного нор-
нормального распределения. Аппроксимация mi = Ф™1'
не искажает существенно критерий W1 [245].
Используя аппроксимацию для квантили стандартного нормального распреде-
распределения (см. раздел 1.1.1), можно записать
.3
и для р = 1- имеем тг = 4,91
п+- i\/ V
В [36] приведена полезная аппроксимация, позволяющая применить критерий
Шапиро—Уилка без помощи таблиц.
3.21
Критерии нормальности распределения
239
Таблица 65
п
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
7
-0,6250
-1,1070
-1,5300
-2,0100
-2,3560
-2,6960
-2,9680
-3,2620
-3,4850
-3,7310
-3,9360
-4,1550
-4,3730
-4,5670
-4,7130
-4,8850
-5,0180
-5,1840
-5,2910
-5,4130
-5,5080
-5,6050
-5,7040
-5,8030
Коэффициенты ту5
п
0,3860
0,7140
0,9350
1,1380
1,2450
1,3330
1,4000
1,4710
1,5150
1,5710
1,6130
1,6550
1,6950
1,7240
1,7390
1,7700
1,7860
1,7980
1,8180
1,8350
1,8480
1,8620
1,8760
1,8900
е
0,7500
0,6297
0,5521
0,4963
0,4533
0,4186
0,3900
0,3660
0,3451
0,3270
0,3111
0,2969
0,2842
0,2727
0,2622
0,2528
0,2440
0,2375
0,2264
0,2207
0,2157
0,2106
0,2063
0,2020
п
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
7 и е [13]
7
-5,9050
-5,9880
-6,0740
-6,1600
-6,2480
-6,3240
-6,4020
-6,4800
-6,5590
-6,6400
-6,7210
-6,8030
-6,8870
-6,9610
-7,0350
-7,1110
-7,1880
-7,2120
-7,2660
-7,3450
-7,4140
-7,5550
-7,6150
-7,6770
7]
1,9050
1,9150
1,9340
1,9490
1,9650
1,9760
1,9880
2,0000
2,0120
2,0240
2,0370
2,0490
2,0620
2,0750
2,0880
2,1010
2,1140
2,1190
2,1280
2,1410
2,1550
2,1830
2,1980
2,2120
е
0,1980
0,1943
0,1907
0,1872
0,1840
0,1811
0,1781
0,1755
0,1727
0,1702
0,1677
0,1656
0,1633
0,1612
0,1591
0,1572
0,1552
0,1548
0,1534
0,1526
0,1499
0,1466
0,1451
0,1436
Для а = 0,05 предлагается статистика
/ 0,6695 W
1 ~ V п0'6518 / В1
где
В=
а0 =
0,899
(п - 2,4H'4162
= п - 2 j + 1
Z^ n-0,5
- 0,02;
Если W\ < 1, то нулевая гипотеза нормальности распределения случайных вели™
чин отклоняется. Модификация критерия Шапиро—Уилка для случая группирован-
группированных данных (что существенно при наличии совпадающих наблюдений) рассмотрена
в [246].
Задача 107. Имеется выборка данных
х: -1, 0, 1, 2, 3, 5, 6, 7, 10, 15.
Проверить гипотезу нормальности распределения случайной величины х критерием
Шапиро-Уилка на уровне значимости а = 0,05.
240 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Таблица 66
Процентные точки критерия W(ct) (a — уровень значимости) [13, 240]
п
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
а
0,01
0,737
0,687
0,686
0,713
0,730
0,749
0,764
0,781
0,792
0,805
0,814
0,825
0,835
0,844
0,851
0,858
0,863
0,868
0,873
0,878
0,881
0,884
0,888
0,891
0,02
0,756
0,707
0,715
0,743
0,760
0,778
0,791
0,806
0,817
0,828
0,837
0,846
0,855
0,863
0,869
0,874
0,879
0,884
0,888
0,892
0,895
0,889
0,901
0,904
0,05
0,767
0,748
0,762
0,788
0,803
0,818
0,829
0,842
0,850
0,859
0,866
0,974
0,881
0,887
0,892
0,897
0,901
0,905
0,908
0,911
0,914
0,916
0,918
0,920
0,10
0,789
0,792
0,806
0,826
0,838
0,851
0,859
0,869
0,876
0,883
0,889
0,895
0,901
0,906
0,910
0,914
0,917
0,920
0,923
0,926
0,928
0,930
0,931
0,933
0,50
0,959
0,935
0,927
0,927
0,928
0,932
0,935
0,938
0,940
0,943
0,945
0,947
0,950
0,952
0,954
0,956
0,957
0,959
0,960
0,961
0,962
0,963
0,964
0,965
п
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
а
0,01
0,894
0,896
0,898
0,900
0,902
0,904
0,906
0,908
0,910
0,912
0,914
0,916
0,917
0,919
0,920
0,922
0,923
0,924
0,926
0,927
0,928
0,929
0,929
0,930
0,02
0,906
0,908
0,910
0,912
0,914
0,915
0,917
0,919
0,920
0,922
0,924
0,925
0,927
0,928
0,929
0,930
0,932
0,933
0,934
0,935
0,936
0,937
0,937
0,938
0,05
0,923
0,924
0,926
0,927
0,929
0,930
0,931
0,933
0,934
0,935
0,936
0,938
0,939
0,940
0,941
0,942
0,943
0,944
0,945
0,945
0,946
0,947
0,947
0,947
0,10
0,935
0,936
0,937
0,939
0,940
0,941
0,942
0,943
0,944
0,945
0,946
0,947
0,948
0,949
0,950
0,951
0,951
0,952
0,953
0,953
0,954
0,954
0,955
0,955
0,50
0,965
0,966
0,966
0,967
0,967
0,968
0,968
0,969
0,969
0,970
0,970
0,970
0,971
0,971
0,972
0,972
0,972
0,973
0,973
0,973
0,974
0,974
0,974
0,974
Имеем s = J^ {x% — x) = 219,6. Используя коэффициенты ап—г+i из табл. 64 для
г=1
п = 10 (fc = — = 5), находим
5
J] Оп-г+1 • (xn-i+i - Xi) = 0,5739 • A5 + 1) + 0,3291 • A0 - 0) + 0,2141 • G - 1) +
г=1
+ 0,1224 • F - 2) + 0,0399 • E - 3) = 14,3274;
I 2
= 205,27439; W = 205;27439 = 0,935.
Из табл. 66 находим И^о@,1) = 0,869.
Так как W = 0,935 > Wio@,l) = 0,869, гипотеза нормальности распределения не от-
отклоняется.
Вычислим точную вероятность получения значения W = 0,935 при условии справед-
справедливости нулевой гипотезы Hq.
Из табл. 65 для п = 10 находим j = -3,262, 77 = 1,471 и е = 0,3660.
Далее получаем z = —3,262 + 1,471 • In I — J = —0,07076. Соответствующая
этой квантили стандартного нормального распределения вероятность Ф(—0,07067) « 0,47
(см. табл. 1). Эта вероятность существенно превышает принятый уровень значимости
а = 0,1, что позволяет уверенно принять нулевую гипотезу нормальности.
3.2] Критерии нормальности распределения 241
Используем теперь критерий W\ для чего предварительно вычислим (по табл. 1 или
с помощью аппроксимаций)
5\ о,14х
10- 10+ -
г = 1, тю = 4,91 • [ | f | - [ —^ | | = 1,5479; i = 2, ш9 = 0,998;
10+ -
г = 3, 7П8 =::: 0,655; г = 4, 7717 = 0,374; г = 5, т® = 0,122; 7717 = --ТП4', тп% =
T7i9 = —-TT12] тпго = —-mi;
mTO^+i тю 1,5479 = 0^48д. ^ = 0?3539; с3 = 0,2323;
5 205 36
С4 = 0,132; С5 = 0,0433; ]Г сп^г+1 • {хп^1+1 - хг) = 14,3322; W' = ^^ = 0,935,
i=i '
что очень близко к точному значению критерия.
В заключение используем приближенный критерий, не требующий применения та-
таблиц. Имеем
«о = A0_°2849)9о,4162 - 0,02 = 0,3665138; z3 = 10 "^ + Х ;
zi = 0,94737; z2 = 0,73684; z3 = 0,52616; z4 = 0,31579; z5 = 0,105263;
[1ДОО IJ-I ?} 10""^^ 1
0,94737 + Штщг + '— —, = 0,584074;
C - 0,94737I0'845 A,1 - 0,94737)8'26 J
a2 = 0,3474026; a3 = 0,2222972; a4 = 0,1278953; a5 = 0,0439392;
В = [0,5847074 • A5 + 1) + 0,347026 • A0 - 0) + 0,2222972 . G - 1) + 0,1278953 • F - 2) +
+ 0,0439392 • E - 3)]2 = 217,934;
(л 0,6695 \ 219,6
W\=\\ n«r;ig * l— = 0,857.
V 100'6518/ 217,934
V 10/ 217,934
Так как W\ = 0,857 < 1, то нулевая гипотеза отклоняется на уровне значимости
= 0,1.
3.2.2.2. Энтропийный критерий нормальности (критерий Васичека)
Критерий основан на том, что энтропия нормального распределения превышает
энтропию любого другого распределения с той же дисперсией.
Энтропия распределения вероятностей с плотностью f(x) равна
оо
Н=- | /(я) log/(ж) da;,
а ее оценка по выборочным данным
п ( л
^ log < J^(Xi+m - Xi-m) >,
п
где Xi = х\ при i < 1; Xi = хп при г > п (xi —г-я порядковая статистика), т — целое
положительное число, меньшее, чем п/2.
242 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Статистика критерия Васичека имеет вид [247]
2ms
ll V^i
где s = —
n -
Если Kmn < Kmn(a), где Kmn(a) — критическое значение статистики, то нуле™
вая гипотеза нормальности распределения отклоняется на уровне значимости а.
Значения Ктп(а) для а = 0,05 приведены в табл. 67. При n, m —^ оо, т/п —>• оо
и справедливости гипотезы Но Ктп —ь л/2тт • е = 4,133 и всегда 0 ^ Kmn ^ 4,133.
Таблица 67
п
3
4
5
6
7
8
9
т
1
1
1
2
1
2
1
2
3
1
2
3
1
2
Значения Kmn(ot)
0,99
1,05
1,19
1,70
1,33
1,77
1,46
1,87
1,87
1,57
1,97
2,05
1,67
2,06
п
9
10
12
14
16
18
т
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2,13
1,76
2,15
2,21
1,90
2,31
2,36
2,01
2,43
2,49
2,11
2,54
2,60
2,18
для
п
18
20
25
30
« =
т
2
3
4
1
2
3
4
2
3
4
5
2
3
4
0,05 [247]
2,62
2,69
2,67
2,25
2,69
2,77
2,76
2,83
2,93
2,93
2,91
2,93
3,04
3,06
п
30
35
40
45
50
т
5
2
3
4
5
3
4
5
3
4
5
3
4
5
Ктп
3,05
3,00
3,13
3,16
3,16
3,19
3,24
3,24
3,25
3,29
3,30
3,29
3,34
3,35
Критерий прост, не нуждается в таблице коэффициентов, как критерий Ша-
пиро^Уилки (см. раздел 3.2.2.1), его асимптотическая эффективность удовлетво-
удовлетворительна. Наиболее эффективен критерий Васичека при проверке нормальности
распределения против альтернатив равномерности и экспоненциальности.
Исследования показали [248], что этот критерий чувствительнее к выбросам
случайных величин, чем критерий Шапиро—Уилка.
Задача 108. В условиях задачи 107 проверить нормальность распределения случайных
величин критерием Васичека на уровне значимости
а = 0,05.
Для примера используем критерий при т = 1 и т = 2. Имеем
1
I
п
г=1
и при т = 1 (п = 10) получаем
Ю
2 • 1 • 4,686
(xi+1 -Xi-г)
= 1,067 • {(ж2 - xi) - (х3 - xi) • (х4 - х2) ... (хю - х8) - (хю - х9)}10 =
= 1,067 • {@ + 1) • A + 1) • B - 0)... A5 - 7) • A5 - 10)} 10 = 2,913.
3.21
Критерии нормальности распределения
243
Из табл. 67 находим !^до@,05) = 1,76.
Так как Kitw = 2,913 > i^i,io@,05) = 1,76, нулевая гипотеза нормальности распреде-
ления не отклоняется.
По аналогии имеем -Ж~2,ю = 2,694 и Ж~2,ю@,05) = 2,15.
Следовательно, и при т = 2 приходим к такому же результату.
3.2.2.3. Критерий Хегази—Грина
Хегази и Грин [249] рассмотрели серию критериев, основанных на статистиках
1 П 1 П
где г/г л =
— \2 —
= Ф (га7-); !%• =
+1
г=1 г=1
Напомним (см. раздел 1.1.1), что квантили uPi могут быть аппроксимированы
по формуле
,= 4,91 р°'14-A-Рг)°Д4 =4,91
0,14
п + 1 — г
0,14'
Критические значения величин Ti(a) и Т2(а) приведены в табл 68. Для а = 0,01
и а = 0,05 имеются весьма точные аппроксимации [249]:
2,8736 8,2894 я
п п2 '
1,9227 5,00677
Ti@,01) = 0,7195 ~~ 0,1751 Inn + 0,0108AптгJ; Г2@,01) = 0,0178 -
Ti@,05) = 0,6027 - 0,1481 Inn + 0,0090(lnnJ; T2@,05) = 0,0126 -
п п
Этот критерий превосходит по мощности критерий Шапиро-Уилка (см. раз™
дел 3.2.2.1) при альтернативах Коши и экспоненциального распределения, но усту-
уступает ему при равномерной альтернативе.
Таблица 68
Критические величины Ti(o) и Тг(а) (а — уровень значимости) [249]
п
5
10
20
40
80
а
0,01
П(а)
0,4563
0,3648
0,2850
0,2090
0,1520
Т2(а)
0,2616
0,2180
0,1462
0,0873
0,0476
0,025
П(а)
0,4212
0,3377
0,2608
0,1912
0,1377
Т2(а)
0,2285
0,1834
0,1181
0,0712
0,0392
0,05
Ща)
0,3871
0,3101
0,2399
0,1770
0,1265
Т2 (а)
0,1974
0,1529
0,0988
0,0599
0,0322
0,10
Ща)
0,3514
0,2822
0,2176
0,1609
0,1159
Т2(а)
0,1683
0,1278
0,0819
0,0490
0,0274
0,50
Ща)
0,3304
0,2683
0,2035
0,1513
0,1091
Т2(а)
0,1509
0,1129
0,0718
0,0429
0,0239
Задача 109. В условиях задачи 107 проверить гипотезу нормальности распределения
критерием Хегази-Грина при а = 0,05.
Имеем
х = 4,8; s = 4,3996; уг =
1
х\ — х
-1-4,8
= -1,17418;
гц = UP1 = 4,91
s 4,9396
0Д4 /io + i^i\0'14]
_ i^Li—i = -1,33508.
V lo + i ' '
Результаты расчетов сведем в таблицу:
244 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
г
1
2
3
4
5
6
7
8
9
10
Xi
-1
0
1
2
3
5
6
7
10
15
Уг
-1,17418
-0,97170
-0,76930
-0,56680
-0,36440
0,04050
0,24290
0,44540
1,05270
2,06490
Pi
0,90900
0,18180
0,27270
0,36360
0,45450
0,54540
0,63630
0,72720
0,81820
0,90910
т
-1,33508
-0,90647
-0,60250
-0,34730
-0,11370
-0,11370
0,34370
0,60250
0,90650
1,33510
Vi—ilil
0,16090
0,06523
0,16680
0,21950
0,25070
0,07320
0,10080
0,15710
0,14620
0,72980
(уг-тJ
0,02589
4,2559- 10~3
0,02780
0,04818
0,06285
5,3589 • 10
0,01016
0,02468
0,02370
0,53260
Получаем Тг =
= 0,2657 и Г2 =
0,2657 и Г2
10 10
Из табл. 68 для а = 0,05 и п = 10 находим
= 0,0763.
Ti@,05) = 0,3101; Т2@,05) = 0,1529.
Так как Тг = 0,2657 < Ti@,05) = 0,3101 и Т2 = 0,0763 < Т2@,05) = 0,1529, гипотеза
нормальности не отклоняется обоими критериями.
Проверим аппроксимацию для критических точек Ti@,05) и Г2@,05).
Имеем
Ti @,05) = 0,6027 - 0,1481 • In 10 + 0,0090 • (In 10J = 0,3094;
Г2@,05) = 0,0126 +
1,9227 5,0067
10
100
= 0,1548.
Видим, что аппроксимации дают достаточно точные приближения к табличным
значениям даже при относительно небольших объемах выборок п.
3.2.2.4. Критерий Али—Чёрго—Ревеса
Али, Чёрго и Ревес [250^252] предложили семейство статистик для проверки
нормалвности распределения случайнвхх величин, основаннв1х на взвешеннвш ква-
квадратах спейсингов (спейсинг — расстояние между соседними порядковыми стати-
статистиками) .
Таблица 69
Критические значения Мп(а)
критерия нормальности Али—Чёрго—Ревеса [252]
к
3
4
5
6
7
8
9
10
11
12
13
14
15
а
0,10
0,182
0,231
0,268
0,291
0,312
0,317
0,329
0,327
0,333
0,339
0,350
0,350
0,348
0,05
0,195
0,268
0,313
0,336
0,370
0,374
0,394
0,378
0,387
0,397
0,417
0,407
0,414
0,01
0,206
0,336
0,407
0,436
0,502
0,487
0,535
0,521
0,510
0,553
0,538
0,544
0,582
к
16
17
18
19
20
30
40
50
60
70
80
90
100
а
0,10
0,348
0,357
0,355
0,352
0,351
0,362
0,363
0,351
0,355
0,357
0,364
0,363
0,359
0,05
0,420
0,417
0,423
0,422
0,414
0,427
0,425
0,426
0,420
0,424
0,429
0,423
0,424
0,01
0,580
0,551
0,580
0,584
0,545
0,561
0,593
0,561
0,598
0,567
0,611
0,604
0,599
3.21
Критерии нормальности распределения
245
Если xi, ..., хп — порядковые статистики наблюдаемого ряда случайных вели™
чин, то статистика критерия записывается в форме
мп = >; {=—- - ф-1 (-^) \ v|ф-
где Ф^1(р)=ир—р™квантиль стандартного нормального распределения;
х = —
s2n =
г=1
i — жJ —оценки соответственно среднего значения
г=1
1 _?
/2тг
и дисперсии; ip(t) =
Критические значения Мп{а) для а = 0,01; 0,05 и 0,10 приведены в табл. 69.
Если Мп < Мп(аI то гипотеза нормальности распределения отклоняется. Мощ-
Мощность М"п~критерия для большинства возможных альтернатив не уступает мощно-
мощности критериев Шапиро^Уилка (см. раздел 3.2.2.1) и Андерсона™Дарлинга (см. раз-
раздел 3.1.2.4).
Задача 110. В условиях задачи 107 проверить гипотезу нормальности распределения
случайных величин Мп критерием Али-Чёрго-Ревеса при а = 0,05.
Вычисления сведем в таблицу:
г
1
2
3
4
5
6
7
8
9
10
Xi
-1
0
1
2
3
5
6
7
10
15
-1,158
^0,955
-0,751
-0,548
-0,142
0,061
0,264
0,467
1,076
2,092
г
п + 1
0,091
0,182
0,273
0,364
0,454
0,545
0,636
0,727
0,818
0,909
-1,33
-0,91
-0,60
-0,35
-0,11
0,11
0,35
0,60
0,91
1,33
0,1647
0,2637
0,3332
0,3752
0,3965
0,3965
0,3572
0,3332
0,2637
0,1647
0,0296
0,00202
0,0228
0,0392
1,02-Ю
2,40 • 10~3
7,396 • 10~3
0,0177
0,0275
0,5806
(*?-фг>.-
4,875 • 10~3
5,34 • 10~4
7,597- 10~3
0,0147
4,06 • 10~4
9,52 • 10
2,774 • 10
5,894 • 10~3
7,266 • 10
0,0956
0,1406
В таблице для удобства записи приняты обозначения
Ф"
Из табл. 69 для п = 10 и а = 0,05 имеем Мю @,05) = 0,378.
Так как Мп = 0,1406 < Мю@,05) = 0,378, гипотеза нормальности распределения слу-
случайных величин отклоняется.
3.2.2.5. Корреляционный критерий Филлибена
Филлибен [253] предложил критерий для проверки сложной гипотезы нормаль-
нормальности (когда параметры распределения не определены), статистикой которого явля-
является коэффициент корреляции г между порядковыми статистиками эмпирического
ряда наблюдений Х{ и медианами порядковых статистик стандартного нормального
распределения (Mi)
- x)(Mi - М)
s) (
г=1
246 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
где Mi = Ф^1 (га^) (Ф — функция Лапласа); ГП{ — медиана г-й порядковой статистики
из равномерного распределения на интервале [0,1].
Так как М = 0 и Щ = —Мп_^+1, то
1
1 ~2
-\2 I
г=1 ^г=-1 г=1 J
Более проста для вычислений статистики критерия формула
г =
Для вычисления тп{ рекомендуется формула [253]
г — mn, г = 1;
г - 0,375
0,365'
г = 2,
В [254] показано, что использование при г = 2, ..., п — 1 упрощенной формулы
г - 0,3
?п,^ = не изменяет существенно результаты. Критические значения крите-
критерия г (а) приведены в табл. 70.
Нулевая гипотеза принимается, если г (а) < г < гA — а). Критерий г имеет вы-
высокую мощность против симметричных альтернатив с длинными „хвостами", по
мощности сравним с критерием Шапиро^Уилка (см. раздел 3.2.2.1). Основные до-
достоинства критерия — возможность проверки сложных гипотез, простота, легкость
вычислений (нет необходимости иметь таблицу коэффициентов), достаточно высо-
высокая мощность. Критерий может быть распространен и на распределения, отлич-
отличные от нормального (тогда Mi = F^1(m^); где F — гипотетическое распределение),
и в этом смысле является общим критерием согласия (см. раздел 3.1). Проверка
гипотезы производится так же, как и для критерия Шапиро^Уилка.
Задача 111. Проверить гипотезу нормальности распределения в условиях задачи 107
критерием Филлибена при а = 0,05.
Вычисляем
% °375 Х °37Б = 0,0603; т2 = 0,15678; т3 = 0,25326;
?г + 0,365 10 + 0,365
т4 = 0,34973; т5 = 0,44621; т6 = 0,54269; т7 = 0,63917; т8 = 0,73565;
т9 = 0,83213; т10 = 0,92860.
Используя аппроксимацию
Mi = ф-\пц) = Umt = 4,91 • К'14 - A - т*H-14] ,
имеем
Mi = 4,91 • @,0603ОД4 - 0,93970'14) = -1,55363; М2 = -1,0061;
М3 = ^0,66213; М4 = ^0,38448; М5 = ^0,13464; М6 = 0,10673;
М7 = 0,35477; М8 = 0,62788; М9 = 0,96076; М10 = 1,46622.
3.21
Критерии нормальности распределения
247
иг
н
ю
Е-"
СО
Ю
й
ш
ю
s
Ч
S
©
S
ш
НИЗ
ш
й
я
ш
И
S
н
а
И
со
СЛ
о
CD
СЛ
О
СО
СЛ
сл
о
см
Is-
сл
о
со
со
сл
о
сл
сл
о
см
СО
о
о
о
т-Н
о
о
о
т-Ч
сл
сл
сл
о
т-Н
сл
00
о
сл
Is-
00
о
сл
со
00
о
СО
СО
сл
as
о
CD
сл
о
СО
сл
сл
о
СП
ь-
сл
о
Is-
OS
о
о
ю
сл
о
СО
00
CD
сл
сл
о
со
CD
сл
о
см
сл
сл
о
сл
00
о
00
CD
00
о
см
см
00
о
СО
сл
сл
о
CD
сл
о
СО
сл
сл
о
со
Is-
сл
о
Is-
со
сл
о
т-Н
>п
сл
о
00
Is-
сл
сл
о
см
CD
сл
о
00
00
сл
о
см
о
о
сл
Is-
00
о
см
см
00
о
ю
со
сл
о
ю
CD
о
СО
as
сл
о
сл
о
on
CD
сл
о
см
m
сл
о
ю
СО
СО
сл
о
о
CD
сл
о
CD
00
сл
о
т-Н
т-Н
сл
о
о
сл
00
о
»о
00
00
о
CD
СО
сл
сл
о
ю
гл
сл
о
сл
сл
о
Is-
сл
о
оо
со
сл
о
00
)П
сл
о
СО
00
ю
сл
сл
о
о
гл
сл
о
со
ОС)
сл
о
СО
т-Н
сл
о
сл
сл
00
о
Is-
00
о
t-
со
сл
сл
о
ю
CD
сл
о
сл
сл
о
ю
г-
сл
о
съ
со
сл
о
ю
ш
сл
о
t-
СО
ю
сл
сл
о
о
CD
сл
о
со
00
сл
о
см
сл
о
ю
о
сл
о
сл
ю
00
о
00
СО
сл
о
со
CD
ел
о
сл
сл
о
Is-
сл
о
о
г-
Os
о
со
ю
сл
о
00
00
^
OS
Os
о
о
CD
ел
о
00
сл
о
CD
см
сл
о
см
т-Н
as
о
00
CD
00
о
сл
со
сл
сл
о
ю
CD
сл
о
сл
сл
о
СО
Is-
сл
о
т—1
Is-
сл
о
Is-
ю
сл
о
сл
СО
^
сл
сл
о
о
CD
сл
о
Is-
00
сл
о
СО
сл
о
Is-
т—1
сл
о
со
JN-
00
о
о
со
сл
сл
о
ю
CD
as
о
сл
сл
о
Is-
Is-
сл
о
ГМ
Is-
сл
о
00
сл
о
о
сл
сл
о
о
CD
as
о
00
00
сл
о
00
00
сл
о
см
см
сл
о
СО
00
00
о
т-Ч
СО
сл
сл
о
ю
CD
ел
о
сл
сл
о
Is-
Is-
сл
о
гм
сл
о
00
>п
сл
о
т-Н
сл
сл
о
о
CD
ел
о
00
00
сл
о
т-Н
сл
о
со
см
сл
о
сл
00
00
о
см
Is-
сл
сл
о
ю
CD
сл
о
сл
сл
о
оо
Is-
сл
о
со
Is-
сл
о
00
in
сл
о
см
сл
сл
о
т-Н
CD
сл
о
00
оо
сл
о
сл
о
т—1
СО
сл
о
ю
00
00
о
СО
Is-
сл
сл
о
ю
CD
сл
о
сл
сл
о
оо
ь-
сл
о
со
Is-
OS
о
as
ю
сл
о
СО
сл
ел
о
т-Н
CD
сл
о
сл
00
сл
о
Is-
ел
о
^
сл
о
т-Н
о
сл
о
Is-
сл
сл
о
ю
CD
сл
о
сл
сл
о
оо
г-
сл
о
со
Is-
сл
о
о
со
сл
о
сл
сл
о
т-Н
CD
сл
о
сл
00
сл
о
о
ю
сл
о
Is-
СО
сл
о
г-
о
сл
о
ю
Is-
сл
сл
о
ю
CD
сл
о
as
сл
о
оо
Is-
Os
о
Is-
сл
о
т-Н
со
сл
о
ю
сл
сл
о
т-Н
CD
сл
о
сл
00
сл
о
см
ю
сл
о
о
сл
о
см
т-Н
сл
о
CD
Is-
сл
сл
о
ю
гл
сл
о
ю
сл
сл
о
Is-
сл
о
Is-
сл
о
см
СО
сл
о
со
сл
сл
о
см
гл
сл
о
о
сл
сл
о
ю
сл
о
см
сл
о
со
т-Н
сл
о
t-
Is-
сл
сл
о
ю
CD
as
о
ю
сл
сл
о
гл
Is-
сл
о
сл
о
00
со
сл
о
ю
сл
сл
о
см
CD
as
о
о
сл
сл
о
СО
ю
сл
о
ю
сл
о
сл
т-Н
сл
о
00
Is-
as
о
со
CD
сл
о
ю
сл
сл
о
о
00
сл
о
г-
Os
о
ОО
СО
сл
о
00
ю
о
см
CD
ел
о
о
сл
сл
о
оо
ю
о
ь-
Os
о
00
см
сл
о
сл
Is-
сл
сл
о
со
CD
сл
о
ю
сл
сл
о
о
сю
сл
о
Is-
Is-
сл
о
со
сл
о
сл
ю
сл
сл
о
см
CD
сл
о
т-Н
сл
сл
о
о
со
сл
о
о
ю
сл
о
ю
см
сл
о
о
I4-
сл
сл
о
со
CD
сл
о
ю
сл
сл
о
т-Н
00
сл
о
Is-
Is-
OS
о
ю
СО
сл
о
о
ю
ю
сл
ел
о
00
CD
сл
о
т—1
сл
сл
о
т-Н
со
ел
о
см
ю
сл
о
00
см
сл
о
т-Ч
Is-
сл
сл
о
со
CD
ел
о
ю
сл
сл
о
см
00
сл
о
оо
сл
о
Is-
СО
сл
о
ю
ю
ю
сл
сл
о
00
CD
ел
о
т-Н
сл
сл
о
т-Н
со
сл
о
см
ю
сл
о
о
СО
сл
о
см
Is-
сл
сл
о
СО
CD
сл
о
ю
as
сл
о
00
сл
о
о
00
сл
о
о
Is-
сл
о
о
CD
»о
сл
сл
о
СО
CD
сл
о
т-Ч
as
сл
о
СО
сл
о
ю
ю
сл
о
СО
00
сл
о
СО
Is-
сл
сл
о
со
гл
сл
о
со
сл
сл
о
00
сл
о
^—I
00
сл
о
см
Is-
сл
о
ю
со
ю
сл
сл
о
00
гл
сл
о
см
сл
сл
о
ю
со
сл
о
Is-
ю
сл
о
со
00
сл
о
оо
сл
сл
о
г-
CD
сл
о
со
сл
сл
о
ю
00
сл
о
гм
00
сл
о
Is-
сл
о
о
Is-
ю
сл
сл
о
СО
CD
сл
о
см
сл
сл
о
СО
со
сл
о
00
ю
сл
о
Is-
СО
сл
о
ю
оо
сл
сл
о
Is-
CD
сл
о
CD
as
сл
о
СО
00
сл
о
со
00
сл
о
LO
Is-
сл
о
ю
Is-
»о
сл
сл
о
СО
CD
сл
о
см
as
сл
о
Is-
СО
сл
о
сл
ю
сл
о
сл
00
сл
о
CD
on
сл
сл
о
ь-
CD
сл
о
CD
сл
сл
о
Is-
00
сл
о
00
сл
о
CD
Is-
сл
о
о
00
ю
сл
ел
о
CD
сл
о
см
сл
сл
о
оо
со
ел
о
о
CD
сл
о
т-Н
сл
о
оо
сл
сл
о
г-
CD
сл
о
Is-
сл
сл
о
Is-
00
сл
о
>п
00
сл
о
г-
сл
о
ю
00
ю
сл
сл
о
CD
сл
о
см
сл
сл
о
гл
со
сл
о
см
со
сл
о
СО
сл
о
00
оо
сл
о
Is-
CD
сл
о
г-
сл
сл
о
оо
00
Os
о
1О
00
сл
о
00
I4-
сл
о
о
сл
ю
о
CD
ел
о
см
сл
сл
о
CD
со
Os
о
см
CD
сл
о
ю
сл
о
сл
оо
сл
сл
о
00
гл
сл
о
Is-
сл
сл
о
гл
00
сл
о
Is-
00
сл
о
т-Н
оо
сл
о
о
о
т-Н
СО
сл
сл
о
гл
сл
о
СО
сл
сл
о
о
Is-
сл
о
3
сл
о
Is-
сл
о
о
СО
сл
сл
о
CD
as
о
СО
сл
сл
о
т-Н
Is-
сл
о
ю
CD
сл
о
00
сл
о
т-Ч
248 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Далее вычисляем
п 10 п
х = 4,8; ]Г (Xi - xf = 219,6; ]Г М? = 7,63472; ^ ж» • М* = 38,37695; г = 0,93725.
г=1 г=1 г=1
Из табл. 70 находим для а = 0,05 г@,05) = 0,917 и г@,95) = 0,99.
Так как г@,95) = 0,99 > г = 0,937 > г@,05) = 0,917, гипотеза нормальности не
отклоняется.
3.2.2.6. Регрессионный критерий нормальности Л а Брека
В [255] Ла Брек рассмотрел серию критериев, основанных на оценке отклонения
от линейности зависимости М(х{) = /л + aM(yi)^ где Х{—порядковая статистика
эмпирического распределения, yi = — порядковая статистика стандартного
нормального распределения.
Критерий позволяет проверять сложные гипотезы нормальности (когда знание
/J, и а не требуется).
Статистики критерия имеют вид
. = 2,4, ...,2k;
s | i=i |
, п = 1, 3, ..., 2k — 1;
r^- -^l H~ ^2 9 1 \r™^ / -\2
K3 = , где s = —j 2^ {Xi - x) .
Необходимо помнить, что щ = an^^+i и bi = 6n_^_|_i.
Критерий со статистикой К\ более чувствителен к асимметричным альтерната™
вам (К\ — это, по существу, квадратичное отклонение от гипотетической линейной
зависимости). Критерий со статистикой К2 более чувствителен к симметричным
альтернативам (он построен на анализе кубических отклонений от линейной зависи™
мости). Комбинированный критерий К% является комбинацией К\ и К^ и применим
при промежуточных альтернативах.
Коэффициенты щ и bi и критические значения статистик Ki(a), K2{o) и К%(а)
приведены соответственно в табл. 71 и 72.
При п > 12 применимы аппроксимации для критических значений статистик:
#i@,90)= 2,682+ 5^5; Кг@,95) = 3,822 - ^2^; ^@,99) = 6,900 - Щ^-;
л/п \/п \/п
ЛГ2@,90) = 2,667 - ^1^1. К2@,95) = 3,815 - ^^; К2@,99) = 6,893 - ^-;
\/П \/П у/П
= 2,331 - 54^; ^з@,95) = 2,992-^^; ^3@,99) = 4,618 -
3.21
Критерии нормальности распределения
249
Мощность критериев Ki, K2j K% не уступает мощности критерия Шапиро-
Уилка (см. раздел 3.2.2.1), превосходя его в среднем. Критерии являются односто-
односторонними, т.е. нулевая гипотеза нормальности отклоняется, если Ki > Ki(a). Более
мощен критерий К%.
Таблица 71
Коэффициенты а% и bi для вычисления статистик Ж°1, Ж°2? -К~з [255]
п
4
5
6
7
8
9
10
11
12
13
г
1
2
1
2
3
1
2
3
1
2
3
4
1
2
3
4
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
7
щ
1,1387
-1,1387
1,2002
-0,7570
-0,9689
1,2266
-0,4545
-0,7721
1,2367
-0,2768
-0,6095
-0,7009
1,2385
-0,1483
-0,4796
-0,6106
1,2298
-0,0512
-0,3753
-0,5245
-0,5691
1,2298
0,0245
-0,2902
-0,4478
-0,5164
1,2225
0,0852
-0,2198
-0,3807
-0,4629
-0,4886
1,2143
0,1346
-0,1606
-0,3222
-0,4125
-0,4536
1,2956
0,1756
-0,1104
-0,2710
-0,3660
-0,4171
-0,4333
к
-0,6261
2,1699
-0,8403
1,9742
0
-0,9701
1,7195
0,6243
-1,0574
1,4962
0,8410
0
-1,1196
1,3092
0,9090
0,3174
-1,1196
1,1527
0,9145
0,4864
0
-1,2010
1,0205
0,8919
0,5771
0,1979
-1,2284
0,9075
0,8564
0,6236
0,3239
0
-1,2501
0,8100
0,8157
0,6441
0,4048
0,1375
-1,2674
0,7249
0,7733
0,6489
0,4566
0,2342
0
п
14
15
16
17
18
19
г
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
щ
1,1966
0,2100
-0,6730
-0,2261
-0,3237
-0,3813
-0,4082
1,1875
0,2393
-0,0299
-0,1865
-0,2854
-0,3473
-0,3815
-0,3925
1,1785
0,2645
0,0027
-0,1513
-0,2507
-0,3154
-0,3548
-0,3736
1,1685
0,2863
0,0315
-0,1199
-0,2192
-0,2858
-0,3289
-0,3532
-0,3611
1,1607
0,3053
0,0571
-0,0917
-0,1905
-0,2583
-0,3040
-0,3324
-0,3461
1,1521
0,3220
0,0798
-0,0663
к
-1,2814
0,6499
0,7313
0,6438
0,4888
0,3027
0,1023
-1,2927
0,5834
0,6906
0,6327
0,5079
0,3512
0,1789
0
-1,3020
0,5240
0,6517
0,6178
0,5177
0,3854
0,2366
0,0797
-1,3095
0,4705
0,6147
0,6006
0,5210
0,4092
0,2802
0,1421
0
-1,3156
0,4222
0,5797
0,5822
0,5198
0,4252
0,3130
0,1911
0,0642
-1,3206
0,3782
0,5467
0,5630
п
19
20
20
21
22
23
ъ
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
щ
-0,1644
-0,2329
-0,0281
-0,3119
-0,3300
-0,3358
1,1436
0,3367
0,1002
-0,0433
-0,1406
-0,2093
-0,2583
-0,2920
-0,3134
-0,3237
1,1363
0,3447
0,1223
-0,0216
-0,1184
-0,1876
-0,2376
-0,2730
-0,2696
-0,3107
-0,3152
1,1283
0,3561
0,1390
-0,0023
-0,0984
-0,1673
-0,2179
-0,2548
-0,2805
-0,2971
-0,3051
1,2050
0,3663
0,1543
0,0151
-0,0798
-0,1485
-0,1995
к
0,5153
0,4354
0,3377
0,2298
0,1162
0
-1,3246
0,3380
0,5156
0,5437
0,5085
0,4413
0,3560
0,2603
0,1583
0,0531
-1,3283
0,3041
0,4834
0,5242
0,5002
0,4440
0,3695
0,2844
0,1926
0,0972
0
-1,3309
0,2705
0,4556
0,5051
0,4906
0,4439
0,3791
0,3031
0,2207
0,1336
0,0451
-1,3329
0,2395
0,4292
0,4864
0,4801
0,4419
0,3854
250 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Продолжение таблицы 71
п
23
24
25
26
27
г
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
a-i
-0,2373
-0,2648
-0,2833
-0,2942
-0,2977
1,1129
0,3754
0,1681
0,0312
-0,0626
-0,1310
-0,1822
-0,2208
-0,2494
-0,2698
-0,2828
-0,2891
1,1056
0,3836
0,1808
0,0460
-0,0466
-0,1147
-0,1661
-0,2050
-0,2347
-0,2563
-0,2713
-0,2798
-0,2875
1,0984
0,3910
0,1926
0,0596
-0,0318
-0,0995
-0,1506
-0,1904
-0,2205
-0,2434
-0,2597
-0,2702
-0,2754
1,0914
0,3977
0,2031
0,0723
-0,0181
-0,0851
-0,1365
-0,1762
к
0,3178
0,2432
0,1644
0,0827
0
-1,3345
0,2107
0,4044
0,4682
0,4692
0,4384
0,3893
0,3291
0,2618
0,1896
0,1148
0,0386
-1,3356
0,1840
0,3809
0,4505
0,4579
0,4337
0,3913
0,3377
0,2766
0,2111
0,1420
0,0715
0
-1,3363
0,1591
0,3586
0,4334
0,4464
0,4282
0,3918
0,3438
0,2888
0,2286
0,1653
0,1000
0,0335
-1,3367
0,1358
0,3376
0,4168
0,4349
0,4220
0,3908
0,3483
п
27
28
29
30
32
г
9
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
щ
-0,2071
-0,2307
-0,2483
-0,2603
-0,2674
-0,2697
1,0845
0,4038
0,2130
0,0841
-0,0054
-0,0717
-0,1229
-0,1628
-0,1941
-0,2186
-0,2371
-0,2503
-0,2591
-0,2633
1,0779
0,4093
0,2221
0,0949
0,0068
-0,0593
-0,1102
-0,1501
-0,1820
-0,2067
-0,2263
-0,2406
-0,2505
-0,2564
-0,2583
1,0714
0,4144
0,2305
0,1052
0,0180
-0,0474
-0,0980
-0,1382
-0,1701
-0,1955
-0,2156
-0,2308
-0,2419
-0,2491
-0,2527
1,0589
к
0,2984
0,2434
0,1849
0,1246
0,0625
0
-1,3369
0,1140
0,3176
0,4007
0,4235
0,4152
0,3888
0,3512
0,3060
0,2556
0,2017
0,1459
0,0878
0,0295
-1,3367
0,0935
0,2985
0,3853
0,4120
0,4081
0,3861
0,3528
0,3117
0,2659
0,2159
0,1639
0,1103
0,0553
0
-1,3364
0,0743
0,2805
0,3703
0,4008
0,4008
0,3827
0,3533
0,3163
0,2741
0,2281
0,1799
0,1294
0,0783
0,0261
-1,3352
п
32
34
36
38
г
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
a-i
0,4232
0,2456
0,1237
0,0384
-0,0259
-0,0759
-0,1159
-0,1483
-0,1743
-0,1953
-0,2220
-0,2247
-0,2341
-0,2402
-0,2432
1,0469
0,4305
0,2587
0,1399
0,0565
-0,0066
-0,5600
-0,0957
-0,1284
-0,1547
-0,1765
-0,1941
-0,2082
-0,2189
-0,2269
-0,2321
-0,2347
1,0356
0,4367
0,2702
0,1543
0,0724
0,0108
-0,0382
-0,0775
-0,1099
-0,1368
-0,1589
-0,1772
-0,1921
-0,2042
-0,2134
-0,2202
-0,2247
-0,2269
1,0248
к
0,0390
0,2468
0,3420
0,3789
0,3855
0,2744
0,3519
0,3217
0,2863
0,2471
0,2051
0,1614
0,1161
0,0701
0,0231
-1,3335
0,0075
0,2162
0,3156
0,3577
0,3701
0,3647
0,3481
0,3236
0,2940
0,2604
0,2241
0,1855
0,1459
0,1048
0,0632
0,0210
-1,3313
-0,0209
0,1881
0,2910
0,3376
0,3545
0,3541
0,3424
0,3230
0,2982
0,2996
0,2379
0,2043
0,1689
0,1326
0,0953
0,0573
0,0193
-1,3287
3.21
Критерии нормальности распределения
251
Окончание таблицы 71
7?
38
40
42
i
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
1
2
3
4
5
6
7
8
9
10
11
12
13
а,
0,4420
0,2803
0,1669
0,0870
0,0264
-0,0219
-0,0609
-0,0934
-0,1199
-0,1425
-0,1615
-0,1769
-0,1897
-0,2003
-0,2081
-0,2142
-0,2180
-0,2199
1,0144
0,4465
0,2890
0,1784
0,1001
0,0402
-0,0071
-0,0457
0,0780
-0,1046
-0,1276
-0,1463
-0,1629
-0,1760
-0,1873
-0,1962
-0,2033
-0,2084
-0,2118
-0,2135
1,0045
0,4501
0,2971
0,1885
0,1118
0,0530
0,0064
-0,0319
-0,0638
-0,0905
-0,1134
-0,1326
-0,1492
h
-0,0465
0,1624
0,2681
0,3182
0,3393
0,3431
0,3356
0,3204
0,3000
0,2755
0,2479
0,2185
0,1874
0,1543
0,1213
0,0868
0,0524
0,1178
-1,3259
-0,0699
0,1388
0,2466
0,2999
0,3245
0,3318
0,3280
0,3166
0,2998
0,2788
0,2553
0,2288
0,2015
0,1721
0,1422
0,1110
0,0800
0,0480
0,0164
-1,3229
-0,0911
0,1167
0,2266
0,2825
0,3100
0,3205
0,3199
0,3117
0,2981
0,2804
0,2599
0,2369
77
42
44
46
г
14
15
16
17
18
19
20
21
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
а{
-0,1632
-0,1746
-0,1847
-0,1923
-0,1986
-0,2031
-0,2061
-0,2076
0,9949
0,4534
0,3040
0,1978
0,1224
0,0648
0,0186
-0,0189
-0,0509
-0,0774
-0,1001
-0,1195
-0,1367
-0,1506
-0,1631
0,1731
-0,1817
-0,1887
-0,1941
-0,1982
-0,2008
-0,2021
0,9858
0,4560
0,3103
0,2062
0,1321
0,0754
0,0301
-0,0074
-0,0387
-0,0651
-0,0881
-0,1074
-0,1245
-0,1390
-0,1516
-0,1624
-0,1713
-0,1789
-0,1852
-0,1899
-0,1935
h
0,2121
0,1865
0,1588
0,1315
0,1025
0,0736
0,0442
0,0150
-1,3197
-0,1107
0,0965
0,2078
0,2660
0,2960
0,3093
0,3115
0,3061
0,2953
0,2805
0,2629
0,2424
0,2208
0,1971
0,1730
0,1476
0,1215
0,0951
0,0681
0,0409
0,0141
-1,3163
-0,1286
0,0775
0,1901
0,2502
0,2825
0,2981
0,3029
0,3000
0,2918
0,2794
0,2642
0,2464
0,2270
0,2061
0,1838
0,1610
0,1373
0,1128
0,0885
0,0633
п
46
48
50
г
22
23
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
а,
-0,1959
-0,1971
0,9770
0,4853
0,3160
0,2137
0,1410
0,0854
0,0403
0,0035
-0,0275
-0,0537
-0,0767
-0,0962
-0,1129
-0,1281
-0,1408
-0,1520
-0,1611
-0,1695
-0,1762
-0,1817
-0,1859
-0,1891
-0,1914
-0,1924
0,9686
0,4602
0,3209
0,2207
0,1490
0,0943
0,0500
0,0138
0,0043
-0,0431
-0,0660
-0,0853
-0,1027
-0,1175
-0,1303
-0,1419
-0,1517
-0,1601
-0,1673
-0,1734
-0,1784
-0,1823
-0,1851
-0,1870
-0,1880
к
0,0381
0,0127
-1,3129
-0,1451
0,0599
0,1735
0,2352
0,2695
0,2873
0,2942
0,2935
0,2875
0,2774
0,2643
0,2491
0,2150
0,2128
0,1926
0,1724
0,1502
0,1280
0,1053
0,0825
0,0594
0,0352
0,0115
-1,3094
-0,1605
0,0435
0,1577
0,2211
0,2570
0,2767
0,2855
0,2869
0,2828
0,2747
0,2637
0,2501
0,2347
0,2182
0,1999
0,1809
0,1613
0,1409
0,1200
0,0985
0,0767
0,0555
0,0331
0,0112
252 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Критические точки критериев
Таблица 72
(a), Ж~2(ок) и Жз(ок) [255]
4
5
6
7
8
9
10
11
12
а = 0,90
Кг
2,730
2,739
2,739
2,736
2,733
2,730
2,726
2,723
2,724
к2
3,419
3,562
3,638
3,684
3,713
3,732
3,745
3,755
3,770
к3
4,379
5,008
5,367
5,594
5,748
5,859
5,941
6,005
6,049
а = 0,95
Кг
2,274
2,490
2,581
2,621
2,638
2,664
2,644
2,641
2,612
к2
3,373
3,425
3,475
3,518
3,554
3,583
3,608
3,628
3,673
к3
5,215
5,247
5,430
5,635
5,825
5,990
6,130
6,249
6,579
а = 0,99
Кг
2,029
2,080
2,109
2,128
2,131
2,142
2,152
2,160
2,167
К2
2,405
2,652
2,769
2,829
2,865
2,872
2,879
2,884
2,889
к3
2,939
3,731
4,165
4,424
4,995
4,974
4,955
4,940
4,296
Задача 112. Проверить гипотезу нормальности распределения случайных величин
в условиях задачи 107 регрессионным критерием Ла Брека на уровне достоверности
а = 0,95.
Используя коэффициенты (ц и bi из табл. 71, имеем
5
]Г <ц • (xi + Жп-i+i) = 1,2298 • (-1 + 15) + 0,0245 • @ + 10) - 0,2902 • A + 7) -
- 0,4478 • B + 6) - 0,5164 . C + 5) = 7,427;
ai ' (Xi + xn-i+i) } = 55,1603;
J
h • {x% + xn-i+1) = -1,201 • (-1 + 15) + 1,0205 • @ + 10) + 0,8919 • A + 7)
+ 0,5771 • B + 6) + 0,1979 • C + 5) = 6,7262; <j ]P h • (Xi + xn^i+1) [> = 45,241;
55,1603 45,241 2,26 + 1,854
Кг = ^^ = 2,260; K2 = ^^ = 1,854; K3 = ^ = 2,057.
Из табл. 72 для а = 0,95ип=10 находим критические значения
lfi@,95) = 3,745; 1^@,95) = 3,608 и i^3@,95) = 2,879.
Так как Кг = 2,26 < #i@,95) = 3,745; К2 = 1,854 < К2@,95) = 3,608 и К3 = 2,057 <
< Ж~з@,95) = 2,879, гипотеза нормальности распределения случайных величин не откло-
отклоняется.
Если бы мы воспользовались аппроксимациями, то получили бы
= 3,822 - ^^ = 3,764; #2@,95) = 3,815 - ^=^ = 3,659;
л/10 л/Ш
К3 = 2,922 - -
л/10 '
Видим, что даж:е при п = 10 аппроксимации достаточно удовлетворительны.
3.2.2.7. Критерий нормальности Лсжка—Спуръе
Весьма эффективный критерий нормальности против асимметричных альтер-
альтернатив предложен в [256]. Его статистики имеют вид
3.21
Критерии нормальности распределения
253
где
Uln =
2n = Л У"
п
-, п
-j n — 1 n
— — V V V--(
где
шг = С?_г - 2(n -
= г
- га -
^ — г~я порядковая статистика.
Математические ожидания и дисперсии статистик равны:
М(Т1п) = 0; D(Tln) = -^з {1,03804 + 0,6Э714(в - 3) + 0,0890805(п - 3)(га - 4)};
М(Т2п) = 0; D(T2n) = ^з {7,03804 + 5,32251(в - 3) + 0,74412(в - 3)(га - 4)}.
При п ^ 5 случайная величина
щ - М(Тш)
распределена как нор™
VD(Tln)
мальная случайная величина и, следовательно, ее критические значения равны
Т\п = M(Tin) + уD(Tin)ua, где гла— «-квантиль стандартного нормального
распределения.
По аналогии, нормальное приближение для Т^п применимо при п ^ 10 и имеет
вид Г2„(а) = М(Г2и) + у/Т>(Т2п)иа.
Критерий Т2п более эффективен для несимметричных альтернатив с „мягкими"
хвостами. Развитие этих критериев для альтернатив с обоими „хвостами", отлича-
отличающимися от нормального распределения, представлено в [257].
Гипотеза нормальности распределения вероятностей случайной величины от™
клоняется, если Tin(T2n) > Tin(a)(T2n(a)), где A — а)—уровень значимости.
Задача 113. Проверить гипотезу нормальности распределения случайных величин
в условиях задачи 107 критерием Локка-Спурье на уровне значимости а = 0,05.
Имеем s2 = 24,4 и s = 4,9396. Используем статистику Т\п.
Предварительно необходимо найти совокупность значений (xk — %Xj + Xi) для всех
возможных сочетаний i,j, к, отвечающих соотношению l^i<Cj<k^.n (всего их
Сп = Сю = 120). Порядок вычислений иллюстрируется в таблице (в ней принято
обозначение Хка = хь — 2xj + хЛ:
г
1
1
1
1
1
1
1
1
1
1
1
1
3
2
2
2
2
2
2
2
2
3
3
3
3
к
3
4
5
6
7
8
9
10
4
5
6
7
хк
1
2
3
5
6
7
10
15
2
3
5
б
Xj
0
0
0
0
0
0
0
0
1
1
1
1
Xi
-1
-1
— 1
-1
-1
-1
-1
— 1
-1
— 1
-1
-1
0
1
2
4
5
б
9
14
-1
0
2
3
г
1
1
1
1
1
1
1
1
1
1
1
1
3
3
3
3
4
4
4
4
4
4
5
5
5
к
8
9
10
5
б
7
8
9
10
6
7
8
Хк
7
10
15
3
5
6
7
10
15
5
6
7
ж,-
1
1
1
CNI
2
2
2
2
CNI
3
3
3
Xi
-1
-1
— 1
-1
-1
-1
-1
— 1
-1
— 1
-1
-1
Xkji
4
7
12
^2
0
-1
2
5
10
-2
-1
0
i
1
1
1
1
1
1
1
1
1
1
1
1
3
5
5
6
6
б
6
7
7
7
8
8
9
к
9
10
7
8
9
10
8
9
10
9
10
10
Хк
10
15
6
7
10
15
7
10
15
10
15
15
Xj
3
3
5
5
5
5
6
6
6
7
7
10
Xi
-1
-1
— 1
-1
-1
-1
-1
— 1
-1
— 1
-1
-1
3
8
-5
-4
-1
4
-6
-3
CNI
-5
0
-6
254 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Окончание
г
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
4
4
4
4
4
4
5
5
5
5
5
6
6
б
6
7
7
7
8
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
6
7
8
9
10
7
8
9
10
8
9
10
9
10
10
Xk
2
3
5
6
7
10
15
3
15
6
7
10
15
5
6
7
10
15
6
7
10
15
7
10
15
10
15
15
Xj
1
1
1
1
1
1
1
2
2
2
2
2
2
3
3
3
3
3
5
5
5
5
6
6
6
7
7
10
X"
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Xkji
0
1
3
4
5
8
13
-1
1
2
3
б
11
-1
0
1
4
9
-4
-3
0
5
^5
-2
3
-4
1
^5
г
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
3
4
4
4
4
4
4
5
5
5
5
5
б
6
6
б
7
7
7
8
8
9
5
5
5
5
5
6
6
к
5
6
7
8
9
10
6
7
8
9
10
7
8
9
10
8
9
10
9
10
10
6
7
8
9
10
7
8
Хк
3
5
6
7
10
15
5
6
7
10
15
6
7
10
15
7
10
15
10
15
15
5
6
7
10
15
6
7
Xj
2
2
2
2
2
2
3
3
3
3
3
5
5
5
5
6
6
6
7
7
10
3
3
3
3
3
5
5
Xi
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
Xkji
0
2
3
4
7
12
0
1
2
5
10
-3
^2
1
6
^4
-1
4
^3
2
-4
1
2
3
б
11
^2
-1
г
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
5
5
5
5
6
6
6
6
6
7
7
7
8
3
6
6
7
7
7
8
8
9
6
6
б
6
7
7
7
8
8
9
7
7
7
8
8
9
8
8
9
9
к
9
10
8
9
10
9
10
10
7
8
9
10
8
9
10
9
10
10
8
9
10
9
10
10
9
10
10
10
Хк
10
15
7
10
15
10
15
15
6
7
10
15
7
10
15
10
15
15
7
10
15
10
15
15
10
15
15
15
Xj
5
5
6
б
6
7
7
10
5
5
5
5
6
6
6
7
7
10
6
6
б
7
7
10
7
7
10
10
Xi
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
5
5
5
5
5
5
6
6
6
7
Xkji
2
7
^3
0
5
^2
3
^3
-1
0
3
8
^2
1
6
-1
4
-2
0
3
8
1
6
0
2
7
1
2
Имеем
= 234;
Используем аппроксимации:
244 I (Ж
•234= - = 1,95; Г1п = ^
= 0,3948.
М(Тт) = 0; D(Tm) = • A,03804 + 0,69714 • 7 + 0,0890805 • 7 • 6) = 0,080495
Для гхо,95 = 1,645 получаем Tin@,05) « 0,2837 • 1,645 = 0,466.
Так как Т\п = 0,3948 < Tin@,05) = 0,466, нормальность распределения вероятностей
случайных величин не отклоняется. К аналогичному выводу (читатель может сам убе-
убедиться) приводит и использование статистики Т2П-
3.2.2.8. Критерий нормальности Ом
Критерий, аналогичный рассмотренному выше (см. раздел 3.2.2.7), использую™
щий анализ комбинаций порядковых статистик, рассмотрен в работах Оя [258—260].
Статистиками критерия являются
#fc - ;
Хк ~
3.21
Критерии нормальности распределения
255
Статистика Т\ эффективна против альтернатив, отличающихся от нормального
распределения коэффициентом асимметрии, а Т2 — коэффициентом эксцесса. При
справедливости нулевой гипотезы М{Т\) = 0,5 и M(T2) = 0,298746 [259], дисперсии
приведены в табл. 73.
Таблица 73
Дисперсии статистик Ом [259]
п
5
6
7
8
9
D(Ti)
0,01512
0,01045
0,00740
0,00575
0,00457
D(T2)
0,01549
0,00800
0,00473
0,00350
0,00248
п
10
15
20
30
оо
D(Ti)
0,00358
0,00218
0,00144
0,00089
0,0214/п
D(T2)
0,00196
0,00098
0,00058
0,00032
0,0026/п
Статистики
т =
Тг - 0,5
Т2 - 0,298746
распределены приближенно нормально, и их критические значения могут быть
вычислены по формулам
fi(a) = 0,5 + >/D(Ti)ua и Т2(а) = 0,298746 + у/Т>(Т2)иа,
где иа — «^квантиль стандартного нормального распределения.
Учитывая независимость статистик Т\, Т2, можно рекомендовать комбинирован™
ный критерий
„2 _ ф2 , f,2
X — il + i2^
имеющий распределение %2 с / = 2 степенями свободы.
Более просты в вычислительном отношении модифицированные критерии [260]
Т[ =
И Т2=
где a,ij = -^(i+j -тг- 1); % = —4 [2(гс - j)(i - 1) - C%_j - С?_х].
При справедливости нулевой гипотезы
М(Т[) = 0; М(Г^) = 0,4523;
D(T[) = А(°'07478СГз + 0,03963С|С^_3 + 2,8979) =
= А [0,11217(п - 4)(п - 3)),0,11889(п - 3) + 2,8979];
= А [0,0874(п - 6)(в - Б)(п - 4) + 0,0435(в - Б)(п - 4) + 5,342(п - 4) + 8,8552].
Как и прежде, Т[(а) = yD(T[)wa, ^(^O = 0^4523 -
256 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Нормальная аппроксимация статистик Т{ и Т'2 несколько хуже, чем Т\ и Т^. По™
прежнему можно использовать критерий
Задача 114. В условиях задачи 107 проверить гипотезу нормальности распределения
вероятностей критерием Оя на уровне значимости а = 0,05 (доверительная вероят-
вероятность 0,95).
Воспользовавшись данными таблицы задачи 113, получим ряд значений Xkji =
Xk - Xj
. Результаты расчетов сведены в таблицу:
XI
г
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
3
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
4
4
4
4
4
4
5
5
5
5
5
6
6
6
6
г
к
3
4
5
6
7
8
9
10
4
5
6
7
8
9
10
5
6
7
8
9
10
6
7
8
9
10
7
8
9
10
Xkji
1/2
2/3
3/4
5/6
6/7
7/8
10/11
15/16
1/3
2/4
4/6
5/7
6/8
9/11
14/16
1/4
3/6
4/7
5/8
8/11
13/16
2/6
3/7
4/8
7/11
12/16
1/7
2/8
5/11
10/16
г
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
7
7
7
8
8
9
3
3
3
3
3
3
3
4
4
4
4
4
4
5
5
5
5
5
6
6
6
6
7
7
к
8
9
10
9
10
10
4
5
6
7
8
9
10
5
6
7
8
9
10
6
7
8
9
10
7
8
9
10
8
9
Xkji
1/8
4/11
9/16
3/11
8/16
5/16
1/2
2/3
4/5
5/6
6/7
9/10
14/15
1/3
3/5
4/6
5/7
8/10
13/15
2/5
3/6
4/7
7/10
12/15
1/6
2/7
5/10
10/15
1/7
4/10
г
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
3
7
8
8
9
4
4
4
4
4
4
5
5
5
5
5
6
6
6
6
7
7
7
8
8
9
5
5
5
5
5
к
10
9
10
10
5
6
7
8
9
10
6
7
8
9
10
7
8
9
10
8
9
10
9
10
10
6
7
8
9
10
Xkji
9/15
3/10
8/15
5/15
1/2
3/4
4/5
5/6
8/9
13/14
2/4
3/5
4/6
7/9
12/14
1/5
2/6
5/9
10/14
1/6
4/9
10/14
3/9
8/14
5/14
2/3
3/4
4/5
7/8
12/13
г
4
4
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
5
5
5
6
6
6
6
6
6
7
7
7
8
3
6
6
6
6
7
7
7
8
8
9
6
6
6
6
7
7
7
8
8
9
7
7
7
8
8
9
8
8
9
9
к
7
8
9
10
8
9
10
9
10
10
7
8
9
10
8
9
10
9
10
10
8
9
10
9
10
10
9
10
10
10
Xkji
1/4
2/5
5/8
10/13
1/5
4/8
9/13
3/8
8/13
5/13
1/3
2/4
5/7
10/12
1/4
4/7
9/12
3/7
8/12
5/12
1/2
4/5
9/10
3/5
8/10
5/10
3/4
8/9
5/9
5/8
Из таблицы находим
хк - '.
= 70,6029 и
• 70,6029 = 0,58836.
Далее МA\) = 0,5 и D(Ti) = 0,00358 (см. табл. 73).
Окончательно (г^эб = 1,645): Ti@,95) = 0,5 + ^ДЩШШ • 1,645 = 0,5984.
Так как Ti = 0,58836 < Ti@,95) = 0,5984, гипотеза нормальности распределения слу-
случайных величин не отклоняется. К аналогичному результату приводят другие критерии
(читатель может это проверить самостоятельно).
3.21
Критерии нормальности распределения
257
3.2.2.9. Критерий среднего абсолютного отклонения (критерий Гири)
Гири [261—263] рассмотрел критерий нормальности распределения случайных
величин, основанный на статистике
1
ns
являющейся отношением среднего абсолютного отклонения — Y1
рочному стандартному отклонению
— X
к выбо™
Статистика Гири распределена асимптотически нормально при п ^ 50 со сред™
M(d) =
-A
тг V ' 8п - 9
0,79788
п ~~ 0,875
га-1,125
и дисперсией
¦ arcsm
n-1
га- 1
n- 1
-i)-J-l«lfo,O45O7-°^V
Более точные аппроксимации приведены в [262]:
M(d) = 0,797885 +
I* П П
0,045070 0,124648 0,084859 0,006323
^— ~ 2 + з + 4 .
гс п п п
п
Для практических расчетов рекомендуется формула Yl \xi ~~ %
г=1
где ^2 х' — сумма значений ж-ов, превышающих ж; п' — количество значений ж-ов,
превышающих ж.
Критерий двусторонний. При п ^ 50 вычисляются квантили
где ua
мости.
-Ьсли d[—
^\ = M(d) +
а-квантиль стандартного нормального распределения; а — уровень значи-
значи- f) = M(d)
то гипотеза нормальности распределения случаи™
ных величин не отклоняется.
Некоторые критические значения d-статистики приведены в табл. 74 (в таблице
приняты обозначения d\(a) и d2(a), соответствующие неравенству d\(a) ^ d ^ ^(сО?
которые удовлетворяются при справедливости нулевой гипотезы).
А. И. Кобзарь
258 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Таблица 74
Критические значения cfi(a) и d^fjcx) критерия Гири
(а — уровень значимости) [262]
ТЪ
11
16
21
26
31
36
41
46
51
61
71
81
91
101
а =
0,1175
0,6829
0,6950
0,7040
0,7110
0,7167
0,7215
0,7256
0,7291
0,7347
0,7393
0,7430
0,7460
0,7487
0,01
d2
0,9359
0,9137
0,9001
0,8901
0,8827
0,8769
0,8722
0,8682
0,8648
0,8592
0,8549
0,8515
0,8484
0,8460
а =
dt
0,7153
0,7236
0,7304
0,7360
0,7404
0,7440
0,7470
0,7496
0,7518
0,7554
0,7583
0,7607
0,7626
0,7644
0,05
d2
0,9073
0,8884
0,8768
0,8686
0,8625
0,8578
0,8540
0,8508
0,8481
0,8434
0,8403
0,8376
0,8353
0,8344
а =
dt
0,7409
0,7452
0,7495
0,7530
0,7559
0,7583
0,7604
0,7621
0,7636
0,7662
0,7683
0,7700
0,7714
0,7726
0,10
d2
0,8899
0,8733
0,8631
0,8570
0,8511
0,8468
0,8436
0,8409
0,8385
0,8349
0,8321
0,8298
0,8279
0,8264
Задача 115. В условиях задачи 107 проверить гипотезу нормальности распределения
случайных величин критерием Гири на уровне значимости а = 0,05.
Имеем
х = 4,8; s =< -
i=l
|0-4,8|-
= 4,686;
-4,8| + ... + |15 -4,8| = 38.
По упрощенной формуле (п = 5 значений превышают х = 4,8; их сумма равна
^ ж; = 5 + 6 + 7 + 10 + 15 = 43) получаем ]Г
Статистика критерия равна d = тт—. • 38 = 0,8109.
= 2- D3-4,8-5) = 38.
Далее
10- 1,686
M(d) = 0,79788
™ 1,125
= 0,8203;
D(d) = 1-
1 ; ю
0,04507 -
ю
= 3,711 . ИГ
/D(d) =0,0609).
Из табл. 74 находим для п = 10 и а = 0,05: d\ « 0,715 и d2 « 0,907.
Так как 0,715 < d = 0,8109 < 0,907, нулевая гипотеза нормальности не отклоняется.
Воспользуемся нормальным приближением (wo,95 = 1,645 и гг,о,о5 = —1,645),
di@,05) = M(d) = +y/T>(d) - С/0,95 = 0,8203 - 1,645 • 0,0609 = 0,720;
d2@,05) = 0,8202 + 1,645 • 0,0609 = 0,920.
Так как 0,720 < d = 0,8109 < 0,920, нулевая гипотеза нормальности не отклоняется.
3.2.2.10. Критерий Дэвида-Хартли-Пирсона
В [264] предложен критерий нормальности распределения вероятностей случай™
ной величины, основанный на распределении отношения размаха к стандартному
отклонению.
3.21
Критерии нормальности распределения
259
Статистика критерия имеет вид
где R = жтах — Жщщ (или {хп — х\) для упорядоченного по возрастанию ряда выбо™
рочных значений)—размах выборки; s — стандартное отклонение.
Таблица 75
Критические границы Ui{ol) и U%(ol)
критерия Дэвида—Хартли—Пиреона
(а — уровень значимости) [9]
п
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
а =
иг
1,737
1,870
2,020
2,150
2,260
2,350
2,440
2,510
2,580
2,640
2,700
2,750
2,800
2,840
2,880
2,920
2,960
2,990
3,150
3,270
3,380
3,470
3,550
3,620
3,690
3,750
3,800
3,850
3,900
3,940
3,990
4,020
4,060
4,100
0,01
и2
2,000
2,445
2,803
3,095
3,338
3,543
3,720
3,875
4,012
4,134
4,244
4,340
4,440
4,520
4,600
4,670
4,740
4,800
5,060
5,260
5,420
5,560
5,670
5,770
5,860
5,940
6,010
6,070
6,130
6,180
6,230
6,270
6,320
6,360
а =
иг
1,758
1,980
2,150
2,200
2,400
2,500
2,590
2,670
2,740
2,800
2,860
2,920
2,970
3,010
3,060
3,100
3,140
3,180
3,340
3,470
3,580
3,670
3,750
3,830
3,900
3,960
4,010
4,060
4,130
4,150
4,200
4,240
4,270
4,310
0,05
и2
1,999
2,429
2,753
3,012
3,222
3,399
3,552
3,685
3,800
3,910
4,000
4,090
4,170
4,240
4,310
4,370
4,430
4,490
4,710
4,890
5,040
5,160
5,260
5,350
5,430
5,510
5,570
5,630
5,680
5,730
5,780
5,820
5,860
5,900
а =
иг
1,782
2,040
2,220
2,370
2,490
2,590
2,680
2,760
2,840
2,900
2,960
3,020
3,070
3,120
3,170
3,210
3,250
3,290
3,450
3,590
3,700
3,790
3,880
3,950
4,020
4,080
4,140
4,190
4,240
4,280
4,330
4,360
4,400
4,440
0,10
и2
1,997
2,409
2,712
2,949
3,143
3,308
3,449
3,570
3,680
3,780
3,870
3,950
4,020
4,090
4,150
4,210
4,270
4,320
4,530
4,700
4,840
4,960
5,060
5,140
5,220
5,290
5,350
5,410
5,460
5,510
5,560
5,600
5,640
5,680
Гипотеза нормальности принимается, если U\(ql) < U < U(a) (a — уровень зна™
чимости). Наиболее полные таблицы критических значений Ui(a) приведены
в [9, 256] (в табл. 75 приведены некоторые значения U\[a) и ^(а)).
260 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
При п —» оо имеют место соотношения [266]
In- 1
при п = 2,4, ..., 2к;
при п= 1,3, . ..,2fc- 1.
Задача 116. Л условиях задачи 107 проверить гипотезу нормальности распределения
вероятностей случайных величин критерием Дэвида-Хартли-Пирсона при а = 0,05.
Имеем R = жтах - xmin = 15 -(-1) = 16; s = 4,686; U = — = —^- = 3,414.
s 4,686
Из табл. 75 для п = 10 и а = 0,05 имеем иг = 2,67 ш U2 = 3,522.
Так как 2,67 < 17 = 3,414 < 3,552, гипотеза нормальности распределения случайных
величин не отклоняется на уровне значимости 0,05.
3.2.2.11. Комбинированный критерий Шпигельхальтера
В [267, 268] рассмотрен комбинированный критерий нормальности против сим-
симметричных альтернатив с неизвестными средним и дисперсией. Критерий основан
на комбинации двух критериев — критерия Гири (см. раздел 3.2.2.9) и критерия
Дэвида-Хартли-Пирсона (см. раздел 3.2.2.10).
Статистика критерия имеет вид
г = {(cnu)-(n-v + g-(n~v
п
У\хг^х\
1 1 R ^
r-y -1 / i\ 7 тт -"- г=1
где Сп = —(n!)"-i; U =—\g= ,
2п s s^fn(n - 1)
Нулевая гипотеза нормальности испытываемого распределения принимается, ес-
если Т1 < Т'{а). Критические значения Т1'(а) на уровнях значимости а = 0,05 и 0,10,
а также значения коэффициента Сп приведены в табл. 76.
Таблица 76
Критические значения Т1 (ol)
критерия Шпигельхальтера [267]
п
5
10
15
20
50
100
а
0,05
1,532
1,453
1,423
1,403
1,337
1,308
0,10
1,512
1,417
1,387
1,369
1,317
1,294
Сп
0,3310
0,2678
0,2445
0,2321
0,2070
0,1971
Критерий обладает хорошей мощностью против симметричных альтернатив.
Задача 117. В условиях задачи 107 проверить гипотезу нормальности распределения
вероятностей случайной величины критерием Шпигельхальтера при а = 0,05.
Имеем R = 15 - (-1) = 16 и s = 4,686.
3.21
Критерии нормальности распределения
261
Из табл. 76 находим Сп = 0,2678 и вычисляем
1
= 0,8548; Т' = {@,2678 • 3,414)^9 + 0,8548^9} 9 = 1,228.
тт R 38
U = —; g = ,
s 4,686 • л/Ю-9
Из табл. 76 для а = 0,05 имеем Г;@,05) = 1,453.
Так как Т' = 1,228 < Т;@,05) = 1,453, гипотеза нормальности не отклоняется.
3.2.2.12. Критерий нормальности Саркади
Саркади [269] предложил критерий нормальности, более совершенный, чем дру-
другие. Предположим, имеется выборка значений случайной величины х\ ^ ж 2 ^ ... ^ хп.
Критерий Саркади строится следующим образом.
Образуем статистику
= Уэ
где
Jn
j = 1,2, ...,n-2),
= m, . ..,n- 1);
77i — произвольное фиксированное число A ^ m ^ n).
Если слохсная гипотеза нормальности верна, то переменные Zj взаимно незави-
независимы и имеют t-распределение (см. раздел 1.1.9) с / = п — j — 1 степенями свободы.
Тогда случайные величины
распределены равномерно на интервале [0,1] (Ff(z) — функция распределения Стью-
дента с / степенями свободы).
Таким образом, задача сводится к проверке равномерности распределения ве™
личин rj по одному из критериев согласия (см. раздел 3.4). Если проверяется
только факт нормальности распределения, то следует выбирать m = п или га = 1,
в ином случае (например, тренд в среднем, изменение дисперсии в альтернативе)
используются другие значения га.
В [270] предлагается использовать для проверки равномерности распределе-
распределения rj „гладкий критерий" Неймана, статистика которого имеет вид
р2_ 1
П ~ п - 2
4 п-2
Е
где
(рг(у) = л/12 f 2/ - 2
ip3(y) = л/7
Ы») = 210B,-1) -45(у-^) +1
— полиномы Лежандра, ортогональные на отрезке [0,1].
Распределение статистики Р| близко к распределению %2 с / = 4 степенями
свободы. Следовательно, если Р^ < X2f(a)i TO на уровне значимости а гипотеза
нормальности не отклоняется.
Функция распределения Стьюдента достаточно полно табулирована в
[25, табл. 3.1а, с. 236]. В связи с большим объемом этой таблицы она здесь не
262 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
приводится, читатель может легко найти ее в [25]. При необходимости можно
воспользоваться аппроксимациями раздела 1.1.9.
Задача 118. Проверить гипотезу нормальности распределения случайных величин
критерием Саркади при а = 0,05.
Выбираем т = п = 10 (^ х% = 48) и вычисляем для j = 1,2, ..., 9
Уз = хз ;—7= 'Y,Xi г- , 1 ' Ж1° = хз - 7,25031;
2/i = -8,25031; у2 = -7,25031; у3 = -6,02531; у4 = -5,02531; у5 = -4,02531;
2/6 = -2,2531; у7 = -1,2531; у8 = -0,2531; у9 = 2,74969.
Далее находим
2 = -1,89577;
1
^2 = 2/2 • | - • (уз + • • • + у1) \ 2 = -1,92842;
z3 = -1,97848; z4 = -2,0652; z5 = -2,2519;
z6 = -1,2859; z7 = -0,6404; z8 = -0,09103.
Переменные rj находим, пользуясь таблицей [25, табл. 3.1а, с. 236] функции t-pacnpe™
деления Стьюдента
т-1 = F8(-l,896) = 1 - F8(l,896) « 1 - 0,956 = 0,044; r2 = F7(-l,928) = 0,049;
гз = F6(-l,978) = 0,046; r4 = F5(-2,065) = 0,048; r5 = F4(-2,252) = 0,044;
r6 = F3(-l,286) = 0,150; r7 = F2(-0,540) = 0,317; r8 = Fi(-0,091) = 0,469.
Теперь вычислим статистику „гладкого критерия" Неймана.
Находим
(fi(n) = л/12 • @,044 - 0,5) = -1,5796; (р2(п) = лД • [@,044 - 0,5J - 0,5] = 1,6717;
ср3(п) = л/7 • [20 • @,044 - 0,5K - 3 • @,044 - 0,5)] = -1,3979;
ip4(n) = 210 • @,044 - 0,5L - 45 • @,044 - 0,5J + - = 0,8477;
8
(fi(r2) = -1,5623; (р2(г2) = 1,61087; (рз(г2) = -1,2744; (f4(r2) = 0,6601;
Vi(r3) = -1,5727; ^2(r3) = 1,6473; (p3(r3) = -1,3480; ^4(r3) = 0,7714;
y?x(r4) = -1,5638; (f2(r4) = 1,6230; (p3(r4) = -1,2988; ^4(r4) = 0,6967;
<Pi(rs) = -1,3979; (р2(г5) = 1,6717; (рз(г5) = -1,3979; (p4(r5) = 0,8477;
<Pi(r6) = -1,2124; <p2(r6) = 0,5255; (p3(r6) = 0,5093; (p4(r6) = -1,2362;
<pi(r7) = -0,6339; <p2{r7) = -0,6687; <p3(r7) = 1,1282; (p4(r7) = -0,1465;
<pi(r8) = -0,1074; (p2{r8) = -1,1051; (рз(г8) = 0,2445; (f4(r8) = 1,0819.
Окончательно получаем
8 8
JZimirj)]2 = 14,2394; УЧ^т,-)]2 = 12,68176;
JZlMrj)]2 = 10,6257; X>4fa)]2 = 5,8756; ?l = \jl Т,Ы{г3)]2 = 5,4278.
3=1 3=1 i=lj=l
Критические значения х4A — а) находим из табл. 55: %4@,95) = 9,488.
Так как Р| = 5,4278 < х4@,95) = 9,488, гипотеза нормальности распределения слу-
случайных величин не отклоняется.
3.2] Критерии нормальности распределения 263
3.2.2.13. Критерий нормальности Лина-Мудхолкара
В [271-273] показано, что если ж1? ..., хп (п ^ 2)—выборка из распределения
1 п
с функцией F{x), то х и s2 = — Yl (xi ~ х>2) независимы тогда и только тогда, когда
п г=1
F(x) —функция распределения нормального закона. Эта характеризация использо-
вана в [274] для построения критерия проверки нормальности распределения про-
против асимметричных альтернатив. Критерий позволяет проверить сложную гипотезу
нормальности распределения с неизвестными средним и (или) дисперсией.
Применение этого критерия не требует ни упорядочения, ни преобразования
переменных, ни выборочной оценки параметров распределения. Распределение ста-
статистики этого критерия при Hq очень близко к нормальному в малых выборках
(тогда как в других критериях это имеет место, как правило, только в асимптотике).
Критерий основан на анализе п средних и дисперсий, рассчитанных по п выбор-
выборкам, образуемым исключением каждый раз одного наблюдения. Хотя полученные
пары значений (ж^> s2) не будут независимыми, их можно использовать для постро-
построения критерия.
Одно из распределений — распределение s2 не является нормальным, а критерий
предполагает использование коэффициента корреляции в нормальной двумерной
совокупности. Поэтому для дисперсии применяется нормализующее преобразова-
преобразование Вилсона—Хилферти
, г = 1, ...,n.
Величину yi можно рассматривать как нормально распределенную случайную ве-
величину.
Таким образом, исследуется корреляция между величинами ги^, оцениваемая
коэффициентом корреляции
Г =
J2(Xi - x)bji -у)
г=1
= \2 \Г^ / -\2
* / / .у \Уг У)
I *
2
i=l г=1
Для построения статистики критерия используется нормализующее преобразование
z = — In . Дисперсия cr2(z) и коэффициент эксцесса (хЦ^) величины z равны
2, _ 3 7,324 53,005 _ 11,7 55,06
гс п2 п3 п п2
Критические значения z(a) могут быть вырахсены через квантили стандартного
нормального распределения иа следующим образом:
z(a) = o-(z)< ui+a + —¦
где а — уровень значимости.
Если х и s2 — среднее и дисперсия полной выборки, то а^, s| — среднее и диспер-
дисперсия по всем наблюдениям, исключая г-е:
1 / _ ч 2 l[/i\2 ГС , х2
264 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Программа расчета и некоторые практические рекомендации по применению этого
критерия рассмотрены в [275, 276].
В конечном итоге статистикой критерия является коэффициент корреляции
между Xi и (sf)^. Если \z\ < z(—-—), то гипотеза нормальности распределения
\ 2i J
случайных величин отклоняется.
В [277] предпринята попытка использовать вместо обычного коэффициента кор-
корреляции коэффициент ранговой корреляции Спирмена (см. раздел 5.2.2.2.2).
Задача 119. Проверить гипотезу нормальности распределения вероятностей случай-
случайных величин в условиях задачи 107 критерием Лина-Мудхолкара при достоверности
а = 0,95.
Имеем х = 4,8; s2 = ^— ?(xi - xf = 24,4.
Вычислим для примера значения х\ и s\:
хг = —!— • [10 • 4,8 —(—1I = 5,444;
10 — 1 L v п
s\ = —!— • A0 - 1) • 24,4 - — .(-l- 4,8J = 22,778.
10 — 2 [ ; ' 9 V ' ; J
Далее по аналогии вычисляем пары значений Xi(si) 3 . Вычисления сводим в таблицу:
г
1
2
3
4
5
6
7
8
9
10
Xi
-1
0
1
2
3
5
6
7
10
15
Xi
5,444
5,333
5,222
5,111
5,000
4,777
4,666
4,585
4,222
3,666
22,778
24,250
25,440
26,361
27,000
27,444
27,250
26,777
23,694
13,000
W = (*?)*
2,835
2,894
2,941
2,976
3,000
3,016
3,009
2,992
2,872
2,351
(Xi -x{yi- у))
^0,03440
0,00286
0,02200
0,02690
0,02200
^0,00326
-0,01644
-0,02250
0,00960
0,61103
48,026
Вычисляем
28,886
г
0,596768 • 1,64265
Далее находим
Ъг= 4,8026; y=-.YtVi = Z'
= 0,596768;
= 0,63995;
= 1 ¦ 1п ' +
2 1 - 0,63995
0,62733
:)з =2,
= 1,64265;
= 0,75809.
а>{х) = А _ L324 53,005 = = _ 11Д 55,06 =
v ; ю юо юоо ' v ; ю юо
Имеем при а = 0595 (критерий двусторонний): ui+a = tio,975 = 1,96.
2
Тогда z@,95) = 0,52893 • j 1,96 + — • (l,963 - 3 • 1,96) • (-0,6194) 1 = 1,01418.
Так как \z\ = 0,75809 < z(a) = 1,01418, нулевая гипотеза нормальности не отклоня™
ется.
3.2] Критерии нормальности распределения 265
3.2.2.14. Критерий нормальности Мартинеса-Мглевича
Критерий применяется против симметричных альтернатив, отличающихся от
нормального распределения „хвостами" или эксцессом. Критерий основан на отно™
шении двух оценок дисперсии — обычной и так называемой „робастной" (устойчи™
вой), двухвесовой.
„Робастная", устойчивая к выбросам, оценка дисперсии имеет вид [278]
I n л\ ~ •> ПРИ
где Zi = < 9med|xi - ж|'
< 1;
x — выборочная медиана, med(...) — медиана ряда в скобках.
В качестве статистики используется отношение дисперсий [278]
При справедливости нулевой гипотезы Hq имеет место МA) = 0,982. Критические
значения статистики для уровней достоверности а = 0,90 и 0,95 могут быть найдены
из соотношений
Г @,9) = 0,6376 - 1Д535п* + 0,126бв*2;
Т*,п п_. _ /1,9065 - 2,5465в* + 0,5652n*2, n > 50;
[0,7824 - 1,1021п* + 0,1021n*2, n < 50;
где п* = lg(n - 1); Г» = lg[I(a) - 0,982].
Этот критерий более мощен для альтернатив с длинными „хвостами", чем многие
другие критерии.
Задача 120. Проверить гипотезу нормальности распределения случайных величин
в условиях задачи 107 критерием Мартинеса-Иглевича при доверительной вероятно-
вероятности а = 0,95.
Для ряда 1, 0, 1, 2, 3, 5, 6, 7, 10, 15 медианой является
х5 + х6 3 + 5
х = = = 4.
2 2
Составляем и ранжируем по величине ряд значений величин
х{ -х\ : 1, 1, 2, 2, 3, 3, 4, 5, 6, 11.
Вычисляем
л л ~ 3+3
А = med|a?i — х = = 3.
Результаты расчетов сводим в таблицу (для упрощения записи приняты обозначения
# = A - z\t) ¦ A - 5zf) и ## = (Xi - i) ¦ A - zlf):
266 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
г
1
2
3
4
5
6
7
8
9
10
Zi
-5/27
-4/27
-3/27
-2/27
-1/27
1/27
2/27
3/27
6/27
11/27
0,0343
0,0220
0,0123
0,0055
0,0014
0,0014
0,0055
0,0123
0,0494
0,1660
(WL
0,8697
0,9150
0,9515
0,9782
0,9945
0,9945
0,9782
0,9515
0,8353
0,4838
#
0,8001
0,8707
0,9267
0,9672
0,9918
0,9918
0,9672
0,9267
0,7200
0,1419
(Xi - xf
25
16
9
4
1
1
4
9
36
121
##
21,7420
14,6400
8,5630
3,9130
0,9945
0,9945
3,9130
8,5630
30,0710
58,5400
Имеем
п
(xi -жJ = 219,6;
г=1 Ы\<1
2\4 / ~ч2
A -ZiL-(xi- xf = 151,934; 1=
1-4) -A-54) = 8,3041;
219,6-8,30412
= 1.107;
10 • 9 151,934
/*@,95) = 1,9065 - 2,5465 • 0,95424 + 0,5652 • @,95424) = -8,8157 • 10" ;
1@,95) = ю"8'8157'10 + 0,982 = 1,962.
Так как I = 1,107 < /@,95) = 1,962, нулевая гипотеза нормальности не отклоняется.
3.2.2.15. Критерий нормальности Д'Агостино
Д'Агостино [279, 280] предложил в качестве статистики для проверки нормаль™
ности распределения использовать отношение оценки Даутона для стандартного
отклонения [281] (см. раздел 2.1.2.1.6.3) к выборочному стандартному отклонению,
оцененному методом максимального правдоподобия,
D =
Г
2 '
п s
где
s = —
Очевидно, что а = —; гт является несмещенной оценкой стандартного откло™
нения а.
Показано, что
п(п — 1)
M(D) =
п-1
Цп - 1) Щп - if 128(п - IK _
1 = 0,28209479;
0,02998598
8,463
л/п
коэффициент ассиметрии;
гг>\ 107'9 л,л,
a4{JJ) = коэффициент эксцесса.
3.21
Критерии нормальности распределения
267
В качестве статистики критерия Д'Агостино используется величина
¦ D - 0,28209479
Y =
0,02998598
критические значения которой приведены в [279, 280] и частично воспроизведены
в табл. 77. Гипотеза нормальности принимается, если Y\{ot) ^ Y ^ Y2{pt), где Yi{a)
и Yi (ol) —критические значения статистики Y при достоверности а.
Таблица 77
Критические значения критерия Д'Агостино [279, 280]
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
60
70
80
90
100
150
200
250
300
350
400
450
500
600
700
800
900
1000
а =
Гг
-2,62
-2,58
-2,53
-2,50
-2,47
-2,44
-2,41
-2,39
-2,37
-2,35
-2,33
-2,32
-2,30
-2,29
-2,28
-2,26
-2,25
-2,24
-2,23
-2,22
-2,21
-2,17
-2,14
-2,11
-2,09
-2,07
-2,00
-1,96
-1,93
-1,91
-1,89
-1,87
-1,86
-1,85
-1,83
-1,82
-1,81
-1,80
-1,79
0,90
Y2
0,235
0,329
0,399
0,459
0,515
0,565
0,609
0,648
0,682
0,714
0,743
0,770
0,794
0,816
0,837
0,857
0,875
0,892
0,908
0,923
0,937
0,997
1,050
1,080
1,120
1,140
1,230
1,290
1,330
1,360
1,380
1,400
1,410
1,420
1,440
1,460
1,470
1,480
1,490
а =
Y1
-3,25
-3,20
-3,16
-3,12
-3,08
-3,04
-3,01
-2,98
-2,96
-2,93
-2,91
-2,88
-2,86
-2,85
-2,83
-2,81
-2,80
-2,78
-2,77
-2,75
-2,74
-2,68
-2,64
-2,60
-2,57
-2,54
-2,45
-2,39
-2,35
-2,32
-2,29
-2,27
-2,25
-2,24
-2,21
-2,20
-2,18
-2,17
-2,16
0,95
Y2
0,299
0,381
0,460
0,526
0,574
0,628
0,677
0,720
0,760
0,797
0,830
0,862
0,891
0,917
0,941
0,964
0,986
1,010
1,020
1,040
1,060
1,130
1,190
1,240
1,280
1,310
1,420
1,500
1,540
1,570
1,610
1,630
1,650
1,676
1,690
1,710
1,730
1,740
1,750
а =
-4,66
-4,63
-4,57
-4,52
-4,47
-4,41
-4,36
-4,32
-4,27
-4,23
-4,19
-4,16
-4,12
-4,09
-4,06
-4,03
-4,00
-3,98
-3,95
-3,93
-3,91
-3,81
-3,73
-3,67
-3,61
-3,57
-3,41
-3,30
-3,23
-3,17
-3,13
-3,09
-3,06
-3,04
-3,00
-2,97
-2,94
-2,92
-2,91
0,99
Y2
0,385
0,479
0,555
0,613
0,667
0,720
0,775
0,822
0,867
0,910
0,941
0,983
1,020
1,050
1,080
1,110
1,140
1,170
1,190
1,220
1,240
1,340
1,420
1,480
1,540
1,590
1,750
1,850
1,930
1,980
2,030
2,060
2,090
2,110
2,150
2,180
2,210
2,310
2,350
268 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Критерий Д'Агостино следует применять, когда нет сведений об альтернатив™
ном распределении. Он показывает хорошую мощность против большого спектра
альтернатив, по мощности немного уступая критерию Шапиро—Yилка [282].
Задача 121. В условиях задачи 107 проверить гипотезу нормальности распределения
вероятностей случайных величин критерием Д^Агостино при достоверности а = 0,95
(s = 4,686).
Вычисляем Г = 5^{г - ^tij . Хг = (\ - —\ .(_!) + ...+ (9 - —\ -15 = 129.
4=1 ^ J \ / \ /
Далее получаем
2-^.129 = 129 =
10-9 100-4,686
0.275288-0,28209479
0,02998598
= _
Из табл. 77 для п = 10 и а = 0,95 находим yi@,95) = -3,25 и у2@,95) = 0,299. Так как
2/1 @,95) = —3,25 < Y = —0,71783 < 2/г@,95) = 0,299, гипотеза нормальности распределе-
распределения случайных величин не отклоняется.
3.2.2.16. Критерии асимметрии и эксцесса
Если распределение случайных величин нормально, то его коэффициент асим-
асимметрии «з = 0 и коэффициент эксцесса «4 = 3. Напомним, что выборочные оценки
коэффициентов асимметрии и эксцесса равны
з
г=1 г=1 г=1
Так как значения «з = 0 и а4 = 3 могут иметь место и для распределений, отличных
от нормального, то критерии этого раздела следует воспринимать как критерии
установления отклонения от нормальности распределения (но не установления
нормальности).
Известно [25], что М(а3) = 0; D(a3) = , ^J2}^ « - (l -
(n + l)(fi + 3) ny ^
В [283] показано, что распределение аз достаточно быстро стремится к нормаль™
ному. Для «4 справедливы соотношения
24n(n-2)(n-3) =24Л_ 225
( ) \ 15 + 2
п
Распределение «4 медленно стремится к нормальному [283].
Рассмотрим использование критерия а% для установления отклонения эмпири-
эмпирического распределения от нормального. Таблицы процентных точек распределе-
распределения «з приведены в [25]. При п > 200 может быть рекомендован грубый критерий:
если
П г,
) >
г=1
то нормальность распределения отклоняется.
На практике применяются нормализующие преобразования для «з • Рассмотрим
некоторые из них. В [284] предложена аппроксимация ? = 5\п(х-\- \/х2 + l) , где
х = —, которая при п —>• со распределена как стандартная нормальная величина
Л
(<5, А — коэффициенты, приведенные в табл. 78).
3.21
Критерии нормальности распределения
269
Таблица 78
п
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
8
5,563
4,260
3,734
3,447
3,270
3,151
3,069
3,010
2,968
2,937
2,915
2,900
2,890
2,870
2,882
2,882
2,884
2,889
2,895
2,902
2,910
2,920
2,930
2,941
2,952
2,964
2,977
2,990
3,003
3,016
3,030
3,044
3,058
3,073
3,087
3,102
Значения коэффициентов S
1/А
0,3030
0,4080
0,4794
0,5839
0,5781
0,6153
0,6743
0,6753
0,7001
0,7224
0,7426
0,7610
0,7779
0,7940
0,8078
0,8211
0,8336
0,8452
0,8561
0,8664
0,8760
0,8851
0,8938
0,9020
0,9097
0,9171
0,9241
0,9308
0,9372
0,9433
0,9492
0,9548
0,9601
0,9653
0,9702
0,9750
п
44
45
46
47
48
49
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
80
82
84
86
88
90
92
94
96
98
100
105
110
115
120
8
3,117
3,131
3,160
3,161
3,176
3,192
3,207
3,237
3,268
3,298
3,329
3,359
3,389
3,420
3,450
3,480
3,510
3,540
3,569
3,599
3,628
3,657
3,686
3,715
3,744
3,772
3,801
3,829
3,857
3,885
3,913
3,940
4,009
4,076
4,142
4,207
1/А
0,9795
0,9840
0,9882
0,9923
0,9963
1,0001
1,0038
1,0108
1,0174
1,0235
1,0293
1,0348
1,0400
1,0449
1,0459
1,0540
1,0581
1,0621
1,0659
1,0695
1,0730
1,0763
1,0795
1,0825
1,0854
1,0882
1,0909
1,0934
1,0959
1,0983
1,1006
1,1028
1,1080
1,1128
1,1172
1,1212
и - [284]
п
125
130
135
140
145
150
155
160
165
170
175
180
185
190
195
200
210
220
230
240
250
260
270
280
290
300
350
400
450
500
600
700
800
900
1000
8
4,272
4,336
4,398
4,460
4,521
4,582
4,641
4,700
4,758
4,816
4,873
4,929
4,985
5,040
5,094
5,148
5,255
5,359
5,461
5,561
5,660
5,757
5,853
5,946
6,039
6,130
6,567
6,976
7,363
7,731
8,149
9,054
9,649
10,271
10,738
1/А
1,1250
1,1285
1,1318
1,1348
1,1377
1,1403
1,1428
1,1452
1,1474
1,1496
1,1516
1,1535
1,1553
1,1570
1,1586
1,1602
1,1631
1,1657
1,1681
1,1704
1,1724
1,1744
1,1761
1,1779
1,1793
1,1808
1,1868
1,1914
1,1950
1,1979
1,2023
1,2058
1,2078
1,2096
1,2111
В [285] предложена следующая нормализующая аппроксимация. Если
t+1H + 3) 3(п2 + 27п-70)(п-
3)
6(n-2)
ш2 = -
а =
тo величина z = <51п< —\-
а
уже при п > 25 может быть аппроксими-
аппроксимирована стандартным нормальным распределением.
270 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Рассмотрим теперь преобразование для коэффициента эксцесса а^ [286]. Рас™
пределение «4 может быть аппроксимировано распределением X2 с / степенями
свободы при
Г ЯР Г =
Д
д /
(гс + 7)(п + 9) V гс(п - 2)(п - 3) *
В [286] предложено весьма эффективное нормализующее преобразование для
коэффициента эксцесса «4- Алгоритм его построения заключается в следующем.
а4 - М(а4)
.Ьсли ж = -; то случайная величина
1
2
9/ '
1-
1 —
VxJ
2
1
Г
f
2
-
>
4 J
11
3
>
B
d =
аппроксимируется стандартным нормальным распределением АГ@,1) у^ке при п > 20.
Нормализующие преобразования позволяют использовать таблицы (или аппрок™
симации) стандартного нормального распределения для проверки отклонения от
нормальности.
Мощность критерия проверки отклонения от нормальности может быть повы-
повышена применением так называемого комбинированного Ж2™критерия [284, 289]
К2 = Х2(а3)+Х2(а4),
где Х(«з) и Х{а.4) — стандартные нормальные эквиваленты распределений «з и«4-
Статистика К2 имеет ^^распределение с / = 2 степенями свободы. Другая
форма комбинированного критерия исследована в [287, 288]. Если q\ = 2р («з < аз)
и q2 = 2р («4 < «4) («з и бц — выборочные оценки параметров «з и «4 соответствен-
соответственно), то статистика q = ^21ngi^2 имеет %2~распределение с / = 4.
Задача 122. В условиях задачи 107 проверить гипотезу нормальности распределе-
распределения случайных величин критериями асимметрии и эксцесса на уровне достоверности
а = 0,90.
Отметим, что задача носит демонстрационный характер, так как применение крите-
критериев такого типа требует объемов выборки не менее 50.
Имеем
х = 4,8; s2 = 21,96 (s = 4,686) ;
ж» ~~ xf = 8,25,84;
г=1
1
(ж* - жL = 13523,952; a3 = т • 825,84 = 0,80258;
V ; 10-4,6863
a4 =
10-21,
—^ • 13523,452 = 2,
804393.
Вычисляем далее
Ща3) =
11 • 13
= 0,33566
М(а4) = 3 - — = 2,4545; D(a4) =
n2il3.15
= 0,56961 (VD(a4) = 0,75473).
3.21
Критерии нормальности распределения
271
Грубый критерий аз = 0,8025 > y/D(oL$) = 0,579 отклоняет гипотезу нормальности
(это применимо для п > 200, поэтому в нашем случае применение критерия некорректно;
однако наша цель — демонстрация техники вычисления — достигается).
Вычислим нормализующие преобразования. Рассмотрим сначала ^-преобразование.
Из табл. 78 для п = 10 находим 8 = 3,734 и - = 0,4794.
А
Далее имеем
х = а3 - 0,4794 = 0,80258 • 0,4794 = 0,384757; С = 3,734 • 1п@,384757 + 1,071465) = 1,4034.
Рассмотрим теперь ^-преобразование:
!° " 70)
у = 0,80258 •
= 1,38527416; /3 =
i • 15 ¦ 17 • 19
• 3,3204334;
ш2 = -1 + у/2 • 3,3204334 = 1,5769879; 6 = (in д/1,5769879) 2 = 2,0953804;
1
2
а =
0,5769879
= 1,8617941;
1,38527416V
1,8617941 )
+ 1 > = 1,4424244.
Теперь рассмотрим преобразование для «4- Сначала вычислим %2-преобразование.
Имеем
6- A00^50 +
17- 19
= 1,3962;
= 6-
1,3962
1,3962
1 +
—V
1,3962/
= 25,47.
Следовательно, величина а^ мо^кет быть аппроксимирована х2~РаспРеДелением
с / та 25,5 степенями свободы.
Наконец, рассмотрим нормализующее преобразование для ос±. Имеем
М(а4) = 2,4545; D(a4) = 0,569161
= 0,75473); х = 2^804393 ~ 2^4545 = 0;4636;
U, 154 (о
d =
9 • 25,47
1 -
9 • 25,47
1 -
25,47
- 0,4636 •
21,47
= 0,644.
Используем нормализующие преобразования для «з и «4 для оценки отклонения
эмпирического распределения отнормального (ito,95 = 1,645 — 95%-я квантиль стандарт-
стандартного нормального распределения. Так как критерий двустронний, при а = 0,90 следует
ПрИМеНЯТЬ Ul + g = U 1+0,90 = 1Ао,95).
2 2
Имеем z = 1,442 < г^о,95 = 1,645. Следовательно, гипотеза нормальности по коэффи-
коэффициенту асимметрии не отклоняется.
По коэффициенту эксцесса имеем d = 0,664 < 11,0,95 = 1,645 и гипотеза нормальности
также не отклоняется.
Рассмотрим теперь комбинированный критерий. Нормализующие преобразования
дают: Х2(а3) = A,403J = 1,9684; Х2(а4) = @,6498J = 0,4222 и К2 = Х2(а3) +
+Х2(«4) = 2,3906. Из табл. 55 для / = 2 имеем критическое значение Хо,эB) = 4,605. Так
как К2 = 2,39 < Хо,э(/ = 2) = 4,605, гипотеза нормальности распределения случайных
величин не отклоняется.
272 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.2.2.17. Критерий характеристической функции (критерий Муроты-Такеучи)
Если Xi (г = 1, ..., п) —выборка из распределения с характеристической функ™
цией c(t), то эмпирическая характеристическая функция определяется как
1 п
cn(i) = -]Texp(itei).
п i=i
В [290^292] исследована возможность применения характеристической функции
для проверки различных гипотез согласия. Для проверки сложной гипотезы нор™
мальности (когда параметры распределения не известны заранее) Мурота и Таке™
учи [293] предложили использовать „стьюдентизированную" форму
=Сп[-
где
-\2
г=1
Введем обозначения a(t) = \c(i)\ и an(t) = \cn(t)\ . В общем случае модуль
характеристической функции \c(i)\ не определяет форму распределения, но для
нормального распределения есть исключение. Распределение с характеристической
функцией c(t) нормально тогда и только тогда, когда величина yj — log |c(t)|2 ли™
нейна при любом t ^ 0 [293].
Для оценки „стьюдентизированного" модуля характеристической функции ис™
пользуется соотношение [293]
1
п
Распределения величин an(t) и an(t) медленно нормализуются с ростом п. Лучшее
приближение к нормальному распределению реализуется при t = 1 -г- 1,5.
Гипотеза нормальности не отклоняется, если а\ ^ an(t) ^ а^ где а\ и а2 —
граничные значения, зависящие от объема выборки и принятого уровня значимости
(приведены в табл. 79).
Таблица 79
Критические значения а\ и аг критерия Муроты^Такеучи
на уровне значимости a = 0,10 [293]
п
10
15
20
35
50
t = 0,5
at
0,7934
0,7871
0,7841
0,7805
0,7793
а2
0,8022
0,7966
0,7935
0,7888
0,7866
t = 1,0
ai
0,3604
0,3512
0,3475
0,3462
0,3466
0,4527
0,4440
0,4365
0,4192
0,4094
t = 1,5
а\
0,0540
0,0545
0,0555
0,0619
0,0660
0,2792
0,2544
0,2349
0,1945
0,1760
t = 2,0
а\
0,0027
0,0022
0,0022
0,0025
0,0024
«2
0,2684
0,1968
0,1640
0,1072
0,0842
Против асимметричных альтернатив критерий лучше, чем критерии асиммет-
рии и эксцесса (см. раздел 3.2.2.16). Критерий демонстрирует результаты не хуже,
чем критерий Шапиро-Уилка (см. раздел 3.2.2.1), но он может быть использован
против более широкого круга альтернатив.
Задача 123. Проверить гипотезу нормальности распределения случайных величин
для данных задачи 107 критерием Муроты-Такеучи на уровне значимости а = 0,1.
Имеем s2 = 24,4 (s = 4,3996); х = 4,8.
3.21
Критерии нормальности распределения
273
Будем использовать значение t = 1. Результаты расчетов сведены в таблицу:
3
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
3
3
3
3
3
3
к
2
3
4
5
6
7
8
9
10
3
4
5
6
7
8
9
10
4
5
6
7
8
9
iCj - Хк
s
-0,20244
-0,4049
-0,6073
-0,8098
-1,2146
-1,4171
-1,6195
-2,2269
-3,2391
-0,2024
-0,4049
-0,6073
-1,0122
-1,2147
-1,4171
-2,0244
-3,0366
-0,2024
-0,4049
-0,8098
-1,0122
-1,2146
-1,8220
(х- — xk \
COS{ s )
0,9796
0,9191
0,8212
0,6896
0,3486
0,0308
-0,0487
-0,6100
-0,9952
0,9796
0,9191
0,8212
0,5300
0,3486
0,1531
-0,4382
-0,9945
0,9796
0,9191
0,6897
0,5300
0,3486
-0,2485
3
3
4
4
4
4
4
4
5
5
5
5
5
6
6
6
6
7
7
7
8
8
9
к
10
5
6
7
8
9
10
6
7
8
9
10
7
8
9
10
8
9
10
9
10
10
Xj — Xk
s
-2,8342
-0,2024
-0,6073
-0,8098
-1,1022
-1,6195
-2,6318
-0,4049
-0,6073
-0,8098
-1,4171
-2,4293
-0,2024
-0,4049
-1,0122
-2,0244
-0,2024
-0,8098
-1,8220
-0,6073
-1,6195
-1,0122
( x- - xi \
rn-f 3 1
COS I 1
V s J
-0,9531
0,9796
0,8212
0,6897
0,5300
-0,0487
-0,8728
0,9191
0,8212
0,6897
0,1531
-0,7569
0,9796
0,9191
0,5300
-0,4382
0,9796
0,6896
-0,2486
0,8212
-0,0487
0,5300
7,6724
Суммируя, находим у
3<к
Окончательно получаем
1 9
о„A) = - + —
п п
cos
7,6857
= 15,3581.
^—— ) = — + — • 15,3581 = 0,40716.
з I 10 100
Из табл. 79 для t = 1 и п = 10 имеем аг = 0,3604 и а2 = 0,4527.
Так как <ц = 0,3604 < апA) = 0,40716 < а^ = 0,4527, гипотеза нормальности распре-
распределения вероятностей случайных величин не отклоняется.
3.2.2.18. Критерии проверки нормальности распределения
по совокупности независимых выборок малого объема
Исследователь или испытатель чаще всего встречается на практике с ситуацией,
когда в его распоряжении находится совокупность малых выборок, поступающих
последовательно в течение длительного промежутка времени наблюдений или не™
пытаний, например, результаты испытаний малых партий изделий по мере их
изготовления. В этом случае появляется необходимость проверки нормальности
распределения случайной величины по совокупности выборок малого объема, в ко-
которых средние и дисперсии в общем случае могут быть разными. Различные методы
установления нормальности распределения наблюдаемой случайной величины в та-
такой ситуации рассматриваются в настоящем разделе.
274 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.2.2.18.1. Применение критерия Шапиро-Уилкаг)
Пусть имеется к независимых выборок объема щ каждая (г = 1, ...,&) и
хи ^ xi2 ^ • • • ^ %im Для каждой г-й выборки. Для каждой выборки вычислим
статистику
Здесь [ •.. ] — наибольшее целое число.
Пусть оц = F(Wi) —уровень значимости W^-статистики; uai —«-квантиль стан-
г к
дартного нормального распределения; U = -^=z y^ uai; q = —21nai—верхняя
к
а^точка распределения %2 с / = 2 степенями свободы и с = ^ Q.
г=1
Идея проверки нормальности распределения заключается в том, что все uai и U
имеют стандартное нормальное распределение, а с имеет распределение %2 с / = 2к
степенями свободы [294].
Ранее [242] была найдена аппроксимация
uai =
коэффициенты которой приведены в табл. 65.
г к
Статистика U = —^= \^ uai имеет стандартное нормальное распределение. От™
клонение распределения от нормального приводит к уменьшению значений W{.
Сдвиг значений uai к малым отрицательным величинам сигнализирует об этом.
Поэтому статистика критерия должна быть интерпретирована в терминах односто™
роннего критерия, т.е. если U < иа, то на уровне значимости а гипотеза нормаль™
ности должна быть отклонена.
к
Во втором варианте критерия вычисляются значения с^ = — 21па^ и с = У^ Cj.
г=1
Если с > x^Bfc), то гипотеза нормальности распределения не отклоняется (с > х2B1с),
критическое значение %2™статистики на уровне значимости ас/ степенями
свободы).
3.2.2.18.2. Применение критерия Саркади2)
В [295] предложено применение модифицированного критерия Саркади для
проверки нормальности распределения случайных величин по совокупности вы-
выборок малого объема. Алгоритм вычисления статистики критерия включает в себя
) См. раздел 3.2.2.1 — основной критерий.
) См. раздел 3.2.2.12 — основной критерий.
3.2]
Критерии нормальности распределения
275
вычисление для каждой г-й выборки величин
1
ч + VfTi^
xik
j = 1, 2, ..., га - 1;
= m, ...,
Пъ - J -
Величины z*- имеют ^-распределение Стьюдента с функцией распределения ве-
вероятностей Fni—j—i(z).
Находим величины гг- = Fni—j—i \zlA и затем объединяем все величины г%- в одну
выборку объема ^(п^ — 2). К ней применяется „гладкий" критерий Неймана для
проверки равномерности распределения величин Tji на отрезке [0,1] со статистикой
pi = -
4 г=1
Е Е
где
= V7 ¦
Если Pi < х^,D), то гипотеза нормальности распределения не отклоняется.
3.2.2.18.3. Критерий Смирнова [12]
Критерий основан на статистике
т =
где Xij—j-e наблюдение г-й вв1борки; Xi,Si—соответственно среднее значение
и стандартное отклонение г-й выборки.
Распределение статистики табулировано в [297]. При щ = п = 4 т имеет
равномерное распределение, а при п ^ 4 статистика t = . имеет
уп — 1 — т2
t-распределение Стьюдента с / = тг — 2 степенями свободы. Проверкой соот-
соответствия распределения величины t распределению Стьюдента и устанавливается
нормальность распределения случайной величины в исходных выборках. Идея
алгоритма такая лее, как и в предыдущем критерии Саркади — проверяется
равномерность распределения величин т (п = 4) или согласие с распределением
Стьюдента величин t (п ф 4).
276 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Задача 124. Имеются 5 выборок по 4 наблюдения в каждой.
Необходимо проверить гипотезу нормальности распределения случайных величин по
приведенной совокупности выборок при достоверности а = 0,95.
#11 = —1, #21 = 6, Ж31 = 7, Ж41 = 0, Ж51 = —3,
#12 — 0? Ж22 = 9, Ж32 = 11, Ж42 = 1, ^52 = —1,
#13 = 1, Ж23 = 11, Жзз = 15, Ж43 = 4, Ж53 = 0,
#14 = 2, Ж24 = 13, Ж34 = 16, Ж44 = 5, Ж54 = 1.
Критерий Шапиро-Уилка C.2.2.18.1)
4
Для 1-й выборки находим х\ = 0,5; ^(#ij — х\) = 5. Из табл. 63 для п = 4 находим
ai = 0,6872 и а2 = 0,1677. Тогда имеем
т = {0,6872.^14-хп)+ 0,1677.(gi3-gia)}a =
Из табл. 65 для п = 4 имеем j = -1,107, 77 = 0,714 и е = 0,6297.
Далее вычисляем
Из табл. 1 находим ai, соответствующее квантили стандартного нормального распре-
распределения ttai = 1,8128 — это ai = 0,965.
Далее по аналогии находим
х2 = 9,75; W2 = 0,9899; иа2 = 1,445; а2 = 0,926;
х3 = 12,25; W3 = 0,9261; гхаз = -0,1152; а3 = 0,460;
Х4 = 2,5; W4 = 0,9127; иа4 = ^0,267; а4 = 0,394;
х5 = -0,75; W5 = 0,9721; wa5 = 0,6832; а5 = 0,751
¦V5 г=1
Из табл. 1 для a = 0,95 находим по,95 = 1,645.
Так как U = 1,5915 < по,95 = 1,645, гипотеза нормальности распределения случайных
величин не отклоняется.
Далее вычисляем
с= ]Г(-21под) = -2- (In0,965 + ... + In0,751) =4,213.
Из табл. 55 находим Хо,9б(/ = 10) = 18,307.
Так как с = 4,213 < Хо,9б(Ю) — 18,307, гипотеза нормальности не отклоняется.
Критерий Саркади C.2.2.18.2)
Выбираем т = п = 4 ш для первой выборки имеем
I
2/2
I 1 f П
2 = -1; 2/з = 0-
3.2] Критерии нормальности распределения 277
Вычисляем
Г 1 (О
[4—1—1 V2
2|/2
+ Уз
Воспользовавшись функцией распределения Отьюдента, имеем (см. табл. 3.1а из [25])
ri = F2 (-2,828) = 0,053 и г2 = 0. Далее по аналогии имеем
1 4 1
2/? = Ж21 - - • ?>2fc - - • Ж24 = -4,833; у2 = -1,833; у\ = 0,1667;
5 fc=i Л
z\ = -3,7131; zl = -11; г2 = 0,032; г2 « 0;
у? = -6,5; г/з = -2,333; у| = 0,6667; z\ = -3,5; v\ = 0,094; ^ = 0,089;
yl = -3,8333; 2/2 = ^0,8333; zl = -2,6919; 4 = -2,20; г\ = 0,06; г\ = 0,136.
Получаем ряд величин:
г\ = 0,053; г\ =0; г? = 0,032; Гз = 0,0444; г| = 0,175;
т\ = 0,084; гз = 0,089; г\ = 0,060; Гз = 0,136.
Находим
<Pi (rl) = -1,548; <р! (гг2) = -1,732; с^ (г?) = -1,621; <рг (г22) = -1,580;
^i (rl) = -1,126; (^i (r-i) = -1,406; (рг (г$) = -1,424; (рг (г5г) = -1,524;
(fi(r2) = —1,261 и ^^ (ft = ^2(^1) = 1,563;
<р2 (rl) = 2,236; (^2 (г2г) = 1,820; ^ (г^) = 2,236; <р2 (г?) = 1,672;
с/?2 (г|) = 0,299; у>2 (г?) = 1,093; ^ D) = 1,148; ^2 (п) = 1,479;
ср2 (rl) = 0,659 и J2 "А = 23,774;
^з (rj) = -1,178; <р3 (гг2) = -2,645; (^3 (rl) = -1,709; ^3 (r-f) = -2,645;
<Рз(г1) = -1,398; у?з(г|) = 0,763; ^3(ri) = -0,319; (f3(rt) = -0,411;
(^3(ri) =-1,015; 993G2)= 0,337 и ^ ^з = 22,251.
Окончательно получаем
1 4
F42 = — • У" У? = 8,527.
Из табл. 55 имеем Хо,9бD) = 9,488.
Так как Р| — 8,527 < Хо,9бD) = 9,488, гипотеза нормальности распределения случай-
случайных величин не отклоняется.
3.2.2.19. Сравнительная мощность различных критериев нормальности
В этом разделе представлены результаты исследования сравнительной мощно-
мощности критериев нормальности распределения вероятностей случайных величин [243]
для различных альтернативных распределений. В табл. 80 представлено ранжиро-
ранжирование 21 критерия нормальности. Критерии по каждой альтернативе представлены
в порядке предпочтения — от наибольшего A) до наименьшего B1). В последней
графе приведено общее ранжирование, соответствующее набранной сумме рангов.
Табл. 80 может быть полезной ориентировкой для пользователя при выборе кри™
терия проверки нормальности распределения вероятностей изучаемой случайной
величины.
278 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Таблица 80
Сравнение критериев проверки
нормальности распределения случайных величин
Наименование критерия (раздел)
Критерий Шапиро-Уилка C.2.2.1)
Критерий К2 C.2.2.16)
Критерий Дарбина C.1.2.7)
Критерий Д'Агостино C.2.2.14)
Критерий «4 C.2.2.16)
Критерий Васичека C.2.2.2)
Критерий Дэвида-Хартли-Пирсоыа
C.2.2.10)
Критерий х2 C.1.1.1)
Критерий Андерсона™Дарлинга C.1.2.4)
Критерий Филлибена C.2.2.5)
Критерий Колмогорова-Смирнова
C.1.2.1)
Критерий Мартинеса—Иглевича
C.2.2.14)
Критерий Лина—Мудхолкара C.2.2.13)
Критерий а3 C.2.2.16)
Критерий Шпигельхальтера C.2.2.11)
Критерий Саркади C.2.2.12)
Критерий Смирнова—Крамера—фон Ми-
зеса C.1.2.2)
Критерий Локка-Спурье C.2.2.7)
Критерий Оя C.2.2.8)
Критерий Хегази-Грина C.2.2.3)
Критерий Муроты—Такеучи C.2.2.17)
Характер альтернативного распределения
асимметричное
а4 < 3
1
7
11
12
14
2
21
9
18
3
16
10
4
8
19
5
17
13
20
6
15
«4 > 3
1
8
7
9
5
14
2
20
3
12
10
16
15
6
13
18
11
4
17
19
21
симметричное
а4 < 3
3
10
7
4
2
8
1
9
5
18
6
13
12
21
11
15
20
19
14
16
17
а4 > 3
2
6
15
5
4
10
9
8
18
1
16
3
12
7
11
14
17
21
13
19
20
я^ нор-
нормальное
«4 ~ 3
2
4
1
12
18
10
1
3
7
9
5
15
16
19
8
13
6
17
14
21
20
Ранг
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
3.3] Критерии проверки экспоненциальности распределения 279
3.3. Критерии проверки экспоненциальности распределения
Экспоненциальный закон распределения вероятностей является базовым зако-
законом, используемым в теории надежности. Его аналитическая простота делает его
привлекательным для инженеров и исследователей. Однако всегда следует пред-
предварительно убедиться в том, что вероятностное поведение случайной величины
(например, моментов отказов изделий) подчиняется „желательному" экспоненци-
экспоненциальному закону. В ином случае выигрыш от простоты расчетов будет многократ-
многократно „скомпенсирован" потерями от ошибочных выводов и заключений, вызванных
отклонением реального распределения вероятностей случайной величины от экспо-
экспоненциального закона.
По-видимому, желанием предостеречь пользователя от таких ошибок объясняет-
объясняется многообразие разработанных на сегодняшний день математиками-статистиками
критериев экспоненциальности, основные из которых представлены в настоящем
разделе.
3.3.1. Критерий Шапиро-Уилка
Критерий предложен Шапиро и Уилком [298]. Предположим, имеется выборка
%\ ^ %2 ^ • • • ^ %nj причем начальная точка распределения неизвестна, т. е. рассма-
рассматривается плотность вероятностей
1 ( х ¦
f(x) = -ехр
v \ v
с неизвестным параметром /л.
Тогда статистика критерия имеет вид
WE =
или при п —У оо (п > 50)
wE= i
Гипотеза экспоненциальности наблюдаемого распределения не отклоняется с до-
достоверностью а, если W\(a) ^ We ^ W^l»), где W\{a) и М^(«) —критические зна™
чения, приведенные в табл. 81.
Для случая цензурированной выборки, когда отсутствуют г\ наименьших и г2
наибольших членов выборки, модификация критерия Шапиро^Уилка рассмотрена
в [299]. Его статистика в этом случае имеет вид
W, =
\ГЬ — Г\—Г2)гр гр
СХ-- -*• ri_i_i-*¦ П + 7
1 = 1
где
Тг = (п-г + 1)(^-^_1), г = 2, ...,п;
(п) _ г — 1 / (п) _ (п). • • _ 9
280 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Таблица 81
Критические значения
критерия экспоненциальности We Шапиро^Уилка [13, 298]
п
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
а =
Шг(а)
0,071
0,062
0,058
0,056
0,052
0,050
0,046
0,043
0,040
0,038
0,034
0,031
0,029
0,028
0,027
0,90
W2(a)
0,358
0,301
0,261
0,231
0,208
0,191
0,173
0,159
0,145
0,134
0,120
0,109
0,102
0,095
0,091
а =
0,062
0,054
0,050
0,049
0,046
0,044
0,040
0,038
0,036
0,034
0,030
0,028
0,026
0,025
0,024
0,95
W2(a)
0,404
0,342
0,301
0,261
0,234
0,215
0,195
0,178
0,163
0,150
0,135
0,123
0,114
0,106
0,101
п
22
23
24
25
26
27
28
29
30
31
32
33
34
35
а =
Шг{а)
0,026
0,025
0,024
0,023
0,022
0,022
0,021
0,021
0,020
0,019
0,019
0,018
0,018
0,018
0,90
W2(a)
0,084
0,078
0,074
0,070
0,066
0,063
0,061
0,058
0,054
0,052
0,050
0,048
0,047
0,045
а =
Wt(a)
0,023
0,022
0,021
0,021
0,020
0,020
0,019
0,019
0,018
0,017
0,017
0,017
0,017
0,016
0,95
W2(a)
0,094
0,087
0,082
0,078
0,073
0,070
0,067
0,064
0,060
0,057
0,055
0,053
0,051
0,049
Критические значения статистики W\ находятся из табл. 81 с заменой п на
п — Г\ — Г2, т. е. гипотеза экспоненциальности не отклоняется, если
W1(n_ri_r2)(a) ^W^ W2(n_ri_r2)(a).
Если начальная точка известна (предположим, /л = 0, что всегда можно сделать
заменой Х{ на Х{ — /i), то статистика Шапиро^Уилка имеет вид
Гипотеза экспоненциальности не отклоняется, если
где Wi(a), W2(a)—критические значения, приведенные в табл. 82.
Вместо статистики We0 можно воспользоваться статистикой [300]
У^ Xi
критические значения которой совпадают с Wi(a) и W~2(a) (см. табл. 81, в которой п
следует заменить на (п + 1)).
Для случая цезурирования справа статистика заменяется на
'if1 г,
Е Е 4Г2
%=2 j=2
8.8]
Критерии проверки экспоненциальности распределения
281
Таблица 82
Критические значения
критерия экспоненциальности We0 Шапиро^Уилка [13, 298]
п
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
а =
Шг(а)
0,033
0,032
0,031
0,030
0,030
0,029
0,028
0,027
0,026
0,025
0,024
0,024
0,023
0,023
0,022
0,90
W2 (a)
0,225
0,200
0,177
0,159
0,145
0,134
0,124
0,115
0,106
0,098
0,093
0,087
0,083
0,077
0,074
а =
0,025
0,025
0,025
0,025
0,025
0,025
0,025
0,024
0,024
0,023
0,023
0,022
0,022
0,021
0,020
0,95
W2(a)
0,260
0,230
0,205
0,184
0,166
0,153
0,140
0,128
0,119
0,113
0,107
0,101
0,096
0,090
0,085
п
22
23
24
25
26
27
28
29
30
31
32
33
34
35
а =
Шг{а)
0,022
0,021
0,021
0,020
0,020
0,020
0,019
0,019
0,019
0,018
0,018
0,018
0,017
0,017
0,90
W2 (a)
0,069
0,065
0,062
0,058
0,056
0,054
0,052
0,050
0,048
0,047
0,045
0,044
0,043
0,041
а =
Wt(a)
0,020
0,019
0,019
0,018
0,018
0,017
0,017
0,016
0,016
0,016
0,015
0,015
0,014
0,014
0,95
W2(a)
0,080
0,075
0,069
0,065
0,062
0,058
0,056
0,054
0,053
0,051
0,050
0,048
0,046
0,045
Ее критические значения совпадают с критическими значениями статистики We0
(см. табл. 82 с заменой п на (п — г2 + 1)).
Задача 125. Имеется ряд наблюдений
хц 1, 2, 4, 5, 9, 11, 18, 21, 29, 35.
Проверить соответствие распределения вероятностей случайной величины^ представ-
представленной этой выборкой^ экспоненциальному распределению при достоверности а = 0,95.
Рассмотреть случаи неизвестного начала распределения (ji неизвестно) и известного
значения fi = 1.
Случай 1 (fi неизвестно)
Вычисляем х = 13,5; (ж - хгJ = C,5 - IJ = 156,25;
10 56?25
Тогда WE =
Xi ~ *) = 1256,5.
5 = 0,138. Из табл. 81 для а = 0,95 и п = 10 находим И^@,95) =
9- 1256,5
= 0,049 и W2@,95) = 0,261.
Так как Wi@,95) < We < W2@,95), гипотеза экспоненциальности распределения не
отклоняется.
Случай 2 (/i = 1)
Находим эквивалентный ряд Х{ — /1 = Х{ — 1:0, 1, 3, 4, 8, 10, 17, 20, 28, 34, для которого
имеем х = 12,5; J2(xi ~ xf = 1256,5 и CExif = 156,25.
1256 5 ~
Тогда WEq = = 0,08. Из табл. 82 для а = 0,95 и п = 10 находим Wt(a) = 0,025
15625
и W2(a) =0,184.
Так как #i@,95) = 0,025 < WEo = 0,08 < #2@,95) = 0,184, гипотеза экспоненциала
ности не отклоняется.
1 КЯ9Я
= 0,101.
IU • ^11 • Z5iy — HOb'ZZ))
Из табл. 81 для п
Вычисляем статистику We^ = ;
J ° 10 • A1 • 2819 - 15625)
= 11 и а = 0,95 имеем Wi@,95) = 0,046 и VF2@,95) = 0,234, что
также не позволяет отклонить гипотезу экспоненциальности, так как We0 не выходит за
пределы критического диапазона.
282 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Задача 126. Проверить гипотезу экспоненциальности для ряда наблюдений, пред-
представленного в задаче 125, при условии, что первое и два последних наблюдения цен-
зурированы (для случая, когда fi неизвестно и а = 0,95).
Имеем п = 1 и гч = 2 (п — г\ — гч = 7). Находим
Т3 = 8 • (х3 - х2) = 8 • 2 = 16; Т4 = 7 • (ж4 - ж3) = 7; Г5 = 6 • (хъ - х4) = 24;
Т6 = 5 • (х6 - хъ) = Ю; Т7 = 4 • (ж7 - ж6) = 28; Г8 = 3 • (х8 - х7) = 9.
Вычисляем
(п-п-^) _ G) _
^~ 1
7 - j + 1 8 - j
a43 = ^5 a53 = ^5 a63 = g? a73 = ^5 a44 = j5 a54 = ^5 a64 = j5
G) 6 G) 4 G) 5 G) 6 G) 5 G) 6 G) 6
a74 — л •) a55 — о ' 5 — о ' 5 ~ о ? a66 ~ r, 5 a76 ~ o ? a77 ~ -, •
4 о о О А А I
Далее получаем
/l 2 3 5 5 6 \
6 . I - . Гз . Гз + - . Гз . T4 + - ¦ T3 . T5 + ... + - . T6 . T7 + - ¦ T7 . T7 + - . T7 . T8 I =
Находим (Г3 + Т4 + ... + Т7 + Т8J = A6 + 7 + ... + 28 + ЭJ = 8836.
Окончательно получаем W\ = = 0,220. Из табл. 81 для П — Г1—Г2 = 7 и а = 0,95
J 40056 '
находим Wi@,95) = 0,062 и W2@,95) = 0,404.
Так как Wi@,95) = 0,062 < WE = 0,220 < W2@,95) = 0,404, гипотеза экспоненциаль-
экспоненциальности распределения вероятностей случайных величин не отклоняется.
3.3.2. Критерии типа Колмогорова—Смирнова
Модификации известных критериев типа Колмогорова^Смирнова для приме-
применения их при проверке экспоненциальности закона распределения вероятностей
(с неизвестными параметрами) наиболее полно представлены в [301, 302].
Предположим, имеет место гипотетический закон распределения вероятностей
F(x) = 1 — ехр| — 1, где \х и v — неизвестные параметры, оценки которых по
выборке могут быть найдены из формул (отметим, что выборка упорядочена, т. е.
хг ^ х2 <* ... ^ хп)
nix — xi) л и
v = — —L\ /л = хг .
п—\ п
Обозначив Wi = ^-^—, переходим к нормированному экспоненциальному рас-
распределению Zi = 1 — exp(^ti^), для которого имеем аналоги известных статистик
критериев согласия
— критерий Колмогорова-Смирнова (см. раздел 3.1.2.1):
\ i 1 Г г- ll
J9+ = max Zi\; D^ = max zi ; Dn = max(J9+, D~) ;
1 ln \ % L n 1
— критерий Андерсона-Дарлинга (см. раздел 3.1.2.4):
А2
.... i-i)l — n;
3.3]
Критерии проверки экспоненциальности распределения
283
— критерий Смирнова-Крамера-фон Мизеса (см. раздел 3.1.2.2):
— критерий Ватсона (см. раздел 3.1.2.5):
2
Yin'
где z = -
— критерий Купера (см. раздел 3.1.2.6):
V = D++D-.
Для случая проверки экспоненциальности распределения с неизвестными пара-
параметрами критические значения перечисленных статистик для различных уровней
значимости приведены в табл. 83.
Таблица 83
Критические значения статистик
критериев согласия типа Колмогорова^Смирнова
для проверки экспоненциальности распределения
с неизвестными параметрами [301]
п
5
10
15
20
25
50
100
оо
5
10
15
20
25
50
100
оо
5
10
15
20
25
50
100
оо
0,25
Уровень значимости
(верхние процентные то
0,15
0,10
0,05
а
чки)
0,025
0,01
Статистика л/пВп
0,683
0,753
0,771
0,786
0,792
0,813
0,824
0,840
0,749
0,833
0,865
0,872
0,878
0,879
0,911
0,927
0,793
0,889
0,912
0,927
0,936
0,960
0,972
0,995
0,865
0,977
1,002
1,021
1,033
1,061
1,072
1,094
0,921
1,048
1,079
1,099
1,115
1,149
1,171
1,184
0,992
1,119
1,163
1,198
1,215
1,257
1,278
1,298
Статистика V
1,098
1,194
1,225
1,245
1,260
1,292
1,310
1,334
1,186
1,294
1,325
1,346
1,366
1,400
1,419
1,444
1,234
1,363
1,392
1,419
1,438
1,481
1,502
1,532
1,314
1,461
1,504
1,536
1,559
1,600
1,647
1,656
1,400
1,556
1,596
1,635
1,658
1,701
1,740
1,770
1,494
1,662
1,701
1,769
1,796
1,847
1,897
1,910
Статистика W
0,083
0,097
0,103
0,106
0,107
0,111
0,113
0,116
0,102
0,122
0,130
0,133
0,135
0,141
0,144
0,148
0,117
0,142
0,151
0,157
0,160
0,166
0,170
0,175
0,141
0,176
0,188
0,195
0,199
0,209
0,215
0,222
0,166
0,211
0,229
0,237
0,247
0,256
0,263
0,271
0,197
0,259
0,281
0,293
0,301
0,319
0,328
0,338
284 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
те
5
10
15
20
25
50
100
оо
5
10
15
20
25
50
100
оо
0,25
Око
нчани
Уровень значимости
е т а б л
и ц ы 83
а
(верхние процентные точки)
0,15
0,10
0,05
0,025
0,01
Статистика U2
0,068
0,075
0,080
0,082
0,083
0,087
0,089
0,090
0,083
0,094
0,099
0,102
0,104
0,108
0,110
0,112
0,093
0,108
0,114
0,117
0,119
0,124
0,126
0,129
0,113
0,131
0,139
0,143
0,146
0,152
0,155
0,159
0,131
0,155
0,165
0,170
0,173
0,180
0,184
0,189
0,153
0,187
0,200
0,207
0,212
0,223
0,229
0,236
Статистика А2
0,460
0,545
0,575
0,608
0,625
0,680
0,710
0,736
0,555
0,660
0,720
0,757
0,784
0,838
0,875
0,910
0,621
0,747
0,816
0,861
0,890
0,965
1,008
1,062
0,725
0,920
1,009
1,062
1,097
1,197
1,250
1,321
0,848
1,068
1,198
1,267
1,317
1,440
1,510
1,591
0,989
1,352
1,495
1,580
1,635
1,775
1,865
1,959
Для п ^ 5 верхние процентные точки распределения статистик вполне удо™
влетворительно совпадают с предельными распределениями при использовании
модификаций, приведенных в табл. 84.
Таблица 84
Процентные точки модифицированных критериев типа
Колмогорова—Смирнова длм проверки экспоненциальности распределения
Статистика
w2
и2
А2
Модификация
/ 9 о о \
W2 | 1 _|_ ' 1
^ + 7"?j
/ 2 3 3 \
V+ ~п~ ~ г?/
\ п тг2/
0,25
0,116
0,090
0,736
Уровень значимости
0,15
0,148
0,112
0,916
0,10
0,175
0,129
1,062
0,05
0,222
0,159
1,321
а
0,025
0,271
0,189
1,591
0,01
0,338
0,230
1,959
Задача 127. Проверить гипотезу экспоненциальности распределения вероятностей
случайных величин в условиях задачи 125 на уровне значимости а = 0,05 критериями
типа Колмогорова-Смирнова.
Имеем х = 13,5; v =
Далее вычисляем
10- A3,5™ 1)
9
= 13,889; Д = 1 -
13,889
10
= -0,3889.
- Д 1 + 0,3889
= 0,1; Zi = 1-е'1 =0,0952;
i> 13,889
W2 = 0,172; z2 = 0,1580; W3 = 0,136; z3 = 0,2709; W4 = 0,388; z4 = 0,3216;
W5 = 0,676; z5 = 0,4913; W6 = 0,820; z6 = 0,5596; FF7 = 1,324; z7 = 0,7339;
W8 = 1,540; z8 = 0,7856; W9 = 2,116; z9 = 0,8795; Wio = 2,548; z10 = 0,9218.
3.3]
Критерии проверки экспоненциальности распределения
285
Критерий Колмогорова-Смирнова
Результаты расчетов представлены в таблице:
г
1
2
3
4
5
6
7
8
9
10
г
п
ОД
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
0,0952
0,1580
0,2709
0,3216
0,4913
0,5596
0,7339
0,7856
0,8795
0,9218
г
%г
п
0,0048
0,0420
0,0291
0,0784
0,0087
0,0404
-0,0339
0,0144
0,0205
0,0782
ъ - 1
п
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
i - 1
п
0,0952
0,0580
0,0709
0,0216
0,0913
0,0956
0,1339
0,0856
0,0795
0,0218
Из таблицы видим, что
D+ max | zA = 0,0784; D~ = max Zi -
Dn = max(D+,D~) = 0,1339.
i- 1
= 0,1339;
Значение статистики критерия равно у/п • Dn = \/Тб • 0,1339 = 0,423.
Из табл. 83 для а = 0,05 и п = 10 находим, что критическое значение статистики
равно 0,97. Так как ^/п • Dn = 0,423 < 0,97, гипотеза экспоненциальное™ распределения
вероятностей случайных величин не отклоняется.
Критерий Купера
Статистика критерия равна
y^-Vn = л/п- (D+ + D~) = \/l0 • @,0784 + 0,1339) = 0,671.
Из табл. 83 для а = 0,05 и п = 10 находим критическое значение, равное 1,461.
Так каку^гг • Vn = 0,671 < 1,461, гипотеза экспоненциальности не отклоняется.
Вычисляем
Критерий Андерсона--Дарлинга
А2 = -— • |l • [1п0,0952 + ln(l - 0,9218)] + 3 • [In0,158 + ln(l - 0,8795)] +
+ 5 • [In 0,2709 + ln(l - 0,8756)] + 7 • [In 0,3216 + ln(l - 0,7339)] +
+ 9 • [In 0,4913 + ln(l ~~ 0,3216)] + 11 • [In 0,5596 + ln(l - 0,4913)] +
+ 13 • [In 0,7339 + ln(l - 0,3216)] + 15 • [In 0,7856 + ln(l - 0,2709)] +
+ 17 • [In 0,8795 + ln(l - 0,158)] + 19 • [In 0,9218 + ln(l - 0,0952)]} - 10 = 0,17988.
Из табл. 83 для п = 10 и а = 0,05 находим критическое значение А2 @,05) = 0,920 или
для модифицированного критерия
(А2У = А2 . A + ** - ^] = 0,17988 . Л + М _ iL) = 0,257,
1 ; V п п2) \ Ю 100/
критическое значение которого из табл. 84 равно 1,321. Далее имеем
А2 = 0,17988 < А2@,05) = 0,920; (А2)' = 0,257 < (А2@,05)); = 1,321,
и гипотеза экспоненциальности не отклоняется.
286 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Критерий Смирнова-Крамера-фон Мизеса
Вычисляем статистики критерия
1 =@,0952-^) +@,158- — ) + @,2709 —^ ) + @,3216-^-
V 20/1 20/1 20/1 20
0,4913-—] + f 0,5596 — — J + f 0,7839 ^ — J + @,7856 - —
2 ( 1 +
+ f 0,8795 1 + f 0,9218 1 + =0,0234
и (W2)' =W2 • [ 1 + — - -^ ) = 0,0234 • A + 0,28 - 0,03) = 0,0295.
V n n ZJ
Из табл. 84 имеем критическое значение статистики
(W2(a))f = 0,222 (для п = 10 ш а = 0,05).
Так как {W2)' = 0,0292 < (М^2@,05)); = 0,222, гипотеза экспоненциальности не отклоня-
отклоняется.
Критерий Ватсона
z=--J2zi =0,52174;
U2 = W2 - п > (z - - ] = 0,0234 - 10 • @,52174 - 0,5J = 0,01877;
(U2)' = U2 • ( 1 + — - АЛ = 0,01877 • A + 0т23 - 0,03) = 0,0255.
х J у п пА)
Из табл. 84 для п = 10 и а = 0,05 имеем критическое значение (U2(a))' = 0,159. Так
как {U2)' = 0,0225 < (С/2(а))' = 0,159, гипотеза экспоненциальности распределения не
отклоняется.
3.3.3. Критерии типа Смирнова-Крамера-фон Мизеса
для пензурированных данных
Рассматривается выборка, в которой все наблюдения, большие, чем некоторая
величина хр, цензурированы, т. е. в распоряжении наблюдателя есть только г на™
блюдений из выборки объема п, удовлетворяющих условию 0^Xi^X2^...^%.
Необходимо проверить гипотезу о том, что ряд наблюдений извлечен из выборки
с функцией распределения вероятностей
F(x) = 1-ехр( -- ] .
Оценкой v по выборке является
1
и = -
г
i + (п ^ г) 2
Оценкой степени цезурирования р является величина
/ j
Применение критерия Смирнова—Крамера—фон Мизеса (см. раздел 3.1.2.2) для
цензурированных выборок рассмотрено в [304]. Полагая, что Zi = 1 ^expj — — 1,
3.3]
Критерии проверки экспоненциалъности распределения
287
запишем статистику критерия в виде
г=1
2г -
1
127*
Критические значения статистики Wjj для выборок со степенью цензурирова™
ния р для различных уровней значимости приведены в табл. 85.
Таблица 85
Критические значения статистики
(а — уровень значимости) [304]
а
0,15
0,10
0,05
0,025
0,01
Степень цензурирования р
0,5
0,0531
0,0635
0,0821
0,1015
0,1279
0,6
0,0720
0,0857
0,1103
0,1359
0,1710
0,7
0,0921
0,1093
0,1401
0,1721
0,2160
0,8
0,1126
0,1333
0,1702
0,2087
0,2613
0,9
0,1321
0,1561
0,1986
0,2433
0,3033
1,0
0,1480
0,1745
0,2216
0,2706
0,3376
Рекомендуется использовать модифицированную форму критерия
2,8 3
\VVp) — Wp \ L + „ 2 '
Естественно, при р = 1 (отсутствие цензурирования) критические значения стати-
статистики совпадают с приведенными в табл. 84.
Задача 128. Проверить гипотезу экспоненциалъности распределения случайных ве-
величин в условиях задачи 125 на уровне значимости а = 0,05 критериями Смирнова-
Крамера-фон Мизеса и Колмогорова-Смирнова при условии, что все наблюдения,
большие хр = 20, цензурированы.
Имеем г = 7 и хр = 20. Вычисляем
v=\
+ (Ю - 7) • 20 =15,71428; р = 1 - ехр(-
Д°
) =
= 1 — exp f —
15,71428/
= 0,06165; z2 = 0,1195; z3 = 0,22473;
0,72;
15,71428
z4 = 0,2725; z5 = 0,4360; z6 = 0,5034; z7 = 0,6819.
Далее
=( 0,06165 - ±
-^] + [0,22473-^
2
0,2775
20
0,4360 - -
0,5034 - g
0,6819 - Н
1
12 -7
- = 0,023
Из табл. 85 для а = 0,05 и р = 0,72 экстраполяцией получаем (Wp @,05)); = 0,15. Так
как (WpY = 0,0308 < (Wp(a))' = 0,15, гипотеза экспоненциальное™ не отклоняется.
288 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.3.4. Критерий Фроцини
В [239] рассмотрен критерий экспоненциальности, основанный на статистике
г -0,5
г=1
l-exp -— -
критические значения которой Вп(а) приведены в табл. 86.
Таблица 86
Критические значения Вп(а) критерия экспоненциальности
Фроцини (а — доверительная вероятность)
п
5
6
7
8
9
10
11
12
13
а
0,90
0,3261
0,3241
0,3292
0,3289
0,3365
0,3377
0,3334
0,3318
0,3313
0,95
0,3687
0,3666
0,3742
0,3740
0,3800
0,3820
0,3790
0,3784
0,3768
0,99
0,4499
0,4495
0,4584
0,4609
0,4660
0,4753
0,4710
0,4641
0,4631
п
14
15
16
17
18
19
20
оо
а
0,90
0,3373
0,3364
0,3345
0,3387
0,3360
0,3370
0,3351
0,3380
0,95
0,3821
0,3837
0,3777
0,3806
0,3814
0,3844
0,3795
0,3840
0,99
0,4656
0,4747
0,4693
0,4716
0,4730
0,4796
0,4738
0,4760
Мощность критерия не уступает всем известным до п ^ 20 и превосходит их при
п > 50.
Задача 129. В условиях задачи 125 проверить гипотезу экспоненциальности рас-
распределения вероятностей случайных величин критерием Фроцини при доверительной
вероятности а = 0,95.
Находим при х = 13,5
10
П ?\
В = ^^ • ( 1 — ехр
13,5
10
1 , - , 1,5
1 — ехр
1 \ 1 q к I in
13,5
10
9 к
¦^1 1 О С I 1П
13,5
10
= 0,0974.
Из табл. 86 для п = 10 находим Бп@,95) = 0,38.
Так как Вп = 0,097 < Вп@,95) = 0,38, гипотеза экспоненциальности распределения
не отклоняется.
3.3.5. Корреляционный критерий экспоненциальности
Рассмотрим функцию распределения
х — .
F(x) = l-exp( -
параметры которой оцениваются по формулам
т(х — х\)
v =
п-1
и IX = Х\ ,
В [301] рассмотрен критерий экспоненциалвности, аналогичнвш корреляционно™
му критерию Филлибена проверки нормальности распределения (см. раздел 3.2.2.4).
3.3]
Критерии проверки экспоненциальности распределения
289
Статистика критерия основана на коэффициенте корреляции г между нормирован™
ной переменной zi = —^т— и математическим ожиданием г-й порядковой етатисти-
ки из экспоненциального распределения, представленного выборкой объема п [303]:
m<j =
Если вместо точного значения mi используется (при п > 20) его аппроксимация
Ы = -1п[ 1
, то соответствующий коэффициент корреляции будем обо-
обозначать r(z,m). Статистика критерия используется в форме
K(z,m) = n[l — r2(z,m)] или K(z,m) = n[l — r2(z,m)] .
Критические значения статистик приведены в табл. 87.
Таблица 87
Критические значения K(zj m, о) и K(z^ m, a)
корреляционного критерия экспоненциальности
(а — уровень значимости) [303]
5
10
15
20
25
50
100
K(z, га, а)
а = 0,10
1,005
1,560
1,935
2,260
2,425
3,350
4,300
а = 0,05
1,305
1,920
2,445
2,820
3,075
4,250
5,700
а = 0,01
1,960
2,720
3,480
4,200
4,725
7,150
10,500
K(z,rh, a)
а = 0,10
0,960
1,540
1,980
2,320
2,550
3,650
5,000
а = 0,05
1,175
1,990
2,550
3,040
3,375
5,050
6,900
а = 0,01
1,760
2,850
3,885
4,820
5,575
8,800
12,900
Задача 130. Проверить гипотезу экспоненциальности распределения в условиях за-
задачи 125 корреляционным критерием на уровне значимости а = 0,10.
Имеем 0 = Ю-A3,5-1) = 13>889; д = ! _ 13^9 = _
Получаем ряд нормированных переменных
zn 0,1; 0,172; 0,316; 0,388; 0,676; 0,820; 1,324; 1,540; 2,116; 2,548.
Вычисляем
10
= — + - =0,2111; ш3 = 0,33611; т4 = 0,47897; т5 = 0,64563;
m6 = 0,84563; m7 = 1,09563;
Тогда
J2(zi ^zf =6,513696;
т8 = 1,42897; т9 = 1,92897; т10 = 2,92897.
(Zi ^z) = 6,66388;
г=1
r(z,m) = 6,66388- F,513696-7,07104)^2 =0,98191;
K(z,m) = 10 • A - 0,981912) = 0,358.
10 А. И. Кобзарь
290 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Из табл. 87 для а = 0,10 и п = 10 находим критическое значение K(z,m,a) = 1,56,
и так как полученное значение K(z, га) = 0,358 меньше критического 1,56, гипотеза
экспоненциальности не отклоняется.
( i \
Если бы мы вместо rrii использовали аппроксимацию тхц = — In I 1 1, то полу-
V п + 1)
чили бы
- — )= 0,0953; m2 = 0,20067;
m3 = 0,31834; m4 = 0,4520; m5 = 0,6061; m6 = 0,7884;
m7 = 1,0116; m8 = 1,2993; m9 = 1,7047; m10 = 2,3979;
-шJ= 4,836; m = 0,887428; ^{Zi - z) • (пц - m) = 5,55767;
г=1 г=1
r(z, m) = 5,55767 • F,513693 • 4,836)" 2 = 0,99023; K(z, m) = 10 • (l - 0,990232) = 0,194,
что меньшее, чем критическое значение K^z,rh,a) = 1,99 (см. табл. 87).
Следовательно, и в этом случае гипотеза экспоненциальности не отклоняется.
3.3.6. Регрессионный критерий Брейна-Шапиро
Если Ж]_, ..., хп — порядковые статистики из экспоненциального распределения
с плотностью
f{x) = Аехр{^А(ж — /i)} ,
то случайные величины у^ = (п — г + 1) (х{ — Xi—\) являются независимыми и иден-
идентично распределенными экспоненциальными величинами.
В [305] предложен весьма эффективный критерий экспоненциальности, основан™
ный на наклоне линии регрессии взвешенных спейсингов у± (т. е. разности смежных
членов выборки) на их порядковые номера г. Так как интенсивность отказов для
экспоненциального распределения А = const, то проверка экспоненциальности эк™
вивалентна проверке равенства нулю угла наклона регрессии у^ = /(г) (о регрессии
можно прочитать в главе 5).
Для общего случая цензурированной выборки, когда отсутствуют s наименьших
и г наибольших наблюдений (га = п — г — s), статистика критерия имеет вид
El ¦ llh \ ( -\
( г - "Т ) (У^+г+1 - У)
-i m — 1
где у = \^ T/S_|_^_|_i, или в более компактной форме
771—1 Z—'
3.3] Критерии проверки экспоненциальности распределения 291
Если ввести обозначения
1 U
^ = Цу*+*+ь (* = 1, •••jra-1); Щ = %_ , (г = 1,...,ш- 2),
J=i *™
то z = у/\2{т - 2) ( U - — 1, где U = ^^ •
Если s = 0 и \л известно, то m = в ^ г + 1 и t{ = ^ t/j (j = 1, ..., га — 1), т. е.
добавляется спейсинг n(#i — /л).
Гипотеза экспоненциальности отклоняется на уровне значимости а, если|^| > и& ,
где и а —( 1 -квантиль стандартного нормального распределения.
2 \ 2 /
z-критерий используется против альтернативы, утверждающей, что интенсив-
интенсивность отказов (параметр Л) монотонно изменяется в выборке.
Для альтернативы, утверждающей, что интенсивность отказов меняется моно-
монотонно, предложена статистика
т — 1 т — 1
12 У o?ys+*+i - т(т - 2) V ye+»+i
Э I i=l г=1
4(m + l)(m - 2)(ife - 3)
где щ = г ——, г = 1, ... ,га — 1, или
I f
2
5^ 2/s+i+i
5(^^2) 14 Q , я, 1WT 12
(m+l)(m-3)
Статистика имеет стандартное нормальное распределение. Если априорные све-
сведения о возможном характере альтернативы отсутствуют, рекомендуется исполь-
использовать комплексную статистику z* = z2 + z2, критические значения которой при
доверительной вероятности а можно вычислить по формулам
4,605 - —, при а = 0,90;
1 2е!
5,991^ —, при а = 0,95:
т
ч ччч
7,378 + , при а = 0,99.
Исследования авторов работы [305] позволяют сделать вывод о высокой мощности
этого критерия.
Задача 131. Для данных задачи 125 проверить гипотезу экспоненциальности ре-
регрессионным критерием Брейна—Шапиро при доверительной вероятности а = 0,95.
Известно, что цензурированию подверглось первое (х\ = 11; s = 1) и два наибольших
(xq = 29 и хю = 35) значения (г = 2).
Имеем т = 10 ^1^2 = 7. Находим ys+i+i = У2+% и для г = 1, ..., 6 получаем:
уз = (Ю - 3 + 1) • (хз - х2) = 8 • D - 2) = 16; у4 = (Ю - 4 + 1) • (х4 - х3) = 7;
2/5 = 24; 2/6 = 10; у7 = 28; у8 = 9;
ю*
292 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
= 2/з = 16; t2 = J2 2/2+i = 2/3 + 2/4 = 23; t3 = ^ y2+j = 23 + t/5 = 47;
t4 = 57; t5 = 85; t6 = 94;
г = — = — = 0,17023; U2 = — = 0,2447; U3 = 0,5; U4 = 0,6064; l/5 = 0,9042;
te 94 94
17 = 0,4851.
Далее вычисляем
z ={12 • G - 2)}i • @,4851 - 0,5) = -0,11541; z2 = 0,01332;
5
Y,i'Ui = 0,1702 + 2 • 0,2447 + ... + 5 • 0,9042 = 9,1062;
7-3 + 6.6.0,4851-у .
= 0,88388 • B1,4636 - 2,4 • 9,1062) = ^0,34584; z* = 0,0133 + 0,1196 = 0,13229.
Так как z* = 0,13229 < z* = 5,991
1 25
= 5,812, гипотеза экспоненциальное™ не откло-
откло3.3.7. Критерий Кимбера—Мичела
Кимбер [306] рассмотрел еще один критерий, основанный на линейной зависи-
зависимости между теоретической F(x) и эмпирической Fn(x) = — функциями распре-
распределения вероятностей случайных величин. Для того, чтобы стабилизировать эту
зависимость и ослабить влияние неравных дисперсий F(x) и Fn(x), Мичел [307]
предложил стабилизирующие преобразования
Si = — arcsln \/F(xi);
При п —)> оо и > р асимптотическая дисперсия
П Si
Статистика критерия имеет вид
D = max Wj ~~ S
j, т. е. не зависит от р.
в т.ч. для случая F(z) = 1 — exp(^z), где z = -г—стандартизированная случай™
ная экспоненциальная величина (у = — ^ xi). Критические значения D-статистики
приведены в табл. 88.
Таблица 88
Критические значения D{ol)
статистики Кимбера—Мичела [307]
п
3
4
5
6
8
10
14
Уровень значимости а.
0,10
0,240
0,232
0,222
0,216
0,198
0,185
0,166
0,05
0,265
0,265
0,251
0,244
0,223
0,208
0,185
0,01
0,301
0,310
0,301
0,296
0,272
0,253
0,226
п
20
30
40
60
80
100
Уровень значимости а
0,10
0,147
0,126
0,113
0,096
0,085
0,077
0,05
0,163
0,140
0,125
0,106
0,094
0,085
0,01
0,199
0,171
0,152
0,129
0,114
0,103
3.3] Критерии проверки экспоненциальности распределения 293
Мощность этого критерия для многих альтернатив выше, чем мощность крите™
риев Колмогорова-Смирнова (см. раздел 3.3.2) и Шапиро-Уилка (см. раздел 3.3.1).
Применение критерия подобного типа для построения критерия согласия с двухпа-
раметрическим распределением Вейбулла рассмотрено в [308].
Задача 132. Проверить гипотезу экспоненциальности распределения случайных вели-
величин для данных задачи 125 критерием Кимбера-Мичела на уровне значимости а = 0,05.
Находим
2 Г / 1 М i
si = - • arcsin 1 - exp = 0,172198;
7Г [ V 13'5Л
s2 = 0,24202; s3 = 0,33804; s4 = 0,37559; s5 = 0,49146;
s7 = 0,65676; s8 = 0,69611; s9 = 0,77805; sio = 0,823609;
n = - • arcsIn@,05J = 0,143564; r2 = 0,253183; r3 = 0,3333; r4 = 0,4030;
7Г
r5 = 0,4681; r6 = 0,5319; r7 = 0,5970; r8 = 0,6666; r9 = 0,7468; no = 0,8564.
Получаем ряд значений
г{-8{\: 0,0286; 0,0112; 0,00471; 0,0274; 0,0404; 0,00464; 0,05976; 0,0295;
0,03125; 0,03279.
Тогда D = max|ri — Si\ = 0,05976. Из табл. 88 для п = 10 и а = 0,05 находим
i
D(pt) = 0,208. Так как D = 0,05976 < D(ot) = 0,208, гипотеза экспоненциальности не от-
отклоняется.
3.3.8. Критерий Фишера
Если мы имеем ряд #i, #2, • • • ? хт то статистика критерия имеет вид
F =
(п -
Эта статистика при справедливости нулевой гипотезы (т. е. экспоненциальности
распределения) имеет ^распределение Фишера с /i = 2n ™ 2 и /2 = 2 степенями
свободы. Если
г=1
(п — 1) xi
где Fa(/i,/2) — а • 100%-е критическое значение F-статистики с /i и /2 степенями
свободы, то нулевая гипотеза экспоненциальности отклоняется.
Критические значения F-статистики могут быть определены по таблицам рас™
пределения Фишера, например, в [24, 25, 29, 57] или с помощью аппроксимаций,
приведенных в разделе 1.1.10.
Задача 133. Проверить гипотезу экспоненциальности критерием Фишера для данных
задачи 125 при уровне достоверности а = 0,95.
135
Имеем п = 10, х\ = 1 и ^ а?г = 135, F = = 15. Из таблиц распределения Фише-
Фишера [25] для Fo,95A8,2) находим Fo,95A8,2) = 19,3.
Так как F = 15 < Fo,95 A8,2) = 19,3, гипотеза экспоненциальности не отклоняется.
294 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.3.9. Критерий Бартлетта-Морана
Статистика критерия, вычисляемая по ряду значений #i,#2> • • • ->хпч имеет вид
[309, 310]
В =
1 +
12n
TnTT
При n ^ 20 распределение статистики В удовлетворительно аппроксимируется
Х2™распределением с f = n — l степенями свободы [95]. Поэтому нулевая гипо™
теза экспоненциальности отклоняется, если В > Х^(п ~ 1) на уровне значимости
()
Задача 134. В условиях задачи 125 проверить гипотезу экспоненциальности крите-
критерием Бартлетта-Морана при а = 0,95.
Имеем
1 п 2 • 100
х = 13,5; In ж = 2,6027; - • ^ 1пж* = 2,1141; В = • B,6027 + 2,1141) = 357867.
Из табл. 55 для / = w- 1 = 9и а = 0,95 находим Хо,9б(9) = 16,919.
Так как В = 13,2867 < %о,95(9) = 16,919, гипотеза экспоненциальности не откло™
няется.
3.3.10. Критерий Климко-Антла-Радемакера-Рокетта
В [311] рассмотрен критерий экспоненциальности, основанный на проверке ра™
венства единице коэффициента формы /3 в распределении Вейбулла с функцией
= 1 - exp j-
Известно (см. раздел 1.1.5), что при /3 = 1 распределение Вейбулла переходит
в экспоненциальное распределение. Поэтому проверка гипотезы Hq : C = 1 про-
против альтернативы Нi: /3 > 1 эквивалентна проверке гипотезы экспоненциальности
распределения против альтернативы, утверждающей, что распределение является
вейбул л овским.
Для оценки параметра C может быть использована аппроксимация [312] с ~ г/'075,
где v = — —коэффициент вариации. В общем виде для трехпараметрического рас-
х
пределения Вейбулла имеем
Критические значения статистики с = -у/n (с — 1) приведены в табл. 89. Если с >
то гипотеза C = 1 (гипотеза экспоненциальности) отклоняется.
3.3]
Критерии проверки экспоненциальности распределения
295
Таблица 89
Критические значения статистики
с = у/гь (с — 1)
(а — уровень значимости) [311]
10
20
30
40
50
100
а
0,20
1,14
1,00
0,94
0,90
0,86
0,81
0,10
1,59
1,41
1,34
1,28
1,24
1,19
0,05
2,05
1,80
1,68
1,60
1,58
1,51
0,02
2,68
2,26
2,09
1,97
1,96
1,87
Задача 135. В условиях задачи 125 проверить гипотезу экспоненциалъности рас-
распределения вероятностей случайных величин критерием Климко-Антла-Радемакера-
Рокетта на уровне значимости а = 0,05.
Имеем
= 11,8157; A=1-
- 'J2(Xi - А) = 13ДШ; с =
_ /ll,8157\
10-9
с_\ -1,075
¦@-
- 28 + 34) = ^0,3889;
13,1111/
= 1,1183; с = 10 • (с - 1) = 0,3741.
Из табл. 89 для п = 10 и а = 0,05 находим co,9sA0) = 2,05. Так как с = 0,3741 <
< со,95(Ю) = 2,05, гипотеза /3 = 1 (гипотеза экспоненциальности) не отклоняется.
3.3.11. Критерий Холлендера—Прошана
В задачах теории надежности экспоненциальное распределение наработки на
отказ f(x) = Аехр(^Аж) характеризуется значением параметра А = const, т.е. по™
стоянством интенсивности отказов изделия во времени. Отсюда следует, что ве™
роятность безотказной работы изделия за время At —> exp(^AAt) определяется
только промежутком времени At и не зависит от того, работало ли изделие раньше
или нет. Другими словами, вероятность безотказной работы нового изделия и из-
изделия, проработавшего часть времени, должна быть одинакова. Проверка этого
обстоятельства и является целью критерия Холлендера^Прошана, рассмотренного
в [313, 314].
Процедура вычисления статистики критерия Холлендера^Прошана включает
в себя вычисление для ряда случайных величин х\ ^ Х2 ^ ... ^ хп статистики
где (p(a,b) =
1 при а > Ь;
Суммирование проводится по всем тройкам г, j, /с, для которых
о
г > j > к.
На уровне значимости а гипотеза экспоненциальности принимается, если
ti(a) ^ Т ^ ^2(а), где t\{ot) и ^(ог)—граничные значения для заданных п и а,
приведенные в табл. 90.
296 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Таблица 90
Граничные значения ti(o) и t^iot)
критерия Холлендера^Прошана [313]
п
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
Уровень значимости а.
0,01
2
7
15
27
42
63
89
122
162
209
260
330
405
490
594
1250
2320
3850
5947
8665
12170
35
55
81
114
155
205
264
334
415
508
613
732
866
1015
2018
3521
5625
8418
12012
16519
0,025
ti
1
5
11
21
34
52
176
405
141
185
236
298
368
446
538
642
1351
2463
4064
6214
9040
12661
t2
2
7
14
54
80
112
152
201
260
328
408
499
603
720
852
998
1986
3461
5546
8301
11864
16310
0,05
ti
25
40
60
86
117
157
204
259
323
397
480
577
685
1427
2574
4215
6434
9341
13020
t2
20
34
53
78
110
150
198
255
322
401
491
593
709
838
982
1956
3411
5464
8189
11709
16085
0,
ti
1
4
9
18
30
47
69
97
131
174
223
282
350
429
518
619
732
1507
2704
4394
6700
9686
13439
10
t2
10
19
33
52
76
107
146
193
249
315
392
480
580
693
820
961
1918
3349
5359
8049
11502
15823
Для случаев совпадения X{ = Xj
(xi,Xj +xk), где
используется замена ip(xi,Xj-\-x^) на
1 при а > 6;
{
i при а = b;
0 при a < b.
Для п > 20 может быть использована аппроксимация
где
Т* =
М(Т) =
Т - М(Т)
=
2592
7(п - 3) J_
432 48
Случайная величина Т* распределена при п ^ 20 как стандартная нормальная
случайная величина, и гипотеза экспоненциальности в этом случае принимается на
уровне значимости а, если |Т*| < и1_& , где и7 —7™квантиль стандартного нормаль™
ного распределения.
8.8]
Критерии проверки экспоненциалъности распределения
297
Задача 136. Для данных задачи 125 проверить гипотезу экспоненциалъности крите-
критерием Холлендера-Прошана на уровне значимости а = 0,05.
Результаты вычислений представлены в таблице, из которой находим
Т= J2 <p(xi,Xj+xk) = 102.
Из табл. 90 имеем ti@,05) = 60 и ?2@,05) = НО.
Так как i\ = 60 < Т = 102 < ti = 110, гипотеза экспоненциальности не отклоняется.
%
3
4
5
6
7
8
9
10
4
5
6
7
8
9
10
5
6
7
8
9
10
6
7
8
9
10
7
8
9
10
8
9
10
9
10
10
4
5
6
7
8
9
10
3
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
4
4
4
4
4
4
5
5
5
5
5
6
6
6
6
7
7
7
8
8
9
3
3
3
3
3
3
3
к
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
Xi
4
5
9
11
18
21
29
35
5
9
11
18
21
29
35
9
11
18
21
29
35
11
18
21
29
35
18
21
29
35
21
29
35
29
35
35
5
9
11
18
21
29
35
Xi +a?fc
3
3
3
3
3
3
3
3
5
5
5
5
5
5
5
6
6
6
6
6
6
10
10
10
10
10
12
12
12
12
19
19
19
22
22
30
6
6
6
6
6
6
6
1
1
1
1
1
1
1
1
1/2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
1
г
5
6
7
8
9
10
6
7
8
9
10
7
8
9
10
8
9
10
9
10
10
5
6
7
8
9
10
6
7
8
9
10
7
8
9
10
8
9
10
9
10
10
6
3
4
4
4
4
4
4
5
5
5
5
5
6
6
6
6
7
7
7
8
8
9
4
4
4
4
4
4
5
5
5
5
5
6
6
6
6
7
7
7
8
8
9
5
к
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
4
Xi
9
11
18
21
29
35
11
18
21
29
35
18
21
29
35
21
29
35
29
35
35
9
11
18
21
29
35
11
18
21
29
35
18
21
29
25
21
29
35
29
35
35
11
Xi + Хк
7
7
7
7
7
7
11
11
11
11
11
13
13
13
13
20
20
20
23
23
31
9
9
9
9
9
9
13
13
13
13
13
15
15
15
15
22
22
22
25
25
33
14
1/2
1
1
1
1
1
1/2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1/2
1
1
1
1
1
0
1
1
1
1
1
1
1
1
0
1
1
1
1
1
0
298 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
г
7
8
9
10
7
8
9
10
8
9
10
9
10
10
7
8
9
3
5
5
5
5
6
6
6
6
7
7
7
8
8
9
6
6
6
к
4
4
4
4
4
4
4
4
4
4
4
4
4
4
5
5
5
Xi
18
21
29
35
18
21
29
35
21
29
35
29
35
35
18
21
29
Xi +a?fc
14
14
14
14
16
16
16
16
23
23
23
26
26
34
20
20
20
1
1
1
1
1
1
1
1
0
1
1
1
1
1
0
1
1
г
10
8
9
10
9
10
10
8
9
10
9
10
10
9
10
10
10
3
6
7
7
7
8
8
9
7
7
7
8
8
9
8
8
9
9
к
5
5
5
5
5
5
5
6
6
6
6
6
6
7
7
7
8
Xi
35
21
29
35
29
35
35
21
29
35
29
35
35
29
35
35
35
Окон
Xi +Хк
20
27
27
27
30
30
34
29
29
29
32
32
40
39
39
47
50
чание
<р(<Р*)
1
0
1
1
0
1
1
0
1ж2
1
0
1
0
0
0
0
0
Для нормального приближения имеем
М(Г) = -
ЩТ) =
3 ¦ 10 • 9 ¦ *
2
2592 432 48
1^= 0,787.
15,248
Из табл. 1 имеем и о,р5 = tio,975 = 1?96.
1 — 2
Так как |Т* = 0,852 < 1,96, гипотеза экспоненциальности не отклоняется.
3.3.12. Критерий Кочара
Критерий, предложешгый Кочаром [315], применяется для проверки постоян-
постоянства интенсивности отказов против альтернативы монотонного увеличения интен™
сивности отказов (т.е. „старения", износа изделия). Статистика критерия (имеется
в виду упорядоченный по возрастанию ряд х\ ^ Х2 ^ • • • ^ хп) имеет вид
-1-71.
где J
= 9
п + 1 — г
п + 1 — г
- 1.
п + 1 ) f V п + 1
При п ^ 20 распределение Тп удовлетворительно аппроксимируется стандарт™
нормалвным распределением. Если Тп ^ Тп(а), то гипотеза экспоненциалв-
ности отклоняется (Тп(а) — критические значения, приведенные для различных
уровней значимости а в табл. 91).
Критерий Кочара обладает высокой мощностью против альтернатив износа
среди критериев подобного типа, рассмотренных в [316—321].
8.8]
Критерии проверки экспоненциалъности распределения
299
Таблица 91
Критические значения Tn(ct) критерия
Кочара (а — уровень значимости) [315]
2
3
4
5
6
7
8
9
10
11
а
0,01
2,2604
2,5321
2,6628
2,7347
2,7814
2,8128
2,8338
2,8481
2,8577
2,8640
0,05
2,2265
2,3923
2,4536
2,4863
2,5006
2,5046
2,5029
2,4976
2,4903
2,4817
п
12
13
14
15
16
17
18
19
20
а
0,01
2,8678
2,8698
2,8705
2,8703
2,8692
2,8676
2,8566
2,8631
2,8604
0,05
2,4724
2,4627
2,4528
2,4429
2,4332
2,4235
2,4141
2,4049
2,3559
Задача 137. Проверить экспоненциальность распределения для данных задачи 125
критерием Кочара на уровне значимости а = 0,05.
Имеем
- \ =4 •
11
J
11
J
J f ^ J = 0,91775; J ( — J = 0,84798; J ( — J = 0,75215;
— J = 0,25415; j(—j= ^0,01645;
— \= 0,62588;
^) = ^0,38220;
—j = 0,46298;
J[ ^— 1 -xi = 0,99147-1 + 0,96473-2 + ...
... + 0,25415 • 21 - 0,01645 • 29 - 0,38220 • 25 = 24,31227.
Получаем
Tn =
17
135
= M35.
Из табл. 91 для п = 10 и а = 0,95 находим Тп@,05) = 2,4903.
Так как Тп = 1,435 < Тп@,05) = 2,4903, гипотеза экспоненциальности распределения
вероятностей случайных величин не отклоняется.
3.3.13. Критерий Эппеа—Палли—Чёрго—Уэлча
Как и критерий Кочара (см. раздел 3.3.12), критерий Эппса^Палли [322] предпо-
предполагает проверку гипотезы экспоненциальности против альтернативы монотонного
изменения интенсивности отказов.
Критерий, подобно критерию Муроты-Такеучи для проверки нормальности
распределения (см. раздел 3.2.2.17), использует выборочную характеристическую
функцию
cn(t) = I
300 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Статистика критерия имеет вид
c=V48n -> ехр -- -- .
Гипотеза экспоненциальности не отклоняется, если с\(а) < с < С2(а), где ci(a)
и С2(а)—критические значения, соответствующие доверительной вероятности а;
они приведены в табл. 92.
Таблица 92
Критические значения ci(ck) и С2(«) критерия
Эппса—Палли (а-
п
7
8
9
10
11
12
14
16
18
20
22
24
26
28
30
35
40
45
50
60
80
100
120
160
200
0,95
с\
-1,64
-1,65
-1,65
-1,66
-1,66
-1,66
-1,67
-1,67
-1,67
-1,67
-1,67
-1,68
-1,68
-1,68
-1,68
-1,68
-1,68
-1,68
-1,68
-1,68
-1,67
-1,67
-1,67
-1,67
-1,67
1,31
1,35
1,38
1,40
1,42
1,44
1,46
1,48
1,49
1,50
1,51
1,52
1,53
1,53
1,54
1,55
1,56
1,57
1,57
1,58
1,59
1,60
1,60
1,60
1,62
- доверительная
а
0,975
с\
-1,81
-1,83
-1,84
-1,85
-1,86
-1,87
-1,88
-1,89
-1,90
-1,91
-1,91
-1,92
-1,92
-1,92
-1,93
-1,93
-1,94
-1,94
-1,94
-1,95
-1,95
-1,95
-1,95
-1,96
-1,96
С2
1,71
1,74
1,77
1,79
1,81
1,82
1,84
1,86
1,87
1,88
1,89
1,89
1,89
1,90
1,91
1,91
1,92
1,92
1,93
1,93
1,94
1,94
1,94
1,96
1,96
вероятность)
0,99
-2,00
-2,02
-2,04
-2,06
-2,08
-2,09
-2,11
-2,13
-2,15
-2,16
-2,17
-2,18
-2,19
-2,19
-2,20
-2,21
-2,22
-2,23
-2,24
-2,25
-2,25
-2,27
-2,28
-2,29
-2,30
2,18
2,22
2,25
2,26
2,28
2,29
2,31
2,32
2,33
2,33
2,34
2,34
2,34
2,34
2,35
2,35
2,35
2,35
2,35
2,35
2,35
2,35
2,35
2,35
2,35
При п > 200с —)¦ JV(O,1) критические значения ci(a) = —Ua и 02@.) = C/a, где
Ua — «-квантиль стандартного нормального распределения.
При сравнительной простоте вычисления с™критерий достаточно мощен, не
уступая критериям Шапиро^Уилка и Кочара против большинства альтернатив.
Критерий, аналогичный критерию Эппса^Палли, рассмотрен Чёрго и Уэлчем [323].
Его статистика имеет вид
М =
sup
I tXi 1
где
71-1
-\2
3.3]
Критерии проверки экспоненциальности распределения
301
Гипотеза экспоненциальности отклоняется, если М ^ Мп(а), где Мп{а)—кри™
тические значения, приведенные для различных уровней достоверности а в табл. 93.
Таблица 93
Критические значения Мп(сх)
критерия "Чёрго^Уэлча
(а — доверительная вероятность)
п
20
50
100
а
0,90
1,11
1,05
1,00
0,95
1,45
1,23
1,16
0,00
2,02
1,67
1,45
Критерий по мощности сравним с критерием Эппса^Палли и равносилен ему,
однако требует значительно больших вычислений.
Задача 138. В условиях задачи 125 проверить гипотезу экспоненциальности распре-
распределения вероятностей случайных величин критерием Эппса-Палли при доверительной
вероятности а = 0,95.
Имеем х = 13,5 и вычисляем статистику критерия Эппса-Палли
—• ехр
10 I \ 13,5
¦ехр -
13,5
+ ехр —
13,5
¦ ... + ехр -
35
13,5
- - ^ = 0,3345.
2 (
Из табл. 92 находим ci@,95) = -1,66 и с2@,95) = 1,38.
Так как ci@,95) = —1,66 < с = ^0,3345 < С2@,95) = 1,38, гипотеза экспоненциально-
экспоненциальности не отклоняется.
3.3.14. Критерий Бергмана
Этот критерий базируется на проверке постоянства интенсивности отказов про™
тив альтернативы „бутылкообразной" зависимости интенсивности отказов от вре-
времени (с участком приработки, когда A;(i) < 0, и износа, когда Xf(t) > 0). Критерий
развит в [323-325].
Определим для выборки объема п: х\ ^ Х2 ^ ... ^ хп переменную
х0 = 0.
1){хз - xj^i
Для экспоненциального распределения — и Щ должны быть связаны строгой линей-
п
ной зависимостью. Отклонения от такой зависимости указывают на отклонение от
экспоненциальности исследуемого распределения и являются источником построе-
построения критерия для установления этого факта.
Бергман [324] предложил простой критерий проверки экспоненциальности рас™
пределения, основанный на числе пересечений прямой
= — графиком зависимо-
302 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Обозначим через Кп число пересечений „снизу", когда для г = 1, ..., п — 1 имеют
г г + 1
место неравенства Щ < — и C/^+i ^ . Статистикой критерия является общее
п п
г
< — и C/^+i ^
п п
число пересечений, определямое как
-1 тт 1 f -I тт
1, если ui < —, г II, если un^i
^ 02 =
гг — 1
О в ином случае;
О в ином случае.
Значения вероятности того, что Ln ^ к при справедливости гипотезв! экспоненци™
альности распределения, приведены в табл. 94.
Таблица 94
Значения ?(Ln ^ к) [324]
п
10
20
30
40
50
60
70
90
100
к
1
0,8000
0,9000
0,9333
0,9500
0,9600
0,9667
0,9714
0,9778
0,9800
2
0,4913
0,7143
0,8019
0,8485
0,8773
0,8969
0,9112
0,9304
0,9372
3
0,2564
0,5324
0,6628
0,7369
0,7844
0,8174
0,8417
0,8750
0,8869
4
0,0959
0,3416
0,4964
0,5945
0,6612
0,7093
0,7455
0,7964
0,8149
5
0,0294
0,2083
0,3617
0,4709
0,5499
0,6089
0,6545
0,7202
0,7445
6
0,0058
0,1068
0,2353
0,3427
0,4272
0,4938
0,5473
0,6269
0,6573
7
0,0008
0,0524
0,1504
0,2470
0,3299
0,3989
0,4563
0,5449
0,5795
8
0,0000
0,0211
0,0846
0,1618
0,2360
0,3023
0,3600
0,4535
0,4914
9
0,0000
0,0081
0,0471
0,1058
0,1690
0,2295
0,2849
0,3787
0,4180
Задача 139. Проверить гипотезу экспоненциальности в условиях задачи 125 крите-
критерием Бергмана на уровне значимости а = 0,05.
ю
Имеем ^2(п — j + 1)(xj — Xj-i) = 135.
i=i
Результаты вычислений сведем в таблицу:
i
1
2
3
4
5
г
п
0,1
0,2
0,3
0,4
0,5
х-
1
2
4
5
9
Ui
0,0740
0,1417
0,2592
0,3111
0,4889
i
6
7
8
9
10
i
п
0,6
0,7
0,8
0,9
1,0
х-
11
18
21
29
35
Ui
0,5630
0,7703
0,8370
0,9555
1,0000
Из таблицы видно, что
= 1 \Ui = 0,074 < ^ = 0Д
= 0 (u9 = 0,9555 > ^- = 0,9
Kn =
7
U6 = 0,5630 < — = 0,6 и U7 = 0,7703 > — = 0,7
Имеем Ln = 1 - 1 + 2 • A - 0) + 0 - 1 = 1. Из табл. 94 находим P(Ln ^ 1) = 0,80, т. е. при
справедливости гипотезы экспоненциальности эта вероятность высока и намного превос-
превосходит заданный уровень значимости. Следовательно, гипотеза экспоненциальности не
отклоняется.
3.3]
Критерии проверки экспоненциалъности распределения
303
3.3.15. Критерий Шермана
Статистика критерия имеет вид [327]
2п х
Критические значения статистики Шермана приведены в табл. 95.
Таблица 95
Критические значения ujn{ot) статистики Шермана
(а — доверительная вероятность) [328]
п
1
2
3
4
5
6
7
8
9
10
а
0,90
0,450
0,484
0,467
0,468
0,462
0,458
0,454
0,451
0,448
0,445
0,95
0,475
0,537
0,518
0,509
0,502
0,494
0,488
0,482
0,477
0,473
0,99
0,495
0,609
0,614
0,589
0,574
0,562
0,551
0,542
0,534
0,527
п
11
12
13
14
15
16
17
18
19
20
а
0,90
0,442
0,440
0,438
0,436
0,434
0,433
0,431
0,430
0,429
0,427
0,95
0?469
0,466
0,463
0,460
0,458
0,455
0,453
0,451
0,449
0,448
0,99
0,521
0,516
0,511
0,506
0,502
0,498
0,495
0,491
0,489
0,486
При п > 20 критерий Шермана удовлетворительно аппроксимируется нормаль-
нормальным распределением со средним М(о;п) и дисперсией D(o;n), где
п+1
- = 0,36788;
е
DW =
2пп
2)(га
чп+2
2п+2
^5 1
о
е п
0,05908
Следовательно, случайная величина ш* =
имеет стандартное нор™
мальное распределение. В [329] рассмотрена аппроксимация распределения
шп-статистики ^-распределением Фишера. Там же предложена очень эффективная
нормальная аппроксимация
0,0955 (тт2 ч
wn = ^- ^ (Z7 - 1) , где U =
оп -0,3679A- —
2п
-( 0,605 \*
г 1
I п )
Статистика шп хорошо аппроксимируется стандартным нормальным распределение
ем уясе при п > 20.
Если шп > шп(а) или 6оп > иа1 то с доверительной вероятностью а гипотеза
экспоненциальное™ отклоняется (иа — а-квантиль стандартного нормального рас™
пределения).
304 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Задача 140. Проверить гипотезу экспоненциальности для данных задачи 125 крите-
критерием Шермана при доверительной вероятности а = 0,95.
Имеем
1
х = 13,5; шп =
2-10- 13,5
- 13,5| + |2 - 13,5|
|35 - 13,5|) = 0,4.
Из табл. 95 для п = 10 находим шп@,95) = 0,473.
Так как шп = 0,400 < сип@,95) = 0,473, гипотеза экспоненциальное™ не отклоняется.
Используем теперь нормальную аппроксимацию
0,4 - 0,3679 • 1 -
U =
2-10/
шп = 0,069914 -
0,2431 ¦ V10 • ( 1 -
0,0995
0,605
10
= 0,069914;
\/То
@,0699142 - 1) = 0,1012,
что существенно меньше, чем и-о,э5 =: 1,645 (однако следует помнить, что пример демон-
демонстрационный и нормальным приближением следует пользоваться только при п > 20).
3.3.16. Критерий наибольшего интервала
Статистика критерия имеет вид [140]
max (pa — Xi-i
Статистика rjn совпадает с известной статистикой Кохрана для проверки одно™
родности нескольких дисперсий (при числе степеней свободы / = 2). Критические
значения г)п{а) приведены в табл. 96.
Таблица 96
Критические значения г)п(сх)
статистики г)п [25]
п
2
3
4
5
6
7
8
9
10
Доверительная
вероятность а
0,95
0,975
0,871
0,768
0,684
0,616
0,561
0,561
0,477
0,445
0,99
0,995
0,942
0,864
0,788
0,722
0,664
0,664
0,573
0,536
п
12
15
20
24
30
40
60
120
Доверительная
вероятность а
0,95
0,392
0,335
0,270
0,235
0,198
0,158
0,113
0,063
0,99
0,475
0,407
0,330
0,287
0,241
0,191
0,137
0,076
Задача 141. Проверить гипотезу экспоненциальности критерием наибольшего ин-
интервала для данных задачи 125 при а = 0,95.
Имеем
хг = 135; г]п = = 0,0592.
Из табл. 96 имеем т?п@,95) = 0,445.
Так как щ = 0,0592 < ?]п@,95) = 0,445, гипотеза экспоненциальности не отклоняется.
3.3]
Критерии проверки экспоненциальности распределения
305
3.3.17. Критерий Хартли [330]
Это один из наиболее простых в вычислительном отношении критериев (однако
его мощность, естественно, уступает рассмотренным ранее). Статистика критерия
имеет вид
max Xi
h(n) = ^<n ,
mm Xi
При справедливости нулевой гипотезы h(n) имеет % -распределение с / = 2
степенями свободы. Критические значения На(п) статистики Хартли приведены
в табл. 97.
Таблица 97
Критические значения ha(n) статистики Хартли
(а — доверительная вероятность) [140]
2
3
4
5
0,95
39
88
142
202
0,99
199
448
729
1036
6
7
8
9
0,95
266
333
403
475
0,99
1362
1705
2063
2432
10
11
12
0,95
550
626
704
а
0,99
2813
3204
3605
При h(n) > Ha(n) гипотеза экспоненциальности отклоняется.
Задача 142. В условиях задачи 125 проверить гипотезу экспоненциалъности крите-
критерием Хартли при а = 0,95.
Имеем h(n) =
= f =35.
Для п = 10 из табл. 97 имеем До,э5(Ю) = 550, что существенно больше полученного
значения h(n) = 35. Следовательно, гипотеза экспоненциальности не отклоняется.
3.3.18. Критерий показательных меток
Применительно к задачам испытаний на надежность постоянство интенсивности
отказов указывает на экспоненциальный закон распределения вероятностей значе™
ний временных промежутков между соседними отказами. В [310] для проверки
экспоненциальности рассмотрен критерий показательных меток. Пусть имеются
моменты появления отказов изделия ti,^, ..., tn и порождаемая ими последова-
последовательность интервалов между отказами
= ti- t
2;
At, =ti+1 -
Каждому интервалу ставится в соответствие его номер и так называемая метка,
равная математическому ожиданию r-й порядковой статистики из единичного экс-
экспоненциального распределения в выборке объема п — sr^n^\ (здесь г — порядковый
номер интервала Air в общем, упорядоченном по возрастанию ряду (п — 1) интер-
интервалов)
П- j
306 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Статистика критерия имеет вид [310]
Критерий применяется при п > 50, его критические значения в этом случае
вв1числяются, исходя из того, что величина s имеет асимптотически нормальное
распределение со средним M(s) = 0 и дисперсией
D(S) =
где
Задача 143. Предположим, что ряд данных задачи 125
хц 1, 2, 4, 5, 9, 11, 18, 21, 29, 35
представляет собой моменты отказов изделий. Проверить гипотезу экспоненциально-
сти распределения Xi критерием показательных меток при доверительной вероятно-
вероятности а = 0,95 (при совпадении рангов интервалов г можно использовать их случайную
последовательную нумерацию).
Результаты расчетов приведены в таблице:
г
1
2
3
4
5
6
7
8
9
10
Xi
1
2
4
5
9
11
18
21
29
35
Axi
1
2
1
4
2
7
3
8
6
г
1
3
2
6
4
8
5
9
7
0,1000
0,3361
0,2111
0,8456
0,4790
1,4290
0,6456
1,9290
1,0956
z%
1
2
3
4
5
6
7
8
9
zi - z
-4
-3
-2
-1
0
1
2
3
4
(z^zf
16
9
4
1
0
1
4
9
16
Sr,n(zi - z)
-0,4000
-1,0083
-0,4222
-0,8456
0
1,4290
1,2912
5,7870
4,3824
+ ± + ...+ i + i) =0,7138.
Далее s = 10,2135; M(s) = 0; DE) = 0,7138 • 60 = 42,828
Случайная величина
= 6,544).
s - M(s) _ 10,2135
\/Щз) ~ 6,544
= 1,5607
имеет стандартное нормальное распределение, 95%™я квантиль которого равна
^о,95 = 1,645 (см. табл. 1). Так как s* = 1,5607 < ^0,95 = 1,645, гипотеза экспоненциаль-
ности не отклоняется.
3.3.19. Ранговый критерий независимости интервалов
Характеристической особенностью экспоненциального распределения случай™
ных величин является независимость интервалов между двумя соседними случай™
ными величинами Axi = Xi — Xi-\.
Для выборок объема п > 30 в качестве оценки такой независимости может
служить ранговый смешанный момент [296, 310]
п-1
г=1
где tj —ранг j-vo интервала в общем упорядоченном ряду значений интервалов.
3.3] Критерии проверки экспоненциальности распределения 307
Например, если были получены величины х\ = 3, ж 2 = 1, #з = 5, Ж4 = 2, а?5 = 11,
то после упорядочения по величине мы имеем #2 = 1, #4 = 2, a?i = 3, Жз=4иж5 = 5.
При справедливости гипотезы экспоненциальности случайная величина
где
М(Лх) = ^(п - 1)(п + 1)Cп + 2);
(п + 1) Eп6 + 21п5 + 501п4 - 823п3 + 1102п2 - 68п - 240)
= 720(n-2)(n-3) '
имеет стандартное нормальное распределение.
(с% \
1 — — 1 -квантиль стан™
дартного нормального распределения, то на уровне значимости а гипотеза экспо-
экспоненциальности не отклоняется.
В [310] рассмотрена модификация этого критерия в форме
п-1
Rl=^2 Sri+ltnSritn,
г=1
Х~^ 1
где sr п = 7 математическое ожидание r-й порядковой статистики из
' 1-^ п — % + 1
г=1
единичного нормированного экспоненциального распределения.
По аналогии рассматривается статистика
где
- ,05772
Правило проверки гипотезы экспоненциальности аналогично случаю крите-
критерия Д*. При совпадении рангов r^ = Tj используются средние ранги (например,
в случае Г{ = rj для обеих величин принимается ранг — -). Следует помнить,
что эти критерии обладают приемлемой мощностью только при п ^ 30.
Задача 144. Проверить гипотезу экспоненциальности распределения вероятностей
случайных величин для данных задачи 125 критериями независимости интервалов
(а = 0,95).
Для ряда
Хг (га =10): 1, 2, 4, 5, 9, 11, 18, 21, 29, 35
имеем ряд интервалов
Axi (n = 9): 1, 2, 1, 4, 2, 7, 3, 8, 6
и соответствующий им ряд рангов
гц 1,5; 3,5; 1,5; 6; 3,5; 8; 5; 9; 7.
Вычисляем
Кг = J2 r*+i • П = 3,5 • 1,5 + 1,5 • 3.5 + ... + 9 • 5 + 7 • 9 = 216,5;
308 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
720-7-6
х [10 • E • 96 + 21 • 95 + 501 • Э4 - 823 • Э3 + 1102 • Э2 ~~ 68 • 9 - 240)] = 2206,5932.
91 б 5 193 3
Тогда R\ = — = 0,494, что меньше иг_а = гхо,975 = 1,96.
Следовательно, гипотеза экспоненциальности не отклоняется.
Вычислим теперь критерий R\. Имеем
sri,n = -= 0,1111; Sr2,n = 0,2361; sr^n = 0,3790; sr^n = 0,5456; sr5,n = 0,7456;
sr^n = 0,9956; sr7jn = 1,329; srg,n = 1,829; sr9,n = 2,829;
sr r,n = ^^—^^ = 0,1736; sr ,n = ^^—^^ = 0,4626;
#i = 0,4626 • 0,1736 + 0,1736 • 0,4626 + 0,9956 • 0,1736 + ... + 1,329 • 2,829 = 8,8728;
М(Ёг) =9-2+i-(ln9 + 0,5772) + ^^ = 7,3144;
• (93 -6-92+24-9) -21n9 = 6,534 (a/d^Ri) = 2,556);
Так как R\ = 0,6097 < иг___а = uo,975 = 1,96, гипотеза экспоненциальности распреде-
распределения вероятностей случайных величин не отклоняется.
3.3.20. Критерии, основанные на трансформации
экспоненциального распределения в равномерное
Если случайные величины #i,#2, -->jxij • • • > хп распределены экспоненциаль™
но, то случайные величины Щ = — должны быть распределены равномерно
i
на интервале [0,1] [231]. В этом случае проверка равномерности распределения
величин Ui эквивалентна проверке экспоненциальности распределения исходных
величин Х{. Рассмотрим серию критериев такого типа.
3.3.20.1. Критерий U
Простейший критерий, основан на статистике
п — 1
1
и= —
г=1
Критические значения статистики Ua приведены в табл. 98.
При п ^ 15 моясно использовать тот факт, что величина
[7* =
распределена как N@,1) и ее квантили тогда могут быть вычислены через квантили
стандартного нормального распределения.
3.3]
Критерии проверки экспоненциальности распределения
309
Таблица Э<!
Критические значения Ua статистики U (а — уровень значимости) [231]
п
5
6
7
8
9
10
11
13
15
17
а
0,01
0,176
0,208
0,232
0,251
0,266
0,279
0,290
0,308
0,322
0,330
0,025
0,221
0,250
0,271
0,288
0,301
0,312
0,322
0,337
0,349
0,359
0,05
0,262
0,287
0,306
0,320
0,332
0,341
0,350
0,363
0,373
0,381
0,10
0,312
0,332
0,347
0,359
0,368
0,376
0,382
0,393
0,401
0,407
п
19
21
26
31
36
41
46
51
61
а
0,01
0,343
0,351
0,366
0,387
0,378
0,394
0,400
0,405
0,420
0,025
0,367
0,374
0,387
0,397
0,404
0,411
0,416
0,420
0,432
0,05
0,388
0,394
0,405
0,413
0,420
0,425
0,429
0,433
0,443
0,10
0,412
0,417
0,426
0,432
0,437
0,441
0,445
0,448
0,456
3.3.20.2. Критерий U
Наиболее простой в вычислительном отношении критерий, основанный на ста-
статистике
U =
(п - г) Ur
r(l-Ur)'
имеющей при справедливости гипотезы экспоненциальности ^распределение
с /i = 2г и /2 = 2(п — г) степенями свободы. Рекомендуется выбирать г = — (п —
четное) или г =
П+1
(в — нечетное).
3.3.20.3. Критерий Гринвуда
Известен ряд весьма эффективных критериев, основанных на спейсингах вели-
величин Ui, равных Di = Ui — Ui-i (i = 1, ..., n; Щ — 0; Un = 1). Здесь Щ следует рас™
сматривать как порядковые статистики (т. е. ряд U{ должен быть предварительно
упорядочен по возрастанию).
Легко видеть, что
В качестве примера критерия экспоненциальности, основанного на спейсин™
rax Di, приведем критерий Гринвуда [331]
?*<
Гипотеза экспоненциальности не отклоняется, если G±(a) ^ G ^ ^(^О? гДе G\(a)
и (jr2(a) — критические значения, приведенные в табл. 99.
310 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Таблица 99
Критические значения Gri(o) и
статистики Гринвуда
(а — доверительная вероятность) [332, 333]
п
3
4
5
6
7
8
9
10
11
13
15
17
19
21
26
31
41
51
61
81
101
201
501
а =
0,694
0,825
0,923
0,997
1,055
1,104
1,145
1,180
1,211
1,272
1,312
1,346
1,375
1,400
1,451
1,490
1,548
1,589
1,621
1,666
1,698
1,781
1,858
0,90
G2
1,539
1,852
2,037
2,160
2,246
2,306
2,349
2,381
2,404
2,441
2,457
2,464
2,466
2,465
2,456
2,443
2,415
2,389
2,367
2,331
2,304
2,226
2,147
а =
Gt
0,680
0,796
0,895
0,954
1,009
1,060
1,095
1,129
1,159
1,234
1,272
1,304
1,332
1,356
1,405
1,444
1,502
1,544
1,577
1,625
1,659
1,750
1,836
0,95
G2
1,673
2,075
2,311
2,461
2,559
2,615
2,670
2,700
2,717
2,693
2,691
2,691
2,685
2,677
2,651
2,624
2,573
2,531
2,495
2,441
2,400
2,289
2,183
a =
Gt
0,672
0,776
0,855
0,919
0,973
1,017
1,055
1,088
1,117
1,198
1,233
1,263
1,288
1,311
1,358
1,395
1,453
1,495
1,529
1,579
1,616
1,714
1,811
0,99
G2
1,780
2,269
2,560
2,737
2,849
2,921
2,967
2,997
3,008
3,015
3,014
3,003
2,988
2,970
2,920
2,873
2,790
2,723
2,669
2,587
2,528
2,371
2,228
Задача 145. Проверить экспоненциальность распределения по данным задачи 125
критериями U и Гринвуда на уровне значимости а = 0,05.
Имеем
Xj = 135. Далее вычисляем
= 0,00741; U2 = -|- = 0,02222; U3 =
135
= 0,05185;
U4 = 0,08889; U5 = 0,15555; U6 = 0,23703; U7 = 0,37037; U8 = 0,5259;
1 9
U9 = 0,74074; U10 = 1,00 и U =-• ]P Ui = 0,2444.
9 i=i
Из табл. 98 для п = 9 и а = 0,05 находим Оо,о5 = 0,332.
Так как U = 0,2444 < f/0,05 = 0,332, гипотеза экспоненциальное™ не отклоняется.
Применим критерий, для которого (при г = — = 5) имеем
U =
(ю -ъ)-иъ
5 -0,1555
= 0,1842.
5 ¦ A — С/5) 5 ¦ A -0,1555)
При а = 0,05, /2 = 2 • A0 - 5) = 10 имеем Fo.osA0,10) = 2?978.
Следовательно, U = 0,18 < 2,98 и гипотеза экспоненциальное™ не отклоняется.
3.3] Критерии проверки экспоненциалъности распределения 311
Рассмотрим теперь критерий Гринвуда. Имеем
D1 = U1= 0,00741; D2 = U2-U1= 0,01481; D3 = U3 - U2 = 0,0295;
D4 = 0,03704; D5 = 0,0666; D6 = 0,08148; D7 = 0,13333; D8 = 0,15555;
10
D9 = 0,08148; D10 = 0,2539 и G = n-^Dt = 1,689.
i=l
Из табл. 99 имеем Gi@,95) = 1,129 и G2@,95) = 2,700.
Так как G\(ot) = 1,29 < G = 1,689 < G^a) = 2,700, гипотеза экспоненциальное™ не
отклоняется.
3.3.21. Критерий Манн-Фертига-Шуера длм распределения Вейбулла
Распределение Вейбулла является обобщающим для экспоненциального распре-
распределения. Закон распределения Вейбулла
/ х
F(x) = 1-ехр --
V а
совпадает при C = 1 с экспоненциальным. Поэтому распределение Вейбулла часто
рассматривается как альтернативное при проверке экспоненциальное™ распреде™
ления.
Учитывая изложенное, критерий согласия для распределения Вейбулла приво-
приводится здесь. Критерий был предложен авторами применительно к задаче испытаний
изделий на долговечность.
Если ti,t2, ..., tr — первые г порядковых статистик наработки на отказ при
испытаниях выборки изделий объема п ^ г, то статистика критерия имеет вид
[Т1 V
— —наибольшее целое число ^ —, щ — коэффициенты, приведенные
в табл. 100.
Гипотеза согласия эмпирического распределения с двухпараметрическим рас™
пределением Вейбулла отклоняется, если
К > Ка(г,п),
где К > Ка (г, п) — критическое значение статистики для доверительной вероятно-
вероятности а (при известных результатах отказов г изделий из п), приведенное в табл. 101.
Задача 146. Проверить гипотезу согласия данных задачи 125 с двухпараметрическим
распределением Вейбулла при доверительной вероятности а = 0,95.
Для ряда значений х% имеем ряд
In ж*: 0; 0,693; 1,386; 1,609; 2,197; 2,398; 2,890; 3,044; 3,367; 3,555.
С учетом коэффициентов а% из табл. 100 для п = г = 10 имеем
JU 1пж»+1 - 1пж» _ 2,890 - 2,398 3,555 - 3,367 _
0,269493 h """H 0,405316
312 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Таблица 100
Коэффициенты о» Ж-критерия согласия
Манн—Фертига—ШСуера для распределения Вейбулла [95]
п
3
4
5
6
7
8
9
10
11
г
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
3
4
5
6
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
9
1
2
3
4
5
щ
1,216395
0,863046
1,150727
0,706698
0,679596
1,115718
0,645384
0,532445
0,583273
1,093929
0,612330
0,474330
0,442920
0,522759
1,079055
0,591158
0,442789
0,387289
0,387714
0,480648
1,068252
0,577339
0,422889
0,356967
0,334089
0,349907
0,449338
1,060046
0,566942
0,409157
0,337763
0,304777
0,297949
0,322189
0,424958
1,053606
0,559013
0,399100
0,324470
0,286163
0,269493
0,271645
0,300869
0,405316
1,048411
0,552769
0,391410
0,314705
0,273245
п
11
12
13
14
15
г
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
щ
0,251386
0,243928
0,251548
0,283879
0,389071
1,044137
0,547721
0,385338
0,307221
0,263737
0,238797
0,226264
0,224477
0,235630
0,269966
0,375356
1,040515
0,543556
0,380417
0,301300
0,256437
0,229515
0,213966
0,207205
0,209131
0,222667
0,258323
0,363582
1,037513
0,540059
0,376352
0,296496
0,250650
0,222377
0,204885
0,195165
0,192209
0,196679
0,211875
0,248409
0,353334
1,034894
0,537085
0,372934
0,292518
0,255180
0,216712
0,197893
0,186266
п
15
16
17
18
г
9
10
11
12
13
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
щ
0,180266
0,180072
0,180072
0,186347
0,239842
0,344309
1,032617
0,534521
0,370021
0,289169
0,242049
0,212103
0,192338
0,179407
0,171667
0,168476
0,170026
0,177619
0,194859
0,232350
0,336283
1,030618
0,532290
0,367507
0,286765
0,238765
0,208278
0,187813
0,173951
0,164928
0,159891
0,158624
0,161559
0,170132
0,188005
0,225729
0,329085
1,028850
0,530332
0,365314
0,283846
0,235958
0,205051
0,184055
0,169504
0,159564
0,153263
0,150176
0,150333
3.3]
Критерии проверки экспоненциалъности распределения
313
Окончание таблицы 100
п
18
19
20
21
i
13
14
15
16
17
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
1
2
3
4
5
6
7
8
9
щ
0,154313
0,163630
0,181971
0,219825
0,322580
1,027277
0,528594
0,363389
0,281692
0,233535
0,202291
0,180882
0,165807
0,155189
0,147984
0,143650
0,142012
0,143250
0,148031
0,157921
0,176611
0,214520
0,316666
1,0,25866
0,527046
0,361682
0,279798
0,231417
0,199905
0,178167
0,162684
0,151549
0,143674
0,138448
0,135580
0,135306
0,137120
0,142527
0,152861
0,171810
0,209721
0,311257
1,024594
0,525657
0,360159
0,278117
0,229551
0,197821
0,175815
0,160009
0,148471
п
21
22
23
г
10
11
12
13
14
15
16
17
18
19
20
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
«г
0,140087
0,134200
0,130451
0,128702
0,129025
0,131756
0,137659
0,148341
0,167481
0,205352
0,306285
1,023439
0,524405
0,358790
0,276618
0,278950
0,195983
0,173760
0,157692
0,145834
0,137052
0,130662
0,126260
0,123640
0,122763
0,123763
0,127019
0,133316
0,144273
0,163552
0,201355
0,301693
1,022380
0,523269
0,357557
0,275268
0,226417
0,194351
0,171948
0,155666
0,143549
0,134451
0,127667
0,122768
0,119503
0,117764
0,117577
0,119120
0,122799
0,129416
0,140590
п
23
24
25
г
20
21
22
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
щ
0,159966
0,197679
0,297435
1,021431
0,522233
0,356436
0,274051
0,225086
0,192892
0,170330
0,153877
0,141549
0,132195
0,125099
0,119811
0,116054
0,113677
0,112638
0,113007
0,114990
0,119014
0,125889
0,137235
0,156679
0,194285
0,293473
1,020551
0,521285
0,355415
0,272945
0,223885
0,191578
0,168899
0,152286
0,139789
0,130219
0,122871
0,117274
0,113132
0,110268
0,108598
0,108124
0,108944
0,111289
0,115596
0,122683
0,134165
0,153650
0,191137
0,289773
314 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
ю
СЛ
ш
е
СЛ
о
95
о
90
о
ft
99
о
,95
о
СЛ
о
СЛ
СЛ
о
,95
о
о
СЛ
о
<ч
СЛ
СЛ
о
95
о
90
о
ю
t-
о
Is-
СО
о
63
о
т-Н
СО
гЧ
3
О
со
00
О
о
00
О
ю
т-Н
ю
00
О
со
о
т—|
о
«
о
т-Н
СЛ
о
95
о
о
СЛ
о
СО
СО
о
о
Is-
о
66
о
Ю
т-Н
СО
00
о
Is-
о
00
СО
о
СО
СЛ
о
СЛ
СО
о
СО
о
о
т-Н
СЛ
СЛ
о
95
о
о
СЛ
о
СО
СО
Is-
о
СО
со
о
62
о
СО
т-Н
СЛ
00
о
т-Н
00
о
ю
Is-
о
Is-
сл
о
ю
о
о
о
СО
т-Н
т-Н
СЛ
00
о
СО
Is-
о
67
о
СЛ
о
ю
о
о
о
СО
t-
т—1
см
00
о
СО
Is-
о
СО
СО
о
00
о
СЛ
о
ь-
о
00
СО
о
СЛ
СЛ
о
95
о
о
о
СО
ю
о
о
00
t-
о
69
о
ю
00
о
ь-
о
t-
о
СЛ
3
о
со
00
о
о
00
о
ю
СЛ
00
о
t-
о
68
о
СЛ
о
Is-
00
о
80
о
ю
СЛ
t-
о
о
t-
о
ю
СО
о
о
СО
00
о
ю
ь-
о
00
СО
о
СО
СЛ
о
96
о
СЛ
t-
о
ю
ю
00
о
Is-
о
68
о
СО
00
о
ь-
о
СЛ
со
о
т—1
СЛ
00
о
т—1
00
о
ю
ь-
о
t-
сл
СЛ
о
95
о
о
о
СО
со
СЛ
00
о
о
00
о
ю
о
Is-
Is-
о
00
СО
о
S
о
см
см
00
о
см
о
СО
СО
о
00
СЛ
00
о
СО
Is-
о
00
СО
о
т-Н
00
о
см
о
66
о
00
СЛ
о
о
ь-
со
о
СО
ю
00
о
ь-
ь-
о
т—1
о
СЛ
СЛ
о
86
о
80
о
ю
ю
00
о
Is-
ь~
о
t-
о
ю
t-
о
t-
СО
о
СО
о
о
о
ь-
о
СО
о
о
1—1
00
о
СО
о
66
о
СО
СЛ
ь-
о
о
Is-
о
65
о
о
СЛ
СЛ
о
ю
о
о
СЛ
о
СО
ю
гЧ
см
00
о
ь-
о
СЛ
СО
о
гЧ
т—1
СЛ
СЛ
о
95
о
о
о
СО
00
о
2*
о
69
о
т-Н
о
СЛ
о
00
о
со
о
СЛ
о
ю
о
о
о
СО
см
т-Н
СЛ
00
о
Is-
Is-
о
68
о
Is-
ь-
о
СЛ
СО
о
64
о
см
СЛ
о
СО
00
о
00
о
ю
СЛ
00
о
00
о
00
СО
о
СЛ
о
СО
00
о
80
о
ю
о
00
о
см
Is-
о
67
о
СО
со
00
о
ю
о
t-
со
о
со
3
о
со
00
о
о
00
о
ю
ю
00
о
t-
о
Is-
СО
о
СО
ю
о
00
СО
о
63
о
СЛ
00
о
т—1
00
о
о
Is-
ю
00
о
о
Is-
СО
о
СО
о
00
о
80
о
Is-
о
t-
ь-
Is-
о
о
Is-
о
66
о
ю
см
00
о
см
Is-
о
СО
со
о
00
СЛ
00
о
т-Н
00
о
ю
Is-
о
ь-
сл
о
ю
СЛ
о
90
о
СО
00
о
СО
СО
о
62
о
СО
ю
00
о
ь-
Is-
о
см
Is-
о
СЛ
см
00
о
см
Is-
о
СО
СО
о
00
о
СЛ
о
Is-
ь-
о
68
о
ю
ь-
о
СЛ
СО
о
65
о
ь-
сл
о
о
о
со
о
о
ю
00
о
ь-
ь-
о
т—1
о
СЛ
СЛ
о
00
00
о
80
о
ю
СЛ
о
ю
СЛ
о
о
о
СО
00
т-Н
00
о
t-
о
СЛ
СО
о
1—1
ь-
о
о
ь-
о
ю
СО
о
о
1—1
ю
00
о
t-
о
ь-
СО
о
СО
о
СЛ
о
ь-
Is-
о
68
о
о
00
со
о
со
о
см
см
00
о
ь-
о
СЛ
СО
о
гЧ
т—1
СЛ
00
о
80
о
ь-
о
ь-
сл
о
СО
00
о
80
о
ю
СЛ
Is-
о
Is-
о
Is-
СО
о
СО
СО
о
00
СО
о
СО
СО
о
см
т-Н
т-Н
00
о
тЧ
Is-
о
59
о
00
CD
00
о
ю
о
67
о
СО
{О
о
ь-
со
о
СО
со
о
СЛ
о
ю
о
о
о
СО
СО
т-Н
СЛ
о
95
о
90
о
СО
СЛ
00
о
г-Н
СО
о
ю
ь-
о
ь-
t-
t-
о
о
t-
о
СО
СО
о
ю
00
о
t-
t-
о
00
СО
о
00
о
ь-
t-
о
68
о
см
00
о
СО
Is-
о
66
о
00
СЛ
СЛ
о
СЛ
о
о
СЛ
о
СО
СО
т—1
СЛ
о
СО
00
о
о
00
о
ю
СЛ
о
86
о
80
о
ю
ю
00
о
t-
t-
о
см
Is-
о
СЛ
00
о
00
Is-
о
СЛ
со
о
СО
00
о
ю
t-
о
00
СО
о
СО
СО
00
о
ю
Is-
о
t-
СО
о
СО
о
00
о
т-Н
Is-
о
65
о
о
3
о
СО
00
о
о
00
о
ю
о
о
т—|
00
о
ю
Is-
о
ь-
сл
00
о
80
о
Is-
о
t-
см
00
о
ь-
о
69
о
1—1
СО
00
о
ю
t-
о
00
СО
о
СО
см
00
о
см
ь-
о
СО
СО
о
00
см
00
о
см
t-
о
66
о
00
t-
ь-
о
СЛ
СО
о
64
о
см
СЛ
00
о
т—1
00
о
ю
ь-
о
ь-
ю
00
о
ь-
ь-
о
см
ь-
о
о»
ю
00
о
СО
о
гЧ
о
СЛ
о
00
о
см
t-
о
68
о
СО
00
о
Is-
о
СО
СО
о
00
СЛ
t-
о
о
t-
о
LO-
LOCO
о
о
т-Н
СЛ
СЛ
о
ю
СЛ
о
06
о
СО
о
т-Н
CD
ь-
о
Is-
CD
о
63
о
00
о
ь-
о
о
СЛ
см
00
о
ь-
о
СЛ
СО
о
т-Н
т—1
о
о
1^
о
68
о
00
t-
о
о
t-
о
66
о
ю
СЛ
t-
о
т—|
t-
о
ю
со
о
о
т-Н
со
о
00
СО
о
СО
о
см
т—1
СЛ
о
СО
00
о
80
о
ю
о
СО
СО
о
62
о
СО
см
00
о
Is-
о
СЛ
СО
о
т—1
т-Н
СЛ
о
см
о
Is-
СО
о
СО
т-Н
ю
00
о
ю
Is-
о
68
о
СО
СО
Is-
о
СЛ
со
о
65
о
t-
Is-
ь-
о
СЛ
со
о
3
о
см
т-Н
СЛ
о
ю
о
о
о
СО
т-Н
СЛ
00
о
т-Н
00
о
ю
Is-
о
t-
т—1
ь-
о
ю
СО
о
62
о
00
00
о
см
Is-
о
00
СО
о
СО
т-Н
о
СЛ
о
ь-
Is-
о
00
СО
о
т-Н
00
о
см
ь-
о
СО
СО
о
00
3.3]
Критерии проверки экспоненциалъности распределения
315
ft
99
о
95
о
о
СЛ
о
ft
СЛ
СЛ
о
,95
о
90
о
СЛ
СЛ
о
,95
о
90
о
Cj
СЛ
СЛ
о
95
о
о
СЛ
о
о
00
О
СО
IN
О
68
о
СО
СМ
LO
о
00
CD
О
CD
О
СЛ
гЧ
см
см
СЛ
ел
о
ю
СЛ
о
о
СЛ
о
СО
т—Н
см
99
о
95
о
90
о
СО
ел
т-Ч
CD
о
00
CD
О
64
о
см
ь-
о
ю
CD
О
т-Ч
CD
О
О
СМ
о
СЛ
о
00
о
СЛ
CD
О
90
о
оо
ь-
о
69
о
О
т-Ч
IN
О
67
о
LO
00
ь-
о
ь-
со
о
3
о
т-Ч
см
СЛ
о
CD
00
о
о
00
о
ю
94
о
86
о
т-Ч
00
о
Ю
о
CD
о
63
о
CD
о
IN
о
CD
о
т-Ч
CD
О
см
см
Ю
00
о
ь-
о
ь-
CD
о
CD
86
о
ю
IN
о
68
о
со
CD
о
СЛ
CD
О
65
о
ь-
О5
СЛ
о
ю
О5
О
о
СЛ
о
СО
СО
СМ
ел
оо
о
о
00
о
ю
ь-
о
ь-
89
о
81
о
ю
Jb-
о
Jb-
СО
о
CD
CD
О
62
О
00
СЛ
00
о
ь~
о
00
CD
О
см
00
о
СО
о
CD
CD
О
00
82
о
см
о
67
о
00
ю
ь-
о
00
CD
О
64
о
О5
'xf
СЛ
о
CD
00
О
о
00
О
ю
ю
00
о
ь-
ь-
о
см
ь-
о
СЛ
85
о
t-
ь-
о
см
ь-
о
СЛ
см
о
LO
CD
о
61
о
о
см
CD
00
о
CD
О
00
CD
О
CD
О
00
о
о
ь-
о
LO
со
о
о
80
о
т-Ч
JN
О
65
о
о
СО
ь-
о
ь-
CD
О
64
о
1—1
см
СЛ
00
о
см
00
о
CD
IN
О
IN
CM
00
о
IN
о
СЛ
CD
О
т—1
82
о
IN
О
69
о
т-Ч
т-Ч
о
CD
О
1—1
CD
О
СМ
см
СО
00
о
СО
ь~
о
CD
О
00
IN
о
СЛ
CD
О
"х*
CD
О
СМ
t-
Jb-
о
69
о
64
о
см
см
ь-
о
CD
CD
О
63
о
СО
СМ
CD
00
О
00
о
см
IN
О
СЛ
ел
ь-
о
см
ь-
о
00
CD
О
СО
80
о
см
ь-
о
68
о
СО
СЛ
со
о
3
о
о
CD
О
см
о
GO
о
т-Ч
IN
О
CD
CD
О
О
ю
ь-
о
ь-
CD
о
СО
со
О
CD
JN-
О
68
о
63
о
СЛ
О5
О
Ю
СЛ
О
90
о
СО
Ю
СМ
см
00
о
ю
IN
О
о
ь-
о
т-Ч
00
ь-
о
о
ь-
о
CD
CD
О
Ю
00
Ь-
О
О
IN
О
66
О
ю
т-Ч
СЛ
о
00
о
69
о
00
о
СЛ
CD
о
CD
О
см
ь-
о
IN
CD
О
СО
CD
О
CD
ь-
О
66
о
62
о
CD
СЛ
о
00
о
т-Ч
00
о
LO
о
00
о
СО
О
00
CD
О
СО
CD
о
О5
CD
О
ю
CD
О
ь-
СО
IN
О
69
о
65
о
CD
00
О
ю
in
о
68
о
со
CD
О
GO
CD
О
СО
CD
О
-xf
СО
О
CD
CD
О
СМ
со
о
00
см
JN-
о
65
о
61
о
00
СЛ
00
О
т—|
00
О
ю
Ь-
О
Ь-
00
IN
о
т-Ч
О
IN
CD
О
LO
ю
ь-
о
00
CD
о
CD
О
СЛ
°
IN
CD
О
64
о
О5
СМ
00
О
см
IN
О
66
о
00
Ю
IN
о
IN
CD
О
СО
CD
О
CD
СМ
ь-
о
ю
со
о
т—1
со
о
о
см
99
о
95
о
о
СЛ
о
СО
о
см
LO
00
о
ь-
t-
о
см
t-
о
СЛ
Jb-
о
СЛ
CD
о
LO
CD
о
ь~
СО
ь-
о
ь-
со
о
СО
CD
о
1—1
см
90
о
оо
о
68
о
о
00
о
о
In
о
65
о
о
СО
о
СО
со
о
см
CD
о
00
СЛ
СЛ
о
ю
СЛ
о
о
СЛ
о
СО
см
см
91
о
86
о
о
00
о
ю
см
00
о
LO
ь-
о
о
ь-
о
т-Ч
LO
о
00
CD
о
3
о
О5
о
СЛ
о
ь-
ь-
о
00
со
о
86
о
LO
о
67
о
со
00
о
СЛ
со
о
64
о
см
см
IN
о
ю
CD
о
т-Ч
со
о
о
см
ел
о
CD
00
о
о
00
о
ю
89
о
81
о
ю
Jb-
о
Jb-
т-Ч
00
о
СО
о
68
о
СО
СО
о
CD
о
СО
CD
о
т-Ч
см
LO
00
о
LO
о
00
CD
о
CD
82
о
со
о
66
о
00
CD
о
00
CD
о
63
о
о
ь-
о
CD
о
о
CD
о
см
см
СЛ
00
о
т-Ч
00
о
ю
ь-
о
ь-
85
о
ь-
о
см
ь-
о
СЛ
о
т-Ч
о
66
о
LO
см
ь-
о
СО
CD
о
СО
CD
о
СО
см
см
00
о
см
ь-
о
CD
со
о
00
80
о
т-Ч
о
65
о
о
о
СО
о
63
о
CD
О5
О5
о
ю
О5
о
о
СЛ
о
СО
"xf
см
Ю
00
о
ь-
ь-
о
см
IN
о
СЛ
83
о
IN
о
69
о
т-Ч
CD
о
СЛ
CD
о
65
о
ь-
о
СЛ
о
00
ь~
о
ел
CD
о
"X*
о
00
о
о
ь-
о
ю
CD
о
о
In
t-
о
69
о
64
о
см
СО
о
CD
со
о
62
о
00
'xf
СЛ
о
СО
00
о
г—1
00
о
ю
см
00
о
ь-
о
СЛ
CD
о
т—1
80
о
см
ь-
о
68
о
СО
LO
о
00
CD
о
64
о
СЛ
LO
00
о
LO
IN
о
00
CD
о
CD
00
о
СЛ
CD
о
со
о
см
CD
JN-
о
68
о
63
о
см
IN
о
Ю
CD
о
61
о
о
см
О5
00
о
т-Ч
00
о
ю
ь-
о
IN
о
00
о
см
ь-
о
00
CD
о
СО
00
о
т-Ч
IN
о
66
о
ю
о
ь-
CD
о
63
о
т—1
см
СО
00
о
СО
IN
о
СО
о
00
ю
ь-
о
00
со
о
СО
CD
о
о
67
о
62
о
CD
т-Ч
о
CD
о
т-Ч
CD
о
см
см
CD
00
о
ь-
о
см
IN
о
СЛ
00
о
т-Ч
ь-
о
ь-
CD
о
ю
CD
IN
о
69
о
65
о
см
о
CD
со
о
63
о
СО
см
о
GO
о
т-Ч
IN
о
СО
CD
о
о
ь-
о
ь-
CD
о
см
со
о
CD
см
JN-
о
66
о
62
о
00
о
о
СО
CD
о
о
CD
О
"xf
СМ
СО
00
о
ю
IN
О
о
ь-
о
т-Ч
т-Ч
CD
о
СЛ
CD
о
Ю
CD
О
ь-
ь-
о
68
о
64
о
СЛ
т-Ч
ь-
о
ю
со
о
62
о
Ю
см
00
t>
о
о
IN
о
СО
О
см
гЧ
СО
о
CD
СО
О
СМ
CD
О
00
т-Ч
о
65
о
т-Ч
CD
О
О
см
316 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
-Inxi 0,693 2,398-2,197
1 3929959 \h +
Е1пжг+1 -Inxi 0,693 2,398-2,197
!±i 1 = 3,929959 -\ ¦ h ... + ¦ = 8,901:
щ ' 1,053606 0,28163
К = ; = 0,441.
8,901
Из табл. 101 для п = г = 10 имеем Ж0,95(Ю,10) = 0,69.
Так как К = 0,441 < Жо,э5(Ю, 10) = 0,69, нулевая гипотеза не отклоняется. Она вклю-
включает в себя и гипотезу экспоненциальное™ распределения, так как экспоненциальное
распределение является частным случаем распределения Вейбулла. Рассмотрим случай
цензурированных испытаний при г = 7 < п = 10. Для этого случая имеем
б б
У ln^+i^ln^ = 4,3402333; V ]nXi+1 ~ lnXi = 6,886416;
К = 4'3402333 = 0,630026.
6,886416
Из табл. 101 для п = 10 и г = 7 находим K0j95G,10) = 0,81.
Так как К = 0,63 < ifo,95G,10) = 0,81, нулевая гипотеза не отклоняется и в этой
ситуации.
3.3.22. Критерий Дешпанде
В [334] Дешпанде рассмотрел класс критериев экспоненциальности против алв™
тернатив распределений с увеличивающейся интенсивностью отказов, основанных
на статистике
т * v^ / к \ / к \ J1' если ж» > Ьж^;
^i71 ~ 1) гф^ [0, еСЛИ Xi ^ fe^j.
В условиях, когда нулевая гипотеза справедлива, величина \jn[ J — ) рас™
пределена асимптотически нормально с нулевым средним и дисперсией [326]
1 М 1 26 26 2
D
26 A + ЬJ 1 + 6 + Ь2
От выбора постоянной Ъ зависит эффективность критерия против различных
альтернатив. Мы воспользуемся рекомендацией авторов работы [326], установив™
ших, что для наиболее распространенной альтернативы вейбулловского распреде-
распределения следует брать Ъ = 0,44.
Тогда критерий отклоняет нулевую гипотезу в случае, если
J2 ^fe 0,44^-) ^ 0,1494^г(^ - 1) иа + 0,694тг(п - 1).
ъфз
Задача 147. В условиях задачи 125 проверить соответствие эмпирических данных
экспоненциальному распределению критерием Дешпанде при а = 0,95.
Имеем для различных сочетаний i и j:
<p(xi] 0,44ж2) = (f(l; 0,44 • 2) = (p(l; 0,88) = 1;
(p(xi\0,Ux3) = у>A; 0,44 • 4) = <рA; 1,76) = 0;
<p(xi\ 0,44ж4) = ... = (p(xi\ 0,44жю) = 0; (p(x2; 0,44x3) = 1;
(f(x2; 0,44ж4) = ... = ip(x2] 0,44жю) = 0; ^(ж3; 0,44^4) = 1;
3.3] Критерии проверки экепоненциальности распределения 317
; 0,44ж5) = (f(x4; 0,44ж6) = 1; (f(x4; 0,44ж7) = ... = (f(x4; ,044жю) = 0;
х5; 0,44х6) = (р(хь; 0,44ж7) = 1; ^(ж5; 0,44х8) = ... = ^(ж5; 0,44жю) = 0;
(р(х6; 0,44ж7) = (f(x6; 0,44ж8) = 1; (р(х6; 0,44ж9) = (р(х9; 0,44жю) = 0;
(р(х7; 9,44ж8) = ... = (f(x7; 0,44жю) = 1;
(^(ж8;0,44ж9) = у?(ж8;0,44ж1о) = <р(х9\0,Ых10) = 1;
В нашем случае 17о,95 = 1,645 и п = 10. Тогда имеем
0,1494 • л/10 • A0 - 1) • 1,645 + 0,694 • 10 • A0 - 1) = 69,454.
Так как J^ (f(xi; 0,44a?j) = 17 < 69,454, гипотеза экепоненциальности распределения слу-
гфз
чайных величин не отклоняется.
3.3.23. Критерий Лоулесса
В работах Лоулесса [336], Энгельгардта и Байна [335] рассмотрен критерий про-
проверки гипотезы относительно величины параметра формы гамма-распределения,
основанный на статистике
где х = I Y\ xi I ; ж = — J^ Xi — соответственно геометрическое и арифметическое
средние ряда х±, #2, • • •, хп.
Напомним, что при равенстве параметра формы гамма-распределения единице
оно переходит в экспоненциальное. Поэтому проверка нулевой гипотезы Н®: к = 1
против альтернативы Н[ : к > 1 или Н": к < 1 эквивалентна проверке гипотезы
экепоненциальности выборочных данных. Гипотеза экепоненциальности принима™
ется на уровне значимости а, если выборочное значение W находится в интервале
M/ri(a) < W < М^2(ск)- Если W < Wi(a), то нулевая гипотеза отклоняется в пользу
гипотезы Н" (т. е. в пользу гипотезы о распределении с уменьшающейся интенсив-
интенсивностью отказов).
Если W > W(ck), to нулевая гипотеза отклоняется в пользу альтернативы Н[
(распределение с увеличивающейся интенсивностью отказов).
Статистика W является обобщением ранее рассмотренной нами статистики
Бартлетта^Морана (см. раздел 3.3.9). Критические значения Wi(a) и W^tt) для
проверки гипотезы экепоненциальности, заимствованные из [337], приведены
в табл. 102.
Задача 148. В условиях задачи 125 проверить соответствие эмпирических данных
экспоненциальному распределению критерием Лоулесса при а = 0,05.
Имеем
/ п \п х
х = I П ж* I = A • 2 • 4 • 5 • 9 • 11 • 18 • 21 • 29 • 35) ю = 8,28257;
* = !.1> = 13,5; W = * = 8-^ = 0,6135.
п р^ х 13,5
Из табл. 102 для п = 10 и а = 0,05 имеем Wx = 0,3758 и W2 = 0,8210.
Так как W\ = 0,3758 < W = 0,6135 < W2 = 0,821, гипотеза экепоненциальности не
отклоняется.
318 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Таблица 102
Критические значения W"i(o) и W^^ol)
критерия экспоненциальности Лоулесса [337]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Уровень значимости а
0,
Шг
0,4359
0,3991
0,3966
0,4006
0,4061
0,4115
0,4165
0,4216
0,4261
0,4302
0,4339
0,4373
0,4405
0,4435
0,4463
0,4487
0,4513
0,4535
0,4556
0,4574
0,4595
0,4613
0,4629
0,4644
0,4662
0,4674
0,4688
0,4700
0,4713
10
w2
0,9950
0,9574
0,9147
0,8794
0,8512
0,8285
0,8099
0,7944
0,7812
0,7699
0,7601
0,7514
0,7437
0,7368
0,7306
0,7350
0,7199
0,7151
0,7108
0,7070
0,7031
0,6998
0,6964
0,6933
0,6906
0,6878
0,6854
0,6830
0,6808
0,
0,3122
0,3058
0,3173
0,3299
0,3413
0,3515
0,3601
0,3684
0,3758
0,3818
0,3877
0,3929
0,3977
0,4019
0,4058
0,4094
0,4130
0,4162
0,4194
0,4219
0,4249
0,4273
0,4296
0,4317
0,4341
0,4360
0,4380
0,4398
0,4416
35
w2
0,9987
0,9790
0,9477
0,9176
0,8915
0,8695
0,8508
0,8348
0,8210
0,8089
0,7982
0,7887
0,7802
0,7726
0,7656
0,7593
0,7536
0,7482
0,7432
0,7388
0,7343
0,7305
0,7265
0,7230
0,7199
0,7167
0,7137
0,7110
0,7083
0,
0,1411
0,1670
0,1927
0,2157
0,2344
0,2505
0,2644
0,2763
0,2876
0,2973
0,3059
0,3139
0,3211
0,3275
0,3334
0,3393
0,3446
0,3491
0,3542
0,3580
0,3619
0,3655
0,3690
0,3724
0,3761
0,3786
0,3817
0,3843
0,3868
31
w2
0,9999
0,9959
0,9826
0,9646
0,9458
0,9280
0,9115
0,8967
0,8832
0,8710
0,8600
0,8500
0,8408
0,8324
0,8241
0,8175
0,8109
0,8047
0,7989
0,7936
0,7885
0,7838
0,7793
0,7750
0,7710
0,7672
0,7637
0,7602
0,7571
3.4]
Критерии согласия для равномерного распределения
319
3.4. Критерии согласия для равномерного распределения
Напомним, если х\, ...,хп—выборка из распределения вероятностей с функ™
цией F(x), то случайная величина yi = F{xi) распределена равномерно на интер™
вале [0,1]. Поэтому установление равномерности распределения у^ является по
существу критерием согласия наблюдаемвж данных с теоретическим распределен
нием F(x). Этим объясняется повышенный интерес к поиску простых в вычисли™
тельном отношении и эффективных критериев равномерности распределения слу-
случайных величин. Можно указать на такие критерии равномерности распределения,
как
— критерий Кимбела [338]
г=1
Un+1 = 1;
— критерий Морана [339]
п+1
в=
— критерий и [340]
г=1
U4 ~~
2г — 1
п
Здесь Ui — порядковая статистика равномерно распределенной случайной ве-
величины. В настоящем разделе мы рассмотрим наиболее эффективные критерии
равномерности распределения случайных величин.
3.4.1. Критерий Шермана
Статистика критерия Шермана для проверки равномерности распределения
имеет вид [327]
п+1
и0 = 1, ип =
Распределение статистики Шермана рассмотрено в разделе 3.3.15, там же приведе-
приведены критические значения (табл. 95) и аппроксимации статистики этого критерия.
Задача 149. Имеется ряд наблюдений над случайной величиной:
Uii 0,047; 0,05; 0,15; 0,18; 0,29; 0,48; 0,52; 0,61; 0,72; 0,91.
Необходимо проверить гипотезу равномерности распределения случайной величины Ui
на интервале [0,1] критерием Шермана при доверительной вероятности а = 0,95.
Находим
1
0,047--
0,5 - 0,047 - jj
0,72 - 0,61 - ^
0,91 - 0,72
= 0,245.
Из табл. 95 для п = 10 имеем сию @,95) = 0,473.
Так как шп = 0,245 < сию @,95) = 0,473, гипотеза равномерности не отклоняется.
320 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Рассмотрим нормальную аппроксимацию шп-распределения.
Имеем (см. раздел 3.3.15)
2 . ю12 + 10 ¦ 912 /10х 22
D(o;n) = — —^ ( — j = G,Q05251 {у/Щшп) = 0,07246).
Вычисляем
u)n-M(ujn) 0,245-0,35049
ш = —1,457.
у/Щшп) 0,07246
Так как \шп\ = 1,457 < t?o,95 = 1,645 (95%-я квантиль стандартного нормального распре-
распределения), гипотеза равномерности распределения не отклоняется.
И еще одна аппроксимация:
и =
Видим, что результаты близки — случайная величина С/', имеющая стандартное нор-
нормальное распределение, находится в пределах 95%-го интервала, что позволяет принять
гипотезу равномерности.
3.4.2. Критерий Морана
Статистика критерия, предложенного Мораном [309], используется в форме
где A = Ui-Ui-U Di = UU Dn+1 = 1 - Un (г = 1, ... ,n + 1).
В [231] показано, что случайная величина
М _
7п
имеет распределение %2 с / = п степенями свободы. Используя аппроксимацию
Вилсона-Хилферти (см. раздел 1.1.8), мо^но получить аппроксимацию
7n +
где z — случайная величина, имеющая стандартное нормальное распределение.
Гипотеза равномерности принимается, если
Мг{а) ^Мп^М2{а),
где Mi (а) и М2(а)—критические значения статистики, приведенные в табл. 103.
Для частного случая, когда Щ = .F(a^), критерий Морана становится критерием
согласия эмпирического распределения с теоретическим F(x). В случае их совпа-
совпадения случайная величина Щ должна быть распределена равномерно на интерва™
ле [0,1].
3.4]
Критерии согласия для равномерного распределения
321
Таблица 103
Критические значения JVfi(cx) и
статистики Морана [341]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Доверительная вероятность а
0
Mi
0,130
0,356
0,643
0,967
1,317
1,687
2,072
2,469
2,876
3,292
3,715
4,145
4,581
5,021
5,466
5,916
6,369
6,825
7,285
90
м2
2,756
3,699
4,573
5,408
6,214
7,001
7,772
8,531
9,279
10,018
10,750
11,475
12,194
12,909
13,618
14,324
15,025
15,721
16,418
0
Мг
0,064
0,215
0,430
0,689
0,979
1,292
1,625
1,973
2,333
2,704
3,085
3,479
3,870
4,272
4,681
5,094
5,513
5,936
6,362
95
м2
3,554
4,592
5,546
6,449
7,319
8,162
8,987
9,795
10,591
11,375
12,150
12,916
13,675
14,428
15,174
15,916
16,652
17,384
18,112
0,99
Mi
0,012
0,070
0,180
0,334
0,523
0,741
0,982
1,242
1,519
1,810
2,113
2,428
2,752
3,085
3,425
3,774
4,128
4,489
4,855
М2
5,370
6,579
7,675
8,705
9,688
10,637
11,559
12,460
13,343
14,210
15,064
15,907
16,740
17,563
18,378
19,186
19,987
20,782
21,571
Если параметры теоретического распределения известны заранее, то критерий
Морана используется в форме [342]
п+1
где Di = Ui-Ui-Ui = l, ...,n + l, E/o = O, Un+1 = 1.
Равномерность распределения Щ на интервале [0,1], а следовательно, и дону™
стимость использования в качестве вероятностной модели распределения функ™
ции -Р(ж), отклоняется, если [342]
>Х(п)
С2
где Cl =
X«(n) — о^квантшть стандартного нормального распределения с / = п степенями
свободы.
Если параметры распределения F(x) определяются по выборке, то критерий
имеет вид
Мп + - - а
—i— > х2»'
где к — число определяемых по выборке параметров.
11 А. И. Кобзарь
322 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Эти аппроксимации, предложенные Ченгом и Стефенсом [342], дают весьма
удовлетворительные результаты уже при п > 5.
Задача 150. Для данных задачи 149 проверить гипотезу равномерности распределе-
распределения случайных величин критерием Морана при доверительной вероятности а = 0,95.
Имеем
D1 = U1 = 0,047; D2 = 0,05 - 0,047 = 0,003; D3 = 0,15 - 0,05 = 0,10;
D4 = 0,18 - 0,15 = 0,03; D5 = 0,11; D6 = 0,19; D7 = 0,04; D8 = 0,04;
D9 = 0,09; Dio = 11; Dn = 0,09.
Тогда
Mn = ^ In [(n + 1) • Di] = -11 In 11-^; In A =
г=1 г=1
= 26,3768 - (In 0,047 + In 0,003 + ... + In 0,19 + In 0,09) = 4,0698.
Из табл. 103 находим Мг = 2,333 и М2 = 10,591.
Так как Mi = 2,333 < Мп = 4,0698 < М2 = 10,591, гипотеза равномерности не откло™
няетея.
Воспользуемся теперь нормальной аппроксимацией и вычислим
1
12-11 \ з / 2
4,0698 - 1- —
J ^^Z = ^0,635,
2
90
что находится в диапазоне Zo,o5 -г- ^о,95 = —1,645 -=- +1,645.
Случайная величина Мп = • Мп = • 4,0698 = 6,887 имеет у2-рас-
7п + 8 78
пределение с / = 10 степенями свободы. При а = 0,95 значение Хо,9бA0) = 18,307
(см. табл. 55), что больше Мп и, следовательно, не отклоняет гипотезу равномерности
распределения.
Применим теперь аппроксимацию Ченга-Стефенса.
11
Имеем Мп = V^lnD^ = 30,4467. Далее вычисляем
г=1
d = A0 + 1) • (In 11 + 0,57722) л/б • 11 • ( — - 1) - — = 15,84026;
с2 = , г • 11 • ( — - 1 ) - — = 1,071176.
л/2^То \ 6 / 2 6'1г
Тогда — = — ' = 13,636 < Хо 95(Ю) = 18,307, и этот критерий не от™
С2 1,071176 '
клоняет нулевую гипотезу.
3.4.3. Критерий Ченга-Спиринга
Критерий равномерности распределения, аналогичный критерию Шапиро-Уил™
ки (см. разделы 3.2.2.1 и 3.3.1), предложен в [343]. Его статистика имеет вид
1 2
?Ур —
где хп — х\ —выборочный размах.
3.4]
Критерии согласия для равномерного распределения
323
Всегда
п(п — 1)
4п(п + 1)
(n = 2,4, ...,2fe);
(ra= 1,3, ...,2fc- 1)
при справедливости нулевой гипотезы (подробнее об этом см. в [211]).
Гипотеза равномерности отклоняется, если W\(a) ^ Wp ^ W(a), где Wi(a)
и W^a)— критические значения при доверительной вероятности а, приведенные
в табл. 104.
Таблица 104
Критические значения Wi(«) и И^г(ск)
критерия равномерности Ченга^С пиринга [143]
п
3
4
5
6
7
8
9
10
11
12
13
14
15
Доверительная
0,90
Шг
6,30
3,74
2,58
2,00
1,64
1,40
1,22
1,08
0,97
0,89
0,81
0,75
0,70
w2
7,97
5,31
4,02
3,23
2,68
2,32
2,04
1,79
1,60
1,45
1,31
1,22
1,12
0,
6,15
3,44
2,42
1,88
1,54
1,32
1,15
1,02
0,92
0,84
0,77
0,71
0,66
вероятность а
95
w2
7,99
5,43
4,18
3,41
2,85
2,47
2,19
1,92
1,73
1,57
1,42
1,31
1,21
0,99
Wx
6,03
3,08
2540
1,71
1539
1,18
1,04
0,91
0,83
0,76
0,69
0,64
0,60
w2
8,00
5,53
4,39
3,67
3,13
2,77
2,46
2,18
1,99
1,79
1,64
1,52
1,39
п
16
17
18
19
20
21
22
23
24
25
30
40
50
Доверительная
0,
Шг
0,65
0,61
0,58
0,55
0,52
0,50
0,47
0,45
0,44
0,42
0,35
0,26
0,21
90
w2
1,03
0,97
0,90
0,85
0,80
0,76
0,72
0,68
0,65
0,62
0,51
0,37
0,29
0,
Wt
0,62
0,58
0,55
0,52
0,50
0,47
0,45
0,43
0,42
0,40
0,33
0,25
0,20
вероятность а
95
w2
1,11
1,04
0,98
0,92
0,86
0,81
0,78
0,73
0,70
0,67
0,54
0,39
0,30
0,
Wt
0,56
0,53
0,50
0,47
0,45
0,43
0,41
0,40
0,38
0,36
0,31
0,23
0,19
99
w2
1,31
1,20
1,12
1,05
0,98
0,92
0,89
0,84
0,80
0,76
0,61
0,44
0,33
Задача 151. Для данных задачи 149 проверить гипотезу равномерности распределе-
распределения случайной величины критерием Ченга-Спиринга при а = 0,95.
ю
Имеем хп = 0,91, ал = 0,047 и ]Р
ж* - жJ = 0,7973241.
Тогда Wp =
@,91 - 0,047) • —
= 1,395. Из табл. 104 для а = 0,95 и п = 10 находим
0,7973241
Wi@,95) = 1,02 и W2@,95) = 1,92.
Так как Wt(a) = 1,102 < Wp = 1,395 < W2(a) = 1,92, гипотеза равномерности распре-
распределения совокупности случайных величин не отклоняется.
3.4.4. Критерий Саркади-Косика
В [344] рассмотрен новый, весьма эффективный критерий равномерности на [0,1],
основанный на модификации критерия Ватсона (см. раздел 1.2.5), со статистикой
где
11*
324 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Распределение признается не противоречащим равномерному на уровне значи™
мости а, если J < «/(а), где J(a) — критическое значение, приведенное в табл. 105.
Таблица 105
Критические значения «/(«)
критерия Саркади—Косика [344]
п
5
10
15
20
25
30
35
Доверительная
вероятность а
0,05
0,499
0,741
0,881
0,931
0,973
1,000
1,020
ОДО
0,408
0,599
0,695
0,748
0,782
0,806
0,823
п
40
50
60
70
80
90
100
Доверительная
вероятность а
0,05
1,040
1,020
1,060
1,070
1,070
1,080
1,080
0,10
0,836
0,823
0,862
0,870
0,876
0,880
0,883
Критерий обладает высокой мощностью против большого спектра альтернатив.
Задача 152. Для данных задачи 149 проверить гипотезу равномерности распределе-
распределения случайной величины критерием Саркади-Косика на уровне значимости а = 0,05.
Вычисления статистики критерия приведены в таблице:
ъ
1
2
3
4
5
6
7
8
9
10
Xi
0,047
0,050
0,150
0,180
0,290
0,480
0,520
0,610
0,720
0,910
г
п + 1
0,0909
0,1818
0,2727
0,3636
0,4545
0,5454
0,6363
0,7272
0,8181
0,9090
г
Х% п+ 1
-0,0439
-0,1318
-0,1227
-0,1836
-0,1645
-0,0654
-0,1163
-0,1172
-0,0981
0,0010
Цп-i + l)
10
18
24
28
30
30
28
24
18
10
di
-0,004390
-0,007322
-0,005110
-0,006557
-0,005480
-0,002180
-0,004150
-0,004880
-0,005450
0,000100
dl
1,927-10^5
5,631 • 10^5
2,614-10^5
4,300 • 10^5
3,010-10^5
4,750 • 10^5
1,720 • 10^5
2,380 • 10^5
2,970 • 10^5
Вычисляем статистику
J = 100 • 2,5028 •
- 10 • @,045419J = 4,399
Легко видеть, что J = 4,399 • 10~~3 < J(ol) = 0,741, что не отклоняет гипотезу равномер-
равномерности.
3.4.5. Энтропийный критерий Дудевича-ван дер Мюлена
По аналогии с критерием нормальности Васичека [247] (см. раздел 3.2.2.2) в [345]
рассмотрен критерий для оценки равномерности распределения.
Пусть х\ ^ ... ^ хп — выборка случайных величин. Ее выборочная энтропия
равна [2471
п
, п) = --
г=1
log2 7^(%i+m - хг^п
т — целое число ^ — (используем Х{ = х\ при г < 1 и Xi = хп при г > п).
3.4]
Критерии согласия для равномерного распределения
325
Распределение случайных величин признается равномерным, если Н{т1п)
На(т,п), где Ha(mJn)—критическое значение, приведенное в табл. 106.
Таблица 106
Критические значения Ша{туп)
статистики Дудевича—ван дер Мюлена [346]
ТЬ
10
20
30
40
тп
1
2
3
4
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
Уровень значимости а
0,01
1,228
0,979
0,951
0,977
0,787
0,588
0,536
0,536
0,543
0,557
0,581
0,605
0,632
0,665
0,540
0,402
0,384
0,384
0,394
0,407
0,420
0,440
0,459
0,569
0,379
0,330
0,316
0,311
0,313
0,318
0,05
0,974
0,766
0,741
0,774
0,658
0,466
0,429
0,428
0,438
0,458
0,481
0,509
0,536
0,544
0,367
0,324
0,312
0,314
0,322
0,335
0,350
0,366
0,383
0,491
0,315
0,270
0,254
0,253
0,257
0,265
0,10
0,845
0,659
0,645
0,681
0,585
0,412
0,378
0,378
0,391
0,410
0,433
0,460
0,489
0,496
0,327
0,287
0,279
0,282
0,291
0,304
0,319
0,336
0,354
0,450
0,283
0,242
0,229
0,228
0,231
0,239
ть
40
50
100
тп
8
9
10
15
1
2
3
4
5
6
7
8
9
10
15
20
1
2
3
4
5
6
7
8
9
10
15
20
30
40
Уровень значимости а
0,01
0,327
0,339
0,350
0,415
0,532
0,342
0,284
0,264
0,257
0,257
0,260
0,266
0,274
0,283
0,337
0,397
0,430
0,353
0,199
0,175
0,165
0,160
0,157
0,157
0,159
0,160
0,180
0,205
0,262
0,325
0,05
0,274
05285
0,297
0,367
0,458
0,282
0,236
0,219
0,214
0,215
0,219
0,226
0,234
0,243
0,295
0,355
0,381
0,219
0,170
0,150
0,140
0,135
0,134
0,134
0,136
0,138
0,159
0,185
0,243
0,314
0,10
0,249
0,260
0,272
0,316
0,422
0,256
0,213
0,198
0,195
0,196
0,201
0,207
0,216
0,224
0,276
0,336
0,360
0,204
0,158
0,138
0,128
0,123
0,122
0,123
0,124
0,128
0,149
0,175
0,233
0,306
Для п > 20 полезна аппроксимация
Х< у^ Iog2(^.
г=0
где
R(l,m- 1) =
_ ) m-l
E
m- j
¦ 2 - m)[log2(ra + 1) + 0,5772 - ДA,га - 1)] > ,
при т = 1 (х0 = 0; жт+1 = 1);
при т ^ 2.
Статистика Н(гп, п) имеет стандартное нормальное распределение. Следует по-
помнить, что Н(т,п) всегда отрицательно и log2 a = 3,3219 lg a.
326 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Задача 153. Для данных задачи 149 проверить гипотезу равномерности распределе-
распределения случайной величины критерием Дудевича-ван дер Мюлена на уровне значимости
а = 0,05.
Выбираем т = 2 и вычисляем статистику критерия
ЯB, Ю) = -^ • |log2 ™ • (х3 - Х1) + ... + log2 И . (Ж10 _ Ж8) J =
= ОД • (log2 0,82 + Iog2 0,3325 + ... + log2 0,75) = 0,20914.
Из табл. 106 для п = 10, т = 2 ш а = 0,05 имеем Я0,о5B,10) = 0,766.
Так как ЯB,10) = 0,209 < Яо,о5B,10) = 0,766, гипотеза равномерности распределен
ния вероятностей случайной величины не отклоняется.
3.4.6. Критерий Хегази-Грина
По аналогии с критерием нормальности Хегази—Грина (см. раздел 3.2.2.3) авто-
авторы работы [249] рассмотрели и критерий равномерности на основе статистик
г=1 г=1
где Xi—порядковые статистики выборки; щ = М(з^)—математическое ожидание
г-й порядковой статистики.
Критерий применим и для случайных величин, распределенных на любом интер-
интервале [а, Ь]. В этом случае следует перейти к переменной у^ = г (г = 1, ..., п)
и объем выборки п заменить на (тг — 2).
В конечном итоге предлагаются статистики
1 \ ' " ГТ1 *-
J-2 = —
771 1-^
г=1
m ^—^ \ m + 1
=1
для переменной ж^ Е [0,1] ;
где т = ^ ж^ _ Ж1
п — 2 для переменной ^ = — •
В [249] рассмотрены так^е модифицированные статистики, которые вместо
математического ожидания г-й порядковой статистики т = используют его
т + 1
модальное значение ^ = г (в силу несимметричности распределения порядко™
вых статистик).
Критерии в этом случае вычисляются по формулам
1
т
\ "\
г —
т —
1
1
1
т
Х^ ( г — 1
Гипотеза равномерности распределения случайных величин а^ принимается на
уровне значимости а, если
TiCTi*) < Тг(а)(Т*(а)) или Т2(Т2*) < Т2(а)(Т2*(а)),
где Ti(a), Тх*(а), Т2(а), Г2*(а) —критические значения соответствующих статистик,
приведенные в табл. 107.
3.4]
Критерии согласия для равномерного распределения
327
Таблица 107
Критические значения Т\(о:), Т]*(о), T^ol) и TJ(q:)
критерия равномерности Хегази—Грина [249]
п
3
8
18
38
78
Уровень значимости а
0,01
Тг
0,3893
0,2590
0,1724
0,1225
0,0853
Т*
0,4277
0,2674
0,1764
0,1224
0,0843
т2
0,1744
0,0822
0,0376
0,0191
0,0096
гр*
А2
0,2807
0,0998
0,0421
0,0188
0,0095
0,05
Тг
0,3254
0,2030
0,1360
0,0950
0,0664
т*
0,3778
0,2142
0,1399
0,0949
0,0663
т2
0,1189
0,0522
0,0240
0,0119
0,0059
0,2059
0,0641
0,0268
0,0123
0,0059
Для промежуточных значений п применима аппроксимация
/п п
коэффициенты а, Ь и с которой для различных статистик и уровней значимости
приведены в таблице:
Статистика
IT (а)
Ща)
Г2*(а)
"Уровень значимости а
0,01
а
-0,0070
-0,0090
-0,0148
0,0047
Ь
0,8373
0,7949
0,1701
-0,0607
с
-0,2500
-0,0782
0,2745
0,9330
0,05
а
0,0003
0,0064
-0,0068
0,0214
ь
0,5876
0,5066
0,0783
-0,1395
с
-0,0425
0,2364
0,2419
0,8212
Мощность критерия достаточно велика по сравнению с другими критериями.
Задача 154. Проверить гипотезу равномерности распределения случайной величи-
величины Х{ на интервале [0,1] для данных задачи 149 критериями Хегази-Грина на уровне
значимости а = 0,05.
Имеем
ю
= 0,1 • @,0439 + 0,1318 + ... + 0,0982 + 0,0083) = 0,1051;
п + 1
1
10
= 0,1 • A,9272 • 10^3 + 0,01737 + ... + 6,889 • 10~5) = 0,0136;
г- 1
- 1
= 0,1 • @,047 + 0,1722 + ... + 0,16888 + 0,09) = 0,1248;
= 0,01764.
Из табл. 107 для а = 0,05 и п = 10 находим (аппроксимацией)
Ti(a) = 0,20; Т*(а) = 0,21; Т2(а) = 0,05; Г2 (а) = 0,06.
Более точные критические значения получим, воспользовавшись аппроксимациями:
71@,05) = 0,0003+^ -Mfi =0,182;
328 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Т;@,05) = 0,0064+ ^ + ^=0,190;
10 Ю
Т2@,05) = -0,0068 + ^ + ^ = 0,042;
vlO Ю
Т2*@,05) = 0,0124 - 2^ + °*™ = 0,050.
lO Ю
Так как
Тг = 0,1052 < Ti@,05) = 0,182; Г* = 0,1248 < 1^@,05) = 0,190;
Т2 = 0,0316 < Т@,05) = 0,042; Г2* = 0,017 < Г2*@,05) = 0,050,
то всеми критериями гипотеза равномерности не отклоняется.
3.4.7. Критерий Янга
В [347] изучен критерий для проверки распределения точек на отрезке. Пусть
на отрезке длиной I с началом в нуле расположено п точек с координатами
х\ ^ ... ^ хп. Определим переменные
Dt = хъ Di = Xi- Xi-i, Dn+1 = l-xn.
Впервые критерии для проверки равномерности, основанные на D-статистиках,
рассмотрены в [348, 349], однако пригодные аппроксимации получены в [347].
Статистика критерия Янга имеет вид
* г=1
п п
Очевидно, что 0 ^ М ^ . При I = 1 имеет место М = ^ mm(D^, A+i)-
г=1
Если I неизвестно, то используется статистика
М* = ^^— J^ min(A, A+i),
Хп ^ Xi , = 2
распределение которой совпадает с распределением М^статистики при замене п на
(п-2).
Гипотеза равномерности не отклоняется, если
Mi (а) <:м<: М2(а),
где Mi (а) и М2(а)—критические значения, приведенные в табл. 108.
При п ^ 15 можно использовать тот факт, что статистика
имеет стандартное нормальное распределение. Если иа — «^квантиль стандартного
нормального распределения, то
, , , ч п . 1 2п — 1
м^а) = 2(^ТТ) * Ui^ 27^ТТ) V ~з~-
Напомним, что
ui-ot = —1,645 при а = 0,90; гы-а = —1,96 при а = 0,95
2 2
и ги^а = ^2,58 при а = 0,99.
2
3.4]
Критерии согласия для равномерного распределения
329
Таблица 108
Критические значения A^i(ck)
статистики Янга [347]
п
2
3
4
5
10
15
20
30
40
Доверительная вероятность а
0,90
Mi
0,090
0,151
0,192
0,220
0,300
0,340
0,370
0,390
0,400
М2
0,545
0,589
0,602
0,610
0,600
0,590
0,590
0,570
0,570
0,95
Mi
0,043
0,104
0,142
0,170
0,260
0,310
0,330
0,360
0,380
М2
0,581
0,627
0,646
0,650
0,640
0,620
0,610
0,600
0,590
0,99
Mi
0,010
0,046
0,073
0,100
0,190
0,240
0,270
0,310
0,340
М2
0,545
0,589
0,602
0,610
0,600
0,590
0,590
0,570
0,570
Более точно распределение Tkf-статистики аппроксимируется бета-распределе-
бета-распределением (см. раздел 1.1.7) с параметрами
а = Ь =
Зп2
2Bгс- 1)
Задача 155. Для данных задачи 149 проверить гипотезу равномерности распределе-
распределения случайной величины критерием Янга при уровне достоверности а = 0,95.
В нашем случае 1 = 1. Имеем ряд
Вг = 0,047; D2 = х2 - хг = 0,05 - 0,047 = 0,003;
D3 = 0,15 - 0,05 = 0,10; D4 = 0,18 ~~ 0,15 = 0,03; D5 = 0,29 - 0,18 = 0,11;
D6 = 0,48 - 0,29 = 0,19; D7 = 0,52 - 0,48 = 0,04; D8 = 0,61 - 0,52 = 0,09;
D9 = 0,72 - 0,61 = 0,11; D10 = 0,91 - 0,72 = 0,19; Dtl = 1 - 0,91 = 0,09,
з которого следует ряд значений:
Mi = mIn(Di,D2) = 0,003; M2 = min(D2,D3) = 0,003; M3 = mm(D3,D4) = 0,03;
M4 = mm(D4, D5) = 0,03; M5 = min(D5,D6) = 0,11; M6 = min(D6, D7) = 0,04;
M7 = mfn(D7, D8) = 0,04; M8 = m!n(D8, D9) = 0,09; M9 = min(D9, D10) = 0,11;
Mio = min(?>iOvDii) = 0,09.
10
Тогда М =J2Mi = 0,546. Из табл. 108 для п = 10 и а = 0,95 имеем Мг = 0,26
, М2 = 0,64. Так как Mi = 0,26 < М = 0,546 < М2 = 0,64, гипотеза равномерности не
отклоняется.
Если воспользоваться нормальной аппроксимацией, то
Mi @.95) =
М2@,95) =
10
1
2-11 \ 3 / 2-11
Видно, что полученные значения близки к табличным.
= 0,266;
= 0,642.
330 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.4.8. Критерии типа Колмогорова-Смирнова
Ранее были рассмотрены критерии типа Колмогорова—Смирнова, основанные
на сравнении теоретической и эмпирической функций распределения (см. разде-
разделы 3.1.2.1 — критерий Колмогорова—Смирнова; 3.1.2.6 — критерий Купера, как об-
общие критерии согласия; 3.2.1.2 — в задачах проверки нормальности распределения;
3.3.2 — в задачах проверки экспоненциальное™ распределения).
Приведем модифицированные формы критериев Колмогорова-Смирнова
+^, D) и Купера (V') для задачи проверки равномерности распределения
D^ = max| —
V = D+ + ?T.
Распределения указанных статистик быстро сходится к предельному, если ис-
использовать их модификации:
D+ =
п
0,4
0,2
0,68
w);
V = IV-
п-1
Критические значения для модифицированных статистик D+, D , D,
дены в табл. 109.
Таблица 109
Критические значения -D~*~, D~, D, V
критериев равномерности [231]
п
D+
D~
D
V
Уровень значимости а
0,01
1,518
1,518
1,628
2,001
0,025
1,358
1,358
1,480
1,852
0,05
1,224
1,224
1,358
1,747
0,10
1,073
1,073
1,224
1,620
0,15
0,973
0,973
1,138
1,537
Задача 156. Для данных задачи 149 проверить гипотезу равномерности распределе-
распределения случайной величины критериями типа Колмогорова-Смирнова на уровне значимо-
значимости а = 0,05.
Результаты вычислений представлены в таблице:
г
1
2
3
4
5
6
7
8
9
10
Щ
0,047
0,050
0,150
0,180
0,290
0,480
0,520
0,610
0,720
0,910
i
п + 1
0,1111
0,1818
0,2727
0,3636
0,4545
0,5454
0,6363
0,7272
0,8181
0,9090
тт. г
п + 1
^0,0641
^0,0404
-0,1227
-0,1836
-0,1645
-0,0654
-0,1163
-0,1172
-0,0981
0,0010
г тт-
п + 1
0,0641
0,1318
0,1227
0,1836
0,1645
0,0654
0,1163
0,1172
0,0981
-0,0010
3.4]
Критерии согласия для равномерного распределения
331
Вычисляем
D+ = 0,001; D~ = 0,1836; D = 0,1836; V = D+ + D^ = 0,1846;
~+ / 04\ / j— 068\
D+ = f 0,001 + -^- 1 • f V10 + 0,2 + -j= J = 0,1466;
= 0,1836-
0,4
To"
0 4
D= @,1836+^-
V = ( 0,1846 - - ] •
10 + 0,2-
0,6
= 0,799;
'2+tS)=0'799;
0,1555+ ^^ ) = 0,264.
Из табл. 109 для а = 0,05 находим D = 1,358 и V = 1,747.
Так как D = 0,799 < Й@,05) = 1,358 и V = 0,264 < F@,05) = 1,747, гипотеза равно-
равномерности распределения не отклоняется.
3.4.9. Критерий Фроцини
Ранее мы рассмотрели критерии Фроцини [239] применительно к проверке со-
соответствия эмпирического распределения нормальному (см. раздел 3.2.1.3) и экс-
экспоненциальному (см. раздел 3.3.4) законам. Для проверки равномерности ряда
Щ: U\ ^ ... ^ Un на отрезке [0,1] статистика критерия Фроцини имеет вид
U4 -
Распределение признается равномерным, если Вп < Bn(ct), где Вп(а) — критиче-
критическое значение статистики Фроцини для проверки равномерности (а — доверитель-
доверительная вероятность), приведенное в табл. 110.
Таблица 110
Критические значения статистики В„(а) критерия Фроцини
для проверки равномерности распределения [239]
п
5
6
7
8
9
10
Доверительная
вероятность а
0,90
0,4964
0,4908
0,4955
0,4933
0,4947
0,4896
0,95
0,5756
0,5700
0,5780
0,5733
0,5764
0,5723
0,99
0,7282
0,7123
0,7428
0,7394
0,7258
0,7310
п
11
12
13
14
15
сю
Доверительная
вероятность а
0,90
0,4948
0,4987
0,4942
0,4956
0,4961
0,4970
0,95
0,5806
0,5790
0,5815
0,5769
0,5730
0,5780
0,99
0,7486
0,7324
0,7441
0,7417
0,7418
0,7440
Задача 157. Для данных задачи 149 проверить гипотезу равномерности распределе-
распределения случайной величины критерием Фроцини при доверительной вероятности а = 0,95.
Вычисляем
Вп = -^= • (|0,047 - 0,05| + |0,05 - 0,15| ¦
vl0
, + |0,91-0,995|) = 0,3298.
Из табл. 110 находим Бп@,95) = 0,5723.
Так как Вп = 0,3298 < ??п@,95) = 0,5723, гипотеза равномерности распределения не
отклоняется.
332 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.4.10. Критерий Грмнвуда-Кэсенберри-Миллера
Ранее, при анализе критериев экспоненциальности, мы рассмотрели критерий
Гринвуда (см. раздел 3.3.20) [331] со статистикой
G = (п
С/о = 0,
В [339] показано, что при п —>> оо распределение (^-статистики медленно стре-
стремится к стандартному нормальному. Критические значения статистики Гринвуда
приведены в табл. 99 (в которой вместо п нужно использовать значения (п — 1)).
В [350] предложен более мощный критерий проверки равномерности распреде™
ления, основанный на статистике
Q =
г=1
Гипотеза равномерности отклоняется, если Q > Q(a), где Q{pt)—критическое
значение статистики на уровне значимости а, приведенное в табл. 111.
Таблица 111
Критические значения Q(ok)
статистики Гринвуда^Кэсенберри^Миллера
для проверки равномерности распределения [346]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
"Уровень значимости а
0,01
0,932
0,831
0,727
0,642
0,573
0,512
0,463
0,423
0,378
0,351
0,318
0,298
0,279
0,259
0,245
0,230
0,218
0,206
0,196
0,187
0,178
0,169
0,163
0,156
0,148
0,144
0,138
0,134
0,130
0,125
0,05
0,859
0,736
0,635
0,551
0,483
0,429
0,387
0,350
0,319
0,294
0,272
0,253
0,237
0,222
0,209
0,197
0,187
0,177
0,168
0,162
0,154
0,147
0,141
0,136
0,131
0,126
0,121
0,117
0,114
0,110
0,10
0,811
0,691
0,586
0,505
0,442
0,393
0,355
0,322
0,294
0,272
0,251
0,234
0,220
0,206
0,195
0,184
0,174
0,166
0,158
0,151
0,144
0,138
0,133
0,128
0,123
0,119
0,114
0,111
0,107
0,104
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
55
60
65
70
75
80
85
90
95
100
"Уровень значимости а
0,01
0,120
0,116
0,112
0,110
0,107
0,103
0,100
0,097
0,095
0,092
0,090
0,088
0,086
0,084
0,082
0,080
0,078
0,077
0,075
0,068
0,062
0,057
0,052
0,048
0,045
0,042
0,040
0,038
0,036
0,05
0,106
0,103
0,100
0,097
0,095
0,092
0,089
0,087
0,085
0,083
0,081
0,079
0,077
0,075
0,074
0,072
0,070
0,069
0,068
0,061
0,056
0,052
0,048
0,045
0,042
0,039
0,037
0,035
0,033
0,10
0,101
0,097
0,095
0,092
0,090
0,087
0,085
0,083
0,081
0,079
0,077
0,075
0,073
0,072
0,070
0,069
0,067
0,066
0,065
0,059
0,054
0,050
0,046
0,043
0,040
0,038
0,036
0,034
0,032
3.4] Критерии согласия для равномерного распределения 333
Задача 158. Проверить гипотезу равномерности распределения случайной величины
для данных задачи 149 критерием Гринвуда-Кэсенберри-Миллера на уровне значимости
а = 0,05.
Вычисляем
п+1
^2(Ui - C/i-iJ = @,047 - ОJ + @,05 - 0,047J + ... + A - 0,91J = 0,127318;
= @,047 - 0) • @,05 - 0,047) + ... + @,91 - 0572) • A - 0,91) = 0,088259.
Тогда Q = 0,127318 + 0,088259 = 0,215577.
Из табл. 111 для а = 0,05 и п = 10 находим Q@, 05) = 0, 319.
Так как Q = 0,215 < Q@,05) = 0,319, гипотеза равномерности распределения не от-
отклоняется.
3.4.11. „Сглаженный44 критерий Неймана-Бартона
Высокую мощность против альтернатив экспоненциального типа имеет крите-
критерий равномерности, предложенный в [346]. Критерий, основанный на отношении
правдоподобия, строится следующим образом. Для ряда величин U\ ^ ... ^ Un
строим ряд
где iTj(Ui) — полиномы Лежандра, ортогональные на отрезке [0,1].
Первые четыре полинома равны
; п2(у) = V5Fy2 - 0,5);
тгз(у) = V7B0y3 - Зу2); тг4(у) = 3G0у4 - 15у2 + 0,375),
где у = U — 0,5.
Статистика Неймана^Бартона имеет вид
J=l
Дэвид [351] показал, что распределение Nk очень хорошо (уже при п ^ 20)
аппроксимируется %2™распределением с / = К степенями свободы.
Если Nk > Nk(cz)i гипотеза равномерности отклоняется на уровне значимо-
значимости а. Критические значения Nk(&) для К = 2,3,4 приведены в табл. 112. При
п > 20 гипотеза равномерности отклоняется, если N^ > Хк(а)^ гДе Хк(а) —
«^квантиль распределения хи™квадрат с / = К степенями свободы.
Задача 159. Проверить гипотезу равномерности распределения случайной величины
для данных задачи 149 критерием Неймана-Бартона на уровне значимости а = 0,05.
Для ряда
Un 0,047; 0,05; 0,15; 0,18; 0,29; 0,48; 0,52; 0,61; 0,72; 0,91
имеем ряд значений г/j = С/г — 0,5:
-0,453; -0,45; -0,35; -0,32; -0,21; -0,02; 0,02; 0,11; 0,22; 0,41.
334 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Таблица 112
Критические значения -2Ук(ск)
критерия равномерности Неймана^Бартона [352, 353]
п
Уровень значимости а,
0,01
0,05
0,10
п
Уровень значимости а
0,01
0,05
0,10
2
3
4
5
6
7
8
9
10
11
12
14
16
10,012
9,717
9,643
9,517
9,384
9,326
0,276
9,208
9,265
9,173
9,170
9,235
9,233
5,903
5,682
5,566
5,573
5,618
5,640
5,683
5,735
5,774
5,790
5,822
5,897
5,908
4,023
4,013
4,116
4,227
4,316
4,382
4,421
4,453
4,476
4,489
4,486
4,517
4,527
18
20
25
30
35
40
45
50
60
80
100
оо
9,235
9,234
9,230
9,230
9,226
9,230
9,221
9,223
9,294
9,218
9,220
9,219
5,918
5,925
5,937
5,947
5,962
5,958
5,961
5,964
5,969
5,974
5,979
5,991
4,536
4,542
4,554
4,562
4,568
4,573
4,576
4,579
4,584
4,589
4,592
4,605
N3
2
3
4
5
6
7
8
9
10
11
13,500
12,870
12,450
12,150
11,950
11,810
11,710
11,650
11,600
11,570
7,400
7,480
7,530
7,570
7,600
7,630
7,650
7,670
7,680
7,690
5,590
5,750
5,910
5,990
6,040
6,070
6,100
6,110
6,120
6,130
12
14
16
18
20
30
40
50
оо
11,560
11,520
11,510
11,500
11,500
11,490
11,490
11,480
11,350
7,700
7,720
7,730
7,730
7,740
7,750
7,760
7,760
7,810
6,130
6,140
6,140
6,140
6,150
6,160
6,170
6,180
6,250
2
3
4
5
6
7
8
9
10
16,140
15,800
15,430
15,120
14,860
14,650
14,470
14,320
14,090
9,520
9,510
9,500
9,490
9,480
9,470
9,470
9,460
9,450
7,190
7,340
7,460
7,530
7,570
7,600
7,620
7,630
7,650
12
14
16
18
20
30
40
50
оо
14,000
13,870
13,780
13,710
13,670
13,580
13,530
13,480
13,280
9,450
9,440
9,430
9,420
9,420
9,400
9,400
9,400
9,490
7,650
7,660
7,660
7,670
7,670
7,680
7,680
7,690
7,780
Вычисляем полиномы для j = 1:
tti(Z7i) = TTi @,047) = 2^3 • (-0,453) = -1,569238;
7n(C72) = -1,55884; тп(С7з) =-1,21243; 7п(С/4) =-1,1085;
7Ti(U5) = ^0,72746; 7п(С76)= ^0,062982; 7п(С/7) = ^0,069282;
тг(С78) = 0,381051; 7п(С/9) = 0,762102; 7n(E/iO) = 1,420282.
Далее по аналогии вычисляем остальные полиномы Hj(Ui). Результаты сведены в та-
таблицу:
3.4]
Критерии согласия для равномерного распределения
335
г
1
2
3
4
5
6
7
8
9
10
-1,569238
-1,558840
-1,212430
-1,108510
-0,727460
-0,069282
-0,069282
0,381051
0,762102
1,420282
1,635133
1,598789
0,525476
0,255806
-0,526370
-1,112667
-1,112667
-0,955695
-0,468680
1,137264
-1,323390
-1,250117
0,509307
0,806000
1,176777
0,158322
-0,158322
-0,802668
-1,182756
0,392680
0,129156
0,623810
-1,236190
-1,280990
-0,451090
0,225033
0,225033
0,611246
-0,561062
-0,505402
-3,751607 0,976389 -1,6741667 -2,220456
Далее вычисляем
]T
F3 =
7i) = -1,18636230; F2 =
= -0,529417995; F4 =
^Г
vlO i=1
= 0,308761312;
7r4(C/*) = -0,70216984;
2 3 4
N2 = J2 Vj2 = !5502789; N3 = J2 vf = 1,783072; JV4 = ^ F/ = 2,2761149.
3=1 3=1 3=1
Из табл. 112 для п = 10 и а = 0,05 находим
Ж2@,05) = 5,774, i?3@,05) = 7,68 и Ж4@,05) = 9,45.
Легко видеть, что N2 < N2{а), N3 < -/Уз(а) и N4 < ./?4@), что не противоречит гипотезе
равномерности распределения.
336 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.5. Критерии симметрии
Если отсутствуют предпосылки для проверки согласия эмпирического распре-
распределения с каким-либо теоретическим, то выявление даже самых общих свойств
эмпирического распределения дает некоторую информацию для выбора приемов
и методов обработки экспериментального материала.
Одним из таких практически важных свойств распределения является его сим-
симметричность относительно центра группирования значений случайной величины.
3.5.1. быстрым44 критерий Кенуя
Критерий применим для быстрой (но грубой) проверки симметричности в вы-
выборках объема п ^ 50 [121].
Статистика критерия стоится следующим образом. Выборочные значения упо-
упорядочиваются по возрастанию: х\ ^ Х2 ^ ... ^ хп, определяются порядковые ста-
п 1Ъп п
тистики с номерами —, —тг? 77? т-е- ЖГ^Ъ #/i5n\, Х(п\.
16 16 2 116/ \Tefj ^2^
По ним вычисляются мера асимметрии А = #/i5n\ —2x/n\Jrx/nm\ и статистика
критерия
3s
где s = — 1 х/15п\ — Х( п_\ I , или А = \/п-
3 V \~^J vieJ/
При п ^ 50 распределение статистики может быть аппроксимировано стандарт-
стандартным нормальным распределением. Тогда гипотеза симметрии отклоняется с до-
достоверностью а, если \А\ > ui+a, где и7 — 7™квантиль стандартного нормального
2
распределения.
Напомним две весьма точные аппроксимации для вычисления нормальных кван-
квантилей (см. раздел 1.1.1)
и7 = 2,0637[1пA - 7) ^ ОДб]0'4274 - 1,5774
с погрешностью менее 0,0008 и и7 = 4,91 7°'14 — A — 7) ' с погрешностью ме-
менее 0,3%.
Задача 160. В выборке объема п = 64 имеются порядковые статистики
ж/15п\ = ЖF0) = 127; х/п\ = ЖD) = 17; х/п\ = ХC2) = 44. Проверить гипотезу симмет-
V 16 J ^ 6 / \2 )
ричности распределения случайной величины критерием Кенуя при доверительной ве-
вероятности а = 0,95.
Находим
жF0) - жD)
Для а = 0,95 имеем (применяя аппроксимацию):
ui+a = uQ 975 = 2,0637 • [ln(l - 0,975)"х - 0,1б]°'4274 - 1,5774 = 1,96.
[ ]
2
Так как А = 4,07 > 1,96, гипотеза симметрии отклоняется.
3.5]
Критерии симметрии
337
3.5.2. Критерий симметрии Смирнова
Проверяется гипотеза Щ: F(a) = 1 — F{a), то есть гипотеза о том, что пред™
полагаемая функция распределения F(x) симметрична относительно центра а.
Для выборки a?i,#2, • • • ixn случайной величины х > 0 статистика Смирнова имеет
вид [354]
тп =
|
ж>0 '
где К^~ —число значений ж, попавших в интервал (а, а + ж); К~ —число значений ж,
попавших в интервал (а — ж, а).
Гипотеза симметричности распределения отклоняется с достоверностью а, если
тп ^ тп(а)ч гДе тп{а)—критическое значение статистики, при п ^ 50 равное [170]
rn[a) =
Задача 161. Имеется ряд выборочных данных
хц 1, 2, 3, 5, 9, 11, 18, 21, 29, 35.
Необходимо проверить гипотезу симметричности распределения случайной величи-
величины х относительно а = 10 критерием Смирнова при доверительной вероятности
а = 0,95.
Имеем для х\ = 1:
— в интервал A0,11) попало К+ = 1 значение;
— в интервал (9,10) попало К~~~ = 1 значение.
Следовательно, при х\ = 1 имеем К+ — К~ = 0.
По аналогии получаем данные, приведенные в таблице:
г
1
2
3
4
5
6
7
8
9
10
Xi
1
2
3
5
9
11
18
21
29
35
К+
1
1
1
1
2
3
3
4
5
5
К^
1
1
1
2
5
5
5
5
5
5
К+ - К^
0
0
0
-1
-3
^2
-2
-1
0
0
Тогда
2 \ 2
rnmax(i^+ - K~) = 3 и rn(o;)=(l0+-
= 3,266 • 1,96 = 6,40.
Так как тп = 3 < тп(а) = 6,40, распределение можно считать симметричным (напомним,
что критерий следует применять при п ^ 50, а настоящий пример следует рассматривать
как демонстрационный).
3.5.3. Знаковый критерий симметрии
Проверяется гипотеза о симметричности распределения относительно центра.
Статистиками критерия являются К+ — число положительных значений величин
yi = Xi — а, и К~ —число отрицательных значений этих величин.
338 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Гипотеза симметричности отклоняется, если
где К (а)—критическое значение, приведенное в табл. 113.
Таблица 113
Критические значения K(ot) критерия знаков
(а — уровень значимости) [12]
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
а
0,01
0
0
0
0
1
1
1
2
2
2
3
3
3
4
4
4
5
5
6
6
6
7
7
7
8
8
0,05
0
0
0
1
1
1
2
2
2
3
3
4
4
4
5
5
5
6
6
7
7
7
8
8
9
9
9
10
0,10
0
0
0
0
1
1
2
2
3
3
3
4
4
5
5
5
6
6
7
7
7
8
8
9
9
10
10
10
11
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
а
0,01
9
9
9
10
10
11
11
11
12
12
13
13
13
14
14
15
15
15
16
16
17
17
17
18
18
19
19
20
20
0,05
10
11
11
12
12
12
13
13
14
14
15
15
15
16
16
17
17
18
18
18
19
19
20
20
21
21
21
22
22
0,10
11
12
12
13
13
13
14
14
15
15
16
16
16
17
17
18
18
19
19
20
20
20
21
21
22
22
23
23
24
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
а
0,01
20
21
21
22
22
22
23
23
24
24
25
25
25
26
26
27
27
28
28
28
29
29
30
30
31
31
31
32
32
0,05
23
23
24
24
25
25
25
26
26
27
27
28
28
28
29
29
30
30
31
31
32
32
32
33
33
34
34
35
35
0,10
24
24
25
25
26
26
27
27
28
28
28
29
29
30
30
31
31
32
32
33
33
33
34
34
35
35
36
36
37
При п > 100 распределение К+ удовлетворительно аппроксимируется нормаль-
нормальным с М{К+) = | и D(K+) = j.
Простая формула для критических значений приведена в [12]: К (а) =
, где [х] —ближайшее целое число к х (с = 1,2879 для а = 0,01;
0,98 для а = 0,05 и 0,8224 для а = 0,10).
Случайная величина F = при справедливости нулевой гипотезы
п — К +1
симметричности имеет ^-распределение Фишера с / = 2(п — К+ + 1) и /2 = 2К+
степенями свободы.
3.5]
Критерии симметрии
339
Критерий прост в вычислительном отношении, но обладает невысокой мощно™
стью. Поэтому его рекомендуется использовать при п > 50 (п — половина объема
выборки).
Задача 162. В условиях задачи 161 проверить гипотезу симметричности распреде-
распределения относительно х = 10 критерием знаков на уровне значимости а = 0,05.
Имеем К+ = 5 и К~ = 5, min(K+, К~) = Ъ. Далее
К@,0Ь) = [^у^ ~~ 0,98 • л/Tlj = 1.
Так как imn(K+^K ) = 5 > Х@,05) = 1, гипотеза симметричности распределения не
отклоняется.
3.5.4. Одновыборочный критерий Вилкоксона
От ряда выборочных величин Х{ переходим к ряду величин у^ = Х{ — а, где
а — предполагаемый центр распределения. Значения у^ упорядочим по абсолют-
абсолютной величине: \yi\ ^ |г/2|
(
\Уп\- В полученном ряду каждому значению \yi\
припишем ранг (от 1 до п), равный его порядковому номеру в упорядоченной
последовательности.
Обозначим через Rf ранги случайных величин t/^, имеющих положительное
значение.
Статистика критерия Вилкоксона задается формулой [355]:
г=1
Гипотеза симметричности отклоняется, если Т+ > Т+(а), где Т+(а) —критическое
значение, приведенное в табл. 114.
Таблица 114
Критические значения Г~*"(а) одновыборочного
критерия Вилкоксона (адаптирована из [24])
п
3
4
5
6
7
8
9
10
11
Доверительная
вероятность а
0,90
6
8
12
17
21
27
33
40
47
0,95
6
9
14
18
23
29
36
43
51
0,99
6
10
15
20
27
34
41
49
58
п
12
13
14
15
16
17
18
19
20
Доверительная
вероятность а
0,90
55
64
73
82
93
103
115
127
139
0,95
60
69
78
89
99
111
123
136
149
0,99
67
77
88
100
111
124
137
151
166
При п > 20 распределение Т+ удовлетворительно аппроксимируется нормаль™
ным с параметрами
М(Т+) =
п(п + 1)
и D(T+) =
24
340 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
т. е. критические значения могут быть вычислены по формуле
п(п + '
Т+ (а) =
+
4 V 24
где [х] —ближайшее целое число к х.
Задача 163. Для данных задачи 161 проверить гипотезу симметричности распреде-
распределения относительно а = 10 критерием Вилкоксона при доверительной вероятности
а = 0,95.
Ряд
xf. 1, 2, 3, 5, 9, 11, 18, 21, 29, 35
преобразуем в ряд
yi = Xi-a: -9, -8, -7, -5, -1, 1, 8, 11, 19, 25.
Ранжированный ряд значений \yi\ имеет вид
1, 1, 5, 7, 8, 8, 9, 11, 19, 25,
для которого имеем последовательность рангов (для одинаковых значений используются
средние ранги):
1,5; 1,5; 3; 4; 5,5; 5,5; 7; 8; 9; 10.
Отмечая в ряду \yi\ значения yi > 0 (они выделены), приходим к последовательности
рангов
Rf: 1,5; 5,5; 8; 9; 10.
Тогда Т+ = J2 Rf = 1,5 + 5,5 + 8 + 9 + 10 = 34.
г=1
Так как Т+ = 34 < Т+(а) = 43, гипотеза симметричности не отклоняется.
Для нормального приближения (гхо,95 :=: 1,645) имеем
что совпадает с табличным результатом.
3.5.5. Критерий Антилла—Керетинга—Цуккини
Критерий, рассмотренный в [356], использует статистику, подобную статистике
Вилкоксона (см. раздел 3.5.4).
Пусть х — эмпирическая медиана ряда х\ ^ х^ ^ • • • ^ хп. Образуем ряд вели-
величин yi = \х{ — ж|, и пусть Ri—ранг величины yi в упорядоченном по возрастанию
ряду значений у^.
Обозначим
Тогда статистика критерия имеет вид
где с7 = mliif а, — 1 при 0 ^ а, 7 ^ «•
Гипотеза симметричности отклоняется, если Ti(j) ^ Ткр(А).
3.5] Критерии симметрии 341
При 7 = 0ип^7 статистика
распределена асимптотически нормально с и = 0 и дисперсией сг2= 0,03156 ехр( ),
V п/
где а = 5,66 для четных п и а = 9,75 для нечетных п. При j = - для Т( - 1 также
6 \6J
применима нормальная аппроксимация при п^7с дисперсией о = 0,01736 ехр I 1,
V п/
где а = 5,77 для четных в и а= 11,11 для нечетных п.
Таким образом, для рассмотренных статистик критические значения могут быть
вычислены по формулам (а — доверительная вероятность):
— для четных п
Гкр@) =0,1776513ехрf-^p) ua; Ткр(±) = 0,131757expf-^) ua;
— для нечетных п
Ткр@) = 0,177613ехр|—^— j U«; Ткр ( - 1 = 0,131757 expf—^— j wa,
где на — а™квантиль стандартного нормального распределения. Критерии этой
группы обладают большей мощностью, чем критерий Вилкоксона (см. раздел 5.4).
Задача 164. Для данных задачи 161 проверить гипотезу симметричности распреде-
распределения критериями Ti@) и Ti(l/6) Антилла-Керстинга-Цуккини при а = 0,95.
Для ряда
хп 1, 2, 3, 5, 9, 11, 18, 21, 29, 35
медиана равна х = = 10. Получаем ряд значений
yi = \Xi -x\ : 9, 8, 7, 4, 1, 1, 8, 11, 19, 25.
Ранжированному ряду
ун 1, 1, 4, 7, 8, 8, 9, 11, 19, 25
соответствует последовательность рангов
Rn 1,5; 1,5; 3; 4; 5,5; 5,5; 7; 8; 9; 10.
Поэтому последовательность рангов jRj, соответствующая последовательности г/$,
имеет вид
7; 5,5; 4; 3; 1,5; 1,5; 5,5; 8; 9; 10.
Для этой последовательности ряд sign(xi — х) будет иметь вид
-1, -1, -1, -1, -1, +1, +1, +1, +1, +1.
Вычисляем статистики критерия:
~ ?) = ^^ х
r^10) = ^'gmin[^IL]'Sign
х Imin (ттп' \)' {~1] + min (гтг' 0 •(-1) + • • •+min (Лт^) •хI =0Д868;
342 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Ti ( - | = —= • 2_, rnin ~~(—"—г 5 " sign ixi — х) -
\ / v ^=1 L v / J
Г / 7 l\ / 55 Л / 10 1\ 1
х min , - • (-1) + min —!—, ~~ • (-1) + ... + min , - ) • 1 = 0,11498.
L \2-11'3/ V ; \2-11'3/ V ; \2-11'3/ J
Для а = 0,95 имеем иа = 1,645, и критические значения статистик равны:
Ткр@) = 0,17765 • expf --^— J • 1,645 = 0,220;
/l\ /2 885\
Гкр [ - ) = 0,131757 • ехр ( - • 1,645 = 0,1624.
V6/ V 10 /
ТаккакГДО) = 0,1868 < Гкр@) = 0,220 и 1\ | - ] =0,115 <Гкр( - ) = 0,162, гипотеза
W V6/
симметричности распределения случайных величин не отклоняется.
3.5.6. Критерий Бхатачарья-Гаствирта-Райта
(модифицированный критерий Вилкоксона)
Критерий является обобщением критерия Вилкоксона (см. раздел 3.5.4) при
проверке гипотезы относительно неизвестного центра распределения [357].
Статистика критерия строится следующим образом. Пусть имеется выборка
xij • • • •,x2n+i и определены вероятности р и д = 1-р @<р<1). Обозначим вы™
борочные квантили Ж[п+1], Ж[пд+1] ж xy2n+i-nq] ix[C] — [/^Ья порядковая статистика
в упорядоченном по возрастанию ряду xf, [... ] — целая часть числа, содержащегося
в скобках).
В [357] предложены две статистики. Первая статистика является модификацией
критерия Вилкоксона (см. раздел 5.4) в форме, рассмотренной авторами рабо-
работы [358].
Обозначим
У{г) = X[nq+1]
1, и < 0;
0
и > 0.
Тогда статистика критерия записывается в форме
Статистика основана на сравнении -q-x верхней и нижней частей данных.
Вторая статистика построена в ранговой форме. Пусть
У {г) = хп+1 — xn+l-i] %{i) = Xn+i-i — Xn+i.
Объединим yf и z' в одну выборку, обозначим через R\^ ..., Rn и Дп+1, ..., i^2n
ранги у'-ов и z'-ов в объединенной выборке. Тогда статистика критерия записыва-
записывается в форме
Л [ п 2п 1
s = г{J2(Ri - 2пр)+ - J2 (Ri - 2пр)+ (' где х+ =
[ J
{J2 J2
Bn+lJ [i=l i=n+l
3.5]
Критерии симметрии
343
При п ^ 10 можно считать, что распределение статистик Т и S нормально со
средними М(Т) = ~~ и М(Я) = 0 и дисперсиями [357]:
^Для q = 0,25: D(T) = 1 и DE) = 0,006;
^Для g = 0,5: D(T) = 0,754 и DE) = 0,9394.
Случай q = 1 соответствует обычному критерию Вилкоксона с центром, оцени™
ваемым выборочной медианой. Критерии рассмотренного типа обладают большей
мощностью, чем критерий Вилкоксона.
Гипотеза симметричности распределения отклоняется с доверительной вероят™
ностью а, если:
— при q = 0,25
\Т\
— при q = 0,5
\Т\
Ткр = 0,5
Ткр =
\S\
\S\
SKp = 0,1985ц i+а,
где и7 — 7™квантиль стандартного нормального распределения.
Задача 165. Проверить гипотезу симметричности распределения критериями Т и S
Бхатачарья-Гаствирта-Райта при д = 0,5 и а = 0,95 для выборки данных
хц 1, 2, 3, 5, 9, 1, 18, 21, 29, 35, 45, 49, 51.
Имеем 2п + 1 = 13, п = 6и
] ^ X[ng+i^i] = Ж[6.0,5 + 1] — Ж
У (г) = X
Вычисляем
-i] = Х[4] ^
Н] -Х[щ.
Т =
1
F.0,5)^ ге^е
— Ж3 — Ж13
(Ж4 — Ж3 — Ж12
— Ж1 — Ж13
= ^ • {хE - 3 - 49 + 35) + хE - 3 - 51 + 35) + ... + хE - 1 - 51 + 35)} =
= I • Ы-12) + х(-14) + ... + х(-12)} = 1.
Тогда при ц 1+0,95 = ^0,975 = 1,96 имеем Ткр = 0,5 + 0,8683 • 1,96 = 2,20.
2
Так как Т = 1 < Ткр = 2,20, гипотеза симметричности распределения не отклоняется.
Рассмотрим теперь Я-критерий. Вычисления, необходимые для подсчета значения
критерия, приведены в таблице (п = б, жп+1 = xj = 18):
i
1
2
3
4
5
6
Xn+l-i
11
9
5
3
2
1
Жп+1+г
21
29
35
45
49
51
7
9
13
15
16
17
(*)
3
11
17
27
31
33
V'(z')
3A)
7B)
9C)
11D)
13E)
15F)
2
3
5
6
l
4
344 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Окончание
г
7
8
9
10
11
12
"@
y'[zf)
16G)
17(8,5)
17(8,5)
27A0)
31A1)
33A2)
7
8,5
8,5
10
11
12
Статистика критерия равна
s = з" * {тахB - 2 • 6 • 0,5; 0) + тахC - 2 • 6 • 0,5; 0) + ... + тахA2 - 6; 0)} =
B-6 + 1J
= 0,2133 • @ + 0 + ... + 2,5 - 0... - 6) = ^0,2982.
Далее имеем Якр = 0,1985 • 1,96 = 0,389. Так как \S\ = 0,298 < Якр = 0,389, гипотеза
симметричности не отклоняется.
3.5.7. Критерий Финча
Критерий рассмотрен в [359]. Основан на интервалах порядковых статистик,
обладает высокой чувствительностью к отклонению распределения от симметрич-
симметричности.
Для выборки х\ ^ Х2 ^ • • • ^ хп введем обозначения
где г = 1, ...,fc; fc = ^ .
L ?> J
Статистика критерия имеет вид V =
, где
; v = 2d2 + A - d2) (am2 + Ьт + =-
I v^ 2
С = > UJJ
V=l /
d = 0,278+^; a = 0,41 + ^f; m=l,47--; 6 = -2ma.
n n n
При п ^ 10 применима аппроксимация критических значений У-статистики
(а — доверительная вероятность)
где иа — «-квантиль стандартного нормального распределения.
Если
\V
то гипотеза симметричности распределения отклоняется с доверительной вероят-
вероятностью а.
3.5] Критерии симметрии 345
Задача 166. Для данных задачи 165 проверить гипотезу симметричности критерием
Финча при доверительной вероятности а = 0,95.
Имеем ряд
хц 1, 2, 3, 5, 9, 11, 21, 29, 35, 45, 49, 51 (п = 13).
Находим
d = 0,278 + — = 0,41646; т = 1,47 - — = 0,8546; а = 0,41 + ^4 = 0,54846;
13 ' ' 13 ' ' ' 132
6= ^2 -0,8546-0,54846 = ^0,93743; v = 3d2 +(l - d2) • (am2 + Ьт + - J = -11,774.
V з /
Далее вычисляем
*=1?|=б;
5+* 1 7 1
ujj = с • 2~2 т' oji = с • 0,16667; Ш2 = с • \J - = с- 0,5095;
Шз = с • 0,8845; ш4 = с • 1,32897; ш5 = с • 1,928968; ш6 = с • 3,01987.
Из равенства ^^ш2 = с2 - 15,6764 = 1 находим с = 0,252567.
Далее
*-J\ *^п — fc-f-1 *^7i — 1 — fc-f-1 i •^'fe-f-2 — 1
i о /iii — t»i о -i ^ i -i — o^/^ i ^ i -4- ner> i i -i nen — O.npi-r -4- т»^> OA — 9.18 -4- 1 1
— = 0,4.
жз — же 21 —
С учетом полученного значения с = 0,25256 имеем
ал = = 0,04209; uj2 = 0,12860; ш3 = 0,22339; ш4 = 0,33564;
6
Ш5 = 0,48718; ш6 = 0,762698.
Вычисляем статистику критерия
\V\ = |-11,774 • @,04209 • (-0,4) + 0128603 • 0,6 + ... + 0,762698 • 0,3333)| = 10,3058.
Далее находим критическое значение (г/о,95 :=: 1,645)
к
Укр —
0,5773- 1,645
= 34,4876.
Так как V = 10,3058 < FKp = 34,4876, гипотеза симметричности распределения не
отклоняется.
3.5.8. Критерий Бооса
Критерий рассмотрен в [360], позволяет проверить симметричность распределе™
ния относительно его центра, в качестве которого используется оценка Ходжеса™
Лемана
х =
n-(n+l) ЛТ „
т. е. медиана всех возмоясных попарных средних Уолша. Статистика
346 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
критерия имеет вид
В = п(
-1-
1 ^\
п
У.
xi +
Xi —
х3 - х
Xj
Для п ^ 10 критические точки В (а) приведены в табл. 115.
Таблица 115
Критические значения jB-критерия Бооса
(а — доверительная вероятность) [360]
а
В(а)
0,90
0,712
0,95
0,899
0,975
1,093
0,99
1,358
Если В > В (а), то гипотеза симметричности отклоняется. Критерий обладает
высокой эффективностью и менее чувствителен, чем другие, к выбросам на хвостах
распределения.
Задача 167. Для данных задачи 165 проверить гипотезу симметричности распреде-
распределения критерием Бооса при а = 0,95.
Имеем ряд
хц 1, 2, 3, 5, 9, 11, 18, 21, 29, 35, 45, 49, 51.
Сначала вычислим оценку Ходжеса-Лемана. Для нахождения медианы расположим
*г + Xj , , _ п(п + 1) _ 13 • 14
= 91) в ряд по возрастанию и найдем
все значения (их будет
2 2 2
медиану х = жп+1 = Ж91+1 = Ж46 = 20 (т.е. 46™ю порядковую статистику).
2 2
Дальнейшие вычисления сведены в таблицу, в которой приняты обозначения
г. 4- т ¦ 9^ • -гIе*. —
i
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
j
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
40
38
37
35
31
29
22
19
11
5
5
9
11
40
37
36
34
30
28
-**
xij
1
2
4
8
10
17
20
28
34
44
48
50
1
3
7
9
г
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
э
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
21
18
10
4
5
10
12
37
36
35
33
29
27
20
17
9
3
7
11
*?;
i6
19
27
33
43
47
49
2
6
8
15
18
26
323
42
46
i
3
4
4
4
4
4
4
4
4
4
4
4
4
4
5
5
5
5
5
3
13
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
13
35
34
33
31
27
25
18
15
7
1
9
13
15
31
30
29
27
23
58
4
6
13
16
24
30
40
44
46
3.5]
Критерии симметрии
347
г
5
5
5
5
5
5
5
5
6
6
6
6
6
6
6
6
6
6
6
6
6
7
7
7
7
7
7
7
7
7
7
7
7
7
8
8
8
8
3
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
21
14
11
3
3
13
17
19
29
28
27
25
21
19
12
9
1
5
15
19
21
22
21
20
18
14
12
5
2
6
12
22
26
28
19
18
17
15
ж*/
2
9
12
20
26
36
40
42
7
10
10
24
34
38
40
3
11
17
27
31
33
г
8
8
8
8
8
8
8
8
8
9
9
9
9
9
9
9
9
9
9
9
9
9
10
10
10
10
10
10
10
10
10
10
10
10
10
11
11
11
3
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
11
9
2
1
9
15
15
29
31
11
10
9
7
3
1
6
9
17
23
33
37
39
5
4
3
1
3
5
12
15
23
29
39
43
45
5
5
7
-**
xij
8
14
24
28
30
33
20
22
10
43
16
г
11
11
11
11
11
11
11
11
11
11
12
12
12
12
12
12
12
12
12
12
12
12
12
13
13
13
13
13
13
13
13
13
13
13
13
13
Оконч
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
xij
9
13
15
22
15
33
39
49
53
55
9
10
11
13
17
19
26
29
37
43
53
57
59
11
12
13
15
19
21
28
31
39
45
55
59
61
ание
*?;
4
6
2
Суммируя столбцы таблицы, получаем
п п
Ч +Х4 - 2х\ = 3532 и
= 1688.
г=1 г=1
Окончательно вычисляем
г<3
Из табл. 15 для а = 0,95 находим Б@,95) = 0,899.
Так как В = 0,6007 < 5@,95) = 0,899, гипотеза симметричности распределения не
отклоняется.
348 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.5.9. Критерий Гупты
Критерий рассмотрен в [314, 361] и обладает достаточной мощностью против
обширного класса альтернатив.
Последовательность процедур вычисления критерия включает в себя следующие
шаги. Для выборки объема х\ ^ ... ^ хп находим медиану
п = 1,3, ...,2k- 1;
2
-(хп +Хп,Л , п = 2,4, ... ,2k.
2\ 2 2+У
Вводим переменную
{1, если Х{ + Xj > 2х;
О, если Х{ + Xj ^ 2х
и находим
1 \nz2\ Гтг]
2 J[2J'
где [у] —наибольшее целое, меньшее или равное у.
Далее вычисляем
2
п(п + 1)
Вводим переменную
{/ _i\ / _i\
1, еСЛИ [X ^ П 5 ) ^ ж^ ^ I ж + п 5 ) ;
V / V /
Находим
{
О, если неравенство не выполняется.
= тах< 1,2^ а» > ; A3=[2n5)D; t =
{ i=l J
где uy — |/~квантиль стандартного нормального распределения; Ах — симметрич-
симметричный двусторонний доверительный интервал для х.
Построение симметричного двустороннего доверительного интервала для х с до™
верительной вероятностью A — а) включает следующие шаги. Находим величину
24
k(a) =
где [... ] — ближайшее целое к числу в скобках.
Далее составляем N = величин z\j = ^~™—-(г < j) и ранясируем их по
возрастанию.
Искомый интервал равен
Ах = цщ — цп, где k = JV + 1 — Aj(q) 5 I '=- k(ct).
Графический метод определения величины Ах изложен в [362].
3.5]
Критерии симметрии
349
Продолжая алгоритм вычисления критерия Гупты, находим
2
Если \J\ ^ гА-|__а, то гипотеза симметричности отклоняется с доверительной веро-
вероятностью 1 — а.
Задача 168. Для выборки
Xii 1, 2, 3, 5, 9, 11, 18, 21, 29, 35
проверить гипотезу симметричности распределения критерием Гупты при довери-
доверительной вероятности 0,90.
9+11
тт / \ ~ Ж5+Ж6 9+11
Находим оценку медианы (п — четное): х = = = 10.
Для вычисления А\ составим таблицу величин Sij при различных сочетаниях г и j:
3
2
3
4
5
6
7
8
9
10
г
1
0
0
0
0
0
0
1
1
1
2
0
0
0
0
0
1
1
1
3
0
0
0
1
1
1
1
4
0
0
1
1
1
1
5
0
1
1
1
1
6
1
1
1
1
7
1
1
1
8
1
1
9
1
Находим А\ = 28 (число единиц в таблице) и Аъ =
Далее вычисляем
2
10-2
10
4- 5
= 10.
B8 - 10) = 0,4; х - п^ 5 = 10 - 10" 5 = 9,369; х + п^ \ = 10,631.
Имеем аг = а2 = ... = а10 = 0; D = тах{1,0} = 1; А3 = 2 • 105 . 1 = 12,619.
Из условия задачи 1 — а = 0,90 (а = 0,10), следовательно, и а = г^о,о5 = —1,645.
п(п + 1) 10-11
=
Найдем ЛГ =
представлены в таблице.
Имеем ряд (равные ранги усредняются):
= 55 значении полусумм Zij =
(г < j), которые
г
1
1
1
1
1
1
1
1
1
1
3
1
2
3
4
5
6
7
8
9
10
1
1,5
2
3
5
6
9,5
11
15
18
Ранг
1
2
3,5
6,5
10,5
13,5
20
24,5
33,5
39,5
ъ
2
2
2
2
2
2
2
2
2
3
j
2
3
4
5
6
7
8
9
10
3
Zij
2
2,5
3,5
5,5
5,5
10
11,5
15,5
13,5
3
Ранг
3,5
5
8
12
12
21,5
26,5
35
30,5
6,5
i
3
3
3
3
3
3
3
4
4
4
j
4
5
6
7
8
9
10
4
5
6
Zij
4
6
7
10,5
12
16
19
5
7
8
Ранг
9
13,5
16,5
23
28
36,5
41,5
10,5
16,5
18
350 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
ъ
4
4
4
4
5
5
5
5
5
j
7
8
9
10
5
6
7
8
9
11,5
13
17
19,5
9
10
13,5
15
19
Ранг
26,5
29
38
43,5
19
21,5
30,5
33,5
40,5
ъ
5
6
6
6
6
6
7
7
7
j
10
6
7
8
9
10
7
8
9
22
11
14,5
16
20
23
18
19,5
23,5
Ранг
47
24,5
32
36,5
45
48,5
39,5
43,5
50
г
7
8
8
8
9
9
10
3
10
8
9
10
9
10
10
Окон
zij
26,5
21
25
23
29
32
35
чание
Ранг
52
46
51
48,5
53
54
55
Находим к (а) =
10-11 /10-11-21
(-1,645) = 11.
2 V 24
Следовательно,
k = N + l- к(а) = 55 + 1 - 11 = 45; 1 = к (а) = 11; Ах = z45
Далее вычисляем
t =
«0,95
Ах-л/^Ы 15-
12 4 \ 12,619/
= 20 - 5 = 15.
=0,3317;
J = ( — ) 2 • (c - 0,25) = f^H) 2 . (o,4 - 0,25) = 0,823.
\nj \ 10 )
Так как J = 0,823 < ^0,95 = 1,645, гипотеза симметричности распределения не откло-
отклоняется.
3.5.10. Критерий Фрезера
Пусть ап(г) = M(xi) — математическое ожидание модуля г-й порядковой ста-
статистики в выборке объема п из стандартного нормального распределения. По
аналогии с критерием знаков (см. раздел 5.3), от переменной Х{ переходим к пере-
переменной yi = Х{ — а (а — предполагаемый центр распределения). Упорядочиваем
(
по абсолютной величине: \у\\ ^ |t/2
Уп\- Пусть Щ —ранг в этом ряду поло-
поло\\ || \\
жительных значений у^ = Х{ — а > 0. Фрезер [363, 364] предложил для проверки
симметричности распределения случайных величин статистику
г=1
Для практических расчетов применима следующая аппроксимация с помощью
квантилей стандартного нормального распределения:
где Pi = \\ ^^ + 1
Напомним ранее приведенные аппроксимации (см. раздел 5.1)
Г _i 10,4247
иа. = 2,0637 ln(l - cti) -0,16 -1,5774
(oti > 0,5; при оц < 0,5 следует вместо oti использовать 1 — щ и поменять знак у uai);
Л П1 Г 0,14 (Л \0,14l
а. =4,91 \а^ -A -аг) J .
3.5] Критерии симметрии 351
При п ^ 10 распределение 5 может быть аппроксимировано нормальным рас™
пределением [365] со средним МEГ) и дисперсией D(S), где
МE) = ^= = 0,399n; DE) = ± ? К№)]2 = | Е
Следовательно, случайная величина ' будет иметь стандартное нор™
0,5 WE ul
мальное распределение. Поэтому критическое значение Я™статистики равно
S(a) = 0,399 • п + 0,5 • Jv^. • иа.
П г———
Если Y1 и% ^ 0,399п + 0,5л/г^.г/а, то с доверительной вероятностью а гипотеза
г=1 V г
симметричности распределения отклоняется.
Задача 169. Для данных задачи 168 проверить гипотезу симметрии распределения
критерием Фрезера при а = 0,95 относительно медианы^ равной 10.
Имеем ряд
»,. — ™. _ ™. _ о. _я. _7« — ^« —1* 1- 7- 11- 1Q- 9^
Строим ранжированный ряд
Ы = \xi -x\: 1; 1; 5; 7; 7; 8; 9; 11; 19; 25.
Ему соответствует последовательность рангов
1,5; 1,5; 3; 4,5; 4,5; 6; 7; 8; 9; 10.
Легко убедиться, что значения yi = х% —- х > 0 (это 1, 7, 11, 19 и 25) имеют в общем
ряду ранги i^i = 1,5; 4,5; 8; 9; 10. Рангам Ri соответствует ряд значений:
A-i-^'J-H^^)-0-""*
А " 3 ¦ (^ + >) " ¦"»>* А " 3 ¦ (^5 +') " °'871Ж;
1 /9-Q.375 Л 1 /ш-ода \
М 2 \ 10,25 ) 2 \ 10,25 /
Соответствующие им квантили г!,/з,; равны
ti^ = 4,91 • [/3i'14 -A - /3iH'14] = 4,91 • [0,55488ОД4 -A - 0,55488H'14] = 0,13738;
и(з2 = 0,52597; щ3 = 1,13446; щА = 1,4104; и^ = 1,87673.
Вычисляем
S = Y, и^ = 5,08494; ]Г и}. = 7,09386.
i i
Для а = 0,95 и 1?q,95 = 1,645 имеем
5@,95) = 8,399 • 10 + 0,5 • G,09386) 2 . 1,645 = 6,1807.
Так как S = 5,085 < 5@,95) = 6,18, гипотеза симметричности распределения совокуп™
ности случайных величин не отклоняется.
352 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3.6. Подбор кривых распределения вероятностей
по экспериментальным данным
Часто инженер или исследователь не имеет достаточных оснований для выбора
того или иного закона распределения вероятностей. Его попытка использовать
критерии нормальности, экспоненциальности или равномерности распределения
случайных величин потерпели неудачу. Что же ему делать? Очевидно, смириться
с тем, что он не сможет применить хорошо известные математические модели для
описания своих экспериментальных данных, и попытаться найти все-таки модель,
которой отвечают его результаты.
Другими словами, ему необходимо подобрать по экспериментальным данным
распределение, которое удовлетворительно описывало бы имеющийся эксперимен™
тальный материал.
3.6.1. Кривые распределения Джонсона
Джонсон [366] предложил для аппроксимации эмпирических распределений
использовать кривые, получающиеся с помощью преобразований плотности нор™
мального распределения.
Пусть х — случайная величина, для которой подбирается распределение Джон™
сона. В общем случае преобразование Джонсона имеет вид
z = 7 + vf(x^ е > А) ? V > 0? ^°° < 7 < °°7 А > 0, ^оо < ? < оо,
где 75 Vi е и А— параметры распределения Джонсона; /(...) —произвольная функ-
функция; z — случайная величина, имеющая стандартное нормальное распределение.
Джонсон [13] предложил три формы функционального преобразования:
/2 (х; е, А) = In I ) , е ^ х ^ е + А;
(х-
/з(ж; е, А) = Arsh —-— ) , ^оо < х < оо.
V л
Им соответствуют семейства кривых 5^, 5^ и Sjj Джонсона.
Подбор кривых распределения Джонсона по экспериментальным данным про-
проводится в два этапа. Сначала определяется, какое из трех семейств распределений
приемлемо. Затем находятся оценки параметров выбранного семейства распреде™
лений (Sl, Sb или Sjj).
Чтобы решить, какое распределение из трех семейств распределения Джонсона
следует использовать для описания полученных экспериментальных данных, вы-
вычисляем эмпирические оценки третьего («з) и четвертого («4) моментов
-I П 1 П -1 П
1 \-^ / -\3 л х \™^ / -\4 2 1 \™^ / -\2
|^Д^ ^ ______ ^^ I ^|^ ^ ^д^ I f^C, ^J. _______ 4^ i ^Д^, ^ ^Д^ la X ^/..Д^У^ C ______ 1? I ^Д^ ^ ^Д^, I ^
ns . -, ns . ., n — I
г==1 г=1 г=1
Далее рекомендуется следующая приближенная процедура выбора типа распре-
распределения:
если «4 > 3(l + 0,641а3) —выбирается семейство Su]
если «4 ~ 3A + 0,641а3) —выбирается семейство Sl]
если «4 < 3(l + 0,641а3) —выбирается семейство Sb-
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 353
При «4 < 1
кривые Джонсона неприменимы. Более точный метод выбора
вида распределения Джонсона по значениям «з -> «4 и коэффициента вариации v = —
s
приведен в [367]. Обширный анализ вопросов, связанных с семейством распределе-
распределений Джонсона, содержится в [368].
3.6.1.1. Семейство распределений Sl Джонсона
Плотность распределения Джонсона семейства S
имеет вид
где г] > 0; ^оо < j = 7 — ^1пЛ < оо; ^оо < е < 77; ™оо < 7 < °°; А > 0 — параметры
распределения и х ^ е.
Распределение, соответствующее кривой /i(x), является логарифмически нор-
нормальным (см. раздел 1.1.3) с параметрами ?]=^,7 = и параметром положе-
ния ?, определяющим начало координат.
Рассмотрим два случая: значение е известно (положим е = 0) и значение па-
параметра неизвестно. В первом случае переходим от переменной х к переменной
™ . . 1 ^ ш
ж = ж — е. 1огда оценки параметров г] ж j имеют вид п=- И7= , где
S S
т = —
п ¦
п(п — 1)
111 Xj —
' In Xj
г=1
Если значение е неизвестно, то оценки параметров находятся по формулам
1,645'
r)= 1,645 In
7 =
1 — ехр —
Т]
Х[0,5п] — ж[0,05п]
? = ,
ехР
где Ж[^] —порядковая статистика эмпирического распределения с номером /3.
Рекомендуется сначала найти квантили распределения случайной величины In x
с помощью таблиц (или формул) стандартного нормального распределения, а затем
потенцированием перейти к квантилям исходной случайной величины х.
Задача 170. В результате испытаний п = 100 изделий получены следующие значения
случайной переменной х (параметра изделия):
1,0
2,0
2,5
3,0
3,5
4,2
4,6
4,9
5,1
5,2
5,3
5,3
5,5
5,6
5,8
6,0
6,3
6,5
6,6
6,7
6,8
7,0
7,0
7 1
7,5
7,5
7,9
7,9
8,0
8,1
8,1
8,3
8,7
8,7
8,8
8,8
8,9
9,0
9,2
9,4
9,6
9,7
9,8
9,9
10,1
10,2
10,2
10,2
10,8
10,9
10,9
11,0
11,0
11,2
11,3
11,5
11,9
11,9
12,0
12,3
12,4
12,5
12,7
12,7
13,5
13,9
14,0
14,1
14,2
14,3
14,4
14,5
15,3
15,9
16,0
16,5
17,0
17,5
18,0
21,2
5,0 6,1
8,4 9,5 10,5 11,7 13,0 14,8 22,3
5,0 6,1 7,3 8,5 9,5 10,6 11,8 13,2 15,2 26,1
12 А. И. Кобзарь
354 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Необходимо выяснить возможность аппроксимации распределения переменной х кри-
кривой из семейства Джонсона и оценить параметры этого распределения. Вычислить
вероятность того, что параметр изделия х ^ 15. Найти значение параметра изделия^
вероятность превышения которого не более 0,05.
Сначала вычислим необходимые исходные данные s2, аз и «4-
Имеем
х = 9,971; s2 =
«3 =
i ~ ХТ = 19,075; S = 4,36749;
i-x) =4,18945.
Находим, что «4 = 4,189 w3*(l + 0,641 • а2.) :=: 4,143. Поэтому для описания получен-
полученных данных применимо семейство Sl Джонсона. Вычисляем параметры распределения
т = —
п
= 2,1915; s =
п(п — 1)
= 0,0505798.
В нашем случае порядковые статистики равны:
Х[0,95-п] = ж0,95 = 17,0; Ж[о,О5-п] = %5 = 3,5; Ж[о,5-п] = х50 = 9,5.
Далее
'17-9,5'
= 1,645- In
9,5-3,5
= 7,3719;
7 = 7,3719 • In
1 - ехр 1 -
7,3719 /
9,5 -3,5
= -25,0732; е = 9,5 - ехр
^jf)
1 = -20,5.
Таким образом, плотность распределения случайной величины может быть описана
функцией
7,3719 ' * г "" п"пп l2
2тг • (ж + 20,5)
-- • 7,37192 • I - ^^ + Ы(х + 20,5)
2 7,3719 v ;
= 2,941 • (ж + 20,5)м1 • ехр{-29,172 • [-3,401 + \п(х + 20,5)]2} .
Случайная величина z = 7 + ^ • 1П(Ж ~ е) имеет стандартное нормальное распределе-
распределение, что позволяет выразить квантили и% распределения случайной величины х через
квантили иа стандартного нормального распределения
[1 / Л]
иа = ехр \- • ^а - 7 П + е.
Этим соотношением можно воспользоваться для ответа на дальнейшие вопросы, постав-
поставленные в задаче. Найдем сначала вероятность того, что х ^ 15. Задача сводится к следу-
следующему— по заданной квантили и^ найти иа и вычислить вероятность, соответствующую
этой квантили. Имеем
15 = ехр [—^ • («о + 25,0732I - 20,5.
Отсюда иа = 1,241, и искомая величина а ищется из условия a = F(ua), где F{y) —
функция стандартного нормального распределения.
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 355
Для вычисления F(y) воспользуемся аппроксимацией (см. раздел 1.1.1)
2,34 ^
g g is a i i " \ i i /1 \
F{y) = 1 - 0,852 •
2,0637 J
и получим
f /l 241 + 1 5774\2'34]
а = F(ua) = 1 - 0,852 • exp<^ - ^ ^ } = 0,893.
1 J ' I \ 2,0637 J J
Следовательно, вероятность того, что ж ^ 15, равна 0,893.
Вторая задача — вычисление значения и^, для которого Р(х > и^) = 0,05, эквива-
эквивалентна поиску квантили и% при а = 1 — 0,05 = 0,95. Имеем г&о,95 = 1,645 и
иха = ехр —-— • A,645 + 25,0732) - 20,5 = 17.
Следовательно, вероятность того, что х ^ 17, не более 0,05.
3.6.1.2. Семейство распределений Sb Джонсона
Уравнение для плотности распределения кривых этого семейства имеет вид
}
где у] > 0, ^оо < 7 < оо, Л > 0, ^оо < е < оо — параметры распределения.
Случайная величина ж, имеющая распределение из семейства Sb Джонсона,
ограничена пределами еие + А.
Возможны три случая:
— оба предела е и е + Л известны (например, если случайной величиной является
доля дефектнвгх изделий в партии, заключенная, очевидно, между 0 и 1);
— известен один предел (например, если х — долговечность изделия, то е = 0);
— оба предела неизвестны.
Если оба предела известны (известны параметры е и Л), то оценки параметров
?7 и 7 находятся по формулам [13, 366]
где иа — а-квантиль стандартного нормального распределения; ха — эмпири™
ческая квантиль ([а(п + 1)]-й упорядоченный по возрастанию член выборки
Х1 ^ Х2 ^ • • • ^ хп)-
Рекомендуется выбирать а' = а, а," = 1-аи уровень а = 0,05.
Квантили аппроксимирующего распределения и^ могут быть выражены через
квантили стандартного нормального распределения иа следующим образом:
<=
1 .
1 + ехр
Если известно только одно крайнее значение ?, то в дополнение к оценкам 7 и
12*
356 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
необходимо найти оценку Л по формуле
с /~ ч (х — е)(ха — е) + (ж — ?){х\-а — s) — 2(жа — e(xi^a — e))
(х - еJ - (ха - ?){xi-ot - e)
где х — выборочная медиана ряда.
Параметры г] и 7 находятся по формулам для случая, когда оба предела извест-
известны (вместо параметра Л используется его эмпирическая оценка Л). Если пределы е
и е + Л неизвестны, то для нахождения оценок параметров необходимо решить
численными методами систему четырех нелинейных уравнений
i = 1'2'3'4'
где uai и xai — «-квантили соответствующих величин.
Однако такая ситуация практически очень редка и здесь не рассматривается.
Задача 171. Наблюдение за временем изготовления п = 50 изделий позволило полу-
получить следующие данные (мин):
0,70 0,93 1,09 1,21 1,41
0,72 0,95 1,10 1,23 1,46
0,75 0,95 1,10 1,23 1,54
0,81 0,96 1,11 1,25 1,55
0,83 0,98 1,12 1,29 1,61
0,84 0,98 1,13 1,32 1,61
0,87 1,02 1,14 1,34 1,62
0,89 1,04 1,15 1,37 1,62
0,90 1,06 1,16 1,38 1,63
0,91 1,08 1,17 1,40 1,63
Необходимо установить возможность аппроксимации распределения времени изготов-
изготовления изделий кривой из семейства Sb Джонсона. Найти параметры распределения^
вычислить вероятность того^ что искомая величина будет находиться в интервале
0,92 ^ х ^ 1,28.
Вычисляем
ж = 1,1628; / = 0,07086; s = 0,26620; ]Г(ж^ - жK = 0,257706; J2(Xi - жL = 0,51103;
г=1 г=1
аз = ~\ • Y(xi - xf = 0,273231; а4 = ^ • Vfc - жL = 2,03551.
Имеем «4 = 2,03551 < 3 • (l + 0,641 • a§) = 3,143, что соответствует области семей-
семейства Sb- В нашем случае по смыслу задачи е = 0 и необходимо найти оценки парамет-
параметров ?], 7 и А. Выбирая а = 0,05, имеем г?о,95 = 1,645 и tto,os = ~ 1,645. Далее находим ста-
статистики с порядковыми номерами [0,05 • 51] = 2 (жг = 0,72); [A — а) • (п +1)] = [0,95 • 51] = 48
( 1,62).
1 1 12 + 1 13
Медиана выборки равна ж = - • (ж25 + Ж2в) = — '— = 1,125.
Тогда для е = 0 находим
А = 1,125 • М25-0,72+ 1,126-1,62-2-0,72-1,62 =
1Д252 - 0,72- 1,62
П
0,72- C,398- 1,62)
= 2,695; -у = 1,645 - 2,695 • Inf lfi2 ) = 1,896.
Г ' \ 3.398-1,62/
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 357
Таким образом, плотность аппроксимирующего распределения есть
/(ж) = ^р^ • ехр\ -- • 11,896 + 2,695 • In
2 I ' ' \ 3,398 -x
3,653
expi- 1,341+ 1,906-In
x -C,398™ x) I L \3,ЗЭ8-ж
Квантиль распределения и^ равна
тг • ехр
fj J _ 3,398 • ехр@,371 • иа - 0,703)
. _^ L t I + ехр@,371 • иа - 0,703)
Вероятность того, что 0,92 ^С х ^ 1,28, равна по определению
Р@,92 ^ х ^ 1,28) = Р(ж ^ 1,28) - Р(ж ^ 0,92).
Задача сводится к тому, чтобы найти вероятности C' = Р(ж ^ 1,28) и /3/; = Р(ж ^ 0,92),
соответствующие квантилям u^i = 1,28 и tto77°'92-
Алгоритм решения этой задачи включает в себя следующие этапы:
— по заданным и^, и u^f, находятся соответствующие им значения upi и гх^//;
— по найденным значениям и^ и и$п вычисляются значения функции стандартного
нормального распределения F(up/) и F(upf/);
— вычисляется искомая вероятность р = /3f -— C".
Теперь, пользуясь аппроксимацией для F(y) (см. предыдущую задачу), вычисляем
},) = F@,5374) = 1 - 0,852 ¦ exp^^^^tJ^^! = 0,704;
= 1 - 0,852 . ехр j^ ^П^^^Х = 0,236.
Окончательно получаем р = J3' - /3ff = 0,704 - 0,236 = 0,468.
Следовательно, вероятность того, что 0,92 ^ х ^ 2,28, равна 0,468.
3.6.1.3. Семейство распределений Sjj Дж:онсона
Уравнение кривых распределения семейства Sjj Дхсонсона имеет вид
I / I Г/ x2lf|\2>
/(Х)= "
Случайная величина, имеющая распределение S\j Джонсона, теоретически
неограничена, и в общем случае все четвхре параметра ^^ ц^ \ ж е неизвестны
и должны быть оценены по выборке. Для оценки параметров rj и j следует исполь™
зовать табл. 116, в которой аз и «4 — соответственно третий и четвертый моменты
распределения вероятностей.
Затем вычисляются оценки
/u[l) где и = ехр -^
358 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Оценки параметров
Таблица 116
и г/ распределения Su Джонсона [369]
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,0
8,2
8,4
8,6
8,8
9,0
«3
0,
^7
0,3479
0,2328
0,1760
0,1421
0,1196
0,1035
0,0914
0,0820
0,0745
0,0684
0,0633
0,0589
0,0552
0,0519
0,0491
0,0466
0,0444
0,0424
0,0406
0,0390
0,0374
0,0361
0,0348
0,0337
0,0326
0,0316
0,0307
0,0298
0,0290
0,0283
0,0276
0,0269
0,0263
0,0257
0,0251
0,0246
0,0241
0,0236
0,0232
0,0277
0,0223
0,0219
0,0215
0,0212
0,0208
0,0205
0,0202
0,0198
0,0195
0,0195
0,0190
0,0185
0,0180
0,0175
0,0171
05
Г]
4,671
3,886
3,396
3,081
2,852
2,676
2,535
2,420
2,324
2,242
2,171
2,109
2,054
2,005
1,961
1,921
1,885
1,852
1,822
1,793
1,767
1,743
1,721
1,699
1,680
1,661
1,643
1,627
1,611
1,596
1,582
1,568
1,556
1,543
1,532
1,520
1,510
1,499
1,490
1,480
1,471
1,462
1,454
1,445
1,438
1,430
1,415
1,415
1,408
1,408
1,395
1,383
1,371
1,360
1,349
0,
^7
0,7373
0,4834
0,3620
0,2905
0,2435
0,2102
0,1853
0,1661
0,1507
0,1381
0,1276
0,1188
0,1112
0,1046
0,0989
0,0938
0,0893
0,0852
0,0816
0,0783
0,0752
0,0725
0,0700
0,0676
0,0655
0,0635
0,0616
0,0599
0,0583
0,0568
0,0553
0,0540
0,0527
0,0515
0,0504
0,0493
0,0483
0,0473
0,0464
0,0455
0,0447
0,0439
0,0431
0,0424
0,0417
0,0410
0,0404
0,0398
0,0392
0,0392
0,0380
0,0370
0,0360
0,0351
0,0342
10
V
4,787
3,927
3,435
3,108
2,872
2,692
2,548
2,431
2,333
2,250
2,178
2,115
2,060
2,010
1,966
1,925
1,889
1,855
1,825
1,796
1,770
1,746
1,723
1,702
1,682
1,663
1,645
1,628
1,613
1,598
1,583
1,570
1,557
1,545
1,533
1,522
1,511
1,501
1,491
1,481
1,472
1,463
1,455
1,446
1,438
1,431
1,423
1,416
1,409
1,409
1,396
1,383
1,372
1,361
1,350
0,
^7
1,2280
0,7747
0,5699
0,4528
0,3776
0,3238
0,2845
0,2542
0,2302
0,2106
0,1943
0,1806
0,1689
0,1588
0,1499
0,1421
0,1352
0,1290
0,1234
0,1184
0,1138
0,1096
0,1057
0,1022
0,0989
0,0958
0,0930
0,0904
0,0879
0,0856
0,0835
0,0814
0,0795
0,0777
0,0760
0,0743
0,0728
0,0713
0,0699
0,0686
0,0673
0,0661
0,0650
0,0639
0,0628
0,0618
0,0608
0,0599
0,0590
0,0590
0,0572
0,0557
0,0542
0,0528
0,0515
15
V
5,004
4,036
3,503
3,156
2,908
2,719
2,571
2,450
2,349
2,264
2,190
2,126
2,069
2,018
1,973
1,932
1,895
1,861
1,830
1,801
1,775
1,750
1,727
1,705
1,685
1,666
1,648
1,631
1,615
1,606
1,586
1,572
1,559
1,555
1,554
1,524
1,513
1,502
1,492
1,448
1,474
1,465
1,456
1,448
1,440
1,432
1,425
1,418
1,411
1,411
1,397
1,385
1,373
1,362
1,351
0,
^7
1,9490
1,1430
0,8166
0,6384
0,5260
0,4487
0,3921
0,3490
0,3150
0,2875
0,2647
0,2456
0,2294
0,2153
0,2031
0,1923
0,1828
0,1743
0,1666
0,1597
0,1534
0,1477
0,1424
0,1376
0,1331
0,1290
0,1251
0,1215
0,1182
0,1151
0,1121
0,1094
0,1067
0,1043
0,1020
0,0998
0,0977
0,0957
0,0938
0,0920
0,0903
0,0887
0,0871
0,0856
0,0842
0,0828
0,0815
0,0802
0,0790
0,0790
0,0767
0,0745
0,0725
0,0707
0,0689
20
7]
5,369
4,208
3,607
3,227
2,960
2,760
2,604
2,477
2,372
2,283
2,207
2,141
2,082
2,030
1,984
1,942
1,904
1,869
1,837
1,808
1,781
1,756
1,732
1,711
1,690
1,671
1,653
1,636
1,619
1,604
1,590
1,576
1,563
1,550
1,538
1,527
1,516
1,505
1,495
1,485
1,476
1,467
1,458
1,450
1,442
1,434
1,427
1,419
1,412
1,412
1,399
1,386
1,374
1,363
1,352
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 359
Продолжение таблицы 116
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7Д
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
«3
0,
-7
3,1890
1,6560
1,1330
0,8620
0,6997
0,5907
0,5125
0,4536
0,4076
0,3707
0,3404
0,3151
0,2937
0,2752
0,2592
0,2451
0,2327
0,2216
0,2117
0,2027
0,1946
0,1872
0,1804
0,1742
0,1684
0,1631
0,1582
0,1536
0,1493
0,1415
0,1380
0,1347
0,1315
0,1286
0,1258
0,1231
0,1206
0,1182
0,1159
0,1137
0,1116
0,1096
0,1077
0,1059
0,1042
0,1025
0,1009
0,0993
25
Г]
5,992
4,469
3,759
3,328
3,033
2,816
2,648
2,513
2,402
2,309
2,229
2,160
2,100
2,046
1,998
1,955
1,916
1,880
1,847
1,817
1,790
1,764
1,740
1,718
1,697
1,677
1,658
1,641
1,625
1,594
1,580
1,567
1,554
1,542
1,530
1,519
1,509
1,498
1,489
1,479
1,470
1,461
1,453
1,445
1,437
1,429
1,422
1,415
0,
^7
6,3890
2,4770
1,5690
1,1480
0,9115
0,7586
0,6515
0,5723
0,5113
0,4629
0,4234
0,3907
0,3632
0,3396
0,3192
0,3014
0,2857
0,2717
0,2592
0,2480
0,2378
0,2285
0,2201
0,2183
0,2052
0,1986
0,1925
0,1868
0,1815
0,1719
0,1676
0,1635
0,1596
0,1560
0,1525
0,1492
0,1461
0,1432
0,1404
0,1377
0,1352
0,1327
0,1304
0,1282
0,1260
0,1240
0,1220
0,1201
30
Г]
7,204
4,875
3,979
3,467
3,132
2,890
2,707
2,561
2,442
2,343
2,258
2,186
2,122
2,066
2,016
1,971
1,930
1,893
1,860
1,829
1,800
1,774
1,749
1,726
1,705
1,685
1,666
1,648
1,631
1,600
1,586
1,572
1,559
1,547
1,535
1,524
1,513
1,502
1,492
1,483
1,474
1,465
1,456
1,448
1,440
1,432
1,425
1,418
0,
-7
2,2360
1,5460
1,1870
0,9681
0,8197
0,7127
0,6304
0,5673
0,5165
0,4747
0,4397
0,4100
0,3844
0,3622
0,3426
0,3354
0,3099
0,2961
0,2836
0,2723
0,2620
0,2525
0,2438
0,2358
0,2284
0,2215
0,2151
0,2035
0,1983
0,1933
0,1887
0,1843
0,1802
0,1762
0,1726
0,1690
0,1656
0,1624
0,1594
0,1565
0,1537
0,1510
0,1485
0,1460
0,1437
0,1414
35
7]
4,300
3,663
3,266
2,989
2,783
2,623
2,492
2,385
2,295
2,217
2,150
2,090
2,038
1,991
1,948
1,910
1,875
1,843
1,813
1,786
1,760
1,737
1,715
1,694
1,674
1,656
1,639
1,607
1,593
1,579
1,565
1,553
1,541
1,529
1,518
1,507
1,497
1,487
1,478
1,465
1,456
1,448
1,440
1,432
1,425
1,418
0,40
^7
3,4840
2,1460
1,5650
1,2380
1,0280
0,8814
0,7733
0,6902
0,6243
0,5708
0,5265
0,4891
0,4564
0,4288
0,4048
0,3836
0,3648
0,3479
0,3328
0,3191
0,3066
0,2952
0,2848
0,2752
0,2663
0,2581
0,2504
0,2366
0,2304
0,2245
0,2190
0,2138
0,2089
0,2043
0,1999
0,1957
0,1918
0,1880
0,1844
0,1810
0,1777
0,1746
0,1716
0,1687
0,1660
0,1633
4,813
3,943
3,448
3,120
2,882
2,701
2,557
2,439
2,340
2,256
2,184
2,121
2,065
2,015
1,970
1,930
1,893
1,859
1,829
1,800
1,774
1,749
1,773
1,705
1,685
1,666
1,648
1,615
1,600
1,586
1,573
1,560
1,547
1,535
1,524
1,513
1,503
1,493
1,483
1,474
1,465
1,457
1,448
1,440
1,433
1,425
360 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,2
8,4
8,6
8,8
9,0
9,2
9,4
Продолжение табл]
яц ы 116
«3
0,45
-7
2,1390
1,6140
1,3020
1,0950
0,9470
0,8363
0,7503
0,6814
0,6251
0,5780
0,5382
0,5040
0,4744
0,4484
0,4254
0,4050
0,3866
0,3696
0,3547
0,3411
0,3286
0,3172
0,3066
0,2967
0,2879
0,2794
0,2716
0,2643
0,2574
0,2509
0,2448
0,2391
0,2337
0,2285
0,2237
0,2190
0,2147
0,2105
0,2065
0,2020
0,1991
0,1956
0,1922
0,1891
0,1860
0,1802
0,1749
0,1699
0,1653
0,1610
0,1570
0,1532
f]
3,705
3,295
3,011
2,801
2,637
2,505
2,396
2,304
2,226
2,157
2,097
2,044
1,997
1,954
1,915
1,880
1,847
1,817
1,789
1,764
1,740
1,718
1,697
1,677
1,659
1,642
1,625
1,610
1,595
1,581
1,568
1,555
1,543
1,531
1,520
1,509
1,499
1,489
1,480
1,471
1,462
1,454
1,445
1,438
1,430
1,416
1,402
1,389
1,377
1,366
1,355
1,345
0,
-7
3,1570
2,1880
1,6870
1,3780
1,1690
1,0180
0,9031
0,8132
0,7407
0,6811
0,6311
0,5886
0,5520
0,5202
0,4922
0,4674
0,4453
0,4255
0,4076
0,3913
0,3765
0,3629
0,3504
0,3385
0,3278
0,3180
0,3088
0,3002
0,2921
0,2846
0,2775
0,2709
0,2646
0,2586
0,2530
0,2476
0,2426
0,2377
0,2331
0,2287
0,2246
0,2206
0,2167
0,2131
0,2095
0,2029
0,1968
0,1912
0,1859
0,1810
0,1764
0,1721
50
Г]
4,087
3,540
3,184
2,931
2,739
2,588
2,465
2,363
2,276
2,202
2,140
2,079
2,028
1,982
1,941
1,903
1,869
1,837
1,808
1,781
1,756
1,733
1,711
1,691
1,672
1,653
1,636
1,620
1,605
1,591
1,577
1,564
1,551
1,539
1,528
1,517
1,506
1,496
1,487
1,477
1,468
1,460
1,451
1,443
1,436
1,421
1,407
1,394
1,381
1,370
1,359
1,348
0
~7
2,2840
1,7830
1,4690
1,2530
1,0960
0,9748
0,8802
0,8033
0,7399
0,6865
0,6410
0,6017
0,5675
0,5274
0,5106
0,4868
0,4653
0,4459
0,4283
0,4122
0,3975
0,3840
0,3714
0,3598
0,3491
0,3390
0,3297
0,3209
0,3123
0,3046
0,2973
0,2904
0,2839
0,2778
0,2719
0,2664
0,2611
0,2561
0,2513
0,2467
0,2423
0,2381
0,2341
0,2266
0,2196
0,2132
0,2072
0,2016
0,1914
0,1905
55
V
3,424
3,105
2,872
2,694
2,552
2,436
2,338
2,255
2,136
2,120
2,065
2,015
1,971
1,931
1,894
1,860
1,830
1,801
1,775
1,750
1,728
1,706
1,686
1,6667
1,649
1,633
1,617
1,602
1,587
1,574
1,561
1,548
1,537
1,525
1,514
1,504
1,494
1,487
1,475
1,466
1,458
1,450
1,442
1,426
1,412
1,399
1,386
1,374
1,363
1,353
0,
-7
3,3830
2,4260
1,9060
1,5770
1,3490
1,1820
1,0540
0,9527
0,9183
0,8024
0,7451
0,6962
0,6539
0,6170
0,5845
0,5556
0,5298
0,5066
0,4856
0,4665
0,4491
0,4331
0,4184
0,4049
0,3923
0,3806
0,3697
0,3595
0,3500
0,3410
0,3326
0,3247
0,3172
0,3101
0,3034
0,2967
0,2907
0,2849
0,2795
0,2742
0,2692
0,2645
0,2599
0,2514
0,2435
0,2362
0,2294
0,2231
0,2172
0,2117
60
7]
3,776
3,346
3,049
2,830
2,662
2,526
2,414
2,320
2,240
2,170
2,109
2,055
2,007
1,963
1,924
1,888
1,855
1,824
1,796
1,770
1,746
1,691
1,673
1,653
1,664
1,647
1,630
1,614
1,599
1,585
1,572
1,559
1,547
1,453
1,524
1,513
1,503
1,493
1,483
1,447
1,465
1,457
1,448
1,433
1,418
1,405
1,392
1,380
1,368
1,357
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 361
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,2
9,4
9,6
9,8
10,0
0,65
^7
2,6210
2,0600
1,7050
1,4600
1,2800
1,1420
1,0330
0,9434
0,8699
0,8083
0,7550
0,7092
0,6693
0,6341
0,6028
0,5749
0,5498
0,5270
0,5063
0,4875
0,4701
0,4542
0,4395
0,4258
0,4131
0,4013
0,3903
0,3799
0,3702
0,3611
0,3524
0,3443
0,3366
0,3293
0,3224
0,3159
0,3096
0,3037
0,2980
0,2926
0,2871
0,2822
0,2724
0,2729
0,2685
0,2643
0,2603
0,2564
0,2526
0,2490
0,2455
0,2389
0,2328
п
3,294
3,013
2,804
2,641
2,510
2,401
2,309
2,231
2,162
2,100
2,049
2,001
1,958
1,919
1,884
1,851
1,821
1,794
1,768
1,744
1,722
1,701
1,681
1,663
1,645
1,629
1,613
1,598
1,584
1,571
1,558
1,546
1,.534
1,523
1,512
1,502
1,492
1,483
1,473
1,469
1,456
1,448
1,440
1,432
1,425
1,418
1,411
1,404
1,398
1,391
1,385
1,373
1,362
0,70
^7
4,1040
2,8860
2,2540
1,8600
1,5890
1,3920
1,2400
1,1210
1,0240
0,9436
0,8761
0,8154
0,7687
0,7252
0,6869
0,6530
0,6226
0,5953
0,5706
0,5482
0,5276
0,5088
0,4915
0,4755
0,4607
0,4470
0,4341
0,4221
0,4109
0,4004
0,3905
0,3812
0,3723
0,3640
0,3561
0,3486
0,3415
0,3347
0,3283
0,3221
0,3163
0,3106
0,3053
0,3001
0,2952
0,2904
0,2859
0,2812
0,2770
0,2730
0,2691
0,2617
0,2548
0,2483
0,2422
0,2365
7]
3,659
3,269
2,996
2,791
2,631
2,502
2,395
2,304
2,226
2,159
2,099
2,045
1,999
1,957
1,918
1,883
1,850
1,820
1,793
1,767
1,743
1,721
1,700
1,681
1,662
1,645
1,628
1,613
1,598
1,584
1,571
1,558
1,546
1,534
1,523
1,512
1,502
1,492
1,483
1,474
1,465
1,456
1,448
1,440
1,433
1,425
1,418
1,411
1,404
1,398
1,392
1,379
1,368
1,357
1,347
1,337
Продолжение таблицы 116
«3
0,75
^7
1,5220
1,3530
1,2210
1,1140
1,0250
0,9509
0,8877
0,8331
0,7586
0,7419
0,7067
0,6735
0,6337
0,6168
0,5924
0,5700
0,5496
0,5308
0,5134
0,4973
0,4824
0,4684
0,4554
0,4433
0,4318
0,4211
0,4110
0,4014
0,3924
0,3838
0,3757
0,3680
0,3607
0,3537
0,3470
0,3407
0,3346
0,3288
0,3232
0,3179
0,3127
0,3078
0,3031
0,2985
0,2941
0,2858
0,2778
0,2706
0,2639
0,2575
п
2,503
2,395
2,305
2,227
2,160
2,100
2,048
2,000
1,958
1,918
1,884
1,851
1,821
1,794
1,777
1,744
1,722
1,701
1,682
1,663
1,646
1,629
1,614
1,599
1,585
1,572
1,559
1,547
1,535
1,524
1,523
1,503
1,493
1,483
1,474
1,466
1,457
1,448
1,441
1,433
1,426
1,419
1,412
1,405
1,399
1,386
1,374
1,363
1,353
1,343
0,
^7
1,9310
1,6760
1,4850
1,3360
1,2150
1,1170
1,0340
0,9642
0,9039
0,8515
0,8055
0,7647
0,7284
0,6942
0,6663
0,6396
0,6152
0,5929
0,5724
0,5535
0,5359
0,5197
0,5045
0,4904
0,4772
0,4648
0,4531
0,4421
0,4318
0,4220
0,4127
0,4039
0,3956
0,3876
0,3800
0,3729
0,3660
0,3594
0,3531
0,3471
0,3413
0,3358
0,3305
0,3253
0,3204
0,3111
0,3025
0,2944
0,2868
0,2798
80
п
2,641
2,511
2,403
2,312
2,234
2,165
2,105
2,052
2,005
1,962
1,923
1,887
1,855
1,824
1,797
1,771
1,747
1,725
1,704
1,684
1,666
1,648
1,632
1,616
1,601
1,587
1,573
1,561
1,548
1,537
1,525
1,515
1,504
1,494
1,485
1,476
1,467
1,458
1,450
1,442
1,435
1,427
1,420
1,413
1,406
1,393
1,381
1,370
1,359
1,349
362 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,2
9,4
9,6
9,8
10,0
Продолжение табл]
яц ы 116
0,
-7
2,6020
2,1670
1,8640
1,6410
1,4690
1,3330
1,2210
1,1280
1,0500
0,9826
0,9243
0,8732
0,8282
0,7881
0,7521
0,7197
0,6904
0,6637
0,6392
0,6150
0,5962
0,5770
0,5592
0,5247
0,5273
0,5130
0,4995
0,4868
0,4749
0,4636
0,4530
0,4429
0,4334
0,4244
0,4158
0,4076
0,3998
0,3923
0,3852
0,3784
0,3719
0,3657
0,3597
0,3539
0,3484
0,3380
0,3283
0,3193
0,3109
0,3030
35
7]
2,828
2,662
2,529
2,418
2,325
2,245
2,176
2,115
2,061
2,012
1,969
1,929
1,893
1,860
1,830
1,802
1,776
1,752
1,729
1,707
1,688
1,668
1,652
1,635
1,619
1,604
1,590
1,576
1,563
1,551
1,539
1,528
1,517
1,507
1,497
1,487
1,478
1,469
1,460
1,452
1,444
1,437
1,429
1,422
1,415
1,401
1,389
1,377
1,366
1,355
0,
~7
4,0290
3,0380
2,4730
2,1000
1,8320
1,6290
1,4700
1,3420
1,2360
1,1470
1,0710
1,0060
0,9485
0,8982
0,8536
0,8138
0,7780
0,7456
0,7161
0,6892
0,6646
0,6419
0,6209
0,5961
0,5835
0,5666
0,5509
0,5362
0,5224
0,5094
0,4972
0,4857
0,4747
0,4644
0,4546
0,4452
0,4364
0,4279
0,4199
0,4122
0,4048
0,3978
0,3910
0,3845
0,3783
0,3666
0,3558
0,3457
0,3363
0,3275
90
V
3,093
2,868
2,694
2,555
2,441
2,344
2,262
2,191
2,128
2,073
2,023
1,979
1,939
1,902
1,868
1,837
1,809
1,782
1,758
1,735
1,713
1,693
1,678
1,656
1,639
1,623
1,608
1,594
1,580
1,567
1,555
1,543
1,531
1,520
1,510
1,500
1,490
1,481
1,472
1,463
1,455
1,447
1,439
1,431
1,424
1,410
1,397
1,385
1,373
1,362
0,
~7
2,4070
2,0710
1,8250
1,6350
1,4840
1,3610
1,2590
1,1720
1,0980
1,0330
1,9765
0,9265
0,8620
0,8420
0,8060
0,7733
0,7436
0,7164
0,6914
0,6683
0,6470
0,6272
0,6087
0,5915
0,5754
0,5593
0,5463
0,5328
0,5203
0,5084
0,4971
0,4864
0,4763
0,4667
0,4575
0,4488
0,4405
0,4325
0,4248
0,4175
0,4105
0,3974
0,3852
0,3839
0,3634
0,3537
Э5
V
2,592
2,472
2,371
2,285
2,211
2,146
2,089
2,038
1,992
1,951
1,913
1,879
1,847
1,818
1,791
1,766
1,742
1,721
1,700
1,681
1,653
1,645
1,629
1,614
1,599
1,585
1,572
1,559
1,547
1,536
1,524
1,514
1,504
1,494
1,484
1,475
1,467
1,458
1,450
1,442
1,434
1,420
1,406
1,394
1,381
1,370
-7
3,5380
2,8320
2,3860
2,0720
1,8390
1,6570
1,5100
1,3900
1,2890
1,2030
1,1290
1,0650
1,0080
0,9581
0,9132
0,8729
0,8364
0,8033
0,7730
0,7453
0,7198
0,6962
0,6744
0,6541
0,6352
0,6171
0,6010
0,5855
0,5709
0,5571
0,5442
0,5309
0,5203
0,5092
0,4987
0,4888
0,4793
0,4702
0,4616
0,4533
0,4454
0,4305
0,4169
0,4042
0,3925
0,3816
30
Ч]
2,799
2,641
2,512
2,406
2,315
2,237
2,170
2,110
2,057
2,009
1,967
1,928
1,892
1,860
1,830
1,802
1,776
1,752
1,730
1,708
1,689
1,670
1,653
1,636
1,620
1,605
1,591
1,578
1,565
1,552
1,541
1,529
1,519
1,508
1,498
1,489
1,479
1,471
1,462
1,454
1,446
1,431
1,416
1,403
1,390
1,379
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 363
«4
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
10,0
10,2
10,4
10,6
10,8
11,0
11,2
11,4
Продолжение табл
ицы 116
1,
^7
2,4030
2,0990
1,8710
1,6920
1,5470
1,4280
1,3270
1,2410
1,1670
1,1020
1,0440
0,9933
0,9477
0,9066
0,8694
0,8356
0,8046
0,7762
0,7500
0,7258
0,7034
0,6825
0,6630
0,6448
0,6278
0,6117
0,5967
0,5825
0,5960
0,5563
0,5443
0,5328
0,5220
0,5099
0,5018
0,4924
0,4834
0,4748
0,4666
0,4587
0,4511
0,4439
0,4369
0,4302
0,4237
0,4175
0,4115
0,4001
0,3895
0,3796
0,3703
0,3615
0,3533
0,3455
05
V
2,450
2,353
2,270
2,299
2,136
2,080
2,031
1,986
1,945
1,908
1,875
1,843
1,815
1,788
1,763
1,740
1,719
1,698
1,679
1,661
1,644
1,628
1,613
1,598
1,584
1,571
1,559
1,547
1,535
1,524
1,514
1,504
1,494
1,484
1,475
1,467
1,458
1,450
1,442
1,435
1,427
1,420
1,413
1,407
1,400
1,394
1,388
1,376
1,365
1,355
1,345
1,335
1,326
1,318
1,
^7
2,5430
2,4780
2,4500
2,1490
1,9210
1,7410
1,5970
1,4750
1,3730
1,2850
1,2100
1,1430
1,0850
1,0320
0,9857
0,9435
0,9053
0,8705
0,8386
0,8093
0,7823
0,7573
0,7342
0,7126
0,6924
0,6736
0,6559
0,6393
0,6237
0,6089
0,5950
0,5818
0,5693
0,5574
0,5461
0,5354
0,5251
0,5154
0,5060
0,4971
0,4885
0,4803
0,4724
0,4648
0,4576
0,4506
0,4438
0,4311
0,4192
0,4082
0,3978
0,3881
0,3789
0,3703
10
7]
2,632
2,505
2,400
2,311
2,234
2,168
2,109
2,056
2,009
1,966
1,928
1,893
1,860
1,830
1,803
1,777
1,753
1,731
1,710
1,690
1,671
1,654
1,637
1,622
1,607
1,593
1,579
1,566
1,554
1,542
1,531
1,520
1,510
1,500
1,490
1,481
1,472
1,463
1,455
1,447
1,440
1,432
1,425
1,418
1,411
1,404
1,398
1,386
1,374
1,363
1,353
1,343
1,334
1,325
1,
^7
2,5350
2,2240
1,9900
1,8050
1,6560
1,5310
1,4270
1,3370
1,2590
1,1900
1,1300
1,0760
1,0280
1,9840
0,9444
0,9083
0,8753
0,8450
0,8179
0,7910
0,7670
0,7445
0,7326
0,7040
0,6857
0,6684
0,6521
0,6368
0,6223
0,6085
0,5955
0,5831
0,5714
0,5601
0,5494
0,5393
0,5295
0,5202
0,5112
0,5027
0,4945
0,4866
0,4790
0,4646
0,4513
0,4389
0,4273
0,4165
0,4063
0,3698
15
п
2,362
2,278
2,206
2,143
2,087
2,037
1,992
1,951
1,914
1,880
1,849
1,820
1,793
1,768
1,745
1,723
1,703
1,683
1,665
1,648
1,632
1,616
1,602
1,558
1,575
1,562
1,550
1,538
1,527
1,517
1,507
1,497
1,487
1,478
1,469
1,461
1,453
1,445
1,437
1,430
1,423
1,416
1,409
1,396
1,384
1,373
1,362
1,352
1,342
1,332
1,
^7
3,8860
3,1240
2,6540
2,3250
2,0790
1,8850
1,7290
1,5990
1,4900
1,3960
1,3150
1,2430
1,1800
1,1240
1,0740
1,0280
0,9871
0,9495
0,9151
0,8834
0,8542
0,8272
0,8020
0,7786
0,7568
0,7464
0,7172
0,6991
0,6822
0,6661
0,6510
0,6366
0,6230
0,6101
0,5978
0,5861
0,5749
0,5642
0,5540
0,5443
0,5349
0,5260
0,5174
0,5012
0,4862
0,4723
0,4593
0,4472
0,4358
0,4252
20
п
2,530
2,423
2,331
2,253
2,184
1,124
2,070
2,022
1,978
1,.939
1,903
1,870
1,840
1,811
1,785
1,761
1,738
1,717
1,697
1,678
1,660
1,644
1,628
1,613
1,598
1,585
1,571
1,559
1,547
1,536
1,525
1,514
1,504
1,495
1,485
1,476
1,468
1,459
1,451
1,443
1,436
1,428
1,421
1,408
1,395
1,383
1,372
1,361
1,351
1,341
364 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Продолжение таблицы 116
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
10,0
10,2
10,4
10,6
10,8
11,0
11,2
11,4
11,6
11,8
12,0
1,25
^7
2,8230
2,4590
2,1920
1,9840
1,8170
1,6790
1,5630
1,4640
1,3790
1,3030
1,2370
1,1780
1,1250
1,0770
1,0340
0,9945
0,9584
0,9251
0,8945
0,8661
0,8397
0,8152
0,7923
0,7709
0,7507
0,7318
0,7140
0,6972
0,6813
0,6663
0,6520
0,6385
0,6256
0,6133
0,6016
0,5904
0,5797
0,5695
0,5597
0,5413
0,5243
0,5086
0,4940
0,4804
0,4678
0,4559
Г]
2,309
2,234
2,168
2,109
2,057
2,011
1,969
1,930
1,895
1,863
1,833
1,806
1,780
1,756
1,734
1,713
1,693
1,675
1,657
1,640
1,625
1,610
1,596
1,582
1,569
1,557
1,545
1,534
1,523
1,513
1,503
1,493
1,484
1,475
1,466
1,458
1,450
1,442
1,435
1,420
1,407
1,394
1,382
1,371
1,360
1,350
1,
^7
5,1110
3,7120
3,0540
2,6350
2,3350
2,1060
1,9240
1,7750
1,6500
1,5440
1,4520
1,3720
1,3010
1,2380
1,1820
1,1320
1,0860
1,0440
1,0060
0,9706
0,9382
0,9083
0,8805
0,8546
0,8304
0,8078
0,7866
0,7667
0,7480
0,7303
0,7136
0,6977
0,6827
0,6685
0,6549
0,6420
0,6297
0,6180
0,6067
0,5857
0,5664
0,5485
0,5320
0,5167
0,5025
0,4891
30
V
2,476
2,378
2,294
2,221
2,156
2,100
2,049
2,003
1,962
1,924
1,890
1,858
1,829
1,802
1,776
1,753
1,731
1,710
1,691
1,672
1,655
1,639
1,623
1,608
1,594
1,581
1,568
1,556
1,544
1,533
1,522
1,512
1,502
1,492
1,483
1,474
1,466
1,458
1,450
1,434
1,420
1,407
1,394
1,382
1,371
1,360
1,35
^7
2,5250
2,2590
2,0550
1,8900
1,7520
1,6360
1,5370
1,4500
1,3740
1,3080
1,2460
1,1920
1,1430
1,0990
1,0580
1,0200
0,9860
0,9542
0,9246
0,8972
0,8716
0,8477
0,8252
0,8042
0,7843
0,7656
0,7480
0,7312
0,7154
0,7003
0,6860
0,6724
0,6594
0,6352
0,6131
0,5927
0,5739
0,5566
0,5404
0,5254
Г]
2,151
2,094
2,044
1,999
1,958
1,921
1,887
1,856
1,827
1,800
1,775
1,751
1,730
1,709
1,690
1,671
1,654
1,638
1,623
1,608
1,594
1,580
1,568
1,566
1,440
1,533
1,522
1,512
1,502
1,492
1,474
1,466
1,456
1,450
1,435
1,420
1,407
1,394
1,383
1,371
1,
^7
3,9290
3,2130
2,7680
2,4550
2,2170
2,0290
1,8750
1,7460
1,6360
1,5400
1,4570
1,3840
1,3190
1,2600
1,2070
1,1590
1,1150
1,0750
1,0380
1,0040
0,9729
0,9436
0,9136
0,8908
0,8669
0,8445
0,8234
0,8036
0,7848
0,7671
0,7503
0,7343
0,7192
0,6910
0,6654
0,6420
0,6205
0,6007
0,5823
0,5653
0,5495
0,5347
0,5209
40
7]
2,281
2,210
2,148
2,093
2,043
1,998
1,958
1,921
1,887
1,856
1,827
1,800
1,775
1,752
1,730
1,709
1,690
1,672
1,655
1,639
1,623
1,608
1,594
1,581
1,568
1,556
1,545
1,534
1,523
1,513
1,503
1,493
1,484
1,467
1,450
1,435
1,421
1,408
1,395
1,383
1,372
1,361
1,351
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 365
Продолжение таблицы 116
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
10,0
10,2
10,4
10,6
10,8
11,0
11,2
11,4
11,6
11,8
12,0
12,2
12,4
12,6
12,8
13,0
1,45
-7
2,4300
2,2020
2,0240
1,8770
1,7520
1,646
1,5540
1,4730
1,4010
1,3370
1,2790
1,2270
1,1800
1,1360
1,0960
1,0600
1,0260
0,9943
0,9651
0,9377
0,9122
0,8882
0,8657
0,8445
0,8245
0,8056
0,7877
0,7546
0,7247
0,6975
0,6727
0,6499
0,6289
0,6095
0,5915
0,5748
0,5592
Г)
2,046
2,001
1,960
1,923
1,889
1,858
1,829
1,802
1,777
1,754
1,732
1,711
1,692
1,674
1,657
1,640
1,625
1,610
1,596
1,583
1,570
1,558
1,546
1,535
1,524
1,514
1,504
1,485
1,468
1,452
1,437
1,422
1,409
1,396
1,.384
1,373
1,365
1,50
^7
3,6690
3,0880
2,7050
2,4260
2,2110
2,0370
1,8930
1,7720
1,6670
1,5760
1,4960
1,4250
1,3610
1,3040
1,2520
2,2040
1,1610
1,1210
1,0840
1,0500
1,0190
0,9892
0,9616
0,9359
0,9117
0,8889
0,8675
0,8280
0,7927
0,7608
0,7318
0,7053
0,6811
0,6588
0,6383
0,6192
0,6016
V
2,157
2,102
2,051
2,006
1,965
1,928
1,894
1,862
1,833
1,806
1,781
1,758
1,736
1,715
1,695
1,677
1,660
1,643
1,628
1,613
1,599
1,586
1,573
1,560
1,549
1,538
1,527
1,506
1,488
1,470
1,454
1,439
1,424
1,411
1,398
1,386
1,375
1,
^7
2,4590
2,2400
2,0670
1,9240
1,8030
1,6980
1,6070
1,5270
1,4560
1,3920
1,3340
1,2820
1,2340
1,1900
1,1500
1,1120
1,0780
1,0460
1,0160
0,9881
0,9619
0,9142
0,8718
0,8338
0,7996
0,7686
0,7403
0,7145
0,6907
0,6688
0,6486
0,6297
0,6122
0,5959
0,5806
0,5662
55
п
1,974
1,936
1,901
1,869
1,840
1,812
1,787
1,763
1,741
1,720
1,700
1,682
1,664
1,648
1,632
1,617
1,603
1,589
1,576
1,564
1,552
1,530
1,509
1,491
1,473
1,456
1,441
1,427
1,413
1,400
1,388
1,377
1,366
1,356
1,346
1,337
1,
-7
3,8130
3,1920
2,7950
2,5100
2,2910
2,1150
1,9690
1,8460
1,7400
1,6470
1,5660
1,4930
1,4280
1,3700
1,3160
1,2680
1,2230
1,1820
1,1440
1,1090
1,0760
1,0170
0,9655
0,9196
0,8785
0,8416
0,8083
0,7780
0,7503
0,7248
0,7014
0,6798
0,6598
0,6411
0,6237
0,6074
60
Г]
2,074
2,028
1,985
1,947
1,911
1,879
1,849
1,821
1,795
1,771
1,748
1,727
1,707
1,688
1,670
1,653
1,637
1,622
1,608
1,594
1,581
1,557
1,534
1,513
1,494
1,476
1,460
1,444
1,430
1,416
1,403
1,391
1,379
1,369
1,358
1,348
Напомним, что
Z ,
e +е
shz =
Квантили и^ эмпирического семейства Sjj выражаются через квантили иа стан™
дартного нормального распределения с помощью формулы
иха = е + Л sh (
иа - 7
V V
366 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
8,6
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
10,0
10,2
10,4
10,6
10,8
11,0
11,2
11,4
11,6
11,8
12,0
12,2
12,4
12,6
12,8
13,0
13,2
13,4
13,6
13,8
14,0
14,2
14,4
14,6
14,8
15,0
Продолжение табл]
яц ы 116
«3
1,65
-7
2,6010
2,3650
2,1810
2,0300
1,9020
1,7930
1,6970
1,6130
1,5390
1,4720
1,4120
1,3570
1,3070
1,2620
1,2190
1,1440
1,0790
1,0220
0,9720
0,9274
0,8874
0,8513
0,8186
0,7888
0,7615
0,7364
0,7132
0,6918
0,6719
0,6533
V
1,925
1,891
1,860
1,831
1,805
1,780
1,757
1,735
1,715
1,696
1,678
1,660
1,644
1,629
1,614
1,587
1,562
1,539
1,518
1,490
1,481
1,464
1,448
1,433
1,419
1,406
1,394
1,382
1,371
1,361
1,
~7
4,6030
3,5820
3,0610
2,7190
2,4670
2,2690
2,1080
1,9730
1,8580
1,7580
1,6700
1,5920
1,5230
1,4600
1,4030
1,3040
1,2200
1,1480
1,0850
1,0300
0,9811
0,9375
0,8983
0,8628
0,8306
0,8011
0,7740
0,7491
0,7261
0,7047
70
V
2,018
1,978
1,940
1,906
1,874
1,844
1,817
1,792
1,768
1,745
1,725
1,705
1,686
1,669
1,652
1,621
1,594
1,568
1,545
1,524
1,504
1,485
1,468
1,452
1,437
1,423
1,410
1,398
1,386
1,375
1,
~7
2,3820
2,2080
2,0620
1,9380
1,8310
1,7380
1,6560
1,5160
1,4020
1,3070
1,2260
1,1560
1,0950
1,0410
0,9928
0,9499
0,9112
0,8761
0,8441
0,8148
0,7879
0,7630
0,7400
0,7187
0,6988
0,6802
0,6628
0,6464
0,6311
0,6166
0,6029
0,5900
75
V
1,831
1,805
1,781
1,758
1,736
1,716
1,697
1,662
1,631
1,602
1,576
1,552
1,530
1,510
1,491
1,474
1,458
1,442
1,428
1,415
1,402
1,390
1,379
1,368
1,358
1,348
1,339
1,330
1,321
1,313
1,305
1,298
1,80
-7
3,6790
3,1470
2,7930
2,5350
2,3350
2,1720
2,0360
1,8190
1,6520
1,5180
1,4080
1,3160
1,2360
1,1680
1,1080
1,0540
1,0070
0,9644
0,9260
0,8910
0,8592
0,8299
0,8030
0,7781
0,7551
0,7336
0,7136
0,6949
0,6774
0,6609
0,6454
0,6308
п
1,910
1,879
1,849
1,822
1,796
1,772
1,750
1,709
1,673
1,640
1,631
1,584
1,560
1,538
1,517
1,498
1,480
1,463
1,448
1,433
1,420
1,407
1,394
1,383
1,372
1,362
1,352
1,342
1,333
1,325
1,316
1,308
Задача 172. В результате наблюдений над случайной величиной х получены следую-
следующие значения (п = 50):
11 16 18 21 21 23 24 24 25 26
27 28 28 28 28 29 29 30 31 31
34 34 35 35
38 39
31
35
40
32
36
41
32
36
42
32
37
42
33
37
45
33
38
46
40
48 55 60
40
62
Найти аппроксимирующее распределение Джонсона^ оценить его параметры и вычис-
вычислить значение х = ж*, для которого а = Р(ж ^ ж*) = 0,95.
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 367
Окончание таблицы 116
10,2
10,4
10,6
10,8
11,0
11,2
11,4
11,6
11,8
12,0
12,2
12,4
12,6
12,8
13,0
13,2
13,4
13,6
13,8
14,0
14,2
14,4
14,6
14,8
15,0
1,85
^7
2,3100
2,0280
1,8200
1,6580
1,5280
1,4200
1,3290
1,2510
1,1830
1,1240
1,0710
1,0240
0,9811
0,9427
0,9078
0,8758
0,8465
0,8195
0,7945
0,7712
0,7496
0,7295
0,7106
0,6929
0,6763
V
1,766
1,723
1,686
1,652
1,622
1,594
1,569
1,546
1,525
1,505
1,487
1,470
1,454
1,439
1,425
1,412
1,400
1,388
1,377
1,366
1,356
1,346
1,337
1,328
1,320
1,
^7
3,4750
2,7260
2,3130
2,0360
1,8320
1,6730
1,5440
1,4380
1,3470
1,2700
1,2020
1,1430
1,0900
1,0430
1,0000
0,9614
0,9263
0,8941
0,8646
0,8373
0,8121
0,7886
0,7668
0,7464
0,7273
90
V
1,834
1,784
1,740
1,701
1,666
1,634
1,605
1,580
1,556
1,534
1,514
1,495
1,477
1,461
1,446
1,431
1,418
1,405
1,393
1,382
1,371
1,361
1,351
1,342
1,333
«3
1,95
-7
2,3310
2,0580
1,8550
1,6960
1,5680
1,4610
1,3700
1,2930
1,2250
1,1650
1,1120
1,0640
1,0210
0,9822
0,9466
0,9141
0,8842
0,8566
0,8310
0,8072
0,7851
п
1,717
1,681
1,648
1,618
1,591
1,567
1,544
1,523
1,504
1,486
1,469
1,453
1,438
1,425
1,412
1,399
1,388
1,377
1,366
1,356
1,346
2,00
^7
3,6120
2,8040
2,3770
2,0960
1,8890
1,7280
1,5980
1,4900
1,3990
1,3200
1,2510
1,1900
1,1360
1,0880
1,0450
1,0050
0,9690
0,9359
0,9055
0,8774
0,8514
п
1,780
1,737
1,698
1,664
1,633
1,605
1,579
1,555
1,534
1,514
1,495
1,478
1,461
1,446
1,432
1,419
1,406
1,394
1,383
1,372
1,362
Находим
х = - • J2 х^ = 33'725 ^ = 100,858; s = 10,0428;
(ж, - xf = 28396,44481;
J2 (%i ~ x) = 1947356,956; a3 = 0,5607; a4 = 3,8287.
Так как a4 = 3,8287 > 3 • (l + 0,641 • a§) = 3,604, применима аппроксимация распре-
распределением из семейства Su Джонсона. Для а4 = 3,83 и аз = 0,56 из табл. 116 (используя
аппроксимацию) находим оценки 7 = ~2,1 и ?) = 3,30.
Далее вычисляем
/ .. \
0,091827 -, АП/-1ТГ
= е = 1,096175;
ch -г =
2- (-2,11)
3,30
= ch(-l,27878) = 1,9353145;
sh[ - ) =sh[ -
= -0,68386.
Тогда
Л =
10,0428
= 25,9209;
1 - ¦ A,09618 - 1) - A,09618 ¦ 1,9353 + 1)
i = 33,77 + 25,9209 • ^/1,09618 • (-0,68386) = 15,2108.
368 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Плотность аппроксимирующего распределения семейства Su Джонсона имеет вид
3,3 1
• — х
д/(ж- 15,21)+25,9212
1 / , х-15,21 /Ж^15,21\2 \
х ехр{ -- • -2,11 + 3,3 • 1п< ¦ Ь \ 1 — + 1 > / •
F j 2 I ' ' | 25,921 YV 25,921 J \) \
Для того, чтобы найти ж*, для которого а = Р(ж ^ ж*) = 0,95, учитывая, что
'J'a = 11,0,95 = 1,645, и полагая по определению ж* = и% = гА§;95? находим
^о,95 = 15Д6 + 25,92 • sh ( 1>645 + 2>1г ) = 51,49.
\ 3,30 J
Следовательно, х ^ 51,49 с вероятностью а = 0,95.
3.6.2. Кривые распределений Пирсона
Наибольшее распространение для аппроксимации эмпирических распределений
получили кривые Пирсона. Плотность вероятности /(ж), график которой принад™
лежит семейству Пирсона, является решением дифференциального уравнения [10]
dy х + Ь
У со + с\х + с2х2
Постоянные 5, cq, ci, c^ выражаются через первые четыре момента распределен
ния (математическое ожидание, дисперсия, коэффициенты асимметрии «з и экс-
эксцесса «4):
„ 6(a4-ag-l)
где К = -^ .
3«з - 2а4 + 6
Выбор из семейства кривых Пирсона такой кривой, у которой первые четыре
момента совпадают с выборочными моментами, определенными по эксперимен™
тальным данным, составляет содержание задачи подбора эмпирической кривой для
распределения вероятностей случайной величины.
Тип кривой из семейства Пирсона определяется значением показателя х [10]
= aj(a4 + 3J= al (К + 2J
Х ~ 4Dа4 - Заз)Bа4 - 3«з - 6) ~ 16 (К + 1) '
На практике различают 7 основных типов кривых Пирсона, которым соответ-
соответствуют различные значения х, а следовательно, «з и «4- Графики для определения
типа кривой Пирсона по значениям аз и «4 приведены в [25], по показателю х —
в [10].
Так как достаточно эффективные и стабильные оценки моментов «з и а4 рас-
распределения достигаются при значительных объемах выборок, то анализу подвер™
гаются, как правило, статистические ряды, разбитые на интервалы равной длины
с = Xi+i — Xi, т.е. статистический ряд представляется своей эмпирической гисто-
гистограммой.
В этом случае границы интервалов разбиения (a^,a^_|_i) фиксируются, а случай-
случайной величиной является количество выборочных значений данных щ, попавших
в тот или иной интервал.
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 369
Далее для всех кривых Пирсона переменная представлена в виде х = ,
с
где ж* —реальное значение переменной; х — мода распределения (значение случай-
случайной величины, соответствующее максимуму плотности распределения); с — длина
интервала, на которые разбит эмпирический статистический ряд.
Напомним порядок вычисления моментов распределения, заданного эмпириче-
эмпирической гистограммой. Гистограмма представлена совокупностью пар
xN
n2/ ' vW ' ' \Щ/ ' ' \nN
где X{ — середина г-го интервала разбиения; щ — количество данных, попавших в г-й
интервал; N — количество интервалов разбиения гистограммы.
Первые четыре момента распределения подсчитываютея по формулам
N \ г N
Xini> & = 1? 2, 3, 4.
Часто вместо переменной х удобнее использовать переменную х = , где
xq —условное начало отсчета (как правило, это величина, соответствующая интер-
интервалу разбиения с наибольшей частотой щ). Тогда х = х® + т\с.
Очевидно, что стп\ = ж, т. е. первый начальный момент равен среднему значе-
значению. Дисперсия а2 выражается через начальные моменты формулой а2 = 7П2 ^тп2^
или а = \/гп2 — тп\. Переход к метрической величине осуществляется по формуле
а' = са.
Коэффициенты асимметрии и эксцесса выражаются через начальные моменты
следующим образом:
З 2т1 А 6 3
з 5 «4 =
(Ш2-ш?J (ma
Легко видеть, что для негруппированного ряда с = 1, П{ = 1. Порядок вычисле-
вычисления mk будет продемонстрирован ниже.
Аппроксимация распределением из семейства Пирсона позволяет подыскать
подходящую кривую для описания плотности распределения эмпирических данных,
что необходимо для выявления основных характеристик распределения (его ход,
симметричность, поведение на хвостах). Однако найти квантиль этого распреде-
распределения по аналитической формуле плотности распределения — задача непростая.
Эту задачу можно решить без подбора распределения, достаточно найти оцен-
оценки «з и а4 и воспользоваться известными таблицами квантилей распределения
Пирсона (табл. 117) для нормированной переменной у = (тогда истинная
квантиль равна х@ = х + sya).
3.6.2.1. Кривые Пирсона типа I
Для кривых этого семейства % < 0- Уравнение кривой имеет вид
где
370 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
ИГ
К
В
S 3
м то
if
и к
а
о н
РЗ К
0 к
\ ГО
1 К
ш
я л
S
в
ф
5
со
1,00
0,90
0,80
0,70
0,60
0,50
,40
о
,30
о
0,20
0,15
о
о
0,05
0,03 1
0,01 |
0,00 1
0,05
II
1,47
1,51
1,35
о
"xt«
1,46
,33
1,41
1,45
,50
1,55
1,55
1,58
1,56
1,59
1,56 1
1,61
00 О
т-Н СМ
1,64
см
см
1,61
1,65
см
,30
,38
1,45
1,49
,53
1,57
1,59
1,61
1,65
со
см
1,29
,35
,42
1,48
1,51
,54
1,57
1,59
1,62
1,65
оо
см
1,27
со
со
,39
,44
1,49
1,52
,55
1,58
1,59
см
со
1,64
о
со
2
1,25
1,31
ь-
со
,42
,46
1,50
1,53
,55
1,58
1,59
т-Н
СО
1,64
см
со
1,19
1,24
1,30
1,35
1,39
,43
,47
1,51
1,53
,55
1,58
1,59
1,61
1,64
со
1,18
1,23
1,28
1,33
1,37
1,41
,45
,48
1,52
1,53
,55
1,58
1,59
1,61
1,63
CD
со
1,23
1,27
гЧ
со
1,35
1,39
1,42
со
,49
1,52
1,54
,55
1,58
1,59
о
со
1,63
оо
со
1,26
1,30
со
1,37
1,40
1,43
со
,49
1,52
1,54
,55
1,57
1,59
о
со
1,62
о
00 гЧ
1,32
1,34
со ь-
со со
О) О
со ^
1,42
1,42
1,33
1,34
LO t-
co со
1,38
1,39
1,43
1,44
1,44
1,45
1,45
1,46
OS О
"хГ1 Ю
1,52
1,52
1,54
1,54
LO LO
LO LO
LO LO
1,58
1,58
о о
со со
см см
CD CD
CM -xf
oo oo
о о
LO LO
CM CM
LO LO
1,35
1,38
1,40
1,42
1,44
1,46
,48
,50
1,52
-xf oo oo
LO LO LO
LO LO
LO LO
LO LO
oo oo
LO LO
1,59
1,59
1,61
1,61
CD 00
,55
1,56
1,57 1
1,58 |
1,60 1
о
LO
a = 0,95
1,72
oz'x
1,66
1,56
1,61
00 О
гЧ CM
1,83
1,80
,77
1,74
t-
1,68
1,64
CM
CM
,87
1,83
1,80
,77
1,74
t-
1,69
1,65
"xf
CM
1,92
О 00
O5 00
1,93
1,90
CO
oo
оо
1,98
1,95
СЛ
1,91
1,98
1,96
LO
СЛ
1,92
1,93
1,93
1,90
Об'Х
1,88
СМ СЛ Ь- Ю
ел оо оо оо
1,88
1,86
1,87
1,85
,84
CD "xf CM О
oo oo oo oo
т-Ч О
oo oo
1,79
1,77
CO LO
oo см
т-Н О
1,68
1,68
ю ю
CD CD
CD 00
CM CM
1,78
CD
b-
,74
b-
1,69
1,77
1,75
со
о
ь-
1,69
1,83
см о
оо оо
,79
1,76
ь-
,72
,77
1,74
оо
со
,71
ел оо
со со
1,84
1,83
1,82
1,80
ел оо
,76
1,73
1,72
,70
,75
1,72
т-Н
ь-
1,91
1,89
1,85
1,88
1,86
1,84
со -xt*
оо оо
1,83
1,82
т-Н О
оо оо
1,79
со
,74
1,71
1,70
1,78
,75
,73
1,70
1,69
сл оо оо
CD CD CD
1,68
1,67
1,68
1,67
1,66
1,66
1,67
1,67
1,66
1,65
1,64
1,64
о
со
см
со
1,64
1,63
CD
со со
1,65
1,64
1,63
1,62
оо
со
о
1,66
1,66
1,65
1,65
1,64
1,63
1,62
см
"xf
1,62
"xf
"xf
см
оо
1,80
1,78
1,76
,74
см
1,70
1,68
,67
1,65
1,64
1,63
1,61
CD
1,85
1,83
т-Н
оо
1,79
ь-
ь-
ю
ь-
,73
т—)
1,69
1,68
со
со
1,65
1,64
1,62
1,61
оо
1,84
1,82
1,80
1,78
1,76
г
,73
ь-
1,68
1,67
,66
1,64
1,63 1
см
со
1,60 1
о
LO
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 371
о
Он
!МСО
0
1,00
0,90
0,80
0,70
0,60
0,50
0,40
,30
о
0,20
LO
0,05 | 0,10
0,03 |
0,01 |
| оо'о
LO
0,0
I
1,56
1,62
1,68
1,65 1
1,76
00 О
т-Н Ol
1,41
1,49
ZS I 99 I
1,71
CD
b-
1,83
Ol
Ol
,39
1,51
1,58
1,73 1,65
114
Ol
oo
1,88
Ol
1,37
,47
1,58
1,64
1,78 1,71
1,82
CD
oo
1,92
CD
Ol
LO
со
1,45
,55
1,65
1,70
Ol
oo
1,85
СЛ
oo
1,94
oo
Ol
1,33
Ol
1,52
о
CO
1,69
1,74
1,84 1,79
1,87
tH
СЛ
1,96
о
со
1,24
1,32
1,40
oo
1,57
,65
1,72
1,77
1,86 1,81
1,89
со
ел
1,97
Ol
со
1,23
1,31
1,39
1,46
1,54
1,61
,68
1,75
1,79
1,88 1,83
1,90
1,94
1,98
«
со
1,23
1,30
1,38
1,44
1,51
1,58
1,65
,71
III
1,81
1,89 1,85
1,91
1,95
oo
oo
CD
со
1,29
1,36
1,43
1,49
1,56
1,62
1,67
,73
1,79
1,82
oo
о
ел
Ol
oo
1,95
oo
oo
oo
со
1,35
1,41
1,47
1,53
1,59
1,64
1,70
,75
1,81
1,84
oo
T—I
СЛ
1,93
1,96
oo
oo
о
-xf"
1,40
1,45
1,51
1,56
1,62
1,67
1,72
,76
1,82
1,84
1,91 1,88
1,93
1,96
2,00
Ol
-xf
1,44
1,49
1,54
1,59
1,64
1,69
1,73
,78
1,83
1,85
1,92 1,88
1,94
1,96
2,00
-xf
-xf"
1,47
1,52
1,57
1,62
1,66
1,70
1,75
,79
1,83
1,86
1,92 1,89
1,94
1,96
2,00
CD
-xf"
1,50
1,55
СЛ
LO
1,64
1,68
1,72
1,76
,80
1,84
1,87
oo
oo
СЛ
1,94
1,97
2,00
oo
1,53
1,57
t—1
CD
1,65
1,69
1,73
1,77
,81
1,85
1,87
со
СЛ
1,94 1
1,97 |
2,00 1
о
LO
LO
b-
0,9
II
e
1,89
1,86
1,82
1,65 1
1,76
00 О
гЧ Ol
2,06
2,04
о
о
Ol
CD
СЛ
1,93
1,89
1,83
Ol
Ol
,25
Ol
2,11
2,08
LO
О
fM
T—I
О
Ol
1,98
1,94
1,88
"xf
Ol
2,22
Д8
Ol
ГМ
2,11
2,03 2,08
о
Ol
1,97
1,92
со
Ol
2,27
2,24
о
Ol
CM
2,15
2,13
2,05 2,09
2,03
1,99
1,94
oo
Ol
2,32
2,28
2,25
,21
CM
2,16
2,13
2,06 2,10
2,04
2,01
1,96
о
со
2,38
2,35
2,32
2,29
2,25
,21
Ol
2,16
2,14
2,07 2,11
2,05
2,02
1,97
Ol
со
2,41
2,38
2,35
2,32
2,28
2,25
,21
Ol
2,16
2,14
2,07 2,11
sot
2,02
1,98
"xt1
со
2,44
2,41
oo
Ol
2,34
2,31
2,28
2,24
,20
Ol
2,16
2,14
2,07 2,11
sot
2,02
66'X
CD
со
2,43
2,40
2,36
2,33
2,30
2,27
2,24
о
Ol
Ol
2,16
2,13
2,07 2,11
2,05
2,03
66'X
oo
со
2,41
2,38
2,35
2,32
2,29
2,26
2,23
Д9
Ol
2,15
2,13
2,07 2,11
2,05
2,03
2,00
о
2,40
2,37
2,34
2,31
2,28
2,25
2,22
Д9
Ol
2,15
2,13
2,07 2,10
2,05
2,03
2,00
Ol
2,39
2,36
2,33
2,31
2,28
2,25
2,22
Д8
Ol
2,15
2,13
2,07 2,10
2,05
2,03
2,00
"xf
2,38
2,35
2,32
2,30
2,27
2,24
2,21
Д8
Ol
ГМ
2,12
2,07 2,10
2,05
2,03
2,00
со
2,36
2,33
2,31
2,29
2,26
2,23
2,21
Д7
Ol
ГМ
2,12
2,07 2,10
2,05
2,03
2,00
oo
2,35
2,33
2,30
2,28
2,25
2,23
2,20
Д7
Ol
ГМ
2,12
2,07 | 2,09
2,05 1
2,03 |
2,00 1
о
LO
372 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
см ее
1,00
0,90
0,80
0,70
0,60
0,50
40
о
0,30
0,20
0,15
о
о
05
о
со
о
о
т-Н
о
о
о
о
о
tf
т-Н
II
62
СЛ
CD
т-Н
ь-
ь-
rH
о ь~
Ь- 00
т-Н т-Н
00 О
гЧ СМ
1,45
LO
ю
64
76
со
оо
т-Н
ел
т-Н
О
см
см
см
1,43
СЛ
LO
оо
со
ь-
ь~
rH
89
LO
ев
т-Н
со
о
см
см
т—1
см
см
т-Н
ю
LO
1,70
ев
ь-
оо
оо
99
LO
СМ
см
см
т-Н
см
см
со
см
1,39
см
LO
1,66
1,81
ев
оо
98
08
см
со
см
СЛ
см
ь~
см
см
оо
см
1,38
1,50
62
^
1,76
1,90
1,97
05
см
т-Ч
СМ
СЛ
т-Ч
см
LO
см
см
оо
оо
см
о
оо
1,26
zs'x
1,48
1,59
т-Ч
IN
1,84
1,96
2,03
т-Ч
т-Н
СМ
ев
т-Ч
СМ
см
см
СЛ
см
см
ь~
оо
см
см
оо
1,26
1,36
1,46
1,57
1,68
СЛ
IN
1,90
2,02
2,09
со
т-Н
СМ
24
см
оо
см
см
оо
оо
см
о
см
оо
1,26
ss'x
1,45
1,55
1,65
1,76
CD
оо
1,96
2,07
2,13
о
см
см
27
см
оо
см
со
оо
см
оо
см
со
оо
1,34
1,43
ss'x
1,62
1,72
1,82
91
^
2,01
2,11
ь~
см
оо
см
см
30
см
оо
см
СЛ
оо
см
ю
см
оо
оо
1,42
1,51
1,60
1,69
1,78
1,87
96
^
2,05
2,15
2,20
со
см
см
33
см
CD
оо
см
см
ь~
см
о
1,49
1,58
1,66
1,75
1,83
1,92
о
о
см
2,09
2,18
2,23
оо
см
см
35
см
оо
оо
см
оо
см
ев
см
см
1,56
1,64
см
ь~
1,80
88'Х
1,96
04
см
2,12
2,21
2,25
31
см
37
см
о
см
см
о
ю
см
"хР
1,62
1,70
ь-
ь~
1,80
1,92
2,00
07
см
2,15
2,23
2,27
32
см
38
см
см
см
со
см
т-Н
ю
см
со
1,67
1,74
т-Ч
оо
1,88
1,96
2,03
о
т—1
см
2,17
2,25
2,29
34
см
40
см
со
см
ь-
см
см
ю
см
оо
1,72
1,79
ю
оо
1,92
1,99
2,06
см
т—1
см
2,19
2,27
2,31
36
см
41
см
см
оо
см
оо
ю
см
о
LO
СЛ
d
оо
о
см
о
о
см
LO
СЛ
т-Ч
о ь-
ь- оо
т-Ч т-Ч
00 О
т-Ч СМ
2,25
2,24
см
см
см
оо
т-Ч
см
LO
т-Ч
см
о
т-Ч
см
т-Н
о
см
см
см
2,40
2,38
2,36
33
см
28
см
LO
см
см
о
см
см
см
т-Ч
см
см
см
LO
см
2,51
2,48
2,45
42
см
36
см
со
оо
см
оо
см
см
т-Ч
см
см
со
см
2,63
61
см
2,59
2,55
2,52
48
см
43
см
СЛ
оо
см
со
см
ь~
<м
см
оо
см
ь~
см
2,70
68
см
2,64
2,59
2,56
со
LO
СМ
48
см
см
о
см
со
оо
см
о
со
2,80
2,79
2,77
2,75
см
см
2,68
2,63
2,60
CD
LO
CM
51
см
GO
CM
44
см
b~
oo
CM
CM
со
2,87
2,86
2,84
2,82
2,79
LO
b~
CM
2,71
2,66
2,63
СЛ
LO
CM
54
CM
T—1
LO
CM
47
CM
о
CM
"xf
со
2,93
2,91
2,90
2,87
2,85
2,81
oo
b~
CM
2,74
2,68
2,65
61
CM
56
CM
со
LO
CM
49
CM
oo
CM
со
со
2,97
2,95
2,92
2,90
2,87
2,83
о
oo
CM
2,75
2,70
2,67
63
CM
58
CM
LO
LO
CM
T—1
LO
CM
LO
CM
oo
со
2,99
2,97
2,94
2,91
2,88
2,85
81
CM
b~
b~
CM
со
b~
CM
2,68
65
CM
о
CD
CM
b-
LO
CM
со
LO
CM
b~
CM
о
3,01
2,99
2,95
2,92
2,89
2,86
82
CM
2,78
со
b~
CM
2,69
66
CM
61
CM
GO
LO
CM
LO
CM
CB
CM
CM
3,02
2,99
2,96
2,93
2,90
2,86
83
CM
2,78
со
b~
CM
2,70
67
CM
62
CM
СЛ
LO
CM
CD
LO
CM
о
LO
CM
"xP
3,03
GO'S
2,97
2,94
2,90
2,87
83
CM
2,79
2,74
b-
CM
68
CM
63
CM
о
CD
CM
b-
LO
CM
1—1
LO
CM
CO
-xP
3,03
GO'S
2,97
2,94
O5
CM
2,87
84
CM
2,80
LO
b~
CM
2,72
68
CM
64
CM
CD
CM
oo
LO
CM
CM
LO
CM
oo
-xP
3,03
GO'S
2,97
2,95
CM
2,88
84
CM
2,80
LO
b~
CM
2,72
69
CM
64
CM
CM
CD
CM
oo
LO
CM
со
LO
CM
о
LO
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 373
n gfgf2 Г(ЛГ) , _ sa3K
Т(^)К2Г( ; Ж Ж
n — объем выборки; с — длина интервала разбиения; I — размах кривой; х — модалв-
ное значение; s = с- а — именованное значение среднеквадратического отклонения.
Для вычисления гамма-функции T(z) приведем ряд полезных соотношений:
T(z) = (z- l)T(z -l) = (z- l){z - 2)T(z - 2) = ..., (z > 1);
Очень полезна аппроксимация
»l-0,427(/3-l)^1>9,
при /3 > 1 ошибка не превышает 0,2%.
В общем случае вычисление гамма-функции по любому аргументу можно про-
производить по формуле (/3 > 1, [z] — целая часть числа)
г|и +1 j = [1 -о,427(/з-1)г1'9] П (и + \ -4-
Например, вычислим значение ГE,6178):
ГE,6178) = ГE + 0,6178) = Г ^5 +
= [1 - 0,427 • 0,6186~1}9] • 4,6178 • 3,6178 • 2,6178 • 1,6178 = 63,26699.
Кривая Пирсона типа I представляет собой бета-распределение (см. раздел 1.1.7),
поэтому ее функция распределения F(x; Ii, I4, #1, ^2? А) модсет быть выражена через
функцию бета-распределения
F{x]lul2,q\,q2, А) = 1г1+ж (gi + l,g2 + 1) •
Задача 173. В результате наблюдений получен статистический ряд^ заданный та-
блицей (п = 1000, с = 5). Необходимо подобрать аппроксимирующую кривую распреде-
распределения Пирсона и найти 95%-ю квантиль распределения.
Сначала найдем моменты распределения. В нашем случае все эмпирические данные
разбиты на 13 интервалов длиной с = 5 каждый. В качестве случайной величины будем
рассматривать середину каждого интервала. Порядок вычислений представлен в таблице
ж^-42,5,
(здесь xi = ).
о
Таким образом, имеем
п п
пц = - • У^ xi - щ = 0,093; т2 = - • Y^ х* • щ = 4,859; т3 = 7,755; т4 = 72,383.
г=1 г=1
374 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
г
1
2
3
4
5
6
7
8
9
10
11
12
13
Xi
22,5
27,5
32,5
37,5
42,5
47,5
52,5
57,5
62,5
67,5
72,5
77,5
82,5
щ
11
93
162
176
178
132
101
67
40
24
12
3
1
Xi
-4
-3
_2
-1
0
1
2
3
4
5
6
7
8
UiXi
-44
-279
-324
-176
0
132
202
201
160
120
72
21
8
riixf
176
837
648
176
0
132
404
603
640
600
432
147
64
TliX^
-704
-2511
-1296
-176
0
132
808
1809
2560
3000
2592
1029
512
2816
7533
2592
176
0
132
1616
5427
10240
15000
15552
7203
4096
Е
100
93 4859
7755 72383
Далее вычисляем
х = 42,5 + mi • с = 42,5 + 0,093 • 5 = 42,965; а2 = т2 - ml = 4,859 - 0,0932 = 4,85;
«4 =
а = 2,202 (s = с • а = 5 • 2,202 = 11,011);
7,755 - 3 ¦ 4,859 ¦ 0,093 + 2 ¦ 0,0932 _
D,850J
72,383 - 4 • 7,755 • 0,093 + 6 • 4,859 • 0,0932 - 3 • 0,0934
4,8502
= 0,3609);
= 2,965.
Имеем
6 • B,965 - 0,3609 - 1)
3 • 0,3609 - 2 • 2,965 + 6
0,3609. B + 8
16 • A + 8,3496)
Так как % < 0, можно применить аппроксимацию эмпирического распределения кривой
Пирсона типа 1.
Выполняем необходимые вычисления:
s-a3 К+ 2 лелГкПГ 11,011-0,60075 10,3496
х = х -— • ^п—г = 42,965 • п I _ = 37,574;
2 К-2
2 • 11,011
6,3496
1 =
^9,3496 • 1,25841 = 15,107;
6,3496 - 8,3496 •
0,60075
4- ^/9,3496- 1,25841
= 1,283;
= -- F,3496 + 3,7837) = 5,067;
h = —
6,3496
= 3,052; h = Б-°
X =
6,3496
1000 1,283х'283 - 5,0675'067
,055 (I = h + h = 3,052 + 12,055 = 15,107);
Г (8,3496)
15,107 6,34966'3496 Г B,283) ¦ Г F,067)'
Г(8,3496) = Г ( 8 + —— ) = [1 - 0,427 • 1,8604 • 2,8604^l!9l x
V ' ; \ 2,8604/ L J
х 7,3496 • 6,3496 • 5,3496 • 4,3496 • 3,3496 • 2,3496 • 1,3496 = 10289,8761;
= [l - 0,427 • 2,5335 • 3,5335m1'9] • 1,283 = 1,156879;
ГB,283) = Г( 2 +
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 375
ГF,067) = ГF+
\ 14,925 /
= [l - 0,427 • 13,925 • 14,925^1;9] • 5,067 • 4,067 • 3,067 • 2,067 • 1,067 = 134,51827;
= 7135 . 10289,8761
1,156879 • 134,51827
Таким образом, уравнение для аппроксимирующей плотности распределения имеет вид
/ ~ \ 1,283 / ~ \ 5,607
у = 179,419962 • [ 1 + ^— j • [ 1 — )
\ 3,052/ \ 12,055/
Напомним, что в качестве переменной мы используем
z = х^ = 0^2 , _ 37^74).
с
Относительно реальной переменной уравнение принимает вид
у = 179,419962 • @,0655 • х - 1,46225I5283 • A,62337 - 0,01659 • жM'067.
Например, для х = 52,5 частота равна
2/E2,5) = 179,419962 • @,0655 • 52,5 - 1/Ш25I'283 • A,62337 - 0,01659 • 52,5M'067 = 101,7,
что совпадает с эмпирической частотой, равной 101.
Для нахождения 95%-й квантили распределения обратимся к табл. 117. Для
Q/3 = 0,359, «4 = 2,965 и а = 0,95 находим, что г/о,95 ^ 1,8. Следовательно,
^„5 = ^р = Ж°-95п4121'965 = 1,8; *о,в5 = 42,965 + 1,8 • 11,011 = 62,78.
Следовательно, вероятность того, что х ^ 62,78, равна 0,95.
3.6.2.2. Кривые Пирсона типа II
Для кривых этого семейства Х = 0, аз = 0 и а^ < 3. Они являются частным
случаем кривых типа I и определяются уравнением
где
/ _ 5ск4-9 п ГBд
q Л
q^ 2C^а4у Л
Криввхе симметричны относительно оси ординат и х = х.
Задача 174. Для статистического ряда, заданного таблицей (п = 205, с = 2) подо-
подобрать кривую распределения из семейства Пирсона.
Вычисление моментов представлено в таблице (здесь xi = — ).
Находим (с = 2)
1 п 1 п
пц = - • У" Зц • гц = 0,0195; т2 = - • V щ • щ = 2,1951;
п f-| та ^
-I П 1 П
тз = — • У"^ ж?- • П{ = 0,3122: Ш4 = — • У^ Хл • щ = 13,2;
те г—^ п ~
г=1 г=1
х = 34 + 0,0195-2 = 34,039.
376 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
i
1
2
3
4
5
6
7
8
9
Xi
26
28
30
32
34
36
38
40
42
щ
1
6
27
40
54
45
23
7
2
Xi
-4
^3
-2
-1
0
1
2
3
4
-4
-18
-54
-40
0
45
46
21
8
16
54
108
40
0
45
92
63
32
-64
^162
-216
-40
0
45
184
189
128
fliXJ
256
486
432
40
0
45
368
567
512
Е 205
450
64 2706
В случае, когда обе ветви кривой асимптотически приближаются к оси абсцисс,
необходимо при оценке четных центральных моментов (/12 = rri2 — т\ и /14 = т^ —
— 4тз • т\ + 6m2 • m\ — Зга4) применять корректирующие поправки Шеппарда [10], с
учетом которых
2 2 2
В нашем случае, полагая с = 1 (половина разряда), имеем
/12 = 2,1951 - 0,01952 = 2,1947; /22 = <т2 = 2,1947 - 0,0833 = 2,1114 (<т = 1,453);
/14 = 13,180656 - 0,5 • 2,1947 + 0,02916 = 12,1125;
Д4 = 13,2 - 4 • 0,3122 • 0,0195 + 6 • 2,1951 • 0,0195 - 3 • 0,01954 = 13,1800656;
/i3 = газ — 3 • wi2
Тогда получаем
„ _ Аз
+ 2 • га? = 0,3122 - 3 • 2,1951 • 0,0195 + 2 • 0,01953 = 0,1838.
-^Щ- = 0,060 (а23 = 0,0036); а4 = § = ??™ = 2;716;
А!
2,11142
6 • B,716 - 0,0036 - 1)
2Д1142
= 17,751; х =
0,0036 • 19,7512
16 • 18,751
= -0,00468.
3-0,0036- 2-2,716 + 1
Так как а4 > 3 и % й 0, для аппроксимации заданного статистического ряда можно
использовать кривую типа П.
Находим параметры кривой:
Я = 7
Л =
-716 =8,063; I = 1,453 .
2C-2,716) ' ' ' V 3-2,716
= 6?354;
205
ГA8,126)
= 225,56210"
ГA8,126)
217'126-6,354 [Г(9,063)]2 —^— [Г(9,063)]2.
Далее вычисляем
ГA8,126) =ГИ8+—— J = [l-0,427-6,9365-7,9365м1'9] • 17,126 ... 1,126 = 5,108028-104;
/ 1 \
Г(9,063) = Г 9 + = [1 - 0,427 • 14,873 • 15,873""l59l • 8,063 ... 1,063 = 46124,251.
Окончательно
Л = 225,562 • 10
^6 5,108028 • 101
46124,2512
= 54,15774468.
Таким образом, уравнение аппроксимирующей кривой имеет вид
~2 \ 8,063
у = 54,15774468 • 1 -
40,373316
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 377
х _ х х — 34 039
Переменной здесь является х = = - .
Окончательно имеем
у = 54,15774468 • @,421553186 • х - 0,0061922 • х2 - 6Д74624)8'063.
Например, для х = 30:
2/C0) = 54,15774468 • @,421553186 • 30 - 0,0061922 • 302 - 6,174624) 8'°63 = 23,
что близко к эмпирической частоте, равной 27.
3.6.2.3. Кривые Пирсона типа III
Для этого типа кривых % = ±оо. Уравнение кривой имеет вид
qx
где
а3
2
X = X —
сааз
Кривые типа III асимметричны и ограничены в одном направлении точкой
х = —I. Кривая типа III совпадает с гамма™распределением. Хорошая аппроксима™
ция эмпирических распределений кривой типа III достигается уже при |%| > 4.
Задача 175. Найти аппроксимирующую кривую для плотности распределения слу-
случайной величины, заданной эмпирическим статистическим рядом (п = 40000, с = 2),
приведенным в таблице.
тэ * ( ж^ - 2,356
Вычисления начальных моментов приведены в таолице (здесь х% = у.
г
1
2
3
4
5
6
7
8
9
Xi
1,5
3,5
5,5
7,5
9,5
11,5
13,5
15,5
17,5
щ
9600
13600
9200
4000
2000
800
400
0
400
Xi
-0,448
0,552
1,552
2,552
3,552
4,552
5,552
6,552
7,552
UiXi
-19200
-13600
0
4000
4000
2400
1600
0
2400
щх^
38400
13600
0
4000
8000
7200
6400
0
14400
-76800
-13600
0
4000
16000
21600
25600
0
86400
153600
13600
0
4000
32000
64800
102400
0
518400
Е
40000
Вычисляем
т\ = — •
п
-18400 92000
ii = —0,46: 7712 = — *
г =1,58:
1
—
63200 888800
= 2,30:
=22,22:
П ^ п -л
г=1 г=1
а2 = [12 = т2 - ml = 2,0884; а = 1,4451;
/i3 = 1,58 - 3 • 2,30 • (-0,46) + 2 • (-0,46K = 4,5593;
/14 = 22,22 - 4 • 1,58 • (-0,46) + 6 • 2,30 • (-0,46J - 3 • 0,464 = 27,9129;
378 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
х = 5,5 - 0,46 • 2 = 4,58; а3 = Щ- = 1,1508; «3 = 2,2825;
27,9129 _ 6.F,4-2,2825-
2,08842 ~ ' ' 3 ¦ 2,2825 -2-6,4 + 6
Q4 = Ц = tUZ^l = 6i400; K= »-w--—-^ = зЭ3,79; х = -56,6.
Так как |х| ^> 4, то приемлема аппроксимация кривой Пирсона типа III.
Вычисляем параметры кривой:
Л 1 1 = 0,752451; I = 1,4451 • ( — Ы^ ) = 0,8213977;
' ' ' \ 15108 2 / '
1 0,752451; I 1,4451 (
2,2822 ' ' ' \ 1,5108 /
2 • 1,4451 • 1,5108
ж = 4,58 ¦ ¦ = 2,3974292;
40000 2,752451 232356451
Л ^^
0,8213977 ехрA,752451) ¦ ГB,752451) ГB,752451)
Находим
ГB,752451) = Г( 2 + ) = [1 - 0,427 • 0,32899 • 1,32899)91 • 1,752451 = 1,6090457;
1,32899 /
Л = 23235Д9417 = 14440,3569.
1,6090457
Уравнение кривой имеет вид
х \°'752451 / 0,752451- х
у = 14440,3589 • Ц • ехр -
0,8213977/ \ 0,5213977
Здесь в качестве переменной используется величина х = = 0,5ж — 1,1925, и относи»
с
тельно нее после преобразований получаем
у = 43052,93758 • @,608718529 • х - 0,451793692H'752451 • ехр(-0,458030866 • ж).
Например, для х = 3,5 имеем
у = 43052,93758 • @,608718529 • 3,5 - 0,451793692H'752451 • ехр(-0,458030866 • 3,5) = 12796,
что близко к эмпирической частоте, равной 13600.
3.6.2.4. Кривые Пирсона типа IV
Для кривых этого семейства имеет место 0 < % < 1. Уравнение кривой типа IV
имеет вид
у = А ( 1 + — ) ехр | -v arctg у ) ,
где
2 + г# б(а4-аз-1) г (г - 2) а3
а=
^ i/) —функция, значения которой по аргументу (р = arctg — приведены в [10].
Уравнение записано относительно переменной х = /.
с г
Кривые асимметричны и имеют неограниченный размах.
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 379
Задача 176. Для эмпирического ряда (N = 1000, с = 2), приведенного в таблице, най-
найти аппроксимирующую кривую из семейства Пирсона.
Вычисление начальных моментов приведено в таблице (xi = —
0,2
i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Xi
0,5
0,7
0,9
1,1
1,3
1,5
1,7
1,9
2,1
2,3
2,5
2,7
2 Ц
3,1
3,3
3,5
3,7
щ
-7
6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
Xi
2
5
14
33
67
123
160
172
153
112
68
41
25
14
7
3
1
HiXi
-14
-30
-70
-132
-201
-246
-160
0
153
224
204
164
125
84
49
24
9
Пгх\
98
180
350
528
603
492
160
0
153
448
612
656
625
504
343
192
81
-686
-1080
-1750
-2112
-1809
-984
-160
0
153
896
1836
2624
3125
3024
2401
1536
729
~ А
fliX^
4802
6480
8750
8448
5427
1968
160
0
153
1792
5508
10496
15625
18144
16807
12288
6561
1000
183 6025
7743 123409
Имеем
т1п = - •
щ = 0,183; т2 = 6,025; т3 = 7,743; т4 = 123,409;
1? = 5,908; /хз = 771з - 3 • 7712 • mi + 2m? = 4,448;
12
A4 = Ш4 — 4 •
• 7711 + 6 • 7712 • 771? - 3 • 77li = 118,948;
= М4 - ^ + — = 118,484;
^ 12 240
= 2,43064;
«з =
Мз
3
А!
= 0,30974;
= 0,096; аА = ^| = 3,407816.
Вычисляем далее:
К =
6 • C,407816 - 0,096 - 1)
3 • 0,096 - 2 • 3,407816 + 6
- = -26,288959; х= -:
16-(К
= -0,139971.
Таким образом, для аппроксимации может быть выбрана кривая типа IV из семейства
Пирсона. Вычисляем ее параметры:
г = ~К = 26,288959; q = 2 + 26-288959 = 14,14444795;
1 =
2,43064
25,288959 - 0,0961 • 24,2889592 = 11,3345908;
26,288959 • 24,288959 • 0,30974
= -10,602238; Л=т
1
8,225505
• 25,288959 - 0,096 ¦ 24,2889592
Находим из [10, таблица XIV, с. 532]: F{r,u) « 1,82 для
v
I F(r, и)
11,12625 о л 88,225505
= arctg — = arctg —^ = 22,6 ; Л = — = 48,4753.
г 226,576 1,82
380 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Далее х =
х - 1,9 10,602238 • 11,3345908
0,2 26,225505
Окончательно получаем уравнение кривой
-14,1444795
= Ъх- 4,928023.
у = 48,4753 • 1
4,3345908^
ехр 10,602238 arctg
11,3345908
= 48,4753 • 11 +
Eж-4,9288023)"
11,3359082
J
• ехр 10,602238 • arctg
5х - 4,9288023
4,3345908
3.6.2.5. Кривые Пирсона типа V
Для кривых этого типа % = 1. Уравнение кривой типа V имеет вид
у = Ах ехр I — y
В}'
где
q = 4 -\
Л = п-
и = a(q — 2)уд — 3 (знак такой лее, как у
д —1
-1)' с ' q-2'
Кривые симметричны и определены для 0 < х < сю.
Задача 177. Для статистического ряда, приведенного в таблице, найти аппроксими-
аппроксимирующую кривую из семейства Пирсона (п = 1000, с = 0,04).
Имеем х% =
0,04
?2
и сводим результаты вычислений в таблицу:
г
1
2
3
4
5
6
7
8
9
10
Xi
0,04
0,08
0,12
0,16
0,2
0,24
0,28
0,32
0,36
040
щ
-4
-3
^2
-1
0
1
2
3
4
5
Xi
3
11
99
346
288
148
83
15
6
1
щх{
-12
-33
-198
-346
0
148
168
45
24
5
Пгх\
48
99
396
346
0
148
332
135
96
25
пгх\
-192
-297
-792
-346
0
148
664
405
384
125
пгх\
768
891
1584
346
0
148
1328
1215
1536
625
1000 -199 1625
99 8441
Находим:
mi = -0,199; т2 = 1,625; т3 = 0,099; т4 = 8,441;
= 1,585;
+ 2т\ = 1?053;
+ 6m2mi — Зт4 = 8,901; а = \J~\Ii = 1,259;
х = 0,20 + с • mi = 0,192; а3 = ^| = 0,528;
/if
= 0,278; «4 = Ч = 3,549.
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 381
Так как % « 1, для аппроксимации может быть использована кривая из семейства
Пирсона типа V.
Вычисляем параметры кривой
=
0,278
= 62 537; и = 1,259 • 60,637 • ^59,537 = 588,085;
11 5 1 V ' 11
Л = 1000.
ГF1,537)
Уравнение кривой принимает вид
=3,5514.10-.
588,085
^ z х- 0,192 588,085
В нашем случае переменная х = 1 = 25ж + 4,9145 и
0,04 60,537
у = 3,5514 • 1090 • B5ж + 4,9145)~62'537
Например, для х = 0,16 имеем
• ехр -
588,085
25ж +4,9145
588,085
8,91456
= 304,
у = 3,5514 • 1090 • 8,91456~62'537 • ехр [ -
что близко к эмпирическому значению 346.
3.6.2.6. Кривые Пирсона типа VI
Для кривых этого типа справедливо неравенство 1 < х < оо.
Уравнение кривой имеет вид
у = Ах [х - I) ,
где
Т(К-2)\;
x); A np; ^ +
F(gi - q2 -2) с qi - q2 - 2
Криввхе асимметричны и ограничены в одном направлении точкой х = I. Если
«з < 0? то Я < 0 и размах распределения находится в пределах (оо, — 1).
Задача 178. Для статистического ряда^ приведенного в таблице^ найти аппрокси-
аппроксимирующую кривую из семейства Пирсона и 99%-w? квантиль распределения (п = 368,
с=1).
Здесь Xi = х — 3.
i
1
2
3
4
5
6
7
8
Xi
1
2
3
4
5
6
7
8
Я-г
^2
-1
0
1
2
3
4
5
Xi
1
56
167
98
34
9
2
1
TliXi
^2
-56
0
98
68
27
8
5
nix\
4
56
0
98
136
81
32
25
ПгЩ
-8
-56
0
98
272
243
128
125
n%x\
16
56
0
98
544
729
512
625
368
148
432
802 2580
382 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Находим
mi = 0,4021; т2 = 1,17391; т3 = 2,17935; т4 = 7,01087.
Учитывая, что размах кривой неограничен, при оценке центральных моментов будем
учитывать поправки Шеппарда (с = 1). Имеем
^2 = щ2 - ml = 1,0121; Д2 - А*2 - — = 0,92883;
/i3 = 2,17935 - 3 • 1,17391 • 0,40217 + 2 • 0,402172 = 0,89310;
М4 = 4,56573; Д4 = /х4 - — + — = 4,088; а = у% = 0,96376;
аз = Щ- = 0,9977; а4 = ^ = 4,7394; х = 3 + 0,40217 • 1 = 3,40217.
Далее
Й
6.D,7394-0,9954-1) = _ 0,9954 - (-31,423)=» =
3-0,9954-2-4,7394 + 6 16 • (-32,423)
Видим, что возможна аппроксимация кривой типа VI. Находим параметры кривой:
1 О QQ77
qi = -- {(^33,423) • (-31,423)} • , ^(^35,423) = 42,031;
2 LV > ' v ^ v/0,9954 ¦ (-31,423) + 16 - (-32,423)
g2 = 6,608; 1 = 2- 0,96376 • ^32,423) • A - 1,761)9,5745;
Л^368" ГC4,423).ГG,608) ^1,5268527-10 ,
xj^ 12 345 = ^—^ + 12,345 = х + 9,345.
1
с ' 1
Окончательно получаем
у = 1,5268627 • 1046 • (ж + Э,345Г42'031 • (х - 1,0383N'608 .
Например, при х = 3 имеем у = 174, что близко к эмпирическому значению 167.
Для нахождения 99%-й квантили обратимся к табл. 117. Из нее следует для
а§ = 0,9954 и а4 = 4,74, что г/0,99 = 3,03 и
жо,ээ = х + а • с • t/o,99 = 3,40217 + 0,96376 • 1 • 3,03 = 6,32236.
3.6.2.7. Кривые Пирсона типа VII
Для этого случая % = 0, «з = 0иа4>3. Уравнение кривой имеет вид
~2 \ —Я
где
Кривые асимметричны относительно среднего значения, совпадающего с модой,
и имеют неограниченный размах. При х = 0? аз = 0и«4 = 3 распределение пере-
переходит в нормальное.
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 383
Задача 179. Для статистического ряда^ заданного таблицей^ найти аппроксимиру-
аппроксимирующее распределение из семейства Пирсона (п = 2886, с = 10).
Здесь жо,99 = х + а • с • y0j99 = 3,40217 + 0,96376 • 1 • 3,03 = 6,6322.
Результаты расчетов сведем в таблицу:
i
1
2
3
4
5
6
7
8
9
10
11
Xi
725
735
745
755
765
775
785
795
805
815
825
щ
^5
-4
-3
^2
-1
0
1
2
3
4
5
4
10
84
270
658
1095
506
152
63
32
12
ЩХг
^20
-40
-252
^540
-658
0
506
304
189
128
60
100
160
756
1080
658
0
506
608
567
512
300
^500
-640
-2268
^2160
-658
0
506
1216
1701
2048
1500
Пгх\
2500
2560
6804
4320
658
0
506
2432
5103
8192
7500
Е
2886 -323 5247
745 40575
Далее:
Я =
2 • D,390574 - 3)
= 4,657382; , = 1,34365 •
1,390574
= 3,376484;
Л =
2886
ГD,657382)
3,376484 ГD,657382) • Г@,5)'
ГD,657382) = [1 - 0,427 • 0,521185 • ^бгпвб'9] • 3,657382 ... 1,657382 = 14,492645;
ГD,157382) = [1 - 0,427 • 5,353967 • 6,353967~159] • 3,157382 ... 1,157382 = 7,3466223;
1-0,427-l-2i»
Г@,5) =
0,5
л =
2886
0,5
14,492645
3,376484 7,3466223 • 1,771176
Имеем уравнение искомой кривой
=
= 951,98444575.
-4,657382
у = 951,9844785 • 11 +
В нашем случае переменной является
х ~~ х
3,376484^
= ОД • (ж - х) ; х = 775 + тг • с = 775 + 10 • (-0,112) = 773,88;
х = ОДж - 77,388.
Относительно реальной переменной уравнение кривой имеет вид
@,1х - 77,-°^-4'657382
у = 951,984475 • ( 1 +
Например, при х = 795 имеем
3,3764842
1/G95) = 951,984475 • @,000877145 • 7952 - 1,3576075 • 795 + 526,3126435)
что находится вблизи эмпирического значения 152.
-4,657382
= 204,
384 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Внимание! Во всех расчетах кривых Пирсона требуется высокая точность
вычислений (необходимо удерживать до 8^-10 знаков после запятой), что объясня-
объясняется мультипликативной схемой накопления ошибок в степенных членах.
3.6.3. Разложение теоретических распределений
Для эмпирического распределения можно получить хорошее аналитическое при™
ближение, если использовать плотность известного теоретического распределения
(f(x) и ее производные.
Для распределений, незначительно отличающихся от нормального, хорошие
результаты дает приближение с помощью рядов Грама^Шарлье [10]
«4^3
24
где
<р(х) =
1 _*±
2 —плотность стандартного нормального распределения;
(р(ж) = — (ж3 — Зх)ср(х)— третья производная от (р(х); (р (ж) = (ж4 — 6ж2
четвертая производная от (р(х).
Переменная используется в нормализованной форме
х =
х — М(ж)
Задача 180. Для статистического ряда, заданного таблицей, найти аппроксими-
аппроксимирующую кривую для плотности распределения с помощью разложения нормальной
плотности распределения вероятностей (п = 2000, с = 40).
Вычисление моментов распределения приведено в таблице (xi = ):
i
1
2
3
4
5
6
7
8
9
10
11
12
13
Xi
175
215
255
295
335
375
415
455
495
535
575
615
655
щ
-6
^5
-4
-3
^2
-1
0
1
2
3
4
5
6
Xi
0
7
22
102
260
386
461
356
239
108
40
15
4
ЩХг
0
^35
-88
-306
^520
-386
0
356
478
324
160
75
24
Пгх\
0
175
352
918
1040
386
0
356
956
972
640
375
144
0
^875
-1408
-2754
^2080
-386
0
356
1912
2916
2560
1875
864
ПгХ,\
0
4375
5632
8262
4160
386
0
356
3824
8748
10240
9375
5184
Е
2000
82 6314
Имеем
mi = 0,041; т2 = 9,157; т3 = 1,49; т4 = 30,271;
li2 = т^т\ = 3,1553; а = 1,77632; s
2980 60542
х = 415 + 40 • 0,041 = 416,64;
: а • с = 71,0528;
fj,3 = т —
2rrii = 1,1018;
= 7П4 ~~
— 3mi = 30,269;
а3 = ^| = 0,1966; а4 = ^ = 3,04.
а6 сг4
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 385
^ ^ х - 416,64
Для аппроксимирующей кривой по переменной х = имеем
f(x) = ф) - 11 + — - (х - Зх) + —^— • (х ^6х + 3I =
= 0,3989 • е" Ж2 • [1 + 0,03276 • (ж3 - Зж) + 1,667 • 10~3 • (ж4 - 6х2 + 3)] .
Например, для х = 495
х = 495 ~ 416'64 = 1Д028; е~^ = 0,54439; х3 - Зх = -1,96721;
I ±y
ж4 - 6ж2 + 3 = -2,81794;
/A,1028) = 0,3989 • 0,54439 • [l + 0,03276 • (-1,96721) + 1,667 • 103 • (-2,81794)] = 0,20214.
Частота в соответствующем интервале равна
п • f(x) = 2000 • 0,20214 = 404.
3.6.4. Метод вкладов
Рассмотренные ранее в разделах 6.1, 6.2 и 6.3 методы восстановления функции
распределения вероятностей требуют большого количества данных и неприменимы
для малых выборок [370, 371]. Поэтому, начиная с 50-х годов, ведутся работы по
поиску эффективных методов построения функций распределения вероятностей
случайной величины по информации, содержащейся в малой выборке [371^373,
382—384]. Среди таких методов можно отметить метод вкладов с использованием
бета^распределения [374, 375], метод структурной минимизации риска [377], метод
уменьшения неопределенности [379], метод нормальных вкладов [380], метод после™
довательных медиан [381].
Широкое распространение получил метод вкладов. Суть метода вкладов заклю-
заключается в том, что каждому выборочному значению случайной величины Х{ ставит-
ставится в соответствие некоторая непрерывная функция tpi(xj)^ называемая функцией
вклада. Наибольшую эффективность демонстрирует метод, в котором в качестве
вкладов используется бета-функция [374]
где сг =
(о — а) г г Т(щ)Т(гПг)
а < х < Ъ — область существования случайной величины; Xj—реализация случай-
случайной величины, совпадающая с модой частного бета-распределения <fi(xj).
Численным экспериментом с использованием оптимизирующих критериев [376,
378] получены следующие оценки параметров частных бета-вкладов
к «¦ 0,5254
щ = 1 + IJn
0,ЗЭЭ6п~0-2335 (хп - х)
_ 0,6286тГ0'2380 - 0,ЗЭ9бг^0'2335 '
A 0,3996п'2335)(хп ^ х
1 - 0,6286п^0'2380 - 0,3996тг^0'2335 '
где п — объем выборки; #i, xn — соответственно наименьшее и наибольшее выбо-
выборочные значения.
13 А. И. Кобзарь
386 Методы анализа законов распределения вероятностей случайных величин [Гл. 3
Итоговая плотность распределения в точке Xj подсчитывается по формуле
1 п
П г=1
Задача 181. В результате эксперимента получено пять значений случайной величи-
величины Xji 1, 2, 4, 7 и 10. Необходимо с помощью метода бета-вкладов построить оценку
плотности распределения вероятностей случайной величины х.
Вычисляем
0,3996-5-°-2335-A0-1)
Сь — JL —
n oQon n поде
- 0,6286 - 5~0'2380 - 0,3996 ¦ 5~0'2335
A - 0,3996 • 50'2335) • A0 - 1)
6=1 + - —тг^ш — iprv^ = 22,98637;
1 - 0,6286 ¦ 5^0'23380 - 0,3996 • 5^0'2335
5 7 . 5
о,5254
пц = 15,2774 - щ.
22,У8оо7 — Xi
Xi + 7,315423
Вычисляем параметры бета-вкладов:
с 7 сгО,5254
щ = 1 + i^^T^;—; = 4,643588; пц = 15,2774 - 4,643588 = 10,633812;
22,98оо7 — I
1 + 7,315423 +
13,2774
П2 = г + 22,98637 - 21 = 5'081765 т^ = ЮД95639;
+1
= ! +
2 + 7,315423 +1
1 Я 2774
22,98637-4
4 + 7,315423 +
7 + 7,315423
_ 13,2774
П5 ~ + 22,98637- 10
10 + 7,315423
Далее вычисляем значения cf.
Г (щ +mi)
ГD,643588 + 10,633812)
B2,98637 + 7,315423L'643588+10'633812^1 • ГF,643588) • ГA0,633812)
ГA5,2773) 1,8380547 • 1011
30,3017914'2773 • ГD,643588) • ГA0б633812) 30,3017914'2773 ¦ ГD,643588) • ГA0,633812)
_ 1,2971 ¦ 10~10
~~ 14,6994- 1541115,637
1,2971 -100 1,2971 -10~10 аЛА 1Л_х8
ж 44 1 С) *
= 5,726-108;
f 44 1 С)
ГE,0817)-ГA0,1956) 27,1584-565781,67
= 1,2971- 10-1° = 1,2971-10-"» = . 17
ГE,9581) -Г(9,31929) 111,71426-80451,32
= 1»2971 • Ю-10 = 1-2971 ¦ Ю-10 = ^ 10^17>
ГG,2726) • Г(8,0048) 1208,4768 • 5085,2762 ' '
3.6] Подбор кривых распределения вероятностей по экспериментальным данным 387
с5 =
1,2971 • 10"
1,2971 • 10"
= 1,8487-10"
ГF,5865) • Г(8,69087) 335,9016 • 20885,6629
Вычисляем значение функции вклада
Pifci) = а • (Х1 - аO11^1 • (Ь - ая)™1 =
= 5,725 • 108 • A + 7,315423K'643588 • B2,98637 - I)9'633812 = 0,109543.
Далее вычисляем функции вкладов по аналогии, используя различные значения Xj,
Ci, rii и mi. Результаты вычислений сведены в таблицу:
(fi(xj)
<pi(xj)
<f2(Xj)
<P3(Xj)
<P4(Xj)
(f5(Xj)
/fe)
Xl = 1
0,109543
0,034305
0,019857
0,005578
0,011499
0,180782
0,036156
x2 = 2
0,105809
0,009948
0,005677
0,001365
0,003068
0,125867
0,025173
хз = 4
0,081900
0,000064
0,000238
3,5-10
1,01 • 10~4
0,082338
0,016467
Ж4 = 7
0,036800
8-10"9
4,887-100
4,103 -lO2
5,31 -lO1
0,036800
0,007360
x5 = 10
0,009938
8,24 -10~6
3,541 • 10
6,52 • 10
1,68 • 10
0,009952
0,001904
Там же приведены оценки плотности распределения вероятностей
f(Xj) = - -Y^lfiiXj).
13*
ГЛАВА 4
ПРОВЕРКА ГИПОТЕЗ О ЗНАЧЕНИЯХ
ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ
Общие положения. Высказывание гипотез о свойствах окружающего нас мира
и проверка их непосредственными наблюдениями или с помощью целенаправлен-
целенаправленного экспериментирования составляет основу того, что мы называем наукой или
научной деятельностью.
Оставляя в стороне проблему формирования гипотез (она лежит за пределами
прикладной математической статистики), рассмотрим процесс проверки их спра-
справедливости по результатам наблюдений.
Проверка научной гипотезы применительно к потребностям ежедневной прак-
практики инженера и исследователя зависит от специфики наблюдаемых процессов
и потребностей практики.
Например, часто встречающаяся на пути инженера задача — проверка соответ™
ствия параметров разработанного изделия предъявляемым требованиям — в мате-
матико-статистической формулировке может звучать так: „необходимо проверить
гипотезу о том1 что параметр е распределения случайной величины х превосхо-
превосходит заданную величину ?qu.
Сколь разнообразен и сложен окружающий нас мир, столь многочисленны
и разнообразны возможные гипотезы о его свойствах. Поэтому настоящая глава
является наиболее объемным разделом настоящей книги. Она содержит в себе
большое количество способов проверки гипотез и примеров их реализации.
Следует всегда помнить о противоречии между категоричностью и надежностью
высказываний по гипотезе: как правило, надежное высказывание некатегорично,
категорическое высказывание ненадежно. Мы выдвигаем гипотезу и отвергаем
ее тогда, когда по выборке получаем результат, маловероятный при истинности
выдвинутой гипотезы. Принятая граница маловероятности называется уровнем
значимости. При превышении этого уровня выдвинутая нулевая гипотеза отклоня-
отклоняется. Иногда пользуются доверительной вероятностью^ являющейся дополнением
уровня значимости до 1. Различие между наблюдаемым и истинным значениями
параметра распределения признается значимым на уровне значимости /3, если
правильная гипотеза будет отклонена в /3 • 100% случаев (мы чаще пользуемся
доверительной вероятностью а = 1 — /3).
При проверке гипотез возможны ошибки двух типов: первого рода — отклонение
верной гипотезы, и второго рода — принятие ложной гипотезы.
Следует помнить, что уровень значимости (или доверительная вероятность)
должен устанавливаться перед (!) получением данных.
Обычно на практике применяются доверительные вероятности 0,95 или 0,99
(уровни значимости 0,05 или 0,01). Важно неукоснительно выполнять основное
требование — гипотезы должны быть выдвинуты перед статистическим анализом,
сам числовой материал не должен быть использован для выдвижения гипотезы.
Гипотезы, выдвинутые на основе анализа полученного материала, могут быть
полезны только в качестве новых гипотез для последующих проверок.
4.1] Сравнение параметров распределений 389
4.1. Сравнение параметров распределений
Рассмотрим в качестве примера однопараметрическое распределение f(x;e) слу-
случайной величины х с параметром е. Относительно е можно выдвинуть три гипотезы
(называемые нулевыми), в соответствии с которыми неизвестный параметр е = ?q,
s > eg или ? < е® (eg — гипотетическое значение параметра). Символически эти
гипотезы обозначаются как Щ: ? = ?q ; Н^: ? > ?® и Hq : ? < ?q . Им противостоят
альтернативы, соответственно записываемые по аналогии символами
Нце^ео; Н[ : е < е0 и Щ: е > е0.
Основой для вынесения суждения по гипотезе является выборочная точечная
оценка параметра, по которой строится доверительный интервал, включающий
с заданной вероятностью неизвестное истинное значение параметра. Методы оценки
параметров распределений подробно изложены в главе 2.
Между нахождением интервальных оценок параметров и проверкой гипотез
об их возможных значениях существует тесная взаимосвязь. Это по сути два
различных способа формулировки одной задачи. Для проверки гипотез о значени-
значениях параметра достаточно найти доверительный интервал параметра и проверить,
попадает ли в него гипотетическое значение параметра.
Например, гипотеза Щ: ? = е0 не отклоняется с вероятностью а, если е0 по™
падает в двусторонний доверительный интервал параметра е с коэффициентом
доверия а. Гипотеза Hq : ? > ?q не отклоняется, если ?® не превышает нижней
границы одностороннего доверительного интервала для е; гипотеза Hq : ? < ?® не
отклоняется, если ?q превосходит верхнюю границу одностороннего доверительного
интервала.
Упрощенное изложение методологии проверки гипотез, изложенное выше, хотя и
отражает суть проблемы, но, конечно лее, не исчерпывает всех возможных ситуаций
(например, когда нужно сравнить несколько (> 2) параметров одновременно и т. п.).
Следует помнить, что суждение по гипотезе приходится выносить по резуль™
татам выборочной реализации наблюдаемых случайных величин. Случайность на™
блюдаемых величин порождает, естественно, и некоторую неопределенность наших
заключений по гипотезе. Привычная классическая формулировке „результаты на-
наблюдений подтверждают выдвинутую гипотез^ должна уступить место фор-
формуле „результаты наблюдений с достоверностью а (заранее принятая величина)
не противоречат выдвинутой гипотезе1'.
4.1.1. Сравнение параметров нормальных распределений
4.1.1.1. Сравнение двух средних значений
Имеются две выборки независимых случайных величин
Xi,Х2, ...,Xn-i,Xn И 2/1,2/2» ••-,Ут-1,Ут-
Необходимо на основе выборочных данных установить наличие значимой разни™
цы в средних двух совокупностей, из которых извлечены выборки, т. е. прове-
проверить нулевую гипотезу Hq : /jli = /j>2 против альтернатив Hi: и± ф /i2, Н[: а\ > /Х2
и H'l: Hi < Ц2-
4.1.1.1.1. Сравнение при известных дисперсиях о"^ и сг^
Статистика критерия проверки нулевой гипотезы имеет вид
(- -J^-L^l"^ - If - !^
z = [х - у) \ — + — > , где x = -y.Xi] У = ^ yyi*
I n га п т
^ ' i=l г=1
390 Проверка гипотез о значениях параметров распределений [Гл. 4
При справедливости нулевой гипотезы z-статистика имеет нормальное распреде™
ление. Гипотеза Щ: /ii = /12 предпочитается альтернативе Hi: /ii / /12 с довери™
тельной вероятностью а, если \z\ < ui+a; альтернативе Н[: /j,i > /12, если z < на;
2
и альтернативе Н": /ii < /12, если z > гхх_а (здесь Uj — 7"квантиль стандартного
нормального распределения).
Задача 182. Имеются две выборки случайных величин:
(гс = 10) хц 1,2; 2,1; 3,2; 3,6; 3,8; 4,4; 6,1; 7,1; 9; 10,2;
(гп = 8) уг: 2,4; 2,8; 4,1; 4,4; 6,8; 7,2; 8,9
с известными дисперсиями о2х = 8,7 г/ <т^ = 6,1. Проверить гипотезу равенства средних
значений Но : fix = fiy в двух выборках при доверительной вероятности а = 0,95 против
альтернативы Hi: Цг Ф fi2-
Вычисляем оценки х = — • У) хг — 5,07; у = — # У^ 2/г = 5,587 и статистику проверки
п т
нулевой гипотезы z = E,07 - 5,587) • \ — + — I = ^0,4046.
[10 8 J
Для а = 0,95 имеем (см. табл. 1) значение tti+a = tio,975 = 1,96.
2
Так как \z\ = 0,4046 < 1^0,975 = 1,96, нулевая гипотеза равенства средних не отклоня-
отклоняется.
4.1.1.1.2. Сравнение при неизвестных равных дисперсиях
Статистика критерия определяется формулой
т — \
т + п
где
п + т-2 ' г п-1^1 7 ' 2 ш-1
г=1 г=1
При справедливости нулевой гипотезы статистика критерия имеет распределе-
распределение Стьюдента (см. раздел 1.1.9) с / = n + m^2 степенями свободы. Проверка
нулевой гипотезы выполняется по аналогии со случаем, когда дисперсии известны,
с заменой квантилей стандартного нормального распределения щ на квантили
распределения Стьюдента t7, значения которых для / $С 30 приведены в табл. 118
(при / > 30 можно принять tj = г/7).
Задача 183. Имеются два ряда выборочных данных:
(п = 12) хц 1, 2, 3, 5, 7, 12, 14, 16, 16, 17, 19, 22;
(т = 10) уц 12, 16, 19, 22, 24, 26, 32, 34, 36, 44.
Необходимо проверить гипотезу равенства средних в обеих выборках Но: /ii = /i2
против альтернативы Hi: ц\ ф Ц2 при доверительной вероятности а = 0,90.
Имеем х = 11,167; у = 26,5; s\ = 52,515 (si = 7,247); si = 98,5 (s2 = 9,925).
Проверкой по критерию Фишера (см. раздел 3.1.1.3.1) убеждаемся в статистической
неразличимости (равенстве) значений s\ и s2- Вычисляем
g2 = A2-1). 52,515+A0-1). 98,5
12 + 10-2
11,167-26,5 \ Г 12 + 10
8^56 ) ' \ 12-10
= 73,21 (s = 8,56);
= -4,18.
4.1]
Сравнение параметров распределений
391
Из табл. 118 для числа степеней свободы / = 12 + 10^2 = 20 и а = 0,90 находим
ti+a = to,95 = 1,725. Так как \t\ = 4,18 > to,95 = 1,725, нулевая гипотеза равенства сред™
2
них должна быть отклонена.
Таблица 118
Таблица квантилей распределения Стыодента tT (ti_7 = —?7)
/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7
0,90
3,078
1,886
1,638
1,533
1,476
1,440
1,415
1,397
1,383
1,372
1,363
1,356
1,350
1,345
1,341
0,95
6,314
2,920
2,353
2,132
2,015
1,943
1,895
1,860
1,833
1,812
1,796
1,782
1,771
1,761
1,753
0,975
12,706
4,303
3,182
2,776
2,571
2,447
2,365
2,306
2,262
2,228
2,201
2,179
2,160
2,145
2,131
0,99
31,821
6,695
4,541
3,747
3,365
3,143
2,998
2,896
2,821
2,764
2,718
2,681
2,650
2,624
2,602
/
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
7
0,90
1,337
1,333
1,330
1,328
1,325
1,323
1,321
1,319
1,318
1,316
1,315
1,314
1,313
1,311
1,310
0,95
1,746
1,740
1,734
1,729
1,725
1,721
1,717
1,714
1,711
1,708
1,706
1,703
1,701
1,699
1,697
0,975
2,120
2,110
2,101
2,093
2,086
2,080
2,074
2,069
2,064
2,059
2,056
2,052
2,048
2,045
2,042
0,99
2,583
2,567
2,552
2,539
2,528
2,518
2,508
2,500
2,492
2,485
2,479
2,473
2,467
2,462
2,457
4.1.1.1.3. Сравнение при неизвестных неравных дисперсиях
Задача сравнения средних двух нормально распределенных совокупностей при
неизвестных и неравных (по выборочным оценкам) дисперсиях известна как про™
блема Беренса^Фишера [5] по имени авторов, впервые ее сформулировавших.
Точного решения этой задачи до настоящего времени нет. На практике обычно
используются различные приближения, некоторые из которых рассмотрены ниже.
4.1.1.1.3.1. Критерий Кохрана-Кокса [386]
1 s2 s2
Статистика критерия 1к = - (х — у), где s2 = — -\—-.
Критические значения статистики вычисляются по формуле
• / т \ , , { т \ 2 2
t'a = via I1+Za 2' где v^8i и и* = Ъ
ta(f) — «-квантиль распределения Стыодента с / степенями свободы (в нашем
случае Д = п — 1 и /2 = т — 1).
4.1.1.1.3.2. Критерий Сатервайта [387]
Статистика критерия совпадает со статистикой критерия Кохрана—Кокс. Кри-
Критическими значениями статистики являются квантили распределения Стьюдента
с числом степеней свободы
392 Проверка гипотез о значениях параметров распределений [Гл. 4
4.1.1.1.3.3. Критерий Уэлча [388]
Отличается от критерия Сатервайта только числом степеней свободы, при ко™
тором определяется критическое значение распределения Стьюдента. В критерии
Уэлча
/у =
Задача 184. Имеются две выборки данных:
(гс = 10) хп 2, 4, 6, 7, 9, 12, 14, 16, 19, 24;
(т = 9) ун 9, 14, 19, 21, 25, 29, 35, 41, 46.
Необходимо проверить гипотезу равенства средних при достоверности а = 0,95.
Вычисляем х = 1,3; у = 26,55. Далее находим:
1 10 1 9
s? = - • J2(Xi - ^f = 49'12' 4 = - - J2(yi - уJ = 1525528;
9 i=l 8 г=1
2 2
щ = -^ = 4,912; i/2 = -^ = 16,947; s2 = щ + и2 = 21,8595 (s = 4,675).
п т
Вычислим теперь статистики критериев для проверки нулевой гипотезы.
Критерий Кохрана-Кокс D.1.1.1.3.1)
Находим по табл. 118 значения to,9s(/i = п. —- 1 = 9) = 1,833 и to,95 (/2 = т —¦ 1 = 9 —
— 1 = 8) = 1,77. Вычисляем статистику критерия и ее критическое значение:
26,55 — 11,33 4,912 • 1,833 + 16,947 • 1,86
К ~~ 4,675 ~~ ' ' °'95 ~~ 4,912 + 16,947 ~~ '
Так как tx = 3,255 > to,95 = 1,853, нулевая гипотеза равенства средних отклоняется.
Критерий Сатервайта D.1.1.1.3.2)
Вычисляем
лак I1 /Ч912У , 1 /152,528\21 '
tc = 4,675 • < - • I I + - • I I ( = 12,57.
Из табл. 118 находим критическое значение: ?о,9б(/ = 12,34) « 1,77, которым также
отклоняется нулевая гипотеза.
4.1.1.1.4. Модифицированный критерий Стьюдента [389]
Статистика критерия
Ш\ + UJ2
где Ш\ = жшах — xmin и 6^2 = I/max "~ 2/min — размахи сравниваемых выборок.
Критические значения Та статистики для выборок одинакового объема п = т
приведены в табл. 119.
Если \Т\ < Ti+g , то гипотеза iifо: /ii = /12 предпочитается альтернативе
2
Л^ : |/1 ф Ц2] если Т < Та — альтернативе iif{ : /zi > /125 если Т > Та — альтернативе
U^ : /ii < /12 (ск — доверительная вероятность).
При п ^ 10 критерий не уступает по эффективности обычному критерию Стьк>
дента [390]. В связи с существенной потерей эффективности пользоваться крите-
критерием при п ^ 20 не рекомендуется.
4.1]
Сравнение параметров распределений
393
Таблица 119
Критические значения модифицированного критерия Стьюдента
для сравнения средних по двум выборкам равного объема [24]
2
3
4
5
6
7
8
9
10
Доверительная
0,95
2,322
0,974
0,644
0,493
0,405
0,347
0,306
0,275
0,250
0,975
3,427
1,272
0,813
0,613
0,499
0,426
0,373
0,334
0,304
вероятность а
0,99
5,553
1,715
1,047
0,772
0,621
0,525
0,459
0,409
0,371
0,995
7,916
2,093
1,237
0,896
0,714
0,600
0,521
0,464
0,419
12
13
14
15
16
17
18
19
20
Доверительная
0,95
0,214
0,201
0,189
0,179
0,170
0,162
0,155
0,149
0,143
0,975
0,260
0,243
0,228
0,216
0,205
0,195
0,187
0,179
0,172
вероятность а
0,99
0,315
0,294
0,276
0,261
0,247
0,236
0,225
0,216
0,207
0,995
0,355
0,331
0,311
0,293
0,278
0,264
0,252
0,242
0,232
Задача 185. Имеются две выборки данных объема п = т = 10:
хщ 2, 4, 6, 7, 9, 12, 14, 16, 19, 24;
xi2: 9, 14, 19, 21, 25, 29, 35, 41, 46, 50.
Необходимо проверить гипотезу равенства средних модифицированным критерием
Стьюдента при а = 0,95 против альтернативы Hi: fii ф цъ-
Имеем xt = 12,3; х2 = 28,9; ал = 24 - 2 = 22; ш2 = 50 - 9 = 41.
12 3 — 28 9
Находим Г = 2 • ^ i J = ^0,527.
22 + 41
Из табл. 119 для
-0,95
= 0,975 находим критическое значение Т-статиетики
2 2
ДЛЯ П = 10 - Т0,975 = 0,304.
Так как \Т\ = 0,527 > То,975 = 0,304, нулевая гипотеза равенства средних откло™
няется.
4.1.1.1.5. Парный t-критерий сравнения средних
Предположим, имеются две выборки случайных величин одинакового объема п,
члены которых расположены в порядке их наблюдения. Требуется проверить ги-
гипотезу равенства средних в этих выборках. В такой постановке двухвыборочная
задача может быть сформулирована как одновыборочная, если в качестве случай™
ной величины рассматривать разности yi = хц — Х{2 наблюдаемых пар
Статистика критерия аналогична обычной статистике Стьюдента (см. раздел
4.1.1.1.3)
t = — у/п, где у = - ^ уг] sy = —
у г=1 ^ г=1
Проверка нулевой гипотезы полностью аналогична обычному критерию Стьюдента.
Задача 186. Проверить гипотезу равенства средних двух выборок в условиях зада-
задачи 185 парным t-критерием.
Имеем последовательность разностей
Уг = хц - xi2 = 7, 10, 13, 14, 16, 17, 21, 25, 27, 26.
394 Проверка гипотез о значениях параметров распределений [Гл. 4
Находим
у = 17,6; 4 = 48>044 (sv = 6>931); * = Т^ ¦ ^10 = 8'03-
Из табл. 118 для п = 10 и а = 0,975 находим ?0,975(Ю) = 1,812.
Так как t = 8,03 > to,975 = 1,812, нулевая гипотеза отклоняется.
4.1.1.1.6. Критерий Уолша, основанный на порядковых статистиках [391]
Рассмотрим следующую ситуацию. Имеется выборка #i, ..., хп объема п из
нормального распределения со средним jii и дисперсией а2. Получено одно неза-
независимое наблюдение у из нормального распределения со средним Ц2 и такой же
дисперсией а2. Необходимо проверить гипотезу Щ: /ii = /л2 против альтернатив
Н[ : ii\ < 112 и Н'{ : iii > Ii2- По сути, нулевая гипотеза утверждает, что независимая
случайная величина у принадлежит распределению, из которого извлечена выборка
Х\, . . . , Хп.
Напомним, что k-й порядковой статистикой называется k-e по величине значение
в выборке упорядоченных по возрастанию случайных величин х\ ^ Х2 ^ ... ^ хп.
Если выборочные значения упорядочены по возрастанию, то порядковые статисти-
статистики просто являются элементами такой выборки.
Проверка гипотезы Hq : /ii = /12 включает в себя проверку справедливости серии
неравенств.
Если
у — х > \/п + 1 (х — хт) или у + х > \/п-\- 1 (х + xn+i^m) ,
где т = 1,..., 4, то нулевая гипотеза отклоняется в пользу альтернативы Hi: /12 > Mi-
Если
у — х < л/п + 1(х - xn+i^m) или у + х < \/п+ 1{х + хт),
то нулевая гипотеза отклоняется в пользу альтернативы Н[: /ii > /z2- В любом
ином случае нулевая гипотеза не отклоняется. Уровень значимости а, принимаемый
для проверки гипотезы, определяется в зависимости от принятого значения т
следующим образом:
@,5)п при т = 1;
а = <
1)@,5)п при т =
(п2 + п + 2)@,5)n+1 при т = 3;
i (n3 + 5п + 6) @,5)п при т = 4.
По сравнению с обычным критерием Стьюдента (см. раздел 4.1.1.1.3) относи™
тельная эффективность критерия Уолша равна от 0,95 при п = 6 до 0,70 при п = 16.
Задача 187. Имеется выборка данных
xf. 7, 10, 13, 14, 16, 17, 21, 26, 26, 27.
Проверить критерием Уолша гипотезу о принадлежности независимо полученного
выборочного значения у = 31 распределению, из которого извлечена выборка х%.
Имеем х = 17,6 при т=1и жю+i-i = жю = 27.
Вычисляем
1 • (ж - xi) = 35,156; V^ + 1 • (х + жю) = 147,92;
(ж - жю) = -31,176; л/п + 1 • (ж + жх) = 81,589.
4.1]
Сравнение параметров распределений
395
Непосредственной проверкой убеждаемся, что
у - ж = 31 - 17,6 = 13,4 > 35,156; у + ж = 31 + 17,6 = 48,6 < 147,02;
у-х = 31- 17,6 = 13,4 > -31,176; у + х = 31 + 17,6 = 48,6 < 81,589.
Видим, что одно из неравенств, а именно у + х < \/п + 1 • (ж + жш), удовлетворяется,
что позволяет отклонить нулевую гипотезу в пользу альтернативы Н\ : fit > /i2- To есть
значение у = 31 взято из распределения со средним, большим, чем среднее распределения
случайных величин Xi. Такой вывод сделан на уровне значимости а = @,5I0 = 0,00097,
т. е. значимым признается событие, вероятность которого не превышает 0,00097.
Это очень низкий уровень значимости (обычно на практике используются значения
0,05 или 0,1). Для а = 0,05 имеем т = 3, жз = 13 и жю+1-з = Ж8 = 25.
Тогда
(х - жз) = 15,25;
1-(х-х8) = ^24,54;
Убеждаемся, что неравенство у + ж <
ж8) = 141,28;
ж3) = 101,48.
выполняется и в этом случае,
что и на уровне значимости а = 0,05 отклоняет нулевую гипотезу в пользу гипотезы
4.1.1.1.7. Двухступенчатый двухвыборочный медианный критерий Волфа [392]
Довольно любопытный критерий сравнения средних двух совокупностей, наи™
более эффективно реализуемый применительно к испытаниям на долговечность
технических объектов.
Процедура проверки гипотезы равенства двух средних заключается в следую™
щем. Фиксируется выборка из первой совокупности объема п: Xi, ... ,жп. Опреде™
ляется ее медиана х = хп+\ (при п нечетном) или х =
Хп + Хп
(при п четном).
2 • • 2
Затем отбираются члены из второй совокупности у до тех пор, пока не будет
получено ровно г значений у-ов, превосходящих медиану.
Статистикой критерия является число Nn значений у-ов, которое необходимо,
чтобы получить ровно г значений у-ов, превосходящих медиану.
Таблица 120
Критические значения Nq (г, п)
для доверительной вероятности а = 0,95 [392]
п
3
5
г
6
7
8
9
10
11
12
13
14
15
16
17
6
7
No
6
7
8
9
10
12
13
14
15
16
17
18
6
7
п
5
7
г
8
9
10
11
12
13
14
15
6
7
8
9
10
11
No
9
10
11
12
13
15
16
17
6
7
9
10
11
13
п
7
9
11
г
12
13
5
6
7
8
9
10
11
12
5
6
7
8
No
14
15
5
6
8
9
10
12
13
14
5
6
8
9
п
11
13
15
17
г
9
10
5
6
7
8
5
7
8
9
5
6
7
8
N0
10
12
5
6
8
9
5
8
9
11
5
7
8
9
396
Проверка гипотез о значениях параметров распределений
[Гл.4
Нулевая гипотеза Но: /лу = /лх отклоняется в пользу альтернативы Hi: /лу > /лх
тогда и только тогда, когда Nn ^ TVq (r, n), где iVo(r, п)—критические значения,
приведенные в табл. 120.
Таблица 121
Значения г и Nq при п ^ 20 для двухступенчатого
двухвыборочного критерия сравнения средних
при доверительной вероятности а = 0,95 [392]
г
No
4
4
5
5
6
7
7
8
8
10
9
12
10
13
11
15
12
17
13
18
14
20
15
21
При п ^ 20 рекомендуемые значения г и No при а = 0,95 приведены в табл. 121.
Задача 188. При испытаниях п = 11 приборов получены значения ресурса
хц 790, 830, 920, 1010, 1080, 1210, 1250, 1300, 1400, 4404 ч.
Необходимо проверить, увеличилась ли долговечность приборов после их усовершен-
усовершенствования.
Для проверки гипотезы были проведены испытания усовершенствованной партии
приборов. В результате испытаний пяти приборов из усовершенствованной партии были
получены следующие значения:
уц 1090, 1100, 1120, 1090, 1200 ч.
Исходя из табл. 120, для выбранного значения г = 5 необходимо, чтобы все первые
пять значений ресурса превосходили медиану, равную в нашем случае 1080 ч. "Убежда-
"Убеждаемся, что Nn = JVo, что позволяет отклонить нулевую гипотезу в пользу альтернативы,
утверждающей значимое смещение ресурса усовершенствованных приборов в сторону
увеличения.
4.1.1.1.8. ^-критерий длм сравнения двух средних с одинаковыми дисперсиями
Критерий эквивалентен t-критерию (ем. раздел 4.1.1.1.2) и использует соотно
шение между распределением Стьюдента и ^-распределением F\j = Й, где F\j —
случайная величина, имеющая распределение Фишера с Д = 1 и /2 = / степенями
свободы.
Достоинством использования такой эквивалентной формы критерия является
экономичность в вычислениях, объем которых снижается на ^ 30%. Если мы име-
имеем выборки
..., х
П1
= /Л2 имеет вид
F =
,|/П2, то статистика критерия проверки гипотезы
¦ 712 — .
ПЩ2
Y1 У^) ~ П2
2/1
Величина F имеет распределение Фишера (см. раздел 1.1.10) с /i = 1 и
f2 = щ + П2 — 1 степенями свободы. При п\ = П2 = n имеет место соотношение
F =
где
4.1] Сравнение параметров распределений 397
Нулевая гипотеза отклоняется, если F > Fa(fi, /2), где ^(/ъ/г)—критическое
значение ^статистики на уровне значимости а при /i и /2 степенях свободы.
Для его нахождения можно воспользоваться таблицами или аппроксимациями,
приведенными в главе 1 (рекомендуется аппроксимация 9).
Задача 189. Проверить F-критерием гипотезу равенства средних в двух выборках из
нормального распределения при а = 0,95 (щ = П2 = 30)
хц 1 3 4 5 7 8 11 14 19 21 23 26 30 35 41
44 49 56 57 58 59 60 63 65 70 71 73 82 84 90;
уц 12 15 19 21 30 40 50 51 52 52 54 55 60 61 62
64 64 65 70 71 73 75 79 80 81 84 85 86 87 90.
Находим J2Xi = 1229' ЛУ^ = 17885 J2x2i = 72805; XZ 2/? = 121146 и вычисляем
Имеем m = гс2 = 30, /i = 1, /2 = 2 • 30 - 2 = 58.
У^ = 17885 J2x2i
C0 - 1) • A229 - 17
1229' ЛУ^ = 17885 J2xi = 72805; XZ 2/?
статистику критерия
788J
F =
30 • G2805 + 121146) - A2292 + 17882)
Для а = 0,95 находим из аппроксимации для F-распределения (см. аппроксимацию 9
в разделе 1.1.10) коэффициенты а = 1,4287, Ъ = 0,95 и с = 0,681. Тогда имеем
h = 2flh = 1,9661; g = ^^А = 0,98276;
/1 + /2 /1 - /2
lgF0,95(l;58) = 1,4287- A,9661 - 0,95)" 2 -0,681-0,98276 = 0,7709;
Fo,95(l;58) = 100'7709 = 5,900.
Так как F = 8,155 > .Fo,95 A; 58) = 5,900, гипотеза равенства средних отклоняется.
4.1.1.2. Сравнение нескольких (к > 2) средних
Имеются к выборок равного объема п из нормалвно распределенной совокупно-
совокупности Жц, #12, • • • ,Х1п1] Ж21,Ж22, • • • ,^2п25 • • • ; Хк1,Хк2, • • • , %кпк •
Проверке подле^кит нулевая гипотеза о статистической неразличимости средних
Но'- fJ>i = /J>2 = • - - = Ук против альтернативы
Hi: |a4+i — fjio\ > 0 (г = 1, ..., к).
4.1.1.2.1. Модифицированный критерий Стьюдента
Статистика критерия имеет вид
к
) (^ j max %jmin)
i=i
где Xjmax, Xjm_in — наибольшее и наименьшее значения j-й выборки.
Если Q > Qa(A;,7i), где Qa(k,n)—критическое значение статистики, приведен™
ное в табл. 122, то нулевая гипотеза отклоняется.
Критерий достаточно прост в применении, но, в связи с большой потерей эф-
эффективности с ростом объема выборки, его рекомендуется применять при п ^ 10.
398
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 122
Критические значения Qa(kjn)
модифицированного критерия Стьюдента [119, 393]
к
п
2
3
4
5
6
7
8
9
10
Доверительная вероятность а = 0,05
1
2
3
4
5
6
7
8
9
10
18,10
3,50
1,79
1,18
0,89
0,71
0,59
0,50
0,44
0,39
7,60
2,50
1,44
1,01
0,78
0,64
0,53
0,46
0,41
0,36
6,20
2,30
1,41
1,01
0,78
0,64
0,54
0,47
0,42
0,37
5,80
2,30
1,43
1,03
0,81
0,66
0,56
0,49
0,43
0,39
5,70
2,40
1,47
1,07
0,84
0,69
0,59
0,51
0,45
0,40
5,70
2,40
1,52
1,11
0,87
0,71
0,61
0,53
0,47
0,42
5,80
2,50
1,57
1,14
0,91
0,74
0,64
0,56
0,49
0,44
5,90
2,60
1,62
1,19
0,94
0,77
0,66
0,58
0,51
0,46
6,00
2,60
1,68
1,23
0,97
0,80
0,68
0,60
0,53
0,47
Доверительная вероятность а = 0,01
1
2
3
4
5
6
7
8
9
10
90,00
8,30
3,40
2,00
1,43
1,09
0,89
0,74
0,64
0,56
17,50
4,00
2,10
1,42
1,07
0,86
0,71
0,61
0,53
0,47
11,20
3,40
1,91
1,33
1,01
0,82
0,69
0,60
0,52
0,47
9,30
3,20
1,87
1,32
1,01
0,82
0,70
0,60
0,53
0,47
8,60
3,10
1,87
1,33
1,03
0,84
0,72
0,62
0,55
0,49
8,20
3,10
1,90
1,36
1,06
0,86
0,74
0,64
0,56
0,50
8,00
3,10
1,93
1,39
1,09
0,89
0,76
0,66
0,58
0,52
8,00
3,20
1,98
1,43
1,12
0,92
0,78
0,68
0,60
0,54
8,00
3,20
2,00
1,47
1,15
0,95
0,80
0,70
0,62
0,55
Задача 190. В результате испытаний пяти выборок приборов объемом п = 8 каж-
каждая, изготовленных разными заводами, получены следующие значения долговечности
приборов (ч):
11
15
8
4
24
14
19
11
5
26
18
21
14
9
32
21
22
19
18
48
30
26
31
24
54
32
38
32
31
62
40
41
44
45
66
45
52
58
61
70.
Требуется проверить гипотезу о статистической неразличимости средних значений
долговечности в выборках на уровне значимости а = 0,05 модифицированным крите-
критерием Стьюдента.
Вычисляем предварительно суммы
J2 хц = 211; J2 х^ = 234' J2 жзг = 217; J2 х^ = 1975 J2 х^ = 3825
Имеем
= 382: mm
in) = 234.
= 197: Q =
382 - 197
224
= 0,8259.
Из табл. 122 для a = 0,05, k = Б и п = 8 находим критическое значение
Go,05 E,8) = 0,91. Так как Q = 0,826 < Qo,o5E,8) = 0,91, нулевая гипотеза равенства сред-
средних не отклоняется, однако критерий находится вблизи критической зоны.
4.1] Сравнение параметров распределений 399
4.1.1.2.2. Критерий „стьюдентизированного" размаха
Статистика критерия
q = ( max Xj — mm
_ l A
где Xj = — y. xij и sf — независимая оценка стандартного отклонения случайных
п ,
величин Xij, полученная на отдельной выборке объема п = / + 1.
Нулевая гипотеза отклоняется, если q > ga(n,/), где qa{nj) —критическое зна™
чение, приведенное в табл. 123.
Для применения критерия необходимо предварительно иметь оценку стандарт-
стандартного отклонения а по отдельной выборке и располагать информацией о том, что
дисперсии во всех выборках одинаковы (методы проверки этого предположения,
т.е. методы сравнения дисперсий, изложены в разделе 4.1.1.4).
Задача 191. Проверить на уровне значимости а = 0,95 гипотезу равенства сред-
средних критерием „стьюдентизированногоа размаха, если оценка стандартного откло-
отклонения Sf получена по выборке
х{: 10, 12, 14, 19, 22, 28, 34, 46, 52, 61, 70.
В качестве выборочного материала использовать данные задачи 190.
Имеем
хг = 26,375; х2 = 29,25; ж3 = 27,125; х4 = 24,625; х5 = 47,75;
f 1 " 2р
z5 = 47,75; min% = 26,375; sf = { • 2^{хг - xf } = 20,868.
г=1
Тогда q = —^ • D7,75 - 26,375) = 3,239.
20,868 v 5;5
Из табл. 123 для а = 0,05, / = 10 и п = 8 имеем go,os(8,10) = 5,30.
Так как q = 3,239 < go,os(8,10) = 5,30, гипотеза равенства средних не отклоняется.
4.1.1.2.3. Дисперсионный критерий
Статистика критерия имеет вид
k
kn (n — 1) j=i
fc-1
где
F =
- if ^ 1
При справедливости нулевой гипотезы статистика критерия имеет распределен
ние Фишера (см. раздел 1.1.10) c/i = fc — 1и/2 = &(п—1) степенями свободы.
При F > Fa(k — 1; к (п — 1)) нулевая гипотеза отклоняется. Здесь -Fa(/i, /2) —
«^квантиль ^^распределения, ее значения могут быть найдены или по соответствую
ющим таблицам, или с помощью аппроксимации.
400
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 123
Жритические значения с|о,(п,, /)
„стьюдентизированного" размаха [119]
п
/
2
5
10
15
20
30
40
60
оо
Доверительная вероятность а = 0,05
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
6,08
8,33
9,80
10,88
11,74
12,44
13,03
13,54
13,99
14,39
14,75
15,08
15,38
15,65
15,91
16,14
16,37
16,57
16,77
3,64
4,60
5,22
5,67
6,03
6,33
6,58
6,80
6,99
7,17
7,32
7,47
7,60
7,72
7,83
7,93
8,03
8,12
8,21
3,15
3,88
4,33
4,65
4,91
5,12
5,30
5,46
5,60
5,72
5,83
5,93
6,03
6,11
6,19
6,27
6,34
6,40
6,47
3,01
3,67
4,08
4,37
4,59
4,78
4,94
5,08
5,20
5,31
5,40
5,49
5,57
5,65
5,72
5,78
5,85
5,90
5,96
2,95
3,58
3,96
4,23
4,45
4,62
4,77
4,90
5,01
5,11
5,20
5,28
5,36
5,43
5,49
5,55
5,61
5,66
5,71
2,89
3,49
3,85
4,10
4,30
4,46
4,60
4,72
4,82
4,92
5,00
5,08
5,15
5,21
5,27
5,33
5,38
5,43
5,47
2,86
3,44
3,79
4,04
4,23
4,39
4,52
4,63
4,73
4,82
4,90
4,98
5,04
5,11
5,16
5,22
5,27
5,31
5,36
2,83
3,40
3,74
3,98
4,16
4,31
4,44
4,55
4,65
4,73
4,81
4,88
4,94
5,00
5,06
5,11
5,15
5,20
5,24
2,77
3,31
3,63
3,86
4,03
4,17
4,29
4,39
4,47
4,55
4,62
4,68
4,73
4,80
4,85
4,89
4,93
4,97
5,01
Доверительная вероятность а = 0,01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
14,04
19,02
22,29
24,72
26,63
28,20
29,53
30,68
31,69
32,59
33,40
34,13
34,81
35,43
36,00
36,53
37,03
37,50
37,95
5,70
6,98
7,80
8,42
8,91
9,32
9,67
9,97
10,24
10,48
10,70
10,89
11,08
11,24
11,40
11,55
11,68
11,81
11,93
4,48
5,27
5,77
6,14
6,43
6,67
6,87
7,05
7,21
7,36
7,49
7,60
7,71
7,81
7,91
7,99
8,08
8,15
8,23
4,17
4,84
5,25
5,56
5,80
5,99
6,16
6,31
6,44
6,55
6,66
6,76
6,84
6,93
7,00
7,07
7,14
7,20
7,26
4,02
4,64
5,02
5,29
5,51
5,69
5,84
5,97
6,09
6,19
6,28
6,37
6,45
6,52
6,59
6,65
6,71
6,77
6,82
3,89
4,45
4,80
5,05
5,24
5,40
5,54
5,65
5,76
5,85
5,93
6,01
6,08
6,14
6,20
6,26
6,31
6,36
6,41
3,82
4,37
4,70
4,93
5,11
5,26
5,39
5,50
5,60
5,69
5,76
5,83
5,90
5,96
6,02
6,07
6,12
6,16
6,21
3,76
4,28
4,59
4,82
4,99
5,13
5,25
5,36
5,45
5,53
5,60
5,67
5,73
5,78
5,84
5,89
5,93
5,97
6,01
3,64
4,12
4,40
4,60
4,76
4,88
4,99
5,08
5,16
5,23
5,29
5,35
5,40
5,45
5,49
5,54
5,57
5,61
5,65
При /2 = fc(n—1)>4 можно использовать упрощенный критерий Романовско™
го [13], основанный на статистике
R =
4.1] Сравнение параметров распределений 401
где
к
п[к(п-1)- 2] j=i 2 (fcn - 3)
к-1
Если R ^ 3, нулевая гипотеза отклоняется.
Изложенная процедура называется однофакторным дисперсионным анализом.
Подробно дисперсионный анализ изложен в главе 5.
Следует помнить, что применение этого критерия при отсутствии нормальности
исходных распределений величин Xij не рекомендуется, так как он становится в этом
случае неустойчивым.
Его устойчивость к отклонениям от нормальности повышается, если использо™
вать модифицированные степени свободы для i^-критерия [87]:
где
, кп +1 с A s2
d=l+ ; с=—; v =
кп — 1 кп — с и кп —
кп(кп + 1)а4 - Цкп - l)s22 _ J^ " .
Задача 192. Проверить в условиях задачи 190 гипотезу равенства средних при дове-
доверительной вероятности а = 0,95.
Имеем
xi = 26,375; х2 = 29,25; х3 = 27,125; х4 = 24,625; ж5 = 47,75;
1 5 8 5 5 8
х= 'J2J2Xii= 315°255 JZ fe ~ xf = 363,66875; ]Г J2 (Xii ~ xjf = 9603,124.
j = l i=l j = l j = l г=1
^ 5-8-7 363,66875
Отсюда F = • = 2,65.
5-1 9603,124
Для а = 0,95, /i = 5 - 1 = 4 и /2 = 5 • (8 - 1) = 35 имеем F0,95D; 35) = 2,67 (см., на»
пример, табл. А7 в [10]).
Так как F = 2,65 < „Fb,95 D; 35) = 2,67, нулевая гипотеза не отклоняется.
Рассмотрим теперь более устойчивый критерий. Вычисляем
5 8 5 8
s2 = J2 J2 (XiJ ~ хзТ = 9602,34; s4 = ]Г J2 (Xii ~~ xif = 5077427,388;
А = 5-8-E-8 + D-5077427,388-3. E-8-l).9602,34^ = _Mg8Q
E • 8 - 1) • E • 8 - 2) • E • 8 - 3) ' '
9602,34 44880,84582
и = '— = 246,2138; с = =~ = ^0,7403;
5-8-1 246,21382
d = 1 + L*±± (-0-7403) =0,98089;
5-8-1 5 • 8 + 0,7403
/i = 0,98089 . E - 1) = 3,923; /2 = 0,98089 • 5 • 7 = 34,3.
Видим, что число степеней свободы несколько снижается, что позволяет отклонить
гипотезу.
402 Проверка гипотез о значениях параметров распределений [Гл. 4
Рассмотрим упрощенный критерий Романовского:
= 8.E-7-2) _ 360,66875 = = / 2 • (Б • 8 - 3) =
5-1 9602,234 v у E - !) • E ' 8 ~ 5 ~ 4)
^ = 3,209.
0,7725
Так как R > 3, нулевая гипотеза отклоняется.
4.1.1.2.4. Критерий Полсона
В [394] Полсоном рассмотрена проблема выделения среди к выборок, по п
наблюдений в каждой, выборки со средним значением, большим, чем у (Aj — 1)
остальных.
Статистика критерия имеет вид
п I max Xi — х ] ь
А = , где х = т
\
Если А ^ Аа, то с вероятностью а справедлива нулевая гипотеза Но : х\ = ... = х^.
В ином случае (А > Ха) выборка с наибольшим средним признается значимо от-
отличной от остальных.
Критическое значение статистики равно
п(к ~~
где Faf — a'-квантиль распределения Фишера с Д = 1 и /2 = кп — 2 степенями
свободы и а' = —^.
к
2а
Значения для а' = — следует брать из обычных таблиц ^-распределения,
используя аппроксимацию по а. Некоторые значения Fa/(l',kn — 2) приведены
в табл. 124, составленной на основе данных таблиц i-статистики Вонферрони [87, 395].
Задача 193. Проверить критерием Полсона в условиях задачи 190 гипотезу равен-
равенства средних против альтернативы, утверждающей, что выборка с наибольшим сред-
ним значимо отличается от остальных (а = 0,95).
5 8
Имеем max х* = 47,75; х = 31,025; \" Y" (хц - жJ = 9602,34.
Находим А = ' = 1,365. Из табл. 124 для к = Ъ, п = 8 ш а = 0,95
'9602,34
имеем F'a = 5,90. Вычисляем критическое значение
А095 =
/ 0927-
5- E-7 + 5-2 + 5,90)
Так как А = 1,365 > Ао,э5 = 0,927, нулевая гипотеза отклоняется и выборка со сред™
ним Xj = 47,75 должна быть признана значимо отличающейся от остальных. Этот вывод
не совпадает с ранее полученным, что может быть следствием отклонения распределения
значений x%j от нормального, а критерий Полсона очень критичен к нормальности
распределения.
4.1]
Сравнение параметров распределений
403
Значения
Таблица 124
; кп — 2) для доверительной вероятности а = 0,95
п
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
30
к
2
7,71
5,99
5,32
4,96
4,75
4,60
4,49
4,41
4,35
4,30
4,26
4,22
4,20
4,17
4,15
4,13
4,11
4,10
4,00
3
7,10
5,91
5,68
5,41
5,29
5,17
5,09
5,01
4,96
4,93
4,89
4,85
4,83
4,81
4,79
4,77
4,76
4,75
4,63
4
6,94
6,30
5,98
5,79
5,66
5,57
5,50
5,45
5,41
5,39
5,35
5,34
5,29
5,26
5,24
5,21
5,18
5,15
5,02
5
7,02
6,51
6,25
6,09
5,98
5,90
5,86
5,81
5,78
5,75
5,71
5,68
5,66
5,63
5,61
5,59
5,57
5,56
5,41
6
7,61
7,11
6,86
6,70
6,59
6,54
6,49
6,45
6,39
6,37
6,35
6,33
6,31
6,29
6,27
6,25
6,23
6,20
6,02
7
7,31
6,93
6,72
6,59
6,49
6,42
6,39
6,37
6,34
6,30
6,28
6,26
6,24
6,22
6,20
6,18
6,16
6,15
6,02
8
7,54
7,16
7,05
6,91
6,85
6,81
6,79
6,77
6,75
6,72
6,70
6,68
6,65
6,62
6,59
6,57
6,55
6,53
6,41
9
7,29
7,30
7,15
7,11
6,95
6,90
6,86
6,82
6,78
6,75
6,72
6,69
6,67
6,65
6,63
6,60
6,59
6,58
6,51
10
7,63
7,35
7,24
7,05
6,95
6,91
6,87
6,85
6,83
6,81
6,79
6,77
6,75
6,73
6,71
6,70
6,68
6,63
6,52
4.1.1.2.5. Метод прямого сравнения (критерий Тьюки)
В [396] рассмотрен критерий, основанный на последовательности статистик
\Xj - X
сравнивающих попарно все исследуемые средние Xj с общим средним. В этом
случае s2 является оценкой общей дисперсии с / = &(п — 1) степенями свободы,
т. е.
-1 к п
-\2
j = li=l
Если Tj < Та для всех j = 1, ..., к, где Та —критическое значение статистики,
приведенное в табл. 125, то нулевая гипотеза не отклоняется. Нарушение нера-
неравенства при любом значении j отклоняет нулевую гипотезу. Предполагается, что
дисперсии s1- всех выборок статистически неразличимы. Этот критерий является
альтернативой дисперсионному анализу (см. раздел 4.1.1.2.3).
Задача 194. В условиях задачи 190 проверить гипотезу равенства средних методом
прямого сравнения при доверительной вероятности а = 0,95.
Имеем
= 26,375; х2 = 29,25; х3 = 27,125; х4 = 24,625; х5 = 31,025;
S2 =
1
= 274,35257.
404
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 125
Критические значения Та критерия Тьюки [396]
/
к
3
4
5
6
7
8
9
10
Доверительная вероятность а = 0,90
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
30
60
120
3,164
2?813
2,629
2,516
2,440
2,385
2,344
2,312
2,286
2,265
2,247
2,232
2,219
2,208
2,198
2,190
2,182
2,175
2,133
2,092
2,068
3,094
2,877
2,744
2,654
2,589
2,540
2,502
2,472
2,447
2,426
2,408
2,393
2,379
2,368
2,357
2,348
2,340
2,290
2,241
2,193
3,054
3,032
2,806
2,734
2,679
2,636
2,602
2,574
2,551
2,531
2,514
2,499
2,486
2,474
2,464
2,455
2,398
2,343
2,289
2,924
2,846
2,787
2,740
2,703
2,673
2,647
2,626
2,607
2,591
2,577
2,565
2,553
2,544
2,482
2,422
2,363
3,020
2,937
2,875
2,826
2,786
2,754
2,727
2,704
2,684
2,667
2,652
2,638
2,626
2,616
2,550
2,486
2,423
3,015
2,949
2,898
2,856
2,822
2,794
2,769
2,748
2,730
2,715
2,700
2,688
2,677
2,607
2,539
2,473
3,014
2,960
2,917
2,881
2,852
2,826
2,804
2,786
2,769
2,754
2,741
2,730
2,657
2,586
2,516
3,015
2,970
2,934
2,903
2,876
2,854
2,834
2,817
2,802
2,788
2,776
2,700
2,627
2,554
Доверительная вероятность а = 0,95
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
30
60
120
4,148
3,565
3,254
3,068
2,944
2,857
2,791
2,741
2,700
2,667
2,640
2,617
2,597
2,580
2,565
2,552
2,540
2,530
2,465
2,404
2,367
3,889
3,527
3,311
3,168
3,066
2,990
2,931
2,884
2,845
2,813
2,786
2,763
2,743
2,726
2,711
2,697
2,685
2,610
2,538
2,497
3,724
3,486
3,327
3,215
3,131
3,066
3,014
2,971
2,936
2,906
2,881
2,859
2,840
2,823
2,808
2,794
2,711
2,632
2,587
3,622
4,453
3,332
3,242
3,172
3,116
3,070
3,032
3,000
2,973
2,949
2,928
2,910
2,894
2,879
2,790
2,704
2,656
3,556
3,428
3,333
3,259
3,200
3,151
3,111
3,077
3,048
3,023
3,001
2,982
2,965
2,949
2,854
2,764
2,713
3,510
3,410
3,333
3,271
3,220
3,178
3,143
3,112
3,086
3,063
3,043
3,025
3,009
2,909
2,814
2,761
3,478
3,397
3,333
3,281
3,237
3,200
3,168
3,141
3,117
3,096
3,077
3,060
2,957
2,857
2,803
3,454
3,388
3,334
3,289
3,250
3,219
3,189
3,164
3,143
3,123
3,106
2,998
2,896
2,839
4.1] Сравнение параметров распределений 405
Вычисляем
|26,375-31,025| |29,25 - 31,025|
Tl= lfisfi2 5-1 =°'888' Т2= 5,23768 =°'339'
|27,125-3?W| = 124,625 - 31,0251 =
5,23768 ' ' 5,23768
т |47-те - 3!:025
5,23768 '
Для / = к • (п — 1) = 5 • (8 — 1) = 35 степеней свободы, а = 0,95 и к = 5 из табл. 125
имеем То,95 = 2,6. Так как Т% = 3,193 > То,95 = 2,6, нулевая гипотеза равенства средних
отклоняется, так как ж5 значимо отклоняется от х.
Этот вывод совпадает с заключением, полученным при использовании критерия
Полсона (задача 193).
4.1.1.2.6. Критерий „стьюдентизированного" максимума
(обобщенный критерий Тьмжи)
Критерий основан на использовании верхней а • 100%-й критической точки
та^*,и модуля „стьюдентизированного" максимума max — с параметрами
к* = — и г/ = Aj (п — 1). Подробно критерий рассмотрен в [397, 398].
Средние г-й и j-й выборок признаются не различающимися, если
,г?3 = 1? • • • 7 ^5 г Т 3)'
Здесь, как и ранее, s2 является оценкой дисперсии объединенной выборки с
у = к(п — 1) степенями свободы, т. е.
i к п
Таким образом, нулевая гипотеза равенства всех j = 1, ..., к средних не откло™
fc(fc-l)
няется только тогда, когда все —- пар средних удовлетворяют вышеприведен™
ному неравенству.
Таблицы значений та^*,и опубликованы в [399, 400], наиболее полные таблицы
содержатся в [398]. Фрагмент этой таблицы воспроизведен в табл. 126.
Задача 195. В условиях задачи 190 проверить гипотезу равенства средних критерием
„стьюдентизированного" максимума при доверительной вероятности а = 0,95.
Имеем
п = 8; к = 5; и = к • (п - 1) = 35; хг = 26,375; х2 = 29,25; ж3 = 27,125;
ж4 = 24,625; ж5 = 47,75; s = 16,563.
Вычисляем = = 10 значений Мц:
2 3 3
Ml2 =
406
Проверка гипотез о значениях параметров распределений
[Гл.4
и далее по аналогии
М13 = 0,091; Мы = 0,212; М15 = 2,585; М23 = 0,257; М24 = 0,559;
М25 = 2,237; М34 = 0,302; М35 = 2,494; М45 = 2,797.
Из табл. 126 для v = k • (п — 1) = 35, & = 5 и а = 0,95 получаем (интерполяцией)
majk*,u = 2,97. Так как все значения Mij < 2,97, следует принять нулевую гипотезу
равенства средних. Необходимо помнить, что применение этого критерия предполагает
равенство (стохастическое ) выборочных дисперсий сравниваемых выборок.
Таблица 126
Критические значения критерия та,к*,и
„стьюдентизированного" максимума [398]
к
к*
5
7
10
i
12
16
20
24
30
60
120
Доверительная вероятность а = 0,95
3
4
5
6
7
8
9
10
12
14
16
18
20
3
6
10
15
21
28
36
45
66
91
120
153
190
3,40
3,93
4,31
4,61
4,85
5,06
5,23
5,38
5,64
5,85
6,03
6,18
6,31
3,05
3,49
3,80
4,05
4,25
4,42
4,57
4,69
4,91
5,08
5,23
5,36
5,47
2,83
3,20
3,47
3,68
3,85
3,99
4,12
4,22
4,41
4,56
4,69
4,80
4,90
2,75
3,09
3,34
3,54
3,77
3,83
3,95
4,05
4,22
4,37
4,49
4,59
4,68
2,65
2,97
3,20
3,38
3,52
3,64
3,75
3,84
4,00
4,13
4,24
4,33
4,42
2,59
2,90
3,11
3,28
3,42
3,53
3,63
3,72
3,87
3,99
4,09
4,18
4,26
2,56
2,85
3,06
3,22
3,35
3,46
3,56
3,64
3,78
3,90
4,00
4,08
4,16
0,52
2,80
3,00
3,16
3,29
3,39
3,48
3,56
3,70
3,81
3,90
3,98
4,06
2,45
2,76
2,90
3,04
3,16
3,25
3,33
3,41
3,53
3,63
3,71
3,78
3,85
2,42
2,72
2,85
2,98
3,09
3,18
3,19
3,33
3,44
3,54
3,62
3,68
3,75
Доверительная вероятность а = 0,90
3
4
5
6
7
8
9
10
12
14
16
18
20
3
6
10
15
21
28
36
45
66
91
120
153
190
2,78
3,24
3,58
3,84
4,05
4,22
4,37
4,51
4,73
4,91
5,06
5,19
5,30
2,55
2,96
3,25
3,48
3,66
3,81
3,94
4,06
4,25
4,41
4,54
4,66
4,76
2,41
2,77
3,03
3,23
3,39
3,53
3,64
3,75
3,92
4,06
4,18
4,28
4,37
2,36
2,70
2,95
3,14
3,29
3,42
3,53
3,63
3,79
3,92
4,04
4,13
4,22
2,29
2,62
2,84
3,02
3,16
3,29
3,39
3,48
3,63
3,76
3,86
3,95
4,03
2,25
2,57
2,79
2,96
3,09
3,21
3,31
3,39
3,54
3,66
3,76
3,85
3,92
2,23
2,53
2,75
2,91
3,04
3,16
3,25
3,33
3,48
3,59
3,69
3,77
3,85
2,21
2,50
2,71
2,87
3,00
3,10
3,20
3,28
3,41
3,52
3,62
3,70
3,77
2,16
2,44
2,63
2,78
2,90
3,00
3,09
3,16
3,29
3,39
3,47
3,55
3,62
2,14
2,41
2,60
2,74
2,85
2,95
3,03
3,10
3,22
3,32
3,40
3,47
3,54
4.1.1.2.7. Критерий Шеффе
Среди к средних значений, предварительно упорядоченных по величине:
%1 ^ ^2 ^ • •. ^ Хк, производится (к — 1) сравнений. Например, для к = 5 произво™
дится к — 1 = 4 множественных сравнения
Если при этом будет превышена критическая разница, то нулевая гипотеза
о равенстве средних /^ и /ij отклоняется.
4.1] Сравнение параметров распределений 407
Шеффе [401] предложил использовать в качестве критического значения вели™
чину
где
к п -I к -|
? ? ^ ~
к (п - 1) ? ? ^ ^ ' ^=fc?^' XJ =
F<x(fii /2) — а-квантиль распределения Фишера с Д = А; — 1 и /2 = А:(тг — 1) сте-
степенями свободы (может быть взята из таблиц или аппроксимирована — см. раз™
дел 1.1.10). Критерий Шеффе является грубым критерием и особенно пригоден
тогда, когда имеется подозрение о неравенстве дисперсий s2- (j = 1, ..., к) между
собой.
Задача 196. В условиях задачи 190 проверить нулевую гипотезу равенства средних
критерием Шеффе при доверительной вероятности а = 0,95.
Имеем
п = 8; к = 5; хг = 26,375; х2 = 29,25; ж3 = 27,125; х4 = 24,625; ж5 = 47,75;
s = 16,563; Д = fc - 1 = 4; /2 = fc • (п - 1) = 35.
Из таблиц ^-распределения для а = 0,95, Д = 4 и Д = 35 находим .Fo,95D; 35) = 2,65.
/24
Следовательно, D\ = 16,563 • 4 / • 2,65 = 26,963.
Имеем ж5 - Ж1 = 47,75 - 24,625 = 23,125 < Вг = 26,963.
Очевидно, что дальнейшая проверка не имеет смысла, и критерий Шеффе не откло-
отклоняет нулевую гипотезу.
4.1.1.2.8. Критерий Стьюдента-Ньюмена-Кейлса
Критерий предложен в [402, 403]. Алгоритм его применения аналогичен крите-
критерию Шеффе (см. раздел 4.1.1.2.7), отличаясь от него только критическим значением
разности средних.
В критерии Стьюдента^Ньюмена^Кейлса критическая разность средних равна
D2 = J-q(k*J,a),
где g(fc*,/, а)—множитель, значения которого приведены в табл. 127; к*—коли-
к*—количество средних значений между сравниваемыми, включая сами эти значения (на-
(например, для разности ж5 — ^4 имеем к* = 2, а для разности х5 — ^2 имеем к* =4);
-< к п
f = к(п — 1) —число степеней свободы при оценке s2; s2 = 77 тт У2 У2 (xij ~~ %) 5
к{<п~^ j=n=i
1 к п
j = l i=l
Задача 197. В условиях задачи 190 проверить гипотезу равенства средних критерием
Стьюдента-Ньюмена-Кейлса при доверительной вероятности а = 0,95.
Из табл. 127 для х5 - хг(к* = 5), / = к • (п ~~ 1) = 35 и а = 0,95 имеем дE,35,0,95) =
= 4,07. Тогда D2 = q • ~4= = 4'07' г^563 = 23,833.
Vn V8
жб^жх = 47,75^24,625 = 23,125 « D2 = 23,833, нулевая гипотеза отклоняется.
408 Проверка гипотез о значениях параметров распределений [Гл. 4
4.1.1.2.9. Критерий Дункана
Дункан [404] предложил модификацию критерия Стьюдента-Ыьюмена-Кейлса,
заменив уровень значимости а на а' = 1 — A — а)
Метод Дункана дает наименьшие допуски для разности средних и наиболее
широко применим. Он позволяет „уловить" различие между средними, которые
„пропускает" критерий Стьюдента—Ньюмена—Кейлса. Алгоритм применения кри-
критерия Дункана D$ идентичен алгоритму критерия Стьюдента—Ньюмена—Кейлса
(см. раздел 4.1.1.2.8), отличаясь от него только использованием вместо множи-
множителя q(k*1f1a) множителя g(fc*,/, а;), значения которого для а = 0,95 приведены
в табл. 128.
Задача 198. В условиях задачи 190 проверить гипотезу равенства средних критерием
Дункана при доверительной вероятности а = 0,95.
Из табл. 128 для х5 — х\ (к* = 5) имеем при f = к • (п — 1) = ЗЪ дE; 35; 0,95) = 3,18.
m ^ s 3,18 • 16,563
Тогда D3 = q • — = ¦=?¦ = 18,622.
\/п V8
Так как х% — х\ = 47,75 — 24,625 = 23,125 > ТK = 18,622, нулевая гипотеза отклоня-
отклоняется (хъ признается с вероятностью 0,95 большим, чем х\).
Для х5 - х2 (к* = 4) имеем q D; 35; 0,95) = 3,12 ш D3 = -?—'-=1 = 18,270.
v 8
Так как х% — Х2 = 47,75 — 26,375 = 21,375, то и разница между х§ и Х2 признается
значимой. Далее по аналогии для
х5 - х3 (к* = 3) имеем D3 = 3'02'^563 = 17,684.
v 8
Имеем xs — х3 = 47,74 — 27,125 = 20,625 > D3l что также позволяет прийти к заклю-
заключению о значимости разности между х§ и х3.
Для х5 - х3 имеем D3 = 16,748 и х5 - х4 = 47,75 - 29,75 = 18,0 > D3 = 16,748.
Таким образом, х§ значимо больше, чем xi, X2, х3 и аЦ- Можсно показать, что
остальные пары средних критерием Дункана статистически не различимы.
Отметим, что, в отличие от ряда ранее использовавшихся критериев, критерий
Дункана, как более чувствительный критерий, отклонил нулевую гипотезу достаточно
уверенно.
4.1.1.2.10. Критерий Л инка-Уоллеса
Критерий предложен в [405, 406] и достаточно полно изложен в [9]. Его приме-
применение предполагает нормальность распределения xij, равенство дисперсий s? и рав™
ные объемы сравниваемых выборок (п). Обозначим через Rj = max хц — mm Xij
размах j-й выборки, а через R = max Xj — min x* размах средних к выборок.
Нулевая гипотеза равенства средних отклоняется, если
К = — > К(п, к, а),
где К(п,к^а)—критические значения, приведенные в табл. 129.
к
У j ^3
Если Xi — Xj > К(п, Aj, a) , то с вероятностью а средние х\ и Xj признаются
статистически различимыми.
4.1]
Сравнение параметров распределений
409
ИГ
s
И
1
s
о- а
к в
Ш
о
CM
on
гЧ
CO
CM
о
О)
сю
со
Ю
со
см
см
т-Ч
т-Ч
00
ел
о
т-Ч
69
о
т—1
35
о
т-Ч
ю
О5
О5
46
ел
00
т-Ч
ел
ю
00
00
48
00
04
00
О
ю
ь-
82
CD
91
ю
о
ю
-xf
СО
СО
СМ
ел
ео
о
О5
OS
b-
00
52
00
т—1
см
00
83
i>
60
ь-
LO
СО
ь-
05
т-Ч
ь~
CD
О5
СМ
СО
CD
Ю
04
Ю
93
СО
т-Ч
СМ
00
00
о
00
83
ь-
60
ь~
см
ОО
ь-
99
CD
80
CD
00
LO
СО
33
CD
03
CD
b-
CO
LO
22
ю
о
CO
63
CO
Ю
СЛ
Ю
b-
CO
b-
CM
b-
03
b-
O5
b-
CD
49
CD
32
CD
CM
t—1
CD
90
ю
63
ю
о
CO
Ю
90
-xf
34
-xf
46
CO
CD
b-
T—1
b-
CM
о
b-
85
CO
66
CD
CO
CO
CO
T—1
CD
О
О
CD
CM
GO
LO
T—1
CD
LO
36
LO
CO
о
LO
68
CD
T—1
34
CO
b-
b-
00
CD
00
b-
CD
b-
Ю
CO
39
CD
GO
t—1
CO
92
ю
b-
b-
Ю
о
CO
Ю
40
Ю
b-
t—1
Ю
O5
00
'xf
53
о
26
CO
00
CD
CD
T—1
Ю
CD
36
CD
O5
T—1
CD
00
O5
LO
Ю
Ю
Ю
CO
Ю
24
Ю
02
Ю
41
-xf
95
CO
О
CM
CO
OS
b-
CD
CO
CD
CD
т-Ч
CO
03
CD
CO
00
LO
60
ю
46
ю
о
CO
LO
CM
t—1
Ю
t—1
LO
CD
33
00
00
CO
LO
т-Ч
CO
О
CO
CO
CD
О
CM
CO
06
CO
90
LO
T—I
b-
LO
49
LO
LO
CO
Ю
О
CM
LO
03
LO
82
b~
LO
26
82
CO
t—1
T—i
CO
T—i
T—1
CM
CD
O5
О
CO
95
LO
80
LO
T—!
CO
LO
39
LO
b-
CM
LO
CM
г—1
LO
95
LO
b-
^
т-Ч
LO
20
b-
b-
00
08
CO
CM
г—1
t—1
CD
O5
CD
Ю
86
ю
t—1
[>
Ю
CO
Ю
Ю
32
Ю
СЛ
T—1
Ю
Ю
о
Ю
00
00
69
-xf
Ю
-f
Ю
t—1
-xf
CO
b-
CO
05
CO
CO
CO
о
CD
т-Ч
O5
LO
OS
b-
LO
64
LO
CO
LO
25
LO
CO
T—1
LO
O5
O5
83
64
т-Ч
i—1
t—1
о
b-
CO
03
CO
CD
Ю
LO
00
LO
CM
b-
LO
57
Ю
о
LO
20
Ю
08
ю
O5
00
b-
^
CD
LO
^
b-
OO
08
67
00
01
CO
Ю
о
O5
Ю
b-
LO
66
LO
52
Ю
LO
CO
LO
Ю
t—1
LO
03
Ю
О
O5
b~
CD
LO
^
CO
CO
05
-xf
65
CO
О
о
CO
CD
00
Ю
CO
b-
LO
т-Ч
CD
LO
47
ю
т-Ч
CO
LO
т—1
т-Ч
Ю
99
CD
00
70
CM
LO
о
CO
CM
о
63
CO
98
CM
b-
СЛ
b-
Ю
O5
со
Ю
b-
Ю
Ю
43
Ю
b-
CM
Ю
07
Ю
96
CM
00
67
49
GO
CM
-xf
о
о
61
00
97
CM
00
LQ
b-
LO
LO
CD
LO
CO
LO
LO
39
LO
CO
CM
LO
04
LO
92
C5
64
47
LO
CM
98
CO
O5
LO
CO
96
CM
OS
T—1
b-
Ю
т-Ч
CD
LO
49
LO
36
Ю
о
CM
LO
T 1
о
Ю
90
b-
b-
62
45
CO
CM
96
CO
00
LO
CO
95
CM
о
CO
LO
CO
Ю
LO
43
Ю
30
LO
Ю
T—I
LO
96
85
CM
b~
58
T—1
о
CM
93
CO
Ю
LO
CO
93
CM
CM
CD
LO
Ю
49
LO
38
LO
25
ю
о
т-Ч
LO
92
81
00
CD
54
37
b-
Т-Ч
90
CO
CO
LO
00
92
CM
Ю
Ю
Ю
CD
Ю
34
ю
T—1
CM
Ю
CD
О
Ю
O5
00
-xf
00
b-
^
Ю
CD
-xf
t—1
Ю
34
-xf
T 1
¦"xf
00
00
CO
t—1
Ю
CO
t—1
СЛ
CM
CD
T—1
LO
LO
CM
LO
О
CO
Ю
GO
T—I
Ю
CO
О
LO
CD
00
^
Ю
b-
^
CM
CO
48
CM
CO
^
CM
т-Ч
^
CD
00
CO
О
LO
CO
90
CM
00
b-
-xf
Ю
00
CO
LO
b~
CM
LO
LO
Ю
о
о
LO
82
CM
b-
о
CD
"xt1
46
30
о
т-Ч
85
CO
49
00
89
CM
о
CD
CO
Ю
b~
CM
Ю
CD
T—1
Ю
04
ю
о
O5
73
-xf
63
CM
Ю
-xf
39
CO
CM
-xf
О
"xf
79
CO
44
CO
86
CM
о
OS
CM
LO
о
CM
LO
о
т-Ч
LO
99
LO
CO
"хЧ
69
00
LO
^
b-
"хЧ
34
OS
т-Ч
О
о
CD
b-
CO
41
CO
84
CM
о
CM
Ю
Ю
т—1
Ю
06
Ю
94
гЧ
00
'xf
65
Ю
Ю
-xf
'xf
'xf
31
CD
t—1
-xf
GO
O5
CO
-xf
b-
CO
о
'xf
00
83
CM
о
CO
т-Ч
Ю
о
LO
95
84
56
-xf
CO
CO
24
о
т-Ч
CM
O5
CO
68
CO
36
CO
80
CM
о
т-Ч
410
Проверка гипотез о значениях параметров распределений
[Гл.4
00
CM
к ю
VO О"
о
оо
со
^
см
о
аз
оо
ь-
ю
ю
«
со
см
см
LO
-xf
52
см
LO
см
ю
-xf
см
ю
'xf
см
ю
^
см
ю
-xf
см
ю
'xf
см
LO
см
ю
'xf
см
LO
'xf
см
Ю
^
см
ю
'xf
о
LO
'xf
СО
СО
о
"xf
03
03
00
о
СО
о
03
-xf
СО
о
"xf
СО
о
03
00
о
СО
о
03
-xf
о
93
00
т-Ч
00
СО
т—1
00
СО
т-Н
00
СО
т-Н
00
СО
т-Н
00
СО
т-Ч
00
СО
т-Ч
00
СО
т—1
00
СО
т—1
00
СО
т-Н
00
СО
т-Н
00
СО
80
СО
ю
ь-
СО
64
СО
ю
о
00
СО
80
ео
о
ь-
00
о
СО
о
О0
о
СО
о
00
о
t-
ео
о
00
аз
CD
ОО
00
СО
О0
65
СО
аз
ю
00
СО
-xf
ео
СО
СО
CD
СО
63
00
63
СО
СО
СО
СО
00
СО
00
63
ОО
СО
со
СО
СО
со
00
см
CD
СО
т-Н
СО
СО
аз
ю
00
Ю
ю
ОО
00
-xf
00
СО
СО
00
Ю
СО
58
00
00
Ю
00
00
ю
СО
00
ю
00
00
LO
СО
00
ю
СО
00
Ю
00
ь-
ю
00
ю
ю
00
СМ
LO
00
48
СО
О
СО
CD
СМ
00
00
Ю
Ю
СО
55
СО
ю
LO
СО
LO
ю
СО
Ю
Ю
СО
Ю
ю
СО
Ю
СО
Ю
СО
СМ
LO
СО
О
ю
СО
'xf
СО
42
СО
СО
СО
О
см
СО
аз
СО
Ю
СО
53
СО
00
Ю
СО
СО
Ю
СО
СО
ю
00
СМ
ю
ОО
СМ
ю
СО
о
ю
00
аз
'xf
СО
CD
СО
СО
00
38
ОО
О5
СМ
00
ю
1—1
СО
О
т-Ч
LO
СО
т—1
LO
ОО
LO
00
т-Н
ю
СО
ю
ео
о
LO
00
49
СО
00
ОО
46
00
44
00
О
-xf
ео
34
00
СО
см
О0
т—1
1—1
00
1—1
о
ю
СО
50
СО
о
ю
СО
о
ю
СО
о
ю
СО
00
-xf
СО
47
СО
СО
СО
"xf
СО
т-Н
СО
t-
СО
СО
т-Ч
СО
СО
СМ
см
СО
08
СО
СМ
аз
со
49
СО
49
СО
аз
СО
00
ОО
ь-
ОО
СО
СО
СО
СМ
СО
аз
оо
ОО
ю
СО
ОО
аз
см
СО
О
СМ
ОО
06
ОО
СО
00
СО
48
СО
00
СО
48
СО
ь-
00
46
СО
44
СО
СО
СО
О
СО
ь-
ОО
СО
СО
СО
00
1>
СМ
00
00
СО
03
00
00
"¦xf
СО
48
00
00
00
48
СО
СО
00
45
СО
43
СО
т—1
00
39
СО
СО
ОО
00
СО
СО
LO
СМ
00
СО
ОО
01
00
Ю
00
СО
48
ео
00
СО
ь-
00
со
О0
СО
СМ
СО
О
ео
00
СО
СО
00
ОО
о
СО
ОО
СМ
СО
00
О
о
ео
СО
О0
СО
48
СО
ь-
'xf
СО
CD
СО
Ю
00
СО
СО
т-Ч
СО
аз
00
СО
ь-
СО
СО
СО
СО
СО
00
СМ
00
СМ
см
ОО
СО
СО
00
аз
см
00
ь-
00
ь-
00
46
СО
ео
см
00
40
СО
00
ео
оо
36
00
СМ
СО
00
ь-
см
ео
т-Ч
СМ
00
СМ
О0
97
см
00
СО
47
СО
ь-
СО
СО
СО
СО
СМ
СО
40
СО
00
СО
СО
35
СО
т-Н
СО
СО
со
СМ
СО
О
СМ
СО
т-Ч
СО
96
см
аз
ь-
00
47
ОО
46
СО
LO
СО
'xf
'xf
ОО
т-Ч
СО
аз
ОО
СО
ь-
00
О0
СО
СО
О
ОО
ОО
'xf
см
ОО
аз
т-Ч
СО
О
ОО
95
см
о
¦*xf
СО
46
СО
46
СО
44
СО
СМ
00
39
СО
ь-
00
СО
СО
СМ
00
СО
00
СМ
СО
СО
СМ
00
СО
т-Ч
СО
О
СО
92
см
"xf
СО
46
СО
ю
СО
СО
'xf
СО
о
'xf
СО
СО
СО
ю
СО
СО
СМ
СО
СО
аз
см
СО
ю
см
СО
о
см
СО
СО
т-Н
СО
'xf
о
СО
89
см
о
ь-
00
46
ОО
'xf
СО
СМ
'xf
СО
аз
СО
ОО
LO
СО
СО
СО
ОО
СО
о
ОО
ОО
ь-
см
СО
см
см
ОО
ь-
т—1
ОО
о
т-Ч
ОО
т-Ч
о
ОО
86
см
о
00
45
СО
ео
00
т-Н
-xf
СО
ь-
00
ео
33
СО
т-Ч
00
СО
00
СМ
ОО
"xf
см
00
О
см
00
-xf
т-Ч
ео
07
00
00
аз
см
00
00
СМ
о
"xf
СО
45
СО
СМ
СО
СО
СО
со
СО
СО
т-Ч
СО
СО
аз
см
СО
ю
см
СО
СМ
ся
СО
т-Н
СО
см
т-Ч
СО
04
СО
ю
аз
см
80
см
о
т-Н
4.1]
Сравнение параметров распределений
411
СЗ
СМ
сб
и
ф
0
х
—1
О,
крите
для
—N
ш
К
го
ф
—
S
II
d
1
0
х
§
а
ш
д
п
Л
е;
ш
S
а
ф
0
S
Oi
п
о
ио
со
см
о
о
00
Jv_
со
ю
^ф
со
см
ь-
см
о
о
СО
о
СО
СО
О
00
СО
О
СП
О
т-Н
ю
о
CD
LO
О
см
со
о
о
о
о
00
о
СЗ
о
т-Н
т-Ч
1,44
о
СЗ
см
ю
см
о
00
см
о
т-Ч
СО
о
ю
СО
о
о
о
г-
о
т-Ч
ю
о
ь-
ю
о
со
СО
о
см
о
00
О
т-Ч
О
т-Ч
ю
см
см
CD
ю
см
О
ь-
см
о
о
СО
о
СО
О
СЪ
СО
О
»о
о
о
ю
о
ю
Ю
о
т—1
CD
О
о
IN-
о
см
00
О
СО
аз
о
аз
СО
LQ
СО
СМ
О
ь-
см
о
о
СО
о
СО
О
СЪ
СО
О
ю
О
О
О
ю
ю
о
т-Ч
CD
О
со
СО
о
о
00
о
ю
аз
о
о
ю
CD
Ю
СМ
о
ь-
см
о
о
СО
о
СО
о
съ
СО
О
ю
о
о
ю
о
ю
ю
о
1—1
СО
о
аз
со
о
о
00
о
ю
аз
о
*!
а>
ю
см
о
00
см
о
СО
о
Ю
СО
О
СЪ
СО
О
СО
О
О
ю
о
ю
ю
о
см
со
о
о
о
т-Ч
00
о
со
СЗ
о
00
ч.
00
ю
см
о
00
см
о
т-Ч
СО
о
ю
СО
о
<-)
о
о
т-Ч
ю
о
СО
ю
О
см
СО
О
т-Ч
JN-
О
СМ
СО
О
h-
аз
о
аз
о
ю
аз
СО
см
о
аз
см
о
см
СО
О
CD
СО
О
т-Ч
о
г-
о
см
ю
о
ь-
ю
о
со
CD
О
СМ
in
о
со
00
о
00
аз
о
1,20
см
ю
о
1^
см
о
аз
см
о
см
СО
О
со
СО
О
т-Ч
"*чР
о
ОО
О
СМ
ю
о
00
ю
О
^
СО
О
СО
IN
о
00
О
СЪ
СО
о
см
см
ю
т—|
г-
см
о
о
СО
о
СО
СО
О
г-
СО
О
ГМ
о
СТ)
О
СО
Ю
О
00
ю
О
ю
CD
О
^
IN-
О
ю
00
О
т-Ч
О
СО
СМ
СО
LQ
СМ
ь-
см
о
о
СО
о
СО
СО
О
Г-
СО
О
ГМ
о
о^
о
LQ
о
О)
LO
о
со
CD
О
ю
JN
о
CD
00
О
СМ
о
1,25
00
ю
СО
00
см
О
О
СО
О
^
СО
О
00
СО
О
СО
О
О
ю
О
Ю
ю
О
о
со
о
h-
CD
О
СО
о
00
О
СО
О
со
см
о
СО
00
см
О
ч—|
СО
О
^
СО
О
00
СО
О
О
т-Ч
ю
о
ю
ю
о
ч—|
СО
о
ОО
СО
О
г-
IN-
О
аз
00
о
»о
о
00
СМ
см
CD
а»
см
о
т-Ч
СО
О
ю
СО
О
СО
СО
О
О
см
ю
о
со
ю
о
см
со
о
съ
CD
о
00
о
о
СО
о
СО
О
о
СО
CD
CD
аз
см
о
см
СО
О
ю
СО
О
аз
СО
О
»П
О
СМ
LO
о
г-
ю
о
СО
СО
О
о
IN
°
аз
IN
о
т-Ч
аз
о
00
о
1,31
СО
CD
сз
см
о
см
СО
о
со
СО
о
о
о
СО
о
со
ю
о
00
ю
о
со
о
1—1
JN
°
О
00
о
см
СЗ
О
СТ)
О
СО
СО
00
CD
00
О
СО
О
СО
СО
О
СО
СО
О
т-Ч
О
со
О
ю
о
аз
ю
о
со
О
см
JN-
О
т-Ч
00
О
СО
аз
о
о
т-Ч
ю
СО
О
JN-
оз
о
СО
О
СО
СО
О
IN-
СО
О
т-Ч
О
IN-
О
LQ
О
СЗ
LQ
о
ю
со
о
СО
JN-
О
СМ
00
О
ю
СЗ
о
см
т-Н
1,36
см
ь-
о
СО
о
СО
о
т-Ч
о
со
о
гм
ю
о
о
CD
о
со
со
о
СО
IN
О
т—1
00
О
т-Н
о
о
ю
о
т-Ч
см
см
ю
см
аз
о
г-~
СО
О
о
о
о
о
ю
о
ю
о
СО
со
о
см
ь-
о
аз
In
О
00
00
О
аз
аз
о
т-Ч
т-Ч
ю
СО
СО
со
00
О
СМ
о
СЗ
СО
О
СО
о
00
О
СО
ю
о
т-Ч
СО
О
т-Н
о
ь-
ь-
о
ю
00
о
СЗ
о
со
о
т—1
см
см
т-Ч
ю
IN
00
см
см
о
о
ю
о
ю
ю
о
о
CD
о
г-
СО
о
г-
IN
о
съ
00
о
1^
аз
о
ь-
о
т-Ч
съ
т-Ч
т-Ч
СО
1—1
ю
ю
т-Ч
со
00
2,23
т—|
00
см
о
т-Ч
412 Проверка гипотез о значениях параметров распределений [Гл. 4
Задача 199. В условиях задачи 190 проверить гипотезу равенства средних критерием
Линка-Уоллеса при доверительной вероятности а = 0,95.
Имеем
#i = 45 - 11 = 34; R2 = 52 - 15 = 37; R3 = 58 - 8 = 50; R4 = 61 - 4 = 57;
5
R5 = 70 ~~ 24 = 46; ]P Rd = 224; Д = max% - min% = 47,75 - 24,625 = 23,125.
i=i
Вычисляем
= 8-23,125 =
224 '
Из табл. 129 для а = 0,95, fc = 5 и п = 8 имеем К(8, 5, 0,95) = 0,81.
Так как К = 0,826 > /?"(8,5,0,95) = 0,81, нулевая гипотеза отклоняется.
Находим критическую разницу средних
Видим, что Х5 — х\ = 47,75 — 24,625 = 23,125 превосходит эту величину.
Следовательно, разность между ж 5 и х\ признается значимой.
4.1.1.3. Сравнение двух дисперсий
Для двух выборок нормально распределенных случайных величин ж1? ..., хп
и 2/1, ..., ут необходимо проверить гипотезу равенства дисперсий о~\ и <т|, опираясь
на их выборочные оценки s\ и s\.
4.1.1.3.1. Критерий Фишера
Если выборочными оценками максимального правдоподобия дисперсий являются
1 п -I га
2
то статистика критерия Фишера записывается как F = -j.
s2
При справедливости нулевой гипотезы Ы®: ®f = o\ статистика критерия имеет
распределение Фишера (см. раздел 1.1.10) с Д = п — 1 и /2 = m ^ 1 степенями
свободы, где п и т — объемы сравниваемых выборок.
Если F > Fi+g (n — 1; ?тг — 1) ж F < Fi~a (п — 1; ?п — 1), то нулевая гипотеза от-
2 2
клоняется в пользу альтернативы Hi: а\ ф (г\.
Если F > Fa(n — 1; ?п — 1), то нулевая гипотеза отклоняется в пользу альтер-
альтернативы Н[: af > <j\ (a — доверительная вероятность). В числителе всегда должна
стоять большая по величине из двух сравниваемых дисперсий.
Критерий Фишера очень чувствителен к отклонениям от нормальности
[407^409] распределения а^, у%. Его устойчивость к отклонениям от нормальности
может быть повышена соответствующей корректировкой степеней свободы [87].
Вместо /i и /2 в этом случае используются степени свободы
f[=df и f2 = bf, где
п + m — F2 — 3)
= 1
4.1] Сравнение параметров распределений 413
В дальнейшем процедура проверки нулевой гипотезы не отличается от обычного
.F-критерия. Критические значения ^статистики приведены в таблицах (ссылки на
таблицы см. в разделе 1.1.10).
Задача 200. Имеются две выборки нормально распределенных случайных величин
(п = т = 10):
хц 2,1; 3,1; 4,8; 6,1; 7,4; 8,5; 10,1; 12,1; 14,0; 15,6;
уц 4,6; 6,1; 8,2; 9,8; 9,9; 10,4; 13,1; 14,5; 16,1; 19,1.
Необходимо проверить гипотезу равенства дисперсий Но: a2 = <j\ против альтерна-
альтернативы Hi: а\ ф о\ при доверительной вероятности а = 0?95.
Имеем
ж = 8,38; у =11,18;
1 10 -I 10
¦4 = j^j ¦ Е (х> - *J = 20>757; *2 = j^j ¦ Е (у* - уJ = 20>419-
Далее F = -^ = —' = 1,016. Из таблиц находим
^ si 20,419 '
F1+a (n - 1; т - 1) = Fi+o!95 A0 - 1; 10 - 1) = F0;975(9; 9) = 4,03.
2 2
Так как F = 1,016 < Fo,975 (9,9) = 4,03, нулевая гипотеза не отклоняется.
Рассмотрим теперь критерий со скорректированными степенями свободы. Имеем
ю ю ю
]Г (хг - xf = 186,813; ]Г (уг - уJ = 183,771; ]Г (Xi - жL = 6439,996;
г=1 г=1 г=1
= 7281,725; Ь2 = A0 + 10) • 6439^96 + 7281^ = lj99832;
' ' 1 ^ A86,813+ 183,771J
d = { 1 + 0,5 • 10 + 1°4 • A,99832 - 3) 1 = 1,802.
[ 10 + 10-3-A,99832-3) v 7J
Окончательно имеем /{ = d • /i = 1,802 • 9 = 16,22 и f2 = d • f2 = 16,22.
Из таблиц [87] для дробных степеней свободы и = 0,975 имеем
F0!975A6,22; 16,22) « 2,65. Так как F = 1,016 < Fo,975 = 2,65, нулевая гипотеза не
отклоняется и в этом случае.
4.1.1.3.2. Критерий Романовского [207]
Статистика критерия:
т-3 si
Если R ^ 3, то нулевая гипотеза равенства дисперсий отклоняется с достовер-
достоверностью не менее 0,89.
Задача 201. Для данных задачи 200 проверить гипотезу равенства дисперсий крите-
критерием Романовского.
Имеем
-=0,7906;
10-1 20,419 ' ' ч У A0-1)-A0-5)
Так как R < 3, нулевая гипотеза равенства дисперсий не отклоняется.
414
Проверка гипотез о значениях параметров распределений
[Гл.4
4.1.1.3.3. Критерий отношения размахов
Статистика критерия имеет вид
где шп = жтах — хш-1П; шт = ?/тах — ут[п — размахи сравниваемых выборок.
Если F* > F?, где F?—критическое значение статистики, то нулевая гипоте-
гипотеза отклоняется с вероятностью а. Критические значения F^(n^m) приведены в
табл. 130, заимствованной из [25]. При п ^ 15 мощность критерия отношения разма-
размахов практически не отличается от мощности критерия Фишера (см. раздел 4.1.1.3.1)
(в числителе всегда должно быть наибольшее из двух значение размаха).
Таблица 130
Критические значения F* (то, тог) отношения размахов
(а — доверительная вероятность) [25]
п
3
4
5
6
7
8
т
2
3
4
5
3
4
5
6
3
4
5
6
7
8
4
5
6
7
8
9
10
5
6
7
8
9
10
11
12
5
0,95
3,90
4,37
5,14
5,71
2,03
2,66
3,07
3,38
1,60
2,06
2,35
2,57
2,74
3,00
1,99
2,16
2,30
2,41
2,51
2,59
2,67
1,92
2,03
2,13
2,21
2,28
2,35
2,40
2,46
1,75
а
0,99
7,37
9,99
11,71
12,98
3,72
4,79
5,49
6,01
2,66
3,32
3,76
4,08
4,36
4,73
2,98
3,22
3,41
3,56
3,70
3,81
3,92
2,74
2,89
3,02
3,13
3,22
3,30
3,38
3,44
2,44
п
8
9
10
11
т
6
7
8
9
10
11
12
5
6
7
8
9
10
11
12
13
14
15
6
7
8
9
10
11
12
13
14
15
8
9
а
0,95
1,85
1,94
2,01
2,08
2,13
2,18
2,23
1,63
1,72
1,80
1,87
1,93
1,98
2,02
2,07
2,10
2,14
2,17
1,63
1,70
1,76
1,81
1,86
1,90
1,94
1,98
2,01
2,04
1,67
1,72
0,99
2,57
2,67
2,76
2,84
2,91
2,98
2,56
2,23
2,34
2,43
2,14
2,20
2,26
2,31
2,75
2,80
2,84
2,88
2,17
2,26
2,33
2,39
2,45
2,50
2,54
2,59
2,62
2,66
2,19
2,25
п
11
12
13
14
15
т
10
11
12
13
14
15
10
11
12
13
14
15
10
11
12
13
14
15
10
11
12
13
14
15
10
11
12
13
14
15
а
0,95
1,77
1,81
1,84
1,88
1,91
1,93
1,69
1,73
1,77
1,80
1,82
1,85
1,63
1,67
1,70
1,73
1,76
1,78
1,58
1,61
1,64
1,67
1,70
1,72
1,53
1,57
1,60
1,62
1,65
1,67
0,99
2,30
2,34
2,39
2,42
2,46
2,49
2,18
2,22
2,26
2,30
2,33
2,36
2,08
2,12
2,16
2,19
2,22
2,25
2,00
2,04
2,07
2,10
2,13
2,16
1,93
1,97
2,00
2,03
2,06
2,08
Задача 202. Для данных задачи 200 проверить гипотезу равенства дисперсий крите-
критерием отношения размахов при доверительной вероятности а = 0,95.
Имеем шп = 15,6 - 2,1 = 13,5 и шт = 19,1 - 4,6 = 14,5.
4.1] Сравнение параметров распределений 415
Далее F* = JJJ = 1,074.
Из табл. 130 для п = т= 10 ша = 0,95 имеем F0*95 A0,10) = 1,86.
Так как F* = 1,074 < Fq g^A0,10) = 1,86, нулевая гипотеза равенства дисперсий не
отклоняется.
4.1.1.3.4. Критерий „стьюдентизированного" размаха
Статистика критерия:
q — •) ГДе Шп — З^гпах «^min? ®m —
Нулевая гипотеза равенства дисперсий отклоняется, если g > ga, где qa—кри™
тическое значение статистики, приведенное в табл. 123 (следует помнить, что здесь
Задача 203. Для данных задачи 200 проверить гипотезу равенства дисперсий крите-
критерием „стъюдентизированного" размаха при а = 0,95.
Имеем
Г 1 10 1 *
Шп = 15,6 - 2,1 = 13,5; у = 11,18; sm = < • ]Г (у* - уJ У = 4,519.
Тогда q = f^ = 2599.
Из табл. 123 для п = 10, / = 10^1 = 9иа = 0,95 имеем до,95 ^ 5,5.
Так как q = 2,99 < до,95 = 5,5, нулевая гипотеза равенства дисперсий не отклоняется.
4.1.1.3.5. Критерий Аризоно-Охты
Предложен в [410] и основан на энтропийном критерии нормальности Васичека
(см. раздел 3.2.2.2).
Если обе выборки упорядочены:
xi ^ х2 ^ • • • ^ хп и уг ^ у2 ^ ... ^ уш,
то статистика записывается в форме
П
где Xij yj —порядковые статистики выборок (т.е. упорядоченные по величине эле-
элементы выборок).
При г, j ^ 1 хг (yj) = хг (уг) и при г (j) > п (т) хг (yj) = хп (ут).
Критерий практически не уступает по мощности критерию Фишера (см. раз™
дел 4.1.1.3.1) при п (т) ^ 20.
При Ki(a) ^ К ^ K2(ol) нулевая гипотеза равенства дисперсий не отклоняется.
Здесь Ki(a) и К2(а) —критические значения статистики, приведенные в табл. 131.
При К < К\(а) или К > К2(о) нулевая гипотеза отклоняется (здесь а — довери™
тельная вероятность).
416
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 131
Критические значения jK"i(q:) (верхняя строка)
и K?(ol) (нижняя строка) статистики Аризоно^Охты
для доверительной вероятности ol = 0,95 [410]
3
5
8
10
15
20
с
1
2
3
3
3
3
m = 3
d=l
0,139
7,425
0,105
2,613
0,087
1,892
0,082
1,619
0,072
1,270
0,069
1,167
5
2
0,316
3,087
0,264
2,045
0,244
1,739
0,218
1,350
0,199
1,205
8
3
0,435
2,316
0,398
1,945
0,360
1,488
0,335
1,346
10
3
0,468
2,101
0,425
1,617
0,408
1,427
15
3
0,559
1,804
0,530
1,576
20
3
0,602
1,692
В табл. 131 указаны соотношения п{гп) и c(d), обеспечивающие максимальную
мощность критерия.
Задача 204. В условиях задачи 200 проверить нулевую гипотезу равенства дисперсий
критерием Аризоно-Охты.
Имеем п = т = 10. Из табл. 131 выбираем с = d = 3.
Вычисляем (имея в виду, что х% = х\ при г ^ 1 и х% = хп при г ^ п):
ю
Д (xi+3 ^ Жг-з) = (х4 - хг) • (х5 - хг) • - • (х10 - х6) • (х10 - х7) =
г=1
= F,2 - 2,1) • G,4 - 2,1) • • • A5,6 - 8,5) • A5,6 - 10,1) = 2,80223251 • 108;
1
B,8023251 • 108I0 = 6,994223;
ю
П B/i+3 - Vj-з) = (9,8 - 4,6) • (9,9 - 4,6) • • • A9,1 - 10,4) • A9,1 - 13,1) = 43770949;
i=i
D3770949) То = 5,8092303.
^ г/ 3 10 6,9944223
Окончательно получаем К = — • — • = 1,204.
3 10 5,8092303
Для п = т = 10, c = d = 3ma = 0,95 из табл. 131 имеем
lfi@,95) = 0,468 и #2 @,95) = 2,101.
Так как #i@,95) = 0,468 < К = 1,204 < 1^@,95) = 2,101, нулевая гипотеза равенства
дисперсий не отклоняется.
4.1.1.4. Сравнение нескольких (к > 2) дисперсий
Пусть sf,s|, • • •, s|—взаимно независимые выборочные оценки дисперсий
-f,a|, ..., G^ по выборкам объема Bi,B2, . ..,п^. Проверяется нулевая гипотеза
q : о\ = сг|+1 против альтернативы Но: af / сг|+1 (для г = 1, 2, ..., Aj — 1).
4.1] Сравнение параметров распределений 417
4.1.1.4.1. Критерий Бартлетта
Предложен в [411], основан на статистике
При щ > 3 (г = 1, ..., Aj) и справедливости нулевой гипотезы величина
Г 1 (к 1 Л)
В = М < 1 -\ j-. г I У^ I } имеет распределение у2 с f = к — 1
[ 3(fc^ 1) у^ гг* — 1 ny j
степенями свободы (о распределении %2 см. раздел 1.1.8).
Если В > Ха(/)? то с достоверностью а нулевая гипотеза отклоняется. Крити™
ческие значения Х«(/) содержатся в табл. 55 или могут быть вычислены с помощью
аппроксимаций.
При / > 30 можно использовать аппроксимацию Вилсона^Хилферти (см. ап™
( 2 / 2 \
проксимацию 3 в разделе 1.1.8) Х«(/) ^ ^114 7+^ai/^I ? гДе иа —квантиль
V 9/ V 9J У
стандартного нормального распределения. Критерий очень чувствителен к откло-
отклонениям от нормальности распределения исследуемых случайных величин. Если
нет уверенности в нормальности распределения (критерии проверки нормальности
распределения рассмотрены в разделе 3.2), им не рекомендуется пользоваться. При
отклонении от нормальности рекомендуется вместо статистики М пользоваться ее
модификацией [22, 87, 412]
М* =
Статистика М* имеет ^-распределение с /i и /2 степенями свободы. Поэтому
нулевую гипотезу следует отклонить, если М* > Fa (/15/2).
Задача 205. Имеются четыре выборки (к = 4) объема п = 5 каждая
хц: 3, 4, 5, 6, 7; xi2: 2, 8, 9, 11, 15;
xi3: 9, 11, 15, 20, 28; xi4: 4, 6, 8, 10, 16.
Необходимо проверить нулевую гипотезу равенства дисперсий в выборках Но: (Т\ =
= а\ = и\ = а! критерием Барлетта при доверительной вероятности а = 0,95.
Имеем
X! =5; х2 = 9; х3 = 16,6; ж4 = 8,8;
1 5
s\ = • J2(Xil - Xlf = 2'5 (Sl = !'581M
1 5
1 5
5з = • У)(ж*з - ж3J = 58,3 (s3 = 7,635);
1 5 9
^(xi4 ~~ хА = 21 2 (s4 =
5 - :
14 А. И. Кобзарь
418 Проверка гипотез о значениях параметров распределений [Гл. 4
Вычисляем
5 -.4 4
га = 53 (п* - 1) = 4 • 4 = 16; М = 16 '1п ~ * J2 4 * ^ ~ J2 4 *ln s* = 456088;
г=1 i=l i=l
c=l+ / • fe ^-- ^ = 1,04; 5 = ^ = 1^=4,474.
3-D-l) 1^5-1 16 I ' ' с 1,104
Из табл. 55 для /=fc^l=4^1=3 находим Хо,9бC) = 7,81.
Так как В = 4,174 < Хоэб(З) = 7,81, нулевая гипотеза не отклоняется. Применим
теперь уточненный критерий. Находим
/i = fc - 1 = 3; /2 = fc + 19 = 4 + 1 9 = 462,28;
(с-IJ A,104™ IJ ' '
ь 462,282 ki^k^ дж* 462,28-4,6088
Ь = = 514,566; М = = 1,393.
462,28 ¦ B,1,104) + 1,104 3 • E14,566 - 4,6088)
Из таблиц находим F0,95C; 462,3) = 2,60. Так как М* = 1,393 < F0,95 = 2,60, нулевая
гипотеза не отклоняется.
4.1.1.4.2. Критерий Кохрана
Для случая выборок равных объемов (тц = п при г = 1,2, ...,&) Кохран [414]
предложил критерий, основанный на статистике
max si
г=1
Если g" > g"a(Aj, гг), то нулевая гипотеза отклоняется. Значения приведены
в табл. 132. Критические значения можно найти также, пользуясь таблицами
F-распределения, с помощью соотношения
Ffc+1_a [п - 1; (п - 1) (fc - 1I
БаУ ' J ~ k^l + Fk^1+a \п - 1; (п - 1) (к - I)] ?
к
где i^7(/i,/2)—7™квантиль ^-распределения с /i и /2 степенями свободы.
Задача 206. Проверить нулевую гипотезу равенства дисперсий в условиях задачи 205
критерием Кохрана при доверительной вероятности а = 0,95.
Имеем J2 s<2i = 2'5 + 22'5 + 58'3 + 21,2 = 104,5; max s\ = 58,3.
Г О О
Тогда g = —— = о,558.
б 104,5
Из табл. 132 для n = 5, k = 4 ш а = 0,95 имеем go,95D; 5) = 0,721.
Так как g = 0,558 < go,95 D; 5) = 0,721, нулевая гипотеза не отклоняется. Если вое™
пользоваться таблицами /^-распределения, то мы бы получили
^4^1+0,95 [E - 1); E - 1) • D - 1)] = F0,987D; 12) « 5,4; go,95D; 5) = 5Л = 0,643.
4 4 — I + 5,4
Естественно, что приближение, дающее удовлетворительные результаты при п ^ 20,
не обеспечило в нашем случае приемлемой точности.
4.1]
Сравнение параметров распределений
419
Таблица 132
Критические значения ^а(к^п) статистики Кохрана
для доверительной вероятности ос = 0,95 [25]
к
2
3
4
5
6
7
8
9
10
12
15
20
30
к
2
3
4
5
6
7
8
9
10
12
15
20
30
п
2
0,999
0,993
0,967
0,928
0,883
0,838
0,794
0,754
0,707
0,653
0,548
0,480
0,363
3
0,995
0,942
0,864
0,788
0,722
0,664
0,615
0,573
0,536
0,475
0,407
0,330
0,241
4
0,979
0,883
0,781
0,696
0,626
0,568
0,521
0,481
0,447
0,392
0,332
0,265
0,191
5
0,959
0,833
0,721
0,633
0,563
0,508
0,463
0,425
0,393
0,343
0,288
0,229
0,163
6
0,937
0,793
0,676
0,587
0,519
0,466
0,423
0,387
0,357
0,310
0,259
0,205
0,145
7
0,917
0,761
0,641
0,553
0,487
0,435
0,393
0,359
0,331
0,286
0,239
0,188
0,133
те
8
0,899
0,733
0,613
0,526
0,461
0,410
0,370
0,338
0,311
0,268
0,223
0,175
0,123
9
0,882
0,711
0,590
0,504
0,440
0,391
0,352
0,321
0,294
0,253
0,210
0,165
0,116
10
0,867
0,691
0,570
0,485
0,423
0,375
0,337
0,307
0,281
0,242
0,200
0,157
0,110
11
0,854
0,673
0,554
0,470
0,408
0,362
0,325
0,295
0,270
0,232
0,192
0,150
0,105
17
0,795
0,606
0,488
0,409
0,353
0,310
0,278
0,251
0,230
0,196
0,161
0,125
0,087
37
0,707
0,515
0,406
0,335
0,286
0,249
0,221
0,199
0,181
0,153
0,125
0,096
0,066
4.1.1.4.3. Критерий Неймана-Пирсона (критерий отношения правдоподобия)
Статистика критерия определяется отношением арифметического среднего
всех sf к их геометрическому среднему (предполагается, что п\ = П2 = ... = п& = п)
Н =
к \ к
ГК
При Н > На нулевая гипотеза отклоняется. Критические значения критерия
приведены в табл. 133. Статистика Н применима и для случая, когда средние зна-
значения сравниваемых выборок значимо отличаются друг от друга (методы проверки
равенства средних см. в разделе 4.1.1).
14*
420
Проверка гипотез о значениях параметров распределений
[Гл.4
При равенстве средних х\ = ... = xj~ применима статистика
1 к
я* =
г=1
Критические значения Н^ приведены в табл. 134.
Таблица 133
Критические значения На критерия Неймана—Пирсона
для доверительной вероятности а = 0,95
к
2
3
4
5
10
20
25
50
п
3
3,21
3,18
3,17
3,05
2,68
2,39
2,31
2,12
4
2,09
2,13
2,08
2,03
1,87
1,75
1,71
1,59
5
1,71
1,74
1,71
1,68
1558
1,50
1,48
1,40
6
1,52
1,54
1,52
1,50
1,44
1,38
1,36
1,31
7
1,41
1,43
1,41
1,40
1,35
1,30
1,28
1,25
8
1,34
1,35
1,34
1,33
1,29
1,25
1,24
1,21
9
1,29
1,30
1,29
1,28
1,25
1,22
1,20
1,17
10
1,25
1,26
1,25
1,25
1,22
1,19
1,18
1,15
12
1,20
1,21
1,20
1,20
1,17
1,15
1,14
1,12
15
1,15
1,16
1,15
1,15
1,13
1,12
1,11
1,09
20
1,11
1,11
1,11
1,11
1,09
1,08
1,08
1,07
Таблица 134
Критические значения Н^ критерия Неймана—Пирсона
для доверительной вероятности а = 0,95
к
2
3
4
5
10
20
25
50
п
3
5,82
5,73
5,42
5,14
4,36
3,79
3,64
3,29
4
3,05
3,12
3,00
2,92
2,64
2,41
2,38
2,15
5
2,26
2,33
2,26
2,22
2,06
2,93
1,87
1,74
6
1,99
2,06
2,01
1,97
1,84
1,74
1,68
1,58
7
1,78
1,84
1,81
1,78
1,66
1,58
1,54
1,48
8
1,62
1,68
1,66
1,62
1,54
1,44
1,42
1,38
9
1,51
1,54
1,54
1,50
1,44
1,38
1,36
1,32
10
1,41
1,43
1,43
1,42
1,38
1,32
1,31
1,27
12
1,33
1,35
1,35
1,34
1,31
1,26
1,25
1,21
15
1,25
1,26
1,26
1,25
1,23
1,20
1,19
1,17
20
1,17
1,18
1,18
1,18
1,16
1,14
1,13
1,12
Задача 207. Проверить нулевую гипотезу равенства дисперсий критерием Неймана-
Пирсона для данных задачи 205.
Имеем
хг =5; х2 = 9; х3 = 16,6; ж4 = 8,8; s? = 2,5; si = 22,5; S3 = 58,3; s\ = 21,2.
Находим
Н =
- V^ ч2 1
4 ^ l --B,5 + 22,5 + 58,3 + 21,2)
П
= 1,609.
B,5 ¦ 22,5-58,3-21,2L
Из табл. 133 для п = 5, к = 4 находим i/o,95 = 1,71.
Так как Н = 1,609 < i?o,95 = 1,T1, нулевая гипотеза не отклоняется.
4.1]
Сравнение параметров распределений
421
4.1.1.4.4. Критерий Блисса-Кохрана-Тьюки
Критерий предложен в [415] как аналог критерия Кохрана (см. раздел 4.1.1.4.2)
и использует статистику
с =
где uji = max Xji — mm x*i—размах г-й выборки.
Если с > ca(n1 Aj), to нулевая гипотеза отклоняется. Критические значения ca(n, Aj)
приведены в табл. 135. Критерий не обладает высокой мощностью и рекомендуется
к применению при п ^ 10.
Таблица 135
Критические значения са(п,к) критерия Блисса—Кохрана—Тьюки
для доверительной вероятности ol = 0,95 [119]
к
3
4
5
6
7
8
9
10
п
3
0,667
0,538
0,451
0,389
0,342
0,305
0,276
0,253
4
0,601
0,479
0,398
0,342
0,300
0,267
0,241
0,220
5
0,563
0,446
0,369
0,316
0,278
0,248
0,224
0,204
6
0,539
0,425
0,351
0,300
0,263
0,234
0,211
0,193
7
0,521
0,410
0,338
0,288
0,353
0,225
0,203
0,185
8
0,507
0,398
0,328
0,280
0,245
0,218
0,197
0,179
9
0,498
0,389
0,320
0,273
0,239
0,213
0,192
0,184
10
0,489
0,382
0,314
0,267
0,234
0,208
0,188
0,172
Задача 208. Проверить нулевую гипотезу равенства дисперсий критерием Блисса-
Кохрана-Тьюки в условиях задачи 205.
Имеем ал = 7 - 3 = 4; ш2 = 15 ~~ 2 = 13; ш3 = 28 ~~ 9 = 19; ш4 = 16 ~~ 4 = 12.
тпя.х UJi
Тогда с =
4+13 + 19 + 12
= 0,396.
Из табл. 135 находим со,9бE;4) = 0,446.
Так как с = 0,396 < со,9бE;4) = 0,446, нулевая гипотеза не отклоняется.
4.1.1.4.5. Критерий Хартли
Критерий основан на статистике [416]
h =
При h > ha(nJk) нулевая гипотеза равенства дисперсий отклоняется. Критиче™
ские значения h > ha(n^k) приведены в [25, 119, 140] и воспроизведены в табл. 136.
Критерий не обладает высокой мощностью и рекомендуется к применению при
к<: ю.
422
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 136
Критические значения ha {n^ к) критерия Хартли
для доверительной вероятности сх. = 0,95 [119]
п
3
4
5
6
7
8
9
10
13
16
21
31
61
к
2
39,0
15,4
9,60
7,15
5,82
4,99
4,43
4,03
3,28
2,86
2,46
2,07
1,67
3
87?5
27,8
15,5
10,8
8,38
6,94
6,00
5,34
4,16
3,54
2,95
2,40
1,85
4
142
39,2
20,6
13,7
10,4
8,44
7,18
6,31
4,79
4,01
3,29
2,61
1,96
5
202
50,7
25,2
16,3
12,1
9,70
8,12
7,11
5,30
4,37
3,54
2,78
2,04
6
266
60,0
29,5
18,7
13,7
10,8
9,03
7,80
5,72
4,68
3,76
2,91
2,11
7
333
72,9
33,5
20,8
15,0
11,8
9,78
8,41
6,09
4,95
3,94
3,02
2,17
8
403
83,5
37,5
22,9
16,3
12,7
10,5
8,95
6,42
5,19
4,10
3,12
2,22
9
475
93,9
41,1
24,7
17,5
13,5
11,1
9,45
6,72
5,40
4,24
3,21
2,26
10
550
104
44,6
26,5
18,6
14,3
11,7
9,91
7,00
5,59
4,37
3,29
2,30
11
626
114
48,0
28,2
19,7
15,1
12,2
10,3
7,25
5,77
4,49
3,36
2,33
12
704
124
51,4
29,9
20,7
15,8
12,7
10,7
7,48
5,93
4,59
3,39
2,36
Задача 209. Проверить нулевую гипотезу равенства дисперсий критерием Хартли
в условиях задачи 205.
Имеем
I = 4 = 58,3;
^ = sx = 2,5; h =
58,3
~2^f
= 23,32.
Из табл. 136 для к = 4 и п = 5 имеем /io,9sE; 4) = 20,6.
Так как h = 23,32 > /10,95 E; 4) = 20,62, нулевая гипотеза отклоняется (т.е. дисперсии
не признаются равными).
4.1.1.4.6. Критерий Кэдуэлла-Лесли-Брауна
Кэдуэлл [147], Лесли и Браун [418] предложили аналог критерия Хартли
(ем. раздел 4.1.1.4.5), основанный на статистике отношения размахов
max uji
к = ls^fc .
Критические значения статистики Ka(nJ fc), превышение которых приводит к от™
клонению нулевой гипотезы, приведены в табл. 137. Критерий применим при к ^ 10,
однако его мощность меньше мощности критерия Хартли.
Таблица 137
Критические значения Ка(п,к) критерия Кэдуэлла^Лесли^Брауна
для доверительной вероятности сх, = 0,95 [119]
п
3
4
5
6
7
8
9
10
к
2
6,28
3,96
3,15
2,74
2,49
2,32
2,20
2,11
3
9,32
5,31
4,02
3,37
2,99
2,75
2,58
2,45
4
11,90
6,32
4,63
3,82
3,34
3,04
2,83
2,68
5
14,20
7,20
5,10
4,16
3,61
3,27
3,03
2,84
6
16,30
7,95
5,53
4,47
3,85
3,46
3,19
2,99
7
18,20
8,63
5,93
4,71
4,04
3,62
3,32
3,11
8
20,00
9,24
6,26
4,93
4,22
3,75
3,44
3,21
9
21,70
9,76
6,55
5,14
4,37
3,88
3,55
3,31
10
23,30
10,30
6,80
5,32
4,51
3,99
3,64
3,39
4.1] Сравнение параметров распределений 423
Задача 210. Проверить нулевую гипотезу равенства дисперсий критерием Кэдуэл-
ла^Лесли^Брауна в условиях задачи 205.
Имеем max ил = шз = 28 — 9 = 19: min из% = ш\ = 7 — 3 = 4.
19
Тогда К = — = 4,75. Из табл. 137 имеем Жо,9бE;4) = 4,63.
Так как К = 4,75 > Жо,95E;4) = 4,63, нулевая гипотеза отклоняется.
4.1.1.4.7. Критерий Самиуддина
Критерий Бартлетта (см. раздел 4.1.1.4.1) очень чувствителен к отклонениям
от нормальности. Поэтому не прекращаются попытки найти альтернативные ему
критерии, отличающиеся повышенной устойчивостью к отклонениям от нормаль-
нормальности. Одна из таких попыток рассмотрена в работах [419, 420]. В них Самиуддином
предложены статистики, основанные на использовании корня кубического из вы-
( s2\^
борочной дисперсии, исходя из того факта, что отношение I —|- I распределено
\ai У
асимптотически нормально.
Пусть sf —выборочные оценки дисперсии с fi = щ — 1 степенями свободы. Обо-
Обозначим
J г=1 i=l J г=1
Тогда В = /(inж2 — t), есть статистика критерия Бартлетта, рассмотренная
в разделе 4.1.1.4.1. Для записи статистик критериев введем обозначения
г=1
Тогда статистики модифицированных критериев Самиуддина имеют вид
1
i X з I
^ Ь{Г 2 ¦__
При к ^> 1 статистики PF* и W** имеют распределение %2(fc — 1). Нулевая
гипотеза равенства дисперсий отклоняется, если
W*(W**)>xl(k-l),
где X2(fc — 1) — «^квантиль распределения %2 с (к — 1) степенями свободы (ее
значения приведены в табл. 55).
Из предложенных критериев наибольшей мощностью обладает критерий W**,
но все они превышают по мощности критерий Бартлетта.
Задача 211. Проверить нулевую гипотезу равенства дисперсий в условиях задачи 205,
используя семейство критериев Самиуддина (а = 0,95).
Имеем
/i = ... = /4=n-l = 5-l = 4; sl = 2,5; si = 22,5; S3 = 58,3; s\ = 21,2;
1 1 i I
ti(sl) 3 = 1,3572; t2 = (si) 3 = 2,8231; t3 = (s23) 3 = 3,8775; t4 = (s24) 3 = 2,7676;
/ 2
61 = ... = 64 = \ -— =0,2357.
424 Проверка гипотез о значениях параметров распределений [Гл. 4
Далее
Ел-.? 4'104'5
i=l
Вычисляем статистики критериев:
;5 = 0,0239; z2 = 0,2153; z3 = 0,5579; z4 = 0,2029.
45
W* = V ——-— = о • V fe - A - 0, 2357) • 2, 754521 = 2, 6027;
^ к-Т 0,2357-2,75452 L J
= 7,638.
Из табл. 55 для f = k — 1 = 3иа = 0,95 находим Хо,9бC) = 7,81.
Так как W* = 2,6027 и W** = 7,638 меньше, чем Хо,9бC) = 7,81, нулевая гипотеза не
отклоняется.
4.1.2. Сравнение параметров экспоненциальных распределений
4.1.2.1. Сравнение двух параметров
Предположим, имеются две выборки случайных величин (например, наработка
на отказ изделия) объемами п и т из экспоненциальных распределений (см. раз-
раздел 1.1.4)
хъх2, ...,а?„ и У1,у2, • ..,Уш,
т. е. из распределений с плотностями
-?) и /B/) =
где i/i и 1/2—параметры распределений (средние значения).
Иногда в практике (задачи анализа надежности объектов) используют параметр
Л = интенсивность отказов. В дальнейшем мы будем уточнять, о каком пара-
параметре идет речь.
4.1.2.1.1. Критерий Фишера
Статистика критерия имеет вид
F=^^
При справедливости нулевой гипотезы статистика F имеет распределение Фише™
ра (см. раздел 1.1.10) с / = 2п и / = 2т степенями свободы. Если F7 — 7™квантиль
распределения Фишера, то с достоверностью а нулевая гипотеза отклоняется:
4.1] Сравнение параметров распределений 425
в пользу альтернативы Hi: v\ / ?2, если
F ^ Fi+a Bn, 2m) или F ^ Fi^a Bгс, 2т) ;
2 2
в пользу альтернативы U{ : vi > i/2, если F > FaBn,2m); в пользу альтернативы
Н'{: i/i < i/2, если F < Fi^aB)
Задача 212. Две партии приборов были испытаны на надежность. В результате
были получены следующие значения моментов их отказов (в условных единицах):
хц 12, 14, 16, 20, 30, 40, 60, 85 (п = 8);
уу. 22, 38, 44, 54, 68, 72 (т = 6).
Необходимо проверить нулевую гипотезу равенства средних Но: v\ = 1/2 против аль-
альтернативы Hi: и\ ф ъ?2 при доверительной вероятности а = 0,95.
а . 977
Имеем ]>>; = 277; Y.Vi = 298; F = ^^ = °>697-
Так как в числителе должно быть большее значение, используем величину
F=^^ = 1,434.
т • 2_j хг
При необходимости найти критическое значение при а = 0,95: Fi+o^s Bга; 2п) =
= Fo,975A2;16).
По таблицам ^распределения (подробнее см. раздел 1.1.10) находим
F0,975A2,16) = 2,90. Так как F = 1,434 < F0,975A2,16) = 2,90, нулевая гипотеза не
отклоняется.
4.1.2.1.2. Критерий Фишера при сравнении интенсивностей отказов (Л)
Рассмотрим сравнение интенсивностей отказов Л в двух экспоненциально рас-
распределенных выборках. Это наиболее распространенный показатель надежности,
используемый при оценке технических объектов. Обычной ситуацией, в которой
получается оценка интенсивности отказов, является испытание объектов, в процессе
которых фиксируется количество отказов за определенный временной промежуток.
Именно в такой интерпретации изложим применение критерия Фишера.
Предположим, были зафиксированы за время испытаний t\ первого объекта
7*1 отказов, а у второго объекта т^ отказов за время t^.
Для проверки нулевой гипотезы Hq : Х± = Х2 используется статистика
71*2 А2 „
К = ^^ = —, имеющая при справедливости нулевой гипотезы г -распределение
7*2*1 Ai
с /1 = 2г2 и /2 = 1тi степенями свободы. При справедливости нулевой гипотезы
( ^2 1 \
(т.е., когда — « 1) должно выполняться неравенство
Ai
Д= Т-Щ- < Fi+aBr2,2r1).
Задача 213. При испытании первого изделия были получены 12 отказов за 210 ч
испытаний. У второго изделия были получены 5 отказов за 100 ч испытаний. Про-
Проверить гипотезу равенства интенсивностей отказов у изделий при доверительной
вероятности а = 0,95.
Имеем п = 5; *i = 100; г2 = 12; *2 = 210; R = U ' 10° = 1,143.
Из таблиц находим jPq,975A0,24) = 2,64.
Так как R = 1,143 < Fq,975A0,24) = 2,64, нулевая гипотеза не отклоняется.
426 Проверка гипотез о значениях параметров распределений [Гл. 4
4.1.2.1.3. Двухвыборочный пуассоновский критерий
Известно (см. раздел 1.1.4), что экспоненциальное распределение порождается
пуассоновским потоком с интенсивностью Л.
Предположим, наблюдаются г\ отказов одного изделия за время i\ и г 2 отказов
второго изделия за время t^. В нашем случае Г\ и г 2—случайные величины,
подчиненные закону Пуассона с параметрами 71 = tiAi и 72 = ^2^2-
В [421] предложен критерий проверки нулевой гипотезы Щ : Х1 = Л2 против аль™
1
тернативы Hi: \\ < Аг, основанный на статистике z = ( г 2 -ri ) \ — (г\ + 1)
V У L J
Нулевая гипотеза отклоняется, если z > гха, где иа—о^квантиль стандартного
нормального распределения, а — уровень достоверности.
Более точный критерий предложен в [422]:
tl
z'= l * '
При z* > ua он также отклоняет нулевую гипотезу.
Задача 214. В условиях задачи 213 проверить нулевую гипотезу равенства интенсив-
ностей отказов двухвыборочным пуассоновским критерием при уровне достоверности
а = 0,95.
210
12 -5
Имеем п = 5; ti = 100; г2 = 12; t2 = 210; z = 10° — = 0,422.
'210 ."
_.E + i)
Из табл. 1 находим г^о,95 = 1,64. Так как z = 0,422 < ^0,95 = 1,64, нулевая гипотеза не
отклоняется.
По аналогии находим
3\ I
12+8 -
210\
1 + Wo)
= 0,179,
что такж:е не отклоняет нулевую гипотезу.
4.1.2.1.4. Сравнение значения параметра с заданным
В практике испытаний на надежность технических объектов особый интерес
представляет проверка гипотез Щ: v ^ щ или Но: v > i/0, где щ — некоторое за-
заданное значение наработки на отказ, являющееся, как правило, нормируемым
количественным показателем надежности.
Рассмотрим методы проверки гипотез о значении интенсивности отказов изде-
изделий (А = —) применительно к различным планам испытаний на надежность (по™
дробнее о планах испытаний на надежность см. в разделе 2.2).
План [N,B,T]
Статистикой критерия проверки нуль^гипотезы является число отказов г за
время испытаний Т. Если г ^ с, где с — приемочное число, удовлетворяющее
4.1]
Сравнение параметров распределений
427
неравенству
Ка{с) > NX0T,
где Ка(с)—коэффициент, значения которого для различных а и с приведены
в табл. 138; Aq— гипотетическое значение интенсивности отказов; а — доверитель™
пая вероятность, то гипотеза Н®: А > Aq отклоняется в пользу альтернативы
Hi: А ^ Ао с достоверностью а.
Таблица 138
Значения коэффициентов Ка(с) [140]
с
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Доверительная вероятность а
0,99
0,01005
0,14855
0,43604
0,82325
1,27911
1,78528
2,33021
2,90611
3,50746
4,13020
4,77125
5,42818
6,09907
6,78235
7,47673
8,18111
8,89457
0,95
0,05129
0,35536
0,81769
1,36632
1,97015
2,61301
3,28532
3,98082
4,69523
5,42541
6,16901
6,92421
7,68958
8,46394
9,24633
10,03596
10,83114
0,93
0,07257
0,43081
0,94223
1,53414
2,17670
2,85488
3,55984
4,28584
5,02895
5,78633
6,55583
7,33581
8,12496
8,92222
9,72672
10,53773
11,35465
0,90
0,10536
0,53181
1,10206
1,74477
2,43259
3,15190
3,89477
4,65612
5,43247
6,22130
7,02075
7,82934
8,64594
9,46962
10,29962
11,13530
11,97613
План [N,B,r]
Статистикой критерия является суммарная наработка изделий до момента на™
ступления г-го отказа Tr = Nr^ критические значения которой находятся по фор-
формуле
где Ka(r — 1) — коэффициент из табл. 138 при с = г — 1.
Гипотеза Но: А < Ао отклоняется в пользу альтернативы Hi: А ^ Ао, если
Тг <Тг(а).
План [N, Б, Т]
Статистикой критерия проверки нулевой гипотезы является число отказов г,
полученное за время испытаний Т.
Если г > с, где с — наименьшее целочисленное решение неравенства
N г
]С CN i1 - е ) е ° ^ а'
i=c+l
то с вероятностью а гипотеза Hq : A ^ Aq отклоняется в пользу альтернативы
Нг: А> Ао.
428 Проверка гипотез о значениях параметров распределений [Гл. 4
План [ЛГ, Б, г]
Статистикой критерия для проверки нулевой гипотезы является суммарная
наработка
Тг = Х> + (ЛГ-г)*Г)
г=1
критические значения которой равны
Если Тг < Тг(а), то гипотеза Но: А < А® отклоняется в пользу альтернативы
Нг: А^ Ао.
Задача 215. Партия электронных приборов была испытана на надеаюность в со-
соответствии с планом испытаний [N,B,T]. При этом испытаниям подвергались
N = 100 ламп в течение Т = 200 ч с заменой отказавших ламп. При испытаниях были
зафиксированы г = 5 отказов. Необходимо с достоверностью а = 0,99 проверить гипо-
гипотезу о том, что интенсивность отказов ламп не превышает величины Ао = 10^4 ч^1.
Вычисляем N • Ао • Т = 100 • 10~4 • 200 = 2.
Из табл. 138 для а = 0,99 видим, что Ж"о,9э(с) ^ 2 при с = 6.
Так как г = 5 < с = 6, гипотеза Но: А ^ Ао не отклоняется.
Находим приемочное число с из условия Ка(с) ^ N • Ао • Т = 2.
Задача 216. На надеаюность была испытана партия электронных ламп в соответ-
соответствии с планом испытаний [N,B,r]. Испытаниям подвергались N= 100 ламп с за-
заменой отказавших ламп. Испытания проводились до появления г = 5 отказов. При
этом пятый отказ наступил при t$ = 200 ч. Необходимо с достоверностью а = 0,95
проверить нулевую гипотезу о том, что интенсивность отказов ламп не превосходит
допустимой величины Ао = 1,3 • 10~4 ч-1.
Из табл. 138 для а = 0,95 иг = 5 (с = г-1 = 4) находим Жо,9бD) = 1,97015 и
Т5@,95)=^95D)= 1'97°154 = 15155 ч.
Ао 1,3 • 10"
В нашем случае Тг = N • tr = 100 • 200 = 20000 ч.
Так как Ts = 20000 > Ts@,95) = 15155, нулевая гипотеза Но: А < Ао не отклоняется,
т. е. с достоверностью 0,95 можно утверждать, что интенсивность отказов ламп не пре-
превосходит 1,3 • 10~4 ч.
Задача 217. Проверить нулевую гипотезу в условиях задачи 216, если испытания
проводились без замены отказавших приборов^ т.е. когда вместо плана [N,B,r] был
реализован план [N, Б, г]. При этом были зафиксированы моменты наступления отка-
отказов ламп
tx = 50, t2 = 60, t3 = 100, U = 180, t5 = 200 ч.
Имеем суммарную наработку до 5-го отказа
5
Т5 = J2 1г + A0° - 5) *5 = 50 + 60 + 100 + 180 + 200 + 95 • 200 = 19590 ч.
г=1
Критическое значение равно
Гв@>95) = К°М4\ = 1'97°154 = 15155.
К } 1,3- 10~4 1,3-10
Так как Тг = 19590 > Т5@,95) = 15155, нулевая гипотеза не отклоняется.
4.1] Сравнение параметров распределений 429
Задача 218. Партия изделий N = 5 была испытана на надежность в течение
Т = 100 ч без замены отказавших приборов (т. е. в соответствии с планом [N,B,T]).
При этом были получены г = 2 отказа. Необходимо проверить гипотезу Но : X < Ао при
доверительной вероятности а = 0,95 и Ао = 6,93 • 10^3 ч.
Находим подбором наименьшее целочисленное решение неравенства
г=с+1
В нашем случае
^ C*.(l_ ^6,93.10^-100^ , ^6,93-100.E^) ^ Q595;
J] CJ • 0, 5г • 0, 5Ж^ = J2 ^5-0,5^ = 0,5-5- 5Z ^5^0,95;
г=с+1 г=с+1 г=с+1
^1 °'55
5 5
Имеем при с = 0: J^ G| = 5 + 10 + 10 + 5 + 1 = 31; при с = 1: ]Г Сг5 = 26 < 30,4. Сле~
г=1 г=2
довательно, с = 1, а так как г = 2 > с = 1, нулевая гипотеза отклоняется.
Задача 219. Партия N = 15 изделий была испытана на надетсность без замены
отказавших ламп до получения г = 5 отказов. Моменты появления отказов равны (ч):
t\ = 100, ?2 = 150, ?3 = 300, ?4 = 400 и tb = 510 (m. e. имеет место план испыта-
испытаний [N,E,r]. Необходимо проверить гипотезу о том, что А < Ао = 1,8 • 10~ ч^ при
а = 0,99.
5
Имеем Tr = J2ti + A5 - 5) ' 510 = 656°-
г=1
Из табл. 138 находим Жо,99E — 1) = Жо,9эD) = 1,279.
1 279
Критическое значение равно Гб@,99) = ' j = 7105,5.
v ; 1,8- 10~4
Так как Ts = 6560 < Т5@,99) = 7105, нулевая гипотеза отклоняется и можно утвер-
утверждать, что интенсивность отказов изделия превышает 1,8 • 10^4 ч.
4.1.2.2. Сравнение нескольких (k ^ 2) параметров
4.1.2.2.1. Критерий Дэвида
Предположим, что к выборок одинакового объема п испытаны в течение фик™
сированного времени t. При этом зафиксированы Г{ отказов в каждой г-й выборке.
Полученные значения г^ упорядочим по убыванию г\ ^ г2 ^ • • • ^ т^.
Дэвид [421] предложил для проверки гипотезы Hq : Xi = A^_|_i (г = 1,2,...,/г — 1)
критерий, основанный на статистике
А = 2
При Di > Dai где Da — критическое значение статистики, приведенное в табл. 139,
гипотеза Но отклоняется в пользу альтернативы Hi: Ai = Л2 = ... = Л^ Ф A^+i =
= ... = Afc.
Если все D{ < Da, то гипотеза Но принимается на уровне достоверности а.
430
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 139
Критические значения Da критерия Дэвида
(а — доверительная вероятность) [421]
к
Dq,95
2
2,77
3
2,48
4
2,28
5
2,13
6
2,02
7
1,93
8
1,86
9
1,81
10
1,76
11
1,72
12
1,69
Задача 220. При испытаниях пяти выборок изделий объемом п = 10 каждая, в тече-
течение одинакового промежутка времени были получены следующие количества отказов
в выборках: т\ = 11, г 2 = 9, гз = 5, г 4 = 4 и г в = 2. Необходимо проверить гипотезу
равенства интенсивностей отказов в выборках при достоверности а = 0,95.
Имеем ряд значений
Di = 2 •
+ 0,5 - 2 • у/г2 + 0,5 = 2 • л/ГЦ) - 2 • ^/9^5 = 0,618;
D2 = 1,474; D3 = 0,448; D4 = 1,080.
Из табл. 139 для к = 5 имеем Do,95 = 2,13. Так как все Di < Do,95, то нулевая гипотеза
равенства интенсивностей отказов не отклоняется.
4.1.2.2.2. Критерий максимального правдоподобия
Статистика критерия имеет вид
к к 1 к
При справедливости нулевой гипотезы U-статистика распределена как %2
с / = Aj — 1 степенями свободы. Поэтому нулевая гипотеза равенства к интенсив™
ностей отказов не отклоняется при доверительной вероятности а, если Н < Х^ (/),
где значения х«(/) приведены в табл. 55.
Если в качестве наблюдаемой случайной величины рассматриваются моменты
наступления фиксированного числа отказов r{trI то iJ-статистика используется
в форме [422]
Я* = 2 <
In —— — к In
к
?<
г=1
где tr{ —момент наступления г~го отказа в i-й выборке.
Задача 221. При испытаниях пяти выборок изделий (к = 5) были получены 4 отказа
в каждой выборке (г = 4). При этом моменты наступления последних по времени
отказов в выборках равнялись
U = 120, t2 = 210, t3 = 340, U = 510, t5 = 520.
Необходимо проверить гипотезу равенства интенсивностей отказов в выборках кри-
критерием максимального правдоподобия при доверительной вероятности а = 0,95.
Имеем
5Я* = 2 • ^ 4 • In — - 5 • 4 • In
t
г=1
= 5,543.
Из табл. 5 для а = 0,95 находим Хо,эб(/ — 4) = 11,14.
Так как Я* = 5,54 < Хо,9бD) = ИД4, нулевая гипотеза не отклоняется.
4.1]
Сравнение параметров распределений
431
Задача 222. Предположим, что в задаче 221 наблюдались не моменты времени до
достижения фиксированного количества отказов в выборках, а количества отказов за
фиксированное время испытаний. Пусть за одно и тоже время испытаний t в выборках
наблюдались следующие количества отказов: г\ = 5, Г2 = 4, гз = 2, г 4 = 6, г^ = 1. Необ-
Необходимо проверить гипотезу равенства интенсивностей отказов в выборках критерием
максимального правдоподобия.
Имеем к = 5; J^ r% = 5 +
г=1
Тогда
Н = 2-
-2 + 6+ 1 = 18.
• In 7*i —
^ = 5,346.
Так как Н = 5,346 < Хо,э5 :=: ИД4, нулевая гипотеза не отклоняется.
4.1.2.2.3. Критерий отношения правдоподобия (критерий Нагарсенкера)
Предположим, имеются к выборок объема п каждая, содержащие экспоненци-
экспоненциально распределенные случайные величины. В [423] для проверки нулевой гипотезы
Hq : v\ = V2 = • • • = v\z равенства средних значений во всех выборках рассмотрен
критерий, основанный на статистике
Их1 ГД6 Xj' n^^j' X nk^Xij'
3 = 1 г=1 г=1
Если L ^ La(n^k), то нулевая гипотеза отклоняется с вероятностью а. Крити-
Критические значения Ьа(п, к) для а = 0,95 приведены в табл. 140.
Таблица 140
Критические значения iya(n, к) критерия отношения правдоподобия
для доверительной вероятности а = 0,95 [423]
п
4
5
6
7
8
9
к
3
0,454
0,535
0,596
0,643
0,681
0,711
4
0,443
0,510
0,563
0,606
0,641
5
0,442
0,498
0,545
0,583
6
0,444
0,492
0,534
п
10
20
40
80
100
к
3
0,736
0,859
0,927
0,963
0,970
4
0,671
0,821
0,906
0,952
0,962
5
0,616
0,787
0,888
0,942
0,954
6
0,569
0,756
0,870
0,933
0,946
Задача 223. Имеются четыре (к = 4) выборки из экспоненциального распределения:
хц: 2, 4, 8, 12, 18; xi2: 5, 7, 11, 19, 21;
ж^3: 11, 17, 21, 22, 29; xi4: 1, 5, 9, 13, 18.
Необходимо проверить гипотезу равенства параметров экспоненциальных распределе-
распределений в выборках критерием Нагарсенкера при доверительной вероятности а = 0,95.
5
Находим х\ = 8,8; х^ = 12,6; хз = 20; Х4 = 9,2; х =
1
= 12,65.
Далее имеем L = I I —^- =
12,6
20
9,2
12,65 12,65 12,65 12,65
= 0,797.
Из табл. 140 находим Ь0,э5E,4) = 0,443.
Так как L = 0,707 > Ьо,э5E,4) = 0,443, нулевая гипотеза не отклоняется.
432
Проверка гипотез о значениях параметров распределений
[Гл.4
4.1.2.2.4. Критерий Чена для двухпараметрических экспоненциальных
распределений
Рассмотрим к независимых экспоненциально распределенных случайных вели™
чин с плотностью распределения вероятностей
Параметр положения Д в практике интерпретируется обычно как гарантийная
наработка, в пределах которой отказы изделия не допускаются.
Чей [424] предложил критерий проверки гипотезы Н®: Д = const, утверждаю-
утверждающей, что гарантийная наработка у всех испытываемых партий изделий постоянна.
Процедура построения статистики критерия Чена включает в себя отбор из
каждой выборки (объема п) наименьшего наблюдения yj = min Xij и определение
размаха совокупности значений yj
Шу = max yj -
Статистика критерия Чена имеет вид
Г к п
[j=n=i
с = кп(п -12)
ул.
J
^ =yj)
-1
Если c>ca(fc,n), то нулевая гипотеза отклоняется на уровне значимости а.
Критические значения статистики Чена са(к,п) приведены в табл. 141.
Таблица 141
Критические значения cCK(fe, n) статистики "Чена [424]
п
3
4
5
6
8
10
16
30
60
3
3,77
3,48
3,34
3,26
3,18
3,13
3,06
3,02
2,99
"Уровень значимости
1
4
4,09
3,83
3,71
3,64
3,56
3,52
3,46
3,41
3,39
5
4,31
4,08
3,97
3,90
3,83
3,79
3,73
3,69
3,67
10
4,92
4,76
4,68
4,64
4,58
4,55
4,51
4,48
4,47
а = ОД
20
5,50
5,40
5,35
5,32
5,28
5,27
5,24
5,22
5,21
30
5,86
5,78
5,74
5,71
5,68
5,67
5,65
5,64
5,63
п
3
4
5
6
8
10
16
30
60
Уровень значимости а = 0,01:
к
3
5,00
4,50
4,28
4,15
4,01
3,93
3,83
3,75
3,71
4
5,23
4,81
4,62
4,50
4,38
4,31
4,21
4,15
4,11
5
5,29
5,02
4,85
4,75
4,63
4,57
4,49
4,43
4,39
10
5,85
5,61
5,50
5,43
5,36
5,31
5,26
5,21
5,19
20
6,34
6,20
6,13
6,08
6,04
6,01
5,97
5,94
5,93
30
6,66
6,55
6,50
6,47
6,43
6,41
6,38
6,36
6,35
Задача 224. В условиях задачи 223 проверить критерием Чена гипотезу равенства
параметров положения (/3i) на уровне значимости а = 0,05 (напоминаем — это озна-
означает, что мы будем принимать значимыми, а не случайными, значения статистики
Чена, вероятность появления которых не превышает 0,05).
Имеем t/i = min хц = 2; г/2 == 5; уз = 11; 2/4 = 1; ojy = 11 — 1 = 10.
l<i<5
4.1]
Сравнение параметров распределений
433
Далее
Е Е
j=n=i=
2/i) = B - 2) + (8 - 2) + ... + A3 ^ 1) + A8 - 1) = 158;
4-5- E™ 1) • 10
158
= 5,063.
Из табл. 141 при а = 0,05 находим со,обD,5) = 4,62.
Так как с = 5,063 > со,о5D,5) = 4,62, нулевая гипотеза отклоняется и гарантийные
наработки у сравниваемых совокупностей следует признать отличающимися.
4.1.2.2.5. Комбинированный критерий Сингха
Обычно мы рассматриваем параметр положения /3 (гарантийный период, когда
отказы не допускаются) и параметр масштаба v (средняя наработка, измеряемая от
параметра положения — гарантийного срока).
Критерий Сингха [437] предполагает проверку гипотезы
Но
= ...= fik= ft]
против общей альтернативы для совокупностей, подчиняющихся экспоненциально™
му закону распределения вероятностей,
Различные варианты критериев проверки такого рода гипотез рассмотрены
в [425—431]. Подробно все эти критерии рассмотрены в [432], там же предложен
один из наиболее мощных критериев для множественного сравнения параметров
экспоненциальных распределений.
Пусть хц ^ X2j ^ ... ^%kj — порядковые наблюдения j'-й выборки (j = 1, 2,..., к).
Предположим, что мы располагаем только первыми (наименьшими) тэ- наблюдени™
ями из каждой j-й выборки.
Оценками максимального правдоподобия для параметров i/j и /3j будут (см. раз™
дел 2.2)
1
bj=xlj; Vj =
Введем обозначения
s =
xij ~ xm) + (rij - rj)(xr.j - Xm)
где xm =
, x12j x13, ..., xlk); R =
Известно [431], что случайные величины
2s* 2Я** 2Я*
и v v
соответственно с / = 2(rj — 1); 2(г — к) и 2 (к — 1) степенями свободы.
распределены как
434 Проверка гипотез о значениях параметров распределений [Гл. 4
Введя обозначение
запишем статистику
(R-\)V
(fc-l)S"
которая распределена как статистика Фишера с Д = 2(А? — 1) и /2 = 2{R — 1) сте-
степенями свободы.
Если С/> Fa[2(fc — 1); 2(i2 — 1)], то с достоверностью а нулевая гипотеза
Hq : v\ = ... = 1/к = v {у и /3 — не определены) отклоняется в пользу альтернативы,
утверждающей, что при равных v по крайней мере две из к выборок различаются
параметрами положения C (т.е. гарантийным сроком).
Для нулевой гипотезы Hq : v\ = ... = v^ = v (/3 не определено) против альтер-
альтернативы, утверждающей, что по крайней мере в двух выборках отличаются пара-
параметры I/, может быть использована модификация критерия Бартлетта (см. раз™
дел 4.1.1.4.1), статистика которого применительно к проверке нашей гипотезы имеет
вид
где
При Q ^ X«(fe ~~ 1) гипотеза Hr0 отклоняется в пользу альтернативы (х«(^ ~~ 1)
для разных а см. в табл. 55).
Совместной проверкой критериев U и Q осуществляется комплексная проверка
гипотез для трехпараметрического экспоненциального распределения.
Задача 225. В результате испытаний на надетсность 4 выборок изделий получены
следующие результаты:
— 1-я выборка (j = 1) — из 7ii = 24 испытанных приборов известны п = 8 первых
наблюдений:
хц = 1, Ж21 = 4, Ж31 = 11, Ж41 = 16, Ж51 = 18, Ж61 = 24, ж71 = 31, Ж81 = 39;
^2~я выборка (j = 2) —из гьч = 30 испытанных приборов известны данные по гч = 5
первым наблюдениям
х\2 = 3, Ж22 = 5, Ж2з = 13, Ж24 = 14, Ж25 = 22;
^3-я выборка (j = 3) —из пз = 10 испытанных приборов известны данные для пер-
первых трех наблюдений (гз = 3):
Ж1з = 10, ж23 = 14, жзз = 20;
^4-я выборка (j = 4) —из п^ = 18 испытанных приборов известны г^ = 6 первых
результатов:
Хы = 20, Ж24 = 25, Ж34 = 31, Ж44 = 42, Ж54 = 44, Ж64 = 49.
Необходимо проверить гипотезу о равенстве параметров положения /3j и масштаба i/j
во всех выборках при доверительной вероятности а = 0,95.
4.1] Сравнение параметров распределений 435
Находим
8
B4 - 8) ' (Ж81 - хи) = 744;
г=1
5
«S2 = J^ (xi2 — Ж12) + C0 — 5) • (Ж52 — Ж12) = 517;
г=1
3
5з = ^2 (Xi3 ~ Ж13) + О-® ~ з) ¦ (Жз3 "¦Ж13)= ^4'
г=1
6
г=1
Далее вычисляем:
S = J2 sj = 744 + 517 + 84 + 439 = 1784; si = -^— = — = 106,2854;
^~ 8 — 1 7
so S4 84 sa 439
„* z 1 on oc. o* ^ /19. o* C7 Q«
S2 — — lZy,ZO, S3 — — — 4Z, S4 — — — r — O'^o?
W ™™. X I X I rys . ___ I 1 _A_ I /n . _ rr* . I I /y» , „_ I 1 I — 1 I / Sr\ * W —
F = V У" щ • (жг7- - X! i - 1) = 492; 17 = -^=—^^^ = 1,513.
^2 \й / B-1)-2276
Находим из таблиц F-распределения Fo59sB • 3; 2 • 21) = Fo,9sF,42) = 2,33.
Так как U = 1,513 < .Fo,95F,42) = 2,33, нулевая гипотеза Но не отклоняется.
Теперь для проверки нулевой гипотезы H'Q вычислим
/ = R - к = 22 - 4 = 18; Д = п - 1 = 7; /2 = г2 - 1 = 4;
/з = г3 - 1; /4 = г4 - 1 = 5;
Тогда Q = • 18 • In 99,111 - У" /-• • In sП = 0,692.
^ 1,1152 l ' Z^JJ 3 '
Так как Q = 0,692 < Хо,9бC) = 7,81, гипотеза Н'о так^е не отклоняется.
4.1.3. Сравнение параметров биномиальных распределений
4.1.3.1. Сравнение двух параметров
Рассмотрим следующую задачу. В выборках объемов п\ и П2 из двух боль™
ших партий изделий зафиксировано соответственно т\ ж т2 дефектных изделий.
Требуется установить значимость различия долей дефектных приборов в партиях
(pi ИР2), что тождественно проверке нулевой гипотезы Н® : рг = р2 против возмож-
возможных альтернатив Н\\ р\ ф Р2-> Н[ : р\ > Р2 и Н": р\ < Р2-
При нормальной аппроксимации биномиального распределения (см. раздел 1.2.1)
436 Проверка гипотез о значениях параметров распределений [Гл. 4
статистикой для проверки Щ является величина
ггц 1 т2 1
z =
/JT) -| J rfYl о Т) -1 —J— T1 о ТП -I ТП о /1
^1+^2 П<1 + П2 \ П
При справедливости нулевой гипотезв! z имеет стандартное нормалвное рас-
распределение. Если \z\ > Ui+a , z > Ua или z < Ui^aj нулевая гипотеза Ы®: рг = р2
отклоняется в пользу альтернатив
Hi: pi ф P2'j H[: pi > р2 и Н" : рг < р2
соответственно (а — доверительная вероятность).
При использовании нормальной аппроксимации с помощью преобразования
arcsln (см. раздел 1.2.1) статистика z имеет вид
1 . 1 /о . /mi
1z arcsin \ / 2 arcsin
\ V
П\
2 \
Задача 226. В двух партиях приборов объемами гц = 100 шт. и П2 = 200 шт. обна-
обнаружены соответственно mi = 3 и rri2 = 5 дефектных приборов. Необходимо проверить
нулевую гипотезу о равенстве долей дефектных приборов в партиях при доверительной
вероятности а = 0,95.
Вычисляем
3 15 1
+ ¦
100 2 • 100 200 2 • 200 _ q 376
3 + 5 100 + 200-3-5/1 1 \
100 + 200" 100 + 200 ' \100 200/
Из табл. 1 находим it 1+0,95 = ^0,975 = 1,96.
2
Так как z = 0,376 < 110,975 = 1,96, нулевая гипотеза не отклоняется.
Аналогично получаем
1 1 / / з / 5 \
1 • 2 arcsin \ / 2 arcsin \ / = 0,37,
100 200 I V ЮО V 200 I
что дает тот же результат.
4.1.3.2. Сравнение значения параметра с заданным
На практике доля дефектных изделий в партии является, как правило, кри-
критерием качества изделий на стадии производства. Основная задача вв1борочного
контроля качества изделий заключается в том, чтобв! по результатам проверки
выборки изделий из партии установить, превосходит ли доля дефектных изделий
в партии некоторую заранее нормированную контрольную величину. В терминах
математической статистики такая задача формулируется как проверка нулевой
гипотезы Щ: р = ро (здесь р — неизвестная истинная доля дефектных изделий
в партии; ро—допустимая величина доли дефектных изделий в партии) против
альтернатив Нi: р > р0 или Н[: р < р0 •
При контроле качества продукции представляет интерес, как правило, гипотеза
Н®: р ^ р® (отклонение этой гипотезы альтернативой Hi: р > р® приводит к бра-
браковке партии изделий).
4.1] Сравнение параметров распределений 437
Статистикой для проверки гипотезы Щ: р ^ р® по выборке изделий объема п
является величина
1
роA — ро)
п
имеющая при справедливости нулевой гипотезы стандартное нормальное распре-
распределение. Гипотеза Щ: р ^ р0 отклоняется в пользу альтернативы Нг: р > pOi если
z > иа1 где иа —«-квантиль стандартного нормального распределения.
При использовании нормализующего преобразования arcsin значения z подсчи-
тываются по формуле
2 ( . [^
z = —р= arcsin \ arcsin -
V*\ V п
где п — объем выборки, т — число дефектных изделий в выборке.
Задача 227. Нормируемый уровень дефектных изделий в партии ро = 0,05. Предпо-
Предположим, что из партии изделий извлечена выборка п = 20 изделий, в которой обнару-
мсены при проверке т = 2 дефектных изделия. Проверить с достоверностью а = 0,95
гипотезу о том^ что доля дефектных изделий в партии не превосходит нормируемого
значения.
Находим
0,05
z= 20 40 ==0,51.
0,05 • A - 0,05)
20
Так как z = 0,51 < 11-0,95 = 1,645, проверяемая гипотеза не отклоняется.
4.1.3.3. Сравнение нескольких параметров (k ^ 2)
Предположим, имеются к выборок из биномиальных совокупностей, объема-
объемами rii, П2, . ..,7ifc. В каждой г-й выборке изучаемое событие наблюдалось mi раз
(г = 1, ..., к). Необходимо проверить гипотезу Hq : pi = Рг+i (fc = l, •••,& — 1) про-
против альтернативы Hi: pi Ф Pi+i-
Статистикой критерия проверки Но является величина
к
9 1 ^^ / ^х2 _ г=1 ГПг
При справедливости нулевой гипотезы величина %2 имеет распределение
хи-квадрат (см. раздел 1.1.8) с f = к — 1 степенями свободы. Поэтому если
X2 ^ Ха(^ ~~ 1)? гДе Х«—а-квантиль распределения хи-квадрат, то с достовер™
ностью а нулевая гипотеза отклоняется.
Если использовать нормализующее преобразование arcsin, то статистика крите™
рия вычисляется по формуле
к
X2 = Y,ndVt -уJ, где
г=1
= 2arcsin 4/—, у =
438 Проверка гипотез о значениях параметров распределений [Гл. 4
Задача 228. Из 8 различных партий изделий извлечены выборки объемами
щ = 10, п2 = 20, п3 = 10, п4 = 50, п5 = 30, п6 = 25, п7 = 10, п8 = 40.
При проверке в них были обнаружены следующие количества дефектных изделий:
ТП\ = 2, 7712 = 5, Шз = 3, Ш4 = 8, Ш5 = 10, Шб = 6, 7717 = 3, mg = 7.
Необходимо проверить гипотезу о равенстве долей дефектных изделий в партиях
изделий с достоверностью а = 0,99.
Имеем
Pi = — = 0,2; р2 = — = 0,4; р3 = — = 0,3; р4 = — = 0,16;
20 20 10 50
10 6 3 7
Р5 = — = 0,33; р6 = — = 0,24; р7 = — = 0,3; р8 = — = 0,175.
Вычисляем
8
i=i * 2 + 5 + 3 + 8 + 10 + 6 + 3 + 7
= 2
20 + 10 + 50 + 30 + 25 + 10 + 40
Далее
1 8 г
X = V п* • (pi - pf = 5,7239 • 10 • @,2 - 0,2256J +
0,2256 • A - 0,2256) r^ L v 7
+ 20 • @,4 - 0,2256J + 10 • @,3 - 0,2256J + 50 • @,16 - 0,2256J + 30 • @,33 - 0,2256J +
+ 25 • @,24 - 0,2256J + 10 • @.33 - 0,2256J + 40 • @,175 - 052256J I = 8,325.
При а = 0,99 имеем Хо,ээ(/ = к - 1 = 7) = 18,48.
Так, как %2 = 8,325 < Хо,ээG) = 18,48, нулевая гипотеза не отклоняется.
4.1.4. Последовательные методы проверки гипотез о значениях параметров
распределений (последовательный анализ Вальда)
Рассмотренные ранее методы проверки статистических гипотез предполагали
фиксированный объем выборки. Вальд [433] предложил теорию последователвной
проверки гипотез (последовательный анализ), существенным отличием которой яв-
является то, что число наблюдений, необходимое для принятия решения по гипотезе,
зависит от исходов испытаний и является случайной, не фиксированной заранее
величиной.
Метод последовательной проверки гипотезы предполагает на каждой стадии
наблюдений (эксперимента) принятие одного из возможных решений: принять
гипотезу, отклонить ее или продолжить наблюдения. Обычно при последователь-
последовательном анализе нулевая гипотеза относительно значения параметра е формулируется
в форме предположения об одном из двух его возможных значений ?® или е\:
Щ: е = е0, Нг: е = ?г.
Задача последовательного анализа в ходе эксперимента — выбрать одну из ги-
гипотез. Вальд [433] показал, что для проверки гипотез методами последовательного
анализа требуется в среднем в два раза меньше наблюдений, чем при проверке
классическими методами, основанными на заранее фиксированном числе наблюде-
наблюдений. Впоследствии было показано [434], что при определенных условиях выигрыш
от применения последовательной процедуры по сравнению с классической теорети-
теоретически неограничен.
4.1] Сравнение параметров распределений 439
Перед планированием процедуры последовательного анализа назначают при™
емлемые величины вероятностей допустимых ошибок: а — вероятность принятия
гипотезы Hi, когда верна гипотеза Hq (ошибка первого рода) и C — вероятность
принятия гипотезы Hq, когда верна гипотеза Hi (ошибка второго рода).
Наибольший выигрыш последовательный анализ дает при а ^> C или а <С /3, т. е.
когда а и /3 являются величинами разного порядка малости.
Так как число наблюдений п в последовательном анализе является величиной
случайной, то необходимо знать либо его функцию распределения вероятностей,
либо параметры этого распределения (например, среднее количество необходимых
наблюдений). Среднее значение зависит только от истинного значения параметра,
относительно которого проверяется гипотеза.
Функция п(е), определяющая зависимость поте, называется функцией среднего
числа наблюдений.
На практике обычно находят средние значения числа наблюдений п(ео) и n(ei)
соответствующие гипотетическим значениям параметра е® и ?]_, между которыми
осуществляется выбор, и максимальное среднее значение числа наблюдений nmax,
необходимое для окончания последовательной процедуры проверки гипотезы.
Если знания только среднего числа наблюдений недостаточно и требуется опре™
делить либо вероятность того, что для завершения последовательной процедуры
понадобится не более некоторого, наперед заданного, числа наблюдений, либо число
наблюдений, соответствующее заданной вероятности завершения последовательной
процедуры, используются таблицы распределения Вальда [435] с функцией
р (х < а) = Wc(a) =
п
где х = ——отношение числа наблюдений к его среднему значению; с — параметр
п
распределения, определяемый видом распределения исследуемой случайной вели™
чины и гипотетическим значением параметра (eq или ?]_).
Вероятность j завершения процедуры последовательного анализа и число испыта™
« / \ ( \ TJ7 П (€)
нии п\е) при некотором значении е (?q или ei) связаны соотношением 7 = Н/С(е) - / \ ?
из которого можно определить либо 75 соответствующее заданному n(e), либо п(е),
соответствующее заданному значению 7-
Некоторые, наиболее употребляемые значения функции распределения Вальда
Wc ( х = з ), приведены в табл. 142.
4.1.4.1. Проверка гипотез о параметрах нормального распределения
4.1.4.1.1. Проверка гипотезы о значении среднего
Проверяется нулевая гипотеза Hq : /л = /iq против альтернативы Hi: /л = /ii
(/хо < fii). Полагается, что дисперсии и\ и а\ известны заранее, причем и\ = сг| = а2.
Введем обозначения
1 — а 2
а 2
Т> О" л I — р flQ + /l\
440
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 142
X
0,006
0,007
0,008
0,009
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,5
3,0
3,5
0,01
0,1986
0,2343
0,2662
0,2948
0,3205
0,4843
0,5693
0,6232
0,6612
0,6899
0,7125
0,7309
0,7465
0,7593
0,7706
0,7805
0,7893
0,7971
0,8041
0,8312
0,8498
0,8635
0,8743
0,8829
0,8901
0,8962
0,9015
0,9060
0,9101
0,9137
0,9169
0,9198
0,9225
0,9249
0,9272
0,9292
0,9329
0,9362
0,9390
0,9416
0,9349
0,9459
0,9478
0,9495
0,9511
0,9526
0,9585
0,9629
0,9663
Функции
0,02
0,0692
0,0928
0,1161
0,1388
0,1605
0,3237
0,4225
0,4891
0,5376
0,5750
0,6048
0,6294
0,6500
0,6677
0,6831
0,6967
0,7087
0,7194
0,7292
0,7667
0,7926
0,8119
0,8270
0,8391
0,8493
0,8578
0,8562
0,8717
0,8774
0,8824
0,8871
0,8912
0,8949
0,8984
0,9016
0,9045
0,9098
0,9143
0,9183
0,9220
0,9252
0,9281
0,9308
0,9332
0,9354
0,9375
0,9458
0,9520
0,9568
[ распределения
0,03
0,0261
0,0396
0,0544
0,0699
0,0858
0,2227
0,3269
0,3981
0,4518
0,4939
0,5281
0,5565
0,5806
0,6013
0,6195
0,6355
0,6498
0,6626
0,6742
0,7192
0,7506
0,7740
0,7923
0,8071
0,8194
0,8300
0,8390
0,8469
0,8590
0,8601
0,8657
0,8707
0,8754
0,8796
0,8835
0,8871
0,8835
0,8991
0,9040
0,9074
0,9124
0,9160
0,9192
0,9222
0,9249
0,9274
0,9376
0,9451
0,9509
с
0,04
0,0102
0,0175
0,0264
0,0364
0,0473
0,1637
0,2582
0,3301
0,3860
0,4309
0,4677
0,4987
0,5252
0,5482
0,5683
0,5682
0,6022
0,6166
0,6297
0,6806
0,7163
0,7431
0,7641
0,7811
0,7953
0,8074
0,8178
0,8269
0,8350
0,8421
0,8486
0,8544
0,8598
0,8646
0,8691
0,8771
0,8807
0,8871
0,8929
0,8980
0,9025
0,9066
0,9104
0,9138
0,9170
0,9199
0,9316
0,9402
0,9468
Wc(x) Вальда [435]
0,05
0,0041
0,0079
0,0130
0,0194
0,0266
0,1196
0,2067
0,2769
0,3334
0,3795
0,4282
0,4508
0,4790
0,5036
0,5252
0,5445
0,5619
0,5775
0,5918
0,6476
0,6870
0,7166
0,7400
0,7589
0,7748
0,7882
0,7998
0,8100
0,8190
0,8270
0,8342
0,8407
0,8467
0,8521
0,8571
0,8618
0,8701
0,8773
0,8873
0,8894
0,8945
0,8991
0,9033
0,9071
0,9106
0,9138
0,9269
0,9365
0,9438
0,07
0,0017
0,0033
0,0057
0,0087
0,0658
0,1357
0,1992
0,2536
0,3000
0,3399
0,3744
0,4046
0,4313
0,4555
0,4764
0,4957
0,5132
0,5292
0,5928
0,6381
0,6725
0,6997
0,7219
0,7405
0,7563
0,7700
0,7819
0,7926
0,8020
0,8106
0,8183
0,8253
0,8318
0,8377
0,8419
0,8530
0,8616
0,8691
0,8758
0,8818
0,8873
0,8922
0,8967
0,9009
0,9047
0,9201
0,9313
0,9398
0,10
0,0017
0,0280
0,0749
0,1256
0,1736
0,2170
0,2559
0,2906
0,3217
0,3498
0,3751
0,3981
0,4191
0,4384
0,4592
0,5277
0,5797
0,6196
0,6514
0,6776
0,6996
0,7183
0,7345
0,7488
0,7614
0,7727
0,7829
0,7921
0,8005
0,8082
0,8153
0,8219
0,8336
0,8439
0,8529
0,8608
0,8681
0,8745
0,8804
0,8858
0,8907
0,8952
0,9134
0,9266
0,9366
0,20
0,0019
0,0120
0,0309
0,0554
0,0826
0,1106
0,1383
0,1652
0,1909
0,2153
0,2385
0,2604
0,2810
0,3006
0,3835
0,4478
0,4990
0,5409
0,5760
0,5958
0,6316
0,6541
0,6739
0,6916
0,7074
0,7218
0,7347
0,7466
0,7575
0,7675
0,7768
0,7934
0,8097
0,8206
0,8319
0,8419
0,8510
0,8592
0,8667
0,8735
0,8798
0,9046
0,9222
0,9353
4.1]
Сравнение параметров распределений
441
X
4,0
4,5
5,0
6,0
7,0
8,0
9,0
10,0
15,0
20,0
25,0
30,0
40,0
50,0
100,0
X
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
1,0
1,1
1,2
1,3
1,4
0,01
0,9690
0,9713
0,9732
0,9762
0,9786
0,9805
0,9820
0,9833
0,9877
0,9903
0,9920
0,9932
0,9949
0,9960
0,9983
0,3
0,0021
0,0083
0,0192
0,0340
0,0515
0,0706
0,0907
0,1112
0,1316
0,1518
0,1715
0,1907
0,2093
0,2926
0,3614
0,4183
0,4662
0,5070
0,5421
0,5727
0,5997
0,6236
0,6450
0,6643
0,6817
0,6976
0,7121
0,7254
0,7490
0,7693
0,7870
0,8025
0,8163
0,02
0,9606
0,9638
0,9663
0,9706
0,9739
0,9765
0,9786
0,9804
0,9863
0,9897
0,9918
0,9932
0,9954
0,9966
0,9990
0,5
0,0025
0,0063
0,0122
0,0201
0,0298
0,0410
0,0533
0,0664
0,0802
0,0945
0,1089
0,1814
0,2492
0,3039
0,3635
0,4109
0,4528
0,4901
0,5234
0,5534
0,5804
0,6048
0,6271
0,6474
0,6661
0,6833
0,7138
0,7400
0,7628
0,7828
0,8003
0,03
0,9555
0,9594
0,9626
0,9677
0,9716
0,9747
0,9772
0,9793
0,9862
0,9900
0,9924
0,9940
0,9961
0,9973
0,9994
0,7
0,0012
0,0031
0,0069
0,0104
0,0159
0,0227
0,0306
0,0395
0,0491
0,0595
0,1175
0,1787
0,2379
0,2930
0,3435
0,3894
0,4310
0,4688
0,5031
0,5343
0,5628
0,5889
0,6128
0,6348
0,6551
0,6911
0,7221
0,7491
0,7726
0,7932
0,04
0,9521
0,9565
0,9601
0,9659
0,9703
0,9738
0,9766
0,9790
0,9865
0,9906
0,9931
0,9947
0,9968
0,9979
0,9996
0,9
0,0064
0,0090
0,0145
0,0199
0,0262
0,0333
0,0778
0,1309
0,1863
0,2406
0,2921
0,3402
0,3878
0,4258
0,4635
0,4981
0,5299
0,5592
0,5861
0,6109
0,6339
0,6748
0,7099
0,7404
0,7669
0,7901
Продолжение табл
0,05
0,9497
0,9545
0,9585
0,9649
0,9697
0,9734
0,9765
0,9790
0,9870
0,9912
0,9938
0,9954
0,9974
0,9984
0,9998
1,0
0,0041
0,0066
0,0100
0,0143
0,0193
0,0251
0,0637
0,1127
0,1657
0,2190
0,2706
0,3194
0,3650
0,4072
0,4464
0,4825
0,5158
0,5464
0,5747
0,6008
0,6250
0,6681
0,7025
0,7372
0,7651
0,7894
0,07
0,9466
0,9522
0,9568
0,9640
0,9694
0,9737
0,9771
0,9798
0,9884
0,9926
0,9951
0,9966
0,9982
0,9990
0,9999
1,2
0,0017
0,0030
0,0049
0,0074
0,0106
0,0144
0,0431
0,0842
0,1322
0,1829
0,2337
0,2832
0,3303
0,3746
0,4162
0,4548
0,4907
0,5239
0,5547
0,5833
0,6097
0,6568
0,6975
0,7325
0,7629
0,7893
0,10
0,9445
0,9508
0,9561
0,9643
0,9704
0,9750
0,9787
0,9816
0,9904
0,9944
0,9966
0,9980
0,9991
0,9995
0,9999
1,4
0,0024
0,0039
0,0058
0,0083
0,0295
0,0634
0,1062
0,1538
0,2033
0,2527
0,3007
0,3466
0,3900
0,4308
0,4690
0,5045
0,5376
0,5683
0,5967
0,6477
0,6915
0,7293
0,7619
0,7902
ицы 142
0,20
0,9454
0,9538
0,9598
0,9694
0,9762
0,9812
0,9849
0,9878
0,9952
0,9979
0,9990
0,9996
0,9999
0,9999
0,9999
1,6
0,0012
0,0020
0,0032
0,0049
0,0202
0,0481
0,0859
0,1301
0,1777
0,2266
0,2750
0,3220
0,3670
0,4096
0,4498
0,4874
0,5225
0,5552
0,5855
0,6400
0,6868
0,7272
0,7619
0,7928
442
Проверка гипотез о значениях параметров распределений
[Гл.4
Продолжение таблицы 142
X
1,5
1,6
1,7
1,8
1,9
2,0
2,5
3,0
3,5
4,0
4,5
5,0
6,0
7,0
8,0
9,0
10,0
15,0
20,0
50,0
X
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
с
0,3
0,8286
0,8396
0,8495
0,8585
0,8667
0,8742
0,9036
0,9240
0,9389
0,9500
0,9587
0,9654
0,9753
0,9819
0,9865
0,9898
0,9922
0,9977
0,9993
0,9996
1,8
0,0028
0,0140
0,0366
0,0697
0,1105
0,1561
0,2039
0,2524
0,3000
0,3464
0,3906
0,4325
0,4720
0,5100
0,5435
0,5757
0,6056
0,6334
0,6831
0,7258
0,7624
0,7939
0,8201
0,8442
0,8643
0,8816
0,9066
0,9096
0,5
0,8160
0,8299
0,8424
0,8536
0,8638
0,8731
0,9086
0,9321
0,9486
0,9604
0,9690
0,9755
0,9844
0,9898
0,9932
0,9954
0,9968
0,9994
0,9999
0,9999
2,0
0,0017
0,0097
0,0280
0,0569
0,0942
0,1375
0,1842
0,2323
0,2806
0,3278
0,3734
0,4168
0,4580
0,4967
0,5330
0,5669
0,5984
0,6277
0,6800
0,7250
0,7634
0,7936
0,8244
0,8484
0,8691
0,8818
0,9020
0,9150
0,7
0,8114
0,8276
0,8420
0,8549
0,8664
0,8769
0,9161
0,9411
0,9578
0,9692
0,9772
0,9830
0,9902
0,9942
0,9965
0,9979
0,9987
0,9998
0,9999
0,9999
2,2
0,0068
0,0215
0,0465
0,0806
0,1215
0,1667
0,2144
0,2629
0,3109
0,2576
0,4025
0,4452
0,4856
0,5235
0,5589
0,.5920
0,6227
0,6776
0,7246
0,7647
0,7989
0,8280
0,8527
0,8738
0,8918
0,9071
0,9218
0,9
0,8105
0,8284
0,8487
0,8585
0,8711
0,8824
0,9240
0,9434
0,9656
0,9762
0,9833
0,9881
0,9939
0,9967
0,9982
0,9990
0,9994
0,9999
0,9999
0,9999
2,4
0,0047
0,0166
0,0382
0,0691
0,1076
0,1513
0,1983
0,2468
0,2953
0,3431
0,3892
0,4334
0,4752
0,5147
0,5516
0,5861
0,6182
0,6755
0,7245
0,7662
0,8016
0,8316
0,8569
0,8784
0,8966
0,9120
0,9250
1,0
0,8108
0,8295
0,8461
0,8608
0,8738
0,8855
0,9278
0,9532
0,9690
0,9791
0,9857
0,9901
0,9951
0,9975
0,9987
0,9993
0,9996
0,9999
0,9999
0,9999
2,6
0,0033
0,0128
0,0314
0,0594
0,0955
0,0138
0,1837
0,2320
0,2810
0,3296
0,3769
0,4223
0,4657
0,5065
0,5450
0,5808
0,6142
0,6738
0,7247
0,7679
0,8044
0,8352
0,8611
0,8828
0,9011
0,9166
0,9295
1,2
0,8123
0,8325
0,8502
0,8658
0,8795
0,8917
0,9350
0,9599
0,9748
0,9838
0,9895
0,9931
0,9969
0,9986
0,9993
0,9997
0,9998
0,9999
0,9999
0,9999
2,8
0,0023
0,0099
0,0259
0,0511
0,0849
0,1253
0,1705
0,2185
0,2678
0,3170
0,3654
0,4121
0,4567
0,4990
0,5387
0,5759
0,6106
0,6725
0,7252
0,7698
0,8073
0,8388
0,8651
0,8872
0,9056
0,9209
0,9338
1,4
0,8148
0,8361
0,8547
0,8701
0,8853
0,8979
0,9416
0,9657
0,9794
0,9875
0,9922
0,9952
0,9981
0,9992
0,9996
0,9998
0,9999
0,9999
0,9999
0,9999
3,0
0,0016
0,0770
0,0214
0,0441
0,0756
0,1143
0,1584
0,2060
0,2554
0,3053
0,3545
0,4024
0,4483
0,4919
0,5330
0,5714
0,6073
0,6713
0,6958
0,7717
0,8102
0,8423
0,8691
0,8913
0,9098
0,9251
0,9378
1,6
0,8177
0,8401
0,8595
0,8764
0,8911
0,9039
0,9476
0,9707
0,9833
0,9903
0,9943
0,9966
0,9988
0,9995
0,9997
0,9998
0,9999
0,9999
0,9999
0,9999
3,2
0,0011
0,0060
0,0177
0,0381
0,0674
0,1044
0,1474
0,1945
0,2440
0,2943
0,3443
0,3932
0,4403
0,4852
0,5376
0,5673
0,6043
0,6704
0,7265
0,7737
0,8131
0,8458
0,8729
0,8953
0,9138
0,9290
0,9415
4.1]
Сравнение параметров распределений
443
X
2,5
3,0
3,5
4,0
4,5
5,0
6,0
7,0
8,0
X
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,5
3,0
4,0
5,0
X
0,30
0,35
0,40
0,45
0,50
0,55
0,60
1,8
0,9530
0,9749
0,9863
0,9925
0,9958
0,9976
0,9992
0,9997
0,9999
3,4
0,0046
0,0146
0,0330
0,0602
0,0955
0,1373
0,1838
0,2332
0,2839
0,3347
0,3846
0,4328
0,4789
0,5225
0,5634
0,6015
0,6700
0,7274
0,7758
0,8160
0,8493
0,8767
0,8992
0,9176
0,9327
0,9450
0,9799
0,9926
0,9969
0,9998
5,0
0,0033
0,0107
0,0251
0,0482
0, 0801
0,1200
0,1666
2,0
0,9578
0,9785
0,9889
0,9942
0,9969
0,9983
0,9995
0,9998
0,9999
3,6
0,0036
0,0121
0,0285
0,0538
0,0874
0,1280
0,1738
0,2231
0,2741
0,3256
0,2763
0,4256
0,4729
0,5176
0,5597
0,6000
0,6691
0,7283
0,7779
0,8189
0,8527
0,8804
0,9029
0,9213
0,9362
0,9483
0,9819
0,9936
0,9992
0,9999
5,5
0,0021
0,0076
0,0192
0,0392
0,0682
0,1058
0,1510
2,2
0,9621
0,9816
0,9909
0,9954
0,9977
0,9988
0,9997
0,9999
0,9999
3,8
0,0028
0,0100
0,0247
0,0481
0,0801
0,1195
0,1645
0,2136
0,2648
0,3169
0,3685
0,4188
0,4671
0,5131
0,5563
0,5966
0,6686
0,7296
0,7800
0,8218
0,8560
0,8839
0,9065
0,9248
0,9395
0,9514
0,9837
0,9945
0,9994
0,9999
6,0
0,0014
0,0054
0,0148
0,0320
0,0582
0,0935
0,1371
с
2,4
0,9659
0,9842
0,9926
0,9964
0,9983
0,9992
0,9998
0,9999
0,9999
4,0
0,0022
0,0084
0,0214
0,0431
0,0735
0,1116
0,1559
0,2046
0,2560
0,3086
0,3610
0,4123
0,4617
0,5087
0,5530
0,5944
0,6682
0,7305
0,7822
0,8247
0,8593
0,8873
0,9099
0,9281
0,9426
0,9542
0,9853
0,9953
0,9995
0,9999
6,5
0,0039
0,0115
0,0261
0,0498
0,0828
0,1248
Продолжение табл
2,6
0,9694
0,9865
0,9939
0,9972
0,9987
0,9994
0,9999
0,9999
0,9999
4,2
0,0017
0,0070
0,0186
0,0386
0,0674
0,1043
0,1478
0,1962
0,2477
0,3007
0,3539
0,4061
0,4565
0,5046
0,5499
0,5923
0,6680
0,7316
0,7844
0,8275
0,8624
0,8906
0,9132
0,9312
0,9455
0,9570
0,9868
0,9959
0,9996
0,9999
7,0
0,0028
0,0089
0,0215
0,0427
0,0735
0,1137
2,8
0,9725
0,9884
0,9950
0,9978
0,9990
0,9996
0,9999
0,9999
0,9999
4,4
0,0013
0,0058
0,0162
0,0347
0,0619
0,0975
0,1402
0,1882
0,2397
0,2931
0,3470
0,4000
0,4515
0,5006
0,5470
0,5904
0,6678
0,7328
0,7865
0,8303
0,8656
0,8939
0,9164
0,9343
0,9484
0,9595
0,9881
0,9965
0,9997
0,9999
7,5
0,0020
0,0069
0,0176
0,0366
0,0653
0,1038
3,0
0,9725
0,9900
0,9959
0,9983
0,9992
0,9997
0,9999
0,9999
0,9999
4,6
0,0010
0,0048
0,0141
0,0311
0,0569
0,0913
0,1330
0,1806
0,2321
0,2859
0,3404
0,3943
0,4467
0,4968
0,5442
0,5886
0,6677
0,7341
0,7887
0,8330
0,8686
0,9870
0,9194
0,9371
0,9510
0,9619
0,9892
0,9970
0,9998
0,9999
8,0
0,0014
0,0053
0,0145
0,0315
0,0581
0,0949
ицы 142
3,2
0,9777
0,9914
0,9966
0,9987
0,9994
0,9998
0,9999
0,9999
0,9999
4,8
0,6677
0,7353
0,7909
0,8357
0,8716
0,9000
0,9224
0,9399
0,9535
0,9641
0,9903
0,9974
0,9998
0,9999
8,5
0,0010
0,0041
0,0120
0,0271
0,0518
0,0869
444
Проверка гипотез о значениях параметров распределений
[Гл.4
X
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,5
3,0
4,0
5,0
X
0,40
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,5
3,0
5,0
0,2180
0,2723
0,3279
0,3834
0,4376
0,4897
0,5390
0,6677
0,7366
0,7930
0,8384
0,8745
0,9030
0,9252
0,9425
0,9559
0,9662
0,9912
0,9977
0,9998
0,9999
9,0
0,0032
0,0234
0,0462
0,0796
0,1235
0,1768
0,2373
0,3026
0,3701
0,4374
0,5028
0,5648
0,6747
0,7636
0,8321
0,8830
0,9197
0,9455
0,9635
0,9757
0,9840
0,9895
0,9988
0,9999
5,5
0,2019
0,2567
0,3135
0,3707
0,4270
0,4814
0,5331
0,6680
0,7399
0,7983
0,8449
0,8815
0,9099
0,9318
0,9485
0,9613
0,9709
0,9932
0,9984
0,9999
0,9999
10
0,0020
0,0174
0,0369
0,0670
0,1084
0,1603
0,2209
0,2874
0,3572
0,4276
0,4963
0,5616
0,6772
0,7701
0,8405
0,8918
0,9279
0,9457
0,9693
0,9802
0,9874
0,9921
0,9993
0,9999
6,0
0,1874
0,2424
0,3002
0,3590
0,4173
0,4738
0,5277
0,6685
0,7433
0,8036
0,8511
0,8880
0,9163
0,9377
0,9539
0,9659
0,9749
0,9947
0,9989
0,9999
0,9999
15
0,0042
0,0124
0,0294
0,0584
0,1015
0,1586
0,2279
0,3057
0,3881
0,4709
0,5507
0,6913
0,7996
0,8758
0,9260
0,9573
0,9760
0,9868
0,9929
0,9962
0,9980
0,9999
0,9999
с
6,5
0,1742
0,2293
0,2879
0,3481
0,4082
0,4668
0,5228
0,6693
0,7467
0,8086
0,8570
0,8941
0,9222
0,9431
0,9586
0,9700
0,9784
0,9959
0,9992
0,9999
0,9999
20
0,0010
0,0045
0,0134
0,0320
0,0864
0,1100
0,1852
0,2310
0,3580
0,4512
0,5441
0,7052
0,8243
0,9022
0,9486
0,9742
0,9876
0,9942
0,9974
0,9988
0,9995
0,9999
0,9999
Окончанр
[ е т а б л
ицы 142
7,0
0,1623
0,2172
0,2765
0,3379
0,3997
0,4602
0,5283
0,6702
0,7501
0,8136
0,8627
0,8999
0,9276
0,9480
0,9629
0,9736
0,9813
0,9968
0,9995
0,9999
0,9999
25
0,0063
0,0131
0,0442
0,0840
0,1528
0,2311
0,3334
0,4284
0,5395
0,7184
0,8452
0,9223
0,9638
0,9842
0,9934
0,9974
0,9990
0,9996
0,9999
0,9999
0,9999
7,5
0,1513
0,2060
0,2658
0,3283
0,3917
0,4541
0,5140
0,6712
0,7535
0,8184
0,8681
0,9053
0,9326
0,9524
0,9666
0,9767
0,9838
0,9975
0,9996
0,9999
0,9999
30
0,0030
0,0064
0,0131
0,0620
0,1273
0,2111
0,3124
0,4250
0,5361
0,7307
0,8631
0,9379
0,9743
0,9902
0,9965
0,9988
0,9996
0,9999
0,9999
0,9999
0,9999
8,0
0,1412
0,1956
0,2557
0,3193
0,3841
0,4482
0,5101
0,6723
0,7569
0,8231
0,8733
0,9104
0,9473
0,9565
0,9700
0,9795
0,9860
0,9980
0,9997
0,9999
0,9999
35
0,0014
0,0064
0,0204
0,0512
0,1068
0,1873
0,2940
0,4120
0,5335
0,7421
0,8795
0,9501
0,9817
0,9939
0,9981
0,9995
0,9998
0,9999
0,9999
0,9999
0,9999
8,5
0,1320
0,1859
0,2462
0,3107
0,3769
0,4429
0,5053
0,6734
0,7603
0,8277
0,8782
0,9152
0,9416
0,9601
0,9730
0,9819
0,9879
0,9985
0,9997
0,9999
0,9999
40
0,0032
0,0140
0,0330
0,0901
0,1640
0,2775
0,3940
0,5313
0,7528
0,8919
0,9597
0,9869
0,9961
0,9990
0,9997
0,9999
0,9999
0,9999
0,9999
0,9999
4.1] Сравнение параметров распределений 445
Если:
п
У^ Xj ^ Д то принимается гипотеза Щ;
п
^ ж^ ^ 5, то принимается гипотеза Н\\
п
А < ^ ж^ < I?, то наблюдения продол^:аются.
г=1
Средние объемы выборок, необходимые для завершения процедуры последова-
последовательного анализа, равны
1 — OL QL
A —- a) In — Ь ol In —
-/ \ о 2 Р 1 ~ Р
1 —- а
(Mi - Mo)
Параметр с распределения Вальда находится по формуле
1 ! -
In —-—, если /1 = /io 1 « <С
: = К-
если/* =
Задача 229. Предположим^ что параметр прибора распределен нормально со стан-
стандартным отклонением а = 200. Необходимо проверить при а = 0,1 и /3 = 0,01 ги-
гипотезу о том, что параметр прибора равен /х = /io = 1800, против альтернативы
ц = 1л1= 2000.
Найти контрольные границы и средние объемы выборок для последовательной про-
проверки гипотезы. Определить объем выборки по,э5, для которого с вероятностью не
менее 0,95 процедура последовательного анализа закончится принятием решения по
гипотезе.
Находим
2002 , 0,01 2000 + 1800
А = • In Ь п • z = -899,96 + 1900 • га;
200 - 1800 0,9 2 ' '
_ 2002 0,99 2000 + 1800
В = In Ь га • = 458,5 + 1900 • п.
2000 - 1800 0,1 2
Далее вычисляем средние объемы выборок (округляем до ближайшего большего
целого):
0,9 0,1
0,9 • In -±- + 0,1 • In ¦
п A800) = 2 . 2002 • °?1 ^^ = 8;
B000 - 1800J
0,01 0,99
0,01 • In — h 0,99 • In ——
п B000) = 2 • 2002 • ^ 3—5^- = 5;
V ; B000 - 1800J
0,01 0,99
inn П 0,9 ' П ОД 1П
nmax = —200 • l V — Ю-
B000 - 1800J
446 Проверка гипотез о значениях параметров распределений [Гл. 4
В нашем случае /3 <^. а, тогда для \х\ = 2000 находим
2000 + 1800
0 99
К = In -?— = 2,2925; с = 2,2925 •
2000-
= 1,14625.
ОД 2000 - 1800
При /i = fjii мы ранее получили n(/ii) = 5. Из табл.142 для с = 1,1462 находим
^0,95 w / ч п ЛС
ж = —-— соответствующее условию Wc{x) = 0,95.
Для с = 1,1462 и 7 = 0,95 имеем (интерполируя) х = —f— = 2,3.
Тогда ?го,95 = 2,3 • п B000) = 2,3 • 5 = 14, т. е. с вероятностью 0,95 для принятия реше-
решения по гипотезе потребуется не более 14 испытаний.
Итак, принимаем гипотезу Но, если
J2xi ^ -899,96 + 1900 • п,
г=1
и принимаем гипотезу Hi, если
JTxi ^ 458,5 + 1900 • п.
г=1
В любом ином случае испытания необходимо продолжить. При Но в среднем пона-
понадобятся 8 испытаний, а при Hi — 5 испытаний. Максимальное среднее число испытаний
не превысит 10.
4.1.4.1.2. Проверка гипотезы о значении дисперсии
Проверяется гипотеза Но: а2 = а\ против альтернативы Нi: а2 = а2 (а\ > (Jq)
при известном среднем /х.
п п
Гипотеза Hq принимается, если J^ х2 ^ А; если ^ х2 ^ В, принимается гипо-
г=1 г=1
п
теза ii/"i; если А < ^ ж| < В, то испытания продолжаются. Здесь
г=1
е70
Средние объемы выборок, необходимые для завершения последовательной про™
цедуры, равны
^JL Ч_Л.у J.JLJL „
й(G2) = 2 L
1 2 ^Л
In —
\
Вероятностные оценки необходимого числа испытаний могут быть найдены, по
аналогии с критерием для проверки гипотезы о среднем значении, с помощью
табл. 142 распределения Вальда при
= к
а —
2 ^O^T^l f_ l-OL
где
In —-—, если сг2 = ctq, а <С /3;
In , если а2 = а2, C <С а.
4.1] Сравнение параметров распределений 447
Если значение среднего /л неизвестно, то все приведенные соотношения сохра™
няются при замене п на (п — 1).
Задача 230. Предположим, что параметр прибора распределен нормально с извест-
известным средним ц. Необходимо проверить при а = 0,01 и /3 = 0,1 гипотезу о том, что дис-
дисперсия значений параметра прибора равна а2 = о% = 25 против альтернативы, утвер-
утверждающей, что а = G\ = 49.
Найти контрольные границы и средние объемы выборок для последовательной про-
цедуры проверки гипотез. Определить объем выборки по,э, для которого с вероятно-
вероятностью не менее 7 = 0,90 процедура последовательного анализа закончится принятием
решения по гипотезе. Определить вероятность того, что последовательная процедура
потребует не более 20 испытаний.
ё-©1
Находим
А = 2 ' 2Б ' 49 . Ь I ^- • [ - ) I = -234,029 + 34,348 • га;
49-25 [Спп |г| '
2'25-49 ¦ Г°'9 ¦'- '=459,354+ 34,348-п.
Если ^2xi ^ —-234, 029 + 34, 348 • п, то принимается гипотеза о том, что а =25;
г=1
п
если ^2 Х1 ^ 459,354 + 34,348 • п, то принимается гипотеза о том, что а2 = 49. В случае
г=1
п
—234,029 + 34,348 • гг < J^ ж^ < 459,354 + 34,348 • п испытания необходимо продолжить.
г=1
Далее вычисляем средние объемы выборок (округляя до ближайшего целого числа)
ОД 0,01 ОД 0,9
0,99 ¦ In — Ь 0,01 • In —— 0,1 ¦ In — h 0,9 • In ^^
nB5) = 2 • ^ J?L = 25; fiD9) = 2 • ^ ^ = 27;
2 • In 1 + ( - ) f-)-l-2-ln-
5 \7j \bj 5
0,1 0,9
2 ¦ In —^— • In ¦
0,99 0,01 ._
= 46.
В нашем случае а <С /3, тогда для а2 = erg = 25 находим
0,1
In-
" 0,99
= 2,292 и с = 2,292 <
49
25 +
2
49
. —- ]_
,146.
Из табл. 142 имеем W1M&(x) = 0,90 при х = -^- « 2,8, тогда по,э = п (сто) • 2,8 = 70.
Теперь определим вероятность окончания последовательной процедуры при п ^ 20. Име-
Имеем х = — = — = 0,8.
п 25
Из табл. 142 находим для с = 1,146: М^1Д4б(ж) = 0,56.
Следовательно, с вероятностью 0,56 для окончания последовательной процедуры
потребуется не более 20 испытаний, при условии, что а2 = ст§ = 25.
4.1.4.2. Проверка гипотезы о параметре экспоненциального распределения
Проверяется гипотеза Hq: Л = Aq (напомним, что Л = \jv — средняя наработка
до отказа, v — интенсивность отказов), против альтернативы Hi: А = Ai > Aq.
448
Проверка гипотез о значениях параметров распределений
[Гл.4
Введем обозначения
А =
Ai fa
1-/3
; 5 =
¦In
Если
принимается гипотеза Н$\ если
Ао V P
2 5, принимается гипоте™
г=1
г=1
за i?i; если А < ^ Х{ < В, испытания продолжаются.
г=1
Средние объемы выборок для последовательной процедуры определяются по
формулам
A — a) In — h a In
Ai 1 .
Т~ ~ г ~ 1п
-; n(\l) = i-
Ао
Ао
Л1
-, Ai
1п Г"
Ао
In
1 2 Al
ln If
Параметр распределения Вальда находится по формуле
^Ар
2
^^—, где К =
Ai
1 — а
In —-—, если А =
ot <C
2 7
In , если А = Ai, /3
Задача 231. Найти параметры плана последовательных испытаний при а = 0,2
и /3 = 0,05 d/L« проверки гипотезы Но о том, что средняя наработка на отказ элек-
электронного прибора равна А = Ао = 100 ч против альтернативы Н\ : А = Ai = 150 ч. Вы-
Вычислить средние объемы выборок, необходимых для окончания последовательного ана-
анализа. Найти вероятность того^ что последовательная процедура позволит принять
решение уже после п = 20 испытаний.
Находим
А =
150 - 100
•In
В =
150 - 100
•In
150 /0,2\"
100 \ 0,95
150 / 0,8 \ п
100 * \ 0,05 у
= 0,00811 «п^ 0,0312;
= 0,00811
0,0554.
Далее вычисляем:
0,8 0,2
0,8 • In — Ь 0,2 • In ^—
1 + In
100 100
0,05 0,95
0,05 • In — h 0,95 • In ——
0,8 ' 0,2
100
50
_
= 19; nmax =
0,8 0,2
2 150
100
= 27.
4.1]
Сравнение параметров распределений
449
Теперь найдем, учитывая, что
= Ai = 150,
150 150 - 100
К = 1п
0,95
= 1,558 и с =1,558 •
In-
' 100
/150- 100 у
V 150 )
= 344,864.
п 20
Имеем х = ——- = — « 1 и из табл. 142 для х = 1 и с = 344 имеем Wc(^) = 0,53, т. е.
n(Ai) 19
с вероятностью 0,53 процедура последовательного анализа закончится при п = 20, если
Л = Ai = 150.
4.1.4.3. Проверка гипотезы о параметре биномиального распределения
Проверяется гипотеза Hq : р = ро против альтернативы Hi: р = р\ > Ро-
Введем обозначения
А =
В =
In
In
In-
Pi !
Po
In
Pi
1 -
In
1 -
¦ a
1 -
1-
a
-In
1-
Po
Pi
Po
1 -;
Po
In
In
In
P1 I
Po
In
Pi
1-
-ln
1 -
1-
Pi
1 -
1 -
Po
Pi
1-
Po '
Pi
-Po *
1-P1
Пусть x — число наступлений наблюдаемого события (например, количество
дефектных приборов в партии). Если х ^ А, то принимается гипотеза Н$\ если
х ^ В, принимается гипотеза ii/i; в случае А < х < В испытания продолжаются.
Средние объемы выборок равны
в(ро) =
A — a) In Ь ск In
1 — а а
1 Pl /1 м Х ^Ро '
ро In A — ро) ш
Ро 1 - Pi
п(рг) =
Ро
1 ^ Pi
1 - a
lnPilni^?o
PO 1 ^ Pl
Параметр распределения Вальда находится по формуле
с = К~
где
Pi
1 Pi (Л u 1Po
pin A -p)ln-
Ро 1 - Pi
In-
<С
<С
15 А. И. Кобзарь
450
Проверка гипотез о значениях параметров распределений
[Гл.4
Задача 232. Необходимо найти параметры плана последовательных испытаний для
проверки гипотезы Но о том, что доля дефектных изделий в партии р = ро = 0,01
против альтернативы Hi: р = рг = 0,02. Определить количество испытаний, для ко-
которого с вероятностью j = 0,95 последовательная процедура закончится принятием
решения (заданы а = ОД и /3 = 0,01).
Находим
0,99
In
А =
В =
0,01
0,9
0,98
0,02 0,99
In — Ь In ——
0,01 0,98
0,02 0,99
In — h In
0,01
In
0,99
0,1
ln-
0,9
0,99
1 0,98
0,02 0,99
In — h In ——
0,01 0,98
In— hln{0,99}0,98
0,01 г J
= -6,399 + 0,0144 • n;
= 3,26 + 0,0144 -n.
Далее
n@,01) =
0,01 0,99
0,9 ¦ In — h 0,1 • In ——
0,9 0,1
(Щ oM
0,01 • In — 0,99 • In ——
0,9 ' 0,98
= 1225;
0,99 0,01
In • In
_ 0,1 0,9
Uinax ~ 0,02 0,99
Вычисляем параметр с (при /3 <С а и р = р\):
0,01 0,99
0,01 • In — h 0,99 • In ——
(ЦJ 0^99"
0,02 ¦ In — 0,98 • In ——
0,01 0,98
= 1466.
= 569;
1 — В
К = In = In
0,1
= 2,2925 и с = 2,2925 ¦
0,02 0,99
0,02 • In — 0,98 • In ——
0,01 0,98
0,02 • 0,98 • In
0,02
0,01
-In
0,99
= 0,65.
Теперь из табл. 142 находим х =
Q,95
, соответствующее условию Wc(x) = 0,95. Име-
Имеем Wo,65(ж) = 0,95 при х к, 3,5, или по,эб = 569 • 3,5 = 1992.
Следовательно, с вероятностью 0,95 при р = р\ = 0,02 процедура последовательного
анализа потребует не более 1992 испытаний.
4.2] Непараметрические критерии однородности статистических данных 451
4.2. Непараметрические (свободные от распределения)
критерии однородности статистических данных
Рассмотренные ранее методы сравнения параметров распределений предполагав
ли, что мы заранее обладаем фундаментальной информацией — нам известен вид
закона распределения вероятностей.
Обычно это требование редко является препятствием для желающих применять
статистику для решения своих проблем. Однако отклонение закона распределения
вероятностей изучаемой случайной величины от нам понравившегося приводит
к искажению вероятностных характеристик наших выводов (вплоть до принятия
решения, противоположного правдоподобному).
В тех случаях, когда наши предположения о гипотетическом законе распреде-
распределения вероятностей не кажутся убедительными, следует применять иные методы
для сравнения случайных величин и проверки гипотез об их значениях.
Методы статистической обработки и анализа результатов наблюдений, закон
распределения вероятностей появления которых неизвестен, объединены единым
направлением математической статистики, получившим название непараметриче-
непараметрическая статистика. Ее приемы и методы, известные еще как методы? свободные от
распределения^ интенсивно развиваются в последние годы.
Любое распределение можно описать параметром положения, характеризую™
щим центр группирования случайных величин, и параметром масштаба, характе-
характеризующим степень рассеяния случайных величин относительно центра группирова-
группирования (например, в случае нормального распределения ими являются соответственно
среднее \х и стандартное отклонение а).
Когда закон распределения неизвестен, гипотезы о параметрах положения и мас-
масштаба проверяются с помощью специальных критериев сдвига и масштаба.
Если fi(x) и /2(х)—неизвестные плотности вероятностей, то гипотеза сдвига
записывается как Hq: fi(x) = /2(ж) против альтернативы Hi: fi(x) = /2(ж — А),
или Н®: А = 0 против альтернативы Hi: А ф 0, где А — сдвиг, определяемый раз™
ностью параметров положения распределений.
Гипотезы о разнице в дисперсиях (при неизвестных распределениях) формули-
формулируются как гипотезы о параметрах масштаба.
Например, если
l(^JL^ и f2(x) = f(x - »),
то гипотеза о параметре масштаба записывается как Hq : т = 1 против альтернати-
альтернативы Hi: т ф 1.
Достоинством рассматриваемых в настоящем разделе непараметрических (сво-
(свободных от распределения) методов проверки статистических гипотез является их
расчетная простота. Однако мощность статистических критериев, построенных на
их основе, уступает аналогичным параметрическим критериям (например, крите-
критериям Стьюдента, Фишера и т. п.). Легко догадаться, что это плата за незнание вида
распределения случайных величин.
Рекомендуется следующий порядок использования непараметрических критериев.
Если распределение случайной величины неизвестно, то непараметрические критерии
являются единственно возможными критериями для проверки различных статистиче-
статистических гипотез. Если распределение известно, то рекомендуется сначала применить про-
простые в вычислительном отношении непараметрические критерии. При отклонении
ими проверяемой гипотезы дальнейшее уточнение не требуется. Если непараметриче-
непараметрический критерий не отклоняет гипотезу, необходимо осуществить ее дальнейшую про-
проверку одним из более точных параметрических критериев, изложенных в разделе 4.1.
15*
452
Проверка гипотез о значениях параметров распределений
[Гл. 4
4.2.1. Непараметрические критерии сдвига
4.2.1.1. Сравнение параметров сдвига двух совокупностей
4.2.1.1.1. Быстрый (грубый) критерий Кенум
Критерий изложен в [121]. Алгоритм его построения состоит в следующем.
Пусть 0 < ж < 1. Черех хж обозначим такое значение случайной величины,
которое превышается [мп] значениями из выборки.
Вычисляется среднее значение
т = 0,2ж j^ + 0 fix 1 + 0,2ж15
16 2 16
со стандартным отклонением
1,1s
где s = - [х± -xi5
J \ 16 16
Для очень несимметричных распределений используются оценки
Ь
+
3 + х is
4 16
1
s = -
4
3 3
-xi - -хз - х is
4 4 4 4 16
16 4 2 4 16 / ^ \ 16
Проверка разности в параметрах положения проверяется критерием
м = ""- -""-
(индексы относятся к номерам проверяемых выборок).
При объемах проверяемых выборок свыше 20 статистика критерия распреде™
лена нормально. Поэтому нулевая гипотеза отсутствия сдвига не отклоняется при
доверительной вероятности а, если \М\ < ui+a .
2
Критерий устойчив к отклонениям от нормальности, имеет эффективность по
сравнению с параметрическим критерием Стьюдента не хуже « 93%.
Задача 233. Имеются две группы наблюдений объема п = 32:
(гр. 1): 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
(гр. 2): 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21,
26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41.
Необходимо проверить отсутствие сдвига меэюду средними критерием Кенуя при
доверительной вероятности а, = 0,95.
Находим для первой совокупности
пц = 0,2 • 30 + 0,6 • 16 + 0,2 • 2 = 16;
13,
29,
22,
14,
30,
23,
15,
31,
24,
16,
32;
25,
xi = 16;
2
ж is = 2;
16
S! =
Для второй совокупности имеем
жх=39;
16
Ж1=25;
2
ж is = 11;
16
S2 = 5
^ = 9,33.
о
т2 = 0,2 • 39 + 0,6 • 25 + 0,2 • 11 = 25;
Н = 9K3.
Далее
М =
nil — ГП2
13,199
= 0,682.
4.2] Непараметрические критерии однородности статистических данных 453
Для а = 0,95 имеем и 1+0,95 = ^о,975 = 1,96.
2
Так как \М\ = 0,682 < г^о,975 = 1,96, гипотеза сдвига отклоняется.
Рассмотрим второй вариант критерия. Для первой выборки имеем
Ж1=28; Жз=4; гпг = -Л 1 1 1 Ж = 30 + 28+^16 + 4 + 2 =
4 4 6 6
si = - • ( 30 + - • 28 - - • 4 - 2 ) = 11,5.
4 \ 4 4 J
Аналогично для второй выборки имеем
xi = 37; хз = 13; т,2 = 25; S2 = 11,5.
4 4
Получаем Af = 0,555; легко видеть, что в силу симметричности наших выборок оба
метода дают одинаковые результаты.
4.2.1.1.2. Ранговые критерии сдвига
Ранговые критерии основываются на последовательности рангов выборочных
значений случайных величин. При этом рассматриваются не сами выборочные
значения, а их ранги, определяемые порядковым номером элемента выборки в об-
общем ряду, упорядоченном по возрастанию. Например, в упорядоченной выборке
%i ^ Х2 ^ • • • ^ %п выборочное значение Х{ заменяется рангом R = г.
4.2.1.1.2.1. Быстрый (грубый) ранговый критерий
Изложен в [121]. Рассматриваются две выборки объемов п и т при п + т = 20
(в, т ^ 4). Их элементы ранжируются по возрастанию совместно. Одинаковым на-
наблюдениям присваивается одинаковый усредненный ранг. Для каждой группы на-
находятся суммы рангов ^ R\ и J^ R2 и средние ранги R± = — ^ Ri и R^ = ~~ J^ Rj •
Вычисляем d = R\ — R2. Статистика d-критерия может быть аппроксимирована
нормальным распределением со средним М(сГ) = 0 и дисперсией
Поэтому при \d*
d
12 \ттг
гипотеза сдвига отклоняется с доверительной
Sd
вероятностью а.
Эффективность критерия для нормально распределенных выборок 0,95 (для
любого другого исходного распределения — не хуже 0,86).
Задача 234. Имеются две выборки случайных величин (п = 12, т = 8):
хщ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12;
x2i: Ю, 11, 12, 13, 14, 15, 16, 17.
Необходимо проверить гипотезу сдвига быстрым ранговым критерием при доверитель-
доверительной вероятности а, = 0,95.
Совместный ранжированный ряд имеет вид (вверху проставлены значения случайной
величины, внизу — принадлежность к выборке):
1 2 3 4 5 6 7 8 9 10 10 11 11 12 12 13 14 15 16 17
Х\ Х\ Х\ Х\ Xi Х\ Х\ Х\ Х\ Xi Х2 Х\ Х2 Х\ Х2 Х2 Х2 Х2 Х2 Х2
454
Проверка гипотез о значениях параметров распределений
[Гл.4
Ранги элементов первой выборки (хц) равны (одинаковые ранги усредняются) 1; 2;
3; 4; 5; 6; 7; 8; 9; 10,5; 11,5; 12,5 и ]Г Пг = 79,5; Кг = 6,625.
Для второй выборки имеем ряд
R2: 10,5; 11,5; 12,5; 13; 14; 15; 16; 17 и
Далее
d =
- R2 = |6,625 - 13,687| = 7,062; \d*
= 109,5; R2 = 13,687.
7,062
2,70
= 2,61.
Так
\d*\ = 2,61 > ui+at = 1,96, гипотеза сдвига не отклоняется.
2
4.2.1.1.2.2. Критерий Манна-Уитни-Вилкоксона
Пусть ж1? . ..,жп и г/!, . ..,ут—упорядоченные по возрастанию выборки. Для
проверки гипотезы сдвига Манн и Уитни [436] предложили ранговый критерий,
основанный на статистике
п т (-1 ^
крити-
критиЗдесь U — точное число пар значений xi и yj, для которых Xi < yj.
Если Ui(a) ^ U ^ ^(а), гипотеза сдвига отклоняется (Ui(a) и ^(
ческие значения, приведенные в табл. 143).
С U-статистикой Манна^Уитни связана статистика Вилкоксона [437], определя-
определяемая суммой рангов элементов одной выборки (предположим, xi объема п) в общей
упорядоченной последовательности элементов совместной выборки объема (m + n):
R = тп -
п(п+
-и.
При п, га > 20 применима аппроксимация
П (п + 771 + 1)
W =
пт (п + т?г + 1)
12
Статистика W аппроксимируется нормальным распределением, и гипотеза сдви™
га отклоняется с достоверностью а, если \W\ > wi+a.
2
Если в двух сравниваемых выборках есть совпадающие значения, то им реко-
рекомендуется приписывать средние ранги (среднеарифметическое для каждой серии
последовательных рангов). При этом в знаменателе статистики следует использо-
использовать величину
12
1-
(т + п)(т + п -— 1)(тт1 + п + 1)
где А; — общее число групп совпадающих величин; t{ — число совпавших величин
в г-й группе (следует помнить, что совпадения учитываются только тогда, когда
совпавшие величины принадлежат различным выборкам, т. е. совпадения, целиком
состоящие из элементов одной и той же выборки, на величину W не влияют).
4.2]
Непараметрические критерии однородности статистических данных
455
Таблица 143
Критические значения U\{ol) и С/г (о) критерия Манна-Уитни
(а — доверительная вероятность) [57]
п
4
5
6
7
8
9
10
т
4
5
6
7
8
9
10
5
6
7
8
9
10
6
7
8
9
10
11
12
7
8
9
10
11
12
13
14
8
9
10
11
12
13
14
15
16
9
10
11
12
13
14
15
16
10
11
12
а
0,90
иг
1
2
3
4
5
6
7
4
5
6
8
9
11
7
8
10
12
14
16
17
11
13
15
17
19
21
24
26
15
18
20
23
26
28
31
33
36
21
24
27
30
33
36
39
42
27
31
34
и2
15
18
21
24
27
30
33
21
25
29
32
36
39
29
34
38
42
46
50
55
38
43
48
53
58
63
67
72
49
57
60
65
70
76
81
87
92
60
66
72
78
84
90
96
102
73
79
86
0,95
иг
0
1
2
3
4
4
5
2
3
5
6
7
8
5
6
8
10
11
13
14
8
10
12
14
16
18
20
22
13
15
17
19
22
24
26
29
31
17
20
23
26
28
31
34
37
23
26
29
и2
16
19
22
25
28
32
35
23
27
30
34
38
42
31
36
40
44
49
53
58
41
46
51
56
61
66
71
76
51
54
63
69
74
80
86
91
97
64
70
76
82
89
95
101
107
77
84
91
п
10
12
14
16
18
20
т
13
14
15
16
17
18
19
20
12
13
14
15
16
17
18
19
20
14
15
16
17
18
19
20
21
22
16
17
18
19
20
21
22
23
24
18
19
20
21
22
23
24
25
26
20
21
22
23
а
0,90
иг
37
41
44
48
51
55
58
62
42
47
51
55
60
64
68
72
77
61
66
71
77
82
87
92
97
102
83
89
95
101
107
113
119
125
131
109
116
123
130
136
143
150
157
164
138
146
154
161
и2
93
99
106
112
119
125
132
138
102
109
117
125
132
140
148
156
163
135
144
153
161
170
179
188
197
206
173
183
193
203
213
223
233
243
253
215
226
237
248
260
271
282
293
304
262
274
286
299
0,95
иг
33
36
39
42
45
48
52
55
37
41
45
49
53
57
61
65
69
55
59
64
69
74
78
83
88
93
75
81
86
92
98
103
109
115
120
99
106
112
119
125
132
138
145
151
127
134
141
149
и2
97
104
111
118
125
132
138
145
107
117
123
131
139
147
155
163
171
141
151
160
169
178
188
197
206
215
181
191
202
212
222
233
243
253
264
225
236
248
259
271
282
294
305
317
273
286
299
311
456
Проверка гипотез о значениях параметров распределений
[Гл.4
Окончание таблицы 143
п
20
22
24
26
28
т
24
25
26
27
28
22
23
24
25
26
27
28
29
30
24
25
26
27
28
29
30
31
32
26
27
28
28
30
31
32
28
29
30
31
а
0,90
иг
169
177
185
192
200
171
179
188
197
205
214
223
231
240
207
217
226
236
245
255
264
274
284
247
257
268
278
289
299
310
291
302
313
325
и2
311
323
335
348
360
313
327
340
353
367
380
393
407
420
369
383
398
412
427
441
456
470
484
429
445
460
476
491
507
522
493
510
527
543
0,
иг
156
163
171
178
186
158
166
174
182
191
199
207
215
223
192
201
210
219
228
238
247
256
265
230
240
250
260
270
280
290
272
282
293
304
95
и2
324
337
349
362
374
326
340
354
368
381
395
409
423
437
384
399
414
429
444
458
473
488
503
446
462
478
494
510
526
542
512
530
547
564
п
28
30
32
34
36
38
40
т
32
33
34
30
31
32
33
34
35
36
32
33
34
35
36
37
38
34
35
36
37
38
39
40
36
37
38
39
40
38
39
40
40
0,90
иг
347
359
370
338
350
362
374
387
399
411
388
402
415
428
441
454
467
443
457
471
485
499
513
527
471
486
500
515
529
563
578
594
628
и2
549
565
582
562
580
598
616
633
651
669
636
654
673
692
711
730
749
713
733
753
773
793
813
833
753
774
795
815
836
881
904
926
972
а
0,95
иг
315
326
337
317
328
340
352
364
375
387
365
378
391
403
416
428
441
418
431
445
458
472
485
499
445
459
473
487
501
533
548
563
596
и2
571
598
615
583
602
620
638
656
675
693
659
678
697
717
736
756
775
738
759
779
800
820
841
861
779
801
822
843
864
911
934
957
1004
Более точная аппроксимация предложена Иманом [438]. В соответствии с ней
гипотеза сдвига отклоняется с достоверностью а', если
\J\=< J(a'),
где
za< —ct'-квантиль нормального распределения; tai(f) — а'-квантиль распределения
Стьюдента с f — п + т — 2 степенями свободы; а' — —-—.
Асимптотическая эффективность критерия Манна—Уитни равна 3/тг « 0,95.
4.2]
Непараметрические критерии однородности статистических данных
457
Одним из вариантов применения рассмотренного критерия является так на™
зываемый ранговый критерий Вилкоксона. Его статистика строится следующим
образом. Для двух выборок х и у одинакового объема п строится ряд разностей
Х{ — у%\, который затем ранжируется по возрастанию.
В упорядоченном ряду значений \х{ — yi\ находится сумма рангов Т величин
Zi = Xi ~ yi > 0. Гипотеза сдвига отклоняется, если Т\(а) ^ Т ^ Т2(а), где Т\(а)
и Т2(а)—критические значения, приведенные в табл. 144.
Таблица 144
Критические значения статистики Т знакового рангового
критерия Вилкоксона (а, — доверительная вероятность) [57]
п
6
7
8
9
10
11
12
а
0,90
2
4
6
9
11
14
18
т2
19
24
30
36
44
51
60
0,95
0
3
4
6
9
11
14
т2
21
25
32
39
46
55
64
п
13
14
15
16
17
18
19
а
0,90
22
26
31
36
42
48
54
т2
69
79
89
100
111
123
136
0,95
Ti
18
22
26
30
35
41
47
т2
73
83
94
106
118
130
143
п
20
22
24
26
28
30
32
а
0,90
Тг
61
76
92
111
131
152
176
т2
149
177
208
240
275
313
353
0,95
Ti
53
66
82
99
117
138
160
т2
157
187
218
252
289
327
368
При п ^ 20 применимо приближение
Г-
п(п+ 1)
Т* =
л/п (п + 1) Bп + 1)
При \Т*\ < ui+a гипотеза сдвига отклоняется (здесь и1 — 7~квантиль стандарт-
2
ного нормального распределения).
Более точно приближение содержится в [439], в соответствии с ним гипотеза
сдвига отклоняется на уровне достоверности а, если
\К\ < К(а),
где
К(а) = \za + \ta(n-l);
za — а-квантиль стандартного нормального распределения; ta(f) — «-квантиль рас-
распределения Стьюдента с / = п™ 1 степенями свободы.
Задача 235. Имеются две выборки случайных величин
(п = 8): 1,2; 2,1; 3,8; 6,4; 7,2; 9; 11; 12,4;
(т=10): 2,1; 2,1; 6,1; 6,3; 9; 9; 11,2; 12,4; 13,6.
Необходимо проверить гипотезу сдвига критериями группы Манна-Уитни-Вилкоксона
при доверительной вероятности а = 0,95.
Применим критерий Манна—Уитни, для чего подсчитаем количество пар, для кото-
которых Хг < у j при всех i = l, . ..,n и j = 1, ..., т. Например, для г = 1 и различных j =
ю
= 1, ..., 10 имеем число таких пар, равное ]Р h\j = 10. Далее по аналогии получаем:
458
Проверка гипотез о значениях параметров распределений
[Гл.4
i
1
10
2
8
3
8
4
6
5
6
6
4
7
4
8
2
8 10
Имеем U =J2J2hiJ = 10'
= 48.
Для а = 0,95 из табл. 143 находим Z7i @,95) = 17 и Е/2@,95) = 63.
Так как 17 < U = 48 < 63, гипотеза сдвига отклоняется.
8 • 9
Для статистики Вилкоксона имеем R = 8 • 10 -\ 48 = 68.
При вычислении W--статистики необходимо иметь в виду, что у нас есть три группы
совпадающих наблюдений B,1; 2,1; 2,1), (9; 9; 9) и A2,4; 12,4), т.е. к = 3, ti = 3, t2 = 3
и t3 = 2.
Вычисляем
8- 10- (8 + 10 + 1)
12
1 -
A0 + 8) • A0 + 8 + 1) • A0 + 8 - 1) ^
8- 19
-2— = -0,714.
= 11,202;
68-
w =
11,202
Имеем tii+o,95 = tio,975 = 1,96. Так как \U\ = 0,714 < 1,96, гипотеза сдвига отклоняет-
2
Используем теперь аппроксимацию Имана. Имеем zi+a = ^0,975 = 1,96.
?о,975(/ = Ю + 8 - 20 = 16) = to,97sA6) = 2,12 (см. таб! 118). Тогда
10-2
¦10-1 -0,714^
= -0,708; J@,975) =
1
2-1,96 2-2,12
= 0,491.
Так как \J\ = 0,708 > J@,975) = 0,491, гипотеза сдвига не отклоняется, т. е. более точная
аппроксимация отклоняет нулевую гипотезу.
Применим теперь знаковый ранговый критерий Вилкоксона (для чего ограничим
в демонстрационных целях выборку yj m = 8 значениями). Находим ряд разностей
Xi-yn -0,9; 0; -2,3; 0,1; -1,8; 0; -0,2; 0.
Ранжируем по величине значения zi = \х% — yi\ (вверху обозначим ранг)
(ранг): 2224 5 6 7 8
(zi): 0 0 0 ОД 0,2 0,9 1,8 2,3
1 + 2 + 3
(для трех равных значений Zi = 0 берем средний ранг =2).
о
Величина z% > 0 в ранжированном ряду имеет ранг Т = 4. Из табл. 144 находим
Ti = 4 и Тч = 32. Так как 2\ = 4 ^ Т = 4 ^ Т^ = 32, гипотеза сдвига отклоняется при
а = 0,95. 8.9
4
Для Т* имеем Т* =
= —0,4. Так как |Т* = 0,4 < 1?о,э75 — 1,96, эта аппроксима™
8 ¦ 9 • 17
ция также отклоняет гипотезу сдвига (однако следует помнить, что Т-аппроксимация
применима только при п ^ 20).
Более точное приближение дает (имеем в виду to,975(/ = 7) = 2,365):
= ^0,389; Ж @,975) =
+
= 0,466.
Так как \К\ = 0,389 < if@,975) = 0,466, гипотеза сдвига отклоняется.
4.2]
Непараметрические критерии однородности статистических данных
459
4.2.1.1.2.3. Критерий Фишера-Йэйтса-Терри-Гёфдинга
Критерий рассмотрен в работах Фишера и Йэйтса [440], Терри [441] и Гёфдин™
га [442] и основан на статистике
г=1
где ат+п{г) = M{zlm+n)—математическое ожидание г-й порядковой статистики
в выборке объема (га + п) из стандартного нормального распределения; Щ — ранг
значений у± в объединенной ранжированной выборке х и у (или ранг Х{ в объеди-
объединенной выборке, тогда суммирование нужно вести по г = 1, ..., п).
Напомним (см. аппроксимацию 5 в разделе 1.1.1), что для ап{г) может быть
использована аппроксимация
\0,14
где р =
Гипотеза сдвига отклоняется, если \S\ < 5(а), где S(a) — критическая величина,
некоторые значения которой приведены в табл. 145.
Таблица 145
Критические значения
статистики Фишера^Йэйтса^Терри^Гёфдинга
(а — доверительная вероятность) [443]
п
5
4
6
5
7
6
5
7
6
8
7
6
т
3
4
3
4
3
4
5
4
5
4
5
6
а
0,90
2,12
2,27
2,33
2,42
2,32
2,46
2,58
2,47
2,60
2,55
2,66
2,75
0,95
2,74
2,59
2,69
2,72
2,66
2,82
2,92
2,92
3,00
3,00
3,10
3,19
п
9
8
7
10
9
8
7
10
9
8
11
10
т
4
5
6
4
5
6
7
5
6
7
5
6
а
0,90
2,62
2,77
2,83
2,67
2,82
2,93
2,95
2,89
3,00
3,06
2,94
3,07
0,95
3,04
3,23
3,29
3,11
3,82
3,40
3,44
3,40
3,52
3,58
3,45
3,59
п
9
8
10
9
10
9
11
10
12
11
10
т
7
8
7
8
8
9
8
9
8
9
10
а
0,90
3,15
3,17
3,22
3,27
3,35
3,38
3,42
3,46
3,50
3,55
3,57
0,95
3,68
3,73
3,78
3,82
3,94
3,96
4,02
4,07
4,11
4,17
4,20
При га, п ^ 10 распределение 5 удовлетворительно аппроксимируется нормаль™
ным со средним /х = МE) = 0 и дисперсией
т-\-п
В этом случае гипотеза сдвига отклоняется, если
S
где ti7 — 7™квантиль стандартного нормального распределения.
460
Проверка гипотез о значениях параметров распределений
[Гл.4
Задача 236. Для двух выборок
(гс = 8) хн 1, 3, 4, 7, 9, 10, 15, 16;
(га = 7) ун 6, 8, 11, 14, 18, 21, 26
проверить гипотезу сдвига критерием Фишера-Йэйтса-Терри-Гёфдинга при довери-
доверительной вероятности а = 0,95.
Ранжируем совместную выборку, отмечая в ней ранги величин жиг/ (вверху отмечен
ранг, внизу принадлежность к выборке х или у)
12 3 4 5 6 7 8 9 10 11 12 13 14 15
1 3 4 6 7 8 9 10 11 14 15 16 18 21 26
хххухухх у у х х у у у
Следовательно, ранги членов выборки х в общем ряду будут
Rii 1, 2, 3, 5, 7, 8, 11, 12.
3
Для них находим а\ь(г) = 4,91 • [р0'14 — A — р)°'14], где р = ^-.
В результате имеем:
г
aib{i)
1
-1,7419
2
-1,2444
3
-0,94388
5
-0,51307
7
-0,16441
8
0
11
0,51307
12
0,71156
Далее вычисляем
S =
i) = -1,7419 - 1,2444 - ... + 0,51307 + 0,71156 = -3,383.
Из табл. 145 для а = 0,90, п = 8шт = 7 имеем 5@,95) = 3,58.
Так как \S\ = 3,383 < 5@,95) = 3,58, гипотеза сдвига отклоняется.
Для нормального приближения вычисляем дополнительно:
г
а\ъ{г)
4
^0,71156
6
^0,33358
9
0,16441
10
0,33349
13
0,94388
14
1,2444
15
1,7419
Имеем
@ = 12,763;
8-7
3,38
(8 + 7) ¦ (8 + 7- 1) 1,845
Так как \S*\ = 1,832 < tio,975 = 1,96, гипотеза сдвига отклоняется.
4.2.1.1.2.4. Критерий Ван дер Вардена [2]
Статистика критерия имеет вид
т
X =
= 1,832.
где Ury — 7™квантиль стандартного нормального распределения.
Для вычисления квантилей и я* может быть применено приближение (см. ап-
аппроксимацию 15 в разделе 1.1.1)
и л, « 4,91
п + т + 1
0,14
т + 1
0,14'
4.2]
Непараметрические критерии однородности статистических данных
461
Гипотеза сдвига отклоняется, если \Х\ < xaj где ха—критическое значение,
приведенное в табл. 146.
Таблица 146
Критические значения Ха статистики Ван дер Вардена
(а — доверительная вероятность) [2, 443]
п
4
4
5
6
5
6
5
7
6
8
7
6
9
8
ТП
3
4
3
3
4
4
5
4
5
4
5
6
4
5
а
0,90
1,82
1,98
1,84
2,05
2,12
2,18
2,29
2,26
2,32
2,32
2,40
2,45
2,36
2,50
0,95
2,14
2,27
2,41
2,37
2,39
2,50
2,60
2,59
2,69
2,69
2,79
2,85
2,76
2,92
п
7
9
8
7
10
9
8
11
10
9
8
12
11
10
тп
6
5
6
7
5
6
7
5
6
7
8
5
6
7
а
0,90
2,56
2,57
2,65
2,69
2,61
2,71
2,76
2,68
2,80
2,87
2,90
2,73
2,86
2,95
0,95
2,98
3,04
3,07
3,12
3,07
3,20
3,25
3,14
3,28
3,36
3,40
3,20
3,36
3,46
ть
9
12
11
10
9
13
12
11
10
14
13
12
11
10
тп
8
6
7
8
9
6
7
8
9
6
7
8
9
10
а
0,90
2,99
2,91
3,02
3,08
3,09
2,97
3,08
3,15
3,19
3,02
3,15
3,23
3,28
3,30
0,95
3,51
3,43
3,54
3,61
3,63
3,49
3,62
3,70
3,75
3,56
3,70
3,80
3,86
3,88
При п, га ^ 20 распределение X удовлетворительно описывается нормальным со
средним ji = М(ж) = 0 и дисперсией
Т>(Х) =
т-\-п
Если X
X
a, гипотеза сдвига отклоняется с достоверностью а.
Вспомогательные величины
К = —?— У и2
то+п
приведены в табл. 147.
При п + га —>• оо эффективность критерия Ван дер Вардена не уступает эффек-
эффективности критерия Стьюдента.
Задача 237. Проверить гипотезу сдвига в условиях задачи 236 критерием Ван дер
Вардена.
Для рангов выборки х в общем ранжированном ряду
Rii 1, 2, 3, 5, 7, 8, 11, 12
находим
i 1 =«1 =4,91- —
8+7+1 16 I \ J-O
0'14
0'14
= -1,5354;
и 2_ = -1Д492; из_ = -0,8851; и^ = -0,4869; uj_ = -0,1566;
16 16 16 16
и^ =0; ми = 0,4869; U12 = 0,6723.
16 16 16
462
Проверка гипотез о значениях параметров распределений
[Гл.4
Имеем X = ]Р ur i
i=1 т + п+1
= ™3,054. Из табл. 146 для п = 8, т = 7 находим жо,95 = 3,25.
Так как |Х| = 3?054 < жо,95 = 3,25? гипотеза сдвига отклоняется.
Используем теперь нормальное приближение. Из табл. 147 находим
К =
т-\-п
Окончательно
D(I) =
п .К= 1^.0,705 = 2,82;
— 1 14
3,054
1,679
= 1,819.
Так как \Х*\ = 1,819 < гйз,95 = 1,96, нулевая гипотеза сдвига отклоняется.
Таблица 147
Вспомогательные величины К критерия Ван дер Вардена [2]
т + п
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
К
0,449
0,497
0,537
0,570
0,598
0,622
0,642
0,661
0,667
0,692
0,705
0,716
0,727
0,737
0,746
0,755
т + п
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
К
0,763
0,770
0,777
0,783
0,789
0,794
0,799
0,804
0,809
0,813
0,817
0,821
0,825
0,829
0,833
0,836
т + п
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
К
0,839
0,842
0,845
0,848
0,850
0,853
0,855
0,858
0,860
0,862
0,864
0,866
0,868
0,870
0,872
0,874
т + п
53
54
55
56
57
58
59
60
62
64
66
68
70
72
74
76
К
0,876
0,877
0,879
0,880
0,882
0,884
0,885
0,887
0,889
0,892
0,894
0,897
0,899
0,901
0,903
0,905
т + п
78
80
82
84
86
88
90
92
94
96
98
100
110
120
130
140
К
0,907
0,908
0,910
0,912
0,913
0,915
0,916
0,918
0,919
0,920
0,922
0,923
0,928
0,933
0,937
0,940
4.2.1.1.2.5. Медианный критерий
Статистика критерия строится следующим образом [365]. Находится медиана
Ме(ж,у) общего упорядоченного ряда (ж, у), и подсчитывается число наблюдений
выборки ж, превосходящих медиану (если (га + п) нечетно и медиана принадлежит
выборке ж, то это число увеличивается на 1/2). Тогда статистика критерия может
быть записана как
S =
г=1
где
При п^т^ 10 распределение S удовлетворительно описывается нормальным [365
со средним \х = МE) = — и дисперсией
- 1)
, если га + n = 2fc;
если m -\- n = 2k — 1.
4.2] Непараметрические критерии однородности статистических данных 463
Если
то с достоверностью а гипотеза сдвига отклоняется.
Иногда применяется другая форма медианного критерия [444]. Пусть А ж С —
количества элементов выборки ж, соответственно больших и меньших медианы
объединенной выборки, а В и D — аналогичные числа для выборки у. Тогда стати-
статистикой критерия сдвига является величина
Y2=
Х
(А + В) (С + D) + (А + С) (B + DY
имеющая, при отсутствии сдвига, распределение хи~квадрат с / = 1 степенью сво-
свободы.
Критерий неприменим, если А, В, С или D < 5 и n + m < 40. Для этих условий
следует пользоваться точным критерием, критические значения которого D и С
для заданных А и В приведены в [44] (из-за громоздкости таблиц мы их здесь не
приводим).
Эффективность медианного критерия по сравнению с критерием Стьюдента
в случае нормального распределения равна 2/тг « 0,64.
Задача 238. Даны две выборки случайных величин:
(ш = 20) х: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20;
(п = 21) у: 9 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49.
Необходимо проверить гипотезу сдвига медианным критерием при доверительной ве-
вероятности а = 0,95.
Ранжируем совместный ряд (ж, у) (вверху обозначен ранг члена выборки в общем
ряду, для совпадающих значений ранги усреднены)
1 2 3 4 5 6 7 8 9,5 9,5 11 12,5 12,5 14 15,5 15,5 17 18,5 18,5 20
12 3 4 5 6 7 8 9 9 10 11 11 12 13 13 14 15 15 16
ххххххххх ух х у х х у х х у х
21,5 21,5 23 24,5 24,5 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
17 17 18 19 19 20 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
х у х х ухууууууууууууууу
Легко видеть, что медианой этого ряда является член выборки с порядковым номером
т + те + 1 20 + 21 + 1 „
= 21, это х = 17.
Вычисляем
20
1L = 3,5;
Тогда 15*1 = — = 4,06. Так как 15*1 = 4,06 > гх1+о,95 = 1,96, гипотеза сдвига не
1,60 —2—
отклоняется.
464 Проверка гипотез о значениях параметров распределений [Гл. 4
Рассмотрим вторую модификацию критерия. В нашем случае А = 3, С = В = 16
ш D = 4. Тогда
B1 + 20) • МЗ • 4 - 16 • 16| -
V
)
B1 + 20) МЗ 4 16 16| )
-у2 — ^ z ?_ — 2694 8
Х C + 16). A6+ 4)+ C + 16). A6+ 4)
что, конечно же, чудовищно превышает критическое значение Xo,9s(l) = 3,84. Следу-
Следует помнить, что критерий применим только при n + m < 40 и А, В, С, D < 5. Мы его
применили некорректно, однако основной цели достигли — продемонстрировали технику
применения критерия.
4.2.1.1.2.6. Критерий Мостеллера
Рассмотрен в [445] и формулируется следующим образом. Гипотеза равенства
средних двух выборок одинакового объема п > 5 отклоняется с доверительной веро-
вероятностью 0,95, если 5 (при п ^ 25) или 6 (при п > 25) наибольших или наименьших
значений содержатся в одной и той же выборке. Критерий имеет низкую мощность
и может быть рекомендован только для быстрой грубой проверки гипотез сдвига.
Задача 239. В условиях задачи 238 {исключив значение у = 49 для того, чтобы выров-
выровнять объемы выборок п = т = 20) проверить гипотезу сдвига критерием Мостеллера.
Видим, что здесь 14 наибольших значений принадлежат выборке у, что намного
превышает критическое значение, равное 5. Следовательно, можно уверенно признать
наличие сдвига в параметре положения двух выборок.
4.2.1.1.2.7. Критерий Розенбаума
Предложен в [446] для двух выборок равного объема. Если не менее 5 (для
в^16иа = 0,95) или 7 (для п^20иа = 0,99) значений одной выборки находятся
вне размаха второй выборки, то нулевая гипотеза отсутствия сдвига на указанных
уровнях достоверности отклоняется.
Критерий рекомендуется использовать для быстрой приближенной проверки
гипотезы сдвига.
Задача 240. Проверить гипотезу сдвига в условиях задачи 238 критерием Розенбау-
Розенбаума.
Вне размаха выборки у (от 9 до 47) находятся 8 значений выборки ж, что больше
критического числа 5 и позволяет предположить наличие сдвига в параметрах положения
двух выборок.
4.2.1.1.2.8. Критерий Хаги
Рассмотрен в [447]. Пусть А и В1— количества наблюдений среди х\, ...,жп?
больших, чем max г/j, и меньших, чем mln у л соответственно, и пусть А' ж В —
количества наблюдений среди г/i, . ..,уп, больших, чем max a^, и меньших, чем
mm Xi соответственно. Критерий Хаги основан на статистике
Т = А + В^ А1 -В1.
Гипотеза сдвига принимается на уровне значимости а, если \Т\ > Та, где Та —
критическое значение, приведенное в табл. 148.
При n, m > 25 применимо соотношение [448]
к) = У+?*У {p2+q)q
(p-q)(l+Py
4.2]
Непараметрические критерии однородности статистических данных
465
Таблица 148
Критические значения Та критерия Хаги (а — уровень значимости) [448]
4
5
6
7
8
9
а
0,05
6
6
6
6
7
7
0,10
5
5
5
5
6
6
10
11
12
13
14
15
а
0,05
7
7
7
7
7
7
0,10
6
6
6
6
6
6
16
17
18
19
20
21
а
0,05
7
7
7
7
7
7
0,10
6
6
6
6
6
6
22
23
24
а
0,05
7
7
7
0,10
6
6
6
где
Гипотеза сдвига принимается, если вычисленное значение Р(Т ^ к) < —, где а —
заданный уровень значимости.
Задача 241. Для данных задачи 238 проверить гипотезу сдвига критерием Хаги на
уровне значимости а = 0,05 (принимаем п = т = 20).
Имеем А = 0, В' = 8, А' = 14, В = 0 и Г = 0 + 0 - 14 - 8 = ^22.
Из табл. 148 для п = т = 20 находим критическое значение Го,о5 = 7.
Так как \Т\ = 22 > To,os = 7, гипотеза сдвига уверенно принимается.
Находим далее
.-6
Р(Г
22) =[ — + !
\ 2 3
= 2,7 • 10~
Легко видеть, что Р(Т ^ 22) <С 0,05/2 = 0,025, что также позволяет принять гипотезу
сдвига.
4.2.1.1.2.9. ^-критерий
Предложен Гаеком и Шидаком [365, 449]. В обозначениях, введенных для кри™
терия Хага (см. раздел 4.2.1.1.2.8), статистика ^-критерия записывается как
Е= \mm(A, В) - min(Af, Вг)\ .
Таблицы критических значений Е^критерия приведены в [450]. Однако мы
рекомендуем вместо таблиц использовать достаточно простую формулу
?(Е
с:
где к = 1, 2, ..., min(ra, n).
Так как ~Р(Е ^ к) = Р(.?7 ^ Aj), to на уровне значимости а гипотеза сдвига будет
принята, если Р(Е ^ к) или P(i? ^ Aj) будет меньше, чем а/2.
Задача 242. Проверить Е-критерием гипотезу сдвига в условиях задачи 238.
Имеем А = 0, В' = 8, А1 = 14 и В = 0.
Тогда ?" = |min@,0) - mln(8,14)| = 8 и
?(Е :> 8) =
^20+20-2-8
20+20
Легко видеть, что ~Р(Е ^ 8) <С а/2 = 0,025, что позволяет уверенно принять гипотезу
сдвига, так как наблюдаемое значение Е = 8 очень маловероятно при отсутствии сдвига
в параметрах положения двух выборок.
466
Проверка гипотез о значениях параметров распределений
[Гл.4
4.2.1.2. Сравнение параметров сдвига нескольких (к > 2) совокупностей
4.2.1.2.1. Критерий Круекала—Уоллиса
Рассмотрен в [451]. Пусть в нашем распоряжении имеются к выборок случайных
величин
1, #12, •••?
#21? #22» •••?#2п2;
Упорядочим все N = ]Р щ элементов выборок по возрастанию и обозначим
г=1
через Rij ранг j-ro элемента г-й выборки в общем упорядоченном ряду.
Статистика критерия Крускала^Уоллиса для проверки гипотезы о наличии сдви-
сдвига в параметрах положения двух сравниваемых выборок имеет вид
N + 1
12
N(N
г=1
где iJi =
i
Легко видеть, что критерий Крускала^Уоллиса является многомерным обобще-
обобщением двухвыборочного критерия Вилкоксона^Манна^Уитни (см раздел 4.2.1.1.2.2).
Гипотеза сдвига отклоняется на уровне значимости а1 если Н ^ На1 где На —
критическое значение, приведенное в табл. 149 для к ^ 5 и п^ ^ 8. При гц ^ 5
применимы различные аппроксимации. Укажем некоторые из них.
Таблица 149
Критические значения критерия Крускала^Уоллиса
(а — уровень значимости) [18, 57, 444]
«i
2
3
3
3
4
4
4
4
4
4
5
5
5
n2
2
2
3
3
2
3
3
4
4
4
2
3
3
пз
2
2
2
3
2
2
3
2
3
4
2
2
3
ОД
4,571
4,500
4,556
4,622
4,458
4,511
4,709
4,555
4,545
4,654
4,373
4,651
4,533
0,05
4,714
5,361
5,600
5,333
5,444
5,791
5,455
5,598
5,692
5,160
5,251
5,648
П\
5
5
5
5
5
5
5
6
6
6
6
6
6
п2
4
4
4
5
5
5
5
2
3
3
4
4
4
пз
к--
2
3
4
2
3
4
5
2
2
3
2
3
4
a
ОД
0,05
= 3
4,541
4,549
4,668
4,623
4,545
4,523
4,560
4,545
4,682
4,590
4,494
4,604
4,595
5,273
5,656
5,657
5,338
5,705
5,666
5,780
5,345
5,348
5,615
5,340
5,610
5,681
«1
6
6
6
6
6
6
6
6
6
7
8
П2
5
5
5
5
6
6
6
6
6
7
8
пз
2
3
4
5
2
3
4
5
6
7
8
а
ОД
4,596
4,535
4,522
4,547
4,438
4,558
4,548
4,542
4,643
4,594
4,595
0,05
5,338
5,602
5,661
5,729
5,410
5,625
5,724
5,765
5,801
5,819
5,805
4.2]
Непараметрические критерии однородности статистических данных
467
Окончание таблицы 149
2
3
3
3
3
4
4
4
4
2
3
п2
2
2
3
3
3
2
пз
2
2
2
3
3
2
п2
4
4
4
2
2
пз
4
4
4
2
2
п4
2
2
2
2
3
2
Q
ОД
5,667
5,664
5,745
5,879
6,026
5,755
п4
2
3
4
2
2
п6
2
2
ОД
5,914
6,042
6,088
6,982
6,955
к =
0,05
6,167
6,333
6,527
6,727
7,000
6,545
к =
а
0,05
6,957
7,142
7,235
7,418
7,682
= 4
4
4
4
4
4
= 5
3
3
3
3
п2
3
3
3
4
4
п3
2
3
3
2
2
п2
3
3
3
3
пз
2
3
3
3
п4
«4
2
2
3
3
2
2
3
2
2
а
ОД
5,750
5,872
6,016
5,808
5,901
«5
2
2
2
3
од
7,026
7,121
7,210
7,333
0,05
6,621
6,795
6,984
6,731
6,874
а
0,05
7,910
8,044
8,200
8,333
Аппроксимация Крускала-Уоллиса [451]
Пусть
м =
N(N + 1) '
V = 2(k-1)-
= (к - 1)
(к-
5iV(iV
Тогда статистика
F =
^V
1)}
М ^к + 1
jfe- I J
будет иметь при отсутствии сдвига i^-распределение с и\ и г/2 степенями сво-
свободы. Таким образом, нулевая гипотеза отклоняется с достоверностью а, если
F>Fa(vuv2).
Аппроксимация Имана-Давенпорта [452]
В соответствии с ней нулевая гипотеза сдвига отклоняется с достоверностью а,
если J ^ Jai где
J = f
- fe)
" 1)} ,
Faifit /2) и Xa(a) —соответственно критические значения статистик Фишера и хи™
квадрат с соответствующими степенями свободы.
Это более точная аппроксимация, чем аппроксимация Крускала^Уоллиса. При
наличии связанных рангов (т. е. когда совпадают значения величин из разных
468
Проверка гипотез о значениях параметров распределений
[Гл.4
выборок и им присваивается одинаковые средние ранги) необходимо использовать
'1
модифицированную статистику Н* = Н < 1 —
v=i
3
7V ~N
5 гДе
= t| —
tj—размер j-й группы одинаковых элементов; q — количество групп одинаковых
элементов.
При щ ^ 20 справедлива аппроксимация распределения статистики Н % -рас-
-распределением с / = & — 1 степенями свободы, т. е. нулевая гипотеза отклоняется, если
Задача 243. В результате наблюдений получены пять выборок случайных величин
(к = 5)
xtji 1, 2, 3, 4, 5, 6 (щ=6); x2j: 3, 4, 5, 6, 7 (п2 = 5); x3j-: 7, 8, 9 (п3 = 3);
x4i: 1, 5, 7, 8, 10, 12 (п4 = 6); ж5,: 10, 11, 13, 14, 16, 18, 20 (га5 = 7).
Необходимо проверить гипотезу об отсутствии сдвига между параметрами положе-
положения в выборках критерием Крускала-Уоллиса на уровне значимости а = 0,05.
5
Ранжируем совместно все N = ]>^Пг = б + 5 + 5 + 6 + 7 = 27 выборочных значений
г=1
Xij (г — номер выборки; Rij—ранг j-ro наблюдения в г-й выборке). Результаты сведем
в таблицу, усредняя ранги совпадающих наблюдений:
г
1
4
1
1
2
1
2
Xij
1
1
2
3
3
4
4
1,5
1,5
3
4,5
4,5
6,5
6,5
i
1
2
4
1
2
2
3
Xij
5
5
5
6
6
7
7
9
9
9
11,5
11,5
14
14
i
4
3
4
3
4
5
5
Xij
7
8
8
9
10
10
11
Ri
14
16,5
16,5
18
19,5
19,5
21
i
4
5
5
5
5
5
Xij
12
13
14
16
18
20
Rt
22
23
24
25
26
27
Далее подсчитываем
36
Кг = У Rtj = 1,5 + 3 + 4,5 + 6,5 + 9 + 11,5 = 36 (#i = — = 6);
r~f 6
R2 = 4,5 + 16,5 + 9 + 11,5 + 14 = 45,5 (R2 = — = 9,1);
R3 = 48,5 (R3 = 16,166); R4 = 82,5 (R4 = 13,75); R5 = 165,5 (Д5 = 23,643).
Тогда
12 5 R2
H = • у -5- - 3 • 28 = 18,562.
27 • 28 ^ rii
Используя аппроксимацию Крускала-Уоллиса, имеем
з
М =
V = 2-4:-
= 24,8095; щ = 3,8274; и2 = 19,91;
\ 5
I - 5. у; — = 6,464.
27-28
2- {3-52 ^6-5 + 27- B-25^6-5
5-27-28
4.2]
Непараметрические критерии однородности статистических данных
469
Учитывая, что у нас были группы совпадающих рангов (всего было q = 8 совпадаю-
совпадающих групп с t\ = 2, ?2 = 2, ?3 = 2, ?4 = 3, ?5 = 2, te = 3, ?7 = 2, tg = 2), находим
Я* =
н
= 18,642;
1 -
27 - 27
18,642 • B4,8095 -5 + 1)
4 • B4,8095 - 18,642) '
Из таблиц F-распределения (или аппроксимаций — см. раздел 1.1.10) находим для
уровня достоверности 1 — а = 0,95: .Fo,95(^1 = 3,83; 1/2 = 19,91) = 3,05.
Так как F = 15,725 > .Fo,95C,83; 19,91) = 3,05, гипотеза сдвига не отклоняется (т.е.
сдвиг признается значимым).
Используем теперь аппроксимацию Имана-Давенпорта:
J =
18,642
1 +
27 - 1 - 18,642
= 37,19; Jo,95 = \ • [4 • F0,95D; 22) + Хо,э5D)] .
Из таблиц находим Fo,95D;22) = 2,82 и Хо,9бD) = 9,49 (аппроксимации см. в разде-
разделах 1.1.8, 1.1.10). Тогда Jo,95 = - • D • 2,82 + 9,49) = 10,385.
Так как J = 37,19 > Jo,95 = 10,385, гипотеза сдвига не отклоняется.
4.2.1.2.2. Критерий Неменьи
Критерий применим для выборок равного объема п (т.е. N = nk). Статистика
критерия, предложенного Неменьи [453], в обозначениях, принятых для крите-
критерия Крускала-Уоллиса (ем. раздел 4.2.1.2.1), имеет вид D^m = \Щ — Rm\, (l ф т;
1,т= 1,2, ...,fc).
Гипотеза сдвига считается принятой, если В^ш ^ ?>/}Ш(а), где D|,m(a) — крити-
критические значения, приведенные в табл. 150.
Задача 244. Для к = 4 выборок равного объема п = 5
xij: 1, 2, 3, 4, 5; x2ji 3, 4, 5, 6, 7;
x3j: 4, 5, 6, 7, 8; x4ji 7, 8, 9, 10, 11
проверить гипотезу сдвига критерием Неменьи при достоверности а = 0,95.
Упорядочиваем по возрастанию ряд j\T = n-lc = 5-4 = 20 значений хц (г — номер
выборки). Результаты сводим в таблицу, ранги совпадающих наблюдений усредняем:
%
1
1
1
2
1
Xij
1
2
3
3
4
Щ
1
2
3,5
3,5
6
г
2
3
1
2
3
Хц
4
4
5
5
5
6
6
9
9
9
i
2
3
2
3
4
Xij
6
6
7
7
7
11,5
11,5
14
14
14
i
3
4
4
4
4
Xij
8
8
9
10
11
Rtj
16,5
16,5
18
19
20
Вычисляем
20
Ri = J2 RlJ = X + 2 + 3'5 + 6 + 9 - 21'5'
j • = 3,5 + 6 + 9 + 11,5 + 14 = 44;
20
i = 6 + 9 + 11,5 + 14 + 16,5 = 57;
^J = I4 +
+ 18 + 19 + 20 = 87,5.
470
Проверка гипотез о значениях параметров распределений
[Гл.4
Критические значения
Таблица 150
критерия Неменьи [9]
п
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
к
3
13,8
20,9
29,0
37,9
47,6
58,0
69,1
80,8
93,1
105,9
119,3
133,2
147,6
162,5
177,9
193,7
210,0
226,7
243,8
261,3
279,2
297,5
316,2
15,7
23,9
33,1
43,3
54,4
66,2
78,9
92,3
106,3
120,9
136,2
152,1
168,6
185,6
203,1
221,2
239,8
258,8
278,8
298,4
318,9
339,8
361,1
4
5
6
7
Доверительная вероятность
20,2
30,9
42,9
56,1
70,5
86,0
102,4
119,8
138,0
157,1
177,0
197,7
219,1
241,3
264,2
287,7
311,9
336,7
362,2
388,2
414,9
442,2
470,0
26,9
41,2
57,2
75,0
94,3
115,0
137,0
160,3
184,8
210,4
237,1
264,8
293,0
323,3
353,9
385,5
417,9
451,2
485,4
520,4
556,1
592,7
630,0
33,9
51,8
72,1
94,5
118,8
145,0
172,8
202,2
233,1
265,4
299,1
334,1
370,4
407,9
446,6
486,5
527,5
568,5
612,6
656,8
702,0
748,1
795,3
40,9
62,6
87,3
114,4
144,0
175,7
209,4
245,1
282,6
321,8
362,7
405,1
449,2
494,7
541,6
590,0
639,7
690,7
743,0
796,6
851,4
907,4
964,6
Доверительная вероятность
22,7
34,6
48,1
62,9
79,1
96,4
114,8
134,3
154,8
176,2
198,5
221,7
245,7
270,6
296,2
322,6
349,7
377,6
406,1
435,5
465,3
495,8
527,0
29,9
45,6
63,5
83,2
104,6
127,6
152,0
177,8
205,0
233,4
263,0
293,8
325,7
358,6
392,6
427,6
463,3
500,5
538,4
577,2
616,9
657,4
698,8
37,3
57,0
79,3
104,0
130,8
159,6
190,2
222,6
256,6
292,2
329,3
367,8
407,8
449,1
491,7
535,5
580,6
626,9
674,4
723,0
772,7
823,5
875,4
44,8
60,6
95,5
125,3
157,6
192,4
229,3
268,4
309,4
352,4
397,1
443,6
491,9
541,7
593,1
646,1
700,5
756,4
813,7
872,3
932,4
993,7
1056,3
8
а = 0,90
48,1
73,8
102,8
134,8
169,6
207,0
246,8
288,9
333,1
379,3
427,6
477,7
529,6
583,3
638,7
695,7
754,3
814,5
876,2
939,4
1001,1
1070,2
1137,6
а = 0,95
52,5
80,4
112,0
147,0
184,9
225,7
269,1
315,0
363,2
413,6
466,2
520,8
577,4
635,9
696,3
758,5
822,4
888,1
955,4
1024,3
1094,8
1166,8
1240,4
9
55,5
85,1
118,6
155,6
195,8
239,0
284,9
333,5
384,6
438,0
493,7
551,6
611,6
673,6
737,6
803,4
871,2
940,7
1012,0
1085,0
1159,7
1236,0
1314,0
60,3
92,4
128,8
169,1
212,8
259,7
309,6
362,4
417,9
476,0
536,5
599,4
664,6
732,0
801,5
837,1
946,7
1022,3
1099,8
1179,1
1260,3
1343,2
1427,9
10
63,0
96,5
134,6
222,3
271,4
323,6
378,8
436,8
497,5
560,8
626,6
694,8
765,2
837,7
912,8
989,7
1068,8
1149,8
1232,7
1317,6
1404,3
1492,9
1591,0
68,2
104,6
145,8
191,4
240,9
294,1
350,6
410,5
473,3
539,1
607,7
679,0
752,8
829,2
907,9
989,0
1072,4
1158,1
1245,9
1335,7
1427,7
1521,7
1617,6
4.2]
Непараметрические критерии однородности статистических данных
471
Далее вычисляем разности D^m = \Щ — Rm\:
1
1
2
3
т
2
22,5
3
35,5
13,0
4
66,0
33,5
30,5
Так как Di,4 = 66 > DiiTn@,95) = 48,1, гипотеза сдвига не отклоняется, между первой
и четвертой выборками существует значимый сдвиг в параметрах положения.
4.2.1.2.3. Критерий Вилкоксона—Вилкокс
Критерий предложен в [454] и подобен критерию Неменьи (см. раздел 4.2.1.2.2).
Пусть имеются к выборок равного объема п и Xij — г-й элемент j-й выборки
(г = 1,2, ..., щ j = 1,2, ..., к). Обозначим через Rij ранг г-го наблюдения j-и вы™
борки в упорядоченном по возрастанию ряду i-x элементов к выборок A ^ Rij ^ к)
и через Rj =
ij сумму рангов j-й выборки.
г=1
Статистикой критерия является разность
критические значения которой приведены в табл. 151.
При Dv^? ^ DVt)?{pt) с доверительной вероятностью а гипотеза сдвига принима-
принимается.
Так лее, как и критерий Неменьи, настоящий критерий позволяет выявить
выборки, приводящие к отклонению нулевой гипотезы.
Задача 245. Для данных задачи 244 проверить гипотезу сдвига критерием Викоксо-
на-Вилкокс.
Ранжируем первые элементы всех 4 выборок. Результаты сведем в таблицу:
г
1
2
3
4
5
3
1
Xij
1
2
3
4
5
1
1
1
1
1
2
Xij
3
4
5
6
7
2
2,5
2
2
2
3
4
4
6
7
8
Rij
3
2,5
3
3
3
4
7
8
9
10
11
Rij
4
4
4
4
4
Далее составляем разности DV? = \RV — Re
и
1
2
3
?
2
5,5
3
9,5
4,0
4
15,0
9,5
5,5
Для fc = 4, n = 5 и a = 0,95 находим из табл. 151 DU?@,9b) = 10,5. Так как
Di?4 = 15 > D^e@,95) = 10,5, сдвиг между параметрами положения первой и четвертой
выборок следует признать значимым (т.е. не случайным).
472
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица
Критические значения .О„>е(сх) критерия
Вилкоксона^Вилкокс [9]
151
п
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
к
3
5,0
5,8
6,5
7Д
7,7
8,2
8,7
9,2
9,6
10,1
10,5
10,9
11,2
11,6
12,0
12,3
12,6
13,0
13,3
13,6
13,9
14,2
14,5
5,7
6,6
7,4
8,1
8,8
9,4
9,9
10,5
11,0
11,5
11,9
12,4
12,8
13,3
13,7
14,1
14,4
14,8
15,2
15,5
15,9
16,2
16,6
4
5
6
7
Доверительная вероятность
7,2
8,4
9,4
10,2
11,1
11,8
12,5
13,2
13,9
14,5
15,1
15,7
16,2
16,7
17,2
17,7
18,2
18,7
19,2
19,6
20,1
20,5
20,9
9,5
11,0
12,3
13,5
14,5
15,6
16,5
17,4
18,2
19,0
19,8
20,6
21,3
22,0
22,7
23,3
24,0
24,6
25,2
25,9
26,4
26,9
27,5
11,9
13,7
15,3
16,8
18,1
19,4
20,5
21,7
22,7
23,7
24,7
25,6
26,5
27,4
28,2
29,1
29,9
30,6
31,4
32,1
32,8
33,6
34,2
14,2
16,5
18,4
20,2
21,8
23,3
24,7
26,0
27,3
28,5
29,7
30,8
31,9
32,9
33,9
34,9
35,9
36,9
37,7
38,6
39,5
40,5
41,1
Доверительная вероятность
8,1
9,4
10,5
11,5
12,4
13,3
14,1
14,8
15,6
16,2
16,9
17,5
18,2
18,8
19,3
19,9
20,4
21,0
21,5
22,0
22,5
23,0
23,5
10,6
12,2
13,6
14,9
16,1
17,3
18,3
19,3
20,2
21,1
22,0
22,8
23,6
24,4
25,2
25,9
26,6
27,3
28,0
28,6
29,3
29,9
30,5
13,1
15,1
16,9
18,5
19,9
21,3
22,6
23,8
25,0
26,1
27,2
28,2
29,2
30,2
31,1
32,0
32,9
33,7
34,6
35,4
36,2
36,9
37,7
15,6
18,0
20,1
22,1
23,9
25,5
27,0
28,5
29,9
31,2
32,5
33,7
34,9
36,0
37,1
38,2
39,3
40,3
41,3
42,3
43,2
44,1
45,0
8
9
а = 0,90
16,7
19,3
21,5
23,6
25,5
27,2
28,9
30,4
31,9
33,4
34,7
36,0
37,3
38,5
39,7
40,9
42,0
43,1
44,1
45,2
46,2
47,2
48,1
19,1
22,1
24,7
27,1
29,3
31,3
33,2
35,0
36,7
38,3
39,9
41,4
42,8
44,2
45,6
46,9
48,2
49,4
50,7
51,9
53,0
54,2
55,3
а = 0,95
18,2
21,0
23,5
25,7
27,8
29,7
31,5
33,2
34,8
36,4
37,9
39,3
40,7
42,0
43,3
44,5
45,8
47,0
48,1
49,2
50,3
51,4
52,5
20,8
24,0
26,9
29,4
31,8
34,0
36,0
38,0
39,8
41,6
43,3
45,0
46,5
48,1
49,5
51,0
52,4
53,7
55,1
56,4
57,6
58,9
60,1
10
21,7
25,0
28,0
30,6
33,1
35,4
37,3
41,5
43,3
44,3
45,1
46,8
48,4
50,0
51,5
53,0
54,5
55,9
57,3
58,6
60,0
61,2
62,5
23,5
27,1
30,3
33,2
35,8
38,3
40,6
42,8
44,9
46,9
48,8
50,7
52,5
54,2
55,9
57,5
59,0
60,6
62,1
63,5
65,0
66,4
67,7
4.2]
Непараметрические критерии однородности статистических данных
473
4.2.1.2.4. „Быстрый66 критерий Кенуя
Среди к выборок равного объема п ^ 20 находятся наибольшее среди наимень-
наименьших значений ж™^. и наименьшее среди наибольших значений x^f* в выборках.
Подсчитываются количества п\ наблюдений, для которых Х{ < ж™^., и П2, для
КОТОРЫХ Х{ < X™f?.
Статистикой критерия Кенуя является сумма п = П1+П2, критические значения
которой п(а) приведены в табл. 152.
Таблица 152
Критические значения n(pt) критерия Кенуя
(а — уровень значимости) [121]
к
а = 0,05
а = 0,01
2
9
12
3
17
22
4
27
33
5
37
45
6
47
57
8
70
83
10
93
110
Задача 246. Имеются три выборки случайных величин объема п = 20 каждая
xtji 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39;
x2j: Ю, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48;
x3j: 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40.
Необходимо проверить гипотезу сдвига критерием Кенуя на уровне значимости
а = 0,05.
Имеем ж?кх = 21 и ж?2Т = 39. Тогда щ = 16, п2 = 6 и п = 16 + 6 = 22.
Из табл. 152 для к = 3 и а = 0,05 находим п(а) = 17.
Так как п = 22 > п(а) = 17, гипотеза сдвига не отклоняется.
4.2.1.2.5. Критерий Фишера-Терри-Йэйтса-Гёфдинга
Вариант критерия Фишера-Терри-Йэйтса-Гёфдинга (см. раздел 4.2.1.1.2.3) для
к > 2 выборок основан на статистике [365]
1 2
к
(JV-l)V-
3 = 1
г=1
где Rij —ранг элементов j-и выборки в общем ряду (N = У^ rij).
3 = 1
При rij > 10 распределение статистики Q может быть аппроксимировано % -рас-
-распределением с / = Aj — 1 степенями свободы. Поэтому нулевая гипотеза отсутствия
сдвига отклоняется с достоверностью а, если Q > Х^{к — 1).
Задача 247. Имеются три выборки случайных величин:
хи: 1, 25 3, 4, 5, 6, 75 8, 9, 10;
x2j: 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25;
x3j: 12, 14, 16, 18, 20, 22, 24, 26, 28, 30.
Необходимо проверить гипотезу сдвига критерием Фигиера-Терри—Йэйтса-Гёфдинга
при доверительной вероятности а = 0,95.
Имеем 7ii = Ю, п2 = 11, п3 = 10 и N = 31.
Строим общий, ранжированный по возрастанию, ряд из элементов трех заданных
выборок (г = 1,2,3 — номер первичной выборки, Xj—элементы объединенной выборки,
j = 1,2, ...,31; Rij —ранг j-ro элемента в объединенной выборке):
474
Проверка гипотез о значениях параметров распределений
[Гл.4
i
1
1
1
1
1
2
1
1
Xij
1
2
3
4
5
5
6
7
1
2
3
4
5,5
5,5
7
8,5
ъ
2
1
1
2
1
2
3
2
7
8
9
9
10
11
12
13
8,5
10
11,5
11,5
13
14
15
16
г
3
2
3
2
3
2
3
2
14
15
16
17
18
19
20
21
Rn
17
18
19
20
21
22
23
24
г
3
2
3
2
3
3
3
Xij
22
23
24
25
26
28
30
25
26
27
28
29
30
31
Далее вычисляем значения (см. раздел 4.2.1.1.2.3)
= 4,91 •
3
0,14
k-3-
1-
включая дробные значения к (дробные ранги).
Результаты сведем в таблицу:
к
1
2
3
4
5
5,5
6
7
8
«31(к)
-2,0567
-1,6276
-1,3788
-1,1943
-1,0434
-0,97634
-0,9134
-0,7974
-0,6913
к
8,5
9
10
11
11,5
12
13
14
15
а3г(к)
-0,6412
-0,5927
-0,4996
-0,4108
-0,3676
-0,3252
-0,2419
-0,1604
-0,0799
к
16
17
18
19
20
21
22
23
24
а3г(к)
0
0,0799
0,1604
0,2419
0,3252
0,4108
0,4996
0,5927
0,6913
к
25
26
27
28
29
30
31
азг(к)
0,7974
0,9134
1,0434
1,1943
1,3788
1,6276
2,0567
Для первой выборки (г = 1) имеем
31
Rij : 1, 2, 3, 4, 5,5, 7, 8,5, 10, 11,5, 13 и ^ a3i(Rij) = ^9,7814.
i=i
Для второй (г = 2) выборки
31
R2j : 5,5, 8,5, 11,5, 14, 16, 18, 20, 22, 24, 26, 28 и ]Г a^{R2j) = 1,6387.
i=i
Для третьей выборки (г = 3)
31
R3j : 15, 17, 19, 21, 23, 25, 27, 29, 30, 31 и ^ a3i(R3j) = 8,1293.
3 = 1
31
Находим ^^ Q-3i@ =:: 28,4186 и вычисляем статистику критерия
Q = ——— • У" —
^ 28,4186 ~_nj
= 17,367.
Находим из табл. 55: Хо,9бB) = 5,99.
Так как Q = 17,367 > Хо,9бB) = 5,99, гипотеза сдвига не отклоняется.
4.2]
Непараметрические критерии однородности статистических данных
475
4.2.1.2.6. Критерий Ван дер Вардена
Статистика Ван дер Вардена для к > 2 выборок имеет вид
-1 т, г 1 2
При справедливости нулевой гипотезы статистика Q* распределена как %
с / = Aj — 1 степенями свободы. Поэтому нулевая гипотеза отсутствия сдвига от™
клоняется, если Q* > Х«(^ ~~ 1)? гДе а — доверительная вероятность.
Задача 248. Проверить гипотезу сдвига в условиях задачи 247 критерием Ван дер
Вардена.
0,14
Вычисляем и % = 4,91 • I I — ) — ( 1 — -^
Результаты сведем в таблицу (включая дробные значения рангов г):
ОД4
г
1
2
3
4
5
5,5
6
7
8
U i
32
-1,8658
-1,5354
-1,3178
-1,1492
-1,0083
-0,9448
^0,8851
-0,7743
-0,6723
i
8,5
9
10
11
11,5
12
13
14
15
U i
32
-0,6723
-0,5771
-0,4869
-0,4006
-0,3586
-0,3173
-0,2362
-0,1566
-0,078
i
16
17
18
19
20
21
22
23
32
0
0,078
0,1566
0,2362
0,3173
0,4006
0,4869
0,5771
г
24
25
26
27
28
29
30
31
U i
32
0,6723
0,7743
0,8851
1,0083
1,1492
1,3178
1,5354
1,8658
Легко видеть, что соотношение и % = —-UN+i-i позволяет ограничиться расчетами
ЛГ+1 ЛГ+1
ЛГ + 1
для г < . Из табл. 147 находим
31
31
31
= 0,817-31 = 25,327.
г=1 32 г=1 М+г
Находим последовательно для г = 1, 2, 3:
31 31 31
J2 и Rlj = -9,293; J2 и R2j = 1,5834; J2 и «3i = 6,1801.
Окончательно получаем
30
25,327
4^
N+1
— • [и д.. = 18,3848.
Так как Q* = 18,38 > хО)95B) = 5,99, гипотеза сдвига принимается, как и ранее.
4.2.1.2.7. Медианный критерий
Для множественного аналога двухвыборочного медианного критерия (см. раз™
дел 4.2.1.1.2.5) используется статистика
476 Проверка гипотез о значениях параметров распределений [Гл. 4
имеющая при щ —>> оо (> 10) распределение хи^квадрат с f = k — 1 степенями сво-
свободы. Здесь rrii—число наблюдений г-й выборки, превосходящих медиану объеди-
к
ненной выборки (N = У^ щ).
г=1
Задача 249. Проверить гипотезу сдвига в условиях задачи 247 медианным крите-
критерием.
Медианой объединенной выборки является х = 13.
Имеем 77ii = 0, W2 = 6, тз = 9, JV = 31. Тогда
X2 = 4 - У -1 - т?^ 31 = 4 • f ^ + ^ + ^)- 31 = 14,492.
Л ^ га* V10 10 10 у
Так как %2 = 14,492 > Xo,9sB) = 5,99, гипотеза сдвига не отклоняется.
4.2.1.2.8. Критерий Хеттманспергера
Критерий рассмотрен в [455]. Используется для проверки равенства параметров
положения Hq : //]_ = ...= //& против альтернатив упорядоченности Hi: \xi ^ ... ^ /i^,
где хотя бы одно из неравенств — строгое. Статистика критерия
Нулевая гипотеза отклоняется с достоверностью а, если
где иа — «-квантиль стандартного нормального распределения,
2
г = п (< = 1,2 fc) D(L)=
Я-
Как и в критерии Крускала-Уоллиса, приняты обозначения ^ = —^, ^ = ]Р Л^j
^ • -I
tj ¦ ¦ « г г J = 1
и ii^j —ранг j-го элемента г™и выборки в общем упорядоченном ряду.
Задача 250. Проверить гипотезу сдвига против порядковой альтернативы крите-
критерием Хеттманспергера в условиях задачи 243.
Имеем (см. задачу 243)
Кг = 5,333; R2 = 9,1; R3 = 16,166; R4 = 13,75; R5 = 23,64.
Тогда
= 0,1924 • [A - 3) • E,333 - 14) + B - 3) • (9,1 - 14) + ... + E - 3) • B3,64 - 14)] = 7,94;
5
D(L) = 5 • ? ^ • (* - 3J = 3'7439 (VDW = 1,935).
Окончательно имеем для а = 0,95: ъйэ,э5 = 1,645 и no,95 * yD(L) = 3,183.
Так как L = 7,94 > 3,183, гипотеза сдвига не отклоняется.
4.2] Непараметрические критерии однородности статистических данных 477
4.2.1.2.9. Критерий Терпстры-Джонкхира
Так же как и критерий Хеттманспергера (см. раздел 4.2.1.2.8), используется
для проверки гипотезы сдвига против альтернатив упорядоченности. Критерий
предложен в [456, 457] и основан на попарных статистиках Вилкоксона^Манна^
Уитни (см. раздел 4.2.1.1.2.2). Статистика критерия имеет вид
г=1 j = l
где dij—количество наблюдений из первых (г — 1) выборок (г > 1), меныних, чем
X{j —j-e наблюдение в г-й выборке.
Гипотеза отсутствия сдвига отклоняется, если S > Sai где Sa—критические
значения, приведенные в табл. 153 и 154.
При щ ^ 10 применима аппроксимация
sa =
где
иа — «-квантиль стандартного нормального распределения.
Легко убедиться, что статистики критериев L — Хеттманспергера ж S — Терпст-
ры-Джонкхира эквивалентны.
Задача 251. Проверить гипотезу сдвига против порядковой альтернативы крите-
критерием Терпстры-Дэюонкхира для данных задачи 243.
Поясним порядок вычисления критерия S. Для ъ = 2 (второй выборки) находим
количество наблюдений первой выборки, меньших, чем x^j-
Для j = 1 имеем #2i = 3 и в первой выборке два значения (жп = 1 и Ж12 = 2) меньше,
чем Ж21 = 3, т. е. «21 = 2.
Далее по аналогии для j = 2 имеем «22 = 3 (предлагается убедиться в этом самому
читателю). Для j = 3 имеем «23 = 4 и далее «24 = 5 и п25 = 6.
При г = 3 находим количества значений в первых двух выборках, меньших, чем x$j
(при различных j): а^\ = 10, аз2 = 11, «зз = И-
Для г = 4 имеем a^i = 0, 042 = 6, 043 = 10, 044 = 12, 045 = 14, а.46 = 14.
Для г = 5 имеем а$\ = 18, пб2 = 19, пбз = 20, as4 = 20, 055 = 20, ase = 20, 057 = 20.
Окончательно находим
5 fii
ij =2 + 3 + 4 + 5 + 6 +10+11+ 11+ ... + 20 +20 = 245-
Далее вычисляем
=
4
DE) = — • [729 • B • 27 + 3) - 36 • B • 6 + 3) - 25 • B • 3 + 3) - ...
( 2i
... - 49 • B • 7 + 3)] = 344,916; уЩЩ = 23,343.
Находим (имея в виду, что гйз,95 = 1,645) 5о,э5 = 143,5 + 1,645 • 23,343 = 181,9.
Так как S = 245 > Яо,э5 = 181,9, имеющиеся результаты наблюдений не противоречат
гипотезе сдвига.
478
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 153
Критические значения Sa критерия Терпстры^Джонкхира для к = 3
(а — доверительная вероятность) [458]
«1
CM
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
см
2
2
2
2
2
2
2
2
2
2
n2
см
2
2
2
2
2
2
3
3
3
3
3
3
4
4
4
4
4
5
5
5
5
6
6
6
7
7
8
ПЗ
2
3
4
5
6
7
8
3
4
5
6
7
8
4
5
6
7
8
5
6
7
8
6
7
8
7
8
8
а
0,90
9
12
15
18
20
23
26
15
19
22
25
29
32
23
27
31
35
38
31
36
40
45
41
46
51
52
57
63
0,95
20
21
16
19
22
25
28
17
20
24
27
31
35
25
29
33
37
41
34
38
43
48
44
49
54
55
61
68
П\
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
п2
3
3
3
3
3
3
4
4
4
4
4
5
5
5
5
6
6
6
7
7
8
4
4
4
4
4
5
5
пз
3
4
5
6
7
8
4
5
6
7
8
5
6
7
8
6
7
8
7
8
8
4
5
6
7
8
5
6
а
0,90
19
23
27
31
35
39
28
32
37
41
46
37
42
48
53
48
54
57
60
66
73
33
38
43
48
53
44
49
0,95
21
25
29
33
38
42
30
35
39
44
49
40
45
51
56
51
57
63
64
70
778
35
41
46
51
57
47
53
П\
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
5
5
5
6
6
6
6
6
6
7
7
7
8
П2
5
5
6
6
6
7
7
8
5
5
5
5
6
6
6
7
7
8
6
6
6
7
7
8
7
7
8
8
Пз
7
8
6
7
8
7
8
8
5
6
7
8
6
7
8
7
8
8
6
7
8
7
8
8
7
8
8
8
а
0,90
55
60
55
62
68
68
75
82
50
56
62
68
63
69
76
77
84
92
70
77
85
85
93
101
94
102
111
120
0,95
58
64
59
66
72
73
80
87
53
60
66
73
67
74
81
81
89
97
74
82
90
90
99
107
99
108
117
127
Таблица 154
Критические значения Sa
критерия Терпстры^Джонкхира
для выборок равного объема
(а — доверительная вероятность) [458]
те
2
3
4
к
4
5
6
4
5
6
4
5
а
0,90
17
27
39
36
58
84
62
99
0,95
18
29
42
39
61
89
66
105
п
4
5
6
к
6
4
5
6
4
5
6
а
0,90
146
94
152
223
133
215
316
0,95
153
99
159
233
140
225
329
4.2] Непараметрические критерии однородности статистических данных 479
4.2.1.2.10. Критерий Мостеллера
Для к выборок равного объема п критерий позволяет ответитв на вопрос: не
является ли одна из к выборок сдвинутой по отношению к (fc — 1) остальнвхм?
Вероятноств того, что в одной из к выборок (равного объема n) r или более чле-
членов больше, чем в (к — 1) оставшихся выборках, равна [455] Р(У) = кС'^^г(С'^п)^1
или при п —>> оо и фиксированных к ж г:
Р(г) = 1
2кп
Если Р(г) < 1 — а, где а — доверительная вероятность, то гипотеза сдвига от™
клоняется.
Задача 252. Для данных задачи 244 проверить гипотезу сдвига критерием Мостел-
Мостеллера.
Проверяем четвертую вв1борку. В ней три члена (9, 10 и 11) превышают все значения
остальных 3 выборок. Имеем jfc = 4, n = 5 и г = 3. Вычисляем
РC) = 4 • Щ^ = 4 • % = 4 • ^^ = 0, 035.
С|.5 С|о 15504
Так как РC) = 0,035 < 1 — а = 0,05, сдвиг четвертой выборки по отношению ко всем
остальным следует признать значимым.
4.2.1.2.11. Критерий Левиса
Критерий аналогичен критерию Мостеллера [459] и использует соотношение
между размахами сравниваемых выборок.
Пусть для г-й выборки имеем min хц = Щ. max Xij = Vi и Щ = V{ — Щ —
размах г-и выборки.
Обозначим max Щ = U и minl^ = V. Параметры положения сравниваемых вы-
выборок не равны между собой (гипотеза Hq отклоняется), если по крайней мере
в двух выборках размахи не пересекаются, т. е. если U > V.
Гипотеза сдвига принимается с достоверностью а, если [459]
?(U > V) < 1-а,
ГДСЗ к г-1
г=2 j = l
При п —>¦ оо (п > 10)
Задача 253. Для данных задачи 244 проверить гипотезу сдвига критерием Левиса.
Имеем Z7i = 1, U2 = 3, U3 = 4, U4 = 7; Vi = 5, F2 = 7, F3 = 8, V4 = 11; C7 = max*/* = 7;
V = minVi = 5.
Находим
i=2j = l °5i
i n2ni 2 n^ni з /^4^i
= E(-D2 • тЙ1 + E(-D3 • Ш + E(-D4 • ^g
j = l °10 i = l °15 j = l °20
Так как Р(С/ > V) = 0,04 < 1 — 0,95 = 0,05, гипотеза сдвига не отклоняется.
480
Проверка гипотез о значениях параметров распределений
[Гл.4
4.2.1.2.12. Х-критерий, основанный на U-статистиках
Пусть имеются к выборок объема щ (г = 1, ..., к) каждая. Из каждой выборки
берем по одному наблюдению. Проделав это всеми возможными способами, в ре~
к
зультате получаем Yi ni выборок одинакового объема к.
г=1
Обозначим через v^j {уц^} количество выборок, в которых наблюдение, взятое
из г-й выборки, было наименьшим (наибольшим). Определим величину щ^ =
Ц
Щк
г
В [461, 462] предложен критерий сдвига, основанный на статистике
L =
i=l
,г=1
где k = -Uij +щк.
При L > La гипотеза сдвига принимается с достоверностью а (здесь La — кри™
тическое значение, приведенное в табл. 155).
Таблица 155
Критические значения La для к = 3
и доверительной вероятности а = 0,95 [460]
711
2
2
2
2
2
2
2
2
3
3
пз
2
3
4
3
4
^0,95
5,33
5,39
6,00
5,85
5,78
711
2
3
3
3
4
712
4
3
3
4
4
пз
4
3
4
4
4
Ьо,Э5
5,55
6,22
6,16
6,22
6,12
При к > 3 справедливо приближение
где Xa(f) — «-квантиль распределения хи™квадрат с / степенями свободы.
Задача 254. Даны три выборки случайных величин е
xxj: 1, 2, 3; x2j: 4, 5, 6; x3j: 7, 8, 9.
Проверить гипотезу сдвига L-критерием при доверительной вероятности а = 0,95
(А; = 3, пг = 3).
В нашем случае следует рассмотреть Y\rii = 3 • 3 • 3 = 27 выборок равного объема
гс = 3.
Имеем выборки:
1.4.7 1,5,7 1,6,7 2,4,7 2,5,7 2,6,7 3,4,7 3,5,7 2,6,7
1.4.8 1,5,8 1,6,8 2,4,8 2,5,8 2,6,8 3,4,8 3,5,8 2,6,8
1.4.9 1,5,9 1,6,9 2,4,9 2,5,9 2,6,9 3,4,9 3,5,9 3,6,9
Находим при г = 1 (первая выборка) иц = 27, ?лз = 0 и по аналогии г>21 = 0, V23 = 0,
^31 = 0, и3з = 27.
4.2] Непараметрические критерии однородности статистических данных 481
Следовательно, имеем
u\\ = = 1; iti3 = 0; U21 = 0; гхгзО; г/31 = 1;
h = -1 + 0 =-1; h = -0 + 0 = 0; /3 =-0 + 1 = 1;
r- 9-5-4.С| /ЛЗ 2 / з
Из табл. 155 для т = П2 = пз = 3 находим Ьо,95 = 6,22; так как L = 8 > Ьо,э5 = 6,22,
гипотеза сдвига не отклоняется.
4.2.1.2.13. Критерий Краузе
Этот критерий является обобщением критерия Вилкоксона^Манна^Уитни (ем.
раздел 4.2.1.1.2.2) на многовыборочный случай. К этому классу относятся кри-
критерии Круекала-Уоллиса (см. раздел 4.2.1.2.1) и Терпстры-Джонкхира (см. раз™
дел 4.2.1.2.9).
Рассмотрим формы обобщения критерия Вилкоксона^Манна^Уитни, порожда-
порождающие различные многовыборочные критерии.
Пусть Wij—статистика Манна-Уитни, возникающая при сравнении выборок
с номерами г и j, т.е. (см. раздел 4.2.1.1.2.2) Wij есть точное число пар значений
Xiv И Xj?, ДЛЯ КОТОРЫХ Xiv < Xj? ПО ВС6М V = 1, 2, . . . , Щ И ? = 1, 2, . . . , flj.
Тогда Wi = J^ Wij будет статистикой Манна-Уитни, сравнивающей г™ю выборку
со всеми остальными. Мо^но показать [463], что
к
где N = J^ rii и Ri — среднее из рангов членов г-й выборки в общем ранжированном
ряду N = J^ n^ значений.
При справедливости нулевой гипотезы (отсутствие сдвига в параметрах поло™
жения к выборок) математическое ожидание M(W^) и дисперсия D(W^) равны
M(Wi) = \nt(N - щ); T>{Wi) = ±nt(N - щ)(М + 1).
В принятых обозначениях рассмотренные ранее статистики Н — Крускала^Уол-
лиса (см. раздел 4.2.1.2.1) и S — Терпстры-Джонкхира (см. раздел 4.2.1.2.9) могут
быть записаны как
г=1
В этом разделе мы рассматриваем статистику критерия, предложенного Краузе
[464, 465]:
2
N + 1
l
Этот критерий эквивалентен критерию Крускала^Уоллиса, но более эффективен
против большого количества альтернатив.
16 А. И. Кобзарь
482
Проверка гипотез о значениях параметров распределений
[Гл.4
При справедливости нулевой гипотезы статистика V распределена как %2
с f = к — 1 степенями свободы. Поэтому гипотеза сдвига отклоняется с достовер™
ностью а, если V < %«(к — 1).
Задача 255. Проверить гипотезу сдвига для данных задачи 243 непараметрическим
критерием Краузе.
Для выборок % = 1 и j = 2. Имеем W12 = 5 + 5 + 4 + 3 + 2 + 1 = 20.
Поясним способ подсчета Wij. Для первого элемента выборки с номером ъ = 1,
равного 1 во второй выборке имеются 5 элементов C, 4, 5, 6, 7), превосходящих его.
Для 2-го элемента выборки, равного 2, во второй выборке находятся также 5 элементов,
превосходящих его по величине. Для 3™го элемента выборки, равного 3, их во второй
выборке уже 4, и т. д.
По аналогии имеем
W13 = 3 + 3 + 3 + 3-
W15 = 7 + 7 + 7 + 7-
W2A = 5 + 5 + 4 + 4-
W34 = 3 + 2 + 2 = 7;
Вычислим теперь
- 3 + 3 + 3 = 18; W14 = 5 + 5 + 5 + 5 + 4 + 4 = 28;
- 7 + 7 = 42; W23 = 3 + 3 + 3 + 3 + 2 = 14;
-4 + 3 = 21; W2b = 7 + 7 + 7 + 7 + 7 = 35;
W35 = 7 + 7 + 7 = 21; W45 = 7 + 7 + 7 + 7 + 6 + 5 = 39.
12
6-5
18-
6-3
6-7
27+1
6-5
6-3
= 19,1.
Из табл. 55 находим Хо,эб(а = 5 — 1 = 4) = 9,49.
Так как V = 19,1 > Хо,9бD) = 9,49, гипотеза сдвига не отклоняется.
4.2.1.2.14. Критерий Пейджа
Используется для выборок равного объема в целях проверки гипотезы отсут™
ствия сдвига Hq : fi\ = ... = /j,k против порядковых альтернатив Hi: \xi ^ \х^ ^
^ ... ^ /ifc, так же как критерии Хеттманспергера (см. раздел 4.2.1.2.8) и Терпстры—
Джонкхира (см. раздел 4.2.1.2.9). Статистика критерия строится следующим обра-
образом. Составляется таблица:
Номер элемента
в выборке
1
2
п
Номер выборки
1
#11
#12
#1п
2
#21
х2п
к
#fci
Xk2
Хкп
Далее ранжируем по возрастанию элементы каждой строки от 1 до к (получаем
п
совокупность рангов Vij). Обозначим через Щ = ^ rij сумму рангов по столбцам.
Тогда статистика критерия Пейджа записывается в форме [466]
Нулевая гипотеза отклоняется с достоверностью а, если
La(Aj,n)—критические значения, приведенные в табл. 156.
где
4.2]
Непараметрические критерии однородности статистических данных
483
Таблица 156
Критические значения La(k^n)
критерия Пейджа
для доверительной вероятности о = 0,95 [18]
п
2
3
4
5
6
7
8
9
10
11
12
к
3
28
41
54
66
79
91
104
116
128
141
153
4
58
84
111
137
163
189
214
240
266
292
317
5
103
150
197
244
291
338
384
431
477
523
570
6
166
244
321
397
474
550
625
701
777
852
928
7
252
370
487
603
719
835
950
1065
1180
1295
1410
8
362
532
701
869
1037
1204
1371
1537
1703
1868
2035
к = 3 п = 13 14 15
La(k,n) = 165 178 190
При п > 10 справедлива аппроксимация
16
202
20
251
где
M(L) =
D(L) =
п(к3 - кJ
Ы4(к - 1)'
При L* ^ иа нулевая гипотеза отклоняется (иа — «^квантиль стандартного нор™
мального распределения).
Задача 256. Проверить гипотезу сдвига критерием Пейджа в условиях задачи 244.
Имеем таблицу:
Номер элемента
в выборке
1
2
3
4
5
Номер выборки
1
1
2
3
4
5
2
3
4
5
6
7
3
4
5
6
7
8
4
7
8
9
10
11
Заменяя элементы выборки по строкам их рангами в строке, получаем таблицу
рангов Rii
3
1
2
3
4
5
г
1
1
1
1
1
1
2
2
2
2
2
2
3
3
3
3
3
3
4
4
4
4
4
4
= 5 R2 = Ю R3 = 15 R4 = 20
16*
484
Проверка гипотез о значениях параметров распределений
[Гл.4
Статистика критерия Пейджа равна
к
L = Yii-Ri = 1-5 + 2- 10 + 3-15 + 4- 20= 150.
г=1
Из табл. 156 для к = 4 ш п = 5 находим Ьо,9бD,5) = 137.
Так как L = 150 > bo,9sD,5) = 137, гипотеза сдвига не отклоняется.
Используем теперь аппроксимацию
= 41,667;
Так как ъг,о,95 = 1,645 и L* = 3,872 > tto,95 = 1,645, то и в этом случае гипотеза сдвига
не отклоняется.
4.2.1.2.15. Критерий Фридмена-Кендалла-Бэбингтона Смита
Обратимся, как и в предыдущем разделе, к таблице:
Номер элемента
в выборке
1
2
п
Номер выборки
1
Хц
Х\1
Xin
2
#21
Ж22
%2п
к
Xkl
Хк2
Хкп
Проран^ируем, от наибольшего к наименьшему, наблюдения внутри каждой
строки. Пусть rij — ранг члена хц в совместной ранж:ировке x\j, ..., Xkj- Обозначим
Для проверки гипотезы сдвига между параметрами положения выборок равного
объема в [467, 468] предложен критерий, основанный на статистике
Гипотеза сдвига отклоняется, если S < Sa(n1 к), где 5а(п, к) —критическое зна-
значение, приведенное в табл. 157, построенной с применением интерполяции по та-
таблице, приведенной в [18].
В связи с тем, что таблицы распределения рассматриваемого критерия со-
составлены для небольшого диапазона значений, широко применяются различные
аппроксимации. Приведем наиболее употребляемые из них.
При п ^ 13 ш к ^ 20 применима аппроксимация
Sa(n,k)=xl(k-1).
Для других значений п и к используется преобразование
F =
п(к- 1M*
4.2]
Непараметрические критерии однородности статистических данных
485
Таблица 157
Критические значения Sq-(ti, k) критерия
Фридмена^Кендалла^Бэбингтона Смита [18]
3
4
5
6
7
8
9
10
11
12
13
Доверительная
вероятность а
= 0,95
к
3
5,82
6,31
6,10
6,33
6,00
6,25
6,00
6,10
6,09
6,08
6,00
4
7,00
7,20
7,32
7,40
7,63
7,50
5
8,30
8,80
8,96
Доверительная
вероятность а
= 0,90
к
3
5,42
5,10
5,21
4,83
4,71
5,00
4,67
4,90
4,91
4,67
4,77
4
6,20
6,00
6,12
6,20
6,26
6,30
5
7,47
7,58
7,61
Гипотеза сдвига отклоняется, если F < .Fa(/i, /2), где -Fa(/i>/2)— «-квантиль
распределения Фишера при Д и /2 степенях свободы.
При 7^к^19шп^13 принимаем f\ = к — 1 и /2 = (к — 1)(п — 1).
При к^8ж7^п^12 принимаем Д = fe - 1 и
(n-1)
где
L=(п ¦
г=1
Если /2 становится дробным, то при использовании таблиц следует применять
интерполяцию.
Весьма эффективны аппроксимации, предложенные Иманом и Давенпор™
том [469]. Для к ^ 7 и п ^ 8 статистика Имана-Давенпорта вычисляется по
формуле J = i[(jfc - 1)F + 5].
Гипотеза сдвига отклоняется с достоверностью а, если J < Jai где /1 = fc — 1,
Здесь Xa (
При 1с
1) — а-квантиль распределения хи^квадрат с (Aj —1) степенями свободы.
6и2^п^6и1с = 5,п = 6,7 вместо J ш Ja следует использовать
К = \ [(к -
486
Проверка гипотез о значениях параметров распределений
[Гл.4
Задача 257. Для трех выборок случайных величин, приведенных в таблице, прове-
проверить гипотезу сдвига критерием Фридмена-Кендалла-Бэбингтона Смита при досто-
достоверности а = О5Э5:
Номер элемента
в выборке
1
2
3
4
5
6
7
8
9
10
Номер выборки
1
2,1
1,8
1,7
1,8
1,9
2,4
1,7
1,6
1,5
1,7
2
3,2
4,1
2,3
2,4
2,5
1,2
1,9
2,3
2,4
2,9
3
4,3
2,3
3,4
3,5
3,6
3,7
3,2
2,8
2,9
3,7
Т '
^3
3,20
2,73
2,47
2,57
2,67
2,43
2,27
2,23
2,26
2,83
Строим таблицу рангов щ по строкам:
3
1
2
3
4
5
6
7
8
9
10
г
1
1
1
1
1
1
2
1
1
1
1
2
2
3
2
2
2
1
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
Имеем
Ri = 11, R2 = 20, R3 = 29.
Вычисляем статистику критерия
12
10-3-4
г2 - 3 • 10 • 4 = 0,1 • (II2 + 202 + 292) - 120 = 16,2.
Находим из табл. 157 So,95A6,3) = 6,1.
Так как S = 16,2 > «So,95 A6,3) = 6,1, гипотеза сдвига не отклоняется.
Продемонстрируем теперь применение аппроксимаций. У нас 1с = 3<7игг=10>
поэтому воспользуемся аппроксимацией J Имана—Давенпорта. Находим
F=
=38,37;
=i. B- 38,37+ 16,2) =46,47.
2 V ' ' ;
Г; =
n-(k-l)-S 10-2-16,2
Из таблиц находим Fo,9sB; 18) = 3,55 и Хо,9бB) = 5,99. Следовательно,
Jo,95 = 0,5 • B • 3,55 + 5,99) = 6,54.
Так как J = 46,47 > Jo,95 = 6,54, гипотеза сдвига не отклоняется.
4.2.1.2.16. Критерий Андерсона-Каннемана-Шэча
Является аналогом критерия Фридмена-Кендалла-Бэбингтона Смита (см. раз™
дел 4.2.1.2.15). Предложен в [470-472]. Для некоторых алвтернатив обладает по
сравнению с критерием Фридмена большей мощностью. Для пояснения последова-
4.2]
Непараметрические критерии однородности статистических данных
487
тельности вычисления статистики критерия воспользуемся обозначениями преды-
предыдущего раздела. Так же, как и в критерии Фридмена—Кендалла—Бэбингтона Смита,
предварительно ранжируем наблюдения в каждой строке. Затем вычисляем эле-
элементы матрицы сопряженности рангов D = ||D^||? гДе Вц —число строк, в которых
столбец г получил ранг I (г, I = 1, 2, ..., к). Правильность вычислений проверяется
условием
1=1 i=l l=li=l
Статистика критерия вычисляется по формуле
к к / х 2 к к к
п
кк
При п ^ 10 гипотеза сдвига отклоняется, если
где Х«(/) — «^квантиль распределения %2 с / степенями свободы.
Задача 258. Проверить гипотезу сдвига для данных задачи 257 критерием Андерсона-
Каннемана-Шэча.
Составляем матрицу сопряженности рангов
1
1
2
3
i
1
9
1
0
10
2
1
8
1
10
3
0
1
9
10
10
10
10
30
Вычисляем статистику критерия
3
А= — -
u] - Ю • 3 = 0, 3 • (92 + I2 + ... + I2 + 92) - 30 = 39;
Из табл. 55 находим Хо,9бD) = 9,49. Так как
k-1
А = 26 > Xo,9sD) = 9,49, наличие
сдвига между параметрами выборок на выбранном уровне значимости 1 — а = 0,05 сле-
следует считать значимым.
4.2.1.2.17. Критерий со взвешенными ранжировками Даны Квейд
Критерий подобен критерию Фридмена (см. раздел 4.2.1.2.15), но позволяет
учесть разброс наблюдений в строках таблицы
3
1
2
п
г
1
Х\х
Xnl
2
#12
Ж22
ХП2
к
Х2к
Хпк
488
Проверка гипотез о значениях параметров распределений
[Гл.4
Критерий предложен в [473, 474]. Ранжирование наблюдений производится вну™
три строк так же, как и в критериях Фридмена (см. раздел 4.2.1.2.15) и Андерсона
(см. раздел 4.2.1.2.16).
Предварительно в качестве „меры доверия" данных выбирается некоторый пока-
показатель, например, Dj —дисперсия в j-й строке таблицы. Затем значения дисперсий
Dj ранжируются рангами qj от наименьшего к наибольшему (j = 1,2, ..., п). Вы™
числяются величина
к
и статистика критерия
W =
72S
k(k + l)n(n + l)Brc +1)
При п ^ 5 справедлива аппроксимация
2Bn
d
где
С — J. О
Зга
5n(n+l)Bn
0 —
(fc -
и — ОС zl
72Cn
Гипотеза сдвига отклоняется с достоверностью а, если W* > Х^(^)? гДе Ха(^) —
а-квантиль распределения хи-квадрат с / = S степенями свободы.
В среднем критерий Д. Квейд мощнее критерия Фридмена по отношению к боль™
шинству альтернатив [475].
Задача 259. Проверить гипотезу сдвига для данных задачи 257 критерием Даны
Квейд.
Подсчитываем дисперсии
по формуле
k
2
Имеем таблицу рангов щ по строкам и дисперсий
внутри столбца от 1 до п:
по строкам, ранжированных
3
1
2
3
4
5
6
7
8
9
10
г
1
1
1
1
1
1
2
1
1
1
1
2
2
3
2
2
2
1
2
2
2
2
3
3
2
3
3
3
3
3
3
3
3
Dj
1,21
1,46
0,74
0,74
0,74
1,56
0,66
0,36
0,50
1,01
8
9
4
5
6
10
3
1
2
7
Вычисляем
з
г=1
, v 2 / Ю
(IZ ^i ' r*i ) = ПС
\i l
= 40442;
4.2]
Непараметрические критерии однородности статистических данных
489
W =
72 • 40442
Далее вычисляем
с= 1-6-
3-4- 10- 11 -21
3-100 + 3-10-1
5-10-11-21
9-4- 11 • 10
2 -21
= 0,829; S =
= 10,758.
2
0,5562
Тогда
= 3- 0,829-2+
(Ю,™-2)-0,829
7-102-112-212
=
= 4,446;
=
0,556
Из табл. 55 находим Хо,95 C,686) « 8,96.
Так как W* = 17,504 > Хо,95 C,686) = 8,96, гипотеза сдвига не отклоняется.
4.2.1.2.18. Критерий Кендалла-Эренберга
Является аналогом критерия Фридмена-Кендалла-Бэбингтона Смита (см. раз™
дел 4.2.1.2.15), превосходя его по мощности [477]. Предварительно наблюдения
ранжируются по строкам, как и в предыдущих критериях. Обозначим через сц
число тех случаев, когда ранг 1-го объекта больше ранга j-vo объекта A^1, j < к)
и Cji —число тех случаев, когда ранг 1-го элемента меньше ранга j-ro.
Предварительно вычисляются элементы матрицы ||qj|| (при этом Cjj = 0). Тогда
статистика критерия имеет вид
К= J2 си(п - cij) = n J2 cij~ J2 сЬ-
Гипотеза не отклоняется, если К > Ка(к,п), где Ка(к1п)—критическое значе-
значение, приведенное для некоторых п и к в табл. 158.
Таблица 158
Критические значения Ка(к,п)
критерия Кендалла^Эренберга
для доверительной вероятности а = 0,95 [119]
к
3
3
3
3
3
п
4
5
6
7
8
^0,95
3
18
14
22
31
к
3
3
4
4
4
п
9
10
3
4
5
^0,95
42
54
4
10
20
к
4
5
5
п
6
3
4
i^0,95
34
8
20
Для выборок большого объема применяется следующее приближение, основан™
ное на статистике U*,
U* = аС/ + /,
где
_ 6Bk+ 5)kn(k- l)(n- l)t
8к
/ =
4(n-2JBA;2
Гипотеза сдвига отклоняется, если U* < Х«(/)? гДе Х«(/) — о^квантиль Х
пределения с / степенями свободы. Следует помнить, что в этом критерии, как и во
всех предыдущих, для одинаковых (связанных) наблюдений применяются средние
ранги (в нашем случае связи сц = 1 и Cj\ = 0 заменяются на сц = Cji = 1/2).
490
Проверка гипотез о значениях параметров распределений
[Гл.4
Задача 260. Проверить гипотезу сдвига для данных задачи 257 критерием Кендалла-
Эренберга.
Восстановим таблицу рангов Гц из задачи 257:
3
1
2
3
4
5
6
7
8
9
10
г
1
1
1
1
1
1
2
1
1
1
1
2
2
3
2
2
2
1
2
2
2
2
3
3
2
3
3
3
3
3
3
3
3
Вычисляем элементы матрицы ||qj||:
1
1
2
3
3
1
*
9
10
2
1
*
9
3
0
1
*
Из элементов второго столбца (г = 2) только один элемент имеет ранг, меньший, чем
элементы первого столбца. Следовательно, с\2 = 1. Аналогичным образом заполняются
все остальные элементы матрицы ||qj||.
Вычисляем
К = Ci2 * С21 + Ci3 ' С31 + С23 * С32 = Ci2 • (п — С12) + Ci3 • (п — С13) + С23 ' (п ~ С2з) =
= 1 • A0 - 1) + 0 • A0 - 0) + 9 • A0 - 9) = 18.
Из табл. 158 для k = 3 ш п = 7 находим Жо,э5 = 22.
Так как К = 18 < Жо,95 = 22, гипотеза сдвига не отклоняется.
Вычислим теперь приближенный критерий. Находим
= 25,9; U=l-
6- 11-3-10-2-9
4-8-B-9 + 6-3 + 7)
2- II3 -3- 10-2 -9
8- 18
3-10-2-9
= 0,7333;
/ =
—з = 3,0369.
4 • 82 • B • З2 + 6 • 3 + 7J
Далее U* = 25,90 • 0,733 + 35037 = 22502. Из табл. 55 имеем Хо,95C) = 7,81.
Так как U* = 22,02 > Хо,9бC) = 7,81, гипотеза сдвига не отклоняется.
4.2.1.2.19. Критерий Ходжеса-Лемана-Сена
Аналог критерия Фридмена--Кендалла--Бэбингтона Смита (см. раздел 4.2.1.2.15),
но обладает по сравнению с ним большей эффективностью. Статистика критерия
строится следующим образом. Находится среднее значение в j-й строке Xj = у
к
г=1
и определяются выровненные наблюдения yij = Xij—Xj. Затем все (п — к) выровнен-
выровненных наблюдений уц ранжируются, что приводит к последовательности рангов Кц.
4.2] Непараметрические критерии однородности статистических данных 491
Далее, пусть
г) J 1, если г/-е наблюдение среди наблюдений ^j относится к г-й строке;
}1J I 0 в противн
Введем обозначения
(г)
}1J I 0 в противном случае (г = 1,2, ..., 2k] v = 1,2, ..., iV).
м =
N(N-1)BN
Тогда статистика критерия имеет вид S = —
' к
Е-
,• -А;
N-
При п ^ 10 гипотеза сдвига отклоняется, если 5 < %^ (& — 1), где %^ — а-кван™
тиль распределения хи-квадрат с / = Aj — 1 степенями свободы.
Следует помнить, что в этом критерии для равных наблюдений не применяются
средние ранги, они просто распределяются между равными величинами случайным
образом.
Задача 261. Проверить гипотезу сдвига для данных задачи 257 критерием Ходэюеса-
Лемана-Сена.
Иллюстрируем вычисления по шагам. Вычисляем величины tjiji
3
1
2
3
4
5
г
1
-1,10
9,93
-0,77
-0,77
-0,77
2
0
1,37
-0,17
-0,17
-0,17
3
1,10
-0,43
0,93
0,93
0,93
3
6
7
8
9
10
i
1
-0,03
-0,57
-0,73
-0,77
-1,07
2
-1,23
-0,37
-0,03
0,13
0,13
3
1,27
0,93
0,47
0,63
0,93
Ранги Rij величин yij составляют следующую таблицу (равным значениям
чайным образом присваиваются последовательные ранги без усреднения):
слу-
слу3
1
2
3
4
5
г
1
2
4
5
6
7
2
18
30
13
14
15
3
28
11
24
25
26
3
6
7
8
9
10
1
16
10
8
9
3
2
1
12
17
19
20
3
29
27
21
22
23
Вычислим теперь значения Zjyu, i = 1,2,3 и и = 1, ...,30. Всего нужно вычислить
nN = 10 • 30 = 300 значений величин < z^ v >. Затем необходимо найти те значения z^ v
(% = 1,2,3), которые равны 1. Результаты сведем в следующую таблицу значений для
различных I/ и i при N = 30:
492
Проверка гипотез о значениях параметров распределений
[Гл.4
у
1
2
3
4
5
6
7
8
9
10
1
1
1
1
1
1
1
1
1
1
2
1
3
у
11
12
13
14
15
16
17
18
19
20
i
1
1
2
1
1
1
1
1
1
1
1
3
1
у
21
22
23
24
25
26
27
28
29
30
%
1
2
1
3
1
1
1
1
1
1
1
1
1
Из таблицы имеем
10
10
5
г
2 + 3 + 4 + 5 + 6 + 7
9 + 10 + 16
12 + 13 + 14 + 15 + 17 + 18 + 19 + 20 -
10
= 15,8
11 + 21 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29
10
= 23,6.
Далее, вычисляя Rj = - • J^i^, имеем J?i = 16; i?2 = 15; R3 = 14; Л4 = 16;
3 i=1
R6 = 15,33; R7 = 16,33.
Тогда
J2 R* = 2407,5845; M = 111,6123; S = 12,366.
Имеем из табл. 55 Хо,9бB) = 5,99. Так как S = 12,366 > Хо,эбB) = 5,99, гипотеза сдви-
сдвига не отклоняется.
4.2.2. Непараметрические критерии масштаба
Непараметрические ранговые критерии сравнения параметров масштаба, как
правило, строятся на базе соответствующих критериев сдвига изменением либо
статистики критерия, либо правил присвоения рангов наблюдениям. При даль-
дальнейшем изложении достаточно широкой гаммы известных критериев масштаба мы
будем специально обращать внимание читателя на это обстоятельство. Напомним,
что критерии масштаба преследуют цель выявить возможные различия в мерах
разброса (изменчивости) наблюдений в двух или более выборках.
4.2.2.1. Сравнение параметров масштаба двух совокупностей
4.2.2.1.1. Критерий Лнсари—Бредли
Является масштабным аналогом критерия Вилкоксона (см. раздел 4.2.1.1.2.2).
Сравниваются две выборки Х{ hj/j, объемами тип соответственно. Пусть Ri —
ранги элементов одной из выборок (предположим, х) в общем упорядоченном по
возрастанию ряду. Статистикой критерия Ансари—Бредли является
S =
г=1
m -
I
2
- 1
D ?7l + П +
2
1
4.2] Непараметрические критерии однородности статистических данных 493
Вычисление статистики критерия может быть выполнено и другим, более
простым методом. Поставим элементам упорядоченной по возрастанию выборки
Х1 ^ Х2 ^ • • • ^ хт+п объема га + п в соответствие ранги по следующему правилу
{. . 1 .771 + П + 1
га + п — г + 1, если г > ;
г, если г ^ .
Тогда статистика критерия равна
г=1
т. е. она определяется суммой специальным образом назначенных рангов одной
выборки.
Легко видеть, что при четном (га + п) последовательность таких рангов имеет
вид
1 2 Ч т + П т + П Ч 2 1
а при нечетном (га + п) —
m + n^ I m + n + 1
i, z, j, ..., - , - , ..., «j, z, i.
Гипотеза равенства параметров масштаба не отклоняется с достоверностью
а, если S\(a) < S < #2@;), где Si (а), ^(а)—критические значения, приведенные
в табл. 159.
При га, п > 10 можно использовать асимптотическую нормальность распределен
ния величины
5, = 5 - M(g)
где
га (га + п + 2)
при га + п = 2/с;
1 при га + п = 2/г — 1;
4(?тг + п)
ттг(т + п - 2)(га + п + 2)
при тв + п =
48(m + n-l)
+ n+l)[(m + nJ + 3] , _. 1
9 при га + n = 2fc — 1.
48( + )
Нулевая гипотеза равенства параметров масштаба в двух выборках принимается
с достоверностью а, если
Эффективность критерия по сравнению с ^критерием в случае нормального
распределения равна — ~ 0,61.
494
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 159
Критические значения Si (о) и ^г(ск) статистики
Лнсари^Бредли (а — доверительная вероятность) [479]
т
2
3
4
п
8
9
10
11
12
13
14
15
16
17
18
6
7
8
9
10
11
12
13
14
15
16
17
5
6
7
8
9
10
11
12
13
14
15
16
а
0,90
Si
2
2
2
2
2
3
3
3
3
3
3
4
5
5
5
5
6
6
6
7
7
7
8
7
7
8
8
9
9
10
10
11
11
12
12
s2
10
11
12
13
14
14
15
16
17
18
19
13
13
15
16
17
18
20
21
22
23
24
25
14
17
19
20
21
23
24
26
27
29
30
32
0,
Si
2
2
2
2
2
2
2
2
2
2
2
4
4
4
4
5
5
5
5
6
6
6
6
6
7
7
7
8
8
9
9
9
10
10
11
Э5
Si
10
11
12
13
14
15
16
17
17
19
19
13
14
16
17
18
19
21
22
23
24
25
26
16
17
19
21
22
24
26
27
29
30
32
33
т
5
6
7
8
9
10
п
5
6
7
8
9
10
11
12
13
14
15
6
7
8
9
10
11
12
13
14
7
8
9
10
11
8
9
10
11
12
9
10
11
10
а
0,
Si
10
1
11
12
13
14
14
15
16
16
17
15
16
17
18
18
19
20
21
22
21
22
23
24
25
26
29
30
31
32
35
36
38
43
90
s2
20
21
24
26
27
29
31
33
34
36
38
27
29
31
34
36
38
40
42
44
35
38
40
43
45
45
48
50
53
56
55
58
61
67
0,
Si
10
10
11
11
12
12
13
14
14
15
15
14
15
16
16
17
18
19
19
20
19
20
21
22
23
26
27
28
29
30
33
34
36
41
95
s2
20
23
24
26
28
30
32
34
36
38
40
28
30
32
35
37
40
41
44
46
37
39
42
44
47
46
49
52
55
58
57
58
63
69
Задача 262. Имеются две выборки случайных величин:
(m = 8)xij: 1,2; 3,4; 6,2; 8,1; 10,2; 11,3; 13,0; 15,9;
(n = 10)x2j: 0,8; 2,4; 4,2; 5,1; 6,8; 11,4; 13,8; 20,1; 24,2; 26,7.
Проверить гипотезу равенства параметров масштаба в выборках критерием Ансари-
Бредли при достоверности а = 0,95.
"Упорядочиваем объединенную выборку по возрастанию (г — номер выборки, Ri —
ранг случайной величины в объединенной выборке). Результаты сведем в таблицу:
4.2]
Непараметрические критерии однородности статистических данных
495
i
2
1
2
1
2
2
0,8
1,2
2,4
3,4
4,2
5,1
1
2
3
4
5
6
г
1
2
1
1
1
2
Xij
6,2
6,8
8,1
10,2
11,3
11,4
7
8
9
10
11
12
i
1
2
1
2
2
2
13,0
13,8
15,9
20,1
24,2
26,7
13
14
15
16
17
18
Далее находим
8 + 10 + 1
Ri-
8 + 10 + 1
= 76 - (|2 - 9,5| + |4 - 9,5| + |7 - 9,5| + ... + |13 - 9,5| + |15 - 9,5|) = 49.
Если бы использовался иной метод присвоения рангов, то имели бы следующую
последовательность рангов:
г: 212122121112121222
Rii 123456789987654321
Сумма таких рангов первой выборки равна S = 2 + 4 + 7 + 9 + 9 + 8 + 6 + 4 = 49, что
естественно совпадает с ранее полученным результатом.
Теперь из табл. 159 для т = 8, п = 10 и а = 0,95 находим Si = 28 и S2 = 52. Так как
Si = 28 < S = 49 < Si = 51, нулевая гипотеза равенства параметров масштаба в выбор™
ках не отклоняется.
Используем теперь нормальную аппроксимацию. Так как (т + п) — четное, имеем
М(Я) =
= 40; DCS) =
' 2°
48-17
= 31, 3725
= 5, 601);
5,601
. 1,606.
Так как Я* = 1,606 < lM(i+a)/2 = ^o,975 = 1596, нулевая гипотеза и в этом случае не
отклоняется.
4.2.2.1.2. Критерий Сижела-Тьюки
Сижел и Тьюки [480] предложили преобразование критериев сдвига в критерии
масштаба. Суть их способа сводится к преобразованию первичной упорядоченной
объединенной выборки. Пусть х\ ^ х^ ^ ... ^ хп—первичная объединенная
выборка. Из нее получаем новую последовательность вида
XI, Хп, Хп-1,Х2, Ж3, Хп^2, %n^3i %4, X&, . . .
(т. е. оставшийся ряд „переворачивается" каждый раз после приписывания рангов
паре краштых значений).
Далее проверка гипотезы о разности параметров масштаба в двух выборках
аналогична проверке гипотезы сдвига в новой последовательности с описанным
правилом нумерации рангов.
Если использовать в качестве критерия проверки нулевой гипотезы сумму ран-
то.
гов (It! = ^ Щ) элементов выборки меньшего объема в такой последовательности,
то нулевая гипотеза принимается, если R\{ot) < R < R2{ol), где R±(a) и
критические значения, которые могут быть получены с помощью табл. 143 крите-
критерия Манна—Уитни (см. раздел 4.2.1.1.2.2). Для этого необходимо из табл. 143 найти
496
Проверка гипотез о значениях параметров распределений
[Гл.4
Ui и U2 для заданных а, га и п и затем вычислить
га(га + 1) ТТ
= nm ¦
= nm ¦
т (га + 1)
-U.
Здесь га — объем меньшей выборки.
При п, га > 10 справедлива аппроксимация
га(п + га + 1)
nm(n + га + 1)
Если |W| > tii+a , нулевая гипотеза равенства параметров масштаба принимает™
ся с достоверностью а.
Задача 263. Проверить гипотезу равенства параметров масштаба критерием Си-
мсела-Тьюки для данных задачи 262.
Строим упорядоченный ряд с нумерацией рангов в соответствии с правилом крите-
критерия Оижела^Тькжи. Результаты сведем в таблицу (г — номер выборки; Ri — ранг члена
объединенной выборки, упорядоченной по правилу Сижела—Тьюки).
г
2
2
2
1
2
2
Xi
0,8
26,7
24,2
1,2
2,4
20,1
Ri
1
2
3
4
5
6
г
1
1
2
2
1
2
Xi
15,9
3,4
4,2
13,8
13,0
5,1
Ri
7
8
9
10
11
12
г
1
2
1
2
1
1
Xi
6,2
11,4
11,3
6,8
8Д
10,2
Ri
13
14
15
16
17
18
Для первой выборки (г = 1) из таблицы имеем
8
= 4 + 7 + 8 + 11 + 13 + 15 + 17 + 18 = 93.
г=1
Из табл. 143 для т = 8, п = 10 и а = 0,95 находим U\ = 17 и 172= 63, откуда
Ri(a) = 80 + — - 63 = 53 и R2 (а) = 80 + — - 17 = 99.
Так как R\(a) = 53 < i? = 93 < i?2(a), нулевая гипотеза принимается.
Используем теперь аппроксимацию
8- 19
93-
W =
= 1,51.
Так как W = 1,51 < гхо,975 :=: 1,96, нулевая гипотеза и в этом случае не отклоняется.
4.2.2.1.3. Критерий Кейпена
Предложен в [481] и является масштабным аналогом критерия Фишера- Йэйтса-
Терри-Гёфдинга (см. раздел 4.2.1.1.2.3).
Если Ri — ранг i-го элемента меньшей по объему выборки х\^Х2^ ...,хш в об™
щем упорядоченном ряду (га + п) значений объединенной выборки, то статистика
критерия может быть записана в виде
К = ]Г am+n(Ri),
г=1
n,
4.2]
Непараметрические критерии однородности статистических данных
497
где ат+п(г) —математическое ожидание квадрата г-й порядковой статистики в вы™
борке объема (га + п) из стандартного нормального распределения (значения а^{г)^
называемые метками критерия, приведены в табл. 160).
Таблица 160
Метки ам(г) критерия Кейпена (все значения умножены на 100) [482]
i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
N
6
202
69
29
29
69
202
7
222
83
34
21
34
83
222
8
240
97
42
21
21
42
97
240
9
256
109
51
25
17
25
51
109
256
10
271
122
61
30
17
17
30
61
122
271
11
285
133
70
36
19
14
19
36
70
133
285
12
298
144
79
43
23
14
14
23
43
79
144
298
13
310
155
89
50
27
15
12
15
27
50
87
155
310
14
321
164
96
57
32
18
12
12
18
32
57
96
164
321
15
331
174
104
63
38
22
13
10
13
22
38
63
104
174
331
16
341
182
112
70
43
26
15
10
10
15
26
43
70
112
182
341
17
351
191
119
77
49
30
18
11
9
11
18
30
49
77
119
191
351
18
360
199
126
83
54
34
21
13
9
9
13
21
34
54
83
126
199
360
19
368
207
133
89
60
39
25
15
10
8
10
15
25
39
60
89
133
207
368
20
376
214
140
95
65
44
28
18
11
8
8
11
18
28
44
65
95
140
214
376
Нулевая гипотеза отклоняется, если
Кг{а) <К <К2{а),
где Ki(a) и К2(а) — критические значения, приведенные в табл. 161.
При га, п > 10 справедливо приближение
К - М(К)
к* =
где
М(К) = га; В(К) =
JV(O,1),
т-\-п
(т + п)(т + п —
¦ГС- 1
При \К*\ < ui+g нулевая гипотеза принимается с достоверностью а.
2
Задача 264. Проверить гипотезу равенства параметров масштаба критерием Кей-
Кейпена для данных задачи 262.
Ранги Ri первой выборки (объема т = 8) в общей упорядоченной последовательности
равны: 2, 4, 7, 9, 10, 11, 13, 15.
Из табл. 160 находим ряд ад
ai8B) = 19
ai8A0) = 9;
= 83; а18G) = 21; а18(9) = 9;
= 13; сы8A3) = 34; сы8A5) = 83.
498
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 161
Критические значения JK~i(a) и K^^pt) статистики Кейпена
(все значения умножены на 100, а — доверительная вероятность) [482]
п
6
5
4
6
5
8
7
6
5
9
8
7
6
10
9
8
7
6
11
10
9
8
7
9
11
т
2
3
4
3
4
2
3
4
5
2
3
4
5
2
3
4
5
6
2
3
4
5
6
8
7
а
0,90
Кг
42
84
181
93
176
34
95
156
247
78
86
139
226
37
80
139
211
297
30
77
139
203
286
423
329
К2
80
577
619
563
672
542
572
694
755
570
589
710
792
442
586
698
826
905
465
620
719
829
927
1186
1101
0,95
Кг
42
84
126
67
144
34
77
125
199
33
69
122
192
28
71
123
173
261
27
57
107
171
243
369
280
к2
80
577
674
621
672
542
603
725
803
570
640
739
843
596
639
763
862
941
620
647
790
877
969
1246
1170
п
12
11
10
9
8
7
13
12
11
10
9
8
14
13
12
11
10
9
8
14
13
11
10
10
9
т
2
3
4
5
6
7
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
6
7
8
9
а
0
Кг
30
76
133
201
276
366
32
70
122
196
270
357
30
68
122
190
264
345
431
69
122
185
335
412
501
90
к2
485
581
717
842
946
1034
505
609
727
851
959
1054
523
593
735
860
970
1072
1167
619
743
863
1090
1203
1297
0
Кг
24
56
113
170
233
313
26
57
102
158
228
308
25
51
99
159
221
300
381
52
99
154
292
360
442
95
к2
642
660
795
895
991
1087
662
679
804
912
1016
1105
523
697
809
929
1030
1126
1217
711
828
947
1158
1266
1356
Тогда К = J2 «is (г) = 199 + 83 + 21 + 9 + 9 + 13 + 34 + 83 = 451.
г=1
Из табл. 161 для а = 0,95, т = 8 и п = 10 находим Кг = 360 и К2 = 1266.
Так как Кг = 360 < К = 451 < К2 = 1266, нулевая гипотеза равенства параметров
масштаба в выборках не отклоняется.
Покажем теперь использование аппроксимации. Необходимо иметь в виду, что
в табл. 160 и 161 приведены значения ajv(z) и Кг(К2), в 100 раз превосходящие реальные
величины. Это не сказывается на проверке критерия, однако должно быть учтено при
использовании аппроксимации (т. е. при вычислении величины К* нужно использовать
значения К и ап+т(г), уменьшенные в 100 раз). Имеем Ш(К) = 8 и (используя табл. 161)
) = 3,62 + 1,992 + 1,262 + 0,832 + 0,542 + 0,342 + 0,212 + ОДЗ2
- ОДЗ2 + 0,212 + 0,342
0,542
0,832 + 1,262 + 1,992
Далее получаем
ЩК) =
8- 10
18- 17
• 39,3458 -
8- 10
17
0,09^ + 0,09^ +
3,62 = 39,3458.
5,5806 (у/ЩК) = 2,362); \К*\ =
4,51 -I
2,362
= 1,478.
Так как \К*\ = 1,478 < иг+а = гк»,975 = 1596, нулевая гипотеза не отклоняется и этим
2
критерием.
4.2]
Непараметрические критерии однородности статистических данных
499
4.2.2.1.4. Критерий Клотпа
Критерий, предложенный Клотцем [483], является масштабным аналогом крите-
критерия Ван дер Вардена (см. раздел 4.2.1.2.6). Его статистика в принятвгх ранее обозна™
чениях имеет вид L =
, где и1 — 7™квантиль стандартного нормального
2
распределения; т^п — объемы сравниваемых выборок; Щ—ранги, полученные
элементами первой выборки (объема га) в общем упорядоченном по возрастанию
ряду. Напомним (см. аппроксимацию 15 в разделе 1.1.1), что можно использовать
аппроксимацию
Метки критерия Клотца и2г приведены в табл. 162.
Таблица 162
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Метки
U i ]
JV
критерия
Клотца (все значения
[ умножены
на 100) [482]
N
6
114
32
3
3
32
114
7
132
46
10
0
10
46
132
8
149
58
19
2
2
19
58
149
9
164
71
28
6
0
6
28
71
164
10
178
83
37
12
1
1
12
37
83
178
11
191
94
46
19
4
0
4
19
46
94
191
12
203
104
54
25
9
1
1
9
25
54
104
203
13
215
114
63
32
13
3
0
3
13
32
63
114
215
14
225
123
71
39
19
6
1
1
6
19
39
71
123
225
15
235
132
79
46
24
10
2
0
2
10
24
46
79
132
235
16
245
141
86
52
29
14
5
1
1
5
14
29
52
86
141
245
17
254
149
94
58
35
19
8
2
0
2
0
19
35
58
94
149
254
18
262
157
101
65
40
23
11
4
0
0
4
11
23
40
65
101
157
262
19
271
164
107
71
46
28
15
6
2
0
2
6
15
28
46
71
107
164
271
20
278
171
114
77
51
32
19
9
1
0
0
1
1
9
19
32
51
77
114
171
278
Гипотеза равенства параметров масштаба двух выборок принимается с досто™
верностью а, если Li(a) < L < L2(aI где Li(a) и L2(a)—критические значения,
приведенные в табл. 163.
При га, п > 10 распределение статистик L удовлетворительно аппроксимируется
нормальным со средним M(L) и дисперсией D(L), где
то+п
M(L) =
т-\-п
т + п
т+п+1
D(L) =
г=1
m+n+l
т(т
m+n
771 "ЧГ""^ о
771 + 71
m + n + l
500
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 163
Критические значения jLi(a) и 1/2 (а) статистики Клотца
(все значения умножены на 100, а — доверительная вероятность) [482]
т
2
3
4
3
4
2
3
4
5
3
4
5
4
5
6
4
5
6
4
5
6
7
4
5
6
7
4
5
6
7
те
6
5
4
6
5
8
7
6
5
8
7
6
8
7
6
9
8
7
10
9
8
7
11
10
9
8
12
11
10
9
а
0,
Ьг
4
23
81
34
83
2
39
76
134
38
69
130
73
124
178
77
121
177
78
123
175
241
74
123
177
238
73
122
177
235
ЭО
ь2
298
356
375
356
427
356
368
451
488
386
474
526
469
560
614
496
570
642
508
593
664
727
523
605
683
753
532
627
720
776
0,95
Ьг
4
23
42
12
62
2
25
51
99
23
54
100
60
90
149
51
95
145
60
98
142
199
52
93
144
199
53
97
140
197
ь2
298
356
414
399
427
356
393
476
523
428
495
568
519
589
643
547
610
673
560
645
702
769
573
652
729
794
581
667
751
820
т
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
2
7
4
5
6
7
8
11
10
8
те
14
13
12
11
10
9
15
14
13
12
11
10
9
15
14
13
12
11
10
18
13
16
15
4
13
12
9
10
8
а
0
Ьг
37
75
122
177
234
298
34
74
120
174
233
296
364
76
122
174
233
294
362
9
35
73
120
172
230
293
359
429
301
90
ь2
442
552
640
719
797
870
459
560
648
736
815
891
962
570
660
751
835
912
986
392
481
578
673
763
849
930
1005
1079
845
0
Ьг
23
56
95
141
198
256
23
54
92
141
192
250
314
51
94
140
193
250
313
3
22
53
92
139
190
247
309
375
257
95
ь2
508
602
694
772
847
919
524
616
704
791
869
943
1012
619
723
811
891
965
1039
449
556
639
737
823
907
986
1061
1133
889
|гаИ |LM(L)|
Если [L \ = J— ^ < иг+а, нулевая гипотеза принимается.
Щь) 2
Критерий Клотца оптимален для распределений, близких к нормальному.
Задача 265. Проверить гипотезу равенства параметров масштаба критерием Клот-
Клотца для данных задачи 262.
Имеем последовательность рангов Щ: 2, 4, 7, 9, 10, 11, 13, 15.
Из табл. 162 находим для N = т + п = 18:
19
2
= 262; и j^ = 65;
= 11;
иш = 0;
19
Вычисляем L = 262 + 65 + 11 ¦
и 11 = 4;
19
19
и\з = 23;
19
и\
= 0;
19
^5 = 65.
19
-0 + 0 + 0 + 4 + 23 + 65 = 430.
Из табл. 163 для m = 8, n = 10 и а = 0,95 находим Ь\ = 250 и L2 = 943.
Так как jLi=250<jL = 430 < L2 = 943, параметры масштаба двух выборок призна-
признаются статистически неразличимыми с достоверностью а = 0,95.
4.2]
Непараметрические критерии однородности статистических данных
501
Используем теперь нормальную аппроксимацию. Вычисляем, используя таблицу 162:
М(Ь) = — • B62 + 157 + 101 + 65 + ... + 157 + 262) = 589,333;
18
D(L) =
8- 10
18- 17
B622 + 1572 + 1012 + 652 + ... + 157+2622) = 55280,087;
/5A) = 235,117; L* =
= 0,678,
235,117
что меньше iio,975 = 1,96; следовательно, и в этом случае нулевая гипотеза не отклоня-
отклоняется.
4.2.2.1.5. Квартальный критерий
Критерий является интуитивным аналогом медианного критерия сдвига (см.
раздел 4.2.1.2.7). Статистика критерия имеет вид
г=1
т + п + 1
т + п + 1
2
где
Название критерия исходит из того, что S приблизительно равно числу на-
наблюдений из первой выборки, лежащих за пределами первой и третьей кварти-
квартилей объединенной выборки. Точнее, S получается, если подсчитать количество
г « с л \ т + п + 1 3(т + ?г + 1)
наблюдении Х{ (г = 1, ..., т), для которых щ < или щ > — -,
4 4
и, если (га + n + 1) делится на 4, прибавить 1/2 в случае, когда Щ = или
3(т + п + 1)
для некоторого г = 1, ..., га, или прибавить 1 в случае, когда оба
последних равенства имеют место для некоторых двух различных индексов г.
При га, п > 20 статистика S имеет приближенно нормальное распределение со
средним М(Я) и дисперсией DEr) [365], где
т(т + п — 1)
МE) =
. т
?гг?г[(т + гг
при га + n = 4fc — 1;
при т-\-п ф 4к -\- 1;
- 2(т + п) - 1]
D(S) =
4(т + п) (пг + гг — 1)
2kmn(rn + гг — 2fc)
при ?п + n = 4Aj — 1;
при ?тг + п т^ 4Aj — 1.
(гтг + п) (гтг + гг — 1)
Поэтому нулевая гипотеза равенства параметров масштаба принимается, если
1 < г/i+a, где а — доверительная вероятность.
yD(S) 2
Эффективность критерия по сравнению с i^-критерием в случае нормального
распределения невелика и равна « 0,37, поэтому им рекомендуется пользоваться
при га, п > 50.
Задача 266. Проверить гипотезу равенства параметров масштаба для данных задачи
262 квартильным критерием.
Имеем ряд рангов Щ: 2, 4, 75 9, 10, 11, 13, 15.
Вычисляем 6 —
Ri-
8 + 10 + 1
8 + 10 + 1
= <5(|2 - 9,5| - 4,75) = EB,75) = 1.
502
Проверка гипотез о значениях параметров распределений
[Гл.4
Далее по аналогии имеем
8(\R2 - 9,5| - 4,75) = E@,75) = 1; 8(\R3 ~~ 9,5| - 4,75) = ?(-2,25) = -1;
S(\R4 - 9,5| - 4,75) = ?(-4,25) = -1; S(\R5 - 9,5| - 4,75) = ?(-4,25) = -1;
S(\R6 - 9,5| - 4,75) = ?(-3,25) = -1; S(\R7 - 9,5| - 4,75) = ?(-1,25) = -1;
S (\R8 - 9,5| - 4,75) = ?@,75) = 1.
Тогда 5 = - • A-1-1-1-1-1 + 1 + 8) = 2,5.
Далее вычисляем, имея в виду, что при k = 4m + п = 41с + 2 (8 + 10 = 4-4 + 2)
8 + 10
- 17
Имеем
12 5 — 3 55|
— -—
1,078
= 0,97. Так как \S*\ = 0,97 < г^о,975 = 1,96, нулевая гипотеза
,
принимается. Следует отметить, что к этому выводу нужно относиться с осторожностью.
Это связано с тем, что точность аппроксимации при наших объемах выборок (т = 8
и п = 10) невелика.
4.2.2.1.6. Критерий Сэвиджа
Для распределений, плотность которых определена на полупрямой @ ^ х < оо),
т. е. экспоненциального типа, Сэвидж [484] предложил критерий масштаба, основан-
основанный на статистике
т п
i=l j=m-\-n — Ri-\-l
где Щ — так же, как и ранее, ранги элементов одной выборки объема т^пв общем
упорядоченном ряду.
Нулевая гипотеза равенства параметров масштаба принимается, если
Ci(a) < С < С^а), где С±(а) и C2(pt) — критические значения, приведенные
в табл. 164.
Применительно к экспоненциальному распределению критерий Сэвиджа позво-
позволяет установить разницу в значениях параметров распределений (Л или v — см.
раздел 1.1.4) в двух совокупностях (например, сравнить средние наработки на отказ
изделий двух выборок).
Задача 267. Даны две выборки случайных величин:
(га = 7) хц: 2,1; 3,2; 4,8; 5,7; 8,1; 9,2; 12,4;
(га = 8) x2j: 0,8; 0,9; 2,6; 4,3; 7,1; 9,4; 12,7; 15,1.
Проверить гипотезу равенства параметров масштаба в выборках критерием Сэвидэюа
при доверительной вероятности а = 0,95.
Ранжируем совместный ряд. Результаты сведем в таблицу (г — номер выборки, Ri —
ранг члена выборки хц в объединенном ряду):
%
2
2
1
2
1
ХЦ
0,8
0,9
2,1
2,6
3,2
Ri
1
2
3
4
5
i
2
1
1
2
1
Xij
4,3
4,8
5,7
7,1
8,1
Ri
6
7
8
9
10
i
1
2
1
2
2
Xij
9,2
9,4
12,4
12,7
15,1
Ri
11
12
13
14
15
Для первой выборки (i = 1) получаем последовательность рангов
Ri = 3, 5, 7, 8, 10, 11, 13.
4.2]
Непараметрические критерии однородности статистических данных
503
Таблица 164
Критические значения Ci(ct) и С2(ок) критерия Сэвиджа
т
3
2
3
2
3
4
2
3
4
2
3
4
5
2
3
4
5
2
3
4
5
6
2
3
4
5
6
2
3
4
5
6
7
2
3
4
5
6
7
(все значения
3
5
4
6
5
4
7
6
5
8
7
6
5
9
8
7
6
10
9
8
7
6
11
10
9
8
7
12
11
10
9
8
7
13
12
11
10
9
8
умножены на 100, а-
а
0,90
Сг
116
45
121
40
119
205
49
110
190
44
109
188
2783
49
106
180
264
44
107
177
256
344
43
102
173
252
338
47
102
169
246
391
420
44
101
167
243
325
414
с2
485
418
494
444
507
595
416
521
623
436
534
636
729
421
547
647
747
437
547
655
758
854
428
559
667
771
871
422
564
672
781
883
979
435
563
677
791
895
994
0,95
Сг
116
45
96
40
83
171
35
90
165
31
92
157
240
28
85
152
233
35
86
148
223
307
33
83
148
219
299
30
81
142
214
294
378
36
81
143
212
288
372
с2
485
418
527
444
566
629
466
566
654
486
571
677
762
504
578
686
784
470
585
699
799
891
486
596
712
816
913
500
603
722
828
927
1021
480
613
727
839
943
1039
— доверительная вероятность) [485]
т
2
3
4
5
6
7
8
2
3
4
5
6
7
8
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
10
п
14
13
12
11
10
9
8
15
14
13
12
11
10
9
16
15
14
13
12
11
10
9
17
17
15
14
13
12
11
10
18
17
16
15
14
13
12
11
10
а
0,90
Сг
42
99
165
240
321
407
498
45
99
164
237
317
402
492
43
97
162
235
314
397
486
578
42
97
161
233
310
393
479
570
44
96
160
230
307
389
475
564
657
с2
431
571
685
798
905
1006
1102
438
572
691
805
913
1017
1116
440
573
696
812
922
1027
1128
1225
438
576
698
815
927
1034
1136
1235
437
578
702
820
933
1041
1145
1246
1342
0
Сг
33
79
140
207
283
365
452
31
79
137
205
279
359
445
30
77
137
202
276
355
439
528
28
77
134
200
272
349
432
520
32
76
133
198
269
346
427
513
603
95
с2
493
619
736
849
955
1054
1148
505
622
743
859
967
1069
1165
491
628
749
868
977
1082
1181
1275
501
632
757
873
985
1091
1192
1288
491
637
761
880
993
1101
1204
1302
1397
Вычисляем статистику критерия
1 1
С =
7+8-3+1
-13 +
= 1,104.
7+8-5+1 7+8-7+1
Из табл. 164 для m = 7, п = 8 и а = 0,95 имеем (учитывая, что в ней приведены
умноженные на 100 критические значения) С\ = 3,72.
504 Проверка гипотез о значениях параметров распределений [Гл. 4
Так как С = 1,104 < С г = 3,72, нулевая гипотеза равенства параметров масштаба
критерием Сэвиджа отклоняется.
Используем теперь нормальную аппроксимацию. При га, п > 10 справедливо нор-
нормальное приближение, в соответствии с которым величина распределена как стандартная
нормальная случайная величина.
Для наших данных вычисляем
7 8 / 1 15 Л
М(С) = т = 7; D(C) = • 1 • V - = 3,115 (\/ЩС) = 1,764).
Имеем [С*1= I1'104'.
1 1,764
Так как |С* = 3,342 > tio,975 :=: 1,96, то и этот критерий отклоняет нулевую гипотезу.
4.2.2.1.7. Критерий Муда
Рассмотрен в [486, 487] в качестве альтернативы критерию, основанному на
i^-статистике Фишера, когда вместо наблюдений используются их ранги. Стати-
Статистика критерия имеет вид
г=1
где Щ —ранги элементов выборки ж1? ..., хт в общем упорядоченном ряду значе™
ний хъ ... ,хт и 2/1, ... ,уп(т ^ п).
Нулевая гипотеза равенства параметров масштаба в обеих выборках принима-
принимается, если rai(a) < М < га2(ск), гДе nii(a) и гп2(а)—критические значения стати™
стики, приведенные в табл. 165.
При га, п > 10 справедлива нормальная аппроксимация [488, 489]
М - Ш(М) + -
м* = 2;
/
где
т(т + п + 1)(т + п - 1) ^ тл(М\ = ™n{m + n + l)(m + n + 2)(m + n - 2)
12 ' v ; 180
Нулевая гипотеза принимается, если
\М*\ < ui+a.
2
Эффективность критерия Муда по отношению к ^-критерию в случае исходного
нормального распределения равна 0,76 [486].
Необходимо отметить, что критерий Муда (как и все ранее рассмотренные
критерии) предполагает равенство средних (параметров положения). Это может
быть обеспечено введением величин Х{ — Дх и у^ — fa вместо величин Xi и у^ (Д]_, fa —
медианы соответствующих выборок).
Задача 268. Поверить гипотезу равенства параметров масштаба в условиях задачи
267 критерием Муда.
Для ряда рангов Щ : 3, 5, 7, 8,10,11,13 имеем
Из табл. 165 для га = 7, п = 8иа = 0,95 имеем Мг = 67 ш М2 = 196.
4.2]
Непараметрические критерии однородности статистических данных
505
Таблица 165
Критические значения M\(ol) и M^^ol) статистики Муда
(а — доверительная вероятность) [488]
т
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
5
5
5
5
5
п
6
7
8
9
10
11
12
13
3
4
5
6
7
8
9
10
11
4
5
6
7
8
9
10
5
6
7
8
9
а
0,
Mi
1
1
2
2
2
3
3
4
3
5
5
5
9
9
9
11
13
9
11
15
15
19
21
23
21
25
29
33
37
90
м2
18
25
32
34
50
57
72
74
15
22
27
34
43
51
63
77
87
33
42
53
66
79
93
107
61
76
91
107
125
0,
Mi
1
1
1
1
1
1
2
2
3
2
3
5
5
5
7
8
9
9
9
11
14
15
15
19
17
20
23
27
31
95
м2
18
25
32
41
50
61
72
80
15
22
31
36
47
57
71
81
93
33
45
55
70
83
101
117
65
79
95
114
135
т
6
6
6
6
6
7
7
7
7
7
7
7
8
8
8
8
8
9
9
5
5
5
6
6
6
6
9
10
п
10
11
12
13
14
7
8
9
10
11
12
13
8
9
10
11
12
9
10
10
11
12
6
7
8
9
11
10
а
0,
Mi
65
74
81
90
99
68
76
86
95
106
116
128
106
117
130
144
158
156
172
42
47
54
41
46
51
59
188
220
ЭО
м2
191
217
245
274
303
160
185
214
243
274
307
342
234
267
302
338
378
328
369
147
107
190
101
123
143
166
410
444
0,
Mi
55
62
69
75
83
60
67
74
83
92
100
110
94
104
116
127
138
140
155
34
39
43
35
39
43
50
168
200
35
м2
203
230
259
291
323
168
196
224
255
290
324
362
246
280
318
356
398
344
386
155
179
203
107
130
151
176
432
464
Так как Mi = 67 < М = 73 < М2 = 196, нулевая гипотеза не отклоняется.
Для нормального приближения имеем
М(М) = 7'16'14 = 130,66; D(M) =
12
|М*
180
|ТЗ —- 130,61|
33,16
= 1100,08
М) = 33,16);
= 1,737.
Так как \М*\ = 1,737 < iio,975 = 1,96, нулевая гипотеза этим критерием не отклоня-
отклоняется.
4.2.2.1.8. Критерий Сукхатме
Критерий является модифицированной формой критерия Вилкоксона-Уитни
(см. раздел 4.2.1.1.2.2). Статистика критерия имеет вид [491, 492]
если0<а<6;
если а < 0,
6.
506 Проверка гипотез о значениях параметров распределений [Гл. 4
При га, п > 10 используется аппроксимация
где
При справедливости нулевой гипотезы Т* распределена как нормальная слу-
случайная величина. Поэтому с вероятностью а нулевая гипотеза отклоняется, если
Т*\ > ui+a. (здесь и7—7™квантиль стандартного нормального распределения).
2
Эффективность критерия Сукхатме для нормально распределенных случайных
величин равна 0,61, для экспоненциально распределенных — 0,94.
Основным неудобством критерия, основанного на Т-статистике, является необ-
ходимость предварительного знания соотношения параметров положения в выбор-
выборках. Этого недостатка лишен модифицированный критерий, предложенный в [490]
(имеем выборки х\, ..., хт и г/i, ..., уп):
п т
2 Y Е
i=pj=i
где
{1, если 0 < и < гу, 0 < v < w
или w < и < 0, ги < г; < 0;
0 в остальных случаях;
{1, если 0 < и < v,
или v < и < 0;
0 в остальных случаях.
Более удобна для практических вычислений другая форма
Г7 = Г[ +Г^,
где
, ^2 m + n-8^o ni(m
212
г=1 г=1
2
-4 ^ , п2(гг2 + l)[3(m + n)+ 8п2 - 14]
^ i2 +
^ i2 + 12
г=1
Здесь Rn —ранг i-то положительного наблюдения у^ в упорядоченных по величине
положительных значениях Х{ и у^\ Ri2 — ранг i-ro отрицательного наблюдения
в упорядоченном по величине ряду отрицательных значений Х{ и у±\ п\—число
положительных наблюдений у {п^ = п — ni); mi —число полож:ительных наблюде-
наблюдений х (ni2 = тп — nil).
При справедливости нулевой гипотезы имеем
М(Т') = ^п [5(w + nf - 3n(m + n) - 2n2 - 12(m + n) + 12n] ;
Щ1 j " 2880 X
x [61(m + nK + 331(m + nf - 120n2 + 480n(m + n) - 2344(m + n) - 600n + 2636] .
Эффективность Т'-статистики по отношению к Т-статистике равна 1,13.
4.2]
Непараметрические критерии однородности статистических данных
507
Задача 269. Проверить гипотезу масштаба критерием Сукхатме для данных зада-
задачи 267.
Имеем выборки
Xii 2,1, 3,2, 4,8, 5,7, 8,1, 8,2, 12,4 (m = 7);
уц 0,8, 0,9, 2,6, 4,3, 7,1, 9,4, 12,7, 15,1 (п = 8).
Значения ф{хг^у^) (г = 1, ..., 7; j = 1, ..., 8) представлены в таблице:
1
2
3
4
5
6
7
1
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
3
1
0
0
0
0
0
0
4
1
1
0
0
0
0
0
5
1
1
1
1
0
0
0
6
1
1
1
1
1
1
0
7
1
1
1
1
1
1
1
8
1
1
1
1
1
1
1
Имеем
-i m n
т ¦ п т-^ .л *' %>
г=1з=1
Окончательно имеем Т*
= 0,482;
45 • 1 ¦ о
= 0,00818
= 0,09).
|0,482 — 0,25|
0^09
= 2,577.
Так как \Т*\ = 2,577 > 11,0,975 = 1,96, нулевая гипотеза отклоняется.
4.2.2.1.9. Критерий Сэндвика—Олесона
Критерий применим для парных выборок равного объема
xli X2i • • • ? xn'i
г/1,2/2, • • • ,2/n-
Пусть тж и Шу — оценки медиан в выборках. Построим последовательность
величин
Cq ™~~™ \ JU q iil/n
- \у{ -
i = 1, . ..,n.
Нулевая гипотеза равенства параметров масштаба принимается, если z^ не
имеют тенденции быть положительными [493]. Для проверки этого используется
критерий знаковых рангов Вилкоксона (см. раздел 4.2.1.1.2.2).
Статистикой критерия является величина
где Ri — ранги неотрицательных значений zi в общем ранжированном по возраста-
возрастанию ряду \zi\.
При п > 20 моясно использовать приближение
^+ п{п+1)
Т* =
п{п+ 1)Bп
24
При \Т*\ > ui+g нулевая гипотеза отклоняется.
2
508
Проверка гипотез о значениях параметров распределений
[Гл.4
Задача 270. Проверить критерием Сэндвика-Олссона равенство параметров мае-
штаба для выборок
хц 1,4, 1,8, 2,7, 3,9, 6,1, 7,8, 7,9;
yii 0,8, 0,9, 2,7, 5,9, 6,1, 8,1, 11,2
при доверительной вероятности а = 0,95.
Для ряда xi имеем медиану тх = 3,9 и, по аналогии, тпу = 5,9. Вычисляем:
zt = \xi - гпх\ - \уг - гпу\ = |1,4 - 3,9| - |0,8 - 5,9| = ^2,6;
z2 = |1,8 - 3,9| - |0,9 - 5,9| = -2,9; z3 = |2,7 - 3,9| - |2,7 - 5,9| = -1,0;
z4 = |3,9 - 3,9| - |5,9 - 5,9| = 0; z5 = |6,1 - 3,9| - |6,1 - 5,9| = 2,0;
z6 = |7,8 - 3,9| - (8,1 - 5,9) = 1,7; z7 = |7,9 - 3,9| - |11,2 - 5,9| = -1,3.
Формируем упорядоченный ряд значений \zi\ (внизу отмечены ранги):
Zi\: 0 1,0 1,3 1,7 2,0 2,6 2,9
Rii 1 2 3 4 5 6 7
Видим, что положительные значения ^@; 1,7; 2,0) имеют ранги Rf. 1, 4 и 5 соответ-
соответственно. Следовательно, Т+ = 1 + 4 + 5 = 10.
Из табл. 144 для п = 7иа = 0,95 имеем Т\ = 4 и Т2 = 24.
Так как Т\ = 4 < Т+ = 10 < Т2 = 24, нулевая гипотеза равенства параметров масшта-
масштаба не отклоняется. Легко видеть, что к такому выводу приводит и аппроксимация
7 •!
= 0,676 < Ui + g = 1^C,975 = 1,96.
4.2.2.1.10. Критерий Краута-Линерта
Большинство из рассмотренных нами ранее критериев предполагали равенство
параметров положения сравниваемых выборок. Краутом и Линертом [494, 495]
рассмотрены критерии масштаба, нечувствительные к сдвигу. Если в нашем распо-
распоряжении находятся две зависимые (парные) выборки
хг: хъх2, ...5ж„;
Vi- 2/15 2/2? • • • ,Уп?
то критерий масштаба строится следующим образом. Сначала случайным образом
тъ
образуем — пар совокупностей
и (жг2?2/г2) и находим
D,=
h - Xj2) - (yix -yi2)
2
Если совокупность величин Di симметрична, то нулевая гипотеза равенства
параметров масштаба не отклоняется. Таким образом, задача сводится к проверке
симметричности распределения совокупности значений Di. Это может быть выпол™
нено одним из критериев, приведенных в главе 3 (см. раздел 3.5).
Для случая независимых выборок критерий строится следующим образом. Каж™
дая выборка случайным образом разбивается на пары наблюдений
( \ ' 1 /
Затем производится сравнение рядов разностей
с помощью любого критерия сдвига.
и Dy.=
(У 31 ™
4.2] Непараметрические критерии однородности статистических данных 509
Задача 271. Для выборок равного объема п = 16
Xii 1, 2, 4, 6, 9, 12, 15, 21, 27, 31, 35, 46, 51, 61, 71, 75;
yji 2, 6, 9, 14, 21, 27, 38, 46, 59, 76, 91, 101, 110, 120, 140, 155
проверить гипотезу равенства параметров масштаба критерием Краута-Линерта
при доверительной вероятности а = 0,95.
Разбиваем выборку хг произвольно на 8 пар:
A,75), B,6), D,61), (9,46), B1,35), A5,51), A2,27), C1,71).
Аналогично поступаем с выборкой у у.
F,9), B,27), B1,155), A4,101), C8,59), D6,140), (91,120), G6,110)
Вычисляем ряд значений
Р., = <«" 7"J -> A -275J = 2738; ^=8;
=1624,5; (9~46J =684,5; B1 ~ ^ = 98;
' ' 2 ' ' 2
648
2
По аналогии получаем ряд
=112,5; C1 ~ llf = 800.
2
^^^=45; ^
^^4,5;
=4,5; ^=312,5;
B1 -2155J = 8978; A4-2101J =3784,5; C8 ^ = 220,5;
D6-214°J=4418; (91-2120J =420,5; (?6 ^ = 578.
Сдвиг рядов _DXi и DVi проверяем критерием Вилкоксона (см. раздел 4.2.1.1.2.2), для
чего строим ряд значений
Z! = 2738 - 4,5 = 2733,5; z2 = 8 - 312,5 = -304,5; z3 = 1624,5 - 8978 = -7353,5;
z4 = 684,5 - 3784,5 = -3100; z5 = 98 - 220,5 = -122,5; z6 = 648 - 4418 = -3770;
z7 = 112,5 - 420,5 = -308; z8 = 800 - 578 = 222.
Ряд значений \zi\ (внизу отмечены ранги) имеет вид:
\zi\ -+ 122,5 222 304,5 308 2733,5 3100 3770 7353,5
i?i^l234 5 6 7 8
Ранги Ri величин z% > 0 (z\ ш zs) в этом ряду: 2 и 5. Применяя критерий Сэндвика—
Олсона (см. раздел 4.2.2.1.9), имеем
Г+ = ]Г 1^ = 2 + 5 = 7.
Zi>0
Из табл. 144 для п = 8 ш а = 0,95 находим Т\ = 4 и Т2 = 32.
Так как Т\ = 4 < Т+ = 7 < Т2 = 32, гипотеза сдвига не подтверждается, а следова-
следовательно, не подтверждается различие параметров масштаба в выборках.
4.2.2.1.11. Критерий Камата
Является интуитивным масштабным аналогом критерия Хага (см. раз-
раздел 4.2.1.1.2.8). Его применение предполагает равенство параметров положения
выборок (т. е. отсутствие сдвига между ними). Предварительно выборки #i, ..., хп
и г/i, ..., уш (jn ^ п) совместно упорядочиваются. Элементы выборки х получают
ранги RXi, а элементы выборки у — ранги Ryi. Находим размахи рангов
Уг )min И ±хш — \-К"Уг /max \-^"Уг Jniin-
510
Проверка гипотез о значениях параметров распределений
[Гл.4
Статистика критерия Камата записывается как [496]
Естественно, что 0 ^ Dnjm ^ т + п- Нулевая гипотеза равенства параметров
масштаба принимается, если D\{ot) < -On,m < D2 («), где D\{ot) и D2{ol)— крити-
критические значения, приведенные в табл. 166.
Таблица 166
Критические значения D\{ol) и Dz(ol) масштабного критерия
Камата (а — доверительная вероятность) [496]
га + п
8
9
10
11
12
13
14
15
16
п
4
4
4
5
3
4
5
3
4
5
6
3
4
5
6
3
4
5
6
7
3
4
5
6
7
3
4
5
6
7
а
0,90
Вг
0
0
0
0
0
0
1
0
0
1
1
0
1
1
1
0
1
2
2
2
0
1
2
2
2
0
1
2
3
3
8
9
10
10
11
10
10
11
11
11
11
11
12
12
12
12
13
13
12
12
13
14
13
13
13
14
15
14
14
13
0,
Вг
0
0
0
0
0
0
0
0
1
1
0
1
1
1
0
0
1
1
2
0
1
1
2
2
95
10
10
11
11
12
12
12
13
12
12
13
13
13
13
15
14
14
14
13
15
15
15
14
14
га + п
16
17
18
19
20
п
8
3
4
5
6
7
8
3
4
5
6
7
8
9
3
4
5
6
7
8
9
3
4
5
6
7
8
9
10
а
0,90
3
0
2
2
3
3
3
1
2
3
3
4
4
4
1
2
3
4
4
4
4
1
2
3
4
5
5
4
4
D2
13
15
15
15
15
14
14
16
16
16
15
15
15
14
16
16
17
16
16
15
15
17
17
18
17
17
16
16
16
0,95
Di
2
0
1
2
2
2
3
0
1
2
2
3
3
3
0
1
2
3
3
3
3
0
1
1
3
4
4
4
4
D2
14
15
16
16
15
15
15
16
17
16
16
16
15
15
17
18
17
17
16
16
16
18
19
18
18
17
17
16
16
При т + п > 20 справедлива аппроксимация [496]
Dt(a) = M(D) - л/ЩЩкг(а); D2(a) = M(D) + л/ЩБ)К2{а),
где
M(D) =m-
2m
2n
п + 1 т + 1'
2m(n-
8mn
(т - lf(m + 2) (т + 1)(п + 1)
4.2]
Непараметрические критерии однородности статистических данных
511
Здесь Ki(a) и К2(а)—коэффициенты, зависящие от и доверительной вероятно™
сти а (для а = 0,95 их значения приведены в табл. 167).
Таблица 167
Значения корректирующих коэффициентов
jftTi@,95) и Ж2@,95) критерия Камата
р -
т
т + п
@,95)
@,95)
0,50
1,99
1,99
0,
1,
2,
55
88
10
0,60
1,77
2,20
0,65
1,67
2,28
0,
1,
2,
70
57
34
0,75
1,50
2,41
Задача 272. Для данных задачи 270 проверить нулевую гипотезу равенства парамет-
параметров масштаба критерием Камата.
Запишем упорядоченный по возрастанию совместный ряд (г — номер выборки, Ri —
ранг элемента в совместной последовательности значений Хг):
г
2
2
1
1
1
Xi
0,8
0,9
1,4
1,8
2,7
Кг
1
2
3
4
5,5
г
2
1
2
1
2
Xi
2,7
3,9
5,9
6,1
6,1
Ri
5,5
7
8
9,5
9,5
г
1
1
2
2
Xi
7,8
7,9
8,1
11,2
Ri
11
12
13
14
Для первой выборки имеем последовательность рангов
RXi -> 3; 4; 5,5; 7; 9,5; 11; 12 и Rn = 12 - 3 = 9.
Для второй выборки имеем
Ry. -> 1; 2; 5, 5; 8; 9, 5; 13; 14 и Rm = 14 - 1 = 13.
Тогда Dn,m = 9 — 13 + 7 = 3. Из табл. 166 имеем для т + п = 14, т = 7 и а = 0,95:
Di = 1 и D2 = 13. Так как D\ = 1 < Dn,m = 3 < D2 = 13, нулевая гипотеза не отклоня-
отклоняется.
Рассмотрим теперь аппроксимацию. Имеем
M(D) = 7 - — + — = 7;
2
82 ¦ 9
2
82 ¦ 9
4+^
8-8 С[4
Жх = 1,99 = К2. Тогда
i = 7 - 1,99 • 2,55 = 2
Из табл.167 для р = 0,5 имеем
и D2 = 7+1,99-2,55 = 12.
Полученный диапазон критических значений несколько уже точных (это следствие
того, что т + п < 20), но и в этом случае нулевая гипотеза не отклоняется.
4.2.2.1.12. Комбинированный критерий Вуша^Вмнда
Ранее мы рассматривали критерии сдвига и критерии масштаба, которые позво™
ляли проверять гипотезы относительно одного из параметров (сдвига или масшта-
масштаба), фиксируя условия для другого параметра (например, полагая их равенство).
Однако на практике возможны случаи, когда нельзя априори знать, какие пара-
параметры сравниваемых выборок могут отличаться между собой. Естественно, в этом
случае целесообразно иметь критерий, позволяющий одновременно проверить сдвиг
512
Проверка гипотез о значениях параметров распределений
[Гл.4
как в параметре положения, так и в масштабном параметре. Одним из таких ранге™
вых комбинированных критериев является критерий Буша—Винда, рассмотренный
в [497].
Статистика этого критерия строится следующим образом. Пусть мы имеем
две независимые выборки х\, ...,хш и г/i, ..., уп и Щ — ранги xi в совокупной
ранжированной по возрастанию выборке.
Введем метки
адг(г) = и г и bN(i) = a%(i),
N+l
где N = т + п и и7 — 7™квантиль стандартного нормального распределения (можно
7
использовать аппроксимацию для квантили и1
дел. 1.1.1). Дисперсии меток
Введем статистики
1,91 [i
°'14-(l-7)°'14
(l-7)°
см. раз-
г И t
N
i=l
равны соответственно:
г=1
w-.-S-'*'
Т —
-1 ran —
Легко видеть, что статистика Smn эквивалентна статистике Ван дер Вардена
(см. раздел 4.2.1.1.2.4), а статистика Ттп — эквивалентна статистике Клотца (см.
раздел 4.2.2.1.4). В качестве статистики комбинированного критерия предлагается
статистика
Wmn = -21n[2 (I - Ф
- 2 ln[2 A - Ф
где Ф(^) — функция стандартного нормального распределения.
Допустимо использование аппроксимации
2,34"
Гипотеза отсутствия сдвига и неразличимости параметров масштаба с достовер-
достоверностью а принимается, если Wmn < Wmn(aI где Wmn(a)—критические значения,
приведенные в табл. 168.
Таблица 168
Критические значения статистики Wmn(€x)
Буша^Винда для т = п [497]
т = п
5
6
7
8
9
10
15
Доверительная
вероятность а.
0,90
7,03
7,19
7,31
7,36
7,45
7,48
7,58
0,95
7,92
8,06
8,20
8,47
8,54
8,65
8,97
0,975
8,57
8567
9,06
9,25
9550
9,65
10,20
т = п
20
25
30
40
50
оо
Доверительная
вероятность ос
0,90
7,65
7,69
7,71
7,74
7,76
7,78
0,95
9,05
9,09
9,24
9,30
9,32
9,49
0,975
10,50
10,50
10,60
10,70
10,90
11,10
4.2]
Непараметрические критерии однородности статистических данных
513
При га, п > 30 справедлива аппроксимация М^теп(а) = х^D), где х
тиль распределения хи-квадрат с / = 4 степенями свободы. Мощность критерия
Буша-Винда весьма высока, что позволяет считать его эффективным критерием
для непараметрической проверки гипотез в выборках из нормального (или близкого
к нему) распределения.
Задача 273. Для данных задачи 270 проверить гипотезу равенства параметров поло-
положения и масштаба в выборках комбинированным критерием Буша-Винда.
Имеем ряд рангов Щ: 3; 4; 5,5; 7; 9,5; 11; 12.
Используя аппроксимацию
14+1
= 4,91 ¦
0,14
15 15
0,14
вычисляем значения а\^(г). Результаты вычислений сводим в таблицу (там же указаны
величины а?4@ и дополнительные величины аы(г) для дробных рангов 5,5 и 9,5):
г
1
2
3
4
5
5,5
6
7
ai4@
-1,5021
-1,1094
-0,8395
-0,6208
-0,4290
-0,3393
-0,2522
-0,0833
al4(i)
2,2563
1,2308
0,7048
0,3854
0,1841
0,1151
0,0636
0,00693
ъ
8
9
9,5
10
11
12
13
14
ai4(i)
0,0833
0,2522
0,3393
0,4290
0,6208
0,8395
1,1094
1,5021
«14@
0,00693
0,0636
0,1151
0,1841
0,3854
0,7048
1,2308
2,2563
Вычисляем
= °'833);
= 0,618 • [ai3C) + oi4D) + oi4E,5) + ... + ai4A2)] = -0,0515
7 • 7 0,833
Далее вычисляем
= 1,021);
= 0,5048 • [a?4C) + %4D) + ... + a?4A2) - 0,5 • a\4(l) - 0,5 • o?4B)
... - 0,5 • o?4 A4)] = -1,235.
Находим аппроксимации
Ф@,0515) = 1 - 0,852 • exp { -
= 0,5205;
Ф A,235) = 1 - 0,852 . exp ^ - ( —
| (Щ^) | = 0,8918.
Окончательно имеем
Wmn = -2 • ln[2 • A - 0,5205)] - 2 • ln[2 • A - 0,8918)] = 3,145.
17 А. И. Кобзарь
514
Проверка гипотез о значениях параметров распределений
[Гл.4
Из табл. 168 для а = О5Э5 и т = п = 7 имеем Штп@,95) = 8,20.
Так как Wmn = 3,145 < Wmn@,95) = 8,20, гипотеза равенства параметров положения
и масштаба в выборках не отклоняется.
4.2.2.2. Сравнение параметров масштаба нескольких (к > 2) совокупностей
критерием Бхапкара-Дешпанде
Рассмотрим совокупность к выборок
^11, #12, • • • 5 Х1п1] #21? Ж22, • • • , %2n2i •••5 #гЪ #г2? • • • ? ^т* 5
• • • 5 %kli хк2? • • • , хкпк-
Пусть Xij —j-e наблюдение в г-й выборке (j = 1, 2, ..., п^). Если мы будем всеми
возможными способами из каждой выборки брать одно наблюдение, то можем
к
получить Yl ni подвыборок.
г=1
Пусть Vij—число таких подвыборок, в которых наблюдение, соответствующее
г-й выборке, было больше, чем (j — 1) наблюдений (или меньше, чем остальные
2
V ¦
(к — j) наблюдений). Определим величины щ* = =г—, которые распределены рав™
i
номерно на интервале [0,1]. Бхапкар [499] показал, что при справедливости нуле™
вой гипотезы Но: F\{x) = F(x) = ... = Fk(x)^ утверждающей, что распределения
в сравниваемых выборках совпадают с точностью до параметров положения и мас-
масштаба, имеет место соотношение иц = -.
к
Там же Бхапкар предложил критерий для проверки сдвига как в дисперсиях, так
и в средних сравниваемых выборок. В случае равенства параметров положения этот
критерий является критерием проверки равенства параметров масштаба. Критерий
Бхапкара основан на статистике
г+1
Дешпанде, Дюфор и Люнг [500, 501] предложили эффективный критерий для
выявления разницы в параметрах масштаба, основанный на статистике
к
п-
к
г=1
1
К
2
г=1
к
г=1
(^il
Л
-y2(fc-l)
D =
{к2
¦d^
гы
где di = иц + щк (г = 1, 2, ..., к).
Ими же предложена статистика для выявления сдвига в к выборках (что полезно
делать перед применением критериев масштаба). Эта статистика имеет вид
fe-1)
L =
где Ii = — г/ii + Wife (г = 1, 2, ..., &).
4.2]
Непараметрические критерии однородности статистических данных
515
В [502] рассмотрена статистика, эквивалентная статистике Крускала-Уоллиса
(см. раздел 4.2.1.2.1). Нулевая гипотеза не отклоняется критериями V^^D, ес-
если У, L, D < Х«(^ ~~ 1)? гДе Ха(^~-0— «-квантиль распределения хи-квадрат с
/ = Aj — 1 степенями свободы.
Для случая А; = 3 критические значения критериев L и D (La и Da) приведены
в табл. 169.
Таблица 169
Критические значения La и Da
для к = 3 [498]
2
2
2
2
2
2
3
3
4
2
2
2
3
3
4
3
4
4
п3
2
3
4
3
4
4
3
4
4
Доверительная
0
L
6,48
7,33
7,40
7,14
7,47
7,21
7,82
8,20
99
D
11,43
13,33
10,00
9,95
8,30
9,38
6,75
7,15
вероятность а
0
L
5,33
5,39
6,10
5,85
5,80
5,55
6,22
6,34
6,15
95
D
10,00
8,00
5,80
5,59
4,54
5,48
4,80
4,18
4,60
Задача 274. Предположим^ что имеются к = 3 выборки по четыре наблюдения
в каждой
хщ 300, 400, 510, 600;
x2i: 250, 440, 570, 900;
x3i: 520, 610, 920, 1070.
Необходимо проверить гипотезу о равенстве параметров масштаба в выборках крите-
критериями V, L и D при доверительной вероятности а = 0,95.
з
В нашем случае щ = 4 и к = 3. Таким образом, мы можем получитв ]~| щ = 4 =64
г=1
подвыборки объема к = 3 каждая (номер столбца в подвыборках соответствует номеру
выборки)
300,250,520 400,250,520 510,250,520 600,250,520 300,440,520
300,250,610 400,250,610 510,250,610 600,250,610 300,440,610
300,250,920 400,250,920 510,250,920 600,250,1070 300,440,920
300,250,1070 400,250,1070 510,250,1070 600,250,1070 300,440,1070
400,440,520 510,440,520 600,440,520 300,570,520 400,570,520
400,440,610 510,440,610 600,440,610 300,570,610 400,570,610
400,440,920 510,440,920 600,440,920 300,570,920 400,570,920
400,440,1070 510,440,1070 600,440,1070 300,570,1070 400,570,1070
510,570,520 600,570,520 300,900,520 400,900,520 510,900,520 600,900,520
510,570,610 600,570,610 300,900,610 400,900,610 510,900,610 600,900,610
510,570,920 600,570,920 300,900,920 400,900,920 510,900,920 600,900,920
510,570,1070 600,570,1070 300,900,1070 400,900,1070 510,900,1070 600,900,1070
Находим уц—число подвыборок, в которых наблюдения в г-й выборке были мень-
меньше, чем 1с — j=3 — 1 = 2 наблюдения. Прямым перебором убеждаемся, что vn = 35,
17*
516
Проверка гипотез о значениях параметров распределений
[Гл.4
у21 = 27, г;з1 = 2. По аналогии находим г^з —число подвыборок, в которых наблюдения
из г-й выборки были больше, чем 3 — 1 = 2 наблюдения из остальных выборок. Имеем
1713 = 3, V23 = 11, ^33 = 50.
Проверкой убеждаемся, что
= 35 + 27 + 2 = 64 и v13 + v23 + v33 = 3 + 11 + 50 = 64.
Далее находим
= — = — = 0,5469; u2i = — = 0,4219; u3i = — = 0,03125;
64 64 ' ' 64 ' ' 64 '
= тт = 0,0469;
64
U23 = ^ = 0,1719;
64
= ^ = 0,78125;
64
= иг1 +
= 0,5469 + 0,0469 = 0,5938; d2 = u2i + u23 = 0,4219 + 0,1719 = 0,5938;
d3 = u3i + г^зз = 0,03125 + 0,78125 = 0,8125;
= -ии +и3 = ^0,5469 + 0,0469 = ^0,5; l2 = -u2i + u23 = ^0,4219 + 0,1719 = ^0,25;
h = -u31 + u33 = -0,03125 + 0,78125 = 0,75.
Вычисляем статистики критериев
V = 64 • B • 3 - 1) ¦
з
E
г=1
1\2 4 Г» 4 / 1
Н1-3) ' 64 ^64 "Г"
= 320-
0,5469
3
16
@,4219
Г з
16
i
0,03125
3
16
-{ — • [@,549 + 0,4219 + 0,03125 -1)]} \ = 2,89;
L =
64 • 5 • 4 • Of
2 ¦ [9 + (9 + 12 + 2) - Of]
16
= 1,82.
Из табл. 169 для а = 0,95 и щ = 4 находим Lo,95 = 6,15 и Do,95 = 4,60.
Так как D = 1,82 < Do,95 = 4,60 и L = 4,67 < Ьо,95 = 6,15, нулевая гипотеза не откло™
няется.
К такому же результату приводит сравнение с Хо,эбB), так как
V = 2,89, L = 4,64, D = 1,82 < Хо,95B) = 5,99.
4.3] Критерии тренда и случайности 517
4.3. Критерии тренда и случайности
Критерии этого раздела предназначены для проверки гипотез о случайности
расположения полученных выборочных данных, т. е. отсутствия взаимосвязи между
значениями реализаций наблюдаемой случайной величины и их номерами в выбо™
рочной последовательности.
В приводимых ниже критериях используются выборочные значения случайной
величины в порядке их появления (т. е. они образуют временной ряд).
Наибольшее применение критерии тренда находят при статистическом контроле
и предупредительном регулировании технологических процессов в промышленное
сти, позволяя заранее статистически обоснованно выявить намечающуюся тенден™
цию ухудшения качества продукции. Для медика наличие тренда в исследуемом
ряду данных о заболеваниях является объективным критерием оценки надвигаю-
надвигающейся эпидемии. Количество возможных ситуаций, в которых выявление тренда
(закономерности, а не случайности появления ряда данных) дает практически
полезную информацию, велико, и каждый инженер или исследователь повседневно
встречается с необходимостью использовать критерии настоящего раздела в своей
работе.
4.3.1. Критерий Аббе-Линника
Пусть #1, ..., хп — ряд значений взаимно независимых нормально распределен-
распределенных случайных величин с математическими ожиданиями //i, ..., /лп соответственно
и одинаковыми (но неизвестными) дисперсиями. Проверяется гипотеза о том, что
все выборочные значения принадлежат одной генеральной совокупности со сред™
ним \х\ (Но: iii = /i, г = 1,2, ..., п) против альтернативы тренда
#i: |//i+i -iii\ >0, i = 1,2, ...,n-l.
Статистика критерия Аббе^Линника имеет вид
п-1
1 §(жг+1"ХгJ 1 п
г=1
Если q > qai то нулевая гипотеза случайности ряда #i, ..., хп отклоняется с до™
верительной вероятностью а (критические значения qa приведены в табл. 170).
При п > 60 справедлива аппроксимация, основанная на том, что случайная
™ /1 \ / 2^ + !
величина Q = — A — q)x ^ имеет стандартное нормальное распределение.
V 2 - A - д)
Поэтому нулевая гипотеза отклоняется, если Q* < и\—а.
В заключение упомянем достаточно простой критерий, приписываемый Кохра™
ну [9], с помощью которого можно установить изменение среднего статистического
ряда скачком после первых щ наблюдений (щ + n^+i = в, г = 2, ..., п — 1). Его
статистики имеют вид
2 _ щ(п - щ) (хгЛ - xiuJ
Хг ~ п х
где хгл = — У2 Xi\ xin = J2 xi'i х = ~ У2
г=1 i=rii + l г=1
518
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 170
Критические значения qa критерия Аббе—Линника [25]
п
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Доверительная
вероятность а
0,95
0,3902
0,4102
0,4451
0,4680
0,4912
0,5121
0,5311
0,5482
0,5636
0,5778
0,5908
0,6027
0,6137
0,6237
0,6330
0,5417
0,6498
0,6574
0,6645
0,99
0,3128
0,2690
0,2808
0,3070
0,3314
0,3544
0,3759
0,3957
0,4140
0,4309
0,4466
0,4611
0,4746
0,4872
0,4989
0,5100
0,5203
0,5301
0,5393
п
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
Доверительная
вероятность а
0,95
0,6713
0,6776
0,6839
0,6893
0,6946
0,6996
0,7047
0,7091
0,7136
0,7177
0,7216
0,7256
0,7292
0,7328
0,7363
0,7396
0,7429
0,7461
0,7491
0,99
0,5479
0,5562
0,5639
0,5713
0,5784
0,5850
0,5915
0,5975
0,6034
0,6089
0,6141
0,6193
0,6242
0,6290
0,6337
0,6381
0,6425
0,6467
0,6508
п
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
Доверительная
вероятность а
0,95
0,7521
0,7550
0,7576
0,7603
0,7628
0,7653
0,7767
0,7698
0,7718
0,7739
0,7759
0,7779
0,7799
0,7817
0,7836
0,7853
0,7872
0,7891
0,7906
0,99
0,6655
0,6659
0,6622
0,6659
0,6693
0,6727
0,6757
0,6787
0,6814
0,6842
0,6869
0,6896
0,6924
0,6949
0,6974
0,6999
0,7024
0,7049
0,7071
Если xf > Ха(-О> то изменение среднего скачком после первых щ наблюдений
признается значимым с достоверностью а, здесь Ха(-0 — а-квантиль распределения
хи-квадрат с / = 1 степенью свободы.
Задача 275. Имеется выборочный ряд значений случайных величин (п = 10)
хц 4,3; 2,1; 0,9; 5,2; 4,8; 1,2; 0,8; 3,0; 6,1; 10,2.
Проверить гипотезу случайности ряда х% критерием Аббе-Линника при доверительной
вероятности а = 0,95.
Вычисляем
1 ю
^ — . V4 гр. — Q Qfl.
dj — > JLj — O.OU.
10 h
9
J2 {xi+i - Xif = B,1 - 4,3J + @,9 - 2,1J + ... + A0,2 - 6,1J = 69,31;
i=l
У (Xi - xf = 77,124; q = i . ^^ = 0,4493.
f^ 2 77,124
Из табл. 170 при п = 10 и а = 0,95 имеем go,95 = 0,5311.
Так как q = 0,4493 < go,95 = 0,5311, нулевая гипотеза отклоняется, и ряд значений х%
с достоверностью 0,95 может быть признан случайным.
Для нормальной аппроксимации имеем
Т = -A-0,4493)
21
2 - A - 0,4493)'
= -1,938.
Так как Q* = —1,938 < Wo,o5 = —1,645, то этим критерием нулевая гипотеза отклоня™
ется.
4.3]
Критерии тренда и случайности
519
Теперь применим критерий Кохрана. Для последовательности пар значений щ и ni+i,
равных B,8), C,7), D,5), E,5), F,4), G,3), (8,2), находим значения:
4,3 + 2,1 00 _ 0,9 + 5,2 + 4,8 + 1,2 + 0,8 + 3,0 + 6,1 + 10,2
ж2л = = 3,2 и ж2п = = 4,025;
Z 5
4,3 + 2,1 + 0,9 5,2 + 4,8 + 1,2 + 0,8 + 3,0 + 6,1 + 10,2
жзл = ~ = 2,433 и жзп = ¦ ¦ '- ¦ = 4,471;
О I
Ж4л = 3,125 и Ж4п = 4,35; х%л = 3,46 и х^п = 4,26; Жбл = 3,083 и жвп = 5,025;
ж7л = 2,757 и ж7п = 6,43; ж8л = 2,787 и ж8п = 8,15.
Далее вычисляем
10
=
3,86
_
= 2,264;
= 0?933; Х1 = 0,414; Хе = 2,344; Х7 = 7?339; Х8 = 11,92.
Из табл. 55 находим, что Хо,9бA) — 3,481 и, следовательно, критерий Кохрана при™
знает скачок среднего после щ = 7 наблюдений.
4.3.2. Критерий Фостера-Стюарта
Предложен в [503] и используется для проверки тренда как средних, так и дис-
дисперсий. Статистики критерия имеют вид
г=2
г=2
где
di = щ — li] Si = щ + li]
{1, если Xi > Xi—i, Xi^2i • - - 5 %i] J 1, если Xi < ж^—i, ж^_2, • • •, ^i;
О, в противном случае; [0, в противном случае.
Статистика S используется для проверки тренда в дисперсиях, статистика d —
для обнаружения тренда в средних. Очевидно, что
0 ^ S ^ п ^ 1 и — (п — 1) ^ d ^ п — 1.
При отсутствии тренда величины
= 7 и ^
где Z =
- 3,4253, /= ^2 Inn - 0,8456,
имеют распределение Стьюдента с v = п степенями свободы. Формулы для / и I
применимы при п > 50, их значения при п < 50 приведены в табл. 171.
Таблица 171
Постоянные / и I критерия Фостера^Стюарта [503]
/
I
10
1,964
1,288
15
2,153
1,521
20
2,279
1,677
25
2,373
1,791
30
2,447
1,882
35
2,509
1,956
40
2,561
2,019
45
2,606
2,072
50
2,645
2,121
Если \t\ (\t\) > ti+a., то с доверительной вероятностью а нулевая гипотеза от™
2
сутствия трендов отклоняется (t7 — 7™квантиль распределения Стьюдента).
520
Проверка гипотез о значениях параметров распределений
[Гл.4
Задача 276. Проверить гипотезу наличия тренда критерием Фостера-Стюарта для
данных задачи 275.
Анализируя ряд а^, получаем значения переменных щ, U, d% и Si.
Результаты сводим в таблицу:
i
2
3
4
5
6
щ
0
0
1
0
0
1
1
0
0
0
-1
-1
1
0
0
Si
1
1
1
0
0
i
7
8
9
10
щ
0
0
1
1
и
1
0
0
0
d%
-1
0
1
1
Si
1
0
1
1
Далее находим 5 =
/ = 1,964 и I = 1,288.
= 6 и d=^di = O. Из табл. 171 для п = 10 находим
Далее имеем t =
0
= 0 и t =
6 - 1,964^
= 1,663.
1,964 1,288
Для ? i+o,95 = to,975(у = 10) = 2,228 (используем таблицы ^-распределения [24-26])
получаем |?| = 0 (|t| = 1,663) < to,975 = 2,228. Следовательно, наличие тренда не подтвер-
подтверждается имеющимися наблюдениями.
4.3.3. Критерий Кокс-Стюарта
В [504] предложена серия быстрых знаковых критериев тренда среднего и дис-
дисперсии в последовательности наблюдений. Для критерия среднего в выборке объема
п предложена статистика
ы
г=1
гДе
Критерий, основанный на статистике 5i, имеет эффективность « 0,86 по отно™
шению к наилучшему параметрическому критерию.
Для проверки гипотезы тренда применяется нормализованная статистика
При
, где MEi) = ^ и D(Si) =
24
гипотеза тренда среднего отклоняется.
Критерий для проверки гипотезы о тренде дисперсии в выборке строится еле™
дующим образом. Выборка х\, ...,хп разбивается на п/k подвыборок жх, ... ,ж^;
ж^+i, ..., Х2к] %2k+ii • • • 5 хзк] xn-k+ii • • • ? жп (если п не делится на fc, отбрасывается
необходимое число наблюдений в центре). Для каждой г-й подвыборки находится
Ы
размах ш^ A ^ г ^ г) (г = — ). Далее размахи ш^ проверяются на тренд крите™
рием *S*i. Рекомендуется выбирать к из следующих соотношений [504]:
п ^ 90 -^ А; = 5; 90 > п ^ 64 -^ А; = 4; 64 > п ^ 48 -^ к = 3; га < 48 ->> А; = 2.
Эффективность дисперсионного критерия « 0,73.
4.3]
Критерии тренда и случайности
521
Задача 277. Имеется выборочная последовательность (п = 48):
г: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
хц 12 1 2 4 6 9 5 3 14 21 24 29 1 3 7 2
г: 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
ж»: 13 21 14 51 1 0 0 17 21 3 4 6 7 8 9 1
г: 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
хц 2 3 12 11 10 21 74 35 28 24 15 О 1 17 19 1.
Необходимо проверить критериями Кокс-Стюарта гипотезу о тренде среднего и дис-
дисперсии в выборке при доверительной вероятности а = 0,95.
Имеем значения hi}fl-i+i для разных г (г = 1, ..., 24):
г
1
2
3
4
5
6
7
8
п — i + 1
48
47
46
45
44
43
42
41
hi,n — i+l
1
0
0
1
1
0
0
0
п — г + 1
9
10
11
12
13
14
15
16
hi,n — i+l
40
39
38
37
36
35
34
33
п - г + 1
0
0
1
1
0
0
1
0
17
18
19
20
21
22
23
24
гг-г + 1
32
31
30
29
28
27
26
25
hi,n — i+l
1
1
1
1
0
0
0
0
Находим
24
Si = J2 D9 - 2i) ' hi,n^i+i = 47 + 41 + 39 + 27 + 25 + 19 + 15 + 13 + 11 + 9 = 246.
г=1
= «1 = 288;
48 • D82 - 1)
24
= 4606 ("v/D(Si) = 67,867);
Так как \Si\ = 0,619 < 1x0,975 = 1,96, гипотеза тренда отклоняется.
Рассмотрим дисперсионный критерий. Выбираем к = 3 и получаем п/к = 16 подвы-
борок:
12, 1, 2; 4, 6, 9; 5, 3, 14; 21, 24, 29; 1, 3, 7; 2, 13, 21; 14, 51, 1; 0, 0, 17;
21, 3, 4; 6, 7, 8; 9, 1, 2; 3, 12, 11; 10, 21, 74; 35, 28, 24 ; 15, 0, 1 ; 17, 19, 1.
Размахи подвыборок образуют ряд
10, 5, 11, 8, 6, 19, 50, 17, 18, 2, 8, 9, 64, 11, 15, 18.
Для полученного ряда находим значения hi^n-V-
= 0,
= 0,
= 0,
Тогда
= 0, he,11 = 1, /17,10 = 1,
|8- 32|
13,038
= 0,
= 0.
16 '
24
= 130,38;
= 1,84.
Так как \S\ = 1,84 < ito,975 — 1,96, гипотеза тренда отклоняется.
= 170;
522
Проверка гипотез о значениях параметров распределений
[Гл.4
4.3.4. Критерий обнаружения сдвига дисперсии в неизвестном точке
(критерий Хсу)
Предположим, что наблюдаемая нами последовательность х\, ..., хп имеет одно
и то же среднее (оцениваемое медианой ряда тх). Необходимо проверить нулевую
гипотезу Hq о неизменности дисперсии в выборке против альтернативы Н\, утвер-
утверждающей, что значение дисперсии меняется в неизвестной точке.
Условно это можно записать так: проверить гипотезу Hq : af = ... = а^ = erg
(<Jq неизвестно) против гипотезы
Я 2 2 2
г: аг = а2 = ... = ак =
>0),
где к неизвестно (l^fc^n — 1).
В [505] предложен критерий для проверки такой гипотезы, основанный на ста™
тистике
Н =
0 < Я < 1.
(n-
i - mx)
Обычно критерий используется в стандартизированной форме
Н -0,5 _/ттЧ п + 1
Я* =
= , где Т>(Н) =
Если Я* < Яа, то с достоверностью а гипотеза изменения дисперсии отклоня™
ется (Яа —критические значения, приведенные в табл. 172). При п > 30 применима
нормальная аппроксимация На « Ua.
Таблица 172
Критические значения (На) Н*-критерия Хсу [505]
п
2
3
4
5
6
7
8
Доверительная
вероятность
0,90
1,345
1,370
1,343
1,325
1,314
1,306
1,303
0,95
1,397
1,613
1,643
1,650
1,652
1,652
1,651
а
0,99
1,414
1,901
2,083
2,170
2,219
2,251
2,260
п
9
10
15
20
25
30
оо
Доверительная
вероятность
0,90
1,301
1,299
1,294
1,290
1,289
1,287
1,282
0,95
1,650
1,650
1,648
1,647
1,647
1,646
1,645
а
0,99
2,266
2,272
2,289
2,298
2,304
2,308
2,326
Определить точку изменения дисперсии позволяет G™критерий, также рассмо-
рассмотренный в [505]. Его статистика строится следующим образом.
Пусть
к
г=1
п — к1
к = 1,2, ...,п- 1,
где к соответствует искомой точке изменения дисперсии.
Пусть далее о^ есть вероятность, соответствующая условию Fak(n — к^к) = W^,
где F1{f\1 J2)—7™квантиль ^-распределения с /i и /2 степенями свободы. Тогда
4.3]
Критерии тренда и случайности
523
О < G € 1.
статистика искомого критерия есть
п-1
к=1 П~ ~
Гипотеза изменения дисперсии отклоняется с вероятностью а, если G < Ga, где
Ga —критические значения, приведенные в табл. 173.
Таблица 173
Критические значения (Ga) G-критерия Хсу [505]
п
2
3
4
5
6
7
8
Доверительная
вероятность а
0,90
0,895
0,838
0,813
0,800
0,792
0,787
0,783
0,95
0,917
0,898
0,874
0,860
0,852
0,847
0,843
0,99
0,989
0,964
0,948
0,938
0,931
0,927
0,926
те
9
10
15
20
30
100
оо
Доверительная
вероятность а
0,90
0,781
0,779
0,774
0,772
0,770
0,768
0,767
0,95
0,840
0,838
0,833
0,831
0,829
0,826
0,825
0,99
0,921
0,920
0,915
0,913
0,911
0,909
0,908
Значение к, для которого величина
ак - о
максимальна, дает оценку точке
изменения значения дисперсии в наблюдаемом ряду. Мощность критериев Н и G
близка.
Задача 278. Для ряда значений
хс 2, 1, 11, 21, 3, 8, 6, 23, 28, 38, 37 (п = 10)
проверить гипотезу о возможном изменения дисперсии ряда критериями Хсу при
доверительной вероятности а = 0,95.
Находим медиану ряда (напомним, что это средний член ранжированного по возра-
возрастанию ряда, если п — нечетное, и полусумма центральных значений, если п — четное).
Q _|_ 1 1
В нашем случае тх = =9,5.
Далее вычисляем
ю
- 9,5J
Н =
1 • A -9,5J + 2- A1 -9,5J
-9-
A0 ^ 1) • ]Г (а^ ^ 9,5J
9 • [B - 9,5J + A - 9,5J + ... + C7 - 9,5J
= 0,831;
В(Я) =
= °'°1697
= 0,130); Н* =
= 2,546.
Из табл. 172 для а = 0,95 и п = 10 находим JIq,95 = 1,65.
Так как Н* = 2,546 > i?o,95 — 1,65, нулевая гипотеза отклоняется в пользу альтерна-
альтернативы изменения дисперсии ряда.
Вычислим теперь статистику (jr-критерия. Находим значения ил и W% (результаты
сведем в таблицу).
Вероятности at находим из соотнош:ений
Fax (9,1) = 3,979; Fa2(8,2) = 3,778; Fa3 G,3) = 6,358;
Fa4F,4) = 4,582; Fa5E,5) = 5,783; Fa6D,6) = 8,60;
Fa7C,7) = 12,776; Fa8 B,8) = 12,498; Fa9(l,9) = 5,179.
524
Проверка гипотез о значениях параметров распределений
[Гл.4
г
1
2
3
4
UJi
56,25
128,50
130,75
263,00
wt
3,979
3,778
6,358
4,582
г
5
6
7
8
UJi
302,25
307,50
319,75
502,00
Wi
5,783
8,600
12,776
12,498
i
9
10
&i
1314,25
2070,50
Wi
5,179
Следует отметить,что имеющиеся таблицы ^-распределения не столь обширны, что-
чтобы по ним можно было быстро определить значения а&. Мы это сделаем интерполяцией
Fa, однако именно из-за отсутствия и громоздкости таких таблиц G-критерий вряд ли
м:ожет быть рекомендован к широкому применению. Тем не менее, используя наиболее
широкие таблицы ^-распределения и применяя интерполяцию, находим:
аг = 0,5675; а2 = 0,7606; а3 = 0,9151; а4 = 0,9137; а5 = 0,9603; а6 = 0,9872;
1 9
а7 = 0,9595; а8 = 0,9995; а9 = 0,9507 и G =
п — 1
= 0,894.
Так как G = 0,894 > Go
гипотезу.
Рассмотрим теперь ряд
,95
= 0,838 (см. табл. 173), этот критерий отклоняет нулевую
• 0,0675; 0,2606; 0,4151; 0,4137; 0,4603; 0,4872; 0,4595; 0,4995; 0,4507.
Из полученного ряда следует, что к:
= max =
Следовательно, начиная с 8™го члена ряда, дисперсия начинает меняться.
4.3.5. Ранговый критерий обнаружения сдвига дисперсии в неизвестной точке
Критерий Хсу (см. раздел 4.3.4) предполагает нормальность распределения слу™
чайной величины. В [506] рассмотрен критерий для решения аналогичной задачи,
но свободный от распределения. Он основан на исполвзовании семейства ранговых
статистик вида
где Щ —ранги выборочных значений в упорядоченном ряду наблюдений.
Метки критерия ап могут быть различными, например
— метки Клотца (см. раздел 4.2.2.1.4) а\п(г) = U2г ;
п+1
— метки Сэвиджа (см. раздел 4.2.2.1.6) a2n{i) = у* :—г-
Обозначим Sj =
), j = 1,2. При отсутствии сдвига дисперсии в ряду на-
i
блюдений Sj-статистики свободны от распределения и симметричны относительно
ajn{i). При справедливости нулевой гипотезы
г=1
4.3]
Критерии тренда и случайности
525
Статистики критериев имеют вид
S3-M(S3)
Нулевая гипотеза отклоняется с доверительной вероятностью а, если \S*\ < *Sj(a),
где Sj(a) — критические значения, приведенные в табл. 174.
Таблица 174
Критические значения рангового критерия
обнаружения сдвига дисперсии [506]
п
5
10
15
20
25
30
40
50
оо
Доверительная
вероятность а = 0,95
Si
1,915
1,928
1,935
1,939
1,942
1,944
1,947
1,949
1,960
s2
1,905
1,923
1,932
1,937
1,940
1,943
1,946
1,948
1,960
Доверительная
вероятность а = 0,90
Si
1,659
1,654
1,652
1,651
1,650
1,650
1,649
1,648
1,645
s2
1,662
1,656
1,653
1,652
1,651
1,650
1,649
1,648
1,645
При п > 20 справедливо приближение Sj(a) ^ иа (иа — «-квантиль стандарт-
стандартного нормального распределения). Статистика S^ имеет наибольшую эффектив™
ность для распределений симметричного типа, Я| —для распределений, скошенных
вправо. Критерии Sf и S^ не уступают по мощности критерию Хсу (см. раз-
раздел 4.3.4) [505], но не требует знания параметров положения.
Задача 279. Проверить гипотезу изменения дисперсии ряда для данных задачи 278
критериями SI и S^-
Ранги выборочной последовательности составляют ряд
хс 2 1 11 21 3 8 6 23 38 37;
Кц 2 1 6 7 3 5 4 8 10 9.
Находим метки ai,n(i) = и2 г , используя аппроксимацию 15 (см. раздел 1.1.1)
п+1
U j =4,91-
п+1
0,14
Вычисляем последовательно метки а\п и а,2П, сводя результаты в таблицу:
п
1
2
3
4
5
o>i,w(i)
1,7822
0,8217
0,3630
0,1206
0,0129
«2Д0(«)
0,1000
0,2111
0,3361
0,4790
0,6456
г
6
7
8
9
10
ai,ioW
0,0129
0,1206
0,3630
0,8217
1,7822
«2,loW
0,8456
1,0956
1,4290
1,9290
2,9290
526 Проверка гипотез о значениях параметров распределений [Гл. 4
Вычисляем статистики критериев
ю
Si = J2 i ' oi,io(#i) = 1 • ai,ioB) + 2 • ai,io(l) + ... + 10 • ai,ioA0) =
= 0,8217 + 2 • 1,7822 + ... + 10 • 0,8217 = 34,804;
10
S2 = Yli • a2,io(Ri) = 1 • 0,2111 + 2 • 0,1 + ... + 10 • 1,929 = 73,295.
Далее находим
II10 11.fi9П1 1П.11
= 55;
D(S2) = 8,051);
|173,29 — 55| _
8,051 ~~ '
Из табл. 174 имеем Si @,95) = 1,928 и S2@,95) = 1,923.
Так как |SJ| = 0,113 < Si@,95) = 1,928 и |S|| = 2,271 > S2@,95) = 1,923, нулевая ги-
гипотеза отклоняется критерием S2 и не отклоняется критерием Si.
4.3.6. Сериальный критерий случайности
Предположим, имеются две выборки случайных величин х и у. Частичная
последовательность элементов одной из выборок в упорядоченной по возрастанию
объединенной выборке, ограниченная с обеих сторон элементами другой выборки
(на границах последовательности — с одной стороны), называется серией.
Например, последовательность
ж, х, у, у, ж, у, х,х,х, у, у
содержит 6 серий C серии элементов уиЗ серии элементов х).
Последовательность ж, ж, ж, у^у^у содержит две серии (одну элементов х и одну
элементов у). Количество и структура серий характеризует случайность появления
последовательности против альтернативы тренда, т. е. наличия закономерности
в расположении элементов одной выборки.
Например, малое число серий будет указывать на тенденцию объединения эле-
элементов одной выборки в группы, т. е. на неслучайный характер их расположения
в общей последовательности.
Большинство сериальных критериев, основанных на числе и структуре серий,
обладает невысокой мощностью, но требует минимальных расчетов.
4.3.6.1. Критерий Вальда-Волфовитца
Имеется выборка значений случайной величины х в порядке их появления; ж —
выборочная медиана. Значения xi ^ ж обозначаем символом а, а значения Х{ < ж
символом Ь. Статистикой критерия является N — общее число полученных серий
элементов а и Ъ.
Гипотеза случайности ряда принимается с вероятностью а, если ni(a) < N <П2(а);
в ином случае она отклоняется в пользу альтернативы неслучайности ряда.
4.3]
Критерии тренда и случайности
527
Таблица 175
Критические значения N±(ol) и N2@1)
сериального критерия Вальда^Волфовитща [25]
т
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
4
4
4
4
те
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
4
5
6
7
8
9
10
11
12
13
14
Доверительная
вероятность а
0,90
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
1
1
1
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
1
2
2
2
3
3
3
3
3
3
3
N2
5
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
7
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
9
9
9
10
10
10
10
10
10
10
10
0,95
Nj
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
2
2
1
1
2
2
2
2
2
2
3
3
3
N2
5
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
7
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
9
9
10
10
10
10
10
10
10
10
10
m
4
4
4
4
4
4
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
7
7
7
7
7
7
7
7
7
7
те
15
16
17
18
19
20
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
7
8
9
10
11
12
13
14
15
16
Доверительная
вероятность а
0,90
Nt
3
4
4
4
4
4
2
3
3
3
3
3
4
4
4
4
4
4
4
5
5
5
3
3
3
4
4
4
4
5
5
5
5
5
5
6
6
3
4
4
4
4
4
15
15
15
16
N2
10
10
10
10
10
10
10
10
11
11
12
12
12
12
12
12
12
12
12
12
12
12
11
12
12
13
13
13
13
14
14
14
14
14
14
14
14
13
13
14
14
14
14
15
15
15
16
0,95
JVi
3
3
3
3
3
3
2
см
2
3
3
3
3
3
3
3
4
4
4
4
4
4
2
3
3
3
3
4
4
4
4
4
4
4
5
5
5
3
3
4
4
4
4
5
5
5
5
N2
10
10
10
10
10
10
10
11
11
12
12
12
12
12
12
12
12
12
12
12
12
12
12
12
13
13
13
14
14
14
14
14
14
14
14
14
14
13
14
14
15
15
15
16
16
16
16
528
Проверка гипотез о значениях параметров распределений
[Гл.4
Продолжение таблицы 175
т
7
7
7
7
8
8
8
8
8
8
8
8
8
8
8
8
8
9
9
9
9
9
9
9
9
9
9
9
9
10
10
10
10
10
10
10
10
10
10
10
11
11
11
11
11
11
11
11
11
п
17
18
19
20
8
9
10
11
12
13
14
15
16
17
18
19
20
9
10
11
12
13
14
15
16
17
18
19
20
10
11
12
13
14
15
16
17
18
19
20
11
12
13
14
15
16
17
18
19
Доверительная
]
0,
Nj
16
16
16
16
14
14
15
15
16
16
16
16
6
7
7
7
7
5
5
6
6
6
7
7
7
7
8
8
8
6
6
7
7
7
7
8
8
8
8
9
7
7
7
8
8
8
9
9
9
зероятность а
ЭО
N2
16
16
16
16
14
14
15
15
16
16
16
16
17
17
17
17
17
15
16
16
16
17
17
18
18
18
18
18
18
16
17
17
18
18
18
19
19
19
20
20
17
18
19
19
19
20
20
20
21
0,95
Nt
5
5
6
6
4
4
4
5
5
5
5
5
6
6
6
6
6
4
5
5
5
6
6
6
6
7
7
7
7
5
5
6
6
6
7
7
7
7
8
8
6
6
6
7
7
7
8
8
8
N2
16
16
16
16
14
15
15
16
16
17
17
17
17
18
18
18
18
16
16
17
17
18
18
18
18
19
19
19
19
17
18
18
19
19
19
20
20
20
20
20
18
19
19
20
20
21
21
21
22
т
11
12
12
12
12
12
12
12
12
12
13
13
13
13
13
13
13
13
14
14
14
14
14
14
14
15
15
15
15
15
15
16
16
16
16
16
17
17
17
17
18
18
18
19
19
20
21
22
23
п
20
12
13
14
15
16
17
18
19
20
13
14
15
16
17
18
19
20
14
15
16
17
18
19
20
15
16
17
18
19
20
16
17
18
19
20
17
18
19
20
18
19
20
19
20
20
21
22
23
Доверительная
вероятность а
0,90
Nt
9
7
8
8
8
9
9
9
10
10
8
9
9
9
10
10
10
10
9
9
10
10
10
11
11
10
10
11
11
11
12
11
11
11
12
12
11
12
12
13
12
13
13
13
13
14
15
16
16
N2
21
19
19
20
20
21
21
21
22
22
20
20
21
21
22
22
23
23
21
22
22
23
23
23
24
22
23
23
24
24
25
23
24
25
25
25
25
25
26
26
26
26
27
27
27
28
28
29
31
0,95
8
7
7
7
8
8
8
8
9
9
7
8
8
8
9
9
9
10
8
8
9
9
9
10
10
9
9
10
10
10
11
10
10
10
11
11
10
11
11
11
11
12
12
12
12
13
14
14
15
N2
22
19
20
21
21
22
22
22
23
23
21
21
22
22
23
23
24
24
22
23
23
24
24
24
25
23
24
24
25
25
26
24
25
26
26
26
26
26
27
27
27
27
28
28
29
29
29
31
32
4.3]
Критерии тренда и случайности
529
Окончание таблицы 175
т
24
25
26
27
28
29
30
31
32
33
34
35
36
37
п
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Доверительная
вероятность а
0,90
Nt
17
18
19
20
21
22
22
23
24
25
26
27
28
29
N2
32
33
34
35
36
37
39
40
41
42
43
44
45
46
0,95
Nt
16
17
18
19
19
20
21
22
23
24
24
25
26
27
N2
33
34
35
36
38
39
40
41
42
43
45
46
47
48
m
38
39
40
41
42
43
44
45
46
47
48
49
50
n
38
39
40
41
42
43
44
45
46
47
48
49
50
Доверительная
вероятность а.
0,90
Ni
30
30
31
32
33
34
34
36
37
38
38
39
40
N2
47
49
50
51
52
53
54
55
56
57
59
60
61
0,95
Nt
28
29
30
31
31
32
33
34
35
36
37
38
38
N2
49
50
51
52
54
55
56
57
58
59
60
61
63
Критические значения п\{а) и П2{сх) приведены в табл. 175. Если т и п —
соответственно количества элементов а и Ъ в последовательности, то при га, п > 20
справедлива аппроксимация
2тп
N -
N* =
+ 1
2тпBтп ~~ т — п)
(га + пJ(т + П — 1)
имеющая стандартное нормальное распределение. Тогда нулевая гипотеза откло-
отклоняется с достоверностью а, если \N*\ > ui+a .
Задача 280. Для ряда значений задачи 278 проверить гипотезу случайности ряда
наблюдений критерием Вальда-Волфовитца при доверительной вероятности а = 0,90.
О _|_ 1 1
Имеем медиану ряда х = =9,5. Обозначим символом а значения Xi < x и сим-
символом Ъ значения х% > х. Получаем ряд символов
а, а, 6, 6, а, а, а, 6, 6, Ь.
В нашем случае имеем т = 5 элементов а и п = 5 элементов Ъ. Всего имеем N = 4
серии элементов — две серии элементов а и две серии элементов Ь.
Из табл. 175 для т = п = Ь и а = 0,90 находим гц = 2 и п2 = 10. Таким образом,
fii = 2<JV = 4<fi2 = Ю, и ряд признается случайным. Следует отметить малую мощ-
мощность таких критериев (их рекомендуется применять при т,п> 50). Для нормальной
аппроксимации имеем
M(N) =
+ 1 = 6; T>(N) =
2-5-5-B-5-5-5-5)
E + 5J • E + 5™ 1)
= 2,222 (y/T)(N) = 1,491);
что меньше ui+a = ti.0,95 = 1,645; следовательно, гипотеза принимается.
2
530
Проверка гипотез о значениях параметров распределений
[Гл.4
4.3.6.2. Критерий Рамачандрана-Ранганатана
В отличие от критерия Вальда—Волфовитца (см. раздел 4.3.6.1) настоящий
критерий учитывает не только количество, но и длины серий (количества элементов
в сериях). Статистика критерия имеет вид
где j— длина серии, п — объем выборки; rij —количество серий длины j.
Гипотеза случайности не отклоняется с вероятностью а при R < R(a). Критиче-
Критические значения R(a) приведены в табл. 176. Критерий обладает большей мощностью
по сравнению с iV-критерием Вальда-Волфовитца.
Таблица 176
Критические значения Ж(о)
критерия Рамачандрана—Ранганатана [14]
п
6
8
10
12
14
16
18
Доверительная
вероятность а
0,90
18
26
34
38
46
54
68
0,95
18
32
38
44
52
60
78
0,99
18
32
50
58
68
80
90
п
20
22
24
26
28
30
Доверительная
вероятность а
0,90
68
76
84
92
98
106
0,95
78
86
94
102
110
118
0,99
100
108
118
128
136
146
Задача 281. Для данных задачи 278 проверить гипотезу случайности ряда критерием
Рамачандрана-Ранганатана.
Имеем две серии элементов длины j = 2 (пг = 2) и две серии элементов длины j = 3
(гс3 = 2). Тогда R = J^f • % = 4 • 2 + 9 • 2 = 26.
з
Из табл. 176 для п = 10 и а = 0,95 имеем R@, 95) = 38.
Так как R = 26 < #@,95) = 38, ряд значений xi признается случайным, а альтерна-
альтернатива тренда отклоняется.
4.3.6.3. Сериальный критерий ЕПахнесси
Критерий Шахнееси [510] является множественным аналогом критерия Вальда™
Волфовитца (см. раздел 4.3.6.1). Если в критерии Вальда^Волфовитца рассматри-
рассматривается количество серий элементов двух „сортов", то критерий Шахнееси предпола-
предполагает анализ серий элементов к „сортов" (к ^ 2). Это делает его более эффективным,
так как позволяет противостоятв большему количеству альтернатив (сдвиг, колеба-
колебания, изменения в определенной точке).
Статистикой критерия остается, как и ранее, N — общее количество серий эле-
элементов. Если количество серий
N<Na(n>,k),
то гипотеза случайности отклоняется с вероятностью а (здесь Na(rii^ к) — критиче-
критические значения, приведенные в табл. 177). В табл. 177 приняты следующие обозна™
чения: rii (г = 1, ..., к) —количество элементов г™го „сорта", к — количество „сортов"
элементов, составляющих ряд.
4.3]
Критерии тренда и случайности
531
Таблица 177
Критические
к
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
3
3
3
и
К
4
4
4
4
4
4
4
4
4
4
4
4
4
и
К
5
5
5
5
5
т
4
4
5
6
6
7
8
8
9
9
п2
4
5
5
6
7
7
8
9
9
10
т
2
q
q
4
с
б
б
711
2
2
2
2
3
3
3
3
4
4
4
4
5
П\
2
2
2
2
2
[
[
[
i значения
а
0,95
2
2
3
3
4
4
5
5
6
6
те2
3
3
3
4
4
4
5
5
5
6
6
6
7
те2
2
2
2
3
3
3
3
4
4
4
4
5
5
П2
2
2
2
2
3
0,9С
Z
(
(
тез
3
3
4
4
4
5
5
5
6
6
6
7
7
тез
3
3
3
3
4
4
4
4
с
1
1
тез
2
2
2
3
3
S
2
4
4
7
г
м-
к
2
2
2
2
2
2
2
2
2
2
п
к)
п\
10
11
11
12
12
13
13
14
15
16
критерия
те2
11
11
12
12
13
13
14
14
15
16
а
0,95
те4
те4
2
2
3
3
3
2
3
3
3
3
4
4
4
4
5
5
5
5
3
4
4
5
5
6
7
7
8
8
9
9
10
0,90
4
4
5
5
6
7
7
8
8
9
10
10
11
а
0,95
4
5
5
6
7
7
8
9
9
10
11
11
12
п5
2
3
3
3
3
0,90
5
5
6
7
7
8
9
9
10
11
11
12
13
а
0,95
6
7
8
8
9
0,90
7
7
8
9
9
Шахнесси
а
0,95
7
7
8
8
9
9
9
10
11
11
3
3
3
3
3
3
3
3
3
3
3
3
3
и
К
4
4
4
4
4
4
4
4
4
4
4
4
i,
Гъ
5
5
5
5
5
0,90
8
8
9
9
9
10
10
11
12
12
711
7
7
7
8
8
8
9
9
10
10
10
11
11
т
5
5
5
6
6
6
6
7
7
7
7
8
711
3
3
3
3
3
к
2
2
2
2
2
2
2
2
2
2
те2
7
8
8
8
9
9
9
10
10
11
11
11
12
п2
те<2
3
3
3
3
4
5
5
6
6
6
6
7
7
7
7
S
3
для
711
16
17
18
19
20
21
22
23
24
25
тез
77
8
8
8
9
9
9
10
10
11
11
11
12
тез
(
(
(
(
<
<
(
тез
3
3
3
4
4
7
7
7
7
к
2
п2
17
18
19
20
20
21
22
23
24
25
510]
а
0,95
12
13
14
14
15
16
17
17
18
19
0,90
13
14
15
16
16
17
18
19
20
21
0,95
те4
Т14
3
3
4
4
4
6
6
6
6
7
7
7
7
8
8
8
8
11
11
12
12
13
13
14
15
16
16
17
18
19
0,90
11
12
13
13
14
14
15
16
17
17
18
19
20
а
0,95
13
13
14
15
15
16
17
17
18
19
19
20
п5
3
4
4
4
4
0,90
13
14
15
15
16
17
17
18
19
20
20
21
а
0,95
10
10
11
12
12
0,90
10
11
12
12
13
532
Проверка гипотез о значениях параметров распределений
[Гл.4
и
к
5
5
5
5
5
5
5
5
4
4
4
4
4
5
5
5
4
4
4
4
5
5
5
5
из
4
4
4
5
5
5
5
5
4
4
5
5
5
5
5
6
4
5
5
5
5
5
6
6
а
0,95
13
14
15
15
16
17
18
18
0,90
14
15
15
16
17
18
18
19
i,
к
5
5
5
5
5
5
5
5
П\
5
5
6
6
6
6
6
7
О к о н ч
Т12
5
6
6
6
6
6
7
7
6
6
6
6
6
7
7
7
ание таблицы 177
6
6
6
6
7
7
7
7
6
6
6
7
7
7
7
7
а
0,95
19
20
21
21
22
23
23
24
0,90
20
21
21
22
23
24
24
25
Задача 282. Дан ряд наблюдений над случайной величиной
хц 12, 8, 6, 0, -4, -3, 1, -2, -6, -10, 8, 4, 2, -1, 5, 15, 21, 32.
Необходимо проверить гипотезу случайности ряда критерием Шахнесси при довери-
доверительной вероятности а = 0,95.
Элементам, для которых Xi < 0, присвоим код а; элементам, у которых 0 ^ Xi ^ 7,
присвоим код 6, а элементам, для которых х% > 7, присвоим код с. Тогда получаем ряд
с^с, 6,6, а,а^ 6, а^а^а, с, 6,6, а, 6, с, с.
Видим, что общее количество серий равно 10 C серии элементов с, 3 серии элементов а
и 4 серии элементов 6). Количества элементов равны п\ =6 (а), П2 = 6 F) ипз = 6 (с).
В табл. 177 для к = 3, гц = 6, П2 = 6 и пз = 6 при а = 0,95 находим па = 9.
Так как п = 10 > па = 9, гипотеза случайности не отклоняется.
4.3.6.4. Критерий Олмстеда
Олмстедом [509] рассмотрена серия критериев случайности, так лее, как и в слу-
случае критерия Рамачандрана-Ранганатана (см. раздел 4.3.6.2) учитывающих длины
серий. В критериях Олмстеда рассматриваются экстремальные длины серий одного
вида, вероятность появления которых связывается с возможным присутствием
тренда в исследуемых рядах. Олмстедом предложено четыре варианта критерия:
наибольшая длина Х\ серии, лежащей по какую-либо одну сторону от медианы;
наибольшая длина \ч серии, лежащей по одну (заранее выбранную) сторону от
медианы; кратчайшая Х^ из обеих наибольших длин серий, лежащих по разные
стороны от медианы; кратчайшая Х± из обеих наибольших длин серий, лежащих по
разные стороны от точки раздела, максимизирующей Х±-
Во всех вариантах для заданных Xi (г = 1,2,3,4) на уровне значимости а ста-
статистикой критерия Олмстеда является наименьший объем выборки п. Гипотеза
случайности отклоняется при п < na(Xi). Критические значения na(Xi) приведены
в табл. 178.
Задача 283. Для ряда наблюдений
Xi : 13, 8, 7, 4, 10, 17, 21, 34, 48, 1, 0, 12, 10, 4, 16, 17, 11, 0, 1, 3, 12, 54, 16, -1
(ji = 24) проверить гипотезу случайности критерием Олмстеда на уровне значимости
а = 0,1.
Находим медиану ряда х = 11. Для значений ряда Xi ^ х примем индекс а, а для
значений х% < х — индекс 6. Получаем ряд
а, 6, 6, 6, 6, а, а, а, а, 6, 6, а, 6, 6, а, а, а, 6, 6, 6, а, а, а, 6,
4.3]
Критерии тренда и случайности
533
в котором 5 серий элементов а и 5 серий элементов Ь, причем h = 4, h = 4, 1з = 4. Из
табл. 178 для а = 0,1, h = I2 = /3 = 4 находим n(h) = 8, п(/г) = 10 и пAз) = 14. Так как
п = 24 > n(Zi), n(h), пAз), то всеми критериями гипотеза случайности не отклоняется.
Легко убедиться, что и последний критерий (I4) также отклоняет гипотезу тренда.
Таблица 178
Критические значения na(li) критерия случайности Олмстеда [24]
/*
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Уровень значимости а
0,10
n(h)
4
6
8
14
20
32
52
86
150
262
500
962
1876
3670
7330
14090
27900
555000
1111000
n(h)
4
6
10
16
26
44
78
142
256
480
930
1838
3630
7160
14190
28100
56100
117300
235000
n(h)
4
8
14
26
50
98
194
390
782
1182
2360
4720
9450
18900
37800
75600
151200
30200
60500
n(h)
4
8
12
18
34
58
108
204
400
790
1568
3130
6220
12490
25000
49900
99900
199800
400000
0,01
n(h)
4
6
8
10
12
16
22
32
42
62
94
156
254
418
766
1472
2860
5570
10860
n(h)
4
6
8
10
14
18
26
38
56
86
140
234
410
748
1446
2830
5530
10860
21500
n(h)
4
6
8
12
20
34
62
116
216
446
884
1762
3510
6990
13930
27900
55500
111000
222000
n(h)
4
6
8
12
16
24
38
66
118
228
444
878
1750
3480
6790
13865
27700
55400
110800
4.3.6.5. Критерий числа серий знаков первых разностей
Для выборки #i, #2, • • • 1 хп вычисляем (п — 1) значений вида
— 1, если Xi+i < Х{\
z% = \ +1, если xi+i > Xi\
0, если я^+i = Х{.
В ряду значений Z{ фиксируем количество серий R, которое и является стати™
стикой рассматриваемого критерия.
Гипотеза случайности ряда не отклоняется при Ri(a) < R < ^(а). Критиче-
Критические значения R\(a) и R^(а) приведены в табл. 179. При п > 30 распределе-
распределение R удовлетворительно аппроксимируется нормальным распределением со сред™
и дисперсией D(.R), где M.(R) = —-—; D(i?) = — . Тогда нулевая
гипотеза проверяется критерием \R*
\R-M(R)\
и при
90
IR* I
гипотеза
случайности отклоняется.
Хальд [51], Уоллис и Мур [413] дополнили критерий числа серий рассмотрением
длин серий знаков + и —. Вероятность появления серий длины I при справедливости
гипотезы случайности ряда равна
2
n
n
(l-
- 1
f 1)!
(
-I
1 +
- 1
2)!
1-2
ЬЗ)!
534
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 179
Критические значения JRi(o) и jR2(ok)
критерия числа серий знаков первых разностей [57]
п
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Ri
1
1
2
2
2
2
4
4
5
5
6
6
7
7
8
8
9
10
10
11
11
12
13
13
14
Доверительная
вероятность а
0,95
Д2
10
11
12
13
14
14
15
16
17
17
18
19
20
20
21
22
23
23
24
0,90
Ri
1
1
2
2
2
3
4
4
5
6
6
7
7
8
8
9
10
10
11
11
12
13
13
14
14
Д2
10
11
12
12
13
14
15
15
16
17
18
18
19
20
21
21
22
23
24
п
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
60
62
64
66
68
70
80
90
100
Ri
14
15
17
18
19
20
21
23
24
25
26
27
29
30
31
32
34
35
36
37
38
45
51
57
Доверительная
вероятность а
0,95
«2
15
26
28
29
31
32
34
35
37
38
40
41
43
44
45
47
48
50
51
53
54
61
68
75
0,90
Ri
15
16
17
19
20
21
22
23
25
26
27
28
30
31
32
33
35
36
37
38
40
46
52
58
д2
24
26
27
29
30
32
33
34
36
37
39
40
42
43
44
46
47
49
50
52
53
60
67
74
Критерий с учетом длин серий основан на статистике
2 _ V^ [п* ~ nP(l)f
Х ^ ^ прA) '
где суммирование ведется для I = 1,2 и ^ 3 (щ —количество серий длины I, рA) -
вероятность появления серии длины I). В частности,
(
гс V 6
24
120
-; рC) = 1-
7 — 15п
12гс *
Правило проверки нулевой гипотезы формулируется следующим образом:
— при х2 ^ 6,3 нулевая гипотеза отклоняется с вероятностью а, если %2 > %2 B,5),
где %2B,5) — а-квантиль распределения хи-квадрат с / = 2,5 степенями свободы;
— при у2 < 6,3 нулевая гипотеза отклоняется, если у2 > -у2B).
6
4.3 ] Критерии тренда и случайности 535
Задача 284. Проверить гипотезу случайности ряда из задачи 283 критерием числа
серий знаков первых разностей при доверительной вероятности а = 0,95.
Ряд знаков первых разностей имеет вид (п = 24):
Из него получаем число серий R = 9 E серий „—" и 4 серии „+").
Из табл. 179 для п = 24 и а = 0,95 имеем Кг = 11 и R2 = 20.
Так как R = 8 < Ri = 11, гипотеза случайности выборки х отклоняется.
Для нормальной аппроксимации имеем
М(Д) = 2'24^г = 15,67; D(R) = W ' 2*~ 29 = 3,944 [л/ЩЩ = 1,986);
= |11-15,7| = Зб6
1 1,986
Так как \R*\ = 2,366 > tto,975 = 1,96, то и этот критерий отклоняет гипотезу случай-
случайности ряда.
Рассмотрим теперь критерий с учетом длин серий. Вычисляем
= 5-24 + 1 = = 11-24-14 = оД736; р [> 3) = 1-0,42-0,1736 = 0,4064.
f\ ) 12-24 ' ' FX J 60-24 ' ' FX^ }
В нашем случае имеются гц = 1 серия длины I = 1, пг = 5 серий длины I = 2 и пз = 3
серии длины 1 = 3. Находим
2 V^hl~^'P@12 (l-24-Q,42J E - 24-0,1736J C - 24 • 0, 4046J
Y = > тт^^ = Ь h — = 12, 983.
^ п-рA) 24 -0,42 24-0,1736 24-0,4046
Так как %2 > 6,3, то используем критическое значение Хо,9бB,5) = 6,903.
Из того, что х :=: 12,983 > Хо,95B,5) = 6,9, следует, что и этот критерий отклоняет
гипотезу случайности.
4.3.7. Критерий инверсий
Если в выборке значений #i,#2, ¦•¦,жп, записанных в порядке их появле™
ния, за некоторым значением Х{ следует меньшее по величине (т.е. Xi > Xj, где
г + 1 ^ j ^ п), то имеет место инверсия. Общее число инверсий J в выборке является
статистикой критерия случайности полученных значений х [14]. Иногда рассматри™
вают статистику Т, определяемую числом обратных инверсий (когда Х{ < Xj, j > г).
Статистика Т совпадает со статистикой U Манна-Уитни (см. раздел 4.2.1.1.2.2),
и ее критическое значение может быть определено по табл. 143 этого критерия.
В качестве третьей меры можно использовать величину К = Т — /, критические
значения которой приведены в работе Кендалла [422].
При п ^ 20 статистика J распределена приблизительно нормально со средним
МA) и дисперсией DG), где
Щ1) = п^1. р 2n3+3n2-5n_
4 11
При |/*| = ^ ui+a. гипотеза случайности отклоняется с вероятно™
стью а. Точные критические значения I\{ol) и /2(tt) приведены в табл. 180 — ги-
гипотеза случайности принимается, если
h(a) < I < 12(а).
Критерий имеет асимптотическую эффективность уЗтг ~ 0,98 относительно
критерия коэффициента регрессии. Следовательно, по эффективности он превос-
превосходит большинство непараметрических критериев для тренда.
536
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 180
Критические значения /i(ck) и /г(ск) критерим инверсий [14]
п
10
12
14
16
18
20
30
Доверительная
вероятность а
0,90
h
13
21
30
41
54
69
171
h
31
44
60
78
98
120
263
0,95
h
11
18
27
38
50
64
162
h
33
47
63
81
102
125
272
n
40
50
60
70
80
90
100
Доверительная
вероятность а
0,90
h
319
514
756
1045
1382
1766
2198
h
460
710
1013
1369
1777
2238
2751
0,95
h
305
495
731
1014
1344
1721
2145
h
474
729
1038
1400
1815
2283
2804
Задача 285. Проверить гипотезу случайности ряда
хц 13, 8, 7, 4, 10, 17, 21, 34, 48, 1, 12, 9, 3, 18, -1, -3, 49, 50, 0, 14
критерием инверсий при доверительной вероятности а = 0,95.
Определяем количества инверсий / для различных значений Жг5 результаты сведем
в таблицу:
г
1
2
3
4
5
6
7
Xi
13
8
7
4
10
17
21
I
11
7
6
5
6
8
9
г
8
9
10
11
12
13
14
Xi
34
48
1
12
9
3
18
I
9
9
3
5
4
3
4
г
15
16
17
18
19
Xi
-1
^3
49
50
0
I
1
0
2
2
0
Сумма инверсий равна /= 11 + 7+... + 2 + 0 = 94. Из табл. 180 для п = 20 и а = 0,95
имеем /i = 64 и /2 = 272.
Так как Д = 64 < / = 94 < /2 = 272, гипотеза случайности не отклоняется.
Используем теперь нормальную аппроксимацию, для чего находим
- 3 •
- 5 • 20
\Г
72
|94 — 95|
= 237,5 (VD(J) = 15,411);
= 0,065.
15,411
Так как |/*| = 0,065 <С 11-0,975 = 1?96, гипотеза случайности также уверенно не откло-
отклоняется.
4.3.8. Критерий автокорреляции
Если выборка значений х случайна, то значение каждого ее элемента не должно
зависеть от величины предшествующего и последующих членов. Для проверки этой
независимости используется статистика [36]
+
4.3]
Критерии тренда и случайности
537
являющаяся коэффициентом корреляции первого порядка между элементами пер™
вичной выборки (жх, #2, • • •, %п) и элементами выборки, полученной из нее сдвигом
на одну единицу (х2,х3, ...,xn,xi).
Гипотеза случайности ряда принимается с вероятностью а при r[ n(pt) < Г\^п <
< т'-1п{а). Критические значения коэффициентов автокорреляции r[ n{pt) и т'^п(а)
приведены в табл. 181.
Таблица 181
Критические значения г[^п(а,) и г"^п((ж) критерия автокорреляции [22, 511]
п
5
10
15
20
25
30
35
Доверительная вероятность а
0,95
Г1,п
-0,753
-0,564
-0,462
-0,399
-0,356
-0,324
-0,299
Г1,п
0,253
0,360
0,328
0,299
0,276
0,257
0,242
0,99
-0,798
-0,705
-0,597
-0,524
-0,473
-0,433
-0,401
Г1,п
0,297
0,525
0,475
0,432
0,398
0,370
0,347
п
45
50
55
60
65
70
75
Доверительная вероятность а
0,95
Г1,п
-0,262
-0,248
-0,236
-0,226
-0,217
-0,209
-0,201
Г1,п
0,218
0,209
0,201
0,193
0,186
0,180
0,174
0,99
Г1,п
-0,356
-0,339
-0,324
-0,310
-0,298
-0,287
-0,276
Г1,п
0,313
0,300
0,288
0,277
0,267
0,258
0,250
При п ^ 75 величину ri?n можно считать распределенной асимптотически нор™
мально со средним M(ri?n) и дисперсией D(ri?n), где
М(п,„) = -
D г,„) =
; D г,„) = \ 2.
п — L (п + 1)(п — 1)
Поэтому критерий случайности может быть записан в форме
П,п -М(Г,П)
< Ul+a .
2
D(r,n)
Среди других удачных нормализующих преобразований укажем результаты
— Люнга-Бокса [500]: rj п = \ ^ \
^Морана [551]: r*n(n — 1)^
[501]: r\ n =
п-1
1,п + 1
п-2 '
п- 1
1).
Для более сложных альтернатив (например, периодические колебания ряда)
более эффективны различные модификации критериев автокорреляции. Укажем
на некоторые из них.
Сумма коэффициентов корреляции первого и второго порядков [513]
п—1 п—2
]Р (Xi - X)(xi+1 - Х) + ]Р (Xi - ж)(Жг+2 - Ж)
(Xi - X)
имеющая при п ^ 20 приближенно нормальное распределение со средним
и дисперсией DfVi^), где
М(п,2) = —
(п- 1)'
¦ 15п + 28?г - 34
п(п-
538
Проверка гипотез о значениях параметров распределений
[Гл.4
Линейная комбинация сериальных коэффициентов
П =
/ -J ^ % '
также аппроксимирующаяся нормальным распределением со средним М(г/) =
= "" Y1 ~( ТТ и дисперсией, приведенной в таблице для различных п:
П ^ = ^ Ъ\ТЬ 1)
п
D(n)
10
0,041
16
0,036
32
0,027
64
0,018
Во всех случаях при п ^ 20 справедливо следующее решение: если г* 2 =
|Г1,2 - М(П,2)| , . * rt — v'MI I ^
i !„* _ I \ "''ta, то нулевая гипотеза случайности
/D(n)
ряда отклоняется.
Задача 286. Проверить гипотезу случайности ряда значений ж, заданных в зада-
задаче 285, критерием автокорреляции при доверительной вероятности а = 0,95.
Находим
20 \ 19
53 ж* = 98956; J]
i=l J i=l
= 5638; J2 хг = Ю254;
г=1
20 • 5638 - 98596 + 20 _
f on =
20 - 10254 - 98596
Из табл. 181 находим ri!20@,95) = ^0,399 и riJ0@,95) = 0,299.
Так как ri;20@,95) = -0,399 < 74,20 = 0,167 < ViJ0@,95) = 0,299, гипотеза случайно™
сти не отклоняется.
Используем теперь аппроксимацию. Имеем
1 20-17
М(п,2о) = ^ = ^0,526; D(ri,20) = ^j^ = 0,0448
, , [0,167 + 0,05261
г 1 on = = 1.UJ7.
1,20 | 0^12
= 0,212);
Так как |r*iJo| — 1,037 < 1x0,975 — 1,96, нулевая гипотеза не отклоняется.
Применим теперь модификацию коэффициента сериальной корреляции. Вычисляем
{xi+2 - Х)
Г-1,2 =
20 19
х = 15,7; ]Г (xi -х) = 5324,3; ]Г (Xi - х) • (xi+1 - х) = 902,61;
Окончательно имеем
902,61 - 1442,8
Г-1,2 =
5324,3
xi - х) • (жг+2 - ж) = 1442,88.
2-20-31
= -0,1014; М(п,2) = = 0,0973;
4.3]
Критерии тренда и случайности
539
2 • 204 - 13 • 203 + 15 • 202 +28-20-34
202 • 19*21
= 0,07338 (у/Т>(п,2) = 0,2709);
—0,101 + 0,097|
= 0,054.
0,0733
Так как |r*ij2| = 0,054 < 110,975 = 1,96, гипотеза случайности ряда принимается.
4.3.9. Критерии ранговой корреляции
4.3.9.1. Критерий Вальда-Волфовигца [514]
Пусть Ri — ранг наблюдения Xi в упорядоченном по возрастанию ряду значе-
значений #i,#2, ... ,хп. В качестве аналога критерия сериальной корреляции (см. раз™
дел 4.3.8) известен коэффициент ранговой сериальной корреляции Вальда^Волфо-
витца [512, 514]
П—1 / \ / N
R _ у^ (R,_ п+г\ (R. п + 1
г=1 ^ ^ ^
При п > 20 распределение R асимптотически нормально [514, 515] со средним
~M(R) и дисперсией D(RI где
Тогда если \R*
М(Д) = 0; B(R) =
\R\
п2(п -
- 3)Erc + 6)
720
a, то с вероятностью а гипотеза случайности
отклоняется. Для распределений нормального типа асимптотическая эффектив-
эффективность R-критерия ^ 0,91 по отношению к сериальной корреляции первого порядка
(см. раздел 4.3.8), для любых других распределений — не менее 0,86 [512].
Задача 287. Проверить гипотезу случайности ряда значений, заданных в задаче 284,
критерием ранговой автокорреляции при доверительной вероятности а = 0,95.
Имеем ряд х% (ъ — порядковый номер х% в последовательности, Ri — ранг х% в после-
последовательности) :
г
1
2
3
4
5
Xi
13
8
7
4
10
Rt
12
8
7
6
10
i
6
7
8
9
10
хг
17
21
34
48
1
Ri
14
16
17
18
4
г
11
12
13
14
15
Xi
12
9
3
18
-1
Ri
11
9
5
15
1
г
16
17
18
19
20
хг
^3
49
50
0
14
Ri
2
19
20
3
13
Вычисляем
19
20 + 1
Ri+l —
20+1
= A2 - 10,5) • (8 - 10,5) • • • C - 10,5) • A3 - 10,5) = 35,25;
202 -21 • 17- E ¦ 20 + 6)
720
= 21033,3 (л/ЩЩ = 144,99);
144,99
и гипотеза случайности не отклоняется.
35 25
\R*\ = 7777^ = °'249 < «о,975 = 1,96,
540
Проверка гипотез о значениях параметров распределений
[Гл.4
4.3.9.2. Критерий Бартелса
Пусть Ri—ранг г-го наблюдения в последовательности п наблюдений Х{. Бар-
телсом [516] рассмотрен ранговый критерий случайности ряда, основанный на
статистике
В =
При совпадении элементов выборки ранги следует случайным образом распре™
12 12
делить среди них. Значение В заключено в интервале —; г < В < 4 -, г.
п(п + 1) п(п + 1)
В пределе при п —> оо имеем 0 < В < 4. Моменты распределения В рав-
равны [516]: М(В) = 2; ТУ (В) =
пределения В равен «з = ~
4(п-2)Eп -2п^
12
i, коэффициент эксцесса «4
. Коэффициент асимметрии рас™
798
. Отсюда
v 17bn
следует, что распределение симметрично, но медленно стремится к нормальному
эксцессу.
Гипотеза случайности отклоняется на уровне значимости а, если B — Ва) <
< В < (Ва + 2). Критические точки Ва определяются по формуле [516] Ва = а +
+ bnc(\nn)d^ где a^b^c^d — коэффициенты, приведенные в табл. 182.
Таблица 182
Коэффициенты аппроксимации критического
значения критерия Бартелса
(а — уровень значимости) [516]
а
а
b
с
d
0,01
-0,023
0,261
-0,345
2,212
0,025
-0,004
0,381
-0,266
1,748
0,05
0,119
0,440
-0,230
1,520
0,1
-0,465
1,184
-0,088
0,674
4 20
При п -Л оо М(Л) = 2 и ТУ (В) = —, или более точно ТУ (В) = .
При п > 100 критерий приобретает вид В* =
В^Ш(В)
Если |В*| < ui+g, то гипотеза случайности не отклоняется.
2
Задача 288. Проверить гипотезу случайности ряда значений, заданных в задаче 285,
критерием Бартелса,
Вычисляем (используем ранги, приведенные в задаче 287)
1
-
п
г) 4-1
= 10,5;
= A2 - 8J + ... + C - 13J = 1327;
= A2 - 10,5J + ... + C - 10,5J = 614,5;
4.3]
Критерии тренда и случайности
541
в =
1327
614,5
= 2,159.
При п = 20 и а = 0,05 из табл. 182 имеем а = 0,119; Ь = 0,440; с = ^0,230 и d = 1,520.
Тогда Во,о5 = 0,119 + 0,440 • 20^0'230 • (In 20I'520 = 1,29.
Так как B - 1,29) = 0,71 < В = 2,159 < B + 1,29) = 3,29, гипотеза случайности не
отклоняется.
4.3.10. Критерий кумулятивной суммы
В [517, 518] изучен критерий отсутствия тренда, основанный на сумме
где х — медиана и S(z) =
г=1
если z ^ 0;
если z < 0.
Статистикой критерия является R— число переходов через нуль суммы V. Кри™
терий тренда отклоняется на уровне значимости а, если Ri(a) < R < .^(ск), гДе
R\{ol) и i?2(oj)—критические значения, приведенные в табл. 183.
Таблица 183
Критические значения JRi(o) и jR2(ok)
критерия кумулятивной суммы [517]
п
10
20
30
40
50
60
70
80
90
100
Доверительная
вероятность а
0,90
Ri
0
0
1
1
1
1
2
2
2
2
6
9
12
14
15
17
19
20
21
23
0,95
Ri
0
0
0
0
1
1
1
1
1
1
д2
6
10
12
15
17
18
20
22
23
25
п
200
300
400
500
600
700
800
900
1000
Доверительная
вероятность а
0,90
Ri
4
4
5
6
7
7
8
9
9
33
40
47
53
58
63
67
71
75
0,95
Ri
2
3
4
4
5
5
5
6
6
R2
36
44
52
58
64
69
74
79
83
Задача 289. Проверить гипотезу случайности ряда значений ж, заданных в зада-
задаче 285, критерием кумулятивной суммы.
В нашем случае медиана ряда есть х = 11. Последовательность значений 8(xi — х)
имеет вид:
+1, -1, -1, -1, -1, +1, +1, +1, +1, -1, -1, -1, -1, +1, -1, -1, +1, +1, -1, +1.
Этот ряд порождает последовательность сумм V%:
+1, 0, -1, -2, -3, -2, -1, 0, +1, 0, -1, -2, -3, -2, -3, -4, -3, -2, -3, -2.
Следовательно, R = 3 (три нуля). Из табл. 183 для п = 20 и а = 0,95 находим J?i = 0
Так как JR1=0<JR = 3<i?2 = 10, исследуемый ряд должен быть признан случай™
ным.
542
Проверка гипотез о значениях параметров распределений
[Гл.4
4.3.11. Знаково-ранговый критерий Холлина
Холлин опубликовал в последнее время ряд работ [552—555], посвященных де-
детальному изучению проблемы использования рангов в критериях случайности. Ука-
Укажем на последний результат [556], в котором предложено в определенном смысле
обобщение рангового критерия Вальда-Волфовитца (см. раздел 4.3.9.1) и знако-
знакового критерия кумулятивной суммы (см. раздел 4.3.10). Предложенный Холлином
знаково-ранговый критерий автокорреляции основан на статистике
r =
fc(n-l)
?
где k — коэффициент, зависящий от объема выборки (некоторые его значения
приведены в табл. 184); х — медиана выборочного ряда х\ ^ ж 2 ^ ... ^ хп; Ri—
ранг величины Zi = \х{ — х\ в общем упорядоченном по возрастанию ряду значений
{1, если у > 0;
-1, если у < 0;
0, если у = 0.
Таблица 184
Значения к для знаково-рангового критерия Холлина [556]
п
к
5
10,11
10
36,95
20
140,62
50
851,62
100
3370
200
13407
400
53480
Ряд значений Х{ признается случайным, если \г\ < га, где га—критические
значения, приведенные в табл. 185 (а — уровень значимости). Критерий Холлина
обладает большей эффективностью среди всех, рассмотренных ранее ранговых
критериев.
Задача 290. Проверить гипотезу случайности ряда значений Xi, заданных в зада-
задаче 285, знаково-ранговым критерием Холлина на уровне значимости а = 0,05.
Медиана ряда равна х = = 11.
Напомним, что медиана ряда равна
полусумме центральных значений упорядоченного по возрастанию ряда при п
четном и центральному значению при п нечетном. Составляем ряд значений z%
(Ri—ранг Zi в последовательности) и соответствующих им значений 5ц = 5(xi — х)
и S2i = 8[(xi - х) (xi^t - х)] = ёц • <5i,i-i:
2
3
4
7
1
Яг
3,5
5,5
7
9,5
1,5
Su
1
-1
-1
-1
-1
s2i
-1
1
1
1
z%
6
10
23
37
10
Яг
8
12,5
17
18
12,5
Su
1
1
1
1
-1
-1
1
1
1
-1
zi
1
2
8
7
12
Яг
1,5
3,5
11
9,5
15
Su
1
-1
-1
1
-1
s2l
-1
-1
1
-1
-1
Zi
14
38
39
11
3
Ri
16
19
20
14
5,5
Su
-1
1
1
-1
1
s2%
1
-1
1
-1
-1
Для равных значений z% применяем средние ранги.
Из табл. 184 для п = 20 находим к = 140,62 и вычисляем статистику критерия
1
140,62 • B0 - 1)
• ^ S[(xi - х) - (Xi-l ~~ Х)] ' Ri ' Ri-1 =
= 3,7428 • 10^4 • (-3,5 • 5,5 + 5,5 • 7 + 7 • 9,5 + 9,5 • 1,5 - ...
... + 19 • 20 - 20 • 14 - 14 • 5,5) = 0,078.
4.3]
Критерии тренда и случайности
543
Из табл. 185 для п = 20 и а = 0,05 находим критическое значение го,о5 = 0,378. Так
как г = 0,078 < го,о5 = 0,378, ряд следует признать случайным.
Таблица 185
Критические значения га
знаково-рангового критерия Холлина [556]
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Уровень значимости а
0,10
0,667
0,608
0,548
0,501
0,467
0,421
0,415
0,394
0,380
0,361
0,349
0,338
0,325
0,317
0,306
0,298
0,292
0,283
0,276
0,270
0,265
0,260
0,255
0,05
0,816
0,749
0,681
0,625
0,587
0,553
0,522
0,498
0,479
0,455
0,442
0,428
0,412
0,402
0,388
0,378
0,370
0,361
0,350
0,343
0,338
0,330
0,323
0,025
0,915
0,834
0,778
0,720
0,682
0,642
0,610
0,583
0,558
0,535
0,518
0,502
0,485
0,472
0,459
0,446
0,436
0,425
0,413
0,404
0,400
0,388
0,323
28
29
30
32
34
36
38
40
42
44
46
48
50
55
60
65
70
75
80
85
90
95
100
Уровень значимости а
0,10
0,250
0,245
0,241
0,233
0,225
0,219
0,213
0,207
0,202
0,197
0,192
0,188
0,184
0,175
0,168
0,161
0,155
0,150
0,145
0,140
0,136
0,133
0,129
0,05
0,317
0,311
0,306
0,296
0,287
0,279
0,271
0,264
0,257
0,251
0,246
0,240
0,235
0,224
0,214
0,206
0,198
0,191
0,185
0,180
0,174
0,170
0,165
0,025
0,374
0,367
0,361
0,349
0,339
0,320
0,320
0,312
0,304
0,297
0,291
0,285
0,279
0,266
0,254
0,244
0,235
0,227
0,220
0,213
0,207
0,202
0,197
4.3.12. Критерии обнаружения выбросов
Среди методов оценки однородности выборочных данных следует выделить
группу методов, связанных с обнаружением аномальных, не согласующихся
с остальными элементами выборки наблюдений.
Результаты проведенных экспериментов или испытаний иногда существенно от-
отличаются от наблюдаемых средних значений. Необходимо быть уверенным, что эти
результаты не являются грубым промахом, ошибкой при фиксировании наблюдае-
наблюдаемой величины. Другими словами, следует убедиться, являются ли эти отклонения
случайными, либо их появление является следствием проявления систематических
(или, по крайней мере, фиксированных) неслучайных процессов.
Для проверки значимости подозрительных экспериментальных данных разра-
разработаны специальные статистические критерии. Если такой критерий подтверждает
гипотезу о том, что подозрительный результат значимо отличается от остальных,
то исследователь должен выявить причину такого отклонения. Если причина со™
держится в нарушении условий эксперимента (скачок напряжения сети, поломка
измерительного прибора), то она должна быть устранена, а полученный выброс
исключается из выборки. Возможно, что причина отклонения содержится в появ-
появлении нового физического процесса. Тогда статистическое установление значимости
выброса привлечет внимание исследователя к этому процессу.
544
Проверка гипотез о значениях параметров распределений
[Гл.4
Рекомендуется проводить обязательный анализ значимости отклонения край™
них значений выборки от остальных, так как если они являются выбросами, то
их использование при оценке выборочных моментов (особенно высших порядков)
и проверка различных статистических гипотез может привести к большим ошибкам.
В рассматриваемых ниже критериях предполагается, что выборки предвари™
тельно ранжированы по возрастанию.
4.3.12.1. Критерии выбросов в случае нормального распределения
4.3.12.1.1. Критерий Шовене
Согласно критерию Шовене [519, 520] элемент выборки х^ объема п является
выбросом, если вероятность его отклонения от среднего значения не больше —-.
Критические значения К* статистики Шовене
К =
s = - Е ж>; s = ^zrj Е ^ - s)
1 1
г=1
г=1
приведены в табл. 186.
Таблица 186
Критические значения К* критерия Шовене [519]
п
К*
4
1,54
5
1,65
6
1,73
10
1,96
15
2,13
25
2,33
50
2,57
100
2,81
300
3,14
Если К > К*, то значение Xi (г = 1, ..., п) должно быть признано выбросом.
Задача 291. Пусть в нашем распоряжении имеется выборка объема п = 10:
Xii -3, 2, 6, 11, 15, 19, 26, 28, 30, 41.
Необходимо проверить наличие выброса в выборке критерием Шовене.
Имеем х = 17,5; s2 = 192,71 (s = 13,882). Вычисляем (для xi = 41)
к =
13,882
= 1>693.
Для п = 10 из табл. 186 имеем К* = 1,96.
Так как К = 1,693 < К* = 1,96, крайнее значение в выборке не является выбросом.
Очевидно, что проверка крайнего левого значения приведет к аналогичному результату.
4.3.12.1.2. Критерий Ирвина
Предложен в [521], используется в случае, когда дисперсия распределения из-
известна заранее. Статистика критерия имеет вид
— для проверки наибольшего значения жп, и
Х2 - X!
— если подозрительным является наименьшее значение х\. При т (г*) < т(а) —
наибольшее (наименьшее) значение признается выбросом с вероятностью а. Кри-
Критические значения т(а) приведены в табл. 187.
4.3]
Критерии тренда и случайности
545
Таблица 187
Критические значения Т{а) критерим Ирвина [29]
п
2
3
10
20
30
40
50
60
Доверительная
вероятность а
0,90
2,33
1,79
1,18
1,03
0,96
0,91
0,88
0,86
0,95
2,77
2,17
1,46
1,27
1,20
1,15
1,11
1,08
0,99
3,64
2,90
2,03
1,80
1,70
1,63
1,60
1,57
п
70
80
90
100
200
300
500
1000
Доверительная
вероятность а
0,90
0,84
0,83
0,82
0,81
0,75
0,72
0568
0,65
0,95
1,05
1,04
1,03
1,02
0,95
0,91
0,87
0,83
0,99
1,53
1,50
1,50
1,47
1,38
1,32
1,28
1,22
Задача 292. Проверить гипотезу о наличии выбросов для данных задачи 291 при
условии, что а = 17 (^принять а. = 0,95 ).
41 — 30 2 + 3
Имеем т = = 0,647 и г* = = 0,294.
Из табл. 187 для п = 10 и а = 0,95 имеем т@,95) = 1,46.
Так как т = 0,647 (г* = 0,294) < т@,95) = 1,46, крайние значения не являются вы-
выбросами.
4.3.12.1.3. Критерий Груббса
Груббсом в [522] предложена серия критериев для обнаружения выбросов, осно-
основанная на статистиках
П =
(Т S
если подозрителвным является наибольшее значение хП1 и
X — Х\
X — Х\
если подозрительным является наименьшее значение х\.
Статистики т\ или т^ применяются, когда дисперсия известна заранее; стати-
статистики т* и г2* — когда дисперсия оценивается по выборке с помощью соотношения
1 П
1 ^^ / -\2
S =
г=1
При т~1 (г*) ^ Ti(a) или Т2 (Т2) ^ Т2(а) проверяемое значение (хп при т\ и т-j*, х\
при Т2 и т|) признается выбросом. Критические значения т±(а) и Т2(а) приведены
в табл. 188.
При п > 25 критические значения т\ мо^но найти, используя приближение [29]
тг(а) =u1+a^i
где Ury — 7™квантиль стандартного нормального распределения.
Для T2{ol) предло^кена аппроксимация [36] при а = 0,95
т2@;95) =
1,31 + 0,4351п(п - 2,7) при 5 ^ п < 35;
1,962 + 0,2811п(п - 15) при 35 < п ^ 500.
18 А. И. Кобзарь
546
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 188
Критические значения ti(ck), Тг(о:) и тз(ск) статистик Груббса [25, 29]
п
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Доверительная вероятность о
0,90
Т\
1,497
1,696
1,835
1,939
2,022
2,091
2,150
2,200
2,245
2,284
2,320
2,352
2,382
2,409
2,434
2,458
2,480
2,500
2,529
2,538
2,555
2,571
2,587
1,406
1,645
1,791
1,894
1,974
2,041
2,097
2,146
2,190
2,229
2,264
2,297
2,326
2,354
2,380
2,404
2,426
2,447
2,467
2,486
2,504
2,520
2,537
тз
1,818
1,943
2,036
2,111
2,172
2,224
2,269
2,309
2,344
2,376
2,406
2,432
2,457
2,480
2,502
2,522
2,541
2,559
2,576
2,592
2,607
2,621
2,635
0,95
т\
1,738
1,941
2,080
2,184
2,267
2,334
2,392
2,441
2,484
2,523
2,557
2,589
2,617
2,644
2,668
2,691
2,712
2,732
2,750
2,768
2,784
2,800
2,815
1,412
1,689
1,869
1,996
2,093
2,172
2,237
2,294
2,343
2,387
2,426
2,461
2,493
2,523
2,551
2,577
2,600
2,623
2,644
2,664
12,683
2,701
2,717
тз
2,121
2,234
2,319
2,386
2,442
2,490
2,531
2,568
2,601
2,630
2,657
2,682
2,705
2,726
2,746
2,765
2,783
2,799
2,815
2,830
2,844
2,857
2,870
0,99
п
2,215
2,431
2,574
2,679
2,761
2,828
2,884
2,931
2,973
3,010
0,043
3,072
3,099
3,124
3,147
3,168
3,188
3,207
3,224
3,240
3,255
3,269
3,282
Т2
1,414
1,710
1,917
2,067
2,182
2,273
2,349
2,414
2,470
2,519
2,562
2,602
2,638
2,670
2,701
2,728
2,754
2,778
2,801
2,823
2,843
2,862
2,880
тз
2,712
2,806
2,877
2,934
2,981
3,022
3,057
3,089
3,117
3,143
3,166
3,187
3,207
3,226
3,243
3,259
3,275
3,289
3,303
3,316
3,328
3,340
3,351
Если наряду с дисперсией заранее известно и среднее значение (/i) совокупности,
из которой извлекается выборка наряду с дисперсией, то используется статистика
критические значения которой тз(ск) также приведены в табл. 188. Если тз ^ т%(а),
то выброс признается значимым.
Задача 293. Проверить гипотезу о наличии выбросов в выборке задачи 291 критери-
критериями Груббса при а = 0,95 (для критериев n, T2 и тз будем считать, что а = 14, для
критерия тз принять /j, = 17).
Вычисляем
s = 13,697; х = 17,4;
17,4 + 3
14
= 1,457;
41 - 17,4
14
17,4 + 3
= 1,686;
= 1,489;
41 - 17,4
13,697
41 - 17
= 1,723;
14
= 1,714,
13,697
Из табл. 188 для а = 0,95 и m = 10 находим
Ti @,95) = 2,441, г2@,95) = 2,294 и т3@,95) = 2,568.
Так как п = 1,686 (т2 = 1,457) < п@,95) = 2,441; п* = 1,723 (т2* = 1,489) < т2@,95) =
= 2,294 и тз = 1,714 < тз@,95) = 2,568, наличие выбросов в выборке отклоняется.
Воспользуемся аппроксимацией для Т2@,95):
т2@,95) = 1,31 + 0,435 • 1пA0 - 2,7) = 2,175,
что близко к табличному значению Т2@,95) = 2,294.
4.3]
Критерии тренда и случайности
547
4.3.12.1.4. Критерий наибольшего абсолютного отклонения
Основан на статистике
т4 =
гДе s = S Г
-\2
При Т4 ^ т(а) значение
приведены в табл. 189).
признается выбросом (критические значения
Таблица 189
Критические значения тДа)
критерия наибольшего абсолютного отклонения [25]
п
3
4
5
6
7
8
9
10
12
Доверительная
вероятность
0,90
1,412
1,689
1,869
1,996
2,093
2,172
2,238
2,294
2,387
0,95
1,414
1,710
1,917
2,067
2,182
2,273
2,349
2,414
2,519
а
0,99
1,414
1,728
1,972
2,161
2,310
2,431
2,532
2,616
2,753
п
14
16
18
20
22
24
25
28
30
Доверительная
вероятность
0,90
2,461
2,523
2,577
2,623
2,664
2,701
2,734
2,764
2,792
0,95
2,602
2,670
2,718
2,779
2,823
2,862
2,897
2,929
2,958
а
0,99
2,859
2,946
3,017
3,079
3,132
3,179
3,220
3,258
3,291
В [36] предложена весьма точная аппроксимация (с точностью до ^J 0,1)
для т±{а) при а = 0,95:
т4@,95) =
1,39 + 0,4621п(гс - 3) при 5 ^ п < 35;
2,136 - 0,2811п(гс - 15) при 35 < п ^ 500.
Задача 294. Проверить гипотезу наличия выбросов в выборке задачи 291 критерием
наибольшего абсолютного отклонения при доверительной вероятности а = 0,95.
41 - 17,5
Вычисляем Т4 =
max Xi — х
= 1,718.
s 13,679
Из табл. 189 для п = 10 и а = 0,95 имеем т4@,95) = 2,414.
Так как Т4 = 1,718 < Т4@,95) = 2,414, гипотеза о наличии выбросов не находит под-
подтверждения.
Вычислим теперь аппроксимацию
т4@,95) = 1,39 + 0,462 • 1пA0 - 3) = 2,289,
что близко к табличному значению.
4.3.12.1.5. Критерий Дэвида
Является модификацией критерия Груббса (см. раздел 4.3.12.1.3), использует
— — 1 т
статистику [523] Тк = — или т! = , где s = ^^(Уг ~ У) —выбо™
s s m — 1 ¦z—-J
г=1
рочная дисперсия, оцениваемая по отдельной независимой выборке (объема га)
значений г/».
18*
548 Проверка гипотез о значениях параметров распределений [Гл. 4
Критические значения т^(а) статистики Дэвида приведены в табл. 190. При
п > 25 применима аппроксимация
где и7 — 7™квантиль стандартного нормального распределения.
При Т5 (те*) ^ т§{а) одно из крайних выборочных значений признается выбросом
с вероятностью а.
Задача 295. Для ряда данных задачи 291 проверить наличие выбросов критерием
Дэвида при доверительной вероятности а = 0,95. Известно, что оценка дисперсии
s' = 182,15 получена по независимой выборке объема т = 10.
Имеем s = 13,496, тогда 75 = ^^f = 1,741 и т| = ^^ = 1,519.
Из табл. 190 для п = 10, т = 10 и а = 0,95 находим т5@,95) = 2,89.
Так как rs = 1,74 < ts@,95) = 2,89, гипотеза о наличии выбросов в выборке отклоня-
отклоняется.
Такой же результат дает аппроксимация. Имеем
и a-i = -и o,95~i = iio,995 « 4,91 • (о,995°д4 - 0,0050'14) = 2,568;
+ 1+ 10
( з Г?\
т5@,95) « 2,568 • 1 + - . л / — = 3,38.
V 9 v 10/
Видим, что ошибка аппроксимации велика (точное значение rs@,95) = 2,89). Это свя-
связано с малым объемом выборки п = 10 (для точной аппроксимации необходимо п > 25).
4.3.12.1.6. Критерии Диксона
Используются для быстрого выявления выпадающих наблюдений по отношению
размаха и подразмахов.
Статистиками критериев являются [524] (в скобках указаны проверяемые на-
наблюдения):
— для проверки одного сомнительного наблюдения
гю = (для проверки х\); Гю = — — (для проверки хп);
Хп — Х\ Хп — Х\
— для проверки одного сомнительного наблюдения независимо от противополож-
противоположного крайнего наблюдения
х2 — х\ , х хп — xn~i ( ,
П X 1 Хл A>] П X X, ^П^
Xn—i Х\ Хп ?2
— для проверки одного сомнительного наблюдения независимо от двух противопо-
противоположных крайних
Х2- X! , , Хп ^ Хп^1 / х
ri2 = х 9 ^ Ж1 (^i); ri2= х ^Хч М;
Хп — 2 XI Хп Хз
— для проверки одного сомнительного наблюдения независимо от следующего по
величине
%3 — Х\ , ч Хп ^ Хп~2 ( \
Г20 = _ {Xl)l Г20 = _ (Хп);
Jyfl Jy\ Jun ^1
— для проверки одного сомнительного наблюдения независимо от следующего по
величине и крайнего противоположного
Хъ~ Х\ ( ч Хп ~~ Хп^2 / х
r2i = х 1 ^ Ж1 (^i); r2i= (a?n);
Хп — 1 Х\ Хп ?2
4.3]
Критерии тренда и случайности
549
Критические значения
Таблица 190
статистики Дэвида
п
га
4
5
6
7
8
9
10
11
13
Доверительная вероятность а = 0,90
10
11
12
13
14
15
16
17
18
19
20
24
30
40
60
120
оо
1,68
1,66
1,65
1,63
1,62
1,61
1,61
1,60
1,59
1,59
1,58
1,57
1,55
1,54
1,52
1,51
1,50
1,92
1,90
1,88
1,86
1,85
1,84
1,83
1,82
1,82
1,81
1,80
1,78
1,77
1,75
1,73
1,71
1,70
2,09
2,07
2,05
2,03
2,01
2,00
1,99
1,98
1,97
1,96
1,96
1,94
1,92
1,90
1,87
1,85
1,83
2,23
2,20
2,17
2,16
2,14
2,12
2,11
2,10
2,09
2,08
2,08
2,05
2,03
2,01
1,98
1,96
1,94
2,33
2,30
2,28
2,26
2,24
2,22
2,21
2,20
2,19
2,18
2,17
2,15
2,12
2,10
2,07
2,05
2,02
2,42
2,39
2,36
2,34
2,32
2,31
2,29
2,28
2,26
2,26
2,25
2,22
2,20
2,17
2,14
2,12
2,09
2,50
2,46
2,44
2,41
2,39
2,38
2,36
2,35
2,34
2,33
2,32
2,29
2,26
2,23
2,20
2,18
2,15
2,56
2,53
2,50
2,47
2,45
2,44
2,42
2,41
2,39
2,38
2,37
2,34
2,32
2,29
2,26
2,23
2,20
2,68
2,64
2,61
2,58
2,56
2,54
2,52
2,51
2,49
2,48
2,47
2,44
2,41
2,38
2,35
2,32
2,28
Доверительная вероятность а = 0,95
10
11
12
13
14
15
16
17
18
19
20
24
30
40
60
120
оо
2,01
1,98
1,96
1,94
1,93
1,91
1,90
1,89
1,88
1,87
1,87
1,84
1,82
1,80
1,78
1,76
1,74
2,27
2,24
2,21
2,19
2,17
2,15
2,14
2,13
2,11
2,11
2,10
2,07
2,04
2,02
1,99
1,96
1,94
2,46
2,42
2,39
2,35
2,34
2,32
2,31
2,29
2,28
2,27
2,26
2,23
2,20
2,17
2,14
2,11
2,08
2,60
2,56
2,52
2,50
2,47
2,45
2,43
2,42
2,40
2,39
2,38
2,34
2,31
2,28
2,25
2,22
2,18
2,72
2,67
2,63
2,60
2,57
2,55
2,53
2,52
2,50
2,49
2,47
2,44
2,40
2,37
2,33
2,30
2,27
2,81
2,76
2,72
2,69
2,66
2,64
2,62
2,60
2,58
2,57
2,56
2,52
2,48
2,44
2,41
2,37
2,33
2,89
2,84
2,80
2,76
2,74
2,71
2,69
2,67
2,65
2,64
2,63
2,58
2,54
2,50
2,47
2,43
2,39
2,96
2,91
2,87
2,83
2,80
2,77
2,75
2,73
2,71
2,70
2,68
2,64
2,60
2,56
2,52
2,48
2,44
3,08
3,03
2,98
2,94
2,91
2,88
2,86
2,84
2,82
2,80
2,78
2,74
2,69
2,65
2,61
2,57
2,52
Доверительная вероятность а = 0,99
10
11
12
13
14
15
16
17
18
19
20
24
30
40
60
120
оо
2,78
2,72
2,67
2,63
2,60
2,57
2,54
2,52
2,50
2,49
2,47
2,42
2,38
2,34
2,29
2,25
2,22
3,10
3,02
2,96
2,92
2,88
2,84
2,81
2,79
2,77
2,75
2,73
2,68
2,62
2,57
2,52
2,48
2,43
3,32
3,24
3,17
3,12
3,07
3,03
3,00
2,97
2,95
2,93
2,91
2,84
2,79
2,73
2,68
2,62
2,57
3,48
3,39
3,32
3,27
3,22
3,17
3,14
3,11
3,08
3,06
3,04
2,97
2,91
2,85
2,79
2,73
2,68
3,62
3,52
3,45
3,38
3,33
3,29
3,25
3,22
3,19
3,16
3,14
3,07
3,01
2,94
2,88
2,82
2,76
3,73
3,63
3,55
3,48
3,43
3,38
3,34
3,31
3,28
3,25
3,23
3,16
3,08
3,02
2,95
2,89
2,83
3,82
3,72
3,64
3,57
3,51
3,46
3,42
3,38
3,35
3,33
3,30
3,23
3,15
3,08
3,01
2,95
2,88
3,90
3,79
3,71
3,64
3,58
3,53
3,49
3,45
3,42
3,39
3,37
3,29
3,21
3,13
3,06
3,00
2,93
4,04
3,93
3,84
3,76
3,70
3,65
3,60
3,56
3,53
3,50
3,47
3,38
3,30
3,22
3,15
3,08
3,01
550 Проверка гипотез о значениях параметров распределений [Гл. 4
— для проверки одного сомнительного наблюдения независимо от следующего по
величине и двух крайних противоположных
Хз - X! , ч Хп - Хп^2 / х
Г22 = {%1); Г22 = (Хп).
Хп^2 ~ Хг Хп - Х3
Критические значения статистик гю(а)^ гц(а), 7*12(ск), Г2о(«), ^2i(«) и 7*22@:),
превышение которых приводит к признанию наличия выбросов в выборке, при-
приведены в табл. 191. Критерий гю рекомендуется применять при 3 ^ п ^ 7;
критерий Гц —при 8 ^ п ^ 10, критерий 7*21 —при 11 ^ п ^ 13; критерий Г22 —ПРИ
14 ^ п ^ 25.
Задача 296. Для выборочного ряда задачи 291 проверить гипотезу о наличии выбросов
критериями Диксона при доверительной вероятности а = 0,95.
Вычисляем:
а?2 - Ж1 2 + 3
Хп -
Х2
Х2
Хп ~
хз
- xi
-X!
2-*i
-хг
-X!
41 + 32
2 + 3
= 0,1136;
= 0,1515;
30 + 3
_ 2 + 3
~~ 28 + 3
г2о = "* "х = ^^ = 0,2045; г20 =
- - 41 + 3 ' ' хп-Х! 41 + 3
~о ~х 6 + 3 хп^хп^ 41-28
7*21 = z Г" = ^^ = 0,2727; г21 = — — = — = 0,3333;
6 + 3 = 0,2903; г22 = Хп^Хп^2 = 41^28 = 0?3714.
х.
х.
хп
х'
Хп
п-хг
п^Х2
п^Х3
Хп — 2
»-Х2
41
41
41
41
41
41
41
-3D
+ 3
- 30
- 2
-30
-6
-28
П О с;.
= 0?282;
= 0,3143;
= 0,2954:
жп^2-Ж1 28 + 3 ' ^ жп-ж3 41-6
Из табл. 191 для п=10иа = 0,95 находим критические значения
7-ю@,95) = 0,412; г20@,95) = 0,531; щ@,95) = 0,477;
7-2i@,95) = 0,612; 7-12@,95) = 0,537; г22@,95) = 0,682.
Сравнением убеждаемся, что (рассматриваются максимальные величины)
По = 0,25 < 7-ю@,95) = 0,412; щ = 0,28 < т-ц@,95) = 0,477;
П2 = 0,314 < п2@,95) = 0,537; г20 = 0,2954 < г20@,95) = 0,531;
г21 = 0,33 < 7-2i@,95) = 0,612; г22 = 0,3714 < г22@,95) = 0,682.
Следовательно, ни одна из статистик не приводит к принятию гипотезы о наличии
выбросов в выборке.
4.3.12.1.7. Критерий Хоглина^Иглевича
В работе авторов критерия [525] рассматривается правило выделения выпада™
ющих наблюдений в нормалвно распределеннвхх выборках с помощью порядковых
статистик. Правило обнаружения выбросов формулируется следующим образом.
Наблюдение признается выбросом, если его значение находится вне интервала,
ограниченного величинами
A + к)хщ - кх[п+1^ц и A + к)х[п+1_г] - кхщ,
где хщ—г-я порядковая статистика (т.е. г-й по величине член выборки, упорядо-
упорядоченной по возрастанию).
4.3]
Критерии тренда и случайности
551
Таблица 191
Критические значения гю(а,)^ гц(«), ri2(o), Г2о(«)?
т2i (ol) и г22 (ol) статистик Диксона (значения приведены
последовательно по строкам в соответствии с порядком записи,
т.е. верхняя строка — гю, ..., нижняя — Г22) [25]
п
6
7
8
9
10
11
12
13
Доверительная
вероятность
0,90
0,482
0,609
0,745
0,670
0,821
0,965
0,434
0,530
0,636
0,596
0,725
0,850
0,399
0,479
0,557
0,545
0,650
0,745
0,370
0,441
0,504
0,505
0,594
0,676
0,349
0,409
0,454
0,474
0,551
0,620
0,332
0,385
0,431
0,449
0,517
0,578
0,318
0,367
0,406
0,429
0,490
0,543
0,305
0,350
0,387
0,411
0,467
0,95
0,560
0,689
0,824
0,736
0,872
0,983
0,507
0,610
0,712
0,661
0,780
0,881
0,468
0,554
0,632
0,607
0,710
0,803
0,437
0,512
0,580
0,565
0,657
0,737
0,412
0,477
0,537
0,531
0,612
0,682
0,392
0,450
0,502
0,504
0,576
0,637
0,376
0,428
0,473
0,481
0,546
0,600
0,361
0,410
0,451
0,461
0,521
а
0,99
0,698
0,805
0,925
0,836
0,951
0,995
0,637
0,740
0,836
0,778
0,885
0,945
0,590
0,683
0,760
0,710
0,829
0,890
0,555
0,635
0,701
0,667
0,776
0,840
0,527
0,597
0,655
0,632
0,726
0,791
0,502
0,566
0,619
0,603
0,679
0,745
0,482
0,541
0,590
0,579
0,642
0,704
0,465
0,520
0,554
0,557
0,615
п
13
14
15
16
17
18
19
20
21
Доверительная
вероятность
0,90
0,515
0,294
0,336
0,369
0,395
0,448
0,492
0,285
0,323
0,354
0,382
0,431
0,454
0,277
0,313
0,341
0,370
0,416
0,454
0,269
0,303
0,330
0,359
0,403
0,438
0,263
0,295
0,320
0,350
0,391
0,424
0,258
0,288
0,311
0,341
0,380
0,412
0,252
0,282
0,303
0,333
0,371
0,401
0,247
0,276
0,296
0,326
0,95
0,570
0,349
0,395
0,432
0,445
0,501
0,546
0,338
0,381
0,416
0,430
0,483
0,507
0,320
0,359
0,388
0,406
0,433
0,490
0,313
0,349
0,377
0,397
0,440
0,475
0,306
0,341
0,367
0,379
0,428
0,462
0,306
0,341
0,367
0,379
0,428
0,462
0,300
0,334
0,358
0,372
0,419
0,450
0,295
0,327
0,349
0,365
а
0,99
0,670
0,450
0,502
0,542
0,538
0,593
0,641
0,438
0,486
0,523
0,522
0,574
0,595
0,426
0,472
0,508
0,508
0,557
0,595
0,416
0,460
0,493
0,495
0,542
0,577
0,407
0,449
0,480
0,484
0,529
0,561
0,398
0,439
0,469
0,473
0,517
0,547
0,391
0,430
0,458
0,464
0,506
0,535
0,384
0,421
0,449
0,455
552
Проверка гипотез о значениях параметров распределений
[Гл.4
21
22
23
24
25
26
Окон
Доверительная
вероятность
0,90
0,363
0,391
0,242
0,270
0,290
0,320
0,356
0,382
0,238
0,265
0,284
0,314
0,349
0,374
0,234
0,260
0,278
0,309
0,343
0,367
0,230
0,255
0,273
0,304
0,337
0,360
0,227
0,250
0,95
0,410
0,440
0,290
0,320
0,342
0,358
0,402
0,430
0,285
0,314
0,336
0,352
0,395
0,421
0,281
0,309
0,330
0,347
0,388
0,413
0,277
0,304
0,324
0,343
0,382
0,406
0,273
0,299
а
0,99
0,496
0,524
0,378
0,414
0,440
0,447
0,487
0,514
0,372
0,407
0,432
0,440
0,479
0,505
0,367
0,400
0,423
0,434
0,471
0,497
0,362
0,394
0,417
0,428
0,464
0,489
0,357
0,389
п
26
27
28
29
30
чание
таблицы 191
Доверительная
вероятность а
0,90
0,268
0,300
0,331
0,354
0,224
0,246
0,263
0,296
0,325
0,348
0,220
0,243
0,259
0,292
0,320
0,342
0,218
0,239
0,255
0,288
0,316
0,337
0,215
0,236
0,251
0,285
0,312
0,332
0,95
0,319
0,338
0,376
0,399
0,269
0,295
0,314
0,334
0,370
0,393
0,266
0,291
0,309
0,330
0,365
0,387
0,263
0,287
0,305
0,326
0,360
0,381
0,260
0,283
0,301
0,322
0,355
0,376
0,99
0,411
05422
0,457
05486
0,353
0,383
0,405
0,417
0,450
0,475
0,349
0,378
0,399
0,412
0,444
0,469
0,345
0,374
0,394
0,407
0,438
0,463
0,341
0,369
0,389
0,402
0,433
0,457
Для выбора значения I используются варианты
, lU + 3!
*1 = о
где [... j — целая часть числа.
Значения коэффициентов к для различных вариантов выбора значений I и ве-
вероятности отсутствия выброса а приведены в табл. 192.
Задача 297. Проверить гипотезу о наличии выбросов в выборке задачи 291 критерием
Хоглина-Иглевича при доверительной вероятности а = 0,95.
тж 1 1 Гю-ьз] „ F
Имеем h = - • —^— = 3; h =
Для а = 0,95 и п = 10 из табл. 192 находим к = 2,4 (для Zi); fc = 2,2 (для Z2) и /с = 1,8
(для 1з). Окончательно имеем
z[^i] - к ' (x[n+i^h) - x[h]) =хз- 2,4 • (х8 - ж3) = 6 - 2,4 • B8 - 6) = -46,8;
X[n+i-h] + 2,4 • (a;[n+i_Zl] - x[h]) = х8 + 2,4 • (ж8 - х3) = 6 + 2,4 • B8 - 6) = 80,8.
Видим, что вне интервала (—46,8; 80,8) нет элементов выборки. Очевидно, что при
|2 = 2 интервал становится еще шире: (—59,6; 91,6).
Следовательно, с вероятностью 0,95 можно утверждать отсутствие выбросов в вы-
выборке.
4.3]
Критерии тренда и случайности
553
Таблица 192
Значения коэффициента к критерия Хоглина—Мглевича [525]
п
7
8
9
10
11
12
13
14
15
16
Доверительная
0,90
к
2,3
1,8
2,7
2,0
2 2
1,8
2,3
2,0
2,1
1,9
h
1,7
1,6
1,7
1,8
1,8
1,8
1,8
1,9
1,8
1,9
h
1,5
1,4
1,4
1,5
1,7
1,6
1,6
1,7
1,7
1,7
вероятность а
0,95
к
3,0
2,2
3,3
2,4
2,7
2,2
2,8
2,3
2,5
2,3
h
2,3
2Д
2,1
0,2
2,2
2,1
2,2
2,2
2,2
2,2
h
2,0
1,8
1,8
1,8
2,1
2,0
1,9
2,0
2,1
2,1
п
17
18
19
20
30
40
50
75
100
200
Доверительная
0,90
к
2,2
2,0
2,2
1,9
2,0
2,0
2,0
2,1
2,1
2,2
h
1,8
1,9
1,9
1,8
1,9
2,0
2,0
2,0
2,0
2,2
h
1,7
1,7
1,8
2,2
1,9
1,9
1,9
2,0
2,0
2,2
вероятность а.
0,95
к
2,6
2,3
2,6
2,3
2,2
2,2
2 2
2,3
2,2
2,4
h
2Д
2,1
2,3
2,1
2,2
2,2
2,2
2,2
2,2
2,4
h
2,0
2,4
2 2
2,1
2,1
2 2
2,2
2,2
2,2
2,4
4.3.12.1.8. Критерий Титьена-Мура для обнаружения нескольких выбросов
Критерий, предложенный Титьеном и Муром [526], является обобщением кри-
терия Груббса (см. раздел 4.3.12.1.3) на случай выявления нескольких выбросов
в выборке. Для выделения к наибольших выбросов используется статистика
L,=
E(*«-
п — к
1 j
= - Е Xi И *k = ^^fc Е
г=1
Для выделения к наименьших наблюдений используется статистика
п
2^ [Xi -х*к) ^
т* i=k+l „„„ =* 1 v^ -.
Если подозрительными являются как наименьшие, так и наибольшие наблюде-
наблюдения, то для их обнаружения используется следующее правило. Находятся абсолют-
абсолютные отклонения di = \xi — х\ и ранжируются по возрастанию от d\ до dn. Обозначим
через Zi выборочное значение Xi, для которого di является г~м по величине. Для
проверки гипотезы исключения к наибольших по модулю наблюдений используется
статистика
п-к
„_*
E(z- - z)
-
zk =
При использовании критерия Титьена—Мура рекомендуется сначала использо-
использовать статистику L^ (Ь^), а затем Е^. Наличие выбросов признается значимым
с достоверностью а, если
Lk (L*k) < Lk(a) или Ек ^ Ек(а),
где Lk(a) и Е^(а) — критические значения, приведенные в табл. 193 и 194.
554
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 193
Критические значения Lk(ot) и L%(ol) критерия Титьена—Мура [526, 527]
п
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
к
1
0,011
0,098
0,200
0,280
0,348
0,404
0,448
0,490
0,526
0,555
0,578
0,600
0,611
0,631
0,648
0,661
0,676
0,688
0,732
0,766
0,792
0,812
0,826
0,840
0,003
0,051
0,125
0,203
0,273
0,326
0,372
0,418
0,454
0,489
0,517
0,540
0,556
0,579
0,594
0,608
0,624
0,639
0,696
0,730
0,762
0,784
0,802
0,820
2
0,003
0,038
0,091
0,148
0,200
0,248
0,287
0,326
0,361
0,388
0,416
0,436
0,458
0,478
0,496
0,510
0,530
0,588
0,637
0,673
0,702
0,724
0,744
0,001
0,018
0,055
0,106
0,146
0,194
0,233
0,270
0,305
0,337
0,363
0,387
0,410
0,427
0,447
0,462
0,484
0,550
0,599
0,642
0,672
0,696
0,722
3
4
5
6
Доверительная вероятность
0,020
0,056
0,095
0,134
0,170
0,208
0,240
0,270
0,298
0,322
0,342
0,364
0,384
0,398
0,420
0,489
0,523
0,586
0,622
0,648
0,673
0,038
0,068
0,098
0,128
0,159
0,186
0,212
0,236
0,260
0,282
0,302
0,316
0,339
0,412
0,472
0,516
0,554
0,586
0,614
0,051
0,074
0,103
0,126
0,150
0,172
0,194
0,216
0,236
0,251
0,273
0,350
0,411
0,458
0,499
0,533
0,562
0,062
0,082
0,104
0,124
0,144
0,165
0,184
0,199
0,220
0,296
0,339
0,410
0,451
0,488
0,518
Доверительная вероятность
0,010
0,032
0,064
0,099
0,129
0,162
0,196
0,224
0,250
0,276
0,300
0,322
0,337
0,354
0,377
0,450
0,506
0,554
0,588
0,618
0,646
0,022
0,045
0,070
0,098
0,125
0,150
0,174
0,197
0,219
0,240
0,259
0,277
0,299
0,374
0,434
0,482
0,523
0,556
0,588
0,034
0,054
0,076
0,097
0,122
0,140
0,159
0,181
0,200
0,209
0,238
0,312
0,376
0,424
0,468
0,502
0,535
0,042
0,060
0,079
0,097
0,115
0,136
0,154
0,168
0,188
0,262
0,327
0,376
0,421
0,456
0,490
7
а = 90
0,068
0,086
0,104
0,125
0,142
0,158
0,176
0,251
0,316
0,365
0,408
0,447
0,477
а = 95
0,050
0,066
0,082
0,100
0,116
0,130
0,150
0,222
0,283
0,334
0,378
0,417
0,450
8
0,073
0,092
0,108
0,124
0,140
0,213
0,276
0,328
0,372
0,410
0,442
0,055
0,072
0,086
0,099
0,115
0,184
0,245
0,297
0,342
0,382
0,414
9
0,080
0,094
0,110
0,180
0,240
0,294
0,338
0,378
0,410
0,062
0,074
0,088
0,154
0,212
0,264
0,310
0,350
0,383
10
0,085
0,152
0,210
0,262
0,307
0,348
0,380
0,066
0,126
0,183
0,235
0,280
0,320
0,356
4.3]
Критерии тренда и случайности
555
Таблица 194
Критические значения Ек(а) критерия Титьена^Мура [526, 527]
те
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
к
1
0,003
0,005
0,127
0,204
0,268
0,328
0,377
0,420
0,449
0,485
0,510
0,538
0,558
0,578
0,594
0,610
0,629
0,644
0,693
0,730
0,763
0,784
0,803
0,820
0,001
0,025
0,081
0,146
0,208
0,265
0,314
0,356
0,386
0,424
0,455
0,484
0,509
0,526
0,544
0,562
0,581
0,597
0,652
0,698
0,732
0,758
0,778
0,797
2
0,002
0,022
0,056
0,094
0,137
0,175
0,214
0,250
0,278
0,309
0,337
0,360
0,384
0,406
0,424
0,442
0,460
0,528
0,582
0,624
0,657
0,684
0,708
0,001
0,010
0,034
0,065
0,099
0,137
0,172
0,204
0,234
0,262
0,293
0,317
0,340
0,362
0,382
0,398
0,416
0,493
0,549
0,596
0,629
0,658
0,684
3
4
5
6
Доверительная вероятность
0,009
0,027
0,053
0,080
0,108
0,138
0,162
0,189
0,216
0,240
0,263
0,284
0,304
0,322
0,336
0,417
0,475
0,523
0,562
0,593
0,622
0,016
0,032
0,052
0,073
0,094
0,116
0,138
0,160
0,182
0,198
0,217
0,234
0,252
0,331
0,391
0,443
0,486
0,522
0,552
0,022
0,036
0,052
0,068
0,085
0,105
0,122
0,140
0,156
0,172
0,188
0,264
0,325
0,379
0,422
0,459
0,492
0,026
0,038
0,052
0,067
0,082
0,095
0,110
0,124
0,138
0,210
0,270
0,324
0,367
0,406
0,440
Доверительная вероятность
0,004
0,016
0,034
0,057
0,083
0,107
0,133
0,156
0,179
0,206
0,227
0,248
0,267
0,287
0,302
0,381
0,443
0,495
0,534
0,567
0,599
0,010
0,021
0,037
0,055
0,073
0,092
0,112
0,134
0,153
0,170
0,187
0,203
0,221
0,298
0,364
0,417
0,458
0,492
0,529
0,014
0,026
0,039
0,053
0,068
0,084
0,102
0,116
0,132
0,146
0,163
0,236
0,298
0,351
0,395
0,433
0,468
0,018
0,028
0,039
0,052
0,067
0,078
0,091
0,105
0,119
0,186
0,246
0,298
0,343
0,381
0,417
7
а = 90
0,029
0,040
0,053
0,064
0,076
0,089
0,102
0,168
0,224
0,276
0,320
0,360
0,396
а = 95
0,021
0,030
0,041
0,050
0,062
0,074
0,085
0,146
0,203
0,254
0,297
0,337
0,373
8
0,032
0,042
0,051
0,062
0,072
0,132
0,186
0,236
0,278
0,320
0,355
0,024
0,032
0,041
0,050
0,059
0,114
0,166
0,214
0,259
0,299
0,334
9
0,034
0,042
0,051
0,103
0,154
0,202
0,243
0,284
0,319
0,026
0,033
0,041
0,089
0,137
0,171
0,223
0,263
0,299
10
0,035
0,080
0,126
0,172
0,212
0,252
0,287
0,028
0,068
0,112
0,154
0,195
0,233
0,268
556
Проверка гипотез о значениях параметров распределений
[Гл.4
Задача 298. Для ряда наблюдений
хц 0,916; 0,944; 1,292; 1,452; 1,524; 1,604; 1,632; 1,812; 2,017; 2,671
проверить наличие нескольких выбросов критерием Титьена-Мура при доверительной
вероятности а = 0,90.
Имеем
=-.уж^ = 1,586; V
г=1 г=1
щ - х) = 2,385;
1
хг =
10-2
жг = 1,397;
• Y" ж* = 1,4569;
г=1
2,385
Е<
0,737
2,385
= 0,309.
Из табл. 193 для к = 1 (п = 10, а = 0,90) находим Li@,90) = 0,490, для к = 2 имеем
Ь2@,90) = 0,287. Так как Li = 0,452 < ь/@,90) = 0,490, наибольшее значение х = 2,671
признается выбросом. Так как L2 = 0,309 > Ь2@,90) = 0,287, второе наибольшее значе-
значение не должно быть признано выбросом.
Для наименьших наблюдений имеем
х\ =
10 10
г=2 г=2
= 1,308;
5 ?
1,886
2,385
= 0,790;
ю-2
1,308
2,385
V хг = 1,750;
= 1,308.
Так как L\ = 0,790 > Li@,90) = 0,490 и L*2 = 0,548 > L2@,90) = 0,287, оба наимень-
наименьших наблюдения не должны признаваться выбросами.
Используем теперь ^-критерий. Имеем d = \хг — х\ = 10,916 — 1,586| = 0,67.
Вычисляя далее по аналогии, получаем ранжированный ряд значений di. Результаты
сведем в таблицу, там же укажем ранги величин Xi, соответствующие значениям di
в ранжировке:
г
1
2
3
4
5
di
0,018
0,046
0,062
0,134
0,226
Ri
6
7
5
4
8
Zi
1,604
1,632
1,524
1,452
1,812
г
6
7
8
9
10
di
0,294
0,431
0,642
0,670
1,805
Ri
3
9
2
1
10
Zi
1,291
2,017
0,944
0,916
2,671
Пользуясь данными таблицы, вычисляем
1
4; Е (^ - z? = 2>386; * = g • Еz* = м66;
i=l i=l
= 1,079; z2 = \-Y,Zi = 1,535; J2 (zi - z2f = 0,748;
El = 1^=0,452; E2=°^
2,386 2,386
= 0,309.
Из табл. 194 для а = 0,90 и п = 10 имеем #i@,90) = 0,420 и ?J2@,90) = 0,214.
Так как Ег = 0,452 > ??i@,90) = 0,420 ш Е2 = 0,309 > ^2@,90) = 0,214, оба проверяв™
мых наблюдения (это 0,916 и 2,671) не являются выбросами.
4.3 ] Критерии тренда и случайности 557
4.3.12.1.9. Критерий Роснера для обнаружения нескольких выбросов
Рассмотренный ранее критерий Титьена-Мура (см. раздел 4.3.12.1.8) предпола™
гает, что количество выбросов к заранее известно. Однако это не всегда так, поэтому
наиболее интересны методы не только выделения самих выбросов, но и выявления
их количества. Такая проблема рассмотрена Роснером [528, 529], который выдвинул
и реализовал интересную идею последовательного применения критерия Груббса
(см. раздел 4.3.12.1.3) для выделения одного выброса, основанного на статистике
* / х — х\ хп — х
тЛ = max , ^-^
у s s
Алгоритм критерия Роснера состоит в следующем. По начальной выборке объ-
объема п вычисляются значения х и s и статистика rj". Затем из выборки удаляется
экстремальный член хш[п (жтах)—в зависимости от того, какое значение более
удалено от среднего. Так повторяется к раз. Полученные значения статистик т*^
(г = 1, ..., к) каждый раз сравниваются с критическими значениями, приведенны-
приведенными в табл. 195 для заданных п, к и вероятности а. Превышение критерием г*^ крити-
критического значения, полученного из табл. 195 для некоторого г, позволяет установить
не только наличие выбросов, но и их количество (равное значению г, при котором
появляется первая значимая величина критерия т^). Вычисление последователь-
последовательных статистик ведется до тех пор, пока т*^,^ > т^.
Задача 299. Для ряда наблюдений (п = 20)
Хг: 0, 15, 16, 22, 22, 23, 26, 27, 27, 28,
28, 31, 32, 33, 35, 37, 38, 41, 56, 58
проверить наличие выбросов и установить их количество критерием Роснера при
доверительной вероятности а = 0,95.
Находим для полной выборки:
х = 29,75; s = 13,122;
= 2Д53; ?^Е1 = 29-75-° = 2,267) = 2,267.
s 13122 )
2Д53;
s 13,122 s 13,122
Исключаем из выборки значение х = 0, соответствующее полученному максимуму.
Для оставшихся членов выборки (п = 19) находим
хг = 31,316; 81 = 11,402; п*2 = max (Ё^^ММ = 2,34; 31?316 15 = 1,4зЛ = 2,34.
' ' у 11,402 ' ' 11,402 ) '
Так как 2,34 > 2,267, продолжаем вычисления. Исключаем из выборки значение х = 58,
соответствующее максимуму.
Для оставшихся п = 18 наблюдений имеем
Х2 = 29,833; s2 = 9,666; тГз = max f56^'833 = 2,707; 29'f3 15 = 1,534) = 2,707.
у 9,666 9,666 J
Так как 2,707 > 2,34, продолжаем вычисления. Исключаем из выборки значение х = 56,
соответствующее максимуму.
Для оставшихся п = 17 выборочных данных находим
х3 = 28,294; s3 = 7,346; т*4 = max f 41 ^ 28'294 = 1?730; 28;294 ~ 15 = 1?810 ) = 1,810.
у 7,346 7,346 J
Так как Т\± = 1,81 < т^3 = 2,707, то дальнейшие вычисления прекращаем.
Проверим теперь значимость последовательности статистик
т*1 = 2,267; т*2 = 2,34; г*3 = 2,707; п*4 = 1,81.
558
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 195
Мритические значения т*± критерия Роснера [529, 530]
п
20
20
20
20
20
20
20
20
20
20
20
20
20
20
30
30
30
30
30
30
10
10
11
11
12
12
13
13
14
14
15
15
16
16
17
17
18
18
19
19
20
20
20
20
20
к
2
2
3
3
3
4
4
4
4
5
5
5
5
5
2
2
3
3
3
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
3
3
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
1
2
3
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
3
2,69
2,41
2,76
2,47
2,34
2,81
2,51
2,38
2,29
2,85
2,55
2,40
2,33
2,27
2,89
2,55
2,97
2,61
2,44
3,02
2,39
2,17
2,45
2,23
2,50
2,27
2,57
2,31
2,62
2,39
2,65
2,42
2,70
2,44
2,75
2,48
2,79
2,46
2,80
2,49
2,83
2,52
2,88
2,60
2,45
п
30
30
30
30
30
30
30
30
40
40
40
40
40
40
40
40
40
40
40
40
20
20
20
20
20
20
20
20
20
25
25
30
30
30
30
30
30
30
30
30
30
30
30
30
30
к
4
4
4
5
5
5
5
5
2
2
3
3
3
4
4
4
4
5
5
5
4
4
4
4
5
5
5
5
5
2
2
2
2
3
3
3
4
4
4
4
5
5
5
5
5
г
тн
п
к
Доверительная ]
2
3
4
1
2
3
4
5
1
2
1
2
3
1
2
3
4
1
2
3
2,65
2,48
2,39
3,05
2,67
2,51
2,42
2,35
3,01
2,72
3,07
2,69
2,52
3,14
2,74
2,57
2,45
3,16
2,76
2,59
40
40
50
50
50
50
50
50
50
50
50
50
50
50
50
50
60
60
60
60
5
5
2
2
3
3
3
4
4
4
4
5
5
5
5
5
2
2
3
3
Доверительная ]
1
2
3
4
1
2
3
4
5
1
2
1
2
1
2
3
1
2
3
4
1
2
3
4
5
2,95
2,63
2,49
2,39
2,97
2,65
2,51
2,42
2,37
2,99
2,62
3,05
2,67
3,12
2,73
2,56
3,16
2,77
2,59
2,49
3,19
2,78
2,60
2,51
2,45
35
35
40
40
40
40
40
40
40
40
40
40
40
40
40
40
45
45
50
50
50
50
50
50
50
2
2
2
2
3
3
3
4
4
4
4
5
5
5
5
5
2
2
2
2
3
3
3
4
4
г
ти
п
к
г
вероятность а = 90
4
5
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
1
2
2,46
2,39
3,10
2,72
3,18
2,76
2,58
3,24
2,81
2,62
2,50
3,28
2,84
2,65
2,52
2,44
3,15
2,77
3,26
2,83
60
60
60
60
60
60
60
60
60
60
80
80
80
80
80
80
80
80
80
3
4
4
4
4
5
5
5
5
5
2
2
3
3
3
4
4
4
4
3
1
2
3
4
1
2
3
4
5
1
2
1
2
3
1
2
3
4
вероятность а = 95
1
2
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
1
2
1
2
3
1
2
3,09
2,74
3,17
2,77
3,22
2,81
2,62
3,32
2,86
2,67
2,55
3,31
2,88
2,69
2,55
2,47
3,17
2,82
3,27
2,85
3,34
2,89
2,68
3,40
2,93
50
50
50
50
50
50
50
60
60
60
60
60
60
60
60
60
60
60
60
60
60
80
80
80
80
4
4
5
5
5
5
5
2
2
3
3
3
4
4
4
4
5
5
5
5
5
2
2
3
3
3
4
1
2
3
4
5
1
2
1
2
3
1
2
3
4
1
2
3
4
5
1
2
1
2
2,64
3,31
2,85
2,67
2,54
3,34
2,77
2,68
2,56
2,48
3,28
2,85
3,32
2,90
2,71
3,40
2,93
2,74
2,61
2,72
2,59
3,45
2,96
2,74
2,61
2,52
3,34
2,90
3,42
2,95
2,73
3,48
2,98
2,77
2,63
3,51
3,01
2,77
2,65
2,56
3,45
3,03
3,49
3,03
п
80
80
80
80
80
100
100
100
100
100
100
100
100
100
100
100
100
100
100
80
80
80
80
80
80
80
80
80
80
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
к
5
5
5
5
5
2
2
3
3
3
4
4
4
4
5
5
5
5
5
3
4
4
4
4
5
5
5
5
5
2
2
3
3
3
4
4
4
4
5
5
5
5
5
г
1
2
3
4
5
1
2
1
2
3
1
2
3
4
1
2
3
4
5
3,44
2,98
2,77
2,63
2,54
3,34
2,92
3,44
2,97
2,77
3,47
3,00
2,79
2,66
3,54
3,04
2,81
2,68
2,59
3
1
2
3
4
1
2
3
4
5
1
2
1
2
3
1
2
3
4
1
2
3
4
5
2,81
3,57
3,05
2,84
2,69
3,61
3,11
2,86
2,72
2,62
3,52
3,03
3,60
3,10
2,86
3,64
3,13
2,89
2,74
3,70
3,16
2,91
2,77
2,67
4.3 ] Критерии тренда и случайности 559
Из табл. 195 для а = 0,95, к = 4 и п = 20 находим критические значения Tii@,95) =
= 2,95; Ti2@,95) = 2,63; пз@,95) = 2,49 и п4@,95) = 2,39.
Так как r*i = 2,267 < Гц @,95) = 2,95; п2 = 2,34 < п2@,95) = 2,63; г*3 = 2,707 >
> 7i3@,95) = 2,49 и Тх*4 = 1,81 < 7i4@,95) = 2,39, то делаем следующий вывод: в выборке
имеются к = 3 значимых выброса и ими являются ж = 0, ж = 56иж = 58.
4.3.12.2. Критерии выбросов для экспоненциального распределения
и распределения Вейбулла
4.3.12.2.1. Критерии выбросов для экспоненциального распределения
4.3.12.2.1.1. Критерий Смоляка-Титаренко
Для экспоненциального распределения с плотностью распределения вероятно-
1 ^^
стей f(x) = т~е а наиболее „подозрительными" естественно считать наибольшие
А
наблюдения, как наименее вероятные. Смоляк и Титаренко [527] рассмотрели кри-
критерий, основанный на отношении величины наибольшего члена выборки к выбо™
рочному среднему:
где Х{ — г-е порядковое значение ряда х\^х^^ ..., а^, ..., хп.
Член выборки xn-k+i признается выбросом при Ск > С к (а). Критические зна-
значения Ckipt) приведены в табл. 196.
Задача 300. Для ряда данных
хц 7, 12, 15, 22, 26, 31, 34, 42, 48, 54, 61, 65, 68, 75, 80, 90, 103, 117, 132, 148
проверить наличие выбросов критерием Смоляка-Титаренко при доверительной веро-
вероятности а = 0,95.
Имеем
х = 61,5; & = — = — = 2,407.
х 61,5
При а = 0,95 и п = 20 из табл. 196 находим Ci@,95) = 5,408. Так как С\ не превы-
превышает соответствующего критического значения, то наибольшее значение не может быть
признано выбросом.
4.3.12.2.1.2. Критерий Бродского^Быцаня^Власенко
Критерии, рассмотренные в работе Бродского, Быцаня и Власенко [531], явля™
ются аналогами критерия Диксона (см. раздел 4.3.12.1.6) для случая экспоненци™
ального распределения.
Для экспоненциального распределения, записанного в форме
f(x) = \е-х*,
где А — интенсивность отказов, статистики критериев проверки выбросов имеют
вид [531]
— для проверки на выброс наибольшего значения хп при известном А:
z\ = Ажп_1, z2 = Х(хп - хп-{);
— для проверки на выброс наибольшего значения хп при неизвестном А:
Z'x ==
— для проверки на выброс наибольшего значения хп и наименьшего значения х\:
хп — хп~г
= .
Х\ — Х2
560
Проверка гипотез о значениях параметров распределений
[Гл.4
s
О
5
о
В
н
ф
ffl
сб
В
л
ч
я
ф
м
Ч
)СТЬ
в
н
о
ф
ffl
сб
в
л
ч
я
ф
ffl
о
ц
СО
со
О
О
СО
о
,_(
о
СО
О
О
о
со
о
ь-
СО
00
Is-
тН
г/)
СО
о
СО
СО
см
т-Н
СИ
ю
О)
СО
СО
СО
Is-
ю
СО
СМ
Is-
о
СО
ю
t—
СО
Си
on
t-
LO
СО
СО
СО
О
СО
т-Ч
^
СО
СЪ
СО
СО
СО
"^f
СП)
СО
С^
т-Ч
"xF
СО
Ю
СМ
Of)
Is-
СО
00
см
00
^
00
СО
t-
СО
Is-
С0
СО
ю
т-Н
СЛ
см
т-Ч
СО
ю
СО
тН
СО
СО
^
Is-
СЛ
СО
СО
СО
О)
т-Ч
00
СО
Is-
СО
00
^
О
т-Ч
ю
Is-
СО
О
СО
СЛ
см
см
^
ю
СО
т-Ч
СО
СО
СО
т-Ч
ю
СО
^
00
см
СЛ
СО
Ir-
ю
ю
00
СО
О
о
Ю
ю
ь-
С7)
СО
СО
СМ
со
см
^
СЛ
о^
т-Ч
СО
Is-
СО
СО
т-Ч
Is-
см
т-Ч
см
СЛ
^
О
00
СО
СМ
ю
см
т-Ч
-XF
00
О>
оо
00
СО
О
СИ
г/)
Ю
t-
о
"XF
СО
см
^
см
со
см
СО
оо
СО
СО
00
СО
СМ
СО
т-Ч
ю
см
см
ю
см
Is-
(Л
СМ
СЛ
ОО
СМ
СО
ю
Is-
со
ГЧ1
со
t-
о
о
LQ
ОО
ю
см
СО
со
см
СО
(Л
СО
СО
СО
о
СО
СО
ю
СО
ю
1—1
со
ю
см
СЛ
"xF
о
со
ю
СО
а>
о
о
ю
СО
со
со
^
о
СО
ю
СО
со
ю
СО
ю
см
СО
о
ю
Is-
т—1
СО
СЛ
СО
Ю
Ю
ОО
СО
СМ
со
00
ю
т-Ч
Is-
00
СЛ
СО
СМ
О
Ю
00
СО
ь-
О5
LQ
LO
00
СО
00
СО
^
СО
см
00
СО
т-Ч
ОО
00
СО
СМ
СО
О
00
00
т-Ч
О
t-
ю
00
СМ
т-Ч
см
ю
Is-
00
см
О)
о
Is-
СМ
СО
т-Н
о
о
ю
СО
СО
Ь-
Is-
00
ю
СО
т-Н
ю
ю
СО
СО
СМ
о
см
о
см
СО
Is-
00
ю
00
т-Ч
СМ
см
ю
Is-
C7i
СМ
т-Н
СМ
00
^
СО
СО
о
со
о
т-Ч
ю
со
СО
Ir-
t-
ю
т-Ч
СО
ОО
СМ
ОО
СО
СО
СО
ю
00
ю
см
00
см
Ю
СО
т-Ч
СО
О)
ю
СО
О
00
СМ
Is-
со
о
СО
см
00
Is-
о
Is-
т—1
ю
О)
т-Ч
•^н
СО
СО
О
Is-
^
СМ
т-Ч
"xt
СО
ю
со
ь-
см
а>
см
СО
СО
СО
т-Ч
О
СО
см
00
СО
СМ
СМ
ю
т-Н
СО
О)
т-Ч
О
ю
ю
Is-
о
1—1
Is-
со
т-Ч
Ю
т-Ч
СП
00
ir-
iron
со
СО
00
Is-
О)
СП
СО
ю
оо
LQ
Is-
см
СО
см
л>-
00
СО
СМ
т-Ч
со
со
LQ
см
см
СО
см
СО
Is-
о
т-Ч
ю
СО
ю
СО
т-Ч
СО
съ
т-Ч
ю
тН
СО
00
Is-
О)
СО
СО
СО
СМ
ю
^
Is-
СО
СО
СО
Is-
СО
00
СМ
т-Ч
т-Н
00
СО
тН
см
СО
со
со
см
ю
см
оо
о
СО
СО
О
О)
т-Ч
ю
t-
см
со
ч—|
см
см
ю
см
съ
00
Is-
т-Ч
I4-
00
00
ю
см
съ
СО
Is-
т—1
т-Ч
05
СМ
СО
СО
СО
00
т-Ч
СО
СО
LQ
см
оо
Is-
СО
СО
Is-
со
см
LQ
00
ел
Of)
т—1
см
ю
см
ю
тН
о»
t-
СО
t—
СО
Is-
ю
^
00
т-Ч
ю
СО
00
Is-
00
см
1—1
Is-
сл
СО
СЛ
О
ю
со
со
ю
СО
см
ю
СО
о
СО
ю
Си
см
см
О)
h-
см
о
(Л
Is-
Is-
со
Is-
СО
00
ю
^
СО
ю
СО
Си
о
ю
о
СО
ю
о
<Л
ю
СО
СО
т-Ч
Is-
см
съ
о
ю
СО
00
О
ю
о
т-Ч
см
^
со
о
СО
ю
00
Is-
О)
Is-
00
см
см
СО
^
Is-
СО
ю
СО
О
ю
^
т-Ч
т-Ч
СО
т-Н
тН
^
Is-
CD
СО
СО
Is-
Is-
см
о
Is-
ю
СО
СО
Is-
"^
ю
т-Ч
см
со
СО
о
СО
Ю
00
о
т-Ч
00
т-Ч
о
СО
СО
Is-
^
СМ
оо
СО
СО
ю
ю
»о
Is-
ч—1
СО
ч—1
00
т-Ч
о
ю
t-
СО
Is-
см
00
СМ
Is-
см
CD
СО
СО
ю
ю
LQ
см
см
Is-
см
ю
ю
со
см
00
см
о
о
Is-
СО
00
^
ю
ОО
Is-
СО
О
СО
СО
СМ
СО
СМ
^
см
см
00
со
СП
Is-
00
см
см
00
СО
СО
СМ
ел
ю
ю
СО
см
Is-
ю
ю
СО
ю
см
СО
СО
00
О)
о
о
СО
^
О
ОО
00
СО
Ю
СО
CD
00
СМ
СО
СО
О
ел
00
СО
О)
см
ел
см
СО
ir-
СО
00
СО
ю
со
сх>
со
Ю
о
со
00
С^
Is-
1—1
со
т-Ч
о
ю
Is-
со
СО
о
Ir-
Iron
СО
СО
СМ
СО
О0
^
ю
ю
СО
Is-
Is-
сл
см
00
СО
т-Ч
О
Is-
ю
ю
сх>
со
см
00
ю
С75
т-Ч
ю
00
00
ю
см
со
о
ю
Is-
о
Is-
ю
tr-
trio
О)
СО
СО
Is-
т—1
со
т-Ч
О
ir-
iron
СМ
о
СО
СО
СО
00
СО
СМ
ю
Is-
ю
СО
сл
см
00
СО
О
сл
ю
см
О
CD
00
СМ
СО
СО
^
О
Is-
ч-Ч
ю
см
см
т-Ч
г-
о
00
СО
О
Is-
'xf
ь-
о
Ir-
Iron
СО
О
СО
CD
Is-
00
СО
О
О
00
LQ
t-
СО
О
^
СМ
оо
ю
О
ОО
СО
00
т-Ч
О
сл
СО
СМ
ю
см
т-Ч
ь-
ю
СО
см
СО
т—1
см
ю
^
см
СО
т-Ч
t-
т—1
т-Ч
т—1
СО
СО
СМ
СО
Is-
00
ю
00
СО
Is-
О)
см
ю
о
СО
см
t-
00
СО
СО
^
ю
о
СО
ю
Is-
ю
см
Is-
о
О)
00
СО
ю
СО
О
Is-
ю
^
со
00
т-Ч
Is-
см
ю
т-Ч
СО
СО
СО
(Л
СО
СМ
сл
00
ю
да
00
СО
О
ю
сл
т-Ч
т-Ч
СО
О
г\1
00
СО
Is-
см
ю
^
Is-
со
СО
ю
О)
т-Ч
00
Is-
ю
см
00
ю
СО
Is-
т—1
СО
^
Is-
СО
СМ
Is-
см
О)
т-Ч
СО
ОО
О
О
^
ю
СО
сл
ю
о
СО
о
ю
ч—1
on
т-Ч
СО
Of)
00
00
00
ю
^
ю
см
ю
00
I4-
СО
Ir-
о
о
т-Ч
ю
см
со
СО
СМ
со
СО
^
Is-
00
СМ
ь-
о
СО
см
СО
ОО
о
Is-
JN-
СЛ
ю
т-Н
Is-
со
CD
СО
СО
о
^
Ю
ОО
СО
ir-
iron
СО
СМ
ОО
СО
00
о
^
о
см
о
СО
см
4.3] Критерии тренда и случайности 561
Для статистик перечисленных критериев получены полезные результаты [531]:
п-2
х) = 1 - {l - d+^j" 2
_ д);
J = l
Р(*2 ? х) = е~х- P(z4 > аг) = (п - 2)!A - ж)"-3 Ц 1 + ^ _
i=i
Если принятый уровень значимости а меньше, чем любая из указанных вероят™
ностей (в зависимости от используемого критерия), гипотеза о наличии выбросов
отклоняется.
Задача 301. Для данных задачи 300 проверить наличие выбросов критериями гз и z^
настоящего раздела на уровне значимости а = 0,05.
1 до -I on 1 до -| on
Имеем z3 = = 0,113; z4 = = 0,1176. Вычисляем ?(z3 ^ 0,113) =
148 —- 7 148 —- 12
1
= B0 - 1)! • A - 0,ИЗI8 • ТТ = 0,7262.
v } l ' ; 11 1 + 7- A-0,113)
j=1 -+j-A-0,113)
Так как Р(^з ^ 0,113) = 0,726 > а = 0,05, то наибольшее значение не является выбро-
выбросом.
Аналогично для z^ = 0,1176 имеем Р(^4 ^ 0,1176) = 0,7207, что также больше 0,05 и,
следовательно, также отклоняет гипотезу наличия выброса.
4.3.12.2.1.3. Критерий Кимбера для нескольких выбросов
Кимбер [532] предложил по аналогии с критерием Роснера (см. раздел 4.3.12.1.9)
последовательную процедуру для выявления нескольких выбросов в выборке из экс™
поненциального распределения. Статистика критерия Кимбера Sj для выделения j
наибольших выбросов имеет вид [532]
г=1
Если Sj(a) — критическое значение статистики, то правило принятия решения
по гипотезе включает в себя следующую последовательность операций. Если для
г = 1,2, . ..,& имеет место Si < ЯДа), то с достоверностью а признается, что к
наибольших наблюдений в выборке не являются выбросами. Если Si > Si (а) для
г = &, & — 1, ..., j + 1 и 5j > Sj(a), то j наибольших наблюдений являются выбро-
выбросами. Если Sk > Sfc(a), то к наибольших наблюдений являются выбросами.
Для выделения нижних выбросов используется статистика
А — 1 *? Г) — Л
Очевидно, что S* = Sn^j. Процедура выделения к нижних выбросов аналогич™
на процедуре выделения к верхних выбросов, но с заменой S^, Sk-i, ..., Si на
Ski^k-ii •••?'S'i- Критические значения Sj(a) для выделения нижних и верхних
выбросов приведены в табл. 197 и 198.
562
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 197
Критические значения Sj(ol) статистики Кимбера
для выделения j верхних выбросов [532]
п
Доверительная
0,95
3
1
2
3
4
вероятность а
0,99
3
1
2
3
4
к = 2
10
11
12
13
14
15
16
17
18
19
20
22
24
26
28
30
35
40
45
50
60
70
80
90
100
120
140
0,4830
0,4530
0,4270
0,4030
0,3830
0,3640
0,3470
0,3320
0,3180
0,3060
0,2940
0,2730
0,2560
0,2400
0,2270
0,2150
0,1900
0,1710
0,1550
0,1420
0,1220
0,1070
0,0960
0,0869
0,0894
0,0679
0,0595
0,4340
0,4010
0,3720
0,3480
0,3270
0,3080
0,2920
0,2770
0,2640
0,2520
0,2410
0,2220
0,2060
0,1930
0,1810
0,1710
0,1500
0,1340
0,1210
0,1110
0,0470
0,0630
0,0740
0,0670
0,0612
0,0523
0,0459
0,5700
0,5360
0,5060
0,4800
0,4560
0,4350
0,4150
0,3980
0,3810
0,3660
0,3530
0,3280
0,3070
0,2890
0,2730
0,2580
0,2290
0,2050
0,1860
0,1710
0,1470
0,1290
0,1150
0,1040
0,0948
0,0809
0,0707
0,5140
0,4750
0,4410
0,4120
0,3870
0,3640
0,3450
0,3270
0,3120
0,2970
0,2840
0,2620
0,2420
0,2260
0,2120
0,2000
0,1750
0,1560
0,1400
0,1280
0,1090
0,0955
0,0885
0,0767
0,0699
0,0597
0,0521
к = 3
15
16
17
18
19
20
22
24
26
28
30
35
40
45
50
60
0,3800
0,3630
0,3470
0,3330
0,3250
0,3130
0,2910
0,2690
0,2510
0,2360
0,2290
0,1980
0,1790
0,1660
0,1470
0,1270
0,3210
0,3040
0,2880
0,2740
0,2660
0,2550
0,2350
0,2140
0,2000
0,1880
0,1800
0,1550
0,1400
0,1280
0,1140
0,0973
0,3060
0,2870
0,2710
0,2570
0,2480
0,2360
0,2160
0,1960
0,1830
0,1700
0,1630
0,1390
0,1250
0,1130
0,1010
0,0860
0,4520
0,4320
0,4120
0,3950
0,3800
0,3660
0,3430
0,3210
0,3020
0,2830
0,2680
0,2390
0,2130
0,1930
0,1790
0,1540
0,3790
0,3590
0,3390
0,3220
0,3070
0,2940
0,2720
0,2520
0,2350
0,2190
0,2060
0,1820
0,1600
0,1450
0,1330
0,1130
0,3590
0,0337
0,3160
0,2990
0,2840
0,2700
0,2480
0,2280
0,2120
0,1960
0,1840
0,1600
0,1410
0,1260
0,1160
0,0983
4.3]
Критерии тренда и случайности
563
п
Доверительная
0,95
3
1
2
3
4
Окончани
е т а б л
вероятность а
нцы 197
0,99
3
1
2
3
4
к = 3
70
80
90
100
120
0,1110
0,1030
0,0932
0,0853
0,0626
0,0852
0,0781
0,0706
0,0636
050476
0,0751
0,0685
0,0706
0,0559
0,0417
0,1330
0,1190
0,1090
0,0994
0,0727
0,0981
0,0873
0,0796
0,0726
0,0532
0,0849
0,0754
0,9685
0,0624
0,0458
к = 4
20
22
24
26
28
30
35
40
45
50
60
70
80
90
100
120
140
0,3210
0,2990
0,2800
0,2630
0,2480
0,2350
0,2080
0,1870
0,1690
0,1550
0,1340
0,1170
0,1050
0,0948
0,0866
0,0740
0,0647
0,2610
0,2400
0,2230
0,2080
0,1950
0,1840
0,1610
0,1440
0,1300
0,1190
0,1010
0,0888
0,0792
0,0715
0,0653
0,0588
0,0488
0,2410
0,2210
0,2030
0,1890
0,1760
0,1660
0,1440
0,1280
0,1150
0,1050
0,0892
0,0779
0,0693
0,0625
0,0571
0,0487
0,0426
0,2350
0,2130
0,1950
0,1800
0,1680
0,1570
0,1360
0,1200
0,1070
0,0974
0,0826
0,0719
0,0639
0,0576
0,0525
0,0447
0,0391
0,3770
0,3510
0,3290
0,3090
0,2920
0,2770
0,2450
0,2200
0,2000
0,1830
0,1570
0,1380
0,1230
0,1110
0,1010
0,0866
0,0756
0,3020
0,2780
0,2580
0,2400
0,2250
0,2120
0,1850
0,1650
0,1490
0,1360
0,1115
0,1010
0,0897
0,0809
0,0737
0,0628
0,0546
0,2770
0,2530
0,2330
0,2160
0,2010
0,1890
0,1630
0,1440
0,1300
0,1180
0,0998
0,0869
0,0772
0,0695
0,0633
0,0538
0,0470
0,2690
0,2430
0,2220
0,2050
0,1900
0,1770
0,1520
0,1340
0,1200
0,1080
0,0915
0,0795
0,0704
0,0633
0,0576
0,0489
0,0270
Задача 302. Для ряда данных задачи 300 проверить наличие выбросов критерием
Кимбера при доверительной вероятности а = 0,95.
Вычисляем
132
?*«
г=1
148 х19
= U,IzU; D2 =
1230
19 1082
?*«
г=1
= 0,122;
= = 0,123;
950
—^ = = 0,124.
!7 833
г=1
Используя табл. 197 для п = 20, а = 0,95, к = 4, убеждаемся, что S^ = 0,124 <
< Я4@,95) = 0,235, и по аналогии S3 < Я3@,95), S2 < Я2@,95), Si < Si @,95). Следо-
Следовательно, верхних выбросов в выборке нет.
Проверяем нижние выбросы. Имеем
Ж1 + Ж2 19
= В= 0,632;
19
о* _
Оч —
Х4
= | =0,393;
^ = Н = 0j441;
Х\ + Х2 + 3?з 34
= * = 0,317.
82
564
Проверка гипотез о значениях параметров распределений
[Гл.4
Обратившись к табл. 198 (к = 4), убеждаемся, что
ЯГ > ЯГ @,95) = 0,596; S%< S?@,95) = 0,717;
*^з < 5*3 @,95) = 0,868; Si < ^4@,95) = 0,988.
Следовательно, только первое нижнее значение (х\ =7) является выбросом.
Таблица 198
Критические значения Sj (еж) критерия Кимбера
для выделения j нижних выбросов [532]
п
Доверительная
0,95
3
1
2
3
4
вероятность а
1
0,
2
99
3
4
к = 2
10
15
20
50
100
200
0,977
0,977
0,976
0,975
0,975
0,975
0,837
0,829
0,825
0,819
0,817
0,816
0,996
0,995
0,995
0,995
0,995
0,995
0,921
0,917
0,915
0,911
0,910
0,910
к = 3
15
20
50
100
200
0,984
0,984
0,983
0,983
0,983
0,855
0,852
0,846
0,845
0,843
0,705
0,698
0,687
0,683
0,681
0,997
0,997
0,997
0,997
0,997
0,931
0,929
0,926
0,925
0,925
0,808
0,802
0,792
0,789
0,788
к = 4
20
50
10
200
0,988
0,987
0,987
0,987
0,868
0,863
0,861
0,860
0,717
0,706
0,702
0,700
0,596
0,580
0,575
0,573
0,998
0,998
0,997
0,997
0,938
0,935
0,934
0,934
0,817
0,807
0,804
0,803
0,693
0,677
0,672
0,671
4.3.12.2.2. Критерии выбросов для распределения Вейбулла
В [522, 534^537] представлен достаточно полный набор различных методов вы-
выявления вв1бросов в выборках, большинство из которых рассмотрено выше. В [533]
рассмотрены методы трансформации статистик известных критериев для обнару-
обнаружения выбросов в выборках, извлекаемых из генеральных совокупностей, имеющих
распределение Вейбулла.
Для выделения верхних выбросов статистиками критериев являются:
— критерии типа Груббса [522]
G =
Si-
'n —fe + l, ...,п
п-к
где S =
— х) :
1
п
п-к
— критерии типа Диксона [524, 636]
Xn - X!
Ч Rs =
4.3]
Критерии тренда и случайности
565
Для выделения нижних выбросов статистиками критериев являются
— критерии типа Груббса
G* =
sl...,k=
i=k+l
i=k+l
— критерии типа Диксона
Xn-l — '•
E* =
Xk + l
Критические значения G(a) и Ri(a) приведены в табл. 199, G^(a) и R*(a) —
в табл. 200.
При G < G(pt) и Rjs > Rkipt) в выборке признается наличие к верхних выбросов.
При Grjf < GJI(a) и R^ > R^(ol) — признается наличие к нижних выбросов.
Задача 303. Для выборки наблюдений (п = 20)
хц 2 3 11 14 19 25 26 31 39 41
46 54 59 65 71 81 95 120 138 154
проверить наличие в выборке выбросов критериями Груббса и Диксона для распределе-
распределения Вейбулла при доверительной вероятности а = 0,95.
В нашем случае п = 20, хп = 154, х\ = 2.
Результаты вычислений сводим в таблицу, используя критические значения из
табл. 199 и 200 при п = 20, к = 1, 2, 3 и а = 0,95:
Статистика
Хп^к+1
Я2
^п-к+1
Хп^к
Ri
Ei @,95)
R<2
Я2@595)
Яз
Яз@595)
Gk
Gk@,95)
к
1
49,474
26459
138
0,105
0,18
0,106
0,21
0,112
0,24
0,718
0,78
2
44,55
18186
120
0,224
0,24
0,225
0,29
0,238
0,29
0,494
0,65
3
40,12
12160
95
0,388
0,29
0,391
0,34
0,412
0,34
0,33
0,54
Статистика
Хк
Я2
^к
Хк + 1
RI
i?i@,95)
Ri
Д5(О,95)
Ез
Дз@,95)
GI
Cfc@,95)
к
1
57,47
33915
3
0,0066
0,46
0,0073
0,49
0,0085
0,51
0,921
0,41
2
60,5
30782
11
0,059
0,56
0,066
0,59
0,076
0,61
0,836
0,27
3
63,42
28188
14
0,079
0,61
0,088
0,64
0,1016
0,67
0,765
0,19
Из таблицы следует, что три наибольших наблюдения Xi = 120, 138 и 154 признаются
выбросами, так как для них G3 = 0,330 < G3@,95) = 0,54 и R1 = 0,388 > #i@,95) = 0,29,
R2 = 0,391 > Д2@,95) = 0,34, R3 = 0,412 > Д3@,95) = 0,34. Так как G*k > G%{ol), to ниж-
нижние выбросы в выборке отсутствуют.
4.3.12.3. Критерий выбросов для любого непрерывного распределения
(критерий Дарлинга)
Для любого непрерывного распределения, определенного с точностью до пара™
метров, Дарлинг [538] предложил критерий, основанный на статистике 1п = У^ттт—Ч"
для проверки на выброс наибольшего (наименьшего) наблюдения.
566
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 199
Критические значения Сг(ск) и Жг(ск) критериев типа
Груббса и Диксона для выявления к верхних выбросов
в выборке, имеющей распределение Вейбулла [533]
п
G
0,
Ri
Доверительная
90
R2
Rs
вероятность а
G
0,
Ri
95
R2
Rs
к = 1
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0,30
0,41
0,49
0,55
0,60
0,64
0,67
0,69
0,71
0,74
0,75
0,77
0,78
0,79
0,80
0,81
0,46
0,38
0,32
0,28
0,26
0,24
0,22
0,20
0,19
0,18
0,17
0,17
0,16
0,16
0,15
0,14
0,67
0,53
0,44
0,38
0,34
0,31
0,28
0,26
0,25
0,23
0,22
0,21
0,20
0,19
0,18
0,18
0,90
0,70
0,57
0,48
0,42
0,37
0,34
0,31
0,29
0,27
0,25
0,24
0,23
0,22
0,21
0,20
0,20
0,31
0,41
0,48
0,53
0,58
0,61
0,65
0,67
0,69
0,71
0,73
0,75
0,76
0,77
0,78
0,55
0,46
0,38
0,34
0,32
0,29
0,27
0,25
0,24
0,22
0,21
0,21
0,20
0,19
0,18
0,18
0,76
0,62
0,52
0,45
0,40
0,37
0,34
0,32
0,30
0,28
0,26
0,25
0,24
0,23
0,22
0,21
0,95
0,79
0,66
0,56
0,49
0,44
0,40
0,37
0,35
0,32
0,30
0,29
0,28
0,26
0,25
0,24
к = 2
8
9
10
11
12
13
14
15
16
17
18
19
20
0,32
0,38
0,42
0,47
0,50
0,54
0,56
0,59
0,61
0,63
0,65
0,67
0,69
0,43
0,39
0,35
0,32
0,29
0,28
0,26
0,25
0,24
0,23
0,22
0,21
0,20
0,56
0,49
0,44
0,40
0,37
0,35
0,32
0,31
0,29
0,28
0,27
0,26
0,25
0,68
0,59
0,52
0,48
0,44
0,40
0,38
0,36
0,34
0,32
0,31
0,29
0,28
0,25
0,31
0,37
0,41
0,45
0,48
0,51
0,55
0,57
0,59
0,62
0,63
0,65
0,49
0,44
0,40
0,37
0,34
0,32
0,31
0,29
0,28
0,27
0,26
0,25
0,24
0,62
0,56
0,50
0,46
0,43
0,40
0,37
0,35
0,34
0,32
0,31
0,30
0,29
0,75
0,66
0,59
0,54
0,50
0,46
0,43
0,40
0,38
0,36
0,35
0,34
0,32
к = 3
10
12
14
16
18
20
0,29
0,38
0,45
0,50
0,55
0,58
0,44
0,37
0,33
0,29
0,27
0,25
0,56
0,46
0,40
0,36
0,33
0,30
0,66
0,54
0,46
0,41
0,37
0,34
0,24
0,32
0,39
0,45
0,50
0,54
0,50
0,42
0,37
0,34
0,31
0,29
0,62
0,52
0,45
0,40
0,37
0,34
0,72
0,60
0,51
0,46
0,41
0,38
Здесь F(xi) = Р(ж < Xi) — функция распределения вероятностей в точке х = Х{.
При п > 3 распределение 1п близко к нормальному со средним МAП) и диспер-
дисперсией D(In), где
МA„) =
D(/n) =
п- 1
4.3]
Критерии тренда и случайности
567
Таблица 200
Критические значения G* (а) и Д*(ск) критериев типа
Груббса и Диксона для выявления к нижних выбросов
в выборке, имеющей распределение Вейбулла [533]
п
0,
щ
Доверительная
90
Щ
Щ
вероятность а
G*
0,
Щ
95
Щ
Щ
к = 1
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0,11
0,16
0,20
0,25
0,28
0,31
0,34
0,36
0,38
0,40
0,42
0,43
0,45
0,46
0,48
0,49
0,67
0,60
0,56
0,53
0,51
0,49
0,47
0,46
0,45
0,44
0,43
0,43
0,42
0,41
0,40
0,39
0,79
0,70
0,64
0,60
0,57
0,54
0,52
0,49
0,49
0,47
0,46
0,45
0,44
0,43
0,43
0,42
0,94
0,80
0,72
0,66
0,61
0,58
0,55
0,53
0,51
0,50
0,49
0,47
0,46
0,46
0,44
0,44
0,07
0,10
0,14
0,18
0,20
0,24
0,26
0,28
0,30
0,32
0,34
0,35
0,37
0,38
0,40
0,41
0,74
0,68
0,64
0,60
0,58
0,56
0,55
0,53
0,52
0,51
0,50
0,50
0,49
0,48
0,47
0,46
0,86
0,77
0,71
0,67
0,64
0,61
0,59
0,56
0,56
0,54
0,53
0,52
0,51
0,50
0,50
0,49
0,97
0,87
0,79
0,74
0,69
0,65
0,62
0,61
0,58
0,57
0,56
0,55
0,53
0,53
0,51
0,51
к = 2
8
9
10
11
12
13
14
15
16
17
18
19
20
0,10
0,13
0,15
0,18
0,20
0,22
0,23
0,25
0,27
0,28
0,30
0,31
0,32
0,67
0,64
0,62
0,60
0,58
0,57
0,55
0,54
0,53
0,52
0,52
0,51
0,50
0,75
0,71
0,68
0,65
0,63
0,61
0,60
0,58
0,56
0,56
0,55
0,54
0,53
0,82
0,76
0,72
0,69
0,66
0,64
0,62
0,61
0,59
0,58
0,57
0,56
0,55
0,07
0,09
0,11
0,13
0,15
0,17
0,18
0,20
0,22
0,23
0,25
0,26
0,27
0,73
0,70
0,68
0,65
0,64
0,62
0,61
0,60
0,59
0,58
0,57
0,57
0,56
0,80
0,76
0,73
0,71
0,68
0,67
0,65
0,64
0,62
0,61
0,60
0,59
0,59
0,86
0,81
0,77
0,75
0,72
0,70
0,68
0,66
0,65
0,64
0,63
0,62
0,61
к = 3
10
12
14
16
18
20
0,08
0,12
0,15
0,18
0,21
0,23
0,70
0,66
0,63
0,61
0,58
0,57
0,76
0,71
0,67
0,64
0,61
0,60
0,82
0,75
0,70
0,67
0,64
0,62
0,06
0,09
0,12
0,14
0,17
0,19
0,75
0,71
0,68
0,65
0,63
0,61
0,80
0,75
0,72
0,68
0,66
0,64
0,86
0,79
0,74
0,71
0,69
0,67
т. е. если
то с вероятностью а нижнее (верхнее) выборочное значение признается выбросом
(ча — «-квантиль стандартного нормального распределения).
568 Проверка гипотез о значениях параметров распределений [Гл. 4
В [539, 540] предложена модификация критерия Дарлинга, имеющая большую
мощность, чем исходный критерий. Предложены статистики:
— для проверки на выброс наибольшего значения хп
для проверки на выброс наименьшего значения х\
При L (L*) ^ xlt [^(п — 1)] в выборке отсутствуют выбросы, при L (L*) < %^[2(п — 1)]
хп (xi) является выбросом. Здесь %^,[2(п —1)] — «-квантиль %2-распределения
с / = 2 (п — 1) степенями свободы.
При нормальном исходном распределении мощность этого критерия по сравне-
сравнению с критерием Груббса падает не более, чем на 20%.
Задача 304. Для ряда значений выборки, взятой из экспоненциального распределения
1 / х\
с плотностью f{x) = — ехр I \ и параметром X = 21,5:
А \ А/
хц 1, 4, 9, 16, 23, 24, 28, 31, 56, 63
проверить наличие выбросов критерием Дарлинга при доверительной вероятности
а = 0,95.
Функция нашего распределения F(x) = 1 —- ехр I —
21,5
Находим
F(Xl) = 1 - ехр (-^) = 0.0454; F(x2) = 1 ^ ехр (-^) = 0Д627;
= 0,342; F(a;4) = 0,5249; F(x5) = 0,6569; F(x6) = 0,67256;
F(x7) = 0,7281; F(x8) = 0,7635; F(x9) = 0,9251; F(x10) = 0,9466.
Далее вычисляем
0,9466 /
=21,736.
Из табл. 55 находим Xo,9sB • 9) = 28,869. Так как L = 21,736 < 28,869, то с вероятно™
стью 0,95 наибольшее значение в выборке хп = 63 следует считать выбросом.
Вычислим теперь
L* = -2 • Y^ In 1 - ~F(Xi+1} = -2 • (-2,03859 - 1,1689 - ... - 0,05756) = 11,4622.
Сравнением L* = 11,46 < Хо,9бA8) = 28,869 убеж:даемся, что наименьюаее значение
х\ = 1 также является выбросом.
4.4] Толерантные пределы 569
4.4. Толерантные пределы
Ценную в практическом отношении информацию о распределении наблюдаемой
случайной величины дают границы интервала, в котором с заданной вероятно™
стью а будет находиться /3-я часть совокупности значений случайной величины.
Такие интервалы (или пределы, в случае односторонних интервалов) называются
толерантными.
Например, широко используемый показатель при нормировании характеристик
надежности технических изделий — 7™РесУРс5 определяемый значением наработки
изделия, при котором доля дефектных изделий в партии не будет превышать
A — 7M в математической статистике интерпретируется как односторонний толе-
толерантный предел при j = /3.
4.4.1. Толерантные пределы в случае нормального распределения
4.4.1.1. Толерантные пределы при известных параметрах распределепим
(// и а2)
Двусторонний симметричный относительно ц интервал имеет вид
2 2
Односторонние толерантные интервалы равны
(-оо; fi + u^a] и [/i - и^а; оо) ,
где и? — е-квантиль стандартного нормального распределения.
Задача 305. Найти двусторонний толерантный интервал^ в котором будет нахо-
находиться 75% всей совокупности значений нормально распределенной случайной величи-
величины с параметрами распределения /л = 101 и а = 24,8.
В нашем случае /3 = 0,75 и
и i+o,75 = ^о,875 « 4,91 • @,875ОД4 - 0Д250'14) = 1,149.
2
Тогда искомый интервал ограничен величинами
101 - 1,149 • 24,8 = 72,5 и 101 + 1,149 • 24,8 = 129,5.
Таким образом, в интервале от 72,5 до 129,5 будет находиться 75% всех значений
случайной величины.
4.4.1.2. Толерантные пределы при неизвестных параметрах распреде лепим
4.4.1.2.1. Среднее /л неизвестно, дисперсим и2 известна
Для односторонних толерантных интервалов (^оо;тв] и [тн;оо), где
тв = х + а(п, а, /3)а и тн = х — а(п, а, /3)сг, справедливо утверждение о том, что /3-я
часть совокупности значений случайной величины х с вероятностью а находится
в каждом из них.
Множитель а(п,а,/3) является решением уравнения
откуда следует, что а(п,а,/3) = и@ -\—т=, где и1—7™квантиль стандартного нор™
мального распределения, Ф — функция Лапласа.
570
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 201
Множители а(те9 ск, /3) длм построения
односторонних толерантных пределов
в случае нормального распределения
(/л неизвестно, сг2 известно) [56]
п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
60
70
80
90
100
200
300
400
500
1000
оо
а
0,90
0,90
2,563
2,188
2,021
1,922
1,855
1,805
1,766
1,735
1,709
1,687
1,668
1,652
1,637
1,624
1,612
1,602
1,592
1,584
1,576
1,568
1,538
1,516
1,498
1,484
1,473
1,463
1,447
1,435
1,425
1,417
1,410
1,372
1,356
1,346
1,339
1,322
1,282
0,95
2,926
2,551
2,385
2,286
2,218
2,168
2,129
2,098
2,072
2,050
2,031
2,015
2,000
1,987
1,976
1,965
1,956
1,947
1,939
1,931
1,901
1,879
1,861
1,847
1,836
1,826
1,810
1,798
1,788
1,780
1,773
1,735
1,719
1,709
1,702
1,685
1,645
0,99
3,608
3,233
3,066
2,967
2,899
2,850
2,811
2,779
2,754
2,732
2,713
2,695
2,682
2,669
2,657
2,647
2,637
2,628
2,620
2,613
2,583
2,560
2,543
2,529
2,517
2,508
2,492
2,480
2,470
2,461
2,455
2,417
2,400
2,390
2,384
2,367
2,326
0,95
0,90
2,926
2,445
2,231
2,104
2,017
1,953
1,903
1,863
1,830
1,802
1,777
1,756
1,738
1,721
1,706
1,693
1,680
1,669
1,659
1,649
1,611
1,582
1,560
1,542
1,527
1,514
1,494
1,478
1,465
1,455
1,446
1,398
1,377
1,364
1,355
1,334
1,282
0,95
3,290
2,808
2,595
2,467
2,380
2,316
2,267
2,226
2,193
2,165
2,141
2,120
2,101
2,084
2,070
2,056
2,044
2,033
2,022
2,013
1,974
1,945
1,923
1,905
1,890
1,877
1,857
1,841
1,829
1,818
1,809
1,761
1,740
1,727
1,718
1,697
1,645
0,99
35971
3,489
3,276
3,149
3,062
2,998
2,948
2,908
2,875
2,846
2,822
2,801
2,783
2,766
2,751
2,738
2,725
2,714
2,704
2,694
2,655
2,627
2,604
2,586
2,572
2,559
2,539
2,523
2,510
2,500
2,491
2,443
2,421
2,409
2,400
2,378
2,326
Значения множителей а(п,а,/3) приведены в табл. 201.
Для двусторонних толерантных интервалов (тВ1тп) справедливы формулы
тв = х + а* (в,
тн = х — а* (п, а, /3) а.
Для них справедливо утверждение, что с вероятностью а /3-я часть распределе-
распределения случайной величины х заключена в промежутке [тн;тв]. Значения множителей
4.4]
Толерантные пределы
571
Таблица 202
Множители а* (П) о, /3) длм построения
двусторонних толерантных интервалов
в случае нормального распределения
(/л неизвестно, сг2 известно) [56]
п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
60
70
80
90
100
200
300
400
500
1000
оо
а
0,90
C
0,90
2,927
2,446
2,236
2,114
2,034
1,977
1,935
1,902
1,875
1,854
1,836
1,821
1,808
1,797
1,788
1,779
1,772
1,765
1,759
1,753
1,732
1,718
1,708
1,700
1,694
1,689
1,682
1,677
1,673
1,670
1,667
1,656
1,653
1,651
1,650
1,648
1,645
0,95
3,290
2,809
2,597
2,473
2,390
2,330
2,285
2,250
2,222
2,198
2,179
2,162
2,148
2,136
2,125
2,115
2,107
2,099
2,092
2,086
2,062
2,046
2,034
2,025
2,018
2,012
2,004
1,998
1,993
1,990
1,987
1,974
1,969
1,967
1,966
1,963
1,960
0,99
3,972
3,490
3,277
3,152
3,068
3,003
2,955
2,917
2,886
2,861
2,839
2,821
2,805
2,790
2,778
2,767
2,757
2,748
2,740
2,733
2,704
2,684
2,670
2,659
2,650
2,643
2,632
2,625
2,619
2,614
2,610
2,594
2,588
2,585
2,582
2,579
2,576
0,95
/5
0,90
3,242
2,668
2,415
2,265
2,165
2,093
2,030
1,996
1,961
1,933
1,900
1,889
1,872
1,857
1,844
1,832
1,822
1,812
1,804
1,797
1,767
1,748
1,733
1,723
1,714
1,708
1,697
1,690
1,684
1,680
1,677
1,661
1,656
1,653
1,651
1,649
1,645
0,95
3,605
3,031
2,778
2,627
2,525
2,451
2,395
2,350
2,313
2,283
2,258
2,236
2,218
2,201
2,187
2,174
2,163
2,152
2,143
2,135
2,102
2,080
2,063
2,051
2,041
2,033
2,022
2,013
2,007
2,002
1,998
1,979
1,973
1,970
1,967
1,954
1,960
0,99
4,287
3,713
3,459
3,308
3,205
3,130
3,073
3,024
2,986
2,954
2,926
2,903
2,882
2,864
2,848
2,834
2,821
2,809
2,799
2,789
2,751
2,725
2,706
2,691
2,679
2,669
2,655
2,644
2,636
2,629
2,624
2,601
2,593
2,589
2,585
2,581
2,576
а*(п, а,/3), являющиеся решением уравнения
Ф[ ui+a —=
—^= - a*(n,a,j3) ) = /3
приведены в табл. 202.
572 Проверка гипотез о значениях параметров распределений [Гл. 4
Задача 306. Имеется выборка из нормального распределения с известной дисперсией
а2 = 54 и неизвестным средним
Хг: 1, 3, 6, 14, 18, 24, 31, 41, 61, 63.
Необходимо найти односторонние толерантные пределы и двусторонний доверитель-
доверительный интервал при а = 0,95 и /3 = 0,90.
Имеем х = 26. Воспользовавшись табл. 201 и 202, находим значения множителей
а(п,а,/3) = аA0; 0,95; 0,90) = 1,802 и a*(n,a,j3) = а*A0; 0,95; 0,90) = 1,933.
Тогда односторонние толерантные пределы равны
тв = 26 + 1,802 • V54 = 39,24; тн = 26 - 1,802 • Vm = 12,76.
Для двустороннего интервала имеем
тв = 26 + 1,933 • \/ы = 40,20; тн = 26 - 1,933 • \/ы = 11,79.
Таким образом, можно утверждать с вероятностью а = 0,95, что в каждом из интер-
интервалов (-оо; 39,24]; [12,76; оо), [11,79; 40,20] находится 90% (/3 = 0,90) всей совокупности
значений случайной величины.
4.4.1.2.2. Среднее /л известно, дисперсия ст2 неизвестна
Односторонние доверительные интервалы находятся по формулам
тв = ц + 6(n, a, /3)s; тн = ц — Ь(п, а, /3)s,
где
Xi-a(n) ~ A ~ ск)-квантиль распределения хи~квадрат с / = п степенями свободы;
up — /3-квантиль стандартного нормального распределения.
Толерантные множители Ь(в,а,/3) приведены в табл. 203.
Двусторонний толерантный интервал определятся из соотношения
тв = /л + Ь*(в,а, /3) s; тн = /х - Ь*(п, а,/3) 5, где Ь*(п, а,/3) = wi+
Толерантные множители Ь*(п,а,/3) приведены в табл. 204.
Задача 307. Для данных задачи 306 найти толерантные пределы, исходя из того,
что среднее ц = 26 считается известным, а значение дисперсии неизвестно (а = 0,95,
/3 = 0,90).
1 ю
Вычисляем Я2 = — • J^(Xi ~ 26J = 49°596 (^ = 21Д)- Из табл- 203 и 204 находим
г=1
толерантные множители Ь(п,а,/3) = 6A0,0,95,0,90) = 2,042 для односторонних пределов
и b*(n,a,f3) = Ь* A0, 0,95; 0,90) = 2,620 для двустороннего интервала.
Окончательно имеем для односторонних толерантных пределов
тв = 26 + 2,042 • 21,7 = 70,31; тн = 26 - 2,042 • 21,7 = -18,31.
и для двустороннего интервала
тв = 26 + 2,620 • 21,7 = 82,85; тн = 26 - 2,620 • 21,7 = -30,85.
Следовательно, можно утверждать, что с вероятностью а = 0,95 в каждом из интер-
интервалов (-оо; 70,31]; [-18,31; оо); [-30,85; 82,85] находится 90% (/3 = 0,90) всей совокупно»
сти значений случайной величины х.
4.4]
Толерантные пределы
573
Таблица 203
Множители &(то9 о, /3) длм построения
односторонних толерантных пределов
в случае нормального распределения
(/л известно, и2 неизвестно) [56]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
60
70
80
90
100
200
300
400
500
1000
оо
а
0,90
/з
0,90
3,948
2,904
2,485
2,258
2,114
2,014
1,940
1,883
1,837
1,800
1,768
1,741
1,718
1,698
1,680
1,664
1,650
1,637
1,625
1,579
1,547
1,523
1,504
1,489
1,476
1,456
1,441
1,430
1,420
1,412
1,371
1,353
1,343
1,336
1,320
1,282
0,95
6,067
3,727
3,190
2,898
2,714
2,586
2,491
2,417
2,358
2,310
2,269
2,235
2,205
2,179
2,156
2,136
2,117
2,101
2,085
2,026
1,985
1,954
1,930
1,911
1,895
1,869
1,850
1,835
1,823
1,812
1,759
1,737
1,724
1,709
1,694
1,645
0,99
7,167
5,271
4,511
4,099
3,838
3,657
3,522
3,418
3,335
3,267
3,210
3,161
3,119
3,082
3,049
3,020
2,994
2,971
2,949
2,866
2,807
2,764
2,730
2,702
2,680
2,644
2,617
2,595
2,578
2,563
2,488
2,456
2,438
2,417
2,395
2,326
0,95
0,90
5,659
3,742
3,040
2,677
2,455
2,303
2,193
2,108
2,042
1,987
1,942
1,904
1,871
1,842
1,817
1,794
1,774
1,756
1,740
1,676
1,632
1,600
1,574
1,554
1,537
1,511
1,491
1,475
1,462
1,445
1,397
1,374
1,361
1,352
1,331
1,282
0,95
7,263
4,803
3,902
3,437
3,151
2,956
2,814
2,706
2,620
2,551
2,492
2,443
2,401
2,364
2,332
2,303
2,277
2,254
2,233
2,152
2,095
2,053
2,020
1,994
1,973
1,939
1,913
1,893
1,877
1,863
1,793
1,764
1,747
1,735
1,708
1,645
0,99
10,272
6,793
5,519
4,860
4,455
4,181
3,980
3,827
3,706
3,607
3,525
3,456
3,396
3,344
3,298
3,257
3,221
3,188
3,158
3,043
2,963
2,904
2,858
2,821
2,790
2,742
2,706
2,678
2,654
2,635
2,536
2,495
2,471
2,455
2,415
2,326
4.4.1.2.3. Среднее /х и дисперсия и2 неизвестны
Односторонние доверительные интервалы находятся по формулам
тв = х + к (п, а, C) s; тн = х — к (п, а, /3) л,
где х = —
г=1
'"
1
, а, /3) = -^= t(n — 1,
^ а);
, q) —
г=1
574
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 204
Множители 6* (то, о, /3) для построения
двусторонних толерантных интервалов
в случае нормального распределения
(/л известно, и2 неизвестно) [56]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
60
70
80
90
100
200
300
400
500
1000
оо
а
0,90
0,90
5,067
3,727
3,190
2,898
2,714
2,586
2,491
2,417
2,358
2,310
2,269
2,235
2,205
2,179
2,156
2,138
2,117
2,101
2,085
2,026
1,985
1,954
1,930
1,911
1,895
1,869
1,850
1,835
1,823
1,812
1,759
1,737
1,724
1,715
1,694
1,645
0,95
6,038
4,441
3,801
3,454
3,234
3,081
2,968
2,880
2,810
2,752
2,704
2,663
2,628
2,597
2,569
2,545
2,523
2,503
2,485
2,414
2,365
2,329
2,300
2,277
2,258
2,227
2,205
2,187
2,172
2,160
2,096
2,070
2,054
2,044
2,018
1,960
0,99
7,936
5,836
4,995
4,539
4,250
4,049
3,900
3,785
3,693
3,617
3,554
3,500
3,453
3,412
3,376
3,344
3,315
3,289
3,266
3,173
3,109
3,060
3,023
2,992
2,967
2,927
2,897
2,874
2,854
2,838
2,755
2,720
2,699
2,686
2,652
2,326
0,95
0,90
7,263
4,803
3,902
3,437
3,151
2,956
2,814
2,706
2,620
2,551
2,492
2,443
2,401
2,364
2,332
2,303
2,277
2.254
2,233
2,152
2,095
2,053
2,020
1,994
1,973
1,939
1,913
1,893
1,877
1,863
1,793
1,764
1,747
1,735
1,708
1,645
0,95
8,654
5,723
4,650
4,095
3,754
3,522
3,354
3,225
3,122
3,039
2,970
2,911
2,861
2,817
2,778
2,744
2,714
2,686
2,661
2,564
2,496
2,446
2,408
2,376
2,351
2,310
2,280
2,256
2,236
2,220
2,137
2,102
2,082
2,068
2,045
1,960
0,99
11,373
7,521
6,111
5,382
4,934
4,629
4,407
4,238
4,103
3,994
3,903
3,826
3,760
3,702
3,652
3,607
3,566
3,530
3,497
3,369
3,281
3,215
3,164
3,123
3,089
3,036
2,996
2,965
2,939
2,918
2,808
2,762
2,736
2,718
2,675
2,326
квантиль нецентрального t-распределения (см. раздел 1.1.23) с / = га степенями
свободы и параметром нецентральности S.
Толерантные множители к(п,а,/3) приведены в табл. 205.
При п ^ 50 справедлива аппроксимация [542]
k(n,a,p) =
2(r»-l)-t*|
4.4]
Толерантные пределы
575
Таблица 205
Множители Jfe(n, о,/3) для построения
односторонних толерантных пределов
в случае нормального распределения
(§л и <х2 неизвестны) [56]
п
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
60
70
80
90
100
200
300
500
1000
сю
а
0,90
0,90
2,745
2,494
2,333
2,220
2,133
2,066
2,012
1,966
1,928
1,896
1,867
1,842
1,820
1,800
1,782
1,766
1,702
1,657
1,624
1,598
1,577
1,560
1,532
1,512
1,495
1,482
1,471
1,412
1,387
1,362
1,338
1,282
0,95
3,402
3,093
2,894
2,755
2,650
2,569
2,503
2,448
2,402
2,363
2,329
2,299
2,273
2,249
2,227
2,205
2,132
2,080
2,041
2,010
1,98 6
1,965
1,933
1,909
1,890
1,874
1,861
1,793
1,765
1,737
1,709
1,645
0,99
4,665
4,243
3,971
3,782
3,642
3,533
3,443
3,370
3,298
3,256
3,211
3,172
3,139
3,105
3,077
3,051
2,952
2,883
2,832
2,793
2,761
2,734
2,693
2,662
2,637
2,617
2,600
2,514
2,477
2,441
2,407
2,326
0,95
0,90
3,413
3,009
2,752
2,582
2,454
2,355
2,276
2,210
2,156
2,109
2,069
2,034
2,002
1,974
1,949
1,926
1,838
1,778
1,733
1,698
1,669
1,646
1,609
1,582
1,560
1,542
1,527
1,450
1,417
1,386
1,355
1,282
0,95
4,209
3,709
3,401
3,188
3,032
2,911
2,815
2,736
2,670
2,614
2,566
2,524
2,486
2,458
2,423
2,396
2,292
2,220
2,167
2,126
2,092
2,065
2,022
1,990
1,964
1,944
1,927
1,832
1,800
1,763
1,727
1,645
0,99
5,746
5,065
4,644
4,355
4,134
3,981
3,851
3,746
3,658
3,583
3,519
3,456
3,414
3,370
3,330
3,294
3,157
3,063
2,994
2,940
2,897
2,862
2,807
2,765
2,732
2,706
2,684
2,569
2,521
2,475
2,430
2,326
Двусторонний доверительный интервал определяется из соотношения
тв = х + к* (п, а, C) s; тн = х — к* (п, а, C) s,
где к*(п,а, C)—толерантные множители, приведенные в табл. 206.
Для множителей &*(п,а,/3) справедливо соотношение
где с — решение уравнения Ф ( —= + с
/п
Ф ( —= — с
V v n
= C.
576
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 206
Множители Jfe*(n, а,/3) для построения
двусторонних толерантных интервалов
в случае нормального распределения
2
и <х неизвестны) [56]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
60
70
80
90
100
200
300
400
500
1000
оо
а
0,90
Р
0,90
15,980
5,847
4,166
3,494
3,131
2,902
2,743
2,626
2,535
2,463
2,404
2,355
2,314
2,278
2,246
2,219
2,194
2,172
2,152
2,077
2,025
1,988
1,959
1,935
1,916
1,887
1,865
1,848
1,834
1,822
1,764
1,740
1,726
1,717
1,695
1,645
0,95
18,800
6,979
4,943
4,152
3,723
3,452
3,264
3,125
3,018
2,933
2,863
2,805
2,756
2,713
2,676
2,643
2,614
2,588
2,564
2,474
2,413
2,368
2,334
2,306
2,284
2,248
2,222
2,202
2,185
2,172
2,102
2,073
2,057
2,046
2,019
1,960
0,99
24,170
8,974
6,440
5,423
4,870
4,521
4,278
4,098
3,959
3,849
3,758
3,682
3,618
3,562
3,514
3,471
3,433
3,399
3,368
3,251
3,170
3,112
3,066
3,030
3,001
2,955
2,920
2,894
2,872
2,854
2,762
2,725
2,703
2,689
2,654
2,326
0,95
/5
0,90
32,020
8,380
5,369
4,275
3,712
3,369
3,136
2,967
2,839
2,737
2,655
2,587
2,529
2,480
2,437
2,400
2,366
2,337
2,310
2,208
2,140
2,090
2,052
2,021
1,996
1,958
1,929
1,907
1,889
1,874
1,798
1,767
1,749
1,737
1,709
1,645
0,95
37,670
9,916
6,370
5,079
4,414
4,007
3,732
3,532
3,379
3,259
3,162
3,081
3,012
2,954
2,903
2,858
2,819
2,784
2,752
2,631
2,549
2,490
2,445
2,408
23,379
2,333
2,299
2,720
2,251
2,233
2,143
2,106
2,084
2,070
2,036
1,960
0,99
48,430
12,860
8,299
6,634
5,775
5,248
4,891
4,631
4,433
4,277
4,150
4,044
3,955
3,878
3,812
3,754
3,702
3,656
3,615
3,457
3,350
3,272
3,213
3,165
3,126
3,066
3,021
2,986
2,958
2,934
2,816
2,767
2,739
2,721
2,676
2,326
При п ^ 50 может быть использовано приближение Боукера [541]
fc*(n,a,/3) =
Yin
Подробные сведения о толерантных пределах для нормального распределения
содержатся в [557, 558], где рассмотрены оценки объема выборки п по заданным /3
и а, оценки толерантных интервалов для нескольких выборок с равными диспер-
дисперсиями [558].
4.4]
Толерантные пределы
577
Задача 308. Для ряда значений (п = 20)
хц 2, 4, 5, 7, 8, 11, 13, 17, 20, 24, 23, 25, 18, 18, 17, 17, 14, 11, 8, 1
найти толерантные пределы при а = 0,95 и C = 0,95.
Вычисляем х = — • ]Г хг = 13,15; s2 =
- 13Д5J = 53,50 (s = 7,314).
20 ^^ь —' —' ~ 20^1 .
г=1 г=1
Из табл. 205 и 206 для га = 20, а = 0,95 и /3 = 0,95 находим толерантные коэффици-
коэффициенты к(п,а,Р) = 2,396 и к*(п,а,Р) = 2,752. Тогда имеем для односторонних толерантных
пределов:
тв = х + к (га, а, /3) • s = 13,15 + 2,396 • 7,314 = 30,67;
тн = ж - к (га, а, /3) • s = 13,15 - 2,396 • 7,314 = -4,374.
Для двустороннего толерантного интервала:
тв =ж + ^*(п,а,/3) -s = 13,15 + 2,752-7,314 = 33,28;
тн = ж - к*(п,а,Р) • s = 13,15 - 2,752 • 7,314 = -6,98.
Следовательно, с вероятностью а = 0,95 в каждом из интервалов (—оо; 30,67];
[—4,37;оо); [—6,98; 33,28] будет находиться 95% (/3 = 0,95) всей совокупности значений
случайной величины.
4.4.1.2.4. Толерантные пределы, основанные на выборочном размахе
Для быстрой оценки толерантных пределов без предварительной выбороч™
ной оценки стандартного отклонения s можно использовать выборочный размах
ujn = хп — Х\ или среднее нескольких выборочных размахов, вычисляемых для т
п 1 т
подвыборок равного объема п' = — [543^545], штп = — J^ Ш{. Границы двусторон-
г=1
Таблица 207
Мнохсители d(l, n, а, /3) для определения
двустороннего толерантного интервала
с использованием размахов
(при га = 1, без разбиения на подвыборки) [543]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
а
0,90
Р
0,90
10,381
2,860
1,753
1,331
1,108
0,970
0,875
0,805
0,752
0,709
0,674
0,645
0,621
0,600
0,95
12,427
3,440
2,118
1,613
1,347
1,182
1,069
0,985
0,922
0,871
0,829
0,795
0,765
0,740
0,99
16,262
4,534
2,806
2,147
1,800
1,583
1,435
1,326
1,243
1,177
1,122
1,077
1,038
1,005
0,95
Р
0,90
20,811
4,109
2,270
15639
1,325
1,137
1,011
0,920
0,852
0,798
0,755
0,719
0,688
0,662
0,95
24,908
4,939
2,738
1,983
1,607
1,382
1,232
1,123
1,042
0,977
0,925
0,882
0,846
0,815
0,99
32,593
6,505
3,642
2,635
2,143
1,848
1,650
1,509
1,401
1,317
1,249
1,193
1,145
1,104
19 А. И. Кобзарь
578
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 208
Множители d(j?ij то', ск, /3) для определения
двустороннего толерантного интервала
с использованием размахов [543]
ТП
а
0,90
Р
0,90
0,95
0,99
0,95
0,90
0,95
0,99
п1 = Ъ
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1,008
0,897
0,838
0,801
05775
0,755
05740
0,727
0,717
0,708
0,700
0,694
0,688
0,683
0,631
0,584
0,558
0,541
0,528
0,519
0,512
0,506
0,501
0,496
0,493
0,489
0,486
0,484
1,237
1,107
1,039
0,996
0,965
0,942
0,924
0,910
0,898
0,888
0,879
0,871
0,865
0,859
0,782
0,727
0,697
0,677
0,663
0,652
0,644
0,637
0,631
0,626
0,622
0,618
0,615
0,612
1,669
1,505
1,418
1,363
1,325
1,296
1,273
1,255
1,240
1,227
1,216
1,206
1,198
1,190
п> = 1С
1,067
0,998
0,960
0,935
0,917
0,903
0,893
0,884
0,877
0,871
0,865
0,861
0,856
0,853
1,154
0,997
0,917
0,867
0,832
0,806
0,786
0,770
0,756
0,745
0,736
0,727
0,720
0,713
)
0,689
0,626
0,592
0,570
0,555
0,543
0,533
0,526
0,520
0,514
0,510
0,506
0,502
0,499
1,412
1,227
1,133
1,075
1,034
1,004
0,980
0,961
0,946
0,933
0,921
0,911
0,903
0,895
0,852
0,778
0,738
0,713
0,694
0,681
0,670
0,661
0,654
0,647
0,642
0,637
0,633
0,630
1,901
1,664
1,543
1,468
1,416
1,377
1,347
1,323
1,303
1,286
1,272
1,260
1,248
1,239
1,160
1,066
1,015
0,982
0,959
0,941
0,927
0,916
0,907
0,899
0,892
0,886
0,881
0,876
него толерантного интервала имеют вид
Тв = х + d(m, п\ а, C)штп; тн = х - d(m, n1', а, 0)штп,
где d (га, в;, а, /3)—толерантные коэффициенты, значения которых приведены
в табл. 207 (при отсутствии разбиения на подвыборки, т. е. когда т = 1) и в табл. 208
(при га > 1).
Задача 309. Для ряда значений задачи 308 построить двусторонний толерантный
интервал с помощью размахов.
Учитывая, что при п ^ 20 существенно уменьшается эффективность оценки s
с помощью размаха, разобьем выборку на две подвыборки (т = 2) равного объема
п = 10 (п = п ] га = 2). Для а = 0,95 и /3 = 0,95, воспользовавшись табл. 208, находим
dB; 10; 0,95; 0,95) = 0,946.
4.4] Толерантные пределы 579
Для подвыборок имеем размахи ил = 24 — 2 = 22, изч = 25 — 1 = 24 и средний размах
22 + 24
a;mn == = 23. Далее вычисляем
тв = 13,15 + 0,946 • 23 = 34,908; тн = 13,15 - 0,946 • 23 = -8,608.
Следовательно, с вероятностью а = 0,95 в интервале [—8,61; 34,91] будет находиться
95% ф = 0,95) всей совокупности значений случайной величины.
Отсюда видно, что толерантный интервал близок к интервалу, полученному в зада-
задаче 308, что свидетельствует о достаточной эффективности использования размахов.
4.4.1.2.5. Толерантные пределы для выборочных дисперсий
Будем искать интервал, который с вероятностью а включает /3-ю часть сово™
кугшости выборочных дисперсий
л ГЦ л Пг
2 1 \~~^ / - \2 - 1 х~^
st = -—т- 22 (xij - х^) > где х* = тг zJ хч-
Очевидно, что Д^квантиль распределения sf есть
¦ = <т
П-1
(п -1) si
так как — j1— имеет распределение хи-квадрат с / = п — 1 степенями свободы.
а
Для оценки а2 используем среднюю оценку по совокупности значений s\, s|, ..., s2^.
Тогда оценкой а будет величина
т(п — 1) т ^ г'
Оценке s2 соответствует f = т(п — 1) степеней свободы. Тогда толерантный
интервал, включающий в себя /3-ю часть всей совокупности значений s\, s|, ..., s2^
(каждая оценка s2 получена по выборке равного объема п) будет равен [546]
отношениями [546] тв = < — ^ \ ; тн = 0.
Для стандартного отклонения s = vs2 толерантный интервал определятся со™
1I.
I су
Напомним, что при / > 30 справедлива аппроксимация %д = - {\/%f — 1 + up) •
Задача 310. В результате наблюдений над т = 10 выборками из нормального распре-
распределения получены следующие выборочные значения дисперсий:
s2: 25, 41, 48, 37, 21, 64, 91, 49, 59, 78.
Оценки sf получены на выборках равного объема п = 20. Необходимо найти толе™
рантный интервал для значений s^ при а = 0,95 и /3 = 0,90.
¦^ ю
Имеем s = — • ^^ s$ = 51,3. По табл. 55 х -распределения (или используем аппрок-
аппроксимации из раздела 1.1.8):
xlin - 1) = Хо,9оA9) = 27,202; Х?-а["» • (» " 1)] = Xo,osA90) = 159,11.
19*
580
Проверка гипотез о значениях параметров распределений
[Гл.4
Вычисляем тв =
10 • 0,946 • 23
159,11
51,3 = 87,71. Следовательно, можно утверждать, что
с вероятностью а = 0,95 в интервале [0; 87,71] находится 90% (/3 = 0,9) всей совокуп-
совокупности значений s'f. Соответствующий интервал для стандартного отклонения s будет
[0; л/ЩТЦ = [0;9,36].
4.4.2. Непараметрические толерантные пределы
Иногда представляет интерес при неизвестном непрерывном распределении
определить тот минимальный объем выборки nmin, при котором можно утверждать,
что с вероятностью а для любой непрерывной совокупности между минимальным
(хш'ш) и максимальным (жтах) значениями выборки, извлеченной из нее, заключена
/3-я доля всей совокупности. В этом случае мы говорим о двустороннем непарамет™
рическом толерантном интервале.
Если через п^п обозначить такой минимальный объем выборки, при котором
можно утверждать, что с вероятностью а в каждом из интервалов (^оо;жтах),
(^min? оо) содержится /3-я доля любой непрерывной совокупности, то говорят о непа-
непараметрических односторонних толерантных интервалах. Между nmin, а и /3 для
двустороннего толерантного интервала справедливо соотношение Уилкса [547]
nmin/3"^-1 - (nmin - 1) 0"»» ^ 1 - а.
Для односторонних интервалов справедливо неравенство /3Пт1п ^ 1 —а. Значения
nmin и в^п, удовлетворяющие приведенным неравенствам приведены в табл. 209.
Таблица 209
Минимальные объемы выборок для построения
непараметрических (двустороннего, пт'1П — верхняя
строка и одностороннего, Timin — нижняя строка)
толерантных интервалов, основанных на
наибольших и наименьших
выборочных значениях [56]
а
0,90
0,95
0,99
0,50
7
4
8
5
11
7
0,70
12
7
14
9
20
3
0,75
15
9
18
11
33
17
0,80
18
11
22
14
31
21
0,90
38
22
46
29
64
44
0,95
77
45
93
59
130
90
0,99
388
30
473
299
662
459
Практический интерес представляет и обратная задача: для заданных значений
п и а определить наименьшую долю C совокупности, относительно которой можно
утверждать, что с вероятностью а эта доля заключена между крайними членами
выборки объема в, либо превосходит наименьшее значение выборки (жт1п), либо
меньше наибольшего значения выборки (жтах).
к
Для двусторонних интервалов при п ^ 50 справедливо соотношение /3 = 1 ,
п
где к является решением уравнения
1 + fc- (l-a)ek = 0.
4.4]
Толерантные пределы
581
Некоторые решения этого уравнения для наиболее употребительных значений а
таковы:
а
к
0,9
3,8897
0,95
4,7439
0,99
6,6384
Для односторонних интервалов справедливо соотношение
В табл. 210 и 211 приведены значения /3, соответствующие различным а и п,
соответственно для двустороннего и одностороннего толерантных интервалов.
Таблица 210
Наименьшая доля /3 совокупности, заключенная внутри
непараметрического двустороннего толерантного интервала
(между жт1п и жтах в выборке объема п) [56]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Доверительная
вероятность
0,90
0,0513
0,1958
0,3205
0,4101
0,4897
0,5474
0,5938
0,6316
0,6632
0,6898
0,7125
0,7322
0,7493
0,7644
0,7778
0,7898
0,8005
0,8102
0,8190
0,8271
0,8344
0,8412
0,8474
0,8531
0,8585
0,8634
0,8681
0,8724
0,8764
0,8802
0,8838
0,8872
0,95
0,0253
0,1354
0,2486
0,3426
0,4182
0,4793
0,5293
0,5709
0,6058
0,6356
0,6613
0,6873
0,7033
0,7206
0,7360
0,7499
0,7623
0,7736
0,7839
0,7933
0,8019
0,8098
0,8171
0,8239
0,8302
0,8360
0,8415
0,8466
0,8514
0,8559
0,8602
0,8641
а
0,99
0,0050
0,0589
0,1409
0,2221
0,2943
0,3566
0,4101
0,4560
0,4956
0,5302
0,5605
0,5872
0,6109
0,6321
0,6512
0,6684
0,6840
0,6982
0,7112
0,7232
0,7342
0,7443
0,7538
0,7625
0,7707
0,7783
0,7854
0,7923
0,8004
0,8043
0,8099
0,9152
п
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
60
70
80
90
100
200
300
400
500
600
700
800
900
1000
5000
Доверительная
вероятность
0,90
0,8903
0,8934
0,8962
0,8989
0,9015
0,9039
0,9062
0,9084
0,9105
0,9125
0,9145
0,9163
0,9181
0,9197
0,9214
0,9229
0,9244
0,9367
0,9456
0,9952
0,9575
0,9617
0,9807
0,9871
0,9903
0,9922
0,9935
0,9945
0,9951
0,9957
0,9961
0,9992
0,95
0,8679
0,8715
0,8749
0,8781
0,8811
0,8840
0,8868
0,8894
0,8920
0,8944
0,8967
0,8989
0,9010
0,9030
0,9049
0,9068
0,9086
0,9234
0,9340
0,9421
0,9484
0,9534
0,9765
0,9843
0,9882
0,9905
0,9921
0,9932
0,9941
0,9947
0,9953
0,9991
а
0,99
0,8202
0,8249
0,8294
0,8337
0,8377
0,8416
0,8453
0,8488
0,8521
0,8554
0,8584
0,8614
0,8642
0,8669
0,8695
0,8721
0,8745
0,8944
0,9089
0,9199
0,9285
0,9355
0,9673
0,9781
0,9835
0,9868
0,9890
0,9906
0,9917
0,9926
0,9934
0,9987
582
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 211
Наименьшая доля совокупности /3, заключенная внутри
непараметрического одностороннего толерантного интервала
(больше жт1п или меньше жтах в выборке объема п) [56]
п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Доверительная
вероятность
0,90
0,3162
0,4642
0,5623
0,6310
0,6813
0,7197
0,7499
0,7743
0,7943
0,8110
0,8254
0,8377
0,8483
0,8577
0,8660
0,8733
0,8799
0,8859
0,8913
0,8962
0,9006
0,9047
0,9085
0,9120
0,9152
0,9183
0,9211
0,9237
0,9261
0,9284
0,9306
0,95
0,2236
0,3684
0,4729
0,5493
0,6070
0,6518
0,6877
0,7169
0,7411
0,7791
0,7791
0,7942
0,8074
0,8190
0,8293
0,8384
0,8467
0,8541
0,8609
0,8671
0,8727
0,8779
0,8827
0,9871
0,8912
0,8950
0,8985
0,9010
0,9050
0,9079
0,9106
а
0,99
0,1000
0,2154
0,3162
0,3981
0,4642
0,5179
0,5623
0,5995
0,6310
0,6813
0,6813
0,7017
0,7197
0,7356
0,7499
0,7627
0,7743
0,7848
0,7943
0,8031
0,8111
0,8185
0,8254
0,8318
0,8377
0,8432
0,8483
0,8532
0,8577
0,8620
0,8660
п
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
60
70
80
90
100
200
300
400
500
700
800
900
1000
Доверительная
вероятность
0,90
0,9326
0,9345
0,9363
0,9380
0,9397
0,9412
0,9427
0,9441
0,9454
0,9467
0,9479
0,9490
0,9501
0,9512
0,9522
0,9532
0,9541
0,9550
0,9624
0,9676
0,9716
0,9747
0,9772
0,9886
0,9924
0,9943
0,9954
0,9967
0,9971
0,9974
0,9977
0,95
0,9132
0,9157
0,9180
0,9202
0,9222
0,9242
0?9261
0,9278
0,9295
0?9312
0,9327
0,9342
0,9356
0,9370
0,9382
0,9395
0,9407
0,9418
0,9513
0,9581
0,9632
0,9673
0,9705
0,9851
0,9901
0,9925
0,9940
0,9957
0,9963
0,9967
0,9970
а
0,99
0,8697
0,8733
0,8767
0,8799
0,8830
0,8859
0,8886
0,8913
0,8938
0,8952
0,8984
0,9006
0,9027
0,9047
0,9067
0,9085
0,9103
0,9120
0,9261
0,9363
0,9441
0,9501
0,9550
0,9772
0,9848
0,9886
0,9908
0,9934
0,9943
0,9949
0,9954
Задача 311. Определить объем выборки х\,хъ, ...,жп, для которой с вероятностью
а = 0,95 между жтт и жтах будет заключаться не менее /3 = 0,99 всей совокупности
значений х.
Из табл. 209 для а = 0,95 и /3 = 0,99 находим nmin = 473, т. е. в выборке объема
п = 473 между жт1П и жтах будет располагаться не менее 99% всех значений х%, извле-
извлеченных из любой непрерывной совокупности.
Задача 312. Определить минимальный объем выборки в условиях задачи 311 для
одностороннего толерантного интервала.
Из табл. 209 находим nmin = 299. Следовательно, для выборки объема п = 299 можно
утверждать, что левее жтах либо правее хт-1П будет находиться 99% всей совокупности.
4.4] Толерантные пределы 583
Задача 313. Определить долю членов непрерывной совокупности^ которая с вероят-
вероятностью а = 0,90 будет заключена между хт\п и жтах в выборке объема п = 49.
Из табл. 210 для п = 49 и а = 0,90 находим /3 = 0,9229. Следовательно, в выборке
объема п = 49 между xmin и xmax будет находиться не менее 92,29% всей совокупности
случайных величин.
По аналогии для одностороннего интервала из табл. 211 получаем для а = 0,90
и п = 49: /3 = 0,9541, т.е. в выборке объема п = 49 справа от жт1п либо слева от жтах
будет располагаться 95,41% всей совокупности.
4.4.3. Толерантные пределы длм будущих наблюдений и прогнозирование
4.4.3.1. Прогнозные интервалы Холла-Прейри
Иногда в практических задачах анализа надежности и долговечности техниче-
технических систем требуется определить границы интервалов, аналогичных толерантным,
но имеющих смысл „предсказывающих".
Сформулируем следующую задачу. Имеется выборка объема п из нормально
распределенной совокупности, по которой определены выборочные среднее х и стан-
стандартное отклонение s. Необходимо найти границу интервала [х ~~ r(ra, n, fc,a); оо)
для которого справедливо утверждение, что с вероятностью а не менее га из к
последующих наблюдений будут превышать значение х — г(гп^ n, k, a)s.
Эта задача рассмотрена в [548]. Коэффициенты оценок r(m1n,kJa)J рассчитан™
ные авторами работы, приведены в табл. 212.
Аналогичная задача рассмотрена в упомянутой работе [548] и для экспонен-
экспоненциального распределения. В этом случае искомый интервал определяется как
п
[Ь(га, п, к, а) ]Р Xi\ оо). Коэффициенты Ь(га, в, &, а) приведены в табл. 213. Табл. 213
г=1
применима и для решения задачи при распределении Вейбулла с известным пара-
параметром /3 (см. раздел 1.1.5). В этом случае искомый интервал будет равен
b (га, n, А;, а) V^ ж •
i=l
; oo
Задача 314. В результате испытаний п = 10 приборов получены следующие резуль-
результаты Xi'. 12, 13, 17, 21, 29, 35, 46, 57, 61, 70. Необходимо определить значение ж@,95),
которое с вероятностью а = 0,95 будет превзойдено не менее^ чем т = 4 приборами из
k = 8 испытанных дополнительно. Задачу решить, исходя из предположений нормаль-
нормальности и экспоненциальности распределения случайной величины х.
Рассмотрим сначала случай нормального распределения.
п
Вычисляем по выборке \°^ х% = 361; s = 21,247. Из табл. 212 для т = 4, п = 10, к = 8
г=1
и а = 0,95 находим коэффициент гD; 10; 8; 0,95) = 1,3.
Следовательно, искомое значение равно жо,э5 = х — rs = 36,1 — 1,3 • 21,747 = 8,479, т. е.
с достоверностью а = 0,95 из 8 испытанных прибора 4 будут иметь параметр х > 8,479.
п
В случае экспоненциального распределения имеем J^ Xi = 361, находим из табл. 213
г=1
коэффициент 6D; 10; 8; 0,95) = 0,030. Тогда искомая величина равна ж@,95) = Ь х
71
х J^ a?i = 0,030 • 361 = 10,83. Следовательно, с вероятностью а = 0,95 у 4 приборов из
г=1
будущих 8 испытываемых значение параметра ж@,95) будет превышать 10,83.
584
Проверка гипотез о значениях параметров распределений
[Гл.4
Таблица 212
Коэффициенты r(m, n, fe, а), для которых вероятность того, что в т или
более из будущих к наблюдений нормального распределения величина ж
будет превышать х — г (га, n, fe, ex.)8, равна ex. [548]
т
п
к
г
т
п
к
г
т
п
к
г
т
п
к
г
а = 0,90
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
2
2
2
2
2
2
2
2
4
4
4
4
4
4
6
6
6
6
8
8
8
8
10
10
10
10
12
12
12
14
14
16
16
16
18
18
20
20
22
24
2
3
4
5
6
8
10
12
4
5
6
8
10
12
8
10
12
16
8
10
12
16
10
12
16
20
12
16
20
16
20
16
20
25
20
25
20
25
25
25
2
1
0,7
0,4
0,2
-ОД
-0,25
-0,3
2,8
2,1
1,5
0,75
0,5
0525
1,6
1
0,75
0,4
3,4
1,9
1,3
0,8
3,5
2
1,2
0575
3,75
1,75
1,1
2,3
1,5
3,5
2
1,25
2,1
1,5
4
2
2,5
3,5
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
2
2
2
2
2
2
2
2
4
4
4
4
4
4
6
6
6
6
6
8
8
8
8
10
10
10
10
12
12
12
14
14
16
16
16
18
18
20
20
22
2
3
4
5
6
8
10
12
4
5
6
8
10
12
6
8
10
12
16
8
10
12
16
10
12
16
20
12
16
20
16
20
16
20
25
20
25
20
25
25
2
1
0,6
0,25
0
-0,2
-0,3
-0,5
2,3
1,5
1,2
0,6
0,3
0,2
2,5
1,5
1
0,6
0,25
2,7
1,5
1
0,5
2,8
1,5
0,9
0,5
2,9
1,3
0,75
1,8
1,1
3
1,5
0,95
2
1,3
3,2
1,5
1,9
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
2
2
2
2
2
2
2
2
4
4
4
4
4
4
6
6
6
6
8
8
8
8
10
10
10
10
12
12
12
14
14
16
16
16
18
18
20
20
22
24
2
3
4
5
6
8
10
12
4
5
6
8
10
12
8
10
12
16
8
10
12
16
10
12
16
20
12
16
20
16
20
16
20
25
20
25
20
25
25
25
1,8
1,1
0,5
0,3
0,15
0
-0,2
-0,4
2,5
1,5
1
0,55
0,3
0,05
1,25
0,75
0,5
0,2
2,5
1,4
1
0,45
2,5
1,5
0,8
0,5
2,5
1,2
0,7
1,6
1
2,3
1,3
0,7
1,7
1
2,5
1,25
1,6
2,2
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
2
2
2
2
2
2
2
2
4
4
4
4
4
4
6
6
6
6
6
8
8
8
8
10
10
10
12
12
12
14
14
16
16
16
18
18
20
20
22
24
2
3
4
5
6
8
10
12
4
5
6
8
10
12
6
8
10
12
16
8
10
12
16
10
12
16
12
16
20
16
20
16
20
25
20
25
20
25
25
25
1,7
1,2
0,6
0,4
0,2
-0,1
-0,3
-0,5
2,1
1,3
1
0,5
0,2
0
2,3
1,25
0,8
0,5
0,15
2,5
1,5
1
0,45
2,5
1,5
0,7
0,5
1,2
0,7
1,7
1
2,5
1,4
0,8
1,8
1
2,5
1,4
1,7
2,3
а = 0,95
5
5
5
5
5
5
2
2
2
2
2
2
2
3
4
5
6
8
3
2,5
1,5
1
0,6
0,4
5
5
5
5
5
5
12
14
14
16
16
16
20
16
20
12
16
20
1
2
1,3
3
1,7
1,15
15
15
15
15
15
15
6
8
8
8
8
10
16
8
10
12
16
10
0,3
2,8
1,7
1,2
0,6
2
20
20
20
20
20
20
4
4
4
4
4
4
4
5
6
8
10
12
2,5
1,7
1,2
0,7
0,4
0,2
4.4]
Толерантные пределы
585
то
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
п
2
2
4
4
4
4
4
4
6
6
6
6
6
8
8
8
8
10
10
10
10
12
12
к
10
12
4
5
6
8
10
12
6
8
10
12
16
8
10
12
16
10
12
16
20
12
16
г
0,1
-од
3,5
2,5
2
1,3
0,8
0,5
4
2,5
1,7
1,2
0,6
4,5
2,7
1,8
1,1
3,5
2
1
0,7
2,5
1,5
то
5
5
5
5
5
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
п
18
18
20
20
24
2
2
2
2
2
2
2
2
4
4
4
4
4
4
6
6
6
6
к
16
20
16
20
25
2
3
4
5
6
8
10
12
4
5
6
8
10
12
6
8
10
12
г
а =
2,1
1,1
3,7
1,7
2,7
2,5
1,5
0,9
0,5
0,3
0,05
-0,1
-0,4
2,5
2
1,3
0,75
0,5
0,2
2,8
1,5
1
0,6
то
0,95
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
20
20
20
20
20
20
20
20
п
10
10
12
12
12
14
14
16
16
16
18
18
20
20
22
2
2
2
2
2
2
2
2
Ок
к
ончание
г
то
12
16
12
16
20
16
20
16
20
25
20
25
20
25
25
2
3
4
5
6
8
10
12
1,8
1
0,6
3,1
1,5
2
1,25
3,2
1
1
2
1,2
3,4
1,55
2
2,5
1,7
1
0,6
0,5
0,2
0
-0,2
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
таблицы 212
п
6
6
6
6
6
8
8
8
8
10
10
10
10
14
14
16
16
16
18
18
20
20
22
к
г
6
8
10
12
16
8
10
12
16
10
12
16
20
16
20
16
20
25
20
25
20
25
25
2,7
1,5
1
0,7
0,3
3
1,5
1,1
0,6
3
1,7
1
0,6
1,9
1,15
3,4
1,5
1
2
1,3
3,2
1,5
2
Таблица 213
Коэффициенты 6(га, n, fe, «), для которых вероятность того, что в т или
более из будущих к наблюдений экспоненциального распределения
п
величина ж будет превышать b(m^nJk1 «) J^ жг, равна ol [548]
т
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
п
2
2
2
2
2
2
2
2
2
2
2
4
4
4
4
4
к
1
2
3
4
5
6
8
10
12
16
20
3
4
5
6
8
Ь
0,015
0,035
0,070
0,100
0,15
0,18
0,20
0,22
0,26
0,28
0,32
0,006
0,015
0,040
0,080
0,100
то
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
п
2
2
2
2
2
2
2
2
2
2
2
4
4
4
4
4
2
3
4
5
6
8
10
12
16
20
25
4
5
6
8
10
ь
а =
0,004
0,021
0,040
0,050
0,070
0,090
0,100
0,111
0,114
0,116
0,118
0,003
0,012
0,020
0,040
0,055
то
= 0,90
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
п
2
2
2
2
2
2
2
2
2
2
2
4
4
4
4
4
2
3
4
5
6
8
10
12
16
20
25
4
5
6
8
10
Ъ
0,004
0,012
0,022
0,032
0,050
0,060
0,070
0,080
0,100
0,110
0,130
0,0015
0,007
0,017
0,028
0,038
т
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
п
2
2
2
2
2
2
2
2
2
2
4
4
4
4
4
4
к
3
4
5
6
8
10
12
16
20
25
4
5
6
8
10
12
Ъ
0,010
0,020
0,026
0,030
0,045
0,052
0,060
0,070
0,080
0,090
0,0015
0,005
0,009
0,020
0,028
0,035
586
Проверка гипотез о значениях параметров распределений
[Гл.4
т
п
к
Ъ
т
п
к
Ъ
т
Продолже
п
к
Ь
н и е
т
табли
п
к
цы 213
b
а = 0,90
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
4
4
4
4
6
6
6
6
6
6
6
8
8
8
8
8
8
10
10
10
10
10
12
12
12
12
14
14
14
16
16
16
18
18
20
20
24
10
12
16
20
5
6
8
10
12
16
20
6
8
10
12
16
20
8
10
12
16
20
10
12
16
20
12
16
20
12
16
20
16
20
16
20
20
0,13
0,18
0,20
0,23
0,004
0,030
0,065
0,080
0,120
0,150
0,180
0,003
0,021
0,045
0,075
0,110
0,150
0,002
0,018
0,050
0,080
0,110
0,001
0,030
0,056
0,085
0,011
0,040
0,068
0,015
0,024
0,050
0,010
0,036
0,001
0,026
0,004
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
4
4
4
4
6
6
6
6
6
6
6
8
8
8
8
8
8
10
10
10
10
10
12
12
12
12
14
14
14
16
16
16
18
18
20
20
22
12
16
20
25
6
8
10
12
16
20
25
8
10
12
16
20
25
10
12
16
20
25
12
16
20
25
16
20
25
16
20
25
20
25
20
25
25
0,070
0,090
0,100
0,120
0,002
0,016
0,030
0,040
0,060
0,075
0,095
0,0015
0,012
0,021
0,040
0,055
0,071
0,001
0,009
0,028
0,040
0,058
0,001
0,016
0,030
0,045
0,0065
0,020
0,035
0,001
0,012
0,026
0,005
0,020
0,001
0,014
0,070
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
20
4
4
4
4
6
6
6
6
6
6
6
8
8
8
8
8
8
10
10
10
10
10
12
12
12
12
14
14
14
16
16
18
18
20
22
2
12
16
20
25
6
8
10
12
16
20
25
8
10
12
16
20
25
10
12
16
20
25
12
16
20
25
16
20
25
20
25
20
25
25
25
2
0,046
0,065
0,075
0,090
0,001
0,011
0,020
0,028
0,044
0,054
0,068
0,001
0,009
0,017
0,030
0,040
0,052
0,001
0,0065
0,020
0,030
0,040
0,001
0,012
0,021
0,033
0,005
0,015
0,027
0,009
0,020
0,037
0,017
0,009
0,049
0,002
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
4
4
4
6
6
6
6
6
6
6
8
8
8
8
8
8
10
10
10
10
10
12
12
12
12
14
14
14
16
16
16
18
18
20
20
22
16
20
25
6
8
10
12
16
20
25
8
10
12
16
20
25
10
12
16
20
25
12
16
20
25
16
20
25
16
20
25
20
25
20
25
25
0,045
0,058
0,068
0,0009
0,009
0,015
0,020
0,030
0,040
0,050
0,0007
0,005
0,010
0,021
0,030
0,040
0,0005
0,004
0,016
0,022
0,030
0,0004
0,008
0,017
0,024
0,003
0,011
0,019
0,0002
0,006
0,015
0,0025
0,010
0,0002
0,006
0,003
а = 0,95
5
5
5
5
5
5
5
5
5
5
5
5
2
2
2
2
2
2
2
2
2
2
2
4
2
3
4
5
6
8
10
12
16
20
25
4
0,004
0,030
0,052
0,080
0,100
0,130
0,180
0,190
0,210
0,250
0,270
0,002
5
5
5
5
5
5
5
5
5
5
5
5
12
12
14
14
14
16
16
16
18
18
20
20
20
25
16
20
25
16
20
25
20
25
20
25
0,050
0,070
0,010
0,033
0,058
0,001
0,020
0,044
0,008
0,031
0,001
0,020
10
10
10
10
10
10
10
10
10
10
10
10
8
8
8
8
8
8
10
10
10
10
10
12
8
10
12
16
20
25
10
12
16
20
25
12
0,001
0,010
0,020
0,036
0,050
0,065
0,001
0,0075
0,022
0,036
0,050
0,001
15
15
15
15
15
15
15
15
15
15
15
15
4
4
4
4
6
6
6
6
6
6
6
8
12
16
20
25
6
8
10
12
16
20
25
8
0,040
0,050
0,061
0,075
0,0006
0,0085
0,019
0,024
0,036
0,047
0,059
0,0005
4.4]
Толерантные пределы
587
т
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
п
4
4
4
4
4
4
4
4
6
6
6
6
6
6
6
8
8
8
8
8
8
10
10
10
10
10
12
12
к
5
6
8
10
12
16
20
25
6
8
10
12
16
20
25
8
10
12
16
20
25
10
12
16
20
25
12
16
Ь
0,020
0,033
0,060
0,090
0,118
0,150
0,180
0,200
0,002
0,022
0,045
0,061
0,097
0,130
0,160
0,001
0,016
0,033
0,065
0,090
0,130
0,001
0,015
0,044
0,070
0,090
0,001
0,025
т
5
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
10
п
22
2
2
2
2
2
2
2
2
2
2
2
4
4
4
4
4
4
4
4
4
6
6
6
6
6
6
6
к
25
2
3
4
5
6
8
10
12
16
20
25
4
5
6
8
10
12
16
20
25
6
8
10
12
16
20
25
Ь
а =
0,012
0,002
0,010
0,029
0,040
0,050
0,070
0,080
0,100
0,130
0,150
0,160
0,002
0,010
0,016
0,030
0,046
0,058
0,078
0,095
0,110
0,001
0,012
0,024
0,036
0,051
0,070
0,080
т
0,95
10
10
10
10
10
10
10
10
10
10
10
10
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
п
12
12
12
14
14
14
16
16
18
18
20
22
2
2
2
2
2
2
2
2
2
2
2
4
4
4
4
4
О
к
16
20
25
16
20
25
20
25
20
25
25
25
2
3
4
5
6
8
10
12
16
20
25
4
5
6
8
10
конча
Ь
0,012
0,026
0,040
0,0045
0,018
0,030
0,010
0,022
0,004
0,017
0,010
0,005
0,0018
0,010
0,020
0,030
0,040
0,050
0,060
0,070
0,080
0,090
0,100
0,0008
0,006
0,010
0,025
0,030
Н И €
т
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
т а б л и
п
8
8
8
8
8
10
10
10
10
10
12
12
12
12
14
14
14
16
16
16
18
18
20
20
22
к
10
12
16
20
25
10
12
16
20
25
12
16
20
25
16
20
25
16
20
25
20
25
20
25
25
цы 213
Ь
0,0065
0,014
0,025
0,035
0,045
0,0004
0,006
0,018
0,026
0,036
0,0003
0,009
0,018
0,028
0,003
0,013
0,022
0,0002
0,0075
0,013
0,003
0,013
0,0001
0,008
0,004
4.4.3.2. Прогнозные интервалы в задачах испытаний на надежность
В [549] рассмотрена задача прогнозирования r-й порядковой статистики хг
в выборке объема п, основанная на величине первых к порядковых наблюдений из
выборки (к < г ^ п). Доверительный интервал для хг может быть использован для
прогнозирования оставшегося времени испытаний на долговечность. Показано [549],
г имеет ^распределение с Д = 2 и /2 = 2 (У — 1)
Xi + ( — к)хк
что статистика U =
г1
степенями свободы. Следовательно, двусторонний интервал для хг с доверительной
вероятностью а будет
¦Fl-g
2
(n — к)
г=1
Fl+g
-•i + (п - к)
„ 1 + а 1 — а
Для односторонних интервалов вместо или используются величи-
ны а или A — а) соответственно.
Хан [550] рассмотрел задачу прогнозирования будущих выборок из экспоненци-
экспоненциального распределения. Задача формулируется следующим образом. По имеющим™
ся данным моментов отказов т изделий необходимо найти нижний доверительный
588
Проверка гипотез о значениях параметров распределений
[Гл.4
интервал с вероятностью а для среднего времени до отказа для к будущих выборок
j т
объема п. Если х = — J^ ж^, то нижняя доверительная граница для средних к вы™
борок объема п будет равна хс(к, га, п, а), где с(к, га, п, а) — коэффициенты оценки.
Справедливы аппроксимации
с(к,т,п,а) ~ —у рг-; c(fc,ra, n, )
(
2m; 2n; A - a) k
F [2m; 2ra; 1 - ^
/i = a
где F(a,b, 7) — 7-квантиль распределения Фишера (см. раздел 1.1.10) с
и /2 = 5 степенями свободы.
Первая аппроксимация точнее, однако весьма затруднен поиск A — а)
лей F-распределения (имеющиеся таблицы недостаточны). Вторая аппроксимация
менее точна, но может быть получена с помощью имеющихся таблиц F-распреде™
ления. Некоторые значения коэффициентов с(&, п, га, а), полученные с помощью
первой аппроксимации, приведены в табл. 214.
Таблица 214
Значения c(fc, тг, ти, а) для прогнозирования при ск = 0,95
нижней границы средней наработки в к выборках объема п
по т ранним моментам отказов [550]
га
3
5
10
20
п = 2
2
0,8
0,5
0,2
0,1
3
1,1
0,7
0,4
0,2
5
1,4
0,9
0,4
0,2
8
1,5
0,8
0,4
0,2
12
1,7
0,9
0,5
09,
п = 5
к
2
1,9
1,1
0,5
0,3
3
2,8
1,6
0,8
04
5
3,6
2,1
1,0
0,5
8
4,0
2,5
1,1
0,5
12
4,7
2,7
1,3
06
п = 10
к
2
3,3
2,0
1,0
0,5
3
4,9
3,0
1,5
0,7
5
6,5
4Д
2,0
0,9
8
7,9
4,9
2,3
1,0
12
9,0
5,6
2,6
1,2
В заключение приведем ряд имеющих практический интерес соотношений, осно™
ванных на гипергеометрическом распределении (см. раздел 1.2.6). Вероятность
того, что среди будущих га наблюдений не менее с величин будут превышать г-й
член упорядоченного по возрастанию ряда в выборке объема п, равна
г —1
\~~^ (с + г — iy.n\ (га + п — с —- г + 1)!га!
Р =
(с + г - 1 - г)\{п - i)\i\ (т + п)\(т - с - г + 1 + г)! *
Вероятность р* того, что среди будущих га наблюдений не менее с величин будут
заключены между крайними значениями ряда, построенного по выборке объема п,
равна
* _ (га-с+2)Ы (п + с-2)\т\
Р ~ (т-с+1)!(га-1)! (ш + га)!(с-1)!'
Задача 315. В результате испытаний п = 10 приборов первые к = 7 отказов получе-
получены в моменты времени t%: 10, 12, 18, 24, 31, 35, 41. Необходимо найти доверительные
интервалы^ в которых находится момент отказа девятого прибора (г = 9), пргх cfeee-
рительной вероятности а = 0,95.
Имеем tfc = ?7 = 41. Из таблиц F-распределения (либо используя аппроксимации из
раздела 1.1.10) имеем (при Д = 2 и /2 = 2 • (9 — 1) = 16)
Fa = F0,95 = 3,63; Fi_a = F0,05 = 0,0515; Fi+a = F0,975 = 4,96;
4.4] Толерантные пределы 589
F 1 = FO!o25 = 0,0253.
1 —а
7
Далее находим J^ U + A0 — 7) 41 = 171 + 13 = 294. Для двустороннего интервала
имеем
41 + 294 • 0,253 = 48,438 <: t9 <: 1419,86 = 41 + 294 • 4,69.
Для односторонних интервалов имеем
t9 ^ 41 + 294 • 0,0515 = 56,141; t9 ^ 41 + 294 • 3,63 = 1108,22.
Задача 316. Для т = 10 изделий получены моменты отказов U: 158, 171, 192, 211,
241, 256, 278, 292, 312, 341. Необходимо с достоверностью а = 0,95 найти нижний
доверительный интервал для средней наработки на отказ в к = 5 выборках объема
п = 10 каждая.
Имеем для а = 0,95 из табл. 214 коэффициент еE,10,10) = 2,0.
1 10
Далее i = — • J^ t% = 245,2, и нижняя граница оценки равна
г=1
t-c(k,n,m,a) = 245,2 • 2,0 = 490,4.
Следовательно, с вероятностью 0,95 средняя наработка на отказ в 5 будущих выбор-
выборках не будет превышать 490,4.
Задача 317. Для данных задачи 316 определить вероятность того^ что среди буду-
будущих трех наблюдений не менее двух будут превышать по величине 5-е наблюдение
U = 241 в
Имеем п = 10, г = 5, т = 3ис = 2. Далее вычисляем
г — 1
1г-л (с + 7* —1)!п! (га + п — с — г + 1)!га!
(с + г - 1-г)! (п-г)!г! (га + п)! (га - с - г + 1 +г)!
6!10! 7!3! =0137
^ F-г)!A0-г)!г! 13! (г - 3)!
Следовательно, с вероятностью р = 0,437 среди трех будущих наблюдений не менее
двух будут превышать величину t$ = 241.
Задача 318. Для данных задачи 316 вычислить вероятность того^ что среди будущих
т = 3 наблюдений не менее с = 2 величин будут заключены между крайними значени-
значениями выборки объема п = 10 (га. е. между t\ = 158 г/ ?ю = 341).
Имеем
C-2 + 2I10! , (Ю + 2-2)!3! =
F C-2 + l)!9! A0 + 3)! B™ г)!
Следовательно, с вероятностью р* = 0,895 из будущих трех наблюдений не менее двух
будут находиться между минимальным t\ = 158 и максимальным ?ю = 341 значениями
выборки объема п = 10.
ГЛАВА 5
МЕТОДЫ ИССЛЕДОВАНИЯ СВЯЗЕЙ
МЕЖДУ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ
Общие положения. В предыдущих главах были рассмотрены различные
методы и приемы математической статистики, позволяющие оценить параметры
статистических совокупностей, сравнивать их между собой. При этом, как прави-
ло, предполагалась взаимная независимость сравниваемых совокупностей. В на-
настоящей главе рассматриваются вопросы оценки связей между статистическими
совокупностями.
Подробно описываются основы и методы дисперсионного, корреляционного и ре™
грессионного анализов, являющиеся последовательными ступенями при исследова-
исследовании связей между случайными величинами.
Методами дисперсионного анализа устанавливается наличие влияния заданно™
го фактора на изучаемый процесс, отображаемый наблюдаемой статистической
совокупностью выборочных данных. Корреляционный анализ позволяет оценить
силу такой связи, а методами регрессионного анализа можно выбрать конкретную
математическую модель и оценить адекватность отражения ею установленной вза-
взаимосвязи случайных величин.
В последние годы стремительно развивается самостоятельное прикладное на™
правление математической статистики — математическая теория активного экспе-
эксперимента. Базируясь на комбинации методов дисперсионного и регрессионного ана-
анализов, методы математического планирования эксперимента дополняют их.
В настоящей главе даются основные понятия и определения математической те-
теории планирования активного эксперимента применительно к изучению механизма
наблюдаемого процесса и построению его статистической модели.
Автор счел уместным изложить в настоящей главе основные сведения по технике
контрольных карт, как самой распространенной форме применения математической
статистики в производстве при предупредительном статистическом контроле каче™
ства продукции. Приводится краткое описание известных методов и примеры их
применения.
5.1. Дисперсионный анализ
Дисперсионный анализ является статистическим методом анализа результатов
наблюдений, зависящих от различных одновременно действующих факторов, с це-
целью выбора наиболее значимых факторов и оценки их влияния на исследуемый
процесс.
Влияние различных факторов на изучаемые случайные величины (например,
влияние технологического способа изготовления или режима нагрузки на долго™
вечность технического изделия) приводит к изменению значений параметров рас-
распределения вероятностей этих величин — среднего, дисперсии или моментов более
высокого порядка.
5.1]
Дисперсионный анализ
591
С помощью дисперсионного анализа устанавливаются изменения дисперсии ре™
зультатов эксперимента при изменении уровней изучаемого фактора. Если диспер-
дисперсии будут отличаться значимо, то следует вывод о значимом влиянии фактора на
среднее значение наблюдаемой случайной величины.
Классические методы дисперсионного анализа основываются на следующих
предпосылках: распределение исходных случайных величин нормально; дисперсии
экспериментальных данных одинаковы для всех условий эксперимента (т. е. для
экспериментов, выполненных на различных уровнях изучаемого фактора).
Поэтому при проведении дисперсионного анализа следует предварительно про™
верить нормальность распределения изучаемой случайной величины (методами,
изложенными в разделе 2.2) и неразличимость дисперсий изучаемых совокупностей
(методами, изложенными в разделе 4.1.1.4).
Подробно теория дисперсионного анализа изложена в [20, 401].
5.1.1. Классический дисперсионный анализ нормально распределенных
случайных величин
5.1.1.1. Однофакторный дисперсионный анализ
Предположим, что анализируется влияние фактора А, изучаемого на к уровнях
(Ai, A2, • • •, Ak). На каждом уровне Ai проведены п наблюдений (хц, з^2, • • •, %in)-
Следовательно, на всех к уровнях фактора А произведены кп наблюдений.
Поясним суть и последовательность проведения дисперсионного анализа. Рас-
Расположим экспериментальные данные в виде таблицы:
Номер
наблюдения
1
2
j
п
Е
Аг
Х\\
Х\2
X!j
Xi
Уровни
А2
Х21
Х22
x2j
Х2п
Х2
фактора А
А{
Хц
Xi2
Xij . . .
Xin . . .
хг
Ак
Xkl
Xk2
Xkj
Хкп
хк
Рассмотрим оценки различных дисперсий, возникающие при анализе таблицы
результатов наблюдений. Для дисперсии, характеризующей изменение данных на
уровне Ai (по строкам таблицы), имеем
1
- 1
Y^
- \2
1
n- 1
1
Из предпосылок дисперсионного анализа следует, что должно иметь место ра™
венство Sf = Я| = ... = 5^, что проверяется соответствующим критерием сравне™
ния (см. раздел 4.1.1.4).
При выполнении условия Sf = const при г = 1, 2, ..., к (что, повторяем весьма
настойчиво, обязательно), находим оценку дисперсии, характеризующей рассеяние
592
Методы исследования связей между случайными величинами
[Гл. 5
значений Xij вне влияния фактора А, по формуле
к п
г=1
г=17=1
(x..^x-f - -
{lJ г) к(п-1)
к п
ъ=13=1
Легко видеть, что, если при оценке Sf мы имеем (п — 1) степеней свободы, то
оценка Sq имеет к (п — 1) степеней свободы.
Общая выборочная дисперсия всех наблюдений равна
s2 г
кп — '.
Следовательно,
с
к п
,2 1
кп-1
к к
ЕЕ
где
4-
j к
г=1
1 1" " ж
1 п
= — У^ х
¦I1
Введем теперь оценку дисперсии SA, характеризующей изменение средних ж^,
связанное с влиянием фактора А:
г=1
Очевидно, что при оценке 5^| используется (Aj — 1) степеней свободы. Теперь
проверка влияния фактора А на изменение средних может быть сведена к сравне™
нию дисперсий S\ и Sq. Влияние фактора А признается значимым, если значимо
S2 S2
отношение —^. Отношение —^. признается значимым с вероятностью а, если
Sq Sq
где i^a(/ij /2) — a-квантиль i^-распределения с /1 и /2 степенями свободы (для нахо-
нахождения .Fa(/i, /2) могут быть использованы либо специальные таблицы, например,
из [24, 25, 29], либо аппроксимации из раздела 1.1.10).
S2
Если влияние фактора А признается незначимым (т.е., когда —^ ^ ^«(/ъ/))?
Sq
то для оценки дисперсии Sq может быть использована более точная оценка 52,
имеющая (кп — 1) степеней свободы против к (п — 1) для Sq.
Для упрощения вычислений приведем алгоритм их выполнения. Вычисляем
последовательно суммы
Далее находим
к-1 '
Сравнением 5^| и Sq устанавливаем наличие влияния фактора А.
5.1]
Дисперсионный анализ
593
Ьсли
к (п — 1)
—^—г^
1
^ 1;
^ l)j, то влияние фактора А признается
ц1 ц2
значимым. В ином случае всю выборку наблюдений можно считать однородной
с общей дисперсией S2 = —^ -^.
fcn — 1
Ранее (см. раздел 4.1.1.2), однофакторный дисперсионный анализ использовался
для проверки гипотезы о равенстве нескольких выборочных средних из нормально-
нормального распределения. Однофакторный дисперсионный анализ и сравнение нескольких
средних являются различными приемами решения одной и той же задачи. Когда
на различных уровнях фактора А проводятся различные количества наблюде-
наблюдений, формулы дисперсионного анализа имеют вид (щ — число экспериментов на
к
уровне
i, N = J2 ni):
г=1
= ??
X
к-1
Отношение —^ сравнивается с Fa(k — 1;N — к).
So
Задача 319. Провести дисперсионный анализ данных, представленных таблицей, при
доверительной вероятности а = 0,95:
1
2
3
4
5
6
Е
Уровни фактора Ai
Аг
3,2
3,1
3,1
2,8
3,3
3,0
18,5
А2
2,6
3,1
2,7
2,9
2,7
2,8
16,8
2,9
2,6
3,0
3,1
3,0
2,8
17,4
А4
3,6
3,4
3,2
3,3
3,5
3,3
20,3
А5
3,0
3,4
3,2
3,5
2,9
3,1
19,1
Вычисляем
= Е Е 4 = 28
x2i=\- A8'5
^° 5-6
Далее вычисляем дисперсии
« 284,87-284,025 =00338;
1
30
284,025 - 282,747
= 284,025;
=282'7
S2A
0,319
= 9,45.
S°- 5.F-1)
Из таблиц для Д = fc — 1 = 4 и /2 = /г • (п — 1) = 25 находим ^о,9бD; 25) = 2,8. Так как
-^ = 9,45 > ^о,95 D; 25) = 2,8, влияние фактора А на поведение наблюдаемых случайных
величин следует признать значимым.
594
Методы исследования связей между случайными величинами
[Гл. 5
5.1.1.2. Двухфакторный дисперсионный анализ
Рассмотренный ранее однофакторный дисперсионный анализ обладает инфор™
мативностью, не большей, чем методы множественного сравнения средних (см. раз-
раздел 4.1.1.2). Информативность дисперсионного анализа возрастает при одновремен™
ном изучении влияния нескольких факторов.
Рассмотрим случай, когда анализируется влияние одновременно двух факторов
А и В на уровнях А\, Ач, ..., А^ и Bi, i^25 • • •, Вт соответственно. Пусть результаты
эксперимента представлены таблицей:
в
Вг
в2
в,
вт
Е
4
4i
хц
#12
xlm
Хг
А2
Х2\
Х2з
Х2т
х2
Хг1
Хг2
х1т
Xi
Хк3
Xkl
Xk2
xkj
Хкт
хк
Е
Xv
Х41
Ху
Дисперсионный анализ для двухфакторных таблиц проводится в следующей
последовательности. Вычисляются суммы
к т
Далее находятся оценки дисперсий
О2 Q1+Q4-Q2- Яз
1 j=i
S2
Если —2" > Fa(fi, /2M где Д = Aj — 1 и /2 = (Aj — 1)(т — 1), то влияние фактора А
So
с достоверностью а признается значимым.
Аналогично значимым признается влияние фактора В^ если
я2
Fa
(/ь /2), где Д = m - 1 и /2 = (А; - 1) (ш - 1) .
Приведенный анализ предполагает независимость факторов А ш В. Если они зави™
симы, то взаимодействие факторов С = АВ также является фактором, которому
соответствует своя дисперсия. Для того, чтобы выделить такое взаимодействие,
необходимы параллельные наблюдения в каждой клетке таблицы, т. е. при каждом
сочетании факторов А и В на уровнях А{ и Bj соответственно необходимо не
одно наблюдение, а серия наблюдений ж^д, Хц2^ ..., хцп. Пусть Xij теперь является
5.1]
Дисперсионный анализ
595
средним из п наблюдений, т. е. Xij =
= — У]
^. Для оценки влияния взаимодействия
17=1
факторов АВ вычисляем дополнительную сумму
к т п
On — V V V X2-
Далее анализ проводится, как и ранее, с той лишь разницей, что в клетках
таблицы вместо отдельных значений Xijv используются их средние значения Xij.
Вычисляется дисперсия
Sab = тк (п - 1)'
и проверяется значимость взаимодействия факторов АВ критерием
r->Fa{fuh),
где
= (к - 1)(т - 1) и /2 = тк(п - 1).
С добавлением каждого нового фактора принципиальная основа дисперсной™
ног о анализа не изменяется, но существенно усложняются формулы и таблицы
для расчетов. Подробное изложение прикладных методов дисперсионного анализа
для случая трех, четырех и более факторов с анализом различных практических
ситуаций содержится в [20, 559].
Задача 320. Провести двухфакторный дисперсионный анализ данных, представлен-
представленных следующей таблицей^ при доверительной вероятности а = 0,95:
В
Вг
в2
Вз
в4
3,6
4,2
3,8
3,4
Аг
3,8
4,0
3,5
3,2
4,1
4,1
3,6
3,2
2,9
3,3
3,6
3,4
А
А2
зд
2,9
3,7
3,6
3,0
3,2
3,5
3,5
2,6
3,7
3,2
3,6
А3
2,5
3,5
3,0
3,8
2,9
3,
3,
з,
6
4
7
Заменяя в клетках таблицы серии значений их средними, получаем следующую
таблицу:
В
Вг
в2
в3
в4
Е
А
Аг
3,83
4,10
3,63
3,27
14,83
А2
3,00
3,13
3,60
3,50
13,23
А3
2,67
3,60
3,20
3,70
13,17
Е
9,50
10,83
10,43
10,47
41,23
Используя данные таблицы, вычисляем суммы
3 4 1 3
х% = 143,34; Q2 = - • J2 Xi = 142,102675;
г=1
i = 141,98157;
4-3
Е xi = 141,6594; Q5 = Е Е Е 4- = 430,79.
г=1j=lu=l
596 Методы исследования связей между случайными величинами [Гл. 5
Далее вычисляем:
а2 Qi + Q4 - Q2 - Q3 143,3745 + 141,6594 - 142,102675 - 141,98157
О _
on :=::::
'=:i 0,15821
(fc-l)-(ra-l) 2-3
Я2 _ Q2 - Qa _ 142,3745 - 141,6594
^ к — 1 2
= Qj^Q* = 141,98157-141,6594 =
771—1 3
= Q.-n.ft = 430,79-3-143,3745 =
rafc • (п - 1) 4-3-2 '
fi| = 0,223675 = 4 = ^^^=0,679; ^# = 3 ' °'1582 = 17,09.
Sg 0,1582 ' ' Si 0,1582 ' ' S2AB 0,02777
Из таблиц (см. раздел 1.1.10) имеем
Fo,95[fc - 1; (А; - 1) • (ш - 1)] = Fo,95B; 6) = 5,1; F0^[m - l; (A; - 1) • (m - 1)] = 458;
^о,95[(^^ 1) -(т- 1);тк- (п - 1)] =F0,95F;24) = 2,5.
Сравнивая, получаем
% = 1,41 < Fo,95B; 6) = 5,1; % = 0,679 < Fo!95C; 6) = 4,8;
о2
^^ = 17,09 > F0,95F; 24) = 2,5.
Следовательно, влияние факторов А и В должно быть признано незначимым. Однако
существенно значимым является взаимодействие факторов А ж В. Это поучительный
пример эффективности двухфакторного дисперсионного анализа по сравнению с про-
простым последовательным повторением однофакторных экспериментов.
5.1.2. Дисперсионный анализ с использованием размахов
Рассмотрим схему двухфакторного дисперсионного анализа с к уровнями фак-
фактора А ж т уровнями фактора В (при каждом сочетании уровней факторов одно
наблюдение или среднее из нескольких наблюдений). В [119] рассмотрено приме-
применение „стьюдентизированного" размаха, как статистики для выявления значимости
влияния изучаемых факторов
max Xi — min
q ъ
Статистика q распределена как статистика „стьюдентизированного" размаха (см.
раздел 4.1.1.2.2), критические точки которой приведены в табл. 123 для различ™
ных т (в табл. 123 следует вместо п использовать т) и /. Количества эквивалент-
эквивалентных степеней свободы / для нашего случая и значения коэффициента с приведены
в табл. 215.
Средний размах ш вычисляется следующим образом. Для каждого уровня Ai
находим
1 т
Х4 = — У^ Xij. г = 1, 2, ..., к.
т ^^ J
i=t
Затем для всех уровней фактора В при г-м уровне фактора А вычисляем т
разностей Axij = x^j — х^, j = 1,2, ..., га. Далее находим
1 т
ujj = max Ахц — min Аж?-7- и ш = — \^ о;,-.
J l^i^k J l^i^k J m f^
5.1]
Дисперсионный анализ
597
Таблица 215
Масштабный коэффициент с и эффективное число степеней
свободы / для двухфакторного дисперсионного анализа [119]
т
2
3
4
5
6
7
8
9
10
20
т
2
3
4
5
6
7
8
9
10
20
/
1,00
1,90
2,70
3,60
4,50
5,40
6,30
7,10
8,10
16,70
i
f
4,70
9,30
13,90
18,50
23,00
27,60
32,10
36,60
41,00
86,00
>
с
1,00
1,05
1,07
1,08
1,09
1,09
1,10
1,10
1,10
11,10
с
1,89
2,12
2,23
2,30
2,34
2,37
2,39
2,41
2,42
2,48
3
/
2,00
3,70
5,40
7,20
8,90
10,70
12,50
14,30
16,10
33,90
7
/
5,50
11,30
16,90
22,40
27,90
33,30
38,70
44,00
49,30
103,00
с
1,35
1,48
1,54
1,57
1,59
1,61
1,62
1,63
1,63
1,66
с
2,00
2,26
2,38
2,45
2,49
2,52
2,55
2,57
2,58
2,64
к
4
f
2,90
5,60
8,20
10,90
13,60
16,30
19,00
21,70
24,40
51,50
к
8
/
6,30
13,40
20,10
26,60
33,00
39,30
45,60
51,80
57,90
119,00
с
1,58
1,76
1,84
1,88
1,91
1,93
1,95
1,96
1,97
2,02
с
2,10
2,37
2,50
2,57
2,62
2,65
2,68
2,70
2,71
2,78
5
/
3,80
7,40
11,00
14,60
18,20
21,80
25,40
29,00
32,60
68,80
с
1,75
1,96
2,06
2,12
2,15
2,18
2,20
2,21
2,22
2,28
9
/
7,00
15,70
23,60
31,10
38,30
45,40
52,50
59,60
66,60
134,00
с
2,18
2,46
2,60
2,68
2,73
2,76
2,79
2,81
2,83
2,90
Превышение выборочной статистикой q ее критического значения qa(mi f)
(из табл. 123) приводит к признанию значимости влияния изучаемых факторов.
Задача 321. Провести дисперсионный анализ в условиях задачи 320 с помощью раз-
махов.
Таблица данных имеет следующий вид:
В
Вг
в2
в4
А
Аг
3,83
4,10
3,63
3,27
А2
3,00
3,13
3,60
3,50
А3
2,70
3,50
3,20
3,70
Имеем к = 3, т = 4. Из табл. 215 для к = 3, т = 4 находим с = 1,54 и / = 5,4.
Далее средние по столбцам (при уровне а» фактора А) равны
3,83 + 4,10 + 3,63 + 3,27
= 3,7075;
3,00 + 3,13 + 3,60 + 3,50
х2 = = 3,3075;
2,70 + 3,50 + 3,20 + 3,70
= 3,275.
Следовательно, max х% — min х% = х\ — хз = 3,7075 — 3,275 = 0,4325.
598
Методы исследования связей между случайными величинами
[Гл. 5
Теперь вычислим т = 4 разностей Axij = хц — xi для всех j = 1, 2, ..., т. Таблица
этих разностей для нашего случая имеет вид.
В
Вг
в2
в3
в4
А
Аг
0,1225
0,3925
-0,0775
^0,4375
А2
-0,3075
-0,1775
0,2925
0,1925
Аз
-0,5750
0,2250
-0,0750
0,4250
0,6975
0,5700
0,3700
0,8625
Для каждого j значения ujj = max Ax^j — min Ax^ приведены в последнем столбце
таблицы. Далее находим
0,6975 + 0,570 + 0,37 + 0,8625 Г 0,4325
ш = = 0,625; q = 1,54 • V4 •
0,625
= 2,13.
Из табл. 123 находим для т = 4 (входим в таблицу с п = 3) / = 5,4 (используем
интерполяцию) и при а = 0,95 находим до,95 D; 5,4) = 5,2.
Так как q = 2,13 < до,9бD;5,4) = 5,2, этот критерий не выявил влияния факторов
А и В на наблюдаемый процесс. К сожалению, выделить влияние взаимодействия фак-
факторов А и В с помощью этого критерия невозможно.
5.1.3. Непараметрический дисперсионный анализ
Использование для однофакторного дисперсионного анализа вместо значений слу™
чайных величин их рангов, назначенных определенным образом, рассмотрено в раз-
разделе 4.2.1.2.15, где приведена подробная информация о критерии Фридмана-Кендал-
ла—Бэбингтона Смита, применяемом в этом случае. Мы отсылаем читателя к разде-
разделу 4.2.1.2.15, где этот критерий рассмотрен применительно к задаче сравнения не-
нескольких средних, что аналогично задаче однофакторного дисперсионного анализа.
Поэтому мы сосредоточимся на изложении пока малоизвестных и в силу этого
обстоятельства редко применяемых методов двухфакторного непараметрического
дисперсионного анализа для неполных данных. Для более глубокого изучения
проблем неполных данных отсылаем заинтересованного читателя к сравнительно
недавно переведенной на русский язык монографии [385].
5.1.3.1. Двухфакторный непараметрический дисперсионный анализ
длм неполных данных
Предположим, имеется таблица дисперсионного анализа с к уровнями факто-
фактора А (г = 1, 2, ..., к) и т уровнями фактора В (j = 1, 2, ..., га). Ранее мы рас-
рассматривали ситуацию, когда в каждой ячейке таблицы было одно наблюдение xij.
Однако в практике часто могут быть случаи, когда часть требуемых значений xij
может по тем или иным причинам отсутствовать: например, когда в эксперименте
не все сочетания факторов Ai и Bj могут быть реализованы. Обычно при обработке
неполных данных используется замена отсутствующих данных средними наблюде-
наблюдениями или средними рангами, вычисленными по некоторому множеству наблюде-
наблюдений. Однако это может приводить к ошибкам. В настоящем разделе приведены
более точные критерии для такой ситуации.
5.1.3.1.1. Критерий Принтиса
Предположим, что двухфакторная таблица имеет т строк и к столбцов, и в каж-
каждой (i^j)-M ячейке находится либо одно наблюдение, либо ни одного. Пусть riij —
число наблюдений в ячейке, расположенной на пересечении j-й строки и г-го столб-
5.1]
Дисперсионный анализ
599
ца (г = 1, 2, ...,1с; j = 1, 2, ..., га). Очевидно, что п^- = 1 или п^- = 0. Обозначим
rij = ^ n^j. В каждой j-й строке ранжируем по возрастанию все гг^ наблюдений
и получаем последователвности рангов Rji, Rj2? • • • ? ^'п^ Для всех j = 1,2,..., га.
Пусть Si — множество строк (а, следовательно, и ранжировок), в которых есть
наблюдение над г-м столбцом (т.е. ранг, относящийся к г~му столбцу). Далее вы™
числяем
% - 1
1
'12
1
% + 1
Построим матрицу W = ||ги^/||, без i/-ro столбца и iz-й строки, где 1 ^ v ^ fc
(т. е. матрица W строится вычеркиванием произвольно выбранных столбца
и строки с одним и тем же номером из матрицы ||ги^'||)- Строим вектор
а = (ai, ..., a^-i, a^+i ..., a^), т. е. удаляется компонента с номером v вычеркнутых
строки и столбца. Вычисляем матрицу W, обратную к матрице W, и квадратич™
ную форму с = aFF^1a/, где а; — вектор-столбец, получаемый транспонированием
вектора-строки а.
При достаточно больших выборках (га ^8, к ^ 6) имеет место приближение
[560, 561], из которого следует, что если с ^ Х«(^ ~~ 1M то гипотеза об отсутствии
влияния исследуемых факторов отклоняется с вероятностью а (здесь Х«(^ ~ 1) —
a-квантиль распределения хи™квадрат с f = к — 1 степенями свободы).
При малых значениях га и к приближение действует плохо, однако таблицы
критических значений этого критерия отсутствуют.
Задача 322. Для данных, представленных в таблице, провести дисперсионный анализ
критерием Принтиса при доверительной вероятности а = 0,95:
3
1
2
3
г
1
3,7
5,6
2
8,2
6,4
2,3
3
7,5
Имеем т = k = 3 ш rij = 2,j = 1,2,3. Производим ранжирование наблюдений по всем
строкам и получаем таблицу рангов:
3
1
2
3
г
1
1
2
2
2
1
1
3
2
Множество строк Si, в которых имеются наблюдения в первом (г = 1) столбце, будет
= {1,3}, и по аналогии S2 = {1,2,3}, S3 = {2}.
Далее вычисляем
ai=
i=i,3
пз +1
Дп
ni + 1
600
Методы исследования связей между случайными величинами
[Гл. 5
а2
= Е
j = l,2,3
Rj2 l\ _ 2 1 1 1 1 1 _ 1
n,- + 1 2/^3 2 3 2 3 2^6'
= ?
3 = 2
Вычислим теперь диагональные элементы матрицы:
1 v^ п7- - 1 1 /l l
12 ^ гц + 1
022 = S ;
.7 = 1,2,3
1
12
12 \3 3
l l :
2
36'
з ш
~ 36'
12
1 1
12 * 3
1
зб7
Далее вычисляем остальные элементы матрицы:
1 ^^ 1 1 v^ 1
12 ^ те,- + 1
ii3 J
W\2 = "Ш21 = * ?
12 ^ rij + 1
jes1ns2 J
= 0
i=i,3
П S2 —пустое мно^кество) ;
12
1 1
" 12 * 3
Таким образом, получаем матрицу
wa =
36
2
36
3
36
о
36
1
36
W21 W22 W23
W31 W32 W33
0
36 36
Отбросим 3-ю строку и 3-й столбец (у = 3), тогда имеем матрицу
2 2
36 36
w =
2
~36
3
36
2
36'
Соответственно имеем вектор а = ( 0, 1 (вместо а = ( 0, , - 1 —так как вычерки-
V 6/ V 6 6/
вается третье значение).
Теперь вычисляем матрицу W", обратную матрице W. Напомним, что обратная
матрица W^1 связана с основной W соотношением W • W^1 = I. Обратная матрица
, где det W — определитель матрицы W, А —
рассчитывается по формуле ,,
присоединенная матрица, являющаяся транспонированной матрицей алгебраических до-
дополнений.
Алгебраическое дополнение Ац элемента aij матрицы равно определителю матрицы,
полученной вычеркиванием в первоначальной матрице г-й строки и j-ro столбца, умно-
женному на (™1)*+J'.
Транспонирование матрицы достигается перестановкой ее строк и столбцов.
Для нашего случая
36-36 I зб/ \ 36/ 36-36
36
2
36
36
3
36
5.1]
Дисперсионный анализ
601
Для матрицы W =
2
36
2
36
2
~36
3
36
матрица алгебраических дополнений имеет вид
3 2
36 36
2 2
36 36
3
36
2
36
2
36
2
36
. Присоединенная матрица получается транспонированием матрицы
Окончательно получаем
A
detW
3
36
2
36
36
2
36
2
36
2
¦36
3-36-36 2-36-36
36-2 36-2
2-36-36 2-36-36
36-2
36
54 36
36 36
Далее вычисляем квадратичную форму (и)ц/ — элементы матрицы W
0 • 36 +0 • \-\) • 36
•36 = 1.
Критическое значение из табл. 55 Xo,9sB) = 5,99.
Так как с = 1 < Xo,9sB) = 5,99, влияние факторов в таблице следует признать незна-
незначимым.
5.1.3.1.2. Критерий Мака—Скиллингса
Обозначения те же, что и в предыдущем разделе. В каждой ячейке допускается
любое число наблюдений riji (j = 1, ..., га; г = 1, ..., к); N = ^2,пз*-- Пр°ЦеДУРа
hi
построения статистики критерия включает в себя следующие шаги. Все наблюдения
к
j-is. строки ранж:ируются по возрастанию от 1 до rij = ^%'i- Обозначим через
г=1
rjiu — ранг наблюдения Xjiv в общей последовательности (j = 1, ..., га; г = 1, ..., к;
у = 1, • • -,riji).
Вычисляем
Будем рассматривать случай пропорциональных частот, т. е. когда п™ =
N
31 тк
т
-, где щ = Y^ riji. Для этого (достаточно распространенного) случая стати-
статистика критерия имеет вид [562]
к
Т =
12
N(N
г=1
J=1
602
Методы исследования связей между случайными величинами
[Гл. 5
При N =
оо (N > 15) справедлива %2™аппроксимация. Влияние изуча™
емых факторов на поведение случайной величины с достоверностью а признается
значимым, если Т ^ ^(к — \).
Критические значения Ta(rn,k,nji) статистики Мака—Скиллингса приведены
в табл. 216.
Таблица 216
Критические значения Та (га, fe, rtji)
статистики Мака^Скиллингса [560, 562]
тп
2
2
2
2
3
3
3
3
4
4
4
4
5
5
5
5
ил
2
3
4
5
2
3
4
5
2
3
4
5
2
3
4
5
Доверительная
0,90
к
2
2,700
3,429
4,375
4,142
3,200
3,571
2,778
3,058
3,750
3,048
3,000
3,153
3,000
2,752
2,817
2,987
3
5,143
4,578
4,635
4,530
4,667
4,662
4,625
4,654
4,587
4,571
4,622
4,580
4,629
4,604
4,669
4,572
4
6,083
6,128
6,243
6,160
6,167
6,231
6,231
6,265
6,250
6,231
6,325
6,243
6,267
6,179
6,287
6,147
5
7,418
7,500
7,664
7,617
7,527
7,633
7,776
7,714
7,500
7,700
7,761
7,782
7,702
7,673
7,746
7,704
вероятность а
0,95
к
2
4,800
4,667
4,167
4,276
5,000
4,587
4,000
3,060
5,400
3,857
4,083
3,938
4,320
4,200
2,267
4,034
3
5,571
5,733
5,846
5,880
6,000
5,896
5,936
5,927
5,786
5,956
5,984
5,955
5,886
5,920
5,977
5,844
4
7,250
7,615
7,577
7,686
7,444
7,479
7,757
7,750
7,625
7,667
7,737
7,717
7,733
7,779
7,747
7,583
5
8,727
8,967
9,036
9,338
9,018
9,089
9,300
9,263
8,918
9,200
9,354
9,404
9,251
9,347
9,317
9,250
Задача 323. Выполнить дисперсионный анализ данных, приведенных в таблице, кри-
критерием Мака-Скиллингса при доверительной вероятности а = 0,95:
3
1
2
3
1
1,2
1,3
1,4
1,5
2,2
2,1
1,5
1,7
1,7
1,6
2,8
2,4
г
2
2,3
2,5
3,7
3,2
1,9
1,6
2,4
2,6
зд
3,4
1,1
1,4
3,1
3,5
2,9
2,2
3,7
3,1
3
3,4
3,3
2,1
2,4
3,9
3,3
Проведя ранжирование данных по строкам, получаем таблицу рангов
3
1
2
3
1
3
1
2
6
5
1
2
4
4
3
8
7
г
2
5
7
12
10
4
3
6
8
9
11
1
2
3
9
11
8
6
11
9
12
10
5
7
12
10
5.1]
Дисперсионный анализ
603
В нашем случае riji = 4; т = 3 и к = 3.
4
Суммы рангов Rji = ]P г^ приведены в следующей таблице:
3
1
2
3
1
10
10
26
2
26
42
10
3
42
26
42
Имеем
N
mk
т. е. имеет место вариант пропорциональных частот.
Далее находим
Вычисляем статистику критерия
Т =
12
N-(N + m) fr{
12- 12
36 ¦ C6 + 3)
11,5-
36 + 3
+ ... + 27,5 -
36 + 3
= 13,128.
Для m = к = 3, riji = 4 и a = 0595 из табл. 216 имеем Т0;95C, 3, 4) = 5,936.
Так как Т = 13,128 > ТЬ,Э5C, 3, 4) = 5,936, следует признать влияние изучаемых фак-
факторов значимым.
5.1.3.1.3. Критерий Лемана-Мака
Обозначения аналогичны критерию Мака^Скиллингса. Ранжируем все
к
rij = ^ riji наблюдений внутри j-й строки и обозначим через Rjiv ранг наблюдения
г=1
Xjiv {и = 1, ... ,га).
Вычисляем сумму и средний ранг наблюдения над j-м столбцом в г-й строке
^i* = ~ Yl Riil/i 3 = 1? • • • 5 т; г = 1, ..., fc.
Далее, вычисляем значение статистики Крускала-Уоллиса (см. раздел 4.2.1.2.1):
2 к
к
щ
1 = 1
12
% К- +1)
Vz^=l
Наконец вычисляем статистику критерия (сумму статистик Крускала-Уоллиса)
604
Методы исследования связей между случайными величинами
[Гл. 5
Громоздкие таблицы критических значений статистики Н приведены в [563].
Для частного случая rij = n (постоянное число наблюдений по строкам)
(т
Обозначим через Zj число пустых ячеек в j'-й строке и введем величины
Тогда статистика Лемана^Мака имеет вид
L =
Ее критические значения равны
m(n-l)f1Fn(f1J2)
/2+/lF«(/i,/2) '
где i^a (/l?/2) — a-квантиль i^-распределения с /1 и /2 степенями свободы; для
нахождения .Fa рекомендуется пользоваться специальными таблицами ([24, 25, 29]
и особенно [87]).
Влияние изучаемого фактора на случайные величины признается значимым
с вероятностью а, если L > La(/i, /2).
Рассмотрим теперь случай, когда хотя бы два числа наблюдений в строках не
равны: rij1 ф rij2; ji,j2 € {1, . ..,га}, j\ /j*2- В этом случае гипотеза о влиянии
факторов принимается, если Н ^ Xa(/i), где X«(/i) — a-квантиль распределения
хи™квадрат с Д степенями свободы.
Задача 324. Выполнить дисперсионный анализ данных^ приведенных в задаче 323,
критерием Лемана-Мака при доверительной вероятности а = 0,95.
Имеем riij =4, rij =n^ = 12,
дены в таблице (см. задачу 323):
= 3. Суммы рангов по ячейкам таблицы приве-
приве3
1
2
3
г
1
10
10
26
2
26
42
10
3
42
26
42
я1 =
Вычисляем
12
т ¦ (щ + 1)
-3-
12
• - • (Ю2 + 262 + 422) - 3 • A2 + 1) = 9,8461.
12-13 4
з
Очевидно, чтоЯ1=Я2=Я3иЯ=У]^=3- 9,8461 = 29,5383.
5.1] Дисперсионный анализ 605
Далее при rij = п = 12 имеем
ЯГ = Я2* = Щ = ^—^ • Нг = 13 • 9,8461 = 127,9993;
ЯГ* = Я2** = Я3** = ^^ • A2 - 1 - 9,8461) = 15,0007.
Число непустых ячеек в j-й строке равно lj = 3 (j = 1, 2, 3).
Находим
? Я** = 45,0021; /i = Е (I, - 1) = 6; /2 = ? A2 - I,) = 27.
j=i i=i j=i
383 9979
Окончательно имеем L = = 38,398. Из таблиц находим Fq 95F,27) = 2,459
6-45,00021 ' ' V ' ;
3 ¦ A2 - 1) ¦ 6 • 2,459
= 11,0.
27 + 6-2,459
Так как L = 38,398 > Lg,95 F,27) = 11,66, влияние изучаемых факторов следует с до-
достоверностью а = 0,95 признать значимым.
606 Методы исследования связей между случайными величинами [Гл. 5
5.2. Корреляционный анализ
Корреляционный анализ предполагает изучение зависимости между случайны™
ми величинами с одновременной количественной оценкой степени неслучайности их
совместного изменения.
Изменение случайной величины у, соответствующее изменению случайной ве-
величины ж, разбивается на две составляющие — стохастическую, связанную с неслу™
чайной зависимостью у от ж, и случайную (или статистическую), связанную со
случайным характером поведения самих у и х.
Стохастическая составляющая связи между у is. x характеризуется коэффици-
коэффициентом корреляции
_ Щ[х-Щх)][у-Щу)]}
Р
где M(z) и D(z) — соответственно математическое ожидание и дисперсия случайной
величины z.
Коэффициент корреляции показывает, насколько связь между случайными ве-
величинами близка к строго линейной. Если у и х распределены нормально, равенство
р = 0 указывает на отсутствие линейной связи между ними. Значение р = =Ы со-
соответствует строго линейной связи между у и х (знак указывает на направление
связи).
Однако коэффициент корреляции р не учитывает возможной криволинейной
связи между случайными величинами. Для учета таких связей используется кор-
корреляционное отношение, введенное К. Пирсоном.
Для двумерного ряда наблюдений, когда на каждом уровне одной переменной у^
наблюдаются щ значений другой переменной Xij (j = 1, ..., щ), корреляционное
отношение определяется следующим образом
где Sq — дисперсия рассеяния значений Х{j, связанная с влиянием группировки
значений X{j по г уровням переменной у\ S2—дисперсия рассеяния значений X{j
без учета их группировки по уровням переменной у.
В нашем случае определено корреляционное отношение х по у. Перестановкой
переменных по аналогии может быть определено г}2 — корреляционное отношение
у по х (тогда на каждом уровне переменной Х{ наблюдается группа значений другой
переменной y%j). В общем случае г}^у ф f]yX.
Если у и х связаны строго линейно, то г]2 = р2 = 1. Если между х и у существует
линейная стохастическая связь, то р2 = г}2 < 1. При нелинейной стохастической свя-
зи р2 < г}2 < 1. В любом случае имеет место неравенство 0 ^ р2 ^ г]2 ^ 1 (равенство
достигается только при строгой линейной связи между у ж х).
5.2.1. Классический корреляционный анализ
нормально распределенных случайных величин
5.2.1.1. Оценка коэффициента корреляции
Рассматриваются нормально распределенные случайные величины у is x —
(#1, т/1), (#2,2/г), • • •; 0*4, Уг)-> - - - ? (xni Уп)- Выборочной оценкой коэффициента корре-
5.2] Корреляционный анализ 607
ляции р является случайная величина
п
J2(Xi ~^){Vi - У)
где х = — > Xi\ у = — > i/«i ^ — объем выборки.
При малых значениях тг (п < 15) лучшей оценкой коэффициента корреляции
является
г* = г|1 +
2(п-3)
При п > 200 распределение выборочного коэффициента корреляции удовлетво-
рительно аппроксимируется нормальным законом [1] со средним М(г) и дисперси™
ей D(r):
M(r) = p; D(r) = ^.
При п > 5 распределение случайной величины [5]
1 1 — г
z = - In = arcth(r)
2 1+r у J
удовлетворительно аппроксимируется нормальным распределением с параметрами
При п > 10 распределение случайной величины [564]
(г — р)\/п — 2
удовлетворительно аппроксимируется распределением Стьюдента с / = п — 2 сте-
степенями свободы.
Приведенные аппроксимации распределения выборочного коэффициента корреля-
корреляции позволяют строить статистические критерии для проверки гипотез о существен-
существенности корреляционной связи и о возможных значениях коэффициента корреляции.
На практике наибольший интерес представляет задача проверки гипотезы о зна-
значимости корреляционной связи между случайными величинами, т. е. значимости
отклонения коэффициента корреляции р от нуля. В принятых обозначениях прове-
проверяется нулевая гипотеза Hq : \р\ =0 против альтернативы Hi: \р\ ф 0.
Эта гипотеза проверяется сравнением выборочного значения коэффициента кор-
корреляции г с его критическим значением га, являющимся а-квантилью распределе-
распределения г при р = 0. Корреляция между случайными величинами признается значимой,
если \r\ ^ га. Критические значения га приведены в табл. 217.
Использование рассмотренных выше аппроксимаций приводит к следующим
оценкам:
— при п > Б
ехр(
та =
ехр(
608
Методы исследования связей между случайными величинами
[Гл. 5
— при п > 10
— при п > 200
гп =
\
п - 2 + t\+a
2
Здесь иа и ta — «-квантили соответственно стандартного нормального распределе-
распределения и распределения Стьюдента с / = п — 2 степенями свободы.
Таблица 217
Мритические значения га
выборочного коэффициента корреляции для р = О [25]
п
3
4
5
6
7
8
9
10
11
12
Доверительная
вероятность а
0,90
0,988
0,900
0,805
0,729
0,669
0,621
0,582
0,549
0,521
0,497
0,95
0,997
0,950
0,878
0,811
0,754
0,707
0,666
0,632
0,602
0,576
0,99
1,000
0,990
0,959
0,917
0,874
0,834
0,798
0,765
0,735
0,708
п
13
14
15
16
17
18
19
20
21
22
Доверительная
вероятность а
0,90
0,476
0,457
0,441
0,426
0,412
0,400
0,389
0,378
0,369
0,360
0,95
0,553
0,532
0,514
0,497
0,482
0,468
0,456
0,444
0,433
0,423
0,99
0,684
0,661
0,641
0,623
0,606
0,590
0,575
0,561
0,549
0,537
Если гипотеза о значимости корреляции между случайными величинами не
отклоняется, то можно построить доверительный интервал для истинного коэффи-
коэффициента корреляции по его выборочному значению. Впрочем, для корреляционного
анализа это уже не столь важно, ибо его основная цель — установление значимости
наблюдаемой связи.
Задача 325. В результате наблюдений над случайными величинами х и у получена
следующая совокупность данных (п = 10):
ж: 2 4 1 7 3 11 14 15 21 4
у: 7 6 4 11 2 21 31 23 40 15.
Необходимо проверить гипотезу о наличии корреляции меэюду случайными величинами
х и у с достоверностью а = 0,95.
Находим
10
г=1
10
г=1
= 8,2;
и - уJ = 1422;
Xi ~~ ж) = 405,6; у = —
ю
= 16,0;
- (Xi - х) ¦ (у* - у) = 723.
Далее получаем оценки коэффициента корреляции
723
г = =
V405,6 ¦ 1422
= 0,952; г* = 0,952 • 1 +
- 0,952"
2-7
= 0,958.
5.2] Корреляционный анализ 609
Из табл. 217 для п = 10 и а = 0,95 находим го,э5 = 0,632.
Так как г (г*) = 05952 @,958) > го,95 = 0,632, наличие зависимости между величинами
х и у следует признать значимой с достоверностью а = 0,95.
Если воспользоваться аппроксимациями (имея в виду, что tti+o,95 = ^о,975 = 1,96),
2
получим
/2- 1,96
ехР —/=
exp
л/7
что близко к точному значению го,95 = 0,632.
С помощью ^-приближения получим (ti+g (/ = п — 2) = to,975(8) = 2,31)
2
1
о 95 =
tg>975(8) J / 2,312
Ю - 2 + tgf975 (8)
— 0,632,
что совпадает с табличным значением.
Наконец, приближение для больших выборок дает
«0,975 1,96
Го,95 = > = ^^ = 0,653.
\/п — 1 3
5.2.1.2. Оценка корреляционного отношения
Предположим, что мы имеем п значений случайной величины у: 2/i, 2/2? • • • ,Ук-
к
При у = yi наблюдаются щ значений случайной величины х. Если п = У^ п^;
1 п'?
ж^-—j™e значение величины ж, наблюдаемое при у = yi (j = 1, 2,..., щ)\ xi = — J^ ж^-;
г j=i
ж = — J^ ж^, то выборочная оценка корреляционного отношения х по у равна [132]
2 г=1
Проверка гипотезы iifg: f}2 = 0 против альтернативы i?i: ?]2 7^ 0 производится
, rj (п — к)
с помощью статистики I = . 9Ч .
(fc-l)(l-r,2)
Если I ^ Fa(fi1 /2), то нулевая гипотеза отклоняется с достоверностью а. Здесь
-Ра(/ъ /2) — а-квантиль i^-распределения cfi = k^lwf2 = n^k степенями сво-
свободы. При линейной связи между случайными величинами tj2 = р2 и 77^ = ^ж-
Следовательно, разность rj2 — р2 может служить мерой нелинейности корреляцион-
корреляционной связи. Проверка гипотезы Щ : 7]2 — р2 = 0 против альтернативы Нi: т]2 — р2 / 0
может быть осуществлена с помощью статистики
_ (ту2 - р2) (п - к)
" (^2)A^2) '
20 А. И. Кобзарь
610 Методы исследования связей между случайными величинами [Гл. 5
имеющей при справедливости нулевой гипотезы ^-распределение с /х = & — 2
и /2 = п — к степенями свободы. Если I* ^ Fa(fi, /2), то с вероятностью а гипотеза
линейности корреляционной связи отклоняется. Следует помнить, что для оценки
корреляционной связи х по у необходимо иметь несколько наблюдений х для
различных у (и наоборот).
Задача 326. Проверить линейность корреляционной связи для выборки
уц 2 4 9 13 15
Xiji 1,3,4 7,8,12 14,19,21 11,9,6 8,7,3
при доверительной вероятности а = 0,95.
Имеем к = 5,Пг = Зшп = 15. Вычисляем далее:
1 + 3 + 4
5 3
X! = — — = 2,66; х2 =9; х3 = 18; х4 = 8,67; х5 = 6; J2J2 ХЬ = 1641'
3 i=ij=i
= 8,864; ^ п* • ж? = 3 • B,662 + 92 + ... + б2) = 1569,2136.
Тогда
, = 1569,2136-15.8,864^ =
у 1641 - 15 • 8,8642
Из таблиц находим Fo^5(fiJ2) = ^0,95 E ~~ 1; 15 — 5) = F0,9sD; 10) = 3,5.
jy j r?-{n-k) 0,845-10
Вычисляем далее I = (fc _ 1} . (l _ ^2) = 4 . A _ Q?845) = 13,629.
Полученная величина больше критического значения i*b,95 D; 10) = 3,5, следователь-
следовательно, необходимо признать наличие существенной нелинейной связи между х и у.
Оценим теперь отклонение связи между жиг/от линейной, для чего оценим коэффи-
коэффициент корреляции. Вместо значений хц на каждом уровне yi будем использовать средние
значения х%. Тогда ряд будет следующим:
хп 2,66 9 18 8,66 6
уц 2 4 9 13 15.
Используя формулы из предыдущего раздела, получаем
1 1 5 5
ж = - • V ж» = 8,864; y=-.\^yi = 8,6; Y" fe - IJ = 130,2187; \" (yi - у) = 125,5;
5 5 »=1 »=1
5
5^ (ж* - ж) • (t/i - у) = (-6,204) • (-6,6) + ... + (-0,204) • 6,4 = 24,775.
г=1
Тогда
24,775
+ _
-v/130,2187- 125,2
@,8448 - 0,0376) ¦ A5 - 5)
=0,194 (г2 = 0,0376);
г
E - 2) • A - 0,8448)
Из таблиц имеем F0,95E - 2; 15 - 5) = F0,95C; 10) = 3,7.
Так как I* = 17,337 > i*o,95C; 10) = 3,7, следует отклонить гипотезу о наличии линей-
линейной корреляционной связи между случайными величинами.
Отсюда следует поучительный вывод — незначимость коэффициента корреляции не
означает отсутствия связи между исследуемыми величинами. Следует говорить об от™
сутствии линейной зависимости, так как незначимость коэффициента корреляции не
исключает наличия нелинейной связи между случайными величинами.
5.2] Корреляционный анализ 611
5.2.1.3. "Частная и множественная корреляции
При необходимости исследования связи между ^ 3 случайными величинами
исполвзуются частные и множественные коэффициентв! корреляции. Рассмотрим
случай трех переменных — ж, у и z (при числе переменнв1х больше трех выражения
для коэффициентов корреляции могут быть выписаны по аналогии).
Зависимость между двумя переменными х ж у при фиксированной третьей
переменной — z оценивается с помощью частного коэффициента корреляции pxy,z-
По аналогии можно определить частные коэффициенты корреляции по остальным
парам переменных pXZiV и pzy^x.
Выборочные частные (парные) коэффициенты корреляции определяются с по-
помощью соотношений
fZy
Так же, как и простые коэффициенты корреляции, парные коэффициенты прини-
мают значения от — 1 до +1. Гипотеза Н®: pxy^z = 0 для коэффициента корреляции
Pxy,z (для остальных аналогично) проверяется с помощью статистики
t =
/1 — г2
' x ' xy,z
где к — число переменных (в нашем случае к = 3).
При справедливости Hq величина t распределена в соответствии с распределе-
распределением Стьюдента при / = п — к степенях свободы.
При \t\ > ti+a (n — к) нулевая гипотеза Hq отклоняется с вероятностью а. Мно-
2
жественная корреляция исследуется в случае, когда необходимо установить су-
существенность взаимосвязи одной переменной с совокупностью остальных. Выбо-
Выборочные множественные коэффициенты корреляции обозначаются rXiVZ1 ry^XZJ rz^xy
и выражаются через парные коэффициенты корреляции с помощью соотношений
1 X
>yz
2
1 xy
h r2xz - 2rxyrZx'i
1-r2
r2 rz
1 z,xy
x ^ i zy
1
2 Г
2
2.2
1
~~ ^VyxVyzTzx
-r2
1 XZ
Между частными, множественными и обыкновенными парными коэффициента-
коэффициентами корреляции имеют место так называемые контрольные соотношения:
г2 = 1- (l^r2 )(l^r2 ) = 1- (l^r2 Ul-
x,yz x V ' rcz/ \ ' xy,z/ х V xy/\
Т„
r2 =1- (l~r2 )(l-r2 ) = 1- (l-r2 Hl-
Г2 = 1- (l^r2 )fl^r2 ) = 1- (l^r2 )fl^r2 )
z,xy ^ V ^2// V zx,yj ^ V 2Ж/ V- zy,xj *
Для проверки гипотезы Uq : px?2/z = 0 используется статистика
rl,yz n-k
имеющая при справедливости Hq i^-распределение cfi = k^lwf2 = n^k степе-
степенями свободы {к — число переменных, в нашем случае к = 3).
20*
612
Методы исследования связей между случайными величинами
[Гл. 5
Таблица 218
Критические значения 7*1,23...fe коэффициента множественной
корреляции (к — число переменных, п — объем выборки)
т U
П К
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
22
24
26
28
30
40
60
Доверительная
0,95
к
3
0,999
0,975
0,930
0,881
0,836
0,795
0,758
0,726
0,697
0,671
0,648
0,627
0,608
0,590
0,574
0,559
0,545
0,532
0,520
0,509
0,488
0,470
0,454
0,439
0,425
0,373
0,308
4
0,999
0,983
0,950
0,912
0,874
0,839
0,807
0,777
0,750
0,726
0,703
0,683
0,664
0,646
0,630
0,615
0,601
0,587
0,575
0,563
0,542
0,523
0,506
0,490
0,476
0,419
0,348
5
0,999
0,987
0,961
0,930
0,898
0,867
0,838
0,811
0,786
0,763
0,741
0,722
0,703
0,686
0,670
0,655
0,641
0,628
0,615
0,604
0,582
0,562
0,545
0,529
0,514
0,455
0,380
6
1,000
0,990
0,968
0,942
0,914
0,886
0,860
0,835
0,812
0,790
0,770
0,751
0,733
0,717
0,701
0,687
0,673
0,660
0,647
0,636
0,614
0,594
0,576
0,560
0,545
0,484
0,406
вероятность а
0,99
к
3
1,000
0,995
0,977
0,949
0,917
0,886
0,855
0,827
0,800
0,776
0,753
0,732
0,712
0,694
0,677
0,662
0,647
0,633
0,620
0,607
0,585
0,565
0,546
0,529
0,514
0,454
0,377
4
1,000
0,997
0,983
0,962
0,937
0,911
0,885
0,860
0?837
0,814
0,793
0,773
0,755
0,737
0,721
0,706
0,691
0,678
0,665
0,652
0,630
0,609
0,590
0,573
0,557
0,494
0,414
5
1,000
0,997
0,987
0,970
0,949
0,927
0,904
0,882
0,861
0,840
0,821
0,802
0,785
0,768
0,752
0,738
0,724
0,710
0,697
0,685
0,663
0,643
0,624
0,607
0,591
0,526
0,442
6
1,000
0,998
0,990
0,975
0,957
0,938
0,918
0,898
0,878
0,859
0,841
0,824
0,807
0,791
0,776
0,762
0,749
0,736
0,723
0,712
0,690
0,669
0,651
0,633
0,618
0,552
0,467
Если F > Fa(fi, /2), то соответствующая корреляция признается значимой. Кри-
Критическое значение коэффициента множественной корреляции равно
п - к + (к - 1) Fa(fu f2)'
Корреляция признается значимой при rx^yz ^ TXiyz(a). Критические значения
1,23...fc (для общего случая к переменных) приведенв! в табл. 218.
Задача 327. Вычислить коэффициенты частной и множественной корреляций и про-
проверить их значимость при доверительной вероятности а = 0,95 для данных, приведен-
приведенных ниэюе (п = 10, к = 3):
Хг\ 1 3 4 7 12 4 19 21 1 3
уц 12 42 58 71 68 50 49 85 18 26
гн 41 12 7 3 14 27 38 13 64 75.
Найдем парные коэффициенты корреляции. Вычисляем коэффициент гху:
10 10 10
J2 (хг ~ xf = 484,5; ]Р (у{ - уJ = 6882,1; J2 (ж* ~ ^) * Ьл ~ у) = 1О915
г=1 г=1 г=1
5.2] Корреляционный анализ 613
10
1 loq
г = 7,5; у = — - Y Уг = 47,9; гху = = = 0,597.
' ' У Ю ^ ' ' ХУ /4845 68821
Y Уг = 47,9; гху = =
Ю ^ ' ' ХУ ^/484,5 • 6882,1
Вычисляем коэффициент rxz:
10 10 10
J2 (%i ~ xf = 484,5; ]Г (z* - zf = 5498,4; ^(ж* - x){Zi - z) = ^519;
i=l i=l г=1
ж = 7,5; z = 29,4; гЖ2 = . 519 = = -0,318.
х/484,5 • 5498,4
ВыЧИСЛЯеМ Туг!
10 10 10
? (Уг - У)" = 6882,1; J2 & ~ zf = 5498,4; ^(г/г - у) • (Zi - z) = -3172,66;
г=1 г=10 г=1
^ = 47,9; z = 29,4; гуг =
Вычислим теперь частные коэффициенты корреляции:
0,597- (-0,318) • (-0,516)
Гху
V
,z
,У
' ху
Гху
— rzx
У2
'ГУХ
= 0,533;
= 0,014;
= -0?429.
J(l - 0,3182) ¦ A - 0,5162)
-0,318-0,597- (-0,516)
^/A-0,5Э72) ¦ A-0,5162)
-0,516- (-0,318) -0,597
yjA ~ Г1х) • i1 ~ гЪх) ^/A-0,3182)-A-0,.
Вычислим множественные коэффициенты корреляции:
2 _ 0,5972 + 0,3182 - 2 • 0,597 • (-0,18) • (-0,516) _
Гх,уг - 1_ Q55162 - »
г2 = °-5972 + °-5162 " 2 • °-597 • ("°'516) • ("°'318) = 0 475 (г =0 689)-
y,xz г _0;3182 ' v y'xz ' ; '
rl xy = 0.3182+0,516^-2-(-0,318). 0,597. (-0,516) = =
' у 1 - 0,5972 V ' У ;
Вычисляем t-статистики для проверки значимости частных коэффициентов корре-
корреляции
л/Ю - 3 • 0,533
— для проверки rXy z: txy z = —, =^~ = 1,667;
л/l - 0,5332
л/7-(-0,014) ллоГ7
— для проверки rxz y: txz у = — = = —0,037;
V1 - 0,0142
\/7-(-0,429)
— для проверки rzv ж: t2t/ ж = — = = —1,256.
л/l - 0,4292
Для а = 0,95 и f = п — к = 7 из табл. 118 для t-распределения имеем 11+0,95 =
= to,975G) = 2,37. Видим, что \txy,z\ , \txzj , \tzy,x\ < 2,37.
Следовательно, наличие частной корреляции отклоняется с достоверностью а = 0,95.
Для коэффициентов множественной корреляции находим критическое значение из
табл. 218 при к = 3, п- к = 7 ш а = 0,95. Имеем гч,2з@,95) = 0,758.
Так как ни один множественный коэффициент корреляции (rx,yz = 0,596,
ry,xz — 0,689 и rZixy — 0,516) не превышает критическое значение 0,758, то и наличие
множественной корреляции отклоняется с достоверностью 0,95.
В заключение проверим правильность вычислений, используя контрольные соотно-
соотношения:
rl,yz = 0,5962 = 0,356 = 1 - A - r2xz) • A - r2xyjZ) = 1 - (l - 0,3182) • (l - 0,5332) = 0,356.
614
Методы исследования связей между случайными величинами
[Гл. 5
5.2.2. Непараметрический корреляционный анализ
Рассмотренные в разделе 5.2.1 методы корреляционного анализа предполагали
нормальность распределения исследуемых величин. Для других распределений бо-
лее эффективны методы изучения связи между случайными величинами, основан-
основанные на применении порядковых статистик, либо на замене наблюдаемых величин
их рангами.
Такие методы, обладая повышенной устойчивостью к отклонениям распреде-
распределения от нормального, в большинстве случаев позволяют упростить вычисления,
оставляя на приемлемом уровне статистические характеристики получаемых за™
ключений по гипотезам.
5.2.2.1. Оценивание корреляции с помощью порядковых статистик
5.2.2.1.1. Оценка корреляции с помощью тренда
Оценка наличия корреляции с помощью критериев тренда основано на сле-
следующей идее. Если значения одной переменной (например, х) предварительно
упорядочить (например, по возрастанию), то поведение второй переменной (напри-
(например, у) может служить индикатором искомой корреляции. В самом деле, наличие
корреляции должно приводить к упорядочиванию значений второй переменной (т. е.
к их тренду), отсутствие корреляции не должно изменять случайный характер
поведения значений у при их размещении вдоль упорядоченной последовательности
значений х.
Отсюда следует, что проверка ряда значений у на тренд любым из критериев
тренда, изложенных в разделе 3.3, эквивалентно проверке наличия корреляции.
5.2.2.1.1.1. Критерий Кенуя
Рассмотрим некоторые из критериев, предложенных Кенуем [121] и предполагав
ющих использование „быстрых" критериев сравнения средних. Значения перемен-
переменной х предварительно проранжируем по возрастанию: х\ ^J X2 ^ •. • ^ хп и зафик-
зафиксируем ряд значений у^, соответствующих Х{. Затем проверим наличие тренда в ря-
ряду значений yi одним из „быстрых" критериев Кенуя [121] или Кокс^Стюарта [565].
Для применения „быстрого" критерия Кенуя поступаем следующим образом.
Разбиваем проверяемую совокупность величин у^ объема п на к групп
У11,У12, • • • ,У\т', У 21, У 22, -", У 2т', •••] У%1, У12 , • • • , Угт\ •••]
Ук1,Ук2, • • •, Укт, (т = п/к) .
В каждой группе фиксируем крайние значения ym{ni и t/maXi для г = 1, ...,&.
Затем отбираем значения max ym{ni и mm ymaXi. Вычисляем количество наблю-
наблюдений п~, для которых yi < max t/min., и п+, для которых ^ > mm ymaXi.
Таблица 219
Критические значения па критерия Кенуя
(а — доверительная вероятность) [121]
а
0,95
0,99
к
2
8
12
3
17
22
4
27
33
5
37
45
6
47
57
8
70
83
10
93
110
5.2]
Корреляционный анализ
615
Статистикой критерия является число п = п + п+. Гипотеза о наличии кор™
реляции принимается с достоверностью а, если п > па. Критические значения па
приведены в табл. 219.
5.2.2.1.1.2. Критерий Коке—Стюарта
Рассмотрим теперь применение критерия Кокс-Стюарта для установления кор™
реляции. Ряд наблюдений yi, соответствующих упорядоченному ряду наблюде™
ний Xi, разбивается на 3 приблизительно равные подвыборки (если в/3— дробное
число, то центральная подвыборка уменьшается (увеличивается) на 1). Сравниваем
попарно п1 ^ п/3 первых и п1 « n/З последних наблюдений. Если наблюдение из
первой трети больше соответствующего наблюдения третьей трети, то поставим
знак +1, в ином случае — 1. Статистикой критерия является сумма Т получаемых
+ 1 и -1.
Корреляция между изучаемыми величинами с вероятностью а признается зна-
значимой, если \Т\ > Та. Значения Та приведены в табл. 220.
Таблица 220
Критические значения Та критерия Кокс^Стюарта
(а — доверительная вероятность)
п'
6
7
8
9
10
11
а
0,95
6
7
8
7
8
9
0,99
8
9
10
11
п'
12
13
14
15
16
17
OL
0,95
8
9
10
9
10
9
0,99
10
11
12
11
12
13
п'
18
19
20
21
22
23
а
0,95
10
11
10
11
12
11
0,99
12
13
14
13
14
15
п'
24
25
26
а
0,95
12
11
12
0,99
14
15
14
Эффективность этого критерия по сравнению с классическим корреляционным
?3 50%, т. е. для обеспечения одинаковых статистических характеристик при провер-
проверке гипотез рассматриваемый критерий требует в 2 раза большего объема выборки.
Задача 328. Для ряда пар случайных величин
(xi,yi): A,51), A9,52), B,48), A9,14), E,51), A7,14), (8,49),
A0,50), A3,33), E1,16), B0,42), B2,31), D8,19), D7,21),
B6,41), B6,53), C0,58), C1,43), D6,21), D5,1), D2,11),
C3,43), C3,51), C5,47), C6,30), D0,19), D1,32), D4,31)
установить наличие корреляции „быстрыми" критериями Кенуя и Кокс-Стюарта.
Ранжируем величины х% по возрастанию и получаем совместный ряд:
Xi
1
2
5
8
Уг
51
48
51
49
Xi
10
13
17
19
Уг
50
33
14
52
хг
19
20
22
26
Уг
14
42
31
41
Xi
26
30
31
33
Уг
53
58
43
43
Xi
33
35
36
40
Уг
51
47
30
19
Xi
41
42
44
45
Уг
32
11
31
1
Xi
46
47
48
51
Уг
21
21
19
16
Используем критерий Кенуя. Разбиваем ряд yi на 4 подвыборки:
2/i: 51 48 51 49 50 33 14
уг: 52 14 42 31 41 53 58
2/з: 43 43 51 47 30 19 32
2/4: 11 31 1 21 21 19 16
616
Методы исследования связей между случайными величинами
[Гл. 5
Имеем
2/mini —
2/min4 = 1; г/тах4 =31; max г/mini = 19;
min г/тах7- =31.
Далее сравнением устанавливаем количество значений, меньших, чем тахут\щ =
= 19 (п~ = 5), и больших, чем mlnt/maxi = 31 (п+ = 16).
Тогда статистика критерия равна Т = п~~ + п+ = 21.
Из табл. 219 для а = 0595 и к = 4 находим То,95 = 27.
Так как Т = 21 < ТЬ,95 = 27, корреляция с достоверностью а = 0,95 признается незна-
незначимой.
Используем теперь критерий Кокс—Стюарта.
Имеем п = 28. Выделим 28/3 ps 9 первых наблюдений г/г и 9 последних наблюдений.
Сравнивая их попарно, получаем последовательность
+1, +1, +1, +1, +1, +1, -1, +1, -1
и Г = 5. Из табл. 220 находим для п = 9 ш а = 0,95: T0)95 = 7.
Так как \Т\ = 5 < То,95 = 7, корреляцию следует признать незначимой на уровне
значимости 0,05.
5.2.2.1.2. Знаковый корреляционный критерий Нелсона
Критерий, предложенный Нелсоном [566], позволяет установить наличие кор-
реляции, непрерывно анализируя совместное поведение пар (#г>2/г) по мере их
появления в эксперименте (в процессе). Критерий основан на числе знаков после-
последовательного изменения величин пар (xi,yi).
Если Xi > Xi-i, yi > yi-i или Х{ < #г-ъ У% < 2/г—1? то паре (xi.yi) приписыва™
ется знак +, в ином случае знак —. Другими словами, если значения пар (а^,у^)
изменились в одном направлении, то это отображается знаком +, в разных направ-
направлениях— знаком —. Если в паре одно или оба значения (xi,yi) не изменились, то
этой паре приписывается значение 0. Статистикой критерия является наименьшее
количество S знаков одного вида (+ или —). Корреляция признается значимой при
S > Sa(Sa—критическое значение, приведенное в табл. 221, п — число анализиру-
анализируемых знаков).
Таблица 221
Критические значения Sa знакового критерия
корреляции Нелсона (а, — доверительная вероятность) [566]
11
12
13
14
15
16
17
18
19
20
21
22
23
а
0,95
2
2
3
3
3
4
4
5
5
5
6
6
7
0,99
1
2
2
2
3
3
3
4
4
5
5
5
6
ТЬ
24
25
26
27
28
29
30
31
32
33
34
35
36
а
0,95
7
7
8
8
9
9
9
10
10
11
11
12
12
0,99
6
7
7
7
8
8
9
9
9
10
10
11
11
ТЬ
37
38
39
40
50
55
60
65
70
75
80
85
90
а
0,95
12
13
13
14
18
20
22
25
27
29
31
34
36
0,99
11
12
12
13
17
19
21
23
25
28
30
32
34
5.2]
Корреляционный анализ
617
При п > 90 сумма S распределена асимптотически нормально [566] и Sa « —
у
Эффективность этого метода ~ 50% от классического. Однако основные его
достоинства — простота и возможность анализировать корреляцию непрерывно (по
мере поступления данных) делает его весьма привлекательным для практического
применения.
Задача 329. Проверить гипотезу корреляции по данным задачи 328 критерием Нел-
сона при доверительной вероятности а = 0,95.
Введем данные анализа появления пар в таблицу:
г
1
2
3
4
5
6
7
Xi
1
19
2
19
5
17
8
Уг
51
52
48
14
51
14
49
Знак
+
+
-
-
-
i
8
9
10
11
12
13
14
Xi
10
13
51
20
22
48
47
Уг
50
33
16
42
31
19
21
Знак
+
-
-
-
-
-
г
15
16
17
18
19
20
21
Xi
26
26
30
31
46
45
42
Уг
41
53
58
43
21
1
11
Знак
-
0
+
-
-
+
г
22
23
24
25
26
27
28
33
33
35
36
40
41
44
Уъ
43
51
47
30
19
32
31
Знак
-
0
-
-
-
+
Из таблицы видим, что наименьшее количество знаков одного вида (в нашем слу-
случае +) равно S = 6. Критическое значение из табл. 221 для а = 0,95 и общего количества
знаков любого вида (в нашем случае оно равно 25, в том числе 6 плюсов и 19 минусов)
равно So,95 = 7.
Так как S = 6 < So,95 = 7, корреляция признается незначимой.
Для нормальной аппроксимации имеем
25
что близко к табличному значению Яо,95 = 7.
5.2.2.1.3. Квадрантный критерий
Рассматривается последовательность случайных величин х и у с выборочными
медианами х и у. Введем обозначения
I 1, если Xi > х и yi > у;
\ 0 в остальных случаях;
1 „
-, если Xi > х и yi = у;
0 в остальных случаях;
1/2, если Xi = х и yi > у;
0 в остальных случаях;
1 „
. -, если Xi = х и yi = у;
0 в остальных случаях.
Статистика S = S± + S2 + *^з + $4 моясет быть использована для оценки корре™
ляции между случайными величинами х и у [365] (при п четном очевидно, что
S = Si). Критерий называется квадрантным, так как статистика S основана на
числе наблюдений в квадрантах, на которые плоскость ху делится прямыми х = х
ж у = у.
Гипотеза о наличии корреляции отклоняется, если Si (a) < S < ^(ск) (критиче-
(критические значения Si (а) и $2 (ок) приведены в табл. 222).
618
Методы исследования связей между случайными величинами
[Гл. 5
Таблица 222
Критические значения Si (а) и ^(ок) квадрантного критерия
корреляции (а — доверительная вероятность) [121]
п
8-
10-
12-
14-
16-
18-
20-
22-
24-
26-
28-
30-
32-
34-
36-
38-
40-
42-
44-
46-
48-
50-
52-
54-
56-
58-
60-
62-
64-
66-
68-
70-
72-
-9
- 11
-13
-15
- 17
-19
-21
-23
-25
-27
-29
-31
-33
-35
-37
-39
-41
-43
-45
-47
-49
-51
-53
-55
-57
-59
-61
-63
-65
-67
-69
-71
-73
а
0,
Si
0
0
0
1
1
1
2
2
3
3
3
4
4
5
5
6
6
6
7
7
8
8
8
9
9
10
10
11
11
12
12
12
13
Э5
s2
4
5
6
6
7
8
8
9
9
10
11
11
12
12
13
13
14
15
15
16
16
17
18
18
19
19
20
20
21
21
22
23
23
0 99
Si
—
0
0
0
0
1
1
2
2
2
3
3
3
4
4
5
5
5
6
6
7
7
7
8
8
9
9
9
10
10
11
11
12
s2
—
5
6
7
8
8
9
9
10
11
11
12
13
13
14
14
15
16
16
17
17
18
19
19
20
20
21
22
22
23
23
24
24
n
74-
76-
78-
80-
82-
84-
86-
88-
90-
92-
94-
96-
98-
100-
110-
120-
130-
140-
150-
160-
170-
180-
200-
220-
240-
260-
280-
300-
320-
340-
360-
380-
-74
-77
-79
-81
-83
-85
-87
-89
-91
-93
-95
-97
-99
-101
- 111
- 121
-131
-141
- 151
-161
-171
-181
-201
-221
-241
-261
-281
-301
-321
-341
-361
-381
400
OL
0,
Si
13
14
14
15
15
16
16
16
17
17
18
18
19
19
21
24
26
28
31
33
35
37
42
47
51
56
61
66
70
75
80
84
89
95
s2
24
24
25
25
26
26
27
28
28
29
29
30
30
31
34
36
39
42
44
47
50
53
58
63
69
74
79
84
90
95
100
106
111
0,
Si
12
12
13
13
14
14
15
15
15
16
16
17
17
18
20
22
24
26
29
31
33
35
40
44
49
54
58
63
67
72
77
81
86
99
s2
25
26
26
27
27
28
28
29
30
30
31
31
32
32
35
38
41
44
46
49
52
55
60
66
71
76
82
87
93
98
103
109
114
При п > 100 может быть использована аппроксимация
S(a) =
при n = 2k — 1.
Гипотеза наличия корреляции в этом случае отклоняется с достоверностью а,
если \S\ < S(a) (u7—7™квантиль стандартного нормального распределения). Кри™
терий обладает эффективностью ^ 41% от классического корреляционного крите-
критерия, однако он очень прост для вычислений.
5.2] Корреляционный анализ 619
Напомним, что медиана упорядоченного ряда z\ ^ z^ ^ ... ^ zn определяется
соотношением
при n = 2Aj — 1;
при п = 2к.
Несколько иная версия квадрантного критерия рассмотрена в [567, 568] — кри™
терий Эландта. Его статистикой при п четном является
и = ±иг, где иг = { р (хг - 5) (Уг - у) > 0;
*=1 [0 ПРИ (xi - Я) (yi -у) ^0.
При справедливости гипотезы о наличии корреляции
Если Р(С/ ^ С/*) > а, то с достоверностью а наличие корреляции отклоняется
(U* —выборочное значение статистики U).
Задача 330. Проверить гипотезу корреляции для данных задачи 328 квадрантным
критерием при доверительной вероятности а = 0,95.
Для упорядоченного ряда значений
хц 1 2 5 8 10 13 17 19 19 20 22 26 26 30
31 33 33 35 36 40 41 42 44 45 46 47 48 51
имеем медиану х = - • (жм + х\$) = = 30,5.
Для упорядоченного ряда
уц 1 11 14 16 19 19 21 21 30 31 32 33
41 42 43 43 48 49 50 51 51 52 53 58
2/14+2/15 33 + 41
имеем у = = = 37. Далее находим количества пар, для которых xi > х
a Vi > у; Xi = х ж yi > у; Xi > х ш yi = у; Xi = х ш yi = у: соответственно Si = 4, S2 = 0,
S3 = 0, S4 = 0. Тогда S = Si = 4. Из табл. 222 для п = 28 и а = 0,95 имеем Si@,95) = 3
и 52@,95) = 11.
Так как Si @,95) = 3 < S = 4 < S2@,95) = 11, с достоверностью а = 0,95 наличие кор-
корреляции отклоняется. Используем теперь аппроксимацию
Так как S = 4 < S@,95) = 9,6, то и в этом случае наличие корреляции отклоняется.
Применим теперь критерий Эландта. Имеем последовательность значений
0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.
Тогда получаем U* = ]>^ Щ = 4. Вычисляем далее
(912 + 3642 + 10012 + ... + 912 + 142 + I2) = 0,999.
40116600
Так как Р(С/ ^ 4) = 0,999 > а = 0,95, гипотеза корреляции отклоняется.
620
Методы исследования связей между случайными величинами
[Гл. 5
5.2.2.1.4. Угловой критерий Олмстеда-Тьюки
Сущность критерия сводится к следующему. Двумерная диаграмма (ж, у) сна-
сначала делится вертикальной прямой х = х на две части и горизонтальной прямой
у = у на две части (ж, i/ — медианы).
Если п — нечетное число, то медианы проходят через одну из точек (ж^,^),
которую следует исключить из рассмотрения. В результате получаем четыре ква-
квадранта. Квадрантам, для которых (xi — ж) (yi — у) > 0 (правый верхний и левый
нижний), приписываем знак +, а квадрантам, для которых (xi — x)(yi — у) < 0
(левый верхний и правый нижний) — знак —.
Затем, двигаясь слева направо (от xmin к жтах), подсчитываем количество встре-
встречающихся подряд точек ai, для которых у^ > у (yi < у). По аналогии, двигаясь
справа налево (от жшах к жт1П), подсчитываем количество встречающихся подряд
точек а2, для которых yi < у (yi > у). Затем, двигаясь сверху вниз (от утах к t/min)?
подсчитываем количество встречающихся подряд точек аз, для которых Х{ < ж
(xi > ж), и, наконец, двигаясь снизу вверх (от ymin к |/тах), подсчитываем количество
встречающихся подряд точек а^^ для которых Xi > ж (ж^ < ж). Знаки значениям ai,
а2? о,з, «4 присваиваются в зависимости от квадранта, в котором располагаются
отобранные точки.
Статистикой критерия является абсолютная сумма
Q =
г=1
критические значения которой приведены в табл. 223.
Таблица 223
Критические значения Qa угловой статистики
Олмстеда—Тьюки
(а — доверительная вероятность) [24]
а
Qa
0,90
9
0,95
11
0?99
14-=-15
0,999
18-=-21
Меньшая величина Qa применяется для выборок большого объема, большая
величина — для выборок малого объема.
При Q > Qa наличие корреляции признается значимым с вероятностью а. Если
Q > 2п при п ^ 6, то критерием Олмстеда-Тьюки пользоваться не рекомендуется.
Критерий обладает низкой эффективностью (« 25% по сравнению с класси-
классическими оценками) и рекомендуется к применению при больших объемах выбо-
выборок (п > 50). При п > 50 вероятность того, что Q > Qa, оценивается по формуле
9Q
168Q + 208
2162-2^
Задача 331. Проверить наличие корреляции мемсду исследуемыми данными крите-
критерием Олмстеда-Тьюки при доверительной вероятности а = 0,95 в условиях задачи 328.
В нашем случае х = 30,5 и у = 37. Движемся слева направо (от жт1п = 1 к жтах = 51)
и подсчитываем количество встречающихся подряд точек (xi,yi), для которых yi < у.
Видим, что таких точек а\ = 5 — это точки A,51), B,48), E,51), (8,49), A0,50). Все эти
точки расположены в левом верхнем квадранте (так как Xi < х и yi > у), значение а\
долж:но учитываться со знаком —.
Движемся теперь справа налево (от жтах = 51 к xmin = 1) и подсчитываем количество
встречающихся подряд точек, для которых у% < г/, — их количество п2 = 10 — это точки
E1,16), D8,19), D7,21), D6,21), D5,1), D4,31), D2,11), D1,32), D0,19), C6,30).
5.2] Корреляционный анализ 621
Так как все эти точки расположены в правом нижнем квадранте (ра > х и yi < у),
то сумма п2 = 10 должна учитываться со знаком —.
Далее движемся сверху вниз (от 2/тах = 58 к ymin = 1) и подсчитываем количество
встречающихся подряд точек аз, для которых xi < x: это точки C0, 58), B6, 53), A9, 52),
A,51). Так как эти точки находятся в левом верхнем квадранте, то значение аз = 4
учитывается со знаком —.
И, наконец, движемся снизу вверх (от t/min = 1 к ушах = 58) и подсчитываем коли-
количество встречающихся подряд точек, для которых Xi > ж, их ац = 2. Это точки D5,1),
D2,11). Все они располагаются в правом нижнем квадранте, и поэтому а^ = 2 также
учитывается со знаком —.
Окончательно имеем Q = \а\ + п2 + аз + ск| = |—5 — 10 — 4 — 2| = 21.
Легко видеть, что критерий приводит к принятию гипотезы о наличии корреляции,
так как Q = 21 > Qo,95 = И- Однако не следует этот вывод считать достоверным, так как
для принятия решения критерием Олмстеда-Тыоки рекомендуется использовать выбор-
выборки объема п > 50 -f- 100 в силу малой эффективности критерия. Здесь мы рассмотрели
пример только для демонстрации вычислительной техники критерия.
Теперь вычислим вероятность
9.213+9.21^168.21 + 208 =
216-221
Так как а = 0,9998 > 0,95, гипотеза корреляции принимается (комментарий см. выше).
5.2.2.1.5. Приближенный критерий Шахани
В совокупности значений пар (x-i^yi) выделим порядковые статистики
Я[о,Зп]>#[о,7п]>У[о,Зп]>2/[о,7п]? т-е- значения хну, которые в упорядоченных по
возрастанию рядах Х{ и yi занимают места с номерами [0,Зп] и [0,7п].
Далее обозначим количество наблюдений, попавших в угол, для которого
Xi < Ж[о,зп]> У > 2/[о,7п]> ч^рез а\] количество наблюдений, попавших в угол х^ > Ж[о,7п]?
У > 2/[о,7п]> через п2] количество наблюдений, попавших в угол х^ > Ж[0,7гф У% < У[о,3п]?
через аз; количество наблюдений в угле Xi < Х[0^п^ yi < У[о,зп] через а±. Статистика
критерия равна q = \а\ + аз — «2 — сц|. Критическое значение g-статистики равно
4
> г/i+a, где w7 — 7-квантиль стандартного нормального распределен
U=i J 2
ПИЯ.
При q > qa корреляция между исследуемыми величинами признается значимой.
Эффективность критерия по сравнению с классическим коэффициентом корреля-
корреляции ^0,67 [121].
Задача 332. Проверить гипотезу корреляции для данных задачи 328 критерием
Шахани.
Имеем Ж[о,зп] — ж[о,з-28] = %9 = 19 ([а]—ближайшее большее целое к а). Далее
X[oj.n] = ^20 = 40; У[0,з-п] = Уэ = 21; г/[0,7п] = 2/20 = 48.
Имеем в угле Xi < 19, у% > 48: ai = 5; в угле х% > 40, у% > 48: аг = 0; в угле Xi > 40,
2/г < 21: аз = 4; в угле ж^ < 19, г/« < 21: а± = 1 точку. Тогда
q = |5 + 4 - 0 - 1| = 8; до,95 = \/Ъ + 4 + 0 + lixo,975 = 3,16 • 1,96 = 6,2.
Так как q = 8 > go,95 :=: 6,2 корреляция признается значимой.
5.2.2.1.6. Сериальный критерий Шведа-Эйзенхарта
Совокупность п пар (xi,yi) разбивается на две равные совокупности, отвечаю™
щие условиям yi > у и yi < у (у — медиана ряда г/^, при п нечетном значение yi = у
исключается). Затем наблюдения ранжируются по возрастающим значениям Х{.
622
Методы исследования связей между случайными величинами
[Гл. 5
Для последовательных пар значений (xi,yi) с yi > у будем применять символ а, для
последовательных пар (жг?2/«) ct/i < у — символ Ь. В результате получим последова™
тельность элементов вида а, 6, 6, а, а, а, 6, .... Последовательность элементов одного
вида, ограниченная с двух сторон элементами другого вида (замыкающие интервал
последовательности одного вида ограничены с одной стороны последовательностям
ми другого вида), называется серией. Количество т серий является статистикой
рассматриваемого критерия [121].
Корреляция признается значимой, если т ^ та (критические значения та
приведены в табл. 224).
Таблица 224
Критические значения пга критерия Шведа^Эйзенхарта
(а — доверительная вероятность) [121]
п
8^9
10-=- 11
12-=-13
14-=-15
16-=-17
18-=-19
а
0,95
2
3
3
4
5
6
0,99
2
2
3
4
4
п
20^21
22^23
24^25
26^27
28^29
30^31
а
0,95
6
7
8
9
10
11
0,99
5
6
7
7
8
9
п
32^33
34^35
36^37
38^39
40^41
а
0,95
11
12
13
14
15
0,99
10
10
11
12
13
При четных п > 40 можно использовать приближения
п + 1 _Л / -1 Г^+ 1
,99 —
где [z] —ближайшее меньшее целое к z.
Задача 333. Проверить гипотезу корреляции для данных задачи 328 критерием
Шведа-Эйзенхарта.
В нашем случае у = 37. Будем обозначать пары (ж^, t/i), в которых yi ~> у = 37, симво-
символом а, а пары, в которых г/^ < у = 37, символом 6. Располагая пары в порядке увеличения
значений ж^,получаем последовательность
ааааа, 66, а, 6, а, 6, ааааааа, ЬЬЬЬЬЬЬЬЬ.
Видим, что в полученной последовательности содержится т = 8 серий D серии
элементов а и 4 серии элементов Ь). Из табл. 224 для п = 28 и а = 0,95 находим
mo5g5 = 10. Так как т = 8 < mo,95 = 10, корреляция признается значимой. Приближение
9Q _|_ 1 1
0,82 • ^28 — 1 = 10 дает такой же результат.
5.2.2.1.7. Критерий автокорреляции Кенуя
Критерий позволяет установить наличие корреляции в ряду пар значений (ж^, г/^),
расположенных по возрастанию одной из величин (например, х). Под автокорреля™
цией понимается наличие зависимости значений переменной величины от порядко-
порядкового номера ее расположения в ряду данных. Проверке такой зависимости и служит
критерий Кенуя.
Критерий строится следующим образом. Все (п—1) пар значений располагаются
в порядке возрастания Xi от хш{п до жтах и разбиваются на две группы, с yi > у
и yi < у (у — медиана). Затем последовательно рассматриваем пары, для которых
справедливо
(xi,yi > y),(xi+uyi+i > у) или (xi,yi < y),{xi+uyi+1 < у).
5.2]
Корреляционный анализ
623
Другими словами, определяется количество последовательных пар точек, на™
ходящихся по какую-либо одну сторону от медианы. Количество таких пар N
является статистикой критерия. Если N > naj то корреляция признается значимой.
Критические значения па приведены в табл. 225.
Таблица 225
Критические значения Na критерия автокорреляции Кенуя
(а — доверительная вероятность) [121]
п
8-
10-
12-
14-
16-
18-
20-
22-
24-
26-
28-
30-
32-
34-
36-
38-
-9
- 11
-13
-15
-17
-19
-21
-23
-25
-27
-29
-31
-33
-35
-37
-39
а
0,95
6
7
9
10
11
12
14
15
16
17
18
19
21
22
23
24
0,99
—
8
10
11
12
14
15
16
17
19
20
21
22
24
25
26
п
40^41
42-
44-
46-
48-
50-
52-
54-
56-
58-
60-
62-
64-
66-
68-
70-
-43
-45
-47
-49
-51
-53
-55
-57
-59
-61
-63
-65
-67
-69
-71
а
0,95
25
26
27
29
30
31
32
33
34
35
36
37
39
40
41
42
0,99
27
28
30
31
32
33
34
35
37
38
39
40
41
42
44
45
п
72-73
74-
76-
78-
80-
82-
84-
86-
88-
90-
92-
94-
96-
98-
100-
-75
-77
-79
-81
-83
-85
-87
-89
-91
-93
-95
-97
-99
- 101
а
0,95
43
44
45
46
47
48
49
51
52
53
54
55
56
57
58
0,99
46
47
48
49
50
51
53
54
55
56
57
58
59
60
62
Задача 334. Проверить наличие автокорреляции для данных задачи 328 критерием
Кенуя.
Для у = 37 и упорядоченной последовательности х\ ^ Х2 ^ ...
вательность пар точек, находящихся по одну сторону от медианы:
хп имеем последо-
последоA,51),
B,48),
E,51),
(8,49),
A3,33),
Всего таких пар
Так как N =
B,48);
E,51);
(8,49);
A0,50);
A7,14);
точек N
20 > По g
B6,41),
B6,53),
C0,58),
C1,43),
C3,43),
= 20. В
B6,53);
C0,58);
C1,43);
C3,43);
C3,51);
табл. 225
C3,51),
C6,30),
D0,19)
D1,32)
D2,11)
для п = 28
C5,47);
D0,19);
D1,32);
D2,11);
D4,31);
находив
D4,31),
D5,1),
D6,21),
D7,21),
D8,19),
I По,95 =
is = 18, корреляция признается значимой.
D5,1);
D6,21);
D7,21);
D8,19);
E2,16).
18.
5.2.2.1.8. Критерий Блума-Кифера-Розенблатта
Статистика критерия, предложенного Блумом, Кифером и Розенблаттом [570],
строится следующим образом. Имеется совокупность точек (ж^, t/i), i = 1, ..., п. Че~
рез точку с координатами (а^, у{) проводятся прямые, параллельные осям координат
(ж, 2/), и подсчитывается количество точек mi (г), находящихся в первом квадранте
(для которого Xj > Xi и i/j > |/i), rri2(i)—находящихся во втором квадранте (для
которого Xj < Х{ и yj > г/^), тз(ъ)—в третьем квадранте (для которого Xj < Х{
и Уз ^ Vi)i rm4(i) —в четвертом квадранте (для которого Xj > Xi и yj < yi).
Статистикой критерия является величина
~1
- m2(i)m3(i)}
г=1
624
Методы исследования связей между случайными величинами
[Гл. 5
Критические значения В (а) при п
В@,95) = 0,0584; В @,99) = 0,868. При В
с вероятностью а.
> ос (п > 30) равны: 5@,90) = 0,0469;
В (а) корреляция признается значимой
Задача 335. Для совокупности п = 10 пар величин
(xi,yi): A,12), B,17), D,8), A2,14), G,1), B,4), A,13), A3,6), D,1), A0,9)
установить наличие корреляции критерием Блума-Кифера-Розенблатта при довери-
доверительной вероятности а = 0,95.
Для пар (жг,г/г) имеем следующие значения mi (г), 777,2B), 7тгз(*) и 7714B):
г
1
2
3
4
5
1
2
4
12
7
12
17
8
14
1
mi (г)
0
0
3
1
6
7712 (г)
2
0
3
0
3
газ (г)
0
2
0
8
0
т4(г)
6
6
2
1
0
г
6
7
8
9
10
Xi
2
1
13
4
10
Уъ
4
13
6
1
9
mi (г)
2
0
6
4
3
7712 (г)
4
2
0
3
1
газ (г)
0
0
3
0
4
т±(ъ)
2
6
0
0
1
Статистика критерия равна
= КГ3 • [@ . 6 - 2 • ОJ + @ • 6 - 0 • 2J + ... + C • 1 - 1 • 4J] = 0,054.
Так как В = 0,054 < 5@,95) = 0,0584, с вероятностью а = 0,95 гипотеза о наличии
корреляции между х и у отклоняется.
5.2.2.2. Ранговая корреляция
Понимая под рангом выборочного значения случайной величины его номер
в упорядоченной по возрастанию выборке, можно рассматривать для оценки силы
связи случайных величин не их численные значения, а соответствующие им ранги.
Подробно методы ранговой корреляции изложены в работе Кендалла [422].
5.2.2.2.1. Коэффициент ранговой корреляции т Кендалла
Предположим, имеется выборка пар случайных величин (ж, у) объема в, кото-
которым соответствуют последовательности рангов R (для ряда х^) и R* (для ряда yj).
Расположим ряд значений Xi в порядке возрастания величины: х\ ^ х^ ^ •. • ^ хп.
Тогда последовательность рангов R будет представлять собой последовательность
натуральных чисел 1,2, ..., п. Значения г/, соответствующие значениям ж, образуют
в этом случае некоторую последовательность рангов R*.
Рассмотрим несколько способов оценки корреляции величин х и у, предложен™
ных Кендаллом [422]. Назовем пару рангов R* и it!* (j < v) инверсией, если в после™
довательности рангов R* наблюдаем R* > iZ* (j = 1, ..., п — 1). Обозначим через Q
число таких пар. Тогда коэффициент корреляции, предложенный Кендаллом [422],
равен
п(п — 1)
Второй способ вычисления т заключается в следующем. В последовательности
рангов R* подсчитываем количество членов, расположенных справа от R* = 1. За-
Затем вычеркиваем R* = 1 и подсчитываем число членов последовательности, распо-
расположенных справа от R* = 2, и т. д. Обозначим сумму чисел, полученных с помощью
5.2] Корреляционный анализ 625
указанной процедуры, через К. Тогда т вычисляется по формуле
1
п(п — 1)
Иногда используются эквивалентные формы записи т:
2S где S = K-Q = 2K-^^^ =
1 - п(п-1У
Коэффициент т принимает значения от — 1 до +1. Равенство т = 1 указывает
на строгую линейную корреляцию. При п ^ 10 распределения т, S и К удовлетво™
рительно аппроксимируются нормальным распределением с параметрами, соответ-
соответственно:
п(п- 1)Bп + 5)ш
М(г) = 0; Р(т)=Г: ¦ 7/; M(S) = 0; DE) =
18
Следовательно, при п ^ 10 наличие корреляции признается значимым с досто-
достоверностью а, если выполняется любое из следующих неравенств:
Яа = г/а
«J;
где ia7 — 7-квантиль стандартного нормального распределения.
Если среди значений х и у есть совпадающие значения (т. е. Xi = ж^ при i ф v или
г/j = у^, при j ф z/), то им приписываются средние ранги (например, если значения 3
и 4-го членов ранжированной выборки совпадают, то им приписывается одинаковый
средний ранг C + 4) : 2 = 3,5). Если наблюдается q связей в ряду х и / связей
в ряду у, то оценка т корректируется следующим образом:
S
1 q I f
где Т = - ]Г ti (U - I); U = -J2ui (ui ~ 1) ; ** (^*) "~ Длина г-й связи в ряду х (у).
г=1 г=1
В случае выборок из нормального распределения коэффициент т может быть
использован для быстрой оценки обычного коэффициента корреляции г по формуле
. Т7Г
Г = Sin .
Задача 336. Имеется последовательность пар (xi, уi):
хц 2 4 7 1 5 9 11 12 17 8
у»: 6 3 5 7 1 2 4 14 18 21.
Используя коэффициент корреляции Кендалла, установить наличие корреляционной
зависимости между х и у с достоверностью а = 0,95.
"Упорядочим ряд значений х% по возрастанию:
хц 1 2 4 5 7 8 9 11 12 17
2/j-: 7 6 3 1 5 21 2 4 14 18.
626 Методы исследования связей между случайными величинами [Гл. 5
Заменяя значения Xi и yj их рангами, получаем последовательность рангов:
Rii 1 2 3 4 5 6 7 8 9 10
Д-: 7 6 3 1 5 10 2 4 8 9.
Далее находим для Ri = 7 число инверсий (когда Ri > R^,, и > 1) равно 6, для
R* = 6 —> 5, для Дз = 3 —» 2, для Д| = 1 —>> 0, для Д| = 5 —» 2, для Rq = 10 —» 4, для
Д? = 2 ->> 0, для Rt = 4 -^ 0, для Дд = 8 -^ 0.
Таким образом, общее число инверсий равно B = 6 + 5 + 2 + 2 + 4 = 19.
4 • 19
Следовательно, т = 1 = 0,155.
' 10-9
Теперь рассмотрим второй способ оценки т. Для первоначальной последовательности
рангов
Rji 7, 6, 3, 1, 5, 10, 2, 4, 8, 9
определяем количество членов, находящихся справа от R% = 1— получаем 6 членов.
Теперь вычеркиваем RX = 1 и получаем ряд
Щ\ 7, 6, 3, 5, 10, 2, 4, 8, 9.
Справа от Rq = 2 находятся 3 члена. Вычеркиваем Rq = 2 и получаем ряд
Rji 7, 6, 3, 5, 10, 4, 8, 9,
в котором справа от R? = 3 находятся 5 членов. Далее, действуя по аналогии, находим
— в ряду R*
— в ряду R*
— в ряду R*
— в ряду R*
— в ряду R*
— в ряду R*
7, 6, 5, 10, 4, 8, 9 справа от R§ = 4 находятся 2 члена;
7, 6, 5, 10, 8, 9 справа от R% = 5 находятся 3 члена;
7, 6, 10, 8, 9 справа от i?J = 6 находятся 3 члена;
7, 10, 8, 9 справа от RI = 7 находятся 3 члена;
10, 8, 9 справа от i?2 = 8 находится 1 член;
10, 9 справа от R% = 9 находятся 0 членов.
Окончательно имеем Ж = 6 + 3 + 5 + 2 + 3 + 3 + 3 + 1 + 0 = 26.
4 • 26
Коэффициент г равен т = 1 = 0,155, что и следовало ожидать.
Далее S = J^Q = 26~19 = 7ht= —2'S . = ^-^ = 0,155.
п • (п — 1) 10-9
Для нормальной аппроксимации находим
= 2- Bп + 5) = ^^ = = n-(n-l)-Bn + 5) = 10-9-25 =
v 7 9п ¦ (п - 1) 9 ¦ 10 • 9 v ; 18 18
= n-(n-l)-Bn + 5) = 10-9-25 = = п ¦ (п - 1) = 10J =
v у 72 72 ' l ; 4 4 '
Далее для гго,95 :=: 1,645 имеем
ГО595 = 1,645 • ^/0,0617 = 0,409; 50,95 = 1,645 • VnE = 18,39;
Жо,95 = 22,5 + 1,645 • д/31,25 = 31,69.
Так как г = 0,155 < го,95 = 0,409; S = 7 < So,95 = 18,39; К = 26 < Ж0,95 = 31,69, с веро-
вероятностью а = 0,95 можно утверждать об отсутствии корреляции между х и у. Оценка
обычного коэффициента корреляции равна
тг • т тг • 0,155
г = sin = sin = 0,241.
2 2 '
5.2.2.2.2. Коэффициент корреляции р Спирмена
Рассматриваем последовательность рангов Ri (величин х^ и R* (величин yj).
Необходимости упорядочивать какую-либо совокупность рядов Х{ и yj нет. Находим
разность рангов di = Ri — Kj, соответствующую паре (жг>2/г)« Коэффициент корре-
5.2] Корреляционный анализ 627
ляции Спирмена определяется формулой [422] р = 1 ^™ .
п(п — 1)
Его значения находятся в интервале от — 1 до +1 (р = О указывает на отсутствие
корреляции).
При п ^ 10 распределение р удовлетворительно описывается нормальным рас-
распределением с параметрами М(р) = 0 и D(p) = -.
Иногда в качестве статистики для проверки значимости р используется сумма
квадратов отклонений рангов
г=1 г=1
При п ^ 10 ее распределение также аппроксимируется нормальным распределе-
распределением с параметрами
DE) = ^
Корреляция признается значимой при \р\ > ра или S > Sai где ра и ?а—кри-
?а—критические значения, равные при п ^ 10
гзт' -« 6
Более точная аппроксимация критических точек р предложена Иманом и Коно-
вером [571]. В соответствии с их аппроксимацией используется статистика
'га-2
. v •- - ¦ л/ 2 1 критические значения которой равны J (а) = —г/а
2 \ V !-Р / 2
+ т^а (^ — 2), где г^а — «^квантиль стандартного нормального распределения; ta —
а-квантиль распределения Стьюдента с / = п — 2 степенями свободы. Если
/1 + оД
J ^ J —-— или J < —J
то гипотеза о наличии корреляции принимается с вероятностью а.
Для выборки из нормальных распределений может быть получена оценка для
обычного коэффициента корреляции г = 2 sin —p.
В заключение приведем ряд полезных соотношений, связывающих между собой
значения коэффициента корреляции тир: неравенство Дэниелса [422]
или при в^оо: — 1 ^ Зт — 2р ^ 1;
неравенства Дарбина^Стюарта
1 1 3 1
при т < 0: -т2 + г - - ^ р ^ -г + -.
628 Методы исследования связей между случайными величинами [Гл. 5
Из приведенных соотношений следует, что хотя коэффициенты гири связаны
между собой, но эта связь не столь элементарна. На практике чаще всего, если
значения обоих коэффициентов не слишком близки к единице, то р « 1,5т.
У читателя может возникнуть вопрос: стоит ли пользоваться коэффициентом г,
если вычисление коэффициента р значительно проще? Почему же тогда коэффици-
коэффициент т применяется на практике чаще? Это связано с тем, что если необходимо учесть
вновь поступившие значения случайных величин, то р в отличие от т приходится
рассчитывать заново по всем выборочным значениям.
Задача 337. Используя данные задачи 336, проверить наличие корреляции с помощью
коэффициента р Спирмена при доверительной вероятности а = 0,95.
Имеем последовательность рангов для х% и г/$:
Rii 2, 3, 5, 1, 4, 7, 8, 9, 10, 6;
Щ: 6, 3, 5, 7, 2, 2, 4, 8, 9, 10.
Вычисляем
J2 (Ri - Ri*J = B - бJ + C - ЗJ + ... + F - 10J = 120; р = 1 ¦ = 0,273.
При а = 0,95 имеем щ+а = ги+0,95 = г^о,975 = 1,96 и
2 2
1,96 „ 10-99 1,645 • 10 ¦ 11 • V9
ро,95 = -Lr= 0,653; So;95 = —— + = 255,47.
Л/9 Ь о
Так как р = 0,273 < ро,95 = 0,653 ш S = 120 < So,95 = 255,47, корреляция незначима. Рас-
Рассмотрим теперь аппроксимацию Имана—Коновера. Находим
=0,811.
2 V V 1-pV 2
При г^о,975 :=: 1,96 и to,975(8) = 2,306 имеем
j (l±EL j = J @,975) = — + ^55 = 2ДЗЗ.
Так как J = 0,811 < J@,975) = 2,133, гипотеза корреляции отклоняется.
Оценка обыкновенного коэффициента корреляции равна
г-= 2. sin"'0'273 =0,285.
6
Легко убедиться теперь, что неравенства Дэниелса и Дарбина—Стюарта выполняются:
3-(п + 2) 2-(п + 1) 3-12-0,155 2-11-0,273
-1 ^ —V ; • т v J • р <J 1; -1 ^ ! ! = ^0,0532 ^ 1;
п-2 w-2r' 8 8
р ^ 1 1^Т • [(п - 1)A - г) + 4] ; 0,273 ^ 1 - Х ~ °ДБ5 • [9 • A - 0,155) + 4] = 0,554;
Зп • т — (п — 2) 3 • 10 • 0,155 — 8
р ^ -^—г-^; 0,273 ^ ¦ = -0,152.
^ 2 • (п + 1) 2-11 '
5.2.2.2.3. Критерий Гёфдинга
Критерий Гёфдинга является ранговым аналогом критерия Блума^Кифера™
Розенблатта (см. раздел 5.2.2.1.8). Статистика критерия строится следующим об-
образом [572]: значения Х{ и у^ предварительно ранжируются, а затем заменяются их
рангами Щ и Щ соответственно.
5.2]
Корреляционный анализ
629
Обозначим через Ci число пар из выборок (xv,yv)i для которых одновременно
xv < Xi и yv < уг:
п I 1, при а < Ь;
Ct = J2 ^(ж^' х^) Ч> {VvtVi) ? г = 1, ..., п, где ср (а, Ь) = I 1/2, при а = Ь;
VjJ^i ^0, при а < Ь.
Положим
Q =
i - 2
* - 1) (R* - 2);
г=1
- 2) (Д* - 2);
г=1
г=1
- 2 (гг - 2) К + (уг - 2) (п - 8) Я
~ п (п - 1) (п - 2) (п - 3) (п - 4)
Гипотеза корреляции принимается, если ?) ^ Da, где Da—критическое значе™
ние, приведенное в табл. 226.
Таблица 226
Критические значения Da критерия независимости
Гёфдинга (а — доверительная вероятность) [18]
0
0
0
а
,90
,95
,99
5
0,03330
6
0,01660
0,03330
0
0
0
п
7
,00635
,00992
,01900
8
0,00476
0,00773
0,01488
0
0
0
9
,00403
,00635
,01217
При п —>• оо может быть использовано предельное распределение для критерия
Блума-Кифера-Розенблатта В, исходя из того, что случайная величина D + ^—
имеет такое же распределение, как и В.
Корреляция признается значимой:
— с вероятностью а = 0,90, если D > 0,0469 -\ ;
— с вероятностью а = 0,95, если D > 0,0584 -\ ;
Збп
— с вероятностью а = 0,99, если D > 0,0868 -\ .
Збп
Задача 338. Для выборочных пар данных
(xi,yt): G,3), G,2), (8,3), (9,4), A0,5), A1,6)
установить наличие корреляции критерием Гёфдинга при доверительной вероятности
а = 0,95.
Находим
d =
C2 =
<p(x5, Xl) • <p(y5,yi)
,x2) • ^B/1,2/2) + (p(x
(x5, x2) • ^B/5,2/2)
- <p(ye,yi) =
+0+0
) • ^ B/4,2/2)
630 Методы исследования связей между случайными величинами [Гл. 5
С3 = (р(х!,х3) • ^р (у 1, Уз) + ^(Ж2,ж3) • у? B/2,2/з) + (р(х4,х3) • <р B/4,2/3) +
+ с^(ж5, ж3) • <р(у5,Уз) + ^(^6, ж3) • <р(уб,Уз) = 1-- + Ы + 0-0 + 0-0 + 0-0 = 1,5.
Вычисляя дальше по аналогии, получаем С4 = 3, С б = 4, Се = 5.
Теперь ранжируем ряд х%:
хц 7 7 8 9 10 11
Ri-. 1,5 1,5 3 4 5 6
и ряд уi:
уц 3 2 3 4 5 6
Д*: 2,5 1 2,5 4 5 6.
(одинаковым значениям присвоены средние ранги).
Далее находим
Q = JZ (Ri ~ 1) • № " 2) • (Щ - 1) • (Я? - 2) =
г=1
= A,5 - 1) • A,5 - 1) • B,5 - 1) • B,5 - 2) + ... + F - 1) • F - 2) • F - 1) • F - 2) = 581,3125;
е
К = J2Ci'(Ri~2)- (Ri ~ 2) = ° • i1^ ~ 2) • B?5 - 2) + • • • + 5 * F - 2) • F - 2) = 128,75;
г=1
6
Я = J^ Сг • (с» - 1) = 0 • (-1) + 0 • (-1) + 1,5 • 0,5 + 3 • 2 + 4 • 3 + 5 • 4 = 38,75;
D = 581,3125-2-4-128,25 + 4-3-38,75 =
6-5-4-3-2 '
Из табл. 226 для п = биа = 0,95 находим Do,95 = 0,0166.
Так как D = 0,0282 > Do,95 = 0,0166, корреляция между жиг/ должна быть признана
значимой.
5.2.2.2.4. Критерий Ширахатэ
Критерий Ширахатэ [573] является аналогом критерия Спирмена (см. раз-
раздел 5.2.2.2.2), асимптотически ему эквивалентен, но обладает большей эффектив-
эффективностью для малых выборок.
Определим ранги случайных величин (а^, г/^), г = 1, ..., в, следующим образом:
п п
R{ = J2 {u(%i - Xj) + u(xi - yj)}; Rn+i = ]Г {и(у{ - x3) + u(y{ -
3=1 j=i
1 при x ^ 0,
где u(a) = <
[0 при x < 0.
Если случайные величины Х{ и у± коррелируют, то будут коррелировать и ранги
Ri и Rn+i.
Статистикой критерия Ширахатэ является сумма
г=1
Если бы мы определили ранги обычным способом:
п п
Ri = J2 U (Xi ~ Хз) И Кг+г = ^2и(У^^ Уз) '
J=l J=l
n
то сумма S* = ^2 ЩЩь+i являлась бы статистикой Спирмена, уже рассмотренной
г=1
ранее в разделе 5.2.2.2.2.
5.2]
Корреляционный анализ
631
Статистики S и S* асимптотически эквивалентны, но если значения статиста-
ки S* находятся в интервале
n(n+l)(n + 2) * n(n+l)Bn+l)
6 ^ ^ 6 '
то статистка S ограничена интервалом
то размах статиста-
Таким образом, если размах статистки 5* равен
-1)
ки S есть
2п(п2 -
6
-, т.е. больше в 4 раза. Следовательно, S-критерий может дать
больше информации, чем критерий, основанный на статистике S*.
При Si(a) < S < 5*2(«) корреляция признается незначимой (критические значе-
значения Si (а) и 5г (а) приведены в табл. 227).
Таблица 227
Критические значения Sa критерия Ширахатэ [573]
п
4
5
6
7
8
9
Доверительная вероятность а
0,90
Si
62
116
199
313
467
664
s2
96
175
195
456
666
932
0,95
Si
61
114
194
302
450
642
s2
97
181
302
468
683
955
n
10
12
14
16
18
20
Доверительная вероятность а
0,90
Si
911
1575
2506
3748
5349
7353
s2
1259
2125
3314
4877
6863
9311
0,95
Si
881
1528
2436
3649
5214
7177
s2
1289
2173
3386
4977
6999
9501
Задача 339. Используя данные и условия задачи 336, проверить наличие корреляции
с помощью критерия Ширахатэ.
Имеем данные (xi,yi)\
хц 1 2 4 5 7 8 9 11 12 17;
Уг\ 7 6 3 1 5 21 2 4 14 18.
Для г = 1 находим
Ri = Yl in ' (Xl ~ хз) +п
= п • (xi - xi) + п - (xi -yi)+n- (xi - x2)
+ n • (xi - 1/2) + n - (xi -хз)+п- (xi - 2/3) + гг • (xi - x4) + n • (xi - г/4) + • • •
... + n • (xi — Ж1О + n • (a?i — 2/i0)) =
= 1 + 0 + 0 + 0 + 0 + 0 + 0 + 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 2.
Далее находим:
R2 =4; Я3 = 7; Д4 = 9; R5 = 12; Д6 = 13; R7 = 14; R8 = 15; Д9 = 16; Rm = 18;
10
#10+1 = #11 + ]P [n - (t/i - ж^) + n • B/1 - 2/j)] =
i=i
= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 0 + 0 + 0 = 12;
Д12 = 10; Д13 = 5; Д14 = 2; Д5 = 9; ,Ri6 = 20; R17 = 4; i?i8 = 7;
Д19 = 17; R20 = 19.
632 Методы исследования связей между случайными величинами [Гл. 5
В результате получаем ряды:
Rii 2 4 7 9 12 13 14 15 16 18;
Rn+i: 12 10 5 2 9 20 4 7 17 19.
Тогда
S = it Ri ' Ri+1 = 2 • 12 + 4 • 10 + 7 • 5+9-2+12-9+13-20+14-4+15-7+16-17+18-19 = 1260.
Из табл. 227 для п = 10 и а = 0,95 находим Si = 881 и S2 = 1289.
Так как Si = 881 < S = 1260 < Si = 1289, корреляция признается незначимой.
5.2.2.2.5. Критерий корреляции Фишера-Йэйтса
Определяется формулой [574]
где ап(г)—математическое ожидание г-й порядковой статистики в вв1борке объ-
объема п из стандартного нормального распределения.
Значения р* заключены между — 1 и +1. Наибольшей эффективностью приме-
применение р* обладает при исследовании зависимости между случайными величинами,
имеющими распределение, близкое к нормальному.
При п ^ 10 распределение статистики
стремится к нормальному со средним М(Я*) = 0 и дисперсией
Корреляция признается значимой с достоверностью а при
\S*\> S(a)Ul±sl^±=jra2n(i).
Здесь, как и ранее, Ri и R* обозначают ранги величин Xi и yi в упорядоченных
рядах х ж у соответственно.
Для нахождения величин ап(г) можно пользоваться либо специальными табли-
таблицами (например, [24] — с. 150), либо аппроксимацией
ап{г) « 4,91 •
Следует учитывать соотношение ап{г) = ап(п + 1 — г), что значительно снижает
необходимый объем вычислений.
5.2]
Корреляционный анализ
633
Задача 340. Используя данные задачи 336, проверить наличие корреляции с помощью
критерия Фишера-Йэйтса.
Для наших данных
Xii 1 2 4 5 7 8 9 11 12 17
уц 7 6 3 1 5 21 2 4 14 18
последовательность рангов будет иметь вид:
Rii 1 2 3 4 5 6 7 8 9 10
Д-: 7 6 3 1 5 10 2 4 8 9
Используя аппроксимацию
ою(г) =4,91
3
0,14
3
г — —
- 1-
вычисляем значения
LV10+4,
и aio(-R*). Результаты сводим в таблицу:
г
1
2
3
4
5
Яг
1
2
3
4
5
Щ
7
6
3
1
5
alo(Ri)
-1,547980
-0,998750
-0,653292
-0,373926
-0,122033
ою(Д?)
0,373926
0,122033
-0,653292
-1,547980
-0,122033
г
6
7
8
9
10
Яг
6
7
8
9
10
Щ
10
2
4
8
9
аю(Д»)
0,122033
0,373926
0,653292
0,998750
1,547980
1,547980
-0,998750
0,373926
0,653292
0,998750
Вычисляем
ю
S* = J2 aio(
= (-1,54798) • 0,373926 + ... + 1,54798 • 0,99875 = 2,44965;
a?o@ = 7,95049;
2 44965
= 0,308.
Для a = 0,95 имеем ио,975 = 1,96 и Я @,95) =
/п-1
= 5,194.
Так как S* = 2,44965 < 5@,95) = 5,194, корреляция признается незначимой.
5.2.2.2.6. Коэффициент корреляции Ван дер Вардена
У^ U r. U щ
Определяется формулой [365] р = %^ п —, где иа — a-квантиль стандарт-
Е2
U_i_
г=1 п + 1
ного нормального распределения. Коэффициент оптимален для оценки корреляции
нормально распределенных случайных величин.
п
При п ^ 10 распределение S = ^ и я^ и r* стремится к нормальному с пара-
метрами
г=1
МE)=0;
634
Методы исследования связей между случайными величинами
[Гл. 5
Отсюда: если \S\ > S(a) = ui
то с вероятностью а корреляция
признается значимой. Для поиска иа могут быть использованы таблицы, либо
аппроксимации (см. раздел 1.1.1), например,
Следует помнить, что иа = —и\-а.
Задача 341. Используя данные задачи 336, проверить наличие корреляции с помощью
критерия Ван дер Вардена.
Используя аппроксимацию и j = 4,91 •
n+l
-
0,14
0,14
, вычисля-
вычисляем значения
в таблицу:
^ (значения FU и В* используем из задачи 340). Результаты сводим
г
1
2
3
4
5
Яг
1
2
3
4
5
Щ
7
6
3
1
5
U Ri
11
-1,335080
^0,906470
-0,602509
^0,347309
^0,113674
ТГ
0,347309
0,113674
-0,602509
-1,335080
-0,113674
г
6
7
8
9
10
Кг
6
7
8
9
10
Щ
10
2
4
8
9
U Ri
11
0,113674
0,347309
0,602509
0,906470
1,335080
11
1,335080
-0,906470
-0,347309
0,602509
0,906470
Вычисляем
10
S = Y1 иЛ^ ' uRi± = (-1,33508) • 0,347309 + (-0,90647) • 0,113674 + ...
i=1 n + l n+l
... + 1,33508 • 0,90647 = 1,65687;
= 6,201377;
6,201373
= - = И0,875.6,201377 =
l ' ; 3
Так как S = 1,656 < Я @,95) = 4,051, гипотеза о наличии корреляции отклоняется
с вероятностью 0,95.
5.2.2.2.7. Коэффициент конкордации Кендалла-Бэбингтона Смита
До сих пор рассматривалась корреляция двух случайных величин. Часто воз-
возникает необходимость исследовать корреляцию нескольких последовательностей
значений случайных величин. Предположим, имеется к последовательностей рангов
с равным числом рангов п в каждой последовательности
R22 ...
Ri
Ri
R.
¦kn-
5.2]
Корреляционный анализ
635
В качестве меры связи к последовательностей Кендалл и Б. Смит [575] предло™
жили коэффициент конкордации (согласованности)
W =
12SW
к2 (п3 — п) '
где Sw = V < V
к(п-
)
Легко видеть, что Sw является суммой отклонений рангов от их среднего
значения. Значения W располагаются в интервале от 0 до 1.
Для п ^ 20 величины W и Sw распределены приблизительно нормально [25]
с параметрами
M(W) = p B(W) = 23(fc ~ ^ ;
В силу несимметричности распределение W при п ^ 20 лучше аппроксимирует™
ся бета-распределением [25].
Точные критические суммы Sw(^) приведены в табл. 228. Если Sw > *5V(a)? TO
наличие согласованности признается значимым с вероятностью а.
Таблица 228
Критические значения Sw(ol) для коэффициента конкордации W [422]
к
3
4
5
6
8
10
15
20
Доверительная вероятность а
= 0,95
п
3
48,1
60,0
89,8
119,7
4
49,5
62,6
75,7
101,7
127,8
192,9
258,0
5
64,4
88,4
112,3
136,1
183,7
231,2
349,8
468,5
6
103,9
143,3
182,4
281,4
299,0
376,7
570,5
764,4
7
157,3
217,0
276,2
335,2
453,1
571,0
864,9
1158,7
Доверительная вероятность а -
= 0,99
п
3
66,8
85,1
131,0
177,0
4
61,4
80,5
99,5
137,4
175,3
269,8
364,2
5
75,6
109,3
142,8
176,1
242,7
309,1
475,2
641,2
6
122,8
176,2
229,4
282,4
388,3
494,0
758,2
1022,2
7
185,6
265,0
343,8
422,6
579,9
737,0
1129,5
1521,9
При п > 10 -т- 15 и отсутствии корреляции величина к(п — 1)W распределена
приблизительно как %2 с / = п — 1 степенями свободы. Отсюда следует, что крити-
2
-V/
ческое значение равно Wa = т / а ^ .
к(п — 1)
Если W > Wai то с вероятностью а корреляция между изучаемыми последова™
тельностями признается значимой.
Если среди последовательностей рангов есть совпадения, то коэффициент кон™
кордации следует вычислять по формуле
W =
12SV
где
(t% — tj}, tj —количество совпавших рангов в j-й последовательности.
Совпавшим рангам, как и ранее, присваиваются средние ранги.
636
Методы исследования связей между случайными величинами
[Гл. 5
Задача 342. Предположим^ что имеются к = 4 последовательности числовых рядов,
объемом п = 10 каждая:
Щ-
z%\
h:
1
7
11
-1
3
8
12
0
7
6
7
1
9
1
6
12
12
4
5
4
14
2
4
5
18
7
3
7
19
0
1
3
21
3
0
2
26;
1;
-i;
-4.
Необходимо проверить согласованность рядов с помощью коэффициента конкордации
Кендалла-Б, Смита при доверительной вероятности а = 0,95.
Имеем совокупность рангов
и квадратов вида
2
fc- (ri-
(riij - 22
J=1
i
1
2
3
4
5
6
7
8
9
10
Rid
j
l
l
2
3
4
5
6
7
8
9
10
2
8,5
10
7
2,5
6
4
8,5
1
5
2,5
3
9
10
8
7
6
5
4
3
2
1
4
2
3
4
10
7
8
9
6
5
1
e
2,25
9
0
2,25
4
1
42,25
16
1
56,25
Далее
fe ¦ (n + 1)
= 134; W = 2 12'134 =0,101.
42 • A000 - 10)
Имея в виду, что Хо,9б(9) = 16,919 (см. табл. 55), получаем
Xo,95 _ 16,919
4-9
36
= 0,470.
Так как W = 0,101 < Wo,95 = 0,470, с вероятностью а = 0,95 можно признать согла-
согласованность рангов незначимой.
5.2.2.2.8. Коэффициент конкордации Шукени-Фроли
Для случая двух групп экспертов Шукени и Фроли [576] предложили аналог
коэффициента конкордации Кендалла—Б. Смита (см. раздел 5.2.2.2.7). Пусть две
группы экспертов численностями тип ставят перед собой задачу проранжиро™
вать к объектов. Обозначим через R^j (г = 1, ..., m; j = 1, ...,&) —ранги, предло™
женные т экспертами первой группы; через R*, A = 1, ..., щ j = 1, ... ^к) —ранги,
предложенные п экспертами второй группы (Rj =
Статистика Шукени—Фроли равна
и R* =
5.2]
Корреляционный анализ
637
Значение статистики L находится в интервале [455]
тпк (к + 1) (к + 2)
тпк (к + 1) Bк + 1)
6 "
Известно [455], что
тпк(к + 1)
M(L) =
Обобщенный коэффициент конкордации Шукени-Фроли определяется соотно™
L - M(L)
шением W =
Z,max-M(L)'
Если p^j—коэффициент корреляции Спирмена (см. раздел 5.2.2.2.2) для i-ro
1 п т
эксперта первой группы и j-ro эксперта второй группы, то [455] W = ]Р ]Р Pij.
j=li=l
Предельное распределение коэффициента Шукени^Фроли отлично от нормаль™
ного и неудобно для применения. Значение W вблизи +1 означает высокую степень
согласованности внутри обеих групп экспертов и между группами; вблизи — 1 —
высокую степень согласия внутри групп и сильное несогласие между группами;
вблизи 0 — либо несогласие внутри групп экспертов, либо согласие внутри групп
экспертов при несогласии между ними.
Задача 343. Две группы экспертов в количествах т = 6 и п = 8 провели ранжи-
ранжирование к = 5 объектов (результаты приведены в таблице). Необходимо проверить
согласованность мнений экспертов критерием Шукени-Фроли.
Номер
эксперта
Ранжировка объектов
Группа 1
1
2
3
4
5
6
Е
1
1
4
1
2
5
Ri = 14
3
2
3
2
1
4
R2 = 15
4
3
2
3
3
3
Rs = 18
2
4
1
4
4
2
#4 = 17
5
5
5
5
5
1
Rb = 26
Группа 2
1
2
3
4
5
6
7
8
Е
1
3
4
1
5
1
3
1
Rl = 19
2
2
5
2
4
2
2
5
Rl = 24
3
1
1
3
2
3
4
4
Rl =21
4
5
2
4
3
4
5
3
Rl =30
5
4
3
5
1
5
1
2
R% = 26
Вычисляем L=J2RJ- Щ = 14 • 19 + 15 • 24 + 18 • 21 + 17 • 30 + 26 • 26 = 2190.
Границы изменения L: = 1680 ^ L ^ 5040 = .
638 Методы исследования связей между случайными величинами [Гл. 5
Далее вычисляем
M(L)=6-845-62=2160;
W = 219°-216° =0,00729.
5040 - 2160
Так как W = 0,00729 ^ 0, согласованность внутри группы экспертов либо между
ними очень низка.
5.2.2.3. Точечно-бмсериальная корреляция
При проведении некоторых исследований часто сталкиваются с проблемой вы™
яснения взаимосвязи между характеристиками, одна из которых может бытв ран™
жирована, а вторая допускает только группировку в две группы по качественному
признаку (дихотомия).
Приведем известные результаты для оценки зависимости в такой ситуации.
Одной из таких оценок является коэффициент точечно-бисериальной корреляции
П = S
где 7ii, П2 — объемы двух групп; п = rii-\-П2', #1, х^— средние значения первой
характеристики в двух группах, образованных в соответствии со второй характе-
характеристикой;
= \2.
г=1 г=1
Значимость корреляции определяется так же, как и для обычного коэффициента
корреляции (см. раздел 5.2.1.1). Если \г$\ > га, то корреляция признается значимой.
Рассмотрим теперь аналогичную задачу для ранговой корреляции, примени™
тельно к коэффициенту ранговой корреляции т Кендалла (см. раздел 5.2.2.2.1).
Напомним, что в случае отсутствия дихотомии
- 2S
п(п — 1) *
Предположим, что дихотомия реализуется в разделении данных по двум при™
знакам в группы объемов п\ и п^ (п\ + П2 = п).
В этом случае коэффициент точечно™бисериальной корреляции Кендалла равен
1
= S I j
1
Проверка значимости т$ проводится аналогично проверке значимости т (см. раз™
дел 5.2.2.2.1).
Задача 344. В нашем распоряжении имеются следующие данные (xi — количествен-
количественный признак^ у —качественный признак^ обозначаемый символом + или —):
хг: 1 2 3 4 5 6 7 8 9 10;
1/:+ + --- + - + --.
Необходимо оценить наличие зависимости между х и у при достоверности а = 0,95.
Используем коэффициент точечно-бисериальной корреляции т§. Имеем гц = 4, п2 = 6
(п\ + П2 = п = 10). Находим далее
1 + 2 + 6 + 8 _ 3 + 4 + 5 + 7 + 9 + 10
Ж1 = = 4,25: Х2 = = 6,33:
4 6
1 4 -.6
Sl = -^2(xi~ ^iJ = Ю?916; Si = - J2 (ж* - ж2J = 9,085; S = 3,014;
3 il 5 il
5.2] Корреляционный анализ 639
3,014
Для а = 0,95 и п = 10 из табл. 217 имеем го,эб = 0,632.
Так как \г$\ = 0,322 < 7*0,95 = 0,632, корреляция признается незначимой.
Теперь вычислим точечнобисериальный коэффициент корреляции Кендалла (см.
раздел 5.2.2.2.1). Имеем последовательность рангов
Rji 1 2 3 4 5 6 7 8 9 10
Rji 2,5 2,5 7,5 7,5 7,5 2,5 7,5 2,5 7,5 7,5
Поясним подсчет рангов Щ. Имеем последовательность членов
что эквивалентно наличию п\ = 4 и П2 = 6 равных элементов, которым приписываем
равные средние ранги. Элементы +, имеющие (условно) номера 1, 2, 3 и 4, получают
1+2+3+4 о^
равный средний ранг = 2,5. Аналогично и элементы — получают равные
5 + 6 + 7 + 8 + 9 + 10 „ к ^ ~
ранги = 7,5. Теперь подсчитаем сумму Q по алгоритму, изложенному
6
в разделе 5.2.2.2.1 (т. е. число инверсий, когда R* < Rt): Q = 6 + 6 + 3 + 2 = 17.
Далее вычисляем
п • (п - 1) 10-9 11
о = J4 = J4 = 11: тл = —, = и.ооо:
I- • 10-9- A0-9-4-3-6-5)
го,95 = ЗД,95 • ХР^Ц = 1,645 • J2-^ = 0,409.
V 9п • (те — 1) V 90 • 9
Так как т$ = 0,335 < 7о,95 = 0,409, точечно-бисериальная корреляция незначима.
5.2.2.4. Статистическая оценка свмзи между качественными признаками
(таблицы сопряженности признаков)
Предположим, что наблюдаемая случайная величина может изменяться в зави™
симости от некоторых признаков — например, долговечность электронного прибора
может зависеть от технологии изготовления, применяемых материалов. По резуль-
результатам наблюдений над случайной величиной, классифицированным по наличию или
отсутствию исследуемых признаков, необходимо ответить на вопрос, существует ли
взаимосвязь между ними, иными словами: связано ли обладание одним признаком
с обладанием другим признаком (в условиях приведенного примера — существует
ли связь между технологией изготовления и применяемыми материалами).
По существу, в данном случае мы имеем переход от точечно-бисериальной кор™
реляции к изучению зависимости между двумя (или несколькими) качественными
признаками.
Таблицы, в которых представлены значения исследуемой случайной величины,
классифицированные по качественным признакам, называются таблицами сопря-
сопряженности признаков.
5.2.2.4.1. Оценка связи признаков в таблицах сопряженности 2x2
Если исследуется взаимосвязь двух признаков А и Л, то таблица сопряженности
называется таблицей 2x2, или четырехклеточной таблицей и имеет вид
а Ь
с d
640
Методы исследования связей между случайными величинами
[Гл. 5
где а — число элементов выборки, обладающим признаками А и В одновременно;
Ь — число элементов выборки, обладающих признаком А, но не обладающих призна-
признаком В; с — число элементов выборки, обладающих признаком В, но не обладающих
признаком A; d — число элементов выборки, не обладающих ни одним из признаков
А и В.
5.2.2.4.1.1. Меры связи в таблицах сопряженности 2x2
Рассмотрим три известнвге меры связи, позволяющие грубо оценить ее наличие.
5.2.2.4.1.1.1. Коэффициент ассоциации [132]
Находится по формуле
_ _ ad — be
^ ~ ad + Ъс
Если признаки А ж В независимы, то Q = 0. В случае полной связи между
признаками Q = ±1. Дисперсия Q равна [132]
Сравнение Q с полученным значением дисперсии (с учетом масштаба
позволяет получить хотя бы первое приближение по оценке связи.
5.2.2.4.1.1.2. Коэффициент коллигации Юла [132]
Находится по формуле
К =
vad — vbc
с дисперсией
fad + vbc
Между Q ж К существует связь
v{k) = Ui-k>)(\ + 1-
Q =
2К
Задача 345. Предположим, что после перепроверки партии электронных ламп из
п = 110 шт., изготовленных по двум технологиям, получены результаты, приведенные
в таблице. Необходимо оценить связь качества ламп с технологией их изготовления
с помощью оценок, изложенных в разделе 5.2.2.4.1.1.
Технология
1
2
Итого
Число
дефектных ламп
95
70
165
Число годных
ламп
15
40
55
Всего ламп
110
110
220
В нашем случае имеем а = 95, b = 15, с = 70, d = 40.
Вычисляем коэффициент ассоциации
95 • 40 - 15 • 70
95 • 40 + 15 • 70
= 0,567;
5.2] Корреляционный анализ 641
Находим коэффициент коллигации Юла
Т>(К) = — . A - 0,3112) • [ — + — + — + — ) = 0,00675 (л/ЩК) = 0,082).
16 v y \95 15 70 40 x
Из анализа полученных оценок можно сделать оценочный вывод о том, что по
вероятности существует связь между технологией изготовления и качеством продукции,
так как коэффициенты Q = 0,567 и К = 0,311 достаточно велики по сравнению со своими
среднеквадратическими отклонениями (превышают их более, чем в три раза).
5.2.2.4.1.1.3. Коэффициент контингенции (сходства) [132]
Основан на формуле
ad — be
На практике для проверки гипотезы о существовании взаимосвязи между изу™
чаемыми признаками используется величина %2 = nF2, имеющая при отсутствии
связи распределение х2 с / = 1 степенью свободы.
С учетом поправки на непрерывность статистика критерия контингенции для
проверки связи признаков имеет вид
Х (а + Ъ) (а + с) (Ъ + d){c + dY
где п — общее число данных в таблице: n = a + 5 + c + d.
Если х2 > ХаA)? то с достоверностью а зависимость признаков А и В признает™
ся значимой. Приведем некоторые полезные значения: Хо 9о(-0 = 2,70; Xq 95A) = 3,85;
Х§,в9A) = 6,58.
Задача 346. Проверить значимость связи признаков в таблице сопряженности 2x2
в условиях задачи 344 коэффициентом контингенции при доверительной вероятности
а = 0,95.
Имеем V = 95 ' 4° " 15 ' 7° = 0,262.
л/ИО- 165-55110
^ 2 220-(95-40-15-70-НОJ
Далее при п = 220 имеем у = = 14,07.
М Р Л 100-165-55-110
Так как х2 = 14,07 > Хо 95 A) =:: 3,85, связь признаков в задаче должна быть признана
значимой.
5.2.2.4.1.1.4. Точный критерий Фишера
Критерий х^х = п^2 применим при п ^ 40 и а, Ь, с, d ^ 5. Если эти условия не
выполняются, то следует воспользоваться точным критерием Фишера, основанном
на статистике
Р =
(а + Ь + с + d)\ f-' {а + Ъ- i)\(a + с - i)\(a + d - i)\
Если р > 1 — а, то с достоверностью а связь признаков признается значимой.
21 А. И. Кобзарь
642
Методы исследования связей между случайными величинами
[Гл. 5
Задача 347. Имеется следующая таблица сопряженности признаков 2x2:
Е
Е
11 6
13 10
24 16
17
23
40
Необходимо при доверительной вероятности а = 0,95 оценить значимость связи при-
признаков в таблице точным критерием Фишера.
_
Вычисляем
A1 + 6)? A3 + 10)! A1 + 13)! F + 10)!
A1 + 6 + 13 + 10)!
f^Q i\ A1 + 6 - г)! A1 + 13 - г)! (И + 10- г)!
= 0,227.
Так как р = 0,227 > 1 — а = 1 — 0,95 = 0,05, связь признаков в таблице следует считать
значимой.
5.2.2.4.1.1.5. Быстрые критерии оценки свмзи в таблицах сопряженности 2x2
При a + 5 + c + d^ 25 и при условии а + Ъ = с + d или а + с = Ъ + d критерием
является величина , ч , ч
_ (а + d) - (b + с)
Va + 6 + с + d
Связь признаков в таблице с достоверностью а признается значимой при z > иа
(иа — «^квантиль стандартного нормального распределения).
При a + Ъ ^ 10 при условии a + 6 <С с + d или а + с <С Ь + d справедлив критерий
(а + с — Ь — а) (а + 6)
a+6+c+d
Если z > гла, то связь признаков признается значимой.
Задача 348. Для таблицы сопряженности
Е
Е
14 28
6 36
20 64
42
42
84
проверить гипотезу о согласованности признаков при доверительной вероятности
а = 0,95.
Имеем а = 14, Ь = 28, с = 6, d = 36. Так как a + 6 = 42 =
36)^B8
d, используем критерий
/84
= 1,745.
Так как z = 1,745 > ^0,95 = 1,645, связь признаков следует признать значимой. Сле-
Следует помнить, что всегда при z берется знак + (это не меняет результат).
Задача 349. Для таблицы сопряженности
15 4
85 77
100 81
19
162
181
проверить гипотезу о согласованности признаков при доверительной вероятности
а = 0,95.
5.2]
Корреляционный анализ
643
В нашем случае
=19<Cc + d = 162, поэтому используем критерий
85-77) ¦ A5 + 4)
= 1,97.
15-4-
15 + 4 + 85 + 77
Так как z = 1,97 > 110,95 = 1,645, связь признаков в таблице следует признать значи-
значимой.
5.2.2.4.1.1.6. Модифицированный критерий знаков Мак-Нимара
Предположим, что над одной и той же группой объектов производятся два экс-
эксперимента и необходимо установить — меняется ли распределение частот от одного
эксперимента к другому. В этом случае мы имеем также таблицу сопряженности
2x2, однако составляющие ее данные, вообще говоря, уже не будут независимыми.
Мак-Ыимар [577] предложил простой критерий проверки изменения соотноше-
соотношения частот в таблице при изменении условий опыта. Пусть мы имеем таблицу:
Опыт 1
+
Опыт 2
+
а
с
b
d
Из нее следует, что значения and соответствуют неизменным условиям опыта
(а — когда и опыт 1 и опыт 2 действуют на объект, d — когда ни один из опытов
не действует на объект). Значения Ъ и с соответствуют условиям, когда действует
только один из опытов. Если Ь « с, то, следовательно, опыты не оказывают влияния
на объект.
Для проверки равенства Ъ = с Мак™Нимар предложил критерий [577]
^/2 — — —, а при Ь + с < 30: х2 =
Ь + с+1' г ' А Ь + с+1 '
Если х2 > Ха (-'-)? РазниЦа меясду Ь и с признается значимой
распределения хи-квадрат с / = 1 степенью свободы).
A) — «-квантиль
Задача 350. Предположим, 30 пациентов начали применять два препарата. При
этом 8 пациентов признали сильным действие как первого, так и второго препаратов;
11 ^слабым действие обоих препаратов; 16 признали действие первого препарата силь-
сильным, а второго слабым] 5 пациентов — наоборот. Необходимо проверить критерием
Мак-Нимара при достоверности а = 0,95 гипотезу о различии в действии препарата.
Имеем таблицу:
Препарат 1
сильное
слабое
Препарат 2
сильное
(а) 8
(с) 5
слабое
1б(ь)
и (d)
Разница между препаратами проявляется в разнице частот (Ь) и (с), так как именно
они фиксируют впечатления пациентов, связанные с различием воздействия исследуе-
исследуемых препаратов. Имеем
2=
Х
(\Ь-С\-1
Ь+с+1
A6- 5^ IJ
16 + 5 + 1
= 4,54.
Так как Хо,9бA) — 3,84 (см. табл. 55), а %2 — 4,54 > Хо,95? то с вероятностью 0,95
следует признать значимой разницу в воздействии препаратов на различных пациентов.
21*
644
Методы исследования связей между случайными величинами
[Гл. 5
5.2.2.4.1.1.7. G-критерий Вулфа
Критерий Вулфа [578] используется вместо критерия х2 Для четыреклеточных
таблиц (см. раздел 5.2.2.4.1.1.3). Он позволяет уменьшить количество вычислений
и лучше обоснован теоретически, чем %2™критерий [9].
Критерий строится следующим образом. В таблице
а Ь
с d
сначала наименьшая из величин увеличивается на 1/2 (так называемая поправка
Йэйтса). Затем соответствующим образом меняются все остальные значения в та™
блице с тем, чтобы величины а + 6, c + d, а + си 5 + cf не менялись. Тогда таблица
принимает следующий вид (считаем, что d является минимальным значением):
Статистика критерия Вулфа равна
чьи
c-fWc-l
- (а + е) ln(a + с) - (Ы- d) 1п(Ь + d) + (а + Ь + с + d) In (а + Ь + с + d) >.
Если G >
), то связь признаков в таблице признается значимой.
Задача 351. Для данных задачи 345 проверить сопряженность признаков в таблице
критерием Вулфа при а = 0,95.
Имеем таблицу:
95^1/2 15 + 1/2
70 + 1/2 40 - 1/2
165
55
110
110
220
Вычисляем
G = 2 • {94,5 • In 94,5 + 15,5 • In 15,5 + 70 • In 70 + 39,5 • In 39,5-
- 110 • In 110 - 110 • In 110 - 165 • In 165 - 55 • In 55 + 220 • In 220 } = 14,337.
Из табл. 55 имеем Xo,9s(l) — 3,85. Так как G = 14,337 > Хо,9бA) = 3,85, следует при™
знать связь частот в таблице значимой.
5.2]
Корреляционный анализ
645
5.2.2.4.1.1.8. Критерий Ле Ром для сравнения двух таблиц сопряженности 2x2
Предположим, что мы имеем в своем распоряжении две таблицы данных 2x2:
a
Необходимо проверить гипотезу о том, что оое таолицы статистически не раз-
различимы и являются выборками из единой совокупности.
Ле Рой [579] предложил для проверки такой гипотезы критерий, основанный на
статистике
R = (аг
¦ а2 + Ь2 + С2 + d2) x
G-2 ~~Ь &2 ~~Ь С2 + 6^2
1
2
а2
а2
с2
+
ь\
- с2
k+d2
- 1
Гипотеза о статистической неразличимости таблиц отклоняется с достоверно™
стью а, если R > Х^(^)ч (Ха(^) — «-квантиль ^-распределения с / = 3 степенями
свободы). Для употребляемых значений а укажем
Хо,9оC) = 6,251; хо)95C) = 7,815; Хо,9вC) = 11,345.
Следует помнить, что ^-критерий применим, если все числа в таблицах превы-
превышают 3.
Задача 352. Проверить гипотезу о статистической неразличимости двух таблиц
сопряженности 2x2 критерием Ле Роя при доверительной вероятности а = 0,90:
Е
15 48
21 71
36 122
Е
63
95
158
Е
27 94
112 456
139 550
Е
121
568
689
Имеем oi = 15, Ьх = 48, а = 21, di = 74, а2 = 27, Ь2 = 94, с2 = 112, d2 = 456.
Вычисляем
R = A5 + 48 + 21 + 74 + 27 + 94 + 112 + 456) х
272
27 + 94 + 112 + 456 \15 +27 48 + 94 21 + 112 74 + 456/
1
1 - li =37,938.
J
15 + 48 + 21 + 74 \15 + 27 48 + 94 21 + 112 74 + 456 у
Так как R = 37,938 > Хо,эоC) = 6,251, следует признать, что таблицы статистически
различимы.
5.2.2.4.1.1.9. Выбор числа наблюдений для анализа
таблиц сопряженности 2x2
Сформулируем следующую задачу. Необходимо для заданных допустимых уров™
ней ошибок — первого рода а (вероятность отклонить верную гипотезу) и второго
646
Методы исследования связей между случайными величинами
[Гл. 5
рода /3 (вероятность принять неверную гипотезу) и заданных значениях р± = —
и р2 = -; при
¦ b = с + d = n определить необходимое число наблюдений — п, ко™
торое требуется провести, чтобы сравнить относительные частоты р\ и р2 между
собой.
Необходимое число наблюдений п рассчитывается по формуле [9] (берется бли™
жайшее целое число): п = ; ; ^ гДе К — коэффициент, приве™
(arcsin у/рг —- arcsin л/р^)
денный в табл. 229.
Таблица 229
Значения коэффициента К [9]
а
0,05
0,01
0,001
0,2
12885
16474
19172
ОД
17250
21369
24426
0,01
30161
35537
43945
Задача 353. Найти объем выборки, позволяющий сравнить относительные частоты
в таблице сопряженности признаков 2 х 2: р\ = 0,61 и р2 = 0,38 при уровнях ошибки
первого рода а = 0,05 и второго рода C = 0,1.
Из табл. 229 имеем К = 17250.
Тогда
= 1™ -2 = 97,55.
E1,3545 - 38,0567)^
Таким образом, необходимо иметь 98 наблюдений. Проверка разницы в таких табли-
таблицах обеспечивает мощность критерия %2, равную 1 — /3 = 0,90.
5.2.2.4.2. Оценка связи признаков в многоклеточных
таблицах сопряженности г X с
Если результаты наблюдений могут быть классифицированы по трем или более
качественным признакам, рассматриваются так называемые таблицы сопряженно-
сопряженности г х с [132]:
Е
П\\
П21
Пг1
П22
ПГ2
Не
П2с
пгс
Ъ
ii
П2
пг
п
Здесь riij—число результатов наблюдений из общего числа в, обладающих
признаками i и j одновременно. В качестве меры связи между признаками
г и с (либо между г и с градациями двух признаков А л В) использует™
/_^ /-^ —^ ~~ I' имеюЩая ПРИ независимости признаков
=ij=i J /
2
ся статистика X п
5.2]
Корреляционный анализ
647
Х2™распределение с / = (г —1)(с—1) степенями свободы. Следовательно, если
X2 > Ха[(г ~~ -0(с ~~ 1)L то с вероятностью а признается зависимость между изучае-
изучаемыми признаками. Однако статистика %2 неудобна при оценке связи признаков, так
как ее значения не нормированы и при п —> оо %2 —> оо (в отличие от рассмотренных
ранее коэффициентов корреляции, значения которых при любых п заключены меж™
ду — 1 и +1). Поэтому для оценки связей в таблицах г х с используются специальные
коэффициенты сопряженности, предложенные Пирсоном и Чупровым [132]. Пирсон
предложил коэффициент сопряженности в виде Кр =
. Значения Кр
зависят от числа изучаемых признаков, что не позволяет использовать его для
сравнения связей в таблицах с различными значениями г ж с. Этого недостатка
лишен коэффициент сопряженности Чупрова [132]
Коэффициент Кr становится равным ±1 в случае полной связи признаков только
при г = с. Так, как коэффициенты сопряженности выражаются через %2, то про-
проверка их значимости может быть осуществлена с помощью критических значений
X2 -распределения.
Если Кр > Кр(а) или К л > Кц{а), то связь признаков признается существен-
существенной.
Задача 354. Предположим, что в результате проверки партии электронных дамп
трех типов (по 100 шт. каждого типа), изготовленных на пяти заводах, получены
следующие количества годных ламп:
Тип
лампы
1
2
3
Е
Завод-изготовитель
1
70
80
30
180
2
60
90
40
190
3
20
100
30
150
4
40
90
20
150
5
30
70
50
150
Е
220
430
170
820
Необходимо проверить гипотезу о наличии связи между качеством ламп различного
типа и заводом-изготовителем при доверительной вероятности а = 0,95.
Имеем г = 3, с = 5, (г - 1) • (с - 1) = 8. Тогда
3 5 2
= 820-
¦ +
180 • 220 190 ¦ 220 150 • 220 150 • 170 150 • 170
.2 /о\ 1С КП7 TU-^ т,«т, ,w2 г л о Л Л \ -.,2
- 1 = 51,244.
Имеем из табл. 55: х§;95(8) = 15,507. Так как %2 = 51,244 > Хо,9б(8) = 15,507, гипотеза
о наличии связи между признаками подтверждается.
Вычислим теперь коэффициенты сопряженности:
51,244
820 + 51,244
= 0,242; KR =
51,244
820 -л/^
= 0,149.
648 Методы исследования связей между случайными величинами [Гл. 5
5.3. Регрессионный анализ
Рассмотренные ранее методы дисперсионного и корреляционного анализа позво-
ляют выявить наличие связи между случайными величинами и оценить силу этой
связи.
Следующей ступенью является выявление конкретного функционального вида
связи между случайными величинами.
При наличии корреляционной связи между х и у имеет место соотношение
F(y) = F(x, у), т. е. функция распределения случайной величины у зависит от зна™
чения случайной величины х. Любая функция распределения полностью определя™
ется своими параметрами. Изменение функции распределения случайной величины
у от х можно задать зависимостями
называемыми соответственно-регрессионной, скедастической, клитической и сина-
гической. На практике обычно предполагается, что дисперсия и моменты высших
порядков распределения у не зависят от значения х. Наибольший практический
интерес представляет определение зависимости \х\у = /(ж), описывающей истинную
зависимость между у и х. Зависимость средних значений у(/лу) называется регрес-
сией у по ж, а методы нахождения таких зависимостей и оценки их статистических
свойств составляют содержание регрессионного анализа.
По выборочным данным можно найти только оценку истинной регрессии, со-
содержащую ошибку, связанную со случайностью выборки.
В основе регрессионного анализа лежит принцип наименьших квадратов, в соот-
соответствии с которым в качестве уравнения регрессии у = f(x) выбирается функция,
п
доставляющая минимум сумме квадратов разностей s = ]Р [yi — / (х{)} . Как пра™
вило, вид функции f(x) определяется заранее, а методом наименьших квадратов
определяются ее коэффициенты, минимизирующие s. Количественной мерой рас-
рассеяния значений yi вокруг регрессии f(x) является дисперсия
где к— число коэффициентов, входящих в аналитическое выражение регрессии
(например, если f(x) — многочлен степени I, то к = I + 1).
В зависимости от вида уравнения регрессии у = f(x) различают линейную
(f(x)—многочлен первой степени) и нелинейную (f(x) — многочлен степени ^ 2)
регрессии.
Вид функции f(x) выбирается исходя из особенностей исследуемого явления
(процесса), а также из общего графического анализа зависимости между у и х.
Подробно выбор формы функциональной зависимости для регрессии рассмотрен
в [9, 14, 580].
Чаще всего ограничиваются рассмотрением линейной регрессионной модели,
а при нелинейной зависимости у = f(x) используют различные линеаризующие пре-
преобразования переменных у жх. Наиболее распространенные из этих преобразований
приведены в табл. 230.
Схема регрессионного анализа включает в себя последовательное решение сле-
следующих задач: нахождение выборочной оценки истинной регрессии; оценки стати-
статистической значимости выборочной регрессии в сравнении с безусловным разбросом
значений у^, характеризующимся дисперсией а2; определение доверительных обла™
стей, с заданной вероятностью включающих в себя истинную регрессию.
5.8]
Регрессионный анализ
649
Таблица 230
Линеаризующие функциональные преобразования
(у* = а* + Ь*х')
Исходная зависимость
У fix)
Ъ
у = а+ -
а
У — и ,
Ь + х
ах
У ~ Ь + х
X
У — . и
а + ох
у = abx
у = ахъ
у = аеЪх
у = а + Ьхп
Преобразование
переменных
2/*
У
1
У
1
У
X
У
Чу
lgy
In у
In у
У
ж*
1
X
X
1
X
X
X
\gx
X
1
хп
Преобразование
коэффициентов
а*
а
а
Ь
Ь
а
а
Iga
Iga
In a
In a
а
Ь*
Ь
1
а
1
а
ь
Ig6
b
ъ
ь
ь
Среди дополнительных задач, позволяющих получить полную статистическую
картину изучаемой регрессии, отметим: анализ так называемых регрессионных
остатков (разница между выборочной регрессией и выборочными значениями функ™
ции); анализ наличия грубых отклонений от регрессии (выбросов); построение
толерантных границ для регрессии.
Эти задачи практически не используются в повседневной работе инженеров
и исследователей, поэтому им далее уделяется необходимое внимание.
Разработанный в настоящее время аппарат регрессионного анализа предпола-
предполагает, что значения у^ взаимно независимы и нормально распределены. Выполне-
Выполнение этих условий должно быть предварительно проверено с помощью критери-
критериев нормальности (см. раздел 3.2.2) и критериев сравнения дисперсий (см. раз-
раздел 4.1.1.4). Наиболее полное изложение прикладного регрессионного анализа со-
содержится в [581].
5.3.1. Линейный регрессионный анализ
Линейный регрессионный анализ исходит из наличия зависимости у = а + /Зж,
где а и C — неизвестные коэффициенты регрессии. Выборочные оценки а и /3
в дальнейшем будем обозначать а и Ь соответственно.
5.3.1.1. Оценка коэффициентов регрессии
5.3.1.1.1. Оценка наименьших квадратов
Оценки наименьших квадратов являются решениями системы нормальных урав-
уравнений, строящихся по совокупности наблюдаемых значений у^ для совокупности
значений xf.
г=1
4=1
650 Методы исследования связей между случайными величинами [Гл. 5
из которой следует система
г=1
г=1 г=1 г=1
Решение системы дает искомые оценки коэффициентов регрессии:
I г=1 г=1 г=1 г=1
6= т^^; а=
г=1 \г=1
Для проверки правилвности вычислений можно использовать соотношения
1 п 1 п
у = а + Ьх, где У=-^У»; ^ = z;l>2xi°
Пг=1 П г=1
Вычисления а и Ъ существенно упрощаются, если интервалы между зна™
чениями независимой переменной х постоянны, т.е., если a^+i — ж^ = / = const
(г = 1, 2,... ,п — 1). Наиболее эффективен метод оценки, предложенный автора-
авторами в [582]. Пусть Xi = ~^— hi, т.е. последовательность #i,#2, • • - ^хп транс-
трансформируется непосредственно в последовательность г = 1,2, . ..,п и зависимость
у = а + Ьх трансформируется в завсимость у = а + 6г. Оценки для этого случая
имеют вид
12f>i-6(n + l)f> E2/i-bE*
7 г=1 г=1 7- г=1 г=1
6 = / 2 ; а = у — ох = ^^^-^^^.
п(п2 - 1) п
Дисперсии этих оценок равны: DF) = ст2: D(a) = 2^^ тт®'2? где сг2—дю>
п — п п(п — 1)
персия остатков.
Для вычисления оценок а и 6 необходимо вычисление сумм J^|/i и Е*2/Ь что
требует п умножений и 2п сложений. Авторы работы [582] предложили более
экономичный линейный метод оценивания, который при незначительной потере
в точности позволяет существенно сократить время вычислений. Эти оценки имеют
вид:
7 4,5 ,„ „ч _ 1 f гу гу гч
Ь = -т (S3 - Si); о = - Si + S2 + S3 -
n n \
к n-k n n
где Si = ]T y- S2 = E 2/*5 ^з = E 2/*' ^^ ближайшее целое к -.
i=l i=fc+l г=п-А;+1
Расчет на ЭВМ этим способом занимает в « 3,2 раза меньше времени, а диспер™
сия оценок возрастает на 12,5% и 9,4% соответственно.
В заключение отметим характерную особенность регрессионных уравнений,
о которой следует помнить инженерам и исследователям. Регрессия у по х:
у = а + /Зх не эквивалентна в общем случае регрессии х по у: ^х = а* + /3*2/.
Если Sy и S^ — стандартные отклонения совокупностей значений у ж х соот™
ветственно (S| = ^—j- J^ (^ -у) ; 52 = ^—у ^ (^ - ж) ), то регрессии у = f(x)
5.3] Регрессионный анализ 651
и х = (р(у) можно записать следующим образом:
S S
У = у + г-^- (х — х) ] х = х + г-^ (г/ — г/) ,
где г — коэффициент корреляции.
Отсюда видно, что регрессии у по х ш х по у совпадают только в одном случае,
когда существует абсолютная корреляция между у ж х^ т.е. когда \г\ = 1. При г = О
S S
прямые регрессии у по х и х по у перпендикулярны. Тогда /3 = г-^~; /3* = ^тг-
При 5^ = ?у коэффициенты корреляции и регрессии совпадают.
Задача 355. В результате наблюдений за зависимостью у = f(x) получены следую-
следующие данные:
ун 2 3 7 10 11 13 18 21 25 31;
хц 8 11 14 18 4 26 31 32 34 41.
Необходимо найти оценку коэффициентов регрессии у по х методом наименьших ква-
квадратов.
10 10 10 10
Находим Y,Xi = 2195 Yl yi = 1415 Y1 ж? = 62195 I] ЖШ = 406°-
г=1 г=1 г=1 г=1
Далее вычисляем оценки
10 • 4060 - 219 • 141 141-0,68318-219
Ь = 5— = 0,68318; а = = ^0,86164.
10-6219-2192 10
Следовательно, уравнение регрессии у по х имеет вид
у = -0,86164 + 0,68318 -ж.
Задача 356. В результате наблюдения за зависимостью у = f(x) получены следую-
следующие данные:
Vi: 13 18 24 21 25 31 36 41 35 41 48 56 61 60 70;
xv 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30.
Необходимо найти оценки коэффициентов регрессии у по х.
Введем замену переменных xi = — Ь 1 = — Ь 1-
Вычисляем оценки наименьших квадратов
15 15
12-У;г.2/*-6.A5 + 1).у>
7 i=i i=i 12 • 5704 -6-16-580
о = ; = = о,о;
15 • B25 - 1) 15 • 224 ' '
580 3,8-A5 + 1)
а = ¦—-—^^ = 8,266.
15 2 '
Воспользуемся теперь линейными оценками. Примем к = п/3 = 5 и вычисляем
5 11 15
г=1 г=6 г=11
b=^--(S -S) = 4l5 'B95 ~ 101) = 3 88-
152 Ч 3 1} 225 ' '
а= — • A01 + 184 + 295-3,88- 15ji? } =7,626.
Видим, что при существенно меньшем количестве вычислений результат практически
не отличается от предыдущего (естественно, что наибольший выигрыш во времени
и наиболее точный результат будут достигнуты при больших объемах выборок).
652 Методы исследования связей между случайными величинами [Гл. 5
5.3.1.1.2. Простейшие оценки коэффициентов регрессии
5.3.1.1.2.1. Метод Бартлеиа—Кенуя
Пары наблюдений (yi,Xi) упорядочиваются по ж и разбиваются на 3 примерно
равные группы (причем первая и последняя группы должны быть обязательно
равного объема). В каждой группе находятся суммы J^2/i и ^#г (обозначим их
соответственно Yi, Y2, У3 и -^"ъ -^2> -^з)-
Тогда коэффициент регрессии оценивается с помощью соотношения [121, 583, 584]:
Ь = — — с ошибкой S^ =
я п I
гдаs = 9 Е Уг wy'+1; а = г/ - ьг-
г=1
Если п пар наблюдений разбиваются на четыре группы, содержащие в себе 1/6,
1/3, 1/3 и 1/6 часть наблюдений, то
с ошибкой ?
\ + Л2 — Аз — ОЛ4 ОЛ1 + А2 — Аз — ОА4
Эти оценки применимы для больших выборок при п ^ 100.
Задача 357. Для данных задачи 356 найти оценку коэффициентов регрессии методом
Бартлетта-Кенуя.
Разбиваем пары наблюдений (г/^, Xi) на три части и находим соответствующие суммы
„ ~ хг
для переменной х% = —.
Xi = 15, Х2 = 40, Хз = 65, Yi = 101, Y2 = 184, F3 = 295.
Тогда имеем
что очень близко к полученному ранее в задаче 355 значению Ь = 3,8.
5.3.1.1.2.2. Метод Керрича
Для частного случая зависимости у = Ьх (а = 0) Керрич [585] предложил еле™
дующий простой метод оценки. Вычисляем разности
г^ gy% gXt1 ~п^г И d^^n(n~l)
Так как любое отношение yi/xi является оценкой 5, то любое значение di явля-
является оценкой lg Ь.
Когда S^/d <^ 1, оценкой lg 6 является величина d. Следовательно, оценка будет
равна Ь = 10d.
Задача 358. Для совокупности значений
хн 1 2 3 4 5 6 7 8 9 10;
ун 3 8 6 16 15 18 21 29 28 32
найти оценку коэффициента регрессии методом Керрича.
Вычисляем последовательность значений di = lg yi -— lg Xi:
dn 0,477; 0,602; 0,301; 0,602; 0,477; 0,477; 0,559; 0,559; 0,493; 0,505.
Далее d = 0,497 и b = Ю0'497 = 3,14, что близко к обычной оценке Ъ = 3,23.
5.8]
Регрессионный анализ
653
5.3.1.1.3. Робастные методы оценки параметров регрессии
Напомним, что одним из важнейших исходных требований регрессионного ана-
анализа является обязательная нормальность распределения наблюдаемых случайных
величин. В связи с тем, что эта предпосылка не всегда выполняется, разработаны
специальные методы, устойчивые (робастные) к отклонениям распределения ис-
исходных величин от нормального распределения. Среди них можно отметить оценки
коэффициентов регрессии с помощью коэффициентов корреляции Кендалла т [586],
„повторных" медиан [587], метода областей Дениэлса [588].
Мы рассмотрим два критерия, наиболее полно отображающих суть подходов
к построению робастных методов оценки параметров регрессии.
5.3.1.1.3.1. Медианный критерий Брауна-Муда
Предположим, мы имеем п пар (п — четное) наблюдений (ж^,^). Разбиваем все
наблюдения на две группы по значению х: группу значений, превышающих ж,
и группу значений Х{ < х. Предположим, что мы располагаем априорными оценками
коэффициентов регрессии ад и Ьд. Для них можно найти регрессию щ = а$ + bgXi
и вычислить регрессионные остатки Ayi = yi — щ. Затем определим количества
положительных (Ayi > 0) остатков mi и т2 в двух группах.
Статистикой критерия Брауна—Муда [589] является величина
2 / \ 21
-?| +
п
ГГЦ--
Гипотеза адекватности регрессии, а следовательно, пригодность выбранных ко-
коэффициентов а® и Ъд отклоняется, если А > %^ (х^, — а-квантиль %2-распределения
с / = 2 степенями свободы). В ряде случаев более эффективной может быть моди-
модификация ^-критерия Брауна—Муда
Критические значения А*»статистики равны Aq 95 = 2,237, Aq 99 = 2,806 [589].
При А* > т4^ гипотеза о пригодности а® и 6q отклоняется с вероятностью а. В этом
случае оценки а® и Ьо заменяются на другие, и итерации продолжаются до тех пор,
пока критерии не будут отклоняться критическими значениями.
Задача 359. При условиях задачи 358 провести оценку коэффициентов регрессии с по-
помощью критериев Брауна-Муда (а = 0,95).
Выберем оценки «о = 1 и bo = 3 и вычислим
щ = q0 + Ь • Xi -+ 4, 7, 10, 13, 16, 19, 22, 25, 28, 31;
Ау{ = у{^у{ -^ -1, +1, -4, +3, -1, -1, -1, +4, 0, -1.
5 + 6
Медиана равна х =
= 6,5. Для Xi > х имеем гп\ = 2 значения Ау > 0 (это 4 и 1).
Для Xi < х имеем ТП2 = 2 (это 1 и 3). Тогда
А= — •
10
А* =
л/т
2 -
10
4
+
2 -
10
4
:-f I 1=0,4;
= 0,632.
Так как А = 0,4 < Хо,9бB) = 6 и А* = 0,632 < А^95 = 2,237, принятые оценки а0 = 1
и Ьо = 3 не отклоняются критерием Брауна-Муда.
654
Методы исследования связей между случайными величинами
[Гл. 5
5.3.1.1.3.2. Оценка Тейла
По п парам (ж^Уг)? где среди значений xi нет повторяющихся, построим
7V = п(п — 1) пар оценок угловых коэффициентов
_ Уз ~ У г
Kj.
Оценкой коэффициента регрессии /3 является медиана [590] b =
N
Так как N — четное , то Ь = - (/Й + /Й+1), где fc = ^-.
Двусторонний а • 100%™й доверительный интервал для оценки Тейла имеет
вид [590]
ГДе Са =
(п- 1)Bга + 5)
18
(при > 10); и7—7™квантиль стандартного нормаль™
ного распределения.
Задача 360. В условиях задачи 358 найти оценку Тейла для регрессионного коэффици-
коэффициента /3 и вычислить его 95%-й двусторонний доверительный интервал.
n-(ra-l) 10-9
=
Найдем
Вычисляем 45 оценок /3ij(i < j) вида (Зц =
в таблицу:
= 45 пар значении (xi,Xj) для различных г:
Уз
-. Результаты вычислений сводим
г
1
2
3
4
5
6
7
8
9
1
-
-
-
-
-
2
5
-
-
-
-
3
3/2
2
-
-
-
-
4
13/3
4
10
-
-
-
5
3
7/3
9/2
1
-
-
-
6
3
10/4
4
1
3
-
-
7
3
13/5
15
5/3
3
3
-
8
26/7
21/6
23/5
13/4
14/3
11/2
8
-
9
25/8
20/8
22/6
12/5
13/4
10/3
7/2
1
10
29/9
24/9
26/7
16/6
17/5
14/4
11/3
3/2
4
Ранжированный по возрастанию ряд значений /3ij имеет вид
3 3 5 7 12 5 5 5 13 13 24 25 29 13
5 ' ' 2' 2' 3 3 5 2' 2' 2' 5 5 9 '894'
13 10 17 7 7 7 11 22 22 22 15 ^ 13 9 14 14 11 п 1П
—, —, —, —, —, —, —, —, —, —, —, 4, 4, 4, —, —, —, —, 5, —, 8, 10.
4 3 5 2 2' 2' 3 6 6 6 4' ' ' ' 3 2 3 3 2'
Медиана этого ряда равна 23-му порядковому значению, т. е. Ъ =
5.3] Регрессионный анализ 655
Для двусторонней оценки при а = 0,95 получаем
10'9'25 =1,96-11,18 = 21,91.
Находим /3 с номерами = — = 11 (ближайшее меньшее целое число)
N + С 45 + 21 91
и — = — = 34 (ближайшее большее целое число).
Имеем /Зц = 2,5 и /З34 = 3,75. Следовательно, искомый доверительный интервал для
коэффициента регрессии равен 2,5 ^ Ь ^ 3,75.
5.3.1.2. Статистическое оценивание регрессии
Статистическое исследование регрессии включает в себя:
— проверку гипотез о значениях коэффициентов регрессии (т.е. о статистиче-
статистической неразличимости выборочных значений у± и у^, вычисляемых по уравнению
регрессии);
— построение доверительных интервалов для коэффициентов регрессии и дове-
доверительных областей для регрессии;
— анализ статистической однородности регрессии (отсутствие выбросов);
— анализ независимости регрессионных остатков.
Ниже рассматриваются различные методы решения перечисленных задач.
5.3.1.2.1. Статистический анализ коэффициентов регрессии
5.3.1.2.1.1. Оценки наименьших квадратов
Статистические выводы относительно коэффициента C регрессии у = а + (Зх
могут быть получены с помощью статистики
t = Ь~Р
где
— а — bxi) ;
г=1
E — истинное значение коэффициента регрессии; Ь — выборочная оценка коэффици-
коэффициента регрессии.
Статистика tp при справедливости нулевой гипотезы Hq : f3 = Ъ имеет распреде-
распределение Стьюдента с / = п — 2 степенями свободы.
Следовательно, с помощью квантилей распределения Стьюдента можно прове-
проверить гипотезу равенства f3 заданному значению, гипотезу о значимости коэффици-
коэффициента регрессии (существенности его отклонения от нуля), построить доверительный
интервал для коэффициента C. Значение коэффициента C регрессии является зна-
значимым с достоверностью а, если \Ъ\ > ti+а Sq.
2
Гипотеза о равенстве коэффициента C заданному значению f3g принимается, если
\Р-Ъ\ <h+ggfl.
2
И, наконец, двусторонний а • 100%-й доверительный интервал для C имеет вид
Ь — Setl + Ot ^/3^6+ Sfttl + QL .
2 2
656 Методы исследования связей между случайными величинами [Гл. 5
Статистические выводы относителвно коэффициента а могут бытв полученв!
с помощвю статистики
гДе ~« - ,, „ ¦ , ,ч c-z:
, — I) Dx
а, а — соответственно выборочная оценка и истинное значение коэффициента а;
S и Sx определены выше для tp.
При Но: а = а статистика ta имеет распределение Стьюдента с / = п — 2 сте-
степенями свободы. Проверка гипотез о значениях коэффициента а и построение
доверительных интервалов для него выполняются по аналогии с коэффициентом /3.
Задача 361. Для совокупности данных
хц 1,2 2,4 2,8 4,2 5,9 6,8 8,1 9,2 10,1 11,0;
ун 7 12 17 24 29 38 46 45 54 68
найти оценки коэффициентов а и /3 регрессии у = а + j3x и провести их статистиче-
статистический анализ при доверительной вероятности а = 0,95 (не путать с а — коэффициен-
коэффициентом регрессии!).
\~^ \~^ \~^
Вычисляем оценку /3 (см. раздел 5.3.1.1.1): b =
Имеем
ю / ю \ 2 ю ю ю
^ ж* = 61,7; ^^ =3806,89; ^ х\ = 486,99; ^ у* = 340; ^ ж^^ = 2695,1.
г=1 \г=1 / г=1 г=1 г=1
Тогда
10 10
10-2695,1^61,7-340 г=1^ i=i^ 340^5,6189-61,7
о = = 5,6189: а = = = ^0,668.
10 ¦ 486,99 - 3806,89 п 10
Проверим теперь значимость полученных коэффициентов (существенность их откло-
отклонения от нуля). Вычислим предварительно
х = 6,17; S2X = ^— -Jt(Xi^ ^f = П?8112; (Sx = 3,3467).
i=l
1 n
Далее вычисляем значение дисперсии S2 = ^2(Уг ~~ УгJ ^ гДе У г = а + Ъ - xi.
П~2 г=1
В нашем случае
щ -л 6,075; 12,818; 15,065; 22,932; 32,484; 37,541; 44,846; 51,027; 56,084; 61,141.
Вычисляем далее
ю
X
= 0,125 • [G - 6,075J + A2 - 12,818J + ... + F8 - 61Д41J] = 13,4755;
я
Sx ¦ л/ri^l 3,3467 -3
+2 3'671 \ + 2'486-
п (n-l)-Sl у 10 9 • 11,8112
Для уровня достоверности а = 0,95 имеем ti~o,95 (п — 2) = to,975(8) = 2,306.
2
5.3] Регрессионный анализ 657
Проверяем значимость коэффициента /3:
\Ъ\ = 5,1689 > to,97s(8) • Яд = 2,306 • 0,3656 = 0,843,
следовательно, с достоверностью 0,95 делаем вывод о значимости коэффициента регрес-
регрессии.
Проверяем гипотезу Н: /3 = /Зо = 5 (о равенстве коэффициента регрессии C® = 5):
|5,619 - 5| = 0,619 < to,975(8) • S$ = 0,843,
т. е. гипотеза о равенстве /3 = 5 не отклоняется.
И, наконец, доверительный интервал для C равен
5,9 - 2,306 • 0,3656 = 4,776 ^ /3 ^ 6,462 = 5,619 + 2,306 • 0,3656.
Аналогичные задачи решаем теперь для коэффициента а. Проверим гипотезу
Но: а = 0 \а\ = 0,668 < to,975 • Sa = 2,306 • 2,485 = 5,73.
Следовательно, коэффициент а с вероятностью 0,95 не отличается значимо от нуля,
т. е. его значение может быть приравнено к нулю.
Двусторонний доверительный интервал для а имееет вид
о, — to,975 -So. ^ а ^ а + to,975 * Sa;
-0,668 - 2,306 • 2,485 = -6,398 <: а ^ 5,602 = -0,668 + 2,306 • 2,485.
Таким образом, уравнение регрессии у по х адекватно отображается уравнением
у = 5,619-ж.
5.3.1.2.1.2. Робастные оценки Тейла
Для робастных оценок f3 Тейла (см. раздел 5.3.1.1.3.2) проверку гипотезы
Hq : /3 = /Зо о равенстве углового коэффициента регрессии /3 заданному значению /3q
проводим следующим образом. Ввгчисляем разности Ayi = у^ — Дзж^ (г = 1, 2, ..., п).
Статистикой критерия для проверки нулевой гипотезв! является величина
1, если х > 0;
С = ]Г 5(Ayj - Ау{), где 5(х) = I 0, если х = 0;
i<3 1^-1, если х < 0.
Гипотеза Н®: C = Cq отклоняется с достоверностью а, если (при п > 10) [18]
га (га- 1)Bга + 5)
Построение доверительного интервала для C рассмотрено в разделе 5.3.1.1.3.2
(см. задачу 360).
Задача 362. Для данных задачи 358 проверить гипотезу о равенстве нулю коэффици-
коэффициента регрессии Но: C = 0 (т. е. гипотезу о значимости регрессии) при доверительной
вероятности а = 0,95.
В нашем случае п разностей Ayi совпадают с п значениями у{. Имеем
ю
«^=«0,975 = 1,96; Н"*);> +5) = 11>180.
2 V 18
Тогда с| = 39 > 1,96-11,180 = 21,913, т. е. значение коэффициента /3 следует признать
отличным от нуля.
658 Методы исследования связей между случайными величинами [Гл. 5
5.3.1.2.2. Статистический анализ уравнения регрессии
Целью статистического анализа уравнения регрессии является установление
его адекватности наблюдаемым экспериментальным данным. Под адекватностью
уравнения регрессии понимается статистическая неразличимость результатов вы-
вычислений по уравнению регрессии и наблюдаемых случайных величин.
5.3.1.2.2.1. Оценка адекватности регрессии
Количественной мерой адекватности является отношение дисперсии S2, опреде-
ляемой рассеянием значений у^ вокруг линии регрессии, к дисперсии *S? естествен-
естественного рассеяния значений у^ вокруг своих средних щ. На привычном для инженера
и исследователя языке это можно сформулировать так: ошибки, обусловленные
заменой истинной зависимости на выборочную регрессию, находятся на уровне
естественного разброса наблюдаемых случайных величин.
S2
Если — > Fa, где Fa — а-квантиль распределения Фишера с /х = п — 2
Sy
и /2 = т — 1 степенями свободы, то ошибка в определении регрессии с доверитель-
доверительной вероятностью а признается статистически значимой (га — объем выборки, по
которой выполнена оценка дисперсии S2 т.е. число дублируемых наблюдений для
каждой серии у±).
Если дисперсия S2 известна заранее (что бывает весьма редко), то /2 —> оо. Если
дисперсия Sy определяется по дублируемым значениям г/^, то ее оценкой является
средневзвешенная дисперсия
¦л п т га
il
Напомним, что S2 =
г=1
Задача 363. Проверить адекватность регрессии для данных задачи 361 при довери-
доверительной вероятности а = 0,95, если для оценки Sy предварительно проводилась серия
наблюдений над случайной величиной у при неизменной величине х (т = 10):
yiji 12 14 11 10 8 6 7 15 13.
Ранее (ем. задачу 361) мы получили S2 = 13,4755. По отдельной серии наблюдений
находим оценку Sy = • ^2(y%j ^ У г) = 11,733 (Sy = 3,425).
С<2 z|75i
Далее имеем F = — = —' = 1,148. Из таблиц ^-распределения находим
Sy 11,733
^0,95 (/1 =n^2 = 8;/2 = m^2 = 8) = 3,438.
Так как F = 1,148 < I7!),95 (8,8) = 3,438, с вероятностью а = 0,95 следует сделать вывод
о статистической неразличимости сравниваемых дисперсий, а следовательно, об адекват-
адекватности уравнения регрессии.
5.3.1.2.2.2. Анализ регрессионных остатков
Определенную информацию об адекватности уравнения регрессии дает иссле-
исследование остатков вида е^ = yi — щ, где щ = а + bxi. Если выборочная регрессия у
удовлетворительно описывает истинную зависимость между у и ж, то остатки е\
должны быть независимыми нормально распределенными случайными величинами
5.8]
Регрессионный анализ
659
с нулевым средним и в значениях в{ должен отсутствовать тренд. Нормальность
распределения остатков е^ может быть установлена одним из критериев согласия
(см. раздел 3.2.2).
Гипотезу о равенстве М(е) = 0 можно проверить любым параметрическим или
непараметрическим критерием сравнения среднего с заданным значением (в нашем
случае с нулем), изложенным в главе 4; гипотезу об отсутствии тренда — одним из
критериев тренда и случайности (см. раздел 4.3).
Независимость в последовательности значений е^ (г = 1, ..., п) может быть про-
проверена с помощью сериального коэффициента корреляции Дарбина-Ватсона [591].
Статистика сериального коэффициента корреляции Дарбина^Ватсона имеет вид
Если D > D\{a) или D > 4 —.Di(a), то с достоверностью а принимается гипотеза
о наличии соответственно отрицательной или положительной корреляции остатков.
Если D2{pt) > D > Di(a) или 4 — D\ (a) > D > 4 — ^(ск), то критерий не по™
зволяет принять решение по гипотезе о наличии или отсутствии корреляции
остатков. Если D2(ol) < D < 4 — D2(ог), то гипотеза корреляции остатков откло-
отклоняется. Критические значения D\{a) и D2(cx) для различных а и числа к ко-
коэффициентов в регрессии (имеется в виду число коэффициентов в регрессии
^ = a + bix + 52X + ... + bkX — такого вида множественную регрессию мы рассмо-
рассмотрим позже), приведены в табл. 231.
Таблица 231
Критические значения статистики Дарбина^Ватсона
(а — доверительная вероятность, к — число коэффициентов
в модели у = а + bixi + 62^2 + ... + bkXk) [591]
п
15
20
25
30
40
50
60
80
100
а
0,95
0,99
0,95
0,99
0,95
0,99
0,95
0,99
0,95
0,99
0,95
0,99
0,95
0,99
0,95
0,99
0,95
0,99
к
]
Вг
1,08
0,81
1,20
0,95
1,29
1,05
1,35
1,13
1,44
1,25
1,50
1,32
1,55
1,38
1,61
1,47
1,65
1,52
L
D2
1,36
1,07
1,41
1,15
1,45
1,21
1,49
1,26
1,54
1,34
1,59
1,40
1,62
1,45
1,66
1,52
1,69
1,56
г
Вг
0,95
0,70
1,10
0,86
1,21
0,98
1,28
1,07
1,39
1,20
1,46
1,28
1,51
1,35
1,59
1,44
1,63
1,50
>
D2
1,54
1,25
1,54
1,27
1,55
1,30
1,57
1,34
1,60
1,40
1,63
1,45
1,65
1,48
1,69
1,54
1,72
1,58
3
Вг
0,82
0,59
1,00
0,77
1,12
0,90
1,21
1,01
1,34
1,15
1,42
1,24
1,48
1,32
1,56
1,42
1,61
1,48
D2
1,75
1,46
1,68
1,41
1,66
1,41
1,65
1,42
1,66
1,46
1,67
1,49
1,69
1,52
1,72
1,57
1,74
1,60
Вг
0,69
0,49
0,90
0,68
1,04
0,83
1,14
0,94
1,29
1,10
1,38
1,20
1,44
1,28
1,53
1,39
1,59
1,46
t
D2
1,97
1,70
1,83
1,57
1,77
1,52
1,74
1,51
1,72
1,52
1,72
1,54
1,73
1,56
1,74
1,60
1,76
1,63
5
Dt
0,56
0,39
0,79
0,60
0,95
0,75
1,07
0,88
1,23
1,05
1,34
1,16
1,41
1,25
1,51
1,36
1,57
1,44
D2
2,21
1,96
1,99
1,74
1,89
1,65
1,83
1,61
1,79
1,58
1,77
1,59
1,77
1,60
1,77
1,62
1,78
1,65
660 Методы исследования связей между случайными величинами [Гл. 5
Задача 364. Для полученных в результате эксперимента данных (п = 15)
хц 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15;
уц 7 8 6 9 11 10 14 13 18 19 11 14 18 16 16
проверить наличие корреляции регрессионных остатков критерием Дарбина-Ватсона
при доверительной вероятности а = 0,95.
Вычислим оценки регрессии методом наименьших квадратов (см. раздел 5.3.1.1)
n-Y^Xi-yi-^Xi-^yi J2vi^b'J2Xl
6 =
Тогда
|>г = 120; X; ж? = 1240; ( ]Г хг) =14400; ]Г хг • уг = 1733;
г=1 г=1 \г=1 / г=1
15-1733-120.190 190-0,7607-120 =
15 ¦ 1240 - 14400 15
Находим регрессионные остатки а = г/г — у% = 6,581 + 0,7607 • жг- — у%\
0,3417; 0,1024; 2,8631; 056238; ™056155; 1,1452; -2,0941; -0,3334;
^4,5727; ^4,8120; 3,848; 1,7094;-1,5299; 1,2308; 1,9915.
Вычисляем статистику Дарбина—Ватсона
15
]Р (а ~~ е^гJ = @,1024 ~~ 0,3417J + B,8631 - 0Д024J + ...
г=2
... + A52308 + 1,5299J + A,9915 - 1,2308J = 149,4087;
Ее? =856,3012; D = ^^ = 1,7515.
^г г ' 85,3012
Из табл. 231 для а = 0,95, & = 1 (так как регрессия у = а + 6 • х имеет один коэф-
коэффициент регрессии 6, не считая свободного члена а) и п = 15 имеем Di@,95) = 1,08
и Аг@,95) = 1,36.
В нашем случае D2@,95) = 1,36 < D = 1,7515 < 4 - ?>i@,95) = 4 - 1,08 = 2,92.
Следовательно, наличие корреляции остатков регрессионной модели
у = 6, 581+ 0,7606-ж
с достоверностью а = 0,95 отклоняется.
5.3.1.2.2.3. Оценка выбросов в регрессии
Наличие грубых отклонений (промахов, выбросов) в значениях у^, не связанных
с естественным разбросом, может приводить к большим ошибкам при построении
регрессии. Учитывая, что в практике регрессионная модель часто используется
для предсказания поведения исследуемой случайной величины, то наличие выброса
в данных может привести к грубым ошибкам прогноза.
Ниже рассмотрены некоторые методы выявления выбросов в регрессии. Бу~
дем использовать следующие обозначения: е^ = г/^ — у{ — остатки в точке х = а^,
5.3]
Регрессионный анализ
661
5.3.1.2.2.3.1. Критерий Эктона
Статистикой критерия является величина [592] V =
-, где ek — остаток
от предполагаемого выброса; е =
среднее по всем другим остаткам;
г=1
гфк
S^ — дисперсия отклонения экспериментальных точек линии регрессии с учетом
отбрасывания подозрительного (fc-го) наблюдения.
Критерий Эктона применим при п ^ 30 для выделения только одного выброса
в простейшей линейной модели у = а + Ъх.
Предположим, что при каждом значении независимой переменной xi получе-
получено mi значений зависимой переменной у^. Тогда оценка для S^ в нашем случае
имеет вид
sl =
гфк
i=l
гфк
г» -2
г=1
гфк
Остаток в{ с вероятностью а признается выбросом, если V > Va, где Уа
критическое значение, приведенное в табл. 232.
Таблица 232
Критические значения Va критерия выбросов Эктона
(а — доверительная вероятность) [14]
п
3
4
5
6
а
0,95
123
7,17
5,05
4,34
0,99
31,4
16,27
9
6,85
п
7
8
9
10
а
0,95
3,98
3,77
3,63
3,54
0,99
5,88
5,33
4,98
4,75
п
15
20
25
а
0,95
3,34
3,28
3,26
0,99
4,22
4,02
3,94
Задача 365. В результате эксперимента были получены следующие значения
соответствующие различным значениям независимой переменной xf.
Xil
Vi-
т
1,2
3,1
4,1
5,6
4,27
2,7
6,1
8,4
9,2
7,9
з,
12
16
9,
12
9
Д
,1
3
,5
5,1
21,3
19,4
18,1
19,6
7,2
27,4
21,5
19,8
22,9
9,
31
36
27
31,
4
,2
,4
,3
63
11,1
41,1
38,2
31,4
36,9
12,4
51,2
48,1
31,4
43,56
16,1
71,1
59,2
63,5
64,6
19,1
91,2
81,2
79,4
83,93.
Необходимо проверить наличие выброса в регрессионной модели при доверительной
вероятности а = 0,95 критерием Эктона.
Вычислим параметры регрессионной модели (см. раздел 5.3.1.1.1):
10
¦г = 88,2; I У" Xi I = 7779,24; V" х\ = 1091,14;
Ш = 4230,223;
Х> = 327,79;
662
Методы исследования связей между случайными величинами
[Гл. 5
10 • 4230,223 - 88,2 ¦ 327,79 327,79 - 4,275 • 88,2
b = ¦ ¦ — = 4,275: а = ' = -4,9265.
10 • 1091,14 - 7779,24 ' 10
Остатки равны а = у г — у г • (у г = —4, 9265 + 4, 275 • хг):
4,066; 1,284; 0,754; 2,724; -2,953; -3,628; -5,626; -4,523; 0,699; 7,204.
Проверяем на выброс максимальный по модулю остаток ею = 7,204. Исключая соот-
соответствующую ему точку хю = 19,1, вычисляем Sw(rrii = 3):
- mf = C,1 - 4,27J + D,1 - 4,27J
¦ F3,5 - 64,6J = 459,2302;
i=lj=l
9
г=1
= 301,9509; S?o = ^02 + 301,9509 = ^ ^ = 55Щ
Среднее по (п —- 1) остаткам, не считая потенциального выброса, равно
\ ¦ ? е{ = -0,80.
г=1
г-л 7,204 + 0,80 i Ae
Вычисляем статистику критерия Эктона V = = 1,45.
5,518
Из табл. 232 для п = 10 и а = 0,95 имеем Fo,95 = 3,54.
Так как V = 1,45 < Fo,95 = 3,54, гипотезу о наличии выбросов в регрессии следует
отклонить.
5.3.1.2.2.3.2. Критерий Титьена-Мура-Бекмана
В работе Титьена-Мура-Бекмана [593] предложен критерий обнаружения одно™
го выброса в линейной модели у = а + кс, основаннвш на статистике
R = max
, где Sf =
гс-2
1- - -
xj - жJ
Если R > Raj то yi, соответствующее максимальному значению отношения —,
признается с вероятностью а выбросом. Критические значения Ra приведены
в табл. 233.
Таблица 233
Критические значения Ra критерия выбросов
в регрессии Титьена—Мура—Бекмана [593]
п
4
5
6
7
8
9
10
11
12
14
Доверительная
вероятность а
0,90
1,41
1,69
1,88
2,01
2,10
2,18
2 24
2,30
2,35
2,43
0,95
1,41
1,71
1,92
2,07
2,19
2,28
2,35
2,43
2,48
2,57
0,99
1,41
1,73
1,97
2,16
2,31
2,43
2,53
2,64
2,70
2,80
п
16
18
20
24
30
36
48
60
100
Доверительная
вероятность а
0,90
2,50
2,56
2,60
2,69
2,79
2,86
2,97
3,04
3,22
0,95
2,64
2,71
2,76
2,85
2,97
3,03
3,15
3,21
3,40
0,99
2,92
2,99
3,06
3,17
3,28
3,35
3,41
3,50
3,75
5.8]
Регрессионный анализ
663
Задача 366. Для данных задачи 365 проверить наличие выброса в регрессионной мо-
модели критерием Титьена-Мура-Бекмана при а = 0,95.
Имеем (используем значения е*, вычисленные ранее в задаче 365)
ю
10
х{ - xf
152,5479
1-0,1
xj - xf
313,216
Вычисляем последовательность значений —:
ei _ 4,066
= 17,1616 - 0,06088 • (Xi - 8,82J .
V17,1616 - 0,06088 • A,28,82)
^ = 0,333; ^ = 0,190; ^ = 0,674; ^ = -0,716;
= 1,01 и по аналогии
Per ft\
- = -0,876;
f = -1,371; f = -1,117; f = 0,187;
0 O
= 2,199.
Находим R = max
= 2,199. Из табл. 233 для а = 0,95 и п = 2,35 находим
^q,95 = 2,35. Так как R = 2,199 < До,95 = 2,35, гипотеза о наличии выброса отклоняется.
5.3.1.2.2.3.3. Критерий Прескотта-Лунда
Прескотт [594] и Лунд [595], учитывая близость значений Si (собственно, эта
близость является одной из предпосылок регрессионного анализа — см. вводную
часть раздела 5.3), предложили упрощенную модификацию критерия Титьена—
Мура—Бекмана, основанную на статистике
R* = max
где S —оценка средней дисперсии остатков I S = S
V п
q — количество пара-
метров в регрессионной модели.
Более удобна эквивалентная форма критерия Прескотта^Лунда
R* =
шах
Гипотеза наличия выброса в линейной регрессионной модели с к параметра-
параметрами (ранее рассматривался случай простейшей модели, когда к = 2; случай к > 2
параметров — множественная регрессия — будет рассмотрен далее в разделе 5.3.2)
отклоняется, если R* < i?^, где R*a—критическое значение, равное
F- 1-
(п - k)F
-квантиль .F-распределения Фишера
= п-^-1 сте-
степенями свободы.
Таблицы критических значений R^ приведены Лундом [595] и воспроизведены
в табл. 234.
664
Методы исследования связей между случайными величинами
[Гл. 5
Таблица 234
Критические значения JR^ критерия выбросов
в регрессии Прескотта^Лунда [595]
п
к
1
2
3
4
5
6
8
10
Доверительная вероятность а = 0,90
5
6
7
8
9
10
12
14
16
18
20
25
30
35
40
45
50
60
70
80
90
100
1,87
2,00
2,10
2,18
2,24
2,30
2,39
2,47
2,53
2,58
2,63
2,72
2,80
2,86
2,91
2,95
2,99
3,06
3,11
3,16
3,20
3,23
1,89
2,02
2,12
2,20
2,26
2,37
2,45
2,51
2,57
2,62
2,72
2,79
2,85
2,91
2,95
2,99
3,06
3,11
3,16
3,20
3,23
1,90
2,03
2,13
2 21
2^33
2,42
2,50
2,56
2,61
2,71
2,77
2,85
2,90
2,95
2,99
3,05
3,11
3,15
3,19
3,23
1,91
2,05
2,15
2,29
2,39
2,47
2,54
2,59
2,70
2,78
2,85
2,90
2,95
2,99
3,05
3,11
3,15
3,19
3,23
1,92
2,06
2,24
2,36
2,45
2,52
2,58
2,69
2,77
2,84
2,90
2,94
2,98
3,05
3,11
3,15
3,19
3,23
1,92
2,17
2,31
2,42
2,50
2,56
2,68
2,77
2,84
2,89
2,94
2,98
3,05
3,11
3,15
3,19
3,23
1,93
2,19
2,34
2,44
2,52
2,66
2,75
2,82
2,88
2,93
2,98
3,05
3,10
3,15
3,19
3,23
1,94
2,23
2,35
2,46
2,63
2,73
2,81
2,87
2,93
2,97
3,04
3,10
3,15
3,19
3,22
Доверительная вероятность а = 0,95
5
6
7
8
9
10
12
14
16
18
20
25
30
35
40
45
50
60
70
80
90
100
1,92
2,07
2,19
2,28
2,35
2,42
2,52
2,61
2,68
2,73
2,78
2,89
2,96
3,03
3,08
3,13
3,17
3,23
3,29
3,33
3,37
3,41
1,93
2,08
2,20
2,29
2,37
2,49
2,58
2,66
2,72
2,77
2,88
2,96
3,02
3,08
3,12
3,16
3,23
3,29
3,33
3,37
3,41
1,94
2,10
2 21
2^31
2,45
2,55
2,63
2,70
2,76
2,87
2,95
3,02
3,07
3,12
3,16
3,23
3,28
3,33
3,37
3,40
1,94
2,10
2,22
2,39
2,51
2,60
2,68
2,74
2,86
2,94
3,01
3,07
3,12
3,16
3,23
3,28
3,33
3,36
3,40
1,95
2,11
2,33
2,47
2,57
2,65
2,72
2,84
2,93
3,00
3,06
3,11
3,15
3,22
3,28
3,33
3,37
3,40
1,95
2,24
2,41
2,53
2,62
2,70
2,83
2,93
3,00
3,06
3,11
3,15
3,22
3,28
3,33
3,38
3,40
1,96
2,25
2,43
2,55
2,64
2,80
2,90
2,98
3,05
3,10
3,14
3,22
3,27
3,32
3,36
3,40
1,96
2,26
2,44
2,57
2,76
2 88
2 97
3,03
3,09
3,14
3,21
3,27
3,32
3,36
3,40
5.8]
Регрессионный анализ
665
Задача 367. Для данных задачи 365 проверить наличие выброса в регрессионной мо-
модели критерием Прескотта-Лунда при доверительной вероятности а = 0,90.
Пользуясь оценками и расчетами, выполненными в задаче 365, получим ряд значений
L (г = 1,2, ...,n) ^
\
0,3292; 0,2563; 0,0610; 0,2200; 0,2390; 0,2937; 0,4555; 0,3662; 0,0566; 0,5830.
Имеем
, *.\ ,
1-0,583 = 1,844.
R* =
Из табл. 234 для а = 0,90, к = 2 и п = 10 имеем Д5,9о = 2,26.
Так как R* = 1,844 < 1?о,эо :=: 2,26, гипотеза о наличии выброса в регрессии отклоня-
отклоняется.
Воспользуемся квантилями ^-распределения.
Находим по таблицам F-распределения (при необходимости интерполяцией)
=F0)99(/1 = 1;/2 =n-2-l) = Fo,9
= 12,246.
Тогда Щу90 =
(n-k)-F
— fe — 1 + F
к табличному значению До,эо = 2,26.
A0 - 2) ¦ 12,246
0 - 2 - 1 + 12,246
= 2,256, что достаточно близко
5.3.1.2.3. Доверительные области и толерантные границы регрессии
5.3.1.2.3.1. Доверительная область простой линейной регрессии
Для линейной регрессии у = а + Ъх доверительная область (с доверительной
вероятностью а ) на заданном отрезке будет ограничена гиперболами
¦ + К
где
С =
и = п —
Х\ ^ X
А Г 1 Г-1 1 + пС
п — 2: А = < - 1 — , 9Ч ,
\Ч A + пС2)A
nCD
D =
(Xi - X)
-nD2
If
u(y, a, A) — коэффициент, зависящий от z/, а и А.
Значения tx(z/, а. А) приведены в табл. 235.
Доверительная зона, рассчитанная по приведенным выше соотношениям, яв™
ляется геометрическим местом доверительных интервалов для различных значе-
значений х.
666
Методы исследования связей между случайными величинами
[Гл. 5
Коэффициенты и{у, «, А) для построения
V
Л
0
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
а = 0,90
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
50
100
оо
6,314
2,920
2,353
2,132
2,015
1,943
1,895
1,860
1,833
1,812
1,796
1,782
1,771
1,761
15753
15746
1,740
1,734
1,729
1,725
1,708
1,676
1,660
1,645
6,625
3,022
2,425
2,192
2,071
1,995
1,944
1,908
1,880
1,859
1,841
1,827
1,815
1,805
1,797
1,789
1,783
1,777
1,772
1,767
1,750
1,716
1,700
1,684
6,922
3,121
2,494
2,250
2,123
2,044
1,991
1,953
1,925
1,902
1,884
1,869
1,857
1,847
1,838
1,830
1,823
1,817
1,811
1,807
1,789
1,753
1,736
1,720
7,203
3,216
2,561
2,306
2,173
2,091
2,036
1,997
1,967
1,944
1,925
1,909
1,897
1,886
1,876
1,868
1,861
1,855
1,849
1,844
1,825
1,789
1,771
1,754
7,470
3,308
2,625
2,360
2,222
2,136
2,079
2,038
2,007
1,983
1,963
1,947
1,934
1,923
1,913
1,905
1,897
1,891
1,885
1,880
1,860
1,823
1,804
1,786
7,724
3,397
2,687
2,412
2,268
2,180
2,120
2,078
2,046
2,021
2,001
1,984
1,970
1,959
1,948
1,940
1,932
1,925
1,919
1,914
1,894
1,855
1,836
1,817
7,965
3,482
2,747
2,463
2,313
2,222
2,160
2,116
2,083
2,057
2,036
2,019
2,005
1,993
1,982
1,973
1,965
1,959
1,952
1,947
1,926
1,886
1,866
1,847
8,192
3,564
2,805
2,511
2,357
2,263
2,199
2,153
2,119
2,092
2,071
2,053
2,038
2,026
2,015
2,006
1,998
1,990
1,984
1,978
1,957
1,915
1,895
1,875
8,407
3,642
2,860
2,558
2,399
2,302
2,236
2,189
2,153
2,126
2,104
2,086
2,070
2,058
2,046
2,037
2,029
2,021
2,015
2,009
1,986
1,943
1,923
1,902
8,609
3,717
2,914
2,604
2,440
2,340
2,272
2,224
2,287
2,159
2,136
2,117
2,102
2,089
2,077
2,067
2,059
2,051
2,044
2,038
2,015
1,971
1,950
1,929
а = 0,95
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
50
100
оо
12,700
4,303
3,182
2,776
2,571
2,447
2,365
2,306
2,262
2,228
2,201
2,179
2,160
2,145
2,132
2,120
2,110
2,101
2,093
2,086
2,060
2,009
1,984
1,960
13,320
4,445
3,271
2,847
2,633
2,504
2,418
2,357
2,312
2,277
2,249
2,226
2,207
2,191
2,177
2,165
2,154
2,145
2,137
2,129
2,102
2,049
2,023
1,998
13,920
4,582
3,356
2,915
2,692
2,558
2,469
2,406
2,358
2,322
2,293
2,269
2,250
2,233
2,219
2,206
2,195
2,186
2,177
2,170
2,141
2,086
2,060
2,034
14,480
4,715
3,438
2,978
2,748
2,609
2,517
2,452
2,403
2,365
2,335
2,311
2,290
2,273
2,258
2,245
2,234
2,224
2,215
2,207
2,178
2,121
2,094
2,068
15,010
4,844
3,518
3,040
2,802
2,659
2,563
2,496
2,445
2,406
2,375
2,350
2,329
2,331
2,295
2,282
2,271
2,260
2,251
2,243
2,213
2,154
2,126
2,099
15,520
4,968
3,594
3,101
2,854
2,706
2,607
2,538
2,485
2,445
2,413
2,387
2,365
2,347
2,331
2,317
2,305
2,295
2,285
2,277
2,246
2,186
2,157
2,128
16,000
5,087
3,668
3,159
2,904
2,751
2,650
2,578
2,524
2,482
2,449
2,422
2,400
2,381
2,365
2,351
2,338
2,328
2,318
2,309
2,277
2,215
2,186
2,156
16,460
5,202
3,740
3,215
2,953
2,795
2,691
2,616
2,561
2,518
2,484
2,456
2,433
2,414
2,397
2,383
2,370
2,359
2,349
2,340
2,307
2,244
2,213
2,183
16,890
5,312
3,809
3,270
3,000
2,838
2,730
2,654
2,597
2,552
2,517
2,489
2,466
2,446
2,429
2,414
2,401
2,389
2,379
2,370
2,336
2,271
2,240
2,209
17,290
5,417
3,875
3,332
3,045
2,879
2,769
2,690
2,632
2,586
2,500
2,521
2,497
2,476
2,459
2,444
2,431
2,419
2,408
2,399
2,364
2,297
0,265
2,234
5.8]
Регрессионный анализ
667
Таблица 235
доверительной
[ области линейной регрессии [25]
Л
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
а = 0,90
8,799
3,788
2,965
2,647
2,480
2,377
2,308
2,258
2,220
2,191
2,168
2,148
2,132
2,119
2,107
2,088
2,080
2,073
2,067
2,044
1,998
1,976
1,954
8,976
3,855
3,015
2,689
2,517
2,412
2,341
2,290
2,252
2,222
2,198
2,178
2,162
2,148
2,136
2,125
2,116
2,108
2,101
2,095
2,071
2,024
2,002
1,979
9,142
3,919
3,061
2,728
2,554
2,446
2,374
2,322
2,283
2,252
2,227
2,207
2,190
2,176
2,164
2,154
2,144
2,136
2,128
2,122
2,097
0,050
2,026
2,004
9,294
3,978
3,105
2,766
2,588
2,478
2,405
2,352
2,312
2,281
2,256
2,235
2,218
2,203
2,191
2,191
2,171
2,162
2,155
2,148
2,123
2,074
2,050
2,027
9,434
4,033
3,146
2,801
2,620
2,509
2,434
2,381
2,340
2,308
2,283
2,262
2,244
2,229
2,217
2,217
2,196
2,187
2,180
2,173
2,147
2,098
2,074
2,050
9,561
4,083
3,184
2,834
2,650
2,538
2,462
2,407
2,366
2,333
2,308
2,287
2,269
2,254
2,241
2,241
2,220
2,211
2,203
2,196
2,170
2,120
2,096
2,072
9,674
4,129
3,218
2,864
2,678
2,564
2,487
2,432
2,390
2,357
2,331
2,310
2,292
2,276
2,263
2,263
2,242
2,233
2,225
2,218
2,192
2,141
2,116
2,092
9,772
4,169
3,248
2,891
2,703
2,587
2,509
2,453
2,411
2,378
2,352
2,330
2,312
2,297
2,283
2,283
2,262
2,253
2,245
2,238
2,211
2,160
2,135
2,110
9,854
4,202
3,274
2,913
2,724
2,607
2,529
2,472
2,430
2,397
2,370
2,348
2,330
2,314
2,301
2,301
2,279
2,270
2,262
2,255
2,228
2,176
2,151
2,126
9,916
4,228
3,294
2,931
2,740
2,623
2,545
2,487
2,444
2,411
2,384
2,362
2,343
2,328
2,314
2,314
2,293
2,284
2,276
2,268
2,241
2,189
2,164
2,139
9,950
4,243
3,305
2,941
2,749
2,632
2,552
2,495
2,452
2,418
2,392
2,269
2,351
2,335
2,322
2,322
2,300
2,291
2,283
2,276
2,249
2,196
2,171
2,146
а = 0,95
17,670
5,517
3,939
3,373
3,089
2,919
2,806
2,726
2,666
2,618
2,582
2,552
2,527
2,506
2,488
2,473
2,459
2,447
2,437
2,427
2,392
2,323
2,290
2,258
10,025
5,612
4,000
3,422
3,132
2,958
2,842
2,760
2,699
2,650
2,613
2,582
2,557
2,536
2,517
2,501
2,487
2,475
2,464
2,455
2,418
2,348
2,314
2,281
18,355
5,701
4,059
3,469
3,173
2,995
2,877
2,793
2,731
2,681
2,643
2,612
2,586
2,564
2,545
2,529
2,515
2,502
2,491
2,481
2,444
2,372
2,338
2,304
18,661
5,785
4,114
3,514
3,212
3,031
2,911
2,826
2,762
2,712
2,673
2,641
2,614
2,592
2,573
2,556
2,542
2,529
2,518
2,508
2,470
2,396
2,361
2,327
18,941
5,864
4,166
3,556
3,249
3,065
2,943
2,856
2,792
2,741
2,701
2,669
2,642
2,619
2,599
2,583
2,568
2,555
2,543
2,533
2,494
2,419
2,384
2,349
19,195
5,935
4,214
3,596
3,284
3,097
2,974
2,886
2,820
2,768
2,728
2,695
2,668
2,645
2,625
2,608
2,593
2,579
2,568
2,577
2,518
2,442
2,405
2,370
19,422
6,000
4,258
3,632
3,316
3,127
3,002
2,913
2,846
2,794
2,753
2,720
2,692
2,669
2,649
2,631
2,616
2,603
2,591
2,580
2,540
2,463
2,426
2,390
19,619
6,058
4,297
3,664
3,345
3,154
3,028
2,938
2,870
2,818
2,777
2,743
2,715
2,691
2,671
2,653
2,638
2,624
2,612
2,601
2,561
2,483
2,446
2,409
19,782
6,107
4,330
3,692
3,371
3,178
3,051
2,959
2,891
2,838
2,797
2,763
2,734
2,710
2,690
2,672
2,657
2,643
2,631
2,620
2,579
2,501
2,463
2,426
19,907
6,144
4,356
3,714
3,390
3,197
3,068
2,976
2,908
2,855
2,813
2,779
2,750
2,726
2,706
2,688
2,672
2,658
2,646
2,635
2,594
2,515
2,248
2,440
19,975
6,164
4,371
3,727
3,402
3,207
3,078
2,986
2,918
2,865
2,823
2,788
2,759
2,735
2,714
2,696
2,680
2,666
2,654
2,643
2,602
2,523
2,485
2,448
668
Методы исследования связей между случайными величинами
[Гл. 5
Для единичного значения щ доверительный интервал будет равен
Щ ±tl±a ± Si,
2
где
i — х)
У2 (xi - xf
J
Легко видеть, что этот интервал будет намного шире, чем границы доверитель-
доверительной зоны для всей регрессии.
Задача 368. По данным задачи 365 построить 95%-к? доверительную зону для регрес-
регрессии на интервале от х\ = 3 до Х2 = 10 и доверительный интервал для yi при Xi = 5,1
(ж = 8,82).
Имеем
3 - 8,82
i/ = 10-2 = 8; С= —
17,6979
— = ^0,329;
D =
17,6979
= 0,066;
п-2
= 30,447; Sy = 5,518;
~~
A + 10 • (-0,329) • 0,0666)
1 -
0,780886
2,08241 ¦ 0,04435
= 0,566.
A + 10 • 0,3292) • A + 10 • 0,06662) _
Из табл. 235 для и = 8, а = 0,95 и Л = 0,566 находим (интерполяцией)
и(8; 0,95; 0,566) = 2,660.
Тогда доверительная зона для регрессии имеет вид (ранее в задаче 365 было получено
уравнение у = —4,9265 + 4,275 • х): г/н ^ у ^ yBj где
^^2
Уш = ^4,9265 + 4,275 • х - 2,66 • 5,518 •
1
1 ] 2
Уъ = ^4,9265 + 4,275 • х + 2,66 • 5,518 •
313,2156 10
(х^хJ , 1
313,2156 10
Для значения yi = 2/E,1) имеем (при / = п — 2 = 8 степенях свободы) t(i+0,95)/2 =
= tO,975 = 2,306 И
1
2
10
313,2156
= 5,902;
- 0,9265 + 4,275 • 5,1 - 2,306 • 5,902 =
= 3,266 ^ у E,1) ^ 30,486 = -4,9265 + 4,275 • 5,1 + 2,306 • 5,902.
Соответствующие границы доверительной зоны будут (подставляем х = 5,1 в урав-
уравнение гиперболы):
у 2 -4,9265 + 4,275 • 5,1 - 14,678
у $ -4,9265 + 4,275 • 5,1 + 14,678 •
^} = 11,30;
1
{ ^^f + ± } * = 22,449.
5.3] Регрессионный анализ 669
Видим, что длина доверительного интервала в этом случае уменьшается в
30,486 - 3,266
22,449^ 11,30 =2-
5.3.1.2.3.2. Оценка обращенного уравнения регрессии
Иногда возникает так называемая обращенная задача оценивания, заключающа-
заключающаяся в ответе на вопрос: если найдена оценка линии регрессии, то каким образом по
некоторому измеренному значению у можно предсказать значение переменной х®^
не являющейся случайной величиной? Браунли [559] и Хальд [51] показали, что а™
доверительный интервал для оценивания значения х® определяется выражением
E"*ft
1+а «
- xf
p= - + —1т+,г "' ; ** = *V^; s2 = ^i^
i=i
m^ — количество наблюдений у± при ж = Х{; то — количество наблюдений ^ при
ж = х®; у о — среднее по т® наблюдениям у^ при х = х®; ta — «^квантиль распреде™
ления Стьюдента при / = п — 2 степенях свободы.
Приведенный доверительный интервал основан на совместном распределении
линии регрессии и у®. Он неприменим для вычисления значений ж, соответствую™
щих ряду значений у, если используется одна и та же линия регрессии.
Укажем еще один способ оценки х®^ предложенный Крючковым и Эйзенхартом
[14], в соответствии с которым оценкой х® служит величина x® = c-^dy®^ где
-у)
d =
Задача 369. По данным задачи 365 найти 95%™й доверительный интервал для вели-
величины хо, если при х = xq были получены следующие значения уст 28,1; 29,2; 25,6.
Имеем
ю
х = 8,82; пи = 3; у= ^ = — • J2 У* = 32,779; S2 = 30,447 E = 0,518);
г=1
10
то = 3; Ь- 4,275; to,975(8) = 2,306; J2 mi ' (ж* ~ ^f = 939,638;
г=1
28,1 + 29,2 + 25,6
2/о = = 27,633.
670 Методы исследования связей между случайными величинами [Гл. 5
Далее
* Уо^У
Ь
Вычисляем:
27,633 -
- 32,779
75
+ зоу *
4,2347
4,275 '
4,275 ^2,3062
' ' 4,275 • 939
G,616 ^8,82J 0о6175
939,638 <Vb475.
• 30,447
,638
¦ g ¦ ^ = 8,82
_ f 1+o .1 • УР = 8,82 + 27'633 32'779 - 2'3°6 5'518 ^^ = 5,990.
^р Ь* VF ' 42347 42347
еду с I —{—¦ f V \ / № ——— vy щ KJ* ju
b* ^p b* vr ' 4,2347 4,2347
Следовательно, 95%-й доверительный интервал для значения жо, соответствующий
измеренным значениям г/ог? имеет вид 5,790 ^ xq ^ 9,419.
Для нахо^кдения оценки Крючкова-Эйзенхарта вычислим
^ т^ • (xi -x)-(yi-y)=3- [A,2 - 8,82) • D,27 - 32?779) + ...
г=1
... + A9,1 - 8,82) • (83,93 - 32,779)] = 4017,3456;
ю
J2 mi • {Ш - yf = 3 . [D,27 - 32,779J + ... + (83,93 - 32?779J] = 17633,3396.
г=1
Тогда имеем
4017,3456
17633,3396
= 0,2278; с = х - d • у = 8,82 + 0,2278 • 32,779 = 1,3529.
Следовательно, хо = 1,3529 + 0,2278-27,633 = 7,65, что очень близко к середине дове-
довела ю / . 9,419 + 5,790
рительного интервала Хальда-Брауна (см. предыдущую задачу, где х = =
= 756045).
5.3.1.2.3.3. Толерантные интервалы длм линейной регрессии
Ранее (см. раздел 4.4) были подробно рассмотрены методы вычисления толе™
рантных пределов для совокупности случайных величин. Напомним, что 7 • 100%-м
толерантным интервалом называется интервал, в границах которого находится
7 • 100% всех возможных значений случайной величины.
В настоящем разделе рассматривается методика построения толерантных ин-
интервалов для линейной регрессии.
Для того, чтобы вычислить толерантные пределы для линейной регрессии, необхо-
необходимо знать дисперсию величины для разных значений независимой переменной х [596].
Эта дисперсия задается формулой Воркинга^Хотеллинга [597]
/ -\2
\Х — X)
+
г=1
Здесь эффективное число наблюдений для некоторой величины х равно
п
n^(Xi -X)
а — хJ + п (х — хJ
5.3] Регрессионный анализ 671
Другими словами, для некоторой величины х средняя величина у определяется
расчетом по линии регрессии столь же точно, как если бы было сделано п* наблю-
наблюдений при заданной величине х.
Теперь для того, чтобы найти толерантный интервал, о котором мы могли бы
с вероятностью а утверждать, что внутри него лежит по крайней мере /Участь
популяции, необходимо найти толерантные интервалы для каждого значения х.
Искомая толерантная область будет геометрическим местом точек толерантных
интервалов для отдельных Х{.
Для определения частных толерантных интервалов следует воспользоваться
методами, изложенными в разделе 4.4.1.2.3 для случая выборок из нормального
распределения с обоими неизвестными параметрами. Односторонние толерантные
интервалы равны (см. раздел 4.4.1.2.3):
верхний: ув = у(х) + S(x)k(n*(x), a,/?);
нижний: |/н = у(х) — 5(ж)&(п*(ж),а,/3).
Двусторонний толерантный интервал имеет вид:
у(х) - k{n*(x),a,p)S(x) ^ у(х) < у(х) + k(n*(x),a,0)S(x).
Эффективный объем выборки п*(х) рассчитывается по вышеприведенной фор™
п
муле, исходя из значений п и ^Р (xi — х) .
г=1
Значение S (х) рассчитывается по формуле
Значения коэффициентов fc(n,a,/3) и fc*(n,a,/3) приведены в табл.203 и 204
соответственно (входом в таблицы являются значения п*). Для п* > 50 справедливо
приближение
к*(п*(х),а,/3) =
Задача 370. Для данных задачи 365 найти двустороннюю толерантную область^
в которой с вероятностью не менее а = 0,95 будет находиться не менее /3 = 0,90 всех
возможных реализаций уравнения регрессии.
Для значения х = 1,2 имеем
ю
Si = 30,447 (Sy = 5,518); х = 8,82; ]Г (х{ - жJ = 313,216;
= 5,518 -\l^+ A 313 2162) = 2'948; п = ^4'9265; b = 4'275;
уA,2) = -4,9276 + 4,275 • 1,2 = 0,2024; п*A,2) = : ; ^ = 3,5.
313,216 + 10- A,2 - 8,2J
Из табл. 204 для а = 0,95, /3 = 0,90 и п* = 3,5 (используем интерполяцию) получаем
к* = 6,885.
Тогда 0,2035 - 2,948 • 6,885 = -20,09 ^ у A,2) ^ 20,50 = 0,2035 + 2,948 • 6,885.
672
Методы исследования связей между случайными величинами
[Гл. 5
По аналогии получаем толерантные интервалы для остальных значений независимой
переменной х. Результаты сведем в таблицу:
X
1,2
2,7
3,9
5,1
7,2
11,1
12,4
16,1
19,1
у{х)
0,202
6,616
11,746
16,876
25,853
42,526
48,083
63,900
76,726
Sy(x)
2,948
2,586
2,323
2,095
2,816
1,884
2,071
1,863
3,649
те*
3,500
4,550
5,640
6,930
9,230
8,580
7,090
3,710
2,290
к*
6,885
4,767
3,914
3,360
3,497
3,040
3,346
6,230
25,160
2/в(ж)
20,500
18,943
20,838
23,915
32,203
48,253
55,010
81,736
168,535
Уш(х)
-20,090
-5,711
2,654
9,837
19,502
36,529
41,150
46,060
-15,083
5.3.1.3. Сравнение линейных регрессий
Сравнение двух регрессионных моделей включает в себя проверку нулевой гипоте-
гипотезы Hq : у\ = у2 о статистической неразличимости линейных регрессий у\ = а\ + Ь\Х
и 2/2 = (i2 + Ь^х. Для проверки If о необходимо последователвно проверить три гипо-
гипотезы: о неразличимости коэффициентов а\ и п2 (Hq : а± = а2)] Ь\ и 62 (Hq : Ъ\ =62)?
и о равенстве остаточных дисперсий, характеризующих разброс значений у^ вокруг
линии регрессии (Hq' : S\ = 5|).
В первую очередь проверяется гипотеза Hq' : Sf = Sf. Для поверки гипотезы
сначала подсчитываются соответствующие дисперсии
S2 =
где rii, гг-2 — объемы выборок, по которым найдены регрессии у\ и г/2 соответственно;
хц (г = 1, ..., ni) и X2i (г = 1, ..., тгг) —значения переменной х в двух выборках.
Затем дисперсии Sf и *S*f сравниваются между собой с помощью критерия
Sf
Фишера. Если —|- > Fa, где .Fa — «-квантиль распределения Фишера с Д = п\ — 2
и /2=П2^2 степенями свободы, то гипотеза Hq' о равенстве двух регрессий
отклоняется, и регрессии признаются статистически различимыми (в числителе
всегда должна быть большая дисперсия).
Если гипотеза Hq' не отклоняется, можно приступить к проверке гипотез H'Q
и Hq . Для проверки равенства угловых коэффициентов Ь\ и ^2 (гипотеза Hq)
используется статистика
h - ъ2
S*
1 ^|
1 i=l
- 1) SZX1 (п2 - 1) St2
1 п2
- \2 • С2 _ ! v^ /
^1 / ч ^г — 7" / \X2i
По — 1 ^
- \2
ni
+ П2 — 4
5.3] Регрессионный анализ 673
При справедливости нулевой гипотезы Hq (т. е. при Ь\ = 62) статистика % имеет
распределение Стьюдента e/ = rii+B2^4 степенями свободы. Если
\tb\ ^ tl + a,
2
то с доверительной вероятностью а гипотеза Hq отклоняется и сравниваемые
угловые коэффициенты Ь\ и ?»2 признаются различными. Если гипотеза Hq не
отклоняется, то проводится проверка гипотезы Hq (проверка равенства а\ = п2)-
Для проверки этой гипотезы используется статистика
tn =
S
Т _ (П1 — 1) ^Х1Ь\ + (П2 — 1) SX2b2 ^ I _ у\ — У2 t
s = ~* ' г
1 ^ 1) Я"х + (П2 - 1) S (Ж1 - Ж2
S**, S^, S^2 определены выше при проверке гипотезы Hq .
При справедливости Hq статистика ta имеет распределение Стьюдента
с/ = щ+В2^4 степенями свободы.
Следовательно, при справедливости \ta\ > ti+a (f) гипотеза Hq отклоняется.
2
Если все гипотезы Н^ Hq и Hq' не отклоняются, то сравниваемые регрессии yi
и у2 признаются неразличимыми.
Задача 371. В результате двух независимых экспериментов получены следующие
результаты (щ = 10, П2 = 6):
хщ 2 4 6 9 11 16 17 20 25 31; х2ц 12 16 21 23 28 31;
ущ 9 19 22 41 49 61 69 83 98 128; y2i: 54 68 87 93 112 130.
Проверить гипотезу о статистической неразличимости регрессионных моделей, полу-
полученных по обеим выборкам при вероятности а = 0,95.
Вычисляем для первой выборки
ю / ю \ ю ю
5^Ж1г = 141; XI = 14,1; Р>] хц \ =19881; ^ а& = 2789; ^ уи = 589;
г=1 \г=1 / г=1 г=1
10
У! = 57,9; ^ хц • у^ = 11361;
г=1
10 ¦ 11361 - 141 • 579 179^3,992-14,1
3; ° 1613;
61 =
10 • 2789 - 19881 10
i «-1
г^2 -1 Ж V
J2
1 г=1
(Xli - п) = 88,989 (Sx! = 9,439).
Аналогично для элементов второй выборки имеем
53^2* = 131; х2 = 21,83; \Y,X2i) = 171615
»=i V=i /
Я|2 = 50,967 (Sx2 = 7,39);
22 А. И. Кобзарь
674 Методы исследования связей между случайными величинами [Гл. 5
б б
J2 2/2* = 5446; у2 = 90,667; ]Г x2i • y2i = 12868;
г=1 г=1
6-12688-131-544 = 544-3,887-131 =
6-3115-17161 6
Далее вычислим дисперсии рассеяния значений yi вокруг линии регрессии:
1 ni 1 10
Я? = • У^ (i/ii — 1,613 — 3,992 • хцJ = - • У^ (г/i* — 1,613 — 3,992 • хцJ = 10,056:
ni - 1 г^ ; 8 г^ ' у ' '
1 1 6 2
Яз = - • У" (уз» - 5,80 - 3,887 • х2%) = 7,0271; Ях = 3,171; S = 2,651.
Проверим гипотезу i/g" • «S'i = Я|. Имеем —|- = — = 1,431. Так как —j = 1,43 <
< -^0,95(8; 4) = 3,838, гипотеза Hq" принимается и дисперсии Si и Я2 с вероятностью
а = 0,95 признаются статистически неразличимыми.
Проверяем теперь гипотезу Hq , для чего вычислим
Далее
Из
таблиц
f («1
1
/
^ 2) ¦ 5?
7?1 +
1
/ (щ - 1) • 5^
находим ti+c
+ (тг2 -
¦ 712 ™" 4
(тг2 -
Af = n1
2)-
1
¦1)
+
J
¦Sx2
1
2
4)
(8 ¦ 10,056 + 4-
ч
7,0271
у 9 • 88,988 5 ¦
= to,975 A2) = 2Д7.
V
)
1
50,967
= 0,0078.
2
Так как \Ьъ\ = 0,0078 < to,975A2) = 2,179, гипотеза Hq не отклоняется, и угловые
коэффициенты Ь\ и &2 признаются неразличимыми с достоверностью а = 0,95. Проверим
гипотезу Hq". Находим:
т 9 • 88,989 • 3,992 + 5 ¦ 50,967 • 3,887 о Л_ ~ у\ - m 57,9 - 50,667
о = = 3,967: о = = = 4,239:
9-88,989 + 5-50,967 Ж1 - ж2 14,1-21,83
5 = 3,008 • 1 + ^ • ( — + - ) Г = 0,2212;
[ 9 • 88,989 + 5 ¦ 50,967 A4,1 - 21,83J \10 6/J
_ 3,967^4,239 _
ta " 0,2212 " ~МЗ-
Сравнивая |to| с to,975A2), имеем \ta\ = 1,230 < to,975A2) = 2,170.
Следовательно, и гипотеза Но" не отклоняется. Таким образом, сравнением эмпи-
эмпирических уравнений регрессий убеждаемся, что они с достоверностью не менее 0,95
статистически эквивалентны.
5.3.1.4. Некоторые специальные задачи линейного регрессионного анализа
В этом разделе мы рассмотрим некоторые частные задачи, возникающие в ли™
нейном регрессионном анализе. В связи с их специфичностью они не рассматрива-
рассматриваются в классических курсах регрессионного анализа.
5.3.1.4.1. Оценка вершины кусочно-ломаной линии регрессии
Предположим, что имеются две пересекающиеся линии регрессии и требуется
определить доверительную зону для точки их пересечения.
Алгоритм получения такой оценки включает в себя ряд последовательных
операций. Сначала строится двусторонний а;-доверительный интервал для двух
5.3]
Регрессионный анализ
675
угловых коэффициентов Ь\ и Ь2 регрессии рассматриваемых прямых у\ = а\ + Ь\х
и у2 = а2 + Ь2х соответственно. С помощью методов, изложенных в разделе 5.3.1.2.1.1,
находим [106]
2 22 2
где t7 — 7~квантиль распределения Стьюдента с / = п — 2 степенями свободы (п —
объем выборки, будем считать его одинаковым для обеих выборок); &i, 62 — оценки
наименьших квадратов соответственно для угловых коэффициентов Ь\ и Ъ2, равные
(см. раздел 5.3.1.1.1)
п п
г=1 г=1
п п
г=1 г=1
V""v 2
nZ_^xu ~
i=i
1 "^^г
Где #1г = ^ 5]
г=1
Spi =
^/32 =
Sx2 yn — 1
1П
sk = 7—J J2 (X
Оценки ai и a2 равны
2
1П 1П
= - J2x^ si = 7—^ J2
Тогда двусторонние «-доверительные интервалы для средних
-< п
и ^2 = — У^ Шг будут иметь вид:
2/1
где
2/1
2 V п
>i ~ Ч Sli
n ~ 1) Sln 2 !
г
22*
676
Методы исследования связей между случайными величинами
[Гл. 5
mi — число параллельных наблюдений над у\ и у2 на уровне Х{ (будем считать для
простоты, что wii = const для всех х^ у\ и у2).
Легко видеть, что S^ и S2i—это дисперсии, характеризующие рассеяние вели™
чин 2/1 и у2 на каждом уровне Х{; Я? и Я|2 — средневзвешенные дисперсии величин
г/1 и у2 по всем Х{.
Следует помнить, что для оценки дисперсий 5|х и 5|2 необходимы параллельные
наблюдения над у на каждом уровне х. В нашем случае t1+a" —соответствующая
квантиль распределения Стьюдента с / =
^ — 1 степенями свободы.
Теперь через каждую точку с координатами (xi,f/f) и (xi,f/J) проведем по две
прямые с угловыми коэффициентами Ь^ и bf (г/J, yf^bfmb® — соответственно нижние
и верхние границы доверительных интервалов). То же самое выполняем и для
второй регрессии — т.е. проведем прямые через точки (х2,у2) и (х2,у2).
Через максимальную область, охватываемую прямыми
y = yl + V?(x-x1); y = yl + bl(x- хг),
будет с вероятностью /3 = afa/f проходить линия регрессии у\ = а\ + Ь\ • х.
По аналогии через максимальную область, охватываемую прямыми
У = §2
2 (X ^ Х2) ; У = У
У = VI + Щ {х - х2); у = у
^ Х2)
- х2) ,
будет с вероятностью /3 = а'а" проходить линия регрессии у2 = а2 + Ъ2х.
Пересечение этих двух областей представляет собой неправильный многоуголь-
многоугольник, который и служит доверительной областью для точки пересечения прямых
регрессии при доверительной вероятности j = j32.
Задача 372. В результате наблюдений были получены две выборки результатов^
представленных в таблице. Необходимо найти 90%-ю доверительную область для
точки пересечения линий регрессии^ пороэюдаемых двумя выборками.
2
3
5
9
11
14
17
20
25
31
Уи
19,21,16
26,21,38
41,38,49
70,61,82
84,71,99
105,91,116
125,109,141
145,131,160
180,161,201
210,191,231
Уи
18,67
28,33
42,67
71,00
84,67
104,00
125,00
145,33
180,67
210,67
о2
6,33
76,33
32,33
111,00
196,33
157,00
256,00
210,33
400,33
400,33
%2i
0,8
1,2
2,0
3,0
4,8
6,9
8,2
10,1
12,0
14,0
У2г
15; 13; 17,1
17; 16,1; 18, 2
18; 17,1; 19,4
21; 19,8; 23,1
27,5; 26; 29
34; 31; 37
38; 36; 41
44; 41,2; 46,1
50; 39; 62
56; 41; 69
Vii
15,03
17,10
18,17
21,30
27,50
34,00
38,33
43,76
50,33
55,33
о2
^2г
4,203
1,110
1,343
2,750
2,250
9,000
6,333
6,043
132,330
196,330
Имеем 7 = Р2 = 0,90 и/3 = л/(Щ « 0,95. Выбираем а = а" = а = л/Р = л/(Щ) « 0,975.
Выполняя необходимые расчеты, получаем
хи
=18769;
уи = 1011,01;
5.3] Регрессионный анализ 677
10 10 10 / 10
Y хц -Ун = 19441,17; V x2i = 63; V ж^ = 594,98; Га
г=1 г=1 г=1 \г=1
10 10
23 Шг = 320,185; 2] ж^ ' У^ = 2634,246.
г=1 1=1
Находим оценки коэффициентов регрессии:
- 10-19441,17-137-1011,01 л 1011,01-6,702-137
bi = ¦ 5 = 6,702; oi = ! ! = 9,2836;
10 - 2711 - 1372 10
- 10 ¦ 2634,246 - 63 ¦ 320,85 ^ ^Л л 320,85 - 3,094 -63
Ъ2 = = 3,094; а2 = = 12,593.
10-594,98-3969 ' 10
Вычисляем дисперсии
Sl = ^— • 23 (Уи - oi - bi • жнJ = 10,6703 (St = 3,2665);
S22 = ^— • jh (y2i -а2-Ъ2> x2if = 0,2737 (S2 = 0,52317);
Slx = ^— • J2 (x^ - ^iJ = 92,678 (SX1 = 9,627);
1 n
/^/ ж "* ( ~ \^ rjf) ллл / Q a Ci.r\-\ \
у \x2i — x2) = 22.uu9; (оЖо = 4,o91);
n
Sl 3,2665 Я2 0,52317
= O.llol; Ь
O.llol; Ьй2 ,
9,627-3 ' ' P2 Sx2-y/n=l 4,691-3
Теперь из табл. 118 (или аппроксимацией из раздела 1.1.9 для а = 0,975) находим
(интерполируя) ?(i+0,975)/2 = ^0,9875 (/ = 8) = 2,798.
Для двустороннего доверительного интервала имеем
Ь" = Ьг - to,9875 • SCi = 6,702 - 2,798 • 0,1131 = 6,385;
bl = bi + to,9875 • S/3! = 6,702 + 2,798 • 0,1131 = 7,018;
Щ = b2 - to,9875 • Я/32 = 3,094 - 2,798 • 0,03717 = 2,990;
Ь1 = Ь2 + to,9875 • SC2 = 3,094 + 2,798 • 0,03717 = 3,198.
Теперь вычислим дисперсии (rrii = 3):
23 таг —
г=1
23 mi — п
г=1
= 184,6313 EЛ = 13,
5^2 = 6,014).
Так как оценки Sy1 и Sy2 используют все 2^ mi ~~ n — 20 степеней свободы, то
г=1
t1 + a// = 11+0,975 = *0,987б(/ = 20 - 1 = 19) = 2,465.
2 2
Далее вычисляем
10
Ш=У1- ^о,9875 • -т= = тт: • У 2/н - 2,465 • ^^ = 101,101 - -> '-==>¦ = 90,509;
л/Г). 10 ^—J л/1П л/1П
% ^ V уи 2,465 ^
/п 10 ^ V10
= уг + to,9875 • % = 101,101 + 2,465 • Щ^- = 111,693;
у/п VI0
678 Методы исследования связей между случайными величинами [Гл. 5
й = ш - w • 5f = й • |>< -2'645 ¦ ^ = 32'085" ^7W^ = 27'397;
= у2 + *0>9875 . % = 32,085 + 2,465 • ^t = 36,773.
/^г VI0
Максимальная область, охватываемая прямыми
у = 90,509 + 6,385 • (х - 13,7); у = 90,509 + 7,018 • (х - 13,7);
у = 111,693 + 6,385 • (ж - 13,7); у = 111,693 + 7,018 • (ж - 13,7) ,
содержит линию регрессии у\ = 9,2836 + 6,702 • х с вероятностью
/3 = а' • а" = 0,9875 • 0,9875 = 0,975.
По аналогии, максимальная область, охватываемая прямыми
у = 27,397 + 2,990 • (ж - 6,3); у = 27,397 + 3,198 • (ж - 6,3);
у = 36,773 + 2,990 • (ж - 6,3); у = 36,773 + 3,198 • (х - 6,3),
содержит линию регрессии у2 = 12,593 + 3,094 • х с вероятностью
/3 = а • а" = 0,9875 • 0,9875 = 0,975.
Поясним максимальную область для первой прямой регрессии — она ограничивается:
-дляж > 13,7 прямыми 2/1 = 111,93 + 7,018-(ж - 13,7) и у[ = 90,509 + 6,385-(ж - 13,7);
-дляж < 13,7 прямыми ух = 111,93 + 6,385-(ж - 13,7) ш у[ = 90,509 + 7,018-(ж - 13,7).
Аналогично, для второй линии регрессии имеем максимальную область:
— для ж > 6,3 между линиями у2 = 36,773 + 3,198 • (ж - 6,3); у'2 = 27,397 + 2,99 х
х (ж -6,3);
— для ж < 6,3 между линиями у2 = 36,773 + 2,99 • (ж - 6,3); у2 = 27,397 + 3,198 х
х (ж -6,3).
Из анализа максимальных областей линий регресии видим, что они пересекаются при
ж < 6,3.
Теперь осталось найти четыре точки пересечения четырех линий, ограничивающих
максимальные области пересекающихся линий регрессии.
Для ж < 6,3 имеем следующие линии:
2/1 = 111,693 + 6,385 • (ж - 13,7); у[ = 90,509 + 7,018 • (ж - 13,7);
у2 = 36,773 + 2,99 • (ж - 6,3); у2 = 27,397 + 3,198 • (ж - 6,3) ,
или
2/i = 24,2185 + 6,385 -ж; у[ = -5,6376 + 7,018 • ж;
у2 = 17,936 + 2,99 -ж; у'2 = 7,2496 + 3,198 • ж.
Находим попарные точки пересечения прямых (г/1,2/2) ?(?/i>2/2) 5(yi52/2) 5B/1? 2/2) , попа-
попадающие в область определения х < 6,3. Прямые г/i и у2 пересекаются в точке ж = -—5,32,
прямые г/i и у2 в точке ж = —1,85, прямые г/i и г/2 в точке х = 5,85, прямые у[ и у2 в точке
ж = 3,37.
Таким образом, мы имеем для описания области пересечения прямых регрессии
четыре точки с координатами (ж = —5,32; у = —9,75), (ж = —1,85; у = 12,4), (ж = 5,85;
у = 35,43), (ж = 3,37; у = 18,01).
С вероятностью 7 = Р2 = @,95 • 0,95J = 0,90 в области, ограниченной этими точками,
находится точка пересечения двух линий регрессии. Отметим, что искомая область
может быть описана и большим количеством точек пересечения.
5.3.1.4.2. Определение объема испытаний для получения заданной точности
оценки коэффициента регрессии
Задача рассмотрена в [598] и формулируется следующим образом. Для извест-
известной заранее стандартной ошибки отдельного наблюдения Уг(сг) необходимо так
спланировать наблюдения, чтобы ошибка в определении углового коэффициента
5.3]
Регрессионный анализ
679
регрессии методом наименьших квадратов при заданной доверительной вероят™
ности а не превышала АЬ (при этом желательно, чтобы число наблюдений п
и интервал изменения независимой переменной х{1) были минимальными).
При наиболее неблагоприятном экстремальном расположении наблюдений (по-
(половина на одном конце интервала, половина на другом) минимально допустимое
соотношение между числом наблюдений п и длиной интервала I для достижения
заданной точности А5 в определении коэффициента регрессии имеет вид [598]
д^КП^ ' ГД6
2ta(n)
2ta(n)
п —
п(п —
1
2)'
п
п = 2т;
п = 2т-1
— коэффициент, зависящий от доверительной вероятности а и числа наблюдений п
(его значения приведены в табл. 236).
Таблица 236
Значения коэффициента fe(a,n) [598]
п
3
4
5
6
7
8
9
10
11
12
13
14
15
Доверительная
вероятность
0,90
10,93
3,58
2,48
1,94
1,69
1,48
1,36
1,25
1,17
1,10
1,04
0,99
0,95
0,95
22,01
18,49
3,35
2,54
2,15
1,87
1,70
1,55
1,44
1,35
1,28
1,21
1,16
а
0,99
55,11
48,58
4,78
3,42
2,82
2,40
2,15
1,94
1,80
1,68
1,58
1,49
1,42
п
16
17
18
19
20
21
22
23
24
25
26
30
60
Доверительная
вероятность
0,90
0,91
0,88
0,85
0,82
0,79
0,77
0,75
0,73
0,72
0,70
0,68
0,63
0,48
0,95
1,11
1,07
1,03
1,00
0,97
0,94
0,91
0,89
0,86
0,85
0,83
0,76
0,52
а
0,99
1,36
1,30
1,25
1,21
1,17
1,14
1,10
1,08
1,05
1,03
1,00
0,92
0,62
По заданным а и АЪ можно найти соотношения между I и А5, между I и п
и, задаваясь одним, выбирать другое.
Задача 373. Известно, что стандартная ошибка измерений у равна а = 5,27. Необ-
Необходимо определить:
— количество наблюдений, обеспечивающих ошибку оценки коэффициента регрессии
не более АЬ = 3,2 на интервале изменения х длиной I = 10 при доверительной вероят-
вероятности а = 0,95;
— наименьшую длину интервала изменения переменной ж, обеспечивающую точ-
точность оценки АЬ = 1,1 с помощью п = 25 наблюдений при доверительной вероятности
а = 0,90.
Отвечаем на первый вопрос. Имеем I = — • к(а,п) и для I = 10, а = 0,95, а = 5,27
АЪ
ж АЪ = 3,2 получаем fc@,95; п) = 10 • 3,2/5,27 = 6,07. Из табл. 236 имеем п = 5.
Отвечаем на второй вопрос. Для п = 25, АЬ = 1,1, а = 0,90 из табл. 236 имеем
^@,90; 25) = 0,70. Тогда I =
= з?35.
680 Методы исследования связей между случайными величинами [Гл. 5
5.3.2. Множественная линейная регрессия
Ранее рассматривались методы оценки и анализа линейной регрессии у = f{x).
Если случайная величина у может зависеть одновременно от двух и более переменных,
возникает задача оценки и анализа множественной регрессии у = f{x\1x2i • • • ->хк)^
где Xj (j = 1, 2, ..., к) —независимые переменные.
Рассмотрим в качестве примера регрессию у = а + f3\Xi + /?2Ж2 для случая двух
независимых переменных х\ и х2. Для большего числа переменных оценки могут
быть получены по аналогии. Для нашего случая оценки коэффициентов f3\ , f32 и а
имеют вид:
_ S(xl)S(xuy)-S(x1x2)S(x2y) _ S(xj) S(x2y) - S(xlX2) S(xiy)
г~ S(x21)S(x22)^[S(x1x2)]2 5 2^ S(x21)S(x22)-[S(x1x2)]2 5
a = y - btxt - b2x2i где
Дисперсия, характеризующая разброс значений у^ вокруг линии регрессии, рав-
равна
1 п 1
52 -L v^4 / г. l \2 J- Го/ 2\ ? о/ Л г. а ( \Л
= > (г/7- — а — Ь\Х\ — Ь2х2) = \Ь[у — bib(xiy) — Ь2Ь\х2у)\ .
п — 3-"-^ n™3L ч 7 J
Проверка гипотез iJq • &i = ^ю и -^о' • ^2 = ^20 (^10? ^20—некоторые заранее за™
данные значения) производится с помощью статистик
ti = ^ъ—^5 h = ^^——, где
i_ 1
( Я(т>2\ 12 f Я(т2\ 1 2
о _ с J у 2/ I а _ с J ^y^ij I
О^! *-> Л / 2\ о/ 2\ го/ \i2 I ' ^2 ^ I о/ 2\ о/ 2\ го/ \т2 f
[ 5(X!J Я(Ж2) "" [S{XlX2)\ J [ D^i) Я(Ж2) — [S (X\X2)\ J
Статистики t\ ж t2 при справедливости гипотез Hq и Uq7 имеют распре-
распределение Стьюдента с / = п^3 степенями свободы. Отсюда: если |5i| >ti±aSb1
2
и |&2| > ti+g Sh2, то коэффициенты 6i и Ъ2 признаются значимыми.
2
Сама регрессия признается значимой, если -^- < Faj где S2.—дисперсия зна-
значений |/г, оцененная ранее или оцениваемая по дублируемым наблюдениям (для Fa
используются степени свободы f\ =n — Зи/2=?71—1, где m — объем выборки, по
которой производилась оценка S2).
Для обнаруясения и устранения выбросов при множественной линейной регрес-
регрессии применяются статистики Прескотта-Лунда (см. раздел 5.3.1.2.2.3.3) с исполь-
использованием соответствующего значения к (в нашем случае к = 3).
Для большего числа независимых переменных расчеты и анализ множествен™
ной регрессии существенно усложняются. Однако в настоящее время разработаны
специальные методы планирования регрессионных экспериментов, позволяющие
упростить оценки коэффициентов регрессии и сократить число необходимых экс™
периментов.
5.3] Регрессионный анализ 681
Некоторые из них будут рассмотрены далее, однако в целом этот обширнейший
раздел современной прикладной статистики останется за бортом нашего труда, так
как он заслуживает самостоятельного скрупулезного и пространного изложения.
В самых общих чертах (на уровне элементарного введения) мы рассмотрим эти
вопросы в разделе, посвященном методам активного планирования эксперимента.
5.3.3. Нелинейный регрессионный анализ
Если линейное уравнение регрессии неадекватно описывает имеющийся стати-
статистический материал, необходимо найти нелинейное уравнение регрессии, удовле-
удовлетворительно описывающее истинную зависимость. Различные приемы нахождения
таких зависимостей рассматриваются ниже.
5.3.3.1. Линеаризация нелинейной модели заменой переменных
Смысл метода ясен из названия — нелинейное уравнение преобразуется в линей-
линейное переходом от исследуемых переменных к новым переменным. Некоторые из
таких преобразований приведены в табл. 230. Обработка результатов наблюдений,
вычисление регрессии и ее статистический анализ для линейно преобразованного
уравнения выполняются методами линейного регрессионного анализа, рассмотрен-
рассмотренными выше. Следует, однако, помнить исходные предпосылки регрессионного ана-
анализа, основная из которых — нормальность распределения изучаемых случайных
величин — должна теперь быть справедлива не для самой случайной величины,
а для ее функционального преобразования, что, к сожалению, далеко не всегда
выполняется. Подбор необходимого линеаризующего преобразования выполняется
первоначально „на глаз" графически. Поясним методику вычисления нелинейной
регрессии примером.
Задача 374. В результате исследования зависимости между случайными величина-
величинами х и у получены следующие результаты (п = 10):
Хц 1 2 3 4 5 6 7 8 9 10
ун 81 19 9 8,5 7 6,6 5 5,8 5,6 5,4.
Необходимо найти регрессию у = f(x) и провести ее статистический анализ.
Предварительным анализом убеждаемся, что можно использовать линеаризующее
преобразование для функции типа у = аех .
Обозначим у* = In г/ и ж* = —. Тогда будем искать линейную регрессию у* = а* +Ь*ж*.
Для х* и у* имеем ряд
* 111111111
23456789 10
у* -+ 4,39 2,94 2,20 2,14 1,94 1,89 1,79 1,76 1,72 1,69
Находим
ю / ю \ 2
J2 xl = 2,92896; ]Г х* \ = 8,578806;
i=l \i=l /
10 10 10
J2 xf = 1,549768; ]Г у* = 22,46; J2 ж** * 2/** = 8,6671587.
г=1 г=1 г=1
Тогда
L* 10-8,6671587™ 2,92896-22,46 orii^ * 22,46-3,019-2,92896
о = = 3,019; а = = 1,361.
10 • 1,549768 - 8,578806 ' 10
682 Методы исследования связей между случайными величинами [Гл. 5
Следовательно, искомая регрессия имеет вид
I 3,019
у* = 1,361 + 3,019 -ж*, или In у = 1,361 + 3,019- -; у = 3,9 • е х .
х
Проверяем значимость коэффициентов регрессии. Имеем
S2 = —!— • V" (у* • 1,361 - 3,019 • ж*J = 0,004 (S = 0,067) ;
! (х* - ж*J = 0,0768 (Sx* = 0,2772); Sb* = S, = 0,0805.
5 Vn^T
п — 1 _
Из табл. 118 для а = 0,95 имеем ?(i+o,95)/2(/ = 8) = to,975(8) = 2,31.
Так как \Ъ*\ = 3,019 > to,97s(8) • Sb* = 2,31 • 0,0805 = 6,186, коэффициент регрессии
признается значимым. Для дисперсии коэффициента а* имеем
1 «Г*2 ) 2 fin 9Q9HQU2 1 2
- + ^} = 0,067 J—+' } =0,0317.
п (п - 1) • S2X* ) X Ю 9 - 0,0768 /
Тогда |а*| = 1,361 > to,975(8) • Яа* = 2,31 • 0,0317 = 0,073, что также приводит к выво-
выводу о значимости коэффициента а* с достоверностью а = 0,95.
5.3.3.2. Полиномиальная нелинейная регрессия (полиномы Чебышева)
При невозможности замены переменных приходится искать оценки нелинейной
регрессии непосредственно по экспериментальным данным.
Как правило, любая нелинейная регрессия может быть представлена полиномом
п
вида у = 5^ сцхг. Если степень полинома к выбрана заранее, то оценки коэффициен-
коэффициента
тов ао, ai, ..., а^ находятся непосредственно методом наименьших квадратов. При
неизвестной степени аппроксимирующего полинома уравнение регрессии ищется
путем последовательных уточнений (последовательного повышения степени по-
полинома). Критерием для прекращения процедуры уточнения степени полинома
является величина остаточной дисперсии
Если *S^+1 > S|, то в качестве регрессии принимается полином степени к. Зна-
Значимость дисперсий S% , х и S% проверяется .F-критерием Фишера при Д = п — к
af2=n^k^l степенях свободы.
При увеличении степени полинома необходимо пересчитывать все коэффициен-
коэффициенты регрессии. Расчеты упрощаются, если значения Х{ являются равноотстоящими
(xi+i — xi = const). Тогда уравнение регрессии к-то порядка может быть представ-
представлено в виде у = ЬоРо(х) + biPi(x) + ... + bkPk(x), где Рк(х) —полиномы Чебышева,
определяемые соотношениями
Р*(гр\ 1 . Р, (~\ гу. ' Р, (~\ Р, (™\ Р- л (гр\ __ V L Р, ^fr}
0\х) — Li Г1\х) — х о ? -гк\х) — ^1\х) гк-1\х) ./.,2 п\ ±к — 2\<Ь)-
* А\4:к — 1]
Коэффициенты регрессии вычисляются по формуле
5.3] Регрессионный анализ 683
Если х* = Ь 1 (х2 — х\ = ... = а^+1 — Xi = ... = хп — хп^\ = const), то х* = г
и уравнение регрессии принимает вид
У = b0P0(i) + biPi(z)(a; -?) + ...+ Ь/ЛООО - x)fc + ..., г = 1, 2, ..., n,
Значения
^ „2,.л (feO
где Bk - 1)!! = 1 • 3 • 5 • ... • Bfc - 1),
можно заранее табулировать для разных п и к, а значения Pj(i) также вычис™
лить, пользуясь приведенными формулами. Для некоторых значений к и п по™
п
линомы Чебышева Pj(i) и ^^-Р^(^) приведены в табл.237. В ней учтено, что
i=l
Рк(г) = —Pk{n + 1 — г) для нечетных Aj, и Pk(i) = Pk(n + 1 ~~ *) Для четных Aj. Оста™
точная дисперсия уравнения регрессии равна
^jdbr5*2' где ^ = ^-1-^1:^@; So^E^if
г=1 г=1 \г=1
Проверка гипотез о значениях коэффициентов регрессии осуществляется с по-
помощью статистик
3 sk
имеющих распределение Стьюдента с f = п — к — 1 степенями свободы.
1
ЕСЛИ \tj\ > tl+a ИЛИ \bj\ > t l+a 5fc
, то с доверительной вероятно™
L»=i
стью а коэффициент регрессии bj является значимым (т. е. существенно отличным
от нуля).
Основным практическим преимуществом полиномов Чебышева является то, что
при повышении степени полинома необходимо вычислять только один дополнитель-
дополнительный коэффициент регрессии без пересчета всех остальных.
Последовательность анализа нелинейной регрессии с помощью полиномов Чебы-
Чебышева состоит в следующем. Сначала находится линейная регрессия низшего поряд™
ка (к = 1) и соответствующая ей дисперсия Sf. Далее вычисляется еще один коэф™
фициент регрессии ?»2 и дисперсия S|, соответствующая квадратичной регрессии.
Затем критерием Фишера проверяется значимость уменьшения дисперсии Щ по
Я2
сравнению с дисперсией Sf. Если -~-j ^ Fa (/i = n — 2; /2 = п — 3), то квадратичная
регрессия предпочтительнее линейной.
S2
Кубическая регрессия предпочитается квадратичной, если -^ ^ F@ (/1 = п — 3;
/2 = п-4).
684
Методы исследования связей между случайными величинами
[Гл. 5
Таблица 237
Полиномы Чебышева
i) ш значения Р* = ^ Р% (г)
г=1
п
3
4
5
6
7
8
9
10
11
i
1
2
3
Р*
1
2
3
4
Р*
1
2
3
4
5
Р*
1
2
3
4
5
6
Р*
1
2
3
4
Р*
1
2
3
4
Р*
1
2
3
4
5
Р*
1
2
3
4
5
Р*
1
2
3
4
5
6
-1
0
1
2
-3
-1
1
3
20
-2
-1
0
1
2
10
-5
-3
-1
1
3
5
70
-3
-2
-1
0
28
-7
-5
-3
-1
168
-4
-3
^2
-1
0
60
-9
-7
-5
-3
-1
330
-5
-4
-3
_2
-1
0
1
-2
1
6
1
-1
-1
1
4
2
-1
-2
-1
2
14
5
-1
-4
-4
-1
5
84
5
0
-3
-4
84
7
1
-3
-5
168
28
7
-8
-17
-20
2772
6
2
-1
-3
-4
132
15
6
-1
-6
-9
-10
-1
3
-3
1
20
-1
2
0
-2
1
10
-5
7
4
-4
-7
5
180
-1
1
1
0
6
-7
5
7
3
264
-14
7
13
9
0
990
-42
14
35
31
12
8580
-30
6
22
23
14
0
Р4(г)
1
-4
6
-4
1
70
1
-3
2
2
-3
1
28
3
— 7
1
6
154
7
-13
-3
9
616
14
-21
-11
9
18
2002
18
-22
-17
3
18
2860
6
-6
-6
-1
4
6
п
11
12
13
14
15
16
17
г
Р*
1
2
3
4
5
6
Р*
1
2
3
4
5
6
7
Р*
1
2
3
4
5
6
7
Р*
1
2
3
4
5
6
7
Р*
1
2
3
4
5
6
7
8
Р*
1
2
3
4
5
6
7
8
9
А К»
110
-11
-9
-7
-5
-3
-1
572
-6
-5
-4
-3
-2
-1
0
182
-13
-11
-9
-7
-5
-3
-1
910
-7
-6
-5
-4
-3
-2
0
280
-15
-13
-11
-9
-7
-5
-3
-1
1360
-8
—7
-6
-5
-4
-3
-2
-1
0
P2(i)
858
55
25
1
-17
-29
-35
12012
22
11
2
-5
-10
-13
-14
2002
13
7
2
-2
-5
-7
-8
728
91
52
19
-8
-29
-44
-56
37128
35
21
9
-1
-9
-15
-19
-21
5712
40
25
12
1
-8
-15
-20
-23
-24
^з(г)
4290
-33
3
21
25
19
7
5148
-11
0
6
8
7
4
0
572
-143
-11
66
98
95
67
24
97240
-91
-13
35
58
61
49
0
39780
-455
-91
143
267
301
265
179
63
1007760
-28
-7
7
15
18
17
13
7
0
Р4»
286
33
-27
-33
-13
12
28
8008
99
-66
-96
-54
11
64
84
68068
143
-77
-132
-92
-13
63
108
136136
1001
-429
-869
-704
-249
251
756
6466460
273
-91
-221
-201
-101
23
129
189
470288
52
-13
-39
-39
-24
-3
17
31
36
5.3]
Регрессионный анализ
685
п
17
18
19
г
Р*
1
2
3
4
5
6
7
8
9
Р*
1
2
3
4
5
6
РФ)
408
-17
-15
-13
-11
-9
—7
-5
-3
-1
1938
-9
-8
-7
-6
-5
-4
7752
68
44
23
5
-10
-22
-31
-37
-40
23256
51
34
19
6
-5
-14
3876
-68
-20
13
33
42
42
35
23
8
23256
-204
-68
28
89
120
126
р4@
16796
68
-12
-47
-51
-36
-12
13
33
44
28424
612
-68
-388
-453
-354
-168
п
19
20
г
7
8
9
10
Р*
1
2
3
4
5
6
7
8
9
10
Р*
О]
Pi(i)
-3
-2
-1
0
570
-19
-17
-15
-13
-11
-9
-7
-5
-3
-1
2660
(онча
Р2(г)
-21
-26
-29
-30
13566
57
39
23
9
-3
-13
-21
-27
-31
-33
17556
ние таблицы 237
Рз(г)
112
83
44
0
213180
-969
-357
85
377
539
591
553
445
287
99
4903140
P4(i)
42
227
352
396
2288132
1938
-102
-1122
-1402
-1187
-687
-77
503
948
1188
22881320
Процесс вычислений заканчивается, как толвко
S^<Fa (f = n-k-l;f2=n-k-2).
^к + 1
Так как поввинение степени полинома от к до к + 1 не уменвшает дисперсию
регрессии, принимается уравнение регрессии, описываемое полиномом степени к.
Задача 375. В результате исследований получена следующая зависимость:
хц 1,1; 3,2; 5,3; 7,4; 9,5; 11,6; 13,7; 15,8; 17,9; 20,0
уц 1,3; 4,75; 6,8; 1,86; -15,6; -51,1; -110,3; -198,6; -321,8; -485,2.
Необходимо найти уравнение регрессии и определить порядок его нелинейности, приняв
достоверность а = 0,95.
ж-1,1 х
Имеем ж* =
1,1
2,1
—, тогда х* = i. Результаты вычислений сводим в та-
таблицу, там же приводим значения полиномов Чебышева для п = 10 и к = 1,2,3,4 из
табл. 237:
xi =i
1
2
3
4
5
6
7
8
9
10
Е
10
ЕА2@
г=1
Уг
1,30
4,75
6,80
1,86
-15,60
-51,10
-110,30
-198,60
-321,80
-485,20
-1167,89
Pi(i)
-9
-7
-5
-3
-1
1
3
5
7
9
330
УгРг(г)
-11,70
-33,25
-34,00
-5,58
15,60
-51,10
-330,90
-993,00
-2252,60
-4366,80
-8063,33
Р2«
6
2
-1
-3
-4
-4
-3
-1
2
6
132
УгР2(г)
7,80
9,50
-6,80
-5,58
62,40
204,40
330,90
198,60
-643,60
-2911,20
-2753,58
Рз(г)
-42
14
35
31
12
-12
-31
-35
-14
42
8580
УгРз(г)
-54,60
66,50
238,00
57,66
-187,20
613,20
3419,30
6951,00
4505,20
-20378,40
-4769,34
Р4«
18
-22
-17
3
18
18
3
-17
-22
18
2860
У iP4.il)
23,40
-104,50
-115,60
5,58
-280,80
-919,80
-330,90
3376,20
7079,60
-8733,60
-0,42
686 Методы исследования связей между случайными величинами [Гл. 5
ю
Вычисляем bo = — • ^ Vi = — • (-1167,89) = -116,79; Ъг = -^ = -8°63;33 =
= -24,4343.
Уравнение регрессии имеет вид
у = -116,79 - 24,434 • (ж* - ж*) = 17,597 - 24,434 • ж*.
Находим дисперсию
2
52 = —Ц-, где Я2 = Sq — Ь2 •
где ?>
г=1
Имеем
Яо = 393510,8521 - — • 1167,892 = 257114,1469;
о ' 10 ' '
\ = 257114,1469 - 24,4342 • 330 = 60097,42942; Я2 = - • 60097,42942 = 7512,1787.
8
Вычислим коэффициент bo = ¦™::= = — = —20,86.
г=1
Далее находим
Si = 60097,42942 - 20,862 • 132 = 2659,002; S% = - - 2659,002 = 379,857.
Из таблиц находим Fq^sC/i = 8, /2 = 7) = 3,726.
й2 7512 1787
Так как -=^ = = 19,776 > ^о,95 (8; 7) = 3,726, следует признать, что диспер-
Sn 379,857
сия §2 значимо меньше, чем Sf. Следовательно, квадратичная регрессия предпочти-
предпочтительнее линейной и на этом этапе следует принять уравнение регрессии у = —106,569 —
- 24,434 х (ж* - ж*) - 20,86 • (ж* - ж*J.
Выполним теперь вычисления для кубической регрессии:
Ьз = ^ = -*™*± = -0,5558;
Ер|« 858°
г=1
10
Si = Sl - bl • J2 рз (*) = 2659,002 - 0,55582 • 8580 = 8,52297;
г=1
Sl = \ ¦ 8,52297 = 1,42049; || = Щ^~ = 267,5.
s2
Отноюаение -^ существенно превышает критическое значение -Fb,95 (/1 = 7,/2 = 6) =
= 4,20.
Продолж:аем вычисления:
0,420 = _ . 4
2860
5.3] Регрессионный анализ 687
ю -,
S2A = Si - A,468 • 10~4) • J2 pl № = 8,5229; §1 = - • 8,5229 = 1,704.
rp Si 1,42
1огда -=2" = < 1, что означает, что увеличение степени регрессионного полинома
свыше трех не уменьшает, а увеличивает дисперсию регрессии.
Поэтому следует принять в качестве адекватной кубическую регрессионную модель
у = ^106,569 - 24,434 • (ж* - ж*) - 20,86 • (ж* - ж*J - 0,5558 • (ж* - ж*K .
х 11
При переходе к натуральной переменной ж* = — имеем
у = -106,569 - 24,434 • ( — - — - 5,5 J - 20,86 • ( — - — - 5,5 J -
- 0,5558 Л — - М _ 5,5 J = -588,328 + 77,344 • ж - 2,36 • ж2 - 0,0581
Проверяем значимость коэффициентов регрессии.
Для Ь\ имеем / = п — 2 = 8, to,975(8) = 2,31 (см. табл. 118) и
|6i| = 24,434 < 2,31 • . 1 = 2,31 • v ^^1Г~" = 31,17.
ю V330
Следовательно, коэффициент Ь\ незначимо отличается от нуля и линейный член
может быть исключен из уравнения регрессии. Далее для коэффициента &2 имеем
/ = п - 3 = 7, to,97sG) = 2,45 и
= 20,86 > 2,37 .
^
/132
Следовательно, коэффициент регрессии &2 значимо отличается от нуля.
Для Ьз имеем / = п — 4 = 6, to,975F) = 2,45 и
|Ьз| = 0,5558 > 2,45 • V**»523 = Q ?^
л/8580
Следовательно, коэффициент регрессии Ьз так^ке значимо отличается от нуля. Итак,
с учетом значимости коэффициентов регрессии, окончательное уравнение регрессии
будет иметь вид
/т 11 \2 /т 11 \3
у = -106,569 - 20,86 • [ - 5,5 1 - 0,5558 • - 5,5 =
у \2,1 2,1 ' у ' \2,1 2,1 ' )
= 735,518 + 88,852 • ж - 2,36 • ж2 - 0,0581 • ж3.
5.3.4. Выбор наилучшей регрессионной модели по Вильямеу—Клуту
Ранее (см. раздел 5.3.1.3) были рассмотрены методы сравнения регрессий в слу™
чае их одинакового функционального вида и одинаковых независимых переменных.
Рассмотрим теперь задачу сравнения любых двух или более регрессий независимо
от их функционального вида и количества независимых переменных.
Из двух любых регрессий наилучшей признается та, которая имеет меньшую
остаточную сумму квадратов (меньшую дисперсию рассеяния зависимой перемен™
ной вокруг линии регрессии).
Вильяме и Клут [14] для сравнения двух любых регрессий у\ и у2 без трудоем-
трудоемкого предварительного подсчета их остаточных дисперсий предложили критерий,
688 Методы исследования связей между случайными величинами [Гл. 5
основанный на оценке с помощью обычной линейной регрессии углового коэффи™
циента Л линии
2/1+2/2 w ч
У 2 = ^2 ~2/!)'
где у — наблюдаемое значение зависимой переменной; t/i, у2—предсказываемые
сравниваемыми регрессиями значения зависимой переменной.
Значимые отрицательные значения углового коэффициента Л указывают на то,
что регрессия у\ лучше, чем регрессия г/2- Значимые положительные значения Л
указывают на предпочтительность регрессии г/2. Если Л незначимо отличается
от нуля, то модели у\ и у2 признаются равноценными. Значимость отклонения
Л от нуля проверяется методами обычного регрессионного анализа для простой
линейной модели. В этом случае испытываемой линейной регрессионной моделью
является
z = Хх, где 2 = у--B/1+2/2); х = |/2- Ш•
Оценка углового коэффициента линейной регрессии подсчитывается по формуле
(см. раздел 5.3.1.1.1)
\ = ^±
п
г=1
Далее находим
— х) : S\ =
г=1 '" " г=1 ^ж
Тогда, если:
—А < —taS\^ то регрессия г/2 предпочитается регрессии г/i;
А > taS\, то регрессия у\ предпочитается регрессии г/2 5
—t l+g *S*a < А < ti+g Яд, то обе регрессии признаются эквивалентными.
2 2
Здесь ta —а-квантиль распределения Стьюдента с / = п — 2.
Задача 376. Выбрать критерием Вильямса-Клута при доверительной вероятности
а = 0,95 лучшую из двух регрессий
2/2 = 1,61 + 3,99 -ж м 2/1 = 1,24 + 2,81 • ж + 0,2 • ж2
для следующего набора данных:
Хц 2 4 6 9 11 16 17 20 25 31;
ун 9 19 22 41 49 61 69 83 98 128.
Результаты промежуточных расчетов приведены в таблице. Имеем ж* = г/2 г — Уи
_ _ УН + У1г ,
10 10 /10 \2
53 4 = 378,845; ]Г ж*2 = 38861,13893; Р>] ж* = 134523,534;
г=1 г=1 \г=1 /
10 10
J2 zi = ^199,55; J2 х*г ' zi = ^19245,586.
г=1 г=1
10 ¦ (-19345,586) - 378,845 ¦ (-199,55) = = _Q
10 • 38861,13893 - 143523,534 ' ' '
5.8]
Регрессионный анализ
689
2
4
6
9
11
16
17
20
25
30
Уг
9
19
22
41
49
61
69
83
98
128
У2г
9,59
17,57
25,55
37,52
45,50
65,45
69,44
81,41
101,36
125,30
У\г
7,66
15,68
25,30
42,73
56,35
97,40
106,81
137,44
196,49
280,55
У 1г + 2/2 г
2
8,625
16,625
26,425
40,125
50,925
81,425
88,125
109,425
148,925
202,925
У2г У\г
-1,930
-1,890
-0,125
5,210
10,850
31,950
37,370
56,030
95,130
155,250
У И + 2/2 г
*г Уг 2
0,375
2,375
-3,425
0,875
-1,925
-20,425
-19,125
-26,425
-50,925
-74,925
378,845
-193,55
Для а = 0,95 и/ = п-2 = 10-2 = 8из табл. 118 имеем ?0,95(8) = 1,86.
Далее вычисляем
S2X* =
п I
- ж*J = 2647 (Sx* = 51,45);
S2 =
- Х •
(S = 3,205) ;
3,205
= 0,027.
Имеем Л = -0,497 < -?0,э5 • 5Л = -1,86 • 0,0207 = -0,039. Следовательно, линейная
регрессия г/2 предпочтительнее квадратичной у\.
5.3.5. Прогнозирование по регрессии
Имеется регрессия у = /(ж), оцененная по равноотстоящим значениям Х{
(г = 1,2, ..., п). Требуется найти значение зависимой переменной уп+/ при х = жп+|
(I — глубина экстраполяции) и оценить ошибку прогноза. Двусторонний а-довери™
тельный интервал для уп+/ имеет вид [600]
f{xn+i) - t±±as\(n,l) = у^+г ^ уп+г ^ 2/°+г = f{xn+i) -\-ti±as\(n,l),
2 2
где f(xn+i) = yn+i—значение г/, вычисленное по регрессии при ж = xn^i; ta —
«^квантиль распределения Стьюдента при / = п — к — 1 степенях свободы;
S2 = —- ^2[yi — f(%i)} —дисперсия регрессии; к — порядок регрессии; Л —
г=1
коэффициент, зависящий от п и I.
Коэффициент Л(п, I) равен:
— для линейной регрессии
Х(п
¦«-{*
'¦У-
-для квадратичной регрессии
Х(щ1) =
1 +
(n±ff
п (п — 1)
i4 - 2 (п + IJ ]Г i2 + п (п +
690
Методы исследования связей между случайными величинами
[Гл. 5
Для удобства вычислений напомним, что
^ .2 _ п (п + 1) Bтг + 1)
4 * б ;
J2
г=1
п(п + 1) Bп + 1) (Зп2 + Зп - 1)
зо
Задача 377. 17о данным эксперимента:
хц 1 2 3 4 5 6 7 8 9 10;
уц 7 9 10 6 6 -4 -10 -22 -33 -47
найти 95%-й доверительный интервал для у = f(x) при х = 15.
Учитывая, что в нашем случае х% = г, применим непосредственно технику полино-
полиномов Чебышева (см. раздел 5.3.3.2). Результаты вычислений (с применением табл. 237
для Pk(i)) приведены в таблице:
Xi = г
1
2
3
4
5
6
7
8
9
10
Е
Уг
7
9
10
6
2
-4
-10
-22
-33
-47
-82
Mi)
-9
-7
-5
-3
-1
1
3
5
7
9
330
ViPi(i)
-63
^63
-50
-18
-2
-4
-30
-110
-231
-423
-994
P2(i)
6
2
-1
-3
-4
-4
-3
-1
2
6
132
ViP2(i)
63
18
-10
-18
-8
16
30
22
-66
-282
-235
Ps(i)
-42
14
35
31
12
-12
-31
-35
-14
42
8580
УгРз(г)
-294
126
350
186
24
48
310
770
462
-1974
8
18
-22
-17
3
18
18
3
-17
-22
18
2860
ViP^i)
126
-198
-170
18
36
-72
-30
374
726
-846
-36
Вычисляем bo = = —8,2; Ъ\ = ^—^—
= = -3,01.
330
Для линейной регрессии (ж = 5,5 —» у = —8,2 — 3,01 • (ж — 5,5)) находим
2
10
10
= $>?"-• (У>1 =4168-672,4 =
Pt{i) = 3495,6 - 3,0Г • 330 = 505,767; S( =
Вычисляем дальше:
132
52 _ ^i _ 505,767
n- 2
= 63,22.
?2 = ^i2 - Я- Т,р2 @ = 505,767 - 1,782 • 132 = 87,538; S22 = 52 ^ 87'538
п - 3
= 12,505.
Критическое значение .Fo,95(/i = 8; /2 = 7) = 3.
5.3] Регрессионный анализ 691
Так как -^ = —-— = 5,055 > .Fo,95(8;7) = 3,7, следует признать, что квадратичная
регрессия предпочтительнее линейной.
Далее находим
ю
10 о2
Sl=Sl^bl'Yl рз № = 87,538 - (9,32 • 1СГ4) • 8580 = 87,530; S| = -^ = 14,588.
i=l
m So 12,505
Так как -^ = < 1, следует признать, что квадратичная регрессия предпочти-
jSo 14,588
тельнее линейной.
Далее находим
2/ = bo + 6i • (ж — х) + &2 • (х — ж) =
= -8,2 - 3,01 • (х - 5,5) - 1,78 • (х - 5,5J = -45,48 + 16,57 - 1,78 • ж2.
Из уравнения регрессии для жю+5 = х\5 = 15 вычисляем yx=i5 = —197,44.
Ранее мы имели Я| = 15,318 (§2 = 3,913). Далее вычисляем:
^=Ю-11-21 g.= Ю-11-21.C00 + 30-1) =
^Ч 6 ' f-? зо
А(Ю,5) = A + ^ + 25333 45° ' 385 + 5Ов25° }1 = 2,234.
I 385 10 • 25333 - 148225 J
Из табл. 118 находим ti+o,95 (/ = п — к — 1); to,975G) = 2,37 (здесь /г = 2 — степень
полинома). Окончательно получаем искомый доверительный интервал:
-197,44 - 2,37 • 3,913 • 2,234 = -218,158 ^ ух=15 ^ -176,722 = -197,44 + 2,37 • 3,913 • 2,234.
5.3.6. Специальные методы сглаживания экспериментальных данных
Рассмотренные в предыдущих разделах оценки коэффициентов регрессии мето-
методом наименьших квадратов хороши только тогда, когда остатки распределены нор™
мально. Если же это не так, если „хвосты" распределения „тяжелы" или в выборке
присутствуют грубые выбросы, то эти оценки быстро теряют свою эффективность.
В таких ситуациях предпочтительнее использовать иные специальные методы
устойчивой (робастной) регрессии.
Для робастной регрессии оценки уравнения регрессии являются решениями
( \
задачи [620] ^ {Р\Уъ~О'0~ J^ ujXij I = mm, где ц>(е) — функция потерь.
V 3=1 )
Очевидно, что (f{s) = ?2 соответствует обыкновенному методу наименьших ква-
квадратов. В некоторых ситуациях более эффективными могут быть иные функции
потерь:
<р{е) = \е
= \е
— метод наименьших модулей;
^, 1 < I/ < 2 — итеративный метод Форсайта [605];
1 — cosf - I , если е < стг:
Vе/
0, если \е > стг (с = 1,5 или 2,1)
. 1 — cosj - I , если е < стг;
(р(?) = < \су —метод Андрюса.
692 Методы исследования связей между случайными величинами [Гл. 5
По скорости вычислений и простоте использования метод наименьших квадра™
тов — наилучший, однако по точности оценивания регрессии такой вывод сделать
нельзя [527, 603]. Сравнение различных методов оценки регрессии приведено в [601].
Ниже мы рассмотрим некоторые из робастных методов оценки регрессии и другие
специальные приемы сглаживания экспериментальных данных.
5.3.6.1. Метод наименьших модулей
В отличие от метода наименьших квадратов, при котором оценка коэффици-
коэффициентов регрессии ищется из условия минимизации суммы квадратов отклонений
экспериментальных точек от выборочной регрессии, в [604, 606, 607, 609] развит
метод наименьших модулей таких отклонений (МНМ). В соответствии с МНМ оцен-
оценки коэффициентов регрессии ищутся из условия минимизации суммы абсолютных
величин отклонений экспериментальных точек от выборочной регрессии.
Для линейной регрессии у = а + /Зх метод наименьших квадратов соответствует
)
= mm.
условию ^2(yi — ol — /Зх{) = min, а МНМ условию 5 = ^2\yi — а — f3x
Замена квадратов отклонений абсолютными вел ч на in в ряде случаев может
оказаться предпочтительнее. Прежде всего, использование МНМ позволяет осла-
ослабить влияние больших отклонений (в методе наименьших квадратов они возводятся
в квадрат). В случае метода наименьших квадратов прямая регрессии имеет вид
- . ху — ху , ч
У = У + q2 (х-х).
В случае же МНМ уравнение линейной регрессии есть
Л _ xkyi - xiyk Ук - yi
хк - хг хк - xi '
где (хк^Ук) и (%i,yi)—некоторые две выбранные из условия S = min эксперимент
тальные точки.
Задача отыскания минимума является типичной задачей кусочно-выпуклого
линейного программирования. В настоящей работе мы не будем излагать основы
линейного программирования, а любопытного читателя отправим к специальной
литературе, например, [610]. Здесь мы опишем только один простейший алго-
алгоритм решения задачи для случая линейной регрессии, рассмотренный в [606]. Для
последовательности пар (#i,i/i), • • •, (хП1 уп) сначала предполагаем, что регрессия
проходит через последнюю точку (xnj yn). Будем искать к ней пару — точку (ж/, у/),
минимизирующую сумму абсолютных величин отклонений S. Для этого вычислим
(п — 1) угловых коэффициентов
о _ Уп -2/1 о _ Уп -2/2 о _ Уп - Уп^1
Л - т Т15 Р2 - ; •••; Рп^г - —7
J XI Х Х2 L Ь l
и упорядочим их по величине (например, C\ < ^2 < • • • < /3n-i)-
Затем в соответствии с упорядоченным рядом /% выстраиваем знакоперемен-
знакопеременный ряд =Ь(жп — #i), =Ь(жп — Х2), • • •, ±(жп — xn-i) и ищем минимум (по абсолютной
величине) суммы величин i(xn — а^), * = 1, ... ,п — 1, с одной переменой знака
в последовательности, выбирая соответствующим образом знаки у суммируемых
величин (у первой величины всегда выбираем +). Фиксируем номера величин /%
и А+ъ меж:ду которыми происходит перемена знака у суммы знаменателей пары
(xi,yi). Если сумма величин ±(жп^з^) отрицательна, то в качестве пары к последней
точке (хП1 Уп) берется точка (ж|, г//), соответствующая угловому коэффициенту A+i,
если сумма полож:ительна, то точка, соответствующая /3{. Если сумма равна нулю,
то берется любая точка ft ^ /3 ^ ft+i-
5.3] Регрессионный анализ 693
На втором этапе считаем, что прямая регрессии проходит через точку (ж/,у/),
и в соответствии с описанным алгоритмом ищем пару к ней. Перебор продолжается
до тех пор, пока не будет получена уже найденная однажды точка. Тогда она
и предпоследняя найденная являются теми двумя точками, через которые проходит
искомая прямая регрессии. Аналитическое описание алгоритма весвма усложнено,
поэтому дадим пояснение его реализации на количественном примере. Напомним
пользователю, что задачи в предлагаемой книге — это не только иллюстрации к из-
изложенному, но и способ пояснения методов и приемов, изложение которых иным
способом слишком громоздко.
Следует отметить, что методы статистического анализа уравнений МНМ-регрес™
сий отсутствуют. Если для способа наименьших квадратов изучены распределения
параметров регрессии и их основные статистические свойства, что, собственно,
и позволяет выполнить необходимый статистический анализ, то для МНМ эти рас-
распределения неизвестны. Поэтому ничего нельзя сказать о статистических свойствах
регрессии, полученной МНМ-методом. Это является существенным недостатком
МНМ-метода, ограничивающим его применение в статистической практике.
Задача 378. Для набора данных:
хц 1 2 3 4 5;
у С 38 24 31 39 48
найти прямую регрессии методом наименьших модулей.
Выбираем в качестве начальной точки последнюю точку с координатами (ж = 5,
у = 48). Вычисляем угловые коэффициенты
48-38 ^ 48-24 ^ 48-31 „ 48-39
А = ——г = 2,5; /32 = ——- =8; /33 = ——- = 8,5; /34 = ——Г = 9'
5—1 5—2 5—3 5—4
Ранжируя полученные значения /3i по возрастанию, получаем знакопеременный ряд
для знаменателей ±4, ±3, ±2, ±1. Его минимальная (по абсолютной величине) сумма
равна +4 — 3 — 2 — 1 = — 2. Перемена знака происходит между j3\ и Д, а так как сумма
отрицательна, то выбираем /З2, т.е. в пару к последней точке E,48) берем пару, соответ™
ствующую 02 —это точка B, 24).
Далее, предполагая, что регрессия проходит через точку B, 24), подбираем пару к ней.
Имеем
38-24 „ 31-24 „ 39-24 „ 48-24
^ 14 * 7 ^ 75 ^ 8
Ранжированием по возрастанию полученного ряда Д приходим к знакопеременному
ряду знаменателей ±1, ±1, ±2, ±3, минимальная сумма которого равна +1+1+2—3=
= +1. Перемена знака в сумме происходит между /Зз и /З4.
Так как сумма положительна, выбираем /Зз и соответствующую точку с координатами
х = 4 и у = 39. Для этой точки имеем ряд /3i
39-38 1 „ 39-24 ^ 39-31 „ 39-48
Для ранжированного по возрастанию ряда /3i получаем знакопеременный ряд ±3, ±2,
=Ы, ±1, для которого наименьшая сумма равна +3 — 2 — 1 — 1 = —1.
Перемена знака происходит между /3\ и 02, и, так как сумма отрицательна, то
выбираем 02 и точку с координатами B,24), но эта точка уже встречалась. Следова-
Следовательно, искомая прямая проходит через две точки — предыдущую D, 39) и полученную
повторением B,24). Отсюда имеем Xk =4, г/д. = 39 и х\ = 2, у\ = 24. Тогда уравнение
прямой регрессии имеет вид
4-24-2-39 39-24 Л
У = 13^ + ^Т^ • я = 9 + 7,5 . я,
694 Методы исследования связей между случайными величинами [Гл. 5
Для нее сумма модулей отклонений от экспериментальных точек равна
5
yi - 9 - 7,5 • х\ = |38 - 9 - 7,5| + |24 - 9 - 7,5 • 2| + ... + [48 - 9 - 7,5 • 5| = 23,5
Для примера: прямая регрессии, полученная методом наименьших квадратов, была
бы у = 25,5 + 3,5 • ж, и для нее
5
J2\Vi - 25,5 - 3,5жг| = |38 - 25,5 - 3,5| + ... + |48 - 25,5 - 17,5| = 36.
г=1
Суммы квадратов отклонений равны
5 5
J2(Vi - 9 - 7'5 • xif = 464,75, и ^2(yi - 25,5 - 3,5 • Xif = 311,5,
г=1 г=1
что соответствует назначению обеих оценок регрессии.
5.3.6.2. Метод последней точки
В ряде задач, в основном связанных с прогнозами в экономике, для линии
регрессии важно получить наибольшее приближение к последним точкам, что
позволяет использовать ее с большей эффективностью для прогноза последующего
поведения изучаемого процесса.
В [606] рассмотрен метод последней точки, когда уравнение прямой регрессии
принудительно приводится в последнюю точку (хП1 уп) за счет некоторого увеличе-
увеличения остаточной дисперсии регрессии. При этом надежда возлагается на то, что
увеличение остаточной дисперсии будет скомпенсировано повышением точности
прогноза в области последней точки. Уравнение регрессии для метода последней
точки имеет вид [606]
^2 Xi ~ ПХп
*=1
У =
Следует отметить, что метод последней точки может быть эффективно ис-
использован совместно с методом наименьших модулей (см. раздел 5.3.6.1). Тогда,
выбрав последнюю точку (жп, уп) в качестве начальной, методами МНМ к ней ищут
оптимальную пару.
Задача 379. Для данных задачи 378 найти прямую регрессии методом последней
точки.
5 / 5 \2
Имеем хп = 5; уп = 48; ]Р хъ = 15; ]Р Vi = 180; ?>г = 225.
г=1 г=1 \г=1 /
Получаем
32 • 150 - 5 ¦ 44 • 32 - 5 ¦ 12 • 150 + 25 ¦ 12 • 44 ,
у = 44 Н • (ж - 12) = 14 + 2,5 • ж.
У 1024 - 2 ¦ 5 • 12 ¦ 32 + 25 ¦ 144 v ; '
5.3.6.3. Метод однозначной аппроксимации
Рассмотренные ранее методы регрессионного анализа на основе принципа наи-
наименьших квадратов не позволяют получить обратимые уравнения регрессии, т. е.
совокупность экспериментальных точек (ж, у) не аппроксимируется однозначно.
5.8]
Регрессионный анализ
695
Регрессии у по х и х по у для одного и того же набора экспериментальных данных
не совпадают.
В [608] рассмотрен метод однозначной аппроксимации, основанный на миними-
минимизации суммы площадей:
S = Е S? = Ё {Уг - Я**)] [*i - ГЧуг)]
где Xi,yi—координаты г-й экспериментальной точки; f(x)—искомая функция;
f~1{x)—функция, обратная к функции f(x).
Для модели у = а-\- /Зх оценки коэффициентов а и C находятся из условия
(
В соответствии с [608] оценки а и /3, удовлетворяющие сформулированным
требованиям, равны соответственно
Ь = ±
а = у — Ъх
(знак + или — выбирается исходя из знака корреляции между переменными у и х).
При оценке коэффициентов по методу однозначной аппроксимации регрессии
у по х и х по у совпадают.
В [602] рассмотрена модификация метода однозначной аппроксимации, пред™
полагающая минимизацию суммы квадратов расстояний от экспериментальных
точек до искомой прямой (ортогональная регрессия). Для случая ортогональной
регрессии оценки равны
Ъ =
г=1 г=1 г=1
л
= ; а = |/ — 6ж.
nGSxSy (SI - SI) + 4 In
тг п
г=1 г=1
Коэффициенты уравнения ортогональной регрессии зависят от масштаба пере-
переменных, в то время как для обычной регрессии и метода однозначной аппрокси-
аппроксимации такая зависимость отсутствует. Корректное обобщение метода однозначной
аппроксимации (и ортогональной регрессии) приведено в работе [638], содержащей
исследование уравнения регрессии в форме нормального уравнения прямой.
Задача 380. Для набора данных (п = 10):
хц 2 4 5 7 6 9 14 21 32 29;
2/»: 8 15 14 16 18 25 31 50 65 61
найти оценки коэффициентов регресии методом однозначной аппроксимации.
Имеем
10 1 10 / 10 \ 10
]Гз^ = 303; х = - • ^ ж» = 30,3; МР хЛ =91809; ]Г х\ = 13097;
*=1 П г=1 \г=1 / г=1
696 Методы исследования связей между случайными величинами [Гл. 5
ю -.ю / ю \ 2 ю
^ = 129; t/ = — • 22 У* = 1^,9; I zJ 2/г I = 16641; ]>J уг = 2713;
г=1 П г=1 \г=1 / г=1
10 -I 10
Y*Xi-yi = 5924; S2X = • У4ж» - жJ = 435,122 (Яж = 20,86);
S2 = ^^ • Y^(yi - yf = 116,54 (Sy = 10,79);
Вычисляем оценки методом однозначной аппроксимации (выбираем знак +, так как
корреляция между у и х положительна)
i_
= 0,517; а = у - Ьх = 12,9 - 0,517 • 30,3 = -2,765.
Следовательно, получаем уравнение регрессии у = ^2,765 + 0,517 • х. Из него можно
непосредственно получить уравнение регрессии х по у: х = 5,348 + 1,934 • у.
Оценки уравнения регрессии у по ж, полученные методом наименьших квадратов
(см. раздел 5.3.1.1.1), привели бы к уравнению у = ^2,701 + 0,515ж.
Легко видеть, что оценки методом однозначной аппроксимации достаточно близки к
оценкам наименьших квадратов.
5.3.6.4. Метод обратных разделенных разностей
Метод предложен в [637]. Его авторы предлагают искать математическую мо-
модель регрессии в классе цепных дробей
Однако приведенные авторами работы [637] численные эксперименты не позво™
ляют сделать вывод о предпочтительности этого метода по сравнению с класси™
ческим методом наименьших квадратов. По крайней мере, возможный выигрыш
в частных задачах никоим образом не компенсируется резко возрастающей слож-
сложностью расчетов.
5.3.6.5. Метод условно-относительных разностей
Завершая настоящий раздел достаточно „экзотичных" методов получения эм™
пирических зависимостей, дополним его кратким указанием на еще один метод,
предложенный недавно — метод условно-относительных разностей [635, 636]. Этот
метод предполагает минимизацию не суммы квадратов вида ^^[уг ~~ f(xi)] =
а квадратов относительных разностей
Естественно, что применение метода условно-относительных разностей обес-
обеспечивает повышение точности аппроксимации в области малых значений г/^, но
снижает ее в области больших значений у^.
Имея некоторые преимущества при решении частных задач, этот метод, в силу
вычислительной сложности и неясности статистических свойств оценок такого вида,
вряд ли может быть рекомендован для широкого применения.
5.4] Контрольные карты 697
5.4. Контрольные карты
Этот раздел обращен прежде всего к инженерам и специалистам производства,
для которых контроль качества создаваемой ими продукции — один из важнейших
заключительных этапов длительного цикла изготовления изделия.
Совокупность контролируемых показателей качества изделия представляется,
если отвлечься от их физической природы, потоком случайных величин, в непре-
непрерывно меняющемся хаосе которого контролер должен своевременно рассмотреть
тревожные симптомы ухудшения качества изделия или признаки нарушения тех-
технологического процесса его изготовления.
Ознакомившись с предыдущими разделами книги, читатель справедливо мо-
жет заключить, что мы рассмотрели столько всевозможных методов сравнения
случайных совокупностей, обнаружения тренда и всего другого, что этого должно
быть вполне достаточно для решения любых задач, в том числе и задач контроля
качества производства. Он будет по сути прав.
Контрольные карты — это прежде всего самая распространенная форма приме™
нения статистики в производстве. Сегодня статистические карты контроля каче-
качества стали настолько общепринятыми, что любая достаточно большая фирма, не
пользующаяся ими в том или ином виде, оказывается в невыгодном положении по
сравнению с конкурентами.
Идея контрольной карты состоит в следующем. Делается предположение о рас-
распределении совокупности или выборочных статистик совокупности. Отбираются
независимые случайные повторные выборки из текущей продукции. Подсчитывав
ются и наносятся на специально подготовленную контрольную карту выборочные
значения контролируемых статистик вместе с дву- или односторонними (в за-
зависимости от специфики контроля) доверительными интервалами. Если текущие
измерения показателей качества продукции находятся внутри доверительного ин-
интервала— процесс производства статистически управляем, качество продукции на-
находится в допустимых пределах; если нет — требуется регулирующее вмешательство
в производственный процесс.
По сути метод контрольных карт — это многократное повторение во времени
метода доверительных интервалов, но в отличие от него он более динамичен.
Динамичность контрольных карт дает возможность фиксировать, когда и где
наблюдаемые величины выходят за рамки случайных колебаний, указывая на необ-
необходимость регулирования технологического процесса.
Техника контрольных карт, организация их внедрения достаточно широко осве-
освещены в литературе [14, 22, 97, 611]. Мы приведем краткие математические и та-
табличные описания наиболее распространенных методов, которые могут служить
кратким введением для инженера или специалиста, не знакомившегося ранее с ни-
ними, и позволят применять их в своей практике.
5.4.1. Контрольные карты Шухарта
Первые контрольные карты предложены Шухартом [612] в 1931 г. Он предложил
состав таких карт, технологию их составления, методы расчета и правила пользо-
пользования.
Контрольные карты можно рассматривать как многократное применение кри-
критерия значимости. Суть контрольных карт состоит в следующем. На карту нано-
наносятся контрольные границы параметра, соответствующие выбранной достоверно-
достоверности контроля. Затем на карту наносятся выборочные значения контролируемого
параметра. Если его положение выходит за контрольные границы — это сигнал
к необходимости вмешательства в процесс.
698
Методы исследования связей между случайными величинами
[Гл. 5
5.4.1.1. х- и Л-карты
Предположим, что в последовательно контролируемых выборках объема п из-
измеряется некоторая характеристика изделия — х. В каждой выборке вычисляется
среднее значение контролируемого признака х и его размах R = жтах — xmin. Обо™
значим их для г-й выборки через Х{ и Щ. В ж™карте контрольные границы для
среднего при достоверности а = 0,997 будут
хш = х — AR (нижняя граница);
- AR (верхняя граница),
где х = — J^ X{ — среднее по к текущим выборка]
мах по к текущим выборкам; А — коэффициент, с
в табл. 238.
1 _
ц — средний раз™
которого приведены
Таблица 238
Коэффициенты для вычисления
границ регулирования контрольных карт Шухарта [1]
Объем
выборки, п
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
ж-карта
А
1,880
1,023
0,729
0,577
0,483
0,419
0,373
0,337
0,308
0,285
0,266
0,249
0,235
0,223
0,212
0,203
0,194
0,187
0,180
0,173
0,167
0,162
0,157
0,153
jR-карта
Вг
0
0
0
0
0
0,076
0,136
0,184
0,223
0,256
0,284
0,308
0,329
0,348
0,364
0,379
0,392
0,404
0,414
0,425
0,434
0,443
0,452
0,459
D2
3,267
2,575
2,282
2,115
2,004
1,924
1,864
1,816
1,777
1,744
1,716
1,692
1,671
1,652
1,636
1,621
1,608
1,596
1,586
1,575
1,566
1,557
1,548
1,541
S- карта
Вг
0
0
0
0
0,085
0,158
0,215
0,262
0,302
0,336
0,365
0,392
0,414
0,434
0,454
0,469
0,486
0,500
0,513
0,525
0,536
0,546
0,556
0,566
в2
2,298
2,111
1,982
1?889
1,817
1,762
1,715
1,676
1,644
1,616
1,589
1,568
1,548
1,530
1,514
1,499
1,486
1,472
1,461
1,451
1,440
1,432
1,422
1,414
С
0,798
0,886
0,921
0,940
0,951
0,960
0,965
0,969
0,973
0,976
0,977
0,980
0,981
0,982
0,984
0,984
0,986
0,986
0,987
0,988
0,988
0,989
0,989
0,990
Для Д-карты средним уровнем (центральным) является R, нижние и верхние
границы регулирования равны соответственно
где D\ и D2—коэффициенты, приведенные в табл. 238.
5.4]
Контрольные карты
699
Задача 381. В результате контроля 25 выборок изделий, при объеме каждой выборки
п = 5, получены следующие значения контролируемого параметра х:
Номер
выборки г
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Выборочные значения Xij
Х\
1
-2
0
1
2
2
-2
1
0
-1
1
2
0
0
-3
0
3
-1
0
0
2
0
3
1
-1
х2
-1
0
0
2
1
-1
-1
1
-2
-1
-1
2
-2
-1
0
-1
1
-2
0
-5
-1
0
1
-3
0
^2
^2
1
-1
-1
2
0
0
1
0
2
-1
2
1
0
0
-3
-1
0
2
-1
-3
4
0
1
2
2
-1
2
1
-1
-2
1
-1
^2
-1
-1
-2
-1
0
1
^2
-1
1
2
0
2
-2
1
0
0
0
3
^2
0
0
0
-1
4
1
0
0
0
2
-1
2
0
0
1
0
0
-3
-1
-1
1
Статистики
Щ
0,0
-0,4
0,6
0,4
0,6
0,4
-1,0
0,4
0,4
-0,6
0,2
0,4
-0,4
0,2
-0,8
0,4
-0,2
-1,0
0,4
-0,2
0,4
-0,8
1,0
-0,4
0,2
R%
4
4
4
4
3
3
2
2
6
3
3
3
4
3
3
3
6
2
1
7
3
5
6
4
2
2,5
2,8
2,3
3,3
1,3
2,3
1,0
0,8
5,3
1,3
1,7
2,3
2,8
1,7
1,7
1,3
5,7
0,5
0,3
8,2
1,3
4,7
6,5
2,8
0,4
Si
1,58
1,67
1,52
1,82
1,14
1,52
1,00
0,89
2,30
1,14
1,30
1,52
1,67
1,30
1,30
1,14
2,39
0,71
0,55
2,86
1,14
2,17
2,55
1,67
0,63
Вычислить границы для контрольных х- и R-карт Шухарта (к = 25).
Имеем х = —
^=0,008;Д=1.
90
25
Контрольные границы для среднего (для п = 5 из табл. 238 находим А = 0,577) будут
равны
хш=й-А-Я = 0,008 - 0,577 • 3,60 = -2,069;
жв = х + А • R = 0,008 + 0,577 • 3,60 = 2,085.
Мы видим, что нигде х% не вышли за контрольные границы.
Теперь для Д-карты из табл. 238 имеем D\ = 0 и D^ = 2,115.
Тогда Ra = 0 и RB = 2,115 • 3,60 = 7,61. Видим, что ни одно значение Ri не выходит
за эти пределы, т. е. процесс статистически управляем.
х- и R-карты Шухарта рекомендуется применять при п < 10 -f- 20.
5.4.1.2. s-карта
s-карта для выборочного контроля среднего квадратичного отклонения более
чувствительна к изменению рассеяния, чем Декарта. Алгоритм построения и ис™
пользования s-карты состоит в следующем. По текущим к выборкам вычисляется
оценка дисперсии контролируемого признака
где
- \2
х)
3=1
700
Методы исследования связей между случайными величинами
[Гл. 5
Если объемы выборок щ одинаковы, то s2 = 7
f. Центральная линия s-
1=1
карты равна s4 = Cs, а границы зоны регулирования равны sH = B\s и sB =
где Bi, B2 и С — коэффициенты, приведенные в табл. 238.
Задача 382. Для данных задачи 381 построить контрольные границы S-карты Шу-
харта.
л 25
Имеем s2 = — • V" S1 = 2,592 (s = 1,610).
25 ^ V ;
Следовательно, для контрольных границ имеем s4 = 0,940 • 1,610 = 1,513;
sH = 0 • 1,610 = 0; sB = 1,889-1,610 = 3,041 (предварительно из табл.238 для п = 5
получили С = 0,940, Вг = 0 и В2 = 1,889).
Видим, что из всех выборок только Si в 20~й выборке близко к sB = 3,04 (впрочем, то
же самое было и для R-карты).
5.4.1.3. ж- и s-карты для выборок неравного объема
Пусть имеем к выборок объемами щ (г = 1, 2, ..., к). Если объемы выборок не
равны между собой, то, естественно, границы регулирования х- и s-карт будут
меняться от выборки к выборке. В этом случае следует поступать следующим
образом. По всем выборкам находим
к к ni k
х =
к
\ п-
i=l
к
\™^ п-
/ v %
г=1
И S =
Для ж^карты имеем
хц = х — центральная линия; хш = х — AiS — нижняя граница;
хв = х + AiS — верхняя граница;
для s-карты имеем
5Ц = CiS — центральная линия; sH = Вцв — нижняя граница;
5В = B2iS — верхняя граница.
Здесь С^, Вц, B2i —коэффициенты из табл. 238, определяемые для объема каждой
выборки; Ai — коэффициенты, приведенные в табл. 239.
Таблица 239
Значения коэффициентов Ai для ж-карт
Щухарта при неравных объемах
контролируемых выборок
щ
2
3
4
5
6
7
8
9
Ai
2,121
15732
1,500
1,342
1,225
1,134
1,061
1,000
щ
10
11
12
13
14
15
16
17
Аг
0,949
0,905
0,866
0,832
0,802
0,775
0,750
0,728
щ
18
19
20
21
22
23
24
25
Ai
0,770
0,688
0,671
0,655
0,640
0,626
0,612
0,600
5.4]
Контрольные карты
701
Задача 383. В результате контроля получены результаты измерений парамет-
параметра х (средние значения и дисперсии, полученные в результате контроля в выборках
разного объема^ приведены в таблице). Необходимо найти контрольные границы для
х~ и s-карт.
Номер
выборки, г
1
2
3
4
5
6
7
8
9
10
Объем
выборки, щ
8
10
12
7
10
6
8
6
5
12
ж-карта
Xi
1356
1380
1448
1358
1372
1430
1356
1426
1444
1404
si
1281
2570
1901
1384
1430
1672
1354
643
3418
1608
35,8 1353
50,7 | 1357,6
43,6 | 1361
37,2 | 1350
37,8 | 1357,6
40,9 | 1346,3
36,8 | 1353
25,3 | 1346,3
58,5 | 1341,5
40,1 | 1361
Xni
1440
1435.4
1432
1443
1435.4
1446.7
1440
1446л
1451.5
1432
s- карта
39.55
39.88
40,05
40.57
40.21
40,25
40.33
40,33
40,42
40,42
Sni
8.18
12.38
14.96
16.07
16.97
17,79
18.61
19.22
19,92
20,49
SBi
70,30
67.39
65» 13
64.27
63.45
62.71
62.06
61.44
60.91
60,34
Для ж-карты имеем среднюю линию
X] Щ • Xi 8 ¦ 1356 + 10 ¦ 1380 + ... + 12 • 1404
Хи =
¦ 10 + ... + 12
= 1396,5.
Коэффициенты А% определяются для каждой выборки по табл. 239. Например, для
первой выборки имеем п\ = 8 и А\ = 1,061, для второй выборки п<2 = 10 и А2 = 0,949,
и т.д.
Находим оценку средней дисперсии
ЕК -1) ¦
= 1680,4 (Я = 40,99).
Тогда для первой выборки имеем
Жн1 = й-A-L-s = 1396,5-1,061-40,99 = 1353; хв1 = Ш+Аг-s = 1396,5+1,061-40,99 = 1440.
Полученные по аналогии результаты для других объемов выборок приведены в таблице.
Для расчета средней линии и контрольных границ s-карты пользуемся коэффициен-
коэффициентами Сг, Вц и B^i из табл. 238, взятыми для соответствующих объемов выборок щ.
Например, для первой выборки имеем щ = 8, С\ = 0,965, Вц = 0,215 и В21 = 1,75.
Следовательно, средняя линия равна
5Ц1 = Сг • s = 0,965 • 40,99 = 39,55,
а границы регулирования равны:
sHi =Bu-s = 0,215 • 40,99 = 8,18; sBl = B2i • s = 1,715 • 40,99 = 70,30.
Вычисленные по аналогии значения Лщ, sH« и sBi для остальных выборок приведены
в таблице.
Из анализа видно, что среднее значение в третьей выборке выходит за границы регу-
регулирования, а все стандартные отклонения находятся в пределах границ регулирования.
5.4.1.4. Контрольная карта для доли дефектных изделий (р-карта)
Предположим, наблюдается к выборок объемами тц, причем в г-й выборке
фиксируется ТП{ дефектных изделий A ^ г ^ к). Оценкой доли дефектных изделий
в г-ж выборке является величина pi = —.
П
702
Методы исследования связей между случайными величинами
[Гл. 5
Оценка среднего значения доли дефектных изделий р =
является цен™
тральной линией р-карты. Границы регулирования определяются формулами
Если все значения щ отличаются друг от друга незначительно, то используется
единая пара контрольных границ
1 1
п, .,. ,- , \n[l-V]> ¦ ГД6 П=1
'}*'
где гс=-
Задача 384. В результате контроля различных партий получены результаты, при-
приведенные в таблице. Найти границы регулирования р~карты.
Номер
партии, г
1
2
3
4
5
6
7
8
9
10
Объем
выборки, щ
981
1422
1174
1524
1353
847
1535
1248
1296
985
Число
дефектов, rrii
27
87
87
76
80
25
37
19
49
42
Доля
дефектных
изделий, pi
0,028
0,061
0,074
0,050
0,059
0,030
0,024
0,015
0,038
0,043
Границы регу-
регулирования
Рт
3,0234
3,0449
),0568
3,0344
3,0425
¦),0091
3,0085
31H22
"),0211
3,0236
Рвг
13,13622
0,0771
0,0917
13,13655
0,0755
0,0509
0,0395
01K22
0,0549
0,0623
Имеем оценку средней доли дефектных изделий
ю
i=i l
27 + 87 + 87 + ... + 42
981 + 1422 + ... + 985
= 0,0428.
Далее, для каждой выборки вычисляется граница регулирования pMi и pBi. Например,
для г = 1 имеем п\ = 981 и
Рн1 = 0,0428 - 3
рв2 = 0,0428 + 3 •
0^28.A-0,0428) | \
}l
981
= 0,0622.
Рассчитанные по аналогии величины для остальных выборок приведены в таблице,
из которой видно, что доли дефектных изделий во всех выборках находятся в пределах
границ регулирования.
5.4]
Контрольные карты
703
5.4.1.5. Контрольная граница числа дефектов (с-карта)
В серии последовательных выборок фиксируются количества дефектных из-
изделий С{. Контрольная карта для регулирования процесса по числу дефектных
изделий включает в себя:
к
1
центральную линию сц = с = —
— нижнюю границу регулирования сп = с — 3-у/с;
— верхнюю границу регулирования св = с-\- 3-\/с.
Рекомендуется при объеме выборок п ^ 30.
Задача 385. Для данных задачи 384 вычислить параметры с~карты.
с* = 52,9; сн = 52,9-3-^52^) = 31,08; св = 52,9 + 3-^52^=74,72.
Имеем с = — • ^
10 '
Видим, что процесс находится в контролируемом состоянии.
5.4.1.6. Карты индивидуальных значений и скользящего размаха
Карты этого типа используются для контроля индивидуальных значений пара-
параметра х и их колеблемости.
Пусть Xi — г-е текущее значение контролируемого параметра, a Ri = \xi-i — Xi\
(г > 1) — абсолютная величина разностей последовательных пар значений х. Кон™
троль значений Х{ и Ri выполняется с помощью карты скользящего размаха.
Абсолютные значения разностей \xi-i ~~ Xi\ можно рассматривать как размахи
последовательных выборок объема п = 2.
Центральной линией карты Xi является величина
ее нижние и верхние границы равны соответственно
хш = х - 2,59675Й; хв = х + 2,5967511
Для R имеем центральную линию Нц = R =
нияснюю границу
г=1
Rn = 0 и верхнюю границу RB = 3,267Й.
Карты индивидуальных значений (з^~карты) и скользящего размаха (i^-карты)
наиболее удобны в тех случаях, когда наблюдения берутся через большие проме™
ясутки времени. Особенно это важно для изделий, выпускаемых штучно, из которых
формирование контролируемых выборок затруднено.
Задача 386. В результате контроля параметра Х{ десяти изделий получены резуль-
результаты, приведенные в таблице. Найти параметры Xi- и Ri-карт и проверить по ним
стабильность параметра изделия.
Номер
изделия, г
1
2
3
4
5
Значение
параметра, Х{
20,1
19,4
18,2
27,4
17,1
Скользящий
размах
Ri = Xi-i — Xi
0,7
1,2
4,2
5,3
Номер
изделия, г
6
7
8
9
10
Значение
параметра, х^
15,1
21,2
24,3
25,1
20,0
Скользящий
размах
Ri = Xi-i - Xi
2,0
6,1
3,1
0,8
5,1
704 Методы исследования связей между случайными величинами [Гл. 5
Находим
х = - • V Xi = — • 202,9 = 20.29: R = - • Y" R{ = — = 3,167.
я g 10 9 ^ 9
Для жi-карты имеем
Жц = § = 20,29; жн = I - 2,6596 • Л = 20,29 - 2,6596 • 3,167 = 11,867;
хв = Ш + 2,6596 • R = 20,29 + 2,6596 • 3,167 = 28,172.
Видим, что все индивидуальные значения Xi находятся в поле регулируемого состо-
состояния.
Для Ri-карты получаем (из таблицы имеем R4 = R = 3,167): RM = 0 и RB = 3,267 х
х 3,167 = 10,346. Ни одно из текущих значений Ri не выходит за пределы зоны
регулируемого состояния.
5.4.2. Контрольные карты накопленных сумм (ККНС)
Контрольные карты накопленных сумм получили широкое применение в послед™
ние 30 лет. Карты этого типа более чувствительны, чем карты Шухарта, к скачко-
скачкообразным изменениям параметров. Теория и практика применения ККНС рассмо-
рассмотрены в [613-615].
Техника ККНС по существу является реализацией последовательной выбороч-
выборочной процедуры. Если в рассмотренных выше картах Шухарта на них наносятся
точки, соответствующие отдельным наблюдениям, то точки, наносимые на ККНС,
не соответствуют отдельным наблюдениям, вычисленным по одной выборке. Все
они, начиная с исходного, дают информацию о наблюдениях от первого до послед-
последнего. В ККНС рассматриваемая точка равняется значению текущего наблюдения
плюс значение некоторой статистики, вычисленной по предшествующей выборке.
Рассмотрим алгоритм формирования ККНС и принятия решения с их помощью.
Через yi будем обозначать значение контролируемого параметра в г-й выборке,
а через Щ —нижние (верхние) контрольные границы, с которыми сравнивается
полученное значение у^.
В отличие от карт Шухарта контролируемый параметр yi является суммой всех
предыдущих наблюдений, а контрольные границы у^ меняются с каждым вновь
полученным наблюдением. Контрольные границы являются линейной функцией
каждого наблюдения, т. е.
?QB' = аш =р Ьг, г = 1, ..., га, где ат = уш =Ь Ь(т + d).
Таким образом, для каждой новой га-й выборки находятся параметры ат и Ь
контрольных границ, с которыми сравниваются все предыдущие значения у±
(г = 1, ..., га — 1) контролируемого параметра.
Если контролируется нижнее значение параметра (т. е. требуется, чтобы хп ^ /л,
где /л — нормативное значение параметра), то используется контрольная граница
Ут = ат - hi = Ут + Ь (ш + d) - Ы
(хп — некоторый контролируемый параметр, например, среднее или дисперсия).
Если при любом г = 1, ..., га — 1 будет наблюдаться неравенство у^ > у^, то
в точке га следует признать значимый сдвиг вниз контролируемого параметра. По
аналогии для контроля верхнего значения (т. е. требуется, чтобы хп ^ /л) использу-
используется неравенство у± < у^ = ут — Ъ (га + d) + Ы (тогда в га-й выборке фиксируется
значимый сдвиг контролируемого параметра вверх).
В случае двустороннего контроля (т. е. когда необходимо фиксировать хп = /л)
используется интервальная оценка у^ < у{ < у^.
5.4] Контрольные карты 705
Если неравенство удовлетворяется, то равенство хп = /л не отклоняется, если
нет — фиксируется значимый сдвиг параметра либо вверх, либо вниз. Параметр Ъ
в уравнении для ут определяется минимальным сдвигом параметра, который дол™
ясен быть выявлен в процессе контроля, и масштабным коэффициентом Aj, равным
отношению числа единиц ординаты ^, приходящихся на единицу абсциссы Х{.
Параметр d определяется выбранным значением ошибки первого рода а (веро-
ятностью отвергнуть правильную гипотезу), а также разбросом значений контроли-
контролируемого параметра хп (при этом предполагается, что ошибка второго рода /3 < 0,01,
т. е. мощность процедуры A — /3) > 0,99). Подробнее технику ККНС продемонстри-
продемонстрируем на примерах конкретных контрольных карт.
5.4.2.1. ККНС для среднего значения
Пусть Xi—среднее г-й выборки объема п. Величиной, подлежащей контролю,
является накопленная сумма
Уг = —
где /л — нормативное значение контролируемого параметра и % — стандартное от-
отклонение среднего. Обычно рекомендуется выполнить оценку % по первым т
выборкам
d = —2 ^па5 гДе ^ = —' а — ошибка первого рода.
S S
п — объем выборки (предполагается, что все выборки равного объема п). Если
тп(п ~~ 1) > 30 ^ 40, то оценка достаточно точна.
Величина D = A/i определяется минимальным недопустимым сдвигом сред-
среднего относительно нормативного значения /л. Параметры Ъ и d равны: Ъ = —,
2 , D
Если производится односторонний контроль (т. е. контроль того факта, что х > /л
или х < /i), то используется значение а. Если контролируется уход среднего в лю-
любую сторону (т. е. контроль того, что х Ф //), то вместо а используется величина 2а.
Таким образом, контрольные границы, полученные после появления га-й выбор-
выборки равны
— для одностороннего контроля
~н- D ( 2 \ D ' " - 1
т т 2 ^ E2/2'
~в _ ^^ 2 I А ^ • • _ 1 о
2/m "~ 2^w о" 1Т7г^72'^11а) "I" "^"г5 г — 1, 2, ..., ??г — 1;
— для двустороннего контроля
Если для некоторого значения yi имеет место одно из неравенств yi > у^;
У г < Ут") Ут < У г ^ ^т? ТО в выборке с номером тп признается соответственно сдвиг
среднего значения вниз, вверх или в любую сторону с вероятностью 1 — а.
Легко видеть, что сдвиг в каждой zz-й выборке контролируется вычислением
~н(в)
по полученному значению yv новых контрольных границ yv и сравнением их
с ранее полученными значениями ^, г < v. Легче всего, естественно, использовать
23 А. И. Кобзарь
706
Методы исследования связей между случайными величинами
[Гл. 5
специальные шаблоны [14, 97], которые позволяют избежать вычислений. Мы же
поясним технику применения ККНС для среднего на конкретном примере.
Задача 387. По данным, приведенным в таблице, найти параметры для ККНС сред-
среднего и проверить стабильность среднего по отношению к нормативному значению
\i = 27, полагая, что недопустимым является отклонение D = А/л = 5 единиц. При-
Принять а = 0.1 и п = 5.
Номер
выборки, i
1
2
3
4
5
Xi
25
36
21
9
31
л
2,4
6,1
4,2
3,8
2,9
Уг
-1,04
3,65
0,52
1,56
2,65
Номер
выборки, г
6
7
8
9
10
Xi
34
16
28
30
24
л
si
3,2
2,1
4,1
4,2
Q Q
О,О
Уг
7,30
1,56
2,08
3,65
2,08
Имеем т = 10 и находим s% = — • ]Р S% = 3,68 (s& = 1,918).
Имеем Ь = D/2 = 5/2 = 2,5. Далее рассмотрим задачу одностороннего контроля ниж-
нижнего значения х% (т. е. контролем должен быть выявлен факт снижения х по сравнению
с /л = 27 более, чем на 5 единиц).
Имеем 5 = — = 2,607; d = —~ • In а = =¦ * 1п0Д = 0,677.
sx <Г 2,6072
Тогда для контроля некоторой j-ш (j = 2,3, ...) выборки имеем порождаемые ею
верхние контрольные границы для г = 1, ..., j — 1 предыдущих значений yi:
В нашем случае они равны
j = 2(i = 1): yf = 3,65 + 2,5 • B + 0,677) - 2,5 • г = 10,34 - 2,5 • г;
yf = 0,52 + 2,5 • C + 0,677) - 2,5 • г = 9,71 - 2,5 • г;
yf = 1,56 + 2,5 • D + 0,677) - 2,5 • г = 13,25 - 2,5 • г;
yf = 3,5 + 2,5 • E + 0,677) - 2,5 • г = 17,84 - 2,5 • г;
yf = 7,30 + 2,5 • F + 0,677) - 2,5 • г = 16,9 - 2,5 • г;
yf = 1,56 + 2,5 • G + 0,677) - 2,5 • г = 29,75 - 2,5 • г;
yf = 2,08 + 2,5 • (8 + 0,677) - 2,5 • г = 23,77 - 2,5 • г;
yf = 3,05 + 2,5 • (9 + 0,677) - 2,5 • г = 27,84 - 2,5 • ц
•, 9): 2/iJ = 2,08 + 2,5 • A0 + 0,677) - 2,5 • г = 28,77 - 2,5 • г.
Порождаемые этими уравнениями переменные верхние контрольные границы
приведены в таблице:
J = 3
j = 4
3 = 5
j = 6
3 = 7
J = 8
j=9
(» = 1
(i = l
(» = 1
(i = l
(г = 1
(i = l
(« = 1
j = 10 (г =
,2):
,2,3)
, • • •
, • ¦ ¦
, ...
, ...
, • • •
1, ..
,4):
,5):
,6):
,7):
,8):
.,9
j
2
3
4
5
6
7
8
9
10
l/i
-1,04
7,84
7,21
10,75
15,34
14,19
18,25
21,27
25,34
26,27
У2
3,65
4,71
8,25
12,84
11,69
15,75
18,77
22,84
23,77
Экспериментальные значения у
Уз
0,52
5,75
10,34
9,19
13,25
16,27
20,34
21,27
2/4
1,56
7,84
6,69
10,75
13,77
17,84
18,77
2/5
3,65
4,19
8,25
11,27
15,34
16,27
2/6
7,30
5,75
8,77
12,84
13,77
2/7
1,56
6,27
10,34
11,27
2/8
2,08
7,84
8,77
2/9
3,65
6,27
5.4]
Контрольные карты
707
Из таблицы видно, что значимый сдвиг среднего вниз произошел в седьмой вы-
выборке, так как ув = 7,3 > t/?6 = 5,75 (выпадающее наблюдение в таблице выделено). Из
примера следует одно основное преимущество ККНС — она фиксирует сдвиг среднего
вниз по двум последовательным значениям контролируемых сумм, что очень важно
при непрерывном контроле производства и позволяет непрерывно и оперативно на него
воздействовать. Уменьшение среднего в седьмой выборке до 16 уверенно выявляется
контролем с помощью ККНС.
Теперь по аналогии (для демонстрации техники и развития навыков вычисления
и анализа ККНС) рассмотрим задачу сдвига среднего вверх. В этом случае необходимо
использовать контрольные границы
У? = Уз - 2,5 • (j + 0,677) + 2,5 • г, г < j.
В нашем случае это приводит к контрольным границам
j = 2(i = l):
j = 3(z = l,2):
3 =4 (i = 1,2,3):
j = 5 (г = 1, ...,4):
j = 6(i = l, ...,5):
j = 7 (i = 1,2, ...,6):
j = 8B = l,...,7):
j = 9(z = l, ...,8):
j = 10 (г = 1, ...,9):
$P = 3,65 - 2,5 • 2,677 + 2,5 • г = -3,04 + 2,5 • г;
Уз'
У?
ш
= 0,52-2,5-3,677-
= 1,56- 2,5 -4,677-
2,5 • г = -8,67 + 2,5 • г;
2,5 • г = -10,13 + 2,5 • ц
= 3,65 - 2,5 • 5,677 + 2,5 • г = -10,54 + 2,5 • г;
уТ = 7,30 - 2,5 • 6,677 + 2,5 • г = -9,39 + 2,5 • г;
у^ = 1,56 - 2,5 • 7,677 + 2,5 • г = -17,63 + 2,5 • г;
Уз* = 2,08 - 2,5 • 8,677 + 2,5 • г = -19,61 + 2,5 • г;
Уэ* = 3,65 - 2,5 • 9,677 + 2,5 • г = -20,54 + 2,5 • г;
yio = 2,08 - 2,5 • 10,677 + 2,5 • г = -24,61 + 2,5 • г.
Вычисленные контрольные границы Щг приведены в таблице:
i
2
3
4
5
6
7
8
9
10
Экспериментальные значения гц
2/1
-1,04
-0,54
-6,17
-7,63
-8,04
-6,89
-15,13
-17,11
-18,04
-22,11
2/2
3,65
-3,67
-5,13
-5,54
-4,39
-12,63
-14,61
-15,54
-19,61
2/з
0,52
-2,63
-3,04
-1,89
-10,13
-12,11
-13,04
-17,11
2/4
1,56
-0,54
-0,61
-7,63
-9,61
-10,54
-14,61
2/5
3,65
-3,11
-5,13
-7,11
-8,04
-12,11
2/6
7,30
-2,63
-4,61
-5,54
-9,61
2/7
1,56
-2,11
-3,04
-7,11
2/8
2,08
-0,54
-4,61
2/9
3,65
-2,11
Из таблицы видно, что сдвиг среднего значения вверх происходит во второй выборке
(г/1 = —1,4 < у\ = —0,54). Таким образом, увеличение среднего с 25 в первой выборке
до 36 во второй выборке является значимым, что и выявила контрольная карта.
5.4.2.2. ККНС выборочных размахов
Карты этого типа используются для контроля изменчивости рассеяния в выбор-
выборках. Контролируемым параметром является сумма размахов
Уъ = 5^^г5 гДе ^i = ^imax ~~ %i min —размах г-Й Выборки.
г
Параметры уравнения для контрольных границ вычисляются по формулам
In —
Ь = а®сь>~
(То
d= -2
In a
(Т\
и ш —
23*
708
Методы исследования связей между случайными величинами
[Гл. 5
Здесь сто — нормативное значение стандартного нормального отклонения (опреде™
ляется предварительно по специально проведенным испытаниям); изменение
значения стандартного нормального отклонения, которое должно быть выявлено
с достоверностью не менее 1 — а; а — ошибка первого рода; с, v — коэффициенты,
зависящие от п (приведены в табл. 240).
Таблица 240
Коэффициенты с и и для ККНС выборочного размаха [97, 617]
п
с
V
3
0,233
7,27
4
0,188
10,95
5
0,16
14,49
6
0,142
17,86
7
0,128
21,08
8
0,118
24,11
9
0,11
27,01
10
0,103
29,82
Практически важно контролировать увеличение разброса значений, чтобы во™
время принять меры для стабилизации контролируемого параметра. Поэтому будем
рассматривать односторонние ККНС для выявления сдвига вверх значения а.
Уравнение для контрольной границы в этом случае имеет вид
Щ = Уз ^Ь (j + d)
Ы,
г <
или для нашего случая
У] = Уз
In —
сто
i-2-
In a
0~\
и ш —
0"о .
1 al
In —
GQ ¦
¦ <JqCI/ —I.
0"!
Если уi < Щ для какого-либо i < j, то в j-й выборке происходит значимое
увеличение разброса значений контролируемой величины.
Задача 388. В результате испытаний т = 10 выборок изделий объемом п = 5 каэюдая
получены следующие результаты:
г
Ri
1
1,4
1,4
2
1,6
3,0
3
1,5
4,5
4
1,8
6,3
5
0,9
7,2
6
3,1
10,3
7
1,5
11,8
8
1,6
13,4
9
1,8
15,2
10
1,4
16,6
Предварительно известно^ что ао = 0,5 и критическое значение <л = 0,72. Выбираем
а = 0,1. Необходимо найти параметры ККНС для размахов и проанализировать с ее
помощью полученные данные.
Выбираем к = 2 и для п = 5 находим из табл. 240 с = 0,160 и v = 14,49.
Далее вычисляем
(П Л 0,72
In — In
ао • с • v
Ь =
= 0,5 • 0,160 • 14,49 •
= 1,384; d = ——¦ = 0,871.
1 -
0,50
14,49 • In
0,72
0,72 0,50
Тогда уравнения для контрольных границ имеют вид
щ = Уз ^ 1,384 • (j + 0,871) + 1,384 • i.
Результаты расчета граничных значений Щ приведены в таблице:
5.4]
Контрольные карты
709
3
2
3
4
5
6
7
8
9
10
У\
1,4
0,41
0,53
-0,86
0,46
2,17
2,29
2,50
2,92
2,94
2/2
3,0
1,91
0,53
1,84
3,56
3,67
3,88
4,30
4,32
Экспериментальные
2/3
4,5
1,91
3,22
4,94
5,06
5,27
5,69
5,70
2/4
6,3
4,61
6,32
6,44
6,65
7,07
7,09
2/5
7,2
7,71
7,83
8,04
8,46
8,47
значения
2/6
10,3
9,21
9,42
9,84
9,85
Уг
2/7
11,8
10,80
11,22
11,24
2/8
13,4
12,61
12,61
2/9
15,2
14,00
Из нее видно, что разброс существенно возрастает в шестой выборке, что фиксируется
переходом значений у г в критическую зону (отмечено жирным курсивом в таблице).
5.4.2.3. ККНС для выборочных дисперсий
Рассматриваем, как и в предыдущем разделе, одностороннюю контрольную кар-
карту, выявляющую увеличение (сдвиг вверх) дисперсии. Контролируемым парамет-
параметром является теперь у^ =
sf, где /^ = п^ — 1, в^ —объем г-й выборки. На оси аб-
сцисс откладывается величина Xi = ]P fi. Параметры для уравнения контрольной
границы находятся по формулам [97], где а^ о\—как и выше (см. раздел 5.4.2.2),
соответственно нормативное (<Tq) и допустимое (erf) значения дисперсии.
Уравнение для контрольной границы имеет вид
В нашем случае Щг = yj —
yf =У3-Ь (Xj + d) + Ьхг, i < j.
In a
О 2 i °
2cr0 In —
In —
(TO .
Если yi < yj1 (i < j), то сдвиг дисперсии вверх (рост разброса контролируемых
величин) признается значимым.
Задача 389. Для данных, приведенных в таблице, найти параметры ККНС для дис-
дисперсий и провести анализ данных при а = 0,1:
Номер
выборки, %
1
2
3
4
5
6
7
8
9
10
щ
5
10
8
9
8
5
5
7
6
7
?(*t -1)
4
13
20
28
33
37
41
47
52
58
3,12
4,10
3,90
5,10
9,20
4,80
4,10
3,80
4,50
5,00
ЕК - 1)*?
12,48
49,38
76,68
117,48
163,48
182,68
199,08
224,16
246,66
276,66
Известно, что сг% = 2 и а\ = 2,5.
710
Методы исследования связей между случайными величинами
[Гл. 5
Вычисляем параметры уравнения контрольных границ:
b =
1- I —
1 -
\ = 4,959; d = -^^ = 10,319.
2,5
Тогда получаем yf = yj - 4, 959 • (j + 10, 319) + 4, 959 • г, г < j.
Результаты расчета контрольных границ у™ приведены в таблице.
3
2
3
4
5
6
7
8
9
10
2/1
3,12
-1,79
^53,80
-52,70
-31,50
-32,10
-35,57
^40,24
-42,50
-42,30
2/2
49,38
^9,20
-8,08
13,13
12,49
9,05
4,38
2,09
2,33
Экспериментальные значения у
Уз
76,68
26,63
47,84
47,12
47,77
39,09
44,63
37,05
2/4
117,48
87,51
86,86
83,44
78,76
79,34
76,72
2/5
163,48
111,71
108,23
103,56
119,02
101,51
2/6
182,68
128,07
123,40
143,81
121,35
г
2/7
199,08
143,24
163,65
141,18
2/8
224,16
193,40
170,94
2/9
246,66
195,73
Из таблицы видно, что все опытные значения лежат выше критической границы.
Следовательно, смещение дисперсии вверх не обнаруживается.
5.4.2.4. ККНС для доли дефектных изделий
В качестве контролируемой величины используется
= ^ Х{, где Х{ — число
i
дефектных изделий в выборке объема п. Так как практический интерес предста™
вляет случай превышения некоторой нормативной доли дефектных изделий ро5 то
будем рассматривать одностороннюю контрольную карту. Цель такой карты — свое-
своевременно зафиксировать превышение нормативной долей дефектных изделий р® ее
допустимого уровня pi.
Параметры такой контрольной карты вычисляются по формулам
nln
ро
ъ =
1~Pi . л^
d= —
In a
In-
nln
1 -po *
po A -po) """ 1-pi
Уравнения для контрольных границ имеют вид
nln
1- Ро
1-Р1
In a
nln
1 ^
1-pi ,
In
Po A -pi)
nln
1 - Po
1-PI
In
Po A -pi)
< j-
Если yi < Щ% ч то следует вывод о значимом росте доли дефектных изделий
в производстве.
5.4]
Контрольные карты
711
Задача 390. В результате испытаний т = 10 партий изделий объема п = 100 каждая
получены количества дефектных изделий в каждой выборке (данные приведены в та-
таблице). Найти параметры ККНС для доли дефектных изделий при а = ОД, ро = 0,02
и р\ = 0,03.
Номер
выборки, i
Xi
1^ хг
1
3
3
2
1
4
3
1
5
4
00 СО
5
2
10
6
2
12
7
5
17
8
1
18
9
3
21
10
2
23
Вычисляем параметры ККНС для доли дефектных изделий
-0,02 х
In 0,1
100 • lr
b =
In
1 - 0,03
0,03 • A - 0,02)
= 2,46716; d= —
100 ¦ In
- 0,02
- 0,03
[0,02- A -0,03),
Следовательно, yf = y, - 2,467 • (j + 2,245) + 2,467 • i.
Расчеты значений контрольных границ у*-г сведем в таблицу.
= 2,245.
J
2
3
4
5
6
7
8
9
10
У1
3
-4,00
-5,47
-4,94
-5,41
-5,87
-3,34
-4,80
-4,27
-4,74
У2
4
-3,00
-2,47
-2,94
-3,41
-0,87
-2,34
-1,81
-2?27
Экспериментальные
Уз
5
-0,01
-0,47
-0,94
1,59
0,13
0,66
0,19
2/4
8
1,99
1,53
4,06
2,59
3,13
2,66
2/5
10
3,99
6,53
5,06
5,59
5,13
значения
2/6
12
8,99
7,53
8,06
7,59
Ш
2/7
17
9,99
10,53
10,06
2/8
18
12,99
12,53
2/9
21
14,99
Из таблицы следует, что ни одно значение yi не попадает в зону контроля, следова-
следовательно, нет оснований считать, что доля дефектных изделий в выборках отличается от
нормативной.
5.4.2.5. ККНС для числа дефектных изделий, основанная на распределении
Пуассона
Координаты точек ККНС те же, что и в предыдущем разделе (г, J^a^). Пара-
Параметры ККНС вычисляются по формулам
In a
b =
d= —
где /jLq — нормативное значение числа дефектных изделий; \i\ — сдвиг числа дефект™
ных изделий, который должен быть обнаружен контролем; а — ошибка первого рода
(рекомендуемые значения 0,01; 0,05; 0,1).
Уравнение для контрольной границы односторонней ККНС с контролем сдвига
вверх числа дефектных изделий имеет вид
Щ% = Uj ~ Ь (j + d) + 6i, i < j.
Если yi < Щг (i < j) , то увеличение количества дефектных изделий признается
значимым.
712
Методы исследования связей между случайными величинами
[Гл. 5
Задача 391. Результаты испытаний партии изделий приведены в таблице. Норма-
Нормативное значение fio = 3, допустимое \х\ = 5, а = ОД. Найти параметры ККНС для
числа дефектных изделий и провести анализ полученных результатов.
Номер
выборки, г
Число
дефектов, xi
?*.
1
3
3
2
4
7
3
2
9
4
2
11
5
3
14
6
4
18
7
9
27
8
3
30
9
2
32
10
2
34
Вычисляем
Ь= — =3,915;
5-3
Тогда t/f = yj - 3,915 • (j + 1,151) + 3,915 • г, г < j
Расчеты контрольных границ t/J* сведем в таблицу.
3
2
3
4
5
6
7
8
9
10
3
-1,42
^3,33
-5,25
-6,17
-6,08
-1,00
-1,91
-3,82
-5,74
2/2
7
0,58
-1,34
-2,25
-2,17
-2,92
2,00
0,09
-1,82
Экспериментальные
2/3
9
2,58
1,66
1,75
6,83
5,92
4,00
2,09
2/4
11
5,58
5,66
10,75
9,83
7,92
6,00
2/5
14
9,58
14,66
13,75
11,83
9,92
значения
2/6
18
18,58
17,66
15,75
13,83
Уг
2/7
27
21,58
19,66
17,75
2/8
30
23,58
21,66
2/9
32
25,58
Из таблицы видим, что в седьмой выборке значимо выросло количество дефектных
изделий B/5 = 15 < f/y = 14,66 и у% = 18 < у? = 18,58). Применение ККНС позволило
оперативно выявить этот сдвиг.
5.4.3. Относительная эффективность контрольных карт
У инженера производства может возникнуть закономерный вопрос: которую из
контрольных карт следует применять? Вообще говоря, для того, чтобы дать более
полный ответ на вопрос, следовало бы знать, чего же хочет инженер: упростить
вычисления, обеспечить высокую эффективность контроля, какие изменения кон™
Таблица 241
Относительная эффективность различных контрольных карт [14]
Причина изменения
Отклонение с пересечением (грубое)
Сдвиг среднего
Сдвиг дисперсии
Медленная флуктуация (тренд)
Быстрая флуктуация (колебания)
Карты Шухарта
ж-карта
1
2
2
i?-карта
2
2
1
1
«s-карта
3
2
ККНС
3
1
1
5.4] Контрольные карты 713
тролируемого процесса хотел бы он зафиксировать? Ответы на эти вопросы может
дать только консультация, проводимая специалистом с учетом всех особенностей
и специфики решаемой задачи. Однако самые общие рекомендации можно дать —
они представлены в табл. 241. В таблице приняты следующие оценки: 1 — наибо™
лее эффективна; 2 — следующая по эффективности; 3 — наименее эффективна; 4 —
(прочерк) неприменима.
5.4.4. Контроль без использования контрольных карт
Для администратора не являющегося статистиком, контрольные карты Шухар-
та, а тем более ККНС, являются трудно усвояемыми, так как требуют привлече™
ния специальных терминов, вычислений по формулам, применения специальных
таблиц. Поэтому были предприняты попытки создать простейшие методы стати-
статистического анализа, которые не требуют ни таблиц, ни вычислений.
Один из таких методов описан в [618]. Правила и логика метода состоят в еле™
дующем. Для непрерывного производства, т. е. когда можно говорить о производ-
производстве с определенной „настройкой", оператор-контролер, работающий с контроль-
контрольным устройством, снабжается следующей инструкцией. На контрольном устройстве
отмечаются красным цветом зоны, соответствующие браку: для одностороннего
контроля — одна зона, для двустороннего контроля — две. Далее на контрольном
устройстве помечаются зеленым и желтым цветами зоны контроля в соответствии
с диаграммой:
— для двустороннего контроля
100%
Красная зона
Желтая зона
25%
Зеленая зона
50%
Желтая зона
25%
Красная зона
-для одностороннего контроля
100%
Зеленая зона
50%
Желтая зона
50%
Красная зона
Для контроля используется правило двух последовательных изделий. Если без
изменения настройки производства последовательно получаем два „зеленых" или
одно „зеленое" и одно „желтое" изделие, то работа продолжается без изменений.
Однако всегда в начале смены и после поступления новой партии изделий
работу следует начинать только после получения пяти последовательных „зеленых"
изделий. Если получается „желтый" результат, следует начать подсчет „зеленых"
изделий заново, и так до тех пор, пока не будут получены пять последовательных
„зеленых" изделий.
Если после настройки в процессе работы получены подряд два „желтых" ре-
результата на одной и той же стороне допуска, то требуется „регулировка в центр"
(это должен уметь делать оператор производства). Затем обязательна проверка по
правилу — пять „зеленых" подряд.
Появление двух „желтых" по разные стороны от центра требует вмешательства
руководителя производства (увеличилось рассеяние результата). После устранения
причины этого увеличения требуется опять получить пять „зеленых" изделий под-
подряд.
714 Методы исследования связей между случайными величинами [Гл. 5
Коротко повторим основные правила метода системв! контроля стабилвности
производства:
— начинать с пяти „зеленых";
— продолжать работу всегда, если подряд получены два „зеленых" либо „зеле-
„зеленое" и „желтое" изделия;
— если получены подряд два „желтых" изделия, регулировать настройку произ™
водства;
— после регулировки снова требуется получить пять „зеленых" изделий подряд.
Естественно, такой метод контроля наиболее эффективен в поточном массовом
производстве однотипных изделий, к производству которых применимо понятие
„настройка".
5.5] Математика-статистические методы планирования эксперимента 715
5.5. Математико-статистичесжие методы
планирования эксперимента
Планирование эксперимента предполагает определение наиболее эффективной
стратегии его проведения с целью получения статистического материала, обладаю-
обладающего заранее заданными свойствами.
С примером такого планирования мы уже встречались в разделе 5.3.3.2 (исполь-
(использование равноотстоящих значений независимой переменной при поиске нелинейной
регрессии).
Планирование эксперимента применяется при решении таких задач, как оценка
параметров распределения, проверка статистических гипотез при заданной мощ-
мощности критерия, нахождение математической модели процесса с заданными ста-
статистическими свойствами, поиск оптимальных по заданным критериям условий
протекания изучаемого процесса.
Многие из методов уже рассматривались нами в соответствующих разделах.
В настоящем разделе мы уделим особое внимание математическим методам плани-
планирования эксперимента для изучения механизма наблюдаемого процесса и построе-
построения его статистической модели.
В последние годы математическая теория активного эксперимента, бурно раз-
развиваясь, оформилась в самостоятельное прикладное направление математической
статистики [619, 620]. Автор далек от мысли изложить стройные основы теории
планирования эксперимента. Скорее всего, он в состоянии предложить читателю
введение в „прихожую" таких основ. Однако автор надеется дать основные понятия
и изложить простейшие прикладные методы планирования эксперимента, вполне
доступные специалистам с общим высшим образованием.
5.5.1. Планирование регрессионных экспериментов
при изучении механизма явленим (статистическое моделирование)
Задача планирования эксперимента может быть сформулирована следующим
образом: требуется получить некоторое представление о поверхности отклика, опи-
описываемой моделью у = /(#1, #2, • • • ? хп) ? гДе У— зависимая переменная-отклик (на-
(например, долговечность изделия); Х{ — независимые переменные — влияющие на от-
отклик факторы, которые можно варьировать в ходе эксперимента (например, пара-
параметры режима нагружения изделия).
Неизвестная функция отклика чаще всего представляется полиномом Aj-й степени
к к к
У = bO + J2 biXi + J2 b^jxixj + J2 ЬИХ1 + * * * >
где 5q, &i> biji bu— коэффициенты полинома.
Планирование эксперимента заключается в выборе на каждом этапе исследова-
исследования оптимального в принятых критериях расположения экспериментальных точек
в пространстве факторов. В качестве критериев оптимальности планов использу-
используются:
— минимизация числа опытов;
— простота вычислений коэффициентов функции отклика;
— независимость оценок коэффициентов функции отклика (ортогональность
плана);
— однородность дисперсий отклика относительно центра плана (ротатабель-
ность плана);
— минимизация объема эллипсоида рассеяния оценок коэффициентов модели
(D-оптимальность плана).
716 Методы исследования связей между случайными величинами [Гл. 5
Наибольшее применение нашли ортогональные планы в сочетании с критериями
D-оптимальности.
Как правило, исследователь ищет поверхность отклика в какой-то определенной
области изменения факторов. Наиболее широко применяется планирование на двух
уровнях (экстремальный эксперимент), когда в эксперименте используются значе-
значения факторов, соответствующие верхней и нижней границам интервала его варьи-
рования. Эти значения называются верхним и нижним уровнями и обозначаются
+1 и — 1 соответственно (или просто + и —). Экспериментальные планы, в которых
все факторы варьируются только на двух уровнях, называются планами 2fe, где к —
число варьируемых факторов.
При построении плана эксперимента исследователь должен исходить из некото™
рого априорного представления о возможном виде функции отклика (линейность,
монотонность и т.п.). Сначала область варьирования факторов определяется исхо-
дя из предположения о линейности поверхности отклика внутри этой области. Если
линейная поверхность отклика описывает экспериментальный материал неадекват-
но, то проводятся дальнейшие эксперименты по уточнению ее вида с помощью
полиномов более высокого порядка.
Более полное изложение математической теории планирования эксперимента
содержится в [621—625].
5.5.1.1. Линейные ортогональные планы (планирование первого порядка)
5.5.1.1.1. Полный факторный эксперимент
Примером плана, позволяющего получить независимые оценки коэффициентов
поверхности отклика, является полный факторный эксперимент (ПФЭ), реализую-
реализующий все возможные неповторяющиеся комбинации уровней независимых факторов
(ранее планы такого типа мы обсуждали применительно к задачам дисперсионного
анализа).
В настоящем разделе ПФЭ рассматриваются применительно к условиям актив-
активного экстремального эксперимента.
Рассмотрим в качестве примера ПФЭ для трех факторов (к = 3). Поверхность
отклика в этом случае имеет вид
У = bo + ^2
г=1
Пусть каждый фактор Х{ варьируется от основного уровня ж^о на величину
. Тогда с помощью преобразования Х{ = —Ц—— можно перейти к кодирован-
ным переменным ж^, принимающим на границах интервала варьирования х\ значе-
значения ±1. План экстремального эксперимента принято записывать в виде матрицы,
определяющей в кодированных переменных Х{ условия проведения эксперимента
(в дальнейшем под Х{ будем понимать кодированные переменные без специаль-
ных оговорок). Пример матрицы ПФЭ для трех факторов приведен в табл. 242.
В литературе принято ^-факторный ПФЭ с изменением факторов на двух уровнях
называть планом типа 2к.
В дальнейшем будем обозначать через y^v значение отклика, полученное в i/-m
эксперименте при условиях (сочетании уровней факторов а^), соответствующих j-й
точке плана, и через хц — значение фактора х\ в j-й точке плана.
5.5]
Математика-статистические методы планирования эксперимента
717
Таблица 242
Матрица полного факторного эксперимента (ПФЭ) 23
Номер точки
плана, j
1
2
3
4
5
6
7
8
Хо
+
+
+
+
+
+
+
+
XI
—
+
+
+
+
х2
—
+
+
+
+
—
+
+
+
+
Х\Х2
+
+
+
+
Х\Х%
+
+
+
+
Ж2Ж3
+
+
+
+
Ж1Ж2Ж3
—
+
+
+
+
Отклик
Уз
2/1
2/2
2/з
2/4
2/5
2/6
2/7
2/8
Для ПФЭ имеют место соотношения (n = 2fc —число точек плана):
что соответствует свойству ортогоналвности столбцов матрицвх плана.
Любой план 2к мож:ет быть построен по следующему простому правилу: в столб-
столбце, соответствующем фактору ж^, знаки + и — чередуются через 2г—1. План 2к
позволяет оценить 2к коэффициентов регрессии Ь\. Однако использовать ПФЭ для
оценки коэффициентов при членах с кратностью нельзя, так как оценки для bo и Ьц
смешиваются (например, столбцы xq и Х{Х{ неразличимы).
Основным преимуществом ПФЭ является ортогональность матрицы плана, что
позволяет существенно упростить вычисление коэффициентов уравнения отклика.
Для любого числа факторов к выборочные оценки bi вычисляются по форму-
формулам [621]
г=1
-I
т — число параллельных опытов в j-й точке плана; п — общее число точек плана.
Дисперсия, характеризующая разброс значений yjv при постоянных условиях экс™
z/=l
перимента (т.е. в одной точке плана), находится по формуле 5| =
Общая дисперсия, характеризующая разброс отклика безотносительно к условиям
-j n -j n m
эксперимента, равна S$ = - J2 S] = п(т^в J2 J2 (Уз» ~ Уз? •
3 = 1
Если количество параллельных опытов в точках плана различно, то
?2 _ J = 1
-, где nij — число опытов в j-й точке плана.
718
Методы исследования связей между случайными величинами
[Гл. 5
Предварительно однородность дисперсий 5| должна быть проверена одним из
методов, изложенных в разделе 4.1.1.4.
Дисперсия коэффициента регрессии bi определяется формулой
n(m-
г Si
Коэффициент Ь{ уравнения отклика с достоверностью а признается значи™
мым, если \bi\ > ti+g (/) Shi•> гДе ^i+<*—квантиль распределения Стьюдента при
2 Ъ 2
f = п(т — 1) степенях свободы.
Для проверки адекватности математической модели отклика используется дис™
п
— Vj) i где d — число коэффициентов аппроксимирующего
персия S2 =
i
полинома; yj—значение отклика, предсказываемое регрессионной моделью. Аде-
Адекватность модели устанавливается сравнением дисперсий S2 и
S
терия Фишера F = — при
S
y с помощью кри-
=n~dnf2 = n (га — 1) степенях свободы.
y
Если все коэффициенты линейной регрессии (в том числе и все коэффициенты
при взаимодействиях) являются значимыми, то d = п и не остается степеней свобо-
свободы для проверки гипотезы адекватности. В этом случае рекомендуется поставить
эксперименты в центре плана (т.е. при значении фактора Xi = 0). Тогда, если
|&о ~~ Уо| < Sy, где |/о — среднее значение отклика в центре эксперимента, линейная
модель признается адекватной.
Задача 392. Построить матрицу ПФЭ 25.
При построении матрицы плана эксперимента будем исходить из правила чередова-
чередования для фактора Xi знаков + и — через каждые 2*™1 знаков. Например, для фактора ж 4
знаки должны чередоваться через 24™1 = 8 знаков. Следуя этому правилу, получаем
матрицу плана эксперимента ПФЭ 25:
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
XQ
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
XI
+
—
+
—
+
—
+
—
+
—
+
—
+
—
+
Х2
+
+
—
—
+
+
—
—
+
+
—
—
+
+
—
хз
+
+
+
+
—
—
—
—
+
+
+
+
—
—
—
Х4
+
+
+
+
+
+
+
+
—
—
—
—
—
—
—
Х5
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
3
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
XI
+
—
+
—
+
—
+
—
+
—
+
—
+
—
+
х2
+
+
—
—
+
+
—
—
+
+
—
—
+
+
—
хз
+
+
+
+
—
—
—
—
+
+
+
+
—
—
—
Х4
+
+
+
+
+
+
+
+
—
—
—
—
—
—
—
Х5
—
—
—
—
—
—
—
—
—
—
—
—
—
—
5.5]
Математика-статистические методы планирования эксперимента
719
Задача 393. Для ПФЭ 23, приведенного в таблице, найти уравнение отклика и про-
провести его статистический анализ.
Уровни факторов и
Уровни факторов
Основной
Интервал варьирования
Верхний
Нижний
интервалы варьирования
Обозначение
0
Axi
+1
-1
Х\
7
4
11
3
х2
2
2
4
0
жз
4
3
7
1
3
1
2
3
4
5
6
7
8
ж0
+
+
+
+
+
+
+
+
XI
+
—
+
—
+
—
+
ж2
+
+
—
—
+
+
—
-
Матрица
жз
+
+
+
+
—
—
—
Х\Х2
+
—
—
+
+
—
—
+
ПФЭ
Ж1Ж3
+
—
+
—
—
+
—
+
2 и результаты
Ж2Ж3
+
+
—
—
—
—
+
+
Ж1Ж2Ж3
+
—
—
+
—
+
+
эксперимента
Уз
34,38,42
15,20,25
19,21,23
30,33,36
-33, -38,-43
28,31,34
-19,-23,-27
10,12,14
Уз
38
20
21
33
-38
31
-23
12
щ
16
25
4
9
25
9
16
4
Уз
37,5
18,5
21,5
34,5
-38,5
29,5
-22,5
13,5
Вычисляем коэффициенты регрессии (уравнения отклика)
94
' Уз = у =
1
&i = -
8
1
Ьо = - ' J
i=
_ 38-20 + 21-33-38-31-23-12
8
38 + 20-21-33-38 + 31 + 23-12
= —12,25:
38 + 20 + 21 + 33 + 38-31 + 23-12
= 1,0;
= 16,25;
1 А
bl2 = о ' /Z
8 з=1
38-20-21 + 33-38-31 + 23 + 12
8
38-20 + 21-33 + 38 + 31 + 23 + 12
= 13,75;
38 + 20 - 21 - 33 + 38 - 31 - 23 + 12
023 = = 0;
8
1 ®
123 = - • J2
_
' хз * х^з ' Уз =
8
38-20-21 + 33 + 38 + 31-23-12
Далее вычисляем S] (значения приведены в таблице) и
2 _ 1 JU ^2 _ 16 + 25 + 4 + 9 + 25 + 16 + 4
о . о
Находим дисперсию коэффициентов регрессии:
я2 —
• Sl = ^т+-т = 0,844 (Я = 0,918).
bi п • (m - 1) у 8 • C - 1)
720 Методы исследования связей между случайными величинами [Гл. 5
Выбираем а = 0,95 и находим из таблиц ti+g = to,975 при / = 8 • C — 1) = 16 степенях
2
свободы: to,975 A6) = 2,12. Вычисляем статистики Стьюдента для коэффициентов модели:
|Ьо| П,75 \h\ 12,25 |Ь2| 1,0
to = ^7 = ^Гв =12'8- h = ^7 = да =13'3' h = ^7 = ^Ts =1'09'
^ 1^ ^ 177 ^ ^ ^=0,54; tl8 = M = ?? = 14,98;
0,918 Sbi 0,918 5Ь. 0,918
, |62з| СЗ |bi23| 8,0
t3 " ^Г " 5Д5 " 0; tl23 " ^7 " 5^S " 8'71-
Видим, что ^2 = 1,09; t\2 = 0,54; ?23 = 0 < to,975A6) = 2,12. Следовательно, коэффи-
коэффициенты &2, &12 и &23 незначимо отличаются от нуля. Тогда уравнение регрессии принимает
вид
у = 11,75 - 12,25 • xi + 16,25 • х3 + 13,75 • xix3 + 8 •
Вычислим теперь ^^{yj — yj) = 10. В нашем случае число значимых коэффициентов
J с О2 т А/- * 42 3-10
модели равно « = 5 и Ь = • > \Vj —- Vj) = = 10.
F n-d t^i 8-5
S2 10
Теперь находим F = — = = 0,74, что, очевидно, меньше критического значения
Sy 13,5
(которое всегда больше единицы). Запишем искомую модель в натуральных переменных:
\ -4Ч
у = 11,75 - 12,25- [ ^^)+ 16,25- (*^*) + 13,75
+ 8- | ^—^ ) Л^—\ • ( ^^li ) = 11,75-12,25-@,25ж1 - 1,75) + 16,25-@,ЗЗж3 - 1533) +
\4/\2/\3/
+ 13,75 • @,25ж1 - 1,75) • @,ЗЗж3 - 1,33) + 8 • @,25xi - 1,75) • @,5ж2 - 1) • @,ЗЗж3 - 1,33) =
= 24,958 - 4,974 • ал + 9,31 • х2 + 2,042 • х3 - 1,33 • xi • х2 +
+ 0,473 • х\ • хз — 2,31 • Х2 - хз + 0,33 • х\ • Ж2 • жз-
5.5.1.1.2. Дробный факторный эксперимент
Если некоторыми взаимодействиями можно пренебречь, то регрессионная мо-
модель, связывающая отклик с основными факторами, может быть получена при
меньшем, чем в ПФЭ, количестве экспериментов с помощью дробного факторного
эксперимента (ДФЭ).
Например, в случае ПФЭ 23, если взаимодействиями х\Хъ-> х\х$, Х2Х% и х 1Ж2Ж3
можно пренебречь, то можно либо использовать 4 оставшихся столбца матрицы
плана для определения коэффициентов регрессионной модели при четырех но-
новых факторах, либо найти модели для трех факторов с помощью четырех, а не
восьми экспериментов. Часть матрицы ПФЭ 2fc, в которой v линейных эффектов
(факторов) приравнены к эффектам взаимодействия, называется дробной репликой
вида 2^.
Соотношения, определяющие правила построения дробных реплик ПФЭ, и ука-
указывающие, какие факторы приравнены к взаимодействиям, называются генериру™
ющими. Например, дробные реплики ПФЭ 23^1 могут быть получены с помощью
генерирующих соотношений х% = Х\Х2 и х% = ^Х\Х2- Матрицы планов, соответствую
ющих этим дробным репликам, приведены в табл. 243.
Очевидно, можно получить еще 4 матрицы дробных реплик 23™1 с помощью
генерирующих соотношений для факторов х\ и х^-
5.5]
Математико-статистические методы планирования эксперимента 721
Таблица 243
Дробные реплики 23
Х3 = Х!Х2
3
1
2
3
4
Х\
+ 1 + 1
Х2
+ 11 +
хз
\
Ж1Ж2ЖЗ
Х3 = ~Х1Х2
j
1
2
3
4
+ 1 + 1
Х2
+ 11 +
хз
хгх2хз
1 1 1 1
Для различения смешанных эффектов по матрице дробной реплики использу™
ется понятие определяющего контраста, характеризующего комбинацию тех фак-
факторов, столбец произведения которых состоит только из плюсов или только из ми-
минусов.
Определяющий контраст J может быть равен +1 или — 1. Например, для дроб-
дробных реплик (табл. 243)
J =
= +1 ИЛИ J =
= —1.
Определяющий контраст позволяет установить систему смешивания основ-
основных факторов с эффектами взаимодействия. Например, если J = Ж1Ж2Ж3 = +1, то
xi = xfx2X% = Ж2Ж3 (так как всегда х\ = +1), т. е. оценка Ь\ смешана с оценкой 623-
Если к эффектам взаимодействия приравнивается не один, а несколько основных
факторов, причем каждому из них соответствует свой частный определяющий
контраст, для полного описания разрешающей способности дробной реплики ПФЭ
используется обобщающий определяющий контраст. Он включает в себя частные
определяющие контрасты и их произведения.
Например, при исследовании 5 факторов можно поставить не 25 = 32 опыта,
а только 8, если реализовать дробную реплику 25^2, т.е. приравнять два фактора
к эффектам взаимодействия. Предположим, что выбраны варианты смешивания
ж4 = Жх^з и Ж5 = Х\Х2Х% с определяющими контрастами J = х\х^х^ и J = x\X2X^x^
соответственно. Тогда обобщающий определяющий контраст может быть записан
следующим образом
J = Ж1Ж3Ж4 = Ж1Х2Ж3Ж5 = Ж2Ж4Ж5.
Теперь для того, чтобы выявить, с чем смешана та или иная оценка коэффици-
коэффициента модели, необходимо умножить комбинацию факторов, соответствующих ей, на
обобщающий определяющий контраст. Например, определим систему смешивания
для оценки коэффициента Ь\2 эффекта взаимодействия Х\Х2- Имеем
т.е. оценка Ъ\2 будет смешанной с оценкой коэффициентов 6234? ^35, ^145- В об-
общем случае получается сложная система смешивания эффектов взаимодействия.
Наиболее эффективными дробными репликами от ПФЭ являются реплики,
у которых линейные эффекты смешаны с взаимодействиями наивысшего порядка.
Различают регулярные и нерегулярные дробные реплики. Регулярные реплики
образуются из ПФЭ делением на число частей, кратное двум. Например, 25™1 —
полуреплика, 25™2—четверть реплики, 27~4 —1/16 реплики от ПФЭ 27. Реплики
типа 3/4, 5/8 и т.д. называются нерегулярными. Дробные реплики позволяют
существенно сократить число факторов и экспериментов для моделирования про™
цесса. Особенно эффективно их применение при планировании экспериментов для
отыскания оптимума отклика.
722 Методы исследования связей между случайными величинами [Гл. 5
5.5.1.2. Нелинейные планы второго порядка
Если линейная регрессионная модель оказывается неадекватной, то в боль-
большинстве практических случаев удовлетворительная аппроксимация поверхности
отклика достигается при использовании полинома второй степени. Математическая
модель поверхности отклика в этом случае имеет вид
к к к
у = Ъ0 + ^2 biXi + Е bijXiXj + J2 Ъцх\.
г=1 i<j i=l
План эксперимента должен обеспечивать получение раздельных (несмешанных)
оценок коэффициентов регрессии Ъ{. Для этого необходимо, чтобы между числом
опытов плана п и числом коэффициентов модели к выполнялось соотношение
(fc + 2)(fc + l) ^ „ ,
п > , и чтобы каждый фактор варьировался не менее, чем на трех
уровнях.
5.5.1.2.1. Симметричные планы второго порядка
Наиболее широкое распространение нашли симметричные планы второго поряд-
порядка [621]. Под симметричным планом понимается план, удовлетворяющий соотноше-
соотношениям
п п
J2 Xij =0; ]Г XeiX^Xvi = 0 (е, 7, ^ = 1, 2, ..., fc; е ф j ф г/ ф е) ;
п п п
Y, %ei%ji = 0 (е Ф 7); Y, x%xii = ° G Ф v); Y1 х% = пХ^
i=l г=1 i=l
г=1 г=1
где п — общее число опытов, выполняемое по плану; j — порядковый номер опыта.
Если в каждой точке плана проводится nij параллельных опытов, то должно
иметь место
п п
п\2 = Y, rrijX^ п\3 = J2 m3x\Jx2lj (e ф 7);
i=i 3=1
где h и n = ^ TBj — соответственно число точек плана и общее число опытов.
Оценки коэффициентов регрессии для симметричного плана второго порядка
вычисляются по формулам
п 1 к п
3=1
j
^ " Е mJ^ij2/i - " Е m3xi3V^
3=1 3=1 3=1
1 п Iй
Ь* = Д^ Е тЗХг03 (* / 0); Ь*е = д^ Е Щ^Хе^ (I ф е),
з=1 3 3=1
5.5] Математико-статистические методы планирования эксперимента 723
1 ^ k\l 1
'J JZ^ A4 — Лз -f- /СЛз — /€A2 ^4 — Аз
A2 , Аз — А2
А4 — Аз + ^Аз — к\2 (А4 — Аз) (А4 — Аз^Аз — к\2)
Контроль правильности вычислений оценок коэффициентов регрессии может
п
быть выполнен с помощью равенства J^ (t/j — yj) = 0, где ijj—предсказываемое
моделью значение отклика.
Выборочные дисперсии и ковариации оценок коэффициентов модели определя™
ются формулами
cov (Ьо, hi) = -~sl', cov iP%u bjj) = ~^sl (i Ф J) 1
где Sy—выборочная дисперсия отклика у, связанная с ошибкой эксперимента.
Значение S2 находится по формуле
- \2
У)
что справедливо в случае однородности дисперсий 5| по точкам плана (эта одно™
родность должна быть предварительно проверена).
Дисперсия 5| предсказываемого моделью значения отклика у определяется
формулой
п
Неадекватность модели второго порядка характеризуется дисперсией
1 " 2
S2 = ^ rrij (tjjyj) , где I — число коэффициентов модели (в случае квадра-
i=i
(fc
тичнои модели / =
S2
Модель с вероятностью а признается адекватной, если — < Fai где Fa — а-
Sy
квантиль распределения Фишера с /i = n -1 и /2 = ^(^' ~ 1) степенями свободы.
i=i
Значимость коэффициентов модели проверяется с помощью статистики ti = 77^ ?
п
имеющей при bi = 0 распределение Стьюдента с / = J^ (г?г^- — 1) степенями свободы.
724 Методы исследования связей между случайными величинами [Гл. 5
5.5.1.2.2. Ортогональные симметричные планы
Наиболее простыми симметричными планами второго порядка являются орто™
гональные планы, предложенные Боксом и Уилсоном [626]. Ортогоналвный план
позволяет найти независимые оценки коэффициентов поверхности отклика. Постро™
ить ортогональный план для получения модели
к к к
У = Ьо + ^2 biXi + J2 hjXiXj + J2 ЬИХ1
i=l i<j i=l
нельзя, так как столбцы матрицы плана, соответствующие х\ и фиктивной не-
ременной ж0? будут неразличимы (оба будут состоять из +1) и, следовательно,
неразличимы будут также оценки bo и Ъц. Для устранения этого смешивания
используется преобразование модели к виду [621]
к к к
где br0 = b0 + A2 Y1 Ь«; (%'iJ = xf - A2;
г=1
Условие ортогональности плана имеет вид Аз = А|. Оценки коэффициентов
регрессии на основе ортогонального плана получаются независимыми и находятся
по формулам:
?'
• / \
Дисперсии оценок коэффициентов регрессии вычисляются по формулам
ь0\, ^«П(л4-Лз)^' ^^^
Оценка коэффициента Ьо находится по формуле
к
h = b'o - А2 Е^«'
г=1
5.5]
Математика-статистические методы планирования эксперимента
725
ее выборочная дисперсия равна
л2
Л2
г=1
S2y (Л4 - Аз + k\l)
п (Л4 — Аз)
Дисперсия предсказываемого значения отклика определяется по формуле
п
г=1
1
А^
т2т2
1
л!
г=1
Проверка значимости коэффициентов регрессии и адекватности поверхности
отклика проводится по аналогии с обычным симметричным планом.
Большинство известных ортогональных планов второго порядка строится по
композиционному принципу, путем достройки ортогонального плана первого по-
порядка. Сначала реализуются опыты, соответствующие полуреплике 23, и опыты
в центре плана для проверки линейности модели. Если модель неадекватна, ставят-
ставятся опыты во второй полу реп лике и в 6 звездных точках. Условие ортогональности
Л3 = А| обеспечивается специальным выбором числа опытов в центре эксперимента
По и величиной звездного плеча а, определяющего координаты звездных точек
плана. Композиционный ортогональный план содержит п = 2к^р + 2к + bq опытов,
где 2к~р — число опытов в звездных точках (дробная реплика ПФЭ, в котором р
линейных эффектов приравнены к эффектам взаимодействия). Для композицион-
композиционного плана имеют место соотношения
Значения %иа, обеспечивающие ортогональность плана, удовлетворяют соот-
соотношению
Bк~р + 2к
2a2J
Параметры и численные значения вспомогательных коэффициентов для ортого-
ортогональных композиционных планов второго порядка при щ = 1 приведены в табл. 244.
Вычисление коэффициентов модели и статистический анализ поверхности отклика
проводятся по формулам для симметричного плана второго порядка.
Таблица 244
Параметры ортогональных композиционных планов
2
3
4
5
fc
2
3
4
5
0
0
0
1
а2
1,000
1,477
2,000
2,392
пХ2
6,000
10,954
20,000
20,785
Распределение опытов
9
15
25
27
пХз
4,000
8,000
16,000
16,000
пХ4
6,000
12,364
24,000
27,446
1
1
1
1
Вершина
куба
4
8
16
16
а
5,000
6,499
9,000
7,989
Ь
3,000
2,510
2,500
1,816
Звездные
точки
4
6
8
10
с
4,500
3,437
3,125
2,359
d
0
0
0
0
726
Методы исследования связей между случайными величинами
[Гл. 5
Задача 394. Для трех переменных был реализован ортогональный план второго по-
порядка, результаты которого приведены в таблице. Найти статистическую модель,
описывающую результаты опытов.
Уровни факторов
Уровни
+ 1
0
-1
XI
15,1
14,7
14,3
х2
36
32
28
жз
1,4
1,2
1,0
Из табл. 244 для по = 1 (один опыт в центре плана) и к = 3 имеем величину звездного
плеча а = ^1,477 = 1,215. Общее число точек плана п = 15, число опытов в каждой точке
плана было rrij =3 (т. е. п = п • rrij = 45). План состоит из 8 точек ПФЭ 23, 6 звездных
точек и одной точки в центре плана (см. табл. 244).
Далее имеем
Л2 =
0,73; Л3
15 15
Матрица плана эксперимента имеет вид:
Л4 =
15
= 0,824.
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Х\
-1
+ 1
-1
+ 1
-1
+ 1
-1
+ 1
-1,215
+1,215
0
0
0
0
0
х2
-1
-1
+ 1
+ 1
-1
-1
+ 1
+ 1
0
0
-1,215
+1,215
0
0
0
хз
-1
-1
-1
-1
+1
+1
+1
+1
0
0
0
0
-1,215
+1,215
0
Ж1Ж2
+ 1
-1
-1
+ 1
+ 1
-1
-1
+ 1
0
0
0
0
0
0
0
х\хз
+1
-1
+1
-1
-1
+1
-1
+1
0
0
0
0
0
0
0
Ж2Ж3
+1
+1
-1
-1
-1
-1
+1
+1
0
0
0
0
0
0
0
Ж1Ж2ЖЗ
0,27
0,27
0,27
0,27
0,27
0,27
0,27
0,27
0,75
0,75
-0,73
-0,73
-0,73
-0,73
-0,73
х12 - Л2
0,27
0,27
0,27
0,27
0,27
0,27
0,27
0,27
-0,73
-0,73
0,75
0,75
-0,73
-0,73
-0,73
Ж22 — А2
0,27
0,27
0,27
0,27
0,27
0,27
0,27
0,27
-0,73
-0,73
-0,73
-0,73
0,75
0,75
-0,73
Уз
16
5
9
5
14
10
17
9
14
8
11
8
16
16
17
Вычисляем коэффициенты модели:
j " X'lj ' Vj =
lj -Л2) -Уз =
611 п • (Л4 - Аз) § mj Xlj Vj 45 • @,824 - 0,53) ^
= 0,227 • [A6 + 5 + 9 + 14 + 10 + 17 + 9) + 0,75 • A4 + 8) -
-0,73 • A1 + 8 + 16 + 16 + 17)] = -2,31;
Ъ22 = 0,227 • [0,27 • A6 + 5 + 9 + 14 + 10 + 17 + 9) -
- 0,73 • A4 + 8 + 16 + 16 + 17) + 0,75 • A1 + 8)] = -3,32;
Ьзз = 0,227 • [0,27 • A6 + 5 + 9 + 14 + 10 + 17 + 9) -
- 0,73 • A4 + 8 + 11 + 18 + 17) + 0,75 • A6 + 16)] = 1,05.
5.5] Математика-статистические методы планирования эксперимента 727
Далее вычисляем
= 0,274 • (-16 + 5-9 + 5™ 14 + 10™ 17 + 9™ 1,215 • 14 + 1,215 • 8) = -9,39;
Ь2 = 0,274 • (-16 - 5 + 9 + 5 - 14 - 10 + 17 + 9 - 1,215 • 11 + 1,215 • 8) = -2,39;
Ьз = 0,274 • (-16 ^5^9 +14+ 10+17+ 9^ 1,215 • 16 + 1,215 • 16) = 4,11;
1 15
Ь12 = — • J2 тз ' Xli ' х*э ' Уз =
п' 3 i=i
3 15
= - ' Yl Xli ' х*э • Уз = О,375 ' A6 - 5 + 9 - 5 + I4 - Ю - 17 + 9) = 1,125;
i=i
Ь13 = 0,375 • A6 - 5 + 9 - 5 + 14 - 10 - 17 + 9) = 1,125;
&2з = 0,375 • A6 + 5 - 9 - 5 - 14 - 10 - 17 + 9) = 3,375.
Искомая модель имеет вид
У = ^о + Ь\ • х\ + Ь2 • х2 + Ь3 - х3 + 6i2 • xix2 + 6i3 • хгхз + b23 • х2х3 +
~~ Л2) + Ь22 • (x\ - Л2) + Ьзз • (х\ - Л2) =
= 11,67 - 9,39xi - 2,39ж2 + 4,11ж3 + 1,12Ъх1х2 + 1,125ж1Ж3 + 3,375ж2ж3 -
- 2,31 • (xl - 0,73) - 3,32 • {х% - 0,73) + 1,05 • (х% - 0,73) = 15,01 - 9,39xi - 2,39ж2 +
+ 4,11ж3 + 1,215ж1Ж2 + 1,215алжз + 3,375ж2ж3 - 2,31ж? - 3,32ж2 + 1,05жз-
5.5.1.2.3. Ротатабельные планы
Существенным недостатком ортогональных планов является то, что полученная
на их основе модель с разной точностью предсказывает значения отклика в раз-
различных точках факторного пространства — т.е. дисперсии 5|. неодинаковы для
различных точек факторного пространства, равноудаленных от центра плана.
Этого недостатка лишены так называемые ротатабельные планы [621], которые
позволяют получить модели с одинаковой дисперсией отклика во всех точках фак-
факторного пространства, равноудаленных от центра плана. Условие ротатабельности
плана имеет вид
п п
А4 = ЗА3, ИЛИ ]Г xfj =^J2 XiJXej'
3=1 3=1
Формулы регрессионного анализа для симметричных планов второго порядка
сохраняются и для ротатабельных планов с учетом условия ротатабельности. Свой™
ство ротатабельности не зависит от числа п® опытов в центре плана (общее число
опытов должно удовлетворять соотношению -—- = [621]).
Д2 к -f- 2
Бокс и Хантер [627] предложили выбирать по, исходя из равномерности дис™
персии предсказания. Такие планы называются униформ-ротатабельными и имеют
\ * Аз
место при значениях А3 = —, удовлетворяющих условию
А2
2А* (А* - 1) (к + 2) + A* (fe + 1) - (fe - 1) = 0.
Например, если ? = 2,3,4,5, то Ад должно соответственно равняться 0,7844;
0,8385; 0,8705; 0,8918. В этом случае отклик оценивается с примерно одинаковой
дисперсией во всех точках шара с радиусом р = л/Х^.
728
Методы исследования связей между случайными величинами
[Гл. 5
Можно выбирать по, исходя из обеспечения ортогональности ротатабельного
плана. Это условие соответствует требованию А| = 1.
Для композиционных планов условие ротатабельности обеспечивается соответ-
соответствующим выбором звездного плеча а = 2 4 .
Число центральных опытов для композиционного ротатабельного ортогональ™
ного плана определяется соотношением
= А* =
42
4} -
- 2к.
При соответствующих значениях А^ можно найти п® для униформ™ и ортого-
ортогональных ротатабельных планов. Параметры и вспомогательные коэффициенты для
некоторых ротатабельных планов приведены в табл. 245.
Таблица 245
Параметры униформ-ротатабельных планов
к
2
3
4
5
к
2
3
4
5
Р
0
0
0
1
а2
2
2,828
4
4
8,000
13,657
24
24
пАз
4
8
16
16
Распределение опытов
п
13
20
31
32
12
24
48
48
а
2,600
3,327
4,429
5,091
по
5
6
7
6
Ь
15300
1,136
1,107
1,091
Вершины
куба
4
8
16
16
с
15625
15250
0,969
1,000
Звездные
точки
d
-0,2438
-0,1378
-0,1153
-0,0900
4
6
8
10
0,81
0,86
0,86
0,89
5.5.1.2.4. D-оптимальные планы
Ортогональность и ротатабельность являются свойствами планов, а не крите™
риями их оптимальности. Эти свойства не имеют количественных оценок.
Кифер [628] предложил выбирать в качестве критериев оптимальности величи-
величины, достигающие экстремума при выборе наилучшего способа обработки экспери-
экспериментальных данных.
Такой величиной может быть объем эллипсоида рассеяния оценок парамет-
параметров математической модели. Планы, минимизирующие объем эллипсоида рассе-
рассеяния, т. е. планы, которые позволяют получить квадратичную модель с наибо-
наиболее точными оценками коэффициентов, называются D-оптимальными. Различа-
Различаются D-оптимальные планы с ограничениями на кубе (—1^з^^+1) и на шаре
Условия
2к + 1^
D-оптимальности плана на
кубе
имеют
вид
лДк2 + 12к + 7
[629]
А2
Последнее равенство выполняется, если план эксперимента содержит только
точки с координатами —1,0, +1. Симметричные D-оптимальные планы построены
Кифером (для к ^ 5) и Коно (для к ^ 9) [629]. Планы Кифера содержат 2к точек
в вершинах куба, к • 2к~1 точек в серединах ребер куба и — L2k~2 точек
5.5]
Математика-статистические методы планирования эксперимента
729
в центрах двумерных граней. Планы Коно включают в себя 2к точек в верши™
нах куба, к • 2к^г точек в серединах ребер куба и одну центральную точку. При
к = 2 планы Кифера и Коно совпадают, D-оптимальность плана обеспечивается
некоторым оптимальным распределением общего числа опытов по точкам плана,
для точного соблюдения которого требуется большое число экспериментов. В связи
с этим возникла задача построения планов, мало отличающихся от D-оптимальных
и содержащих меньшее число опытов. Такие планы называются почти D-оптималь-
ными и обозначаются Bi (г — число параметров модели) [630]. Матрицы планов В±
и В$ приведены в [630].
План второго порядка D-оптимален на шаре только тогда, когда он ротатабелен.
Условия ?)™оптимальности на шаре имеют вид
(* + l)(fc + 2)'
(fc + 1) (fc + 2)
Ал — ЗАч —
3 (к + 3)
D-оптимальным планом на шаре будет композиционный план, включающий
в себя 2к точек в вершинах куба, вписанного в сферу единичного радиуса, 2к точек
на единичной сфере и одну центральную точку. При этом на каждую вершину
* а - (fc + 3) к2
куба должна приходиться доля наблюдении, равная 2~к> на кажДУю
звездную точку — доля
-^ина центральную точку — доля
" (к + 1) (к + 2J .—г-—., ^ ,,— (fc + !) (fc + 2) •
Практически обеспечение требуемого соотношения числа опытов в точках такого
плана связано с необходимостью проведения большого количества экспериментов.
Поэтому для обеспечения D-оптимальности на шаре обычно используется ротата™
бельное планирование, в котором число опытов в центре плана выбирается из усло-
условия ^оптимальности с отказом от требований ортогональности и униформности.
Характеристики ротатабельных планов с числом центральных опытов, выбранным
из условия Х)™оптимальности, приведены в табл. 246.
Таблица 246
Характеристики D-оптимального плана
к
2
3
4
5
к
2
3
4
5
Р
0
0
0
1
с
п\2
8
13,657
24
24
:к2
2
8
4
4
Распределение опытов
п
11
16
26
27
пЛз
4
8
16
16
пХ4
12
24
48
48
710
3
2
2
1
а
3,667
7,953
13
21
Вершины
куба
4
8
16
16
6
1,833
2,715
3,25
4,5
Звездные
точки
4
6
8
10
с
1,3750
1,0000
0,8125
0,8438
d
-0,5729
-0,7270
-0,6770
-0,8438
5.5.1.2.5. Несимметричные планы второго порядка
Симметричные планы второго порядка позволяют большую часть оценок коэф-
коэффициентов регрессионной модели определить независимо друг от друга (коррели™
руются только оценки коэффициентов 5q и Ъц, Ьц и bjj^ i / j). Отказ от требования
730 Методы исследования связей между случайными величинами [Гл. 5
симметричности позволяет в некоторых случаях получитв более эффективные пла™
ны. Наибольшее распространение получили несимметричные планы второго поряд™
ка, предложенные Хартли [631]. Планы Хартли экономичны, число экспериментов
в них равно числу коэффициентов модели или ненамного превосходит его. Они
близки к D™ оптимальным, построены по композиционному принципу и состоят
из дробной реплики ПФЭ, звездных точек и опытов в центре, число которых
выбирается из условия D-оптимальности.
Планы Хартли нельзя сделать ортогональными или ротатабельными (кроме
случая к = 5) выбором звездного плеча а. Если план Хартли образован на основе
дробной реплики с генерирующим соотношением, не содержащим тройного вза-
взаимодействия, то он становится симметричным и регрессионный анализ функции
отклика проводится по формулам симметричного планирования второго порядка.
Коэффициенты Ьд, Ьц, а также Ь{ и Ь?1/ для переменных ж^, же и ж^, не входящих
в тройное взаимодействие генерирующего соотношения, подсчитываются по фор-
формулам
к п 7 п п 7 к
= - Е Уз - - Е Е хиу^ ь» = -- Е Уз + - Е хпУз - - Е Е хи
п 1 к п 7 п
Е Уз Е Е иу^ ь» Е Уз + Е хпУз - - Е Е х
j = l i=l j=l j=i jz=i
Ф
где a, 6, c, d — коэффициенты, определенные ранее для симметричных планов.
Оценки коэффициентов hi и Ь?1/, входящих в тройное взаимодействие определя™
ющего контраста J = XiX?xv1 вычисляются по формулам
\i=i
1 - Аг Аг
где е = ; / = — е =
Л2 — Аз Аз A3 (A2 — Аз]
Дисперсии этих оценок равны соответственно S^ = е— и ^~ = — Я^. Диспер™
сии остальных коэффициентов модели вычисляются по формулам
q _ о _ о _ _
Ь0 - -\; йь„ - -^-Лу; bbi - —; йЬу - —.
Дисперсия предсказываемого значения отклика определяется формулой
q2
п
Параметры и вспомогательные коэффициенты некоторых планов Хартли для
к
ограничений на кубе (—1 ^ Х{ ^ +1) и на шаре {^2,xi ^ ¦'-) пРивеДены в табл. 247.
г=1
Матрицы планов Хартли приведены в [630] для к = 5 и к = 6, там же приведены
экономичные несимметричные планы Вестлейка (к = 5), Дрейпера, Хартли—Коно.
5.5]
Математика-статистические методы планирования эксперимента
731
Таблица 247
Параметры планов Хартли
к
3
4
5
к
3
4
5
Р
1
1
1
1
1
пХ2
10
10
16
18
28
сг
3
1
4
1
5
пХз
4
8
8
16
16
2
Генератор
Х1х2х3
хгх2х3
Ж1Ж2ЖЗ
Ж1Ж2ЖЗЖ4Ж5
Ж1Ж2ЖЗЖ4Ж5
пА4
22
10
40
18
66
а
11
3,247
17
3,727
27
Распределение опытов
п
Ь
3,667
0,955
4,25
0,818
5,4
11
17
17
27
27
с
0,611
8,5
0,531
13,5
0,54
по
1
1
1
1
1
-1,14
1,719
-0,996
2,455
-1,014
Куб
4
8
8
16
16
е
1,833
8,5
2,125
-
Звезда
6
8
8
10
10
f
4,5833
10,625
4,25
-
Тип
плана
сфера
куб
сфера
куб
сфера
Задача 395. Для плана Хартли на кубе для пяти переменных построить матрицу
плана и по результатам его реализации найти поверхность отклика (в каждой точке
плана проводились rrij = 3 измерения).
Из табл. 247 находим для к = 5 (куб) п = 27, по = 1, куб—16, звезда—10, т. е. всего
проводятся 27 экспериментов, в том числе 1 — в центре плана, 16 — в точках куба, 10 —
в звездных точках (звездное плечо а2 = 1, а = 1).
Матрица плана и результаты эксперимента приведены в таблице:
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
XI
+
—
—
+
—
+
+
—
—
+
+
—
—
+
х2
+
—
+
—
+
—
+
—
+
—
+
—
+
хз
+
+
—
—
—
—
+
+
+
+
—
—
+
+
Ж4
+
+
—
—
+
+
—
—
+
+
—
—
—
-
Х5
+
+
—
—
+
+
—
—
—
—
+
+
+
+
Уз
1320
257
434
465
451
467
1222
257
511
493
407
183
471
442
Уз
1288
265
443
478
445
465
1205
280
509
494
386
202
460
435
3
15
16
17
18
19
20
21
22
23
24
25
26
27
XI
+
—
0
+
—
0
0
0
0
0
0
0
0
х2
+
—
0
0
0
+
—
0
0
0
0
0
0
хз
—
—
0
0
0
0
0
+
—
0
0
0
0
Х4
+
+
0
0
0
0
0
0
0
+
—
0
0
Х5
—
—
0
0
0
0
0
0
0
0
0
+
—
Уз
1015
202
427
511
293
498
312
475
379
412
337
329
508
Уз
1002
230
380
590
266
591
230
513
353
431
330
381
468
Вычисляем оценки коэффициентов регрессии (в нашем случае п = п • rrij = 27 • 3 = 81).
Тогда имеем из табл. 247
Л2 = — = 0,667; Аз = — = 0,592; А4 = — = 0,667;
Вычисляем:
* Уз
а = 3,727; 6 = 0,818; с = 13,5; d = 2,455.
3,727 iZ,o_ 0,818 ^
' Уз • тз =
27
хЬ • Уз =
732 Методы исследования связей между случайными величинами [Гл. 5
0,818 Л, 13,5 ^* _ 2,455 * Л, 2 _
?j~ Е 3Уз + "^- ' Z) 3x*i ' Уз ~ "^ ¦ J2 Е 3хИ ¦ Уз\
3=1 3=1 i=lj=l
|1 13,5 Л, _ 2Д55 * ^ 2 _
^ Z, 32/i + "?f * 2^ Зж^' ' Уз ^р * Z, Z, 3xii * 2/i = 27'95
i=i j=i i=ij=i
622 = 30,9; Ьзз = 52,9; 644 = 0,4; b55 = 44,4;
27 27
* Уз = °5°555 • J2 х*зуэ ; fei = 0,0555 • ^ XU ' Уз = 18254; &2 = 180?6;
bi J2
18 i=i j=i 3=1
b3 = 80,3; b4 = 50,6; b5 = 43,3;
¦^ 27 27 27
^' = 7^^ * 1Z 3xi3 ' х*з ' Уз = 0,0625 • J2 xiJ ' х^з ' Уз*ч bl2 = °,0625 • J2 XlJ ' Х2з ' Уз =
lb'S 3 = 1 3 = 1 3 = 1
bis = 56,1; бы = 42,7; b15 = ^32,3; b23 = 67,8; b24 = 43,2;
b25 = -29,1; 634 = -28?6; b5 = 38,4; b45 = 71,8.
Искомая регрессионная модель имеет вид
у = 380,1 + 182,4xi + 180,6ж2 + 80,Зж3 + 50,6ж4 + 4353ж5 + 27,9^? + 30,9^2 +
+ 52,9жз + 0,4^4 + 44,4^5 + 7
+ 67,8ж2ж3 + 43,2ж2ж4 - 29,1ж2ж5 - 28,6ж3ж4 + 38,4ж3ж5 + 71,8ж4ж5.
Вычисленные по полученной регрессионной модели значения отклика близки к экс-
экспериментальным реализациям наблюдаемой случайной величины.
5.5.2. Планирование экспериментов по поиску оптимума
Традиционные методы экспериментального нахождения оптимума функции нес-
нескольких переменных у = /(#i, #2, • • • 5 хп) предполагают последовательное изучение
зависимостей у = fi(xi) от каждого из факторов при фиксированных значениях
остальных. Недостатком таких методов является большое количество необходимых
экспериментов и невозможность учесть взаимодействие факторов.
В последние годы разработаны специальные методы поиска оптимума, базиру™
ющиеся на математической теории экстремального эксперимента. Подробное изло-
изложение таких методов содержится в [631, 632].
5.5.2.1. Метод крутого восхождения
Бокс и Уилсон [626] предложили метод планирования экспериментов по поиску
оптимума, сочетающий движение по градиенту функции отклика с ортогональным
линейным планированием, — метод крутого восхождения. В соответствии с этим ме-
методом сначала проводится ПФЭ или ДФЭ с центром в некоторой точке факторного
пространства с координатами Жю,Ж2о, • • • ?хко- Методами линейного регрессионно™
го анализа вычисляются оценки коэффициентов модели отклика bi (г = 1, ...,&).
Дальнейшее движение к оптимуму осуществляется изменением интервалов варьи-
варьирования основных факторов в соответствии с уравнением
причем используются некодированные значения переменных. Параметр А выби-
выбирается следующим образом. Вычисляются произведения 5^Аж^, и определяется
базовый фактор х§, для которого biAx§ является наибольшим по абсолютной
величине в сравнении с остальными факторами. Выбирается значение А = Ai = .-=—г,
5.5]
Математика-статистические методы планирования эксперимента
733
где 0 < е < 1 (рекомендуется выбирать е = 0,5 + 0,8), Ь? —коэффициент линейной
модели при факторе х?. Затем вычисляются шаги и координаты первой точки
крутого восхождения по формуле xj = Ai (Ъ{Ах{) + ж^о- Шаги и координаты по-
последующих точек на линии крутого восхождения подечитываются по формуле
х\ = jAi {b\Ax\) + Xio^ где j = 1,2, ... —номер шага в направлении крутого вос-
восхождения.
Из всех реализованных опытов выбирается тот, который дал наилучшие резуль-
результаты (например, максимальный отклик). Условия наилучшего опыта принимаются
за основной уровень факторов, и цикл крутого восхождения повторяется до тех
пор, пока все коэффициенты линейной модели Ъ{ не будут признаны незначимыми.
При движении к оптимуму значения параметра А должны уменьшаться от цикла
к циклу. Выбор величины шага при движении по градиенту производится из пред-
представлений исследователя о возможном характере оптимума.
При достижении оптимума для описания функции отклика используются ме™
тоды планирования экстремальных экспериментов второго порядка. Движение по
градиенту наиболее эффективно для симметричных регрессионных моделей, у ко-
которых коэффициенты Ь{ различаются несущественно.
Задача 396. Необходимо найти оптимум отклика у в зависимости от трех фак-
факторов (ж1,Ж2,жз) методом крутого восхождения Бокса-Уилсона. Результаты после-
последовательного экспериментирования по реализации крутого восхождения приведены
в таблице:
Реализация трехфакторного крутого восхождения
Номер по
порядку
1
2
3
4
5
6
7
8
9
10
11
12
Последовательность операций
крутого восхождения
Основной уровень, хю
Интервал варьирования, Axi
Верхний уровень
Нижний уровень
Кодовое значение переменных
Опыты ПФЭ 23
1
2
3
4
5
6
7
8
h
hAxi
Ai = O,S/\bs
Шаг « Ai(biAA?i)
,1ты на линии восхождения
9
3
Факторы
132
7
139
125
хг
+ 1 1 + 1 + + 1
80
560
3
135
138
141
16
5
21
11
х2
+ + + 1 1 + 1 1
136
680
0,8/136
4
20
24
28
0585
0,10
0,95
0,75
х3
+ + 1 1 + 1 + 1
97
9,7
0,06
0,91
0,97
..L03
Отклик
Уг
251
303
310
324
434
470
490
1127
1455
1627
1594
734
Методы исследования связей между случайными величинами
[Гл. 5
По результатам ПФЭ 23 находим коэффициенты регрессии при линейных парамет-
параметрах:
1
Ь\ = —
Xl ' Уз = 80;
= 136; b3 = -
n
= 97.
Далее вычисляем произведения (указаны в таблице). Наибольшее значение произве-
произведения ^2 • Аж2 = 680. Поэтому выбираем фактор Х2 за базовый.
тэ * , Л 0,8 0,8
Выоираем для первого шага А = Ai = ;—- = .
\bs\ 136
136
Тогда шаг в направлении крутого восхождения равен Ai
{Ь\
П Я ЯП 7
—
lot)
= 3,0;
А2 • (Ь2 • Аж2) =
Координаты
\
= 4,0; Ai • (Ь3 • Аж3) = 0,06.
136
точек крутого восхождения рассчитываем следующим образом:
х\ = Ai • (bi • Axi) + жю = 3 + 132 = 135; ж^ = 4 + 16 = 20; х\ = 0,06 + 0,85 = 0,91.
Второй шаг: х\ = 2Ai • (Axi) + жш = 2 • 3 + 132 = 138, и т.д. Результаты опытов при™
ведены в таблице, из которой видно, что второй опыт на линии крутого восхождения дает
наибольший результат. Следовательно, максимум достигается при значениях координат
точки х\ = 138, Х2 = 24 и хз = 0,97. В окрестности этой точки можно теперь строить
план второго порядка для уточнения поверхности отклика.
5.5.2.2. Симплексное планирование
Эффективным методом планирования эксперимента по поиску оптимума явля™
ется последовательный симплексный метод, предложенный Спендли, Хексто и Хим~
суортом [634].
^мерным симплексом называется выпуклый многогранник, образованный (к + 1)
вершинами в fc-мерном пространстве. Например, на плоскости (к = 2) симплек-
симплексом будет треугольник. Симплекс называется правильным, или регулярным, если
все его ребра равны между собой (например, равносторонний треугольник на
плоскости). Из любого правильного симплекса можно, заменив одну точку на ее
зеркальное отображение относительно границы или ребра симплекса, построить
новый симплекс. Путем последовательной замены вершин можно осуществить пе-
перемещение симплекса в факторном пространстве.
Координаты вершин правильного ^-мерного симплекса с единичным ребром
и центром в начале координат определяются строками матрицы
Ri -r2 -r3
0 R2 -r3
0
0
1
/( ) J{)
Координата новой вершины симплекса после замены определяется формулой
Xik+2 = т yZ xij ~ xii ГДе xi — координата заменяемой вершины; — У^ж^- —среднее
3 3
значение координат всех точек симплекса, кроме заменяемой; Xik+2 — координата
новой верп1ины.
Последовательное симплексное планирование эксперимента осуществляется еле™
дующим образом. Сначала ставятся эксперименты в вершинах симплекса (их число
5.5]
Математика-статистические методы планирования эксперимента
735
на единицу больше числа факторов). Затем выявляется и отбрасывается верши™
на с минимальным (если необходимо найти максимум) или максимальным (если
необходимо найти минимум) значением отклика. На оставшейся грани строится
симплекс с новой вершиной, являющейся зеркальным отображением отброшенной.
Затем проводится эксперимент в новой вершине симплекса, и цикл его перемещения
повторяются до тех пор, пока симплекс не начнет „вращаться" вокруг вершины
с экстремальным значением отклика.
Симплексное планирование имеет ряд существенных достоинств — оно обладает
свойством самоконтроля, исключает влияние ошибок эксперимента на конечный
результат оптимизации; на любом этапе экспериментирования можно включить
в рассмотрение еще один фактор, добавив только одну вершину (эксперименталь-
(экспериментальную точку), увеличивающую размерность симплекса на единицу.
Метод не предъявляет жестких требований к точности фиксирования значений
отклика (он требует только ранжирования их по величине). Отсутствует необходи-
необходимость описания поверхности отклика. Симплекс-планирование безразлично к фор-
форме поверхности отклика. Подробно метод симплекс-планирования изложен в [621].
Задача 397. Рассмотрим пример поиска оптимума симплекс-планированием. Пред-
Предположим^ имеются два фактора х\ и х2 с основными уровнями хю = 1000 и х2о = 1
и интервалы варьирования Axi = 500 и Ах2 = 0,2 соответственно.
Симплексом в нашем случае является треугольник ABC. Будем ставить эксперимент
в точке А с координатами в кодированной форме
Х\ =
х2 =
Затем ставим экспериментв! в точках В с координатами х\ = 0,5 ж х2 = 0,86 и в точ-
точке С с координатами х\ = 1 и х2 = 0.
Дальнейшее движение симплекса приведено в таблице:
Номер
опыта, j
1
2
3
4
5
6
7
8
Симплекс
ABC
ABC
ABC
ВСА1
ВС А'
В'С'А1
В'С'А"
В'С" А"
Вершина, в которой
ставится опыт
А
В
С
А'
С
В1
А"
С"
Код
0
0,5
1
1,5
1
2
1,5
2,5
Значение
1000
1250
1500
1750
1500
2000
1750
2250
Х2
Код
0
0,86
0
0,86
1,72
1,72
2,58
2,58
Значение
1
1,172
1
1,172
1,344
1,344
1,516
1,516
Отклик,
Уз
9
13
11
17
18
21
24
20
Видим, что из точек стартового комплекса ABC наименьший отклик имеется в точ™
ке A (yj = 9). Так как ищется максимум, то будем искать точку А\ симметричную
к точке А относительно грани ВС симплекса. Имеем координаты искомой точки
Ж14 = ^ • @,5 + 1) - 0 = 1,5; ж24 = ^ • @,86 + 0) - 0 = 0,86.
¦л / \ Х\ X\Q „ а ~
he натуральные (некодированные) координаты равны х±4 = z ш х± = i\x\ x
х Ж14 = 500 • 1,5 + 1000 = 1750; х2 = Ах2 • х24 + х20 = 0,86 • 0,2 + 1 = 1,172.
Далее по аналогии рассчитываются остальные точки симплекс-планирования (ре-
(результаты последовательного симплекс-планирования приведены в таблице).
Видим из таблицы, что наибольшее значение достигается в точке А" с координатами
X! = 1,5; х2 = 2,58.
Очень короткое послесловие
Уважаемый читатель! Лежащая перед тобой книга — не классическое исследова-
исследование, по окончании которого уместно делать вывод о том новом, что автору удалось
вырвать у природы. Эта книга — и не учебник, призванный системно ввести тебя,
мой читатель, в предмет. Скорее всего, эта книга — справочник с комментариями,
заменяющими изложение основ теории обработки результатов наблюдений.
Однако пространные комментарии, большое число и подробное описание приме-
примеров позволяют автору надеяться на то, что его труд может претендовать на статус
пособия или руководства, т. е. быть чем-то средним между классическим учебником
и ординарным справочником.
Автор хотел бы ограничиться одной ремаркой, цель которой — ответить на веро-
ятный вопрос оппонента-профессионала: почему пропущены (или недостаточно пол-
полно изложены) некоторые разделы прикладной математической статистики? Такие,
например, как многомерная статистика, временные ряды, методы распознавания
незрительных образов, теория обслуживания и очередей и т. п.
Вопрос естествен. Однако автор хотел бы обратить внимание оппонента на
вводную часть книги. Цель книги — дать инструмент в руки инженера или ис-
исследователя, не имеющего горячего стремления погружаться в математические
глубины теории вероятностей и математической статистики. Автор исходил из
того, что математика перечисленных выше разделов прикладной статистики весьма
„тяжела" для среднего инженера или исследователя и вряд ли будет им воспринята.
Впрочем, может быть, это слабый аргумент, и дело скорее в неспособности автора
соответствующим образом изложить эти разделы прикладной статистики.
Так или иначе, автор сделал всё, что мог, и надеется, что тем самым внес свой
скромный вклад во введение инженеров и исследователей в увлекательный мир
обработки результатов наблюдений.
Последние строки книги автор считает своим долгом посвятить словам благо-
благодарности ее научному редактору B.C. Ароловичу, чей напряженный труд немало
способствовал превращению исходного авторского текста в книгу, достойную вни™
мания читателя.
Список литературы
1. Крамер Г. Математические методы статистики / Пер. с англ. — М.: Мир, 1975.
2. Ван дер Варден Б. Л. Математическая статистика / Пер. с нем. — М.: ИЛ, 1960.
3. Колмогоров А.Н. Основные понятия теории вероятностей. — М.: Наука, 1974.
4. Гнеденко Б. В, Курс теории вероятностей. — М.: Наука, 1965.
5. Кендалл М., Стъюарт А. Теория распределений / Пер. с англ. — М.: Наука, 1966.
6. Уилкс С. С. Математическая статистика / Пер. с англ. — М.: Наука, 1967.
7. Юл. Д. Э., Кендалл М. Д. Теория статистики / Пер. с англ. — М.: Госстатиздат, 1960.
8. Джини К. Средние величины / Пер. с итал. — М.: Статистика, 1970.
9. Закс Л. Статистическое оценивание / Пер. с нем. — М.: Статистика, 1976.
10. Митрополъский А. К. Техника статистических вычислений. — М.: Наука, 1971.
11. Идье В., Драйад Д., Дмсеймс Ф., Рус М., Садуле Б. Статистические методы в экспе-
экспериментальной физике. — М.: Атомиздат, 1976.
12. Смирнов Н. В., Дунин-Барковский И. В. Курс теории вероятностей и математической
статистики. — М.: Наука, 1969.
13. Хан Г1., Шапиро С. Статистические модели в инженерных задачах / Пер. с англ.—
М.: Мир, 1969.
14. Химмельблау Д. Анализ процессов статистическими методами / Пер. с англ. — М.:
Мир, 1970.
15. Шторм Р. Теория вероятностей. Математическая статистика. Статистический кон-
контроль качества / Пер. с нем. — М.: Мир, 1970.
16. Справочник по надежности. Т. 1 / Пер. с англ. — М.: Мир, 1969.
17. Хастингс Н., Пикок Дмс. Справочник по статистическим распределениям / Пер.
с англ. — М.: Статистика, 1980.
18. Холлендер М., Вулф Д. Непараметрические методы статистики / Пер. с англ. — М.:
Финансы и статистика, 1983.
19. Йэйтс Ф. Выборочный метод в переписях и обследованиях. — М.: Статистика, 1965.
20. Пустылъник Е. И. Статистические методы анализа и обработки результатов наблю-
наблюдений. — М.: Наука, 1968.
21. Мот Ж. Статистические предвидения и решения на предприятии.—М.: Прогресс,
1966.
22. Коуден Д. Статистические методы контроля качества / Пер. с англ. — М.: Наука, 1961.
23. Абезгауз Г. Г. и др. Справочник по вероятностным расчетам.—М.: Воениздат, 1970.
24. Оуэн Д. Н. Сборник статистических таблиц / Пер. с англ. — М.: ВЦ АН СССР, 1966.
25. Большее Л. Н., Смирнов Н.В. Таблицы математической статистики.—М.: Наука,
1965.
26. Келли Т. Л. Статистические таблицы / Пер. с англ. — М.: ВЦ АН СССР, 1966.
27. Митрополъский А. К. Интеграл вероятностей. Л.: Изд-во ЛГУ, 1972.
28. Таблицы нормального интеграла вероятностей, нормальной плотности и ее нормиро-
нормированных производных. — М.: Изд-во АН СССР, 1960.
29. Янко Я, Математико-статиетические таблицы / Пер. с чеш. — М.: Госстатиздат, 1961.
30. Дьяконов В. Л. Справочник по расчетам на микрокалькуляторах. — М.: Наука, 1986.
31. Цветков A. Н., Епанечников В. А. Прикладные программы для микро-ЭВМ „Элек-
„Электроника БЗ-34", „Электроника-МК-56", „Электроника МК-54".— М.: Финансы и ста-
статистика, 1984.
32. Справочник по специальным функциям / Под ред. М. Абрамовица и И. М. Стиган. —
М.: Наука, 1979.
33. Епанечников В. А., Цветков А.Н. Справочник по прикладным программам для
микрокалькуляторов. — М.: Финансы и статистика, 1980.
24 А. И. Кобзарь
738 Список литературы
34. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. —
М.: Наука, 1971.
35. Hastings С. Approximations for digital computers, Princeton Univ.Prtss., 1955.
36. Казакавичюс К. А. Приближенные формулы для статистической обработки резуль-
результатов механических испытаний // Завод, лаб. 1988. Т. 54, № 12. С. 82—85.
37. Надежность и эффективность в технике. Справочник / Под ред. Б. В. Гнеденко. —
Т. 2. —М.: Машиностроение, 1987.
38. Kennedy W.«/., Gentle J. E. Statistical computing, Marcel Dreker Inc., New York and
Basel, 1980.
39. Joiner B. I., Rosenblatt J. R. Some properties of the in samples from Tukey's symmetric
lambda distribution // JASA. 1971. V. 66. P. 394-399.
40. Lin Jinn-Ту an. Approximating the normal tall probability and Its inverse for use on a
pocket calculator // JRSS. Sec. С 1989. V. 38, №1. P. 69-70.
41. Goldwaite L. R. Failure rate study for the lognormal lifetime model // Proc. Symp.
Reliability Quality Control, Philadelphia, 1961.
42. Aitchison J., Brown J. The lognormal distribution. London: Cambridge Univ. Press, 1951.
43. Венецкий И. Г., Венецкая В. И. Основные математико-статистические понятия и фор-
формулы в экономическом анализе. — М.: Статистика, 1982.
44. Шор Я. Б., Кузьмин Ф. И. Статистические методы анализа и контроля качества
и надежности.—М.: Сов. радио, 1968.
45. Пагурова В. И. Таблицы неполной гамма-функции. — М.: ВЦ АН СССР, 1963.
46. Шор Я. Б. Статистические методы анализа и контроля качества и надежности. — М.:
Сов. радио, 1962.
47. Слуцкий Е. Е. Таблицы для вычисления неполной Г-функции и функции вероятно-
вероятностей. — М.: Изд-во АН СССР, 1950.
48. Лившиц И. Г. Обобщенное гамма-распределение // Надежность и контроль качества.
1975. №7. С. 28-34.
49. Stacy E. W. A generalization of the gamma-distribution // AMS. 1962. V. 28. P. 1187-1192.
50. Пирсон К. Таблицы неполной бета-фукнции.— М.: ВЦ АН СССР, 1974.
51. Хальд А. Математическая статистика с техническими приложениями. —М.: ИЛ, 1956.
52. Cadwell L, H, An approximation to the symmetrical incomplete beta function // Biometri-
ka. 1952. V. 39. P. 204-207.
53. Wise M. E. The Incomplete bet a-function, as a contour Integral and a quickly conversing
series for Its inverse // Biometrika. V. 37. 1950. P. 208-218.
54. Wise M. E. On normalizing the Incomplete bet a-function for fitting to dosage response
curves // Biometrika. 1969. V. 47. P. 173-175.
55. Molenar W. Approximations to the Polsson, binomial and hypergeometric distribution
function, Math. Center tracts., 31, Amsterdam, 1970.
56. Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике. — М.:
Финансы и статистика, 1982.
57. Ликеш Ж., Ляга Й. Основные таблицы математической статистики. — М.: Финансы
и статистика, 1985.
58. Boyd W. С. A nomogram for chl-square // JASA. 1965. V. 60. №309. P. 344-346.
59. Fisher R. A., Yates F. Statistical tables for biological, agriculture and medical research.
Edinburgh & London: Oliver and Boyd, 1963.
60. Fisher R. A. Statistical tables for research workers. Edinburgh: Oliver and Boyd, 1925.
61. Wilson Т. В., Hilferty M. M. The distribution of chi-square // Proc. of the national
Academy of sciences. 1931. V. 17, № 12. P. 684-688.
62. Hawkins D, M., Wixley R.A.J, A note on the transformation of the normality // AS.
1986. V. 40, №4. P. 296-298.
63. Hernandes F., Johnson R. A, The large-sample behavior of transformations to normality
// JASA. 1980. V. 75. P. 855-861.
64. Taylor J. M. G. Power transformations to symmetry // Biometrika. 1985. V. 72. P. 145-152.
65. Goldstein R. B. Chi-square quantlles, Algorithm 51 // Commun. Assoc. Сотр. 1973.
V. 16. P. 483-485.
Список литературы 739
66. Sever о N. С, Zelen V. Normal approximation to the chi-square and non-central
Improbability function // Biometrika. 1960. V. 47. P. 411-416.
67. Haldane J. B. S. The approximate normalization of the class of frequency distribution //
Biometrika. V. 29, 1937. P. 392-404.
68. Golberg H., Levine H. Approximate formulas for the percentage points and normalization
of t and x2 // AMS. 1945. V. 17. P. 216-225.
69. Gilbert R. J. A sample formula for cuterpolating tables of x2 // Biometrics. 1977. V. 33.
P. 383-385.
70. Hoagling D. C. Direct approximations for chi-square percentage points // JASA. 1977.
V. 72, №359. P. 508-515.
71. Aroian L. A. A new approximation to the levels of significance of the chi-square distribu-
distribution // AMS. 1973. V. 14. P. 93-95.
72. Peizer D. В., Pratt J. W. A normal approximation for binomial, F, beta and other
common, related tall probability, 1 // JASA. 1968. V. 63, №324. P. 1416-1456.
73. Pratt J. W. A normal approximate for binomial, F, beta and other common, related tall
probability, 2 // JASA. 1968. V. 63, №324. P. 1457-1483.
74. Ling R. F. A study of the accuracy of same approximations for ?, x2 and F tail probability
// JASA. 1978. V. 73, №362. P. 274-283.
75. Zar J. H, Approximations for the percentage points of the chi-square distribution // JRSS.
Sec. C. 1978. V. 27, №3. P. 280-290.
76. Fisher R. A. Expansion of „Student's" integral in power of n^1 // Metron. 1926. №5.
P. 109-112.
77. Koechler K. J. A simple approximations for the percentage of t distribution, // Techno™
metrics. 1983. V. 25, №1. P. 103-105.
78. Koechler K. J. A simple approximations for the percentage of t distribution // JRSS.
Sec. C. 1978. V. 27, №3. P. 280-290.
79. Nelson L. S. Same notes of Student's // J. of Quality Techn. 1984. V. 16, № 1. P. 64-65.
80. Nelson L. S. Standardizing Student's t // AS. 1973. V. 27. P. 93.
81. Gentleman W. M., Jenkins M. A. An approximation for Student's ^-distribution // Bio-
Biometrika. 1968. V. 55. P. 571-572.
82. Scott A., Smith T.M.E. A note on Moran's approximation to Student's // Biometrika.
1970. V. 57, №3. P. 681-682.
83. Dawson F. H. Alternatives to the use of tabulated values of distribution In statistical
programs // Nature. 1975. V. 256. P. 148.
84. Мог an P. A. P. Accurate approximation for t-test, in Festschrift for J. Nayman: Research
papers in statistics, ed. F. N. David. — N. Y.: Wiley, 1966. P. 225-230.
85. Wang Y. Y. Probability the type 1 errors of the Welch tests for the Behrens-Fisher
problem // JASA. 1971. V. 66. P. 605-608.
86. Fenstad G. U. A comparison between the U and V tests In the Behrens-Fisher problem
// Biometrika. 1983. V. 70, №1. P. 300-302.
87. Мардиа К., Земроч П. Таблицы F-распределений и распределений, связанных с ни™
ми.^М.: Наука, 1984.
88. Paulson E. An approximate normalization of the analysis of variance distribution // AMS.
1942. V. 13. P. 233-235.
89. Haines P. D. A closed form approximation for calculating the percentage points of the F
and t distributions // JRSS. Sec. C. 1988. V. 37, №1. P. 95-100.
90. Carter A. H. Approximation to percentage points of the z-dlstrlbution // Biometrika.
1947. V. 34. P. 352-358.
91. Hald A. D. Statistical tables and formulas, New York, 1952. P. 47-59.
92. Cochran W. G. Note on an approximate formula for the significance levels of z // AMS.
1940. V. 11. P. 93-95.
93. Бородачев Н. А., Абдрашитов Р. М., Веселова И. М. Точность производства в маши™
построении и приборостроении. — М.: Машиностроение, 1973.
94. Гумбель Э. Статистика экстремальных значений.—М.: Мир, 1965.
24*
740 Список литературы
95. Капур if., Ламберсон Л. Надежность и проектирование в технике. — М.: Мир, 1980.
96. Owen D. В. The power of Student's t-test // JASA. 1965. V. 60, №309. P. 320-333.
97. Джонсон H., Лион Ф. Статистика и планирование эксперимента в технике и науке.
Методы обработки данных. — М.: Мир, 1980.
98. Pearson E. S. Note on an approximation to the distribution of non-central %2 // Biometri-
ka. 1959. V. 46. P. 364-366.
99. Patnaik E. S. The norbcentral %2 and F distribution and their applications // Biometrika.
1949. V. 36. P. 202-232.
100. Pearson E. S., Hartley H. O. Charts of the power function for analysis of variance test,
derived from the non-central iF-distribution // Biometrika. 1951. V. 38. P. 112—130.
101. Tiku M.L. Laguerre series forms of non^central x2 and F distribution // Biometrika.
1965. V. 52. P. 415-427.
102. Tiku M. L. A note on approximating to the non^central F distribution // Biometrika.
1966. V. 53. P. 603-610.
103. Судаков Р. С. и др. Статистические задачи обработки систем и таблицы для числовых
расчетов показателей надежности. — М.: Высшая школа, 1975.
104. Большее Л. Н. Асимптотические пирсоновские преобразования // Теор. вероятн. и ее
примен. 1963. №8. С. 129-155.
105. Браунли К. А. Статистическая теория и методология в науке и технике. — М.: Наука,
1977.
106. Рао С. Р. Линейные статистические методы и их приложения. — М.: Наука, 1968.
107. Anscomb F. J. The transformation of Poisson, binomial and negative-binomial data //
Biometrika. 1948. V. 35. P. 246-254.
108. Черницкий П. И. Таблицы вероятностей. — М.: Воениздат, 1957.
109. Binns M. R. Approximating the negative binomial via the positive binomial // Techno-
metrics. 1974. V. 16. P. 323-324.
110. Best D. J., Gipps P. G. An improved gamma approximation to the negative binomial //
Technometrics. 1974. V. 16. P. 621-624.
111. Liberman G. J., Owen D. B. Tables of the hypergeometric probability distribution. Stan-
Stanford Univ. Press, Stanford, Calif., 1961.
112. Vilaplana J. H. A tables of the hypergeometric probability distribution, Publ. Lab. Ing.
Ind. Panama, s. B, r. 2, 1976, P. 1-2095.
113. Беляев Ю.К. Вероятностные методы выборочного контроля. — М.: Наука, 1975.
114. Локтев А. Л. Аппроксимационные формулы для распределений нормального, Стыо-
дента, хи-квадрат // Надежность и контроль качества. 1990. №5. С. 22-25.
115. Редько М. Ю. Об аппроксимациях нецентральных F-распределений центральным //
Надежность и контроль качества. 1990. №5. С. 52-59.
116. Вульфович Б. А. Оценивание параметров малой выборки. — Деп. во ВНИЭРХ 22.10.91,
№1180-рх9.
117. Dixon W. J. Estimation of the mean and standard deviation of a normal population //
AMS. V. 28. P. 806-809.
118. Боярский Э.А. Порядковые статистики.—M.: Статистика, 1972.
119. Введение в теорию порядковых статистик / Пер. с англ. — Под ред. А. Сархана
и Б. Гринберга. — М.: Статистика, 1970.
120. Pearson E. S., Tukey J. W. Approximable means and standard deviations based on
distances between persenage points of frequency // Biometrika. 1965. V. 52. P. 533-546.
121. Кенуй М. Г. Быстрые статистические вычисления. "Упрощенные методы оценивания
и проверки. — М.: Статистика, 1979.
122. Дэйвид Г. Порядковые статистики / Пер. с англ. — М.: Наука, 1979.
123. Eisenberger /., Posner E. S. Systematic statistics used for data compression in space
telemetry // JASA. 1965. V. 60. P. 97-133.
124. Walsh J. E. Some significance tests for the median, which are valid under very general
conditions // AMS. 1949. V. 20. P. 64-81.
125. Ашмарин И. П., Васильев Н. Н., Амбросов В. А. Быстрые методы статистической
обработки и планирования экспериментов.—Л.: Изд-во ЛГУ, 1971.
Список литературы 741
126. Фишбейн В. И. Номограмма, реализующая функцию биномиального распределения
// Надежность и контроль качества. 1972. № 12. С. 51-63.
127. Herrey E. M. J. Confidence intervals based on the mean absolute deviation of normal
sample // JASA. 1965. V. 60. P. 257-269.
128. Krutchkoff F. G. The correct use of the sample mean absolute deviation In confidence
intervals for a normal variate // Technometrics. 1966. V. 8. P. 663-67.
129. Peters C. A. F. Uber die Bestimmung des Wahrscheinlichen Fehlers einer Beobachtung aus
den Abweichungen der Beobachtungen von ihrem arithmetischen Mittel // Astronomische
Nachrichten. 1956. 44. S. 30-31.
130. Gutterman H. E. An upper bound for the sample standard deviation // Technometrics.
1962. V. 4. P. 134-135.
131. Dawton F. Linear estimates with polynomial coefficients // Biometrlka. 1966. V. 53.
P. 129-141.
132. Кендалл М.Дою., Стьюарт А, Статистические выводы и связи. — М.: Наука, 1973.
133. Зелингер Г. Я. Построение кратчайших доверительных интервалов для ереднеквадра-
тического отклонения нормального распределения // Завод, лаб. 1983. №3. С. 64—66.
134. Iliescu D. F., Voda V. Ch. On the estimation of standard deviation for a normal popula-
population, Trab. estadlst, J. Invest. Oper. 1974. V. 25. P. 71-98.
135. Gohen A. C. Tables for maximum likelihood estlmates-singly truncated and singly cen-
censored samples // Technometrics. 1961. V. 3. P. 535-541.
136. Schmee J., Gladsiein D., Nelson W. Confidence limits for parameters of a normal distri-
distribution from singly censored samples, using maximum likelihood // Technometrics. 1985.
V. 27. P. 119-128.
137. Gupta A. K. Estimation of the mean and standard deviation of a normal population from
a censored sample // Biometrika. 1952. V. 39. P. 260-273.
138. Sarhan A. E., Greenberg B. G. Estimation of location and scale parameters by order
censored sample, part 3, Techn. Report, 4, OOR Project, 1957.
139. Dixon W. J. Simplified estimation from censored normal samples // AMS. 1954. V. 25.
P. 610-614.
140. Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д. Математические методы в теории
надежности. — М.: Наука, 1965.
141. Pandley В. Ж., Srivostava R. A shrinkage estimator for scale parameter of an exponential
distribution // Microelectron Reliability. 1987. V. 27. P. 949-951.
142. Barter H. L. Estimating the parameters of negative exponential populations from one or
two order statistics // AMS. 1961. V. 32. P. 1078-1090.
143. Epstein B. Estimation from life test data // Technometrics. 1960. V. 2. P. 447-454.
144. Ogawa J. Determination of optimal spacing for the estimation of the side parameters of
an exponential distribution based on sample quantiles // Ann. Inst. St. Mat. 1960. V. 12.
P. 11-155.
145. Harber H. L. Best linear unbiased under symmetric censored of the parameters of a double
exponential population // JASA. 1961. V. 32. P. 1078-1084.
146. Kuldorff G. Estimation of one or two parameters of exponential distribution on the basis
of suitably chosen order statistics // AMS. 1963. V. 34. P. 1419-1431.
147. Siddiqui M. M. Optimal estimators of the parameters of negative exponential distribution
from one or two order statistics // AMS. 1963. V. 34. P. 117-121.
148. Saleh A. K., Ali M. M. Aslmptotic optimum quantiles for the estimation of the parameters
of the negative exponential distribution // AMS. 1966. V. 37. P. 143-151.
149. Hassanein К. М. Estimation of the parameters of the extreme values distribution by use
of two or three order statistics // Biometrika. 1969. V. 56. P. 429-436.
150. Weissman I. Estimation of parameters and large quantiles based on the К largest
observations // JASA. 1978. V. 73. P. 812-815.
151. Kubai P., Epstein B. Estimation of quantiles of location-scale distribution based on two
or three order statistics // Technometrics. 1980. V. 22. P. 575-581.
152. Кудлаев Э. М. Оценивание параметров распределения Вейбулла-Гнеденко (обзор) //
Изв. АН СССР: Техн. кибернет. 1986. №6. С. 5-18.
742 Список литературы
153. Мартыненко Ю. Н. Ускоренная оценка параметров распределения Вейбулла мето-
методом максимального правдоподобия // Надежность и контроль качества. 1987. №6.
С.11-13.
154. Подольский Ю. М. О точном вычислении некоторых решеточных функций Грина //
Укр. физ. ж. 1972. Т. 17, №2. С. 240-260.
155. Тonaka S., Ichiakawa М. Approximate formula of coefficient of variation for Weibull
distribution // Reliability Eng. 1983. V. 4. P. 141-143.
156. Глушко В. Т., Бобро Н. Т., Рубец Г. Т., Гажемон Л. И. Некоторые методы оценки
параметров обобщенного распределения Вейбулла // Надежность сложных техниче-
технических систем: Сб. — Киев: Наукова думка, 1974. С. 83-91.
157. Один И. М. Определение параметров распределения Вейбулла методом наименьших
квадратов // Надежность и контроль качества. 1975. №7. С. 45—48.
158. Багно А. Н. Об одном методе оценки параметров распределения Вейбулла // Надеж-
Надежность и контроль качества. 1975. №7. С. 25-32.
159. Балицкая Е. О., Золотухина Л. А. Асимптотическая эффективность моментных
и квантильных оценок параметров распределения Вейбулла // Завод, лаб. 1988. Т. 54,
№3. С. 92-96.
160. Bain L. J. Inferences based on censored sampling from the Weibull or extreme-value
distribution // Technometrics. 1972. V. 14. P. 693-702.
161. Engelhart M. On simple estimation of the parameters of the Weibull or extreme™value
distribution // Technometrics. 1975. V. 17. P. 369-373.
162. Mann N. R., Fertig K. W. Simplified efficient point and Interval estimators for Weibull
parameters // Technometrics. 1975. V. 17. P. 361-368.
163. Engelhart M., Bain L, J. Some complete and censored sampling results for the Weibull or
extreme-value distribution // Technometrics. 1973. V. 15. P. 541-549.
164. Engelhart M., Bain L. J. Some results on point estimators for the two-parameter Weibull
or extreme-value distribution // Technometrics. 1974. V. 16. P. 49-56.
165. Mann N. R. Best linear invariant estimation for Weibull parameters under progressive
censoring // Technometrics. 1971. V. 13. P. 521-533.
166. Балицкая Е. О., Золотухина Л. А. Оценка параметров распределения Релея // Завод,
лаб. 1992. Т. 58, №5. С. 54-57.
167. Мапп N. Д., Fertig К. W. Tables for obtaining Weibull confidence bounds and tolerance
bounds on best linear invariant estimates of parameters of the extreme™value distribution
// Technometrics. 1973. V. 15. P. 87-101.
168. Stasy E. W. Quasymaximum likelihood estimations for two-parameter gamma-distribution
// IBM J. Res. And Develop. 1973. V. 17. P. 115-124.
169. Shenton L. IL, Bowman К. О. Further remarks on maximum likelihood estimator for
gamma-distribution // Technometrics. 1972. V. 14. P. 725-733.
170. Рудых Г. А. Оценки максимального правдоподобия двухпараметрического гамма-
распределения // Надежность и контроль качества. 1977. №1. С. 60-65.
171. Мартыненко Ю. Н. Ускоренная оценка параметров гамма-распределения // Надеж-
Надежность и контроль качества. 1984. №12. С. 10—11.
172. Буймов А. Г., Буймова Н. А. Об имитации и оценивании параметров гамма-распреде-
гамма-распределения // Исследование корреляционно-экстремальных систем, Томск, 1987, С. 8—11.
173. Wang Wenjun. Scale parameter of gamma-distribution and its autocovariance estimation
// Chin. J. Appl. Prob. and Stat. 1987. V. 3. P. 193-202.
174. Clopper C. /., Pearson E. S. The use of confidence or fiducial limits illustrated in the case
of the binomial // Biometrika. 1934. V. 26. P. 404-413.
175. Чурилов В. И, Об использовании приближенных зависимостей для определения до-
доверительных границ параметра биномиального распределения // Надежность и кон-
контроль качества. 1972. №12. С. 51-63.
176. Blyth С. R. Approximate binomial confidence limits // JASA. V. 81, 1986. P. 843-855.
177. Hall P. Improving the normal approximation when constructing one-sided confidence
intervals for binomial and Poisson parameters // Biometrika. 1982. V. 69. P. 647-652.
Список литературы 743
178. Paulson E. An approximate normalization of the analysis of variance distribution // AMS.
1942. V. 13. P. 233-235.
179. Camp В. Н. Approximation to the point binomial // AMS. 1951. V. 22. P. 130-131.
180. Pratt J. W. A normal approximation for binomial, F, beta, and other common related tail
probabities. 2 // JASA. 1968. V. 63. P. 1457-1483.
181. Титенко И. М. Оценка доверительных границ параметра биномиального распреде-
распределения // Надежность и контроль качества. 1983. № 12. С. 31—36.
182. Дамидович Н. О., Курский И.Ю. и др. О приближенных формулах вычисления
доверительных границ вероятностей при биномиальном плане испытаний // Завод.
лаб. 1988. Т. 54, №3. С. 95-98.
183. Noether G. E. Some simple distribution free confidence intervals for the center of a
symmetric distribution // JASA. 1973. V. 68. P. 716-719.
184. Багдонавичюс В., Адоменас В. Исследование одного распределения и оценок его
параметров // Применение теории вероятностей и математической статистики: Сб.
Вып. 5. Вильнюс, 1983.^ С. 123-130.
185. Hahn G. J. A simultaneous prediction limit on the means of future samples from an
exponential distribution // Technometrics. 1975. V. 17. P. 341-345.
186. Nelson W.B. Two-sample prediction, General Elect. Сотр., TIS Rep., 68-C-40.
187. Green J. Asymptotic sample size for given confidence intervals length // JRSS. Sec. C.
1982. V. 31. P. 298-300.
188. Нейман Ю. Вводный курс теории вероятностей и математической статистики / Пер.
с англ. — М.: Сов. Радио, 1962.
189. Леман Э.Л. Проверка статистических гипотез / Пер. с англ. — М.: Физматгиз, 1964.
190. Чернов Г., Мозес Л. Е. Элементарная теория статистических решений / Пер. с англ. —
М.: Сов. Радио, 1962.
191. Закс III. Теория статистических выводов / Пер. с англ. — М.: Мир, 1975.
192. Де Гроот М. Оптимальные статистические решения. — М.: Мир, 1974.
193. Pearson К. Experimental discussion of the (x , p) test for goodness-of-fit // Biometrika.
1932. V. 24. P. 351-381.
194. Gochran W. G. The chi-squared test of goodness-of-fit // AMS. 1952. V. 23. P. 315-345.
195. Gochran W. G. Some methods for strengthening the common chi-squared tests // Bio-
Biometrika. 1954. V. 10. P. 417-451.
196. Kallenberg W. C. M., Oosterhoff J., Schrever B. F. The number of classes in chi-squared
goodness-of-fit tests // JASA. 1985. V. 80, №392. P. 959-968.
197. Mann H. В., Wald A. On the choice of number of intervals in the application of the chi-
square test // AMS. 1942. V. 18. P. 50-54.
198. Щербинин А. Ф. Об относительной эффективности критерия хи-квадрат и его ана-
аналогах // Надежность и контроль качества. 1986. №2. С. 13-17.
199. Dahiya R. С, Gurland J. How many classes in the Pearson chi-square test? // JASA.
1973. V. 68, №343. P. 707-712.
200. Hamdan M. A, The number and width of classes in the chi-square test // JASA. 1963.
V. 58, №303. P. 678-679.
201. Best D. J., Rayner J.G.M. Are two classes enough for the goodness-of-fit test? //
Statistica Neerlandica. 1981. V. 35. P. 157-163.
202. Dahya R. C, Gurland J., Pearson K. Chi-squares test of fit with random intervals //
Biometrika. 1972. V. 59, №1. P. 147-153.
203. Lawal H. J9., Upton G. J. G. An approximation to the distribution of the %2 goodness-of-fit
statistic for the use with small expectations // Biometrika. 1980. V. 67, №2. P. 447-453.
204. Larntz K. Small-sample comparisons of exact levels for chi-square goodness-of-fit statistics
// JASA. 1978. V. 73. P. 253-263.
205. Yarnold J. K. The minimum expectation in %2 goodness-of-fit tests and the accuracy of
approximations for the accuracy of approximations for the null distribution // JASA.
1970. V. 65. P. 864-886.
206. Wishart J. x2 probabilities for large number of degrees of freedom // Biometrika. 1956.
V. 43. P. 92-95.
744 Список литературы
207. Романовский В. И. Элементарный курс математической статистики. — M.-JL: Госпла-
низдат, 1939.
208. Barnett A., Eisen E. A quartile test for differences in distribution // JASA. 1982. V. 77,
№377. P. 47-51.
209. Орлов А, И, Распространенная ошибка при использовании критериев Колмогорова
и омега-квадрат // Завод, лаб. 1985. Т. 51, №1. С. 60-62.
210. Kolmogorov А. N. Confidence limits for an unknown distribution function // AMS. 1941.
V. 12. P. 461-463.
211. Смирнов Н. В. Оценка расхождения между эмпирическими кривыми распределений
в двух независимых выборках // Бюллетень МГУ. Сер. А. Вып. 2. 1939. С. 13—14.
212. Stephens M. A. Use of Kolmogorov-Smirnov, Oramer-von Mises and related statistics
without extensive tables // JRSS. S. B. 1970. V. 32. P. 729-731.
213. Chandra M., Singpurwalla N. D., Stephens M. A. Kolmogorov statistics for tests of fit for
the extreme»value and Weibull distributions // JASA. 1981. V. 76, №375. P. 729-731.
214. Koziol J. A., Byar D. P. Percentage points of the asymptotic distributions of one and two
sample K—S statistics for truncated or censored data // Technometrics. 1975. V. 17, №4.
P.507-510.
215. Stephens M. A. EDF statistics for goodness-of-fit and some comparisons // JASA. 1974.
V. 69. P. 730-737.
216. Смирнов Н. В, О распределении пш -критерия Мизеса // Математический сб. 1937.
2D4), №5. С. 973-993.
217. Смирнов Н. В. О критерии Крамера—фон Мизеса // Успехи матем. наук (новая
серия). 1949. Т. 4, №4C2). С. 196-197.
218. Мартынов Г. В. Критерии омега-квадрат. — М.: Наука, 1978.
219. Tiku M. L. Ohi-square approximation for the distributions of goodness-of-fit statistics UN
and Wjj /I Biometrika. 1965. V. 52, №3-4. P. 630-633.
220. Renyi A. On the theory of order statistics // Acta Mathem. Acad. Scientiarum Hungarical.
1953. V. 4. P. 191-232.
221. Залесский Б, А., Ольшевская О. В. О функции распределения статистики омега-
квадрат при малых выборках // Завод, лаб. 1989. №7. С. 103-105.
222. Goto Ishii. On the exact probabilities of Renyi tests // Annal. Inst. Stat. Math. 1959.
V. 2. P. 17-24.
223. Anderson T. W., Darling D. A. A test for goodness-of-fit // JASA. 1954. V. 49. P. 765-769.
224. Lewis P. A. W. Distribution of the Anderson-Darling statistic // AMS. 1961. V. 32.
P. 1118-1123.
225. Watson G. S. Goodness-of-fit tests on a circle // Biometrika. 1961. V. 48, №1-2.
P. 109-114.
226. Щербинин А. Ф. Критерии согласия омега-квадрат по группированным наблюдениям
// Надежность и контроль качества. 1983. №1. С. 11-18.
227. Sinclair CD., Spurr В. D., Ahmad V.I. Modified Anderson-Darling test // Commun.
Stat.-Theor. Meth. 1990. V. 19, №10. P. 3677-3686.
228. Мардиа К. Статистический анализ угловых наблюдений.—М.: Наука, 1978.
229. Kuiper N. Н. Tests concerning random points on a circle // Proc. Konikl. Nederl. Akad.
Van Wettenschappen. 1960. S. A. V. 63. P. 38-47.
230. Stephens M. A. The goodness-of-fit statistic Fn-distribution and significance points //
Biometrika. 1965. V. 52. №3-4. P. 309-321.
231. O'Reilly F. J., Stephens M. A. Characterization and goodness-of-fit tests // JRSS. 1982.
232. Darling J. The Kolmogorov-Smirnov, Cramer-von Mises tests // AMS. 1957. V. 28.
P. 823-838.
233. Durbin J. Some methods of constructing exact tests // Biometrika. 1961. V. 48, №1-2.
P. 41-57.
234. Pearson K. On a method of determining whether a sample of size n supposed to have
been drawn from a parent population having a known probability integral has probably
been drown of random // Biometrika. 1933. V. 25. P. 379-410.
Список литературы 745
235. Pearson E. S. The probability integral transformation for testing goodness-of-fit and
combining independent tests of significance // Biometrika. 1939. V. 30. P. 134-148.
236. Kaizenbeisser W., Hackl P. An alternation to the Kolmogorov-Smirnov two-sample test
// Commun. Stat.-Theor. Meth. 1986. V. 15, №4. P. 1163-1177.
237. Anderson T. W. On the distribution of the two-sample Cramer-von Mises criterion //
AMS. 1962. V. 33. P. 1148-1159.
238. Frozini B. V. A survey of a class of goodness-of-fit statistics // Metron. 1978. V. 36, № 1-2.
P. 3-49.
239. Frozini B. V. On the distribution and power of a goodness-of-fit statistic with paramet-
parametric and nonparametric applications, „Goodness-of-fit" / Ed. by Revesz P., Sarkadi K.,
Sen P. K., Amsterdam-Oxford-New York: North-Holland. Publ. Сотр., 1987, P. 133-154.
240. Shapiro S. S., Wilk M. B. An analysis of variance test for normality (complete samples)
// Biometrika. 1965. V. 52, №3. P. 591-611.
241. Lloyd E. N. Least-squares estimation of location and scale parameters using order statistics
// Biometrika. 1952. V. 39. P. 88-95.
242. Shapiro S. 5., Wilk M. B. Approximations for the null distribution of the W statistic //
Technometrics. 1968. V. 10, №4. P. 861-866.
243. Shapiro S. 5., Wilk M. В., Chen H. J. A comparative study of various tests for normality
// JASA. 1968. V. 63, №324. P. 1343-1372.
244. Shapiro S. Я., Francia R. S. An approximate analysis of variance test normality // JASA.
1972. V. 67, №337. P. 215-216.
245. Weisberg S., Bingham C. An approximate analysis of variance test for non-normality
suitable for machine calculation // Technometrics. 1975. V. 17, №1. P. 133-134.
246. Royston J. P. Correcting the Shapiro-Wilk test W for ties // J. Stat. Comput. Simul.
1989. V. 31, №4. P. 237-249.
247. Vasicek O. A test for normality based on sample entropy // JRSS. 1976. V. 38, №1.
P. 54-59.
248. Prescott P. On a test for normality based on sample entropy // JRSS. 1976. V. 38, №3.
P. 254-256.
249. Hegazy Y. A. S., Green J. R. Some new goodness-of-fit tests using order statistics // Appl.
Statist. 1975. V. 24, №3. P. 299-308.
250. С sorgo H., Revesz P. Quantile processes and sums of weighted spasing for composite
goodness-of-fit. In: Statistics and Related Topics, North Holland, Amsterdam, N. Y., 1981.
P. 69-87.
251. Aly E.-E., С sorgo M. Quadratic nuisance parameter-free goodness-of-fit tests in the
presence of location and scale parameters // CJS. 1985. V. 13. P. 53-70.
252. Aly E.-E., Shayib M. A. On some goodness-of-fit tests for the normal, logistic and extreme-
value distributions // Commun. Stat.-Theor. Meth. 1992. V. 21, №5. P. 1297-1308.
253. Filliben J. J. The probability plot correlation coefficient test for normality // Technomet-
Technometrics. 1975. V. 17, ЛН. P. 111-117.
254. Gulledge T. Rn Looney S. W. An alternative test for normality Comput. Sci. And Statist //
Proc. 16-th Symp. Interface, Atlanta, Ga, Marth 1984, Amsterdam e.a., 1985. P. 265-267.
255. La Brecque J. Goodness-of-fit tests based on nonlinearity in probability plots // Techno-
Technometrics. 1977. V. 19, №3. P. 293-306.
256. Locke C, Spurrier J. D. The use of [/-statistics for testing normality against nonsymmetric
alternative // Biometrika. 1976. V. 63, №1. P. 143-147.
257. Locke C, Spurrier J. D. The use of [/-statistics for testing normality against alternatives
with both tails heavy or both tails light // Biometrika. 1977. V. 64, №3. P. 638-640.
258. Oja H. Two location and scale goodness-of-fit tests // Biometrika. 1981. V. 68, №3.
P. 637-640.
259. Davids С. Е., Quade D. [/-statistics for skewness or symmetry // Commun. Stat.-Theor.
Meth. 1978. V. A7, №5. P. 413-418.
260. Oja H. New tests for normality // Biometrika. 1983. V. 70, №1. P. 279-299.
261. Geary R. C. The ratio of the mean deviation to the standard deviation as a test of
normality // Biometrika. 1935. V. 27. P. 310-322.
746 Список литературы
262. Geary R. С. Moments of the ratio of the mean deviation to the standard deviation for
normal samples // Biometrika. 1936. V. 28. P. 295-307.
263. Geary R. С Testing for normality // Biometrika. 1947. V. 34. P. 209-242.
264. David H. A., Hartley H. 0., Pearson E. S. The distribution of the ratio, in a single normal
sample, of range to standard deviation // Biometrika. 1954. V. 41. P. 482-493.
265. Pearson E. S., Stephens M. A. The ratio of range to standard deviation in the same normal
sample // Biometrika. 1964. V. 512, №3-4. P. 484-487.
266. Thomson G. W. Bounds for the ratio of range to standard deviation // Biometrika. 1985.
V. 42, №1-2. P. 268-269.
267. Spiegelhalter D. J. A test for normality against symmetric alternatives // Biometrika.
1977. V. 64, №2. P. 415-418.
268. Spiegelhalter D. J. An omnibus test for normality for small samples // Biometrika. 1980.
V. 67, №2. P. 493-496.
269. Sarkadi K. On testing for normality, A Magyar Tud. Akad., Matem. Kutato Intezet.
KozlemenyeL, V. A5, 1960. P. 269-275.
270. Золотухина Л. А., Винник Е. В. Эмпирическое исследование мощности критерия
Саркади и его модификации // Завод, лаб. 1985. Т. 52, №1. С. 51-55.
271. Kawata Т., Sakamoto H. On the characterization of the normal population by the
independence of the sample mean and the sample variance // J. Math. Soc. Japan. 1949.
ЛН. P. 111-115.
272. Заингер А. А. О независимых выборках из нормалвной совокупности // Успехи
матем. наук. 1951. Т. VI. Вып. 5. С. 172-175.
273. Коган А. М., Ландеман Э. М. Информационный аналог теоремы о независимости
среднего и дисперсии // Проблемы устойчивости стохастических систем: Тр. семи-
семинара. — М.: ВНИИСИ, 1985. —С. 763-767.
274. Lin Ch.-Ch.y Mudholkar G. S. A simple test for normality against asymmetric alternatives
// Biometrika. 1980. V. 67, №2. P. 455-461.
275. Nelson B. B. Testing for normality // J. of Quality Technology. 1983. V. 15, №3.
P.141-143.
276. Nelson L. S. A simple test for normality // J. of Quality Technology. 1983. V. 13. P. 76-77.
277. Mudholkar G. 5., Lin G. C. On two applications characterization theorems to goodness™
of-fit // Goodness-of-fit, Amsterdam, 1987. P. 395-414.
278. Martinez J., Iglewicz B. A test for departure from normality based on a biweight estimator
of scales // Biometrika. 1981. V. 68, № 1. P. 331-333.
279. DyAgostino R.B. An omnibus test of normality for moderate and large size samples //
Biometrika. 1971. V. 58, №2. P. 341-348.
280. DyAgostino R. B. Small sample probability points for the D-test of normality // Biometri-
Biometrika. 1972. V. 59, №1. P. 219-221.
281. Dawton F. Linear estimates with polynomial coefficients // Biometrika. 1966. V. 53.
P. 129-141.
282. D'Agostino R. B. Monte Carlo power comparisons of the Wf and D tests of normality //
Common. Stat. 1973. V. 1. P. 545-551.
283. Pearson E. S. A further development of tests for normality // Biometrika. 1930. V. 22.
P. 239-249.
284. D'Agostino R. В., Pearson E. S. A further development of tests departure from normality.
Empirical results for the distribution of 62 and \fb\ // Biometrika. 1973. V. 60, №3.
P. 613-622.
285. D'Agostino R. B. Transformation to normality of the null distribution of gi // Biometrika.
1970. V. 57. P. 679-681.
286. Anscombe F. J., Glynn W. J. Distribution of the kurtosis statistic bi for normal samples
// Biometrika. 1983. V. 70, №1. P. 227-234.
287. Bowman K. 0., Stenton L. R. Omnibus test contours for departures from normality based
on л/К and b2 II Biometrika. 1975. V. 62, №2. P. 243-249.
288. Littele R. G., Folks J. L. Asymptotic optimality on Fisher's method of combining inde-
independent tests. 11 // JASA. 1973. V. 68. P. 193-194.
Список литературы 747
289. Jarque С. М., Вега А. К. A test for normality of observation and regression residuals //
Internat. Stat. Review. 1987. V. 55, Ш2. P. 163-172.
290. Fenerverger A., Mureika R. A. The empirical characteristic function and its application
// Annal. Statist. 1977. V. 5. P. 88-97.
291. Heaihote C. R. A test of goodness-of-fit for symmetric random variables // Austr. J.
Statist. 1972. V. 14. P. 172-181.
292. Kontrouvelis LA. A goodness-of~fit test of simple hypothesis based on the empirical
characteristic function // Biometrika. 1980. V. 67. P. 138-240.
293. Murota K., Takeuchi K. The Studentized empirical characteristic function and its appli-
application to test for the shape of distribution // Biometrika. 1981. V. 68. P. 55-65.
294. Wilk M. В., Shapiro S. S. The joint assessment of normality of several independent samples
// Technometrics. 1968. V. 10, №10. P. 825-839.
295. Винник Е. Вп Золотухина Л. А. Применение модифицированного критерия Саркади
для проверки гипотезы нормальности по совокупности малых выборок // Завод, лаб.
1987. Т. 53, №7. С. 51-54.
296. Wald A., Wolfowitz J. An exact test of randomness in the nonparametric case based on
serial correlation // AMS. 1943. V. 14. P. 378-388.
297. Арлей Н., Бух К. Введение в теорию вероятностей и математическую статистику /
Пер. с англ.^М.: ИЛ, 1951.
298. Shapiro S. S., Wilk M.B. An analysis of variance test for the exponential distribution
(complete samples) // Technometrics. 1972. V. 14. P. 355-370.
299. Samanta M., Schwarz С J. The Shapiro-Wilk test for exponentiality based on censored
data // JASA. 1988. V. 83, №402. P. 528-531.
300. Stephens M. A. On the W test for exponentiality with origin known // Technometrics.
1978. V. 20. P. 353-357.
301. Spinelli J. J., Stephens M. A. Tests for exponentiality when origin and scale parameters
are unknown // Technometrics. 1987. V. 29, №4. P. 471-476.
302. Spurrier J. D. On overview of tests of exponentiality // Commun. Stat.-Theor. Meth.
1984. V. 13. P. 1635-1654.
303. Sarhan A. E. Estimation of the mean and standard deviation by order statistics // 1954.
AMS. V. 25. P. 317-328.
304. Peitit A, N. Tests for the exponentiality distribution with censored data using Cramer-
von Mises statistics // Biometrika. 1977. V. 64, №3. P. 629-632.
305. Brain C. W., Shapiro S. S. A regression test for exponentiality: censored and complete
samples // Technometrics. 1983. V. 25, №1. P. 69-76.
306. Kimber A. C. Tests for the exponential, Weibull and Gumbel distributions based on the
stabilized probability plot // Biometrika. 1985. V. 72, №3. P. 661-663.
307. Michael J. R. The stabilized probability plot // Biometrika. 1983. V. 70. P. 11-17.
308. Coles S. G. On goodness-of-fit tests for the two-parameter Weibull distribution derived
from the stabilized probability plot // Biometrika. 1989. V. 76, №3. P. 593-598.
309. Moran P. A. P. The random division of an interval, 11 // JRSS. 1951. V. 13. P. 147-150.
310. Кокс С, Льюис П. Статистический анализ последовательностей событий / Пер.
с англ. — М.: Мир, 1969.
311. Klimko L, Л., Antle С. Е., Rademaker A. W., Rockette H. E. Upper bounds for the power of
invariant tests for the exponential distribution with Weibull alternative // Technometrics.
1975. V. 17, №3. P. 357-360.
312. Tanaka S., Ichikawa M. Approximate formula of coefficient of variation for Weibull
distribution // Reliability Engineering. 1983. V. 4, №3. P. 141-143.
313. Hollander M., Proshan F. Testing whether new is better than used // AMS. 1972. V. 43.
P. 1136-1146.
314. Siurges H. A. The choice of a class interval // JASA. 1926. V. 21. P. 65-66.
315. Kochar S. C. Testing exponentiality against monotone failure rate average // Commun.
Stat.-Theor. Meth. 1985. №2. P. 381-392.
316. Klefsjo B. Some tests against aging based on the total time on test transform // Commun.
Stat.-Theor. Meth. 1983. V. 14, №12. P. 917-927.
748 Список литературы
317. Deshande J. V. A class on tests for exponentiality against Increasing failure rate average
alternative // Blomertlka. 1983. V. 70. P. 514-518.
318. Barlow R. E. Likelihood ratio tests for restricted families of probability distributions //
AMS. 1968. V. 39. P. 547-560.
319. Bickel P. J., Doksum K. Tests for monotone failure rate based on normalized spacing //
1969. AMS. V. 40. P. 1216-1235.
320. Klefsjo B. Testing exponentiality against HNBUE // Scand. J. Statist. 1983. V. 10.
P. 67-75.
321. Hollander M., Proshan F. Tests for the mean residual life. A methods and corrections //
Biometrika. 1980. V. 67. P. 259-261.
322. Epps T. W., Pulley L. B. A test of exponentiality vs. monotone-hazard alternatives from
the empirical characteristics function // JRSS. Sec. B. 1986. V. 48, №2. P. 206-216.
323. Bergman B. On the replacement and the total time on test concept // Scand. J. Statist.
1979. V. 6. P. 161-168.
324. Bergman B. Crossings In the total time on test plot // Scand. J. Statist. 1977. V. 4.
P. 171-177.
325. Barlow R. E., Campo R. Total time on test processes and applications to failure data
analysis // Reliability and fault free analysis (ed. Barlow, Fussel and Singpurwalla), SIAM,
Philadelphia, 1975.
326. Dipankar Bandyopadhyay^ Basu A. P. К note on tests for exponentiality by Deshpande
// Biometrika. 1989. V. 76, №2. P. 403-405.
327. Sherman B. A random variable related to the spacing of sample values // AMS. 1950.
V. 21, №3. P. 339-361.
328. Sherman B. Percentlles of the шп statistic // AMS. 1957. V. 28, №1. P. 257-261.
329. Bartholomew D. J, Note on the use of Sherman's statistics as a test for randomness //
Biometrika. 1954. V. 41. P. 556-558.
330. Hartley H. O. The maximum F^ratio as a short-cut test of heterogeneity of variance //
Biometrika. 1950. V. 37. P. 308-312.
331. Greenwood V. The statistical study of Infection disease // JRSS. Sec. A. 1946. V. 109.
P. 85-110.
332. Stephens M. A. Further percentage points for Greenwood's statistics // JRSS. Sec. A.
1981. V. 144. P. 364-366.
333. Burrows P. M. Selected percentage points of Greenwood's statistics // JRSS. Sec. A. 1981.
V. 142. P. 256-258.
334. Deshpande J. V. A class of tests for exponentiality against increasing failure rate average
alternatives // Biometrika. 1983 V. 70. P. 514-518.
335. Engelhardt M. E., Bain L. J. Uniformly more powerful unbiased tests for the parameters
of the gamma distribution // Theory and Applications of Reliability. V. 1. N. Y.: Acad.
Press. — P. 307-314.
336. Lawless J. F. Statistical models and methods for lifetime data. — N. Y.: J. Welley, 1982.
337. Keating J. P., Glaser R. E., Ketchum N. S. Testing hypotesis about the shape parameter
of a gamma distribution // Technometrics. 1990. V. 32, № 1. P. 67-82.
338. Kimball B. F. Some basic theorems for developing tests of fit for the case of the non-
parametric probability distribution function. 1 // AMS. 1947. V. 18. P. 540-548.
339. Moran P. A. P. The random division of an Intervals // JRSS. 1947. Sec. B. V. 9. P. 92-98.
340. Smirnoff N. Sur la distribution de nuj2 // Compte Rendus de l'Academie des Sciences.
Paris, 1932. №202. P. 449.
341. Cheng R.C.H., Thornton K.M. Selected percentage points of the Moran statistic //
J. Stat. Comput. Simul. 1988. V. 30. P. 189-194.
342. Cheng R. С. Н., Stephens M. A. A goodness~of™fit using Moran's statistic with estimated
parameters // Biometrika. 1989. V. 76, №2. P. 385-392.
343. Cheng S. W., Spiring F. A. A test to Identify the uniform distribution with applications
to probability plotting and other distributions // IEEE Trans. Reliability. 1987. V. R-36,
№1. P. 98-105.
Список литературы 749
344. Kosik P., Sarkadi К. A new goodness-of-fit test // Proc. of 5-th Pannonian Symp. of
Math. Stat., Visegrad, Hungary, 20-24 May, 1985. P. 267-272.
345. Dudewicz E.«/., van der Meulen E. C. Entropy-based tests of uniformity // JASA. 1981.
V. 76, №376. P. 967-974.
346. Neyman J. „Smooth" tests for goodness-of-flt // Scand. Aktuarietidsrlft. 1937. V. 20.
P.149-199.
347. Young D. L. The linear nearest neighbour statistic // Biometrika. 1982. V. 69, №2.
P. 477-480.
348. Clark P. J., Evans F. C. Distance to nearest neighbour as a measure of spatial relationships
in populations // Ecology. 1954. V. 35. P. 445-457.
349. Finder D. A., Witherick M.E. Nearest-neighbour analysis of linear point patterns //
Tijdshrlft voor Economischl th social Geografie. 1973. V. 64. P. 160-163.
350. Quesenherry G. P., Miller F. L. Power studies of some tests for uniformity // J. Statist.
Comput. Simul. 1977. V. 5. P. 169-191.
351. David F. N. On Neyman's „smooth" test for goodness-of-fit // Biometrika. 1939. V. 31.
P.191-199.
352. Miller F. L., Quesenberry G. P. Power studies of some tests for uniformity, 11 // Commun.
Stat.-Simul. Comput. 1979. S. B. V. 8, №3. P. 271-290.
353. Solomon H., Stephens M. A. On Neyman's statistics for testing uniformity // Commun.
Stat.-Simul. Comput. 1983. V. 12. P. 127-134.
354. Смирнов H. В. О критерии симметрии закона распределения случайной величины //
ДАН СССР. 1947. Т. 56, №1. С. 13-16.
355. Wilcoxon F. Individual comparisons by ranking methods // Biometrics, Bull. 1945. V. 1.
P. 80-83.
356. Antille A., Kersting G., Zucchini W. Testing symmetry // JASA. 1982. V. 77, №379.
P. 639-646.
357. Bhaitacharya P. K., Gastwirth J. L., Wright A, L. Two modified Wilcoxon tests for sym™
metry about an unknown location parameters // Biometrika. 1982. V. 69, № 2. P. 377-382.
358. Antille A., Kersting G. Tests for symmetry // Zeitschrift fur Wahrscheinliehkeitstheorie
und Verwandte Gebiete. 1977. V. 39. P. 235-255.
359. Finch S. J. Robust univariate test of symmetry // JASA. 1977. V. 72, №358. P. 387-392.
360. Boos D. D. A test for symmetry associated with the Hodges-Lehmann estimator // JASA.
1982. V. 77, №379. P. 647-651.
361. Gupta M.K. An asymptotically nonparametric test of symmetry // AMS. 1967. V. 38.
P. 849-866.
362. Moses L. E. Query: Confidence limits from rank tests // Technometrics. 1965. V. 7.
P. 257-260.
363. Frazer D. A. S. Most powerfull rank-type tests // AMS. 1957. V. 28. P. 1040-1043.
364. Klotz J. Smoll sample power and efficiency for the one sample Wicoxon and normal scores
test // AMS. 1963. V. 34. P. 624-632.
365. Гаек Я., Шидак 3. Теория ранговых критериев / Пер. с англ. — М.: Наука, 1971.
366. Johnson N. L. Systems of frequency curves generated by methods of translation //
Biometrika. 1946. V. 36. P. 146-148.
367. Висленев Ю. С, Самосейко В. Ф. О выборе закона распределения по моментам слу-
случайной величины // Надежность и контроль качества. 1987, №5. С. 21-24.
368. Бостандэюиян В. А. Распределение Джонсона (препринт), ИХФ АН СССР, Черного™
ловка, 1978.
369. Johnson N. L. Tables to facilitate fitting Su frequency curves // Biometrika. 1965. V. 52.
P.547-558.
370. Демаков И. П., Потепун В. Е. Графоаналитический метод построения полуэмпири-
полуэмпирических функций распределения малых выборок // Труды метрологических институ-
институтов СССР. Общие вопросы метрологии: Сб.^Л.: ВНИИМ, 1972.^ С. 96-102.
371. Статистические методы оценки качества и надежности промышленных изделий по
результатам малого числа испытаний: Методологические указания.—Уфа: Изд-во
УАИ им. С. Орджоникидзе, 1983.
750 Список литературы
372. Демаков И. П. Проблема принятия решения по малому числу наблюдений (обзор
состояния и перспективы) // Методы статистического анализа и обработки малого
числа наблюдений при контроле качества и надежности приборов и машин: Сб. — Л.:
ЛДНТП, 1974. —С. 4-18.
373. Гаскаров Д. В., Шаповалов В. И. Малая выборка. — М.: Статистика, 1978.
374. Королькова Л. И. Непараметрическое оценивание функции распределения по малой
выборке. — Челябинск, 1988, ВИНИТИ, №6602-888.
375. Корольков И. В., Королькова Л. И. Оценивание по малой выборке с использованием
бета-распределения // Проблемы разработки и использования гибких автоматизиро-
автоматизированных производств на предприятиях уральского региона: Сб. — Свердловск: УНЦ
АН СССР. —С. 12.
376. Горский Л. К. Статистические алгоритмы исследования надежности. — М.: Наука,
1970.
377. Алгоритмы и программы восстановления зависимостей / Под ред. В. Н. Вапника. —
М.: Наука, 1984.
378. Еременко И. В., Свердлик А. Н. Об одном методе построения законов распределения
величин при малом числе испытаний // Некоторые вопросы специального приме-
применения вычислительной техники: Сб.—Л.: ЛВИКА им. А. Ф. Можайского, 1963.—
С.18-29.
379. Демидович Б. П., Марон И. А., Шувалова Э. 3. Численные методы анализа. — М.:
Физматгиз, 1963.
380. Попов С. А., Шаповалов В. И. Об оценивании закона распределения по ограниченным
данным // Надежность и контроль качества. 1982. №11. С. 29-32.
381. Дружинин Г. В., Воронова О, В. Сравнение методов построения эмпирической функ-
функции распределения по малому числу наблюдений // Надежность и контроль качества.
1983. №1. С. 11-18.
382. Чавчанидзе В. В., Кумсенишвчлч В. А. Об определении законов распределения на
основе малого числа наблюдений // Применение вычислительной техники для авто™
матизации производства. — М.: Машгиз, 1961.
383. Гаскаров Д. В., Голинкевич Т. А., Мозгалевский А. В. Прогнозирование технического
состояния и надежности радиоэлектронной аппаратуры. — М.: Сов. радио, 1974.
384. Гаскаров Д. В., Мозгалевский А. В., Шаповалов В. И. Некоторые вопросы прогнози-
прогнозирования по ограниченной информации // Электронная техника. 1975, с. 8, вып. 4C4).
С.15-20.
385. Диттл Р. Даю. А., Рубин Д. Б. Статистический анализ данных с пропусками / Пер.
с англ. — М.: Финансы и статистика, 1991.
386. Cochran W. G., Сох СМ. Experimental design. N.Y.: J. Willey a. Sons, 1957.
387. Satterwaite R. An approximate distribution of estimates of variance components //
Biometrics. 1946. V. 2. P. 110.
388. Welch B. L. The generation of „Student's" problems when several different population
variance are involved // Biometrika. 1947. V. 34. P. 28-35.
389. Lord E. The use of range in place of standard deviation, in the t-test // Biometrika. 1947.
V. 34. P. 41-67.
390. Daly J. F. The use of the sample range in an analogue of Student's t-test // AMS. 1946.
V. 17. P. 71-74.
391. Walsh J.E. Some significance tests based on order statistics // AMS. 1946. V. 17, №1.
P. 44-52.
392. Wolfe D.A. Two-stage two^sample median test // Technometrics. 1977. V. 19, №4.
P. 495-501.
393. Артемьев Е. JO., Мартынов Е. М. Вероятностные методы в психологии. — М.: Изд-во
МГУ, 1975.
394. Paulson E. On optimum solution to the ^-sample slippage problem for the normal
distribution // AMS. 1952. V. 23, 4. P. 610-616.
395. Baily R. Tables of the Bonferroni t statistic // JASA. 1977. V. 72, №358. P. 469-478.
Список литературы 751
396. Nelson P. R. Exact critical points for the analysis of means // Oommun. Stat.-Theor.
Meth. 1982. V. 11, №6. P. 699-709.
397. Hochberg Y. Some generalization of the T-method in simultaneous inference // J. Multi-
var. Anal. 1974. №4. P. 224-234.
398. Stoline M.R., Ury H. K. Tables of the studentIzed maximum modules distributions and
an application to multiple comparisons amond means // Technometrics. 1978. V. 21, № 1.
P. 87-93.
399. Half G. J., Hendricson R. W. A table of percentage points of the largest absolute value
of k Student t variates and its applications // Biometrika. 1971. V. 58. P. 323-332.
400. Pillai К. С S., Ramachandran K. V. On the distribution of the ratio of the г-th observation
In an ordered sample from a normal population to an Independent estimate of the standard
deviation // AMS. 1954. №3. P. 565-572.
401. Шеффе Г. Дисперсионный анализ. — М.: Физматгиз, 1963.
402. Newman D. The distribution of the range in samples from normal populations, expressed
In terms of an Independent estimate of standard deviation // Biometrika. 1939. V. 31.
P. 20-30.
403. Keuls M. The use of the studentized range in connection with an analysis of varianse //
Euphytlca. 1952. V. 1. P. 112-122.
404. Duncan D. B. Multiple range and multiple F test // Biometrics. 1955. V. 11. P. 1-42.
405. Link R. F., Wallace D. L. Some short cuts to allowances, Princeton Univ., March, 1957.
406. Kurtz Т.Е., Link R. F., Tukey J. W., Wallace D.L, Short-cut multiple comparisons for
balanced single and double classification: part 1, Results // Technometrics. 1965. V. 7.
P. 95-161.
407. Pearson E. S. The analysis of variance in classes of non-normal variation // Biometrika.
1931. V. 23. P. 114-134.
408. Geary R. C. Testing for normality // Biometrika. 1947. V. 23. P. 209-241.
409. Gay en A. K. The distribution of the variance ratio in random samples of any size drawn
from non-normal universes // Biometrika. 1950. V. 37. P. 236-255.
410. Arizono /., Ohia M. A test of homogeneity of variances based on sample entropy // Bull.
Osaka Prefect. A, v. 36, №1, 1987. P. 29-37.
411. Bartlett M. S. Properties of sufficiency of statistical tests // Proc. Roy. Soc. 1937. A 160.
P. 268-287.
412. Box G. E. P. A general distribution theory for a class of likelihood criteria // Biometrika.
1949. V. 36. P. 317-346.
413. Wallis W. A., Moore G. H. A significance test for time series analysis // JASA. 1941.
V. 36. P. 401-409.
414. Cochran W. G. The distribution of the largest of a set of estimated variances as a fraction
of their total // Annals of Eugenics. 1941. V. 11. P. 47-52.
415. Bliss G. /., Gohran W. G., Tukey J. W. A rejection criterion based upon the range //
Biometrika. 1956. V. 43. P. 418-422.
416. Hartley H. O. The maximum F-ratio as a short-cut test of heterogeneity of variance //
Biometrika. 1950. V. 37. P. 308-312.
417. Gadwell J. H. Approximating to the distributions of measures of dispersion by a power
of x2 // Biometrika. 1952. V. 40. P. 336-346.
418. Leslie R. Т., Brown В. М. Use of range In testing heterogeneity of variance // Biometrika.
1966. V. 53. P. 221-227.
419. Samiuddin M., Atiqullah M. A test for equality of variance // Biometrika. 1976. V. 63,
№1. P. 206-208.
420. Samiuddin M., Hanif M., Asad H. Some comparisons of the Bartlett and cube root tests
of homogeneity of variance // Biometrika. 1978. V. 65, № 1. P. 218-221.
421. David H. A. The ranking of variance in normal population // JASA. 1956. V. 51.
P. 112-116.
422. Кэндэлл М. Ранговые корреляции. — M.: Статистика, 1975.
423. Nagarsenker P. B. On a test of equality of several exponential survival distributions //
Biometrika. 1980. V. 67, №2. P. 475-478.
752 Список литературы
424. Chen H. J. A new range statistic for comparisons of several exponential location parame-
parameters // Biometrika. 1982. V. 69, ЛН. P. 257-260.
425. Sukhatme P. V. On the analysis of k sample from exponential populations with especial
reference to the problems of random intervals // Statist. Reseach. Memoric. 1936. V. 1.
P. 94-112.
426. Epstein В., Tsao С. К. On the tests based on ordered observation from two exponential
populations // AMS. 1953. V. 24. P. 458-466.
427. Perng S. K. A test for equality of two exponential distributions // Statist. Neerlandica.
1978. V. 32. P. 93-102.
428. Hseih H. K. On testing the equality of two exponential distributions // Technometrics.
1981. V. 23. P. 265-269.
429. Hogg R. V., Tanis E, A, An iterated procedure for testing the equality of several exponen™
tial distributions // JASA. 1963. V. 58. P. 435-443.
430. Singh N., Nagaran P. The likelihood ratio test for the equality of k [^ 2] two parameters
exponential distributions based of type 2 censored samples // J. Stat. Comput. Simul.
1983. V. 18. P. 373-381.
431. Epstein В., Sohel M. Some theorems relevant to life testing from on exponential popula-
populations // AMS. 1954. V. 25. P. 373-381.
432. Singh N. A simple and asymptotically optimal test for the equality of k [^ 2] exponential
distributions based on type 2 censored samples // Commun. Stat.-Theor. Meth. 1985.
V. 14, №7. P. 1615-1625.
433. Вальд А. Последовательный анализ / Пер. с англ. — М.: Физматгиз, 1960.
434. Башаринов А. Е., Флейшман Б. С. Об эффективности метода последовательного ана-
анализа в устройствах обнаружения слабых сигналов в шумах // Радиотехн. и электрон.
1958. Т. 3, №8. С. 42-47.
435. Крапивин В. Ф. Таблицы распределения Вальда. — М.: Наука, 1965.
436. Mann H. Bn Whitney D. R. On a test of whether one of two random variables is stochas-
stochastically larger than the other // AMS. 1947. V. 18. P. 50-60.
437. Singh N. The ratio test for the parameters exponential distributions // Commun. Stat.™
Theor. Meth. 1985. V. 13, №6. P. 116-119.
438. Iman R. L. An approximation to the exact distribution of the Wilcoxon-Mami-Whitney
rank sum test statistic // Commun. Statist. 1976. A5. P. 587-598.
439. Iman R. L. Use of a t-statistic as an approximation to the exact distribution of the
Wilcoxon signed rank test statistic // Commun. Statist. 1974. V. 3. P. 795-806.
440. Fisher R. A., Yates F. Statistical tables for biological, agricultural and medical research.
Edinburgh & London: Oliver and Boyd, 1946.
441. Terry M.E. Some rank order test which are most powerfull against specific parametric
alternatives // AMS. 1952. V. 23. P. 346-366.
442. Hoeffding W. Optimum non-parametric tests // Proc. 11-th Berkley Symp., 1950. P. 83-92.
443. Sidak Z. Tables for two normal-scores rank tests for two-sample location problem // Appl.
Math. 1973. V. 18, №5. P. 333-345.
444. Бернстейн Ф. Сборник статистических таблиц / Пер. с англ. — М.: Статистика, 1968.
445. Mosteller F. A ^-sample test for an extreme population // AMS. 1948. V. 19. P. 58-65.
446. Rosenbaum S. Tables for a nonparametric test of location // AMS. 1954. V. 25. P. 146-150.
447. Haga T. A two-sample rank test on location // Annal. Inst. Stat. Math. 1959/60. V. 11.
P.211-219.
448. Hojek S. Tables for the two-sample Haga test of location // Aplikate Mat. 1978. V. 23,
№4. P. 237-247.
449. Sidak Z., Vondrauek J. A sample non-parametric test of the difference in location of two
populations // Appl. Mat. 1957. V. 2. P. 215-221.
450. Sidak Z. Tables for the two-sample location E-test based on exceeding observations //
Appl. Mat. 1977. V. 22, №3. P. 166-175.
451. Kruskal W. H., Wallis A. Use of ranks in one criterion variance analysis // JASA. 1952.
V. 47. P. 583-621.
Список литературы 753
452. Iman R. L., Davenport J. M. New approximations to the exact distribution at the Kruskal-
Wallis test statistic // Commun. Stat.-Theor. Meth. 1976. V. 5. P. 1335-1348.
453. Nemenyi P. Distribution-free multiple comparisons. New York, State Univ., Downstate
Medical Center, 1963.
454. Wilcoxon F., Wilcox R. A. Some rapid approximate statistical procedures, Lederle Labo-
Laboratories, Ptarl River, New York, 1964.
455. Хеттманспергер Т. Статистические выводы, основанные на рангах / Пер. с англ. —
М.: Финансы и статистика, 1987.
456. Terpstra Т. J. The asymptotic normality and consistency of Kendall's test against trend,
when ties are present In one ranking // Indagationes Math. 1952. V. 14. P. 327-333.
457. Jonckheere A.R. A distribution™free Ic-sample test against ordered alternatives //
Biometrlka. 1954. V. 41. P. 133-145.
458. Odeh R. E. On Jonckheere's Ic-sample test against ordered alternatives // Technometrics.
1971. V. 13, №4. P. 912-918.
459. Lewis J. L. A k sample test based on range Intervals // Biometrika. 1972. V. 59, №1.
P.155-160.
460. Bhapkar V. P., Deshpande J. V. Some nonparametric tests for multisample problems //
Technometrics. 1968. V. 10, №3. P. 578-585.
461. Deshpande J. V. Some nonparametric tests of statistical hypotheses, Dissertation submit™
ted for the Ph. D. degree to the Univ. of Poona, 1965.
462. Deshpande J. V. A nonparametric test based on [/-statistics for the problem of several
samples // J. Indian Statist. Assoc. 1965. V. 3. P. 20-29.
463. Barbur A. D., Cartwright D. /., Donnely J. В., Eagleson G.K. A new rank test for the
fc-sample problem // Commun. Stat.-Theor. Meth. 1985. V. 14, №6. P. 1471-1484.
464. Usawa H. Locally most powerfull rank tests for two-sample problems // AMS. 1960. V. 31.
P. 685-702.
465. Crouse C. F. Distribution free test based on the sample distribution function // Biometri-
ka. 1966. V. 53. P. 99-108.
466. Page E. B. Ordered hypotheses for multiple treatments: A significance test for linear ranks
// JASA. 1963. V. 58. P. 216-230.
467. Frideman M. The use of ranks to avoid the assumption of normality implicit in the analysis
of variance // JASA. 1937. V. 32. P. 675-701.
468. Kendall M. G., Babington Smith. The problem of m rankings // AMS. 1939. V. 10.
P. 275-287.
469. Iman R. L., Davenport J. M. Approximations of the critical region of the Friedman statistic
// Commun. Stat.-Theor. Meth. 1980. V. 9. P. 571-595.
470. Anderson R. L. Use of contingency tables In the analysis of consumer preference //
Biometrics. 1959. V. 15. P. 582-590.
471. Kanneman K. An incidence test for k related samples // Blom. Zeitschrift, ed. 18, 1976.
S. 3-11.
472. Schach S. An alternative to the Friedman test with certain optimality properties // Annal.
of Statistics. 1979. V. 7, P. 537-550.
473. Quade D. Analyzing randomized blocks by weighted rankings, Report SW 18/72, Math.
Center Amsterdam, 1972.
474. Quade D. Using weighted ranking In the analysis of complete blocks with additive block
effects // JASA. 1979. V. 74, №370. P. 680-683.
475. Quade D., Silva С Evaluting of weighted rankings using expected significance level //
Commun Stat.-Theor. Meth. 1980. V. 9. P. 1087-1096.
476. Ehrenberg A. S. C. On sampling from a population of a rankers // Biometrlka. 1952. V. 39.
P. 82-87.
477. Alvo M., Cabilio P., Feigin P. D. Aslmptotlc theory for measures of concordance with
special reference to average Kendall tau // Annal. of Stat. 1982. V. 10, №4. P. 1269-1276.
478. Нискина Н. 17., Тейман А. И., Шмерлинг Л. С. Непараметрические методы статисти-
статистики, основанные на рангах, их применение. — Препринт / ВНИИ системных исследо-
исследований. — М., 1986.
754 Список литературы
479. Ansari A. R., Bradley R. A. Rank-tests for dispersions // AMS. 1960. V. 31, №4.
P. 1174-1189.
480. Siegel S., Tukey J. W. A nonparametric sum of ranks procedure for relative spread in
unpaired samples // JASA. 1960. V. 55, №291. P. 429-445.
481. Capon J. Asymptotic efficiency of certain locally most powerfull rank tests // AMS. 1961.
V. 32, №1. P. 88-100.
482. Sidak Z. Tables for two normal-scores tests for the two-sample scale problem // Aplik.
Matematlky. 1973. V. 18, №5. P. 346-363.
483. Klotz J. Nonparametric tests for scale // AMS. 1962. V. 33, P. 498-512.
484. Savage I. R. Contributions to the theory of rank order statistics — the two-sample case //
AMS. 1956. V. 27. P. 590-615.
485. Sidak Z. Tables for the two-sample Savage rank test optimal for exponential densities //
Aplik. Mat. 1973. V. 18, №5. P. 364-374.
486. Sukhatme B. V. On certain two-sample nonparametric tests for variances // AMS. 1957.
V. 28, №1. P. 188-194.
487. Mood A. On the asymptotic efficiency of certain nonparametric tests // AMS. 1954. V. 25.
P. 514-522.
488. Laubsher N. F., Sieffenc F. E., De Lange E. M. Exast critical values for Mood's distri-
distribution-free test statistic for dispersion and its normal approximation // Technometrics.
1968. V. 10, №3. P. 497-507.
489. Welchser S. Mood's test for dispersion as a counting of triplets // Commun. Stat.-Theor.
Meth. 1985. V. 14, №2. P. 303-306.
490. Sukhatme B. V. A two-sample distribution™free test for comparing variances // Biometri-
ka. 1958. V. 45. P. 544-548.
491. Sukhaime B. V. Testing the hypothesis that two population differ only In location // AMS.
1958. V. 29, №1. P. 60-78.
492. Sukhatme B. V. On certain two-sample nonparametric tests for variances // AMS. 1957.
V. 28, №1. P. 188-199.
493. Sandvik L., Olsson B. A nearly distribution-free test for comparing dispersion in paired
samples // Biometrlka. 1982. V. 69, 32. P. 484-485.
494. Krauih J., Lieneri G.A. Eln lokatlonslnsensltlver DIspersIontest fur zwel unabhanglge
Stichproben [DP-test] // Biometr. Z. 1974. V. 16, №2. S. 83-90.
495. Krauih J., Lienert G.A. Ein lokatlonslnsensitlver DIspersiontest fur zwel abhangige
Stichproben // Biometr. Z. 1974. V. 16, №2. S. 91-95.
496. Kamat A. R. A two-sample distribution-free test // Biometrika. 1956. V. 43. P. 377-387.
497. Bush J. R., Wieand H.S. An asymptotically optimal nonparametric statistic for testing
equally of two normal population means and variances // Commun. Stat.-Theor. Meth.
1982. V. 11, №1. P. 1-12.
498. Bhapkar V. P., Deshpande J. V. Some nonparametric tests for multlsample problems //
Technometrics. 1968. V. 10, №3. P. 578-585.
499. Bhapkar V. P. A nonparametric test for the problem of several samples // AMS. 1961.
V. 32. P. 1108-1117.
500. Ljung G. M., Box G. E. P. On a measure of lack of fit In time-series models // Biometrika.
1978. V. 65. P. 197-203.
501. Dufor J.-Af., Roy R. Some robust exact results on sample for randomness // J. of
Econometrics. 1985. V. 29. P. 257-273.
502. Bhapkar V. P. A nonparametric test for the several sample location problem, Univ. of
North Carolina, Inst. of Statistics, MImeo series, №411, 1964.
503. Foster F. G., Stuart A. Distribution-free tests In tlmeserles dated on the breaking of
records // JRSS. 1954. V. B16, №1. P. 1-22.
504. Cox D. R., Stuart A. Quick sing tests for trend In location and dispersion // Biometrika.
1955. V. 42. P. 80-95.
505. Hsu D. A. Tests for variance shift at an unknown time point // Appl. Statist. 1977. V. 26,
№3. P. 279-284.
Список литературы 755
506. Hsieh Н. К. Nonparametric tests for scale shift at a unknown time point // Commun.
Stat.-Theor. Meth. 1984. V. 13, №11. P. 1335-1355.
507. Wald A., Wolfowitz J. On a test whether two samples are from the some populations //
AMS. 1940. V. 11. P. 147-162.
508. Ramachandran G., Ranganathan J. // J. Madras Univ. 1953. Sec. B. V. 8. P. 76. (Цит.
no [14]).
509. Olmsted P. S. Runs determined in a sample by an arbitrary cut // Bell. System. Techni-
Technical J. 1958. V. 37. P. 55-82.
510. Shaughnessy P. W. Multiple runs distributions: Recurrence and critical values // JASA.
1981. V. 76, №375. P. 732-736.
511. Anderson R.L. Distribution of the serial correlation coefficient // AMS. 1942. V. 13.
P. 34-43.
512. Knoke J. D. Testing for randomness against autocorrelation: Alternative tests // Biometri-
ka. 1977. V. 64, №3. P. 523-529.
513. Knoke J. D. Testing for randomness against autocorrelation: The parametric case //
Biometrika. 1975. V. 62. P. 571-575.
514. Wald A., Wolfowitz J. An exact test for randomness in the non^parametric case based on
serial correlation // AMS. 1943. V. 14. P. 378-388.
515. Stuart A. The efficient of tests on randomness against normal regression // JASA. 1956.
V. 51. P. 285-287.
516. Bariels R. The rank version of von Neimann's ratio test for randomness // JASA. 1982.
V. 77, №377. P. 40-46.
517. Me Gielchrist C. A., Woodyer K. D. Note on a distribution-free CISIM technique //
Technometrics. 1975. V. 17, №3. P. 321-325.
518. Woodward R. H., Goldsmith P. L. Cumulative sum techniques, ICI Monograph., №3,
Oliver and Boyd, London, 1964.
519. Шенк X. Теория инженерного эксперимента / Пер. с англ. — М.: Мир, 1972.
520. Уорсинг Ф., Геффнер Л. Методы обработки экспериментальных данных / Пер.
с англ. —М.: ИЛ, 1949.
521. Irwin J. О. On a criterion for the rejection of outlying observations // Biometrika. 1925.
V. 17. P. 238-250.
522. Grubbs F. E. Simple criteria for testing rejection of outlying observations // AMS. 1950.
V. 21. P. 27-58.
523. David H. A. Revised upper percentage points of the extreme studentized deviate from the
sample mean // Biometrika. 1956. V. 43. P. 450-461.
524. Dixon W. J. Rations involving extreme values // AMS. 1956. V. 22. P. 68-76.
525. Hoaglin D. C, Iglewicz B. Fine-tuning some resistant rules for outlier labeling // JASA.
1987. V. 82, №400. P. 1147-1149.
526. Tietjen G., Moore H. Some Grubb's type statistics for the detection of several outliers //
Technometrics. 1972. V. 14. P. 583-597.
527. Смоляк С. А., Титаренко Б. П. Устойчивые методы оценивания. — М.: Статистика,
1980.
528. Rosner В. On the detection of many outliers // Technometrics. 1975. V. 17. P. 221-227.
529. Rosner B. Percentage points for the RST many outlier procedure // Technometrics. 1977.
V. 19, №3. P. 307-312.
530. Goodness~of-fit techniques, ed. D'Agostino R. B. and Stephens M. A., Marcel Dekker Inc.,
New York and Basel, 1986.
531. Бродский Я. С, Быцань Н. Н., Власенко В. М. Об исключении экстремальных значе-
значений // Завод, лаб. 1975. №7. С. 847-849.
532. Kimber А. С. Tests for many outlier on a exponential sample // JRSS. Sec. C; Appl. Stat.
1982. V. 31. №3. P. 263-271.
533. Fung Karen Yuen, Paul S. R. Comparisons of outlier detection procedures in Weibull
or extreme™value distributions // Commun. Stat.-Simul. Comput. 1985. V. 14, №4.
P. 895-917.
756 Список литературы
534. Mann N. R. Optimal outlier tests for a Weibull model-to identify process changes or
predict failure times // Studies in the Management Sciences. 1982. V. 19. P. 261-270.
535. Bartlett V., Lewis T. Outlier in statistical data // N. Y.: J. Willey, 1978.
536. Dixon R. J. Analysis of extreme values // AMS. 1950. V. 21. P. 488-506.
537. Beckman R. J., Cook R. D. „Outlier... s" // Technometrics. 1983. V. 25. P. 119-163.
538. Darling D. A. On a test for homogeneity and extreme values // AMS. 1952. V. 23, №3.
P. 450-456.
539. Аронов И. З., Золотарев А. О. К вопросу оценки однородности экспериментальных
данных об отказах изделий // Надежность и контроль качества. 1987. №7. С. 3—6.
540. Бахмутов В. Ф., Аронов И. 3. Общий критерий оценки однородности и методика
обработки результатов усталостных испытаний // Надежность и контроль качества.
1986. №5. С. 25-29.
541. Bowker A. H. Computation of factors for tolerance limits on a normal distribution when
sample is large // AMS. 1946. V. 17. P. 238-240.
542. Stange K. Angewandte Statistik, 1 und 2, Berlin-Heidelberg-New York, 1970/1971.
543. Frawwley W. H., Kapadia C. H., Rao J. N., Owen D. B. Tolerance limits based on range
ang mean range // Technometrics. 1971. V. 13. P. 651-655.
544. Mitra S. K. Tables for tolerance limits for normal population based on sample mean or
mean range // JASA. 1957. V. 52. P. 88-94.
545. Resnikoff G. L. Two-sided tolerance limits for normal distribution using the range, Appl.
Mathem. And Statistics Laboratory, Stanford Univ. Technical Report, №33, 1957.
546. Tietjen G. L., Johnson M.E. Exact statistical tolerance limits for sample variances //
Technometrics. 1979. V. 21, №1. P. 107-110.
547. Wiles S. S. Statistical prediction with special reference to the problem of tolerance limits
// AMS. 1942. V. 13. P. 400-409.
548. Hall I. J., Prairie R. R. One-sided prediction interval to contain at least m out of к future
observations // Technometrics. 1973. V. 15, №4. P. 897-914.
549. Lawless J. F. A prediction problem concerning samples from the exponential distribution,
with application in life testing // Technometrics. 1971. V. 13, №4. P. 725-730.
550. Hahn G. J. A simultaneous prediction limits on the means of future samples from an
exponential distribution // Technometrics. 1975. V. 17, №3. P. 341-345.
551. Мог an P. A. P. Some theorems on time series 2: The significance of the serial correlation
coefficient // Biometrika. 1948. V. 35. P. 255-260.
552. Hollin M"., Ingeubleek J.-F., Puri M. L. Linear serial rank tests for randomness against
ARMA alternatives // Ann. Statist. 1985. V. 13. P. 1156-1181.
553. Hollin M., Ingenbleek J.-F., Puri M. L. Linear and quadratic serial rank tests for random-
randomness against social dependence // J. Of Time Serial Annal. 1987. V. 8. P. 409-424.
554. Hollin M., Merald G. Rank-tests for randomness against first order serial dependence //
JASA. 1988. V. 83. P. 1117-1129.
555. Hollin M., Puri M. L. Optimal rank-based procedures for time series analysis: Testing on
ARMA model against other ARMA models // Annal. Statist. 1988. V. 16. P. 402-432.
556. Hollin M., Laforet A., Merald G. Distribution-free tests against dependence: signed or
unsigned ranks? // J. of Stat. Planning and Inference. 1990. V. 24. P. 151-165.
557. Mee R. W. Simultaneous tolerance intervals for normal population with common variance
// Technometrics. 1990. V. 32, №1. P. 83-92.
558. Odeh R. E., Chou Youn-Min, Owen D. H. Sample-size determination for two-sided
/3-expectation tolerance intervals for a normal distribution // Technometrics. 1989. V. 31,
№4. P. 461-468.
559. Браунли К. А. Статистические исследования в производстве. — М.: ИЛ, 1949.
560. Нискина Н. П., Тейман А. И., Шмерлинг Л. С. Двухфакторный дисперсионный ана-
анализ для неполных данных / Препринт. — М.: ВНИИСИ, 1986.
561. Prentice M. J. On the problem of m incomplete ranking // Biometrika. V. 66, P. 167-177.
562. Mack D. A., Skillings J. H. A Friedman-type rank test for main effects in a two-way
ANOVA // JASA. 1980. V. 75, 3372. P. 941-947.
Список литературы 757
563. Mack D. A. A quick and easy distribution-free test for main effects in a two-way ANOVA
// Commun. Stat. 1981. V. 10, №6. P. 571-591.
564. Stange K. Uber einen zweiseitigen Test fur die Korrelationszahle einer zweidimensionalen
Normaverteilung // Statist. H. 1973. V. 14, №3. S. 206-236.
565. Cox D. Д., Stuart A. Quick tests for trend in location and dispersion // Biometrika. 1955.
V. 42. P. 80-95.
566. Nelson L.S. A sign test for correlation // J. of Quality Technology. 1983. V. 15, №4.
P.199-200.
567. Elandt R. С Exact and approximate power function of the non-parametric test of tendency
// AMS. 1962. V. 33, №2. P. 471-481.
568. Kruskal W. H. Ordinal measures of association // JASA. 1958. V. 53. P. 814-861.
569. Olmstead P. S., Tukey J. W. A comer test for association // AMS. 1947. V. 18. P. 495-513.
570. Blum J. R.^ Kiefer J., Rosenblatt M. Distribution-free tests of independence based on the
sample distribution function // AMS. 1961. V. 32. P. 485-498.
571. Iman R. L., Conover W. J. Approximation of the critical region for Spierman's rho with
and without ties present // Commun. Stat.-Simul. And Comput. 1978. V. 7. P. 269-282.
572. Hoeffding W. A non-parametric test of independence // AMS. 1948. V. 19. P. 546-557.
573. Shirahate S. Intraclass rank tests for independence // Biometrika. 1981. V. 68, №2.
P. 451-456.
574. Fieller E. C, Pearson E. S. Tests for rank correlation coefficients. 2 // Biometrika. 1961.
V. 48, №1-2. P. 29-40.
575. Kendall M. G., Babington Smith. The problem of m rankings // AMS. 1939. V. 10.
P. 275-287.
576. Schucany W. R., Frawley W. H. A rank test for two group concordance // Psichometrika.
1973. V. 38. P. 249-258.
577. McNemar Q. Note on sample error of the differences between correlated proportions or
percentages // Psychometrika. 1947. V. 12. P. 153-154.
578. Woolf B. The log likelihood ratio test [the G-test]. Methods and tables for tests of
heterogeneity in contingency tables // Ann. Human Genetics. 1957. V. 21. P. 397-409.
579. Le Roy H. L. Ein einfacher x -Test fur den Simultanvergleich der inneren Struktur
von zwei Analogen 2x2, Haufigkeitstabellen mit freien Kolonnen und Zeilentotallen,
Schweizer. Landw. Forchg., 1, 1962, S. 451-454.
580. Kvetom K. Formation of empirical regression curves and surfaces using power function //
Acta Technica. 1988. №2. P. 141-157.
581. Дрейпер Н.у Смит Г. Прикладной регрессионный анализ / Пер с англ. — М.: Стати-
Статистика, 1973.
582. Иоала В., Ольман В. Метод оценивания коэффициентов линейной одномерной ре-
регрессии // Изв. АН ЭССР: Физика. Математика. 1987. Т. 36, №4. С. 422-424.
583. Маслов П. П. Замена способа наименьших квадратов простейшим расчетом // Вест-
Вестник статистики. 1973. №5. С. 18-20.
584. Bartlett M. S. Fitting a straight line when both variables are subject to error // 1949.
Biometrics. V. 5. P. 207-212.
585. Kerrich J. E. Fitting the line у = b • x when errors of observation are present in both
variables // The Amer. Statistician. 1966. V. 20. P. 24.
586. Sen P. K. Estimates of the regression coefficient based on Kendall's tau // JASA. 1968.
V. 63, №324. P. 258-264.
587. Siegel A. F. Robust regression using repeated medians // Biometrika. 1982. V. 69, №1.
P.242-244.
588. Daniels H. F. F distribution-free test for regression parameters // AMS. 1953. V. 25, №3.
P. 499-513.
589. Brown G. W., Mood A. M. On median tests for linear hypotheses // Proc. of the Second
Berkeley Symp. on Math. Stat. And Prob., Univ. of Calif. Press., 1950. P. 159-166.
590. Theil H. A rank-invariant method of linear and polynomial regression analysis. 1 // Proc.
Kon. Ned. Akad. V. Weetenseh. 1950. A53. P. 386-392.
758 Список литературы
591. Durhin J., Watson G. S. Testing for serial correlation in least-squares regression //
Biometrika. 1951. V. 38. P. 159-178.
592. Acton F.S. Analysis of straight line data.^N.Y.: Welly, 1959.^ P. 261.
593. Tietjen G. L., Moore R. H., Beckman R. J. Testing for a single outlier in simple linear
regression // Technometrics. 1973. V. 15, №4. P. 717-721.
594. Prescoti P. An approximate test for outlier in linear models // Technometrics. 1975.
V. 17, №1. P. 129-132.
595. Lund R. E. Tables for an approximate test for outliers in linear models // Technometrics.
1975. V. 17, №4. P. 473-476.
596. Wallis W. A. Tolerance intervals for linear regression // Proc. of the Second Berkley Symp.
on Math. Statist. And Probability, Univ. of Calif. Press., Berkley and Los Angeles, 1951.
P. 43-51.
597. Working H., Hotelling H. Applications of the theory of error to the interpretation of trends
// JASA. 1929. V. 24. P. 73-85.
598. Пустылъник Е. И. Две задачи, связанные с обработкой линейных зависимостей //
Завод, лаб. 1981. Т. 47, №3. С. 52-53.
599. Янкаускас В. Модель регрессии с автокоррелированными остатками в условиях ма-
малых выборок // Применение теории вероятностей и математической статистики: Сб.
1983. Вып. 5. Вильнюс, 1983.^ С. 86-94.
600. Четыркин Е.М. Статистические методы прогнозирования. — М.: Статистика, 1975.
601. Петрович С. Л., Шлеч Г. К. Робастная регрессия: оценки и сравнения методом
Монте-Карло // Завод, лаб. 1987. №3. С. 41-48.
602. Айвазян С, Л., Енюков И. С, Мешалкин Л. Д. Прикладная статистика. Исследование
зависимостей.—М.: Финансы и статистика, 1985.
603. Демиденко Е. 3, Линейная и нелинейная регрессия. — М.: Статистика, 1981.
604. Мудрое В. Ж., Кушко В. Л. Метод наименьших модулей. — М.: Знание, 1971.
605. Forsythe А. В. Robust estimation of straight line regression coefficients by minimizing
p-th power deviations // Technometrics. 1972. V. 14. P. 159-166.
606. Епишин Ю. Р. Регрессионный метод наименьших абсолютных отклонений // Завод,
лаб. 1974. № 10. С. 1227-1232.
607. Епишин Ю. Г. Об оценках параметров наименьших абсолютных отклонений // Эю>
номика и математические методы. 1974. Т. X, №54. С. 1023. Р. 1028.
608. Дронов В, С, Целищев В. Д. О сглаживании экспериментальных зависимостей мето-
методом однозначной аппроксимации // Завод, лаб. 1975. Т. 41, №7. С. 844-846.
609. Планирование эксперимента в исследовании технологических процессов / Хартман К.
и др. — Под ред. Э.К. Лецкого. — М.: Мир, 1977.
610. Шиндовский Э., Щюрц О. Статистические методы управления качеством. — М.: На-
Наука, 1964.
611. Дэюонсон Н., Мюн Ф. Статистика и планирование эксперимента в технике и науке.
Методы обработки данных / Пер. с англ. — М.: Мир, 1980.
612. Shewhart W. A. Economic control of quality of manufactured product, van Nostrond, New
York, 1931.
613. Barnard G. A. Cumulative charts and stochastic processes // JRSS. Ser. B. 1959. V. 21.
P.148-159.
614. Goldsmit P. L., Whitfield H. Average run lenght in cumulative sum chart when a F™mask
is used // Technometrics. 1961. V. 3. P. 441-447.
615. Johnson N. L., Leone F. C. Cumulative sum control charts // Industr. Quality Contr.
1962. V. 18-19 [three papers].
616. Page E. S. Cumulative sum charts // Technometrics. 1961. V. 3. P. 511-518.
617. Cox D. R. The use of range in sequential analysis // JRSS. 1949. Ser. B, V. 11. P. 921-929.
618. Shainin D. How to improve upon the benefits of the good old and control charts // Proc.
World Quality Congress, Braiton, 1984, V. 2. P. 48-56.
619. Налимов В. В. Планирование эксперимента. — М.: Наука, 1971.
620. Налимов В. В., Голикова Т. И. Логические основания планирования эксперимента. —
М.: Изд-во МГУ, 1971.
Список литературы 759
621. Налимов В. В., Чернова Н. А. Статистические методы планирования экстремальных
экспериментов. — М.: Наука, 1965.
622. Адлер Ю.П. Введение в планирование эксперимента. — М.: Металлургия, 1969.
623. Финни Д. Д. Введение в теорию планирования эксперимента. — М.: Наука, 1970.
624. Федоров В. В. Теория оптимального эксперимента (планирование регрессионных экс-
экспериментов).— М.: Наука, 1971.
625. Хикс Ч. Р. Основные принципы планирования эксперимента. — М.: Мир, 1967.
626. Box G. E. P., Wilson К. В. On the experimental attainment of optimum conditions //
JRSS. 1951. V.B13, №1. P. 1-17.
627. Box G. E. P., Hunter J. S. Condensed calculation for evolutionary operation programs //
Technometrics. 1959. V. 1. P. 77-84.
628. Kiefer J. // JRSS. 1959. V.B21. P. 272.
629. Голикова Т. Ж., Микешина Н. Г. Свойства 1)™оптимальных планов и методы их по-
построения // Новые идеи в планировании эксперимента: Сб. — М.: Наука, 1969.—
С.21-58.
630. Андрукович П. Ф., Голикова Т. И., Костина С. Г Планы второго порядка на ги-
гиперкубе, близкие по свойствам к D-оптимальным // Новые идеи в планировании
экспериментов: Об.^М.: Наука, 1969.^0. 140-153.
631. Hariey H. О. Smallest composite design for quadratic response surfase // Biometrics. 1959.
V. 15. P. 611-622.
632. Адлер Ю. П., Маркова E. Bn Грановский JO. В, Планирование эксперимента при по-
поиске оптимальных условий. — М.: Наука, 1970.
633. Уайльд Д. Дж. Методы поиска экстремума / Пер. с англ. — М.: Наука, 1967.
634. Spendley W., Hext G. R., Himsworth F. R. Sequential application of simplex design in
optimization and evolutionary operations // Technometrics. 1962. V. 4. P. 441.
635. Копаев Б. В. К вопросу использования относительных разностей в методе наимень-
наименьших квадратов // Геодезия и картография. 1991. №6. С. 9—13.
636. Копаев Б. В. Использование условно-относительных разностей при определении ко-
коэффициентов полинома методом наименьших квадратов // Надежность и контроль
качества. 1991. №12. С. 3-12.
637. Штефан В. В., Карташев В. Я. Исследование статистических зависимостей методом
обратных разделенных разностей. — Препринт / ВИНИТИ. №1105-В 92. — С. 2—19.
638. Абдуллаева В. Г., Володченко А. П. Определение параметров уравнения регрессии
в форме нормального уравнения прямой. — Препринт / ВИНИТИ. №1246-1989.
1989. —С. 2-11.
Сокращенные названия использованных журналов
AMS — The Annals of Mathematical Statistics
JRSS — Journal of the Royal Statistical Society
JASA — Journal of the American Statistical Association
CS — Communication In Statistics
JSCS — Journal of Statistical Computation and Simulation
RISI — Review of the International Statistical Institute
SJS — Scandinavian Journal of Statistics
SASJ — South African Statistical Journal
SN — Statistical Neerlandica
JIS — Journal of the Institute of Statisticians
AS — The American Statistican
AISM — Annals of the Institute of Statistical Mathematics
CJS — The Canadian Journal of Statistics
Перечень демонстрационных задач
Стр.
Исходная информация
Содержание задачи
1. Вычисление вероятностей для полностью определенных
законов распределения вероятностей
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
28
30
31
32
34
35
36
38
39
43
43
44
48
54
59
60
62
Нормальное распределение
Нормальное распределение
Нормальное распределение
Нормальное распределение
Равномерное распределение
Логарифмически нормальное расп-
ределение
Экспоненциальное распределение
Распределение Вейбулла
Гамма-распределение
Бета-распределение
Бета-распределение
Бета-распределение
X2-распределение (распределение
Пирсона)
Распределение Стьюдента (t-pacn-
ределение)
Распределение Фишера (F-pacnpe-
деление)
Распределение Фишера (F-pacnpe-
деление)
Усеченное нормальное распределе-
распределение
Вь числение значения ф> нкц - \ ас™
пределения
Вь числение квантилей
Вь числение математическ х с ж ' да™
н t порядковых статист к
Комплексное вычислен' е вероят-
ностных характеристик
Комплексное вычисление вероят-
ностных характеристик
Вычисление значения функции рас™
пределения
Вычисление вероятностных характе™
ристик применительно к испытани-
испытаниям приборов
Вычисление вероятностных характе-
характеристик
Вычисление вероятностных характе-
характеристик
Вычисление квантилей распределе-
распределения
Вычисление квантилей распределе-
распределения
Вычисление квантилей распределе-
распределения
Вычисление квантилей распределе-
распределения
Вычисление квантилей распределе-
распределения
Вычисление квантилей распределе-
распределения
Вычисление квантилей распределе-
распределения
Вычисление изменения параметров
при усечении нормального распре-
распределения
762
Перечень демонстрационных задач
Продолжение таблицы
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Стр.
63
64
66
68
69
71
72
72
73
74
78
78
79
79
79
Исходная информация
Распределение модуля случайной
величины, i аспределенно" нср-
мально
Распределен е, п рождае ое нср-
мальной плотностью с линейным
дрейфом среднего
Распределение, порождаемое нор-
нормальной плотностью с линейным
дрейфом среднеквадратического
отклонения
Распределение Рэлея
Распределение Максвелла
Распределение экстремального зна-
значения
Треугольное распределение (расп-
(распределение Симпсона)
Распределение Коши
Логистическое распределение
Распределение Парето
Композиции законов распределе-
распределения вероятностей случайных вели-
величин, возникающие при расчете на-
надежности по схеме „нагрузка^на-
пряжение"
Композиции законов распределе-
распределения вероятностей случайных вели-
величин, возникающие при расчете на-
надежности по схеме „нагрузка^на-
пряжение"
Композиции законов распределе-
распределения вероятностей случайных вели-
величин, возникающие при расчете на-
надежности по схеме „нагрузка-на-
пряжение"
Композиции законов распределе-
распределения вероятностей случайных вели-
величин, возникающие при расчете на-
надежности по схеме „нагрузка^на-
пряжение"
Композиции законов распределе-
распределения вероятностей случайных вели-
величин, возникающие при расчете на-
надежности по схеме „нагрузка^на-
пряжение"
Содержание задачи
Вычисление вероятностей и парамет-
параметров распределен я
Вь ч слен е ве] оя не с нь х xaj ак-
теристик
Вычисление вероятностных харак-
характеристик
Вычисление функции распределения
и квантилей
Вычисление функции распределения
Вычисление функции распределения
и квантилей
Вычисление функции распределения
Вычисление вероятностных харак-
характеристик
Вычисление функции распределения
и квантилей
Вычисление вероятностных харак-
характеристик
Вычисление вероятности безотказ-
безотказной работы, когда прочность и на-
нагрузка распределены нормально
Вычисление вероятности безотказ-
безотказной работы, когда прочность и на-
нагрузка распределены логарифмиче-
логарифмически нормально
Вычисление вероятности безотказной
работы, когда прочность и нагрузка
распределены экспоненциально
Вычисление вероятности безотказ-
безотказной работы, когда прочность рас-
распределена нормально, нагрузка —
экспоненциально
Вычисление вероятности безотказ-
безотказной работы, когда прочность имеет
гамма-распределение, нагрузка рас-
распределена экспоненциально
Перечень демонстрационных задач
763
Продолжение таблицы
33
34
35
36
37
38
39
40
41
42
43
С р.
79
80
81
82
86
88
89
91
91
92
94
Исходная нфор > ац я
Ко по^ ц законов распределе-
распределения вероятностей случайных ве-
величин, возникающие при расчете
надежности по схеме „нагрузка-
напряжение"
Нецентральное распределение
Стьюдента (нецентральное ^рас-
^распределение)
Нецентральное распределение Пир™
сона (нецентральное хи-квадрат
распределение)
Нецентральное распределение Фи-
Фишера (нецентральное F-распреде-
ление)
Биномиальное распределение (рас-
(распределение Бернулли)
Биномиальное распределение (рас-
(распределение Бернулли)
Распределение Пуассона
Отрицательное биномиальное расп-
распределение
Распределение Паскаля
Геометрическое распределение
(распределение Фарри)
Гипергеометрическое распределе-
распределение
Содержан е зада11 '
Вь ч слен е ве!оятнсст без тказ-
ной работы, когда прочность име-
имеет распределение Вейбулла, нагрузка
распределена нормально
Вычисление параметра нецентраль-
нецентральности
Вычисление квантили распределе-
распределения
Вычисление квантили распределе-
распределения
Вычисление функции распределения
Вычисление функции распределения
аппроксимацией Моленара
Вычисление функции распределения
Вычисление функции распределения
Вычисление функции распределения
Вычисление плотности и функции
распределения
Вычисление функции распределения
2. Оценка параметров распределения вероятностей
44
45
46
47
48
49
50
51
103
109
116
121
131
131
132
137
Нормальное распределение
Нормальное распределение
Нормальное распределение
Нормальное распределение
Нормальное распределение (усечен-
(усеченная выборка)
Нормальное распределение (непол-
(неполностью определенная выборка)
Нормальное распределение (цензу™
рированная выборка)
Экспоненциальное распределение
Точечная оценка среднего значения
Интервальная оценка среднего зна-
значения при неизвестной дисперсии
Точечная оценка дисперсии и стан-
стандартного отклонения
Интервальная оценка стандартного
отклонения
Оценка параметров распределен я
Оценка параметров распределения
Оценка параметров распределен я
Точечная оценка интенсивности от-
отказов при испытании партии прибо-
приборов до заданной наработки с заменой
отказавших приборов
764
Перечень демонстрационных задач
Продолжение таблицы
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
Стр.
137
137
137
139
139
144
144
144
144
145
145
173
173
174
175
Исходная информация
Экспоненциальное распределение
Экспоненциальное распределение
Экспоненциальное распределение
Экспоненциальное распределение
Экспоненциальное распределение
(цензурированная выборка)
Экспоненциальное распределение
Экспоненциальное распределение
Экспоненциальное распределение
Экспоненциальное распределение
Экспоненциальное распределение
Экспоненциальное распределение
Распределение Вейбулла
Распределение Вейбулла
Распределение Вейбулла
Распределение Вейбулла
Содержание задачи
Точечная оценка интенсивности от-
отказов при испытании партии прибо-
приборов до заданного числа отказов с за-
заменой отказавших приборов
Точечная оценка интенсивности от™
казов при испытании партии прибо-
приборов до заданной наработки без заме-
замены отказавших приборов
Точечная оценка интенсивности от-
отказов при испытании партии прибо-
приборов до заданного числа отказов без
замены отказавших приборов
Двухстадийная оценка среднего зна-
значения
Точечная оценка параметра (средне-
(среднего значения) с помощью порядковых
статистик
Интервальная оценка среднего зна-
значения
Интервальная оценка интенсивности
отказов при испытании партии при-
приборов до заданной наработки с заме-
заменой отказавших приборов
Интервальная оценка интенсивности
отказов при испытании партии при-
приборов до заданного количества отка-
отказов с заменой отказавших приборов
Интервальная оценка интенсивности
отказов при испытании партии при-
приборов до заданного количества отка-
отказов без замены отказавших приборов
Интервальная оценка интенсивности
отказов при испытании партии при-
приборов до заданной наработки без за-
замены отказавших приборов
Интервальная оценка наработки на
отказ
Точечная оценка параметра а при
известном параметре /3
Совместная точечная оценка пара-
параметров распределения
Совместная точечная оценка пара-
параметров распределения (метод момен-
моментов)
Совместная точечная оценка пара-
параметров распределения по одной по-
порядковой статистике
Перечень демонстрационных задач
765
Продолжение таблицы
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
Стр.
175
176
177
177
177
178
178
178
178
181
187
191
193
194
195
196
Исходная информация
Распределение Вейбулла
Распределение Вейбулла
Распределение Вейбулла
Распределение Вейбулла (выборка
цензурирована)
Распределение Вейбулла
Распределение Вейбулла
Распределение Вейбулла (выборка
цензурирована)
Распределение Вейбулла
Экспоненциальное распределение.
Распределение Вейбулла с из-
известным параметром /3 (выборка
цензурирована)
Гамма-распределение
Биномиальное распределение
Гипергеометрическое распределе-
распределение
Закон распределения вероятностей
неизвестен (известна только
дисперсия)
Закон распределения вероятностей
неизвестен (известна только
дисперсия)
Экспоненциальное распределение
с изменяющейся интенсивностью
отказов
Экспоненциальное распределение
Содержание задачи
Точечная оценка параметров рас™
пределения методом наименьших
квадратов
Точечная оценка параметров распре™
деления методом аппроксимации
Точечная оценка параметров распре™
деления
Точечная оценка параметров распре-
распределения
Интервальная оценка параметра а
при известном параметре /3
Совместная интервальная оценка па-
параметров распределения
Интервальная оценка квантили рас-
распределения
Интервальная оценка квантили рас-
распределения
Оценка экономии в продолжительно-
продолжительности испытаний приборов при цензу-
цензурировании выборов
Точечная оценка параметров а и f3.
Интервальная оценка параметра /3
при известном параметре а
Интервальная оценка параметра
распределения
Оценка верхней границы количе-
количества дефектных изделий изделий
в партии
Интервальная оценка центра рас-
распределения
Оценка квантили распределения
Оценка интенсивности отказов изде-
изделия в период приработки
Прогнозирование средней наработки
для будущих испытаний
3. Определение объема выборки, необходимого для оценки
параметра распределения с заданной точностью
83
197
Нормальное распределение (дис-
(дисперсия известна)
Определение объема выборки, необ-
необходимого для оценки среднего значе-
значения с заданной абсолютной ошибкой
766
Перечень демонстрационных задач
Продолжение таблицы
84
85
86
87
88
89
90
Стр.
198
198
200
200
200
201
201
Исходная информация
Нормальное распределение (дис-
(дисперсия неизвестна)
Распределение Вейбулла (параметр
формы /3 известен)
Биномиальное распределение
Биномиальное распределение
Биномиальное распределение
Экспоненциальное распределение
Гамма-распределение
Содержание задачи
Определение объема выборки, необ-
необходимого для оценки среднего значе-
значения с заданной предельной относи-
относительной ошибкой
Определение объема выборки, необ-
необходимого для оценки среднего зна-
значения с заданной относительной
погрешностью
Определение объема выборки, необ-
необходимого для контроля заданной до-
доли дефектных изделий в партии
Определение объема выборки, обес-
обеспечивающего заданную длину дове-
доверительного интервала для оценки
параметра распределения
Определение объема выборки, необ-
необходимого для прогнозирования чис-
числа дефектных изделий в партии
Определение объема выборки для
оценки интенсивности отказов
Определение объема выборки, необ-
необходимого для оценки среднего значе-
значения с заданной предельной ошибкой
4. Проверка согласия эмпирического распределения
с предполагаемым теоретическим законом
91
92
93
94
95
96
207
211
212
215
217
219
Распределение вероятностей неиз-
неизвестно (одна выборка)
Распределение вероятностей неиз-
неизвестно (две выборки)
Распределение вероятностей неиз-
неизвестно (две выборки)
Распределение вероятностей неиз-
неизвестно (одна выборка)
Распределение вероятностей неиз-
неизвестно (одна выборка)
Распределение вероятностей неиз-
неизвестно (одна выборка)
Проверка критерием % гипотезы
о согласии эмпирического распреде-
распределения с нормальным законом
Проверка гипотезы согласия эмпири-
эмпирического распределения с экспоненци-
экспоненциальным с помощью критерия числа
пустых ячеек. Проверка совпадения
распределений в двух выборках
Проверка совпадений эмпирических
распределений в двух выборках кри-
критерием Барнетта-Эйсена
Проверка совпадения эмпирического
распределения с нормальным (при
заданных параметрах) критерием
Колмогорова-Смирнова
Проверка совпадения эмпирического
распределения с нормальным зако-
законом критерием Смирнова-Крамера-
фон Мизеса
Проверка совпадения эмпирического
распределения с нормальным зако-
законом критерием Реньи
Перечень демонстрационных задач
767
Продолжение таблицы
97
98
99
100
Стр.
221
223
224
226
Исходная информация
Распределение вероятностей неиз-
неизвестно (одна выборка)
Распределение вероятностей неиз-
неизвестно (одна выборка)
Распределение вероятностей неиз-
неизвестно (одна выборка)
Распределение вероятностей неиз-
неизвестно (одна выборка)
Содержание задачи
Проверка совпадения эмпирического
распределения с нормальным зако-
законом критерием Андерсона—Дарлинга
Проверка совпадения эмпирического
распределения с нормальным зако-
законом критерием Ватсона
Проверка совпадения эмпирического
распределения с нормальным зако-
законом критерием Купера
Проверка совпадения эмпирического
распределения с нормальным зако-
законом критерием Дарбина
5. Проверка совпадения функций распределения вероятностей
в двух выборках
101
102
103
228
229
230
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Проверка совпадения эмпирических
распределений критерием Колмого-
Колмогорова-Смирнова
Проверка совпадения эмпирических
распределений критерием Катцен-
байссера-Хакля
Проверка совпадения эмпирических
распределений критерием Андер-
Андерсона
6. Проверка совпадения эмпирического распределения вероятностей
с нормальным законом
104
105
106
107
108
109
110
232
234
235
239
242
243
245
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Проверка нормальности эмпиричес-
эмпирического распределения критерием х2
Проверка нормальности крите! я-
ми Колмогорова—Смирнова и пш^ с
оценкой параметров гипотетического
распределения по выборке
Проверка нормальности эмпири-
эмпирического распределения критерием
Фроцини
Проверка нормальности эмпиричес-
эмпирического распределения критерием Ша-
пиро-Уилка
Проверка нормальности эмпири-
эмпирического распределения критерием
Васичека
Проверка нормальности эмпиричес-
эмпирического распределения критерием Хега-
зи—Грина
Проверка нормальности эмпиричес-
эмпирического распределения критерием Али-
Чёрго-Ревеса
768
Перечень демонстрационных задач
Продолжение таблицы
111
112
113
114
115
116
117
118
119
120
121
122
123
124
Стр.
246
252
253
256
258
260
260
262
264
265
268
270
272
276
Исходная информация
Распределение вероятностей неиз-
неизвестно (одна выборка)
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно (совокупность выборок ма-
малого объема)
Содержание задачи
Проверка нормальности эмпири-
эмпирического распределения критерием
Филлибена
Проверка нормальности эмпиричес-
эмпирического распределения критерием Ла
Брека
Проверка нормальности эмпиричес-
эмпирического распределения критерием Лок-
ка-Спурье
Проверка нормальности эмпиричес-
эмпирического распределения критерием Оя
Проверка нормальности эмпиричес-
эмпирического распределения критерием Гири
Проверка нормальности эмпиричес-
эмпирического распределения критерием Дэви-
да^Хартли-Пирсона
Проверка нормальности эмпири-
эмпирического распределения критерием
Шпигельхальтера
Проверка нормальности эмпири-
эмпирического распределения критерием
Саркади
Проверка нормальности эмпиричес-
эмпирического распределения критерием Ли-
на-Мудхолкара
Проверка нормальности эмпиричес-
эмпирического распределения критерием Мар-
тинеса-Иглевича
Проверка нормальности эмпири-
эмпирического распределения критерием
Д'Агостино
Проверка нормальности эмпириче-
эмпирического распределения критериями
асимметрии и эксцесса
Проверка нормальности эмпиричес-
эмпирического распределения критерием Му-
роты-Такеучи
Проверка нормальности эмпиричес-
эмпирического распределения по совокупности
независимых выборок малого объема
7. Проверка совпадения эмпирического распределения
с экспоненциальным законом
125
281
Распределение вероятностей неиз-
неизвестно
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Шапиро-Уилка
Перечень демонстрационных задач
769
Продолжение таблицы
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
Стр.
282
284
287
288
289
291
293
293
294
295
297
299
301
302
304
Исходная информация
Распределение вероятностей неиз-
неизвестно (выборка цензурирована)
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно (выборка цензурирована)
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно (выборка цензурирована)
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Содержание задачи
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Шапиро-Уилка
Проверка экспоненциальности эмпи-
эмпирического распределения критерями
типа Колмогорова-Смирнова
Проверка экспоненциальности эмпи-
эмпирического распределения критери-
критериями типа Смирнова-Крамера-фон
Мизеса и Колмогорова-Смирнова
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Фроцини
Проверка экспоненциальности рас-
распределения корреляционным крите-
критерием
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Брейна—Шапиро
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Кимбера-Мичела
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Фишера
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Бартлетта-Морана
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Климко-Антла-Радемакера^Рокетта
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Холлендера-Прошана
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Кочара
Проверка экспоненциальности рас-
распределения критерием Эппса—Палли
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Бергмана
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Шермана
25 А. И. Кобзарь
770
Перечень демонстрационных задач
Продолжение таблицы
141
142
143
144
145
146
147
148
Стр.
304
305
306
307
310
311
316
317
Исходная информация
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Содержание задачи
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
наибольшего интервала
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Хартли
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
экспоненциальных меток
Проверка экспоненциальности эмпи-
эмпирического распределения критерия-
критериями независимости интервалов
Проверка экспоненциальности эмпи-
эмпирического распределения критерия-
критериями Un Гринвуда
Проверка гипотезы согласия эмпи-
эмпирического распределения с двухпа-
раметрическим распределением Вей-
булла (частный случай экспоненци-
экспоненциального распределения) критерием
Манна-Фертига-Шуера
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Дешпанде
Проверка экспоненциальности эмпи-
эмпирического распределения критерием
Лоулесса
8. Проверка совпадения эмпирического распределения
с равномерным законом
149
150
151
152
153
154
319
322
323
324
326
327
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Проверка равномерности эмпири-
эмпирического распределения критерием
Шермана
Проверка равномерности эмпири-
эмпирического распределения критерием
Морана
Проверка равномерности эмпиричес-
эмпирического распределения критерием Чен-
га—С пиринга
Проверка равномерности эмпиричес-
эмпирического распределения критерием Сар-
кади-Косика
Проверка равномерности эмпиричес-
эмпирического распределения критерием Дуде™
вича—ван дер Мюлена
Проверка равномерности эмпиричес-
эмпирического распределения критерием Хега-
зи—Грина
Перечень демонстрационных задач
771
Продолжение таблицы
155
156
157
158
159
Стр.
329
330
331
333
333
Исходная информация
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Содержание задачи
Проверка равномерности эмпиричес-
эмпирического распределения критерием Янга
Проверка равномерности эмпиричес-
эмпирического распределения критериями ти-
типа Колмогорова^Смирнова
Проверка равномерности эмпири-
эмпирического распределения критерием
Фроцини
Проверка равномерности эмпиричес-
эмпирического распределения критерием Грин-
вуда—Кэсенберри—Миллера
Проверка равномерности эмпириче-
эмпирического распределения „сглаженным"
критерием Неймана—Бартона
9. Проверка симметричности эмпирического распределеним вероятностей
160
161
162
163
164
165
166
167
168
169
336
337
339
340
341
343
345
346
349
351
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Проверка симметричности эмпири-
эмпирического распределения „быстрым"
критерием Кенуя
Проверка симметричности эмпири-
эмпирического распределения критерием
Смирнова
Проверка симметричности эмпири-
эмпирического распределения критерием
знаков
Проверка симметричности эмпири-
эмпирического распределения критерием
Вилкоксона
Проверка симметричности эмпири-
эмпирического распределения критерием
знаков Антилла—Керстинга—Цукки-
ни
Проверка симметричности эмпири-
эмпирического распределения критерием
Бхатачарья-Гаствирта-Райта
Проверка симметричности эмпири-
эмпирического распределения критерием
Финча
Проверка симметричности эмпири-
эмпирического распределения критерием
Бооса
Проверка симметричности эмпири-
эмпирического распределения критерием
Гупты
Проверка симметричности эмпири-
эмпирического распределения критерием
Фрезера
25*
772
Перечень демонстрационных задач
Продолжение таблицы
Стр.
Исходная информация
Содержание задачи
10. Подбор кривых распределения вероятностей по эмпирическим данным
170
171
172
173
174
175
176
177
178
179
180
181
353
356
366
373
375
377
379
380
381
383
384
386
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Распределение вероятностей неиз-
неизвестно
Аппроксимация эмпирического рас-
распределения кривой из семейства Sl
Джонсона
Аппроксимация эмпирического рас-
распределения кривой из семейства Sb
Джонсона
Аппроксимация эмпирического рас-
распределения кривой из семейства Su
Джонсона
Аппроксимация эмпирического рас-
распределения кривой Пирсона типа I
Аппроксимация эмпирического рас-
распределения кривой Пирсона типа II
Аппроксимация эмпирического рас-
распределения кривой Пирсона типа Ш
Аппроксимация эмпирического рас-
распределения кривой Пирсона типа IV
Аппроксимация эмпирического рас-
распределения кривой Пирсона типа V
Аппроксимация эмпирического рас-
распределения кривой Пирсона типа VI
Аппроксимация эмпирического рас-
распределения кривой Пирсона типа VII
Аппроксимация эмпирического рас-
распределения с помощью разложе-
разложения нормальной плотности распре-
распределения
Оценка плотности эмпирического
распределения методом бета-вкладов
11. Сравнение параметров нормально распределенных совокупностей
182
183
184
185
186
390
390
392
393
393
Нормальное распределение (две вы-
выборки с известными дисперсиями)
Нормальное распределение (две вы-
выборки с неизвестными, но равными
дисперсиями)
Нормальное распределение (две вы-
выборки с неизвестными и неравными
дисперсиями)
Нормальное распределение (две вы-
выборки)
Нормальное распределение (две
парные выборки)
Проверка гипотезы равенства сред-
средних в двух совокупностях
Проверка гипотезы равенства сред-
средних в двух совокупностях
Проверка гипотезы равенства сред-
средних в двух совокупностях
Проверка гипотезы равенства сред-
средних в двух совокупностях модифици-
модифицированным критерием Стьюдента
Проверка гипотезы равенства сред-
средних в двух совокупностях парным
t-критерием
Перечень демонстрационных задач
773
Продолжение таблицы
187
188
189
190
191
192
193
194
195
196
197
198
199
Стр.
394
396
397
398
399
401
402
403
405
407
407
408
412
Исходная информация
Нормальное распределение (одна
выборка и одно независимое значе-
значение случайной величины)
Нормальное распределение (две вы-
выборки)
Нормальное распределение (две вы-
выборки с равными дисперсиями)
Нормальное распределение (более
двух выборок с равными дисперси-
дисперсиями)
Нормальное распределение (более
двух выборок с равными дисперси-
дисперсиями)
Нормальное распределение (более
двух выборок с равными дисперси-
дисперсиями)
Нормальное распределение (более
двух выборок с равными дисперси-
дисперсиями)
Нормальное распределение (более
двух выборок с равными дисперси-
дисперсиями)
Нормальное распределение (более
двух выборок с равными дисперси-
дисперсиями)
Нормальное распределение (более
двух выборок с равными дисперси-
дисперсиями)
Нормальное распределение (более
двух выборок равного объема с рав-
равными дисперсиями)
Нормальное распределение (более
двух выборок равного объема с рав-
равными дисперсиями)
Нормальное распределение (более
двух выборок равного объема с рав-
равными дисперсиями)
Содержание задачи
Проверка гипотезы о принадлежно-
принадлежности независимого выборочного зна-
значения к первичной выборке крите-
критерием Уолша
Проверка гипотезы равенства сред-
средних в двух совокупностях двухсту-
двухступенчатым критерием Волфа
Проверка гипотезы равенства сред-
средних в двух совокупностях ^-крите-
^-критерием
Проверка гипотезы равенства сред-
средних в более, чем двух совокупно-
совокупностях модифицированым критерием
Стьюдента
Проверка гипотезы равенства сред-
средних в более, чем двух совокупно-
совокупностях критерием „стьюдентизирован-
ного" размаха
Проверка гипотезы равенства сред-
средних в более, чем двух совокупностях
дисперсионным критерием
Проверка гипотезы равенства сред-
средних в более, чем двух совокупностях
критерием Полсона
Проверка гипотезы равенства сред-
средних в более, чем двух совокупностях
методом прямого сравнения Тькжи
Проверка гипотезы равенства сред-
средних в более, чем двух совокупно-
совокупностях критерием „стьюдентизироваы-
ного" максимума (обобщенный кри-
критерий Тьюки)
Проверка гипотезы равенства сред-
средних в более, чем двух совокупностях
критерием Шеффе
Проверка гипотезы равенства сред-
средних в более, чем двух совокупно-
совокупностях критерием Стьюдента-Ньюме-
на^Кейлса
Проверка гипотезы равенства сред-
средних в более, чем двух совокупностях
критерием Дункана
Проверка гипотезы равенства сред-
средних в более, чем двух совокупностях
критерием Линка—Уоллеса
774
Перечень демонстрационных задач
Продолжение таблицы
200
201
202
203
204
205
206
207
208
209
210
211
Стр.
413
413
414
415
416
417
418
420
421
422
423
423
Исходная информация
Нормальное распределение (две вы-
выборки)
Нормальное распределение (две вы™
борки)
Нормальное распределение (две вы-
выборки)
Нормальное распределение (две вы-
выборки)
Нормальное распределение (две вы-
выборки)
Нормальное распределение (более
двух выборок)
Нормальное распределение (более
двух выборок равного объема)
Нормальное распределение (более
двух выборок равного объема)
Нормальное распределение (более
двух выборок равного объема)
Нормальное распределение (более
двух выборок равного объема)
Нормальное распределение (более
двух выборок равного объема)
Нормальное распределение (более
двух выборок)
Содержание задачи
Проверка гипотезы равенства дис-
дисперсий в двух совокупностях крите-
критерием Фишера
Проверка гипотезы равенства дие-
персий в двух совокупностях крите-
критерием Романовского
Проверка гипотезы равенства дис-
дисперсий в двух совокупностях крите-
критерием отношения размахов
Проверка гипотезы равенства дис-
дисперсий в двух совокупностях кри-
критерием „стьюдентизированного" раз-
размаха
Проверка гипотезы равенства дис-
дисперсий в двух совокупностях крите-
критерием Аризоно-Охты
Проверка гипотезы равенства дис-
дисперсий в более, чем двух выборках
критерием Бартлетта
Проверка гипотезы равенства дис-
дисперсий в более, чем двух выборках
критерием Кохрана
Проверка гипотезы равенства дис-
дисперсий в более, чем двух выборках
критерием Неймана—Пирсона
Проверка гипотезы равенства дис-
дисперсий в более, чем двух выборках
критерием Блисса-Кохрана-Тьюки
Проверка гипотезы равенства дис-
дисперсий в более, чем двух выборках
критерием Хартли
Проверка гипотезы равенства дис-
дисперсий в более, чем двух выборках
критерием Кэдуэлла—Лесли—Брауна
Проверка гипотезы равенства дис-
дисперсий в более, чем двух выборках
критерием Самиуддина
12. Сравнение параметров
экспоненциально распределенных совокупностей
212
213
425
425
Экспоненциальное распределение
(две выборки)
Экспоненциальное распределение
(две выборки)
Проверка гипотезы равенства сред-
средних в двух совокупностях критерием
Фишера
Проверка равенства интенсивностей
отказов критерием Фишера
Перечень демонстрационных задач
775
Продолжение таблицы
214
215
216
217
218
219
220
221
222
223
224
Стр.
426
428
428
428
429
429
430
430
431
431
432
Исходная информация
Экспоненциальное распределение
(две выборки)
Экспоненциальное распределение
(одна выборка и заданное значение
интенсивности отказов)
Экспоненциальное распределение
(одна выборка и заданное значение
интенсивности отказов)
Эксп ненц альное распределен е
(одна выборка и заданное значение
интенсивности отказов)
Экспоненциальное распределение
(одна выборка и заданное значение
интенсивности отказов)
Экспоненциальное распределение
(одна выборка и заданное значение
интенсивности отказов)
Экспоненциальное распределение
(более двух выборок равного
объема)
Экспоненциальное распределение
(более двух выборок). Фиксируются
моменты наступления заданного
количества отказов
Экспоненциальное распределение
(более двух выборок). Фиксируются
количества отказов в выборках за
заданное время испытаний
Экспоненциальное распределение
(более двух выборок равного
объема)
Экспоненциальное распределение
(более двух выборок равного
объема)
Содержание задачи
Проверка равенства интенсивностей
отказов в двух совокупностях двух»
выборочным пуассоновским крите-
критерием
Сравнение интенсивности отказов
с заданным значением при испыта-
испытании приборов до заданной наработки
с заменой отказавших приборов
Сравнение интенсивности отказов
с заданным значением при испыта-
испытании приборов до заданного количе-
количества отказов с заменой отказавших
пр сборов
Вариант решения задачи 216 без за-
замены отказавших приборов
Сравнение интенсивности отказов
с заданным значением при испыта-
испытании приборов до заданной наработки
без замены отказавших приборов
Сравнение интенсивности отказов
с заданным значением при испыта-
испытании приборов до заданного количе-
количества отказов без замены отказавших
Проверка гипотезы равенства интен-
интенсивностей отказов в более, чем двух
совокупностях критерием Дэвида
Проверка гипотезы равенства ин-
интенсивностей отказов в более, чем
двух совокупностях критерием мак-
максимального правдоподобия
Проверка гипотезы равенства ин-
интенсивностей отказов в более, чем
двух совокупностях критерием мак-
максимального правдоподобия
Проверка гипотезы равенства ин-
интенсивностей отказов в более, чем
двух совокупностях критерием от-
отношения правдоподобия (критерий
Нагарсенкера)
Проверка гипотезы равенства пара-
параметра положения (гарантийной нара-
наработки) в более, чем двух совокупно-
совокупностях критерием Чена
776
Перечень демонстрационных задач
Продолжение таблицы
225
Стр.
434
Исходная информация
Экспоненциальное распределение
(более двух выборок)
Содержание задачи
Проверка гипотезы равенства пара-
параметра положения (гарантийной нара-
наработки) и параметра масштаба (сред-
(средней наработки, отсчитываемой от га-
гарантийной наработки) в более, чем
двух совокупностях комбинирован-
комбинированным критерием Сингха
13. Сравнение параметров биномиально распределенных совокупностей
226
227
228
436
437
438
Биномиальное распределение (две
выборки)
Биномиальное распределение (одна
выборка и заданное значение пара-
параметра)
Биномиальное распределение (бо-
(более двух выборок)
Сравнение параметров распределе-
распределений в двух совокупностях
Сравнение параметра распределения
с заданным значением
Сравнение параметров распределе-
распределения в более, чем двух совокупностях
14. Проверка гипотезы о значениях параметров распределения
методом последовательного анализа Вальда
229
230
231
232
445
447
448
450
Нормальное распределение с из-
известным стандартным отклонением
Нормальное распределение с из-
известным средним
Экспоненциальное распределение
Биномиальное распределение
Проверка гипотезы о значении сред-
среднего нормально распределенной со-
совокупности. Вычисление параметров
последовательной процедуры
Проверка гипотезы о значении дис-
дисперсии нормально распределенной
совокупности. Вычисление парамет-
параметров последовательной процедуры
Проверка гипотезы о значении пара-
параметра экспоненциально распределен-
распределенной совокупности (средняя наработ-
наработка на отказ). Вычисление параметров
последовательной процедуры
Проверка гипотезы о значении пара-
параметра биномиально распределенной
совокупности (доля дефектных из-
изделий в партии приборов). Вычис-
Вычисление параметров последовательной
процедуры
15. Непараметрические (свободные от распределения) критерии сдвига
233
234
235
452
453
457
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Проверка гипотезы сдвига меж-
между двумя совокупностями быстрым
(грубым) критерием Кенуя
Проверка гипотезы сдвига меж-
между двумя совокупностями быстрым
(грубым) ранговым критерием
Проверка гипотезы сдвига между
двумя совокупностями критериями
группы Манна—"Уитни—Вилкоксона
Перечень демонстрационных задач
777
Продолжение таблицы
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
Стр.
460
461
463
464
464
465
465
468
469
471
473
473
475
476
476
Исходная информация
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (более двух выборок)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок)
Распределение совокупности неиз-
неизвестно (более двух выборок)
Распределение совокупности неиз-
неизвестно (более двух выборок)
Распределение совокупности неиз-
неизвестно (более двух выборок)
Содержание задачи
Проверка гипотезы сдвига между
двумя совокупностями критерием
Фишера—Йэйтса—Терри—Гёфдинга
Проверка гипотезы сдвига между
двумя совокупнс стя ' кр тер е
Ван дер Вардена
Проверка гипотезь сдв' а ежду
двумя совокупностями медианным
критерием
Проверка гипотезы сдвига между
двумя совокупностями критерием
Мостеллера
Проверка гипотезы сдвига между
двумя совокупностями критерием
Розенбаума
Проверка гипотезы сдвига между
двумя совокупностями критерием
Хаги
Проверка гипотезы сдвига между
двумя совокупностями .Е-критерием
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Крускала-Уоллиса
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Неменьи
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Вилкоксона-Вил-
кокс
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями „быстрым" критерием Кенуя
Проверка гипотезы сдвига между
несколькими (более двух) совокуп-
совокупностями критерием Фишера—Терри—
Йэйтса-Гёфдинга
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Ван дер Вардена
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями медианным критерием
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями против порядковой альтерна-
альтернативы критерием Хеттманспергера
778
Перечень демонстрационных задач
Продолжение таблицы
251
252
253
254
255
256
257
258
259
260
261
Стр.
477
479
479
480
482
483
486
487
488
490
491
Исходная информация
Распределение совокупности неиз-
неизвестно (более двух выборок)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок)
Распределение совокупности неиз-
неизвестно (более двух выборок)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Распределение совокупности неиз-
неизвестно (более двух выборок равного
объема)
Содержание задачи
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями против порядковой альтерна-
альтернативы критерием Терпстры-Джонк-
хира
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Мостеллера
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Левиса
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями L-критерием, основанным на
[/-статистиках
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Краузе
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Пейджа
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Фридмеыа-Кендал-
ла—Бэбингтона Смита
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Андерсона—Канне-
мана-Шэча
Проверка гипотезы сдвига между
несколькими (более двух) совокуп-
совокупностями критерием Даны Квейд со
взвешенными ранжировками
Проверка гипотезы сдвига меж-
между несколькими (более двух) со-
совокупностями критерием Кендалла—
Эренберга
Проверка гипотезы сдвига между
несколькими (более двух) совокупно-
совокупностями критерием Ходжеса—Демана—
Сена
16. Непараметрические (свободные от распределения) критерии масштаба
262
494
Распределение совокупности неиз-
неизвестно (две выборки)
Проверка гипотезы равенства пара-
параметров в двух совокупностях крите-
критерием Ансари—Вредли
Перечень демонстрационных задач
779
Продолжение таблицы
263
264
265
266
267
268
269
270
271
272
273
274
Стр.
496
497
500
501
502
504
507
508
509
511
513
515
Исходная информация
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно, но известно, что оно огра-
ограничено полупрямой (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две парные выборки равно-
равного объема)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (две выборки)
Распределение совокупности неиз-
неизвестно (более двух выборок)
Содержание задачи
Проверка гипотезы равенства пара-
параметров масштаба в двух совокупно-
совокупностях критерием Сижела—Тьюки
Проверка гипотезы равенства пара-
параметров масштаба в двух совокупно-
совокупностях критерием Кейпена
Проверка гипотезы равенства пара-
параметров масштаба в двух совокупно-
совокупностях критерием Клотца
Проверка гипотезы равенства пара-
параметров масштаба в двух совокупно-
совокупностях квартальным критерием
Проверка гипотезы равенства пара-
параметров масштаба в двух совокупно-
совокупностях критерием Сэвиджа
Проверка гипотезы равенства пара-
параметров масштаба в двух совокупно-
совокупностях критерием Муда
Проверка гипотезы равенства пара-
параметров масштаба в двух совокупно-
совокупностях критерием Сукхатме
Проверка гипотезы равенства пара-
параметров масштаба в двух совокупно-
совокупностях критерием Сэндвика—Олсона
Проверка гипотезы равенства пара-
параметров масштаба в двух совокуп-
совокупностях критерием Краута-Линерта,
нечувствительным к сдвигу
Проверка гипотезы равенства пара-
параметров масштаба в двух совокупно-
совокупностях критерием Камата
Проверка комбинированной гипоте-
гипотезы равенства положения и масштаба
в двух выборках комбинированным
критерием Буша^Винда
Проверка гипотезы равенства пара-
параметров масштаба в нескольких (бо-
(более двух) совокупностях критерием
Бхапкара—Дешпанде
17. Оценка случайности эмпирических данных, выявление тренда в них
(критерии тренда и случайности)
275
518
Ряд взаимонезависимых нормаль™
но распределенных случайных ве-
величин с одинаковыми (неизвестны-
(неизвестными) дисперсиями
Проверка гипотезы случайности эм-
эмпирического ряда критерием Аббе—
Линника
780
Перечень демонстрационных задач
Продолжение таблицы
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
Стр.
520
521
523
525
529
530
532
532
535
536
538
539
540
541
542
Исходная информация
Ряд нормально распределенных
случайных величин
Ряд нормально распределенных
случайных величин
Ряд нормально распределенных
случайных величин с одинаковыми
средними
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд нормально распределенных
случайных величин
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд случайных величин с неизвест-
неизвестным законом распределения
Ряд случайных величин с не звест-
ным законом распределения
Содержание задачи
Проверка гипотезы наличия трен-
тренда в средних и дисперсиях эмпи-
эмпирического ряда критерием Фостера—
Стюарта
Проверка гипотезы наличия тренда
в средних и дисперсиях эмпиричес-
эмпирического ряда критерием Кокс—Стюарта
Проверка гипотезы наличия сдвига
дисперсии в неизвестной точке кри-
терием Хсу
Проверка гипотезы наличия сдвига
дисперсии в неизвестной точке ран-
ранговым критерием
Проверка гипотезы случайности эм-
эмпирического ряда критерием Валь-
да-Волфовитца
Проверка гипотезы случайности эм-
эмпирического ряда критерием Рама-
чандрана-Ранганатана
Проверка гипотезы случайности эм-
эмпирического ряда критерием Шах-
несси
Проверка гипотезы случайности эм-
эмпирического ряда критерием Олм-
стеда
Проверка гипотезы случайности эм-
эмпирического ряда критерием числа
серий знаков первых разностей
Проверка гипотезы случайности эм-
эмпирического ряда критерием инвер-
инверсий
Проверка гипотезы случайности эм-
пирического ряда критерием авто-
автокорреляции
Проверка гипотезы случайности эм-
эмпирического ряда критерием ранго-
ранговой сериальной корреляции Вальда™
Волфовитца
Проверка гипотезы случайности эм-
эмпирического ряда критерием Бар-
телса
Проверка гипотезы случайности эм-
эмпирического ряда критерием куму-
кумулятивной суммы
Проверка гипотезы случайности эм-
п рического ряда знаково-ранговым
кр fтерием Холлина
Перечень демонстрационных задач
781
Продолжение таблицы
Стр.
Исходная информация
Содержание задачи
18. Выявление грубых результатов наблюдений (выбросов) в выборке
291
292
293
294
295
296
297
298
299
300
301
302
303
304
544
545
546
547
548
550
552
556
557
559
561
563
565
568
Выборка нормально распределен™
ных случайных величин
Выборка нормально распределен-
распределенных случайных величин с известной
дисперсией
Выборка нормально распределен™
ных случайных величин (вариан-
(варианты— дисперсия известна и неиз-
неизвестна)
Выборка нормально распределен-
распределенных случайных величин
Выборка нормально распределен-
распределенных случайных величин (дисперсия
оценивается по отдельной выборке)
Выборка нормально распределен-
распределенных случайных величин
Выборка нормально распределен-
распределенных случайных величин
Выборка нормально распределен-
распределенных случайных величин (число вы™
бросов принимается заранее)
Выборка нормально распределен-
распределенных случайных величин (число вы-
выбросов заранее не известно)
Выборка экспоненциально распре-
распределенных случайных величин
Выборка экспоненциально распре-
распределенных случайных величин
Выборка экспоненциально распре-
распределенных случайных величин
Выборка случайных величин, име-
имеющих распределение Вейбулла
Выборка случайных величин из
непрерывного распределения с из-
известными параметрами
Проверка гипотезы наличия выброса
в выборке критерием Шовене
Проверка гипотезы наличия выброса
в выборке критерием Ирвина
Проверка гипотезы наличия выброса
в выборке критериями Груббса
Проверка гипотезы наличия выбро-
выброса в выборке критерием наибольшего
абсолютного отклонения
Проверка гипотезы наличия выброса
в выборке критерием Дэвида
Проверка гипотезы наличия выброса
в выборке критерием Диксона
Проверка гипотезы наличия выбро-
выброса в выборке критериеями Хоглина—
Иглевича
Проверка гипотезы наличия несколь-
нескольких выбросов в выборке критерием
Титьена-Мура
Проверка гипотезы наличия несколь-
нескольких выбросов в выборке критерием
Роснера
Проверка гипотезы наличия выбро-
выбросов в выборке критерием Смоляка™
Титаренко
Проверка гипотезы наличия выбро-
выбросов в выборке критерием Бродского™
Быцаня—Власенко
Проверка гипотезы наличия несколь-
нескольких выбросов в выборке критерием
Кимбера
Проверка гипотезы наличия выбро-
выбросов в выборке критериями Груббса
и Диксона
Проверка гипотезы наличия выбро-
выбросов в выборке критерием Дарлинга
19. Вычисление толерантных пределов, содержащих заданную долю
генеральной совокупности
305
569
Выборка случайных величин, име-
имеющих нормальное распределение
с известными параметрами
Вычисление толерантных пределов
для совокупности случайных вели-
величин
782
Перечень демонстрационных задач
Продолжение таблицы
306
307
308
309
310
311
312
313
314
315
316
317
318
Стр.
572
572
577
578
579
582
582
583
583
588
589
589
589
Исходная информация
Выборка случайных величин, име-
имеющих нормальное распределение
с неизвестным средним и известной
дисперсией
Выборка случайных величин, име-
имеющих нормальное распределение
с известным средним и неизвестной
дисперсией
Выборка случайных величин, име-
имеющих нормальное распределен' е
с неизвестными параметра
Выборка случайных вел - ^ н, - е-
ющих нормальное распределение
Выборка случайных величин, име-
имеющих нормальное распределение
Выборка случайных величин с неиз-
неизвестным распределением
Выборка случайных величин с неиз-
неизвестным распределением
Выборка случайных величин с неиз-
неизвестным распределением
Выборка случайных величин, име-
имеющих нормальное или экспоненци-
экспоненциальное распределение
Выборка случайных величин, име-
имеющих экспоненциальное распреде-
распределение
Выборка случайных величин, име-
имеющих экспоненциальное распреде-
распределение
Выборка случайных величин, име-
имеющих экспоненциальное распреде-
распределение
Выборка случайных величин, име-
имеющих экспоненциальное распреде-
распределение
Содержание задачи
Вычисление толерантных пределов
для совокупности случайных вели-
величин
Вычисление толерантных пределов
для совокупности случайных вели-
величин
Вычисление толерантных пределов
для совокупности случайных вели-
ч н
Вь ч сление толерантных пределов
для совокупности случайных вели-
величин с помощью выборочного размаха
Вычисление толерантных интерва-
интервалов для выборочных дисперсий
Вычисление объема выборки, в ко-
которой с заданной вероятностью бу-
будет находиться заданная доля сово-
совокупности
Вычисление минимального объема
выборки для одностороннего толе-
толерантного интервала
Вычисление доли непрерывной сово-
совокупности, которая с заданной веро-
вероятностью будет находиться между
крайними членами выборки
Определение границ интервала, в ко-
котором будут находиться т из к буду-
будущих наблюдений
Вычисление прогнозных интервалов
для нижней границы средней нара-
наработки по ранним моментам отказов
Вычисление нижнего доверительно-
доверительного интервала для средней наработки
на отказ
Вычисление вероятностей появле-
появления заданных величин в будущих
наблюдениях
Вычисление вероятности попадания
будущих наблюдений в заданный
интервал
20. Дисперсионный анализ данных
319
593
Совокупность данных, полученных
при различных уровнях изучаемого
фактора (распределение нормаль-
нормально)
Однофакторный дисперсионный ана-
анализ данных
Перечень демонстрационных задач
783
Продолжение таблицы
320
321
322
323
324
Стр.
595
597
599
602
604
Исходная информация
Совокупность данных, полученных
при различных уровнях двух фак-
факторов (распределение нормально)
Совокупность данных, полученных
при различных уровнях двух фак-
факторов (распределение нормально)
Совокупность данных, полученных
при различных уровнях двух фак-
торов (распределение неизвестно,
в данных возможны пропуски)
Совокупность данных, полученных
при различных уровнях двух фак-
факторов (распределение неизвестно,
в данных возможны пропуски)
Совокупность данных, полученных
при различных уровнях двух фак-
факторов (распределение неизвестно,
в данных возможны пропуски)
Содержание задачи
Двухфакторный дисперсионный ана-
анализ данных
Двухфакторный дисперсионный ана-
анализ данных с помощью размахов
Двухфакторный дисперсионный не-
непараметрический анализ для непол-
неполных данных критерием Принтиса
Двухфакторный дисперсионный не-
непараметрический анализ для непол-
неполных данных критерием Мака-Скил-
лингса
Двухфакторный дисперсионный не-
непараметрический анализ для непол-
неполных данных критерием Лемана—
Мака
21. Корреляционный анализ данных
325
326
327
328
329
330
331
332
333
334
608
610
612
615
617
619
620
621
622
623
Две выборки нормально распреде-
распределенных случайных величин
Две выборки нормально распреде-
распределенных случайных величин
Несколько (более двух) выборок
нормально распределенных случай-
случайных величин
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Проверка гипотезы о наличии кор-
корреляции между случайными вели-
величинами
Оценка корреляционного отношения
(оценка линейности корреляционной
связи)
Вычисление показателей частной
и множественной корреляции и оцен-
оценка их значимости
Установление значимости корреля-
корреляции „быстрыми" критериями Кенуя
и Кокс—Стюарта
Установление значимости корреля-
корреляции знаковым критерием Нелсона
Установление значимости корреля-
корреляции квадрантным критерием
Установление значимости корреля-
корреляции угловым критерием Олмстеда—
Тькжи
Установление значимости корреля-
корреляции между случайными величинами
приближенным критерием Шахани
Установление значимости корреля-
корреляции между случайными величинами
критерием Шведа-Эйзенхарта
Установление значимости корреля-
корреляции между случайными величинами
критерием автокорреляции Кенуя
784
Перечень демонстрационных задач
Продолжение таблицы
335
336
337
338
339
340
341
342
343
344
345
346
347
Стр.
624
625
628
629
631
633
634
636
637
638
640
641
642
Исходная информация
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Две выборки случайных величин
с неизвестным распределением
Несколько (больше двух) выборок
случайных величин с неизвестным
распределением
Несколько (больше двух) выборок
случайных величин с неизвестным
распределением
Одна выборка случайной вели™
t 'Ны — количественная, и соответ-
соответствующая ей выборка, содержащая
качественные признаки
Таблица сопряженности признаков
2x2
Таблица сопряженности признаков
2x2
Таблица сопряженности признаков
2x2
Содержание задачи
"Установление значимости корреля-
корреляции между случайными величина-
величинами критерием Блума-Кифера^Ро-
зенблатта
Установление значимости корреля-
корреляции между случайными величинами
с помощью рангового коэффициента
корреляции Кендалла
Установление значимости корреля-
корреляции между случайными величинами
с помощью рангового коэффициента
корреляции Спирмена
Установление значимости корреля-
корреляции между случайными величинами
критерием Гёфдинга
Установление значимости корреля-
корреляции между случайными величина -
критерием Ширахатэ
Установление значимости корреля-
корреляции между случайными величинами
критерием Фишера—Иэйтса
Установление значимости корреля-
корреляции между случайными величинами
критерием Ван дер Вардена
Установление корреляции между
несколькими совокупностями слу-
случайных величин с помощью коэф-
коэффициента конкордации Кендалла-
Вэбингтона Смита
Установление корреляции между
несколькими совокупностями слу-
случайных величин критерием Шуке-
ни-Фроли
Установление значимости точечно-
бисериальной корреляции (зависи-
(зависимости между качественным и коли-
количественным признаками)
Установление связи признаков в та-
таблицах 2x2
Установление значимости связи при-
признаков в таблицах сопряженности
2x2 с помощью коэффициента
контингенции
Установление значимости связи при-
признаков в таблицах сопряженности
2x2 точным критерием Фишера
Перечень демонстрационных задач
785
Продолжение таблицы
348
349
350
351
352
353
354
Стр.
642
642
643
644
645
646
647
Исходная информация
Таблица сопряженности признаков
2x2
Таблица сопряженности признаков
2x2
Таблица сопряженности признаков
2x2 (наблюдения проводятся над
одним и тем же объектом)
Таблица сопряженности признаков
2x2
Две таблицы сопряженности при-
признаков размера 2x2 каждая
Допустимые уровни ошибок перво-
первого и второго рода при принятии ре-
решения о наличии связи между ка-
качественными признаками
Таблица сопряженности признаков
г х с
Содержание задачи
"Установление значимости связи при-
признаков в таблицах сопряженности
2x2
Установление значимости связи при-
признаков в таблицах сопряженности
2x2
Установление значимости связи при-
признаков в таблицах сопряженности
2x2 модифицированным критерием
знаков Мак-Нимара
Установление значимости связи при-
признаков в таблицах сопряженности
2x2 критерием Вулфа
Проверка гипотезы о статистической
неразличимости двух таблиц соп-
сопряженности размером 2x2 каждая
критерием Ле Роя
Определение объема выборки, по-
позволяющего сравнить относительные
частоты в таблицах 2 х 2 с заданны-
заданными ошибками первого и второго рода
Проверка гипотезы о наличии связи
в таблице сопряженности г х с
22. Регрессионный анализ данных
355
356
357
358
359
651
651
652
652
653
Совокупность выборочных значе-
значений случайной величины, получен-
полученных при фиксированных значена ях
второй случайной величины
Совокупность выборочных зна11 е-
ний случайной величины, получен-
полученных при фиксированных значениях
второй случайной величины
Совокупность выборочных значе-
значений случайной величины, получен-
полученных при фиксированных значениях
второй случайной величины
Совокупность выборочных значе-
значений случайной величины, получен-
полученных при фиксированных значениях
второй случайной величины
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение неизвестно), полученных при
фиксированных значениях второй
случайной величины
Оценка коэффициентов регрессии
методом наименьших квадратов
Вь числение коэффициентов регрес-
с с помощью линейных оценок
Оценка коэффициентов регрессии
методом Бартлетта—Кенуя
Оценка коэффициентов регрессии
методом Керрича
Оценка коэффициентов регрессии
с помощью робастного критерия
Брауна-Муда
786
Перечень демонстрационных задач
Продолжение таблицы
360
361
362
363
364
365
366
367
368
369
Стр.
654
656
657
658
660
661
663
665
668
669
Исходная информация
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение неизвестно), полученных при
фиксированных значениях второй
случайной величины
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение нормально), полученных при
фиксированных значениях второй
случайной величины
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение неизвестно), полученных при
фиксированных значениях второй
случайной величины
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение нормально), полученных при
фиксированных значениях второй
случайной величины
Совокупность выборочных значе-
значений случайной величины получен-
полученных при фиксированных значениях
второй случайной величины
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение нормально), полученных при
фиксированных значениях второй
случайной величины
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение нормально), полученных при
фиксированных значениях второй
случайной величины
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение нормально), полученных при
фиксированных значениях второй
случайной величины
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение нормально), полученных при
фиксированных значениях второй
случайной величины
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение нормально), полученных при
фиксированных значениях второ"
случайной величины
Содержание задачи
Оценка регрессионного коэффициен-
коэффициента с помощью метода Тейла
Вычисление и статистический ана-
анализ оценок коэффициентов регрес-
регрессии
Проверка гипотезы о равенстве нулю
коэффициента регрессии, оцененно-
оцененного с помощью метода Тейла
Проверка адекватности регрессион-
регрессионной модели
Проверка гипотезы о наличии корре-
корреляции регрессионных остатков кри-
критерием Дарбина—Ватсона
Проверка гипотезы о наличии вы-
выброса в регрессионной модели крите-
критерием Эктона
Проверка гипотезы о наличии вы-
выброса в регрессионной модели крите-
критерием Титьена-Мура-Бекмана
Проверка гипотезы о наличии вы-
выброса в регрессионной модели крите-
критерием Прескотта-Лунда
Построение доверительной зоны для
уравнения регрессии
Оценка обращенного уравнения ре-
регрессии (с заменой переменных)
Перечень демонстрационных задач
787
Продолжение таблицы
370
371
372
373
374
375
376
377
378
379
380
Стр.
671
673
676
679
681
685
688
690
693
694
695
Исходная информация
Совокупность выборочных значе-
значений случайной величины (распреде-
(распределение нормально), полученных при
фиксированных значениях второй
случайной величины
Две выборки случайных величин,
полученные при фиксированных
значениях другой случайной вели-
величины
Две выборки случайных величин,
порождающие регрессионные моде-
модели
Известно стандартное отклонение
изучаемой регрессионной последо-
последовательности
Совокупность выборочных значе-
ний случайной величины (нормаль-
(нормальное распределение), полученных
при фиксированных значениях вто-
второй случайной величины
Совокупность выборочных значе-
значений случайной величины (нормаль-
(нормальное распределение), полученных
при фиксированных значениях вто-
второй случайной величины
Две регрессионные модели и неза-
независимая выборка значений случай-
случайной величины
Совокупность выборочных значе-
значений случайной величины, получен-
полученных при фиксированных значениях
второй случайной величины
Двумерная выборка случайных ве-
величин
Двумерная выборка случайных ве-
величин
Двумерная выборка случайных ве-
величин
Содержание задачи
Вычисление толерантной области
для линейной регрессии
Проверка гипотезы о неразличи-
неразличимости регрессионных моделей, по-
полученных по двум независимым
выборкам
Оценка доверительной области для
точки пересечения двух линий ре-
регрессии
Определение объема испытаний для
получения заданной точности оцен-
оценки коэффициента регрессии
Построение нелинейной регрессион-
регрессионной модели и ее статистический
анализ
Построение и статистический анализ
нелинейной регрессии с помощью по-
полиномов Чебышева
Выбор лучшей регрессионной моде-
модели критерием Вильямса-Клута
Вычисление прогнозируемых значе-
значений случайной величины по уравне-
уравнению регрессии
Вычисление регрессии методом наи-
наименьших модулей
Вычисление прямой регрессии мето-
методом последней точки
Вычисление регрессии методом одно-
однозначной аппроксимации
23. Вычисление параметров контрольных карт
381
382
383
699
700
701
Выборочные значения контролиру-
контролируемого параметра
Выборочные значения контролиру-
контролируемого параметра
Выборочные значения контролиру-
контролируемого параметра
Вычисление границ для контроль-
контрольных карт х и jR-карт Шухарта
Вычисление границ для контроль-
контрольных Я-карт Шухарта
Вычисление контрольных границ
для х- и Я-карт Шухарта по выбор-
выборкам неравного объема
788
Перечень демонстрационных задач
Окончание таблицы
384
385
386
387
388
389
390
391
Стр.
702
703
703
706
708
709
711
712
Исходная информация
Выборочные значения контр л ру-
емого параметра
Выборочные значения контролиру-
контролируемого параметра
Выборочные значения контролиру-
контролируемого параметра
Выборочные значения контролиру-
контролируемого параметра
Выборочные значения контролиру-
контролируемого параметра
Выборочные значения контролиру-
контролируемого параметра
Выборочные значения контролиру-
контролируемого параметра
Выборочные значения контролиру-
контролируемого параметра
Содержание задачи
Вь *- ' слей е границ для контроль-
контрольных карт доли дефектных изделий
(Р-карта Шухарта)
Вычисление границ для контроль-
контрольных карт числа дефектных изделий
(С-карта Шухарта)
Вычисление границ для контроль-
контрольных карт индивидуальных значе-
значений и скользящего размаха (xi- и
Ri-карты Шухарта)
Вычисление параметров контроль-
контрольной карты накопленных сумм для
контроля среднего значения
Вычисление параметров контроль-
контрольной карты накопленных сумм для
контроля разброса по выборочным
размахам
Вычисление параметров контроль-
контрольной карты накопленных сумм для
контроля разброса по выборочным
дисперсиям
Вычисление параметров контроль-
контрольной карты накопленных сумм для
контроля доли дефектных изделий
Вычисление параметров контроль-
контрольной карты накопленных сумм для
контроля доли дефектных изде-
изделий, основанного на распределении
Пуассона
24. Математическое планирование эксперимента,
построение планов и анализ моделей
392
393
394
395
396
397
718
719
726
731
733
735
Число изучаемых независимых па-
параметров-факторов
Матрица и результаты реализац
полного факторного эксперимента
Матрица и результаты реализации
ортогонального плана второго по-
порядка
Построение матрицы полного фак-
факторного эксперимента
Определение уравнения отклика
проведение его статистического
анализа
Определение статистической модели,
описывающей результаты опытов
Построение матрицы плана Хартли на кубе для пяти переменных и вы-
вычисление поверхности отклика
Результаты последовательного экс-
экспериментирования при поиске оп-
оптимума
Результаты последовательного экс-
экспериментирования при поиске оп-
оптимума
Определение оптимума отклика (три
фактора) методом крутого восхо-
восхождения Бокса-Уилсона
Поиск оптимума отклика методом
симплекс-планирования
Перечень математико-статистических таблиц
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Стр.
26
41
47
67
76
100
101
102
102
105
106
107
107
108
112
Наименование
Квантили стандартного нормаль-
нормального распределения
Значения (р(у)
Значения функции Gi (ж)
Значения функции F(z\ А)
Значения A — R), умноженные
на 104
Оптимальные порядковые стати-
статистики Диксона
Значения коэффициентов оценки
Огавы для различного числа оп-
тимально расположенных порядко-
порядковых статистик
Оценка /г по двум статистикам
Оценка /i по четырем совместным
квантилям
Значения коэффициентов k(pi,p2)
Критические значения G1
Значения R1
Значения Жо,э75
Доверительный интервал для ме-
медианы (номера порядковых стати-
статистик)
Значения А
Область применения
Общее применение
Аппроксимация Кэдуэлла для бета-
распределения
Аппроксимация Корниша—Фишера
для распределения хи-квадрат
Вычисление функции распределе-
распределения, порождаемой нормальной
плотностью с линейным дрейфом
среднеквадратического отклонения
Вычисление вероятности отказа из-
изделия, прочность которого распре-
распределена по закону Вейбулла, а напря-
напряжение распределено нормально
Точечная оценка среднего нормаль-
нормальной совокупности
Точечная оценка среднего нормаль-
нормальной совокупности
Оценка среднего нормальной сово-
совокупности
Оценка среднего нормальной сово-
совокупности
Оценка среднего нормальной сово-
совокупности
Интервальная оценка среднего нор-
нормальной совокупности по выбороч-
выборочному размаху
Интервальная оценка среднего нор-
нормальной совокупности по интер-
квартильной широте
Интервальная оценка среднего нор-
нормальной совокупности по среднему
абсолютному отклонению
Интервальная оценка среднего нор-
альной совокупности по медиане
Оценка среднеквадратического от-
отклонения нормальной совокупности
по выборочной дисперсии
790
Перечень математике™ статистических таблиц
Продолжение таблицы
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Стр.
112
113
114
114
115
116
118
119
119
120
122
124
124
125
126
127
Наименование
Значения 1/d
Значения коэффициента f(pi,P2)
Значения к% • (—10 ) для оптималь-
не " л не " но " с ценки а
она^ ен я Хг /Зг для оценки Огавы
Оценки а по подразмахам
Оценка а по двум статистикам
Значения it7
Значения квантилей распределен
ния размаха а; G)
Значения квантилей распределе-
распределения среднего абсолютного отклоне-
отклонения 771G)
о In - 1
Значения * / —^— для интерваль-
ной (двусторонней) оценки а
Коэффициенты z\ и Z2 кратчайших
доверительных интервалов
Значения функции z = f{y)
Значения функции g(z)
Значения функции z = f{h^y)
Значения функции t/j(z)
Значения k(h,j)
Область применения
Оценка среднеквадратического от-
отклонения нормальной совокупности
по выборочному размаху
Оценка среднеквадратического от-
отклонения нормальной совокупности
по шаблону
Оценка среднеквадратического от™
клонения нормальной совокупности
с помощью порядковых статистик
Оценка среднеквадратического от-
отклонения нормальной совокупности
с помощью порядковых статистик
Оценка среднеквадратического от-
отклонения нормальной совокупности
по размахам
Оценка среднеквадратического от-
отклонения нормальной совокупности
Квантили стандартного нормаль-
нормального распределения для вероятно-
вероятностей, используемых в раз л' ^ нь х
аппроксимациях
Оценка и проверка статист '^есК'Х
гипотез, основанных на при енен
размахов
Интервальная оценка среднеквадра-
среднеквадратического отклонения нормальной
совокупности
Интервальная оценка среднеквадра-
среднеквадратического отклонения нормальной
совокупности
Интервальная оценка среднеквадра-
среднеквадратического отклонения нормальной
совокупности
Оценка параметров усе^ енно не \ -
мального распределения
Оценка параметров усе^ енно не \ -
мального распределения
Оценка параметров в неполностью
определенных выборках
Оценка параметров в неполностью
определенных выборках
Оценка параметров нормального
распределения в цензурированных
выборках
Перечень математика-статистических таблиц
791
Продолжение таблицы
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
Стр.
128
129
130
138
141
142
143
148
149
150
153
163
167
168
170
Наименование
Коэффициенты х'(а:,7г,71) и
X (а, п, г)
Коэффициенты t;(a,n,r) и
(-1) -t"(a,n,r)
Коэффициенты к% и к[ для п = 10
Значения коэффициентов bi и Si
Значения коэффициентов кш и кв
Значения коэффициентов ca(d) и
c'a(d) для а = 0,90
Значения коэффициентов bfa(d) и
b'a(d) для а = 0,95
Зависимость параметра /3 распре-
распределения Вейбулла от коэффициен-
коэффициента вариации v = s/x
Значения аз,/3,6 и с, используемые
при оценке параметров распределе-
распределения Вейбулла
Значения G, /3 и Ь; для оценки па-
параметров распределения Вейбулла
Значения коэффициентов щ и q
Значения коэффициентов к\ и fe
Значения коэффициентов с'а и с^
Значения коэффициентов d'a и d^
Коэффициенты к'{е,а) и fc/;(e,a)
Область применения
Оценка параметров нормального
распределения в цензурированных
выборках
Оценка параметров нормального
распределения в цензурированных
выборках
Оценка параметров нормального
распределения в цензурированных
выборках с помощью порядковых
статистик
Оценка параметров экспоненциаль-
экспоненциального распределения с помощью по-
порядковых статистик
Интервальная оценка наработки на
отказ
Интервальная оценка интенсивно-
интенсивности отказов
Интервальная оценка интенсивно-
интенсивности отказов
Оценка параметров распределения
Вейбулла
Оценка параметров распределения
Вейбулла
Оценка параметров распределения
Вейбулла
Оценка параметров распределения
Вейбулла с помощью порядковых
статистик
Оценка параметров распределения
Вейбулла с помощью порядковых
статистик
Совместная интервальная оценка
параметров распределения Вейбул-
Вейбулла с помощью порядковых статис-
статистик
Совместная интервальная оценка
параметров распределения Вейбул-
Вейбулла с помощью порядковых статис-
статистик
Интервальная оценка наработки
компонента при заданной вероят-
вероятности безотказной работы
792
Перечень математике™ статистических таблиц
Продолжение таблицы
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
Стр.
173
196
198
199
200
201
215
217
219
220
222
224
231
232
233
233
Наименование
Значения г) = — -
; t(r,r)
Значения 1' = Fy 2m, 2n; a^ J для
а = 0,95
гл tot М
Значения —)=*-
л/п
Значения п для распределения
Вейбулла
Значения а (г, а)
Значения Ь(г, а)
Процентные точки статистик Dn и
Квантили распределения пш2
Квантили распределения %2
Квантили предельного распределе-
распределения статистики nQ2
Нижние критические точки стати™
стики Ватсона U2
Критические значения V^ (а) для
верхних процентных точек стати™
стики Купера
Значения коэффициентов ci моди-
модифицированного х -критерия нор-
нормальности для к = 3 -^ 15
Критические значения dkict) моди-
модифицированного %2-критерия нор-
нормальности
Критические значения статистики
пш2 для проверки нормальности
распределения
Критические значения статисти-
статистики Колмогорова—Смирнова, моди-
модифицированной для проверки нор-
нормальности распределения
Область применения
Оценка сокращения продолжитель-
продолжительности испытаний за счет цензуриро-
цензурирования испытываемой выборки
Прогнозирование средней наработ-
наработки до отказа в экспоненциальных
выборках
Определение объема выборки для
оценки среднего нормального рас-
распределения при неизвестной дис-
дисперсии
Определение объема выборки, необ-
необходимого для оценки среднего рас-
распределения Вейбулла
Планирование испытаний для оцен-
оценки интенсивности отказов с задан-
заданной точностью
Планирование испытаний для оцен-
оценки интенсивности отказов с задан-
заданной точностью
Проверка гипотезы нормальности
гипотетического распределения
Проверка гипотезы нормальности
гипотетического распределения
Проверка гипотезы согласия
Проверка гипотезы согласия
Проверка гипотезы согласия гипо-
гипотетического распределения с теоре-
теоретическим
Проверка гипотезы согласия гипо-
гипотетического распределения с теоре-
теоретическим
Проверка совпадения эмпирическо-
эмпирического распределения с нормальным
Проверка совпадения эмпирическо-
эмпирического распределения с нормальным
Проверки гипотезы нормальности
распределения
Проверка гипотезы нормальности
распределения
Перечень математика-статистических таблиц
793
Продолжение табл ць
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
Стр.
235
236
239
240
242
243
244
247
249
252
255
258
259
260
267
269
272
278
Наименование
Критические значения статистики
Фроцини Вп для проверки нори-
альности распределения
Коэффициенты an^j+i (xlO4) кри-
критерия Шапиро—У илка
Коэффициенты 77, j и е
Процентные точки критерия И7"(а)
Значения Ктп(а) для а = 0,05
Критические значения Ti(a) и
Т2(а)
Критические значения Мп(а) кри-
критерия нормальности Али—Чёрго—
Ревеса
Критические значения г (а) крите-
критерия Филлибена
Коэффициенты щ и Ь% для вычис-
вычисления статистик Ki, Ж~2, Кз
Критические точки критериев
Кг(а), К2(а) и К3(а)
Дисперсии статистик Оя
Критические значения di(a) и
d2{a) критерия Гири
Критические значения U\(ot) и
U2 (а) критерия Дэвида-Хартли-
Пирсона
Критические значения Т' (а) крите-
критерия Шпигельхальтера
Критические значения критерия
Д'Агостино
Значения коэффициентов 8 is. —
А
Критические значения а\ и п2 кри-
критерия Муроты—Такеучи на уровне
значимости а = 0,10
Сравнение критериев проверки
нормальности распределения слу-
случайных величин
Область применения
Проверка гипотезы нормальност
распределения
Проверка гипотезы нормальности
распределения
Аппроксимация критических точек
критерия Шапиро—"Уилка
Проверка гипотезы нормальности
распределения
Проверка гипотезы нормальности
распределения критерием Васичека
Проверка гипотезы нормальности
распределения критерием Хегази-
Грина
Проверка гипотезы нормальности
распределения
Проверка гипотезы нормальности
распределения
Проверка гипотезы нормальности
распределения
Проверка гипотезы нормальности
распределения
Проверка гипотезы нормальности
критерием Оя
Проверка гипотезы нормальности
критерием Гири
Проверка гипотезы о нормальности
распределения критерием Дэвида-
Хартли-Пирсона
Проверка гипотезы нормальности
распределения критерием Шпигель-
Шпигельхальтера
Проверка гипотезы нормальности
распределения
Аппроксимация распределения ко™
эффициента эксцесса нормального
распределения
Проверка гипотезы нормальности
распределения критерием Муроты—
Такеучи
Сравнение различных критериев
нормальности по мощности
794
Перечень математике™ статистических таблиц
Продолжение таблицы
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
Стр.
280
281
283
284
287
288
289
292
295
296
299
300
301
302
303
304
305
Наименование
Критические значения критерия
экспоненциальное™ We Шапиро™
Уилка
Критические значения критерия
экспоненциальное™ We0 Шапиро™
Уилка
Критические значения статистик
критериев согласия типа Колмого-
Колмогорова-Смирнова для проверки экс™
потенциальности распределения с
неизвестными параметрами
Процентные точки модифициро-
модифицированных критериев типа Колмогоро-
Колмогорова-Смирнова для проверки экспо-
ненциальности распределения
Критические значения статистики
W2
Критические значения Вп(а) кри-
критерия экспоненциальности Фроци-
ни
Критические значения K(z, га, а) и
K(zJm,a) корреляционного крите-
критерия экспоненциальности
Критические значения D(pt) стати-
статистики Кимбера-Мичела
Критические значения статистики
с = л/п(с — 1)
Граничные значения t\(a) и ?г(а)
критерия Холлендера-Прошана
Критические значен я Тг(а) кри-
критерия Кочара
Критические значения ci(ct) и сг(а)
критерия Эппса—Палли
Критические значения Мп(о) кри-
критерия Чёрго-Уэлча
Значения Р(ЬП ^ к)
Критические значения шп (а) стати-
статистики Шермана
Критические значения г]п(а) стати-
статистики Г]п
Критические значения ha (n) стати-
статистики Хартли
Область применения
Проверка гипотезы экспоненциаль-
экспоненциальности распределения критерием
Шапиро—Уилка
Проверка гипотезы экспоненциаль-
экспоненциальности распределения критерием
Шапиро—Уилка
Проверка гипотезы экспоненциаль-
экспоненциальности распределения критериями
типа Колмогорова-Смирнова
Проверка гипотезы экспоненциаль-
экспоненциальности распределения критериями
типа Колмогорова-Смирнова
Проверка гипотезы экспоненциаль-
экспоненциальности распределения критериями
типа Крамера-фон Мизеса-Смир-
нова по цензурированным выборкам
Проверка гипотезы экспоненциаль-
экспоненциальности критерием Фроцини
Проверка гипотезы экспоненциаль-
экспоненциальности корреляционным критерием
Проверка гипотезы экспоненциаль-
экспоненциальности критерием Кимбера-Мичела
Проверка гипотезы экспоненциаль-
экспоненциальности критерием Климко—Антла—
Радемакера—Рокетта
Проверка гипотезы экспоненци-
экспоненциальности критерием Холлендера-
Прошана
Проверка гипотезы экспоненц аль-
ности критерием Кочара
Проверка гипотезы экспоненц аль-
ности критерием Эппса—Палли
Проверка гипотезы экспоненциаль-
экспоненциальности критерием Чёрго-Уэлча
Проверка гипотезы экспоненциаль-
экспоненциальности критерием Бергмана
Проверка гипотезы экспоненциаль-
экспоненциальности критерием Шермана
Проверка гипотезы экспоненци-
экспоненциальности критерием наибольшего
интервала
Проверка гипотезы экспоненциаль-
экспоненциальности критерием Хартли
Перечень математика-статистических таблиц
795
Продолжение таблицы
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
Стр.
309
310
312
314
318
321
323
324
325
327
329
330
331
332
334
338
Наименование
Критические значения Ua стати-
статистики и
Критические значения G\(pt) и
G2{pt) статистики Гринвуда
Коэффициенты щ JiT-критерия со™
гласия Манн—Фертига—Шуера для
распределения Вейбулла
Критические значения Ка (г, п)
критерия Манн—Фертига—Шуера
Критические значения W\{a) и
И^(ск) критерия экспоненциально-
сти Лоулесса
Критические значения М\ (а) и
M2(ct) статистики Морана
Критические значения W\{a) и
W2 (а) критерия равномерности
Ченга-Спиринга
Критические значения J(a) крите-
критерия Саркади-Косика
Критические значения На(т,п)
статистики Дудевича—ван дер Мю-
лена
Критические значения Ti(a),
Ti(a), T2(ot) и Tj(a) критерия
равномерности Хегази-Грина
Критические значения Mi (a),
M2{pt) статистики Янга
Критические значения J9+, D~, D,
V критериев равномерности
Критические значения Вп(а) кри-
критерия Фроцини для проверки рав-
равномерности распределения
Критические значения Q(ot)
статистики Гринвуда—Кэсенберри—
Миллера для проверки равномер™
ности распределения
Критические значения Nk(cv)
критерия равномерности Неймана—
Бартона
Критические значения К (а) крите™
рия знаков
Область применения
Проверка гипотезы экспоненциаль-
ности критерием U
Проверка гипотезы экспоненциаль-
ности критерием Гринвуда
Проверка гипотезы согласия эмпи-
эмпирического распределения с распре-
распределением Вейбулла
Проверка гипотезы согласия эмпи-
эмпирического распределения с распре-
распределением Вейбулла
Проверка гипотезы экспоненциаль-
ности критерием Лоулесса
Проверка гипотезы равномерности
распределения критерием Морана
Проверка гипотезы равномерности
распределения критерием Ченга-
Спиринга
Проверка гипотезы равномерности
распределения критерием Саркади-
Косика
Проверка гипотезы равномерности
критерием Дудевича—ван дер Мю-
лена
Проверка гипотезы равномерности
распределения критерием Хегази—
Грина
Проверка гипотезы равномерности
распределения критерием Янга
Проверка гипотезы равномерности
критериями Колмогорова-Смирно-
Колмогорова-Смирнова
Проверка гипотезы равномерности
распределения критерием Фроцини
Проверка гипотезы равномерности
распределения критерием Гринву-
да-Кэсенберри-Миллера
Проверка гипотезы равномерности
распределения критерием Неймана—
Бартона
Проверка гипотезы симметрии эм-
эмпирического распределения крите-
критерием знаков
796
Перечень математике™ статистических таблиц
Продолжение таблицы
114
115
116
117
118
119
120
121
122
123
124
125
126
127
Стр.
339
346
358
370
391
393
395
396
398
400
403
404
406
409
Наименование
Критические значения Т+ (а) одно-
выборочного критерия Вилкоксона
Критические значения JB-критерия
Бооса
Оценки параметров j ш г] распреде-
распределения Su Джонсона
Значения квантилей уа = (ха — x)/s
нормированного распределения
Пирсона
Таблица квантилей распределения
Стьюдента t1
Критические значения модифици™
рованного критерия Стьюдента для
сравнения средних по двум выбор-
выборкам равного объема
Критические значения Nq (г, п)
для доверительной вероятности
а = 0,95
Значения г и No при п ^ 20
для двухступенчатого двухвыбо-
рочного критерия сравнения сред-
средних при доверительной вероятно-
вероятности а = 0,95
Критические значения Qa(k^n) мо-
модифицированного критерия Стью-
Стьюдента
Критические значения <?а(^,/)
„стьюдентизированного" размаха
Значения F^(l; kn — 2) для довери-
доверительной вероятности а = 0,95
Критические значения Та крите-
рия Тыоки
Критические значения rria,k*,v
„стьюдентизированного" максиму-
максимума
Множители g(ifc*,/,a) для кри-
критерия Стьюдента-Ньюмена-Кейл-
са при доверительной вероятности
а = 0,95
Область применения
Проверка гипотезы симметрии эм-
эмпирического распределения крите-
критерием Вилкоксона
Проверка гипотезы симметрии эм-
эмпирического распределения крите-
критерием Бооса
Аппроксимация эмпирического рас-
распределения кривой из семейства Su
Джонсона
Нахождение квантилей эмпиричес-
эмпирического распределения с помощью кри-
кривых распределения Пирсона
Проверка статистических гипотез
Сравнение средних значений двух
нормально распределенных выбо-
выборок модифицированным критерием
Стьюдента
Сравнение средних значений двух
нормально распределенных выборок
двухступенчатым критерием Волфа
Сравнение средних значений двух
нормально распределенных выборок
двухступенчатым критерием Волфа
Сравнение средних нескольких (> 2)
нормально распределенных выборок
равного объема
Сравнение средних нескольких (> 2)
нормально распределенных выборок
равного объема
Сравнение средних нескольких (> 2)
нормально распределенных выборок
равного объема критерием Полсона
Сравнение средних нескольких (> 2)
нормально распределенных выборок
равного объема методом прямого
сравнения (критерий Тьюки)
Сравнение средних нескольких (> 2)
нормально распределенных выборок
равного объема критерием „стью-
„стьюдентизированного" максимума
Сравнение средних нескольких (> 2)
нормально распределенных выборок
равного объема критерием Стью-
дента—Ньюмена—Кейлса
Перечень математика-статистических таблиц
797
Продолжение таблицы
128
129
130
131
132
133
134
135
136
137
138
139
Стр.
410
411
414
416
419
420
420
421
422
422
427
430
Наименование
Множители q(k*, /, с/) для крите-
критерия Дункана при доверительной ве-
вероятности а = 0,95
Критические значения К(п,к,а)
для критерия Линка—Уоллеса
при доверительной вероятности
а = 0,95
Критические значения F* (п, га) от-
отношения размахов
Критические значения К\(сх) и
К.2(ct) статистики Аризоно—Охты
для доверительной вероятности
а = 0,95
Критические значения ga(k,n) ста-
статистики Кохрана для доверитель-
доверительной вероятности а = 0,95
Критические значения На крите-
критерия Неймана-Пирсона для довери-
доверительной вероятности а = 0,95
Критические значения Ы^ крите-
критерия Неймана-Пирсона для довери-
доверительной вероятности а = 0,95
Критические значения са(п,к)
критерия Блисса-Кохрана-Тьюки
для доверительной вероятности
а = 0,95
Критические значения па(п^к)
критерия Хартли для доверитель-
доверительной вероятности а = 0,95
Критические значения Ка(п^к)
критерия Кэдуэлла-Лесли-Брауна
для доверительной вероятности
а = 0,95
Значения коэффициентов Ка(с)
Критические значения Da крите-
критерия Дэвида
Область применения
Сравнение средних нескольких (> 2)
нормально распределенных выборок
равного объема критерием Дункана
Сравнение средних нескольких (> 2)
нормально распределенных выборок
равного объема критерием Линка—
Уоллеса
Сравнение дисперсий двух нормаль-
нормальных выборок критерием отношения
размахов
Сравнение дисперсий двух нормаль-
нормально распределенных выборок крите-
критерием Аризоно-Охты
Сравнение дисперсий нескольких
(> 2) нормально распределенных
выборок равного объема критерием
Кохрана
Сравнение дисперсий нескольких
(> 2) нормально распределенных
выборок равного объема критерием
Неймана-Пирсона
Сравнение дисперсий нескольких
(> 2) нормально распределенных
выборок равного объема критерием
Неймана-Пирсона
Сравнение дисперсий нескольких
(> 2) нормально распределенных
выборок равного объема критерием
Блисса-Кохрана^Тькжи
Сравнение дисперсий нескольких
(> 2) нормально распределенных
выборок равного объема критерием
Хартли
Сравнение дисперсий нескольких
(> 2) нормально распределенных
выборок равного объема критерием
Кэдуэлла-Лесли-Брауна
Сравнение выборочной интенсивно-
интенсивности отказов (параметр экспоненци-
экспоненциального распределения) с заданным
значением
Сравнение параметров нескольких
(> 2) экспоненциальных распреде-
распределений
798
Перечень математике™ статистических таблиц
Продолжение таблицы
140
141
142
143
144
145
146
147
148
149
150
151
152
153
Стр.
431
432
440
455
457
459
461
462
465
466
470
472
473
478
Наименование
Критические значения La(n,k)
критерия отношения правдоподо-
правдоподобия для доверительной вероятности
а = 0,95
Критические значения са(к^п) ста-
статистики Чена
Функция распределения Wc(x)
Вальда
Критические значения U\(a) и
Ui (а) критерия Манна-Уитни
Критические значения статисти-
статистики Т знакового рангового критерия
Вилкоксона
Критические значения статистики
Фишера-Йэйтса-Терри-Гёфдинга
Критические значения Ха стати-
статистики Ван дер Вардена
Вспомогательные величины К кри-
критерия Ван дер Вардена
Критические значения Та крите-
критерия Хаги
Критические значения критерия
Крускала—"Уоллиса
Критические значения D^m(a)
критерия Неменьи
Критические значения Du,e(pL) кри-
критерия Вилкоксона-Вилкокс
Критические значения п(сч) крите-
критерия Кенуя
Критические значения Sa кри-
критерия Терпетры—Джонкхира для
к = 3
Область применения
Сравнение параметров нескольких
(> 2) экспоненциальных распреде-
распределений
Сравнение гарантийных наработок
нескольких экспоненциально рас-
распределенных выборок критерием
Чена
Последовательные методы проверки
гипотез о значениях параметров рас-
распределений критерием Вальда
Сравнение параметров сдвига двух
совокупностей критерием Манна-
Уитни
Сравнение параметров сдвига двух
совокупностей с неизвестным рас-
распределением критерием Вилкоксона
Сравнение параметров сдвига сово-
совокупностей с неизвестным распреде-
распределением критерием Фишера—Йэйтса—
Терри-Гёфдинга
Сравнение параметров сдвига двух
совокупностей с неизвестным рас-
распределением критерием Ван дер
Вардена
Вычисление статистики критерия
Ван дер Вардена (см. выше)
Сравнение параметров сдвига двух
совокупностей с неизвестным рас-
распределением критерием Хаги
Сравнение параметров нескольких
(> 2) совокупностей с неизвестным
распределением критерием Круска-
Крускала—Уоллеса
Сравнение параметров нескольких
(> 2) совокупностей с неизвестным
распределением критерием Неменьи
Сравнение параметров нескольких
(> 2) совокупностей с неизвестным
распределением критерием Вилкок-
Вилкоксона—Вил коке
Сравнение параметров нескольких
(> 2) совокупностей с неизвестным
распределением критерием Кенуя
Сравнение параметров нескольких
(> 2) совокупностей с неизвестным
распределением критерием Терп-
стры—Джонкхира
Перечень математика-статистических таблиц
799
Продолжение таблицы
154
155
156
157
158
159
160
161
162
163
164
165
166
Стр.
478
480
483
485
489
494
497
498
499
500
503
505
510
Наименование
Критические значения Sa крите-
критерия Терпстры-Джонкхира для вы-
выборок равного объема
Критические значения La для
к = 3 и доверительной вероятности
а = 0,95
Критические значения La(k,n)
критерия Пейджа для доверитель™
ной вероятности а = 0,95
Критические значения Sa(n^k)
критерия Фридмана—Кендалла—
Бэбингтона Смита
Критические значения Ка(к1п)
критерия Кендалла-Эренберга
для доверительной вероятности
а = 0,95
Критические значения Si(a) и
&(«) статистики Ансари-Бредли
Метки a,N{i) критерия Кейпена
Критические значения К\(а) и
.Кг (ck) статистики Кейпена
Метки U i критерия Клотца
~N
Критические значения L\(ot) и
L2 (а) критерия Клотца
Критические значения С\{а) и
С2 (а) критерия Сэвиджа
Критические значения Mi (а) и
M2(pt) статистики Муда
Критические значения Di(ct) и
1>2(«) масштабного критерия Ка-
мата
Область применения
Сравнение нескольких (> 2) со-
совокупностей по выборкам равно-
равного объема критерием Терпстры—
Джонкхира
Сравнение параметров нескольких
(> 2) совокупностей с неизвестным
распределением Ь-критерием
Сравнение параметров нескольких
(> 2) совокупностей с неизвестным
распределением по выборкам равно-
равного объема критерием Пейджа
Сравнение параметров нескольких
(> 2) совокупностей с неизвестным
распределением по выборкам рав-
равного объема критерием Фридмана—
Кендалла-Бэбингтона Смита
Сравнение параметров нескольких
(> 2) совокупностей с неизвестным
распределением по выборкам рав-
равного объема критерием Кендалла-
Эренберга
Сравнение параметров масштаба
двух совокупностей с неизвестным
распределением критерием Ансари-
Бредли
Сравнение параметров масштаба
двух совокупностей с неизвестным
распределением критерием Кейпена
Сравнение параметров масштаба
двух совокупностей с неизвестным
распределением критерием Кейпена
Сравнение параметров масштаба
двух совокупностей с неизвестным
распределением критерием Клотца
Сравнение параметров масштаба
двух совокупностей с неизвестным
распределением критерием Клотца
Сравнение параметров масштаба
двух совокупностей с неизвестным
распределением критерием Сэвиджа
Сравнение параметров масштаба
двух совокупностей с неизвестным
распределением критерием Муда
Сравнение параметров масштаба
двух совокупностей с неизвестным
распределением критерием Камата
800
Перечень математике™ статистических таблиц
Продолжение таблицы
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
Стр.
511
512
515
518
519
522
523
525
527
530
531
533
534
536
537
540
541
Наименование
Значения корректирующих коэф-
фициентов ifi@,95) и 1^@,95) кри-
критерия Камата
Критические значения Wmn(a) ста-
статистики Вуша-Винда для т = п
Критические значения La и Da для
fc = 3
Критические значения qa критерия
Дббе-Динника
Постоянные / и 1 критерия
Фостера-Стюарта
Критические значения (На) Н*-
критерия Хсу
Критические значения (Ga) G-кри-
G-критерия Хсу
Критические значения рангового
критерия обнаружения сдвига дис-
дисперсии
Критические значения JVi (a)
и N2{cx) сериального критерия
Вальда-Волфовитца
Критические значения R(a) крите-
критерия Рамачандрана—Ранганатана
Критические значения Na(ni, к) се-
сериального множественного крите-
критерия Шахнесси для к = 2 -f- 6
Критические значения na(li) кри-
терия случайности Олмстеда
Критические значения Ri(a) и
i?2 («) критерия числа серий знаков
первых разностей
Критические значения Д (а) и /г (а)
критерия инверсий
Критические значения г[^п(а) и
ri,n(a) критерия автокорреляции
Коэффициенты аппроксимации
критического значения критерия
Бартелса
Критические значения Ri(a) и
i?2 («) критерия кумулятивной сум™
мы
Область применения
Сравнение параметров масштаба
двух совокупностей с неизвестным
распределением критерием Камата
Сравнение параметров положения
и масштаба двух совокупностей с
неизвестным распределением ком-
комбинированным критерием Буша—
В инд а
Сравнение параметров положения
нескольких совокупностей с неиз-
неизвестным распределением
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы сдвига диспер-
дисперсии выборочного ряда в неизвестной
точке
Проверка гипотезы сдвига диспер-
дисперсии выборочного ряда в неизвестной
точке
Проверка гипотезы сдвига диспер-
дисперсии выборочного ряда в неизвестной
точке
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Перечень математика-статистических таблиц
801
Продолжение таблицы
184
185
186
187
188
189
190
191
192
193
194
195
196
197
Стр.
542
543
544
545
546
547
549
551
553
554
555
558
560
562
Наименование
Значения к для знаково-рангового
критерия случайности Холлина
Критические значения га знако-
во-рангового критерия случайно-
случайности Холлина
Критические значения К* крите-
критерия Шовене
Критические значения т(а) крите-
критерия Ирвина
Критические значения ri(a), Т2(а)
и тз(а) статистик Груббса
Критические значения т^а) крите-
критерия наибольшего абсолютного от-
отклонения
Критические значения т$(а) стати-
статистики Дэвида
Критические значения гю(ск),
гц(а), Г12 (а), г20(а), r2i(a) и
^22 (аг) статистик Диксона
Значения коэффициента к крите-
критерия Хоглина—Иглевича
Критические значения Lk{pt) и
L%(a) критерия Титьена-Мура
Критические значения Ek(cx) кри-
критерия Титьена—Мура
Критические значения т^ крите-
критерия Роснера
Критические значения С к (а) кри-
критерия Смоляка-Титаренко
Критические значения Sj (а) крите-
критерия Кимбера для выделения j верх-
н' х выбросов
Область применения
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы случайности вы-
выборочного ряда
Проверка гипотезы наличия выбро-
выброса в выборке, имеющей нормальное
распределение
Проверка гипотезы наличия вы-
выброса в выборке, имеющей нор-
нормальное распределение с известной
дисперсией
Проверка гипотезы наличия выбро-
выброса в выборке, имеющей нормальное
распределение
Проверка гипотезы наличия выбро-
выброса в выборке, имеющей нормальное
распределение
Проверка гипотезы наличия выбро-
выброса в выборке, имеющей нормальное
распределение
Проверка гипотезы наличия выбро-
выброса в выборке, имеющей нормальное
распределение
Проверка гипотезы наличия выбро-
выброса в выборке, имеющей нормальное
распределение
Проверка гипотезы наличия нес-
нескольких выбросов в выборке, имею-
имеющей нормальное распределение
Проверка гипотезы наличия нес-
нескольких выбросов в выборке, имею-
имеющей нормальное распределение
Проверка гипотезы наличия нес-
нескольких выбросов (количество вы-
выбросов априори неизвестно) в выбор-
выборке, имеющей нормальное распреде-
распределение
Проверка гипотезы наличия выбро-
выбросов в выборке, имеющей экспоненци-
экспоненциальное распределение
Проверка гипотезы наличия нес-
нескольких выбросов в выборке, име-
имеющей экспоненциальное распределе-
распределение
26 А. И. Кобзарь
802
Перечень математике™ статистических таблиц
Продолжение таблицы
198
199
200
201
202
203
204
205
206
207
Стр.
564
566
567
570
571
573
574
575
576
577
Наименование
Критические значения S* (а) кри-
терия Кимбера для выделения j
нижних выбросов
Критические значения G(a) и
Ri(a) критериев типа Груббса и
Диксона для выявления к верхних
выбросов в выборке, имеющей
распределение Вейбулла
Критические значения G* (а) и
R*(ot) критериев типа Груббса и
Диксона для выявления к нижних
выбросов в выборке, имеющей рас™
пределение Вейбулла
Множители а(п,а,/3) для постро-
построения односторонних толерантных
пределов в случае нормального
распределения (// неизвестно, а2
известно)
Множители а*(п,а,/3) для построе-
построения двусторонних толерантных ин-
тервалов в случае нормального
распределения (// неизвестно, а
известно)
Множители Ь(п,а,/3) для постро-
построения односторонних толерантных
пределов в случае нормального
распределения (/i известно, а2
неизвестно)
Множители Ь*(п, ск,/3) для постро-
построения двусторонних толерантных
интервалов в случае нормально-
нормального распределения (/i известно, а2
неизвестно)
Множители к(п,а, C) для постро-
построения односторонних толерантных
пределов в случае нормального
распределения (fi и а2 неизвестны)
Множители к*(п,а,/3) для построе-
построения двусторонних толерантных ин-
интервалов в случае нормального ра-
сределения (/i и а2 неизвестны)
Множители d(l,n,a,/3) для опреде-
определения двустороннего толерантного
интервала с использованием разма-
хов (при т = 1, без разбиения на
подвыборки)
Область применения
Проверка гипотезы налич я нес-
нескольких выбросов в выборке, име-
имеющей экспоненциальное распреде-
распределение
Проверка гипотезы наличия нес-
нескольких выбросов в выборке, имею-
имеющей распределение Вейбулла
Проверка гипотезы наличия нес-
нескольких выбросов в выборке, имею-
имеющей распределение Вейбулла
Вычисление толерантных пределов
нормально распределенной случай-
случайной величины (среднее неизвестно,
дисперсия известна)
Вычисление толерантных пределов
нормально распределенной случай-
случайной величины (среднее неизвестно,
дисперсия известна)
Вычисление толерантных пределов
нормально распределенной случай-
случайной величины (среднее известно,
дисперсия неизвестна)
Вычисление толерантных пределов
нормально распределенной случай-
случайной величины (среднее известно,
дисперсия неизвестна)
Вычисление толерантных пределов
нормально распределенной случай-
случайной величины (среднее и дисперсия
неизвестны)
Вычисление толерантных пределов
нормально распределенной случай-
случайной величины (среднее и дисперсия
неизвестны)
Вычисление толерантных интер-
интервалов нормально распределенной
случайной величины с помощью
размахов
Перечень математика-статистических таблиц
803
Продолжение таблицы
208
209
210
211
212
213
214
215
216
Стр.
578
580
581
582
584
585
588
597
602
Наименование
Множители cf(m,r/, а,/3) для опре-
определения двустороннего толерантно-
толерантного интервала с использованием раз-
махов
Минимальные объемы выборок
для построения непараметри-
непараметрических (двустороннего, nmin и
одностороннего, n^m) толерантных
интервалов, основанных на наи-
наибольших и наименьших выбороч-
выборочных значениях
Наименьшая доля /3 совокупности,
заключенная внутри непараметри-
непараметрического двустороннего толерантно-
толерантного интервала (между хт'1П и жтах в
выборке объема п)
Наименьшая доля /3 совокупности,
заключенная внутри непараметри-
непараметрического одностороннего толерант-
толерантного интервала (больше xmin или
меньше жтах в выборке объема п)
Коэффициенты г(т,п,к,а), для
которых вероятность того, что в
т или более из будущих к на-
наблюдений нормального распределе-
распределения величина х будет превышать
х — г (т, п, к, a) s, равна а
Коэффициенты Ь{т1 п,к,а), для
которых вероятность того, что в т
или более из будущих к наблюде-
наблюдений экспоненциального распреде-
распределения величина х будет превышать
п
Ь (га, п, к, a) Yl xij равна а
г=1
Значения с(к, п, т, а) для прогно-
прогнозирования при а = 0,95 нижней
границы средней наработки в к вы-
выборках объема п по т ранним мо-
моментам отказов
Масштабный коэффициент с и эф-
эффективное число степеней свобо-
свободы / для двухфакторного диспер-
дисперсионного анализа
Критические значения Та(т, к, fiji)
статистики Мака-Скиллингса
Область применения
Вычисление толерантных нте! -
валов нормально распределенной
случайной величины с помощью
размахов
Вычисление толерантных интерва-
интервалов для случайной величины с
неизвестным законом распределе-
распределения вероятностей
Вычисление доли совокупности с
неизвестным законом распреде-
распределения вероятностей, заключенной
между крайними значениями вы-
выборки
Вычисление доли совокупности с
неизвестным законом распределе-
распределения вероятностей, заключенной вне
крайних значений выборки
Прогнозирование значений будущих
наблюдений нормально распреде-
распределенной совокупности по результатам
наблюдения над выборкой
Прогнозирование значений будущих
наблюдений экспоненциально рас-
распределенной совокупности по ре-
результатам наблюдения над выбор-
выборкой
Прогнозирование результатов испы-
испытаний изделий на надежность
Двухфакторный дисперсионный
анализ с использованием размахов
Двухфакторный дисперсионный
анализ при неизвестном распре-
распределении данных и при наличии
пропущенных наблюдений
26*
804
Перечень математика-статистических таблиц
Продолжение таблицы
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
Стр.
608
612
614
615
616
618
620
622
623
629
631
635
646
649
659
661
662
664
Наименование
Критические значения га выбо-
выборочного коэффициента корреляции
для р = 0
Критические значения r*i?23...fe ко-
коэффициента множественной корре-
корреляции
Критические значения па крите-
критерия Кенуя
Критические значения Та крите-
рия Кокс-Стюарта
Критические значения Sa знаково-
знакового критерия корреляции Нелсона
Критические значения Si(a) и
5*2 (а) квадрантного критерия кор-
корреляции
Критические значения Qa угловой
статистики Олмстеда-Тыоки
Критические значения тпа крите-
критерия Шведа—Эйзенхарта
Критические значения Na крите-
критерия автокорреляции Кенуя
Критические значения Da крите-
критерия независимости Гёфдинга
Критические значения Sa крите-
критерия Ширахатэ
Критические значения Sw(<x) для
коэффициента конкордации W
Значения коэффициента К
Линеаризующие функциональные
преобразования (у* = а* + Ь*ж*)
Критические значения статистики
Дарбина-Ватеоыа
Критические значения Va крите-
критерия выбросов Эктона
Критические значения Ra крите-
критерия выбросов в регрессии Титьена-
Мура—Бекмана
Критические значения R^ крите-
критерия выбросов в регрессии Прескот-
та-Лунда
Область применения
Проверка гипотезы о наличии кор-
корреляции между случайными величи-
величинами
Проверка гипотезы о наличии мно-
множественной корреляции между слу-
случайными величинами
Оценка корреляции между пере-
переменными с помощью порядковых
статистик
Оценка корреляции между пере-
переменными с помощью порядковых
статистик
Оценка корреляции между случай-
случайными величинами
Оценка корреляции между случай-
случайными величинами
Оценка корреляции между случай-
случайными величинами
Оценка корреляции между случай-
случайными величинами
Оценка корреляции между случай-
случайными величинами
Проверка гипотезы о независимости
случайных величин
Проверка гипотезы о наличии
корреляции
Проверка гипотезы о наличии свя-
связей (согласованности) для несколь-
нескольких последовательностей
Выбор числа наблюдений для анали-
анализа таблиц сопряженности 2x2
Выбор типа кривой регрессии
Проверка гипотезы о наличии кор-
корреляции регрессионных остатков
Проверка гипотезы о наличии вы-
выброса в регрессионной моделили
Проверка гипотезы о наличии вы-
выброса в регрессионной модели
Проверка гипотезы о наличии вы-
выброса в регрессионной модели
Перечень математика-статистических таблиц
805
Окончание таблицы
235
236
237
238
239
240
241
242
243
244
245
246
247
Стр.
666
679
684
698
700
708
712
717
721
725
728
729
731
Наименование
Коэффициенты 11G,«, А) для по-
построения доверительной области
линейной регрессии
Значения коэффициента к(а,п)
Полиномы Чебышева Pj(i) и значе-
нияР-=;?р„2(;)
г=1
Коэффициенты для вычисления
границ регулирования контроль-
контрольных карт Шухарта
Значения коэффициентов Аг для
ж-карт Шухарта при неравных объ-
объемах контролируемых выборок
Коэффициенты ежи для ККНС
выборочного размаха
Относительная эффективность
различных контрольных карт
Матрица полного факторного экс-
эксперимента (ПФЭ) 23
Дробные реплики 2 ~~
Параметры ортогональных компо-
композиционных планов
Параметры униформ-ротатабель-
ных планов
Характеристики D-оптимального
плана
Параметры планов Хартли
Область применения
Построение доверительной области
для линейной регрессии
Определение объема испытаний для
получения заданной точности оцен-
оценки регрессии
Вычисление и анализ нелинейных
регрессионных моделей
Построение контрольных карт Шу-
Шухарта для регулирования технологи-
технологических процессов
Прстроение контрольных карт Шу-
Шухарта для регулирования техноло-
технологических процессов по выборкам
неравного объема
Построение ККНС для контроля
разброса случайной величины по
размаху
Выбор типа контрольной карты
для контроля технологического
процесса
Математическое планирование экс-
экстремального эксперимента
Математическое планирование экс™
тремального эксперимента
Математическое планирование экс-
экстремальных экспериментов
Математическое планирование экс-
экстремального эксперимента
Математическое планирование экс-
экстремального эксперимента
Математическое планирование экс-
экстремального эксперимента
Предметный указатель
Вейбулла распределение, оценка парамет-
ров 146
— интервальные оценки 165
— метод максимального правдоподобия
146
— метод моментов 147
— метод наименьших квадратов 150
— оценка а при известном /3 165
— оценка по квантилям 151
— оценка по порядковым статистикам 152
— планирование эксперимента по оценке
параметров 198
— совместная оценка параметров 166
— точечные оценки 146
Выбросы, критерии обнаружения 543
— для нормального распределения 544
— критерии для экспоненциального рас-
распределения 559
— критерий Бродского-Быцаня-Власенко
559
— критерий Диксона 548
— критерий для непрерывного распределе-
распределения (Дарлинга) 565
— критерий для распределения Вейбулла
564
— критерий Ирвина 544
— критерий Кимбера 561
— критерий наибольшего абсолютного от-
отклонения 547
— критерий Роснера 557
— критерий Смоляка-Титаренко 559
— критерий Титьена—Мура 553
— критерий Хоглина-Иглевича 550
— критерий Шовене 544
Гамма-распределение, оценка параметров
179
— /3 при известном а 179
— интервальная оценка /3 180
— оценка для малых выборок 180
— оценка максимального правдоподобия
179
— оценка методом моментов 180
— планирование эксперимента при оценке
параметра 201
— совместная оценка параметров 179
— точечные оценки 179
Гипергеометрическое распределение, оцен-
оценка параметров 191
Дискретные распределения вероятностей
84
— биномиальное 84
— геометрическое 92
— гипергеметрическое 92
— отрицательное биномиальное 90
— распределение Паскаля 91
— распределение Пуассона 88
Дисперсия (стандартное отклонение) нор-
нормального распределения 24
— интервальная оценка а по точечной
оценке 119
— интервальная оценка дисперсии а2 118
— интервальная оценка по среднему абсо-
абсолютному отклонению 118
— интервальная оценка стандартного от-
отклонения а по размаху 118
— оптимальная линейная оценка 113
— оценка Джини 115
— оценка Диксона 115
— оценка максимального правдоподобия
111, 123
— оценка Огавы 114
— оценка по выборочной дисперсии s2 111
— оценка по размаху 112
— оценка по среднему абсолютному откло-
отклонению 112
— оценка по шаблону 112
— оценки в неполных выборках 123
— точечная оценка 111
Интенсивность отказов с периодом прира-
приработки 195
Контрольные карты 697
Контрольные карты Шухарта 697
— карты с 703
— карты р 701
— карты s 699
— карты х и R 698
— карты индивидуальных значений и
скользящего размаха 703
Контрольные карты накопленных сумм
(ККНС) 704
— выборочных дисперсий 709
— выборочных размахов 707
— доли дефектных изделий 710
— среднего значения 705
Предметный указатель
807
Корреляционный анализ 606
— анализ по тренду 614
— квадрантный критерий 617
— корреляционное отношение 609
— коэффициент корреляции 606
— критерий Блума-Кифера-Розенблатта
623
— критерий Кенуя 614
— критерий Кенуя (автокорреляции) 622
— критерий Кокс-Стюарта 615
— критерий Олмстеда-Тьюки 620
— критерий Шахани 621
— критерий Шведа-Эйзенхарта (сериаль-
(сериальный) 621
— непараметрический корреляционный
анализ 614
— частная и множественная корреляции
611
Критерии согласия 204
— двухвыборочные критерии 227
— двухвыборочный критерий Колмогоро™
ва-Смирнова 227
— критерий х2 204
— критерий Андерсона 229
— критерий Андерсона™Дарлинга 220
— критерий Барнетта—Эйсена 211
— критерий Ватсона 222
— критерий Дарбина 224
— критерий Катценбайссера-Хакля 228
— критерий Колмогорова-Смирнова 227
— критерий Купера 223
— критерий Реньи 218
— критерий числа пустых интервалов 209
— одновыборочные критерии 204
Критерии нормальности 231
— критерий Али-Чёрго-Ревеса 244
— критерий асимметрии и эксцесса 268
— критерий Васичека 241
— критерий Гири 257
— критерий Д'Агостино 266
— критерий Дэвида—Хартли—Пирсона 258
— критерий Колмогорова-Смирнова 233
— критерий Ла Брека 248
— критерий Лина—Мудхолкара 263
— критерий Локка-Спурье 252
— критерий Мартинеса—Иглевича 265
— критерий Муроты-Такеучи 272
— критерий Оя 254
— критерий Саркади 261
— критерий Филлибена 245
— критерий Фроцини 235
— критерий Хегази-Грина 243
— критерий Шапиро-Уилка 238
— критерий Шпигельхальтера 260
— критерий, основанный на совокупности
малых выборок 273
— модифицированный %2-критерий 231
Критерии экспоненциальности 279
— корреляционный критерий 288
— критерий Бартлетта-Морана 294
— критерий Бергмана 301
— критерий Брейна-Шапиро 290
— критерий Дешпанде 316
— критерий Кимбера-Мичела 292
— критерий Климко-Антла-Радемакера-
Рокетта 294
— критерий Колмогорова-Смирнова 282
— критерий Кочара 298
— критерий Смирнова—Крамера—фон Ми-
зеса 286
— критерий Манна—Фертига—Шуера для
распределения Вейбулла 311
— критерий наибольшего интервала 304
— критерий показательных меток 305
— критерий типа Крамера-фон Мизеса 286
— критерий Фишера 293
— критерий Фроцини 288
— критерий Хартли 305
— критерий Холлендера—Прогнана 295
— критерий Шапиро-Уилка 279
— критерий Шермана 303
— критерий Эппса—Палли—"Чёрго—Уэлча
299
— ранговый критерий 306
— трансформация в равномерное распре-
распределение 308
Критерии равномерности распределения
319
— критерий Шермана 319
— критерий Гринвуда-Кэсенберри-Мил-
лера 332
— критерий Дудевича—ван дер Мюлена 324
— критерий Морана 320
— критерий Неймана—Бартона 333
— критерий Саркади-Косика 323
— критерий типа Колмогорова-Смирнова
330
— критерий Фроцини 331
— критерий Хегази—Грина 326
— критерий Ченга-Спирмена 322
— критерий Янга 328
Математическое планирование экспери-
эксперимента 715
— D-оптимальные планы 728
— линейные ортогональные планы 716
— метод крутого восхождения 732
— нелинейные планы второго порядка 722
— несимметричные планы 729
— ортогональные симметричные планы
724
— планы поиска оптимума 732
Предметный указатель
— ротатабельные планы 727
— симметричные планы 724
— симплексное планирование 734
Непараметрические критерии сдвига 452
— ^критерий 465
— Ь-критерий 480
— быстрый ранговый критерий 453
— критерий Левиса 479
— критерии сдвига для двух совокупностей
452
— критерии сдвига для нескольких (> 2)
совокупностей 466
— критерий Андерсона—Каннемана—Шэча
486
— критерий Ван дер Вардена 475
— критерий Вил коксона-Вил кокс 471
— критерий Даны Квейд 487
— критерий Кендалла—Эренберга 489
— критерий Кенуя 452
— критерий Краузе 481
— критерий Крускала—Уоллиса 466
— критерий Манна-Уитни-Вилкокеона
454
— критерий Мостеллера 464
— критерий Неменьи 469
— критерий Пейджа 482
— критерий Розенбаума 464
— критерий Фишера—Йэйтса—Терри—Гёф-
динга 459
— критерий Фишера-Терри-Йэйтса-Гёф™
динга 473
— критерий Фридмена-Кендалла-Бэбинг-
тона Смита 484
— критерий Хаги 464
— критерий Хеттманспергера 476
— критерий Ходжеса-Лемана-Оена 490
— медианный критерий 462
Непараметрические критерии масштаба
492
— квартальный критерий 501
— критерии масштаба для двух совокупно™
стей 492
— критерий Ансари-Бредли 492
— критерий Буша—Винда 511
— критерий Камата 509
— критерий Кейпена 496
— критерий Клотца 499
— критерий Краута—Линерта 508
— критерий масштаба для нескольких со™
вокупностей (> 2) 514
— критерий Муда 504
— критерий Сижела—Тьюки 495
— критерий Сукхатме 505
— критерий Сэвиджа 502
— критерий Сэндвика—Оллсона 507
Непрерывные распределения вероятно-
вероятностей 24
— Х2"неЦентРальное 80
— ^-нецентральное 81
— ^-распределение (Фишера) 56
— t-нецентральное 79
— ^-распределение (Стьюдента) 51
— бета-распределение 39
— Вейбулла 37
— гамма-распределение 38
— композиция распределений „нагрузка-
напряжение" 74
— Коши 72
— логарифмически нормальное 35
— логистическое 73
— Максвелла 68
— нормальное 24
— нормальное с линейным дрейфом сред-
среднего 64
— нормальное с линейным дрейфом сред-
неквадратического отклонения 65
— Парето 73
— равномерное 34
— распределение х (Пирсона) 44
— распределение модуля случайной вели-
величины, распределенной нормально 62
— распределение экстремального значения
70
— Рэлея 68
— треугольное 71
— усеченное нормальное 61
— экспоненциальное 36
Оценки при неизвестном законе распреде-
распределения вероятностей 192
— оценка Кантелли 192
— оценка Мей дел я 192
— оценка "Чебышева 192
— оценки Нётера 193
Параметр распределения 96
Подбор кривых распределения по экспери-
экспериментальным данным 352
— кривые Джонсона 352
— кривые Пирсона 368
— метод вкладов 385
— разложение теоретических распределе-
распределений 384
Последовательный анализ Вальда 438
— биномиальное распределение 449
— нормальное распределение 439
— экспоненциальное распределение 447
Ранговая корреляция 624
— коэффициент конкордации Кендалла-
Бэбингтона Смита 634
Предметный указатель
809
— коэффициент конкордации Шукени™
Фроли 636
— коэффициент корреляции Кендалла 624
— коэффициент корреляции Спирмена 626
— критерий Ван дер Вардена 633
— критерий Фишера-Йэйтса 632
— критерий Ширахатэ 630
— точечно-бисериальная корреляция 638
Регрессионный анализ 648
— анализ регрессионных остатков 658
— анализ уравнения регрессии 655
— выбросы в регрессии 660
— доверительные области и толерантные
границы регрессии 665
— линейный регрессионный анализ 649
— медианный метод Брауна-Муда 653
— метод Бартлетта—Кенуя 653
— метод Керрича 652
— метод наименьших квадратов 649, 655
— метод наименьших модулей 692
— метод однозначной аппроксимации, ме-
тод обратных разделенных разностей
694, 696
— метод последней точки 694
— метод Тейла 654
— метод условно-относительных разностей
696
— множественная регрессия 680
— нелинейная регрессия 681
— оценка коэффициентов регрессии 649
— оценка адекватности 655
— оценка наименьших квадратов 649
— оценка Тейла 654
— специальные методы сглаживания 691
— сравнение линейных регрессий 672
— статистический анализ коэффициентов
регрессии 655
Симметричность распределения, крите-
критерии оценки 336
— знаковый критерий 337
— критерий Антилла—Керстинга—Цуккини
340
— критерий Бооса 345
— критерий Бхатачарья—Гаствирта—Райта
342
— критерий Вилкоксона 339
— критерий Гупты 348
— критерий Кенуя 336
— критерий Смирнова 337
— критерий Финча 334
— критерий Фрезера 350
Сопряженность признаков, оценка таблиц
сопряженности 639
— 6?-критерий Вулфа 644
— коэффициент контингенции 641
— критерий Ле Роя 645
— критерий Мак-Нимара 643
— критерий Фишера 641
— оценка связей в таблицах г х с 646
— оценка связи в таблицах 2x2 642
Среднее нормального распределения,
сравнение средних 389
— ^-критерий 396
— дисперсионный критерий 399
— критерий „стьюдентизированного" раз-
размаха 399
— критерий Волфа 395
— критерий Дункана 408
— критерий Липка-Уоллеса 408
— критерий Полсона 402
— критерий Стьюдента—Ньюмена—Кейлса
407
— критерий Тькжи 403
— критерий Уолша 394
— критерий Шеффе 406
— модифицированный критерий Стьюден-
та 392
— парный ?-критерий 393
— сравнение средних двух совокупностей
389
— сравнение средних нескольких (> 2) со-
совокупностей 397
— сравнение средних при известных дис-
дисперсиях 389
— сравнение средних при неизвестных
неравных дисперсиях 391
— сравнение средних при неизвестных рав-
равных дисперсиях 390
Сравнение дисперсий нормально распреде-
распределенных совокупностей 412
— критерий „стьюдентизированного" раз-
размаха 415
— критерий Аризоно-Охты 415
— критерий Бартлетта 417
— критерий Блисса-Кохрана-Тьюки 421
— критерий Кохрана 418
— критерий Кэдуэлла-Лесли-Брауна 422
— критерий Неймана^Пирсона 419
— критерий отношения размахов 414
— критерий Романовского 413
— критерий Самиуддина 423
— критерий Фишера 412
— критерий Хартли 421
— сравнение дисперсий двух совокупно-
совокупностей 412
— сравнение нескольких (> 2) совокупно-
совокупностей 416
Сравнение параметров экспоненциальных
совокупностостей 424
— критерий Дэвида 429
810
Предметный указатель
— критерий максимального правдоподо-
правдоподобия 430
— критерий Нагарсенкера 431
— критерий Сингха 433
— критерий Фишера 424
— критерий Чена 432
— пуссоновский критерий 426
— сравнение параметров двух совокупно-
совокупностей 424
— сравнение параметров нескольких (> 2)
совокупностей 429
— сравнение с эталоном 426
Сравнение параметров биномиальных со™
вокупностей 435
— сравнение параметров двух совокупно-
совокупностей 435
— сравнение параметров нескольких (> 2)
совокупностей 437
— сравнение с заданным значением 436
Толерантные пределы 569
— для нормальных совокупностей 569
— ц и а2 неизвестны 569
— /i известно, а2 неизвестно 572
— известны /i и а2 569
— непараметрические пределы 580
— пределы в задачах испытаний на надёж-
надёжность 587
— пределы для будущих наблюдений 583
— пределы для выборочных дисперсий 579
— пределы Холла—Прейри 583
— пределы, основанные на размахе 577
Тренд и случайность, критерии оценки 517
— критерий Аббе-Линника 517
— критерий автокорреляции 536
— критерий Бартелса 540
— критерий Вальда-Волфовитца 526
— критерий знаков первых разностей 533
— критерий инверсий 535
— критерий Кокс-Стюарта 520
— критерий кумулятивной суммы 541
— критерий Олмстеда 532
— критерий Рамачандрана-Ранганатана
530
— критерий ранговой корреляции 539
— критерий Фостера-Стюарта 519
— критерий Холлина (знаково-ранговый)
542
— критерий Хсу 522
— критерий Шахнесси 530
— ранговый критерий оценки сдвига в дис-
дисперсии 524
— сериальный критерий 526
Экспоненциальное распределение, оценка
параметров 134
— двухстадийная оценка 135
— интервальная оценка параметра 141
— оптимальная линейная оценка 135
— оценка максимального правдоподобия
134
— оценка Огавы 137
— оценка по одной порядковой статистике
136
— оценка Эпштейна 119
— планирование эксперимента по оценке
параметра 200
— точечная оценка 134
Именной указатель
Аббе (Abbe) 517
Али (А1у) 244
Андерсон (Anderson) 213, 220, 229, 486
Ансари (Ansari) 492
Анскомб (Anscomb) 89
Антилл (Antille) 340
Антл (Antle) 294
Аризоно (Arizono) 415
Ароян (Arolan) 47
Байн (Bain) 317
Барнетт (Barnett) 211
Бартелс (Bartels) 540
Бартлетт (Bartlett) 294, 417, 652
Бартон (Barton) 333
Бекман (Beckman) 662
Бергман (Bergman) 301
Бернулли (Bernulli) 84
Блисс (Bliss) 421
Блум (Blum) 623
Бокс (Box) 727, 732
Боос (Boos) 345
Боукер (Bowker) 576
Браун (Brown) 422, 653
Браунли (Browlee) 669
Бредли (Bradley) 492
Брейн (Brain) 290
Бродский 559
Буш (Bush) 511
Бхапкар (Bhapkar) 514
Бхатачарья (Bhatacharya) 342
Быцань 559
Вальд (Wald) 438, 526, 539
Ван дер Варден (Van der Varden) 460, 475,
633
Васичек (Vasicek) 241, 324
Ватсон (Watson) 213, 222, 659
Вейбулл (Weibull) 36, 37, 146, 198
Вилкокс (Wilcox) 471
Вилкоксон (Wilcoxon) 339, 454, 471
Вилсон (Wilson) 45, 263
Винд (Wieand) 511
Власенко 559
Волф (Wolfe) 395
Волфовитц (Wolfowitz) 526, 539
Вонг (Wang) 53
Воркинг (Working) 670
Вулф (Woolf) 644
Гаек (Hajek) 465
Гаствирт (Gastwirh) 342
Гёфдинг (Hoeffding) 459, 473, 628
Гири (Geary) 257
Голдштейн (Goldstein) 45
Грин (Green) 243, 326
Гринвуд (Greenwood) 309, 332
Груббс (Grabbs) 545, 564
Гупта (Gupta) 348
Д'Агостино (D'Agostino) 266
Давенпорт (Davenport) 467, 485
Дарбин (Durbin) 224, 627, 659
Дарлинг (Darling) 213, 220, 565
Даусон (Dawson) 53
Даутон (Dawton) 115, 266
Дешпанде (Deshpande) 316, 514
Джини (Gini) 115, 213
Джонсон (Johnson) 107, 352
Джонкхир (Jonckheere) 477
Диксон (Dixon) 100, 115, 131, 548
Дудевич (Dudewicz) 324
Дункан (Duncan) 408
Дэвид (David) 258, 429
Дюфор (Dufor) 514
Закс (Sachs) 185
Мглевич (Iglewicz) 265, 550
Иман (Iman) 456, 467, 485, 627
Ирвин (Irwin) 544
Йэйтс (Yates) 459, 473, 632
Камат (Kamat) 509
Каннеман (Kanneman) 486
Кантелли (Cantelli) 192
Картер (Carter) 59
Катценбайссер (Katzenbeisser) 228
Квейд (Quade) 488
Кейлс (Keuls) 407
Кейпен (Capon) 496
Кендалл (Kendall) 484, 489, 535, 624
Кенуй (Kenuai) 101, 336, 452, 614, 622, 652
Керрич (Kerrich) 652
Керстинг (Kersting) 340
Кёхлер (КоесЫег) 52
812
Именной указатель
Кимбел (Kimball) 319
Кимбер (Kimber) 292, 561
Кифер (Kiefer) 623, 728
Климко (Klimko) 294
Клотц (Klotz) 499
Кокс Д. (Сох D.) 520, 616
Кокс К. (Сох С.) 391
Колмогоров 213, 214, 225, 234, 330
Коно (Копо) 730
Косик (Kosik) 323
Кохран (Cochran) 304, 391, 418
Кочар (Kochar) 298
Коши (Cauchy) 72
Крамер (Cramer) 213, 216, 286
Краузе (Crouse) 481
Краут (Krauth) 508
Крускал (Kruskal) 466
Крючков (Kruchkoff) 669, 670
Купер (Kulper) 213, 223, 330
Кэдуэлл (Cadwell) 41, 422
Кэмп (Camp) 186
Кэсенберри (Quesenberry) 332
Ла Брек (La Brecque) 248
Ле Рой (Le Roy) 645
Левис (Lewis) 479
Леман (Lehmann) 103, 490, 603
Лесли (Leslie) 422
Лин (Lin) 263
Линерт (Lienert) 508
Линк (Link) 408
Линник 517
Локк (Locke) 252
Локтев 54
Лоулесс (Lawless) 317
Лунд (Lund) 663, 680
Люнг (Ljung) 514
Мак (Mack) 601, 603
Мак-Нимар (McNemar) 643
Максвелл (Maxwell) 68
Манн Н. (Mann N.) 166, 311
Манн X. (Mann H.) 454
Мартинес (Martinez) 265
Мейдель (Meidel) 192
Мизес, фон (von Mises) 213, 216, 286
Миллер (Miller) 332
Мичел (Michael) 292
Моленар (Molenar) 85, 185
Моран (Moran) 294, 320
Мостеллер (Mosteller) 464, 479
Муд (Mood) 504, 653
Мудхолкар (Mudholkar) 263
Мур (Moore) 553, 662
Мурота (Murota) 272
Мюлен, ван дер (van der Meulen) 324
Нагарсенкер (Nagarsenker) 431
Нейман (Neyman) 261, 333, 419
Нелсон (Nelson) 616
Неменьи (Nemenyi) 469
Нётер (Noether) 193
Ньюмен (Newman) 407
Огава (Ogawa) 101, 114, 137
Олмстед (Olmsted) 532, 620
Олссон (Olsson) 507
Охта (Ohta) 415
Оя (Oja) 254
Палли (Pulley) 299
Парето (Pareto) 73
Паскаль (Pascal) 48, 91
Пейдж (Page) 482
Пейзер (Peizer) 47, 53, 58
Пирсон (Pearson) 44, 80, 101, 258, 368, 419,
647
Полсон (Paulson) 42, 57, 186, 402
Пратт (Pratt) 47, 53, 58, 186
Прейри (Prairie) 583
Прескотт (Prescott) 663, 680
Принтис (Prentice) 598
Прошан (Proshan) 295
Пуассон (Poisson) 48, 86, 88
Радемакер (Rademaker) 294
Райт (Wright) 342
Рамачандран (Ramachandran) 530
Ранганатан (Ranganathan) 530
Ревес (Revesz) 244
Реньи (Renyl) 218
Розенбаум (Rosenbaum) 464
Розенблатт (Rosenblatt) 623
Рокетт (Rockette) 294
Романовский 207, 413
Роснер (Rosner) 557
Рэлей (Rayleigh) 68
Самиуддин (Samiuddln) 423
Саркади (Sarkadi) 261, 274, 323
Сатервайт (Satterwaite) 391
Сен (Sen) 490
Сижел (Siegel) 495
Сингх (Singh) 433
Скиллингс (Skillings) 602
Смирнов 213, 214, 216, 225, 234, 275, 282,
330, 337
Смит Б. (Babington Smith) 484, 634
Смоляк 559
Спендли (Spendley) 734
Спиринг (Spiring) 322
Спирмен (Spierman) 626, 630
Именной указатель
813
Спурье (Spurrier) 252
Стьюдент (Student) 51, 79, 392, 407
Стюарт (Stuart) 519, 520, 615
Сукхатме (Sukhatme) 505
Сэвидж (Savage) 502
Сэндвик (Sandvik) 507
Такеучи (Takeuchi) 272
Тейл (Theil) 654, 657
Терпстра (Terpstra) 477
Терри (Terry) 459, 473
Тику (Tiku) 82
Титаренко 559
Титенко 186
Титьен (Tietjen) 553, 662
Тькжи (Tukey) 101, 403, 495, 620
Уайз (Wise) 42
Уилк (Wilk) 238, 274, 279
Уилкс (Wiles) 580
Уилсон (Wilson) 732
Уитни (Whitney) 454
Уоллес (Wallace) 408
Уоллис (Wallis) 466
Уолш (Walsh) 103, 394
Уэлч (Welch) 299, 392
Фертиг (Fertig) 166, 311
Филлибен (Filliben) 245, 288
Финч (Finch) 344
Фишер (Fisher) 40, 52, 56, 81, 293, 412, 424,
459, 473, 632, 641
Фостер (Foster) 519
Франчиа (Francia) 238
Фрезер (Frazer) 350
Фридмен (Friedman) 484, 488
Фроли (Frawley) 636
Фроцини (Frozini) 213, 235, 288, 331
Хага (Haga) 464
Хакль (Hackl) 228
Хальд (Hald) 669
Хан (Hahn) 587
Хантер (Hunter) 727
Хартер (Harter) 136
Хартли (Hartley) 258, 305, 421, 730
Хегази (Hegazy) 243, 326
Хейнс (Halnes) 58
Хекст (Hext) 734
Хеттманспергер (Hettmannsperger) 476
Хилферти (Hilferty) 45
Химсуорт (HImsworth) 734
Хоглин (Hoaglin) 550
Ходжес (Hodges) 103, 490
Холл (Hall) 184, 583
Холлендер (Hollander) 295
Холлин (Hollin) 542
Хотеллинг (Hotelling) 670
Хсу (Hsu) 522
Хэлден (Haldane) 46
Цуккини (Zucchini) 340
Чебышев 192, 682
Чен (Chen) 432
Ченг (Cheng) 322
Чёрго (Csorgo) 244, 299
Чупров 647
Шапиро (Shapiro) 238, 274, 279, 290
Шахани (Shahani) 621
Шахнесси (Shaughnessy) 530
Швед (Shved) 621
Шерман (Sherman) 303, 319
Шеффе (Scheffe) 406
Шидак (SIdak) 465
Ширахатэ (Shlrahate) 630
Шовене (Chauvenet) 544
Шпигельхальтер (Spiegelhalter) 260
Шуер (Shuer) 311
Шукени (Schucany) 636
Шухарт (Shewhart) 697
Шэч (Schach) 486
Эйзенхарт (Elsenhardt) 621, 669
Эйсен (Eisen) 211
Эктон (Acton) 661
Энгельгардт (Engelhardt) 317
Эппс (Epps) 299
Эпштейн (Epstein) 136
Эренберг (Ehrenberg) 489
Янг (Young) 328
Научное издание
КОБЗАРЬ Александр Иванович
ПРИКЛАДНАЯ МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.
ДЛЯ ИНЖЕНЕРОВ И НАУЧНЫХ РАБОТНИКОВ
Редактор B.C. Аролович
Оригинал-макет: А.А. Пярнпуу
Оформление переплета: А.Ю. Алехина, Л.А. Гусева
Подписано в печать 05.05.06. Формат 70x100/16. Бумага офсетная.
Печать офсетная. Усл. печ. л. 65,79. Уч.-изд. л. 72,4. Тираж 1500 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ОАО «Московская типография № 6»
115088, г. Москва, Ж-88, ул. Южнопортовая, 24
ISBN 5-9221-0707-0
9 785922 107075м