АКАДЕМИЯ ФЕДЕРАЛЬНОЙ СЛУЖБЫ ОХРАНЫ
РОССИЙСКОЙ ФЕДЕРАЦИИ
В. М. Радыгин, С. И. Федорова
Тригонометрические ряды
и интеграл Фурье
Пособие
Орел 2010
. - м	омам
-: й 6 Я А Я
*отв«л Г
•3W-A4L-
00117013
УДК 517.443
ББК 22.161.1
Р159
Радыгин, В. М.
Р159 Тригонометрические ряды и интеграл Фурье : пособие / В. М. Рады-
гин, С. И. Федорова. — Орел : Академия ФСО России, 2010. - 70 с.
Пособие написано в соответствии с программами по дисциплинам "Математи-
ка" и "Математический анализ" для подготовки курсантов по специальностям
210404-210406, 230102, 090106. Помимо теоретического материала оно содержит
большое число примеров, которые призваны оказать помощь курсантам в овладении
навыками в разложении функций в тригонометрические ряды. Значительное место в
пособии отводится гармоническому анализу и спектральному представлению наи-
более типичных сигналов.
Обсуждено и рекомендовано к изданию на заседании кафедры № 4, протокол № 7
от 10 июня 2009 г.
УДК 517.443
ББК 22.161.1
© Академия ФСО России, 2010
СОДЕРЖАНИЕ
§ 1.	Периодические функции и некоторые их свойства..........4
§ 2.	Гармонические колебания................................6
§ 3.	Сложение гармонических колебаний. Тригонометрический ряд.9
§ 4.	Ортогональность функций тригонометрической системы....10
§ 5.	Коэффициенты Фурье. Ряд Фурье..........................13
§ 6.	Достаточные условия разложения функции в ряд Фурье.
Теорема Дирихле.............................................17
§ 7.	Ряд Фурье для функции, заданной на промежутке длины Т..22
§ 8.	Ряды Фурье четных и нечетных функций .................26
Г Т
§ 9.	Ряды Фурье функции, заданной на промежутке 0; — ......31
2
§ 10.	Ряд Фурье в комплексной форме........................36
§11.	Гармонический анализ периодических функций............40
§ 12.	Формула Парсеваля-Ляпунова............................47
§ 13.	Обобщенный ряд Фурье...............................  49
§ 14.	Интеграл Фурье. Теорема Фурье........................52
§ 15.	Интеграл Фурье четных и нечетных функций.............57
§ 16.	Комплексная форма интеграла Фурье....................59
§ 17.	Преобразования Фурье.................................65
БИБЛИОГРАФИЧЕСКИЙ СПИСОК...................................69
§ 1.	ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
И НЕКОТОРЫЕ ИХ СВОЙСТВА
Многие важные процессы, с которыми приходится сталкивать-
ся при изучении различных явлений в физике и технике совершают-
ся циклически, т. е. воспроизводятся в прежнем виде через опреде-
ленный промежуток времени Т, называемый периодом рассматри-
ваемого процесса.
Периодическими, в частности, являются многочисленные ко-
лебательные процессы, происходящие в электрических и радиотех-
нических цепях. Различные величины, характеризующие такие про-
цессы, представляют собой периодические функции времени t. Так,
сигналы, с которыми приходится иметь дело в современной теории
связи, как правило, являются изменяющимися во времени токами
или напряжениями и весьма часто представляют собой периодиче-
ские функции времени.
Напомним, что функция /(х) называется периодической, если
существует действительное число Т тН), такое, что при любом х из
области определения данной функции числа х-Т и х + Т принад-
лежат этой области и выполняется неравенство
/(ЛТ) = /(Л) = ./'(Л- + Т).	(I)
Число Т называют периодом функции. По определению, для
того чтобы получить представление о функции /(х), достаточно
изучить ее на любом интервале длины Т. За такой интервал чаще
всего принимают один из двух интервалов (0; Т)
или
а - 2Т а — Т 0 а
Рис.1
4
Примерами периодических функций могут служить тригоно-
метрические функции j = sinx, j = cosx с периодом Т = 2л,
j = tgx, у = ctgx с периодом л. Периодической функцией будет и
функция у = с (с - константа), ее периодом является любое дей-
ствительное число Т.
В дальнейшем будут широко использованы следующие свой-
ства периодических функций:
1.	Если Т - период функции /(х), то любое число кТ, где к -
целое число, также является периодом функции.
2.	Сумма, разность, произведение и частное двух периодиче-
ских функций периода Т есть периодическая функция периода Т.
3.	Сумма сходящегося ряда функций периода Т также есть
функция периода Т.
4.	Если функция /(х) имеет период Т, то функция
Т
ф(х) = f (сох) имеет период —.
со
Действительно,
= /(сох + Т) - f (сох) = ф(х).
5.	Интеграл от периодической функции /(х) по любому про-
межутку [а; ос + 77], длина которого равна периоду Т, имеет одно и
то же постоянное значение:
а+Т	Т
\f{x)dx = J/(x)c/x.
а	О
(2)
Геометрически равенство (2) выражает равенство площадей
заштрихованных криволинейных трапеций с основаниями [0; Г] и
ос; ос + г] (рис. 2).
5
Рис. 2
§ 2.	ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Простейший периодический процесс - гармоническое колеба-
ние. Опишем этот процесс математически.
Предположим, что точка z движется по окружности радиуса А
с постоянной угловой скоростью со (рис. 3).
Рис. 3
Ее проекции zx и zv на
ось Ох и Оу соответственно
будут совершать при этом ко-
лебательные движения. Най-
дем законы движения точек
Z И Z у .
Пусть в начальный мо-
мент времени t = 0 точка z
занимает положение zq, ее ра-
диус-вектор составляет с осью
Ох угол (pg.
По прошествии времени t радиус-вектор точки z составит с
осью Ох угол со/1 + (pg • Абсцисса точки z изменяется по закону
х = zx = A cos(co^ + фо),
а ордината - по закону
у = z у = A sin(co/ + Фо) •
(3)
(4)
6
Колебания, описываемые функциями (3) и (4), называются
гармони ч еским г i.
Итак, при равномерном движении точки z по окружности ра-
диуса А ее проекции zx и zy на оси координат совершают гармо-
нические колебания. При этом А называют амплитудой, (pg - на-
чальной фазой, а со - угловой частотой гармонического колебания.
Период гармонического колебания равен промежутку времени
со
за который точка z, двигаясь по окружности, возвратится вновь в
свое исходное положение zq.
В соответствии с этим угловая частота гармонического коле-
бания
2п
(0 =—
Т
равна тому углу, на который поворачивается радиус-вектор Oz дви-
жущейся точки z за одну секунду.
Любую из гармоник (3) и (4) всегда можно записать в виде
a cos coz + b sin со/,
где а и b - некоторые постоянные числа.
Например,
A sin (со/ + (pg) — A sin cpg cos со/ + A cos фд sin со/ =
- a cos со/ + b sin со/,
где а = A sin (pg, b = Л cos (pg.
Справедливо и обратное утверждение: всякая функция вида
a cos со/ + b sin со/
7
/2	2
представляет собой гармонику с амплитудой А = уа +Ь , угловой
частотой (pg, определяемой из условий а = Язтфф, b = Лсозфф:
a cos coz + /?sin со/ = Л5ш(со/ + фо).
При описании закона движения точки z по окружности вместо
двух действительных функций (3) и (4) удобно рассматривать одну
комплексную функцию действительного переменного:
^(cos(co/ + 9o) + /sin(cD/ + 9o))=	(5)
Эту функцию называют комплексной гармоникой.
Действительные гармоники (3) и (4), выражающие законы из-
менения координат вектора (9z, можно представить в виде действи-
тельной и мнимой части функции (5):
Л cos (со/ + фо) = Re(y4ez(wz+<*>°)),
Л8т(сп/ + фо)=
Комплексную гармонику (5) можно представить в виде
Z =	= Ае1™,
где А = Ае1(?° - так называемая комплексная амплитуда гармоники.
Комплексная амплитуда А геометрически изображается ра-
диусом-вектором Ozq начального положения zq движущейся точки
z по окружности. Этот вектор вращается с постоянной угловой ско-
ростью (0.
8
§ 3.	СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИИ.
ТРИГОНОМЕТРИЧЕСКИЙ РЯД
Задача исследования периодических процессов, описывающих
работу современной аппаратуры связи, значительно облегчается, ес-
ли эти процессы представимы в виде наложения гармонических ко-
лебаний, а величины, их характеризующие, в виде суммы гармоник.
Рассмотрим следующую последовательность гармоник:
= А\ sin(cox + cp| )= <7} coscox + Z>i sin сох,
у2 — ^2 sin(2cox + <р2)= cos 2сох + ^2 s^n 2cox,
yn = An sin(/?cox + <pw) - an cos ncox + bn sin /7 cox.
(6)
Независимая переменная здесь обозначена через х. Нулевая
гармоника - постоянная А. Она же обозначена и через —— для еди-
2
нообразия приводимых в дальнейшем формул. Последующие гар-
моники имеют частоты, кратные со: со, 2со, ..., исо.
Периоды этих гармоник:
5
2л
n(i)
2л
Очевидно, что число Т = — будет общим периодом для всех
со
гармоник.
Сумма этих гармоник
Aq + ^Afc sin (Acox + <р£) = —— +	а к cos Acox + sin k(dx (7)
к=]	2	А=1
9
есть, согласно свойству периодических функций (3), периодическая
.	2л
функция с периодом Т = —.
со
Замечено, что суммы гармоник приводят к самым разнообраз-
ным периодическим функциям, отнюдь не похожим на гармоники.
Естественно возникает вопрос: нельзя ли произвольную перио-
дическую функцию представить в виде суммы гармоник или, как
говорят, разложить на гармоники? Оказалось, что этого, как прави-
ло, сделать нельзя, если ограничиться конечной суммой гармоник.
Если же привлечь к рассмотрению ряды, членами которых являются
гармоники, то практически любую периодическую функцию можно
разложить на гармоники.
Итак, рассмотрим функциональный ряд
ОО	OQ
Aq + ^Ап sin(«COX + Фн) = — + ^r//?COS/?01Y + ^Sin/7(D.r, (8)
гг=1	2	п=1
составленный из гармоник (6).
Этот ряд называется тригонометрическим рядом, а числа
6/q,с/] ,6/2носят название коэффициентов триго-
нометрического ряда. Если этот ряд сходится, то его сумма S(x) бу-
дет периодической функцией периода Т =
2л
со
§ 4.	ОРТОГОНАЛЬНОСТЬ ФУНКЦИЙ
ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ
В основании любого тригонометрического ряда
— + 2L ап cos п^х + sin «сох
2	/7 = 1
лежит тригонометрическая система функций
10
—, cos cor, sin cox, cos 2a)x, sin 2cox,..., cos ий)х, sin и nix...
(9)
Эта система обладает одним замечательным свойством, кото-
рое служит стержнем всей теории тригонометрических рядов.
Прежде чем сформулировать это свойство, введем:
Определение. Система функций Ф1(х),ф2(х),...,фл(х)... назы-
вается ортогональной на отрезке [«;/?], если
Ь
/фл (х)фш(х)с/х =
а
О прии /и; п,т = 1, 2, 3...
с > 0 при/? = /и; п = 1, 2, 3...
(10)
Убедиться в том, что тригонометрическая система функций ор-
тогональна, нетрудно. Для этого надо показать, что для функций
системы выполняются условия (10).
В самом деле
2
j — cosncnxt/x =
-----sin /7 (lit
2тссо
— sin исо— = — sin ил = 0,
ий) 2 ий)
f — sinncoxcZx — 0,
так как подынтегральная функция нечетна.
Применяя известные формулы тригонометрии:
cos а • cos р = - (cos(oc - р) + cos(a + р)),
cos а • sin Р = - (sin(a - р) + sin(a + Р)),
sin ос • sin p = — (cos(ot - P) - cos(ot + P)),
получим при натуральных к и I
f cos kaxx cos Iwxdx
— jcos(£ — /)сох<7х +
fcos(A: + l)(j)xdx — О
2
f cos Acox sin laxxdx
T k*l
2
js in(Zc - l)oxxdx + —
2
Jsin(£ + l)(jixdx — 0,
T
2
2
f sin kcax sin ktoxdx =
k*l
— jcos(£ - l)(tixdx — jcos(£ + /)сох<Ух = 0.
Кроме того,
г 2
I cos и(охах =
L
2
j.
2
2
j(l + cos 2n($x)dx =
2
2	1 2r
sin nmxdx = — J(1 - cos 2hcdx)<7x =
12
Заметим, что в силу периодичности подынтегральных функций
полученные равенства справедливы для любого другого отрезка
длины Т.
Следовательно, тригонометрическая система функций ортого-
нальна на любом отрезке длины Т.
§ 5.	КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
Пусть тригонометрический ряд правильно сходится на всей
числовой оси к периодической функции /(х) с периодом Г, т. е.
оо
-----1- 2, ап cos исох + bn sin яшг = /(х).
2	/7-1

Выразим коэффициенты ряда а$,ап,Ьп через сумму ряда /(х).
Для нахождения коэффициента проинтегрируем в пределах
от----до — равенство (11):
OQ
2	2	2
Jcos nttixdx + bn Jsin ясохс/х = [f (x)<7x.
T	T	T
В силу ортогональности тригонометрической системы все сла-
гаемые, стоящие под знаком суммы, равны нулю, поэтому
13
Учитывая, что
Та^
---, получаем
^0=-
(12)
Определим коэффициент ап (п - целое положительное чис-
ло). Для этого умножим обе части равенства (И) на costar и про-
интегрируем полученное равенство по отрезку
[ f(x) cos k(f>xdx = f
00
^0	7	,7 V4
— cos kttixdx +
[cos «arc cos koxxdx +
2
+ bn [sin лсох cos kwxdx.
> £ I
у?
В силу ортогональности тригонометрической системы все ин-
тегралы в правой части равны нулю, кроме одного - при коэффици-
енте который равен —. Будем иметь
f (x) cos kdixdx = Ofc
2
или, заменив к на и,
14
2
J f (x) cos nayxdx.
T
(13)
2
Для отыскания коэффициента bn обе части равенства (11) ум-
ножим на sin/xox и проинтегрируем в пределах от-до —:
2	2
J/(х)sinkcaxdx - J — sinktiixdx + ^an (cosrztDxsinkayxdx +
T	_T 2	n=X _T
2	2	2
T
2
+ bn (sin «coxsin AclhyA.
T
Все интегралы в правой части равны нулю, кроме интеграла,
Т
являющегося коэффициентом при Ьп, равного —:
J f (х) sin kitixdx — b^ ~ или

2
Т
2
(/(х) sin natxdx.
Т
(14)
Определение. Коэффициентами Фурье функции f (х) называ-
ются числа ао,апфп, вычисленные по формулам
15
а0
2
\f(x)dx; ап
2
Т
2
J/(x) cos n(dxdx; bn
T
2
T
2
{/(x)sin nfjyxdx,
T
где T =
2л
co
Тригонометрический ряд, коэффициенты которого являются
коэффициентами Фурье для функции /’(х), называется рядом Фурье
для функции /(х).
Замечание. В силу известного свойства интеграла от периоди-
ческой функции /(х) при вычислении коэффициентов Фурье вме-
сто промежутка
можно брать любой другой промежуток
длины Т:
2 а+Т
«0 = — |/(х)с/х J
ос+Г
f / (х) cos noxxdx;
а
2
Т
а+Т
f/(x)sin ntnxdx.
а
Пусть функция /(х) такова, что для нее можно найти коэффи-
циенты Фурье.
Тригонометрический ряд
оо
cos п сох + bn sin п сох,
(15)
16
где a§,an,bn - коэффициенты Фурье функции /(х), будет рядом
Фурье для этой функции независимо от того, сходится он или рас-
ходится, и независимо от того, совпадает ли его сумма 5’(х) с функ-
цией / (х), для которой он составлен, или нет.
§ 6. ДОСТАТОЧНЫЕ УСЛОВИЯ РАЗЛОЖЕНИЯ
ФУНКЦИИ В РЯД ФУРЬЕ. ТЕОРЕМА ДИРИХЛЕ
Какие же требования надо предъявлять к функции /(х), чтобы
составленный для нее ряд Фурье сходился и его сумма 5(х) совпа-
дала с/(х)?
Для этого, очевидно, достаточно предположить, чтобы функ-
ция /(х) была интегрируема на отрезке
. Ведь для любой
интегрируемой, в частности, непрерывной или кусочно-
непрерывной функции /(х) можно вычислить коэффициенты Фурье
ац,ап,Ьп и формально записать соответствующий ей ряд Фурье:
f (х) ~ —— + 22 ап cos п сох + bn sin п сох.
2	И = 1
(16)
Однако нельзя утверждать, что формально записанный ряд
Фурье для функции /(х) сходится. Он может расходиться для всех
х. Более того, даже в случае сходимости ряда его сумма £(х) может
не совпадать с / (х).
В этой связи возникает вопрос о том, какие условия следует
наложить на функцию /(х), чтобы составленный для нее ряд Фурье,
во-первых, сходился и, во-вторых, его сумма S(x) совпадала с /(х).
Только в этом случае можно считать решенной задачу о разложении
функции /(х) в ряд Фурье и в соотношении (16) символ соответ-
ствия заменить знаком равенства:
./«=?
оо
+ 22 ап cos сох + sin и шх.
Л? = 1
(17)
17
На поставленный вопрос отвечает теорема Дирихле, которую
ниже приводим без доказательства. Но прежде дадим определение.
Определение. Функция /(х) кусочно-монотонна на отрезке
[«; />], если этот отрезок можно разбить конечным числом точек
XI, Х2,..., хн-| на интервалы (а; х0, (х^ х2; b) так, что на
каждом из интервалов функция монотонна, т. е. либо невозрастаю-
щая, либо неубывающая.
Из определения следует, что если функция /’(х) монотонна и
ограничена на отрезке [о; b], то она может иметь только точки раз-
рыва первого рода.
Теорема Дирихле. Пусть периодическая функция /(х) с пе-
риодом Т на каком-либо отрезке длины Т монотонная и ограничен-
ная. Тогда ряд Фурье, составленный для функции / (х), сходится на
всей числовой прямой, причем его сумма S(x) равна функции /(х)
во всех точках непрерывности этой функции
5(л) = Дх)
и равна среднему арифметическому пределов слева и справа во вся-
кой точке х разрыва функции
S(.v) =
Дх - 0) + Дх + 0)
Замечание. Условия монотонности и ограниченности называ-
ются условиями Дирихле.
Пример 1. Осциллограмма напряжения, зарегистрирован-
ная на экране осциллографа, представляет периодическую последо-
вательность импульсов
г/(х) = <
0 при - 2 < х < 0
1 при 0 < х < 2
с периодом Т = 4.
Разложить в ряд Фурье функцию z/(x).
18
Решение. Условия теоремы Дирихле для функции w(x) вы-
полнены. Период функции г/(х) Т = 4, поэтому со = — = —- = —.
Вычислим коэффициенты Фурье:
«О =
\и(х)с1х = — ]м(х)б/х =
пл
-2
пл ,
 cos — хах =
1 . пл
—sin —
пл 2
---(sin 71/7-0) = 0 прии = 1, 2, 3...
пл
ш(х) sin nuxxdx —
плх ,	1
---dx = —
2	2
пл
Г1 . пл . I
IJ • sin — xdx =------cos плх
О 2	пл
=-----(cos пл — I) =
о
при п четном,
пл
при п нечетном.
Следовательно, в точках непрерывности
71	. Зя .571
-x + sin—x + sin —
2	2	2
и т J
1 гр
2
п
5
О
Т
2
п
2
О
о
О
19
В точках разрыва х = 2п при п = 0, ± 1, ± 2... сумма ряда равна
полусумме левого и правого пределов:
S(2n) =
2
На рисунке 4 изображены графики частичных сумм получен-
ного ряда:
2
2 . Зя
—sin —
С увеличением числа входящих в них гармоник суммы S|(x),
(х), *?з(х) начинают все точнее и точнее воспроизводить осцил-
лограмму импульсного напряжения.
Пример 2. Разложить в ряд Фурье функцию
1,если 1
с периодом Т - 2.
20
Решение. Построим график функции (рис. 5).
/(*)
Рис. 5
Заметим, что данная функция на промежутке [0; 2] удовлетво-
ряет условиям теоремы Дирихле. Период функции Т = 2, поэтому
2л
0) = — = л.
Т
Найдем коэффициенты Фурье:
2	2	1		1	3
а0 = ~ J~ ff (x)dx = [xdx + jl-dx = - + l = -,
1 0	20	0	1	2	2
2T	22	1
an =— J/(x) cos ntnxdx = — J/(x) cos mixdx = Jx cos ллхт/х +
T 0	20	0
ИЛ
COS/7HX
JO
— sin mix
rm
0
(cos Л2Л — 1) =
при n четном
при n нечетном,
т. e. U2n 0,	1 —
21
2Т	22	1
bn = — J/(х) sin ntaxdx = — J j (x) sin nnxdx = x • sin mtxdx +
T 0	20	0
---COSHflX +
mt
Sin /7ЛХ
— cos лях
mt
ПТ1
Следовательно, во всех точках непрерывности функции /‘(х)
имеем разложение
3	00
4	Л?=1
cos(2h - 1)лх +
— sin лях.
Ttn
В точках разрыва х = 2£, к = 0, ± 1, ± 2... сумма ряда равна по-
лусумме левого и правого пределов
S(2k) =
f(2k - 0) + f(2k + 0) _ 0 + 1
§ 7. РЯД ФУРЬЕ ДЛЯ ФУНКЦИИ, ЗАДАННОЙ
НА ПРОМЕЖУТКЕ ДЛИНЫ Т
В приложениях часто возникает задача о разложении в триго-
нометрический ряд функции /(х), заданной лишь на некотором
промежутке длины Т, например [oc;a + 7j (рис. 6), и удовлетво-
ряющей на этом промежутке условиям Дирихле. О периодичности
/(х) здесь, следовательно, не может быть и речи.
22
--•
а-Т
О
ос + Т
Рис. 6
Поступим следующим образом. Будем рассматривать функцию
j(x) как "участок" некоторой периодической функции ср(х) с пе-
риодом Т, которая в промежутке [а; а + Т) совпадает с функцией

<р(х + Г) = <р(х), если хе
— со*
ф(х) = /(х), если хе [а; а + Г].
(18)
Такую функцию ф(х) естественно называть периодическим
продолжением функции /(х) на всю ось Ох (рис. 7).
Рис. 7
Вычислим коэффициенты Фурье ф(х):
tf0=- |ф(х)<7х,
а
23
а+Т
j ср(х) cos ntsyxdx,
01
2
T
a+T
jcp(x) sin nwxdx.
a
Запишем ряд Фурье для функции ср(х):
со
СЮ	1
—— + £_,ап cos п сох + bn sin и сох.
2	п=\
Этот ряд во всех точках непрерывности промежутка (ос; ос + Т)
имеет суммой значение функции /(х). Посмотрим теперь, чему
равна сумма ряда на концах промежутка [ос; ос + 7]. Здесь возможны
два случая:
1)	/(ос) = /(ос + Т) - в этом случае точки а + кТ
(к = 0, ±1, ±2...) будут точками непрерывности функции ср(/), а по-
этому сумма ряда в этих точках будет /(ос) или / (a + Т);
2) /(ос) Ф /(а + Т) - в этом случае точки а + кТ окажутся точ-
ками разрыва 1-го рода, а поэтому сумма ряда в этих точках будет
l(/(a) + /(a + T)).
Таким образом, ряд Фурье функции /(х), заданной на проме-
жутке длины Т, есть ряд Фурье для функции, полученной из /(х)
периодическим продолжением на всю числовую ось.
Пример 3. Разложить в ряд Фурье функцию
/« = 3 1--
если хе [0; 2].
Решение. График функции /(х) вместе с ее периодическим
продолжением изображен на рисунке 8.
24
На промежутке [0; 2] функция /(х) ограничена и монотонна.
Длину промежутка, на котором задана функция /(х), примем за пе-
2л
риод Т, т. е. Т = 2, тогда частота со = — = л.
Найдем коэффициенты Фурье ац,ап,Ьп:
cos rmxdx = 0,
— sin rmxdx =----
2)	rm
COSMTEX
Sin /77LXJq =
3
rm
Отсюда в промежутке (0; 2) имеем разложение
25
На концах промежутка [О; 2] ряд Фурье сходится к среднему
арифметическому пределов функции слева и справа:
5(0) = 5(2) =
/(0 + 0) + /(2-0) _ 3 + 0 _ 3
2	2 ~ 2
§ 8. РЯДЫ ФУРЬЕ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
Функция /(х), определенная на симметричном относительно
начала координат промежутке [-а; а|, называется четной, если
/(~х) = /(х), Vx G
[— а; а ,
и нечетной, если
f (—х) = -/’(х), Vx е [— сг, а .
(19)
График четной функции симметричен относительно оси Оу
(рис. 9), а график нечетной функции симметричен относительно на-
чала координат (рис. 10).
Рис. 9
Рис. 10
Нетрудно убедиться в том, что произведение двух четных и
двух нечетных функций есть функция четная, а произведение двух
26
функций, из которых одна четная, а другая нечетная, есть функция
нечетная.
Кроме того, если /(х) интегрируема в промежутке [-о; а], то
а
2 |/(х)б/х
если f(x) четная,
О
О, если /(х) нечетная.
Пусть функция /(х) является четной на промежутке
2’ 2
и удовлетворяет в нем условиям Дирихле.
Так как cos мох - функция четная, a sin max - нечетная, то
произведение /(х) cos «сох будет функцией четной, а /(x)sinHCOx -
нечетной.
На основании предыдущего замечания для коэффициентов
Фурье четной функции /(х) будем иметь формулы
2	4 2
J/(x)dx = - J/(x)t/x;
T 1 о
ап - — j/ (х) cos исохб/х =
j f (х) cos noxxdx;
О
п
2
— J/(x)sinHcav6/x = 0.
Соответственно этому разложение в ряд Фурье четной функ-
ции /(х) в точках ее непрерывности имеет вид
27
оо
ДД = ~^ + Е ап COS MDX .
п=\
В случае нечетной функции /(х) получим:
«О = — f f(x)dx - 0;
п
f (x) cos nttixdx = 0;
T
Т
п
j f (х) sin ntisxdx = — J/(х) sin ntoxdx
и поэтому для нечетной функции /(х) в точках непрерывности бу-
дем иметь
оо
f W = X bn sin «сох.
/7 — 1
Итак, как говорят, четная функция раскладывается в ряд Фурье
"по косинусам", а нечетная - "по синусам".
Пример 4. Разложить в ряд Фурье функцию
ДД = 1
1, если хе (-2; 0),
-1, если хе [0; 2).
Решение. График функции изображен на рисунке 11.
28
Рис. 1 1
Функция f(x) кусочно-монотонна, ограничена на промежутке
(-2; 2) и является нечетной.
2л 71
Примем Т = 4, поэтому со = — = —. Найдем коэффициенты
Фурье функции /(х). В силу четности функции f(x) получим:
^0 Q @ п 0 ’
Л71
при п четном,
при п нечетном .
Таким образом, при хе (-2; 0)и(0; 2) будет
.71	1.3л
sin—x + -sin—
2	3	2
1 . 5л
-sin — х
5	2
В точке х = 0 сумма ряда Фурье равна 0 и не совпадает со зна-
чением функции /(х) в этой точке.
2
Пример 5. Разложить в ряд Фурье функцию у~х ,
хе [-1; 1].
Решение. График функции изображен на рисунке 12.
29
Принимая Т = 2 (длину промежутка, на которой задана функ-
ция), найдем коэффициенты Фурье
«О
2	1 2
j f (%) cos nisxxdx = 2 Jxz
T	О
cos mixdx =
sin mix +
mi
2x
cos mix -
sin mix
bn = 0, так как f(x) - четная функция.
Следовательно, внутри промежутка (—1; 1) имеем разложение
cos их +—cos 2лх + — cos 3 лх +...
4	9
Ввиду того что /(-!) = /(1), полученное разложение справед-
ливо и на концах промежутка.
30
§ 9. РЯДЫ ФУРЬЕ ФУНКЦИИ, ЗАДАННОЙ
НА ПРОМЕЖУТКЕ 0;-
Пусть функция /(х) задана на промежутке 0; — и удовле-
творяет на нем условиям Дирихле. При помощи какой-либо функ-
ции <?(х), не нарушающей условий Дирихле, "продолжим" функцию
/(х) на промежуток---; 0 (рис. 13).
В результате получим функцию
q(x), если хе--------;0
(р(х) =
f (х), если хе 0; —
2
определенную на промежутке длины Т (рис. 13) и удовлетворяю-
щую там условиям Дирихле.
Ряд Фурье функции <р(х) на отрезке 0;
во всех внутренних
точках непрерывности этой функции будет сходиться к заданной
функции /(х).
31
Поскольку существует бесконечное множество продолжений
д(х) для функции /(х) на промежуток
то и рядов Фурье
для функции /(х), заданной на промежутке 0;
можно полу-
чить бесконечно много.
На практике чаще всего используют четное (рис. 14) или не-
четное (рис. 15) продолжение.
Рис. 14
Рис. 15
Ряд Фурье для четного продолжения функции /(х) будет со-
держать только косинусы. Но так как в промежутке
четное
продолжение совпадает с функцией /(х), то во всех точках непре-
рывности промежутка
будем иметь разложение ,/(х) в ряд
Фурье только по косинусам
«0
/(*) =
оо
+	COS И сох.
/1=1
32
Если же функцию f(x), определенную в промежутке
продолжить нечетным образом на промежуток
то рассуж-
дая аналогично, можно получить ее разложение в ряд Фурье по си-
нусам
сю
/(х) = bn sin исох,
И = 1
справедливое во всех точках непрерывности внутри промежутка
Пример 6. Функцию /(х) =---------, заданную в промежутке
0; л], разложить в ряд Фурье по косинусам.
Решение. График функции f (х) вместе с ее периодическим
продолжением изображен на рисунке 16.
Жирной линией обозначен график функции /(х), а тонкой -
график ее четного периодического продолжения с периодом 2л.
Функция /(х) монотонна и непрерывна в промежутке [0; я], следо-
вательно, удовлетворяет условиям Дирихле. Учитывая, что
2л 2л ,
О) = — = — = 1
Т 2л
, вычислим коэффициенты Фурье:
33
т
= “ \f\x)dx - J
О

J f (x) cos nwxdx = — J
0	Ko
cos nxdx ~
cos nx
при n четном,
при n нечетном,
bn —0.
0
Таким образом, разложение функции f(x) на отрезке [0; п
имеет вид
Л -X
л
4
Ъх +
25
cos5x + ...
2
Здесь учтено, что периодическое продолжение функции /(х)
является непрерывной на всей числовой оси функцией. Поэтому ряд
Фурье /(х) на концах промежутка [0; л] в точках х-0 и х = л,
сходится к значению функции /(х) в соответствующих точках.
л — х
пр и м е р 7. Функцию f (х) =----, заданную в промежутке
[0; л], разложить в ряд Фурье по синусам.
Решение. График функции /(х) вместе с ее нечетным пе-
риодическим продолжением изображен на рисунке 17. Жирной ли-
нией обозначен график самой функции /(х).
34
Рис. 17
Как и в предыдущем примере, /(х) на промежутке [0; л] удов-
летворяет условиям Дирихле, а периодическое продолжение имеет
гр >-р	2л 2л
период 7 = 2л. Тогда со = — = — = 1.
Найдем коэффициенты Фурье:
п
= — j/(x) sin nuxxdx — ~f
Т О
sin nxdx =
О
— cos пх----— sin пх
"	л2
О ”
Запишем разложение функции f (х) в ряд Фурье по синусам
sin 2х
sin3x
которое имеет место во всех внутренних точках промежутка [0; л].
Выясним, будет ли справедливо это разложение на концах
промежутка [О; л].
Точка х = л является точкой непрерывности периодического
продолжения, поэтому 5(л) = /(л). В точке х = 0 периодическое
продолжение терпит разрыв, поэтому сумма ряда находится как по-
35
лусумма левого и правого пределов функций в этой точке. Отсюда
5(0) = 0, что не совпадает со значением f (0).
Итак, найденное разложение функции /(х) в ряд Фурье по си-
нусам верно для всех точек промежутка (0; л .
Одну и ту же функцию f(x) =-----, заданную на промежутке
0; л], мы представили и рядом Фурье по косинусам, и рядом Фурье
по синусам.
§ 10. РЯД ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ
Пусть функция f(x) в промежутке
удовлетворяет
условиям Дирихле. Тогда в точках непрерывности этого промежутка
справедливо разложение
/ (х) = — + 22 ап cos + bn s*n n<jXx ’
2
где ап
2
J f (х) cos naxxdx
5
п
j/(x)sin ntitxdx
По формулам Эйлера
cos исох
—in(Ax
in(f)x
36
1 i moir -zTzgix |	1 I in(Ax . —in(AK
smn(Ax =—e -e = — -e + e
2Г	1 2v
Подставив эти выражения для coshCDx и sin/7 сох в (17),
получим
«О
оо
ШОХ
—inox
in (АХ
—inox
_"0
со
in ОХ
-1П(АХ
(20)
п
п
п
п
Введем обозначения
(21)
Тогда разложение (17) можно записать в виде
оо
/ / ,х .	. V ЭПОХ
/(х) — cq +
Л — 1
оо
/7=—оо
(22)
Правая часть этого равенства называется комплексной формой
ряда Фурье для функции f (х), а коэффициенты сп (п = 0, ± 1, ±2...),
вычисляемые по формулам (21), называются комплексными коэф-
фициентами Фурье для функции / (х).
Очевидно, что коэффициенты являются комплексно-
сопряженными коэффициентам сп:
Для коэффициентов сц, сп, с_п можно получить интегральные
представления.
37
Действительно,
с0 =
J/(x)t7x
n ~
j/(x) cos nttixdx — i j/(x)sin/?0)хб/х =
Г f (x)(cos n($x — i sin n($x)dx =
~z7?cox
“n
—n ~
n
J f (x) cos nwxdx 4- i
\f (x) sin z?G)xc/x —
2	1 2
\f (x)(cos «cox + i sin n(f)x)dx = — \f (x)ein(i)xdx
Эти формулы можно объединить в одну формулу
L
1 2
сп=- \f(x)e~m(,ixdx, (И = о,+1,±2,±3...),	(23)
1 JL
7
38
в которой п принимает все целочисленные значения (положитель-
ные, отрицательные и нулевое).
П р и м е р 8. Разложить функцию
/(V) =
-1, если - л < х < О,
1, если0 <х <п
с периодом Т - 2л в ряд Фурье в комплексной форме.
Решение. Функция удовлетворяет условиям Дирихле
(рис. 18).
Рис. 18
Учитывая, что Т = 2тг, со = 1 согласно формулы (23), найдем
комплексные коэффициенты Фурье
39
inn
- inn
inn
—inn
2nni
nni
—(1 — cos ил) =
nni
nm
Следовательно
oo
inx
711
Это разложение справедливо для всех х, кроме х = пк, где
§ 11. ГАРМОНИЧЕСКИМ АНАЛИЗ ПЕРИОДИЧЕСКИХ
ФУНКЦИЙ
Большинство периодических функций, встречающихся при
исследовании периодических процессов, особенно в теории связи,
таковы, что их можно представить в виде суммы тригонометриче-
ского ряда
„ 00
+ У
(24)
Членами тригонометрического ряда являются гармоники
cos «сох + bn sin ждх = Ап sin(//cox +	)
fl	fl-	fl-	  с г
с амплитудами А
2	2л
п , угловыми частотами со - —
4л
2/77Г
Пв) =------
начальными фазами (рл, определяемыми из
условии
п -Sin<pH =
П COS (pw
40
В соответствии с этим, разложение (24) можно записать в виде
оо
/'(х) = Aq + Ап sin (//сох 4- <р/7).
п=1
(25)
Физический смысл равенства (25) состоит в том, что периоди-
ческая функция /’(х), быть может довольно сложная по своей при-
роде, оказалась представленной в виде суммы бесконечного числа
более простых гармонических колебаний.
В этой связи представление периодической функции /(х) в
виде суммы тригонометрического ряда (24) или ряда (25) называется
гармоническим анализом периодической функции
Постоянная составляющая, или "нулевая гармоника",
Т
= -у- = 7 \fO)dx
2	1
т
2
является средним значением функции ,/(х) в промежутке
Первую гармонику Л] sin(wx + (pi) называют основной гармо-
никой, а ее угловую частоту со =
2л
Т
- основной частотой. Угловые
частоты /до последующих гармоник Ап sin(ncox + срл) кратны угло-
вой частоте со основной гармоники.
Очевидно, что разложение (25) функции /(х) на составляю-
щие гармоники полностью определяется набором чисел
Aq,A[,^2,...,Ап... - амплитуд гармоник и чисел ср|,ср2,---,(Р/7 ••• _
начальных фаз гармоник.
Совокупность амплитуд Aq, Ai , Л2,..., Ап ... гармоник, входя-
щих в разложение (25), называется амплитудным спектром, а сово-
купность их начальных фаз ср|,(р2,---,(Рл	_ фазовым спектром пе-
риодической функции /(х).
41
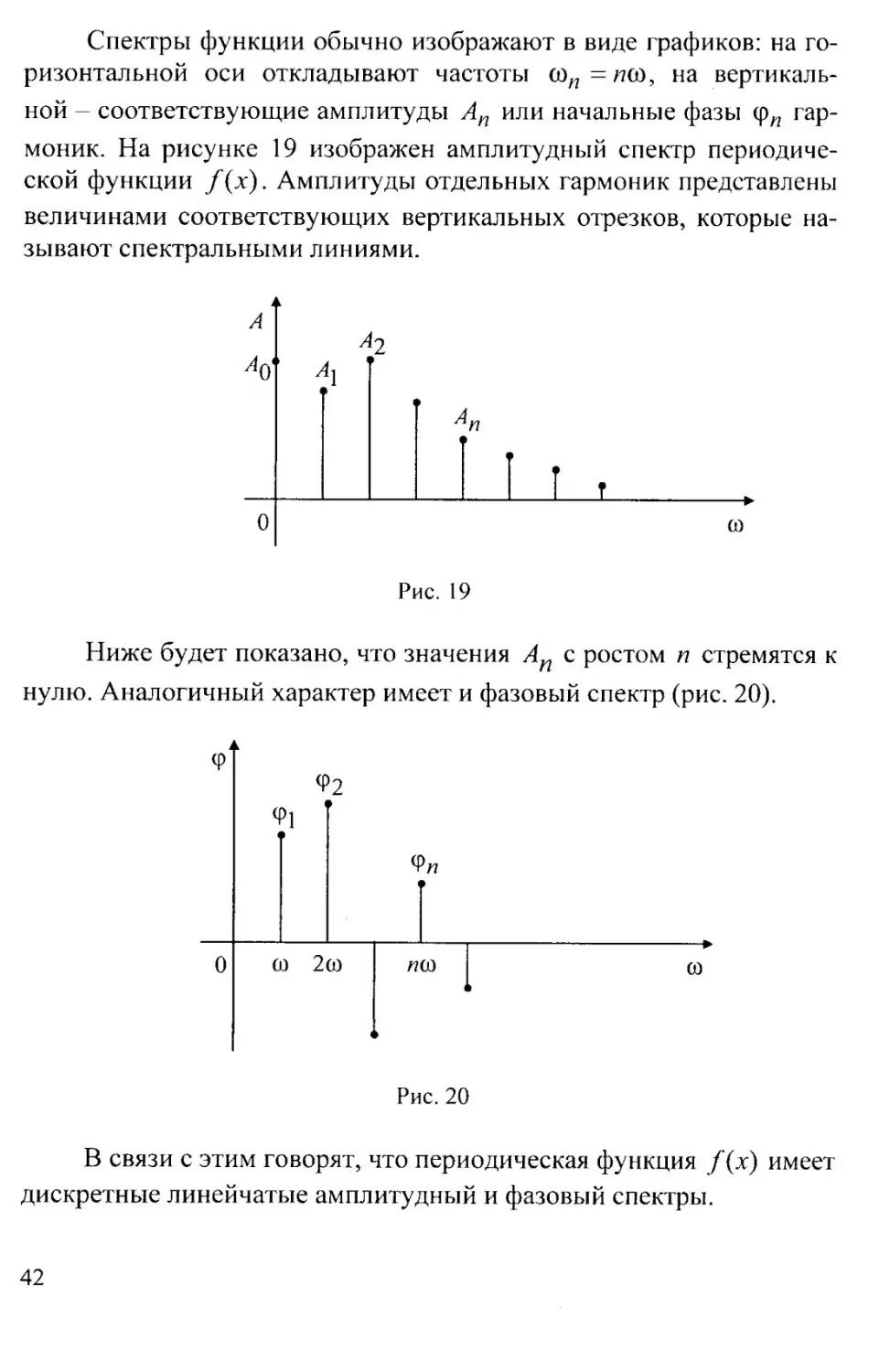
Спектры функции обычно изображают в виде графиков: на го-
ризонтальной оси откладывают частоты соп=/7со, на вертикаль-
ной - соответствующие амплитуды Ап или начальные фазы ф/7 гар-
моник. На рисунке 19 изображен амплитудный спектр периодиче-
ской функции /(х). Амплитуды отдельных гармоник представлены
величинами соответствующих вертикальных отрезков, которые на-
зывают спектральными линиями.
Рис. 19
Ниже будет показано, что значения А„ с ростом п стремятся к
нулю. Аналогичный характер имеет и фазовый спектр (рис. 20).
Рис. 20
В связи с этим говорят, что периодическая функция /(х) имеет
дискретные линейчатые амплитудный и фазовый спектры.
42
В тех же самых условиях функция f (х) может быть представ-
лена рядом Фурье в комплексной форме:
4-00
/(х)=
П = — оо
(26)
с комплексными коэффициентами
Если наряду с частотами со, 2со,...,/?со... комплексных гармоник
1П(ИХ	П	п	~
спе рассматривать отрицательные частоты - со, - 2со,...,-/7С0...,
то шкалу частот нужно дополнить отрицательной полуосью.
Совокупность модулей сп
при п = 0, ± 1, ± 2, ±3... комплекс-
ных амплитуд сл, отложенных против соответствующих частот
сон - nd) при п = 0, ± 1, ± 2, ± 3..., составит линейчатый амплитуд-
ный спектр функции /(%).
Ввиду того что


и точки соп = исо находятся на оди-
наковом расстоянии со друг от друга, амплитудный спектр будет
располагаться симметрично относительно оси ординат (рис. 21).
Рис. 21
43
Коэффициенты сп гармоник могут, в частности, оказаться дей-
ствительными числами. В этом случае, при построении амплитудно-
го спектра функции f(x), можно не переходить к модулям коэффи-
циентов откладывая соответствующие спектральные линии с
г t
учетом знаков чисел сп.
Для построения соответствующего фазового спектра нужно
найти аргументы ф„ комплексных коэффициентов сп. Ввиду со-
пряженности сп и с_п их аргументы отличаются лишь знаками. По-
этому линейчатый фазовый спектр функции ,/(х) будет распола-
гаться симметрично относительно начала координат (рис. 22).
Рис. 22
Таким образом, в зависимости от представления периодиче-
ской функции f{x) рядом Фурье в тригонометрической или ком-
плексной форме получаются спектры: либо на положительной полу-
оси, либо на обеих полуосях частот.
С увеличением периода Т функции /(х) уменьшается рас-
2л
стояние со = —- между соседними спектральными линиями. При
Т —> сю расстояние между спектральными линиями будет безгранич-
но сокращаться. Естественно ожидать, что амплитудный и фазовый
спектры, все более и более сгущаясь, перейдут в пределе в непре-
рывные или, как говорят, выродятся в непрерывные амплитудный и
фазовый спектры.
44
При исследовании процессов, характеризующих работу совре-
менных средств связи часто приходится иметь дело с сигналами, яв-
ляющимися периодическими функциями времени. Для того чтобы
изучить структуру и свойства сигнала, прибегают к его гармониче-
скому анализу.
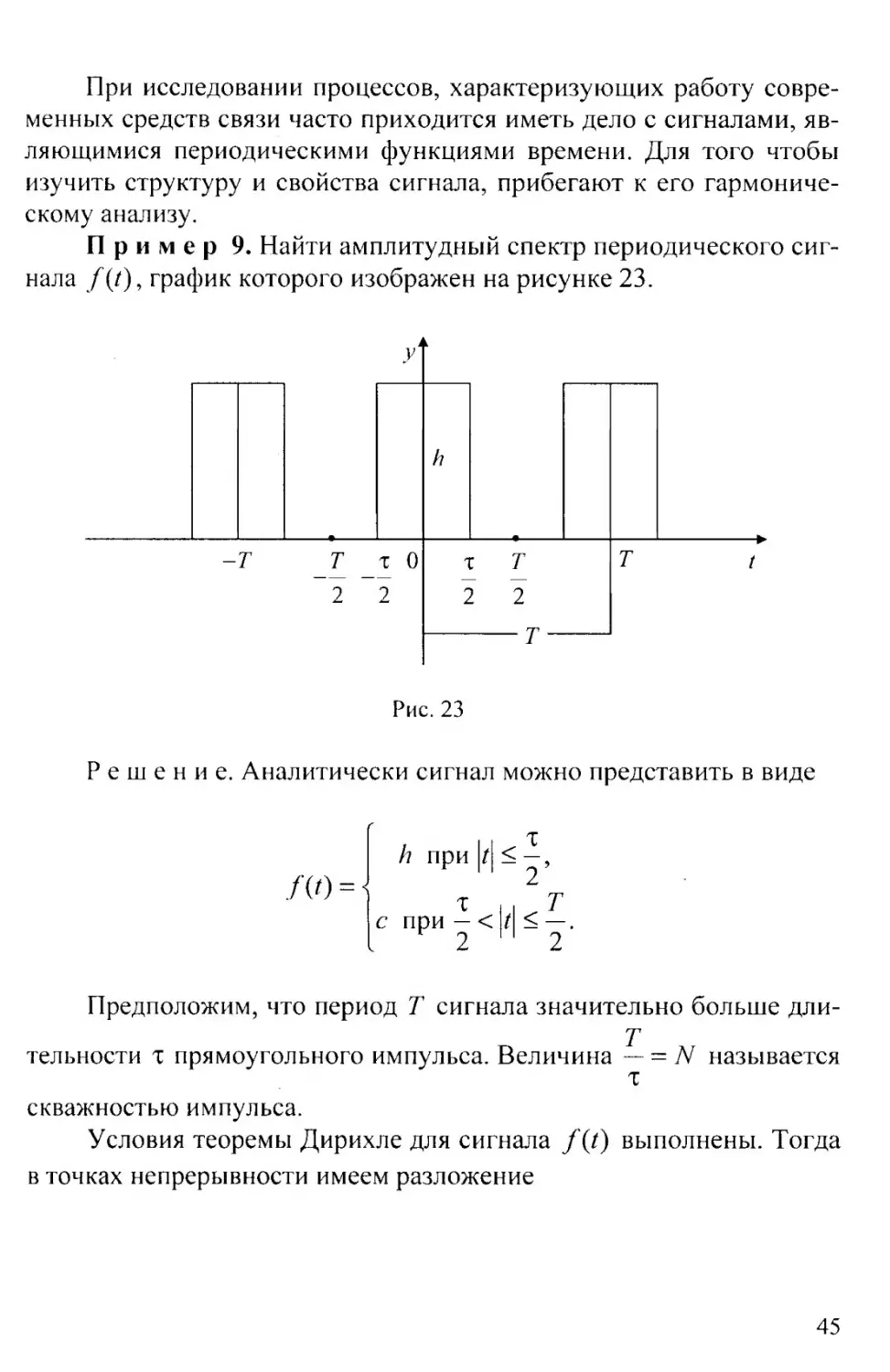
Пример 9. Найти амплитудный спектр периодического сиг-
нала f (/), график которого изображен на рисунке 23.
Рис. 23
Решение. Аналитически сигнал можно представить в виде
./(О =
с при —
Предположим, что период Т сигнала значительно больше дли-
тельности т прямоугольного импульса. Величина — = N называется
скважностью импульса.
Условия теоремы Дирихле для сигнала /(/) выполнены. Тогда
в точках непрерывности имеем разложение
45
сю
Найдем
п ~~
'7 -inoM
Tino
ТпО
inco—
—ino—
2
2П . ПОП
---sin---
Тпо 2
. пот
sin ——
non
Спектральные линии
обращаются
нуль при
пот ,
----= ЛА',
2л
—intfrf

2
2
/7(0 =
на шкале частот. Эти точки не зависят от величины периода Т, так
как определяются лишь длительностью т импульса.
( 2л
В промежутке 0;
между началом координат и первым ну-
2л	2л
лем — располагается п — —
т	тсо
= N спектральных линий
,	2л
(включая нулевую линию, приходящуюся на точку —
При Т —> оо или, что одно и то же, при увеличении скважности
f.. 2л
импульса число спектральных линий в промежутке 0;
как и в
других подобных промежутках, безгранично растет, а расстояние
46
между ними со = — безгранично сокращается. Дискретный спектр
сп сигнала сгущается, вырождаясь в пределе в непрерывный спектр.
§ 12. ФОРМУЛА ПАРСЕВАЛЯ-ЛЯПУНОВА
Пусть периодическая функция /’(х) периода Т непрерывна на
всей числовой оси и на любом отрезке длины Т кусочно-монотонна.
Тогда по теореме Дирихле при всех х имеет место равенство
со
f (х) = — + cos + bn sin исйх) .
2	/7 = 1
Умножая обе части этого равенства на — /(х) и интегрируя
полученное равенство по промежутку [0; Г], получим
I J./'2	= "0'7 J/(х№х + £ "/7 7 J7 W cos ntoxdx +
7 0	7 0	/7 = 1у	1 о
2Г .	.
+ Ьп —- J/(х) sin /7(Дх<Тх .
7 0	)
Учитывая формулы (12, 13, 14), для коэффициентов а$,ап,Ьп
будем иметь
т
\f\x)dx
0
И
2
Т
(27)
Полученное равенство называется равенством Парсеваля-
Ляпунова. Если учесть, что
47
где Ап (п = О, 1, 2...) - амплитуда л-й гармоники, то равенство Пар-
севаля-Ляпунова можно записать в другом виде
1	| оо
J/2(.v)dx = ^02+-XA,2
о	2и=1
(28)
Левая часть этого равенства есть конечная величина, следова-
тельно, ряд в правой его части сходится. Тогда, согласно необходи-
мому признаку сходимости числовых рядов при д—его общий
член А„ —> 0. Это означает, что амплитуда Ап с ростом п (что то
же самое при со/7 —» «=) стремится к нулю (заметим, что при п —> о©
коэффициенты ап и Ьп также стремятся к нулю).
Рассмотрим пример использования равенства Парсеваля-
Ляпунова.
Пусть сигнал описывается напряжением г/(0, которое является
2
периодической функцией с периодом Т. Тогда p(t) = u (/) есть
мгновенная мощность, выделяемая на сопротивление в 1 Ом. Энер-
гия колебания Е на отрезке [0; Т] определяется формулой
Е = \p2(t)dt = \u2dt.
О	О
Средняя мощность колебания на промежутке [0; Т] есть
Из равенства Парсеваля-Ляпунова следует, что
48
Полученное равенство дает представление о распределении
средней мощности сигнала по диапазону частот и позволяет опреде-
лить среднюю мощность по известному амплитудному спектру.
Если, например, функция описывает сигнал-помеху, то
можно выделить полосы частот, в основном образующие данный
сигнал. Построив тот или иной фильтр, не пропускающий в прием-
ник эти полосы частот, можно свести к минимуму действие помехи.
§ 13. ОБОБЩЕННЫЙ РЯД ФУРЬЕ
Рассмотренный ранее ряд Фурье функции / (х)
со
cos п(х)х + b„ sin п(йх
f I-
в основе своей имеет основную тригонометрическую систему функ-
ций —, cosoix, sin ок, cos2oir, sin 2сох..., ортогональную на отрезке
длины Т =
со
Поэтому точнее такой ряд следует называть триго-
нометрическим рядом Фурье, ибо ряд Фурье можно строить и на ос-
нове других систем функций.
Пусть на отрезке [а; 6] задана система непрерывных функций
Ф1(*)> Ф2(Д-> ФмМ-
(29)
Нормой какой-либо функции этой системы называется число
Г
Фи(Х) = {фл? (х)с/х (и = 1,2...).
V и
49
Определение. Система функций {ф/7(х)} называется ортонор-
мированной, если нормы всех функций этой системы равны 1 и лю-
бые две ее функции ортогональны, т. е. при к Ф т
tyk(x)'tym(x)dx = 0.
Теорема. Если функция f(x) представлена в виде суммы
функционального ряда
/(*) = Хап<?п(х)
/7 = 1
(30)
где фл(х) (и = 1, 2, 3...) образуют ортогональную на отрезке [я; b
систему, то такое разложение единственно и коэффициенты ап мо-
гут быть определены по формуле
Ь
|/(х)ф„(х)б7х
(31)
[фя(х)<7х
а
Коэффициенты, вычисленные по формуле (31) называются ко-
эффициентами Фурье, а ряд с такими коэффициентами - обобщен-
ным рядом Фурье данной функции /(х), соответствующим системе
функций {фи(х)}.
Доказательство. Умножим обе части равенства (30) на
ФА- (х):
/(х)Фа (х) = Х"пФ«(х)Фа(х).
/7 = 1
50
Проинтегрируем обе части этого равенства на промежутке
[б/; b], при этом предположим, что ряд можно почленно интегриро-
вать:
h	оо b
Е 1<рп (х) 9 к (x)dx 
а	п—\ а
В силу ортогональности системы функций ср] (х),(р2 (*)•• все
слагаемые в правой части при пФ к обращаются в ноль, поэтому
Ь	Ь
(xXv = ак J<P£2 (x)dx>
а	а
откуда и вытекает формула (31).
Отметим, что знаменателем этой формулы является квадрат
нормы функции (х) (тем самым эта величина отлична от нуля и
коэффициент определяется однозначно).
Обобщенный ряд Фурье широко используется в теории пере-
дачи сигналов, при этом используются разнообразные системы
функций: полиномы Чебышева, Эрмита, Лаггера, Лежандра, функ-
ции Уолша и др.
В 1933 г. выдающийся отечественный ученый В. А. Котельни-
ков, получивший мировое признание за свои работы, доказал сле-
дующую теорему.
Теорема Котельникова. Если колебание w(/) задается на ин-
тервале (- оо; + ©о) и имеет спектр, ограниченный сверху частотой
F, то его можно представить обобщенным рядом Фурье:
w(0 =
~ , д ч sin 2nF(t - кМ)
У г/(ЛА/)------------------,
X 2tcF(z - W)
(32)
где AZ = —
2F
Разложение в данном случае выполнено по ортогональной (но
ненормированной) системе функций:
51
<?к (0 =
sin 2nF(t - кМ)
2nF(t-kM) ’
называемых функциями отсчета.
Равенство (32) позволяет восстановить непрерывное колебание
u(t) по его отсчетам, взятым через интервалы А/. Таким образом,
можно передавать не весь сигнал, а лишь его мгновенные значения,
взятые через промежутки времени А/. Такой процесс в теории пере-
дачи сообщений называют дискретизацией сигнала по времени t.
§ 14. ИНТЕГРАЛ ФУРЬЕ. ТЕОРЕМА ФУРЬЕ
Пусть функция f (х) удовлетворяет условиям Дирихле на вся-
ком конечном промежутке
и абсолютно интегрируема на
всей числовой оси, т. е. существует несобственный интеграл
-рОО
j|/(x)| dx = Q.
— оо
По теореме Дирихле в каждой точке х ряд Фурье этой функ-
ции сходится и его сумма
ST (х) ~	+ X (ап cos п^х + s^n ясох).
2 W = 1
Подставим сюда выражения для коэффициентов Фурье:
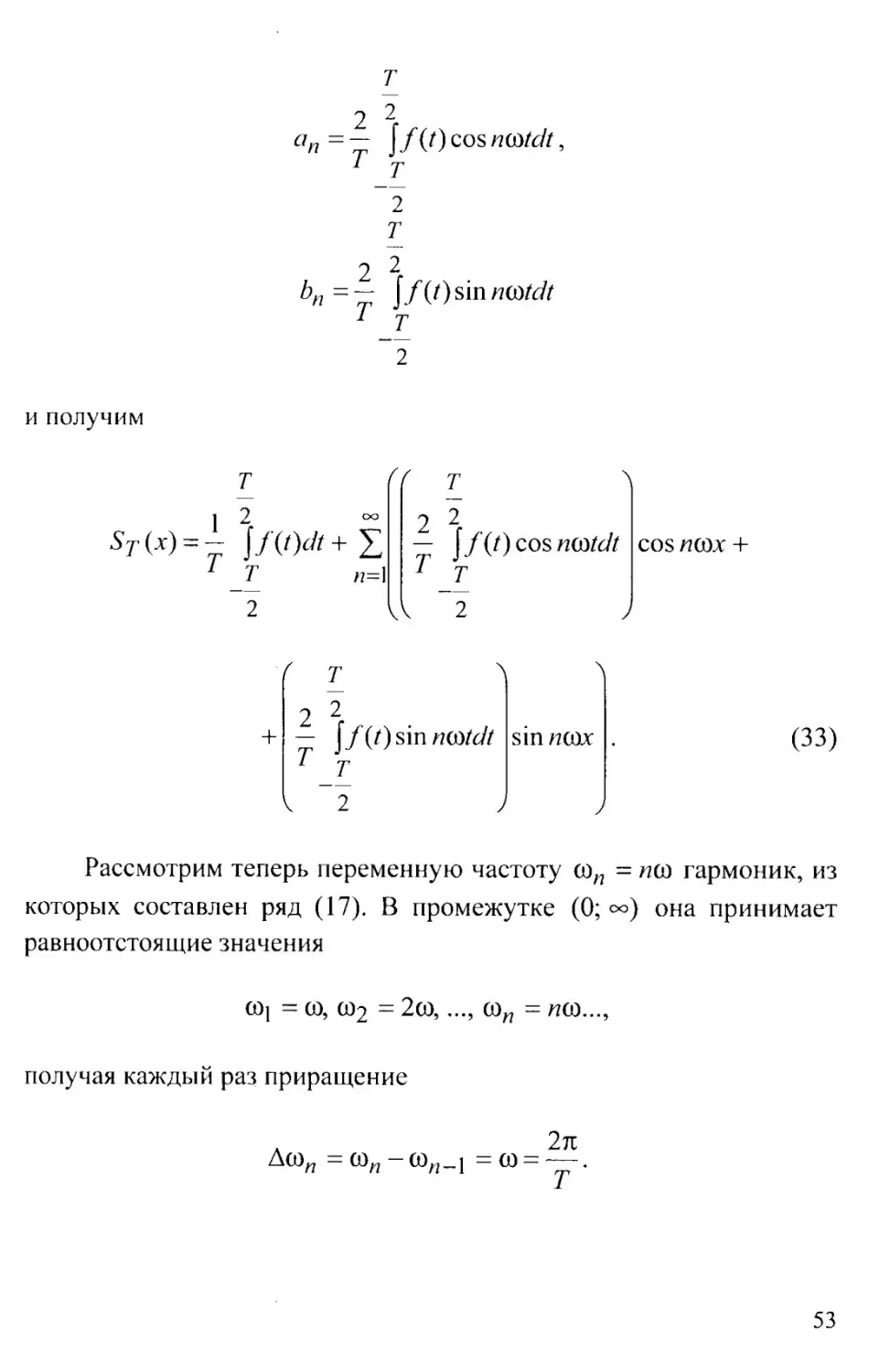
2 2
//('Ж
1 _т
2
52
т
и получим
ап
2
J/(Z) cos noMdt,
Т
2
[/(/) sin noMdt
Т
сю
2
Т
2
J f (/) cos nortdt cos a? cox +
Г
2	J
ff (7) sin nortdt sin aicox .
(33)
Рассмотрим теперь переменную частоту (0Z2 = лсо гармоник, из
которых составлен ряд (17). В промежутке (0; оо) она принимает
равноотстоящие значения
(О] = со, 0)2 = 2со,сон ~ 77(0...,
получая каждый раз приращение
Д(О„ = со/7 — (0л_| = со =
53
Отсюда
= Дсо„ • -.
Г t
л
В соответствии с этим равенство (33) можно записать в виде
оо
И
п •
(34)
Посмотрим, что произойдет с этой формулой при Т —> «>. Пер-
вое слагаемое правой части этого равенства стремится к нулю,
так как
/(О dt =
— оо
Ввиду того, что точка х считается фиксированной, а интегри-
рование ведется по переменной /, интегралы, стоящие под знаком
суммы в равенстве (34), будут функциями со„.
Обозначим:
Т
j 2
— ]/(/) COS — £7у (оЭ/7 ),
71 _т_
2
54
2
f/(Z) sin (f)ntdt = b? ((f) n),
т
тогда сумму в правой части равенства (34) можно записать в виде
OQ
cos солх + h'p ((f) п )sin cd^x^co^.
/7 = 1
(35)
Эта сумма напоминает интегральную сумму для функции
fl((o)cos сох + b((f))sin сох
на промежутке [0; оо). Поэтому можно допустить, что сумма (34)
при Т -> оо будет интегралом"
СО
/(х) - J(c/((o)coscox + Z?(co)sincox)c/co,
О
(36)
— со
Z?(co) = —
—со
f/'(Z) sin (f)tdt.
— со
Интеграл /(х) называется интегралом Фурье.
Заметим, что формула (36) получена из разложения функции
/’(х) в ряд Фурье в результате предельного перехода при Т —> со,
поэтому в точках непрерывности функции /(х) значение /(х) равно
Строгое доказательство предельного соотношения (36) содержится в подробных
курсах анализа.
55
/(х), а в точках разрыва 7(х) = | (/(х - 0) +/(х + 0)), т. е. имеет
место формула
оо
I(x) = J(<i(co)cos (fix + b(co)sin сох)с/со =
0
/(х), если х - точка непрерывности,
1	(37)
+ /(х + 0)), еслих — точка непрерывности.
Формула (37) называется интегральной формулой Фурье.
Итак, вышеописанное позволяет сформулировать теорему
Фурье, которую приводим без доказательства.
Теорема Фурье. Если функция /(х) удовлетворяет условиям
Дирихле на всяком промежутке и абсолютно интегрируема на всей
числовой оси, то
оо
j(<7(co)cOS сох + /фсо)sin (ox)Jco =
0
/(x), если x - точка непрерывности,
1 (/(X - 0) +/(x + ОД если х - точка непрерывности.
Интеграл Фурье можно представить и в другом виде. Учиты-
вая, что
я (со) cos (fix + Z?(co)sin сох = /i((o)sin(cfix — (pg),
где Л((о) - амплитуда и фо - начальная фаза, соответствующие час-
7 2	2
а (со) + b (со), а фд определяется из ус-
ловий <7(со) = Л(со)с08фо, 6(С0) = Л(со)5тфо-
Интеграл Фурье дает разложение, вообще говоря, непериоди-
ческой функции на непрерывную "сумму" гармоник
56
.1 (co)sin(шл' - фф), частоты которых также изменяются непрерывно.
Зависимость амплитуды Л (со) от частоты (амплитудный спектр)
изображается непрерывной линией. Анализируя эту зависимость
можно выделить те полосы частот, которые играют наибольшую
роль в формировании данной функции.
§ 15. ИНТЕГРАЛ ФУРЬЕ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
Случаи четной и нечетной функций рассматриваются анало-
гично ряду Фурье. Пусть /(х) - четная функция, тогда
cz(co) = — J / (х) cos сохб/х = — [/ (х) cos сохс/х
— сю	О
= ~ J/(x)sincoxc/x = 0.
—оо
(38)
(39)
Следовательно, интеграл Фурье функции /(х) имеет вид
оо
[<7(CO)COS СОХб/CD.
О
(40)
Аналогично, если /(х) - нечетная функция, то интеграл Фурье
примет вид
оо
fZ?(co) sin сохс/со,
о
(41)
где
Z>(cd) =
оо
[ / (х) sin ош/х.
0
(42)
), то доопределяя ее
Если f (х) определена на полуоси [0; + <*>
произвольным образом (с соблюдением требуемых ограничений) на
57
промежутке (-	0) получим представление ее интегралом Фурье
(естественно, оно не будет однозначным). Практически удобно
брать либо четное, либо нечетное продолжение.
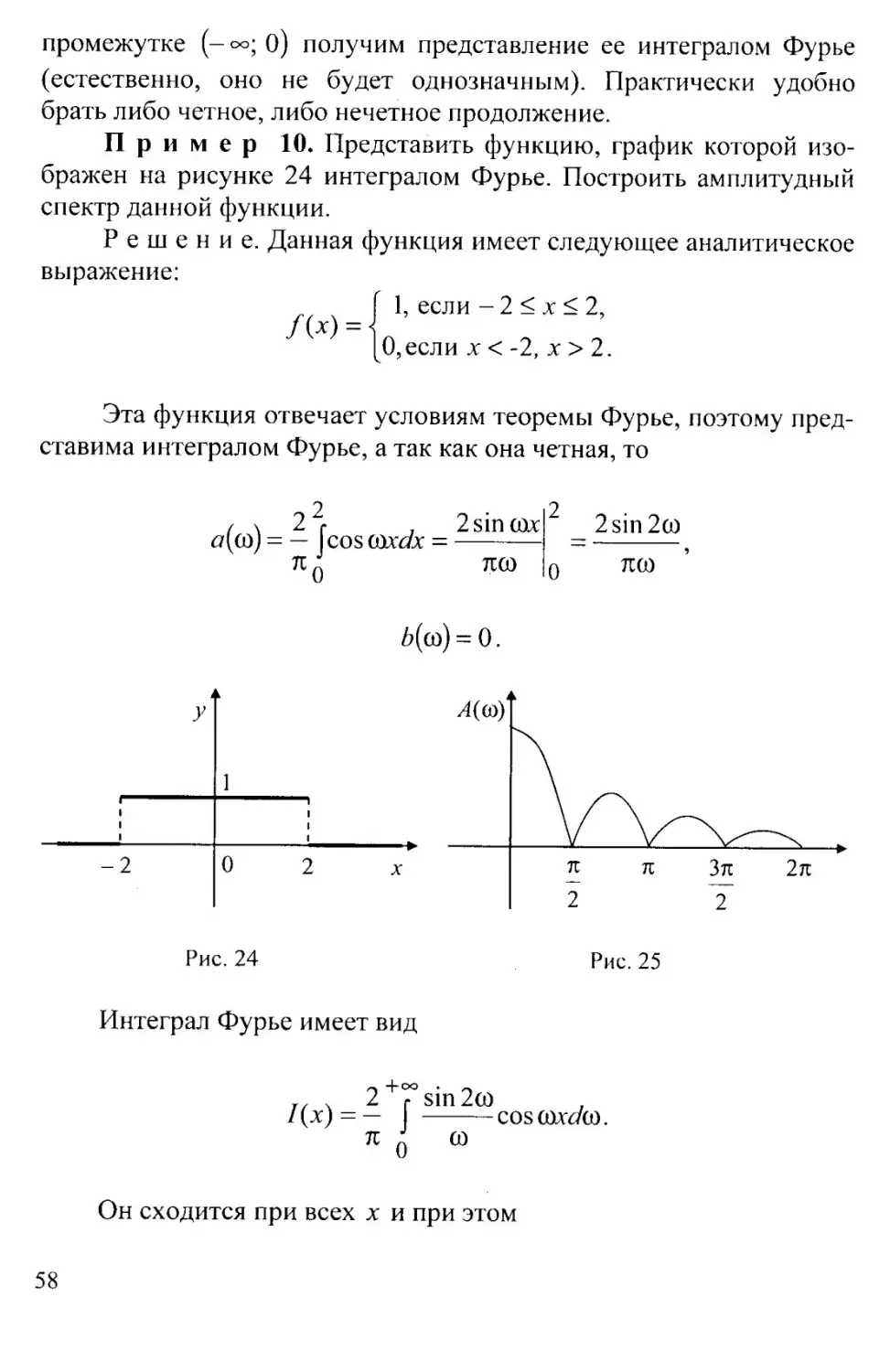
Пример 10. Представить функцию, график которой изо-
бражен на рисунке 24 интегралом Фурье. Построить амплитудный
спектр данной функции.
Решение. Данная функция имеет следующее аналитическое
выражение:
/« =
I 1, если - 2 < х < 2,
0, если х <-2, х > 2.
Эта функция отвечает условиям теоремы Фурье, поэтому пред-
ставима интегралом Фурье, а так как она четная, то
2sinuix
2sin 2со
тгсо
JLCD
0
Рис. 24
Рис. 25
Интеграл Фурье имеет вид
/(х) = -
к
COS
Он сходится при всех х и при этом
58
1, если
/(л) =
2

О, если х
Амплитуда Л (со)
в данном случае равна я(со) так как
(/?(со) = 0). График этой функции - амплитудный спектр (рис. 25).
§ 16. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ
В электротехнике и теории цепей широко используется ком-
плексная форма интеграла Фурье. Аналогично ряду Фурье исполь-
зуем формулы Эйлера
cos сох = - (е/Сйг 4- е-/03х )
2\	/’
sin сох =	(e/01Y - e-/Oir).
2V	'
Подставим их в интеграл Фурье:
ОО Z	J /
7(х)= j (a(co))--(e/OXY
0<	2
1 ОО /
= - Д(с/(со) - /7>(со)>/ок
2 о
+ (я(со) +/£>(со))е ZOir)(7co.
Обозначим <?(со) -/Ь(со) = S(co), тогда
j т*00	। Н-оо
5(со) = — J/(x)coscoxJx-z — f/(x)sincox<7x =
— оо	—оо
| Ч“°°	J ~|-оо
~ — [/(x)(cosсох - i sin cox)cZx = — [ f (x)e-/cox dx.
л	л J
— co	—oo
59
Соответственно
S (со) = «(со) + /Л (со),
тогда
1 Ч- °°
5(<о) = - [ f(x)eiVKdx = S(- со).
71
— оо
Теперь интеграл Фурье примет вид
/(х) = - °f (s(co)e'“¥ + S(-W)e_'“v )<Ло =
2 О
= - [$Хю>'&к<Ло + -pI-coK itaxdw.
2 о	2 о
Во втором интеграле сделаем замену: -co=z, d($=-dz и по-
лучим
1 00	1 о	1 00
/(х) = - p(C0)e'“vc7w— fS(z)e'“zdz = - JS(w)e'“'Jco.
2	2	2
Итак, интеграл Фурье представлен в виде
1 + оо
/(х) = - f S(<o)eiwcdu,
— оо
(43)
где
1 т °°
5(со) = - (
л
— оо
/(х)е"'“хг/х.
(44)
Форма интеграла Фурье (43) называется комплексной формой,
а функция 5(со) - спектральной функцией (или спектральной плот-
ностью).
Отметим, что
S(co) =
(со) + b (со) = Л (со)
60
т. е. модуль спектральной функции равен амплитуде гармоники, со-
ответствующей частоте со. Поэтому при нахождении амплитудного
спектра удобно пользоваться именно комплексной формой интегра-
ла Фурье.
Пример 11. Найти амплитуду A((i)) для функции
/(X) =
при х < О,
при х > 0.
Р е ш е н и е. По формуле (44) найдем :
Тогда
Я(со) = 5(со) =
В теории цепей достаточно часто приходится иметь дело с им-
пульсными непериодическими сигналами. Амплитудные и фазовые
спектры сигналов позволяют всесторонне изучить их свойства и на
этой основе конструировать более совершенную аппаратуру связи
для приема и передачи информации.
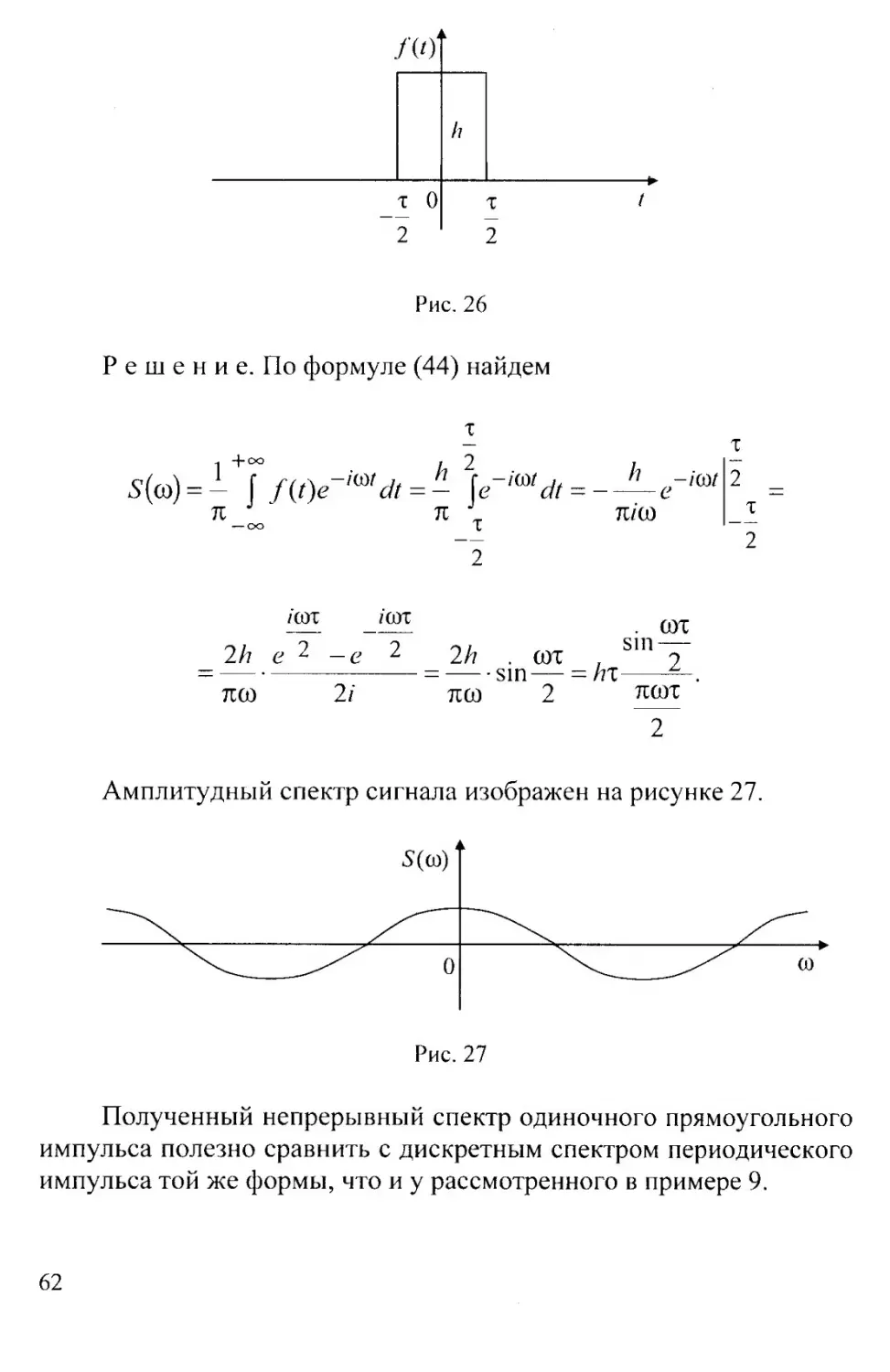
Пример 12. Найти спектральную плотность прямоугольно-
го импульса высоты h и длительности т (рис. 26)
/(О =
0, при t
61
Рис. 26
Решение. По формуле (44) найдем
т
к J	л J_	л/со 1
— оо	I
2
2
/СОТ /СОТ
2/7
Л (О
2/? . (от
----sin —
лсо 2
. сот
sm —
— fa----2_
Л(ОТ
Амплитудный спектр сигнала изображен на рисунке 27.
£((0)
Рис. 27
Полученный непрерывный спектр одиночного прямоугольного
импульса полезно сравнить с дискретным спектром периодического
импульса той же формы, что и у рассмотренного в примере 9.
62
Пример 13. Импульс напряжения на выходе дифференци-
рующей цепочки изменяется по закону (рис. 28)
г/вых
ае~ш
О при
при t > 0 (а > 0),
КО.
11 в,х
Рис. 28
Найти спектральную характеристику, амплитудный и фазовый
спектры импульса.
Решение. Находим спектральную плотность (характеристи-
ку) импульса:
5(ю) =
4ZCD
(a+ild)t
0
63
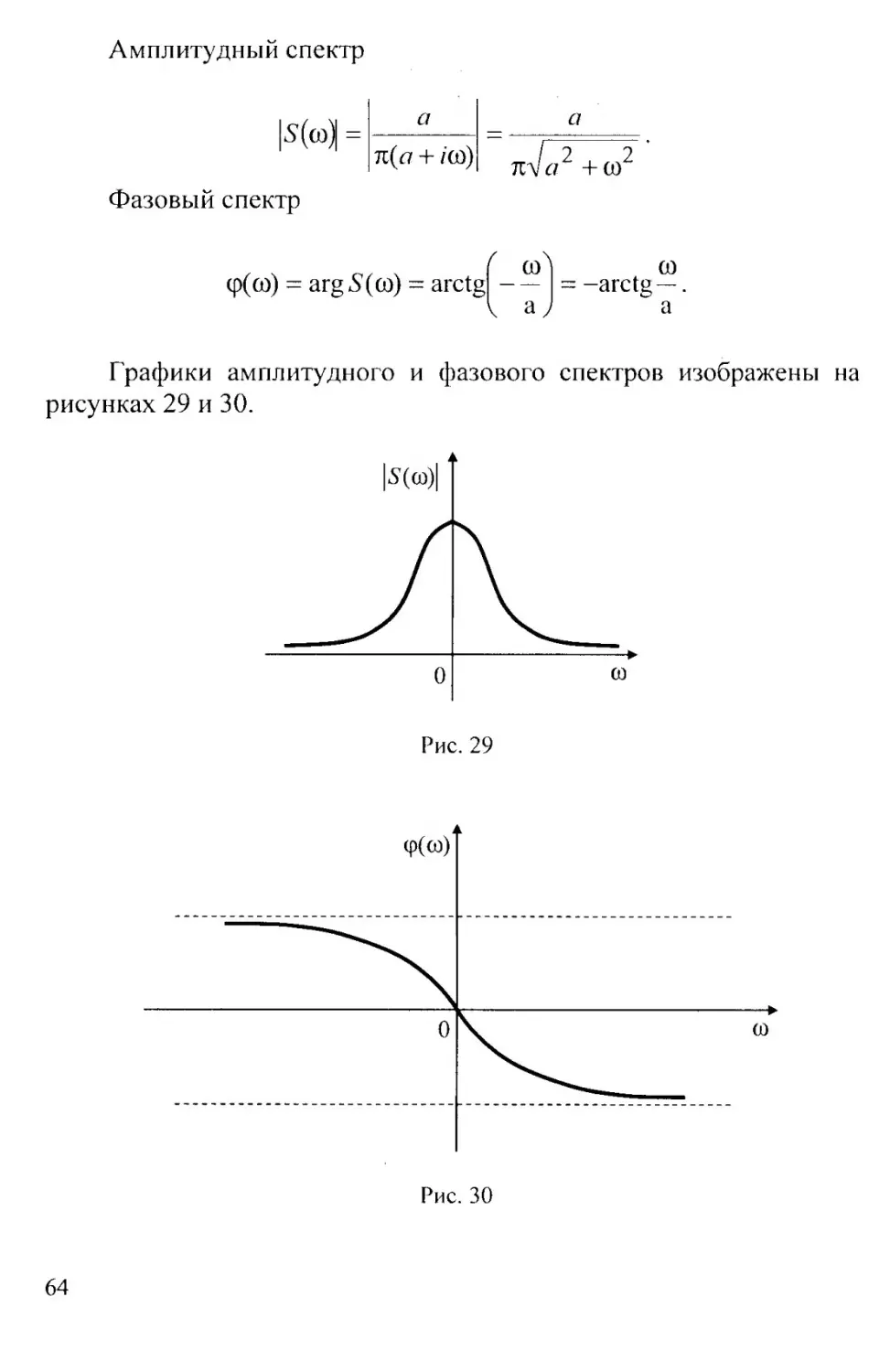
Амплитудный спектр
5(а>)
а
7l(<7 + /СО)
а
Фазовый спектр
ср(со) = argS(co) = arctg
со
со
= -arctg—
а
Графики амплитудного и фазового спектров изображены на
рисунках 29 и 30.
64
§ 17. ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Представим интеграл Фурье в комплексной форме в следую-
щем виде:
• е/Сйгс7со.
—сю
Обозначим
1
F(co) = -—= f f(x)e~i<Mdx.
а/2тс j
(45)
Функция ^(co) называется образом /(x) по Фурье (от спек-
тральной функции 5(со) она отличается только постоянным множи-
телем). Переход от / (х) к F(co) называют преобразованием Фурье.
Здесь видна аналогия с преобразованием Лапласа: /(х) - оригинал,
F(w) - изображение.
Предполагая, что функция /(х) непрерывна, можно записать
J 4~ОЭ
,/(л) = ^= J F(w)t>'Ao.
(46)
Эта формула представляет обратное преобразование Фурье.
Она позволяет по образу F(yri) найти оригинал /(х).
Аналогично вводятся косинус и синус преобразования Фурье.
Пусть /(х) - четная функция (либо задана на полуоси [0; ©о)),
тогда
65
f(x)= j(7(to) COS G)X<7CO = j — j/(x) COS (llWx COS GJt/(D -
0	>
о
f (x) COS (DXc/x
V
0
COSGX/O).
Выражение
Fc (CD) =
+ oo
J/(x) coscmz/x
0
(47)
называется косинус-образом Фурье функции /(х), а переход от
/(х) к Fc(cd) - косинус-преобразованием функции /(х).
Формула

4“ОО
fF(o))coscoxJco
о
(48)
определяет обратное косинус-преобразование Фурье.
Аналогично, если функция /(х) - нечетна либо задана на по-
луоси [0; с»
), то формулы
Fc (со) = — [ f (х) sin сшх/х
VTt 0
(49)
г^"+со
f (х) - Л — fF(co) sin oixz/co
Мтг 0
(50)
определяют прямое и обратное синус-преобразование Фурье.
Эти преобразования непосредственно используются при реше-
нии дифференциальных и интегральных уравнений, уравнений ма-
66
тематической физики. Кроме того, они нашли широкое применение
в различных вопросах радиотехники, автоматического регулиро-
вания.
Идея заключается в следующем. На вход некоторого преобра-
зователя В (например, усилителя) подается известная функция /(х)
(например, напряжение переменного тока). Преобразователь В пре-
вращает функцию /(х) в другую функцию ср(х) = £?(/(х)). При этом
известна спектральная характеристика преобразователя - функция
В(со), которая описывает воздействие преобразователя на функцию
входа, точнее на ее спектральную функцию 5(со) или амплитуду
И((о). Требуется найти функцию ср(х) по заданным функциям /(х)
и /?(со).
Эта задача решается по такому плану:
1.	По функции /(х) находим ее образ по Фурье F(co) (либо,
если это удобнее, Fc(co) или Fs,(co)).
2.	Зная воздействие преобразователя на 5(со) (функция F(co),
как известно, отличается от £(со) лишь постоянным множителем),
* *
находим 5 (со) (и соответственно F (со)), являющуюся спектраль-
ной функцией функции ср(х) на выходе.
*
3.	С помощью обратного преобразования Фурье по F (со) на-
ходим <р(х).
П р и м е р 14. На вход преобразователя поступает функция
/(*) =
Преобразователь действует таким образом, что все колебания с
частотами со> 1 гасятся, а при 0 < со< 1 амплитуда колебания 5(со)
умножается на множитель ———. Найти функцию <р(х) на выходе,
sin лсо
Решение. Данная функция четная, поэтому будем использо-
вать косинус-преобразование
67
z ч |2V	,	|2 sin сох
K.(co)= — 2-coscoxax= — 2-------
VTCq	h CO
n 2 sinrcco
= 2J----------
V я co
Эта функция отличается от амплитуды Л(со) (в полосе
О < со < 1) только постоянным множителем, поэтому функция
*
Fc (со) имеет вид
(«•) =
со
sinrcco
при 0 < со< 1,
при (О> 1,
т. е. Fc* (со) = 2 — при сое [О; 1].
V я
Для нахождения функции ф(х) на выходе сделаем обратное ко-
синус-преобразование
ср(х) =
1~2+°° [2
(со) cos сохб/со = J— I 2 J— cos coxJco =
библиографический список
1.	Бугров, Я. С. Высшая математика (в 3-х томах), т. 3 / Я. С. Бугров,
С. Н. Никольский. - М. : Дрофа, 2004. - 512 с.
2.	Гаврилина, Н. П. Сборник задач по математике, ч. IV / Н. П. Гаври-
лина, С. И. Федорова. - Орел : ВИПС, 1994.
3.	Ильин, В. А. Основы математического анализа / В. А. Ильин,
Э. Г. Позняк. - М. : Наука, 2000.-447 с.
4.	Кудрявцев, Л. Д. Математический анализ / Л. Д. Кудрявцев. - М. :
Высшая школа, 1973.-481 с.
5.	Колмогоров, А. И. Элементы теории функций и функционального
анализа / А. Н. Колмогоров, С. В. Фомин. - М. : Наука, 1989. - 623 с.
6.	Письменный, Д. Т. Конспект лекций по высшей математике, ч. 2 /
Д. Т. Письменный. - М. : Рольф, 2000. - 256 с.
7.	Титчмарш, Э. Н. Введение в теорию интегралов Фурье / Э. Н. Тит-
чмарш. - М. : Ком Книга, 2007. - 480 с.
8.	Федорова, С. И. Ряды Фурье. Интеграл Фурье / С. И. Федорова. -
Орел : ВИПС, 1994.- 50 с.
9.	Харди, Г. Г. Ряды Фурье / Г. Г. Харди, В. В. Рогозинский. - М. : Ком
Книга, 2006.- 158 с.
Учебное издание
Радыгин Владимир Михайлович
Федорова Светлана Ивановна
Тригонометрические ряды
и интеграл Фурье
Пособие
Технический редактор М. Г. Лобанова
Корректор О. Н. Горбачева
Выпускающий Е. Н. Оброткина
Компьютерная верстка М. М. Мухиной
Подписано в печать 08.12.2009 г. Формат 60x84/16. Печать офсетная.
Бумага офсетная. Гарнитура «Times New Roman».
Усл. печ. л. 4,06. Уч.-изд. л. 3,20. Тираж 102 экз. Заказ № 419.
Отпечатано в типографии Академии ФСО России
302034, г. Орел, ул. Приборостроительная, 35.