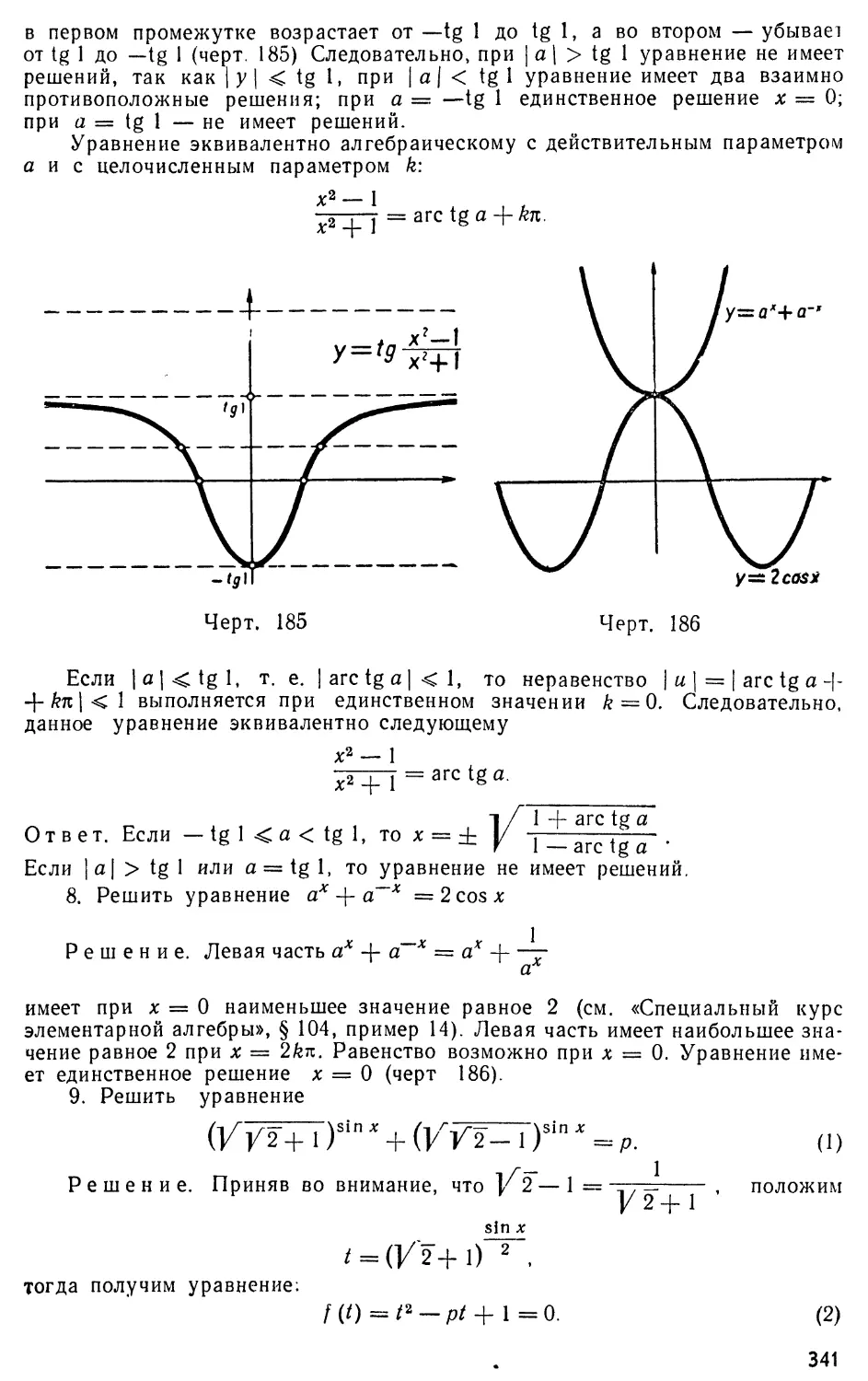
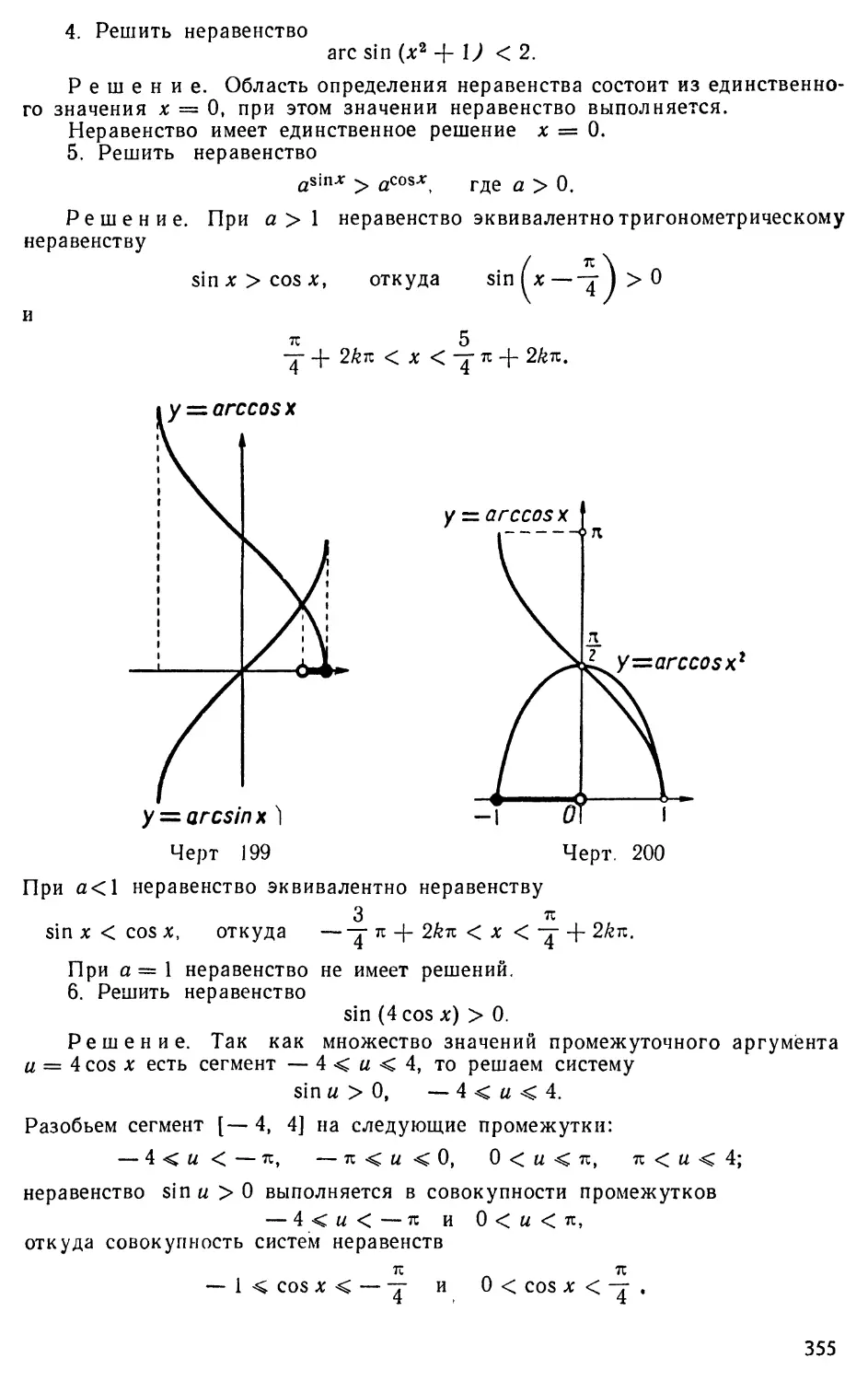
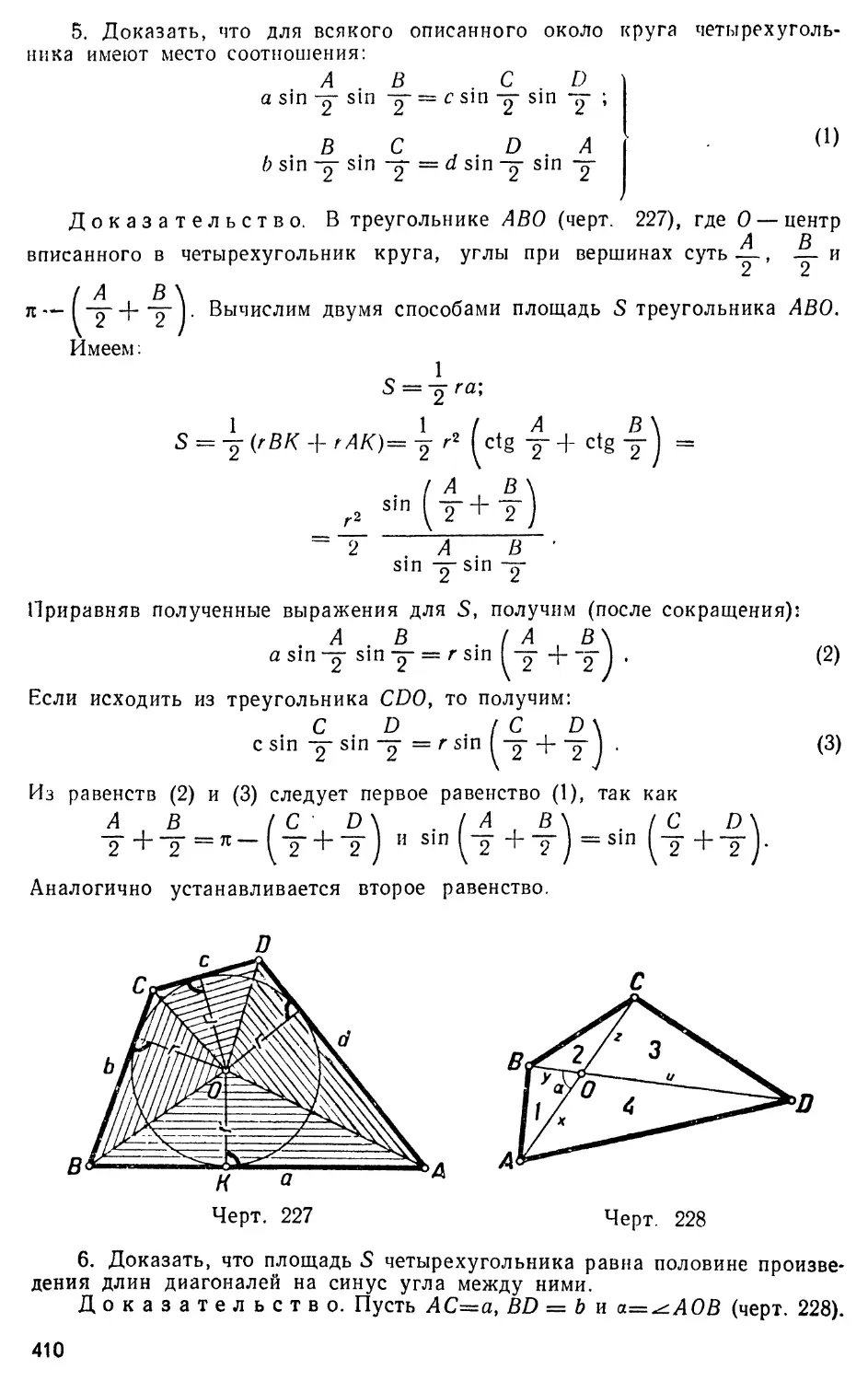
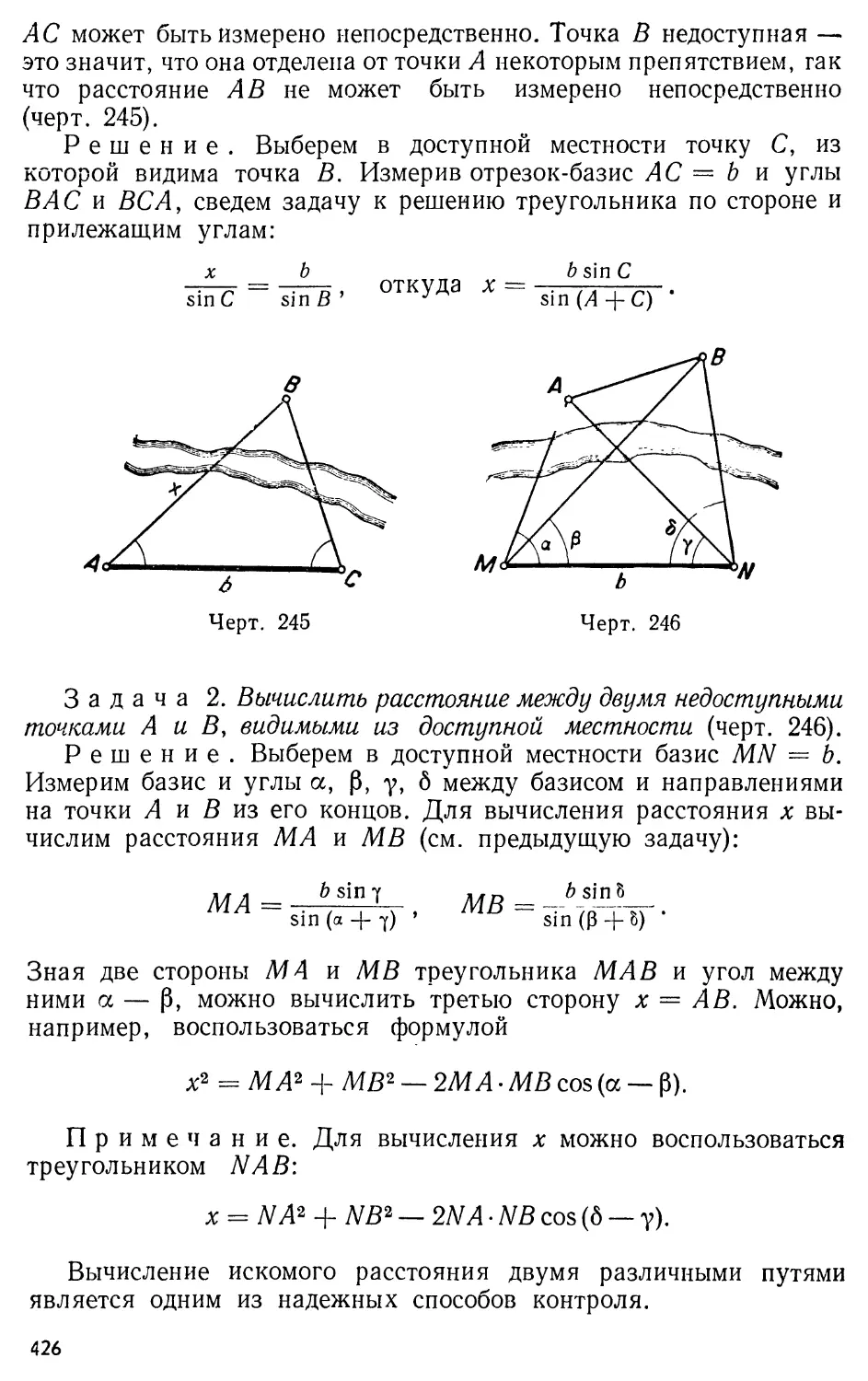
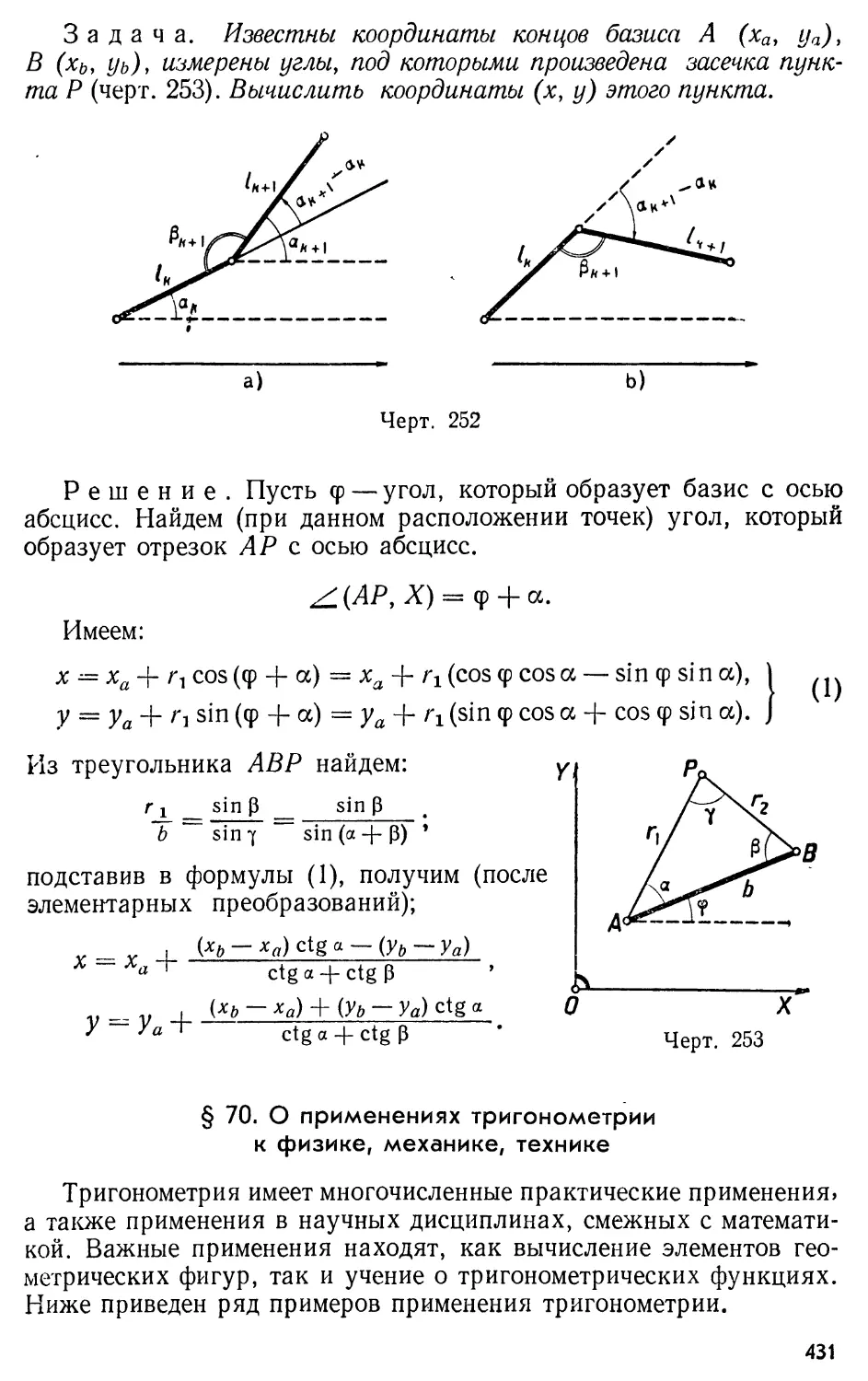
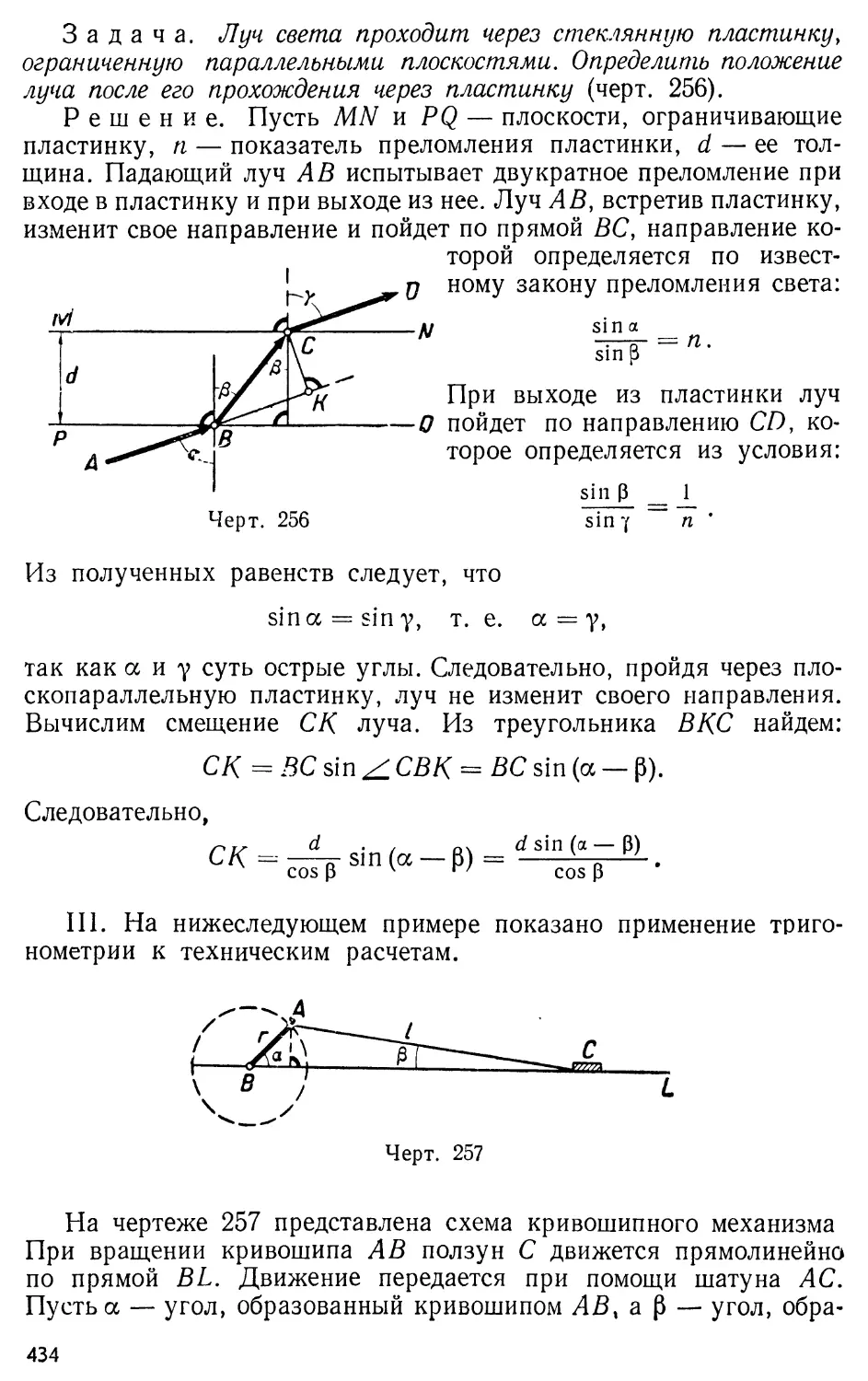
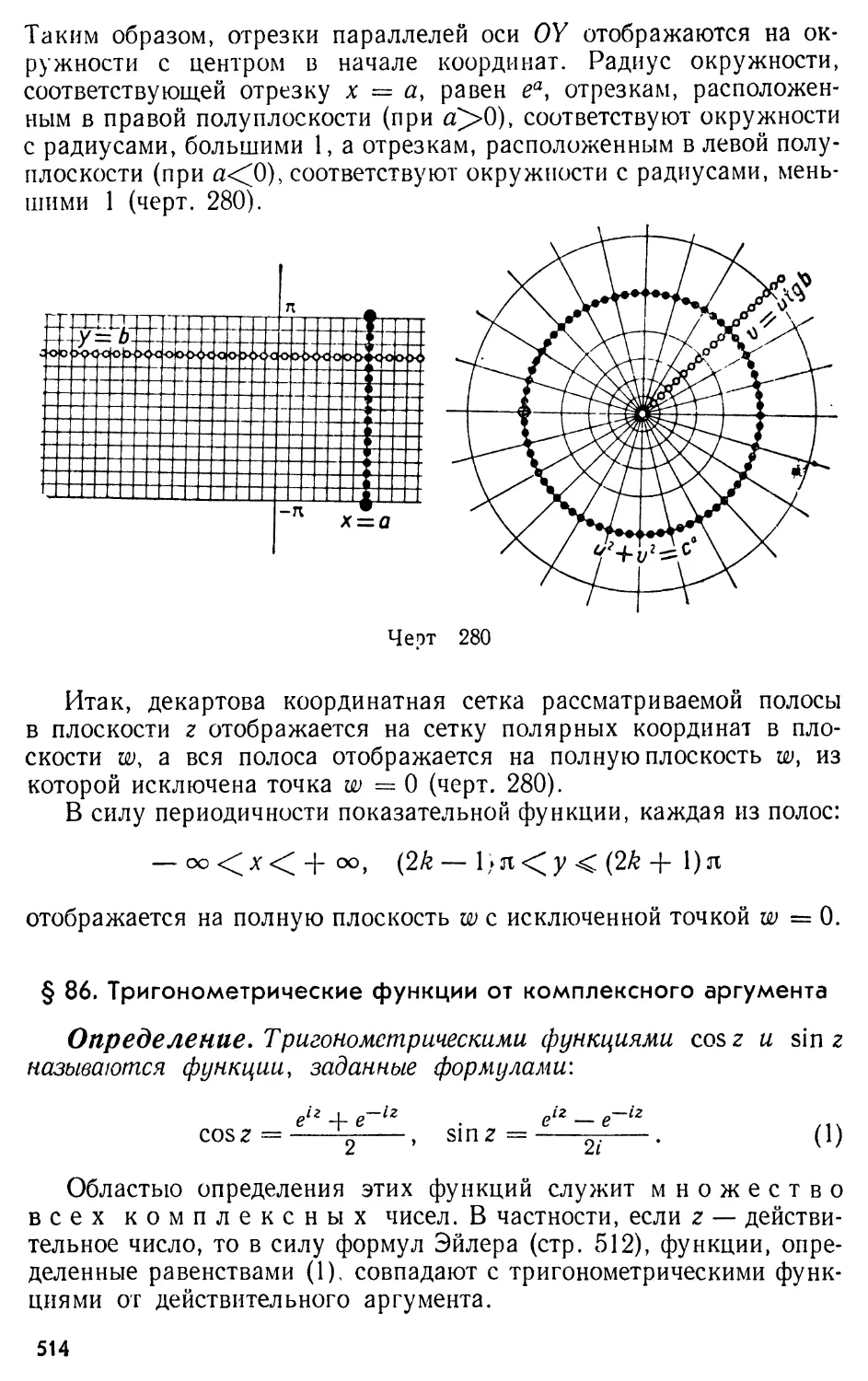
Text
СИ НОВОСЕЛОВ
специальный
курс
тригонометрии
Издание пятое
Допущено
Министерством высшего
и среднего специального
образования СССР в качестве
учебного пособия
для педагогических институтов
и государственных университетов
ИЗДАТЕЛЬСТВО
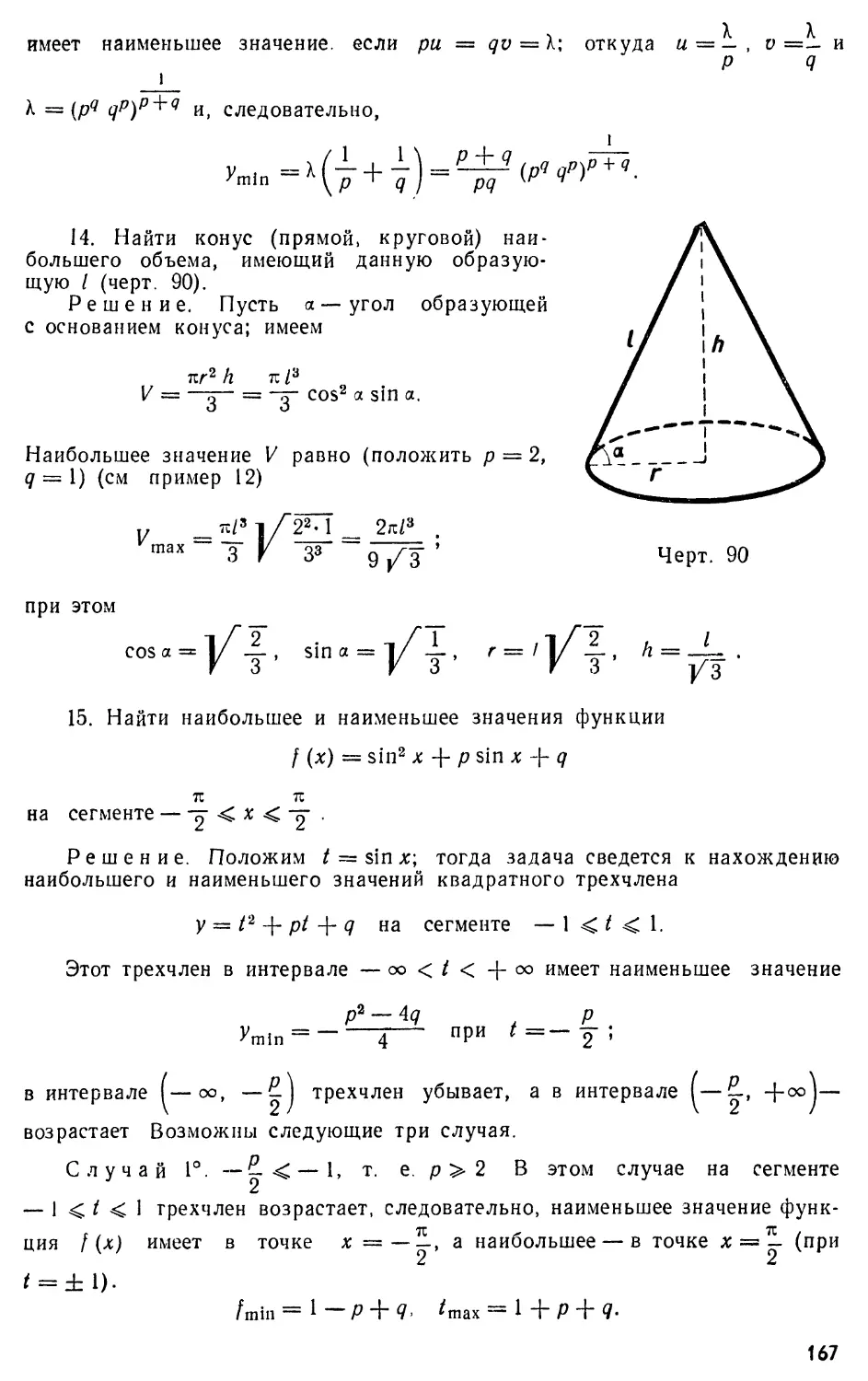
«ВЫСШАЯ ШКОЛА»
Москва —1967
УДК 514. 0(075.8)
Новоселов Сергей Иосифович
СПЕЦИАЛЬНЫЙ КУРС
ТРИГОНОМЕТРИИ
Редактор А. И. Селиверстова
Переплет художника А. Е. Григорьева
Технический редактор В. А. Зорина
Корректор Р. И. Самофатова
Τ-02760. Сдано в набор 14/ХН— 65 г.
Подписано к печати 15/1II—67 г.
Формат 60X90Vie. Объем 33,5 печ. л.
Уч.-изд. л. 31,52. Изд. № ФМ—298
Тираж 30 000 экз. Цена 98 коп.
Тематический план издательства
«Высшая школа» (вузы и техникумы)
на 1966 г.
Позиция № 55
Москва, К -51, Неглинная ул., д. 29/14,
Издательство «Высшая школа» 3.597
Московская типография № 4
Главполиграфпрома
Комитета по печати
при Совете Министров СССР,
Б. Переяславская, д 46
2—2—2
55-66
ПРЕДИСЛОВИЕ
Настоящая книга предназначается в качестве учебного пособия
для физико-математических факультетов педагогических институ-
тов и университетов по разделу «Тригонометрия» — специального
курса элементарной математики. При написании настоящей книги
я руководствовался теми же принципами, которые положены
в основу моей книги «Специальный курс элементарной алгебры»
и которые подробно высказаны мною в предисловии к упомянутой
книге.
Едва ли нужно доказывать необходимость углубленного и систе-
матического изучения студентами элементарной математики, т. е.
той дисциплины, которую они станут преподавать в школе. Раз-
личные курсы «высшей» математики, при всем их огромном значе-
нии, не могут сами по себе обеспечить необходимой профессиональ-
ной подготовки будущего учителя.
Было бы ошибкой думать, что студент изучает элементарную
математику только лишь при прохождении дисциплины, значащей-
ся в учебном плане под названием «Специальный курс элементарной
математики». Эта дисциплина содержит лишь сравнительно немно-
гие основные вопросы элементарной математики, изучаемые в их
взаимной связи и в связи с дисциплинами «высшей» математики.
Изучение методики математики, прохождение педагогической прак-
тики и работа в специальных семинарах требуют от студента серьез-
ного самостоятельного изучения элементарной мате-
матики. По этой причине учебная литература по элементарной
математике, как я полагаю, не может строго ограничиваться рамками
программы «Специального курса», а должна содержать систе-
матическое, углубленное, научно обоснованное и
полное изложение элементарной математики. В учебниках и посо-
биях по элементарной математике студент должен находить ответы
на самые разнообразные вопросы, которые могут у него возник-
нуть по содержанию школьного курса математики. Эти соображения
и побудили меня при написании настоящей книги дать достаточно
полное изложение тригонометрии, тогда как в программе
«Специального курса» вопросы тригонометрии занимают сравни-
тельно небольшой удельный вес,
Настоящую книгу следует рассматривать как продолжение
моей книги «Специальный курс элементарной алгебры», поэтому
вопросы (например, общие положения теории уравнений и нера-
венств), содержащиеся в указанной книге и необходимые для тех
или иных разделов курса тригонометрии, в тексте не излагаются,
а делаются ссылки на соответствующие параграфы «Специального
курса элементарной алгебры» (изд. начиная с 1956 г.).
Последняя IX глава настоящей книги содержит основы теории
элементарных трансцендентных функций над полем комплексных
чисел, т. е. материал, не относящийся собственно к тригоно-
метрии. Этот материал отнесен мною к курсу тригонометрии потому,
что невозможно изучать показательную, логарифмическую, триго-
нометрические и обратные тригонометрические функции над по-
лем комплексных чисел независимо друг от друга.
В четвертом издании книга подверглась переработке, которая
в основном выражается в следующем:
I. Структура курса приближена к структуре современного
школьного курса тригонометрии.
a) Учение о тригонометрических функциях последовательно из-
лагается на координатной основе.
b) Теоремы сложения и их следствия используются в качестве
аппарата для исследования тригонометрических функций.
c) Материал, посвященный исследованию тригонометрических
функций, выделен в особую главу.
d) Расширен вопрос о гармонических колебаниях, как имею-
щий важное прикладное значение.
II. Учтены требования современной программы педагогических
институтов.
a) Аналитические определения тригонометрических функций
при помощи степенных рядов даны независимо от аксиоматического
определения.
b) Введено интегральное представление обратных тригонометри-
ческих функций.
III. Несколько изменено расположение глав: глава «Элементы
сферической тригонометрии» непосредственно следует за главой
«Вычисление элементов геометрических фигур». Такое расположе-
ние в большей степени соответствует логике предмета.
IV. Внесены отдельные изменения, улучшающие (по мнению
автора) изложение. Так, например, в большей мере систематизиро-
ван подбор примеров на тригонометрические уравнения, урав-
нения, содержащие параметры, рассмотрены особо, уточнен вопрос
об исследовании вычислительных задач, исключены некоторые
второстепенные детали и т. п.
В настоящем издании исправлен ряд погрешностей и в отдельных
местах уточнен текст.
Выражаю благодарность П. С. Моденову за ценные советы, ко-
торыми я пользовался при составлении книги,
Автор
ВВЕДЕНИЕ
§ 1. О содержании курса тригонометрии
Возникновение тригонометрии обусловлено потребностями вы-
числительной практики, а именно, необходимостью создания аппа-
рата для вычисления элементов различных геометрических фигур
по достаточному количеству их заданных элементов. Еще в древней
Греции, в связи с решением ряда вычислительных астрономических
задач, тригонометрия достигла значительного развития. Осново-
положное значение в формировании тригонометрии как само-
стоятельной науки имели труды среднеазиатских ученых
IX—XIII вв. Хотя тригонометрия и получила самостоятельное
значение как научная дисциплина, располагающая собственными
методами исследования, все же ее конечная цель усматривалась
в выработке методов вычисления элементов «простейших» геомет-
рических фигур: плоских и сферических треугольников. В основу
учения о тригонометрических функциях неизменно полагались гео-
метрические построения; установленные геометрически алгебраи-
ческие соотношения между тригонометрическими функциями поз-
волили применять алгебраические методы к исследованию этих
функций, к выполнению преобразований, к установлению различ-
ных соотношений между элементами геометрических фигур. Так
сложился своеобразный характер тригонометрии, основывающейся
на геометрии и вместе с тем широко применяющей алгебраические
методы.
Дальнейшее развитие науки показало, что значение тригономет-
рических функций заключается не только в выработке аппарата,
для решения вычислительных геометрических задач; эти функции
получили важное значение в механике и физике при исследовании
периодических процессов. Таким образом, теория три-
гонометрических функций получила самосто-
ятельное значение, и возникла потребность в аналитическом
построении этой теории, не опирающемся на геометрию.
Начала аналитической теории тригонометрических функций
были положены трудами великого ученого, члена Петербургской
Академии наук Л. Эйлера.
Поставив задачу определить тригонометрические функции не-
зависимо от евклидовой геометрической системы, великий русский
математик Н. И. Лобачевский создал аналитическую тео-
рию этих функций, в основу которой был положен аппарат степен-
ных рядов.
В настоящее время тригонометрия как самостоятель-
ная наука не существует: вопросы, связанные с вычис-
лением элементов геометрических фигур, относятся к геомет-
рии, здесь тригонометрия выполняет «служебную» роль; с дру-
гой стороны, аналитическая теория тригонометрических функций
включилась в ту главу математического анализа, которая
посвящается общей теории элементарных функций. Несмотря на то,
что в настоящее время тригонометрия перестала существовать как
самостоятельная наука, она продолжает оставаться весьма важ-
ной самостоятельной учебной дисциплиной. В школьном курсе ма-
тематики тригонометрия по справедливости имеет значительный
удельный вес.
Поскольку достаточно развитый аналитический аппарат, не-
обходимый для построения аналитической теории тригонометри-
ческих функций, далеко выходит за пределы программы, школьный
курс тригонометрии неизбежно строится на геометрической основе.
Кроме того, геометрическая теория тригонометрических функций
в большей степени соответствует практическим приложениям три-
гонометрии.
В современном школьном курсе тригонометрии находят отра-
жение две линии, а именно: функциональная и вы-
числительная. Первая линия, выражающаяся в исследо-
вании тригонометрических функций как функций числового аргу-
мента, имеет важное принципиальное значение, поскольку эти
функции играют существенную роль в современном математическом
анализе, физике, механике, технике. Вторая линия, выражающая-
ся в вычислении элементов геометрических фигур, имеет важное
практическое значение, как дающая вычислительные средства,
необходимые для геометрии, физики, техники, астрономии, геоде-
* Правильное сочетание в школьном курсе обеих указанных линий есть
задача методики математики. Заметим лишь, что нижеследующие две
крайние точки зрения в равной мере являются порочными.
Первая крайность выражается в игнорировании функциональной линии
и в сведении тригонометрии лишь к «решению треугольников».
Другая крайность выражается в игнорировании вычислительной линии.
Решение треугольников, изучаемое в тригонометрии, имеет существенное
значение и поскольку к вычислению элементов треугольников обычно сво-
дится решение различных вычислительных планиметрических и стереомет-
рических задач. Пренебрежительное отношение к разделу, дающему вычис-
лительные средства для геометрии, физики, механики, астрономии и т. д.,
глубоко ошибочно.
В соответствии с общими задачами специального курса элемен-
тарной математики педагогических институтов и университетов,
специальный курс тригонометрии ставит своей целью углубление,
развитие и научное обоснование школьного курса тригонометрии,
а также знакомство с практическими приложениями тригономет-
рии. Специальный курс тригонометрии охватывает в расширенном
изложении все вопросы школьного курса, а потому имеет, наряду
с прочими разделами специального курса элементарной математики,
весьма важное значение с точки зрения профессиональной подго-
товки учителя школы.
В настоящей вводной главе в конспективном изло-
жении указаны те сведения, которые будут считаться извест-
ными из прочих дисциплин, изучающихся в педагогических инсти-
тутах и университетах, и которые послужат основанием для изло-
жения курса тригонометрии в последующих главах.
§ 2. Основные понятия теории проекций
Чтобы отрезку, ограниченному точками А и В, приписать на-
правление, его граничные точки А и В задаются в определенном
порядке; первая точка (пишется на первом месте) называется н а-
чалом отрезка, вторая (пишется на втором месте) — его кон-
цом (черт. 1). Направленный отрезок называется вектором.
Черт. 1 Черт. 2
В кинематической интерпретации вектор АВ рассматривается
как путь, пройденный прямолинейно движущейся точкой от на-
чального положения А до конечного положения В.
Пусть АВ — данный вектор; прямая /, проходящая через точ-
ки Л и β, содержит все точки отрезка АВ. Начальная точка А век-
тора АВ делит прямую / на два луча, один из которых содер-
жит конец В вектора, говорят, что этот луч одинаково
направлен с вектором АВ; другой луч не содержит точку В\
говорят, что этот второй луч противоположно направлен с век-
тором А В (через 2).
Если точки А и В совпадают, то говорят, что А В есть нуль-
вектор.
Примем некоторый отрезок е за единицу длины. Длина отрезка
АВ (при данной единице измерения) называется длиной или м о-
д у л е м вектора АВ. Модуль вектора будем обозначать так: | АВ |.
Пусть АВ и CD — два вектора, расположенные на одной
прямой/, причем каждый из них отличен от нуль-вектора; эти
векторы могут быть либо одинаково направлены, либо про-
тивоположно направлены. Это означает следующее: в пер-
вом случае луч прямой /, одинаково направленный с АВ, и луч,
одинаково направленный с CD, имеют общую часть, являющуюся
также лучом прямой / (черт. 3); во втором случае общей частью
этих двух лучей является либо отрезок, либо точка (общее начало),
либо пустое множество (лучи не имеют общей части) (черт. 4).
D А С В
В
В
СС А
В
Черт. 3
Черт. 4
Пусть АВ и CD — два параллельных вектора, каждый из кото-
рых отличен от нуль-вектора; векторы АВ и CD могут быть направ-
лены либо одинаково, либо противоположно.
Это означает следующее: в первом случае концы В и D данных век-
торов расположены на плоскости по одну сторону относитель-
но прямой АС, соединяющей их начала (черт. 5), во втором случае
точки В и D расположены по разные стороны относительно
прямой АС (черт. 6).
Черт. 5
Черт. 6
Черт. 7
Два вектора считаются равными тогда и только тогда, когда
они параллельны или лежат на одной прямой, одинаково направлены
и равны по длине (черт. 7).
Замена вектора вектором, ему равным, называется перено-
сом вектора.
Пусть / — данная прямая, на которой заданы две точки: на-
чальная точка О и единичная точка Е, так что отрезок ОЕ по
длине равен 1. Заданием точек О и Ε устанавливается положи-
тельное направление на прямой: всякий отличный от
нуля вектор на прямой / считается положительно (отри-
цательно) направленным, если его направление одинако-
во (противоположно) с направлением единичного век-
тора ОЕ (черт. 8).
ч т
о ε
Черт. 8 Черт 9
Нуль-вектору не приписывается никакого направления.
Прямая, на которой установлено положительное направление
и выбран единичный отрезок, называется осью.
Пусть А В — вектор, расположенный на оси /; величиной
вектора будем называть его длину, если он имеет положительное
направление, его длину, взятую со знаком, — если он имеет отри-
цательное направление; величина нуль-вектора считается равной
нулю. Величину вектора АВ будем обозначать так: АВ.
Сложение векторов производится по следующему правилу:
чтобы сложить данные векторы, следует приложить (посредством
переноса) начало второго вектора к концу первого, начало третьего
к концу второго и так далее и построить вектор, соединяющий
начало первого слагаемого с концом последнего.
Пусть Аи Аг, ..., Ап, Ап+\ —данные точки; тогда, согласно
изложенному правилу сложения векторов, имеем
AjA2+ А2А3 + ... + АЛАЛ+, = Aj Ал+1. (черт. 9)
Правило применимо, в частности, если точки Ль Л2.··» Ап+\
расположены на одной прямой (черт. 10, η = 4). Если аь аг, ..., ап
суть величины векторов ΑιΑ2, А2А3, ..., А„Ая+ь расположенных на
оси, то величина вектора-суммы равна сумме величин векторов-
слагаемых:
Лх Ап+\ = Аг А2 + А2 А3 + ...
или
А, А„м\ = ах + а2 + ... + ап
Ап Лп.
ι+1·
Это последнее равенство устанавливается в геометрии для случая
двух слагаемых путем непосредственного рассмотрения всех возмож-
ных взаимных расположений (десять случаев) точек Аи Аъ Аъ
(теорема Шаля) и распространяется для произвольного числа
слагаемых методом математической индукции.
Как известно:
1°. проекцией точки А на ось 1 называется основание А{ перпен-
дикуляра, опущенного из точки А на ось 1.
2°. проекцией вектора А В называется величина вектора А4ВЬ
соединяющего проекцию начала вектора с проекцией его конца
πρ,ΑΒ = Α1Βι. (черт. 11)
Ради краткости, нередко как величину А{В{ вектора AiBb так и
сам вектор А^ называют общим термином проекция.
При параллельном переносе вектора его проекция на данную ось
не меняется: если АВ = CD, то и ΑιΒι = CiDi (черт. 12).
Пусть AiA2 ... Аг+i — произвольная ломаная линия, располо-
женная на плоскости. Звенья этой ломаной будем рассматривать как
векторы ΑιΑ2, Α2Α3, ..., Ап Ал+ь направления которых опреде-
ляются порядком задания вершин. Вектор-сумма
*ι ™η+1 — А] А2
/in ·»»ο
и ό
^м+1
называется также замыкающей данной ломаной. Имеет место
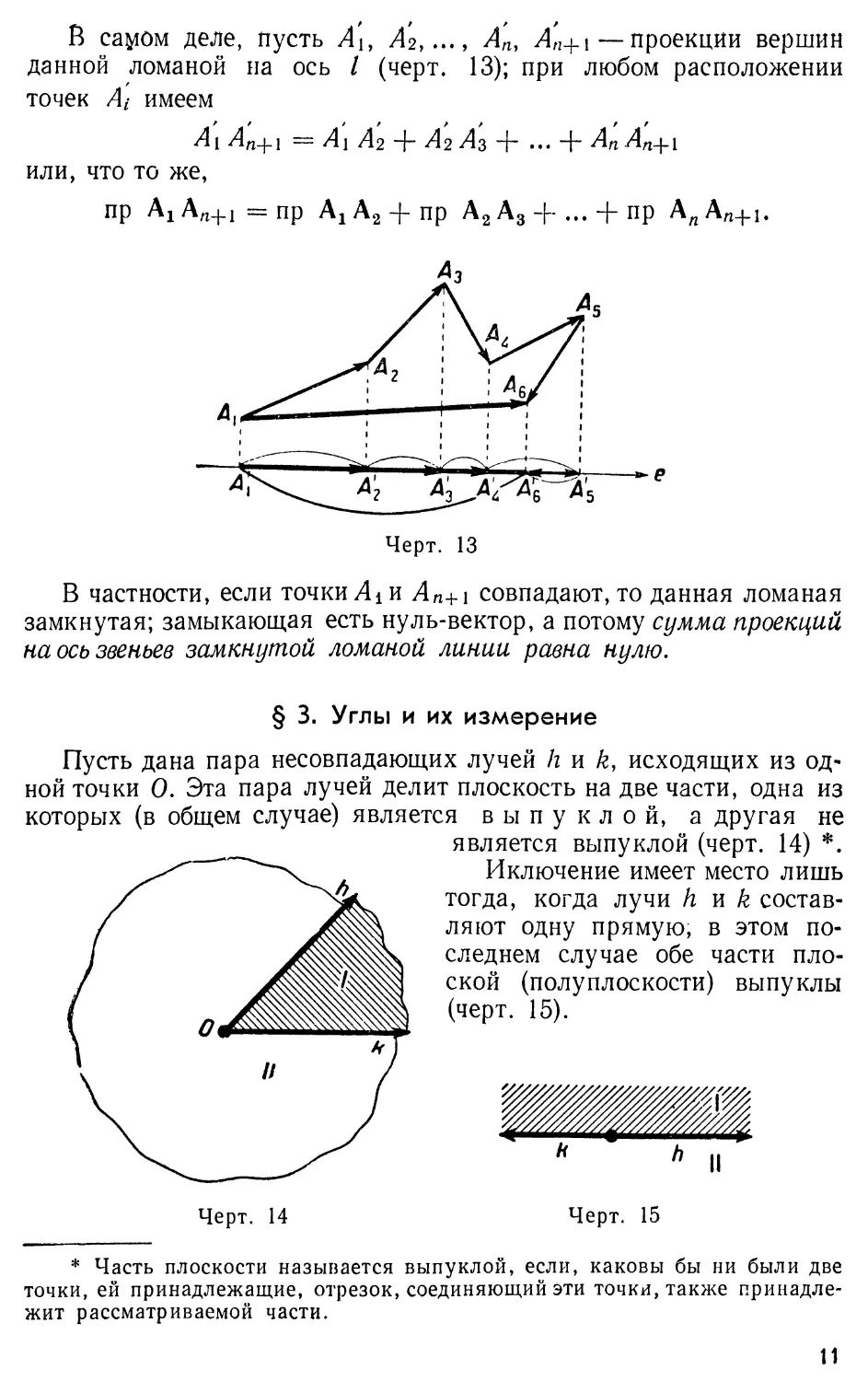
следующая основная теорема о проекции ломаной (черт. 13).
Теорема. Сумма проекций на ось звеньев ломаной равна проек-
ции на туже ось замыкающей; или в другой формулировке: проекция
вектора-суммы равна сумме проекций векторов-слагаемых.
ю
β са^ом деле, пусть А\, А2,..., А'п, А'п+\ —проекции вершин
данной ломаной на ось / (черт. 13); при любом расположении
точек Αι имеем
А\А'п+х =А\А2 + А2Аз + ... + А'
или, что то же,
πρ ΑχΑπ+1 = пр
А2 Ао -}-"
пр
Черт. 13
В частности, если точки Л ι и Ап+\ совпадают, то данная ломаная
замкнутая; замыкающая есть нуль-вектор, а потому сумма проекций
на ось звеньев замкнутой ломаной линии равна нулю.
§ 3. Углы и их измерение
Пусть дана пара несовпадающих лучей /г и k, исходящих из од-
ной точки О. Эта пара лучей делит плоскость на две части, одна из
которых (в общем случае) является выпуклой, а другая не
является выпуклой (черт. 14) *.
Иключение имеет место лишь
тогда, когда лучи h и k состав-
ляют одну прямую, в этом по-
следнем случае обе части пло-
ской (полуплоскости) выпуклы
(черт. 15).
Черт. 14
Черт. 15
* Часть плоскости называется выпуклой, если, каковы бы ни были две
точки, ей принадлежащие, отрезок, соединяющий эти точки, также принадле-
жит рассматриваемой части.
11
В геометрии углом называется система двух различных лучей А и
k, исходящих из одной точки О, причем указывается, какая из двух
частей, на которые делится плоскость данными лучами, считается
внутренней относительно угла. Эта часть плоскости называется
внутренней областью угла, другая часть плоскости—
внешней областью, лучи А и k — сторонами, а точ-
ка О — вершиной угла.
Иногда углом называют не только систему двух лучей А и k, но
и часть плоскости, которую составляет внутренняя область угла
вместе с его сторонами.
В тригонометрии под углом будем понимать множество всех лучей,
исходящих из некоторой точки О и расположенных во внутренней
области некоторого угла с вершиной в точке О, вместе с его сторонами
h и k (черт. 16). Это соответствует кинематическому
представлению угла как «пути», описанного лучом, вращающимся
в плоскости вокруг точки О; при этом стороны А и k суть начальное
и конечное положения вращающегося луча, а прочие «внутренние»
лучи суть его промежуточные положения.
Два различных луча А и k, исходящие из точки О, определяют
два угла; внутренняя область для одного из них является внешней
для другого; эти углы будем называть взаимно дополнитель-
ными.
Черт 16 Черт. 17
Если лучи А и k совпадают, то в этом случае также говорят о двух
взаимно дополнительных углах; один из этих углов нулевой,
для него внутренняя область есть пустое множество;
внутренняя область другого угла есть вся плоскость за
вычетом луча А = k\ этот последний угол называется полным
(черт. 17).
Рассмотрим один из лучей, например А, ограничивающих данный
угол, который предполагается отличным от нулевого и от полного.
Если продолжить луч А (за точку О), то плоскость разделится полу-
ченной прямой на две части — полуплоскости. Одна из этих полу-
плоскостей I либо содержит внутреннюю область данного угла, либо
сама содержится в этой области-, другая полуплоскость II либо содер-
\2
жит внутреннюю область дополнительного угла, либо сама содер-
жимся в этой области (черт. 18).
Будем говорить, что полуплоскость I располагается во внут-
реннем направлении, а полуплоскость II — во в н е ш-
нем направлении относительно стороны А данного угла.
Для нулевого угла по-
нятие полуплоскости, рас-
положенной во внутрен-
нем направлении, не имеет
смысла. Для полного угла
следует дать специальное
указание, какая именно из
полуплоскостей считается
расположенной во внут-
реннем направлении.
Пусть О и О' — верши-
ны двух углов на плоско-
сти, а A, k и A', k! — их стороны. Совместим две какие-либо сто-
роны, например Аи /ι',этих углов так, чтобы совпали и полупло-
скости, расположенные во внутреннем направлении относительно
этих сторон *. Иными словами, приложим углы друг к другу сто-
ронами А и А' так, чтобы совпали и полуплоскости, расположен-
ные во внутреннем направлении. Если при таком совмещении
совместятся стороны k и k' (черт. 19), то углы ^(А, k) и ^(А', k')
равны (конгруэнтны), если же стороны k и k' не совместятся, то
углы не равны. Пусть, например, сторона k' окажется во
Черт. 18
Черт. 19
внутренней области угла ^(Л, &), тогда (черт. 20) ^(А, k)
при этом угол ^(А, k) рассматривается как сумма угла ^(А\ kr) и
угла </.{k\ k), где внутренней областью угла </(kr, k) считается та
* Для этого совмещения возможно пользоваться как движением, так и
отражением, «переворачиванием» плоскости.
13
часть плоскости, которая содержится внутри угла
образом, имеем
к).
, k). Таким
Измерение углов производится по общим принципам измерения
скалярных величин. Приняв некоторый угол за единицу измерения,
относят всякому ненулевому углу положительное число —его меру,
Черт. 20
или величину. При этом, как обычно, равные углы имеют равную
величину, величина суммы двух углов равна сумме их величин
(аддитивность меры); величина угла, принятого за единицу изме-
рения, равна 1; величина нулевого угла равна 0.
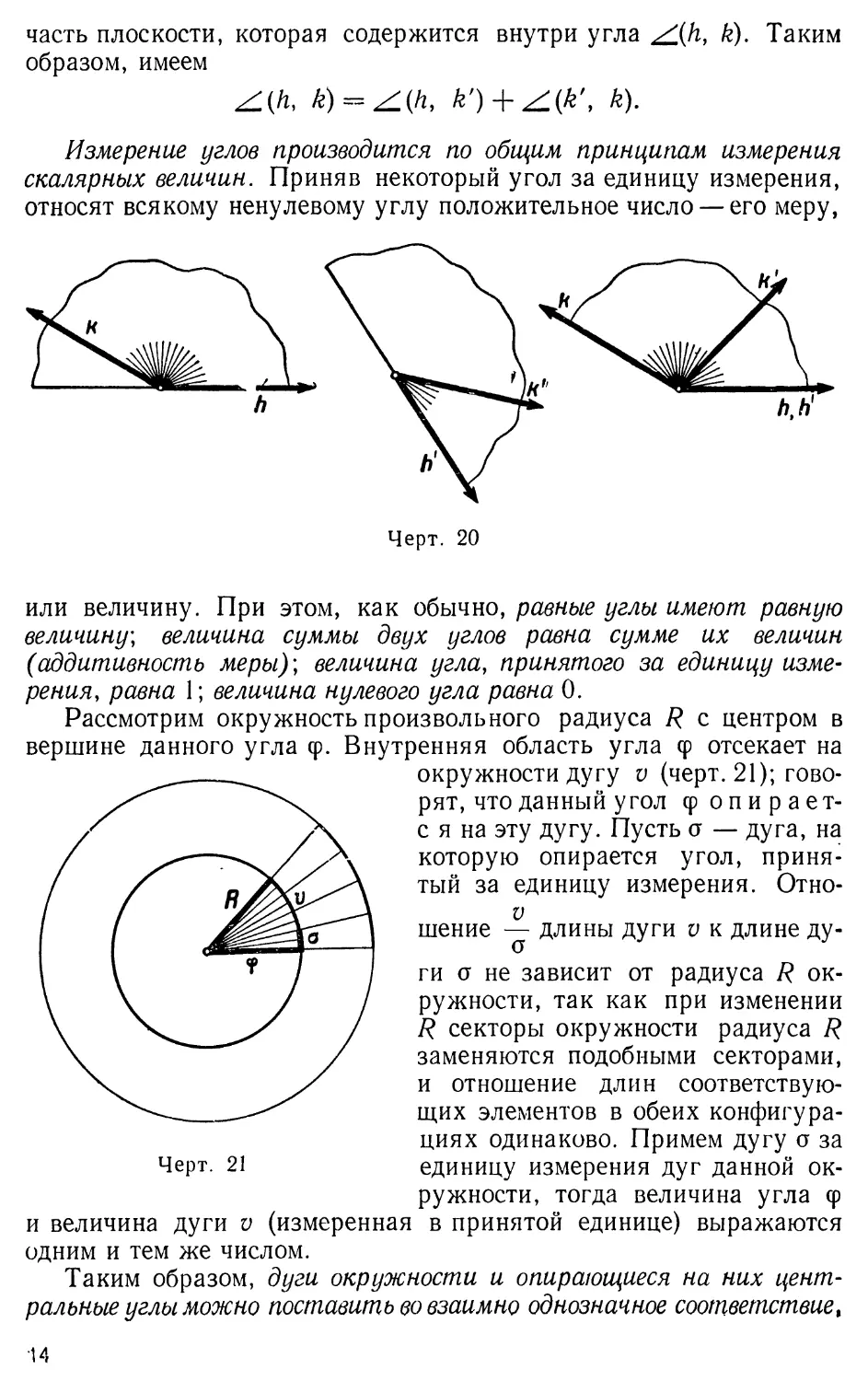
Рассмотрим окружность произвольного радиуса R с центром в
вершине данного угла φ. Внутренняя область угла φ отсекает на
окружности дугу ν (черт. 21); гово-
рят, что данный угол фопирает-
с я на эту дугу. Пусть σ — дуга, на
которую опирается угол, приня-
тый за единицу измерения. Отно-
V
шение — длины дуги υ к длине ду-
ги σ не зависит от радиуса R ок-
ружности, так как при изменении
R секторы окружности радиуса R
заменяются подобными секторами,
и отношение длин соответствую-
щих элементов в обеих конфигура-
циях одинаково. Примем дугу σ за
Черт. 21 единицу измерения дуг данной ок-
ружности, тогда величина угла φ
и величина дуги ν (измеренная в принятой единице) выражаются
одним и тем же числом.
Таким образом, дуги окружности и опирающиеся на них цент-
ральные углы можно поставить во взаимно однозначное соответствие,
14
при этом соответственные угол и дуга измеряются одним и тем же
числом в угловой и соответственной ей дуговой единице.
В вычислительной практике обычно за единицу измерения углов
о 1
принимают угол, равный ™ части полного угла, этот угол назы-
вается градусом. Нередко в элементарной геометрии величина
угла выражается «в долях d» — это значит, что за единицу измерения
принимается прямой угол. В математическом анализе и в различных
теоретических рассуждениях за единицу измерения углов (или дуг)
принимается радиан (дуговой радиан). Введение радианной меры
основано на следующем предложении.
Отношение длины дуги окружности, на которую данный угол,
как центральный, опирается, к радиусу окружности не зависит от
величины радиуса и определяется данным углом.
В самом деле, при изменении радиуса это отношение, будучи от-
ношением сходственных линий в подобных фигурах (дуги и радиусы,
ограничивающие подобные секторы) (см. черт. 21), не меняется.
Радианной мерой угла (и соответствующей дуги) называется от-
ношение длины дуги, для которой данный угол φ является централь-
ным, к ее (дуги) радиусу.
В радианном измерении за единицу измерения углов принимает-
ся угол (центральный), опирающийся на дугу, длина которой равна
радиусу. Этот угол называется угловым радианом, а соот-
ветствующая дуга — дуговым радианом. При обозначе-
нии радианной меры не принято ставить наименование
единицы измерения.
Введение радианной меры целесообразно при изучении тригоно-
метрических функций числового аргумента средствами математи-
ческого анализа; градусное измерение углов и дуг удобно на прак-
тике тем, что в нем единица измерения (градус) соизмерима
с полным оборотом.
Углы и дуги можно рассматривать как направленные
величины (в предыдущих рассуждениях мы рассматривали их как
величины ненаправленные). Чтобы ненулевому углу со сторонами
h и k придать направление, стороны h и k задаются в определенном
порядке, первая сторона (пишется на первом месте) называется н а-
чальной, а вторая (пишется на втором месте) — конечной
сторонами данного угла. С кинематической точки зрения направ-
ленный угол можно представить себе, как «путь», описанный лу-
чом, вращающимся вокруг точки (вершины угла) в определен-
ном направлении; начальная и конечная стороны угла суть
начальное и конечное положения этого луча. Для обозначения на-
правленного угла на чертежах ставят стрелку в направлении от
начальной стороны к конечной.
Пусть /JJx, k) и /JJi', k') — два направленные угла на плос-
кости; при помощи движения первого рода («переворачива-
ние» плоскости не допускается) можно совместить их начальные
15
стороны, тогда полуплоскости, расположенные во внутреннем на-
правлении относительно начальных сторон данных углов, либо сов-
местятся (черт. 22, а), либо не совместятся (черт. 22, 6), оказавшись
по разные стороны от прямой, на которой будут лежать лучи h и К
после их совмещения. В первом случае углы ^(Л, k) и ^/(/г\ k') на-
зываются одинаково направленными (или ориентированными),
а во втором — противоположно направленными *.
а)
Черт. 22
Будем считать некоторый данный направленный угол на плос-
кости положительно направленным; говорят, что тем са-
мым на плоскости задается положительное направление вращения.
* Таким образом, одинаковая или противоположная ориентация углов
различается по тому, каким движением первого или второго рода
могут быть совмещены начальные стороны и полуплоскости, расположенные
во внутреннем направлении относительно этих сторон. В элементар-
ной геометрии считается очевидным, что совмещение двух конгруэнт-
ных фигур может осуществляться либо движением в плоскости без «перево-
рачивания» (движение первого рода), либо, кроме того, для совмещения не-
обходимо «перевернуть» плоскость «'другой стороной». В основаниях геомет-
рии, напротив, понятие одинаковой и противоположной ориентации пред-
шествуют различению движений на движения первого и второго рода Пер-
вое определяется как движение, сохраняющее ориентацию треуголь-
ника, второе — как изменяющее ее на противоположную. Не имея
возможности входить в подробности, относящиеся к основаниям геометрии,
в тексте мы сформулировали лишь окончательный результат, который полу-
чится после обоснования понятия двух родов движения.
16
Плоскость, на которой задано положительное направление вра-
щения, называется ориентированной плоскостью. Всякий
угол, одинаково направленный с данным, также называется положи-
тельно направленным', всякий угол, противоположно направленный
с данным, называется отрицательно направленным. Нулевому углу
не приписывается никакого направления.
При измерении углов на ориентированной плоскости принимают
некоторый положительно направленный угол за единицу изме-
рения. Если данный угол положительно направлен, то его величи-
ной считается положительное число, равное результату
измерения; если данный угол отрицательно направлен, то
его величиной считается отрицательное число, равное результату
измерения, взятому со знаком минус.
Практические потребности физики, механики, техники приводят
к необходимости дальнейшего расширения понятия угла. Углы,
которые мы рассматривали в предыдущих рассуждениях, по абсо-
лютной величине не могли превосходить полного угла. С кине-
матической точки зрения полный (положительный или отрицатель-
ный) угол есть «путь», пройденный вращающимся около точки лу-
чом, который, описав в плоскости полный оборот (в положительном
или отрицательном направлении), вернулся в первоначальное по-
ложение. Винт, пропеллер самолета, маховое колесо машины и т. п.
могут совершать любое количество полных оборотов в том или ином
направлении. Исходя из сказанного, считают, что всякое действи-
тельное число (при выбранной единице измерения углов) взаимно од-
нозначно определяет некоторый угол. Примем для определенности
радианную систему измерения углов. Пусть φ — данное положи-
тельное число; если φ<2π, то это число определяет тот угол, кото-
рый им измеряется; если φ>2π, то представим φ в виде суммы
φ = 2kn + α,
где 0<^α<2π, a k —целое положительное число (это представление
единственно). Тогда рассматриваем угол, определяемый числом φ,
как состоящий из k положительных полных углов и угла ос. Анало-
гично, если φ — отрицательное число и | φ | >2π, то можно предста-
вить φ в том же виде φ == 2kn + а, где —2π<α<0, a k — целое
отрицательное число; в таком случае рассматриваем угол φ, как со-
стоящий из k отрицательных полных углов и угла а.
Итак, введение в рассмотрение углов любой величины позволяет по-
ставить во взаимно однозначное соответствие множество всех дейст-
вительных чисел и множество всех углов на плоскости, в силу которого
всякому действительному числу соответствует некоторый угол
ориентированной плоскости, и обратно — всякому углу соответству-
ет некоторое действительное число.
Дуги окружности также можно рассматривать как направлен-
ные величины, а именно дуга считается положительно (отрлцатель-
2 Зак. 597 17
но) направленной, если опирающийся -на нее центральный угол по-
ложительно (отрицательно) направлен (черт. 23). Наконец, можно
рассматривать дуги любой величины. Так, например, дугу, измеряю-
щуюся числом 2kn + α (где k —
натуральное число, а 0<α<Ί2π)
можно представить себе как ре-
зультат наматывания на окруж-
ность радиуса R нерастяжимой
нити, имеющей длину, равную
(2kn +a)R, а дугу, измеряющуюся
числом — (2Ы 4- а) — как резуль-
тат наматывания на окружность
той же нити, но в противополож-
ном направлении.
Расширение понятия угла (ду-
ги) позволяет складывать направ-
ленные углы (дуги) произвольной
величины; имеем всегда
Черт. 23
где ^(Λι, Α/ι+ι) есть угол со сторонами hu hn+\> измеряющийся чис-
лом, равным сумме (алгебраической) величин углов-слагаемых.
§ 4. Координатная плоскость
Рассмотрим плоскость, на которой задана прямоугольная декар-
това система координат XOY (черт. 24); такую плоскость будем на-
зывать координатной плоскостью. Всякой паре (а, Ь) дей-
ствительных чисел взаимно однозначно соответствует точка коор-
динатной плоскости, для которой число а является абсциссой, а
b — ординатой. Координатная плоскость является ориентиро-
ван н о й, а именно: положительно направленным считается прямой
угол XOY, для которого начальной стороной служит положительная
полуось абсцисс, а конечной — положительная полуось ординат.
В тригонометрии нередко, в соответствии с распространенным
изображением на чертежах, ось абсцисс называют горизонталь-
н о й, а ось ординат — вертикальной.
Пусть М(а, Ь) — произвольная точка координатной плоскости;
вектор ОМ, соединяющий начало координат с точкой М, называ-
ется рад и усом-вектором этой точки.
Пусть F — произвольный вектор (черт. 25) на координатной
плоскости, Fx и Fy — его проекции на оси ОХ и OY, тогда длину дан-
ного вектора можно вычислить по формуле
(1)
18
В самом деле, достаточно перенести вектор F так, чтобы его начало
совпадало с началом координат, тогда \FX | и \Fy | суть катеты прямо-
угольного треугольника, для которого \F\ является гипотенузой,
откуда следует справедливость формулы (1). Исключение представ-
ляется лишь в случаях, когда вектор F лежит (после переноса) либо
на оси абсцисс (тогда Fx = 0), либо на оси ординат (тогда Fy = 0),
в этих случаях треугольник вырождается в отрезок, а справедли-
вость формулы (1) устанавливается непосредственно.
\F*\
Черт. 24
Черт. 25
Пусть А(хи уд и В(х2, У2) —Две произвольные данные
точки, Ах и Вх — их проекции на ось абсцисс;
имеем
пр^ А В = ОВХ — ОАХ = х2 — хг
и аналогично
Расстояние d между точками А и В есть длина вектора АВ:
Последняя формула верна при произвольном положении
точек А и В на плоскости.
Примем положительную полуось ОХ за начало отсчета углов,
т. е. будем рассматривать множество всех углов (направленных),
для которых луч ОХ является начальной стороной (черт. 26). Вся-
кому действительному числу φ соответствует некоторое вполне
определенное положение конечной стороны угла, измеряющегося этим
числом. Это соответствие не является взаимно однозначным,
так как двум углам, отличающимся целым числом полных углов, т. е.
слагаемым 21гл (k — целое число), кратным 2π, соответствует одно
и то же положение их конечных сторон, и обратно: величины двух
углов с совпадающими конечными сторонами отличаются на сла-
гаемое вида 2kn.
2*
19
Рассмотрим круг с центром в начале координат и с радиусом 1;
на окружности этого круга примем точку Л(1, 0) за начало отсчета
дуг и установим положительное направление, соответствующее
ориентации координатной плоскости. Пусть φ — данное действи-
тельное число; отложим от точки А (в положительном либо в отри-
цательном направлении) ду-
гу, величина которой равна
φ, длина этой дуги равна | φ .
Центральный угол, опираю-
щийся на эту дугу, изме-
Черт. 26
Черт. 27
ряется (в радианной мере) тем же числом φ. Точку Μ — конец
отложенной дуги — будем рассматривать как изображение на еди-
ничной окружности числа φ (черт. 27). Ориентированную единичную
окружность, точками которой изображаются действительные числа,
будем называть также числовой окружностью, а ограниченный
ею круг — единичным кругом. Два различных действи-
вительных числа φΑ и φ2 изображаются одной и той же точкой еди-
ничной окружности в том и только в том случае, если
<Р2 — φι =
т. е. если φ2 =
где k — целое число.
Координатные оси делят единичный круг (окружность) на че-
тыре части: I, II, III и IV (черт. 28), называемые четвертями
единичного круга (единичной окружности). Точки пересечения ко-
ординатных осей с единичной окружностью, разделяющие ее на
четыре дуги, могут причисляться, а могут не причисляться к этим
дугам. В первом случае четверти единичной окружности называ-
ются замкнутыми, а во втором — открытыми. Рас-
смотрим, например, первую четверть единичной окружности. Чис-
ловой сегмент Ο^φ^^" изобразится на единичной окружности
в виде замкнутой первой четверти, а числовой — интер-
вал 0<^ф<С"9 — в виДе открытой первой четверти (черт. 29).
20
Сегменту -|<φ<π соответствует вторая замкнутая четверть, а ин-
тервалу -^<φ<π — вторая открытая четверть и т. д. Всякий чи-
словой интервал 2kn <С ф <С(2£ + Π л; (k — произвольное целое
if
IV
Черт. 28
Черт. 29
число) изображается на единичной окружности ее первой открытой
четвертью, интервал ( 2k-\- γ) я < φ <[ {2k + 1) π изображается вто-
рой четвертью и т. д. Первая и вторая четверти (вместе с их общей
граничной точкой φ = ^-J образуют в сумме полуокружность, назы-
ваемую верхней полуокружностью. Числовому интервалу
О < ψ <С Ц (сегменту 0 <; φ <; π) соответствует открытая
(замкнутая) верхняя полуокружность, к которой не причис-
ляются (причисляются) ее концы. Третья и четвертая четверти
образуют в сумме нижнюю полуокружность;
эта полуокружность (открытая) соответствует а
интервалу π < φ < 2π. Аналогично опреде-
ляются правая и левая полуокружности, пер-
вая соответствует интервалу —^ < φ < |- ,
вторая — интервалу ^ < φ < ^ π (^ля замк-
нутых полуокружностей надо брать соответ-
ствующие сегменты).
Если конечная сторона угла (или конец
дуги) содержится в некоторой четверти, то
говорят, что данный угол (дуга) оканчи-
вается в этой четверти. Пусть а и b — два действительных чис-
ла, взятые при условии 0<α<6<2π; числовой промежуток (от-
крытый или замкнутый), ограниченный этими числами (снизу чис-
лом а, сверху числом Ь), изображается на единичной окружности
дугой с концами в точках, изображающих числа а и b (черт. 30).
Черт. 30
21
Той же самой дугой изобразится всякий промежуток, ограничен-
ный числами а + 2Ы и Ь f 2&jt, где k — произвольное целое
число. Сопоставим способы изображения действительных чисел
точками окружности и точками прямой линии при помощи следую-
щей наглядной иллюстрации. Представим себе числовую ось в виде
тонкой нерастяжимой бесконечной нити. Совместив начальную
точку прямой с начальной точкой /1(1, 0) единичной окружности,
будем наматывать нить на окружность, тогда точки числовой пря-
мой и точки окружности, изображающие одно и то же число, со-
вместятся.
§ 5. О монотонных функциях
Мы предполагаем известным общее понятие функции, а также
связанные с ним основные понятия учения о функциях: область
определения функции, множество ее значений, ограниченность и
неограниченность числовой функции, непрерывность.
В тригонометрии особо важную роль играют монотонные
функции. Как известно, функция f (х) называется возрастающей
(убывающей) в данном промежутке, если при произвольных двух
различных значениях аргумента, принадлежащих данному проме-
жутку, большему значению аргумента соответствует большее
(меньшее) значение функции
f(x1)<f(x2)> если хг<х2
для возрастающей функции, и
), если *!<*<,
для убывающей функции.
Возрастающая и убывающая функции относятся к классу м о-
нотонных функций.
При изучении действительных функций от дейст-
вительного аргумента мы будем рассматривать лишь о д-
нозначные функции, т. е. функции, для которых каждому
значению аргумента соответствует единственное значение функции*.
Будем говорить, что функция f(x) на сегменте аКх<Ь возра-
стает (убывает) от т до М, если:
1° функция f(x) возрастает (убывает) на сегменте \а, Ь]\
2° в концах а и Ь сегмента имеет значения, равные (соответст-
венно) т и Μ
f(a) = m
* Понятие многозначной функции встретится в данной книге в гл. VIII,
где идет речь об элементарных функциях от комплексного аргу-
мента.
22
3° всякое значение г, промежуточное между т и М:
т<^с<^М (для возрастающей функции)
или
• Μ (для убывающей функции),
функция f(x) имеет при некотором значении х = 1 в интерва-
ле (а, Ь):
= с, где α<ξ<& (черт. 31).
Mmf(b) м
M-f(b)
Черт. 31
В силу монотонности функции, это значение ^единствен-
н о.
Из математического анализа известно, что если функция f(x)
возрастает (убывает) и непрерывна на сегменте [а, Ь], то она воз-
растает (убывает) на этом сегменте от f (а) до f(b). Для моно-
тонных функций справедливо и обратное:
если функция f(x) возрастает (убывает) от f (а) до f (b) на сег-
менте [а} Ь]9 то она непрерывна на этом сегменте.
Аналогично определяется понятие функции, возрастающей
(убывающей) от т до /И в и н τ е ρ в а л е (а, Ь)\ в этом случае ус-
ловие 2° заменяется следующим условием 2':
2',
lim/(χ) = m,
==M.
Следует иметь в виду, что интервал (а, Ь) может быть как ко-
нечным, так и бесконечным, а т и Μ могут быть как
действительными числами, так и иметь беско-
нечные значения ±оо. Так, например, функция 2х в интервале
(—оо, + оо) возрастает от 0 до + оо, функция \gx в интерва-
ле (0, + оо) возрастает от —сю до + оо, функция - в интервале
(О, 1) убывает от +оо до 1 (черт. 32).
В математическом анализе доказывается следующая георема
об обратной функции.
Теорема. Всякая возрастающая (убывающая) функция имеет
обратную функцию. При этом обратная функция также возраста-
ет (убывает).
Если функция f(x) на сегменте a<jt<fc возрастает (убывает)
от т до М, то обратная на сегменте m<y<7W (на сегменте М<у<га)
у=/5х
г
Черт. 32
функция возрастает (убывает) от а до Ь (с надлежащим изменением
последнее утверждение справедливо для функции, монотонной в
интервале)
Черт. 33
Функция немонотонная может не иметь обратную функцию,
так как данное ее значение функция может иметь при нескольких
(быть может, на бесконечном множестве) значениях аргумента, и
тогда каждому значению функции у нельзя поставить в соответ-
ствие единственное значение дс. при котором
у = /(*).
24
Предположим, что область определения функции y=zf(x)
можно разбить на промежутки монотонности, т. е.
на такие промежутки, в каждом из которых она либо возрастает,
либо убывает. В этом частном случае переход к обратной функции
возможен в каждом данном промежутке монотонности функции
f(x) (черт. 33). Так, например, для функции у = х2 в интервале
— оо <х< +оо невозможен переход к обратной функции, так как
всякое положительное значение у функция имеет при двух
различных значениях χ = ±l/y. Интервал (-—оо, +оо)
можно разбить на два промежутка: —оо < χ <0 и 0 <; χ < +°°;
в первом из этих промежутков функция у = х2 убывает и имеет
обратную функцию
X
— Vyi
во втором из этих промежутков функция у = х2 возрастает и имеет
обратную функцию
§ 6. Периодические функции
Определение. Функция f {x) называется периодической, если су-
ществует положительное число I (хотя бы одно) такое, что при
любом значении аргумента χ значения функции f {x) в точках х,
χ + Ι, χ — I равны
f(x)=f(x+l)=f(x-l).
Из этого определения следует, что если точка χ принадлежит области
определения функции f(x), то точки х±1 также принадлежат обла-
сти ее определения. На том же основании точки χ±21, χ±3/ и
вообще χ + kl (где k — произвольное целое число) вместе с точкой
χ принадлежат области определения функции /(#), и имеет место
равенство: ?·
f(x + kl)--
В самом деле
Рассмотрим двустороннюю последовательность сегментов
..., [-/, 0]; [0, /]; [/, 2/]; [2/, 3/],...,
каждый из которых (кроме [0, /]) может быть получен из «началь-
ного» сегмента [0, I] переносом вдоль оси абсцисс. График перио-
дической функции у = f (x) одинаков на каждом из этих сегментов;
2В Зак. 597 25
в этом смысле говорят, что графиком перрюдической функций
является линия, «повторяющаяся» бесконечное множество раз
(черт. 34).
Черт. 34
Если f {χ) есть периодическая функция с периодом Ζ и т — не-
которое действительное число, то для отыскания множества всех
значений аргумента х, при которых значение функции равно т,
т. е., иными словами, для решения уравнения
f(x)=m (1)
достаточно найти множество хи Хъ ··· всех искомых значений аргу-
мента лишь на полусегменте 0<*</. Множество всехрешений урав-
нения (1) получится, если к каждому найденному решению приба-
вить произвольное слагаемое, кратное периоду (черт. 35)
А
и
Черт. 35
Следовательно, уравнение (1) либо не имеет решений, либо имеет
бесконечное множество решений.
Если периодическая функция с периодом I обладает некоторыми
свойствами (например, монотонна, непрерывна, ограничена) в не-
котором промежутке [α, β], принадлежащем начальному сегменту:
0<α<β</,
U
то она обладает тем же свойством в каждом из промежутков
(черт. 36)
/, β+ /],.... [α
» + Щ.
Заметим, что при исследова-
нии свойств периодической
функции вместо начального
сегмента 10, /] можно взять
любой сегмент [а, а + /],
охватывающий ее полный пе-
риод.
Если число / есть период
функции f(x), то любое из
чисел 2/, 3/, ..., и/, также яв-
Черт
ляется ее периодом.
Если среди всех периодов данной функции существует наи-
меньшее положительное число, то этот наименьший
положительный период обычно кратко называется перио-
дом *.
* Из курса математического анализа известно, что если для непре-
рывной периодической функции не существует наименьшего положитель-
ного периода, то данная функция постоянна Таким образом, всякая непрерыы
пая непостоянная периодическая функция имеет наименьший положительный
период.
Глава первая
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
И СООТНОШЕНИЯ МЕЖДУ НИМИ
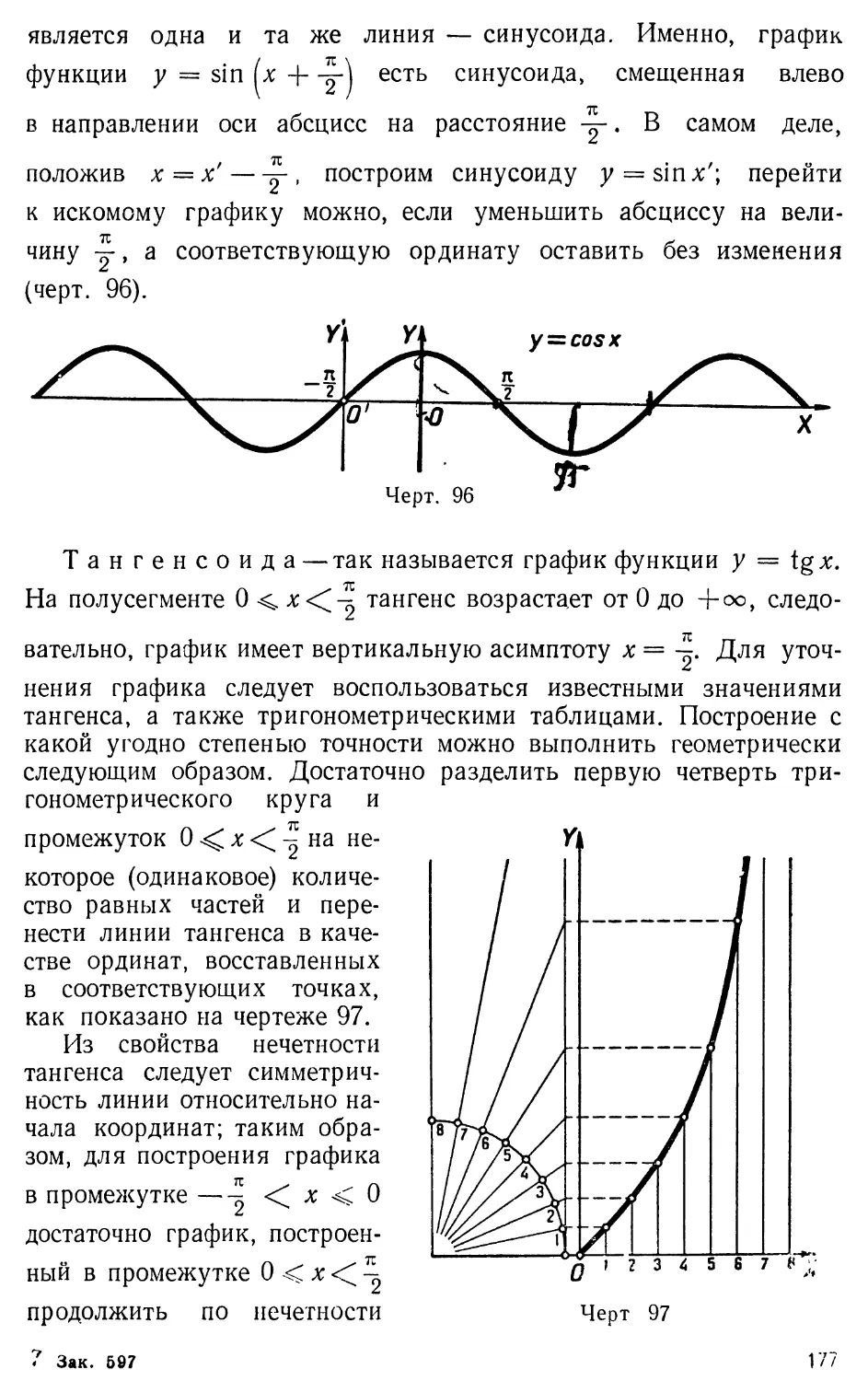
Му\
§ 7. Тригонометрические функции угла
Пусть а — произвольный данный (направленный) угол на ори-
ентированной плоскости. Установив на плоскости произвольную
декартову прямоугольную систему координат, отложим угол а,
приняв начало координат за его вершину, а положительную по-
луось абсцисс — за начальную сторону
(черт. 37).
Выберем произвольную точку МфО на
конечной стороне угла а. Таким образом,
ОМ есть произвольный радиус-вектор на
координатной плоскости, образующий угол
а с положительной полуосью абсцисс. Этот
радиус-вектор называется также подвиж-
церт 37 ным радиусом. Пусть χ и у — абсцисса и
ордината точки М, а р = \ОМ\ =
= Ух1 + >'2 —длина радиуса-вектора ОМ.
Теорема. Для произвольного радиуса-вектора, образующего дан-
ный угол а с осью абсцисс, каждое из отношений
У
У_
X
(1)
либо имеет одно и то же значение, либо не существует.
Разъяснение. Теорема утверждает, что каждое из от-
ношений (I) при данном угле ос не зависит от длины подвижного ра-
диуса ОМ и определяется исключительно величиной а.
Доказательство. Случай Г. Конечная сторона угла α
не принадлежит ни одной из координатных осей, т. е.
k — целое число).
2 (гАе
28
Возьмем на конечной стороне угла α две любые точки М(х, у) и
М'{х', У')> отличные от точки О (черт. 38, а и Ь). Если из точек Μ
и М' опустить перпендикуляры на ось абсцисс, то получатся π ο-
лобные прямоугольные треугольники ОММХ. и ОМ'МХ. Кате-
ты треугольника ОМХМ суть абсолютные величины координат
Черт. 38
точки М, т. е. \х\ и |у|, гипотенуза равна длине ρ радиуса-вектора
ОМ. Катеты и гипотенуза треугольника ОМ'МХ суть |х'|, |/j и р'.
Равенство
Ρ Ρ
выражает равенство отношений сходственных катетов к гипоте-
нузе. Векторы ОМК и ОМХ на оси ОХ одинаково направлены, так
как лучи, соединяющие точку О с точками Мх и М'х, совпадают
между собой, являясь проекцией конечной стороны угла α на его
начальную сторону. Абсциссы χ и х' суть числа одного и того же
знака как величины двух одинаково направленных векторов ОМХ
и 0Мх оси абсцисс, поэтому отношения - и —, совпадают не только
по абсолютной величине, но и по знаку, т. е. i- = -.
Ρ Ρ
Итак, отношение - при данном угле а одно и то же, незави-
симо от длины радиуса-вектора ОМ. Аналогично доказывается
теорема и для трех остальных отношений.
Случай 2°. Конечная сторона угла а принадлежит либо го-
ризонтальной, либо вертикальной оси, т. е. а = k% . Треугольники
ОММХ и ОМ'МХ вырождаются в отрезки; этот случай требует
специального рассмотрения.
29
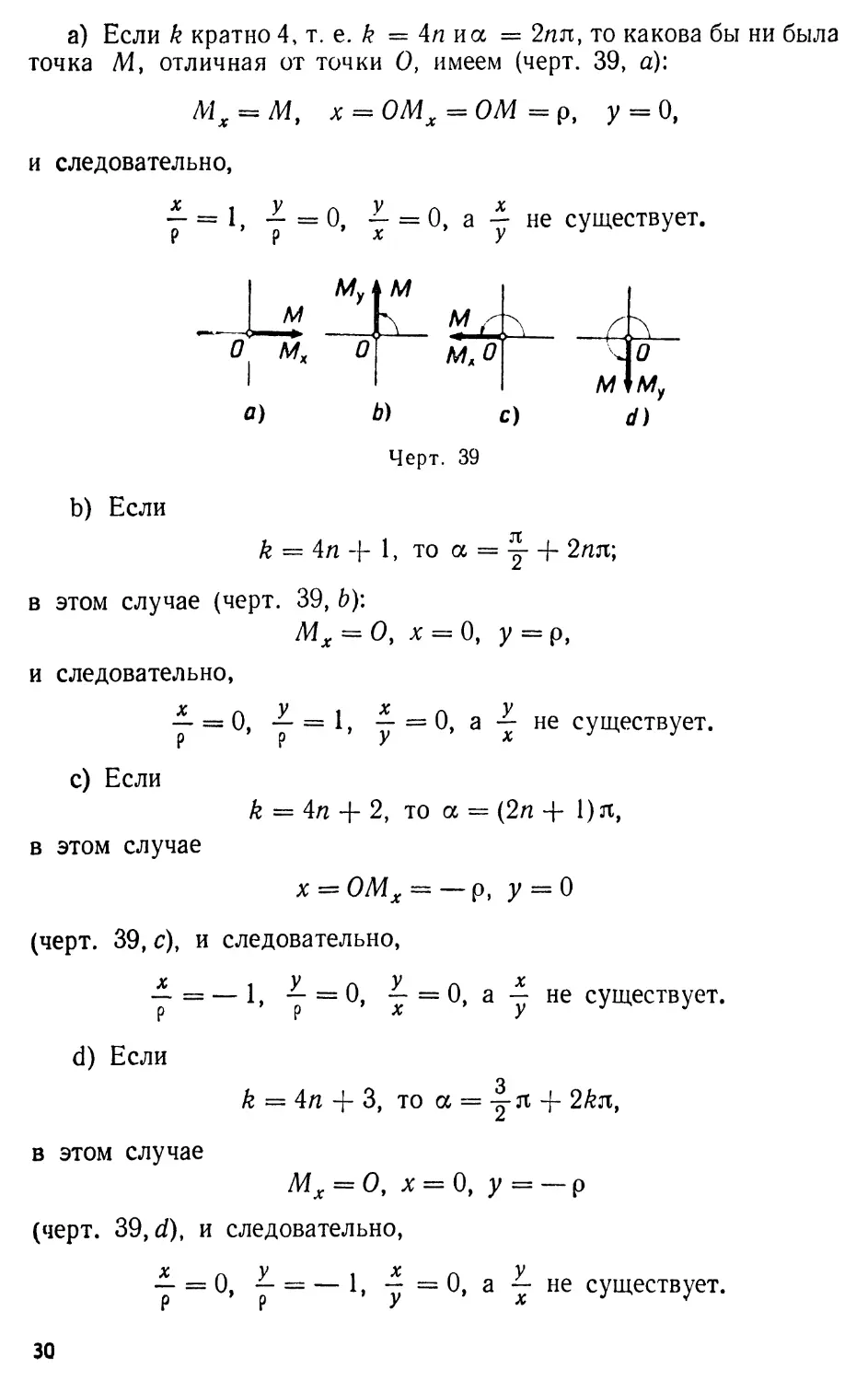
а) Если k кратно 4, т. е. k = An и α = 2ηπ, то какова бы ни была
точка /И, отличная от точки О, имеем (черт. 39, а):
Мх = М, х== ОМХ = ОМ = р, у = О,
и следовательно,
7" = 1, — = 0, — = 0, а — не существует.
Μ
Mj.
a) b) с) d)
Черт. 39
b) Если
k = 4п + 1, то α = у + 2шг;
в этом случае (черт. 39, Ь):
МХ = О, х = 0, у = р,
и следовательно,
-- = 0, f- = 1, - = 0, а ή- не существует.
с) Если
в этом случае
2, то а = (2п+ 1)π,
(черт. 39, с), и следовательно,
7
d) Если
j = — 1, у = 0, ^- = 0, а -£ не существует.
= 4п + 3, то α = -ό-π +
в этом случае
(черт. 39, d), и следовательно,
Χ Γι У 1 Х П У
j = 0, — = — 1, - = 0, а ~ не существует.
30
Итак, во всех случаях при данном угле а каждое из отноше-
ний (1) либо имеет одно и то же значение, либо не существует,
независимо от выбора точки М, на конечной стороне угла а.
ч. т. д.
Для двух различных углов отношения (1) (каждое) имеют,
вообще говоря, различные значения.
Определения: 1°. Отношение абсциссы χ конца радиуса-
вектора, образующего угол а с осью абсцисс, к длине ρ радиуса*
вектора называется косинусом угла а.
2°. Отношение ординаты у конца радиуса-вектора, образую-
щего угол а с осью абсцисс, к длине ρ радиуса-вектора называется
синусом угла а.
3е. Отношение ординаты у к абсциссе χ конца радиуса-вектора,
образующего угол а с осью абсцисс, называется тангенсом угла а.
4°. Отношение абсциссы χ к ординате у конца радиуса-вектора,
образующего угол а с осью абсцисс, называется котангенсом угла а.
Косинус, синус, тангенс и котангенс обозначаются (соответ-
ственно) так:
Значение каждого из этих отношений определяется только лишь
углом а, поэтому они (отношения) суть функции угла а — эти
функции называются тригонометрическими функциями угла.
Определения 3° и 4° можно заменить следующими эквивалент-
ными определениями:
3'. Тангенс угла а есть отношение синуса этого угла к его коси-
нусу, т. е.
, Sin α
tga
4'. Котангенс угла α есть отношение косинуса этого угла к его
синусу, т. е.
, cos a
ctga
В самом деле,
COS α χ χ
7
и аналогично:
х
COS a
Sin α у у
Ρ
31
Так как |*|"<р, |у|<р. то при всех значениях а имеем
|cosa|< 1, | sin ос | < 1.
Знаки тригонометрических функций (по четвертям) определя-
ются в соответствии со знаками координат точек в различных чет-
вертях координатной плоскости.
Косинусы углов положительны (отрицательны) для углов, окан-
чивающихся в той части координатной плоскости, в которой абс-
циссы точек положительны (отрицательны).
Следовательно, косинусы углов, оканчивающихся в правой (откры-
той) полуплоскости (I и IV четверти), положительны, а углов,
оканчивающихся в левой (открытой) полуплоскости (II и III четвер-
ти), отрицательны.
Аналогично знак синуса определяется по знаку ординаты:
синусы углов, оканчивающихся в верхней (открытой) полуплоскости
(I и II четверти) положительны, а углов, оканчивающихся в нижней
- Μί (открытой) полуплоскости (III
и IV четверти), отрицательны.
Тангенсы и котангенсы по-
ложительны (отрицательны) в
тех четвертях, в которых коор-
динаты точек одинаковы (про-
тивоположны) по знаку.
Следовательно, тангенсы и
котангенсы углов, оканчиваю-
щихся в I и III (открытых)
четвертях, положительны, а уг-
лов, оканчивающихся во II и IV
(открытых) четвертях, отри-
цательны (черт. 40).
Кроме указанных четырех
основных тригонометрических
Черт. 40 функций, введены специальные
названия и обозначения для
функций, по величине обратных косинусу и синусу. Первая назы-
вается секансом, seca = nntt_ , а вторая — косекансом,
—
1
с
■ >ч
о
1
+
+ 1
I cos a
+
т и
Π
и
-
(
—
не сущ(
+
+
— —
sin a
)
+
ствует
tga
cos a
coseca =-
Sin a
Знание свойств основных тригонометрических функций позво-
лит без труда устанавливать соответствующие свойства секанса и
косеканса. Поэтому интереса для специального изучения эти функ-
ции не представляют; нередко при различных тригонометрических
преобразованиях ими пользуются как удобным обозначением
для и -—.
COS a -sin a
В старых учебниках секанс и косеканс причислялись к числу
основных тригонометрических функций и изучались особо, наряду
с прочими функциями. Сколько и какие функции относить к числу
основных является делом условным. Так, например, во мно-
гих старинных руководствах, кроме шести тригонометрических
функций, рассматривалась седьмая функция синус-версус
(обращенный синус), которая определялась следующим образом
(черт. 41):
sin versa = ^, =>—.
синус-версус выражается через косинус сле-
дующим образом
sin vers a = 1 — cos a;
специальное изучение функции sin vers α вы-
звало бы лишнее загромождение курса три-
гонометрии вопросами, не имеющими прин- « δ Μ
ципиального значения. '
Многочисленные теоретическиие и практи- Черт 4ι
ческие применения тригонометрии показали
целесообразность изучения (в качестве основ-
ных) четырех тригонометрических функций, определения
которых 1°—4° даны в настоящем параграфе.
Практически значения тригонометрических функций находятся
по таблицам, в которых с данной степенью точности даются значе-
ния тригонометрических функций от значений аргумента, взятых
в некоторой арифметической прогрессии. Устройство тригономет-
рических таблиц изложено в § 71.
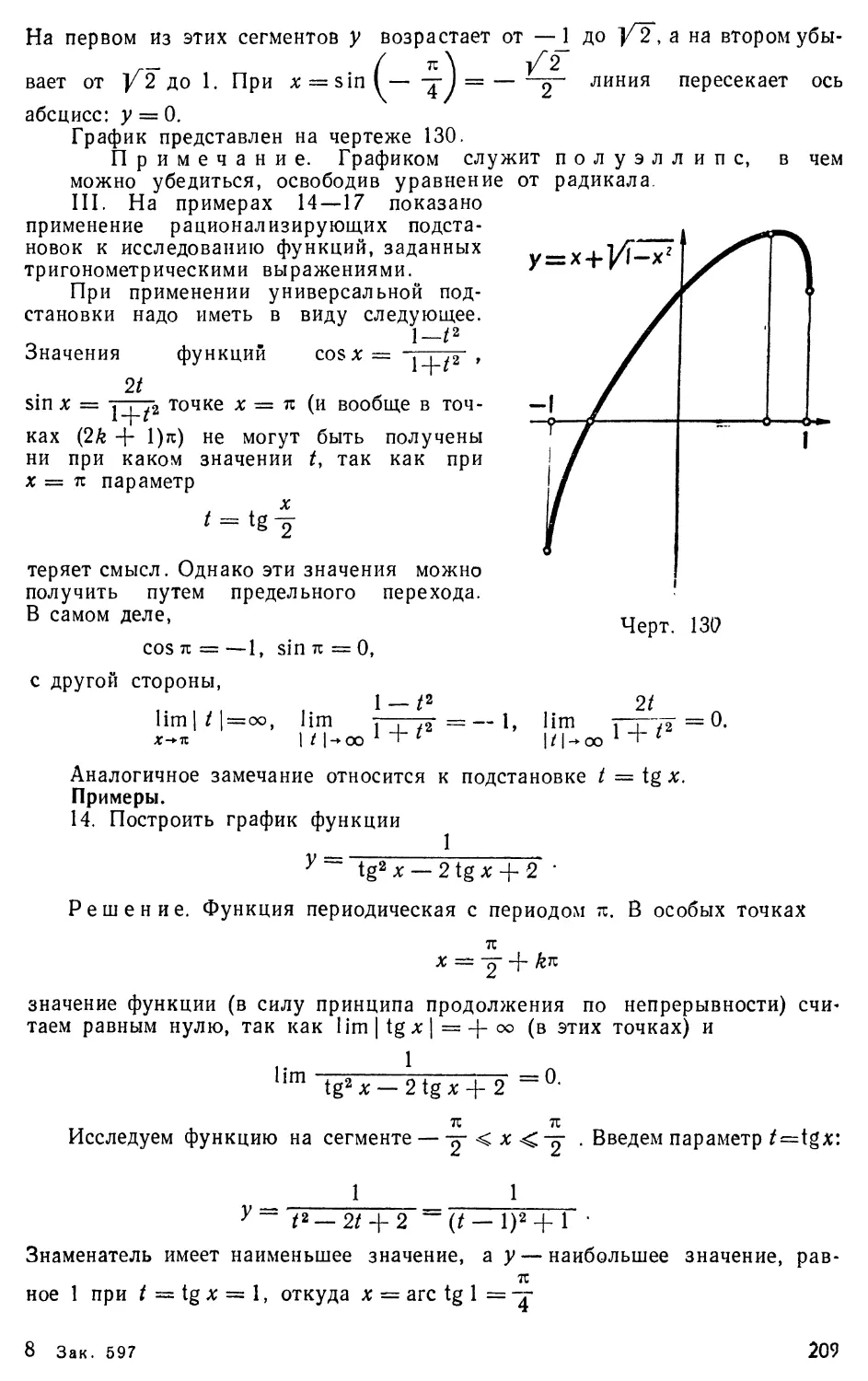
§ 8. Различные определения
и интерпретации тригонометрических функций
Многообразные применения тригонометрии в математических
дисциплинах и в физике, механике и технике вызвали потребность
в различных интерпретациях тригонометрических функций. В свя-
зи с различными интерпретациями определения тригонометриче-
ских функций могут формулироваться в различных равносильных
между собой формах.
I. Определение тригонометрических функ-
ций с помощью единичного круга.
В силу независимости значений тригонометрических функций
от длины радиуса-вектора можно условиться выбрать все радиусы-
векторы равными по длине. Если (в частности) все радиу-
сы-векторы берутся по длине равными 1, то их концы расположатся
на единичной окружности. Данный угол а отложится на коорди-
33
натной плоскости в виде угла, образованного двумя радиусами
единичной окружности: начальным радиусом ОА (черт. 42) и ра-
диусом ОМ, образующим с О А угол а. Пусть χ и у — координаты
точки Μ (конца рассматриваемого радиуса); так как ρ = | ОМ | = 1,
то— = л; и - = у, а потому
Следовательно, косинус и синус угла а суть абсцисса и ордината
(соответственно) конца Μ радиуса единичного круга, образующего
угол а с осью абсцисс.
4(1,0)
Черт. 42
Черт. 43
Эта интерпретация получена как следствие определений
1° и 2°, принятых в предыдущем параграфе; однако она может быть
принята и в качестве определения косинуса и синуса. В самом деле,
положим по определению χ = cosa, у = sina; если OMi — произ-
вольный радиус-вектор, образующий угол α с осью абсцисс
■й*
(черт. 43), то в силу теоремы о независимости отношений -π-
οτ длины ρ радиуса-вектора имеем
cos a =
X Хг
= -г- = — , sin a
-'-*-*·
где jcif У\ и pi — координаты конца и длина радиус-вектора OMit
Итак, отправляясь от равенств (1), как от определений, можно
получать в качестве следствия равенства, принятые (см. предыдущий
параграф) в качестве определения косинуса и синуса.
Тангенс и котангенс суть отношения ординаты к абсциссе и
абсциссы к ординате конца радиуса единичного круга, образую-
щего данный угол α с начальным радиусом.
Функциям tga и ctga можно дать и другую интерпретацию.
Рассмотрим ось AT, касающуюся единичной окружности в на-
чальной точке Л(1, 0). На этой оси примем направление, образую-
щее угол ^ с осью абсцисс за положительное, а за начало — точ-
34
ку А. Ось AT называется осью тангенсов. Ось тангенсов
параллельна оси ординат и одинаково с нею направлена (черт. 44).
Рассмотрим центральную проекцию Mt (из точки О) конца ра-
диуса ОМ единичной окружности, образующего данный угол α с
осью абсцисс. Возможны следующие три случая (черт. 43).
м,
Υ ι
4(1,0) _[_
χ Τ
ν.
0
ч^
τ
he*?
у
A
Χ
Г. Угол α оканчивается в правой полуплоскости, в этом случае
точки Μ и Mt расположены на одном и том же луче, исходящем из
начала координат и образующем угол а с осью абсцисс. Обозначим
через Υ ординату точки Mt, имеем (по определению тангенса):
С л у ч а й 2°. Угол α оканчивается в левой полуплоскости (черт.
44, 2°); в этом случае радиусы-векторы ОМ и OMt противоположно
направлены. Отношения
МХМ у
х ■=— и
омл
AMt
ол
равны по абсолютной величине (в силу подобия треугольни-
ков ОММХ и 0AMt) и одинаковы по знаку (их числители и знаме-
натели соответственно имеют противоположные знаки); следова-
тельно, tga= -χ = Υ.
Случай 3°. α =±^ + 2kn. В этом случае радиус ОМ пер-
лендикулярен к оси ОХ, центральная проекция точки Μ на ось
тангенсов не существует, tga также не существует (черт. 44,3°).
Итак, при всех допустимых значениях угла а тангенс этого угла
равен ординате точки, в которой ось тангенсов пересекается с про-
должением радиуса единичной окружности, образующего угол а
с осью абсцисс.
35
Эта интерпретация может быть принята в качестве определения
тангенса (провести подробно рассуждения предоставляем учащим-
ся).
Функцию ctga можно интепретировать следующим образом.
Рассмотрим ось ВС, касающуюся единичной окружности в точке
β (0, 1) и одинаково направленную с осью абсцисс (черт. 45). Эта
ось называется осью котангенсов. При всех допустимых значениях
угла α (т. е. а Ф kn) котангенс этого угла равен абсциссе X точки
Мс, в которой ось котангенсов пересе-
кается с продолжением радиуса еди-
ничной окружности: ctga = X.
Эту интерпретацию можно принять
в качестве определения котангенса.
Интепретация с помощью единично-
го круга удобна при изучении свойств
тригонометрических функций геометри-
ческими средствами.
На чертеже 46 представлены еди-
ничный круг, данный угол а, соответст-
вующая точка единичной окружности,
ее координаты и точки осей тангенсов и котангенсов. Направ-
ленные отрезки ОМХ} МХМ, AMt и ВМС иногда называются соот-
ветственно линиями косинуса, синуса, тангенса и котангенса
данного угла. Из изложенного следует, что значения тригономет-
рических функций равны величинам соответствующих тригоно-
метрических линий.
II. Интерпретация при помощи круга про-
извольного радиуса.
В рассуждениях, изложенных в предыдущем пункте I, можно
вместо единичного круга брать круг произвольного радиуса (т. н.
тригонометрический круг). Это равносильно соглашению считать
все радиусы-векторы равными по длине числу R. При такой замене
единичного круга чертеж 46 претерпевает преобразование гомоте-
тии с центром в точке О и с коэффициентом R и получается чертеж 47.
Сказанное в предыдущем пункте остается в силе, но лишь со сле-
дующими изменениями. Имеем
хх. у у
Черт. 45
Следовательно, косинус и синус суть отношения абсциссы и орди-
наты конца радиуса-вектора ОМ к радиусу круга.
Определения тангенса и котангенса как отношений координат
конца радиуса-вектора остаются прежними.
Тангенс и котангенс равны отношениям соответствую-
щих координат точек осей тангенсов и котангенсов к радиусу R
круга.
36
Тригонометрические функции можно определить как отноше-
ния соответствующих тригонометрических линий ΟΜλ (линия ко-
синуса), МХМ (линия синуса), AMt (линия тангенса) и ВМС (ли-
ния котангенса) к радиусу /? тригонометрического круга
cos α =
ОМ*
R
sin α =
MM
R '
R
R
В старых учебниках тригонометрический круг обычно не свя-
зывается с системой координат В этом случае, выбрав начальный
радиус и установив положительное направление отсчета углов,
Черт 46
Черт 47
надо ввести специальные соглашения относительно знаков, с ко·
торыми должны браться величины тригонометрических линий (см.,
например, учебник тригонометрии Н. Рыбкина). По сути дела эти
соглашения представляют собой введение системы координат, но
лишь в «замаскированном» виде.
III. Векторная интерпретация.
Пусть α — данный угол. Рассмотрим на координатной плоско-
сти произвольный вектор АВ, образующий угол α с осью
абсцисс (черт. 48). Перенесем параллельно вектор АВ, поместив
его начало в начале координат; пусть после указанного переноса
вектор АВ займет положение ОМ. Известно, что при параллельном
переносе вектора его проекция на данную ось не изменяется, сле-
довательно, спроектировав векторы АВ и ОМ на ось абсцисс, по-
лучим: пр*АВ =прдг0М. Но так как проекция радиуса-вектора ОМ
на ось абсцисс равна абсциссе χ его конца М, то пр*АВ = х. Ана-
логично проекция вектора АВ на ось ординат равна ординате у
конца радиуса-вектора ОМ, т. е. пруАВ = у.
Имеем далее ρ = | ОМ | = | АВ |.
Из изложенного следует, что
х прд:АВ у πρν АВ
= ; sina = —=
Итак, косинус угла а есть отношение проекции вектора, обра-
зующего угол а с осью абсцисс на эту ось, к длине вектора.
Синус а есть отношение проекции вектора на ось ординат к
длине вектора.
Тангенс и котангенс суть отношения проекций:
tga =
пру АВ
пргАВ '
ctga = -■
пру АВ
Μ
Черт 48
Черт 49
Иногда векторная интерпретация тригонометрических функций
формулируется в форме, не требующей предварительного введения
координатной системы:
косинус угла а есть отношение проекции вектора на произволь-
ную ось /, образующую с данным вектором угол а, к длине вектора]
синус угла а есть отношение проекции вектора на произвольную
ось т, образующую угол +^ с осью /, к длине вектора:
cos a =
ПР/ АВ
ТавТ
sin а =
i АВ | ' О111^ ~~ 1 АВ | '
Тангенс и котангенс суть отношения проекций'.
t« пр^АВ . __ пр/АВ
пр/ АВ '
пР/яАВ'
Заметим, что выбор двух взаимно перпендикулярных осей /
и т на ориентированной плоскости равносилен установлению ко-
ординатной системы тО1, а при различных способах выбора осей
/ и т происходит параллельный перенос осей координат, от чего
проекции вектора на оси не изменяются (черт. 49).
Последнюю формулировку можно видоизменить следующим
образом:
косинус угла а есть отношение проекции произвольного вектора,
направленного вдоль конечной стороны угла а на начальную сторону,
к длине вектора;
синус угла а есть отношение проекции произвольного вектора,
направленного вдоль конечной стороны угла а на ось, образующую
угол + |- с начальной стороной, к длине вектора.
Векторная интерпретация получена исходя из координатного
определения тригонометрических функций; обратно, можно при-
нять векторную интерпретацию в качестве основного определения
и получить координатное определение в качестве следствия. В са-
мом деле, примем равенства
пр ^ АВ
cos α =
|-ΑΒΓ· Slna==
в качестве определения; если (в частности) условиться выбирать
все векторы с началом в одной и той же точке О, то свободный вектор
заменится радиусом-вектором. Проекции вектора на оси координат
являются координатами его конца и векторное определение триго-
нометрических функций получит координатную интерпретацию,
принятую в § 7 в качестве основного определения.
Таким образом, координатное и векторное определения тригоно-
метрических функций эквивалентны.
Векторная интерпретация имеет многочисленные применения в
геометрии, в механике и в физике. Она удобна в тех случаях, когда
в рассуждениях пользуются свободными векторами.
Из векторного определения тригонометрических функций выте-
кают нижеследующие теоремы о проекциях, имеющие многочислен-
ные применения в геометрии и в смежных дисциплинах.
Теорема 1°. Проекция вектора на ось равна (по величине)
длине вектора, умноженной на косинус угла между осью и данным
вектором:
πρ,ΑΒ = |AB|cos(ABO)·
Доказательство. В самом деле, из равенства
cos a = Var^B вытекает Пр, АВ = I А В | cos ос, где а=/(АВ,/)
|Ad| *—
есть угол между данным вектором и осью / (черт. 50), ч. т. д.
Теорема 2°. Проекция вектора А В, расположенного на некото-
рой оси т, на другую ось I равна произведению величины этого век-
тора на косинус угла, образованного осью т с осью I.
Теорема 2° является обобщением теоремы Г.
Доказательство. Обозначим через α угол, который
образует ось т с осью /.
Если направление вектора АВ совпадает с направлением оси т,
то его величина равна положительному числу — его длине, в этом
случае | АВ| = ρ (черт. 50). Вектор АВ образует угол а с осью /,
а потому
пр, АВ = р cos a = | АВ | cos a = АВ cos a.
39
Если направление вектора А В противоположно направлению
оси т, то величина А В характеризуется отрицательным числом
АВ= — | АВ | = — р. В рассматриваемом случае направление век-
тора ВА совпадает с направлением оси т (черт. 51). Проекции
векторов АВ и ВА на ось / равны по абсолютной величине
и противоположны по знаку; имеем:
пр, А В = — пр/ В А = — ρ cos α = АВ cos a.
Черт. 50
Черт. 51
Таким образом, теорема справедлива при любом расположе-
нии точек Л и β на оси т, ч. т. д.
Рассмотрим вектор АВ, образующий с некоторой координатной
осью, например с осью абсцисс, угол φ. Пусть xi и х2 — коорди-
наты (соответствующие данной оси) его начала и конца. В таком
случае проекция вектора на данную координатную ось равна
х2 — Χι, но, с другой стороны, эта же проекция равна ρ cos φ, следо-
вательно,
χ2 — χ\ = Ρ cos φ, откуда х2 = Χ\ + ρ cos φ.
Эти формулы часто применяются в аналитической геометрии.
IV. Интерпретация тригометрических
функций острого угла. Во многих геометрических и
прикладных вопросах достаточно оперировать с тригонометриче-
скими функциями лишь острых углов. Так, нередко элементы
геометрической фигуры можно рассматривать как элементы ряда
прямоугольных треугольников.
Пусть ABC — произвольный прямоугольный треугольник, один
из острых углов которого (например, А) равен данному углу а
(черт. 52). Для острого угла значения всех тригонометрических
функций положительны; в этом случае имеем:
Ь а
— = cos α, — =
с с
40
Итак, определения тригонометрических функций острого угла
могут быть сформулированы в следующем сокращенном и легко за-
поминаемом виде:
Косинус острого угла есть отношение прилежащего (к данному
углу) катета к гипотенузе.
Синус есть отношение противолежащего ка- β
тета к гипотенузе.
Тангенс есть отношение противолежащего
катета к прилежащему.
Котангенс есть отношение прилежащего ка-
тета к противолежащему.
Если угол α заменить другим острым углом
треугольника равным ^ ■— а, то прилежащий
катет станет противолежащим, а противолежа- церт 52
щий — прилежащим, а потому:
cos (γ—a j = since, sin /у -—α) = cos а,
В дальнейшем, в зависимости от потребности, будут применяться
различные интерпретации тригонометрических функций.
Наличие разнообразных интерпретаций для тригонометрических
функций указывает на их многочисленные применения в матема-
тике и смежных дисциплинах. Для успешного изучения и приме-
нения тригонометрии необходимо уметь пользоваться всеми этими
интерпретациями.
§ 9. Аргумент тригонометрической функции
Соответствие между углами и значениями данной тригономет-
рической функции позволяет всякую тригонометрическую функцию
рассматривать как функцию, для которой значениями аргумента
являются углы, а значениями функции — числа.
Будем рассматривать дуги (ориентированные) единичного круга
с общим началом отсчета в точке /1(1, 0). Всякой данной дуге σ вза-
имно однозначно соответствует опирающийся на нее (в единичном
круге) центральный угол а, а этому углу соответствует значение
данной тригонометрической функции (если, разумеется, угол яв-
ляется допустимым значением аргумента для рассматриваемой
тригонометрической функции). Следовательно, всякой дуге σ
может быть поставлено в соответствие значение данной тригономет-
рической функции от угла а (опирающегося на дугу σ). Поэтому
тригонометрические функции можно рассматривать как функции
Оуги.
41
Черт 53
Соответствие между дугами и значениями тригонометрических
функций может быть установлено и непосредственно без примене-
ния угла как промежуточного аргумента; для этого достаточно от-
ложить на окружности единичного круга данную дугу от начальной
точки А (1, 0), построить радиус-вектор ОМ, соединяющий начало
координат с концом Μ дуги и рассмо-
треть координаты точки /И (черт. 53).
Пусть χ — произвольное действитель-
ное число; данному числу соответствует
угол (дуга) а, измеряющийся (в принятой
системе измерения углов или дуг) числом
х, а углу (дуге) соответствуют значения
его тригонометрических функций. Таким
-образом, всякому действительному числу χ
соответствуют значения тригонометриче-
ских функций угла, измеряющегося этим
числом.
При рассмотрении тангенса, а также
котангенса предполагается, что измеряю-
щийся числом χ угол а, является допустимым значением
аргумента для данной функции.
Следовательно, тригонометрические функции можно рассмат-
ривать как функции числового аргумента, именно, они суть слож-
ные функции, для которых промежуточным аргументом является
угол (дуга)
cos α
sin α
tga
ctga
Таким образом, в итоге получается cooTBeTcfBne между числами:
всякому (допустимому) действительному числу χ соответствует
число — значение тригонометрической функции.
При рассмотрении тригонометрических функций как функций
числового аргумента условились в качестве единицы измерения дуг
и углов принимать радиан. В силу этого соглашения символ sin 2
следует толковать как синус угла (дуги), радианная мера которого
выражается числом 2, символ cos (—5) означает косинус дуги,
радианная мера которой выражается числом — 5 и т. д.
Выбор единицы измерения дуг и углов не имеет принципиаль-
ного значения. Выбор радиана не диктуется необходимостью.
Радиан оказывается лишь удобной единицей, так как в радианном
измерении формулы математического анализа, относящиеся к три-
гонометрическим функциям, принимают наиболее простой вид.
Если Μ — точка единичной окружности, изображающая данное
число х, то косинус и синус суть абсцисса и ордината точки М>
число угол
a -»
42
а тангенс и котангенс — отношения ее координат. Длина дуги AM
с точностью до слагаемого, кратного 2л. равна |х|.
Из изложенного следует, что аргумент тригонометрической
функции может быть истолкован как угол, либо как дуга, либо
число — мера угла (дуги). В различных вопросах тригонометрии
и в ее приложениях все эти интерпретации находят применение.
Так, например, в формулах решения треугольников под аргу-
ментами тригонометрических функций обычно подразумеваются
углы, а в формуле гармонического колебания s = A sin at аргу-
мент / есть число, измеряющее время (коэффициент а — число,
характеризующее частоту колебания).
При изучении тригонометрических функций от числового ар
гумента нередко (для удобства) сохраняется геометрическая тер-
минология. Называя аргумент тригонометрической функции дугой
или углом, подразумевают под ним (аргументом) не саму дугу
(угол), а число, ее измеряющее. Сохраняя геометрическую терми-
нологию, мы позволим себе вместо, например, такой фразы «си-
нус числа х», говорить «синус дуги а:» или «синус угла х».
В геометрической теории тригонометрических функций οι
числового аргумента закон соответствия между значениями аргу-
мента и тригонометрической функции устанавливается не пря-
мым указанием математических операций (формулой), которые
надлежит выполнить над аргументом, а геометрически. Однако,
чтобы иметь возможность говорить о функции, необходимо нали-
чие закона соответствия, в силу которого каждому (допустимому)
значению аргумента соответствует определенное значение функции,
но не существенно, каким способом этот закон устанавливается.
Определение тригонометрических функций, не зависящее от гео-
метрии и не связанное с геометрическими интерпретациями, дает-
ся в аналитической теории тригонометрических функций
(см. гл. VIII).
Построить формулы, выражающие значения тригонометриче-
ских функций посредством только лишь алгебраиче-
ских действий над аргументом, невозможно (см. § 36), по-
этому элементарная математика (в частности, школьный курс)
вынуждена строить тригонометрию на базе геометриче-
ской теории.
Ниже приведена мотивировка целесообразности введения радианного
измерения углов и дуг
Примем за единицу углов некоторый угол е. Пусть в принятой единице
положительный полный оборот (полная окружность) измеряется числом k.
Известно, что предел отношения длины хорды к длине стягиваемой ею
малой дуги равен 1:
h
где υ и h — длины дуги и соответствующей хорды.
43
Пусть число χ является мерой угла (дуги) при единице измерения е (черт.
54) Не нарушая общности рассуждений, примем радиус окружности равным
1; тогда длина полной окружности равна 2π; длина дуги, на которую опи-
рается (как центральный) единичный угол е, равна -^ ; длина дуги, на кото·
2π
рую опирается угол, измеряющийся числом х, равна —^ х. Рассмотрим дугу,
на которую опирается угол 2х, и стягивающую ее хорду. Длины рассматри-
ваемых дуги и хорды соответственно суть:
2π
Имеем:
откуда
Черт. 54
Вычислив производные (непосредственно путем приращений), получим:
d sin χ 2π
') =
lim
k '
h
υ
lim
лг-О
2x,
= lim
лг-О
sin χ
X
h =
sin
2*
k
- =
= 2 sin x.
X
— 1»
X
2π
k '
dx
d cos χ
~dx~~
и далее:
k С k
sin χ dx = — 2^ cos χ -f С и I cos * dx = ^ sin χ + С.
Соответствующие коэффициенты появятся в формулах дифференциаль-
ного и интегрального исчисления, содержащих обратные тригонометрические
функции. Разложения в степенные ряды косинуса и синуса примут следующий
вид:
cos χ = 1 —
2πχ\2
2πχ /2πχ\3 1
Все эти формулы получат наиболее простой вид, если выбрать единицу
измерения углов (дуг) при условии
2π
откуда
Итак, мера полного оборота долоюна выражаться числом 2π, что имеет место,
если за единицу измерения углов (дуг) принят радиан.
С изложенной точки зрения радиаиная система измерения углов и дуг
является наиболее естественной.
В частности, есль за единицу измерения углов (дуг) принять градус,
то к = 360°, а соответствующий коэффициент равен
§ 10. Тригонометрические функции
от некоторых частных значений аргумента
Если известна сторона ап правильного я-угольника, вписан-
ного в единичный круг, то легко вычислить значения тригономет-
рических функций от угла
180°\
Примем за начальный радиус, делящий пополам сторону впи-
санного я-угольника, тогда Ц явится синусом угла ~, а апофе-
Г 2
ма 1п = 1/ 1 ~- — его косинусом:
sm- = f. cos- =
Черт. 55
Воспользуемся формулами геометрии, выражающими стороны не-
которых вписанных правильных многоугольников через радиус
круга:
1°. При η = 3 имеем: а3 = |/3 , /3 = у (всюду считаем ради-
ус круга R = 1).
Следовательно,
ii = sin 60° =
2°. При η = 4 имеем: α4 = Υ 2 , /4 =
Следовательно,
3. При /2=5 имеем:
-±/ ,
3-ψ- - 4 (νττ
(Применить формулу преобразования сложного квадратного
радикала см. «Специальный курс элементарной алгебры», § 40»)
Следовательно,
, к _ 2 У 5 - \Г~Ь _ УТ/Ъ
g 5 ~/Т(|Г5 + 1)~
4®. При ^ = 6 имеем: ап = 1, /Л = '-^— ·
Следовательно,
sinT - sin 30° = 7, cos-g «V"· tg-g- =-7=r
5е9. При я = 8 имеем: α8 = |/"2 — |/ 2 · /8 = 2'
Следовательно,
sin |= sin 22,5- ^ΙΞΖΣ, cos4 = -^P
._ = У 2 - 1.
6°. При η = 10 имеем: ап = ^Т2~ } , 1„ = -| Кю+2/"5~.
Следовательно,
π 1
C0SIO=T
g Ю ~ ιΑϊο
π у 5 —
Ϊ0 """ /ΪΟ + 20
79. При η = 12 имеем: α12=κ2-/3 , /Λ =
46
Следовательно,
sin^ == sin 15° =
I/2-/3 __ /б — /2
π __ J/2+/3 __ γ 6 + У 2
)ЬТ2~" 2 ~ 4
.„ π 1/2 -VT
V2+V3
= 2-1/3.
Примечание. Для найденных частных значений тригономет-
рических функций мы не пишем их приближенных значений в виде де-
сятичных дробей. Эти приближенные значения даются в тригонометри-
ческих натуральных таблицах
Найденные значения тригонометрических функций дают воз-
можность определить значения функций от ряда других углов,
дополнительных до у.
π
8°. Так как -J — ~ = ^ = 54", то (в силу 3°):
3π г ло · π 1 - / 5 — ι/" 5 .3π лГЬ + 1
, jq = cos54° = sin -g- = "2 ! / " cin— —-—x—
π π ζπ
9°. Так как-| —^=^ = 72°, то (в силу 6°):
cos 24 = cos 72° = sin 18Ф - ^Ъ ГХ
10е. Так как J—^=|? =75°, то (в силу 7°):
C0ST2 Τ—■ sln== ^"""^
Вычислив координаты вершин правильных многоугольников,
расположенных в различных четвертях координатной плоскости,
можно найти тригонометрические функции для ряда углов, окан-
чивающихся во II, III и IV четвертях.
2π 1 2π γ~ξ 2π _
11° cos -£=- —-j , sin з~=~~2~ tg "З" = "~ ^ 3 '
cos -^= —у , sin •^■= g- , tg У == "^"З" (черт. 56).
3π γ-ζ Зл: /Τ 3π
12°. sin-j=-2— , cos j= 2~~, tg j = — 1;
47
sin j=—-
V~2 5k Y~2
—- ■ cosT ?—, tg -y = 1;
slnT=-T
> . 4π 1
• sln"5 =7
6π
sin y =
τ_/τ
7π
cos j~ -
5-/5
tg -j = — 1 (черт 55, /г = 4).
4π
COS "r~ = —
/5·
5-/5
6π
cos -5 = -
8π
/"5 +1
in - = - -j у 10 + 2 / 5 , cos -f- =
sin
(черт, 57).
Черт 56
Черт. 57
§ 11. Четность и нечетность тригонометрических функций
Теорема. Косинус является четной функцией, /п. е.
cos (—α) = cosa; синус, тангенс и котангенс являются нечетны-
ми функциями, т. е.
sin(~- a) = — sin a, tg(—a) = —tgat ctg(—a) = — ctga.
Μ
Черт 58
Черт 59
Доказательство. Точки Μ и /Иь единичной окруж-
ности, изображающие взаимно противоположные значения аргу-
мента а и —а, симметричны относительно оси ОХ (черт. 58). Сле-
довательно, точки Μ и М{ имеют одну и ту же абсциссу χ =« OB и
48
взаимно противоположные ординаты у == В Μ и —у = Б/Иь от-
куда
jt = cos α = cos (—α) и sin (—a) = —у = —sin a.
Для функции tga имеем
4. / ч sin (—a) —Sin , , re\\
tg(—«)=53i^=^-=-E^r. = —tga (черт. 59)
и аналогично: ctg(—a)= —ctga, ч. т. д.
Примеры.
;)—.
sin I к / = — 1, sin
cos( — T) = cos(T ]=-5-f tg(^ —-« ) = -tg-fi =
3π ι
sin I TJ = — sin-r=-
2 ·
1
§ 12. Нахождение угла (дуги)
по данному значению его тригонометрической функции
Пусть /(а)-—данная тригонометрическая функция, am —
заданное число; требуется найти все те углы (дуги), для которых
значение рассматриваемой функции /(а) равно т.
Иными словами, требуется найти множество всех решений
уравнения
Это уравнение называется простейшим тригонометриче-
ским уравнением.
Мы будем рассматривать следующие четыре простейшие три-
гонометрические уравнения (по числу основных тригонометриче-
ских функций):
cosa = m, sina=m, tga = m, ctga==m.
Геометрическое решение.
Геометрическое решение простейшего тригонометрического урав-
нения заключается в построении угла (дуги) по данному
значению его тригонометрической функции.
1.° Уравнение cos а = т. Для построения угла, косинус
которого равен т, строим на оси абсцисс точку Р(т, 0) с абсциссой
равной т (черт. 60).
При|т|<1 точка Ρ (т> 0) лежит внутри единичного круга.
Параллель оси ОУ, проходящая через точку Р, пересечет единич-
3 Зак 097 49
ную окружность в двух точках Μ и Мь симметричных относи-
тельно оси абсцисс (черт. 60).
Радиусы ОМ иОУИ] определяют (в общем случае) два геометри-
чески различные положения для конечной стороны искомого угла.
При 0 < m < 1 радиусы ОМ и ОМХ расположены в I и IV
(черт. 60, а) четвертях, а при —1<Γ.#*<Ό — во II и III четвертях
(черт. 60,6). Все углы, косинус которых равен т, имеют конечной
стороной либо радиус ОМ, либо радиус OMt.
При т = 1 для конечной стороны искомого угла возможно
лишь одно положение ОА. В этом случае будем говорить, что
точки Μ и Mi совпали с точкой Л, а радиусы ОМ и ОМ{ совпали
с радиусом ОА. При т = — 1 точки Μ и М{ совпадают с точкой
Λι(-1,0).
Если | /721 >1, то точка Р(т, 0) лежит вне единичного круга;
в этом случае параллель оси ΟΥ через точку Ρ не пересекает еди-
ничной окружности, а потому не существует дуг, имеющих данное
значение косинуса.
Итзк, простейшее уравнение cosa =m имеет решения при
| т \ < 1 и не имеет решений пои \ т | > 1.
5(0,1)
Μ
Черт. 60
Уравнение sina = /и · решается аналогично предыду-
щему (черт. 61). Достаточно на оси ординат построить точку
Р(0, т) и провести через нее параллель оси абсцисс. При |т|<]1
получим в пересечении с единичной окружностью две различные
точки Μ и Μι в правой и левой полуокружностях (соответственно),
а для конечной стороны искомого угла два возможные положения
ОМ и OMi. При т = 1 точки Μ и МА совпадут с точкой β(0, 1),
а при т= —1 — с точкой В{(0, —1). При | т \ >1 простейшее урав-
нение sin a = m не имеет решений.
Уравнение tga = т. Построим на оси тангенсов точку Τ
с ординатой равной т (черт. 62). Прямая, соединяющая точку
Т(1, т) с центром единичного круга, пересечет единичную окруж-
ность в двух диаметрально противоположных точках Μ и Μ χ.
50
Радиусы ОМ и 0М{ суть геометрически различные положения ко-
нечной стороны искомого угла.
Итак, уравнение tga = m имеет решения при произвольном дей-
ствительном т.
Уравнение ctga = m решается аналогично, геометриче-
ское построение представлено на чертеже 63.
Т(\.т)
4(1,0)
Μ
Черт. 62
Черт. 63
Главные решения и формулы общего ре-
шения
Уравнение cosa = т (где \т\ <1). Все углы, имеющие ко-
синус равный т и оканчивающиеся в верхней замкнутой полу-
плоскости (для этих углов ОМ служит конечной стороной, черт. 60),
отличаются друг от друга на целое число полных оборотов. Наи-
меньший положительный из этих углов содержится на сегменте
[0, π], этот угол называется главным решением простей-
шего уравнения cosa = m или кратко главным углом (ду-
гой) и обозначается символом arc cos m.
Итак, arc cos m есть угол (дуга), содержащийся на сегменте
[0, π], косинус которого равен т
0 < arc cos m < π; cos (arc cos m) = m,
где \m\ < 1.
При |т|;>1 символ arc cos m не имеет смысла.
Практически для нахождения значения arc cos m при заданном
значении т пользуются тригонометрическими таблицами.
Примечание. При рассмотрении тригонометрических
функций как функций числового аргумента неизвестное
а в простейшем уравнении сор-α = т следует считать „ч и с-
л о м, в соответствии с этим под arc cos m следует также понимать
число: меру угла (дуги), а не с а м угол (дугу). Однако в ма-
тематической литературе принято сохранять геометрическую
терминологию.
Примеры.
1. Имеем
π . 1 π
arc cos 0 = у , arc cos 1 = 0, arc cos y=-g-;
1 π У 3" _ π ΥΤ + 1 _ π
arc cos 77=^=-7- , arc cos—ό -g- , arc cos ^ у
Ϋ2 + Υ 2 π
arccos о =="8" ' arc cos (— 1) = π> arc cos
/ 1 \ 2π
arc cos( ~ 7^=- )=T , arc cos ^ *Tj=T l
3π
Λ Y~2 Г4
Ι Υ 5 + 1 λ 4π
arc cos I ξ )=Tj
arc cos I — 2~-— / = Τ ί;"
2. arc cos -g- ж arc cos 0,3333 » 70°32'.
Зная главное решение, можно найти множество всех решений
простейшего уравнения cosa = m. В самом деле, все искомые дуги
оканчиваются в двух точках (М—в верхней полуплоскости и М{ —
в нижней полуплоскости, черт. 64), симметричных относительно оси
абсцисс (совпадение точек Μ и Μι не исключается). Множество
всех дуг, оканчивающихся в верхней полуплоскости, получим,
прибавив к дуге arc cos m любое целое число полных оборотов:
arc cos m + 2kn. Множество всех дуг, оканчивающихся в нижней
полуплоскости, получим, прибавив к симметричной относитель-
но оси ОХ дуге —arccos m произвольное целое число полных обо-
ротов: —arc cos m + 2kn.
Формула
α = ± arc cos m + 2kn
(k — произвольное целое число)
дает множество всех решений простейшего уравнения cosa = m
Примеры.
Уравнение Общее решение
1 π
1. cos x = -g- . * = ±"3" + 2βπ.
2. cos χ = |/ 3 . χ = ± ■£ + 2kn.
3. cos χ = 1. χ = 2£π.
1 2
4. cos χ = — -ζ . λ=±τπ + 2^·
52
5. cos χ — 0.
4k ± 1 2n ■
■. —-— π =
6. cos χ = — 1.
7. cos χ = -q· .
произвольное целое число, так как 4k db 1
изображает произвольное нечетное число:
4/г± 1 = 2л+ 1.
а; = ^ π -f- 2&π = (2/2 + 1) π, η — произволь-
ное число, так как 2k ± 1 — нечетное число
* = ± arc cos j + 2kiz = ± 70°32' + 360°«
(см. пример 2, стр. 52)
π —
Черт. 65
Уравнение sina = m решается аналогично предыдущему.
Среди углов, служащих решением этого уравнения и оканчиваю-
щихся в правой полуплоскости, наименьший по абсолютной ве-
личине угол принадлежит сегменту —-^, π- . Это решение назы-
вается главным: arc sin m (черт. 65).
Итак, arc sin m есть угол (дуга), содержащийся на сегменте
\—Ι· Τ г синУс которого равен т:
— -^ < arc sin m < γ , sin (arc sin m) = m,
где \m\ < 1.
При |т|>1 символ arc sin m не имеет смысла.
Примеры.
1.
π 1 π
arc sin 0=0, arc sin 1= -j , arc sin-o"=-g-;
arc sin
. ΥΊ
2 "=*t , arc sin .
= -q- , arc sin
ίητ|/
5-/5
π
arc sin (— 1) = — -η-, arc sin
• ( l\
ιη\-2)=~~τ;
53
Л / /3 \ π
arc sin I —"~~γ~ )— 4 arc sinl Y~j Τ
arc sin ( — -j
i3
2. arc sin ί — γJ « arc sin ( — 0,4286) « — 25°23'.
Угол 25°23', имеющий синус, равный 0,4286, находим по таблицам и поль-
зуемся свойствами нечетности синуса.
Зная главное решение, можно найти множество всех решений
уравнения sina = т. Две дуги arc sin m и π —arc sin m, оканчива-
ющиеся в точках Μ и Λίι, симметричных относительно оси ординат
(первая в правой полуплоскости, а вторая в левой) имеют синус
равный т (по построению)
sin (arc sin m) = m, sin (π — arc sin m) = m.
Множество всех искомых решений найдем, прибавив к каждой
из этих дуг произвольное целое число полных оборотов
__ fare sin m + 2kn,
[(я — arc sin m) -f- 2kn.
Это выражение можно записать в виде одной формулы, заметив,
что в верхней строке слагаемое arc sin m берется со своим знаком,
а коэффициент при π — четное число 2k\ в нижней строке arc sin m
берется с обратным знаком, а коэффициент при π есть нечетное
число 2k + 1.
Выражение
χ = (— 1)" arc sin т + пл
дает при четном η = 2k верхнюю строку, а при нечетном η — 2k + 1
нижнюю строку.
Примеры.
Уравнение* Общее решение
ίη χ = 4. *=(— 1)Л7Г +
1/2 π
2. sin^-^-o— . х = ( - 1)" "4 + пк.
-<-Κ-ϊ)
3. bin x = — —2— ·
ι/"2 _ т/""з"
4. sin * = - ■* ^—L~ . * = (— Vn+1 Ϊ2
54
7t ΊΠ -f- \— \)a
5. sin χ = 1. χ = (— 1)" -κ + «π = о
так как при я четном /2 = 2& и при η нечет-
ном η = 2k + 1, имеем:
2/2 + (—1)л = 4k + 1.
6 sin лс = — 1. *== (— l)n+1 у + mt = — у + 2^π.
7. sin л: = - у . л: = (— 1)"+ι 25°23' + 180° /г
(см. пример 2. стр. 54).
Уравнение tga = т. Точка β(0,1) и В{ (0, —1), в кото-
рых оканчиваются дуги, не имеющие тангенса, разделяют единич-
ную окружность на правую и левую (открытые) полуокружности;
из двух диаметрально противоположных точек (см. черт. 62), в ко-
торых оканчиваются дуги, имеющие данный тангенс, первая рас-
положена в правой, а вторая в левой (открытой) полуокружности.
Дуга arctgm, оканчивающаяся в правой полуокружности, имеет
наименьшую абсолютную величину и называется главным решением.
Итак, arctgm есть угол {дуга), содержащийся β интервале
\—Τ' Ύγ тангенс которого равен т
— y<arctgm<-|; tg(arctgm) = /я,
где — сю <^ т <d оо.
Примеры.
π 1 τ
1. arc tg 0 = 0, arctgl=-y, arc!
arc tg (/"2-1)= f-, arctg(-
2. arc tg 3 « 7Γ34' (по таблицам).
Общее решение простейшего уравнения tgoc = т находится
по формуле
а = arc tgm + kn
(где k — произвольное целое число).
55
В самом деле, при четном k = 2п получается дуга, оканчиваю*
щаяся в той же точке, что и arc tg m, а при нечетном k = 2п + 1
(прибавляется нечетное число полуоборотов)—дуга, оканчиваю-
щаяся в диаметрально противоположной точке.
Примеры.
Уравнение Общее решение
1. tg*= 1. * = "4~ + £π.
2. tg* = — 1. * = — J + ^π.
3. tg * = /Т. * = -g- + *π.
5. tg * = 2. * = 63°26' + 180°л.
Уравнение ctgcc = m. Точка А и Ль в которых оканчива-
ются дуги не имеющие котангенса, разделяют единичную окруж-
ность на верхнюю и нижнюю (открытые) полуокружности, в соот-
ветствии с этим главное решение arcctgm выбирается в верхней
(открытой) полуокружности.
arc ctg т есть угол (дуга), содержащийся в интервале (О, π),
тангенс которого равен т\
О < arc ctg m<^ny ctg (arc ctg m) = mt
где — oo <] m <C °° ·
Формула общего решения имеет вид:
α = arcctgm + kn.
Примеры.
Уравнение Главное решение Общее решение
π π
1. ctg x = 0, arc ctg 0 = у , x = γ + &π.
π π
2. ctg * = 1, arc ctg 1 = -j , д: = -j + ^π.
3π 3
3. ctg χ = — 1, arc ctg (— 1) = -j , ^ = -ξ π -f ^π.
4. ctg χ = — / 3 , arc ctg (— / 3 ) = -g-, χ = -g· π + kn.
Теорема. Какова бы ни была система двух действительных
чисел (и, ν), удовлетворяющих условию
56
существует единственная дуга в промежутке ϋ^α<2π (т. е. в
пределах первой окружности), косинус и синус которой имеют дан-
ные значения а и ν:
cosa = и, sin a = и. (1)
Доказательство. На плоскости существует единствен-
ная точка Μ с абсциссой и и с ординатой ν. Точка Μ лежит на еди-
ничной окружности, так как
ρ = | ОМ | = yu2 + v2 = 1.
Радиус ОМ определяет единственный угол а в промежутке
0<л:<2л, для которого косинус и синус имеют данные значения и
и и, ч. т. д.
В поле действительных чисел существует бесконечное
множество значений аргумента, удовлетворяющих условию
(1); каждое из этих значений отличается от α на слагаемое вида
2kn (где k — целое число).
Следствие. Какова бы ни была система действительных
чисел «, v, до, ζ> взятых при условиях
в промежутке 0<α<2π существует единственное значение аргу-
мента а, при котором
cosa = и, sina = u, tga=z, ctga=^.
В самом деле, поставленным условиям удовлетворяет дуга, для
которой выполняются равенства (1).
§ 13. Соотношения между тригонометрическими функциями,
тригонометрические тождества
Мы будем рассматривать выражения вида
U (cosa, sin a, tga, ctga), (U)
получающиеся из некоторого аналитического выражения
U(u, υ, w, z)
заменой его аргументов и, v, w, z посредством подстановки
w=cosa, u = sina, до = tga, 2= ctga.
Для выражения
i/(cosa, sin a, tga, ctga) (U)
SB Зак. 597 57
допустимым считается произвольное значение а, при котором вы-
полнимы все математические операции, содержащиеся в (U) (со-
ответствующее значение U является действительным числом).
Примечание. В частности, выражение (U) может не
содержать некоторых тригонометрических функций, в этом
случае выражение U(u} v, w, ζ) не содержит соответствующих
промежуточных аргументов.
Выражение (U) называется алгебраическим выраже-
нием от тригонометрических функций, если U(u, v, w, ζ) есть ал-
гебраическое выражение от промежуточных аргументов и, vt w, z.
В частности, выражение (U) называется многочленом,
дробным рациональным и иррациональным
выражением от тригонометрических функций, если выражение
U(u, vf w, z) является (соответственно) многочленом, дробным или
иррациональным от промежуточных аргументов.
При совместном задании двух или нескольких выражений до-
пустимыми считаются значения аргумента, допустимые для каж-
дого из данных выражений (в отдельности). Множество всех таких
значений предполагается непустым.
Равенство
£/(cosa, sina, tga, ctga) = l^(cosa, sin a, tga, ctga) (I)
называется тригонометрическим тождеством, если оно
выполняется при всех допустимых значениях а, при которых пра-
вая и левая части рассматриваются совместно.
Если выражения
£/(cosa, sina, tga, ctga) и V(cosa, sina, tga, ctga)
тождественны, то множества допустимых значений аргумента a
для каждого из них в отдельности могут быть различными.
В самом деле, могут существовать такие значения а, при которых
одно из выражений U и V теряет смысл, а другое смысла не теряет,
но вместе с тем существует непустое множество значений а, при
которых оба данные выражения имеют смысл и тогда их значения
равны между собой.
Замена выражения другим, ему тождественным, называется
тождественным преобразованием данного выражения. При выпол-
нении тождественного преобразования множество допустимых зна-
чений аргумента α может измениться.
Рассмотрим некоторое тригонометрическое тождество (I); воз-
можен один из следующих случаев:
Случай 1°. Равенство (1) не является тождеством относи-
тельно промежуточных аргументов ut v, w, z.
Случай 2°. Равенство (1) является тождеством относительно
промежуточных аргументов a, v, w, z
U (ιι, υ, w,z) = V (и, ν, wy z).
58
В первом случае тригонометрическое тождество называется
нетривиальным, а во втором — тривиальным.
Примерами тривиальных тождеств могут служить следующие
тождества:
(cos α -f- sin α)2 = cos2 α + 2 cos α sin α -f sin2 α;
_J ■ 1_ = tg a + Ctg a
tg« Ctg α tg"Ctga #
В самом деле,
(и + ν)2 = «Ч 2uv + ν2;
1,1 w + ζ
w ζ wz
Тривиальные тригонометрические тождества не представляют
интереса; а потому ниже будут рассматриваться нетривиаль-
ные тождества.
Все изложенное выше относится (с надлежащими корректива-
ми) к аналитическим выражениям, содержащим (в качестве проме-
жуточных аргументов) тригонометрические функции от нескольких
различных аргументов. Примером такого выражения может слу-
жить выражение
sin2 α + sin2 β + 1
tg « - tg β + 1 '
содержащее тригонометрические функции от аргумента α и от
аргумента β.
Основные соотношения.
Теорема. При произвольном значении аргумента а имеет
место тождество
sin2 α -f cos2 α = К
Доказательство. Точка с координатами
χ = cos а, у = sin а
расположена на единичной окружности, а потому квадрат ее рас-
стояния до начала координат равен 1
л;2 -\- у2 _- ^ или Cos2 α + sin2 α = 1, ч. т. д.
Левую часть доказанного тождества принято называть τ ρ и-
гонометрической единицей.
Присоединив к доказанному тождеству равенства, определяю-
щие тангенс и котангенс, получим систему трех основных
соотношений, связывающих значения четырех тригонометрических
функций:
(1)
ЗВ* 59
Из основных тождеств (1) можно в качестве следствия вывести
сколько угодно других тригонометрических тождеств. Мы отметим
наиболее часто встречающиеся следствия тождеств (1).
Г. Из второго и третьего тождеств следует:
tga.ctga = 1 (2)
при всех значениях а, для которых имеют смысл тангенс и котан-
генс.
2°. Разделив первое тождество (1) почленно на sin2a (если
sina=^0), а затем на cos2a (если cosa=^=0), получим
1 = -V и ctg2 a + 1 = -Л- ί (3)
COS ОС einer» * \ /
или в другом обозначении
tg2 a + 1 = sec2 α и ctg2 a + 1 = cosec2 a. (3')
Из соотношений (1) можно выразить значение произвольной
тригонометрической функции через соответствующее значение лю-
бой другой функции.
Из первого тождества (1) можно выразить косинус через синус
и, подставив остальные два соотношения, получить выражения для
тангенса и котангенса через синус:
'!-«"■«. **а~±У|-_ .,„..' (4)
ctga= ±VT=^
Sin a
(знак во всех равенствах берется либо верхний, либо нижний).
Аналогично получаются выражения тригонометрических функ-
ций через косинус:
sin a = ± ]' 1 —cos? a, tga =
COS a
= ± V\ —COS2 a
ctga =
± Y\ —COS2 a
(5)
Первое соотношение (З), являющееся следствием (1), позволяет
выразить косинус через тангенс, из второго и третьего соотноше-
ний (1) найдем выражение синуса и котангенса через тангенс.
Имеем:
cosa = , sina = —_ ga ctga = τ—. (6)
60
Аналогично находятся выражения тригонометрических функ-
ций через котангенс:
cos α =
ctga
±/l+ctga<z'
sin α = —
*в« = й?г· (?)
Формулы (4), (5), (6) и (7) позволяют по заданному (возможному)
значению одной из тригонометрических функций найти значения
других функций. Произвол в выборе знака показывает, что задача
(в общем случае) имеет два решения, т. е. при данном значении од-
ной функции возможны две различные системы значений всех четы-
рех функций. В самом деле, по заданному значению одной из три-
гонометрических функций можно построить (в общем случае) два
геометрически различные положения конечной стороны углы. До-
полнительным условием для определения положения конечной
стороны может служить указание четверти, в которой она распо-
ложена; этим условием определится знак перед радикалом.
Примеры.
1. Найти множество допустимых значений аргумента для выражения
sin a + ctg a
l+tga ·
Решение. Из множества допустимых значе-
ний α следует исключить те значения, при кото-
рых:
π
a) tg α теряет смысл, т. е. значения γ + kn\
b) ctga теряет смысл, т. е. значения вида kx π;
c) tg a = — 1, т. е. значения вида:
arc tg (—1) + ^π = -Τ+^π.
Черт. 66
На чертеже 66 отмечены концы дуг, не принадлежащих множеству до-
пустимых значений а. В частности, в пределах первой окружности [0,2 π]
данное выражение имеет смысл в следующих интервалах:
2. Доказать тождество
1 — (sin6 a -f COSn о.) = 3 sin2 a cos2 a.
Решение.
sin6 a -f COS6 a = (cos2 a -f- sill2 a) (cos4 a — sin2 a COS2 a -f- sin4 a) =
(разложение на множители)
= COS4 a — sin2 α-cos2 a -f sin4 a =
— (COS4 a -f- sin4 a) — sin2 a COS2 a =
= (cos2 a -f si°2 a)2 — 3 sin2 a cos2 a = (выделение полного квадрата)
= 1 —3 Sin2 a COS2 a,
откуда следует доказываемое тождество.
3. Дано
sin χ -f cos χ = a
Найти
sin5 я + cos5 x.
Решение. Имеем
sin5 χ -\- cos5 χ = (sin χ + cos *) (sin4 * — sin3 л; cos χ + sin2 * cos2 * —
— sin χ cos3 a; + cos4 ^) == (sin a: -f- cos *) ((sin4 χ + cos4 x) —
— sin χ cos χ (sin2 χ -\- cos2 *) + sin2 * cos2 *].
Возведя почленно в квадрат заданное соотношение, получим
(sin2 χ -f cos2 χ) -\- 2 sin к cos x = a2,
откуда
a2- 1
sin χ cos * = —2— »
имеем далее (выделяем полный квадрат)·
(sin4 x + cos4 χ) = (sin2 *■+ cos2 *)2 — 2 sin2 * cos2 * =
(a2—!)2 14. 2a2 — a4
= 1- 2 = 2
Подставив в искомое гыражение, получим
Ί + 2а2 — а4 а2— 1 , (а2- 1
sin- χ + cos5 ^ = а
4. Положим
#1 = Sincp1, #2 = COS φχ Sin φ2» *3 = COS <ρχ COS φ2 Sin φ3,
Α:λ_ ! = COS φι COS φ2 ...
Χη = COS φ! COS φ2 ...
Доказать, что при всех значениях срх. φ2, ..., уп_{ имеет место тождество
Решение.
4~i + ^==cos2cPicos2cP2 ... cos2cpA1_2(sin29^_1 +cos29/2_1) =
= COS2 cpx COS2 φ2 ... COS2 ср„ _ 2.
Далее
x2n_2 + x2n__l + x2n = cos*<?lcos2<?2 ... cos2cprt_
+ COS2 φχ COS2 φ2 ... COS2 φΑΖ_ 3 COS2 ср„_2 == Cos2 ¥l cos2 ?2 ·- cos2?/j—3
и так далее, пока не получим
*? + *!+ ... +^ = 5ίη2φι+εθ52φι= 1.
5... Доказать, что если имеет место равенство
(1 + cos α) (1 + cos β) (1 + cos γ) = (1 — cos a) (1 — cos β) (1 — cos γ),
то значение каждой части равно | sin α |·| sin β |·| sin γ |.
Решение. Умножим обе части на (1 + cos α) (1 + cos β) (1 + cos γ):
[(l+cosa)(l+cosP)(l b cosy)]2 = (1 — COs2a)(l — cos2 β) (1 - cos2 γ) =»
= sin2 a.sin2 β-sin2 γ.
Выражение
(1 + cos a) (1 + cos β) (1 -f cos γ)
неотрицательно при любых значениях α, β и γ (так как | cos χ | < 1), сле-
довательно:
(1 +cosa)(l + cos?) (I +COS7) = | sin a |.| sin β |·| sin γ |.
Если sin a, sin β, sin γ положительны, например, в случае острых углов
α, β и γ, то знак абсолютной величины излишен.
6. Упростить выражение
sin2 χ sin * -f- cos x
U W ^sin* — cos д;~" tg2 λ; — 1 '
Решение. Преобразуем вторую дробь:
sin * +cos* cos2 x (sin χ + cos χ) cos2 x
tg2 χ — 1 sin2 χ — cos2 χ sin χ — cos x'
Следовательно,
sin2 λ: cos2 χ sin2*—cos2 χ
и \X) sin* — cos χ sin*—cos a; sin* — cos*
= sin * + cos *.
Имеем окончательно
sin2 * sin * -(-cos *
sin *
Примечание. В полученном тождестве множества допустимых
значений аргумента для левой и правой частей (рассматриваемых
по отдельности) различны. В самом деле, выражение
sin * + cos * имеет смысл при всех значениях *, а выражение в левой
части имеет смысл при всех *, кроме значений, удовлетворяющих хотя
бы одному из следующих условий:
π
sin* = cos*, tg* = ±l, х = ~2'-{-кк.
π 3 π
Так, в частности, значения: * = -j; * = ^-π; * = у не являются
допустимыми для левой части.
63
Следовательно, в данном случае в результате выполнения тождествен-
ного преобразования множество допустимых значений аргумента * расши-
рилось.
7. Выразить через tg и ctg дробь sin2aCOS2a .
Решение. Введем в числителе квадрат тригонометрической единицы!
1 (COS2 α + sin2 α)2 cos4 α + 2 COS2 α si Π2 α + sin4 α
Si η2 α COS2 α = COS2 α Sin2 α ~~ COS2 α sin2 α ^
COS4 α sin4 α
- COS2asin2a ^2+ COS2«sin2a = ctg2 a + tg2 a + 2,
8. Выразить через tga дробь
1
Ρ =
" a sin2 a + b sin a cos a + с cos2 * '
Решение. Разделим числитель и знаменатель на cos2ai
1
COS2a I + tg2a
= atg2a+ 6tga + с ^ atg2a-\- ^ tg a + о *
π
Примечание. Если а Ф 0, то при a = тр + kn данное выра-
жение не теряет смысла, но выражение, полученное в качестве оконча-
тельного результата, теряет смысл.
9. Доказать тождество
l + tg*+ctg* ctg*
cosec2 χ + tg2 χ - ctg2 χ -sin*c°s*·
Решение. Преобразуем слагаемые левой части!
1 + tg х + ctg χ 1 + tg* + t^7 1
a) sec2 χ + tg χ ~ (1 + tg2 x) + tg χ — tg χ " sin χ *
ctg λ: ctg*
b) Tosec2 χ + tg2 χ - ctg2 χ ~~ (1 + ctg2 x) + tg2 χ - ctg2 χ =
ctg a: cos3^
^ 1 + tg2 χ = sin* '
Преобразуем левую часть:
cos л; cos3 χ cos χ (1—cos2*)
ΙΠΓΪ-ΙΠΓΓ^ ΪΪΪΤί =cos*sin*; чт. д.
10. Выразить
U (х) = cosec * ]/ j + JQS ^ + γΖΓ— ~ Ζ5"
через ctg*.
Решение. Имеем:
1/" ι , ' _Ί/ 2 _ >"2 _= V*
V 1 + cosx "*" 1 — cos jc Г I — cos2 χ J/ sin2 л; |sin*|
Следовательно
Для дуг, оканчивающихся в верхней полуокружности 2kiz < χ < (2к -f
имеем sin χ > 0 и | sin χ | = sin x, а потому
Для дуг, оканчивающихся в нижней полуокружности
(2А+ \)π<χ <2(k+ 1)π,
имеем sin*<0 и | sin χ | = — sin x, а потому
Итак,
( yTctg2 χ, если 2kn < χ < (2k + 1) π;
Ι— /2 (ctg2 α: + 2), если (2k + 1) π < * < 2 (k + 1) π
11. Упростить выражение
_ fi/1 —sinT _ -|/l + sincp\ Λ/l-cos φ ^ -1/1+cos φ
\Г 1 + Sincp Г 1 —8ίηφ/\Γ Ι + ΰΟβφ Γ 1 — COS φ
Решение. Так как |sin<p|<l и |coscp|<l, то все подкоренные
выражения неотрицательны, а потому применимы правила действия над
радикалами. Имеем!
/1 — Sin φ Tj/Ί + Sin φ (1 — Sl'n φ) — (1 -f Sin φ) 2 Sin φ
1 4- Sin φ "~ V I—Sin φ = 1^1 — Sin2 φ ~ "" |COS φ| *
Аналогично получим
/1 — COS φ -Ι ί\ + COS φ 2 COS φ
1+COSCp ~~ У 1 — COS φ "~ "" I Sin φ Ι *
Следовательно,
*4 Sin φ COS φ COS φ Sin φ
= [COS φ j | Sin φ | = | COS φ | | Sin φ | '
Для дуг, оканчивающихся в верхней открытой полуокружности, имеем
sincp>0, а потому | sin φ | = sin φ; для дуг, оканчивающихся в нижней
полуокружности, sin φ < 0, а потому | sin φ Ι = — sin φ.
Для дуг, оканчивающихся в правой полуокружности, | cos φ ) = cos φ, а для
дуг, оканчивающихся в левой полуокружности, |cos φ | == — cos φ.
Следовательно,
4, если 2kn < φ <-£--]- 2kn (I четверть);
Ρ(φ) =
π
—4, если ~2 + 2&π < φ < (2k -f- 1)π (II четверть);
3
4, если (2k -f- 1)π < φ < γ π ψ 2kiz (Π Ι четверть);
3
—4, если τ>·π + 2Λπ <φ <2(£-f- 1)π (IV четьерть).
65
График функции, определяемой выражением Ρ (φ), представлен на черте-
же 67, точки φ = k _ί- являются точками разрыва I рода.
12. Исключить χ из системы равенства
tg2* + ctg2 x = a, tg4 χ + ctg4* = 6.
Решение. Требуется найти соотношение между параметрами а и bf
являющееся необходимым (но в общем случае недостаточным), существова-
ния значения дс, при которых выполняются оба данные равенства.
Возведи в квадрат первое равенство, получим
tg4 χ + ctg4 χ + 2 tg2 x ctg2 χ = α2.
В силу второго равенства и основного тож-
дества tg χ ctg x = 1 получим искомое соот-
ношение:
6+ 2 = а*.
13. Исключить χ из системы равенств
cosec χ — sin x = т, sec χ — cos χ = η.
Решение. Умножим первое на sinjt,
а второе на cos x
1 — sin2 χ = m sin x, 1 — cos2 χ = л cos л: (1)
(2)
или
cos2 χ = т sin л:, sin2 л: = /? cos x.
Перемножим почленно и сократим на sin x cos x*
sin λ: cos χ — mn.
(3)
Умножив почленно равенства (2) на равенство (3), после сокращения по-
лучим
cos3 χ = m2n, sin3 χ = n2my
откуда
^ —— ч ———
cos2 χ — т γίηιη2, sin2 χ = π yfm2n-
Сложив почленно, получим искомое соотношение между параметрами т
и η
т
5 + АгуЛ/п2« = 1.
В некоторых случаях тригонометрические тождества могут быть интер-
претированы геометрически в предположении, что аргумент является острым
углом.
Примеры. 14. Доказать тождество
sin α 1 -f- cos α
1 — COS α sin α
и истолковать его геометрически для острого угла а.
* Значения х, при которых cos χ = 0 или sin χ = 0, не принадлежат
множеству допустимых значений аргумента для левых частей равенств (1)
(рассматриваемых совместно).
Решение. Для доказательства тождества преобразуем левую часть
следующим образом:
Sin a (I -f- COS α)
(1 —COS α) (1 + COSa)"
sin a (1 +cos a) 1 -f- cos a
1 — COS2 a
Sin a
Предположим, что a — острый угол, построим прямоугольный треуголь
ник ABC с гипотенузой, равной 1, и с острым углом, равным а. Из по-
строения, представленного на чертеже 68, следует, что /\ADiC ^ /^ ACD2,
а потому
АС АР2
ADX~ AC ;
l = l— cos а, ЛО2 = Ι+cosa, получим данное
: sin a,
подставив /
тождество.
Примечание. Изложенные геометрические рассуждения дока
зательством тождества служить не могут, так как тождество верно
при произвольных допустимых значениях а, а в геометри
ческих рассуждениях считается, что 0<a<_IL.
Черт. 68
Черт. 69
15. Истолковать геометрически тождество
sin a + cos a
sec a -f- cosec a
= Sin a COS a,
считая а острым углом.
Решение. Рассмотрим Δ ABC с гипотенузой, равной 1, и с острым
углом, равным α (черт. 69). Построим Δ ADE, у которого А — прямом
угол и DE _1_ АВ\ имеем: ^ DEA = ^ ВАС (углы с перпендикулярными
сторонами), следовательно, Δ ABC ~ Δ AED, а потому
АС+ ВС
AD + АЕ~~
АВ
'"DE'
Но ЛС = cos a, £C = sina, AB = \\ AD =
sin α ι cos л 1
DE = DB + BE = tg a + ctg a = __+_„-_.
Подставив в (1), получим данное тождество.
Глава в то рая
АППАРАТ ТРИГОНОМЕТРИИ
§ 14. Теоремы сложения
Теоремы сложения для тригонометрических функций утвержда-
ют, что тригонометрические функции от суммы (разности) двух
слагаемых выражаются алгебраически через значения тригонометри-
ческих функций от слагаемых*.
Доказательство теорем сложения заключается в установлении
соответствующих формул.
Теорема сложения для косинуса. При произвольных зна-
чениях а и β имеют место теоремы сложения, выражающиеся сле-
дующими формулами:
cos (α + β) = cos α cos β — sin α sin β, (Ca +β);
cos (a — β) = cos a cos β + sin a sin β. (Ca_p).
Доказательств о**. Пусть М и
Λ/ — точки единичной окружности, изобра-
X жающие данные значения α и β. Коорди-
наты точек Μ и N соответственно суть
(черт. 70)
N
Черт. 70
ί = sin a;
= sin β.
* He следует считать очевидным существование таких формул. Так,
например, логарифм от суммы log (x + у) невозможно выразить алгебра-
ически через log x и log у. В этом смысле и следует понимать часто
применяющуюся (неудачную) фразу: «сумму нельзя логарифмировать».
** За основу мною принято изложение, данное в работе П. М. К о-
тельникова с упрощением, предложенным Н. И. Фломиным
(журн. «Математика в школе» № 5, 1958).
68
Вычислим квадрат расстояния между точками Μ и N по общей
формуле расстояния между двумя точками на плоскости (см. § 4):
= (χμ~χν) + (Ум-У ν)2 = (cos α-cos β)2 +
+ (sina-~ sin β)2 = 2(1 — cos a sin β — sin a sin β).
Рассмотрим разность данных дуга и β, это есть дуга с началом
в точке N и с концом в точке Л4, измеряющаяся числом а — β.
Отложим дугу ΝΜ от начальной точки Л(1, 0). Пусть R — конец
отложенной дуги, по построению имеем ^jAR = \jMN'. Хорды AR
и ЛШ, соединяющие концы равных дуг kjAR и w МЛ/, равны между
собой AR = NM*.
Точка R имеет координаты
χ = cos (a — β), у = sin (a — β).
Вычислим квадрат расстояния между точками А и R:
2= [cos(a — β)— l]2+sin2(cc — β)=2[1 —cos (α —β)].
Подставив в равенство NM2=AR2 найденные выражения для
его левой и правой частей, получим формулу (Οα_β).
Заменив β на — β в формуле (Са- β), получим формулу
(C. + β)
cos (а + β) = cos [a — (— β)] = cos a cos (— β) + sin a sin (— β) =
= cos a cos β — sin a sin β, ч. т. д.
В изложенном доказательстве не налагается никаких
ограничений на аргументы α и β; это могут быть дуги произвольной
величины. Формула расстояния между двумя точками на координат^
ной плоскости верна при любом расположении данных точек,
а потому приведенное доказательство носит общий характер, оно
справедливо при произвольных значениях α и β**.
Следствие (формулы дополнительных аргументов): если
сумма двух аргументов а и β равна -^-, то косинус одного из
этих аргументов равен синусу другого, т. е.
если α+β = -£-, tno ^5α = $ίηβ, ^$β = $ίηα.
* Каковы бы ни были дуги ΝΜ и AR, они конгруэнтны, а в конгруэнт-
ных фигурах расстояния между соответствующими точками равны
** Мы рекомендуем учащимся построить чертеж 70, придавая а и β раз-
личные конкретные значения, например a = 30°, β = 150°, a = —45°
р ши — 50°, α -в 150°, β = —280° и т. п.
69
В самом деле, вычислим, например, cos a = cos (-^ β] по
формуле (Са_р):
cos a = cos (~ β ) = cos -£- cos β + sin -£- sin β = sin β.
Теорема сложения для синуса. При произвольных зна-
чениях а и β имеют место теоремы сложения, выражающиеся
следующими формулами:
sin (а + β) == sin α cos β + cos α sin β, (5α + β)
sin (а — β) = sin α cos β — cos α sin β. (Sa-β)
Доказательство. Синус суммы α + β равен косинусу
дополнительного до -ψ аргумента -^ (α + β). Этот последний
аргумент можно представить в виде разности следующим об-
разом:
π
"2
Следовательно,
sin
ίη(α+ β) = cosi-f - 'α + β)1 = cos Γ/^- _aj -βΐ =
2 aj cos β + sin f -g- — a\ si
sinP =
sin a cos β + cos a sin β.
Заменив в формуле β на —β, получим формулу синуса раз-
ности
sin (a — β) = sin a cos (— β + cos a sin (— β) =
= sin a*· cos β — cos a sin β, ч. т. д.
Другое доказательство теорем сложения. Это
доказательство опирается на основные положения теории проекций.
Выведем формулу (Са+(э). Отложим от конечной стороны угла α угол β
(черт. 71). Пусть OS есть положение конечной стороны угла β. На луче 05
возьмем точку Μ на расстоянии, равном 1 от точки О: | ОМ | = 1. Косинус
угла α + β есть проекция радиуса-вектора ОМ на начальную сторону ОХ
угла а: прд. ОМ = cos(a + β). Для угла β роль горизонтальной оси играет
ось ОХ', совпадающая с конечной стороной угла а. Система взаимно перпен-
дикулярных осей ΧΌΥ' может быть получена из системы Χ0Υ поворотом
на угол а.
Пусть ON есть проекция радиуса-вектора ОМ на ось 0Xf. Радиус-вектор
ОМ есть замыкающая ломаной ONM. Спроектируем эту ломаную на ось ОХ.
По теореме о проекции ломаной имеем
cos (a + β) = прд. ON + пр^ NM. (1)
Отрезок ON лежит на оси ОХ', и его величина равна
Otf=np/OM = cosp,
70
поэтому
прд. ON = ON cos (XOXf) = cos β cos a.
Отрезок NM параллелен оси ОУ, величина его равна пру'ОМ = sin β.
Направление оси ОУ образует с осью ОХ угол, равный а-\- — \
^(ХОУ)
Следовательно,
; (ХОХ') + ^ (Х'ОУ) = а + —.
/ π Ч
прд. NM = NM cos (ХОУ) = sin β cos α + -γ J.
Подставив в равенство (1), получим
COS (α + β) = COS α COS β + COS ί α + ~γ\ Sl'n β.
(2)
Положим α = _ в формуле (2)
COS
Ы)-
cos π sin β = — sin β.
Полученное равенство справедливо при произвольном β. Заменив
/ π λ
в равенстве (2) cos (α + ~2~) на — sin α, получим формулу (βα+β).
Заменив в формуле (^+β) аргумент β на —β, получим формулу (£α__β)%
Формулы (5α+β) и (5α_β) устанавливаются так же, как в первом дока-
зательстве, ч. т. д.
Примечание. Доказательство основано на общих положениях тео-
рии проекций, а потому применимо при любых значениях аргументов аир.
В качестве упражнения рекомендуем воспроизвести доказательство форму-
лы (Са+о), пользуясь чертежом 72.
71
Теорема сложения для тангенса. Для всех значений
а и β, при которых существуют tg(a + β), tga u tgβ, имеет
место формула
tgfa + β) tga + tgP
1 — tg a tg β ·
Доказательство. Воспользовавшись формулами (Sa+э)
и (Ca+rj), для всех значений α и β, для которых существует
tg(a + β), получим
f α ι β\ __ sln (a ~Ь Ρ) Sin a COS Э +COS a sin 3
&l I r'~"cos(a + p) cos a cos Э — sin a sin Ь*
cos a cos Э — sin a sin [
Если существуют tga и tg β, то cosa^=0 и α)5β^=0. Раз-
делив почленно числитель и знаменатель на cos a cos β, получим
формулу (Та+з), ч. т. д.
Следствие. Если существуют tg(a — β), tga и tg β, то,
заменив β на — β, получим формулу
Формулы сложения для котангенса предлагаем вывести уча-
щимся.
Примеры.
В нижеследующих примерах даны значения тригонометрических функ-
ций некоторых таких дуг, для которых эти значения могут быть выражены в
радикалах (т. е посредством четырех арифметических действий и извлечения
корня над целыми числами). Приведенные ниже формулы могут служить
средством приближенного вычисления с любой степенью точности значений
тригонометрических функций от ряда дуг.
1. Вычислить sin3° и cos3°.
Решение. Зная, что 3J = 18° — 15°, и воспользовавшись найденными
в § 10 значениями тригонометрических функций — углов 18° и 15°, получим
sin 3° = sin -j|r = sin 18° cos 15° — cos 18° sin 15° =
~~ 4
— JL [(/"5- l) (/"6 + YD -У10 + 2/1 (/~6 + /I?)] ^0,05234.
16
И аналогично
cos 3° = — [1Ло + 2 /~5(/6 + YD + (/"5 - 1) (/6 - YD] «0,99863.
16
2. Вычислить sin 6° и cos 6°.
72
Решение. Имеем: 6° = 36° — 30°; зная тр игонометрические функции
углов 36° и 30° (см. § 10), получим
sin 6° = sin 36° cos 30° — cos 36° sin 30° =
«0,104528.
И аналогично:
1
cos6°=-g- [/3(1/5+ l) +1/"2'1/δ —/~б] ^0,99452.
3. Вычислить sin 9° и cos 9°.
Решение. Решение аналогично предыдущему примеру. Исходя из
равенства 9°=45°—36°, получим:
sin9° = sin-^-=-y [/"2(/Ί>+ l)~ 2Vb—V~b] ^0,15643;
cos 9° = -γ [/1 (/1 + l) + 2 Кб —/l] « 0,98769.
4. Вычислить sin 12° и cos 12°.
Решение. Исходя из равенства 12° = 30°—18°, получим
cosl2° = cos-^=-g- [ /1 ]Λθ + 2 /"5 + (/"б — l)] _ 0,97815;
sin 12° = γ [Y\0+2Vb - /"3 (/"5 — l) » 0,20791.
Различные интерпретации теорем сло-
жения.
При некоторых частных предположениях отно-
сительно значений α и β формулы сложения можно установить
различными способами непосредственно геометрически. Эти спо-
собы можно встретить в ряде школьных учебников и пособий.
Однако надо иметь в виду, что все эти способы доказатель-
ствами теорем сложения служить не могут, так как
теоремы сложения верны при произвольных значениях аргументов
α и β; а не только при тех частных предположениях, которые обу-
словлены применимостью данного геометрического рассуждения.
Эти геометрические рассуждения следует толковать лишь как и н-
терпретации теорем сложения при тех или иных частных
предположениях*.
Ниже указаны некоторые из наиболее распространенных ин-
терпретаций теорем сложения.
1. Предположим, что α и β суть произвольные острые углы.
Рассмотрим треугольник ABC (черт. 73), у которого J^B = a+ β;
* Авторы учебников, в которых некоторая геометрическая интерпрета-
ция положена в основу доказательства теорем сложения, вынуждены про-
водить дополнительные рассуждения, устанавливающие общность теорем
сложения (см., например, школьный учебник тригонометрии Рыбкина).
73
причем стороны с и а образуют с высотой h = BD углы α и β (этими
условиями Δ ABC определяется с точностью до подобия).
С одной стороны (черт. 73)
пл. Δ ABC = \ac sin (α + β)*.
С другой стороны
пл. Δ ABC = пл. AABD + пл. Δ DBC,
но пл. AABD = -jADh} ил. ι
(1)
Имеем h = α cos β = с cos α, /4D = с sin α, CD = a sin β.
Следовательно,
пл. Δ AMD = ~ac sin α cos β и пл. Δ DBC = -^-accosasin β.
Подставив в (1) и сократив обе части на у ас, получим фор-
мулу (Sa+β).
В В
о ь
Черт. 73
D b
Черт. 74
II. Несколько видоизменив предыдущее построение, мож-
но получить формулу (Са_р). Для этого вычислим площадь
Δ ABC, изображенного на чертеже 74 в предположении, что
0<β<α<-|. Имеем
пл. Δ ABC = γ ас sin (^ — а + β] =
= ^ас sin !"-£ — (a — β)Ί = 1 ас cos (a — β).
При данном построении
h = с sin a = a cos β, AD = с cos a, DC = asin β.
Дальнейшие рассуждения проводятся так же, как в предыдущем
примере.
* Мы пользуемся известной формулой для площади треугольника по
данным двум сторонам и углу между ними (см. § 61).
74
В виде упражнения рекомендуем учащимся получить формулу
ϊ+β), исходя из чертежа 75.
III. Для интерпретации теорем сложения можно исходить
из непосредственного построения тригонометрических линий суммы
(или разности) углов. Таково, например, распространенное в учеб-
ной литературе построение, относящееся к случаю, когда α и β —
острые углы, причем α + β < -^ . Это построение представлено на
чертеже 76. По построению CD J_ OBy DM J_ CN, CN ±_ OA, сле-
довательно, /^MCD =a; имеем:
sin (α + β) = СЛ/ = ЛШ4 МС. (i)
Далее:
MM = DK = OD sin a = cos β sin a
и
MC = CD cos a = sin β cos a.
Подставив в (1), получим формулу (Sa+β).
Предоставляем учащимся получить из того же чертежа формулу
(Ca + β).
IV. Теоремы сложения можно интерпретировать при помощи
теоремы Птолемея, утверждающей, что произведение диаго-
налей вписанного четырехугольника равно сумме произведений
противоположных сторон*.
Пусть α и β —данные острые углы. Рассмотрим построение, пред-
ставленное на чертеже 77, где АС = 2R —диаметр; имеем по теореме
Птолемея
AC-BD - AB-CD + ВС-AD. (1)
Из прямоугольных треугольников ABC и ACD найдем
CD = 2# sin β, /1Ο = 2^ο$β, BC = 2Rslna.
* Еще в древней Прении теорема Птолемея применялась для составле-
ния «таблии хорд» (т е. по сути дела тригонометрических таблиц). Подроб-
нее см. В. П. Шереметьевский. Очерки по истории математики.
Учпедгиз, 1940
75
Из треугольника ABD получим: BD = 2R s\n{a-\-$) *.
Подставив в (1) и сократив обе части на 4/?2, получим формулу
(S.+p).
Черт. 77
Черт. 78
V. Аналогично можно интерпретировать формулу (S«_p); рас-
суждения предлагаем провести учащемуся в виде упражнения, поль-
зуясь чертежом 78.
§ 15. Обобщение теорем сложения
Последовательным применением формул (Sa+β), (Са+р), (Τ«+β)
можно выразить тригонометрические функции от суммы любого
числа дуг (углов) через тригонометрические функции дуг α, β
и у. Например,
sin (a + β + γ) = sin [(a + β) + у] = sin (a + β) cos у +
+ cos (a + β) sin γ = sin a cos β cos γ + cos a sin β cos у +
+ cos a cos β sin у — sin a sin β sin y.
Подобным же образом найдем:
cos (a + β + γ) = cos [(a + β) + γ] = cos 4a + β) cos у —
— sin (a + β) sin γ = cos a cos β cosy —sin a si η β cosy —
— sin a cos β sin у — cos a sin β sin γ,
и, наконец,
5 V- -г м г r/ cos (σ + β + γ) 1 - tg a tg β - tg a tg γ - tg β tg γ
Общие формулы для
η
sin (a-, + a2 + ... + an) = sin 2 ^
* В силу известной формулы, а = 2# sin А (см. § 58).
76
cos(aj+a2+ .··+«„) = cos 2j at
можно вывести методом математической индукции. Представим фор-
мулы для двух и трех слагаемых в следующем виде, удобном для
выяснения их структуры:
sin (a + β) = cos a cos β (tg a -f tg β);
cos (a + β) = cos a cos β (1 — tga tg β);
sin (a + β + γ) = cos a cos β cos γ [tg a + tg β +
+ tgY-tgatgptgY)]; (S)
cos (a + β + γ) = cos a cos β cos γ [ 1 — (tg a tg β -f
* (C)
Слагаемые в квадратных скобках (объединенные в круглые скоб-
ки) суть основные симметрические функции от тангенсов данных ар-
гументов, взятые через один и с чередующимися* знаками.
Докажем, что имеют место формулы
sin2 «i = cosatcosa2 ...cosап1рг—рг + ръ — ...]; (S)
η
cos 2 ai = cosajcosas... cosart[l — p2 + p4—...], (C)
где
Pi = tga, + tga2 + ... + tg<v,
Рг = tg ax tg2 + tg аг tg a3 + ... + tg an- x tg an;
и вообще
P* =
есть сумма всевозможных произведений тангенсов, взятых по k.
Применим метод математической индукции. Предположим, что
формулы (S) и (С) верны при некотором η (и при произвольных а/),
докажем, что в этом предположении они верны для случая η + 1
произвольных слагаемых аь а2, ..., ая+1.
* В силу принципа продолжения по непрерывности, наличие особых
значений, при которых хотя бы один из тангенсов теряет смысл, несущест-
венно.
77
Имеем:
sin (αχ + α2 + ... + αΛ + α/ι+1) = sin
\/=ι
η
= cos aj cos a2... cos art+i [p, — p3 + pb —... +
+ (1—P2 + P4 —-..)tgan+1] (в силу (S) и (С)).
Выражение, заключенное в квадратные скобки, преобразуется сле-
дующим образом:
Выражение p2k+\-\-p2k tgos/2+1 есть сумма всевозможных произ-
ведений, составленных из tgalf tga2, ..., tga^i, взятых по 2k+L
В самом деле, слагаемое p2k+\ содержит все такие произведения,
в которые не входит tga^+i, а слагаемое p2klg&n+\ состоит из
всех произведений, в которые входит tgart_f-i. Следовательно,
формула (S) верна для суммы η + 1 слагаемых а,, а2> ..., ал,
απ+ι в предположении, что она верна для суммы η слагаемых.
Аналогично (предоставляем подсчет учащимся) в том же предполо-
жении устанавливается справедливость формулы (С) для η + 1
слагаемых. Будучи верными при η=2, формулы (S) и (С) верны
при произвольном натуральном η > 2, ч. т. д.
Общие формулы (S) и (С) можно вывести другим способом, опираясь
на правило умножения комплексных чисел, заданных в тригонометрической
форме *.
Рассмотрим η комплексных чисел:
гх = cosаг + /sinalt г2 — cosa2 + i sina2> ..., zn = cos an + i sin ол.
Перемножив эти числа, получим:
(cos αχ + i sin ax) (cos a2 + i sin a2) ... (cos an -ψ- ί sin αΛ) =
= COS(a1 + aa+ ... +dn) + /Sin (αχ + α2+ ... + an).
Перемножив скобки в левой части и приравняв действительную часть
cos (αχ -)- α2 + ··· + ап)> а коэффициент при мнимой единице sin (αχ -}- α2 +
+ ··· + αη)» получим формулы (С) и (S).
Примеры.
1. Дано tga = a, tg β = 6, tg γ = с, где a > 0, b > 0, с > 0, а α, β и γ —
острые углы. Установить необходимое и достаточное условие, при котором
сумма S = α + β + γ есть острый угол.
* Для умножения двух комплексных чисел это правило выводится
посредством основных формул (Sa_j_p) и (Ca_j_p), а для любою числа сомно-
жителей распространяется методом математической индукции.
78
Решение. В силу условий задачи
О < α < у , 0<β<~, 0<γ<~
возможны следующие два исключающие друг друга случая:
a) сумма S = α -|~ β + γ либо принадлежит первой четверти (открытой)
0<α + β + γ<"2*(τ. е. S — острый угол), в этом случае cos S > 0;
b) сумма S принадлежит левой полуокружности (полуоткрытой)
JL <S < — π, в этом случае cos S < 0.
Условия cos 5 > 0, cos S < 0, имеющие место в случаях а) и Ь), также
взаимно исключают друг друга, а потому искомое необходимое и доста-
точное условие выражается неравенством cos S > 0 или
COS (α + β + γ) = COS α COS β COS γ (1 — tg α tg β — tg β tg γ — tg α tg ) =
= cos α cos β cos γ [ 1 — (ab + be + ас)] > 0.
Искомое условие принимает следующий вид:
ab + be + ас < 1.
§ 16. Формулы приведения
Формулами приведения называются формулы, дающие выраже-
ние тригонометрических функций от аргументов
через функции от аргумента а.
Все формулы приведения выписаны в таблицу, помещенную на
странице 81. Этой таблицей пользуются следующим образом. Пусть,
например, требуется вычислить δίηί^π+α); берем строку с по-
меткой у + α (шестая строка) и столбец с пометкой sin (второй
столбец); на пересечении взятых строки и столбца написано—cosa.
Соответствующая формула приведения пишется так:
/з \
sin (-77 π + a = —cosa.
Формулы приведения, записанные в первой строке таблицы,
выражают свойство четности и нечетности тригонометрических
функций (доказательство см. в § 11); остальные же формулы при-
ведения являются следствием теорем сложения для косинуса и си-
нуса. Для образца выведем формулы для аргумента ——ее
(7-я строка):
/3 \ 3π , . 3
cos у π—a) = cos γ cosa + sin -^ π sin a = — sin a,
. / 3 \.3 3
sin ί у π — a) =sin-2" π cos a — cos γ π sin a = — cosa.
79
Для tgj—jt— αj формула тангенса суммы неприменима, так
, з
как tgyJi не существует; поэтому выразим сначала тангенс через
синус и косинус:
• /3 "\
Sin 7Г π — α
4 / COS ί γ π — α
COS α
и аналогично
(τπ ~~α)
ι / ό \ \ζ / — Sin α
-—COS a
Формулы приведения, будучи следствиями теорем сложения,
справедливы при произвольном (допустимом) значении
аргумента а.
Геометрическая интерпретация формул приведения для случая
острого угла представлена в последнем столбце таблицы; равенст-
ва, выражающие формулы приведения для косинуса и синуса,
можно установить из рассмотрения равных треугольников (на чер-
тежах заштрихованы).
При пользовании формулами приведения можно пользоваться и
следующим правилом:
если угол а откладывается от оси абсцисс (формулы для углов
—α, π ^ а, 2я=)=а>), то наименование приводимой функции сохра-
няется; если же угол а откладывается от оси ординат (формулы для
углов ^±а, 2" ±а). то наименование приводимой функции заменя-
ется сходным (синус и косинус, тангенс и котангенс).
Чтобы определить знак перед приведенной функцией, достаточно
определить знак приводимой функции, считая угол а острым.
гт 'л. (3π \
Для примера составим по этому правилу формулу для cosl о a 1.
Угол а откладывается от оси ординат, поэтому косинус следует
заменить синусом. Если а — острый угол, то угол ~ —а
оканчивается в III четверти, в этой четверти косинус отрицателен,
поэтому в правой части следует поставить знак минус. Итак,
/3π \
cos тг —a = — sin a
80
Аргумент
радианы (градусы)
1
— а
2
тс
у + α (90° + α)
3
тс
у —α (90°—α)
4
π + α (180° + α)
5
π— α (180° —α)
6
3
у π + α (270° + α)
7
3
γ π — α (270° — α)
8
2π -|- α (360° + «)
9
2π — α (360° — α)
Таблица формул
приведения
Функция
COS
COS α
— sin α
sin α
— COS α
— COS α
sin α
— sin α
COS α
COS α
sin
— Sin α
COS α
COS α
— Sin α
Sin α
— COS α
— COS α
sin α
— Sin α
— tgot
— Ctga
Ctga
tga
— tga
— Ctga
Ctga
tga
-tga
ctg
— Ctga
— tga
tg a
Ctga
— Ctga
— tga
tga
Ctga
— Ctga
\
\
1
\
С
\
\
\
η
/η
к.
7
/
/
\ ι
Τ
/
/
Ό
4 Зак. 597
Не следует, однако, думать, что правая часть всегда отрица-
тельна, так как в зависимости от значения а могут представиться
разные случаи. Например, при α =-^π получим
cos (у тс — -—jt) = — sin-jjt^O, так как sin-^π<^0.
Следует заметить, что в практике не всегда целесообраз-
но пользоваться готовыми формулами приведения или применять
изложенное правило. Применение формул и правила нецелесооб-
разно, например, при преобразовании тригонометрических функций
от аргумента π + α. В самом деле, точки единичной окружности
а и π -\- а диаметрально противоположны, их координаты (соот-
ветственно) равны по абсолютной величине и противоположны по
знаку:
cos (π -f- a) = — cos α, sin (π -f a) = — sin α,
а отношения (соответственных) координат равны
tg (π + α) = tg α; ctg (π + α) = ctg α.
Точно также непосредственно ясно, что тригонометрические
функции от аргументов 2π + α и а (соответственно) равны между
собой, ибо дуги единичной окружности, соответствующие этим ар-
гументам, оканчиваются в одной и той же точке. По тон же причи-
не ясно, что тригонометрические функции от аргументов α и 2kn +α
(где k — любое целое число) равны между собой.
cos (α + 2kn) = cos α, sin (α + 2&π) = sin a.
На практике часто формулами приведения пользуются в пред-
положении, что α является острым углом. Пусть требуется вычис-
лить тригонометрическую функцию произвольного аргумента β.
Формулы для аргументов 2π + а и —а позволяют заменить угол β
положительным углом, содержащимся в пределах первой окруж-
ности. Поэтому можно считать, что 0<;β<2π (или в градусной мере
0<β<360°). Рассмотрим два острых угла, которые образует конеч-
ная сторона β с осями координат (при этом направления осей во вни-
мание не принимаются). Обозначим через α наименьший из них (или
один из них, если оба равны 45°), тогда имеем 0 <а < ^. Соответст-
вующая формула приведения выражает тригонометрические функции
угла β через тригонометрические функции угла а. Обычно заранее
составляются таблицы значений тригонометрических функций
(а также их логарифмов), которыми и пользуются в готовом виде.
Эти таблицы обычно даются для значений углов в градусной мере.
Предыдущие рассуждения показывают, что вполне достаточно
составить таблицу значений тригонометрических функций лишь
для углов, взятых от 0° до 45Q,
Примеры.
1. Ниже даны примеры приведения тригонометрических функций раз-
личных углов к функциям угла, меньшего 45°.
a) sin 72° = sin (90° — 18°) = cos 18°;
b) cos 1000° = cos (2-360° + 280°) = cos 280° = cos (270° + 10°) = sin 10°;
c) tg 520° = tg (360° + 160c) = tg 160° = tg (180° — 20c) = — tg 20°.
2. Вычислить
Решение. Имеем:
. /3 \ /3 \ . /3 \
tg ( у π —. α J cos ί у π — α J = sin ( у π — α 1 = — cos a;
COS (2π —· a) = COS a; COS fa — у ) = cos ( у — « ) = sin a;
sin (π —a) = sin a; COS (π + a) =— COS a;
. / Λ . /π \
Sin ί a —· у J = — sin ί у — a I = — COS a.
После подстановки получим
Ρ = — 1 + sin2 a + cos2 a = 0.
3. Доказать, что
cos (χ + ηκ) = (— \)n cos χ и sin (χ + ηπ) — (— \)n sin χ.
Решение. В самом деле, если η = 2k — четное число, то
(— \)п = 1 и cos (χ + 2kn) = cos x, sin (* + 2kn) = sin x;
если п нечетное число, то
cos (x -f 2kn + π) = cos (χ -^ π) = — cos χ.
Аналогично устанавливается второе равенство.
4, Доказать, что
/пк 13 \ ,
cos ( — — у^ я 1 + cos
/3 3 \
(Τ ηπ~Τ4π)
если целое число /г при делении на 7 дает в остатке одно из следующих
чисел: 1, 3, 4.
Решение. Разделим число η с остатком на 7:
η = 7k + η
/tnrni \ 13
члены данной суммы имеют вид: cos ( —γ- — a j, где /тг=1, 3, 5 и α~τιπ
или α = — π.
14
Подставив η = 7k -\- r, получим
(7k -{- г) /ηπ \ /гтк
— сА = (— l)*m cos (^р- — a ) .
cos I
\ / \ ' / \ ' /
4* 83
Так как т — нечетное число, то для всех трех слагаемых множитель
(— \}km __ ^— 1^/г ОдИН и тот Же. Следовательно, достаточно доказать, что
гъ 13 \ /Зт 3 \ /5т 3
при г = 1, 3, 4.
а) Полагаем л=1; преобразуем каждое слагаемое отдельно:
13
cos( у — γ^π J = cos
11 \ 11 3
— Ϊ4π J ==cos Ϊ4 π== — οοδϊ4π;
'3 3 \ 3
cos | у π — — 7i]=cos π '
COS ( у π — γ^π )= cos -7Γ==(
Сумма этих чисел равна нулю.
Случаи Ь) г = 3 и с) г = 4 рассматриваются аналогично (предоставляем
вычисление учащимся).
/ π\ / π\
5. Преобразовать cos ί χ + η γ J и sin f x + η -ζ Ι.
Решение. Если /г — четное число (я = 2k), то
/ π \ . -ή
cos I л: + η ~2 I = cos (χ + &π) = (— \)R cos ^ = (—1) cos *;
и аналогично
η
(ηπ\ -κ*
λ: + у ) = (— 1) sin a:.
Если л — нечетное число (п = 2k -\- 1), то:
cos ( χ + η -ζ ):= cos ( χ + ^π + ~2~ j = — sin (χ + &π) =
= (_ ])*+! Sin д; = (—1) 2 sin λ;;
и аналогично
м— 1
sin ί χ-\- η γ\ =
cos (* + Α;π) = (— 1) 2 cos α:.
§ 17. Тригонометрические функции кратных дуг;
полиномы Чебышева
Если в формулах сложения (Οα+β), (Sa+p) и (Ta^) положить
β—α, то получатся формулы, выражающие тригонометрические
функции от двойного аргумента 2а через тригонометрические
функции аргумента а. Имеем:
sin 2а = 2 sin a cos a; (S2a)
cos 2a = cos2 a — sin2 а; (Сга)
tg2« = Tl^I. (Т„)
8Ί
Формулы для тригонометрических функций от За, 4а и т. д.
могут быть получены последовательным применением теорем сло-
жения. Так, например,
sin За = sin (2а -J- а) = sin 2а cos а + cos 2а sin а = ή~ ji H ί
= 2 sin α cos2 α -f- (cos2 а — sin2 α) sin а =
= 3 sin α cos2 а — sin3 а = 3 sin а — 4 sin3 а.
Аналогично найдем 2 jtv**«C C*iJ· * =1//- (М^Л*/% Со
cos 3 α = 4 cos3 α — 3 cos α.
Чтобы получить общие выражения для cos па и sin na, до-
статочно в общих формулах сложения (С) и (S) (стр. 77) поло-
жить а, = а2 = ... = ап = а. Тогда получим:
cos па == cosna — С η sin2 a cos"""2 a + C^ sin4 a cos""4 a — ... (Cm)
п-Л_
(последний член равен (—1) 2 . η cos a si η""1 α при нечетном п и
(—I)2 sin"α при четном" ri)\
sin na = Cn sin a cos""1 a — Czn sin3 a cos""3 a +
+ C* sin5 a cos""5 a — ... (S«a)
/2-1
(последний член равен (—1) 2 sin" α при нечетном п и
η—2
(—1)~ η sin""1 a cos a при четном п).
Формулы (Ст) и (Sna) можно получить другим способом, вос-
пользовавшись известной из теории комплесных чисел формулой
Моавра
(cos a + i sin a)" = cos na + i sin ш.
Преобразовав левую часть по формуле бинома Ньютона и при-
равняв действительные части и коэффициенты при i правой и левой
частей, получим формулы (Спа) и (Sna).
Формулы (Спа) и (Sna) выражают тригонометрические функции
от я-кратного аргумента через степени синуса и косинуса простого
аргумента. Так, например, при η = 4 получим
cos 4 a = cos4 a — 6 sin2 a cos2 a -f sin4 a;
sin 4a = 4 sin a cos3 a — 4 sin3 a cos a.
При я = 5 получим
cos 5 a = cos5 a — 10 sin2 a cos3 a 4- 5 sin4 a cos a;
sin 5a = 5 sin a cos4 a— 10 sin3 a cos2 a + sin5 a.
Из рассмотрения левых частей тождеств (Спа) и (Srta) следует,
что cos η α и sin па можно преобразовать в однородные многочлены
степени η относительно cosa и sina.
85
Левая часть тождества (С„а) содержит только лишь четные
степени синуса; эти степени можно выразить через косинус по
формуле
sin2*a = (l — cos2 α)*.
Следовательно, cosna может быть представлен в виде многочле-
на относительно косинуса следующим образом:
cos па — cos" а —С2п cos"~2 a (1 — cos2 a) -f-
+ C£cos"--4a(l-cos2a)2-...
Многочлен
Tn (x) = x«-C2n xn~2 (1-χη + Ο4η xn~4 (1 - x2)2 - ... (T)
называется м-ным полиномом Чебышевапо имени ве-
ликого русского ученого П. Л. Чебышева (некоторые заме-
чательные свойства полиномов Чебышева изложены ниже, см. § 43).
Формула (Ст) примет вид:
cos па = Τп (cos a). (С„а)
Тождество (Srta) можно переписать так:
sin па = sin a (Cln cos""1 a — Съп sin2 a cos""3 a +
Выражение, заключенное в скобки, содержит si η α только лишь в
четных степенях, а потому оно может быть представлено в виде
многочлена относительно косинуса. Многочлен
и η (χ) = схпхп-х-с1п- х*) хп~ъ + с*п- χ*? *п~ь -... (U)
называется n-ным полиномом Чебышева второго рода.
Формула (S^a) примет вид:
sin па ·= sin a Un (cos a). (S*na)
Степень полинома Тп(х) равна п. В самом деле, из формулы (Т)
видно, что аргумент χ содержится в правой части не выше, чем в
степени п. Подсчитаем коэффициент при хп
(сумма биномиальных коэффициентов четного номера).
Так как этот коэффициент отличен от нуля, то степень Тп(х)
равна п.
Аналогично докажем, что полином Un(x) имеет степень η — 1;
коэффициент при хп~] равен
86
Примеры.
1. Ниже составлены выражения для четырех первых по порядку поли-
номов Чебышева.
Так как cos 0* = 1, то считают То (х) = 1; имеем далее:
cosl-a = cosa и Тх (χ) = χ;
cos 2α = 2cos2 a — 1 и T2(x) = 2x2 — 1;
cos 3α = 4 cos3 α — 3 cos аи T3 (χ) — 4*3 — Зл:;
COS 47 = COS4 а — 6 Sin2 α COS2 α -f sin4 а = COS4 а — 6(1 — COS2 α) COS2 ι +
+ (1 — cos2 а)2 = 8 cos4 а — 8 cos2 а + 1 и Г4 = 8л:4 — 8*2 + 1.
Составим выражения для четырех первых полиномов Чебышева вто-
рого рода:
sin 1 ·α = sin α и Vу (х) = 1;
sin 2α = 2 sin α cos α и Uo (χ) = 2χ\
sin 3α = 3 Sill α COS2 a — sin3 α = sin α (3 COS2 α — sin2 a) =
= sin a (4 cos2 a — 1) и U3(x) = 4x2 — 1;
Sin 4a = sin a (4 cos3 a — 4sin2 a cos a) =
= sin a (8 cos3 a — 4 cos a) и U^(x)=8x3 — Ax.
2. Найти значения п, при которых cos na и sin πα могут быть представ-
лены в виде многочленов относительно синуса
Решение. Заменив в общих формулах (С^) и (S*a) α на у — а, по-
лучим тождества
/ π \ / π \
COS I П -γ — П1 \ = Tn(s\U α) И Sin ( П ~γ — Па I =
= Un (sin a) COS a.
Случай 1°. n = 2k — четное число; имеем:
cos 2Ь = (—1)Л T2k (sin a); sin 2H = (— \)k+l cos a[/2jfe (sin a).
Случай 2°. /2 = 2/г + 1— нечетное число; имеем:
sin (2* -f- 1)2 = (—1)*Г2Л+1 (sin a);
и
cos (2/г + 1) a = (—1)^ cos a U2k+\ (sin a).
Из полученных тождеств видно, что cos 2/га и sin (2/г+1) а можно пред-
ставить в виде многочлена относительно синуса.
Так, в частности, имеем:
cos 2a = 1 — 2 sin2 a; sin 3a = 3 sin a— 4 sin3 a;
COS 4a = COS4 a — 6 sin2 a COS2 a + sin4 a =
— (1 — sin2 a)2 —6 Sin2 a (1 — sin2a) + sin4a = 8sin*a — 8 sin2 a + 1.
3. Вычислить произведение
Ρ = cos a cos 2i cos 4a ... cos 2k a ... cos 2n a.
87
Решение. Перемножив почленно тождества
2 Sin α COS α = sin 2α,
2 sin 2α cos 2α = sin 4α,
2 sin 4α cos 4α = sin 8α,
2 sin 2" α cos 2na = sin2"+1a,
после сокращения получим:
2n+1 sin a.P = sin 2n+l a,
откуда
sin 2"+! a
Если, в частности,
то
sin2"+1a= sin (π —
и, следовательно, получим
π 2π 4π
COS -ТТЛ CCS -ΓΤΊ COS -ΤΓί ...COS ·
Так, в частности, при η = 1 получим
π 2π Ι
cos-g-cos-β-**—.
При п = 2 получим
π 2π 4π 1
cos-g- cos -g- cos -g- = -g- ,
или в градусах
cos 20° cos 40° cos 80° = -ψ .
§ 18. Формулы деления аргумента
Формулы тригонометрических функций от половинного аргу-
мента дают выражения тригонометрических функций от аргумента
|- через тригонометрические функции от аргумента а.
Заменив в формуле (С2а) аргумент α на —, получим
cos2 -| sin2 -^- = cos a;
к этому соотношению присоединим тождество
cos«-i- + sin«-^=l.
88
Решив относительно cos -|· и sin -^, получим
А также
tgl^ij/"1-003*
COS-
sin-
1 + COS α \ 2
Знаки перед радикалами должны выбираться в соответствии с
тем, в какой четверти расположен аргумент ^ .
В формулах (С«\, (Sec] и (Та\ тригонометрические функции
от половинного аргумента у выражены через косинус аргумен-
та а. Если известно значение cos а, то по этим формулам мож-
но вычислить абсолютные величины тригонометрических функций
и
Заданием значения косинуса cosa = m определяется бесконеч-
ное множество дуг
а.= ± arc cos m + 2кл.
Соответствующие половинные дуги
α arc cos m . *
J =* ± о ^ kK>
COS
sin
α
2
α
Τ
ι/ 1 + COS α
~ Ι 2
ΐ/ 1 —COS α
~ Г 2
в зависимости от выбора знака и значения k, мо'гут в общем случае
оканчиваться в л ю б о й четверти единичного круга. В самом деле,
если—l<m<4, ToO<arccosm<^, a^-^-s~ есть острый угол. Если
выбрать знак +, то дуга -^ будет оканчиваться в первой или третьей
четверти, в зависимости от четности или нечетности k. Если выбрать
знак —, то получится дуга, оканчивающаяся во второй или в четвер-
той четверти. При т = ±1 получаются дуги, оканчивающиеся в кон-
цах горизонтального или вертикального диаметра. Следовательно,
в общем случае при данном cosa = т в формулах (Caj и (S «) воз-
можна любая комбинация знаков. 2
Представим данный аргумент α в виде α =а0 + 2knt где а0
выбирается в промежутке—π<αο<π; в таком случае формула
4В Зак. 597 89
К)
может быть записана в виде:
cos-в- = (--- - ■•cos*
2
В самом деле, γ < Ц- < -£-, а потому угол -|- = Ц + &я
оканчивается в правой полуокружности при четном k и в левой
полуокружности при нечетном k\ в первом случае cos у ^> О, а во
втором cos -у < 0.
Аналогично, если а представить в виде
α == α0 + 2£π, где 0 < α0 < 2π,
то формулу /S α \ можно записать в виде
В самом деле, 0<уО, а потому угол у = у + kn оканчива-
ется в верхней полуокружности при четном k и в нижней полу-
окружности при нечетном k\ в первом случае siny^-Ο, а во вто-
ром sin γ<0.
Выражения для tg -^ можно получить в другом виде, а имен-
но:
. a =slnJ 2sin|cos|- sina
Ь 9 ^у rr 1 _L глс η ( —)
x α 1 + COS α
cos у 2 cos2 γ
α sin| 2sin2| ^^^
2 a a a. sin a I —)
cosy 2cos-2sin-nr \ 2/
Из формул /Τα\ и (Та\ вытекает следствие: тангенс по·
\ Т/ \ Т/
ловинного аргумента tg у выражается рационально через sin α
α cos α.
Из тождеств
2 sin у cos у = sin α и sin2 у -f cos2 у = 1
можно выразить косинус и синус половинного аргумента через
sina. В самом деле, складывая и вычитая, получим эквивалент-
90
иую систему уравнений:
/ sin-j +C0S-2" =l+sina, [sin у—cos у ι =1—sin α,
откуда
sin γ + cos у = ± ]Λ +sina
и
cos -у — sin у = ± у 1 — sin a.
Складывая и вычитая, получим формулы:
a __ ± К 1 + Sina ± К i —Sina
COS -75- г
• a __ ± У 1 + sin a =p V 1 — Sin a
5)
2 2
При данном а знак перед каждым из радикалов выбирается в
соответствии с тем, какие знаки имеют sin-|· и cos γ, при этом
всегда в формулах (Са) и (S'a) знаки перед вторым радикалом
противоположны. Формулы (С'«) и (S'a) менее удобны, чем
формулы 1Са\ и /S а ^, они не имеют широкого применения.
Примечание. Формулы (Са\ и is'a) можно получить
из формул /С а \ и (S а \ посредством алгебраических преобра-
зований. В самом деле, имеем
Применив формулу преобразования сложного квадратного
Радикала (см. «Специальный курс элементарной алгебры»,
§ 40), получим равенство (Со).
Из формулы
tga =
l-tg2-S-
2
можно получить формулу, выражающую tg γ через tg α. Из
квадратного уравнения
tgatg2|- + 2tg|--tga=0 (1)
4В*
91
найдем
t*4-=-
2 tga
Корни уравнения (1) (за неизвестное считается tg-^ j обратны по аб-
солютной величине и противоположны по знаку. Это можно объяс-
нить геометрически: если дано tga = m, то a = arctg m + ηπ,
откуда, при четном η = 2k:
или при нечетном n=2k-\-l
, α , /arc tg m , π - \ , arc tg m
tg T = tg (^—f- + у + &tj = — ctg —f— .
Эти значения обратны по величине и противоположны по знаку,
то или другое из них выбирается при д а н н о м α в зависимости
от знака tg-|.
Построение формул, выражающих тригонометрические функ-
ции, от дуги -^ через функции дуги α встречает затруднения алге-
браического характера, связанные с необходимостью решать урав-
нения высших степеней. Если в формуле (С*т)(стр. 86) заменить па
на а, а α на -, то для нахождения неизвестного χ = cos- по задан-
ному значению cosa получится уравнение
Это уравнение в общем случае имеет η действительных раз-
личных корней. В самом деле, множество всех дуг, имеющих
данный косинус cosa = m, определяется по формуле
a = ± arc cos т+2/гл,
откуда
α __ arc cos m , 2Ы
~к - ± л h~7T ·
Если выбрать знак +, то получится бесконечное множество дуг
α arc cos т , 2Ы ~
η
которые оканчиваются на единичной окружности лишь в η геомет-
рически различных точках при k = 0, 1, 2, η — 1, ибо прибавление
к числу k любого целого слагаемого, кратного п, вызывает прибав-
ление к - слагаемого, кратного 2π (τ. е. получается дуга, оканчи-
92
вающаяся в той же точке). Следовательно,
/arccos m , 2kn \
COS ( ) ,
где k = 0, 1, 2, ..., η—1 (в общем случае), имеет η различных
значений. Аналогично, все дуги вида
α arc cos m ι 2Ы /Q4
τ η— ~γ ~τ~ w
оканчиваются в п геометрически различных точках. Дуги серии
(2) и серии (3) попарно симметричны относительно оси абсцисс, а
именно, заменив в (3) произвольное целое число k на — £, получим
дугу, противоположную некоторой дуге серии (2), но изменение
знака дуги не изменяет косинуса. Поэтому χ = cos— в общем случае
имеет η различных действительных значений.
Например, при η = 3 получим кубическое уравнение
* q о о 3 COS α г.
cosa=4;r — Зл: или х3 τ χ — = 0.
4 4
Это уравнение можно решить в радикалах, однако, здесь (в общем
случае) имеет место неприводимый случай, характеризующий на-
личие трех действительных корней. Формула К а р д а н о дает:
3 г " 3 /
ι / COS α ι / COS2 а — 1 -* г COS α Ί / COS2 a — 1
X=V nr + V—64— + ]/ -8--K —64— ·
Так как cos2a — l<0, то в общем случае (приа=^=2йя) под знака-
ми кубических радикалов содержатся мнимые числа и выразить χ
посредством действительных радикалов невозможно.
В частном случае при я—2k последовательным применением
формул (Са\ и (S^\ можно получить формулы, выражающие
в квадратных радикалах тригонометрические функции аргумента
-^ через функцию аргумента а.
Так, например,
cos-г =<
{·-
-\i I + cos a
Примеры.
1 Вывести формулы [Та ) и [Та ), исходя из формулы (Тс
\ τ/ Ι т/ V ι
Решение. Освободив в правой части равенства (Ta j знаменатель
"2"/
93
от радикала, получим:
α ±/ 1— COS α ± У 1—COS2 α ± sin α
+ cos a 1 + COS α 1 + COS a '
Из двух знаков в числителе следует взять знак +» так как при всех
допустимых значениях α (т. е. α ψ (2k + 1) π) знаменатель положителен,
a sin α и tg iL имеют одинаковые знаки. В самом деле, если 2kn < α <
< (2k -f- 1) π, то sin α > 0, но тогда &π < ϋ < —Х_ π, т. е. дуга -1
оканчивается в I или III четверти (в зависимости от четности или нечет-
ности k), в этом случае также tg — > 0; аналогично, если (2£+1)π<
<α<2(£+1)π, то sina<0, в этом случае "^ 1 π < — < (k -f- 1) π,
дуга -ί- оканчивается во II или IV четверти, но тогда tg a < 0.
Аналогично, формула [Та ] может быть получена из (τ α ] путем
\т/ V ту
освобождения в правой части числителя от радикала.
2. Найти выражение для cos — и sin — .
2п 2п
Решение. Имеем:
16 "~ 2
Обозначим для кратности
(й = 1, 2, 3, ...),
где символ извлечения квадратного корня применяется η раз.
В этом обозначении имеем:
#2
Применим метод математической индукции. Предположим, что
cos трг = —2— и S1 n ул" = "
В этом предположении имеем:
и аналогично
π
Sill 7~Г =
DilJ 2"+1
' 2
1 2
1/2 +
2
"_ ,/2
2
мулы верны при произвольном я > 3.
§ 19. Формулы преобразования произведения
тригонометрических функций в сумму
Теорема. При произвольных а и β имеют место тож-
дества:
_ cos (α + β) + COS (α - β) .
— 2 ' V^'W
— COS (α - β) - COS (a + β) .
— 2 » (P*^/
Доказательство. Сложив почленно равенства (0α+β) и
(0α_β), выражающие косинус суммы и косинус разности, получим:
cos (α+β) + cos (a — β) = 2 cos a cos β.
Откуда следует формула (С-С).
Если почленно вычесть равенства (Са_^) и (0α_β), то полу-
чается формула (S-S). Тождество (S-C) устанавливается почлен-
ным сложением равенств (Sa+β) и (Sa-β), ч. т. д.
Доказанные формулы позволяют заменить вычисление произ-
ведения синусов и косинусов вычислением суммы этих функций (но
от других аргументов).
Следствие. Последовательным применением формул (С-С),
S-S) и (S-C) любое произведение
cosa^cosaa·..^^^^^!^ ...§ίηβΛ
можно преобразовать в сумму косинусов и синусов.
Геометрическая интерпретация. Пусть a —
произвольный, а$ — острый угол. Построим ромб, смежными сто-
ронами которого являются радиусы единичного круга, образующие
углы ±β с конечной стороной угла α (черт. 79). Диагональ ромба
95
ОМ есть замыкающая ломаной OLM. Спроектировав на ось абс-
цисс, получим:
npOL+npLM=npOM.
Векторы OL и LM образуют с осью ОХ углы α+β и α —β,
поэтому:
пр OL = cos (а + β), npLM = cos (а — β) и прОМ = 20К cos а,
где К — точка пересечения диагоналей ромба, имеем: OK = cos β.
Подставив в равенство (1) и сократив на 2, получим формулу (С-С).
Проектированием на ось ординат получим формулу (S«C).
Вторая диагональ NL· ромба образует с осью ОХ угол α +-%>
отрезок ОЬ служит замыкающей ломаной ONL·.
Имеем:
пр.* NL=2np NK=2 sin β cos ί-^- + α\ = — 2 sin β sin α
и
cos (α + β) = πρ^ OL = πρ^ ON + πρ^ NL = cos (α — β) — 2 sin α sin β.
Откуда получается формула (S-S).
В качестве упражнения предлагаем вы-
полнить построение в случае, когда β не
является острым углом (например, β — ту-
пой угол).
Примечание. Изложенная интер-
претация доказательством рассматривае-
мых формул служить не может, так как
формулы верны при произвольных а и
β, а не только для случая острого угла β.
Ч1срт. ι у
Примеры.
1. Вычислить (без таблиц) произведение
Ρ = tg 20° tg 40° tg 60° tg 80°.
Решение. Имеем:
si π 20° si η 40° si π 60° si η 80°
Ρ =
cos 20° cos 40° cos 60° cos 80°
как показано в примере, рассмотренном на стр. 88,
cos 20°cos 40°cos 80° = -g-.
Следовательно, знаменатель равен — . Для вычисления числителя при-
16
меним формулу (S*S):
sin 20° sin 40° = ~к (cos 20° — cos 60°);
и далее:
1 (cos 20°— cos 60°) ^ sin 80° = J-SL [cos 20° sin 80° — 1 sin 80°] =
2 2 4 L 2 J
sin 100° + sin 60°
Л 1
J-16
(принять во внимание, что sin 100° = sin 80°).
Следовательно: Ρ = 3.
2. Доказать, что:
cos (α + β) sin (α — β) — cos (β + γ) sin (β — ι
+ cos (γ + δ) sin (γ — δ) + cos (δ + a) sin (Ь — α) = 0.
Решение. Преобразуем каждое слагаемое е сумму по формуле (S»C):
sin (α — β) cos (α -f β) == γ (sin 2α — sin 2β).
Написав аналогичные равенстра для остальных трех слагаемых и сложив
их почленно, получим нуль в правой части.
3. Преобразовать в сумму cos a cos β cos γ.
Решение. Применим формулу (С·С) сначала к произведению двух
первых сомножителей:
COS (а + β) + COS (α - β)
cos α cos β cos γ = 2 cos ϊ ^
= у cos (α + β) cos γ + if cos (α — β) cos γ;
снова применим формулу (С«С):
cos α cos β COS γ = -j COS (α + β + γ) + -j cos (a + β — γ) +
§ 20. Тригонометрические многочлены и их преобразование
Определение. Выражение вида
Ρ (а) = а0 + (aiCosa+6, sin a) -f- ... + (akcoska-{-bk sin ka) -f-
+ ... (anQos na-\- b ns\n l
называется тригонометрическим многочленом п-го порядка; при
этом предполагается, что \ ап \ + | bn \ =/= 0*.
Иными словами, тригонометрический многочлен есть линейная
комбинация, составленная из функций
1, cosa, sina, ..., cosfcx, sin&a, ..., cosna, sinrca.
Примерами тригонометрических многочленов могут служить
следующие выражения:
1 + cosa + sina, cosa + 3sin2a + cos3a и т. п.
* Это условие выражает, что хотя бы один из коэффициентов ап и Ьп
не равен нулю.
97
Теорема. Всякая целая неотрицательная степень косинуса и
синуса cos" χ и sinm χ, а также всякое произведение этих степеней мо-
жет быть преобразовано в тригонометрический многочлен.
Доказательство. В самом деле, всякое произведение
cosatcosa2, ..., cosocn sin βι-sin β2, ♦ ·, sin $mможно преобразовать
в сумму косинусов и синусоь (см. § 19, следствие), аргументами
которых служат алгебраические суммы вида
«1 ± «2 ± .- ± *п ± βΐ ± β2 ± Рз ± ..· ± βΛ.
В частности при а4 = а2 = ... = ая= β4 == β2 =...= β^ =а по-
лучатся формулы преобразования произведений cos" a sin'71 α (в част-
ности, может быть η = О или т = 0), в линейную комбинацию ко-
синусов и синусов дуг, кратных а, т. е. в тригонометрические много-
члены, и т. д.
На практике для выполнения этого преобразования целесооб-
разно пользоваться формулами
1 . о о 1 +COS 2а . 0 1—COs2a
sin a cos a = у sin 2a, cos2a=—i—^ , sin2 a = ^—
в целях упрощения алгебраических выкладок (см. ниже примеры).
В элементарной математике преобразование степеней cos" a,
sinma и cos" a sin™ а в тригонометрические многочлены называется
также преобразованием понижения степени.
В общем виде формулы преобразования степеней cos" a и sin" a
в тригонометрические многочлены удобно получить, воспользовав-
шись формулами Μ о а в ρ а.
Положим
и =cos a-\-i sin α, υ=cos a — i sin a;
тогда имеем
и Α-ν . и — и
cosa = —ψ- , sina=—^-,
un __ CQS na _j_ £ sjn na> υη =tC0S flQf j Sjn na>
откуда
cos na = у (мл+ул), sin ш = у (ил — у").
Следовательно,
cos" a =
■Ή-Ο"):
!У21
[cosna+C^cos(n—2)a+C^cos n — 4)a+
9?
Аналогично
sin«a = Л-(и-vY = Л- [ия-С\ип-Х v+C2nun-2υ2-...].
При четном n=2k получим:
sin a = -—кг- [(и -\-υ ) — C2k uv (и ~~ -\-v "~ ) + ...] =
2
= 2kJx [cos2^a—C2^cos 2k — 2)a-\-C2k^os(2k — 4)a— ...j.
При нечетном n=2k-\-\ получим:
sin2A+la = J=:""b
i "-J 22yfe
ι sin(2ft— l)a+CL+isin(2* — 3)a+ ...].
Предлагаем учащимся в виде упражнения доказать получен-
ные равенства методом индукции, исходя из равенств:
cos"+I a=cos'*a-cosa; sinn+1 a^sin^a-sina;
из выражений (по предположению) для cos"a и sin^a и из фор-
мул (С-С), (S-C), (S-S).
Примеры.
1. Преобразовать в тригонометрический многочлен sin3a.
Решение.
sin3 a = sin2 a sin a = "о" (1 — COS 2a) sin a = "o" sin a — ~o sln a COS 2a =
J^ . 1 sin3a+sin(—a) 3 . 1
= 2 sin a— 2 2 ~ 4 sln a— 4
2. Преобразовать в тригонометрический многочлен sin4 a.
Решение.
sin4 a =
/1 — cos2a\2 ι
2 I =-4"(l — 2cos2a + cos22a) ==
1 1 1 l+cos4a 3 1 1
= ~ξ — у cos 2a + -j 2 = ~g" — ~2 cos 2a -f -g- cos 4rc.
3. Преобразовать в тригонометрический многочлен si n3 a cos5 a.
Решение
sin3 a COS6 a = (sin a COS a)3 COS2 a =
в= jg sin3 2a (1 + cos 2a) = jt» sin2 2a (sin 2a -f sin 2a COS 2a) =
= 32 (1 — cos 4a) ί sin 2a-f--^ sin 4a I =
= 32 sin 2a-f у sin 4a — cos 4a sin 2a — у COS 4a sin 4a .
Имеем:
л sin 6α — sin 2α . · 1 .
cos 4α sin 2α = ^ и COS 4α sin 4α = γ sin 8α;
после подстановки получим:
3 111
sin3 α cos6 α = 7τ sin 2α -f- ττ: sin 4α — rj sin 6α — too sin 8α.
Теорема. Всякий тригонометрический многочлен может быть
преобразован в многочлен относительно косинуса и синуса:
Ρ (а) = Q(cosa, sin α),
где Р(а) — тригонометрический многочлен, a Q(x, у) — некоторый
многочлен от двух аргументов.
При этом порядок тригонометрического многочлена Ρ (а) равен
степени соответствующего многочлена Q(x, у).
Обратно: всякий многочлен относительно косинуса и синуса мо-
жет быть преобразован в тригонометрический многочлен.
Доказательство. Пусть
Ρ (а) = а0 + (ajcosa+ftj sin a) + ... + (akcoska+bhsinka) + ... +
+ (an cos na -f bn si η ηα)
—данный тригонометрический многочлен; преобразуем каждый его
член по формулам (см. § 17):
cos ka=Tk (cos a); sin ka =sm aUh (cos a);
просуммируем, тогда получим
Ρ (α) = [ао + аг Т, (cos a) + ... + ak Tk(cosa) + ... + an Tn(cosa)] +
+ sina[&1+62i/2(cosa) + ... + bnUn (cosa)].
Правая часть этого тождества есть многочлен Q(cosa, sin a)
относительно cos α и sin α; группа старших членов относи-
тельно (cosa и sina) есть 2n~l a^cos^a + 2n~l &/2sinacosn"~1 a;
так как | ап \ + | bn \ =f= 0, то эта группа членов не может обра-
титься в нуль-многочлен; следовательно, степень Q(x, у) равна п.
Обратно: для преобразования многочлена Q(cosa, sina) в три-
гонометрический многочлен достаточно преобразовать каждый его
член в тригонометрический многочлен и выполнить приведение
подобных членов.
Примечание. Представление тригонометрического
многочлена Р(а) в виде многочлена Q (cosa, sina) не единственно,
так как всякую содержащуюся в Q четную степень косинуса
(синуса) можно выразить через синус (косинус).
Примеры. 1. Преобразовать тригонометрический многочлен
Ρ (а) = 1 + COS α φ (2 COS 2a + 3 Sin 2a) + (COS 3a — sin 3a)
в многочлен относительно cosa и sina.
100
Решение. Имеем
2 COS 2α + 3 sin 2α = 2 cos2 α —2 sin2 α -f 6 COS α sin α;
cos 3a — sin 3a = (4 cos3 a — 3 cos a) — (3 sin a — 4 sin3 a) =3
= 4 sin3 a + 4 cos3 a — 3 cos a — 3 sin a
Подставив, получим
Ρ (α) = 1 — 2 COS a — 3 Sin a + 2 COS2 a + 6 COS a sin a —
— 2 sin2 a + 4 cos3 α φ 4 sin3 a
Заменив, например, cos3 α на cos a (1 — sin2 α), получим (после подста-
новки) другое представление Ρ (α) в виде многочлена относительно коси-
нуса и синуса.
2. Преобразовать в тригонометрический многочлен
Q (COS a, sin а) = 2 COS а — sin a COS a -f COS3 a — sin4 a.
Решение. Подставив
1 3 cos За
Sin a COS а = -ψ SIП 2а, COS3 a = -j COS a + 7— I
3 1 1
Sin 4a = -q — ТГ COS a + "о* COS 4a
Ο Δ Ο
(см. примеры 1 и 2 на стр. 99),
получим
3,11 /1 1 \
Q (COS a, sin а) = ~β\~~ξ COS a -f ( "Tf Sin 2a —у COS 2a J -|-
-\—j COS За + -д- COS 4a.
§ 21. Формулы преобразования суммы
тригонометрических функций в произведение
Теорема. При всех значениях а и β имеют место ра-
венства:
I ft ft
cos a + cos β = 2 cos α—γ- cos σ-γ^; (С -f С)
cos α — cos β == — 2 sin —ρ· sin -γ1-; (C — C)
sin a + sin β = 2 sin ^i- cos ^^; (S -f- S)
sina —sinp=2sin^cos^. (S — S)
При всех значениях а и β, отличных от γ + Απ, имеют
место равенства:
Sin (JC + β) /Τ1 ι Τ\
ll^; (T + T)
tga-tgp= 5ί"(*-ξ>. (Τ-Τ)
& δΜ COS a COS β ν '
101
Доказательство. Для доказательства четырех первых
формул введем вспомогательные аргументы φ и ψ, связанные с ар-
гументами α и β линейными уравнениями:
φ -{- ψ = α, φ — ψ = β. (L)
При всех значениях α и β уравнения (L) можно решить относительно
φ и ψ
φ = 1±ί, ψ=^.* (L')
Формулы (L) и (L/) устанавливают взаимно однознач-
ное соответствие между множеством всевозможных пар значений
аргументов α и β и множеством пар значений аргументов φ и ψ.
Имеем:
cos a + cos β = cos (φ + ψ) -f- cos (φ — ψ) = 2 cos φ cos ψ =
= 2 cos
cos
2 wo 2 '
Аналогично доказываются следующие три формулы.
Равенства (Т + Т) доказываются формальными преобразова-
ниями:
t cos β db cos ol sin β
f _i t ft — S*n α 4- S*n ^ —
6 — ® Ρ ~~ COS α ^° COS β ~
COS α COS β
Sin(a± β)
4. Т. Д.
COS a COS β
Выведенные формулы преобразования суммы тригонометриче-
ских функций в произведения называются также формулами приве-
дения к логарифмическому
виду. При вычислениях с таблицами
логарифмов всегда удобно вместо сложе-
ния пользоваться умножением, а потому
при логарифмических вычислениях целе-
сообразно суммы представлять в виде про-
изведений.
Геометрическая интер-
претация. Построим радиусы еди-
ничного круга, образующие углы α и β с
Черт. 80 горизонтальной осью; угол, образован-
ный этими радиусами, равен α — β. Огра-
ничимся рассмотрением случая, когда 0<α— β<π. Диаго-
наль OL ромба, построенного на радиусах-векторах ОМ« и
ΟΜβ образует угол ^-—^ с осью ОХ; ее длина равна (черт. 80)
|OL| = 21 OK I =^
* Точки (φ, ψ) и (α, β) посредством невырожденного аффинного преобра-
зования (Ζ/) взаимно однозначно преобразуются друг в друга.
102
Спроектировав ломаную OM$L· на ось абсцисс, получим
пр ΟΜβ + пр Щ L == пр OL, (1)
но
пр ΟΜβ = cos β, пр Μβ L = пр ΟΜα = cos α,
Подставив в равенство (1), получим формулу (С + С). Спроек-
тировав на ось ординат, получим формулу (S + S).
Вторая диагональ Щ М« образует с осью ОХ угол
γ +^-?г-> ее длина равна 2 \Щ К |=2 sin ^тр-, радиус-вектор ОМ«
есть замыкающая ломаной ΟΜβ Μα.
Имеем:
пр ОМ« = пр ΟΜβ + пр Μβ Μα
или
cos α = cos β -f 2 sin —γ- cos у + ~γ^
Откуда, приняв во внимание, что
а 4-
получим формулу (С — С). Спроектировав на ось OY, получим
формулу (S — S).
Примечание. Изложенная интерпретация доказатель-
ством формул приведения к логарифмическому виду служить
не может (см. аналогичное примечание на стр. 96).
Следствия из основных формул:
1. cos α + sin β = cos α -f cos ί γ — β J
В частности, при α = β
cos α + sin α = Υ2 cos (α — ~ ].
2. Положим β = j в (Τ 4- Ό и (Τ — Τ)
"sin(a + -J) V~2 Sin (-J - α)
1 tg α = -~
( J)
1 ^ ι^α cos α » 1 1ё«- cosoc
Sin α + Sin Ρ ^2sin~2~COS-^- , α +
COS α + COS β α + β α — μ g 2
2 cos —g— cos —2~
103
4. Аналогично получим:
rtJa + P f «+
COS α + COS β __ Clg 2 Sin α + Sin β _ tgΊ
COS α —COS β ~~~ α — β ' sin α — sin β α — β #
tg —g— ' tg —2~
5. 1 + sin α = sin у + sin α =
= 2 sin (-J + οΛ cos (^ — α) ;
так как sin( -^ + οΛ = cos ί^- — αV το
1 + sin α = 2 sin21i + сЛ = 2 cos2 (-J — α).
6. Аналогично
1 — sin α = 2 sin2 (£ — αJ = 2 cos2 (-J + α) ·
Примеры.
1. Представить в виде произведения
sin2 α— sin2 β.
Решение. Первый cnoco6i
sin2 α — sin2 β = (sin α + sin β) (sin α — sin β) =
. α + β α—β . α —β α + β
= 2 sin 2~" cos 2 sln ~T~ cos ~~2~~ =
/α+β «ψβ\/α-β α + β\
= ί 2 sin —2— cos —2—) ι sin —2—cos —2—) ==!
= sin (α + β) sin (α— β).
Второй способ! Применив преобразование понижения степени,
получим:
sin2 α — sin2 β == γ (cos 2β — cos 2α) = sin (α + β) sin (α — β).
2. Упростить выражение
5 = sin2 (α — 30°) + sin2 (α + 30°) — sin2 α.
Решение. Применим к каждому слагаемому преобразование пониже-
ния степени.·
1 — cos (2α — 60°) 1 —cos (2α+ 60°) 1 — cos 2α
S= 2 + 2 — 2 =
l_ COS 2α COS (2α — 60°) + COS (2α + 60°)
^ 2 + 2 ~~ 2
Преобразуем числитель последней дроби в произведение:
cos (2α — 60°) + cos (2α + 60°) = 2 cos 2α cos 60° == cos 2α;
подставив, получим S = -γ .
3. Представить в виде произведения
S = sin α -f- cos α -f- sin 2α + cos 2α + sin 3α + cos 3α.
104
Решение. Группируем слагаемые и преобразуем после группировки
в следующем порядке:
sin α + sin За = 2 sin 2а cos α; cos а + cos За = 2 cos 2а cos а.
Следовательно,
S — (2 sin 2α cos α -f sin 2α) -f- (2 cos 2a cos a + cos 2a).
Имеем·
2 sin 2a cos a -f- sin 2a = 2 sin 2a ( cos a + -—) = 2 sin 2a ( cos a 4- cos ό~ I =
(α π \ /α π \
и
(α π \ /α π \
~2 "^ "б" / C0S I ~o" ~— ~6~ J '
(α π\ /α π \
γ+ "6")COS("2*"- "g" I (sin 2a + cos 2a) =
- /α π \ /α π\ / π \
■=4 У2 cos [j+τ)cos (2 - 6 Jcos (2a - tj ·
откуда
4. Преобразовать в произведение
S = sin a + sin β + sin γ — sin (a + β + ϊ)·
Решение. Преобразуем выражение S по формулам (S -f- S) и (S — S)
сгруппировав первое слагаемое со вторым, а третье — с четвертым*
5 = (sin a + sin β) — [sin (a + β + γ) — sin γ] =
a + Β α — β /α + β \ α + β
= 2 sin -ρ cos —^ - 2cos ί —ρ + TJsin -~^ =
α φ β Γ α — β /a-f-β \Ί α 4~ β α ~\~ Ί
=2 sin 2 cos—γ- — cos ί —γ- + γ ) = 2 sin 2 2 sin —y1 sin
Следовательно,
sin a + sin β + sin γ — sin (a + β + γ) = 4 sin 4jr- sin ^-g-^ sin
5. Преобразовать в произведение?
Решение.
По формуле
sin (α + β + γ) == COS α COS β COS 7 [tg α + tg β + tg 7 ·— tg α tg β tg γ]
(стр. 76) получим
S = tg α tg β tg γ.
6. При каких условиях имеет место равенство
sin χ + sin у = sin (x -(- у)?
10b
Решение. Преобразуем левую и правую части:
χ -\-у χ —у
sin χ + sin у — 2 sin —?>— cos —j— *
x + У ■ х + У
sin (χ + у) = 2 sin —2~ cos —jr~ .
Данное равенство можно переписать так:
/ х— У х+У\ .
I cos 2 ~~cos 2 j =
2
или
. χ-{-у . χ . у
2 sin —о— sin ^г sin -к — 0.
Приравнивая поочередно сомножители нулю получим;
a) sin —Ρ = 0, -ψ- = ^π χ + у = 2Ы; (1)
b) sin ~к = 0, л: = 2&π, у—произвольная дуга; (2)
у
c) sin "τ?" = 0' у = 2^π, а: — произвольная дуга. (3)
Итак, для выполнения данного равенства необходимо и достаточно,
чтобы пара чисел χ и у удовлетворяла хотя бы одному из условий (1), (2),
(3), т. е. или дуги χ и у оканчиваются в точках, симметричных относительно
оси абсцисс, либо одна из дуг оканчивается в точке (1, 0).
§ 22. Примеры выполнения
различных тригонометрических преобразований
Теоремы сложения и вытекающие из них следствия (формулы
приведения, формулы тригонометрических функций от кратного
и половинного аргумента, формулы преобразования произведения
в сумму и суммы в произведение) вместе с основными тригонометри-
ческими тождествами (см. § 13) служат основанием для выполнения
различных тождественных преобразований аналитических выра-
жений, содержащих тригонометрические операции. Эти тождествен-
ные преобразования как по своей цели, так и по методам выполне-
ния могут быть весьма разнообразными. В практике выполнения
тождественных преобразований основные формулы и отдельные
частные приемы применяются в различных комбинациях; частные
свойства преобразуемых выражений нередко позволяют рациона-
лизировать вычисления. Эти упрощающие моменты никакой общей
теорией предусмотрены быть не могут. Навыки в рациональном вы-
полнении преобразований достигаются практикой.
В настоящем параграфе на примерах показаны различные прие-
мы выполнения тригонометрических преобразований.
106
Примеры.
В примерах 1—7 показаны различные приемы преобразования сумм
в произведения и произведений в суммы.
1. Преобразовать в произведение
S = (cos χ + cos у)2 + (sin x + sin у)2.
Решение. Преобразовав возводимые в квадрат суммы в произведе-
ния, получим:
χ _L_ у % у χ _L у χ у γ , у
5 = 4 cos2 —тр- cos2 —γ1 +4 sin2 —~ cos2 -γ1 = 4 cos2 —^ .
2. Преобразовать в произведение
(sin α + cos 2α -f- sin 3α)3 — sin3 α — sin3 2α — sin3 3α.
Решение. Применим следующую формулу разложения на множители:
(х + У + г)3 - Xs - у3 - ζ3 = 3 (х + у) (у + ζ) (ζ + *);
имеем:
S = 3 (sin α -f sin 2α) (sin 2α -f sin 3a) (sin 3a + sin a) =
3 a 5 a
= 3·2 sin -γα cos y2 sin γ a cos у 2 sin 2a cos a =
3 5 a
«= 24 sin yasinya sin 2a cos2 ~к COS a.
3. Доказать тождество:
',ι,ι
sin (a — b) sin (a — c) "^ sin (6 — c) sin (b — a) "*" sin (c — a) sin {c — b) β
1
"~ a — b a — с b — с '
2 cos —2~ cos —2— cos —2—
Решение. Приведем к общему знаменателю левую часть:
sin(a-6)sin(fe-c)sin(a-c) lsin (6 - с) ~ sin (а ~ О + sin (a - b)].
Преобразуем в произведение выражение, заключенное в квадратные
скобки:
• »и ч · / ч о a+b — 2c . b — a
sin (о — с) — sin (a — с) = 2 cos ?> sln —2—
и далее:
a + b — 2c . 6 — β
2 cos 2 sln ~2~ + sin (a — 6) = : ,-r
b — a\ a^ b — 2c b — a
= 2 sin о cos к — cos —^—
- cos
b —a b — с а — с
= — 4 sin —η— sin —η— sin ·
2 am 2 M!1 о— ·
Преобразовав каждый из множителей в знаменателе по формуле
α α
sin α = 2 sin -χ cos ~n , получим после сокращения правую часть доказывае-
мого тождества
4. Доказать тождества:
sin α sin β sin γ
a) sin (α — fi) sin (a — γ) + sin(p —7)sin(p —a) + sin (γ—a) sin (γ—β) = °·
107
., cos« , Cos? , C0ST _n
b) lin(a —β)8ίπ(« —γ) + sin (β — γ) sin (? -a) "+" sin (γ—a) sin (γ—β) " U'
Решение. Докажем тождество а). После приведения к общему зна-
менателю и сложения получим в числителе следующее выражение:
sin a sin (β — γ) + sin β sin (γ — α) + sin γ sin (a — β),
в котором всякое последующее слагаемое получается из предыдущего кру-
говой перестановкой аргументов α, β и γ. Преобразуем первое слагаемое
по формуле (S-S):
sin a sin (β — γ) = у [cos (a — β + γ) — cos (a + β — γ)].
Прочие слагаемые преобразуются посредством круговой перестановки аргу-
ментов: как нетрудно проверить, сумма всех этих слагаемых тождественно
равна нулю
Тождество Ь) получится заменой в тождестве а) аргументов α, β и γ
π π π
соответственно на γ — α, у — β, у— Τ·
5. Доказать тождество:
sin За sin 3b
sin (с — a) s\n(a — b) "*" sin (a — 6) sin (b — c) ~^~
sin 3c
Решение. Приведем дроби к общему знаменателю, тогда для первой
дроби получим в числителе произведение, которое преобразуем в сумму:
cos (За — b + с) — cos (3a + b — с)
sin За sin (b — с) = * ' g — L . (1)
Числители остальных дробей получим круговой перестановкой аргу-
ментов:
cos (3b — с 4- а) — cos (3b 4* с — а)
sin 3b sin (с — а) = !—'—^ ! , (2)
cos (Зс — а ^ Ь) — cos (Зс + а — Ь)
sin Зс sin (a — 6) = 2 · (3)
Отнеся общий множитель у к знаменателю, перегруппируем слагаемые
числителя следующим образом: первое слагаемое (1) сгруппируем со вто-
рым слагаемым (2)
cos (За — b + с) — cos (3b ψ с — а). (4)
Первое слагаемое (2) сгруппируем со вторым слагаемым (3) и первое
слагаемое (3) — со вторым слагаемым (1). Преобразовав разность (4) в про-
изведение, получим:
— 2 sin (a + b + с) sin (2a — 2b).
Выполнив круговую перестановку аргументов, получим два остальные
произведения Сложив все эти произведения, получим числитель
— 2 sin (a + b + с) [sin (2a — 2b) + sin (2b — 2c) + sin (2c — 2a)].
108
Преобразуем в произведение сумму, заключенную в квадратные скобки!
[sin (2а — 2ft) + sin (26 — 2с)] + sin 2 (с'.— а) =*
= 2 sin (а — с) cos (α — 2b -f с) + 2 sin (с — a) cos (с — α) = 2 sin (α
X [cos (a — 2b -\- с) — cos (c — a)]— — 4 sin (c — a)sin (ft — c) sin (a — ft).
Итак, числитель левой части доказываемого тождества равен
8 sin (а + b + с) sin (a — ft) sin (ft — с) sin (с — a)
Знаменатель равен 2 sin (a — ft) sin (ft — c) sin (c —- a).
Сократив на общие множители, получим 4 sin (a + b + с), ч. т. д.
6. Установить соотношения между значениями аргументов α, β и γ,
при которых имеет место равенство:
cos2a + cos2 β -f- cos2 γ -f- 2 cos a cos β cos γ = 1. (1)
Решение. Преобразуем в произведение следующую сумму;
5 = cos2 a + cos2 β + cos2 γ + 2 cos a cos β cos γ — 1;
имеем:
a) cos2 β + cos2 γ — 1 = cos2 β — sin2 γ =
= j [cos 2β + cos 2γ] = cos (β + γ) cos (β — γ);
b) cos2 a + 2 cos a cos β cos γ = cos2 a + cos a [cos (β + Τ) + cos (β — Τ)»
c) S = cos (0 + 7) cos (β — γ) + cos2 a + cos a [cos (β + γ) + cos (β — γ)] =
= [cos a -f cos (β + γ)] [cos a + cos (β — γ)].
Откуда получим
S = 4 cos з^ * cos з ^ * cos ψ-± cos
Условие (1) равносильно равенству S = 0. Необходимым и достаточным
условием последнего равенства является обращение в нуль хотя бы одного
из множителей на которые разложено выражение S, Приравняв нулю пер-
α + β+ 7
вый множитель, получим: cos ^ = 0, откуда
« + β + γ = (2*,+ Ι)π (2)
Аналогично, приравняв нулю поочередно прочие множители, получим:
-« + β + 7 = (2£2+ 0 ^ (3)
« — β + Ύ = (2^з + Ι) π; (4)
* + β-7 = (2*4+1)π, (5)
где ki, k2, ks, &4 — произвольные целые числа.
Искомым необходимым и достаточным условием является существование
такой системы целых чисел къ k2, k3. k±, при которой выполняется хотя бы
одно из равенств (2)—(5).
Допустим, ρ частности, что α, β и γ — острые углы
0<а<-^, 0<β<γ.. 0 < γ < у ; (6)
в этом случае ни одно из равенств (3). (4), (5) не может выполняться.
В самом деле, из неравенств (6) получим
109
и, следовательно, равенство (3) невозможно. Аналогично устанавливается
невозможность выполнения равенств (4) и (5). Из неравенств
0<α + β + γ < ут:
следует, что для острых углов α, β и γ может выполняться лишь условие (2)
при ki = 0:
α + β + Τ = π.
Следовательно, для острых углов α, β и γ равенство (2) выполняется тогда
и только тогда, когда α, ρ и γ в сумме составляют π (т. е. α, β и γ суть
углы треугольника).
7. Представить в виде произведения сумму
/l —cos χ + /l +cos%.
Решение. Для каждого из радикалов подкоренное выражение не-
отрицательно. Преобразуем отдельно каждый радикал:
Y\ — cos χ
-ν
ν
Χ r
2 sin2-η =/2
= 1/2 cos2 -~ = / 2
Sin T7
cos -κ
следовательно,
— cos χ + /1 + cos χ = Υ 2 ( sin -χ
+
COS 7Γ
Дальнейшие преобразования проводятся в зависимости от того, в какой
χ
четверти оканчивается дуга γ . Возможны следующие случаи:
χ
a) Akn < χ < (4k-{- 1)π, тогда -g оканчивается в первой четверти:
— cos χ + Υ\ + cos * = /Τ ί sin у + cos у J =
χΥΊ χ ΥΎ\ η . ( χ π
n у -у- +cos γ — ] =2 sin ^y+ -j
л:
b) (4/г + 1) π < я < (4k + 2) я, тогда у оканчивается во второй чет-
верти:
sin ί у — -j ) ;
Υ\ — cos* + ]Л φ cos* =
sin у — cos у j = 2 sin
с) (4^ + 2) π < д: < (4k + 3) π; дуга у оканчивается в третьей чет-
верти:
Υ1 — cos χ ^ ]Λ ψ cos x = — /Τ (cosy + sin у) =
л:
d) (4^ + 3) π < л: < 4 (k 4- 1) π; дуга у оканчивается в четвертой чет-
верти:
р
. г г— ( χ χ \ ( π χ \
Υ1 — cos χ 4- /1 + cos χ = у 2 ί cos у — sin у j = 2 sin I -j — у j .
no
В примерах 8—11 рассмотрены различные тригонометрические преоб-
разования, связанные с исключением неизвестных из системы уравнений.
Требуется найти необходимые (в общем случае недостаточные)
условия в виде уравнений, которым должны удовлетворять значения па-
раметров, чтобы данная система имела решения
В практике исключения неизвестных надлежит руководствоваться сле-
дующими указаниями:
1) Так как ищутся лищь необходимые условия совместности си-
стемы, то допустимы преобразования уравнений, в результате которых мно-
жество всех решений системы расширяется (т. е. возможно появ-
ление посторонних решений), но недопустимы преобразования, при которых
происходит потеря решений.
2) Преобразования уравнений выполняются с тем расчетом, чтобы в ка-
честве следствий из данных уравнений получились уравнения между пара-
метрами, не содержащие неизвестных и не обращающиеся в тождество.
Примеры.
8. Исключить χ из системы уравнений:
sin χ + cos χ = т, sin3 χ -\- cos3 χ = η.
Решение. Имеем:
sin3 χ + cos3 χ = (sin χ + cos χ) (sin2 χ + cos2 χ — sin χ cos χ) =
= tn (1 —- sin x cos χ).
Возводим обе части первого уравнения в квадрат:"
1 + 2 sin л: cos χ = tn2.
В качестве следствия из данной системы получим:
2 sin χ cos χ = tn2— 1, tn sin χ cos χ = tn — п.
Подставив выражение для произведения sin x cos x из первого уравнения
во второе, получим в качестве следствия искомое уравнение между парамет-
рами:
тз__зт+ 2я = 0. (1)
Примечание. Поскольку уравнение (1) отыскивалось в качестве
необходимого условия, мы не учитывали неравенств, которым долж-
ны удовлетворять значения параметров. Так, например, из первого уравнения
получим
т ·■
■ Y2 sin ί χ-\- -ξ- j, откуда | т | < ]/~2.
Мы не принимали во внимание также, что почленное возведение уравне-
ния в квадрат может привести к посторонним решениям.
Аналогичное примечание следует иметь в виду при решении всех приве-
денных ниже примеров на исключение неизвестных.
9. Исключить φ из уравнений:
COS (а — 3φ) sin (а — 3φ)
COS3 φ ~~~ Sin3 φ ~^'
Решение. Имеем:
COS (а — 3φ) = tn COS3 φ; (1)
sin (а — 3φ) = m sin3 φ. (2)
Умножим уравнения (1) и (2) соответственно на cos 3φ и sin 3φ и выч-
тем почленно:
cos (α — 3φ) cos 3'f — sin (a — 3<f) sin 3-f = m (cos3 у cos 3-f — sin3 φ sin 3?)
111
или
COS α = m (COS3 φ COS 3φ — Sin3 φ Sin 3φ).
Имеем:
COS 3φ = — 3 COS φ + 4 COS3 φ,
sin 3φ = 3 sin φ — 4 sin3 φ,
откуда
cos a = — 3m (cos4 φ + sin4 φ) + 4m (cos6 φ 4- sin6 φ) (3)
Возведем (1) и (2) почленно в квадрат и сложим, тогда получим
COS6 φ +
Подставив в равенство (3), получим
COS6 φ + Sin6 φ = "^ . (4)
4
cos α = — 3m (cos4 φ + sin4 φ) + — , (5)
Итак, из равенств (1), (2) следуют равенства (4), (5).
Примем во внимание следующее тригонометрическое тождество:
COS6 φ + Sin6 φ = 1 — 3 COS2 φ Sin2 φ
(см. пример 2, стр. 61). В силу (4) имеем:
•^2 = 1 —3C0S2cpsin2cp И COS2 φ Sin2 φ = —g—2—· (б)
Имеем далее
COS4 φ -f Sin4 φ = 1 — 2 COS2 φ Sin2 φ = 1 — 2 ^ = —~ξ^Γ~ -
Подставив в (5), получим (после упрощения правой части) требуемый
результат
2 —т2
10. Исключить χ из уравнений:
cos (χ — a) == a, sin (χ — β) = b.
Решение. Имеем:
cos x cos a -(- sin χ sin a = a II sin β
sin χ cos β — cos χ sin β = b || cos a
cos β;
— sin a.
Умножив данные уравнения (соответственно) на sin β и cos α, а затем на
cos β и на — sin α, после почленного сложения получим:
sin χ cos (a — β) = a sin β + b cos a;
cos χ cos (a — β) = a cos 3 — b sin a.
После почленного возведения в квадрат и сложения получим:
cos2 (а — β) = а2 + Ь2 — 2ab sin (a — θ).
11. Исключить неизвестные л; и у из системы уравнений:
sin χ + sin у = 2a, (1)
cos χ + cos у = 26, (2)
tg * + tg у = 2c, (3)
где a2 + б2 ^ 0
112
Преобразуем левые части уравнений (1) и (2) в произведения:
. х + У х — У /1/ч
sin—2—cos—2—==а> ( '
Х + У Х — У . /о,ч
cos —2— cos —2— = ^ '
Возведем (Г) и (2') почленно в квадрат и сложим:
cos2 ^L = α2 + ^ (4)
а затем вычтем
cos* ^±Z _sin2 ^+
Перейдем к аргументу * + у и примем во вниманием (4):
б2 — а2
cos (* + у) = а2+6а .
Перемножим почленно (Г) и (2'), приняв во внимание (4), найдем
2ab
sin (x+y) = fl2 + ба . (6)
Преобразуем левую часть равенства (3) так:
8 T S/" COS X COS У COS (Х + У) + COS (* — У)
2 sin (jc + y)
= jzrz ·
cos (x + y)+ 2 cos2 —2"^- — 1
Воспользовавшись равенствами (4), (5) и (6), исключим из равенства (3)
аргументы * и у:
2ab
или после преобразований
В примерах 12—15 приводятся доказательства некоторых условных
равенств, т. е. равенств, имеющих место при всех значениях аргументов,
удовлетворяющих одному или нескольким уравнениям.
Примеры.
12. Доказать, что
sin8 χ cos8 x 1
а3 + b3 = (a + b)3
при всех значениях ху удовлетворяющих условию
sin4* cos4 x 1
u~*"b~r~<x + bi
где а > 0, b > 0.
5 Зак. 597 113
Решение. Равенство (1) можно переписать в следующем виде:
Ь а
sin4 χ + cos4 χ -f- — sin4 x + -γ cos4 χ = (sin2 χ -f- cos2 x)2
или после преобразований:
Asin2* — l/iLcos2*) =0, откуда λί — sin2 л; = l/iL cos2 χ,
α Υ b j Υ α ψ b
а потому
sin2 л: cos2 л:
λ
Подставив в (1), получим: λ = . , , и, следовательно,
sin8* cos8 a: /sin2x\3 /cos2*\3
+ i2(J +cosl (]
13. Дано:
α cos α + b sin α = с (1)
и
a cos β + b sin β = ct (2)
где α φ β ~j- 2kn и хотя бы одно из чисел а или 6 отлично от нуля. Дока-
зать, что
COS ή — Z2 i Ш~ ·
Решение. Складывая и вычитая соотношения (1) и (2), получим
ал- β α __β α + β α—β
a cos —2— cos —2— + ^ sin —2— cos —2— = c; ^
a_LR a — β α + β α~β
sinsin * + ^ cos —sin° *4^
β + β
— a sin—2— sin —2~*~ + ^ cos —2— sin—2— = °* *4^
α —β
Из условия α — β =£ 2/е;г следует, что sin —^— ^ 0. Из (4) получим
α+β α+β
a sin 2 = 6 cos —2— · (5)
Допустим для определенности, что а Ф 0; из последнего равенства
найдем:
sin
α + β
Докажем, что при данных условиях cos —-^— Φ 0. В самом деле,
в противном случае α + β = (2&+ 1)π, и тогда соотношение (2) примет вид'
— a cos a -f- b sin a = c\ (2')
из (1) и (2') получим 2a cos a = 0. Так как а Ф 0, то cosa=0, откуда
π
a = -γ + ki π; и, следовательно,
a — β =_ 2α — (α + β) = 2 (Λ, — k) π,
что противоречит условию.
114
Из (5) найдем
Из равенства (3) получим
« + I
с*
с2 sec2
a cos
α + β
• b sin ·
αψθ\2
Γ\2
С1
а2 + б2
Геометрическая интерпретация Уравнения
*cosa 4- У sin α = с и * cos β + ν sin β = <?
выражают нормальные уравнения двух
прямых, касающихся окружности ра-
диуса с. с центром в начале координат;
перпендикуляры, опущенные из начала
координат на эти прямые, по длине
равны с и образуют углы а и β с осью
абсцисс Условия (1) и (2) выражают,
что данные прямые пересекаются в точ-
ке /И(а, Ь) Угол, образованный пер-
пендикулярами на данные прямые из
начала координат, равен а — β Из
чертежа 81 найдем
cos ·
С
■ /а2 + Ь* '
14. Доказать, что при
имеют место тождества:
Черт. 81
М(а.Ь)
sin2 В + sin2 С — 2 sin В sin С cos Л = sin2 A,
cos2 В + cos2 С + 2 cos В cos С cos Л = sin2 А.
Решение. Положим
X = sin2 В + sin2 С — 2 sin В sin С cos /4 — sin2 Л;
Υ = cos2 θ + cos2.C + 2 cos β cos С cos Л — sin2 Л.
Сложим и вычтем почленно эти равенства:
Х+ Υ =2+ 2 cos A (cos В cos С — sin В sin С) — 2 sin2 Л =
= 2 fcos2 Л + cos Л cos (В + С)];
но так как
cos (В -\- С) = cos (π — Л) = — cos Л,
то
X + У = 0;
— А = (cos2 В — sin2 β) + (cos2 С — sin2 С) + 2 cos (β — С) cos Л =
= cos 2β + cos 2C + 2 cos (β — С) cos Л =
= 2 cos (β + С) cos (β — С) + 2 cos (β — С) cos Л =
= 2 cos (β — С)·[cos (β + С) + cos A] = 0.
Итак, X + Y = 0 и Κ = Χ=0, откуда X = Υ = 0, ч. т. д.
5*
115
15. Доказать, что
α β 1+е
при условии
е2 — 1 1 + 2е cosk -\-e2
1 + 2^ cos а + б2 = б2 — 1 '
где ^ > 1.
Решение. Заметим, что знаменатель
1 + 2е cos а-\- е2 — (е + cos α)2 + sin2 α
положителен при всех значениях а, так как ни при каком значении α pa*
венства
sin α = е -f cos a = 0
не могут иметь места Составим производные пропорции, воспользовав-
шись следующим свойством)
а с а + с а — с
если ύ=ύ· το τη = τ=Ί>
получим (после сокращения на числовые множители))
е + cos β — 1 — б cos β
£ + cos a ~~ 1 + e cos α
Составим вторично производную пропорцию по тому же способу?
(1 — g) (1 — cos3) (I +g)(l +cosp)
(l + *)(l+cosa) — (1—e)(l —cosa)
Следовательно,
!_οοδβ 1-COSa /1+β\2 _ _ _ В _ a / 1 + в \2
т. e.
•2
1+cosa —^ 1 — e; ' K c· l8 2 l« 2 "
Отсюда следует доказываемое условное равенство.
§ 23. Рационализирующие подстановки
Пусть /?(cosa, sina) — рациональное выражение отно-
сительно cos a и sina. Рассмотрение функций, рациональных отно-
сительно sina, cosa, tga, ctga не представляет специального инте-
реса, так как tga и ctga — рационально выражаются через косинус
и синус.
Примерами функций, рациональных относительно косинуса и
синуса, могут служить:
1 sin a
sin a cos a, :— , o . » : ^—.
' COSa — Sina' 2sin2a — Sin a COS a — COS2 a
Определение. Если функция R (cosa, sina) может быть пред-
ставлена в виде сложной функции от промежуточного аргумента
/=/(а):
R (cos a, sin a) = Rx (/),
116
где /?ι (Ο — рациональная функция, то введение промежуточного
аргумента t посредством формулы
называется рационализирующей подстановкой.
Теорема. Для всякой функции /?(cosa, sin α), рациональной
относительно cos α и sin α, подстановка
является рационализирую1цей.
Доказательство. Достаточно доказать, что функции
cos α и sin α рационально выражаются через тангенс половин-
ного аргумента / = tg-|-. В самом деле, имеем:
. а « cos^-sin* у i~tg*y
cos a = cos^ -τ2 sm2 -y = - = ;
cos* у + sin2 у 1 + tg2 у
α σ α
ο . α α 2SW-2-COS-5- 2 tg -y
sin α = 2 sm -у- cos -^- = : — =
cos2-^- +sin2 ^- i + tg«-|-
Положив i = tgy, представим функции cos α и sin α в виде
рациональных функции от аргумента t:
cos a = i=^J и sin a - j^ . (R)
Эти равенства имеют место при всех значениях a ^ (2&-J- 1)π;
при a = (2^+1) л выражение tg -^- теряет смысл.
Заменив в данном выражении /?(cosa, sin α) функции cos a
и sin α их выражениями через ty получим рациональное выраже-
ние от аргумента t, ч. т. д.
Подстановка t = tg-| называется универсальной, так
как всякое выражение вида R (cos a, sin а) она преобразует в
рациональное выражение от аргумента t.
Геометрическая интерпретация. Промежу-
точный аргумент / изображается отрезком, отсекаемым на оси тан-
генсов биссектрисой угла а (черт. 82).
Универсальная подстановка обладает следующим свойством:
значения промежуточного аргумента / = tg-^- выражаются ра-
117
ционально через cos α и sin α. Β самом деле, согласно формулам
У А и (УА § 18 (стр. 90), имеем
, a sin α 1 — cos α
cos α"
Система функций
1 + t2'
Sill α
It
+t2
(1)
(2)
устанавливает взаимно однозначное соответствие между значениями
t в интервале — оо < t < со и точками единичной окружности
с исключенной точкой Л±(— 1, 0). В самом деле, всякой точке
#= cos a, y=sin а единичной окружности (где — π<α<π соответст-
вует значение / = tg^ (формулы (1)), при-
чем координаты этой точки выразятся фор-
мулами (2). Обратно, всякому действи-
тельному значению / соответствует дуга
а = 2 arc tg t, оканчивающаяся в точке
M(cosa, sinoc) единичной окружности.
Уравнения (2) позволяют находить на еди-
ничной окружности «рациональные точки», т. е.
точки с рациональными кординатами. В самом
деле, всякому рациональному значению t, в си-
Черт. 82 Лу уравнений (2), соответствует точка М(х, у)
окружности с рациональными координатами. Об-
ратно, всякой рациональной точке окружности, отличной от точки (—1, 0).
соответствует согласно формуле (Τ \ рациональное значение параметра
2/
Полученному результату можно дать другое геометрическое толкование.
Примем за 1 гипотенузу о прямоугольного треугольника, тогда формулы
а =
1 + ι2
1
дают возможность отыскать в общем виде все прямоугольные треугольники,
катеты которых соизмеримы с гипотенузой Итак, мы получаем следующие
общие выражения катетов «рациональных» прямоугольных треугольников:
2/ . 1 - t2
откуда
a\b
— t2)
t2).
Придавая t всевозможные рациональные значения, будем получать все-
возможные рациональные треугольники. Так, при t = 2 можно получить
118
й= 4, b — 3, с= 5 (мы получим по формуле Ь<0, однако знак не существен,
поскольку речь идет о длинах сторон треугольника), при / = 3 получим
а = 6, Ь — 8, с = 10, при *=0 и t=\ треугольник вырождается в отрезок.
Ниже указаны случаи, в которых рационализация может быть
достигнута при помощи более простых подстановок.
Г. Если выражение R (cos α sin а) содержит функцию cosa
(или sin а) только в четных степенях, то можно положить
/=sina (соответственно /=cosa). В самом деле, достаточно
принять во внимание, что четные степени косинуса (синуса) рацио-
нально выражаются через синус (косинус)
cos2* a = (1 — sin2 a)* = (1 — t2)kt
а потому
Я (cos2 a, sin a) = R(\ — t2, t).
2°. Если числитель и знаменатель выражения R (cosa, sin a),
являющегося алгебраической дробью относительно cosa и sin a
суть однородные многочлены одной и той же степени k относитель-
но cosa и sin α, то можно положить / = tga (либо t ~ ctga). В са-
мом деле, имеем
sin a = /cosa.
После этой замены все члены числителя и знаменателя будут
иметь общий множитель cos*a; сократив дроби на этот множитель,
представим R cosa, sin α в виде рациональной функции от аргумен-
та t.
3°. Если все члены числителя и знаменателя выражения
R (cosa, sin α) имеют четную (либо нечетную) степень относительно
cos χ и sin Xy то можно положить /=tg a. В самом деле, степени двух
различных членов числителя и знаменателя отличаются на четное
число единиц, а потому можно заменить числитель и знаменатель
тождественными однородными многочленами. Для этого доста-
точно умножить члены более низких степеней на некоторую степень
тригонометрической единицы sin2 a + cos2 α (см. ниже пример 4).
4°. Пусть R есть рациональное выражение относительно три-
гонометрических функций кратных дуг
R = R (cosnAa, sin Alia, cosAZ2a, sinn2a, ..., cosn^a, sinn^a),
где пл, п2> ..., п/г — целые числа. Если тригонометрические функции
кратных дуг выразить через степени sin a и cosa, то R представит-
ся в виде рациональной функции от sin a и cosa и рационализация
сводится к рассмотренному случаю.
Если Aii, Az2, ..., nk — рациональные (дробные) числа
Пл . /ίο . .... flu ,
1 Я\ 2 ?2 ' ' h Як'
то, положив a = Αζβ, где η — наименьшее общее кратное знаме-
нателей, представим тригонометрические функции, находящиеся
119
под знаком функции R, в виде тригонометрических функций от
аргументов кратных β, τ. е.> получается предыдущий случай.
Теорема. Если функция R (cosa, sin а) четная, то она может
быть рационализирована подстановкой t =cosa.
Доказательство. Универсальная подстановка ii=tg~>
где—π<^α<^π преобразует данную функцию в рациональную
от аргумента /4
/?(cosa, sin a) ^R^t^.
При замене α на —α значение t^ заменится на —tu а значение
Rl не изменится (в силу условия теоремы) *.
Следовательно, Ri (^) есть четная функция от tt> а потому
где R2 — некоторое рациональное выражение.
Из равенств
,2 j 2 _а_ J_--COSa 1—/
следует, что R2(t\) = R2( l Tt ) есть рациональная функция па-
раметра / =cosa, ч. т. д.
Практически рационализация выполняется описанным выше
способом Г.
Примечание. Доказательство основано на следующем
положении, известном из алгебры: если рациональная функция
R(x) четная, то она может быть представлена в виде рациональ-
ной функции от х2.
Р(х)
В самом деле, пусть R (х)= -^-' Отделим в многочленах
Ρ (χ) и Q (л;) члены с четными и с нечетными степенями х:
Ρ (х) = Pi (х2) + хРг (х2)\ Q (х) = Qi (х2) + xQ* (х2)
(аргумент х2 многочленов Рь P2i Qi, Q2 для краткости писать
не будем). Итак,
Заменив χ на — ху получим (в силу четности R(x))
* Заметим, что t\ может быть произвольным действительным числом,
так как по заданному значению tx определяется a = 2агс tg tv
120
откуда (после умножения и преобразований)
2x(P,Q2-Q1P2) = 0\ PiQ2 = QiP* и |j=-g
где К — некоторое рациональное выражение, но тогда
Следствие. Если /?(cosa, sin a) — нечетная функция, то
——^(cosa, si η α) является четной функцией. По доказанному
-т^-# (cos a, sin a) = /^(cosa),
откуда
/?(cosa, sin a) = sin a /?3 (cos a).
Примеры.
l Преобразовать выражение Ρ = sjn X\QOSX
посредством универсальной подстановки
Решение Имеем:
2.
rz= 2t
Л-
Рационализировать функцию
1 (
Решение. Положив / =
3.
Ре
4.
Ре
к
/(*) =
tg
Рационализировать
ш е н и е. Положив / -
tg χ cos6 χ
sin4 λ:
Рационализировать 5 =
ш е н и е. Положив t =
sin
COS
sin χ
COS X
X COS6
sin4 a;
= tgJC,
sin3
= tg jc,
sin x (sin2 λ: + cos2 χ)
° sin3 jc + cos3
X
1 — t2 ~ 1 +2^ — t*
sin .t
sin χ — cos jc
получим
JC
\x ■ t
- ι '-1"
1
ПОЛучИМ:
tg* ι
4A:sec2A: /J (1 + ia) ·
sin jc
JC + COS3 JC
получим:
tgA;(tg2A: + l) /(/2 + l)
tg3 АГ+1 /8+1
COS2 X
Решение. Положив / = sinjc, получим:
I—/2 1— t'
+ Г
5B Зак 597 121
6. Дано:
sin χ -f sin у = a, cos χ -f cos у = Ь\
вычислить sin (χ -f- У) и cos (χ -|- у)
Решение. Введем рационализирующий параметр / = tg х ~т~ У , тогда
будем иметь:
2/ 1 — /а
sin (χ + у) = у '_j772 cos (* + у) = t + /3.
Согласно условию
sin л: + sin у а х -\- у а
——J——=— или tg ——=— = <,
откуда
2α6 /?2— α2
sin (χ + у) = ^qr^' cos U + У)
7. Рационализировать выражение
а:
cos -Q-
2
χ
cos -γ + 1
Решение. Положив х = 6у, получим:
sin 2y 2 sin у cos у
v cos3y+l cos3 у — 3 cos у sin2 у + Г
Для рационализации следует применить универсальную подстановку,
положив
1 — i2 2/ ух
cos у = γτρΤ^" · sin v = Г+Т2' где l e tg Τ" = *δ "Ϊ2"
(предлагаем учащимся произвести подстановку).
8. Доказать тождество
1 + ctga + ctg (45°— α)
2 Si"2 ^ ctgI cos 2α - 2 + 2 Sin 2« = ^ 2^ **' «5°+ «>-
Решение. Заметим, что обе части доказываемого тождества рацио-
нально выражаются через / = tg α; имеем:
tg2a t2 1
Sin2 cc- l + tg2a=T+72> Ctga = —, ctg (45°- a) =
1+/ 1—^2
= tg (45° + a) = узту, ctg 2a = -^ρ-,
I-/2 2/
COS 2a = 1 _|_ /2> Sin 2a = ] ^2.
Выполнив подстановку (элементарные выкладки опускаем), докажем,
что обе части равны одной и той же алгебраической дроби
4/2(1 + 0
(Г-О5 '
122
§ 24. Введение вспомогательных углов
и тригонометрические подстановки
Преобразование посредством введения вспомогательного угла
в общем виде можно характеризовать следующим образом: данное
число или данное выражение рассматривается как значение тригоно-
метрической функции от некоторого аргумента, называемого вспо-
могательным углом (вспомогательным аргументом). Из множества
всех возможных значений для вспомогательного угла выбирается
одно, вполне определенное значение (например, наименьшее по
абсолютной величине), этим выбором вспомогательный угол по задан-
ному значению его тригонометрической функции вполне определя-
ется и в дальнейших преобразованиях считается известным.
1. Переход к полярным координатам. Это
преобразование основано на следующем предложении.
Если хотя бы одно из чисел а и Ь отлично от нуля, то
в промежутке О < φ < 2π (или в промежутке — π << φ < π)
существует единственное значение φ, при котором
b = r sin φ,
(1)
где г =
b2.
В самом деле, построим на координатной плоскости точку
Λί(α, b) (черт. 83). Заданием точки Μ определяется ее расстояние
до начала координат
г = | ОМ | = /а2+ Ь2 М(а,Ь)
и единственный угол φ между ОМ и
осью ОХ, если значение φ выбирать в
промежутке [0, 2π) (или в промежутке
(—π, π]), ч. т. д.
Точка М' (cos φ, sin φ) есть точка
пересечения луча ОМ с единичной ок-
ружностью.
Если вместо угла φ взять угол
то формулы (1) примут вид:
Черт. 83
а = г cos φ, b — г sin φ,
где
г = — /α2+ b2,
В этом случае направление радиуса-вектора ОМ заменяется проти-
воположным. Нередко в целях единообразия в выборе вспомога-
тельного угла φ этот угол определяют по формуле
φ = arc tg — , если а
О,
5В*
123
<ρ
-|- при
γ при
если а — 0.
При таком выборе имеем всегда γ <; φ < -=- ■
Формулы (1) можно записать таким же образом:
а = г cos φ, b —r sin φ,
при этом следует считать
Va2+ b2, если α> 0, . ь
г - \ г где φ - arc tg — ;
-Ya2+b\ если α<0, α
при α = 0 выбор угла φ указан выше.
В самом деле, при а>0 точка М' принадлежит правой единич-
ной полуокружности и за вспомогательный угол берется угол, за-
ключенный в пределах от — ^ до ~, образованный ОМ с осью абс-
цисс. Если же а<4), то точка М' принадлежит левой полуокружно-
сти и за вспомогательный угол берется угол, заключенный в тех
же пределах, образованный продолжением ОМ (за точку О) с осью
абсцисс.
Примечание. Если данные действительные числа а
и b суть действительные и мнимые части комплексного числа
ζ = а + Ы, то переход к полярным координатам означает пе-
реход к тригонометрической форме комплексного числа
ζ r= r (cos φ -|- /sin φ).
II. Преобразование суммы вида a sin ах + bcosax.
Введем полярные координаты точки М(а, Ь) по формулам (1),
тогда данное выражение преобразуется следующим образом:
asinou: + bcosax = г (cos φ cos αχ + sin φ sinax) = r sin (αχ + φ).
Если ввести полярные координаты точки N(b, a), положив
b=r cos ty, a = г sin ψ, где г = Уа2+ Ь2,
то получим
a sin ах + b cos ax = г cos (ax — ψ).
Это преобразование часто применяется в физике (см. § 34).
III. Различные приемы преобразования
алгебраических сумм в произведения. Ниже
указаны некоторые приемы введения вспомогательного угла, по-
средством которых алгебраическую сумму можно представить в виде
произведения, содержащего в качестве множителей известные числа
и тригонометрические функции от вспомогательного аргумента.
124
1°. Дана сумма а + Ь\ введем вспомогательный аргумент,
положив α = arctg — (слагаемые предполагаются отличными от
нуля), тогда, приняв во внимание, что 1 = tg-^-, получим:
a J \ ■ о / cos a
2°. Разность а — b можно преобразовать аналогично:
г- Ιπ \
У 2 α sin ί-^- — αϊ
a — b =— '
COS α
. Ь
где a = arctg
3°. Если а и b — числа одного знака, то —>0, и для пре-
образования суммы а ± Ь можно положить а = arc tg у — ,
тогда получим:
а + b ^a(l + tg2a) = asec2a;
а cos 2a
а — b = а (I — tg2 a) =
sec2 a
4°. Отношение a~~ A посредством подстановки a — arctg —
преобразуется следующим образом:
α +&~l + tga bl^ 4
5°. Разность α2 —62, где |6|<|α|, можно преобразовать
посредством вспомогательного угла α = arc sin—, тогда получим:
а2_&2=агЛ _ii\ = α2 (I— sin2а) = α2 cos2 а.
Можно также положить β = arc cos —, тогда получим
α2— b2 -α2sin2β.
6°. Разность а2—Ь2, где |6|<|α|, можно посредством
цста но:
образом:
подстановки β = arc cos— преобразовать также и следующим
а2_ Ь2 = Й2М _ ι j = Ъ2 (sec2 β - I) = б2 tg2 β.
7°. Сумма a2-\r b2 преобразуется подстановкой α = arctg —
(пункт 3°):
125
Для различных сумм более сложного вида могут применяться
самые разнообразные и нередко искусственные способы введения
вспомогательных углов.
В старых руководствах, в которых логарифмическим вычисле-
ниям придавалось большое значение, преобразование сумм в про-
изведения или «приведение к логарифмическому виду» играло су-
щественную роль. При современной вычислительной технике по-
добные преобразования (с целью производства вычислений) утра-
тили свою ценность.
Введением вспомогательного аргумента пользуются для пре-
образования некоторых иррациональных выражений в
рациональные выражения относительно тригонометриче-
ских функций от вспомогательного аргумента.
Рассмотрим, например, функцию
R (ху \?а2—х2), (R)
где uf>0, R(uy ν) — рациональная функция от аргументов и и ν.
Функция (R) имеет действительные значения лишь на сегменте
Согласно подстановке 5°, положим
*=acos/, где / = arc cos—
тогда получим
\/а2— χ2 = Υ аЦ\ —cos2/) =a|sin/| = asin/
(следует принять во внимание, что значение / находится в верхней
полуокружности, но тогда sin/>0).
Тригонометрическая подстановка
χ = a cost, /= arc cos—
а
устанавливает взаимно однозначное соответствие между сегмен-
тами— α<^χ<α и 0</<;π.
Данное выражение (R) представится в виде выражения
R (a cos /, α sin /), рационального относительно cos/ и sin/.
Для выражения вида
R (х, V*2— я2), где \х\>а,
согласно подстановке 6°, можно положить / = arc cos — или
χ = α sec ty и тогда
atg/ в промежутке' а<л:<^-[-°о,
У χ2__ а2 ^ а I tg t\ =
1 ( — atg/ в промежутке —оо<^х<—а.
Для выражения вида R (x, Yx2 -f· а1), согласно подстаиов-.
ке 7°, можно положить / = arc tg —, откуда χ = atg/ и
Yx2+ a2 = a sec /.
126
Указанные подстановки применяются в математическом ана-
лизе при интегрировании выражений, содержащих радикалы вида
Υ± α2 ± х2.
Примеры.
1. Имеем:
а)
3 sin лг+cos χ = 2 I i— sin χ + ~γ cos x I = 2 sin I x + -g-Jr=
b) sin χ — /~3cos χ = 2sin I x — "ό");
(2 3 \
—7= sin χ — —r=r cos χ) = -/"13 sin (χ *~ α).
/13 ν 13 /
В случае с) вспомогательный угол определяется из условий
2 3 3
cos а =^= г— , sin a = г— , положим a == arc sin .— . Пользуясь четырех-
у 13 К 13 /13
значными таблицами найдем: аж56°18';
итак,
2 sin χ — 3 cos χ = |/Ί3 sin (* — 56O18').
На примерах 2 и 3 показано применение преобразования перехода к по-
лярным координатам к исследованию функций двух аргументов.
а:4 + у4
2. Доказать, что Jim γ2\ν2 =0·
* .> о ^ ТУ
Решение. Положив χ = г cos φ, у = г sin φ, получим:
Следовательно, неравенство
<ε
выполняется, если г—расстояние точки М(х, у) до начала координат мень-
2j^v
3. Доказать, что функция __——- не имеет предела в точке 0(0, 0).
Χ -ρ χ
Решение. Преобразовав к полярным координатам, получим:
2ху
f (χ> У) = ^2j~y2 = 2 cos cpsin φ = sin 2φ.
При данном значении φ функция f(x, у) постоянна, т. е. она постоянна на
любом данном луче, исходящем из начала координат. Однако вдоль различных
лучей, исходящих из точки О, значения /(*, у) различны при этих условиях
(как известно из теории пределов) предел \imf(x, у) в точке О(0, 0) не су-
ществует.
4. Дано:
127
Доказать, что
Решение. Введем вспомогательные углы α и β из условий:
cosa = a1, sina=61} cos β = α2 sin β = 62>
тогда третье условие примет вид
а1 а2 +^1^2 = COS φ — a) = О,
откуда
π π
β —- a = -ψ -j- &π и ρ = a + -у + ^π,
и, следовательно,
/π \
a2 == cos rf = cos ( a -J- ~7T 4~ ^π )= (— 1) sin a;
V 2 /
/ π \
b2 = sin β = sin ί a -|- -pp + £π J = (— 1)* cos a.
Справедливость доказываемых равенств устанавливается проверкой.
5. Формулы корней кубического уравнения в непри-
водимом случае.
Как известно (из курса высшей алгебры), приведенное кубическое
уравнение с действительными коэффициентами
при Я— 4~ -^—- < 0 имеет три действительные корня, однако, эти корни не
могут быть выражены через коэффициенты посредством действительных
радикалов. Рассмотрим формулу Кардано
x = u + v,
где
Представим подкоренное выражение первого кубического радикала в три-
гонометрической форме положив
2" = ρ cos φ, "4~ + "27' = — Ρ2 sin2 Ϋ.
и, следовательно,
ρ3 <7
— -^—-, cos φ = — -те—' φ = arc cos
27 ^P
имеем: « = Υ ρ (cos φ 4- i sin φ); а для υ следует брать комплексно сопря-
женные значения:
3/-— / ? , . . ? \ 3/~ / φ . φ \
иг = у р ( cos -j 4- ί sin -g- J, Cx = у ρ ί cos -g- — ί sin -5- J;
i/2 = -|/" ρ ί cos —g— 4-*' sin —3—I. U2= Y~9 (cos —g— — / sin —5—- J j
3 / φ4- 4π γ-|-4π\ з.._ / φ 4~ 4η
u3 = |/ ρ I cos —2— + ' sln —3— )> ^з— К Ρ 1 cos —3— —
128
откуда
д^! = 2 ϊ/ ρ cos -7г, дг9 = 2 у ρ cos —ό—» л:3 = 2у ρ
cos
§ 25. Вычисление некоторых тригонометрических сумм
и произведений
В настоящем параграфе показаны на ряде примеров методы сум
мирования некоторых конечных рядов (о суммировании конечных
рядов в общем виде см. «Специальный курс элементарной алгеб-
ры», § 114) и вычисления произведений, членами которых являются
тригонометрические функции
1. Вычисление суммы косинусов и сипу
сов дуг, образующих арифметическую про-
грессию.
Первый способ. Рассмотрим сумму
cos а + cos (α + h) + cos (α + 2A) + ··- + cos (α + nh) =
= 2 cos (α + kh)\
имеем:
sin 4 cos a = -ir I sin ( a + ^ ) — sin la~ ^
sin| cos(a + A) = yisin^a + -| ftj— sin ^a +
. /2 7 . . ν 1 Г · / , 2/7 -Ь 1
in cos(a + /i/i) sin ία + f
1 Г · / , 2/7 -Ь 1 , \ . / , 2л — 1 ; Μ
= —sin ία + —f- hj— sin [a -| ^— AJ ;
. /2
сложив почленно и разделив на sin γ. получим:
cos (a + kh) = _i_ [sin fa + %±±± h) ~ sin (a - |)1
2sin-o-L ^ У V ^J
z
Откуда окончательно:
^y cos I a -f -γ h\ sin ■ 2
2j cos (a + kh) = —
sin _
Если в этой формуле заменить α на -= аи А на — А, то
получим
я . / , η \ . п+1
sin I <7 4- γ Λ ] sin ■ 2 гс
= —^ 4 <2',)
Σ, sin(a +
, ' sin JL
129
Второй способ. Вычислим по формуле Моавра k-ю сте-
пень комплексного числа ζ = cos ft + is\nh и умножим ее на чис-
ло cos α + / sin a:
(cos α -f/sin α) г* === (cosa+/sina)(cos£/z+*sin&/i) =
= cos (a+kh)-\-i sin (a -f kh).
Искомые суммы (2) и Qj) суть действительная и мнимая части
суммы п+1 членов геометрической прогрессии:
(со a -f- t sin a) (1 -|-г+г2+ ... +гп) =
2л+|- 1
= (cosa +- ί sin a) г_ —;
имеем:
г"+1 — 1^ cos (η + 1) /г — \+ι s\n(n + \)n _
ζ — 1 sin ^7 — 1 + i sin h
sin 1±± h - sin £±1Ά + < cos H±i ft
^(sin^A-tcos^A^sfn-i+icosA^
sin
= ;—-h— ί cos γ h + ι sin -ψ h \.
s η —
Умножив на cosa + i'sina, получим в произведении:
sin i±i h sin 1+1 h
^ )
Действительная часть есть сумма (2ι), а коэффициент при
ί —сумма (по-
следствие. Положим, в частности, а = 0, тогда полу-
чим:
cos A h sin
1 +COS /2 +COS 2/2+ .., +COS AZft ==
sin JL
sin — h sin
2 2
sin ft + sin 2ft + ... +sin /гЛ =
.in-
130
2. Разделив почленно (2**) на (2*). получим
sin h + sin 2/z -f ... + sin nh __ . η , /VM
1 + cos h + cos 2Λ + ... + cos /ιΑ "" ^T ^2'
3. Вычислить сумму
/г
2 cos kx = cos χ -f cos 2x + ... + cos nx. (2з)
Имеем:
η η
2 cos Ал: = 2 cos Ax — 1.
Воспользовавшись формулой (2*)> получим (после преобразо-
ваний):
cos — χ sin ~*~ χ cos "* χ sin—я
\1 и 2 2 ι 2 2
2j COS Ax = 1 =
Так, в частности,
4π . 3π
cos __ sin —
2π . 4π . 6π 7 7
COS -γ- -f COS -у- + COS -=- =-
sin— sin —
2 2
sin —
π
COS —
η
cos
- +
3π
"Τ
sin
COS
cos
sin.
π
Τ
/2
/1.
2 '
З^с
7
+
η
6π
2/г
η
. π
2Κ
4. Вычислить суммы: (
sin x-\- sin3^+.. .+sin (2/2 — 1) χ = 2 sin (2^ —
cos
(Σί)
131
Решение. Положив в формулах (2л) и (σ^ а = х, п = 2х и заме-
нив η на я—-1, получим:
η
sin [* + (η — 1) χ] sin ηχ sin2nx
sin (2ft-1)*- ^(sin; =-5^
^ri cos nx sin nx sin 2λζλ:
2C0S (2k~ ° *= —ш^—=жт
5. Вычислить сумму
1 —cos χ + cos 2л: —cos 3* +...+ (—0л cos дгд:.
Решение. Достаточное формуле [σ\) положить h = x
η ί ηχ \ηπ\ ίη+\ (η+\)
cosl-yT--lsin l~^~ ^+ —§
(~1)Л cos kx=s
\
Преобразуем числитель в сумму:
1 \ (пхАпк
t
sin
(—2~ л; + —2~
2л + 1 2п +
§ 2
1 Г 2/2 + 1 д: Ί
= у (— 1)л cos —£— дг + cos -γ ,
откуда
(-,)<>cos ^+!*+cos !-
2cos^
*=о 2
Примечание. Этим же способом вычисляется сумма
2 (— 1)α— * sin ЛЛ
k=\
(предоставляем вычисления учащимся).
6. Вычислить суммы:
и
η
cos2 a + cos2 (a + /г) + ... + cos2 (a + п/г) = 2 cos2 <a + ^Л)·
132
Решение. Выразим каждое слагаемое через косинус двойного аргу-
мента. Имеем:
2;9/ , tn τπ \ — cos (2а + 2kh) η + 1 1 ν
sin2 (α + kh) = > γ-£ *- = -I- _ — > cos (2α +
Для вычисления последней суммы достаточно в формуле (2ι) заменить
α на 2α, /ζ на 2Л, тогда получим:
η
ж-^ cos (2а + nh) sin (n + 1) /ι
^ cos (2α 4- 9£Μ = *—-2-—/ . ν ^ ;
и, следовательно,
sin2 (α+ £//)=_ 2 — 2sin/z
/fe=0
В частности,
/2+1 cos nx sin (/2 + 1) χ
sin**-|-sin'2*+...+ sin',»; = -2-- 27ΠΤΤ—·
Посредством несложных тригонометрических преобразований правой части
получим другую формулу для этой же суммы
V ,,ntbr=s JL _cos(« + l);tsln« f .х
Подобным же образом вычисляется вторая сумма
/2+1 cos (2a-f /2/j) sin (/2 + \)h t /ν
kh) = -f- + ^2,{n/ ^ . (Σ6)
η
+ cos (2a-f /2/j) sin (/2 + \)h
cos' (« + kh) -f- + ^{/ ^
Примечание. Зная одну из рассматриваемых сумм, нетрудно найти
другую, так как:
2 sin2 (a+ kh) + 2 cos2 (a + kh) = n + l.
Пример. Решить линейную систему:
хх sin -^- + х.г sin 2— +...+ *„_ J sin (η — 1) — = аг,
2π 2π 2π
ΛΓχ sin — + χ2 sin 2 —+...+ *я_, sin (л — 1) — = а2;
/2—1 /2—1 /2 —1
sin —^-π + .ν25ίη2 —jp- * + ...+ *„_! sin (/2 — 1) n
133
Решение. Умножим данные уравнения соответстве нно на множители
k
sin k , sin k—,..., sin k
η η
η ' η '"' η
и сложим почленно. Коэффициент при хт в полученном уравнении равен:
η— ι
sin *-£- sin «-£-.
Если /e=m, то получим:
""' . cosn-^sin/"-"^
^з,п,(____- __ =_.
ί==) /г
(формула Σ*6)
Если кфт, то получим:
« — 1 гс — 1 /7—1
V^ ^π ^π 1 ν^ ^ —^ ^ ^Ί k -\- πι
2i sini ΊΓ8ΪΏί~Ίι Υ Ζέ C0Si~7rn~T 2d cos/ Τ~~πζ=°·
f. = \ i = 1 / = 1
(применить формулу 2з)
Таким образом, выводное уравнение примет вид:
п— 1 гг — 1
п ν^ кк 2
ϊ= ^ a'"slru Tf 0ТКУда хь = ΊΓ 2а a'sln~7T·
/ = ι /= ι
7. Вычисление сумм вида:
η η
2 cosp kh и 2 sin/? ^ (ГДе Р — натуральное число).
6=0 6=0
Обозначим через Sp н Sp следующие суммы:
Sp = 1 + cos ph -\- cos 2ph +... + cos nph\
S"p= sin ph + sin 2/?/z +...+ sin nph.
Эти суммы вычисляются по формулам (2*) и (Σ**) (заменить h на ρ/ζ):
cos 2£A sin Ιΐ+ΆΕΐ sin IE! sin (H±1L£>L
2 2 2 9
sin— sin _
Для вычисления суммы
выразим степени косинуса посредством тригонометрических функций крат-
ных дуг (см. § 20, стр. 98):
= -ψζτ [ cos pkh + Clp cos (p - 2) kh + C2p cos (p — 4) kh+...];
134
положив последовательно k=0, 1, 2, ... η и просуммировав по k, по
лучим:
Тем же методом вычисляется ^
Положив, в частности, ρ = 3, вычислим сумму
^ sin3 /?/i = sin3 h + sin3 2Λ + ... + sin* nh.
Имеем
3 1
sin3 kh = j sin kh~ j sin ЗЛЛ.
Просуммировав по k, получим:
η
sin3 kh = —г / sin kh = τ / sin 3kh =
3 sin .1 h sin l±i Λ sin ill /> sin ii!L±Ji
2 2 2 2
4 sin A 4sin^L
2 2
8. Вычислить суммы:
S' = cos л: + 2 cos 2л· 4- 3 cos Здг + ... -f η cos ял;;
S" = sin χ + 2 sin 2л: 4-3 sin 3x 4- ... 4-/1 sin ял:.
Решение. Первый способ. Перепишем сумму следующил»
образом:
S' + cos χ 4- cos 2л: 4 cos Зл: + . .. 4· cos пх +
4- cos 2л: + cos 3 х-\- . .. + cos nx -f-
4- cos я*.
^-я строка есть сумма п — k -f- 1 косинусов, аргументы которых образуют
арифметическую прогрессию; эту сумму вычисляем по формуле (2ι) (заме-
ним а на kx, h на χ, η на η — k)i
ί η—/? \ η — £4-1
cos I £x 4- —ψ- χ I sin 2 *
cos kx 4- cos (& 4 1) * + · · ·+ cos ^^ = =
sin -i-
2
cos -
sin J 2sin-£-
Γ . 2" 4 1 . /. 1
sin —2—л: —sin(^ —γ
135
Полагая к = 1, 2 ...пи суммируя получим:
η
sin ί—у x + kx\
S' =
Вычисляем
η
2 sin -y
сумму;
2n
+ 1
2
1
2 sin
X
Σ. / 1 \ χ 3 2/г-1 Si"
sin ί А?*— у *J = sin -y + sin у * + .. · + sin —-.— * =
2
[формула
Следовательно.
· 2
* sln
2 ^
2 * sln2
2 sin JL 2 sin2 A
Тем же методом вычисляется вторая сумма (вычисления предоставляем
учащимся):
(п + 1) sin nx — n sin (η + 1) χ ,.
4 sin2 -y
Второй способ. Рассмотрим сумму
г + 2г2 + Зг3 + . . . + nzn — - z г
г-1 (г-
(см. «Специальный курс элементарной алгебры^ 114)
Положим ζ = cos χ + i sin χ, тогда имеем:
г^ = cos бх + i sin /?jc ,
и, следовательно,
„/l+l 7rt+l _2
г-1 (г-1)2
Вычисляем правую часть последнего равенства
χ ( χ
b)
а) г — 1 = cos χ — 1 + ι: sin л: = — 2 sin у ( sin у — / cos у j;
1 η [cos (η + 1) χ + ι sin (η + 1) χ]
ι χ Γ χ jc "] ==Β
— 2 sin -у sin -у — ί cos у
ai[cos (η + Ι) χ + ί sin (/г + 1) χ] siny + ί cos -
г —
λ:
— 2 sin -y
χ
2 sin -y
/ 1 \ / П Ί
sini л + у 1 * — ί cos I/1+ у)*;
136
c) г(гл — 1) = — 2 sin -у (cos x+ /sin x) ( sin у — /cos yj;
d) (2— 1>2 = Γ— 2 sin у (sin — - i cos уΥΓ =
χ
= — 4 sin2 -y (cos л; + г sin л:);
. η* / nx nx\
sin -y lsin-y — ί cos-y 1
= .
nx
n+1 sin -y lsin-y — ί cos-y 1 2sin2~2- —r sin
(Z 1)2 2sln«-j- 4 sin· -|-
Следовательно,
.*>+*.■-naln(n+:*)x si"2^ +1( s[nnx _ C0S(n+iJ*
χ χ \ χ χ
2 sin у 2 sin2-у γ 4 sin2-у 2 sin y
Отсюда найдем выражения для 5' и S".
9. Вычислить суммы:
51 = 1 + a cos χ + a2 cos 2x + ... + an cos nx;
52 = a sin χ + a2 sin 2x -f- ... + an sin лд:.
Решение. Рассмотрим сумму п + 1 первых членов геометрической
прогрессии
1 + αζ + α2 ζ2 + · ·. + αη ζη = αη+1 ζ*+1 — 1 ^
Если положить г = cos д: ^ / sin χ, то последнее равенство примет вид:
Вычислим правую часть последнего равенства:
- 1> лг — 1 + ш"+ * sin (π + 1) * __
аг — 1 β cos * — 1 + ia sin л:
= cos (n + 1) л: — 1 + fa"*1 sin (n + 1) *] (a cos χ — 1 — ia sin л:)
"~ ea2 — 2a cos л: + 1
Действительная часть полученного выражения равна Sb а коэффициент
при / равен 52:
с aAZ+2cos/iA:--a'I+1 cos (л+1) х — a cos * + 1 /v, ч
Sl = a'-2flcos*+l (Σβ)
c α"+2 sin ηχ — αη+χ sin (л + 1) χ + α sin χ /κ, ,.
Sz α»-2αcos*+1 (Σί1 }
Различные частные приемы вычисления сумм показаны на примерах
10- 13.
10. Вычислить сумму
η
sin·· ^+3sin^+...+ 3"-Isin»-^= 2 a^'sinsA.
137
Решение. Исходим из тождества
sin Зх = 3 sin χ — 4 sin3 x.
h h h
Полагая последовательно χ = -g-, -ψ-, .. ., „_ j , получим:
sin h =3 sin -5- — 4 sin3 -q-
o ο
h h h
sin -3- = 3 sin -ga" — 4 sin3 -^r
Л h h
s in -qT- — 3 sin -03- — 4 sin3 -00-
o о О
h h h
sin ^,t = 3 sin -ψ- — 4 sin3 -^тг
1
3
з2
oAZ-1
— 1
Умножив последовательно эти равенства на 1, 3, З2, ..., 3" 'и сло-
жив почленно, получим после сокращения:
sin /г = 3" sin Ji - 4 У З^""1 sin3 A,
откуда
ok— 1
sin3 —^ = -ξ- Зп sin -^тг — qf sin /г.
11. Вычислить суммы:
51 = cos χ + С^ cos 2д; + С2п cos Зл: + ... + Спп cos (/ζ +1) χ;
52 = sin x + Cln sin 2л: + C2n sin 3^ + ... + Cnn sin (n + 1) *.
Решение. Рассмотрим равенство:
ζ + φ2 + С^ г3 + ... + Cnn zn+l = г (1+ г)п.
При г =в cos л: + / sin л: это равенство примет вид:
Si + f'S2 = (cos χ + ί sin χ) (cos лг + 1 + i sin л:)п;
но
[(cos a; + 1) + i sin *f = 2Л cos" у cosy + ί sin Ц-\ .
ьно,
У П fi I О ц I Q "Ι
+ iS2 = 2" cos" γ cos —y- χ + ί sin —γ- α: ,
Следовательно,
откуда
Si = 2" cos" γ cos ^-γ- xt S2 =2л cos72 γ
(Σιο)
138
12. Найти сумму
"Г
° — COS α COS (α + β) "Γ" COS (a + β) COS (α + 2β)
1
+ COS [α +(/ι — 1) β] COS (α + /ιβ) *
Решение, Имеем:
tg (α + Ρ) — tg α =
"*" ' # ' "Γ"
sin
COS a COS (a + β) '
sin β
: COS (a + β) COS (a + 2,3) ;
sin
= cos fg + (n _ i
Сложив почленно, получим:
tg (α+Αζβ) — tg a -= S- sin β,
откуда
5=777
sin
" sin β COS α COS (α + Αζβ) '
13. Вычислить сумму
,_',', , !
cos χ + cos Зх * cos χ + cos 5a: '···"' cos χ -f- cos (2/z + 1) x'
Решение. Преобразуем в знаменателях суммы в произведения:
ς ι
О = "77
1
1
1
2 у cos х cos 2x ' cos 2x cos Зх "*" ' *' "" cos пх cos (/ι + 1) χ
Положив в предыдущем примере α = β = Λ:, получим:
)■
с ==
si
sin пх
sin 2x cos (η + 1) χ'
14. Доказать что
Решение. Имеем:
2 ctg 2α — Ctg α = — tg α.
χ χ
Заменив в этом тождестве последовательно α на χ, -тг , -ζ,
следующие равенства:
получим
2 ctg 2х — ctg л: = — tg л:
X X
2 ctg χ — ctg -^ = — tg-g
2 ctg γ — ctg j = — tg j
139
Умножив эти равенства на I, у. -j ψϊ и сложив почленно,
получим:
i χ ^ 1 а
2ctg 2* - тщ ctg тр* = — JJ^ ^5 tg ^
откуда и следует подлежащее доказательстьу равенство.
В рассмотренных ниже примерах показаны приемы вычисления различ-
ных тригонометрических произведений. На первых дну χ примерах иллю-
стрирован один из простейших приемов. В последующих примерах вычисление
произведений основано на теоремах о разложении многочлена на множи-
тели.
Вычислить произведение!
Р= (2 cos x — 1) (2 cos 2х — 1) ... (2 cos 2я·1 χ — i) =»
« Π (2cos2A χ - 1).
Решение. Предположи^ что cos хФ— тг , умножим обе части на
? cos χ 4- 1, тогда получим:
(2 cos + 1)Р= (2cosx+l) (2 cos χ — 1) (2 cos 2*— i) ... (2 cos 2я""1 χ—l). (1)
Примем ео внимание следующее тождество:
(2 cos 2* χ + I) (2 cos 2* * -- 1) » 4 cos2 2Λ χ — 1 =
= 2 (cos 5Λ+Ι χ + 1) — 1 = 2cos 2Λ+1 jc + 1.
Выполнив последовательно умножения е правой части равенства (1),
получим:
(2 cos χ + 1) Ρ = 2cos 2я χ ^ 1.
Итак, имеем окончательно!
2 cos 2я * + 1
2 cos χ + 1 '
16. Вычислить произведение:
а Ь\ ( а Ь\ j a
Y + cosyj fcos-j + cos -^J... (cosgTi
a b
Решение. Умножив обе части на cos ^ — cos ψι получим:
(a b\ I a b\ I a b\
cos j + cos j) ... Icosyt+cos^nj (cos 2«-cos272j =
==i cos ^— cos ψ\ P.
140
Приняв во внимание тождество
(а Ь\ ( a b
[COS ~k + COS ^J ^COS jj - COS ~
a b
a b
COS* - - COS* ψ
и выполнив умножения, получим!
( a b\ 1
I cos ψ — cos ψ 1 Ρ = (cos a — cos b) ψ,
откуда
η
cos a — cos 6
17. Вычислить произведение<
Г / 2π\Ί Г / 2π(/ι—1)
[1 ^ COS?j[l - COS ^φ + -JJ ... 1^1 -COS ^φ + "~ 7
^ JJ 1^ ^
n [>-«
Решение. Уравнение Tn (χ) — cos α,
рде
Г„ (jc) — л/1 —C*(l — λ:2) λ:^2 + С^ (1 - jc2) λ:^4 - ...
— полином Чебышева (см. § 17) служит для определения всех возможных
значений *=cos«, при этом дуга и определяется из условий cos пи = cos α
Положив α = φ/г получим уравнение
ГЯ(Х)—СО «φ = 0,
корнями которого служат значения χ = cos и, где дуга и определяется из
условия
cos пи = cos η γ;
последнее условие перепишется так:
пи = i я? + 2&π,
откуда
2/гтс
«=» ±φ + — .
Для χ = cos и возможны η следующих различных (в общем случае) значе-
ний:
/ 2π\ / 4π\
Хо = COS φ, ХХ = COS ί φ + — 1 , Χ2 = COS ί φ + ~ 1 , .. .,
Χη-1 = COS |^φ + 2 J .
141
Следовательно, имеет место разложение на множители:
Тп (х) - cos щ = 2п~1 (х - х0) (х - хг) ...(*- *„_,) =
(коэффициент при хп равен 2п \ см. § 17).
Положив в этом тождестве х — 1, получим искомое произведение
Π Г / 2kn\~] 1 — cos ην
1-COS φ + —j = , . (Π17)
18. Вычислить произведение
- Π-.(.+?).
Решение. Положив в формуле (Н17) предыдущего примера φ = 2xt
преобразуем в произведение правую часть, а также каждый двучленный
сомножитель в левой части; тогда получим:
Π/ &π\ 2s\n2nx
sin' * + -== х .
k=0 Х J
откуда (извлекая корень) получим:
\ sin
k—l
П
19. Вычислить следующие произведения:
ΠΙ kn\
cosb+- I;
b)flsin^+^,); с) П si
k=0
η . 2n—l
Решение, а) Если в формуле предыдущего примера заменить χ на
π
л;+ -η", то общий член произведения преобразуется следующим образом:
142
а потому
η—
П(. кк\ ( π \ / (η — 1)π\
COSr+ H ^cosxcos U+- ) · cos(* + =
ь ^ \ ι \ / \ /
/ π
in ί ηχ -\- η -ο*
(— I)^sin2mjc
, если η = 2m,
(— l)mcos(2m+ 1) χ
, если я = 2т + 1.
22/тг
π
b) Если в формуле предыдущего примера заменить χ на χ + ^ , то
общий член произведения преобразуется следующим образом:
sin (χ + ^"Ь j) = sin (^ + ~2^- π ) ,
а потому
η
sin ί χ+ -2^~"π J=sin l^+2njsin( ^ + 2^lsl
π \ / π | π
^jsin^ + ^-h-
Sin I лт ~ iw ι —= от | л. τ 2/2 j
X sin [x+oz-rrr ... smhf+r-i—— ■
/ ^ ι 2π\
V /
cos ηχ
2η—\
Π/ ^π\
sin I x~\~~^j на две группы, одна
из этих групп выписана в верхней строчке, а другая — в нижней следую·
щим образом:
/ π\ / 2π\ / η — '
sinA: sin(x+-T] sin ( x-\- — j ... sin f
/ /ιπ\ / л + 1 \ / я + 2\ / 2n
sin ί x+ —j sin f л:-!- —^— π^δίη Ix + -^— π^... sin ί x+ —
Члены, подписанные друг под другом, взаимно противоположны
sin {*+ ~ίγ π)β sin
следовательно,
2/г-) Г/г-1
Π .·η (* + ?)-(-D- Π
143
20. Вычислить произведение
/2—1
Решение. Найдем корни уравнения х2П — 1. Искомыми корнями
служат значения комплексных корней степени 2/г из 1. Занумеруем эти
корни следующим образом (черт. 84):
ε0 = 1,
π ... π
ε, = cos — -}- ί sin —
2π
2π
2π 2π
ε2 = COS — + i Sin — , ...,
= —1. ε—i=cos— — £ sin —
2τΐ
2π
e_2 = cos—— tsin—, ..
Разложим двучлен х2П — 1 на действитель-
ные множители; для этого сгруппируем по-
парно линейные комплексно сопряженные
множители, на которые разлагается этот дву-
член.
—*-\) X
Черт. 84
X (х -
Так как
- ε_2)... (χ - εΛ-1) (^- ε_^
= л:2 — 2jccos— + I,
то имеем:
—1 ==(a:2_
-2, cos
— 2л: cos
/7—1
= (*2-1)П (*2~2
/е=1 Ч
2π \
Ί + ή
Откуда найдем искомое произведение:
21. Вычислить произведение
п—\
X2 — 2л: COS
2k + 1
2/г
144
Решение. Поступим также, как в предыдущем примере: разложим
двучлен х2П + 1 на действительные множители
х'2П + 1 =
Откуда
4=0
Аналогично получаются следующие формулы:
ΐ~ΐ / 2k 4- 1 \
Π (*»-2xcos-^-«+l) = Jt*"+l. (П21)
= *2ι4*2η-Ι + ... + ΐ: (π'2Ι)
π
Формула (^2ΐ) получится разложением на множители двучлена
+1-- 1.
Для получения формулы (Π^ι) разложим на множители двучлен
* + ι *=
далее замечаем, что
2ft + 1 \ 2(n — k)
полагая /г = 0, 1, ..., я, — 1, /2, получим для η—k множество тех же значе-
ний n — k — n, η —1, ..., 1, 0, следовательно, произведения (П^) и (П^)
равны.
22. Доказать справедливость следующих равенств:
П. kn . π . 2π . (/г — 1) π /η
Sln Υπ = sln 2^ ' sln 2^ -· sln л ^^T : (Пи)
Υπ
Π
ы
η
1η 2η+ 1 ~sln 'V
2π ηπ У 2η+ \
sin
= 2"
. (2/г—1)π π. . 3π . (2η—1) π УТ
П. (2/е—1)π . π. 3π (2лг— 1) π У 2 , „,
^~Ύη ==sln4^sin4^--sin τΤ~=ζ-ψ-> (Π22)
б Зак 597 145
1 I
(2k-\) π π Зл: (2/2-1) π /2
cos""4^ = (:ο5^0054^··· C0S~~^ = "2^"
Π
C0S *Γ+\ = C°S 2^ΤΊ C0S
(— \)m
22/72+1 при 2m + 1 = л;
(_l)m (Π2θ)
22m при η = 2m.
Решение. Для вычисления (П22) положим в формуле (П2о) -зс = 1,
тогда получим:
f = П ИЛИ
откуда следует справедливость формулы (П22).
Аналогично доказываются прочие формулы (n22j, (^22)» (^22)> (^22)·
Следует положить (соответственно) х= 1 в формуле (Π2ι) ; х = 1 в фор-
муле (П21); х = —1 в формуле (П21); х = г в формуле (Π2ι).
23. Доказать, что при четном η имеет место тождестзо
ft-2
Т~ Л sin2
sin nx — η sin χ cos χ { [
. 1 \ л .
Решение. Рассмотрим формулу
sin nx = C^ sin λ: cos" ! л; — Czn sin3 л: cosn 3 χ +
/г—2
+ Cjj sin5 jc cosn~5 ^ — ... + (— 1) 2 я sin"""1 χ cos jc
(ci.
sin /гх = sin χ cos χ V С' cos" 2 χ — С3 sin2 χ c#)s"~ 4
ИЛИ
... + (- 1) 2 C^-^in"-
Так как четные степени косинуса выражаются через четные степени
синуса (в виде многочленов от этих степеней), то
sin nx = sin x cos л:· Р (sin2 χ)
или, положив ζ = sin χ, получим
sin ял; = sin л: cos xP (ζ2)
где
/г—2 η—4 я—2
Ρ (ζ*) = Cj (1 - г*)~ - С,з ζ2 (1 - г2)~+... + (- \)~ Сп~' г""2.
Всякое значение z=sin χ, при котором sin/zx=0, но sin x i= 0 и cos χ φ 0,
служит корнем многочлена Ρ (ζ2).
Из условия sin nx = 0 найдем:
βπ /2 — 2 /г
χ = - , где Л = 0, ± 1, ± 2, . ., ± —j- , у .
146
При k — Ο и & = у множители sin лг и cos x обращаются в нуль, а при
прочих значениях k эти множители в нуль не обращаются. Следовательно:
π 2гс (п — 2) π
2! = sin-, г2 = sin -,..., 2^= sin—^ ,
2
2π (η — 2) π
zsin
z_1==-sin-, 2_2 = — sin — , ^^γη
2
суть я—2 различные корни многочлена Ρ(ζ2) степени η — 2; следовательно,
имеет место разложение
(Λ — коэффициент при старшем члене Ρ (ζ2))
Λ-ΐΓΪ A(z\-z*){zl-z>)...(*U-*2y
(так как zk = — z_k)
sin2 л: \ / sin2^ \ / sin2 χ
И1 М
I 7TA sin27TJ I Sin2-2F-/
(так как ζ = sin x).
В самом деле,
/г—2
(—1) 2i Z2 •••^«_2 = г1 г-1 ··· 2/1-2· J/z-2
2 2 2
есть произведение корней Ρ (г2), равное свободному члену, деленному на
Л, т. е.
/ п~72 2 _2 Р (°) - п
2
Подставив в равенство (*), получим доказываемое тождество. Аналогично
доказываются следующие тождества:
η
2"
Π /ι sin2 * \
1 (2£-ΐ)π I* (n~ четное)
\ Sin2)
2
sinnx = /г sin χ
П/ sinz jc \
/ 1 — ^ I; (n — нечетное)
*-. I sin2^j
П/. sin2 л: \
1 — Топ—ПГГ \l (n— нечетное)
/г—1
2
sin2:
2/г
Глава третья
ИССЛЕДОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
ЧИСЛОВОГО АРГУМЕНТА
В настоящей главе будут рассматриваться тригонометрические
функции от числового аргумента. В соответствии с условием, при-
нятым в § 9, значения тригонометрических функций от числового
аргумента χ определяются как ее значения от угла, радианная
мера которого равна числу х.
Ряд свойств тригонометрических функций был уже установлен
в предыдущих главах; в настоящей главе эти свойства будут сфор-
мулированы в функциональной терминологии.
§ 26. Области определения и множества значений
тригонометрических функций
1°. Областью определения функций cos χ и sin л: является мно-
жество всех действительных чисел, т. е. интервал (—оо, оо).
В самом деле, будучи координатами конца дуги, измеряющейся
числом ,ν, эти функции имеют определенное значение, каково бы
ни было действительное число х.
2°. Областью определения функции tgx является бесконечное
множество интервалов
_3 π \ / π π \ /π 3π
(π ι U π ι /
— -^ + £π, —+
В самом деле, функция tgx имеет смысл для любых дуг,
кроме дуг, оканчивающихся в точках β (0,1) и ВЛ (0,— 1); эти
последние дуги измеряются числами у + kn. Исключив числа
148
Υ -f kn из множества всех действительных чисел, получим бес-
конечное множество интервалов (— у + £л;, -^
Аналогично устанавливается, что
3Q. Областью определения функции ctgx является бесконечное
множество интервалов (kn, (k + 1)π).
4°. Множеством значений функции cos Jt, а также функции ύηχ
является сегмент [—1, 1].
В самом деле, в § 12 установлено, что при заданном значении т
косинуса (синуса) соответствующий угол существует в том и толь-
ко в том случае, если —1< т<1. Иными словами, косинус (синус)
может принимать любое действительное значение, принадлежащее
сегменту [—1, 1 ].
5°. Множеством значений функции tgx, а также функции ctg jt
является множество всех действительных чисел (—оо, оо).
В самом деле, в § 12 установлено, что при заданном значении
т тангенса (котангенса), соответствующий угол может быть по-
строен, каково бы ни было действительное число т. Иными слова-
ми, тангенс (котангенс) может принимать любое действительное
значение.
Из изложенного следует, что функции cosx и sin x ограничены,
так как |cos*| <1, |sinx|<l, а функции tgx udgx неограничены
(в соответствующей области определения).
Примеры.
I Областью определения каждой из следующих функций
sin a:2, cos 2х, cos (sin x), sin (χ + χ2)
является множество всех действительных чисел.
Рассмотрим, например, функцию sin*2. Представим ее в виде сложной
функции sin и с промежуточным аргументом и = х2. Областью определения
промежуточного аргумента и = х2 является интервал —оо< χ < оо, функ-
ция sin и определена при всех значениях и, следовательно, сложная функ-
ция определена при всех значениях х.
2. Установить (в общем случае) область определения следующих слож-
ных функций sin u(x) и cos u(x).
Решение.
Выражение sin и или cos и имеет смысл при всех значениях аргумента,
при которых промежуточный аргумент и имеет смысл. Следовательно, об-
ласть определения функции sin и (х) или cos и (х) совпадает с областью опре-
деления и (х)
На основании сказанного, имеем:
функция промежуточный область определения
аргумент
l)coslg* и = lg χ 0 < χ < оо
2) sin — и = ~г (— оо, 0) и (0, оо)
Л X
3) sin (ctg χ) и = ctg x kK < χ < (k + 1) π
\) cos lg / 1 - χ2 u = \gV(i-x2) —\<x<\
149
3) Установить область определения функции igu(x).
Решение. Область определения находится из следующих условий:
1) промежуточный аргумент имеет смысл и 2) значение промежуточного ар-
гумента должно принадлежать области определения тангенса, т. е.
π
a) у = tg sin χ, промежуточный аргумент и = sin x имеет смысл при
— оо < χ < оо. Так как | sin χ \ < 1, то sin χ Φ γ + kn. Область определе-
ния: интервал — оо < χ < оо ;
b) у = ctg cos χ, промежуточный аргумент и = cos x определен при
— оо < х< оо. Если « = £π, то у теряет смысл; решаем уравнение
cos χ = &π; так как при | k \ > О имеем | &π | > 1, то это уравнение имеет
π
решения лишь при k = 0, соответствующие значения χ = γ + ηπ (η—целое
число) следует исключить из множества всех действительных чисел. Область
определения есть бесконечное множество интервалов
π π
-y + mr, ~2+>
c) функция tg ~ , промежуточный аргумент и = γ имеет смысл при
1 π 2
χ φ 0. Если и = — = γ + «π, откуда * = ^ ι η π . то у == tg л: теряет
смысл. Исключив из множества всех действительных чисел числа χ = 0 и
2 1
х = (2^4- η тс » найдем область определения функции у = tg — в виде бес-
конечного множества интервалов
[ 3π '
4. Найти множество значений функций:
a) у = sin2 χ. Так как множество значений sin χ есть сегмент [—1, 1],
то множество значений sin2 χ есть сегмент 0 < у < 1;
b) У = tg2 *. Так как множество значений tg x есть множество всех
действительных чисел, то множество значений tg2 x есть множество всех
неотрицательных чисел 0 < у < оо;
c) у = sec χ = CQS;c . Так как cos x может иметь произвольное значение,
не большее по абсолютной величине, чем 1, то | sec χ \ > 1. Множество зна-
чений состоит из двух промежутков — оо <у < — 1 и 1 < у < оо ;
d) y = 2sin*. Имеем у = 2W, где и = sin x. Множество значений проме-
жуточного аргумента и = sin χ есть сегмент — 1 < и < 1, а множество зна-
1
чений функции у есть сегменту < у < 2.
§ 27. Периодичность тригонометрических функций
Теорема Г. Функции cos* a sinx периодические, их наимень-
ший положительный период равен 2π.
Разъяснение. Из изложенного выше (см., например, § 16,
стр. 82) вытекает, что всякое число вида 2kn (в частности 2π),
150
где k — произвольное целое число, есть период косинуса и сину-
са, ибо
cos (χ -f 2&jt) = cos x, sin (χ + 2kn) — sin χ
(дуги х и х + 2kn оканчиваются в одной и той же точке).
Докажем, что никаких других периодов функции cos* и sin л;
не имеют.
Доказательство. Число l=j=0 служит периодом функ-
ции cos x в том и только в том случае, если имеет место тождество
(по определению периода)
cos (χ + Ι) = cos x или cos {x + /) — cos λ: ξ 0.
Преобразовав в произведение левую часть последнего тождества,
получим:
(l)n^- = 0. (1)
Так как сомножитель sini* + -^) не равен тождественно нулю,
то тождество (1) выполняется в том и только в том случае, если
sin-n = 0, откуда / = 2kn. Следовательно, периодами синуса яв-
ляются числа 2kn\ среди этих чисел наименьшим положительным
является 2π.
Для функции sin л: теорема доказывается аналогично, ч. т. д.
Теорема 2°. Функции \gx и dgx периодические, их наимень-
ший положительный период равен п.
Доказательство. Число I является периодом тангенса
в том и только в том случае, если при всех допустимых значениях
аргумента χ имеет место равенство:
tg(*+/) = tgA: или —г-^4 = 0.
te v ' ' fe cos (a: + /) cos χ
Последнее равенство выполняется тождественно в том и только
в том случае, если sin/ = 0, откуда I = kn. Если χ принадлежит
области определения тангенса, то число χ + / = χ + kn также
принадлежит этой области. В самом деле, в противном случае
χ + kn было бы числом вида χ + kn = -^ + пп (п — целое число),
но тогда и число χ = -^ + (п — k)n не принадлежало бы (вопреки
условию) области определения тангенса.
Итак, всякое число вида kn является периодом функции tgx,
наименьшее из этих чисел есть п.
Для функции ctgx теорема доказывается аналогично, ч. т. д.
Теорема. Всякая функция вида
= U (cosx9 sin x, tg xt ctg x)
есть периодическая функция аргумента х, одним из периодов которой
является 2п.
151
Доказательство. В самом деле, при замене значения
аргумента χ на χ + 2kn значения промежуточных аргументов
и = cos χ, ν = sin jc, w = tg χ, ζ = ctg χ
не меняются, а потому не меняется значение функции f(x)y ч. τ . д.
Заметим, что число 2π, будучи периодом функции f(x)y может
не быть ее наименьшим положительным периодом.
Так, например, функция f(x) = sin x cos x периодическая, но 2π
не является ее наименьшим периодом. В самом деле,
/ (л: + π) = sin (χ + π) cos (χ -f π) = (— sin χ) (— cos χ) =
= sin λ: cos χ = / (χ).
Следовательно, число π является периодом функции f(x).
Примеры.
1. Нижеследующие функции, будучи сложными функциями от перио-
дических функций, являются периодическими:
2·'»*,
_ cos χ ·
2. Доказать, что функция | sin л: | периодическая и найти ее наименьший
жительный период.
Решение. Число π является периодом данной функции., так как
| sin (χ + π) Ι = I — sin χ | = | sin χ \.
Докажем, что это число есть наименьший положительный период. В са-
мом деле, если бы число 0</<π было бы периодом, то имело бы место тож-
дество | sin(* -f /) I = I sin * |, положив в частности χ = 0у получим | sin /1 =
= 0, что невозможно, так как при 0</<π имеем sin/>0.
3. Доказать, что функции а) *+ sin* и b) sin*2 непериодические
Доказательство, а) Если функция * -f sin * периодическая,
то существует число 1фО такое, что
(х + 0 + sin (* + /) == * + sin * или / + 2cos I*+γ] sin γ = 0. (1)
Если sin у φ 0 (т. е. / φ 2&π), то cos I *+ yl^1 J~ = const,
\ ' 2sin-2"
что на самом деле не имеет места; если же sin у = 0, то из (1) найдем
/ = 0, что противоречит условию, / φ 0.
b) Рассуждаем аналогично: тождество
sin (* + /)2 = sin *2 или 2 cos ( *г -\- 1х + -к ) sin ( /* + "лГ I = 0
не имеет места, так как ни один из сомножителей тождественно не равен нулю,
а каждый из них обращается в нуль лишь на множестве изолированных точек.
Можно рассуждать иначе: если бы данная функция была периодической,
то множество корней уравнения sin *2 = 0 также было бы периодическим. Ре-
152
шим это уравнение Получим последовательность (двустороннюю) корней
χ — ±|/"&π. Найдем расстояние между двумя «соседними» корнями
V(k+ 1)π — Vkk = г = -> 0, при 6 -> со.
Это показывает, что точки ± "|//ггс расположены непериодически на число-
вой оси.
§ 28. Интервалы знакопостоянства
тригонометрических функций
Функция cos х. В § 7 установлено, что косинус положите-
лен (отрицателен) для дуг, оканчивающихся в правой (левой) от-
крытой полуокружности. Следовательно, в интервале (—-|-, -|Λ
и (в силу периодичности косинуса) во всех интервалах вида
( — γ + 2/гп, γ + 2£π) (правая полуокружность) cosx>0.
В интервале (γ , у я ] и во всех интервалах
(γ + 2kn, γ π -}- 2kn j имеем cos л: < 0.
Φ у н к ц и я sin χ. Синус положителен (отрицателен) для дуг,
оканчивающихся в верхней (нижней) полуокружности; следователь-
но, в интервале (0, π), а также во всех интервалах (2knf(2k+l) π)
функция sin л: положительна. В интервале (—я,0) во всех интер-
валах ((2k — 1)π, 2kn) функция sin л: отрицательна.
Функция tgx. Для дуг, оканчивающихся в I четверти (откры-
той), тангенс положителен, а для дуг, оканчивающихся в IV чет-
верти (открытой), тангенс отрицателен, поэтому tgx>0 в интер-
вале (0, |Л и tgχ< 0 в интервале ( — ~, 0). Рассмотрение функ-
ции tg.x: в интервалах, соответствующих остальным четвертям,
излишне; в силу того, что π есть период тангенса, имеем
tg^>0 в интервалах fkn, γ +кл\ (I и III четверти) и tgjc<0
в интервалах (— γ + kny kn\ (II и IV четверти).
Функция cigx положительна (отрицательна) в тех же ин-
тервалах, что и tgA;.
Примеры.
1. Найти область определения функции T^cos x*
Решение. Искомая область определения находится из условия
cos χ > 0, откуда получим бесконечное множество сегментов
6В Зак. 597 153
2. Найти область определения функций
В каких промежутках справедливы тождества
a) lg tg χ = lg sin χ — lg cos x, b) lg tg χ = Ig | sin χ \ — lg | cos χ \ ?
Решение. Области определения функций yLi у2 и у3 находятся из
неравенств cosa:>0, sin*>0, tgx>0. Получим соответственно для функции
/π π \
Ух множество интервалов I ^ + ^π, у + 2&π Ι (для функции у2 множе-
ство интервалов (2βπ, (2& + 1) π), для функции у3 множество интервалов
( π
Тождество а) имеет место при условиях sin χ > 0, cos χ > 0, tg χ > О,
/ π \
т. е. в интервалах !2£π, -2" + 2^πΙ (дуги, оканчивающиеся в I четверти).
Тождество b) имеет место при условии tg χ > 0, т. е. в интервалах
:, ί^ + "2')π)· ^ самом деле, если tg χ < 0 то lg tg x не имеет смысла.
Если же tg χ > 0, то
tg χ = | tg χ Ι = ι cQS χ ι и lg tg x= lg | sin *| — lg | cos χ |.
§ 29. Промежутки монотонности тригонометрических функций,
наибольшие и наименьшие значения
Теорема. На всяком сегменте [2&л, (2й + 1)π] (изображаю-
щимся верхней замкнутой полуокружностью) функция cos x убывает
от 1 до—1; на всяком сегменте [(2k — 1)π, 2kn] (изображающим-
ся нижней замкнутой полуокружностью) функция cos x возрастает
от — 1 до 1.
Доказательство. В силу периодичности косинуса доста-
точно доказать теорему лишь для двух сегментов [0, π] и [—π, Ο],
составляющих в сумме период косинуса.
Докажем, что функции cos χ на сегменте [0, л] убывает от 1 до
—1, для этого надо доказать следующие три положения.
1°. На сегменте [0, я] функция cos а: убывает.
2°. В граничных точках сегмента значения косинуса суть +1 и
1
Это положение установлено выше: известно, что
cos 0 = 1, cos л = —1.
3°. Произвольное значение т, промежуточное между —1 и 1,
функция cos л: принимает в некоторой точке с сегмента !0, л1.
Это положение установлено выше (см. § 12); в самом деле, на
сегменте [0, л ] существует дуга (и притом единственная) с= arc cos m,
косинус которой равен т
cos с = пи
154
Остается доказать положение 1°. Пусть х{ и х2 — два произволь-
ные различные значения аргумента, взятые на сегменте [0, π],
пусть 0 <;*! <[ х2 <; я. Для сравнения соответствующих значений
косинуса составим разность cos*2 — cos xi и преобразуем ее в про-
изведение:
cosх2 — cosjcj = — 2 sin*2 g Kl si
sin
χ* -f
(1)
Из неравенств 0<л:1<л:2<л следует, что 0< *ι + *а <^ π и
О < *2~*1 <C-f > Следовательно, оба сомножителя sin x*~Xl- ■ и
sin *2 ^ ** положительны, а потому
cos х2 — cos хл < 0 и cos х2 < cos jc1#
Итак, большему значению аргумента соответствует меньшее
значение косинуса, следовательно, на данном сегменте функция
cosjc убывает.
Аналогично доказывается, что функция cos χ на сегменте[—π, Ο]
возрастает от —Л до 1.
1°. Если — π < хг < х2 < 0, то
следовательно, в равенстве (1) сомножитель sin
*2
и cos
^ отрицате-
следовательно,
лен, а потому cos хг—cos
cosx возрастает.
2°. Известно, что cos (—π) = —1, cos 0 = 1.
3°. Если —1 < m< 1, то в точке с = —arccos m, принадлежа-
щей сегменту [—π, 0], имеем cose = т, ч. т. д.
Примечание. Доказать возрастание функции cos x
на сегменте [—π, 0] можно и так:
Пусть х{ и хг — два значения аргумента, взятые при усло-
вии —π < х{ <#2<^0. Противоположные значения аргумента
—Χι и —х2 расположены на сегменте [0, π] и 0<—х2<С—#1-^я.
В силу убывания функции cos χ на сегменте[0, π] и ее четности
имеем:
cos (—x2)>cos (—х^ или cosa:2>cosa:i.
Изложенные результаты могут быть представлены в виде сле-
дующей таблицы:
Значения ар
гумента χ
Функция
у = cos χ
...
...
- 2π
1
< к <
\
— π
—1
< X <
/
0
1
< χ <
\
π
—1
< χ <
/
2π
1
...
...
6В*
155
Геометрическое доказательство. Теорему
можно доказать геометрически, исходя из интерпретации косинуса
как абсциссы точки единичной окружности. Докажем геометриче-
ски убывание косинуса на сегменте [0, π].
Разобьем сегмент [0, π] на два сегмента Г0, у] и | у , π 1;
исследуем cos χ на каждом из этих сегментов отдельно.
Пусть 0 <; Χι < х2 <С-у- \ изобразим значения аргумента Х\ и х2
в виде дуг единичной окружности (черт. 85). Из геометрии извест-
** - но, что для двух дуг, меньших полуокруж-
ности, хорда, стягивающая большую дугу,
удалена от центра круга на меньшее расстоя-
ние.
Абсциссы Xi^cosxi и X2 = cosa;2 кон-
цов дуг Х\ и х2 суть расстояния от центра
круга хорд, стягивающих дуги, по величине
равные 2хх и 2хъ Так как
2л;1<2л:2, то Хг^>Х2>
а потому
cos хл > cos х2 при Х\<1х2.
Черт. 85
Если дуги х1 и х2 содержатся во второй четверти у <*j<a:2<ji,
то дуги φα и φ2, дополняющие χλ и х2 до полуокружности,
удовлетворяют неравенствам 0 < φ2 < уг < у .
Расстояния до центра хорд, стягивающих дуги 2φ2 и 2ψί
соответственно суть
|Д, | = |cos*i| и \Х2\ = | cosх21,
следовательно, |cosχλ \ <i \ cosx2\; но так как во второй (замкну-
той) четверти косинус не положителен, то
cos χ, > cos x2 при χλ < х2
(установить геометрически возрастание косинуса на сегменте
[—π, Ο] предоставляем учащимся в виде упражнения).
Теорема. На всяком сегменте — у + 2£л, -^ + 2kn (изобра-
жающемся правой замкнутой полуокружностью) функция sin л:
возрастает от — 1 до 1; на всяком сегменте ^ + 2£π, -^ -f 2knI
(изображающемся левой замкнутой полуокружностью) функция
sin л; убывает от 1 до — 1.
Доказательство. В силу периодичности синуса, доста-
Г π π Ι
точно доказать теорему лишь для сегментов γ, -у
и Ι~Τ· ΤI' состав;ню щих в сУмме период синуса. Доказатель-
156
ство аналогично изложенному выше доказательству монотонно-
сти косинуса.
1°. Пусть хг < хъ тогда имеем
sin х2 — sin χ, = 2 cos
sin
если
— ·η-<*ΐθ2<*-77. TO —
если же у <
0 <
3 π _
"2"^> то -ζ <
~ и sinA:2
2 ^ 2 ^ 2 '
sin x2 — sin хг > 0;
- ΛΤι ^ 3π
Следовательно, на сегменте —у, у функция sin x возрастает,
а на сегменте у, у — убывает.
2°. Граничные значения функции sin x на рассматриваемых
сегментах суть — 1 и 1, а именно:
= — 1, siny = 1,
для сегмента
а для сегмента
L 2> 2
Л 3π]
2 ' 2 J
имеем sin
имеем
π t . 3π 1
sin — = I, sin ~2= — Ι.
3°. Пусть m — произвольное число на сегменте [—I, I], тог-
да значение т функция sinx принимает на сегменте —У» Τ |
Γπ 3π1
в точке с = arc sin m, а на сегменте у, у — в точке
Cj = π — arc sin m, ч. т. д.
Изложенные результаты могут быть представлены в виде сле-
дующей таблицы:
Значения ар
гумента χ
Функция
у = sin χ
...
'·
3π
2
1
<х<
\
π
— 1
<х<
/
π
1
<х<
\
3
τπ
— 1
<π<
/
5
τπ
1
...
...
Промежутки монотонности синуса можно установить геометри-
чески, для этого следует рассмотреть функцию y=sin x «по четвер-
тям». Для примера рассмотрим эту функцию на сегменте [0, ~]
157
(1 замкнутая четверть). Пусть yj=sinA:1, y2=sin #2 и 0<"^
Тогда (см. черт. 85) 2у4 = 2Ап\\ и 2у2 — 2 sin х2 суть длины
хорд, стягивающих дуги 2χι и 2х2. Так как большую хорду стя-
гивает большая дуга, то sin 'i<sinx2.
Возрастание синуса в 1 четверти следует также из равенства
sin л: = γ\ — cos2x.
Так как cos* убывает и cos χ > 0 в первой замкнутой четверти, то
cos 2x убывает, подкоренное выражение возрастает, а следователь-
но, sin* также возрастает.
Наконец, можно воспользоваться формулой приведения
sin а: = —cos (χ + у) . Пусть —- -^ <4*ι < *2<^ у > положим
U} = xi -f ~ и «2 = ^2+у. получим 0<^ иг < и2 < π. Составим
разность sinx2 — si η лг5:
sin x2 — sin χΊ = — cos w2 + cos r/j = — (cos w2 — cos иг) > 0
(в силу убывания функции cos и на сегменте [0, π]), откуда сле-
дует возрастание функции sinx на сегменте —~, ~ .
Теорема. Во всяком интервале (— γ+kn, γ + kn\
(изображающемся правой либо левой открытой полуокружно-
стью) функция tgx возрастает от — со до оо .
Таким образом, функция tgx возрастает от — оо до со во
всяком интервале, из которых состоит ее область определения.
Доказательство. В силу периодичности тангенса доста-
точно доказать теорему лишь для интервала / — у, ~\ равно-
го по длине периоду тангенса.
Требуется установить нижеследующие положения.
1°. В интервале (— -^, ~) функция igx возрастает.
В самом деле,
COS X2 COS Χι
Если — у < хг < х2 < ~, то 0 < х2 — χ, < π, а потому
sin (х2 — л^) > 0, cosa:2>0, cosx^O,
и следовательно, tg χ2 — tg χ, > 0, т. е. tg x возрастает.
158
2°. Каково бы ни было действительное число т, в интервале
( — т» ■§) существует точка с, в которой функция igx принимает
значение т.
В самом деле, в § 12 установлено, что с = arctgm.
3°. limtgx = oo, limtgx = —oo*.
π _ _*_ ,
Χ-+ -у- *- 2 t-
Это положение является следствием Г и 2°. Для доказательства
lim tg χ = оо надо установить следующее. Пусть N > 0 — произволь-
ное заданное (как угодно большое) число; существует число ξ такое,
что ξ <-^ и в интервале (ξ, ~) выполняется неравенство
В самом деле, поставленному условию удовлетворяет число
ξ =arctg/V **. В силу возрастания тангенса имеем в интервале
Далее, в интервале — γ < χ < — ξ имеем tg χ < tg (— ξ) =
= — tg ξ = — Ν у следовательно, lim tgx = — оо.
Изложенное доказательство пояснено геометрически на черте-
же 86.
Полученные результаты можно представить следующей таб-
лицей:
Значения ар
гумента χ
Функция
...
...
3
2
+00
—оо
<х<
/
π
+^
—оо
<х<
/
π
Τ
+ ОО
ОО
<л:<
/
3
Τπ
ОО
<*<
/
5
+ «>.
—ОО
...
Примечание. Распространенное утверждение, что
«тангенс есть возрастающая функция» или «тангенс всегда воз-
растает», ошибочно. Во всей области определения тангенс
* Символы lim tg л: и lim tg дс обозначают односторонние преде-
лы Первый предел, левый, вычисляется в предположении, что χ < ~к
второй предел, правый, вычисляется в предположении, что χ > —-к .
** А также всякое число, большее ξ, но меньшее ir.
159
не обладает свойством монотонности. В самом деле, возьмем, на-
пример, следующие значения аргумента: 0, ~, -^π; имеем
0<-^< -^п и вместе с тем tgO<tg-^, a tg~>tg-^:rt; этого не
может быть для монотонной функции.
ни)
Черт. 86
Черт 87
Интервалы монотонности тангенса можно установить геомет-
рически. На чертеже 87 показано геометрически возрастание
тангенса на полусегменте
Можно также исходить из равенства tg л: =
sin χ
cos χ
Рассмотрим, например, tg* на полусегменте 0, £) ; при
0<*i<*2<y имеем 0<sinA:1<sinx2 и cos хг > cos х2 > 0,
откуда
sin χλ ^ sin х2 х ^ ι
< ИЛИ tg^<tgX2.
sin χλ
COS Хх
• cos х2
Теорема. Во всяком интервале (&π, (k + 1)π) (изображаю-
щемся верхней либо нижней открытой полуокружностью) функция
ctgx убывает от сю до —оо.
Таким образом, функция ctg# убывает от оо до —оо во всяком
интервале, из которых состоит ее область определения.
Доказательство. В силу периодичности котангенса до-
статочно доказать теорему лишь для интервала (0, π) равного по
длине периоду котангенса,
160
Доказательство аналогично доказательству соответствующих
свойств функции tgx.
Г. В интервале (О, π) функция ctgx убывает.
Это следует из неравенства
j , sin (х2 — Х\) ^ гл
ctg Ч — ctg хЛ = L-2 < О,
& * ъ J cos а;2 cos Xj ^ '
где
2°. Каково бы ни было действительное число т> в интервале
(0, π) существует число с = arc ctg т такое, что ctg с = т.
3°. lirn ctg χ = оо и lim ctg л; = —оо.
() +
* - π —
+
В самом деле, неравенство ctgx>A/ выполняется в интер-
вале (0, arc ctg N), а неравенство ctgx< — Л/-— в интервале
(π — arc ctgm, π).
Предоставляем учащимся геометрически установить интервалы
монотонности котангенса.
Наибольшие и наименьшие значения. Про-
веденное выше исследование тригонометрических функций на моно-
тонность позволяет во многих случаях элементарными
средствами находить наибольшие и наименьшие значения функций,
заданных выражениями, содержащими тригонометрические опера-
ции.
Так, например, выше установлено, что 1 и —1 суть наибольшее
и наименьшее значения функций cosx и sin r, отсюда следует, что
функция у= acosx+ b (или as\nx-\- b) имеет наибольшее и наи-
меньшее значения, равные
Функция y=asin*+ bcosx введением вспомогательного ар-
гумента, преобразуется к виду
у = /а2 + b2 sin (χ + а).
Наименьшее и наибольшее ее значения равны
-Vci2 + b* и утах = V а2 + б2.
Следовательно, имеют место неравенства
— /а2 + ^2 < ^ sin χ + b cosx < /а2 + б2.
Примеры на отыскание наибольших и наименьших значений
приведены ниже.
Примеры.
1. Установить промежутки монотонности функции | cos χ |.
Решение. На всяком сегменте \-^ + kn} (k-\-\)n\ (II и IV четвер-
ти), на которых cos;: возрастает от 0 до 1 или убывает от 0 до —1, функ-
161
ция
I cos л: I возрастает от 0 до 1. На всяком сегменте \kn, "Tj" + £π О И
III четверти), на котором cos л: убывает от 1 до 0 или "возрастает от —1
до 0, функция | cos л: | убывает от 0 до 1. Наибольшие и наименьшие зна-
чения суть Утах=1, Утт=0.
2. Определить промежутки монотонности функции / (х) = sin 2х.
Решение. Функция периодическая, с периодом π, ибо
sin 2 (а: + π) = sin (2x + 2π) = sin 2x.
Введем промежуточный аргумент w, положив:
= sin«, и — 2х. На
сегменте -— Л < и < Л функция sin и возрастает от —1 до 1. Этому
сегменту соответствует сегмент
-— < χ < — . Аналогично сегменту
4 4
— < и < — π соответствует сегмент — < χ < — π, на котором функция
2 2 4 4
убывает от 1 до —1. Эти сегменты охватывают полный период функции.
Изложенные результаты можно представить в виде следующей таблицы:
Аргумент
X
Промежуточ-
ный аргумент
и --= 2х
Функция
у — sin и
...
...
4
3
- 2π
1
<х<
\
\
π
~" Τ
π
""Τ
—1
<х<
/
/
π
Τ
π
ΊΓ
1
<*<
\
\
3π
4
3π
2
j
...
...
...
3. Установить промежутки монотонности функции у — sin (cos x).
Решение. Функция периодическая, с периодом 2гг установим про-
межутки монотонности в пределах одного периода. На сегменте 0<Λτ<π
промежуточный аргумент и убывает от 1 до —1; в соответствии с этим у
убывает от sin 1^0,84 до sin(—1)^—0,84.
На сегменте — π<*^0 функция возрастает от sin(—1) до sinl. Наи
большие и наименьшие значения суть
Ушах = Sin 1,
= —Sinl.
Аргумент
X
Промежуточ-
ный аргумент
и = cos χ
Функция
у = sin и
...
...
...
—π
—1
—sinl
<χ<
/
/
0
1
sin 1
<*<
\
π
— 1
—sinl
<x<
/
/
2π
1
sin 1
...
...
...
162
4. Установить промежутки монотонности функции
Решение. Формула, определяющая функцию, имеет смысл при не-
отрицательных значениях χ Из промежутка 0 < χ < + оо следует исклю-
чить значения х, при которых тангенс теряет смысл. Эти значения опре-
·./— π . и /2/5+1 \2 ^
деляются из условия ух= — + &π, откуда χ = I—ή—π) · Введем про-
межуточный аргумент, положив
у = tg u\ u = /"F; χ = и2
Область определения данной функции состоит из бесконечного множе-
ства интервалов
(2k — 1)2π2 (2k + Ι)2 π2)
4 ' 4
Эти интервалы являются промежутками возрастания, имеем:
π2\ /π2 9π2\ /
°· τ) · (τ τ) (
■)■
Аргумент χ
Промежуточный ар-
гумент и =у χ
Функция
У =,tg и
0
0
0
<х<
/
/
π2
Τ
π
У
+ 00
—оо
<х<
/
/
9π2
4
3π
2
+ ос
—оо
<х<
/
/
25π2
4
5π
2
+ 00
—оо
• · ·
...
...
5. Доказать, что уравнение
sin x = cos*
Γ π1
О, ~к\ имеет единственный корень.
на сегменте
Решение. При χ = — значения синуса и косинуса равны
4
sin!!- =cos^. = —— Кроме — данное уравнение не может на сегменте
4 4 2 4
И]
иметь никакого другого корня. В самом деле, разность sin лг—cos χ
на сегменте
Го, у! воз
возрастает, ибо уменьшаемое возрастает, а вычитаемое
убывает, следовательно, равенство sin я — cos χ = 0 может выполняться
лишь при единственном значении аргумента.
6 Установить промежутки монотонности функции
Решение. Имеем
■и2, u==tgx.
163
На всяком промежутке вида Ы <# < у + kn, на котором и = tgx воз-
растает от 0 до + оо, функция у = и2 возрастает от 0 до + оо. На всяком про-
π
межутке вида ^—"о+ &π < χ < ^π> на котором ы = tg* возрастает от — оо
до 0, функция у е=а ы2 убывает от оо до 0.
Наименьшее значение ут\п = 0, наибольшее значение утах не существует.
7. Найти наибольшее значение периметра прямоугольного треугольника,
имеющего данную гипотенузу.
Решение. Периметр прямоугольного треугольника, гипотенуза ко-
торого равна с, а острый угол равен а, выражается формулой
2р = с + С COS α + с sin α = с\\ + У
Наибольшее значение периметра р = с (l +
π
бедренного прямоугольного треугольника, α = -j .
COS ία — -^ J .
реализуется для равно-
b. Снаряд вылетел из орудия с начальной скоростью v0 под углом а к гб»
ризонту. Вычислить угол а, при котором дальность полета является наиболь-
шей (сопротивление воздуха не принимается во внишшие).
Решение, Рассмотрим параметрические уравнения траектории сна-
ряда (черт. 88)
х = tv0 cos α, у = tv0 sin α — -j- ,
(где время t — параметр). Время полета снаряда есть положительный ко-
рень уравнения у = 0, откуда t = v° sln α . Дальность полета равна
g
ν π sin 2α
χ = .
g
Из смысла задачи ясно, что достаточно считать α острым углом 0 < α < ϋ.
Дальность полета является наибольшей, если дс = — ; имеем: *шах = —.
Черт*
Р. Картина повешена на стену так, что ее нижний край на а м,
а верхний край на b м выше глаза наблюдателя. На каком расстоянии χ
164
от стены должен стать наблюдатель, чтобы картина была видна под
наибольшим углом.
Решение. Из чертежа 89 найдем тангенс угла зрения φ:
+ ^ 7^ ( > ' > '
X2 X
Так как tg φ —- возрастающая функция аргумента φ, то наибольшее
значение φ имеет место при наибольшем значении tg φ Наибольшее значе-
ние tgcp имеет место при том значении х, при котором х + — имеет наи-
х
меньшее значение. При данном произведении
аЬ
л>— =ао
л
сумма *+~ имеет наименьшее значение, если
аЬ ,/
χ — —, откуда χ = у ab.
10. Найти наименьшее и наибольшее значения однородного тригономе-
трического трехчлена второй степени
у = a sin2 χ + b sin χ cos χ -f· с cos2 x
Решение. Выразим трехчлен через тригонометрические функции двой-
ного аргумента
У = 2"(1 — cos 2х) + у sin 2* + у (1 + cos 2*) =
α + с 1
= —2~ + 2" [(с ^ а) cos 2^ + 6 sin 2л:].
Наибольшее и наименьшее значения выражения, заключенного в квадрат
ные скобки, суть
γ а* -\-Ь2-\-с2 — 2ас и — /а2 + Ь2 + с2 — 2ас ;
следовательно,
( a -
h с
+ γ α2
— /a2
+
2
+
b*
b2
+
+
o* — 2ac
c2 — 2ac
11. При каких значениях параметра т уранение
sin2 χ — sin x cos χ — 2 cos2 χ = m
имеет решения?
Решение. Однородный тригонометрический трехчлен, находящийся
в левой части, имеет следующие наибольшее и наименьшее значения (см. пре-
дыдущий пример) -"1-
165
Следовательно, чтобы уравнение имело решение необходимо и доста-
точно, чтобы значение т принадлежало сегменту
2 ^ 2
12. Найти наибольшее и наименьшее значения произведения
у = cos^7 χ sin'7 χ
на сегменте 0 < χ < — , где ρ и ? — данные положительные рациональные
числа.
Решение. Примем во внимание основное тождество
cos2 χ -f- sin2 x = 1
и обозначим cos2 χ = и, sin2 x = ν, тогда получим:
Ε 1
у = и2 и2 ; w -f ϋ — 1·
Но, как известно из алгебры (см. «Специальный курс элементарной алгебры»,
§ 60), произведение у при заданной сумме аргументов и и и имеет наиболь-
шее значение, если
- = - или « = λ 2" . ν=\^ ,
где λ — коэффициент пропорциональности, который определяется из условия:
\р \q 2
т + т = 1, откуда λ = ^-ρ^ .
Выполнив подстановку, получим:
Λί
* = arccos]/ ^^Tq , ymax = ^
Наименьшее значение ymin =0, при х = 0 и л; = -^ .
π
Следовательно, на сегменте 0 < χ < -^ имеют место неравенства
0 < cosp χ
ъ\п<1 χ < 1 / -
13. Найти наименьшее значение выражения
y==[gP х + ctgQ х
в интервале 0 < χ < £., где ρ и ^ — положительные рациональные числа.
Решение, аналогичное решению предыдущей задачи. Положим
α = tg^ jc, ν = ctg? jc; сумма у = и + ν при данном произведении иР vq = 1
166
имеет наименьшее значение, если ри = αν = λ; откуда и == _ , υ =— и
Ρ <7
и, следовательно,
1
14. Найти конус (прямой, круговой) наи-
большего объема, имеющий данную образую-
щую / (черт. 90).
Решение. Пусть а — угол образующей
с основанием конуса; имеем
V =
= -J· COS2 α Sin α.
Наибольшее значение V равно (положить ρ = 2,
7 = 1) (см пример 12)
ι/ _π/8
max~"T
Черт. 90
при этом
15. Найти наибольшее и наименьшее значения функции
/ (х) = sin2 χ + ρ sin χ + <7
π π
на сегменте — -о- < х < "ό" ·
Решение. Положим t — s\n x\ тогда задача сведется к нахождению
наибольшего и наименьшего значений квадратного трехчлена
у = t2 + pt + <7 на сегменте -— 1 < t < 1.
Этот трехчлен в интервале — оо < / < -J- °° имеет наименьшее значение
. Ρ
при t =— у;
в интервале ί— оо, —-] трехчлен убывает, а в интервале ί—^-, +°°J—
возрастает Возможны следующие три случая.
Случай 1°. — - < — 1, т. е. ρ > 2 В этом случае на сегменте
ция f (х) имеет в точке χ =——, а наибольшее — в точке * = — (при
— 1 < t < 1 трехчлен возрастает, следовательно, наименьшее значение функ-
—
/min = 1 — Ρ + Я
167
Случай 2°. — £-> \, т. е. ρ < — 2. В этом случае на сегменте
·— 1 < t < 1 трехчлен убывает, следовательно, наименьшее значение / (х)
имеет в точке χ = ~к , а наибольшее — в точке χ = — -^ ;
/mln = 1 + Ρ + <7. /max =* 1 - Ρ + <7·
Случай Зэ, —2 < ρ < 2. В этом случае наименьшее значение функ-
р
ция / (х) имеет в точке χ = — arc sin -к :
А · Р
= / \- агс sin T
4·
Наибольшим значением / (я) является большее из граничных значений
f(~l) И f{j)'T β· /тах= 1 + 1 Ρ 1+9
§ 30. Непрерывность тригонометрических функций
Теорема. Каждая из тригонометрических функций непрерыв-
на в любой точке, принадлежащей ее области определения.
Справедливость теоремы вытекает из общей теоремы математи-
ческого анализа о непрерывности монотонной функции. Эта теоре-
ма сформулирована во введении (см. § 5, стр. 26).
Непрерывность тригонометрических функций можно устано-
вить из непосредственного вычисления их приращений, таким спо-
собом непрерывность тригонометрических функций обычно дока-
зывается в общих курсах математического анализа.
Ниже приводится геометрическое доказательство непрерывно-
сти тригонометрических функций, основанное на их интерпрета-
ции при помощи единичного круга.
Функция cos χ. Областью определения косинуса является
множество всех действительных чисел; требуется доказать, что
функция cos л: непрерывна при любом значении аргумента.
Пусть а — произвольно заданное значение аргумента; надо дока-
зать, что приращение косинуса по абсолютной величине меньше лю-
бого заданного (как угодно малого) числа ε > 0
| cos χ — cos a | < ε
при условии, что приращение аргумента по абсолютной величине
меньше некоторого числа δ
(число δ определяется заданием ε).
Предположим сначала, что точка, изображающая значение ар-
гумента а, не совпадает с концами горизонтального диаметра еди-
ничного круга а=Ф=Ы. Возьмем число ε настолько малым, чтобы
обе точки cos α — ε и cosa + ε помещались внутри интервала
(—1, 1) оси ОХ, т. е. |cosa ± в| < 1.
168
Рассмотрим точки а.\ и а2, лежащие на той же полуокружности
(верхней или нижней), на которой лежит точка а (черт. 91), и про-
ектирующиеся в точке cos α + ε и cos α —ε (соответственно). Обо-
значим через δ длину наименьшей из дуг а^а и аа2. При всех значе-
ниях аргумента, удовлетворяющих неравенству |х —α|<δ, со-
ответствующая точка единичной окружности лежит на дуге, огра-
ниченной точками а{ и аъ а потому проектируется на ось абсцисс
внутрь отрезка, ограниченного точками cos α — ε и cos α + ε,
и следовательно,
I cos χ— cos α
при |χ—
Если точка а на единичной окружности совпадает с концом гори-
зонтального диаметра, например, с точкой Л(1, 0), то в этом слу-
чае cos α = 1
I cos χ — cos a | = 1 — cos χ < ε,
если |x — α|<δ, где достаточно положить δ = arc cos (1 — ε).
sma+ε
Черт. 91
Черт. 92
Функция sin*. Областью определения синуса является
множество всех действительных чисел; требуется доказать, что функ-
ция sin x непрерывна при любом значении аргумента. Доказатель-
ство проводится точно так же, как и для функции cosx, с той лишь
разницей, что проектирование следует производить не на ось абс-
цисс, а на ось ординат (черт. 92). Провести подробно рассуждения
предоставляем учащимся в виде упражнения.
Итак, будучи непрерывными в каждой точке, функции sin x и
cos л: непрерывны в интервале — оо < χ < + оо.
Функция tgx. Требуется доказать, что функция tg.x не-
прерывна в каждом из интервалов у—ψ -f kn, ^ + kit).
Рассмотрим сначала интервал^—^, jj. Пусть α — данное зна-
чение аргумента в интервале у—^, jj. Возьмем на оси танген-
169
сов три точки iga — ε, iga и tga + ε и соединим эти точки
с началом координат: пусть аъ а и а2 — соответствующие точки
единичной окружности. Пусть δ — длина наименьшей из дуг ααλ
и аа2. Если | χ — α | </δ, то точка л: лежит на дуге аг аъ а соот-
ветствующая точка tg* лежит на оси тангенсов в интервале
(tga — ε, tga + ε), τ. е.
| tg*— tga|<e, если |*— α|<δ.
Следовательно, функция tg* непрерывна в (—~, ^-). Будучи
периодической с периодом π, функция tg* непрерывна в любом
интервале у—| + kit, ^ + kit).
Функция ctg*. Непрерывность котангенса устанавливается
аналогично, ч. т. д.
Функция tgA: не является непрерывной в интервале (—оо, +оо);
в самом деле, точки -^ + kn не принадлежат ее области определения
и в окрестности каждой из этих точек функция неограничен^, так
как
lim | tg jc I = -+ оо.
χ - \ + *«
Следовательно, точки ~ + kit являются точками разрыва тангенса.
Для котангенса точками разрыва служат точки kn; в окрест-
ности каждой из этих точек котангенс неограничен, так как
lim | ctgx I = + оо.
Теорему о непрерывности тригонометрических функций иначе
можно сформулировать следующим образом.
Если число а принадлежит области определения тригонометри-
ческой функции, то предел тригонометрической функции в точке а
равен ее значению в этой точке, т. е.
lim cos χ = cos a, lim sin χ = sin a,
lim tg x = tg a, lim ctg χ = ctg a.
(1)
Пределы различных выражений, содержащих тригонометри-
ческие функции, находятся на основании соотношений (1) и общих
теорем теории пределов об операциях над пределами (теоремы о
пределе суммы, произведения, частного, сложной функции и т. д.).
Примеры.
1. Найти
sin χ + cos x
Um l-tgx ·
170
Решение. По общим правилам теории пределов найдем:
нη χ + cos χ lim sin χ -f- Hm cos χ
llm 1 —tg* "= 1-limtg* =
π
ι , Уз
Т + "Г _Уз"(1 + Уз) У
= _J_ ~ 2(VT-l) ~ 2
2. Функция
1 — 2 sin χ
разрывна в точках, в которых:
2k+\
a) tg χ теряет смысл, откуда х = —^—π»
b) I — 2sin* = 0, откуда sin л: = ^ и χ = (—\)п§ + "π-
Во всех остальных точках, будучи частным непрерывных функций, дан-
ная функция непрерывна.
3. Функция
у = sin χ2
непрерывна в любой точке, так как она может быть представлена в виде слож-
ной функции
у = sin и, и = я2,
непрерывной от промежуточного аргумента и, а аргумент и есть непрерывная
функция от χ (в силу теоремы о непрерывности сложной функции).
Принцип продолжения по непрерывности,
особые значения аргумента
В математическом анализе принцип продолжения по непрерывности
в общем виде формулируется следующим образом:
Если при χ = а функция { (х) не определена и, таким образом f (а) не имеет
смысла, но конечный предел Пт/(л;) = А в точке а существует, то принято
Х-уп
значение χ = а включать в область определения функции, при этом считается
Принцип продолжения по непрерывности заключается в замене функции
f(x) функцией, совпадающей с нею при всех допустимых значениях аргумен-
та хфа и непрерывной в точке а.
Если функция / (х) имеет предел в точке а, то этот предел является един-
ственным, а потому продолжение функции по непрерывности возможно
лишь единственным образом (если только оно возможно), независимо
от способа, которым выполнялось отыскание предела.
В тригонометрии принцип продолжения по непрерывности применяется
к функциям, заданным при помощи формулы, содержащей тригонометриче-
ские операции над аргументом. Если при подстановке в формулу значения
х = а формула теряет смысл, такое значение аргумента в дальнейшем будем
называть особым, то исследуют (по общим правилам), имеет ли
171
данное выражение предел в точке а\ этот предел (если он существует и ко-
нечен) рассматривается как значение данного выражения в точке χ = а
Применение принципа продолжения по непрерывности позволяет во
многих практически важных случаях производить сокращение дробных вы-
ражений на общие функциональные множители числителя и знаменателя
Пусть, например, функции Fi(x)> F2(x) и φ(χ) определены в некоторой окре-
стности точки а и непрерывны в этой точке, причем φ(α) = 0, F2(fl) Φ Ο
и у(х)фО в некоторой окрестности точки а (кроме точки а). В этом слу-
чае выражение
φ(χ) Ft (χ)
при подстановке х = а теряет смысл. Выражение
равно (во всяком случае в некоторой окрестности точки а) выражению U(x)
при значениях хфа и не теряет смысла в точке χ = а. Применим принцип
продолжения по непрерывности; имеем:
Следовательно, равенство
у (х) Ft (х) Ft (x)
φ (χ) F2 (χ) - F2 (χ)
имеет место при всех значениях χ (во всяком случае в некоторой окрестности
точки а), чем обосновывается возможность сокращения числителя и знаме-
нателя на общий множитель φ(χ).
Примечание. В курсе средней школы, обычно из педагогиче-
ских соображений, отказываются от применения принципа про-
должения по непрерывности. Как бы методика ни решала этот вопрос,
ни при каких обстоятельствах недопустимо наивное протаскивание вся-
кого рода «раскрытия» неопределенностей», нахождения «истинных зна-
чений» и т. п., как чего-то очевидного «само по себе».1
Примеры.
1. Равенство
считалось первоначально справедливым при всех значениях х, при которых
обе функции tg χ и ctg x имеют смысл. Принцип продолжения по непрерыв-
ности позволяет не исключать из рассмотрения значения χ = kn, при
которых ctg χ теряет смысл. В самом деле, при χ = kn значение левой части
равно 0, значение правой части также равно 0, ибо
Ii — 0 (так как iim I C*S х I == + °°).
2. Для выражения
sin2 χ sin χ -f cos χ
'*' ~~ sin χ — cos χ ~~ tg2 χ — 1
172
особыми значениями являются следующие значения ху при которых
π
a) sin χ = cos xt откуда χ = -j + &π;
π
b) tg χ = ± 1, откуда ^ = ± -j + ^πί
π
c) tg χ теряет смысл, откуда х = у + kiz.
Выполнив тождественные преобразования, получим (см. пример 6, стр. 63)
sin2 χ sin x + cos x
sin*-cos*- tg'x-1 -s'n*
Правая часть этого тождества непрерывна при произвольном действитель-
ном значении х, при этом
lim U {х) = sin α -f- cos #»
значит, для вычисления V (а) достаточно положить в правой части х=-а.
Так, в частности,
3. Равенство
1 1 + tg2 x
a sin2 x + b sin χ cos * φ с cos2 λ; α tg2 л; + 6 tg x + с
π
при а=£0 справедливо также и при значениях χ = γ + kn, особых для
π
правой части. В самом деле, при χ — γ + kiz левая часть непрерывна и
имеет значение, равное — . Следовательно, это же значение является пре-
делом правой части и, согласно принципу продолжения по непрерывности
оно является также и значением правой части в рассматриваемых осо-
бых точках.
Примечание. То же самое получится, если находить предел
правой части непосредственно!
,· 1 + tg2* L±i!±
llm a tg2 χ + b tg x + с - lim
_L±i!___±
a tg2 χ + b tg x + с - lim az2 + bz + с ~ а '
π
При <г = 0 в точках χ — γ-{-к% правая и левая части теряют смысл
и так как
1
lim
b sin x cos* -I- с cos2 χ
= +oo,
то в этих точках данное выражение не имеет никакого значения (принцип
продолжения неприменим).
4. Исследовать особые значения аргумента для функции, заданной
формулой
i + t
' w
cos χ + ctg χ '
173
Особыми значениями аргумента являются значения, изображающиеся кон-
цами горизонтального и концами вертикального диаметров:
π
а) точки χ = 2 + ^π (концы вертикального диаметра) не принадлежат
области определения / (х), так как
lim |/(x)|= + oo;
Ь) точки χ — Ы (концы горизонтального диаметра) следует включить
в область определения f(x), ибо
/ (Ы) ^llmf (χ) = lim ™f +с\** = 0.
5. Для функции, заданной формулой
-\f\ +
T=:'cosx -\f\ + cos x
V
π
(см. пример 11, стр. 67), точки k γ (изображающиеся концами горизон-
тального и вертикального диаметров) не принадлежат области определения.
В самом деле, эти точки суть точки разрыва 1-го рода (см. черт. 67), а по-
тому lim Ρ (λ:) не существует.
6. Рассмотрим тождество
lg sin2 χ = 2 lg sin χ.
Левая часть, рассматриваемая в отдельности, имеет смысл в ин-
тервалах (kKt (k + 1)π)
Правая часть, рассматриваемая в отдельности, имеет смысл в
интервалах (2&π, (2k + 1)π), в которых sinA;>0. Рассмотрим произвольную
3
точку, в которой sin *<0; положим, например, χ =-^ π. В этой точке левая
часть имеет смысл, а правая часть смысла не имеет. В данном случае принцип
продолжения правой части по непрерывности неприменим. В самом деле,
предел lim lg sin χ не имеет смысла, ибо не только точка к π, но и некоторая
ее окрестность не принадлежат области определения функции lg sin л;.
7. Значение функции
равно 0 в точке χ = 0. В самом деле, согласно принципу продолжения по
непрерывности,
f (0) = lim x sin — = 0
x-+Q x
(множитель х имеет предел равный нулю, а второй множитель sin- ограни-
чен).
174
§ 31. Графики тригонометрических функций
Для построения графика тригонометрической функции достаточ-
но выполнить построение на каком-либо сегменте, охватывающем
период данной функции, и затем периодически продолжить постро-
енный график. Если выполнено построение графика в первой чет-
верти, то, пользуясь известными свойствами тригонометрических
функций, можно выполнить построение графика и в других четвер-
тях.
Синусоида (обыкновенная) — так называется линия, явля-
ющаяся графиком функции: у = sin χ в интервале (—оо, +оо).
Рассмотрим функцию sin χ на сегменте 0 < χ < -^; на этом сегменте
она возрастает от 0 до 1. Для уточнения формы линии можно вос-
Черт. 93
пользоваться известными значениями синуса (см. § 10). Для более
точного построения графика следует воспользоваться таблицами
значений тригонометрических функций. Построение графика мож-
но выполнить геометрически с любой степенью точности. Это пояс-
нено на чертеже 93. Первая четверть единичной окружности и от-
резок 0< *<С"5 разделены на одинаковое количество равных час-
тей (на чертеже 93 на 8 частей). Перпендикуляры, опущенные из
концов точек деления дуги на ось абсцисс (т. е. значения синуса),
снесены в виде ординат, восставленных из соответствующих точек
отрезка 0 < χ <!-|. Концы построенных отрезков принадлежат ли-
нии. Во второй четверти синус убывает от 1 до 0. В точках χ и
дх—xt расположенных на единичной окружности симметрично от-
носительно оси ординат, значения синуса равны:
sin л: = sin (π — χ).
Следовательно, график синуса во второй четверти симметричен
графику в первой четверти относительно параллели оси ординат,
проходящей через точку (-^, 0). Из свойства нечетности синуса
sin(—χ) = —sin jc следует, что синусоида симметрична относитель-
но начала координат. Построив график на сегменте 0 < χ < π и
175
продолжив его по нечетности на сегмент —л <; х^О, получим график
на сегменте —л < χ < л, охватывающем полный период синуса.
Для дальнейшего построения синусоиды достаточно последователь-
но продолжить по периодичности полученную линию на сегменты
[л, Зл], [Зл, 5л], ,.., [—Зл, —л], (—5л, —Зл], ...
(черт. 94).
у= stnx
Я π-л
ЗтхХ
Черт. 94
Примечание. На сегменте [0, л] функция у = sin*
вогнута (см. «Специальный курс элементарной алгебры»,
§ 58, стр. 205—208). В самом деле, при 0<α:ι <л:2< л имеем
Sill
-cos
-<sin:
График функции у = cos* можно построить непосред-
ственно. Характер линии ясен из известных свойств косинуса:
функция cos χ на сегменте 0, ~ убывает от 1 до 0, а на сегменте
1π ι I. J
s, л убывает от 0 до —1. График симметричен относительно оси
- ординат, так как функция
cos а: является четной. Для
уточнения линии следует во-
спользоваться таблицей зна-
чений косинуса. Можно вы-
полнить построение линии
геометрически тем же спосо-
бом, каким была построена
синусоида, при этом, в силу
Срждества cos χ = sin (j — χ\
перенос ординат можно производить^ 1^к, как показано на чер-
теже 95. |
Из тождества sinu;+ у) =cosa: следует, что графиком функ-
й i
ций sin χ и
у = cos χ = sin (χ + γ
176
является одна и та же линия — синусоида. Именно, график
функции у = sin (χ + γ\ есть синусоида, смещенная влево
в направлении оси абсцисс на расстояние ~. В самом деле,
положив χ = х' — γ , построим синусоиду у = sin x'\ перейти
к искомому графику можно, если уменьшить абсциссу на вели-
чину —, а соответствующую ординату оставить без изменения
(черт. 96).
П У*
Черт. 96
Тангенсоид а — так называется график функции у = tgx.
На полусегменте 0<.х<-^ тангенс возрастает от 0 до +оо, следо-
вательно, график имеет вертикальную асимптоту χ = -g. Для уточ-
нения графика следует воспользоваться известными значениями
тангенса, а также тригонометрическими таблицами. Построение с
какой угодно степенью точности можно выполнить геометрически
следующим образом. Достаточно разделить первую четверть три-
гонометрического круга и
промежуток 0 < χ < ^ на не-
которое (одинаковое) количе-
ство равных частей и пере-
нести линии тангенса в каче-
стве ординат, восставленных
в соответствующих точках,
как показано на чертеже 97.
Из свойства нечетности
тангенса следует симметрич-
ность линии относительно на-
чала координат; таким обра-
зом, для построения графика
в промежутке —-^ < х < О
достаточно график, построен-
ный в промежутке 0 < χ < ~2
продолжить по нечетности Черт 97
Зак. 597
177
(симметрично относительно начала координат). Построив график
в интервале (—~, -|j и продолжив его периодически (с периодом
π), получим представленную на чертеже 98 линию.
Построение графика функции y=ctgA; на основе известных
свойств котангенса предоставляем учащимся.
Тождество ctgx = —tgi-sH-*) показывает, что для построения
графика котангенса достаточно сместить тангенсоиду влево на рас-
стояние j и отразить ее симметрично, как в зеркале, относительно
оси абсцисс (черт. 99, пунктиром помечена ветвь тангенсоиды).
Черт. 98
Черт. 99
Примечание. В промежутке ίθ, γ\ функция
выпукла (см. «Специальный курс элементарной алгео-
ры», § 58, стр. 205).
Пусть 0<*1<*2<-|-,
неравенство
эквивалентно следующему:
и далее
. X2 — ·
Sin ?r~
cos x2cos■
sin
COS Χι COS -
χ2
ί 78
Сократив последнее неравенство на положительные мно-
жители, получим очевидное неравенство
COS Х2
COS
§ 32. Простейшие тригонометрические неравенства
Простейшим тригонометрическим неравенством называется не-
равенство вида
t(x)\/mf (f)
где f(x) — данная тригонометрическая функция. В силу периодич-
ности тригонометрических функций, достаточно найти множество
всех решений неравенства (f) в пределах какого-либо промежутка,
охватывающего полный период данной функции.
Рассмотрим простейшие тригонометрические неравенства.
1°. Неравенство cos χ > т.
Если т<—1, то решением служит произвольное действительное
число: —оо<^л:<^ + оо, так как при всех значениях аргумента
cosx> —1 > т.
Если т>1, то неравенство не имеет решений.
Пусть —1</72<Ч; рассмотрим функцию cos* на сегментах
[О, π] и [—π, Ο], составляющих в сумме ее период. На сегменте
[0, π] функция cos* убывает, при χ = arc cos m имеет место равен-
ство cos χ = m, следовательно, если 0 < χ < arc cos /я, то cos x > /и,
если же arc cos ггк^х < π, то cos*<^m.
На сегменте [—π, 0] неравенство cosx>m выполняется
в промежутке — arc cos m < χ < 0.
Следовательно, на сегменте [—π, π] неравенство выполняется
в интервале
—arc cos т < χ <^ arc cos m.
Общим решением служит бесконечное множество интервалов
(—arc cos m -j- 2kn, arc cos m -f- 2kn).
Черт. 100
На чертеже 100 показано графическое решение неравенства.
Параллель оси ординат, проведенная через точку (т, 0), отсечет
от единичной окружности дугу (справа), точки которой имеют абс-
циссы большие, чем т.
Τ 179
Неравенство cosa;< m выполняется на дуге единичной окружно-
сти, дополнительной к дуге — arc cos m < χ < arc cos m (черт. 101).
В пределах одной окружности эту дополнительную дугу можно
задать, например, таким неравенством:
arc cos m < χ < 2π — arc cos т.
Общее решение состоит из бесконечного множества интервалов:
(arc cos m + 2kn, —arc cos m + 2(k + 1)π).
2q. Простейшее неравенство sin χ > т. Анало-
гично предыдщуему, получим (черт. 102):
arccosm
arcslnm
sinx<m
Черт. 102
m < — I
интервал
(— oo, oo)
— 1 < m < 1
Множество интервалов
arc sin m + 2Ы < χ <
< (π — arc sin m) + 2&π
m > 1
нет решений
Неравенство sin%<^ m (где —1 <C tn<^ 1) выполняется на дуге,
дополнительной к дуге arc sin m < χ < π — arc sin /τζ, эту дугу
можно задать неравенствами
—π — arc sin m
arc sin
3. Простейшее неравенство tgx^> m (где m — произвольное
действительное число) в правой полуокружности выполняется (в си-
лу возрастания тангенса) в интервале arc tgm<x<-^.
180
Общим решением служит бесконечное множество интервалов:
arctgm
Примеры.
π, (черт. 103).
a)
b)
с)
d)
e)
f)
1. Неравенство
sin χ > -γ-
Vs
sin x*< — —2~-
cos χ < — y
tg x > 2
sin * < sin 0,3
ctg χ > /3"
Общее решение
π
2
2
arc tg 2 + &π
-0,3 + (2k -
βπ < χ
3π
π
<! χ <^ — ~ο" -f- 2«тс
4
χ < -ο* π + 2^π
1)π<*<0,3 + 2£:π
π
Черт. 103
На чертеже 104 показаны дуги единичной окружности, на которых
выполняются эти неравенства.
2. Установить область определения функции
' = у sin χ — γ .
181
Решение. Область определения находится из условия
1
sin χ—-^ > О или
1
Г π 5π Ί
откуда получим бесконечное множество сегментов \-г-\-2Ы, -тг- -f- 2&π .
§ 33. Неравенства, содержащие аргумент
и его тригонометрические функции
В настоящем параграфе будут рассмотрены основные неравен-
ства, связывающие аргумент и значения тригонометрических функ-
ций от этого аргумента.
1. При всех действительных значениях χ имеет место неравен-
ство
| sin л: | <|*|; (1)
равенство имеет место при единственном значении χ = 0.
Иными словами, синус по абсолютной величине не превосходит
аргумент.
Доказательство. Если 0 < χ < —, то неравенство вы-
полняется, так как длина половины хорды ΒΒχ единичной окруж-
ности (черт. 105), т. е. sin x меньше длины половины стягиваемой ею
дуги, т. е. χ (где л: — радианная мера дуги А В). Итак, приО<х<-^
имеем 0 < sin χ < χ.
Если —у<л;<0, то длина половины дуги и полухорды
выразится числами \х\ и |sinxj, в этом случае неравенство
также очевидно.
182
Если I χ Ι > γ,
I sin* |< 1.
то подавно | sin χ |
так
как у.
| |
Итак, неравенство (1) имеет место (строго) при всех значениях
хфО. При χ = 0 имеет место равенство, ч. т. д.
Графическая интерпретация. Так как при д£>0
имеем sin χ < *, а при л; < О имеем л: < sin x, то в правой коорди-
натной полуплоскости (х > 0) синусоида расположена ниже биссек-
трисы координатного угла у = х, а в левой полуплоскости (*<0)
выше этой биссектрисы (черт. 106).
2. В интервале 0 < χ < у имеет место неравенство
'■■
(2)
А.
Черт. 105
Черт. 106
Доказательство. В самом деле, треугольник О АС
(см. черт. 105) содержит круговой сектор ОАВ единичного круга,
следовательно, пл. сект. ОАВ < пл. Δ О АС.
Имеем
пл. сект.
пл.
откуда следует неравенство (2), ч. т. д.
На чертеже 107 представлена графическая интерпретация нера-
венства (2).
Г, В интервале 0<л:<у имеет место система
Следствия:
неравенств
2°. При | χ | φ 0 имеет место неравенство [ χ |
Это неравенство получится, если в неравенстве
положить у = arc sin χ (где — 1
[ arc sin χ |.
|sinyK|y|
183
3°. При всех значениях χ имеет место неравенство
1 — cos χ < γ или 1 — γ < cos x, (3)
равенство при χ = 0.
Доказательство. В самом деле,
0< 1— cos χ < 2 sin2 4,
но в силу (1) имеем: sing -γ < -j-, откуда следует неравен-
ство (3), ч. т. д.
Графическая интерпретация. Линия у = cosx
заключена между прямой у = 1 и параболой у = 1 — j (черт. 108).
4°. β интервале (0, π) £шшт? же-
неравенство'
х3
χ ^-<sinA:. (4)
Доказательство. Имеем
А
В силу неравенств (1) и (2)
Черт. 107
t§4>4 и
sin 2^4'
/ АГ2\
откуда sinx>A:il — —I, ч. т. д.
Графическая интерпретация. Из неравенств
Xs
χ— т^ sin л: < л; следует, что в окрестности точки 0 синусоида
л:3
заключена между прямой у=х и параболой 3-й степени у = χ —
(черт. 109).
5°. В интервале (0, π) имеют место неравенства
16·
(5)
184
Доказательство. Имеем:
cos x — (1 —-^-] = у — (1 —cosx) =
В силу (4) и (1) получим следующее неравенство, эквивалентное (5):
1. X
"32* 2
Ч. т. д.
Черт 108
Доказанные неравенства
Черт. 109
имеют многочисленные применения в приближенных вычисле-
ниях.
Так, в частности, приближенное равенство sinx ^ х имеет ме-
х'3
сто для малых углов с ошибкой, меньшей чем j, приближенное
X2
равенство cosa: ж 1 (для малых углов) с ошибкой, меньшей чем -^;
х2 л:4
и, наконец, cosa:^1 —у с ошибкой, меньшей чем у^.
Эти приближенные равенства широко применяются при состав-
лении тригонометрических таблиц (подробнее см. ниже § 71).
Приближенная замена синуса малого угла его радианной мерой
применяется в физике, например, при выводе формулы периода ка-
чания математического маятника.
Установленные неравенства служат обоснованием возможности
применения в графике упрощенных, приближенно вер·
7В Зак 597
185
н ы х изображений. Поясним последнее следующим примером.
На чертеже 110, а изображено ортогональное проектирование шара
на плоскость. При малом отклонении плоскости экватора от гори-
зонтальной плоскости смещение P'Q' точки Ρ экватора равно since
(радиус шара считаем равным 1) или P'Q' = α с ошибкой, меньшей
чем ~. Смещение же Ν'Ν\ полюса от абриса равно 1 — cos α с ошиб-
кой, меньшей чем ^-,— это смещение можно считать равным нулю.
Так, например, при α = 15" имеем (по четырехзначным таблицам)
α = 0,2618 (радиан), P'Q' = sina = 0,2588, N[N' = 1 — cosa =
= 0,0341, ^ =0,1318.
При a = 10е получим ρψ- = 0,0876.
Ν
Ν
9'
Черт. 110
Этими расчетами обосновывается возможность при малых углах
наклона α в целях упрощения чертежа прибегать кприближен-
но верным изображениям (черт. ПО, Ъ - полюс шара изо-
бражен на абрисе), на чертеже НО, с представлено верное изображе-
Доказанные неравенства позволяют вычислить некоторые заме-
чательные пределы, имеющие широкое применение в математиче-
ском анализе. Так, например, из неравенств (при малых значениях
1*1/
sin*
— 1
<Т и |(l_cosx)|—i-
следует, что
lim 5^ = 1 и lim!=««£. '
186
Примечание. Доказанные в настоящем параграфе,
а также аналогичные более точные неравенства без труда мо-
гут быть установлены применением аппарата степенных рядов
(см. ниже § 80),
Ряд неравенств более точных, чем (1) — (5), может быть установлен
элементарными средствами при помощи применения различных искусствен-
ных приемов. Ниже приведен пример применения таких искусственных
приемов.
Примеры.
1. Доказать, что на сегменте 0 < χ < γ имеют место неравенства
х — -§ < sin* < * — "(з"~1"~у2О ' ^
Доказательство. Г. Воспользуемся тождеством
Зп sin ψ — 4[sin3у + 3sin3^-+ ··· +3n~~l sin3^) = sin*
\ /
(cm. § 25. пример 10, стр. 137).
В силу равенства (4)
х —
В силу неравенства (1) имеем:
т=ъ)<
27
1_2+ \-χ8( ι )-χ3
Подставив в тождество, получим неравенство
JL»3 γ3
χ — -g- — 4Т32Л ^ sin *.
Так как п — произвольное натуральное число, то получим в пределе
/ уЗ уЗ ~
π
2°. По доказанному при 0 < χ < γ имеем:
0 < χ — -7г < sin χ*
*3
а:3 / χ2 \
* Неравенство χ — -g- = a: I 1 — -g- j > 0 выполняется в интервале
/ π\
0 < х < у 6 и, в частности, в интервале 10, γΙ.
7В* 187
а также
χ χ3
0<Т~2П
Χ Χ3
0<Τ~2^
χ
sin -ή-,
sin γ.
Возведя почленно последнее неравенство в квадрат, получим:
х2 χ4 ι
2* з«28 ·
214·32
sin 7 '
откуда и подавно
х
О < 24
х
sln ~4 -
Перемножив почленно неравенства (а) и (b), получим:
— ~™~~ —— <* I — * ·— ι I — ■ ι s* с ΐ η — q i η 2 ——
26 29 V 2 23· 6 / 121 3· 28 / 2 4 '
Приняв во внимание тождество
. х . 9 * 1 . * 1 .
Sin у Sin2 -^-rrr-g- Sin у -ζ
й неравенства (с), получим:
X X3
sin χ < 2sin-2" — Ψ
Аналогично имеем:
χ χ χ3
Sin о ^С ^ Sin ~Т т ?>о 5
sin χ
sin -ζ < 2sin-g—
хь
27·25'
■27.45
Sln
23 (η-ΐ
2$ («—Π 27
nfl— 1
Умножив неравенства (6Х) — (6Л) соответственно на 1, 2, 3, 4,
π просуммировав, получим
on - * ^3/. . 1 ι 1
Sin X < 2п Sin Kfi
(а)
(Ь)
(с)
(6,)
(6t)
(6з)
(6»)
Просуммировав прогрессии, получим:
X X3
sin χ < 2п sin ^тт—"FT"
+ 2^( 1 + §4 Τ2Γ + ··· + 24/1 —4 )
120· 24/г
Приняв во внимание неравенство 2п s'm ^п < χ и осуществив переход
к пределу (при п^ + °°)» получим неравенство
sin χ < χ
"β~ι~ Ton '
ч. т. д.
188
π
2. При О < χ < -к имеет место неравенство
Доказательство. Имеем в силу неравенств (5) и (6)
i?
sin* *~~ 6
π
Так как при 0 <х < у
то
*~~ б
1 2 +16
откуда (и подавно) следует неравенство (7), ч. т. д.
3. Доказать, что при | χ | < уг2т имеет место неравенство
Где m — произвольное натуральное число.
Доказательство. В силу неравенств (1) sin2g^ < -т—^, воспользо-
вавшись последним неравенством, получим:
__m(m —
+ 1-2
(-1)*— ft] (^2m2J + ··· +
m(m-l)... (m-
+ (1}
+ (~1} m!
m x2 , / a:2 \s ki χ2Ϋ
* \k
Просуммировав геометрическую прогрессию (сходящуюся при \х\ <^2т),
получим
тх_ х2 *!___
тт>{~„ (. х2\-~1~2гп — х2'
ч. т. д.
189
§ 34. Гармонические колебания
В математике простым гармоническим или синусоидальным ко-
лебанием называется всякая функция (а также график) вида
у = A sin (ωχ + α),
где A=j= О, ω>0*.
Теорема. Функция у = A sin (ωχ + α) является периодиче-
скои с наименьшим положительным периодом — .
Доказательство. Достаточно применить способ, изло-
женный в § 27 (стр. 151). Если число T=j=O есть период данной
функции, то имеет место тождество
A sin [ω (χ + Τ) + α] = A sin (ωχ + α)
или
(. ω/\ . ω/ л
ωχ + а + -γ sin -у = 0.
Последнее тождество выполняется в том и только в том
случае, если sin^- = 0, откуда Τ = -^-. Наименьшим положи-
2π
тельным периодом является число —, ч. т. д.
Простейшее гармоническое колебание с заданным периодом Τ
можно представить в виде
„ . /2πχ .
y Asm[ +
М'
В физике и технике гармонические колебания играют важную роль
в изучении периодических процессов, как, например, распростра-
нение волн, движение механизма паровой машины, сила и напря-
жение переменного электрического
тока и т. п.
Функция A sin (ωχ + а) имеет сле-
дующую кинематическую интерпрета-
цию. Рассмотрим отрезок ОМ длины А,
вращающийся вокруг своего конца О
с постоянной угловой скоростью ω.
Следовательно, точка Μ равномерно
движется по окружности радиуса А.
Проекция М! точки Μ на некоторую
прямую / (на черт. 111 прямая /
изображена в вертикальном положе-
нии) совершает гармоническое коле-
О'
/L
J
I 0
J
Черт. 111
* Предположение, что ω > 0 не нарушает общности, так как случай
ω < 0 можно свести к предыдущему A sin (ω* -\- а) = — Л sin (—ω* — α).
Случай ω =μ 0 исключается, ибо тогда у = const.
190
бательное движение. В самом деле, пусть О' — проекция на
прямую / точки О, а (начальная фаза) — угол, образованный на-
чальным положением радиуса с горизонтальным диаметром. За
промежуток времени χ (от начального момента) подвижной радиус
опишет угол ωχ и будет образовывать с горизонтальным диаметром
угол, равный ωχ + а. Отклонение у точки М' от точки О' выразится
формулой
у = Л sin (ωχ + α).
Точка Μ' совершает периодическое [с периодом -^-) колебатель-
ное движение на отрезке [—Л, Л] оси /. Наибольшее отклонение
вверх (вниз) от точки О достигается в моменты времени х,
при которых sin (ωχ + α) = 1 (соответственно — 1), откуда
ωχ + α = —~— η [соответственно —т~~\
и
(4k+\) π — 2α / (4k — 1) π —. 2α \
χ = л l_^ соответственно χ = χ .
2ω \ 2ω )
Тригонометрический двучлен
у = a sin ωχ + b cos ωχ,
где хотя бы одно из чисел аи b отличны от нуля: | а | + | b \ Φ О,
есть гармоническое колебание. В самом деле (см. § 24, стр. 124),
если ввести вспомогательный угол а, определяемый условиями
а . ь
cos а = , , sin а = —
то получим
у = Л sin (ωχ + а), где Л = >Аа2 + б2.
Рассмотрим некоторые частные виды гармонических колебаний
и их графики.
1°. Φ у н к ц и я у = A sin x.
Если Л>0, то данная функция имеет те же промежутки возра-
стания и убывания, что и sinx, наибольшее значение A sin x есть Л,
а наименьшее — Л. График получается растяжением обыкновен-
ной синусоиды у = sin χ в Л раз от оси абсцисс *. При Л<4) следует
выполнить растяжение от оси абсцисс в | А | раз и зеркальное отра-
жение в оси абсцисс. Число | А | называется амплитудой, или
* При Л < 1 соответствующее растяжение принято называть сжатием
Так растяжение в γ раз есть сжатие в 2 раза.
191
«размахом» синусоиды, а рассматриваемое преобразование называ-
ется также преобразованием амплитуды.
На чертеже 112 представлены графики функций
у = -^ sin x.
2°. Функция у = sin (л; + а).
График данной функции получается из обыкновенной синусоиды
параллельным переносом начала координат в точку О'(—а, 0).
Число а называется начальной фазой, а рассматриваемое
преобразование синусоиды — сдвигом фазы.
Черт. 113
3°. Функция у = sin ωχ, где αΓ> 0, — периодическая с наи-
меньшим положительным периодом Τ = —.
График получается при помощи растяжения обыкновенной си-
нусоиды в - раз от оси ординат (или при помощи сжатия в ω раз).
В самом деле, если обыкновенную синусоиду (в системе координат
ΧΌΥ) у = sin x' подвергнуть растяжению в — раз, положив
х =- χ\ то получим (в системе ΧΟΥ) у = sin аи. Это преобразование
называется также преобразованием периода.
На чертеже 113 представлены синусоиды: а) обыкновенная,
б) сжатая к оси ординат в два раза: у= sin 2х (период Τ = π),
с) растянутая от оси ординат в два раза: y = sln~ (период
Τ = 4π).
Выбрав подходящим образом коэффициент растяжения -, можно
получить синусоиду с любым заданным периодом Т. Так, например,
при ω = ^ получим синусоиду у = sin 2πχ с периодом, равным 1.
В пределах одного периода функция sin ωχ имеет следующие про-
Г π π Ί
межутки монотонности: на сегменте —^-, с—\ она возрастает от
— I до 1, а на сегменте I ~, ^ она убывает от 1 до —1; при этом
JW = 1 При Х = £-+^; Ут1п=— 1 ПрИХ = ~^2{\
При переходе от одной системы измерения углов (дуг) к другой триго-
нометрические функции претерпевают преобразование периода. Пусть угол
et принятый за новую единицу измерения, измеряется в старой единице е
числом k:
ех = ke,
тогда угол, измеряющийся в старой системе измерения числом х, в новой
системе будет измеряться числом х' = ^ . Следовательно, функция sin x пре-
образуется в функцию sin kx'> что равносильно преобразованию периода.
В частности, если за единицу измерения принять не радиан, а градус,
то получим
х — 180 х '
где χ и х' — радианная и градусная меры дуги, а потому
π
у = sin χ = sin yg^ x'
Следовательно, график синуса, начерченный при градусной системе измере-
ния получается из обыкновенной синусоиды растяжением от оси ординат в
180
— раз.
Рассмотрим гармоническое колебание в общем виде
у = A sin (ωχ +α).
График этой функции получается из обыкновенной синусоиды
У-sinX (1)
193
путем последовательного выполнения рассмотренных простейших
преобразований (черт. 114).
&&
Черт. 114
В самом деле, имеем
у =
Эту функцию можно получить, выполнив последовательно
над обыкновенной синусоидой (1) следующие простейшие преобра-
зования:
1. Χ=ωχ', Y = sm(x)x'
2. */=*+~, Y = sin
(преобразование периода),
(перенос начала координат в точку — -^, т. е. сдвиг фазы).
3. у == AY\ у = A sin (ω* + α) (преобразование амплитуды).
Примеры.
1. На чертеже 125 представлен график функции
у = sin χ +cos χ = γ2 sin ( х-\- -г)
(пунктиром намечена обыкновенная синусоида).
Черт. 115
2. Исследовать на монотонность функцию у = cos2 x, построить ее
график.
Решение. Имеем
у = у (1 ψ cos2*).
194
Функция периодическая с периодом π. На сегменте 0, ~- убывает от
1 до 0, а на сегменте \ -^ , π возрастает от 0 до I. График можно полу-
чить из обыкновенной синусоиды путем следующих преобразований:
a) у = sin X, X = χ' + -^ (сдвиг фазы);
b) y=cos*', x' = 2* (преобразование периода);
c) Y= cos 2х, у' = Υ + 1 (перенос в направлении оси ординат),
d) у' = cos 2x + 1, У = ~2 У' (сжатие к оси абсцисс).
Эти преобразования представлены на чертеже 116.
Черт. 116
Аналогично строится график функции
у = sin2 л: = -2 (1— cos 2*)
с той разницей, что после преобразования с) следует выполнить зеркальное
отражение в оси абсцисс.
195
Сложение гармонических колебаний
Сложение колебаний с одним и тем же
периодом (наименьшим положительным). Если два гармони-
ческие колебания
У\ — Аг sin (ωΎ χ -f ν-ι) и у2 = Л2 sin (ω2 χ + α2)
П Г)
имеют один и тот же период Г, то Τ = — = —- , откуда
ωχ=ω2, тогда
yi 4- у2 = (Л1 cos oci -f- Л2соз сс2) sin ωχ 4~ (Лх sin αχ -|~Л2 sin α2) cos ωχ,
где ω = ω1 = ω2.
Получился линейный тригонометрический двучлен относительно
sin ωχ и cos ωχ:
У\ + У2 = a sin ωχ + b cos ωχ,
где
a = Ал cos α, -f- Л2 cos α2, b = Αλ sin aj + Л2 sin a2.
Следовательно, в силу изложенного
У] + Уъ = Л sin (ωχ + α),
где
cos a =
= ]/~Л^ + Αϊ + 2Л! Л2 cos (a2 — а^
cos aT 4- А2 cos a2 О1-„ Αι sin αχ + A2 sin a2
sin a =
Черт. 117
Амплитуду Л результирующего
колебания можно построить геомет-
рически, как показано на черте-
же 117: Л есть диагональ паралле-
лограмма, стороны которого равны Л ι
и Л 2 й образуют между собой угол,
равный α2 —αι.
Сложение колебаний
с различными периодами.
Лемма. Если ω, Φ ω2, то тож-
дественное равенство двух тригоно-
метрических двучленов
flj sin ω1 x+b) cos ω3 x=a2 sin ω2 x-f b2 cos ω2χ
имеет место в том и только в том случае, если
а, = &! = аа = 62 = 0.
О)
(2)
Доказательство. Допустим, что хотя бы один из четы-
рех коэффициентов аь а2, bu Ь2 отличен от нуля. Пусть, например,
|fli| + I bi\ =£ 0, тогда первый двучлен есть гармоническое колеба-
ние
у^=а\ sin ω3 x+b-ι coso^ix=A1 sin (ω! х-\-аг)\
так как функция yt не равна тождественно нулю, то из тожде-
ства (1) следует, что хотя бы одно из чисел а2 и Ь2 отлично от нуля.
Тогда второй двучлен также является гармоническим колебанием:
у2=а2 sin ω2 x-\-b2 sin ω2 χ~Α2 sin (ω2 ,v-f α2).
В силу тождества (1) двучлены ух и у2 изображают одну и ту же
функцию. Эта функция периодическая с наименьшим положитель-
ным периодом / = — = —, откуда (вопреки условию) ω} = ω2.
111
Следовательно, допущение, что хотя бы один из коэффициентов дан-
ных двучленов отличен от нуля, приводит к противоречию с усло-
вием леммы, а потому имеет место равенство (2), и т. д.
Теорема. Сумма двух гармонических колебаний с различными
периодами (наименьшими положительными) является периодической
функцией в том и только в том случае, если их периоды соизмеримы.
Доказательство. Условие необходимо.
Пусть
fi (χ) = α3 sin coj χ + bi cos ω, χ и /2 (χ) = α2 sin ω2 χ -f b2 cos ω2 χ
— два данные гармонические колебания, при этом ω] =f=- ω2.
Сумма fi(x) + f2(x) является периодической функцией в том и
только в том случае, если существует число ТфЬ такое, что имеет
место тождество
h (х + Τ) + h(x + T) = ft (x) + Ш
или
α, sin со, (x + T) + ft, cos (йг (χ + Τ) + α2 sin ω2 (χ+Τ) +
+ b2 cos ω2 (χ + Τ) = α, sin o>j χ + bx cos щ х + α2 sin ω2 χ +
Последнее тождество (после элементарных преобразований)
можно заменить следующим эквивалентным ему тождеством:
Τ— 1) — &, sin03 Τ I sina)j α: + [aj sino)! Τ -\- b^ (cosω] Τ1 —
== [a2(l — со$ш2Г) + 62sino2 Л δίηω2^+
[— a2 sin ω2 71 + й2 (1 — cos ω2 Τ)} cos ω2 χ.
197
В силу доказанной леммы последнее тождество имеет место в
том и только в том случае, если
а3 (cos cuj Τ — 1) — Ьг sin ω1 Τ = О, )
aisin(*1T+ ^(coscujT·— 1) =0; J
a2 (1 — cos ω2 T) + b2 sin ω2 Τ = 0,
— a2 sin ω2 Τ + b2 (1 — cos ω2 Γ) = 0.
Первые два равенства образуют систему линейных однородных
уравнений относительно коэффициентов а4 и &4; эта система должна
иметь нетривиальные решения, так как хотя бы один из этих коэф-
фициентов отличен от нуля (тривиальный случай /±(jc) = 0 не рас-
сматривается), последнее имеет место в том (и только в том) случае,
если
' 1
sin ω, 7, cos ω, Г — 1
откуда
" = ι и 7 =
где ΤΊ = -^ — период первого колебания, &х — целое число.
Аналогично из второй системы уравнений получим
Τ = k2 T2t
где Т2 = — период второго колебания, k2 — целое число.
Следовательно,
T = kxTx = k2 T2, откуда γ^ = η^,
т. е. периоды 7Ί и Тг соизмеримы.
Условие достаточно. Предположим обратное, что
периоды данных колебаний /4(jc) и /2(jt) соизмеримы, т. е. =г = ^,
У 2 «1
где Αι и k2— целые числа; имеем ^Τλ — k2T2\ число Αι Γι, будучи
кратным Γι периода первого колебания, является также его пе-
риодом. По той же причине число k2T2 является периодом второго
колебания. Сумма двух периодических функций ft(x) + f2(x) с общим
периодом Τ также является периодической функцией с тем же пе-
риодом Г, ч. т. д.
Из изложенных рассуждений следует, что общим периодом суммы
двух гармонических колебаний с соизмеримыми периодами является
общее кратное их периодов.
Наименьшим положительным периодом суммы двух гармоничес-
ких колебаний является наименьшее общее кратное их периодов (наи-
меньших положительных).
198
Примеры.
χ
1. Функции sin ~2" и cos x имеют общий (наименьший) период 4π, так
как 4π есть период первой из них, а 2π — второй.
2. Сумма sin 10* + cos 15* есть периодическая функция с периодом
2π 2π 2π
-g—. В самом деле, -ттг есть период первого слагаемого, -уг —период
2π
второго. Наименьшим общим кратным этих периодов является -f- .
2х 7х
3. Сумма cos -g- + cos -утр является периодической функцией с перио-
дом (наименьшим положительным) Τ = 24π. Период 3π первой функции в Τ
24
содержится 8 раз, а период -у π второй функции — 7 раз.
Пусть у = /(*) — уравнение произвольного периодического
движения с наименьшим положительным периодом Г. Нижесле-
дующие тригонометрические функции имеют период Т:
-^-A: + a2) ..., sin ί —* +
..., sin
ί
причем, для первой из них Τ является наименьшим периодом. В
весьма многих встречающихся в приложениях случаях функция
f(x) может быть представлена в виде суммы бесконечного ряда Фу-
рье *:
f(x) = Ао + Л, sin^* + αχ| + ... + Ansin^x + αλ + ...
Таким образом, сложное периодическое движение представляется
как результат совместного действия (наложения) простейших гар-
монических колебаний с периодами (наименьшими), равными
Τ ΐ- — —
' 2 ' 3 · "tf n ' '··
Гармоническое колебание Ап sin i-^ψ- + an) называется п-й гар-
моникой функции f(x).
Для приближенного представления движения, харак-
теризующегося функцией f(x) в виде суммы синусоидальных колеба-
ний, может служить сумма (конечная) некоторого числа η первых
членов ряда Фурье, т. е. некоторый тригонометрический многочлен
(см. § 20) от аргумента ~.
Для нахождения гармоник функции f(x), заданной графически
(например, в результате экспериментальных исследований), скон-
струированы приборы — гармонические анализа·
* Условия разложимости функции / (х) в тригонометрический ряд уста-
навливаются в курсе математического анализа.
199
торы, дающие автоматически некоторое количество первых
гармоник функции f(x) по ее графику.
Из доказанной теоремы следует, что при сложении двух гармо-
нических колебаний с несоизмеримыми периодами получается непе-
риодическая функция. Так, например, функции sin χ + sin nx
или cos л: + sin j/2 x — непериодические.Пусть
у, = Аг sin (ω1 χ + αχ), и у2 = А2 sin (ω2 χ + α2)
уравнения двух колебательных движений (χ — время).
Обозначим через φ разность аргументов
φ = (ω2 χ + а2) — (ω, χ + аг) = (ω2 —- ω^ χ + (α2 — α^,
тогда результирующее движение можно представить в виде
Уг + Уч = Л sin (ah χ + аг) + А2 sin (ω^+α, + φ) =
= {Αλ + Α2 cos φ) sin (ω, χ + аг) + Л2 sin (pcos^Oj x + α^.
Если по обычным правилам ввести вспомогательный угол, то по-
лучим
У1 + У2 = Л sin (ω, л; + а),
где «амплитуда»
А = У А\ + А\ + 2Αί Α2 cos φ,
а также «фаза» а суть функции времени х.
Если периоды данных колебаний близки между собой, то раз-
ность со2 — со! мала, в этом случае «амплитуда» А и «фаза» α ре-
зультирующего колебания медленно меняются. На протяжении
небольшого промежутка времени результирующее движение вос-
принимается как синусоидальное колебание. Однако с течением
времени амплитуда меняется, ее наибольшее и наименьшее значе-
ния суть А\ + А2 и |Л1 — А2\ (при cos(p=:M). Описанное
явление носит в физике название биения: суммарное колебание
воспринимается как колебание с амплитудой, меняющейся пе-
риодически, то возрастающей, то затухающей. В частности, бие-
ние можно наблюдать, слушая результирующий звук, исходящий
из двух источников, дающих колебания с близкими, но различ-
ными периодами.
§ 35. Примеры исследования функций и построение графиков
На примерах, приведенных в настоящем параграфе, показаны
различные приемы исследования и построения графиков функций,
заданных формулами, содержащими тригонометрические операции.
I. В примерах 1—9 показано исследование функции на осно-
вании непосредственного рассмотрения формулы, при помощи ко-
торой задана функция.
200
Примеры.
1 Построить график функции y=sec#.
Решение. Областью определения является бесконечное множество
π π
интервалов — у + &π < х < у + kn. Функция четная и периодическая
с периодом 2π. поэтому достаточно ее исследовать в двух промежутках
π \ / π π
0. — I и I тг , π . На полусегменте О < χ < -χ функция cos χ убывает от 1
до 0, следовательно, у =
1
cos л:
возрастает от 1 до -f- oo
/π Ί
В полуинтервале ( у, π в силу тождества sec (π — *) = — seca: ли·
/π \
ния симметрична относительно точки (у, 01 оси абсцисс; в этом полуин-
тервале cos л: убывает от 0 до — 1, a sec χ возрастает от — оо до— 1. На
Г π\ / π Ι
промежутки —π, —у I и I— -о". О линия продолжается по четности, а
далее—по периодичности.
График секанса представлен на чертеже 118; для уточнения линии сле-
дует воспользоваться частными значениями функции.
2. На чертеже 119 представлен график функции у = cosec x. Подробные
рассуждения представляем учащимся.
Черт. 118
3. Построить график функции у = log^ (sin χ) (где а > 1).
Решение Область определения состоит из бесконечного множества
интервалов (2&π, (2β+1)π). Функция периодическая с периодом 2π; доста-
точно исследовать ее в интервале, в котором она имеет смысл в пределах
π
одного периода. В полуинтервале 0 < χ < -у синус возрастает от 0 до 1,
a loga sin χ возрастает от —оо до 0, На полусегменте -к < х < π синус убы-
201
вает от 1 до 0 a logasin* убывает от 0 до — оо Из неравенства sin χ < 1
следует, что у < О и что утах = 0 ( при χ = ·|-Υ
Черт. 119
График представлен на чертеже 120 (рекомендуем составить таблицу
значений функции lg sin χ при значении аргумента χ = 0; 0,1; 0,2;... и
т. д., пользуясь таблицами логарифмов тригонометрических функций).
y~lgsinx
2π Ύη
π
Черт. 120
4. Построить график у = y\oga sin *.
Решение. Область определения находится из условия log^ sin x > 0.
Но (см, предыдущий пример) log^sinA:<0, и равенство нулю имеет место
π
лишь в точках Λ: = -2" + 2£π, поэтому область определения состоит из изо-
π
лированных точек χ = -^ + 2βπ, в которых у = 0, все же прочие точки не
принадлежат области определения функции. График состоит из изоли-
рованных точек оси абсцисс (черт 121).
5. Построить график функции y = 2cosx.
Решение. Область определения есть интервал (—оо, +оо).
202
Имеем:
Аргумент χ
Промежуточный аргу-
мент и = cos χ
Функция у = 2"
0
1
2
<х<
\
\
π
1
1
<*<
/
/
2π
1
2
Наибольшее и наименьшее значения суть Углах = 2, Ут\п == "о"
-?«
f
о
Черт. 121
Дальнейшее исследование функции излишне, так как сегменты [0, т.)
и [π. 2π] охватывают полный период функции. График представлен на чер
теже 122.
6. Построить график функции у = sin(sin x).
Решение. Область определения — интервал (—оо, +оо). Функция
π
нечетная и периодическая с периодом 2π. На сегменте 0< χ < -g функция
sin χ возрастает от 0 до 1, а у = sin(sin л;) возрастает от 0 до sin 1^0,84
(сравнить с примером 3 на стр. 162).
На сегменте ->π данная функция убывает от sin 1 до 0 (черт. 123),
Черт. 123
203
пунктиром намечена синусоида. Для построения графика на сегменте
|—π, 0] достаточно продолжить график, построенный на сегменте [0, π],
симметрично относительно начала координат. Для всего интервала (—оо, +°р)
график получится путем периодического продолжения.
7. Построить график функции у = sin χ2 (кривая Френеля, имею-
щая применения в физике).
Решение. Область определения есть интервал (—оо, + оо). Данная
функция четная, поэтому достаточно исследовать ее в промежутке 0<*< +oo.
Введем промежуточный аргумент у = sin и, и = х2· Определим промежутки
монотонности:
Аргумент χ
Промежу-
точный ар-
гумент
и = х2
Функция
у = sin и
0
0
0
/
/
V\
π
ΊΓ
1
<д:<
/
\
η
3π
ΊΓ
1
<Χ<
/
/
V4
5π
Τ"
1
V4
7π
2
—1
...
...
...
Функция у возрастает от —1 до 1 на сегментах
[/
4k—I
-π,
и убывает от 1 до — 1 на сегментах
Наибольшее и наименьшее значения суть ymax = l, ymin = — 1.
Линия пересекает ось абсцисс в точках, в которых и = х2 = Ы, от-
куда χ = гЬУ^л (см. пример 3 на стр. 153).
Построив линию в промежутке [0, + оо) следует продолжить ее на про-
межуток (—оо, 0] симметрично относительно оси ординат (черт. 124).
Черт. 124
Примечание. Неравенство | sin χ21 < χ2 показывает, что в окрест-
ности начала координат линия расположена между параболой у = х2 и осью
абсцисс.
8. Построить график
функции у = cos —.
204
Решение. Область определения состоит из двух интервалов
— оо < л: < 0 и 0 < л: < + оо. Функция четная, достаточно исследовать ее
в интервале (О, -J- оо). Точки пересечения линии с осью абсцисс определя-
1 1 π 2
ются из условия cos ~ = 0, откуда — = -^-\-k,K и х= ,g^ ι ηπ ' ФункЧия
ограничена, так как —1 < cos —■< 1, следовательно, линия заключена в по-
лосе, ограниченной прямыми у=±1· Наибольшее значение, равное 1,
1 1
функция имеет в точках, в которых cos — = 1, откуда — = 2&π и
Xz==-~j-- . Наименьшее значение, равное — 1, функция имеет в точках, в ко-
торых cos — = —1, откуда — = (2k + 1) π и χ = ^ ι \\ π· Для нахождения
промежутков монотонности введем промежуточный аргумент и = —. Имеем:
Аргумент χ
Промежу-
точный ар-
гумент
1
α = ΊΓ
Функция
COS U
...
...
...
1
4π
4π
1
<χ<
\
\
1
3π
— 1
<х<
\
/
1
2π
2к
1
<х<
\
\
1
π
π
— 1
<х<
\
/
оо
0
1
График функции представлен на чертеже 125. Точка χ = 0 является точкой
y=cosx!
IF!)
Черт 125
205
разрыва (2-го рода); в этой точке функция не имеет предела (ни конечного,
ни бесконечного).
9. Исследовать на монотонность функцию
у = χ — sin χ
и построить ее график.
Решение. Область определения — интервал—оо < χ <οο Докажем,
что у возрастает в интервале (—оо, оо).
Составим разность
— /(*ι) = (*2 — sin *2) ~
~ sin xl)l
где Χι и х2 — два любые действительные числа, причем Χι<χ2
Имеем
/ 1^2/ "^" / \^1/ "™" V^2 "*"" ^1/ ~"~ ^olll ^2 "~~ bill &\) ^=z
= (л:2 — Χχ) — 2 sin -^—η—-
По условию, х2 — X\ > 0,
имеем далее:
cos
2sin-
, — Χχ Χ2 — <
—s cos —s~"
< 2
sin
Следовательно, знак разности / (x2) — f (χι) определяется первым сла-
гаемым x2 — Χι, т. е. f(x2) —/(^ι)<0, значит, функция f(x) возрастает
Функция f(x) нечетная, ее график пред-
y=zx--Sinx ставлен на чертеже 126. Следует принять во
внимание, что в силу неравенства
О < χ — sin л: < —ζ- (при χ > 0)
в окрестности начала координат линия заклю-
чена между кубической параболой
х3
У = "Τ-
Η осью абсцисс и что разность между орди-
Черт. 126 натами биссектрисы координатного угла Υ—χ
и линии у = f(x) есть периодическая функ-
ция У — у = sin χ.
II. На примерах 10—13 показано применение тригонометрических под-
становок к исследованию алгебраических функций.
10. Исследовать функцию
и построить ее график.
Решение. Введем тригонометрическую подстановку χ ·,
t=aTctgx, тогда пелучим:
1
у= 2" sin 2/.
tg t, где
206
Аргумент х есть возрастающая функция от t. Сегменту 0<*<1 соответству-
ет сегмент
4 '
на котором у возрастает от 0 до ~к . Промежутку 1 < χ < + оо соответ-
ствует промежуток
на котором у убывает от ~к до 0.
Итак, в промежутке 0 < χ < 1 функция у возрастает от 0 до -g*,
в промежутке 1 < χ < + оо убывает от -х до 0.
Данная функция нечетная, ее график
представлен на чертеже 127.
11. Исследовать функцию
1 — χ
Решение. Воспользуемся той же под-
становкой, что в предыдущем примере, тогда
получим*
1
У=-
Черт. 127
у = у tg 2/, где χ = tg /, / = arc tg x.
Результат исследования запишем в таблицу:
x = tgt
У
0
0
0
<t<
/
/
π
1
+ ОО
—оо
<i<
/
/
π
Τ
+ 00
0
Итак, в интервале 0<*<1 функция у возрастает от 0 до оо, а в интервале
1< χ <оо возрастает от —оо до 0.
Функция нечетная, ее график представлен на чертеже 182.
12. Исследовать функцию
1
Решение. Воспользовавшись той же подстановкой χ = tg tt получим
2
: sin 2t
I
207
имеем».
t
У
о
0
+ оо
<х<
/
\
1
π
Τ
2
/
/
-Η ο
π
Τ
Η-ос,
функция нечетная, ее график (гипербола) представлен на чертеже 129
Черт. 128
Черт. 129
Примечание. Исследование функций, рассмотренных в при-
мерах 10, 11, 12, может быть выполнено другим способом — чисто ал-
гебраически (см. «Специальный курс элементарной алгебры»). Реко-
мендуем учащимся сопоставить оба способа исследования.
13. Исследовать функцию
у = Х + У \— Х2
Решение Областью определения функции служит сегмент —1 <* < 1.
Воспользуемся тригонометрической подстановкой, положив χ = sin t на
π π
сегменте — у < t < -у, т. е. t = arc sin x Таким образом, сегменту
π π
— 1 < χ < 1 взаимно однозначно соответствует сегмент — у< /< γ .
Имеем:
у = sin t + cos t = j/"2"sin I / + -^· J.
π π
Эта функция на сегменте — -к < t < -τ возрастает от у = — 1 до у 2, а
π π .—
сегменте -^ < t < -^ убывает от V 2 до 1.
на
Перейдя к аргументу х, получим соответственные сегменты)
-<A;<l.
/2" . π
1 < л: < -у = sin -j и
208
у=х+УГ-хг
На первом из этих сегментов у возрастает от —J до ]/Т, а на втором убы-
( Л /2
вает от У 2 до 1. При * = sinl— ~ξ) — — ~~2~ линия пересекает ось
абсцисс: у = 0.
График представлен на чертеже 130.
Примечание. Графиком служит полуэллипс, в чем
можно убедиться, освободив уравнение от радикала.
III. На примерах 14—17 показано
применение рационализирующих подста-
новок к исследованию функций, заданных
тригонометрическими выражениями.
При применении универсальной под-
становки надо иметь в виду следующее.
l—t2
Значения функций cos* = . . μ ,
sin χ = TTT2 точке χ = π (и вообще в точ-
ках (2k + \)к) не могут быть получены
ни при каком значении t, так как при
χ = π параметр
' 1
теряет смысл. Однако эти значения можно
получить путем предельного перехода.
В самом деле,
cos π == —1, sin π = 0,
с другой стороны,
\ t2
lim|/|=oo, lim «
Χ-+π Ι /|-00 [
Аналогичное замечание относится к подстановке t = tg x.
Примеры.
14. Построить график функции
1
У— tg2* — 2igx + 2 '
Решение. Функция периодическая с периодом π. В особых точках
π
X — у + кк
значение функции (в силу принципа продолжения по непрерывности) счи-
таем равным нулю, так как lim j tg χ | = + оо (в этих точках) и
lim
1
tg2 χ — 2 tg x + 2
= 0.
Исследуем функцию на сегменте — -к < χ <£-к . Введем параметр t=igx:
1 1
У ~~~ t2—2t + 2 """ (t — I)2 + 1 '
Знаменатель имеет наименьшее значение, а у — наибольшее значение, рав-
π
ное 1 при t = tg x = 1, откуда χ = arc tg 1 = -г
8 Зак. 597 209
Имеем:
Аргумент χ
Промежуточный аргу-
мент / = tg χ
1
Функция и- ^ _{yjr[
1
π .
~ Τ
—сю
0
<х<
/
/
тс
Τ
1
1
< л<
/
\
тс
τ
00
0
График представлен на чертеже 131.
7
ν К71\
4 2
Черт. 131
1 -j- cos x
15. Исследовать функцию У — 2 — s\r\ χ и П0СТР0ИТЬ ее график.
Решение. Применим универсальную подстановку
в интервале —π < χ < π, равном по длине периоду функции. Имеем
χ = 2 arc tg / и
1 1
-2J +4
где — оо < t < оо.
1 4
В промежутке — сю < * < -^ функция у возрастает от 0 до у,
1 4
а в промежутке -к < ^ < оо функция убывает от -т ДоО. Наибольшее зна-
чение
Ушах — з *
Промежутку —оо < t < -^ соответствует промежуток —π < χ <?агс tg *к" ι
1 1
а промежутку γ < / < ос — промежуток 2 arc tg -к < χ < π. Следователь-
Г
|
П
Г П 4
но, на сегменте | — π, 2 arc tg -g" I функция возрастает от U до γ , а на
210
сегменте
1 Ί 4
,-?>·, π убывает от у до 0. График представлен на черте-
же 132 (принять во внимание, что 2 arc tg -^-^О^З I .
16. Исследовать функцию у = cos χ + cos 2* и построить ее график.
Решение. Имеем
у = cos χ + 2 cos2 a; — 1.
Введем рационализирующий параметр, положив £ = cos x, тогда получим
у = 2*» + *-1. (1)
На сегменте 0 < χ < π параметр t убывает от 1 до — 1, а на сегменте
— π < дс < 0 возрастает от — 1 до 1. Исследуем трехчлен (1) на сегменте
—1 </<1; корни трехчлена (1) суть ^ι= тт и t2 — — 1.
Имеем
К1\2 91
2' + т)-т]·
1 9
При t = — -ζ трехчлен имеет наименьшее значение ymin = — ~g"> на сег-
1 9
менте —1 < t < — -ξ- трехчлен убывает от 0 до — -g-, а на сегменте
1 9
— т- < / < 1 возрастает от— -g- до 2. Данная функция четная, поэтому доста-
точно исследовать ее на сегменте 0 < χ < π. Этому сегменту взаимно одно-
значно соответствует сегмент — 1 < t < 1. На сегменте 0<*< arc cos ί — -^
промежуточный аргумент t убывает от 1 до —-^-, а у убывает от 2 до
9 / 1\ 1
— -jp на сегменте arc cos ί— -^-J < д: < π аргумент t убывает от — -j до
9
—· 1, а у возрастает от —"тг до 0. На сегменте —π < χ < 0 (приняв во
внимание свойство четности данной функции) имеем следующее:
9 / 1 \
у убывает от 0 до — -g· на сегменте — π < χ < — arc cos ί — -j 1 ;
9 / 1 \
у возрастает от — -g- до 2 на сегменте — arc cos ί — -j)<*<0.
δ* 211
На сегменте 0 < χ < π ордината у обращается в нуль в точках
1 π
х = arc cos ~к = "з и У == arc cos (—1) = π
Исследуемая функция периодическая с периодом 2π, сегмент [— π, π] охва-
тывает полный ее период.
График представлен на чертеже 133. Значение
arc cos
(- j) » 1,82 («
104°)
находим по таблицам
cos2x
Черт. 133
7. Построить график функции
у = / (#) = sin χ + sin Зх.
Решение. Функция нечетная, периодическая с периодом 2π.
График симметричен относительно прямой χ — —t так как
/ (π — χ) = sin (π — χ) -f- sin (3π — Зх) = sin л: -f- sin Зх = / (я),
π
а потому достаточно выполнить построение лишь на сегменте 0< χ < -=■.
В концах этого сегмента функция обращается в нуль: / (0) = / ( у I = 0.
Введем рационализирующую подстановку, положив t =sin*, тогда получим
у = 4 sin* — 4 sin3 л: = 4/ (1 — t2).
Многочлен
ρ (/)=/(! — t2)
на сегменте [0, 1] имеет наибольшее значение, равное
12 2/3" 1
---п¥Чк=-~сГ ПРИ * = 77Ψ-
212
1 О ^ Q
На сегменте О < t < —jr=. многочлен Ρ (t) возрастает от 0 до —g— , а
V 3
1 2/3"
на сегменте -γ= < t < 1 убывает от —q— до О*.
/3 у
В соответствии с изложенным функция / (х) возрастает от 0 до
81^3
8/3
до 0 на сегменте
на сегменте 0 < χ < arc sin —p= и убывает от
1 π
arc sin -γζζ < χ < -χ .
/3 ^
График представлен на чертеже 134 (значение arc sin—n=r^ 1,61 (-^35°)
находим по таблицам I
у = s/7?л -f- 5/лЗх
Черт. 134
* Исследовать Ρ (/) можно обычными методами дифференциального ис-
числения. Можно исследовать Ρ (t) и элементарными средствами В самом
деле,
ι
а потому наибольшее значение Ρ (t) имеет, если 2/2 = 1 — t2 (см. «Специ-
альный курс алгебры», § 88), откуда t = -=. Составим разность:
Δ = Ρ (t2) - Ρ (tj = (t2-t1)(\-t2]-t1t2- t\Y
1 1
если 0 < tx < t2 < гг^-, то Δ > 0, если же -γ= < tx < t2 < 1. το Δ < О
Следовательно, Ρ (/) возрастает на сегменте 0, —^ и
L уЗ J
менте I —т= ,
убывает на сег·
213
§ 36. Трансцендентность тригонометрических функций
Свойство трансцендентности тригонометрических функций вы-
ражается следующей теоремой.
Теорема. Ни одна из тригонометрических функций не удов-
летворяет никакому алгебраическому уравнению.
Доказательство. Рассмотрим, например, функцию
cosx. Требуется доказать, что не существует многочлена Р(ху у),
отличного от нуль-многочлена и такого, что в результате подста-
новки у =cosx получится тождество
Р(ху cos*) = 0. (1)
Предположим противное, что многочлен Р(х, у) (отличный от
нуль-многочлена), для которого имеет место тождество (1), суще-
ствует. Расположим многочлен Ρ (ху у) по степеням х:
Ρ (X, у) ΞΞ Рп (у) X" + р„_, (у) χη-l + ... + рЛ (у) χ + pQ (у), (Ρ)
где рп, рп-\9·*., Pi, Po — многочлены от аргумента у:
Рп (У) = ck yk + ck-x у*-1 + ... + cQ9
Рп~\ (У) - d/ У1 + di-ι yl~] + ... + d0>
(Ρ)
Пусть m — произвольное число сегмента [—1, 1 ]; значение т
функция у= cos χ принимает при бесконечном множестве
значений аргумента х& = arc cos m + 2kn и xl = —arc cos m +
+ 2kn. Положим у = т в выражении (Р), тогда получим алгебра-
ическое уравнение
рп (т) хп + рп-\ (т) хп~1 + ... + р, (т) χ + р0 = О,
имеющее бесконечное множество корней Xk и х^. Это возможно
лишь при условии рп (т) = рп-\ (т) = ... = р0 (т) = 0. Получает-
ся, что для каждого из уравнений
рп{у) = О, Ря-1(У) = О,..., ро(У) = О.
Произвольное число т сегмента [—1, 1] является корнем.
Это возможно лишь при условии, если все многочлены (р)
являются нуль-многочленами, но тогда (вопреки предположению)
Р(х, у) также является нуль-многочленом. Следовательно, функ-
ция cos л: не удовлетворяет никакому алгебраическому уравнению.
Трансцендентность остальных тригонометрических функций
доказывается так же, ч. τ . д.
Следствие. Закон соответствия тригонометрических функ-
ций не может быть выражен посредством алгебраических действий
над аргументом.
В самом деле, если бы, например, функция cos x могла быть
представлена формулой
cos a; = Q{x),
где Q{x) — некоторое алгебраическое выражение, то она (.вопреки
доказанному) удовлетворяла бы некоторому алгебраическому урав-
нению Р(х, у) = 0.
Это последнее уравнение можно было бы получить, освободив
уравнение
у - Q(X) = 0
от радикалов и дробей (если они содержатся в выражении Q{x)).
Итак, тригонометрические функции не могут быть выражены
формулами, содержащими лишь алгебраические действия над аргу-
ментом. Известное из математического анализа представление
тригонометрических функций при помощи степенных рядов, кро-
ме алгебраических действий над аргументом, содержит операции
предельного перехода (суммирование бесконечного
ряда).
Глава четвертая
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
§ 37. Аркфункции
Арксинус. Для тригонометрической функции у = sin*,
рассматриваемой в интервале —оо< χ <оо, переход к обратной
функции невозможен. Так как функция sinx всякое ее зна-
чение т принимает на бесконечном множестве значений
аргумента, то по данному значению у = т нельзя найти одно
единственное значение х. Переход к обратной функции ста-
нет возможным, если рассматривать у = siη л: не при произвольных
значениях х, а на каком-либо промежутке монотонности синуса.
Промежутками монотонности синуса служат сегменты:
— ^ + 2kn, у + 2£π , на которых sin χ возрастает от — 1 до 1,
и сегменты у + 2&π,-^-jt-f 2&π , на которых sin x убывает от 1
до — 1 (см. § 29); эти сегменты в сумме составляют интервал
(— оо, + оо), т. е. множество всех действительных чисел. На
каждом из этих сегментов функция у = sin x имеет обратную
функцию.
Рассмотрим функцию y=sinx на сегменте —-^ ^ χ < у ;
известно, что (см. § 12, стр. 53), при любом значении у, взятом
при условии — 1 < у < 1, на сегменте —^ ^ х ^ "о" существует
единственная дуга χ = arc sin у, синус которой равен у*. Сле-
* Считаем уместным напомнить, что здесь и ниже мы пользуемся гео-
метрической терминологией лишь ради ее удобства и краткости. Называя
χ = arc sin у дугой, следует иметь в виду, что, в зависимости от толкования ар-
гумента тригонометрической функции, χ может иметь тот или иной конкрет-
ный смысл. Если мы рассматриваем тригонометрические функции от чис-
лового аргумента, то χ есть число, а не дуга (в геометрической теории это
есть радианная мера дуги, но не сама дуга). В вопросах, связанных с иссле-
дованием функций, такое именно толкование и должно быть принятр.
216
довательно, функция, обратная относительно у = sin x на сегмен-
те — у < χ < у, выражается формулой
χ = arc sin у,
где — 1 < у < 1.
Зная функцию, обратную относительно sin л: на сегменте
—2 ^ х ^ Т' можно (на основании формул приведения) постро-
ить обратную функцию относительно синуса на любом его
промежутке монотонности. В самом деле, дуга arcsiny + 2&π
имеет синус, равный у:
sin (arc sin у -j- 2kn) = sin (arc sin у) = y,
и заключена на сегменте —^ + 2kn} у + 2kn , следовательно
λ: = arc sin у + 2kn
есть обратная функция относительно функции у = sin x на сег-
менте
Дуга (π — arc sin у) + 2kn имеет синус, равный у:
sin [(π — arc sin у) + 2kn\ = sin (π — arc sin y) =
= sin (arc sin y) = y,
и расположена на сегменте \~ -f- 2£π, -^ + 2&π , следовательно,
х = (π — arc sin у) + 2&π
есть функция, обратная относительно у = sin x на этом сегменте.
Так, в частности, х = п — arc sin у есть функция, обратная
Γπ 3 I
синусу на сегменте у, у π .
Из изложенного следует, что достаточно ограничиться иссле-
дованием функции
у = arc sin л;
(следуя привычке в обозначениях, мы переставили местами буквы
у и х).
Функция arc sin x обладает следующими свойствами:
Iе. Область определения функции у = arc sin x есть сегмент
-—1 <х<1> так как множество значений синуса есть этот сегмент.
8В Зак. 597 217
2°. На сегменте — 1 < χ < 1 функция y=arcsin x возрастает
от —у до у. В самом деле, во-первых, будучи обратной функци-
ей относительно возрастающей на сегменте —у, у функции
л: = sin у, функция arc sin x также возрастает, и, во-вторых, про-
извольное значение т, взятое на сегменте —^ » у » функция
arc sin χ имеет в точке χ = sin m.
Итак, множество значений арксинуса есть сегмент
3°. arc sin л: шпь нечетная функция.
Доказательство. Так как —у < arcsin*<-|-, то дуга
— arc sin л: заключена в промежутке от —у до -^-:
— у<— arc sin л: <у .
Далее, sin (— arc sin x) = — sin (arc sin χ) = — χ.
Следовательно, дуги arc sin (—л:) и —arc sin л: имеют одина-
ковый синус, равный —х, и обе расположены на сегменте
— у, у, потому они равны: arc sin (— χ) = — arc sin χ, ч. т.д.
4°. Функция у = arc sin χ непрерывна на сегменте —1<х<1.
Доказательство. Можно применить тот же метод
доказательства, которым установлена непрерывность синуса
(см. стр. 168). Если Χι и х2 — проекции на ось ординат концов дуг
у—еиу+ε, то приращение дуги
Ау по абсолютной величине мень-
ше ε:
е, если |Δχ|<δ,
где в качестве δ может быть взята
наименьшая из разностей χ — Х\
и х2 — х (черт. 135).
y—arcsinx
Черт. 135
218
Если точка χ совпадает с одним из концов сегмента [—1, 1].
то следует брать соответствующие односторонние окрестности это
го конца.
Примечание. Непрерывность функции у= arc sin x
следует также из общей теоремы математического анализа о
непрерывности функции, обратной относительно непрерывной
монотонной функции.
Из изложенного следует, что взаимно обратные функции
у = arc sin x и χ = sin у
гомеоморфно (т. е. взаимно однозначно
и непрерывно) отображают друг на
друга сегменты
< X < 1 и — у < J/ < -£■
(черт. 136).
Для построения графика функции
#= arc sin x построим график функции
#=sini/, т. е. синусоиду с волнами
О X
I
/
<
Υ
η
2
/
"Τ
y=arcsinx
j
/ι.
ο χ
Черт. 137
Черт 138
расположенными вдоль оси ΟΥ (черт. 137). Выделив на полученной
линии дугу, для которой ординаты заключены на сегменте —^, ~ ,
получим график арксинуса (черт, 138).
Арккосинус. Функция у = cos χ в качестве промежут-
ков монотонности имеет сегменты [2&π, (2k + 1)π], на которых
она убывает от 1 до —1, и сегменты [{2k ■— 1)π, 2&π], на которых
она возрастает от—1 до 1 (см. § 29). Эти сегменты в сумме состав-
ляют всю область определения косинуса, т. е. множество всех дей-
ствительных чисел. На каждом из этих сегментов функция
y = cosx имеет обратную функцию.
8В*
219
Рассмотрим функцию у = cos χ на сегменте 0 < χ < π. Если
— 1<у<^1, то на сегменте |0, л| существует единственная дуга
arc cosy, косинус которой равен л:. Следовательно, функция, обрат-
ная относительно у = cos χ на сегменте 0 <х < π, выражается
формулой
χ =* arc cos у, где — 1 < χ < 1.
Зная обратную функцию на сегменте [0, π], можно (на основа-
нии известных свойств косинуса) построить обратную функцию от-
носительно косинуса на любом его промежутке монотонности.
В самом деле, дуга arc cos у + 2kn имеет косинус равный у и
заключена на сегменте [2£π, (2k -f 1)π], следовательно, -
χ = arc cos у + 2kn
есть обратная функция относительно у = cos x на сегменте
Дуга — arc cos у + 2kn имеет косинус, равный у, и заключена
на сегменте {(2k — 1)π, 2kn], следовательно,
х = —arc cos у + 2kn
есть функция, обратная относительно y=cosx на этом сегменте.
Итак, достаточно ограничиться исследованием функции (меняем
местами χ и у)
у = arc cos x.
Функция у = arc cos л: обладает следующими свойствами (эти
свойства устанавливаются аналогичными рассуждениями как для
арксинуса: провести их во всех подробностях предлагаем уча-
щимся).
1°. Область определения функции у = arc cos x есть сегмент
2°. На сегменте —1<* < 1 функция у = arc cos x убывает от
π до 0.
3°. Имеет место равенство
arc cos (— χ) = π — arc cos x.
Из этого тождества следует, что функция arc cos x не являет-
ся ни четной, ни нечетной.
Доказательство. Дуга arc cos (—x) заключена на сег-
менте [0, π], в силу определения арккосинуса. Дуга π — arc cos x
заключена в том же промежутке: это следует из неравенств
0 < arc cos у < π; обе дуги имеют одинаковый косинус:
cos [arc cos (— χ)] = — χ и cos (π — arc cos x) =
= — cos (arc cos л:) = — x\
следовательно, эти дуги равны, ч. т. д.
220
4°. Функция у = arc cos χ непрерывна на сегменте — 1<*
Взаимно обратные функции
у = arc cos χ и χ = cos у
гомеоморфно отображают друг на друга сегменты — 1 <л:
и 0<у <π (черт. 139).
у== а г ее os χ
Черт. 139
Для построения графика функции у = arc cos x достаточно
взять выделенную на чертеже 140 дугу синусоиды, изображаю-
щейся уравнением χ = cos у.
Арктангенс. Точки
χ = -? + kn (k — любое целое
число) разделяют множество
всех действительных чисел
на интервалы, в каждом из
которых тангенс возрастает от
—оо до +оо. Следователь-
но, в каждом из интервалов
Л-| + Ы, ^ + kn\ функ-
ция у = igx имеет обратную
функцию.
При произвольном дей-
ствительном у в интервале
- JL , ^) существует един-
— cosy
ственная дуга arctgy, тан-
генс которой равен у. Следо-
вательно, функция, обратная
относительно у = tgx в ин-
тервале — у < χ < у, выра-
жается формулой
х = arc tgy,
где — oo<y<oot
ч
-1
к,
<
\
0
η
y=zarccosx
1 JT
Черт 140
221
Зная функцию, обратную относительно тангенса в интервале
—-к < χ < -|, можно построить обратную функцию в любом интер-
вале монотонности тангенса. В самом деле, дуга arc tg у -f kn
имеет тангенс равный у и заключена в интервале
следовательно,
х = arc tgy -\~ kn
есть обратная функция относительно y = tgx в интервале
Функция у = arc tg x обладает следующими свойствами:
1°. Область определения функции y=arctg* есть множество
всех действительных чисел, т. е. интервал — оо < χ <^ + оо, так
как множество значений тангенса есть этот интервал.
2°. В интервале — оо<<л;< + оо функция y = arctgx воз-
растает от —у до ~.
В самом деле, во-первых, будучи обратной функцией относи-
тельно возрастающей в интервале —~<у <-^ функции х= tg у,
функция arctg* также возрастает, во-вторых, произвольное дей-
ствительное значение m в интервале (—j, j) функция arc tg* име-
ет в точке χ = tgm и, наконец,
lim arc tg x = -н- и lim arc tg л: = ^ .
В самом деле, пусть ε > 0 — произвольное заданное число; при
произвольном значении *>tg(y— ε"\ имеем у — ε <arc tgx<—.
Следовательно, lim arc tg x = -£■.
3°. arc tg x — нечетная функция:
arctg(—x) = —arctgA:
(доказательство такое же, как доказательство нечетности арк-
синуса).
4°. Функция у= arc tg# непрерывна в интервале — οο<χ< +оо.
Доказательство аналогично доказательству непрерывности арк-
синуса; можно применить также общую теорему анализа о не-
прерывности обратной функции.
Из изложенного следует, что взаимно обратные функции
у = arc tg χ и χ = tg у
гомеоморфно отображают друг на друга интервалы —- оо<х<-{~ оо
и -^<у<|- (черт. 141).
О
Черт. 141
Я у = a ret g x
x=tgy
Для построения графика функции у = arc tgx следует построить
график функции х= tg у и выделить ветвь, которая заключена в
полосе—~<у<-^ (черт. 142).
"2 y—arctgx
Черт. 142
Арккотангенс. Рассуждения, лежащие в основе опре-
деления и изучения свойств арккотангенса, аналогичны соответ-
ствующим рассуждениям, относящимся к арктангенсу, поэтому
мы ограничимся кратким перечислением основных положений.
Функция у = arc ctg x есть обратная функция относительно
х = ctgy в интервале О <У <π.
Функция у = arc ctg x + кл есть обратная относительно
л: = ctg у в интервале ктк^у <^(k-\-1)п.
1°. Область определения функции у = arc ctg x есть интервал
— оо <^ χ
оо.
<^ χ <^ + ,
2°. В интервале — оо <л;< + сю функция у = arc ctg я убы-
вает от π до 0.
223
Имеем:
lim a
3°. Имеет место равенство
= 0 и lim arc ctg χ = π.
ж->—оо
arc ctg (— χ) = π — arc ctg a;.
4°. Функция у = arc ctg χ непрерывна в интервале— оо<х<+
+ оо. Взаимно обратные функции y=arcctgA: и х— ctgy го-
меоморфно отображают интервал — оо < л: < + оо на интервал
0<у<я. ^ ^ V
График функции у = arc ctg x можно построить, выделив ветвь
котангенсоиды *=ctgy, заключенную в полосе О <Г у < π
(черт. 143). ч/ч
о
Черт. 143
Примечание. В некоторых старых учебниках рекомен-
дуется значение функции arc ctg л: выбирать в интервале
(-—·, ^); это мотивируется тем, что в интервале (—ϊ-, ^ ко-
тангенс может иметь любое заданное значение. Однако такой
выбор был бы неудобен, так как интервал (-—ρ -|) содержит
точку разрыва котангенса. Если бы мы условились выбирать
значение арккотангенса в этом интервале, то функция arc ctg x
оказалась бы разрывной. График этой функции изображен на
чертеже 144.
Черт. 144
224
Рассмотренные в настоящем параграфе функции
arc sin х> arc cos χ, arctg# и arcctg*
называются обратными тригонометрическими функциями, или
кратко аркфункциями.
Примеры. В нижеследующих примерах приведены образцы исследова-
ния элементарных функций, заданных формулами, содержащими обратные
тригонометрические операции.
1. Исследовать функции arc sin _L и arc cos -i и построить их гра-
фики.
Решение. Рассмотрим подробно первую функцию у = arc sin -L.
χ
Область определения устанавливается из условия
1
< 15 откуда
\х\> 1; областью определения служит совокупность двух промежутков
— со < χ < — 1 и 1<а:<+оо. Функция нечетная; на полусегменте
1 < χ < + оо промежуточный аргумент -- убывает от 1 до 0, а у убывает
от ~ до 0. В промежутке — оо < χ < — 1 функция убывает от 0 до — 1
(черт. 145).
Черт. 145
Заметим, что функция у = arc cosec x определяется из условий cosec y=x
и——<у<— , но из условия cosec у —χ следует sin у = JL, откуда
2 2 χ
у = arc sin J- . Итак, arc cosec x *= arc sin —
χ x
На чертеже 146 представлен график функции у = arc cos — = arc sec χ.
Область ее определения есть совокупность двух промежутков — оо < *< — 1
и 1 < χ < оо. В первом промежутке у возрастает от Л до π, а во вто-
ром возрастает от 0 до — ·
2. Исследовать функцию
arc cos x*.
225
Решение. Область определения — сегмент — 1 < χ < 1, функция чет-
ная, на сегменте 0 < χ < 1 убывает от ί до 0, а на сегменте — 1 < χ < О
возрастает от 0 до — (черт. 147).
-ι Ο ι
Черт. 146
3. Исследовать функцию
> = arc cos2 x.
Решение. Имеем: у = и2, где « = arc cos я, на сегменте [—1,1] аргу-
мент и убывает от π до 0, а у убывает от π2 до 0 (черт. 148).
Черт. 148
Черт. 149
4. Исследовать функцию у — log arc tg x (основание логарифмов считаем
большим 1).
Решение. Область определения находится из условия arc tg χ > 0, от-
куда 0 < χ < + °°· В интервале 0 < χ <+ <*> арктангенс возрастает от 0 до
i , а у возрастает от — оо до log ^-. Линия пересекает ось абсцисс в точке
Σ (черт. 149).
226
5. Исследовать функцию у == arc cos (arc sin χ)
Решение. Область определения находится из условия — 1 <arc sin <
откуда —sin I < χ < sin 1. На сегменте I—sin 1, sin 1] промежуточный ар-
гумент arc sin л; возрастает от -— 1 до 1, а у убывает от π до 0 (черт. 150).
y-=zarccos(arcsin x)
— sin\
sin\
Черт. 150
y=z(arcsinx—\)2
Черт. 151
6. Исследовать функцию у — (arc sin χ — I)2.
Решение. Область определения — сегмент — 1 < χ < 1.
Положим и — arc sin a: — 1 На сегменте — 1 < χ < sin 1 аргумент и
возрастает от— — — 1 ж — 2,57 до 0, а у убывает от (—2,57)2 ж 6,60 до 0;
на сегменте sin 1 < χ < 1 аргумент и возрастает от 0 до — — 1 л? 0,57, а у
возрастает от 0 до (0,57)2^0,32 (черт 151).
7. Исследовать функцию
у = arc sin (χ2 — 3* + 1)·
Решение. Область определения находится из условия:
|*а —3* + 1| < 1,
откуда получим систему квадратных неравенств:
χ2 — Зх + 1 < 1
χ2 — Зх + 1 > —
или
х2 — Зл: < 0
о)
Первое неравенство выполняется на сегменте 0 < χ < 3, второе в каждом
из двух промежутков — оо < л: < 1 и 2 < χ < +эо. Областью определе-
ния служит их общая часть, т. е. совокупность двух сегментов:
0<*<1 и 2<*<3;
/ 3\2 5
имеем: у = arc sin и, где и = х2 -—Зх + I = 1х — -^ ) — -ξ .
227
Результаты исследования даны в таблице:
X
и=д2—3jc+1
у = arc sin и
0
1
π
ΊΓ
<*<
\
1
j
π
""" ΊΓ
—
•2
— 1
π
<*<
/
/
3
1
π
"2
График представлен на чертеже 152.
8. Исследовать функцию
У = arc tg -ΓΖΓ
Черт. 152
Черт. 153
Решение. Областью определения служит множество трех интервалов
— оо<*< —1, — 1 < χ < 1, 1 < χ < + оо.
S силу четности достаточно исследовать функцию в двух промежутках
0<л:<1 и 1<*<+оо;
имеем:
X
1
и - х2 - 1
у = arc tg и
0
— 1
π
<х<
\
\
1
+ оо
— оо
π
π
<χ<
\
\
00
0
0
График представлен на чертеже 153.
228
§ 38. Тригонометрические операции над аркфункциями
Тригонометрические функции от одного и того же аргумента
выражаются алгебраически одна через другую, поэтому в резуль-
тате выполнения какой-либо тригонометрической операции над
любой из аркфункций получается алгебраическое выражение.
В силу определения аркфункций
sin (arc sin χ) = χ, cos (arc cos x) = χ
на сегменте — 1 <ζ χ < 1 и
tg(arc \gx) = χ, ctgfarcctgx) =x
(1)
(2)
в интервале — oo < χ < + oo.
Равенства (1) не являются справедливыми при всех действи-
тельных значениях х. Так, при |*|>1 выражение arc sin х, а сле-
довательно, и sin (arc sin л:) теряют смысл.
Равенства (1) суть тождества на сегменте —1< * < 1. На чер-
теже 154 графически показано различие между функциями, задан-
ными формулами
у = х и у = sin (arc sin x),
у = χ y=sin (a res in x)
Черт. 154
В
Черт. 155
первая изображается биссектрисой координатного угла, а вторая —
отрезком этой биссектрисы. Равенства (2) справедливы при всех
действительных значениях х.
Каждое из равенств (1) и (2) является тождеством в том смысле,
что оно справедливо при всех значениях х, содержащихся в об-
ласти определения как правой, так и левой частей.
Ниже приведены всевозможные случаи выполнения тригономет-
рических операций над аркфункциями.
1. Положив в формуле cos φ = ± Vl — sin2 φ (выражающей
косинус через синус), φ = arc sin x получим
cos (arc sin x) = ± ]/l — [sin (arc sin a:)]2 = ± ΥI — x2.
229
Перед радикалом следует взять знак-)-, ибо дуга φ = arc sin x
принадлежит правой полуокружности (замкнутой) — ~ <ζ φ ^у ,
на которой косинус неотрицателен. Итак, имеем:
cos (arc sin) χ = j/1 — χ2.
Геометрическая интерпретация (черт. 155).
Число χ есть ордината точки β, угол АОВ = arc sin x\ величина
отрезка ΟΒι есть косинус этого угла: cos ЛОВ = ОВХ.
По теореме Пифагора ОВг = У\ — ВВ\ = V\ — χ2 , откуда
cos (АОВ) = cos (arc si η χ) = ]/1 — χ2.
2. Подобным же образом найдем:
si n (arc cos x) = Υ1 — cos2 (arc cos χ) = ]/1 — χ2.
В силу неравенств 0 < arc cos χ < π имеем sin (arc cos χ) > 0,
а поэтому перед радикалом необходимо взять знак +.
Геометрическая интерпретация аналогична
предыдущему случаю.
3. Из тождества tg φ = ^—т следует:
1
4. Имеем
, , sin (arc sin x)
tg (arc sin X) = —-. :—f- =
° ^ ' рлс lam cm vi
cos (arc sin χ) γ~\ X2
5. Положим в формуле sin φ = ± gcp =- (выражающей
синус через тангенс) cp=arctg.x;. Так как в правой полуокруж-
ности синус и тангенс имеют одинаковые знаки, то перед ради-
калом следует взять знак+. Следовательно,
sin(arctgA:)= __ll__ .
Ниже дана сводка формул, получающихся в результате вы-
полнения простейших тригонометрических операций над аркфунк-
циями. Справедливость всех этих формул может быть установлена
при помощи рассуждений, подобных приведенным выше.
230
sin (arc sin) χ = χ
sin (arc cos x) = \f\ — x2
sin (arc tg*) /ι+χ,
sin (arc ctg x) ^+^
tg (arc sin x) -: .- -
/ 1 — л:2
/1 -л:2
tg (arc cos дс) — χ
tg(arctg x) = χ
tg (arc ctg x) = —
cos (arc sin *) = |/Ί — л;2
cos (arc cos x) = χ
cos (arc tg x) - -.rr-.—
Τ 1 + χ2
cos (arc ctg *) ^l + jt8
V\ — x2
ctg (arc sin x) =
ctg (arc cos *)— γ·γ-ζ:Γ^
ctg (arc tgx) = —
ctg (arc ctg ;f) = χ
Выражения, находящиеся в правых частях каждого из напи-
санных в таблице равенств, — алгебраические. Эти фор-
мулы являются лишь иначе написанными формулами, при помо-
щи которых тригонометрические функции выражаются одна через
другую.
Ниже приведены образцы выполнения различных преобразова-
ний посредством выведенных формул.
1. Преобразовать выражение sin (2 arc sin x).
Применив формулу sin 2φ = 2 sin φ cos φ, имеем:
sin (2 arc sin x) = 2 sin (arc sin x) cos (arc sin x) = 2x \f\ — г2.
2. Подобным же образом устанавливается справедливость
тождеств:
cos(2arccos;t) = cos2 (arc cos jc) — sin2 (arc cos x) = 2x2 — 1;
\a (9 ягг to y\ - 2 tg (arc \g x) __ 2x
tg(2 arctgx)- ^tg.jarctg^ -fZ?·
3. Пользуясь теоремой сложения, получим:
sin (arc sin л: + arc sin у) = si η (a re si η χ) cos (arc si η у) -f-
+ cos (arc sin x) sin (arc siny) = χ γ\ —у2 -\- у ΥΙ — χ2.
231
4. Следуя приему, указанному в предыдущем примере, можно
доказать следующие тождества:
cos (arc cos χ + arc cos у) = xy — ]/" 1 — χ2 |/Ί — у2;
sin (arc cos χ -f arc sin y) = ]/Ί —χ2 \f\ — у2 + xy\
sin (arc sin л:-—arc sin y) = χ |/l — y*~y \/Ί —χ2;
tg (arc tg л: — arc tg y) =
— У.
tg(arcsinx + arc sin yH sin (arcsin, +arc siny) ^
&v ' 7/ cos (arc sin * +arc sin y)
5. Положив в формулах
λ: /l — у2 + у VY^
• о 2 tg φ 1 — tg2 φ
sin 2φ = , , , \ и cos φ = , ■ 4 2
l-ftg2cp τ 1 4- tg2 cp
φ == arc tgx, получим:
sin(2arctgx) = р|~2, cos (2 arc tg χ) = |^2.
6. Преобразовать cos (-~ arccosx).
Положив в формуле
φ . -- ί\ + COS Φ
cos |- = ± у -ry-1 . φ = arc cos x,
получим:
cos (γ arc cos χ) =|/"i+i .
Перед радикалом взят знак -К так как дуга у arc cos x при-
надлежит первой четверти, а потому левая часть неотрицательна.
7. Чтобы преобразовать выражение sin ί-γ arc sin x ), поло-
жим в формуле (стр. 91)
232
: arc
sin л:,
sin JL
2
тогда
sini
fy\
получим
-ζ arc sin л
+ sii
.)_
Γΐφ— |
2
V ι +
/1 — si
χ — /
2
)
1 —x
(sf)
(1)
В общей формуле (S*_ j следует в правой части взять знак +;
в самом деле, функция sin (-^ arc sin χ) положительна при
<0
отрицательна при х<0; такое же распределение знаков имеет
место и для правой части равенства (1).
Аналогично устанавливается равенство
cos ί γ arc sin x) =
2
8. Для преобразования выражения cos (n arc cos χ), где п — на-
туральное число, положим в тождестве (§ 17)
cosna = cos" α — С^ cos"-2 α sin2 α + С* cos"-4 α sin4 α— ...(Cncc)
a = arc cos x. Если степени синуса выразить через косинус, то
получим
cos (n arc cos x) = Tn (cos (arc cos χ)) = Τη (χ),
где Тп(х) есть n-й полином Чебышева.
Следовательно, функция cos (η arc cos x), определенная на сег-
менте [—1, 1], совпадает на этом сегменте с многочленом п-й
степени Тп(х).
Аналогичное выражение sin (n arc cos л;) можно преобразовать,
положив в тождестве (см. § 17)
sin (па) =· sin aUn (cos a)
а = arc cos x, тогда получим:
sin (n arc cos x) = ]/l — χ2 Un (χ).
Если положить в тождестве
sin па = Cln cos"-1 α sin α — Съп cos"~3 a sin3 a +
+ Съп cos"-5 a sin5 a — ... (Sna)
a = arc sin x, то получим:
η— 1 /г —3
sin (narc sinx) =Cln( 1-х2) 2 χ— C2n{\— χ2)~Ύ~χ^ + ...
9. Преобразовать tg(narc tgx). При всяком целом п эта функ-
ция является рациональной.
В самом деле,
Cl Sin α COS"-1 α — Cl Sin3 α cos""3 α + ...
tg па = о к =
to COS" а — С2 Sin2 α COS""2 а + ...
C1tga--C3tg3a+...
гзз
Положив в формуле (Тпа) а = arctgx, получим:
С1 X — С3 у.3 4- ...
tg(rtarctg*) = -;—-к-
Преобразования рассмотренного вида можно разнообразить,
если брать различные комбинации аркфункций и теорем сложения.
§ 39. Соотношения между аркфункциями
Соотношения первого рода. Соотношениями
первого рода будем называть соотношения между аркфункциями,
вытекающими из зависимости между тригонометрическими функ-
циями дополнительных дуг.
Теорема. При всех допустимых значениях χ имеют место
тождества:
arc sin x -f arccosx = ^ ; (1)
arc tg χ + arc ctg χ = ~ . (2)
Доказательство. В самом деле, дуги arc sin x и
^ —arccosA; имеют одинаковый синус:
sin (arc sin χ) =χ (по определению арксинуса);
-| — arc cos a: ) = cos (arc cos x) = χ
(формула приведения).
Обе дуги заключены на сегменте — γ , ~
L г г.
так как
—^ < arc sin χ ^ -j (по определению арксинуса);
О <; arc cos x < π (по определению арккосинуса),
откуда — ^-<-| ~-arccosx<-|.
Следовательно, эти дуги равны
arc sin χ = -χ — arc cos x.
Аналогично доказывается второе тождество (2), ч. т. д.
На чертеже 156 дано геометрическое пояснение равенства (1).
Соотношения второго рода. Соотношениями вто-
рого рода будем называть соотношения между аркфункциями, вы-
текающие из соотношений между значениями тригонометричес-
ких функций от одного и того же аргумента. Посредством соотно-
шений второго рода производятся преобразования одной аркфунк-
ции в другую (но от различных аргументов).
С л у ч а й 1. Значения двух данных аркфункций заключены в
одной и той же полуокружности.
Пусть, например, рассматривается дуга а, заключенная в ин*
тервале
jirccos χ
\arcsin χ
arccosx
'arcsin χ
χ>0
Данная дуга может быть представлена как в виде арксинуса,
так и в виде арктангенса. В самом деле, дуга arc sin (since) имеет
синус равный sin α и заключена, так же как и а, в интервале
(—|-, |j, следовательно,
а = arc sin (sin α).
Аналогично можно дугу а представить в виде арктангенса:
а = arctg(tga).
Если дуга а заключена в интервале (0, π), то она может быть
представлена как в виде арккосинуса, так и в виде арккотангенса:
a = arc cos (cos α) = arc ctg (ctg a).
Так, например:
π . /2"
-г = arc sin ^-
= arc tg 1;
— ~ = arc sin ί — — J = arc tg ί —
Аналогично
3π /
-г- = arc cos -
Ниже приведены формулы преобразования одних в другие
аркфункций, значения которых содержатся в одной и той же полу-
окружности (правой или верхней).
1. Выражение arc sin x через арктангенс.
Пусть у — arc sin x, тогда
Дуга arc tg -y=JL·^-, по определению арктангенса, имеет
тангенс равный г и расположена в интервале (— 2. э ΐ.) .
У1 — χ2 \ ι ΔΙ
В силу (*) дуга arc sin а: имеет тот же тангенс и расположена
/ π π\
в том же интервале I—^ » у
Следовательно,
(в интервале (—1,1).
2. Выражение arctgx через арксинус.
Так как
У \ + х2
то
(2)
в интервале (— оо, + оо).
3. Выражение арккосинуса через арккотангенс.
Из равенства ctg(arccosx) = —^ следует тождество
У 1 — х2
arc cos x = arc ctg . (3)
у l — χ
Случай II. Рассмотрим две аркфункции, значения которых вы-
бираются в различных промежутках (например, арксинус и арк-
косинус, арккосинус и арктангенс и т. п.). Если аргумент какой-
либо аркфункции (т. е. значение тригонометрической функции)
положителен, то соответствующая аркфункция (дуга), заключен-
ная в первой четверти, может быть представлена при помощи любой
аркфункции; так, например,
^ = arc sin у = arc cos -γ- = arc tg -^= = arc ctg "/3.
Поэтому каждая из аркфункции от положительного аргумента
может быть выражена посредством любой другой аркфункции.
Значение какой-либо аркфункции от отрицательного аргумента
принадлежит либо промежутку от —^ до 0, либо промежутку от
- до л и не может быть представлено в виде аркфункции, значение
которой принадлежит другому (из этих двух) промежутку.
/ 1 \ 2
Так, например, дуга arc cos [ — -тН^'о11 не может быть значе-
нием арксинуса. В этом случае
2 π . /З
уя=л — -g· = π — arc si n -у-.
Ниже приведены формулы преобразования одних в другие арк-
функции, значения которых выбираются в различных полу-
окружностях.
4. Выражение арксинуса через арккосинус.
Пусть у = arc sin х\ если 0 < л: < 1, то 0 ^
у <Г ^-
Дуга у имеет косинус, равный ]/1—х2, а потому
arc sin = arc cos |/1 — χ2.
При —1 <;*<() это равенство выполняться не может. В са-
мом деле, в этом случае —-^ <^arcsinA;<0, а для функции
arc cos l/l — x2 имеем:
0 < arc cos Yl—x2 < Ί ,
так как аргумент -арккосинуса есть арифметический корень
Υ\—χ2, т. е. число неотрицательное.
Расположение рассматриваемых дуг пояснено на чертеже 157.
х>0 х<0
Черт. 157
При отрицательных значениях χ имеем
arc sin χ = — arc sin (— χ) = — arc cos ΥI — χ2.
Таким образом, имеем окончательно:
Черт. 158
а —х>0 и
arc sin л: =
arc cos Υ\ — л:2, если 0<х<1,
— arc cos УI — а:2, если — 1 < χ < 0.
(4)
На чертеже 158 представлен график функции arccos]/!—χ2.
237
Область определения есть сегмент [—1,1]; согласно равенству (4),
закон соответствия можно выразить следующим образом:
( arc sin χ, если 0<х<1,
arc cos J/1 — χ2 = { . t . . Α
ψ { — arc sin λ:, если— 1<л;<0.
5. Аналогично установим, что при 0 < χ < 1 имеем:
arc cos л: = arc sin γ\ —χ2,
если же — 1 <; χ <! 0, то
arc cos χ = π — arc cos (—χ) = π — arc sin }Λ — x2.
Таким образом,
ί arc cos |/l — x\ если 0<л:<1, „
arc cos χ = | (o)
[π—arc sin J/Ί—x2, если —10
6. Из соотношения
1
cos (arc tgx)
VT+T*
при χ > 0 имеем:
arc tgx = arc cos . .
Если же х<0, то
1
arc tg χ = — arc tg (— χ) = — arc cos
VT
Итак,
arc tgx =
arc cos - , если χ > О,
У 1 + χ2
— arc cos -г, - , если χ < 0.
7. Если 0<х<;1, το arc cos χ = arc tg
При — 1<л;<0имеем:
агссо5л:=л — arc cos (—χ)=η — arc tg- =
"~~* X
= π + arc tg-
Итак,
(6)
arc tg ^1~χ2 , если 0 < χ < 1,
arc cos χ = I η\
π + arc tg ——— , если — 1 < χ < 0.
χ
238
Следуя методу, выясненному на приведенных примерах, уста-
новим справедливость следующих равенств:
arc tg* =
arc ctg — , если х > О,
arcctg π, если
(8)
При л;>0 равенство (8) легко установить: если же х<^0, то
arc tgx= — arc tg(— x) = — arcctg— = — (π —arcctg—^
— x у χ /
arcctg , если 0<;х<1)
9. arc sin* = { * (9)
ι Λ/ ι ___ y2
arc ctg π, если — 1 <; χ <* 0.
ι χ
\ arc sin тттр" · если 0<х'
10. arc ctg λ: = \ χ (10)
| π — arc sin уТ~Т~Г, если х<^0.
ι arc tg 4 , если χ > 0,
11. arcctg* = <; χ (Π
j π +arctg— , если х-
ι
Примеры.
1. Исследовать функцию у =« arc tg л: — arc ctg — .
Решение. Эта функция определена для всех значений ху за исклю-
чением значения χ = 0 (при χ = 0 второе слагаемое теряет смысл). Восполь-
зовавшись формулами (8), по-
лучим У
0, если χ > 0,
(
— π, если χ < 0.
На чертеже 159 изображен
график данной функции. ..
2. Исследовать функцию
у = arc sin VV^lc -f y~Grctgx-arcctg\
+ arcsin)/V Черт. 159
Решение. Первое слагаемое определено для значений 0 < χ < 1, вто-
рое—для тех же значений аргумента. Преобразуем первое слагаемое по
формуле (4). Так как 0 < |^1 — χ < I, то получим
arc sin Vi — χ = arc cos У 1 — (1 — χ) — arc cos Vx,
239
откуда:
у = arc sin V\ — χ 4- arc sin V χ = arc cos Ух -f arc sin Ул: = у на сег-
менте [0, 1].
3. Исследовать функцию
у = arc sin r — arc cos ;
Решение. Выражения, стоящие под знаками аркфункции, не пре-
восходят по абсолютной величине единицы, поэтому данная функция опре-
делена для всех значений х. Преобразуем первое слагаемое по формуле (4):
arc sin —_L__ = arc cos
/ι = arc cos "l/ -
1 l + x2 V 1
1*1
= arc cos r
Приняв во внимание равенство
f arc cos 6, если ξ > 0,
arc cos Ι ί | = {
(π— arc cos ξ, если ξ < О,
получим:
О, если л: > О,
У =
π — 2 arc cos,/- если χ < 0.
V 1 + *2
§ 40. Выполнение обратных тригонометрических операций
над тригонометрическими функциями
При преобразовании выражений вида
arc sin (sin л;), arc cos (cos л:), arctg(tgjc), arcctg(ctgA;)
следует принимать во внимание, в какой четверги находится ар-
гумент л: и в каком промежутке находится значение данной арк-
функции. Рассмотрим, например, первое из данных выражений
у = arc sin (sin x).
Согласно определению арксинуса, у есть дуга правой полуокруж-
ности (замкнутой), синус которой равен sinx;
sin у = sin χ и —у^У^у·
Областью определения функции arc sin (sin x) служит интервал
— oo<jt<^+oo, так как при всех действительных значениях χ
значение промежуточного аргумента и= sin x содержится на сег-
менте —1 < и <1. При произвольном действительном χ значение у
(в общем случае) отлично от значения х.
Так, например, при χ = — имеем:
у = arc sin (sin ~ j = arc sin j = -^ = x\
240
5
но при χ = -f
. / . 5 λ .1 π .
у = arc sin i sin -g- π j = arc sin -^ = -g- =f= x.
В силу периодичности синуса функция arc (sin x) также яв-
ляется периодической с периодом 2π, поэтому достаточно иссле-
довать ее на сегменте — у , -ψ π величиной 2π.
Если значение χ принадлежит сегменту — у,-| , то у = х\
на этом сегменте график функции совпадает с биссектрисой ко-
ординатного угла.
Если значение χ принадлежит сегменту Ur , -^ π , то в этом
ίζ Δ J
Г π π1
случае дуга π — χ принадлежит сегменту —~2~ > "И > и» так как
sin (π — χ) =sin;c, то имеем у = я — χ;
в этом промежутке график функции совпадает с прямой линией
у = п — х. Если значение χ принадлежит сегменту -^ π, -г π ,
то, пользуясь периодичностью или путем непосредственной про-
верки, получим:
у = χ — 2π.
Если значение χ принадлежит сегменту —γ л, —~ , то
у = — π — χ.
Если значение χ принадлежит сегменту — -£ π; — -^ π L то
у = л: 4- 2π.
Вообще, если — у + 2&π < χ < -^ + 2Απ, то
у = χ —
и если ~ + 2^π < χ < -^ π + 2&π, то
у = (я—х) -J-
График функции
у = arc sin (sin л:)
представлен на чертеже 160. Это ломаная линия с бесконечным
множеством прямолинейных звеньев.
Рассмотрим функцию
у = arc cos (cos jc),
6 Зак. 597 241
Согласно определению арккосинуса, имеем
cos у = cos xt где 0 < у < π.
Областью определения данной функции является множество всех
действительных чисел; функция периодическая с периодом равным
2π. Если значение χ принадлежит сегменту [0, π], то у = х. Если
χ принадлежит сегменту [π, 2π], то дуга 2π —χ принадлежит
сегменту [0, я] и cos(2jt — x) =rcosx, поэтому
arc cos (cos χ) = 2π — χ.
Следовательно, на сегменте [π, 2π] имеем
у = 2π — χ.
y~arcs/n(sinx)
/
/
Черт. 160
Если х принадлежит сегменту [2π, 3π], то
у =х— 2π.
Если χ принадлежит сегменту [3π, 4π], то
у = 4π —■ χ.
Вообще, если 2kn < χ < (2& + 1), то
у = χ — 2£π;
если же (2k — 1) π < χ < 2йл, то у = — * +
Графиком функции у = arc cos (cos x) является ломаная линия
(черт. 161).
y=zorccos(cosx)
Рассмотрим функцию
у =arctg(tgx).
Согласно определению арктангенса
где — у
.242
Выражение arctg(tgAr) имеет смысл при всех действительных
2&-J- 1
значениях х, за исключением х =—γ- π. Следовательно, областью
определения данной функции служит бесконечное множество
интервалов
_3 π_\ / _π π\ /π 3 \
2 π' 2)> [ 2'Ύ)> \Ύ> Ύη>)> ·"»
Данная функция периодическая с периодом равным π.
Имеем:
у = х, если —- <^ χ < —,
у = х — я, если γ<ΧτΓπ>
у=х + я, если —-jt<i< — у,
и вообще
у = л: — £я, если — у4-&я<^<^- + ^π·
Для построения графика функции достаточно построить отре-
зок биссектрисы координатного угла у = χ в интервале [—^-, ·|
(концы отрезка к графику не причисляются), а затем продолжить
график периодически с пе-
y-arctg(tgx)
ΊΓ7
риодом равным π (черт. 162).
График состоит из бесконеч-
ного множества параллель-
ных между собой прямоли-
нейных отрезков.
Точки ~ + kn являются
точками разрыва первого ро- Черт. 162
да функции у = arctg(tgx),
так как в этих точках предел функции не существует, но сущест-
вуют различные между собой правые и левые пределы. Так,
в точке ~2 левый предел равен считаем х<^-^ I:
lim [arc tg (tg x)\ = lim χ = у ,
а правый предел равен ι считаем ^/>-γ
lim [arc tg (tg x)\ = lim (x — π) = — γ .
9* 243
На чертеже 163 представлен график функции у= arc ctg(ctgx);
исследование этой функции предоставляем учащимся в виде уп-
ражнения.
Отметим, что исследование функций
arc cos (sin x) и arcctg(tgx)
не представляет затруднений, так как, пользуясь соотношениями
arc sin (sin χ) + arc cos (sin χ) = -|·
arc tg (tg x) + arc ctg (tg x) = |-,
v = arcctq(ctqx) можно пРивести рассмотре-
7 σ σ ние этих функций к уже
Ρ Ρ J* изученным функциям.
г / / Примеры.
&L (^—^ 1. Исследовать функцию
π χ у — χ—arc tg (tg x) и построить ее
график.
Решение. Областью опре-
деления является бесконечное
множество интервалов
2k + 1
Черт. 163
{ 2 π'
в зтих интервалах
arc tg (tg χ) — χ — Ы и у = kn.
Графиком является изображенная на чертеже 164 ступенчатая разрыв-
ная линия. /л
Yk y = x — arctg(tgx)
ч°
Черт. 164
2. Исследовать функцию у=х — arc sin (sin x) и построить ее график.
Решение. Если -l-f2b<^<|-f 2£π, то
arc sin (sin x) = χ — 2kn и у == 2kn;
если
у + 2&π < χ < -£ π -f 2&π, το arc sin (sin χ) — (π — χ) + 2kn
Графиком является изображенная на чертеже 165 ломаная линия.
у=х—arcsin(sinx)
2πΑ
"Г"*
Черт. 165
3. Исследовать функцию у = χ arc sin (sin x).
Решение. Если — JL + 2/гт: < л: < ϋ + 2Λπ, то
π
если ~2
3
у π + 2^π, то у = л: [(2^ + 1) π — л:).
Графиком является ломаная линия, состоящая из параболических дуг
(черт. 166).
yz^xarcsin(sinx)
Черт. 166
245
§ 41. Формулы сложения
Формулы сложения дают выражения для суммы или разности
двух (или нескольких) аркфункции через какую-либо данную арк-
функцию. Пусть дана сумма двух аркфункции; над этой сум-
мой можно выполнить любую тригонометрическую операцию
(см. § 38). В соответствии с этим дуга-сумма может быть выражена
посредством любой данной аркфункции. Однако в различных слу-
чаях (при одних и тех же аркфункциях) могут получаться различ-
ные формулы в зависимости от промежутка, в котором заключена
сумма, и от промежутка, в котором берется значение рассматривае-
мой аркфункции.
Сказанное пояснено ниже на числовых примерах.
Примеры.
1. Преобразовать в арксинус сумму γ = arc sin JL+ arc sin — .
о 2
Решение. Эта сумма является суммой двух дуг α и β, где
а == arc sin -о- , β = arc sin -к .
π ί 1 V"2
В данном случае а<-^-(так как у < - , а следовательно,
1 π \ π π π
arc sin -Q- < -j ι , а также ρ ~ -g- < -j , поэтому Τ < "о" ·
Вычислив синус дуги γ, получим:
sinT + \\
7 3 2 ^ 2 У Ж
Г π π]
Так как сумма γ заключена на сегменте —~9~' ~9" > то
Г π π]
—~9~' ~9" >
2. Представить дугу γ, рассмотренную в предыдущем примере, в виде
арктангенса.
Решение. Имеем:
tg (arc sin у) + tg (arc sin у) ^ + 2 y~
1 — tg (arc sin yjtg fare sin-|Л 2 ]/ 6"—1
откуда
γ = arc sin -Q- + arc sin -77 = arc tg ' ^ ,
d J 2/6-1
3. Представить посредством арктангенса сумму
γ = arc tg 1 + arc tg 2.
246
Решение. В данном случае (в отличие от предыдущих) дуга γ окан-
чивается во второй четверти, так как arc tg 1 = ~ , a arc tg 2 >— # вы_
числяем
В рассматриваемом примере γ Φ arc tg (—3), так как дуги γ и arc tg (—3)
заключены в различных интервалах,
2
В данном случае
-к < γ < π, а — -о- < arc tg (— 3) < 0.
= π -f- arc tg (— 3) = π — arc tg 3.
4. Представить дугу γ, рассмотренную в предыдущем примере, в виде
арккосинуса.
Решение. Имеем
cos γ = cos (arc tg 1 + arc tg 2) = — ,._. .
Обе дуги γ и arc cos I— ,— ) расположены в верхней полуокружно-
сти и имеют одинаковый косинус, .следовательно, эти дуги равны:
7 = arccos( — -r=~
Так как суммы и разности любых аркфункций можно выражать
при помощи произвольной аркфункций, то можно получать самые
разнообразные формулы сложения. Однако все эти формулы выво-
дятся посредством однотипных рассуждений. Ниже в качестве
образца даются некоторые из формул сложения, по этим образ-
цам можно получить аналогичные формулы в различных прочих
случаях.
Формулы сложения аркфункций от поло-
жительных аргументов. Пусть α и β — две дуги, за-
ключенные в промежутке от 0 до -^ (первая четверть):
0<а<| и
Сумма α + β заключена в верхней полуокружности: 0<α + β<π,
следовательно, ее можно представить в виде аркфункций, значение
которой выбирается в том же интервале, т. е. в виде арккоси-
нуса, а также в виде арккотангенса:
α -f β = arc cos [cos (α + β)] .= arc cos (cos a cos β — sin a sin β);
α + β = arc ctg [ctg ( α + β)] - arc ctg c*fgagcg [^ .
Разность a — β заключена в правой полуокружности:
247
следовательно, она может быть представлена в виде аркси-
нуса, а также в виде арктангенса:
α — β = arc sin [sin (α — β) ] = arc sin (sina cos β — cosa sin β),
a - β - arc tg [tg (a - β)] - arc tg , '^ ~ fg\ ,
Так как значение всякой аркфункции от положитель-
ного аргумента заключено в интервале (0, -|), то сумму двух
аркфункции от положительных аргументов можно представить в
виде арккосинуса, а также в виде арккотангенса, а разность двух
аркфункции от положительных аргументов можно представить
в виде арксинуса, а также в виде арктангенса.
Ниже приведены образцы соответствующих преобразований.
1) Преобразовать в арккосинус arc sin x -f- arc sin у, где 0<a:<^1
и 0<у<1.
Имеем:
cos (arc sin л: + arc sin у) = ]/l — χ2 ]/1 — у2 — ху
(см. § 38), откуда
arc sin л: + arc sin у = arccos(]/l — χ2 ]/Ί — у2— ху).
2) Преобразовать в арксинус arc sin χ — arc sin у, где 0 < χ < 1
и 0<у<1.
Имеем:
sin (arc sin χ — arc sin у = χ ]/1 — у2 — у j/1 — χ2,
откуда
arc sin χ — arc sin у = arc sin (a:]/ 1 —y2 — y |/1 — χ2).
3) Преобразовать в арктангенс arc cosa: — arc cos у, где
<1 и 0<<1
Имеем:
ν V1 ν2 χ V \
tg (arc cos χ - arc cos у) = y v' x\l
\l=T ·
xy + У 1 — хгу 1 —ν2
откуда
у У] ХЪ χ ЛГ\ V2
arc cosa: — arc cos у = arctg^ r y
Изложенным способом устанавливаются прочие различные
формулы сложения аркфункции от положительных ар-
гументов; нескольких таких формул приводятся ниже.
4) arc cos x + arc cos у = arc cos (xy — j/1 — χ2 Υ \ — y2).
5) arc tg χ 4- arc tg у = arc cos» —r==- r
148
~ч . , . x — yVl—x2
0) arc sin χ — arc tg у = arc sin —r>——τ— .
Формулы сложения аркфункций от про-
извольных аргументов.
1) Выразить сумму
γ = arc sin x + arc sin у
через арксинус.
По определению арксинуса,
— у < arc sin л: < у и — -| <агс sin у< ~ ,
откуда
— η <; arc sin χ -f arc sin y <ζ π.
Для дуги у возможны следующие три случая.
Случаи I: — у < γ <у .
Если числа χ и у разных знаков или хотя бы одно из них равно
нулю, то имеет место случай I. В самом деле, приО<л:<;1и
—1 <J'<0 имеем:
<y и —~ < arc sin у < О,
откуда
π ^ ^ π
При jc > О, У > 0 для дуги γ имеет место одна из следующих
двух систем неравенств:
а) 0 < γ < у или Ь) ~ < γ < π.
Необходимым и достаточным признаком, позволяющим отличить
один от другого случаи а) и Ь), является выполнение неравенства
cosy>O в случае а) и cos у < 0 в случае Ь).
В самом деле, взаимно исключающие друг друга соотношения
а) и Ь) влекут за собой взаимно исключающие следствия cos γ > О
и cos γ <0 (соответственно), а потому эти следствия служат необ-
ходимыми и достаточными признаками наличия дан-
ных соотношений.
Вычислив cos γ, получим:
cos γ = cos (arc sin χ + arc sin y) = l/1 — χ2 Υ \ — y2 — xy.
При *>0, y>0 наличие случая I означает выполнение неравенств
а), т. е. cos γ > 0 или
откуда (1 — х2) (1 — у2) >*2у2 и, следовательно, х2 + у2 < 1.
9В Зак. 597 249
Наличие случая I при χ < О, у < О означает выполнение нера-
венств
— -к К arc sin x -f~ arc sin у < 0;
но тогда для положительных аргументов —χ и —у имеет место
случай I, а потому
(■— xf + (— у)2 < 1 или х2 + у2<1.
Случай II: γ<γ<^.
В этом случае х>0, у>0, т. е. выполняются неравенства Ь);
из условия cos γ < 0 получим л:2 + у2>1.
Случай III: — π<γ< — у.
Этот случай имеет место при #<0, у<0 и
— π <; arc sin χ + arc sin у < —^ .
Изменив знаки на противоположные придем к предыдущему
случаю:
π > arc sin (— χ) + arc sin (■— у) > 5-,
откуда χ2 + у2 > 1.
Из сопоставления результатов следует, что признаком случая I
при одинаковых по знаку значениях аргументов (т. е. при
л:у>0) может служить неравенство х2 + у2 < 1. Случай II имеет
место, если х^>0, у^>0 и х2 + у2^>1. Случай III имеет место,
если л:<;0, у<^0 и х2 -\- у2^> \.
Дуги у и у' = arc sin (xY 1 — у2 + у Υ \ -—χ2) имеют оди-
наковый синус, но (по определению арксинуса) — γ^ν'< 5-,
следовательно, в случае I 7 = 7'; в случае II γ=π — γ' ив слу-
чае III γ = —π —γ'.
Итак, имеем окончательно:
arc sin (χ Υ\ — у2 + yj/l —- я2);
xy < 0 или χ2 + V2< 1.
arc sin χ + arc sin у =
Пример.
π — arc sin (xYl — у2 + у |/1 — χ2);
(1)
ι · 3 , .5 · 56 /3\2 . / 5\2
1. arc sin ^ + arc sin Гз = arc sin ^; (τ) + (is)
2S0
2. Заменив в формуле (1) χ на —х. получим:
arc sin a;— arc sin у
arc sin (*|/Ί —у2 — у j/Ί —χ2);
ху> 05 или x2-fy2< 1.
π — arc sin (xj/ 1 — y2 — у }/Ί — x2);
(2)
x>0, y<0 и *2 + у»>1.
— π —arc sin (χ}/Ί — у2— у j/l — х2);
\ л: < 0, у > 0 и х2 + у2 > 1.
3. Выразить сумму γ = arc cos x + arc cos у через арккосинус.
В силу основных неравенств
О <ζ arc cos χ <^ η и 0 ^ arc cos у < π,
имеем
О < arc cos x + arc cos у < 2π.
Возможны следующие два случая.
Случай I: 0 < γ < π. Если 0 < arc cos x + arc cos у < зт, то
arc cos x < π — arc cos y.
Приняв во внимание, что обе дуги arc cos χ и я — arc cos у
расположены в промежутке [0, π] и что в этом промежутке ко-
синус убывает, получим:
χ > cos (π — arc cos у) = — cos (arc cos y) = — y,
и, следовательно: χ>—у, откуда х + у > 0.
Случай II: π<^γ^2π. Если
π < arc cos x -f arc cos у <^ 2π,
то
π — arc cos у < arc cos x,
откуда при помоши рассуждений, аналогичных предыдущим,
получим л: + у<0. Из сопоставления результатов следует, что
случай 1 имеет место, если χ -f- у > 0, а случай IIv если χ -f
Из равенства
cos (arc cos χ + arc cos у) = xy — ]/" 1 — л:2 ]/"l — у2
следует, что дуги
γ = arc cos χ + arc cos у и у' = arc cos (xy — ]/1 — л:2 j/
имеют одинаковый косинус.
В случае Ι γ = γ'; в случае II γ = 2π — γ', следовательно,
у2)
arc cos χ + arc cos у =
arc cos (xy — |/1 —· χ2 γ 1 — у2);
x + y>0.
2π — arc cos (xy — j/l — x2 j/"l —
(3)
9B*
251
4. Заменив у на — у и приняв во внимание, что
arc cos (—у = π — arc cos у
и
arc cos(— ху — ]/Ί —χ2' j/l — у2) =
= π — arc cos {xy + j/Ί — χ2 ]^1 — у2),
получим:
[—arc cos (ху -f |/l — x2Y\ — }Ч х> у.
arc cos л: — arc cos у = \ (4)
[arc cos (ху + γΐ —χ2 /1 —у2), * < у.
Пример.
3 , 9 / 13\
arc cos -ψ -f- arc cos γζ = arc cos — == .
5. Выразить сумму γ = arc tgx + arc tgy через арктангенс.
Из неравенств
— 2-<arctgx<T и _<a
следует
— π < arc tg x + arc tg у < π.
Дальнейшие рассуждения аналогичны соответствующим рас-
суждениям, относящимся к сумме арксинусов.
Возможны следующие случаи:
случай I: — |-<γ<-| ;
случай II: γ<γ<π;
случай III: —Ж^У<С—-^ -
В случае I дуга γ оканчивается в правой (замкнутой) полуок-
ружности и в случаях II и III — в левой (открытой) полуокруж-
ности. В случае I имеем cosy >0, а в случаях II и ill cosy<^0.
Так как
1 — ху
cos у = - — ,
то в случае I ху < 1. В случаях II и III xy^>\.
Следствия:
а) Если числа л: и у разных знаков или хотя бы одно из них
252
равно нулю, то имеет место случай I. Если к и у — числа одного
знака, то случай I имеет место при ху < 1
b) Случай II имеет место при х>0, у>0, если л;у>1.
c) Случай III имеет место при *<0, у<0, если ху >1.
d) Равенство γ = ±-у имеет место при ху=\ (тогда созу=0);
если же
то
Дуга
содержится в интервале
(~Τ' τ) и tg7 =
γ'. Следовательно,
γ = γ' в случае I, у = π -j- у' в случае II и у = — π + γ'
в случае III. Из сопоставления изложенного получим формулу:
arctgA:+arctgy =
arc
, ху>\ (5)
j*~
не имеет смысла, в этом
Если ху=1, то выражение arc tg j_
случае дуга γ не имеет тангенса и не может быть представлена
в виде арктангенса.
Так, например,
arctg3-|-arctg-^ = π+агс tg(— 7) = π —arctg7.
В данном случае 3 · у > 1.
6. Заменив у на —у, получим:
arctgx—arctgy =
arctg
π+arctg
— π+arctg
—У
χ —у
\+ху
, ху<—
(6)
253
Если в выведенных формулах сложения положить χ = у, то
получим следующие формулы «удвоения»:
2 arc sin x =
arcsin(2xj/l— л;2); \х\<-
η — arc sin [2χγ\ —χ2);
V2
2 arc cos χ =
— π — arc sin (2* |Λ —χ2
fare cos (2x2— 1);
2π-
2arctgx ='
- arc cos (2x2 — 1); — 1 < χ < 0.
arctg-r^r; И<1
arc
arc tg
2x
1 —χ
2x
(7)
(8)
(9)
- π; χ < — 1.
Следуя методу, изложенному на рассмотренных выше при-
мерах, можно установить формулы деления пополам (см. стр. 232):
-7Г arcsinx=arc sin
•7Г arccosA:=arccos
l/L±£.
Г 2 '
-s-arc sin л: =
arc cos
— arc cos-
если 0<л:<1,
если — l<Ji<0,
(И)
(12)
Выведенными формулами не ограничиваются возможные пре-
образования суммы аркфункций. Не обязательно рассматривать
сумму или разность одноименных аркфункций. Так, например,
можно вывести формулы преобразования суммы arcsinx + arctgy
в любую другую аркфункцию. Можно было бы рассмотреть форму-
лы преобразования суммы большего числа, чем двух аркфункций.
Приемы выполнения подобных преобразований выяснены на рас-
смотренных случаях.
§ 42. Примеры преобразования сумм аркфункций
При преобразовании суммы аркфункций с конкретными
числовыми данными следует по возможности избегать поль-
зования громоздкими общими формулами, и нет необходимости пом-
нить эти формулы наизусть. Вычисление тригонометрических
254
функций от аркфункции и их сумм выполняется на основе теорем
сложения и известных соотношений, имеющих место для тригоно-
метрических функций. По конкретным числовым данным во многих
случаях бывает возможно непосредственно установить, в какой
четверти оканчивается рассматриваемая сумма аркфункции.
Примеры.
В примерах I—5 показаны различные преобразования сумм и разностей
аркфункции с числовыми данными.
1. Доказать, что
arc sin.
2
Решение. Имеем:
J^-=arctg(r2+l)3
^, a arctg
ибо У-— < 1 и arc tg J-— < arc tg 1 = — . Следовательно, сумма дуг
в правой части доказываемого равенства заключена в первой четверти
Взяв тангенс от левой части, получим:
tg (arc sin J^L + arc tg IjL) = tg (iL + arc tg ΪΣ.
^ 2 2 + /2 Ϋ2
j__j/2_ 2-/2 /2—1
2
Следовательно, правая и левая части равны (как дуги в 1 четверти).
2. Доказать, что
1 1 / 11 \
arc cos -к + arc cos у== arc cos I — Т7 I ·
Решение. Левая часть есть дуга, содержащаяся в верхней полу-
окружности. Вычислим косинус левой части:
_\ __УЪ /48 11
14 2*7 14'
Правая часть также содержится в верхней полуокружности, имеет тот же
косинус, что и левая, следовательно, дуги равны.
3. Доказать, что
1 1 32
2 arc tg -g- -+- arc tg -j = arc tg ^ .
Решение. Так как —- < 1, το arc tg — < — , а потому дуга 2 arc tg —-
содержится в первой четверти. Следовательно, левая часть содержится
255
в верхней полуокружности. Имеем
25
Вычисляем тангенс левой части
(2arctgT +arctgTj=
Ц *2 4 =32
11 43*
""12 · 4
Так как тангенс левой части положителен, то она содержится в первой
четверти. Левая и правая части суть дуги первой четверти, имеющие оди-
наковый тангенс, следовательно, эти дуги равны.
4. Доказать, что
Ί/Τ /ёГ+i π
arc cos I/ _—arc cos·
2/3
Решение. Левая часть заключена в правой полуокружности; вы-
числим ее синус:
Τ/ — —
sin ( arc cos Ί/ — — arc cos
V6 +1
3 2/3
V* l/K_9,/i
Следовательно, левая часть равна — .
6
5. Доказать, что
arc tg -g- + arc tg -g- + arc tg у -f arc tg -g- = -j-.
Решение. Каждая из дуг в левой части меньше, чем—, а потому
4
левая часть содержится в верхней полуокружности. Вычисляем (последова-
тельно) тангенс левой части:
/ 1 1 \ 4
tg i arc tg -3- + arc tg 1Н=у J
Г/ 1 1\ 11 У + У 7
tg (arc tg j + arc tg у 1 + arc tg у = ^- = -g- j
Kl 1\ 11 "9"+8"
arc tg -3 + arc tg yj + arc tg у J = у j- = 1.
256
Единственная дуга в интервале (О, π), имеющая тангенс, равный 1.
есть —
4
Непосредственное преобразование сумм аркфункций (без пользования
готовыми формулами) можно успешно применять также и в ряде случаев,
когда аргументы аркфункций являются буквенными выражениями (т. е. со-
держат буквы-аргументы либо параметры)
Примеры. 6. Вычислить сумму
у = arc tg x -f- arc 1
U+ χ '
Решение. Имеем:
1 —χ
tgy = -
— χ
1 + х
Так как — π < у < π, то ' у = — либо у = ■— -2_ π, Равенство у = — £
4 4 4
может иметь место лишь при условии, если выражения:
знаками обоих арктангенсов, отрицательны:
находящиеся под
χ <0 и
Зта система неравенства удовлетворяется, если χ < — 1,
Итак имеем:
π
-^-, если *> —1,
— ~Τπι если
На чертеже 167 представлен график данной функции.
7 Доказать тождество
F 1 ~| Л
2 arc tg у = arc cos x
ι -\- Χ
Решение. Область оп-
ределения левой части нахо-
дится из условия """ х > О,
откуда
1 — χ > О
ι + χ > о
или
II) 1-.
-1
о
-
Черт. 167
1 + х<0
Первая система неравенств имеет общее решение — 1
противоречива. Областью определения правой части служит сегмент
257
а вторая
—-1<*<1. Следовательно, совместное рассмотрение левой и правой ча-
стей доказываемого тождества возможно в промежутке —1 < χ < 1. Левая
и правая части содержатся каждая в промежутке [0, π]. Для доказатель-
ства тождества достаточно установить равенство косинусов от правой и от
левой частей. Имеем:
cos (2 arc tg l/ 1 """* ) = 2 cos2 (arc tg l/ Llli j — 1 =
\ V l + x / \ V i + x I
= 2 -!-*.
откуда следует справедливость доказываемого тождества
Примечание. Тождество можно доказать, положив в формуле
= arccos*.
8. Вычислить сумму
arc tg -l + l.2.xt + arc tg 1 + 2.3a.2 + ... + arc tg j + „ (*+ 1} χί ■■
+
6=1
Решение. Рассмотрим разность
γ = arc tg (k + 1) χ — arc tg kx,
где k — натуральное число; эта разность содержится в интервале
/ π π \
ί — у , γ Ι. Так, при χ > 0 имеем:
π
О < arc tg kx < arc tg (k + 1) χ < -γ
и 0 < γ < ^~ . Аналогично при *<0 получим — JL < γ < 0. Следователь-
но, дугу γ можно преобразовать в арктангенс:
Положив последовательно k = \t 2, ..., η:
arc tg 2x — arc tg * = arc tg
у
arc tg 3* — arc tg 2* = arc tg j + 2.3^2 ·
arc tg (n + 1) χ - arc tg я* = arc tg
n {n +
25?
и, просуммировав, получим!
η
Harctg
пх
Положив, в частности, *=1, получим}
9. Вычислить сумму
Srt = arctg у
у + arctg уу^ + ··· + arctg y^-·
Решение. Каждое из слагаемых меньше, чем —. Суммируем по-
следовательно;
5χ = arc tg у , 52 = arc tg у + arc tg yyj- = arc tg у < "f"}
1 2 1
S3 = S2 + arc tg y^g- = arc tg у + arc tg y^" =
= arc tg 1 = arc tg _<-?-.
j 1 4 4
Применим метод математической индукции. Допустим, что при некотором
k имеем
Sk = arc tg £-q7j »
тогда получим;
k 1
SkjL\ = arc tg T-r-j + arc tg 0(bJL n2 =
1 _Jl_
Л+1 2(Л+ I)2
Согласно принципу математической индукции формула
верна при произвольном натуральном п.
На примерах 10—13 показано исследование некоторых функций, задан-
ных формулами, содержащими обратные тригонометрические операции.
10. Исследовать функцию
χ + У 1 — х2
у = arc cos x -j- arc cos = »
?59
Решение Преобразуем второе слагаемое Имеем:
arc cos χ — arc cos —f-=r = arc cos *—--£- =
— arc cos ·
/2
arc cos -
/2
χ <
/2 '
1
/2'
Это преобразование можно выполнить либо непосредственно, заметив что
при χ > —т=г дуга arc cos x — —р= оканчивается в четвертой четверти,
а при χ < г—- в первой, либо можно воспользоваться готовой форму-
лой (4) (см предыдущий параграф).
Следовательно,
1
arc cos
- arc cos χ + -j ; χ > γγ »
1
/2
arc cos χ — -j ;
2 arc cos л: — ■
π
Построим график данной функции Областью опре-
деления служит сегмент (—1 1J. На сегменте
— l> 47Ίτ\ Функция
у = 2 arc cos χ — —ζ
убывает от jn до j. На сегменте —j=- \
Черт. 168
11. Исследовать функцию
функция имеет значение равное — (черт. 168).
4
у = arc sin
2х
Решение. Область определения находится из условия
2х
< 1 или 2 |*| < (1 + х2).
Последнее неравенство справедливо при всех значениях х. Следовательно,
областью определения служит интервал — оо < χ < -f- oo.
26Q
Воспользуемся формулой (стр 232).
sin (2 arc tg x) —
2х
Рассмотрим две дуги. 2 arc tg x и arc sin
2x
. имеющие одинаковый
1 + χ2
синус. Для дуги 2 arc tg л: имеют место неравенства — к < 2 arc tg x< к,
для второй дуги имеем:
π 2χ π
—- 2 < arc sin ι _j_ д.2 < 2
Если — 1 < * < 1, то — — < arc tg χ < i .
4 4
Следовательно,
π π
·-- γ < 2 arc tg a: < γ и 2 arc tg л: =
arc sin
2x
Для значений х < — 1 имеем —π < 2 arc tg χ < —— , а потому
2x
arc sin
= — π —2 arc tg λ:.
2*
Если χ > 1 то arc sin = π — 2 arc tg χ.
1 + χ2
Итак, получим:
ί — π — 2arctg χ; χ < — 1;
2 arc tg χ; — 1 < χ < 1;
π — 2 arc tg χ; 1 < χ
Откуда имеем:
X
у
— oo
0
<x<
\
— 1
π
<X<
/
1
π
"2
<,<
0
График данной функции получается путем соединения дуг трех линий
как показано на чертеже 169.
Υ
169
261
Примечание. Наличие угловых точек при х = ^-\ можно обна-
ружить методом дифференциального исчисления Вычислив производ-
ную, получим1
__ 2 (1 + а:2) — 2лг2 _
dx
Г \ 1 ~|~ X )
+
2(1— χ2)
Правая производная в точке I равна /_j_(l) = — 1, а левая равна
/1_(1)=1. Следовательно, χ = 1 есть угловая точка
12. Исследовать функцию
2
Решение. Так как при любом значении χ
\ 1 - х2 | < 1 + х2,
то областью определения служит интервал —оо < χ < + оо. Воспользуемся
формулой (стр. 232):
1-х2
cos (2 arc tg *) = j _|_ ^2 ·
Рассмотрим две дуги, имеющие одинаковый косинус?
1-х2
2 arc tg л: и arc cos ^ , ^2 i
1 — х2
в силу определения аркфункций имеем.
1 х
— π < 2 arc tg χ < π и 0 < arc cos j . ^2 < π·
Функция четная. Следовательно,
1 ·— χ2 [ 2 arc tg χ; χ > О,
{
arc cos
{
\+x2 1 — 2arctgx; χ < 0.
Отсюда находим:
У
—с»
π
<х<
\
0
0
<х<
/
-Н оо
π
График представлен на чертеже 170 (начало координат является угловой
точкой).
13. Исследовать функцию
у = arc sin χ + 3 arc cos χ + arc sin (2x Vl — x2).
262
Решение. Согласно формуле (7) (стр 254)
2 arc sin χ;
arc sin (2xV\ — χ2)-
π — 2 arc sin x;
Vf,
< χ < 1;
— π —2arc sin λ:; — 1 < χ < — -~т=г
Черт 171
Приняв во внимание, что arc sin лг + arc cos χ = — , получим:·
3
"2" π;
w<x<wl
-γ + 4 arc cos χ; γ=· < χ < U
3
— "ο* π + 4 arc cos x; — 1 < χ < —
График представлен на чертеже 171.
§ 43. Некоторые свойства полиномов Чебышева
Известно, что n-й полином Чебышева
Τ γ\ — γη — Γ2 γη~2() — у2) -4- Γ4 гп~4(\ г2)2
совпадает на сегменте [—1; 1] с функцией, заданной формулой
cos (n arc cos x)y что позволяет установить ряд замечательных
свойств полиномов Чебышева.
263
Теорема. Для последовательности {Тп(х)} полиномов Чебы-
шева имеет место рекуррентная формула
х)-Тп^(х). (1)
Доказательство. Положим в тождестве
cos 72+1) φ = 2 cos ηφ cos φ — cos (η — 1)φ
φ = arc cos χ, тогда получим.
cos[(Az-f 1) arc cos χ] = 2 cos |η arc cos x] cos (arc cos x) —
— cos [(η — 1) arc cos χ],
откуда следует справедливость тождества (1) на се ι менте
[—1, 1J. Левая и правая части (1) суть многочлены, значения
которых равны при бесконечном множестве значений аргумента
— 1<[x<1, следовательно, многочлены тождественны над
полем действительных (комплексных) чисел, ч. т. д.
Пользуясь рекуррентной формулой (1), можно последова-
тельно вычислять полиномы Чебышева. Первые два полинома
найдем непосредственно:
Го (х) = cos (0 arc cos x) = 1, Тг (χ) = cos (arc cos χ) = χ.
Для нахождения следующих полиномов применяем формулу (1):
Т2 (х) = 2x7, (х) - Го (х) = 2*а - 1;
Г3 (х) = 2хТ2 (х) — Тг х) = 4х3 — Зх;
Г4 х) - 2хТ9 (х) — Г2 (*) = 8х4 — 8х2+1
и т. д.
Теорема. Многочлен Тп(х) имеет η различных действитель-
ных корней; все корни Тп(х) содержатся в интервале (—1, 1).
Доказательство. Из формулы
Тп (х) = cos (n arc cos x)
следует, что Тп (х) = 0, если
2k —\ (2^ — 1) те
п arc cos χ — —ό— π, откуда χ = cos —^— ·
Полагая k = 1, 2, 3, ... η, получим п различных корней
Х\у Х%> ··*> ^п'
2k — I
Х* = cos -27Г π·
2^ ι 2/ 1
В самом деле, если 1 < k < / < η, то 0 < 2п л < -^— π < π,
а потому xk'^>xl. При значениях /г, отличных от рассмотренных,
никаких новых значений для хп получено быть не может, так как
264
многочлен Тп(х) не может иметь больше, чем η различных дей-
ствительных корней. Это же видно и из общей формулы для xk
χ , Λ = cos
η+ρ
= cos π —
(2ρ-\)π\__
2η
Так, например, *я+1=*л; *η+2 =*„_,; *я+8 = *„^2 и τ· д·
Числа л:,, х2, ..., л:Л суть простые корни, ибо все они раз-
личны, ч. т. д.
Для построения корней Тп можно поступить следующим
образом: разделим полуокружность единичного радиуса на 2п
равных частей, занумеруем точ-
ки деления в направлении, ука-
занном на чертеже 172, и от-
метим точку Л, ближайшую к
точке В с абсциссой 1. Затем,
начиная с точки Л, спроекти-
руем на отрезок [—1, 1], через ί|
одну, точки деления. Полу- х^х7 х6
ченные в проекции точки и яв-
ляются геометрическим изобра-
жением корней полинома Тп(х).
На сегменте — 1 <*<1 значения
Черт. 172
полиномов Чебышева
принадлежат тому же сегменту [—1; 1]
Это следует из равенства Тп(х) = cos (я arc cos х) на сегменте
Вычислим те значения χ на сегменте |—1, 1], для которых
7л(л:) = ±1; так как Тп(х) = cos (n arc cos х), то
Tn(x)=\f если π arc cos л: = 2kn\
7ΊΛ(χ) = — 1, если я arc cos λ: = (2k + 1)я.
Таким образом,
Τ η (χ>η) = (— 1)ΓΙι если η arc cos x'm = mn.
Отсюда найдем:
x'o = 1; Χ\ = cos -^ ; x2 = cos Ц-;...; *„ = —!.
Итак,
я(х\) = -1; Тп (х2) == 1, ...,
265
Из формулы
у = Τп (х) = cos (n arc cos χ)
получим промежутки монотонности полиномов Чебышева:
χ
...
5π
cos —
η
J
/
4π
cos —
η
1
3π
со? —
η
—]
/
2π
cos —
η
ι
Ν.
π
COS
η
— 1
/
ι
ι
Графики шести первых полиномов Чебышева представлены
на чертеже 173.
Черт. 173
Теория многочленов Тп(х) была разработана П. Л. Чебышевым
в его труде «Вопросы о наименьших величинах, связанных с приб-
лиженным представлением функции». П. Л. Чебышевым была по-
ставлена и решена следующая задача: среди многочленов вида
найти такой многочлен, который на данном сегменте имеет наи-
меньшее уклонение от нуля, т. е. для которого наибольшее значение
его абсолютной величины на данном сегменте является наименьшим.
266
Многочлены, обладающие этим свойством, играют важную роль
в анализе и в его приложениях. Докажем, что полиномы Чебышева
решают изложенную задачу для сегмента [—1, 1].
Теорема. Из всех многочленов степени п, имеющих коэффициент
при хп равный единице, наименьшее отклонение от нуля на сег-
менте [—1, 1] имеет полином
Τη(χ)τλΤηχ).
Доказательство. Коэффициент при хп многочлена Тп(х)
равен 1, так как старший коэффициент Тп(х) равен 2п~Л (§ 17).
Наибольшее значение |Гл/а:)| на сегменте [—1, 1] есть -—j-,
так как наибольшее и наименьшее значения Тп(х) суть ± 1·
Итак, отклонение от нуля на сегменте [—1, 1] многочлена
-—^ Тп (х) равно -^ц. Предположим, вопреки утверждению тео-
ремы, что некоторый многочлен
имеет на сегменте f—1, 1] отклонение от нуля меньшее, чем
-Tfrr· Согласно этому предположению, многочлен Рп{х) отличен
от многочлена Тп(х) и на сегменте [—1, 1] удовлетворяет не-
равенствам:
^Μ<^γϊ. (2)
Рассмотрим точки
« π ' 2π ' -
χ0 =ζ [у χ\ = COS — , Χ2 — COS — , ..., Xn = — 1.
В этих точках имеем:
Tn{x'n) = (-^f. (3)
Разность R (χ) = Тп (χ) — Рп (χ) есть многочлен степени не
выше η—1. Согласно неравенствам (2) и неравенствам (3), будем
иметь
#(*о)>О, /?(*!)< О, /?(^)>0,...
267
Сегмент [—1, 1] разбит при помощи точек лго, х\.*.,х'п на η
сегментов. Рассмотрим один из этих сегментов; его границами
служат две соседние точки xi+i и X/, разность R(x) обращается
в нуль по крайней мере в одной точке каждого из сегментов
[*/+!, χ'ι]· В самом деле, R(x) в концах сегментов [*j+i, xt] имеет
разные знаки, а потому, в силу непрерывности, обращается
в нуль по крайней мере в одной внутренней точке каждого
сегмента. Следовательно, /?(*) = О, так как, будучи многочленом
степени не выше η—1, он имеет по меньшей мере η корней,
а потому
что противоречит сделанному предположению. Следовательно, не
существует многочлена, имеющего на сегменте [—1, 1| отклоне-
ние от нуля меньше, чем -—j , а потому Тп (л;) есть многочлен,
наименее уклоняющийся от нуля, ч. т. д.
Глава пятая
УРАВНЕНИЯ И НЕРАВЕНСТВА
§ 44. Тригонометрические уравнения
Уравнение
F(x, у, ...,*) = О (F)
называется элементарным трансцендентным, если
F(x, у. ..., г) есть элементарная трансцендентная функция. Следо-
вательно, функция F(x, у, ... г) содержит элементарные трансцен-
дентные операции над неизвестными и не может быть представлена
никаким алгебраическим выражением*.
Система уравнений
F, = О, F2 = 0, .... Fk = 0 (Ft)
называется трансцендентной, если хотя бы одно из уравне-
ний, входящих в ее состав, является трансцендентным.
Уравнение
F, (х, у, ... z) = F2(x, у, ..., ζ)
называется трансцендентным, если эквивалентное ему уравнение
Fx (χ, у, ..., ζ) — F2 (χ, у, ..., ζ) = О
трансцендентно**.
* Так, например, уравнение
Ig 10^2+1 = 1
не является трансцендентным, ибо его левая часть, хотя и содержит транс-
цендентные операции, но на самом деле трансцендентной функцией не
является:
lglO*4""1 = *2+1.
** Так, например, уравнение
х* + 2х = 1 + 2х
эквивалентно алгебраическому уравнению х2 —1=0, а потому и не счи-
тается трансцендентным.
269
В тригонометрии рассматриваются трансцендентные уравне-
ния, содержащие тригонометрические и обратные тригонометриче-
ские операции над неизвестными.
В общем случае элементарное трансцендентное уравнение нель-
зя решить элементарными средствами, т. е. нельзя установить пра-
вил, позволяющих получить общее решение уравнения путем после-
довательного выполнения ряда арифметических действий и элемен-
тарных операций над данными (известными) числами (коэффици-
енты, параметры и пр.). Однако в ряде частных случаев общее реше-
ние трансцендентного уравнения можно выразить одной или не-
сколькими формулами, содержащими только лишь элементарные
операции над известными числами.
В тригонометрии под названием тригонометрических уравнений
рассматриваются частные виды уравнений (систем), содержащих
тригонометрические операции над неизвестными. Мы не даем опре-
деления понятия тригонометрического уравнения в общем
виде по следующей причине: это определение было бы плодотвор-
ным, если бы выделение класса уравнений, названных тригономе-
трическими, связывалось с установлением общих методов их реше-
ния и исследования; на самом же деле речь идет лишь о тех или
иных частных видах уравнений (называемых тригонометрическими)
и специальных (а не общих) приемах их решения.
Примечание. Принятые во многих старых учеб-
никах определения нельзя признать удачными. Например,
под определение тригонометрического уравнения, как содер-
жащего неизвестное под знаками тригонометрических функ-
ций, подойдут многие уравнения, неразрешимые элементар-
ными средствами. Так, например, уравнение
χ + sin л: = 1
линейное относительное χ и sinx, неразрешимое элементар-
ными средствами, обычно не называют тригонометрическим.
С другой стороны, если сделать оговорку, что неизвестные
должны содержаться только лишь под знаками триго-
нометрических функций, то под это определение не подойдет,
например, такая система:
sin χ + sin у = α, χ + у = b,
приводимая обычно в учебниках среди тригонометрических
уравнений.
Вопрос о том, следует или не следует данное
уравнение, содержащее тригонометрические функции, считать
тригонометрическим, не имеет принципиального значения;
и нет никаких неудобств, когда этот термин применяется к тем
уравнениям, которые рассматриваются в каждом данном
случае.
270
В практике решения тригонометрических уравнений наиболее
часто встречаются уравнения вида
где f(x) — периодическая функция. Период / функции f(x) (обычно
наименьший положительный) будем называть периодом урав-
нения (/). Для уравнения, обладающего периодом,
достаточно найти все его решения, принадлежащие какому-либо
полусегменту равному подлине периоду уравнения, например полу-
сегменту 0< %</. Пусть χι, хъ ..., xk9 ....— множество всех решений
уравнения (/) на полусегменте [0, /] (для уравнений, рассматривае-
мых в элементарной математике, это множество, как правило, к о-
н е ч н о); тогда, в силу периодичности данного уравнения, множе-
ство всех его решений составится из двухсторонних арифметических
прогрессий Xi + kj, x2 + k2l, Хз + &з1> ··· (где kit k2, A3).··—про-
извольные целые числа) с разностью равной /. Так, например, пер-
вую прогрессию в развернутом виде можно записать следующим
образом:
... хх — 2/, хг — Z, хъ хг + /, хг + 2/, ...
Из изложенного следует, что множество (если оно непусто) всех
решений уравнения, обладающего периодом, можно представить в ви-
де совокупности двухсторонних арифметических прогрессий с раз-
ностью равной периоду уравнения.
В частности, в § 12 для простейших тригонометрических урав-
нений были получены следующие формулы общих решений:
Уравнение
a) cos х = т
период 2π
b) sin χ = m
период 2π
с) tg χ = m
период π
d) ctg χ = m
период π
Общее решение
χ = i arc cos m + 2&π, если | m\ < 1
не имеет решений, если \т
χ = (—1 )п arc sin m + ηπ, если
не имеет решений, если \т
> 1
т < 1
> 1
χ = arc tg m + &π, где т — произвольное дей-
ствительное число
х = arc ctg m + kn, где т — произвольное дей-
ствительное число
271
Так, при |/я|>1 множество решений уравнения а) пусто,
при \пг\ <. 1 состоит из двух арифметических прогрессий (двухсто-
ронних):
..., arc cos m — 2π, arc cos m, arc cos m + 2π, ...,
„.., — arc cos m — 2π, — arc cos m, — arc cos m + 2π, ...
Эти прогрессии в общем случае различны, однако, в частных случаях
могут совпадать. Так как для обеих прогрессий разность одинакова: d=2n,
то для совпадения прогрессии необходимо и достаточно равенство какого-
либо члена первой прогрессии какому-либо члену второй прогрессии;
arc cos m + 2&π = — arc cos m + 2/π,
откуда
arc cos tn = (/ — k) π.
Так как 0 < arc cos m < π, то значения k и / должны удовлетворять
системе неравенств
0< (i—k)< 1.
Следовательно, или / = k или / — k — 1.
В первом случае arc cos m = 0, т = 1 и обе прогрессии обращаются
в одну: {2&π}. Во втором случае arc cos m = π, m = — 1 и обе прогрессии
обращаются в одну: {(2& + 0π}·
При т=0 обе прогрессии хотя и различны, но их члены можно объе-
динить в одну прогрессию с разностью π. В самом деле, в этом случае
arccosm=u и общие члены первой и второй прогрессий соответственно
суть:
и —γ + 2/π = γ+(2/-1)π.
Это суть числа вида — + ηπ — при η четном получаются члены первой
прогрессии, а при η нечетном — второй.
Аналогично общее решение уравнения Ь) либо пусто, либо (в об-
щем случае) состоит из двух арифметических прогрессий.
Общее решение уравнения с), а также уравнения d) есть дву-
сторонняя арифметическая прогрессия с разностью π.
Решение уравнения вида
(1)
равносильно нахождению общего решения уравнения
/ (х) = ± arc cos φ (χ) -f- nnt (2)
с целочисленным параметром п.
Сказанное (с надлежащим изменением) относится к прочим
уравнениям того же вида, но для которых вместо cos f(x) берется
какая-либо другая тригонометрическая функция от функции /(*).
В частности, если функция f(x) алгебраическая, а функция
<р(*) постоянная: φ(χ) = m( = const), то уравнение (2) является ал*
гебраическим.
т
Всякое множество решений тригонометрического уравнения,
заданное формулой, содержащей целочисленный параметр, будем
называть серией решений. Серия решений может быть общим реше-
нием, а может являться некоторой частью (правильной) множества
всех решений уравнения. Так, для уравнения sin χ = 0 серия реше-
ний χ = 2kn есть часть множества всех решений χ = ηπ.
Примеры. 1 Решить уравнение sin (kx + b) = т (где k=£0).
Общее решение состоит (вообще говоря) из двух арифметических про-
грессий или пусто. В самом деле, уравнение
sin (kx + b) = т
при | т | > 1 не имеет решений, а при | т | < 1 имеет бесконечное мно-
жество решений
kx + b = (— \)п arc sin m -{-ηπ,
откуда
arc sin m b ηπ
* = (-!)« — -T + —·
Одну прогрессию получим при п четном, а другую —при η нечетном,
для каждой из прогрессий разность равна .
k
Примерами уравнений этого типа могут служить:
/ π\ 4 π 4
a) cos I 2x -f- -j I = -g-, откуда 2x + -j = ± arc cos -g- + 2&π
и * = ± — arc cos -_ — -^. -f- &π, или в градусной мере χ ж ± 18°26' —
— 22°30' + 180°^;
(π \ /— π π π π
3* — -g-1 *= |/ 3 , откуда 3χ—-β =-^-\-Ы или x = -^--\-k-j .
2. Решить уравнение sin 2* = —J- .
Решение.
2х = (— 1)" arc sin (—у) + ηπ
или
где η — целое число. Условие 2х > 0 показывает, что последнее уравнение
(эквивалентное данному) имеет решения лишь при тех значениях п, при
которых его правая часть положительна. Это уравнение не имеет решений
при значениях η = 0, —1,-2, ..., при которых его правая часть отрицательна.
Ответ.
' = log. [(-I)"*1 у+ /1*1.
где η — произвольное натуральное число.
3. Решить уравнение cos (sin x) = r ,
10 Зак. 597 273
Решение.
sin χ —
2/ζπ.
Последнее уравнение имеет решение при условии
откуда найдем единственно возможное значение k = 0.
Итак данное уравнение эквивалентно следующему
-\-2kn
Ответ.
π
sin x= ± -g-.
π
х == -(- arc sin -£- +
arc sin — можно приближенно найти по таблицам:
arc sin -g- ж arc sin 0,5236 ж ЗГ34' ж 0,5509 (радиан)
4. Решить уравнение 1
cos χ2 = -к·.
Решение.
л:2 = ± 4 + 2£π.
Правая часть последнего уравнения неотрицательна при k > 1; кроме
того, при β = 0 она содержит неотрицательное число — . Общее решение
о
данного уравнения состоит из серии
где к — натуральное число, и из двух решений χ = ± 1/ — .
г о
§ 45. Об особых случаях решения уравнений
Понятие корня уравнения (см. «Специальный курс элементарной ал-
гебры», § 55)
h W = /2 (χ) (f)
может быть расширено в так называемых особых случаях, когда хотя бы од-
на из функций fi(x) и f2(x) теряет смысл. Именно, вводится следующее до-
полнительное определение — принцип предельного перехода:
Если в точке χ = а хотя бы одна из функций fi(x) и ί%(χ) теряет смысл, но
то число а считается корнем (особым) уравнения (i)*.
* При этом предполагается, что точка а является предельной точкой
для множества допустимых значений аргумента. В противном случае прин-
цип предельного перехода теряет смысл.
374
Это дополнительное определение принимается обычно в анализе Однако
школьный курс элементарной математики вынужден отказаться от приме-
нения принципа предельного перехода *. В силу сказанного, возможны две
точки зрения на случай, когда при некотором значении χ = α, хотя бы одно
из выражений f^x) или /2(х) теряет смысл.
I. Согласно первой точке зрения, дополнительное определение кор-
ня в особом случае не принимается, а потому, χ = а не считается корнем
уравнения.
II. Согласно второй точке зрения, надо произвести исследование пре-
дела ^,a[fi — /2]: если этот предел не существует, или не имеет смысла,
или отличен от нуля, то а не есть корень уравнения', если же этот предел равен
нулю, то а есть корень (особый).
Возможно придерживаться как той, так и другой точке зрения, но во
избежание недоразумений (там, где они могут возникнуть) надо указывать,
какая из этих точек зрения принимается.
Примеры.
1. Решить уравнение
1— cos 2jc sin 2л:
2 sin л: 1 + cos2a:
(1)
Решение. Выполним последовательно преобразования, заменяющие
данное уравнение уравнениями ему эквивалентными:
1 —cos 2л: sin 2л:
2 sin л: ~~ 1 + cos 2л: = 0;
2 sin2 χ cos2 χ — sin x sin 2л:
2 sin χ cos2 χ ~~ *
είπΛ: sin 2л; (cos χ — 1)
2 sin л: cos2 л: ~ * *'
Приравниваем поочередно нулю множители числителя!
sin χ = 0, sin 2л; = 0, cos χ — 1=0,
откуда найдем:
х == /271, х == k -£, χ = 2тл.
Первая и третья серии решений содержатся во второй (k — четное и k = 4m),
π
поэтому все три серии можно объединить в одну χ = k ^.
При таком способе могут появиться посторонние решения, это суть те
решения, при которых знаменатель левой части уравнения (2) (эквивалент-
ного (1)) обращается в нуль. В данном случае любое значение χ из серии
*= k-κ является особым При k четном, k = 2п, левая часть уравнения (1)
теряет смысл, а при k нечетном, k = 2п + 1, — правая.
Согласно первой точке зрения, уравнение (1) не имеет решений и все ре-
π
шения χ = k к следует считать посторонними.
* Обоснование и применение принципа предельного перехода требуют
знакомства с понятием предела функции и наличия навыков в нахождении
пределов, что зыходиг за рамки школьной программы,
W \ 275
Согласно второй точке зрения надо исследовать предел левой части
уравнений (2), т. е предел
[sin a:· sin 2х (cos χ — 1)1
lim [ 2 sin* cos»* J = Hm [sin * ~ tg *!
в каждой из точек * = -χ-.
При k четном этот предел равен нулю, при k нечетном этот предел (ко-
нечный) не существует:
lim [sin а: — tg χ] = + оо.
2+*
Следовательно, числа вида χ = kn суть корни (особые) уравнения (1)
и формула χ — Ы дает его общее решение
2. Решить уравнение lg cos χ — 0.
Решение. Область определения правой части устанавливается из
условия cosx>0, откуда получим совокупность интервалов
— у + 2£π< χ < ^+2Ы.
Из данного уравнения найдем общее решение:
cos χ -.= 1 и χ = 2kiz.
Рассмотрим любое значение *, при котором cos*<0. Положим для опре-
деленности χ = π. При χ = π левая часть данного уравнения теряет
смысл, однако число π не может служить особым корнем. В самом деле, левая
часть не определена не только в точке π, но и в некоторой ее окрестности, а
потому lim lg cos x не имеет смысла, и следовательно, теряет смысл примене-
ние принципа предельного перехода.
2£+1
Точки χ = —η— Λ (концы интервалов, составляющих область опреде-
ления) также не являются решениями уравнения, так как в каждой из этих
точек
lim lg cos x = — оо.
§ 46. Соотношения между двумя дугами,
имеющими одинаковое значение
данной тригонометрической функции
Теорема. Необходимым и достаточным условием того, чтобы
Г две дуги и и ν имели одинаковый синус
sin и = sin v,
является наличие соотношения:
и = (—1)ην + ηπ;
2s чтобы дуги и и ν имели одинаковый косинус:
cos и = cos vt
является наличие соотношения:
и = ±υ + 2kn;
276
2k -4- 1
3° чтобы дуги и и ν, отличные от дуг вида —~-, имели
одинаковый тангенс, является наличие соотношения
• и = V -J- ППУ
где η — некоторое целое число.
Доказательство. Докажем утверждение 1°.
Условие достаточно. В самом деле, если имеет ме-
сто соотношение и = (—\)ηυ + ηπ, то в зависимости от четности
или нечетности η имеем:
. [υ + 2kn (n = 2k),
sin и =sin 1
[(л — υ) + 2kn (n=2k + 1),
в обоих случаях sin и = sin ν.
Условие необходимо. Пусть sin и = sin v; обозначим
через т общее значение синуса двух дуг и и ν:
sin и = т, sin ν = т.
Рассмотрим множество всех дуг, имеющих синус, равный т:
(— l)"arc sin m + пп)\ (1)
каждая из дуг и и ν содержится в выражении (1) при некотором зна-
чении п:
и =(—l)*iarcsinm + /ZiJi, |
ν = (— 1 У1* arc sin m + η2 τί. J
Если числа П\ и м2 одинаковой четности (т. е. оба четные или не-
четные), то вычтем почленно равенства (2):
и — ν = (П[ — /г2)я = 2kn,
где пл — п2 есть некоторое четное число 2k. Если п\ и пг — числа
различной четности, то сложим почленно (2):
и + υ = (tii + ^2)^ = (2k + 1)π, .
где Πι + η2 = 2k + Ι есть некоторое нечетное число. Итак, если
дуги и и ν имеют одинаковый синус, то либо их разность равна це-
лому числу периодов 2kny либо их сумма равна нечетному числу
полупериодов (2k + 1)π.
Следовательно,
[v + 2kn . nn .
и = I = (— \)ηυ + tin.
1 + (2*+1)
Утверждение 2° доказывается аналогично.
Условие достаточно. В самом деле, если
и = ± υ
277
то
cos и = cos (± ν 4- 2£π) = cos (± у) = cos υ.
Условие необходимо. Обратно, если cos и = cost^ = /я,
то
и = ± arc cos tn -f 2ηΊ π,
ν = ± arc cos m -f 2n2 π.
Складывая или вычитая (в зависимости от знаков при arc cos m
в правых частях), получим:
и ±. ν = 2 (ti] ± п2) л = 2пл,
где п = ftj ± п2 — целое число.
Также доказывается утверждение 3°, если
и = υ + пи, то tgw=tgu.
Обратно, если tgu = tgv = т, то и = arc tgm -f -Л, π и
у ·-= arc tg /и + &2 π> откуда
^ = у + (кг — k2) я = ν + ля, ч. т. д.
Сформулировать и доказать соответствующую теорему для котан-
генса предоставляем учащимся.
Если в случае 3° одна из дуг, например и, имеет вид —ί-~π»
то при наличии соотношения и = υ + ηπ дуга и имеет тот же
вид:
В этом случае tg и и tg и не существуют.
Обратно, если tg и и tgu не существуют, то дуги и и ν имеют вид:
_ 2kx + 1 __ 2&2+ 1
# 2 Я, U — 2 Я.
В этом случае
и = ν + (&J — &2)π = ϋ + яя.
Таким образом, в общем случае соотношение и = ν + ηπ
служит признаком (необходимым и достаточным) того, что либо
дуги и и ν имеют одинаковый тангенс, либо ни для одной из них
тангенс не существует.
Примечание. Теорему можно доказать другим способом.
Например, утверждение 1° можно доказать так:
рассмотрим равенство
и — ν и + ν
sin и — sin ν = 0 или 2 sin—^—cos—^— = 0,
278
откуда (необходимое и достаточное условие):
. и — υ и -φ- ν
sin— "2— = 0 или cos—2—— 0·
и, следовательно,
w — ν = 2/гл или м + и = (2& -f~ 1) π.
Объединив формулы в одну, придем к тому же окончательно-
му результату.
Рассмотрим уравнение
sin/(x, у, ..., z) = sin φ (*, у, ..., ζ),
выражающее равенство синусов от двух функций. Это уравнение
равносильно уравнению с целочисленным параметром п:
f = (_ ΐ)*φ -j- nn
(для краткости аргументы не пишем).
Аналогично, уравнение
cos/ = cos φ
эквивалентно уравнению
/ = ± φ + 2/ιπ.
Уравнение
tg/ = ίβφ (3)
не всегда эквивалентно уравнению
/ = φ + пп. (4)
В самом деле, всякое решение уравнения (3) есть решение урав-
нения (4), но н е всякое решение (4) служит решением (3).
Всякое решение уравнения (4), при котором tg/ и tg<p не имеют
смысла, является посторонним для уравнения (3).
Решения уравнения (4), посторонние для (3), находятся из ус-
ловия
π .
φ = -ζ- +
или из равносильного ему условия
Примеры.
1 Решить уравнение
sin χ = cos x.
Решение. Имеем:
/ π \
cos l-g- —a: = cos x,
откуда
π
279
выбрав в правой части знак +, получим
π 7t
2х = -у — 2&π, откуда χ = — — kn.
Заметив, что коэффициент— £ можно заменить на к (ибо — к, равно
как и к, может иметь произвольные целые значения), получим серию
решений:
π
X = -f + kn.
Выбор знака минус в правой части (1) приводит к противоречивому урав-
нению.
2. Решить уравнение
s\n3x + sin 12° = 0.
Решение.
sin Зл: = — sin 12° или sin Зх = sin (—12°),
откуда
Зд; = (— \γ (_ 12°) + п-180° и, следовательно, χ = (— 1)"+1 4° + 60°·/г.
3. Решить уравнение
cos Зх + cos 5* = 0.
Решение.
cos Зх = — cos 5л:
или
cos (За: + π) = cos 5лг,
откуда
Зх -f π = ± Ъх + 2^π.
Уравнение имеет две серии решений
(2/г—1) π (2&—1) π π
* ~J^ и a:v ' (2^+l)
(заменим /г на — ^).
4. Решить уравнение
Решение. Заменим данное уравнение следующим
2
t
(1)
(2)
При переходе от уравнения (1) к (2) область определения изменилась:
из области определения (1) исключились значения вида Ιπ и, с другой
π Г
стороны, к этой области присоединились значения вида -у + /π где / —
2 / π \ Ι
целое число и -q- ~тг + /π Ы= ηπ .
0 \ l I J
Решаем уравнение (2):
— -t (— \
1 _Л , у Зъ(2к+\)
3 χ _ 2 д: -f- Λπ, ^ — 10
280
В полученной серии могут содержаться решения, посторонние для
уравнения (3), которые находятся из уравнения
π π
γ — χ = -ζ + /π, это числа вида χ — Ы.
Таких чисел в рассматриваемой серии не содержится, уравнению (1) чис-
ла этого вида не удовлетворяют.
Числа вида
π /3 \
χ = -γ + /π I тогда γ χ = kv π
могут появиться в качестве посторонних решений уравнения (1). Это будет
иметь место, если
3π(26+1) π
ϊο =γ + ι*
или
3k-51 = 1. (4)
3* —1
Следовательно, —g— должно быть целым числом /, что имеет место для
чисел
k = 2 + 5t,
дающих при делении на 5 остаток 2. Эти значения k дают посторонние
решения уравнения (1).
§ 47. Решение уравнений посредством подстановок
В настоящем параграфе будут рассматриваться тригонометри-
ческие уравнения вида
F(sin*, cosx, tg*, ctg*)=O, (F)
где F(uy υ, до, ζ) есть некоторое аналитическое выражение от аргу-
ментов ut v, до, 2, не содержащее никаких других аргументов.
В частных случаях уравнение (F) может содержать не все, а лишь
некоторые из тригонометрических функций.
Рассмотрим частный случай, когда уравнение (F) содержит лишь
одну тригонометрическую функцию. Возьмем, например, уравне-
ние
/(cos*) = 0. (f)
Выполним подстановку cosx = t, тогда получим:
/(0 = 0. (fj
Составим смешанную систему
/(0=0, _1</<1. (ft, t)
Всякое решение t = tt смешанной систе^мы (ft, t) дает серию
решений (f), которую найдем, решив простейшее уравнение:
cos χ = tlt откуда χ = ± arc cos tt + 2kn.
Множество всех решений уравнения (f) состоит из множества
всех серий, соответствующих всевозможным решениям смешанной
ЮВ Зак. 597 281
системы (ft, t). Если смешанная система не имеет решений, то дан-
ное тригонометрическое уравнение также не имеет решений. В част-
ности, если (f) есть алгебраическое уравнение (не обращающееся
в тождество) относительно косинуса, то (it) также является алгеб-
раическим уравнением. В этом случае система (ft, t) имеет конечное
(быть может, пустое) множество решений, тогда и данное уравнение
(f) либо не имеет решений, либо имеет бесконечное множество ре-
шений, состоящее из конечного числа серий.
Аналогично, решение уравнения вида
/ (sin *) = О
подстановкой
sin χ = t
приводится к решению смешанной системы и к решению ряда
простейших тригонометрических уравнений.
Решение уравнения
/ (tg x)=0
приводится к решению уравнения
f(t) = О
без присоединения неравенств, так как тангенс может принимать
произвольное действительное значение.
Рассмотрим уравнение
F(s'\n xy cos χ, tg x, ctg x) = О,
содержащее несколько тригонометрических функций от неизвест-
ного. Все содержащиеся в уравнении функции можно выразить че-
рез одну из них, а потому решение уравнения (F) приводится к ре-
шению уравнения (fi). Однако формулы, выражающие тригонометри-
ческие функции друг через друга, содержат радикалы, и преобразо-
вания, связанные с освобождением от них, могут внести посторон-
ние решения. Эти решения должны быть устранены проверкой.
Примеры.
1. Решить уравнение
2 cos2 χ + 3 cos χ — 2 = 0.
Решение. Положив cosa; = /, составим смешанную систему
2/2 + 3/—2 =0, — 1 < / < 1.
Корни квадратного уравнения суть ^=~9~ и /= — 2. Смешанная систе-
1
ма имеет единственное решение t ==—у откуда найдем:
1 π
cos χ = γ и я = ± -д- + 2&π.
2. Решить уравнение
tg3 x + tg2 χ — 3 tg χ — 3 = 0.
282
Решение. Положив t = tg χ, получим:
t3 + t2 — 3/ — 3 = 0 ~·
или, разложив (над полем действительных чисел) на множители левую
часть:
(/ + 1) (t — /3) (/ + УЗ ) = О,
откуда
tg л; = — 1 и tg * = ± У~3,
и следовательно,
π π
х = — -ξ + kn и χ = ± — + ηπ.
3. Решить уравнение
sin χ + cos x = 1. (1)
Решение. Выразим косинус через синус:
cos л: = ± |/ 1 — sin2 x.
Положив sin# = /, составим смешанную систему
освободив уравнение от радикала, получим
2/2 — 2/= 0, откуда ^ = 0 и /а=1.
Значение / = sin* = 0 удовлетворяет уравнению (1) при cos χ = 1.
Следовательно, для решения ^=0 следует взять знак + перед радика-
лом. Решения уравнения (1), соответствующие корню tL = 0, суть
χ = 2kn,
так как из общей формулы χ = ηπ следует исключить нечетные значения
п, дающие для косинуса значение — 1.
Значение t2=l удовлетворяет уравнению (2), откуда найдем
π
sin л; = 1 и χ = -к + 2/гк.
Итак, имеем две серии решений:
π
x== Ύ
§ 48. Рационализирующие подстановки
Рассмотрим уравнение
R (cos х, sin л:, ...) = 0,
рациональное относительно содержащихся в левой части тригоно-
метрических функций. Если для выражения R известна рационали-
зирующая подстановка, т. е. все входящие в него тригонометриче-
ские функции выражаются в виде рациональных функций от неко-
торого промежуточного аргумента /, то применение этой подстанов-
ки приведет к рациональному уравнению относительно t.
ЮВ* 283
В соответствии с перечисленными в § 23 основными рационали-
зирующими подстановками, отметим следующие способы рациона-
лизации тригонометрических уравнений.
1) Универсальной подстановкой / = tg ^ приводится к рацио-
нальному относительно / всякое уравнение
R (cosχ, sin*, tgx, ctg*) = O, (R)
рациональное относительно тригонометрических функций одного
итого же аргумента х. Всякое (действительное) решение
t=t\ уравнения (R) (после подстановки) дает серию решений три-
гонометрического уравнения
χ = 2arctg/x + 2kn.
Посредством универсальной подстановки могут быть найдены
все решения уравнения (R), за исключением решений вида
χ = (2&+1) π (в этом случае tg-^ не существует). Наличие или от-
сутствие решений этого вида может быть установлено проверкой.
Применим универсальную подстановку к решению уравнения*
линейного относительно косинуса и синуса
a sin x-\- b cos χ = с, (1)
(где афО и b=j=O)
Положив tg γ — t, получим:
Сократив на ί2φθ, получим квадратное уравнение:
t2 (с + Ь) — 2at + с — b = 0. (2)
Числа вида χ = (2k + 1)π удовлетворяют данному уравнению,
если — b — с, поэтому исследованию подлежат два случая.
Случай 1Q Если а2 + Ь2 > с2, то корни (действительные)
квадратного уравнения (2) находятся по формуле
__ а±
с + Ь
Общее решение данного уравнения есть
284
Если с2 > а2 + Ь2У то уравнение (1) не имеет решений, так
как корни уравнения (2) мнимые.
Случай 2°. b = — с. В этом случае данное уравнение имеет
серию решений:
χ =(2k+ 1)π.
Уравнение (2) обращается в уравнение 1-й степени, из которого
найдем вторую серию решений:
х= — 2arctg-^- + 2£π.
П. Уравнение R (cos к, sin χ) = О, содержащее cos χ (или sin x),
лишь в четных степенях рационализируется подстановкой
/ = sin χ (или / = cos x).
III. Уравнение
aosin"A; + ajsin"-1 xcosx + a2 smn~2 cos2 χ -f- ... +
+ ancosnx = 0 (1)
называется однородным тригонометрическим
уравнением.
Случай Г. Оо^О.
Умножив обе части уравнения (1) на —^-, получим
COS X
«otg/2x + a1tg«-1x+ ... +ал = 0. (2)
Так как Φ 0, то появление посторонних корней произойти
не может. Область определения уравнения (2) уже области опреде-
ления уравнения (1) так как левая часть уравнения (2) теряет
смысл при значениях χ = ~2 + kn, а левая часть уравнения (1)
имеет смысл при всех значениях х. Однако, ни одно из чисел
ψ + kn не удовлетворяет уравнению (1); в самом деле, положив
в (1) χ = ~ + kn, получим противоречивое следствие cos χ =
= sin x = 0. Следовательно, потери решений произойти не может,
а потому уравнения (1) и (2) эквивалентны.
Случай 2°. Несколько первых коэффициентов равно нулю
а0 = αλ = ... = dk—x = 0; но ah Φ 0.
В этом случае уравнение примет вид:
cosk x(aksinn-k х +ak+\sinn~k-1 xcosx+ ... + ап cos"-* χ) = 0;
285
оно эквивалентно совокупности двух уравнении:
cos л: = 0 и aks\nn-f* χ + a,k+\ s\nn~k~l xcosx-f- ... -f-
+ ап cos"~* x = 0,
первое из которых есть простейшее уравнение, а для второго
имеет место случай 1°.
Примечание. Однородное уравнение может быть
сведено к алгебраическому подстановкой / = ctg x (два
возможные случая предгалгаем рассмотреть учащимся).
Ниже указаны некоторые тригонометрические уравнения, при-
водящиеся к однородным:
1°.
a sin2 x-\- b sin x cos x + с cos2 x = d.
Достаточно правую часть заменить на d (sin2 x + cos2 x)t чтобы по-
лучить однородное уравнение 2-й степени.
2°.
α sin4 x + Ъ sin3 x cos χ + с sin2 x cos2 ,ν -{- rfsin л: cos3 л; -f
Достаточно правую часть заменить на /-(sin2 χ -f cos2 л-)2, чтобы
получить однородное уравнение 4-й степени.
3°.
a sin2* + b sin 2 л: + с cos 2x + с/cos2* = е.
Достаточно преобразовать sin 2x и cos 2x по формулам двойного
аргумента и заменить е на е (sin2 χ + cos2 x), чтобы получить одно-
родное уравнение 2-й степени.
Примеры.
1. Решить уравнение
(cos χ — sin *) (2 tg χ + sec χ) + 2 = 0.
Решение. Применив универсальную подстановку, после преобразо-
ваний получим:
2 — 2t— 3
0
откуда (разложив числитель на множители):
(ЗР _ ]) (/2 _[_ 2t + 3) = 0.
1
Действительные корни последнего уравнения суть t =
Уз '
откуда
Данное уравнение не имеет решений вида (2k + 1) π, а потому полу-
ченная серия является общим решением.
2. Решить уравнение
3·— 7 cos2 χ sin л: — 3 sin3 χ = 0.
286
Решение. Положим / = sin χ, заменим cos2 χ на 1 — t2 и составим
смешаннию систему:
4/з _7/ +3 = 0, — 1 < t < 1.
Кубическое уравнение имеет три действительные корня:
неравенствам удовлетворяют два первые, откуда:
π π
тг + 2#π и χ = (—l)n~F· + ηκ.
Δ ο
3. Решить уравнение
Решение. Для рационализации достаточно положить tg а: = ^, так
как
рационально выражается через t. Имеем:
\ + t 2/
откуда
2(1 +/) /2 = 0.
Из последнего уравнения найдем два различные решения
/ = — ι и * = 0,
откуда:
π
х — — -j- + &rc и л: = /?π.
4. Решить уравнение
5 cos 2х = 4 sin x.
Решение. Так как cos 2x выражается рационально через sin x:
cos 2x = cos2 χ — sin2 χ = 1 — 2 sin2 x,
то для рационализации достаточно положить / = sin*, тогда получим:
до/2+ 4/ — 5 = 0,
откуда:
= (— \)п arc sin
δ. Решить однородное уравнение
2 sin3 * — sin2 cos χ + 2 sin χ cos2 л: — cos3 χ = 0.
Решение. Разделив обе части на cos3 л: и положив / = tg x, получим:
2/3_/2 + 2ί — 1 = 0
или, разложив левую часть на множители,
(<! + 1) (2/ - 1) = 0.
287
1
Это уравнение имеет один действительный корень t = -у» которому соот-
ветствует серия решений:
χ = arc tg у + kn.
6. Решить уравнение
6 sin2 *+3 sin χ cos χ — 5 cos2 x = 2.
Решение. Заменив правую часть на 2 cos2 χ + 2 sin2 *, после пере-
носа всех членов в левую часть получим однородное уравнение
4 sin2 χ + 3 sin x cos χ — 7 cos2 χ = 0;
положив t = tg x, получим:
At2 + 3* — 7 = 0, откуда ^ = — -j , /2 = 1
и, следовательно,
7 π
χ =— arc tg-j-)-^π и ΛΓ=~τ"+&π.
7. Решить уравнение
sin 2х = cos 2л: — sin2 χ + 1.
Решение. Преобразуем функции двойного аргумента и свободный
член:
2 sin χ cos л; = (cos2 χ — sin2 л;) — sin2 χ + (cos2 л: + sin2 χ)
или
sin2 x + 2 sin a; cos a: — 2 cos2 χ = 0.
Положим tg # = /:
/2 + 2* — 2 = 0, откуда / = — 1 ± VH
И χ = arc tg (— 1 ± Уз) + *π.
§ 49. О преобразовании формул общего решения
тригонометрического уравнения
Во многих практически часто встречающихся случаях общее
решение тригонометрического уравнения может быть задано при
помощи конечного числа серий решений. Разбиение
общего решения на серии можно осуществить различными способа-
ми, а потому общее решение тригонометрического уравнения можно
задать различными системами формул. Пусть, например, некото-
рая серия решений задана формулой
χ = f(n)
(где η — целочисленный параметр).
Разбив все целые числа на четные и нечетные η = 2k и
η = 2&ι + 1, можно разбить данную серию на две серии
г = f (9Ь) и у = f (9k* 4- IV
можно разбить данную серию на три серии, например, так:
χ = / (3k), χ = / (3k + 1), χ = / (3k + 2) и т. д.
288
Возможно также преобразование, при котором несколько серий
объединяются в одну, т. е. задаются одной формулой.
Возможно, что в двух сериях окажутся одинаковые решения,
в таком случае можно, оставив эти решения в одной серии, исклю-
чить их из другой.
Мы ограничимся рассмотрением лишь частного случая, когда
общее решение тригонометрического уравнения можно составить из
конечного множества двухсторонних арифме-
тических прогресси й*.
Ниже указаны некоторые общие положения, относящиеся
к двусторонним арифметическим прогрессиям, часто применяю-
щиеся при преобразовании формул решений тригонометрических
уравнений.
Рассмотрим произвольную двустороннюю арифметическую про-
грессию
..., а — 2d, а — d, α, а + d, а + 2d, ..., а + nd, ..., {a + nd}.
1°. За начальный член этой прогрессии (соответствующей значе-
нию η = 0) можно принять любой ее член. Положим, например,
Ь = а + kd (где k — произвольное целое число), тогда прогрессия
.... b — d>b,b + d,b + 2d, ..., b + Id, ... {b + Id}
состоит из тех же членов, что и первая прогрессия. В самом деле,
Значит, член а + nd, содержащийся в первой прогрессии под но-
мером п, содержится во второй прогрессии под номером η — k,
а всякий член b + ld = a + (/ + k) d второй прогрессии содержит-
ся в первой под номером / + k.
Тгк, например, общее решение простейшего уравнения
tg*= — γ"3 может быть представлено в виде:
х = — ~ + kn или в виде χ = -г- π + пп (здесь k = η + 1).
О о
2е. Если 6 = Ы, то все члены прогрессии
..., а — 26, а — ό, α, α + δ, α + 2δ, ... {α+ηδ}
содержатся среди членов прогрессии {а + nd}. В самом деле,
а + ηδ = а + nkdy т. е. л-й член прогрессии {а + ηδ) содержится
в прогрессии {а + nd} под номером nk.
Так, например, общее решение уравнения
sin jc-sin Зл: = 0
состоит из двух прогрессий:
х = kn и χ = /ζ ~,
* Этим случаем обычно ограничивается школьная учебная литература
289
a,
a
{a
a
+ d,
+ 2rf),
+ (k-
\)d,
a -\
(a A
(a A
\a-
-kd,
hd)
-2d
f (k
.
+ kd, ...
+ kd, ..
-\)d\-
Vkd,
(к
Φ)
('■)
(2)
-i)
Члены первой прогрессии содержатся во второй, а потому общее
решение может быть задано формулой χ = -^ (здесь ό = 3d).
3°. Пусть k — некоторое натуральное число; члены прогрессии
{а + nd} можно разбить на k арифметических прогрессий с разно-
стью kd следующим образом:
..., a — kd,
..., [a + {k—l)d] — kdf
Эти k прогрессий составлены из членов прогрессии {a -f nd},
причем всякий член прогрессии {а + nd} содержится среди членов
одной из этих прогрессий. В самом деле, разделим число η на k
(с остатком):
η — sk 4 г
(где г = 0, 1, 2, ..., k — 1), тогда член а + nd содержится в г-й
прогрессии под номером s.
Обратно, если даны k прогрессии с общей разностью kd, содер-
жащие члены а, а + d, a + 2d, ..., а + (k — \)d (каждый из этих
членов может содержаться лишь в одной прогрессии), то такие
прогрессии можно объединить в одну прогрессию с разностью d.
Так, например, двустороннюю прогрессию с разностью 2:
..., —7, —5, —3, —1, 1, 3, 5, 7, 9, И, 13, 15, ..., которую образуют
нечетные числа, можно разбить на следующие три прогрессии
с разностью
6:
1
—
1,
9,
7,
—5,
-1,
1,
з,
5,
7,
9,
п.
13,...,
15
17,...
Если периодом (не обязательно наименьшим положительным)
уравнения является 2π, то множество всех его решений в пре-
делах одного периода удобно изображать точками единичной окруж-
ности. Число прогрессий с разностью 2π, из которых состоит общее
решение, равно числу геометрически различных точек единичной
окружности.
Чтобы показать, что различные формулы изображают одно
и то же множество решений, достаточно убедиться, что на единич-
ной окружности эти формулы определяют одно и то же множество
точек.
Примечания: I. Для уравнений с периодом н е
равным 2я применение указанной геометрической интер-
290
претации может привести к ошибкам. Так, например, мно-
жество всех решений уравнения cos ·£ = 1 есть χ = Akzi (пе-
риод уравнения равен 4π). На единичной окружности полу-
чим точку Л(1, 0), однако, не всякая дуга 2ηπ, оканчиваю-
щаяся в точке Л, служит решением уравнения. Для геоме-
трического изображения корней уравнений с периодом не рав-
ным 2π следует пользоваться не единичной окружностью, а
числовой прямой.
II. Вопрос о преобразовании формул общего решения не
имеет принципиального значения. Вовсе не обязательно
подвергать каким-либо преобразованиям правильно
составленные формулы общего решения.
При решении уравнения различными способами его общее
решение может оказаться представленным посредством раз-
личных формул; в связи с этим иногда и возникает потреб-
ность в преобразовании друг в друга полученных формул.
Примеры.
1 Общее решение уравнения 2 sin2 χ— 1 (период уравнения π можно
задать) формулами
(I)
χ = (—
(II)
(черт. 174, римскими цифрами отмечены номера серий). Разобьем общее
решение на четыре арифметические прогресии:
3π
Χ ==
τ+(2/2+1) π
-τ- π -f- 2ηπ (свойство 1°
5
+ 2
Все четные прогрессии можно объединить в одну:
π π
χ = -τ -\-k ~2 . (свойство 3°)
Объединение серий (I) и (II) можно выполнить также следующим
образом:
* = ±т·
= (4* ± 1) χ .
291
Две прогрессии {4/г+1} и {4k—1} образуют множество всех нечетных
чисел {2п+1} (при n — 2k получим первую прогрессию, при n = 2k—\
— вторую), а потому
π π π
χ = (2л -φ- 1) -ξ = -ξ + η у .
на
2. Общее решение уравнения, рассмотренного на стр. 273 (пример 1а),
основании свойств Г может быть преобразовано так5
— 4° 4' + 180°/г f 175°56' + 180°η
х = ± 18°26' — 22°30' + 180° η = ί
^ — 4U όο
3. Решить уравнение
180°/г \ 139°24;
sin2 χ — cos2 χ = cos χ.
Черт. 174 Черт. 175
Решение. Положив t = cos x, получим^
2t2 + t— 1=0, откуда tx = у и /а = —1.
Следовательно, получим две серии решений;
и х = (2&+1) π. (черт. 175)
Полученные три арифметические прогрессии можно объединить в одну;
π
• =.
π
π
-тг + 2Ы = .
π 2π (2π — 1)π
-Т+-з /ι= 3 ·
4. Общее решение уравнения
sin -g- sin -g- = 0
состоит из двух геометрических прогрессий:
χ = 3/ζπ и jc = 5/π.
292
Однако эти прогрессии имеют общие члены: при k, кратном числу 5, чле-
ны первой прогрессии содержатся во второй, а при /, кратном числу 3,
члены второй прогрессии содержатся в первой. Общее решение может быть
представлено при помощи семи прогрессий, не имеющих попарно общих
членов:
χ = 15£π, χ = 3π (5k + 1), χ = 3π (bk + 2),
χ = 3π(5& + 3), Χ = 3π(5& + 4), χ = 5π (3k -f 1), χ = 5π (3k + 2).
Эти прогрессии можно представить в виде следующих четырех серий:
*=15&π, * = 3π(5&±1), χ = 3π (5k ± 2), χ = 5π (3k ± 1),
объединив попарно в одну формулу 2-ю и 5-ю, 3-ю и 4-ю, б-ю и 7-ю прог-
рессии.
5. Решить уравнение
2 cos2 4л; + sin2 3* = 1.
Решение. Выполнив рационализирующую подстановку t = cos 2x
2 cos2 Αχ = 2 (2/2 — I)2 = &4 — 8/2 + 2;
sin23A; = γ(1 — cos6*) == -g [1 —
-2- (1 — 4 cos3 2x + 3 cos 2*) =
получим уравнение
16/4 — 4/3 — 16*2 + Ы + 3 = 0 или (4/2 — 3) (4/2 — t — 1) = О,
/3 „ _в о_ 1 ± /Ϊ7
cos 2jc =
и cos 2лс =
следовательно,
*-±£+
— π+£π и χ = ± arc cos -
12
Первые две серии решений можно объединить в одну. Имеем*
12
_5_
12
π ·$- kn
Χ
(ь
/ π
π
"Ϊ2
+
— -
)+
π)
π
Ϊ2"
π
Ϊ2"
f- Ant
\-kitt
π
To +(2*-l)
π
•D-2-
π
(Ι)
(Η)
Д93
Эти четыре прогрессии с разностью π можно объединить в две с раз-
π
ностью ~2 :
и- и
π
ί2 "
π
Ϊ2 "
(- η
Τ" Λ
π
ΊΓ
π
72
π
±ΐ2~
π
Выполненное преобразование пояснено на чер-
теже 176, число 2π есть период уравнения (хотя и
не наименьший положительный).
Черт. 176
§ 50. Различные частные приемы
решения тригонометрических уравнений
При решении тригонометрических уравнений широко применя-
ется разложение левой части уравнения
/W=0 (f)
на множители. Из общих положений теории уравнений известно,
что если левая часть уравнения (f) представлена в виде произведе-
ния
= М*)М*).../л(*).
то достаточно решить совокупность уравнений
(fi)
объединив в одно множество все решения каждого из уравнений
(fi).
При решении совокупности уравнений (fj) следует брать лишь
те корни, которые принадлежат общей части областей определения
всех уравнений (fj). Если, например, при некотором значении χ = а
удовлетворяется какое-либо (хотя бы одно) из уравнений (fj), а ле-
вая часть некоторого другого уравнения теряет смысл, то значение
χ = а н е может служить решением данного уравнения (по-
сторонний корень).
При разложении на множители левой части данного уравнения
f(x) = 0 широко применяются формулы преобразования сумм три-
гонометрических функций в произведения.
В практике решения тригонометрических уравнений дробных
рациональных относительно содержащихся в них три-
гонометрических функций пользуются общими правилами пре-
294
образования дробных выражений с целью их упрощения.
Обычные преобразования уравнений, заключающиеся в сокращении
дробных выражений на общие функциональные множители числи-
теля и знаменателя, в сокращении взаимнопротивоположных (функ-
циональных) слагаемых, в применении законов арифметических
действий, в «отбрасывании» общего знаменателя, в возведении в на-
туральную степень обеих частей уравнения, не могут сузить
область определения данного уравнения, а могут лишь ее расши-
рить, поэтому применение указанных преобразований может
повлечь за собой появление посторонних решений, но не может
привести к потере корней. Отсюда вытекает следующее практически
важное указание: если при решении уравнения применяются пре-
образования, не сужающие его область определения, то в процессе
решения нет необходимости следить за изменением области опреде-
ления уравнения, а достаточно решить преобразованное уравнение
и проверить его корни подстановкой в данное уравнение.
Если кроме «упрощения» уравнения (сокращение на функцио-
нальные сомножители, сокращение взаимно-противоположных сла-
гаемых, «отбрасывание» общего знаменателя) не применялись ни-
какие другие преобразования, то посторонними решениями могут
оказаться лишь те значения неизвестного, при которых левая
или правая части данного уравнения теряют смысл.
При проверке корней полезно (в целях сокращения работы)
иметь ввиду следующие указания: для уравнения f(x) = О, обла-
дающего периодом, достаточно подвергнуть испытанию корни на
каком-либо промежутке, например, —^, -Л равном по длине пе-
риоду уравнения.
Если кроме того функция f(x) является четной (либо нечетной),
то наличие корня χ = а влечет за собой наличие взаимно-противо-
положного корня х = —а. В этом случае достаточно ограничиться
проверкой лишь неотрицательных корней на сегменте
по длине равном полупериоду уравнения.
Примечание. Если применяется принцип предельного пе-
рехода, то испытанию подлежат все те значения неизвестного (в пре-
делах периода либо полупериода уравнения), при которых теряет
смысл левая либо правая часть исходного уравнения
Примеры. В примерах 1 и 2 показано применение формул преобразования
сумм в произведения с целью разложения левой части уравнения на мно-
жители.
1. Решить уравнение
sin χ + sin 2x + sin Зх = 1 + cos x + cos 2x.
Решение. Преобразуем левую часть:
sin χ -|- sin 2x + sin 3x = (sin χ -f sin 3*) + sin %x —
= 2 sin 2x cos χ + sin 2x = 2 sin χ cos χ (2 cos χ -f 1).
29*
Преобразуем правую часть:
1 + cos χ + cos 2x = (1 -f cos 2x) + cos x = 2 cos2 χ + cos л: =
= cos a: (2 cos χ + 1).
Перенесем все члены в левую часть и представим данное уравнение
в виде
(2 cos χ + 1) cos a: (2 sin а: — I) = 0.
Приравнивая поочередно нулю три сомножителя получим три серии
решений:
2 π π
x=±-g-n + 2knt χ=γ+Ιϊπ, χ= (— \)n-Q-\-kTz.
2. Решить уравнение
sin2* + sin2 2a: = sin2 3a:
Решение. После переноса всех членов в левую часть, разложим ее
на множители следующим образом:
sin2 χ — sin2 Зх + sin2 2х = (sin χ — sin За:) (sin χ -f- sin 3 χ) + sin2 2a: =
= — 4 cos 2a: sin χ sin 2a: cos χ + sin2 2a: = — 2 cos 2a: sin2 2a: -f- sin2 2a: =
= sin2 2л: (1 —2 cos 2 x).
Данное уравнение эквивалентно совокупности двух уравнений:
ktz π
sin 2а: = 0 и 2cos2a: = 1, откуда χ = -γ и χ = ± -g- + kn
В примерах 3—6 показано применение преобразования произведений
в суммы и в частности преобразования понижения степени.
3. Решить уравнение
sin a:+2 sin x cos (α — χ) — sin a = 0.
Решение. Преобразуем в сумму средний член; тогда уравнение
примет вид:
sin χ + sin (2a: — а) = 0 или sin (2л: — а) = sin (— x)t
откуда
4. Решить уравнение
sin л: sin 7х = sin За: sin 5л:.
Решение. Преобразуем в сумму правую и левую части:
cos 6 χ — cos 8а: cos 2а: — cos Sx
__ _ или cos 6jc = cos 2Xf
откуда
6a: = ± 2a: + 2кк и χ = -g- , a: = -j- .
Первая серия содержится во второй (при четном п) и потому общее
ηπ
решение выражается формулой χ = -j-.
296
5. Решить уравнение
χ
sin2 χ — cos2 χ =r cos -χ .
Решение. Применив формулу косинуса двойного аргумента, получим
χ
~К H./JJH t-иэ \δ.λ, -γ· nj = tus ρ
x x
— cos 2x = cos -χ или cos (2x -f- π) = cos -χ ,
откуда
и, наконец,
2χ + π = ± γ + 2kn,
(4± 1)* = (46 —2) π
2(2*--1) π
и я =
2(2*—1) π
λ- 5 η Λ— 3
6. Решить уравнение
cos2 χ + cos2 2* + cos 23* + cos2 4x = 2.
Решение. Применив преобразование понижения степени, получим
эквивалентное уравнение:
cos 2х + cos 4х + cos 6* -f- cos 8^ = 0.
Для разложения левой части на множители группируем первое сла-
гаемое со вторым, третье с четвертым
cos Зх cos χ + cos x cos 7*=0
или
cos χ (cos 3x + cos Ix) = 0
и окончательно
cos χ cos 2x cos 5* = 0,
откуда найдем три серии решений!
π π
* = "2 + *π, χ =-J
Решения первой серии содержатся в третьей (черт. 177). В самом деле,
χ = γ
5π
2л_
5
общее решение состоит из двух серий!
π
• π π
=Τ+*"9" и
7. Решить уравнение
sin χ sin Зх — γ т
Решение. Преобразуем левую часть
в сумму
cos 2х — cos 4х = 1,
Черт. 177
297
Подставив в левую часть cos 4х = 2 cos2 2х — 1, получим уравнение
(2 cos 2а:— 1) cos 2х = О,
из которого найдем две серии решений
π π π
Ниже приведены примеры преобразования уравнений, изменяющие
область определения уравнения.
8. Решить уравнение
sin 2x cos χ tg χ = 0. (1)
Решение. Сократив левую часть уравнения на cos x, получим
/равнение
sin χ sin 2x = 0 или 2 sin2 x cos л; = 0. (2)
Общее решение найдем из уравнения
sin л: = 0, откуда χ = Ы.
Уравнение cos χ — 0 можно не рассматривать, так как если cos χ = 0,
то левая часть уравнения (1) теряет смысл
Примечание. Применение метода предельного перехода дает
lim sin 2x cos x tg x— lim 2 sin2 χ cos * = 0.
π
Следовательно, -к , а также все числа ~п -{- Ы суть особые решения
уравнения.
9. Решить уравнение
Решение. Умножим обе части на 1 + sin x, а затем на cos л:.
Получим последовательно
tg χ -f- sin x tg χ + cos χ = 2 (1 + sin x),
sin λ: + sin2 χ + cos2 * =·2 cos χ (1 + sin #),
(sin * + 1) (1 — 2 cos χ) = 0. (2)
Уравнение (2) есть следствие уравнения (1) с более широкой областью
определения.
Общее решение (1) найдем, решив уравнение
π
1—2 cos χ = 0, откуда χ = ± у + 2&π.
Уравнение (1) имеет период 2я; для проверки полученной серии корней
π π
достаточно проверить лишь два корня * = "з" и * = — ~з"
4U 2 -^- *
-±/3 + (2Т
298
Уравнение sin χ -f 1 = О дает серию посторонних решений.
10. Решить уравнение
tg 4л:
Решение. Имеем последовательно
tg 4а: — tg χ = 0, откуда
4л: = χ + kn и χ = -о~ .
В процессе решения уравнения область его определения расширилась.
Левая часть данного уравнения есть четная периодическая функция с пе-
риодом π, а правая — постоянна. Поэтому достаточно испытать лишь два
π Γ πΐ
корня 0 и -д-, принадлежащие полупериоду 0, у данного уравнения.
Корень χ = 0 посторонний.
π
Корень * = "з" удовлетворяет уравнению.
/π π\
В промежутке ( — -^ , γ) равном по длине периоду уравнение имеет
π
два корня ±-^ ·
Серия χ =
И. Решить уравнение
Серия а: = ± — + #π дает общее решение уравнения.
о
+ tg2A: + tg3* = 0. (1)
Решение. Выполняем последовательно тождественные преобразо-
вания:
sin За: sin За:
cos χ cos 2л: ' cos Зх ~~ ' ' '
sin За: [cos За: -f cos x cos 2a:]
cos χ cos 2a: cos 3x ~ W
Разложим на множители числитель:
cos За: + cos x cos 2a: = (4 cos3 χ — 3 cos χ) + cos χ (2 cos2 χ — 1) =
= 2 cos a: (3 cos2 a: — 2).
Подставив в левую часть уравнения (2), после сокращения получим
sin За: (3 cos2 а: —2)
cos 2a: cos 3 χ
= 0,
откуда sin За: = 0 и 3cos2a: —2 = 0. Из этих уравнений найдем две серии
решений: _
x = k-j, х = ± arc cos l/ _ + kn.
Левая часть уравнения (1) —нечетная функция с периодом π. Поэтому
достаточно проверить три корня, принадлежащие положительному полупе-
риоду
Ml·
ι / 2
I/ — .
π
= "з" и A:2 = arscos
299
-ctg
Для проверки можно воспользоваться уравнением (3) эквивалентным
уравнению (1) Корни xit х2 и х3 получены из условия обращения в нуль
числителя, при этом (как легко проверить) ни один из множителей знамена-
теля не равен нулю. Следовательно, xit x2 и хъ удовлетворяют уравнению (3)
и эквивалентному ему уравнению (1).
12. Решить уравнение
π\ / π\ 4 cos2 л:
Решение. Выполняем последовательно тождественные преобразова-
ния и упрощения уравнения:
4 cos2 a: sin — cos—
. 2 2
— cos χ
tg χ = 2 sin χ cos #,
sin* (1 —2 cos2 λ:)
cos χ ~ *
sin χ cos 2* = 0, (2)
откуда
π π
Уравнение (2) есть следствие (1) с более широкой областью определения.
Число π — период уравнения (1), обе его части суть нечетные функции,
π
поэтому достаточно проверить лишь два корня уравнения (2) х^ = 0 и х2 =7"»
содержащиеся на сегменте 0, — . Оба эти корня для уравнения (1) являют-
ся посторонними.
Уравнение (1) не имеет решений.
На примерах 13 и 14 показан прием решения некоторых тригонометри-
ческих уравнений посредством введения вспомогательного угла.
Примеры.
13. Решить уравнение
a sin χ + Ь cos χ — с, (1)
где | а | + | b | Φ 0.
Решение. Введем вспомогательный угол φ (см. § 24):
b
φ = arc tg — .
Разделив обе части уравнения на ±j/~a2 + 62 (взятый с надлежащим
знаком, см. стр. 124), получим:
и, наконец,
300
х = (- 1)" arc sin -±γ±—— +ηπ- arc tg — .
Исходное уравнение эквивалентно (2), а потому имеет решения, если
с
Уа2 + Ь2
< 1
или с2 ·< а2 + б2. Если с2 > a2 -f- 62, то уравнение не имеет решений.
Рассмотрим, например, уравнение
sin v
sin а; = 1.
π
Разделив обе части на 2, положим φ = -ψ, получим
π \ 1 π π
J = 2"' 0ТКУда x = i"-""1)" "б""~ "з" + Ππ·
2"' 0ТКУда x = i"-""1) "б"
Геометрическая интерпретация Решение уравнения (1)
можно толковать как отыскание точки X = cos х} Υ = sin x, в которой
прямая линия
ЬХ + αΥ = с (3)
пересекается с единичной окружностью
Ь
Введение вспомогательного угла из условий cos φ = г— -=
У CL «-J— и
sin φ = /- = есть приведение уравнения прямой (3) к нормальному виду.
У a2 -J- о2
с
При этом
есть расстояние прямой (3) от начала координат.
V a2 + b2
Прямая имеет с единичной окружностью общие точки в том и только в том
случае, если
с
-g-J = 0.
Так, например, чтобы решить уравнение
cos a + sin α = 1,
достаточно найти точки пересечения прямой X + Υ = 1 и окружности
Χ2 -\-Υ2 = \. Искомые точки суть Л (1,0) и В (0,1), в этих точках оканчи-
ваются дуги 2Ы и -g + 2kn.
14. Решить уравнение
(π \ / π \ /
χ — -jj + 4 sin ух + -g· J + 5 sin ^5 д; ■
Решение. В силу формул приведения
sin
Введем вспомогательный угол, определяемый из условий
3 4 4
cos φ = τ-, sin ф= -ξ-, т. е. φ = arc tg -gr #
0 0 ύ
Преобразуем данное уравнение следующим образом:
/ π\ / π\ /π
sin ί jc — -g-1 cos φ + cos I # — -g J sin φ = — sin ί 5 χ + -g·
301
или
— ^Л = sin Г
sin ( χ + φ — -ίτ ) = sin ( — Ъх — -F-
откуда получим две серии решений
π π π φ kit
χ + ?— "β" ~ ~~ΡΧ ~~~β + 2кк и, наконец, χ = gg — "g" + "3
π φ π (2£ + 1)
ν + φ = 5χ + g- + (2/5 + 1) π, откуда л; = 4" — 24 + 4 π*
Указанные выше и другие частные приемы решения тригоно-
метрических уравнений применяются обычно в их различных ком-
бинациях. Умение целесообразно пользоваться различными част-
ными приемами приобретается лишь в результате длительной прак-
тики. Никакими общими правилами невозможно предусмотреть
также различные искусственные приемы, вносящие упрощения в
процесс решения тригонометрических уравнений.
Нередко одно и то же тригонометрическое уравнение может
быть решено различными способами, при этом сравнительная про-
стота процесса решения (вообще говоря) зависит от выбора способа
решения. Так, например, уравнение линейное относительно сину-
са и косинуса
a sin χ + b cos x = с
можно решить следующими способами:
1°. Посредством универсальной подстановки (см. стр. 284).
2°. Посредством введения вспомогательного угла (см. стр. 300):
±V α2+ b2 sin (x + φ) = с.
3°. Можно выразить одну тригонометрическую функцию через
другую, например,
cos л: = i ]/l —sin2 л:.
4°. Можно возвести обе части в квадрат, тогда получится урав-
нение, приводящееся к однородному:
a2sin2x + 2 ab cos x sin χ ~\- b2cos2x = с2.
В частном случае при а = b последнее уравнение примет особо
простой вид:
ab sin 2x — с2 — а2
5°. Рассмотрим тождество
(a sin χ + b cos χ)2 + (a cos χ — b sin χ)2 = a2 + b2.
В силу данного уравнения получим
(a cos χ — b sin xf = a2 -f- δ2 — с2.
302
Значения sin л: и cos x определяются из системы уравнений
a sin χ + bcosx = с;
— b sin χ + a cos л: = ± j/α2 + б2 + с2.
Неизвестное л; определяется по найденным значениям синуса и ко-
синуса.
Первый способ не приводит к появлению посторонних решений,
потеря решений имеет место лишь при Ь — —с (см. стр. 284).
Второй и пятый способы также не приводят ни к потере, ни к
появлению посторонних решений.
При третьем (а также при четвертом) способе возможно появ-
ление посторонних решений, что показано на примере решения
уравнения sin χ + cos x = 1 (см. стр. 283, пример 3).
Рассмотрим еще следующий пример, уравнение
tg χ = —tg χ
решается непосредственно:
2tg* = 0, tg* = 0, χ = kn.
Однако это же уравнение можно решить другим способом:
Применение второго способа нецелесообразно, так как оно искус-
ственно и, кроме того, вносит посторонние решения (см. стр. 279).
Посторонние решения получаются при нечетных значениях
n=2k + 1, так как тогда теряют смысл левая и правая части урав*
нения.
Выбор наиболее целесообразных способов решения достигается
практикой.
Примеры.
15. Решить уравнение
3
sin3 χ cos Зх + cos3 x sin Зх = -q .
о
Решение. 1-й способ. Выразим степени тригонометрических функ-
ций через функции кратных дуг:
cos3 χ = -ζ [cos Зх + 3 cos χ],
sin3 χ ζ= —[3 sin x — sin За:];
подставив в уравнение, получим:
3 3
-т [sin χ cos 3 χ + cos x s\n3 x] = -g
или
1 π ηπ
sin 4*=-£ , откуда χ = (— \)η Tg + -ζ .
303
2-й способ. К тому же результату придем, применив формулу для
тригонометрических функций тройного аргумента:
sin Зх = 3sin χ — 4sin3 x, cos Зх = 4cos3 χ — 3cos χ;
после подстановки получим:
3 1
3sin* cos χ (cos2 χ — sin2 я) = тг, или sin 4x = ?г.
В данном примере оба способа равноценны в смысле простоты решения.
15. Решить уравнение
sin χ + cos x + sin x cos χ = 1.
Решение. 1-й способ. Перепишем уравнение в виде
sin χ + cos χ — 1 — cos x sin χ. (1)
После возведения в квадрат обеих частей и тождественных преобразований,
получим:
1 + sin 2х = 1 — sin 2х+ -ξ sin2 2x (2)
или
sin 2д; (8 — sin 2x) = 0.
Так как второй множитель положителен, то
π
sin 2x =■ 0, откуда * = &-£.
При переходе от уравнения (1) к (2) возможно появление посторонних корней
(возведение обеих частей в квадрат).
π 3
Достаточно испытать корни 0, -g , π, и ^π в пределах одного периода
уравнения.
π
Уравнению удовлетворяют два корня 0 и ^.
Следовательно, получим две серии решений
π
х = 2kn и χ = -к- + 2kn.
2-й способ. Положим
cos χ + sin x = t\
имеем:
t2 = 1 + 2 sin χ cos jc,
откуда cos χ sin χ = —f>— ·
Данное уравнение примет вид:
μ _[_ 2t — 3 = 0,
откуда / = 1 и t = — 3.
Следовательно, получим совокупность двух уравнений
cos л: -f sin # = 1 и cos x + sin x = — 3.
Первое уравнение было решено выше (стр. 283). Второе уравнение не
имеет решений, так как каждое из слагаемых в левой части по абсолютной
величине не превосходит 1 и в сумме не может получиться число —3.
Второй способ более искусственен, чем первый, но зато он не вносит
посторонних решений.
16. Решить уравнение
304
Решение. Если применить универсальную подстановку / = tg UL t
то получится рациональное уравнение, однако, проще поступить иначе.
Преобразуем правую часть следующим образом:
,π Λ1 sinM —~ —
tg2li-T)tg
4 *
cos (тт
/π \ χ . λ:
—cos^— χ) cos g- -sm
2 1 — sin л: 1 — sin x
/π \ χ χ
cos ^γ — a:J cos 2" + s in у
1 + sin χ ' cos λ:
Данное уравнение примет вид
sin χ (1 — sin x)2
cos дс (1 + sin л;) cos χ ·
освободившись от знаменателя, получим:
3 sin лс = 1, откуда χ = (—\)п arc sin тг + «π.
о
17. Решить уравнение
sin (л + 20°) 2
sin (л:+ 22°) = 3 *
Решение. Составим следующую производную пропорцию:
sin(* + 20°) + sin (χ + 22°) _5
sin (χ + 22°) — sin (χ + 20°) = 1 *
Разложив на множители числитель и знаменатель, получим
tg(* + 21°) __.
откуда
tg(jc + 21°) =5 tg 1°
х = — 21° + arc tg (5 tg 1°) + 180°.k.
18. Решить уравнение
/ π\ 1
sin4x+ sin^Ar + yj =y .
Решение, Выразим левую часть через функции двойного аргумента
следующим образом:
(1 — cos2*)2
sin4 χ = ~λ ;
-с" (2*+ ^)Т -о + . ■■
4/ 4 4
После подстановки и тождественных преобразований, получим:
cos 2х — sin 2х = 1 или cos [ 2 л: + - I = —· ·
\ 47 2
Π Зак. 597 305
π ι π
2χ + 4" = ± Τ
π
χ = £π и α: = — ξ-
откуда
Следовательно
19. Решить уравнение
29
sin10 χ + cos10 χ = j-g cos4 2a:.
Решение. В качестве рационализирующего параметра удобно при-
нять / = cos2 2л:, так как
1 — cos2*\5 /l+cos2*\5 I + 10/ + Ы2
§ J +(^ 2 ) = Гб ·
Подставив в данное уравнение, получим смешанную систему:
24/2 — 10/ — 1 =0, 0</ <1,
которая имеет единственное решение / = тр следовательно,
1 π π (2fc+l)«
cos 2x = ± ψψ , 2x=j + kj, x = g .
/
20. Решить уравнение
sin" χ + cos" χ = 1,
где η φ 2—натуральное число.
Решение, η = 2т + 1 — нечетное число.
Положим X = cos xt Y = sin л;. Уравнению могут удовлетворять только
лишь дуги, оканчивающиеся в I четверти, так как во II, III и IV четвер-
тях хотя бы одна из координат отрицательна: следовательно, хотя бы одно
из чисел Хп и Уп также отрицательно. Кроме того, | X \п < 1, | Υ \п < 1,
а потому Хп+ Υη < 1.
Искомая дуга χ не может оканчиваться внутри I четверти. В самом
деле, при η = 1 уравнение примет вид X -J- Υ = 1, но, с другой стороны,
X и Υ суть катеты прямоугольного треугольника с гипотенузой равной 1,
а потому X + Υ > 1.
Если n = 2k + I > I, то η > 3, имеем:
Хп = Х2-Хп~2 < X2, так как 0 < X < 1.
По той же причине УЛ < У2, но тогда
χη _|_ у/г < Х2 + у2 = ι
Уравнению удовлетворяют дуги χ = 2kn и jc = — + 2βπ, оканчиваю-
щиеся в граничных точках I четверти.
Пусть η = 2m — четное число. Искомая дуга л: не может оканчиваться
ни в какой внутренней точке четвертей единичного круга, так как
ХП = | χ \П < Х2, УП = | у |/1 < у2 и тогда χ/I + y/I < L
= | \ | | +
Уравнению удовлетворяют дуги χ = -И , оканчивающиеся в граничных
точках четвертей единичного круга.
21. Решить уравнение
(sin χ -J- cos а;) К2 = tg x -J- ctg a:.
306
Ре шение. После преобразований получим эквивалентное уравнение
♦ / тг \ ι
Так как при произвольном χ
sin
< 1,
1
sin (x-\--j-) = \ и sin 2a; = 1
sin 2jc
то уравнение может удовлетвориться лишь теми значениями х, при которых
а)
или
b) sin ί χ + j J = — 1 и sin 2л: = — 1.
В случае а)
π π
первое уравнение дает: χ = -ξ + 2&π, а второе: * = — + шт.
Множество всех решений, общих для обоих уравнений, определяется фор-
мулой
В случае Ь)
первое уравнение дает: χ = — — π -f- 2kn, а второе х = — — + ηπ. Β этом
4 4
случае уравнения не имеют общих решений.
Итак, общее решение данного уравнения есть χ = — + 2&π.
22. Решить уравнение
cos (π sin χ) = sin (π cos x).
Решение. Имеем:
cos (π sin χ) = cos ί — —
откуда
π
к — π cos χ = ± π sin λ; -f· 2βπ
или
± 2 sin χ + 2 cos a; = 1 — 4k.
Получилось уравнение вида
a sin x + b cos л: = с, где α = ±2, 6 = 2, г = *— 4k ·\-\.
Равенство b + с = 0, т. е. 3 = 4k, не выполняется ни при каком значении k.
Общее решение данного уравнения находится по формуле (стр. 284)
у +
4« — о
где /г — любое целое число, удовлетворяющее условию
11* 307
а /г —произвольное целое число. Следовательно, допустимые значения*?
суть целые числа, содержащиеся между корнями квадратного уравнения
16&2 — 86 — 7 = 0.
Корни последнего уравнения суть ki ж — 0,45 и £2~0,95.
Следовательно, к — 0 есть единственное допустимое значение &,
откуда
χ = 2 arc tg ± 2±*7 + 2пл.
§ 51. Тригонометрические уравнения, содержащие параметры
Решение тригонометрических уравнений, содержащих пара-
метры, может представить значительные трудности, связанные с
необходимостью решать неравенства и системы неравенств. В ряде
случаев приходится решать уравнения и неравенства в целых чис-
лах. Никакой общей теории решения тригонометрических уравне-
ний с параметрами не может быть построено.
Представление о решении уравнений, содержащих параметры,
дано на рассмотренных ниже примерах.
Примеры.
1. Решить уравнение
χ
α sin x = b cos γ . 0)
Решение. Имеем последовательно
xx χ
2α sin у cos γ — ο cos γ = 0, (2)
X f X \
cos 2~ ί 2α sin "2 —/? J = 0. (3)
Уравнение (3) эквивалентно совокупности уравнений:
A) cos 2" = 0, В) 2а sin |· = b.
Общее решение уравнений А) есть χ — (2k-\-\) π.
Ъ
\)
Решаем уравнение В): если a=f=O, то sin-=— , последнее уравнение
имеет решение в том и только в том случае, если
2а
или | b |< 2\ а |.
При \Ь\> 2а уравнение В) противоречиво
Особый случай для уравнения В):
При а = 0, Ь=/=0 уравнение В) противоречиво.
При а =з b = 0 — удовлетворяется тождественно.
Объединив множества решений уравнений А) и В), получим общее
решение уравнения (1).
Ответ. 1°. При |6|<2|а|иафО две серии решений x — (2k-\- Ι; π
и * = ( I)*2i
308
2°. При I b I > 2 | a \ одна серия решений (2k + 1)π (в частности, если
fl = 0, ЬфО).
3°. а = b = 0. Уравнение удовлетворяется тождественно.
2. Решить уравнение
migx + ncigx = 2. (1)
Решение. Умножив обе части на tg χ, получим
т tg2 χ — 2 tg л: + η = 0.
(2)
Уравнение (2) с более широкой областью определения. Посторонними
для (1) являются те решения (2), для которых tg χ = 0.
Решив уравнение (2) как квадратное от-
носительно tg χ, получим:
ι±/ι-
тп
где тфО и тп < 1.
Уравнению (2) удовлетворяет tg χ = 0,
если η = 0, тогда при тфО получим
m tg2 χ — 2 tg * = 0, откуда
.*=- и tg*=O;
второе простейшее уравнение дает серию по-
сторонних решений.
Ответ. 1°. Если тфО, пфО и
тп < 1, то
arctgVf
Черт 178
2°. Если т=£0, η = 0, то χ = arc tg — + kn.
: 0, η φ 0, το λ: = arc ctg —- + kn.
η
3° Если т ■
4°. Если т = п = 0 или яш > 1, то уравнение противоречиво.
Геометрическая интерпретация.
Пусть т > 0, я>0и0<л;<2", тогда произведение
(т tg χ)* (η ctg χ) = тп = const.
Сумма положительных слагаемых у = т tg я + η ctg jc имеет минимум
ymin при m tg * = η ctg #, откуда х = arc tg I/ HI, при этом у — 2 l^m/г
(черт. 178). Линия у = т tg * + η ctg а: пересекается с прямой у = 2 лишь
при условии V тп < 1, т. е. тп < 1.
3. Решить уравнение
cos (χ — а) = m sin χ — η cos л:.
Решение. Применив к левой части формулу (Са«), получим однород-
ное тригонометрическое уравнение первой степени
cos a: (cos а + п) -\- (sin а —» m) sin л: = 0;
30?
если
cos a + η
тфвта, то tg*= m_sina i
если
m = sin α, η φ — cos α, το cos χ = 0;
если
т = sin α, η = — cos α,
то уравнение удовлетворяется тождественно.
Ответ.
1°. Если т =£sin α, то
cos a + я
* = агс '§ m-sina + Ы-
2°. Если m = sin α, η φ. — cos а, то
3°. Если m = sina, η — — cos α, то уравнение удовлетворяется тожде-
ственно.
4. Решить уравнение
cos (ах + Ь) = cos (αχ * + ^х).
Решение. Имеем
ax + b=±(alx + bl) + 2&π,
откуда
(flTCi)^=-6±6,-|-2k (1)
(знаки берутся либо верхние, либо нижние). При | а Ι φ Ι αλ \ получим:
Особые случаи: Ι α | = | ах \. Пусть, например, а = а1ф0, тогда, взяв в ле-
вой части равенства (1) знак + перед аъ получим:
x = 2a(-b-b1
Если взять верхние знаки, то получим:
0 = — b-\-b1 + 2kn.
Последнее соотношение противоречиво, если разность bx — b не равна
кратному 2π; если же 63 =6 + 2/ζπ, то (при а = ах) данное уравнение удов-
летворяется тождественно.
Ответ.
1°. Если | а \ф\ ах |, то χ =JJ-^ (— b ψ bx + 2ηπ).
2°. Если а = ахф0 и b — Ьхф2пп, то
3°. Если ах = — аф0 и Ь-\- Ь1ф2пк, то
x = fa(-b + bx + 2kn).
4°. Если а = ахф0 и 6 — 6t = 2/ιπ или а = — βιΦΟ и b + 6х = 2/ζπ,
то уравнение удовлетворяется тождественно.
5°. Если а = аА = 0 и 6 =/= ± ^ι + 2/ζπ, то уравнение противоречиво.
310
6°. Если а — аг = О и 6 = ± ^ + 2ηπ, то уравнение удовлетво ряется
тождественно.
5. Решить уравнение
т η (cos χ — sin x)
tg x + ctg 2x = ctg*—1 ' W
Решение. Выполним последовательно тождественные преобразования
т cos л: sin 2х η (cos * — sin *) sin x
cos a:
cos χ — sin χ
откуда
m sin 2x — η sin χ = 0 или sin χ (2m cos χ — η) = 0.
Последнее уравнение эквивалентно совокупности двух уравнений
sin χ = 0 и 2m cos * — /2 = 0.
(2)
Первое уравнение дает серию посторонних решений χ = kn. Второе урав-
нение при | η | < I 2т \ и тфО дает серию решений
x = ± arc cos к- + 2£π.
(3)
Если Ι η I > I 2m |, то второе уравнение (2) не имеет решений.
Исследуем, при каких значениях параметров тип серия (3) содержит
посторонние решения.
При переходе от (1) к (2) область определения последовательно расши-
рялась за счет упрощения уравнения. Поэтому из серии (3) следует исклю-
чить те значения ху при которых левая или правая часть уравнения (1) те-
ряет смысл, т. е. (черт. 179):
a) теряет смысл tg χ либо ctg x, либо
ηπ
ctg 2x, откуда χ = -у \
π
b) ctg χ = 1, откуда χ = - + ππ.
c) tg χ = — ctg 2χ или tg x = t
откуда χ = к + ηπ'·> этот случай включается в
случай а).
В соответствии с этим серия (3) содержит
посторонние решения в следующих случаях:
A) arc cos — = 0 или π, тогда η = ± 2т; все решения посторонние
2т
(случай а);
B) arc cos— =— , тогда η ~ 0, тфО все решения посторонние (слу-
чай а);
η π Γ—
C) arc cos ^ = j, тогда η = т ν 2.
В серии (3) посторонними решениями являются —-\-2kn (случай Ь);
η ?π лГ-
D) arc cos 2^ = "ζ » тогда η = — т У 2 .
3π
В серии (3) посторонними являются решения —-7-~\-2kn.
311
Ответ.
1°. Если тфО, | я | < 21 /я | и | я | =£ | /я | V2. то
2
χ = ± arc cos 2^ + 2kn.
2°. Если Ι η Ι > 21 m I (в частности m = 0, пфО) или я = 0, тфО>
то уравнение противоречиво.
3°. Если я = т1ЛГ=£0, то jc = — ϊ" + 2Λπ·
о
4°. Если я = — m V2 =£ 0, л; = ^ π + 2&π.
5. Если m = л = 0, то уравнение удовлетворяется тождественно.
6. Решить уравнение
sin mx cos mx
sin jt "~" cos* " * '
Решение. Умножив обе части на sin x cos x, получим
sin (/я— 1)* = 0. (2)
Если тф\, то из уравнения (2) найдем
В множестве всех решений уравнения (2) могут содержаться решения
посторонние для уравнения (1), это те значения х, при которых cos χ = 0
/π
либо sin χ — 0, т. е. значения вида χ = -«г- (/ — целое число).
Итак, в серии (3) посторонними являются те корни, для которых
kn Ιπ
^ЗТ^Т или 2* = /(т-1). (4)
Иными словами, в серии (3) посторонними являются те корни, для кото-
рых уравнение (4) имеет решения в целых числах относительно к и /
(т — данное число).
При произвольном т следует исключить значение к = 0.
В частности, при т = 2 исключаются все значения k, так как уравне-
ние (1) при любом к имеет решения в целых числах: / = 2/г.
На том же основании при т = 3 исключаются все значения к При т— 4
уравнение (1) примет вид 2k = 3/. Оно имеет решения в целых числах при /г,
кратном числу 3: к = Ъки эти значения к исключаются.
При т = У2 уравнение (4) не имеет решений в целых числах, кроме
к = I = 0, а потому серия (3) содержит лишь один посторонни корень χ = 0.
При m = — уравнение (4) примет вид 6£ = — 2/, или 3k = — /; оно
о
имеет решения при любом k, все значения к исключаются.
Особый случай при /72 = 1; уравнение (1) удовлетворяется тождест-
венно всеми допустимыми значениями х.
7. Решить уравнение
sin4 χ -f cos4 χ + sin 2x + a = 0.
Решение. Выделим полный квадрат из первых двух членов:
sin4 χ + cos4 x == (sin2 x + cos2 χ)2 — 2 sin2 χ cos2 * = 1 — j sin2*2*.
Данное уравнение примет вид:
sin2 2x — 2 sin 2* — 2 (1 + α) = 0.
312
Положив / =* sin 2х, составим смешанную систему
/2_2/ — 2(а+1)=0, —1</<1. П)
Уравнение имеет в поле комплексных чисел решения:
/ = 1 ± У2а — 3.
3
Значения t действительны, если 2а + 3 > 0, откуда а > —^ ·
Найдем значения параметра а, при которых хотя бы один из корней
удовлетворяет неравенствам— 1 < t < 1.
Полусумма корней равна 1:
h + h
—к = 1» следовательно, t1 < 1 < /2·
3
Равенство корней имеет место при а = —7>» и Т0ГДа ^ι = /2 = 1 -
о
Если а > —— , то ίχ < 1 < /2ί больший корень смешанной системе не
удовлетворяет. Меньший корень удовлетворяет системе (1) в том и только
в том случае, если число — 1 расположено вне сегмента корней или в его
левом конце. Положив t= — 1 в левой части уравнения (1), получим иско-
мое условие
1 — 2а > 0, откуда а < j .
3 1
Ответ. 1°. Если — — < а < —, то данное уравнение имеет общее ре-
шение
х = (~l)« arc sin (1 — V2а + 3) + ηπ.
3 1
2°. Если а < — 2" или а > 2"» то Уравнение не имеет решений.
8. Решить уравнение
COS2 (* + α) + COS2 (Х — α) = sin 2α. (1)
Решение. Применим к левой части преобразование понижения сте-
пени:
cos (2х + 2а) + cos (2х — 2а) = 2 (sin 2а — 1).
Преобразовав левую часть в произведение, получим
cos 2α cos 2x = sin 2α — 1. (2)
Обе части уравнения (2) суть периодические функции относительно
параметра α с периодом π, поэтому достаточно ограничиться промежутком
π π
-2 <α<2 ·
Если cos 2a=f=0, т. e. α φ ± j , το
sin 2α — 1
cos 2x =
cos 2α
Заметив, что при α φ ± j (выразить обе части через tg α)
sin 2α — 1
-«•(-г).-
COS 2α
I IB Зак. 597 * 313
получим
cos 2х = tg (а - \ V (3)
Последнее уравнение имеет решения в том и только в том случае, если
+ 1. (4)
η π 3π π π
Так как (по условию) — -^ < a < ^ , то— -ζ < a — j < j .
Аргумент ξ = α — — в промежутке —L. π < ξ < — удовлетворяет уело·
4 4 4
вию (4): — 1 < tg S<1, если (черт. 180) —-
4
- или
4
UL<a — ^<!1и, наконец, 0<a<!L, при этом α =£ Ξ.. Откуда получим
4 4 4 2 4
два промежутка 0 < a < — и —
—
Приняв во внимание периодичность уравнения относительно параметра,
получим совокупность промежутков
π π π
me < a < τ + me, у + ηπ < a < κ + ηπ.
(Δ)
Если α принадлежит какому-либо промежутку этой совокупности, то
соответствующая серия решений находится из уравнения (3).
Особые случаи. При α = _ + kn уравнение (2), эквивалентное (1),
4
π
удовлетворяется тождественно, при α =— -ξ -f- ηπ противоречиво.
Ответ. Уравнение (1):
1°. имеет серию решений
1
х = ± ^ агс cos
/ π\
( α — J 1
если α принадлежит совокупности промежут-
ков (Δ);
2°. удовлетворяется тождественно, если
a = - + ππ;
3°. противоречиво, если аф—-{-пк не при-
надлежит совокупности промежутков (Δ).
9. Решить уравнение
tg (« + X) tg (a — *) = 1 — 2 COS 2*. (1)
Решение. Уравнение имеет период π относительно параметра a,
π π
поэтому его достаточно рассмотреть в промежутке — -^ < a < 77 .
Переписав уравнение в виде
sin (a+ x) sin (а— χ) 1 — 2 cos 2л
cos (a + χ) cos (a — χ) = 1 · ί2)
314
составим производную пропорцию по правилу
а с b -j- a
если τ = τ-, то
6 — α α* — с
получим:
cos 2л: 1 — cos 2a:
cos 2α = cos 2л: ' ^
Применим подстановку / = cos 2х и составим смешанную систему:
*2+7 cos 2а — cos 2а = 0, — 1</<1. (4)
Корни уравнения (4) действительны, если
Δ = cos2 2α + 4 cos 2α = cos 2α (cos 2α + 4) > 0.
Так как cos 2α + 4 > 0, то это неравенство эквивалентно следующему
cos 2α > 0, последнее неравенство в промежутке —— < α <ί. выполняется,
π π
если — -ζ < α < -ξ .
1°. Если α = ± —, то уравнение (4) имеет двойной корень /=0
4
— этот случай рассмотрен ниже как особый.
2°. Если —— < α < 5., то корни уравнения (4) противоположны по
4 4
знаку: tl < 0 < /2·
Подставив в левую часть / = 1, получим /(1) = 1 > 0, следовательно,
положительный корень t2 меньше 1.
Подставив в левую часть t = — 1, получим / (—1) = 1 — 2 cos 2α:
a) если / (— 1) > 0 и Δ > 0, то меньший корень содержится в проме-
жутке [—1,0). Имеем cos 2α ·< jr , откуда получим два промежутка:
π π π π
-g-<a<-^H—^-<α<—у. (δ)
В этом случае
— 1 < ^<0</2< 1;
b) если /(—!)< 0, Δ > 0, т. е. cos 2a > L, откуда — 1 < a < !L, то
2 об
меньший корень расположен вне сегмента [—1, 1]. В этом случае имеем
tx < — 1 < 0</2< 1.
Корни квадратного уравнения (4) суть
^ _ — COS 2a ± V cos 2a (cos 2a + 4)
4,2 s ·
В совокупности промежутков (δ) смешанной системе удовлетворяют оба
корня.
π . . π
В интервале — ~б~ ΊΓ смешаннои системе удовлетворяет корень t2.
Среди решений смешанной системы (4) могут быть решения посторонние
для (1). Это имеет место, если tg(a + *), либо tg (a — χ) теряет смысл,
т. е если * = ±а+у+/я (/ — целое число), откуда
2х = ± 2а + 2/π + π и cos 2x = — cos 2a,
следовательно,
t± = — COS 2a < 0.
ИВ* 315
В этом случае
откуда
t\ -f tx cos 2α — cos 2α = — cos 2α = О,
Значения вида χ => ± - -f kn не могут удовлетворять уравнению (3),
4
но они могут быть решениями (1); это имеет место, если
„ π π
Последнее не может иметь места при — -т < α < -τ , так как
i) —ι.
π
Случай же α = i "Τ должен рассматриваться особо.
Итак, особые случаи следующие)
COS (2а = 0, α = ± -ζ .
Уравнение (1) примет вид
tg (Л + *) tg (j - χ) = 1 - 2cos 2аг,
откуда
1 = 1 — 2 cos 2л;, cos 2x = О
и χ = ± "ξ* + пк ~ это серия посторонних корней.
Ответ. Г. В совокупности промежутков
π π π π
, [_ arc CQS — cos 2α db V cos 2α (cos 2α + 4)
2°. В совокупности интервалов
π π
— "7Г ~г ^я <С ot <C ~ic" —f- ^Я
3е. В совокупности сегментов
π π π π
-^- + /ιπ<α<-2- + Α2π и **γ + «π<α< —-ζ + >*π.
Уравнение не имеет решений (либо корни (4) мнимые, либо особый
случай).
Примечание. При составлении промежутков для значений α
следует принять во внимание периодичность (период π) уравнения от-
носительно параметра.
316
10. Найти условия, при которых уравнение
sin2 χ -f- 2р sin χ -\- q = О
имеет решения.
Решение. Заменим уравнение смешанной системой
(a) t2 + 2pt + q = 0. \
(b)
—1</
Если Δ = ρ2 — <7<0, то квадратное уравнение не имеет действительных
корней, данное уравнение не имеет решений В дальнейшем будем предпо-
лагать, что Δ>0, τ. е. что p2>q.
Случай Г. Оба корня уравнения (1) содержатся на сегменте [—1, 1)
(черт. 181). В этом случае (см «Специальный курс элементарной алгебры»,
§ 83), подставив в левую часть £=1
и / = —1, получим неравенства
(возможность кратного корня не
исключается):
и
и,
1 +
1 —
кроме того,
— 1
наконец,
2р 4-
2р +
<Р <
Я<
Я *
г 1,
>о
(3)
(4)
(5)
Я <
(6)
Черт. 181
Требуется решить систему неравен-
ств (3)—(6). Воспользуемся графи-
ческим способом (считаем ρ абсцис-
сой, a q — ординатой точки пло-
скости).
Прямые 1±2р + g = 0 пересекаются в точке (0, —1) и служат каса
тельными к параболе р2 = q в точках (±1, 1). В самом деле, если решать сов-
местно уравнение параболы и уравнение какой-нибудь из этих прямых, то
получится двукратный корень.
Искомые точки должны: 1) располагаться выше (или на) прямой 1 +
+ 2р + q = 0; а также выше (или на) прямой 1 — 2р + q = 0; 2) принад-
лежать полосе, ограниченной прямыми ρ = ±\\ 3) располагаться ниже (или
на) параболы q = ρ2 Перечисленным условиям удовлетворяют точки обла-
сти (замкнутой) I (черт. 182) Аналитически эта область может быть задана
неравенствами:
если — 1 < ρ < 0, то
— 2q — 1 < q < ρ2,
если 0 < ρ < 1, то
2р — 1 < q < ρ2
(1)
При указанных условиях тригонометрическое уравнение имеет две се-
рии решений, соответствующие двум корням квадратного уравнения.
С л у ч а й 2°. Одни из корней принадлежат сегменту [—1, 1]. Возмож-
но одно из двух расположений корней:
a) — 1 < *, < 1 < /2,
b) tx < — 1 < t2< 1.
При расположении а) имеем.
1 - 2р + q > 0, (3)
1 + 2р + q < 0. (7)
317
Искомые точки расположены выше (или на) прямой 1 — 2р -f- q = 0 и ниже
прямой 1 + 2/7 + q = О, при этом неравенство (6) удовлетворяется автома-
тически На чертеже получаем область II. При расположении Ь) получим
неравенства
1 — 2р + Р<0 и 1 + 2р +
что на чертеже определяет область (III). Аналитически полученные условия
выразятся так:
а)
b)
р<0, — \+2p<q
р>0, — 1 — 2р <q
Черт. 182
■—2/0 — 1; (И)
:2р-1. (Ill)
При указанных условиях
тригонометическое уравнение
имеет одну серию решений,
соответствующую единственно-
му решению смешанной си-
стемы.
Случай 3°. Оба корня
квадратного трехчлена (1)
расположены вне сегмента
[ —1,1]. Возможно одно из
трех расположений корней:
a) /1<ί.<-1<1,
b) - 1< 1< /χ < /2,
c) t1 < — 1 < 1 <t2.
При расположении а) выпол-
няются неравенства
1 + 2р + q > О,
1 — 2p + q> 0, р> 1.
На чертеже 166 получим
область IV. Аналогично при
расположении Ь) получим об-
ласть V.
При расположении с) выполняются неравенства:
1 + 2р + q < О, 1 — 2р + q < 0.
На чертеже 166 получим область VI. Аналитически полученные условия
выразятся так:
a) 1 < ρ < + оо, 2р — 1 < q < ρ2;
b) — оо < ρ < — 1, — 2ρ — \<q<p2.
с)
f
■oo < ? < — 1,
< ρ < —
B этом случае тригонометрическое уравнение не имеет решений.
Если точка (р, q) расположена выше параболы (область VII), то квад-
ратное уравнение имеет мнимые корни, тригонометрическое уравнение не
имеет решений.
11. Решить уравнение
tgfatg*) = ctg (π ctg λ:).
Решение. Перепишем уравнение так:
(1)
= tg [j — ncigxj ,
318
откуда
tg*=-2--ctg* + fc, (2)
где k — произвольное целое число.
Значения х, при которых tg χ = 0, не удовлетворяют уравнению. Ум-
ножив обе части (2) на tg*, получим эквивалентное уравнение, квадратное
относительно tg x:
2 tg2 χ — (2k + 1) tg x + 2 = 0.
Решив это уравнение относительно tg x, получим:
tgx = j(2k+\± V (2k+l)*-\6). (3)
При k = 0, ± 1, —? уравнение (3) не имеет решений, так как
(2k + I)2— 16 <0.
При переходе от уравнения (1) к уравнению (2) возможно появление по-
сторонних решений. Это суть такие решения уравнения (2), при которых
tgfatg х) теряет смысл (см. стр. 279), т. е. при которых
tg χ = m + 2" ,
где т — целое число. Найдем из формулы (3) всевозможные рациональные
значения tg x, среди которых содержатся (в частности) и значения вида
1
т + 2 .
Значение tg x рационально тогда и только тогда, когда подкоренное
выражение в формуле (3) есть квадрат целого числа:
(2k + I)2— 16 = г2 или (2k + I)2 — z2 = 16. (4)
Перепишем последнее уравнение так:
[(2*+1) + г][(2*+1)-г] = 16. (5)
Из уравнения (4) следует, что ζ — нечетное число, а потому множители (за-
ключенные в квадратные скобки), на которые разложено число 16, должны
быть четными числами. Разложение числа 16 на произведение четных чисел
возможно четырьмя способами: 2-8; 4-4; (—2)·(—8); (—4) (—4); в соответ-
ствии с этим возможны следующие случаи:
(26+1)-ζ = 8 J W (2k + \)z = 2 J l }
<2*+l) + * = 4 j (2A+0 + Z —2J
(2Λ+ 1) —2 = 4 J V (2*+l)-z = -8J K )
(2*+l) + z 8J (2*+1) + ,==_4j
(2*+l)-z = -2l { } (2ЛЧ-1)—г = —4J K }
Из этих систем найдем следующие возможные значения для k:
2kx + 1 = 5, kx = 2 и 2/^0 -J- 1 = — 5, ife2 = — 3.
При k — 2 соответствующие значения \gx суть
1
tg x == 2 и tg д: = g" ·
из которых второе дает посторонние решения.
31$
При k = — 3 соответствующие значения ig x суть
1
l§ X == "~~ Δ И 1§ Χ — —-— "η t
из которых второе дает посторонние решения.
Ответ.
= arc
+ „π>
4
£=£0, ±1, ±2, — 3,
х = i arc tg 2 + шг (β = 2, — 3).
§ 52. Некоторые системы тригонометрических уравнений
и методы их решения
Решение и исследование тригонометрических систем уравнений
может представить значительные трудности даже в тех сравнитель-
но редких случаях, когда это решение выполнимо элементарными
средствами. Ниже мы ограничимся (в основном) системами, которые
наиболее часто встречаются в приложениях тригонометрии к вы-
числениям элементов геометрических фигур.
При рассмотрении однотипных систем мы не будем проводить
подробных исследований для каждой системы, а будем ограничи-
ваться указанием на методы решения и исследования ранее рас-
смотренных примеров.
Примеры.
•1. Решить систему
sin# + siny = a (I) \
х + у=Ь (2) Г
Решение. Преобразуем в произведение левую часть уравнения (2):
о · Х + У Х~~~У
2 sin —2— cos —2— ^ °"
Воспользовавшись уравнением (2), получим эквивалентную систему:
b χ — у
2 sin-^ cos—2— = я; χ + у = b (Г)
Случай 1°. sin γφΟ, т. е. Ьф2кк и
а
b
2sin -J7
<1
В этом случае, заменив первое уравнение эквивалентным ему уравнением
(с целочисленным параметром), получим линейную систему:
п
х — у =± 2 arc cos ^- -f 4/?π, χ + У = b,
из которой найдем общее решение:
b a b a
χ = γ ± arc cos -ζ- + 2kn, y = —± arc cos γ — 2Ы
(перед арккосинусом знаки либо верхние, либо нижние).
320
Случай 2°. b — 2kn, a =f= 0 — система не имеет решений.
Случай 3°. b = 2kK, α Φ 0. Всякое решение уравнения (2) удовлет-
воряет (I), а потому общее решение системы может быть записано в виде
х, у = 2kn — χ (где я — произвольное число).
Случай 4°
Ь
2 sin -g-
> 1 — система не имеет решений.
Решить и исследовать данную систему можно методом подстановки.
Выразим, например, у из второго уравнения и подставим в первое, тогда
получим систему
(1 е- cos b) sin χ + sin b cos χ = α, у = 6 — лс,
в которой первое уравнение—линейное относительно косинуса и синуса.
Предлагаем в виде упражнения исследовать полученную систему и сравнить
выводы с полученными выше результатами.
По тому же образцу решаются и исследуются системы:
sin χ ± sin у = а | cos x ± cos у = α λ
χ±у = ь ) l x±y = bj'
Система (и аналогичные системы)
sin χ -f cos у = at χ + у — Ь
сводится к предыдущей введением вместо у нового неизвестного ζ = -ρ- .—у,
2. Решить систему
мп χ sin у = α, χ + у = 6.
Решение. Преобразовав в сумму левую часть первого уравнения,
получим:
cos (χ — у) — cos (χ + у) = 2α. * + у = 6,
откуда
cos (a: — у) = 2а + cos b, χ + у = 6.
Дальнейшее решение и исследование проводится по образцу предыдущего
примера.
Применение метода подстановки приведет к уравнению линейному от-
носительно косинуса и синуса двойного аргумента (доказать).
Тем же способом решаются системы, у которых левая часть первого урав-
нения имеет вид
cos χ cos у, cos л; sin у
и т. п., а второе уравнение
х± У = Ь.
3. Решить систему
tg л: — tg у = а, х-\-у = Ь.
Решение. Применив способ подстановки, получим (после упрощения)
систему
tg Ь tg2 χ + 2 tg χ — a tg b tg χ — tg b — a = 0, у = b — x.
Первое уравнение решается как квадратное относительно tg χ.
Особые случаи. Г. tg b = 0, b = nn, tg д: — tgy=a, χ + у = ηπ
(η — данное целое число),
откуда
2 tg χ = α, у = ηπ — χ;
а а
χ = arc tg -γ-{- k*t у = — arc tg -γ -f (n — β) π.
321
π
2°. tg b не существует b = ~^- -]- ηπ,
π
tg χ — tg у = α, у = -у + я* — х.
Подставив в первое уравнение, получим tg χ — ctg χ = а (последнее урав-
нение решается без труда).
Рассмотренным в настоящем примере способом решаются и исследуются
системы
tg χ ± tg у = а | ctg χ ± ctg у = а |
* ± у = 6 J ' *±У = & J '
4. Решить систему
sin χ
Решение. Применив способ подстановки, получим систему эквивалент-
ную данной
sin b ctg у — a -f cos b, x = b — у.
Первое уравнение при sin b φ О приводится к простейшему относительно
котангенса.
Особый случай: sin b = 0, b = ηπ.
1°. Если η = 2m — четное число, то χ = 2/ηπ — у (из второго уравне-
ния), откуда sin а: = —sin у. При аФ —1 первое уравнение системы противо-
речиво, система не имеет решений. При а = —1 первое уравнение удовлетво-
ряется тождественно, общее решение имеет вид χ = 2тк — у, где у — про-
извольное число неравное 1гк (где k — целое число).
2°. Если η = 2m — 1 нечетное число, то аналогично получим следую-
щее: при а Ф 1 система противоречива, а при а = 1
х = (2т — ί)π — у, где у Φ kn.
Этим же приемом решаются и исследуются следующие тригонометриче-
ские системы:
cos л: sin a:
5. Решить систему
tg л: tg у = α, χ -f у = 6.
Способом подстановки уравнение приводится к квадратному относи-
тельно тангенса (исследование представляем учащимся в виде упражнения).
6. Решить систему
sin2 χ + sin2 у = а, х + у = Ь.
Решение. Введем двойные аргументы, тогда получим систему
cos 2х + cos 2у = 2(1 —а), 2х + 2у = 2Ь,
способ решения которой показан в примере 1.
7. Решить систему
sin χ sin у = a, cos л: cos у = 6. (1)
Решение. Путем почленного сложения и вычитания получим систему
cos (xr\-y) — b — a, cos (χ —- у) — b -f a (2)
эквивалентную данной. Эта система имеет решение в том и только в том
случае, когда а и b удовлетворяют неравенствам:
— 1 < 6 — α < 1, —i<b + a<\.
322
ъ
Из этих неравенств получим (соответственно):
α — 1 < 6 < α + 1 ■ — а — 1 < 6 < — а -\- \
Множество точек М(а, Ь) плоскости, удовлетворяющих обоим этим неравен-
ствам, образует квадрат (замкнутый, черт. 183); этот квадрат может быть за-
дан следующими неравенствами (алгебраиче-
ское решение предоставляем учащимся, см.
«Специальный курс элементарной алгебры»):
— а — 1 < b < а + 1, — 1 < а < О,
а — 1<6< — α+1, 0<α<1
Если значения параметров а и b удовлет-
воряют условиям (3), то данная тригономет-
рическая система эквивалентна следующей си-
стеме двух линейных уравнений с двумя це-
лочисленными параметрами:
х + У = ± arc cos (b -— a) -f- 2/ηπ;
* —у = ± arc cos (6 + я) + 2ππ,
откуда
X =
— α) ± arc cos (6 + a)
± arc cos (b — a) =F arc cos (b +
где тип — произвольные целые числа, а знаки перед арккосинусами в одной
из формул (например, в верхней) могут быть взяты в произвольной комбина-
ции (возможны 4 такие комбинации), а в другой формуле первый арккосинус
берется с тем же, а второй — с обратным знаком (что в первой формуле).
Можно вместо т + η и т — η ввести другие параметры, положив
т4-я = /г, т — η = I.
Но тогда k и / не могут считаться произвольными целыми числами, а должны
быть числами одинаковой четности (т. е. оба четные либо оба нечетные), так
как только при этом условии тип будут целыми.
8. Решить систему
sin χ cos у = a, cos x cos у — b.
Решение. Случай Г. Предположим, что b φ 0 и а ф 0.
Заметив, что значения χ и у, при которых cos χ = 0 или cosy = 0, не могут
служить решениями системы, разделим почленно первое уравнение на второе:
а а ,
tg χ = -г , откуда χ — arc tg -г- -г
(1)
Подставив в первое уравнение, получим
(-1)"
cosy = 1 при b > 0
или
=1 npHi<0·
323
Получилось простейшее уравнение относительно у, которое имеет решения
при j/α2 + б2 < 1 (считаем, например, Ь > 0):
у = ± arc cos (—1)* V а2 + b2 -f /2π, (2)
формулы (1) и (2) дают общее решение системы. Если j/α2 + б2 > 1, то си-
стема не имеет решений.
Примечание. При указанном способе решения, система
f=a, y = b (I)
заменяется системой
При α =j£= 0 и b =£ 0 эти системы эквивалентны, что нетрудно уста-
новить (в общем виде) непосредственно.
Случай 2°. Одно из чисел а и b равно нулю. Пусть, например, b = 0,
но α φ 0, тогда из второго уравнения найдем
π
cos *=0 и χ = γ + kn
(при cosy = 0 первое уравнение не может удовлетворяться). Подставив в пер-
вое уравнение, получим простейшее уравнение (—l)^cosy = a, откуда при
а\ < 1
у = ± arc cos (— \)k a + 2/ηπ.
Если \а\ > 1, система не имеет решений.
Случай 3°. а = b = 0. В этом случае две серии решений системы
определяются следующим образом:
π
1) cosy = 0, у = -γ + кк, χ — произвольное число;
?' sin χ = 0, cos у = 0, χ = Ы, у = — -\~ Ы.
Но решения второй серии содержатся в первой, а потому вторую серию можно
не учитывать.
9) Решить систему
sin χ + sin у = a, cos χ + cos у = &.
Решение. Преобразовав левые части в произведение, получим си-
стему:
χ -f у # — у α * + У * — У δ
cos cos Cos
f у у + У
sin —2— cos —2— = ΊΓ ' cos —2— Cos 2Υ
которая решается и исследуется способом, изложенным в предыдущем при-
/ х+У х—У\
мере можно положить и = —о— , ν = —о—) ·
10. Решить систему
6. (Г)
Решение. Если ввести новые неизвестные
u = tgx, ν = tgy,
то получится алгебраическая система
и + υ = α, -^ + -^ = ^. (2)
324
которую можно заменить системой
откуда a=buv, и если b=f= 0, то и ν служат корнями квадратного урав-
нения
bz2 — abz + a = 0. (3)
Решение и исследование квадратного уравнения проводятся по обычным
правилам.
Этот способ решения может внести посторонние решения, посторонним
является всякое решение, для которого и = 0 или ν = 0. Квадратное урав-
нение (3) имеет корень, равный 0, в том случае, если а = 0.
Итак, особому рассмотрению подлежат следующие случаи:
1°. Ь == 0, а Ф 0. В этом случае, алгебраическая система (2), а также
и тригонометрическая система противоречивы.
2°. (3 = 0, b Φ 0. Аналогично и в этом случае система противоречива
3°. а — b = 0 Система (2) имеет бесконечное множество решений
ν = —и, где и — произвольное отличное от нуля число. В этом случае общее
решение тригонометрической системы дается формулой
у = — χ -f kn,
π
где χ — произвольное число, отличное от чисел вида η -q- .
11. Решить систему
tg* :tgy 5 tgz = a : b : с, χ + γ + ζ = π. (\)
Решение. Если χ + у+2 = тс, то из условия tg (x -f у + ζ) = 0 (при-
менить формулу, стр. 76). найдем условное соотношение
tg х + tg у + tg z ^ tg x tg y tg z; (2)
обозначим через t коэффициент пропорциональности, тогда первые два
уравнения запишутся в виде
igx= at, igy=btt igz^ct. (3)
Подставив в соотношение (2), получим:
t [abet2· — (а + b + с)] = 0,
откуда или
abet2· — (а + b + с) = 0, (4)
или /=0. Если / =0, то tg χ = tgy = tg 2 = 0, т.е. x = kx, у = ш,
z = шс; подставив в последнее уравнение (1), получим k-\- т-\- η == 1, от-
куда найдем серию решений:
х = /гтг, у = /τζπ, 2 = (1 к /72) π, (5)
где k и /тг — произвольные целые числа.
При нахождении прочих решений подлежат рассмотрению следующие
случаи.
Случай 1°, Ни одно из чисел a, b и с не равно нулю, тогда
<.--*±*±£
abc
Если
325
Из равенства (3) найдем:
χ = arc tg at + £π, у = arc tg bt -f ran, ζ = arc tg ct -f- ^π,
Коэффициент / определен из условия tg (* + у + ζ) = 0, а потому
|
arc tg at + arc tg bt -f- arc tg ct = < 0.
Ι
π
Так, в частности, при α > О, b > 0 и с > 0 сумма арктангенсов равна π,
если перед радикалами взят знак +, и —π, если взят знак —. Из условия
х Н~ У + ζ = π один из целочисленных параметров может быть выражен
через два другие произвольные целочисленные параметра.
Случай 2°. Если хотя бы одно из чисел a, b и с равно нулю, но
a -f b + с Φ О, то уравнение (4) не имеет решений.
Случай 3°. Если хотя бы одно из чисел a, b и с равно нулю, а также
а + b + с = 0, то уравнение (4) удовлетворяется тождественно. Рассмот-
рим, например, случай а — О, Ь = — с Φ 0 (аналогично рассматриваются
прочие случаи). Имеем
tg χ = 0, tg у = —tg 2, откуда * = βπ; у=—2 + miz>
Из последнего уравнения (1) найдем:
соответствующая серия решений выражается формулами
х = &7с, у = — 2 + (1 — &) π,
π
где 2— произвольное число, неравное -к" + ηπ·
Заметим, что в этом случае последние формулы дают общее решение си-
стемы, ибо при 2 = пп получаются решения серии (5).
12. Решить систему
cos χ '. cos у : cos z = а : b : с, л: + У + 2 = -γ , (1)
где а, 6 и г — положительные числа.
Решение. Имеем: ζ = -γ — (χ + у),
откуда в качестве следствия получим:
cos 2 = sin (χ -j-y) = sin * cos у + cos л: sin у (2)
и аналогичные равенства получим при помощи круговой перестановки
аргументов х, у и 2. В равенстве (2), линейном однородном относительно ко-
синусов, можно эти косинусы заменить пропорциональными им числами,
а потому получим:
с = b sin x + a sin у;
а = с sin у + 6 sin 2;
6 = α sin 2 + с sin x.
Умножив первое уравнение на с, второе уравнение — на — а и третье —
на Ь, иосле почленного сложения получим:
c2 + b2_a2==2bcsinx} откуда sin χ = С* + ^~ а>
Аналогично найдем следующие два простейшие тригонометрические урав-
нения:
а2 + с2 — б2 б2 + а2 — с*
: о^ > sin 2 = к-т .
326
При данном способе возможно появление посторонних решений. В самом
деле, в качестве следствия получится то же соотношение (2), если послед-
нее уравнение (1) заменить уравнением χ + У + ζ = ~о~ + 2&π.
§ 53. Уравнения, содержащие неизвестные
под знаками аркфункций
Рассмотрим сначала простейшие уравнения:
arc sin χ = т, arc cos χ = m,
arc tg χ = m, arc ctg χ = my
в которых требуется найти неизвестное по заданному значению од-
ной из аркфункций. Рассмотрим подробно одно из этих уравнений
arc sin л: = m.
Так как значение арксинуса принадлежит сегменту ^-, ~ ,
то это уравнение имеет решение лишь при условии |т|<!-^- .
При соблюдении этого условия единственное (в силу монотонности
арксинуса) решение есть
χ = sin т.
Аналогично рассматриваются прочие простейшие уравнения.
Уравнение arc cos χ = т имеет единственное решение к = cos m
при условии 0<ш<л и не имеет решений, если т не принадлежит
сегменту 10, π].
Уравнение
arctg* = т имеет единственное решение χ = tg m
при условии, если т принадлежит интервалу ί—~, -^j.
Уравнение
arc ctg л: =/л имеет единственное решение χ = ctg m, если т
принадлежит интервалу (0, π).
Решение уравнения вида
/ (arc sin x) = 0
(по знаком функции / может быть любая другая аркфункция) по-
средством подстановки приводится к решению смешанной системы
/(0 = 0, —L<*<JL
с последующим решением простейших уравнений (по числу реше-
ний смешанной системы).
327
Решение уравнения
/ (arcsinχ, arc cos*) = О
в силу тождества arc cos л: = ~ — arc sin χ приводится к предыдуще-
му случаю. Аналогичное замечание относится к уравнению
/ (arc tg x, ate ctg χ) — 0.
Одним из наиболее распространенных приемов решения урав-
нений, содержащих обратные тригонометрические функции, яв-
ляется выполнение некоторой тригонометрической операции над
обеими частями данного уравнения. Этот способ решения приводит
(в общем случае) к уравнению не эквивалентному дан-
ному. Рассмотрим, например, уравнения
/(*)=Ф(*), (I)
sin/(x) = sin φ (χ). (II)
Уравнение (II) есть следствие (I). Обратное не имеет места; в самом
деле, уравнение (II) эквивалентно уравнению
/(*)=(—1)я φ (*) + /ιπ (И*)
с целочисленным параметром, и всякое решение (Пп) при n=f=O
является посторонним для уравнения (I). Для устранения посто-
ронних решений необходима проверка путем подстановки в урав-
нение (I).
Уравнение (I) также (в общем случае) не эквивалентно уравнению
tg/(*)=tg<p(*). (Ill)
В самом деле, во-первых, всякое решение уравнения (I) (если та-
кие решения существуют), при котором обе его части имеют зна-
чения вида —ί— я, является посторонним для уравнения (III)*,
и, во-вторых, всякое решение (если оно существует) уравнения
f(x) = cp(x) + rm (ШЛ)
при n-f=0 есть решение уравнения (III) (если только не имеет места
особый случай), но не является решением уравнения (I), все так-
кие решения должны быть устранены проверкой. Итак, при пере-
ходе от уравнения (I) к (III) возможны как потеря, так и появление
посторонних решений.
Так, например, уравнение
х = я — χ (1)
* В общем виде мы не касаемся вопроса о применимости принципа
предельного перехода.
328
имеет единственно решение χ = —, а уравнение
tg* = tg(ji — x) (2)
имеет серию решений χ = kn. При переходе от уравнения (1) и
(2) появилась серия посторонних решений χ = kn, а решение
х = ~ потеряно.
Во многих случаях в результате выполнения какой-либо три-
гонометрической операции над обеими частями уравнения, со-
держащего аркфункции, получается алгебраическое уравнение.
В каждом таком случае все корни данного уравнения содержатся
среди корней алгебраического уравнения, за исключением, быть
может, случая перехода от уравнения (I) к уравнению (III), когда
возможна потеря некоторых решений. Следовательно, для решения
данного уравнения достаточно найти все решения алгебраического
уравнения в поле действительных чисел и подвергнуть их проверке
посредством подстановки в исходное уравнение. Алгебраические
функции (получающиеся в результате выполнения тригонометри-
ческих операций над аркфункциями, вообще говоря, являются
иррациональными. Следовательно, уравнения, получающиеся после
выполнения тригонометрических операций над обеими частями дан-
ного уравнения, в общем случае будут также иррациональными.
Для получения алгебраического уравнения необходимо еще (в об-
щем случае) освобождение иррационального уравнения от радика-
лов, что в свою очередь может привести к появлению посторонних
решений.
Источником появления посторонних решений могут быть 1акже
тождественные преобразования. Так, например, для уравнения
arc sin f(x) = arc sin φ(χ)
множество допустимых значений неизвестного определяется из
двух условий:
Г. значения χ должны принадлежать области определения
функций f (χ) и φ (χ), рассматриваемых совместно;
2°. должны выполняться неравенства
При переходе к уравнению
f Μ = φ W
(если это последнее уравнение рассматривать вне связи с данным)
условия 2° отпадают. Изменение множества допустимых значений
обусловлено тождественными преобразованиями:
sin (arc sin / (*)) = f {x)t sin (arc sin φ (χ)) = φ (jt).
329
Примеры.
1. Решить уравнение
3 arc sin VH — π = 0.
Решение.
arc sin Vχ = -5- , Vχ = -?г и x = Τ ·
2. Решить уравнение
4 arc tg (лг2 — 3* + 3) — π = >
Решение.
arc tg (л:2 — За: + 3) = -£■, *2 — 3* + 3 = 1,
откуда
«, 1 „ о
Л^ — 1, Л2 — ^#
3. Решить уравнение
2 arc sin л: = 8.
Решение. Уравнение не имеет решений, так как оно имеет противо-
речивое следствие
π
arc sin x = 4, но 4 > -у .
4. Решить уравнение
π — arc sin χ = arc cos x. (1)
Решение. Возьмем синус от обеих частей:
sin (π — arc sin x) ■= sin (arc cos x)t
откуда
sin (arc sin *) = sin (arc cos x)
или
x = Y\ —л;2. (2)
Возведя в квадрат обе части, получим:
2л:2 = 1,
откуда
1 1
*= ут и*==~Ί7Τ-
Значение — тр=- не есть корень иррационального уравнения (2). Это есть
постороннее решение, появившееся в результате возведения в квадрат обеих
частей уравнения (2). Значение χ = -γ=. есть корень иррационального урав-
нения, но не есть решение данного уравнения (1), так как данное уравнение
не имеет решений. В самом деле, противное предположение противоречит
тождеству
π
arc sin χ + arc cos x = -н*
1
=· удовле·
arc sin χ = arc cos xm
Значение х = г— · удовлетворяет другому уравнению;
330
Если взять синус от обеих частей этого последнего уравнения, то получится
то же самое иррациональное уравнение.
5. Решить уравнение
arc tg (x + 2) — arc tg (χ + 1) = -£- .
Решение. Взяв тангенс от обеих частей, получим квадратное урав-
нение:
х2 + Зх + 2 = О,
которое имеет корни х{ = — 2, х2 = —1.
Оба найденные значения удовлетворяют уравнению.
6. Решить уравнение
arc cos χ — arc tg χ.
Решение. Взяв косинус от обеих частей, получим:
1
откуда
х2 (х2 + 1) = 1 или хх + х2 — 1 = 0.
Последнее уравнение имеет два действительные корня:
и *2 = -J/ "
из которых данному уравнению удовлетворяет первый.
7. Решить уравнение
2 arc sin x = arc cos 2x. (1)
Решение. Имеем:
cos (2 arc sin x) = cos (arc cos 2x),
откуда
1 — 2x2 = 2x, 2x2 + 2x — 1 = 0, (2)
следовательно,
*ι -— 2 » *2 = 2
Область определения уравнения (1) устанавливается системой двух
неравенств:
1*1 < 1 и | 2х | < 1, откуда — γ < х< у .
Этим условиям удовлетворяет корень #2, который является решением урав-
нения (1), так как дуги 2 arc sin х2 и arc cos 2х2 содержатся в интервале (0, π)
и имеют одинаковый косинус, а потому они равны. Корень х^ является посто-
ронним для уравнения (1), так как | *41 > 1; этот корень появился в резуль-
тате расширения области определения при переходе от уравнения (1) к (2).
8. Решить уравнение
arc sin mx = arc cos nx.
Решение. Возьмем синус от обеих частей (1):
sin (arc sin mx) = sin (arc cos nx)\
331
откуда получим иррациональное уравнение
тх = W— п2х2.
По возведении обеих частей в квадрат, получим:
= 1, откуда χ = ±
г 2 д
Возможны следующие случаи:
Г. т > О, η ;> 0, но, по крайней мере, одно из чисел т или /г отлична
от нуля. В этом случае уравнению может удовлетворить только положитель-
ное значение х, так как при χ < 0 дуги arc sin χ и arc cos nx расположены
в различных промежутках.
Единственным решением уравнения является
1
*~~ Vm2 + п* '
2°. т < 0, η < О, но, по крайней мере, одно из чисел т или η отлично
от нуля. В этом случае уравнение не может иметь положительных решений,
и единственным его решением является
//л2 + л2
3°. т > 0, η < 0. В этом случае уравнение (1) не имеет решений, так
как аргументы аркфункций тх и п% имеют разные знаки, а поэтому дуги
arc sin тх и arc cos nx расположены в различных промежутках. То же самое
имеет место в случае т > 0, η < 0.
4°. т = η == 0. В этом случае уравнение противоречиво.
9. Решить уравнение
π
arc sin 2x + arc sin x ь= -5- , (1)
Решение. Приравняв косинусы обеих частей:
cos (arc sin 2х -f- arc sin χ) = -к ,
получим иррациональное уравнение:
Vl — 4л:2 VY^l? — 2х* = у ; (2)
освободив от радикалов, получим:
28х2 —3 = 0.
Решив это квадратное уравнение, найдем
1
1 ι/Τ
Значение л: = —у I/ -у не может служить корнем данного уравне-
( i/~^ ( 1 -ι/"3"\
ния. В самом деле, дуги arc sin у— у γ) и arc sin ^— ~ζ у γ) содер-
/ π \ π
жатся в интервале!— -γ > 01 и их сумма не равна -у .
332
1 Ί/"3
Значение χ = γ Ι/ у является корнем данного уравнения: достаточно
заметить, что при этом значении косинус от обеих частей уравнения (1)
1
равен -χ .
Примечание I. Взятие косинуса, а не какой-нибудь
другой тригонометрической операции, удобно (в данном случае), так
как получается только одно слагаемое, содержащее радикалы, что
позволяет освободить уравнение от иррациональности однократным
возведением в квадрат обеих частей. Если, например, взять синус от
обеих частей, то в левой части получатся два слагаемых, содержащие
радикалы. ·
Примечание II. Значение х~ — у у γ удовлетворяет
уравнению, которое получается из (1) заменой его правой части на
π
— -тр; иррациональное уравнение (2) получится то же самое.
о
10. Решить уравнение
arc sin x + arc cos (1 — χ) = arc sin (— x). (I)
Решение. Выполнив преобразования, получим эквивалентное урав-
нение
2 arc sin x + arc соз (1—*) = 0,
откуда
2 arc sin x = — arc cos (1 — χ).
Приравняв косинусы обеих частей, получим:
cos (2 arc sin x) = 1 — χ, откуда 2х2 — χ = 0. (2)
Корни уравнения (2) суть χ = 0 и χ— -j. Подстановкой в данное урав-
ние установим, что ему удовлетворяет только первый корень χ — 0. Вто-
1
рое значение χ = γ является решением уравнения
arc sin χ — arc cos (1 — χ) = arc sin (— x).
11. Решить уравнение
2 . 1
arc sin——?=- — arc sin У 1 — χ = arc sin -^ . (1)
Решение. Приравняв синусы обеих частый, получим:
После освобождения от радикалов и преобразований получим квадрат-
2
ное уравнение 9jc2 — 12* + 4 = 0, имеющее двукратный корень χ = ?г .
о
Подстановкой убедимся, что он удовлетворяет уравнению (1).
Примечание. То же самое квадратное уравнение полу-
чится, если уравнение (1) заменить уравнением
2 . 1
arc sin ,- + arc sin У 1 — χ = arc sin у . (2)
333
2
Значение χ = -^ не удовлетворяет уравнению (2). В этом случае ирра-
циональное уравнение примет вид:
~9x X 3 ;
последнее уравнение решений не имеет.
12. Решить уравнение
2 arc cos x = arc sin (2x V\ — x2). (1)
Решение. Имеем:
sin (2 arc cos x) ~ 2x V\ — x2\
2x V\ —x2 = 2x V\ — x2.
Последнее уравнение удовлетворяется тождественно на сегменте
— 1 < χ < 1. При χ < г— дуга 2 arc cos а: оканчивается за пределами пер-
вой четверти, и уравнение (1) не удовлетворяется; при произвольном
х> г.— эта дуга содержится в первой (замкнутой) четверти; уравнение
(1) удовлетворяется.
Итак, множество всех решений уравнения (1) есть сегмент —-f=<a:<1;
множество посторонних решений есть полусегмент — 1 < χ < ~~т= .
13. Решить систему
π2
arc sin x arc sin у = -ттг ,
arc cos x arc cos у = -кг ,
π
Решение. Воспользовавшись тождеством arc cos a = -ψ — arc sin a,
выразим левую часть второго уравнения через арксинусы.
/π \ / π \ π2
\-γ — arc sin x\ Ι -γ — arc sin yj = -gj .
Выполнив подстановку и = arc sin χ, ν == arc sin у и тождественные преоб-
разования, получим систему:
π2 π 5
uv = 12"' uv ~~ (" + ϋ) Τ" + ~2ΐ π2 = °·
Вычислив « + ϋ и uu, составим квадратное уравнение, корнями кото-
рого являются и и ν.
12г2 — 7π2 + π2 = 0,
π π π π
откуда Ui = -у , Ci=-4~h w2 = -j- , ^2=~з".
334
Следовательно, получим совокупность двух систем:
π \ . π \
arc sin χ = -g- I arc sin χ = —ξ- j
i и I .
arc sin у = -τ- Ι arcsiny = -q-|
Данная система имеет два решения:
/3" /2" VI /3"
Х\ = —γ", У ι = —γ- и х2 = -γ- г Уг = —2~ ·
14. Решить уравнение
arc sin mx = 2 arc tg /ζ*. (1)
Решение. Взяв синус от обеих частей, получим:
sin (arc sin mx) = sin (2 arc tg nx), (2)
откуда
2/2 X
(3)
Это уравнение, а также и (1) имеет очевидное решение χ = 0. Для отыска-
ния прочих решений (сократив на х) получим уравнение
2п
или
тп2х2 = 2п — т. (4)
Если тфО и η φ 0, то уравнение (4) имеет в поле комплексных чисел
следующие корни:
2п— т
2п — т
Значения χ действительны, если ——— > 0, откуда
т>0 ) т< 0 )
либо (I), либо (II).
т < 2п J m > 2a2 J
Подлежат рассмотрению следующие случаи:
Случай 1° т > 0, п> 0 Из неравенств (I) найдем 0 < т < 2я; при
этом условии из формулы (5) получим два действительных значения х\
1 -1/г2п-т 1 ί/
:-7гУ —— и ^ = — К
2n —m
m
Множество допустимых значений неизвестного для уравнения (1) нахо-
дится из условия | mx \ < 1
Это последнее неравенство есть следствие уравнения (3), так как при
всех значениях χ
335
Чтобы положительный корень х2 удовлетворял уравнению (1), необходи-
мо и достаточно выполнения неравенства
2 arc tg пх2 < -у , откуда Н<~
или
2л — т
т
< 1, т. е.
Если 0 < л < т < 2/г, то дуги arc sin тх2 и 2arctgrtx2 имеют одинаковый
синус; обе эти дуги содержатся в первой четверти, а потому равны, т. е х2
удовлетворяет уравнению (1).
Отрицательный корень jq = — х2 в данном случае также удовлетворяет
уравннению (I).
Из изложенного следует, что при т > О, η > 0 уравнение имеет:
а) единственный корень χ = 0, если 2п < т (корни уравнения (4) мни-
мые), а также, если 2п = т (тогда xt = х2 = 0);
b) три действительные корня, если η < т < 2п\
c) единственный корень χ = 0, если η > т.
В последнем случае дуга 2 arc tg *2 оканчивается во второй четверти
π
и аналогично 2 arc tg χ4 < —-g ·
Примечание. Если η — т> то xt = —
В этом случае «граничном» для Ь) и с) имеем
m
arc sin
2 arc tg m# = ± ~оГ
a)
2/7 < m
b)
4 n < m < 2 /7
/77 = ΛΪ
Черт 184
Результаты исследования пояснены графически на чертже 184.
Случай 2°. m < 0, я < 0 рассматриваются аналогично предыдущему
случаю. Уравнение (1) можно заменить эквивалентным уравнением
arc sin (—тх) = 2 arc tg (—пх),
что равносильно замене т и η на —m и —л.
336
Случай 3°. Числа тип — противоположных знаков. Уравнение (1)
имеет единственное решение χ = 0.
Случай 4°. т = 0, η Φ 0 либо т Φ 0, η = 0.
Уравнение имеет единственное решение л: = 0.
Случай 5°. m = я = 0. Уравнение (1) удовлетворяется тождественно.
При изложенном способе при переходе от уравнения (1) к уравнению
(2) могут появиться посторонние решения, что и имело место в случае 1с).
В этом случае корень х{ удовлетворяет уравнению
arc sin mx = — π — 2 arc tg nx,
а корень х2 — уравнению
arc sin mx = π — 2 arc tg nx.
Примечание. Переход от уравнения (1) к уравнению (2)
путем вычисления синуса от обеих частей удобен тем, что в результате
получается рациональное уравнение.
§ 54. Примеры решения некоторых трансцендентных уравнений
В настоящем параграфе приведены примеры решения некоторых транс-
цендентных уравнений, содержащих различные сложные трансцендентные
функции от неизвестного.
Примеры.
1. Решить уравнение
\oga (sin x + cos x) — Ъ.
Решение. Данное уравнение эквивалентно уравнению
л ( к \ сР
sin χ + cos χ = а° или sin [χ + ~j"l = г— . (2)
Чтобы уравнение (2) имело решения, необходимо и достаточно выполне-
ния условия
/2
< 1 или 0 < аь < /2. (3)
Если основание логарифмов а > 1, то неравенства (3) эквивалентны
неравенствам
— °° < b <-γ \oga2.
Если а < 1, ίο -γ \oga 2 < b < + °°·
При соблюдении условия (3) имеем серию решений:
аь π
χ = (—\)п arc sin -y= — -j- + пк.
2. Решить уравнение
1^3 sin ax-\- cos ах = Ь. (I)
Решение. Решаем уравнение, эквивалентное данному:
(π \ Ь
12 Зак. 597 337
Если I b I > 2, то уравнение (2) не имеет решений, если |6|<2, то
получим эквивалентное уравнение с целочисленным параметром:
Ь π
ах = (—1)" arc sin -γ — -g- + ηπ.
Последнее уравнение эквивалентно совокупности двух уравнений
Ь π
ах = arc sin -γ — -jr + 2&тг; (3)
α* = -g- — arc sin у + 2/fit. (3')
Из неравенства ах > О определяются условия, при которых уравнения
(3) и (3') имеют решения:
1°. Для уравнения (3)
Ъ η
arc sin -у — ~g~ + 2&π > О,
откуда
_ ί 0, 1,2 л если 1 < Ь < 2,
~~ 1 1,2 m если —2 < 6<1;
2°. Для уравнения (3')
5π г>
-g- — arc sin -g- + 2^π > О,
откуда fe = 0, 1, 2, . . ., т, . . .
Итак, если | Ь \ < 2, то уравнение имеет две серии решений:
х = loga I arc sin-у — -у + 2focl и л: = loga f -γ — arc sin-у + 2kn\ ,
где значения k для каждой серии определяются соответственно условия-
ми 1° и 2°.
3. Решить уравнение
sin (π arc tg χ) = cos (π arc tg *),
Решение. Положив м = π arc tg *, получим:
π
sin и = cos и, откуда и = -τ- + kn.
Для вычисления * получим уравнение
arc tg* =-j + &.
Значения &, при которых последнее уравнение имеет решение, опреде-
ляются из условия
π Ι π
"~"2~<Т"^^<~2~' отку да k = 0> *' "" J *
Уравнение имеет три решения:
1 . 3 5
^ = tg-4-, x = — tg-j, x = tg-y.
4. Решить уравнение
lg (arc tg x) + lg (arc ctg *) = a. (1)
338
Решение. Найдем область определения уравнения:
arc tg x > 0, arc ctg x > 0, откуда χ > 0.
Уравнение (1) эквивалентно следующему:
arc tg x arc ctg x = 10α.
Положив / = arc tg x, получим смешанную систему:
Корни квадратного уравнения суть:
п± Уп2— 16-10°
«- 4 · -
Корни действительны, если
π2— 16-10" > 0, откуда Ж 2 lg-j- .
При этом условии корни tx и t2 квадратного уравнения положительны
π
-у й
"О"(τ) -Τ·Τ
π ίχ -\-t2 τι π
0 < ?ι < ί2 < "у » так как —2— = ~4~ < ~2~ *
Следовательно, при а < 2 lg -τ- уравнение имеет два решения:
5. Решить уравнение
Решение. Область определения уравнения находится из условия
cos χ > 0. При этом условии, прологарифмировав обе части, получим:
(cos 3* + 2 cos x) lg cos χ = 0.
Последнее уравнение эквивалентно совокупности двух уравнений:
cos 3* + 2 cos χ = 0 и lg cos χ == 0.
Первое уравнение после преобразования примет вид
(4 cos2 χ — 1) cos χ = 0,
откуда получим три серии:
+ 2k (2fe + 1)
χ = ± -у + 2*π, χ = ± у π + 2kn, x = (2fe + 1) γ-
Из второго уравнения найдем четвертую серию:
cos χ = 1 и χ = 2/ети.
Для решений первой серии условие cos χ > 0 выполняется. Для решений
второй серии имеем cos χ < 0, следовательно, вторая серия является посто-
ронней.
U· 139
Для решений третьей серии левая часть уравнения принимает вид 0°,
т. е. теряет смысл, следовательно, эта серия является серией посторонних
решений.
Четвертая серия удовлетворяет уравнению.
Итак, имеем две серии решений:
* = ± -g- + 2kn и χ = 2kn.
Примечание. Применим к решениям третьей серии принцип
предельного перехода:
lim (cos x)cos x{4 cos2 *-1) = lim гг{АгШ'{) = lim 10(422~1)2 lg г = 1,
(2k+l)n iim2^2- i)
x ~* 2 *-o
ибо limzlgz = 0 (см. «Специальный курс элементарной алгебры»,
§ 108). Следовательно, третья серия состоит из особых решений.
6. Решить уравнение
=l. (1)
Решение. Область определения уравнения (1) находится из условия
0 < sin χ < 1.
Преобразуем левую часть, перейдя к логарифмам при основании 2
log2 sin χ 2 log2 sin χ
откуда
log2 sin χ = ζ
данное уравнение эквивалентно смешанной системе
±γψ
sin* = 2 Δ , 0 < sin χ < 1.
Эта последняя система имеет серию решений, дающую общее решение
данного уравнения
- V-тг ι°ζ* 3
х = (—l)n arc sin 2 ν 2 +ηπ.
7. Решить уравнение
Решение. Введем промежуточный аргумент:
*2 — 1 2
" ~ х2 + 1 ~" * "" х2 + 1 *
В промежутке 0 < χ < -f- °° аргумент и возрастает от —1 до 1,
промежутке — оо < χ < 0 убывает от 1 до —1; сложная функция
340
в первом промежутке возрастает от —tg 1 до tg 1, а во втором —убывает
от tg 1 до —tg 1 (черт. 185) Следовательно» при | а \ > tg 1 уравнение не имеет
решений, так как |у| < tg I, при \а\ < tg 1 уравнение имеет два взаимно
противоположные решения; при а = —tg 1 единственное решение χ — 0;
при а — tg 1 — не имеет решений.
Уравнение эквивалентно алгебраическому с действительным параметром
α и с целочисленным параметром k:
χ2 — 1
= arc tga
χ2\
4-
tg)
-tg\T
Черт. 185
Черт. 186
Если |a|<tgl, т. е. |arctga|<l, то неравенство | и \ = | arc tg a -|-
+ £π|<1 выполняется при единственном значении k = 0. Следовательно,
данное уравнение эквивалентно следующему
Ответ. Если — tg 1 < а < tg I, то χ = ;
arc tg a
! — arc tg a '
Если | α | > tg 1 или α = tg 1, то уравнение не имеет решений.
8. Решить уравнение ах -f- a~x =2 cos*
Решение. Левая часть ах + а~х = ах + —
ах
имеет при χ — 0 наименьшее значение равное 2 (см. «Специальный курс
элементарной алгебры», § 104, пример 14). Левая часть имеет наибольшее зна-
чение равное 2 при χ = 2kn. Равенство возможно при χ = 0. Уравнение име-
ет единственное решение χ = 0 (черт. 186).
9. Решить уравнение
= р.
1
Решение. Приняв во внимание, что у 2 — 1 = , —
sin χ
/=0/2+1)
тогда получим уравнение:
=0.
(1)
положим
(2)
341
Левую часть уравнения (1) можно представить в следующем виде:
у = asin х + a~sin * , где а = VVT+T,
эта функция четная, наименьшее ее значение есть у = 2 при sin л = 0, а
наибольшее
7===
У/2 + 1
2+1
при sin*=l. Следовательно, график пересекается с прямой у —ρ при
условии 2 < ρ < /2" VV~2+ 1 (черт 187).
Черт 187
При соблюдении этого условия имеет место следующее расположение кор-
ней квадратного уравнения (2):
<h = т-< к/. < V7T+T.
Ответ. Если
то уравнение имеет серию решений
§ 55. Приемы решения тригонометрических
и некоторых других трансцендентных неравенств
I. Неравенства, приводящиеся к простей-
шим
Рассмотрим неравенство вида
где fix) — данная тригонометрическая функция, а — данное для
определенности положительное число. Рассмотрим, например, не-
равенство
cos ^
342
Имеем:
откуда
— arc cos m + 2kn < αχ < arc cos m + 2&π,
arc cos m
, 2kn
' a
arc cos m
4_ ^
Предположим, в частности, что а — ρ есть натуральное число;
в этом случае функция cos px имеет период — ; любой сегмент дли-
ной 2π содержит ρ периодов левой части. Следовательно, на единич-
ной окружности существует ρ геометрически различных дуг, на
которых выполняется данное неравенство. Эти дуги определяются
неравенствами
arc cos m . 2kn ^ ^ arc cos m . 2kn
при k = 0, 1, 2, ..., ρ — 1.
На чертеже 188 изображены дуги единичной окружности, на
которых выполняется неравенство cos 5лГ>
Черт. 188
Примеры.
Решить систему неравенств
tgx>
Черт. 189
cos Зх > — -
Решение. Число 2π является общим периодом функций tg x и cos Зх.
Найдем дуги в пределах одного (общего) периода, на которых выполняются
оба данные неравенства.
Первое неравенство выполняется в двух интервалах:
5π 3π
-Τ<Χ<Ύ· 0)
-j-< x< -γ и
Второе неравенство выполняется в трех интервалах (черт. 189)
2π
10
14
Χ< -FT'i
(2)
343
Две системы интервалов (1) и (2) имеют общую часть в виде следующих
двух интервалов:
4π π 5π 3
~9~ < * < ~2Г и Τ < х < ~2п'
Общее решение системы есть совокупность интервалов
4π π
-g- + 2kn < χ < -γ + 2kn,
5π
2. Решить неравенство
3
-γπ + 2kn.
cos χ Ι < т.
n-arccosm
arccosm
Решение. 1°. При т>\ неравенство выполняется тождественно.
2°. При т <; 0 неравенство противоречиво.
3°. При 0 < т < 1 неравенство эквивалентно системе
— т < cos χ < т.
Функция | cos л: | периодическая
с периодом π. На сегменте [0, π] по
длине равном периоду неравенства,
оно выполняется в интервале (черт 190)
arc cos m < χ < π — arc cos т.
Общее решение есть совокупность ин-
тервалов
arc cos m + kn < χ < — arc cos m +
Черт. 190
П. Основываясь на общих законах монотонности арифмети-
ческих действий, на неравенствах, содержащих абсолютные ве-
личины, на свойствах тригонометрических функций: ограничен-
ность
— 1 < cos χ < 1, — 1 < sin χ < 1,
монотонность, знакопостоянство в данных промежутках и т. п.,
можно непосредственно устанавливать различные неравенства,
связывающие значения тригонометрических функций в различных
промежутках. Ниже приводятся примеры непосредственного уста-
новления различных неравенств; соответствующие приемы никакой
общей теорией предусмотрены быть не могут.
Примеры.
1. Доказать, что для любого острого угла χ
sin x + cos χ > 1.
Решение. Рассмотрим тождество
sin2 χ + cos2 χ = 1.
Для острого угла 0 < sin χ < 1, а потому sin2 χ < sin x, а также
cos2 χ < cos χ, откуда и следует доказываемое неравенство (истолковать
344
геометрически). Для острых углов также непосредственно устанавливаются
следующие неравенства:
sin χ
2. sin χ < tg x, так как tg x = CQg χ и 0 < cos χ < 1.
3. sin (χ -f У) < sin a: -f- sin у (применить формулу (Sa ι β)).
4. sin 2jk < 2 sin χ, так как sin 2x — 2 sin * cos x и 0 < cos χ < 1.
π 2tg a:
5. tg 2* > 2 tg at, если 0 < χ < -j , так как tg 2л: = t __ t 2 ^ ·
I!I. Неравенство рациональное относительно некоторой три-
гонометрической функции
решается подстановкой f(x) = t\ при этом к неравенству
R
следует присоединить неравенства —1<7<1, если f{x) обозначает
синус либо косинус. Решив неравенство (R) относительно промежу-
точного аргумента t, сведем задачу к решению простейших триго-
нометрических неравенств.
Если левая часть является рациональным выражением относи-
тельно нескольких функций, то применением рационализирующей
подстановки (случаи применимости этих подстановок указаны в
§ 23) неравенство может быть приведено к предыдущему виду.
Примеры.
1. Решить неравенство
sin χ > cos2 x.
Решение. Применив рационализирующую подстановку t = sin л\ по-
лучим систему неравенств:
t2 + t — 1 > 0, —1 < / < 1.
Решением первого неравенства является множество двух интервалов
— ос < t < 2 и 2 <*<+°°·
Общей частью системы этих двух интервалов и сегмента [ — 1, 1] является
промежуток
Следовательно, данное тригонометрическое неравенство эквивалентно про-
стейшему неравенству:
У "-1
откуда
У"Ъ— 1 УЬ 1
arc sin 2 + 2^π < л: < — arc sin ^ + 2 (2Л + 1) π
V~5-l \
arc sin 2 ^0,66 найдем по таблицам ),
123 Зак. 597 345
2. Решить неравенство
sin χ -f- cos χ — 1
sin χ — cos χ + 1 '
χ
Решение. Положим t = tg γ , тогда получим (после подстановки
и преобразований):
sin χ + cos χ— 1 1 — /
sin лс — cos χ + 1 ~~ 1 + / »
откуда получим две линейные системы:
Первая система имеет решение —1 <t < 1, а вторая не имеет решений.
Следовательно,
-К tgy < 1,
откуда (в пределах одного периода)
π χ π π π
~4"<*2~<~4" и — IT ^ * ^ IT '
Переходя к данному неравенству, заметим, что при χ = 0 его левая
часть теряет смысл, а потому его решение (в пределах одного периода) со-
стоит из двух интервалов
— γ < х <0 и 0 < χ < j .
Общее решение есть совокупность интервалов
Примечание. Если в точке χ = 0 значение левой части данного
неравенства найти по принципу продолжения по непрерывности, то по-
лучим
sin χ + cos χ — 1 1 — t
i1™) sin*-cosA: + l =|^0Γ+7 = 1·
В таком случае точку χ — 0 исключать не следует.
IV. При решении тригонометрических неравенств можно при-
менять следующий общий прием.
Предположим, что решено уравнение
/W=0, (f)
т. е. что известны все его корни и что, будучи расположены в по-
рядке возрастания, эти корни делят область определения функ-
ции / (х) на конечное или бесконечное множество промежутков.
Пусть χ/_ι и Χι —два соседние корня уравнения (f); если функция
f(x) непрерывна, то в интервале (*/_ь Χι) она знакопостоянна, так
как в этом интервале она не обращается в нуль. В рассматриваемом
346
случае корни уравнения (f) разбивают область определения функ-
ции / (*) на интервалы знакопостоянства. Общим решением нера-
венства
служит множество всех интервалов, в которых функция f(x) по-
ложительна.
Если функция f{x) разложена на множители: f = fi/2···/* и для
каждого множителя (в отдельности) установлены интервалы зна-
копостоянства, то, объединив в одно множество концы всех эт?.х
интервалов, получим разбиение области определения f(x) на ин-
тервалы знакопостоянства.
Неравенство
/М>0 (или f(x)<0)
выполняется в тех интервалах, в которых число отрицательных
сомножителей четно (нечетно).
Примеры.
Решить неравенство
sin χ > sin 3*.
Решение. Решаем эквивалентное неравенство:
sin χ —sin3x > 0 и — 2 cos 2х sin χ > 0;
последнее неравенство эквивалентно неравенству
cos 2x sin χ < 0. (1)
Найдем корни уравнения
cos 2*«sin x = 0
на сегменте [—π, π], охватывающем период левой части.
π 3
Решив уравнения cos 2х = 0 и sin χ — 0, получим χ = ± f» x=± jk,
;t = 0 и χ=±π. Составим таблицу распределения знаков для каждого из
интервалов, на которые делят найденные корни сегмент [—π, π|Ί
χ
cos 2x
sin χ
cos 2x sin χ
—π
+
0
0
<*<
+
—
—
3π
4
0
—
0
<x<
—
—
+
π
— τ
0
—
0
<x<
+
—
—
0
+
0
0
+
+
+
π
Τ
0
+
0
<ΛΓ<
—'
+
—
3π
4
0
+
0
<*<
+
+
+
π
-4-
0
0
12Β*
347
Следовательно, неравенство (1) выполняется в интервалах
/ 3 \ f π \ π 3 \
(-π. -Ίή, (_τ. θ), Τ. τή.
Общее решение состоит из трех серий интервалов
-l)«,(2*-4)«|; [(2ft—!")«. 2ta]; ^2k + |) π, (2* + |) π] .
2. Решить неравенство
χ
Решение. Рассмотрим левую и правую части в пределах промежут-
ка, охватывающего их общий период 3π. Имеем:
2
tg χ — tg ~n > 0 или
cos a: sin -Q-
Составим таблицу распределения знаков множителей числителя и знамена-
теля:
X
2
sin -^χ
cos χ
X
cosT
2
sin -q-a:
χ
cos χ cos —$-
ό
0
0
I
+
0
<χ<
+
+
+
π
+
0
+
<χ<
+
—
3
Τπ
0
0
0
<*<
—
+
—
+
5π
2
—
0
—
<χ<
—
—
. —
—
3π
0
—
—
0
/ π\ /3 5 \
Неравенство выполняется в интервалах [О» ~о/ и Ι Τπ» "9"π]*
V. Применение координатной интерпретации. Так как cos φ
и sin φ суть абсцисса и ордината точки единичной окружности, то
решение неравенства
/ (cos φ, sin φ)>0
равносильно решению смешанной алгебраической системы
/(х, У)>О, *2 + у2 = 1;
348
Эта система определяет ту часть единичной окружности, которая
содержится в области f (х, у)^> О (черт. 191).
Решения системы уравнений
f{x, у) =0,*2 +у2 = 1
суть концы дуг, на которых выполняется данное тригонометричес-
кое неравенство.
Примеры.
1. Решить неравенство
COS φ -f- sin φ > 1.
Решение. Решаем смешанную систему
х + у— 1 > 0 и A:2 + y2 = l.
Черт. 191
Надо найти дугу окружности, лежащую выше прямой
дим точки пересечения прямой и окружности:
= — х+\. Нахо-
Из этой системы найдем координаты концов дуги
*ι = 1. У1 = 0 и х2 = 0, у2 = 1
(черт. 192)
В верхней полуплоскости относительно прямой у = — χ + 1 лежит дуга
π
О < φ < -ζ . Общим решением неравенства служит бесконечное множество
интервалов I
/ π
I 2Ы, -^
\
+ 2kn\ (дуги, оканчивающиееся в первой четверти).
2. Решить неравенство
Sin φ > 4 V 3 COS3 φ.
Решение. Составляем смешанную систему:
349
Решением этой смешанной системы служит дуга единичной окружности,
расположенная выше кубической параболы у
ресечения параболы и окружности:
4|/Л3*3. Находим точки пе-
X2 +
hy2 = i г
откуда 48х* -f- χ2 == 1.
Последнее уравнение имеет два действительных корня χ =± -j . Дуга
π 4π
■g" < ? < "з" расположена на единичной окружности выше данной кубиче-
ской параболы, общим решением служит бесконечное множество интервалов
(черт. 193)
VI. На нижеследующих при-
мерах показано решение триго-
нометрического неравенства с дву-
мя неизвестными.
Черт. 193
Примеры.
1. Решить неравенство
Решение. Имеем
Черт. 194
sin (χ + у) > 0.
< х + у<(2к+\)к
или
2Ы — χ < у < (2k + 1) π — χ.
При данном целом значении к полученные неравенства определяют на пло-
скости полосу, ограниченную двумя параллельными прямыми: снизу пря-
мой у = —χ + 2kn и сверху прямой у = —χ -j· (2/г + 1)π. Придавая
к произвольные целочисленные значения, получим бесконечное множество
параллельных полос (черт. 194).
350
2. Решить неравенство
sin χ > sin у.
Решение. Ниже изложено решение неравенства в геометрической
форме. Имеем!
χ _1_ у χ у
sin х — sin у > 0, откуда cos —?>— s^n —9— > ^·
Первый множитель положителен, если
π х 4-у π
+ 2kn < ρ1 <
откуда получим бесконечное множество полос!
(4/г — 1) π — х < у < (4k + 1) π — х.
В полосах
(4* + 1) π — χ < у < (46 + 3) π — χ
первый множитель отрицателен.
у — χ
Второй множитель положителен, если sin —r>— < 0» откуда
или
(4fc + 2) π + * < у < 4 (Λ + 1) π + χ.
В полосах
46π + χ < у < (4k + 2) π + χ
второй множитель отрицателен. Полосы,
в которых оба множителя имеют одина-
ковый знак, в пересечении образуют мно-
жество квадратов, расположенных «в шах-
матном порядке»; на чертеже 195 эти квад-
раты заштрихованы.
3. Решить неравенство
ЗГС tg Τ > Ь Черт. .95
Решение. Данное неравенство эквивалентно неравенству -j <
При χ > 0 получим -j ж < у < -{- оо;
π
при χ < 0 получим — оо < у < -т- х.
Геометрически общее решение изображается двумя областями (I)
образованными точками, лежащими внутри двух вертикальных
(черт. 196).
У_
χ '
и (II),
углов
351
4. Решить неравенство
sin π (χ2 4- У2) < 0.
Решение. Имеем;
(2k + 1) π < π (χ2 + у2) < 2 (k + 1)π,
где k = 0, 1, 2, 3, ..., так как *2 + у2 > 0. Следовательно,
V(2k + 1) < ϊΛχ2 + у2 < V2(k + 1);
геометрически множество всех решений состоит из бесконечного множества
концентрических колец (открытых) с центром в начале координат (на чертеже
197 эти кольца отмечены знаками +).
Черт. 196
Черт. 197
VII. Простейшие неравенства, содержащие обратные триго-
нометрические функции, решаются непосредственно: достаточно
воспользоваться свойством монотонности и принять во внимание
область определения и множество значений данной функции. Так,
в частности, неравенство
arc sin χ < а
при я>-75г удовлетворяется во всей области определения аркси-
нуса, т. е. на сегменте — 1<*<1; при — -^<α
arc sin x< arc sin (sin α), откуда — 1 <x<<sin а\ при
γ имеем
γ
неравенство не имеет решений, так как —γ < arc sin x.
352
Примеры
1
2
3
4
5
6
7
8
9
10
11
Неравенстве
arc sin χ < 1
arc sin x < 5
1
arc cos χ > arc cos -g
arc tg χ > 5
arc tg < 5
arc cos > 0
π
arc cos χ <— -y
π
arc sin ^ < — -g-
3
arcctg * > -4-π
π
arc ctg * > "2
arc sin л: < — 2
Общее решение
— 1 < χ < Sin 1
— 1 < Χ < 1
1
не имеет решений
—оо < χ < -\- оо
— 1 < * < 1
не имеет решений
1
— 1 < χ < — ~2
— оо < χ < — 1
—оо < л: < 0
не имеет решений
12 Решить неравенство
arc tg2 л: — 4 arc tg x + 3 > 0 (1)
Решение. Положив / = arc tg x, решаем систему
о, — -ή <t <-к.
(2)
Решением квадратного неравенства служит система двух интервалов:
— оо</<1 и 3</< + оо Решением системы (2) служит интервал
— iL < t < 1. Решение (1) найдем из условия — — < arc tg л: < 1,
откуда — оо < χ < tg 1.
353
VIΠ Ниже приведены примеры решения различных неравенств, содержа-
щих сложные трансцендентные функции от неизвестных.
1 Решить неравенство arc sin χ < arc sin (1 — χ).
Решение. Областью определения левой части служит сегмент
—1 < χ < 1, областью определения правой части —сегмент 0 < χ < 2,
общей частью этих сегментов служит сегмент 0 < χ < 1. В силу возрастания
арксинуса данное неравенство эквивалентно следующей системе»
* < 1 — χ и 0< * < 1,
откуда получим полусегмент 0 < χ < -*· (черт. 198).
y=arcsin(\—x)
Черт. 198
2. Решить неравенство
arc sin χ > arc cos χ.
Решение. Если χ < 0, то неравенство не может выполняться, так
как arc sin дс<0, a arc cos x > 0. Поэтому достаточно найти решение неравен-
ства на сегменте 0 < χ < 1. В этом предположении левая и правая части
принадлежат первой (замкнутой) четверти, в которой (в силу монотонности
синуса) имеем:
sin (arc sin χ) > sin (arc cos *) или χ > V 1 — χ1 ,
откуда χ2 > 1 — χ2 и, наконец, r— < χ < 1 (черт. 199).
Неравенство
V~2
arc sin χ < arc cos χ
1
выполняется в промежутке — 1 < χ < г— .
3. Решить неравенство
arc cos χ > arc cos χ2.
Решение. Областью определения неравенства служит сегмент
— 1<х<1. В силу убывания арккосинуса данное неравенство эквива-
лентно системе
χ < х1 и — 1 < χ < 1,
откуда — 1 < χ < 0 (черт. 200).
354
4. Решить неравенство
arc sin (χ2 + IJ < 2.
Решение. Область определения неравенства состоит из единственно-
го значения χ = 0, при этом значении неравенство выполняется.
Неравенство имеет единственное решение χ = 0.
5. Решить неравенство
asin* > flcos* где α > о.
Решение. При а>\ неравенство эквивалентно тригонометрическому
неравенству
sin Г jc—-ξ ) > 0
sin χ > cos χ, откуда
iy=zarccosx
y=.arccosx[
y = arcsinx) -T 01 I
Черт 199 Черт. 200
При а<\ неравенство эквивалентно неравенству
sin x < cos x, откуда
3 π
— -г π + 2kn < χ < -j +
При α = 1 неравенство не имеет решений.
6. Решить неравенство
sin (4 cos χ) > 0.
Решение. Так как множество значений промежуточного аргумента
и = 4 cos χ есть сегмент — 4 < и < 4, то решаем систему
sin w > 0, — 4 < и < 4.
Разобьем сегмент [— 4, 4] на следующие промежутки:
— 4 < ы < — π, —π<«<0, 0<«<π, π<«<4;
неравенство sin и > 0 выполняется в совокупности промежутков
— 4<«<—π и 0 < и < π,
откуда совокупность систем неравенств
— 1
cos χ < —
0 < cos χ < -τ .
355
В пределах одного периода косинуса первая система неравенств выполняет-
ся в интервале
π π
π — arc cos -τ < χ < π + arc cos -τ .
Вторая система неравенств выполняется в интервалах
π π π π
arc cos -τ < χ < ~2 и — -к < χ < — arc cos —г .
Общее решение состоит из трех серий интервалов:
π π
(2ft + 1)π — arc cos -j < x<(2k + 1)π + arc cos -ζ,
π Ak + 1 4ft — 1 π
arc cos -ζ + 2&π < χ < —^— π и —?>— π < χ < 2&π — arc cos -χ .
7. Решить неравенство
πχ
tg4(x+l) >L «)
Решение. Неравенство выполняется, если
π πχ π
T+kn<4(x+\) <T +*«.
откуда
1 + 4^ < 7Τ1 < 2 + 4Λ. (2)
Примем во внимание, что при произвольном (заданном) целом k
1+Ч& и 2+4yfe суть числа одного знака. В самом деле,
1 + 4/? > 0, если β > —-ζ , т. е. если Л > 0;
2 + 4& > 0, если k > — у , т. е. если & > 0,
и аналогично, оба эти выражения отрицательны при k < 0. Следовательно,
при любом целом k неравенства (2) эквивалентны неравенствам
1 1 1 — Ak I —4ft— I
Г+~4£> 1+Т> 2~F4£ или nr4fe>7 (3>
r4fe>7> 2 + Ak ; (3>
_ 4ft — 4ft — i
числа \ 4. 4^ и 2 4- 4ft ПРИ любом ^елом ЬфО имеют один и тот же
знак —оба отрицательны. В самом деле, при ft>0 числители обеих дро-
бей отрицательны, а знаменатели — положительны, а при ft < 0 числители
попожчтельны, а знаменатели — отрицательны. Следовательно, при произ-
вольном целом ft фО неравенства (3) эквивалентны неравенствам
Н-4ft 2 +4ft
4ft < х < ~" 4ft + 1 ;
при ft = 0 из неравенств (3) получим}
0>у> — у или — оо < л; < — 2.
Общее решение (1) состоит из бесконечного множества интервалов (4)
и интервала (— оо, —2).
356
§ 56. О приближенном решении трансцендентных уравнений
Вопрос об элементарных графических и численных
(приближенных) приемах решения уравнений изложен в учебнике
по специальному курсу элементарной алгебры (см. «Специальный
курс элементарной алгебры», § 66). Напомним, что обычно графи-
ческий прием позволяет в первом приближении определить про-
межутки, в которых заключаются корни уравнения; последующее
применение метода деления промежутка позволяет вычислить дан-
ный корень с требуемой степенью точности.
Пусть f(a) и f{b) (где а<6) — числа разных знаков и в интер-
вале (а, Ь) содержится лишь один корень уравнения
fix) =0.
Вычислив значения функции f(x) в промежуточных точках интер-
вала (а, Ь), можно вычислить искомый корень с любой степенью
точности.
При применении линейной интерполяции в качестве прибли-
женного значения корня берут абсциссу точки пересечения оси
абсцисс и хорды, соединяющей концы (a, f (а)) и (ft, /(Ь))дуги линии
у= f (χ). Это приближенное значение находится по формуле
(Ь - a) f (a)
слагаемое
(Ь - a) f (а)
— а = —
f(b)-f (a)
называется поправкой, эту поправку следует прибавить к первона-
чальному значению χ = а (см. «Специальный курс элементарной
алгебры», § 66).
Примеры.
1. Рассмотрим уравнение
sin я —х-\- 1 = 0.
Из чертежа 201, на котором представлены графики функций у = sin x
и у = χ—1, видно что корень данного уравнения находится в интервале
Вычислив значения непрерывной функции / (х) = sin χ — χ -{- 1
(г- ·>
π
в точках "о" и π, получим числа, противоположные по знаку.
2 — γ>0 и /(π) =—π+1 < 0.
/π \
Вычислив значение функции / (χ) в середине интервала I у, тИ, полу-
чим отрицательный результат:
з \ VI з
/==~2~~Τπ+ 1 = — 0 64 <0.
/π 3 \
Следовательно, искомый корень содержится в интервале (у, ~Τπ) Вы"
357
числив значение функции в промежуточной точке
жительный результат:
3 \ У~Ъ 2
Ы
= -^π, получим поло-
/2 3 \
1"3*π» fπ ) ·
Следовательно, искомый корень содержится в интервале
Продолжая вычисление промежуточных значений, можно найти как угодно
малый интервал, содержащий искомый корень, и вычислить этот корень
с любой данной степенью точности.
y=sinx
Черт. 201
2. Рассмотрим уравнение tg χ = χ. В силу нечетности данных функций
представляет интерес отыскание лишь положительных корней. Как
показывает черт. 202 уравнение имеет бесконечное множество положитель-
ных корней. В интервале (0, у) корней нет, ибо χ < tg x; первый поло-
/ 3 \
жительный корень содержится в интервале [π, ~пк\> второй — в интер-
вале (2π, "2"πΙ, третий — в интервале (3π, ^-π) и τ д.; k-й корень со-
(2k 4- 1 \
кк, —о—π)> причем по крайней мере увеличения
2k + 1
k корень приближается к —о—π·
Вычислим приближенно с точностью до 0,1 наименьший положительный
корень. Заменим данное уравнение эквивалентным уравнением
sin χ — jccos χ = 0,
левая часть которого не имеет разрыва на сегменте
[π, -Ι*]·
Положим
f (χ) — sin χ—λ; cos*. В точке ~г π = 3,9250 (=225°)* (т. е. в середине сег-
мента), имеем:
(-j π ) = sin (225°) (1 — 3,9250) = 2,068 > 0.
* В скобках даны значения аргументов тригонометрических функций
в градусах лишь потому, что распространенные тригонометрические табли-
цы составлены в градусной мере.
358
/5 3 \
(τκ· τη-
Так как /Ι"ο"π) =— 1 < 0. то искомый корень содержится в интервале
Черт. 202
/ 5
Вычисляем поправку при линейной интерполяции ί положив а = -ξ- π,
/3 5 \ / 5 \ π
(т*-4«)>(т*)_т·2·068
°'5292 (- 30°19')·
Следовательно, Х\ — -j" π + Δ* = 4,4542 (= 255°19') Вычислим / (х^);
имеем;
/ (xt) = sin 255°19' — 4,4542 cos (255°19') =
= —cos 14Ο4Γ + 4,4542 sin 14Ο41' = 0,161 > 0.
/ % \
Так как / -^-π = — 1, а / (4,4542) = 0,161, то искомый корень лежит
/ 3 λ
ε интервале (4,45; "у π) · Значение /(4,4542) близко к нулю, поэтому ес-
тественно ожидать, что искомый корень ближе к 4,45, чем к ~к π = 4,71.
Предлагаем читателю проверить, что /(4,5) < 0. Искомый корень ξ содер-
жится между 4,45 и 4,50. Более точные вычисления дают ξ = 4,4934..,
Глава шестая
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ГЕОМЕТРИЧЕСКИХ ФИГУР;
ПРИМЕНЕНИЯ ТРИГОНОМЕТРИИ
§ 57. Общие понятия
В геометрии рассматриваются различные элементы геометричес-
ких фигур, как, например:
в планиметрии — стороны, углы (внутренние и внешние), пло-
щадь, периметр данного многоугольника, высоты, медианы, бис-
сектрисы, радиус вписанного круга данного треугольника и т. п.;
в стереометрии — ребра, грани, двугранные и линейные углы
данного многогранника и т. п.
Тригонометрия изучает различные задачи на вычисление
значений искомых элементов геометрической фигуры по достаточ-
ному количеству значений заданных элементов этой фигуры.
Для краткости в тригонометрии принято (в случаях, когда это
не может повлечь недоразумений) сам элемент фигуры и его меру
(численное значение) называть одним и тем же термином. Так,
например, слово «сторона» может означать как сам геометрический
элемент (т. е. отрезок), так и его длину; термин «боковая поверх-
ность» может означать как саму поверхность, так и ее площадь,
и т. п.
Наиболее подробно в тригонометрии изучается «решение тре-
угольников», т. е. вычисление различных элементов треугольника
по достаточному количеству данных его элементов. Это обусловлено
тем, что вычисление элементов более сложных фигур (плоских и
пространственных) обычно сводится к вычислению элементов цепи
треугольников, дающей возможность последовательно перейти от
данных элементов к искомым.
Опрелделение. Стороны и углы треугольника называются его
основными элементами.
Различные прочие элементы треугольника будем называть его
неосновными элементами.
330
Если Л, S, С — вершины данного треугольника, то принято
теми же буквами А В. С обозначать его углы (а также их величины),
имеющие вершинами эти точки, строчными буквами а, Ь, с обозна-
чать стороны (а также их длины), проти-
волежащие углам, обозначенным теми же
прописными буквами (черт. 203).
Допустимые значения основных элемен-
тов треугольника определяются следую-
щими условиями:
Г. Углы А, В и С всякого треугольни-
ка С положительны и (в евклидовой гео-
Черт 203 метрии) в сумме составляют л:
Л>0, β>0, С>0; А + В + С = л.
2°. Всякая сторона треугольника меньше суммы двух его других
сторон.
§ 58. Соотношения между основными элементами треугольника
I. Теорема синусов. Во всяком треугольнике стороны
пропорциональны синусам противолежащих углов.
sin A sin В sin С А>
где R — радиус круга, описанного около данного треугольника.
Доказательство. Пусть Л — произвольный
угол треугольника; для доказательства достаточно установить
справедливость равенства
a =2R sin Л. (1)
Случай 1°. Угол Л — острый (черт. 204). Через одну из
вершин, отличную от Л, например через β, проведем диаметр В А'
описанного круга. Рассмотрим вспомогательный треугольник Л'ВС.
В этом треугольнике угол А' равен углу Л, так как оба эти угла
опираются на одну и ту же дугу ВС. Из прямоугольного тре-
угольника А'ВС найдем равенства (1).
Случай 2°. Угол Л — тупой (черт. 205). Выполним то же
построение. В этом случае угол Л' опирается на дугу ВАС, допол-
нительную до 2л по отношению к дуге, на которую опирается
угол Л. Следовательно, А' = π — Л. Из треугольника А'ВС най-
дем:
а = 2/? sin A' = 2/? sin Л.
Случай 3°. Угол Л — прямой (черт. 206). Из треугольника
ABC найдем непосредственно:
a = 2R = 2R sin -J = 2R sin Л.
361
Систему равенств
sin Л sin В sin С :
А+В+С=п
(I)
будем называть основной системой соотношений между элемен-
тами треугольника.
Черт. 205
Черт. 206
Черт. 207
II. Теорема проекций. Для всякого треугольника име-
ет место система соотношений
а = b cos С -f с cos В
Ъ = с cos A + a cos С
с = a cos В + 6 cos A
(И)
Доказательство. Пусть ABC — данный треугольник;
проекция ломаной CAB на ее замыкающую СВ равна СВ, т. е. а.
Итак (черт. 207):
пр CAB = пр С А + пр АВ = b cos С + ccosB = а.
362
Аналогично устанавливаются два прочие соотношения системы
(II), ч. т. д.
III. Теорема косинусов. Для всякого треугольника
имеет место система соотношений
а2 =
с2 — 2bc cos Л;
(Ill)
'■ — 2abcosC.
Доказательство. Из геометрии известно, что (черт. 208)
a) а2 = Ь* + с2 — 26AD, если А < -ϊ-;
b) а2 = б2 + с2 -(- 26D/1, если Л > ■£;
c) а2 = Ьъ + с2,
S В
если Л = -5-.
A b С А Ь С
b) с)
Черт. 208
Эти три равенства можно объединить в одно, заметив, что
AD = прас АВ:
а2 = Ь2 + с2 — 2Ь-прАСАВ
(в слу чае Ь)пр ас А В <С0). Приняв во внимание, что прлс^4 В = с cos Л,
получим первое равенство (III). Аналогично устанавливаются
прочие равенства, ч. т. д.
Теорема. Если система шести чисел а> Ь, с, А, В, С удовлетворя-
ет условиям:
2) 0<Л<я, 0<β<π, 0<С<я
и если для нее выполняется какая-либо одна из систем соотношений
(I), (II) и (III), то для нее выполняются и две другие системы этих
соотношений.
Разъяснение. Если углы измеряются не в радианной мере,
то вместо л должна быть взята соответствующая мера развернутого
угла. В частности, при градусной мере неравенства 2) запишутся
так:
0° < Л < 180°; 0° < В < 180°; 0° < С < 180°.
363
Таким образом, теорема утверждает, что системы (I), (II)
(111) эквивалентны между собой. Если принять за основу какую-
либо одну из этих систем, то две дугие можно получить как ее
следствия.
Доказательство. Г. Докажем, что из системы (I)
следуют системы (II) и (III). В самом деле, имеем:
А = π —-Β — С,
откуда
sin A = sin В cos С + cos В sin С. (I)
Обозначив через 2R коэффициент пропорциональности (вне зави-
симости от его геометрического смысла для равных отношений
системы (I), получим:
а = 2/? sin Л, b = 2Rs\nBy с = 2/? sin С,
умножив обе части (I) на 2Rt получим первое соотношение (II), ана-
логично получаются прочие соотношения (II).
Возведем почленно в квадрат равенство (I) и выполним следую-
щие преобразования:
sin2 A = sin2 В cos2 С + cos2 В sin2 С + 2 sin В sin С cos В cos С =
= sin2 В (1 — sin2 С) + (1 — sin2 В) sin2 С + 2 sin В sin С cos В cos С =
= sin2 β -f sin2 С + 2 sin В sin С (cos В cos С — sin В sin С) =
= sin2fi -f sin2C + 2 sin β sin С cos (β+ C).
Приняв во внимание, что В + С = π — Л, получим оконча-
тельно:
sin2 Л = sin2fi + sin2 С —2 sin β sin С cos Л.
Умножив обе части на (2i?)2, получим первое равенство системы
(III). Аналогично устанавливаются прочие равенства системы (III).
Т. Докажем, что из системы (II) следуют системы (I) и (III).
Исключим с из равенств (II): умножим первое из этих равенств
на а, второе — на 6 и вычтем почленно, тогда получим:
а2 — Ь2 = с (a cos В — Ь cos Л).
Подставив с из третьего равенства, получим:
а2 — Ь2 = а2 cos2 β — б2 cos2 Л,
откуда
a2 sin2 β = b2 sin2 Л; α sin В = b sin Л
(так как α, 6 sin А и sin β положительны), а потому
а _ 6
sin A ~~ sin β ·
364
Так же доказываются равенства
а с Ь
sin A sin С ' sin В sin С *
Остается доказать, что Л + В + С = π.
Заменив в первом равенстве (II), линейном однородном отно-
сительно ау b и с, эти числа пропорциональными им числами
sin Л sin β и sin С, получим:
sin Л = sin В cos С + sin С cos В,
откуда
sin A =sin(fi + C).
Приняв во внимание, что 0 < Л < π и 0<β + Ο<[2π>
получим:
а) либо А == В + С, либо Л + В + С = π.
Допустим, что
А + В + Сф π,
тогда
Л = β + С.
Воспользуемся вторым и третьим равенством (II). Взяв для
определенности второе равенство, получим аналогично
sin β = sin(i4 + C),
и так как по предположению
то
В = А + С.
Из системы уравнений
В=А+С
следует С = 0, что противоречит условию С>0. Итак, предположе-
ние, что А+В+Сфп ведет к противоречию, а потому Л + В+С=п.
Следовательно, если выполняются соотношения (II), то выпол-
няются все соотношения системы (I), т. е. система (I) есть след-
ствие системы (II).
Так как (по доказанному) из системы (II) вытекает система (I),
а из системы (I) вытекает система (III), то система (III) есть след-
ствие системы (II).
Примечание. Это нетрудно обнаружить непосред-
ственно,
365
Умножив равенства (II) соответственно на а, Ь, —с и сложив
почленно, получим:
а2 + Ь2 — с2 = (аЬ cos С + ас cos В) + {be cos A + ba cos С) —
— (са cos В -\- cb cos Л) = 2αύ cos С,
откуда
с* = а2 + б2 — 2а6 cos С.
Аналогично выведем остальные равенства системы (III)
3°. Докажем, что из системы (III) следуют системы (I) и (II).
Сложив два первые равенства системы (III), после сокращения
получим третье равенство системы (II); аналогично получатся ос-
тальные равенства.
Так как из системы (111) следует (II), а из системы (II) следует
I), то из системы (III) следует система (I).
Примечание. Равенства (1) можно вывести из равенств
(III) непосредственно.
В самом деле, из первого равенства (III) найдем
sin A *= 1/1-cosM = ]/1 - (*'+^-fl1)' =«·/<,
где
К = Д- К(а + 6 + с)(а + 6-с)(а + с —6)(6 + с —с),
так как множитель К есть симметрическая функция аргументов
а, 6, с, то
sin A sin В sin С ^
Сложив последние два равенства (III) и заменив а, Ь, с
пропорциональными им числами sin Л, sin β, sin С, получим
sin Л = sin(B + С).
Доказательство заканчивается так же, как в пункте 2°.
В пунктах Г, 2°, 3° рассмотрены все случаи возможные согласно
условию теоремы, ч. т. д.
Теорема. Если для шести величин а, 6, с, Л, В, С, удовлетво-
ряющих условиям:
Г. а>0, 6>0, с>0;
2°. 0<Л<л, 0<β<π, 0<С<>,
выполняется какая-либо одна из систем соотношений (I), (II), (III),
то существует единственный треугольник, стороны которого суть
a, by ct а противолежащие им углы А, В, С (соответственно).
Разъяснение: конгруэнтные, но различно расположенные
треугольники не считаются различными.
366
Доказательство. Если выполняется одна из систем (I),
(II), (III), то в силу эквивалентности этих систем выполняются и
две другие. Из первого равенства системы (II) имеем:
а <b | cos С | + с | cos В |< b + с.
Из двух других равенств этой системы получим:
£<с + а, с<а + Ь.
Следовательно, числа а, Ъ и с таковы, что любое число из них мень-
ше суммы двух других. Из геометрии известно, что при этом уело*
вии существует единственный треугольник, стороны которого вы-
ражаются числами a, b и с. Пусть А\ В' и С — углы полученного
треугольника, противолежащие его сторонам a, b и с (соответ-
ственно). В таком случае из системы соотношений (III), которая
имеет место для всякого треугольника, найдем (в частности) для
треугольника А'В'С
л,
А = arc cos
По условию для чисел а, Ь} с, А, В, С выполняется система со-
отношений (III), из которой найдем
^2 + С2 _ а2
4=arccos 2b~c
Следовательно, А = Л'; аналогично найдем В =В\ С = С".
Треугольник ABC есть искомый, ч. т. д.
Системы основных соотношений могут служить для вычисле-
ния основных элементов треугольника по трем данным его
основным элементам (из которых хотя бы один элемент — сторона,
см. ниже § 64).
§ 59. Тригонометрические тождества и неравенства,
имеющие место для углов треугольника
В настоящем параграфе приводятся некоторые тригонометри-
ческие соотношения (равенства и неравенства), выполняющиеся
тождественно для углов произвольного (в общем случае) треуголь-
ника.
Доказанные ниже равенства имеют место при более общих пред-
положениях: они выполняются для произвольной (допустимой)
системы трех углов Л, β, С, составляющих в сумме π:
А + В + С = п.
В частности, эти тождества справедливы, если А, В и С суть углы
треугольника. Условные тригонометрические тождества приме-
367
няются в различных преобразованиях формул, содержащих три-
гонометрические функции от углов треугольника *.
1. Из соотношения А = π — (В + С) на основании формул
приведения следуют тождества:
sin A = sin (В + С), cos А = — cos (В + С),
tg4=-tg(fl + C). (1)
При помощи круговой перестановки аргументов А, В и С уста-
навливаются еще шесть аналогичных формул.
2. Из соотношения у = γ у— следуют тождества:
sinl=cos^, cosA = sin^, tg*=ctg*±£. (2)
При помощи круговой перестановки аргументов устанавлива-
ются еще шесть аналогичных формул.
3. Для углов косоугольного треугольника:
tg A + tgfi + tgC - tg A tgfitgC. (3)
Доказательство.
\alA 4- R -U П = tg Л + tg Б + tg С — tg Л tg Β tg С _ Ω
щ^-ru-p^) ι _ tg Л tg β — tg β tg С — tg С tg Л ~"υ>
откуда следует (3), ч. т. д.
А В ВС С А
4 tg — tg l· tg — tg l· tg — tg — =1 (4)
• о О Lo Ο ι δ Ο δ Ο Ι δ Ο ιδ О V '
ττ ^ Л , Β . С π
Доказательство. Так как у + у + у^у» то
/Л . В . С\ Л В С /, , А , В
COS/ y + y + yj =COSyCOSyCOSyM— tgytg у —
откуда следует тождество (4), ч. т. д.
ABC
5. sin Л + sin В + sin С = 4 cos — cos у cos у =
= 4 sin —у— sin —у— sin —у— . (5)
Доказательство.
sin A + sin В + sin С = sin Л + sin В + sin (Л + В) =
о . Л + β Л —β , о Л + в . А + В
= 2 sin X cos —s h 2 cos —J5— sin —£— = ·
~ . A + B/ A — B, A + B\ л . А + В А В
= 2sin—y— (cos-y f- cos—^-j =4sin —y-cos у cos у.
y (
* Приводимая ниже сводка формул может служить для справок. За-
поминать все эти формулы не следует.
368
Для получения тождества (5) достаточно воспользоваться ра-
венствами (2), ч. т. д.
ЛВС
6. cos A + cos В + cos С = 1 +4 sin у sin у sin у , (6)
Доказательство,
cos А + cosB + cos С = 2cos ^-±-^cos ^T~ + (l ~
A A+B . A . В . t
= 4 cos—γ- sin у sin у + 1,
откуда в силу (2) следует тождество (6), ч. т. д.
Аналогично доказываются следующие тождества:
ЛВС
7. sin A + sin В — sin С = 4 sin у sin у cos у. (7)
arc
8. cos A -f- cos В — cos С = 4 cos у cos у sin у — 1. (8)
9. sin 2Л + sin 2В + sin 2C = 4 sin A sin В sin С
(воспользоваться тождеством 2А + 2В + 2С = 4π). (9)
10. cos2,4 + cos2B + cos2C = — 1 — 4cos Л cosBcosC. (10)
11. sin2 A + sin2 В — sin2 С = 2 sin Л sin β cos С
(см. предыдущий параграф, стр. 364). (11)
12. sin2 Л -bsin2B + sin2C = 2(l + cos Л cos В cos С). (12)
Доказательство. Достаточно выразить левую часть через
функции от двойного аргумента и воспользоваться формулой (10).
13. cos2 Л -f- cos2В + cos2С = 1 — 2cos Л cosBcosC. (13)
14. sin Л cos β cos С + sin β cos Л cos С + sin С cos Л cos β =
= sin Л sin β sin С. (14)
Доказательство. Достаточно воспользоваться условием
sin (Л +В + С) =0.
15. sin у sin у cos у + sin у cos у sin у +
+ cos у sin у sin у = cos у cos у cos у . (15)
Доказательство. Достаточно воспользоваться условием
13 Зак. 597 369
Ниже приводятся некоторые тригонометрические неравенства,
имеющие место для углов треугольника.
16. tg^ + tg2§ + tga£>l. (16)
Воспользуемся тождеством (4) и неравенством Буняковского
(см. «Специальный курс элементарной алгебры», § 58):
ч. т. д.
17. sinysin|-siny<-i-. (17)
Доказательство. Обозначим буквой k левую часть дока-
зываемого равенства; будем иметь:
1 / А— В . С\ . С
= у (COS —2 Sin у \ Sin у .
Q
Положив χ = sin -^-, получим следующее квадратное уравнение:
+ 2£==0.
Так как корни этого уравнения должны быть действительны, то
Δ = cos2 ^=-5 — 8k > О,
откуда:
k < -g- cos2 2 < у
ч. т. д.
18. cos A + cos В + cosC<; -r-. (18)
Доказательство. Воспользовавшись тождеством (6) и не-
равенством (17), получим:
1 3
cos A + cos β-J-cosC^ 1 + 4 · -~ — -к >
ч. т. д.
19. sin A + sin В + sin С <Ц^. (19)
370
Доказательство. Воспользовавшись теоремой о выпук-
лых функциях (см. «Специальный курс элементарной алгебры»,
§ 58), получим: __
. „ , . η , · />/о . Л + В+С 3/3
smA + sin β + sin С <3sin—Ly-J— = —^—,
4. Т. Д.
20. cos £ cos | cos § < Ц1. (20)
Доказательство. Достаточно воспользоваться тождест-
вом (5) и неравенством (19).
21. tgiitgftgf <i-ir. (21)
Доказательство. При данной сумме
произведение
имеет наибольшее значение, если
. А . в , В > С , С , Л
Т0 τ0 —— \0 ТСГ — —- TCf —^ tf^ ——
& Q о О о О & О о О о О 9
откуда А = В = С = — . Для равностороннего треугольника имеет
место равенство
δ 2 lg 2 lg 2 3 /3 ·
Для всякого неравностороннего треугольника имеет место нера-
венство, ч. т. д.
22. Доказать, что
>2Э если треугольник
остроугольный,
sin2 A + sin2 S + sin2 С
, если треугольник
тупоугольный,
= 2, если треугольник
прямоугольный.
(22)
Доказательство. В силу тождества (12)
sin2 A + sin2 В + sin2 С — 2 = 2 cos /4 cos β cos С,
Для остроугольного треугольника правая часть последнего тож-
дества положительна, для тупоугольного треугольника — отри-
13* 371
цательна (один из косинусов отрицателен), а для прямоугольного
треугольника — равна нулю, это утверждение равносильно дока-
зываемому, ч. т. д.
§ 60. Элементы различных измерений
Определение. Выражение
F(a, 6, с, А, В, С),
составленное из основных элементов треугольника, называется эле-
ментом п-го измерения, если оно является положительно-однородной
функцией п-го измерения от аргументов a, b и с.
Иными словами, при замене аргументов а, Ь и с числами ka,
kby kc выражение умножится на kn:
F(ka, kb, kct А, В, С) = knF(a, b, с, А, В, С),
где k — произвольное положительное число.
В частности, элементы нулевого измерения называются угловыми
элементами. Элементы первого измерения называются линейными
элементами.
При растяжении сторон треугольника в k раз их длины а, Ь, с
заменяются числами ka, kb, kc, а сам треугольник подвергается
преобразованию подобия с коэффициентом k. При таком преобра-
зовании всякий элемент п-го измерения изменяется в kn раз.
При преобразовании подобия треугольника его угловые эле-
менты не меняются (в этом случае η = 0 и kn = 1):
если F — угловой элемент, то
F(a, b, су Α, В, С) = F(ka, kb, kc, А, В, С).
Примерами угловых элементов могут служить углы треуголь-
ника А, В, Су их тригонометрические функции, выражение °^-т
и т. п.
При преобразовании подобия треугольника каждый из его ли-
нейных элементов изменяется в k раз (в этом случае η = 1 и kn = k):
если F — линейный элемент, то
F(ka, kb, kc, А, В, С) = kF(a, b, с, А, В, С).
Примерами линейных элементов могут служить стороны, бис-
сектрисы, медианы, высоты треугольника, радиусы вписанного
и описанного кругов, периметр.
Примером элемента второго измерения может служить площадь
треугольника, она изменяется в k2 раз при преобразовании подо-
бия с коэффициентом k.
Теорема. Элемент U является угловым в том и только в том
случае, если он может быть выражен посредством формулы, содержа-
щей только лишь углы треугольника.
372
Доказательство. Если элемент U может быть выражен
формулой
U = F(A, β, С),
не содержащей сторон, то при замене сторон а, 6, с числами ka,
kb, kc он не меняется, значит, U есть угловой элемент.
Обратно, если U = F (а, Ь, с, Л, β, С) есть угловой элемент,
то (по условию) он не изменяется, если в нем а, Ь и с заменить
пропорциональными числами:
s\nA = ^\ sin£ = 2/?; sinC = ^,
ПОЛОЖИВ k — ^5 ·
Следовательно,
,c,A,B,C) = F^, ±, ±, Л, В, с) =
= F(s\nAy sin β, sin С, Л, В, С), ч. т. д.
Так, например,
2р __ 2 (sin Л + sin В + sin С)
а ~~ sin A
(где ρ — полупериметр) есть угловой элемент.
Теорема. Отношение двух элементов одного и того же измерения
есть угловой элемент.
Доказательство. Если
Ft (а, 6, су Л, β, С) и F2(a, Ь, с, Л, β, С)
— два элемента измерения м, то их отношение не изменяется при
преобразовании подобия треугольника
Fl(ka, kb, kc, А, В, С) _ kn F1(af b, с, А, В, С) __
f 2 (ka, kb, kc, А, В, С) ~~ kn F2 (a, b, с, А, В, С) ~~
_ T7! (g, b, с, Л, В, С)
~~ F2(a, b, с, А, В, С) '
Следовательно, это отношение есть угловой элемент, ч. т. д.
Следствие. В частности, отношение двух линейных эле-
ментов есть угловой элемент.
Пусть L =L(a, b, с, Α, β, С) — некоторый линейный элемент
треугольника. Заменим a, b и с на 2R siaA, 2R smB и 2R sinC. Если
вынести множитель 2^, то получим:
Ца, Ь} с, Л, β, С) =2R-L(sinA, sinfi, sinC, Л, β, С). (1)
Выражение L(sinA, sinfi, sinC, Л, β, С) есть угловой элемент.
Определение. Угловой элемент Ц8тЛ, sinfi, sin С, Л, β, С)
называется угловым элементом, соответствующим линейному эле-
менту L(a, b, с, А, В, С), и обозначается символом U(L).
373
В силу равенства (1) имеем:
L = 2R.U(L). (2)
Так, например, угловой элемент, соответствующий периметру
треугольника 2р = а + Ъ + с, есть
U (2р) = sin A + sin В + sin С.
Угловой элемент, соответствующий сумме сторон а + Ьу есть
U(a + b) = s\nA + sinB.
ι
Если F есть элемент порядка пф\у то Fn есть линейный
элемент.
Угловой элемент, соответствующий F, определяется как угло-
/ 1\ 1
вой элемент U\FnJ линейного элемента Fn .
§ 61. Соотношения между различными элементами треугольника
I. Теорема тангенсов. Разность двух сторон тре-
угольника относится к их сумме, как тангенс полуразности проти-
волежащих углов к тангенсу полусуммы этих углов
a-b
(две аналогичные формулы получатся посредством круговой пере-
становки букв в обеих частях).
Доказательство. Преобразуем угловые элементы, со-
ответствующие полусумме и полуразности сторон треугольника:
а + Ь = 2R (sin A + sin В) = 4/? sin ^y-^cos ^=^;
a — b = 2R (sin Л — sin β) = 4R cos^±^- sin
откуда следует теорема тангенсов, ч. т. д.
Геометрическое доказательство. Предпо-
ложим для определенности, что а>&. На чертеже 209 построены
отрезки BD == а + b и Bi( = а — b.
Имеем: ^ ЛСО = π — С;
374
Проведем отрезок KL·, параллельный AD. Треугольники DAK
и AKL — прямоугольные. Из подобия треугольников DAB и
LKB имеем:
а — Ь
ВК
DB
KL
AD
AKtg
А —В
tg
А — В
AKtg·
А + В*
II. Формул ы Μ о л ь в е й д е. Сумма (разность) двух
сторон треугольника относится к третьей стороне, как косинус
(синус) полуразности противолежащих им углов относится к си-
нусу (косинусу) половины угла, противолежащего третьей сто-
роне, т. е.
cos -
А —В
а — Ь
sin
А — В
С
cos~2*
Доказательство. Приняв во внимание, что
= 4/? cos у. cos
, λ η . С
а — b = 4R siny
А — В
С С
с = 47? cos у sin ~2 ,
получим доказываемые формулы, ч. т. д.
Геометрическое доказательство. Вос-
пользуемся чертежом 209. Применив теорему синусов к треуголь-
нику ADB, получим:
a + b
sinM + yl sin(^ + 2 J
А —В
с
sin "тг
С
sin тг
Вторую формулу получим, применив теорему синусов к тре-
угольнику КАВ.
III. Формулы, выражающие тригономет-
рические функции углов треугольника че-
рез его стороны.
375
Из формулы косинусов (§ 58, соотношения III) можно выразить
косинусы углов треугольника через его стороны:
^±. ,1,
Из формулы (1) получим:
Α Ί /Ί + cosA
COS
Α Ί /
/(
Abe
Обозначив через 2р = а + Ь-\- с периметр треугольника, получим:
cos L -
C0S 2 "~
2 "~ V be ф
Посредством аналогичных преобразований получим:
и, наконец,
A ^_ Ί /(ρ - b) (ρ - с) = 1 Ί / (ρ - о) (ρ - 6) (ρ - с)
Щ 2 Г Ρ(ρ-α) p-aV p
Прочие шесть формул могут быть выведены из этих круговой
перестановкой букв.
.. ι Г(р — а) (р — Ь) (р —с)
Множитель г = I/ —^- -^ - есть симметрическая
функция от аргументов a, b и с, а потому:
° 2 р—а7 ° 2 ρ—-^?' σ 2 ρ —с
(множитель г один и тот же).
IV. Формулы, выражающие различные эле-
менты треугольника через его основные
элементы.
Периметр. Имеем:
2p = a + b + c = 2R (sin A + sin В + sin С) =
= 8R cos у cos у cos у
(см. формулу 5, § 59).
Угловой элемент, соответствующий периметру, есть
ARC
U (2р) = sin Л + sin В + sin С = 4 cos у cos у cos у.
376
Высоты. Пусть АН = 1га — высота, опущенная из вершины А
на сторону а. Из треугольника ВАН найдем:
ha = csinB — в случае острого угла (черт. 210);
ha = с sin (π — В) = с sin В — в случае тупого угла (черт. 211 а);
ha~c~c sin^· = с sin В— в случае прямого угла (черт. 2116).
Итак, независимо от величины угла В имеем:
ha = с sin В.
Точно так же из треугольника САН получим ha = bsinC.
Итак;
= bsinC = 2RsinBsinC.
Угловой элемент высоты ha равен
U(ha) = sin В sin С.
Формулы для других высот получатся круговой перестановкой
букв.
Площадь. Теорема. Площадь треугольника равна половине
произведения двух смежных сторон треугольника на синус угла
между ними:
S = "коЬ sin С = —be sin A = γ ас sin В.
Доказательство. Пусть hb — высота, опущенная на
сторону Ь\ имеем: hb = a sin С, следовательно,
S = у bhb —-y-ab sin С.
Аналогично находятся два другие выражения для площади, ч. т. д.
Площадь есть элемент второго измерения, >Л§~ есть линейный
элемент; соответствующий угловой элемент находится по формуле
U
(/s) = γ
γ sin A sin β sin С .
13В Зак. 597
377
Известная из элементарной геометрии формула Г е ρ о н а
S = Vp(p-a){p — b)(p — cf
дает выражение площади треугольника через его стороны.
Биссектрисы. Пусть AD — Ъа — биссектриса угла А.
Из треугольника BAD найдем (черт. 212):
(2)
sin
sin(//4D£) '
ко
Из
А
/V
В D
Черт
пропорции
R ^
2 π
а С
. 212
(2) найдем:
D'
π —
(у
ψ-
β
Черт.
π В —С
"2 2 #
Q 1
213
* с sin β
а "" В — С '
cos —2—
Угловой элемент биссектрисы Ьа равен
,j,i ч __ sin В sin С
β/ Б — С
cos —2—
Пусть b'a — внешняя биссектриса угла, проходящая через вершину А.
Если В = С, то Ьа не существует. Допустим, что В > С, тогда из тре-
угольника D'AB найдем (черт. 213):
sin (π — В) ~~ sin (AD'В) '
но
Следовательно (в общем случае),
sin В _ ,/ч sin С sin j
. \в-с\
sin J—f;
sin
Медианы. Пусть AM = та — ме-
диана треугольника, проведенная из вер-
шины А (черт 214).
378
Продолжим медиану та на расстояние МА\ равное МА.
Четырехугольник А'ВАС есть параллелограмм. Сумма квадратов
сторон равна сумме квадратов диагоналей, откуда
4т2а + а2 = 2Ь2 + 2с2
и, следовательно,
Угловой элемент медианы та равен
U (ma) = у γ2 sin2 В + 2 sin2 С — sin2 A .
Радиус вписанного круга. Пусть г — радиус кру-
га, вписанного в треугольник ABC. Соединив центр вписанного
круга с вершинами треуголь-
ника, разобьем ABC на три
треугольника: ОАВ, ОВС и
О АС. Пусть S — площадь /7//Д^К/'
треугольника ABC; имеем
(черт. 215):
S = iui. АОАВ+ил. АОВС+ ^ _^
+ пл. АОАС = ±гс + ±-га+ °~ ~ с ^*
т 215
Итак, имеем:
5
Ρ
Воспользовавшись формулой Герона, получим:
г = ί/(ρ- д) (р — 6) (р — g)
У ρ
Подставив выражения для S и ρ через углы треугольника
получим:
г =
-у sin A sin β sin С
Л В С~
2 COS γ COS у COS у
= 2 sin 4- sin I sin -J · (2R).
Угловой элемент радиуса г равен
U (г) = 2 sin у sin у sin у.
Примечание. В формулах, дающих выражение tgy,
tgy, tgy через стороны треугольника (стр. 376), числитель г
есть радиус вписанного круга.
13В*
379
Пусть га—радиус вневписанной окружности, касающейся стороны а.
Из чертежа 216 найдем:
S = пл. АВОа + пл. АСОа— пл. ВСОа =
+ К
= ~2 fa (b + с — а) = (ρ — а) га.
Итак,
Так как
(р-а)
в
в
= 4R cos у cos γ cos γ , г = 4/? sin у sin γ sin
B
ρ — а = 2R ( 2 cos -^ cos -^- cos γ — sin Л j
A ( В С А\
: 4/? cos -ο" ί cos ~n cos -q* — sin -y I =
A I В С
·. 4R cos γ ( cos у cos γ — cos
C\ AD A . В . С
= 4/? cos -о" sin -о" sin -9-,
TO
ra = 47? sin -y cos у cos -g·
ABC
U (га) = 2 sin -γ cos -j cos γ .
Примечание. Формулы для тангенсов половин углов треуголь-
ника можно преобразовать следующим образом:
В гь
= ~ё; tg 2 = ρ ; tg 2 "■
§ 62. Ряд равных отношений
Пусть L — произвольный линейный элемент треугольника ABC.
По определению углового элемента, соответствующего L, имеем
или
Присоединим к основным элементам треугольника произволь-
ные линейные элементы Liy L2, ..., Lk, ... и соответствующие им
угловые элементы i/(Li), U(L2), ..., U{Lk)y тогда можно составить
соответствующий ряд равных отношений, связывающий основные
380
линейные и угловые элементы с элементами Lb L2, ..., Lk и их уг-
ловыми элементами:
* x ~ sin Л sin В' sin С ί/ (Li) U (L2) — U (Lk)
Если вводится в рассмотрение элемент F — измерения п, то
ι
рп
в ряд равных отношений следует включить отношение -
Воспользуемся выражениями для различных угловых элемен-
тов, составленными в предыдущем параграфе:
/
U (2р) - 4 cos у cos у cos у; U (\/S) = ]/у sin A sin В sin С,
ττ/f ч г> · а> г?/» \ sin β sin С
U (ha) = sin β sin С, ί/ (6J =
Б —с
cos—ъ—
U (та) = ~ γ 2 sin2 В + 2 sin2 С — sin2 А ,
Включив в ряд равных отношений периметр, площадь, высоты,
биссектрисы, медианы и радиус вписанного круга, получим
лвс /ι
2 cos -g· cos γ cos γ |/ у sin Л sin β sin С
sin В sin С sin В sin С 1
γ /2 sin2 β + 2 sin2 С — sin2 Л
cos ■
ft . Л . В . С
2 sin -g- sin -g- sin -£
В этом ряде содержатся также и все отношения, получающиеся
из данных одновременной круговой перестановкой букв а, Ъ, с и
Л, β, С. Так, например, вместе с отношением DainC в ряде равных
отношений содержатся и следующие два отношения:
sin С sin A sin Л sin β *
381
Ряд равных отношений позволяет решать различные задачи
на треугольники. Эти задачи могут носить весьма разнообразный
характер, как, например: установление соотношений между раз-
личными элементами треугольника, определение вида треуголь-
ника при заданных соотношениях между его элементами, задачи
на наибольшие и наименьшие значения и т. п.
Примеры
1. Доказать, что
Решение. Имеем:
_L _L i_ 1 / 1 1 1
Kl "*" hb + Tc = 2R V sin θ si ^ +
hb + Tc = 2R V sin θ sin С "^ sin С sin A + sin Л sin В
sin A -\- sin В -f sin С
2i?sin Л sin β sin С
ABC
4 cos -у cos ~2 cos -j
lftD . A . β . С А В С
ibR sin γ sin γ sin γ cos у cos у cos y
А В . С
4R sin у sin у sin у
2, Доказать, что имеет место равенство отношений:
a b с
X = X = X
ha hb hc
Решение. Имеем:
1 1
' ha ZRs'm β sin С '
Отношение
-у = 4R2 sin A sin В sin С
есть симметрическая функция от основных элементов, а потому для всех
трех сторон это отношение одно и то же.
Примечание. Доказываемое равенство отношений следует
также из равенств
ha a = hb Ь == hc с — 2S.
3. Доказать, что для элементов треугольника справедливо тождество
a2 sin (В — С) fr2 sin (С— Л) с2 sin (Л — В) _
sin В + sin С "I" sin С + sin Л "*" sin Л + sin β ~
S82
Решение. Слагаемые левой части получаются друг из друга одно-
временной круговой перестановкой аргументов а, Ь, с и Л, В, С, поэтому
преобразуем первое слагаемое.
a2 sin (В — С) 4/?2 sin2 A sin (В — С)
sin В + sin С ~~ . θ+C В—С^
2 Sin о COS f;
β— С В —С
sin2 Л sin —τ;— cos —is—
= 4R2·
COS тт COS
— С
2 ^a 2
/ ^ ^ β £\
= 4#2 (4 sin2 γ cos j sinr—2— = 4/?2 [(1 — cos A) (cos С — cos B)] =
= 4^2 [cos C —cos В —cos Л (cos С — cos B)].
Выполнив последовательно круговую перестановку букв и сложив, полу-
чим тождественно нуль.
4. Вычислить углы равнобедренного треугольника, для которого отно-
шение η является наибольшим (наименьшим).
π А
Решение. Пусть В = С; в этом случае В = -^ — -ζ ·
Имеем:
г ABC А В
„г = 4 sin ysin у sin у == 4sin^- sin2 γ =
Л Л / Л \
= 2 sin -о" (1 — cos В) = 2 sin γ Ι 1 — sin у 1 =
г
Отношение тг имеет наибольшее значение, если
А
ζ— Л 1 π
У 2 sin -у — Т7~ = 0» откуда Л = -j ,
π
и, следовательно, В = С = q- , искомый треугольник — равносторонний.
sI.-toF,in4-4=Y
Выражение - — I]/2 sin — — —-р=- \ на сегменте [ 0,π ], имеет наименьшее
с< \ £ у Δ J
значение, равное 0 при Л = 0. Это случай вырождения треугольника в от-
резок.
5. Вычислить углы прямоугольного треугольника, стороны которого
образуют арифметическую прогрессию.
Решение. Пусть Л — меньший угол треугольника, ас — его гипо-
тенуза. По условию стороны треугольника с sin Л, с cos Лис образуют ариф-
метическую прогрессию, откуда получим тригонометрическое уравнение:
с sin А + с .
с cos А = 2 или 2 cos Л — sin Л = 1.
Применив универсальную подстановку / —tg-^-, получим:
3/2 _{_ 2/ — 1 = 0.
383
Это уравнение имеет единственный положительный корень t = -j , и сле-
А 1
довательно, tg у = -тт; угол В найдем из условия
В_ ( π Α \ 1
Итак,
А = 2 arc tg -g- » В = 2 arc tgy .
6. Вычислить отношение площади треугольника ABC к площади тре-
угольника AiBiCi, вершинами которого являются точки касания круга,
г
вписанного в данный треугольник с его сторонами, зная отношение р.
Решение. Пусть S и 52 — площади треугольников ABC и AxBiCi.
Найдем выражение для элемента второго измерения Slt Имеем (черт. 217)!
Si = пл. Д О Α χ Βγ + пл. Д О А х Сг + пл. Д Ofii C7 =
= у г2 sin (π — А) + у г2 sin (π — θ) + у г2 sin (π — С) =
1 Л j5 С
= у г2 (sin Л + sin В + sin С) = 2r2 cos у cos у cos у .
(§ 59, формула 5
Следовательно,
ς 2r2 cos у cos у cos у
1Г = 2R2 sin Л sin В sin С ^
г2
А В С ==
8/?2 sin у sin у sin у
>я
27? ί 4/? sin у sin у sin у j
Черт. 217 Г2 г
= 2R*r ==='2R·
7. Доказать, что
Решение. Имеем:
/ д ^ С \ ί А В С \
г*Га*гь'гс= 28^4 (sin у sin у sin у j ί sin у cos у cos у ) χ
/ A . В С\/ А В С\
χ f cos у sin у cos у j ί cos y cos у sin у J =
= 22Ris\n2A sin2 В sin2 С = >
384
Другое решение. Имеем:
г" (р-а)(рР-.Ь)(р-с) = (™· СТР·
(ρ - af (ρ - fr)2 (ρ - cf ^ρ*
ρ2 '(ρ-α) (ρ _б) (р-
= р(р~а)(р-6)(р-с) = 52.
8. Доказать, что
\ 1_ J_ _1_
r ~~ ra^~ rb + rc '
Решение. Имеем:
Ι .Α
, !
С"1" Л В
cos γ sin y cos
COS γ COS
ABC ABC ABC
cos γ sin γ sin γ + sin γ cos γ sin γ -f- sin γ sin γ cos γ
= Л В С А В С
sin γ sin γ sin γ cos γ cos γ cos γ . 4#
= д g С'— у (равенство 15, § 59).
4/? sin γ sin γ sin γ
Другое решение. Имеем!
111 р—а ρ — b р — с Зр — (а + Ь + с) ρ 1
га fb 'с ~~ rP rP rP ~ rP ~~ rp~ r '
§ 63. Общий принцип Торопова решения треугольников
Принцип решения треугольников Торопова указывает
общий прием составления уравнений для вычисления иско-
мых элементов треугольника по трем его данным элементам.
Из геометрии известно, что по заданным (допустимым) зна-
чениям двух углов треугольник определяется по форме, с точностью
до подобия. Это значит, что всякие два треугольника с двумя со-
ответственно равными углами подобны между собой. Если известны
два угла треугольника, то из равенства А + В + С = я опреде-
ляется его третий угол; зная же углы треугольника, можно вы-
числить произвольный данный угловой элемент (как значение дан-
ной функции углов).
Рассмотрим следующую задачу: даны значения двух угловых
элементов Ui(A, β, С) = mi} U2(A, В, CJ= ш2; вычислить углы
А, В, С треугольника.
385
Для нахождения искомых углов составим следующую смешан-
ную систему, состоящую из трех уравнений и трех неравенств:
U\(A, В}С) = тъ U2(A9B,C) = m2\] гтч
А + В + С=п, Л>0, S>0, С>0. J
Всякое решение системы (V) (если оно существует) определяет
бесконечное множество подобных между собой треугольников. В ча-
стности, если система (U) не имеет решений, то треугольников с дан-
ными соотношеними между его углами не существует.
Зная углы треугольника, можно вычислить его произвольный
угловой элемент, при этом линейные элементы определятся из
ряда равных отношений с точностью до положительного
числового множителя:
а = k sin Л, Ь = k sin В, с = k sin С
и вообще L = kU(L)t где k( = 2R) — произвольное положитель-
ное число.
Если множителю k придать некоторое численное значение,
то из множества всех подобных между собой треугольников дан-
ной формы выделится некоторый определенный треугольник, иными
словами, треугольник определится не только по форме, но и по
размерам.
Разобьем различные задачи на решение треугольников на пере-
численные ниже три группы.
Задачи I типа
Даны два угловых элемента U\ = mb U2 = т2 и один линейный
L = п.
Зная Uι и U2, можно составить систему (U) для нахождения Л,
В и С. Зная Л, δ и С, можно вычислить любой угловой элемент и
в частности, элемент U (L), соответствующий L. Знание L дает
возможность вычислить любой его линейный элемент ΖΛ В самом
L ,
деле, из равенства yjp- = k найдем для искомого треугольника
коэффициент пропорциональности ряда равных отношений. Зная
k и угловые элементы треугольника, можно вычислить любой его
линейный элемент L' = Ш (Lf).
В частности, можно вычислить стороны треугольника:
г sin Л , ___ г sin В ^_ г sin С
Число различных решений задачи определяется следующим
образом: всякое решение А, В, С смешанной системы (U) опреде-
ляет треугольник по форме. Если отношение k заданного значе-
ния η элемента L к значению соответствующего углового элемента
U (L) положительно:
>0,
U(L)
366
то треугольник, определяемый этим значением k, дает решение
задачи.
Если отношение г^ут < 0, то соответствующее решение смешан-
ной системы (U) не дает решения задачи.
Итак, число решений задачи равно числу решений смешан-
ной системы (U), для которых отношение т-^-т положительно.
Пример. Приведем пример противоречивой задачи.Пусть L = a— 6=5,
π π 1 " V~2 \ — V2
A = -g- , £= -j , тогда U (Li) = sin Λ — sin В = γ — -ψ = —?> <0
5 10
Так как Л < Б, то должно быть α < 6 и α— 6 < 0, но в условии
а —6 = 5 > 0.
Искомый треугольник не существует.
Задачи II типа
Даны два линейных элемента L\ и L2 и один угловой U = т^
Задача сведется к предыдущей, если будет найден какой-либо
другой угловой элемент. В качестве известного второго углового
элемента можно взять отношение
В качестве известного линейного элемента можно взять либо
Lu либо L2.
Задачи III типа
Даны три линейных элемента Lu L2 и L3.
Задача сведется к случаю I, если будут известны два угловых
элемента. В качестве известных угловых элементов можно взять
отношения:
Таким образом, принцип Торопова дает общий способ составле-
ния смешанной системы (U), соответствующей данной задаче.
Решение и исследование системы (U) производится особо в каждом
конкретном случае, так как вид этой системы зависит от того, какие
элементы являются заданными.
С точки зрения вычислительной практики не безраз-
лично, в какой форме представлено окончательное решение за-
дачи. Так, например, при вычислении при помощи натуральных
таблиц (и арифмометра) желательно формулу решения представить
в виде суммы. При вычислениях с логарифмическими таблицами
(заметим, что в настоящее время эти таблицы все более утрачивают
387
свое значение) желательно формулу решения представить в виде
произведения.
В ряде случаев целесообразно, в целях упрощения процесса
решения уравнений и формы окончательного ответа, заменить за-
данные элементы другими непосредственно выражающимися через
данные.
§ 64. Основные случаи решения треугольников
Основными случаями решения треугольников называются за-
дачи на вычисление элементов треугольника по трем данным его
независимым основным элементам*.
Ниже мы ограничимся вычислением трех основных эле-
ментов по заданным трем прочим основным элементам, так как вы-
числение различных других элементов принципиальных затруд-
нений не вызывает и может быть выполнено по формулам, связы-
вающим их с основными элементами.
Решение прямоугольных треугольни-
ков**. В прямоугольном треугольнике известен один из его эле-
ментов С = -^, а потому достаточно задать два его элемента, кото-
рые вместе с С образуют систему трех данных элементов. В учебной
литературе решение прямоугольных треугольников рассматривается
особо, ибо в этом частном случае вычисление неизвестных элементов
треугольника можно выполнить непосредственно на основании
определения тригонометрических функций острого угла (см. §8,
стр. 41) и теоремы Пифагора и нет необходимости прибегать к общим
формулам, относящимся к произвольным треугольникам.
По определению тригонометрических функций острого угла,
имеем:
а = с sin А = с cos В, b = с sin В — с cos A;
а = b tg A = b ctg Б, b = a tg В = a ctg A.
Перечислим основные задачи на решение прямоугольных тре-
угольников.
1°. Даны гипотенуза с и острый угол А.
Остальные элементы вычисляются по формулам:
a = csh\A\ b = ccosA\ Β=γ — Α.
* Известно, что, в евклидовой геометрии углы треугольника не являются
независимыми элементами, ибо они связаны соотношением А + В + С = π.
Если же заданы три угла, удовлетворяющие этому соотношению, то треуголь-
ник определяется лишь с точностью до подобия.
** Выделение задач на решение прямоугольных треугольников имеет
под собой педагогическое основание, так как задачи на прямо-
угольные треугольники, весьма важные с точки зрения приложений три-
гонометрии, могут решаться на ранних стадиях изучения тригонометрии
независимо от последующего рассмотрения задач на решение косоугольных
треугольников.
388
2°. Даны катет а и один из острых углов, например угол А.
Остальные элементы вычисляются по формулам:
В=$-А, b=actgA, c = -,
sin А
3°. Даны катет а и гипотенуза с.
Остальные элементы вычисляются по формулам:
А = arc sin у, B=-j—A, b = Vc^^a2,
Примечание. Если отношение — близко к 1, то для большей
с
точности вычислений по таблицам вместо угла А можно вычислить угол
—, воспользовавшись формулой
в г
•Ί-V-
1 — cos В
1 + cos В
ίΊΞΙ
4°. Даны катеты а и Ь.
Остальные элементы вычисляются по формулам:
Решение косоугольных треугольников.
Задача I типа. Даны два угла и одна из сторон тре-
угольника-, вычислить остальные основные элементы.
Пусть, например, даны Л, В и а\ требуется вычислить С, b и с.
Решение.
sin В
sin Л * sin С sin A '
откуда
С =
я sin (Л + В)
sin A ' sin Л
Задача имеет единственное решение
при условиях:
Л>0, β>0, Л + Б<я.
Если значения А и В этим неравенст-
вам не удовлетворяют, то искомый тре-
угольник не существует.
Черт. 218
Примечание. Если А = В, то треугольник равнобедренный,
в этом случае решение упрощается (черт. 218).
С = π — 2,4, Ь = а, с = 2а cos Л
Задачи II типа. Существуют следующие две задачи этого
типа.
389
Задача Hi. Даны две стороны треугольника и угол между
ними; вычислить остальные основные элементы.
Пусть, например, даны a, b и С, требуется вычислить Л, В и с.
Ρ е ш е н и е. Общий принцип Торопова дает возможность со-
ставить тригонометрическое уравнение для одного из искомых углов.
Имеем:
a sin Л sin Л sin Л
Τ = sin В = sin (Л+ С) ^ sin Л cos С + cos Л sin С ' ('
Откуда
(a cos С — 6) sin Л + я sin С cos Л = 0.
Это линейное однородное относительно sin Л и cos Л уравнение,
из которого найдем:
, „ Ь — a cos С
С^Л= asinC >
остальные элементы найдем по формулам:
a sin С
= π — С — Л, с =
sin Л
Для вычисления стороны с и углов можно воспользоваться фор-
мулами косинусов:
_ 2ab cos С, Л -arc cos
При логарифмических вычислениях удобно поступить иначе.
Если угловой элемент -2 заменить элементом ^-^, который также
можно считать известным, то, воспользовавшись теоремой танген-
сов (§61, стр. 374), получим:
Л— в л —в
а-Ъ tg ~~2~ ^ —γ~
a+b A+B - С
tg —γ- ctg -т>
откуда
А + В =r-jt—C.
390
Из этой системы вычисляются углы Л и В. Сторону с можно вы-
числить по теореме синусов
a sin С
с =
sin Л
Задача 114 имеет единственное решение при произвольных дан-
ных, удовлетворяющих условиям а>0, £Г0 0С
Примечание. Если α — b, то треугольник равнобедренный
β этом случае решение упрощается:
π С С
А= В = -ζ — у, с = 2а sin у.
Задача П2. Даны две стороны и угол, противолежащий одной из
данных сторон; вычислить остальные основные элементы.
Пусть, например, даны: а, Ь и Л; требуется вычислить С, В и с.
Решение. Для вычисления углов составим смешанную
систему:
sin β = 4 sin Л, А + В + С = п, β>0, C>0. (U)
Сторону с можно найти по теореме синусов
__ a sin С
~~ sin Л Ф
Исследуем смешанную систему (U). Если b sin A < α, то
— sin A < 1; простейшее тригонометрическое уравнение
sin β = — sin Л в интервале (0, π) имеет два решения:
Вг = arc sin i— sin A\ , Β2 = π — arc sin j— sin Л).
Рассмотрим следующие случаи:
1°. b<^a\ в этом случае
sin В < sin Л, В3<Л и βϊ<γ.
Следовательно, всегда β, < л — Л, т. е. βχ + Л < π, и
Значения Bj и С, удовлетворяют всем соотношениям системы (U).
Рассмотрим другое решение:
В2 = л — Вг\ имеем Л + В2 =π + (Л — Вг)
поэтому соотношения системы (U) не удовлетворяются.
391
2°. a = b и Л<-|-; в этом случае 5, = Л, С=п — (Л+
+ /?!)>(). Значение В2 не удовлетворяет соотношениям системы
(U), ибо A -f- В2 = π. При Л ^>тг задача не имеет решения.
3G. 6sirii4<[a<& и Л<-|-. В этом случае sinB>sinA#
Имеем
Все соотношения системы (U) удовлетворяются.
Рассмотрим другое решение:
В2 = п — В1; имеем С2 = π — (Л + Б2) = Вг — Л>0.
Все соотношения системы (U) выполняются. При Л^-γ задача
не имеет решения.
4Q. b sin Л = α и Л < ~. В этом случае Вг = В2 = -^,
с= |—л.
Решением служит прямоугольный треугольник. При Л>-о задача
не имеет решения.
5. b sin Л>а. В этом случае первое уравнение системы (U) не
имеет решений; задача не имеет решений.
Итак: 1°. Если из двух данных сторон аи b угол Л противолежит
большей стороне, то задача имеет единственное решение.
2Q. Если а = bt задача имеет единственное решение (равно-
бедренный треугольник) при Л<у и не имеет решений при
3Q. Если угол Л противолежит меньшей стороне, причем
bsmA<^a<^b, то задача имеет два решения, если Л<у, и не
имеет решений, если Л>-~.
4°. Если b sin Л = α, то задача имеет единственное решение
(прямоугольный треугольник), если Л<-|-, и не имеет решений,
если Л > γ .
5ς. Если b sin Л > α, задача не имеет решений.
392
Результаты исследования представлены на чертеже 219.
Задача III типа. Даны три стороны а, 6, с треугольника',
вычислить его углы А, В, С.
Решение. Непосредственное применение теоремы синусов
по принципу Торопова приводит к смешанной системе, неудобной
для практического вычисления углов. Однако вместо системы ос-
новных соотношений (I) между элементами треугольника можно
взять эквивалентную ей систему (III), тогда
Черт. 219
получится следующая смешанная система для вычисления углов
треугольника;
а2 = Ъ2 + с2 — 2bc cos Л, Ь2 = с2 + а2 — 2са cos В,
С2 =dl2+ b2— 2ab cos С,
О < A < π, 0 < β < π, 0 < С < π.
(U')
Углы треугольника определяются как главные решения простей-
ших тригонометрических уравнений
А= arc cos
с1 — а2
и т. д.
(1)
Из геометрии известно, что треугольник (и притом единствен-
ный) со сторонами а, Ь, с существует в том и только в том случае,
если
+ а, с<а + 6, (2)
393
Неравенства (1) суть необходимые и достаточные
условия существования решения (и притом единственного) си-
стемы (U'), ибо всякое решение этой системы определяет треуголь-
ник со сторонами а, Ь, с (см. стр. 367), и обратно, углы всякого та-
кою треугольника удовлетворяют системе (U').
Можно доказать аналитически, что при соблюдении системы неравенств
(2) смешанная слстсма (£/') имеет единственное решение.
ПростеГплее уравнение (1) имеет ре.хкчие в интервале 0 < Л < π,
если выполняется неравенство
| ь2 + с2 — а21 < 2Ьс. (3)
Докажем, что это неравенство следует из неравенств (2).
Из неравенств (2) имеем;
b — с < а и с — b < a
и, следовательно,
\Ь — с\<ау откуда Ь2 + с2 — 2Ьс < а2
Ь* + с2 — а2< 2bc. (4)
Возведя в квадрат первое неравенство (2), получим:
а1 — (Ь2 + с2) < 2Ьс. (5)
Из неравенств (4) и (5) следует неравенство (3).
Существование главных решений для уравнений, определяющих осталь-
ные углы треугольника, устанавливается круговой перестановкой букв
а, Ь, с.
При логарифмических вычислениях обычно пользуются фор-
мулами:
1Ь 2 ~~ ρ — α' & 2 ~ ρ — b > ι& 2 ~ ρ — с '
α + b + c
где ρ = ——ψ1 полупериметр и
г = I/ -—^-^ ——^ — радиус вписанного круга (см. §61,
стр. 376).
§ 65. Неосновные случаи решения треугольников
Неосновными случаями решения треугольников будем называть
задачи на вычисление различных элементов треугольника по трем
данным его элементам, среди которых хотя бы один не является ос-
новным. Общий принцип Торопова решения треугольников
(см. § 61) указывает способ составления смешанной тригонометри-
ческой системы для вычисления углов искомого треугольника.
394
В рассмотренных ниже примерах неосновных случаев будем
считать задачу решенной, если указан способ ее сведения к одному
из основных случаев решения треугольников.
Задачи I типа. Простейшими среди задач этого типм
являются такие задачи, в условиях которых непосредственно за-
даются два угла треугольника. В этом случае вычисление любого
линейного элемента производится непосредственно по данному
линейному элементу.
Примеры.
1. Даны Л, Вир; вычислить стороны и площадь треугольника.
Ρ е ш е н ν е. Угол С находится непосредственно: С — π — (Л + В).
Будем предполагать, что Л + В < π, так как при Л + В > π задача не
имеет решения.
Имеем
sin Л
ABC -./"-τ
2cos _cos _cos_ у у sin Л sin β sin С
Следовательно,
A
•л psin-ο-
p sin A z
А В С" = В A + В '
2 cos у cos у cos у cos у sin —^—
p2sin A sin β sin С ABC
-- P2tg tgtg
8 cos2 y cos2 -g cos2 ~2
По этому образцу решаются различные такого же рода задачи, как
например: определить стороны треугольника, зная его углы и площадь,
углы и радиус вписанного круга, углы и биссектрису и т. п.
На нижеследующих примерах 2 и 3 рассмотрено решение двух задач
первого типа, в которых угловые элементы (хотя бы один) заданы в виде
некоторых функций от углов треугольника.
2. Найти стороны треугольника, если даны г, отношение b "^ с = k
и В.
Решение. Представляем угловой элемент b ~*" с в виде функции от
b -f- с
углов треугольника. Имеем
hb-\-hc sin A sin С + sin A sin В
b + c = sin В + sin С = sin A'
Итак,
sin A = k и Л = агс$1п/г, С=и — Л — В
395
(чтобы задача имела решение, необходимо выполнение условия О < k < 1);
имеем далее»
а г
откуда
sin Л
r sin A
А
2 sin 2 sin
2 sin
β
2 sln
γ si
С
2
β
η -ζ sin
С '
2
rcos
β
sin -у
cos
Л
2
Л
+ β
2
Аналогично вычисляются другие стороны.
3. Задача Паскаля. Даны А и отношение разности сторон b-— с
к высоте ha, т. е. k =—~~ ?-. Найти В и С.
ha
Решение. Имеем:
β + C В—С
2 cos—о—sin—η—
sin B-~ sin С гг
k
_
sin В sin С = sin β sin С
А
, · А · БС . . А ·
4sin-ysin—2— 4 sin -^ sin
^~cos(£ — С) — cos (β + С) ~ cos (β— С) + cos A '
откуда для разности В—С получаем тригонометрическое уравнение:
k cos (В — С) — 4 sin A sin В ~~ С + * cos Л == 0.
Заменив cos (Б — С) на 1 — 2 sin2 и положив / = sin , получим
квадратное уравнение:
А А
kt2 + 2 sin γ t — k cos2 -y = 0.
Вычислив β —С и присоединив уравнение Β-\-0=π — Л, найдем β и С.
Задачи II типа. Простейшими задачами этого вида яв-
ляются задачи, в которых непосредственно задается один из углов
треугольника и два его линейных элемента.
Иногда в целях упрощения решения отношение двух данных
линейных элементов L\ и L2 заменяют отношением . ,а (см.,
lx — l2
например, основную задачу II, когда даны стороны треугольника
и угол, заключенный между ними). Этот прием бывает обычно по-
лезен в случае, когда дан угол А и одноименные элементы
Li = Lb и L2=LO соответствующие искомым углам В и С (например:
hb й hc или гь и rCt или Ьь и Ьс и т. п.).
396
Примеры.
1. Вычислить основные элементы треугольника, если даны 2р, г и А.
Решение. Известным угловым элементом является
А В С
2Р 4«»TcosTcoeT
=лвГ T TT
2 sin у sin у sin у
Для вычисления углов В и С получается система
А В i С 2р А В С π А
ctg yctg-y = —tg-y; у + -у ^T-y ·
Способ решения этой системы см. в § 52. Однако в данном случае
можно не прибегать к общему методу решения треугольников, а восполь-
зоваться соотношением
. А г
из которого найдем
а = ρ — г ctg -у .
Далее Ь + с = 2р — а. Воспользовавшись формулой Мольвейде (стр 375),
получим следующую систему для углов В и С:
В —С b + c A B+ С π А
cos —2— = —а— sin Ύ * —2— = ~2"~~ΊΓ' β>0' С>0.
Решение и исследование этой системы выполняется обычными приемами,
после чего задача сведется к основному случаю 1 решения треугольников.
2. Вычислить основные элементы треугольника, если даны:
а2 _ Ь2 = k2y с и а.
Решение. Отношение а — есть известный угловой элемент!
а* — b* k^_ sin2 Л— sin2 θ k2
~d* ==72"' или sin2 С в с2 ·
но sin2 A — sin2 β = у (cos 2β — cos 2A) = sin (Л — B) sin (Л + θ),
и, следовательно,
sin (А —В) b*_ sin (A — B) k2
^iFC = с2 или sin (A + θ) = c2 ·
Составив производную пропорцию, получим:
sin (Л — θ)— sin (Л + £) _ k2 — с2 cos Л sin В __ с2 — ft2
sin (Л — β) + sin (Л + θ) = fc2 + с2 или sin Л cos β ~ с2 + k2 '
откуда
с2 — к2
*ββ= c2 + fe2 tg Л.
397
Это уравнение относительно В надо решать при условиях 0 < В < π — Л,
после чего задача сведется к основной задаче первого типа.
3. Вычислить углы треугольника, если даны та, т^ и С.
т2 — т2
Решение. Можно считать известным угловой элемент —^ ь- _ £.
К + ть
имеем
(2 sin2 Б + 2 sin2 С — sin2 Л) — (2 sin2 С+ 2 sin2 Л — sin2 В)
k== (2 sin2 β + 2 sin2 С — sin2 Л) + (2 sin2 С + 2 sin2 Л — sin2 β) ·
или
3 sin2 β —3 sin2 Л
k = sin2 В + 4 sin2 С + sin2 Л '
Заметив, что
sin2 В — sin2 Л = sin (Л + В) sin (В — Л) = sin (β — Л) sin С
и
sin2 β + sin2 Л = 1 — cos (Л + β) cos (Л — В) = 1 + cos С cos (β — Л),
получим
3sinC sin (В —А)
k== 1 + cos С cos (B — A) + 4 sin2 С
Это уравнение, линейное относительно sin (В—А) и cos (β — Л), совместно
с уравнением А -\- В = π — Сие неравенствами Л > О, В > 0 составляют
систему для вычисления углов.
Задачи III типа представляют обычно наибольшие труд-
ности, обусловленные необходимостью решать тригонометрическую
систему уравнений, служащую для вычисления углов треуголь-
ника. Составление этой системы на основе принципа Торопова за-
труднений не представляет, однако так составленная система может
оказаться менее удобной для решения, чем некоторые эквивалент-
ные ей системы, которые можно составить применением различных
искусственных приемов. Эти искусственные приемы никакой общей
теорией предусмотреть нельзя.
Примеры.
1. Вычислить основные элементы треугольника по двум сторонам b и о
и биссектрисе Ьа угла между ними.
Решение. Из ряда равных отношений имеем:
В— С
b = 2R sin β, с = 2R sin С, ba cos —γ- = 2Я sin В s in С,
откуда
b + с = 2R (sin β +sin C)= AR sin ^ cos —g— =■
Л β—С
= 47? cos γ cos —τ,— · (1)
398
Умножив третье равенство на 4R, получим
В—-С
4Rba cos —2— = 8/?2 sin B sin С·
Воспользовавшись равенством (1), получим
Ьа (Ь + с) А Ьа (Ь + с)
д = 2Ьс, откуда cos -ζ = ^
COS -γ
ba(b + с) . A
Если —кг < 1, то, найдя из полученного простейшего уравнения -^ г
ba(b + с)
сведем задачу к основному случаю; если же —ψτ > 1, то задача не имеет
решения
2. Вычислить основные элементы треугольника, если даны три его
высоты ha, hb и hc.
Ρ е ш е н и е. Для нахождения углов А, В и С применим следующий
искусственный прием. Восиользуемся соотношениями
a b с
апа = bhb = chc или, что то же -г = -г = -г
ha hb hc
(см пример 2, стр. 382). Следовательно, если существует треугольник ABC
с данными сторонами а, Ьу с, то существует треугольник А^В^С^ стороны
которого измеряются числами:
I 1 I
Обратно, если существует треугольник АХВ^СХ со сторонами <7t, 6lt cu
то существует треугольник ЛВС с данными высотами ha, hb, hc; при этом
ААВС — bAxBid.
В самом деле, рассмотрим треугольник AiBiCi, пусть /ια , hb t hc — вы-
соты этого треугольника, тогда имеем alha = b^hb = Cj/ι^ ; выполним пре-
образование подобия Ai4i8tCi с коэффициентом подобия, равным -А- = /г,
тогда получим треугольник со сторонами, равными:
а ■= kau b = kbu с = kclt
и с высотами, равными:
и аналогично fe/i^. -= Λ^.
Итак задача имеет решение (и притом единственное) в случае, если
существует треугольник со сторонами — , —, Если ha < hb < he>
ha hb hc
то полученное необходимое и достаточное условие запишется в виде нера-
венства — < -— + —. Для вычисления углов искомого треугольника
ha hb hc
39?
достаточно вычислить углы подобного треугольника AiB\Cx (по трем его
сторонам)!
2
•Ί ϊ Гх
ν·
К - ha
— -4-— - —)(— 4- — -
hb hc ha }\hc r ha hb }\ha ^ hb
X IE Ζ
hn hh hr
Для вычисления сторон α, b и с достаточно воспользоваться формулой
a hb hb I hc \
iTO^sin/isinc · 0ТКУда a = 5Έχ Η ИгГё
§ 66. О применениях тригонометрии к геометрии
Тригонометрия имеет многочисленные применения к геометрии:
с помощью тригонометрии можно доказывать различные геометри-
ческие положения, устанавливать свойства геометрических фигур,
находить зависимости между их элементами, решать вычислитель-
ные задачи. Тригонометрическими методами устанавливаются за-
висимости между элементами различных измерений и угловыми
элементами. Так, например, в предыдущих параграфах были уста-
новлены соотношения между линейными и угловыми элементами
треугольника.
Вычислительные геометрические задачи, которые решаются
при помощи тригонометрии, могут быть весьма разнообразными,
в этих задачах требуется по достаточному числу заданных
(известных) элементов фигуры данного вида вычислить некоторые
указанные в условии (неизвестные) элементы этой
фигуры (примеры таких задач были рассмотрены выше примени-
тельно к треугольникам)*. Методы решения вычислительных гео-
метрических задач также могут быть самыми разнообразными.
Решение вычислительной задачи с применением тригонометрии,
как правило, содержит в себе две части: геометрическую и
вычислительную. Следует, однако, иметь в виду, что обе
эти части тесно связаны между собой и составляют вместе одно целое,
так что не всегда можно их точно разграничить.
К геометрической части можно отнести геометрическое обосно-
вание решения, т. е. доказательство тех свойств рассматриваемых
геометрических конфигураций, которые используются при решении,
выполнение геометрических построений, рассмотрение геометри-
* Различные геометрические задачи, решаемые с применением тригоно-
метрии, известны из школьных учебников и задачников.
400
чески различных (возможных) случаев расположения элементов
данной фигуры, доказательство (геометрическими средствами) су-
ществования тех или иных фигур или их элементов (например, воз-
можности провести сечение).
К вычислительной части можно отнести вывод формул, связы-
вающих искомые элементы с данными, преобразование полученных
формул к виду, удобному для вычислений, выполнение вычислений
при заданных численных значениях (известных) элементов.
При решении задач средствами тригонометрии широко при-
меняется следующий общий прием: отправляясь от данных эле-
ментов, строится цепь примыкающих друг к другу треугольников
с тем расчетом, чтобы в результате последовательного вычисления
некоторых элементов этих треугольников можно было вычислить
искомые величины.
При решении задачи с числовыми данными задаются чис-
ленные значения ее известных элементов, при этом возможно,
что фигура с данными значениями из-
вестных элементов существует (хотя
бы одна), либо возможно, что такой
фигуры не существует, несмотря на
то, что по соответствующим форму-
лам значения неизвестных элементов
можно вычислить. Таким образом,
в процессе решения задачи входит
исследование, которым либо доказы-
вается, что фигура, соответствующая
условию задачи, существует, либо вы-
ясняется, что такой фигуры не су-
ществует. Это исследование, как пра-
вило, относится к геометриче-
ской части решения.
Пример. Вычислить полную поверхность правильной треугольной
пирамиды, если сторона основания равна а = 25 см, а боковое ребро обра-
зует с этой стороной угол α = 15° (черт. 220).
Решение. Вычислим площадь равнобедренного треугольника BSC.
Имеем 5* = —·α· — tg α= Ι_ί .
Полная поверхность пирамиды равна
при а = 25, а = 15° все вычисления выполнимы: S ^ 396,1.
Однако пирамида, о которой идет речь в условии, не существует. В са-
мом деле, плоские углы трехгранного угла при вершине В (согласно условию)
должны иметь следующие величины: 60°, 15°, 15°, но трехгранный угол с
такими плоскими углами не существует, ибо 60° > 15° + 15°.
Задача не имеет решения.
14 Зак. 597
401
Вопрос об исследовании существования фигуры отпадает,
если заранее известно, что эта фигура существует (на-
пример, имеется в природе, является техническим сооружением или
его частью, начерчена на чертеже или представлена на модели),
а ее известные элементы найдены путем измерения.
В задачах с параметрическими данными известные элементы,
называемые параметрами, задаются в общем виде (буквами), им
можно придавать произвольные числовые значения.
Если каждому из параметров, содержащихся в условии, при-
дать некоторое значение, то задача превратится в задачу на вычис-
ление с числовыми данными. Эта задача может иметь решение (хотя
бы одно), а может не иметь ни одного решения. Иными словами,
геометрическая фигура с данными значениями параметров может
существовать, а может ни одной такой фигуры не существовать.
Система значений параметров называется допустимой,
если существует хотя бы одна фигура указанного в условии вида.
Множество всех допустимых систем значений параметров назы-
вается областью определения задачи.
Множеству всех допустимых систем значений параметров со-
ответствует некоторое множество фигур, называемое семей-
ством фигур данной задачи.
Решение задач с параметрическими данными может выполняться
без исследования либо с исследованием.
Решение задачи без исследования соответствует следующей по-
становке вопроса: даны в общем виде (на буквах) значения известных
элементов некоторой существующей в действительности фигуры,
требуется составить формулы для вычисления указанных в условии
неизвестных элементов этой фигуры*.
Решение задачи с исследованием соответствует следующей по-
становке вопроса: установить способ вычисления неизвестных эле-
ментов для произвольной фигуры семейства.
В этой постановке вопроса исследование, заключающееся в ус-
тановлении области определения задачи и числа решений для
каждой допустимой системы значений параметров, является состав-
ной частью решения.
Возможно, что в семействе фигур, определяемых условием за-
дачи, окажутся фигуры с различным расположением элементов,
так что все семейство разобьется на части и для фигур, принадлежа-
щих различным частям, получатся различные формулы вычисле-
ния искомых элементов. Рассмотрение всевозможных геометри-
ческих различных случаев расположения элементов фигур, опре-
деляемых условием задачи, относится к геометрической части
решения.
* Если возможны геометрически различные расположения рассматри-
ваемых элементов (известных и неизвестных) фигуры, то можно указать
чертежом, какое именно расположение рассматривается,
402
Без ограничения общности будем предполагать, что формула,
дающая решение задачи, применима к произвольной фигу-
ре семейства*.
Эта формула, рассматриваемая аналитически, вне связи с гео-
метрической задачей, имеет свою собственную область определения.
Так как формула решения применима к произвольной
фигуре семейства (или к выделенной его части), то область опреде-
ления формулы не может быть уже области определения задачи.
Следовательно, для всех тех систем значений параметров, при кото-
рых формула теряет смысл, соответствующая фигура не существует.
Роль тригонометрии в исследовании геометрических задач с па-
раметрическими данными заключается в исследовании формулы ре-
шения как функции угловых параметров.
Исследования формулы производятся с учетом ограничений
для значений параметров, вытекающих из их геометрического
смысла (например, плоские углы выпуклых многоугольников мень-
ше 180°, угол между прямой и плоскостью не больше 90°) и из
свойств рассматриваемой геометрической фигуры.
Область определения формулы, установленная с учетом указан-
ных ограничений, может оказаться шире области определения зада-
чи (т. е. все вычисления по формуле могут быть выполнимыми,
а фигура данного вида может не существовать; пример такого слу-
чая приведен на стр. 401). Чтобы убедиться в том, что исследованием
формулы найдена истинная область определения задачи, надо
геометрическими средствами (например, описанием построения)
доказать существование соответствующей геометрической фигуры
при произвольной системе значений параметров из найденной обла-
сти определения формулы. Этот вопрос относится к геометричес-
кой части решения.
Исследование, о котором шла речь, вытекающее из требования
«решить задачу», будем называть основным исследованием.
Кроме основного исследования решения задачи, можно выпол-
нять дополнительное исследование, т. е. исследование, не выте-
кающее из требования «решить задачу». Дополнительное исследова-
ние не имеет определенного содержания, если не указано, что именно
является предметом исследования. Так, при решении геометриче-
ских задач можно ставить, например, следующие вопросы, найти
наибольшие или наименьшие значения данных элементов, иссле-
довать эти элементы на монотонность (как функции парамет-
ров), выяснить применимость формул к вырожденным фигурам
и т. п.
В последующих параграфах приведен ряд вычислительных гео-
метрических задач, при этом рассматривается по преимуществу
* Если для различных частей семейства имеют место различные формулы,
го можно части этого семейства рассматривать по отдельности.
14* 403
вычислительная часть решения, поскольку тригонометрия находит
применение именно в этой части, геометрическая же часть пред-
ставляет интерес с точки зрения геометрии*.
§ 67. φ задачах на решение многоугольников
Пусть Ρ — произвольный многоугольник, ограниченный про-
стой (т. е. не имеющей точек самопересечения) замкнутой ломаной
линией. Из геометрии известно, что я-угольник имеет 2я основных
элементов, я углов и я сторон, при этом в общем случае
я-угольник определяется заданием 2я — 3 его основных элементов.
Пусть, например, задана ломаная ΑίΑ2Α3... Αη, эта ломаная
определяет я-угольник с вершинами в точках Аи Л2, ..., An
(черт 221). При этом длины звеньев ломаной и углы между ними
можно задавать произвольно (из множества их допустимых зна-
чений). Зная длины звеньев ломаной линии ΑιΑ2 = аи А2А3 =
= а2,... Ап-\ Ап--=ап-\ и величины углов Л2, А3) ..., Ап-\ (углы
будем обозначать теми же буквами, что и вершины), можно по-
строить саму ломаную линию и многоугольник ЛИ2, ..., АпА\\
при этом определяются три остальных основных элемента я-уголь-
ника — сторона ап = ΑηΑι и два угла Л ι и Ап.
Черт. 222
Можно установить общие соотношения, имеющие место для
основных элементов произвольного я-угольника. Из геометрии
известно, что сумма углов я-угольника (при данном п) постоянна:
А1 + А2+... + Ап = п(п — 2). (1)
Для получения соотношений между линейными и угло-
выми элементами спроектируем контур многоугольника на две
взаимно перпендикулярные оси. Для простоты примем за оси про-
екций одну из сторон многоугольника, например сторону ЛИ2,
и перпендикулярную ей прямую (черт. 222). Установим на плоскости
прямоугольную систему координат, приняв за ось абсцисс прямую,
* Ряд задач, интересных с точки зрения геометрии, рассмотрен в статье
И. И. Гайдукова, журнал «Математика в школе» № 2 за 1959 г.
404
на которой расположен вектор ΑιΑ2, и установив на ней положи-
тельное направление, совпадающее с направлением этого вектора.
Спроектируем А2А3 ... А\ на ось ОХ. Подсчитаем углы, которые
образуют звенья ломаной с осью абсцисс:
Сторона
Л3 Л4
Л4 Аъ
АПАХ
(π-
(«-
Угол
π -
с ЛА Л2
-л.
Косинус
— COS Л 2
cos (Л2 + А3)
—cos (Л 2 + А3 + А4)
+ ..· +ЛЛ)
Имеем:
пр А2А3 + пр А3А4 + ... + пр Ап А, = пр Α2Αχ;
(А)
проекция звена Af A/+i равна его длине, умноженной на коси-
нус угла, образованного этим звеном с осью ОХ.
пр
=aicos{AlAi+uOX) = α,(— I)'-1
2+ As
Аг).
Подставив в формулу (1) и приняв во внимание, что
пр А2 Αχ = — пр Aj A2 = — аъ получим:
аг = а2 cos Л2 — а3 cos (А2 + А3) + я4 cos (А9 + А3 +
Проектируем ту же ломаную на ось ΟΥ. Звено АгА/+1 обра-
зует с осью ординат угол, равный
у.-^
Α,+ь ОХ).
Следовательно,
прА.А/+1 =flicos[-| —
- a, sin (A4 A/+lf OX) = (— 1)'—Ёа4 sin (Ля + Л3 + ... + At).
Воспользуемся общей формулой (Л), приняв во внимание, что
пр А2 Aj = 0, получим:
а2 sin Л2 — а3 sin (Л2 + А3) + а4 sin (Л2 + Л3 + Л4) + ... +
+ (— \)"ап sin^2 + Л3 + ... + Ап) = 0. (III)
405
Система соотношений (I), (И) и (Ш) при заданных 2п — 3
основных элементах обращается в систему трех уравнений, кото-
рая может служить для вычисления трех неизвестных элементов.
Формулы (I), (II) и (III), будучи применены (в частности)
к треугольнику, дают следующую систему соотношений:
А + В + С = л; (Г)
а = с cos В — b cos (В + А) или а = Ъ cos С -\- с cos В (IV)
-bsm(B + A)=O или -^ = -^ . (ИГ)
Из этой системы соотношений можно вывести все установленные
в § 57 формулы, связывающие основные элементы треугольника.
Так, подставив с из формулы (НГ) в (ΙΓ), получим:
а = Ь cos С Η ^— cos В = -г—^ [cos С sin В + sin С cos β] =
sin (S + C)l = -^sin A.
v ' J sin В
sin J
Следовательно, имеет место теорема синусов, откуда (см. § 58)
вытекают все прочие соотношения между основными элементами
треугольника.
Пример. Положим, например, η = 4, тогда формулы (II) и (III) примут
вид,
а = b cos В — с cos (В + С) + d cos (В + С + D);
О = 6 sin В — с sin (Б + С) + d sin (В + С + £>).
После почленного возведения в квадрат, сложения и преобразования полу-
чим формулу, выражающую квадрат стороны четырехугольника:
a^ = b2 + c2 + d2 — 2bc cos С + 2bd cos (С + D) — 2cd cos D.
В практике решения различных задач на вычисление элемен-
тов многоугольника обычно разбивают многоугольник на треуголь-
ники и сводят задачу к последовательному вычислению элементов
треугольников. В зависимости от взаимного расположения задан-
ных элементов разбиение многоугольника можно производить раз-
личными способами (диагоналями, прямыми, параллельными сто-
ронам или перпендикулярными им и т. п.). Ниже мы ограничимся
рассмотрением ряда задач на четырехугольники.
Примеры. 1. Даны две стороны а и b параллелограмма и угол, образо-
ванный ими. Вычислить острый угол γ между диагоналями.
406
Ре ш е н и е. Предположим для определенности, что а — большая сто-
рона: а > Ь. Разобьем параллелограмм на треугольники при помощи диагона-
лей (черт. 223). Из треугольников ABD и ABC найдем диагонали:
d\ = BD2 = a2
• 2abcos A;
d\ = AC2 = a2 + b2 + 2ab cos Л
Искомый угол между диагоналями найдем, применив теорему косину-
сов к треугольнику АОВ:
cos γ = .
2d} d2 γ (α2 _|_ £2)2 __ 4α2 b2 cos2 A
Область определения задачи устанавливается следующими неравен-
ствами:
О < Ь<а, 0 < /1 < 180°.
Проведем такое дополнительное исследование. Установить множество
допустимых значений для угла γ, в зависимости от длин сторон паралле-
лограмма.
Из формулы (1) следует, что при данных а и b в полуинтервале
0 < А < 90° косинус угла γ убывает от 1 (предельное значение при /4—0)
до а2 ~~ b (при А = 90°), а в промежутке 90° < А < 180° возрастает от
до 1. Следовательно,
-<cos7< 1 иО<7<агс cosi
а2 _|_ 1)2 ~~ ■' " ' а2_)_^2" ^ »" »-^ι (Х2-\-Ь2
Значению А = 0 соответствует вырождение параллелограмма в отрезок
при возрастании А от 0 до 90°, угол между диагоналями возрастает от 0
до arc cos α2 + b2 .
Итак, угол между диагоналями параллелограмма с данными сторонами
не может быть произвольным.
Так, например, не существует параллелограмма со сторонами а = 3 м,
b = 1 м и γ = 45°.
В самом деле,
Ь γ 4
а2 4-
γ2
~ ΊΓ' но 45О==агс cos -2~-
Черт. 223
F а
Черт. 224
2. Даны основания а и b трапеции и ее боковые стороны cud. Вычислить
углы трапеции и ее площадь.
Решение. Предположим для определенности, что а — большая сто-
рона (черт. 224). Пусть А — угол, образованный сторонами а и с. Прямая
407
BF, параллельная стороне d, разбивает трапецию на треугольник ABF
и параллелограмм BCDF. В треугольнике ABF известны три стороны с, d
и (а — Ь)\ по трем сторонам можно вычислить угол А:
cos A =
и аналогично
cosD== 2d(a^W
и далее, В = 180° — А, С = 180° — D.
Для вычисления площади воспользуемся формулой
S = -^ (а + b) h = у (а + 6) <г sin A
(где Л — высота трапеции). Имеем:
(я
(а
-*)2 +
2с (а —
-*)· + .
с·2 —
■ft)
с2
1
sin A = V\ — cosM = 2c\a — b\ ^ ^ (a "" b^ "~ l(a ~~ b
откуда после преобразований получим формулу, выражающую площадь
трапеции по ее сторонам:
Х
_±_
~4|α — Ь\
X V[(c+d)+(a— b)] [(c+ d)- (α- b)) [(a- b)+(c- d)} [(a- b)-(c- d)}.
l r ^· Доказать, что для произволь-
ζχ ной трапеции существует следующая
зависимость между сторонами и диаго-
С/ f-i ^^\^i Χσ налями:
/l + fl = c* + d2 + 2ab, (1)
0 *>υ
где а и Ь — основания, с и d — не-
Черт. 225 параллельные стороны. /, и /2 — диа-
гонали.
Решение. Найдем диагонали из треугольников ABD и ABC
(черт. 225):
f22 = b2 + c2 + 2bccosA.
Исключив из этих соотношений cos Л, получим
bf\ + af\ == (α2 6 + с2 b + б2 α + с2 а)
или
6/? + af22 = (α + 6) (с2 + α&) (2)
Воспользовавшись треугольниками /4CD и BCD, получим:
<>ή + bfl = (α + *) ί^2 + ab); (3)
сложив равенства (2) и (3), получим равенство (1J.
408
4. Даны стороны а, Ь, с и d четырехугольника, вписанного в круг; найти
углы этого четырехугольника и его площадь.
Углы вписанного в круг четырехугольника удовлетворяют условиям
(черт. 226)
Л -f С = π, В + D = π.
Применив теорему косинусов к треугольникам ABD и BCD, получим два
выражения для квадрата длины диагонали BD\ приравняв эти выражения,
получим
а2 + d2 __ 2ad cos A = b2 + с2 + 2bc cos A
(принять во внимание, что cos С = —cos Л), откуда найдем
(а2 + d2) — (b2 + с2)
cos A = 2 (be + ad) ;
и далее:
(a -f d)2 — (b — с)2 (а + d + с — b) (a + d + b —с)
1 + cos A = 2(bc+ ad) ~~ 2 (be + ad) ;
1 -cos A = 2 (be + ad) ^ 2 (be + ad) ·
Обозначим через 2р периметр вписанного че- -
тырехугольника:
тогда a + 6+£ — d = 2(p — d),
и аналогично преобразуются прочие выраже-
ния. Откуда получим:
А
cosy =
Л
jin —
2
V*
[p — t
be
э — а]
tg-
>)(*> — <
+ «d
) (p — d
-■■
—:
r (p —
(Ρ-
α)
b)
\
(p — d)
(p-c) '
Ч^^4
Черт.
226
2 2 bc+ ad
В этих формулах α и d — стороны, образующие угол А, а с и Ь — про-
тиволежащие им стороны.
Вычислим площадь 5 четырехугольника:
1
S = пл. аЛ££> + пл. δ BCD = γ fad sin Л + 6с sin (π— Л)] =
sin Л > ·—
= -γ- (ad + bc)= V(p -a) (p - b) (p - c) (p-d).
MB Зак. 597 409
5. Доказать, что для всякого описанного около круга четырехуголь-
ника имеют место соотношения:
А . В .CD
a sin у sin у — с sin у sin у ;
β С J D , А
b sin -у sin у = d sin у sin у
(1)
Доказательство. В треугольнике АВО (черт. 227), где О — центр
вписанного в четырехугольник круга, углы при вершинах суть—, — и
π — [ -g- + "2~ ) · Вычислим двумя способами площадь S треугольника АВО.
Имеем.
S = у (rBK + гАК)= \ г* ( ctg γ + ctg
Т+ 2J
sin
sin у sin у
Приравняв полученные выражения для S, получим (после сокращения):
. А . В .
a sin у sin у = г sin
( А В\
I у + у J .
Если исходить из треугольника CDO, то получим:
С D (С D\
sin у sin у = г sin ί у + у J .
с sin
Из равенств (2) и (3) следует первое равенство (1), так как
А В I С D\ (А В
Ύ+Ύ=π-[Τ + Ύ) и i^+
В\ /С
+y)=sin ^у
D
Аналогично устанавливается второе равенство.
D
В
Черт. 227
Черт. 228
(2)
(3)
6. Доказать, что площадь 5 четырехугольника равна половине произве-
дения длин диагоналей на синус угла между ними.
Доказательство. Пусть АС=а, BD = Ь и а=^АОВ (черт. 228).
410
Точка пересечения диагоналей делит каждую диагональ на две части:
а ==л; + 2, b = у-{-и Разбив четырехугольник на 4 треугольника, получим
1 1 1
пл. δ χ = -ζ ху sin α; пл. Δ4 = ^· У2 sin (π —- α)==-^"Уг sin α.
. 1
пл. Δ3 = ~2 zu sln α; пл· Δ4 = ~2 xu Sin α,
откуда
S = у sin α (ry -\- yz -\- zu -\- xu)— γ (x -\- z) (у + м) sin a = γ ab sin a,
ч т. д.
7. Доказать, что из всех четырехугольников A BCD с данными сторонами
А В — Ь, ВС — с, CD = d, DA = а наибольшую площадь имеет четырехуголь-
ник, который может быть вписан в круг.
Задачу можно кинематически интерпрети-
ровать следующим образом: пусть A BCD—дан-
ный шарнирный четырехугольник, т. е.
четырехугольник, составленный из стержней
данной длины a, b, с, d, последовательно скреп-
ленных в концах в заданном порядке, так что
эти стержни, оставаясь в одной плоскости, мо-
гут вращаться вокруг вершин. Требуется уста-
новить, при каком условии площадь шарнирно-
го четырехугольника будет наибольшей.
Доказательство. Разобьем четы-
рехугольник A BCD диагональю АС на два
треугольника (черт. 229); имеем
5 = пл. Δ ABC + пл. Δ ACD = у (be sin В + ad sin D). (1)
Для преобразования полученного выражения найдем (по теореме коси-
нусов) А С2 из двух треугольников ABC и ACD:
АС2 = Ь2 + с2 — 2bc cos В = а2 + d2 — 2ad cos D. (2)
из (1) и (2) получим соответственно:
be sin В + ad sin D = 2S;
be cos В — ab cos D = -g (&2 + c2 — a2 — d2).
Возведем почленно в квадрат и сложим; после преобразований получим:
16S2 = 4(Ь2с2 + a2d2) — 8abcd cos (В + D) — (b2 + с2 — a2 — d2).
Наибольшее значение для 16S2, а следовательно, и для S, получится,
когда cos (В + D) имеет наименьшее значение Наименьшее значение
cos (В + D) есть —1, при В + D = π, что имеет место для вписанного че-
тырехугольника.
§ 68, Применение тригонометрии к стереометрическим задачам
При помощи тригонометрии решаются разнообразные стерео-
метрические задачи, как, например, установление соотношений
между углами (плоскими и двугранными) в различных пространст-
венных конфигурациях, вычисление элементов многогранника (дан-
14В· 411
кого вида) по достаточному числу заданных его элементов, вычисле-
ние элементов тел вращения, вычисление площадей плоских сече-
ний в данных телах и т. п. Методы решения этих задач могут быть
самыми разнообразными.
Никаких общих принципов решения стереометрических задач
установить невозможно; различные частные случаи этих задач
показаны ниже на примерах.
Примеры.
1. В плоскости Ρ проведена прямая / под углом β ίгде 0 < β <-ί|
к проекции на плоскость Ρ наклонной, образующей угол а с плоскостью Р.
Вычислить угол φ между прямой и наклонной.
Решение. Без ущерба для общности будем считать, что прямая
/ проходит через основание наклонной. Пусть 0 < β < т>, точка В —основа*
Черт. 230 Черт. 231
ние наклонной, АВ — произвольный отрезок наклонной, AD — перпенди-
куляр к прямой /, проведенный из точки А, С — проекция точки Л на Ρ
(черт. 230).
Имеем:
ВС = ABcosa, BD = ВС cos?
(так как CD J_ BD),
BD = AB cos φ
Откуда получим
COS φ = COS α COS β. (1)
В предельных случаях при β = 0 и β = -g рассуждения неприменимы,
так как при этих значениях треугольник CBD не существует, однако форму-
ла (1) остается в силе. В самом деле, при β = 0 имеем φ = α, а при β = -χ
π
имеем φ = -о , в обоих случаях равенство (1) остается в силе.
Примечание. Формула (1) может применяться при решении раз*
личных стереометрических задач.
Следствие 1. Если прямые /4 и 1ч β плоскости Ρ образуют равные
углы, β4 = β2 с проекцией наклонной, то эти прямые образуют равные углы
с наклонной (черт. 231).
В самом деле,
COS φι = COS α COS βχ = COS α COS β2 = COS f2»
412
откуда
φι = φ2.
Следствие II. Если две прямые Ιχ и 12 в плоскости Ρ образуют
равные углы с наклонной, то они образуют равные углы с ее проекцией.
ЕСЛИ φι = φ2, το
COScpx COS φ2
COS α ~ COS α
cos pj =
= COS βχ И βχ = β2.
2. Доказать теорему.
Площадь проекции фигуры F в
плоскости Ρ на плоскость Q равна
произведению площади F на коси-
нус двугранного угла, образованно-
го плоскостями Ρ и Q*.
Доказательство. Пусть
F] — проекция фигуры F на пло-
скость Q (черт. 232), φ—угол между
плоскостями Ρ и Q, требуется до-
казать, что
пл.
пл. F cos φ.
π
Если φ = -g , то Ρ _J_ Q, в этом
π
случае φ = -у и cos φ = 0, фигура Т7!
Черт. 232
вырождается в некоторое множество точек, лежащих на линии пересечения
Ρ и Q, поэтому пл. Fi = 0.
Таким образом, формула (1) справедлива.
Пусть 0 < φ < ~2 . Рассмотрим сначала частный случай, когда Fi есть
квадрат, одна из сторон которого параллельна линии пересечения плоскостей
Ρ и Q. Если а — сторона квадрата, то пл. F = а2; фигура Fi есть прямоуголь-
ник со сторонами, равными а и a cos φ. Следовательно (черт. 233),
пл. Fi = a cos φ·α = a2 cos φ = пл. F
acos<f
i Ρ
Черт. 233
Пусть F — произвольная (квадрируемая) фигура. Рассмотрим на пло-
скости Ρ две системы параллельных прямых; прямые первой системы парал-
лельны линии / пересечения плоскостей Ρ и Q и удалены друг от друга на
расстояние а; прямые другой системы перпендикулярны линии / и удалены
* Фигура F предполагается квадрируемой.
413
друг от друга на то же расстояние. Плоскость Ρ разобьется рассматриваемы-
ми прямыми на бесконечное множество конгруэнтных квадратов со сто-
роной, равной а. Множество всех квадратов, внутренних относительно
фигуры F, образует многоугольник П, содержащийся внутри F. Согласно
определению площади,
lim пл Π = пл. F.
Квадраты, на которые разбита плоскость Р, спроектируются на плоскость
Q в виде прямоугольников со сторонами, равными α и α cos φ (черт. 234).
Множество всех рассматриваемых прямоугольников, содержащихся внутри
фигуры Fb образует многоугольник Пь являющийся проекцией многоуголь-
ника П. Площадь фигуры F4 есть предел площади многоугольника П^
пл. F1 = lim (пл Пх) = lim (пл. Π cos <р) = cos φ lim (пл. Π) = cos φ пл. F.
3. Плоские углы трехгранного угла равны at b, с; вычислить двугранные
углы
Решение Пусть Л, В и С —двугранные углы, противолежащие
углам a, b и с соответственно (черт. 235). Пусть L — точка, взятая на ребре
угла Л; положим для простоты OL ш 1. Проведем через точку L плоскость,
414
перпендикулярную ребру угла О А. Эта плоскость может пересекать либо сами
ребра ОВ и ОС (каждое), либо их продолжения, либо может не пересекать
(хотя одно из них). В соответствии со сказанным следует раздельно рассмот-
реть все возможные случаи.
Предположим, что углы Ь и с острые, тогда плоскость пересекает ребра
ОВ и ОС] в сечении трехгранного угла получится треугольник LMN, в ко-
тором ^NLM = Л. Из треугольника LNM найдем
NM2 = LN* + LM* — 2LN-LM cos Л.
Из треугольника OMN найдем
NM2 = ON2 + OM2 — 2ON.ОМ cos a.
Приравняем полученные два выражения для /V/И2:
LN2 + L/W2 — 2LN-LM cos Л = ΟΛΓ2 + ОМ2 - 20N-0M cos α.
Приняв во внимание, что
ON* — LN2 = 1, ОМ2 — Z,M2 = 1.
перепишем полученное равенство в следующем виде (сократив все члены
на 2)1
ON ОМ cos a 1
A
Приняв во внимание, что
NL = ON sin b, ML
получим
■ ОМ sin.
1
LN
= ctg
1
Ζ,ΛΓ
: ctg
или
cos Л
cos a — cos b cos с
sin b sin с
Если угол b — тупой, ас — острый, то
плоскость пересечет продолжение ребра ОС.
В этом случае
= π — Л, ^NOL^k — Ь,
(i)
= π —α.
Нетрудно убедиться (подробности пред-
ставляем учащимся), что формула (1) останет-
ся в силе.
Аналогично устанавливается справедли-
вость формулы (1) в случаях, когда угол
b — острый, ас — тупой или оба угла Ь и
с — тупые.
Случай, когда хотя бы один из углов b
или с — прямой, предлагаем рассмотреть уча-
щимся в виде упражнения.
4. Грани параллелепипеда суть равные
между собой ромбы и расположенные так,
что встречаются вместе три плоских острых
угла. Вычислить объем параллелепипеда, если
сторона ромба равна а, а острый угол
равен а.
Решение. Пусть A BCD А' В'CD' — данный параллелепипед, через
Л обозначена одна из вершин, при которой три плоских угла равны
(черт. 236). Прямые А В и AD в плоскости основания образуют равные углы
Черт. 236
415
с наклонной А А' к этой плоскости. Поэтому проекцией А А' является бис-
сектриса угла BAD, т. е. диагональ основания (см. задачу 1, стр. 412).
Пусть φ—угол наклона АА' к плоскости основания, тогда имеем
COS φ =
COS α
cos-j
Из прямоугольного треугольника AA'L найдем высоту h параллелепипеда»
h = a sin ср = α Ϋ\ — cos2 φ = ι
cosy
Следовательно,
V = β« sin a _JL
a
cos -77
■·/-(·
COS α
α
cos тг
|asin| = 2as sin |
Параллелепипед указанного в условии вида можно построить при про-
извольных α и а, удовлетворяющих неравенствам a>0, 0<a < -^. Это и есть
область определения задачи.
При a -* 0 параллелепипед вырождается в отрезок.
5. Сторона основания правильной треугольной пирамиды равна я,
двугранный угол между боковыми гранями равен а; вычислить объем
и боковую поверхность пирамиды
Решение (черт. 237). Проведем плоскость СКВ, перпендикулярную
41$
ребру SA, тогда ^СКВ = α. Пусть KL — высота треугольника СКВ. Из
прямоугольного треугольника LKB найдем:
α α
KL = yctgy .
Из прямоугольного треугольника AKL найдем угол φ между ребром SA
и плоскостью основания:
KL
Сторона основания Л β образует с проекцией ребра AS угол -g·, следо-
вательно, можно найти угол β между ребрами SA и АВ (см. задачу 1):
π ]/ 3 cos φ
COS β = COS φ COS -g" = η ·
Зная угол β и сторону α основания, найдем боковую поверхность пира-
миды?
п
Из треугольника OS/4 найдем высоту пирамиды /г= 05 = О A tg φ = гт= tg φ
и вычислим ее объем?
1
V = у пл.
а3
= J2 tg φ.
Для получения окончательного результата надо исключить вспомогатель-
ные углы φ и β; имеем!
COS φ — Г 1 -
ctg2
/Τ
α
2
2
α
sin —
Ι π
sin I "g" +
-]/sin
— с
α \
sin
( α
/α π ^
α
~2
Μ · ία
CNI
l/ctg4"-ctg^
* Знак абсолютной величины излишен, ибо 0 < ц. < л и sin у > 0.
417
tgp = -
— -Τ COS2 φ
VS 1 i/ , (α π
—2~cos? у sin^y + -6
sin -^
1
Ί/ f a π\ f α π
J/ sin^y+_Jsin^.___
Окончательно получим следующие выражения для боковой поверхности
и объема:
8
α
α3 cos -ξ
| α π
^K sin lT + ¥
Для выполнения основного исследования рассмотрим полученные фор-
мулы.
Из геометрического смысла α следует, что 0 < α < π. При этом условии
значения S и V положительны, если
откуда γ < α < π. Это же ясно и из геометрических соображе-ний так
как |
π
Если 'а > 0, ~о < α < π, то соответствующую пирамиду можно построить.
Исследование формулы дало истинную область определения задачи
В качестве дополнительного исследования рассмотрим вырожденные
фигуры.
π
При α-^ΊΓ пирамида вырождается в ограниченную снизу и неограни-
ченную сверху призму; имеем:
Jim S
π
= +
И
а-*··
1
π
1
При α->π пирамида вырождается в плоскую фигуру — в правильный
(сдвоенный1) треугольник со стороной основания а. В этом предельном
случае имеем:
и liml/=0.
α-*·π
6. В правильной четырехугольной пирамиде двугранный угол при осно-
вании равен о; через ребро этого угла проведена плоскость, образующая
с апофемой противоположной боковой грани угол φ. Вычислить площадь се
чения.
Черт. 238
Решение. Возможны два расположения секущей плоскости
(черт. 238, I и черт. 238, II).
Рассмотрим сначала расположение I.
В сечении получается трапеция BEFC (доказать!).
Через высоту SO пирамиды проведем сечение SGK, перпендикулярное ребру
ВС, отрезок GL есть высота трапеции BEFC.
На чертеже 239 представлены отдельно сечения BFEC и SKG и грань
SAD:
= π — (α + φ).
F L
HOG
Черт. 239
Η
Из треугольника KLG найдем
__ KG
~ sin^KLG
sin α =
a sin α
sin φ
Треугольники SAD и SFE подобны, следовательно,
EF SL „„ AD(SK-KL)
AD = JR> откуда
SK
Имеем: 1) ЛО = а;
2>SK =
3) /и-
Sin φ
Искомая площадь сечения равна
(из треугольника SKO)',
(из треугольника KLG).
)= у I
BC+AD^-KL)}LG;
SK
после подстановки и преобразований получим
a2 cos (φ + α) si
(I)
Для расположения И все рассуждения остаются в силе, но угол φ следует
заменить на π — φ:
a2 cos (α— φ) sin2 α
Ρ = *
(Π)
Рассмотрим условия, при которых существуют сечения вида I. Эти
сечения существуют, если //C5G=180° — 2α < 90°, т. е. если 45° <а<90°.
Допустимые значения для углов α и φ определяются неравенствами
(черт. 240)
180° — 2α < φ < 90°; 45° < α < 90°.
а>аЪ
Черт. 240
Сечения вида (II) существуют (черт. 241),
( 0 < α < 45° при α < φ < 2а;
1 45° < а < 90° при а < φ < 90°.
если
Основное исследование, заключающееся в установлении условий, при
которых существуют рассматриваемые сечения, проведены геометрическими
средствами. В данном случае исследование формулы не даст истинной области
определения задачи. Так, например, формула (I) при 0 < α < 90° и
0 < φ< 90° имеет смысл и дает положительные значения для Р, если
90° — α < φ < 90°.
420
Этим условиям удовлетворяет, например, пара значений: а = 30°, φ = 80е,
однако при α = 30° сечений вида I не существует.
7. В правильную четырехугольную пирамиду вписан шар радиуса /?.
Вычислить боковую поверхность пирамиды, если двугранный угол между
боковыми гранями равен а.
45°<a<90c
Черт. 241
Решение. Пусть О — центр шара, вписанного в пирамиду SABCD,
а Οι — центр основания пирамиды; через диагональ основания проведем
сечение АМС плоскостью, перпендикулярной ребру SB; имеем ^АМС = <*
(черт. 242).
S
Черт. 242
421
Рассмотрим сечение пирамиды плоскостью, проходящей через высоту
пирамиды и через боковое ребро SB, и сечение плоскостью OiSL, проходящей
через высоту пирамиды и перпендикулярной стороне основания ВС.
Обозначим: h — Ofi — высота пирамиды, ρ = ΟιΜ, φ = ^SLOi — угол
наклона боковой грани к основанию, δ = ^SBO± — угол наклона бокового
ребра к основанию, а — сторона основания.
Имеем последовательно:
φ
а = 2R ctg -ζ (из треугольника L00{);
α αγ~2
h~-^\g^ = —2—tg δ (из треугольников SOiL и SOiB).
Следовательно,
tg<p
a V~2 a a V~2
ρ = —£— ctg γ — —2— s^n "J (из тРеУгольников ОМС и θ! MB).
Следовательно,
sinb = ctg-^- .
Проекцией боковой поверхности является основание, а так как все че-
тыре боковые грани наклонены к основанию под одним и тем же углом φ,
то (см. пример 2, стр 414)
бок ~~
исключим вспомогательный
Г» Г» О г η
ctg·
Следовательно,
1
sin2 δ
ώ 1 — sin2
г φ cos2
2
COS φ
угол φ:
1
/ι
δ
φ
2
У
ν-
1 + COS φ
1 — COS φ
COS φ
1
l/l+2tgn
1
α
a
l + V-
ι-V-
-cosa )
cos a
COS α
Для нахождения допустимых значений α обратимся к полученной фор-
муле. По смыслу задачи 0 < α < π. Значение 5б<ж положительно, если
cos а < 0, откуда у < α < π. Из геометрического рассмотрения фигуры сле-
дует, что при R > 0 и "2~<α<π рассматриваемая пирамида существует.
422
В данном случае исследование формулы дает истинную область определе-
ния задачи.
В качестве дополнительного исследования рассмотрим вырожденные
фигуры.
π
При данном а ->-£ пирамида вырождается в ограниченную снизу и не-
ограниченную сверху призму:
При а -> π поверхность пирамиды вырождается (при данном R) в пару
параллельных плоскостей lim S^0K = + оо.
α-»- π
8 Вычислить двугранный угол между основанием и боковой гранью пра
вильной четырехугольной пирамиды, если отношение радиуса описанного
шара к радиусу вписанного шара равно η (черт. 243).
Решение. Пусть φ — искомый угол, R и г — радиусы описанного
и вписанного шаров, h — высота пирамиды, / — боковое ребро, а — сторо-
на основания, О — центр вписанного и О' описанного шаров.
Из прямоугольного треугольника SKD найдем:
или l2 =
и R = 2h
0)
Из треугольника SEF найдем:
SF = EFtgq> или h = -ξ tg φ.
Из треугольника SDF найдем:
или /2 =
аУ~2
423
Подставив в равенство R = ^ , получим:
Из треугольника OFE найдем:
OF = EF ig-^ или г = у tg у .
По условию
1 φ
R =nr или ctg φ 4- у tg φ = η tg γ .
φ
Выполнив универсальную подстановку t = ig~2 , получим биквадратное
уравнением
(2л + 1) t* — 2я/2 +1=0.
Согласно геометрическому смыслу задачи, 0 < φ < у , а потому 0 < i < 1.
Определим значения параметра п, при которых квадратное уравнение
(2п + 1)г2 — 2яг + 1 =0 (2)
имеет корни (хотя бы один), содержащиеся в интервале (0, 1). Корни урав-
нения (2) действительны, если
П2 —(2/г + 1) > 0 или п2 — 2п — 1 > 0,
и так как по смыслу задачи η > 0, то
1 + -/~ΊΓ < а? < + оо.
При этом условии оба корня уравнения (2) положительны. Подставив в ле-
вую часть (2) 2 = 1, получим положительный результат / (1) = 2 > 0. Сле-
довательно, число 1 лежит вне интервала корней, т. е.
либо 0 < Ζχ < г2 < 1. либо 1 < гх < г2.
η
Так как при η > 0 выполняется неравенство 2п ι j < 1, то имеет место
первое расположение. Следовательно, при η < 1 -|- V 2 задача не имеет ре-
шений, при η > 1 -f- У 2 задача имеет два решения:
/!
п± Уп2 — 2п —
При η = 1 + V 2 задача имеет единственное решение:
φ = 2 arc tg
ΑΊΑ
При этом значении φ отношение радиусов η имеет наименьшее значение.
При η -*> -f оо (для определенности считаем R данным) получим предель-
ные случаи (черт. 244); lim φ2 = 0 и Птф2 = -у, соответствующие вырож-
дению пирамиды в точку и в отрезок.
Черт. 244
§ 69. Понятие о геодезических задачах
Методы тригонометрии находят широкое применение при ре-
шении различных практических задач по производству - измере-
ний на местности, как, например, вычисление расстояния между
различными пунктами земной поверхности, если это расстояние
нельзя измерить непосредственно, вычисление высоты данного
предмета (горы, здания и т. п.), составление планов и карт и т. д.
Описание необходимых измерительных инструментов, правил
пользования ими, учет погрешностей, пользование различными гео-
дезическими теблицами и различные способы практического выпол-
нения измерений излагаются в курсах геодезии. Ниже мы рас-
смотрим ряд простейших геодезических задач с точки зрения их
математического содержания. Мы будем предполагать, что измере-
ния производятся на достаточно малом участке земной поверхности,
так что эту поверхность можно считать плоской и не учитывать ее
кривизны.
Задача 1. Вычислить расстояние от доступной точки
А до некоторой недоступной точки В, видимой из точки А.
Разъяснение: точка А доступная — это значит, что в ней
может находиться наблюдатель вместе с измерительными инстру-
ментами. Кроме того, будем предполагать, что доступной является
не только точка Л, но и некоторая область —доступная
местность,— содержащая точку А. Будем считать, что всякая
точка С доступной местности видима из точки А и что расстояние
425
АС может быть измерено непосредственно. Точка В недоступная —
это значит, что она отделена от точки А некоторым препятствием, гак
что расстояние А В не может быть измерено непосредственно
(черт. 245).
Решение. Выберем в доступной местности точку С, из
которой видима точка В. Измерив отрезок-базис АС = Ъ и углы
ВАС и ВС А, сведем задачу к решению треугольника по стороне и
прилежащим углам:
sin С sin В
откуда χ =
6 sin С
sin (A + С)
Черт. 245
Черт. 246
Задача 2. Вычислить расстояние между двумя недоступными
точками А и В, видимыми из доступной местности (черт. 246).
Решение. Выберем в доступной местности базис MN = Ь.
Измерим базис и углы α, β, γ, δ между базисом и направлениями
на точки Л и β из его концов. Для вычисления расстояния χ вы-
числим расстояния Μ А и MB (см. предыдущую задачу):
__ Ьsinγ
~ Sin (α + γ) ·
Sin~(Β + δ)
Зная две стороны Μ А и MB треугольника МАВ и угол между
ними а — β, можно вычислить третью сторону χ = АВ. Можно,
например, воспользоваться формулой
х2 - Μ А2 + MB2 — 2МА · MB cos (α — β).
Примечание. Для вычисления х можно воспользоваться
треугольником ΝΑΒ:
x = NA2 + NB2 — 2NA · NB cos (δ — γ).
Вычисление искомого расстояния двумя различными путями
является одним из надежных способов контроля.
426
Предлагаем в виде упражнения рассмотреть случаи различного
взаимного расположения базиса и измеряемого отрезка (черт. 247).
/И
N
Μ
Задача 3. Вычислить высоту вертикального предмета, ос-
нование которого недоступно.
Решение. Задача решается просто, если можно выбрать го
ризонтальный базис А В, из концов которого видна вершина из-
меряемой высоты 05 (черт. 248) и который находится в одной верти-
кальной плоскости с этой высотой на уровне ее основания.
Пусть h — высота угломерного инструмента. Вычислив
углы α и β (см. черт. 245), из треугольника 5^4ιβι найдем:
sin (α-β)
и OS ==А + Аг S sin а.
Черт. 248
Задача Π о τ е н о τ а , Известны три опорные пункта А,
В и С, которые нанесены на план. Из некоторой тонки Μ измерены
углы а и β, под которыми видны отрезки А В и ВС (черт 249), На-
нести на план точку М.
427
Предполагается, что точки Л, β и С, расположенные в гори-
зонтальной плоскости на местности, даны (например, специально
сооруженные и издалека видимые геодезические знаки) и все эле-
менты базисного треугольника ABC измерены с надлежащей сте-
пенью точности. Решение задачи Потенота позволяет найти поло-
жение пункта М, из которого видны вершины базисного треуголь-
ника и который лежит в плоскости этого треугольника. Для на-
несения на план точки Μ достаточно знать углы χ — ^МАВ и
у=^ВСМ. В соответствии со сказанным задача Потенота геометри-
чески формулируется так: Известны стороны четырехугольника
АВСМ: АВ = а, ВС = b и угол между ними ^.АВС =γ. Кроме
того, известны углы, образованные диагональю ВМ со сторонами
AM и СМ-.^АМВ =а, ^_ВМС = β, вычислить углы χ и у при
вершинах А и С.
Решение. Из треугольников АВМ и ВМС имеем:
nw sin x ', sin у
ВМ = а -— = b -7-^-.
sin α sin β
Сумма углов четырехугольника равна 360°, а потому
x + y = 360°-(a + p + v). (1)
Для нахождения χ и у получим систему двух уравнений
(1) и (2)
sin χ b sin a
siny ~~ a sin β " ' '
Введем вспомогательный угол φ, положив
, bslna , bs\na
и составим из (2) производную пропорцию:
t *-У
sin*—siny tg φ — 1 s 2
sin χ + siny e tgcp+1 ИЛИ х + У =*§(?— 45°).
откуда
tg^ = tg(V-45°)tgi^. (3)
Из последнего соотношения в силу (1) получим:
Это уравнение и (1) составляют линейную систему для на-
хождения χ и у.
428
у -Х- ν
Особому рассмотрению подлежит случай, когда "Г = 90°,
тогда невозможен переход к уравнению (3). В этом особом слу-
чае
χ + у = 180°, а значит α + β + У = 180°.
Следовательно, вокруг четырехугольника МЛЯС можно описать
окружность. Пусть R — радиус описанной окружности, тогда
ВМ = 2R sin x = 2R sin у, a = 2#sina, .6= 27? sin β.
В данном случае уравнение (2) есть следствие уравнения (1). За-
дача имеет бесконечное множество решений, тогда Μ может зани-
мать произвольное положение на описанной около треугольника
ABC окружности.
Понятие о триангуляции. Способ триангуляции
заключается в разбиении местности, на которой производятся из-
мерения, на треугольники таким образом, что кажый пункт рас-
сматриваемой местности принад-
лежит хотя бы одному треуголь-
нику и каждые два треугольника
не могут иметь общих внутрен-
них точек, а могут иметь лишь
общую сторону либо общую верши-
ну. На чертеже 250 представлено
разбиение многоугольного участ-
ка на треугольники, это разбие-
ние называется тригономет-
рической сетью, а вер- Черт. 250
шины треугольников, входящих
в состав сети, — тригонометрическими пунктами.
При съемке планов больших участков из каждого данного тригоно-
метрического пункта могут не быть видимы все прочие пункты, одна-
ко необходимо, чтобы с каждого пункта были видимы не менее четы-
рех соседних пунктов. Примем сторону АВ одного из треугольни-
ков за базис и измерим ее непосредственно. Помещая угломерные
инструменты в различных вершинах треугольников сети, можно
измерить их углы. Стороны треугольников, образующих сеть, могут
быть найдены вычислением. Так, зная в треугольнике ABC углы
и базис b = А В, можно вычислить стороны ВС и АС. Зная в тре-
угольнике АСЕ сторону АС и углы, можно вычислить стороны АЕ
и СЕ и т. д. Стороны треугольников тригонометрической сети могут
служить базисами при производстве измерений на более мелких
участках. В случае надобности треугольники основной тригономет-
рической сети можно разбивать на более мелкие треугольники и
строить более мелкую «вторичную» тригонометрическую сеть.
429
Понятие о полигонометрии. В полигонометрии
в качестве геодезической опоры принимается некоторая ломаная
линия. Предположим, что измерены расстояния между пунктами
Л, В, С, D, Е, F, G, ..., в таком случае звенья ломаной ABC...
могут служить базисами для производства измерений на местности.
Продолженная на местности ломаная ABC... называется поли-
гоном или магистралью (черт. 251).
Черт. 251
При составлении планов в геодезии широкое применение имеет
метод координат.
Рассмотрим несколько простейших задач полигонометрии.
Если известны координаты (х0, у0) начальной точки Ло, длина
/ι отрезка А0А^ и угол аи который этот отрезок образует с прямой,
принятой за ось абсцисс, то координаты конца отрезка АОАХ на-
ходятся по известным формулам:
к cos
ί= у0
sin
Если для полигона A0Ai... An известны длины его звеньев ll9
h, ---у In, углы αϊ, α2, ..., ccrt, которые эти звенья образуют с осью
абсцисс, и координаты (х0, у0) начальной точки Ао, то координаты
вершин вычисляются последовательно:
У\ =
= χι + 4 cos α2,
sin α2;
χη = χη_ι + ln cos αη, yn = yn-\
sin
Если угломерным инструментом измерен угол β^+ι между
звеном lk+\ и звеном lk> то, как нетрудно видеть (черт. 252, а
и Ь):
± 1809, откуда
= α^ + βΑ+1 ± 180°.
430
Задача. Известны координаты концов базиса А (ха, уа)у
В (хь> Уь), измерены углы, под которыми произведена засечка пунк-
та Ρ (черт. 253). Вычислить координаты (х, у) этого пункта.
а)
Ь)
Черт. 252
Решение. Пусть φ — угол, который образует базис с осью
абсцисс. Найдем (при данном расположении точек) угол, который
образует отрезок АР с осью абсцисс.
Имеем:
х = χα -f- гл cos (φ + α) = χα -f rx (cos φ cos α — sin φ si η α),
у = ya + r5 sin (φ + α) = Уа + /Ί (sin φ cos α + cos <
Из треугольника АВР найдем:
Γχ sin β sin β
Ύ ~~ sin γ ~~5Ϊη(α4-β) э
подставив в формулы (1), получим (после
элементарных преобразований);
a — (yb— у а)
У
ctg а + ctg β
~~ Ха) + ^Уь ~ Уа) Ctg a
ctg α + ctg β
Черт. 253
§ 70. О применениях тригонометрии
к физике, механике, технике
Тригонометрия имеет многочисленные практические применения,
а также применения в научных дисциплинах, смежных с математи-
кой. Важные применения находят, как вычисление элементов гео-
метрических фигур, так и учение о тригонометрических функциях.
Ниже приведен ряд примеров применения тригонометрии.
431
1. При разложении силы (или какой-либо другой векторной
величины) на составляющие по двум (или трем в пространстве)
взаимно перпендикулярным направлениям, приходится вычислять
проекции силы на данные направления. Пусть под действием по-
стоянной силы F тело движется прямолинейно, примером может
служить движение тела по наклонной плоскости. Если сила образует
с прямой, по которой движется тело, угол φ, то для вычисления ра-
боты следует найти проекцию силы F на прямую / (черт. 254)
= Z7 cos φ.
Если длина пути, пройденного телом по прямой / равна s, то со·
ответствующая работа выразится формулой:
А = |F|scos(p.
S Fcosy
Черт. 254
Черт. 255
Задача. Тело движется по наклонной плоскости под дейст-
вием силы тяжести с ускорением в η раз меньшим ускорения, сво-
бодного падения, коэффициент трения равен k. Вычислить угол х,
образованный наклонной плоскостью с горизонтом.
Решение. Разложим вес Ρ данного тела на две взаимно
перпендикулярные составляющие, одна из которых N = Ρ cos x
перпендикулярна наклонной плоскости (черт. 255). Другая состав-
ляющая, направленная вдоль наклонной плоскости, равна Ρ sin χ.
Сила трения / пропорциональна нормальной составляющей
/ = kP cos x.
Движение по наклонной плоскости происходит под действием
силы Ρ sin л: — kP cos x с ускорением, равным
Ρ sin χ — k Ρ cos x
= g(s\nx —
где т —масса тела, a g — ускорение силы тяжести. По условию
откуда получим уравнение
sin л; — A cos л: = —.
η
432
Введем вспомогательный угол, положив
ι
а = arc cos
/ι
тогда полученное уравнение примет вид:
sin(*a)
По смыслу задачи: 0<&<1, я>1, 0<><-|- и 0<а<-|-.
Уравнение (1) имеет решение в том и только в том случае, если
1
η V\ + k2 ^ '
это последнее условие выполнено, так как п^>\. При данных
допустимых значениях неизвестного и параметров
— -^-О— а<£, а потому
nVl
χ — α = arc sin—г и χ = α + arc sin
Из условия 0<х<у найдем:
α + arc sin— <-^- f или α < arc cos—-
или, что то же, arc cos —= < arc cos—Γ ,
откуда
это условие выполнено, так как п^>1.
Итак, имеем:
χ = arc cos r + arc sin
+k2)
_ arc cin
- arc sin
II. Тригонометрия широко применяется в различных задачах
геометрической оптики. Для иллюстрации рассмотрим следующую
задачу.
15 Зак 597 433
Задача. Луч света проходит через стеклянную пластинку\
ограниченную параллельными плоскостями. Определить положение
луча после его прохождения через пластинку (черт. 256).
Решение. Пусть MN и PQ — плоскости, ограничивающие
пластинку, η — показатель преломления пластинки, d — ее тол-
щина. Падающий луч АВ испытывает двукратное преломление при
входе в пластинку и при выходе из нее. Луч АВ, встретив пластинку,
изменит свое направление и пойдет по прямой ВС, направление ко-
торой определяется по извест-
ному закону преломления света:
tvi ' ^
—_ , __ M-V^El >f ΟΙ 11 ^
. Q = п.
sin β
При выходе из пластинки луч
— О пойдет по направлению CD, ко-
торое определяется из условия:
Черт. 256
Из полученных равенств следует, что
sin β
sin γ
siny, т. е. а = γ,
так как α и γ суть острые углы. Следовательно, пройдя через пло-
скопараллельную пластинку, луч не изменит своего направления.
Вычислим смещение СК луча. Из треугольника ВКС найдем:
С К = ВС sin ^ СВК = ВС sin (α — β).
Следовательно,
d sin (α—β)
d . , оч d sin (α
= a Sin (α — β) = ν Q
cos β ν ^; cos β
III. На нижеследующем примере показано применение триго-
нометрии к техническим расчетам.
Черт. 257
На чертеже 257 представлена схема кривошипного механизма
При вращении кривошипа АВ ползун С движется прямолинейно
по прямой BL. Движение передается при помощи шатуна АС.
Пусть α — угол, образованный кривошипом АВ, а β — угол, обра-
434
зованный шатуном с осью BL. Если г и / — длины кривошипа и
шатуна, то зависимость между α и β можно найти из треугольника
ABC:
' 0ТКУда *ιηβ = ^ΐ
Во многих механизмах j = -^ , а потому β = arc sin ^—-, Для
практических расчетов можно составить, например, такую таб-
лицу приближенных значений β:
α
β
0°
0°
10°
2°
20°
4·
30°
5,5°
40°
7,5°
50°
9°
60φ
10°
70°
11°
80°
11,5°
90°
11,5°
При α = 0 шатун и кривошип занимают положение, изображен-
ное на чертеже 258, начальное расстояние ползуна от точки В
Черт. 25е
равно г -\- I. Если кривошип повернется на угол а, то расстояние
ползуна С от точки В сделается равным
г cos a + I cos β;
отклонение S = С0С ползуна от его начального положения вы-
разится формулой:
S = г (1 — cos α) + / (1 — cos β).
IV. Тригонометрические функции находят широкое применение
при изучении периодических процессов, о чем было сказано выше
(см. гл. III, § 34).
§ 71. Вычисления при помощи тригонометрических таблиц
Для производства вычислений пользуются таблицами значений
тригонометрических функций или их логарифмов. Обычно тригоно-
метрические таблицы составляются для значений аргумента, вы-
раженных в градусной мере, так как при практических расчетах
удобно за единицу измерения углов принимать угол, соизмеримый
с полным оборотом.
15*
435
Таблицы называются натуральными, если в них даются
значения тригонометрических функций, и логарифмиче-
скими, если в них даются значения логарифмов этих функций.
Для составления тригонометрических таблиц достаточно вы-
числить значения тригонометрических функций (или их логариф-
мов) лишь для значений аргумента от 0° до 45°. В самом деле, зная
тригонометрические функции острых углов, не больших 45°, можно,
пользуясь формулами приведения, вычислить их от любого дан-
ного значения аргумента.
На основании формул приведения cos a = sin (90° —α),
tg a = ctg (90°—α) значения тригонометрических функций, до-
полнительных до 90° дуг, могут быть записаны в одну строку, как
например:
38°
sin
0,616
cos
COS
0,788
sin
tg
0,781
ctg
ctg
1,280
tg
52°
Синус угла 38° есть в то же время косинус дополнительного
угла 52°
sin 38° =cos 52° =0,616.
В силу этого свойства, во многих таблицах тригонометрические
функции даются для углов от 0° до 45°. Эти же таблицы служат для
вычисления тригонометрических функций от 45° до 90°.
Для составления тригонометрических таблиц достаточно вы-
числить тригонометрические функции углов от 0° до 30°. В самом
деле, тождества:
sin (30°+α) =cos α — sin (30°—α),
cos (30° + α) = — sin α + cos (30° — α)
позволяют вычислить синус и косинус угла а + 30°, зная значения
этих функций от углов а и 30° — а.
При помощи аппарата степенных рядов (см. ниже, §80) можно
вычислять значения тригонометрических функций с любой задан-
ной степенью точности, а потому можно составить тригонометри-
ческие таблицы с любым данным числом значащих цифр.
Тригонометрические таблицы можно составить элементарными
средствами, однако, при современной вычислительной технике эти
средства не имеют практического значения, и могут (в разумной
мере) служить лишь учебно-педагогическим целям.
436
Ниже изложено краткое описание способов вычисления зна-
чения функций элементарными средствами.
Если известны (т. е. могут быть вычислены с любой степенью
точности ) since и cos а, то можно вычислить с любой степенью точ-
ности тригонометрические функции от аргументов ~, 4'···» L· Для
этого достаточно последовательного применения формул тригоно-
метрических функций от половинного аргумента:
а -ж Г\ —COS α α "l/l+COSa
s\n-^=y 2 , cos 2"= у —Ц>— и т. д.
Так как извлечение квадратного корня можно выполнить (эле-
ментарными средствами) с любой степенью точности, то и искомые
значения тригонометрических функций также можно вычислить
с любой данной степенью точности. Таким образом, не представляет
принципиальных затруднений (если не считаться с громоздкостью
вычислений) вычисление тригонометрических функций как угодно
малых углов.
В § 10 и 14 было показано, как можно элементарными средствами
вычислить тригонометрические функции от углов:
45°, 36°, 30°, 24°, 22°30', 18°, 15°, 12°, 9°, 6°.
Далее, исходя из углов 9° и 6°, можно вычислить тригонометри-
ческие функции от угла 9° — 6° = 3°. Исходя из угла 3°, можно
вычислить значения функций для углов ГЗО' и 45'. Зная тригоно-
метрические функции от угла 45', можно составить таблицы значе-
ний синуса и косинуса через каждые 45'.
Способ составления таблиц (близкий к описанному) через каж-
дые 45' изложен в известном учебнике тригонометрии М. Голо-
вина «Плоская и сферическая тригонометрия, с алгебраическими
доказательствами, собранными Михаилом Головиным, Надворным
советником, Академии наук членом, учительской семинарии про-
фессором в Санкт-Петербурге при Императорской Академии наук,
1789 г.». Далее для вычисления значений функции через каждые
15' Головин рекомендует применение линейной интерполяции.
При составлении тригонометрических таблиц для вычисления
тригонометрических функций малых углов широко пользуются
приближенными равенствами:
sin л; ж я, cos.v»l—γ·
Неравенства
Ι τι γ ^" с ί Π γ <S^ V
437
дают следующие оценки погрешностей (см. § 33):
X3
sin χ = χ с ошибкой, меньшей -js
X2 Я4
cos χ = 1 — — с ошибкой, меньшей -^ .
2 1о
Если данный угол содержит а градусов, то его радианная мера
выразится числом χ = -щ, и для погрешности рассматриваемых
приближенных формул получаются следующие оценки [принять
во внимание, что щ <С ей ) '·
- - ] ( к Υ а
4 4 \180)
3
- ( Υ а ^ —
4 4 \180) ^ 22·53·103 ~ 106
.аз.
16 ~~ Тб
Вычислив по приближенной формуле sin 1°, получим
sin 1° = sin ш = Ш = '
2
с ошибкой, меньшей чем ^<0,000005. Допустим, например, что
приближенная формула sin χ = χ применяется для составления
трехзначных натуральных тригонометрических таблиц. Неравенст-
во (при α = 7)
χ — sin x < 2j~ < 0,000686
показывает, что в данном случае приближенная формула пригодна
для вычисления синусов углов от 1° до 7°. Воспользовавшись най-
денным значением -^=0,01728, получим (округлив результаты
до 3-го знака):
sin 1° - щ = 0,017; sin 5° = 5 щ = 0,086;
sin 2° - 2 щ - 0,035; sin 6° = 6 щ = 0,104;
sin 3° - 3 jjL - 0,052; sin V = 7^ = 0,121;
sin4° = 4j^ = 0,069.
438
Приближенная формула для косинусов малых углов cos χ = 1 — —
обладает большей степенью точности. Так, при составлении трех-
значных таблиц этой формулой можно пользоваться непосредствен-
но для вычисления косинусов углов до 15°. В самом деле, для по-
грешности получим следующую оценку:
10^<1015<
Как было указано выше, путем применения формул деления
аргумента пополам и теорем сложения можно вычислить непо-
средственно (с любой степенью точности) тригонометрические функ-
ции от довольно большого числа углов:
3°, 6°, 9°, 12°, 15°, 18°, 22°30\ 24° и т. д.
Эти непосредственно вычисленные значения, с одной стороны,
могут служить средством контроля, а с другой стороны, зная эти
значения и значения функций от малых углов, можно, пользуясь
теоремами сложения:
sin (x ± h) = sin x cos h ± cos χ sin h,
cos (χ ± h) = cos χ cos h ψ sin χ sin /z,
вычислить значения тригонометрических функций для промежуточ-
ных аргументов. Таким образом, элементарными средствами без
особого труда можно составить трехзначные тригонометрические
таблицы.
В вычислительной работе применяются различные таблицы,
например: четырехзначные таблицы Б ρ а д и с а , пятизначные
таблицы Пржевальского, семизначные таблицы В е г а
и пр. Мы не останавливаемся на описании пользования таблицами,
поскольку к каждым таблицам прилагается соответствующее руко-
водство, в котором и излагаются правила их применения. Заметим,
что в зависимости от устройства таблиц эти правила могут быть
несколько различными. В таблицах обычно даются значения три-
гонометрических функций (или их логарифмов) через некоторый
интервал. Так, например, значения логарифмов тригонометрических
функций в таблицах Брадиса даются через 6', в таблицах Прже-
вальского через Г, а в таблицах Вега через 10".
Для вычисления значений функций от промежуточных значений
аргумента обычно применяется линейная интерполяция. Как из-
вестно, при линейной интерполяции приращение функции прибли-
женно считается пропорциональным приращению аргумента.
Пусть, например, по таблицам Пржевальского требуется найти
Ig sin 37°10' 32", непосредственно из таблицы найдем lg sin 37°10' =
439
= 1,78113. Табличная разность (т. е. разность между найденным и
непосредственно следующим значением функции) равна 17:
d = lg sin 37Ο1Γ — lg sin 37°10' = 17.
Таким образом, 17 стотысячных приходятся на 60", а на 32" при-
ч 17.32 п .
дется (приближенно) -^- = 9 стотысячных; прибавив наиденную
поправку, получим:
lgsin 37°10'32" = 1,78113+0,00009 = Г,78122.
Для облегчения вычислений, поправки обычно даются в готовом
виде.
Так, в таблицах Брадиса нахождение поправок не требует ни-
каких дополнительных вычислений: эти поправки включаются
в таблицу. В таблицах Пржевальского даются значения поправок
для Г', 2", ..., 9" в виде маленьких табличек, помещенных сбоку
основной таблицы (partes proportionalis). Для рассмотренного при-
мера вычисления расположатся так:
lgsin37°10' = Г, 78113
+ 30" 8,5
+ 2" 0,57
lgsin37°10'32" = 1,78122
Для убывающих функций cos x, ctg x, lg cos x и lg ctg x поправки
следует не прибавлять, а вычитать.
Линейная интерполяция может внести значительную погреш-
ность, если табличная разность изменяется быстро. Так для сину-
сов и тангенсов углов, близких к нулю (а также для косинусов,
тангенсов и котангенсов углов, близких к 90°), табличная разность
изменяется настолько быстро, что линейная интерполяция, при-
меняемая в этих участках таблицы, может внести погрешности боль-
шие по сравнению с погрешностями на прочих участках. Этим объ-
ясняется, что, например, в таблицах Брадиса логарифмы синусов
даются для углов от 0° до 14° с интервалом через 1', а для углов от 14°
до 90° — с интервалом через 6'. К таблицам Вега, составленным
с интервалом 10", приложены специальные таблицы, в которых
лешрифмы синуса и тангенса углов от 0° до 5° вычислены через
интервал 1".
Для вычисления логарифмов синусов (тангенсов) углов, близких к нулю,
применяется также следующий прием (если нет в распоряжении более под-
робных таблиц): так как
sin χ ж χ (и tg χ ^ х),
440
то считают приближенно синусы (тангенсы) малых углов пропорциональными
аргументу; поэтому можно составить пропорцию (приближенную):
s\n(x + h) x+h ( tg(* + /Q *+A\
: = и аналогично —г = .
sin л: х \ *£х х J
Заметим, что, так как в правой части находится отношение дуг x-\-h
и х, то безразлично, в какой единице эти дуги измерены: будем считать,
например, что дуги измерены в секундах. Пусть известен, например, lgsinjt,
тогда, прологарифмировав первую пропорцию, получим:
lg sin (χ + h) = lg sin χ + Ig (x + h) — lg x.
Значения \g(x + h) и lg* находятся по таблицам логарифмов чисел.
Пусть, например, требуется найти lg sin 1°22'36". Из таблиц найдем не-
посредственно:
lg sin 1°22' =2,37750.
Так как Г22' = 4920" и Г22'36" = 4956", то положив
х= 4920, х + h = 4956,
получим:
lg sin 1°22'36" = lg sin 1°22' + lg 4956 — lg 4920 = 2,38066.
О точности вычисления при помощи таблиц можно судить по таб-
личной разности, т. е. по разности двух соседних указанных в таб-
лице значений функций. Так как в различных частях таблицы эта
разность неодинакова, то и точность вычислений различна в зави-
симости от значений углов. Пусть, например, в пятизначных таб-
лицах логарифмов, составленных через интервал Г, табличная
разность d (стотысячных), тогда изменение угла на k" вызовет
в мантиссе логарифмов изменение на ^ k стотысячных. Таким обра-
зом, чем меньше табличная разность, тем меньшее влияние оказы-
вают погрешности, получающиеся благодаря округлению данных.
При нахождении угла по данному его логарифму ошибка, выз-
ванная изменением на 1 последнего десятичного знака (т. е. ошибка
на 1 стотысячную), вызовет изменение угла на i-j-j . Чем больше
табличная разность, тем точнее можно вычислить угол по логариф-
му его тригонометрической функции. Так, например, для пяти-
значных таблиц логарифмов синусов для углов до 12° ошибка в ман-
тиссе на 0,00001 вызовет погрешность, меньшую 1"; для углов,
близких к 30°, погрешность доходит до 3"; для углов, близких
к 45°, — до 5", а для углов, близких к 89°, —.до 5'.
Для нахождения углов по их тригонометрическим функциям
или их логарифмам пользуются теми же тригонометрическими таб-
лицами, но с той лишь разницей, что данными считаются не углы,
а их тригонометрические функции (или логарифмы этих функций).
Найдя по таблицам значение, наиболее близкое к данному, и со-
ответствующий угол, применяют принцип линейной интерполяции
и вносят надлежащую поправку (подробности см. в приложенных
к таблицам описаниях). Следует учитывать также ошибки, обус-
15В Зак. 597 441
ловленные самими таблицами, так как в них значения функций да-
ются до 0,5 последнего десятичного знака.
Указанным приемом может быть оценена погрешность в каждом
конркетном вычислении.
При решении задач на вычисление элементов геометрических
фигур методами тригонометрии обычно поступают следующим обра-
зом: сначала решают задачу в общем виде, обозначив буквами дан-
ные и искомые элементы, и составляют формулы, выражающие иско-
мые элементы через данные (либо выписывают готовые формулы).
Общие формулы преобразуют (по возможности) к виду, наиболее
удобному при вычислениях по данным таблицам. Так, при пользо-
вании натуральными таблицами лучше всего, когда окончательный
результат дан в виде суммы легко вычислимых слагаемых; напротив,
при пользовании логарифмическими таблицами лучше всего окон-
чательный результат представить в виде произведения сомножи-
телей, логарифмы которых непосредственно находятся по таблицам.
После составления общей формулы решения подставляют в нее чис-
ловые значения данных элементов и производят вычисления по
таблицам, соблюдая правила пользования таблицами и правила
приближенных вычислений.
В настоящее время техника вычислений при помощи логариф-
мических таблиц отживает свой век. Однако во многих распростра-
ненных математических таблицах на первое место ставятся именно
логарифмические таблицы. Это соответствует тому положению ве-
щей, что еще до сравнительно недавнего прошлого эти таблицы счи-
тались единственным вычислительным средством. В настоящее
время следует избегать применения логарифмических таблиц в тех
случаях, когда вычисления с помощью натуральных таблиц не вы-
зывают особых затруднений. При производстве вычислений следует
широко пользоваться различными имеющимися в распоряжении
математическими таблицами.
Так, в таблицах В. М. Брадиса, кроме логарифмических таблиц,
содержатся многие другие таблицы (квадратов, кубов, квадратных и
кубических корней, обратных величин и пр.). Использование раз-
личных таблиц дает возможность многие вычисления в школьной
практике производить, не прибегая к таблицам логарифмов. При
наличии же арифмометра таблицы логарифмов становятся почти
бесполезными.
Для вычислений, не требующих большой точности (не более
трех значащих цифр), удобно пользоваться логарифмической линей-
кой. При помощи линейки быстро находятся квадраты, кубы, квад-
ратные и кубические корни, обратные величины, а потому линейка
может заменить двух-трехзначные математические таблицы. Так
как при помощи логарифмической линейки весьма просто решаются
пропорции, то удобно пользоваться теми формулами, которые за-
писываются в виде равенства отношений (теорема синусов, тан-
генсов, формулы Мольвейде).
442
В приведенных ниже примерах показано применение натураль-
ных и логарифмических таблиц и логарифмической линейки к ре-
шению вычислительных задач.
Примеры.
1. Вычислить по четырехзначным таблицам основные элементы треуголь-
ника, если дано а ^ 225,2; 6 ж 798,2; С = 36°44'.
Решение. При вычислении с помощью натуральных таблиц восполь-
зуемся формулой косинусов
с = Уа2 + Ъ2 — 2ab cos С,
а2 ^50760, б2 ^637 100 (по таблицам квадратов).
Далее (умножение выполнено на арифмометре)
2ab cos С =2-225,2-798,2-0,8015 = 288180,
и наконец,
с ^У 399 700 ^632,3
(по таблицам квадратных корней)
sin Л i^asinC· —- « 225,2-0.5981-0,001581 ^ 0,2129
о
| — найдем по таблицам обратных величин J, и наконец, А ж 12°18',
β = 180° — (А + С) « 130°58'.
При помощи логарифмической линейки решение примет следующий
вид.
Округляем данные а « 225, Ь ж 798, С «36е 40'.
Далее, а2 ^50 800, Ь2^ 637 000 найдем при помощи шкалы квадратов.
Производим умножение 2ab cos С » 288 000 и по шкале квадратов нахо-
дим с = "К 400 000 ^632.
Далее воспользуемся теоремой синусов
sin Л sin β sin С
устанавливаем пометку с ^632 основной шкалы против С ^36°40' шкалы
синусов На шкале синусов читаем А ж 12°18' (против пометки ^225).
Угол А острый как лежащий против меньшей стороны.
Против пометки b ж 798 читаем 49°; чтобы выполнялось условие
А+В+ С = 180°, следует взять В ж 180° — 49° = 131°.
2. Вычислить при помощи пятизначных таблиц логарифмов основные
элементы треугольника, если дано А =61°40'30", 6=375,44, с=278,20.
Решение. Для логарифмических вычислений лучше всего восполь-
зоваться формулой тангенсов:
в-с
b — c_tg 2 В —С Ь — с В+С Ь — с А
Т+7 sTc· откуда iz^~ = F+-ciz-^- = τη^Ύ-
tg-тг-
Имеем;
д
»— с = 97,24; Ь + с = 653,64; -тг = 30°50Ч5".
15В* 443
Выполняем логарифмические вычисления:
\g(b — c) = 1,98784
— lg (6 +с) = 3,18466
lgctg30°5Q'15" = 0,22402
В
2
* — С
= 1,39652
= 13°59'32"
lg (6 + с) = 2,81534.
Итак
В — С
2
В+ С
= 13°59'32"
==90°——= 59Ο9'45",
откуда
β = 73°9Ί7", C=45o1043".
Для вычисления а можно воспользоваться формулой Мольвейде:
Ь-\-с
cos -
В—С
откуда
(b + c) sin -γ
В—С
sin-
cos ·
Имеем:
lg (b + e) = 2,81534
lg sin -γ = Γ,70978
— lgcos
= 0,01308
= 1,98692.
lg α = 2,53820
α = 345,30
3. Основанием четырехугольной пирамиды служит квадрат, две боко-
вые грани пирамиды перпендикулярны к плоскости основания, две другие
боковые грани образуют с плоскостью основания
равные двугранные углы, каждый из которых ра-
вен а = 53°46/, высота пирамиды h = 24,15. Вычис-
лить посредством четырехзначных таблиц боковую
поверхность.
Решение. Сначала решаем задачу в общем
виде. Из геометрических соображений следует, что
(черт. 259):
5б = 2 пл. AASB+2 пл. aSAD.
Имеем:
пл. AASB= -γ*
1
пл. aSAD= -γ AD
/z2ctga
AS^^-hz\ga.-^.
444
Составляем формулу решения задачи в общем виде:
sin a
Sin a
Для сравнения произведем вычисления при помощи как натуральных,
так и логарифмических таблиц.
Вычисления при помощи натуральных таблиц:
имеем:
/г2 ^ 24,152 ^ 583,2, ctg a = ctg 53°46' ^0,7328,
1
sin a = sin 53° 46'^ 0,8067;
Sin a
+ 1 ж 2,240,
S6 = 583,2 · 0,7328- 2,240^ 957,3 (кв. единиц).
Вычисления при помощи таблиц логарифмов.
Приведем результат к логарифмическому виду:
2/г2 ctg a cos2
sin a
Производим вычисления по таблицам:
lg 24,15 = 1,3829= lg/г,
lg 2 = 0,3010
2 lg 24,15 = 2,7658
Igctg53°46' =Г,8649
2 1gcos 18°07'= Г, 9560
— lg sin 53°46' = 0,0933
lg cos ( 45° — ·|Λ = lg cos 18°07' = 1,9780,
Igsin53°46' = Γ.9067.
lgS6 = 2,9810
Откуда 5б = 957,2 (квадратных единиц).
Глава седьмая
ЭЛЕМЕНТЫ СФЕРИЧЕСКОЙ ТРИГОНОМЕТРИИ
§ 72. Основные понятия
В настоящем параграфе будут (в конспективном изложении)
указаны те положения из сферической геометрии, которые
служат основой сферической тригонометрии. Элементы сфери-
ческой геометрии излагаются в специальном курсе геометрии, по-
этому мы ниже ограничимся лишь перечислением необходимых для
дальнейшего сведений, опуская их доказательства*.
I. Известно, что через вся-
кие две данные не диаметрально
противоположные точки сфери-
ческой поверхности проходит
единственная окруж-
ность большого круга; через
две диаметрально противопо-
ложные точки проходит бес-
конечное множество
таких окружностей (черт. 260).
Две не диаметрально про-
тивоположные точки разбивают
проходящую через них окруж-
ность большого круга на две
дуги, одна из этих дуг мень-
Черт 260 ш е, а другая больше по-
луокружности.
Всякой дуге большого круга соответствует центральный угол,
образуемый радиусами сферы, соединяющими ее центр с концами
дуги.
Дуги большого круга принято измерять в дуговой мере
(например, в радианах или градусах); в соответствующей угло-
вой мере измеряется опирающийся на нее центральный угол.
* См. Д. И. Перепелки н,
Гостехиздат.
Курс элементарной геометрии, т. II,
446
Если R — радиус сферы, а α — радианная мера дуги АВ, то
длина этой дуги ν вычисляется по формуле
υ =aR.
Пусть Л, В, С — три точки сферы, не лежащие (все три) на
одной и той же окружности большого круга; соединив попарно эти
три точки тремя дугами большого круга, каждая из которых мень-
ше π, получим на поверхности сферы фигуру, называемую эйле-
ровым сферическим треугольником или крат-
ко — сферическим треугольником (черт. 261). Точ-
ки Л, β, С называются вер-
шинами, а соединяющие их
дуги сторонами сфериче-
ского треугольника. Стороны
сферического треугольника, про-
Черт. 261
Черт. 262
тиволежащие вершинам Л, В и С, обозначаются соответственно
малыми буквами a, b и с. Углом сферического треугольника
при данной его вершине называется угол, образованный сторо-
нами, пересекающимися в этой вершине; это есть угол, образо-
ванный к а с а т е л ь н ы м и в данной вершине к пересекающим-
ся в ней сторонам. Угол сферического треугольника есть линейный
угол двугранного угла, образованного пересечением пло-
скостей больших кругов, в которых расположены стороны, обра-
зующие данный угол (черт. 262). При этом внутренней областью
угла считается та область, в которой расположена сторона треуголь-
ника, противолежащая вершине. Углы и стороны сфе-
рического треугольника будем называть его основными эле-
447
ментами. Из сказанного следует, что величина каждого из основ-
ных элементов эйлерова треугольника заключается в интервале
от 0 до π*.
II. Всякому сферическому треугольнику соответствует трех-
гранный угол, вершина которого находится в центре сферы, а реб-
рами служат радиусы, соединяющие центр сферы с вершинами тре-
угольника. Обратно, всякому трехгранному углу с вершиной в центре
сферы соответствует сферический треугольник, который высекает
этот угол на поверхности
сферы (черт. 263).
Элементы взаимно соответ-
ственных сферического тре-
угольника и трехгранного уг-
ла связаны между собой сле-
дующим образом: величины
Черт. 263
Черт. 264
углов А, В и С треугольника суть величины двугранных
углов трехгранного угла, а величины сторон а, Ь, с треуголь-
ника суть величины плоских углов трехгранного угла.
Всякое соотношение между элементами сферического треугольника
(трехгранного угла) может быть интерпретировано как соотношение
между элементами соответствующего трехгранного угла (сфери-
ческого треугольника).
III. Пусть АВ — дуга большого круга, тогда диаметр, пер-·
пендикулярный плоскости большого круга, в которой содержится
дуга АВ, пересечет поверхность сферы в двух точках С\ и С\, кото-
рые называются полюсами данной дуги (черт. 264).
* В чисто теоретических исследованиях иногда рассматриваются сфери-
ческие треугольники, так называемые треугольники Μ е б и уса, элементы
которых могут иметь произвольную величину. Изучение таких
треугольников практического значения не имеет.
448
Если вершины треугольника AxBxCi служат полюсами сторон
треугольника ABC, то треугольник ΑχΒχύχ называется полярным
относительно треугольника ABC (черт. 265).
При этом приняты такие обозначения: точка Αι есть полюс
ВС, точка Вх есть полюс АС, точка Сх есть полюс АВ. Вершины
полярного треугольника принято выбирать так, чтобы вершины Л4
и А лежали с одной стороны относительно плоскости дуги ВС.
Аналогичное указание относится к выбору остальных вершин поляр-
ного треугольника.
Черт. 265
В сферической геометрии доказывается, что если треугольник
A\BiCi полярен относительно ABC, то и треугольник ABC полярен
относительно Α χΒ {С{.
В силу изложенного, вершина А треугольника ABC есть полюс
стороны αχ треугольника А\В£и а вершина Αχ треугольника
АхВхСх есть полюс стороны а треугольника ABC.
В сферической геометрии доказывается, что соответственные
угол и сторона взаимно полярных треугольников в сумме составля-
ют π (черт. 266):
Вх-\-Ь =π, С -\-с1=л9 С1-\-с==п.
На чертеже 266 дуга ВхСх есть суть экватора относительно
полюса в точке Л; величина этой дуги (в радианах) равна αχ.
Эта дуга состоит из двух дуг равных ~ (точка Βχ есть полюс отно-
сительно дуги Ь, а точка С4 есть полюс относительно дуги с), час-
тично наложенных друг на друга так, что их общая часть равна ли-
нейному углу двугранного угла с ребром О А, т. е. углу А.
449
IV. Во всяком сферическом треугольнике:
1°. Каждая сторона меньше суммы двух других сторон
2°. Каждая сторона больше разности двух сторон.
3°. Сумма сторон треугольника положительна и меньше 2п
0<а+ Ь + с<2л.
Примечание. Эти предложения известны из стерео-
метрии как свойства плоских углов трехгранного угла.
4Θ. Сумма углов сферического треугольника больше пи меньше Зк
(применить свойство 3° к сторонам аи Ь\ и с{ полярного треуголь-
ника).
Примечание. В отличие от прямолинейного треу-
гольника сферический треугольник может иметь два, а так-
же все три угла тупые или прямые.
5°. В сферическом треугольнике против большей стороны (боль-
шего угла) лежит больший угол (большая сторона).
Πротив равных сторон (углов) лежат равные углы (стороны).
6°. Углы сферического треугольника удовлетворяют неравен-
ствам:
А + В — С<я, А — В + С<п, В+С — А<л.
Так, для получения первого неравенства достаточно применить
условие Г к сторонам полярного треугольника: a^bi + cu а затем
выразить стороны треугольника А^В{С{ через углы данного тре-
угольника ABC.
Указанные соотношения Г — 6° служат для определения мно-
жества допустимых систем значений для элементов сферического
треугольника. В задачах на вычисление элементов сферического
треугольника эти соотношения позволяют установить, имеет ли за-
дача решение приданных условиях, а также число ее решений.
V. Если элементы сферического треугольника ABC равны со-
ответственным элементам треугольника А'В'С:
А = А', В=В\ С = С\
а = а', Ь = Ь'у с = с',
то такие треугольники либо равны (могут быть наложены друг на
друга движением в пространстве), либо зеркально равны. Два зер-
кально-равные треугольника движением в пространстве не могут
450
быть наложены друг на друга, а могут быть приведены в положение,
изображенное на чертеже 267, при котором соответственные вер-
шины являются диаметрально противоположными. Зеркально-
равные треугольники называются также симметричными.
VI. В сферической геометрии рассматриваются следующие зада-
чи на построение сферических треугольников: по трем сторонам;
по трем углам; по стороне и прилежащим углам; по углу и приле-
жащим сторонам; по двум сторонам и углу, противолежащему одной
из них; по двум углам и стороне, противолежащей одному из них.
При этом равные и зеркально-равные треугольники не рассмат-
риваются как различные
решения задачи. Если произ-
вольно заданы три элемента сфе-
рического треугольника, то за-
дача построения треугольника
по этим элементам может не
иметь решения (заданная систе-
ма трех элементов не является
допустимой), может иметь един-
ственное решение, может иметь
два различных решения.
В соответствии с изложен-
ным в сферической тригономет-
рии рассматриваются задачи
на вычисление основных элемен-
тов сферического треугольника
по заданной системе значений
трех его основных элементов.
VII. Сумма углов всякого сферического треугольника больше π
Черт. 267
Разность
А + В + С>л.
ε - (А + В + С) — π
между суммой углов и π называется эксцессом или сферическим избыт-
ком треугольника.
Плошадь сферического треугольника равна произведению эксцесса
на квадрат радиуса
§ 73. Соотношения между основными элементами
сферического треугольника
В настоящем параграфе выведены соотношения между основ-
ными элементами произвольного эйлерова треуголь-
ника, применяющиеся в сферической тригонометрии при решении
треугольников (сферических).
451
Формулы косинуса стороны
Теорема 1. Косинус стороны сферического треугольника равен
произведению косинусов двух других сторон плюс произведение сину-
сов тех же сторон на косинус угла между ними:
cos a = cos b cos с + sin b sin с cos Л, '
cos b = cos с cos a + sine sin a cos B,
cos с = cos α cos ft + sin α sin 6 cos C. .
(I)
Эти формулы можно получить из какой-либо одной путем одно-
временной круговой перестановки букв а, Ь, с и Л, В, С.
Доказательство. Для доказательства достаточно рас-
смотреть соответствующий трехгранный угол. Так как а, 6, с и
Л, β, С равны по величине (соответственно) плоским и двугранным
углам трехгранного угла, то, как известно,
- cos a — cos b cos с
C0S Л = sin b sin с
(доказательство дано в § 68, пример 3, стр. 414) это равенство рав-
носильно первому доказываемому соотношению. Аналогично уста-
навливаются прочие формулы, ч. т. д.
Другое доказательство. Из векторной алгебры известна сле-
дующая общая формула преобразования скалярного произведения двух
векторных произведений:
([ab][xy]) = (ах) (by) - (ay) (bx). (*)
Обозначим через гА% гв и гс радиусы-векторы точек А, В, С, т. е. векто-
ры, соединяющие центр сферы с вершинами данного треугольника. Пре-
образуем по формуле (*) следующее произведение ([Гагв][гагс])· ^ез
ущерба для общности считаем радиус сферы равным 1, тогда получим:
\[ГЛ гв\\ = sln с> | [rA rc]\ ^ s*n b\ векторные произведения [гА гв] и [гА гс]
перпендикулярны к плоскостям двугранного угла при вершине Л и угол
между этими произведениями равен углу А (принять во внимание, что
угол А меньше π).
Следовательно,
([ГА гв\ [ГА гс\) — sin с sxn b cos А'*
имеем далее:
(ГА ГС) = C0S Ь ' (ГВ ГЛ)=
Подставив в формулу (*), получим равенство
sin с sin b cos A — cos a — cos b cos с,
эквивалентное первому равенству (J). Аналогично доказываются прочие
разекства, ч. т. д,
452
Формулы синусов
Теорема II. Синусы сторон сферического треугольника про-
порциональны синусам противолежащих им углов:
sin A sin В sin С
sin a sin b sin с
(П)
Доказательство. Формулы синусов можно вывести из
формул косинусов.
Имеем:
COS а — COS Ь COS С \2
ί/sin2 b sin2 с — cos2 b cos2 с — cos2 #+ 2 cos a cos b cos с
V sin2 b sin2 с
У
(1 — cos2 b) (1 — cos2 c) — cos2 b cos2 с — cos2 a + 2 cos α cos 6 cos с
sin2 b sin2 с
Vl — cos2 α — cos2 b — cos2 с + 2 cos й cos 6 cos с r, .
= sin a : · и ■ = К sin a.
sin a sin b sin с
Множитель /С (в окончательном выражении) при sin а есть
симметрическая функция аргументов а, бис, не меняющаяся
при их перестановке, поэтому все отношения (II) имеют одно и то
же значение, равное этому множителю, ч, т. д.
Примечание. Перед радикалом берем знак +, так как аргументы
в пределах от 0 до π имеют положительные синусы.
Формулы пяти элементов
Теорема III. Произведение синуса стороны сферического тре-
угольника на косинус прилежащего угла равно произведению косинуса
противолежащей этому углу стороны на синус третьей стороны
минус произведение синуса противолежащей стороны на косинус
третьей и на косинус угла между ними:
sin a cos В = cos b sin с — sin b cos с cos Л,
sin /; cos С = cos с sin α — sin с cos a cos B,
sin с cos A = cos a sin b — sin α cos b cos C,
(III)
sin α cos С = cos с sin b — sin с cos bcosA,
sin b cos A = cos a sin с — sin α cos с cos 5,
sin с cos В = cos 6 sin a — sin b cos a cos C.
Доказательство. Для доказательства первой формулы
воспользуемся равенствами:
cos a = cos b cos с + sin Ь sin с cos Л,
cos Ь = cos a cos с + sin a sin с cos β.
453
Исключим из этих равенств cos а, для чего умножим первое на cos с
и сложим со вторым; тогда получим:
cos b = cos b cos2 с + sin b sin с cos с cos А + sin a sin с cos В.
Заменив в правой части cos2 с на 1 — sin2 с, получим (после сокра-
щения) равенство, эквивалентное первому доказываемому соотно-
шению. Прочие формулы доказываются аналогично, ч. т. д.
Заметим, что для получения второй и третьей формул достаточно
произвести в первой формуле одновременную круговую переста-
новку букв а, Ь, с и Л, β, С, а для получения двух последних формул
достаточно произвести круговую перестановку букв в четвертой
формуле.
Теорема IV. Произведение синуса угла на косинус прилежащей
стороны равно произведению косинуса угла, противолежащего этой
стороне, на синус третьего угла плюс произведение синуса противо-
лежащего угла на косинус третьего угла и на косинус стороны между
ними:
sin A cos b = cos В sin С + sin В cos С cos α,
sin Β cos с = cos С sin A + sin С cos A cos 6,
sin С cos a = cos A sin В + sin A cos В cos c,
\ (IV)
sin Л cose = cos С sin θ + sin С cos β cos α,
sin В cos a = cos A sin С + sin A cos С cos by
sin С cos 6 = cos В sin Л + sin β cos Л cos с
Доказательство. Заметив, что равенство
sin с cas В = cos b sin α — sin b cos α cos С
является линейным однородным относительно синусов сторон, за-
меним в нем sin a, sin b, sin с пропорциональными числами sin A,
sin β, sin С, тогда получим равенство:
sin С cos В = cos 6 sin A — sin В cos a cos С,
эквивалентное первому доказываемому равенству. Аналогично дока-
зываются прочие равенства, ч. т. д.
Формулы косинуса угла
Теорема V. Косинус угла сферического треугольника равен про-
изведению косинусов двух других углов, взятому с обратным знаком,
плюс произведение синусов тех же углов на косинус стороны между
ними:
cos А = — cos β cos С + sin В sin С cos a,
cos β = — cos C cos A + sin С sin A cos b, \ (V)
cos С = — cos Л cos β + sin Л sin В cos c,
454
Доказательство. Исключим из равенств (формулы
(IV) пяти элементов, вторая серия)
sin Л cos Ь — cos θ sin С + sin β cos С cos α,
sin Β cos a = cos A sin С -f- sin A cos С cos b,
произведение sin A cos b путеАм подстановки из первого равенства во
второе, тогда получим:
sin β cos α = cos A sin С + (cos β sin С -f sin β cos Ccos α)-cos С
или
sin β cos α = cos A sin С + cos В cos С sin С + sin β cos α (1 —sin2 С).
Откуда (после сокращения) получим равенство, эквивалентное пер-
вому доказываемому соотношению. Аналогично доказываются две
прочие формулы, ч. т. д.
Другое доказательство. Рассмотрим треугольник
AiBiCi, полярный для данного. Применив к полярному треуголь-
нику формулу косинуса стороны, получим:
cos аг = cos bx cos cx + sin bx sin cx cos Au
Приняв во внимание, что
а1 = л — Л, bx = π — β, Cj = Jt — С, А1=л — аъ
получим первую доказываемую формулу, ч. т. д.
Формулы котангенсов
Рассмотрим четыре рядом лежащие элемента сферического тре-
угольника; существуют следующие шесть возможных комбинаций
(черт. 268):
АсВа, сВаС, ВаСЬ,
аСЬАу СЬАс, ЬАсВ.
В каждой из этих комбинаций противо-
лежащие друг другу элементы (т. е. А и
а, с и С и т. д.) будем называть крайними,
а два другие элемента средними (т. е. с и
β, В и а и т. д.).
Теорема VI (правило Непера). Раз-
ность между произведением синуса средней Черт. 268
455
стороны на котангенс крайней и синуса среднего угла на котан-
генс крайнего, равна произведению косинусов средних элементов:
(VI)
sin с ctg α— sin β ctg Л = cos с cos β,
sin a ctg b — sin С ctg В = cos a cos C,
sin b ctg с — sin A ctg С = cos b cos Л,
sinactgc— sinBctgC = cosacos/?,
sin b ctg a — sin С ctg A = cos b cos C,
sin с ctg & — sin A ctg β = cos с cos A
Доказательство. Рассмотрим равенство, выражающее
формулу пяти элементов:
sin b cos A = cos a sin с —- sin a cos с cos β,
и равенство, являющееся следствием теоремы синусов:
sin b sin A — sin a sin β.
Разделив почленно эти равенства, получим равенство, эквивалент-
ное первой доказываемой формуле. Аналогично устанавливаются
прочие формулы, ч. т. д.
§ 74. Соотношения между элементами
прямоугольного треугольника
Рассмотрим прямоугольный сферический треугольник, т. е.
треугольник, хотя бы один из углов которого прямой. При-
нято обозначать данный прямой угол треугольника буквой Л,
противолежащая сторона а называется гипотенузой, а про-
чие стороны — катетами. Углы β и С называются косвен-
ными углами, среди косвенных углов могут быть как прямые,
так и тупые.
Если в общих формулах (I) — (VI), содержащих элемент Л,
положить А = -^ , то эти формулы упростятся и примут следующий
вид (после незначительных преобразований):
cos а = cos b cos с,} (I')
sin b = sin a sin β, | ..,.
sine = sin a sin C, J
cos β = cos b sin C,
cos С = cos с sin β, [ (V)
cos a = ctgfictgC,
456
cos β = ctga tge,
sin b = tgcctgC,
cos С = tgftctga,
sine = tgftctgS
(в приведенном списке формулы (Г) суть следствия формул (I),
формулы (II') суть следствия (II) и т. д.).
Равенства (Г), (1Г), (V) и (VI') называются десятью фор-
мулами прямоугольного треугольника.
Формула (Г), выражающая гипотенузу прямоугольного сфе-
рического треугольника через его катеты, играет роль теоремы
Пифагора в евклидовой геометрии, а потому называется сфе-
рической формулой Пифагора.
Следствия: 1°. Если оба катета меньше -у, либо больше
-γ, то гипотенуза меньше —у если же один катет больше γ ,
а другой меньше γ, то гипо-
тенуза больше -^-.
В самом деле, из сфериче-
ской формулы Пифагора
cos a = cos b cos с
следует, что если знаки cosft
и cos с одинаковы, т. е. либо
0<6<-|-и 0<с<-|-, либо
(черт. 269).
и -γ-<^<π, то
cosa>0 и 0<a<-y; если
же знаки cosb и cose противо-
положны, то cos а < 0 и -γ<^α<
2~. Из (формулы
cos a =ctg£clgC
следует (рассуждения такие же, как и в предыдущем случае),
что если косвенные углы оба меньше чем -^- или оба больше
чем -γ, то гипотенуза меньше -γ, если же один угол меньше,
а другой больше -£-, то гипотенуза больше -^-.
457
3°. Катет и противолежащий угол либо оба меньше -γ,
либо оба равны -γ, либо оба больше -γ-
В самом деле, из формулы
cos β = cos b sin С
следует, что cos β и cos& одинаковы по знаку (так как sinC>0),
это равносильно доказываемому утверждению.
§ 75. Решение прямоугольных треугольников
Различные задачи на вычисление основных элементов прямо-
угольных сферических треугольников решаются при помощи десяти
формул.
Для облегчения пользования десятью формулами для прямо-
угольного сферического треугольника существует мнемоническое
правило Непера, которое делает излишним заучивание
этих формул.
Заменив элементы b и с соответственно на -^ b и -^ с,
перепишем десять формул прямоугольного сферического треуголь-
ника следующим образом:
cos a = sin ί-| b j sin j -| c\ cos α = ctg β ctg С,
cosi-|- — b) = sin α sin β, cos β = ctg α ctg |-| c\
cos f-|- — с \ = sin a sin C, cos ί-γ — b\ = ctg ίΛ- — c\ ctg C,
y —fcjsinC, cos С = ctg ij —b\ ctg a,
cosC = sin i-| cjsinfi, c
Начертив прямоугольный треугольник (пло-
ский), отметим в нем гипотенузу буквой а,
острые углы буквами В η С (черт. 270), ка-
теты, противолежащие этим углам, отметим
соответственно надписями -^— b и \ — с (при
этом, прямой угол, будучи известным элемен-
п *β том, не отмечается никак). Для всякого из
1~с пяти элементов имеются два смежные и два
Черт. 270 несмежные элемента, смотря по расположе-
нию соответствующих пометок на вспомога-
тельном плоском треугольнике. Так, например, для элемента С
смежные элементы суть а и ~— 6, а несмежные — суть β и-^ — с.
458
Из рассмотрения десяти формул вытекает мнемоническое пра-
вило:
Правило Непера: косинус каждого элемента равен произведе-
нию котангенсов смежных элементов; равен произведению синусов
несмежных элементов.
Сферический треугольник определяется заданием допустимой
системы значений трех его основных элементов, в случае же пря-
моугольного треугольника один из элементов известен (угол
л К\
А = 2~), поэтому прямоугольный треугольник определяется заданием
системы (допустимой) значений двух его основных элементов.
В соответствии с изложенным существуют следующие шесть
основных случаев решения прямоугольных сферических треуголь-
ников:
Г. по двум катетам:
даны b и с, вычислить а, В, С;
2°. по катету и гипотенузе:
даны а и ft, вычислить с, В, С;
или
даны а и с, вычислить ft, В, С;
3°. по катету и противолежащему углу:
даны ft и В вычислить а, с, С;
или
даны с и С, вычислить а, Ь, В\
4°. по катету и прилежащему углу:
даны ft и С, вычислить а, с; В;
или
даны с и В, вычислить a, ft, С;
5°. по гипотенузе и прилежащему углу:
даны а и С, вычислить ft, с, β;
или
даны а и В, вычислить ft, с, С;
6°. по двум углам:
даны β и С, вычислить a, ft, с.
Десять формул прямоугольного сферического треугольника свя-
зывают во всех возможных сочетаниях три элемента прямоуголь-
ного треугольника из пяти его элементов a, ft, с, 5, С. Число всех
возможных таких сочетаний равно 10; число формул также равно
10. Для вычисления искомых элементов прямоугольного треуголь-
ника берут три формулы, которые связывают два данных эле-
мента с одним из искомых. Эти три формулы и образуют сис-
тему уравнений для вычисления искомых элементов. Выразив
явно тригонометрические функции от искомых элементов через
тригонометрические функции от заданных элементов, получим
систему простейших тригонометрических уравнений, которая обра-
459
зует смешанную систему вместе с неравенствами, характеризующими
допустимые значения искомых элементов.
Выбор формул для решения задачи производится по правилу
Непера. Формула, связывающая три искомых элемента, может
служить средством контроля.
Поясним сказанное рассматриванием нескольких задач на ре-
шение прямоугольных сферических треугольников.
Задача. Даны катеты b и с, вычислить гипотенузу а и
косвенные углы В и С.
Решение. Применив правило Непера, пишем формулы,
связывающие каждый из искомых элементов с данными элементами.
Для вычисления а
cos a = sin (-| b | sin |-| с
\ c\ = z\g[~- — b\zigB
sine = tgbctgfi;
или
cos a = cosb cos c\
для вычисления В
cos
или
для вычисления С
cos (-| b \ = ι
или
sin 6 = ctg Ctg с.
Откуда найдем окончательно:
cos a = cosb cos с, tg β = -I— , tg С = -1Ц-
' & sine ' & sin b'
0<α<π, 0<β<π, 0<С<л.
Эта смешенная система имеет единственное решение.
Контрольной формулой может служить соотношение между иско-
мыми тремя элементами:
cos a = ctg В ctg С.
Задача. Даны катет и гипотенуза а и Ь, вычислить другой
катет с и косвенные углы В и С.
460
Решение. По правилу Непера имеем:
cos (-^ b j = sin a sin β,
cos a = sin (~ b) sin (~ c).
z 1 l
Для вычисления с, В и С получим смешанную систему:
• г» sin b л tgl) cos a
sinfi = -—, cosC=t§—, cosc = —-u
sin a' iga' cos b'
0<с<л, 0<β<π, 0<C<n.
Чтобы первое из простейших уравнений этой системы имело реше-
ние, необходимо и достаточно выполнения условия sin6<sin a.
При соблюдении этого условия
|cosa|<|cos6| и |tg6|<|tga|.
Следовательно, второе и третье уравнения также имеют решение.
Первое уравнение имеет в интервале (0, π) два решения:
D sin b n sin b
Вл = arc sin—— и Во = л — arc sin ——.
1 sin a z sin a
Если Bj=f=B2 (равенство возможно при β, = Β2 = -~J, то из двух
значений Вг и В2 следует взять значение Въ меньшее -2-, если
b<i~Y и значение В2 больше -|-, если &>-у, так как катет и
противолежащий угол должны быть либо оба большими -—-, либо
оба меньшими -^-.
Задача. Даны катет b и противолежащий угол β, вычис-
лить а, с и С.
Решение. Применив правило Непера (по образцу, указан-
ному в предыдущих задачах), составим смешанную систему:
sin b . igb . п cos В
SIna = -_ sinf= 6^ sinC = —τ-,
sin θ ' tg В ' cos 6 '
0<α<π, 0<^<π, 0<β<π.
Первое уравнение имеет решение при условии sin 6<sin В и, так
как допустимые значения Ь и В оба одновременно содержатся либо
в первой, либо во второй четверти, то либо 6<β<-^, либо
!. Иными словами, задача может иметь решение лишь при
461
условии, если значение В заключено между значением b и -^. При
указанном условии каждое из простейших тригонометрических
уравнений имеет два, в общем случае, различные решения.
Из первого уравнения для гипотенузы найдем следующие зна-
чения:
__ . sin 6 ___ ■ sin b
Предположим, что эти значения различны:
αι <. -γ- <. "2
(равенство п\ = а2 = \ имеет место при sin Ь = sin β). При
α=αί<^~ катеты и косвенные углы содержатся в одной четверти либо
в первой, либо во второй. Поэтому из двух решений второго (треть-
его) уравнения следует взять то, которое находится в одной четверти
с катетом b (углом В). При а = cl%^>-T) катеты и косвенные углы
содержатся в различных четвер-
тях, поэтому из двух решений
второго (третьего) уравнения
следует взять то, которое на-
ходится в различных четвертях
с катетом b (углом В). Таким
образом в общем случае задача
допускает два различных реше-
ния (черт. 271).
По указанному образцу ре-
шаются и исследуются прочие
задачи на вычисление основных
элементов прямоугольного сфе-
рического треугольника по за-
данным дбум его основным эле-
ментам.
Решение прямосторонних сфе-
рических треугольников, т. е.
треугольников, для которых хотя бы одна сторона равна -^, при-
водится к решению прямоугольных треугольников. В самом деле,
если а = -н , то полярный треугольник является прямоугольным,
Черт. 271
так как для него
= π — -^ = ^.
Для углов, близких к -η , синус, а для углов, близких к 0, косинус из-
меняется очень медленно, а потому пользование таблицами в некоторых слу-
462
чаях не может обеспечить требуемой точности. В этих случаях искомьГе эле-
менты можно вычислять по тангенсам, преобразовав надлежащим образом
основные формулы. Так, в случае вычисления катета с по гипотенузе а
и катету b можно поступить следующим образом Воспользуемся формулой
tg- = 1/ _Ш ; положив cose '= с s а , получим,
2 г 1 + cos с cos b
β 2 У ь 2 ь 2
Для вычисления угла В воспользуемся формулой
• sin В
sin b
Положив в этой формуле sin В = ^—,
получим
-и / tg~~2~
f tg —ϊч—
—_Ь_
2~~
Знак перед радикалом можно определить, зная, что b и В содержатся
в одной четверти.
§ 76. Понятие о решении косоугольных
сферических треугольников
В основе решения косоугольных сферических треугольников
лежит тот же общий принцип, который применяется при решении
прямолинейных треугольников. Остановимся кратко лишь на ос-
новных случаях. Если дана система (допустимая) значений трех
основных элементов, то взяв систему трех основных соотношений
(например, формулы I косинуса стороны) и подставив значения из-
вестных элементов, получим тригонометрическую систему трех
уравнений для вычисления трех искомых элементов. Присоединив
к этой системе уравнений неравенства, связывающие допустимые
значения для элементов сферического треугольника, получим сме-
шанную систему для решения и исследования задачи. Основные со-
отношения, служащие для вычисления значений искомых элемен-
тов, можно выбирать в различных видах (см. §71); этот выбор сле-
дует производить с тем расчетом, чтобы сделать наиболее удобными
решение тригонометрических уравнений и последующие вычисления.
В некоторых случаях целесообразно путем проведения сферическо-
го перпендикуляра из вершины на противоположную сторону раз-
бить данный косоугольный треугольник на два прямоугольные
треугольника. После этого задача сводится к решению двух пря«
моугольных треугольников (вернее к вычислению некоторого числа
их необходимых элементов).
Существуют следующие шесть типов основных задач на решение
треугольников.
46Э
Г: По трем сторонам: даны а, Ь, с, вычислить Л, β, С.
2°. По трем углам: даны А, В, С, вычислить а, Ь, с.
3°. Яо <5βί/Λί сторонам и углу между ними: например, даны а,
6, С, вычислить Л, β, с.
4°. По двум углам и стороне между ними: например, даны Л,
β, су вычислить а, 6, С.
5°. Яо <3##ж сторонам и углу, противолежащему одной из них:
например, даны а, 6, Л, вычислить В, С, с.
6°. Яо двум углам и стороне, противолежащей одному из них:
например, даны Л, В> а, вычислить Ь, с, С.
Задача Г. Вычисления можно производить по формулам
косинусов сторон. Из равенства
cos a = cos Ъ cos с + sin b sin с cos A
для вычисления угла Л получим следующее простейшее тригоно-
метрическое уравнение:
cos a — cos b cos с
COS Л =
sin b sin с
Для вычисления прочих углов получим аналогичные уравнения;
к этим уравнениям следует присоединить неравенства:
0<Л<я, 0<β<π, 0<С<я, Л+В+С>л.
Эта система формул удобна для вычислений на арифмометре.
Задача 2°. Вычисление сторон по данным углам можно про-
изводить по формулам (V) косинусов углов, из равенства
cos Л = — cos В cos C+sin В sin С cos α,
получим
cos Л + cos в cos С
cos a = ■
sin В sin С
Для прочих сторон получим два аналогичных простейших уравнения.
Задача 3°. При данных a, b и С сторона с может быть вычис-
лена по формуле:
cos с = cos a cos b + sin a sin b cos С.
Углы Л и β можно найти из формул котангенсов (VI) (см. § 73).
, „ sin Ь ctga , , ^
ctg A = sinCe cos b ctgC,
, r> sin a oXub , ^
cteB- sine ~ cosactgc
(эти формулы удобны для вычислений на арифмометре).
464
Эту задачу можно решить путем разбиения данного треуголь-
ника на два прямоугольных треугольника сферическим перпенди-
куляром, опущенным из вершины Л, на сторону а. Однако этот
способ представляет неудобство, связанное с необходимостью раз-
личать два случая, изображенные на черт. 272.
Черт. 272
Задача 4* решается подобно предыдущей задаче. Для вы-
числения элементов а, Ъ и С достаточно воспользоваться форму-
лой косинуса угла и формулами котангенсов:
cos С = — cos A cos В + sin A sin В cos c\
Задача 5е. Для вычисления угла В при данных а, Ь и А
можно воспользоваться формулой синусов:
η · л sin b
sin S = sin A-.—.
sin a
Для вычисления стороны с и угла С можно воспользоваться фор-
мулами III пяти элементов:
sin a cos В = cos b sin с — sin Ь cos с cos A
(уравнение для вычисления с по данным Л, 6, В и а):
sin с cos В = cos Ь sin a — sin b cos a cos С
(уравнение для вычисления С по данным β, fc, а и с).
Задача 6° решается аналогично предыдущей.
Как видно из изложенного, по основным формулам может быть решена
любая основная задача 1° —6° на вычисление элементов сферического тре-
угольника, однако, для вычислений по логарифмическим таблицам указан-
16 Зак 597
465
ные формулы неудобны, а потому в сферической тригонометрии выводятся
специальные серии формул, которые и применяются при логарифмических
вычислениях. Ниже указаны эти формулы и методы их доказательств (эле-
ментарные выкладки опущены, они могут быть выполнены учащимися в виде
упражнения). Подставив в формулы
sin4=j/·
COS
1 + cos A
2 2 V 2 ' β 2
значение cos Л, найденное из неравенства
cos a = cos b cos с + sin b sin с cos Л
после элементарных преобразований, получим:
-v\
— cos A
1 + cos A
in Λ = ]/sin(p — 6) sin (ρ —
2 г sin 6 sin с
sin
и
j4_ = -i/sin ρ sin (p-a)
2 V sin 6 sin с
Λί
' sin (ρ — a) *
[τ]
где
2P^a + b + c и M-l/sm(p-a)s\n(p-b)sin(p-c)
V sin ρ
и аналогичные формулы для тригонометрических функций углов о" и о" (при
этом ρ и М, как симметричные функции сторон, имеют одно и то же значение).
Эти формулы применяются при вычислении углов треугольника по его
сторонам.
Аналогично из формулы косинуса угла:
cos Л = — cos В cos С + sin θ sin С cos a
и из 'общих формул половинного аргумента могут быть получены формулы,
выражающие тригонометрические функции половины стороны:
sin
где
i-V
— cos Ρ cos (Ρ —А)
sin В sin С
*-]β
(р — в) cos (p— С)
sin β sin С
tg -γ = К cos (Ρ — Л),
2Ρ = Л + В + С
—cos P
cos (Ρ — A) cos (Ρ — В) cos (Ρ —С)9
аналогичные формулы имеют место для тригонометрических функций -^
466
и 2" (в виде упражнения вывести эти формулы из предыдущих путем перехо-
да к полярному треугольнику).
Эти формулы применяются при вычислении сторон сферического тре-
угольника по его углам.
Формулы Деламбра, так называются нижеследующие фор-
мулы:
А + В
sin —2— :
sin
Л —В
cos
cos
a
cos
cos
a
sin
sin
a
cos
cos ·
a
sin
—
2
с
~2
—
2
с
~2
+
2
с
Ύ
+
2
b
b
b
b
с
C0S-7T
С
cos-jt-
A + B ^a 2 С
sin -Q-,
С
sin -y»
sin-
а также аналогичные формулы для прочих комбинаций сторон и углов.
Для вывода первой формулы подставим в тождество
А + В А В А В
sin —2— = sin -у cos -у + cos у- si n -у
выражения синусов и косинусов половинных углов через стороны треуголь-
р у у у
ника (формулы -gr )· Приняв во внимание, что
cos
sin a sin
после преобразований радикалов, получим:
sin
А + В sin (ρ — b) + sin (p — a)
sin с
■cos -
2 sin -|- cos
cos ■
cos
Тем же способом выводятся прочие формулы.
16*
467
Аналогии Непера. Так называются следующие четыре формулы:
а— Ь
A + B cos 2 i С
^ —9— = 7ΓΊΓΪΓ ctg "о".
cos ■
a+b
tg-2- =
sin ·
a — b
T~ С
4Г7ГС^ ~9~'
sin
2
A — B
tg—
cos
A + B
sin
Л —
(N)
а также аналогичные формулы для прочих комбинаций сторон и углов.
Аналогии Непера являются следствиями формул Деламбера, достаточно
разделить почленно формулы Деламбера, взяв их по две в надлежащих соче-
таниях.
Теорема тангенсов:
А—В
a — b
tg:
tg
a + b
выводится почленным делением второй аналогии Непера на первую (или чет-
вертой на третью).
Аналогии Непера применяются при решении основных задач 3°—6°
с помощью логарифмических таблиц. Эти формулы играют ту же роль, что
формулы Мольвейде в прямолинейной тригонометрии. При решении задачи
3°, при данных a, b и С, первые две аналогии дают систему уравнений для
углов А и В. Сторона с может быть найдена по третьей (или по четвертой) ана-
логии или по теореме синусов
При решении задачи 4° при данных А, В и с третья и четвертая аналогии
дают систему уравнений относительно а и Ь.
При решении задачи 5° при данных a, b и А угол В находится по теореме
синусов, а угол С и сторона с по аналогиям Непера:
— b
С ♦
-γ = ctg
cos
cos -
a + b
* cosd±^
» tg ~9~ = tg о
cos
A—B
(можно взять две другие аналогии).
Задача 6° решается аналогично предыдущей задаче 5*.
468
§ 77. Формулы эксцесса и площади сферического треугольника
Эксцесс сферического треугольника определяется как разность между
суммой углов и π:
(Л + Я + С) — π = 2Ρ — π.
Если из этого равенства выразить Ρ через эксцесс: Р= у +~о~ и под-
[ а 1
ставить в формулы у- (см. предыдущий параграф), выражающие три-
гонометрические функции половин сторон через углы, то (после преобразо-
ваний) получим:
а у sinτsin(А-τ)
SIn1~= sin β sinC '
cos 2
2 sin β sin С
I/
tg-£- = I/
sin [В— —
где
sin у
ini А — у Jsini В— у I sin (С —у J
Аналогичные формулы имеют место для других сторон.
α . Ъ
Перемножив почленно формулы для sin у и sin -γ, получим
α b sin~T V ^[*-T}sin[»-T) sin γ
sin γ sin γ = sinC sin Л sinS = "1THC~ cos Ύ~
Отсюда следует формула К а н ь о л и:
b
sin С, (К)
sin -γ sin -γ
2 с
cos-у
ε
а также две аналогичные формулы для у, получающиеся круговой пере-
становкой букв.
Подставив в формулу (К)·'
sin С = 2 sin A cos Jg- = 2 ^sin Ρ sin (Ρ ~ α> sin (f ~ 6> sin <Ρ ~ c> ,
2 2 sin α sin 6
469
получим выражение для sin-о- в виде симметричной функции сторон:
Sin ε — Vsin ρ sin (ρ — a) s\n (ρ — b) sin (ρ-^Τ)
~ΊΓ α b с
2 cos -γ cos -γ cos -γ
Это — вторая формула К а н ь о л и.
Заменив в формулах Деламбера (D) для sin—^— и cos —2— полу-
А + В π С—ε
сумму —2— через -g* — —g—» представим эти формулы в виде пропорций
следующим образом:
С —ε α — b . С—ε a+b
COS—оГ~ COS—?Г~ Sin ~75— COS—o~"
С - с С - с
cos -γ cos -ψ sln~2~ cos ~2~"
Составим следующие пропорции:
С—ε С a—b с
cos —γ- — cos -γ cos —γ- — cos -γ
С —ε С ~~ a—b с
cos —γ- + cos -γ cos —γ- + cos -g-
C—ε С a+b с
~ ~γ cos —γ- — cos -γ
. С-ε , . С ~ a+b с
si η —η— + sin -ο- cos —ft— + cos -ft-
Δ Δ Ζ Ζ
Представив числители и знаменатели в виде произведений, получим
(после преобразований):
ε p—bi ρ—α
I С ε\ ε ρ ρ—с
ctg j^-g-~ Τ j tg Τ = tg-|-tg ^у-.
Умножив почленно последние равенства, получим после извлечения корня
следующую формулу Л ю и л ь е:
Перед радикалом следует взять+, так как π
откуда
ε π — (А + В + С) п
<
Зная эксцесс, можно вычислить площадь сферического треугольника,
так как
где /^—радиус сферы.
470
§ 78. О различных применениях сферической тригонометрии
1. Применение к решению стереометриче-
ских задач. Основные элементы сферического треугольника:
его стороны а, Ьу с и углы А, В, С суть (соответственно) плоские
и двугранные углы соответствующего трехгранного угла, поэтому
сферическая тригонометрия находит применение при вычислении
элементов трехгранных углов.
Примеры.
1. Вычислить двугранные углы правильных многогранников: тетра-
эдра и додекаэдра.
Решение. Плоские углы правильного тетраэдра равны:
Воспользовавшись формулой косинуса стороны, получим:
π π 1 1
cos Α = !ϋΐΖϋίΐ = ΙΖΐ = 1
Следовательно,
А = В = С = arc cos -g- « 70°31 '43".
Для додекаэдра плоские углы при вершинах суть углы правильного
пятиугольника, поэтому
3π
имеем:
cos 55 - cos2 —
л 5 5
cos Л =
Подставив значения
получим:
1
cos A = — rnF и Л = В = С = arc cos
2. Плоский угол правильного трехгранного угла равен а, вычислить
угол при вершине описанного конуса.
Решение. Вычислим двугранный угол трехгранного угла, применив
формулу косинуса стороны (черт 273):
COS α — COS2 α cos α
cos A = cos В = cos С == -r-a- = —
2 cos2 -y
471
Рассмотрим трехгранный угол SOAB; в этом угле плоские углы суть а,
L·, L· (где χ — искомый угол при вершине конуса), а противолежащие
им двугранные углы соответственно суть _ΐ, _ и _ = _ . Вычисление
о Ζ 2 2
угла -£ равносильно решению сферического (равнобедренного) треуголь-
А В А
ника по стороне α и прилежащим к ней углам — и __ = —. Применив
теорему
Ч
синусов,
А
в
Sin α
«η-
•i" \
. А ·
sm-γ
- \ D
is
i
/
1
/
A
I
ы
i !
A !
ο /ι
l^T!JM!/}l/HMllf/lfW/ll/l/llflfllfIWlifll/ll/l/llllllllli 1
Черт. 273
Черт. 274
получим (элементарные преобразования опускаем):
sin
Sina
sin
2π
sin
A 2 УЗ
2 - 3
• ΐ/Γ
Sin α у —
- cos A
2 sin £
2
3. Яа плоское зеркало падает световой луч; угол падения равен а. Затем
зеркало поворачивают на угол β вокруг проекции падающего луча в плоскость
зеркала (в первоначальном положении зеркала). Найти угол, на который от-
клонится отраженный луч от первоначального направления*.
Решение. Пусть АО — падающий луч (черт. 274), ОВ — отражен-
ный луч при первоначальном положении зеркала, 0D — перпендикуляр
к плоскости зеркала в первоначальном положении, ОС — перпендикуляр
к плоскости зеркала в новом положении, ОЕ — новое положение отраженно-
го луча, тогда ^.AOD = a, ^DOC = β, требуется вычислить угол χ = ^lBOE,
Пусть γ = -£ АОС — новый угол падения. Рассмотрим два трехгранных
угла OACD и ОАВЕ; эти углы имеют общий двугранный угол при ребре ОА,
* Эта задача составлена редактором книги П. С. Моденовым.
472
обозначим этот угол через А. В первом трехгранном угле плоские углы суть
α, β и γ, поэтому (из формулы косинуса стороны):
cos A
cos β — cos α cos γ
sin a sin γ
Во втором трехгранном угле плоские углы суть х, 2зс и 2γ, поэтому
cos A —
cos x — cos 2α cos 2γ
sin 2a sin 2ύ
Так как OD есть проекция ОС на плоскость ОАВ и луч О А составляет
углы γ и α с наклонной ОС и с ее проекцией 0D, то (см. стр. 413)
cos γ = cos α cos β.
Приравняв значения cos А, получим:
cos β — cos α cos γ
sin α sin γ
cos χ — cos 2α cos 2γ
sin 2α sin 2γ
откуда
cos χ = 4 cos α cos γ (cos β — cos α cos γ) + cos 2α cos 2γ =
= 4 cos α cos γ (cos β — cos α cos γ) + (2 cos2 α — 1) (2 cos2 γ — 1) =
= 4 cos α cos β cos γ — 2 cos2 α — 2 cos2 γ + 1.
Заменив cosy на cos η cos β, получим:
cos χ = 4 cos2 α cos2 β — 2 cos2 α — 2 cos2 α cos2 β + 1 =
= 2 cos2 α cos2 β — 2 cos2 α + 1 = 1 — 2 cos2 α sin2 β.
4. Вычислить объем наклонного параллелепипеда, если даны длины его
ребер, выходящих из одной вершины, и плоские углы при этой вершине.
Черт. 275
Решение. Введем обозначения, как показано на чертеже 275, теми
же буквами А, В, С обозначим двугранные углы при ребрах О А, ОВ и ОС.
Обозначим через /, т, η длины ребер ОЛ, ОВ и ОС, имеем:
V = (нл OABD) · h = (/m sin с) (η sin a sin В) — Imn sin a sin B.
R R
Воспользуемся формулами, выражающими sin -— и cos— через стороны
16В Зак 697
473
сферического треугольника, т. е. через углы а, Ь, с (см. стр. 466):
sin В — 2 sin ^ с s ^ — 2 l/"5*11 ^ ~ а^ sin (Р ~~ с) l/^sin p sin (p — b) _
2 2τ sinasinc V sinasinc
__ 2Vs\n ρ s\n(p—a) sin (ρ — b) sin (ρ— с)
sin a sin с
где 2p — a -{- b -\- с.
Следовательно, получим окончательно:
V — 2lmn\/ sin a\ - ~т c sjn ~v c a s\n a +—^f sin α "~ ~^" g .
ij/sin*
II. Применение сферической тригономет-
рии в геодезии и астрономии. Сферическая триго-
нометрия применяется к решению различных геодезических задач
в тех случаях, когда измерения и вычисления производятся для
столь больших участков земной поверхности, что невозможно пре-
небречь ее кривизной. Сферическая тригонометрия находит широ-
кое применение при решении различных задач теоретической и при-
кладной астрономии.
Примеры.
1. Задача. Известны географические координаты двух пунктов А
и В земной поверхности, вычислить расстояние между данными
пунктами.
Решение. Пусть φΛ и φΒ—широты, а \л и λβ— долготы данных
пунктов (черт. 276). Расстояние d между А и В измеряется длиной дуги
большого круга земного шара. Рассмотрим сферический треугольник, вер-
шинами которого служат полюс и данные пункты А и В. В этом треуголь-
нике стороны РА и РВ соответственнно суть Л — φ^ и — — φβ, угол
между ними равен j\A λβ | Искомое расстояние равно длине стороны А В.
Пусть d — дуговая (радианная или градусная) мера А В, тогда по формуле
косинуса стороны имеем:
cos d = cos I γ — φΑ j cos I у — φΒ Ι + sin I -j — φΑ J sin I у — φΒ j X
X cos (Хл — λΒ)
или
cos d = sin фл sin φΒ + cos фл cos φΒ cos (Хл — λβ),
искомое расстояние равно Rd, где d — радианная мера дуги АВ, a R — ра-
диус земного шара.
Вычислим, например, расстояние между Ленинградом и Берлином.
Координаты Ленинграда φΑ = 59°56' северной широты и Хл = 30°18'
восточной долготы.
Координаты Берлина суть φΒ = 52°30' северной широты и \в = 13°18'
восточной долготы:
cos d = sin 59°56' -sin 52о30г + cos 59°56' cos 52ο30' cos 17° «
« 0,8655-0,7934 + 0,5010-0,6088.0,9563 ж 0,9784,
474
откуда
d ^ arc cos 0,9784 = 11Ο56' = 0,2883 (радиан).
Зная радиус земного шара R ^ 6370 (км), получим:
AB^Rd = 6370-0,2883 « 1330 км.
Вычисления выполнены на арифмометре при помощи четырехзначных
натуральных таблиц.
\
4 Χ
..Ν
^ \
\ 4
ι * ^ Ι
\ \
-4. i
IS
χ"
4 \
1 /
Черт. 276
Черт. 277
2. В Харькове наблюдали звезду при часовом угле t = 50°27'32" и при
азимуте а = 89°7'16"; вычислить зенитное расстояние звезды и ее склонение Ь,
Широта Харькова равна φ = 50°0'10".
Решение. Рассмотрим на небесной сфере треугольник, вершины
которого суть небесный полюс Р, зенит Ζ и наблюдаемая звезда S (черт. 277).
В сферическом треугольнике PZS сторона ΡΖ равна 90° — φ, сторона ZS есть
искомое зенитное расстояние г, сторона PS равна 90° — δ, угол при полюсе
Ρ есть часовой угол t, угол при вершине Ζ равен 180° — а. Следовательно,
в треугольнике PZS известны сторона ΡΖ и два прилежащих к ней угла Ρ
и Ζ, требуется вычислить сторону PS и сторону ZS. Перейдя к привычному
обозначению, положим:
а = RZ = 90° — φ = 39°59'50", B = t = 50°27/32", С = 180° — а = 90°52'44".
Для вычисления сторон Ь и с воспользуемся аналогиями Непера:
tg
Ь + с
cos-
В—С
В
— с
sin
COS
Β+ С
sin
В + С tg 2 '
Производим вычисления:
D Q
Б —С = —40°25Ч2"; —ψ- = — 20° 12 '36"; В + С = 14Γ20Ί6";
70°40'8"; у = 19°59'55",
16В*
475
Igcos
Я-С -
= 1,97240
— Igcos
=0,48014
lgtg 1 = Г,56104
=0,01358
— (b + с) = 45Ο53'44Λ
Ig
sin-
— lgsin
= 1,53840
= 0,02520
lgtg|-= 1,56104
— с
= 1,12464
—с
= — 7Ο35'22".
Из (*) и (**) получим: 6 = 38°18'22", г == 53°29'6";
z = 6 = 38°18/22", δ = 90° — с = 36°30'54ff
(**)
Глава восьмая
АНАЛИТИЧЕСКАЯ ТЕОРИЯ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
§ 79. Определение тригонометрических функций
при помощи степенных рядов
В предыдущих главах (см. гл. II и III) тригонометрические
функции изучались на основе их геометрического опре-
деления. Однако в науке возникла необходимость в определении
тригонометрических функций чисто аналитическими средствами,
независимо от геометрии.
Создание неевклидовой геометрической системы поставило ее
творца — великого русского ученого Н. И. Лобачевского
перед проблемой определения тригонометрических функций ана-
литячески, вне зависимости от геометрии Евклида. В своих тру-
дах Н. И. Лобачевский определяет тригонометрические функции
при помощи степенных рядов; этими трудами положены основы со-
временной аналитической теории тригонометрических функций.
В § 36 доказано, что в силу трансцендентности тригонометри-
ческих функций, эти функции невозможно представить при помощи
формул, содержащих только лишь алгебраические опе-
рации над аргументом. Если к алгебраическим операциям присое-
динить операцию предельного перехода, то представ-
ление тригонометрических функций при помощи формул окажется
возможным. В самом деле, в общем курсе математического анализа
доказывается следующая теорема: тригонометрические функции
cos χ и sin χ разлагаются в следующие степенные ряды:
1— ίρ + J- —..., (С)
! + £!
(S)
В общем курсе математического анализа тригонометрически,
функции считаются известными из элементарной математикие
а в элементарной математике эти функции определяются геометри-
477
чески. Таким образом, определенные геометрически функции cos χ и
sin x могут быть разложены в степенные ряды (С) и (S).
Обратно, можно принять за основу аналитическое определение
тригонометрических функций как сумм степенных рядов (С) и (S)
и доказать, что так определенные функции имеют ту самую геомет-
рическую интерпретацию, которая в геометрической теории при-
нимается за определение тригонометрических функций. Это поло-
жение будет доказано в настоящем параграфе.
Определение. Аналитическим косинусом и аналитическим сину-
сом называются (соответственно) функции, заданные следующими
формулами:
~ 1 оГ ~Ь ··· · ( 1/ ТоглГ "^ ···» ν"1)
Установим основные свойства аналитического косинуса и си-
нуса, исходя из этого определения.
Г. Областью определения функций С (х) и S (х) является мно-
жество всех действительных (комплексных) чисел.
В самом деле, степенные ряды (С) и (S) сходятся (и притом
абсолютно) при произвольном действительном (комплексном) зна-
чении х. Чтобы в этом убедиться, достаточно применить признак
абсолютной сходимости Даламбера. Так, для ряда (С) имеем:
lim
«и
| =1ίΠΊ
Ι χ I
2°. Функция С (χ) — четная, а функция S (х) — нечетная.
Это очевидно, так как ряд (С) содержит только лишь четные, а ряд
(S)—только лишь нечетные степени аргумента.
3°. Имеют место формулы сложения, выражающиеся следующими
тождествами:
C(x-y)=C(x)C(y)
S(x + y) = S (χ) С(у) + С (х) S (у). (Sx+y)
Доказательство. В справедливости доказываемых тож-
деств можно убедиться проверкой, выполнив соответствующие
действия над рядами. Для примера докажем первое тождество.
Имеем в левой части:
(х — у)2П
4
478
Правую часть вычисляем путем умножения рядов (что воз-
можно в силу их абсолютной сходимости). Выполнив умноже-
ние рядов:
получим ряд — произведение с общим членом:
[У2П 2п-2 2 2л-2/г 2k y2n "1
(2/г)! ^ (2/г — 2)! 2! ^ "' ^ (2л — 2Л)! (2k)\ ^ '" ^ (2я)1 J'
Аналогично, выполнив умножение рядов
„2/г—1
получим ряд — произведение с общим членом:
(— П*-1
х2п~х у х2п~ъ у3
(2/г —1)! "·" (2/г — 3)! 3! + '"
'" "^~ (2/г —2^ + 1)! (2Л — 1)! ~^~ '" ^ (2/г — 1)! J *
Выполнив сложение С (х)С (у) + S(x)S(y), получим ряд с общим
членом:
L· J -
[(2/i)! (2/2 — 1)! "*" (2/г — 2)! 2!
Таким образом, получился ряд тождественный ряду, изобра-
жающему левую часть доказываемого равенства (Сдг-у), ч. т. д.
Следствия.
I. Положив у=х в тождестве (C*-y), получим тождество:
В самом деле
С(х — х) =
(положить χ = 0 в ряде (С).
II. Заменив в тождествах (Сх-У) и (Sx+y) аргумент у на —у
и воспользовавшись четностью аналитического косинуса, и нечет-
479
ностью аналитического синуса, получим две следующие форму-
лы сложения
С(х + у) = С (х) С (у) — S (х) S (у) (Сх+у),
S(x — y) = S(x)C (у) — C(x)S (у) (Sjr-y).
III. Таким образом, для аналитического косинуса и аналити-
ческого синуса имеют место те же самые формулы сложения, ко-
торые в гл. II доказаны для тригонометрических функций, доста-
точно лишь заменить cos χ на С (х), a sin χ на S (χ). В качестве след-
ствий теорем сложения, путем формальных преобразований были
получены формулы преобразования сумм в произведения и произ-
ведений в суммы, формулы удвоения и деления пополам аргумента
для функций cos v и sin χ. Так как формулы сложения имеют место
для функций С (х) и S (х), то указанные следствия этих формул ос-
таются в силе (для доказательства нет надобности воспроизводить
изложенные в гл. II выкладки).
Формулы преобразования произведений в суммы:
S(x)S(y) =
С (χ-у)-с (χ + у)
+ y)-S(x-y)
Формулы преобразования сумм в произведения:
(А)
С(х) + С(у) =
х + у
(В)
Формулы удвоения и деления пополам аргумента:
S (2а:) = 2S (х) С (х)\ С (2х) = С2 (х) — S2 (х)\
(С)
IV. Функции С (х) и S (х) имеют в интервале — оо < к <<х>
производные любого порядка. Эти производные можно получить поч-
ленным дифференцированием (соответствующее число раз) рядов
(С) и (S).
480
Это свойство вытекает из общей теоремы анализа о дифферент
цируемости степенного ряда в интервале сходимости.
В частносги» имеем:
V. Уравнение С (х) = 0 имеет наименьший положительный ко-
рень. Обозначим через λ этот корень, тогда
a) в интервале (0, λ) обе функции С (х) и S (х) положительны,
b) на сегменте 10, λ] функция С (х) убывает от 1 до 0, а функ-
ция S (х) возрастает от 0 до 1.
Доказательство. Имеем:
При достаточно малых положительных значениях χ все члены
этого последнего ряда положительны, а потому
Это неравенство будет наверное выполнено, если О<
Итак, в интервале (0, 2) функция S (х) положительна. Докажем,
что в этом интервале функция С (х) убывает, для этого достаточно
установить, что ее производная отрицательна. В самом деле:
С (х) = -S (л)<0
в интервале (0, 2).
Вычислим значение функции С (х) в точках 0 и 2:
С(0)=1, g Jg
— 3 61 у 7-8у \01\ι \\-\2
Следовательно, в концах сегмента [0, 2] функция С (*) имеет
противоположные знаки:
С(0)>0 и С(2)<0.
В силу непрерывности и монотонности этой функции на данном
сегменте существует единственное значение аргумента
* = λ, 0<λ<2,
при котором функция С (л;) обращается в нуль:
С(К) = 0;
при этом
С(х)>0
в интервале
0<χ<λ.
481
Итак, обе функции С (χ) и S(x) положительны в интервале
Ο<λ.
Положив χ = λ, в тождестве
получим S(k)= 1 (принять во внимание, что )^
Так как S' (х) = С(*)>0 в интервале (ОД), то на сегмен-
те [0, λ] функция S(x) возрастает.
VI. Имеют место формулы приведения:
C(x+ λ)
С (х + 2λ)
С (х + 3λ)
С (χ -f- 4λ)
< азател
= — S (x)\
= -C(x)\
= S(x);
= ОД;
5(x +
S(x +
S(x +
S(x +
ьство. Вычислим
λ)=.
2λ) =
3λ) =
4λ) =
С (ж).
-S(x).
значения
[χ + λ]
к). [χ — 2λ]
с). [χ + 3λ]
[χ + 4λ]
функций С (χ) и
и 5 (х) в точках λ, 2λ, 3λ и 4λ; имеем:
С(2Х) = С2(λ) — 52(λ) -= — 1, 5(2λ) = 0;
С (3λ) = С(Х)С (2λ) — 5 (λ) S (2λ) = 0;
и, наконец:
С (4λ) - С2 (2λ) — S2 (2λ) = 1, 5 (4λ) = 2S (2λ) С (2λ) = 0.
Для доказательства формул приведения достаточно воспользо-
ваться теоремами сложения. Так, например:
С(х+ λ) = С (х)С (λ) — S (χ) S (λ) = —S (χ).
Следствие. Функции С (χ) и S(x) периодические. В самом
деле, тождества [χ + 4λ1 показывают, что число 4λ является перио-
дом для каждой из этих функций.
VII. В каждом из интервалов (£λ, (k + 1)λ) (где k—произволь-
ное целое число) каждая из функций С (х) uS (x) знакопостоянна.
В силу периодичности рассматриваемых функций, достаточно
установить их знакопостоянство лишь в следующих четырех ин-
тервалах:
(0, λ), (λ, 2λ), (2λ, 3λ), (3λ, 4λ);
a) в интервале (0, λ), где функции положительны:
C(x)>09 S(x)>0;
b) в интервале λ, 2λ):
С (χ) < 0, S (χ) > 0,
482
В самом деле, если λ<χ<2λ, то χ = λ + α, где 0<α<λ.
Воспользовавшись формулами приведения, получим:,
С (л:) = — S (а)< О, S (х) - С (а) > 0.
Аналогично доказываются следующие утверждения:
c) в интервале (2λ, 3λ):
С (χ) < 0, S(x) < 0;
d) в интервале (3λ, 4λ):
Следствие. Функция S(x) положительна в интервале
(0, 2λ) и отрицательна в интервале (2λ, 4λ).
В силу периодичности, S (х)>0 в интервалах (4 £λ, (4& + 2)λ)
и S(x)<0 в интервалах ((4й + 2λ), 4 (& + 1) λ). В частности,
S<O в интервале (— 2λ, 0).
Функция С(х) четная, поэтому она положительна в интервале
(— λ, 0). Из изложенного следует, что функция С (х) положительна
в интервале (— λ, λ) и отрицательна в интервале (λ, 3λ).
В силу периодичности,
С(х)>0 в интервалах ({4k— 1)λ, {4k + 1)λ)
и
С(х)<0 в интервалах ((4k + 1)λ, (4k + 3)l).
VIII. На сегменте [0, 2λ] функция С (χ) убывает, а на
сегменте [2λ, 4Ц — возрастает.
Доказательство. Пусть, например, 0<^хг <χ2<2λ.
Составим разность С (х2) — C(Xi)9 преобразуем ее в произведение:
С (χύ - С (χύ = - 2S
Так как
то
а потому
483
Откуда
С(х2)-С(хг)<0
C(x2)<C(Xl),
т. е. функция С (х) убывает на сегменте [0, 2λ]. Возрастание функ-
ции С(х) на сегменте [2λ, 4λ] доказывается аналогично.
Тем же методом доказывается следующее утверждение:
в интервале (— λ, λ) функция S(x) возрастает, а в интервале
( λ, 3λ) — убывает.
Теорема. Аналитический косинус и аналитический синус совпа-
дают с тригонометрическими функциями cos χ и sin x:
С (χ) = cos x, S (χ) = sin χ.
Доказательство. Достаточно доказать следующие по-
ложения:
a) уравнения
Х = С(х), Y = S(x). (1)
Суть параметрические уравнения единичной окружности
X2 + У2 = 1;
b) аргумент χ есть длина дуги AM единичной окружности от
точки А (1, 0) до точки Μ (Χ, У).
а) Рассмотрим простую дугу, определяемую уравнениями (1)
на сегменте 0 <лг <λ (четверть периода). На этом сегменте функции
С (х) и S (х) непрерывны и монотонны (первая убывает, вторая воз-
растает), следовательно, система (1) определяет на плоскости не-
которую простую дугу.
При произвольном значении параметра х, где 0 <* <λ, соответ-
ствующая точка дуги расположена в первой четверти единичной
окружности, так как
Х=С(х)>0\ Υ = S(x;>0.
Обратно, пусть Μ(Χ,Υ)—точка, расположенная в первой
четверти единичной окружности:
Υ = J/T^A"2,
где
0<Х< 1;
эта точка соответствует тому значению параметра χ на сегменте
0 < χ < λ,
при котором функция С (х) имеет значение равное X.
484
Концами дуги служат точки:
а: = О, X =С(0)= 1, Υ -5(0) -0
а: = λ, X = С (λ) = 0, К = δ(λ) = 1 (черт. 278).
Точно так же докажем, что сегменту
λ < χ < 2λ соответствует вторая, сег-
менту 2λ<!Λ:<;3λ — третья, а сегменту
3λ<Α:<4λ — четвертая четверти еди-
ничной окружности.
Таким образом, система (I) на сег-
менте 0 < χ < 4λ дает параметрическое
представление полной единичной ок-
ружности.
Ь) Докажем что параметр χ есть дли-
на дуги s единичной окружности, отсчи-
тываемой от точки А (1, 0). Имеем
4(1,0)
Черт. 278
s =
— C(x)]*+[S(x)]*dx =--
Значит х есть радианная мера угла, образованного отрезком ОМ
(черт 278) с осью абсцисс. Отсюда вытекает интерпретация функций
С (χ) и S (х) как «линии косинуса» и «линии синуса» угла х, ч. т. д.
Из изложенного следует, что геометрическое определение функ-
ций cos л: и sin а: и аналитическое определение функций С (х) и
S (х) являются лишь различными способами задания одних и тех
же функций. Свойства этих функций можно изучать как геометри-
ческими, так и чисто аналитическими средствами.
§ 80. Вычисление значений тригонометрических функций
аналитическими средствами
Представление тригонометрических функций при помощи сте-
пенных рядов дает удобный аппарат для вычисления значений этих
функций с любой заданной степенью точности. Как известно, чтобы
вычислить значение тригонометрической функции от произвольного
данного значения аргумента, достаточно уметь вычислять значения
тригонометрических функций от значений аргумента, заключенных
на сегменте 0<а:<-| (для значения аргумента вне этого сегмента
достаточно воспользоваться формулами приведения; см. § 23).
Поэтому таблицы значений тригонометрических функций состав-
ляются обычно для углов от 0° до 45°. Итак, будем считать, что
485
0<х<-; так как -т<О> то и подавно 0<х<1; при этом усло-
вии ряды
~Х~3\ Ы ••• + V— (2/1 — 1)1 "'
= ! ~2[ +-4J —··· + (— U (2л)] + ·-
являются знакопеременными рядами с убывающими по абсолют-
ной величине членами. Из теории рядов известно, что сумма знако-
переменного ряда с убывающими (по абсолютной величине) членами
заключена между двумя его последовательными частными сум-
мами. Следовательно, имеем в частности:
х
χ тг- <^ sin x
Аналогичные неравенства имеют место для косинуса.
Если для вычисления значения тригонометрической функции
от данного значения аргумента (считаем0<jt<l) заменить соответ-
ствующий ряд некоторой его частной суммой, т. е. сохранить неко-
торое количество его первых членов и отбросить все последующие
члены, то допущенная от такой замены ошибка меньше абсолютной
величины первого отброшенного члена. Пусть, например, требуется
составить пятизначные таблицы значений синуса. Сохраним в ряде
четыре первые члена, тогда получим приближенное равенство
X3 . Хъ X1
ъ\х\х~х — -β]- i- -gj ТГ
с ошибкой, не превосходящей-gj-. Так как 0 < χ<-ξ-<0,8, то
имеем следующую оценку погрешности:
Таким образом, приближенная формула (1) вполне достаточна для
составления пятизначных таблиц значений синуса. Следует заме-
тить, что при малых значениях аргумента можно пользоваться мень-
шим числом членов.
Примеры. 1. Показать, что для составления четырехзначной таблицы
значений синусов углов от 0° до 15° достаточно пользоваться приближен-
ной формулой sin χ — χ — -4^ .
6
486
Угол 15° в радианной мере измеряется числом — «0,2618 < 0,3 При
пользовании данной формулой допущенная ошибка будет меньше, чем
_**_ (0,3)5 З5 З4
5! < 1ШГ ^ 120-105 ^ 4-10е < °'00002·
2. Вычислить с точностью до пяти десятичных знаков 24°30'.
Решение. Угол 24°30' в радианной мере измеряется числом 0,427606.
Воспользуемся приближенной формулой
с ошибкой, меньшей чем
*8 (0,5)8 5«
"8Г < ~W = 8! 108 < 0,0000005.
Положив χ = 0,427606, произведем вычисления по общим правилам
приближенных вычислений с шестью десятичными знаками:
положительные слагаемые
1 = 1,000000
_ =0,001393
4!
1,001393
отрицательные слагаемые
χ2
-^j- = 0,091 422
— = 0,000008
6!
0,091430
Откуда после вычитания и округления получим
cos 24°30;« 0,90996.
§ 81. Аксиоматический метод в тригонометрии
В настоящем параграфе будет дано аксиоматическое
определение тригонометрических функций как функций, обладаю-
щих некоторыми точно описанными характеристическими свойст-
вами, на основании которых можно установить все прочие свойства
этих функций*.
При этом, в приведенных ниже рассуждениях совершенно без-
различно, какими средствами эти функции могут быть заданы.
Определение. Аналитическим косинусом С (х) и аналитическим
синусом S (х) называются функции:
I определенные для всех действительных значений х\
II удовлетворяющие функциональному уравнению:
С(х-у)=С(х)С (у) + S(x)S (у); (С, _у)
(иными словами, равенство (Сх^у) выполняется тождественно при
всех значениях χ и у);
* При написании настоящего параграфа я пользовался ценными сове-
тами редактора книги П. С. Моденова.
487
III положительные в интервале 0<*<λ, где λ — некото-
рое положительное число
С(х)уО и 5(л-)>0 при 0<χ<λ;
IV в граничных точках интервала (О, λ) имеют место сле-
дующие равенства:
C(0)=S(k = 1.
Сформулированное определение не дает ответа на вопрос, су-
ществует ли хотя бы одна система функций С (х) и S (х), удовлетво-
ряющая перечисленным условиям.
Предметом специального исследования должен явиться также
вопрос, является ли построенная (каким-либо способом) пара функ-
ций С{х) и S (х) единственной (приданном λ), удовлетворяющей
всем перечисленным условиям I — IV.
В настоящем параграфе мы, не касаясь вопроса о существовании
функций С {х) и S (л:), установим свойства этих функций, вытекаю-
щие только лишь из основных условий I — IV. Таким образом,
следующие ниже рассуждения настоящего параграфа будут носить
условный характер: в них будут установлены свойства функций
С (х) и S (х) в предположении, что эти функции существуют.
Г. Имеют место следующие равенства граничных значений:
5(0) =Ο(λ; = 0.
Доказательство. Положив в основном тождестве (II)
С(х-у)=С{х)С (у) + S (х) S (у) (Сх-У)
χ -ζ у = 0, получим:
С(0) = C2(0) + S2(0), откуда в силу IV
1 = 1 + S2 (0) = 0 и 5 (0) = 0.
Положив в II χ = у = λ, получим:
откуда 1 + С2 (λ) = 1 и С (λ) = 0.
2Q. Имеет место тождество
Доказательство. Достаточно положить в основном соот-
ношении (II) χ = у и принять во внимание условие (IV).
Следствие. Функции С(х) и S(x> ограничены:
3°. Имеют место следующие тождества, выражающие функ-
ции С(х) и S(x) одна через другую:
488
Доказательство. Заменив в основном соотношении (II)
χ на λ, а у на х, получим:
Заменив в полученном равенстве χ на λ — у, получим:
C(y)=S{X-y)y
ч. т. д.
4°. Для функции S(x) имеет место формула сложения:
S(x + y,=S(x)C (у) + S(y)C (χ. (Sx+y)
Доказательство. Воспользовавшись доказанным свой-
ством 3е, получим:
S(x + у) = С[\ — (х + у)] = С [(λ — *) — у] =
ч. т. д.
5°. Функция С (х) четная, а функция S(x) нечетная.
Доказательство. Положив в основном соотношении (II)
χ = О, получим:
Итак, С (л:) — четная функция.
Положив у = — х, в формуле (Sx+y) получим:
0 = S(x — x) = S(x)C(—x) + C(x)S(— jc) =
= C(x)[S(x) + S(— *)]=0.
Возможны два случая:
Случай а): С (х) =£ 0; тогда
S(x) + Sx— х) = 0 или S(x) = —S(—x).
Случай Ь): С(х) = 0.
Пусть у — произвольное число, взятое в интервале (0, λ). Примем
во внимание, что S (— у) = — S (у), ибо С (у) > 0 [в силу преды-
дущего пункта а)\ и что S(x)=j=Oy так как в силу пункта
2° S(x) = ± 1.
Имеем далее
С(х + у) = С{х-(-у))=С(х C(y)+S(x)S(-y) = ±S(y)=f=O.
В таком случае
S(x + y) = —S(— x — у). Последнее равенство перепишется так:
S(x)C(y) = -S(-x)C(y)
[принять во внимание, что С(—х) = С(х) = 0 и С(—у) = С(у)],
откуда и в этом случае 5 х) = —S(—χ).
Следовательно, 5 (χ) — нечетная функция.
489
6°. Для функций С (χ) и S (х) имеют место все четыре формулы
сложения, (Сх±у), (S^y), а также все их следствия, т. е. формулы
приведения, формулы удвоения и деления аргумента пополам, фор-
мулы преобразования произведений в суммы и сумм в произведе-
ния (все эти формулы в принятом обозначении выписаны в парагра-
фе 79; изложенное их обоснование остается в силе).
Следствия: I. Функции С (х) и S (л:) периодические с пе-
риодом 4λ (см. паграграф 79).
II, Остается в силе пункт VIII параграфа 79, в котором уста-
новлены промежутки монотонности функций С (х) и S(x).
Т. Функции С (х) и S (х) непрерывны в интервале (— со, + оо).
Докажем следующую лемму.
Лемма. Функция С(х) непрерывна в точке х= 0.
Доказательство. Так как С (0) = 1, то для доказатель-
ства леммы надо установить, что
*- о
Достаточно рассмотреть правый предел lim С (χ), считая, что
^0, так как если этот правый предел существует, то, в силу свой-
ства четности С (х):
С(х) = С ( - *),
существует и имеет то же значение и левый предел С (х) в точке 0.
Так как в интервале (0, λ) функция С (х) монотонна (убывает)
и ограничена, то правый предел функции С (х) существует, а сле-
довательно, существует предел (двусторонний) С (х) в точке χ = 0;
обозначим через / этот предел:
lim С (*) = /.
χ - 0
Так как в интервале (0, λ) функция С(л:)>0 и убывает, то 1ф0.
Перейдя к пределу в тождестве С(2х) = 2С2(х) — 1, получим
21imC2(A:)~-l или / = 2/2—1.
Это квадратное уравнение имеет один положительный корень
1 = 1. Следовательно,
/ = НтС(лг) = 1 и С(0) = 1,
х-+0
т. е. функция С (х) непрерывна в точке 0, ч. т. д.
Следствие. Функция S (х) непрерывна в точке χ = 0.
В самом деле,
limS(x) = lim(± γ\— С2(χ)) = 0.
х-+0
490
Значение функции S(x) в точке χ = О также равно О
= limS(*)=0.
0
х-+0
Теорема. Функции С (х) и S(x) непрерывны в каждой точ-
ке х.
Доказательство. Требуется доказать, что
НтС(х + А) = С(*) и \\mS(x + h) = S(x).
Докажем первое равенство. Имеем:
C(x + h) = C(x)C(h) — S(x)S(h)
и
lim С {х + К) = С (л;) lirn С (А) — S (x) lim S (h) = С (х),
так как limC(A) = l, limS(A)=0.
Второе равенство доказывается тем же методом, ч. т. д.
Функция аналитический тангенс Т(х) определяется формулой:
Τ (χ) — S M ·
С (х) ·
изучение ее свойств не представляет затруднений и может быть
выполнено обычными способами (см. гл. I и III) на основании опре-
деления и известных свойств косинуса и синуса. Это же замечание
относится к котангенсу.
§ 82. Теорема единственности
Теорема единственности. При данном положительном λ не
существует двух различных систем функций С(х), S (х) и С\(х),
S\(x), удовлетворяющих основным условиям I — IV.
Доказательство. Требуется доказать, что если (при
данном λ>0) как для функций С (х), S(x), так и для функций
Ci(jc), Si (χ) выполняются основные условия I — IV, то имеют
место тождества:
1°. Рассмотрим последовательность значений аргумента:
λ λ λ
л λ λ λ j λ
Докажем, что в точках этой последовательности значения функций
С (х) и Ci (x) равны. В силу условия IV, имеем:
С{Х) = 0, d (λ) = 0.
491
Последовательным применением формулы деления аргумента по-
полам получим:
и в общем виде:
где sn = V 2 + ]/2+... + 1^2 (п — радикалов; применить метод
математической индукции).
Точно так же найдем, что
2
2°. Пусть т — произвольное целое число, а п — произвольное
натуральное число; докажем, что в точках ^λ значения функций
С (х) и Οχ (χ) (а также S (х) и Si (*)) равны. По доказанному при
т = 1 имеем равенства
Допустим, что равенства:
верны для некоторого целого т; докажем, что в этом предположении
они будут верны для числа т + 1. В самом деле, применим фор-
мулы сложения;
=с (| м- i) -с (| я) с (»,) - s ψλ) s (i
Для функции S (х) рассуждения аналогичные.
В силу принципа математической индукции, равенства (1)
справедливы при произвольном натуральном т.
При т = 0 имеет также:
^ ("2й) = ^1("2Й) ^'» ^\~оп
492
Если ггк^О— целое отрицательное число, то для доказательства
равенств (1) достаточно воспользоваться свойствами четности и не-
четности рассматриваемых функций. Так, например:
T)=L ( j = С [
Ψ
р (ml\
= С* [ψ) '
3°. Пусть χ — произвольное действительное число. Достаточно
доказать равенства
С(х) =CtW; S(jc)=Si(jc)
для случая х>0, так как, в силу свойств четности и нечетности рас-
сматриваемых функций, эти равенства будут верны и при значе-
нии — х.
Разложим отношение ~ в двоичную дробь:
— = Ро + -ψ + -ψ + · · · или
где р0 — целое число, а рь р2,..., рп — двоичные знаки,
т. е. либо р* = 0, либо pfe = l. Если двоичная дробь конечна,
пусть, например, рпф0, но р„+] = рп+2 = ...== 0, то х есть
число вида -^-λ, и для этого случая утверждение доказано.
Предположим, что двоичная дробь бесконечна; положим:
ρ D~ λ
χη = Ρο^ Η—ο~ ^ ~t" · · · Η
Имеем: limxn= χ, и в силу непрерывности рассматриваемых
функций (пункт 7° предыдущего параграфа) получим:
= 1\тС(хп) и C1(x)
но так как
С(хп) = С,(хп)у то limC^-limC,^), т. е. С(х)=С,(х).
Для функции S (л:) и Si (л:) доказательство аналогичное.
Итак, доказываемые равенства имеют место при произвольных
действительных значениях аргумента, ч. т. д.*
* Для доказательства С (я) = Ci(jc) достаточно заметить, что значения
тк
аргумента -ψ. ПРИ которых функции Си Ct равны, образуют всюду плотное
в интервале (— оо, + оо) множество. Из общей теоремы теории функций сле-
дует, что при этом условии две непрерывные в интервале (—· оо, + оо) функ-
ции С(х) и Ci(x) тождественны в этом интервале.
493
Примечание.
Если при двух различных значениях λ= λ4 и λ = λ2 суще-
ствуют системы функций
Cxt(*), SXl(x) и Сх,(*), SK(x)y
то эти системы различны. Это следует хотя бы из того, что при
λχ <λ2 имеем: Сх2 (λ4) > 0, тогда как С^ {к{) = 0.
Теорема. Если при некотором значении λ=λ0 существует со-
ответствующая система функций:
удовлетворяющая условиям I — IV, то я/ш произвольном λ>0
существует единственная система функций С\(х) и S\(x), удов-
летворяющая условиям I — IV.
Доказательство. Достаточно применить преобразова-
ние периода, положив
В самом деле:
I. Областью определения функций С\ и S\ служит интервал
( — оо, + оо), так как функции Сх0 и S\o определены при про-
извольном действительном значении х.
II. Имеем:
III. Если: 0<χ<λ, то 0<-^-x<X0, а потому
x.(4)>0 и Sx(x)=S
IV. Имеем:
6\(0) = СХо(0) = 1; 5λ(λ) = 5χο (λ0) = 1.
Таким образом, система функций Сх(х), S\(x) удовлетворяет всем
условиям I—IV.
В силу теоремы единственности, никаких других функций
Сх (х) и Sx (χ), кроме Сх0 (-— х\ и 5χ0 ί-^- χ\, не может существо-
вать ч. т. д.
494
§ 83. Различные конкретные определения
тригонометрических функций
В аксиоматической теории особого рассмотрения требует во-
прос о существовании объектов, удовлетворяющих дан-
ной системе аксиом. Так, в данном случае из рассуждений двух
предыдущих параграфов не следует, что функции С (х) и S(x)>
удовлетворяющие заранее поставленным условиям I—IV, суще-
ствуют. В изложенных выводах из аксиом I — IV мы не встретили
противоречий, однако, быть может, эти противоречия встретятся
при дальнейшем развитии теории, и тогда вся теория окажется не-
состоятельной. Существование функций С (х) и S (х) будет доказа-
но, если будет сконструирована конкретная система функций, об-
ладающая характеристическими свойствами I — IV. Тем самым
будет установлена непротиворечивость условий I — IV. Построить
функции S (х) и С (х) можно различными способами. Ниже указаны
наиболее распространенные способы этого построения.
I. Геометрическая теория. Эта теория была изложена
в главе I. Косинус и синус, определенные геометрически, суть
функции С*_(л;) и S±(x):
= Ck (x)y s\nx = S% (х)\
Ύ Ύ
функции С\(х) и S\(x) суть:
Сх (х) = cos -|j- xt Sx (x) = sin -i χ.
В силу теоремы единственности, никаких других функций, удов-
летворяющих условиям I — IV, не существует.
В параметрическом представлении окружности:
х = cos /, у = sin /
параметр t есть длина дуги, отложенной от начальной точки А (1,0)
до точки Μ (χ, у), соответствующей значению параметра t. Если
λφ7^-, то в параметрическом представлении окружности:
χ = cosx /, у = sinx /, т. е. χ = cos -£-t, у = sin -^ t9
длина s дуги AM равна s = -2^> откуда / = — s, т. е. пара-
метр пропорционален длине дуги AM с коэффициентом пропор-
циональности, отличным от 1.
II. Определение тригонометрических функций
как степенных рядов.
В этой теории, изложенной в § 79, при помощи степенных
рядов строятся функции CJL(x) = cosx и S^(x) =sin.x;,
2 2
495
III. Τ ρ и г о н о м е τ ρ и ч е с к и е функции как ре-
шения линейного дифференциального урав-
нения. Тригонометрические функции можно определить как
частные решения некоторого линейного дифференциального урав-
нения второго порядка, при этом их свойства можно установить на
основании общих теорем теории дифференциальных уравнений.
Рассмотрим следующее линейное однородное уравнение с по-
стоянными коэффициентами:
S + r-a (1)
Согласно общим теоремам теории дифференциальных уравнений,
существуют два частные решения С (х) и S (х) уравнения (1), удов-
летворяющие следующим начальным условиям*:
С (0) = 1, (7(0)= 0, 5(0)=: 0, S'(0)=l.
Функции С {х) и S (х) линейно независимы, так как начальное
значение вронскиана отлично от нуля:
С (0) 5 (0)
С'(0) S'(0)
1 0
0 1
= 1,
а потому общее решение уравнения (1) можно представить в виде
где Ci и с2 — произвольные постоянные. Функции С (х) и S (х)
непрерывны в интервале (— оо , + оо).
Следовательно, эти функции удовлетворяют первому характе-
ристическому условию I, присущему аналитическим косинусу и
синусу (см. § 81).
Дифференциальное уравнение (1) можно заменить системой
линейных уравнений
dx ' dx / v '
с постоянными коэффициентами. Существует единственное решение
этой системы
у = у{х), z = z(x),
удовлетворяющее начальным условиям
у(0) = 0, г(0) = 1.
Функция у (х) [в силу способа составления системы (2)] удовле-
творяет дифференциальному уравнению (1) и начальным условиям
■у(0) = 0, y'(0)=z(0) = l.
Следовательно,
y(x)=S(x). (3)
* В данном рассуждении функции С (х) я S (х) (пока) никак не связы-
ваются с тригонометрическими функциями.
496
Функция ζ (χ) также удовлетворяет уравнению (1)
d2z __ _d_(dz_\ __ d(—у) _ dy_
dx2 ~~ dx \dx) ~~ dx ~~ dx~~ Z
и начальным условиям
z(0) = l, z/(0)=-y(0) = 0f
а потому
)
(4)
Итак, в силу системы (2), имеем
S'(x) = C(x), C'(x) = -S(x).
Умножив первое уравнение (2) на у, а второе на·г и сложив,
получим:
у ^ + 2^ = 0 или ^.(у2 + г2) = 0
' dx * dx dx v/ ' ' *
откуда
У2(х) + г2{х) -const.
Положив (в частности) y = C(x)f z=S(x), получим:
C2(x) + S2(x) -const,
но при χ = 0 значение левой части равно 1. Следовательно, име-
ет место тождество:
C«(*) + S«(;c) = l. (5)
Следствие. Функции С(х) и S(x) ограничены.
Пусть ξ — произвольное действительное число; функция:
f(x) = C(x-l)
(при данном ξ) удовлетворяет уравнению (1). В самом деле,
а потому
f"(x) + f(x) = C(x-l)-C(x-l) = O.
Следовательно, функция f(x) при некоторых значениях сг и
с2 содержится в общем решении (у) уравнения (1):
C(x-l) = ClC(x) + c2S(x). (6)
Продифференцируем последнее равенство
С (х — I) = CjC (χ) + c2S' (χ) = — CjS (jc) + caC («).,. (7)
и положив в равенствах (6) и (7) χ = ξ, получим:
17 Зак. 597 49?
откуда (принять во внимание (5)), получим:
*i = C(S), cs = S(g).
Равенство (6) примет следующий вид:
Последнее равенство есть тождество, так как χ и ξ — произволь-
ные числа.
Следствие. Для функций С{х) и S(x) удовлетворяется
условие II, которым обладают аналитические косинус и синус.
Теорема. Существуют положительные значения аргумента х,
при которых функция С(х) обращается в нуль.
Доказательство. Предположим противное, что С (х) =£=0
при произвольном значении х^>0. Тогда С(х)^>0 в интервале
(0, + оо). В самом деле, если бы существовало значение хи при ко-
тором С (χι) <Ч), то (в силу непрерывности) в промежутке, ограни-
ченном точками χ = 0 и χ = xly существовала бы точка ξ (по край-
ней мере одна), в которой С (£) = 0 (ибо С (χι)<0, а С (0) = 1> 0),
что противоречит предположению.
Так как S' (х) = С(х)>0, то функция S (х) возрастает. Следо-
вательно, S (*)>0 при х>0, ибо S (0) = 0 и S (0) <5 (х). Так как
S (х) — возрастающая положительная и ограниченная в интервале
(0, + оо) функция, то существует конечный предел:
= /2>0.
Из тождества С (х) = — S (х) и неравенства S (*)>0 следует,
что С (χ) <Ό,Ή значит С (х) есть убывающая функция. Будучи убы-
вающей и положительной (а потому ограниченной), функция С (х)
имеет предел в бесконечности:
Рассмотрим разность
С(х+1)
эта разность в бесконечности имеет предел равный 0:
lim[C(x+ l) — C(x)] =/! — /, =0.
ЛГч-ОО
Но, с другой стороны, применив теорему Лагранжа:
C(x+l)-C{x) = C'(l) = -S(t)
(где χ <^ ξ <С -^ + О, получим:
+ 1) —C(jc)]= —HmS(g) = —/2<0.
Х-+ 00
Следовательно, предположение, что функция С (х) отлична от
нуля при всех положительных значениях аргумента, привело к про-
тиворечию, откуда следует справедливость теоремы, ч. т. д.
498
Обозначим через λ наименьший положительный корень функ-
ции С (.ν)*, тогда С (λ) =0 и С (*)> 0 при 0 <л: <λ. В интервале (0, λ)
функция S (х) возрастает (как имеющая положительную производ-
ную) и S (0) = 0, а потому S (λ)>0**:
Положив χ = λ в тождестве С2(х) -\-S2{x) = 1, получим
S (λ) = 1. Итак, имеем
С (0) = S (λ) = 1
и в интервале (0, λ) функции С (х) и S (х) положительны.
Следовательно, эти функции удовлетворяют характеристическим
условиям III — IV.
Функции С (х) и S(x), как удовлетворяющие условия I — IV,
суть аналитический косинус и аналитический синус:
С (jc) = Сх (х), S(x)=Sx(x).
Докажем, что λ =|· . Рассмотрим параметрические уравнения
окружности (см. стр. 495):
x = Cx(t), y = Sx(O, где 0</<4λ.
Вычислим длину дуги σ с началом в точке А (1, 0), соответствую-
щей значению параметра / = 0, и с концом в точке Μ (χ, у), соответ-
ствующей произвольному значению параметра t. Имеем:
Следовательно, C\(f) и S\(t) суть абсцисса и ордината конца
дуги длины t единичной окружности, отложенной от точки Л,
а потому
При / = λ имеем σ = λ =
* Наименьший положительный корень существует, так как множество
точек, в которых непрерывная функция С (х) обращается в нуль, замкнуто
*· Значение S (λ) есть предел возрастающей положительной в интер-
вале (0, λ) функций: S (λ) = lim S (χ).
17* 499
IV. Определение тригонометрических
функций при помощи обращения интегра-
лов. В этой теории сначала определяются обратные тригонометри-
ческие функции, а затем тригонометрические функции как им
обратные.
В данной аналитической теории рассматривается функция, аргу-
ментом которой является верхний предел следующего интеграла
f dz
= J γγζτ
Этот интеграл рассматривается (пока) вне связи с известными
из элементарной математики тригонометрическими и обратными три-
гонометрическими функциями.
Областью определения подынтегральной функции является
интервал ( — 1,1).
ι о
Оба несобственные интеграла 1 у _ 2 и \ -., 2 сходят-
о -ι
ся*. Таким образом, областью определения функции As (x) слу-
жит сегмент [—1, 1]. Обозначим \ ζ = λ и введем в рас-
b
смотрение функцию Ас (я) = λ — As (χ) = Г ., dz . Имеем
х l ~ Z*
As(x) + Ac(x) = k.
Из общих теорем интегрального исчисления следует, что обе
функции As(x) и Ас(х) непрерывны на сегменте [—1, 1].
Так как подынтегральная функция положительна, то на сег-
менте — 1 < χ < 1 функция As (x) возрастает, а функция Ас (х)
о
убывает. При этом первая возрастает от I — z = — λ до λ,
Jl 1/ 1 — г2
ι
а вторая убывает от \ = 2λ до 0.
* Сходимость интегралов можно установить, применив степенной приз-
нак сходимости. Так, например, Jim (1—ζ)2. Ί/- · = —γ=-, следо-
г-ι γ I —· ζ2 γ 2
dz
вательно, I Ά/Λ ο- сходится,
509
Функция у = As(x) как возрастающая и непрерывная на
сегменте [ — 1,1] имеет обратную функцию
непрерывную и возрастающую от — 1 до 1 на сегменте —
Функция у = Ас{х) имеет обратную функцию
непрерывную и убывающую от 1 до — 1 на сегменте 0 <# <2λ.
Будем рассматривать функции S(a) и С (а) совместно на сегменте
О <α<λ.
Теорема. Функции С (а) и S(cc)
суть тригонометрические функции
С (а) = cos α, «S (α) = sin α,
рассматриваемые на сегменте
Доказательство. Рассмотрим
первую четверть единичной окружности
(черт. 179)
у = у 1 — χ*9 где 0 < χ < 1.
Вычислим длину дуги от точки В (0, 1) до произвольной точки
(ху у) (черт. 279), имеем
ВМ =
rf*
Вычислим длину четверти окружности
ι
dx
ВА =
= λ; итак, λ = -«-.
о
Пусть α есть длина дуги AM, тогда
-5-
и х =
Вычислим длину а дуги ЛУИ следующим образом:
у у
откуда y = S(a).
501
Итак, С (α) и S (α) суть абсцисса и ордината точки Μ (χ, у) еди-
ничной окружности, в которой оканчивается дуга а, отложенная от
начальной точки А (1, 0), ч. т. д.
Следствие. Функции As и Ас суть обратные тригоно-
метрические функции:
As (х) = arc sin χ, Ас (χ) = arc cos χ.
При помощи интегрального представления функции As{x)
и Ас {х) можно изучать аналитическими средствами свойства обрат-
ных им функций С {х) и S (х). Для примера установим аналитически
теоремы сложения для тригонометрических функций.
Пусть t =X|/l —у2-)- у |/ 1 — х2, тогда имеем:
dt __ d (jc/1 — у2 + у V\ — χ2) __ </*
(элементарные выкладки опущены) или
rf (arc sin /) = d (arc sin χ) -\- d (arc sin y),
otk уда
arc sin / = arc sin χ + arc sin у + С,
где С = const; положив * = у = 0, получим С = 0. Итак,
arc sin x + arc sin у = arc sin (х у/ 1 — у2 + у |/l — x2)
Положим далее
arc sin χ = α, тогда л: = S (α), /"1 —л:2 = С(а);
arc sin у = β, тогдау = 5(Р), y^l —у2 = С (β);
тогда получим
α + β = arc sin [S (α) С ф) + С (a) S (β)]
и наконец
5 (α + β) = 5 (α) С (β) + С (α) S (β) (8α+β)
эта формула выведена при условиях
Аналогично (при соответствующих условиях) выводятся осталь-
ные формулы сложения.
Функции С (а) и S (а) определены совместно лишь на сегменте
О, -2 и совпадают на этом сегменте с тригонометрическими функ-
циями. Распространим функции С (а) и S (а) на все множество дей-
ствительных чисел так, чтобы при этом сохранились формулы сло-
жения (Caii3) И vSa±p).
502
Например, потребовав выполнения формулы S(a + β), поло-
жим β =^- , тогда получим (формула приведения):
« + -f) = S(a)c(-f) + C(a)S(-f) = С (a).
Этим равенством функция S(x) распространяется на сегмент
\ < χ < π (если * = α + JL , то 0 < a < -|-
Положив а = 0, β = —а, получим 5 (0 —a) =S (0)-С (а) —
— С (0) S (а) = — S (а), т. е. S (а) есть нечетная функция и т. д*.
Точно таким же условиям (в силу формул приведения) подчи-
няются тригонометрические функции sin α и cos α. Следовательно,
S (a) = sin α, С (a) = cosa в интервале — oo <a<^oo.
Примечание. При построении теории можно исходить
χ
С* и
из интеграла Ат (х) = \ . ,2 2. Несобственный интеграл
о
сю
сходится. Функция Ат(х) определена на множестве
1 + ζ2
всех действительных чисел. Функция Ат(х) может служить
средством аналитического определения арктангенса.
§ 84. О различных способах построения теории
тригонометрических функций
Изложенная в § 81 аксиоматическая теория тригонометрических
функций не предрешает вопроса о том, какими средствами
можно построить эти функции. Приняв за основные (характеристи-
ческие) некоторые свойства данных функций, аксиоматическая тео-
рия устанавливает все прочие их свойства как следствия основных
свойств и общих теорем алгебры, анализа, теории функций, неза-
висимо от того или иного способа представления этих функций.
Теорема единственности доказывает, что различные способы зада-
ния тригонометрических функций равносильны, поскольку они не
могут привести к различным функциям, обладающим данными ха-
рактеристическими свойствами.
Из § 83 известно, что функции, обладающие характеристиче-
скими свойствами I — IV, могут быть построены различно: гео-
* Можно доказать (аналогичные рассуждения см., например, в учебнике
Н. Рыбкина), что после указанного распространения тригонометрических
функций теоремы сложения останутся в силе для произвольных α и β.
503
метрически, посредством степенных рядов как решения дифферен-
циального уравнения, как обращения интегралов.
Существуют и другие способы построения теории тригонометри-
ческих функций (например, при помощи бесконечных произведе-
ний). В § 83 показано, что исследование свойств тригонометри-
ческих функций может производиться различными средствами в за-
висимости от способа их задания. Так, например, приняв за основу
геометрическую теорию тригонометрических функций, можно вы-
вести их разложения в степенные ряды, этот путь (при помощи фор-
мулы Тейлора) известен из общего курса математического анализа
(а потому и не излагается в настоящем курсе). Напротив, если при-
нять за основу представление тригонометрических функций при
помощи степенных рядов, то можно установить (см. § 79), что эти
функции имеют геометрическое толкование, принимаемое в геоме-
трической теории в качестве их определения.
С точки зрения аксиоматической теории различные способы опре-
деления тригонометрических функций суть лишь различные их
конкретные интерпретации. Для установления свойств тригоно-
метрических функций, в зависимости от целесообразности, можно
пользоваться какой-либо (безразлично, какой именно) одной или
несколькими различными их интерпретациями.
Исторически аксиоматическая теория является завершающим
этапом в развитии теории тригонометрических функций, и по своей
сущности она не могла появиться прежде других теорий. Тригоно-
метрия возникла из практических потребностей, вызвавших необ-
ходимость решать задачи на вычисление элементов геометрических
фигур, а потому геометрическая теория исторически сложилась
прежде других теорий.
Многообразные применения, которые получили тригонометри-
ческие функции в анализе, в геометрии, в механике, в физике и
в Других дисциплинах, обусловили возникновение различных путей
построения теории этих функций. Аксиоматическая теория возникла
в результате отвлечения от различных конкретных построений тео-
рии тригонометрических функций, в ней эти функции определяются
посредством описания характеризующих их основных свойств
(см. § 81, условия I — IV), не зависящих от способа их построения.
При этом ясно, что перечень характеристических свойств возник на
базе уже развитой теории тригонометрических функций.
В качестве аксиом, определяющих тригонометрические функ-
ции, могут быть приняты различные их свойства. Иными словами,
в основу теории тригонометрических функций может быть положена
различная система аксиом, однако эта система не может быть
установлена произвольно.
Во-первых, совокупность характеристических свойств не
должна быть противоречивой. Так, например, мы получили бы про-
тиворечивую систему аксиом, если бы к условиям I — IV присое-
динили какое-нибудь свойство, которым тригонометрические функ-
504
ции не обладают. Если бы мы, например, присоединили такое
условие V:
ПтС(х) = + оо,
то это условие находилось бы в противоречии с неравен-
ством | С (х) |<1, вытекающим из прочих аксиом (см. §81, пункт
2°). Следовательно, не существует ни одной пары функций, удов-
летворяющей условиям I — V. Непротиворечивость принятой си-
стемы аксиом решается (как это было отмечено выше) путем построе-
ния конкретной пары функций, для которой все аксиомы выпол-
няются.
Во-вторых, система характеристических свойств (аксиом)
должна быть полной, а именно ей не должны удовлетворять никакие
две различные системы функций. Это свойство полноты имеет место
в силу доказанной (см. § 82) теоремы единственности.
Если бы за основу теории принять непротиворечивую, но и не-
полную систему характеристических свойств, то кроме тригономет-
рических функций всеми этими свойствами обладали бы и некото-
рые другие функции. Такая аксиоматика не могла бы служить
достаточным основанием для построения тригонометрии.
Две различные системы характеристических свойств, при по-
мощи которых можно определить тригонометрические функции,
должны быть эквивалентны. Пусть А и В — две различные эквива-
лентные системы аксиом, в таком случае, приняв за основу систе-
му Л, можно получить как следствия все свойства, перечисленные
в системе β, и обратно, приняв за основу систему 5, можно полу-
чить как следствия все свойства, перечисленные в системе А.
Примеры. Примем за основу следующие свойства функций С(х) и S(x):
условия I, III и IV оставим без изменения, а свойство II заменим формулой
сложения для синуса:
ΙΓ При всех значениях χ и у имеет место тождество:
π
Для простоты положим λ = ~2. Тригонометрические функции cos x
и sin а; удовлетворяют всем четырем условиям, I и IP, III и IV. Докажем,
что кроме тригонометрических функций всем перечисленным условиям удов-
летворяют функции
π
С (х) — ах cos χ и S (х) = а 2 sin x.
Справедливость условий I, III и IV очевидна. В справедливости условия II
убедимся проверкой:
S(x
17В
+ У)
Зак.
= а
597
1 J
( Л
\а
2
π
sin
sin
(χ
+
(о
У) =
1У COS
ι [а * sin у) =
505
При различных значениях а соответствующие системы функций различны;
при а = 1 получается тригонометрическая система. Таким образом, условиям
Ι, ΙΓ III и IV удовлетворяет бесконечное множество систем функций, а по-
тому эти условия не могут быть положены в основу аксиоматической теории
тригонометрических функций.
2. Примем в качестве характеристических следующие свойства функций
С(х) и S(x):
Г. Областью определения служит интервал (— оо, + оо).
ΙΓ. Имеют место формулы сложения:
5 (х + У) = 5 (х) С (у) + С (x)S (у);
C(x + y) = C(x)C(y)-S(x)S(y).
III'. Имеет место тождество
S2 (
IV. В промежутке 0 < χ < λ функция S (χ) положительна
5 (χ) > 0.
V. С (0) = 1; С(Х)=0.
Свойства Г—V суть следствия свойств I—IV, принятых в § 81 за основ-
ные. Докажем, что, приняв свойства Г—V за основные, можно получить
I—IV как следствия.
Свойства I и Г формулируются одинаково.
Положив в ИГ χ = 0, получим
52(0) + С2(0) = 1, откуда 5(0) = 0.
Положим в II' у = —х, тогда получим:
0 = S(x)C(-x) + C(x)S(-x);
1 = C(x)C(—x) — S (x) S (— χ).
Из этой системы найдем:
Следовательно, функция С(х) четная, а функция Six) нечетная.
Заменив во втором тождестве II' у на —у и воспользовавшись свойством
четности и нечетности, получим
Следовательно, выполняется условие II.
Положив в ИГ χ = λ, получим S2(l) = 1, и так как (в силу IV')S(X) > 0,
то 5(λ) = 1.
Следовательно, функции С(х) и S(x) удовлетворяют условиям IV.
Если значение χ принадлежит интервалу (0, λ), то этому же интервалу
принадлежит значение λ — χ, а потому S(K — л;) > 0. Имеем в интервале
(0, λ):
5(λ — χ) = S(X) C(x) — C(k)S(x) = С (χ) > 0.
Следовательно, условие III также выполняется.
Итак, из условий Г—V вытекают условия I—IV.
Свойства Г—V, как эквивалентные условиям I—IV, могут быть приняты
в качестве характеристических свойств тригонометрических функций.
Относительно независимости между собой условий I — IV
заметим, что мы не имели в виду сформулировать минималь-
ное число свойств, характеризующих тригонометрические функ
506
ции. В выборе свойств I — IV мы руководствовались стремлением
дать по возможности легко обозримую, симметричную и простую
в применении систему аксиом. Число условий, содержащихся в ак-
сиомах I — IV, можно уменьшить. Так, например, в условии III
достаточно потребовать положительность лишь какой-либо одной
из функций С (х) и S (х) в интервале (0, λ). Потребуем, например,
выполнение неравенства С (х)^>6\ тогда неравенство S (х)^>0 можно
вывести как следствие. В самом деле, достаточно принять во вни-
мание, что при 0<#<λ имеем также 0<λ — χ<λ, а потому:
При помощи задания характеристических свойств можно определять
тригонометрические функции не только совместно, но и каждую по отдель-
ности. В качестве примера рассмотрим аксиоматическое определение косину-
са*.
Определение. Аналитическим косинусом называется функция С (х)
A) Непрерывная в интервале (—о°, -f- оо);
B) Удовлетворяющая функциональному уравнению
С (х + у) + С (х - у) = 2С (*) С (у);
C) Существует наименьший и положительный корень λ уравнения
С (х) = 0, т. е. С (λ) =0, но С (χ) φ 0, если 0 < χ < λ;
D) С (0) > 0.
С л едет в ия:
Г. Функция С (х) положительна в интервале (0, λ), ибо С (0) > 0 и
С(х)фЪ в этом интервале.
2°. С (0) = 1. В самом деле, положим в В) х — у — 0\
2С(0)=2С2(0),
откуда, приняв во внимание условие D), получим С (0) = 1.
3° Функция С (л;) четная. Положив в тождестве В) χ = 0, получим
С(у) + С (- у) = 2С (у), откуда С(-у)=С (у).
4°. Имеет место тождество
В самом деле,
С (χ + 2λ) + С (х) = 2С(х + \)С (λ) = 0.
Положив х = 0, получим С (2λ) = — 1.
5°. Имеет место формула удвоения аргумента
С (2дс) =-= 2С« (дс) — 1.
В самом деле,
С (2*) + 1 = С (2х) + С (0) = 2С2 (*).
6°. Имеет место формула деления аргумента пополам
с(тг)-: '
X
Достаточно в предыдущем равенстве заменить χ на -„- ,
* См. Ю. М. Гайдук, Журнал «Математика в школе» № 4, 1953.
17В* 507
7°. Функция С (χ) ограничена
Допустим противное, что при некотором значении χ = а имеем
| С (а) | > 1, тогда (в силу тождества В)
2С (λ + а) С (к — а) = С (2λ) + С (2а) = 2 [С2 (а) — 1] > О,
но с другой стороны
2С (λ — а) С (к + а) = 2С (2λ — (λ + а)) С (λ + а) = — 2С2 (λ + а) < 0.
8°. Функция С (х) периодическая, с наименьшим положительным перио-
дом равным 4λ.
Во-первых, 4λ есть период, так как
С (χ + 4λ) = С ((χ + 2λ) + 2λ) = — С (χ + 2λ) = С (*).
Во-вторых, не существует положительного периода /, меньшего 4λ.
Допустим противное, что такой период / существует; имеем:
С (/) = С (0 + /) = С (0) = 1
и
С (/) + С (0) = 2С2 (γ\ откуда с(~А=±\. Если с(-А =
то
Но, с другой стороны,
значит, С2 (λ——τ 1 = 0, что противоречит основному условию С).
0 = С ^4) + С (0)
откуда С |-т-1 = 0, что также противоречит условию С.
9°. Теорема единственности. Не существует двух различных функций
С(х) и С4(Х), удовлетворяющих (при данном I) условиям А), В), С) и D),
Доказательство (с некоторыми несущественными изменениями) теоремы
единственности, изложенное в § 82, остается в силе.
Следствие. Функция С^(х), определенная в § 81, удовлетворяет
условиям А)} В), С) и D), а потому не существует никакой другой функции,
определяемой этими условиями:
С (х) = Сх (*) = cos -^ χ.
Глава девятая
ЭЛЕМЕНТАРНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
НАД ПОЛЕМ КОМПЛЕКСНЫХ ЧИСЕЛ
В настоящей главе даны краткие (по возможности элементар-
ные) сведения об элементарных трансцендентных функциях от ком-
плексного аргумента. Всестороннее изучение элементарных функ-
ций над полем комплексных чисел является одной из задач тео-
рии аналитических функций и излагается в руководствах по этой
дисциплине*. В нижеследующих параграфах основное внимание
обращено на рассмотрение элементарных трансцендентных функций
с точки зрения исследования тех их свойств, которые известны из
элементарной алгебры и тригонометрии.
§ 85. Показательная функция над полем комплексных чисел
и ее связь с тригонометрическими функциями
В качестве одного из свойств, характеризующих показательную
функцию, примем функциональное уравнение:
/(*,+*a) = /to)/(*a), (1)
которому (по условию) должна удовлетворять, эта функция при
произвольных комплексных значениях г} и г2.
Будем искать функцию от комплексного аргумента, удовлетво-
ряющую следующим условиям:
1. Функция \(г) является целой трансцендентной функцией,
т. е. она может быть представлена в виде суммы степенного ряда,
сходящегося при всех (комплексных) значениях аргумента.
И. Функция f(z) удовлетворяет функциональному уравнению
(1) при произвольных комплексных значениях г4 и z2.
* См. например, И. И. Привалов, Введение в теорию функций
комплексного переменного или В. И. Смирнов, Курс высшей матема-
тики, том. III.
509
Для доказательства существования функции / (ζ) построим сте-
пенной ряд, сумма которого удовлетворяет условиям I и П. По-
ложим
+ + az» + ;
этот ряд по условию I должен сходиться при всех значениях ζ.
Вычислим отдельно левую и правую части равенства (1); имеем
в левой части
/ (*ι + г2) = ао + а} (г, + г2) + а2 (ζ, + z2f + ... + ап (гх + ζ2)η + ...
Для вычисления правой части выполним умножение степенных
рядов по общему правилу
/(га) = ао + ал Ч + ··> +anzn2+ ...
Группа членов n-й степени ряда-произведения есть однородный
многочлен
αοαηζΊ + агап-\ ζ}"1 ζ2 + а2ап-2 ζηΓ2ζ\ + ... + ап αοζη2-
По условию, эта группа членов при произвольном целом неотри-
цательном η должна быть тождественна многочлену
ап (ζ, + ζ2)η = ап г*} + апС\ гТх г2 + ... + ап Скп г?"* ζ\ + ... + ап ζη2.
Необходимые условия, которым должны удовлетворять
искомые коэффициенты аи получим, приравняв соответственные
коэффициенты в двух полученных выражениях для группы членов
п-й степени (при η = 0, 1, 2, ...). В частности, при произвольном η
имеем аоап = ап. По условию, ряд бесконечен (т. е. an=f=O для бес-
конечного множества значений п), поэтому а0 = 1. Приравняв
коэффициенты при ζ"""1 г2, получим рекуррентную формулу:
откуда
а
Допустим, что ап-\ = ,п_ χ)1, тогда из соотношения ахап-\=пап
найдем ап — —у-. Таким образом, найдена единственно воз-
можная система значений для коэффициентов искомого ряда.
Докажем, что ряд
удовлетворяет всем поставленным условиям.
510
Условие I выполнено, так как ряд (2) сходится при всех зна-
чениях ζ (достаточно, например, применить признак абсолютной
сходимости Даламбера). Следовательно, сумма ряда (2) есть целая
трансцендентная функция / (ζ). Условие II выполнено, в чем можно
убедиться, перемножив ряды:
ι + ^ι ^ι Η ρ2 ·" "· "* ~η\ ■" '··
1 Ι π у Ι (^1 Ζ2)2 I I (fll г*)П Ι
ι + βι ^2 i jT2 f" ·*· "I }R г" -·
Выполнив умножение, получим ряд с общим членом
(ахгл)п . (αλζγ)η-{ αχζ2 (αιζλ)η-* (ахг%)к , , (gt г2)п
az! "Ч" (я — 1)! 11 "τ" ··· "*" (n — k)\k\ "" «I ~~
Сумма ряда-произведения есть значение суммы ряда (2) при
ζ = г4 + z2, ч. т. д.
При различных значениях а4 получаются различные функции,
удовлетворяющие условиям I и II. Положив, в частности, а{ = 1,
получим функцию, которая обозначается символом ехр ζ:
expz= 1+Z + -J+ ... +-ζ-+ ...
Функция ехр ζ действительна при всех действительных значениях
ζ = χ, непрерывна (как сумма всюду сходящегося степенного ряда)
и удовлетворяет функциональному уравнению (1). Следовательно
(см. «Специальный курс элементарной алгебры» § 110), функция
ехр ζ, рассматриваемая над полем действительных чисел, является
(над этим полем) показательной функцией
ехр χ = ах,
где
a = expl = l + I + ± + ... + Л. + ...
Сумма ряда 2 4- -хт + ··· + -^г + ··· есть число е — основание
натуральных логарифмов, ибо, как известно из теории пределов:
2 + 4 + 4+ + +
Таким образом, при всех действительных χ имеем
ехр χ = е*.
511
Изложенное выше служит мотивировкой следующего определе-
ния.
Определение. Показательной функцией ez над полем комплекс-
ных чисел называется целая трансцендентная функция, опреде-
ляемая формулой:
Ad
Пусть ζ — чисто мнимое число: ζ = iy\ подставив в степенной ряд
и отделив действительную и мнимую части, получим формулу:
= cosy 4* * sin у,
дающую выражение показательной функции от чисто мнимого аргу-
мента через тригонометрические функции.
Для показательной функции от произвольного комплексного
аргумента ζ = χ + iy получим формулу:
ez — ех eiv _ ex (CQS у _j_ I sjn y^
При ζ = ± iy имеем:
e*y = cos у + i sin y, e~iy = cos у — ί sin у. (Л)
Из этих последних формул получим выражение тригономет-
рических функций через показательную:
в'у + в-/у . eiy—e-iy
cosy = —-il , siny = 27 · (β)
Формулы (А) и (В) называются формулами Эйлера — по
имени великого ученого, члена Российской Академии наук Л. Эйлера
(1707—1783).
Примеры.
1 е1 = cos 1 + i sin 1.
2. el+/ = <?(cos 1 +i sin 1).
3. βπί = cos π + / sin π = —1.
4. β ' 2 = cos -5. — / sin Ξ- = — i.
Основные свойства показательной
функции.
1°. Показательная функция отлична от нуля при всех значе-
ниях ζ.
512
В самом деле, предположение ег = О противоречит равенству
ег-е~2 = 1.
2°. Функция ег — периодическая с мнимым периодом I = 2т.
В самом деле
ег+2*1 = ^. ^2π/ = е2 (cos 2л 4- i sin 2π) = е2.
В частности, е2ш = 1, где /г — произвольное целое число.
3°. Всякий период ω показательной функции е2 есть число,
кратное 2ni, т. е. ω = 2kni. В самом деле, если ω =α + /β есть
период показательной функции, то
£>ω = еа+^ = еа (cos β + / sin β) = 1,
откуда
£αα)5β = 1, ^α sin β = 0.
Следовательно, sin β = 0 и β == ηπ. Из условия eacos/m =1
получим: еа = 1, cos пл = 1, а поэтому α = 0, число и = 2k
—четное и ω =а + /β = 2&π/.
4°. Всякое комплексное число ζ — а + Ы можно представить
в следующей показательной форме: ζ = re1*?, где г = | г| φ = arg z,
ηρα .этож аргумент φ определен с точностью до слагаемого, крат-
ного 2ju.
В самом деле, достаточно представить г в тригонометрической
форме ζ =. г (cos φ + / sin φ) = re^ (если ζ = 0, то г == 0, а в ка-
честве φ может быть взято произвольное число).
5. Отображение, реализуемое показа-
тельной функцией. Пусть w = ez\ положим
ζ = χ + iyy w = и + iv, тогда
и + iv = ех (cos у + / sin у) или и = е* cos #, α = е* sin у.
Так как ez — периодическая функция с периодом 2ш, то достаточно
рассмотреть ее лишь в полосе (замкнутой сверху):
— oo<*<-f- оо, —Я
Положив у = Ь, где —π<^ί?<;π, получим
и — ех cos fr, ϋ = е* sin 6.
В плоскости i7OV это суть параметрические уравнения луча
v = u tg b. проходящего через начало координат и образующего угол
b с осью абсцисс. Таким образом, прямые, параллельные оси ОХ,
отображаются на лучи, проходящие через начало координат пло-
скости w (само начало исключается, w=j=0). Положив х = а, полу-
чим параметрические уравнения окружности:
и = е° cos у, υ = еа sin у, где —· η < у < π.
513
Таким образом, отрезки параллелей оси 0Y отображаются на ок-
ружности с центром в начале координат. Радиус окружности,
соответствующей отрезку χ = α, равен еа, отрезкам, расположен-
ным в правой полуплоскости (при а>0), соответствуют окружности
с радиусами, большими 1, а отрезкам, расположенным в левой полу-
плоскости (при а<0), соответствуют окружности с радиусами, мень-
шими 1 (черт. 280).
γ=ΰ—
χ = α
Черт 280
Итак, декартова координатная сетка рассматриваемой полосы
в плоскости ζ отображается на сетку полярных координат в пло-
скости w, а вся полоса отображается на полную плоскость до, из
которой исключена точка w = 0 (черт. 280).
В силу периодичности показательной функции, каждая из полос:
— оо<л:<
(2А
отображается на полную плоскость w с исключенной точкой w = 0.
§ 86. Тригонометрические функции от комплексного аргумента
Определение. Тригонометрическими функциями cos ζ и sin z
называются функции, заданные формулами:
.—/2
COS Ζ =
sin г = ·
eiZ - e
,-iz
(1)
Областью определения этих функций служит множество
всех комплексных чисел. В частности, если ζ — действи-
тельное число, то в силу формул Эйлера (стр. 512), функции, опре-
деленные равенствами (1). совпадают с тригонометрическими функ-
циями от действительного аргумента.
514
Если показательные функции etz и e~iz разложить в степенные
ряды (по степеням ζ) и подставить в формулы (1), то получим разло-
жения косинуса и синуса в степенные ряды:
справедливые при произвольном комплексном зна-
чении ζ.
Из формул (1) следует, что равенства:
eiz = cos z + / sin ζ и е~/г = cos г — ί sin z
справедливы при произвольном комплексном зна-
чении ζ.
Примеры.
2е
2/ 2 2е
= Τ е* + ~Ъ> е~1 = ~2 (cos ! + f sin 1J + "27 ^cos * ""ί# sin ^ =
* e2 + 1 e2 — 1
= 2g cos 1 + ι 2g sin 1.
Основные свойства тригонометрических
функций.
1°. Теоремы сложения, имеющие место для трцгонометрических
функций от действительного аргумента, остаются в силе. Так, на-
пример:
el (zx—z2) , e~i{zx-z2) eizt e~iz2 , e~izx βίζ2
cos (г, — г2) = -^ = -^— =
__ (cos zx + i sin 2!) (cos г2 — ί sin г2) + (cos гг — ί sin ζ ι) (cos г2 + ί sin z2)
~~ 2 " "~
= cos г2 cos z2 + sin ^j sin z2.
Аналогично можно вывести остальные теоремы сложения.
Примечание. Теоремы сложения можно вывести пу-
тем непосредственного умножения рядов (рассуждения, изло-
женные на стр. 478 и 479 остаются в силе).
2°. И з формул (1) следуют тождества:
cos (— ζ) = —- cos z, sin ( — ζ) = — sin ζ, sin2z + cos2z = 1.
515
3°. Функции cos ζ и sin ζ неограничены во всей комплексной пло-
)сти*.
Рассмотрим, например, функцию cos z на мнимой оси; имеем
е-у 4- еу
cos iy = ψ-— и lim cos/y = + °°·
4°. Из теоремы сложения (также, как в §16) можно вывести
формулы приведения.
5°. Функции sin ζ и cos z — периодические с действительным
периодом, равным 2π. Так, например:
ezl еЫ + e-iz e-2ic/ ezi + e~iz
cos (2 + 2π) = L2 = ~2 = cos ζ.
Всякий период синуса и косинуса есть число 2kn, кратное 2я.
Так, например, если ω — α + /β есть период косинуса, то
cos ω = cos 0 = 1, откуда е2ы — 2еы +1=0,
значит, еы = 1 или (см. стр. 513) ίω = 2kni, т. е. ω = 2kn.
6°. Функция cos z = cos (λ: + iy) действительна на действи-
тельной оси у = 0 и .на прямых χ = kn\ во всех прочих точках ζ
косинус имеет мнимые значения.
Доказательство. Отделив действительную и мнимую
части косинуса, получим:
e(x+iy) I j_ e(-x—iy)l р-У pix ι РУ Р—1х
iy =~ %f- =-i—e ^e e =
__ e~y (cos χ -f i sin x) + ey (cos χ — /sin x) __
~ 2 -~
= cos λ: !g 1 sin λ: ^ = cos^chy — ι sinxsh y**.
Значения cos г действительны в том и только в том случае, если
еу е—у
либо sinx = 0, либо р> = 0»
а потому, в силу известных свойств синусов от действительного
аргумента:
либо χ = £π, либо еу = ^~у, откуда у = 0, ч. т. д.
* Неограниченность тригонометрических функций вытекает также из
общих теорем теории аналитических функций о целых трансцендентных
функциях.
ех ι ρ—χ ех ρ—χ
** Как известно, функции —И_— и — называются гипербо-
лическим косинусом и гиперболическим синусом и обозначают-
ся так: ch χ и sh x.
516
Из формулы
sin г = cos
~\
следует, что значения sin ζ действительны на действительной
оси у = 0 и на прямых χ = kit —~ = —ψ— л.
Найдем, в частности, все комплексные значения ζ = χ + iy,
при которых cos z = 0. Эти значения находятся из системы урав-
нений:
cos χ ch у = 0, sin x sh у = 0.
Так как chy>0, то из первого уравнения найдем cosx = 0
и χ =—γ—π. Из второго уравнения найдем shy=O, откуда
еу = етУ или у = 0. Следовательно, z = —i— π. Итак, уравне-
ние cos г = 0 не имеет мнимых корней.
Чтобы найти все значения г, при которых sin ζ = 0, достаточно
решить уравнение:
+ 1
cos
г + у = 0,
откуда ζ + Ύ =
и ζ =
7°. Об отображении, реализуемом триго-
нометрическими фукциями. Ограничимся рассмотре-
нием функции cos 2. Положив
w = и + w = cos г,
получим (см. предыдущий пункт)
и = cos a: ch у, а= — sin x sh у.
В силу периодичности, достаточно рассмотреть функцию cos z
лишь в полосе — π <# < π. В силу свойства четности cos z =
cos( — ζ), точки ζ и — ζ, симметричные от-
носительно начала координат плоскости ΧΟΥ,
отображаются в одну и ту же точку w плоско-
сти UOV (черт 281), поэтому достаточно рас-
смотреть cos z лишь в полосе 0<je<Jt.
При χ = 0 имеем
и = ch у = ■
х= π
В промежутке — оо <j/<0 функция ch у
убывает от + оо до 1, а в промежутке
0<^/<С + °° возрастает от 1 до + оо, сле-
довательно, мнимой оси OY соответствует
Черт. 281
517
в плоскости UOV луч (дважды покрытый) действительной оси:
1 < и < + оо, 0 = 0.
При χ = π имеем:
и = — ch у, 0 = 0.
Аналогично докажем, что прямой χ = π соответствует луч (дважды
покрытый) действительной оси
Отрезку у = с, 0<jt<Jt, где с=^0, параллельному действитель-
ной оси, соответствует линия
и = ch с cos χ, υ = — sh с sin xt
это есть дуга эллипса
и2 ν2 _ -
соответствующая сегменту 0<^χ^π. При с^>0 имеем ν<Ί), а при
c<O имеем 0>О; следовательно, прис^>0 получается нижняя, а при
с<4) —верхняя половина эллипса. При с = 0 эллипс вырождается
в отрезок действительной оси: — 1<^<1, 0=0. Прямой χ = с,
где 0<!с<:я и с=/=^у параллельной мнимой оси, соответствует
линия
и = cos с ch у, 0 = — sin с sh у,
где— оо <у<+ оо, это есть ветвь гиперболы
cos2 с sin2 с
.π
При этом, если 0<с<~, то получается правая ветвь, ибо «>0,
если же -ο<^<^π' то получается левая ветвь, ибо ιι<Ί). Если с =
= ~, то гипербола вырождается в мнимую ось и = 0. Таким обра-
зом, декартова координатная, сетка рассматриваемой полосы отоб-
ражается на семейство эллипсов и гиоербол, имеющих (как не-
трудно проверить) фокусы в точках ± 1 (черт. 282).
Функция tg z определяется формулой;
, sin z I eiz—e~iz
cos ζ ι
Принять во внимание тождество:
519
tl
li "
II
к
1°
■■
—
—
ивя
—
RID
(■
-
CO
■ 1
Щ
-*
• i 0
:
:
:
•
:
о
о
о
о
О
?
о
§
с=,.
3CZ
'=
Тангенс имеет смысл при всех значениях ζ, отличных от кор-
ней уравнения cosz = 0, т. е. от чисел ζ — —ί—π·
Теоремы сложения для тангенса устанавливаются обычным
способом.
Тангенс есть периодическая функция; всякий ее период кратен π.
В самом деле, чтобы число ω было периодом тангенса, необходимо и
достаточно наличия тождества
-tg2=0 или
откуда sin ω = 0 и ω = kn.
Значения tg ζ действительны при действительных значениях ζ,
а при мнимых ζ значения tg г мнимы. В самом деле, если ζ = χ +
+ iyy то
, _1_ e{ ^
~~ i el (x+ly) -\- e~L (*+'y) i cos χ ch у — / sin χ sh у *
Приравняв нулю мнимую часть tg z, получим (элементарные вы-
кладки опускаем):
cos2 χ sh у ch у + sin2 x sh у ch у = sh у ch у =0.
Так как ch ί/>0, то sh у = 0, откуда у = 0.
§ 87. Логарифмическая функция
Пусть ζ — г (cos φ + /sin φ) произвольное отличное от нуля ком-
плексное число. По определению, натуральным логарифмом числа ζ
называется число до, удовлетворяющее уравнению
z = ew. (1)
Если до = и + ш, то имеем:
г (cos φ + i sin φ) = eu (cos v+i sin у),
откуда найдем:
eu = r, υ = φ + 2&π
или
и = In г, у = φ + 2&π и до = In r -f- (φ + 2kn) i, (2)
1 де In r — натуральный логарифм в поле действительных чисел,
a k — произвольное целое число.
При ζ = 0 уравнение (1) не имеет решений, так как еш=1=0 при
произвольном значении до. Таким образом, число 0 не имеет лога-
рифма.
Из формул (2) следует, что всякое отличное от нуля комплексное
число имеет бесконечное множество логарифмов, значения которых
составляет двустороннюю арифметическую прогрессию с мнимой раз-
ностью, равной 2пг. Это объясняется периодичностью показательной
520
функции. Множество всех значений логарифма числа ζ будем обозна-
чать так:
Ln z = In г + (φ + 2&π) i = In | ζ | + i arg г,
где под arg ζ подразумевается множество всех значений аргумента.
Если для arg z выбирается вполне определенное значение в проме-
жутке от —π до л (или от 0 до 2π):
— π < φ < π (или 0 < φ < 2π),
то из множества всех чисел Ln z выделится значение, называемое
главным значением логарифма
In г = In г + ί'φ, где г = |г| и —π<^φ<;π.
Множество всех чисел Lnz есть арифметическая прогрессия:
..., In <г — 4ш\ In 2 — 2ш, In г, inz-\-2nit In z -f 4ш, ...
Примеры. 1. Имеем:
In (— 1) = ln 1 -f-πι = m\
Ln(—1) = (2£ + 1)πί.
2. Пусть α — произвольное отрицательное число; имеем:
\а\ =—a, arg а = π + 2kn;
ln а = ln (—а) + πι
и
Ln а = ln (— а) + (2k + 1) πί.
3. ln ί = ln 1 + i y = ί ~2
Ln ί =
4. ln (1 + 0 = ln J/2 (cos j+ i sin -jjl = у In
2
ϋΥΙ-Ι,-ο , ,_
4
2 + / ~
Ln (1 + 0 = у In 2 + i-| + 2£n) i.
Если ζ — положительное число, ζ = ау где а>0, то φ = О,
а потому in а совпадает со значением логарифма в поле действи-
тельных чисел, все прочие значения логарифма мнимые. Обратно,
если главное значение 1η ζ есть действительное число, то φ = О,
т. е. ζ есть положительное число. Следовательно, действительные
значения логарифма имеют лишь положительные числа.
Основное свойство логарифма:
Ln г, z2) = Ln z1 + Ln z2 (3)
остается в силе. При этом равенство (3) понимается в следующем
смысле: левая и правая его части обозначают одно и то же мнооюе-
ство чисел. В самом деле, пусть
Zi = h (cos φχ -j- i sin φι); г2 =s r% (cos <p? + i sin φ2),
18 Зак. 597 521
тогда
г, z2 = r, r2 [cos (φ! + ф2) + i sin (φ, +
имеем
Ln (ζ, га) = In (r, ra) + (ψχ + φ2 + 2£π) Ι (3')
и
Ln г, + Ln z2 = [In r, + (φχ + 2^ι π) ί] + [In r2 + (φ2 + 2&2 π) i] =
- In r, + ln r2 + [(Φι + φ2) + 2(*! + k2)n] L (3")
В силу свойств логарифмов действительных чисел имеем
In (гг г2) = In Γι + ln r2.
Всякое число из множества чисел (3") содержится в множестве
(3')> ибо k\ + k2 есть целое число ki -\- k2 = k. Обратно, всякое
число из множества (3") содержится в множестве (3'), так как произ-
вольное целое число к можно (бесконечным множеством способов)
разбить на два целых слагаемых k = ki + k2. Итак, множества
(30 и (3") состоят из одних и тех же чисел. Аналогично доказывается
равенство:
Ln — = Ln ζλ — Ln z2.
Примечание. Равенство
ln (ζι z2) = \nzx-\- In z2
имеет место не. всегда, так как сумма φ! + Фг может вый-
ти из промежутка ( — π, π], в котором выбираются главные
значения аргументов. Если (в частности) гА и ζ2 положитель-
ны, то это равенство справедливо, ибо тогда
ф1=<р2 = φΐ + ψ-2 = 0.
Равенство
Lnzm = m Ln г,
вообще говоря, места не имеет. Рассмотрим случай натурального т.
Пусть ζ = г (sin φ + / sin φ), тогда:
zm _ rm (cos m(p _|_ l sjn my}
И
Ln zm = m ln r -f- (my + 2kn) iy
но
m Ln ζ = m In г + m (φ + 2йх π) i = mln г + (ту + 2^ /ηπ) ι.
Всякое значение mLnz содержится среди значений Lnzm, но зна-
чение Ln zm содержится среди значений mLn z лишь при значениях
к, кратных т. Так, в частности
Ln (— 1) = Ln i2 = (2k + 1) ш,
но
2Ln i = 2 (ξ- + 2кг π\ i = (4kx + 1) ш.
522
Следовательно, множество значений т Ln z составляет правиль-
ную часть множества Ln zm.
Логарифмическая функция
1 + (φ + 2kn)i = lnr + iargz
w = Lnz = 1π/- + (
есть бесконечнозначная функция от комплексного аргумента 2.
Всякому значению z=£=0 соответствует бесконечное (счетное) мно<
жество значений wm, где
wk = w0 + 2kni и оуо = In z.
Пусть Ζ./0 —- некоторое значение аргумента; соответствующее зна"
чение w0 изображается точкой плоскости UOV, расположенной в по"
лосе Do, определяемой неравенствами — η<^υ^η. Значение Wk
расположено в полосе (2£ —1) я<^<(2& + 1) я. Пусть z=£Q —
данное комплексное число; возьмем в качестве argz главное его зна-
чение.
5д
Черт. 283
Рассмотрим окружность Кг (черт 283) радиуса | ζ \ с центром в на-
чале координат. Положение произвольной точки Ζ этой окружности
определяется центральным углом /, который будет отсчитывать от
радиуса-вектора точки ζ. Сегменту 0<^<2я соответствует полная
окружность, при этом концам сегмента t = 0 и t = 2π соответ-
ствует одна и та же точка ζ. В качестве аргумента Ζ возьмем вполне
определенное значение φ-W, где 0</<2π. На плоскости UOV
точке ζ соответствует точка w0, лежащая в Do, а точке Ζ — точка
значению t = 0 соответствует точка w0 в полосе Do, а значению
/ = 2π — точка α;4 в полосе Du а всей рассматриваемой окружности
соответствует отрезок, соединяющий точки w0 и wi. Кратко принято
18*
523
говорить так: если точка ζ, описав в плоскости XOY в положитель-
ном направлении окружность с центром в точке О, возвращается
в первоначальное положение, то значение логарифма w0 переходит
в значение W\. Аналогично можно показать, что значение Wk пере-
ходит в значение
§ 88. Обратные тригонометрические функции
от комплексного аргумента
Найдем множество всех значений аргумента ζ, при которых
тригонометрическая функция cos ζ имеет данное значение w
COSZ ИЛИ ГО) = е + е (1)
Для вычисления ζ получим уравнение, квадратное относительно eiz\
£>2/z _ 2weiz +1=0, откуда eiz = w + Yw2 — 1.
Следовательно, для ζ получается бесконечное множество значений:
z = jLn{w + Yw2 — 1)*.
Уравнение (1) имеет решения относительно ζ при произволь-
ном w, так как w + Yw2 — 1 =j= 0 ни при каком значении w.
В самом деле, уравнение w = — Yw2— 1 имеет противоречивое
следствие: w2 = w2 — 1.
Бесконечнозначная функция (меняем местами буквы ζ и w)
является обратной относительно функции ζ = cos wh обозначается
символом:
w = Arc cos z = 4- Ln (ζ + Υ ζ2 — ΐ).
Областью определения функции Arc cos ζ служит множество всех
комплексных значений г; это находится в соответствии с тем фак-
том, что косинус (над полем комплексных чисел) может иметь про-
извольное комплексное значение.
Будем под символом Υ ζ2—1 подразумевать одно какое-
либо из двух значений радикала, тогда другое значение равно:
* В этой формуле радикал рассматривается над полем комплексных
чисел, он является двузначным символом, а потому двойной знак не ставится.
524
Из тождества
г —
: + Vz* - 1
следует, что числа, находящиеся под знаком логарифма в выражении
для Arc cos г, взаимно обратны. Следовательно, главные значения
аргументов (взятые в пределах от — π до π) чисел:
ζ + V?2 — 1 и ζ — Υ ζ2 — 1
противоположны, если
arg [ζ + V ζ2 - 1) = φ, (2)
где — π < φ < π, тогда
arg(z-l/>— l)=— φ.
Для определенности условимся значение радикала выбирать таким
образом, чтобы при 0<φ<[π имела место формула (2). Иными сло-
вами, выбирается то значение радикала, при котором число
ζ + \ίζ2 — 1 изображается точкой, расположенной в верхней
(замкнутой) полуплоскости.
Если ζ + j/ ζ2 — 1 = а есть действительное число, что воз-
а2 + 1
можно, если значение ζ действительно, ζ = —χ—, то под
γζ2—\ будем подразумевать арифметическое значение ра-
дикала.
Все множество значений Arc cos z можно представить в сле-
дующем виде:
Arccosz =X-Ln{z ± Yz2 — l) =
4-Ln·
Λ- [Ln 1 — Ln (z + Yz2— 1)1 = —I Ln (z + Yz2— l) -f- 2nn
(ибо Ln 1 = 2nm).
Ho
Ln [z + Yz2—\) = ln | ζ + \/Ί2~\ Ι + (φ + 2mn) t,
откуда
Arc cos г = ± j- (ln | ζ + Yz2— 11 -f ίφ) +
525
(полагаем k — т ± η) и, наконец:
Arc cosz = ± (φ — i In ί ζ + Υ г2— 11) +
Значение Arc cos ζ, получающееся при k = 0 и при выборе зна-
ка + , называется главным значением арккосинуса и обозначается
символом:
arc cos z = φ — ι In | ζ -|- ]/z2— 1 |'.
значение arc cos ζ расположено в полосе 0< α<π плоскости UOV,
ибо и = φ, где 0<φ<π.
Все множество значений функции Arc cos z определяется фор-
мулой
Arc cos z = ± arc cos z
В этой формуле значение—arc cos ζ, противоположное главному
<0
значению, заключено в полосе —
τ
-2п
arccosz+ 2п
-arccosz+ In
получим
Xs
Черт. 284
а прочие значения арк-
косинуса получаются из
этих двух прибавлением
произвольного слагаемого
кратного периоду ко-
Функция Arc sin ζ οπ-
•V ределяется как обратная
фу нкция относительно
ζ = sin w. Решив относи-
тельно w уравнение
2ί
w = Arc sin z = Ln [iz +
Воспользовавшись формулой
sin w = cos(-^ —
получим
— ζ2]
(3)
—. — w = Arc cos ζ
или
■ = у — Arc cos w = у ± j Ln (z + j/z2— 1).
(4)
Примечание. Равенство (4) также можно получить
из равенства (3) путем формальных преобразований (предо-
ставляем это учащимся в виде упражнения).
526
Если взять главное значение арккосинуса, то получим одно-
значную функцию
arc sin г = ~ — arc cos г,
называемую главным значением арксинуса. Так как значение
arc cos г заключено в полосе, ограниченной прямыми и = О и
и = π, то значение arc sin ζ заключено в полосе, ограниченной
прямыми
= -Ύ и
и = у (черт. 285).
Если ζ = χ — действительное число, не превосходящее по
абсолютной величине 1, то
Точка Μ с координатами
расположена на единичной
окружности. Значение
φ == arg (χ + ί]/Ί — χ2) есть ме-
ра угла, образованного радиу-
с ом-вектором ОМ с осью абс-
цисс. Так как j/Ί — х2 > 0, то
точка Μ лежит в верхней (замк-
нутой) полуплоскости. В рас-
сматриваемом случае
Черт 285.
arc cos z = arc cos χ = φ, где 0 < φ < π.
Таким образом, на отрезке действительной оси — 1<;*<1 у = О
функция arc cos г имеет геометрическую интерпретацию, которая
в геометрической теории принимается в качестве определения этой
функции. В этом случае (в частности) множество значений
Arc cos x = ± arc cos x + 2kn
есть множество всех решений простейшего тригонометрического
уравнения
cos w = χ
(где w рассматривается в качестве неизвестного).
Аналогично, функция
arc sin ζ = у — arc cos г
при ζ = χ, где—1<х<1, имеет геометрическую интерпретацию,
которая принимается за основу в геометрической теории.
527
Функция Arc tg ζ определяется как обратная функция отно-
сительно
Выразив w через ζ, получим:
2/^"1-ίζ 2/
Эта функция бесконечнозначная; областью ее определения служит
множество всех комплексных чисел, неравных ± /. При г = ± ί
арктангенс теряет смысл. Если ζ = χ — действительное число, то
\i — χ I = I i 4- а: I и
— д;
= 1:
в этом случае, как нетрудно проверить, значения Arc tg z действи-
тельны.
Примеры.
1. Пусть ζ = χ, где \х\ > 1. В этом случае:
О при χ > 1,
О при χ < — 1.
Следовательно,
|0, если χ > 1,
(π, если χ < — 1,
а потому
— i In (* + Υ χ2 — 1), если д: > 1,
arc cos # =
π — i In (— * — }A*2— l), если χ < — 1.
Так, например:
arc cos 2 = — i In (2 + ]/Τ), arc cos (— 2) = π—Π η (2—
arc sin 2 = -|- -f ί In (2 + /У), arc sin (— 2) = γ + Πη (2 —
2. Положив ζ — i, получим:
Следовательно,
arc cos i = 2~— / In (l + ]/ T),
arc sin i = i In (l + V~2).
Тождества
Arc sin ζ = Arccos]/l—z2, Arc sin г = Arc tg ——z- ;
Arc sin zl + Arc sin z2 = Arc sin (г, Vl—zl + z2 V 1
528
и прочие аналогичные тождества, вытекающие из соотношений меж-
ду тригонометрическими функциями и из теорем сложения, имеют
место в том смысле, что правая и левая части каждого из этих тож-
деств представляют собой одно и то же множество чисел.
§ 89. Степенная, общая показательная
и общая логарифмическая функции
Пусть
ζ = χ + iy = ρ (cos φ + i sin φ)
(где — π<φ<;π) — произвольное комплексное число.
Определение. Степенью числа z=f=O с показателем а = а + /β
называется множество всех чисел, определяемых формулой:
ga ___ £>о Ln z
В частности, если г=л;>0, число α =α действительно и если
берется главное значение логарифма In г, то получим тождество
д-ОС __ £>0t In Χ
имеющее место над полем действительных чисел.
Рассмотрим следующие возможные случаи.
Случай Г. а = η —целое число.
В этом случае
гп = еп Ln? = еп (\пг+2Ы)= βη (In 9+Ιψ + 2ΗΙ) = βη 1« Ρ (COS Λφ + ί Sl'n Лф) =
= pn (cos ηφ + ί sin /ζφ).
Таким образом, получается то же значение г/г, которое находится
по формуле Моавра. В данном случае
W = Ζη
есть однозначная степенная функция комплексного аргумента.
Случай 2°. а = -
В этом случае имеем:
Случай 2°. α = — , где — — несократимая дробь и
гя =е" =eq = ец
я ^ ч
Если, в частности, р= 1, то получим:
) У -
529
Таким образом, значения zq суть значения комплексного ра-
дикала ;/ ζ. При произвольном р, взаимно простым с q, полу-
чим:
ζ я =[у' г ) = \/~ζΡ.
Таким образом, данное определение дробной степени комп-
лексного числа совпадает с определением, принятым в алгебре
(см. «Специальный курс элементарной алгебры», § 46).
Функция w = ζ? есть ^-значная функция аргумента ζ.
С л у ч а й 3°. ζ =α, гдеа — действительное иррациональ-
ное число. В этом случае
z* = pa jcos ^αφ _j_ 2Α»πα) -f- ί sin (αφ -f- 2/гяа)]. (1)
Придавая k произвольные целые значения, получим бесконеч-
ное (счетное) множество значений иррациональной степени ζα.
При различных k получаются различные значения ζα. В самом деле,
если бы при k = ki и k = k2 получились одинаковые значения ζα,
то имело бы место равенство:
αφ -f- 2k1 πα = αφ + 2й2 πα + 2^π
(где η — некоторое целое число), но тогда, вопреки условию,
α = , ^_k было бы рациональным числом. Таким образом,
функция
w = ζ*
является бесконечнозначной функцией комплексного
аргумента ζ. Различные ветви этой функции получаются по фор-
муле (1) при различных целых значениях k.
Рассмотрим, в частности, иррациональную степень отрицатель-
ного ζ =— b (где b">0). Имеем: ρ = b, φ = π. Следовательно:
(_ Ь)а = ba[cos(2k + 1)απ -f i sin(2& + 1)απ];
так как (2k + 1) na=f=nn (где п — целое число, иначе α было бы
рациональным), то все значения иррациональной степени отрица-
тельного числа мнимы. По этой причине иррациональные степени
отрицательных чисел над полем действительных чисел не рассмат-
риваются.
Случай 4°. а = α + /β — мнимое число, β=^=0. В этом
случае
ζα _ £(<Η-''β) [In ρ + (φ+2£π)/] _ βο. In ρ-β (φ+2£π). βΙ [β 1η ρ+α ( φ+ 2kκ)] __.
= ρ°β-β (v+2kK) [cos (β In ρ + αφ + 2/?πα) + i sin (β In ρ + αφ+2Λπα)].
530
Функция za при мнимом а — бесконечнозначная; при различ-
ных k получаются различные значения za, ибо значения модуля
\za\ = \z\a e-^+2kK> при различных k различны.
Примеры.
Таким образом, все значения степени il действительны.
2 Найти общее выражение степени \а+1?.
Имеем: ]«+# = 6<*+*β) Ι-η Ι _ β2 (α-Μβ) «π/ = β-2β*π^2α*π/ β
= —^ fcos 2/?πα -(- ί sin 2^πα].
В частности, при α = 0 получим 1^ = e2kli^ (заменяем k на — k, ибо /fe
—произвольное целое число). Таким образом, все значения чисто мнимой
степени единицы действительны.
Определение. Общей показательной функцией с произвольным
комплексным основанием a=f=O называется функция, заданная
формулой
w = аг = ez Ιηα.
Пусть ρ=|α|, а φ — главное значение аргумента а; тогда
имеем:
w = ег [In
Следовательно, общая показательная функция является беско-
нечнозначной, при различных значениях k получаются различные
ее ветви.
До настоящего времени символом ez обозначалась однозначная
функция, определенная как сумма степенного ряда
1+г + '¥ + ... + '-1 + ...
или посредством формулы Эйлера
^ (cosy + i sin у).
Однако, если в формуле (2) положить а = е, то символ ez приобре-
тет другой смысл, он будет обозначать бесконечнозначную функцию.
Во избежание недоразумений (там, где они могут возникнуть) при-
нято показательную функцию в первоначальном смысле
обозначать символом:
ехрг = 1 +z + ... +^у+ ... =expx(cosy + isin у),
а символом е\—общую показательную функцию при основании,
равном е. В этом обозначении формулу (2) следует писать так:
w = а2 = ехр {г [1η ρ + (φ + 2kn) /]},
531
и, в частности.
ez -ехр {zfLn£]} = ехр [г (1 + 2kni)].
Надо заметить, однако, что общая показательная функция с основа-
нием е рассматривается редко.
Примеры:
1. Составить формулы для общей показательной функции при а=1.
Имеем:
\г ^ ]*+/у ^ ехр (_ 2kny)- [cos 2knx + i sin 2knx\.
При k — 0 получим ветвь этой функции, тождественно, равную 1. Прочие
ветви функции 1~ мнимы и не являются постоянными.
2. Имеем:
/* = ехр |г | γ + 2kn) i\ =
/π \ /π \
= cos ί -g- + 2kn 12 + ί sin Ι γ + 2^π I 2.
Определение. Общим логарифмом Loga Л/ ^асла N = т i~ in
при основании а^О называется множество всех решений простей-
шего показательного уравнения
aw = N.
Перепишем это уравнение так:
ехр(оу Lna) = Л^,
откуда
wLna = LnN и о; = Loga Л/ = t£^.
Пусть
а = ρ (cos φ + i sin φ), Ν = R (cos Φ + i sin Φ),
тогда имеем
Таким образом, множество всех значений общего логарифма
определяется формулой, содержащей два целочисленных параметра
Общая логарифмическая функция
является бесконечнозначной.
Примеры.
1. При а — е получим
LnA/
l+2/πί ·
532
Таким образом, над полем комплексных чисел Lo&, N и LnN — не одно и то
же. Значение Ln,V содержится (при / = 0) среди значений N
2. Составить формулу для Logj/V.
Решение. Имеем:
где / — произвольное целое число, отличное от 0, a к — произвольное целое
число. Если | N | = R = 1, то значения LogtA/ действительны.
3. Решить уравнение в поле комплексных чисел:
10г = 100
Решение. Имеем:
LnlOO 21nlO
с ~ Ln 10 ~ In Ю+2/πί '
Значение г действительно, если (2 In 10+ 2kni) (ln 10 — 2/π/) действительно,
что будет иметь место, если
2k — 4/ = 0,
откуда к = 2/, и тогда
2 1п10+4Ы
In 10 + 2/тп
2.
4. Основание логарифмов отрицательно; найти условие, при котором
положительное число А имеет хотя бы одно действительное значение лога-
рифма.
Решение. Имеем:
In Л + 2Ш
Lo&-aA - lna + (2/+ \)ni '
Значение Log__a Л действительно при условии если
(In Л + 2kni) [In α—(2/ + 1) πι)
есть действительное число, откуда
2Ыпа — (2/ + 1)1пЛ =0
и
2k
1ΛΙ 4Ι7ΤΤ
Так, например:
__ 21п2
Log_2(4)_ ιη2 + (2/+1)π/ 1п2 + (2/ + 1)ш
действительное значение логарифма получится, если
kji In 2 = (2/ + 1) πΐη 2, т.е. при к = 21 + 1, и тогда значение log 2 (4)
будет равно 2:
(-2)2 = 4.
Число 3 при основании — 2 не имеет действительных логарифмов
Итак, при отрицательном основании —а действительные логарифмы
имеют лишь те положительные числа, которые можно представить в виде сте-
пени а с показателем, равным дроби с четным числителем и нечетным знаме-
нателем.
ОГЛАВЛЕНИЕ
Стр
Предисловие 3
Введение 5
§ 1. О содержании курса тригонометрии 5
§ 2. Основные понятия теории проекций 7
§ 3. Углы и их измерение 11
§ 4. Координатная плоскость 18
§ 5. О монотонных функциях 22
§ 6. Периодические функции 25
Глава I. Тригонометрические функции и соотношения между ними
§ 7. Тригонометрические функции угла 28
§ 8. Различные определения и интерпретации тригонометрических
функций 33
§ 9. Аргумент тригонометрической функции 41
§ 10. Тригонометрические функции от некоторых частных значений
аргумента 45
§ 11. Четность и нечетность тригонометрических функций .... 48
§ 12. Нахождение угла (дуги) по данному значению его тригонометри-
ческой функции 49
§ 13. Соотношения между тригонометрическими функциями, тригоно-
метрические тождества 57
Глава II. Аппарат тригонометрии
§ 14. Теоремы сложения 68
§ 15. Обобщение теорем сложения 76
§ 16. Формулы приведения 79
§ 17. Тригонометрические функции кратных дуг; полином Чебышева 84
§ 18. Формулы деления аргумента 88
§ 19. Формулы преобразования произведения тригонометрических
функций в сумму 95
§ 20. Тригонометрические многочлены и их преобразование ... 97
§ 21. Формулы преобразования суммы тригонометрических функций
3 произведение ° 101
§ 22. Примеры выполнения различных тригонометрических преобра-
зований 106
§ 23. Рационализирующие подстановки 116
§ 24. Введение вспомогательных углов и тригонометрические под-
становки 123
§ 25. Вычисление некоторых тригонометрических сумм и произведе-
ний 129
534
Глава III. Исследование тригонометрических функций числового
аргумента
§ 26. Области определения и множества значений тригонометрических
функций 148
§ 27. Периодичность тригонометрических функций 150
§ 28. Интервалы знакопостоянства тригонометрических функций . 153
§ 29. Промежутки монотонности тригонометрических функций, наи-
большие и наименьшие значения 154
§ 30. Непрерывность тригонометрических функций 168
§ 31. Графики тригонометрических функций 175
§ 32. Простейшие тригонометрические неравенства 179
§ 33. Неравенства, содержащие аргумент и его тригонометрические
функции 182
§ 34. Гармонические колебания . 190
§ 35. Примеры исследования функций и построений графиков . . . 200
§ 36. Трансцендентность тригонометрических функций 214
Глава IV. Обратные тригонометрические функции
§ 37. Аркфункции 216
§ 38. Тригонометрические операции над аркфункциями 229
§ 39. Соотношения между аркфункциями 234
§ 40. Выполнение обратных тригонометрических операций над три-
гонометрическими функциями 240
§ 41. Формулы сложения 246
§ 42. Примеры преобразования сумм аркфункции 254
§ 43. Некоторые свойства полиномов Чебышева 263
Глава V. Уравнения и неравенства
§ 44. Тригонометрические уравнения 269
§ 45. Об особых случаях решения уравнений , . 274
§ 46. Соотношения между двумя дугами, имеющими одинаковое
значение данной тригонометрической функции 276
§ 47. Решение уравнений посредством подстановок 281
§ 48. Рационализирующие подстановки 283
§ 49. О преобразовании формул общего решения тригонометрического
уравнения 288
§ 50. Различные частные приемы решений тригонометрических урав-
нений 294
§ 51. Тригонометрические уравнения, содержащие параметры . . , 308
§ 52. Некоторые системы тригонометрических уравнений и методы их
решения 320
§ 53. Уравнения, содержащие неизвестные под знаками аркфункции 327
§ 54. Примеры решения некоторых трансцендентных уравнений . 337
§ 55. Приемы решения тригонометрических и некоторых других
трансцендентных неравенств 342
§ 56. О приближенном решении трансцендентных уравнений 357
Глава VI. Вычисление элементов геометрических фигур;
применения тригонометрии
§ 57. Общие понятия 360
§ 58. Соотношения между оснозными элементами треугольника . 361
§ 59. Тригонометрические тождества и неравенства, имеющие место
для углов треугольника 367
§ 60. Элементы различных измерений 372
§ 61. Соотношения между различными элементами треугольника 374
§ 62. Ряд равных отношений 380
535
§ 63. Общий принцип Торопова решения треугольников 385
§ 64. Основные случаи решения треугольников 388
§ 65. Неосновные случаи решения треугольников 394
§ 66. О применениях тригонометрии к геометрии 400
§ 67. О задачах на решение многоугольников 404
§ 68. Применение тригонометрии к стереометрическим задачам 411
§ 69. Понятие о геодезических задачах 425
§ 70. О применениях тригонометрии к физике, механике, технике 431
§ 71. Вычисления при помощи тригонометрических таблиц .... 435
Глава VII. Элементы сферической тригонометрии
§ 72. Основные понятия 446
§ 73. Соотношения между основными элементами сферического тре-
угольника 451
§ 74. Соотношения между элементами прямоугольного треугольника 456
§ 75. Решение прямоугольных треугольников 458
§ 76. Понятие о решении косоугольных сферических треугольников 463
§ 77. Формулы эксцесса и площади сферического треугольника . . 469
§ 78. О различных применениях сферической тригонометрии . . . 471
Глава VIII. Аналитическая теория тригонометрических функций
§ 79. Определение тригонометрических функций при помощи степен-
ных рядов 477
§ 80. Вычисление значений тригонометрических функций аналитиче-
скими средствами 485
§ 81. Аксиоматический метод в тригонометрии 487
§ 82. Теорема единственности 491
§ 83. Различные конкретные определения тригонометрических функ-
ций 495
§ 84. О различных способах построения теории тригонометрических
функций 503
Глава IX. Элементарные трансцендентные функции над полем
комплексных чисел
§ 85. Показательная функция над полем комплексных чисел и ее
связь с тригонометрическими функциями 509
§ 86. Тригонометрические функции от комплексного аргумента ... 514
§ 87. Логарифмическая функция 520
§ 88. Обратные тригонометрические функции от комплексного аргу-
мента. 524
89. Степенная, общая показательная и общая логарифмическая
функции 529