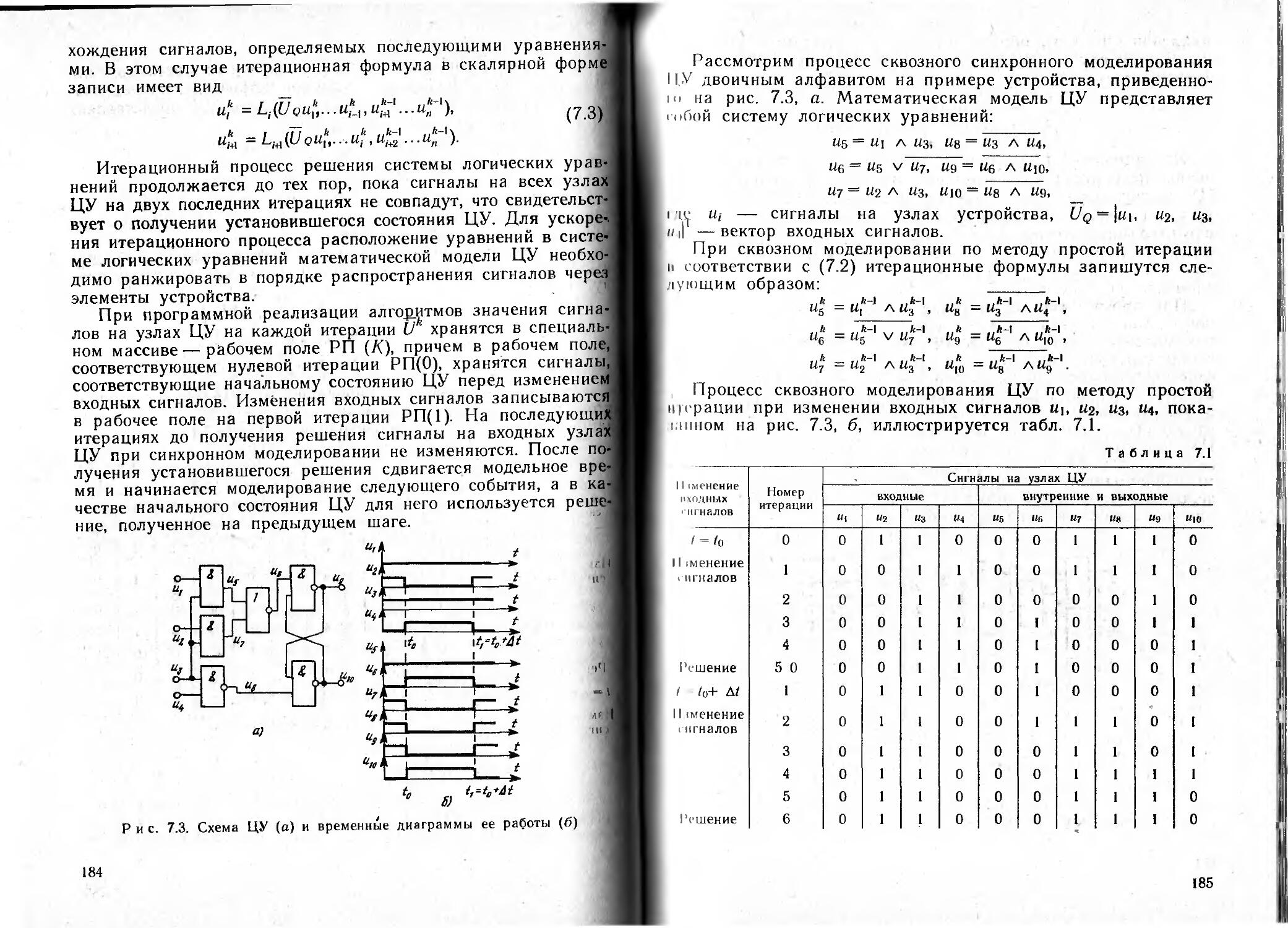
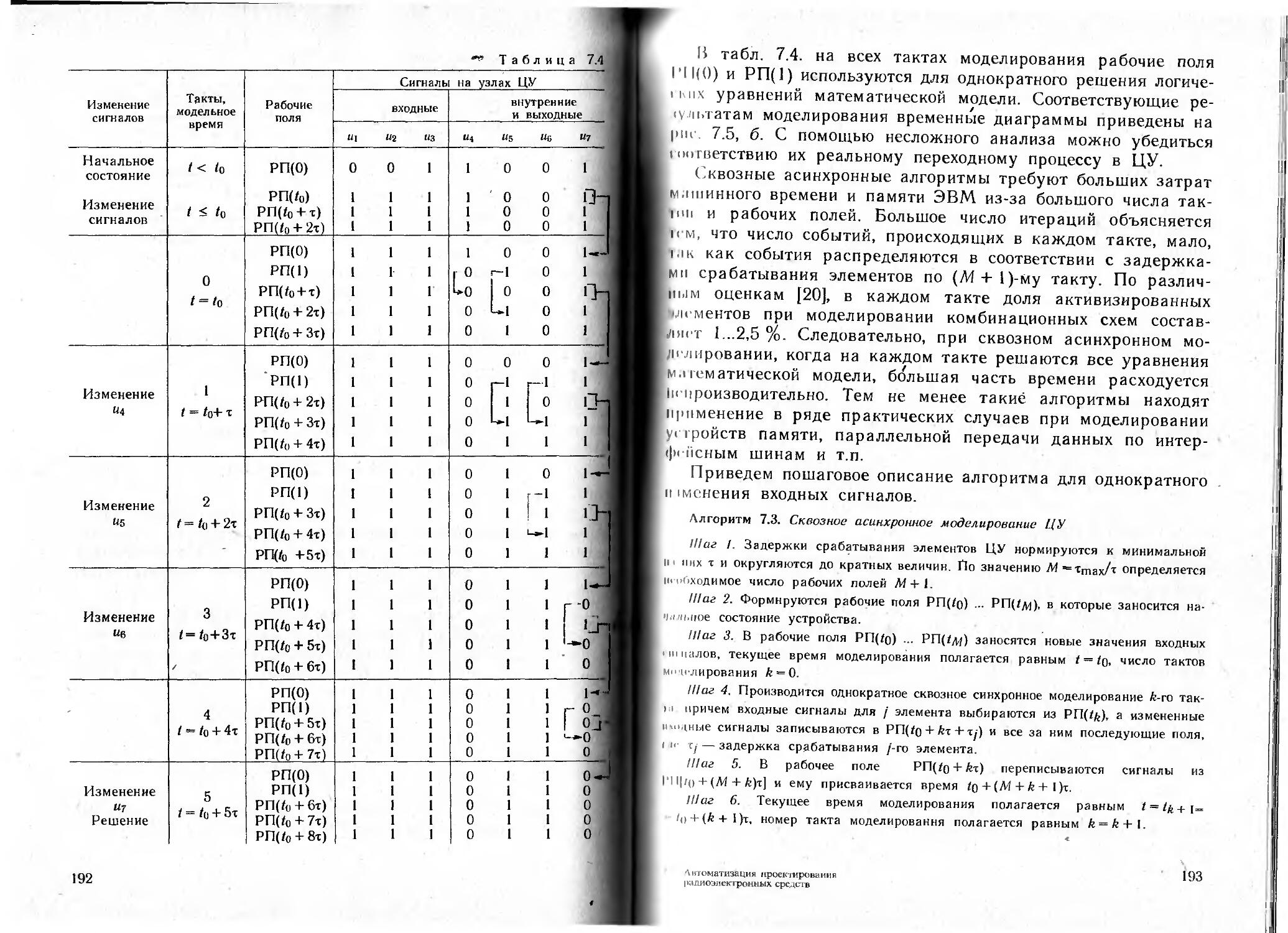
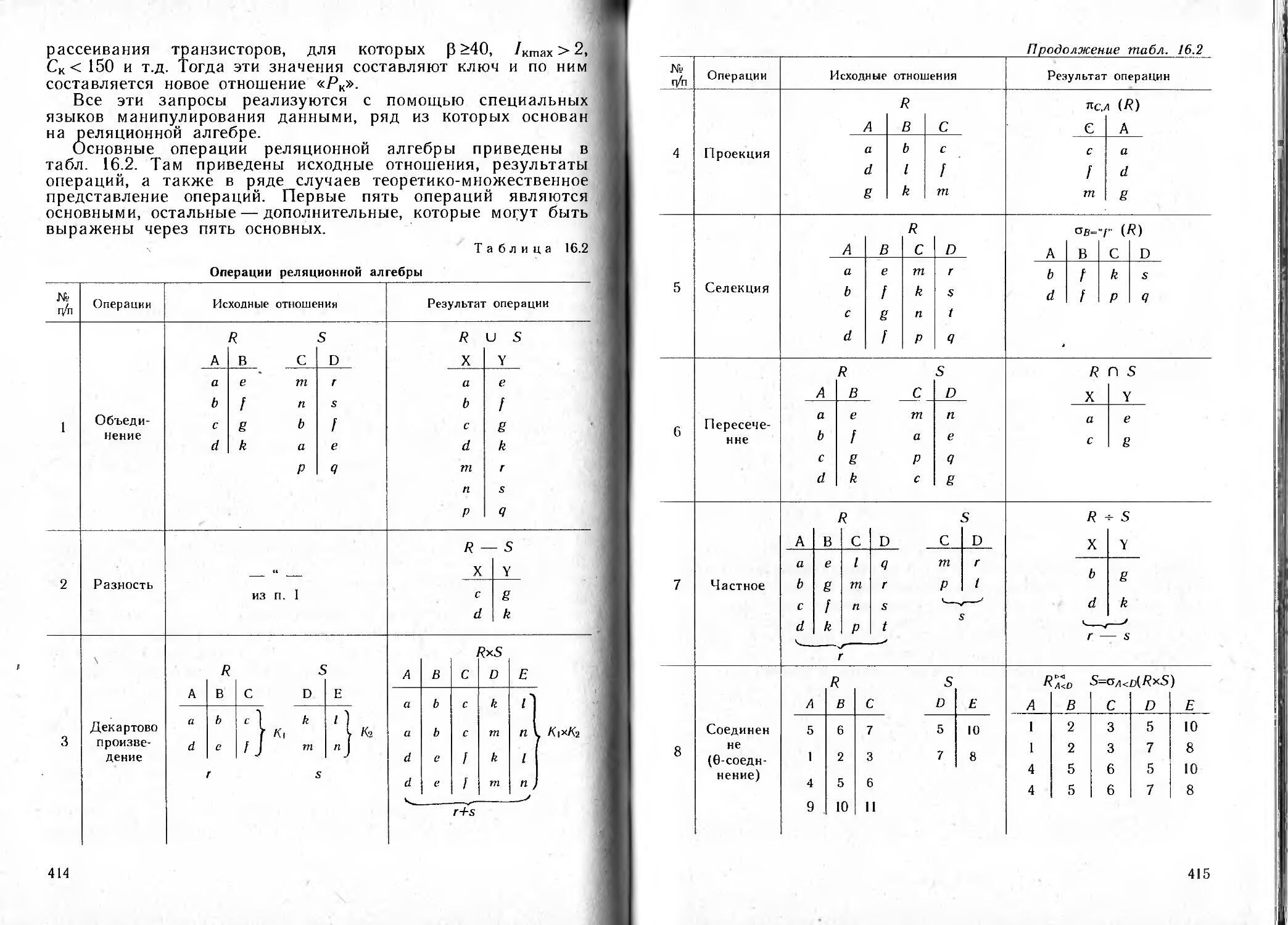
/
Author: Алексеев О.В.
Tags: компьютерные технологии проектирование радиотехника радио радиоэлектронные аппараты
ISBN: 5-06-002691-4
Year: 2000
Text
АВТОМАТИЗАЦИЯ ПРОЕКТИРОВАНИЯ РАДИОЭЛЕКТРОННЫХ СРЕДСТВ
ВЫСШ АЯ ШКОЛ А
/Автоматизация ПРОЕКТИРОВАНИЯ РАДИОЭЛЕКТРОННЫХ СРЕДСТВ
Под редакцией доктора технических наук, профессора О.В. Алексеева
Рекомендовано
Министерством образования Российской Федерации в качестве учебного пособия для студентов вузов, обучающихся по специальности «Радиотехника»
НАУЧНАЯ БИБЛИОТЕКА брянского,государственного технич , университета
Уч ^АЯ itf*'
Москва «Высшая школа»
2000
УДК 681.3
ББК 30.2-5-05
А 22
О.В. Алексеев!, А.А. Головков, И.Ю. Пивоваров, Г.Г. Чавка
I* е цензентц кафедра САПР ВС Рязанского радиотехнического института (зав. кафедрой — д-р техн, наук, проф. В.К Корячко); кафедра радиопередающих и антенно-фидерных устройств Московского авиационного института (.зав. кафедрой — д-р техн, наук, проф. Д.И. Воскресенский)
Автоматизация проектирования радиоэлектронных средств: А 22 Учеб, пособие для вузов/О.В. Алексеев, А.А. Головков, И.Ю. Пивоваров и др.; Под ред. О.В. Алексеева. —- М.: Высш, шк., 2000.— 479 с., ил.
ISBN 5-06-002691-4
В книге рассмотрен® общие принципы построения САПР радиоэлектронных средств (РЭС); обобщены и систематизированы наиболее употребительные методы н алгоритмы математического моделирования функциональных элементов, радиоустройств и радиоснстем Изложены вопросы проектирования, построения банков данных элементов РЭС, применения ЭВМ в САПР РЭС.
Для студентов радиотехнических специальностей вузов. Может быть полезна аспирантам и научным работникам.
УДК 681.3
ББК 30.2-5-05
ISBN 5-06-002691-4
© Коллектив авторов, 2000
Оригинал-макет данного издания является собствеииостью издательства «Высшая школа» и его репродуцирование (воспроизведение) любым способом без согласия издательства запрещено.
ПРЕДИСЛОВИЕ
Необходимость проектирования сложных радиоэлектронных средств (РЭС) и требования к сокращению сроков их проектирования и повышению качества проектных работ противоречивы. Удовлетворить их можно лишь при широком использовании вычислительной техники в процессе проектирования. В связи с этим автоматизированные методы проектирования РЭС различного назначения широко внедряются в практику радиопромышленности. Будущие радиоспециалисты должны изучить теоретические основы автоматизации проектирования радиоаппаратуры, чтобы успешно работать в условиях функционирования систем автоматизированного проектирования (САПР) на предприятии.
Целью настоящего пособия является систематическое изложение вопросов, связанных с автоматизацией системотехнического, схемотехнического и конструкторского проектирования радиоэлектронных средств в тех объемах, которые отведены па дисциплины «Математические основы САПР» и «Основы автоматизации проектирования РЭС» в учебном плане базового высшего образования по направлению «Радиотехника». Задачей этих дисциплин является изучение методов моделирования радиотехнических систем и устройств и их конструкций, методов оптимизации проектных решений, наиболее употребительных вычислительных методов и проектных процедур, а также основ машинной графики, информационного обеспечения и др. Материалы пособия максимально ориентированы на использование рабочих станций и персональных ЭВМ.
При дальнейшем обучении материалы пособия могут быть дополнены монографиями и специализированными учебными пособиями, посвященными автоматизированнсму проектированию антенн и устройств СВЧ, радиопередающих и радиоприемных устройств, автоматизации проектирования конструкций и т.п., опубликованными к настоящему времени.
Материалы пособия базируются на публикациях отечественных и зарубежных авторов и оригинальных результатах,
3
полученных в Санкт-Петербургском государственном электротехническом университете в процессе выполнения научно-исследовательских работ, и представляют собой изложение курсов лекций, читаемых авторами студентам радиотехнического факультета университета в течение ряда лет. Кроме теоретических основ в пособии приводятся контрольные вопросы и задачи для самостоятельного изучения материала и углубления знаний в области САПР, а также краткие характеристики наиболее распространенных отечественных и зарубежных пакетов прикладных программ для персональных ЭВМ для проектирования радиоаппаратуры.
Авторы надеются, что пособие будет полезно также широкому кругу специалистов, занимающихся проектированием радиотехнических устройств и систем.
Предисловие, введение и глава 1 пособия написаны О.А. Алексеевым, глава 2 по просьбе авторов написана С.В. Кузнецовым, главы 4, 5, 7, 9, 11, 14, 15 — А.А. Головковым, главы 3, 12, 16, 17—; Г.Г. Чавкой, главы 10 и 13 — И.Ю. Пивоваровым, главы 6 и 8 — А.А. Головковым и Г.Г. Чавкой, глава 18 — авторами совместно. Общее редактирование пособия выполнено О.В. Алексеевым.
Авторы выражают глубокую признательность рецензентам: кафедре САПР ВС Рязанского радиотехнического института (зав. кафедрой проф., д.-р техн, наук В.П. Корячко) и кафедре радиопередающих и антенно-фидерных устройств Московского авиационного института (зав. кафедрой проф., д.-р техн, наук Д.И. Воскресенский) за ценные замечания и рекомендации, которые были учтены авторами при доработке рукописи.
Отзывы, замечания и предложения по содержанию книги просим направлять по адресу: 101430, Москва, ГСП-4, Неглинная ул., д. 29/14, изд-во «Высшая школа».
Авторы
ВВЕДЕНИЕ
Под радиоэлектронным средством (РЭС) понимается изделие или составные части его, в основу функционирования которых положены принципы радиотехники и электроники. Существуют различные уровни разукрупнения РЭС по функциональной сложности: радиоэлектронные системы, комплексы, устройства и функциональные узлы. Уточним эти йонятия в соответствии с существующими стандартами.
Радиоэлектронная система — это радиоэлектронное средство, представляющее собой совокупность функционально взаимодействующих автономных радиоэлектронных комплексов и устройств, образующих целостное единство, и обладающее свойством перестроения структуры в целях рационального выбора и использования входящих в нее средств при решении технических задач.
Радиоэлектронный комплекс — это радиоэлектронное средство, представляющее собой совокупность функционально связанных радиоэлектронных устройств, обладающее свойством перестроения структуры в целях сохранения работоспособности и предназначенное для решения технических задач. В зависимости от сложности решаемых задач радиоэлектронная система (комплекс) может быть автономной или частью другой радиоэлектронной системы (комплекса).
Радиоэлектронное устройство—это радиоэлектронное средство, представляющее собой функционально законченную сборочную единицу, выполненную на несущей конструкции, и реализующее функции передачи, приема, преобразования информации.
Радиоэлектройный функциональный узел — это радиоэлектронное средство,- представляющее собой функционально законченную сборочную единицу, выполненную на несущей конструкции, реализующее функцию преобразования сигнала и не имеющее самостоятельного эксплуатационного применения.
По конструктивной сложности радиоэлектронные средства имеют также ряд уровней: шкаф, блок, модуль, ячейка и др.
5
Отдельные радиоэлектронные устройства или функциональные узлы могут составлять класс укрупненных базисных элементов, в значительной степени определяющих характеристики сложных систем и комплексов. К базисным элементам можно отнести цифровые и аналоговые блоки формирования и обработки сигналов, усилители, излучающие устройства, различные фильтры, частотно-разделительные, согласующие устройства и др. Значительная часть их работает в радиодиапазоне частот и образует основу для построения радиочастотных трактов систем и комплексов.
В последние годы значительное распространение нашли широкополосные радиочастотные тракты, позволяющие реализовать современные требования к системам связи, радиолокации, навигации и др. Это почти мгновенная смена рабочих частот, одновременная работа на нескольких сильно разнесенных частотах рабочего диапазона, многоканальная работа радносрсдств и т.д.
Протее автоматизации проектирования радиоэлектронных средств но содержанию и последовательности решаемых задач может быть весьма разнообразен в зависимости от функциональной и конструктивной сложности разрабатываемых радиотехнических систем, комплексов, устройств и узлов.
В настоящем учебном пособии сделана попытка учесть специфику автоматизации проектирования РЭС различного уровня сложности, рассмотрен с общих позиций процесс проектирования радиоэлектронных средств, включая этапы моделирования, анализа, синтеза и оптимизации на основе математического, программного, информационного обеспечения с использованием современных средств машинной графики.
В учебном пособии представлены все основные аспекты построения и использования САПР РЭС — от общих вопросов обеспечения САПР и математического моделирования РЭС различного уровня сложности до решения задач оптимального проектирования РЭС с применением современных средств машинной графики и баз даных при диалоговом взаимодействии пользователя с ЭВМ.
Глава 1
ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ РЭС
§1.1. ОПИСАНИЯ РАДИОЭЛЕКТРОННЫХ СРЕДСТВ
В основе функционирования РЭС лежат передача, извлечение и обработка информации, а также преобразование и передача электромагнитной энергии. Электромагнитные поля, волны и сигналы — фундаментальные понятия радиоэлектроники, с которыми приходится оперировать при создании и использовании РЭС.
Радиоэлектронное средство, как правило, бывает весьма сложным техническим объектом, включающим большое число составных частей с многообразными связями между ними. Описание таких объектов в процессе их создания и использования должно быть согласовано с возможностями их восприятия человеком.
По характеру отображаемых свойств описания разделяют на функциональные, конструкторские и технологические.
Функциональное описание оюбражает основные принципы работы и протекающие в РЭС физические и информационные процессы.
Конструкторское описание отображает материальную реализацию РЭС, его геометрические формы, расположение в пространстве, используемые материалы и компоненты и т.п.
Технологическое описание относится к методам и средствам изготовления РЭС.
Для упрощения восприятия описаний, их систематизации они разделяются на иерархические уровни. Каждый уровень описания отличается степенью детализации отображаемых свойств РЭС. На всех уровнях описания стремятся представить РЭС в виде совокупности связанных блоков, которые являются обособленными составными частями, причем это, как правило, делается таким образом, чтобы отдельные блоки были самостоятельными материальными объектам^. Каждый блок данного иерархического уровня описания представляет собой
7
описание следующего, более низкого иерархического уровня, который в свою очередь представляется в виде совокупности блоков. Такое разукрупнение (декомпозиция) доводится до уровня, у которого составляющие блоки дальнейшему делению не подлежат.
По функциональному описанию РЭС уровни разукрупнения включают систему, комплекс, устройство и функциональный узел (рис. 1.1).
Нижний иерархический уровень — радиоэлектронный функциональный узел — представляет собой функционально законченную сборочную единицу, выполненную на несущей конструкции и не имеющую самостоятельного эксплуатационного применения (например, усилитель, модулятор и т.п.). Однако функциональный узел также может быть представлен в виде составных частей — компонентов, таких как интегральные схемы, транзисторы, резисторы, конденсаторы, печатные платы, подложки и т. п., с определенными связями между ними, т.е. узел может быть описан с различной степенью детализации, так же, как его компоненты.
Рис. 1.1. Иерархическая структура РЭС (функциональный аспект)
8
Конструкторское описание РЭС обычно состоит из следующих уровней: шкаф, блок, модуль, ячейка. Модули также разукрупняются на модули 3, 2, 1-го и нулевого уровня. Все уровни конструкторского описания выполняются на основе своей несущей конструкции, т.е. на совокупности конструктивных элементов, предназначенных для размещения средств, обеспечения их устойчивости и прочности в заданных условиях эксплуатации (например, рама, корпус, кассета, стойка, пульт и т.п.). Радиоэлектронные модули обладают свойствами конструктивной и функциональной взаимозаменяемости.
Окончательное описание радиэлектронного средства как законченного изделия представляет собой полный комплект технической документации, включающий в себя текстовой материал, схемы, чертежи, рисунки, фотографии, технологические карты и т.п., оформленные в соответствии с требованиями ЕСКД. Этот комплект документации необходим для изготовления и эксплуатации РЭС. Он может быть выполнен как на традиционных бумажных, так и на машинных носителях (магнитных дисках, лентах и др.).
При проектировании широко используются промежуточные описания РЭС и его составных частей. Важнейшее место среди них занимают модели различных классов. Например, представления о свойствах РЭС могут быть получены с помощью натурной модели (макета, стенда и т.д.) или другой физической модели, представляющие собой некий «образ» РЭС. Свойства РЭС на таких моделях изучаются путем эксперимента.
При широком использовании ЭВМ для проектирования РЭС доминирующую роль среди промежуточных описаний играют математические модели.
Математическая модель РЭС — совокупность математических объектов (например, чисел, переменных и их массивов), отражающая свойства радиоэлектронного средства и отношения между ними. Математические модели, как и сами РЭС, обычно строятся по блочно-иерархическому принципу и могут отражать различные аспекты описаний (функциональный, конструкторский и др.).
И сходным (первичным) описанием РЭС является техническое задание (ТЗ) на проектирование. ТЗ представляет собой некоторую совокупность документов, определяющих цели и задачи, решаемые РЭС, требования к ним, условия использования, экономические ограничения и т.п.
9
§ 1.2. СУЩНОСТЬ И ЭТАПЫ ПРОЕКТИРОВАНИЯ РЭС
Сущность процесса проектирования РЭС заключается в разработке конструкций и технологических процессов производства новых радиоэлектронных средств, которые должны с минимальными затратами и максимальной эффективностью выполнять предписанные им функции в требуемых условиях. Следует подчеркнуть, что в результате проектирования создаются новые, более совершенные РЭС, отличающиеся от своих аналогов и прототипов более высокой эффективностью за счет использования новых физических явлений и принципов функционирования, более совершенной элементной базы и структуры, улучшенных конструкций и прогрессивных технологических процессов.
По степени новизны проектируемых изделий различают следующие задачи проектирования [38]:
1. Частичная модернизация существующего РЭС (изменение его параметров, структуры и конструкции), обеспечивающая сравнительно небольшое (несколько десятков процентов) улучшение одного или нескольких показателей качества для лучшего решения тех же или новых задач.
2. Существенная модернизация, которая предполагает значительное улучшение (в несколько раз) показателей качества.
3. Создание новых РЭС, основанных на новых принципах действия, конструирования и производства для резкого увеличения (на несколько порядков) показателей качества при решении тех же или существенно новых задач.
Проектирование является сложным многоэтапным процессом, в котором могут принимать участие большие коллективы специалистов, целые институты и научно-производственные объединения, а также организации заказчиков, которым предстоит эксплуатировать разработанную аппаратуру.
С точки зрения последовательности выполнения различают основные стадии проектирования:
1. Предварительное проектирование, результатом которого являются технические предложения (аван-проект). Эта стадия в наибольшей степени насыщена элементами научного поиска, теоретическими расчетами, экспериментальными исследованиями. Они завершаются обычно созданием лабораторных макетов.
2. Эскизное проектирование, результатом которого является эскизный проект. На этой стадии усилия разработчиков во многом направлены на поиски эффективных конструкторских решений. Она также связана с большим объемом теоретичес-
10
кпх изыскании, сложных расчетов и заканчивается созданием жспериментального образца проектируемого изделия и его Тщательными экспериментальными исследованиями (натурным модел ированием).
3. Техническое проектирование, при котором выполняется тщательная проработка всех схемных, конструкторских и технологи-и'ских решений. На стадии технического проектирования создается техническая документация на разрабатываемую аппаратуру и процессы ее производства. Итогом является технический проект, содержащий необходимую документацию и опытный образец изделий, прошедший всесторонние испытания в реальных условиях эксплуатации. Следует подчеркнуть чрезвычайную важность и трудоемкость создания технической документации, на основе которой происходит в дальнейшем единичное, серийное или массовое производство РЭС.
С точки зрения содержания решаемых задач процесс проектирования можно разбить на следующие этапы'.
1. Системотехническое проектирование, при котором выбираются и формулируются цели проектирования, обосновываются исходные данные и определяются принципы построения системы. При этом формируется структура проектируемого объекта, его составных частей, которыми обычно являются функционально завершенные блоки, определяются энергетические и информационные связи между составными частями. В результате формулируются частные технические задания на проектирование отдельных составных частей объекта.
2. Функциональное проектирование, применительно к РЭС называемое также схемотехническим., имеет целью аппаратурную реализацию составных частей системы (комплексов, устройств, узлов). При этом выбирают элементную базу, принципиальные схемы и оптимизируют параметры (осуществляют структурный и параметрический синтез схем) с точки зрения обеспечения наилучшего функционирования и эффективного производства. При выборе элементной базы и синтезе схем стремятся учитывать конструкторско-технологические требования.
3. Конструирование, называемое также техническим проектированием, решает задачи компоновки и размещения элементов и узлов, осуществления печатных и проводных соединений для РЭС всех уровней (модулей, ячеек, блоков, шкафов), а также задачи теплоотвода, электрической прочности, защиты от внешних воздействий и т.п. При этом стремятся оптимизировать принимаемые решения по конструктивно-технологическим, экономическим и эксплуатационным показателям.
11
На этом этапе проектирования разрабатывают техническую документацию, необходимую для изготовления и эксплуатации РЭС.
4. Технологическая подготовка производства обеспечивает разработку технологических процессов изготовления отдельных блоков и всей системы в целом. На этом этапе проектирования создается технологическая документация на основе предшествующих результатов. Каждый этап проектирования сводится к формированию описаний проектируемого РЭС, относящихся к различным иерархическим уровням и аспектам его создания и работы.
Этапы проектирования состоят из отдельных проектных процедур, которые заканчиваются частным проектным решением. Типичными для проектирования РЭС процедурами являются анализ и синтез описаний различных уровней и аспектов.
Процедура синтеза заключается в создании проектного рейн пня (описания) по заданным требованиям, свойствам и ограничениям. Например, широко используются при проектировании РЭС процедуры синтеза электронных схем по их заданным характеристикам в частотной или временной области. При этом в процессе синтеза может создаваться структура схемы (структурный синтез), либо определяться параметры элементов заданной схемы, обеспечивающие требуемые характеристики (параметрический синтез).
Процедура анализа состоит в определении свойств заданного (или выбранного) описания. Примерами такой процедуры могут служить расчет частотных или переходных характеристик электронных схем, определение реакции схемы на заданное воздействие и др. Анализ позволяет оценить степень удовлетворения проектного решения заданным требованиям и его пригодность. Процедуры синтеза и анализа в процессе проектирования тесно связаны 1 между собой, поскольку обе они направлены на создание приемлемого или оптимального проектного решения.
Типичной проектной процедурой является оптимизация, которая приводит к оптимальному (по определенному критерию) проектному решению. Например, широко используется оптимизация параметров электронных схем с целью наилучшего приближения частотных характеристик к заданным. Процедура оптимизации состоит в многократном анализе при целевом изменении параметров схемы до удовлетворительного
12
приближения к заданным характеристикам. В сущности, оптимизация обеспечивает создание (синтез) проектного решения, по включает поэтапную оценку характеристик (анализ).
Проектные процедуры состоят из отдельных проектных операций. Например, в процессе анализа математических монелей РЭС приходится решать дифференциальные и алгебраические уравнения, осуществлять операции с матрицами, и т.п. 1акие операции могут иметь обособленный характер, но в целом они образуют единую проектную процедуру.
Проектные процедуры и операции выполняются в определенной последовательности, называемой маршрутом проектирования.
Маршруты проектирования могут начинаться с нижних иерархических уровней описаний' (восходящее проектирование) либо с верхних (нисходящее проектирование).
Следует особо подчеркнуть, что между всеми этапами проектирования существует глубокая связь и взаимосвязь. Так, определение окончательной конструкции и разработка всей технической документации часто не могут быть выполнены до окончания разработки технологии. В процессе конструирования и разработки технологии может потребоваться коррекция принципиальных схем, структуры системы и даже исходных данных. Поэтому процесс проектирования является не только многоэтапным, по и многократно корректируемым по мере его выполнения, т.е. процесс носит итерационный характер.
В процессе проектирования необходимо не просто создать аппаратуру, которая будет обеспечивать заданное функционирование, но и оптимизировать ее по широкому спектру функциональных, конструкторско-технологических, эксплуатационных и экономических показателей. На отдельных этапах для отдельных частных задач оптимизацию можно осуществить на основе разработанных формальных математических методов. Однако применительно к комплексным РЭС задача оптимизации часто не поддается формализации. Встречаясь с такой ситуацией, разработчики обычно рассматривают несколько вариантов решения поставленной задачи, подсказанных, как правило, предшествующим коллективным опытом, интуицией, и выбирают лучший из них. Такой подход называется эвристическим многовариантным анализом. Однако в связи со все возрастающей сложностью РЭС, с повышением требований к ним необходимые расчеты оказываются все более трудоемкими, а количество вариантов, целесообразных для рассмотрения, катастрофически возрастает. Эта ситуация получила название «тирания альтернатив». Часто на этапе проектирования
13
i
трудно предвидеть некоторые требования, вытекающие из условий эксплуатации. В результате всего этого создание нового РЭС затягивалось на долгие годы. Представляемые к испытаниям опытные образцы часто оказывались не удовлетворяющими заданным требованиям, а доводка аппаратуры происходила в процессе испытаний, что удорожало проектирование во много раз.
Подобное положение не было виной разработчиков. Это результат возникшего принципиального несоответствия традиционного подхода к проектированию и сложности современных радиоэлектронных средств. Указанное противоречие и вызвало интенсивное развитие новой технологии проектирования РЭС, базирующейся на системном подходе и совершенствовании процессов проектирования с применением математических методов и средств вычислительной техники, комплексной автоматизации трудоемких и рутинных проектных работ, замены макетирования и натурного моделирования математическим моделированием, использованием эффективных методов многова-риантпого проектирования и оптимизации, а также повышением качества управления проектированием.
Системный подход позволяет найти оптимальное, в широком смысле, решение задачи проектирования за счет всестороннего, целостного рассмотрения как проектируемого изделия, так и самого «процесса проектирования и способен привести к подлинно творческим новаторским решениям, включая крупные изобретения и научные открытия.
Главным средством автоматизации проектирования являются ЭВМ и управляемые ими другие технические средства, которые создают необходимую основу для полной реализации потенциальных возможностей системного подхода.
§1.3. ПРИМЕНЕНИЕ ЭВМ ДЛЯ АВТОМАТИЗАЦИИ ПРОЕКТИРОВАНИЯ
Различные вычислительные средства уже давно используются специалистами в проектно-конструкторских работах. Быстродействие современных ЭВМ позволяет решать такие задачи, которые в принципе недоступны для «ручных» методов расчета, дает возможность учесть значительно большее число факторов, влияющих на функционирование и производство РЭС, резко повысить число рассматриваемых вариантов при проектировании. С помощью ЭВМ осуществляются анализ и синтез схем, их оптимизация, компоновка и размещение элементов конструкции РЭС, находятся оптимальные варианты электрического соединения элементов (трассировки) и решаются многие другие сложные задачи.
14
Широко используются автоматизированные средства для подготовки Технической документации. Так, для изготовления чертежей и описательных документов (электрических схем, сборочных чертежей, таблиц соединений, спецификаций) применяются специальные чертежные автоматы, графопостроители и алфавитно-цифровые печатающие устройства, управляемые с помощью ЭВМ.
На первом этапе применения ЭВМ для автоматизации проектирования дело сводилось к решению частных задач проектирования, носивших главным образом расчетный характер. Для каждой задачи строилась ее математическая модель, выбирался численный метод и разрабатывался алгоритм решения. На основе алгоритма создавалась программа на одном из алгоритмических языков. Полученные от ЭВМ результаты подвергались необходимой обработке «вручную».
Однако при описанном «позадачном» подходе к автоматизации ЭВМ решают весьма ограниченный круг вопросов, не соответствующий их потенциальным возможностям, по существу отсутствует взаимодействие разработчиков с ЭВМ, не учитывается сильная взаимосвязь между различными этапами и уровнями проектирования.
Так, этап конструкторского проектирования часто сводится к решению задач, оторванных от электрической природы аппаратуры и ее функционирования. Критерии оптимизации конструкции в большинстве случаев не учитывают функциональных факторов. В то же время электромагнитные связи элементов конструкции существенно проявляются во многих случаях на функционировании РЭС.
С другой стороны, схемотехнический этап проектирования во многих случаях не учитывает конструкторско-технологических, эксплуатационных и экономических факторов. В результате этого разрыва спроектированная аппаратура по эффективности оказывается далекой от оптимальной, хотя на каждом этапе принимаются меры и затрачиваются большие интеллектуальные и материальные средства на оптимизацию.
При традиционном методе вмешательство проектировщика в автоматические процедуры проектирования не предусматривается, хотя это может обеспечить значительный эффект.
Все эти трудности и противоречия привели к необходимости решения задач автоматизации проектирования на основе системного подхода как в части его организации, так и в части аппаратных вычислительных средств и их программно-ма
15
тематического обеспечения. Это породило новый этап автоматизации проектирования — этап создания систем автоматизированного проектирования (САПР).
Каковы основные черты систем автоматизированного проектирования и их принципиальные отличия от «позадачных» методов автоматизации?
Первой характерной особенностью является возможность комплексного решения общей задачи проектирования, установления тесной связи между частными задачами, т.е. возможность интенсивного обмена информацией и взаимодействие не только отдельных процедур, но и этапов проектирования. Например, применительно к техническому (конструкторскому) этапу проектирования САПР позволяет решать задачи компоновки, размещения и трассировки в тесной взаимосвязи, которая должна быть заложена в технических й программных средствах системы.
Применительно к системам более высокого уровня можно говорить об установлении тесной информационной связи между схемотехническим и техническим этапами проектирования. Такие системы позволяют создавать радиоэлектронные средства, более эффективные с точки зрения комплекса функциональных и конструкторско-технологических требований.
Вторым отличием САПР является интерактивный режим проектирования, при котором осуществляется непрерывный процесс диалога «человек—машина». Сколь ни сложны и изощренны формальные методы проектирования, сколь ни велика мощность вычислительных средств, невозможно создать сложную аппаратуру без творческого участия человека. Системы автоматизации проектирования по своему замыслу должны не заменять конструктора, а выступать мощным средством обеспечения его творческой деятельности.
Третья особенность САПР заключается в возможности имитационного моделирования радиоэлектронных систем в условиях работы, близких к реальным [39]. Имитационное моделирование дает возможность предвидеть реакцию проектируемого объекта на самые различные возмущения, позволяет конструктору «видеть» плоды своего труда в действии без макетирования. Ценность этой особенности САПР заключается в том, что в большинстве случаев крайне трудно сформулировать системный критерий эффективности РЭС. Эффективность связана с большим числом требований различного характера и зависит от большого числа параметров РЭС и внешних факторов. Поэтому в сложных задачах проектирования практически невозможно формализовать процедуру поиска оптимального по
16
критерию комплексной эффективности решения. Имитационное моделирование позволяет провести испытания различных вариантов решения и выбрать лучший, причем сделать это быстро и учесть всевозможные факторы и возмущения.
Четвертая особенность заключается в значительном усложнении программного и информационного обеспечения проектирования. Речь идет не только о количественном, объемном увеличении, но и об идеологическом усложнении, которое связано с необходимостью создания языков общения проектировщика и ЭВМ, развитых банков данных, программ информационного обмена между составными частями системы, программ проектирования, коррекции работы машины, ее обучения, систематизации и обобщения опыта, усовершенствования стратегии принятия решений.
Пятая особенность заключается в значительном усложнении технических средств САПР. Системы автоматизации проектирования требуют применения машин высокой производительности, многомашинных комплексов, разветвленной системы периферийных устройств, в частности устройств отображения информации, диалога и изготовления документации.
И наконец, последняя особенность САПР, которую можно отметить, заключается в замкнутости процесса автоматизированного проектирования. Под этим подразумевается, что проектировщик вводит в машину информацию на уровне замысла, а в результате диалогового процесса проектирования машина выдает технические решения и документацию, необходимую для изготовления РЭС и автоматизированного управления технологическими процессами ее производства.
§ «.4. СОСТАВ И ПРИНЦИПЫ ПОСТРОЕНИЯ САПР
САПР создаются в проектных, конструкторских, технологических организациях и на предприятиях с целью повышения качества, технико-экономической эффективности проектируемых и выпускаемых РЭС, уменьшения затрат на их создание и эксплуатацию, сокращения сроков и трудоемкости проектирования, а также повышения качества проектной документа
ции.
го и
Системы автоматизированного проектирования состоят из совокупности средств метод шеского||\^е^|гцч£|ского, л1 нгви-стического, программного, техни«|£^£эд,||^1^|,м|щионг' организационного обеспечь ^янского государственного [ технического университета
17
Методическое обеспечение (МО) САПР включает в себя теорию процессов, происходящих в схемах и конструкциях РЭС, методы анализа и синтеза схем и конструкций радиоэлектронных устройств, систем и их составных частей, их математические модели, математические методы и алгоритмы численного решения систем уравнений, описывающих схемы и конструкции РЭС. Указанные компоненты МО составляют ядро САПР. В методическое обеспечение САПР входят также алгоритмические специальные языки программирования, терминология, нормативы, стандарты и другие данные. Очевидно, что разработка методического обеспечения САПР РЭС требует глубоких специальных знаний в областях радиотехники, электроники, в частности системотехники, схемотехники и микроэлектроники, конструирования и технологии производства РЭС. Отсюда вытекает, что разработка методического обеспечения САПР РЭС — прерогатива специалистов в области радиотехники и электроники.
Обычно в качестве, обособленных блоков в методическом обеспечении выделяются математическое и лингвистическое обеспечения.
Математическое обеспечение — это совокупность математических моделей, методов и алгоритмов для решения задач автоматизированного проектирования.
Лингвистическое обеспечение представляет собой совокупность языков, используемых в САПР для представления информации о проектируемых объектах, процессе и средствах проектирования и для осуществления диалога между проектировщиками и ЭВМ.
Если математическое и лингвистическое обеспечения являются полностью самостоятельными в составе САПР, под методическим обеспечением понимается совокупность документов, описывающих состав, правила отбора и эксплуатации средств автоматизированного проектирования.
Компоненты МО создаются на основе перспективных методов проектирования, поиска новых принципов действия и технических решений, эффективных математических и других моделей проектируемых объектов, применения методов многовариантного проектирования и оптимизации, использования типовых и стандартных проектных процедур, стандартных вычислительных методов.
Методическому обеспечению САПР в широком его понимании посвящена основная часть книги.
П рограммное обеспечение (ПО) включает в себя документы с текстами программ, программы на машинных носителях (магнитных лентах, дисках и др.) и эксплуатационные документы, обеспечивающие функционирование САПР.
Программное обеспечение подразделяется на общесистемное и прикладное. Компонентами общесистемного ПО являются, например, операционные системы, трансляторы с алгоритмических языков, супервизоры и т.п., то есть совокупность программ, которая осуществляет управление вводом и обработкой информации в ЭВМ, диалоговый режим работы и другие обслуживающие функции независимо от объекта проектирования. Прикладное ПО включает программы и пакеты прикладных программ, предназначенные непосредственно для получения проектных решений. Прикладное ПО разрабатывается обычно совместно специалистами в области проектируемых РЭС и системного программирования.
Техническое обеспечение (ТО) САПР включает в себя устройства вычислительной и организационной техники, средства передачи данных, измерительные и другие устройства или их сочетания.
И нформационное обеспечение (ИО) САПР состоит из описания стандартных проектных процедур, типовых проектных решений, типовых элементов РЭС, комплектующих изделий и их моделей, материалов, числовых значений параметров и других данных. Эти данные в закодированной форме записываются на машинных носителях: магнитных лентах и магнитных дисках.
Основное назначение информационного обеспечения САПР— это уменьшение объемов информации, требуемой в процессе проектирования от разработчика РЭС, и исключение дублирования данных в прикладном ПО и ТО САПР.
Данные ИО обычно группируются в отдельные массивы, каждый из которых относится к определенному объекту описания. Такие массивы называются файлами. Вся совокупность файлов образует базу данных, которую можно многократно использовать при проектировании различных РЭС для различных этапов и уровней. Для создания, расширения, корректировки и коллективного использования данных создаются специальные системы управления базами данных (СУБД). Совокупность баз данных, систем управления ими, а также относящихся к ним программных, языковых, технических и организационных средств называется банком данных.
Организационное обеспечение САПР включает методические и руководящие материалы, положения, приказы, инструкции, штатные расписания, квалификационные требования и
19
другие документы, обеспечивающие необходимую деятельность и взаимодействие различных подразделений организации и отдельных пользователей при создании, эксплуатации и развитии САПР.
Основными структурными звеньями САПР являются подсистемы. Подсистемой называется выделенная по некоторым признакам часть САПР, обеспечивающая получение законченных проектных решений и соответствующих проектных документов. Различают объектно-ориентированные (объектные) и объектно-независимые (инвариантные) подсистемы.
Объектные подсистемы осуществляют непосредственное проектирование. Применительно к САПР; осуществляющим комплексное проектирование РЭС, объектными являются, например, подсистемы схемотехнического и конструкторского проектирования. Для конструкторских САПР объектными являются подсистемы компоновки, размещения, трассировки и т.п.
Инвариантные подсистемы выполняют функции управления и обработки информации, не зависящие от объекта проектирования. Таковыми являются, например, подсистемы управления САПР, диалоговых процедур, оптимизации, подсистемы ввода, обработки и вывода графической информации, подсистемы информационно-поисковых процедур и др.
Каждая подсистема, в свою очередь, состоит из компонентов, объединенных общей для подсистемы целевой функцией. Под компонентом обычно понимают элемент средства обеспечения, выполняющий определенную функцию. Так, например, компонентами подсистемы схемотехнического проектирования являются: методическое обеспечение анализа схем; программы, реализующие те или иные алгоритмы анализа; графические дисплеи, обеспечивающие отображение самих схем и, например, частотных характеристик этих схем; файлы, содержащие модели транзисторов; совокупность их основных характеристик и т.п. Очевидно, что все указанные компоненты связаны между собой внутри подсистемы. На рис. 1.2 приведена обобщенная структурная схема САПР, отражающая ее составные части и связи между ними. На этом рисунке компоненты подсистем обозначены тремя знаками. Первый знак характеризует разновидность обеспечения, к которому относится данный компонент, второй указывает номер компонента для данного вида обеспечения, а третий — к какой подсистеме относится данный компонент, например М1А первый компонент методического обеспечения подсистемы А; И2Н — второй компонент информационного обеспечения подсистемы Н и т.п.
20
М1А, П1А,..., O2H - компоненты подсистем САПР.
Рис. 1.2. Обобщенная структурная схема САПР
САПР создается и функционирует в проектной организации как самостоятельная система. Однако она может быть связана с подсистемами и банками данных других автоматизированных систем предприятия: автоматизированной системой управления технологическими процессами (АСУ ТП), автоматизированной системой для научных исследований (АСНИ). В частности, основная задача АСНИ может состоять именно в том, чтобы получать и отрабатывать математические модели для САПР. На крупных предприятиях АСНИ, САПР и АСУ могут функционировать как взаимосвязанные на уровне технических средств и банков данных.
21
При создании САПР руководствуются следующими общесистемными принципами:
1. Принцип включения состоит в том, что требования к созданию, функционированию и развитию САПР определяются со стороны более сложной системы, включающей в себя САПР в качестве подсистемы. Такой сложной системой может быть, например, комплексная система АСНИ — САПР — АСУ ТП предприятия, САПР отрасли и т.п.
2. Принцип системного единства предусматривает обеспечение целостности САПР за счет связи между ее подсистемами и функционирования подсистемы управления САПР.
3. Принцип комплексности требует связности проектирования отдельных элементов и всего объекта в целом на всех стадиях, проектирования.
4. Принцип информационного единства предопределяет информационную согласованность отдельных подсистем и компонентов САПР. Это означает, что в средствах обеспечения компонентов САПР должны использоваться единые термины, символы, условные обозначения, проблемно-ориентированные языки программирования и способы представления информации, которые обычно устанавливаются соответствующими нормативными документами. Принцип информационного единства предусматривает, в частности, размещение всех файлов, используемых многократно при проектировании различных объектов, в банках данных. За счет информационного единства результаты решения одной задачи в САПР без какой-либо перекомпоновки или переработки полученных массивов данных могут быть использованы в качестве исходной информации для других задач проектирования.
5. Принцип совместимости состоит в том, что языки, коды, информационные и технические характеристики структурных связей между подсистемами и компонентами САПР должны быть согласованы так, чтобы обеспечивалось совместное функционирование всех подсистем и сохранялась открытая структура САПР в целом. Так, введение каких-либо новых технических или программных средств в САПР не должно приводить к каким-либо изменениям уже эксплуатируемых средств.
6. Принцип инвариантности предусматривает, что подсистемы и компоненты САПР должны быть по возможности универсальными или типовыми, т.е. инвариантными к проектируемым объектам и отраслевой специфике. Применительно ко всем компонентам САПР это, конечно, невозможно. Однако многие компоненты, например программы оптимизации, обработки массивов данных и другие могут быть сделаны одинаковыми для разных технических объектов.
22
7. Принцип развития требует, чтобы в САПР предусматривалось наращивание и совершенствование компонентов и связей 'между ними. При модернизации подсистемы САПР допускается частичная замена компонентов, входящих в подсистему, с изданием соответствующей документации.
Приведенные общесистемные принципы являются чрезвычайно важными на этапе разработки САПР. Контроль за их соблюдением обычно осуществляет специальная служба САПР предприятйя.
Вопросы и упражнения для самопроверки
1. Какие существуют виды описания радиоэлектронных средств и какова их связь с математическими моделями различных уровней иерархии?
2. Дайте характеристику основных задач, стадий и этапов проектирования радиоэлектронных средств.
3. Что такое проектная процедура? Приведите примеры проектных процедур на этапах системотехнического и функционального проектирования.
4. Охарактеризуйте возможности применения ЭВМ иа различных этапах проектирования.
5. Каковы основные черты САПР?
6. Опишите содержание методического, математического, лингвистического, программного, технического, организационного и информационного обеспечения САПР.
7. Какими основными системными принципами руководствуются при создании САПР?
Глава 2
ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ САПР
§2.1. СОСТАВ, ОРГАНИЗАЦИЯ И РЕЖИМЫ РАБОТЫ ТЕХНИЧЕСКИХ СРЕДСТВ САПР
Технические средства САПР — это совокупность взаимосвязанных и взаимодействующих аппаратных средств, предназначенных для выполнения автоматизированного проектирования.
Технические средства делятся на две основные группы:
— центральные средства, включающие собственно ЭВМ, осуществляющие прием данных, их программную обработку, накопление и выдачу информации на устройства отображения и в каналы связи;
— периферийные (терминальные) средства, используемые для подготовки и ввода данных, отображения и документирования данных и результатов проектирования, хранения информации, оперативного общения пользователя с системой в процессе проектирования.
Основой технических средств САПР является базовая ЭВМ, содержащая процессоры, запоминающие устройства, устройства управления и каналы ввода-вывода информации.
За десятилетия своего развития технические средства САПР прошли ряд этапов, в значительной степени связанных со сменой поколений ЭВМ и совершенствованием периферийных устройств. Базовые ЭВМ первых поколений САПР РЭС представляли собой автоматизированные рабочие места (АРМ) на основе универсальных ЭВМ среднего класса и мини-ЭВМ с расширенным набором периферийных устройств ввода-вывода графической информации (АРМ на базе ЭВМ IBM-360 и PDP-11 за рубежом, АРМ на базе БЭСМ-6, МИР, ЕС ЭВМ, СМ ЭВМ, «Электроника» у нас в стране). Характерной чертой развития технических средств этих поколений было стремление максимально приблизить АРМ к проектировщику РЭС с помощью САПР. Возникшее при этом противоречие между требованием относительно низкой стоимости, габаритов и потребления и требованием сохранения высоких тех-
24
пических параметров базовых ЭВМ из-за сложности решаемых задач САПР привело к созданию мощных децентрализованных систем ЭВМ, объединенных локальными вычислительными сетями (ЛВС).
К настоящему времени сложился устойчиво растущий рынок сбыта аппаратных и программных средств в области САПР, который выработал собственные требования к базовым ЭВМ, периферийным устройствам и ЛВС. В качестве эталонных базовых ЭВМ, находящихся непосредственно на столах проектировщиков РЭС, выступают в течение уже длительного времени рабочие станции (PC), связанные ЛВС между собой п с другими ЭВМ.
PC имеют существенные отличия от персональных компьютеров (ПК), поскольку требования к PC формируются рынком в области САПР, а требования к ПК — в значительной степени рынком в области конторского оборудования, бытовой техники, средств связи и коммуникаций. PC развивались независимо от ПК, однако удешевление элементной базы PC и повышение требований к техническим характеристикам ПК привели к тому, что наиболее мощные модели ПК проникли па рынок средств САПР, конкурируя с недорогими PC.
Особенности архитектуры и технических характеристик PC с точки зрения их применения в качестве базовых вычислительных систем в области САПР РЭС наиболее ясно проявляются при их сравнении с ПК.
1. Вычислительным ядром большинства PC является RISC-процессор, т.е. процессор с сокращенным набором команд и повышенным быстродействием за счет того, что большинство его команд выполняется за один период тактового генератора частоты, синхронизирующего работу такого микропроцессора (МП). Большинство ПК имеет в качестве вычислительного ядра МП со сложным набором команд (CISC-процессор), у которого каждая команда выполняется за несколько тактов генератора частоты. При этом сравнительно более низкая производительность ПК компенсируется более простым программным обеспечением и совместимостью с более ранними моделями ПК-
2. Все современные PC имеют большой объем оперативного запоминающего устройства (ОЗУ) и работают под управлением сложных многозадачных операционных систем (ОС) с соответствующими аппаратными средствами поддержки. Большая часть ПК имеет несколько меньший об„ъем ОЗУ и работает под управлением более простых однозадачных ОС типа
25
MS-DOS, хотя и имеет средства аппаратной поддержки многозадачности ОС. Эта особенность PC обусловлена сложностью задач и иерархичностью пакетов САПР. \
3. Наличие в PC мощных графических процессоров с поддержкой высокоскоростной и высококачественной графики с разрешением не менее 1000x1000 и цветовой палитрой до 1,5 млн. цветовых оттенков. В большинстве ПК используется менее высококачественная графика стандарта VGA, SVGA. Эта особенность PC обусловлена тем, что большинство задач САПР требует высококачественного графического ввода-вывода информации.
4. В базовый комплект PC обязательно встраивается аппаратура высокоскоростной связи со стандартной ЛВС — сетевой адаптер. В базовом комплекте ПК обычно не предусмотрено наличие сетевого адаптера. Такая особенность PC обусловлена тем, что PC не может работать эффективно в автономном режиме, без взаимодействия с другими PC и типами ЭВМ через ЛВС. ПК спроектирован как автономное, самодостаточное устройство, поэтому даже при объединении ПК в локальную сеть большинство операций с информацией ПК проводит автономно.
Структурная схема типичной PC с подключенными к ней периферийными устройствами показана на рис. 2.1.
Базовый набор компонентов PC составляют:
— системная плата, содержащая RISC-процессор с аппаратно реализованным сопроцессором арифметики с плавающей точкой (САПТ), оперативное и постоянное запоминающие устройства (ОЗУ и ПЗУ) и, как правило, графический адаптер с подключенным к нему монитором;
— платы сопряжения с периферийными устройствами, образующие подсистему ввода-вывода с клавиатурой, манипулятором типа «мышь», иногда с автоматическим сканером, графопостроителем или лазерной печатью;
— платы сопряжения с внешними запоминающими устройствами (ВЗУ), плата сетевого адаптера.
Основой системной платы является базовый МП, осуществляющий арифметические и логические операции, а также управление PC. На одном кристалле современного RISC-МП расположен целочисленный процессор, часто сопроцессор арифметики с плавающей точкой, а иногда и графический процессор обработки изображений (от сотен, тысяч до миллионов транзисторов на одном кристалле). В некоторых недорогих ва-
26
Рис. 2.1. Архитектура рабочей станции
риантах базовых ЭВМ САПР на основе ПК используются МП со сложным набором команд. Основные данные для различных типов МП PC и ПК приведены в табл. 2.1.
Таблица 2.1
Тип МП, фирма-разработчик Конструктивное исполнение САПТ Разрядность Быстродействие, млн. ком ан д/с Емкость ОЗУ, Мбайт Производительность с САПТ МФЛОПС
SPARC, Калифорнийский ун-т, RISC Отдельная БИС 32 15...20 4096 5...7
MIPS, Стенфордский ун-т., RISC То же 32 20...28 4096 3...7
MC68040, Motorola, CISC Встроен в МП 32...64 20...28 4096 3...5
180486, Intel, CISC То. же 32...64 25...33 4096 4...6
Mc88000, Motorola, RISC » 32...64 33..40 8192 7. .12
180860, Intel, RISC » 64 33... 120 4096 7...66
Быстродействие целочисленного процессора в МП зависит как от тактовой частоты задающего генератора, так и от организации процессора. У процессора с сокращенным набором команд типа RISC среднее число приходящихся на одну команду тактов генератора менее 1,3, а у RISC-процессоров с внутренней параллельностью функционирования некоторых аппаратных средств оно меньше единицы, достигая 0,5...0,25. Для CISC-процессоров типов MC68040 и 180486 со сложным набором команд среднее количество тактов генератора на одну команду приближается к 1,3 за счет такой же, как у RISC-процессоров, конвейерной организации функционирования аппаратуры, при которой команда разбивается на ряд этапов выполнения. Каждый этап текущей команды выполняется своей частью аппаратуры МП параллельно с выполнением этапов предыдущих и последующих команд.
Для ускорения выполнения арифметических операций над числами с плавающей точкой используются аппаратно реализующие операции САПТ, как встроенные внутрь кристалла МП, так и выпускаемые отдельными большими интегральными схемами (БИС). Арифметический сопроцессор — это процессор,
28
Работающий совместно с целочисленным процессором под объединенным управлением. Выполнение операций плавающей арифметики осуществляется сопроцессором параллельно с работой целочисленного процессора. Непрерывная обработка своих команд целочисленным процессором прерывается только на этапе передачи ему результата операции плавающей арифметики из сопроцессора.
При параллельной работе целочисленного процессора и сопроцессора производительность ЭВМ следует оценивать с помощью специальных тестовых задач. Одним из наиболее популярных тестовых пакетов для оценки производительности является пакет Linpack, измеряющий быстродействие ЭВМ при решении систем линейных алгебраических уравнений. В этом случае производительность машины выражается в специальных единицах — миллионах операций с плавающей точкой в секунду (МФЛОПС). Производительность определяется отношением общего числа операций, используемых в тестах пакета при решении систем линейных уравнений, к времени работы процессора с сопроцессором при решении задач пакета.
На системной плате PC основной МП соединен широкой 64-разрядной и наиболее быстродействующей шиной с ОЗУ и графическим адаптером, т.е. с устройствами, требующими максимальной скорости обмена друг с другом. Устройства управления ВЗУ на основе жестких и гибких дисков, а также сетевой адаптер имеют собственную 32-разрядную быструю шину, которая через буферные устройства соединяется с основной 64-разрядной шиной системной платы. Остальные, более медленные периферийные устройства соединены низкоскоростной 8-разрядной шиной, которая через буферные схемы также соединяется с основной шиной. Такое иерархическое построение шин PC позволяет существенно снизить ее стоимость при сохранении высоких скоростей обмена информацией.
Все устройства управления периферией в современных PC и ПК строятся на основе собственных, менее мощных, чем центральный, микропроцессоров, берущих на себя значительную часть функций обмена данными основного МП, разгружая его для вычислительной работы. Такая концепция построения PC и ПК, при которой обработка данных производится в ряде взаимосвязанных интеллектуальных центров, называется распределенной обработкой данных.
В ЭВМ обычно используется два типа памяти: ПЗУ и ОЗУ. Процессор в ЭВМ считывает данные и команды из ОЗУ и ПЗУ и выполняет их. В ПЗУ хранятся подпрограммы— драйверы, организующие ввод-вывод информации со
29
стандартных периферийных устройств PC, входящих в ее минимальный базовый комплект. Эти периферийные устройства имеют ограниченную номенклатуру, а ввод-вывод с них должен обслуживаться максимально быстро, что и обеспечивают ПЗУ-драйверы. В ОЗУ хранятся и выполняются программы и драйверы, загружаемые с ВЗУ, так как содержимое ОЗУ стирается при отключении питания.
В современных ПК и PC ОЗУ имеет сложную иерархич-ную организацию, что связано с двумя причинами:
— повышенные требования к защите данных при многозадачном режиме работы ЭВМ.
— растущий разрыв между быстродействием МП и микросхем ОЗУ при организации больших объемов памяти.
Первая причина обусловила наличие виртуальной адресации памяти и соответствующей аппаратуры преобразования виртуальных адресов программы в физические адреса ОЗУ, как показано на рис. 2.2. Виртуальный адрес программы всегда начинается с нулевого адреса. Он суммируется с содержимым регистра базы, базовый адрес которого указывает, в какое место поместить программу в физической памяти. Аппаратура управления памятью включает в себя также регистр границы, с помощью которого проверяются обращения программы за пределы области разрешенных для данной задачи адресов ОЗУ, и регистр кода доступа к области ОЗУ, с помощью которого разрешается доступ на чтение-запись в ОЗУ, только чтение из ОЗУ либо полный запрет обращения к данной области памяти. Аппаратура сравнения адресов проверяет разрешение на доступ данной задачи к данной области адресов ОЗУ. Если сформированный физический адрес находится вне диапазона разрешенных адресов либо код доступа задачи не соответствует коду доступа к данной области ОЗУ, устройство управления памятью инициирует прерывание по ошибке доступа к ОЗУ. Аппаратура управления памятью обеспечивает с помощью кодов доступа сегментацию ОЗУ, т.е. деление памяти на различного размера сегменты для совместного использования несколькими задачами. Для организации более быстрого обмена с ВЗУ виртуальная память делится на страницы. Страницы — это блоки последовательных адресов равного размера в ОЗУ. Страница является минимальной единицей обмена данными между ОЗУ и ВЗУ. Типичный размер страницы — 4 и 8 Кбайт.
30
Рис. 2.2. Функциональная схема устройства преобразования адресов и управления ОЗУ
Разрыв между быстродействием МП и относительно медленным циклом обращения к ОЗУ устраняется введением блока юполнительной быстродействующей памяти (КЭШ-памяти) между МП и основным ОЗУ. КЭШ-память может входить как непосредственно в состав МП, так и выполняться в виде отдельных БИС. Чтобы процессор не загружать управлением данными в КЭШ-памяти, она имеет собственное устройство управления. Аппаратура такого устройства обеспечивает следующие функции:
— перезапись областей основного ОЗУ в КЭШ-память при отсутствии в ней данных, необходимых МП;
— устранение неоднозначности данных КЭШ-памяти и основного ОЗУ при записи в КЭШ из МП и при записи в основное ОЗУ из ВЗУ или других периферийных устройств новых данных.
В современных МП с тактовой частотой свыше 20...30 МГц помимо КЭШ-памяти вводится еще один промежуточный блок сверхоперативной регистровой памяти — очередь предварительной выборки команд или данных между КЭШ-памятью и собственно процессором. Эта сверхоперативная память находится всегда на одном кристалле с процессором, организуя опережающую выборку команд или данных до эт.апа их выполнения в процессоре.
31
Рис. 2.3. Структурная схема иерархии систем оперативной памяти рабочих станций и персональных компьютеров
Иерархия системы ОЗУ PC и ПК показана на рис. 2.3. Такое построение системы ОЗУ позволяет обеспечить высокое быстродействие МП и большой объем ОЗУ при сохранении относительно невысокой цены на весь компьютер.
Кроме оперативной памяти ЭВМ содержит ВЗУ. В ПК и PC наибольшее распространение в качестве ВЗУ получили накопители на жестких и гибких магнитных дисках (НЖМД и НГМД) [35]. В жестких дисках с несменными пластинами, называемых винчестерами, удается достичь высокой плотности записи
информации, в десятки и сотни раз превосходящей плотность записи на гибких дисках. Существенно меньше и время доступа к информации у НЖМД по сравнению с НГМД.
Конструктивно винчестер содержит пакет вращающихся магнитных дисков (обычно 4...8 пластин), размещенный вместе с блоком магнитных головок в герметизированном корпусе. Прецизионно выполненные механизмы позволяют добиться высо-
кой плотности записи, которая постоянно растет с раз- витием технологической базы. Объем винчестера достигает 10 000 Мбайт и более при габаритах, позволяющих уместить такое ВЗУ в корпусе настольного варианта PC или ПК. Такая емкость внешней памяти позволяет создавать и эксплуатировать большие программные системы и пакеты САПР, сосредоточивая большую часть данных на ВЗУ PC проектировщика аппаратуры и обеспечивая при необходи- мости оперативный доступ к ним. Существенный недостаток винчестеров — невоз
можность смены дисков.
Перспективы развития внешней памяти PC и ПК связывают с технологией ВЗУ на оптических дисках. Конструктивно ВЗУ на оптическом диске близко к ВЗУ типа «винчестер», но вместо магнитных головок записи-чтения используются оптические лазерные устройства. В ВЗУ на неперезаписываемых и несменных оптических дисках достигнуты объемы памяти до нескольких Гбайт. Разработаны также магнитооптические перезаписываемые диски, которые по параметрам аналогичны дискам типа «винчестер», но имеют большую надежность и сменные оптические диски емкостью 600 Мбайт.
32
НГМД имеют худшие параметры, чем НЖМД, но отличаются дешевизной и используются для хранения и переноса данных и программных пакетов с компьютера на компьютер. I ибкие диски также называют флоппи-дисками. В настоящее время распространены три стандарта накопителей на дисках (жестких и гибких): диаметр диска 8 дюймов (200 мм), 5,25 ,пойма (133 мм) и 3,5 дюйма (89 мм). Гибкие диски размером 5,25 дюйма и менее называются дискетами. При обычной плотности записи на 5,25-дюймовой дискете помещается 360 Кбайт, при повышенной плотности записи— 1,2 Мбайт. Для 3,5-дюймовой дискеты используется обычно повышенная плотность шписи, обеспечивающая объем 1,44 Мбайт.
Рассмотренные устройства определяют вычислительные параметры нижнего уровня технических средств САПР — PC и ПК- Основные параметры наиболее популярных PC приведены в табл. 2.2. Более полные данные о PC и ПК, используемых в области САПР, приведены в [36]. Следует заметить, что па рынке средств САПР в нашей стране выбор весьма ограничен и ни один тип ЭВМ пока не соответствует по своим параметрам и идеологии построения зарубежным рабочим станциям.
Таблица 2.2
Параметры PC Тип PC, фирма
Decstation-5500, DEC RS-6000, PS-320, IBM Sparc station-2, SUN
Тип процессора MIPS, R3000A IBM Power-RISC SPARC
Операционная система ULTRIX AIX 3.0 Sun OS, UNIX V.O
Тактовая частота, МГц 30 20 40
Быстродействие, млн. ко-манд/с 28 27 28,5
Производительность с САПТ, МФЛОПС 7,0 7,4 4,2
Объем КЭШ-памяти, Кбайт 128 8 - команды 32 - данные 16
Объем основного ОЗУ, Мбайт 32..256 8...32 До 207
Суммарный объем НЖМД, Гбайт 4,4 640 7,6
Тип ЛВС, обслуживаемый сетевым адаптером Ethernet Ethernet, Token Ring Ethernet
Автоматизация проектирования радиоэлектронных средств
33
Данные табл. 2.2 показывают, что современные PC используют в качестве ОС многозадачные ОС, часто совместимые с ОС UNIX. Многозадачные ОС PC функционируют в режиме разделения времени. В таком режиме процессорное время де лится специальным системным таймером-счетчиком на небольшие равные кванты. Они предоставляются по очереди всем задачам, решаемым процессором. Все ресурсы PC во время отведенного текущей задаче кванта доступны ей. Процессор переключается в режиме разделения времени с задачи на задачу настолько быстро, что, с точки зрения медленной реакции человека, задачи в ОС решаются «параллельно». Наиболее существенный выигрыш в производительности многозадачной ОС происходит за счет разделения во времени и параллельного использования периферийного оборудования, например, пока одна задача занимает процессор, другая задача обеспечивает обмен с печатающим устройством, а третья — осуществляет обмен между ВЗУ и ОЗУ.
PC и ПК являются нижним уровнем, технических средств САПР, непосредственно доступным проектировщикам РЭС с помощью САПР. Часть задач в САПР требует более высокой производительности, что достигается использованием ЭВМ других классов и их комплексированием вместе с PC и ПК на базе ЛВС.
•
§2.2. ВЫСОКОПРОИЗВОДИТЕЛЬНЫЕ ТЕХНИЧЕСКИЕ СРЕДСТВА САП» И ИХ КОМПЛЕКСИРОВАНИЕ
PC и ПК имеют традиционную архитектуру, ориентированную на последовательные вычисления, т.е. одним потоком команд они обрабатывают один поток данных. Такая организация вычислений была предложена фон-Нейманом и названа его именем. Усложнение решаемых задач и вычислительных алгоритмов САПР привело к внедрению в эту область более высокопроизводительных ЭВМ, организация вычислений в которых основана на множественности потоков команд, обрабатывающих множество потоков данных. Архитектура этих ЭВМ называется параллельной — иефон-неймановской. По множест-венности-одиночности потоков команд и данных ЭВМ можно разделить на четыре класса, но на практике используются ЭВМ трех классов [40]. На рис. 2.4 показаны упрощенные структурные схемы трех классов ЭВМ, вклщчающие в себя следующие блоки: ОЗУ команд (ОЗУк), ОЗУ данных (ОЗУд), устройство управления (УУ), центральный процессор (ЦП), а также потоки команд (К) и потоки данных (Д).
34
ЭВМ класса ОКОД—это । радиционныё фон-нейма-новские машины с одиночным потоком команд и одиночным потоком данных. К ним относятся PC и НК. окмд ЭВМ —это параллельные компьютеры с одиночным потоком команд и множественными потоками данных. МКМД , ‘ВМ — это многопроцессорные ЭВМ с множественными потоками команд и множественными потоками па иных.
На рис. 2.4,. а, б, в пока-•аны также соответствующие трем классам ЭВМ алгоритмы организации вычислений. Стрелками в них обозначены потоки команд п данных, кружками — выполняемые операторы. В случае ОКОД ЭВМ исполь-|уется обычный последо-нательный алгоритм вычислений.
Для организации вычислений в ЭВМ класса <>КМД используется последовательно-групповой алгоритм. В этом случае группе выполняемых операто-
ров соответствуют операции над векторными и матричными данными. ОКМД ЭВМ реализуются в виде векторных и матричных ЭВМ. Поскольку производительность таких машин велика, их называют суперЭВМ.
Матричная суперЭВМ представляет собой матрицу одинаковых процессорных элементов с собственными локальными ОЗУ, причем каждый из процессоров матрицы выполняет в каждый момент времени одну и ту же команду над разными элементами векторных (матричных) данных. Недостаток матричных ЭВМ — ограниченное количество процессорных элемен
Рис. 2.4.
а)
б)
Классификация параллельных ЭВМ:
а —ЭВМ класса ОКОД, алгоритм последовательный, б-ЭВМ класса ОКМД, алгоритм последовательно-групповой, в-'ЭВМ класса МКМД, алгоритм параллельный, слабосвязаниый
35
тов в матрице ограничивает производительность ЭВМ: чем длиннее векторы обрабатываемых данных, тем ниже выигрыш в производительности такой матричной суперЭВМ перед обыч-1 ной ОКОД ЭВМ, называемой обычно скалярной машиной.
От этого недостатка свободны векторные суперЭВМ класса ОКМД. Р отличие от матричной векторная суперЭВМ имеет один процессор, но его аппаратура разбита на отдельные сек-, ции, причем каждая секция обрабатывает элемент векторный данных за один и тот же такт времени своей логической подфункцией, на которые разбивается общая логическая функция, описывающая работу векторного процессора. Элементу векторов передаются от секции к секции с каждым новым тактом времени, формируя таким образом непрерывный конвейер обработки векторов. Секции конвейера называют его ступенями. Такие векторные конвейерные суперЭВМ оказываются тем более производительнее по сравнению со скалярными, чем длиннее обрабатываемые векторы. Существенный недостаток векторных суперЭВМ — резкое снижение производительности при нарушении непрерывного потока данных, поступающих на вход конвейера.
Поскольку алгоритм организации вычислений для ОКМД ЭВМ имеет специальный вид—последовательно-групповой, ЭВМ этого класса называют специализированными, так как они достигают своей пиковой производительности лишь на определенного класса задачах. В области САПР такие супер ЭВМ успешно применяются для формирования реалистичных трехмерных графических изображений и решения ряда задач конструкторского проектирования сложных изделий, где требуется обработка векторов и матриц.
СуперЭВМ класса МКМД называют суперскалярными высокопараллельными многопроцессорными системами. Поскольку эти ЭВМ реализуют алгоритм вычислений со слабосвязанными множественными потоками команд и данных общего вида, они являются универсальными и обеспечивают выигрыш в производительности по сравнению со скалярными на большинстве задач, решаемых в области САПР. СуперЭВМ этого класса имеют множество процессоров, причем каждый из процессоров обрабатывает свои данные под управлением свое с потока команд. Наиболее сложной проблемой для таких суперЭВМ является синхронизация обмена данными между задачами, запущенными на нескольких процессорах, и синхронизация ожидания одних запущенных задач (процессов) другими.
Аппаратная связь между процессорами МКМД ЭВМ осуществляется тремя способами:
— использование общей шины, соединяющей несколькс процессоров;
— использование общего многопортового ОЗУ, доступногс для всех МП;
36
— использование микросхем коммутации перекрестных «вязей, осуществляющих переключения информационных свя-|<-й МП между собой по принципу «каждый с каждым».
При наличии общей шины, соединяющей несколько МП, возникают конфликты между МП за право монопольного обмена по шине, что снижает эффективность такой ЭВМ. Этот ш-достаток привел к тому, что в настоящее время такой вид связи между МП почти не используется.
Использование общего многопортового ОЗУ предъявляет очень жесткие требования к устройству управления ОЗУ и к надежности самой памяти. Несмотря на этот недостаток, МКМД суперЭВМ с общей многопортовой памятью довольно широко используются в САПР.
Наиболее перспективны многопроцессорные комплексы, в которых отдельные МП соединяются друг с другом с помощью коммутаторов перекрестных связей на основе быстро развивающихся КМОП-переключателей.
Поскольку в параллельных ЭВМ трудно теоретически оценить производительность для решения различного класса задач, их производительность оценивается экспериментально с использованием текстовых пакетов и выражается в миллионах операций с плавающей точкой в секунду — МФЛОПС. В габл. 2.3 приведены данные для параллельных суперЭВМ различных классов. Более полные данные приведены в [40].
Таблица 2.3
Параметры Тип суперЭВМ, фирма
МРР Goodyear Aerospace SX-3 NEC GC-5/16K Parsytec
Класс суперЭВМ Матричная ОКМД Векторная ОКМД Многопроцессорная МКМД
Количество процессоров (ступеней конвейера) 16 384 4x4x2 1 16 384
Тип одного процессорного элемента 1-разрядный процессор с ОЗУ 1 Кбайт 4-ступенчатый векторный кон-. вейер МП-транспыотер Т9000, 32...64 разряда, САПТ
Пиковая производительность, МФЛОПС 160..290 20 000 400 000
Объем ОЗУ, Мбайт 8 2048 4192
Скорость ввода-вывода данных, Мбайт/с 160 400 102 000 *
37
Параллельные суперЭВМ — это уникальные дорогие компьютеры, поэтому они являются ЭВМ коллективного пользова ния, работающими под управлением ОС с разделением времени. Они оснащены высокоскоростными адаптерами связи с peJ гиональными и глобальными вычислительными сетями и связаны с PC разработчиков РЭС с помощью САПР через сетевые каналы связи.
Промежуточным уровнем технических средств САПР между суперЭВМ и PC, ПК выступает ЭВМ среднего класса^ типа ЕС-ЭВМ у нас в стране и ES-9000 за рубежом либо су-пермини-ЭВМ типа «Электроника-82» у нас в стране и VAXj microVAX за рубежом. Эти ЭВМ обладают производительностью выше, чем PC и ПК (свыше 5...10 МФЛОПС), требуюц существенных эксплуатационных расходов, являются компьютерами коллективного пользования с ОС разделения временц и выполняют функции обслуживания внутренних ЛВС фирм и выхода на глобальные и региональные сети при необходимости ведения расчетов, на суперЭВМ. В’ последнее время в связи с использованием САПР средними и мелкими фирмами падает спрос на эти дорогостоящие промежуточные ЭВМ на рынке технических средств САПР. В качестве промежуточных звеньев для предоставления сетевых соединений выступают различного рода РС-серверы. 1 :
РС-сервер — это PC с расширенным набором (по объему или номенклатуре) периферийных устройств. В качестве одной из задач в ОС такой станции запускается процесс-сер-, вер — программа, обслуживающая пользователей других PC через сеть, предоставляя им периферию данной PC либо сетевое соединение через региональную сеть с суперЭВМ. В соответствии с этим различают файл-серверы (PC с дополнительными ВЗУ), серверы сетевой связи (PC с расширенным набором сетевых адаптеров данной ЛВС с другими — ЭВМ-шлюз), вычислительные серверы (PC с повышенной производительное тью) и т.д. Все эти PC, ПК и ЭВМ других классов объединяются (комплексируются) для эффективного использования в области САПР вычислительными сетями.
Преимущества такого комплексирования заключаются в расширении функциональных возможностей САПР (каждый пол J зователь в том или ином подразделении имеет доступ к базам данных и программным средствам в других территориально удаленных подразделениях), оптимизации распределения нагру." ки между различными ЭВМ, в коллективном использовании дг рогостоящей графической периферии, в повышении надежности функционирования технических средств САПР.
38
Р и с. 2.5. Комплекс технических средств САПР RS-6000 фирмы IBM
Существует следующая классификация вычислительных се-I.и [3]:
— по топологии связей — радиальные (звездообразные), магистральные, кольцевые, радиально-кольцевые, древовидные, полные (многосвязные) и др.;
— по составу ЭВМ — однородные и неоднородные;
— по способу передачи данных — сети с коммутацией каналов, сообщений или пакетов;
— по способу управления — централизованные (с централизованным управлением) и децентрализованные;
— по удаленности узлов — локальные (в пределах здания, ряда зданий), региональные (охватывающие регион, область) и 1лобальные (охватывающие страны и континенты).
Примеры построения сетей на базе отечественных и зарубежных ЭВМ приведены в [4, 36].
Локальные вычислительные сети объединяют PC, ПК и серверы в пределах одного предприятия, фирмы. На рис. 2.5 пока <ан комплекс технических средств САПР средних и крупных фирм RS-6000, поставляемый корпорацией IBM.
39
В комплексе ведущей является шлюз-ЭВМ среднего класса ES-9000 для выхода через региональные сети к мощным суперЭВМ. В пределах фирмы отдельные подразделения и группы разработчиков объединены ЛВС среднего уровня типа Ethernet Эта сеть в качестве канала связи использует коаксиальный кабель со скоростью передачи 10 Мбит/с и имеет шинную (магистральную) организацию типа моноканала. Моноканал — это сетевой канал связи, использующий монопольный способ передачи сообщений по коаксиальному кабелю на одной центральной частоте, называемой тональной. Аппаратура пользователей (абонентов сети) подключается к центральной жиле коаксиального кабеля с помощью блика доступа, соеди ненного сетевыми адаптерами для связи по моноканалу ЭВМ. При передаче по моноканалу два абонента на какое-то время занимают целиком весь канал. Остальные абоненты, желающие передать данные, ждут освобождения канала, затем в свою очередь занимают его и передают данные. В процессе ожидания аппаратура абонентов такой сети должна прослушивать моноканал до его освобождения. В качестве абонентов сети Ethernet комплекса RS-6000 выступают файл-серверы PS-520 подразделений и групп разработчиков. PS-520— это PC с дополнительной ОЗУ и ВЗУ. В пределах подразделения организуется своя высокоскоростная ЛВС типа «циклическое кольцо» — Token Ring. В сети типа «циклическое кольцо» каналом является также коаксиальный кабель, но образующий топологическую фигуру — кольцо. Время доступа к кольцу поделено на жесткие Дискреты и засинхронизировано. Аппарату-! ра абонентов подключается к кольцу через специальные усилители-повторители, задерживающие сигнал, распространяю^ щийся по кольцу, на время дискрета (в это время считывается-записывается информация абонента из сети). В кольце циркулирует специальная кодовая группа — маркер. Абонент сети приняв такой маркер, получает доступ в кольцо и посылает за ним свою информацию. Абонент-получатель принимает ин-1 формацию и добавляет код получения сообщения к маркеру. Передавший данные абонент получает прошедший по кольцу маркер, убеждается в успешном приеме получателем данных и освобождает маркер. Теперь другой абонент может, получив свободный маркер, занять кольцо. В высокоскоростных коль-< цевых сетях в кольце может циркулировать несколько марке ров. Такая кольцевая сеть в подразделении фирмы объеди-i няет до пяти рабочих станций PS-320. К каждой PC можно подключить нисколько ПК PS-2 фирмы IBM. Непосредственно в кольцевую сеть можно подключить до 50 ПК типа PS-2. , 40
§2.3. ПЕРИФЕРИЙНОЕ ОБОРУДОВАНИЕ САПР
Помимо PC, ПК и других ЭВМ для организации САПР f 1’.-)С требуется дорогостоящее периферийное оборудование. Периферийное оборудование ЭВМ — это совокупность технических и программных средств, обеспечивающих взаимодейст-иие ЭВМ с пользователем и внешней средой, а также хранение, подготовку и преобразование информации к виду, удобному для ввода-вывода.
Периферийное оборудование подразделяется на две группы: локальное, устанавливаемое рядом и подключаемое непосредственно к ЭВМ, и удаленное (терминальное). По выполняемым функциям и локальное, и терминальное оборудование пключает в себя средства хранения, телеобработки и ввода-нывода информации. Средства взаимного общения с пользова-|слем должны осуществлять представление и ввод информации в основном в графической форме.
В настоящее время существуют различные методы ввода и регистрации графической информации: высвечивание точек и пиний на экране монитора, нанесение точек, вычерчивание линий и символов изображения на бумаге (в том числе специальной), изменение цвета бумаги путем химической (термической) реакции, электризация поверхности фотополупроводника, проецирование изображения с помощью луча лазера и др.
Каждый метод и устройства, реализующие его, имеют свои юстоинства и недостатки. Основными критериями для их сравнения являются:
— качество изображения;
— скорость формирования изображения;
— стоимость оборудования и его эксплуатации;
— особенности программного обеспечения.
По программному обслуживанию периферийные устройства САПР делятся на два класса: растровые и координатные (нектарные).
В растровых устройствах выводится мозаичный рисунок п < отдельных точек — пикселов, или ПЭЛов (от англ, picture dement), по типу телевизионной развертки. При этом осущес-тляется последовательный перебор элементов мозаики и выделение пикселбв, составляющих изображение. Время вывода» изображения постоянно, не зависит от сложности рисунка и определяется только числом элементов мозаики (пикселов) и скоростью их перебора.
При векторном способе осуществляется последовательное пычерчивание линий, составляющих изображение. Время вво
41
да-вывода изображения пропорционально суммарной дли линий (в том числе с учетом «невидимых» линий). Для сложных изображений время вывода может быть достаточно велико.
В современных САПР широкое применение находят оба типа устройств. Все периферийные устройства делятся на три основные группы [35]:
— средства ввода-вывода с машинных носителей;
— средства ввода-вывода с документов;
— средства непосредственного взаимодействия с ЭВМ.
Первая группа средств включает в себя накопители на магнитных дисках или накопители на магнитных лентах (стриммеры), представляющие собой обычные ВЗУ.
Средства ввода-вывода с документов имеют свою специфику для ввода-вывода текста и графической информации. К ним относятся различные печатающие устройства (принтеры), графопостроители, планшеты, сканеры и др.
Средства непосредственного взаимодействия с ЭВМ включают в себя устройства отображения алфавитно-цифровой и графической информации (дисплеи, проекционные системы и др ), акустические устройства ввода-вывода информации, устройства связи с реальными объектами (датчики, исполнительные устройства), а также средства ручного ввода информации: алфавитно-цифровую клавиатуру, различные планшеты и манипуляторы (электронная «мышь», управляющие ручки— джойстики, управляющий шар — трекболл и др ).
Наиболее распространенным электронным средством отображения информации является дисплей. Большинство современных дисплеев PC и ПК строятся на основе платы графического адаптера (графического процессора) и монитора.
Требования к качеству графического изображения в задачах САПР весьма велики, поэтому обычные графические адаптеры ПК стандарта VGA (640x480 точек разрешения, 256 цветов и ниже) не подходят для визуализации изображений. Существует несколько видов изображений в пакетах САПР:
— высококачественные черно-белые двухмерные изображения (чертежи, эскизы и т.д.);
— цветные или полутоновые двухмерные изображения (топология БИС, печатных плат и т.д.);
— каркасные трехмерные проекции конструкторских чертежей, эскизов и т.д. с удалением и без удаления невидимы) линий;
— проекции трехмерных изображений с закрашивание»! поверхностей;
42
— проекции реалистичных трехмерных изображений с уче-н>м отражательных характеристик поверхностей объектов и формированием светотеней.
Наиболее простые черно-белые изображения и каркасные ||>ехмерные изображения могут строиться векторными методами. Остальные виды изображений требуют растровой цветной (полутоновой) графики с высоким разрешением и богатой цве-|овой палитрой.
Для изображений среднего качества могут быть использованы графические адаптеры мощных ПК типа SVGA с разрешением не менее 1024x768 точек, 256 цветов и адаптеры наиболее недорогих PC, например семейства SUN с разрешением 1152x900, 256 цветов.
Для визуализации реалистичных трехмерных изображений, конструкций сложных объектов и многослойных топологий ВИС требуются более высокие быстродействие и разрешение |рафических адаптеров. Такие графические адаптеры называют графическими процессорами, а PC с графическим про-ш'ссором и цветным монитором повышенного разрешения и размера по диагонали (19 дюймов и выше) — графической рабочей станцией. Так, в графической PC фирмы IBM PS-730 используется плата графического процессора, обеспечивающая разрешение 1280x1024 точки с более чем 4 млрд, оттенков цветов. Быстродействие такой графической станции при ви-<уализации изображений — 990 тыс. трехмерных графических преобразований в секунду, что эквивалентно воспроизведению 120 тыс. трехмерных треугольников с закрашиванием в секунду
В связи с высокими требованиями к качеству изображений и области САПР доминируют цветные и полутоновые мониторы на электронно-лучевых трубках с повышенными разрешением и строчной и кадровой развертками, хотя ведутся интенсивные разработки и высококачественных мониторов на жидких кристаллах. Следует отметить быстрое развитие лазерных проекционных систем визуализации изображений на больших плоских экранах с повышенным разрешением до 1024x1024 точек. В этом случае развертка луча лазера ведется зеркальными механическими отклоняющими системами либо электронными системами на базе а кустооптических дефлекторов.
Устройства графического вывода (печатающие устройства — принтеры, графопостроители и т.д.) занимают ведущее место среди номенклатуры периферийных устройств на рынке технических средств САПР (более 2/з от всей оконечной аппаратуры). Сложилось разделение устройств вывода на печатающие устройства и графопостроители, однако границы их использования для вывода текста и графики в прследнее время все более размываются.
43
Печатающие устройства по порядку вывода делятся на: — посимвольные, в которых вывод алфавитно-цифровой информации осуществляется последовательно символ за символом за один цикл печати;
— построчные, которые формируют и выводят за один цикл печати всю строку;
— постраничные, которые формируют и выводят целиком всю страницу за один цикл печати.
По физическому принципу различают печатающие устройства ударного и безударного действия. В первом случае изображение получают в результате удара по носителю записи специальным органом — молоточком, стержнем, иглой и др. В устройствах безударного действия изображение выводится в результате физико-химического, электрического и другого воздействия на оконечный носитель записи (бумагу) или некото рый промежуточный носитель (специальную пленку, различные барабаны, пластины и др.).
Наиболее популярны среди принтеров ударного действия матричные печатающие устройства, в которых изображения (знаки) формируются специальной головкой, содержащей стержни-иглы, возбуждаемые электромагнитным или пьезоэлектрическим приводом. В простых моделях головок 9... 12 игл, в более сложных— 18...24. Сложные модели обеспечивают достаточно высокое качество печати, но низкое быстродействие.
К недостатку печатающих устройств ударного действия относится также наличие большого количества механических
элементов, работающих при высоких динамических нагрузках и связанный с этим ограниченный ресурс, повышенный уровень шума и ненадежность.
Печатающие устройства безударного действия относятся к матричным устройствам. Изображение формируется из отдельных точек с четкостью от 3 до 32 точек на мм. В большинства из них используется одинаковый принцип: формирование скрытого электрического или магнитного изображения на промежуточном носителе, далее его визуализация и перенос на бумагу. Среди безударных печателей наиболее популярны термопечати, струйные печатающие устройства и лазерные печати.
Термопечатающие устройства используют термопечатные головки (терморезисторы) и копировальные пленки (5... 10 мкм) с легкоплавким красящим слоем. Локальный нагрев пленки у красителя приводит к переносу отпечатка на бумагу. В таких устройствах достигаются высокая четкость (6... 12 точек на 1 мм), высокая контрастность, легко реализуется многоцветность изображения.
44
Струйные печатающие устройства относятся к посимвольным матричным устройствам. Существует два типа таких печатей: с непрерывной капельной струей и импульсные (ждущие). В первых заряженные капельки красителя летят мимо отклоняющей системы и формируют символы (графику) на бумаге. Скорость такой печати до 300 см2/мин при разрешении '.’О точек на 1 мм. В ждущих принтерах капли вылетают лишь тогда, когда необходимо сформировать символ. В них исполь-|уются многосопловые (до 9...12 сопл и более) струйные головки, обеспечивающие плотность записи 4...12 точек на 1 мм. Возбуждение капсул-инъекторов осуществляется пьезоэлемен-гом или нагревом микрорезистора.
Наибольшую популярность в настоящее время имеет лазерная печать, обеспечивающая очень высокую скорость печати (до 10 страниц в минуту) при высокой четкости — до 32...40 точек на 1 мм. В таких устройствах изображение регистрируется (лектрографическим способом. Лазер создает скрытое изображение на барабане, а его визуализация осуществляется специальным порошком — тонером с тепловым закреплением на оумаге. При этом луч лазера по одной координате разворачивается механически с помощью зеркальной многогранной призмы, а по другой координате — электронным способом с помощью акустооптического дефлектора. Управляет работой лазерной печати мощная микроЭВМ, формируя страницы вывода, получаемые от PC или ПК. К недостаткам лазерной печати следует отнести ее относительно высокую стоимость и сложность формирования цветных изображений. Лазерные принтеры обычно используются коллективно несколькими пользователями через ЛВС. Лидером в производстве лазерных печатей является фирма Hewlett-Packard. Параметры одного из относительно недорогих лазерных принтеров HP Laserjet IIP:
номинальная скорость печати — 4 стр/мин; емкость лотка для подачи бумаги — 50 листов; емкость приемного лотка — 20, 50 листов;
минимальная емкость буферной памяти — 512 Кбайт; максимальная емкость буферной памяти — 4,5 Мбайт; интерфейсы с ЭВМ — последовательный и параллельный; ресурс кассеты с тонером — 3500 страниц;
масса — 10 кг.
Графопостроители подразделяются на два основных типа: растровые и векторные (координатные).
Растровые устройства по своей конструкции близки к принтерам безударного действия и используют электрохимический, электротермический и другие принципы работы. Пишущий
45
узел в них представляет собой гребенку электродов, образующую растр во всю ширину бумаги. Специальная бумага перемещается в одну сторону ведущим барабаном; при подаче напряжения на те или иные электроды и общий электрод проходит химическая или термическая реакция и возникает отпечаток на бумаге. Разрешающая способность таких устройств — 4...8 точек на 1 мм. Достоинства растровых устройств — высокая скорость работы, не зависящая от сложности изображения; недостаток — сложность конструкции системы управления напряжением на электродах гребенки.
Векторные (координатные) графопостроители относятся к электромеханическим устройствам и выполняются в двух видах: планшетном и рулонном. В планшетном графопостроителе бумага фиксируется, а пишущий узел закреплен на каретке, установленной, в свою очередь, на движущейся планке. Тем самым каретка может перемещаться в любую точку планшета. Используется векторный способ управления графопостроителем путем подачи аналоговых или дискретных (шаговых) сигналов, пропорциональных изменениям координат при перемещении пишущего узла. Для вывода сложных кривых применяется линейная, линейно-круговая или параболическая интерполяция с помощью специальной управляющей микроЭВМ, входящей в состав графопостроителя.
В рулонном графопостроителе планка неподвижна, а барабан или валик перемещает бумагу. Рулонный графопостроитель более автоматизирован в работе, чем планшетный, однако нельзя использовать произвольные листы, бланки и т.п.
Основное назначение устройств ввода графической информации заключается в преобразовании аналоговых объектов изображения в дискретную форму представления в ЭВМ. Устройства ввода включают в себя как средства ввода информации с документов, так и органы ручного ввода при непосредственном взаимодействии с ЭВМ.
При вводе осуществляются две основные операции: поиск, выделение (считывание) изображения и кодирование информации. По степени автоматизации операции считывания изображения устройства ввода разделяются на полуавтоматические и автоматические. В первых поиск элементов осуществляется вручную, а кодирование информации— автоматически; во вто^ рых устройствах и считывание, и кодирование информации производятся автоматически с помощью ЭВМ.
Для управления маркером на дисплее и ввода команд используются ручные манипуляторы: электронная «мышь», управляющая ручка — джойстик, управляющий шар — трек-
46
<юлл. Во всех манипуляторах вращение сферы передается на твижки потенциометров — валюаторов, тем самым изменяются сигналы, соответствующие текущим координатам. Такие устройства относятся к дисплейным указателям, так же как алфавитно-цифровая и функциональная клавиатура, световое перо, сенсорный экран и др.
Среди полуавтоматических устройств ввода изображений наиболее популярны полуавтоматические сканеры, в которых чувствительный элемент считывания изображения перемещается по элементам изображения рукой человека. Автоматические устройства ввода изображений выполняют считывание информации без участия человека. Существует два типа автома-гических устройств ввода: следящие — аналог векторных устройств вывода и сканирующие (растровые).
Следящие устройства ввода выполняют слежение за линией и устанавливаются либо на графопостроитель, либо на специальную координатную систему. Возможности следящей системы ограничены сложностью рисунка, числом пересечений, типом линий и т.д.
В сканирующих устройствах (сканерах) осуществляется растровое представление вводимого документа, выполняется распознавание образов, символов, знаков; далее изображение может быть графически отредактировано на дисплее и выведено па растровое устройство вывода. В автоматических и полуавтоматических сканерах в качестве чувствительного элемента используется однокоординатная линейка фотоприемников или линейка приемников на основе приборов с зарядовой связью (ПЗС). По другой координате перемещение линейки осуществляется вручную или автоматически с помощью шагового двигателя. Поверхность считываемого изображения освещается светодиодами, что улучшает равномерность засветки и качество считываемого изображения. Сканеры на основе таких систем позволяют получать четкость картинки до нескольких десятков точек на мм. Для быстрого ввода в ЭВМ изображений, сравнимых по четкости с телевизионным, используются автоматические сканеры на основе телевизионных камер с приемной ПЗС-матрицей и высококачественной широкоугольной оптикой.
К средствам непосредственного взаимодействия с ЭВМ относятся и акустические системы ввода-вывода информации. Средства акустического ввода подразделяются на устройства ввода изолированной и дискретной речи (отдельные команды) и устройства ввода слитной речи. Средства акустического вывода делятся на устройства синтеза звуков, устройства синтеза речи по правилам синтеза и по образцам. Синтез по правилам ведет к созданию искусственной речи; синтез по образ
47
цам заключается в кодировании естественной речи для последующего воспроизведения (так называемые компилятивные синтезаторы).
Технические средства САПР динамично развиваются в сторону максимально быстрой реакции на любую команду человека и организации ввода-вывода любой информации в виде, естественном для специалиста проблемной области, в которой функционирует конкретная САПР.
В связи с быстрым развитием технических средств САПР при написании этой главы были использованы материалы журналов «Электроника», «Интерфейс» и «Мир ПК»-
Вопросы и упражнения для самопроверки
1. Перечислите основные особенности рабочих станций (PC) по сравнению с персональными компьютерами (ПК). Чем они определяются?
2. Чем вызвана необходимость введения виртуальной адресации и аппаратуры управления памятью в архитектуру высокопроизводительных МП?
3. Сформулируйте основные требования к архитектуре рабочей станции, обусловленные концепцией распределенной обработки данных.
4. Перечислите основные виды параллельных суперЭВМ. К какому классу с точки зрения множественности-одиночности потоков команд и данных они относятся?
< 5. Как оценивается производительность параллельных ЭВМ и рабочих станций. имеющих сопроцессор арифметики с плавающей точкой.
6. Выберите вид периферийного оборудования для:
— оперативного вывода оператору из ЭВМ реалистичной трехмерной сцены;
— регистрации в виде твердой копии трехмерной реалистичной сцены;
- — регистрации в виде твердой копии каркасного трехмерного изображения;
— оперативного ввода в ЭВМ изображения динамично меняющего форму предмета;
— ввода в ЭВМ чертежа;
— ввода в ЭВМ текстового документа.
7. Выделите особенности формирования состава технических средств САПР для небольшой фирмы с малым количеством сотрудников, специализирующейся на разработке и выпуске малы$ партий радиоэлектронного оборудования. Выберите виды необходимых технических средств САПР, тип базовой ЭВМ фирмы. Объедините выбранное оборудование в единый комплекс технических средств САПР.
Глава 3
ЛИНГВИСТИЧЕСКОЕ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ САПР
\
§3.1. КЛАССИФИКАЦИЯ И ОСОБЕННОСТИ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И ПРОЕКТИРОВАНИЯ
Лингвистическое обеспечение САПР — это совокупность языков, используемых в процессе разработки и эксплуатации САПР для обмена информацией между человеком и ЭВМ [1, 3]. Термином «язык» в широком смысле называют любое средство общения, любую систему символов или знаков для обмена информацией.
Лингвистическое обеспечение САПР состоит из языков программирования, проектирования и управления.
Языки программирования служат для разработки и редактирования системного и прикладного программного обеспечения САПР. Они базируются на алгоритмических языках — наборе символов и правил образования конструкций из этих символов для задания алгоритмов решения задач.
Языки проектирования — это проблемно-ориентированные языки, служащие для обмена информацией об объектах и процессе проектирования между пользователем и ЭВМ.
Языки управления служат для формирования команд управления технологическим оборудованием, устройствами документирования, периферийными устройствами ЭВМ и др.
Существуют различные уровни языков программирования: высокие, более удобные для пользователя, и более низкие, близкие к машинным языкам.
Программа, записанная на некотором языке программирования высокого уровня, называется исходной. Прежде чем исходная программа будет исполнена, она должна быть преобразована в машинную форму, соответствующую ЭВМ данного типа. Подобные преобразования осуществляются специальными программами, называемыми языковыми процессорами.
Основные типы языковых процессоров — трансляторы и интерпретаторы; соответственно преобразования программ называют трансляцией и интерпретацией. 11
49
Рис. 3.1 Классификация язиков программирования
Трансляцией называют перевод всего текста программы на исходном языке (исходной программы) в текст на объектном языке (объектную программу). Если исходный язык является языком высокого уровня, а объектный — машинным, то транслятор называют компилятором. Если исходный язык—машинно-ориентированный (в автокоде), а объектный — машинный, то транслятор называют ассемблером. Если исходный и объектный языки относятся к одному уровню, то транслятор называют конвертером.
По методу трансляции (компиляции) сначала исходная программа переводится на машинный язык, а затем скомпилированная рабочая программа исполняется.
При интерпретации перевод исходной программы в рабочую совмещены во времени; очередной оператор исходной программы анализируется и тут же исполняется.
В большинстве случаев применение трансляторов приводит к меньшим затратам машинного времени, но к большим затратам машинной памяти, чем при интерпретации.
Совокупность языка программирования и соответствующего ему языкового процессора называют системой программирования.
Классификация языков программирования представлена на рис. 3.1 [36].
Класс машинно-зависимых языков представлен ассемблером (макроассемблером). Он относится к языкам низкого уровня и используется для написания программ, явно использующих специфику конкретной аппаратуры.
50
К машинно-ориентированным языкам относится язык СИ (разработан в 1972 г.) В нем объединяются достоинства низкоуровневых возможностей ассемблеров и мощных выразительных средств языков программирования высокого уровня. Язык СИ является одним из претендентов на роль основного языка программирования в САПР и ориентирован на разработку системных программ. Он, в частности, послужил главным инструментом для создания операционных систем для ПЭВМ UNIX и MS DOS.
Язык Фортран является первым универсальным языком высокого уровня (с 1954 г.). Фортран — самый примитивный из распространенных алгоритмических языков общего назначения. Наиболее эффективен при численных расчетах, прост по структуре и эффективен при выполнении программ. Несмотря на свои недостатки, этот язык получил большое распространение при разработке прикладных программ для решения научных задач. Наиболее популярная в настоящее время версия этого языка — Фортран-77.
Идеи Фортрана получили развитие в языке PL/1 (создан в 1964 г.). В нем сделана попытка преодолеть некоторые недостатки, свойственные языкам для больших ЭВМ и использованы идеи структурного программирования. В настоящее время имеются различные версии этого языка: PL/M, PL/Z, PL/65 и др. Как язык программирования PL/М, в частности, значительно уступает конкурирующим с ним языкам Паскаль и Модула-2.
Язык Паскаль является одним из наиболее популярных языков программирования и используется для разработки системных и прикладных программ, в частности для персональных ЭВМ. Язык Паскаль создан вначале исключительно для учебных целей и изящно реализовал большинство идей структурного программирования. Достоинства языка оказались столь значительными, что он приобрел огромную популярность для самых различных приложений. В частности, компилятор Turbo Pascal, снабженный интерактивным редактором, позволяет создавать достаточно сложное программное обеспечение — системы управления базами данных, графические пакеты и др
Развитием Паскаля являются языки Модула-2 (в Европе) и Ада (в США). Язык Модула-2 обладает лучшими средствами для обработки больших программных комплексов и позволяет более эффективно использовать особенности аппаратуры. Таким образом, этот язык призван заполнить ниши между Паскалем и СИ. По оценке специалистов, язык Модула-2 через несколько лет станет наиболее популярным среди всех языков программирования. • /
51
Язык Ада можно назвать наиболее универсальным среди созданных языков. Однако трансляторы с этого языка пока не получили достаточного распространения.
Язык Алгол — общепризнанный язык для публикации алгоритмов решения научных задач, построен на четких и полных определениях. Для Алгола характерны строгие, но негибкие структуры данных и программ. Алгол труден для реализации на большинстве ЭВМ, поэтому используются неполные варианты языка или его расширения.
Язык Кобол, разработанный для решения экономических задач, широко распространенный на больших и средних ЭВМ прошлых лет, на персональных ЭВМ почти не используется. На ПЭВМ имеются интегрированные системы, базы данных и другие типы прикладных систем, используемые в задачах экономического и управленческого характера.
Самыми распространенными на ПЭВМ являются различные версии языка Бейсик, простота которого делает его превосходным средством для начинающих программистов. В языке встроены удобные функции для работы с экраном дисплея, клавиатурой, внешними накопителями, принтером, каналами связи. Это позволяет относиться к Бейсику как к продолжению аппаратуры ПЭВМ. Системы Бейсика работают в режиме интерпретации, что способствует сокращению характерного цикла в работе программиста: составление программы — пробное исполнение — исправление ошибок — повторное исполнение.
Бейсик наряду с Паскалем принят во многих учебных заведениях как базовый язык для изучения программирования.
Язык АПЛ применяется для обработки структурных данных (векторов, матриц) и использует иероглифическую запись программных текстов. Из-за большого числа иероглифов (около 100) его иногда называют китайским Бейсиком [36].
К классу проблемно-ориентированных языков можно отнести Лого, CPSS, Форт и Смолток.
Язык Лого — диалоговый процедурный язык, реализованный на принципе интерпретации и работающий со списками, текстами, графическими средствами и др. Язык очень перспективен для обучения, создания электронных игрушек и т.д.
В системах программирования GPSS легко описывается и исследуется класс моделей массового обслуживания.
Развитием проблемно-ориентированных языков является объектно-ориентированный подход (языки Смолток, Форт, Модула и Ада). Отличительными особенностями таких языков являются модульность построения процедур, абстракция данных,
52
динамическая связка программ, что позволяет отказаться от перекомпилирования всей программы при внесении изменений в отдельные модули, и использование механизма наследования иерархического типа.
К недостаткам таких языков относится некоторая замедленность выполнения программ из-за их динамической связи и сложность трансляторов.
Язык Смолток предназначен для решения нечисловых задач при построении систем искусственного интеллекта. В языке Форт применены структурное программирование и очень компактный машинный код.
Для разработки систем искусственного интеллекта также используются функциональные языки Лисп, Пролог и Снобол. Эти языки ориентированы на обработку символьной информации, требуют больших массивов данных и стали применяться в ПЭВМ в связи с появлением дешевой полупроводниковой памяти, позволяющей довести объем ОЗУ до нескольких Мбайт. Языки этого класса относятся к так называемым языкам представления знаний.
Язык Лисп применяется для программирования интеллектуальных задач — общение на естественном языке, доказательство теорем, принятие решений и т.п.
Язык Пролог приобрел в последние годы большую популярность в связи с японским проектом создания вычислительных систем пятого поколения. Он предназначен для создания широкого класса систем искусственного интеллекта, в том числе и персональных экспертных систем.
При использовании САПР приходится решать задачи не только вычислительного характера и обработки данных, но и автоматизировать описание объектов, процессы ввода, вывода и редактирования данных, ввода графических изображений, схем, чертежей и т.п. Для этой цели служат языки проектирования. Классификация языков проектирования приведена на рис. 3.2 [1, 3, 6].
Языки проектирования делят на языки входные, выходные, сопровождения, промежуточные и внутренние.
Входные языки служат для задания исходной информации об объектах и целях проектирования. Во входных языках можно выделить две части: непроцедурную, служащую для описания структур объектов, и процедурную, предназначенную для описания заданий на выполнение проектных операций и процедур. Этим частям соответствуют языки описания объектов и языки описания заданий. Разновидности первых: схемные, графические языки и языки моделирования (рис. 3.2).
53
Языки проектирования
Рис. 3.2. Классификация языков проектирования
Схемные языки применяются для описания электрических и электронных схем и содержат данные об элементах схем и их связях друг с другом.
Графические языки используются для ввода чертежей, геометрических изображений, деталей и т.п. Задание геометрии деталей осуществляется различными способами: координатным, структурно-символическим (методом типовых графических элементов), аналитическим (математическими уравнениями поверхностей и линий) и рецепторным (мозаичным). При этом используются графические примитивы и элементарные графические операции. Разработаны специальные системы графического программирования (см. гл. 17).
Языки моделирования близки к алгоритмическим языкам и применяются для описания процессов в моделируемом объекте.
Выходные языки используются для представления результатов проектирования в удобном для разработчика виде. Возможные формы представления — таблицы, графики, чертежи, диаграммы, текстовые сообщения. При этом необходимо обеспечить эффективность понимания разработчиком проектных результатов (желательно в графической форме), соблюдение требований стандартов при формировании подлинников конструкторской, программной и технологической документации.
Языки сопровождения служат для непосредственного общения пользователя с ЭВМ и применяются для корректировки и редактирования данных при выполнении проектных процедур. В диалоговых режимах работы с ЭВМ средства языков вход
54
ного, выходного и сопровождения тесно связаны и объединяются под названием диалогового языка. Современные диалоговые языки широко используют средства машинной графики (графический диалог). Диалог с ЭВМ может быть пассивным, когда инициатор диалога — система, и от пользователя требуются только простые ответы, и активным при двусторонней инициативе диалога. Наиболее распространенная форма пассивного диалога — это система встроенных, в том числе иерархических, директивных меню.
Недиалоговые системы языков сопровождения ориентированы на пакетный режим работы ЭВМ.
Промежуточные языки используются для описания информации в системах поэтапной трансляции исходных программ. Введение таких языков облегчает адаптацию программных комплексов САПР к новым входным языкам, т.е. делает комплекс открытым по отношению к новым составляющим лингвистического обеспечения.
Внутренние языки устанавливают единую форму представления данных (текстовой и графической информации) в памяти ЭВМ по подсистемам САПР. Принимаются определенные соглашения об интерфейсах отдельных программ, что делает САПР открытой по отношению к новым элементам программного обеспечения.
В качестве примера современного языка проектирования можно указать язык VHDL (VHSIC — hardware description language) — язык описания аппаратуры на базе сверхвысокоскоростных интегральных схем. Этот язык принят в качестве стандарта как инструментальное средство автоматизации проектирования СБИС, ориентированное на методологию нисходящего проектирования. Он является достаточно универсальным, чтобы охватить все аспекты проектирования изделий области цифровой электроники.
§3.2. СИСТЕМНОЕ ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ САПР РЭС
Программное обеспечение — это совокупность программ, процедур и правил, написанных на том или ином языке, предназначенных для использования в САПР. Программное обеспечение делится на общее (системное) и прикладное (специальное) [1, 3, 4, 6, 36].
Системное программное обеспечение включает программы, осуществляющие управление, контроль и планирование вычислительного процесса, распределение ресурсов, ввод-вывод дан
55
ных и другие операции в подсистемах САПР. Его делят на общесистемное, представляемое операционными системами, используемыми в САПР, и базовое, включающее программы обслуживания подсистем САПР (мониторные системы, СУБД, графические и текстовые редакторы и т.п.).
Прикладное программное обеспечение состоит из прикладных программ, реализующих алгоритмы решения проектных задач. В подсистемах САПР программы обычно объединяются в пакеты прикладных программ (ППП).
К программному обеспечению предъявляются следующие требования: экономичность (эффективность по быстродействию и затратам памяти); удобство использования, применение простых проблемно-ориентированных языков, наличие средств диагностики ошибок пользователя и т.п.; надежность и правильность получения результатов проектирования; универсальность по отношению к тем или ином ограничениям решаемых задач; открытость (адаптируемость) относительно внесения изменений в процессе эксплуатации программ; сопровождаемость, характеризующая работоспособность программ при внесении изменений в них; мобильность при перестройке программ с ЭВМ одного типа на ЭВМ другого типа.
Программное обеспечение целесообразно разрабатывать на основе принципов модульности и иерархичности.
Операционная система является основным компонентом системного программного обеспечения САПР. Структура операционной системы показана на рис. 3.3 [1].
Рис. 3.3. Структура общесистемного программного обеспечения САПР
56
Операционные системы включают в себя программы двух групп:
• — обрабатывающие программы, составляющие подсистему подготовки программ пользователя (внешнее программное обеспечение);
— управляющие программы, образующие группу исполнения программ пользователя (внутреннее программное обеспечение).
К обрабатывающим программам относятся трансляторы с алгоритмических языков, библиотеки стандартных программ и системные обслуживающие программы.
Группа управляющих программ включает в себя программы управления задачами, заданиями и данными.
Программа управления задачами (супервизор, диспетчер, монитор, резидентная программа) находится в оперативной памяти и выполняет все необходимые диспетчерские функции — переключение с выполнения одной программы на другую, распределения ресурсов времени и оперативной памяти между программами. Именно супервизор реализует мультипрограммный режим работы ЭВМ или режим разделения времени.
Программы управления заданиями выполняют интерпретацию директив языка управления заданиями — ввод, трансляция, загрузка в память ЭВМ, решение, вывод информации.
Программы управления данными обеспечивают поиск, хранение, загрузку в оперативную память и обработку файлов.
Функции и структуры операционных систем имеют различия в одно- и многопроцессорных вычислительных системах, многомашинных комплексах и вычислительных сетях. Соответственно этому операционная система должна обеспечить одно-или мультипрограммный режим работы ЭВМ, режим мультиобработки задач, совместное функционирование уровней и подсистем САПР через специальную мониторную систему.
Для персональных ЭВМ наибольшее распространение получили операционные системы UNIX, MS DOS, WINDOWS и др. [36].
Система UNIX достаточно проста по организации, легко переносится с одной машины на другие, ориентирована на пользователя— программиста. Система UNIX — это мультипрограммная система с коллективным доступом. Она обладает целым рядом достоинств — возможностью организации многоуровневой и многозадачной работы, высокой мобильностью, иерархической файловой структурой, гибким и богатым командным языком, бо1атой библиотекой сервисных процедур и функций. Эта система в настоящее время главным образом используется в исследовательских и учебных целях.
.57
'I
Широкое распространение в ПЭВМ получила операционная система MS DOS, являющаяся базовой для ЭВМ серии IBM PC, стандартом операционной системы для 16- и 32-раз-рядных персональных компьютеров. Система имеет развитый командный язык, возможности организации многоуровневых каталогов, работы с последовательными устройствами как с файлами, подключения дополнительных драйверов внешних устройств и др. Имеются трансляторы практически для всех популярных языков высокого уровня.
Важным достоинством операционных систем является возможность поддержки в ОЗУ так называемых виртуальных дисков. Под виртуальным диском понимается область ОЗУ, обращение к которой происходит точно так же, как если бы это был реальный физический диск. Подобное построение системы позволяет существенно повысить скорость записи и доступа к информации и значительно снизить нагрузку (число обращений) на реальный диск.
Для персональных ЭВМ разработан новый класс общесистемного программного обеспечения — так называемые программы-оболочки, которые существенно расширяют и дополняют понятие операционной системы. В традиционных операционных системах управляющие команды вводятся с клавиатуры; такой способ взаимодействия не нагляден и недостаточно удобен. С использованием программ-оболочек в полноэкранном режиме выполняются наиболее часто встречающиеся операции при работе с системой: просмотр содержимого каталога на дисках, переход из одного каталога в другой, копирование, перемещение и удаление файлов, запуск программ и т.д. Примерами таких программ-оболочек являются Norton Commander, Windows. Некоторые современные операционные системы имеют собственные программы-оболочки.
В последние годы началось активное вторжение персональных ЭВМ в обработку текстов, графических данных и др. В связи с этим специальным классом программного обеспечения выделились интегрированные пакеты программ, текстовые редакторы и динамические электронные таблицы.
Располагая текстовым редактором, персональную ЭВМ с печатающим устройством можно легко превратить в электронную пишущую машинку, по своим возможностям намного превосходящую обычные машинки: легкость изменения текста, исправления ошибок, вставка и удаление текста, распечатка в любом числе копий в различных форматах с использованием различных шрифтов и др.
58
Известны текстовые редакторы Лексикон, Chi-Writer, Word, Multi-Mate и др. [36].
Интересными программами являются динамические электронные таблицы, в ячейках которых могут помещаться тексты, числа и математические формулы, устанавливающие взаимосвязь между элементами ячеек. При работе программы может быть построена и рассчитана модель сложной системы, например предприятия, учреждения, другого экономического объекта. Современные динамические электронные таблицы (например, Lotus 1-2-3 FRAME WORK) включают в себя кроме собственно таблицы также текстовой редактор, СУБД, подсистему машинной графики, полиэкранный интерфейс, средства телекоммуникационной связи. Примеры системного программного обеспечения приведены также в гл. 9, 16, 17 настоящего пособия.
§3.3. ПРИКЛАДНОЕ ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ САПР РЭС
Прикладное программное обеспечение представляют пакеты прикладных программ (ППП) для выполнения различных проектных процедур [1, 3, 6, 36]. Оно разрабатывается на основе единого внутреннего представления графической и текстовой информации, единого входного языка, строится по модульному принципу и ориентировано на использование непрограммистом-проектировщиком.
Различают несколько типов ППП в зависимости от состава пакета. Пакеты прикладных программ простой структуры характеризуются наличием только обрабатывающей части — набора функциональных программ (модулей), каждая из которых предназначена для выполнения только одной проектной процедуры. Объединение нужных модулей осуществляется средствами операционной системы ЭВМ.
Пакеты прикладных программ сложной структуры и программные системы появились в результате развития прикладного программного обеспечения. В первых из них имеется собственная управляющая часть — монитор, во вторых, кроме того, языковой процессор с проблемно-ориентированным входным языком. Программные системы вместе с соответствующим лингвистическим и информационным обеспечением называют программно-методическими комплексами САПР.
Управляющая часть программного обеспечения имеет иерархическую организацию и в общем случае в ней можно выделить различные уровни: уровень операционных систем вычислительной сети, операционных систем отдельных ЭВМ, мониторных систем САПР и мониторов отдельных ППП.
59
Основные функции управляющей части: связь с пользователем в режиме диалога, планирование вычислительного процесса, распределение вычислительных ресурсов, динамическое распределение памяти и др.
Принципы модульности и иерархичности позволяют организовать коллективную параллельную разработку различных частей программного обеспечения, создавать открытые программные системы, облегчают их комплексную отладку и информационное согласование.
Выделяют системный уровень разработки прикладного программного обеспечения, уровень прикладных программ и уровень подпрограмм (модулей).
Связи между отдельными программными модулями могут быть реализованы по управлению, информации, размещению и воздействию.
Связи модулей по управлению могут быть двух типов: последовательные связи между модулями без возврата в. предыдущий модуль и иерархические связи с подчиненностью модулей различных уровней.
Связи модулей по информации проявляются в передаче числовых массивов в несколько модулей пакета. Этот аспект взаимодействия модулей затрагивает проблемы построения информационного обеспечения САПР.
Связи модулей по размещению указывают группы модулей, одновременно размещаемых в оперативной памяти на различных этапах проектирования.
Связи модулей по воздействию отражают такие воздействия одних программ на другие, которые приводят к изменению самих программ, например воздействие языковых процессов на рабочие программы. Внутри рабочих программ связи модулей по воздействию стараются исключить.
К настоящему времени разработано большое, количество пакетов прикладных программ САПР электрических и электронных средств. В качестве примеров можно привести ДИСП, САМРИС-2, СПАРС, АРОПС, КРОСС и др. [1]. Из зарубежных систем можно отметить пакеты MicroCAP, PSPICE, P-CAD, SPADE и др. (подробнее см. гл. 18 настоящего пособия).
Значительное число этих пакетов ориентировано на автоматизацию проектирования печатных плат, цифровых и аналоговых интегральных схем, операционных усилителей, низкочастотных радиотехнических устройств. В то же время весьма недостаточно разработано пакетов программ проектирования радиочастотных, в том числе мощных устройств, радиоэлект
60
ронных средств СВЧ, пакетов, посвященных комплексному построению и интеграции радиочастотных средств, включающих н себя как усилители, так и пассивные радиочастотные устройства, вплоть до антенн и СВЧ-устройств.
Развитие программного обеспечения САПР требует все более значительных затрат высококвалифицированного труда. Стоимость многих промышленных САПР составляет миллионы долларов. Поэтому актуальной становится разработка САПР второго порядка, или САПР САПРов. Пока таких систем еще не существует, но прогресс в этом направлении имеется. В отличие от традиционных САПР в таких системах результат имеет нематериальный (информационный) характер. Различие результатов вызвано различными языками описания предметных областей: в-одном случае — чертежи, схемы, устройства, а в другом — программа проектирования. Однако и в том, и в другом случае возможен единый системный методологический подход к проектированию; становится актуальным создание и развитие банка инженерных знаний, необходимых для проектирования.
Вопросы и упражнения для самопроверки
1. Поясните состав лингвистического обеспечения САПР.
2. Приведите основные типы языковых процессоров; укажите разницу между трансляцией., компиляцией и интерпретацией программ.
3. Перечислите основные группы языков программирования.
4. Назовите типы и основные характеристики языков программирования.
5. Перечислите наиболее распространенные языки программирования, используемые в САПР.
6. Укажите основные типы языков проектирования САПР, приведите примеры языков.
7. Приведите структуру общесистемного программного обеспечения САПР.
8. Назовите основные классы системного программного обеспечения САПР, приведите Примеры операционных систем для ПЭВМ.
9. Приведите основные характеристики и примеры прикладного программного обеспечения САПР РЭС.
Глава 4
МАТЕМАТИЧЕСКИЕ МОДЕЛИ РАДИОЭЛЕКТРОННЫХ ОБЪЕКТОВ ПРОЕКТИРОВАНИЯ
§4.1. ОБЩИЕ СВЕДЕНИЯ О МАТЕМ,АТИЧЕСКИХ МОДЕЛЯХ РЭС
Проектирование радиоэлектронных средств с применением ЭВМ требует описания этого объекта на языке математики в виде, удобном для его алгоритмической реализации.
Математическое описание проектируемого объекта называют математической моделью. Математическая модель — это совокупность математических элементов (чисел, переменных, векторов, множеств и т.п.) и отношений между ними, которые с требуемой для проектирования точностью описывают свойства проектируемого объекта. На каждом этапе проектирования используется свое математическое описание проектируемого объекта, сложность которого должна быть согласована с возможностями анализа на ЭВМ, что приводит к необходимости иметь для одного объекта несколько моделей различного уровня сложности.
В общей теории математического моделирования математическую модель любого объекта характеризуют внутренними, внешними, выходными параметрами и фазовыми переменными. Внутренние параметры модели определяются характеристиками компонентов,, входящих в проектируемый объект, например номиналы элементов принципиальной схемы. Если проектируемый объект содержит п элементарных компонентов, то и его математическая модель будет определяться парамет-рами_оц...щп, которые образуют вектор внутренних параметров 117= |ац...&уп|т. Каждый из параметров w\, в свою очередь, может быть функцией, вектором или еще более сложным математическим функционалом в зависимости от объекта проектирования.
Выходные параметры модели — это показатели, характеризующие функциональные, эксплуатационные, конструкторско-технологические, экономические и другие характеристики проектируемого объекта. К таким показателям могут относиться
62
коэффициенты передачи, масса и габариты проектируемого объекта, надежность, стоимость и т.п. Понятия внутренних и выходных параметров инвариантны, при моделировании на более сложном уровне выходные параметры могут стать внутренними и наоборот. Например, сопротивление резистора является внутренним параметром при моделировании усилительного устройства, компонентом которого он является, но это же сопротивление будет выходным параметром при моделировании самого резистора, что требуется при пленочном его исполнении Вектор выходных параметров Модели будем обозначать F = |/.1..Л|т.
Внешние параметры модели — это характеристики внешней по отношению к проектируемому объекту среды, а также рабочие управляющие воздействия. Вектор внешних параметров в общем случае содержит множество самых различных составляющих, к его составляющим с полным правом можно отнести все, что говорилось ранее о составляющих вектора внутренних параметров. Будем обозначать его Q = ]qi...qm^.
Уравнения математической модели могут связывать некоторые физические характеристики компонентов, которые полностью характеризуют состояние объекта, но не являются выходными или внутренними параметрами модели (например, токи и напряжения в радиоэлектронных устройствах, внутренними параметрами которых являются номиналы элементов электрических схем, а выходными параметрами — выходная мощность, коэффициент передачи и т.п.). Такие характеристики называют фазовыми переменными^ Минимальный по размерности вектор фазовых переменных V = |vi...ur|T, полностью характеризующий работу объекта проектирования, называют базисным вектором. Например, при составлении уравнений математической модели_радиоэлектронных устройств в качестве базисного вектора V можно использовать вектор узловых потенциалов либо вектор напряжений на конденсаторах и токов в индуктивностях— переменные состояния. Использование вектора фазовых переменных позволяет упростить алгоритмическую реализацию программ, составляющих уравнения математической модели устройства.
В общем случае выходи ьш параметры F представляются операторами от векторов V, W, Q и могут быть определены из решения системы уравнений математической модели устройства. С учетом вышесказанного математическая модель любого радиотехнического объекта может быть представлена в виде следующих систем уравнений:
63
ч
(р (К IF, Q) - 0 ; (4.1)
F=V(V), (4-2)
где <р и *|/ — операторы, определяющие вид систем уравнений модели.
Система уравнений (4.1) может представлять собой систему линейных алгебраических уравнений, нелинейных уравнений различного вида, дифференциальных в полных или частных производных и представляет собой собственно математическую модель проектируемого объекта. В результате решения системы (4.1 ^определяются действующие в устройстве фазовые переменные V. Система уравнений (4.2) определяет зависимость выходных параметров объекта от фазовых переменных V.
В частных случаях составляющие вектора V могут являться внутренними или выходными параметрами объекта и тогда системы уравнений (4.1), (4.2) упрощаются.
Отметим, что часто моделированием называют лишь составлен ие_системы (4.1). Решение уравнений (4.1) и отыскание вектора F с помощью уравнения (4.2) называют анализом математической модели.
На каждом уровне моделирования различают математические модели проектируемого радиотехнического объекта и компонентов, из которых состоит объект. Математические модели компонентов представляют собой системы уравнений, устанавливающих связь между фазовыми переменными, внутренними и внешними параметрами, относящимися к данному компоненту. Эти уравнения называют компонентными, а соответствующую модель — компонентной.
Математическую модель объекта проектирования, представляющего объединение компонентов, получают на основе математических моделей компонентов, входящих в объект. Объединение компонентных уравнений в математическую модель объекта осуществляется на основе фундаментальных физических законов, выражающих условия непрерывности и равновесия фазовых переменных, например законов Кирхгофа. Уравнения, описывающие эти законы, называют топологическими, они отражают связи между компонентами в устройстве. Совокупность компонентных и топологических уравнений для проектируемого объекта и образует систему (4.1), являющуюся математической моделью объекта.
Исходя из задач конкретного этапа проектирования математическая модель проектируемого объекта должна отвечать самым различным требованиям: отражать с требуемой точностью зависимость выходных параметров объекта от его внутренних
64
ii внешних параметров в широком диапазоне их изменения; им(ть однозначное соответствие физическим процессам в объеме; включать необходимые аппроксимации и упрощения, ко-шрые позволяют реализовать ее программно на ЭВМ с различными возможностями; иметь большую универсальность, т.е. быть применимой к моделированию многочисленной группы однотипных устройств; быть экономичной с точки зрения зат-р г машинных ресурсов и т.п. Эти требования в своем большинстве являются противоречивыми, и удачное компромиссное удовлетворение этих требований в одних задачах может ока-ыгься далеким от оптимальности в других. По этой причине для одного и того же компонента или устройства часто приходится иметь не одну, а несколько моделей. В связи с этим классификация моделей должна выполняться по множеству признаков, чтобы описать все возможные случаи.
По уровню сложности различают полные модели и макромодели. Полные модели объекта проектирования получаются путем непосредственного объединения компонентных моделей в общую систему уравнений. Макромодели представляют со-оой упрощенные математические модели, аппроксимирующие полные.
В свою очередь, макромодели делят на две группы: факторные и фазовые модели.
Факторные модели предназначены для использования на следующих этапах проектирования в качестве компонентных моделей. Их выходными параметрами являются фазовые пере-м(нные полных математических моделей для следующего этапа проектирования.
Фазовые макромодели предназначены для использования на том же этапе проектирования, на котором их получают, для сокращения размерности решаемой задачи:
По способу получения математические модели радиотехнических объектов делят на физические и формальные. Физические модели получают на основе изучения физических закономерностей функционирования проектируемого объекта, так что структура уравнений и параметры модели имеют ясное физическое толкование. Формальные модели получают на основе п (мерения и установления связи между основными параметрами объекта в тех случаях, когда физика работы его известна недостаточно полно. Как правило, формальные модели тре-оуют большого числа измерений и по своей природе являются локальными, справедливыми вблизи тех режимов, в которых производились измерения. В литературе иногда такие модели называют моделями «черного ящика». '
Автоматизация проектирования радиоэлектронных средств
65
В современных системах автоматизированного проектирования формирование системы уравнений математической модели проектируемого объекта выполняется автоматичес-ки с помощью ЭВМ. В зависимости от того, что положено в основу алгоритма формирования системы уравнений, модели радиотехнических объектов можно разделить на электрические, физико-топологические и технологические.
Понятие электрической модели включает либо систему уравнений, связывающих напряжения и токи в электрической схеме, являющейся моделью объекта, либо саму электрическую схему, составленную из базовых элементов (резисторов, конденсаторов и т.п.), на основе которой можно в ЭВМ получить систему уравнений, связывающих напряжения и токи в модели объекта.
В физико-топологических моделях исходными параметрами являются геометрические размеры определяющих областей проектируемого объекта и электрофизические характеристики материала, из которых они состоят. В результате решения системы уравнений этой модели поля находятся внутри и на внешних выводах устройства. Такие модели применяются при разработке полупроводниковых приборов, СВЧ-устройств и в ряде других случаев.
Технологические модели основываются на параметрах технологических процессов изготовления проектируемого объекта (температура и время диффузии, концентрация диффузанта и т.п.). Выходные параметры такой модели — совокупность физико-топологических либо технологических параметров.
По способу задания внутренних и внешних параметров математические модели делят на дискретные и непрерывные.
Различают модели статические и динамические в зависимости от того, учитывают ли уравнения модели инерционность процессов в проектируемом объекте или нет. Статические модели отражают состояние объекта проектирования при неизменных внешних параметрах и не учитывают его переходные характеристики. Динамические модели дополнительно отражают переходные процессы в объекте, происходящие при изменении во времени внешних параметров.
Существуют и другие варианты классификации математических моделей элементов и узлов радиоустройств.
При проектировании радиотехнических объектов наиболее широкое распространение получили электрические модели. Поэтому в настоящей книге основное внимание будет уделено именно этому виду моделей проектируемых объектов.
66 ।
Программа моделирования радиотехнических и других объектов должна автоматически формировать систему уравнений математической модели из базового набора элементарных схемных элементов, компонентные уравнения для которых хранятся в библиотеке программы. Для синтеза адекватных реальному объекту моделей большинства радиотехнических устройств пазовый набор должен содержать по крайней мере пять типов сосредоточенных схемных элементов, перечисленных в табл. I I. В таблице приведены и компонентные уравнения для каждого из элементов базового набора.
Таблица 4.1
Базовые элементы Компонентные уравнения
в операторной форме во временной форме в частотной форме
1 Резистор:
линейный и = Ri(s) u(m) = Ri(a>)
управляемый током и = r(i)i(s) u(a) =
управляемый напряжением i = G(u)u(s) i(t) = G[u(l)]u(t) t(co) = G[u(co)]u(co)
2 Конденсатор:
линейный i = Csu(s) i(t) = cdu/dt i(co) = /<оСи(ш)
управляемый током u = -^-s C(i) u(t)= f-^-d/ J C(i) , > 1'(“) u(co) = —
управляем ый напряжением i = sC(u)u(s) /(/) WM dt i(<o)=/<oC(u)u(<b)
3. Индуктивность:
линейная и = Lsi(s) u(<b) =
управляемая током и = sL(i)i(s) dt u(a>) — jaiL(i)i((ti)
управляемая потоком и — s<P(s) dt «(<в) = /а>Ф(а>)
67
Продолжение табл. 4.1
Базовые элементы Компонентные уравнения
в операторной форме во временной форме в частотной форме
4. Источник напряжения:
независимый u=E(s) и = E(t) u(®) — Е(а>)
управляемый ТОКОМ tab и = £!»„„(«)] u(t) - Ер0(,(/)] и(а) -
управляемый напряжением иаь « = £!«„»(*)] и(<а) - Ejuebt®)]
5. Источник тока:
независимый t = /(s) » = /(/) '(®) - /(®)
управляемый током 1аъ « =/[»<(.(«)] Щ) =1[1М] i(<o) = /[U( w)]
управляемый напряжением Uab i(w) = /[«<,(,{о>)]
Компонентные уравнения могут связывать мгновенные значения напряжений и токов, действующих на базовом элементе, либо их комплексные амплитуды. В первом случае говорят О; моделировании во временной области, во втором — в частот ной. Чем больший набор базовых компонентов позволяет испо? льзовать данная САПР, тем более многофункциональной она^ является. В табл. 4.1 отсутствуют распределенные и излучаю щие элементы, ряд специальных элементов теории цепей (транс’ форматоры, преобразователи импедансов и т.д.), которые будут описаны в последующих главах по мере необходимости.
Рассмотрим теперь примеры электрических моделей различу ных функциональных компонентов, из которых состоят радио технические устройства.
§4.2. ПРИМЕРЫ МОДЕЛЕЙ ДИСКРЕТНЫХ ЭЛЕМЕНТОВ РАДИОЭЛЕКТРОНИКИ
При разработке электрических моделей функциональных компонентов радиоэлектроники (после подробного изучения физических основ его функционирования) стремятся отразить основные зависимости, наиболее сильно влияющие на работу
68
самого компонента и связанных с ним других компонентов. Характерной особенностью радиоэлектронных компонентов является зависимость их основных характеристик от конструктивного исполнения. Эта зависимость естественным образом должна учитываться и в его электрической модели. Так, если ком
понент выполнен дискретным, то его электрическая модель должна учитывать влияние корпуса и выводов. Если компонент является составной частью интегральной схемы, то модель должна учитывать, каким образом изготовлена эта схема. При гибридно-интегральной технологии необходимо учитывать влияние подложки и физические свойства материалов, из которых выполнены отдельные элементы схемы. В монолитной монокристальной микросхеме модели компонентов должны отражать способы изоляции их друг от друга, электрофизические свойства подложки, технологйческий процесс изготовления элементов. В связи с этим современные САПР содержат по нескольку электрических моделей\ компонентов, выполняющих в устройствах одну и ту же функцию.
Рассмотрим примеры электрических моделей дискретных компонентов радиоэлектроники при различном их конструк-
тивном выполнении.
Модель пленочного резистора. Пленочные резисторы представляют обычно узкие полоски высокоомной резистивной пленки, нанесенной на диэлектрическую подложку, снабженные низкоом-пыми контактными площадками, как показано на рис. 4.1, а. Сопротивление такого резистора рассчитывается по известной формуле 7? = RqI/w, где Rq— поверхностное сопротивление резистивного слоя; /, w— длина и ширина резистивной полоски. Высокоомные резисторы выполняются в виде змеек с прямоугольными или закругленными изгибами, и их сопротивление рассчитывается по аналогичным формулам, но с поправочными коэффициентами, зависящими от конкретной топологии резистора. В электрической модели обычно учитывают наличие паразитных шунтирующих емкостей между выводами резистора C~Ewd/l и „ wl
па корпус Ск ~ в—, где £ — диэлектрическая проницаемость d
подложки, a d — ее толщина. Глобальная модель пленочного
резистора, справедливая в широком диапазоне рабочих частот, таким образом, примет вид, показанный на рис. 1.1, б. Локальная модель, предназначенная, например, для цепей постоянного тока, будет содержать только один резистор R.
Рис. 4.1. Пленочный резистор (а) и его электрическая модель (б)
69
Р и с. 4.2. Диффузный резистор (а) и его электрические модели (б), (в)
Модель диффузного резистора. Диффузные резисторы представляют собой резистивные полупроводниковые слои, созданные в кристалле в результате локальной диффузии и изолированные от остального объема кристалла р-п-переходом. Выводы резистора создаются металлизацией на поверхности структурных областей. Наиболее распространенная структура диффузного резистора, сочетающая высокое сопротивление с хорошей температурной стабильностью, показана на рис. 4.2, а.
При построении электрической модели диффузного резистора необходимо учитывать, что обратносмещенный р-п-переход обладает током утечки и распределенной емкостью вдоль его длины. Глобальная модель будет представлять собой распределенную цепь (рис. 4.2, б), описываемую уравнением в част-t ных производных
л2»
— = г, [С, (u) du/dl + /, (и)] dz
с граничными условиями u(zi, = u(z2, /)=U2(0. где Г|/
Ci, /] — удельные на единицу длины сопротивление, емкость И ток утечки диффузного резистора; Z\, z-A—координаты вывоА дов резистора; щ, иг—напряжения на выводах относительнд подложки. у
Если пренебречь током подложки, то локальная модель тая, кого резистора может быть представлена в виде рис. 4.2, в.
Модель пленочного конденсатора. Пленочные конденсатов ры формируются последовательным нанесением на диэлектрин четкую подложку металлической, диэлектрической и опять мен таллической пленок (рис. 4.3, а). Удельное поверхностное сопротивление металлических пленок достаточно велико (0,1...3,0 Ом/мм ), и потери в них становятся заметными уже на частотах порядка единиц мегагерц. На высоких частотах существенную добавку вносят релаксационные потери R, связанные с поляризацией диэлектрика. В глобальной электрической модели такого конденсатора помимо полезной емкости С необходимо учесть и паразитные эффекты, обусловленные потерями в металлических электродах г и диэлектрике R.
70
R
Рис. 4.3. Пленочный конденсатор (а) и его электрические модели (б)
На рис. 4.3, б представлена глобальная электрическая модель пленочного конденсатора. Величины R и L определяются экспериментально, а значения Сиг можно найти по формулам С = zS/d', г = 2Rolw, где S — площадь перекрытия обкладок, d— толщина диэлектрической пленки, Ro — поверхностное сопротивление пленок металлизации, /, w — длина и ширина обкладок. Для создания малогабаритных конденсаторов с большой емкостью могут применяться многослойные структуры, состоящие из нескольких последовательно наносимых диэлектрических и металлических слоев, и тогда в модели приходится учитывать распределенный характер конденсатора.
Локальная модель пленочного конденсатора представляется обычно просто конденсатором с соответствующей емкостью.
Модель диффузного конденсатора. Диффузные конденсаторы представляют собой барьерную емкость р-п-перехода, в котором диэлектриком является обедненный носителями слой. Такой конденсатор может быть реализован на различных типах переходов, например когда одной из обкладок является базовая область p-типа, а второй — область «-типа (рис. 4.4, а). В электрической модели диффузионного конденсатора кроме паразитных элементов следует учесть нелинейность емкости р /г-перехода, зависящей от приложенного напряжения: (>'([/) — Со/(1—и/ут)у—). где Со — емкость перехода при п = 0; у = 0,3...0,5 — коэффициент, зависящий от характера распределения примесей в зоне перехода. Глобальная электрическая монель такого конденсатора для случая изоляции структуры диэлектрическим слоем приведена на рис. 4.4, б. Здесь R — нелинейное сопротивление р-и-перехода, г —объемное сопротивление //'-области, С — емкость, «-область — подложка.
Рис. 4.4. Диффузный конденсатор (а) и его электрическая модель (б)
71
Модель биполярного транзистора. К настоящему времени известно много электрических моделей биполярных транзисторов. В САПР радиоэлектронных средств наиболее часто используются модели Эберса — Молла, обобщенная модель управления зарядом Гуммеля — Пуна, модель Линвилла, а также локальные П- и Т-образные модели линейных приращений Джиаколлето. Рассмотрим, например, один из вариантов модели Эберса — Молла (рис. 4.5, а), отражающей свойства транзисторной структуры в линейном режиме работы и в режиме отсечки. На рисунке гэ, г6, гк — сопротивления эмиттер-ной, базовой и коллекторной областей транзистора и контактов к ним, /б> А — управляемые напряжением на входном переходе и„ источники тока, отражающие передачу тока через транзистор, /?Эб — сопротивление утечки перехода база-эмиттер. Ток источника /б связан с напряжением на переходе соотношением
Рис. 4.5. Электрические модели биполярного транзистора: а — модель Эберса
Молла, б — глобальная модель дискретного транзистора; в
интегральный
транзистор, г — модель интегрального транзистора, д — модель Джиаколетто
72
/б = /б.,[ехр(ип/(тут))— 1], где /бо — ток насыщения перехода, ут = (0,3...1,2)В— контактная разность потенциалов, т - эмпирический коэффициент.
Параллельно переходу база-эмиттер включены барьерная емкость Сбэ и диффузионная емкость Сдэ перехода. Величина Сб, определяется обратным напряжением на переходе ип и зависит от него по закону
Сбэ = Соб/(1—ип/ут)\
где Соб — емкость перехода при ип = 0; у = 0,3...0,5 — коэффициент, зависящий от распределения примесей в области базы транзистора.
Диффузионная емкость является функцией тока /б, протекающего через переход, и определяется выражением
Сдэ = Alft,
|де А— коэффициент, зависящий от свойств перехода и его температуры.
Коллекторно-базовый переход моделируется аналогично, отличие состоит лишь в учете только барьерной емкости перехода С'кб =-----25----, так как при работе транзистора в линейном
(1-«п / Yt)Y
режиме и режиме отсечки коллекторного тока этот переход (акрыт. Выражение для тока управляемого источника коллекторного тока, моделирующего усилительные свойства транзистора, имеет вид
/к = р/бо[ехр(ип/(тУт))—1],
। де Р — коэффициент усиления транзистора в схеме с общим ,миттером.
Параметры модели Эберса — Молла могут быть получены либо расчетным путем на основе анализа физико-топологической модели транзистора, либо измерены экспериментально. Наиболее легко определяются статические параметры модели па постоянном токе.
Для дискретного биполярного транзистора глобальная электрическая модель получается добавлением к модели Эберса — Молла паразитных параметров: индуктивностей выводов и емкостей на корпус, как показано на рис. 4.5, б. При использовании модели рис. 4.5, а для моделирования бескорпусно-го транзистора необходимо учесть лишь индуктивности выводов, кроме индуктивности общего электрода.
Биполярные интегральные транзисторы обычно выполняют по планарно-эпитаксиальной технологии. Если изоляция тран
73
зисторов в микросхеме друг от друга и от подложки осуществляется с помощью диэлектрической изоляции, то структуры транзисторов формируются в специальных «карманах»—г однолегированных областях, предварительно изолированных - оч поликристаллической подложки слоем диэлектрика (обычйо оксидом кремния) (рис. 4.5, в). Электрическая модель такого транзистора должна учитывать возникновение /?-С-структуры, образованной распределенным по длине коллекторной области объемным сопротивлением изолирующего слоя и емкостью коллектор—‘подложка. Влияние изолирующего слоя может быть учтено в модели транзистора (рис. 4 5, а) подключением к коллекторному выводу параллельного соединения конденсате
Г и резистора /?п (рис. 4.5, г).
11 образная электрическая модель линейных приращений еДжиаколлето) для биполярного транзистора по схеме с общим эмиттером показана на рис. 4.5, д. Эта модель включает семь параметров:
г-„ го, гк — распределенное сопротивление материала базы, е Л
эми гера и коллектора и их выводов, 8 =—— = —-— кру
dU4
тизна транзистора по току в рабочей точке /?бэ = (1 + ₽o)/S — дифференциальное сопротивление эмиттерного перехода, n al а (1
ро =—- = у-------коэффициент передачи транзистора по току
й(/6 1-а0
в схеме с общим эмиттером на постоянном токе, <зд—коэффи* циент передачи тока транзистора в схеме с общей базой!; Гбк — дифференциальное сопротивление коллекторно-б,,зовогс перехода, возникающее вследствие модуляции ширины'базы; /?кэ —’ сопротивление, учитывающее конечную проводимость я выходной цепи транзистора; Сбк— барьерная емкость обра: несмещенного коллекторно-базового перехода; СбЭ — суммар> ная емкость эмиттерного перехода, включающая диффузиощ ную и барьерную емкости перехода, тэ- — коэффициент.
Такая электрическая модель транзистора отражает его работу в режиме линейного усиления без захода рабочей точки в область отсечки. (!
Электрические модели линейных приращений для дискретного и интегрального биполярных транзисторов получают и: базовой модели (рис. 4.5, д) добавлением соответствующих паразитных реактивных элементов, подобно тому, как это делалось для модели Эберса — Молла.
Физико-топологическая модель транзистора. Рассмотриь теперь для примера построение физико-топологической модели биполярного транзистора в диффузионно-дрейфовом прибл,
74
/Кении. Это приближение основано на локальной и феноменологической зависимости плотности тока в полупроводнике от градиента потенциала электрического поля и концентрации носителей заряда, причем коэффициенты пропорциональности содержат в качестве множителя подвижность носителей заряда. В предположении невырожденного полупроводника и малости электрического поля плотность тока в полупроводнике складывается из плотностей тока проводимости (дрейфовой составляющей) и диффузии. Выражение для плотностей электронного и дырочного токов имеют такой вид:
in = е[цппЕ + Dn V м);
jp = Dp V р);
dn/dt = -V in-Rn-е
dp/dt=-^ jp-Rp, е
где е — заряд электрона; ц„, — подвижность электронов и
дырок соответственно, п, р — концентрация электронов и дырок н материале полупроводника; Е — напряженность электрического поля; Dp, Dn — коэффициенты диффузии носителей;
п - п р-р
V — оператор Гамильтона; Rn =----Rp = -------- —скорости
т т
п р
рекомбинации носителей; пр, рр — равновесные концентрации носителей; хп, хр—время жизни электронов и дырок.
Для упрощения задачи рассмотрим одномерную модель транзистора, которую разделим на ряд характерных областей, как показано на рис. 4.6. Каждую из областей будем рассматривать по отдельности. В базовой области можно считать, что электронный ток отсутствует и для базового тока можно записать
jp = e\ippE —eDp -^ = О, dx
откуда для напряженности электрического поля в базе транзистора несложно получить
F-Dp 1 dp 1 dNP — j т *
р dx Np dx
где Np — избыточная концентрация дырок в области базы, ут = —- —контактная разность потенциалов.
75
Рис. 4.6. Физико-топологическая модель транзистора
С учетом последнего выражения исходная система уравнений диффузионно-дрейфового приближения упрощается и базовая область транзистора будет описываться краевой задачей относительно распределения концентрации носи-
телей n(x, t) из системы уравнений
dn(x,t) _ 1 d/„ п~пр.
dt е dx тп
/„ = ерппЕ + eDn^ dx при следующих граничных условиях у эмиттерной и коллекторной границ базовой области:
п(хээб,0 = п^хбэб) ехр[иэб(0Лт] = пэ(0;
и(хбкб, 0 = Пр(хбкб)ехр[иКб(О/тт] = «к(0.
где пэ(0> пк(0 — полная концентрация электронов в эмиттере и коллекторе, пр — равновесная концентрация носителей в базе, т„ — время жизни электронов в базе, ут—контактная разность потенциала, иэб, иКб — напряжения база — эмиттер и база — коллектор.
На практике удобнее иметь систему уравнений относительно избыточной концентрации электронов: N(x,t) =n(x,t)—пр(х).
Граничные условия для N (x,t) имеют вид
7УЭ = Пр(хбЭб)ехр[(иэб(ОЛт)— 1 ];
NK = Пр(хбКб)ехр[(икб(ОЛт)— 1].
Сформулируем теперь краевую задачу для эмиттерной области транзистора в предположении прямого смещения н!а входном р-п-переходе. Считая, что в «-области электронны' ток отсутствует, запишем систему уравнений:
1 d/P _ P(x,t)-Pp(x) ।
е dx
г
т₽
/рэ = —e\ipp{x.t)yjNр —— - еД ах ах
Граничные условия для данной системы характеризуют концентрацию дырок в эмиттере на границе перехода база — эмиттер
р(хээб) = рр(хэб)ехр[(иЭбЛт)— 1]
)
76
г
и плотность тока, обусловленного поверхностной рекомбинацией:
jps — sSpp3(0).
Совместное решение краевых задач для областей базы и миттера позволяет полностью описать работу транзистора.
Как видно из приведенных выше соотношений, даже упрошенная физико-топологическая модель транзистора требует решения краевых задач, что затрудняет использование подобных моделей при моделировании радиоэлектронных устройств, многие из которых содержат большое количество (до нескольких тысяч) полупроводниковых приборов.
Поэтому такие модели в основном используются при разработке самих радиоэлектронных компонентов.
Модель полупроводникового диода. Основой полупроводникового диода является р-п-переход на границе двух слоев полупроводникового материала с различными типами проводимости. В качестве модели диода можно использовать модель Эберса — Молла для одиночного перехода, показанную па рис. 4.7, а. Здесь Сд—сумма барьерной и диффузионной емкостей перехода, Ro—сопротив- ление утечки, г— объемное сопротивление тела ^базы, завися- щее от геометрических размеров и степени легирования полупроводника, /у—управляемый напряжением на переходе источник тока, ток которого подчиняется закону
/^ = Л/0[ехр(и117’/М)—1], |де /0 — ток насыщения перехода, обусловленный тепловой генерацией неосновных носителей в слоях полупроводника, А и V — эмпирические коэффициенты, Т — абсолютная температура.
Данная модель хорошо аппроксимирует вольт-амперную характеристику диода, кроме области пробоя (рис. 4.7, б), являющуюся для большинства диодов нерабочим режимом. В электрической модели дискретного диода необходимо учесть наличие индуктивностей выводов L\ и L%, емкости корпуса и контактов Ск и Сп (см. рис. 4.7, в).
Интегральный диод обычно представляет собой полную структуру биполярного транзистора, изолированную от подложки и используемую в диодном включении. Возможные варианты такого включения показаны на рис. 4.7, г, при этом рабочим является лишь один из переходов, второй переход либо не используется вовсе, либо подключается параллельно первому. Структура электрической модели такого диода зависит от способа изоляции перехода и от включения диода. Так, если в транзисторной структуре вообще не используется коллекторная область, то для такого диода справедлива модель, приведенная на рис. 4.5, а без дополнительных паразитных элементов.
77
I
Модель
ЗЛрса -Молла
в)
Рис. 4.7. Электрические модели полупроводникового диода:
а — модель Эберса — Молла, б — вольт-амперные характеристики диода и его модели, в — глобальная модель дискретного диода, г — варианты выполнения интегрального диода
г)
Модель МДП-транзистора. Рассмотрим электрическую модель полевого МДП-транзистора. МДП-транзистор в отличие от биполярного является четырехполюсным прибором, типовая структура которого показана на рис. 4.8, а. Кроме трех основных выводов — истока, стока и затвора — он имеет и четвертый — подложку. Структура электрической модели МДП-транзистора, аналогичной модели линейных приращений биполярного транзистора, представлена на рис. 4.8, б. Здесь элементы Ск — учитывают инерционные свойства носителей в канале, представляя собой сосредоточенный эквивалент распределенной емкости и сопротивления, межэлектродные емкости С'зи и
6)
Рис. 4.8. МДП-транзистор и его модель:
а — структура МДП-транзистора, б — электрическая модель конечных приращений
78
С'зс обусловлены перекрытием областей стока и истока областью затвора, а С"-мСзс — влиянием частей канала, находящихся под управляющим воздействием затвора, г311 и г,с — сопротивления утечек, гс и ги — объемные сопротивления областей стока и истока, на которые распространяется влияние затвора, Rtn, — сопротивление p-области между подложкой, стоком и истоком. Для управляемого генератора тока, отражающего усилительные свойства транзистора, используется несколько видов соотношений, из которых большую известность получила уточненная модель Хофстайна:
it, = |(2Д, + Кг\и3—иы)—2Дщси]исц при ис< и3—иоэ);
if. = 1Д1(Мз—«<>э) + ^2«сиКиз—Иоэ) при ис > и3—иаз,
где Д1 — р-,ф£/,2/(2£W7) — удельная крутизна, L, Z — длина и ширина области канала, W, — толщина и диэлектрическая проницаемость слоя диэлектрика под затвором, — эффективная подвижность носителей в канале, К2— удельная выходная проводимость, обусловленная модуляцией длины канала., ис, ии, — напряжения на стоке, истоке и затворе соответственно,
Иоэ = 6(7^1! + 2Ф - 4%Ф) + u0> ь = 72£пеМ1 / со • ф = yjln(Nn/Ni'), Со — удельная емкость диэлектрика, Nn, еп — концентрация примеси и диэлектрическая проницаемость подложки, Но—пороговое напряжение при ип = 0.
Электрические модели дискретных МДП-транзисторов получаются по аналогии с моделями дискретных биполярных транзисторов, моделью же интегрального МДП-транзистора может служить непосредственно модель, показанная на рис. 1.8, б, ибо канал транзистора изолирован от основного объема подложки слоем объемного заояда и взаимным влиянием тран-и1 сто ров можно пренебречь.
В заключение заметим, что при топологическом формировании системы уравнений математической модели к электрическим моделям могут предъявляться специальные требования, например могут не допускаться нелинейные пассивные пазовые компоненты электрических моделей. Однако это не приводит к большим трудностям в моделировании, ибо, согла-। ио [8, 14], любой нелинейный пассивный компонент может быть представлен в виде линейного элемента той же природы и нелинейного источника тока или напряжения.
§4.3. ЭЛЕКТРИЧЕСКИЕ МОДЕЛИ ИНТЕГРАЛЬНЫХ СХЕМ
Моделирование интегральных схем (ИС) в радиоэлектронных устройствах, включающих несколько десятков или даже сотен корпусов интегральных схем, представляет собой неп
79
ростую задачу, прежде всего из-за ее размерности. ИС или другой крупный электронный функциональный узел состоит из тех же компонентов, примеры электрических моделей которых рассмотрены в предыдущем параграфе. В принципе, разделив ИС на простейшие компоненты, можно получить ее модель из электрических моделей этих компонентов, как это делается при формировании моделей радиоэлектронных устройств в целом. Для ИС средней и высокой степени интеграции такой путь построения электрической модели связан с неоправданно большими вычислительными затратами. Это объясняется слишком высоким порядком системы уравнений математической модели для таких схем и значительными трудностями определения номиналов элементов электрических моделей отдельных компонентов, из которых состоит ИС. Поэтому более рациональным представляется использование для моделирования ИС в радиоэлектронных устройствах макромоделей, имеющих в пределах требуемой точности такие же внешние характеристики, как и реальное устройство.
Один из возможных путей построения электрических макромоделей ИС состоит в том, чтобы на первом этапе разработать наименее подробную локальную макромодель ИС, отражающую главные особенности работы ИС в радиоэлектронных устройствах. На втором этапе в модель добавляются элементы, моделирующие неидеальнбсть характеристик реальной ИС: конечные входное и выходное сопротивления, частотные зависимости характеристик, задержки в срабатывании и т.п. Достоинством такого подхода к построению макромоделей является явный физический смысл каждого базового элемента в электрической модели, недостатком — неформализованность подхода и, как следствие, необходимость определения номинала ряда базовых элементов путем измерений.
Рассмотрим примеры такого подхода при разработке макромоделей аналоговых и цифровых ИС.
Модель операционного усилителя. Одним из самых распространенных в современной схемотехнике устройств является операционный усилитель. Для него характерны наличие двух дифференциальных входов, большой коэффициент усиления (30... 100 дВ), частотная зависимость коэффициента усиления, смещение выходного напряжения относительно нуля при нулевых напряжениях на дифференциальных входах усилителя, конечные значения, входных и выходного сопротивлений, входные токи смещения [13].
В локальной модели идеального операционного усилителя не учитываются частотные зависимости коэффициента передачи, смещение выходного напряжения, входные токи смещения.
80
Электрическая макромодель из базовых элементов, отражающая указанные свойства операционного усилителя, показана на рис. 4.9, а. Здесь резистор R\ отражает конечное входное сопротивление между двумя дифференциальными входами щ и /<2. управляемый источник напряжения Ut= К(и.\—112)— усилительные свойства (К = пы*_ — крутизна по входному сиг-палу), резистор /?2 — конечную нагрузочную способность операционного усилителя (зависимость выходного сигнала от сопротивления нагрузки усилителя).
Реальная амплитудная передаточная характеристика операционного усилителя показана на рис. 4.9, б, а частотная характеристика — на рис. 4.9, в. Возможный вариант глобальной макромодели операционного усилителя для линейного режима работы в диапазоне частот приведен на рис. 4.9, г.
Здесь смещение выходного сигнала относительно нуля учитывается с помощью постоянного источника напряжения (7'1= Д(/ на одном из входов модели. Входные токи смещения, необходимые для базового смещения транзисторов во входном шфференциальном каскаде операционного усилителя, отражены источниками постоянного тока /| и /2 на входных зажимах
Рис. 4.9. Макромодель операционного усилителя:
а—локальная модель усилителя, б —- амплитудная характеристика, в — частотная характеристика, г — глобальная модель операционного усилителя
81
модели. Частотную зависимость коэффициента передачи операционного усилителя целесообразно учитывать с помощью промежуточного управляемого источника I^SU с комплексным Сопротивлением нагрузки А?з—Сз, напряжение на котором имеет такую же частотную зависимость, как и коэффициент передачи усилителя. Усложнением этого сопротивления можно обеспечить практически любую частотную характеристику коэффициента передачи. Если это сопротивление нагрузки будет нелинейным, то можно будет учесть и нелинейность амплитудной передаточной характеристики операционного усилителя. Источник напряжения Ui — KU?,, управляемый напряжением {/3, характеризует усилительные свойства, а резистор А?4 и конденсатор С4 — нагрузочную способность операционного усилителя.
На основе электрической модели рис. 4.9, г можно разрабатывать макромодели и множества других устройств радиоэлектроники, реализуемых на основе операционных усилителей: умножителей, делителей, сумматоров напряжения, логарифмических и антилогарифмических устройств, интеграторов, дифференциаторов, компараторов и ряда других устройств. Для построения моделей этих устройств макромодель операционного усилителя должна быть дополнена электрическими моделями элементов, подключаемых к входным и выходным зажимам усилителя для реализации требуемой функции.
Используя аналогичный подход, можно разрабатывать электрические макромодели и цифровых ИС. Такие модели, несмотря на функциональное различие цифровых ИС, будут похожи друг на друга по принципам построения. Поэтому далее рассмотрим только макромодели сумматора с инверсией ИЛИ-HE и JKRS-триггера [13, 20].
В локальных макромоделях цифровых функциональных элементов не конкретизируется физическая природа сигнала (ток или напряжение), уровни логического нуля или единицы считаются фиксированными и функциональный элемент описывается соответствующим логическим уравнением либо таблицей истинности. Такие макромодели функциональных элементов используются на начальных этапах проектирования цифровых устройств, когда наиболее важным фактором представляется правильная работа всего цифрового устройства. Вопросы моделирования цифровых устройств на логическом уровне рассматриваются в гл. 7.
82
a)
Рис. 4.10. Двухвходовой инвертирующий сумматор и его макромодель: и сумматор, б-временные диаграммы работы инвертирующего сумматора, в - макромодель сумматора
В электрических моделях цифровых функциональных элементов конкретизируется природа сигналов в устройстве, учитываются задержки в срабатывании цифровых элементов, их конечные входные сопротивления и нагрузочная способность, допускается, что уровни логической единицы и нуля могут изменяться в некотором интервале, например при изменении напряжения питания, который можно установить экспериментально или моделированием цифрового элемента на уровне отдельных компонентов, из которых он состоит.
Модель элемента ИЛИ-HE. Логическое функционирование двухвходового инвертирующего сумматора (рис. 4.10, а) описывается логическим уравнением и = ui U «2 либо таблицей истинности (табл. 4.2). При подаче на входы ui и «2 напряжений, соответствующих уровню логического нуля в цифровом устройстве, на выходе сумматора и будет напряжение, соответствующее уровню логической единицы, во всех остальных случаях уровень и будет соответствовать уровню логического нуля.
Т а б л и ц а 4.2 Та б л и ц а 4.3
«1 «2 и UR US
Запрещенная комбинация
0 0 1 0 0
0 1 0 0 1 0 1
1 0 0 1 0 1 0
1 1 0 1 1 Запоминающая комбинация
83
Временные диаграммы работы инвертирующего сумматора показаны на рис. 4.10, б, где /о и /j — максимальные задержки в срабатывании сумматора_при спаде и нарастании выходного сигнала (в дальнейшем для упрощения положим и~i и и ] — минимальное и максимальное напряжения, соответствующие логической единице в моделируемом цифровом устройстве, ио, но = 0— аналогичные напряжения для уровня логического нуля.
Один из возможных вариантов электрической макромодёли инвертирующего сумматора, учитывающей перечисленные выше особенности его работы, представлен на рис. 4.10, в. Здесь элементы Ri, Ci, и R%, Сч отражают полные входные сопротивления элемента, логические значения уровней напряжения на которых и\ и и?. определяются по следующему правилу: если напряжение на любом из входов больше и~\ и меньше и то на этом входе присутствует уровень логической единицы, в противном случае — уровень логического нуля. Зависимый источник, отражающий логические свойства сумматора /2, определяется соотношением.
_______; • /2 = («а + d)/R,
где и = «| U и.2 — логическое состояние на выходе сумматора, определяемое логическим уравнением либо табл. 4.2 в зависимости от логических уровней напряжений на входах элемента,
Рис. 4.11. JKSR-триггер и его макромодель:
а — триггер, б, в — временные диаграммы работы триггера, г — макромодель JKSR-триггера
84
а и d — коэффициенты, определяемые из условия равенства напряжения «з уровню, соответствующему логическому нулю на выходе сумматора при и = 0, (н0 < н3 < и^) и уровню единицы при и = (ut~ £ и3 < и,).
Элементы /?з и С3 (R3C3 = т/3) служат для моделирования задержки в срабатывании сумматора. Ток второго зависимого источника /; определяется соотношением Источник /(
совместно с резистором /?( моделирует конечную нагрузочную способность элемента.
Приведенная модель по переходным характеристикам хорошо согласуется с характеристиками реального инвертирующего сумматора..
Модель JKRS-триггера. Рассмотрим пример построения электрической макромодели более сложного цифрового элемента— JKRS-триггера (рис. 4.11, а). Триггер имеет два информационных входа: J и К. Входы установки и сброса S и R при работе триггера в асинхронном режиме устанавливают триггер в состояние 1 или 0 в. соответствии с таблицей переходов (табл. 4.3). В синхронном режиме работой триггера управляет вход С в соответствии с таблицей переходов (табл. 4.4)-, причем переключение триггера происходит по фронту синхронизирующего импульса. Сигналы установки и сброса на входах S и R имеют приоритет по сравнению с тактовыми сигналами на входе С. Временные диаграммы, поясняющие работу JKRS-триггера, показаны на рис. 4.11, б, в.
Таблица 4.4
«с «/ «к UQ UQ
0 0 0
1 0 0 Предыдущее состояние
0 1 1
1 0 1
0 0 1 0 1
1 1 0 0 1
0 1 0 1 0
1 1 1 1 0
0 1 1 0 1
1 1 1 0 1
0 1 1 1 , 0
85
На диаграммах выделены задержки в установлении выходного напряжения для сигналов установки или сброса S и R (t'i и /'о) и задержки в установлении выходного напряжения для тактовых сигналов С (£"i и /"0).
Работу JKRS-триггера можно описать системой логических уравнений:
Fi = u^U/fUc; F3 = F2qt;
Ql = ^2^2ы/’ 93 =
F2 = F 4 =
<72 = Q\F}uk\ q$ = uKFAq3,
где нд, us, uc, uj, uk — логические уровни напряжений на входах R, S, С, J, К соответственно.
В макромодели триггера необходимо учитывать конечные входные сопротивления элемента по всем входам, логические функции триггера, задержки установления выходного напряжения для логического нуля и единицы при подаче тактовых сигналов, сигналов установки и сброса, а также конечную нагрузочную способность триггера.
Электрическая макромодель триггера, учитывающая все указанные эффекты, приведена на рис. 4.11, г. Здесь входные сопротивления всех управляющих и информационных входов моделируются параллельными соединениями резисторов и конденсаторов R\...R$, и С1...С5. Подобно предыдущему случаю, логические уровни сигналов иа этих входах (/ определяются по правилу: если напряжение на входе больше или равно некоторому минимальному пороговому уровню то сигнал на данном входе принимается равным логической единице, в противном случае считается, что на входе присутствует сигнал логического нуля.
Токи зависимых источников 1\ и /2, моделирующих логическую функцию элемента, определяются соотношениями
Л =(я| <7з + di)/R&
/2 = (02*72 + di)/R3,
где логические функционалы q3 и определяются из решения приведенной выше системы логических уравнений, коэффициенты «1, «2, d\, di определяются из условия равенства aiq3 + d\ и «2<74 + di напряжению логического нуля и < ио, если q — 0, и напряжению логической единицы и >и[, если q=\.
Времена задержки переключения триггера по сигналам установки и сброса 5 и R и по синхросигналам входа С ‘моделируют интегрирующими цепочками RyC& и R$Ci. Для упроще
86
ния модели, приведенной на рис. 4.11, г, задержки установки логического нуля и: единицы на выходе JKRS-триггера принимаются для S — R- и С-йходов одинаковыми.
Токи управляемых источников /з = 5«б и l^Su? моделируют выХодйые цепи триггера, а резисторы Rio и /?ц — нагрузочные способности по выходам Q и Q.
Таким образом, электрическая модель рис. 4.11, г отражает основные особенности работы JKRS-триггера и может быть использована для моделирования цифровых устройств на их основе.
Электрические макромодели других цифровых элементов различной сложности приведены в [20].
§4.4. ТОПОЛОГИЧЕСКИЕ ОСНОВЫ АВТОМАТИЗИРОВАННОГО ФОРМИРОВАНИЯ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ РЭС
I
Как указывалось ранее, процесс формирования уравнений математической модели радиоэлектронного устройства на основе электрической модели этого устройства, состоящей из базовых элементов (см. §4.1), выполняется с помощью ЭВМ. Общие методы решения задачи формирования системы уравнений математической модели основываются на теории графов. Теория графов—обширная область математики, имеющая множество инженерных и вычислительных приложений. Здесь нас будут интересовать только 'машинные методы формирования уравнений модели объекта проектирования, поэтому ограничимся теми разделами этой теорий, которые имеют непосредственное отношение к материалам данной главы. >
Для формирования уравнений математической модели иа основе электрической модели ^устройства, состоящей из базовых элементов (см. табл. 4.1), йсйользуются направленные графы G(V, S), в которых каждая ветрь Vq соответствует двухполюсному базовому элементу модели, а ее направление/ совпадает с направлением действия* на этом элементе фазовой переменной (направлением протекания тока или напряжения). Каждая вершина графа s, соответствует узлу электрической модели — точке соединения двух иди более базовых элементов. Таким образом* направленный граф полностью описывает топологию электрической модели. Для полного описания модели ее граф необходимо дополнить, списком типов и номиналов базовых элементов в ветвях графа. Приведем ряд определений, которые понадобятся для дальнейшего изложения материала.
Путь. Путем в графе между вершинами s, и S/ называют множество ветвей, в котором, двигаясь по смежным ветвям,
87
можно перейти из вершины s, в вершину sj. Графически путь представляется отрезком между двумя вершинами без ответвлений.
Связный граф. Направленный граф G(V, S) называют связным, если можно указать путь между двумя любыми вершинами графа S/ и sj.
Инцидентность. Ветвь называют инцидентной вершине, если она начинается или заканчивается в этой вершине.
Контур. Контуром называют связный подграф, в котором каждой вершине инцидентно ровно две ветви.
Дерево. Деревом связного графа называют связный подграф, включающий все узлы графа, но не имеющий контуров. Дерево графа, соответствующего электрической модели с т + 1 узлами, содержит т ветвей. Ветви графа, вошедшие в дерево, называют ребрами графа. Ветви графа, не вошедшие в дерево, образуют дополнение к графу и называются хордами графа.
Главное сечение. Главным сечением графа назы
вают сечение, проходящее через одно ребро и через столько хорд графа, сколько требуется для разделения графа на отдельные части. Так как в дерево с т + 1 вершинами входит т ребер, то в связанном графе существует тп главных сечений.
Для примера на рис. 4.12, а показана электрическая модель фазового контура, используемого для коррекции фазовых характеристик радиотрактов, а на рис. 4.12, б — соответствующий ей направленный граф. Выбор дерева неоднозначен, и в качестве ребер графа могут быть выбраны «ю, Р24, Рзо> tMo-Ветви ^12, ^23. ^34 являются хордами графа. Главные сечения
графа показаны стрелками.
Хотя направленный граф полностью описывается соедине-' ниями и направлениями ветвей, такая форма неудобна дл представления и хранения в памяти ЭВМ. Для записи в ЭВМ' о графе в виде!
наиболее удобно представление информации
Рис. 4.12. Фазовый контур:
а — схема фазового контура, 6 —направленный граф схемы, в — главные сечения графа
88
ыблицы. Содержащаяся в графе информация может быть полностью представлена матрицей, называемой матрицей акциденций. Для направленного графа G(V, S) с |S| = т + 1 поршинами и |V| = п ветвями матрицей инциденций является матрица А = [а(/фт + i)n, в которой ац=\, если ветвь инцидентна вершине и направлена от нее, а,/ = -1, если ветвь инцидентна вершине и направлена к ней, ац = 0, если ветвь не инцидентна вершине. Например, для графа, приведенного на рис 4.12, б, матрица инциденций имеет такой вид:
Вершины Ветви
V10 1*30 »24 V40 »12 V23 ^34
1 -1 0 0 0 1 0 0
2 0 0 1 0 -1 1 0
А = 3 0 1 0 0 0 -1 1
4 0 0 -1 1 0 0 -1
0 1 -1 0 -1 0 0 0
Графы электрических моделей радиоэлектронных устройств не содержат собственных контуров (ветвь называют собственным контуром, если оба ее конца инцидентны одному и н>му же узлу), вследствие чего каждый столбец матрицы ин-пнденций [а(/] содержит только два ненулевых элемента 1 и 1, а остальные элементы равны нулю. Это позволяет без потри информации исключить любую строку матрицы инциденты, так как содержащаяся в ней информация может быть несложно восстановлена. Обычно исключают строку матрицы, < <ютветствующую нулевому узлу. Матрица, полученная путем исключения одной из строк, называется редуцированной. Для 1вязного графа ранг матрицы инциденций А равен числу вершин графа без единицы: т.
В [13] приводится доказательство двух важных теорем о < нойствах строк и столбцов матрицы инциденций связного |рафа. В первой из них доказывается, что для связного графа набор всех строк редуцированной матрицы инциденций являет-о| линейно-независимым.
Вторая теорема постулирует важное свойство столбцов ре-|уцированной матрицы инциденций: в редуцированной матрице инциденций связного графа с т + 1 узлами т столбцов ма-||)ицы линейно независимы, если соответствующие этим столбцам веТви образуют дерево в графе.
89
Матрица инциденций, описывая нам топологическую структуру электрической модели, имеет ясный физический смысл, ибо с ее помощью „может быть записан заког сохранения заряда для электрической цепи (первый закон Кирхгофа для токов). Действительно, так как строки редуцированной матрицы описывают ветви, подключенные к соответствующим вершинам графа, и направление токов в них, То, умножив каждую строку матрицы на вектор токов в ветвях /в, получим алгебраическую сумму токов в узлах электрической модели, которая по первому закону Кирхгофа равна нулю. В результате можно записать
A,/,1T0v (4.3)
где /,< = [йой/—й, п— (Г — вектор токов через ветви графа, соответствующего электрической модели.
Для электрической модели фразового контура, на рис. 4.12, а, запись первого закона матрицы инциденций име^т вид t
показанной
Кирхгофа с помощью
0
0
0
0
0
О
С
0
о 1
о -1
0 .ȣ).
1 о
-1
0
йо i.3O *24 Йо Й2 ЙЗ *34
= 0.
О
о о
В скалярной форме нений:
эта запись соответствует системе урав-
-йо + ' 12 - Й)
Й4 - Й2 + .f2-3 = 0;
йо - йз + Й4 = 0;
—/24 + ЙО — *34 — 0. I
С помощью матрицы индиденций может быть записан Л второй закон Кирхгофа — закон равновесия напряжений. Дей-1 ствительно, напряжение на Vq ветви электрической модели через узловые потенциалы м, и, можно определить равенством иц = I/,—и,. В векторной форме это равенство может быть записано следующим образом:
и(/= |О...О1О...О— 1О....ОЙ7о, где l/o = |«i.м„Г — вектор узловых потенциалов.
Сравнивая строку в последнем равенстве с соответствующим столбцом матрицы инциденций, можно заметить, что они являются транспонированными по отношению друг к другу.
90
Обобщая этот результат на все ветви графа электрической модели, окончательно запишем
(7в = АЧ, (4.4)
i;ie и„ = |ню ...ипп—||т — вектор напряжений на ветвях графа <лектрической модели устройства, т — знак транспонирования матрицы.
Для нашего примера рис. 4.12 уравнения (4.4) запишутся
в виде
«Ю -10 0 0
изо о' 0 1 0
W24 0 10-1 U]
^4(1 = 0 0 0 1 и2
и12 1-1 0 0. из
и2:) 0 1-10 «4
U34 0 0 1-1
Для того чтобы использовать при составлении системы уравнений более общую форму записи закона Кирхгофа для iokob, а именно: алгебраическая сумма токов через любое сечение электрической цепи всегда равна нулю, введем другую матрицу графа, называемую матрицей главных сечений. Для ее получения необходимо выделить дерево графа и дополнение к нему (см. выше). Направление сечения будем считать совпа-цнощим с направлением ребра, его образующего.
Матрицей главных сечений направленного графа называют матрицу D = [d(/], в которой элемент dt/= 1, если ветвь / находится в сечении i и ориентация ветви совпадает с ориентацией сечения, задаваемой ребром, d(/ — -1, если ветвь / находится в сечении i и их ориентации противоположны, <1Ч = 0, если ветвь / не находится в сечении i.
Например, для графа рис. 4.12, б один из возможных вариантов дерева и соответствующего этому дереву набора главных сечений показан на рис. 4.12, в (хорды показаны пунктиром), а матрица главных сечений имеет вид
Сечения Ветви
изо 1»24 *40 И 23 »34
1 1 0 0 0 -1 0 0
D= 2 0 1 0 0 0 -1 1
3 0 0 1 0 -1 1 0
4 0 0 0 1 -1 1 -1
91
Общая форма первого закона Кирхгофа с помощью матрицы главных сечений D может быть записана следующим образом:
D-/B = 0 (4.5)
где /в =\iio,...iij,...in — вектор токов в ветвях графа, состав-
ляющие которого перечислены в порядке нумерации столбцов в матрице D.
Нетрудно убедиться, что для графа, приведенного на рис. 4.12, б, общая форма первого закона Кирхгофа в матричной и скалярной формах имеет вид 000-1 о 100 0-1
010-1 1
0 0 1-1 1
1
о
0
0
йо- Й2=0;
1зо-«2з+«34=О; 1'24-1’12+«23=0; «40_« 1 г+«2з+«34=0.
Ветви дерева удобно нумеровать в следующем порядке: вначале ребра, потом хорды графа. В этом случае вектор токов в ветвях и матрицу главных сечений можно представить в блочном виде следующим образом:
= 0,
(4-6)
где индекс «р» относится к ребрам графа, а индекс «х» соответствует хордам. Исходя из метода получения матрицы главных сечений D, можно заключить, что подматрица Dp всегда будет единичной: Dp = [l]; следовательно, можно записать равенство (4.6) следующим образом:
= 0.
Выполнив в последнем равенстве матричные действия, приведем запись общей формы закона Кирхгофа (4.6) к более удобному для практики виду:
7p = -Dx7x. (4.7)
92
Последнее соотношение представляет собой выражение токов ребер графа через токи его хорд. Так как токи, протекающие в базовых элементах электрической модели, представляют собой токи ребер и хорд графа, то из (4.7) можно записать
D
(4-8)
Следовательно, токи хорд можно рассматривать как независимые переменные, решив систему уравнений математической модели относительно которых можно рассчитать токи во всех базовых элементах, если воспользоваться (4.8). При этом матрица главных сечений позволяет записать относительно токов в ветвях /в минимальную по размерности и линейно независимую систему уравнений.
Так, для графа, показанного на рис. 4.12, б, последовательно записав выражения (4.6), (4.7) и (4.8), можно убедиться в < праведливости сказанного выше относительно свойств матрицы главных сечений графа на конкретном примере:
-10 0
0-1
1 1 о
*12
*23 >
*34
‘1 О О О'
_ 0 100
р ” 0 0 10’
0 0 0 1
«ю
*30
1 р *24
*40
*10 -1
*30 0
*24 -1
*40 -1
о о
1 1
1 о
Последнее равенство при скалярной форме записи приводит к системе уравнений закона токов для модели рис. 4.12, а в виде:
йо = «12;
«зо = «23—«34; .
«24 = «12—«23!
«40 ~ «12—«23 + «34-
93
Для упрощения записи второго закона Кирхгофа введем еще одну матрицу, характеризующую граф электрической модели — главную матрицу контуров. Метод построения главной матрицы контуров основан на выделении дерева в графе G(V,S). Подключение к дереву любой хорды приводит к образованию главного контура для этой хорды, ориентация которо-| го выбирается по направлению обхода, задаваемого хордой. В связном графе с тп + 1 вершинами и п ветвями можно выде-, лить п—т хорд и, следовательно, п—т главных контуров,. Поочередно подключая хорды к дереву графа, будем последовательно. выделять главные контуры графа, на основе которых и строится матрица контуров.
Матрицей главных контуров В называют матрицу [Ьц^п-т где Ьу—1, если ветвь i входит в /-й главный контур и ее направление совпадает с направлением обхода контура, задаваемым хордой, bij = -\, если ветвь входит в главный контур и; ее направление противоположно ориентации контура, Ьц = О, если ветвь не входит в главный контур.
Для нашего примера матрица главных контуров будет иметь вид
Контуры Ветви в контурах
Изо U24 1»40 UI2 V23 ^34
1 -1 0 -1 -1 1 0 0
В - 2 0 -1 1 1 0 1 0
3 0 1 0 -1 0 0 I
Очевидно, что по способу формирования матрицы главных контуров В ее столбцы, соответствующие хордам, всегда будут содержать только один отличный от нуля и равный 1 элемент. Поэтому, подобно (4.6), при формировании матрицы главны^ контуров ветви графа также удобно будет перечислять в таком( порядке: ребра графа, затем его хорды в порядке нумерации, главных контуров графа. Именно в таком порядке и сформиро-j вана матрица главных контуров для нашего примера.
При указанном порядке перечисления ветвей матрица глав^ ных контуров может быть записана в виде двух подматриц;^ В = [ВР|ВХ], где подматрица Вх, соответствующая хордам гра* фа, является единичной: Вх = 1. Эта подматрица определяет! рднг матрицы В, который для связного графа равен п—т+ 1.
94
Матрица главных контуров позволяет компактно записать икон напряжений Кирхгофа, устанавливающий, что алгебраическая сумма напряжений в каждом контуре любой сложной схемы всегда равна нулю:
В-(/в=0, (4.9)
। де (7В = |«io...un n—1|Т — вектор напряжений на ветвях графа.' Это выражение легко может быть доказано, читатель найдет доказательство, в частности, в [14]. Отметим, что матрица главных контуров позволяет записать относительно напряжений па ветвях t/в минимально возможную по размерности и линейно независимую систему уравнений математической модели [14].
Если при формировании матрицы главных контуров нумерация ветвей была упорядочена, как указывалось выше, то равенство (4.9) можно преобразовать к виду
t7₽
Z7x
[Вр|Вх]Ов = [Вр|1]
- о,
и„
1
А.
и
|де, как и ранее, индекс «р» относится к напряжениям на ребрах графа, а «х» — на хордах.
После выполнения действий над матрицами из последнего равенства получим систему уравнений, связывающую напряжения на ребрах и хордах графа:
t7x = -Bp-t7p. (4.10)
Подобно (4.8), учитывая, что действующие на базовых элементах электрической модели напряжения представляют напряжения на ребрах и хордах графа, из (4.10) можно записать
йР. (4.Н)
Следовательно, напряжения на ребрах графа являются независимыми переменными, определив которые из решения сис-ц'мы уравнений (4.11) можно найти все остальные напряжения, действующие на элементах электрической модели радиоустройства.
Напряжения и токи на базовых элементах электрических моделей представляют собой фазовые переменные этих моделей, ибо они полностью описывают работу моделируемого устройства. Связь напряжений и токов на базовых элементах представляет собой соответствующие компонентные уравнения, которые могут быть заранее записаны в память ЭВМ.
95
Выражения (4.8) и (4.11), связывающие фазовые переменные, действующие на различных базовых элементах электрической модели устройства, по сути своей представляют матричную запись топологических уравнений модели. Таким образом, для автоматизированного получения в ЭВМ системы уравнений математической модели устройства необходимо сформировать матрицы главных сечений D или главных контуров В и компонентные уравнения для каждого базового компонента (см. табл. 4.1). После подстановки компонентных уравнений в (4.8) или (4.11) получается система уравнений, представляющих математическую модель нашего устройства.
Рассмотрим методы получений в ЭВМ главных матриц сечений и контуров для графа электрической модели радиоустройств.
Между матрицами главных сечений и главных контуров существует фундаментальное соотношение, доказательство которого приводится в [13]. Если столбцы матриц расположены 6 одинаковой последовательности, то эти матрицы связаны соотношениями
BDM,
(4-12)
DBT = 0.
Справедливость соотношений графа рис. 4.12, б, матрицы В выше:
(4.12) можно проверить для и D для которого получены
10 0-1 0-1-1
0 10 0-11 1
0 0 1 0 1 0-1
-10 0
0 -1 1
-1 1 0
-1 1-1
1 0 0
0 1 0
0 0 1
0 0 0
0 0 0
0 0 0
Из
соотношений главных контуров и
(4.12), используя сечений в блочном
1 D
представление матри виде, можно записать
[Вр|1]
= B₽+D
= 0;
в;
= Bp+Dx =0,
1
96
откуда следует, что между блоками матриц выполняются соотношения
ВР = -DTX;
(4.13)
Dx = -BTp.
Из выражений (4.13) в свою очередь можно получить два важных равенства:
B = [-DTX|1);
(4.14) О = 11|-Втр].
Равенства (4.14) свидетельствуют, что в ЭВМ матрицу В можно получать из матрицы D и наоборот. Справедливость •того покажем на примере матриц контуров и сечений для графа рис. 4.12, б:
г . а . л Г10 0 0 -I О О'
0 0 0 1 -1 1 -1
что совпадает с матрицей D для графа, полученной ранее.
В свою очередь, существует также связь между матрицей пнциденций и главной матрицей контуров, которая при одинаковой последовательности столбцов матриц может быть записана в виде такого равенства.
А-Вт = 0. (4.15)
Равенство (4.15) следует непосредственно из правил формирования матриц А и В, и его доказательство приведено в [14].
В том случае, если в графе электрической модели выделено дерево, матрицы А, В и D можно записать в блочном виде (см. выше):
А = [АР|АХ];
В = [Вр}1];
d = uIdx].
Из последних равенств и (4.15) имеем
[Ар|ах]
в;
= а₽-в; + АХ = о,
откуда следует, что блоки матрицы инциденций Ар и Ах и блок матрицы контуров Вр связаны соотношением
Втр = —Атр-Ах. ' (4.16)
Автоматизация проектирования радиоэлектронных средств
97
I
Из (4.12), (4.14), (4.15), (4.16) запишем выражения, связы-! вающие матрицу инциденций с матрицами главных контуров и сечений графа:
В—[-А'1 • Ах|1);
(4.17) D = -А-р‘[Ар|Ах] = Ар-’А.
Уравнения (4.17) показывают путь автоматизированного получения матриц В и D в ЭВМ. Для этого необходимо опи-1 сать в ЭВМ граф электрической модели с помощью матрицы инциденций, выделить в графе дерево и после разделения ма-| трицы А на блоки Ар и Ах с помощью равенств (4.17) найти матрицы контуров и сечений графа, которые, как подчеркива-1 лось выше, представляют собой одну из форм записи тополо-1 гических уравнений электрической модели.
Запись матрицы инциденций в ЭВМ может быть осуществ-1 лена с помощью программы, использующей один из видов диа-| лога, в том числе и графического. Этот вопрос относится к проблемам выбора языка описания электрических моделей [7, 8], поэтому здесь рассматриваться не будет, а основное внимание уделим вопросам выделения с помощью ЭВМ дерева графа. 1
Электрическая модель радиоустройства может содержать! независимые источники тока и напряжения. Уравнения (4.8) показывают, что токи, соответствующие хордам графа, являют-1 ся независимыми переменными. Поскольку ток независимого источника не может быть зависимой переменной, эти базовые элементы всегда должны являться хордами графа и не могут] входить в дерево.
Аналогично, уравнения (4.11) показывают, что независимыми переменными являются напряжения, соответствующие ребрам графа. Следовательно, все базовые элементы, представляющие’ независимые источники напряжения, должны являться ребрами! графа электрической модели, т.е. входить в дерево графа. . При этом предполагается, что в электрической модели не-] допустимы контуры, состоящие только из независимых источ-| ников тока или напряжения. Образующие контуры независи-1 мые источники тока или напряжения могут быть исключены! без последствий для результатов моделирования, так как поя-| вление подобных контуров означает параллельное включение двух или более идеальных источников, которые всегда могут! быть приведены к одному эквивалентному.
В ряде случаев к дереву графа предъявляются совершенно! определенные требования по порядку его формирования. Так,! для моделирования методом переменных состояний дерево графа должно быть выбрано таким образом, чтобы в него во-! шли все независимые источники напряжения, за ними все воз-] можные зависимые источники напряжения, конденсаторы, ре-
98
пн-торы и индуктивности. В частном случае дерево графа мо-zkcr не содержать всех типов указанных выше базовых он ментов либо включать другие их типы.
Для нахождения дерева графа электрической модели устройства обычно используется свойство столбцов матрицы инциденций, о котором упоминалось выше: в графе с т+\ i/.ijiumu m линейно независимых столбцов матрицы инци-дгпций соответствуют ветвям, образующим дерево графа. Пшестно, что столбцы у единичной матрицы линейно независимы 130]. Следовательно, нахождение дерева графа можно ।нести к диагонализации первого блока матрицы инциденций А~|АР|АХ], Ар=1. Ветви графа, соответствующие линейно иг1ависимым столбцам, входящим в единичную матрицу, и пудут образовывать дерево графа.
Если обратиться к записи закона токов Кирхгофа с помощью матрицы инциденций (4.3), то процесс формирования единичной подматрицы Ар = 1 будет представлять собой исключение из первого уравнения для всех токов ребер, кроме первого, из второго уравнения — всех токов ребер, кроме второго ребра, и т.д. В ходе этих преобразований можно исполь-ювять следующие операции: перестановки строк и столбцов, гуммирование и вычитание строк матрицы, умножение их на I Допустимость этих действий следует непосредственно из I.HIIICII первого закона Кирхгофа (4.3). Действительно, перес-i.топка строк в матрице А представляет перестановку уравнении в системе (4.3), перестановка столбцов - перестановку чпепов в уравнениях (4.3), суммирование или вычитание строк соответствует суммированию или вычитанию уравнений । истомы (4.3) друг из друга.
Так как матрица А включает элементы 1, -1, 0, то формирование единичной подматрицы Ар можно свести к формированию диагональной матрицы. В настоящее время известно много алгоритмов диагонализации матриц на основе перечис-п'нных выше преобразований. Рассмотрим один из них, опи-। анне которого приводится ниже.
Алгоритм 4.1. Диагонализация матрицы инциденций
Шаг 1. Столбцы матрицы инциденций располагаются в порядке, заданном тре-оуемым приоритетом для составления дерева графа, например источники напря-юппя. конденсаторы, резисторы, источники тока, индуктивности.
Шаг 2. Последовательно просматривают столбцы недиагонализированной час-||| матрицы до первого ненулевого элемента а,* в недиагонализированной строке /.
Шаг 3. Если k * /, то столбец сдвигается на место /. остальные столбцы, па п ленные для формирования дерева от / до й-l. сдвигаются на один вправо.
Шаг 4. Если i > /. то меняются местами строки i и /.
Н1аг 5. Если в столбце / имеются ненулевые элементы, кроме диагонального и,,, го они устраняются прибавлением строки / с соответствующим знаком к строгач с ненулевыми элементами.
Шаг в. Если то строка / умножается на -1.
Шаг 7. Если / < in (in + I —число вершин), то переходим-к шагу 2, иначе подматрица А,, единичная и переходим на конец.
г 99
/77 О
п б)
Рис. 4.13. Четырехполюсник («) и его направленный граф (б)
Отметим, что в описанном алгоритме при диагонализации предпочтительными столбцами являются наиболее левые. Та кпм образом, заданная приоритетность базовых элементов для составления дерева расположением столбцов сохраняется.
До сих пор все изложение материала велось применитель' ио к двухполюсным базовым элементам электрических моде лей. Однако полученные результаты могут быть обобщены и на случай базовых элементов с произвольным числом пар вы кодов, описываемых матрицами классической или волновой теории цепей. Рассмотрим для примера четырехполюсный ба зовый элемент, характеризуемый матрицей сопротивлений Z г включенный между парами узлов k, I и т, п (рис. 4.13, а) Компонентные уравнения для четырехполюсника в этом слу чае могут быть записаны через элементы матрицы Z в еле дующем виде:
«I = Z|J»I + 212*2 = им = Uk—
U = ZI
**2 ^211) + 222*2 Umn **»;
где ii\. ii2, ii, i'2—напряжения и токи на входе и выходе че тырехполюсника, ищ, итп— напряжения на ветвях, ит, un, Uk ui—напряжения на узлах, к которым подключен четырехпо
люсиик
Приведенная выше пара компонентных уравнений позволяв’
представить каждую пару зажимов
Р п с. 4 14. Детектор амплитудно-модулирован-иых колебаний
четырехполюсника ветвьн графа, как показан» на рис. 4.13, б, харак теризуемой своим ком понентным уравнением При нумерации ветве! графа электрической моде ли этим ветвям необхо димо будет присвоит! два числа. По анало гии можно получить I граф базового элемен
та с произвольным чи слом входов.
100
Подведем краткие итоги полученным в этом параграфе ре-•ультатам. В электрических моделях, сформированных на осцине базовых элементов теории цепей, фазовыми переменными ппняются напряжения и токи, действующие на элементах. I' 1>М11онентные уравнения, связывающие эти токи и напряжения для каждого компонента, хранятся в памяти ЭВМ. Опи-i.iii электрическую модель с помощью матрицы инциденций, дпнол тенной списком типов и номиналов базовых элементов, Мы получаем в ЭВМ полную информацию о модели проекти-щ-емого устройства. На основании матрицы инциденций формируются главные матрицы контуров и сечений графа, с помощью блоков которых записываются топологические уравнения, представляющие собой запись двух фундаментальных чпищов для электрической цепи — законов равновесия напря-Ькспий и токов Кирхгофа. Дополнением топологических уравнений компонентными формируется в ЭВМ система уравне-Hii.i, представляющих математическую модель проектируемого I (ройства.
Вопросы и упражнения для самопроверки
I. Выберите фазовые переменные, внешние и внутренние параметры в модели ц...... Эберса — Молла, показанной на рис 4.5, а.
2. Выделите все возможные деревья и независимые контуры в графе фазового bun । ура, схема которого приведена на рис. 4.12, б.
.1 . Докажите, что сумма любого столбца нередуцированиой матрицы инциден-iiiiii равна нулю.
4. Что характеризует сумма модулей элементов строки матрицы инциденций ипнравленного графа, а также суммы отрицательных и положительных элементов?
5. Используя модель диода Эберса — Молла, получите электрическую модель о н-ктора AM-колебаний с разделенной нагрузкой, схема которого приведена на ри< 4 14.
6. Постройте направленный граф электрической модели детектора АМ-колеба-iiuii из п. 5, выделите ребра (дерево графа) и хорды.
7. Для направленного графа из п. 6 запишите матрицы иицидеиций, главных i синий и главных контуров, перечисляя ветви графа в порядке ребра — хорды.
8. Разделите матрицы иицидеиций, главных сечений и контуров в п. 7 иа бло-iiii согласно (4.6), (4.10), (4.15). Проверьте совпадение выражений (4.13), (4.16), ( I 17) для графа электрической модели АМ-детектора.
9. Запишите уравнения математической модели детектора для токов ветвей ( I 10). используя блоки матрицы главных контуров из п. 8.
Глава 5
МАТЕМАТИЧЕСКИЕ МОДЕЛИ РЭС ВО ВРЕМЕННбЙ ОБЛАСТИ
В гл. 4 было показано, что независимая система уравнс ний, описывающая математическую модель устройства, може быть получена топологическими методами с помощью теори графов. Конкретный вид алгоритма формирования систем) уравнений математической модели зависит от выбранной вектора фазовых переменных — набора параметров, характе ризующих функционирование моделируемого устройства. 1 зависимости от того, являются ли фазовые переменные функ циями времени или комплексной частоты, различают матемд тические модели устройств во временной и частотно областях. В обоих случаях при формировании системы уран нений математической модели обычно используют операторну| форму записи компонентных уравнений для базовых элементе электрических моделей. Это объясняется удобством алгори-, . мического преобразования системы интегродифференциальны: уравнений, записанных в операторной форме, к виду, наибе лее удобному для численного решения, удобством перехода о операторной формы записи к частотным моделям замене оператора s на мнимую частоту /со, а также целесообраз ностью использовать обратное преобразование Лапласа.
Модели во временной области наиболее удобны для аналц за переходных процессов в радиоустройствах, моделированг статического режима, моделировании нелинейных устройств. I настоящей главе рассматриваются алгоритмы формированц системы уравнений математической модели радиоустройств в временной области, а также ее решения численными метода ми относительно выбранных фазовых переменных.
§5.1. ТАБЛИЧНЫЙ МЕТОД ФОРМИРОВАНИЯ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Многие методы автоматизированного формирования сист< мы уравнений математической модели проектируемого устроц ства во временной и частотной областях можно получить I
102
।''иного метода, называемого в литературе табличным [14]. В ним методе при формировании системы уравнений математической модели в качестве фазовых переменных используются ||>кп ветвей /„ и напряжения на них Un, а также узловые потенциалы Uo, отсчитанные от заземленного узла электрический модели.
Рассмотрим самый общий вариант табличного метода формирования системы уравнений математической модели для люктрической модели, содержащей элементы С, L, R и источники тока и напряжения I(t), E(f). Первый (4.3) и второй (4.4) 1к<1ны Кирхгофа запишем через матрицу инциденций следующим образом:
А7В = 0; UB - Ат Uo = 0,
вцссь индекс «в» соответствует ветвям, а индекс 0 — узловым и шряжениям, отсчитанным от нулевого узла.
В общем случае система уравнений, описывающая базовый двухполюсный элемент электрической модели, подключенный между узлами i и /, может быть записана в виде.
k2
б, Z//(s)
Kif
(5.1)
Ц,,, +
= ^,
'J
। nc ijij(s) и Zij(s) — проводимость и импеданс базового элемен-ы. записанные в операторной форме, k\ = k% = 1 — безразмер-
—о ni.ie константы, 1Г>7
-—токи и напряжения независимых
источников, в том числе учитывающих начальные условия в Пазовом элементе — токи в индуктивностях и напряжения на конденсаторах (см. табл. 4.1). Для всех базовых элементов равенство (5.1) запишем в матричном виде:
(5.2)
Р£7В + R7B = U7° =
YB = [Уь„1 — Дка’
। опальная подматрица проводимостей включенных в ветвях "а ювых элементов, ZB = [Zb ] — Диагональная подматрица пмпедансов в ветвях, 1-—единичные подматрицы соответствующего размера, Е , I — векторы, учитывающие источники напряжения и тока.
103
Уравнения законов Кирхгофа для электрической модели i компонентные уравнения (5.2) перепишем в такой последов^ тельности:
UB-fiJu0 = 0;
YE(7E + ZB7B = №°;
А/в = 0.
Последнюю запись можно представить в матричной форме которая и является обобщенной системой уравнений таблична
го метода:
§ о 3 S 1 > з* 4 I и 1 °'
V 7 0 / - ж вл хл ^влхл v(wz+l)xn 1 Б w ^лх(?п+1) ^(ш+1)х(т+1) U $
Размерности всех подматриц указаны в (5.3), где п— числ; ветвей в графе, соответствующем электрической модели устрой' ства, т — число вершин графа, исключая заземленную.
Чтобы оператор Лапласа s всегда входил в числитель, емкости в (5.3) будем определять через проводимости конденсаторов, а индуктивности — через импедансы катушек индуктивности (см. табл. 4.1). Так как оператор s эквивалентен диффё ренциальному оператору во временной области, то систем^ уравнений (5.3), полученная табличным методом, в общел случае будет представлять собой систему дифференциально! алгебраических уравнений, позволяющую моделировать проем тируемый объект во временной области. Достоинства такой подхода составления системы уравнений математической модели на основании электрической — отсутствие необходимое™ различать ветви с пассивными компонентами, источникам» тока и напряжения, произвольные нумерация ветвей и описания матрицы инциденций графа электрической модели i ЭВМ.
Однако табличный метод имеет и ряд существенных недос татков, из-за которых он практически не используется в систе| мах автоматизированного проектирования радиотехнически) устройств.
Как видно из (5.3), блочная матрица в левой части систе мы уравнений имеет на главной диагонали квадратные под матрицы, в том числе и нулевую, нулевые подматрицы имеют ся и вне главной диагонали. Наличие нулевых диагональных » недиагональных блоков затрудняет использование специаль ных алгоритмов для работы с разреженными матрицами.
104
Главный же недостаток этого метода заключается в большой размерности системы уравнений, так как подобное описание электрических моделей приводит к появлению излишних фазовых переменных в системе уравнений, что, естественно, ыгрудняет решение задачи. В §4.4 было показано, что часть переменных в системе (5.3) может быть исключена путем под-i 1 шовки и тем самым будет уменьшен порядок системы уравнений математической модели устройства. Так, если модель характеризовать только потенциалами узлов, отсчитанными от нулевого Uo, то от системы уравнений (5.3) придем к системе уравнений по методу узловых потенциалов, а если в системе уп 1внений (5.3) оставить в качестве фазовых переменных только напряжения на ветвях модели UB, то получим систему уравнений по методу контурных токов.
Рассмотрим эти методы более подробно.
J5.2. ТОПОЛОГИЧЕСКИЕ МЕТОДЫ ФОРМИРОВАНИЯ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПО МЕТОДУ УЗЛОВЫХ ПОТЕНЦИАЛОВ И КОНТУРНЫХ ТОКОВ
Использование фазовых переменных только . одного iiiiia — токов ветвей либо напряжений на узлах электрической модели — позволяет сформировать машинными методами болте компактные системы уравнений математической модели проектируемого устройства, с меньшей размерностью вектора фа ювых переменных и меньшим числом нулевых элементов в ма.рицах. Такие модели на основе практически одних и тех же алгоритмов могут быть сформированы как цо временной, 1ак и частотной областях, что является несомненной ценнос-|ыо такого подхода.
В случае моделирования во временной области по методу у 1ловых потенциалов в качестве вектора фазовых переменных Г выбирается вектор узловых напряжений, отсчитанных от одного из узлов электрической модели, потенциал которого пола-ыется равным нулю: Uo = |»zi...uJT. Вектор Uo полностью опи-гыпает электрическую модель, а значит, и работу устройства п целом.
Для формирования системы уравнений математической мо-лгли по методу узловых потенциалов необходимо, чтобы электрическая модель устройства не включала источников напряли пня. Перед моделированием все источники напряжения должны быть преобразованы в источники тока по теореме об шпивалентном генераторе (теореме Тевенина). Таким образом, |.пектрическая модель будет содержать только пассивные ба-кшые элементы и источники тока (см. табл. 4.1).
105
Рис. 5.1. Электрическая модель:
а-—исходная схема, б — модель с источниками тока, в — модель с источниками напряжения
Для любого пассивного базового элемента связь тока ветви iu и напряжения иа ней ив_ в операторной форме записывается чёрез проводимость y^s) с’'помощью соотношения iB y4(s}uB 1 В матричной форме для всех пассивных элементов''эти выр^> жения можно записать в следующем виде:
Ynt7nB = /nB + r0, (5.4)
где Yn — диагональная матрица проводимостей пассивных ветвей электрической модели, £7ПВ, /Пв—векторы напряжений и тока на пассивных ветвях графа модели, IF* — вектоп независимых источников, в том числе учитывающих начальные условия в реактивных элементах в соответствии с (5.1).
Для примера на рис. 5.1, а приведена электрическая модели содержащая зависимые и независимые источники тока и напряжения, на рис. 5.1, б показана та же модель после преобразования по теореме Тевенина источников напряжения в источники тока. Матрица Yn проводимостей пассивных ветвей элект рической модели рис. 5.1, б в операторной форме имеет вид
106
Согласно выражению (4.5), запись первого закона Кирхгофа через матрицу главных сечений графа электрической модели такова:
D/B = 0.
Вектор токов через ветви графа /в сформируем в следующем порядке: вначале перечислим все токи через пассивные >лементы электрической модели, потом токи всех зависимых и независимых источников тока. Разделив матрицу главных сечений на .блоки [Dn|Dz], относящиеся к ветвям, характеризующим пассивные базовые элементы, и источникам тока соответ-г! ченно, последнее равенство можно записать как
[D.I D,) _
ИЛИ
Dn /пв — — D j I j,
(5.5)
|дс /пв — вектор токов через пассивные элементы модели, 11 — вектор токов источников тока.
Воспользовавшись выражением (5.4), преобразуем уравнения (5.5) и запишем их относительно вектора напряжений на пассивных ветвях графа электрической модели UnB:
Dn Yn t/nB-Dnr° =-D/У/. (5.6)
Как_показано в гл. 4 (см. 4.5), напряжения на ветвях । рифа UK связаны с узловыми потенциалами Uo соотношением 77в = ATt70.
Разделив вектор UB и матрицу инциденций на блоки по аналогии с (5.5), последнее выражение можно записать в виде
U Jb
а;
С/о
или (5.7)
Una U Jb — A} U 0 ,
। де Uв — вектор напряжений на источниках тока, входящих в >лектрическую модель устройства, Ап, А/ — блоки матрицы инциденций, относящиеся к пассивным ветвям и ветвям, содержащим источники тока.
После подстановки (5.7) в (5.6) получаем систему уравнений относительно вектора узловых потенциалов электрической модели устройства:
Dn-Yn-ATn(7To-D>J = -D/7/. (5.8)
Полученная в (5.8) система уравнений представляет собой истему дифференциально-алгебраических уравнений матема-
107
гнческой модели относительно вектора неизвестных фазовых переменных — узловых потенциалов Uq. На_пряжения, дейст-1 вующие на пассивных элементах модели /7ПВ и источника тока UjR, могут быть найдены с помощью (5.7) после решения системы уравнений (5.8) относительно Uq.
Как видно из (5.8), запись компонентных уравнений длс пассивных базовых элементов в форме (5.4) предполагает, что нелинейности в электрической модели могут здесь моделиро-ваться только с помощью нелинейных источников тока, что накладывает некоторые ограничения на структуры электрических моделей компонентов устройства.
Для нашего примера рис. 5.1, б система уравнений математической модели методом узловых потенциалов из (5.8) имеет вид
или
11 110
0 0-1-11
+ хСдИ, + «СДц - и2) + («] - и2) / sL5 - Ц;
-sCi(ul -ц2)-(и, -м2)/ sL5 +и2 / Rg - 12.
Заметим, что система уравнений математической моде. (5.8) может быть получена и на основании (4.3) с помоцц матрицы инциденций графа электрической модели, однако этом случае матрицы в левой части системы будут содержа большее число нулевых элементов, что приводит необходимости использования специальных алгоритмов рабо' с разреженными матрицами. Вывод уравнений узлов! потенциалов через матрицу инциденций читатель может най в [8, 14].
Алгоритм 5.1. Моделирование радиоустройства во временной облас методом узловых потенциалов.
Шаг /. Столбцы матрицы инциденций располагаются в порядке: пассивные ба зовые элементы, затем зависимые и независимые источники тока,- Выделяются под матрицы Ап и А/, относящиеся к пассивным ветвям и к ветвям с источниками тока
108
Шаг 2. Находится дерево графа и формируется матрица главных сечений графа D । принятым на первом шаге приоритетом базовых элементов (см. (4.17)]. Выделяются подматрицы Dn и D/, относящиеся к пассивным ветвям и источникам тока.
Шаг 3. В цикле формируется диагональная матрица проводимостей пассивных о,новых элементов Yn в соответствии с принятым на первом шаге порядком их перечисления. ।
Шаг 4. Формируются векторы узловых потенциалов Uq и токов источников п>ка lj в соответствии с записью строк и столбцов матрицы инциденций.
Шаг 5. Согласно (5.8), производятся матричные операции и формируются левая к правая части системы уравнений относительно вектора узловых потенциалов Uq.
Шаг 6. Переход к решению системы дифференциально-алгебраических уравнений <п посительно вектора фазовых переменных — узловых потенциалов V =Uq.
При моделировании радиоустрой^тв по методу контурных юков в качестве вектора фазовых переменных выбирается век-юр токов в хордах графа электрической модели /х. При. этом к е зависимые и независимые источники тока, имеющиеся в модели устройства, должны быть преобразованы в эквивалентные источники напряжения на основе теоремы Тевенина.
Для примера на рис. 5.1, в показана электрическая модель рис. 5.1, а после преобразования по теореме Тевенина источников тока в эквивалентные им источники напряжения.
Подобно (5.4), для всех пассивных разовых элементов элек-|рпческой модели связь токов ветвей /Пв с действующими на них напряжениями UnB может быть записана в матричной форме в виде _ ___
Zn 7ПВ = UnB + №°, (5.9)
। ле Zn — диагональная матрица сопротивлений пассивных вет-п< li электрической модели в операторной форме, IVй — вектор ниточников, учитывающих начальные условия в реактивных >лементах (5.1).
Для нашего примера рис. 5.1, в уравнения. (5.9) имеют
109
Согласно (4.9), запись второго закона Кирхгофа через матрицу главных контуров электрической- модели В может быть представлена в следующей форме: В(7в = 0.
При формировании матрицы инциденций графа электрической модели А, а значит, и матрицы главных контуров В, согласно §4.4, вначале опишем все независимые источники напряжения, потом все зависимые источники, затем пассивные ветви графа электрической модели устройства. Это позволит разделить матрицу главных контуров В на блоки В =[|Ве|Вп], относящиеся к ветвям с источниками напряжения и к ветвям с пассивными элементами. На две составляющих разделим и вектор напряжений на ветвях модели U»= |(/Т/?|//тпв|, первая из которых будет описывать независимые и зависимые источники напряжения, а вторая — напряжения на ветвях, содержащих пассивные элементы электрической модели. В результате запись закона равновесия напряжений Кирхгофа можно будет представить в следующем виде:
IBjBnl
и ™
или
= -Вп(Л»
(5.10)
Подставляя в (5.10) выражение (5.9), запишем систему уравнений относительно вектора токов_через пассивные элементы электрической модели устройства /пв:
Bn-Zn-7nB-BnF = -B£{7f. (5.11)
Первый закон Кирхгофа из (4.8) и (4.14) можно записать как 7В = вт7х, или после разделения вектора /в и матрицы В на блоки 7 л
BI
в;
где /х — вектор токов через хорды графа электрической модели устройства, /л—вектор токов, протекающих через источники напряжения.
Последнее выражение можно записать в виде двух подсистем уравнений:
7е = Вт£/Х;
/пи “ В п/х.
После подстановки (5.12) в (5.11) получим систему уравнений математической модели устройства относительно неизвестных токов хорд графа электрической модели /х:
(5-12)
1 ю
BnZn-BTn7x-BX = -ЬЕиЕ. (5 13)
Система уравнений (5.13) представляет собой искомую запись уравнений математической модели методом контурных токов, удобную для алгоритмической реализации на J9BM. Токи, протекающие через пассивные элементы модели /пв, и токи, протекающие через источники напряжения, могут быть найдены после решения системы уравнений (5 13) с помощью (5.12).
Необходимо заметить, что запись уравнений (5.13) не совпадает с общепринятой записью уравнений по методу контурных токов, которая приводится, например, в [8]. Это объясняется тем, что здесь контуры сформированы на основе хорд графа электрической модели, что обеспечивает минимальную размерность системы уравнений (5.13) и удобство моделирования не только планарных, но и непланарных моделей. Отме-1пм также, что запись компонентных уравнений (5.9) и топологических уравнений (5.13) предполагает, что нелинейности в «лектрической модели могут присутствовать только в источниках напряжения Не, что, естественно, накладывает ограничения на возможные электрические модели компонентов проек-шруемого устройства.
Для конкретного примера электрической модели, приведенной на рис. 5.1, в, система уравнений по методу контурных KiKdB (5 13), если за ребра выбрать Е\, Сз, С4, Еу, а за хор-1ы — R2, L5, будет иметь вид
11 000
0 0-1 10
01-101
------------------------
I |Дс3
I |Дс4
I st5
о_________________________
1 о
о о
О I
или
Приведем укрупненную пошаговую схему алгоритма.
111
Алгоритм 5.2. Моделирование радиоустройств по методу контурных токов i во временной области
Шаг /. Столбцы матрицы инциденций располагаются в таком порядке независимые источники напряжения, зависимые источники напряжения, пассивные элементы I
Шаг 2. С помощью описанного в §4.4 алгоритма выделяется дерево графа с заданным на первом шаге приоритетом ветвей. Выделяется вектор токов хорд графа 7х-
Шаг 3. Формируется матрица главных контуров графа В с принятым на первом шаге расположением столбцов согласно выражению (4.17). Выделяются подматрицы В/f и Вп, относящиеся к ветвям с источниками напряжения и к ветвям с пассивными элементами.
Шаг 4. Формируется диагональная матрица сопротивлений пассивных базовых элементов Zn в операторной форме в соответствии с принятым порядком их перечисления.
Шаг 5. Формируется вектор напряжений источников напряжения Up.
Шаг 6. Согласно (5.13), формируются левая и правая части системы уравне- I ний относительно вектора токов хорд электрической модели V = /х-
Шаг 7. Переходим к решению системы дифференциально-алгебраических урав-1 нений относительно вектора фазовых переменных /х.
Если положить в алгоритмах 5.1 и 5.2 s = /со, то получим! системы уравнений математической модели устройства по ме-1 тодам узловых потенциалов и контурных токов в частотной области.
§5.3. МОДЕЛИРОВАНИЕ РЭС МЕТОДОМ ПЕРЕМЕННЫХ СОСТОЯНИЯ
Рассмотренные в предыдущем параграфе методы автома-1 тизированного формирования системы уравнений математиче-| ской модели радиоустройства на основе его электрической мо-1 дели, несмотря на удобство алгоритмической реализации, обладают тем существенным недостатком, что приводят к математи-1 ческим моделям в виде систем дифференциально-алгебраичес-1 ких уравнений высокого порядка, решение которых зачастую! связано с большими вычислительными трудностями.
С середины 50-х годов в автоматизированном проектирова-1 нии начал широко применяться метод переменных состояния,' позволяющий получить систему уравнений математической модели в виде двух систем матричных уравнений:
A(j7) = lJ + MQ;
о/
112
F = F(V,Q,V ,...), (5.14)
i де V—вектор_фазовых переменных, называемых переменными состояния, Q—вектор, характеризующий входные воздействия, F—вектор выходных параметров, L, М— постоянные юйствительные матрицы соответствующего размера.
Уравнения (5.14) представляют собой систему дифференциальных уравнений первого порядка, называемую системой уравнений для переменных состояния в нормальной форме, численное решение которой относительно вектора фазовых переменных V самое простое из всех методов моделирования. Кроме того, уравнений в (5.14), как правило, оказывается меньше, чем при использовании метода узловых потенциалов либо контурных токов, что также облегчает процесс моделирования, особенно нелинейных устройств.
Алгоритмическую реализацию метода во многом определяет выбор вектора переменных состояния V. За вектор переменных состояния могут быть, например, выбраны узловые потенциалы, при этом размерность системы (5.14) будет равна количеству узлов в электрической модели, контурные токи либо другие переменные [14]. При моделировании переходных процессов в радиоэлектронных устройствах за переменные состояния рационально выбирать вектор, состоящий из напряжений на всех конденсаторах электрической модели устройства Uc и токов во всех индуктивностях II, позволяющий для динамических моделей получить систему дифференциальных уравнений первого порядка минимально возможной размерности.
Для электрических моделей, состоящих из базовых R, С, L, М, I, {/-элементов, такой выбор вектора переменных состояния возможен только для электрических моделей без особенностей: в графе модели должны отсутствовать контуры, состоящие только из независимых или управляемых источников напряжения и только из конденсаторов, в графе не должно быть сечений, содержащих только независимые или управляемые источники тока, а также сечений, составленных только из индуктивностей либо индуктивностей и источников тока [14]. В дальнейшем ограничимся рассмотрением только моделей без особенностей, топологические же методы формирования уравнений переменных состояния для электрических моделей с особенностями можно найти, например, в [14].
В случае электрической модели без особенностей в ней можно выделить специальное дерево графа, называемое нормальным, в котором ребра выбираются в следующем порядке: все независимые и управляемые источники напряжения, все воз-
113
можные конденсаторы, все возможные резисторы и минимально необходимое для составления дерева число индуктивностей.
' из (4.7), (4.10) и (4.12) ирхгофа могут быть записаны в матрицы главных сечений следую-
При выборе нормального дерева графа » первый и второй законы Кирхгофа мог блочном виде с помощью щим образом:
Ip —
!и
Ug
Ul и, и.
D
D
D
D
D О D, D
СМ &EL Dt7 /с
UG ^VL Dw Dt/y 11 - _
CG Det D« 1
RC Url Dr/ Dw. J
EG DjyG Dcg £
ЕЕ D^t Все Dk U =
EI Dy/ DL D«, Uc
EJ D„ Dw u R
Dx7x;
d:(/₽>
(5.15)
7 R
и
токов, протекающих через независимые и источники напряжения, Jc— вектор через конденсаторы, //? — вектор
где lE, Iи — векторы
управляемые источники напряжения, Jc—вектор токов, протекающих через конденсаторы, /«— вектор токов, протекающих через резисторы, включенные в дерево графа, 1с, — вектор токов, протекающих через резисторы, включенные в хорды графа, //,— вектор токов, протекающих через индуктивности в хордах, /, / — векторы локов_ независимых_и управляемых источников тока, Е, U, Uc, Ur, Ug, Ul, Ui, Uj — векторы напряжений на соответствующих элементах в ребрах и хордах графа, Djrs — блоки матрицы главных сечений, отвечающие за взаимодействие соответствующих базовых элементов в ребрах и хордах.
Выполняя в (5.15) матричные действия, запишем уравнения для токов, протекающих через резисторы в ребрах графа, и напряжений, действующих на хордах графа:
U с, = DT£Gf + ОТс/ц(/ + DTcg(/c + DTrgUr.
В матричном виде связь напряжений на резисторах с токами, протекающими через них, можно записать как компонентные уравнения: _
Ur - Hr[r, Ug = Rg/g.
где R/?, Rg — диагональные матрицы, состоящие из сопротивлений резистивных ребер и хорд графа.
(5.16)
I 14
Подставив последние соотношения в уравнение (5.16), получим 1
®RG / R
DkgRg J/g
Для упрощения записи введем ipnu.:
о -D«, Е
’o
Pgg 0 J7
О “ D RL U с PcG 0 _ 11-следующие обозначения ма-
Г1
DflG
~ Rc
О - Dw
_^cg О
• т
> *2
[PIg О - Dw DJ/g о
о
о
Кроме того, будем полагать, что управляемые источники кжа и напряжения зависят линейно только от токов в резисторах модели Ir, Ig, напряжений на конденсаторах Uc и токов и индуктивностях U переменных состояния:
IR
+ N2 - >
I с
U
1
= N, и_С
(5.17)
где N|, N2—матрицы, которые определяются по известным зависимостям для напряжений и токов управляемых источников.
В результате можно записать выражения для токов через резисторы электрической модели_устройства в зависимости от
нектора переменных состояния
Uc
11
вектора токов независи-
и
мых источников напряжений и токов
Е
Й
Е
пли
Т,!*
I с
— Uc
+ тз-
тм Ус + T4Ni
+ TN
(5.18)
Е |Дс
= [Т, -Т^.Г'гЛ +[Т, -T4N,r‘[T3 +T4N,]_.
Il
Ir
7C
Для нашего примера, приведенного на рис. 5.1, а, эта имеет вид ,
запись
= т
*2
Е
/
115
Deg D£/
Pcg Dc/ Dc/
R% 0
.0 Re _ iRi.
-1 0
0 0
Et Г-1 0 0
i7 +[-i-i о
'e5
Из (5.15) можно получать также и выражения для напряжений на индуктивностях Ul в хордах графа и токов через конденсаторы 1с в ребрах:
El = DT£L Е + V)1 иl-U + D1cl:Uс + DTRlUr,
(5-19)
/с = -Dcg’/g-Dcl-/£-Dc/7 -Dcj J.
Используя компонентные уравнения, выразим напряжения на сопротивлениях в ребрах графа UR через протекающие в них токи: UR = RrIr — и запишем (5.19) в виде одного матричного уравнения:
и
7
Ul
1с
+ Р3
/ R
1g
+ Р<
(5.20)
I L
где введены обозначения:.
'Rr 0 р _ 0
0 -DcgJ 4 1° ~ Da
запись имеет вид
Для нашего
Н/.Г1
1С,
примера рис. 5.1 эта
116
Подставляя в (5.20) выражение для токов в резисторах в ребрах и хордах графа (5.18) и выражение для напряжений и пжов управляемых источников (5.17), запишем систему урав-пс||ий_для Ul и 1с относительно вектора переменных состоя-
Uc
и вектора напряжений и токов независимых источни-
ков
Ul
/ с
- {р,+p4n2+[р.(+р4\,]м,'м2}л/с
11.
{Р2 + [Р3 +
। де ЛА। = Ti—T4N2; M2 = T3 +T4N!.
Компонентные уравнения для емкостных элементов в ребрах и индуктивных элементов в хордах графа таковы:
7С= С—(77с); Ul = L —(7с), d/ dZ
1 де С, L — диагональные матрицы конденсаторов и индуктивностей. Последнее выражение можно объединить в одно мат-
ричное равенство:
Ul
Ic
0 1 h с J di и с
(5.22)
После подстановки (5.22) в (5.21) получим окончательную нтись уравнений переменных состояния с помощью топологи-
ческих методов:
L
0 С_ и с
= {р, + P4N, + [Р3 +
Uc
II
P4NJM1‘M2}_
(5.23)
+ {Р2+[Р3
p4n,]M;'t2}
Е
1
р P4N1]m1‘T2}_,
L
0
+
Е
1
Решение системы дифференциальных сительно вектора переменных состояния
уравнений (5.23) относе
может быть выпо-
лнено с минимальными затратами по сравнению с другими алгоритмами автоматизированного формирования системы
117
уравнений уравнений - Ue. , V = _ фор /л
математической модели. После решения системы математической модели относительно вектора
мируется система уравнений относительно вектора
выходных параметров модели F = F(V, Q, V',....), формирование
которой существенно зависит от моделируемого устройства, поэтому рассматриваться здесь не будет, Частные случаи формирования уравнений для определения F можно найти в [7].
Для нашего примера электрической модели, показанной на рис. 5.1, а, с учетом полученных ранее выражений система уравнений по методу переменных состояния может быть записана в виде
О
Сл о_____с4
I
В заключение приведем укрупненную схему алгоритма.
Алгоритм 5.3. Моделирование радиоустройств методом переменных состояния
Шаг /. Формируется нормальное дерево графа электрической модели устройства, включающее все источники напряжения, все конденсаторы и необходимое для формирования дерева число резисторов, используя алгоритм 4.1.
Шаг 2. На основании выражения (4.7) по матрице инциденций и выбранному дереву графа формируется матрица главных сечений D — [1|DXJ.
Шаг 3. Матрица главных сечений разбивается на блоки в соответствии с (5.15).
Шаг 4. Используя блоки матрицы главных сечений D, формируем вспомогательные матрицы Т4....Т4, Р1...Р4, N], N2 в соответствии с выражениями (5.16), (5.17), (5.20), (5.22).
Шаг 5. Формируются диагональные матрицы индуктивностей, емкостей, резисторов L, С, R/?. Rg.
Шаг 6. На основаи. и выражения (5.23) формируется правая часть уравнений переменных состояния.
Шаг 7. Переходим к решению системы уравнений переменных состояний отно
сительно вектора состояний
(7с
/
Вопросы решения систем дифференциальных уравнений при моделировании переходных процессов в радиоустройствах рассматриваются в §5.5.
118
§5.4. МОДЕЛИРОВАНИЕ СТАТИЧЕСКОГО РЕЖИМА РЭС
Моделирование статического режима — режима работы по постоянному току любого радиоустройства — необходимо для р<счета рабочих точек отдельных каскадов радиоустройств, (оставления карты режимов работы компонентов устройства, определения рассеиваемых мощностей в компонентах и т.п. 'го моделирование может быть выполнено на основании глобальной модели радиоэлектронного устройства во временной или частотной областях, которые могут быть получены одним ш описанных в настоящей главе и гл. 6 методов. Для моделирования на постоянном токе в этих случаях в системе уравнений математической модели устройства следует положить оператор Лапласа $=.О, исключив тем самым из системы дифференциально-алгебраических уравнений производные по времени, гак как в статическом режиме токи и напряжения в модели не зависят от времени. При этом получается модель устройства в виде системы нелинейных уравнений относительно выбранного вектора фазовых переменных, например узловых потенциалов, или переменных состояния.
Возможно и специальное формирование электрической мо-гели устройства по постоянному току, которая может быть получена на основе моделей отдельных компонентов, из которых исключены реактивные элементы.
В первом случае отпадает надобность в специальных моделях радиоустройств по постоянному току, но зато усложняются алгоритмы получения системы уравнений математической модели, во втором случае упрощаются алгоритмы моделирования статического режима, но требуется использование специализированных моделей компонентов по постоянному току, из которых состоит устройство.
Проблему моделирования статического режима будем рассматривать на примере моделирования устройства по методу узловых потенциалов, хотя все результаты могут быть перенесены и на другие алгоритмы формирования системы уравнений математической модели устройства. Как указано выше, математическая модель любого радиоустройства по постоянно-мутоку представляет собой систему нелинейных уравнений /'({/)= 0, решив которую, находят потенциалы на узлах электрической модели. В скалярном виде эта система уравнений может быть записана в виде
119
lAui.....u„) = /i(«) =0;
Ш «„) = /2(«) = 0;
/>,.......«„) = /„(«) = о.
(5.24)
Процедуры решения систем нелинейных уравнений численными методами достаточно глубоко разработаны в математике, поэтому рассмотрим только алгоритмические аспекты моделирования РЭС на постоянном токе, математическое же обоснование методов можно найти, например, в [26, 27].
В отличие от систем линейных уравнений, методы решения которых описаны в гл. 6, для систем нелинейных уравнений неизвестны прямые методы решения и для нахождения узловых потенциалов в устройстве на постоянном токе приходится использовать итерационные методы.
Одним из наиболее- простых итерационных методов решения систем нелинейных уравнений является метод простой итерации. Он основан на допущении, что систему нелинейных уравнений относительно узловых потенциалов (5.24) можно привести к виду
= £,(<......<');
«2 =^(«|.«Г'...«Г');
<
=gnM........
Используя значение UkA на предыдущей, (/г-1}-й итерации из соответствующего уравнения вычисляют новые значения н,-па последующей /г-й итерации, при этом при вычислениях н\-используют значения uh\, иг,..., ukj.\, вычисленные из предыдущих уравнений. Процесс останавливается, когда разность между значениями переменных на соседних итерациях оказывается меньше требуемой точности <е.
__Близость полученного на /г-й итерации вектора переменных Uk к решению системы нелинейных уравнений (5.24) можно оценить и по величине нормы вектора левых частей уравнений системы: Nh = 2 ((7 )• Очевидно, что равенству О/г корням
V 1=1
системы уравнений (5.24) соответствует Nl! — 0.
120
Несомненным достоинством метода простой итерации яв-имется отсутствие в нем производных. Этот метод приводит к решению системы при близких начальных приближениях, однако с увеличением числа переменных и сложности уравнений опласть сходимости уменьшается и при выборе начального приближения необходимо руководствоваться опытом и здравым смыслом инженера
Более быструю сходимость к решению системы обеспечивает метод Ньютона. Итерационная формула для метода Ньютона может быть получена, если решение на каждой итерации представить как сумму предыдущего решения и добавки. Uk + i = Uk + AUk— и разложить левые части уравнений сис-н'мы (5.24) на (k + 1 )-й итерации в многопараметрический ряд 1ейлцра вокруг значений переменных на предыдущей итерации U11:
/,iu™) = / (йк + д7) = /,(й") + £®Нд ик + — t /|(^ W Д^;
6 а«,. 2 !<=!/=! du,Suj 1
— А’+1 _ —k —k —k n ) /. 1 и П (U ) Ь b
/,(U )=f2(U +ли ) = f2(U ) + s-'2( «•+ — ££ M —Wa»/-;
<=i dii: 2 !>=/=! du, du,
— k n k
/„«A =/,,o7+A u‘) = f„(yk)+ +^ tY^^^kiAuki.
<=i 2!f=i/=i dufiUj
Если итерационный процесс является сходящимся к точному решению системы уравнений > Uo, то при /г —> со приращения переменных будут малы, а сами перемейные бу-тут близки к значениям корней системы и можно считать, что левые части разложений обращаются в нули. В силу малости л(/й отбросим все члены разложения начиная с квадратичного и приведенная выше запись сводится к системе линейных_ура-впений относительно приращений искомых переменных &U.
/=| OUj
f (и' ) = ) Ли'1-
M ’ tr du, ” (5.26)
;=l du.
121
или F(U ) =-
ди.
AU , где
Ц(Ц ) dut
— матрица первых
производных (матрица Якоби).
Уравнения (5.26) позволяют формально ционную формулу метода Ньютона в виде
записать
им = ик
)
dUj
итера-
(5.27)
На __практике sfi(ukf dui
же обычно обращение
вызывает трудности и система
матрицы Якоби
(5.26) решается
относительно вектора приращений узловых потенциалов одним из известных методов решения систем линейных алгебраических уравнений (см. гл. 6), а_затем _н а ходится значения переменных на новой итерации Uk+} = Uk + £JUk.
Так как цель итерационного решения заключается в наискорейшем уменьшении от итерации к итерации нормы вектора левых частей системы уравнений математической модели устройства (5.24), что автоматически может и не выполняться на каждой итерации, то на практике чаще используют модифицированную форму метода Ньютона:
— /г+1 — k
и =и -tk
ди.
(5.28)
где коэффициент tk выбирается из условия минимизации нормы вектора ошибки , на очередной итерации: Л/*+1 = +tk*uk) -4
_ v 1=1
—> min . Так как значения Uk и At/* могут быть вычислены на каждой итерации, то величина tk может быть найдена методами однопараметрической оптимизации (см. гл. 12).
Для случая одного уравнения с одним неизвестным /(«) = 0 итерационная формула Ньютона (5.27) принимает вид
uk+ ' = uk- tkf(uk)/f\uk).
На рис. 5.2, а иллюстрируется Поиск корня уравнения /</(«) = О методом Ньютона от начального приближения и. Поиск корня по модифицированной формуле метода Ньютона (5.28) с оптимизацией коэффициента tk показан на рис. 5.2, б.
122
Рис. 5.2. Графическая интерпретация метода Ньютона — Рафсона
Приведем пошаговое описание работы алгоритма.
Алгоритм ' 5.4. Решение системы нелинейных уравнений модифицированным
истодом Ньютона
Шаг 1. Задается вектор начальных значений переменных.
Шаг 2. Вычисляются значения левых частей системы уравнений (5.24) и формируется вектор F(U ).
Шаг 3. Методом левых, правых или центральных разностей вычисляются все
ш> «можные- значения
производных
—-----. Формируется матрица
dUj
Якоби
диЛ
Шаг 4. Уравнения (5.26) решаются относительно вектора приращений перемен-пых Д U .
Шаг 5. Одним из методов однопараметрической оптимизации находится оптимальное значение коэффициента Ц, минимизирующего норму вектора левых частей - + 1 . , । истемы уравнении N на данном шаге Л+ 1.
Шиг 6. Вычисляются уточненные значения переменных U =U + ti{&U и Норма вектора левых частей уравнений N
Шаг 7. Если уточненное значение нормы N больше заданной точности N' > е. то переходим к шагу 2, иначе получено решение системы уравнений (5.24) относительно вектора узловых потенциалов U.
Заметим, что хотя метод Ньютона и имеет квадратичную 'ходимость, тем не менее для него_тоже существует проблема выбора начального приближения £/°. Можно считать [27], что величина области сходимости обратно пропорциональна числу уравнений и степени сложности системы, поэтому при моделировании устройства по постоянному току следует тщательно выбирать начальное приближение для итерационного процесса.
Метод возмущения, часто применяемый для решения задач моделирования сложных РЭС в статическом режиме, свободен от указанного недостатка, хотя и требует больших затрат машинного времени на получение решения. Суть этого метода шключается во введении наряду с системой уравнений мате-
123
магической модели устройства на постоянном токе F(U) = О, которую необходимо решить относительно вектора узловых потенциалов U второй системы <р((/) = 0 такого же порядка, как и исходная, решение которой известно. ____
Поиск решения исходной системы уравнений F({/) = 0 выполняется за п последовательных шагов решения деформированных систем уравнений u\U) = 0, которые на /г-м шаге деформации могут быть записаны в виде
rflft(i7) = <pl(U)+^[/l(D)-<pi(L7)] = o, п
d* (Z7) = ф2 (67) + * [f2 (Z7) - ф2 ((/)] = о,
• п (o.zy;
^(^) = Ф„(^) + -[/л(^)-Фй(^)1 = 0. п
При /г=1, поскольку число уравнений п велико, известное решение системы уравнений ф((7) = 0-UФо может быть использовано как хорошее начальное приближение для итерационного решения систем_ы на первом шаге деформации D(U) = 0. Так как_система £/((7) = 0 мало отличается от известной системы ф(С/) = О, то сходимость метода Ньютона будет обеспечена. Продолжая формировать деформированные системы D\U) = 0 и используя для их решения в качестве начального приближения решение, полученное на предыдущем, (7?-1)-м шаге деформации, повторяем этот процесс п раз. Когда k = п, деформированная система уравнений становится эквивалентной исходной системе F({7) = Lf\U) = 0 и решение последней из деформированной систем Cf\U) = 0 будет являться искомым решением для модели на постоянном токе.
Так как при большом числе переменных для выполнения последовательных деформаций может понадобиться большое число шагов, то это приводит к увеличению затрат машинного времени. С другой стороны, при большом числе переменных искажение системы на каждом шаге будет мало и решение ее может быть получено всего за несколько итераций методом Ньютона.
В [27] показано, что метод возмущений особенно эффективен при моделировании технических систем, в том числе и радиоэлектронных, при этом систему уравнений с известным решением можно получить, рассматривая любое устройство подобного же типа.
124
Приведем шаговое описание работы алгоритма.
Алгоритм 5.5. Решение системы нелинейных уравнений методом возмущений
Шаг 1. Формируется система уравнений с известным решением <р((7) —0 того *г порядка, что и модель радиоустройства на постоянном токе.
Шаг 2. Полагается ft—1.
Шаг 3. В соответствии с (5.29) формируется деформированная система на k-м иг.не деформации D (U) —0.
Шаг 4. Выполняется решение деформированной системы нелинейных уравнений методом Ньютона с использованием в качестве начального приближения решения системы иа предыдущем. (й-1)-м шаге деформации.
Шаг 5. Если k<n, то полагается k — k+ I и переходим к шагу 3, иначе имеем 1><'1ненне исходной системы нелинейных уравнений.
Ряд сложностей при моделировании РЭС на постоянном тке возникает, если устройство включает модели активных приборов, характеризующиеся экспоненциальными функциями. При итеративном решении систем уравнений математической модели в этом случае возможно переполнение разрядной сетки, так как экспоненциальная функция очень быстро возрастет при положительных значениях показателя степени. Возникают трудности и при больших отрицательных смещениях на полупроводниковых приборах, так как вычисляемые для матрицы Якоби производные имеют здесь очень малые значения. Один из возможных путей борьбы с этими трудностями включается в использовании при прямых и обратных напряжениях, превышающих некоторые значения, кусочно-линейной аппроксимации характеристик приборов.
Кусочно-линейную аппроксимацию целесообразно использовать и тогда, когда уравнения, описывающие нелинейности, известны не в аналитической форме, а заданы в виде таблиц измеренных значений. Алгоритмы, моделирующие нелинейнос-III с помощью кусочно-линейной аппроксимации, описаны, например, в [27].
§5.5. МОДЕЛИРОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В РЭС
Для моделирования переходных процессов в радиоустройст-нах необходимо решить систему математической модели, описывающей поведение моделируемого устройства во времени, с учетом начальных условий и временной зависимости входных сигналов. Как показано в §5.1—5.3, модель устройства представляет собой в этом случае систему дифференциально-алге-ораических или просто дифференциальных уравнений относительно фазовых переменных, являющихся функциями времени. К
125
настоящему времени разработано много подходов к решению таких систем на ЭВМ. Подобно предыдущему параграфу, ограничимся рассмотрением алгоритмической реализации наиболее распространенных из этих методов, математическое же обоснование их можно найти в [13, 27].
Для расчета переходных процессов в радиоустройствах, описываемых линейными электрическими моделями, обычно используется метод преобразований Лапласа, особенно удобный в связи с представлением уравнений модели в операторной форме и в равной мере применимый к моделям во временной и частотной областях. Специально разработанный для реализации на ЭВМ метод обратного преобразования Лапласа не требует определения полюсов и вычетов функции выходного параметра, применим к жестким системам и системам с распределенными постоянными. Как известно [13], временной отклик электрической модели определяется обратным преобразованием Лапласа:
= <5.30)
где F(s)— операторное изображение выходного параметра, полученное из математической модели.
Классический метод вычисления обратного преобразования требует нахождения полюсов и вычетов функции F(s), что неудобно при реализации его на ЭВМ. Чтобы избежать этого, заменим в (5.30) переменную интегрирования s на z = ts, а
р (Z)
функцию ez заменим отношением полиномов —-------, имеющих
QmW
степени п и т соответственно. Эта аппроксимация известна как аппроксимация Паде [14]. Коэффициенты полиномов Рп и Q„, в аппроксимации Паде могут быть найдены, если приравнять аппроксимирующую функцию ряду Тейлора для экспоненты ez:
Л j
Р (z) n+wi , 00 i
n>ZL - —!=«___________ = Ус z + Ус-Z
Q,„(z) '="+'n+1'
где о/, bi—коэффициенты полиномов в аппроксимации Паде, Ct— коэффициенты ряда Тейлора для ez. Приравнивая в последнем равенстве коэффициенты при одинаковых степенях z\ можно получить систему линейных уравнений для определения коэффициентов сц и Ь\. Для примера в табл,- 5.1 приведе-
шь
па аппроксимирующая функция шачений п и т.
P„(z)
для различных
<?,„(*)
Таблица 5.1
п 01 0 1 2
1 1 + г 1 + г + г2/2
0 —-
1 1 1
1 1 + г/2 1 + 2 г-/3 + 22/б
1
1-2 1-2/2 1-г/З
1 1 + 2/3 1 + г/2+г2/18
2 1-2 +г2/2 1 - 2г/3 + г2/6 1-2/2 + 2’718
После подстановки ег в (5.30) получим аппроксимирующее выражение для определения временного отклика модели через обратное преобразование Лапласа:
ДО =
I (-С+ /00 р <г}
2пу/ *7'°°
(5.31)
Интеграл в (5.31) может быть вычислен с помощью вычеши, расположенных внутри бесконечного замкнутого контура интегрирования справа и слева от оси координат. Чтобы инте-||трование вдоль бесконечно удаленного контура не давало вклада в значение интеграла, пит выбираются такими, что-z Р (zj
оы у подынтегральной функции F(—) " число полюсов
было больше числа нулей по крайней мере на два. Тогда в соответствии с теоремами операционного исчисления
f F(z/t} dz = ±/2+£ Rk. (5.32)
< к
। не знак плюс берется, когда контур интегрирования с располагается в левой полуплоскости и обходится против часовой « грелки, а знак минус — при расположении контура в правой полуплоскости и при том же направлении обхода, /?* — выче-|ы в полюсах подынтегральной функции, расположенные внутри контура интегрирования. Для п < т имеем
127
PnW k>
Qm(z) mZ-Z,.’
(5.331
p (z) где Zi — полюсы аппроксимирующей функции Паде —-—kt —
Qm(z) соответствующие им вычеты. Полюсы zt и вычеты kt для различных п и т рассчитаны с высокой точностью, и их значения, можно найти в [14]. Если в (5.32) и (5.33) замкнуть контур интегрирования в правой полуплоскости, то для временной зависимости выходного параметра модели получим выражение, Z(0=|£w,/0. (5-34)!
Выражение (5.34) представляет основную формулу прибли-] женного обратного преобразования Лапласа, которая исполь-^ зуется для моделирования переходных процессов в линейных электрических моделях. Определив из системы уравнений математической модели .операторное изображение выходного параметра F(s) и задавшись пит, можно найти с требуемой, точностью его временную зависимость.
Приведем пошаговое описание работы алгоритма.
Алгоритм 5.6. Моделирование переходных процессов в линейных моделях с по-мощью обратного преобразования Лапласа.
Шаг /. Из системы уравнений математической модели получаем операторное изображение выходного параметра модели.
Шаг 2. .Задаемся п и т и определяем полюсы zi и вычеты в них kp
Шаг 3. Делим каждое значение z(- на t и заменяем з в F(s) на Zi/t. Полагаем
текущее время моделирования t = Iq.
Шаг 4. В цикле т раз умножаем функцию F на и суммируем результаты]
2.F k, t ‘
Выделяем действительную часть суммы
и делим
на t.
Шаг 5. Если t< то увеличиваем t на At и переходим к шагу 4, иначе р»] счет переходного процесса окончен.
Описанный метод особенно удобен при моделировании ли! нейных устройств с непериодическими входными сигналами (одиночными импульсами, скачками потенциалов и т.п.). Оипы бки в расчетах вначале растут, потом стабилизируются даж! для очень больших значений времени, что позволяет увеличит! допустимый интервал расчета переходных процессов /кон за счет увеличения пит. Для контроля ошибок выполняютс'1 расчеты с выбранными значениями пит, затем расчеты а тем же значением т, но на единицу Меньшим значением сте' пени п. Если результаты совпадают, то расчет сделан прави льно.
128
I'и v 5.3. Графическая интерпретация методов решения дифференциальных уравнений:
и— метод Рунге — Кутта первого порядка, б —решение уравнения явным методом Эйлера. « — решение уравнения неявным методом
11 < других алгоритмов, используемых для решения систем диф-||н реициальных уравнений математической модели линейных ра-11н'устройств, можно отметить метод вариации произвольных по-< юяиных, описание которого приведено, например, в [13].
При моделировании во временнбй области нелинейных уст-ронств нельзя использовать метод обратного преобразования Л.шласа и приходится решать системы дифференциальных шик) дифференциально-алгебраических уравнений численными мг годами. Алгоритмы интегрирования систем дифференциаль-ш./к уравнений описаны во множестве учебников [27], мы расширим здесь некоторые из них, наиболее удобные для моде-ипрования радиоустройств. Для упрощения описания алгоритмов будем рассматривать их на примере одного уравнения с ошой неизвестной, затем распространим результаты на системы уравнений.
11усть требуется найти функцию и, удовлетворяющую уравнению
= и' = f(u, I) (5.35)
и принимающую при t— Zq заданное начальное значение и (Zo) = Ио-
V к । оматизаиия проектирования I». । ди оэлек тройных средста
129
Выбор начального значения ио служит для выделения одной из кривых семейства, задаваемого уравнением (5.35), как показано на рис. 5.3, а. Эта задача в математике известна как задача Коши. Для ее решения широко используются разностные методы.
В разностных методах решение задачи получают в дискретном ряде значений аргумента to, Z|, /&, Z„, отличающихся на шаг интегрирования А/. В одношаговых разностных метода! для нахождения следующего значения Uk = u(tk) требуется информация только об одном предыдущем шаге. Из одношаговых методов наибольшую известность получил метод Рунге — Кутта, который на самом деле является целым семейст] вом методов, представляющих аппроксимацию методов, осно! ванных на рядах Тейлора, но без явного вычисления производных, за исключением первой.
Для пояснения методов Рунге-—Кутта представим значе! ние искомого решения уравнения в точке разложением в ряд Тейлора вокруг предыдущей точки /*_/, u(tk) = uk = u(tk-i + А/) = «*_( + A/^rll + , (5.36)1
d/ 2! d/
Если шаг интегрирования А/ мал, то всеми членами разложения высокого порядка можно пренебречь и представит.', (5.36) в виде
= +А/~^ =иА | + А//(нй.|, tk\), (5.37)
dZ
где tk-i)—первая производная в предыдущей
dZ
точке Z*_|. Если процесс продолжить, то для любой последую щей точки задания аргумента получим итерационную формулу
Uk\ — Uh + tk), n.
Полученные выражения (5.37) для определения переменно! Ии известны как явный метод Эйлера, а по своей сути он пред ставляет метод Рунге—Кутта первого порядка. Графически выражение (5.37) проиллюстрировано на рис. 5.3, а, начиная точки /1, ui, где видно, что на каждом новом шаге определе ния приближенного решения переходим на другую кривую се мейства. Систематическая ошибка метода (ошибка дискрети зации) имеет порядок А/2, так как члены разложения (5.36^ содержащие степени А/ выше вт.орой, отбрасываются. Кровд систематической ошибки, в процессе вычисления появляетс: .ошибка округления, величина которой определяется ЭВМ 1 программой и которая накапливается с ростом числа шагов!
130
Точность метода можно значительно повысить, если сохрани и. член с Дг, однако для этого необходимо знание второй „ d2w(Z/;)
производной Величину второй производной можно ап
проксимировать конечно-разностным выражением
U ~ Ч (fk) _ ~ /0^’ /;)
d/z Д/ Д/
I и' для вычисления f(uk+\, tk+i) используется приближенное пычение Uk + 1 = iik + Atf(iik,tk), вычисленное по методу Эйлера. Подставив это выражение в ряд Тейлора и отбросив члены Hi.iiiie третьего порядка Д/3, можно получить
uk + I = iik +~[f(uk + Д/ - f(uk, tk),tM) + f(uk, tk)]. (5.38)
Выражение (5.38) известно как модифицированный метод Эплсра и по своей сути представляет метод Рунге—Кутта пороге порядка. Ошибка дискретизации для этого метода Пропорциональна Д/3 [14].
< /чевидно, что чем выше порядок вычисляемой конечно-раз-1ПН1ИЫМ методом производной, тем больше дополнительных вычислений правой части уравнения (5.35) необходимо сделать. Метод Рунге — Кутта дает набор формул для расчета коорди-н.и точек внутри интервала tk—tk + i для реализации этой и/ion Для примера приведем распространенную формулу меры а Рунге—Кутта четвертого порядка
Uk + । = Uk + — [/г(| + 2/г, + 2k2 + /г3], •
6
В"- /го = /(нЛ, tk), ki= f(uk + ^- k0,
(5.39)
f(llk+ ~ f-k + ^“)’ = f^Uk + Д^2, Zfe+l).
Заметим, что в методе Рунге — Кутта четвертого порядка пн.шале вычисляется величина /го для предыдущей точки tk l.i гем, используя это значение /го, аргумент смещают на пол-пипа вперед Ik + — и получают значение k\. На основе k\ из
||'Г1 точки tk опять со смещением на половину интервала ин-п-1 рирования вычисляют значение /гг и, наконец, сделав полный шаг вперед от точки tk, вычисляют значение /гз- Значения
A’i, k% k$ затем суммируются с весами 1/6, 1/3, 1/3, 1/6.
131
Шаг интегрирования выбирается из максимально допусти мой ошибки на каждом шаге интегрирования. Оценка ошибш приводится в [27] и в современных алгоритмах обычно оцени вается автоматически, позволяя автоматически изменять дли ну шага. Недостатком методов Рунге — Кутта высокого поряд ка является необходимость вычисления большого числа значе ний правой части уравнения (5.35) для каждого шага, причел эти вычисленные значения не используются на последующи^ шагах.
Одношаговые методы легко распространяются на системь обыкновенных дифференциальных уравнений. Если в резуль тате работы программы моделирования система уравнений модели получилась более высокого порядка, то с помощью под становок ее всегда можно свести к системе обыкновенны дифференциальных уравнений. Например, в дифференциаль ном уравнении второго порядка —- - f(u, t) можно воспользо dt
.. du 1
ваться подстановкой-— = v и получить систему двух обыкно d/
венных дифференциальных уравнений:
du
— = v, dt
%
Пусть после подобных подстановок система уравнений ма тематической модели приведена к системе обыкновенных диф ференциальных уравнений вида
= F(U, t), dt
где U — вектор переменных, F(U, t)
— вектор правых час
т
тей уравнений системы.
Воспользовавшись для простоты модифицированной форму лой Эйлера (5.38), запишем итерационную формулу для реше ния системы обыкновенных дифференциальных уравнений од пошаговым методом второго порядка:
и k +, = U(tk +,) = vk + у [I] |7((7/г. t k) + F(Uk + дфйёЛ, tk), tM)], где [1] — единичная матрица.
132
’(ля сравнения различных одношаговых методов по эффек-||ичк>сти рассмотрим решение этими методами уравнения
2/2 +2и при следующих начальных условиях: t = 0, и = 1
|11| Аналитическое решение этого уравнения с учетом задан-lii.ix граничных условий имеет вид
u= l,5e2t-/2-/-0,5.
Ниже в табл. 5.2 приведены результаты численного решения ^того уравнения с шагом интегрирования А/ = 0,1 различными методами.
Таблица 5.2
б Метод Эйлера Метод Рунге — Кутта четвертого порядка Точное решение
0.1 1,2000 1,2221 1,2221
0,2 1,4420 1,4997 1,4997
0,3 1,7348 1,8432 1,8432
0,4 2,1041 2,2783 2,2783
1,0 7,0472 8,5834 8,5836
Как видно из табл. 5.2, точность полученного результата •jiiiicht не только от величины шага интегрирования А/, но и pi количества шагов, и при большом числе шагов точность получаемого результата снижается из-за накопления ошибок инна рирования.
Алгоритм 5.7. Интегрирование системы дифференциальных уравнений метода» Рунге—Кутта второго порядка
Шаг /. Полагаем, что время .интегрирования равно началу процесса интеграции.ишя й = 0. ty = to, а переменные U(to) = Uo — их начальным _условиям.
Шаг 2. Вычисляем вектор правых частей системы уравнений F(Uy, tk) в момент ll|li'M(41H ty.
Шаг 3. Вычисляем вектор значений переменных по методу Рунге—Кутта in рного порядка, используя вычисленные на втором шаге значения правых частей Vo пшений Uk +1 =Uk + A/[1]F(£7/j, t-kY
Шаг 4. Вычисляем вектор правых частей системы в момент времени >1 , । - lk + Kt при F(Uk+ ь tk+i).
Шаг 5. Вычисляем решение системы уравнений для момента времени tk+i, io пользуя выражение (5.38).
Шаг 6. Если ty+i < <кон. т0 увеличиваем t на шаг интегрирования AZ и передним к шагу 2, иначе расчет закончен.
133
Для рассмотрения многошаговых разностных методов вер] немея опять к задаче Коши (5.35). Будем полагать, что нам известны значения решения уравнения в г предыдущих точкая соответственно равные Uk-\...Uk-r- Значения Uk-i...Uk-l можно вычислить, например, с помощью метода Рунге—Кутта. В многошаговых методах новое значение переменной Uk н следующей точке интегрирования вычисляется с помощью рекуррентного соотношения:
- bof(uk, th) + bj(uk_v tk_x) + brf(ut_r, tk_r), (5 40) AZ
где ah bi—коэффициенты, не зависящие от k, i = 0,..., г, при чем «о * 0.
Из (5.40) видно, что в многошаговых методах допускаете!, вычисление Uk только в регулярных точках интегрирования Ц и изменять шаг интегрирования, подобно методам Рун] ге — Кутта, затруднительно. Если йо = 0, то значение Uk выра] жается явным образом через предыдущие значения Uk-\...Uk-r и производные в этих точках f(uk-\, tk-i) и мы имеем дело с явным многошаговым методом. Когда же b^Q, для нахождения Uk приходится решать нелинейное уравнение:
aouk-bot!df(uk, tk) = -'£uk~iai +
/=1 <=i
В этом случае метод называют неявным.
В практике вычислений наибольшее распространение полу чили методы Адамса, которые представляют частный случаи многошаговых методов (5.40), когда ao = -ai = l, и* = 0 npj] k = 2, 3,...., г, т.е.
uk = Uk-t + А^6,/(ма_,,
(5.41)
(5.42)
i=0
В случае b = 0 методы Адамса будут явными, в противном случае — неявными. Описание различных вариантов явных методов Адамса можно найти в [27].
Рассмотрим неявные варианты многошаговых методов, koj торые применяются для решения жестких систем дифференциальных уравнений. Дифференциальное уравнение и система таких уравнений называются жесткими, если они описываю] разномасштабные по времени процессы, протекающие в моделируемом объекте. Другими словами, жесткими системами уравнений являются системы, постоянные времени в который разнятся во много раз. Такие случаи часто встречаются практике моделирования радиочастотных устройств, когда по, стоянные времени цепей питания во много раз превышают пс
134
। кшпные времени цепей радиочастоты. Решение таких систем п/шошаговыми и явными методами приводит к значительным ошибкам. Рассмотрим для примера систему
— = 998и + 1998гц — = -999и - 1999о. d/ dt
Гели полагать ио = Vo = 1, то решение системы нетрудно найти аналитически и оно будет равно
u = 4et-3e'ooot-, о =-2e‘z + 3e'l000z.
Попробуем решить эту систему методом Эйлера. Дискретное решение можно записать формулами
Uk + I = Uk + Д/(998ы^ + 1998щ);
Vk + i = Vk + At(-999uk - 1999о^),
i не wo = «о = Г Если шаг интегрирования At = 0,01 то
ui = 1 + 0,01(998 + 1998) = 30,96;
vt = 1 + 0,01(-999 - 1999) = -28,98
место точных значений и\ =3,96, Hi =-1,98. Если сделать еще п< сколько шагов интегрирования, то расхождение с точным решением принимает катастрофический характер. На начальных шагах интегрирования ошибку можно уменьшить исполь-ншлнием меньшего значения At, однако постепенно ошибки округления и дискретизации накопятся в такой степени, что • нова приведут к неустойчивому решению. Графически решение системы явным методом Эйлера показано на рис. 5.3, б.
В настоящее время для решения жестких систем дифференциальных уравнений математической модели радиоустройств широко используется метод Гира, в основу которого положены И! явные многошаговые методы. Формулу Гира можно получить hi (5.40), если положить Ь\ = = ••• = Ьг = 0, bo = 1. Тогда для
<и искания очередного значения переменной Uk получаем нелинейное уравнение
a0Uk - Atf(uk, tk) = -^UjUk-i- (5.43)
(=i
Коэффициенты сц в правой части (5.43) выбираются из ус-1<|нпя минимальной погрешности аппроксимации. Это условие |'.|7| приводит к линейным уравнениям относительно коэффициентов ас.
ao = -^jai\ =-1; =0, I =2,3...г.
/=1 /=| с=1
135
Если эти уравнения записать в виде системы, то получим
tii + 2а2 +... + гог =1;
<2, + 2? 0-2 + ... + г2 о.г = <2о;
О] + 23«2 + ... + г^аг — 0; (5.44)1
<2| + 2Г 0-2 + ... + г'о.г = 0.
где г — порядок аппроксимации, учитываемый в конкретном случае. Эта система линейных уравнений имеет однозначно,1 решение,- так как ее определитель отличен от нуля. Так, прй
3 1
г = 2 коэффициенты будут равны <2о = -~ , «i=-2, «2 = — •
и тогда уравнение для оп
Для г = 3 из (5.44) можно получить значения коэффициен] тов ап = — , а\ = -3, «9 = —, аз — — 6 2 3
ределения Uk получим в виде
- Mf(uk,tk} =~3uk^ о
3 1
— uk_2 + uk^. Z* О
Неявные разностные методы обладают хорошими свойства ми устойчивости при решении жестких уравнений, что компен сирует необходимость решения на каждом шаге интегрирова ния нелинейного уравнения. Графически решение систем! уравнений из вышеприведенного примера неявным методе! первого порядка (г=1) показано на рис. 5.3, в.
Полученные выше формулы несложно распространить и н систему дифференциальных уравнений. Воспользовавшис! приведенной выше формулой Гира для г = 2 для одного урай нения, запишем итерационную формулу для решения система на k-м шаге интегрирования:
а _ ---- _ 1 _
|[Д -M[l]F(Uk,tk) = 2Uk-i (5 45
Система нелинейных уравнений (5.45) на каждом шаге до^ жна решаться относительно значений искомых переменных L в очередной точке интегрирования tk. Это решение можВ быть выполнено, например, методом Ньютона, если в качеств начального приближения для Uk использовать Uk-\-
Алгоритм 5.8. Интегрирование жесткой системы дифференциальных уравн ний методом Гира второго порядка
136
nine I. Определяем ц.|‘|.1.лы1ые значения in |н-мепных в узлах ин-1'1 рпрования /о и Рп Н| Полагается те-I пит время интегри-I Ц1.Н1ПЯ / = 1\.
Ill иг 2. В соответствии! г (5.45) формируем Lii'iiyto часть системы !* пшенных уравнений
Н1))1)гнтельно неизвестных
Рис. 5.4. Двухтактный пиковый детектор радиоимпульсов
значений переменных в точке /j»;
3 — ----
-Uk-M[\y(Uk. tk)-
Шаг 3. Формируем вектор правой части системы нелинейных уравнений отно-Ihkou.iio Uk'. 2Uk—l~ ~+'k-~2-
Шаг 4. Систему нелинейных уравнений, сформированную на предыдущем > ин решаем относительно Uk методом Ньютона,
Шаг 5. Если tk < /кои- то увеличиваем tk на шаг интегрирования Д/ и переходим к шагу 2, иначе моделирование переходного процесса закончено.
Оценка ошибок многошаговых методов интегрирования сис-ji mi.i дифференциальных уравнений и областей их устойчивос-HI юстаточно сложна и существенно зависит от характера ин-1< । рыруемой системы. Эти материалы можно найти в [27].
Вопросы и упражнения для самопроверки
I. Какова размерность вектора фазовых переменных при формировании систе->-ы уравнений математической модели рис. 5.1. а табличным методом?
Сформируйте электрическую модель двухтактного пикового детектора ра-щпимпульсов РЛС, схема которого приведена на рис. 5.4, используя модель полу-1ipi.ii тикового диода Эберса — Молла. Получите для электрической модели пико-пн штектора блоки матриц инциденций и главных сечений согласно (5.8) и запиши ш систему уравнений по методу узловых потенциалов.
3. Преобразуйте источники тока в эквивалентные источники напряжения (теорем.i Гевенина) и получите для графа модели пикового детектора блоки матрицы ..in ц’нций и главных контуров согласно (5.11). Запишите систему уравнений Mali м.1 гической модели для пиковогб детектора по методу контурных токов.
1 Какова размерность вектора фазовых переменных при формировании систе-.. уравнений математической модели по методу переменных состояния?
.1. Пусть статический режим участка интегральной схемы описывается систе-||.и нелинейных уравнений
2
3%| + 2х 2 — 5х2 + 15 =0;
2 2 *
2х । — Зх| + х 2 + 2x2—= О-
137
Выполните несколько шагов решения системы (Х| = I. Х2 — 2) методом простой ита рации и Ньютона при различных начальных приближениях и проследите за сход! мостыо.
6. Что достигается использованием аппроксимации Паде при моделировании переходных процессов в линейных устройствах?
7. Пусть математическая циальных уравнений вида
модель устройства описывается системой дифферен
dxs/dl “(Л| + Х2)1;
dxi/(il - (%2—xi)t.
интегрирования системы, используя метод Рун
Выполните несколько шагов
ге — Кутта второго порядка при %|(0) — хг(0)= 1 Д<“1.
8. Выполните несколько шагов интегрирования методом Гира второго порядкя для системы дифференциальных уравнений из п. 7, используя два первых значения из предыдущего решения.
Глава 6
МАТЕМАТИЧЕСКИЕ МОДЕЛИ РЭС В ЧАСТОТНОЙ ОБЛАСТИ
Как указывалось в гл. 4 и 5, фазовые переменные, полнос-ii.io характеризующие состояние объекта проектирования в частотной области, являются функциями комплексной частоты А /со. Этот случай соответствует анализу установившегося р< жима при возбуждении линейной или нелинейной цепи ис-[очпиками синусоидального сигнала.
В настоящей главе рассматриваются основные алгоритмы моделирования различного уровня в частотной области, методы решения систем линейных уравнений, а также алгоритмы моделирования нелинейных радиочастотных трактов.
§0.1. МЕТОДЫ МОДЕЛИРОВАНИЯ РЭС В ЧАСТОТНОЙ ОБЛАСТИ
При моделировании РЭС в частотной области используется mi год комплексных амплитуд, суть которого заключается в him, что в установившемся режиме в любой сложной электрической цепи при синусоидальном воздействии напряжения и кжи могут быть представлены в виде суммы синусоидальных । оставляющих: основной (со) и высших (2со, Зсо, ...) гармоничес-гих составляющих. Подобный подход также называют спектральным анализом устройства.
Наиболее часто такой подход применяется при анализе ра-пючастотных трактов, в которых и протекают такие периодические синусоидальные токи.
В качестве фазовых переменных в частотной области применяются напряжения и токи не только на отдельных элемен-|.|х, но и на входах четырехполюсников и многополюсников, а ыкже линейные комбинации напряжений и токов цепи.
К выходным параметрам радиоэлектронных средств в час-ниной области относятся различные функции цепей — входные и передаточные комплексные сопротивления и проводимости, коэффициенты отражения и передачи по напряжению и нжу, коэффициенты усиления радиоэлектронных средств и др.,
139
причем для цепей с сосредоточенными элементами эти функ-1 ции являются дробно-рациональными относительно комплекс-! вой частоты.
Рассмотрим связь между некоторыми выходными параметрами. Так, если K(jw)—комплексный коэффициент передачи цепи, то частотная Л'(/со) и импульсная характеристики g(t) связаны между собой парой преобразований Фурье:
K(jw) = J g(t)e 'M'd/, g(t) = Xf (6.1)
Если используются аналоговые сигналы, то соотношения! (6.1) — непрерывные; для импульсных сигналов применяются! специально разработанные алгоритмы дискретного (в том чис! ле быстрого) преобразования Фурье.
Представив комплексный коэффициент передачи /\'(/ы) = К(а>)е'^ю\ отмечаем, что — амплитудно-частотная! характеристика, ср(со)— фазочастотная характеристика цепи. I
Импульсная g(t) й переходная /?(/) характеристики связашЛ друг с другом соотношениями
g(t) = ±h(t), ft(/) = Jg(T)dT. (6.2)
d/
При подаче па устройство произвольного входного сигналJ хт(1) выходной сигнал во временной области можно найти с помощью интеграла свертки (Дюамеля):
I
*вых(0 = J - т)бт. (6.3)
(I
Этому соотношению в частотной области соответствует
ХВЫх(/ш) = К(^) Хвх(/со), (6.41
где Хвх(/со) и XBi,ix(/“)—спектры входного и выходного сигналов.I Методы моделирования РЭС в частотной области можн! разбить на две группы; в первой из них используется связи между временными и частотными характеристиками цепей, в<| второй — выполняется непосредственное моделирование выход! пых параметров радиотехнических устройств.
Методы моделирования первой группы заключаются в огн ределении по прямому преобразованию Фурье (6.1) частотно™ коэффициента передачи и затем расчете по (6.4) спектров вы! ходных сигналов по заданным входным. Наконец, с помощьга обратного преобразования Фурье (6.1) можно найти времен! ные характеристики выходных сигналов.
140
В методах второй группы для анализа устройств исполь-lyeicH выражение (6.4), причем частотные функции цепи непосредственно моделируются по внутренним параметрам устройств.
В подавляющем большинстве случаев используются мето-п.| второй группы, в которых для различных значений рабочих частот вычисляются значения частотных характеристик V« ipoiicTB [12, 13, 21], так называемый численный спектральный подход.
большое достоинство частотных методов анализа по сравнению с временными — высокое быстродействие, возможность нпализа устойчивости и др. Они наиболее удобны при использовании матриц классической и волновой теории для моделирования РЭС, радиочастотных и излучающих устройств, комплексов радиоэлектронных средств и др.
§6.2. ПРИМЕНЕНИЕ МАТРИЦ КЛАССИЧЕСКОЙ И ВОЛНОВОЙ ТЕОРИИ ДЛЯ МОДЕЛИРОВАНИЯ РЭС
При частотных методах анализа все двухполюсные элементы, вхо-iHiniie в схему, характеризуются своим комплексным сопротивлением (/<о)= г (го) + /х (го) или проводимостью у (]'(&)= I/z (/го) = g (го) + I //>(ю), зависящими в общем случае от частоты.
Четырехполюсные и многополюсные элементы электрических । м м описываются соответствующими матрицами параметров.
Все матрицы делятся на две основные группы: матрицы, соответствующие классической теории четырех-1юл юсника;
матрицы, соответствующие волновой теории четырехполюсника.
В первую группу входят матрицы сопротивлений (импедан-i.i) Z, проводимости Y, передачи А, гибридная Н и др.
Во вторую — матрица рассеяния S и волновая матрица пе-]ц чачи Т.
Элементы и структуру матриц рассмотрим на примере че-п.||>ехполюсника N (рис. 6.1). Пусть к обоим входам четырехполюсника подключены два независимых источника с активным внутренним сопротивлением.
Матрицы классической теории четырехполюсника. В этом ыпучае фазовыми переменными, полностью описывающими н< пь (рис. 6.1), являются частотные характеристики комплексных токов и напряжений на входах четырехполюсника. Соответствующие элементы матриц связывают эти две пары пере-м< иных в виде двух уравнений, поэтому при известных матрицах две из фазовых переменных являются зависимыми, а inc — независимыми (источниками).
141
+ 4
Рис. 6.1. Напряжения и токи на входах четырехполюсника
Z, 2
В зависимости от того, какая пара фазовых переменных выбирается независимой, формируется та илй иная матрица классической теории. Возможны шесть комбинаций пар зависимых и независимых парамет ров. Все элементы матриц в общем случае также являются функциянЛ
комплексной частоты.
В матрицах сопротивления (холостого хода) Z независи мыми считаются токи на входах, поэтому напряжения равны
(7| — zi|7| + 2(2/2, .(^2 ~Z2lA +^22 ^2’
(6.5
или
U = Zl, U =
Z =
2И 212
матрицы в режиме
- 212 ~
2
/4. Z
холостого хода
.2
= о 21
г21 222_
I =
называются
того
z-параметрами или иного входа:
2
= О
2
2 22 “
'2
(6.1 /, = О
Элементы определяются
I, I, - О
Сопротивления z\\ и Z2j — передаточными, матрица Z является сопротив- ления равны
Для определения матрицы проводимости (короткого замь1 кания) Y задаются напряжения U\ и U2 на входах четырехпс люсника,
^22
Для
симметрической
Zl2=« 221-
или
Элементы ляются в
называют i взаимного
a zl2
входными, । четырехполюсник
и передаточны
тогда токи равны
7| = «/ц^7| + У\2^2’ t/2 = //21(/| +Д/22И2,
I = \и,
У\\ У12
. Уи У22 _
(6.7
матрицы Y называются //-параметрами и опред! короткого замыкания того или иного
/, /, /,
= — «/,. = У* =
режиме
входа
«/.2
I/, П2 = О Проводимости «/21 — передаточными. Для взаимного четырехполюсника
U,, |С/| <= о
I/, U2 = О
и., ut = о
(6.;
У\\ и «/22 называют входными, а
«/J2
142
и.1грица Y является симметричной и передаточные сопротивления равны. Отметим, что i/ц * 1/гц и т. д., так как эти пзраметры определяются в разных режимах, в то же время ими матрицы являются взаимно обратными: Z = Y .
Матрица передачи (цепная матрица) А соответствует пере-ине сигнала с левого входа на правый; следовательно, незави-। имыми фазовыми переменными считаются выходные (для че-и.фехполюсника) напряжения U2 и ток (-/2). а входные равны
{/| = auU2 — ^|2^2> ч
/| = a2iU2 ~а22^2
(6-9)
и,
= А
А
ап а12
.А.
Элементы матрицы передачи А и определяются частью в режиме режиме короткого замыкания второго хода:
_°21 °22 _
называются «-параметрами холостого хода, частью — в
и
U,
,«2, = ~ и7 = о и..
.а. 4=0
‘22
-ь .(6.10)
~/2 и2 = о
Элементы матрицы ац и «22 называют коэффициентами перс гачи соответственно по напряжению в режиме холостого ко । । и по току в режиме короткого замыкания на втором вхо-|г Элементы «12 и «21 — передаточные соответственно сопро-।пиление и проводимость при коротком замыкании и холостом Й<> ю на втором входе (см. (6.6), (6.8)). Знак минус в формулах (Ь1*), (6.10) указывает на то, что направление тока /2 удобнее ыменить на обратное; тогда минус исчезнет. Для взаимной воин определитель матрицы detA=l.
Гибридная матрица Н получается, когда независимыми фазовыми переменными считаются ток на первом входе 1\ и напряло ние на втором входе U2, тогда остальные переменные равны
U, - h.. I, + /z.9f/9;
. *11 1 12 2’ (6.11)
/2 —h2\l} + h22U 2
и ни
н =
/2 _ U2
h h
Kll rLl2 h h
L/42l ft22J
-Элементы гибридной матрицы H называются //-параметрами и определяются в режиме холостого хода по первому входу и короткого замыкания — по второму входу:
./г.,., .(6 12)
/, U., = 0 ~ и2 /, = о
143
Элементами гибридной матрицы Н являются «и р /?2j — соответственно входное сопротивление и коэффициент передачи по току при коротком замыкании на выходе, h\2 t hi2 — соотйетственно коэффициент передачи по напряжению ь передаточную проводимость при холостом ходе на входе. Дл» взаимного четырехполюсника действует условие hi2 + /?2i = 0.
Области применения рассмотренных матриц различны прь разном включении отдельных четырехполюсников в состав; общей схемы. Так, матрица сопротивлений удобна при после довательном соединении обоих входов четырехполюсников < общими токами на их входах, тогда общая матрица Z цет равна сумме матриц Z, отдельных четырехполюсников; Z =
Матрица проводимости удобна при параллельном соедине нии отдельных четырехполюсников с общими напряжениями на их входах, тогда общая матрица Y-цепи равна сумме мат риц У, отдельных четырехполюсников: У = У,-.
Цепная матрица удобна при каскадном соединении отдель ных четырехполюсников, когда выходные напряжения и toi предыдущего четырехполюсника совпадают с входными нап ряжением и током последующего; тогда матрица передачи / каскадного соединения равна произведению матриц передачи А,- отдельных четырехполюсников: А=]^А,.
Гибридная матрица Н удобна для макромоделированш транзисторных каскадов, так как условия определения элемен тов гибридной матрицы близки к физическим режимам работы транзисторов. Гибридная матрица применяется при сме шанном соединении четырехполюсников: последователь ном — по входу, параллельном — по выходу. Тогда матрица Ь общей цепи равна сумме матриц Н, отдельных четырехполюс ников: Н =^НР >=|
Связь между элементами рассмотренных матриц отражен^ в табл. 6.1. Определители матриц связаны следующими соот ношениями:
det Z = —— = = = = =
det У a2l h22 z2l y2i ^21
(6.13)
Z22 Ун tz22
144
Таблица 61
Связь между элементами классических матриц четырехполюсника
Z Y А Н
Z 1 2HZi2 1 _Z21 222. Z22 ~ ZV2 1 У22 Уп ГУ 21 Ум. Ун У12 1 ан detA С121 1 Д22 1 а22 -detA ] detH /г,2 /г22 — й21 1 II — Д2
detY
Y А Н det 2 £ z2i £ 2 22 —Z2| Z|| г,, detZ 1 222_| detZ z12 —z2, 1 -1 У2, 1 У 11 У'21 У 22. У22 । detY уи 1 ~У,2 У 21 detY а12 L~1 1»ц J ап Я12 1а21 а22. 1 а)2 detA а22 1 а21 /гн [/г2) detH 1 [detH /г,, /г2( h.a 1 /г„ /г,2 _/г2| /г22
По табл. 6.1 легко получить связь между элементами матриц при условиях:
— взаимности четырехполюсника: 212 = 221, у\2 = У2\, detA=l, h 12 + hsi= 0;
— симметрии четырехполюсника: zij = Z22, У\\ — У22, аи = ^22, <1НН = 1.
Возможны еще два типа уравнений, соответствующих двум комбинациям пар зависимых и независимых параметров, но
они не получили широкого распространения:
И,
,G =
£11 £(2
S22.
а12
tz 21 а
. (6.14)
22.
G
2
= Н 1
П2
Первая из них есть гибридная матрица, обратная матрице II, вторая — обратная матрица передачи, соответствующая поправлению передачи справа налево (рис. 6.1).
Матрицы параметров наиболее часто применяемых четырехполюсников приведены в табл. 6.2 [12, 13].
Пример 6.1. Приведем частотные характеристики рассмотренных параметров |ля чебышевского фильтра 5-го порядка со следующими данными: граничная час-н>та — 10 МГц, неравномерность характеристики передачи в полосе пропускания— 0,1 дБ. сопротивления нагрузки и генератора — 75 Ом.
Схема фильтра, его характеристики затухания (Да) и коэффициента бегущей полны (КБВ) приведены на рис. 6.2, а, б. Легко подсчитать, что заданная неравномерность соответствует KBBmin = 0,74.
145
Р и с. 6.2. Схема (а), частотные характеристики затухания и КБВ (б) чебышевского фильтра
Рис. 6.3. Комплексный коэффициент передачи (а), переходная и импульсная характеристики (б) фильтра
На рис. 6.3, а. б изображены характеристики комплексного коэффициента передачи фильтра, а также его импульсная и переходная характеристики. Вид последних тесно связан с граничной частотой, видом аппроксимации и неравномерностью характеристики передачи фильтра.
Таблица 6.2
Матрицы простейших четырехполюсников____ ______
Вид четырехполюсника Элементы матрицы
Z Y А
Не существует У —у —у У 1 2 0 1
• X- • Z -Z -z Z Не существует I 0 У 1
146
П родолжение табл. 6.2.
Вид четырехполюсника Элементы матриц
Z Y A
_ 1 -/UMry/ sin у/ /IV'clgy/ Sill у/ -/cig у/ / CSC у/ W W j CSC у I /cig у I w w cos у/ /IFsin у/ / sin у/ . — cos yl Ц7
Длинная линия Волновое сопротивление W Постоянная распространения у
»?/»!=// Нтеальный трансформатор Не существует He существует n 0 0 1/n
р/ Не существует He существует l/p o 0 0
112=1X11 \ Источник напряжения. управляемый напряжением
4 Не существует 0 0 a 0 0 -1/g 0 0
4“/ (
12= Источник тока, управляемым напряжением
0 0 г 0 He существует 0 0 1/7 0
ii4=ri 1 Источник напряжения. управляемый током .
Не существует He существует 0 0 0 -l/p
(2=Р6 Источник тока, управляемый током
147
Рис 6.4. Характеристики z-параметров (а) и (/-параметров (б) фильтра
Рис. 6.5. Характеристики a-параметров фильтра
рис. 6.4, 6.5, 6.6 показаны частотные характеристики
На рис. 6.4, 6.5, 6.6 показаны частотные характеристики элементов матриц Z, Y, А и Н фильтра. Все они являются параметрами импеданса, проводимости или передачи фильтра при холостом ходе или коротком замыкании входа или выхода фильтра. Так как рассматривается схема фильтра без потерь, то характеристики передачи — элементы «ц и «22 на рис. 6.5 и элементы П\%, hz\ на рис. 6.6 — являются вещественными, а остальные — входные или выходные сопротивления или проводимости — чисто мнимыми величинами. Легко проследить связь между приведенными элементами матриц согласно табл. 6.1, а также условиями взаимности и симметрии схемы фильтра.
Матрицы волновой теории четырехполюсника. Эти матрицы вводятся для нагруженного четырехполюсника (рис. 6.7). В этом случае в качестве фазовых переменных принимаются комплексные «падающие» и -------------"" ----- ------”---
комбинации нормированных четырехполюсника:
«отраженные» волны — линейные напряжений и токов на входах
а2
(Ц ~Ш
I-- (^2 + ^Г2^2)>
(6.15)
I---(^2 ~ ^/2 ^2 )•
27^7
148
Рис.-6.6. Характеристики ft-параметров фильтра
Используются два типа волновых уравнений, соответствующие двум комбинациям пар падающих и отраженных волн, матрица рассеяния S и волновая матрица передачи Т.
Матрица рассеяния S связывает падающие волны (независимые переменные) и отраженные волны (зависимые переменные) в виде уравнений
ft, = sun, + si2a,', b2 - s21ci( + s.„a..
(6.16)
пли
b -Sa,
SI2 a
S2I S22J LG2.
Элементы матрицы рассеяния называются s-параметрами и определяются в режиме наличия и отсутствия падающей волны с того или иного входа (наличия или отсутствия императоров Е\ или Ег, рис. 6.7):
Рис. 6.7. Нагруженный четырехполюсник
149
bt
, «12 = —
Ь2
S22 = —
I fl2
= L
" «, а., = О’
Подставив (6.15) в (6.17), получаем:
Z. - R.. Z., - R 2UП
= -----L • S* = ----=- «21 = —А
Z, + /?,, Z, + /?,s £, V
где Z| и Z2 — входные сопротивления соответственно с первого или второго входа, когда источник на противоположном входе замкнут накоротко. Следовательно, диагональные элементы хц и s’22 матрицы рассеяния есть коэффициенты отражения по первому или второму входам, а внедиагональные S12 и л’21 — коэффициенты передачи в прямом или обратном направлениях.
Для взаимного четырехполюсника матрица рассеяния является симметричной и коэффициенты передачи равны: Л12 = л’21. Для четырехполюсника без потерь матрица рассеяния унитарна: SS=1, где + означает комплексно-сопряженную транспонированную матрицу.
Матрица рассеяния удобна для анализа энергетических характеристик радиочастотных трактов (см. §6.3).
Волновая матрица передачи Т связывает волны на одном входе с волнами на другом входе. При этом в качестве «падающих» волн принимают волны, идущие в одном направлении, а отраженных—в другом. Если принять за независимые фазовые переменные «выходные» волны 62 и 02, то «входные» волны «I и Ь\ определяются решением системы уравнений:
а2
л’ 521 fl, = О
ь2
fl, а2 = о'
n <617> a, = 0
S,
или
a
а, = ttlb2 + /|2а2; + br>ti
b. = L,b.
(6.19)
= т
A J
А’ а., ’
|_u2 j
Элементы волновой матрицы раметрами и определяются или отражений от него:
при
А1 /|2
/2| <22-
передачи Т называются /-па-отсутствии второго генератора
T =
I = ^-*11 .
, > Аг
Ь„ а., =0
_ n.
a„
,1 ь., = о
> ‘21 _
= А_.
Ь2 а2 = О
2
t = А > ‘22
a.,
. (6.20)
Ь2 = О I
Волновая матрица передачи, как и матрица А, наиболее удобна при каскадном соединении четырехполюсников. Общая матрица в этом случае также равна произведению соответствующих матриц: Т = Вт,.
15()
Элементы волновых матриц рассеяния S и передачи Т свя-
1.Н1Ы соотношениями
S =
sn
_S2I
s1Z
S22
1 ^21 detT . -p _ ^i2
Ai J — Аг_ J21 ^22 _
1 1
s2( xI(
S22 detS
(6.21)
Формулы связи между элементами классических матриц и матрицы рассеяния S приведены в табл. 6.3.
Таблица 6.3
< вязь между элементами классических и волновых матриц четырехполюсника
Z A H
р detZ+zi j+z22+1 detY+yn+^i+l O)l+Oj2+021+O22 detH+/o 1+/122+1
Yi detZ+2||-Z22-l -detY-i/ii+j/22+l ail+«l2-C2|-a22 detH+/i|i-ft22-l
Y2 detZ-zn+z22-l -detY+{/n-j/2i+l -O|l + O|2-O21+O22 —det Н+Л| (—A22+1
S 2 Yl 2г12 P Y2 1 Yi ~ 2z/i2 1 y, 2detA ₽L2 Y, . 2 Yi 2^2 P 2/*2i Y2 .
Рассмотренные выше матрицы параметров для четырехполюсников могут быть распространены на случай произвольно-ю многополюсника. При каскадном соединении произвольных многополюсников наиболее часто используются матрицы рассеяния S и неопределенные Y-матрицы.
В случае неопределенных Y-матриц фазовыми переменными модели являются напряжения на входах многополюсника (рис. 6.8). Тогда Y-матрица связывает напряжения и токи на входах многополюсника:
7 = YL/, 7 = [/1/2.../J, U = {щи2...ип]\ (6.22)
Так как сумма всех токов, втекающих в многополюсник, равна нулю: = О, то
;=|
=0, (6.23)
<=1 /=1
г е. определитель неопределенной Y-матрицы равен нулю. Так как напряжения и, могут быть произвольными, то
£1.
i=l
151
Рис. 6.8. Неопределенная Y-матрица
т.е. сумма элементов любого столбца или любой строки матрицы равна нулю. Если один из узлов (например, /г-й) может быть заземлен, как обычно и бывает в РЭС, то все напряжения можно отсчитывать относительно него. В матрице Y это эквивалентно вычеркиванию k-ro столбца и k-й строки. Сумма элементов оставшейся матрицы не равна нул'ю и называется определенной Y-матрицей. Она связывает внешние токи (токи внешних узлов) с узло
выми напряжениями, отсчитываемыми относительно заземленного узла. Такая матрица и была рассмотрена выше на примере четырехполюсника.
Неопределенную Y-матрицу несложно получить, даже если в модели РЭС используются модели базовых компонентов с
различным числом полюсов: двухполюсники, четырехполюсники и т.д. При наличии в модели РЭС только пассивных компонентов неопределенная Y-матрица будет симметричной. Эта симметрия нарушается при наличии в РЭС моделей активных
компонентов.
Как будет показано далее, процесс формирования Y-мат-рицы легче выполнить для ее неопределенной формы, хотя для нахождения выходных параметров устройства необходимо использовать определенную Y-матрицу.
Рассмотренные матрицы классической и волновой теории нашли широкое применение при решении различных задач моделирования РЭС.
Рис. 6.9. Характеристики «параметров фильтра
152
Рис. 6.10. Характеристики /-параметров фильтра
Пример 6.2. Рассмотрим частотные характеристики элементов матриц S и Т |ли примера чебышевского фильтра (см. рис. 6.2).
Комплексные характеристики «ц и s,2 приведены на рис. 6.9 Как и ранее, использованы условия взаимности S|2 = S2i и симметрии sn = S22 фильтра. Для заданных параметров фильтра максимальное значение модуля коэффициента отражения фильтра равно |зц|тах = 0.15; неравномерность характеристики передачи Is^l—0,1 ib. Из условия унитарности для схемы без потерь получаем |s(I| + |sig| — 1.
Характеристики /-параметров фильтра показаны на рис. 6.10. Из условия |1шимности фильтра получаем detT = I, а симметричности — /^ = /21 = 0. Видно, но для схемы без потерь коэффициенты передачи /12 и /21 являются чисто мнимыми величинами.
§6.3. ФОРМИРОВАНИЕ СИСТЕМЫ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ РЭС В ЧАСТОТНОЙ ОБЛАСТИ
Электрическую модель любого сложного радиоэлектронного устройства всегда можно представить состоящей из четырех-нолюсных или двухполюсных моделей более простых базовых компонентов (см. табл. 4.1 и 6.2), соединенных произвольным образом. Соотношения для элементов результирующих матриц при различном соединении четырехполюсников приведены в нтбл. 6.4 [12, 15].
Используя табл. 6.2, в которой приведены элементы матриц пазовых четырехполюсников, табл. 6.1 и 6.3 для связи элементов матриц классической и волновой теории четырехполюсников, а также табл. 6.4 с соотношениями между элементами ма-гриц при различном соединении четырехполюсников, можно получить выражения для элементов результирующей матрицы, описывающей все устройство. Как указано в предыдущем параграфе, на основе результирующей матрицы классической либо волновой теории многополюсника могут быть вычислены
153
любые выходные параметры устройства. Таким образом, процесс формирования уравнений математической модели РЭС в частотной области сводится к нахождению элементов результирующей матрицы модели устройства, состоящей из моделей базовых четырехполюсников, вычислению выходных параметров по элементам результирующей матрицы и дальнейшему анализу устройства с помощью выражений (6.1) — (6.4).
Таблица 64
Соединения простейших четырехполюсников
Однако такой подход к моделированию не очень удобен для алгоритмической реализации. Это объясняется необходимостью разбиения сложной модели на простые четырехполюсники, что чревато появлением ошибок, а также необходимостью алгоритмизировать более 30 таблиц межматрнчных преобразований. 11а практике для упрощения алгоритмической реализации обычно выбирают матрицу передачи А в качестве промежуточной и преобразование матрицы D в матрицу С выполняют по следующей схеме: тип D е А, А е тип С. В этом случае все возможные преобразования, которые необходимо алгоритмизировать, можно свести к следующим:
(Z, Y, Н, S, Т) е А,
A e.(Z, Y, Н, S, Т).
154
Следовательно, в этом случае необходимо алгоритмизировать лишь 10 возможных межматричных преобразований. Ма-ipima передачи имеет преимущества перед другими матрицами классической теории многополюсников, поскольку она может быть получена для большего числа базовых четырех- по-люсников по сравнению с другими (см. табл. 6.2).
В некоторых программах взаимные преобразования полнос-11.Ю исключены. Это достигается описанием базовых четырехполюсников только в параметрах матрицы передачи А и выражении результирующих матриц всех схем различных соединений четырехполюсников, приведенных в табл. 6.4, через матрицы четырехполюсников, записанных в параметрах матрицы пере-•|.1чи А. Например, для различных схем соединения двух четырехполюсников, матрицы передачи которых записаны в виде
д/ _ QI1 а12 . ДИ _ б(11 а12
а21 «22 a2i аи
и соответствии с табл. 6.4 можно получить результирующие матрицы A-параметров в следующем виде:
для последовательного соединения четырехполюсников
(«и____ °П )(°21 °22 )
^11^21 ^11 ^21
А = О21 + °21 Г // П2|а21 ^12 и12 t П И I X а2|а22 + а21 а22 ) а21 + а21
а2| + a2i f ; W ‘ ^21
для параллельного соединения
а||а|2 Gll ^12 «12«|2
А = «12 + «|2 а' + а" — «II )(«22 ~а22 ) «;2 + а" а(2 «22 + а;'2а22
а12 + Й|2 aj2 +а"2
(6.24)
(6.25)
для последовательного соединения по входу и параллельно-ю соединения по выходу
1 i и (^12 а\2 Ха21 а21 ) fll2a22 + fl!2 G2I
А = ull + ац a2l&22 + ^21^21 °22 + а22 а22 + а22 «22«22 . (6.26)
«22 + а22 ^"22 ^22
155
Применение выражений (6.24) — (6.26) позволяет существенно сократить затраты на формирование результирующей матрицы моделируемого устройства. На основе библиотеки базовых четырехполюсников и приведенных выражений в настоящее время разработано большое число эффективных работающих программ для моделирования РЭС в частотной области.
Рис. 6.11. Формирование неопределенной Y-матрицы
Еще большей простотой отличается алгоритм формирования неопределенной Y-матрицы, что и обусловило широкое применение этого метода моделирования в различных пакетах прикладных программ моделирования и оптимизации радиоустройств. Как указано в §6.3, в основе этого метода моделирования лежит обобщенная запись первого закона Кирхгофа для многополюсника. Рассмотрим подробнее алгоритм формирования неопределенной Y-матрицы.
На рис. 6.11 показана часть модели устройства, состоящей из двухполюсников и имеющей п узлов. Предположим, что выделенный /-узел модели соединен с каждым i-узлом модели ветвью с проводимостью Y. Очевидно, что если два узла модели непосредственно не соединены между собой, то соответствующая проводимость ветви может быть приравнена нулю. Кроме того, к /-узлу подходит ток от внешнего источника тока. При отсутствии такого источника у какого-нибудь узла его значение без потери общности может быть приравнено нулю.'
По первому закону Кирхгофа с учетом алгебраической записи токов для /-узла можно записать
-/ j + i/i + i/2 + .... + i/n = 0, /; = £i/k. (6.27)
На основании закона Ома для каждой ветви с проводимое тью Yjk можно записать
ijk = (urUk)Yjk. (6.28)
Подставляя (6.28) в (6.27), получим
// = £(«, - u„)Yik = u,±Yik -iukYjk. (6.29)
k=i *=l
k*i k*j
156
Здесь выражение yn = 2-jYjk определяют как собственную Л=1
проводимость /-узла, выражение ——как взаимную проводимость
Л=1
между /- и /г-узлами. Записывая аналогичным образом уравнения для всех узлов модели, можно получить систему уравнений (6.23).
Проведенные преобразования позволяют получить простой алгоритм формирования неопределенной Y-матрицы для модели, содержащей только пассивные двухполюсники. Диагональные элементы Уц получают как сумму проводимостей всех ветвей,, подходящих к /-узлу; недиагональные элементы y,k— как гумму проводимостей всех ветвей, соединяющих i- и /-узлы, тятую с обратным знаком. Поэтому для описания моделей в виде неопределенной Y-матрицы часто используется табличный способ описания модели в виде соединений узел — ветвь.
При соединении произвольных многополюсников с известными неопределенными Y-матрицами Y' и Y" (рис. 6.12) общая Y-матрица может быть получена простым включением запанных параметров матриц многополюсников в соответствующие позиции общей Y-матрицы. Элементы матриц, попадающие в одни ячейки, суммируются. Так, для соедине-
ним многополюсников, показанного на рис. 6.12, получаем
У\х У'и Уъ 0
Уч\ У 24 У25 0
V О У 31 У.34 У 35 0
Y = = .^41 ••• У 44 + У 44 У 45 + У 45 У 46 У 47 (6.30)
О Y" У 5\ У 54 + Уб4 Уб5 + У55 Убб У 51
0 У 64 У 65 У 66 У 61
0 У 74 У15 У16 У11
Доказательство этого положения можно найти в [12, 15].
Для нахождения выходных характеристик радиоустройства ||>ебуется определенная матрица Y, которая может быть получена из неопределенной путем исключения из нее строки и < голбца, соответствующих заземленному узлу. Методы решения получающейся при этом системы уравнений (6.23) описаны в §6.6.
В заключение рассмотрим алгоритм формирования Y-мат-рнцы радиоустройства.
157
Рис. 6.12. Соединение многополюсников
Шаг 4. Исключаются из полной
Алгоритм 6.1. Формирование определенной Y-матрицы
Шаг 1. Формируется неопределенная Y-матриЦа части модели РЭС. составленной из пассивных двухполюсников в соответствии с (6.29).
Шаг 2. Формируются неопределенные Y-матрицы для базовых многополюсников, входящих в модель устройства.
Шаг 3. Суммируются неопределенные Y-матрицы пассивной части устройства с неопределенными Y-матрицами базовых многополюсников в соответствии с выражением (6.30). неопределенной Y-матрицы устройства строка
и столбец, соответствующие заземленному узлу.
Шаг 5. Переходим к решению системы уравнений относительно напряжений на
входах многополюсной модели устройства для нахождения его выходных параметров.
§6.4. ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ НЕЛИНЕЙНЫХ РЭС В ЧАСТОТНОЙ ОБЛАСТИ
Особый класс при моделировании радиоэлектронных, средств в частотной области составляют нелинейные устройства, внутренние параметры которых зависят от напряжений и токов схемы.
На рис. 6.13 приведена классификация методов моделирования и анализа нелинейных устройств в частотной области. Используются различные признаки для классификации методов: режимы малого и большого сигналов; явные и неявные методы, моделирование безынерционных (резистивных) и инерционных цепей; использование различного математического аппарата — ряды Тейлора, Фурье, Вольтерра и др.
При подаче на вход нелинейного радиотехнического устройства нескольких сигналов с частотами «ч, (02, в схеме возникают колебания на высших гармониках тп\(й\, т^, ... и на комбинационных частотах micoj ± тгсог ± —.Если амплитуды этих новых гармоник малы по сравнению с амплитудами основных гармоник сон юг-., то говорят, что схема работает в режиме малого сигнала, в противном случае — в режиме большого сигнала.
В режиме малого сигнала схемы делятся на безынерционные, содержащие только нелинейные резистивные элементы, и инерционные, содержащие линейные или нелинейные индуктивности и емкости.
158
I' и с. 6-13. Классификация методов моделирования и анализа нелинейных устройств в частотной области
Разработаны явные методы моделирования и анализа нелинейных устройств в режиме малого сигнала. Термин «явные методы» означает, что известно возбуждение (например, u(t) па рис. 6.14, а), подаваемое непосредственно на нелинейный лемент, необходимо лишь найти реакцию нелинейного элемента i(f) на заданное воздействие. В неявных методах и воздействие ид(/), и реакцию z(0 необходимо определить (например, при подсоединении резистора к диоду) (рис. 6.14, б).
В явных методах характеристика нелинейного элемента аппроксимируется степенным полиномом (рядом Тейлора) и за-’ |ем вычисляются амплитуды высших гармоник с требуемой ючностью. Подставляя функцию возбуждения в полином, выполняя необходимые действия и группируя члены с частотами <i>i, 2о>1, Зсоь легко определить амплитуды колебаний на выходе с этими частотами.
Реализация неявных методов моделирования в инерционных цепях осуществляется двумя способами (см. рис. 6.13). По первому из них через переходный процесс предварительно временными методами находится установившийся режим (см. |л. 5), определяется временная функция сигнала на выходе и । помощью преобразования Фурье определяются амплитуды ирмоник сигнала. Достоинствами такого подхода являются общность и универсальность, так как при этом используется наиболее общее описание нелинейной цепи — система нелинейных дифференциальных уравнений — и наиболее прямой путь
159
* КВ
u(t)\7
u.9(t)
о
О----
а)
Рис. 6.14. (6) подходы
Явный (о) и неявный к моделированию нелинейных устройств
того, для
поиска решения этой систе-мы — численное интегрирование. Метод в принципе позволяет решить задачу анализа нелинейной' цепи для любых уровней входного воздействия как при одно-, так и при многосигнальном воздействии. К недостаткам метода относится необходимость расчета переходного процесса в нелинейной цепи, который сам по себе часто не представляет интереса. Кроме цепей и при многосигнальном’ воз-1 действии этап анализа является длительным и весьма неэко«| номичным с точки зрения вычислительных затрат.
По второму способу неявного подхода используется опера-1 тор передачи в виде функционального ряда Вольтерра, кото-1 рый является обобщением интеграла Дюамеля (6.3) на случай! нелинейной инерционной цепи и связывает выходной и вход-1 ной сигналы в виде [5, 18]
МО =£«/„(0 = f +
(6-31) cr,
+ j J /z2(T|,T2)x(/-T1)x(/—T2)dTldT2 + —00
где x(t)—входной сигнал; /г„(ть..т»)— ядро Вольтерра — нели-1 нейная импульсная характеристика м-го порядка. При п — 11 /zi(t) — обычная импульсная характеристика. Добавление членов при п > 1 соответствует учету нелинейных преобразований.I Если входной сигнал и нелинейности схемы не слишком вели-] ки, то достаточно использовать лишь несколько первых членом ряда.
Выполнив преобразование Фурье, получим связь между! входным и выходным сигналом в частотной области:
У(/(01, /С02. (/(0|, /а>2, .. , /со») I1-V,.(/CO1), (6.32)
*=i /=1
где ja>2, .... /со,J—передаточная функция и-го порядка!
функционального ряда Вольтерра.
Анализ нелинейной схемы заключается в итерационном решении системы уравнений типа (6.32) с последовательным оп« ределением частотных ядер Вольтерра и уточнением воздейст! вия и реакции нелинейного элемента.
160
Метод функционального pH'ia Вольтерра применяется iinii.KO при относительно ма-лых сигналах, так как при "плыиих сигналах ряды Воль-leppa расходятся.
В режиме большого сиг-iin.ua также разработаны яв-
‘Ые И неявные методы. Рис. 6 15 Примеры моделирования
К обоим ТИПаМ методов нелинейной цепи
<нносятся методы, основан-iii.li- па кусочно-линейной аппроксимации характеристик нелинейного элемента. При этом в чином случае задается воздействие на нелинейный элемент
к режиме большого сигнала и затем определяются гармоники |н акции нелинейного элемента на заданное воздействие. Подоб-
in.ii'i подход применяется при расчете режимов генераторных приборов радиопередающих устройств, анализе вентильных гхсм и др. [12, 17].
При неявном задании возбуждения на нелинейном элемен-н обычно выделяют линейную инерционную часть схемы и от-дглыю нелинейные элементы (рис. 6.15). Разработаны алгоритмы анализа нелинейных схем такой структуры, заключающие-
। и и итерационном решении соответствующих операторных уравнений при кусочно-линейной аппроксимации характерис-|пк нелинейного элемента [5, 7, 12, 13].
К неявным методам анализа нелинейных схем в режиме (шльшого сигнала относятся также поисковые методы. Суть их включается в прямом определении установившегося режима и нелинейной цепи без предварительного расчета переходного процесса. При этом осуществляется итеративный поиск таких начальных условий для решения нелинейных дифференциальных уравнений, которые непосредственно соответствуют установившемуся режиму. В ряде задач такой подход дает существенный выигрыш в вычислительных затратах перед методами < расчетом переходного процесса.
Одним из самых распространенных неявных методов анализ нелинейных схем при периодическом воздействии являет-1)1 метод гармонического баланса [5, 7, 18]. При этом предпо-л.нается, что в любом сечении анализируемого устройства искомый ток или напряжение можно представить в виде укороченного ряда Фурье с неизвестными амплитудами. Затем ни ряды подставляются в систему дифференциальных уравнений, описывающих нелинейную схему, после чего приравни-
f \ и 1 оматизация проектирования г । июэлскгроииых средств
161
ваются коэффициенты, соответствующие гармоникам едина! нового порядка. В итоге для каждой переменной получаю'1 систему алгебраических, в общем случае нелинейных гармониче-1 ских компонентных уравнений и проводят решение одним из численных методов. Таким образом, осуществляется переход от! системы нелинейных дифференциальных уравнений во времен-| ной области к системе нелинейных алгебраических уравнений в частотной области, что сильно упрощает анализ.
Метод гармонического баланса может быть применен при! любом количестве входных сигналов с различными частотам» необходимо только учесть соответствующие гармонические ком понентные уравнения.
Главный недостаток метода гармонического баланса — большое количество уравнений. В то же время этот метод в отли чие от методов анализа в режиме малого сигнала связан не fl разложением в ряд Тейлора, а с разложением в ряд Фурье, и поэтому его точность зависит не от амплитуды сигнала, а от количества учитываемых гармоник.
К методу гармонического баланса примыкают проекцией, ные (вариационные) методы, которые построены на основ' итерационной процедуры с последовательным увеличением чйЬ1 ла учитываемых гармоник. Используются также укороченный ряды Фурье с неизвестными коэффициентами — амплитудами! В ряде случаев анализ удобно начать с первого шага в виде] линейного приближения и далее, увеличивая число гармонии на каждом шаге, вариационными методами определять неизвестные коэффициенты ряда Фурье. на I
Рассмотренные методы моделирования и анализа нелин^Й! ных каскадов радиочастотных средств находят широкое прцч менение при разработке САПР РЭС. i ]
I' l; И
§6.5. ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ КОМПЛЕКСОВ , t I РЭС В ЧАСТОТНОЙ ОБЛАСТИ „
Под комплексом радиотехнических устройств понимает» многоканальный радиочастотный тракт, содержащий совокупность усилителей (генераторов, передатчиков), пассивных, уем ройств согласования, фильтрации, фазирования, управлеййя совместно работающих на многополюсную комплексную й'аИ рузку, например фазированную антенную решетку (ФАР): I
Целью построения комплекса в его передающем варианте Является сложение мощностей отдельных усилителей в общей антёв ной системе в широком диапазоне частот и обеспечение необходи*1 мой направленности излучения антенной системы для максимизм ции энергетического потенциала комплекса [12, 19, 21].
162
Преимущества использования широкополосных каскадов несомненны. Это почти мгновенная смена рабочих частот гене-p.норов, возможность одновременной работы комплекса на не-(ьольких сильно разнесенных частотах рабочего диапазона, многоканальная работа радиосредств, высокие уровни эквивалентной излучаемой мощности и коэффициента усиления при щ пользовании ФАР и др.
В качестве многополюсной нагрузки может быть задана не ылько антенная решетка, но и произвольный многополюсный I атпотехнический объект, в том числе с экспериментально (пятыми частотными характеристиками: схемы сложения мощ-Ihoctii, электрофизические установки, объекты ВЧ-индукцион-.... нагрева и др.
Структурно комплекс можно представить в виде генераторов с комплексным внутренним сопротивлением, подключенных через распределительно-согласующий многополюсник свяли к многополюсной нагрузке.
В многополюсник связи входят линейные базисные элемен-|ы комплексной связи R-, L-, С-элементы, фильтры, частотно-р । (делительные и селективно-согласующие устройства, линии Передачи, мосты, схемы сложения и разделения мощности, широкополосные трансформаторы, частотные и фазовые пммутаторы и др. [12, 19].
Основные базисные элементы комплексов радиотехнических кч ipoficTB изображены на рис. 6.16. К ним относятся как прос-|ые четырехполюсные элементы (см. табл. 6.2), так и соединения их в виде многополюсников. При моделировании и проек-|провании широкополосных радиокомплексов используются сле-иующие укрупненные базисные элементы [12].
блок многополюсных антенн-, используются электродинамические модели антенных решеток (см. гл. 8), излучатели ко-юрых произвольно расположены в пространстве; при проектировании выполняется анализ матриц импеданса и рассеяния ни генных решеток, учитывающий взаимное влияние между излучателями в рабочем диапазоне частот.
Лестничный четырехполюсник, с помощью которого могут 01,1 гь представлены модели октавных фильтров, диплексеров, широкополосных селективно-согласующих устройств и т.д.
Отрезок линии передачи, который может использоваться как самостоятельный элемент связи антенной решетки и генераторов, так и в качествё элемента синтеза более сложных миогополюсных устройств (широкополосных гибридных трансформаторов, мостов, схем сложения и деления мощности, фа-><>пых коммутаторов и др.) [12].
163
Рис. 6.16. Базисные элементы комплексов радиотехнических устройств
Гибридный трансформатор, используемый как в идеальном варианте, так и при реализаций на линиях передачи. Гиб-.| ридный трансформатор имеет два входа и два выхода и яв-^ ляется двухканальным фазовым коммутатором (см. рис. 6.16): при синфазном питании входов сигнал выделяется на одном из выходов,, при противофазном — на другом. При питании одного входа мощность сигнала делится поровну между двумя выходами и на выходах выделяются синфазные сигналы, при питании другого входа — противофазные. Гибридный трансфер^ матор может быть использован для построения многоканалЬ^ ных фазовых коммутаторов и развязывающих устройств pal диотехнических комплексов [12].
Фазовый контур, обеспечивающий необходимую фазочастот! ную характеристику канала. Могут быть использованы как симметричные, так и несимметричные варианты реализации фазового контура, а также в комбинации с гибридным трансформатором или фазовым коммутатором — двух- или многока-j нальные фазоразностные цепи, обеспечивающие постоянную! линейную или произвольную зависимость разности фаз от частоты.
Кольцевой диплексер — двухканальное частотно-разделительное устройство, содержащее две пары фильтров нижних и ве-. рхних частот и фазоинвертирующий трансформатор. Фильтры нижних и верхних частот имеют общую частоту стыка, поэто
164
му при питании того или иного входа диплексера сигнал вы-н ляется на первом или втором выходе в зависимости от того, ниже или выше рабочая частота сигнала частоты стыка филь-ip<>B. При моделировании используются как идеальные, так и / ( реализации фильтров различного порядка. Кольцевой дип-iKi.cep также является развязанно-согласованным восьмиполюсником; по существу, это двухканальный частотный комму-|.нор, идеально согласованный по всем входам, поэтому может быть использован для проектирования частотных комму-fa юров с любым числом входов.
Приведенные укрупненные базисные элементы могут служи 1ь основой для моделирования комплексов радиоэлектронных средств как со структурной и частотной развязней. так и комбинированного типа для различного прикладною назначения [12, 19].
§6.6. МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Как указывалось ранее, при моделировании РЭС в частотной области обычно используется численный спектральный под-Li/i. Наибольшие преимущества такой подход обеспечивает при моделировании линейных устройств. В связи с этим при вычислении выходных параметров часто встает задача обра-11и пня матриц и решения систем линейных уравнений.
Обратной матрицей по отношению к данной матрице А и.। и.шают матрицу А'1, которая, будучи умножена на данную матрицу (справа или слева), дает единичную матрицу:
АА' = А'А=1. (6.33)
Нахождение обратной матрицы А'1 называют обращением м.ирицы А Обратная матрица существует, если. исходная м.нрица А — квадратная и неособенная (detA 0). Определи-it-.ni. обратной матрицы равен det(A'’) = 1/detA.
Система линейных уравнений в общем случае имеет вид АХ = К
пли
«цХ1 +«12X2 + ••• + О.\пХп = Ь\,
) «21X1 + «22X2 + ... + «2лХ„ = (?2, (6.34)
_ С «Л1Х1 + «„2X2 + ... + аппхп = Ьп, _
I и X — вектор неизвестных переменных, В—вектор
п шестных констант, А — квадратная матрица с элементами — номер строки, /— номер столбца).
‘Нормально эту систему_можно_решить, обратив матрицу А:
X = Д 'В. ' (6.35)
165
Рис. 6.17. Классификация методов решения системы линейных уравнений
Решение систем линейных уравнений производится прямыми или итерационными методами (рис. 6.17).
Прямыми методами называют такие методы, которые позволяют за конечное число действий получить точное решение системы. Термин «точное решение» следует понимать условно как характеристику алгоритма, а не реального вычислительного процесса. Алгоритмы, лежащие в основе прямых методов, дают точное решение, если все величины в системе заданы и все вычисления проводятся абсолютно точно, без ошибок округления. К прямым методам относятся правило Крамера, методы Гаусса, Жордана и LU-разложения в различных модификациях [6, 14, 30].
Итерационные методы основаны на построении итерационной последовательности, сходящейся к искомому решению. Выполнив определенное число итераций и обрывая процесс, можно получить приближенное решение системы с любой наперед заданной точностью. Итерационные методы просты н реализации и требуют минимальных затрат оперативной памяти. Они применяются в основном для регнения задач сверхвысокой размерности, когда число неизвестных изменяется oi нескольких тысяч до миллионов К итерационным методам от носятся метод простой итерации, методы Якоби, Гаусса —Зей-деля и релаксационные [6, 30].
Рассмотрим прямые методы.
Правило Крамера используется, когда при решении сис| темы (6.34) требуется найти только одну неизвестную—переменную. По этому правилу k-я компонента Xk вектора X рав-на отношению определителя матрицы А, в которой k-й стоД бец заменен вектором В, и определителя матрицы А [14, 30]:
det (матрицы А с k- м столбцом, замененным на В) 1Г.
Xfe =-------------------------------------. (6.36)
det А
166
Правило Крамера используется для решения уравнений пи <кого порядка и при теоретических исследованиях. Однако йог метод требует больших затрат машинного времени, очень чувствителен к ошибкам округления й редко применяется в вычислительных программах. Так, общее число умножений в методе Крамера -2(п + 1)!; например, при л =10 число умно-к< ний около 80 млн. При обращении матриц недостатки те ко и число операций еще более возрастает.
Алгоритм 6.2. Решение системы линейных, уравнений по правилу Крамера
Шаг /. Вычислить detA.
Шаг 2. Положить к = I.
Шаг 3. Заменить /г-й столбец матрицы А столбцом свободных членов.
Шаг 4. Вычислить определитель этой матрицы.
Шаг 5. Вычислить /г-ю неизвестную.
Шаг 6. Если к — п. вычисления закончить, в противном случае положить
к + 1 и перейти к шагу 3. '
Пример 6.3. Пусть задана система
х, + 2х, + Зх, = 4 12 3
2х, + 4х, + 5х., =3 А = 2 4.5
Зх, + 5х2 + 6х, = 6, 3 5 6
4'
3
6
Тогда, по правилу Крамера,
'4 2 3'
det 3 4 5
6 5 6
1 2 3 ‘
det 2 4 5
3 5 6
Аналогично можно найти = -9, хз = 5.
Метод Гаусса—один из лучших численных методов решения линейных систем уравнений невысокого порядка. Он основывается на том факте, что сложение одного уравнения системы с другим, умноженным на константу, не изменяет решения < п< темы [6, 14, 30]..
Метод Гаусса состоит из прямого и обратного ходов. Прямо й ход выполняется за (п—1) шагов (где п — порядок । истемы), на каждом k-м шаге исключается очередная неизвестная xft из уравнений, начиная с (/г + 1)-го и ыканчивая n-м, по формуле
'b/./z+l (4ik,k ' ^kj.k/^-hk.k' k~\, 2, ...,И, i, j k + 1, .... tl, (6.37)
167
где ciijjt, aik.k и Щ/, л+i— соответственно элементы матрицы А,( преобразованной на ft-м и (ft + 1)-м шагах; амг. k и а^, ь— диа-!| тональные и внедиагональные элементы на ft-м шаге преобразования. В соответствии с (6.37) пересчитываются и константы правых частей системы (6.34):
bi,k+ 1 = ft/, k~bk, fe cikj, fe /cikk. fe, (6.38)
где Ьм, bk,k и ft/.fe+i — соответственно правые части системы, преобразованные на ft-м и (ft+l)-M шагах.
Элемент k в формулах (6.37), (6.38) называется глав-н ы м элементом на ft-шаге исключения по Гауссу и должен быть отличен от нуля: ctkk.k * 0.
Так, например, на первом шаге исключается первая переменная из всех уравнений^начиная со второго. Для этого, сос-. тавив отношения т.ц = -ац/ап (i = 2, 3, ..., п), прибавим к t-му уравнению системы первое., уравнение, умноженное на тц. Выполнив это, получаек^преобразованную систему вида
ДцХ| + а|2х2 + al3x3 +...+ ainxn = b^,
а^х2 + а2з,1хз + - •+ a2n,ixn ~b2i '
ап2’^Х2 ~^ап3.1Х3 + °пп, 1Хп ~Ьп1
Здесь fl,;], ft,.! (г, j) =2,3, ..., п — новые значения коэффи-1 циентов системы и правых частей, которые получаются после выполнения первого шага прямого хода Гаусса. На втором
шаге аналогичным преобразованиям подвергаем систему уравнений (п—1)-го порядка начиная со второго (6.39) и т. д.
верхнюю треугольную матрицу U, а вектор
В результате выполнения (п-1) шагов исходная матрица А преобразуется_в В — в вектор Bf.
(6.40)1
!1Ч
Обратный ход заключается в последовательна, (од, определении неизвестных из системы (6.40): из последнег^ уравнения определяем хп = Ь'п1ипп, по найденному хп й? (n-l)-ro уравнения определяем x„-i, по найденным хп и x„_i цз (п-2)-го уравнения определяем хп-2 и т. д. В общем виде обратную подстановку можно записать так:
Xi = u-i,n+ i-^UjjXj, i - п-I, п-2,1, (6.41)'i
/=ы
168
। и- Uij — элементы верхней треугольной матрицы U (6.40). Последовательное вычисление неизвестных продолжается до тех нор, пока не определим из первого уравнения хь На этом процесс решения системы (6.34) с помощью эквивалентной ей нстемы (6.40) заканчивается.
Алгоритм 6.3. Решение системы линейных уравнений методом Гаусса
Шаг 1. По формулам (6.37), (6.38) вычислить элементы верхней треугольной м<прииы и столбца свободных членов — прямой ход алгоритма.
Шаг 2. По формулам (6.41) вычислить переменные — обратный ход алгоритма.
Отметим, что метод исключения Гаусса (прямой ход) требует выполнения щп IXw + 4)
------- операции, где п — порядок матрицы, а обратная подстановка может
п(п + 1)
ni.ui, выполнена приблизительно за ----- операции
При реализации метода Гаусса на ЭВМ имеет большое значение выбор III.итого элемента; наибольшая точность реализуется, если на k-м шаге главным выпирается элемент в k-м столбце с наибольшим абсолютным значением из всех пиментов в строках от k до п. В случае разреженных матриц разработаны ч иоритмы определения главного элемента и компактной записи матриц в память HIM (1. 14, 16, 22].
Пример 6.4. Решим методом Гаусса систему из примера 6.3, предварительно in pi iтавив для наглядности вторую и третью строки. Тогда после прямого хода ||11'|уЧ||М
%1 + 2х2 + З*3 = 4.
х2 + Зх3 = 6,
*3 = 5.
Обратный ход приводит к соотношениям
*3 = 5,
4 X 2 ~ 6 ” 3 X g «
/| = 4 - Зх3 - 2х2.
(качение третьей переменной получилось сразу; подставив х% = 5 во второе ||.ц|нение. получим х-2=-9 и из последнего х/ = 7.
В методах Крамера и Гаусса непосредственно определяет -> я решение системы уравнений (6.34). Если заданы различные ы-кгоры правых частей В, то для каждого из них необходимо ргшать всю систему уравнений. В ряде случаев боле^ экономичным бывает сначала найти обратную матрицу А , а за-п м, используя (6.35), найти решение системы для любой задан-iliiii правой части. Кроме того, обратная матрица часто пред-। । шляет собственный интерес в различных прикладных । । шчах. Одним из широко используемых методов вычисления обратной матрицы является метод Жордана [7, 30].
Метод Жордана базируется на формуле связи прямой и оьратной матриц (6.33). Обозначив элементы искомой обратит! матрицы через с^, по (6.33) получаем
169
«II ... fl1H
«21 a22- -a2ll
C|, C12...c„,
Si c2, ...c2„
I 0 0...0
0 I 0...0
(6 42)
Si S2-S,,
0 0 0...1
a , a о ...a
L ul vv«2 .
Разобьем эту систему на п систем линейных уравнений от поситсльно столбцов неизвестных элементов с,у обратной матрицы А . Тогда первая система имеет вид
«и «12 - «о,
«21 «22 •••«2„
L«,a ««2 ••«,»,
сн
С21
S1 .
(6.43)
Во второй системе в качестве неизвестных бу (ут столбец [cj с’22 ••• <’„2]т и правая часть [0 1 0 Of (единица во второй позиции), для третьей системы — третий столбец матрицы А" и единица в третьей позиции и т.д.
Решив составленные системы уравнений, например методом Гаусса, вычисляем элементы обратной матрицы. ТакиМ| образом, по методу Жордана, нахождение обратной матриць, сводится к /i-кратному решению систем линейных уравнений поэтому при больших п требуемое4 число операций можно при ближешю оценивать величиной п .
Алгоритм 6.4. Обращение матрицы методом Жордана
Шаг /. Положить /г=1.
Шаг 2. Составить систему линейных уравнений вида (6.42), вставив в npaByid часть на /г-ю позицию единицу, а в остальные — нули.
Шаг 3. Решить систему уравнений, записать найденные неизвестные в виД| /г-го столбца искомой обратной матрицы.
Шаг 4. Если /г =п, вычисления закончить, в противном случае положить к .= к + 1 и вернуться к шагу 2.
Пример 6.5. Найдем матрицу, обратную матрице А из примера 6.4. Тогда пер воя система уравнений вида (6.65)
< ц + 2с.,| + 3f.il - 1. 2<ц + 4<’2i + 5с(| = О, Зс 11 + 5с2| + без, = 0.
ГОиепие этой системы дает первый столбец А .
СП = 1, <•_>, =-3. ед, = 2.
Из второй системы
«12 + 2<Э2 + Зои "= 0.
< 2с,2 + 4с22 + 5С;й = I.
3ci2 + 5с22 + 6с,32 = 0.
170
Определяем С|2 = -3, С22 = 3. <’32 = -1-Наконец, из третьей системы
С|.ч + 2^23 + Зс.чз ~ О, - 2С|2 + 4с*2з + 5сзз = б. k Зс]з + 5с2з + бсзз = I
iini'iiii-ляем Г|з=2, С23 = ~1- G33~ 0.
1аким образом, обратная матрица равна
-3 2’
3 - 1
- 1 0
Прпш-рим
1-3 2‘ 1 2 3 ' 1 0 О’
А'А = -3 3-1 2 4 5 = 0 I 0
2 - ! 0 3 5 6 0 0 1
— — —
‘lpiuii-рим решение системы уравнений. Умножением А 1 в 1 в соответствии с
IO.V.) получаем
V 1-3 2 '4 ’ 7
X = л-2 -3 3 - 1 3 = -9
X. 2 - 1 6 5
Метод LU-разложения наиболее предпочтителен, если тре-бу< гея найти решение системы линейных уравнений (6.34) для (мпюе чем одного вектора В. Алгоритмы этого метода близки к мг|«>ду исключения Гаусса, хотя вычисления могут проводить-। и в различной последовательности. При этом методе матрица А разлагается на нижнюю треугольную матрицу L (lower) и Верхнюю треугольную матрицу U (upper) так, чтобы
‘'и 0 .. . 0 1 н12 . «In’
А = LU = /21 /22 • . 0 0 1 . •• U2n (6.44)
А. • hm 0 0 . . 1
I in ла уравнение (6.56) принимает вид
LUX = ~В. (6.45)
Г< шение этого уравнения получают в два этапа. Сначала, как и методе Гаусса, методом прямого исключения получают ре-
шение относительно соответствующее уравнению
Lp = В . (6.46)
171
На втором этапе с помощью процесса обратной подстановки находят решение относительно X:
UX - ~у. (6А7)
Элементы треугольных матриц рассчитывают по формулам
lik = aik-^limumll, i > k, uhj = (akj - ^ltmuml) / lkk,j > k, (6.48) rn=l m=l
где lik — элементы матрицы L; tikj—элементы матрицы U. Эти уравнения описывают так называемый алгоритм Краута разложения на треугольные матрицы [14]. Его выполнение осуществляется при задании k=l, 2, ... ,п и поочередным использованием формул (6.48); требуемые в них значения элементов матриц L и U рассчитываются на предыдущих этапах процесса. Каждый элемент а1у- исходной матрицы А требуется для вычисления только соответствующих элементов матриц L и U. Так как нулевые элементы матриц L и U, а также еди ничную диагональ матрицы U запоминать не нужно, в процес се вычислений матрицы L и U могут быть записаны на мест! матрицы А и занесены в те же ячейки памяти, причем L рас положена в нижнем треугольнике (i > /), a U — соответствен но в верхнем треугольнике (i </) матрицы А.
Существуют другие формы алгоритма разложения, связан иые с рассмотрением по строкам или столбцам матрицы / Так, записав матрицы L и U, как сказано выше, в виде, oi щей квадратной
н12 и13 ... и]п
/21 /22 u23 ...u2n
матрицы, получаем
*21
^31
°12 / ^11
а22 ~ ^21 / W!2
° 32
12
(fl23 ^21Н1з) / ^22
(° 33 “ ^3IWI3 ~^32U32)--'
. (6.49)
/п! ^«2 ^пЗ • •" ^пп
Видно, что первые столбцы матриц А и L совпадают, еле довательно, 1ц = a,i; вычислив и.\2= а\%/l\i, находим элемент! второго столбца матрицы L, далее последовательно элемента третьего столбца и т.д. Эти действия могут быть сведены | алгоритм.
Алгоритм 6.5. IAJ-разложения (по столбцам)
Шаг I. Положим й=1.
Шаг 2. lik = aik; i k.
Шаг 3. Ukj “ akj/lkk' i>k.
Шаг 4. Itj = aij-likUkj', i, j>k.
Шаг 5. Если k = n, процедуру разложения заканчиваем; в противном случя положим £ = А+1 и перейдем к шагу 2.
172
После разложения матрицы А на треугольные L и U промежуточные пере-м< паые у из системы (6.46) определяются прямой подстановкой (прямым ходом):
У\ = &|/й|.
У1 “ (bf—^Х</,) / 1ц. I = 2,3.п.
(6.50)
Решение исходной системы (6.34) в соответствии с (6,47) вычисляется обратной нипстановкой (обратным ходом):
хп ~ Уп.
Xi = yi—^luijxi, i = п - I,и - 2....I.
(6.51)
Описанный алгоритм LU-разложения эквивалентен приведению матрицы к верхней треугольной форме с помощью процедуры Гаусса. Отличие заключается в том, что элементы под I дивной диагональю в треугольной матрице замещаются не пулями, а элементами матрицы L.
С использованием LU-разложения легко вычисляется опре-щлитель матрицы:
det А = detL = lu
(6.52)
Кроме того, если требуется найти решение для другого векто-Р-| В в правой части, то не нужно повторно проводить разложение матриц на треугольные, а достаточно только произвес-||| прямую (6.50) и обратную подстановки (6.51).
Алгоритм 6.6. Решение системы линейных уравнений методом LU-разложения
Шаг 1. Произвести LU-разложение матрицы А системы уравнений.
Шаг 2. Вычислить промежуточные переменные yi по (6.50).
Шаг 3. Вычислить неизвестные системы уравнений по (6.51).
С точки зрения объема вычислений метод LU-разложения имеете с прямой и обратной подстановками эквивалентен метолу исключения Гаусса и требует также около пА/3 операций.
Пример 6.6. Найти решение системы из примера 6.3 методом LU-разложения и переставленными 2-й и 3-й строкой).
В соответствии с алгоритмом 6.2 получаем
L =
’ I 0 О' 3-1 о 2 0-1
1 2 3
0 1 3
0 0 1
, и =
Непосредственным умножением проверяем, что
173
I
A=LU= 3
2 3'
5 6
4 5.
Тогда для вектора B=[4 6 3J промежуточные переменные У1 в соответствии с (6.46) и (6.50) вычисляем из системы
' У1 = 4.
31/!—(/2 = 6, v 2(/|—(/з = 3. откуда у\ = 4, (/2 = 6, 1/з = 5.
Окончательное решение системы в соответствии с (6.46) и (6.51) получаем из системы
I Х| + 2%2 + Зхз = 4.
1 Х2 + Зхз = 6, I %з = 5,
откуда хз = 5, хг = -9, Х| = 7.
Обращаем внимание, что последняя система точно совпадает с системой из примера 6.3.
Как и в методе Гаусса, при использовании LU-разложения для сильноразреженных матриц число операций можно значительно сократить, если использовать специальные алгоритмы упорядочения для выбора на каждом шаге главного элемента матрицы [1, 14, 16, 22].
При использовании точных методов надо большое внимание обращать на устойчивость получившегося решения. Последняя связана с плохой обусловленностью матрицы системы уравнений. Матрица называется плохо обусловленной, если определитель ее почти равен нулю. В этом случае небольшие вариации коэффициентов матрицы приводят к значительным ошибкам при вычислении решения. Сказанное поясним примером.
Пример 6.7. Найти решение системы уравнений и проверить устойчивость решения при вариации коэффициентов системы уравнений.
Пусть задана система уравнений
I Зх] + 4x2 ~ 7, | X] + Х2 — 2.
Точное решение: Х|=1, хг=1.
Увеличим коэффициенты при X] на I %; тогда получаем систему
। 3,03х| + 4x2 = 7,
) I.OIxj + хг = 2.
Ее решение (Х|==0.99. хг= 1) также в одном компоненте отличается от первоначального на I %.
174
Определитель первоначальной системы равен -I, и она. следовательно, являет-. » хорошо обусловленной, а решение системы устойчиво.
1еперь рассмотрим плохо обусловленную систему
' 1 Зх| + 4x2 = 7,
\ Х1 + 1,33X2 = 2,33.
lie решение также Х| = 1, хг=1. Сделав вариации некоторых коэффициентов чин системы, найдем соответствующие решения:
I 3xj + 4x2 = 7,
Xi + 1.33x2 = 2.32;
Ге решение: Х|=-3, хг = 4;
) Зх| + 4x2 ” 7,
Х| + 1.32x2 = 2,33;
ki решение: Xi = 2; хг = 0.5;
| Зх| + 4x2 “ 7.
Х[ + 1.32x2 = 2.34.
Be решение Х| = 3. Х2 = -0,5.
Видно, что при изменении первоначальных коэффициентов плохо обусловлен-iinii системы на доли процента решения изменяются в 2...4 раза. Это связано с 1см что определитель системы очень мал; в нашем случае равен -0,01.
Таким образом, при реализации на ЭВМ необходимо постоянно проводить ана-Н11 обусловленности системы и в необходимых случаях принимать соответствую-iiiiii' меры: изменять координатный базис, вводить весовые функции и др.
Итерационные методы, как отмечалось выше, основаны пл построении итерационной последовательности X , X ,Х , < хидящейся к искомому решению X. Каждый такой метод характеризуется своей итерационной формулой, позволяющей вычислять очередное приближение по ранее найденным. Так । ьк точное решение системы уравнений неизвестно, то для оценки точности метода вводится вектор приращений A\=Xfe+1-Xfe. Когда норма вектора приращения ||ДХ|| < е, где । заданная точность, итерационный процесс считается оконченным.
По методу простой итерации исходная система уравнений (1156) приводится к виду
%! = Х2 + Х3 + ••• + &! »
х2 = а'21х{ + а2зхз + + Ь'2 ,
х3 + й32х2 + ... +Ь'3 , (6.53)
Х„ = О',,Х. +а'„9Х9 +а'„3Х3 + • + Ь'„ , п т I л по о и ’
175
где коэффициенты а(/- получены делением элементов исходно^ матрицы на ап и переносом в правую часть" В матричной форме систему (6.53) можно представить как
X*+1 = A'Xk + B'. (6.54)
Тогда, задавшись вектором Xk, подставляем его компоненты в правую часть уравнения (6.73) и вычисляем значения компонент вектора Хк+ . Далее порученные значения вектора Xk снова подставляем в правую часть уравнений (6.53) и получаем новые значения переменных и т. д. При некоторых условиях доказана принципиальная сходимость этого итерационного процесса.
Метод Зейделя отличается от описанного тем, что уточненное значение компоненты xi вектора Xfc + I сразу же использует-! Ся для вычисления компоненты хг, найденные компоненты xi и Х2 — для вычисления Хз и т.д.
В матричной неявной форме решение по методу Зейделя может быть представлено в виде
(L + D)X* + 1 + UX* = В, (6.55)
где L, D, U — соответственно нижняя треугольная, диагональная и верхняя треугольная матрицы, полученные из исходной матрицы А:
А = L + D + (J . (6.56)
Условия сходимости метода Зейделя иные, чем для метода простой итерации, поэтому каждый из методов может сходиться там, где другой расходится. Для улучшения сходимости метода Зейделя в него вводят свободные параметры.
Другим вариантом соотношения (6.55) является итерационная процедура метода Якоби:
DX* + ' + (L + U)X* = В. (6.57)
Этот метод точно сходится для матриц со строгим диагональным преобладанием, в которых
tail > i = l,2,...,n. (6.58)
/=1 «*/
Обобщением метода Зейделя является метод последовательной релаксации, по которому процесс итерации происходит в соответствии с неявным матричным уравнением
(aL + D)X*+1 + [aU-(l-a)D]X* = аВ, (6.59)
где а—параметр релаксаций, причем 1< а< 2. Существует оптимальное значение параметра релаксации а0Пт. соответствующее на каждом этапе наибольшей скорости сходимости.
176
Рис. 6.18. Примеры схем четырехполюсников
.bin многих практических случаев аопт = 2/( 1 +Jl-ц ), где о максимальное собственное значение матрицы D'’(L+U) |гм. (6.56)]. Отметим, что при а=1 метод последовательной |н'/шксации сводится к методу Зейделя.
Рассмотренные методы решения систем линейных уравне-liiiii получили широкое распространение при моделировании и пнализе радиоэлектронных средств, к
Вопросы и упражнения для самопроверки
I. Назовите способы моделирования РЭС в частотной области.
2. Назовите режимы определения параметров матриц Z, Y, А и Н четырехпо-чик инков.
3, В чем отличие при вычислениях параметров классических и волновых матриц четырехполюсников?
4. Сформулируйте условия, налагаемые требованиями взаимности и симметрии '|ги.1рехпол1осников на элементы классических и волновых матриц.
5. Определите элементы классических матриц для реактивной цепи, изображен-....... на рис. 5.1.
6. Определите элементы волновых матриц для схемы из п.5.
7. Определите элементы матриц импеданса Z и передачи А для цепи (рис. 13. «).
К. Определите элементы матриц проводимости Y и передачи А для цепи (рис. 1. 1.4. б).
9. Перечислите явные и неявные методы при моделировании нелинейных v< ipoiiCTB в режиме малого и большого сигналов.
10. Решите методом Гаусса систему линейных алгебраических уравнений
'3 9 6 12
4 12 12 х2 = 12
1 - I 1 Х-, I
II. Решите систему из n il методом LU-разложения.
177
Глава 7
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ
Целью моделирования цифровых устройств (ЦУ) является получение картины логико-временного поведения ЦУ при различных входных воздействиях. Модели ЦУ, используемые при проектировании радиоустройств, можно разделить на две ос-новные группы: физические и логические.
В первом случае отдельные элементы, из которых состоит ЦУ, представляются их электрическими макромоделями, сос тоящими из базовых элементов теории цепей (см. гл. 4), на ос! новании которых формируется полная электрическая моделы ЦУ. Система уравнений во временной области, соответствующая полной электрической модели ЦУ, может быть получена одним из алгоритмов, описанных в гл. 5 и 6 и обычно пред ставляет собой систему дифференциальных уравнений высоко го порядка, решение которой требует больших затрат машинного времени. Алгоритмы решения систем дифференциальных уравнений рассмотрены в § 5.5.
Физические модели ЦУ позволяют наиболее полно представить работу устройства во времени с учетом реальных задержек срабатывания элементов, но их целесообразно использО1-' вать на заключительном этапе проектирования из-за больших, затрат времени на моделирование, когда необходимо иметь данные об устройстве, которые нельзя получить с помощью! более простых моделей. >м
В моделях логического уровня каждый элемент ЦУ предстат! вляется упрощенной формальной моделью в виде логического соотношения, описывающего логику функционирования элемент, та. При меньшей детализации работы по сравнению с физич₽"-. кими моделями логические модели обладают во много раз боль^ шим быстродействием и позволяют на начальных этапах проеш тирования ЦУ решить ряд важных для практики задач:
— проверить правильность логического функционирования ЦУ;' — сравнить характеристики различных вариантов схемных решений;
178
— разработать процедуры тестового контроля ЦУ и проверить их правильность и полноту;
— проверить работу цепей установки ЦУ в начальное сос-тояние.
В настоящее время разработано много алгоритмов, пакетов прикладных программ и даже специализированных языков для моделирования ЦУ на логическом уровне. Рассмотрим некоторые из них применительно к комбинационным цифровым устройствам.
§7.1. ОПИСАНИЕ ЯЗЫКОВ МОДЕЛИРОВАНИЯ И ЭЛЕМЕНТОВ ЦИФРОВЫХ УСТРОЙСТВ
В МОДЕЛЯХ ЛОГИЧЕСКОГО УРОВНЯ
При моделировании на логическом уровне физическая природа сигналов (ток или напряжение), распространяющихся в ЦУ, не конкретизируется. Сигналы задаются символами, совокупность которых описывает состояние и работу элементов, из которых состоит ЦУ. Совокупность различных символов, используемых при моделировании, называют алфавитом логического моделирования. Между реальными сигналами и символами алфавита всегда можно установить однозначное соответствие [20].
Простейший из используемых алфавитов для моделирования ЦУ на логическом уровне — двоичный, включающий всего два символа: 0 и 1. Он обеспечивает максимальную скорость
моделирования, но не позволяет выявить неоднозначность ра-
боты ЦУ и характер переходных процессов.
Моделирование мно-юзпачными алфавитами позволяет получить больше информации о ЦУ, по и требует больших с.ятрат машинного времени. Для анализа сос-(язаний сигналов на |дементах ЦУ исполь-|уют троичный алфавит, содержащий кроме 0 и I еще символ неопределенного состояния X, ко-юрому ставится в соответствие процесс перехода из 0 в 1 и обратно либо безразличное сос-
Р и с. 7.1. Алфавиты моделирования:
а - трехзначный, б - пятизначный, в - девятизначный
179
тояние сигнала (рис. 7.1, а). Для примера на рис. 7.2, а приведены таблицы истинности для наиболее распространенных базовых элементов цифровых схем И, ИЛИ, НЕ при моделировании трехзначным алфавитом. При этом полагалось, что Х=Х.
Для уточнения характера процесса смены состояний элементов ЦУ используется пятизначный алфавит, показанный на рис. 7.1, б, в котором символы 0, 1 и X имеют тот же смысл что и в трехзначном алфавите, а символ Е описывает гладкую смену сигнала из 0 в 1. Соответственно символ Е будет описывать обратное изменение сигнала из 1 в 0. Таблицы истинности для элементов И, ИЛИ, НЕ при моделировании их пятизначным алфавитом приведены на рис. 7.2, б.
Более подробно характер переходных процессов в 1_1Д описывается при использовании-.девятизначного алфавита, включающего символы 0, 1, X, Е, Е, G, G, F, F. По сравнению с пятизначным алфавитом здесь добавлены символы G и F соответствующие статическим и динамическим сбоям при переключении из 0 в 1 и из 1 в 0 (рис. 7.1, в).
При моделировании ЦУ с помощью многозначных алфавитов отдельные элементы моделируются многозначными таблицами истинности, что приводит к увеличению времени моделирования и требуемого объема памяти. В настоящее время разработаны и другие, в том числе бесконечнозначные, алфавиты,
и-и,лиг
А, О X /
0 0 0 0
X О X л
7 О л 7
и-1и
Ur О X 1
и 7 А 0
0 Е Л Ё 7
0 0 0 0 0 0
Е 0 Е л X Е
Л О X л X X
Ё О X л Ё Ё
7 О Е X Ё 7
U; 0 £ X Е 1
и 7 Ё X Е О
Рис 7.2. Таблицы истинности простых логических элементов для трехзначно! (о) и пятизначного (б) алфавитов
180
Как указывалось выше, в качестве моделей элементов ЦУ и.। логическом уровне используются формальные модели «чер-..... ящика» (см, гл. 4), в которых связь между входными и выходными сигналами элемента задается с помощью булевых уравнений либо таблиц истинности. Это прежде всего относит-1Я к простейшим базовым элементам цифровых схем И, ИЛИ, 111', сложению по модулю два и др., в виде комбинаций которых может быть, реализовано любое цифровое устройство. Более сложные элементы цифровых устройств — триггеры, регистры, устройства памяти и т.п.— в одних случаях представляют-гч комбинациями простейших базовых компонентов, в других, и.। уровне регистровых передач, их описывают в терминах выполняемых им'и операций, не прибегая к разложению на сос-ывляющие их простейшие элементы. Такой подход оказывается наиболее эффективным при моделировании цифровых устройств на основе микросхем средней или большой степени интеграции, позволяя существенно сократить время моделирования. Возможна, и комбинация обоих подходов, когда в одних и тех же программах моделирования используются модели простейших базовых элементов цифровых схем и модели, более сложные на уровне регистровых передач. Описание соединений элементов цифровых устройств в ЭВМ может быть выполнено в форме списков [20], логической сети [5] либо таблиц в i.i виси мости от конкретного языка описания ЦУ, используемо-к> в программе.
Как следует из вышесказанного, математическая модель ЦУ будет представлять собой систему булевых уравнений, каждое из которых описывает один элемент ЦУ, либо многомерных таблиц истинности. Такие математические модели могут оыть организованы в ЭВМ различным образом.
В зависимости от способа организации модели ЦУ можно разделить на компилирующие и интерпретивные. В моделях компилирующего типа исходное описание ЦУ в виде логической сети или таблицы транслируется на язык машинных копт и оформляется в виде объектного модуля, который затем и выполняется в ЭВМ в процессе моделирования. Для такого перевода описания ЦУ на язык машинных кодов используется < пениальный компилятор, являющийся частью моделирующей программы. Достоинством такого подхода является большая । корость работы программы моделирования, недостатком — необходимость разработки компилятора, что представляет собой сложную задачу, а также необходимость повторных компиляций при внесении изменений в'ЦУ.
181
В моделях ЦУ интерпретивного типа связи между отдель-1 ними элементами ЦУ представляются в виде таблиц, описание ЦУ в машинные коды не переводится, и каждое логическое уравнение, представляющее математическую модель того или иного элемента ЦУ, решается с помощью специальной подпрограммы. Выбор очередной подпрограммы производится специальной интерпретирующей программой, которая исполь зует записанные в таблицу адреса перехода от одного элемен-1 та ЦУ к другому. Обращение к подпрограмме, моделирующей элемент, будет происходить всякий.раз, когда интерпретатору понадобится выполнить данную логическую операцию. Модели интерпретивного типа оказываются более простыми и менее трудоемкими в разработке, однако они имеют меньшее быстродействие по сравнению с компилятивными.
В зависимости от учета или неучета задержек в срабаты вании ЦУ при моделировании модели ЦУ подразделяются на синхронные и асинхронные, а по способу организации процес-! са решения системы уравнений — на сквозные и событийные. 1
Описание особенностей всех видов моделей ЦУ приводится в следующих параграфах.
§7.2. СИНХРОННОЕ МОДЕЛИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ ДВОИЧНЫМИ АЛФАВИТАМИ
При синхронном моделировании ЦУ на' логическом уровне не учитываются задержки срабатывания отдельных элементов, из которых состоит ЦУ. Это позволяет свести моделирование к последовательному вычислению сигналов на выходах элементов ЦУ по значениям сигналов на их входах с помощью булевых уравнений или таблиц истинности, моделирующих кажЛ дый элемент. При этом считается, что независимыми перемен* ными, синхронизирующими работу модели устройства/ являются события — изменение сигналов на входах ЦУ. После определения состояния, в которое перейдет ЦУ при очередной, смене входных сигналов, осуществляется сдвиг модельного времени до момента наступления очередного события. В про-; межутке между двумя событиями смены сигналов на входах ЦУ не происходит, а если на входах устройства появятся новые сигналы, то они будут отнесены к началу следующего такта моделирования. Контроль временного интервала между со-1 бытиями необходим для построения временных диаграмм, наглядно представляющих работу ЦУ в предположении нулевом длительности переходных процессов.
По принципу* работы такая модель соответствует работе синхронного цифрового автомата [20], в котором сигналы на
182
п оды ЦУ поступают только в моменты подачи синхросигна-1ПЦ, в остальное время входные сигналы не могут изменять |<>яние ЦУ. Переходные процессы в устройстве обязательно ыкапчиваются к моменту прихода следующего синхросигнала.
Синхронные модели можно использовать для моделирования i инхронных и асинхронных цифровых автоматов и термин «син-Ьрошюе моделирование», общепринятый в литературе, означает IO./H.KO неучет задержек в работе отдельных элементов ЦУ.
Как показано в §7.1, математическая модель ЦУ без учета i.ru-ржек представляет собой систему булевых уравнений, гп',| (ывающих между собой сигналы на входах и выходах эле-MI нгов ЦУ. В общем виде такая система может быть записана следующим образом:
F = F(U),
I ш Uq — вектор сигналов на входах ЦУ, U — вектор сигналов и.। внутренних узлах схемы ЦУ (входах и выходах элементов), логический функционал, F—вектор выходных сигналов, iin i ересующих разработчика.
Система логических уравнений (7.1) при каждом собы-HHI — изменении входных сигналов решается итерационно относительно вектора U, по координатам которого определяются требуемые выходные сигналы устройства F.
Алгоритмы решения системы логических уравнений делят и.। две группы: сквозные и событийные. В первом случае при п ।грационном решении системы логических уравнений матема-ц|'1сской модели ЦУ на каждой итерации решаются .все логические уравнения и процесс решения системы U = L(Uq, U) во многом напоминает решение итерационными методами системы линейных алгебраических уравнений. Сквозное моделиро-н.шие может выполняться методом простой итерации, когда 1ля определения сигналов в ЦУ на последующей _итерации /' используются сигналы на предыдущей итерации Uk~\ Итерационный процесс решения системы логических уравнений по методу простой итерации может быть записан в виде
Uk = L(UQ, Uk~}), (7.2)
или в скалярном виде
ик = Lt (Uq, ик~', .... ик~', где i = 1 ... п.
Если решение системы логических уравнений ведется по методу итерации Зейделя, то сигналы, определенные при решении предыдущих уравнений системы, используются для на
183
хождения сигналов, определяемых последующими уравнениями. В этом случае итерационная формула в скалярной форме записи имеет вид
и- = {73)
< = Lm(Uqu{,...u*, и%-..uk~'Y
Итерационный процесс решения системы логических уравнений продолжается до тех пор, пока сигналы на всех узлах ЦУ на двух последних итерациях не совпадут, что свидетельствует о получении установившегося состояния ЦУ. Для ускорения итерационного процесса расположение уравнений в системе логических уравнений математической модели ЦУ необходимо ранжировать в порядке распространения сигналов через элементы устройства.
При программной реализации алгоритмов значения сигналов на узлах ЦУ на каждой итерации и хранятся в специальном массиве—рабочем поле РП (Л), причем в рабочем поле, соответствующем нулевой итерации РП(0), хранятся сигналы, соответствующие начальному состоянию ЦУ перед изменением входных сигналов. Изменения входных сигналов записываются в рабочее поле на первой итерации РП(1). На последующих итерациях до получения решения сигналы на входных узлах ЦУ при синхронном моделировании не изменяются. После получения установившегося решения сдвигается модельное время и начинается моделирование следующего события, а в качестве начального состояния ЦУ для него используется решение, полученное на предыдущем шаге.
Рис. 7.3. Схема ЦУ (а) и временные диаграммы ее работы (б)
184
Рассмотрим процесс сквозного синхронного моделирования ЦУ двоичным алфавитом на примере устройства, приведенно-||| на рис. 7.3, а. Математическая модель ЦУ представляет собой систему логических уравнений:
U-5 = U] А из, Us = из Л Щ,
Us~ U§ V Uy, Ug = Us Л U]0,
U7 — и% A U3, U10 — Us л ид,
। и, — сигналы на узлах устройства, Uq = |«|, и%, из, и J —вектор входных сигналов.
При сквозном моделировании по методу простой итерации и соответствии с (7.2) итерационные формулы запишутся сле-лующим образом:
11^ — 1 I л ft I I I - f / ' Л It I
44g — 4Z| Л f 44 g — Z\ f
11k — 1lk~] X/ ffk — A I/*"1
flA „ t,k-\ . t.k-l t.k _ A-1 Л-1
44y , ^чО ~~ ^8 •
Процесс сквозного моделирования ЦУ по методу простой in грации при изменении входных сигналов «ц U2, из, «4, пока-laiiHOM на рис. 7.3, б, иллюстрируется табл. 7.1.
Таблица 7.1
11 <менение входных сигналов Номер итерации . Сигналы на узлах ЦУ
входные внутренние и выходные
ча «2 «3 44 «5 «г> «7 и» «9 «Ю
/ = /о 0 0 1 1 0 0 0 1 1 1 0
11 ,менение 1 0 0 1 1 0 0 1 1 1 0
сигналов 2 0 0 1 1 0 0 0 0 1 0
3 0 0 1 1 0 I 0 0 1 1
4 0 0 1 1 0 1 0 0 0 1
Решение 5 0 0 0 1 1 0 1 0 0 0 1
1 /0+ Д/ 1 0 1 1 0 0 1 0 0 0 1
111менение 2 0 1 1 0 0 1 1 1 0 1
сигналов 3 0 1 1 0 0 0 1 1 0 1
4 0 1 1 0 0 0 1 1 I 1
5 0 1 1 0 0 0 1 1 I 0
Решение 6 0 1 1 0 0 0 1 1 I 0
185
Временные диаграммы, соответствующие приведенным результатам моделирования, показаны на рис. 7.3, б.
Сквозное моделирование по методу простой итерации может использоваться для синхронных и асинхронных моделей ЦУ, недостатком его является большое время, затрачиваемое на решение системы логических уравнений, представляющих математическую модель ЦУ на логическом уровне из-за большого числа итераций. Существенно сократить время моделирования можно за счет выполнения итерационного процесса по методу итерации Зейделя. В соответствии с (7.3) для нашего примера итерационные формулы запишутся следующим образом: ______
A U3 , «8 ли*,
If k k .Ji
V и7 , ид A U|0
.Ji ..fi .Ji .Ji
«7 = и2 ли3, — Ug A Ug .
Процесс сквозного.моделирования ЦУ, показанного на рис, 7.3, а, по методу итерации Зейделя при таком же изменении входных сигналов, что и в предыдущем случае, приведен 1 табл. 7.2.
Таблица 7 Л
Изменение входных сигналов Номер итерации Сигналы на узлах ЦУ
входные внутренние и выходные
«1 W2 «з t/4 «5 «6 "7 «8 «9 «ю!
t = /о 0 0 1 1 0 0 0 1 1 1 0
Изменение сигналов 1 0 0 1 1 0 0 0 0 1 1
2 0 0 1 1 0 1 0 0 0 1
Решение /=/0 + А/ 3 0 0 0 1 1 0 1 0 0 0 )
Изменение сигналов I 0 1 1 0 0 1 1 1 0 1 I
2 0 1 1 0 0 0 1 1 I 0 1
Решение 3 0 1 1 0 0 0 1 1 1 0 i
Как видно из табл. 7.2, решение системы логических урав^ нений по методу итерации Зейделя позволяет существенно са кратить число итераций, однако этот метод неприменим пр» асинхронном моделировании ЦУ с учетом задержек срабаты вания элементов.
186
Приведем пошаговое описание алгоритма для разового изменения входных сигналов.
Алгоритм 7.1. Сквозное моделирование ЦУ двоичным алфавитом по методу ii/’iii той итерации
Шаг /. Формируется рабочее поле на нулевой итерации РП(0). соответствую-III < начальному состоянию устройства.
Шаг 2. Фиксируется изменение входных сигналов, формируется рабочее поле 1Ы первой итерации РП( 1).
Шаг 3. Номер итерации k полагается равным 2.
Шаг 4. Начиная с первого логического уравнения системы уравнений матема-приткой модели ЦУ определяется новое значение сигналов на выходе элемента IIS' описываемого данным уравнением.
Шаг 5. Если сигнал на выходе элемента изменился, то в рабочее поле для и итерации РП(£) вносится новое значение сигнала, иначе переписывается । hi пал из рабочего поля РП(£-1). соответствующего предыдущей, (Л—I )-й итерации.
Шаг 6. Если вычислены все сигналы на k-к итерации, то переходим к шагу 7. lin.i'ie к шагу 4.
Шаг 7. Сравниваются рабочие поля на k-н и (й-1)-й итерациях; если они cob-mi i.iiiiT. то моделирование отклика ЦУ на разовое изменение входных сигналов па..(ено, иначе увеличиваем номер шага итерации на I и переходим к шагу 4.
Значение сигнала на выходе элемента ЦУ может изменить-111 только в том случае, если изменился сигнал по крайней м< рс на одном из его входов. Это обстоятельство положено в <нпову работы событийных алгоритмов синхронного моделирования ЦУ, в которых в отличие от алгоритмов сквозного моделирования на каждой итерации решаются не все логические уравнения системы, а только уравнения для тех элементов, у вторых на предыдущей итерации изменились входные сигна-fi.i Для организации такого вычислительного процесса в кон-|ц каждой итерации решения системы логических уравнений шиле сравнения рабочих полей на соседних итерациях формируется список изменившихся сигналов, по которому можно определить активизированные элементы, т.е. элементы, на вхо-।а\ которых изменился сигнал и для которых на последующей пгерации необходимо решать логические уравнения. Итера-....пный процесс прекращается, когда в модели ЦУ не будет и тенившихся сигналов и активизированных элементов.
Процесс моделирования событийным алгоритмом ЦУ, схема которого представлена на рис. 7.3, а, приведен в табл. 7.3. Начальные условия, изменения входных сигналов и временные in.праймы совпадают с предыдущими примерами.
187
Таблица 7.3
Изменение входных сигналов Номер итерации Сигналы на узлах ЦУ
входные внутренние н выходные изменившиеся сигналы активизированные элементы
«1 «2 из «4 «5 иъ «7 Us «10
t = to 0 0 I 1 0 0 0 1 1 1 0 — —
Изменение сигналов 1 0 0 1 1 0 0 1 1 1 0 «2» Щ «7, «8
2 0 0 1 1 0 0 0 0 1 0 U7, ив «6, «10
3 0 0 1 1 0 1 0 0 1 1 и6, «10 «9
4 0 0 1 1 0 1 0 0 0 1 «9 «10
Решение 5 0 0 0 1 1 0 1 0 0 0 1 — —
t = + Д/ Изменение сигналов 1 0 1 1 0 0 1 0 0 0 1 «2, «4 «7, ‘ «8 1
2 0 ' 1 1 0 0 1 1 1 0 1 «7. ив «6, «10
3 0 1 1 0 0 0 1 1 0 1 ив «9
4 0 1 1 0 0 0 1 1 1 1 «9 «10
к 5 0 1 1 0 0 0 1 1 1 0 «10 «9
Решение 6 0 1 1 0 0 0 1 1 1 0 — 1 .1
Как видно из работы событийного алгоритма, здесь наибоп] лее удобной представляется интерпретивная организация ма-, тематической модели ЦУ, однако событийное моделирование,] может быть и компилятивным. Как и сквозное моделирование,(1 событийное может выполняться методами простой итерации и' итерации Зейделя. Событийное моделирование целесообразно применять в тех случаях, когда выигрыш от уменьшения чйс-Ч ла решаемых уравнений на всех итерациях превышает затраЯ ты на анализ активизации элементов ЦУ.
Приведем пошаговое описание работы алгоритма для раза-н вого изменения входных сигналов.
Алгоритм 7.2. Синхронное событийное моделирование ЦУ двоичным алфавитом по методу простой итерации
188
Шаг I. Формируется рабочее поле на нулевой итерации РП(0). соответствующее начальному состоянию ЦУ, списки изменившихся сигналов и активизированных элементов полагаются пустыми: Ik = 0. Aft = 0.
Шаг 2. Фиксируется изменение входных сигналов, формируется рабочее поле ил первой итерации РП(1). Номер итерации полагается равным k — 2.
Шаг 3. Сравниваются рабочие поля на (й-1)-й и (Л-2)-й итерациях РП (fe-1) и l'll(fe—2). формируется список изменившихся сигналов если /ft = 0. то переходим и тагу 8.
Шаг 4. На основании /ft и описания ЦУ определяется список активизированных элементов Ak
Шаг 5. Начиная с первого элемента списка Ak решается логическое уравнение. моделирующее активизированный элемент ЦУ, и определяется новое значение пинала на его выходе.
Шаг 6. Если сигнал иа выходе элемента изменился, то в рабочее поле для fc-й ик'рации РП(/г) вносится новое значение сигнала, иначе переписывается выходной пинал из рабочего поля РП(Л—I).
Шаг 7. Если промоделированы все элементы из списка Ak. то полагаем А - It + I и переходим к шагу 3, иначе к шагу 5.
Шаг 8. Фиксируем состояние ЦУ после изменения входных сигналов на шаге 2.
Рассмотренные выше алгоритмы синхронного моделирования ЦУ двоичным алфавитом обладают высоким быстродействием, однако результаты моделирования ими не всегда могут пыявить ошибки в работе ЦУ, которые могут возникнуть из-за ыцержек в срабатывании элементов ЦУ, кроме того, синхронное моделирование не позволяет выявить характер переходных процессов в устройстве.
§7.3. АСИНХРОННОЕ ДВОИЧНОЕ МОДЕЛИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ
Упоминавшиеся недостатки синхронных алгоритмов моделирования ЦУ обусловили разработку более медленных, но biro более адекватных реальной работе ЦУ асинхронных ал-н>ритмов, учитывающих задержки срабатывания отдельных •.цементов. Задержка срабатывания элемента цифрового устройства зависит от многих факторов: от того, на каком входе •лсмента и каким образом произошла смена сигнала, от начального состояния элемента, цепей питания и т.д. В дальнейшем будем полагать задержки срабатывания не зависящими от нпда переключения, а задержками в линиях передачи будем пренебрегать, хотя описываемые далее алгоритмы несложно распространить и на более общий случай. Кроме того, для упрощения описания алгоритмов будем полагать, что переходные процессы в ЦУ завершаются до следующей смены входных сигналов.
С учетом сделанных допущений в асинхронных моделях 11,У модель каждого элемента может быть представлена в кнде каскадного соединения идеального безынерционного логи-
189
Рис. 7.4. Модель логического элемента для асинхронного моделирования
ческого элемента и линии задержки, реализующей функцию U(t) = U'(t—т/) (рис. 7.4), где т;— задержка срабатывания элемента. Независимой пе-1 ременной при асинхронном моделировании является время, которое в моделирующей ЦУ программе продвигается с шагом, равным минима-1 льной задержке срабатывания элементов в устройстве т. Задержки всех элементов округляются до значений, кратных т, что позволяет считать задержку срабатывания / элемента равной Ti = rjt, где г, — целое число. Асинхронное моделирование может быть сквозным и событийным, причем в отличие от синхронных моделей здесь алгоритмы существенно отличаются.
Рассмотрим принципы организации сквозного асинхронного моделирования ЦУ. При сквозном асинхронном моделировании работы ЦУ при каждой смене входных сигналов необходимо наличие в моделирующей программе не одного рабочего поля, а М + 1, где М = ттах/т, а т|Пах—максимальная задержка срабатывания элемента в устройстве. Каждое из рабочих полей будет характеризовать нам состояние устройства в раз-4 личные моменты времени, отличающиеся на т. Так, РП (/о)—В момент смены сигналов i -/о, РП(/|)—в момент / = /г=^о + т и т.д. Перед началом моделирования в рабочие поля РПЦо) -1 РП(/м) заносятся сигналы, соответствующие начальному сос-| тоянию устройства, затем текущее время полагается равным моменту поступления входных сигналов и во все рабочие полй заносятся новые сигналы на входных узлах ЦУ.
Далее • однократно решаются логические уравнения* моделирующие работу безынерционных элементов устройству* исходя из состояния, задаваемого РП(/о). Если при этом на выходах элементов изменяются сигналы, то их новые значеци^ заносятся в РП(/|)... РП(/л<) в зависимости от задержки срабатывания элемента, а также во все последующие рабочие поля. После решения всех логических уравнений для сое- тояниЯ ЦУ, описываемого РП(/о), ему присваивается время РП(/м +1), где (tM + i) =/о + (М + 1 )т и в него записываются значения сигналов на узлах ЦУ из предыдущего рабочего поля РПЦм). 1 Описанный процесс повторяется с рабочим полем РП(/|), потом с РП(/г) и т.д. На любом k-м такте моделирования, соответствующем времени /* = 7о + Лт. сигналы на входах элемента ЦУ для решения /-логического уравнения берутся из РП(/Ц, и изменившиеся сигналы на его выходах заносятся в РПЦ^ + т/)
190
I’ и с . 7.5. Асинхронная модель ЦУ (а) и временные диаграммы ее работы (б)
и нее последующие за ним рабочие поля, где Ту— задержка i|>.|батывания /-го элемента. Процесс моделирования продолжается до тех пор, пока на последнем такте не совпадут все рабочие поля.
В скалярном виде работа сквозного асинхронного алгоритма моделирования ЦУ на любом &-м шаге может быть запитана следующим образом:
Uj(to + kx + ту) = Lj(U(to + kx)), (7.4)
I /1<‘ k = 1, ..., n.
Описанный алгоритм допускает как компилятивную, так и ппгерпретивную организацию моделирования, однако в отличие от синхронного моделирования здесь нельзя использовать для решения системы логических уравнений итерационный процесс по методу Зейделя.
Для примера на рис. 7.5, а показана модель ЦУ с определенными задержками срабатывания элементов. Процесс итерационного решения уравнений математической модели для каждого такта сквозного асинхронного моделирования ЦУ можно записать следующим образом:
щЦо + kx + т) = иi(/q + kx) v uz(to + kx),
Ub(to + kx + 2т) = U2(to + kx) л Из(/о + kx), u&(to + kx + 2т) = щ(/р + kx) л ujfjo + kx), uj(to + kx + 2x) = U5(to + kx) л ue{to + kx).
Результаты моделирования для изменения входных < in налов, показанного на рис. 7.5, б, приведены в табл. 7.4.
191
Таблица 7.4
Сигналь на узлах ЦУ
Изменение сигналов Такты, модельное Рабочие поля входные внутренние и выходные
время «I «2 «3 и4 «5 «6 «7
Начальное состояние /< to РП(0) 0 0 1 1 0 0 1
Изменение сигналов t < to РП(/0) РП(/о +• т) РП(/0 + 2т) 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1
РП(0) 1 1 1 1 0 0 1—
Q РП(1) 1 1 1 10 -1 0 1
РПЦо + т) 1 1 1 со 0 0 ГН
РП(/о 4" 2т) 1 1 1 0 Li 0 1
РП(/о 4- Зт) 1 1 1 0 1 0 1
РП(0) 1 1 1 0 0 0 1-*—
РП(1) 1 1 1 0 г* г—1 1
Изменение Щ 1 t = /о+ т РП(4) 4- 2т) 1 1 1 0 1 0 ГН
РПЦо + Зт) 1 1 1 0 Ц -«-1 i
РП(Г0 + 4т) 1 1 1 0 1 1 i
РП(0) 1 1 1 0 1 0 i-»-
РП(1) 1 1 1 0 1 г-1 i
Изменение U5 2 t = to 4- 2т РПИо + Зт) 1 1 1 0 1 1 1 ]-1
РП(/0 + 4т) 1 1 1 0 1 -»1 1
РП(/0 +5т) 1 1 1 0 1 1 1
РП(0) 1 1 1 0 1 1 1—J
РП(1) 1 1 1 0 1 1 г0
Изменение U6 3 t — /о+Зт РП(/0 + 4т) 1 1 1 0 1 1 1J-I
Р1+ 5т) 1 1 1 0 1 1 -*о
/ РП(«о + 6т) 1 1 1 0 1 1 0 !
РП(0) 1 1 1 0 1 1 1-.-J
4 РП(1) РП(4> + 5т) 1 1 1 1 1 1 0 0 1 1 1 Г °-J 0j<
РП(/0 + 6т) 1 1 1 0 1 1 —0
РП(/0 + 7т) 1 1 1 0 1 1 0
РП(О) 1 1 1 0 1 1 о-J
Изменение 5 РП(1) 1 1 1 0 1 1 0
«7 РПЦ0 + 6т) 1 1 1 0 1 1 0
Решение РП(/0 + 7т) 1 1 1 0 1 1 0
РП(/о + 8т) 1 1 1 0 1 1 0
192
В табл. 7.4. на всех тактах моделирования рабочие поля 1'11(0) и РП(1) используются для однократного решения логиче-। них уравнений математической модели. Соответствующие ре-<у./п>татам моделирования временные диаграммы приведены на рис. 7.5, б. С помощью несложного анализа можно убедиться соответствию их реальному переходному процессу в ЦУ.
Сквозные асинхронные алгоритмы требуют больших затрат машинного времени и памяти ЭВМ из-за большого числа так-|пи и рабочих полей. Большое число итераций объясняется (гем, что число событий, происходящих в каждом такте, мало, мк как события распределяются в соответствии с задержками срабатывания элементов по (М 4- 1)-му такту. По различным оценкам [20], в каждом такте доля активизированных Элементов при моделировании комбинационных схем составляет 1...2,5%. Следовательно, при сквозном асинхронном моделировании, когда на каждом такте решаются все уравнения м.нематической модели, большая часть времени расходуется Непроизводительно. Тем не менее такие алгоритмы находят применение в ряде практических случаев при моделировании устройств памяти, параллельной передачи данных по интерфейсным шинам и т.п.
Приведем пошаговое описание алгоритма для однократного и (мснения входных сигналов.
Алгоритм 7.3. Сквозное асинхронное моделирование ЦУ
Шаг I. Задержки срабатывания элементов ЦУ нормируются к минимальной и них т и округляются до кратных величин. По значению Л4=ттах/т определяется необходимое число рабочих полей Л1 + 1.
Шаг 2. Формируются рабочие поля РП(<о) ... РПЦм), в которые заносится на-bi ii.uoe состояние устройства.
Шаг 3. В рабочие поля РП(/о) РП(/д/) заносятся новые значения входных • in налов, текущее время моделирования полагается равным t = to, число тактов Моделирования k — 0.
Шаг 4. Производится однократное сквозное синхронное моделирование k-ro так-> । причем входные сигналы для / элемента выбираются из РП(^), а измененные иодные сигналы записываются в РП(/о + fex + т,) и все за ним последующие поля, in су — задержка срабатывания /-го элемента.
Шаг 5. В рабочее поле РПЦо + бт) переписываются сигналы из 1'11|/() + (Л! + /г)х| и ему присваивается время to + (М + k + I)т.
Шаг 6. Текущее время моделирования полагается равным t = tk+\= /о + (k + 1 )т, номер такта моделирования полагается равным k = k + l.
'\ втоматизация проектирования радиоэлектронных средств
193
Шаг 7. Производится сравнение РП(/^ + 1) ... РПро + (М + k + I )т]. Если они не совпадают, то переходим к шагу 4. иначе моделирование отклика ЦУ на изменение входных сигналов закончено.
Указанные выше недостатки сквозного асинхронного моделирования обусловили широкое применение при асинхронном моделировании ЦУ событийных алгоритмов. При произвольных задержках срабатывания элементов асинхронное событийное моделирование обычно организуется интерпретивными методами. Рассмотрим примерную организацию событийных интерпретив-ных алгоритмов моделирования ЦУ с учетом задержек.
Для организации событийных алгоритмов асинхронного моделирования ЦУ в программе формируется массив, хранящий очереди совершения событий и два рабочих поля, в одном из которых, РП(1), хранятся текущие значения сигналов на выхо-1 дах безынерционных логических элементов, а во втором, РП(2),— значения сигналов на выходах элементов задержки (см. рис. 7.4). Каждое'событие в очереди совершения событий содержит номер элемента, сигнал на выходе которого должен измениться, и номер такта моделирования, в котором это событие должно произойти. События в очереди упорядочены в порядке возрастания времени их наступления.
На каждом k-м такте работы алгоритма из очереди совершения событий выбираются события, которые должны произойти в текущий момент времени t = to + ki, и сигналы на выходах задержек в РП(2) устанавливаются такими, как и сигналы, записанные для этих элементов в РП(1). Далее производится решение логических уравнений для активизированных изменениями сигналов элементов в РП(2). Если при этом на выходах активизированных элементов изменяются сигналы, то новые значения сигналов заносятся в первое рабочее поле РП(1), а сами элементы — в очередь совершения событий, где располагаются в порядке, определенном задержкой срабатывания данного элемента. В результате моделирования длина очереди совершения событий возрастает на число элементов, на выходе которых в результате моделирования на данном такте изменился выходной сигнал.
Для примера в табл. 7.5 приведен процесс событийного асинхронного моделирования ЦУ, показанного на рис. 7.5, а, при тех же изменениях входных сигналов, что и в предыдущем случае.
194
Т а б л и ц а 7 5
11гменение in валов Такты, модельное время Рабочие поля Сигналы на уалах ЦУ Очередь совершения событий
входные внутренние, выходные
W| W2 м3 «4 «5 «6 «7
11 1чальное < «н тояние t< to РП(0) 0 0 1 10 0 1 —
11<менение ।игиалов 0 t = to РП(2) РП(1) 1 1 1 1 1 1 10 0 1 0 10 1 |(U4,/0 + т), («5,/о + 2т)]
11 (менение и4 1 t = to + T РП(2) РП(1) 1 1 1 1 1 1 0 0 0 1 0 111 [GWo + 2т), («6,/о + Зт)]
11 иченение ^5 2 t = to + 2т РП(2) РП(1) 1 1 1 1 1 1 0 10 1 0 111 [(«бДо + Зт)]
111менение 3 t = + 3т РП(2) РП(1) 1 1 1 1 1 1 0 111 0 110 ](U7,/o + 5t)]
4 t — to + 4т РП(2) РП(1) 1 1 1 1 1 1 0 111 0 110 |(«7, to +5т)]
11 1менение «7 1 ’•шение 5 t = to + 5t РП(2) РП(1) 1 1 1 1 1 1 0 110 0 110 —
Временные диаграммы работы ЦУ, полученные по резуль-i him моделирования, приведены на рис. 7.5, б. Нетрудно у(н литься в совпадении результатов, полученных с помощью Акцизного и событийного алгоритмов, и в упрощении процесса tn пнхронного моделирования при использовании событийных м« годов.
В событийных алгоритмах возникает ряд сложностей при наработке одновременных событий. В описанном выше алгорит-м. последовательность одновременных событий, происходящих н одном такте, не анализировалась. Известны более совершенные алгоритмы, позволяющие учитывать очередность событий н каждом такте моделирования [20], однако и более сложные к алгоритмической реализации.
Наибольших затрат машинного времени при работе собы-..... алгоритма требует процедура включения — выключение события в очередь совершения событий. Каждое новое corn и не должно быть включено между двумя соседними со
195
бытиями^ которые должны произойти в предыдущий и последующий моменты времени. Так как события в очереди расположены в порядке возрастания времени и для поиска места включения должны просматриваться поочередно, то время включения — выключения оказывается пропорциональным длине очереди совершения событий и в сложных ЦУ этол процесс занимает много машинного времени.
Алгоритм 7.4. Событийное асинхронное моделирование ЦУ
Шаг /. формируются рабочие поля РП(1) и РП(2), характеризующие состояние элементов ЦУ без учета задержки и с ее учетом, содержание которых соответст! вует начальному состоянию ЦУ.
Шаг 2. В РП( 1) заносятся изменившиеся входные сигналы, и из сравнении РП( I) и РП(2) формируется очередь совершения событий Q.
Шаг 3. Текущее модельное время полагается равным / = <0-
Шаг 4. Из очереди совершения событий Q выделяется список элементов, события на выходе которых должны произойти в текущий момент времени.
Шаг 5. Производится запись в РП(2) новых значений сигналов для очередных событий из РПЦ).
Шаг 6. Выполняется решение логических уравнений для активизированный элементов ЦУ. на входы которых поступают сигналы, выбранные из очереди совершения событий. Изменившиеся сигналы заносятся в РП( I).
Шаг 7. Уточняется очередь совершения событий, в которую заносятся в соответси вин с задержками срабатывания элементов изменившиеся сигналы с шага 6. I
Шаг 8. Проверяется очередь совершения событий. Если очередь не является пустой Q * 0, то увеличивается модельное время / = / + т и переходим к шагу 4, иначе моделирование ЦУ окончено.
Асинхронные алгоритмы двоичного моделирования позволяют более полно описать работу ЦУ и переходные процесс^ в нем, выявить статические и динамические риски сбоя, а I ряде случаев и состязания сигналов в ЦУ. Недостатками этий алгоритмов являются невозможность учета разброса задерже) срабатывания элементов ЦУ и существенно большие затрат! машинного времени на моделирование, чем в синхронных ал горитмах.
§7.4. МОДЕЛИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ МНОГОЗНАЧНЫМИ АЛФАВИТАМИ
Алгоритмы двоичного синхронного моделирования не позв<
ляют выявить возможную неоднозначность в поведении ЦУ, во
зникаюшую, например, из-за неопределенного состояния ЦУ
перед подачей входных сигналов, наличия элементов памяти.
196
< истязаний сигналов на рходах элементов и т.п. Асинхронное шоичное моделирование ЦУ не учитывает разброса задержек । рабатывания элементов и поэтому может выявлять неоднозна-.... поведения устройства не во всех случаях, кроме того, uno требует больших затрат машинного времени для моделирования. Моделирование многозначными алфавитами (см. §7.1) при умеренных затратах машинного времени на моделирование, всего в 4...6 раз больших, чем при синхронном моделировании, позволяет обнаруживать состязания сигналов на входах vie ментов ЦУ, оценить характер переходных процессов в нем.
При моделировании многозначными алфавитами задержки срабатывания элементов принимаются произвольными, а модели Элементов характеризуются многозначными таблицами in чинности, подобно приведенным на рис. 7.2. Для простоты в ыльнейшем ограничимся только моделированием ЦУ троичным алфавитом.
Моделирование ЦУ многозначными алфавитами производится в два этапа. На первом из них всем входным сигналам, ко-1<>рые должны измениться на данном такте моделирования, присваивается неопределенное значение X и выполняется синхронное моделирование ЦУ с использованием многозначных |.|<>лиц истинности. Состояние, в которое перейдет устройство, фиксируется.
На втором этапе на входных узлах ЦУ устанавливается (ребуемый набор входных сигналов и опять выполняется моли.пирование устройства с использованием многозначных таблиц истинности, в котором в качестве начального состояния Н.У используется состояние, полученное на предыдущем этапе моделирования. Символы неопределенного состояния X, оставшиеся на узлах ЦУ после получения установившегося решения, будут свидетельствовать о возможности состязаний сигналов на входах элементов, выходные сигналы которых имеют потения X. На элементах,' получивших в результате второго папа моделирования, значения сигнала 0 или 1 состязания п< возможны. Если же в результате моделирования сигналы на in ех узлах ЦУ определены, то при таком наборе входных сигналов состязания в устройстве невозможны.
Для примера выполним моделирование трехзначным алфавитом ЦУ, схема которого показана на рис. 7.6, а. Итерационные формулы для моделирования этого устройства по методу простой итерации имеют такой вид: *
197
Ы5 ~ U2 V U3 ' >
W6 “ Ui ~l Л W5~' > u7 ~ U3 ~l л w4 '
,.k - „*-* л ,,k-'
,,k _
1л-ц — bly /\ Wg
Результаты моделирования сигналов, показанной на рис.
устройства
при
смене входны!
7.6, б, приведены в табл. 7.6.
Таблица 7 6
Этап троичного моделирования Изменение сигналов, время Номер итерации Сигналы на узлах
входные внутренние и выходные
W[ U2 «3 u4 «5 ^6 Н7 «8 «9
1 Начальное 0 1 0 1 1 1 1 0 0 1
состояние
Изменение 1 X X 1 X 1 1 0 0 1
сигналов 2 X X 1 X 1 X X 0 1
t<to 3 X X 1 X 1 X X X 1
4 X X 1 X 1 X X X X
Решение 5 0 X X 1 X 1 X X X X
2 Изменение 1 0 1 1 0 1 X X X X
сигналов 2 0 1 1 0 1 0 1 X X
/=/о 3 0 1 1 0 1 0 1 1 X
4 0 1 1 0 J 0 1 1 0
Решение 5 0 1 1 0 J 0 1 1 0
Рнс. 7.6. Моделирование ЦУ трехзначным алфавитом:
а-схема устройства, б
результаты моделирования при отсутствии состязаний, в моделирования при наличии состязаний
результаты
198
Временные диаграммы, иллюстрирующие работу ЦУ при । а кой смене входных сигналов, показаны на рис. 7.6, б. Не-|рудно заметить, что при выбранном наборе входных сигналов состязания сигналов в ЦУ будут отсутствовать, что и под-терждается результатами моделирования.
Рассмотрим теперь процесс моделирования этого же устройст-иа в том случае, когда набор входных сигналов приводит к появлению состязаний сигналов. Состязания можно получить при следующем наборе входных сигналов: и\ = 1, U2~ 1, «3 = 0, »1 = 0 (рис. 7.6, .в). Выполним троичное моделирование устройства по той же схеме, что и в предыдущем случае, с указанным выше набором входных сигналов. Результаты моделирования сведены в табл. 7.7.
Таблица 7.7
Этап I рентного моделирования Изменение сигналов, время Номер итерации Сигналы на узлах ЦУ
входные внутренние и выходные
«1 «2 Ил U4 «5 «6 «7 «9
Начальное 0 , 1 0 1 1 1 1 0 0 1
состояние 1 i X X X 1 1 0 0 1
Изменение 2 1 X X X X 1 X 0 1
1 сигналов 3 1 X X X X X X 0 1
1 <1о 4 1 X X X X X X X 1
5 1 X X X X X X X X
Решение 6 0 1 X X X X X X X X
Изменение 1 1 1 0 0 X X X X X
9 сигналов 2 1 1 0 0 1 X 1 X X
Z t=tu 3 1 1 0 0 1 1 1 X X
Решение 4 1 1 0 0 1 1 1 X X
Как видно из табл. 7.7, в установившемся решении сигналы па узлах и& и ид ЦУ не определены, что и свидетельствует и наличии предсказанных состязаний в устройстве при таком напоре входных сигналов. Временные диаграммы, иллюстрирующие работу ЦУ для этого случая, показаны на рис. 7.6, в.
Троичное моделирование позволяет обнаружить любые опасные состязания сигналов, которые могут иметь место в устрой-। । не при сравнительной простоте алгоритмической реализации и относительно небольших затратах машинного времени. Не-1п>| гатком моделирования троичным алфавитом является то, чю из-за допущения произвольности задержек срабатывания ^цементов оно может указывать на состязания, отсутствующие и реальном устройстве. Это часто наблюдается при моделировании сложных ЦУ с разветвлениями и счетными входами, I 'н любое переключение счетного входа приводит при троичном моделировании к состязаниям.
199
Алгоритм 7.5. Моделирование ЦУ трехзначным алфавитом
Шаг 1. Изменяющимся сигналам на входных узлах ЦУ присваиваются неопре-деленные значения X. сигналы на внутренних и выходных узлах сохраняют знач< ния. соответствующие начальному состоянию устройства.
Шаг 2. Выполняется синхронное моделирование ЦУ троичным алфавитом одним из описанных в §7.2 алгоритмов от состояния, определенного на шаге 1. I
Шаг 3. Сигналам на входных узлах ЦУ присваиваются изменившиеся значения, сигналы на внутренних и выходных узлах сохраняют значения, полученные при моделировании на шаге 2.
Шаг 4. Выполняется синхронное моделирование ЦУ троичным алфавитом от состояния, определенного на шаге 3.
Шаг 5. По результатам моделирования исследуется возможность состязаний в ЦУ.
Несколько по-другому производится моделирование троич-1 иым алфавитом установочных последовательностей на ЦУ Перед подачей входных сигналов элементы ЦУ могут находить-1 ся в одном из устойчивых состояний, и разработчиков интере-1 сует, в каком состоянии окажется ЦУ при подаче ему на входные узлы того или йного набора входных сигналов.
При моделировании установки ЦУ от неопределенного сос тояния всем сигналам на внутренних и выходных узлах ЦУ присваивается неопределенное значение X, затем в один этап выполняется троичное моделирование при заданном наборе сигналов на входных узлах устройства. Если по окончании мо делирования сигналы на каких7то узлах ЦУ окажутся неопре-1 деленными, то данный набор входных сигналов не является для ЦУ установочным.
Более подробные сведения о работе устройства можно получить при использовании многозначных алфавитов: пятизнач! ного, семизначного и девятизначного. По принципу работы алгоритмы моделирования ЦУ этими алфавитами мало чем от личаются от троичного моделирования, за исключением] таблиц истинности для элементов (см. §7.1). Подробное описание особенностей моделирования ЦУ многозначными алфавитами можно найти в [20]. Так же как и при троичном моде-1 лировании, допущение о произвольности задержек при моде-| лировании многозначными алфавитами может привести к. выявлению маловероятных в реальных схемах случаев статич ческих и динамических рисков сбоя и состязаний сигналов. Д
Таким образом, моделирование ЦУ многозначными алфа-] витами позволяет определить всевозможные, даже маловероят ные в реальных устройствах, риски сбоя и состязания сигналов. Асинхронное моделирование двоичным алфавитом никогда не указывает на ложные состязания и сбои, но позволяет
200
обнаруживать их не во всех случаях. Это привело к разработке методов логического моделирования ЦУ, занимающих промежуточное положение между многозначным моделированием и асинхронным моделированием двоичным алфавитом. Из них методов наибольшую известность получили алгоритм мо-лелирования с нарастающей неопределенностью и алгоритм Л троичного моделирования, в которых принят троичный алфавит моделирования, но возможности изменения задержек GPa-О.и ывания элементов ограничены [20]. Естественно, что устранение недостатков, присущих асинхронным алгоритмам и монтированию с помощью многозначных алфавитов, получается .1.1 счет увеличения затрат машинного времени, и усовершенствованные алгоритмы используют в тех случаях, когда необходимо особо тщательное исследование работы устройства.
§7.5. МОДЕЛИРОВАНИЕ НЕИСПРАВНОСТЕЙ В ЦИФРОВЫХ УСТРОЙСТВАХ И СИНТЕЗ ДИАГНОСТИЧЕСКИХ ТЕСТОВ
В процессе разработки, производства и эксплуатации ЦУ в «пставе различных радиоэлектронных средств возникают задачи проверки правильности функционирования цифровых устройств и отыскания неисправностей в них. Фактически эти вопросы можно свести к решению двух задач: построению набора входных сигналов, проверяющих правильность работы устрой-i nia, и разработке входных наборов, позволяющих локализовать тип и место неисправности в ЦУ. При этом контролирующие и диагностические тесты должны выявлять как устойчивые, так и перемежающиеся неисправности. Разработка i сетов является трудоемкой задачей, решение которой в большинстве случаев возможно лишь с применением двоичного, реже троичного алфавитов.
Поведение неисправного элемента в составе ЦУ можно ими-। кровать, изменив соответствующим образом математическую модель устройства. Логическое уравнение, отражающее правильную работу элемента, заменяется другим, которое отражает поведение элемента в данном неисправном состоянии. Недостатком такого подхода к моделированию неисправностей в ЦУ являются большие затраты машинного времени на модификацию моделей при внесении — исключении неисправностей.
В последнее время чаще отображают неисправность элемента ЦУ логическим сложением или умножением его входных сигналов с соответствующей маской. Например, при моделировании в схеме ИЛИ неисправности типа «постоянная 1 на выходе» достаточно каждый раз при моделировании этого эле-
201
мента в набор его входных сигналов вводить логическую еди ницу сложением набора выходных сигналов с маской, содер жащей символ логической единицы. Используя логическое ум ножение, можно задать неисправность типа «постоянный 0 н; выходе», для чего следует произвести умножение входных сиг налов на маску, содержащую только символы логическою нуля. В этом случае оказываете^ ненужной отдельная програм ма, управляющая моделированием дефектов, а устанавливат| и отменять неисправности можно в любом месте, не затраги вая структуру математической модели ЦУ.
Для комбинационных схем ЦУ существует ряд хорошо раз работанныХ'методов построения контролирующих и диагности ческих тестов, описанных в [20]. По способу формирования и можно разделить на две группы: алгоритмы случайного поис ка и направленные алгоритмы.
В первом случае, задав в ЦУ некоторую неисправность, помощью датчиков случайных чисел формируют наборы вход ных сигналов и для каждого из них анализируются диагности ческие способности. Способность набора входных сигнал выявлять неисправности в ЦУ проверяют сравнением отклика ЦУ при отсутствии неисправностей и при их наличии. Разли чие откликов свидетельствует о возможности диагностирова ния неисправности. После моделирования ЦУ неэффективны! наборы входных сигналов отбрасывают исходя из следующь: правил: набор входных сигналов должен обнаруживать макси мальное число неисправностей, а число наборов, проверяющ работу всех элементов ЦУ, должно быть минимальным.
Направленные алгоритмы, наоборот, формируют набор» входных сигналов, предназначенные для выявления либо опре деленной неисправности, либо проверки данного участка ЦУ По результатам моделирования определяется эффективное той или иной комбинации входных сигналов и решается воп рос о включении ее в набор контролирующих и диагностичев ких тестов. Все направленные алгоритмы связаны с большйм перебором вариантов наборов входных сигналов, поэтому В{ мя поиска оптимального входного набора обычно ограничивав тся программно. Наиболее полно теория построения тест I для комбинационных ЦУ изложена в [20].
Построение тестов для ЦУ с памятью является более слоги ной задачей, чем для комбинационных устройств. Это объяс няется тем, что для проверки ЦУ с памятью обычно необходи мо использовать не один набор входных сигналов, а последи вательность таких наборов, кроме того, дополнительные трудности вносит возможная неоднозначность поведения yci ройства и необходимость учета состязаний сигналов в испрап 202
ним и неисправном устрой-। । нах. По этим причинам п1>|.ем моделирования при подборе тестов для ЦУ с памятью в несколько раз Поныне, чем для комбинационных. Алгоритмы, используемые пни отыскания тестов для 1I.V с памятью, как прави-ю. представляют собой ра-ннггие соответствующих ал-1о|)птмов для комбинационных ЦУ.
В заключение качествен-
Р и с . 7.7. Эффективность алгоритмов
случайного н направленного поиска диагностических тестов
по сравним эффективность алгоритмов случайного и направ-ннного поиска диагностических тестов. При использовании алгоритмов случайного поиска время генерации случайного набора входных сигналов много меньше времени моделирования ЦУ || ui короткое время можно получить тестовые входные наборы,
Проверяющие неисправности, для которых число проверяющих Напоров велико. Затем эффективность работы алгоритма резко
11пыкается, так как остаются неисправности, проверяющиеся м 1лым числом входных наборов, вероятность генерации которых мала. Это иллюстрируется пунктирной кривой на рис. 7.7.
Для направленных алгоритмов время получения каждого
напора входных сигналов 11.1ВИЯ либо значительно больше его. Направленные алгоритмы поиска ипагностических тестов, таким образом, работают медленнее, чем алгоритмы случайного поиска, но обеспечивают большую полноту тестов (сплошная кривая на рис. I /). Наиболее целесооб-р.| ню совместное исполь-ншание алгоритмов: на начальных этапах исполь-|уются алгоритмы случайного поиска, а затем ।в пользуются направленные алгоритмы.
сравнимо с временем моделиро-
Р и с. 7.8. Дешифратор цифровых кодов
203
При производстве сложных ЦУ и БИС обычно разра7 ботанные тесты с помощью систем АСНИ под управлением ЭВМ через интерфейсные устройства подаются на входные узлы ЦУ и используются для поиска и устранения неисправностей. Реакция ЦУ на поданные входные сигналы вводится в ЭВМ, где и производится анализ работы ЦУ сравнением отклика реального устройства с теоретически полученными значениями. Вопросы реализации подобных программно-аппаратных комплексов описаны в [20].
Вопросы и упражнения для самопроверки
1. Составьте таблицы истинности для двухвходовых элементов ЦУ, реализующих логические функции И — НЕ, ИЛИ — НЕ при троичном и пятизначном алфавитах моделирования.
2. Составьте таблицы истинности для двухвходового элемента ЦУ. реализующего функцию сложения по модулю 2 (исключающее ИЛИ), при троичном н пятизначном алфавитах моделирования.
3. Выполните сквозное и событийное моделирование двоичным алфавитом схемы дешифратора кодов, показанной иа рис. 7.8, при смеие входных сигналов С 001III на 101000.
4. Выполните сквозное моделирование троичным алфавитом для задания из п. 3. |
5. Проверьте, является ли набор входных сигналов 101001 установочным для дешифратора из п.З.
Глава 8
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭЛЕКТРОДИНАМИЧЕСКИХ ОБЪЕКТОВ
§8.1. ПРИМЕНЕНИЕ МЕТОДОВ ДЕКОМПОЗИЦИИ ПРИ МОДЕЛИРОВАНИИ СВЧ-УСТРОЙСТВ
Одна из важнейших задач проектирования РЭС — это моделирование в радиоаппаратуре полей, как динамических (электромагнитных, тепловых и др.), так и статических (электрических, м.нпитных, механических и т.д.).
Как и в любой физической системе, между полями сущест-I уют причинно-следственные связи, поэтому здесь также можно говорить о внутренних параметрах модели (конфигурации '.цементов, создающих поля), внешних параметрах — воздейст-ннях (точках, зарядах и пр.), возмущающих поля, и выходных П.1 p.iметрах—реакциях результирующего поля на возмущения.
Законы сохранения энергии и непрерывности применимы к Любому виду поля — электрическому, тепловому, акустическому и т.д., поэтому топологические уравнения для моделирования системы полей будут инвариантны относительно физичес-|к>н природы пол'я.
Как правило, при моделировании электронных схем исполь-•уются фазовые переменные только одного типа и математиче-> к.1я модель получается в виде обыкновенных дифференциальных (либо алгебраических) уравнений (см. гл. 4, 5, 6). Решение их сводится к разделению переменных и определению реакции на заданное воздействие.
При моделировании полей используются фазовые переменные двух типов: скалярные и векторные, так как изменение фа-1НПЫХ переменных по пространству и времени имеет сравнимую величину. Обычно, если внешние воздействия заданы в виде переменных одного типа, фазовые переменные, определяющие реакцию системы, относятся к другому типу, и наоборот.
При моделировании электродинамических объектов (антенн, у< фойств СВЧ и др.) используется система уравнений Максвелла [23]:
205
rot E =
8B dt
- rot /7 = -----+ J.
dt
div D - p.
(8-1)
div В = 0,
D = eE, B = \xH, J-csE, (8.2)
причем уравнения (8.1) — уравнения Максвелла в дифференциальной форме; (8.2) — материальные уравнения, зависящие от свойств среды. _ ____
В соотношениях (8.1), (8.2) E_=E(r,t)— вектор напряженное' ти электрического_ поля, Н = H(r,t)—вектор напряженности магнитного поля, D = D(r,f) — вектор электрической индукции,' В = B(r, t) — вектор магнитной индукции, J = —ректор
плотности тока проводимости; символ радиуса-вектора г означает зависимость от пространственных координат, t — от времени; р — плотность заряда в заданном объеме; виц — соответственно электрическая и магнитная проницаемости среды, с—удельная проводимость среды. Обозначение rot£—ротор вектора напряженности электрического поля:
rot Е =
ех еу ez д/дх о/су д/Дг Ех Еу Ег
(8.3)
— объемная производная вектора Е\ е*,еу,ег —единичш векторы (орты) на координатных, осях, Ех, Е„, jEz — соответствующие составляющие вектора Е Вектор rot И определяет соотношением, аналогичным равенству (8.3). Скаляр divD — ди-t вергенция вектора электрической индукции:
- ДО, dD 8D /олч'1
div о = —-+—- +—- (8.4) 1
Дх су Дг
— дифференциальная операция над компонентами вектора £>, значение divB определяется аналогично (8.4).
К системе уравнений Максвелла (8.1), (8.2) добавляются граничные условия для нормальных и тангенциальных составляющих полей на границе объема, где моделируется поле, I внутри — на поверхностях характерных подобластей.
206
Решение всех этих уравнений с учетом граничных условий (краевая задача математической физики) возможно аналитически только для простейших объемов, когда поверхности раздела совпадают с координатными плоскостями.
Реальные объекты электродинамики достаточно сложны, усложнение их конфигурации ведет к быстрому росту трудоемких вычислительных процессов при решении единой краевой шдачи.
Поэтому наиболее универсальным методом моделирования и анализа СВЧ-устройств является декомпозиционный подход—разбиение сложного устройства на ряд более прос-ii.ix устройств, допускающих независимый анализ и характе-рн |уемых теми или иными матрицами параметров. Эти прос-ii.ie устройства называют базовыми элементами (блоками).
Используется два способа анализа базовых элементов. По первому из них заменяют каждый базовый элемент некоторой схемой замещения, состоящей из сосредоточенных элементов I /, С и /?, а также регулярных отрезков линии передачи, четырехполюсников и многополюсников. Электродинамические расчеты каждого из базовых элементов выполняют заблаговременно, а результаты представляют в виде приближенных формул и справочных таблиц, определяющих связь номиналов I >лементов схемы замещения с геометрическими размерами ба-loiioro элемента, частотой, свойствами среды.
По второму способу СВЧ-устройство разбивается на автономные блоки в виде определенных геометрических конфигураций, допускающих аналитическое или численное решение краевой задачи и определение матриц параметров. Далее, как и по первому способу, составляется модель всего устройства.
В настоящей главе моделирование СВЧ-устройств описывается с точки зрения второго (электродинамического) подхода.
В качестве моделей отдельных блоков СВЧ-устройств обычно используют матрицу рассеяния (см. |л 6). Тогда суммарная матрица рас-11яиия получается в результате объе-иппения матриц рассеяния отдельных fi ПИКОВ.
Пример разбиения полоскового । ВЧ-устройства показан на рис. 8.1 Г’З]; соответствующее ему каскадное । оединение матриц рассеяния блоков—-на рис. 8.2. В частности, для ивух матриц рассеяния блоков А и В
Рис. 8.1. Пример полоскового устройства
207
_Spa
S«P
SB
S₽p S₽r
_S7P Srr
(8.5)
где a, p и у — соответствующие сечения соединения (рис. 8.2), элементы суммарной матрицы рассеяния
FsE S
q ° aa ° ay
АВ~ т
К J
равны
^аа = Saa + SapSpp(l - S ppS pp ) Spa.
saT =sap(i-sX)-1Spr
А В -I (8-6)
Sya ~ STpO -SppSpp) Spa-
4 =S„ +sTPs£5(i-s*s*)-,s(}r.
Далее к блокам А и В необходимо поочередно подсоединить блоки С, D и т.д. В результате получим матрицу рассеяния S устройства (рис. 8.1) в целом.
Возможны также описания каскадного соединения блоков на основе матриц Z и Y [23].
Пример 8.1. Приведем параметры матрицы рассеяния по методу декомпозиции для полоскового чебышевского фильтра (рис. 8.3. а). Выбраны отдельные элементарные блоки в виде разомкнутых шлейфов и каскадно включенных отрезков линии передачи. Элементы матриц рассеяния одного из шлейфов (2-й блок) и линии передачи (3-й блок), а также всего фильтра приведены на рис. 8.3, б, в, г. Видно, что так как элементарные блоки и фильтр в целом не содержат потерь, т2о матрицы рассеяния их унитарны, что приводит к условиям I-Slll +IS12I =1. 4’11—4’12= ±я/2.
Основные проблемы декомпозиции — это оптимальное разбиение на блоки и определение матриц рассеяния блоков, кото-1 рые можно получить из решения краевой задачи для каждого из них. При этом используются два подхода к решению задач. По первому из них выбирается система базисных функций, описывающих электродинамические процессы в блоке. Затем решается задача для базисных функций и составляется модель
208
Г и с. 8.3. Конструкция (а) и элементы матрицы рассеяния отдельных блоков (б. в) и всего полоскового фильтра (г)
блока. В качестве базисных часто используют собственные функции (или моды), например для токов, протекающих по фрагментам базисного элемента при отсутствии возбуждения. Моды пжа ортогональны, поэтому энергия, излучаемая одной из мод, нс зависит от любых других мод, которые могут существовать.
По второму подходу используют функцию Грина, соответствующую полю точечного источника, которая является решением потенциального уравнения
V 2G—k2G = /fi>pS(r-r0), (8-7)
|де G— искомая функция Грина,_ 5(r—го) — дельта-функция шчечного возбуждения в точке го- Тогда напряжение на любом выводе блока Ui, обусловленное током на /-м выводе плотностью Tj, определяется интегралом
M^l^. <М>
209
где Wj — размеры вводов-выводов.
Элементы Z-матрицы вычисляются по аналогичным соотношениям:
ztj = —— f j G(s)ds. (8.9)
По матрице Z можно найти матрицу рассеяния блока.
Как указывалось ранее, решение электродинамических задач традиционно проводят с использованием векторных и скалярных фазовых переменных; при этом искомые поля выражаются через электродинамические скалярный и и векторный /1 потенциалы:
Б . • ЗА
с =-grad и-——,
В = rot А (8.10)
.. -т ди
<11V/4 = —LIE , dt
причем последнее условие (калибровка Лоренца) налагается для упрощения решения, так как переменных больше, чем уравнений. При этом первое и четвертое уравнения Максвелла (8.1) удовлетворяются автоматически, а второе и третье— преобразуются к симметричному виду:
„2 д2и р V IZ-ЦЕ — =-И, а/2 е
У2Л-це^| = -цЛ а/2
(8.И)
где
„2 . д2и д2и д2и 1О,
Viz = divgradw = —- +—- +—- (8.12)
ах2 ду2 dz2
— оператор Лапласа (лапласиан) скалярного потенциала и. 1
Уравнения (8.11) называют уравнениями Даламбера: векторным относительно Л и скалярным относительно и. Так как уравнения Даламбера симметричны, то можно рассмотреть методы решения одного из них, например для скалярного потенциала и. Решение для векторного потенциала А будет_аналогич-но. По найденному распределению потенциалов и и. А в_прост-рапстве можно определить напряженности полей Е и Н.
Решение уравнений должно выполняться с учетом граничных условий. В частности, для идеальной поверхности граничные условия в потенциальных терминах можно записать следующим образом.
Граничные условия первого рода
210
u = F(x, у, z, J, t), (8.13)
i те / —плотность поверхностного тока. Тангенциальная составляющая магнитного поля может иметь разрыв на идеально проводящей поверхности. Размер скачка численно равен плотности поверхностного тока J и может изменяться в пространстве. Тангенциальная составляющая электрического поля равна пулю.
Граничные условия второго рода
— = F(x,y, z,p,t), (8.14)
дп
। те р — поверхностная плотность зарядов. Нормальная составляющая вектора электрической индукции на идеальной поверхности может иметь разрыв, численно равный поверхностной плотности зарядов. Нормальная составляющая магнитного поля равна нулю.
В общем случае уравнения (8.11) представляются в виде
V и = а—- + b— + cu + d. (8.15)
8t2 dt
В зависимости от вида правой части уравнение относительно потенциала будет описывать тот или иной вид волнового процесса:
11азвание процесса Математическая форма Поля и процессы
Лапласа 3 = 0 Статические электрическое, магнитное, акустическое, тепловое и другие поля. Распространение Т-волны в области, свободной от зарядов
11уассона с If —d Электрические поля при наличии зарядов в моделируемой области, тепловые поля с внутренними источниками тепла и т.п.
Диффузии II S ,du о— dt Нестационарные электрические и тепловые поля
Волновое уги = dPu dt2 Распространение электромагнитного, теплового, акустического полей в области, свободной от зарядов
При решении задач электродинамики для базовых блоков используются различные проекционные методы: метод Бубно-U.I — Галеркина, метод частичных областей (Трефтца), метод минимальных автономных блоков, и численные методы: конечных разностей, конечных элементов и др.
Анализ этих методов приведен в следующих параграфах нлстоящей главы.
2Н
§ 8.2. МЕТОДЫ НАХОЖДЕНИЯ СОБСТВЕННЫХ ФУНКЦИЙ БЛОКОВ
Рассмотрим так называемые проекционные методы решения электродинамических задач для отдельных базовых блоков СВЧ-устройства.
В случае применения метода Бубнова — Галеркина, неизвестное решение задачи представляется в виде сумм рядов:
£ = = (8.16)
/=| Г=1
где множества {£,}, {Hi}— системы векторных функций, которые получаются при решении краевой задачи для заданного блока V при отсутствии в нем возбуждений (собственные волны), либо, если это невозможно, для упрощенной по конфигурации идеализированной области Vo, охватывающей исходный блок V (рис. 8.4); коэффициенты a,, bt выполняют роль некоторых проекций в выбранном базисе._
В качестве собственных функций {£,}, {/£} нередко используются системы векторных функций, порождаемых следующей
краевой задачей для Vo:
rot £, + = 0,
dt
< rot Hi - = 0, dt (8.17)
£т = 0 на Si;.
В простейшем случае Vo совпадает с V, но V может быть частью Vo- В ряде важных случаев вместо £т = 0 берутся иные краевые условия.
Значения коэффициентов di, bi в (8.16) определяются_из условия ортогональности решения собственным функциям {£/}, {Hi} в основной области V.
— - 8еЕ -•
f (rot— )EkdV =0,
v _dt (8.18)
j (rot Ё + ^-)HkdV =0, k =1,2.n.
dt
Подставляя £ и H в виде рядов (8.16) в условия ортогона льности (8.18), получаем систему п линейных уравнений относительно а, и bi.
212
Таким образом, система дифференциальных уравнений Максвел-ча сводится к системе линейных уравнений, решение которой является приближенным решением исходной системы (8.1). Полученная система является проекционной моделью физической системы, и разложение (8.16) иллюстрирует проекционный подход к решению >лсктродинамических задач.
Метод Бубнова — Галеркина
Р н с . 8.4. Исходный (а) и идеализированный базисный (б) блоки СВЧ-устройства
весьма универсален и используется в произвольных случаях. I ели же среда обладает какими-либо простыми свойствами, например однородна, то возможны упрощения этого метода.
Если устройство разбивается на сравнительно небольшое число автономных блоков и для каждого из них может быть найдена методом разделения переменных система собственных функций, удовлетворяющих краевой задаче на всей поверхности блока, кроме области соединения с соседним блоком, то иля решения можно использовать метод частичных областей (метод Трефтца) (рис. 8.5). При этом для областей V] и Кг_за-лаются_ системы базисных функций (базисы Трефтца) {£ц} {£д} {Hi2}. И затем минимизируются (ортогонализируются) отклонения на связывающей поверхности S12 (рис. 8.5, а):
J (£«, £/! -7)£*л2 ds =0, s12 -=1
(8.19)
। i.e k= 1, 2, ..., n берется по собственным функциям второго блока.
Комбинированным методом называют методом Трефтца, в котором базисы Трефтца не могут быть получены в замкнутой
шалитической форме, а определяются каким-либо иным мето-|ом, например методом Бубнова — Галеркина. Комбинирован-
ный метод играет большую роль при гких моделей в САПР устройств СВЧ [23].
Для моделирования микрополос-ковых (^ВЧ-устройств (интегральных ( чем СВЧ) особый интерес представляет модифицированный метод Треф-iiia. В этом случае базисы Трефтца не применяются непосредственно, а <лужат для формирования новых ба-И1СОВ, удовлетворяемых только на
построении математиче-
Р и с. 8.5. Идея (а) и применение (б) метода частичных 4 областей
213
Рис. 8.6. Минимальный автономный блок
внутренних и. внешних границах областей. Показано [23], что при этом получаются алгебраические формы, в точности совпадающие с теми, которые возникают при применении метода Бубнова — Галеркина к специальным интервальным адмитанс-ным и импедансным уравнениям электродинамики [23].
Реализация на ЭВМ реше ний электродинамических задач рассмотренными методами может привести к большим затра
там машинного времени. Если сокращать размеры автономных блоков, то число простейших автономных блоков, подлежащих одновременной обработке, с увеличением сложности и размеров СВЧ-устройства быстро перейдет допустимые пределы. Поэтому естественным является иерархический принцип в виде первичной и вторичной композиции. Простейшие блоки, получаемые при вторичной композиции, называют минимальными автономными блоками.
В методе минимальных автономных блоков (метод вторичной декомпозиции) каждый первичный блок разбивается на подблоки таким образом, чтобы их размеры были достаточно малы и можно было считать, что поля на внешних поверхностях каждого подблока однородны и определяются двумя ортогональными составляющими (рис. 8.6); при этом изменение полей происходит только внутри блока. Выделенный минимальный блок является действительно независимым и автономным, он описывается своей матрицей рассеяния, известной заранее, независимо от того, в какой конкретной структуре этот блок выделен.
Каждый минимальный автономный блок имеет выходы на шесть волновых каналов, соединяющих его с соседними блоками. Длина этих каналов нулевая, поэтому поля на границах блоков равны.
Для каждого из минимальных автономных блоков решение может быть получено аналитически. Записав матрицы рассеяния минимальных автономных блоков (они просты, так как содержат только по две компоненты полей) и свернув их, получим матрицу рассеяния всего первичного блока.
214
§8.3. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Метод конечных разностей относится к численным методам решения электродинамических задач, при этом в уравнениях (Н 11) для скалярного или векторного потенциалов использует-<я аппроксимация непрерывных функций левой части уравнений их дискретными образами; область непрерывного изменения аргумента заменяется дискретным множеством точек, напиваемым сеткой (рис. 8.7, а). Тогда все производные в уравнениях (8.11) заменяются их конечно-разностными анало-taMH и исходная задача сводится таким путем к системе линейных алгебраических уравнений относительно потенциалов в у 1лах сетки. Значения потенциалов в узлах сетки и являются искомыми величинами.
Для иллюстрации метода конечных разностей рассмотрим решение уравнения Лапласа в двумерной области с равномерной сеткой
. а и/dx + auldy =0, (8.20)
описывающее статические электрическое или магнитное поля, 1 де и — искомая скалярная потенциальная функция.
Разобьем область решения на ряд прямоугольных областей > шагом h (рис. 8.7, а); тогда для точки поля (х,, //,) определим разностные аналоги частных производных; возможны правый аналог (пр и левый 1лев первой частной производной, например, по х:
u(.xs, yf) - i^Xj h
(821)
Тогда аналог второй
производной в точке (х(-, yt) будет
I а к же строится производная по у:
д2и ~ tz(x„ yt + h)- ‘2u(xh у.) + tz(x;, t/, - Za.)
Sr/2 ~ h2
Xi, yt
(8.23)
215
Рис. 8.7. Метод конечных разностей: а - пятиточечная аппроксимация, б - семиточечиая аппроксимация, в - асимметричная сетка, г - учет криволинейной границы
Подставив (8.22), (8.23) в заданное уравнение (8,20), получаем
В2 и । 82и 8х2 + 8у2
и(х,- + й, у,) + н(х,- - й, t/,) + ы(хъ yt + h) +
У,
+tt(xi,yi -Иу-Щх^у,) = 0. (8.24)
Точно так же можно записать уравнение для любой другой точки пространства; например, для точки (xt- + й, yi)
д2и д2и
дх2 ду2
~ и^х, + 2й, у,) + н(х,-, у,) + и(х,- + й, z/, + й) + X, Ч; Й, у.
+и(Х/ + h,yt -h)~ 4u(x, + й, yt) = 0. (8.25)
Действуя по аналогии, получим такие уравнения для всех точек координатной сетки, связывающие значение потенциальной функции в этих точках. В результате получим систему линейных алгебраических уравнений относительно н(х, у), где х, у берутся в анализируемом пространстве с шагом й. Матрица этой системы будет очень разреженной: для всех внутренних точек — независимо от числа узлов — количество отличных от нуля элементов матрицы в строке равно пяти. Это так называемая пятиточечная аппроксимация частотных производных. Здесь же отметим, что для решения трехмерного уравнения Лапласа необходимы кубическая сетка и семиточечная аппро ксимация частных производных (рис. 8.7, б).
Итак, решая систему уравнений типа (8.24), (8.25) относите-^ льно и(х, у), получим распределение," например, электрического потенциала, а по нему находим остальные характеристики поля.
Сетку пространства не обязательно выбирать прямоуголь ной, возможны другие варианты, которые наилучшим образом моделируют объем: треугольные, косоугольные, круговые, эллиптические и др.
216
Часто возникает необходимость в использовании неравномерных (асимметричных) сеток (рис. 8.7, в). Такие сетки осо-пенно полезны при более тщательном исследовании полей в и сдельных подобластях. В этом случае при выводе аналогов частных производных необходимо использовать члены ряда Гейлора более высокого порядка. Так, для плоского случая (рис. 8.7, в) частные производные равны
~ ^12(пз -Цр)-/г22(ц -Цр) дх ^(hi + hz)
У<
(8.26)
д2и -u^ + h^Us -Up)
dx2 + hz)
Xt, Di
|де «о. «ь «2 — искомые значения потенциала -в узлах сетки (рис. 8.7, в). В выражениях (8.26) отображены члены 3-го порядка. Легко проверить, что при h\ = h% = h первое уравнение (8.26) сводится к так называемой двусторонней производной, а птрое — к формуле (8.22).
Весьма важным моментом при разработке программ для решения конечно-разностных уравнений является учет криволинейной границы, на которой задаются значения потенциала (рис. 8.7, г). Для этого в разностной записи частных производных следует участь вклад узлов, лежащих на границе области.
Так, для точки (х,, yt) (рис. 8.7, г) вторые производные бучу г равны
ua - u(xit y,) u(x,., yi) - u^Xj - h, yt)
д2и дх2
ah______________________й
0,5/г(1 + а)
(8.27)
х„у,
иь - н(х,., У;) и(х,- ,У')- l^X,: У' - й)
д2и ду2
Ыг___________________h
0,5й(1 + Ь)
(8.28)
xt,yi
Подставив (8.27), (8.28) в (8.20), получаем уравнение
217
— + я 2 [»(*< ~h<y,) . “а , Ц> yi - fl) _ дх2 ду2 h2 1 + a tz(l + а) 6(1 + b) 1 + 6
(8.29) а + 6 J
----— и(хпУ,) =0, ab
где иа, иь задаются граничными условиями (обычно либо 0, либо константа). Отметим, что при а = 6=1 уравнение (8.29; переходит в полученное ранее (8.25) для равномерной сетки. , Решение систем линейных уравнений, полученных конечноразностным методом, обычно проводится одним из описанных в §6.6 прямых или итерационных методов с учетом разрежен ности матрицы системы. В качестве прямого используется метод прогонки, являющийся разновидностью метода Гаусса для трех- или пятидиагональных матриц [I].
Разностные схемы — распространенный метод алгоритмиза-1 ции краевых задач. Поскольку аппроксимации подвергается дифференциальный оператор задачи, число узлов оказывается большим и порядки систем весьма велики по- сравнению с проекционными методами. Но значительная разреженность матриц помогает преодолевать эту трудность.
Метод конечно-разностной аппроксимации имеет ясную электрическую аналогию, позволяющую для моделирования полей использовать методы моделирования сложных электри-’ ческих схем. Рассмотрим схемные модели конечно-разностногО подхода.
Так, например, потенциальную функцию на узлах сетки можно отождествить с напряжениями на узлах электрической схемы (рис. 8.8, а).
Сравнив (8.24) с обозначениями на рис. 8.8, а, легко получить ii + (г—13—1'4 = (8.30)
где ii = [u(xi, yi)—u(xi—h, yi)]/Я и т.д.
Элементы Я одинаковы для изотропных сред, в противном случае они различны.
Заменяя резисторными звездами каждую из элементарных областей поля, получим электрическую модель поля в виде сет! ки резисторов. Анализ этой модели можно проводить топологическими методами, описанными в гл. 4, 5.
Граничные условия на поверхности моделируются источни ками напряжения или тока. В случае граничных условий первого рода (8.13) на конечных выводах резисторов электрической модели должен присутствовать источник напряжения (рис. 8.8, б); нулевой потенциал соответствует заземленному выводу.
218
Рис. 8.8. Электрические аналоги конечно-разностиого подхода: и уравнение Лапласа, б-учет граничных условий, о-уравнение Пуассона, г-уравнение диффузии, <?-дуальное уравнение диффузии, е- волновое уравнение
Граничные условия второго рода эквивалентны подключению к выводам источников тока, моделирующих нормальную (оставляющую поля.
Если моделируемое поле имеет внутренние источники энер-1П11 (уравнение Пуассона V2u = -k), то соответствующая схем-п.(я модель конечно-разностной аппроксимации имеет вид, и юбраженный на рис. 8.8, в. Таким образом, в узлах сетки |к чисторов включаются источники тока.
Уравнение диффузии (V2u = b-du/dt) описывает нестационарные процессы в электромагнитных полях и указывает на апериодическое накопление энергии. Выполнив конечно разностную аппроксимацию, такую же, как и для уравнения Лапласа, приходим к эквивалентной электрической схеме (рис. 8.8, г). Здесь в узлах сетки должны включаться конден-|.| горы C=o i^/R, моделирующие накопление энергии. Возможна дуальная электрическая схема для уравнения диффузии, пн* накопление моделиоуется индуктивностями (рис. 8.8, д).
219
Наконец, для волнового
уравнения^
2u = ad2-“7) dt2>
электрическая модель, полученная конечно-разностной аппрокси-1 мацией, имеет вид рис. 8.8, е. Легко показать, что вторая производная по времени в исходном уравнении эквивалентна наличию двух видов накопителей энергии в схеме модели.
Рассмотренный метод конечных разностей и соответствующие ему электрические модели полей находят применение в системах автоматизированного проектирования, так как в рам-1 ках этих методов удобно формализуются сложные границы и неоднородные среды.
Процесс моделирования поля можно представить в неско-1 лько этапов:
— вычисление в узлах координатной сетки искомой потен! циальной функции;
— определение промежуточных значений потенциала между узлами сетки методами интерполяции;
— построение эквипотенциальных линий (поверхностей).
При использовании этого метода в САПР необходимо обращать внимание на точность, сходимость и устойчивость конечно-разностных аппроксимаций.
Основными причинами ошибок являются замена дифферен! циальных уравнений конечно-разностными и отличие в интер! полирующих и исходных функциях ПОЛЯ.
Казалось бы, обе составляющие ошибок могут быг сведены к минимуму с уменьшением шага сетки. Однако при этом появляется неустойчивость решений, так как размер! шага стоит в знаменателе формул аппроксимации и резко возрастает объем вычислений.
Оценим погрешность при достаточно грубом шаге сетки.! Для этого сравним значения потенциала в узловой точке со значением, полученным через потенциал в соседней точке, и его производные. Обратившись снова к рис. 8.7, а, обозначим^ потенциалы в трех соседних точках:
ui = u(xi~h, yi), uq = u(xi, yt), U2 = ufxi + h, yi). (8.311 Тогда, использовав разложения в ряд Тейлора, получаем
, ди h2 д2и "'‘'•-'•ах + 0 /г3 д3» 3! дх3 0 /г4 д4и + 4! дх4 0 0
, ди —11 -4- И - h2 д2и /г3 З3и /г4 54и (8.32Я
дх 2! дх2 1 3! дх3 1 4! дх4
0 0 0 0
220
। io индекс получим
Io означает точку (х/, г/,). Сложив эти
выражения,
<>|куда
a2
ui + «2 = 2«o + Л2— dx2
h4 d4u
+ 12 dx4 0
(8.33)
d2u _ 1
dx2 h‘
h2 d4u
'o
Uj + U2 2Uq —..
»-2 12 дх4 0
(8.34)
О
i равняв пней для для ошибки получим
это выражение с конечно-разностной аппроксима-второй производной d u/dx = \/h (uj + uj—2uq) (8.22),
h2 d4u £ = —
2Л4 дби
.12 дх4 0 6! дх6 О
(8.35)
11 < этого выражения видно, что если производные искомой по-|епциальной функции выше 3-го порядка близки к нулю, то конечно-разностная аппроксимация дает точные результаты и при большом шаге сети h. В противном случае неизбежны ...бки, которые тем выше, чем большее значение имеют высшие производные искомой функции.
При моделировании нестационарных полей возникают проблемы устойчивости и сходимости решения.
Устойчивость решения — это отсутствие накопления ошибки интегрирования при различных шагах интегрирования по времени и пространственным координатам. Устойчивость решения уравнений при использовании конечно-разностных .пшроксимаций тесно связана с устойчивостью электрических моделей полей (рис. 8.8). Если электрическая модель устойчива, то устойчиво и решение соответствующей полевой задачи К примеру, решение уравнения Лапласа всегда устойчиво, |.ш как его электрическая модель состоит из пассивных резисторов.
Исследование электрической модели на устойчивость возможно различными методами, и это, как правило, не приво-III г к вычислительным трудностям.
Проблема сходимости приближенного решения при конечно разностной аппроксимации к точному определяется устойчивостью решения. Если конечно-разностная аппроксимация у< гойчива, то она и сходится к точному решению. Устойчивость предполагает сходимость, но не наоборот. „
221
Сходящееся решение всегда может обеспечить получение результата с необходимой точностью.
Таким образом, алгоритм моделирования полей методом конечных разностей может быть представлен следующим об-| разом.
Алгоритм 8.1.
Шаг I. Ввод геометрии устройства, граничных условий.
Шаг 2. Выбор вида сетки и шага, построение сетки.
Шаг 3. Выделение внутренних и граничных узлов.
Шаг 4. Формирование электрической модели.
Шаг 5. Проверка устойчивости модели: если модель устойчива, перейти к следующему шагу, в противном случае вернуться к шагу 2.
Шаг 6. Формирование матрицы числовых коэффициентов и вектора граничных условий.
Шаг 7. Решение системы линейных уравнений.
Шаг 8. Поверка сходимости и точности решения, если точность удовлетворительна, перейти к следующему шагу, в противном случае вернуться к шагу 2.
Шаг 9. Проведение интерполяции значений поля между узлами.
Шаг 10. Расчет эквипотенциалов поля.
Описанный алгоритм может быть реализован в САПР электродинамических объектов.
§8.4. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
В процессе дискретизации решения уравнений поля можно] использовать не только сетку из точек, но и некоторые элемен-1 ты конечных размеров.
В последние годы разработан метод конечных элементов] называемый также проекционно-сеточным, под которым понимают процесс Бубнова — Галеркина для некоторой краевой задачи, в котором базис формируется из функций, определена ных не во всей области задачи, а на специально построение'' системе носителей в ней. В качестве носителей могут быть треугольные или криволинейные образы, что существенно рам ширяет класс решаемых задач. Искомые поля также представляют^ в виде сумм (проекций) (8.16), однако базисные функции {Е,} {Hj} отличны от нуля только на своих носителях. Неизвестные коэффициенты (проекции) определяются методом Бубнова — Галеркина [23].
Таким образом, метод конечных элементов является комбинацией как проекционных, так и конечно-разностных методов моделирования электродинамических объектов.
222
Рис. 8.9. Метод конечных элементов: а - разбиение, б - один элемент, в - объединение элементов
Рассмотрим подробнее метод конечных элементов на при-f"‘pc двумерного уравнения Лапласа V2u = О (8.20) с граничным условием 1-го рода и = ио на So. Эта задача известна как и чача Дирихле. Обычно метод конечных элементов комбинируется с некоторой вариационной задачей в пределах моделируемой области.
11звестно, что распределение потенциала в некоторой обла-i ।и в стационарном состоянии соответствует минимуму потенциальной энергии поля. Решим уравнение Лапласа при усло-iiiin минимизации энергии поля в моделируемой области:
W(u) = - J|Vt<|2ds min, (8.36)
,, - ди - ди „
। не vu^L-вх — + еу--------оператор Гамильтона в плоском
ду
пространстве, Е —вектор электрического поля в области, s поверхность моделируемой области.
аким образом, поиск и(х,у) можно сформулировать в виде вариационной задачи: найти функцию и(х, у), удовлетворяющую уравнению Лапласа, граничным условиям и =ио на So и ыкую, что W(u) минимальна.
Разобьем моделируемую область на треугольные элементы, л<н гаточно малые, чтобы считать, что внутри треугольника по-к'пциал изменяется линейно от координат (рис. 8.9, а)
и = а + Ьх + су. (8.37)
Следовательно, истинная гладкая поверхность фактического распределения потенциала в плоскости (х, у) заменяется мно-нн ранной поверхностью, кусочно-планарно аппроксимирующей ш гпнное решение. Чтобы не было разрывов на стыке элемен-||>н, необходимо однозначно задать потенциалы в вершинах со-'Г'ших элементов. Тогда распределение потенциала вдоль лю-Гюп стороны элемента в соответствии с (8.37) будет определять-। и линейной интерполяцией между двумя вершинами.
223
Коэффициенты а, b, с в интерполирующей плоскости для и могут быть найдены по заданным потенциалам в вершинах элементов и\, «2 и из (рис. 8.9, б):
Подставив решение из (8.38) в (8.37), получаем уравнение для конечного элемента интерполирующей планарной поверх* ности:
(8.39'
можно записать в виде
В скалярном виде это равенство
и - ы,а i (х> У) - и}а 1 (х> У) + и2а 2 U> У) + иза з (х> У)> ' (‘
где
«1U. У) =^[(х2Уз ~ хзУг) + (Уг - Уз)х + (*з - х2)у1 /1
arfx, У) = -7 [U3«/i - xiУз) + (Уз ~ У0х + Ui - хз)У)’ /1
«з(^, У) = 4 [U,у2 - х2у}) + (г/, - уг)х + (х2 - х,)у\, /1
1 xi У,
A = 1 x2 У2 — определитель матрицы, равный удвоенной
1 -^з Уз
площади конечного элемента (рис. 8.9, б). Можно отметин, что формулы для a,, i= I, 2, 3, получаются с помощью цикли ческой перестановки индексов.
Подставив выражение (8.40) в (8.36), получим выражения для энергии одного конечного элемента через потенциалы узловых точках:
W(u) ~ | f |Vu|2ds = | f £|u,.Va,.(x, z/)|2ds =
~>A ‘-'A
(8.41)
= | Ё £“/«/ f lVa < U.«/)] [Va ;. (x, t/)]ds = U/U/S,, ,
/=1 /=! 5 i=\ /=1
224
। !< обозначено
St, = J [Va f (x, t/)] [Va(x, #)]ds, 5л
(8.42)
- площадь плоского конечного элемента. В матричной формц выражение (8.41) имеет вид
№(u) = lt7T[S,]t7, (8.43)
। к элементы S(/ получаются циклической перестановкой
мп к-ксов, в частности
512 = \(У2 - «/з)(«/з “«/>) + (*з - х2)(х, - *з)] и Т-Д-
л/х
11олная энергия совокупности всех конечных элементов p.iKiia сумме энергий каждого элемента:
(8-44)
При объединении Двух соседних элементов (рис. 8.9, в) из Li ловия непрерывности потенциалов (щ = uq, «2 = щ) можно ыписать связь между разделенными и объединенными элеме-III. 1ми:
’1 0 0 0'
и2 0 10 0 U,
и3 и4 = 0 0 10 0 10 0 «2 «3 = с «2 «3 (8.45)
«5 0 0 0 1 _и4_ _и4_
и6_ 1 0 0 0
। . С — матрица связи элементов, [uj и2 из urf — вектор потенциалов для объединенного конечного элемента.
Энергия для двух раздельных элементов (рис. 8.9, в) опре-
л< ляется выражением
и, и2 «з н4
U5
Уб
(8.46)
по ставив в которое соотношение (8.44), получаем
\л।оматизация проектирования
[•а тоэлектронных средств
225
W = - [u, u2 u3 u4 ] C
S|-3 0
Ul u2
u3 «4
= 2 [«I «2 «3 UJS
«i
U2
«3
«4.
. (8.47)
Аналогично можно присоединить к двум конечным элемсн там третий, четвертый и тд.
Чтобы минимизировать запасенную в конечных элемента' энергию, необходимо решить систему уравнений:
— =0, k = 1,2,...,н, (8.48)1
где п — число внутренних вершин объединенных конечных эле ментов. Так как W зависит от и* квадратично, то систем| уравнений (8.48) линейна и имеет единственное решение, со<и
ветствующее минимуму энергии при заданных граничных ш тенциалах.
Проведем учет граничных условий: для, этого запише! вектор U в блочном виде: U = [t/Bt/3f, где UB — варьируемы потенциалы внутренних узлов, U3 — заданные потенциал) граничных узлов. Тогда матрицу S надо представить тоже блочном виде:
блоки ее соответствуют только внутренним (S4B), только гр ничным (S33) узлам или связям внутренних и граничных узло| (SB3 и S3B). Тогда система уравнений (8.48) примет вид
Раскрыв произведение и выполнив дифференцирование, получи!
[SBDSJ
U«
й3
-0 или SBBt/B = -SB3Z73.
Матрица SBB—квадратная и неособенная, поэтому решепИ для потенциалов внутренних узлов определяется выражением ив = -S;bSB3(7b = -S'KBSB3U3. (8.52
Это решение единственное и точно определено везде, в toi числе и на границах области, где задан потенциал.
22(5
К сетке из треугольников не предъявляется требования ।''<>метрической равномерности и регулярности, поэтому раз-iiiH-nne обычно производится произвольно, с тем чтобы наи-лучшим образом вписаться в заданные границы моделируемой области. Единственным требованием к сетке является сопи. |дение смежных сторон и вершин.
В то же время в методе конечно-разностной аппроксимации! число узлов обычно больше, порядок линейных систем иычительно выше, а к самой сетке предъявляется требование |Ч । улярности.
Рассмотрим применение метода конечных элементов для решения уравнения Пуассона:
V2u = p/е. (8.53)
||.ля двумерной задачи в этом случае минимизируемый функционал будет иметь вид
№(u) = -f|Vu|2 ds-lj up ds—> min. (8.54)
2 s e s
Плотность заряда в моделируемой области задана и ее Пылогично потенциалу можно аппроксимировать по верши-п. 1м треугольного конечного элемента:
Р(*> У) = (8.55)
/=|
I if р,(х. у) — коэффициенты, характеризующие плотности зари ia в вершинах элемента. Тогда второй интеграл в выражении (8.53) примет вид
J up ds = JaiPyds. (8.56)
,5 Л /=' 5
Обозначив Т//= j a,P; ds, образуем квадратную матрицу Т третьего S
порядка; тогда выражение (8.56) можно привести к виду
Pi
| и р ds = th Тр = [uj u2 u3] T p2 .
О
Рз
(8.57)
Подобно уравнению Лапласа для объединения конечных элементов, можно записать
227
s s
s s
° ЗВ ° 33
ив
й3
- 1 [t/в t/з] Е
т
ив
т
L ЗВ
Т„з Рв
Тзз J _р3
—> min|8.58i
Условие минимизации энергии
^=0, k = l, 2,...,«,
(8.59)'
где п — число внутренних узлов.
После дифференцирования
имеем
1 Твв 4тзв
Твз Рв
Тзз. рз
= 0.
(8.60)
Отсюда можно найти потенциалы внутренних узлов, соответст вующие минимуму энергии в моделируемой области, грани» ным условиям и заданному возбуждению:
и. =--s;l £
т
вв
т
. ЗВ
Т„з
Таз JLPa J
Рв
-S 'S и,.
вв вз
(8.61)
Алгоритм 8.2. Метод конечных элементов
Шаг 1. Ввод исходных данных.
Шаг 2. Построение сетки из конечных элементов.
Шаг 3. Формирование матрицы S.
Шаг 4. Нумерация узлов и потенциалов.
Шаг 5. Разбиение матрицы S на блоки, соответствующие внутренним
граничным узлам.
Шаг 6. Определение внутренних потенциалов.
Шаг 7. Определение напряженности поля.
Шаг 8. Построение эквипотенциален.
При реализации на ЭВМ для удобства работы алгорит!.. внутренние узлы, потенциалы в которых являются варьируй мыми, нумеруются первыми, а узлы с заданными потенциала ми — последними.
§8.5. МОДЕЛИРОВАНИЕ ИЗЛУЧАЮЩИХ УСТРОЙСТВ
В предыдущих параграфах настоящей главы изложены во просы моделирования электродинамических устройств закр» того типа. Рассмотрим кратко этапы моделирования и авто матизации проектирования антенных устройств. Современный проблемам антенной техники посвящено значительней количество работ. Методики автоматизированного проектири
228
П.И111Я антенн и СВЧ-устройств, а также примеры проектиро-И.Н1НЯ широкого класса излучающих и распределительных уст-|ц>1итв приведены в учебном пособии [21].
При автоматизированном проектировании любой антенной »in гемы приходится решать внешнюю и внутреннюю задачи.
Первая формулируется как определение геометрии антенной гпсгемы и оптимального амплитудно-фазового распределения (Л'1>Р) поля (тока) на элементах антенны, обеспечивающих пцанные требования к характеристикам излучения антенной гпсгемы. К таким задачам относятся задачи проектирования и игельных излучателей и антенных решеток по заданным , пебованиям как к амплитудной диаграмме направленности 1'UI), так и амплитудно-фазовой ДН или к интегральным параметрам ДН (коэффициент направленного действия, mi ‘ффициент рассеяния и т.п.). При решении внешней задачи чисто необходимо оптимизировать также и геометрию излучающей системы.
Внутренняя задача сводится к проектированию распреде-||н‘льной системы, реализующей АФР, найденное при реше-tiiiiii внешней задачи. Подобная проблема тесным образом примыкает к задачам проектирования активных и пассивных упройств, моделированию которых посвящены гл. 4, 5, 6-нас-рющего пособия. При решении внутренней задачи необходимо учитывать специфику построения излучающей системы в виде фа шрованных или многолучевых антенных решеток с учетом п i.iимовлияния между излучателями, их конструктивных осо-Ги ипостей и др.
Для решения внешней задачи необходимо выполнить этап мл тематического моделирования антенной системы.
Решая уравнения Максвелла (8.II1) для случая однородной и изотропной среды с временной зависимостью возбуждающих шектрических токов в виде ехр(/со/), для векторного пшенциала электромагнитного поля получаем
- 1г-
А(х, у, z) = — ( /(%', у', z')-d V, (8.62)
4л£ ' г
। не г = [(х—х0)2 + (у—уо)2 + (z—z0)2]1/2 — расстояние между ..ками наблюдения и интегрирования, р = 2л/Х; V — объем, ыпимаемый токами излучающей системы.
Выражение (8.62) представляет собой строгое решение не-ол породных уравнений (8.11) и является единственным, поскольку удовлетворяет условию излучения на бесконечности и имеет всюду конечное значение.
229
Подставляя решения типа (8.62) в выражения (8Л0), полу чаем векторные распределения полей Е(х, у, z) и Н(х, у, г) для произвольной точки пространства Зная распределения полей, можно в принципе найти любые характеристики излу чения антенной системы. Однако из-за математических слож ностей по этим точным распределениям не удается получит простых замкнутых выражений даже для сравнительно прос
тых излучающих систем. Поэтому для упрощения решения этой задачи разбивают все пространство излучения на даль нюю, промежуточную и ближнюю области.
Решение, как правило, выполняют в сферической системе координат, поэтому области дальнего поля (часто называемой дальней зоной или областью Фраунгофера) предполагают R»R', где R — расстояние до точки наблюдения, R’ — д< точки интегрирования излучающей системы. Тогда выражен.., (8.62) упрощается и принимает вид
A„(R, 0, <р) = ----( /(%', у', z') е~/|Wcns“dV, (8.63)
4tiR I
где а — угол между векторами R и R ; 0 и ср — сферически) координаты. Подставляя выражение (8.63) в (8.10) и отбрасы вая члены с множителями 1/R2 и 1//?3, получаем расчетам) соотношения для составляющих полей Eq, Ev, Hq, в дальней зоне. Анализ этих соотношений показывает, что в дальней зоне:
— поле имеет поперечный характер, т.е. составляющие Е1 ///? векторов полей в направлении распространения волны от сутствуют;
— поле в окрестности точки наблюдения носит характ I плоской электромагнитной волны, т.е. компоненты Eq и I также £<, и Hq находятся в фазе и их отношение равно харйг теристическому сопротивлению среды;
— зависимость поля от расстояния R имеет вид расходи шейся сферической волны exp(-j$R)/R. _
Угловое распределение составляющих вектора Е в далыц‘1 зоне не зависит от расстояния R и характеризуется функциями W°|EE°T г = I ^Omax (®l*fPl )1
------------------, (8 64
.ртах (^2> Ф2 )1
Oniax(®l| Ф1)1
где 0|, ф1, 02, ф2 — направления максимального излучения дл» соответствующих компонентов. Функции Ее(0, <р) и Еф(0, ср) и] зывают нормированными диаграммами направленности ш полю для соответствующих составляющих.
230
Поток мощности излучения в дальней зоне всегда направлен радиально. Плотность потока мощности равна радиальной «оставляющей вектора Пойнтинга: .
П /? = 0,5/?е(£еН*ф—£<рЯ*е) = (|£е|2 + \e/)/(2Zc) (8.65) l ie Zc — характеристическое сопротивление среды. Мнимая ч.кть вектора Поинтинга в дальней зоне равна нулю. Угловая ыкисимость
F\e, ф) = П/?(0, ф)/П/?тах(0О, фо), (8.66)
ric П/?тах — модуль вектора Пойнтинга в направлении миксимального излучения 0о, фо, называется нормированной диаграммой направленности по мощности.
Показано, что граница дальней зоны определяется неравенством R>2D2/X , где D — наибольший размер излучающей ип-темы. При R <20/7. дальняя зона плавно переходит в промежуточную область, иногда называемую областью Френеля. В этой области зависимость поля от расстояния уже нс имеет характера сферической волны ехр(-/р/?)/R, так как р.п-стояние R дополнительно входит в показатель степени выражения (8.62). Поэтому в промежуточной области на монотонное убывание поля по закону 1/R накладывается и» коллирующее затухающее колебание. Угловое распре-игление составляющих векторов поля зависит от расстояния R г.е. диаграммы направленности излучающей системы в пой области искажаются тем сильнее, чем меньше R. Размеры промежуточной области определяются неравенствами
D D(dV3 п 2D2 4 2(2) X
На расстояниях, меньших нижней границы промежуточной области, располагается ближняя зона излучающей системы. В пой области электромагнитное поле имеет сложный характер и при его моделировании необходимо пользоваться строгим выражением (8.62). В общем случае в ближней зоне присутствуют все компоненты поля, зависимость поля от расстояния R носит нерегулярный характер, вектор Пойнтинга 11.ПЮВИТСЯ комплексным и гщ направлению может не ытпадать с радиусом-вектором R.
В ближней зоне излучающей системы сосредоточивается пычительная реактивная часть электромагнитной энергии, что ыгрудняет широкополосное согласование антенны с фидерным трактом [12].
После моделирования электромагнитного поля излучающей «пггемы можно определить различные вторичные параметры П1лучения — КНД, ширину луча, уровень боковых лепестков и ip . а также входной импеданс антенной системы. По послед
231
нему параметру антенная система стыкуется с остальными базисными элементами комплекса радиоэлектронных средств, определяющими его эксплуатационные свойства (см. §6.3, 6.Е настоящего пособия).
При моделировании излучающих устройств на ЭВМ снача ла составляется формализованное задание, выбирается физй' ческая модель устройства, затем строится математическая м,1 дель, адекватная принятой физической модели, и, наконец, реализуется параметрический синтез устройства [21] .
Часто вопросы математического моделирования излучающих устройств бывают тесно связаны с приемами конструиро! вания РЭС. Так, при проектировании модульных ФАР СВЧ диапазона необходимо уже при системном и функциональном проектировании ФАР в целом, а также ее основных частей (полотна модулей ФАР, излучателей, устройств СВЧ-тракта т.д ) решать конструкторские задачи, в первую очередь опр* делять топологию проектируемых объектов. При изменении частотного диапазона должна существенно меняться и тополи гия устройств. Поэтому собственно САПР ФАР должна быт. интегрированной системой с собственной системой управле-ния. Практика показывает, что на стыках проектных рабо1 различных уровней проектирования потеря времени не мены ше, чем на стыке проектирования и изготовления.
В дальнейшие этапы проектирования, как правило, должн| входить макетная отработка модулей ФАР с автоматизировав ной передачей данных в интегрированную САПР. Эксперимей тально полученные характеристики модуля могут быть входными данными математической модели ФАР в целом, на базе ко-торой решаются основные задачи системного проектировани”
Вопросы и упражнения для самопроверки
1. Приведите примеры фазовых переменных при решении задач моделиро ния электродинамических объектов.
2. Объясните принцип декомпозиции при анализе СВЧ-устройств.
3. Установите связь между элементами матрицы рассеяния реактивия четырехполюсников по условиям унитарности S-матрицы.
4. Выведите и объясните структуру дифференциальных уравнений относится но векторного и скалярного потенциала для решения задач моделирования поЛя различного типа.
5. Приведите основные методы определения собственных функций блоков СРМ устройств; объясните разницу между ними.
6. Поясните применение метода конечных разностей для моделирования пл ких и трехмерных полей.
7. Приведите основные схемные модели при конечно-разностном подходе к ай! лизу полей различного типа.
8. Приведите основные соотношения и объясните алгоритм применения метид( конечных элементов для моделирования полей.
9. Поясните алгоритмы решения внешней и внутренней задачи при модели вании излучающих устройств.
232
Глава 9
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАДИОСИСТЕМ
§9.1. ВВЕДЕНИЕ В МОДЕЛИРОВАНИЕ СЛОЖНЫХ ТЕХНИЧЕСКИХ СИСТЕМ
В соответствии с определением (см. гл. 4) система предста-Вюпют собой совокупность находящихся в определенной взаи-I Мхснязи компонентов, которые принадлежат части реального iK ipa. являющейся объектом исследования. Это определение Lсражает две содержательные стороны понятия системы — на-лпчие множества компонентов и определенных взаимосвязей I М< иду ними, за счет которых система имеет новые свойства, I ннорых может и не быть у входящих в нее компонентов. I ' нойства системы в равной степени определяются как характеристиками составляющих ее компонентов, так'и характеристиками взаимосвязей между ними.
Можно показать [11], что с увеличением числа компонентов li in гемы количество всевозможных парных связей между ними I р.п гот асимптотически как квадрат их числа. Таким образом, I и .1 же если влияние на работу системы каждой взаимосвязи |Су.'|.ет невелико по сравнению с влиянием компонентов, коли-I *1«ч гненное преобладание связей приведет к существенному, а I 1лч.1стую и преобладающему их влиянию на функционирова-I )ш<- системы. Отсюда следует, что систему нельзя рассматри-ln.iii.. а значит и моделировать, диакоптически, т.е. -по отдель-I iii.iM образующим ее компонентам, так как при этом могут по-। риться существенные свойства системы, определяемые ее I и инмосвязями. Это обстоятельство является одним из отличи-I и льных свойств системных моделей и объясняет трудности, I ш> шикающие при моделировании больших систем по сравне-I пик) с моделированием отдельных компонентов.
Цля формального описания факта наличия у системы как I см и кого целого новых свойств, отсутствующих у составляющих ci компонентов, обычно используется определитель ковариа-I ннопной матрицы R параметров компонентрв системы или
233
сигналов на их выходах. Величина определителя detR зависит от количества элементов в матрице R и от значений Гу коэффициентов ковариации между выходными парамет- рами компонентов системы. Чтобы проиллюстрировать вышесказанное, рассмотрим удобный для вычислений случай равенства всех коэффициентов ковариации, образующих ковариационную матрицу R. Значения определителя detR в зависимости от числа компонентов системы п и величин Гц приведены в табл. 9.1.
Таблица 9.1
п detR
Г,1
0 0,1 0,5 1,0
2 1 1 0,25 0
4 1 0.8 0.3 0
8 1 0,63 0,036 0
12 1 0,5 0,004 0
Как видно из табл. 9.1, по мере увеличения взаимно! ковариации между выходными сигналами компонентой, составляющих систему, величина определителя ковариацион! ной матрицы detR уменьшается от единицы (отсутствие связей между компонентами Ч/= 9) до нуля в случае макси мально возможной связи компонентов rf7=l. Из таблицы также видно, что detR убывает и по мере увеличения чис компонентов в системе, даже при сравнительно слабых связях между ними. В первом случае систему часто называет сложной, во второй — большой. Совокупность компонента и будет проявлять себя как система при условии detR« 1, и 1 этом случае ее нельзя рассматривать диакоптическч независимо от того, чем обеспечивается малая величиня определителя detR — большим числом компонентов или сильными связями между ними.
Кроме большой размерности и сложности отметим еще ряд характерных особенностей больших и сложных систем: слабую структурированность теоретических и фактических знаний 4 системе и ее компонентах, физическую разнородност подсистем и компонентов,’ образующих систему, случайность и неопределенность факторов, действующих в систем», многокритериальность оценок качества функционирований системы.
Радиосистемы относятся к специфичному классу большци систем, что объясняется их информационной сущностью, статистическим характером связей между компонентами; эт(1
234
(н.п гродействующие системы, в которых имеют место быстрые преобразования радиосигналов наряду со сравнительно медленно протекающими информационными * процессами; это । иск мы, находящиеся под постоянными случайными воздействиями.
11митационное моделирование на ЭВМ является одним из । ажнейших инструментов изучения системы, позволяющим во цюгом преодолеть трудности, возникающие при их проекгиро-ь ищи из-за перечисленных выше особенностей больших и сложных систем. Вычислительные эксперименты с математической моделью системы позволяют сделать выводы о поведении |м- гемы в различных ситуациях без ее построения, если это проектируемая система; без вмешательства в ее работу, если мю действующая система, экспериментирование с которой рого и небезопасно; без разрушения системы, если цель |п:т юдования состоит в определении предельных условий ее Ьнооты. Процесс моделирования системы включает построение (модели, организацию вычислительных экспериментов с ней, |н апизацию программного обеспечения моделирования.
Процесс построения модели состоит из ряда этапов, из которых можно выделить два: построение формальной аналити-'рч кой или алгоритмической модели на основе знаний о моде-мруемой системе и формирование машинной модели по построенной формальной. Второй этап построения модели являет- и предметом рассмотрения специалистов по программированию и здесь рассматриваться не будет. Построение же формами. пой модели системы производится ее разработчиком и пред-। ынляет собой сложную научную задачу. В последнее время чшпе используются алгоритмические формальные модели бо-bli.iniix систем на основе специальных средств автоматизации h u< гемотехнического моделирования, в состав которых входят: MU.IK описания моделируемых систем; средства обработки язы-। иных конструкций языка описания (компилятор, транслятор иди интерпретатор); управляющая программа моделирования, ш уществляющая имитацию моделирования системы во времени набор стандартных программных средств, используемых 1'1я организации вычислительных экспериментов с моделью. .1 окне специализированные средства моделирования обладают п< |>ед моделями, реализованными с помощью универсальных Hii.iKOB программирования, рядом преимуществ: меньшими заир нами на программирование, возможностью использовать Iмилели стандартных компонентов, автоматическим формированием данных, соответствующих принятому способу моделирования системы, и удобством их накопления и представления.
•in средства будут рассмотрены в последующих параграфах н.п гоящей главы.
235
Вычислительные эксперименты с любой системой вообще и радиотехнической в частности проводятся для получения информации о ее поведении, а эта информация довольно многообразна и характеризует различные стороны функционирования радиосистемы. На основании этой информации вычисляются показатели эффективности для системы, что представляет собой сложную задачу, которая решается пи этапе организации вычислительных экспериментов и требует привлечения теории планирования.эксперимента, статистики к других математических методов. В связи с тем что радиосио темы работают в условиях действия случайных факторон значения многих функционалов, характеризующих эффектиН' ность функционирования системы, могут оказаться случай ными величинами. Поэтому при выборе показателей эффек-тивности обычно пользуются средними значениями соответсТ вующих функционалов, либо вероятностями совершения неко-торых случайных событий, либо строятся совокупности функционалов, характеризующие свойства системы интегралы»: такие, как помехозащищенность, надежность и т.п.
В качестве примера рассмотрим возможную оценк помехозащищенности радиосистемы. Пусть функционал А’ i=l, .... п, является одним из показателей эффективност сложной системы и его значение F’t, найденное в результат моделирования, соответствует функционированию системы условиях действия помех с заданными характеристиками, значение г также найденное в результате моделирование относится к нормальным условиям функционированИ системы, когда помехи отсутствуют. Тогда в качестй показателя помехозащищенности моделируемой системы можно выбрать взвешенную сумму:
где у,—коэффициенты, характеризующие важность того ил иного показателя эффективности, определяемы разработчиком. Величина а будет показывать, наскольк изменяется эффективность системы под влиянием помех заданными характеристиками. В некоторых случаях I качестве могут выбираться показатели, ,соответствующи идеальному варианту системы, который определяется ограни чениями на физическую реализуемость системы или отдельны ее компонентов и не может быть реализован на практик Подробно вопросы выбора показателей эффективности систсч при их моделировании и организации вычислительных эксп( риментов с моделями рассматриваются в [24].
236
Проблемы организации программного обеспечения модели-....алия заключаются в необходимости учета множества раз-। |н>образных и противоречивых требований к программному i (>f>< течению, таких, как структурированность программ, просопи, совместимость с другими видами программного обеспе-||Ц11ия, возможность генерирования случайных чисел и процес-11<>н и т.п. Перечисленные проблемы характерны не только I применительно к моделированию систем, но и к программно-I гу обеспечению любого назначения, и для их изучения можно |(П>р атиться, например, к [2].
(2 точки зрения целевого назначения и описательных свойств I р । (личные уровни моделирования систем имеют свои характерные Особенности. Можно выделить ряд характерных уровней моделирования радиосистем, каждому из которых соответствуют I < ион формальные модели системы. Отметим прежде всего 11 к-дующие: модели потенциальной предельной достижимости, 11 нс гемотехнические модели, функциональные модели.
Модели потенциальной предельной достижимости характеризуют потенциальные возможности моделируемой радиоси-11 и мы в целом или отдельных ее подсистем и компонентов на I огниве изучения фундаментальных достижений науки в дан-1>। области.
Системотехнические или имитационные модели описы-I ii.iior функционирование системы в кибернетических терминах, 11 помощью этих моделей выполняется имитационное моделй-Iронание радиосистем. Термин «имитационное моделирование» | и тачает, что при системотехнических моделях результат моде-I пирования нельзя вычислить или предсказать заранее и необ-|моапм вычислительный эксперимент на модели, чтобы иссле-| (опять поведение проектируемой, системы.
Имитационные модели в свою очередь можно разделить на |лпскретно и непрерывно изменяющиеся. Эти определения, ра-I |умеется, относятся к поведению зависимых переменных модели. а не к самой системе. При дискретной имитации зависи-I мыс переменные изменяются дискретно в определенные мо-1м'-пты имитационного времени, называемые моментами со-I ш-ршения событий в системе. Время в такой имитационной I модели может изменяться непрерывно или дискретно в зави-|(нмости от того, могут ли дискретные изменения зависимых I ш-ременных происходить в любые моменты времени или толь-I ко в моменты совершения событий. Пример изменения зависи-I mi.ix переменных в дискретной имитационной модели показан и.। рис. 9.1, а. Модели дискретных систем обычно являются I алгоритмическими.
237
Рис. 9. Г Графическое представление отклика в имитационных моделях
При непрерывной имитационной модели зависимые пере' менные изменяются непрерывно в течение имитационного вре' мени. Сама непрерывная имитационная модель системы МО1 жет быть непрерывной во времени либо дискретной в зависи' мости от того, доступны ли значения зависимых переменных в любой момент времени или только в определенные моменты имитационного времени. Примеры изменения зависимых переменных при непрерывной имитации показаны на рис. 9.1, б, в, При непрерывной имйтации обычно используются аналитические модели радиосистем в виде систем , или нелинейных уравнений. Описанные в гл шения таких систем при большом числе переменных привели . к тому, что при моделировании радиосистем непрерывная имитация, как правило, не используется.
В ряде случаев применяются комбинированные модели, при которых зависимые переменные могут изменяться дискретно, непрерывно или непрерывно с наложенными дискретными скачками. Это позволяет организовать взаимодействие между дискретно и непрерывно изменяющимися переменными, с ОД' ной стороны, и понизить порядок решаемой системы дифференциальных уравнений — с другой, за счет дискретной ими1 тации части зависимых переменных. В дальнейшем будем ра-осматривать только дискретные или комбинированные матр матические модели, как наиболее распространенные и имею-щие наибольшую алгоритмическую поддержку.
В основу построения функциональных моделей радиосистСМ положены макромодели отдельных компонентов и подсистем, При классификации функциональных моделей радиосистем обычно учитывают способы получения и свойства макромоде-лей отдельных компонентов, а также способы описания сигналов и помех в системе. Подобные системные модели имею! большую конкретность по сравнению с имитационными и благодаря этому позволяют уточнять характеристики отдельных компонентов системы в процессе проектирования, а также изучать их влияние на работу системы в целом. Однако ош требуют больших затрат на программирование и организации вычислительных экспериментов.
дифференциальных 'л. 5 трудности ре-
238
V’2. МОДЕЛИ ПОТЕНЦИАЛЬНОЙ ПРЕДЕЛЬНОЙ ДОСТИЖИМОСТИ
Потенциальная предельная достижимость в задачах моделирования имеет два аспекта. Первый из них заключается в гом, что использование математических моделей на всех уровнях моделирования для отражения процессов, протекающих в реальных радиосистемах, предполагает, что модельные представления не противоречат законам природы вообще и конкретным законам, присущим моделируемым компонентам и системам, в частности. Выполнение этого требования обязательно и может быть достигнуто различными путями: либо в самих моделях должна быть предусмотрена проверка соответствия результатов моделирования физическим законам, либо на параметры модели накладываются ограничения, автоматически обеспечивающие выполнение предельных фундаментальных законов.
В то же время при проектировании больших радиосистем необходимо представлять те предельные условия, за границы которых не могут выходить параметры проектируемой системы. Задача определения потенциальных характеристик систем решается с помощью моделей систем и компонентов потенциальной предельной достижимости. Существует ряд методологических подходов к построению таких моделей. Рассмотрим некоторые из них.
В одних случаях потенциальные математические модели компонентов радиосистем могут представляться в виде математических выражений, связывающих входные и выходные параметры компонента через запись физических и информационных законов, которые определяют основную суть преобразования информации,, либо каких-то физических параметров в лапном устройстве без учета мешающих факторов.
В других случаях математические модели компонентов пред-। (являются как некоторые логические высказывания, которым предписываются значения «истинно» или «ложно» в ивисимости от того, выполняются или не выполняются некоторые критерии. В качестве основы для таких критериев пыбираются физические законы, которым должны удов-летворять математические модели компонентов радиосистем.
Описываемое такими потенциальными моделями радиоустройство будет иметь ясную физическую интерпретацию, и его функционирование не будет противоречить фундаментальным иконам природы. Состоящая из таких компонентных моделей модель системы будет функционировать с предельно возможными параметрами, удовлетворяющими предельным фундаментальным законам природы (законам сохранения энергии,
239
второму началу термодинамики, возрастания энтропии и т.п.). Результаты моделирования могут использоваться для оценки характеристик эффективности проектируемой системы.
Разработчиков часто интересует проблема технической реа-1 лизуемости системы, которая определяется прогнозируемым уровнем развития технического прогресса. Если условия потенциальной реализуемости компонентов радиосистемы могут быть предметом общетеоретических исследований в области физики и математики, то для технической реализуемости это сущест! венно усложняется, поскольку конкретная технология может зависеть от таких ненаучных и субъективных факторов, как нали-1 чие определенной технологии, материальной базы, квалифика-1 ции персонала и т.п. Отсюда следует, что если разработчиков системы интересуют предельные характеристики системы на данном уровне развития техники, в математических моделях компонентов системы следует установить проверку на соответ ствие параметров компонента реальным физическим устройствам, реализуемым по конкретным технологиям. В подав-J ляющем большинстве случаев это достигается сравнением пове дения компонента или его ближайшего аналога и его потен-] циальной модели в одинаковых условиях. Проверенное в результате эксперимента соответствие абстрактной модели реально-1 му компоненту может использоваться, например, в качеств критерия истинности высказывания, которым интерпретируется потенциальная математическая модель компонента.
Рассмотрим в качестве примера модель потенциальной пре дельной достижимости для оптической системы связи, упрощен! ная структура которой показана на рис. 9.2. Система состоит из оптического передатчика, открытого оптического канала, оп-| тического приемника и связей между ними. Будем рассматрив вать простейший случай передачи двоичной информации, в которой передатчик в дискретные моменты модельного времени,// излучает импульс с оптической энергией Е„о или £nj при передаче оптических нуля или единицы, После прохождения опти ческого импульса по каналу связи его энергия становится ран ной £ф, которая и поступает на фотодетектор.
Рассмотрим потенциальную модель фотоприемного уст ройства. Если на фотодетектор падает оптическая энергия Я то в нем образуются электронно-дырочные пары, причем их число определяется следующим распределением вероятности:
Лп).|Е/(ВД1-ехр|-Е/(ВД| (9|)
п!
где п — число генерируемых электронно-дырочных пар, h — постоянная Планка, hf — энергия фотона на частоте f. I
240
Оптический * передатчик
^п -Д»
Рис. 9.2. Оптическая система связи
Без утраты общности допустим, что даже при генерации одной электронно-дырочной пары ее можно зарегистрировать и интерпретировать как наличие импульса двоичной единицы. Тогда единственный вариант ошибки — отсутствие электроннодырочных пар в детекторе при наличии излученного передатчиком оптического импульса. Вероятность такого события можно определить, положив в (9.1) п = 0:
р(0) = ехр[-Е/(Л/)]. (9.2)
Это позволяет сформулировать потенциальную математиче-(кую модель фотоприемного устройства следующим образом: если энергия, поступившая из канала, E^ = 2lhf, то фотоприемник срабатывает и выдает импульс двоичной единицы на своем электрическом выходе u(t) с вероятностью, равной р = 1 —1-10‘9, иначе импульс на выходе отсутствует, что интерпретируется как передача двоичного нуля.
В приведенной потенциальной модели фотоприемного устройства сделаны следующие идеализации: пренебрежение фоновым шумом, т.е. при передаче двоичного нуля на фотоприе-мное устройство поступает нулевая энергия, отсутствие темнового тока в фотоприемнике, а также допущение о том, что даже одна электронно-дырочная пара может быть обнаружена и зарегистрирована как наличие оптического импульса.
Одним из наиболее распространенных передатчиков для оптических линий связи является светоизлучающий диод. Такие диоды представляют собой, по сути дела, широкополосные шумовые излучатели. Шумопэдобный характер излучения диода определяет фундаментальный предел, являющийся основой для модели потенциальной предельной достижимости. Отсчеты светового поля на выходе источника шумоподобного сигнала с ограниченной шириной спектра, взятые в фиксированной точке в фиксированный момент времени, можно записать в виде
Еп(Л) = Ее{(Л +/В1е'2я/Ш). (9-3)
где f — номинальная частота излучения диода, А . и В — независимые гауссовы случайные переменные с нулевыми средними значениями и одинаковыми дисперсиями сто. «(О— модулирующий двоичный сигнал.
241
Плотность мощности в данной точке в данный момент времени определяется как квадрат комплексной амплитуды поля: /I2 + В. Так как А и В — случайные величины, то плотность мощности также будет случайной величиной, среднее значение которой равно 2о2о, а дисперсия — 2 Vo о-
Выражение (9.3), определяющее распределение во времени выходной энергии передатчика при передаче двоичного нуля или единицы в соответствии со значением н(/,), можно использовать как потенциально достижимую модель передающего устройства. Ясно, что в случае модуляции такого шумоподобного излучения двоичным сигналом его выходная энергия определяется случайным распределением Л(/,) и B(tt). Если импульс логической единицы будет достаточно коротким, т.е. модуляция осуществляется высокими частотами, то энергия сигнала на выходе передатчика, определяемая (9.3), может оказаться соответствующей нулевому сигналу, что и определяет фундаментальное ограничение для передающего устройства оптической системы связи.
Рассмотрим теперь модель потенциальной предельной достижимости для открытого оптического канала связи. В открытых оптических каналах связи фундаментальное ограничение на модель налагается дифракцией. Минимальная расходимость светового излучения передатчика даже при идеальной пространственной когерентности определяется соотношением Х/Оп, где Л. —длина волны оптического излучения, a Dn — апертура передающей линзы. Так, при заданных диаметрах передающей линзы Dn и линзы фотоприемника £)ф коэффициент передачи оптического канала' длиной d можно найти по формуле
2 1
+ 101g
/<(дБ) = -101g
я£П2Т 1П|
-101g
4Z2
4Л2
n2d2 4Л2
(9.4>
где три члена в правой части равенства представляют собой усиление передающей линзы, приемной линзы и потери при распространении в канале.
При выводе уравнения математической модели потенциальной предельной достижимости для оптического канала (9.4) в качестве допущений было принято, что оптический передатчик, фотоприемное устройство и обе линзы расположены на одной оптической оси, а искажения светового пучка из-за турбулентности атмосферы и несовершенства линз не происходит.
Используя полученные выше потенциальные модели компонентов оптической системы связи (9.2)—(9.4), можно
242
организовать имитационное моделирование работы такой системы (методом Монте-Карло) и определить предельно возможные вероятности правильного функционирования, на которые могут ориентироваться разработчики при проектировании реальной системы.
В настоящее время модели потенциальной предельной достижимости получают широкое распространение, ведется разработка теоретических основ построения подобных моделей |25], проводятся практические исследования и определяются фундаментальные пределы в различных областях радиоэлектроники.
§9.3. АГРЕГАТИВНЫЕ ИМИТАЦИОННЫЕ МОДЕЛИ РАДИОСИСТЕМ
Наиболее известным общим подходом к формальному описанию процесса функционирования компонентов и систем является агрегативный подход, предложенный Н.П. Бусленко |1 1, 25]. Этот подход позволяет моделировать функционирование непрерывных и дискретных, детерминированных и стохастических систем. При агрегативном моделировании радиосис-гсма декомпозируется на конечное число подсистем или компонентов с сохранением связей, обеспечивающих их таимодействие. Для каждого из компонентов системы имитационная модель строится по унифицированной алгоритмической схеме, называемой математическим агрегатом.
Математический агрегат представляет математическую схему, с помощью которой может быть описано функционирование большого круга компонентов технических систем. Понято математического агрегата является достаточно широким, поэтому рассмотрим только его частный случай — кусочно-линейные агрегаты (КДА).
КЛА представляется в виде многополюсника, характеризующегося своими входными зажимами, на которые поступают входные сигналы ц,-, i=l, ..., п, и выходными зажимами, с которых снимаются выходные сигналы wt, j= 1, В каждый момент имитационного времени t КЛА характеризуется своим, внутренним состоянием Z(/), содержащим k оставляющих £/(/), и принимающим одно из
качений из пространства допустимых состояний Z(/)e Z. Так как вектор состояний Z имеет k составляющих, то пространство Z будет представлять собой многогранник, заданный системой линейных уравнений. Для упрощения изложения материала в дальнейшем будем полагать, что многогранник Z образован k плоскостями Z\ = const, /=
243
Связи между входными зажимами одних агрегатов и выходными зажимами других называют каналами, по которым агрегаты в определенные моменты имитационного времени t могут обмениваться сигналами, при этом взаимное влияние вне механизма обмена сигналов не учитывается. Кроме того, на каналы накладывается еще ряд ограничений: ко входу агрегата подключается не более одного канала, к выходу — любое конечное число, передача сигналов в каналах происходит мгновенно и без искажений, любой сигнал описывается конечным набором характеристик.
Для описания соединений в декомпозированной на агрегаты радиосистеме обычно используется таблица, столбцы и строки которой пронумерованы двойными индексами i, г и /, q, где i и г — номера входного зажима и агрегата Аг, к которому он относится; / и q—номера выходного зажима и агрегата Aq, которому он принадлежит. Элементами таблицы являются 1 для зажимов, ..соединенных каналами, и 0, если такое соединение отсутствует. Очевидно, что составленная таким образом таблица будет представлять собой матрицу смежности направленного графа, вершинами которого являются входные и выходные зажимы агрегатов, а ветвями — соединяющие их каналы.
Взаимодействие моделируемой системы с внешней средой рассматривается как обмен сигналами между внешней средой и агрегатами, соединение которых моделирует систему. В соответствии с этим внешнюю среду обычно представляют в виде фиктивного агрегата Ло, выходными сигналами которого яв-, ляются сообщения в систему извне, а входными сигналами — сигналы, выдаваемые системой во внешнюю среду. Таким образом, агрегативная модель системы является замкнутой.
Рассмотрим процесс функционирования КЛА. Пусть в момент времени /о агрегат находится в состоянии Z(/o), где Z(/o) принадлежит пространству Z, ограничивающему воз можные состояния агрегатов. При i >/о состояние агрегата линейно изменяется во времени внутри пространства Z до тех< пор, пока хотя бы по одной из составляющих Z/ (/) не достигнет граничного значения Z/. Пусть это произойдет в момент времени t\. Тогда при to < t < t\ линейное изменение состояния агрегата можно описать следующим выражением: j
Z(t) = Z(t0) + (t—Ш (9.5)
где у = |'У1-..у*|Т — вектор скоростей изменения составляющих агрегата.
Значение момента времени t\ л^ожет быть найдено из (9.5) следующим образом:
244
z^) + (/-ш = Zf, t = [z,-zx^)1/yi + k, (9.6) ।де I — номер составляющей вектора состояния, которая дос-।игла граничного значения.
В момент времени t\ состояние агрегата скачком изменяется и становится равным Z(7j). Переход агрегата из одного состояния в другое зависит только от предыдущего состояния Z(/o) и от того, какая из составляющих вектора состояний Z/ достигла своего граничного значения Z/, и определяется оператором перехода Я:
Z(f1) = 771[Z(/0), 4]. (9.7)
Оператор Н\ может быть статистическим или детерминированным в зависимости от того, какое реальное устройство моделирует данный агрегат. В этот же момент времени t\, когда скачком изменяется состояние КЛА, на его выходных шжимах может _выдаваться сигнал, который зависит от состояний Z(/o) и Z(/j):
W1) = FI|Z(/o), Z(/i)J- (9.8)
Оператор F\, как и Hi, может быть статистическим или детерминированным в зависимости от условий работы агрегата.
При t>t\ изменение состояния агрегата вновь происходит в соответствии с соотношениями (9.5)—(9.8) до очередного момента достижения граничного состояния КЛА по одной из (оставляющих вектора состояний.
Простые формулы для определения моментов времени дос-шжения граничных состояний, являющиеся следствием кусочно-линейной аппроксимации закона изменения состояния агре-। ата, обеспечивают простоту алгоритмической реализации мо-1ели КЛА и системы, • составленной из таких агрегатов.
Обратимся теперь к случаю поступления на входные (ажимы агрегата входного сигнала._ Если в момент to на агрегат,_находящийся в состоянии Z(/o), поступает входной сигнал V(to), то он может вызвать как изменение состояния КЛА, так и появление на его выхрдных_ зажимах сигнала
в соответствии с операторами и F}.
Z(t0 +_0) = H\Z(FF), Wo)], (9.9)
Wo + 0) = F2{Z(to), V(/o), Z(t0 + 0)].
После момента времени to и отработки поступившего на вход КЛА сигнала начинается в соответствии с приведенными выше формулами изменение состояния агрегата до следующего момента поступления входного сигнала на его входы либо достижения граничных значений по одной из составляющих вектора состояний.
245
• Рис. 9.3. Арегативная имитационная модель системы связи
Из приведенного описания функционирования КЛА видно, что в виде подобных агрегатов может быть формализованно описано функционирование различных компонентов радиосистем: цифровых автоматов, процессов передачи и обмена информацией в каналах и сетях связи, вычислительных систем, систем массового обслуживания и др.
Для примера рассмотрим реализацию с помощью агрегативной системы модели оптической системы связи из §9.2. Очевидно, что наиболее простой представляется организация модели системы в виде соединения четырех агрегатов, каждый из которых моделирует генератор передаваемой двоичной информации (внешнюю среду), оптический передатчик, открытый оптический канал связи и фотоприемное устройство, как это показано на рис. 9.3.
* КЛА1, моделирующий внешнюю среду, выдает на своих выходах в соответствии с' требуемым случайным распределением сигналы v(t), эквивалентные импульсам двоичных нулей и единиц. Причиной для выдачи КЛА1 выходных сигналов может служить достижение им граничных состояний по различным составляющим вектора состояний. Эти сигналы поступают на вход КЛА2, моделирующего оптическое передающее устройство, на выходе которого получаются случайные сигналы, причем оператор £2 определяется выражением (9.3). Здесь операторы //|, F\, Н2—нулевые, т.е. изменения состояния агрегата во времени не происходит.
Выходной сигнал КЛА2 поступает на вход агрегатам моделирующего открытый оптический канал. Вектор состояний этого агрегата включает в качестве составляющих количество оптических импульсов k, распространяющихся по оптическому каналу, и время ДО, которое осталось каждому /-му импульсу, находиться в канале. Время определяется длиной канала d, скоростью распространения излучения в нем с и временем появления этого импульса на входе канала tf. At/ = // + d/c—t.
Вектор состояний КЛАЗ линейно изменяется во времени по закону: Z/(/) = |/, ti + d/c-t], /= 1, ... k.
В момент достижения граничного состояния Z/(/) = 0 по одной из составляющих / вектора состояний, т.е. в момент появления оптического импульса у фотоприемного устройства
246
КЛАЗ скачком меняет свое состояние: количество распространяющихся по каналу импульсов уменьшается на единицу, а и.। выходе КЛАЗ появляется сигнал W(t + 0) = Fi[Z/(t)], в шльнейшем поступающий на вход чет- вертого агрегата, моделирующего фотоприемное устройство. Если помехи в канале отсутствуют, то оператор /д будет простой, и выходной сигнал W(t + 0) будет повторять входной сигнал, умноженный на коэффициент передачи канала, определяемый выражением
W(l + 0) = V(/—d/c)K. Если же в модели необходимо учесть помехи в канале, то оператор F] будет статистическим < жданным распределением для имитации помех в открытом оптическом канале. Оператор Ег У этого КЛА будет нулевым, । е. при поступлении сигнала на вход агрегата выходной, сигнал отсутствует, изменяется только вектор состояний и регата Z(/), который будет содержать на один сигнал <>ольше.
Аналогично можно представить в виде КЛА и фотоприем-ное устройство. ,У моделирующего его агрегата не будет линейно изменяться вектор состояний (у = 0), операторы Hi, F\, Н% |.1кже будут нулевыми, оператор же F% определяется из следующих соображений: если энергия оптического сигнала с выхода предыдущего КЛАЗ превышает 21/г/, то на выходе агрегата появляется сигнал и(/), соответствующий логической с шпице, в противном случае — логическому нулю. Если оператор F‘2 выбрать статистическим, то можно имитировать шумы фотоприемного устройства. Таким образом, с помощью КЛА описывается динамика работы оптической системы I вязи.
Опишем схематически организацию имитационного моде-шрования в агрегативной системе. Так как агрегативная модель является замкнутой, то имитация функционирования । пстемы возможна лишь за счет возникновения внутренних 1 обытий. Допустим, что на выходе одного из агрегатов, например Ао, в момент / появляется выходной сигнал. Тогда цравляющая программа моделирования переводит агрегат Ао и список ожидающих обслуживания и составляет список а ктивизированных агрегатов, на входы которых поступит нгпал с выхода Ао- После этого управление поочередно передается подпрограммам, имитирующим функционирование .1 ктивизированных агрегатов. В процессе обслуживания каждому агрегату определяется время следующей активизации из-за достижения вектором состояний граничного значения, либо появления входных сигналов. Когда обслуживание всех агрегатов, на входах которых изменился сигнал, будет окончено, управляющей программой проверяется условие окончания моделирования, и если оно не выполняется, то
247
выполняется, то управление передается подпрограмме активизации агрегатов во времени имитации. Эта программа выбирает минимальное время в упорядоченном списке моментов времени изменения состояний агрегатов Tmin, определяет имя активизируемого агрегата Ад и одновременно производит сдвиг имитационного времени на тП1|П, полагая его равным t = to + Тщ|Г|- Затем управляющая программа моделирования составляет список агрегатов, у которых момент активизации совпадает с новым модельным временем, и приступает к поочередной активизации подпрограмм обслуживания активизированных агрегатов. Активизация любого Aq состоит в передаче управления подпрограмме имитации функционирования агрегата, обеспечивающей выполнение операторов Hi, Fi или Н%, F%. В результате агрегат переходит в новое состояние и формирует выходные сигналы. Дальнейший процесс обслуживания агрегатов управляющей программой моделирования аналогичен описанному выше.
Приведем пошаговое описание имитации событий в агрегативной модели. •
Алгоритм 9.1. И митация функционирования системы агрегативным методом
Шаг /. Производится начальная установка состояний агрегатов.
Шаг 2. Определяются момент времени t, когда произойдет следующее событие в агрегатах за счет линейного изменения вектора их состояния, и имя активизируемого агрегата Ад. Текущее время моделирования'полагается равным t.
Шаг 3. Определяются новые состояния всех агрегатов, время активизации которых равно I, и фиксируются их новые состояния на момент времени t. Формируются выходные сигналы всех активизированных агрегатов
Шаг 4. По матрице смежностей определяются каналы и агрегаты, на входы которых поступят сигналы с активизированных агрегатов.
Шаг 5. Определяются новые состояния агрегатов, активизированных поступившими на них входными сигналами, формируется новое множестве выходных сигналов ,и состояний этих агрегатов.
Шаг 6. Проверяются условия окончания моделирования, если они не выполняются, то переход к шагу 2.
Шаг 7. Оформление результатов моделирования. П
Описание поведения каждого агрегата реализуется <5 помощью специализированных систем имитационного модеи лирования. При этом приходится укалывать _спосрб выдачи сигналов и характеристики агрегатов Hi, Fi, Н%, F%, а также матрицу смежности для задания коммутации входных . ц выходных зажимов агрегатов. Далее система моделирования строит программные модели агрегатов, а управляющая программа моделирования стандартным образом организует имитацию событий в системе и сбор информации. В настоящее время известно несколько систем имитационного моделирования, реализующих имитацию агрегативным способом, наибольшую известность из них получили системы АИС и САПАС. ,
248
§9.4. ДИСКРЕТНЫЕ ИМИТАЦИОННЫЕ МОДЕЛИ РлДИОСИСТЕМ
Как указывалось в §9.1, при дискретном имитационном моделировании радиосистем воспроизводятся взаимодействия, и которых участвуют компоненты системы и которые приводят к изменению состояний компонентов и системы во времени в целом. Таким образом, дискретная имитация позволяет воспроизвести поведение моделируемой системы во времени, т.е. представить динамику ее функционирования. Для пояснения сущности алгоритмов дискретного имитационного моделирования уточним важные понятия «событие», «действие» и «процесс». Действие — это изменение состояния компонентов или системы в целом. Событие—начало или конец любого действия, т.е. при моделировании событие происходит в тот момент, когда принимается решение о начале или окончании какого-либо действия. Процесс—это упорядоченная во времени последовательность событий или действий, которая может включать несколько действий сразу. Взаимосвязь этих понятий поясняется рис. 9.4.
При дискретной имитации функционирования системы спишется, что ее состояние может изменяться только в моменты времени совершения событий. Между этими моментами времени состояние системы и ее компонентов полагается неизмен
ным. Для получения картины поведения системы во времени в модели организуется продвижение имитационного времени ог одного события к другому при обязательном учете возможности параллельного выполнения в реальной системе.нескольких действий сразу. Очевидно, что в алгоритмических реали-шциях моделей систем этот параллелизм действий может (пять реализован лишь за счет последовательного обслуживания событий или действий, одновременно возникающих в разных компонентах реальной системы. Когда имитация одновременно появившихся событий в системе будет завершена и бу-чут определены моменты совершения следующих событий, начала или завершения следующих действий или процессов,
тогда производится сдвиг молельного времени до момента совершения ближайшего по времени события. По способу организации квазипараллелизма действий в имитационной модели различают четыре ме-юдологических подхода к построению дискретных моделей
Процесс
Действие 7 Действие Z
Событие/ Событие2 Событие 4 Событие б
Рис. 9.4. Взаимосвязь между событиями, действиями й процессами
249
систем: событийный подход; подход, ориентированный на действия, называемый часто подходом сканирования активностей; транзактный подход и процессорно-ориентированный подход. Рассмотрим эти подходы подробнее.
Событийный подход к построению дискретных имитационных моделей. При этом подходе функционирование системы моделируется путем идентификации происходящих и ней изменений в моменты совершения событий. При этом предполагается, что с формальной точки зрения действия всех компонентов, приводящие к изменению состояния системы, одинаковы, связи между отдельными действиями, которые выполняются независимо одно от другого, отсутствуют, а в результате одних и тех же событий происходят одинаковые действия. В этом случае имитационная модель системы представляет собой набор процедур проверки возможности совершения событий, алгоритмов имитации выполнения действий и управляющей программы моделирования. Задача исследователя заключается в описании взаимосвязи событий между собой и временных характеристик действий различных компонентов системы. Имитация функционирования системы осуществляется путем выполнения упорядоченной во времени последовательности событий.
Перед началом имитации управляющая программа моделирования устанавливает начальные состояния моделей компонентов системы и задает начальные параметры, определяющие условия совершения событий и времени t = /о, затем управление передается на программу проверки выполнимости условий совершения событий. В процедурах поверки появления события реализуется зависимость выполнения соответствующего этому событию действия от конкретной ситуации, имеющей место в реальной системе. Имена тех событий, для которых эти условия выполнены, заносятся в список инициализируемых, т.е. совершившихся, событий. Если этот список содержит хотя бы одно событие, то начинается последовательное выполнение процедур обслуживания событий, каждая из которых реализует алгоритм, имитирующий соответствующее действие компонента системы В большинстве случаев имитация действия происходит путем временной задержки т, равной времени совершения этого действия компонентом в реальной системе. Завершается работа алгоритма имитации действия оператором, который модифицирует значение момента совершения этого действия и будущем ta = to + т и возвращает управление на выполнения следующей по порядку процедуры обслуживания событий, имя которой определяется управляющей программой моделирования.
250
Как только будут выполнены все процедуры обслуживания событий, находящихся в списке совершившихся событий, управляющая программа моделирования начинает корректировать модельное время. Корректировка осуществляется специальной подпрограммой, которая ищет в списке запланированных событий минимальное значение момента инициализации to + Tmjn, которое и становится новым значением модельного времени t. После корректировки модельного времени, если не выполняется условие завершения имитации, управление вновь передается на программу проверки выполнимости условий совершения событий и весь описанный процесс имитации функционирования системы повторяется вновь.
Когда условие завершения имитации выполнено, она прекращается и управление передается подпрограмме, которая вычисляет результаты моделирования и выводит их исследователю.
Для иллюстрации событийного подхода к моделированию гнетем вновь рассмотрим оптическую систему связи, показанную на рис. 9.2.
Событийная модель в этом случае состоит из описания /гействий, происходящих в момент генерирования оптического импульса передатчиком, прихода импульса по оптическому каналу на фотоприемное устройство и, наконец, выдачи выходного электрического импульса с выхода фотоприемного устройства. Изменения состояния системы могут происходить юлько в моменты совершения этих событий, и имитация с использованием событий «генерирование оптического импульса», «достижение оптическим импульсом фотоприемника» и выдача выходного электрического импульса» полностью обеспечивают воспроизведение динамики функционирования системы.
На первом шаге планируется генерирование очередного оптического импульса, что в ходе имитации при неоднократном обращении к процедуре обслуживания этого события позволяет организовать непрерывный поток информации, поступающий па вход оптической системы связи. Будем полагать, что эти события совершаются в моменты модельного времени / —
Рассмотрим теперь логику второго события — достижение оптическим импульсом фотоприемника. Условиями совершения и ого события, очевидно, являются наличие оптического импульса излучения, распространяющегося по оптическому каналу, т.е. совершение первого события, и значение модельного времени, равное t = tt + тк, где к — моменты совер
251
шения первого события, тк — время распространения оптического излучения по каналу в идеальных условиях, равное тк — d/c. Процедура имитации действия, инициа лизированного этим событием, заключается во временной задержке второго события относительно первого на время тк, т.е. время распространения оптического излучения по открытому оптическому каналу. Обычно оно распределено по гауссовому закону с математическим ожиданием тк из-за флуктуаций показателя преломления среды, обусловленных турбулентностью атмосферы.
Аналогично по логической взаимосвязи и третье событие— выдача фотоприемником выходного электрического им-| пульса. Для того чтобы совершилось это событие, необходимо предварительное совершение второго события, т.е. появление оптического импульса на входе фотоприемника и модельного времени, равного t = tt + тк + Тф, где Тф — время задержки срабатывания фотоприемного устройства, зависящее от многих внешних условий, в которых работает система, и обычно рас-1 пределенное по закону Рэлея.
В ходе имитации по различным законам будет возникать первое событие «генерирование электрического импульса» и после выполнения остальных событий в упорядоченной во времени последовательности можно проверить пропадание импульсов в системе при больших скоростях передачи информации из-за нестабильности задержек в распрост-1 ранении оптического излучения и фотоприемного устройства
Приведем описание алгоритма имитационного моделиро-1 вания при событийном подходе.
Алгоритм 9.2. Имитационное моделирование систем способом составлении расписания событий
Шаг 1. Устанавливаются начальные состояния компонентов системы и исходные значения параметров, определяющих инициализацию событий, устанавливается начальное значение модельного времени t = tg.
Шаг 2. Проверяются условия выполнимости- всех событий и составляется список событий, для которых выполнены условия инициализации.
Шаг 3. Если список пустой, то переход к шагу 4, иначе передается управление на выполнение процедуры обслуживания первого события из списка Модифицируется время совершения данного события в будущем tj = t + tj, и ом исключается из списка. Переход к шагу 2.
Шаг 4. В списке запланированных событий находится событие, имеющем| минимальное время инициализации tj, и корректируется модалоное время, котор'* полагается равным этому моменту времени.
Шаг 5. Проверяется условие окончания имитационного моделирования, если оно не выполняется, то переход к шагу 2.
Шаг 6. Оформляются результаты моделирования.
252
В настоящее время разработан ряд систем имитационного моделирования, обеспечивающих разработчика систем программными средствами для программирования последовательности событий, продвижения имитационного времени и описания инициализируемых событиями действий и взаимосвязи со-оытий. Наиболее распространенными имитационными системами, ориентированными на событийный подход, являются HASP и SIMSCRIPT [24].
Подход сканирования активностей. При использовании >гого подхода для имитации функционирования системы разработчик описывает действия, в которых участвуют компонен-п.| системы, и задает условия начала и окончания этих дейст-пнй. При этом полагается, что с формальной точки зрения чсйствия компонентов системы, независимы друг от друга, мо-1 у г быть различными, а условия их совершения могут быть представлены алгоритмически. В результате совершения к йствий в системе будут происходить различные события, ко-|<>рые заранее не планируются, а инициализируются по условиям, определенным для данного действия.
Имитационная модель системы представляет собой набор процедур, моделирующих действия, и процедур проверки выполнимости условий начала или завершения действий. Условия начала или окончания действий проверяются после оче-р< того продвижения имитационного времени. Для того чтобы могло быть выполнено каждое действиё в модели, проверка условий (сканирование) производится для всего множества к пствий при каждом продвижении имитационного времени.
Поясним упрощенно работу управляющей программы мо-рлирования при имитации сканированием активностей. Перед началом имитации соответствующая подпрограмма устанавливает начальные состояния компонентов системы и задает начальные условия инициализации действий. Затем начинает-< я проверка условий инициализации всех действий. Обычно и । проверка производится по параметрам модели либо по моментам модельного времени, когда должно начаться выполнение действия. По аналогии с событийным подходом составляется список действий, для которых выполнены условия инициализации, и затем управление поочередно передается процедурам, имитирующим эти действия. Каждая процедура, моделирующая действие, завершается вычислением момента времени следующей инициализации, а также параметров мокли компонента, изменившихся в результате совершения дей-||ния. Все действия заносятся в список в соответствии с моментами их последующей инициализации. *
253
После окончания имитации всех инициализированных дейс твий управляющая программа моделирования пересчитыва<1 модельное время, принимая его равным минимальному значению момента инициализации действий.
Если после корректировки модельного времени условие завершения имитации не выполняется, то управление имитацией вновь передается процедуре проверки условий инициализации действий.
Так как в результате выполнения алгоритмов, имитирующих действия, могут возникнуть условия для инициализации других действий, то в управляющей программе моделирования должны быть предусмотрены повторные циклы провер.,' выполнимости условий инициализации действий.
Обратимся вновь к рассмотрению примера — оптической системе связи, показанной на рис. 9.2. При моделировании с методом сканирования действий можно выделить два основных действия: прохождение сигнала через оптический ка нал связи и выделение и преобразование оптического сигнала в электрический сигнал в фотоприемном устройстве.
Процедура имитации первого действия будет заключаться
в задержке светового импульса на выходе оптического канала на время распространения тк в соответствии с заданным рас пределением длительностей и ослаблению оптического сигналя по случайному, заданному заранее закону. Условие начала действия — появление сигнала на выходе оптического передат, чика, условие окончания первого действия определяется по времени t\ = t + тк.
Второе действие по описанию имитирующей программы аналогично первому и заключается в пороговом обнаружении оптического сигнала, задержке его по заданному случайному закону Тф для имитации срабатывания фотодиода и усилителя и выдаче электрического сигнала на выход системы. Условие начала этого действия — завершение первого действия, т.е. появление оптического сигнала на .входе приемного устройст ва, условие окончания определяется по модельному времеп|1 /2 = t + Тк + Тф.
Так как здесь действия совершаются друг за другом, то модельное время будет продвигаться поочередно после имита
ции каждого из них.
Подход к имитационному моделированию систем сканиро-
ванием активностей наиболее эффективен для моделировани! систем, в которых продолжительность действия определяется и
что обеспечивает
зависимости от состояния системы,
простуц
схему моделирования в информационных системах, частным
случаем которых являются радиосистемы.
254
Приведем пошаговое описание алгоритма сканирования ак-।нвностей.
Алгоритм 9.3. Имитационное моделирование системы сканированием актив-41 и тей
Шаг /. Устанавливаются начальные состояния компонентов системы, параметрон, определяющих условия инициализации действий, и начальное значение модельного времени t = t().
Шаг 2. Для заданного момента модельного времени / производится проверка пыиолнения условий начала или завершения всех действий и составляется список н йствий. которые необходимо инициализировать.
Шаг 3. Если этот список пустой, то переход к шагу 4, иначе управление пере-i.u-гся подпрограмме имитации первого действия из списка; определяется время .ыи-ршения этого действия в будущем tj=l + xj и затем оно исключается из списка инициализированных действий. Переход к шагу 2.
Шаг 4. Корректируется модельное время заменой текущего времени на время, инициализации ближайшего действия I = t + Tymin-
Шаг 5. Проверяется условие окончания процесса имитации; если оно не вы-|кь'1няется. то переход к шагу 2.
Шаг 6. Оформляются результаты моделирования.
Имитация функционирования радиосистем способом сканирования активностей требует больших временных затрат, чем при событийном подходе, однако такое моделирование позволяет получить больше информации о работе моделируемой системы. Из систем имитационного моделирования, ориентированных на данный подход, можно отметить CSL, SMPL.
Транзактный подход к организации дискретных имитационных моделей. В ряде случаев функциональные действия всех компонентов однотипны и представляют собой набор про- лейших операций, алгоритмы выполнения которых лишь из.-мспяют временю' е координаты компонентов системы. При ном необходимо учитывать зависимость выполнения действий ipyr от друга. Такие процессы функционирования системы по своей сути являются процессами массового обслуживания [11, ’5|. В виде процесса обслуживания могут быть представлены различные по своей природе процессы функционирования технических, производственных и других систем. Характерны для i.iKnx процессов случайное появление заявок на обслуживание, называемых транзактами, и завершение обслуживания в i пучайные моменты времени, т.е. стохастический характер процесса функционирования.
В любом элементарном процессе обслуживания всегда мокко выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание. Элементарный прибор массового обслуживания показан на рис. 9.5 и состоит п । накопителя заявок (Н), в котором может одновременно на-
255
ходиться, ожидая обслуживания, несколько транзактов; кана ла обслуживания заявок (К), в котором происходит задержка заявки на время обслуживания, имитирующая действие ком понента, и который может управляться управляющими сигналами Пу.
Кратко процесс функционирования элементарного прибора массового обслуживания вида рис. 9.5 можно описать следую щим образом. Путем обращения к генератору случайных чи сел с заданным законом распределения определяется длитель ность времени обслуживания транзакта в канале п вычисляется время окончания процесса обслуживания. До па
ступления этого момента модельного времени канал считается занятым и обслуживание следующей заявки не производится, При поступлении заявки на вход прибора она заносится и очередь на обслуживание в накопитель (Н), где и находится до начала обслуживания в канале (К). Таким образом, для каждого прибора массового обслуживания транзактный подход сочетает в себе черты событийного подхода и подхода сканированием активностей. Достоинством такого подхода является то, что логика событий в имитационной модели может быть заложена в самом имитационном языке.
Для описания имитационной модели радиосистемы имеется широкий набор стандартных приборов обслуживания, на которые декомпозируется модель системы. Схема соединения приборов отражает образование и уничтожение транзактов, занятие и освобождение ими приборов массового обслуживания, управление движением транзактов в системе, имитацию задержек в продвижении транзактов и по виду близка к структуре моделируемой системы.
Алгоритм работы имитационной модели при транзактном подходе состоит в следующем. В начале моделирования упра вляющая программа устанавливает приборы обслуживания п модельное время в начальное состояние. Затем управление передается программе проверки источников транзактов. Эта
программа просматривает
Рис. 9.5. Простейший прибор обслуживания заявок
условия создания новых транзактов каждым источником, и при их выполнении подпрограмма создания транзактов генерирует новые транзакты и помещает их в спи сок активизированных транзактои для данного момента модельною времени I. Затем управление ими тацией передается программе уничтожения транзактов, которая
256
I
просматривает очереди транзактов и выбирает те, чье время пребывания в модели истекло. Эти транзакты также помешаются в список активизированных. Когда просмотрены все вновь генерируемые и уничтожаемые транзакты, подпрограмма инициализации начинает поиск транзактов, завершивших к моменту I пребывание в канале какого-либо прибора массово-|о обслуживания либо поступившего в очередь на обслуживание в накопитель прибора. Эти транзакты дополняют список 1кти визированных.
Если в списке активизированных имеется хотя бы один раизакт, то управляющая программа моделирования передает управление подпрограмме обслуживания транзактов. Эта подпрограмма находит по списку активизированных транзактов .1 ipec прибора, в канале которого завершилось обслуживание ранзакта, выбирает из очереди к этому каналу новый тран-i.ikt и закрепляет за ним освободившийся канал, определяя при этом момент будущей активизации транзакта при освобождении им канала: /а = t + тк, где тк — время выполнения дейс-ПП1Я, которое имитируется обслуживанием транзактов этим каналом. После того как все транзакты, обслуживание которых и вершилось, освободят каналы и произойдет передвижка оче-ргчей транзактов, управление передается программе передвижения транзактов. Эта подпрограмма определяет адрес прибора обслуживания, на который должен поступить обслуженный i раизакт, и организует его перемещение по схеме модели. Если га нал прибора, на который поступает транзакт, свободен, то । раизакт его занимает, при этом определяется время завершения обслуживания транзакта каналом, если же канал занят, то । раизакт поступает в очередь на обслуживание к нему в соот-||| гствии со своим приоритетом. Если транзакт поступает на уничтожение, то специальная программа формирует статистику пребывания транзакта в модели системы.
Для оптической системы связи имитационная модель при раизактном подходе может быть представлена в виде четырех приборов массового обслуживания, как показано на рис. 'и> На вход первого прибора, имитирующего оптический передатчик, поступают по случайному во времени закону тран-1.1КТЫ, атрибут которых случайным образом помечается сим-полами логического нуля или единицы, чтобы имитировать пе-ре !зваемую цифровую информацию.
Второй прибор имитирует оптический канал. В этом приборе время обслуживания каждого транзакта каналом равно времени распространения сигнала по каналу минус время и мщания обслуживания в накопителе. Время обслуживания можно изменять случайным .образом, чтобы имитировать распространение оптического излучения в турбулентной атмосфере.
257
\и।>>\|д।и шипя ироекi иронии ия радиоэлектронных среде) в
\При6ор 7 |
I------------1
1’ранзак/пы I ,———s I x Т/1сметкп\1_
| Прибор! |
| Прибор J ‘ ।
|*
। трап-1,6 о —i--». ^u^j"2
Рлс. 9.6. Транзактная имитационная модель системы связи
Третий и четвертый приборы имитируют фотоприемйое устройство. В них отсутствуют накопители, а транзакт после окончания обслуживания в канале третьего прибора приобре тает дополнительную случайную задержку, имитирующую время срабатывания фотоприемного устройства. Четвертый прибор представляет собой логический переключатель, который направляет транзакт на уничтожение по различным пу тям в зависимости от того, помечен ли атрибут транзакта логическим нулем или единицей в первом приборе.
Описание этой модели операторами языков логического моделирования не представляет трудности.
Алгоритм 9.4. И митационное моделирование систем при транзактном подтдо
Шаг 1. Производится начальная установка приборов и модельного времени.
Шаг 2. Передается управление программе сканирования источников транзик тов, которая проверяет условия создания новых транзактов и генерирует их с тр»-буемыми характеристиками. Формируется список активизированных транзактов.
Шаг 3. Передается управление программе уничтожения транзактов. Форми< •руется список уничтожаемых транзактов. корректируется список активизированных транзактов.
Шаг 4. Передается управление программе инициализации транзактов в приборах массового обслуживания, корректируется список активизированных транзактов.
Шаг 5. Проверяется список активизированных транзактов, если список пусг, то переход к шагу 7, иначе передача управления программе обслуживания тря» зактов.
Шаг 6. Передача управления программе продвижения транзактов.
Шаг 7. Из списка моментов активизации транзактов выбирается минимально» время, модельное время полагается равным этому времени.
Шаг S. Если условие окончания моделирования ие выполняется, то переход I шагу 2..
Шаг 9. Оформление результатов моделирования.
Как видно из описания алгоритма работы управляющей
программы моделирования, при сравнительной простоте они
сания имитационной модели системы при транзактном подхо
де появляются дополнительные расходы машинного времени на просмотр транзактов и приборов по сравнению с двумя предыдущими подходами. Несмотря на этот недостаток, трап
258
шктный подход в настоящее время широко используется для моделирования систем различного назначения. Наиболее распространенными системами имитационного моделирования, ориентированными на транзактный подход, являются GPSS, SIMULA, Q-GERT и др.
Процессорно-ориентированный подход к построению дискретных имитационных моделей. Этот подход используется, ко-|да функциональные действия различных компонентов системы неодинаковы, причем у каждого компонента может существовать своя последовательность элементарных действий, которые последовательно выполняются во времени. Это позволяет рассматривать функционирование компонента системы как единый процесс, а всю имитационную модель представить и виде набора описаний процессов и информационных и управляющих связей между ними.
Так как в процессы объединяются действия, которые определяют функционирование одного компонента модели, то имеет место полное соответствие компонентов физической сис-к мы и ее имитационной модели, что делает такие модели особенно наглядными и удобными для поиска узких мест в рабо-|е системы.
Рассмотрим упрощенную схему работы управляющей прог-1> 1ммы моделирования при процессорно-ориентированном под-юде к имитационному моделированию. После установки начального состояния имитационной модели и начального ими-।анионного времени t = to управляющая программа моделирования составляет список активизированных процессов, для действий которых время активизации ts<t. Далее управляющая программа выбирает первый из активизированных процессов и проверяет выполнение условий начала или окончания действия из этого процесса, для которого истек по время ожи-'мния. Если эти условия выполняются, то управление передается подпрограмме, имитирующей данное функциональное действие. Работа подпрограммы, имитирующей действие, завершается модификацией времени следующей активизации >гого действия /а = / + т, где т — сдвиг времени. Если после 1апершения работы подпрограммы имитации действия выполняются условия для совершения следующего действия этого № процесса, то управление передается подпрограмме, имитирующей последующее действие, и т.д. до окончания процесса. После того как будут выполнены все действия выбранного ра-iii'c активизированного процесса, начинается проверка условий выполнения действий из следующего активизированного процесса и т.д. Когда будут выполнены подпрограммы имита
259
ции действий всех активизированных процессов, управляющая программа моделирования осуществляет сдвиг модельного времени. За новое модельное время принимается минимальное время новой активизации действий, и далее процесс имитации повторяется. Запишем этот процесс пошагово.
Алгоритм 9.5. Имитационное моделирование системы процессорно-ориентированным^ подходом
Шаг 1. Устанавливаются начальные состояния процессов и начально* модельное время I == to-
Шаг 2. Поверяется список активизированных процессов. Если список пуст. То переход к шагу 4.
Шаг 3. Выбирается первый элемент списка активизированных процессов и управление передается подпрограммам имитации действий этого процесса, для кото-| рых выполнены условия совершения. После завершения работы подпрограмм имитации действий устанавливается новое время их активизации и данный процесс исключается из списка активизированных. Переход к шагу 2.
Шаг 4. Осуществляется сдвиг модельного времени, которое выбирается ранным минимальному времени активизации процессов: / = / + тт1п-
Шаг 5. Проверяется условие завершения моделирования. Если условие выполнено. то переход к шагу 6,. иначе формируется список активизированных процессов. в который заносятся все процессы, время активизации действий в которых ta </, и располагаются в списке согласно приоритетам процессов. Переход к шагу 2.
Шаг 6. Оформляются результаты моделирования.
Очевидно, что в рассматриваемом ранее примере оптической системы связи (см. рис. 9.2) работа системы представляй-, тся в виде одного процесса из ряда последовательных дейст вий, имитирующих работу оптического передатчика, канала связи и фотоприемного устройства.
При процессорном способе имитации близость модели к физической системе облегчает отладку модели и введение до лущений, что особенно удобно для проектирования, когда при-J ходится вносить в модель много изменений и дополнений. Особенно эти преимущества сказываются по мере роста размеров модели. Из систем моделирования, использующих для описа-| ния реальных объектов процессы, можно отметить СЛАМ. PLSIM, SOL, ASPOL, DISLIN и др.
§9.5. ФУНКЦИОНАЛЬНЫЕ МОДЕЛИ РАДИОСИСТЕМ
Функциональные модели занимают промежуточное положение между системотехническими и схемотехническими моделями. Им присуща большая конкретность в представлении npoJ цесса функционирования радиосистемы по сравнению с систе-' мотехническими моделями, что позволяет с их помощ, уточнять требования к отдельным радиоустройствам, в то ж» время в них отсутствует излишняя детализация, свойственниц схемотехническим моделям, что позволяет реализовать такие модели даже на персональных ЭВМ.
260
Функциональные модели отражают процесс функционирования реальной радиосистемы, представлением ее в виде напора функциональных блоков, каждый из которых выполняет шданную функцию по формированию или преобразованию радиосигналов или информационных процессов. Для матема-i пческого моделирования на функциональном уровне радиоси-<к му следует декомпозировать на ограниченное число таких функциональных блоков. При этом физические устройства мо-i у г и не совпадать с функциональными, на которые декомпо-шруется система. К функциональным блокам, например, можно отнести совокупность радиоустройств, осуществляющих оперирование информационных процессов и радиосигналов; у< гройств, осуществляющих прием и демодуляцию радиосигналов, и т.п. Располагая набором различных функциональных блоков, из них можно составлять функциональные модели широкого класса радиосистем. Очевидно, что декомпозиция реальной системы и составление функциональной модели требуют более детальных знаний о системе, чем при системотехническом подходе к моделированию. Для радиосистем определенно-ю класса обычно реализуют адаптивное автоматизированное разбиение ее модели на функциональные блоки.
Алгоритмически функциональная модель радиосистемы представляет совокупность библиотеки функциональных блоков, подпрограммы-интерпретатора связей между ними, управляющей программы моделирования, осуществляющей продвижение имитационного времени и передачу управления на подпрограммы, имитирующие функционирование блоков, а ыкже набора стандартных подпрограмм для организации вычислительного эксперимента, представления результатов моделирования и т.п.
Воздействия на входах и выходах функциональных блоков будут представлять собой фазовые переменные модели,- Способ описания фазовых переменных существенно влияет на состав модели и макромодели функциональных блоков. Из исполь-|усмых в настоящее время методов описания входных воздействий и фазовых переменных необходимо отметить следующие:
— метод несущей, когда используются мгновенные шачения фазовых переменных, входных сигналов и их смеси с помехами u(t)+
— метод комплексной огибающей, когда фазовые переменные и входные сигналы описываются с точностью до их комплексных огибающих U(t);
— метод статистических эквивалентов, когда реальные <лучайные процессы в радиосистеме представляются своими
261
статистическими характеристиками, например математическим ожиданием, дисперсией и т.д.,. либо когда реальные процессы заменяются другими, но статистически адекватными им в рамках выбранного критерия, например по совпадению определенного числа моментов;
— метод информационного параметра, когда вместо исследования прохождения реального сигнала в модели системы изучается прохождение через модель информационного параметра, для приема и обработки которого эта система предназначена.
Независимо от способа описания фазовых переменных и разбиения модели системы на функциональные блоки макромодели отдельных функциональных блоков обычно представляют в виде динамических звеньев, чтобы проследить функционирование системы во времени. В самом общем случае в динамическом звене входные и выходные переменные связаны системой дифференциальных уравнений. В простейшем случае функционального блока с одним входом — выходом (рис. 9.7, а) при использовании метода несущей эта связь может быть записана в виде
£afe(0d\-(-f) = (9.10)
Л=о к At 1=0 dr
Уравнение (9.10) описывает линейное нестационарное звено с сосредоточенными постоянными. В случае стационарных звеньев а^(/) = я* = const, bi(t) = bi = const и можно использовать не эту запись, а более простую запись связи входных и выходных переменных через обобщенные характеристики звена: импульсную 3(/), переходную h(f), передаточную /C(jco) и т.д., что позволяет при моделировании избежать интегрирования систе мы дифференциальных уравнений. Если звено, моделирующее функциональный блок, является стационарным и безынерцион* ным, то (9.10) превращается в нелинейное уравнение.
г)
Рис. 9.7. Модели функциональных блоков радиосистем
262
Если функциональный блок моделируется нелинейным динамическим звеном, то связь входных и выходных переменных может быть записана в виде системы нелинейных дифференциальных уравнений соответствующего порядка. Одномерные безынерционные нелинейные звенья (рис. 9.7, б) описываются нелинейной зависимостью мВых(0 = G[wBX(/)J, где функцию G стремятся аппроксимировать удобными для вычислений математическими формулами. Инерционное нелинейное звено обычно представляют в виде каскадного включения нелинейного безынерционного звена и линейного инерционного (рис. 9.7, в) для упрощения моделирования системы.
Для нахождения отклика системы на сложное входное воздействие в методе несущей при линейных моделях функциональных блоков обычно используется интеграл свертки. Если модели функциональных блоков нелинейны, то для определения отклика системы приходится решать систему нелинейных дифференциальных уравнений.
Дискреты продвижения имитационного времени при моделировании по методу несущей выбираются более жесткими, чем требует теорема Котельникова, так как для точного представления непрерывного процесса рядом его дискретных значений необходима специальная обработка дискретных выборок с помощью оптимальных фильтров. Такая обработка в ЭВМ не предусмотрена, и интервал дискретизации фазовых переменных выбирается из условия
М = tk-tk-i < 1/(у/Гр), У = 5... 10,
। де /гр — верхняя граничная частота спектра сигнала. При моделировании по методу несущей /гр определяется радиочас-।отами, на которых работает радиосистема, и поэтому значе-* пне А/ оказывается малым, что затрудняет использование это-к> метода для моделирования больших систем.
Для примера рассмотрим функциональную модель оптической системы связи рис. 9.2, построенную по методу несущей. В качестве фазовых переменных, зависящих от времени, и модели системы рационально выбрать: u(t) — подлежащий передаче информационный случайный двоичный сигнал, £(г, I) —напряженность электрического поля световой волны в раскрыве передающей линзы, £п(/)— шумы открытого оптического канала связи, £$(/) — напряженность электрического поля в раскрыве приемной линзы, ип(<)—собственные шумы приемного устройства, Мф(/)—выходной сигнал фотоприемного устройства.
263
Рис. 9.8. Функциональная модель системы связи по методу несущей
В качестве функциональных блоков выберем: передающе! устройство вместе с оптикой, математическое описание функ ционирования моделирующего его звена на основании (9.3) имеет вид E(t) = /siw(/)sincoZ (со — частота, световой несущей); оптический канал, для моделирующего звена которого из (9.2) получим £ф(<) = k$En(r,t+ ?^-) + E(t + ^^-, г)]; фотоприемнос
X X
устройство, работа которого характеризуется следующим математическим выражением: u$(t)= «л(/)+| О|£ф(/)]/г(< - т)с!т, гд h(t) — переходная характеристика выходного фильтра детектора, G — нелинейная функция детектора светового излучения, k[, Л2 — коэффициенты пропорциональности. Результирую- щая схема модели оптической системы связи, состоящая из набора перечисленных функциональных блоков, показана на рис. 9.8. При имитации управляющая программ» модели- рования для каждого момента имитационного времени £-, связанного с тактами посылок двоичного сигнала, будет ге- нерировать по заданным законам значения шумовых сос- тавляющих £п(£), ип(б) и затем поочередно передавать управ- ление подпрограммам, имитирующим работу звеньев, моделирующих функциональные блоки в соответствии с вышеприведенными выражениями,ч по результатам моделирования можно будет оценить эффективность оптической системы свя-] зи и требуемые характеристики ее отдельных блоков.
11ри моделировании радиосистем по методу комплексной огибающей фазовые переменные представляются в виде их комплексных огибающих а модели функциональных
блоков представляются эквивалентными низкочастотными и не всегда физически реализуемыми звеньями, выполняющими над огибающей радиосигнала ту же функцию, что и исходное звено над полным радиосигналом. Для моделирования методом комплексной огибающей разработан ряд методов описания функциональных блоков и фазовых переменны? Применительно к задачам радиотехники наиболее рационален метод, разработанный Евтяновым на основе метода медление
264
меняющихся амплитуд Ван-дер-Поля. При использовании >гого метода любое динамическое звено может быть описано шфференциальным уравнением относительно комплексных медленно изменяющихся вместе с информационным процессом амплитуд U(t). В случае линейного звена, как и в методе несущей, возможно использование переходных, импульсных или передаточных характеристик, записанных для комплексных огибающих. Связь между, например, переходными характеристиками функциональных блоков по методу несущей //(/) и по методу комплексной огибающей hKo(t) определяется соотношением
^ко(^) = Л(/)ехр(-/Дсо/),
। дс Дю = Ц)Гр-®о. <оо — частота несущей, соГр — верхняя
гмничная частота спектра радиосигнала.
При моделировании по методу комплексной огибающей широко используются спектральные методы. В соответствии с Теоремой смещения преобразования Фурь^, если для переходной характеристики по методу несущей h(t) передаточная функция звена равна /((/со) (они, как известно, связаны преобразованием Фурье), для переходной характеристики по методу комплексной огибающей Лко(() передаточная функция будет равна
/C(jQ) = Л] jcoo + £2].
Два последних выражения свидетельствуют, что уравнению, характеризующему функциональный блок по методу несущей в виде стационарного линейного радиозвена рис. 9.7, и, всегда соответствует уравнение модели эквивалентного олока для комплексной огибающей и нахождение его не составляет трудностей. Большую сложность вызывает отыскание уравнений для нелинейных звеньев, но и здесь разработаны эффективные методы для их определения [25].
При моделировании радиосистем по методу комплексной шибающей дискреты продвижения имитационного времени ш раничиваются шириной спектра информационного сигнала, а так как информационные процессы протекают во много раз медленнее несущей, то этот метод допускает существенно (юльшую скорость имитации, чем предыдущий, хотя и не столь универсален. Примеры математических моделей функциональных блоков радиосистем по методам несущей и комплексной огибающей приведены в [1, 17, 25].
При моделировании по методу статистических экви-||.ментов реальные случайные процессы на входах — выходах функциональных блоков заменяются другими процессами, имеющими такие же статистические характеристики. Таким
265
образом, статистический эквивалент функционального блока обеспечивает лишь в статистическом смысле с точностью до выбранных статистических характеристик адекватность выходного сигнала реальному процессу.
В настоящее время известно много методов получения статистических эквивалентов моделей функциональных блоков радиосистем: статистической линеаризации, генерации, фильтрации информационного параметра и др., но наибольшее распространение получили различные варианты метода статистической линеаризации.
При использовании этого метода нелинейные динамические звенья, моделирующие функциональные блоки радиосистем, заменяются линейными, безынерционными, обеспечивающими совпадение заданных статистических характеристик входной и выходной фазовых переменных. Например, можно потребовать, чтобы выполнялось равенство математических ожиданий и корреляционных функций и, как уледствце, дисперсий с реальными процессами: иъыг[1)= П2л(0> Мб. ^)=Пл(б»
б?)> гвь.х(6, /2) = Г2л(Л. б>) (см. рис. 9.7, г).
После замены нелинейного звена по методу статистической линеаризации математические ожидания и коореляционные функции* входной и выходной фазовых переменных модели функционального блока оказываются связанными линейно через коэффициенты линеаризации кц.
П2л(П = к\jf/|Л(0 + k\2r\n(t), ^2л(/) = k2\U |л(0 + &22Лл(0-
С математической точки зрения метод статистической линеаризации эквивалентен разложению плотности вероятности реальной выходной переменной в ряд по моментам распределения входной переменной и усечения разложения линейными членами ряда.
Метод гармонической статистическо!! линеаризации пред ставляет развитие этого метода на функциональные блоки с колебательными процессами на .входе и выходе. Однако нахождение коэффициентов линеаризации здесь значительно более затруднено, так как в ряде случаев, например при преобразовании частоты или детектировании, сигнал на выходе блока будет содержать составляющие, отсутствующие зо входном сигнале. В этом случае для получения линейности звена, моделирующего функциональный блок, приходится вводить обратные связи либо включать ряд звеньев параллельно, причем каждое звено передает или генерирует свою статистическую составляющую выходной переменной. Для нахождения коэффициентов линеаризации здесь приходится использовать метод контурных интегралов.
266
I1 и с. 9.9. Система ФАП и ее модель по методу информационного параметра
Метод статистических эквивалентов обеспечивает большую < корость моделирования радиосистем при случайных воздействиях, однако он менее информативен, чем оба предыдущих метода, а модели будут адекватны реальным функциональным блокам только в сравнительно небольшом диапазоне изменения фазовых переменных.
Метод информационного параметра широко применяется 1ЛЯ построения математических моделей систем и функциональных блоков следящего типа, в частности радиоустройств слежения за параметрами движения цели, систем радиоуправления и наведения, систем автоматического слежения за час-югой и фазой, оптимальных демодуляторов сигналов с угло-|«н"( модуляцией и в других случаях. В таких системах информационными параметрами, ради слежения за которыми и <<ндается система, могут являться частота, фаза колебания, наложение цели в пространстве и т.п., а измеренным параметрам является оценка отслеживаемого параметра.
Сущность информационного метода заключается в замене реального входного воздействия в системе новым входным на {действием в виде информационного параметра, т е. ос^ ванной информационной характеристики системы. Этот подход шнволяет моделировать только преобразование информации в • нстеме и, следовательно, работать с низкочастотными моделями функциональных блоков, моделируя только преобра-и>вание информации в них. В результате появляется возможность увеличить дискрет имитационного времени, а значит, и ускорить процесс моделирования. Так, на рис. 9.9, а наказана схема реальной системы фазовой автоподстройки частоты, находящейся под воздействием сигнала с переменной фазой = t/sin<p(/) и шума а на рис. 9.9, б
приведена модель этой системы по методу информационного параметра, когда на вход системы подается сигнал рассогласования фаз между входными колебаниями и колебаниями ‘ выхода управляемого генератора Дер.
267
В настоящее время разработано достаточно большое число пакетов программ и специализированных систем для функционального моделирования больших систем набором функциональных блоков из области радиоэлектроники, из которых следует отметить ДИС, СИМУЛУ, МИК и др.
Вопросы и упражнения для самопроверки
1. Какие этапы можно выделить в процессе имитационного моделировании больших систем?
2. Как влияет на каждый из этапов процесса имитационного моделирования метод построения дискретной имитационной модели?
3. Опишите работу РЛС при случайном потоке целей в секторе обзора в терминах событийного подхода, подходов сканированием активностей и процессоржг ориентированного.
4. Приведите пример моделей компонентов радиосиртем, когда окончание действия заранее не планируется, а основывается на состоянии системы.
5. Опишите модель цифрового дешифратора импульсно-кодового сигнала в системе опознавания «свой — чужой» в виде кусочно-линейного агрегата.
6. В многопользовательской вычислительной системе реального времени происходит активизация задач пользователями по случайному закону. Если процессор занят решением другой задачи, то очередная активизированная задача ставится и очередь на решение со своим приоритетом. Если количество задач, ожидающих решения, превышает некоторое число, то система не допускает активизации задачи. Время решения каждой задачи процессором также распределено по случайному закону.
Разработайте имитационную модель вычислительной системы, основанную пи транзактиом подходе.
Глава 10
УЧЕТ ВЛИЯНИЯ РАЗБРОСА ПАРАМЕТРОВ ЭЛЕМЕНТОВ НА ХАРАКТЕРИСТИКИ РЭС
§10.1. ФОРМУЛИРОВКА ЗАДАЧ УЧЕТА ВЛИЯНИЯ РАЗБРОСА ПАРАМЕТРОВ
Ни один параметр элемента РЭС не может быть реализован со значением, в точности равным номинальному. На отклонения будут влиять технологические погрешности изготовления самого элемента, разброс параметров материалов, из которых <>п выполнен, а также условия эксплуатации (старение >лемента, температура, влажность и т.п.).
Следовательно, параметры элементов РЭС есть случайные величины с определенными статистическими характеристиками. Наличие разброса параметров элементов неминуемо приводит к появлению разброса внешних характеристик РЭС, поэтому последние тоже случайные величины, но уже с неизвестными статистическими характеристиками. Конечно, найти разброс внешних характеристик можно, изготовив опытную партию разработанного компонента РЭС, экспериментально исследовав их внешние характеристики и выполнив статистическую обработку результатов измерений. Однако такой подход требует значительных затрат времени, материалов и тру-ia. а в результате компонент может оказаться непригодным к серийному выпуску.
Поэтому встает задача учета влияния разброса параметров с помощью ЭВМ при замене изготовления и испытания образцов их математическим моделированием. При этом можно ввести следующую классификацию решаемых задач.
1. Допусковый анализ — заданы структура компонента РЭС и его номинальные параметры, а также допуски на них. I ребуется найти возникающие допуски внешних характеристик компонента. Данная задача решается, когда устройство полностью спроектировано и необходимо лишь проанализировать влияние разброса параметров для оценки и щелия при его выпуске в серию и необходимости введения подстроечных элементов.
269
2. Допусковый синтез — заданы структура компонента РЭС и его номинальные параметры, а также допуски на внешние характеристики. Требуется найти допуски на параметры элементов. Данная задача обратна допусковому анализу и возникает, когда устройство спроектировано, но ещё- не выбраны требования на точность изготовления элементов.
3. Статистический параметрический синтез — заданы структура компонента РЭС, допустимые границы его параметров и допуски на них, а также требуемые уровни и допуски для внешних ‘характеристик. Требуется найти номинальные параметры. Данная задача возникает, когда наличие разброса параметров необходимо учесть еще на этапе проектирования компонента.
4. Статистический структурный синтез — заданы лишь требуемые уровни внешних характеристик компонента РЭС и допуски на них. Требуется найти структуру -компонента и номинальные параметры. Учитывая, что проблема структурного синтеза на ЭВМ, даже по детерминированной модели, в настоящее время решена лишь для ограниченных классов цепей, данную задачу в дальнейшем рассматривать не будем.
Наиболее наглядное решение указанных задач можно было бы получить, найдя в явном виде связь допусков на параметры с допусками на внешние характеристики.
Введем понятие функции качества F(V)—-некоторой функции, зависящей от вектора параметров V и являющейся интегральной оценкой качества всех интересующих нас внешних характеристик компонента РЭС (при этом не конкретизируя способ построения данной функции). Пусть известен также вектор номинальных значений параметров Vo. которому соответствует номинальная функция качества F(Vo). Вследствие наличия разброса конкретная реализация вектора параметров компонента отличается от номинальной jia веюгор отклонений AV, а функция качества для него есть F(Vo + AV)
Разложим данную функцию качества в многопараметрический ряд Тейлора вокруг номиналов Ро в виде
F(V0 + AV) = Vo) +1 Av + l!./=i dvi
, 1 ^F(b) 2!i=i/=i dvi8v/
(Ю.1)
АцАо+.
где Ащ, i=l, 2, .., n —компоненты вектора отклонений AV.
270
Данный ряд содержит бесконечное число членов и неприго-ien для практического решения поставленных задач. В зависимости от значений отклонений параметров можно выделить та случая:
1. Случай малых отклонений. Отклонения ДУ малы насколько, что в данном выражении можно пренебречь всеми членами ряда, кроме первых двух. Этот случай характерен в основном для пассивных схем, выполненных на дискретных •лементах или по гибридной технологии. Как будет показано ниже, основным методом решения задач учета разброса параметров элементов при этом будет являться метод коэффициен-|ов чувствительности.
2. Случай больших отклонений. Компоненты вектора ДУ юстаточно велики, и пренебрежение высшими членами ряда невозможно. Такие разбросы характерны для полупроводниковых приборов, и для их учета необходимо использовать мето-ия статистического моделирования.
Необходимо отметить, что граница между «малым» и большим» отклонением достаточно условна и определяется не юлько собственно вектором ДУ, но и значениями частных производных функции качества, т.е. чувствительностью цепи к и (менению параметров. Поэтому отклонение в единицы процентов для элемента, входящего в высокодобротный колеба-к-льный контур, уже может считаться «большим». В среднем же за границу этих двух случаев принимают разброс порядка 5%.
Рассмотрим более подробно пути решения указанных задач.
§ 10.2. МЕТОД КОЭФФИЦИЕНТОВ ЧУВСТВИТЕЛЬНОСТИ
Итак, пусть разбросы параметров элементов достаточно м злы и можно пренебречь высшими, членами ряда Тейлора. 1 <>гда будет справедливо приближенное равенство
— — — п 8F(V о)
F(V0 + ДУ) « Г(У0) + Е—Ш Av, ‘=i 8vi
или _ (Ю.2)
ДР(ДУ)= Л(У0+ДУ) -Г(У0) = £^§^Дц.
i=l OV,
Это выражение и представляет собой искомую связь раз-ороса параметров с разбросом внешних характеристик
Входящие в (10.2) частные производные функции качества по и раметрам называются коэффициентами чувствительности
«,= dF(Vo)/dVi, г = 1, 2, ..., п.
271
Отметим, что абсолютное значение коэффициента чувствительности а, характеризует степень влияния отклонения параметра Vi на функцию качества, а знак — «направление» влияния (при а,>0 функция качества с увеличением Vi возрастает, а при а, < 0 — уменьшается).
Однако введенные таким образом коэффициенты чувствительности at обладают существенным недостатком — их нельзя сравнивать для различных параметров, ибо значение коэффициента зависит от значения самого параметра. Поэтому для целей сопоставления влияния различных параметров (например, при выделении элементов подстройки) пользуются нормированными коэффициентами чувствительности
bi_SF(V0)/ F(V0) _а dvt / о0; ‘ F(Vo) ’
Если функция F(V) может быть получена аналитически, то и коэффициенты также можно вычислить непосредственно. В противном случае необходимо будет воспользоваться методами численного дифференцирования (см. § 13.2). При это_м потребуется многократное _вычисление функции F(V) — один раз для определения F(Vo) и п раз для определения ее значения при отклоненных параметрах vt (при условии использования односторонних разностей) или 2п раз при двусторонних разностях.
Рассмотренный способ вычисления коэффициентов чувствительности при помощи численного дифференцирования получил название метода приращений. Его основным достоинством является универсальность, а недостатками — значительные вычислительные затраты и невысокая точность. В САПР РЭС применяются еще несколько методов определения коэффициентов чувствительности — метод присоединенной схемы, вариационный метод и т.п., однако они предназначены для работы лишь с моделями устройства в виде системы ОДУ. Следовательно, эти методы обладают ограниченными возможностями (хотя и обеспечивают большую точность и малые вычислительные затраты), поэтому здесь подробно не рассматриваются.
Пусть в итоге коэффициенты щ, i = 1, 2, ..., п, определены. Тогда формула (10.2) приведется к виду
ДЕ(ДЦ) = Дие = Хс , (10.3)
i=i 1=1
где с, — частные отклонения, характеризующие вклад i-ro параметра в изменение функции качества..
272
Применим найденные коэффициенты для решения задач чпнускового анализа и синтеза.
Допусковый анализ. Подставляя в выражение (10.3) в качестве отклонения Лгу допуск на соответствующий параметр Ли, = (±Е/), находим допуск на функцию качества Ер в виде = ±«,.(±е,). (10.4)
г=|
В зависимости от способа выбора знака перед допуском е( щиможны два частных случая:
1. «Наихудший случай». Знак перед допуском принимается шишаковым со знаком соответствующего коэффициента Чувствительности Ер — Ё|п,|е,, т.е. направление отклонений 1=1
Параметров выбирается таким, чтобы Ер имела максимальное значение. Такая оценка является граничной и, следовательно, излишне жесткой.
2. «Случай граничных пар». Необходимо вычислить гпьшение Ер при всех возможных комбинациях знаков L,впусков с/ (для этого потребуется выполнить вычисление Ер раз; при не слишком большом числе параметров эта La чача вполне реальна, ибо собственно коэффициенты а, /ребуется определять лишь однажды), а затем найти, к примеру, математическое ожидание Ер, его дисперсию и т.п.
Важной особенностью этих способов допускового анализа является то, что они не требуют задания статистических характеристик параметров устройства, а используют лишь информацию о величине допуска.
Допусковый синтез. Формула (10.3) не обеспечивает воз-мп/кности непосредственного решения задачи допускового син-к- /а, ибо приводит к одному уравнению с п неизвестными. • ледовательно, необходимы дополнительные условия. В зави-11/мости от их определения различают несколько методов син-II' ш.
Метод равных отклонений. Принимаем допуски на все параметры равными, т.е. £, = 8 = const, i=l, 2, ..., п.
Тогда (10.4) преобразуется к виду £ г = е £|а,|, откуда /==1
(.лгдует тривиальное решение задачи допускового синтеза: • Ел/
/=|
Подобно «наихудшему случаю» при допусковом анализе, 1Л1ШЫЙ метод дает слишком жесткие ограничения на разброс параметров, ибо ориентируется на наиболее сильно влияющие •лементы.
273
Этот метод можно несколько усовершенствовать. Ориентируясь на коэффициенты чувствительности, разобьем все параметры на две группы: П] «сильновлияющих» и и2 = п—п\ «слабовлияющих» — и зададимся допустимым относительным вкладом каждой группы в полное отклонение функции качества (например, соответственно k\ и k%, причем «i + fe2=l). Тогда и допуск для каждой группы также получится свой:
Ei = ,
Ml
е2 = (1—£i)£f/ a,I.
Варьируя величиной k\, можно итеративно подобрать приемлемое соотношение допусков ej и е2. Естественно, возможно разбиение и на большее число групп.
Метод равных влияний. Здесь равным для всех параметров принимается не допуск е, а частное отклонение с, = |(?(|ei = с = const, i==l, 2, п.
Тогда из (10.4) определяем с=Ер/п, откуда искомое выра* жеиие для допуска на параметр Vt находим как Ei = с/|а,| =Е f/(n|d)-
Этот метод дает значение Е/, уже гораздо более близкое к реальным условиям, но и оно еще далеко от оптимального. При необходимости в этом методе также можно воспользоваться разбиением параметров на группы с различной степенью влияния на функцию качества.
Другим способом получения более реалистичных требований на допуски элементов является учет статистического характера параметров. Так, если предположить, что все параметры распределены внутри интервала частного отклонения с,= |n,|£i по равномерному закону, то дисперсия этого распределения будет равна <т2(-= |о,|2е2(/3, а дисперсия функции качества найдется как <т2/.= .
Mi
Предположим далее, что допускается некоторая вероятность брака (т.е. невыполнения условия допускового синтеза) Рб- Тогда из интеграла вероятности можно найти соответствующие допустимые значения £f/6f- Так. при Рб = 0,003 получим Ер/ср = 3, а при Рб = 0,05 имеем £ г/аг = 2. Т^к к^к частные отклонения для всех параметров равны, то <5 1 = ср1п, откуда окончательно получаем е, = л/ЗаДРБ)/(л/п|с1,|). Можно показать, что полученный таким образом допуск существенно больше, чем найденный ранее. Предположение о нормальном законе распределения внутри частного отклонения вместо равномерного дополнительно смягчает требования к допускам.
274
Оптимизационные методы. Наиболее универсальным спо-гобом осуществления допускового синтеза с применением коэффициентов чувствительности является способ, основанный па поиске условного экстремума (минимума_или максимума) некоторой вспомогательной функции R(X), называемой целевой функцией (методы поиска экстремума будут рассмотрены подробно в гл. 11 и 12). При этом целевая функция есть функция от допусков на параметры, в качестве условия ограничения будет выступать выражение (10.4), а сам поиск будет производиться не в пространстве параметров Уе IVmin. VmaxL 3 В Пространстве допусков £ G [£min, €П1ах].
Простейшим случаем является случай^ максимального <уммарного допуска, когда принимается /?(Х )=££,., и задача спускового синтеза запишется в виде max{££,}, i = 1, 2, и; /=1
£ |a,|et =Е г-
<=1
Как сама целевая функция, так и ограничения являются линейными функциями относительно допусков е,. Следовательно, ось можно применить методы решения задачи линейного программирования (см. гл. 11).
Более сложным случаем является формирование целевой функции не непосредственно по допускам £„ а через некоторые ывисящие от допусков вспомогательные функции. Так, например, целью допускового синтеза можно поставить минимизацию । кшмости изготовления радиоэлектронного изделия в целом. При этом необходимо задать функциональную связь стоимости реализации каждого параметра s(- с его допуском е,: s(-=/((е<), I -- 1, 2, ..., п, и записать задачу допускового синтеза в виде min{£ /,{£,)}, /=|
£ We<=£r-<=|
В зависимости от вида функции ф (е<) данная формулировка приводит к задаче линейного (гл. 11) или нелинейного (гл. 12) программирования.
Таким образом, в случае малых отклонений с помощью коэффициентов чувствительности можно решить задачи допускового анализа и синтеза.
275
§ 10.3. СТАТИСТИЧЕСКИЕ МЕТОДЫ УЧЕТА РАЗБРОСА ПАРАМЕТРОВ
В случае больших разбросов параметров пренебречь высшими членами ряда Тейлора не удается и для решения задач допускового анализа и синтеза необходимо использовать методы статистического моделирования, наиболее известным из которых является метод Монте-Карло. По своей сути этот метод аналогичен натурному макетированию, однако вместо изготовления макета из элементов с разбросом используется генерация вектора случайных параметров с заданными статистическими характеристиками (средним, дисперсией и т.п.), а вместо измерения внешних характеристик макета — их вычисление с помощью алгоритмов моделирования. Несомненным преимуществом метода Монте-Карло перед методом коэффициентом чувствительности (вынуждающим зачастую использовать его и в случае не очень больших разбросов параметров) является возможность учета любых статистических законов распределения параметров, любой функциональной (в том числе и корреляционной) связи параметров, а также любых дополнительных условий-ограничений на параметры компонента РЭС и его внешние характеристики.
Рассмотрим применение метода Монте-Карло для допускового анализа и синтеза.
Допусковый анализ. Метод Монте-Карло для решения задачи допускового анализа функционирует следующим образом; ,
1 Выполняется генерация случайной реализации вектор» параметров компонента РЭС И . При этом каждая компонента вектора 1=1, 2, ..., п, генерируется с соответст-1 вующими статистическими характеристиками (закон распре-' деления, математическое ожидание, дисперсия, корреляция и T.n.)J
2. Проводится моделирование компонента РЭС с данным вектором параметров и определяется реализация внешних характеристик H(k\
3. По полученным внешним характеристикам вычисляется реализация функции качества
4. Заданное число раз повторяются шаги 1...3. Число повторений М зависит от требуемой точности статистического) моделирования.
Для ориентировочной оценки необходимого значения М можно воспользоваться формулой М> 1/[Д2( 1-Рд)], где Д— требуемая относительная погрешность, Рл — доверительная вероятность.
276
Из анализа данного выражения видно, что метод Монте-Карло при высокой точности требует очень большого объема испытаний (до 109 и более), однако уже при 1000 испытаниях обеспечивается точность порядка 1%, что вполне достаточно 1ля практики.
Возможно применение и другого критерия завершения испытаний. Для этого на каждом испытании оценивают ккущую дисперсию функции качества и процесс моделирования прекращается, когда относительное изменение шсперсии по сравнению с предыдущим испытанием окажется меньше заданной точности Ад, т.е. когда выполнится < AD, где i — номер испытания.
В любом случае обычно число повторений требуется порядка 500... 1000.
5. По найденной совокупности реализаций внешних характеристик H(k\ k=l, 2, ..., М, выполняется их статис-гпческая обработка. Например, определяются математическое ожидание, дисперсия, их доверительные интервалы, границы нолей допусков и т.д.
6. По полученной совокупности реализаций функции качества /н‘\ k=l, 2, ..., М, строятся гистограммы распределения.
Статистическая обработка внешних характеристик особенностей не имеет. На построении же гистограмм необходимо остановиться особо. Оно состоит в следующем:
В результате статистического моделировайия находится совокупность значений функции качества Р, Л=1, 2, .... М.
2. Вычисляются минимальное T^min = min{F(fe)} и максимальное Fmax = max{F(A:)} значения функции качества.
3. Интервал Fmin-.-Z'max разбивается на заданное число подынтервалов с границами F\, Fz,..., Fl + i, где L — количество о।счетов гистограммы.
4. Определяется Li—число попаданий отсчетов функции качества в каждый из подынтервалов. Это можно сделать 'Шим из двух способов:
— границы каждого подынтервала известны, ибо F\ = Fmin, //ci ^max> (Zmax — Тогда значе-
ние каждой реализации Рк’ последовательно сравнивается с |раницами каждого подынтервала и находится тот подын-|срвал, для которого выполняется условие Ft < < Fi + |. В
среднем для такого метода потребно около kL операций 1 равнения.
— номер подынтервала i, в который попадает отсчет функции качества F*k\ вычисляется из соотношения i=int{( F^k}~Fmi„)L/(Fmm-Fmiri)}.
277
Данный способ, без сомнения, более экономичен по времени, • 5. Разделив число попаданий отсчетов функции качества в данный i-й подынтервал L, на общее количество отсчетов L ht = Lj/L и сопоставив полученному значению Л, высоту некоторого прямоугольника с основанием на интервале [Fj...Fl+ J, получаем гистограмму плотности вероятности распределения отсчетов F<k\ Используя ее, можно оценить закон распределения функции качества.
6. Находим pi = £ hj, i = 1, 2, ..., L, и, приняв pt за
/=|
высоту прямоугольника (аналогично п. 5), строим гистограмму вероятности реализации. Пользуясь ею, получаем следующую информацию:
— отложив на гистограмме значения функции качества, соответствующие номинальным параметрам, можно узнать, какой процент изготовленных компонентов РЭС буцет иметь функцию качества хуже номинальной;-
— отложив некоторые классификационные значения функции качества (например, соответствующие границам между группами компонентов), получаем процент выхода компонентов в каждой группе и выход в брак.
При необходимости непосредственно по результатам работы алгоритма Монте-Карло возможно вычислить и коэффициенты чувствительности п,-, i = 1, 2, ..., п. В отличие от определенных в § 10.2 эти коэффициенты будут учитывать реальные законы распределения параметров, а также при необходимости и наличие корреляционной связи между ними Порядок их определения состоит в следующем:
1. Оцениваются коэффициенты корреляции функции ка-| чества с каждым из параметров по формуле
G = (Е F*fc}v k=l
где М — число статистических испытаний; тр и ср—определенные по результатам статистического моделирования 'математичес кое ожидание и дисперсия функции качества; те,- и ст,-—заданные математическое ожидание и дисперсия t-ro параметра.
2. Решается система п линейных уравнений Dp = R, где D — матрица коэффициентов корреляции значений парамет-ров устройства; R — матрица коэффициентов корреляции функции качества и параметров, определенных на шаге 1; р—-искомый вектор вспомогательных коэффициентов.
278
Очевидно, что в случае некоррелированности параметров устройства имеем ц = И и решение системы не требуется.
3. Вычисляются абсолютные и относительные коэффициен-н>1 чувствительности:
Ui =
bi = aimF/ т,.
Допусковый синтез. Решить задачу допускового синтеза методом Монте-Карло можно, к сожалению, лишь итерационно При этом решение будет следующим:
1. Задаются некоторые исходные разбросы параметров элементов.
2. Выполняются шаги 1...6 метода Монте-Карло для допусконого анализа.
3. Результаты допускового анализа сравниваются с критериями допускового синтеза. Вид этих критериев может быть р.инообразен, например:
— критерии по статистике внешних характеристик: математическое ожидание или границы поля допусков должны быть не ниже (не выше) заданного уровня; дисперсия или ширина поля допусков — не больше заданных и т.п.
— критерии по статистике функции качества: процент выхода компонентов с функцией качества не выше (не ниже) некоторого уровня не менее заданного значения и т.д
4. Если результат статистического моделирования признан н< удовлетворительным (критерии синтеза не выполняются), то разбросы некоторых параметров (каких именно, можно оцепить, например, по максимальным коэффициентам чувстви-нльности) увеличиваются и алгоритм повторяется начиная с и 2. Если же критерии выполнены, то текущие разбросы параметров и принимаются за результат допускового синтеза.
§10.4. СТАТИСТИЧЕСКИЙ СИНТЕЗ КОМПОНЕНТОВ РЭС
Согласно введенной в § 10.1 классификации, задачей ста-। истического синтеза является отыскание таких номинальных шачений параметров элементов, которые при заданных ста-।истических характеристиках этих параметров обеспечивали ом получение оптимальных (наилучших в некотором смысле) ।. мистических оценок внешних характеристик компонента I1 >С. В качестве критерия оптимальности обычно использует-< я один из трех основных вариантов:
— процент выхода годных схем (отношение числа схем, 1ля которых выполняются все условия работоспособности, к нищему числу изготовленных схем);
279
— процент выхода взаимозаменяемых схем (отличается от предыдущего тем, что проверяется не только работоспособность данного экземпляра схемы, но и условия его стыковки по внешним характеристикам с соседними узлами РЭС);
— надежность (вероятность того, что за заданное время эксплуатации внешние характеристики схемы не выйдут за границы условий работоспособности и, если требуется, условий стыковки).
Первый критерий является базовым для остальных, поэто-’ му дальнейшее рассмотрение проблемы будем вести применительно к максимизации процента выхода годных схем.
В зависимости от условий производства и эксплуатации возможны два подхода к решению задачи статистического синтеза:
— в разрабатываемом устройстве нет подстроечных эле ментов;
— в разрабатываемом устройстве есть некоторое число подстроечных элементов.
Очевидно, что обеспечение 100 %-ной заменяемости компонентов без подстройки устройства возможно лишь за счет худ ших (в среднем) характеристик устройства, чем при втором подходе; следовательно, и применять первый подход нужно! лишь в исключительных случаях.
В свою очередь, проектирование устройства с элементами подстройки может выполняться также двумя способами:
— последовательный способ — сначала выполняется параметрический синтез устройства без разброса параметров, за-1 тем выделяются подстроечные элементы и, наконец, отыски-1 ваются границы варьирования подстраиваемых параметров, обеспечивающих заданную настройку при наличии разброса параметров остальных элементов;
— параллельный способ — поиск границ варьирования подстраиваемых параметров выполняется одновременно с поиском оптимальных номинальных статистически заданных па-| раметров.
По возрастанию степени сложности решения указанных за-1 дач их можно расположить в следующем порядке:
1) последовательный способ проектирования подстраиваемых схем;
2) проектирование схем без элементов подстройки;
3) параллельный способ проектирования подстраиваемых схем.
Как указано выше, критерием оптимальности проектирования (функцией качества) является процент выхода годных схем
280
В отличие от параметрического синтеза устройства с детерминированными параметрами, когда для определения функции ачества требуется, как правило, однократное моделирование устройства, при статистической оптимизации функция качества может быть найдена лишь в результате допускового анализа (методом коэффициентов чувствительности или статистическим моделированием). Следовательно, вычислительные затраты при ri 1тистическом синтезе существенно больше, чем при детерминированном, причем тем в большей степени, чем больше ста-гистических параметров будет учитываться. Собственно же поиск экстремума функции качества может производиться теми же методами, что и для детерминированной задачи.
Рассмотрим алгоритмы решения поставленных задач более подробно.
Последовательный способ проектирования подстраиваемых схем. Пусть выполнен параметрический синтез устройства без учета разброса параметров и выделены элементы подстройки, ’(ля определенности будем считать, что всего параметров п, н< них первые /г, параметров — неподстраиваемые, а параметры czi+l, ..., п— подстраиваемые.
В случае малых отклонений поиск границ подстройки можно выполнить с использованием коэффициентов чувствительно-< । и. Для этого:
— вычисляем отклонение функции качества вследствие p.i <броса параметров неподстраиваемых элементов для наихудшего случая: ДЕр=£ |щ|_
/=1
— это отклонение должно быть скомпенсировано перестройкой подстраиваемых параметров на некоторую величину До, относительно номинального значения. Следовательно, должно выполняться соотношение ДЕ/? = £ |а,|Дц, из которого и +!
шобходимо определить значения Дг\. Эта задача подобна ^пусковому синтезу, но не относительно допусков е(, а в пространстве Дщ. Следовательно, и решена она может быть о/шим из рассмотренных ранее способов.
В случае же больших отклонений найти границы подстройки возможно, применяя алгоритмы статистического моделирования.
Простейшим из этих алгоритмов синтеза элементов подстройки является алгоритм, основанный на совместном применении метода Монте-Карло и методов параметрического синтеза ш'терминированной модели компонента РЭС. Суть алгоритма । а нова:
281
1. Выполняется параметрический синтез компонента РЭС без учета разброса параметров по критерию оптимизации поведения внешних характеристик. Найденные параметры — суть их номинальные значения.
2. Определяются коэффициенты чувствительности и выделяются подстраиваемые параметры (при этом следует учитывать не только собственно значения коэффициентов, но и практическую возможность подстройки того или иного элемента: при этом общее число подстроечных элементов должно быть малым).
3. В соответствии с методом Монте-Карло выполняется генерация реализации вектора параметров неперестраиваемых элементов, и эти параметры отмечаютс: как неварьируемые.
4. Выполняется параметрический синтез компонента РЭС в пространстве только перестраиваемых параметров по прежнему критерию. Оптимальные значении перестраиваемых параметров запоминаются.
Временные затраты иа выполнение данного шага не слишком велики по двум причинам:
— малое число варьируемых параметров:
— наличие хорошего начального приближения, в качестве которого принимаются обычно номинальные,значения подстраиваемых параметров, полученные в п. 1.
Вследствие этого можно применять "росгые методы синтеза (обычно градиентные), описанные в гл. 12.
5. Заданное число раз повторяются шаги 3 и 4.
6. По полученной (см. п. 4) совокупности оптимальных перестраиваемых параметров определяются требуемые границы их перестройки min{i?i) и rrtax{oj. -
В случае неудовлетворительности результата (например, границы перестройки1 оказались слишком широкими) необходимо изменить выбор базиса элементом подстройки и повторить алгоритм с п. 3.
Проектирование схем без элементов подстройки. Подобно детерминированным методам синтеза, алгоритмы статистичес-| кого синтеза можно разделить на регулярные (не использую» щие производные функции качества, использующие голькр первые производные, использующие высшие производные и т.д.) и случайные (слепого поиска и с самообучением). Рассмот рим кратко, как функционируют алгоритмы статистического синтеза различной сложности.
Регулярные алгоритмы, не использующие производным Простейшим из алгоритмов этой группы является следующий:.
I. Задаются начальные параметры устройства, их статистические характеристики. а также совокупность условий работоспособности.
2. Выполняется допусковый анализ методом Монте-Карло, при этом запоминаются реализации вектора параметров, при которых выполняются вг* условия работоспособности. Если условия работоспособности не выполнились им при одной случайной реализации вектора параметров, то необходимо изменит начальные значения параметров и повторить п. 2.
282
3. Вычисляется математическое ожидание каждого параметра по совокупности шпомненных векторов и текущее значение параметра принимает значение математического ожидания.
4. Повторяются п. 2 и 3 до тех пор, пока процент выхода годных схем не достигнет максимума. На этом синтез заканчивается.
Необходимо отметить важные особенности данного алгоритма:
— вектор, проходящий через два последовательных приближения вектора параметров, является статистическим градиентом функции качества и совпадает с истинным, если число испытаний бесконечно, а параметры некоррелированы и распределены по нормальному закону. Следовательно, достоинством этого алгоритма является определение градиента оез вычисления частных производных функции качества;
— в том случае, когда область разброса параметров существенно меньше области работоспособности, найденное данным алгоритмом решение не будет оптимальным, ибо область разброса расположится на краю, а не в центре области работоспособности. Поэтому, если в процессе синтеза процент выхода приблизился к 100 %, необходимо искусственно увеличить область разброса (пропорционально по всем параметрам) и продолжить поиск. По окончании процесса разброс параметров снова устанавливается равным исходному.
Регулярные алгоритмы, использующие производные функции качества. Для функционирования этих алгоритмов необходимо вычисление частных производных функции качества. Конечно, подобно детерминированному случаю, эти производные можно найти численно, задавая последовательно приращение каждому из параметров. Однако, поскольку в данном случае шачение функции качества находится как результат допуско-ного анализа методом Монте-Карло, такое определение производных потребовало бы чрезмерных вычислительных затрат
Известны, однако, способы определения производных ста-шстической функции качества — процента выхода годных схем по результатам однократного применения метода Монте-Карло.
Так, в простейшем случае некоррелированных нормально распределенных параметров первая производная может быть найдена в виде
5F(V0)_ 1
__ д. А/ >
Л4ст, /=| о,
। ш М— число испытаний, Ро< и ст,— математическое ожидание и среднеквадратичное отклонение i-ro параметра, а коэффициент К/ равен 1, если /-е испытание успешно, и равен 0, гели нет.
283
При аналогичных условиях и обозначениях вторая производная будет равна
d2E(Ko) = ' 1 vi ~ v°t
dV'dVj Mopj '=i ст,- cSj
Данные выражения дают возможность использовать обычные регулярные алгоритмы (градиентные, Ньютона и т.п.) для поиска экстремума статистической функции качества.
Алгоритмы случайного поиска. Наиболее прост в реализации метод слепого поиска экстремума статистической функции качества:
1. Задаются границы допустимых значений параметров vj e[vHi. Veil. ,= б 2« п, и их статистические характеристики
2. Генерируется случайная реализация вектора номинальных значений параметров, причем каждая компонента вектора считается распределенной по равномерному закону в диапазоне t»Hi—Овй
3. Выполняется допусковый анализ методом Моите-Карло, при этом составляющие вектора параметров .генерируются в соответствии со своими статистическими характеристиками.
4. Вычисляется текущий процент выхода годных схем и сравнивается с предыдущими. Вектор номинальных значений, при котором процент выхода максимален, запоминается.
5. Повторяются п. 2...4 заданное число раз или до тех пор. пока функция качества не достигнет некоторого граничного значения. За вектор оптимальных номиналов принимается запомненный вектор.
Недостатком данного метода является его низкое быстродействие.
Известно большое число алгоритмов случайного поиска с самообучением для нахождения экстремума детерминированной функции качества. Практически все и< них могут быть применены и для статистической оптимизаций простой заменой вычисления детерминированной функций качества на ее статистическое моделирование методом Монте-Карло. Естественно, что элементы самообучения повышают быстродействие алгоритмов по сравнению с методом слепого поиска.
Для примера рассмотрим алгоритм, основанный на комбинации метода Монте-Карло с методом искусственного отбора. Данный алгоритм характеризуется высокой вероятностью нахождения глобального экстремума функции качества в условиях сильной неопределенности по параметрам и не нуждается в задании начального приближения:
1. Задаются границы допустимых значений параметров [с>ц<. г?в(], i—1. 2.л, К
их статистические характеристики.
284
2. Текущие границы варьирования параметров принимаются равными границам допустимых значений, т.е.
v Hi “ рнй п si — г’в/. i~ 1. 2. п.
3. Все параметры проектируемого устройства разделяются на четыре группы:
1) неварьируемые детерминированные параметры. К ним относятся параметры. которые нельзя изменять в процессе синтеза и у которых разброс равен нулю пли мал по сравнению с другими параметрами. В дальнейшем они генерируются как фиксированные значения, равные номиналу;
2) неварьируемые статистические параметры. Эти параметры также не меняются, но имеют существенный разброс. Генерируются как случайные числа с за-щнными статистическими характеристиками;
3) варьируемые детерминированные параметры. В процессе синтеза будут генерироваться по равномерному закрну на интервале варьирования;
4) варьируемые статистические параметры. Будут генерироваться на интерва-III варьирования по специальному закону распределения. Математическое ожидание этого закона равно середине интервала варьирования, а вид закона зависит от отношения ширины интервала варьирования параметра к его допуску. Когда ин-к-рвал варьирования много шире допуска, закон распределения близок к равномерному. По мере уменьшения интервала варьирования закон стремится к нормальному и при равенстве интервала варьирования и допуска превращается в нормальный. Одновременно данный параметр переводится в группу неварьируемых ста-। нстических.
4. Заданное число раз выполняется генерация случайных реализаций векторов параметров устройства, при этом генерация значений параметров выполняется в кютветствии с приведенным выше алгоритмом. Для каждого вектора вычисляется и* терминированная функция качества.
5. Выделяется заданное число наилучших значений функции качества и соответствующих им векторов параметров. По этой совокупности векторов находятся новые интервалы варьирования — нижняя и верхняя границы интервала прини-м.потея равными соответственно наименьшему и наибольшему случайным значениям параметра.
6. Повторяются п. 4 и 5 заданное число раз или пока функция качества не до-। пп нет порогового значения, или пока все параметры четвертой группы не перей-IVT во вторую, а интервал варьирования параметров третьей группы не окажется v/ке технологических ограничений.
§10.5. АЛГОРИТМЫ ГЕНЕРАЦИИ СЛУЧАЙНЫХ ЧИСЕЛ С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ
При реализации метода Монте-Карло для допускового анализа и синтеза, а также алгоритмов статистической оптимизации требуется генерация последовательности случайных чисел < (аданным законом распределения. Из трех возможных спо-гибов генерации (с помощью физических датчиков, табличный и программный) б САПР РЭС применяется лишь последний, ибо первый способ не обеспечивает необходимой стабильности результата, а второй требует слишком большого объема памя
285
ти ЭВМ. Правда, полученные программным путем числа ян ляются, вообще говоря, псевдослучайными, ибо, задав конкретное число, всегда можно повторить всю последовательность. Поэтому самой важной характеристикой качества генерации случайных чисел является интервал апериодичности — длина последовательности неповторяющихся случайных чисел. Чем этот интервал больше, тем выше качество генератора.
В основе программных генераторов различных распрг делений случайных чисел. лежит генератор равномерного распределения в интервале 6 е [0,1], входящий обычно и состав стандартного программного обеспечения ЭВМ. Способы построения такого генератора можно разбить на три группы:
1. Способы усечения случайных чисел (алгоритмы Лемера).| Имеется несколько разновидностей.
Способ середины квадрата (способ Неймана). Задается исходное «-разрядное двоичное число to. Оно возводится квадрат, получается.2«-разрядное число, средние п разрядов которого принимаются за t\, и т.д. В качестве исходного желательно брать какое-либо иррациональное число. Основ ной недостаток способа — малый интервал апериодичности, не превышающий 2 .
Способ середины произведения. Здесь в качестве hobi 1 случайного числа ti+i принимаются средние п разрядов 2«-разрядного числа, являющегося произведением дву, «-разрядных предыдущих чисел ti-x и to Интервью апериодичности этого алгоритма больше, но по-прежнему (л превышает 2".
Способ усечения целого. Целое число s(- умножается ня целую константу k, из произведения выделяются « младшЯ разрядов, которые принимаются за новое «/-ц. Это значенш s(+i рассматривается как дробная часть очередного генерИ«| руемого вещественного числа /,+ j. Константа k определяете! соотношением 8р±3, где р — любое целое. В качеств#' начального значения so используется любое нечетное число. I
2. Способы с использованием специальных функций,. Наиболее часто используются линейные алгоритмы, которые и общем виде можно записать в виде
s, + 1 = [ Т. aiSi-f + &](inodn2), /=о
ti+i = Si+ \т *,
где Si — целая переменная; /, щ, k, т — некоторые целые чис ла; функция X(mod т) означает операцию нахождения дробной части частного Л/пг.
286
Способы различаются выбором преобразующих функций. Например, наиболее часто используются следующие разновидности генераторов:
— мультипликативный генератор s/ + 1 = [a-st](modra);
— смешанный генератор s/ + i = [as, + £](modm);
— генератор Фиббоначчи (аддитивный генератор) s<+i =[Sj + Si— i] (mod m).
Интервал апериодичности зависит от выбора коэффи-niii нурв a, k и^я. Так, у мультипликативного генератора при а 5 и т = 242 интервал аперидичности равен 10 , а в случае а = 513 и т = 236 — уже 2-10 .
3. Способы перемешивания. Основаны на имитации хаотического перемешивания содержимого разрядов случайного числа.
Полученное одним из рассмотренных способов равномерное распределение в диапазоне [0,1] может служить исходным для получения других законов распределения.
Так, равномерное распределение чисел в произвольном диапазоне Х/е[а, 6] получают с помощью преобразования = а + (b-a)ti.
Нормальное распределение с математическим ожиданием ///, и дисперсией сгЛ находят на основании центральной предельной теоремы, суммируя некоторое М (обычно 'll =5...10) равномерно распределенных в диапазоне [0,1] чисел п воспользовавшись выражением Xi = тх + <зх(2/M^t, -1).
/=1
Более сложные законы распределения получают способом («•ратной функции. Вид наиболее часто встречающихся в ' АПР РЭС законов распределения tp(x) и соответствующих им преобразующих функций приведен ниже.
I. Экспоненциальный закон:
tp(x) = Xexp{-X(x-/j)}, х,- = b-\п(/,)Д.
2. Закон Вейбулла:
<р(х) = m(x-y)'”“'lexp{-(x-y)m/m^}/mx,
= 1п(1-/,.) +у.
3. Закон Рэлея:
<р(х) = хехр{-х2/2сг2)}/сг2,
х, = ст
Тля генерации распределений произвольной формы (в том числе и не имеющих аналитического описания) используется । пособ, основанный на использовании гистограммы требуемого ыкопа распределения.
287
Вопросы и упражнения для самопроверки
1. Сформулируйте основные задачи учета влияния разброса параметров.
2. Выполните разложение функции качества в ряд Тейлора.
3. Когда применим метод коэффициентов чувствительности? Его применение для решения задач допускового анализа и синтеза.
4. Дайте сравнительную характеристику методов допускового синтеза с применением коэффициентов чувствительности.
5. Опишите алгоритм Монте-Карло для выполнения допускового анализа.
6. Как но результатам работы алгоритма Монте-Карло формируется гистограмма распределения?
. 7. Как по результатам работы алгоритма Монте-Карло определяются коэффициенты чувствительности?
8. Как с помощью алгоритма Монте-Карло можно решить задачу допускового синтеза?
9. Сформулируйте задачу статистического синтеза РЭС и укажите основные пути ее решения.
10. Дайте сравнительную характеристику алгоритмам статистического синтезе РЭС с элементами подстройки.
И. Дайте сравнительную характеристику алгоритмам статистического синте-" РЭС без подстраиваемых элементов.
12. Перечислите основные способы построения программных генераторов рл« личных распределений случайных чисел. Дайте их сравнительную характеристику,Я
Глава 11
ОПТИМАЛЬНОЕ ПРОЕКТИРОВАНИЕ РЭС НА ОСНОВЕ РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
§11.1. ПРИМЕРЫ СВЕДЕНИЯ ЗАДАЧИ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ РЭС К ЗАДАЧЕ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Основные идеи линейного программирования возникли во время второй мировой войны в связи с поиском оптимальных стратегий при ведении военных операций и в дальнейшем пыли использованы для решения многих задач из области управления, торговли и техники. В частности, линейное програм.-мпрование широко используется для проектирования радио->/!сктронных средств и систем, конструкций и технологических процессов производства радиоаппаратуры [26, 28].
Задачи, в которых отыскивается минимум или максимум некоторой функции, зависящей от многих переменных при наличии ограничений на эти переменные, объединяются под общим названием задачи математического программирования. Частным случаем этих задач, когда минимизируемая-(макси-мпшруемая) функция и ограничения линейно зависят от переменных, являются задачи линейного программирования. В 1ильнейшем функцию, максимум или минимум, которой необходимо найти, будем называть целевой функцией. При проек-шровании радиоэлектронных средств целевая функция будет лрактеризовать качество работы, стоимость аппаратуры либо иные характеристики, зависящие от параметров составляющих компонентов, оптимальные значения которых в результате решения задачи необходимо найти. Ограничения же, присутст-нующие в задаче, представляют систему соотношений, сужающих допустимую область изменения параметров компонентов при решении задачи оптимизации.
Таким образом, задача линейного программирования ыключается в нахождении вектора переменных V = |^i...un|T, минимизирующего линейную целевую функцию
Ач i оматизания и рос к i ирона пня радиоэлектронных средств
289
F =2_tcjvj -> min f=I
при наличии ограничений равенств:
£Z11UI + aI2v2 + ... + ainvn =Л1,
а/г|^1 + O-k2V2 + ... + ClknVn = Ak', линейных ограничений неравенств:
/>nui + bi2v2 + ... +binvn > Bi,
b2ivi + b22v2 + ... + brtlvn >Br
H общей неотрицательности элементов: u(>0, i= 1, ..., п. Значения Л,, В,, а,/, bij. Ci, где i, j = 1, ..., п, полагаются известными.
Это общий вид задачи линейного программирования, часто называемый основной задачей. В математике различают нес колько видов формулировки задачи линейного программирования: задача оптимального планирования, транспортная зада-i ча, задача о назначениях и т.д. [28]. В большинстве случаен они сводятся к основной задаче, поэтому в дальнейшем будем! рассматривать только этот вариант задачи линейного програ ммирования.
В отличие от формулировки задачи (11.1) в практически! задачах могут встречаться ограничения только равенства либя только неравенства, переменные могут принимать отрицатели пые значения, а целевая функция может максимизироваться Такое разнообразие форм записи задачи линейного программирования затрудняет разработку общих алгоритмов ее реи— ния, поэтому при решении задачи сводят к стандартной фор ме, в которой целая функция минимизируется, а все ограничс-] пня заданы в виде равенств с положительно определенны!...: переменными. Привести задачу линейного программировании к стандартной форме возможно, если использовать следующие правила [28]:
а) максимизация целевой функции F = civi + c2v2 + равносильна минимизации функции F' = -CiVi-c2v2-...-cnvn;
б) ограничение в виде неравенства b\ivt + b\2v2 +...+ binvn > /Я может быть приведено к стандартной форме в виде равенстня введением новой неотрицательной переменной n,!+i >0: /’п&Л +bi2u2+...+bi„vn-v,i+i=Bi; по аналогии ограничение-неравенстчя вида b2[Vi + b22v2 + ...+ b2nv„ < В2 приводится к стандартной форме введением переменной пп+2>0: b2iVi + 622^2+-+ ^„+2 =° В
290
। и* новая переменная v„ + 2 ^0 также неотрицательна. Введенные таким образом дополнительные переменные n„+i и vn+2 оудут входить в минимизируемую целевую функцию F с нулевыми коэффициентами, чтобы они не влияли на ее нигимальное значение;
в) если некоторая переменная по условиям исходной ыдачи может принимать любые значения, то ее можно представить в виде = vn + з-и„ + 4 с последующей подстановкой в целевую функцию и ограничения новых неотри-П1гельных переменных vn + 3 и vn + 4.
Таким образом, приведение задачи линейного программирования к стандартной форме может потребовать введения юполнительных неотрицательных переменных, увеличивающих p.i (мерность задачи. В окончательном виде стандартная форма задачи линейного программирования в матричной записи может быть представлена следующим образом:
F = СТ'/ -> min;
A:V = А; (11.2)
V > 0;
I IV С = |ci-..c„|T, V = |ui...u„|T, /1= Hi...Am|TA = [щ7]—матрица
коэффициентов в_левой части уравнений-ограничений размера iiixii, причем в V наряду с исходными переменными будут входить дополнительные, появившиеся в результате приведения задачи к стандартной форме. Коэффициенты при дополнительных переменных будут входить и в матрицу А.
Рассмотрим примеры постановки задачи линейного программирования, возникающие при проектировании радиоэлектронных устройств.
Пусть проектируется система командной радиосвязи, вклю-ч.нищая п различных видов связи (коротковолновые и ультракоротковолновые радиостанции, радиорелейные средства свя-III. спутниковая связь и т.д.). Число параллельно работающих каналов в каждом виде связи будет равно vt, i=l, ..., п. Каждый из видов связи имеет свои преимущества и недостатки при работе в различных вариантах помеховой обстановки, ра (лична и стоимость организации одного канала для каждо-|о вида связи с,.
Проектируемая система должна устойчиво работать при p.i 1личных уровнях помех в эфире и в каждом случае должна ын-спечивать вероятность правильной передачи сообщения не хуже чем pjy j = 1, ..., т.
291
Вероятность правильной передачи сообщения одним каналом каждого i-ro вида связи при /-ом варианте помеховой обстановки в эфире известна и равна рц. Вероятность того, что сообщение не будет принято абонентом при передаче его одним каналом, соответственно составит 1—рр. Если же это сообщение передается vi некоррелированными каналами, то вероятность его непередачи составит (l-pij)v‘. Поскольку по условиям задачи одно и то же сообщение должно передаваться не одним, а п видами связи, то полная вероятность, что сообщение не дойдет до абонента, в приближении статистической независимости каналов и видов связи будет равна ...{\-рп^^.
Это позволяет для т вариантов помеховой обстановки и эфире записать систему неравенств-ограничений, исходя из правильной передачи сообщения при каждом /-м уровне помех
1-( 1-/W2 -(\-ртпУ'‘>рт.
После логарифмирования и выполнения несложных математических преобразований полученная выше система нера! венств-ограничений может быть приведена к следующему виду:
bnvi.+h\2^2 + + binvn <В\',
bmlVl + bm2V2 + ... + Ь тпРп <вп,
где bij= \n(\-pij), Bj = Infl—/?/), i=\...n, j=\...m.
Последние соотношения позволяют сформулировать задачу проектирования оптимальной системы радиосвязи как задачу определения количества каналов в каждом виде связи] минимизирующего суммарную стоимость средств связи при обеспечении вероятностей передачи сообщений не хуже заданных для вариантов помеховой обстановки в эфире:
F = C[V[ + C2V2 +...+cnvn -> min;
+ bi2V2 + ... + binvn <В\',
bml^i + bm2V2 + ... + bmnVn <Bp,
Vj >0, i = l...n.
Очевидно, что эта формулировка задачи проектирования оптимальной системы радиосвязи полностью эквивалент" основной задаче линейного программирования, определяемой
292
соотношениями (11.1). Возможны и другие варианты формулировки этой задачи. Например, если в качестве коэффициентов целевой функции с, выбрать энергетические ютраты на организацию одного канала каждого i-ro вида связи, то получим задачу линейного программирования, решение которой позволит определить количество каналов в каждом виде связи, при которых при всех уровнях помех сообщение с заданной вероятностью будет передано с минимальными энергетическими затратами.
В качестве еще одного примера рассмотрим сведение к основной задаче линейного программирования задачи покрытия функциональной схемы цифрового устройства шданным набором (серией) микросхем.
Пусть имеется функциональная схема цифрового устройства, каждый элемент которой выполняет какую-нибудь логическую функцию И, ИЛИ, НЕ-И и т.д. Каждой логической функции ср,- можно в бинарное отношение сопос-ювить число kj, i=l, .... т, представляющее количество логических элементов ср,- в функциональной схеме цифрового устройства.
Задан тайже набор микросхем, ч)/-/, /=1> п> на базе которого необходимо реализовать цифровое устройство. Каждая микросхема реализует одну или несколько логических функций ср,; следовательно, каждой /-Й микросхеме можно сопоставить ряд чисел /?/,-, характеризующих, сколько и каких логических функций ср,- реализуется в микросхеме /-го типа, '(ля каждой микросхемы Нц образуют строку из п чисел, все //,, образуют матрицу Н размером тггхп.
Пусть нам известна стоимость каждой микросхемы с;-. При каких условиях задача реализации функциональной схемы цифрового устройства с помощью заданного набора микросхем мелет быть сформулирована как задача линейного программирования, минимизирующая оптимальным выбором количества микросхем каждого типа Vj стоимость цифрового устройства:
F = CjVj -> min;
/=i
h\iVi + hnV2 + ... + h\nvn > ki;
hmlVl + hm2V2 + ... + h mnPn —
Vj >0, j = l...n, i де Vj — количество микросхем /-го типа, используемых для реализации цифрового устройства, заданного функциональной г\емой.
293
Если все Cj = 1, то записанная выше задача линейного программирования представляет собой задачу минимизации числа микросхем, с помощью которых реализуется цифровое устройство.
Особенность задачи состоит в том, что искомые переменные представляют собой целые числа. В простейшем случае решение, полученное в непрерывном пространстве, может быть округлено до ближайшего большего целого, обеспечивая некоторую избыточность покрытия.
К подобным задачам могут быть сведены задачи оптимального проектирования частотно-избирательных фильтров, размещения микросхем на печатной плате, трассировки проводников в каналах и ряд других. К задачам линейного программирования сводятся и некоторые алгоритмы решения задачи нелинейного программирования с ограничениями, которые рассматриваются в последующих главах.
§11.2. СИМПЛЕКС-МЕТОД И ОСНОВНЫЕ УТВЕРЖДЕНИЯ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Нетрудно заметить, что классический метод отыскания экстремумов функции многих переменных, заключающийся и дифференцировании целевой функции по всем переменным, приравнивании нулю производных и решении полученной системы уравнений относительно оптимальных значений перемен ных, неприемлем для решения задачи линейного программи рованияД 11.2), так как функция F линейно зависит от переменных V и ее производные по всем переменным о, постоянны и нигде не обращаются в нуль.
Для решения задач линейного программирования Г. Данцигом была разработана специальная вычислительная проце дура, называемая симплекс-методом и основанная на ряде теоретических утверждений линейного программирования. Дли лучшего понимания этих утверждений и существа симплекс-метода рассмотрим геометрическую интерпретацию задачи линейного программирования и метода ее решения.
Пусть требуется минимизировать функцию
F = -Зщ-4п2 -> rnin при наличии следующих ограничений:
V! + V2 < 20;
-Vi + 4^2 20;
vi, v2 £ 0.
294
Так как целевая функция и ограничения <ависят всего лишь от твух переменных, то их можно представить в виде прямых на плоскости ViOv2- Эта графическая интерпретация мдачи показана на рис. 11.1, где определяемые прямыми ограничения показаны сплошными линиями, а линии равного уровня целевой функции— пунктирными. Стрелки на каждой граничной прямой показывают, с какой стороны прямой выполняется ограничение. Для точек внутри заштрихованной области ОАВС и на ее
Рис. 11.1. Графическая интерпретация задачи линейного программирования
границах выполняются ограничения
ыдачи. Эта область называется допустимой, а точки внутри области и на ее границах представляют собой допустимые решения задачи. Допустимых решений множество, и необходимо найти одно из них, минимизирующее целевую функ-
цию F.
Штриховыми линиями на рис. 11.1 изображены прямые /'=-Зщ-4г>2 = 0 и F" =-За 1-4^2 = _68. Эти прямые параллельны и представляют собой две линии равного уровня /' со значениями 0 и -68 соответственно. Целевая функция убывает в направлении вектора, обратного градиенту
cF
дщ dF dv2
показанному на рис. 11.1 широкой стрелкой.
Линией уровня F с наименьшим значением целевой функции, имеющей хотя бы одну общую точку с областью допустимых значений, является прямая, проходящая через точку В с координатами (12,8). Минимальное значение целевой функции равно -68. Заметим, что оптимальное решение
295
задачи достигается в вершине допустимой области, а сама область является выпуклой, причем решение соответствует строгому выполнению равенств для ограничений задачи и число переменных, не равных нулю, равно числу ограничений в задаче. Это эквивалентно равенству нулю двух добавочных переменных, которые необходимо было бы ввести в ограничения задачи для приведения ее к стандартной форме. Такие решения, в которых не равны нулю столько переменных, сколько в стандартной форме задачи ограничений-равенств, а остальные переменные равны нулю, называются опорными решениями задачи линейного программирования; они всегда соответствуют одной из вершин многоугольника ограничений. Переменные, не равные нулю, называются допустимым базисным решением задачи или просто базисом, остальные переменные — небазисными или нулевыми.
Эти выводы можно распространить и на случай многомерной задачи. В случае п переменных каждое уравнение-ограничение представляет собой плоскость в п-мерном пространстве. Фигура, образованная этими плоскостями, образует область допустимых значений переменных и называется симплексом. Для нашего частного случая двумерной задачи симплекс представляет собой многоугольник на плоскости.
Одно из основных утверждений линейного программирования показывает, что, для того чтобы задача линейного программирования имела оптимальное решение, симплекс должен быть выпуклым, т.е. допустимая область определения переменных является выпуклым множеством.
Опорные решения задачи линейного программировании соответствуют вершинам симплекса ограничений, в которых не равны нулю и положительны т переменных по числу уравне-i ний-ограничений, образующих допустимое базисное решение, и равны нулю остальные п—т переменных, образующих неба зисное решение.
Оптимальное решение задачи линейного программирования,) если оно существует, является одним из опорных решений.
Эти утверждения подтверждаются рассмотренным ранс< графическим примером. Оптимальное решение задачи было получено в одной из вершин симплекса ограничений и представляют собой одно из опорных решений.
Приведенные утверждения свидетельствуют, что при поис ке оптимального решения достаточно вычислить только все опорные решения и определить значение целевой функции и них. Однако с возрастанием числа переменных и ограничений
2!И>
>ги вычисления оказываются очень трудоемкими. Более рациональное решение обеспечивает симплекс-метод, который позволяет, отправляясь от какого-либо допустимого базисного решения, т.е. вершины симплекса, перейти к соседнему базисному решению, в котором значение целевой функции будет меньше, причем остальные варианты не вычисляются. Оптимальное решение задачи линейного программирования симп-чекс-методом получается за конечное число шагов. Рассмотрим процедуру симплекс-метода подробнее.
Работа, симплекс-метода начинается с выбора опорного решения Ко, содержащего т базисных ненулевых переменных и п-т небазисных нулевых переменных щ, /= 1, ..., п. Для упрощения записи положим, что базисные переменные представляют собой первые т переменных вектора Ко в шдаче (11.2). Так как в задаче имеется т уравнений-ограничений, то т базисных переменных V\...vm могут быть выражены через оставшиеся п-т небазисных переменных >>,„и уравнения-ограничения могут быть преобразованы <>| (11.2) к виду
ОI D | ССI, т + I + I-Ct 1, т + 2^ tn + 2 ••• ОС j«0^,
............................................. (ИЗ)
D т + 1&т + I-OCm, т + 2^ 0С?п. п^п>
। ie Di—постоянные, ос,/—преобразованные коэффициенты матр