Text
С. Э. ФРИШ и А. В. ТИМОРЕВА
КУРС
ОБЩЕЙ ФИЗИКИ
ТОМ I
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
МОЛЕКУЛЯРНАЯ ФИЗИКА
КОЛЕБАНИЯ И ВОЛНЫ
ИЗДАНИЕ ОДИННАДЦАТОЕ,
СТЕРЕОТИПНОЕ
Допущено
Министерством высшего и среднего
специального образования РСФСР
а качестве учебника для государственных
университетов
ш
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1962
530.1
Ф 90
V
ОГЛАВЛЕНИЕ
Введение
§ 1. Физика; ее содержание, связь с другими науками и с тех-
техникой 7
§ 2. Физические законы Ю
§ 3, Единицы измерения 12
ЧАСТЬ ПЕРВАЯ
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
Глава I. Кинематика
§ 4. Общие замечания . 15
§ 5. Прямолинейное равномерное движение 17
§ 6. Прямолинейное неравномерное движение . . 20
. § 7. Равнопеременное прямолинейное движение. Ускорение 22
¦ § 8. Ускорение произвольного прямолинейного движения 25
§ 9. Скорость и ускорение как векторы 26
§ 10. Криволинейное движение 29
§ 11. Ускорение при криволинейном движении 32
§V 12. Кинематика твердого тела. Угловые скорость и ускорение . . 37
§ 13. Угловая скорость как вектор 41
Глава 11. Динамика
§ 14. Первый закон Ньютона 44
§¦¦15. Второй закон Ньютона. Сила и масса 46
V § 16. Силы трения , 49
- §у17. Количество движения. Импульс силы 52
-¦•§ 18. Единицы силы и массы. Примеры 53
••¦ § 19. Механический принцип относительности 53
§,/20. Третий закон Ньютона. Сохранение количества движения ... 59
§ 21. Силы, действующие при криволинейном движении . , 64
§ 22. Ускоренные системы. Инерционные силы . 67
' -§/23. Зависимость силы тяжести от широты местности 71
§ 24. Силы Кориолиса 73
Глава 111. Работа и энергия
^§ 25. Работа и мощность 78
V§ 26:> Кинетическая энергия механической системы 84
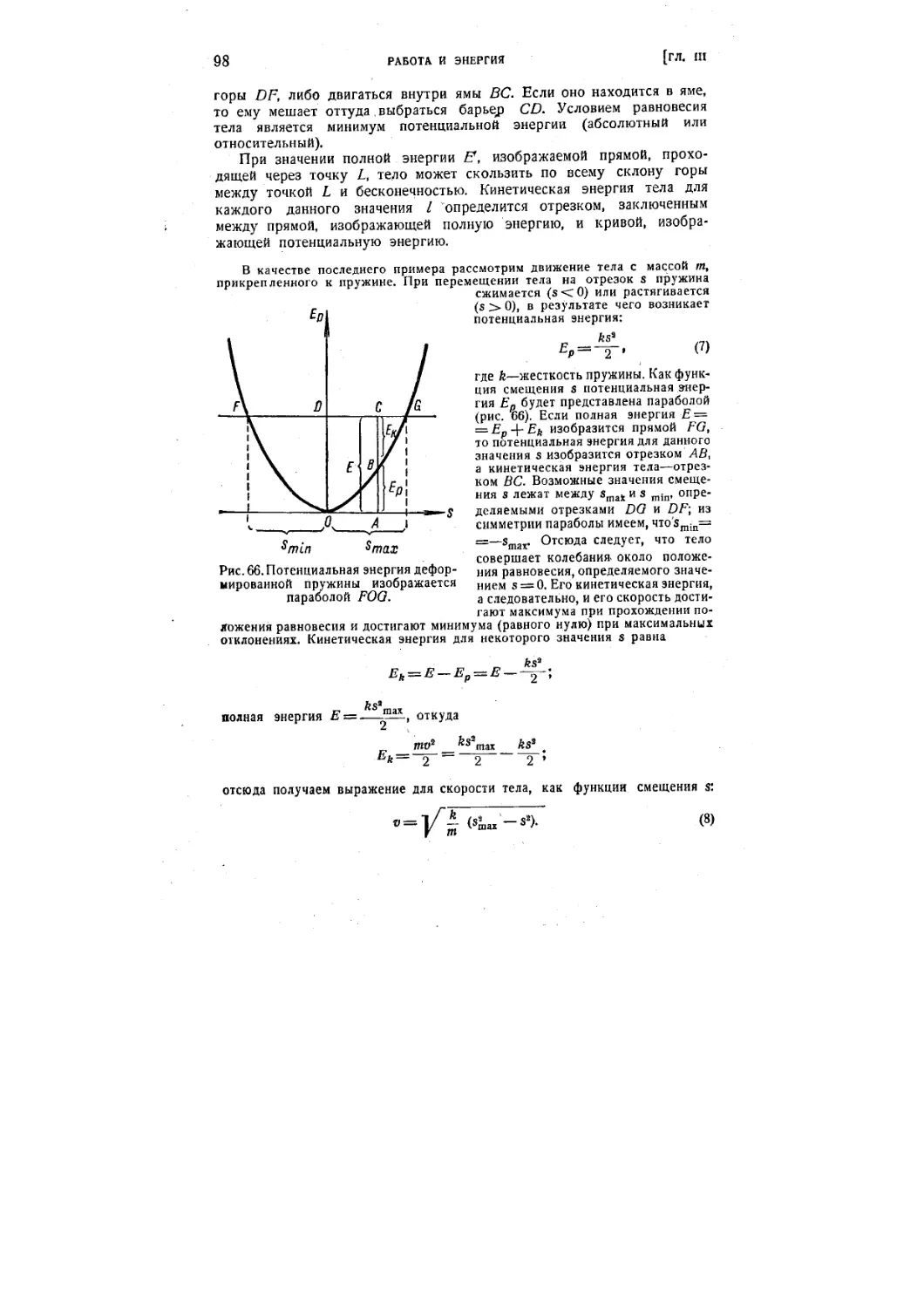
w§ 27:, Потенциальная энергия механической системы 89
\/ § 28,-Законы сохранения и изменения механической энергии си-
системы Г 92
§ 29. Графическое представление энергии 95
§ 30, Формулы размерности 99
§ 31. Границы применимости классической-механики . . .' 102
4 ОГЛАВЛЕНИЕ
Глава IV. Силы тяготения
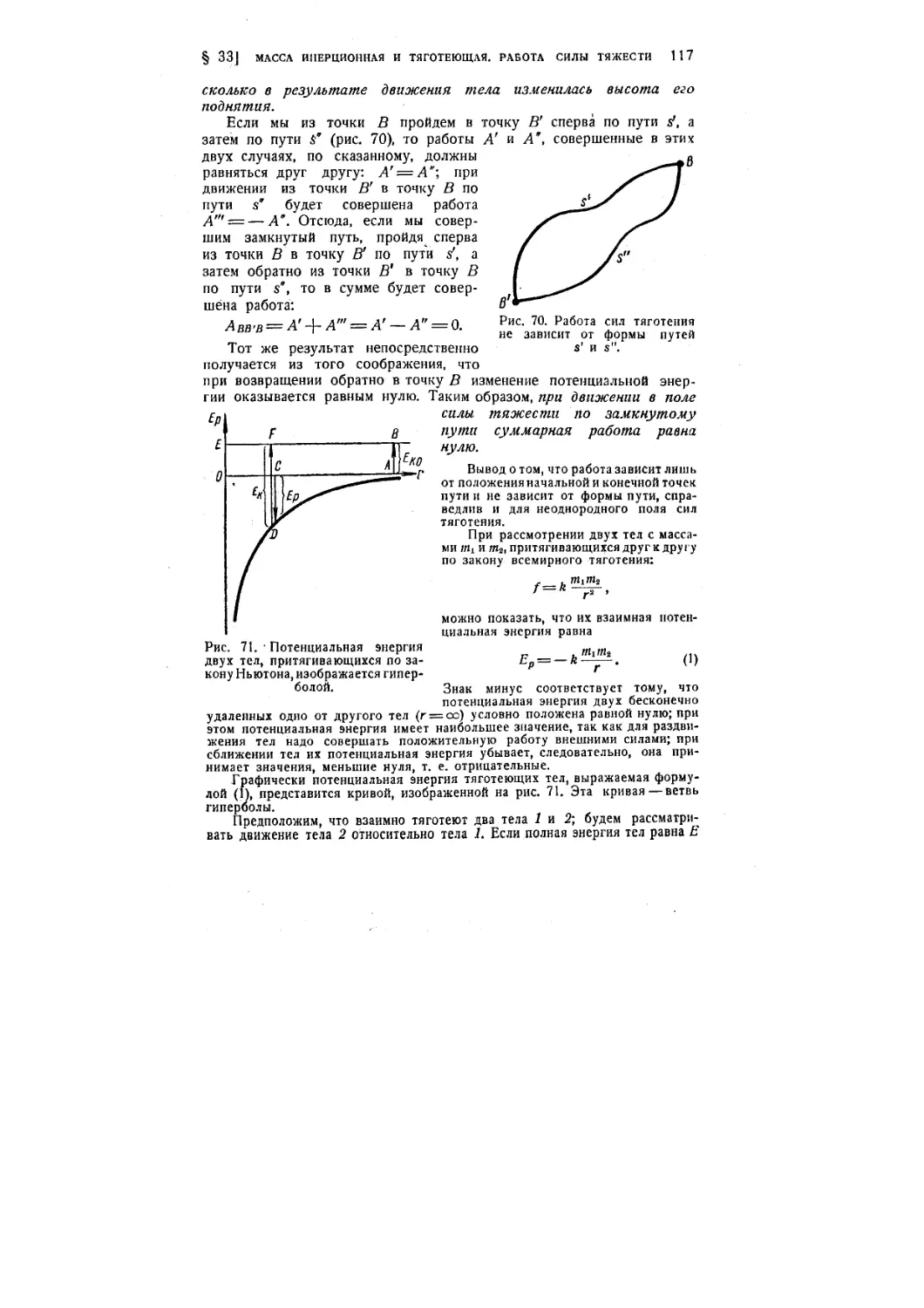
§ 32. Силы тяготения 110
§ 33. Масса инерционная и тяготеющая. Работа силы тяжести. ... 115
Глава V. Движение твердого тела
§ 34УДвижение твердого тела 119
§ Зб^Вращение твердого тела. Момент силы и момент инерции. . . 121
§ 36. Моменты инерции некоторых тел 125
§ 37}/Момент количества движения 127
§ 38. Гироскопы 131
§ 39.\/Кинетическая энергия вращающегося твердого тела 134
Глава VI. Движение жидкости
§ 40. Движение идеальной жидкости. Линии и трубки тока 139
§ 41. Применение закона сохранения количества движения к теку-
текущей жидкости 4 144
§ 42. Движение вязкой жидкости 148
ЧАСТЬ ВТОРАЯ
МОЛЕКУЛЯРНАЯ ФИЗИКА
Глава VII. Газы
§ 43. Атомно-молекулярная теория строения вещества . . ". . J57
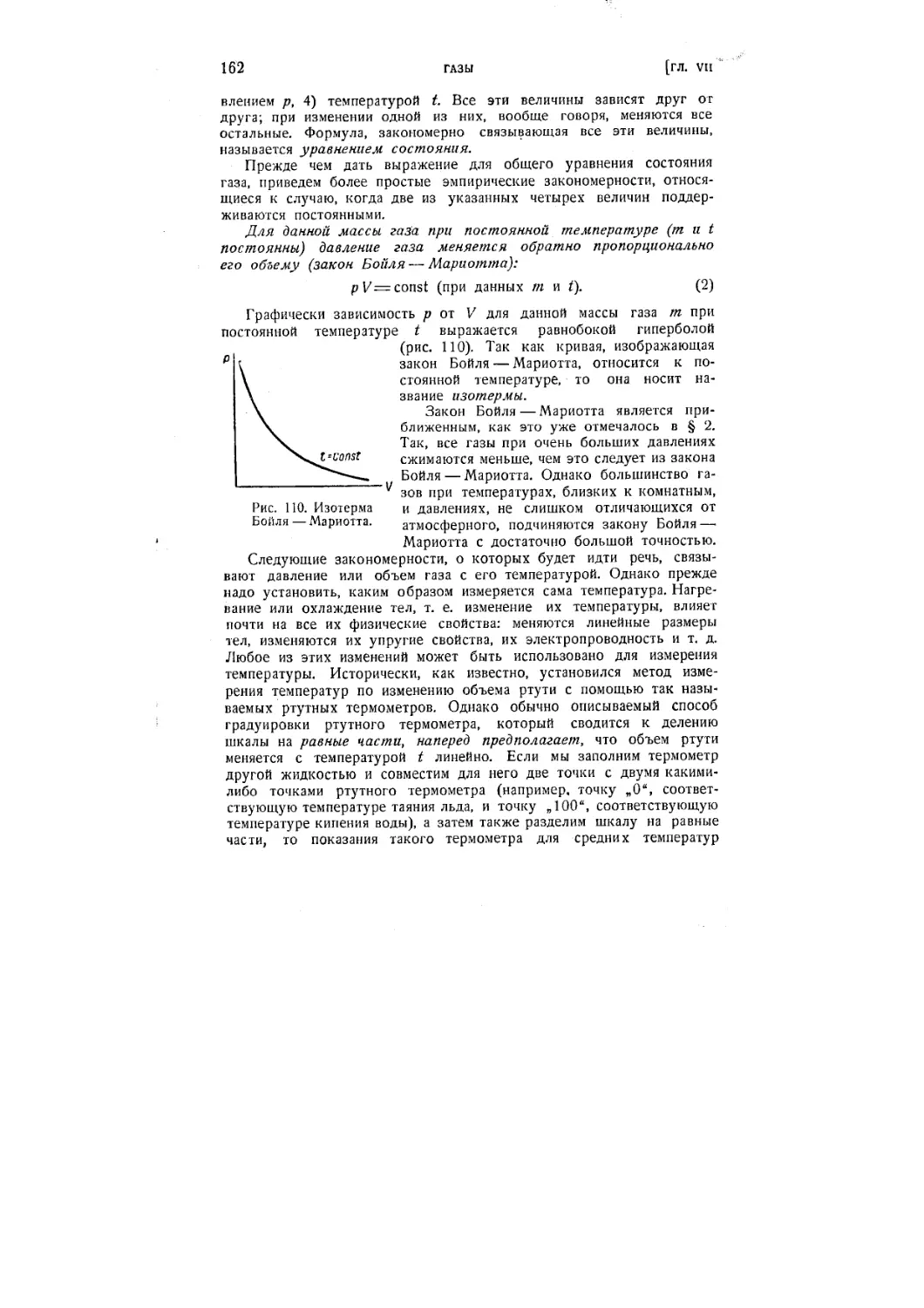
§ 44. Законы Бойля — Мариотта и Гей-Люссака. Определение тем-
температуры 161
§ 45. Уравнение состояния идеальных газов. Плотность газов .... 167
§ 46. Основные представления кинетической теории газов 170
§ 47. Парциальные давления в газовых смесях 176
§ 48. Внутренняя энергия газа. Число степеней свободы 178
§ 49. Теплоемкость газов : 180
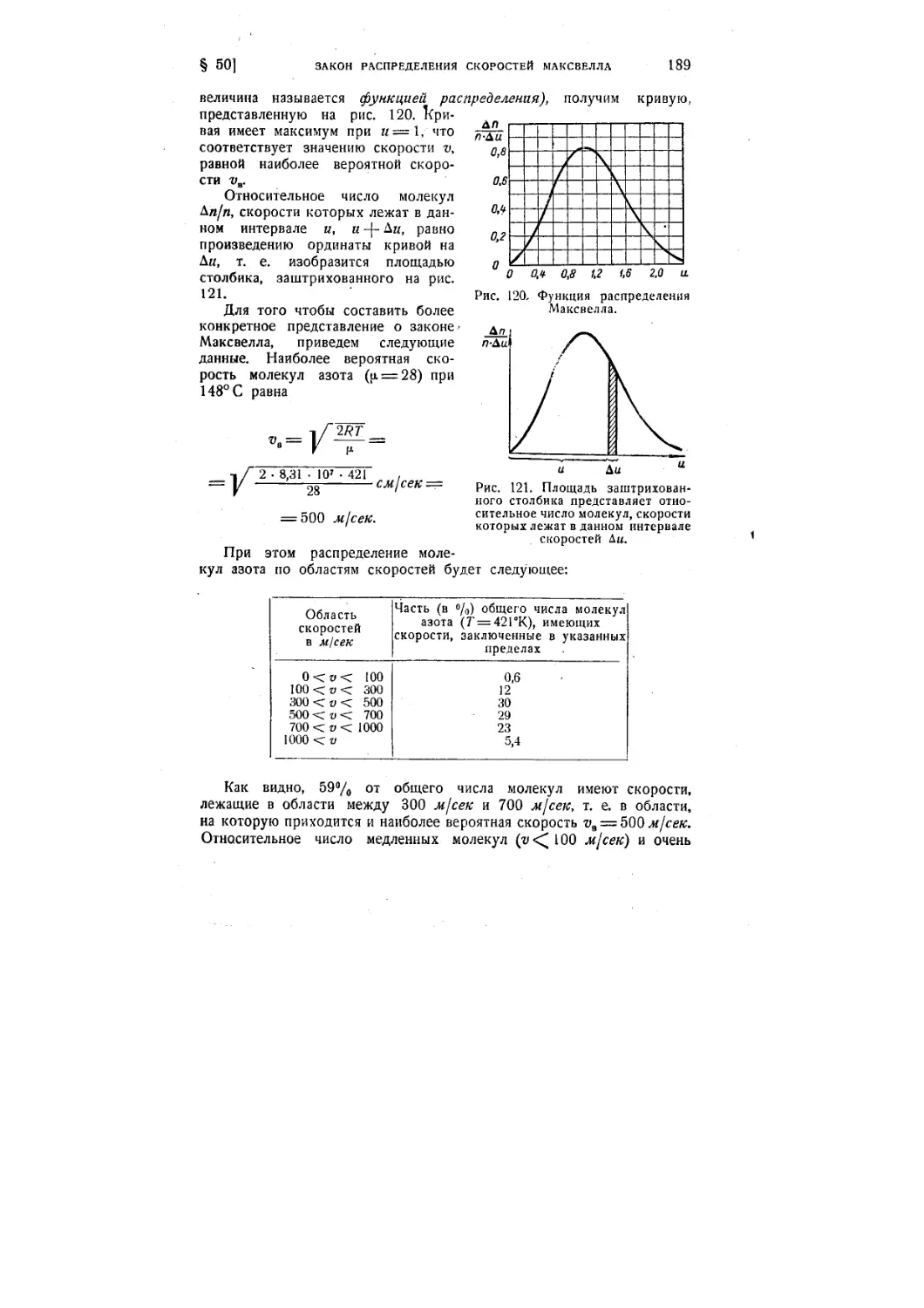
§ 50. Закон распределения скоростей Максвелла 182
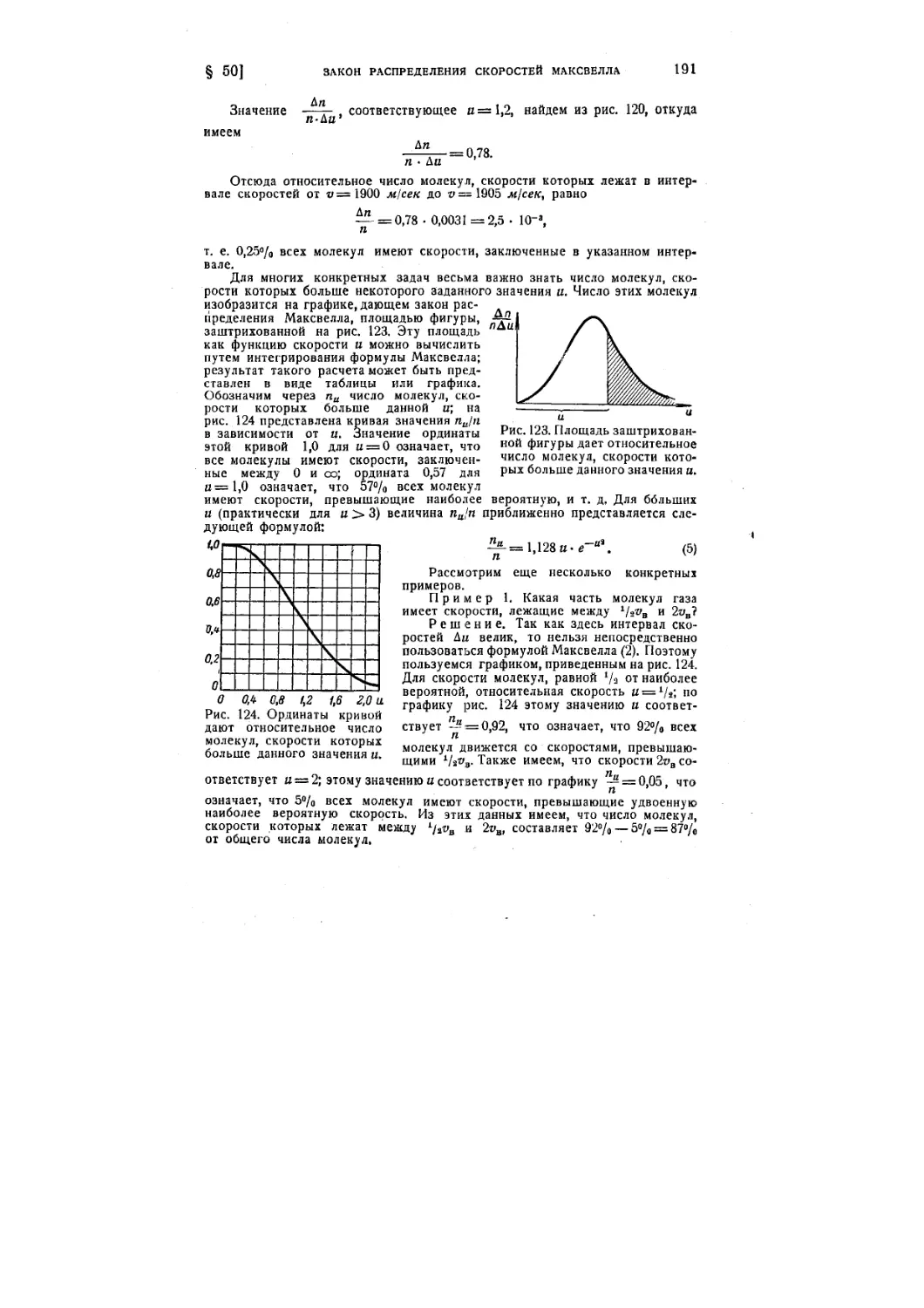
§ 51. Распределение частиц с высотой 194
§ 52. Определение числа Авогадро . . . 195
§ 53. Длина свободного пути молекул 199
§ 54. Опыты с молекулярными пучками 202
§ 55. Явления переноса в газах. Диффузия 205
§ 56. Внутреннее трение и теплопроводность газов . . 209
§ 57. Теплопроводность и внутреннее трение в газах при очень
низком давлении 217
§ 58. Получение и измерение низких давлений . 219
§ 59. Свойства газов при очень низких давлениях 225
§ 60. Реальные газы. Уравнение Ван-дер-Ваальса 222
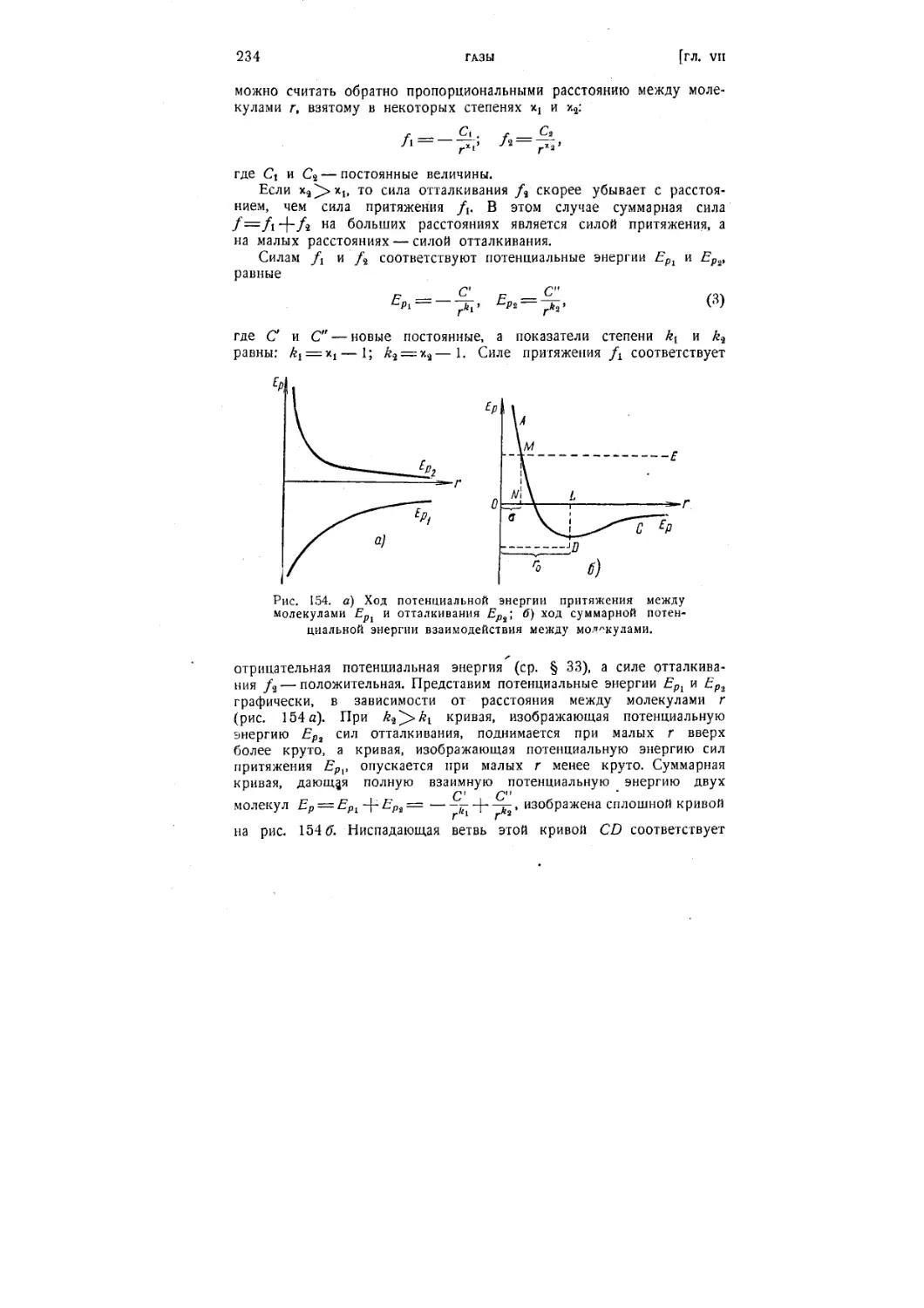
§ 61. Более точный учет характера поправок Ван-дер-Ваальса .... 231
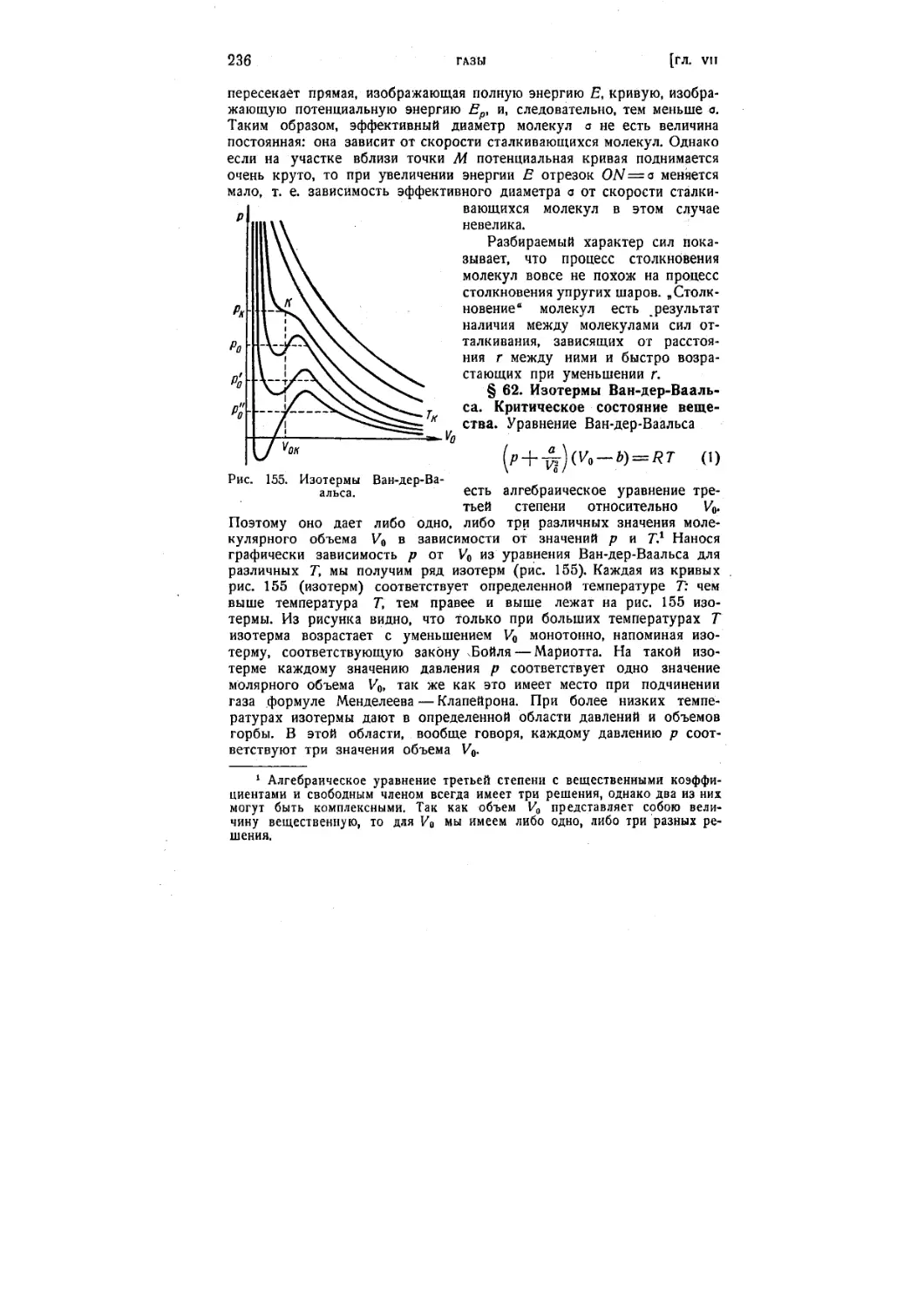
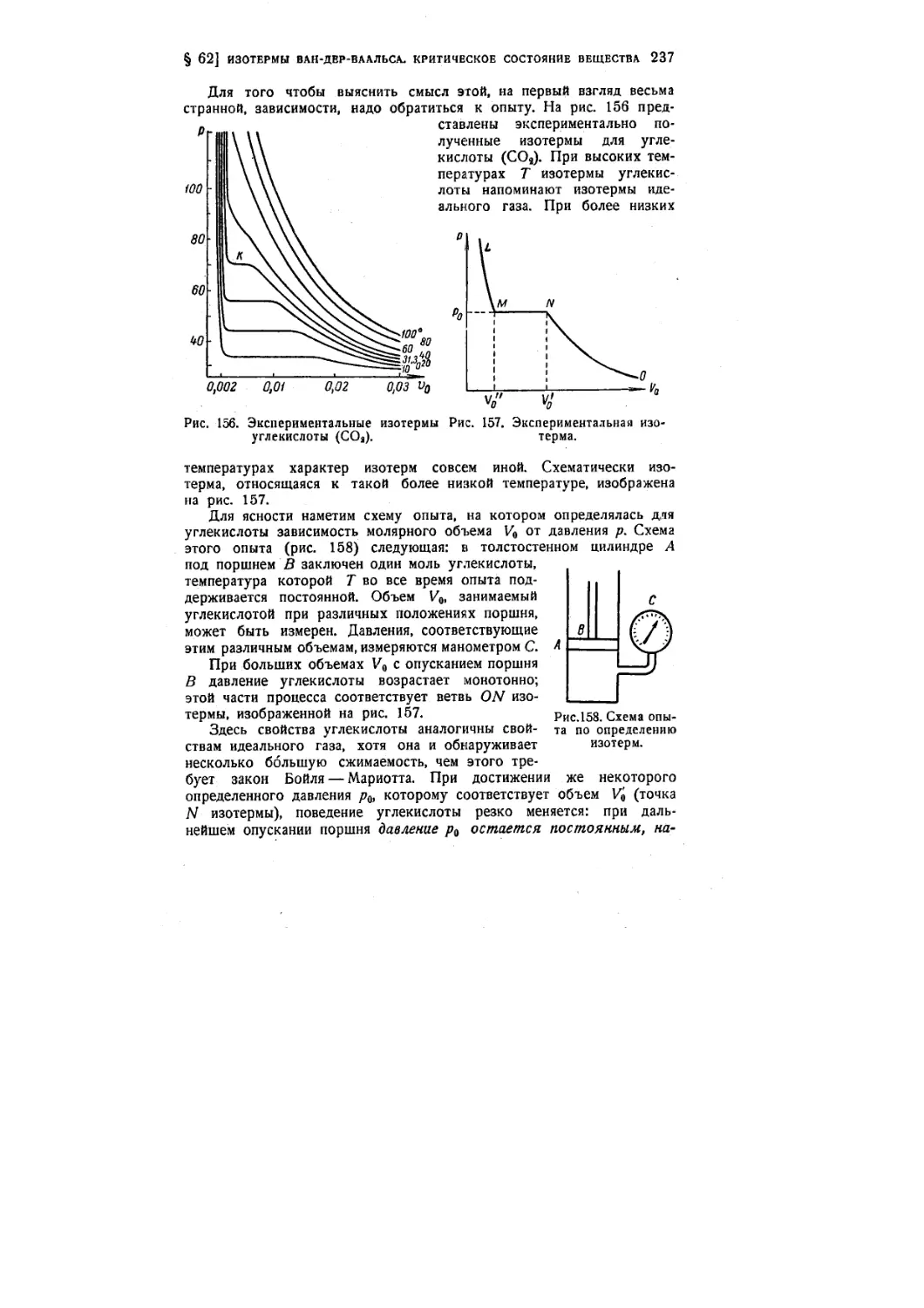
§ 62. Изотермы Ван-дер-Ваальса. Критическое состояние вещества. . 236,
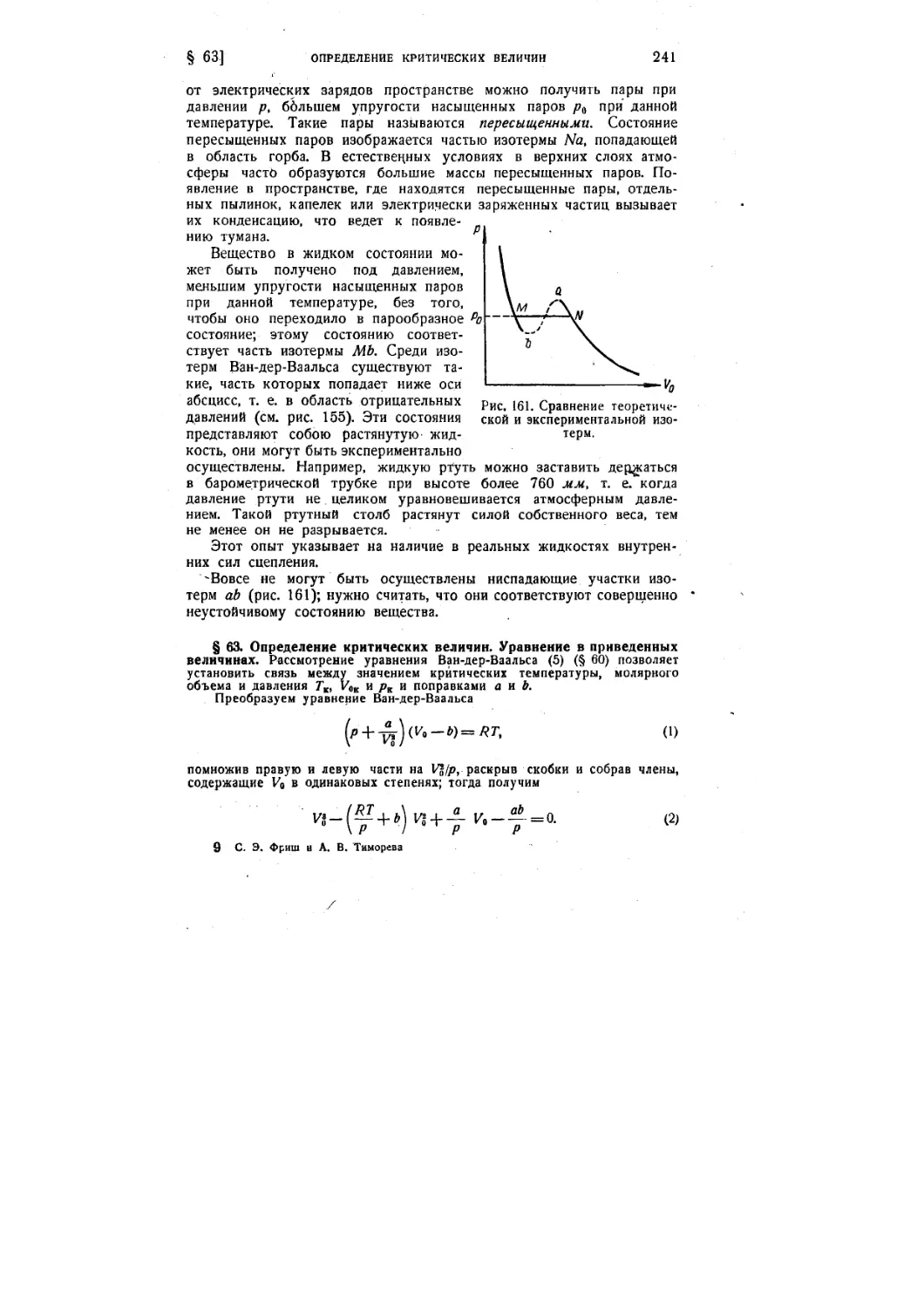
§ 63. Определение критических величин. Уравнение в приведенных
величинах 241
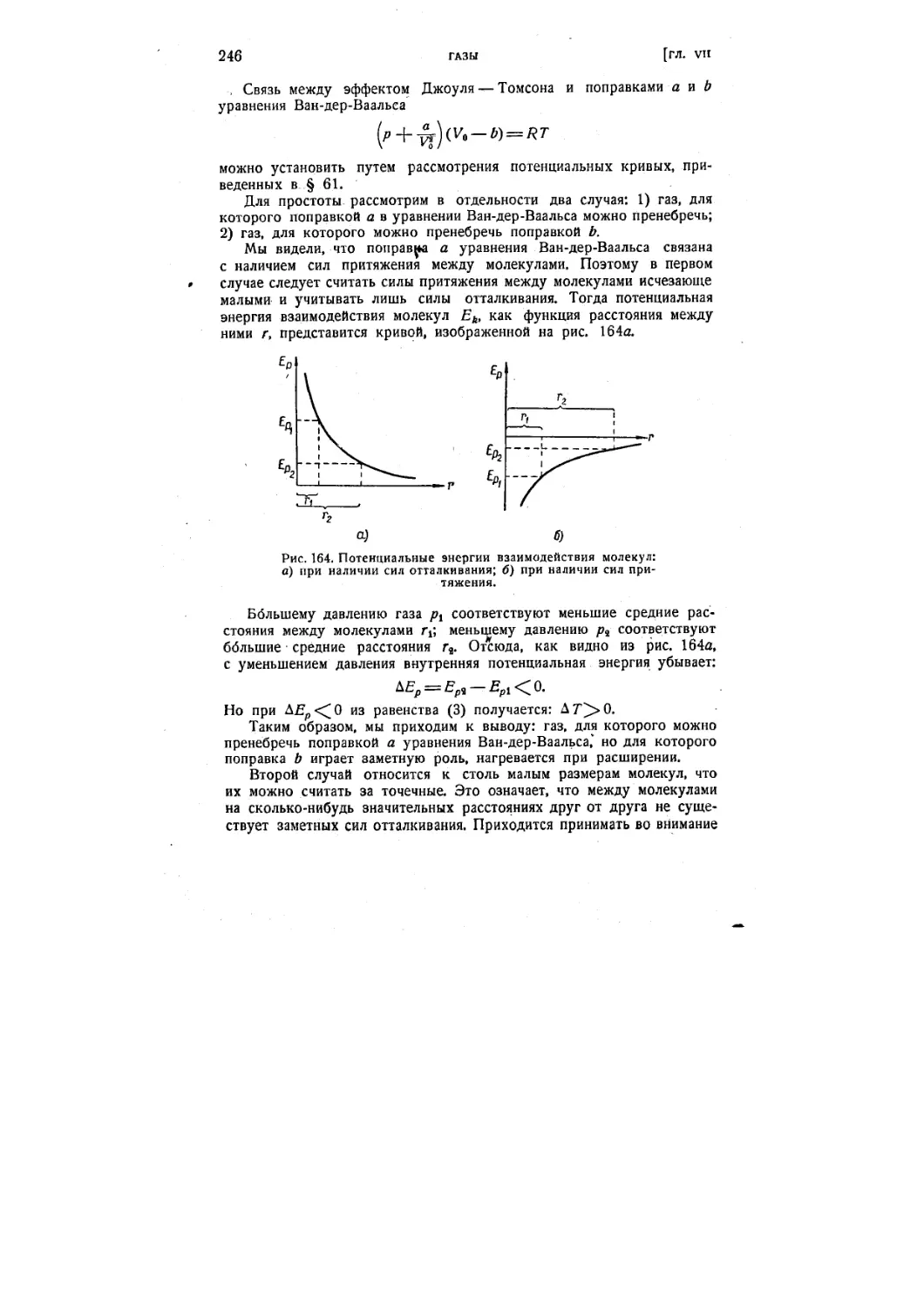
§ 64. Внутренняя энергия реального газа. Эффект Джоуля—Том-
сона 244
§ 65. Ожижение газов 247
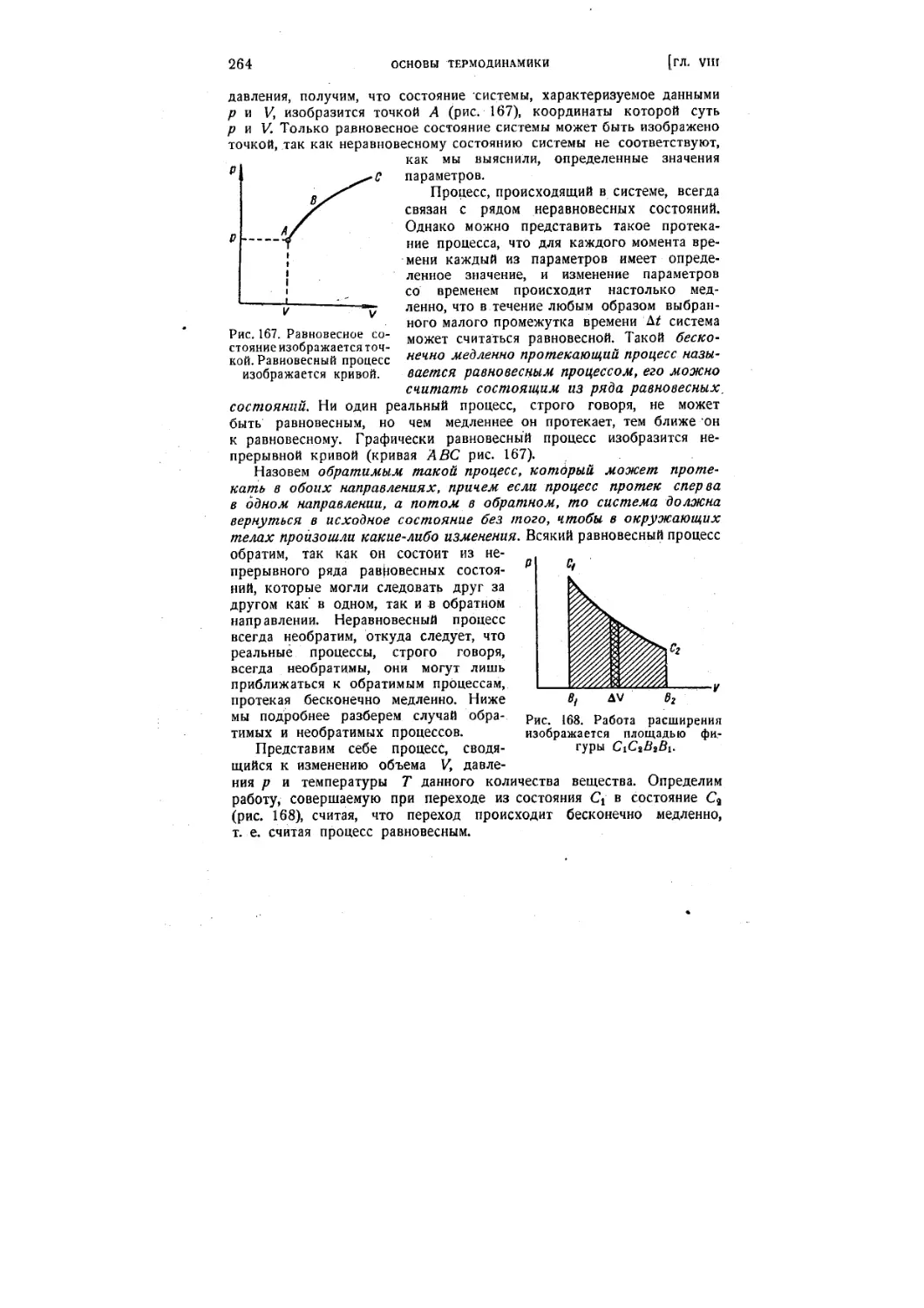
Глава VIII. Основы термодинамики
§ 66. Молекулярно-кинетическое и энергетическое описание про-
процессов 252
§ 67, Эквивалентность количества переданного тепла и работы . . . 253
ч
ОГЛАВЛЕНИЕ . 5
§ 68. Первое начало термодинамики 256
§ 69. Круговые процессы (циклы) 262
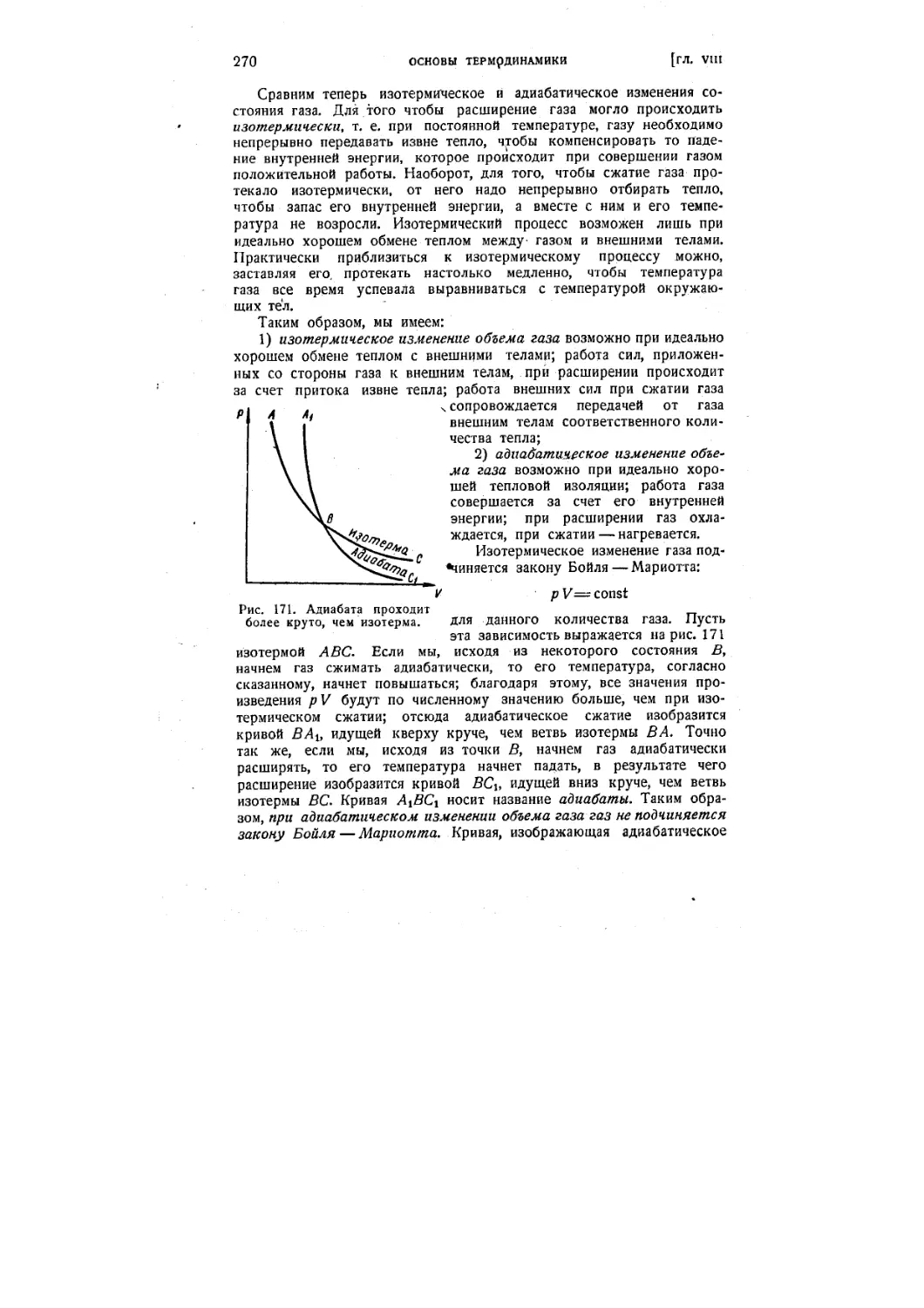
V § 70. Адиабатические процессы. Уравнение адиабаты 268
§ 71. Работа при адиабатическом и изотермическом изменениях
объема газа 273
§ 72. Второе начало термодинамики 277
§ 73. Цикл Карно. Коэффициент полезного действия тепловой ма-
машины 278
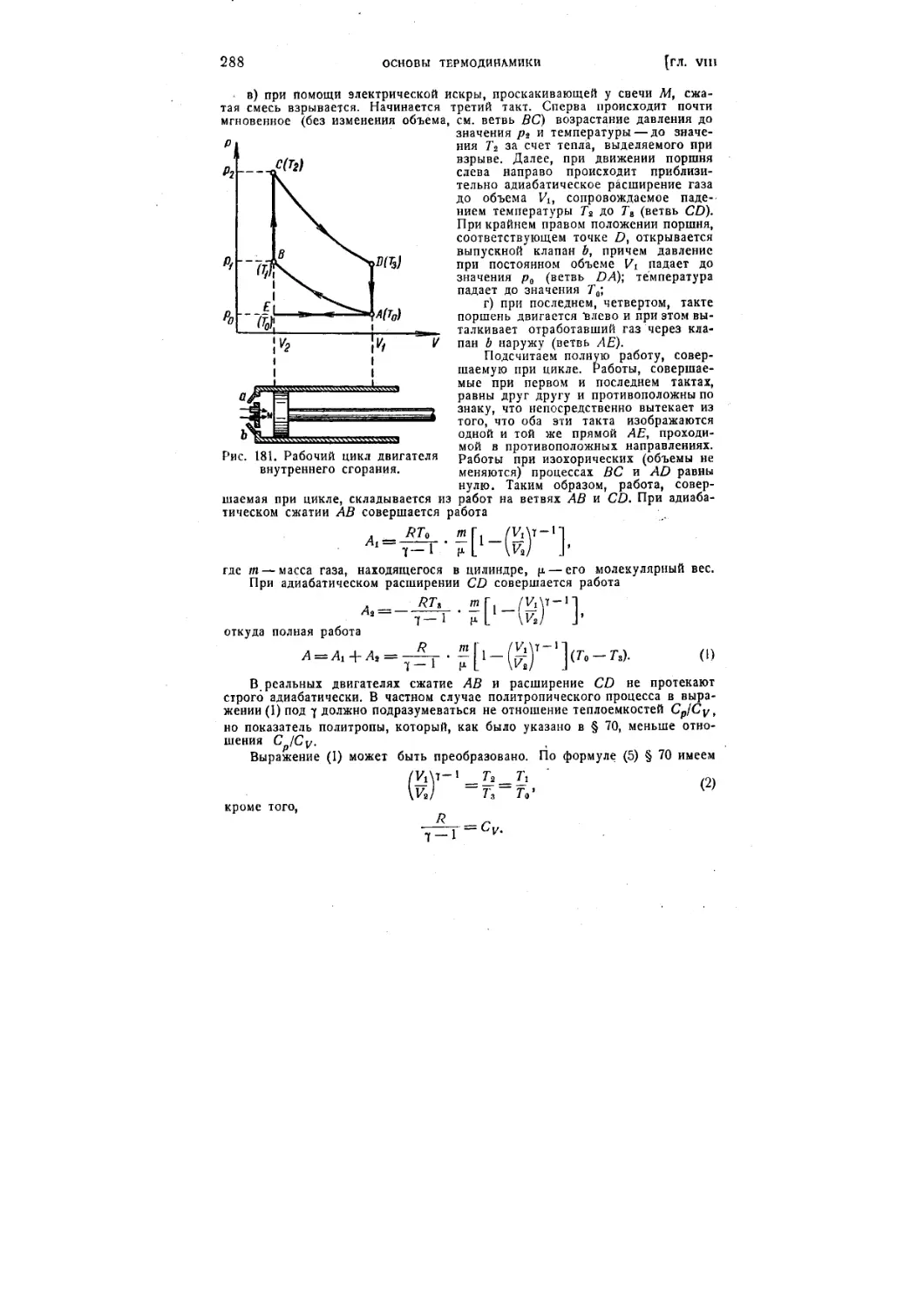
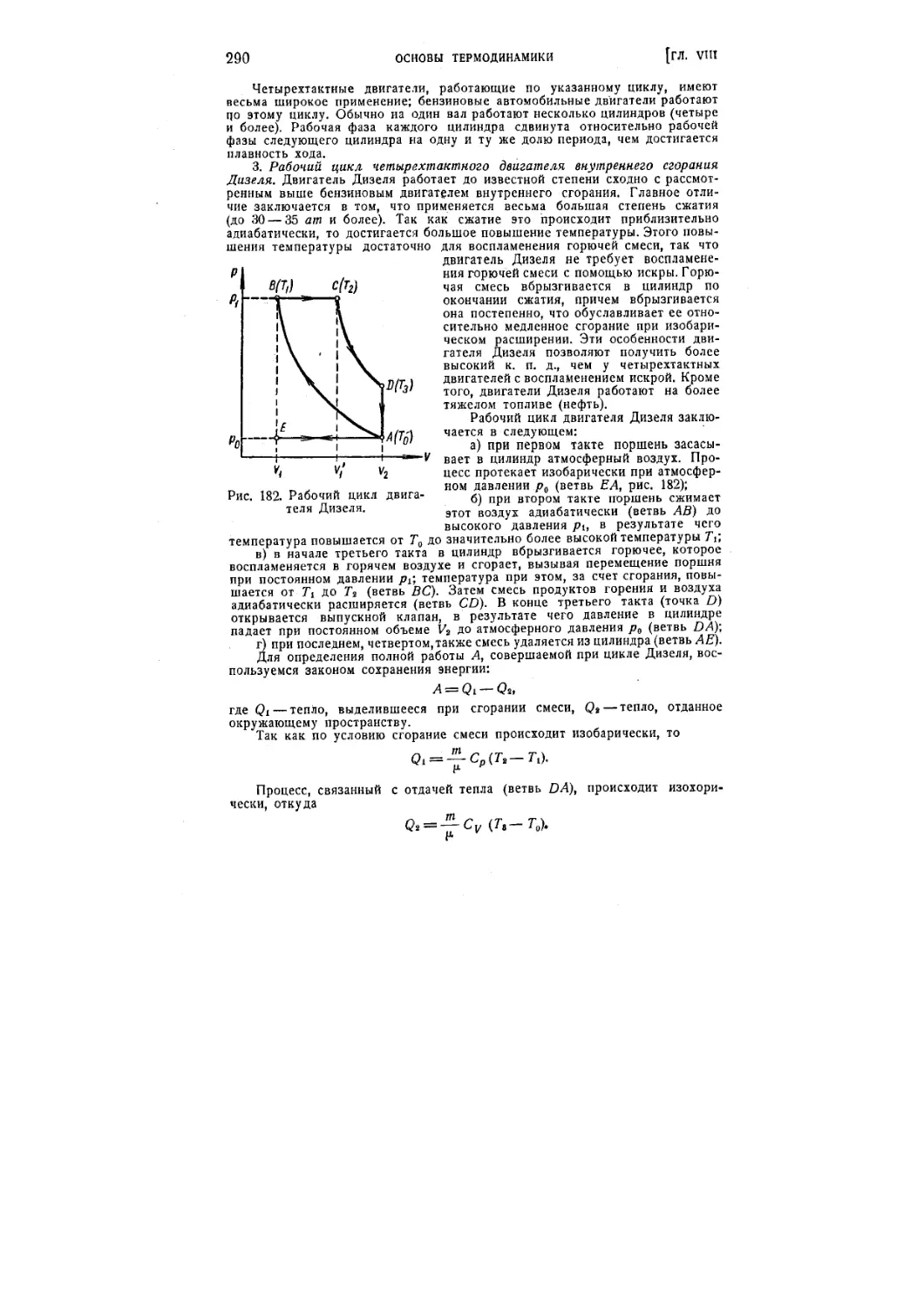
§ 74. Технические циклы 285
§ 75. Обратимые и необратимые процессы 292
§ 76. Статистический смысл второго начала термодинамики .^. . . 294
§ 77. Неравенство Клаузиуса. Энтропия .
^/Глава IX. Молекулярные явления в жидкостях ',
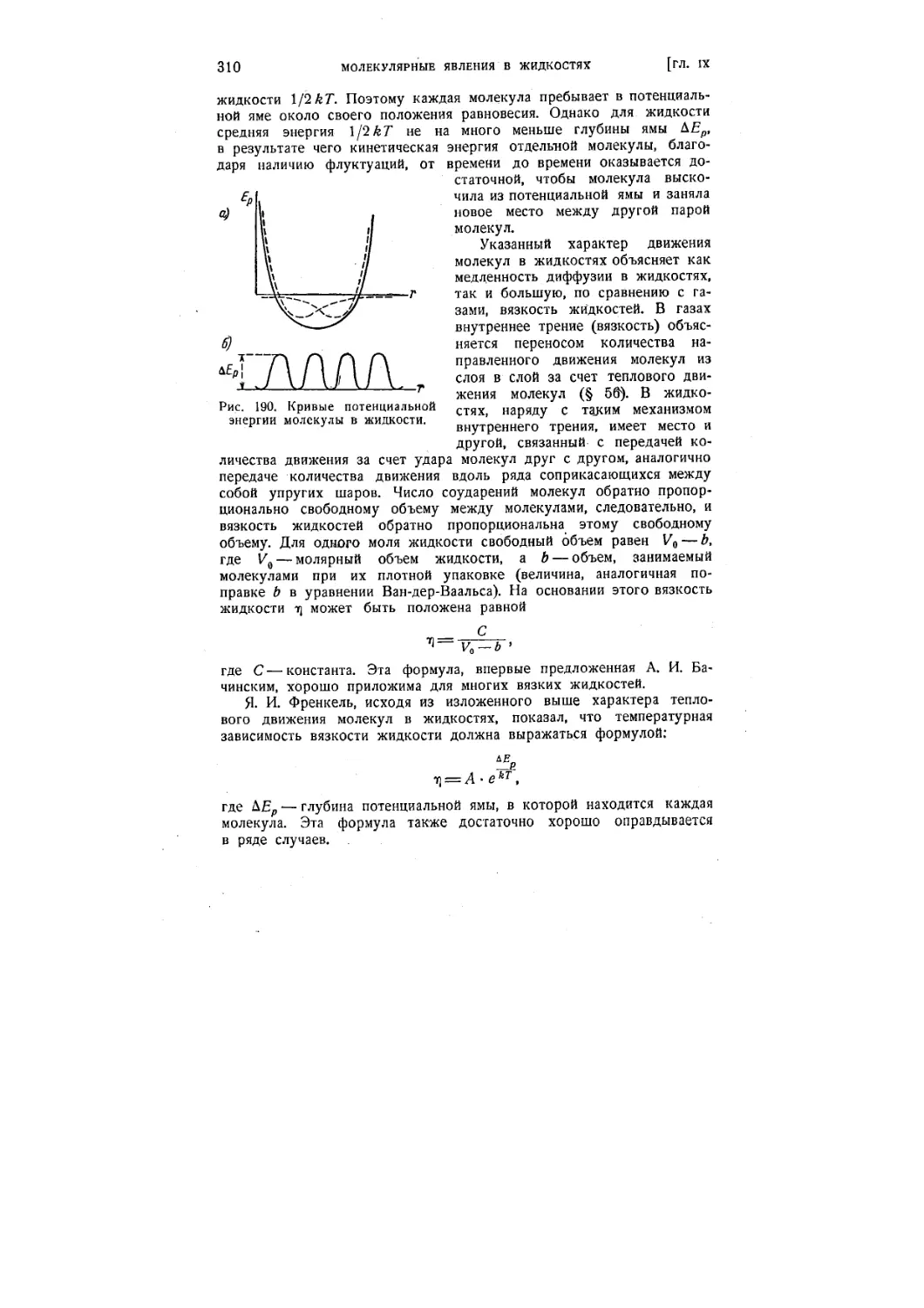
§ 78. Строение жидкости. Молекулярное давление 308
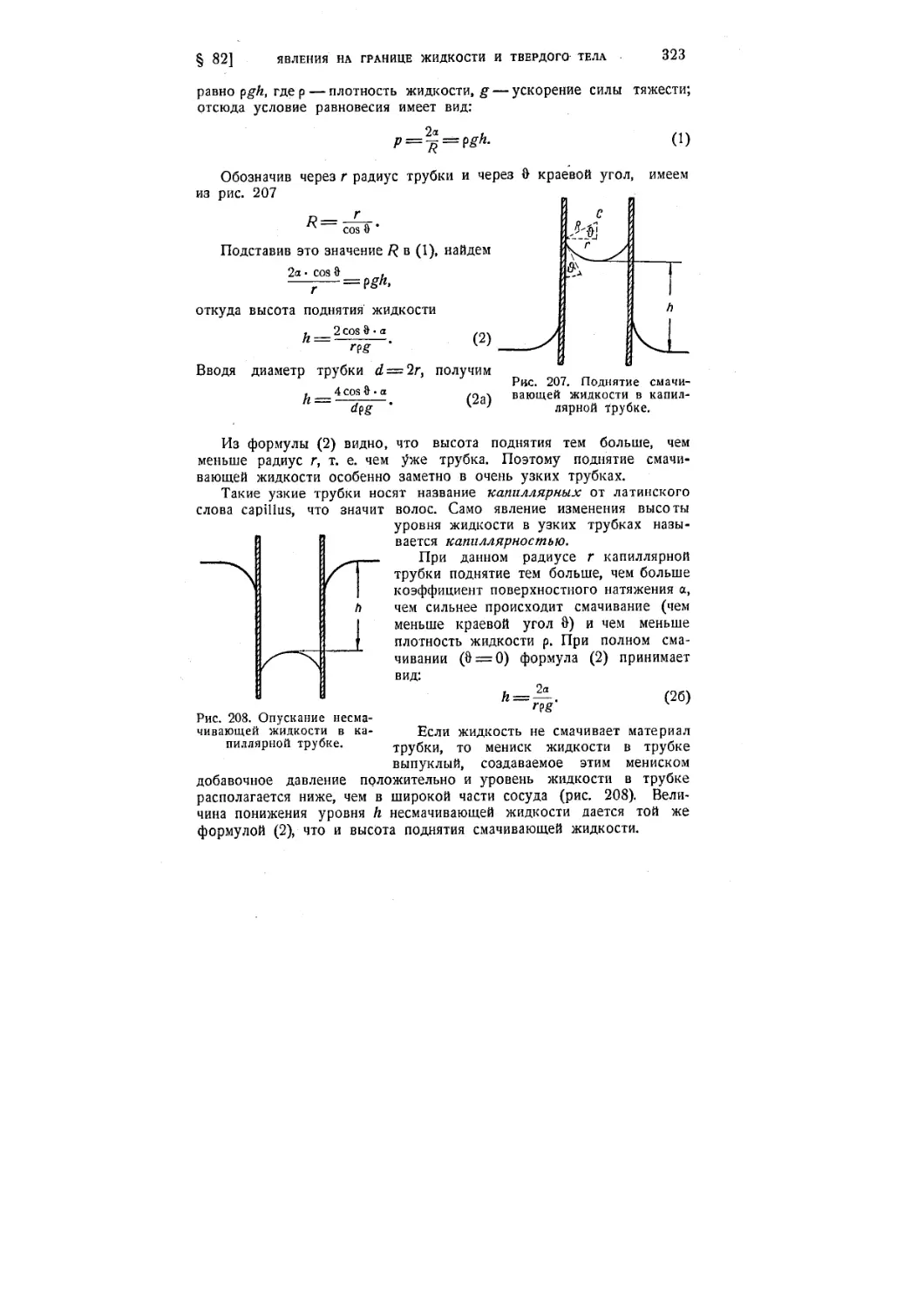
§ 79. Поверхностное натяжение 313
§ 80. Давление под изогнутой поверхностью жидкости 316
§ 81. Давление под изогнутой поверхностью жидкости любой формы 319
§ 82. Явления на границе жидкости и твердого тела. Капилляр-
Капиллярность 321
§ 83. Растекание капли по поверхности жидкости. Мономолекуляр-
Мономолекулярные пленки . . . 326
§ 84. Испарение жидкостей 328
§ 85. Растворы. Осмотическое давление '331
§ 86. Давление насыщенных паров под искривленной поверхностью
и над раствором 335
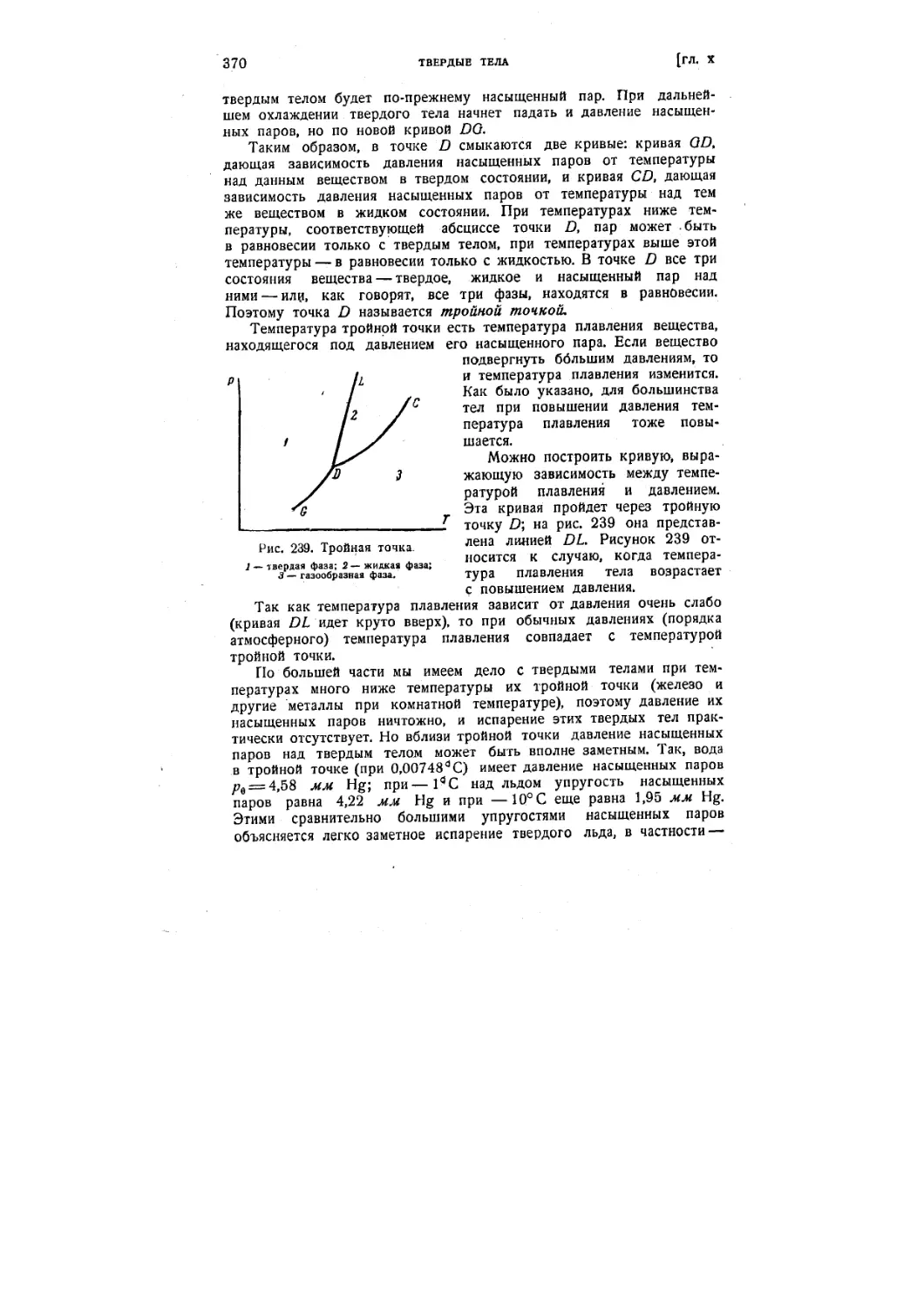
\/ Глава X. Твердые тела ;;j.
§ 87. Кристаллические и аморфные тела 340
§ 88. Энергия кристаллической решетки 344
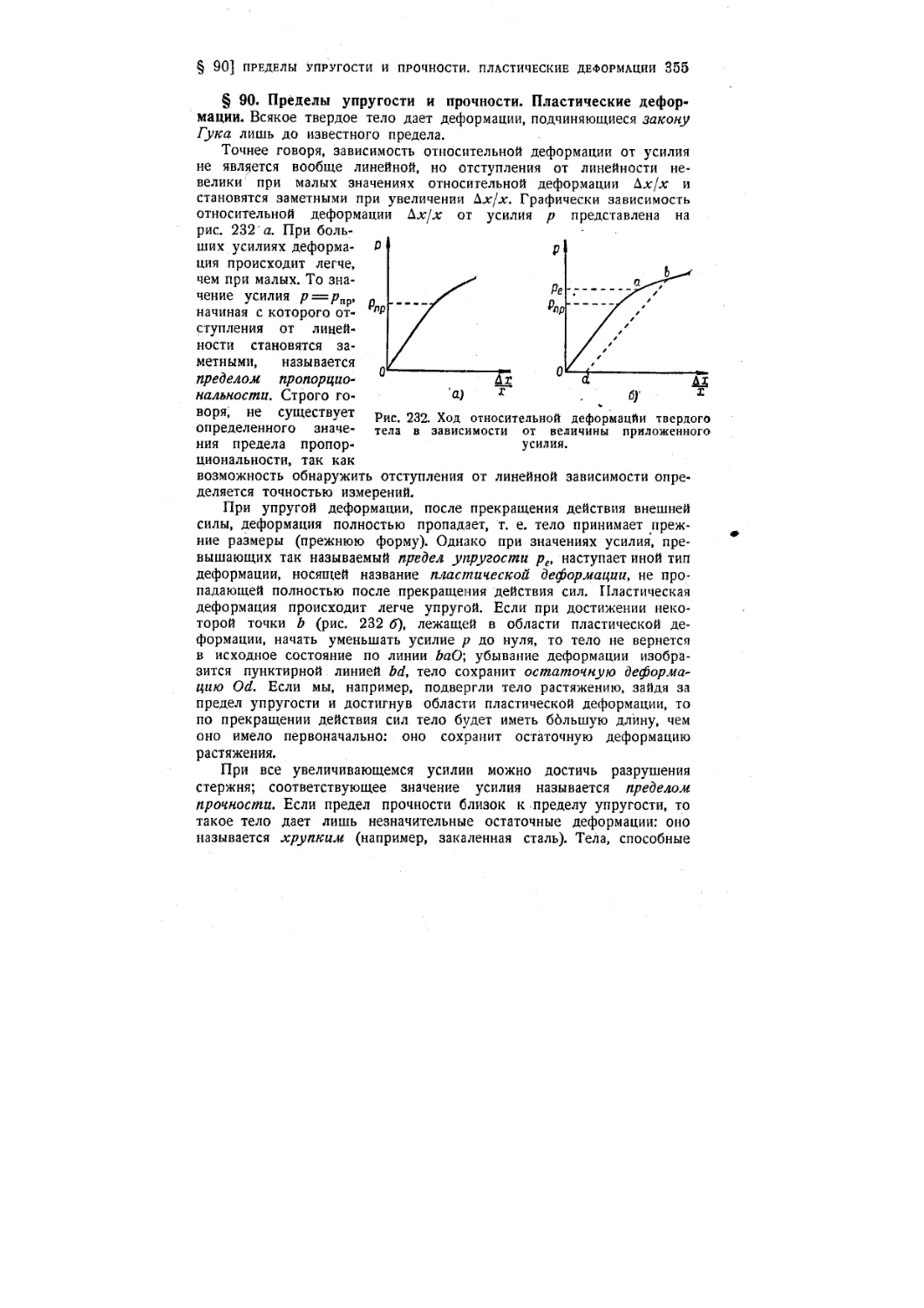
§ 89. Деформация твердых тел 348
§ 90. Пределы упругости и прочности. Пластические деформации . . 355
§ 91. Деформации с точки зрения кристаллической структуры твер-
твердых тел 358
§ 92. Тепловое движение в твердых телах. Расширение твердых тел 361
fj § 93. Теплоемкость твердых тел 363
§ 94. Плавление и испарение твердых тел 367
§ 95. Квазикристаллическое строение жидкостей 371
§ 96. Абсорбция и адсорбция газов твердыми телами 373
ЧАСТЬ ТРЕТЬЯ
КОЛЕБАНИЯ И ВОЛНЫ
Глава XI. Гармоническое колебательное движение
- // § 97. Гармоническое колебание 376
S/ § 98. Скорость и ускорение при гармоническом колебательном
движении. Примеры 381
V § 99. Энергия гармонического колебательного движения 385
V § 100. Сложение колебаний, происходящих вдоль одной прямой . . . 387
•¦ § 101. Сложение взаимно перпендикулярных колебаний 391
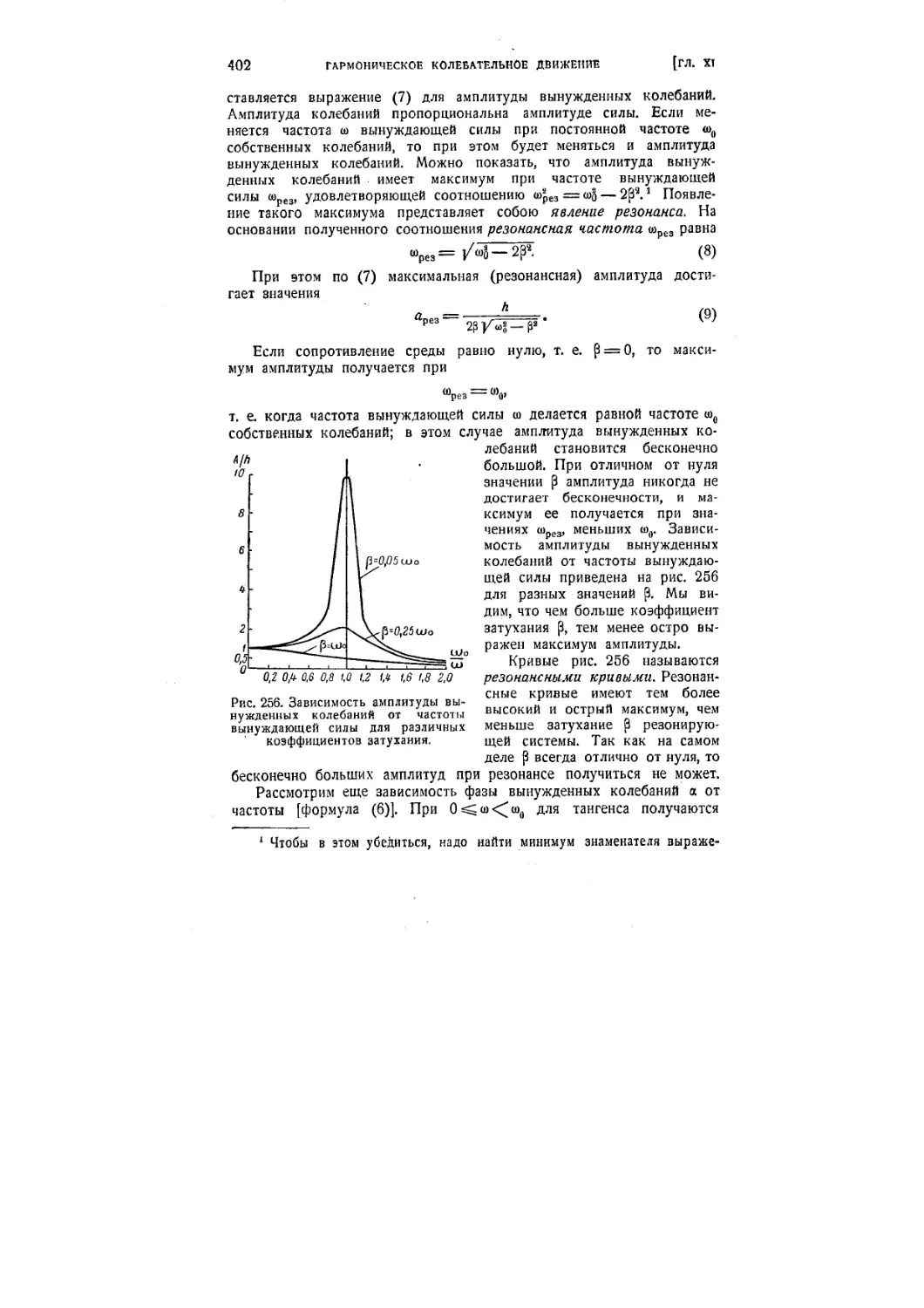
V § 102. Затухающие колебания 395
yj § ЮЗ. Вынужденные колебания 399
§ 104. Представление негармонических колебательных процессов
при помощи гармонических колебаний 405
X § 105. Представление колебательных процессов с помощью комплекс-
комплексных чисел 411
О ОГЛАВЛЕНИЕ
Глава XII. Волны
V § 106. Распространение волн в упругой среде 414
V § 107. Принцип Гюйгенса 417
у § 108. Уравнение волны 419
^ § 109. Интерференция волн 422
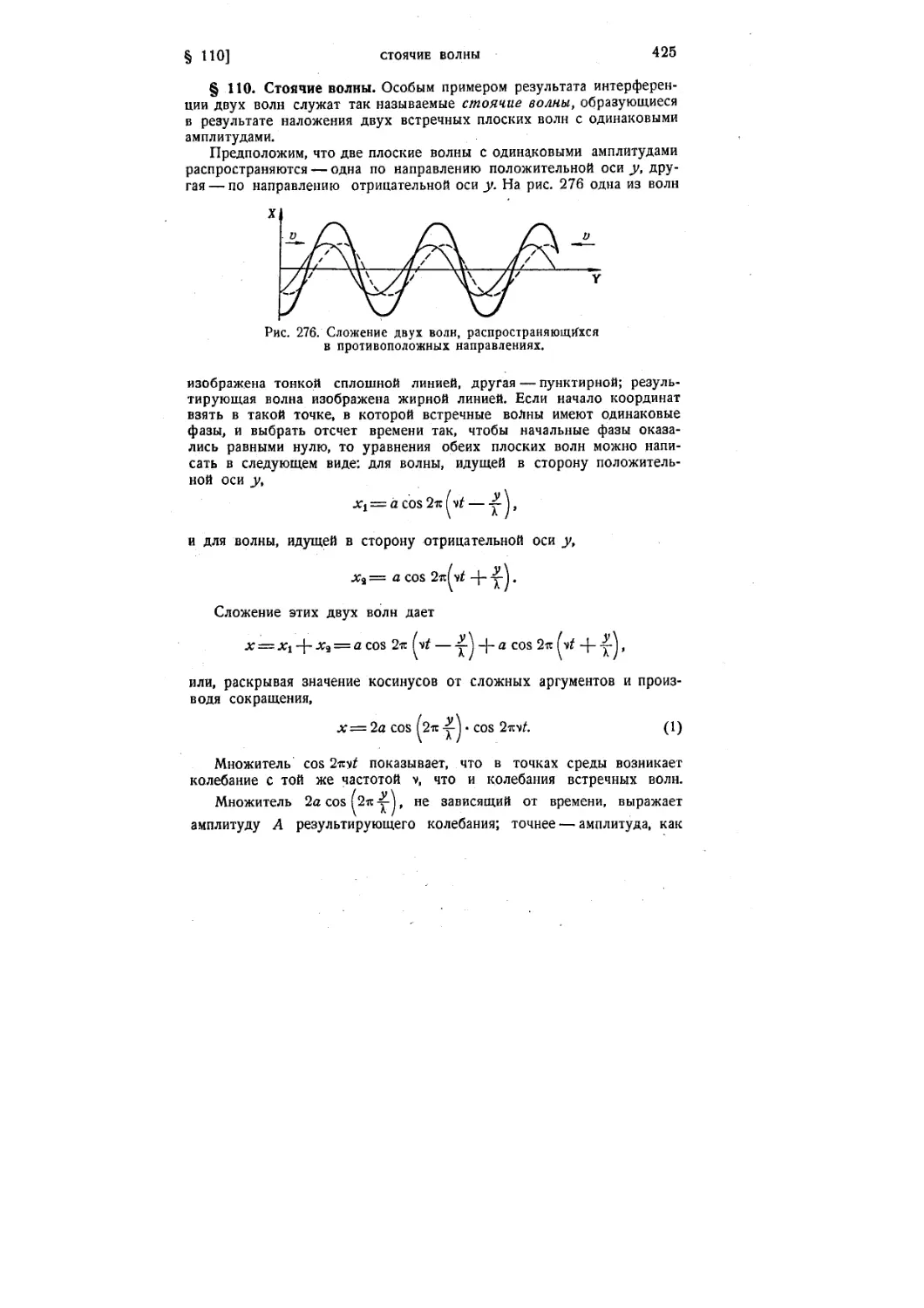
§ НО. Стоячие волны 425
V § 111. Динамика распространения колебаний в упругой среде. . . . 429
^ § 112. Энергия волны 432
§ 113. Явление Допплера 436
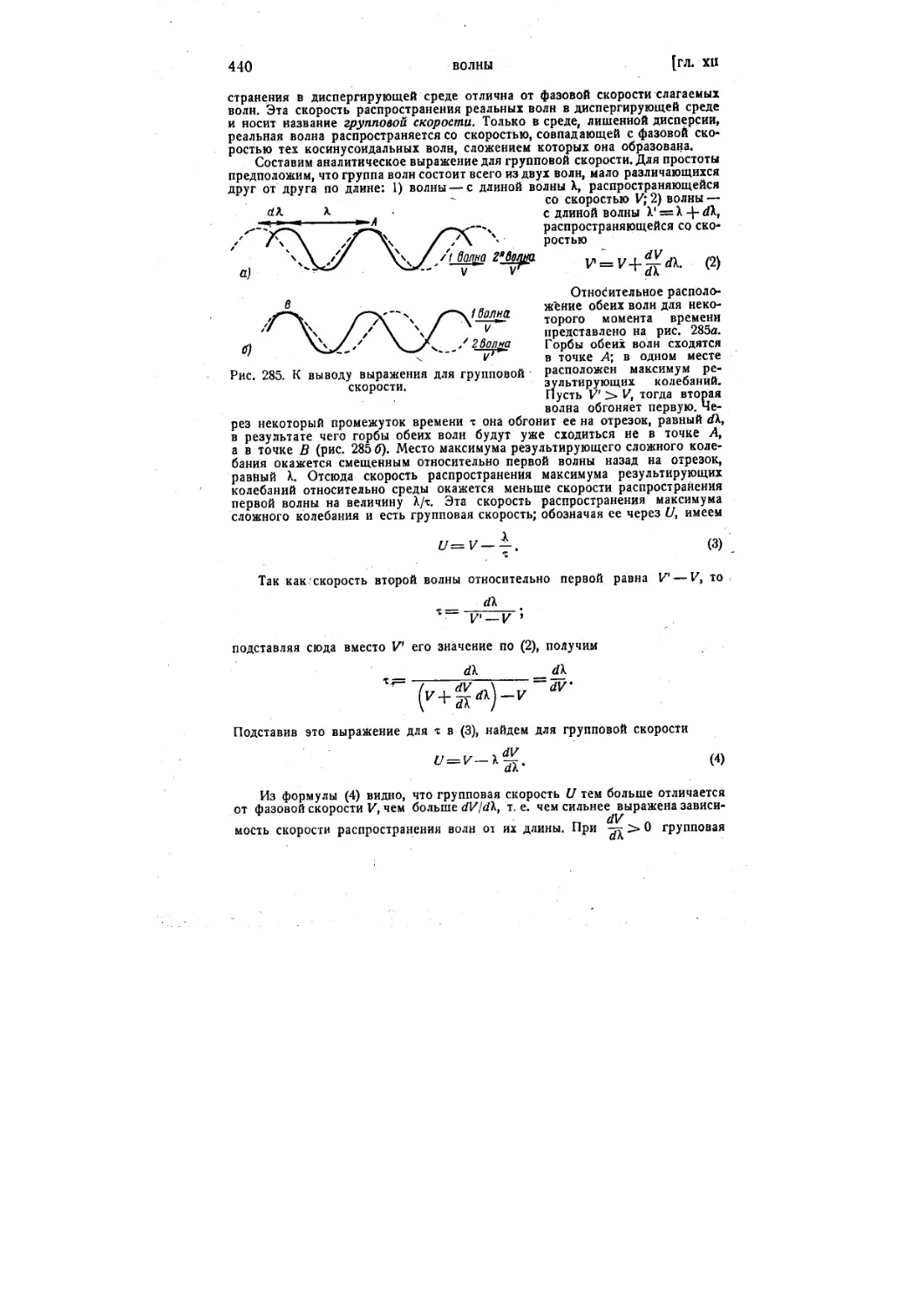
§ 114. Групповая скорость 438
Глава XIII. Акустические колебания
§ 115. Звуковые колебания и их распространение 442
§ 116. Интерференция звуковых волн 445
§ 117. Восприятие звуков 448
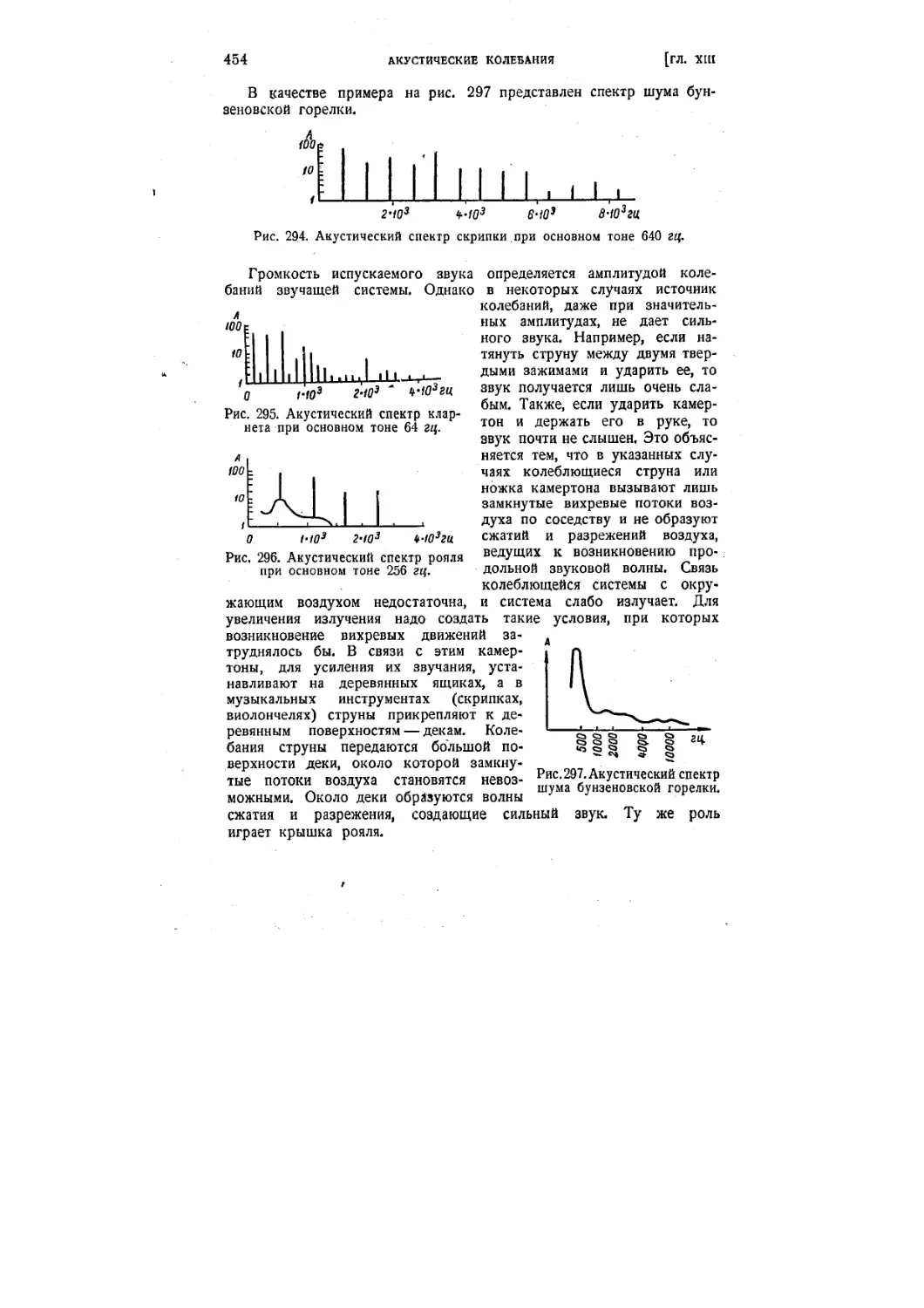
§ 118. Источники звуков. Получение ультразвуков 453
§ 119. Отражение и поглощение звуковых волн . 457
Алфавитный указатель 460
00
ВВЕДЕНИЕ
§ 1. Физика; ее содержание, связь с другими науками и с тех-
техникой. Физика, наряду с другими естественными науками, изучает
объективные свойства окружающего нас материального мира. По-гре-
По-гречески слово cpuct? означает природу.
Физика изучает наиболее общие формы движения материи (механи-
(механические, тепловые, электромагнитные и т. д.) и их взаимные превра-
превращения. Изучаемые физикой формы движения присутствуют во всех
высших и более сложных формах движения (в химических, биологи-
биологических процессах и др.) и неотделимы от них, хотя и никоим образом
не исчерпывают их. Так, открытому физикой закону всемирного тяго-
тяготения подчиняются все известные тела земные и небесные, незави-
независимо от того, являются ли они химически простыми или сложными,
живыми или мертвыми. Установленному физикой закону сохранения
энергии подчиняются все процессы, независимо от того, носят ли они
специфически химический, биологический и т. д. характер. Высшие,
более сложные формы движения являются предметом изучения дру-
других наук (химии, биологии и др.).
Границы между физикой и некоторыми другими естественными
науками не могут быть установлены резко. Существуют обширные
пограничные области между физикой и химией, возникли даже особые
науки: физическая химия и химическая физика. Области знания, где
физические методы применяются для изучения более или менее част-
частных вопросов, также соединяются в особые науки: так возникают,
например, астрофизика, изучающая физические явления, протекающие
в небесных объектах, и геофизика, изучающая физические явления,
протекающие в атмосфере Земли и в земной коре. Физические откры-
открытия часто давали толчок к развитию других наук. Изобретение ми-
микроскопа и телескопа ускорило развитие биологии и астрономии.
Открытый физиками спектральный анализ стал одним из основных
методов астрофизики и т. д.
Развитие физики и химии, наряду с другими естественными науками,
сыграло крупную роль в развитии материалистического мировоззрения.
Последовательно развитая материалистическая философия, высшей
ступенью которой является диалектический материализм, широко ис-
использовала для обоснования своих положений физические открытия,.
ВВЕДЕНИЕ
Физика, проверяя свои теории непосредственным критерием опыта и
практики, всегда шла по пути раскрытия объективных свойств мира,
и этим объясняется то, что подавляющее большинство физиков фак-
фактически оказывались стихийными материалистами. Однако слабость
стихийного материализма, заключающаяся в его бессознательности и
неумении философски осмыслить опытные данные науки, вела к тому,
что часть буржуазных ученых, под влиянием реакционной идеологии
господствующих классов, неоднократно пыталась использовать физи-
физические открытия для обоснования идеалистических воззрений. Такие
попытки встречаются особенно часто в периоды крупных открытий,
когда старые положения подвергаются пересмотру, а новые еще недо-
недостаточно выяснены. Так, в самом конце XIX и в первых годах XX
столетий, когда возникло учение об электронах и были открыты
факты, легшие в основу теории относительности, появились много-
многочисленные „обоснования" идеализма, якобы базирующиеся на новых
физических открытиях. Несостоятельность этих „обоснований" была
с исключительной последовательностью и полнотой вскрыта Лениным
в его книге „Материализм и эмпириокритицизм". По поводу выска-
высказываний ряда буржуазных философов, утверждавших, что новые
открытия физики повели к представлению об исчезновении материи,
Ленин писал: «„Материя исчезает"—это значит исчезает тот предел,
до которого мы знали материю до сих пор, наше знание идет глубже;
исчезают такие свойства материи, которые казались раньше абсолют-
абсолютными, неизменными, первоначальными (непроницаемость, инерция, масса
и т. п.) и которые теперь обнаруживаются, как относительные, при-
присущие только некоторым состояниям материи. Ибо единственное
„свойство" материи, с признанием которого связан философский
материализм, есть свойство быть объективной реальностью, суще-
существовать вне нашего сознания».J
Сказанное Лениным около сорока лет тому назад по поводу кри-
кризиса физики того времени целиком применимо и к современному этапу
развития физики, когда изучение внутриатомных процессов заставляет
ограничить старые представления механики и электродинамики и вве-
ввести новые представления квантовой механики. Критический анализ, ¦
последовательно проведенный с точки зрения диалектического мате-
материализма, позволяет отделить ценное физическое содержание новых
теорий от той идеалистической шелухи, в которую иногда облекают
их авторы.
Толчком к развитию физики, как и всех других наук, послужили
практические требования людей. Механика древних египтян и греков
возникла непосредственно в связи с теми запросами, которые были
поставлены тогдашней строительной и военной техникой. Также под
влиянием развивающейся техники и военного дела были сделаны
крупные научные открытия конца XVII и начала ХУЩ^толетий,
» Э. И> Ленин, Сочинения, 4-е изд., т. 14, стр. 247,
§ 1] ФИЗИКА; ЕЕ СОДЕРЖАНИЕ, СВЯЗЬ С ДРУГИМИ НАУКАМИ И С ТЕХНИКОЙ 9
Основоположник русской физики и химии М. В. Ломоносов сочетал
свою научную работу с требованиями практики. Его многочисленные
и разнообразные исследования по природе твердых и жидких тел,
оптике, метеорологии, атмосферному электричеству были связаны
с теми или другими практическими задачами.
В начале XIX столетия применение паровых машин сделало необ-
необходимым решение вопроса о наиболее выгодном превращении тепла
в механическую работу. Этот вопрос не мог быть решен при узко-
узкотехническом подходе. После того как в 1824 г. французский инже-
инженер Сади Карно в общем виде рассмотрел проблему о переходе тепла
в работу, можно было действительно увеличить коэффициент полез-
полезного действия тепловых машин. Одновременно работа Карно послу-
послужила фундаментом для возникновения общего учения о передаче и
превращении энергии, получившего впоследствии название термоди-
термодинамики. Таким образом, требования практики приводят к новым
физическим открытиям, а эти последние служат базой для дальней-
дальнейшего развития техники. Нередко весьма теоретические и отвлечен-
отвлеченные на первый взгляд физические открытия со временем находят
самые разнообразные и важные технические применения.
Открытие в 1831 г. Фарадеем электромагнитной индукции сделало
возможным широкое практическое использование электрических
явлений.
Открытый в 1869 г. Д. И. Менделеевым периодический закон не
только сыграл исключительную роль и развитии учения об атомах и
природе химических явлений, но и является руководящим при решении
огромного количества практических задач химии и физики.
В семидесятых годах прошлого столетия Максвелл создал общую
теорию электромагнитных процессов. Исходя из этой теории, он при-
пришел к выводу о возможности распространения электромагнитной энер-
энергии в виде волн. В 1888 г. Герц экспериментально подтвердил правиль-
правильность этого вывода Максвелла. Несколькими годами позже открытие
Максвелла — Герца было использовано А. С. Поповым для осуще-
осуществления радиотелеграфии. В свою очередь развитие радиотехники
открыло перед физиками новые, исключительно широкие эксперимен-
экспериментальные возможности в изучении свойств природы.
Исследования А. Г. Столетова по „актино-электрическим" явле-
явлениям A888—1889) сыграли существенную роль в выяснении природы
фотоэлектрического эффекта, широко применяемого в современной
технике (телевидение, автоматика и т. д.).
Примеры взаимного влияния техники и физики в процессе их раз-
развития весьма многочисленны, и нет надобности их все приводить.
Отметим только, что в настоящее время исключительно важные про-
проблемы, которые способны в корне изменить технику, как, например,
непосредственное практическое использование солнечной энергии или
получение энергии за счет термоядерных реакций требуют для своего
решения дальнейшего глубокого изучения физических явлений.
10
ВВЕДЕНИЕ
§ 2. Физические законы. Физические законы устанавливаются
путем обобщения опытных данных, и их правильность проверяется
на соответствии выводов из них с опытом. Физические законы выра-
выражают объективную внутреннюю связь между физическими явлениями и
реально существующие зависимости между физическими -величинами.
По большей части содержание физических законов выражается
в математической форме как зависимость между численными значе-
значениями а и b данных физических величин А и В. Отсюда становится
ясной принципиальная важность для установления физических законов
измерения физических величин.
Измерить какую-либо физическую величину — зьачит определен-
определенным образом сравнить ее с однородной величиной, принятой за еди-
единицу. Например, измерение длины некоторого тела мы производим
путем последовательного прикладывания к нему определенного другого
тела, длина которого выбрана за единицу длины.
Очевидно, результат измерения никогда не может быть абсолютно
точен; степень его точности зависит от развития техники измерения
и от той тщательности, с которой измерение произведено. Поэтому
результат любого измерения может быть дан лишь в следующем виде:
численное значение а данной физической величины заключено между
приближенными значениями ах и at; чем меньше разность La = ax — at
по отношению к а, тем точнее оказывается измеренной физическая
величина А. Уже из одного этого следует, что устанавливаемые на
основании опытов физические закономерности не могут быть абсо-
абсолютно точными.
Таким образом, физические законы, выражающие в математической
форме количественные связи между физическими величинами, не
являются абсолютно точными; их точность всегда соответствует уровню
развития науки и техники данного времени.
Рассмотрим, например, зависимость объема данной массы газа от
давления при постоянной температуре.
Предположим, что мы имеем 8 л газа, находящегося под давле-
давлением р = — ат при некоторой постоянной температуре. Будем менять
давление, придавая ему определенные значения, например: р = 1 am,
4
-5- am, 2 am и т. д., и измерим объемы газа V, соответствующие
о
этим давлениям (при одной и той же температуре).
Тогда мы получим экспериментальные результаты, которые могут
быть записаны в виде следующей таблички:
Давление газа р в атмосферах ....
Соответствующие объемы газа V
в литрах
8
1
4
4/.
3
2
2
4"
1
8
§ 2] ФИЗИЧЕСКИЕ ЗАКОНЫ 11
Из этой таблички легко видеть, что для данной массы газа про-
произведение из давления газа р на его объем V остается постоянным:
р V = const.
Этот результат представляет собою известный закон Бойля — Ма-
Мариотта. Однако этот закон оказался установленным в результате
измерений, произведенных лишь с ограниченной степенью точности и
в ограниченном интервале давлений. Можно поэтому ожидать, что
закон Бойля — Мариотта не окажется верен, если мы произведем изме-
измерения значительно более точно или распространим их на более высо-
высокие и более низкие давления. И, действительно, более точные изме-
измерения обнаруживают отступления от закона Бойля — Мариотта; эти
отступления малы в тех интервалах давлений, к которым относились
опыты, и велики при очень больших давлениях. Можно показать, что
связь между давлением и объемом газа при постоянной температуре
лучше выражается формулой, называемой формулой Ван-дер-Ваальса:
+ ?) (V-ft) = const,
где gj и Ь — некоторые поправки. Если объем газа V велик по сравне-
сравнению с поправками ^-а и />, то членами р, и Ъ можно пренебречь по
сравнению с р и V, и тогда мы снова получим закон Бойля—Ма-
Бойля—Мариотта: pV = const. Таким образом, формула Ван-дер-Ваальса не
только лучше отображает реальные свойства газа, чем формула
Бойля — Мариотта, но она вместе с тем и указывает, в каких преде-
пределах формула Бойля — Мариотта является достаточно хорошим прибли-
приближением и где она уже не может применяться.
Подобные же рассуждения можно привести и по поводу других
физических законов, в том числе и механических (см. § 4).
Приближенный характер физических законов не умаляет их объек-
объективного значения: физические законы, хотя и не абсолютно точно,
но приближенно и относительно верно выражают объективные свойства
материи, и степень их точности повышается в процессе познания окру-
окружающей нас природы. Наука на каждом данном историческом этапе
своего развития дает нам приближенный „снимок" с действительности,
но со временем снимки эти улучшаются и полнее и лучше отражают
объективные свойства мира, который в своей совокупности остается
неисчерпаемым. „Признание теории снимком, приблизительной копией
с объективной реальности, — в этом и состоит материализм0.1
Часто забвение приблизительного характера физических законов,
приписывание им абсолютной точности и экстраполяция их на те
области, для которых их применимость не проверена, может повести
к грубым ошибкам. Например, установив закон, по которому при
1 В. И. Ленин. Сочинения, 4-е изд., т. 14, стр. 252.
12 ВВЕДЕНИЕ
температурах, близких к комнатной, всякий газ при понижении тем-
температуры на 1° С при постоянном давлении уменьшается в объеме на
~-5 объема, который он занимал при 0° С {закон Геа-Люссака), мы
можем, путем незаконной экстраполяции на очень низкие темпера-
температуры, прийти к выводу, что при охлаждении до температуры —273° С
вещество газа должно вовсе исчезнуть. На самом деле, значительно
раньше, чем будет достигнута такая температура, газ перестанет под-
подчиняться закону Гей-Люссака (см. § 44).
§ 3. Единицы измерения. Выбор единиц измерения может быть
произведен произвольно. Исторически их выбор тесно связан с сообра-
соображениями практического характера: например, такие единицы измере-
измерения, как старинная русская единица длины „локоть" или английский
„фут" (по-английски foot — стопа), связаны с размерами человеческого
тела.
В XVIII столетии французскими учеными была сделана попытка
установить „абсолютную" систему, связав единицы измерения с такими
объектами, которые не могли бы с течением времени подвергнуться
изменениям или быть утерянными. Так, за единицу длины было решено
выбрать 40000Q00 долю Длины меридиана. Однако изготовление такой
линейки неминуемо сопряжено с погрешностями. С аналогичными
трудностями встретились попытки установить и другие „абсолютные"
единицы. Поэтому, начиная с конца прошлого столетия, единицы стали
определяться образцовыми (эталонными) телами. Например, единица
длины метр определялась как расстояние между двумя черточками
на линейке из иридиевой платины, хранящейся в Международном
бюро мер и весов. Однако в настоящее время используется в извест-
известном смысле „смешанная" система, где часть единиц определяется
эталонными телами, а часть — с помощью определенных, воспроиз-
воспроизводимых физических явлений. Так, по международной системе
единиц (сокращенно обозначается MS), принятой Международной кон-
конференцией в 1960 г., за единицу длины (метр) принимается длина,
на которой укладывается 1 650 763,73 длин световых волн оранжевой
линии изотопа криптона 86 (Кг86) в пустоте (см. т. III):
1 ж =1650 763,73 Х.(Кг86).
Определенный таким образом метр очень близок к старому метру,
соответствующему расстоянию между черточками на эталонной ли-
линейке. Но по сравнению со старым метром он имеет то преимуще-
преимущество, что не может быть утерян и испорчен; со временем он не будет
меняться, как может меняться длина эталонной линейки в результате
„старения" материала, из которого она сделана. Всегда можно вновь
и вновь сравнить какую-либо длину с длиной световой волны оран-
оранжевой линии изотопа 86 криптона.
Для измерения таких длин, которые выразились бы слишком боль-
большим числом метров или слишком малой долей метра, употребляются
§ 3] ЕДИНИЦЫ ИЗМЕРЕНИЯ 13
другие единицы, образованные из единицы длины — метра по деся-
десятичной системе:
\ км = \ 000 м; \ см = -щ- м; 1 мм = -тщ: м;
1 микрон (сокращенно мк), равный щ мм, и т. д.
За единицу массы в международной системе единиц принята мас-
масса тела из иридиевой платины, хранящегося в Международном
бюро мер и весов и называемого килограммом (сокращенно кг).
Масса килограмма близка к массе 1000 см3 чистой воды при 4°С.
Единицы ббльшие и меньшие килограмма устанавливаются также по
десятичной системе:
1 тонна = 1000 кг; I г = щ кг и т. д.
За единицу времени принимается время, равное
ol ООи yzOj У/4/
доле тропического года на 1 января 1900 г. Под тропическим годом
понимается промежуток времени между двумя последовательными
прохождениями Солнца (в его видимом движении по эклиптике) через
точку весеннего равноденствия. Таким образом, единица времени свя-
связана со временем обращения Земли вокруг Солнца. Эта единица вре-
времени носит название секунды.
Для всякой иной физической величины можно было бы установить
свои собственные, вообще говоря, произвольно выбранные единицы
измерения. Например, для единицы площади можно было бы выбрать
площадь любого данного тела, без всякого отношения к уже выбранной
единице длины. Однако такой способ выбора единиц был бы весьма
неудобен. Поэтому, например, за единицу площади выбирают площадь
квадрата с длиной стороны, равной единице длины. Аналогично по-
поступают и с прочими физическими величинами, устанавливая для них
единицы измерения на основании закономерных связей, которыми эти
величины связаны с теми, единицы измерения для которых уже выбраны.
Поясним это примером. Пусть требуется установить единицу изме-
измерения для физической величины, называемой плотностью. Под плотно-
плотностью d подразумевается такая физическая величина, характерная для
данного однородного тела, которая прямо пропорциональна его массе
т и обратно пропорциональна его объему V. Поэтому численное зна-
значение плотности d равно
<* = *?. (О
где k — численный коэффициент, значение которого зависит от тех
единиц, в которых измерены d, m и V.
Имея уже наперед установленными единицы измерения массы т
и объема V, мы можем выбрать единицу плотности так, чтобы равен-
равенство A) выполнялось при некотором определенном значении коэффи-
коэффициента k. Обычно для установления единицы вновь вводимой в рас-
14 ВВЕДЕНИЕ
смотрение физической величины принято полагать А = 1. Тогда фор-
формула A) примет вид:
d=%, B)
и для того, чтобы она численно оправдывалась, за единицу плотности
мы должны выбрать плотность такого тела (независимо от того,
существует оно в природе или нет), единица массы которого занимает
единичный объем.
Таким же образом вводятся единицы измерения и других физиче-
физических величин.
В международной системе единиц за основные единицы приняты
шесть следующих:
единица длины — 1 метр A л)
единица массы — 1 килограмм A кг)
единица времени — 1 секунда A сек.)
единица температуры — 1 градус Кельвина A°К) (см. § 44)
единица силы тока — 1 ампер A а) (см. т. II)
единица силы света — 1 свеча A ев) (см. т. Ш)
Единицы измерения других величин вводятся на основании физи-
физических закономерностей, связывающих эти величины с основными.
В механике достаточно пользоваться, в качестве основных, единицами
трех физических величин — длины, массы и времени. В международ-
международной системе за эти единицы, как сказано, принимаются: метр,
килограмм, секунда. Сокращенно эта система может быть обозначена
как УИ/СЗ-система.
Однако можно строить и другие системы, иначе выбирая основ-
основные единицы. Например, в физике широко используется так называе-
называемая CGS-система, в которой за основные единицы принимаются:
единица длины — 1 сантиметр A см)
единица массы — 1 грамм A г)
единица времени — 1 секунда A сек.)
Очевидно, COS-система является кратной от международной си-
системы (MS).
Кроме того, применяется так называемая техническая система,
в которой за основные единицы приняты единицы длины A м), вре-
времени A сек.) и силы, причем за единицу силы принята та сила,
с которой земной шар притягивает тело с массой в 1 кг на уровне
моря на широте 45°. Эта единица силы называется килограмм-сила
(сокращенно обозначается 1 кГ; подробнее см. § 17). Таким образом,
в технической системе единиц основными единицами являются:
единица длины — 1 метр A м)
единица силы —1 килограмм-сила A кГ)
единица времени — 1 секунда A сек.)
ЧАСТЬ ПЕРВАЯ
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
ГЛАВА I
КИНЕМАТИКА
§ 4. Общие замечания. Механика есть учение о простейшей
форме движения материи, которое состоит в перемещении тел или их
частей друг относительно друга.
Механика, как и все остальные естественные науки, устанавливает
свои положения в результате обобщения опытных данных. Опыты
над перемещением тел относятся к простейшим. Человек наблюдает
перемещение тел повседневно в обыденной жизни, при любых произ-
производственных процессах, — отсюда следует наглядность механических
представлений. Этим же объясняется и то, что из всех естественных
наук механика прежде других получила широкое развитие. Основные
законы механики были в значительной мере выяснены Галилеем
A564—1642) и окончательно сформулированы Ньютоном A642—1727).
Леонард Эйлер A707—1783), работавший в течение многих лет
в Петербургской Академии наук, впервые придал законам механики
аналитический вид и сыграл большую роль в ее развитии. Однако
механика Галилея — Ньютона, получившая название „классической",
возникла в результате наблюдения лишь над ограниченным типом
движений, а именно, движений тел, сравнимых по размерам с раз-
размерами человеческого тела (брошенный камень) или очень больших
по сравнению с ними (движение планет) и движущихся со скоро-
скоростями, не очень большими. Отсюда — приближенный характер клас-
классической механики. Дальнейшее развитие науки показало, что клас-
классическая механика является прекрасным приближением к действи-
действительности только до тех пор, пока мы не имеем дело с движением тел,
состоящих из большого числа атомов (макроскопических тел) и ско-
скорости которых малы по сравнению со скоростью света. Ленин писал:
„.. .механика была снимком с медленных реальных движений, а новая
физика есть снимок с гигантски быстрых реальных движений".1
Законы движения макроскопических тел со скоростями, сравни-
сравнимыми со скоростью света, даются теорией относительности, уста-
установленной Эйнштейном.
1 В. И. Лени н. Сочинения, 4-е изд., т. 14, стр. 252.
16 КИНЕМАТИКА [ГЛ. t
Законы классической механики перестают также быть справед-
справедливыми, когда мы переходим к движению отдельных атомов или
элементарных частиц (микроскопических тел).1 Законы движения
микроскопических тел устанавливаются так называемой квантовой
механикой. Ниже мы дадим границы применимости классической
механики, пока же будем предполагать, что речь идет всегда о движе-
движении макроскопических тел со скоростями, малыми по сравнению со
скоростью света.
Привычность механических явлений и их наглядность, а также
успехи в объяснении некоторых физических явлений (например
звуковых) с помощью чисто механических представлений привели
к тому, что в XIX столетии для многих физиков объяснить какое-
либо явление — означало свести его к явлениям механическим. Эта
точка зрения соответствовала философскому механическому мате-
материализму. Однако все дальнейшее развитие физики, особенно раз-
развитие учений о свете и об электричестве, показало, что многие
явления подчиняются своим собственным законам и не могут быть
сведены к простейшему типу движения — механическому. Механи-
Механический материализм должен был уступить место диалектическому
материализму, рассматривающему более общие типы движения мате-
материи, учитывающему все разнообразие реального мира.
Энгельс писал по этому поводу: „У естествоиспытателей движение
всегда отождествляется с механическим движением, перемещением...
Движение, в применении к материи, — это изменение вообще. Из
подобного же недоразумения вытекает и яростное стремление свести
все к механическому движению..., чем смазывается специфический
характер прочих форм движения".52
Механическое движение может быть весьма различных видов
и носить достаточно сложный характер. Поэтому механика разбивает
реальные движения на более простые, а изучив их, переходит затем
снова к более сложным движениям. Наиболее простым механическим
движением является движение так называемой материальной точки.
Под материальной точкой понимают в механике такое тело,
размерами и формой которого можно пренебречь в данной задаче.
Одно и то же реальное тело, в зависимости от постановки задачи,
часто рассматривается либо как материальная точка, либо как тело
конечных размеров. Например, рассматривая задачу, о полете артилле-
артиллерийского снаряда, мы в первом приближении можем пренебречь его
формой и размерами и рассматривать снаряд как материальную точку.
Но если необходимо учесть влияние сопротивления воздуха на полет
снаряда и роль вращения во время полета, то мы уже не вправе
1 Слово „микроскопический" здесь не означает, что частицу можно видеть
в микроскоп, но что она представляет собою элементарную частицу—электрон,
протон и т. д., или частицу, состоящую из небольшого числа элементарных
частиц, например атом или отдельную молекулу.
* Ф. Энгельс, Диалектика природы, 1950, стр. 197.
§ 5] ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ 17
рассматривать снаряд как материальную точку: мы должны учесть
его форму, размеры и т. д. Наряду с этим, астрономы, рассматривая
движение земного шара по орбите вокруг Солнца, могут считать зем-
земной шар за материальную точку.
Из определения механического движения как простого перемеще-
перемещения явствует, что это перемещение может происходить лишь отно-
относительно каких-либо других материальных тел. Поэтому для того,
чтобы получить возможность характеризовать движение какого-либо
тела, прежде всего следует условиться, относительно какого другого
тела (или группы неподвижных друг относительно друга тел) мы
будем отсчитывать перемещение данного тела. Это тело (или группа
тел) образует систему отсчета. Таким образом, каждое движение
должно рассматриваться относительно какой-либо определенной
системы отсчета. В разных случаях система отсчета может выби-
выбираться различным образом, но определенно характеризовать данное
движение мы можем, только твердо выбрав систему отсчета. Напри-
Например, бросив какой-либо предмет, мы можем рассматривать его дви-
движение относительно комнаты; в этом случае систему отсчета обра-
образуют стены, пол и другие части комнаты. Мы можем, однако, рас-
рассматривать движение того же тела и относительно Солнца или
какой-либо определенной звезды, только мы должны вперед точно
условиться, относительно чего именно мы рассматриваем движение
нашего предмета.
Практически для описания движения приходится связывать с телами,
образующими систему отсчета, какую-либо координатную систему,
например обычную прямолинейную прямоугольную систему координат.
При рассмотрении движения относительно комнаты можно, например,
поместить начало координат в одном из углов комнаты, а оси на-
^ править вдоль стен; или начало координатной системы можно поме-
помеху стить на Солнце, а оси провести в направлении определенных звезд.1
*w В дальнейшем мы поставим вопрос о выборе системы отсчета, пока же
-^ будем подразумевать, что нам всегда дана система отсчета и твердо
•»— связанная с ней координатная система, которой мы будем пользо-
"" ваться для характеристики движения.
Механику принято делить на две части: кинематику, рассматри-
рассматривающую лишь само перемещение в зависимости от времени, и дина-
динамику, учитывающую взаимодействия тел, ведущие к изменению их
состояния движения.
§ б. Прямолинейное равномерное движение. Рассмотрим дви-
движение тела, трактуемого как материальная точка, сводящееся к его
равномерному перемещению вдоль некоторой прямой OD (рис. 1).
В любой данный момент времени t, когда движущееся тело нахо-
находится в некоторой точке А, мы можем определить его положение
1 Координатную систему можно связать также с какой-либо материальной
сплошной средой. Например, можно рассматривать движение рыбы относи-
относительно воды, а которой она плавает.
2 С. Э. Фриш и А. В. Тиморева
18
КИНЕМАТИКА
[ГЛ. I
отрезком s, отсчитанным от некоторой точки О, условно принятой
за начало отсчета. Очевидно, s меняется со временем. Отрезок s
совпадает с путем, фактически
пройденным прямолинейно движу-
движущимся телом, если в начальный
момент (t — О) тело находилось
в точке О. Проводя координатную
систему OXYZ, можно охаракте-
охарактеризовать также положение тела
в каждый данный момент его коор-
координатами х, у и г. При сделанном
на рис. 1 выборе координатной
х,
и
Рис. 1. Положение тела А при
прямолинейном движении опреде-
определяется либо отрезком s, либо его
проекциями на координатные оси
системы координаты тела
z совпадают с проекциями пути sx,
sy и s2 на координатные оси. Таким
образом, положение движущейся
точки можно характеризовать либо
отрезком s, который будет некото-
некоторой функцией от времени t:
A)
либо ее координатами
от времени:
х, у и z, которые также будут функциями
Так как рассматриваемое движение происходит вдоль прямой, то
оно носит название прямолинейного.
Движение называется равномерным в том случае, если движущееся
тело в произвольные, но равные промежутки времени проходит
одинаковые отрезки (пути).
Движения очевидным образом различаются друг от друга тем,
что тела могут проходить за одинаковые промежутки времени раз-
разные пути, или (говоря другими словами) тем, что одинаковые пути
могут быть пройдены за различные промежутки времени. Эти раз-
различия в движениях мы характеризуем, вводя понятие скорости. Под
скоростью равномерного движения подразумевается физическая вели-
величина, тем большая, чем больший путь проходит тело за данный
промежуток времени, или, другими словами,;— физическая величина,
тем большая, чем меньший промежуток времени необходим для
прохождения данного пути. Таким образом, скорость равномерного
движения v есть физическая величина, прямо пропорциональная
пройденному пути и обратно пропорциональная тому промежутку
времени, за который этот путь пройден.
Пусть положение прямолинейно движущегося тела в некоторый
момент времени tu определяется отрезком -ед—з-в момент времени
§ 5] ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ 19
t — отрезком s. Тогда за время t — tn тело проходит путь s — sB,
и математическое выражение для скорости v может быть записано
в виде:
где k — коэффициент пропорциональности. В частном случае, если
f, = 0 и 5,-0, то.
v = k±. (За)
Здесь s представляет собою путь, пройденный за время /. Скорость
равномерного движения есть величина постоянная. Пользуясь соот-
соотношением C), можно измерять скорость ¦», отрезок s и время t
в любых единицах. Если же заранее придать коэффициенту k какое-
либо определенное значение, то, как указывалось в § 3, нельзя
выбирать единицы измерения для всех трех физических величин v,
s и t произвольно. Произвольно могут быть выбраны лишь единицы
для двух величин, а для третьей величины единицы измерения дол-
должны быть выбраны так, чтобы соотношение C) численно выполня-
выполнялось при данном коэффициенте k. Так, положив k = 1 и, следова-
следовательно, переписав формулу C) в виде:
можно лишь для двух из фигурирующих в ней величин выбирать
произвольно единицы. Если мы выберем за единицу длины санти-
сантиметр (см), за единицу времени секунду (сек.), то, пользуясь фор-
формулой D), мы обязаны взять в качестве единицы скорости скорость
такого равномерного движения, при котором за 1 сек. проходится
путь в 1 см. Это есть единица скорости в CGS-системе; сокращенно
она обозначается см/сек. В других системах единиц за единицу
пути берут метр (м) или километр (км), а за единицу времени —¦
секунду (сек.) или час, тогда соответственно получаются единицы
скорости м/сек и км/час.
Из формулы D) имеем
(t — U). E)
Если 4 = 0 и s0 = 0, то формула E) примет вид:
s = vt; Ea)
здесь s — путь, пройденный телом за время t.
Сравнивая Eа) с A), мы видим, что в случае равномерного
движения тела его путь есть линейная функция от времени.
Можно изобразить линейную зависимость пути от времени
графически. Отложим по оси абсцисс время t (рис. 2), а по оси
20
КИНЕМАТИКА
[ГЛ. I
ординат — путь
симость пути s
s. Тогда, в соответствии
от времени
с формулой Eа), зави-
t выразится прямой ОВ, проходящей
через начало координат. За некоторый
промежуток времени t, изображаемый
на оси абсцисс отрезком Ob, тело
"пройдет путь s, который изобразится
отрезком Оа или равным ему отрез-
отрезком ЬВ.
Из рис. 2 имеем
, ЬВ s .„,
t
Рис. 2. При равномерном дви-
движении зависимость пройден-
пройденного пути s от времени t изо-
изображается прямой ОВ,
Таким образом, на нашем графике
скорость v изобразится тангенсом угла а;
чем больше скорость v, тем ббльший угол
а составит прямая ОВ с осью времен t.
§ 6. Прямолинейное неравномерное движение. При неравно-
неравномерном движении за одинаковые промежутки времени тело проходит
неравные пути. В этом случае можно ввести понятие о средней
скорости движения. Средняя скорость неравномерного движения за
данный промежуток времени t —1$ равна скорости такого равно-
равномерного движения, при котором тело прошло бы тот же путь s — s0
за тот же промежуток времени t —1$, что оно проходит, двигаясь
неравномерно. Таким образом, обозначая среднюю скорость движения
через v, имеем
Значение средней скорости v зависит от того промежутка вре-
времени, за который она берется. Поэтому средняя скорость является
недостаточной характеристикой неравномерного движения. Например,
при движении поезда на перегоне между двумя станциями нас может
интересовать не только его средняя скорость на всем перегоне, но
и скорости, которые поезд имел на отдельных участках пути. Для
этого мы должны, очевидно, разбить путь на отдельные участки As
и измерить те промежутки времени М, в течение которых эти участки
проходились, тогда
*=& 0)
представит собою среднюю скорость на некотором данном участке
пути Д5.
Мы получим тем более точную характеристику движения, чем
короче выберем те промежутки времени М, для которых будем
определять среднюю скорость v. В принципе промежуток времени Д^
может быть выбран настолько малым, что движение в течение этого
промежутка времени можно будет практически считать равномерным.
§ б]
ПРЯМОЛИНЕЙНОЕ НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
21
Тогда средняя скорость v за этот малый промежуток времени даст
нам достаточную характеристику движения в данный момент времени;
другими словами, она представит скорость v в данной точке пути.
Таким образом, скоростью неравномерного движения в данной
точке пути (или в данный момент времени) является предел,
к которому стремится средняя скорость при бесконечном убы-
убывании промежутка времени At, за который она определяется.
Математически это выражается следующим образом:
¦в = пред.
/As
= пред. -г-
Из дифференциального исчисления известно, что пред.
B)
есть произ-
водная от пути по Бремени; таким образом, скорость численно равна произ-
производной от пути по времени:
ds
Bа)
Сказанное может быть пояснено графическим построением.
Графически зависимость пути от времени при неравномерном
движении выразится кривой. Вид этой кривой различен для различных
движений; для некоторого частного
случая он изобразится кривой О А В,
представленной на рис. 3.
Средняя скорость v за проме-
промежуток времени М есть:
О
Рис. 3. Скорость неравномерного
движения определяется тангенсом
угла а, образованного касательной
с осью Ot.
Вводя среднюю скорость v, мы
заменяем хордой АВ действитель-
действительную зависимость пути от времени,
выражаемую за промежуток времени
Д? дугой А В, т. е. неравномерное
движение заменяем равномерным.
Бесконечно уменьшая промежуток
времени kt, по сказанному, получим
скорость в данный момент времени t, причем секущая АВ в пределе
станет касательной AD, хорда А В и дуга АВ сольются, т. е. нерав-
неравномерное движение за бесконечно малый промежуток времени Д?
будет совпадать с равномерным.
Таким образом:
'As'
v = пред.
At -.0
= tga,
где a — угол между осью Ot и касательной к данной точке А кри-
кривой, изображающей зависимость пути от времени.
22
КИНЕМАТИКА
[ГЛ. I
Посмотрим, как изобразится при неравномерном движении прой-
пройденный путь в зависимости от скорости.
Построим график, отложив по оси абсцисс время t, а по оси
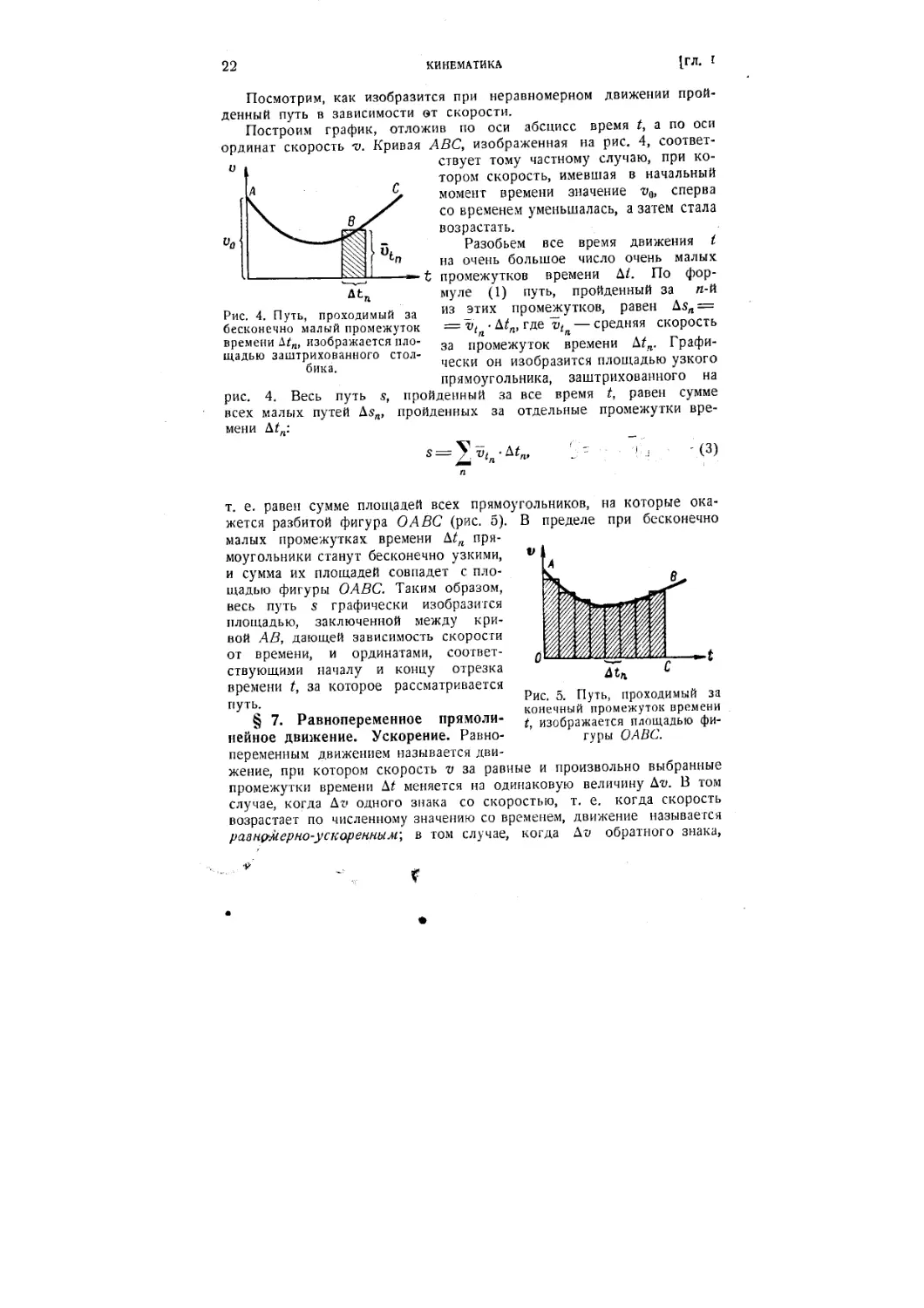
ординат скорость -о. Кривая ABC, изображенная на рис. 4, соответ-
соответствует тому частному случаю, при ко-
котором скорость, имевшая в начальный
момент времени значение г»0, сперва
со временем уменьшалась, а затем стала
возрастать.
Разобьем все время движения I
на очень большое число очень малых
t промежутков времени Ai. По фор-
формуле A) путь, пройденный за и-й
Рис. 4. Путь, проходимый за из этих промежутков, равен Asn =
бесконечно малый промежуток = vt/i ¦ Atn, где vt/i — средняя скорость
времени Atn, изображается пло- за промежуток времени Atn. Графи-
щадью заштрихованного стол- ,.
нбика чески он изобразится площадью узкого
прямоугольника, заштрихованного на
рис. 4. Весь путь s, пройденный за все время t, равен сумме
всех малых путей Asn, пройденных за отдельные промежутки вре-
времени At-
s =
C)
т. е. равен сумме площадей всех прямоугольников, на которые ока-
окажется разбитой фигура ОАВС (рис. 5). В пределе при бесконечно
малых промежутках времени Atn пря-
прямоугольники станут бесконечно узкими,
и сумма их площадей совпадет с пло-
площадью фигуры ОАВС. Таким образом,
весь путь s графически изобразится
площадью, заключенной между кри-
кривой АВ, дающей зависимость скорости
от времени, и ординатами, соответ-
соответствующими началу и концу отрезка
времени t, за которое рассматривается
путь.
§ 7. Равнопеременное прямоли-
прямолинейное движение. Ускорение. Равно-
Равнопеременным движением называется дви-
движение, при котором скорость v за равные и произвольно выбранные
промежутки времени At меняется на одинаковую величину Av. В том
случае, когда Дг> одного знака со скоростью, т. е. когда скорость
возрастает по численному значению со временем, движение называется
раанрЖерно-ускоренным; в том случае, когда Av обратного знака,
Рис. 5. Путь, проходимый за
конечный промежуток времени
t, изображается площадью фи-
фигуры ОАВС.
§ 7] РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ. УСКОРЕНИЕ 23
т. е. когда скорость убывает по численному значению со временем,
движение называется равномерно-замедленным.
Для характеристики того, насколько быстро со временем меняется
скорость, вводится физическая величина, называемая ускорением..
Ускорение w равнопеременного прямолинейного движения есть физи-
физическая величина, прямо пропорциональная приращению скорости и
обратно пропорциональная тому промежутку времени, за который
произошло это приращение.
Пусть в момент времени ^0 скорость имела значение v0, а в момент
времени t — значение ¦», тогда за время t — tu скорость изменилась
на v — ¦»(,. и математически ускорение w представится соотношением:
™ b k^ A)
где k — коэффициент пропорциональности, зависящий от выбора
единиц, в которых измеряются скорость v и время L Ускорение
равнопеременного движения есть величина постоянная. Если поло-
положить коэффициент пропорциональности k=l, то ускорение
Av
при этом в CGS-системе за единицу ускорения должно быть при-
,, нято ускорение такого движения, при котором скорость меняется
¦5 на 1 см/сек за каждую секунду; сокращенно эта единица ускорения
обозначается 1 смIсек2. В ЖЛ^-системе единиц за единицу ускорения
применяется ускорение такого движения, при котором скорость
меняется на 1 м/сек за каждую секунду (сокращенно 1 м/сек'х).
Из формулы A) при k — \ имеем
v = vt + w(t — ta). B)
Таким образом, при равнопеременном движении скорость меняется
со временем линейно. Если ?0^0, то по B):
Ba)
наконец, если начальная скорость va = 0, то
v = wt. B6)
Ускорение w имеет тот же знак, что и изменение скорости Av,
поэтому при равномерно-ускоренном движении ускорение w поло-
положительно, а при равномерно-замедленном — отрицательно.
Определим путь, проходимый при равнопеременном движении.
Положим для простоты начальную скорость ¦»0^0, тогда
по B6) графически зависимость скорости от времени (считаем ^
24
КИНЕМАТИКА
[ГЛ. I
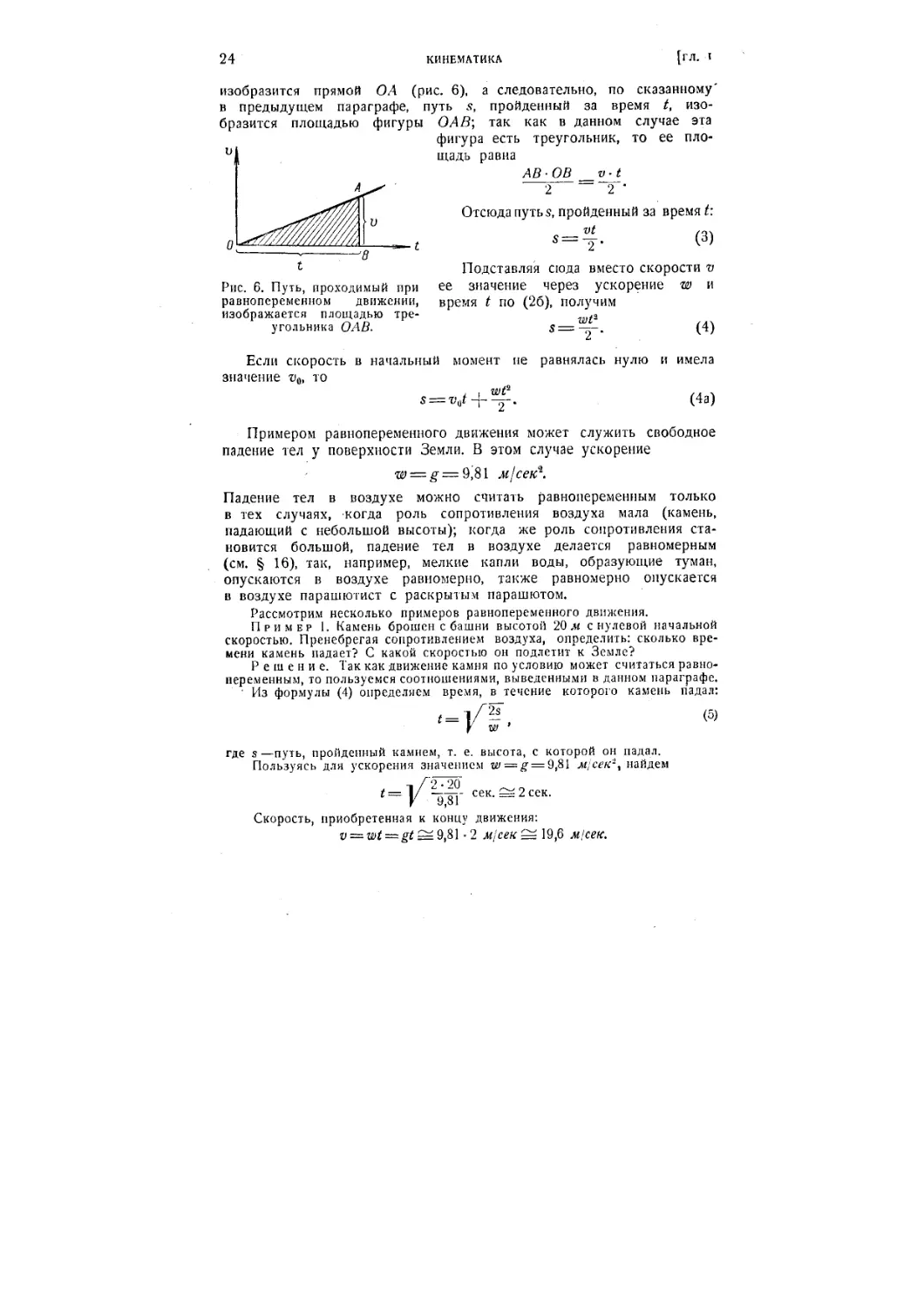
изобразится прямой ОА (рис. 6), а следовательно, по сказанному'
в предыдущем параграфе, путь s, пройденный за время /, изо-
изобразится площадью фигуры ОАВ; так как в данном случае эта
фигура есть треугольник, то ее пло-
площадь равна
АВ-ОВ _v-t
2 ~~ 2 "
Отсюда nyrbs, пройденный за время t:
C)
•=т-
Подставляя сюда вместо скорости v
Рис. 6. Путь, проходимый при ее значение через ускорение w и
равнопеременном движении, время t no B6), получим
изображается площадью тре- ,2
угольника ОАВ. s=—-. D)
Если скорость в начальный момент не равнялась нулю и имела
значение v0, то
s = »o*-f^. Dа)
Примером равнопеременного движения может служить свободное
падение тел у поверхности Земли. В этом случае ускорение
¦aj = g- = 9,81 м/сек*.
Падение тел в воздухе можно считать равнопеременным только
в тех случаях, когда роль сопротивления воздуха мала (камень,
падающий с небольшой высоты); когда же роль сопротивления ста-
становится большой, падение тел в воздухе делается равномерным
(см. § 16), так, например, мелкие капли воды, образующие туман,
опускаются в воздухе равномерно, также равномерно опускается
в воздухе парашютист с раскрытым парашютом.
Рассмотрим несколько примеров равнопеременного движения.
Пример 1. Камень брошен с башни высотой 20 м с нулевой начальной
скоростью. Пренебрегая сопротивлением воздуха, определить: сколько вре-
времени камень падает? С какой скоростью он подлетит к Земле?
Решение. Так как движение камня по условию может считаться равно-
равнопеременным, то пользуемся соотношениями, выведенными в данном параграфе.
' Из формулы D) определяем время, в течение которого камень падал:
t=l/^ E)
Y w
где s —путь, пройденный камнем, т. е. высота, с которой он падал.
Пользуясь для ускорения значением w = g = 9,81 м;сек'\ найдем
I 2 сек.
Скорость, приобретенная к концу движения:
v = wt = gt = §,%\ -2 MJceK= 19,6 м/сек.
§ 8] УСКОРЕНИЕ ПРОИЗВОЛЬНОГО ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ 25
Скорость v, приобретенную к концу пути s, можно выразить и алгебраи-
алгебраически через пройденный путь s и ускорение w. Для этого подставляем
в выражение v = wt вместо t его значение по E), тогда
v = wt = w 1/ — ,
X W
откуда
v= Y2sw. F)
Пример 2. Камень, брошенный вертикально вверх, достигает высоты
30 м. Через сколько времени он достигнет этой высоты и через сколько вре-
времени он упадет обратно на Землю? Какую начальную скорость надо ему
сообщить?
Решение. Движение камня, брошенного вертикально вверх, будет
в той своей части, где камень поднимается кверху, равномерно-замедленным,
поэтому его ускорение да = — g и высота его поднятия
s = vot — ~ , G)
где v0 — начальная скорость камня и t—время, в течение которого он под-
поднимается вверх. Начальную скорость va определим из условия, что скорость vs
в наивысшей точке равна нулю, т. е.
откуда
vo=gt (8)
и, следовательно, по G),
откуда искомое время поднятия камня на высоту s равно
<=/!¦
Сравнивая это время с временем, определяемым равенством E), находим,
что время поднятия камня на высоту s равно времени его свободного паде-
падения с той же высоты. Подставляя найденное значение t в (8), получим
Wo = V2sg.
Следовательно [ср. с формулой FI, и скорость, с которой камень надо бро-
бросить вертикально вверх, равна скорости, какую он приобретает, свободно
падая с той же высоты s. Пользуясь выведенным соотношением и численным
значением, данным в примере, находим:
v0 = V2sg= ]/2-30-9,81 м1 сек Q^ 24,2 м/сек;
§ 8. Ускорение произвольного прямолинейного движения. В об-
общем случае неравномерного прямолинейного движения можно ввести
понятие о среднем ускорении. Среднее ускорение w за данный
промежуток времени At равно ускорению тела, движущегося равно-
равнопеременно и приобретающего за тот же промежуток времени Д? то
же приращение скорости Av, что и рассматриваемое тело:
— До ,,,
26
КИНЕМАТИКА
[ГЛ.
Понятие об ускорении в данный момент вводится так же, как
и понятие о скорости в данный момент. Мы уменьшаем промежуток
времени At настолько, чтобы движение за этот промежуток времени
можно было практически считать равнопеременным. Среднее уско-
ускорение гг> за такой промежуток времени и даст нам ускорение в дан-
данный момент. Таким образом, под ускорением в данный момент под-
подразумеваем предел, к которому стремится среднее ускорение w при
бесконечном убывании того промежутка времени Д^, за который оно
берется:
w — пред. (w) = пред. (-^), B)
где Дг>— бесконечно малое изменение скорости за бесконечно малый
промежуток времени Д^.
Из дифференциального исчисления имеем
(Av\ dv
* = "?«; 77 =7*.
Bа)
т. е. ускорение численно равно производной от скорости по времени. Так как
d's
0О
w = - ¦¦ B6)
т. е. ускорение численно равно производной от пути по времени. .
Эти соотношения так же, как и в случае скорости, мы можем
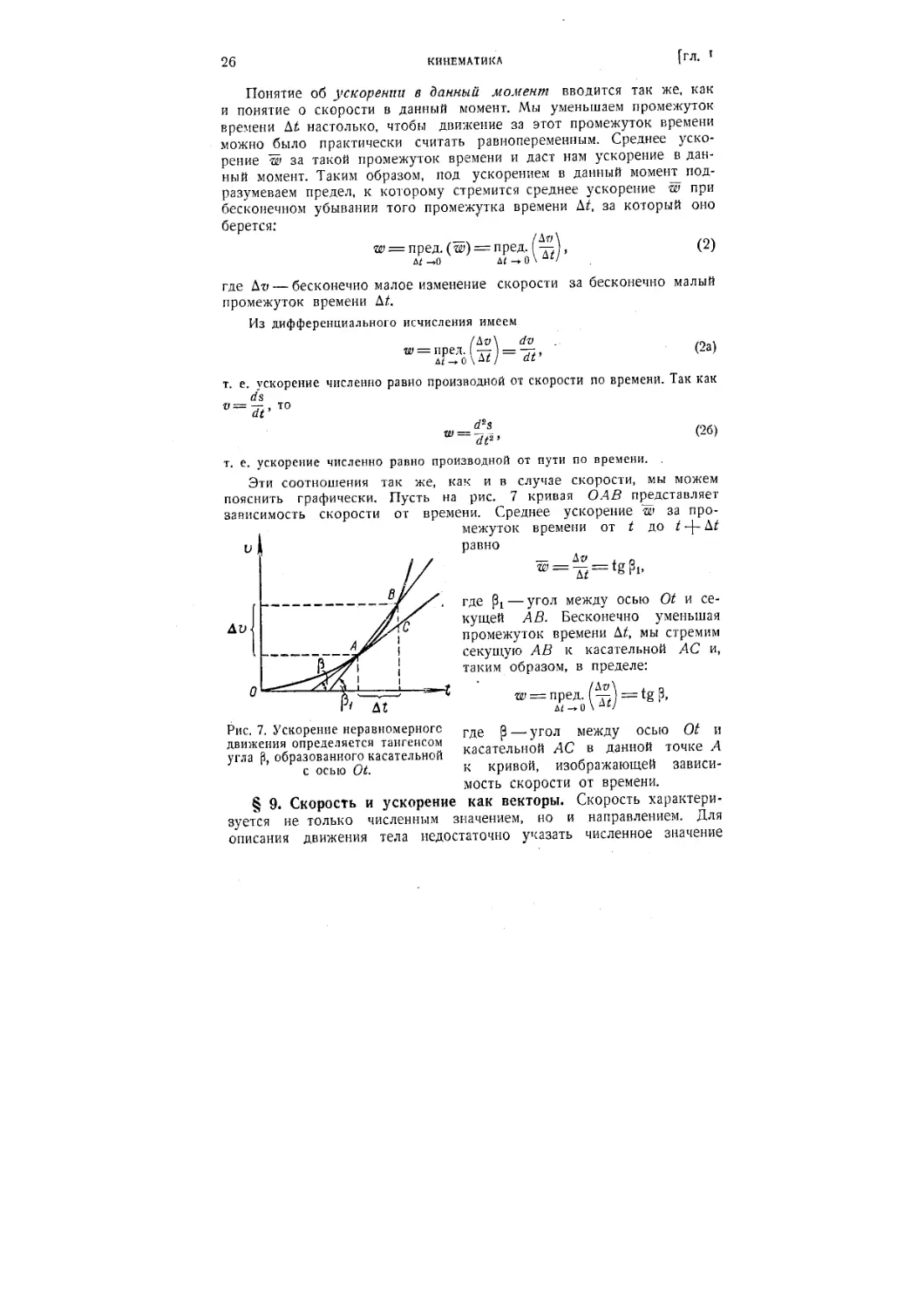
пояснить графически. Пусть на рис. 7 кривая ОАВ представляет
зависимость скорости от времени. Среднее ускорение гг> за про-
промежуток времени от t до t -\- At
v ) равно
где pt — угол между осью Ot и се-
секущей АВ. Бесконечно уменьшая
промежуток времени At, мы стремим
секущую АВ к касательной АС и,
таким образом, в пределе:
; = пред. — =
Рис. 7. Ускорение неравномерногс
движения определяется тангенсом
угла р, образованного касательной
с осью Ot.
где р — угол между осью Ot и
касательной ЛС в данной точке А
к кривой, изображающей зависи-
зависимость скорости от времени.
§ 9. Скорость и ускорение как векторы. Скорость характери-
характеризуется не только численным значением, но и направлением. Для
описания движения тела недостаточно указать численное значение
§ 9]
СКОРОСТЬ И УСКОРЕНИЕ КАК ВЕКТОРЫ
27
Рис. 8. При сложении
двух векторов А и В
результирующий век-
вектор С изображается
диагональю паралле-
параллелограмма, сторонами
которого служат век-
векторы А и В.
его скорости, необходимо еще указать, в каком направлении оно
движется.
Величины, характеризуемые не только численным значением, но
и направлением, называются векторами. Величины, для определения
которых достаточно задать только их численное значение, называются
скалярами (например, промежуток времени,
масса, плотность и т. д.).
Вектор может быть изображен стрелкой,
длина которой в некоторых произвольных еди-
единицах длины равна численному значению ве-
вектора, а направление совпадает с направле-
направлением вектора. Векторы принято обозначать
жирными буквами, а их численные значения —
теми же обычными буквами; например, буква А
означает вектор, а А — его численное значе-
значение. Знак минус перед вектором означает, что
вектор — А направлен в сторону, противопо-
противоположную вектору А, будучи одинаковой с ним
длины.
Опыты показывают, что физические вели-
величины, являющиеся векторами, складываются
иначе, чем алгебраические величины. Способ сло-
сложения векторов определяется правилом параллелограмма: при сложении
двух векторов А и В суммарный вектор С определяется диагональю
параллелограмма, сторонами которого слу-
служат векторы А и В (рис. 8).
При сложении более чем двух векто-
векторов можно найти суммарный вектор путем
последовательного применения правила
параллелограмма. Тот же результат полу-
получится, если построить ломаную, соста-
составляющие которой по величине и напра-
направлению совпадают со слагаемыми векто-
векторами А, В, С, D (рис. 9). Суммарный
Рис.9. ВекторF,являющийся вектор F определится замыкающей, прове-
суммой векторов А, В, С, D, денной от начала ломаной к ее концу,
изображается замыкающей Разность двух векторов А и В можно
ломаной линии, составляю- определить, введя вектор В' = —В, тогда
щие которой — векторы А. ^ у
В, С, D. А — В = А + В'. A)
Построив вектор В', численно равный вектору В, но направлен-
направленный в противоположную сторону, найдем вектор С, являющийся
суммой векторов А и В'. В силу равенства A), вектор С представит
одновременно и разность векторов А — В.
Вектор можно определить либо непосредственно, задав его по
величине и направлению, либо задав его проекции на координатные
28
КИНЕМАТИКА
[гл. 1
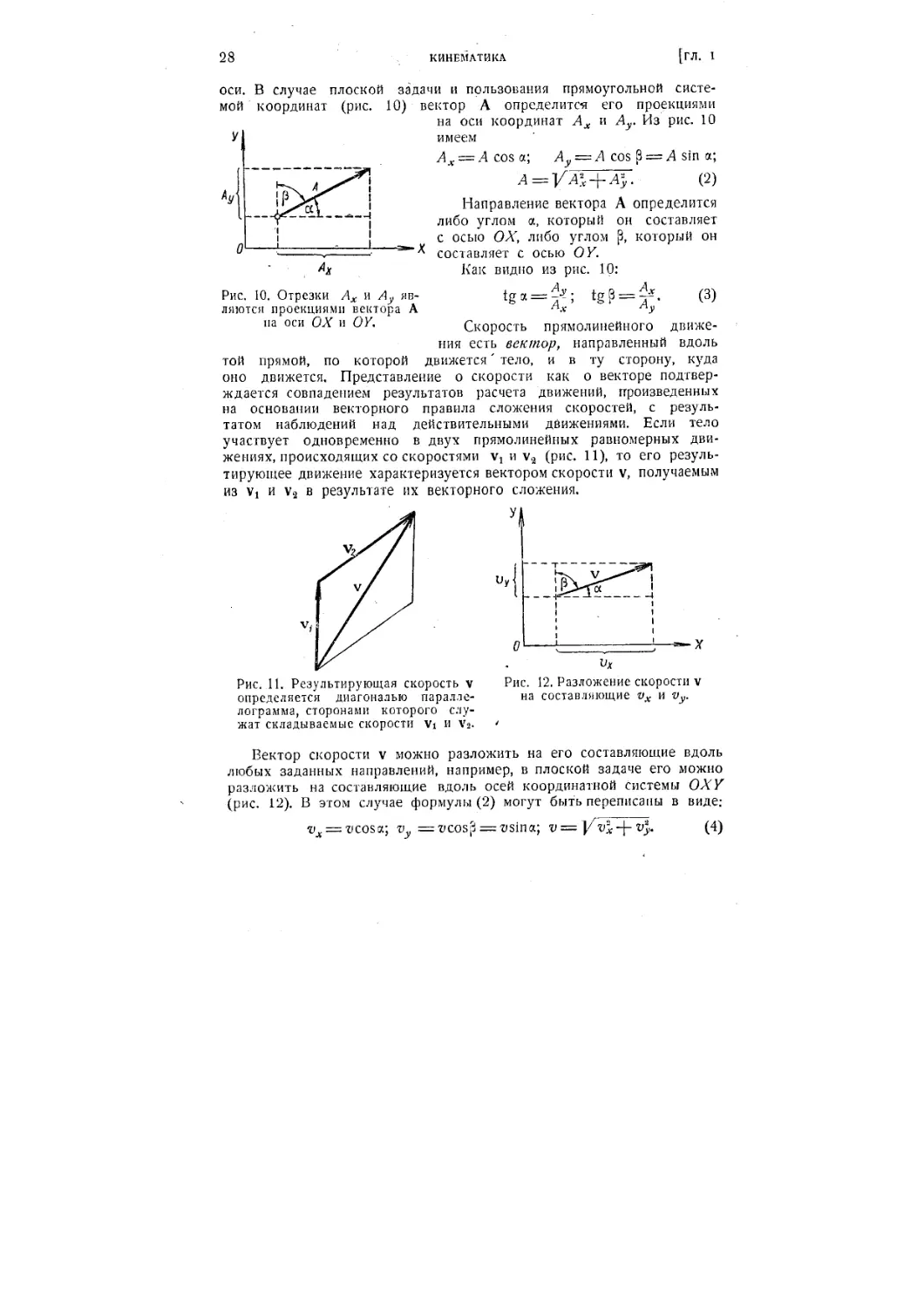
оси. В случае плоской задачи и пользования прямоугольной систе-
системой координат (рис. 10) вектор А определится его проекциями
на оси координат Ах и Ау. Из рис. 10
имеем
Ах -= A cos а; Ау = A cos C = A sin а;
B)
Направление вектора А определится
либо углом а, который он составляет
с осью ОХ, либо углом р, который он
составляет с осью OY.
Как видно из рис. 10:
Рис. 10. Отрезки Ах и Ау яв- tga = -^; tgP = —. C)
ляются проекциями вектора А &х Ау
па оси ОХ и OY. Скорость прямолинейного движе-
движения есть вектор, направленный вдоль
той прямой, по которой движется' тело, и в ту сторону, куда
оно движется. Представление о скорости как о векторе подтвер-
подтверждается совпадением результатов расчета движений, произведенных
на основании векторного правила сложения скоростей, с резуль-
результатом наблюдений над действительными движениями. Если тело
участвует одновременно в двух прямолинейных равномерных дви-
движениях, происходящих со скоростями v, и v, (рис. 11), то его резуль-
результирующее движение характеризуется вектором скорости v, получаемым
из V! и Vj в результате их векторного сложения.
Рис. 11. Результирующая скорость v
определяется диагональю паралле-
параллелограмма, сторонами которого слу-
служат складываемые скорости Vi и v2.
Рис. 12. Разложение скорости v
на составляющие vx и vy.
Вектор скорости v можно разложить на его составляющие вдоль
любых заданных направлений, например, в плоской задаче его можно
разложить на составляющие вдоль осей координатной Системы OXY
(рис. 12). В этом случае формулы B) могут быть переписаны в виде:
v = Vvx-^Vy. D)
§
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
29
Рис. 13. Определение результирующей
скорости.
Пример. Найти по величине и направлению относительно берега ско-
скорость v человека, движущегося поперек парохода со скоростью vt = 2 м/сек;
пароход движется со скоростью t»a = 8 м/сек.
Решение. Скорость v человека относительно берега является век-
векторной суммой скоростей Vi и Va_ (рис. 13). Ее численное значение
v== Yv\ + v\ = 1^4 -f- 64 м/сек = ]Л38 м/сек = 8,25 м/сек. Направление ско-
скорости v определится углом а,
который она составляет с на- - Y? Направление движения
правлением движения паро- v(
хода; из рис. 13:
tg а = ^! = -|- = 0,25,
откуда о = 14°03'.
Ускорение, как и ско-
скорость, есть вектор, так
как оно характеризуется,
кроме численного значе-
значения, еще и направлением.
В случае прямолинейного движения ускорение всегда направлено вдоль
той же прямой, вдоль которой направлена скорость и вдоль которой
совершается движение. При этом ускорение, как мы уже отмечали,
может быть направлено либо в ту же сторону, что и скорость (уско-
(ускоренное движение), либо в обратную (замедленное движение). Если
ускорение направлено под некоторым углом к скорости, то ско-
скорость меняется не только по вели-
величине, но и по направлению. В этом
случае тело движется криволинейно.
§ 10. Криволинейное движение.
Если линия, описываемая материальной
точкой при ее движении, или как го-
говорят, ее траектория, представляет
собою кривую линию, то движение
называется криволинейным. Для того
чтобы определить вектор скорости
при криволинейном движении, рассмо-
рассмотрим малый промежуток времени Дг;
за этот промежуток времени материальная точка пройдет малую
дугу As (рис. 14). Если мы будем бесконечно уменьшать промежу-
промежуток времени, то и дуга As станет бесконечно уменьшаться и в пре-
пределе сольется со стягивающей ее хордой As. Криволинейное дви-
движение в пределе совпадает на бесконечно малом участке с прямо-
прямолинейным. Поэтому скорость криволинейного движения в данной
точке А численно окажется равной
Рис. 14. Вектор скорости v на-
направлен при криволинейном дви-
движении по касательной к траек-
траектории.
г. = пред.
и -, о
Д8
¦)¦
A)
30
КИНЕМАТИКА
[гл. i
а ее направление совпадет с направлением бесконечно малой
хорды As, стягивающей бесконечно малую дугу As. Но так как бес-
бесконечно малая хорда в пределе совпадает по направлению с каса-
касательной к данной точке А, то вектор скорости v при криволиней-
криволинейном движении направлен в каждый данный момент по касатель-
касательной к траектории тела, проведенной в направлении движения.
Если скорость v при криволинейном движении имеет постоянное
численное значение, т. е. если за одинаковые и произвольно выбранные
промежутки времени материальная точка проходит дуги одинаковой
длины, то криволинейное движение называется равномерным. Однако
надо помнить, что по направлению скорость и в этом случае непре-
непрерывно меняется: в каждой точке пути она направлена по касатель-
касательной, а для криволинейного пути в разных точках касательная имеет
разные направления.
Таким образом, при криволинейном движении вектор скорости
никогда не остается постоянным: он все время меняется. В слу-
случае равномерного криволинейного движения он меняется только по
направлению, сохраняя постоянное
численное значение; в общем слу-
случае неравномерного криволинейного
движения он меняется и по вели-
величине и по направлению.
Для рассмотрения криволиней-
криволинейного движения весьма удобно опре-
определять положение тела с помощью
координат, например, в случае пло-
плоского движения — с помощью коор-
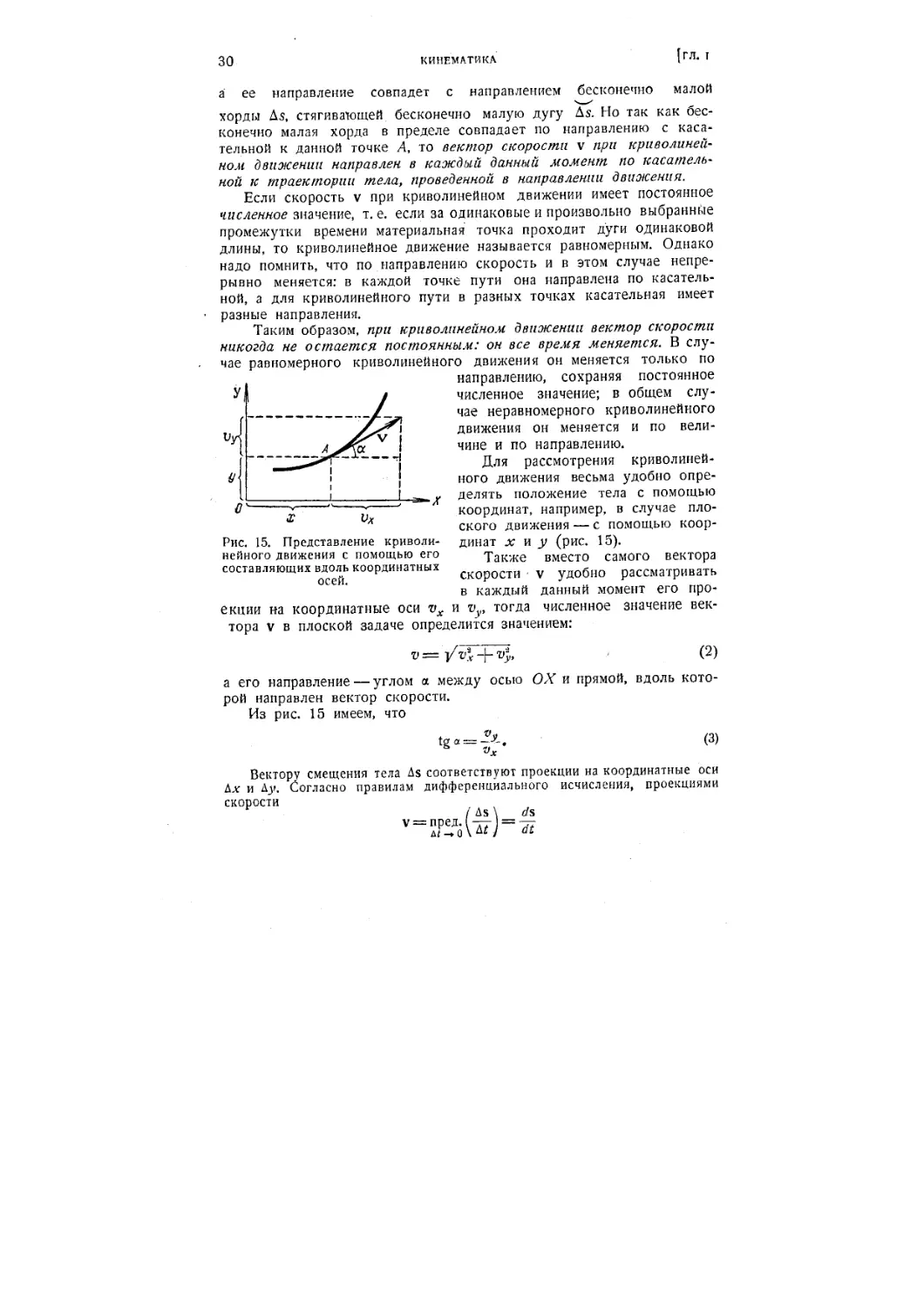
Рис. 15. Представление криволи- динат х и у (рис. 15).
Также вместо самого вектора
скорости v удобно рассматривать
в каждый данный момент его про-
проекции на координатные оси vx и vy, тогда численное значение век-
вектора v в плоской задаче определится значением:
нейного движения с помощью его
составляющих вдоль координатных
осей.
v = yvl -)- vy, - B)
а его направление — углом а между осью ОХ и прямой, вдоль кото-
которой направлен вектор скорости.
Из рис. 15 имеем, что
tg а = -•«-. C)
Вектору смещения тела As соответствуют проекции на координатные оси
Ах и Ду. Согласно правилам дифференциального исчисления, проекциями
скорости
§ Ю]
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
31
будут величины
Д_у\ dy
D)
Здесь dxjdt и dyjdt представляют собой производные координат по вре-
времени. Их можно вычислить, если координаты движущегося тела заданы
в виде определенных функций от времени: x=ft (t); у =/2 (t).
Рассмотрим несколько примеров криволинейного движения.
Пример 1. Тяжелое тело брошено с начальной скоростью, численно
равной v0 и составляющей угол а с горизонтом. Найти: 1) вид траектории,
2) высоту наибольшего подъема,
3) дальность полета.
Решение. Вводя коорди-
координатные оси, как показано на
рис. 16, имеем следующие выра-
выражения для составляющих скорости
тела (сопротивлением воздуха пре-
пренебрегаем): Утах\
vx = va cos а, \
vy = v0 sin a — gt, J
где g—ускорение силы тяжести.
Координаты х и у тела, как функ-
функции времени, выразятся:
х = щ cos a • t,
• t — ^~. |
F)
'•max
Рис. 16. Траектория тела, брошенного
под углом а к горизонту.
у = v0 sm a •
Исключая из выражений для х и у время t, получим уравнение траектории:
t(r ? Л*
У а ' 2t^cos2a
Так как а есть заданный угол и v0 — значение начальной скорости, то коэф-
коэффициенты при х и х* являются постоянными величинами; обозначая их
через а и Ъ, получим
у = ах — Ьх2,
что представляет собой уравнение параболы. Таким образом, тяжелое тело,
брошенное под углом к горизонту, движется по параболе.
В высшей точке траектории vy = 0, откуда
v0 sin a — gt = 0,
и время V поднятия на наибольшую высоту равно
г»0 sin а
Наибольшая высота поднятия
g
Тело упадет на горизонтальную плоскость через время
2о0 sina
G)
= 2t', откуда
Дальность полета получим, подставляя это значение t в выражение для х:
Ъ. (8)
g
g
32
КИНЕМАТИКА
[гл.
баллистическая
кривая
Парабола
Из последней формулы имеем, что при данном v0 наибольшая дальность
полета достигается при а = 45°.
Все полученные формулы справедливы лишь для движения тел в пустоте.
При бросании тяжелых тел в воздухе существенную роль играет сопроти-
сопротивление воздуха. Из-за сопротивления
воздуха скорость во время полета
убывает, и траектория не является
больше параболой: ее нисходящая
ветвь идет круче (баллистическая
кривая, см. рис. 17); дальность полета
и высота подъема становятся меньше.
Характер баллистической кривой
сильно зависит от формы брошен-
брошенного тела. Роль сопротивления воз-
воздуха можно видеть из следующего
примера: из формулы (8) для тела,
движущегося в пустоте, при началь-
начальной скорости z>0 = 550 м/сек и угле бросания 20°, дальность полета полу-
получается 19,8 км. Артиллерийский снаряд, имеющий вид цилиндра с конической
передней частью, весом 82 кГ, при тех же начальных условиях имеет даль-
дальность полета всего 8,1 км.
Пример 2. Тяжелое тело брошено с начальной скоростью, численно
равной vg и составляющей угол а с горизонтом. Пренебрегая сопротивле-
сопротивлением воздуха, найти по величине и но направлению скорость: 1) в высшей
точке подъема, 2) в точке падения на горизонтальную плоскость.
Решение. Определим сперва направление вектора скорости v в наи-
наивысшей точке подъема, для которой vv = 0:
0
Рис. 17. Сравнение параболической
траектории и баллистической кривой.
tg
= S = 0,
откуда
= 0.
Таким образом, в наивысшей точке подъема скорость направлена гори-
горизонтально. Численно она равна:
Vi = Yv% + vy = Vvt cos2 a = vo COS a-
Определим теперь по направлению и
по величине скорость в точке падения.
Воспользовавшись выражениями для vy и
для времени t, через которое тело упадет,
выведенными в предыдущем примере, по-
получим, что в точке падения vy =— v0 sin a,
откуда следует, что угол <х2, определяющий
направление скорости в этой точке, будет
дан соотношением:
vv va sin a
tg a2 = -« = = — tg a,
Vx v0 COS a b
Рис. 18. Скорость vs, с которой
тело падает, численно равна
начальной скорости v0.
отсюда получаем: а2 = — а, т. е. скорость тела в точке падения составляет
угол с горизонтом, численно равней углу, который составляла с горизонтом
начальная скорость, но только направлена она вниз (рис. 18).
Скорость в точке падения тела равна
Vi = Yv2x + vy = У vl cos2 a + vl sin2 a = va,
т. е. скорость в точке падения численно равна начальной скорости.
§ 11. Ускорение при криволинейном движении. Как было ука-
указано в предыдущем параграфе, при неравномерном криволинейном
движении вектор скорости меняется и по величине, и по направлению.
§ 11] УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ 33
Изменение вектора скорости Av за некоторый промежуток времени
от t до t-\-At представится векторной разностью скоростей v2 и v,,
которые тело имело в моменты времени t-\-kt и t. Ускорение при
этом численно будет равно
4?|^ О)
где | Av | — численное значение изменения вектора скорости v; напра-
направлено ускорение в ту сторону, куда направлено бесконечно малое
изменение скорости Av. Таким образом, равенство A) может быть
записано также в векторном виде:
чг = пред. (^r). (la)
Раньше чем более подробно рассмотреть ускорение при криволи-
криволинейном движении, разберем понятие о кривизне кривой линии.
В случае окружности кривизна определяется величиной 0 = -^,
н
где R — радиус рассматриваемой окружности. Если а есть централь-
центральный угол, соответствующий
дуге окружности s, то, как
известно, между R, а и s
имеет место соотношение:
~s=R«. B)
Кругом кривизны пло- f/
ской линии в некоторой точ- /
ке А называется предельное
положение окружности, про-
проходящей через точку А и
две другие точки Вх и Вг чч ^,У
при их бесконечном прибли- ^- "
жении к точке А (на рис. 19 рис jg Нахождение радиуса кривизны
кривая проведена сплошной ДуГИ д"8_
линией, а круг кривизны —
пунктирной). Радиус круга кривизны дает радиус кривизны рассма-
рассматриваемой кривой в точке А, а центр этого круга — центр кривизны
кривой для той же точки А.
Проведем в точках By и /?2 касательные B^D и ВйЕ к окруж-
окружности, проходящей через точки ??,, А и В,г. Нормали к этим каса-
касательным В^С и ВгС представят собой радиусы R окружности и
пересекутся в ее центре С. Введем угол Да между нормалями Bfi
и BiC; очевидно, он равен углу между касательными ByD и В.гЕ.
По формуле B): _
г, As
34
КИНЕМАТИКА
[ГЛ. I
где через As обозначена дуга круга BiAB^. При As -*¦ О, по ска-
сказанному, радиус окружности определяет радиус кривизны кривой
д в точке А. Таким образом, для радиуса
кривизны кривой имеем
; = пред.
Д5-.0
Bа)
Величина, обратная R, даст кри-
кривизну линии в данной точке: С = -^.
Из рис. 20 видно, что в точке Аи
где кривая проходит более полого,
радиус кривизны имеет ббльшее зна-
значение /?!, а в точке Л2, где кривая
загибает круче, — меньшее значение
/?4. Для крицой в точке А3, где вы-
Рис. 20. Радиусы кривизны кри- пуклость обращена в другую сторону,
вой в разных точках. чем в точках At и Л2, центр кривизны
также лежит по другую сторону кривой.
Теперь рассмотрим более подробно ускорение тела, движущегося
неравномерно по плоской кривой. Пусть у, есть вектор скорости
и точке А кривой (рис. 21), а у3 — вектор скорости в точке В.
Вектор v3 отличается от vt и по величине и по направлению. Про-
Проведем из точки А отрезок АС,
равный и параллельный отрез-
отрезку BD, изображающему вектор
скорости v2. Тогда отрезок
ЕС, равный разности векторов
va и V!, представит изменение
скорости Ду на пути АВ. При-
Приближая точку В к точке А, Рис. 21. Изменение скорости Ду при
мы будем тем самым стремить криволинейном движении.
к нулю и промежуток времени
At, который телу необходимо затратить, чтобы пройти от точки А
до точки В. При этом по формуле Aа) мы получим для ускорения
в точке А выражение:
ш = пред. т-
At->0 \ас
Отложим вдоль АС отрезок AF = vy и разобьем Ду на две соста-
составляющие: A\t и Ду2. Тогда ДУ( характеризует изменение скорости
по направлению, а Дуа — изменение скорости по величине. Очевидно,
Ду = Ду, -\- Ду2; подставляя это значение Ду в выражение для уско-
ускорения w, получим
w = пред. (?) = пред. /Ду'+А^ — ^Л ' — '^
At -» 0 \al I At-, 0
U -> 0
р
U -. 0
§ 11] УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ 35
Сложение здесь повсюду векторное. Величина
C)
и-.о
представляет собою ту часть ускорения, которая характеризует изме-
изменение скорости только по направлению.
Обозначим угол между АЕ и АС через Да; по построению это
tCTb угол между векторами скоростей V] и v2, а следовательно, и
между касательными к нашей кривой в точках А и В. При малом
угле Да, как видно из рис. 21, можно написать:
EF=AE -Да,
но так как EF=Av1 и AE = vlt то
Воспользовавшись этим выражением для At>j, получим по C) для
численного значения составляющей ускорения wn:
> о
Величину, стоящую под знаком предела, помножим и поделим на
длину дуги As = AB; кроме того, заметим, что при Д^-> 0 и As->0.
Тогда находим
/ Да As\ /A~s\ /Да
и>л = пред. lt>! — • дт-1=1»! пред. I тг I • пред.^
Но пред. (~)= Vi, a по Ba) пред. [^-)=-^-. Воспользовавшись
этими выражениями, получим для wn:
где vl — скорость тела в точке A, a R — радиус кривизны кривой
в той же точке. В пределе при Да—»0 мы имеем, что /_ AEF-* 90° и,
следовательно, вектор Avj располагается нормально к скорости v,,
которая направлена по касательной к кривой в точке Л. Таким
образом, wn, совпадающее по направлению с Avb оказывается рас-
расположенным нормально (перпендикулярно)к скорости и направленным
к центру кривизны пути в данной точке. В соответствии с этим
часть полного ускорения wn носит название нормального или центро-
центростремительного ускорения. Из приведенных рассуждений мы легко
определим' и направление-второй части ускорения wt; в самом деле,
при Да —> 0 отрезок АС стремится по направлению к Vi, откуда А\г,
а следовательно, и xvt оказываются направленными вдоль той же
прямой, что и скорость Vj, т. е. вдоль касательной к кривой в точке А.
36 КИНЕМАТИКА [ГЛ. Г
¦Поэтому часть ускорения w, носит название касательного или тан-
тангенциального ускорения.
Резюмируя, мы можем сказать: при криволинейном движении
полное ускорение w может быть разбито на две составляющие:
1) тангенциальное ускорение w(, характеризующее изменение ско-
скорости по величине, и 2) нормальное ускорение wn, характеризую-
характеризующее изменение скорости по направлению. При этом
где R — радиус кривизны траектории в данной точке и v — значение
скорости тела в этой точке; направлено нормальное ускорение по
нормали к кривой (к центру кривизны).
Тангенциальное ускорение:
где Дт) — изменение численного значения вектора скорости; направлено
тангенциальное ускорение по касательной к траектории. Очевидно
(рис. 22), нормальное ускорение wn и тан-
тангенциальное Wj взаимно перпендикулярны,
отсюда полное ускорение w численно равно
w = у w'n -\- w\. G)
Направление вектора полного ускорения
w определится либо углом {3, который w
составляет с радиусом кривизны, либо углом
а, который w составляет с касательной:
Рис. 22. При криволиней- w w
ном движении полное ус- tg р = —, tg а = —- . (8)
корение w разлагается на wn wt
IT^^JoTiZt При равномерном движении по кривой
тростремительное) ш„. wt = 0 и w = wn; таким образом, при равно-
равномерном криволинейном движении танген-
тангенциальное ускорение раино нулю, и полное ускорение, совпадая
с нормальным, направлено в каждой точке траектории по нор-
нормали к ней, к центру кривизны. Оно выражает в этом случае тот
факт, что скорость, оставаясь постоянной по величине, все время
меняет свое направление.
Полученные нами формулы относятся к движению по плоской
кривой, однако их легко обобщить и на случай неплоского криво-
криволинейного движения.
Пример. Найти нормальное и тангенциальное ускорения тяжелого тела,
брошенного горизонтально с начальной скоростью vt (пренебрегая сопроти-
сопротивлением воздуха).
§ 12] КИНЕМАТИКА ТВЕРДОГО ТЕЛА. УГЛОВЫЕ СКОРОСТЬ И УСКОРЕНИЕ 37
Решение. Полным ускорением в данном случае будет ускорение силы"
тяжести g; оно направлено вертикально вниз и постоянно по величине. Отсюда
(рис. 23) имеем для нормального ускорения
выражение
wn = gsina (9)
и для тангенциального
Wt = gcosa. A0)
Значение угла а определим из того со-
соображения, что скорость нашего тела v на-
направлена так же, как W/, и что ось OY на
рис. 23 направлена вертикально вниз; тогда
vx = v0\ vv=gt,
откуда
vx
-
v
COS a = -
V
;_ §*_
Рис. 23. Ускорение горизон-
горизонтально брошенного тела.
vl + tf2
Подставляя эти значения для sin a и cos a в (9) и A0), найдем
При ^ = 0, т. е. в начальный момент, когда ш^ = 0 и wn = w — g, нормаль-
нормальное ускорение совпадает с полным. По мере падения тела нормальное уско-
ускорение убывает (увеличивается радиус кривизны, траектория брошенного тела
становится менее искривленной) и начинает возрастать тангенциальное уско-
ускорение. При t —- оо имеем: да/—->w — g и wn—» 0.
§ 12. Кинематика твердого тела. Угловые скорость и ускоре-
ускорение. Все реально существующие твердые тела более или менее де-
деформируются под влиянием приложенных к ним сил; отдельные их
части могут смещаться друг относительно друга. Для того чтобы упро-
упростить рассуждение, введем понятие об абсолютно твердом теле. Под
абсолютно твердым телом подразумевается такое воображаемое тело,
которое вовсе не деформируется под влиянием приложенных к нему
сил. В абсолютно твердом теле не-
невозможны перемещения отдельных его
частей друг относительно друга. Дви-
Движение абсолютно твердого тела сво-
сводится к поступательному движению
и к вращению.
Поступательное движение твердого
тела — это такое движение, при кото-
котором любая прямая линия, проведенная
в теле и неизменно связанная с ним,
Рис. 24. Поступательное движе-
движение твердого тела.
перемещается, оставаясь параллельной самой себе (рис. 24). При
поступательном движении все точки твердого тела обладают одина-
одинаковыми скоростями v и одинаковыми ускорениями w.
38
КИНЕМАТИКА
! [ГЛ. I
Вращательное движение — это такое движение, при котором все
точки твердого тела описывают окружности, центры которых лежат
на одной прямой, являющейся осью вращения (рис. 25).
В общем случае твердое тело может одновременно совершать и
поступательное и вращательное движения. Наконец, и сама ось вра-
вращения может менять' свое положение
относительно тела; в этом случае для
каждого данного момента времени го-
говорят о вращении вокруг мгновенной
оси.
Введем понятие об угловой скорости.
Для этого определим положение неко-
некоторой точки В вращающегося тела
(рис. 25) углом <р, который образован
радиусом ОВ с некоторым начальным
радиусом ОА. При вращении тела угол
9 непрерывно меняется. Угловой ско-
скоростью равномерно вращающегося тела
Рис. 25. Вращательное дви- называется физическая величина <л, про-
жение твердого тела. порциональная углу Дер, на который по-
повернется радиус ОВ, и обратно про-
пропорциональная промежутку времени At, за который радиус повер-
повернулся на этот угол Дер:
<° = kbt, О)
где k — коэффициент пропорциональности. Если положить k=\, то
А<Р
==7
B)
при этом, измеряя А<р ш At в определенных единицах, мы должны
выбрать для измерения (о такие единицы, чтобы равенство B)
выполнялось. Измеряя, как обычно, углы в радианах, а время
в секундах, мы должны за единицу угловой скорости выбрать
угловую скорость такого движения, при котором угол ср меняется
на один радиан за одну секунду; эту единицу угловой скорости
можно обозначить радиан/сек, обычно ее обозначают просто ¦—
или сек'1.
Значение угловой скорости ш данного вращающегося твердого
тела не зависит от выбора точки В, так как угол Дер, на который
поворачивается за данное время At радиус ОВ, не зависит от поло-
положения точки В.
Найдем связь между линейной скоростью v точки В и угловой
скоростью вращения тела ш.
сти дугу As, тогда ее линейная скорость численно равна
с другой стороны (см. рис. 25),
Д? = -д-. откуда v = д|- • /?,
или по B)
v = <aR, C)
где /?—расстояние точки 5 от оси вращения. Чем дальше отстоит
точка В от оси вращения, тем больше, при данной угловой скоро-
скорости <о, ее линейная скорость v. Различные точки вращающегося твер-
твердого тела' имеют различные линейные скорости.
Свяжем угловую скорость с периодом обращения тела Т. За время
At=T тело совершает полный оборот, а угол <р возрастает на 2тс,
т. е. Д<р = 2л, откуда по B):
<•> = т . D)
Наконец, введем в рассмотрение число оборотов п в единицу
времени. Так как один оборот совершается за время Т, то, следо-
следовательно, за единицу времени будет совершено оборотов:
п=~. E)
Отсюда по D) получаем еще одно выражение для угловой ско-
скорости вращения тела:
со = 2ии. F)
Каждая точка вращающегося тела, двигаясь по окружности, имеет
нормальное ускорение:
где v — ее линейная скорость, a R — расстояние от оси вращения.
Подставляя сюда вместо линейной скорости v ее значение через
угловую скорость (о по C), найдем
да„ = «*/?. ' G)
Так как все точки вращающегося твердого тела обладают одной
и той же угловой скоростью ш, то из формулы G) видно, что чем
дальше от оси вращения отстоит рассматриваемая точка вращающе-
вращающегося твердого тела, тем большее нормальное ускорение она имеет.
40
КИНЕМАТИКА
[ГЛ. I
Используя формулы E) и F), мы можем придать выражению G)
еще следующий вид:
wn — —fr (8)
ИЛИ
wn = ii^n^R. (8a)
В случае неравномерного движения по окружности вводим по-
понятие об угловой скорости ш в данный момент:
СО
ш = пред. -rj
Д/--.0 \ЛС
При этом связь между угловой скоростью <о в данный момент и ли-
линейной скоростью v в данный момент сохраняется та же, что между
ш и v при равномерном вращении [формула C)].
При неравномерном вращении угловая скорость ш меняется со
временем. Для характеристики этого изменения вводится угловое
ускорение C, представляющее собою, в случае равнопеременного
вращения, физическую величину, прямо пропорциональную изменению
угловой скорости Дш и обратно пропорциональную тому промежутку
времени At, за который это изменение произошло. В общем случае
неравномерного вращения угловое ускоре-
ускорение в данный момент равно
A0)
Из дифференциального исчисления имеем
« = §? (9а)
и для углового ускорения
„dad
A0а)
Рис. 26. Точка А, находя-
находящаяся на земном шаре на
широте <р, описывает окруж-
окружность радиуса Ri.
Пример 1. Определить угловую и линей-
линейную скорости точек на поверхности земного
шара, а также их нормальное ускорение.
Решение. Угловая скорость:
« = Т = 247Ш7бб «кг'^7,3. 10- сек-
она одна и та же для всех точек земного шара.
Линейная скорость точек на широте <р (рис. 26) равна
v = ы/Zi — &R cos <?,
где ^? — радиус земного шара. Подставляя вместо а ее численное значение
6370 637 10°
? ру р
и зная, что /? = 6370 км = 6,37 • 10° м, получим
v = 4,65 • 102 costp Mjсек.
Нормальное ускорение wn на широте <р равно
wn = <оа/?.[ = ш2/? cos у.
wn = 3,4 cos у см/сек2.
Пример 2. Колесо радиуса г = 10 см вращается ускоренно так,
его число оборотов возрастает на яо = — оборота за каждую секунду. Найти
к концу второй секунды: 1) угловую скорость колеса, 2) линейную скорость
точек на его ободе, 3) нормальное, тангенциальное и полное ускорения точек
на ободе.
Решение. Число оборотов п к концу второй секунды будет
п = not = 4- ¦ 2 — = 1 сек-1.
2 сек.
Угловая скорость ш к концу второй секунды:
ы = 2тш = 2r.nat = 2 • 3,14 • 1 сек. = 6,28 сек..
Линейная скорость точек на ободе колеса к концу второй секунды:
v ==ш7? = 6,28 • 10 см/сек = 62,8 см/сек — 0,628 м/сек.
Нормальное ускорение точек на ободе:
м>„ = <оа# = 6,282 ¦ 10 см/сек* = 394,4 см/сек*.
Тангенциальное ускорение wt найдем из того соображения, что
v = aR = 2ъпаМ,
т. е. v возрастает равномерно со временем, следовательно, для него, как
для случая равнопеременного движения, должно иметь место равенство
v = wtt, где wt — искомое тангенциальное ускорение, откуда
«^ = 2яяо/? = 6,28 • -j • 10 см/сек'" —31,4 см/сека.
Полное ускорение
w = Ywl + w\ — j/^94,42 + 31,4- см/сек2 = 396,5 см/сек*.
Направление лолного, ускорения определим из рис. 22, откуда видно, что
угол а, который оно составит с касательной к окружности, определится ра-
равенством:
wn 394,4 . АП„_
sin a = —? = —^- -~ 0,9965,
w 396,5
откуда а = 85°30'. Таким образом, полное ускорение направлено подуглом 85°30'
к касательной, или, что то же самое, под углом р = 4°30' к радиусу.
§ 13. Угловая скорость как вектор. Движение по окружности заданного
радиуса R будет в том случае полностью охарактеризовано, если заданы: \)угло-
\)угловая скорость (о (или линейная скорость v), 2) плоскость, в которой лежит окруж-
окружность, и 3) направление вращения. Последняя характеристика необходима, так
¦ как движение по окружности, рассматриваемое с определенной стороны
плоскости, может происходить либо по часовой стрелке, либо против часовой
стрелки. Однако все эти три характеристики могут быть даны с помощью одного
42
КИНЕМАТИКА
[гл. i
вектора, если условиться проводить этот вектор перпендикулярно к плоскости
и сопоставлять направлению вектора определенное направление вращения.
Последнее делается по правилу буравчика: сопоставляем направление век-
вектора с поступательным движением буравчика, а вращение — с направле-
направлением вращения ручки буравчика (рис. 27). Тогда для характеристики вращения
Рис. 27.
Правило
бурав-
буравчика.
Рис. 28. Вектор угловой скорости проводится пер-
перпендикулярно к плоскости, в которой происходит
вращение, и в такую сторону, что рассматри-
рассматриваемое с его конца вращение представляется
происходящим против часовой стрелки.
вводим такой вектор <о, называемый вектором угловой скорости, что: 1) его
численное значение равно численному значению угловой скорости и>, 2) про-
проведен он нормально к плоскости, в которой лежит окружность, по которой
происходит вращение, и 3) рассматриваемое с конца этого вектора вращение
представляется происходящим против часовой стрелки (рис. 28). Изображение
угловой скорости с помощью вектора оправдывается тем, что в случае, если
тело принимает участие одновременно в двух вращениях, его результирующее
вращение характеризуется вектором, получаемым сложением векторов угловых
скоростей слагаемых вращений по правилу параллелограмма.
В векторном анализе вводится понятие о так называемом векторном
произведении. Под векторным произведением векторов А и В подразумевается
вектор С, численное значение кото-
С рого равно:
С = А ¦ fisin(Z А, В),
где А и В— численные значения век-
векторов А и В, a (Z. А, В)— угол между
ними (угол а на рис. 29). Вектор С
направлен перпендикулярно к пло-
плоскости, содержащей векторы А и В,
и в такую сторону, чтобы при рас-
рассматривании с его конца вектор А мог
быть совмещен с вектором В путем
вращения против часовой стрелки
(в сторону меньшего угла; см. рис. 29). Другими словами: при вращении
ручки буравчика в направлении от А к В (в направлении меньшего угла)
поступательное движение буравчика определит направление вектора С.
Векторное произведение обозначается символом:
С==АХВ.
Рис. 29. Векторное произведение.
§ 13]
УГЛОВАЯ СКОРОСТЬ КАК ВЕКТОР
43
Векторное произведение не обладает свойством коммутативности: векторы
С = АхВ и С' = ВхА совпадают лишь по численному значению, но на-
направлены'в противоположные стороны.
Введение представления об угловой ско-
скорости как о векторе позволяет удобно связать
вектор линейной скорости v с вектором угло-
угловой скорости ю и радиусом-вектором г, опреде-
определяющим положение материальной точки отно-
относительно оси вращения.
Как видно из рис. 30:
v = ш X г,
т. е. v является векторным произведением
миг.
При рассмотрении угловой скорости как
вектора и угловое ускорение C должно рас-
рассматриваться как вектор, потому что в этом случае в равенстве
Рис. 30. Связь между векто-
векторами Ы, V И Г.
1 = пред. —
величина Д<о представляет собою векторное изменение угловой скорости а.
ГЛАВА П
ДИНАМИКА
§ 14. Перзый закон Ньютона. До сих пор мы рассматривали
лишь перемещение тел в зависимости от времени, т.е. рассматривали
задачи кинематики. Вопросов же, связанных с взаимодействием тел,
которое ведет к изменению состояния движения, мы не касались
вовсе. Эти вопросы относятся к области динамики. Основные поло-
положения динамики были сформулированы Ньютоном в его „Матема-
„Математических началах натуральной философии" A687) в виде трех за-
законов движения.
Первый закон Ньютона может быть сформулирован следующим
образом: всякое тело сохраняет состояние покоя или равномер-
равномерного и прямолинейного движения, пока воздействие со стороны
других тел не заставит его изменить это состояние.
Здесь тело рассматривается как материальная точка, т. е. из рас-
рассмотрения исключается вращательное движение. В § 35 мы увидим,
что тело может без воздействия со стороны других тел находиться
также в состоянии равномерного вращения.
Из первого закона Ньютона следует, что тело может только
тогда изменить состояние покоя или равномерного и прямолиней-
прямолинейного движения, когда на него воздействуют другие материальные
тела.
Проверить первый закон Ньютона непосредственными опытами
невозможно, так как в реально окружающей нас обстановке нельзя
поставить тела в такие условия, когда на них вовсе не воздействуют
другие тела. Однако путем обобщения ряда фактов мы убеждаемся
в правильности первого закона Ньютона. Обычно наблюдаемое со-
состояние покоя окружающих нас предметов обусловлено тем, что
воздействия различных тел компенсируют друг друга, например, при-
притяжение со стороны земного шара и реакция опоры или подвеса
в случае покоящегося тяжелого тела. При движении тело тем дольше
сохраняет свою скорость, чем слабее на него воздействуют другие
тела: брошенный с некоторой начальной скоростью камень, сколь-
скользящий по поверхности Земли, тем дольше движется, чем ровнее эта
поверхность, т. е. чем меньше на него воздействие других тел.
§ Н] ПЕРВЫЙ ЗАКОН НЬЮТОНА 45
Окончательно в справедливости первого закона Ньютона нас убеждает,
косвенным образом, совпадение всех вытекающих из него следствий
с опытными данными.
Останавливаясь более подробно на первом законе Ньютона, надо
поставить вопрос: относительно какой системы отсчета (какой коор-
координатной системы) устанавливается тот покой или то равномерное
и прямолинейное движение, о котором идет речь в первом законе
Ньютона. Сам Ньютон подразумевал, что дело здесь идет о неко-
некотором абсолютном движении в абсолютном пространстве. Он писал:
„Абсолютное пространство по всей своей сущности, безотносительно
к чему бы то ни было внешнему, остается всегда одинаковым и не-
неподвижным.. .. Абсолютное движение есть перемещение тела из одного
абсолютного его места в другое". Такая точка зрения метафизична
и не соответствует действительности. Свойства объективно суще-
ствугощего реального пространства определяются самой материей.
Положение тел и их движение, как мы уже подчеркивали, могут
быть определены лишь относительно других материальных тел; по
отношению к различным телам одно и то же тело может двигаться
по-разному.
Наблюдения показывают, что первый закон Ньютона справедлив
не по отношению к каждой системе отсчета. Рассмотрим несколько
примеров. Положим, что системой отсчета является прямолинейно и
равномерно движущийся вагон. Тогда, если отвлечься от сотрясений,
первый закон Ньютона выполняется: покоящиеся относительно вагона
тела не приходят в движение без воздействия на них со стороны
других тел и т. д. Но стоит вагону начать заворачивать, тормозить
. или ускорять ход, как появятся явные нарушения первого закона
Ньютона: покоившиеся до того тела могут отклониться или упасть
без видимого воздействия на них со стороны окружающих тел.
Возьмем в качестве системы отсчета земной шар; в этом случае
первый закон Ньютона выполняется гораздо точнее, чем в случае
движущегося вагона, где даже при равномерном движении сказы-
сказывается тряска, но и здесь достаточно тонкие наблюдения над неко-
некоторыми процессами (качание маятников, распространение воздушных
и океанских течений и т. д.) выявляют отклонения от первого за-
закона Ньютона или, вернее, от следствий из него. Но если мы
выберем в качестве системы отсчета гелиоцентрическую систему,
начало которой помещено па Солнце, а оси направлены па опреде-
определенные звезды, то в такой системе первый закон Ньютона выпол-
выполняется практически вполне точно. Система отсчета, по отношению
к которой выполнен первый закон Ньютона, носит название инер-
инерциальной, системы. Сам первый закон Ньютона иногда называется
принципом инерции.
Как указано, инерциальной системой практически вполне точно
является гелиоцентрическая система; инерциальной будет также и
всякая система, движущаяся относительно нее равномерно и прямо-
46 динамика [гл. и
линейно. Всякая же система, имеющая относительно одной из инер-
циальных систем ускорение, сама не будет инерциальной. Более
подробно вопрос об ускоренных системах мы рассмотрим ниже.
§ 15. Второй закон Ньютона. Сила и масса. Второй закон
в формулировке, данной самим Ньютоном, гласит: изменение движе-
движения пропорционально приложенной силе и происходит в том на-
направлении, в каком действует сила.
Таким образом, второй закон Ньютона вводит понятие о новой
физической величине — силе.
Из первого закона Ньютона, как мы видели, следует, что только
воздействие одних материальных тел на другие способно изменять
состояние их движения. Это воздействие одних тел на другие,
ведущее к изменению состояния их движения, и характеризуется
физической величиной, называемой силой. Изменение состояния дви-
движения означает, что тело выходит из состояния покоя или равно-
равномерного и прямолинейного движения, т. е. что меняется его ско-
скорость, что тело приобретает ускорение. Отсюда следует, что
физическая величина — сила характеризует то воздействие одних тел
на другие, в результате которого тела приобретают ускорение.
Возьмем какое-либо определенное тело и будем на него воздей-
воздействовать каким-либо другим телом (или другими телами) так, чтобы
оно приобретало различные ускорения w. Очевидно, чем сильнее
воздействие, тем большее ускорение w приобретает тело. Отсюда
естественно принять за силу, с которой другие тела воздействуют
на рассматриваемое тело, физическую величину /, пропорциональную
тому ускорению, которое данное тело приобретает:
f=k'w, A)
где k' — коэффициент пропорциональности.
Равенство A) позволяет нам сравнивать между собою силы, дей-
действующие на какое либо данное тело, по тем ускорениям, которые
они ему сообщают. Так как ускорение имеет направление, то сила
также должна быть величиной направленной. Опыты показывают, что
при одновременном действии нескольких сил тело получает такое же
ускорение, какое оно получает под действием одной силы, равной
векторной сумме данных сил. Отсюда следует, что сила есть
вектор; направлен вектор силы так же, как и вектор вызываемого
им ускорения.
Таким образом, равенство A) может быть записано в векторном
виде:
i = k'w. (la)
Воздействие тел друг на друга не ограничивается только тем,
что тела сообщают одно другому ускорения. Некоторые другие воздей-
воздействия также характеризуются силой и могут быть, в свою очередь, исполь-
использованы для уточнения понятия силы. Вообще говоря, тела, взаимо-
§ 15]
ВТОРОЙ ЗАКОН НЬЮТОНА. СИЛА И МАССА
47
действуя друг с другом, вызывают изменения формы или, как говорят,
деформируют друг друга. Эти деформации могут быть использованы
для сравнения сил. Предположим, что тело А (рис. 31 а), воздей-
воздействуя на тело В путем непосредственного соприкосновения, сообщает
ему ускорение w (толкает тело В). Если мы поместим между те-
телами А и В какое-либо упругое тело, например пружину р (рис. 31 б),
то, когда тело А будет толкать тело В, пружина сожмется. При этом
пружина сожмется тем сильнее, чем большее ускорение тело А
сообщает телу В, т. е. чем с большей
силой тело А воздействует на тело В.
Измеряя эту силу по вызываемому ею
ускорению по равенству A), мы можем
проградуировать пружину и дальше
пользоваться ею для измерения сил.
Пружина явится прибором для измере-
измерения сил; такой прибор принято называть
динамометром.
Пользуясь указанным способом изме-
измерения сил с помощью пружинного ди-
динамометра, мы можем поставить такой
опыт: воздействовать на разные тела
одной и той же силой и сравнить те Рис. ЗГ. Тело А, толкая тело
ускорения, которые они получают. ?- сообщает ему ускорение w.
¦L г > у j ПрИ этом пружина, помещен-
Оказывается, что, вообще говоря, раз- н{я между теламИ) оказывается
ные тела под влиянием одинаковых сжатой,
сил приобретают различные ускорения.
Таким образом, ускорения, приобретаемые различными телами, опре-
определяются не только действующими на них со стороны других тел
силами, но и некоторым собственным [свойством тел. Это свойство
тел характеризуется особой физической величиной, называемой
массой.
Чем меньшее ускорение приобретает тело под влиянием данной
силы, тем больше его масса. Следовательно, мы можем положить, ¦
что массы различных тел обратно пропорциональны тем ускорениям,
которые эти тела приобретают под влиянием равных сил:
пн
Wy
B)
Масса тел зависит от размеров тел и от природы их вещества.
~ Масса является одной из самых основных характеристик тел.
Ньютон считал, что масса есть мера количества материи в теле. Это
определение, долго удерживавшееся в науке, носило неправильный
метафизический характер. Также порочной была точка зрения тех
физиков-идеалистов, которые приписывали массе лишь формаль-
формальный характер некоторого „коэффициента", фигурирующего в уравне-
уравнениях механики.
48 динамика [гл. п
Диалектический материализм учит нас, что свойства материи
неисчерпаемы и поэтому ни одна из физических характеристик дви-
движущейся материи не может служить ее полной мерой. Говоря о ма-
материи, как о философской, гносеологической категории, Ленин ука-
указывал, что нельзя смешивать философское понятие о материи с теми
или другими конкретными характеристиками различных видов материи;
он писал:1 „Но совершенно непозволительно смешивать, как это.
делают махисты, учение о том или ином строении материи с гносео-
гносеологической категорией, — смешивать вопрос о новых свойствах новых
видов материи (например, электронов) с старым вопросом теории
познания, вопросом об источниках нашего знания, о существовании
объективной истины и т. п.".
Понятие о массе, как и о всякой другой физической величине,
может быть установлено лишь через совокупность объективных за-
закономерных взаимосвязей этой величины с другими физическими
величинами. По отношению к массе одна из таких взаимосвязей
дается вторым законом Ньютона, который вводит понятие об инерт-
инертности тел. При этом, говоря об инертности тел, имеют в виду, что
тела различаются неким объективным свойством, проявляющимся
в том, что они приобретают неодинаковые ускорения при одинаковых
внешних воздействиях. Это свойство, присущее всем телам, характе-
характеризуется определенной физической величиной, которая и является
массой. Соотношение B) позволяет количественно сравнивать массы
различных тел. Измеряемая* таким образом масса может быть названа
тинерцпонной массой", поскольку она измеряется на основании инер-
инерционных явлений.
Более полное содержание понятия массы вскрывается в резуль-
результате рассмотрения широкой совокупности фактов. Одним из наиболее
основных из таких фактов является установленный М. В. Ломоно-
Ломоносовым закон сохранения масс: масса изолированной системы тел
остается постоянной при всех происходящих в ней изменениях.
В § 17 мы укажем связь между массой и физической величиной,
называемой количеством движения; эта величина, носящая векторный
характер, также подчиняется закону сохранения. Кроме того, масса
проявляется в гравитационных явлениях (закон всемирного тяготения,
§ 32 и 33). Наконец, теория относительности приводит к выводу
о наличии глубокой взаимосвязи массы и энергии. При скоростях,
приближающихся к скорости света в пустоте, масса тел не остается
постоянной, но возрастает с увеличением скорости. Постоянной
остается масса системы, полностью изолированной, т. е. такой, по
отношению к которой не имеет место обмен не только веществом
(атомы, молекулы и т. д.), но и энергией.
Сопоставляя равенства A) и B), мы приходим к выводу; уско-
ускорение w, приобретаемое телом, прямо пропорционально силе \,
1 В. И. Ленин. Сочинения, 4-е изд., т. 14, стр. 116.
§ 16] СИЛЫ ТРЕНИЯ 49
действующей на тело, и обратно пропорционально массе тела т:
где k — коэффициент пропорциональности.
Равенство C) имеет векторный характер. Оно выражает точное
содержание второго закона Ньютона.
При решении многих физических задач величина и направление
действующей силы оказываются известными, например, в случае сил
всемирного тяготения (§ 32) или упругих сил, подчиняющихся закону
Гука (§ 89). Тогда равенство C) позволяет найти ускорение и, сле-
следовательно, определить характер движения.
Равенство C) является основным уравнением динамики.
§16. Силы трения. Наряду с силами, возникающими при дефор-
деформациях тел (упругие силы), и силами тяготения существуют и другие
силы, вызванные молекулярными взаимодействиями между соприка-
соприкасающимися телами или отдельными частями одного и того же тела.
Эти силы, проявляющиеся при относительном перемещении соприка-
соприкасающихся тел или частей одного и того же тела друг относительно
друга, носят название сил трения.
Силы трения, возникающие при соприкосновении различных тел,
называются силами внешнего трения. Эти силы не пропадают и тогда,
когда оба соприкасающихся тела неподвижны одно относительно
другого (трение покоя). Силы, вызванные перемещением частей
одного и того же тела друг относительно друга, называются силами
внутреннего трения (наиболее часто они проявляются при движении
жидкостей и газов). \
Силы трения играют большук) роль в нашей повседневной прак-
практике и в технике, поэтому уменье их учитывать существенно для
правильного применения второго закона Ньютона во многих практи-
практически важных случаях. \
Силы трения направлены тангенциально к соприкасающимся по-
поверхностям тел и зависят от их отно^тельных скоростей. Последним
они существенно отличаются от упругих сил и сил тяготения. Силы
трения могут возникать не только между соприкасающимися твердыми
телами, но и между твердым телом и жидкостью или твердым телом
и газом. \
Так как при всяком реальном движении в земных условиях воз-
возникают те или иные силы трения, то для определения ускорения
тела необходимо учитывать, кроме действующей на него заданной
силы f, еще силу трения fip, которая возникает при наличии отно-
относительной скорости v.
Пусть некоторое тело А движется относительно другого тела,
с ним соприкасающегося, с относительной скоростью v. Опыт показы-
показывает, что сила трения fip, действующая на тело А, всегда направлена
в сторону, противоположную скорости v. Предположим, что на тело А,
3 С. Э. Фриш и А. В. Тиморева
50 динамика [гл. И
кроме силы трения fTp, действует какая-либо другая сила f. Тогда
ускорение w, приобретаемое телом А, определится суммарной силой
По второму закону Ньютона:
где т — масса тела, k — коэффициент пропорциональности.
Для того чтобы в реальных условиях тело двигалось с постоян-
постоянной скоростью v, к нему необходимо приложить силу f, уравнове-
уравновешивающую силу трения fTp. Только тогда в равенстве A) результи-
результирующая сила f -j- fTp равна нулю и, следовательно, равно нулю и
ускорение w, т. е. тело движется равномерно.
Тело движется прямолинейно и равномерно, когда внешняя
сила уравновешивает возникающую в результате движения силу
трения.
Рассмотрим, например, пароход, движущийся прямолинейно под
влиянием постоянной толкающей силы винта /, которую будем счи-
считать положительной. Как только пароход сдвинется с места, воз-
возникнет сила трения, зависящая от скорости парохода v. Так как сила
трения направлена противоположно толкающей силе винта /, то обо-
обозначим ее через —/тр. Пароход будет двигаться под влиянием резуль-
результирующей силы /—/тр. В начале движения, пока скорость v мала,
результирующая сила /—/тр положительна, и пароход движется
ускоренно. По мере возрастания скорости v возрастает по числен-
численному значению и сила трения, и ускорение становится меньше.
Наконец, разность /—/тр примет значение нуль, и тогда пароход
пойдет равномерно. Если толкающая сила винта по какой-либо при-
причине уменьшится, то разность/—/тр может оказаться отрицательной,
и тогда пароход начнет двигаться замедленно.
В качестве второго примера рассмотрим падение тяжелого тела
в воздухе с учетом сопротивления воздуха. Если тяжелое тело начнет
падать с нулевой начальной скоростью, то на него действует лишь
сила тяжести Р, и оно приобретает ускорение w, равное ускорению
свободного падения g. По мере возрастания скорости падения появится
сила трения о воздух, результирующая сила Р—/тр окажется меньше
силы тяжести, и ускорение w станет меньше ускорения свободного
падения g. При дальнейшем возрастании скорости падения сила
трения, наконец, уравновесит силу тяжести Р, и тело будет падать
равномерно с постоянной скоростью. Величина этой скорости рав-
равномерного падения зависит от формы и размеров падающего тела.
Опыт, например, показывает, что для падающего человека эта ско-
скорость равна приблизительно 60 м/сек. Такой именно скорости до-
достигают парашютисты при „затяжном прыжке". После раскрытия
парашюта сила сопротивления воздуха резко возрастает, и скорость
падения („спуска") снижается приблизительно до 5—6 м[сек.
§ 16] СИЛЫ ТРЕНИЯ 51
Сила трения, возникающая при скольжении сухих поверхностей отно-
относительно друг друга, в большой степени зависит от состояния этих поверх-
поверхностей (их шероховатости). Величина силы трения зависит и от нормальной
составляющей Fn силы, сжимающей поверхности. При увеличении нормаль-
нормальной составляющей Гя сила трения возрастает приблизительно пропорцио-
пропорционально Fn:
Лр = ^я- B)
Коэффициент х в формуле B) называется коэффициентом трения. Зна-
Значение коэффициента трения -/ зависит не только от характера соприкасаю-
соприкасающихся поверхностей, но и от их относительной скорости v.
Величина силы трения (при данной нормальной составляющей силы Fn)
для твердых соприкасающихся поверхностей в довольно широких пределах
не зависит от величины соприкасающихся поверхностей.
Если, например, параллелепипед с одинаково обработанными поверхно-
поверхностями, скользящий по твердой поверхности, перевернуть на другую гра.нь,
имеющую другие размеры, то сила трения /тр при той же относительной
скорости v останется неизменной.
Трение между соприкасающимися сухими поверхностями, как было ска-
сказано, не пропадает, когда относительная скорость v становится равной нулю.
Чтобы тело начало скользить по какой-либо поверхности, к нему надо при-
приложить внешнюю силу /, параллельную поверхности и большую некоторого
определенного для данного случая значения ft. Пока" внешняя сила f<Cfu
тело остается неподвижным, что означает, что между ним и поверхностью,
с которой оно соприкасается, возникает сила /тр, называемая силой трения
покоя, уравновешивающая внешнюю силу.
Сила трения покоя может принимать любые значения, заключенные между
О и /i, в зависимости от величины приложенной внешней силы. Максималь-
Максимальное значение силы трения покоя численно
равно той силе /(, под влиянием которой fmp
тело начинает скользить. Оно удовлетво-
удовлетворяет соотношению B); при этом коэффи-
коэффициент х называется коэффициентом тре-
трения покоя. Значение коэффициента трения ft---
покоя зависит только от природы соприка-
соприкасающихся поверхностей. При соприкосно-
соприкосновении сухих поверхностей дерева коэффи-
коэффициент трения покоя приблизительно равен
0,6; при соприкосновении стальной поверх- ..
ности со льдом коэффициент трения покоя
равен приблизительно 0,03. Рис. 32. Зависимость силы тре-
Когда внешняя сила / превышает мак- ния /тр от относительной ско-
симальную силу трения покоя, тело начи- рости v.
нает скользить, и появляется сила тре-
трения при скольжении. Эта сила трения
при скольжении сперва меньше силы трения покоя и с возрастанием отно-
относительной скорости v вначале продолжает убывать; затем с возрастанием
относительной скорости v возрастает и сила трения. Графически зависимость
силы трения от относительной скорости изображена на рис. 32. При v — 0
сила трения покоя может принимать любое значение между нулем и ft
(отрезок ОА по оси ординат) в зависимости от значения приложенной внеш-
внешней силы. Дальнейшая зависимость силы трения от относительной скорости v
представляется кривой ABC.
В технике между трущимися поверхностями вводят смазку, т. е. вязкую
жидкость, которая образует тонкий слой между твердыми поверхностями.
Теория смазки была впервые развита русским инженером Н. П. Петровым,
который показал, что при наличии смазки мы имеем дело с внутренним
3«
52 ДИНАМИКА [ГЛ. II
трением. Ближайший к твердому телу слой смазывающей жидкости прилипает
к нему; скольжение происходит лишь между слоями жидкости. В случае вала,
расположенного соосно с подшипниками, сила трения пропорциональна вяз-
вязкости смазочного вещества, числу оборотов вала в единицу времени и
обратно пропорциональна ширине зазора между поверхностями вала и под-
подшипника.
ч* § 17. Количество движения. Импульс силы. Рассмотрим вна-
вначале движение, происходящее под влиянием постоянной силы f, т. е.
движение, характеризуемое постоянным значением вектора ускоре-
ускорения w. Пусть за промежуток времени Д^ скорость тела меняется на
величину Av = va — vlF тогда
At ~~ U '
подставляя это значение ускорения w в выражение второго закона
Ньютона:
w = k —,
т '
получим
Vo — V! , f mva — mvi ,. ,,,
* . -=k— ИЛИ —г-, ==k\. A)
Mm At v '
Следует иметь в виду, что mva — т\1 есть векторная разность
величин /wv2 и т\у Величину т\, равную произведению вектора
скорости тела v на его массу, принято называть количеством дви-
движения К- Количество движения
K = mv B)
есть величина векторная, она имеет то же направление, что и вектор
скорости v.
Вводя в выражение A) количество движения, получим
¦^i = *f или **=Ы, C)
где ДК есть изменение вектора количества движения. Равенство C)
означает: при равнопеременном движении изменение количества
движения за единицу времени пропорционально приложенной силе
и происходит в том же направлении, в каком действует вектор
силы.
Пользуясь равенством C), можно также дать следующее опре-
определение силы: сила есть векторная величина, численно пропорцио-
пропорциональная вызываемому ею изменению количества движения за единицу
времени и направленная в ту же сторону, в которую направлено
изменение количества движения.
Обобщим выражение C) на случай любых неравномерных дви-
движений, когда сила f меняется со временем. Тогда в равенстве C)
§18] ЕДИНИЦЫ СИЛЫ И МАССЫ. ПРИМЕРЫ 53
мы должны подразумевать под М бесконечно малое изменение вре-
времени, т. е. писать:
пред. ~ = ki, (За)
где вектор f есть значение силы в данный момент времени.
Равенство (За) так же, как и равенство C) § 15, выражает вто-
второй закон Ньютона.
С точки зрения приведенных рассуждений равенства C) § 15
и (За) настоящего параграфа вполне эквивалентны одно другому, так
как второе из них было непосредственно выведено из первого; оба
они выражают точное содержание второго закона Ньютона. Однако
указанная эквивалентность имеет место при предположении, что масса
тела т есть величина постоянная, не зависящая от его скорости.
Это справедливо, пока скорости тел малы по сравнению со скоростью
света. При движениях, происходящих со скоростями, сравнимыми
со скоростью света, масса т не остается постоянной: она зависит от
скорости v. Движения при таких скоростях подчиняются механике
теории относительности. При этом, однако, выражение (За) сохра-
сохраняет смысл; таким образом, оно является более общей формули-
формулировкой второго закона Ньютона, чем равенство B) § 15. Наряду
со значением силы в данный момент времени мы можем рассма-
рассматривать и среднее значение^силы f за некоторый конечный проме-
промежуток времени Д^, тогда вместо (За) получим
-? = kt, или f Д* = А'ДК = k' (mv2 — mvi), D)
где *=4\
Величина f Д^, равная произведению из среднего значения силы
f на промежуток времени Д?, за который рассматривается ее действие,
называется импульсом силы. Импульс силы есть величина векторная.
Равенство D) утверждает, что вектор импульса силы пропорционален
по величине векторному изменению количества движения, происхо-
происходящему за тот промежуток времени, за который берется импульс
силы, и направлен в ту же сторону, куда направлено изменение
количества движения.
§ 18. Единицы силы и массы. Примеры. Полагая в равенстве C)
§ 15 коэффициент пропорциональности k=\, получим
Этим соотношением можно воспользоваться для установления единиц
для измерения силы / или массы т.
54 ДИНАМИКА [ГЛ. II
В системе CGS за единицу массы принят грамм (см. § 3), а за
единицу ускорения 1 см/сек'*; отсюда, пользуясь равенством A), мы
должны в CGS-системе за единицу силы выбрать такую силу, под
влиянием которой тело с массой в \ г приобретает ускорение
в 1 см/сек'К Эта единица силы называется диной.
Положив в формуле (см. § 17)
Ш z='k' (mv.2 — /OTj)
коэффициент k'=\, получим
f — JL_^ L
откуда следует, что дина равна такой силе, под влиянием которой
количество движения тела меняется на 1 г • см/сек за одну секунду.
В МKS-сжтеме за единицу силы должна быть выбрана такая
сила, под1 влиянием которой тело с массой в 1 кг приобретает уско-
ускорение в 1 м\сек1. Эта единица силы называется ньютон. Как легко
сосчитать:
1 ньютон = 0,001 стена— 10s дин.
В технической системе единиц единица силы выбирается как
одна из основных единиц независимо от второго закона Ньютона.
Очевидно, любая определенным образом фиксированная сила может
служить единицей силы. В качестве такой силы в технической системе
выбирается определенная сила тяжести. На все тела, находящиеся
у поверхности Земли, действует со стороны Земли сила притяжения
(сила тяжести, или вес, как ее называют). Сила тяжести различна для
различных тел, и для данного тела она зависит от того, в каком месте
земного шара и на какой высоте над поверхностью Земли находится
это тело. Однако, если выбрать вполне определенное тело и фикси-
фиксировать его положение на земной поверхности, то тем самым будет
вполне определена и действующая на него сила тяжести (его вес),
которая может быть выбрана за единицу. Так именно и поступают:
в технической системе за единицу силы принимают ту силу,
с которой притягивается к земному шару гиря, служащая эта-
эталоном массы в 1 кг, расположенная на широте 45° и на уровне
моря (более точно за единицу силы в технической системе прини-
принимается сила, сообщающая массе в 1 кг ускорение gQ = 9,80665 м/сек1).
Эта единица силы называется килограмм, т. е. называется тем же
самым словом, что и единица массы килограмм; для избежания пута-
путаницы мы будем эти две единицы совершенно различных физических
величин обозначать разными сокращениями: единицу массы в один
§ 18] ЕДИНИЦЫ СИЛЫ И МАССЫ. ПРИМЕРЫ 55
килограмм обозначим кг, а единицу силы в один килограмм обо-
обозначим кГ. Сила, равная -т-^ кГ, называется Грамм и обозначается Г
IUUU
(в отличие от единицы массы грамма, обозначаемой г). Сила в 1000 кГ
называется Тонна-сила (обозначается 7"). Так как под влиянием силы
в 1 кГ тело с массой в 1 кг приобретает ускорение 981 смjсек'1
(ускорение силы тяжести), то
1 кГ=981000 дин, 1 Г= 981 дин.
Так как изменения веса тел для различных точек поверхности
земного шара невелики, то при решении задач по большей части
можно считать, что на Земле тело с массой ъ \ кг весит 1 кГ. Для
широты 45° и уровня моря это соотношение, по определению,
выполняется точно.
Выбрав в технической системе указанным определенным образом
единицу силы и измеряя ускорение в м/сек*. мы не можем уже,
пользуясь формулой A) настоящего параграфа, произвольно устана-
устанавливать единицу массы. За единицу массы в технической системе
должна быть выбрана масса тела, которое под влиянием силы
в 1 кГ приобретает ускорение в 1 м/сек'К Эта единица массы не
имеет специального названия.
Так как масса в 1 кг под влиянием силы в 1 кГ, т. е. под влия-
влиянием собственного веса, приобретает ускорение свободного падения,
равное 9,81 м/сек1*, то, следовательно, техническая единица массы,
которая под влиянием силы в 1 кГ приобретает ускорение в 1 м/сек',
должна быть в 9,81 раза больше 1 кг. Таким образом:
1 техн. ед. массы ==9,81 кг.
Остановимся еще несколько подробнее на соотношении между
весом и массой тел. Вес некоторого тела Р есть сила, с которой
это тело притягивается к земному шару, следовательно, ускорение
w = g, которое тело с массой т приобретает под влиянием соб-
собственного веса, по формуле C) § 15 равно
р
g = k — , откуда P — k'mg, B)
где k' — коэффициент пропорциональности.
Формула B) дает общую связь между весом тела Р и его мас-
массой т, независимо от выбора единиц, в которых измеряются вес
тела Р, его .масса т и ускорение силы тяжести g; численное зна-
значение коэффициента пропорциональности k' зависит от выбора этих
единиц. Если мы положим А'=1, тогда
P=mg, Ba)
50 ДИНАМИКА [ГЛ. II
но в этом случае мы уже не вправе измерять Р, mage произволь-
произвольных единицах, а должны пользоваться какой-либо одной системой
измерения. Например, в CGS-системе т. измеряется в граммах,
g — в см/сек1, Р—в динах; в технической системе: т — в техни-
технических единицах массы, g—в м\сек%, Р — в кГ. В каждой из этих
систем выполняется соотношение Bа). Но если мы воспользуемся
смешанной системой единиц, например будем измерять т. в кило-
килограммах массы (кг), g—в м\сек1 и Р—в килограммах веса (кГ),
то коэффициент пропорциональности k' уже нельзя положить равным
единице; в этом случае он примет значение:
9,81 #
Тогда
Р(кГ) = щ • т(кг) • g (м/сек*).
Положив здесь т=\ кг, g- = 9,81 slceKL, получим: Р=\ кГ, как
и следовало ожидать.
Ввиду важности соотношений, выиеденных в § 15 и 17, и необходимости
уметь правильно пользоваться системами единиц, приведем несколько при-
примеров.
Пример 1. Вагон весом 16 Укатится с начальной скоростью 5 м/сек.
Определить среднее значение силы, действующей на вагон для трех случаев:
а) вагон останавливается под влиянием сил трения в течение 1 мин.; б) вагон
затормаживается в течение 15 сек.; в) вагон останавливается, натолкнувшись
на препятствие, в течение 0,5 сек.
Решение. Находим среднее значение силы, действующей на вагон,
из соотношения между импульсом силы и изменением количества движе-
движения D) § 17:
fA? = mva — mvi, откуда f= i— -.
В наших случаях вагон останавливается, так что его конечная скорость v2 = 0,
откуда
знак минус означает, что сила, действующая на вагон, направлена в сторону,
.противоположную направлению скорости вагона Vi. Пользуясь технической
16 000 ,_^
системой единиц, имеем, что масса вагона m = ~—j-.— техн. ед. массы ^
?Ё 1632 техн. ед. массы, откуда в случае а) численная величина среднего
значения силы f равна
в случае б):
-„ 1632-5 _ ,лл _
/=—пг—кГ = 544 кГ;
10
в случае в);
18]
ЕДИНИЦЫ СИЛЫ И МАССЫ. ПРИМЕРЫ
57
-«—/V
Ду
Рис. 33. Упругий удир мяча о стену.
Таким образом, при одном и том же изменении количества движения
сила зависит от времени, в течение которого это количество движения из-
изменилось: при медленной остановке из-за сил трения эта сила оказалась
равной всего 139 кГ, при ударе о
препятствие, когда количество движе-
движения изменилось до нуля за короткий
промежуток времени в 0,5 сек., сила
превысила 16 Т.
Пример 2. Мяч весом 200 Г
ударяется о стену и отскакивает от нее
без потери скорости, так что угол а,
образованный траекторией мяча с нор-
нормалью к стене (рис. 33 а) до удара,
равен углу, образованному траекто-
траекторией с нормалью после удара. Ско-
Скорость мяча 5 м/сек, продолжитель-
продолжительность удара о стену Дг = 0,05 сек.
Определить силу удара для а = 60°.
Решение. Из формулы D)
§ 17 имеем:
f A? = m(v2 — Vj) = »i Av, C)
где v2—Vi представляет собою векторную разность. Считая положительным
направление нормали, внешней к стене (рис. 33 б), получим
Av = v2 cos а — (— г»! cos а) = а2 cos а -\-а, cos а.
По условию задачи мяч отскакивает от стены без потери скорости, т. е.
г»1 = vs = v, откуда Av = 2v cos a;
направлено Av по нормали к стене. Подставляя это значение
Av в C), найдем, что среднее значение силы /, действующей
на мяч во время удара, равно
- 2mv- cos a
f~ Д! '
где At— время удара. Для численных значений, приведенных
в примере, имеем
2-0.2-5 —
Т~ 9,81-0,0.5" Kl =lKl-
Пример 3. Через неподвижный блок (рис. 34) пере-
перекинута веревка, к концам которой подвешены грузы весом Pt
и Р2. Предполагая, что движение происходит без тренин, опре-
определить ускорение, с которым будут двигаться грузы.
Г2 Решение. На каждый из грузов действует сила тяжести
Рис 34 и сила натяжения веревки/н. Будем считать направление вниз
Движение положительным. Тогда
ГруЗОВ, ПрИ- /Я2Ш = Р2—fu, —/HiKJ = Pi—/н,
КкевеоевкеХ где т' и Ш2 — массь| грузов, w — численное значение их уско-
пепекинутои Рения- Вычитая почленно из первого равенства второе, получим
через блок. (mL -\- m2) w = Ра—Рй
но силы тяжести Р2 и Р( соответственно равны m2g и m^g, где g — уско-
ускорение силы тяжести, откуда
nil —nil ' ..
58 динлмикл [гл. п
Такого рода блок с перекинутой через него веревкой с двумя грузами
представляет собой демонстрационный прибор ^машина Атвуда"), служащий
для иллюстрации второго закона Ньютона.
Если оба груза взять одинаковыми, то ш2 = rnL, и по D) ускорение гру-
грузов да = 0. Подтолкнув в этом случае грузы, т. е. сообщив им некоторую
скорость v, легко наблюдать при малом трении в блоке, что грузы будут
двигаться-равномерно. Взяв один груз немного тяжелее другого, получим,
что ffls — mi много меньше, чем тг-\-ти откуда по D) ускорение грузов w
будет невелико. В этом случае легко зарегистрировать пути, проходимые гру-
грузами за равные промежутки времени, и убедиться, что они соответствуют
случаю равномерно-ускоренного движения.
; § 19. Механический принцип относительности. В § 14 мы ви-
видели, что первый закон Ньютона выполняется в инерциальной системе
отсчета; то же относится и ко второму закону Ньютона. Первый
закон Ньютона может, вообще, рассматриваться как частный случай
второго закона; в самом деле, положив в выражении второго закона
f = /и«/ силу f = 0, получим w = 0, что и означает, что тело, на
которое не действуют никакие силы (т. е. не воздействуют никакие
другие тела), имеет ускорение, равное нулю, т. е. пребывает в со-
состоянии покоя или прямолинейного и равномерного движения.
Нами также было указано, что всякая система, движущаяся пря-
прямолинейно и равномерно относительно инерциальной системы, сама
тоже является инерциальной системой.
Рассмотрим движение одного и того же тела относительно двух
различных инерциальных систем; очевидно, это движение будет
различаться лишь на некоторую постоянную разность скоростей:
ускорения одного и того же тела в различных инерциальных
системах одинаковы. Отсюда по второму закону Ньютона и силы,
действующие на одно и то же тело, в обеих инерциальных системах
одинаковы. Если мы находимся внутри прямолинейно и равномерно
движущегося вагона, то для сообщения определенного ускорения
относительно вагона какому-либо телу надо приложить к нему те же
силы, какие надо приложить в том случае, когда вагон покоится.
Другими словами, внутри прямолинейно и равномерно движущегося
вагона все механические процессы происходят точно так же, как и
в неподвижном вагоне. Это означает (отвлекаясь, конечно, от тряски
и от возможности взглянуть в окно), что, находясь внутри равно-
равномерно и прямолинейно движущегося вагона, нельзя с помощью каких бы
то ни было механических опытов определить скорость вагона и
вообще установить факт его прямолинейного и равномерного движе-
движения. Эта невозможность определить с помощью механических опы-
опытов, проведенных внутри системы, ее прямолинейное и равномерное
движение была впервые выяснена Галилеем. В 1632 г. Галилей,
рассматривая явления, происходящие в закрытой каюте корабля,
писал: „И вот (если только движение корабля равномерное), вы не
заметите ни малейшей перемены во всех явлениях и ни по одному
из них не в состоянии будете судить — движется ли корабль или
стоит на месте: вы, прыгая, будете проходить по полу те же самые
§ 20] ТРЕТИЙ ЗАКОН НЬЮТОНА. СОХРАНЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ 59
пространства, как и при покое корабля, т. е. вы не сделаете —
оттого, что корабль движется весьма быстро — ббльших прыжков
к корме, чем к носу корабля, хотя в то время, когда вы находитесь
в воздухе, пол, находящийся под вами, бежит в сторону, противо-
противоположную прыжку, и, бросая какую-нибудь вещь приятелю, вам не
нужно будет с большей силой кидать ее, если он будет около носа
корабля, вы же около кормы, чем если бы вы стояли наоборот;
капельки из подвешенной к потолку кружки с водою будут падать
вертикально на пол, и ни одна из них не упадет по направлению
к корме, хотя, покуда капля находится в воздухе, корабль уходит
вперед. Мухи будут продолжать свои полеты безразлично во все
стороны, и никак не случится, чтобы они (как будто уставши сле-
следовать за быстрым бегом корабля) собрались к той стороне, которая
ближе к корме". '
Резюмируя, мы можем сказать: никакими механическими опы-
опытами, произведенными внутри системы, нельзя решить — нахо-
находится ли жерциальная система в состоянии покоя или она равно-
равномерно и прямолинейно движется. С механической точки зрения
все инерциальные системы совершенно эквивалентны. Любую из них
можно положить покоящейся, а скорости всех остальных инерциаль-
ных систем определять относительно нее.
Это положение носит название механического принципа отно-
относительности, или принципа относительности Галилея.
Теория относительности Эйнштейна обобщает этот результат,
утверждая, что вообще никакими опытами, произведенными внутри
системы, будь то электрические,
световые и т. д., нельзя установить ^ ^ А
прямолинейное и равномерное
движение системы.
§ 20. Третий закон Ньютона. Г"*"
Сохранение количества движе- 2
ния. Третий закон Ньютона
дополняет содержание второго Рис. 3,5. Тело В воздействует на тело
закона, он подчеркивает то об- А с силой tt; в свою очередь, тело А
стоятельство, что воздействие тел, воздействует на тело В с силой U, чис-
численно равной fi и направленной в про-
ведущее к изменению состояния тивоположную сторону.
их движения, носит характер
взаимодействия; он гласит: если тело В (рис. 35) воздействует на
тело А с силой f1; то тело А, в свою очередь, воздействует на
тело В с силой \%, численно равной силе fj и направленной в про-
противоположную сторону:
f| = -f* (О
Существенно подчеркнуть, что силы f, и fa, о которых идет речь
в третьем законе Ньютона ^„действие" и „противодействие"), при-
приложены к разным телам.
60 ДИНАМИКА [ГЛ. П
Приведем несколько примеров: а) человек толкает вагонетку
(рис. 36), при этом к вагонетке приложена направленная вперед сила f,;
равная ей и направленная в противо-
противоположную сторону сила f2 приложена
к рукам человека; б) молоток уда-
ударяет о гвоздь: сила f4 действует со
стороны молотка на гвоздь; равная ей
и направленная в противоположную
сторону сила f9 приложена к мо-
Рис. 36. Человек толкает вагонетку лотку; в) из колодца за веревку
с силой t,; сила f2, численно рав- поднимается кверху ведро: сила f,
ная силе fi и направленная в про- г j r i
тивоположную сторону, приложена приложена к ведру и направлена
к рукам человека. вверх; равная ей и направленная
вниз сила f2 приложена к веревке.'
Оба взаимодействующих тела приобретают ускорения. Если массы
тел т, и ть а приобретаемые ими ускорения wi и w2, то по вто-
второму закону Ньютона:
nil' т%' - Д' ^
откуда по A) ~
W2 /04
т. е. взаимодействующие тела приобретают ускорения, направленные
в противоположные стороны и обратно пропорциональные их массам.
Из третьего закона Ньютона вытекает весьма важное следствие.
В случае взаимодействия двух тел А а В изменение количества
движения тела А по формуле C) § 17 равно
AKA = fi-A*b C)
где ft — сила, действующая на тело А со стороны тела В, а Д^ —
время, в течение которого действует сила fj. При этом предполага-
предполагалось, что сила ft постоянна в течение промежутка времени Д^. Из-
Изменение количества движения тела В равно
1 Силу U, которая по третьему закону Ньютона приложена к тому телу В,
которое приводит в движение тело А, иногда называют силой инерции. Однако
очевидно, что такое разделение сил il и fa на „движущую" силу fi и „силу
инерции" (г возможно лишь в том случае, если сами тела Л и fi по какому-
либо иризваку могут быть разделены на „двигаемое" и „движущее", как это
имеет место в случае человека, опирающегося о землю, и сдвигаемой с места
вагонетки. Стоит же представить себе случай столкновения двух одинаковых
шаров, чтобы стало ясно, что оба тела А и В и обе силы ft и Ь, фигурирую-
фигурирующие в третьем законе Ньютона, вполне „равноправны". Поэтому и термин
„сила инерции" в указанном смысле (в ньютоновом смысле) нет оснований
удерживать, и мы им здесь не будем пользоваться.
О другом смысле термина „сила инерции" см. § 22.
§ 20] ТРЕТИЙ ЗАКОН НЬЮТОНА. СОХРАНЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ 61
где fa — сила, действующая на тело В со стороны тела А, а ДЛ,—
время, в течение которого действует сила f9. По третьему закону
Ньютона:
кроме того, время Д^, в течение которого тело В действует на
тело А, очевидно, равно времени М2, в течение которого тело А
действует на тело В, откуда fl\ti = — !2Д^ и, следовательно,
ДКд = — ДКя. D)
Это равенство, которое, мы получили для случая постоянной силы
взаимодействия между телами, легко обобщить и на случай, когда
сила f( меняется. Для этого время взаимодействия между телами
надо разбить на столь малые промежутки Д^-, чтобы в течение каж-
каждого из них силу можно было считать постоянной. Для каждого от-
отдельного бесконечно малого промежутка времени Д?(- будет выполнено
равенство D), а следовательно, оно будет выполнено и для всего
времени взаимодействия. Таким образом, равенство D) носит общий
характер. Оно означает: насколько в результате взаимодействия
количество движения одного тела увеличилось, настолько коли-
количество движения другого тела уменьшилось, т. е. произошла пере-
передача количества движения.
Формулу D) можно переписать:
ДКд + ДКв = 0, E)
т. е. при взаимодействии двух тел общее изменение их количества
движения равно нулю, откуда следует, что их общее количество
движения К = Кл-+-Кв остается постоянным. Этот результат может
быть обобщен на любое число тел, образующих замкнутую систему,
т. е. таких тел, которые взаимодействуют друг с другом, но не
взаимодействуют ни с какими внешними по отношению к системе
телами. Полагая, что система состоит из п тел, и обозначая их коли-
количества движения соответственно через К), Ка> Кз, .... Кя. получим
K = K1 + K, + K3 + ... + K« = const, F)
т. е. полный вектор количества движения замкнутой системы,
представляющий собою векторную сумму количеств движения тел,
образующих замкнутую систему, остается постоянным во все
время движения.
Этот закон, носящий название закона сохранения количества
движения, является одним из основных законов физики. Он спра-
справедлив не только в случае взаимодействия макроскопических тел,
но и в случае взаимодействия микроскопических частиц, т. е. отдель-
отдельных атомов, атомных ядер, электронов и т. д.
Для иллюстрации закона сохранения количества движения рас-
рассмотрим следующий пример: человек, масса которого ть неподвижно
62 динамика [гл. ii
стоит на тележке, покоящейся относительно Земли; масса тележки т.г.
Их общее количество движения равно нулю. Если человек начнет
бежать по тележке со скоростью vt по отношению к Земле (рис. 37),
то он приобретет количество движения mxvy, при этом тележка
при отсутствии сил трения также приобретет количество движения
=—/»,¦»!, так как общее количество движения т{о^-\-т^
должно остаться равным нулю. Та-
v> JJk ким образом, тележка приобретает
\ относительно Земли скорость, рав-
Рис. 37. Человек бежит по тележке да с 03Начает, что ско-
со скоростью Vij тележка откаты- 3 '
вается в противоположную сторону рость v3 направлена в сторону,
со скоростью va. противоположную той, в которую
бежит человек. Тележка будет
двигаться, пока бежит человек. Когда человек остановится на тележке,
его количество движения станет снова равным нулю, тогда станет
равным нулю и количество движения тележки: она остановится.
Рассмотрим еще неупругое столкновение шаров. Закон сохранения
количества движения позволяет определить скорость ¦», которую
приобретут после неупругого центрального (скорости шаров напра-
направлены по прямой, соединяющей их центры) удара два шара С мас-
массами mi и тъ имевшие до столкновения скорости vt и в9.
При неупругом ударе оба шара после столкновения движутся.
с одинаковой скоростью v. Кроме того, так как удар центральный, то
все три скорости vlt т>2 и v направлены вдоль одной прямой.
Отсюда, в силу сохранения количества движения, имеем
= (nil ~\~ тг) v> откуда v =
Разберем теперь случай, когда на два тела А и В, кроме сил
их взаимодействия fi и f2, действуют еще внешние силы Fi и F2;
тогда для каждого из тел имеем:
Складывая эти равенства почленно и замечая, что по третьему закону
Ньютона fi-j-f2 = 0, получим
Вводя полное количество движения обоих тел К = Кл-ЬКв и
равнодействующую внешних сил F = Ft -(- F2, напишем
ДК = Р-Д^. , G)
Такое же равенство имеет место и для любого числа взаимодей-
взаимодействующих тел. Таким образом, изменение полного количества дви-
§ 20J ТРЕТИЙ ЗАКОН НЬЮТОНА. СОХРАНЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ 63
эюения системы тел определяется импульсом равнодействующей
внешних сил. Если равнодействующая внешних сил равна нулю, то
равно нулю и изменение полного количества движения, и, следова-
следовательно, полный вектор количества движения системы остается по-
постоянным: равенство G) снова ведет к равенству F).
Называя силы взаимодействия между телами, образующими систему,
внутренними силами, мы можем сказать: под влиянием внутренних
сил система не может изменить своего полного количества дви-
движения. Под влиянием внутренних сил могут лишь прийти в движение
отдельные части системы друг относительно друга. Например, паро-
паровоз под влиянием лишь сил, действующих со стороны пара на пор-
поршень, не может прийти в целом в. движение; он приходит в движе-
движение оттого, что появляется внешняя сила в виде силы трения между
колесами и рельсами. Сила, возникающая благодаря трению и при-
приложенная к колесам, сдвигает паровоз. Равная ей сила, возникающая
по третьему закону Ньютона и направленная в противоположную
сторону, приложена к рельсам; она отталкивает рельсы в обратную
сторону. Так как рельсы скреп-
скреплены с земным шаром, то их
смещение не играет роли. Коли-
Количество движения, приобретенное
паровозом, равно количеству дви-
движения, переданному земному
шару. Так как масса земного шара
чрезвычайно велика по сравне-
сравнению с массой паровоза, то ско-
скорость, приобретенная земным ша-
шаром, ничтожно мала.
Рис. 38. Проекция Кх результирую-
результирующего вектора К равна сумме проекций
слагаемых векторов.
Так как проекция результирую-
результирующего вектора на какое-либо направле-
направление (рис. 38) равна сумм.е проекций слагаемых векторов на то же направление,
то из равенства G) следует, что и изменение суммы проекций количеств
движения тел, образующих систему, на любое направление определяется сум-
суммой проекций импульсов внешних сил на то же направление. Если за такие
направления мы примем оси OX, OY и OZ прямолинейной прямоугольной
координатной системы, то получим для системы из п тел:
21
»=1
yi= 23
23 д**1=
j=i j
Переходя к бесконечно малым промежуткам времени и соответственно
к бесконечно малым изменениям составляющих количеств движения, получим:
<=i i
(8a)
т. е. сумма производных по времени от проекций количеств движения на каждую
из координатных осей равна сумме проекций внешних сил на ту же ось.
64 ДИНАМИКА [ГЛ. II
Если равна нулю сумма проекций внешних сил на одну из осей, то по
равенствам (8) сумма проекций количеств движений тел, образующих систему,
на ту же ось остается постоянной. При равенстве нулю суммы внешних сил
остается постоянной сумма проекций количеств движения тел на каждую из
осей:
п п п
Кх= S^i = const, Kv= ^Kyi = const, K2= 2гАГгг = const. Fa)
i=l i=l i=I
§ 21. Силы, действующие при криволинейном движении. Связь
между вектором силы f и вызываемым им ускорением w, выражаемая
вторым законом Ньютона:
t = mw, A)
является общей и справедлива для любого движения, как прямоли-
прямолинейного, так и криволинейного. Однако ввиду важности различных
типов криволинейного движения, рассмотрим действующие при этом
силы несколько подробнее. Равенство A) показывает, что сила и
ускорение в каждый данный момент имеют одинаковое направление.
При криволинейном движении, как мы видели
в § 11, ускорение w направлено не по каса-
касательной к траектории, но составляет с нею
некоторый угол и может быть разложено
на две составляющие: тангенциальную wt
и нормальную wn. Отсюда следует, что и
сила f, действующая на тело, движущееся
криволинейно, направлена в каждый данный
момент под углом к направлению движения
и может быть разложена на две составляю-
г, „„ „ щие: тангенциальную h и нормальную f_.
Рис. 39. Разложение силы „ *
на тангенциальную и нор- Первая составляющая ft направлена по
мальную составляющие, касательной к траектории, вторая /„ — по
нормали к ней, т. е. по радиусу кривизны,
по направлению к центру кривизны (рис. 39), поэтому нормальную
составляющую силы fn называют также центростремительной со-
составляющей силы.
Из рис. 39 видно, что численное значение полной силы f
равно:
V B)
Тангенциальная и нормальная составляющие силы ft и /„ связаны
соответственно с тангенциальной и нормальной составляющими
ускорения wt и wn соотношениями:
C)
§ 21] СИЛЫ, ДЕЙСТВУЮЩИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ 65
Так как по равенству E) § 11 нормальная составляющая уско-
ускорения wn=-p, где v — линейная скорость тела, a R — радиус
кривизны траектории в данной точке, то
/„ = «?• D)
При равномерном движении по кривой (скорость постоянна по
величине, тангенциальная составляющая ускорения равна нулю) тан-
тангенциальная составляющая силы равна нулю, и вся сила есть сила
центростремительная. Эта сила, действуя по нормали к траектории,
заставляет тело непрерывно заворачивать, не изменяя его скорости
по величине; если бы эта сила отсутствовала, то тело двигалось бы
прямолинейно.
В случае движения по окружности можно в выражении D) заме-
заменить линейную скорость v угловой скоростью си или выразить ее
через период обращения Т или число оборотов п. Тогда, в силу
соотношений v = wR = 1-к ^- = 2i:nR (см. § 12), получим для цен-
центростремительной силы:
fn == inw'R = 4я2/« Yi= 4и2/яя2/?. Dа)
По третьему закону Ньютона, наряду с центростремительной
силой, приложенной к движущемуся по кривой телу, существует
вторая сила, равная ей по величине, направленная в обратную
сторону и приложенная к тому телу (к тем „связям"), которое
заставляет движущееся тело заворачивать. Эта сила называется
центробежной. Таким образом, центростремительная и центробеж-
центробежная силы — это те две силы, существование которых обусловлено
третьим законом Ньютона; приложены они к разным телам. Напри-
Например, в случае вращения камня, привязанного к веревке, центростре-
центростремительная сила приложена к камню, а центробежная — к веревке;
в случае трамвая, идущего по закруглению, центростремительная
сила приложена к трамваю, а центробежная — к рельсам; в случае
Луны, обращающейся вокруг Земли, центростремительная сила при-
приложена к Луне, центробежная — к Земле.
О так называемой инерционной центробежной силе будет ска-
сказано ниже (§ 22).
Разберем несколько примеров.
Для уменьшения бокового давления колес поезда на рельсы на закругле-
закруглениях железнодорожное полотно делают несколько наклонным. Рассчитаем,
на какой угол а надо наклонить к горизонту полотно железной дороги на за-
закруглении радиуса кривизны R, чтобы нагон, идущий по закруглению со ско-
скоростью v, не оказывал бокового давления на рельсы.
Вагон не будет оказывать бокового давления на рельсы в том случае,
когда неуравновешенная реакцией полотна составляющая ij силы тяжести Р,
66
ДИНАМИКА
[ГЛ. II
направленная к центру кривизны (рис. 40), явится центростремительной силой,
вызывающей заворачивание вагона. Отсюда должно быть выполнено условие:
где т — масса вагона. Так как вес вагона
р = mg, то по E) искомый наклон пути опре-
определится углом а, удовлетворяющим равен-
равенству:
ШЖШШШШШШШШ/Л
Рис. 40. Составляющая силы
тяжести \i заворачивает вагон.
В формулу F), как видно, не входит
масса вагона, а входят только радиус за-
закругления Д и скорость v. На железнодо-
железнодорожных путях наклон пути выбирается
в соответствии с той средней скоростью,
с какой поезда проходят закругление; тогда
поезда, идущие более медленно, оказывают
боковое давление на внутренний рельс,
а идущие более быстро — на наружный.
В качестве второго примера рассмотрим действие центробежного регу-
регулятора паровой машины, схема которого представлена на рис. 41. К верх-
верхнему концу Л вертикального стержня АВ прикреплены шарнирно два стержня
одинаковой длины /, на концах которых находятся тяжелые шары d и Сч.
Со стержнями ACi и АСз соединены
шарнирно два других стержня, нижние
концы которых несут муфту S. Регулятор
вращается вокруг вертикальной оси АВ.
При изменении скорости его вращения
изменяется угол расхождения стержней
ACi и Ad, что влечет за собой сдвиг
муфты S; муфта S соединена с механиз-
механизмом, регулирующим впуск пара в цилиндр
паровой машины.
Определим угол а расхождения стер-
стержней АСх и АСз при заданной угловой
скорости вращения регулятора <л.
При отклоненном положении стержня
сила тяжести шара Си равная
p=mg и направленная вертикально
вниз, не уравновешивается реакцией
стержня; разложим силу Р на две со-
составляющие: N' — вдоль направления
стержня и fj — направленную горизон-
горизонтально. Составляющая N' уравновесится реакцией стержня; составляющая fi
явится той центростремительной силой, которая заворачивает шар. заставляя
его двигаться по окружности вокруг стержня АВ. Отсюда следует, что должно
быть выполнено условие:
Рис. 41. Центробежный регулятор.
Но из рис. 41 имеем
/
откуда по G)
= lsina,
2 sin а / 1 lu>* \ .
. или sin о = 0.
g \ COS а g )
§ 22] УСКОРЕННЫЕ СИСТЕМЫ. ИНЕРЦИОННЫЕ СИЛЫ 67
Отсюда получаем два решения:
и второе решение: sin а = 0, т. е. а = 0. Это пторое решение не предста-
представляет интереса, так как конструкция регулятора не допускает значения
а = 0; первое решение определяет искомое значение о: при возрастании а
возрастает и угол а.
§ 22. Ускоренные системы. Инерционные силы. Как мы видели,
на основании рассуждении, приведенных в § 19, никакими механи-
механическими опытами, производимыми внутри некоторой системы отсчета,
нельзя установить — движется ли система прямолинейно и равномерно
или нет. Всякое же ускорение системы сказывается на происходящих
в ней механических явлениях.
Рассмотрим теперь более подробно влияние ускорения системы
на происходящие в ней процессы. Для этого снова обратимся к при-
примеру движущегося вагона. Пусть перво-
первоначально вагон движется прямолинейно
с постоянной скоростью v, в направлении,
указанном стрелкой на рис. 42"" У перед-
передней стенки вагона на горизонтальной
полке лежит шар А с массой т. Полку
будем считать абсолютно скользкой, так
что между ней и шаром не возникает
никаких сил трения. Рассмотрим явления, Рис. 42. Шар А отстает от
происходящие внутри вагона, по отноше- ускоренно движущегося ва-
нию к одной из двух следующих систем гона,
отсчета: 1) по отношению к системе
отсчета, связанной с полотном железной дороги, и 2) по отноше-
отношению к системе отсчета, связанной с вагоном. При прямолинейном и
равномерном движении в обеих системах на шар не действуют ни-
никакие силы (кроме уравновешивающих друг друга силы тяжести и
силы реакции опоры). Предположим теперь, что вагон приобрел
постоянное ускорение w, направленное в ту же сторону, куда
направлена и скорость вагона v; вагон начинает идти в_се скорее
и скорее.
Как проявляется в этом случае движение шара по отношению
к обеим указанным системам отсчета?
Выясним сперва характер движения шара по отношению к системе
отсчета, связанной с полотном железной дороги. Относительно полотна
шар продолжает двигаться с первоначальной скоростью V, так как
никакие горизонтальные силы на него не действуют, но так как вагон
начинает идти скорее, то шар отстает от вагона.
Таким образом, шар, ранее покоившийся относительно полки
вагона, теперь начинает скользить по ней в направлении, обратном
движению вагона. Отсюда следует, что относительно системы отсчета,
связанной с вагоном, шар приобрел ускорение — w.
68
ДИНАМИКА
[гл. н
Если допустить, что в системе отсчета, связанной с вагоном
(которая не инерциальна), справедлив второй закон Ньютона, то
появление в этой системе ускорения можно формально объяснить
действием на шар силы
Г = т(— w),
где т — масса шара и — w — его ускорение относительно вагона,
численно равное ускорению самого вагона. Эта фиктивная сила,
которую приходится вводить в ускоренной системе отсчета, чтобы
в ней выполнялся второй закон Ньютона, называется инерционной
силой или силой инерции.
Предположим теперь, что шар, лежащий на полке, скреплен со
стенкой вагона пружиной С (рис. 43). Тогда при ускорении вагона
шар будет отставать от вагона лишь до тех пор, пока пружина не
растянется настолько, что появившаяся, бла-
благодаря растяжению пружины, сила не ока-
окажется достаточной, чтобы сообщить шару
ускорение w, равное ускорению вагона.
Другими словами: пружина тянет шар за
вагоном с силой f; эта сила приложена к
шару, направлена в сторону ускорения ва-
вагона w и численно равна mw, где т —
масса шара. По третьему закону Ньютона
существует вторая сила ft =— f, приложен-
Рис. 43. Пружина тянет ная к ПруЖИне и направленная в сторону,
шар за ускоренно движу- *
щимся вагоном с силой f; обратную направлению ускорения вагона.
По отношению же к системе отсчета,
связанной с вагоном, шар, после того как
пружина растянулась, снова окажется отно-
относительно вагона в состоянии покоя. Следовательно, в этой системе
отсчета, согласно второму закону' Ньютона, сумма сил, приложен-
приложенных к шару, должна равняться нулю. Этому требованию можно
удовлетворить, если приложить к шару инерционную силу f и
считать, что она уравновешивает силу f, с которой растянутая
пружина тянет шар. Эта инерционная сила f = ft; таким образом,
силу ft, появление которой обусловлено выполнением третьего '
закона Ньютона и которая приложена к пружине („связям") в уско-
ускоренной системе отсчета, мы прилагаем к самому телу (шару А).
Пользуясь ускоренной системой, связанной с вагоном, мы заме-
заменяем динамическую задачу задачей статистической, задачей о равно-
равновесии шара. Для этого,, как сказано, мы считаем приложенной
к шару А не только действующую на него действительную силу f,
но и силу flt действующую на связь. Такая замена динамической
задачи статической возможна для любого случая ускоренного дви-
движения.
с такой же силой V шар
растягивает пружину.
§ 22]
УСКОРЕННЫЕ СИСТЕМЫ. ИНЕРЦИОННЫЕ СИЛЫ
69
Пусть на материальную точку с массой т. действует сила f.
Уравнение движения этой материальной точки выразится вторым за-
законом Ньютона:
f = mw,
где w — ускорение, приобретенное материальной точкой. Это урав-
уравнение можно переписать:
W
Величина fi^ — mw по третьему закону Ньютона представляет
собою силу, действующую на те тела, которые, воздействуя на рас-
рассматриваемую материальную точку, сообщают ей
ускорение. Прилагая же мысленно силу f' = fi
к самой материальной точке и называя ее силой
инерции, мы получим
f + f'=o,
т. е. в каждый данный момент сила инерции
и сила, приложенная к материальной точке,
уравновешиваются. Это положение носит назва-
название начала Даламбера.
Рассмотрим еще несколько примеров возник-
возникновения инерционных сил. Предположим, что на
полу лифта лежит груз с массой т. Если лифт
поднимается кверху с ускорением w, то такое же
ускорение приобретает и груз. Груз приобретает
это ускорение в результате давления со стороны рис 44 Ускоренно
пола, добавочного по отношению к тому давле- движущийся вверх
нию, которое уравновешивает вес груза. Сила лифт ускоряет груз.
этого давления i = mw. По третьему закону На груз действует
., г j j сила {. с такОй же
Ньютона груз в свою очередь давит на пол с до- силой 'fi rpy3 давит
бавочной силой fj = — f. Если груз лежит не на чашку весов,
прямо на полу, а на чашке пружинных весоп
(рис. 44), то эта сила fj давит на весы; пружина весов сожмется
сильнее, и если весы при отсутствии ускорения лифта указывали
вес груза Р, то теперь они укажут вес Р' = Р -j— f, где f' = ft.
В случае, если лифт опускается с ускорением w, то с таким же
ускорением будет двигаться вниз вместе с лифтом и груз. Часть
силы тяжести, действующей на груз, будет сообщать ему ускорение.
Эта часть силы равна f = /ww, откуда давление груза на весы ока-
окажется равным Р' = Р — f.
В обоих случаях показания весов отличны от того показания
(равного Р), которое они дают при отсутствии ускорения у лифта,
благодаря тому, что мы имеем дело с динамической задачей — с дви-
движением груза с ускорением w. По отношению же к системе отсчета,
связанной неизменно с лифтом, груз продолжает в обоих случаях
покоиться и изменение показаний весов может быть истолковано как
70
динамика
[гл. п
изменение веса груза, вызванное тем, что к его истинному весу Р
прибавилась инерционная сила f (направленная в ту же сторону, что
и Р, если ускорение лифта w направлено вверх, и направленная
в сторону, противоположную Р, если w направлено вниз).
Совершенно аналогичным образом объясняется возникновение
инерционных сил во вращающейся системе. Пусть сидящий на
карусели человек держит в руках камень с массой т (рис. 45). Для
того чтобы камень дви-
двигался вместе с каруселью,
т. е. описывал круг ра-
' диуса R (где R — рас-
расстояние от оси карусели
до камня), необходимо
камню сообщать центро-
центростремительное ускоре-
ускорение wn = ш'2/?, где ш —
угловая скорость враще-
., ., ., „ ния карусели. Для этого
Рис. 45. Человек, сидящий на карусели, тянет 3 * '
к себе груз с силой f, чтобы заставлять его к камню должна быть
заворачивать. приложена центростре-
центростремительная сила /=
= /иша/?. Человек должен непрерывно тянуть камень к себе, чтобы
заставлять его заворачивать. Не будь силы f, камень начал бы
двигаться по касательной t. По третьему закону Ньютона камень
действует на руки челонека с силой f! = —f; эта сила f, прило-
приложена к рукам человека и направлена от центра карусели наружу;
в § 21 эта сила была названа центробежной.
Однако, если рассматривать весь процесс по отношению к си-
системе отсчета, вращающейся вместе с диском, то камень остается
при вращении неподвижным в этой системе и необходимость при-
прилагать к нему силу f может быть истолкована как результат того,
что к самому камню оказалась приложенной сила f' = flt направлен-
направленная от центра карусели наружу. Это есть инерционная сила, совер-
совершенно аналогичная инерционным силам, рассмотренным нами в при-
примерах с ускорениями вагона и лифта.
Инерционную силу, действующую во вращающейся системе, иногда
называют инерционной центробежной силой. Ее не следует сме-
смешивать с той действительной центробежной силой, о которой шла
речь в § 21.
В повседневной жизни нам часто приходится встречаться с инер-
инерционными силами. Например, когда трамвай начинает резко тормозить
или поворачивать на большом ходу, мы оказываемся соответственно
отброшенными, по отношению к трамваю, вперед или в сторону,
наружную по отношению к завороту; это является следствием того,
что мы сохраняем скорость, которую имели раньше, вагон же при-
приобретает ускорение. По отношению же к системе отсчета, связанной
§ 23]
ЗАВИСИМОСТЬ СИЛЫ ТЯЖЕСТИ ОТ ШИРОТЫ МЕСТНОСТИ
71
с вагоном, эти относительные смещения объясняются действием сил
(инерционных сил). Эти инерционные силы приходится учитывать во
всякой ускоренной системе, как добавочные по отношению к силам,
действующим в инерционной системе.
Особое освещение вопросу о силах инерции пытался придать
Эйнштейн в общей теории относительности. С точки зрения Эйн-
Эйнштейна силы инерции эквивалентны силам тяготения. Мы уже видели,
что ускорение лифта ведет к тому же результату, как если бы груз
становился тяжелее или легче (в зависимости от направления ускорения
w), т. е. силы инерции оказываются эквивалентными силам тяжести.
Таким образом, выходит, что ускорение какой-либо системы эк-
эквивалентно появлению в этой системе сил тяготения. Однако, как
показал В. А. Фок, такая эквивалентность несправедлива в пределах
больших пространственных и временных масштабов. Инерциальная
система отсчета, т. е. связанная с совокупностью неподвижных звезд,
является преимущественной, и ускорение в этой системе не имеет
того относительного характера, который имеет скорость.
§ 23. Зависимость силы тяжести от широты местности. Пользование
инерционными силами весьма удобно для решения различных механических
задач в ускоренной системе, в част-
частности, во вращающейся системе. Та-
Такого рода вращающейся системой
является, между прочим, земной шар,
совершающий суточное вращение.
Поэтому при точном рассмотрении
различных механических процессов,
происходящих на поверхности Земли,
следует принимать во внимание инер-
инерционные силы, возникающие от су-
суточного вращения. Эти силы неве-
невелики, поэтому во многих случаях мы
можем ими пренебрегать и прибли-
приближенно считать, как было указано,
Землю за инерциальную систему от-
отсчета. Однако в ряде случаев суточ-
суточным вращением Земли пренебрегать
нельзя.
Рассмотрим влияние суточного
вращения Земли на силу тяжести.
Пусть тяжелое тело А с массой т
находится на широте <р (рис. 46). Решая задачу по отношению к координатной
системе, вращающейся вместе с Землей, мы должны учесть инерционную силу
/=ты*Яи A)
где <й — угловая скорость вращения Земли и Л?1—расстояние от земной оси
до тела. Сила i направлена перпендикулярно к земной оси. Эта сила f
складывается с силой тяжести тела Ро, направленной к центру Земли.
Отсюда кажущийся вес тела Р<р на широте <р равен
P9 = Po + f- B)
В этом равенстве справа стоит векторная сумма.
Из рис. 46 имеем: Ri = R cos <р, где R—радиус Земли, откуда по A)
Рис. 46~. Влияние суточного вращения
Земли на силу тяжести.
72
ДИНАМИКА
[гл. н
Эта сила весьма мала по сравнению с силой тяжести. В самом деле,
Ре = mgo, откуда
если подставить вместо <д, R и g0 (истинное ускорение силы тяжести) их
<¦>*# 1
численные значения, то окажется, что — = o«oi косинус же угла 9
go -toa
всегда sg 1, т. е. действительно сила / много меньше силы
f, f тяжести Ро. Поэтому для определения кажущегося веса Р9
по равенству B) мы воспользуемся следующим приближенным
расчетом. Разложим силу f на две составляющие: fj— на-
направленную вертикально вверх (для данной точки земного
шара), и f2 —направленную горизонтально. Тогда приближенно
можно считать, что составляющая /2 изменяет силу тяжести
лишь по направлению, а составляющая /i — лишь по вели-
величине. Отсюда приближенно:
Р9 = Ро _/,.
Но из рис. 47 имеем, что /1=/costf>, откуда
Р<р—Р0 —/COS if,
или по C) *
Р9 — рй — mM2/?cosaep.
Вынося Ро за скобку и замечая, что ра = mg0, получим
рщ = р0 A —
\
So
D)
Рис. 47.
Определение
веса тела Р?
на широте <р.
Формула D) дает зависимость кажущегося веса Р? от широты
местности <j>. Величина есть постоянная, равная gtm,
так что
Р9 — Ро 1 — 9Яо
1
Dа)
На самом деле надо еще принять во внимание, что Земля
не представляет собою правильной сферы, но приплюснута
у полюсов, что ведет к увеличению у полюсов силы тяжести. Правильная
зависимость веса тела от широты <р имеет вид:
На полюсе Р„ совпадает с Ро; на экваторе Р^ наиболее отличается от Ро.
Угол а, который составляет направление кажущегося веса Р^ с земным
радиусом, как видно из рис. 47, определится соотношением:
Л
Sin а = -
Заменяя приближенно Р9 через Ро и замечая, что /2=/sin<pr получим
/ sin и тш2/? cos со sin <p
sm а = -J т. = 1 1 1-
или
Sin a =
COS <f SHI <f.
E)
Таким образом, кажущаяся сила тяжести Р9 направлена к центру Земли
и на полюсе и на экваторе; наибольшее отклонение она имеет на широте
<Р = 45°.
§ 24]
СИЛЫ КОРИОЛИСА
73
Если тело двигается вдоль экватора с линейной скоростью v (отсчитан-
(отсчитанной в инерциальной системе координат, связанной с центром земного
шара), то на него будет действовать инерционная сила /,- направленная
против силы тяжести и равная:
ти*
Эта сила окажется численно равной силе тяжести Ро при условии
откуда для v получаем значение:
Так как ^0 = 981 см/сек1 и /? = 6 370 км — 6,37- 10s см, то
см
км
»= 1/981-6,37-1Оа —=7,91.10s -i^-^7,9
' сек сек сек"
Таким образом, при отсутствии силы трения со стороны воздуха, тело,
брошенное горизонтально со скоростью а =7,9 км/сек, стало бы двигаться
у поверхности Земли не падая, т. е. в виде спутника. Эта скорость носит
название „первой космической скорости".
При движении спутника над поверхностью Земли на высоте h по кру-
круговой орбите, как легко подсчитать, его скорость будет меньше. При
Л = 250- км получим w = 7,76 км/сек, а при Л = 2000 км—к = 6,9 км/сек.
; § 24. Силы Кориолиса. Покажем, что во вращающейся системе
на тело, перемещающееся относительно этой системы, действует,
кроме центробежной, еще добавочная сила. Эта сила, носящая наз-
название корполисовой силы (в честь французского математика Корио-
Кориолиса, 1795—1843), зависит от скорости v' тела относительно враща-
вращающейся системы и от угловой скорости вращения системы ш.
Рассмотрим сперва частный случай. Пусть система представляет
собою диск, вращающийся с постоянной угловой скоростью <о вокруг
вертикальной оси О (рис. 48) в на-
направлении, указанном стрелкой. Пусть
тело а перемещается равномерно из
точки А вдоль радиуса ОС со скоростью
•»' относительно диска. За время At тело
а пройдет отрезок Al = AB = v'At.
За это время At в неподвижной си-
системе координат радиус ОС, благо-
благодаря вращению диска, повернется на
угол Д<р = wAt, и тело передвинется
из А в D. В неподвижной системе
координат тело а принимает одно-
одновременно участие в двух движениях:
в движении относительно диска со скоростью г»' и в движении
вместе со вращающимся диском. Линейная скорость вращения диска
различна для различных мест диска. Обозначим ее значение
в точке А через vr Двигаясь лишь со скоростью вращения vn тело а
Рис. 48. Движение тела вдоль
радиуса вращающегося диска.
74
ДИНАМИКА
[ГЛ. И
описало бы дугу А А' и пришло бы в точку А'. Двигаясь одновре-
одновременно со скоростью vr, и относительной скоростью v', тело а должно
было бы попасть в точку В' (отрезок А'В' || АВ). На самом деле
тело а переходит в точку D. Это происходит за счет того, что
линейная скорость вращения vr возрастает по мере удаления точки а
от центра вращения. Таким образом, относительно неподвижной
системы, координат тело а, двигаясь вдоль радиуса, непрерывно
меняет свою скорость: оно движется ускоренно. Величина этого
ускорения w может быть определена по тому добавочному пути
As = B'D, который тело а прошло за время At. Из рис. 48 имеем:
или, так как А'В' = Al=v' At и Дср = шД?, то
Следовательно, добавочный путь As возрастает пропорционально
квадрату времени At. Но пропорциональность пути квадрату вре-
времени At имеет место при движении с постоянным
ускорением w (равномерно-ускоренном движении)
при котором
1
Рис. 49. Напра-
Направление силы
Кориолиса при
движении тела
вдоль радиуса
вращающегося
диска.
Сравнивая это выражение для As с A), полу-
получим, что тело а испытывает ускорение
w = 2zi'(o. B)
Это ускорение направлено перпендикулярно к
относительной скорости v', и в нашем случае —
направо. Для того чтобы сообщить телу а это уско-
ускорение, к нему необходимо приложить силу /, на-
направленную направо и равную /= mw, где т — масса
тела. Не будь силы/, тело отклонилось бы во вращаю-
вращающейся вместе с диском системе координат от своего
„прямолинейного" движения вдоль радиуса диска.
Сила fk, равная силе /, но направленная в противоположную
сторону, будет действовать по третьему закону Ньютона на те связи,
которые удерживают тело а при его движении на радиусе. Совер-
Совершенно аналогично, как в ранее рассмотренных случаях ускоренных
систем, пользуясь координатной системой, вращающейся вместе с дис-
диском, будем считать, что сила fk приложена к самому телу а. Таким
образом, во вращающейся системе к телу, движущемуся вдоль
радиуса со скоростью v', приложена „инерционная" сила
fk = 2zi'uot, C)
направленная перпендикулярно к v' (в нашем примере налево, см.рис. 49).
Сила fk и носит название силы Кориолиса.
§ 24]
СИЛЫ КОРИОЛИСА
75
Покажем теперь, что сила Кориолиса существует и в том случае,
когда тело а движется на диске по окружности с центром на оси вра-
вращения (рис. 50). При движении тела а относи-
относительно диска со скоростью v' полная скорость
в неподвижной системе координат равна
vr-\-v', где vr — линейная скорость вращения
диска в том месте, где находится тело а. Сле-
Следовательно, на тело а действует центростреми-
центростремительная сила
где R — расстояние от оси вращения до тела.
Возводя в этой формуле сумму (vr -f- v') а квад-
квадрат, получим
Рис. 50. Движение тела
на вращающемся диске
по окружности, кон-
концентрической с диском.
В координатной системе, связанной с диском, член
mv-r
IT
опреде-
определяет инерционную центробежную силу, вызванную вращением диска
О с угловой скоростью <и; член -^— определяет центро-
центробежную силу, вызванную относительным движением тела
по кругу радиуса R. со скоростью v'\ член
Рис. 51. Раз-
Разложение от-
относительной
скорости на
составляю-
составляющую V1, вдоль
радиуса и со-
составляющую
vi,перпенди-
vi,перпендикулярную к
радиусу.
определяет добавочную силу, вызванную одновремен-
одновременным наличием как вращения диска, так и движения
тела относительно диска.
Сила fk, равная силе /, но направленная в проти-
противоположную сторону, даст для этого случая силу
Кориолиса.
Эта сила совпадает по величине с силой, возни-
возникающей при движении вдоль радиуса [формула C)],
и направлена также перпендикулярно к относитель-
относительной скорости.
Теперь рассмотрим случай, когда тело а движется
с относительной скоростью v', направление которой
составляет угол E с радиусом ОС (рис. 51).
В этом случае скорость v' можно разложить на две
составляющие: на составляющую вдоль радиуса v\ =
= v'cos C и составляющую, перпендикулярную к радиусу,
Составляющей v[ по формуле C) соответствует кориолпсова
сила fH = 2v'u) cos §-т, составляющей v'3 — сила /Л2 = 2v'u> sin $-m;
76
ДИНАМИКА
[гл. и
полная сила Кориолиса
Таким образом, и для произвольного направления относительной
скорости v' для силы Кориолиса сохраняется выражение C).
Наконец, рассмотрим самый общий случай, когда тело движется
в направлении, составляющем угол а с осью вращения (рис. 52).
Тогда разложим скорость v' на составляю-
составляющую vj, перпендикулярную к оси вращения,
и составляющую \'а, параллельную оси вра-
вращения. Эта последняя составляющая не обус-
обусловливает никакого изменения расстояния от
оси и, следовательно, не может вести к появ-
появлению добавочных ускорений и сил. Отсюда
величина силы. Кориолиса определяется лишь
составляющей t\ = i/'sin а. Заменяя в фор-
формуле C) v' через v\ = v' sin а, получим общее
выражение для силы Кориолиса
fk = 2v'ш sin a • т. D)
Рис. 52. Разложение отно-
относительной скорости на
составляющую vj, периен-
дикулярную к оси, и со-
составляющую V» — вдоль
оси вращения.
Во всех случаях сила Кориолиса направлена
перпендикулярно и к переносной скорости v' и к
оси вращения. Для определения направления силы ffe
введем в рассмотрение вектор угловой скорости ш
(см. § 13). Тогда кориолисова сила f^ направлена
перпендикулярно к плоскости, содержащей векторы в> и v1 (рис. 53), и так,
что если сопоставить направление поворота головки буравчика от вектора v'
к вектору ы (в направлении меньшего угла), то направление силы ik опре-
определится направлением поступательного движения
буравчика.
Если воспользоваться обозначениями вектор-
векторного анализа, то \k определится через векторное
произведение векторов v1 и to (см. § 13):
Сила Кориолиса проявляется при движе-
движениях по поверхности земного шара, обладаю-
обладающего определенной угловой скоростью, бла-
благодаря суточному вращению. Предположим,
например, что поезд идет в северном полу-
полушарии в меридиональном направлении на
север (точка а на рис. 54). При этом вектор
относительной скорости v' составляет острый угол а с вектором угло-
угловой скорости о), и кориолисова сила ik направлена касательно к
земной поверхности направо, если встать лицом по ходу движения
поезда. Поезд оказывает на правый рельс большее давление, чем на
левый. В южном полушарии, при движении поезда к югу (точка а'
на рис, 54), v' составит с ш тупой угол, и сила Кориолиса направ-
Рис. 53. Определение на-
направления силы Корио-
Кориолиса 1к.
§ 24]
СИЛЫ КОРИОЛИСА
77
лена налево относительно хода движения. Существованием силы Ко-
риолиса объясняется подмывание реками в северном полушарии пра-
правого, а в южном — левого берегов (закон Бера), возникновение северо-
северовосточных пассатов в северном полушарии и т. д.
Другим примером влияния сил Кориолиса на движение тел у по-
поверхности земного шара являются: отклонение свободно падающих
тел к востоку от вертикали и отклонение
плоскости качаний маятника. Разберем по-
последний случай несколько подробнее. Пред-
Предположим для простоты, что маятник совер-
совершает колебания на северном полюсе. Тогда
скорость груза маятника v' все время перпен-
перпендикулярна к оси земного шара (при большой
длине нити) и, следовательно, v' J_ <u, где со —
по-прежнему вектор угловой скорости вра-
вращения Земли. В результате на груз маятника
действует сила Кориолиса, численно равная
fk = Imv'uy, лежащая в горизонтальной плос-
плоскости и направленная вправо по отношению
к вектору v'. Под действием этой силы груз
маятника при каждом размахе отклоняется
вправо. В результате плоскость качаний маят-
маятника будет поворачиваться относительно Зем-
Земли в направлении часовой стрелки и по-
повернется на угол 2и за сутки. В случае ка-
качаний маятника на широте <р плоскость качаний повернется в сутки
на угол 2тс sin ср.
Наблюдение отклонения плоскости качаний маятника было впервые
проведено Фуко в 1851 г. и послужило прямым доказательством
существования суточного вращения Земли.
Рис. 54. Направление сил
Кориолиса, действующих
на тела, движущиеся по
поверхности Земли.
ГЛАВА III
РАБОТА И ЭНЕРГИЯ
§ 25. Работа и мощность. В окружающей нас обстановке мы
имеем дело с телами, взаимодействующими друг с другом теми или
иными силами (упругие силы, силы тяготения, силы трения и т. д.).
Поэтому перемещения тел в таких условиях осуществляются лишь
под влиянием сил. Отсюда, естественно, возникает потребность дать
характеристику того действия сил, которое связано с перемещением
тел. В механике за такого рода характеристику принимается вели-
величина, тем большая, чем больше составляющая сила вдоль направле-
направления перемещения и чем на больший отрезок перемещается точка ее
приложения. Эта величина называется работой. Полностью физиче-
физический смысл работы может быть выяснен после того, как будет уста-
установлена связь между совершаемой работой и изменением энергии.
Тогда становится ясн*ым, что работа есть
Jj мера изменения энергии (§ 28).
' ^ простейшем случае прямолинейного
J движения и постоянной силы, направлен-
' ной вдоль перемещения, работа пропор-
*"$ циональна произведению силы / на лере-
""s мещение s точки ее приложения:
Рис. 55. Работу производит
лишь составляющая силы fs A = kfs, A)
вдоль направления переме-
перемещения s. где k — коэффициент пропорциональности.
В том случае, если сила, приложенная
к телу, составляет угол а с направлением перемещения (рис. 55),
разложим силу f на две составляющие: is — направленную вдоль
перемещения, и f, — перпендикулярную к нему.
По сказанному, работу совершает лишь составляющая fs, поэтому
A = kfss,
или, так как /s=/cosa, то
А = kfs cos a. (la)
Полагая коэффициент пропорциональности k = l, получим
A =fs cos a. B)
§ 25] РАБОТА И МОЩНОСТЬ 79
Таким образом, в случае произвольно направленной силы, работа
численно равна произведению из силы f, перемещения s ее точки
приложения и косинуса угла а. между направлением силы и пере-
перемещения.
Работа характеризуется лишь численным значением и поэтому
представляет собою величину скалярную.
В векторном анализе скалярную величину С, равную произведению из
численных значений векторов В и D и косинуса угла между ними, называют
скалярным произведением:
C = B-D cos а.
Из равенства B) следует, что работа представляет собою скалярное
произведение вектора силы f и вектора перемещения s.
Когда угол а<^90с, то cos а ^> О, и работа положительна; в этом
случае составляющая силы fs направлена в сторону перемещения.
При а]>90° имеем cos а <^ 0, работа в этом случае отрицательна;
при этом составляющая силы fs направлена в сторону, противопо-
противоположную перемещению. Поясним сказанное примерами: 1) к телу,
лежащему на шероховатой поверхности, приложена сила /, которая
перемещает его по этой поверхности; сила / направлена вдоль пере-
перемещения и совершает положительную работу. Одновременно к телу
приложена сила трения /тр, она направлена в сторону, противопо-
противоположную перемещению тела; совершаемая ею работа отрицательна;
2) подброшенное тяжелое тело летит вверх, сила тяжести напра-
направлена вниз, т. е. в сторону, противоположную направлению движения;
работа силы тяжести отрицательна; 3) тяжелое тело падает вниз;
в этом случае сила тяжести направлена в ту же сторону, куда про-
происходит перемещение тела; работа силы тяжести положительна;
4) тело под влиянием центростремительной силы равномерно дви-
движется по окружности; в этом случае сила все время перпендикулярна
к направлению движения (а = 90°), и работа по формуле B) равна
нулю.
Рассмотрим теперь случай, когда сила не постоянна и движение
происходит по криволинейному пути. Возьмем столь малую дугу As,
чтобы ее можно было считать совпадающей с хордой As. Пусть
/j — составляющая сила f вдоль касательной к дуге As. Тогда зна-
значение /j на длине пути As можно считать постоянным, и элементар-
элементарная работа АЛ, совершенная на этом пути, будет равна
ДЛ=Л-А*. C)
Всю работу Л, совершаемую на конечном пути s, получим, раз-
разбив путь s на отдельные бесконечно малые элементы As, определив
элементарные работы АЛ и сложив их:
Л = 2 A As. D)
80
РАБОТА И ЭНЕРГИЯ
[гл. ш
0
Полную работу Л можно представить графически. Отложим по
оси абсцисс длину пути s (рис. 56), а по оси ординат — значение
составляющей силы fs. Пусть кри-
кривая АВ представляет значения со-
составляющих силы fs для различных
точек пути для некоторого частного
случая. Разобьем всю длину пути,
изображаемого отрезком ОС, на
элементарные отрезки As. Элемен-
Элементарная работа ДЛ, совершаемая на
одном из этих отрезков As, равна
Рис. 56 Работа графически опре- fs^s, т. е. изображается площадью
деляется площадью фигуры О ABC. густо заштрихованного столбика.
Вся работа на пути s равна сумме
всех элементарных работ ДЛ, т. е. графически изображается пло-
площадью всей заштрихованной фигуры О ABC.
Определим работу, совершаемую при одновременном действии на тело
нескольких сил \и f2, f3 и т. д. (рис. 57). Элементарная работа ДЛ равно-
равнодействующей равна
ДЛ =/ cos a As,
где f—равнодействующая сил lu h, U, a a — угол, который она составляет
с направлением перемещения As. Величина /cos а есть проекция fs силы f
на направление s. Но мы видели
(см. § 20), что проекция резуль-
результирующего вектора на некоторое
направление равна сумме проекций
его слагаемых на то же направле-
направление, откуда
fs=fl
и, следовательно,
AA=fsAs =
т. е. работа результирующей силы
равна алгебраической сумме работ
составляющих сил.
Рис. 57. Работа результирующей силы t
равна сумме работ слагаемых сил ftI
hi '«¦
Воспользовавшись этим положением, мы можем преобразовать выраже-
выражение для работы. Разложим силу f, действующую в некотором направлении,
на составляющие вдоль координатных осей fx, fyi fz, тогда по доказанному:
ДЛ =fxcos av As+/j,cosa2 As+ZjCOS а3 As,
где oj, о2 и о8 — соответственно углы'между составляющими силы fx, fy, fz
и направлением перемещения As. Но направление составляющих fx, fy, fz
совпадает с направлением осей А", У, Z, откуда Ascos aL = Ax, Ascoso2 = A^»,
As cos a3 = Да, где Ах, Ay, Аг — проекции перемещения As на координатные
оси. Отсюда
z. E)
Для переменной силы следует брать бесконечно малое смещение ds
с составляющими dx, dy, dz, тогда
z. Ea)
§25] РАБОТА И МОЩНОСТЬ 81
Вся работа на конечном перемещении s выразится суммой элементарных
работ dA, т. е. криволинейным интегралом:
А = ^ (fxdx +fydy -\-fzdz), F)
где Bt и Bt — начальная и конечная точки пути S.
Практически часто весьма важно знать не только работу, совер-
совершенную силами, но и то время, за которое работа произведена.
Очевидно, из двух механизмов, совершающих одну и ту же работу,
ценнее тот, который совершает эту работу за меньший промежуток
времени. Поэтому наряду с работой вводится в рассмотрение новая
величина, называемая мощностью. Мощное тью W называется физи-
физическая величина, пропорциональная работе ДА и обратно пропор-
пропорциональная тому промежутку времени Д^, за который эта работа
совершена:
W = kA^, G)
где k — коэффициент пропорциональности. Полагая k=l, получим
* = ?. Gа)
Если сила меняется со временем, то мощность тоже не остается
постоянной; в этом случае имеет смысл говорить о мощности в дан-
данный момент, подразумевая под ней тот предел, к которому стре-
стремится отношение ДА/Д/ при бесконечном убывании промежутка вре-
времени At:
1Г=пред. №). (8)
Пользуясь обозначениями дифференциального исчисления, получим
W = A^, (8a)
т. е. мощность численно равна производной от работы- по времени.
Так как элементарная работа ДЛ =fshs, то по (8)
№=пред. (¦тт1)=Л-пред.(^), но пред. №) =
где v есть значение скорости в данный момент. Отсюда
W=ft-v. (9)
т. е. мощность в каждый данный момент пропорциональна произае-
дению проекции силы на направление движения на скорость движения.
4 С. Э. Фриш и А. В. Тнмореаа
82 РАБОТА И ЭНЕРГИЯ [ГЛ. Ш
Ввиду практической важности величин работы и мощности истори-
исторически возникло большое количество единиц для их измерения. При-
Приведем эти единицы.
1) Единица работы в CGS-системе. Пользуясь равенством B),
в котором полагаем <х = 0, получим: за единицу работы в CQS-cu-
стеме принимается работа, совершаемая силой в 1 дину на пути
в 1 см, при условии, что сила действует в направлении переме-
перемещения. Эта единица работы называется эрг.
Наряду с этим употребляется более крупная единица работы
джоуль:
1 джоуль = 107 эргов.
2) В MKS-системе за единицу работы принимается работа,
совершаемая силой в 1 ньютон на пути в 1 м. Так как 1 h=10s дин
и 1 .и =10* см, то эта единица работы равна 107 эргов, т. е.
1 джоулю.
3) В практической технической системе за единицу работы
принимается работа, совершаемая силой в 1 кГ на пути в 1 м.
Эта единица работы называется килограммометр (сокращенно кГм).
Так как 1 кГ=Ш 000 дин и 1 л* = 100 см, то 1 кГм =
= 981000-100 5^гов = 9,8Ы07 эргов = 9,81 джоуля;
1 джоуль = <щ кГм = 0,102 кГм.
4) Единица мощности в CGS-системе. За единицу мощности
в CGS-системе принимается мощность механизма, совершающего
работу в 1 эрг за 1 сек. Эта единица мощности обозначается эрг1сек.
Наряду с единицей мощности эрг/сек употребляется более круп-
крупная единица мощности, называемая ватт:
1 ватт = 10' эрг/сек — 1 джоуль/сек.
Таким образом, мощностью в 1 вт обладает механизм, совер-
совершающий работу в 1 дж за 1 сек.
100 ватт называются 1 гектоватт (сокращенно гвт),
1000 ватт называются 1 киловатт (сокращенно кет).
5) В MKS-cncitue за единицу мощности принимается мощность
механизма, совершающего работу в 1 джоуль за 1 сек., т. е. 1 ватт.
6) В технической системе за единицу мощности принимается
мощность механизма, совершающего работу в 1 кГм за 1 сек.
Эта единица мощности сокращенно обозначается кГм/сек.
Очевидно:
1 кГм/сек = 9,81 ватта,
= <щкГм/сек = 0,102 кГм/сек.
§ 25] РАБОТА И МОЩНОСТЬ 83
Кроме того, исторически возникла единица мощности, называемая
„лошадиной силой",1 равная 75 кГм/сек. Таким образом:
1 л. с. = 75 кГм/сек = 736 ватт = 0,736 киловатта.
7) В современной практике весьма часто употребляют еще две
следующие единицы работы:
а) равную работе, совершаемой механизмом с постоянной мощ-
мощностью в 1,-гектоватт за время в 1 час. Эта единица работы назы-
называется гектоватт-час:
1 гектоватт-час = 100 ватт -3600 сек. = 3,6-10" джоулей;
б) равную работе, совершаемой механизмом с постоянной мощ-
мощностью в 1 киловатт за время в 1 час. Эта единица работы назы-
называется киловатт-час:
1 киловатт-час = 1000 ватт-3600 тс. = 3,6-106 джоулей.
Рассмотрим несколько примеров на определение работы и мощности.
Пример 1. Электропоезд весом 500 Г проходит равномерно путь в
3 км в гору с уклоном 4 м на I км пути. Коэффициент трения ч. = 0,002.
Определить: а) работу, совершенную поездом; б) мощность, развиваемую
электропоездом, зная, что путь э 3 км был пройден за 5 мин.
Решение. Работа совершается
против силы трения:
где Pi — давление, оказываемое поездом
на путь (рис. 58), и против составляющей
силы тяжести Р2, параллельной пути. Та-
Таким образом, искомая работа А равна
s. A0)
Из рис. 58 имеем
р _ , Рис. 58. Работа совершается про-
"'— г cos or, Pt = И зт а, тив силы трения и против скатывакь
где Р-вес поезда и а-угол, под щей назад силы Р3.
которым путь наклонен к горизонту.
Подставляя эти значения Pt и Р2 в A0), получим
А = Р (х cos а -\- sin a) s. A1)
Величины sin а и cos а определим из условия, что подъем равен 4 м на 1 км
пути, откуда
= yA_ = 0,004 и cosa= |Л — sin8 a = /l—0,004s = 0,99992,
т. е. приближенно единице. После этого по равенству A1) имеем
А = 5 • 10» @,002 + 0,004) • 3000 кГм,
1 В среднем лошадь при длительной работе действительно даег мощность
около 75 кГм/сек, однако кратковременно лошадь может развить мощность
в несколько „лошадиных сил".
84
РАБОТА И ЭНЕРГИЯ
[ГЛ. Ill
откуда
Искомая мощность
кдж.
W = — = 8'83'10<
ИЛИ
300
2,94-10»
: 0,736
кет = 2,94- 10s кет
л. с. — 399 л. с.
Пример 2. Определить работу, совершаемую при сжатии пружины
на 10 см, если известно, что сила пропорциональна сжатию пружины и что
для сжатия пружины на 1 см необходима сила
в 2 кГ.
Решение. Здесь мы имеем случай работы
переменной силы; сила возрастает пропорционально
сжатию пружины. Обозначив сжатие через s,
имеем, что сила
/ = *«, A2)
где k—коэффициент1, определяемый степенью жест-
жесткости пружины.
Графически зависимость силы / от сжатия s
изображается прямой ОА, проходящей через на-
начало координат (рис. 59).
Если пружина сжата на величину s, то s и
представляет собою тот путь, на котором рассма-
рассматриваемая переменная сила совершала работу. По
сказанному на стр. 80, работа изобразится пло-
площадью заштрихованной фигуры. Так как эта фигура есть треугольник, то ее
площадь равна—^ , но OS = s и AB = ks, откуда искомая работа
0
S в
Рис. 59. Работа упругих
сил растянутой пружины
равна площади треуголь-
треугольника (DAB.
ks-s
A3)
Численное значение k определим по A2) из условия, что/=2 кГ при
s=l см; однако желая воспользоваться технической системой, переведем s
в метры, тогда s == 0,01 м и
k = — = Q^ry кГ1м = 200 кГ\м.
Подставляя это значение k в A3), получим
, 200- @,1)а „ , '„
А = ^-^ кГм — 1 кГм.
§ 26. Кинетическая энергия механической системы. Тело, рас-
рассматриваемое как материальная точка, движущееся под действием
силы, меняет свою скорость. Работа приложенной силы связана
с изменением скорости тела. Эта связь выражается через физическую
величину, называемую кинетической энергией материальной точки.
Для определения кинетической энергии материальной точки
сосчитаем, какую работу надо совершить для того, чтобы изменить
скорость материальной точки с массой т. от значения vY до значе-
§ 26] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ 85
ния щ. Для этого приложим к материальной точке постоянную
силу f, параллельную вектору скорости Vj, которая за некоторый
промежуток времени t изменит скорость от значения vt до значе-
значения Vi. За это время t материальная точка пройдет путь s, и сила f
совершит работу
A=fs. A)
Ввиду постоянства силы движение будет равноускоренным, причем
ускорение его
а следовательно, сила
B)
Путь, пройденный материальной точкой за время t, определим
через среднюю скорость v== а"Г ', откуда получаем
C)
Подставляя наиденные значения силы / и пути 5 по B) и C)
в формулу A), найдем
. „ Pa —Pi Pa + Pi v ^(Pa
/i in • ^ ¦ I rrl ^ ,
откуда
. _/яр| mv\ -
Таким образом, работа силы f численно равна приращению вели-
величины ?тг-, которая называется кинетической энергией. Обозначим
кинетическую энергию через Ek:
Тогда равенство D) можно переписать в виде:
A = Ek, — Ekl = AEk. F)
Из равенства D) следует, что для того, чтобы тело, движущееся
со скоростью v, остановилось (zij = u, г>2 = 0), сила, приложенная
к этому т^лу, должна совершить отрицательную работу, численно
равную кинетической энергии тела Ek = -7—\ обратно, чтобы телу
с массой in сообщить скорость v, приложенная сила должна совер-
совершить положительную работу, равную ~^~.
86 РАБОТА И ЭНЕРГИЯ ' [ГЛ. III
Если в выражении ^— все величины выражены в CGS-системе,
т. е. м — в граммах, v — в см/сек, то энергия выражается в эргах.
В технической системе v выражается в м/сек, т — в технических
единицах массы (равных 9,81 кг); энергия ..получается в кГм. На
практике часто пользуются смешанной системой: скорость v выра-
выражают в м/сек, массу т — в кг, а энергию Ek желают получить в
кГм. Тогда в формулу E) должен быть введен коэффициент про-
пропорциональности k, который в данном случае будет иметь численное
значение g-кт, таким образом:
р /,.г,л_ т (кг) [у (м/сек)}1 ¦
ck(Ki м) — 981-2 '
Соотношение D) может быть легко получено и для случая переменной
силы и криволинейного движения. Пусть за произвольный малый промежуток
времени A't тело проходит малый путь As (рис. 60).
Тогда работа АА на этом пути равна
ДЛ=/соза-Дз, G)
где а — угол, которой сила f составляет с направле-
направлением перемещения As.
По второму закону Ньютона f = m-w, где w —
ускорение, вызываемое рассматриваемой силой; напра-
Рис. 60. Малый путь вление вектора w совпадает с направлением силы.!.
As, проходимый при Отсюда выражение G) перепишем:
криволинейномдвиже- AA = mw cos a-As. (8)
Величина w cos а есть проекция вектора ускорения на
малое перемещение As, которое совпадает по напра-
направлению с касательной к траектории. Таким образом, w cos а есть касательная
составляющая ускорения Wj, которая равна Av/At, где Av— изменение чис-
численного значения v. Подставляя это значение w cos а в (8), получим
Наконец, замечая, что &s = vht, найдем
&.А = mv Av. (9)
Чтобы получить полную работу А, совершаемую на конечном пути s,
надо просуммировать выражение (9J:
А = 2 ДЛ"= 2 mv Av.
Вынося массу т, как величину постоянную, за знак суммы, получим
А = т 2 v До. (9а)
Для того 'чтобы сосчитать эту сумму, положим изменение скорости бес-
бесконечно малым, тогда сумма заменится интегралом
?
[ = т \ vdv,
§ 26] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ 87
взятым в пределах от скорости vu соответствующей началу пути, до ско-
скорости v%, соответствующей концу пути. Выполняя интегрирование, получим
m \ vdv = m\-7r\ = -^ ^, откуда A = -~- ^.
Приведем несколько примеров на определение кинетической энергии.
Пример 1. Поезд весом 600 Г отходит от станции и через 5 мин.
после отхода имеет скорость 60 км/час, пройдя путь, 2,5 км. Какую среднюю
мощность развивал паровоз, если коэффициент трения % постоянен и равен
0,005,
Решение. Работа, совершенная паровозом, складывается из работы
против силы трения и работы, идущей на сообщение поезду запаса кинети-
кинетической энергии, откуда
* A-f .s + "^
Л —Утр s п 2 •
где /тр==%Р есть сила трения, т — масса поезда, v — его скорость в конце
пути s.
Отсюда искомая мощность W равна
или
\F = 0,005-6-106--^|^—^'~^Wr2^.W=5'3'W
или
Пример 2. Определить скорости, приобретаемые шарами после цен-
центрального упругого удара; массы шаров mt и /па и их скорости до удара щ
и»,.
Решение. Обозначим скорости шаров после удара через v\ и v'a. Упру-
Упругий характер удара означает, что сумма кинетических энергий шаров после
удара должна равняться сумме их кинетических энергий до удара:
33 miaf , m^vl /in\
2~~ + ~2~* К '
Кроме того, должен выполняться закон сохранения количества движения
(см. § 20), по которому:
1 Следует иметь в виду, что равенство A0) имеет скалярный характер;
оно осталось бы справедливым и при не центральном ударе, т. е. когда ско-
скорости шаров Vi и Vi имеют разные направления. Равенство же A1) имеет
векторный характеров том виде, как оно приведено в тексте, оно справед-
справедливо лишь для центрального удара, когда все скорости г\, г»а, v\ и fj напра-
направлены вдоль одной прямой.
88 РАБОТА И ЭНЕРГИЯ [ГЛ. III
Решая два уравнения A0) и A1) относительно двух неизвестных v\ и
у'г, найдем:
. (w2 — mi) v,
f9 =: ;
+ ms ' mi + m2
( 1 Z.)
Пример 3. Определить потерю кинетической энергии при неупругом
центральном ударе двух шаров. Массы шаров mi и т2, их скорости до
столкновения vt и z/a.
Решение. Кинетическая энергия шаров до столкновения:
„ mi»; . mty\
После неупругого удара оба шара катятся с одинаковой скоростью о',
равной (см. § 20):
+
Изменение кинетической энергии при ударе равно
.„ р р (mi -f- /п2)у'2 !тху\ . m2vl\
Подставляя сюда »' по A3), найдем
"" '3 . (И)
Таким образом, при неупругом столкновении шаров происходит умень-
уменьшение кинетической энергии. Это изменение энергии идет на работу, совер-
совершаемую при неупругой деформации шаров во время удара. В конечном счете
эта работа ведет к нагреванию шаров.
Переходя от рассмотрения одной материальной точки к рассмот-
рассмотрению системы материальных точек, мы применим соотношение D)
к каждой точке системы:
Л; = ^-^!. A5)
Здесь индекс I отмечает данную материальную точку, а А-% означает
работу сил, приложенных к этой точке.
Кинетической энергией системы Ек называется сумма кинетиче-
кинетических энергий всех материальных точек, образующих систему:
2 ту)
A6)
Суммируя почленно равенства A5) для всех материальных точек,
получим:
EM — Eki = A, A7).
где A = 2j &i есть сумма работ всех сил, приложенных ко всем
материальным точкам, образующим систему. Равенство A7) выра-
§ 27] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ 89
жает один из основных законов механики: изменение кинетической
энергии системы равно работе всех сил, приложенных к мате-
материальным точкам, образующим систему.
§ 27. Потенциальная энергия механической системы. Предпо-
Предположим, что тело, рассматриваемое как материальная точка, переме-
перемещается из одного места в другое, взаимодействуя с окружающими
телами. На тело, следовательно, действуют силы; в этом случае
говорят, что тело перемещается в силовом поле. Характер сил,
действующих на рассматриваемое тело, может быть весьма разно-
разнообразным, например, эти силы могут быть силами тяготения, силами
трения, электрическими силами и т. д.
Рассмотрим работу, совершаемую при движении материальной
точки в однородном поле силы тяжести. Такое поле силы тяжести
существует вблизи поверхности
Земли, где сила тяжести практи-
практически не зависит от высоты над
поверхностью Земли (пока высота h
мала по сравнению с радиусом зем-
земного шара /?). Пусть материальная
точка движется по некоторой кри-
кривой ВХВ9 (рис. 61). Разобьем эту
кривую на элементарные отрезки,
настолько малые, чтобы каждый из
них можно было считать прямоли- Рис 61 Определение работы
нейным. Тогда элементарная работа сил тяготения.
ДЛ, совершаемая при передвижении
по отрезку As, будет &А = Р&$ cos а, где Р—вес тела, а а — угол,
который направление силы тяжести составляет с направлением пере-
перемещения. Из рис. 61 видно, что As cos a = ДА, где ДА — изменение
высоты тела при перемещении на отрезок As.
Вся работа перемещения из точки В^ в точку ?а будет
но 2Д^ Дает отрезок А, указывающий, насколько точка В\ лежит
выше точки В& таким образом,
A = Ph, A)
т. е. работа силы тяжести при перемещении тела по любой кривой
линии равна работе при перемещении вдоль вертикали на отрезок А,
равный разности высот начальной и конечной точек пути тела.
Работа в поле силы тяжести не зависит от формы и длины
пути, а только от того, насколько выше лежит конечная точка
пути по отношению к начальной точке. Оказывается, что в при-
природе существуют и другие силы, кроме силы тяжести, обладающие
тем же замечательным свойством: работа сил при перемещении мате-
материальной точки зависит только от положения начальной и конечной
90 РАБОТА И ЭНЕРГИЯ " [ГЛ. Ш
точек пути и не зависит ни от вида пути, ни от скорости движе-
движения. Такие силы носят название потенциальных сил. При движе-
движении материальной точки в поле потенциальных сил можно ввести
понятие о потенциальной энергии, через разность которой будет
определяться работа сил. Пусть материальная точка перемещается
из некоторой точки пространства (/) в другую точку пространства B)
и пусть при этом действующие на нее силы совершают работу Aifi.
По сказанному, для потенциальных сил эта работа характеризуется
только положениями начальной и конечной точек пути, т. е. поло-
положением точек (/) и B). Это означает, что можно ввести такую
величину Ер, характеризующую положение материальной точки
в поле потенциальных сил, что работа Ах$ будет равна разности
вначений Ер1 и Epi, которые величина Е„ принимает в точках
(/) и B):
Epi — Epi = Al2. B)
Величина Ер называется потенциальной энергией.
Равенство B) определяет лишь разность потенциальных энер-
энергий в двух точках; саму потенциальную энергию можно определить,
если условно принять за нуль значение потенциальной энергии
в какой-либо точке пространства.
В качестве примера определим потенциальную энергию матери-
материальной точки в поле силы тяжести. По равенству A) работа силы
тяжести при перемещении тела между двумя точками простран-
пространства В\ и Bq, из которых вторая лежит на отрезок h ниже первой,
равна A = Ph или A = mgh, если через т обозначить массу тела,
а через g—ускорение силы тяжести. Обозначим высоту точки Ву,
отсчитанную от некоторой нулевой высоты, через hb а точки Вг —
через А3, тогда h = hx — А2 и
А = mghi — mgh2.
С другой стороны, по формуле B)
А = Ер1 — Epi.
Если условно принять, за нуль значение потенциальной энергии ма-
материальной точки на высоте А2 = 0, то из сравнения двух послед-
последних равенств получаем
Eph = mgh. C)
Таким образом, потенциальная энергия тела с массой т, поднятого
на высоту h, оказывается равной mgh. При этом потенциальная
энергия тела, лежащего на поверхности Земли, условно принята
равной нулю. Если тело падает с высоты ft, то сила тяжести совер-
совершает положительную работу А = Ph. Потенциальная энергия при
этом убывает. При поднятии тела на высоту h работа силы тяжести
отрицательна. В этом случае из равенства B) получим, что
ЕрХ — Epi<C.O, т. е. что потенциальная энергия возрастает.
§ 27] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ 91
В качестве второго примера рассмотрим потенциальную энер-
энергию сжатой пружины. В примере 2 § 25 мы видели, что работа,
которую необходимо затратить для сжатия упругой пружины на
ftsa
величину s, равна А = -у, где k — коэффициент жесткости пру-
пружины. На такую же величину возрастет потенциальная энергия
пружины. Если потенциальную энергию не сжатой пружины мы по-
положим равной нулю, то потенциальная энергия пружины, сжатой на
величину s, окажется равной:
Е --
р— 2 *
Здесь потенциальная энергия пропорциональна квадрату сжатия
пружины.
Переходим к рассмотрению системы материальных точек. Пред-
Предположим сперва, что система материальных точек изолирована, т. е.
что ее точки взаимодействуют только друг с другом и не испыты-
испытывают воздействия внешних по отношению к системе тел.-| Силы
взаимодействия материальных точек пусть зависят от их расстояния
друг от друга. Условимся называть конфигурацией системы опреде-
определенное расположение материальных точек. Всякое перемещение
материальных точек друг относительно друга ведет к изменению
конфигурации системы. При переходе системы из какой-либо кон-
конфигурации (/) в другую конфигурацию B) силы, действующие на
все материальные точки системы, совершат работу, которую мы
обозначим через Л^- Если все силы ноСят потенциальный харак-
характер, то работа Л^ будет зависеть только от того, какова на-
начальная и какова конечная конфигурация системы. В этом случае
работа А\^ может быть представлена как разность потенциальных
энергий системы, находящейся соответственно в конфигурациях
(/) и B):
Л1|2 = ?„! — ?> D)
Как и выше, соотношение A) определяет лишь разность потен-
потенциальных энергий; для определения самой потенциальной энергии
следует принять за нуль энергию какой-либо определенной конфи-
конфигурации системы.
Разобранный выше пример с потенциальной энергией тела в поле
силы тяжести Земли можно рассматривать и как пример на потен-
потенциальную энергию системы, образованной совокупностью: Земля и
рассматриваемое тяжелое тело. В случае падения тяжелого тела
с высоты А, первоначальной конфигурацией будет: Земля и тело на
высоте h над ее поверхностью, конечной конфигурацией: Земля и
тело на ее поверхности. Работа силы тяжести выразится через раз-
разность потенциальных энергий в этих двух конфигурациях:
92 РАБОТА И ЭНЕРГИЯ [ГЛ. Ш
Отметим еще раз, что соотношение D) имеет смысл только при
условии, что работа сил не зависит от способа перемещения мате-
материальных точек при переходе системы из одной конфигурации
в другую. Это условие не всегда выполнено. Не все силы, встре-
встречаемые в природе, потенциальны. Работа сил трения, например, за-
зависит от длины пройденного пути. Поэтому при наличии сил тре-
трения нельзя выражать работу через разность потенциальных энергий.
§ 28. Законы сохранения и изменения механической энергии
системы. Предположим, что мы имеем изолированную систему мате-
материальных точек, в которой действуют только потенциальные силы.
Состояние системы будет определяться ее конфигурацией а ско-
скоростями материальных точек, образующих систему. При пере-
переходе системы из одного состояния в другое силы, приложенные
к материальным точкам, образующим систему, совершают работу,
которую мы снова обозначим через А^л, считая, что индекс 1 отно-
относится к начальному состоянию системы (/), а индекс 2 — к ее конеч-
конечному состоянию B). В каждом из этих состояний, различающихся
скоростями материальных точек и их расположением, система будет
характеризоваться соответственными значениями кинетической энер-
энергии Eki и Eki и потенциальной энергии Epi и Ер2. Тогда работа Ац
может быть выражена двояким способом: либо через разность кине-
кинетических энергий
А\,2== Eki Рк\< j (')
либо через разность потенциальных энергий
АУЛ = Ер1 — Ер,. . B)
Из этих двух равенств имеем
Е -\- Е = Е . -4- Е C)
Сумма кинетической и потенциальной энергий системы называется
ее полной механической энергией Е:
Ek-\-Ep = E. D)
Тогда равенство C) принимает вид:
"?, = ?» E)
т. е. мы получаем, что полная энергия изолированной системы,
в которой действуют только потенциальные силы, остается по-
постоянной. Это положение называется законом сохранения механи-
механической энергии. Оно является одним из наиболее важных следствий
основных законов механики.
При переходе из одного состояния в другое могут меняться
кинетическая и потенциальная энергии, взятые в отдельности, но их
сумма остается постоянной. Если произошло, например, увеличение
кинетической энергии на некоторую величину h.Eh, то на такую же
§28] ЗАКОНЫ СОХРАНЕНИЯ И ИЗМЕНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ 93
величину Д?р = Д?'к должна уменьшиться потенциальная энергия.
Следует, однако, помнить, что закон сохранения механической энер-
энергии изолированной системы только тогда имеет место, когда силы,
действующие в системе, являются силами потенциальными. При на-'
личии непотенциальных сил, например сил трения, сумма кинетиче-
кинетической и потенциальной энергии системы не будет оставаться по-
постоянной. Обобщение закона сохранения энергии на любые системы
будет дано в § 68.
Рассмотрим случай падения тела, пренебрегая трением.
Пусть тело массы т поднято на высоту h, тогда его потенци-
потенциальная энергия
Ep = mgh.
При падении тела с высоты h его потенциальная энергия убы-
убывает, но зато тело приобретает скорость, а следовательно, и запас
кинетической энергии. В конце падения эта кинетическая энергия
будет
р mv%
где v = yigh — та скорость, с которой тело подлетает к Земле.
Подставляя это значение v в выражение для кинетической энергии,
найдем
т. е. к концу падения вместо потенциальной энергии возникло рав-
равное ей количество кинетической энергии. Энергия перешла из одного
вида в другой, но общее ее количество осталось неизменным.
Для замкнутой механической системы ее полная энергия Е, рав-
равная сумме кинетической энергии Ek и потенциальной энергии Ер,
остается постоянной:
Е = Ek -f- Ep = const.
Убывание кинетической энергии ведет к увеличению потенциаль-
потенциальной, и обратно. Как и в случае падающего камня, в общем случае
замкнутой механической системы процессы сводятся лишь к пере-
переходу энергии из кинетической в потенциальную и обратно.
Предположим, что в замкнутой механической системе все тела
сперва покоятся, тогда Ek = 0 и потенциальная энергия Ер = Е,
т. е. представляет собой полный запас энергии. Так как кинетиче-
кинетическая энергия Ek всегда положительна, то она может возникнуть
лишь за счет убывания потенциальной энергии Ер. Отсюда мы по-
получим: если в начальный момент потенциальная энергия Ер имеет
минимальное возможное значение, и тела, образующие механиче-
механическую систему, находились в покое (Ек = 0), то в последующие
моменты времени они не смогут прийти в\ движение, так как
94
РАБОТА И ЭНЕРГИЯ
[гл. ш
не сможет возникнуть, без внешних воздействий, кинетическая энер-
энергия Ек. Другими словами: замкнутая механическая система, по-
потенциальная энергия которой имеет минимальное значение и
в которой отсутствуют движения тел, находится в состоянии
равновесия. Примером может служить тяжелый шар, неподвижно;
лежащий на дне ямы: его потенциальная энергия Ер имеет мини-
минимальное значение, и он находится в равновесии; без воздействия
извне шар не может выкатиться из ямы.
Рассмотрим несколько частных примеров.
Пример 1. Камень весом 2 кГ, падающий с высоты 5 м, вдавливается
в мягкий грунт на 5 см. Чему равна средняя сила удара?
Решение. Камень, поднятый на высоту Л, имел запас потенциальной
энергии Ep = Ph, где Р—вес камня. За счет этой потенциальной энергии
совершилась работа вдавливания камня в грунт,
откуда
где/—средняя сила удара и s — глубина вдавли-
вдавливания в грунт. Отсюда:
7=Р~=2
'0,05
кГ=200 кГ.
Рис. 62. Баллистиче-
Баллистический маятник.
Пример 2. Для измерения скорости пули поль-
пользуются баллистическим маятником. Это—ящик с пе-
песком, подвешенный на нити. Пуля, попадая в ящик,
застревает в нем, но при этом ящик оказывается
отброшенным на некоторую высоту (рис. 62). Определить скорость пули v
по следующим данным: масса пули ти масса ящика от2, высота подъема
ящика Л.
Решение. Когда пуля попадает в ящик, она начинает двигаться вместе
с ящиком с общей скоростью »', определяемой из условия, что столкновение
между пулей и ящиком неупругое:
ttl\
-V.
Кинетическая энергия ящика вместе с пулей
(nti + w»a) v'a
Ek= 2 '
Подставляя сюда значение »', получим
с* — 2 (От! + т2) *
При отклонении ящика на высоту Л вся эта кинетическая энергия перей-
перейдет в потенциальную, откуда следует:
отсюда получаем, что искомая скорость пули
§ 29] ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЭНЕРГИИ 95
Так как обычно масса пули ntj, очень мала по сравнению с массой ящика /п2.
то приближенно
Рассмотрим теперь неизолированную систему и допустим, что
среди внутренних сил имеются и силы трения (непотенциальные
силы). При этом мы ограничимся учетом только механических явле-
явлений и не будем принимать во внимание тепловые и другие немеха-
немеханические явления, о которых речь будет ниже (§ 68). Разобьем
силы, действующие на материальные точки, на три группы: 1) силы
внутренние потенциальные, 2) силы трения (внутренние непотенци-
непотенциальные) и 3) внешние, вызванные воздействием со стороны тел, не
входящих в рассматриваемую систему. Тогда и в равенстве A) разо-
разобьем работу на три части, соответствующие этим трем группам
сил, в результате чего получим
• Ею — Eki = А внутр. пот -f- А гр -+- А внеш. F)
Изменение же потенциальной энергии будет связано лишь с ра-
работой потенциальных сил:
?pl ?-р2== АВНуТр. пот. (')
Из равенств F) и G) получаем:
Ею + ЕРъ — (ffti + ЕрХ) =- Авкеш ~\- Атр.
Но сумма кинетической и потенциальной энергий Ек-\-Ер есть
полная механическая энергия системы Е, поэтому имеем:
?а_?1 = Лвнеш + Лтр. . (8)
1 Из равенства (8) вытекает, чт,о изменение полной механической
\ энергии системы, равно сумме работ внешних сил и сил трения.
Следовательно, полная механическая энергия системы представляет
собой такую физическую величину, изменение которой обусловлено
работой внешних сил и сил трения. Энергия неизолированной меха-
механической системы возрастает, если сумма работ внешних сил и сил
трения положительна, и убывает, если эта сумма отрицательна.
Заметим, что работа сил трения всегда отрицательна, так как сила
трения для каждой материальной точки направлена в сторону,
противоположную ее скорости, т. е. против направления ее переме-
перемещения. Таким образом, сила трения всегда обуславливает уменьше-
уменьшение полной механической энергии системы.
§ 29. Графическое представление энергии. Потенциальная энер-
энергия тела весом Р, поднятого над поверхностью Земли на высоту ft,
равна
Ep = Ph = mgh, A)
где т. — масса тела.
96
РАБОТА И ЭНЕРГИЯ
[гл. ш
Представим зависимость Ер от А графически, отложив по оси
абсцисс значение А и по оси ординат значение Ер; тогда, согласно
формуле A), зависимость Ер от А представится прямой О А (рис. 63),
проходящей через начало координат; угол, составляемый этой пря-
прямой с осью абсцисс, тем больше,
чем больше вес тела Р.
Пусть рассматриваемый процесс
представляет собой подбрасывание
камня весом P=mg вертикально
вверх. Если пренебречь сопроти-
сопротивлением воздуха, то можно считать,
что движение камня происходит без
совершения внешних работ. Тогда
полная энергия камня
. ' р р I р (<Г\
птах
О
Рис. 63. Потенциальная энергия
поднимаемого тела изображается
прямой ОА.
постоянна; графически она пред-
представится прямой CD, параллельной
оси абсцисс. Так как кинетическая
энергия Ек ~5^ 0, то по B) макси-
максимальное возможное значение потенциальной энергии будет Ер = Е
(нся энергия перешла в потенциальную). Отсюда максимальная вы-
высота подъема камня Атах определится абсциссой точки пересечения
прямых ОА и CD. Движение камня возможно лишь для значений А,
заключенных между нулем и Атах. Для некоторого определенного
значения А, заключенного в этих пределах, отрезок BF изобразит
потенциальную энергию камня и отрезок FQ — его кинетическую
энергию. График вполне наглядно показывает, как при поднятии
камня кверху (А возрастает) возрастает потенциальная энергия
камня Ер и убывает кинетическая Ек; при
вает), наоборот, убывает Ер и возрастает
наоборот, убывает Ер
все время постоянна.
Максимальная высота поднятия
полную энергию:
Ep-\-Ek
М
падении камня (А убы-
Ek. Сумма их значений
камня
Е_
mg'
определится через
C)
Кинетическая энергия для некоторой высоты A<^Amaj[, изобра-
изображаемая отрезком FG, равна
Ek = E — Ep = mghma% — mgh. D)
Обозначая скорость, которую камень будет иметь на высоте А,
то1
через v, имеем ?¦(, = ——; получим по D):
mv2
~2~
— mgh, откуда v =
— А).
E)
§ 29j
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЭНЕРГИИ
97
При поднятии камня эта скорость направлена вверх, при его
падении — направлена вниз.
Эту же скорость можно выразить и через начальную скорость
камня г»0, тогда
' _ _ ¦ mvl , mv* mvl
Ek = E — Ep = -^ — mgh, откуда —2~=-y-—
и, следовательно,
I
Рис. 64. Тяжелое тело на на-
наклонной плоскости.
F)
Тот же рис. 63 представляет и соотно-
соотношения между энергиями в случае сколь-
скольжения без трения тяжелого тела Р по
наклонной плоскости. Однако, в случае
наклонной плоскости, в качестве незави-
независимой переменной мы можем выбрать
не только /г, но, например, и отрезок / (рис. 64), откладываемый
по основанию наклонной плоскости от ее начала. В силу соотно-
соотношения /г = Alga, где а —угол, составляемый наклонной плоскостью
с горизонтом, потенциальная энер-
энергия, как функция /, представится:
Ep = mg-tga.-l.
Таким образом, графически Ер
изобразится в зависимости от /
также прямой, проходящей через
начало координат, только ее наклон
будет иной, чем на рис. 63.
Этот же прием изображения
энергий можно использовать и для
случая скольжения- без трения тя-
тяжелого тела по поверхности любого
профиля. Пусть тело скользит без
трения по горе, профиль склона
которой представлен на рис. 65а.
Тогда потенциальная энергия Ер,
как функция расстояния i, откла-
откладываемого вдоль основания горы,
изобразится кривой ABCDF (рис. 65<J). Местам более крутого подъ-
подъема горы соответствует более крутой подъем кривой на рис. 656,
яме на горе соответствует „потенциальная яма" на кривой ABCDF.
Пусть полная энергия тела Е изображается прямой QE. В силу со-
соотношения ?р<? из рис. 656 сразу видим, что в этом случае /
может иметь значения, либо заключенные между точками Hal,
либо заключенные между точкой К и бесконечносхью. Это означает,
что тело может при таком значении Е либо скользить по склону
IN
1 1
I |
{ i
Bf
\
|
б)
с'
с
F
МН 1
Рис. 65. Потенциальная энергия
тела, скользящего по склону горы,
изображается кривой ABCDF.
98
РАБОТА И ЭНЕРГИЯ
[ГЛ. Ш
горы DF, либо двигаться внутри ямы ВС. Если оно находится в яме,
то ему мешает оттуда,выбраться барьер CD. Условием равновесия
тела является минимум потенциальной энергии (абсолютный или
относительный).
При значении полной энергии Е, изображаемой прямой, прохо-
проходящей через точку L, тело может скользить по всему склону горы
между точкой L и бесконечностью. Кинетическая энергия тела для
каждого данного значения / определится отрезком, заключенным
между прямой, изображающей полную энергию, и кривой, изобра-
изображающей потенциальную энергию.
В качестве последнего примера рассмотрим движение тела с массой т,
прикрепленного к пружине. При перемещении тела на отрезок s пружина
сжимается (s<0) или растягивается
(s ;> 0), в результате чего возникает
потенциальная энергия:
Ер = \. 0)
где к—жесткость пружины. Как функ-
функция смещения s потенциальная энер-
энергия Ер будет представлена параболой
(рис. %6). Если полная энергия ? =
= ?„ + ?* изобразится прямой FG,
то потенциальная энергия для данного
значения s изобразится отрезком АВ,
а кинетическая энергия тела—отрез-
тела—отрезком ВС. Возможные значения смеще-
смещения s лежат между smaX и s min, опре-
определяемыми отрезками DQ и DF; из
симметрии параболы имеем, 4io'smin=
=—smax. Отсюда следует, что тело
совершает колебания, около положе-
положения равновесия, определяемого значе-
значением s = 0. Его кинетическая энергия,
а следовательно, и его скорость дости-
достигают максимума при прохождении по-
Яожения равновесия и достигают минимума (равного нулю) при максимальных
отклонениях. Кинетическая энергия для некоторого значения s равна
Рис. 66. Потенциальная энергия дефор-
ыированной пружины изображается
параболой FOQ.
полная энергия Е —
ks*
, откуда
2
аЬ = 2 ~~ 2
отсюда получаем выражение для скорости тела, как функция смещения s:
§ 30] ФОРМУЛЫ РАЗМЕРНОСТИ 99
§ 30. Формулы размерности. Изученный нами в предыдущих
параграфах материал позволяет поставить вопрос о так называемой
размерности физических величин и о формулах размерности.
До сих пор единицу для измерения какой-либо физической вели-
величины мы устанавливали на основании закономерной связи этой ве-
величины с другими, для которых единицы измерения уже известны,
полагая в соответствующей формуле коэффициент пропорциональности
равным единице. Таким образом, устанавливалась определенная си-
система единиц, связанная с некоторым определенным выбором основ-
основных величин и единиц для их измерения. Так, в CGS-системе за
основные физические величины избрана длина, время и масса и за
единицы их измерения, соответственно, — сантиметр, секунда и грамм.
О возможном выборе других основных величин мы уже говорили в § 3.
При данном выборе основных физических величин возможен
различный выбор единиц их измерения, и, таким образом, возникает
вопрос, как зависят производные единицы от единиц основных ве-
величин. Остановимся на системах, где за основные величины выбраны
длина, время и масса, и обозначим единицы их измерения соответ-
соответственно через L, Т и М.
Если производная единица А меняется пропорционально р-й сте-
степени единицы длины L, q-й степени единицы*массы М и r-й сте-
степени единицы времени Т, то говорят, что единица А имеет размер-
размерность р относительно единицы длины, размерность q — относительно
единицы массы и размерность г — относительно единицы времени.
Такую зависимость единицы А от единиц основных величин выра-
выражают символической формулой (формулой размерности):
[A] = LP-Mq-Tr. A)
Например, если формула размерности для некоторой определен-
определенной единицы А имеет вид:
что также может быть записано в виде:
то это означает, что данная производная единица А меняется про-
пропорционально единице массы, пропорционально квадрату единицы
длины и обратно пропорционально квадрату единицы времени. На-
Например, если мы единицу массы увеличим в 1000 раз, единицу
длины—в 100 раз и единицу времени — в 60 раз, то рассматри-
1000-1002
ваемая производная единица А увеличится в —™—¦ раз, т. е.
в 2,78-103 раза.
Если производная единица вовсе не зависит от какой-либо из
основных единиц, то говорят, что она нулевой размерности относи-
относительно этой основной единицы.
100 РАБОТА И ЭНЕРГИЯ [ГЛ. III
Знание размерности физических величин существенно не только
потому, что оно позволяет легко подсчитать, как меняется единица
измерения данной физической величины при изменении единиц из-
измерения основных величин, но и потому, что сравнение размерности
величин позволяет контролировать правильность расчетов. Этот
контроль основан прежде всего на следующем очевидном положе-
положении: складывать, вычитать и связывать знаком равенства можно
только величины одной размерности.
В самом деле, нельзя складывать, например, массу с какой-либо
длиной или утверждать, что площадь некоторой фигуры может
равняться длине какого-либо отрезка и т. д.'
Далее, можно указать, что в показателе степени может стоять
лишь кисло, т. е. величина, лишенная размерности.
Определим размерность ряда уже известных нам физических
величин.
о
Размерность скорости: исходя из соотношения v = у-, видим,
что единица скорости меняется пропорционально единице длины и
обратно пропорционально единице времени, откуда
[v] = L.T-\ B)
Размерность ускорения: исходя из соотношения w = ~, полу-
получаем
[w\ = L.T~\ C)
Размерность силы: исходя из соотношения f=mw и пользуясь
уже найденной размерностью ускорения w, получим
[f] = MLT-\ D)
Размерность работы: исходя из соотношения A=fs, получим
[A] = ML*T~\ E)
Такую же размерность имеет и энергия.
Размерность мощности: исходя из соотношения W = —, по-
получим
[W] = ML%'T-\ F)
Однако существуют такие физические величины, единицы изме-
измерения которых не зависят от единицы длины, времени и массы.
Например, угол, измеряемый отношением длины дуги к длине ради-
радиуса, будет нулевого измерения относительно всех трех основных
единиц L, М, Т. За единицу для измерения угла выбирается цен-
центральный угол, стягивающий дугу, длина которой равна радиусу;
эта единица измерения угла, называемая радианом, одна и та же
во всех системах. Наряду с радианом, однако, углы измеряют также
и в градусах; в этом случае за единицу угла выбран центральный
§ 30] ФОРМУЛЫ РАЗМЕРНОСТИ . 101
угол, стягивающий дугу, длина которой равна ^ длины полной ок-
окружности. Поэтому для однозначности можно в формулы размерно-
размерности вводить еще символ единицы угла.! Обозначим этот символ
буквой Ф. В формулы размерности приведенных выше величин —
скорости, ускорения, силы и т. д. — он не должен входить, так как
все эти величины нулевой размерности относительно угла. Но если.
мы захотим написать размерность угловой скорости'ш==-^-, то в нее
можно ввести символ Ф, так как единица угловой скорости зависит от
того, какой единицей для измерения угла мы пользуемся; таким образом:
Однако обычно принято указывать размерность лишь по отноше-
отношению к единицам длины, времени и массы, тогда
[*\=Т-\ G)
Так же мы получим размерность углового ускорения
№=т-\ (8)
Из рассмотрения размерности величин иногда можно указать
точный характер закономерности, если предварительно известен ее
приближенный вид. Например, естественно положить,. что скорость v,
лриобретаемая свободно падающим вблизи земной поверхности
камнем, должна быть тем больше, чем больше высота падения h и
чем больше ускорение силы тяжести g.
Таким образом, полагая что v должно быть пропорциональным g
и h, взятым в некоторых степенях щ и пь получим
v = k-gn^hn*,
где k — численный коэффициент. Размерность скорости [v] = L- Т~и,
такова должна быть и размерность gn^hn*. Но {g\ = LT~x и [h] = L.
Отсюда видно, что для того, чтобы размерности времени в обоих
выражениях были одинаковы, должно «i = -«-. Но, при я, = у и щ
должно равняться -у, так как иначе не совпадут размерности
длины. Отсюда видим, что требование об одинаковости размер-
размерности величин, связанных знаком равенства, будет выполнено при
1
и1=яа = у, т. е.
В самом деле, из формул равномерно-ускоренного движения
(§ 7) мы получаем, что ;
v=Y2gh ^ 1,41 Vgh.
1 Из других физических величин нулевой размерности относительно
длины, времени и массы укажем температуру.
102 РАБОТА И ЭНЕРГИЯ [ГЛ. III
§ 31. Границы применимости классической механики. Как мы
уже указывали в § 4, классическая механика применима лишь к мак-
макроскопическим телам, т. е. телам, состоящим из большого числа
атомов и движущимся со скоростями, малыми по сравнению со ско-
скоростью света. Так как скорость света равна приблизительно
300 000 лм/сек-, то классическая механика применима ко всем обыч-
обычным телам, движущимся с практически достижимыми скоростями.
Однако весьма точные наблюдения над некоторыми небесными
объектами (планета Меркурии, скорость которой при движении по
орбите вокруг Солнца достигает 100 км [сек) позволяют заметить
отклонения от следствий из классической механики. Эти отклоне-
отклонения объясняются механикой теории относительности. Весьма резко
проявляются отклонения от классической механики при наблюдении
отдельных атомов, электронов и других элементарных частиц.
Механика больших скоростей, т.е. скоростей, сравнимых со ско-
скоростью света, дается теорией относительности.
Теория относительности, как и всякая другая теория, ломающая
старые представления, поставила на очередь решение ряда важных
методологических вопросов. Многие буржуазные физики и философы
пытались использовать теорию относительности для обоснования
своих порочных ' идеалистических воззрений, в частности философ-
философского релятивизма. В действительности содержание теории относи-
относительности ни в коей мере не ведет к философскому ' релятивизму.
Теория относительности изучает преимущественно явления, обна-
обнаруживающиеся при скоростях, близких к скорости света, существую-
существующие объективно и, следовательно, не зависящие от нашего произвола
и в этом отношении не являющиеся „относительными". Ленин, как
мы указывали в § 4, отме-
тил, что новая физика (он
подразумевал при этом
теорию относительности)
S'
быстрых реальных дви-
движений, в то время как
старая классическая ме-
механика была снимком с
и "' * медленных движений.
„ „., „ о Содержание теории
Рис. 67. Система S, движущаяся относительно г ,
системы S' со скоростью щ. относительности будет
более подробно рассмо-
рассмотрено в т. III, здесь же мы лишь остановимся на некоторых
следствиях теории относительности и используем их для определе-
определения границ применимости классической механики. Начнем с рас-
рассмотрения некоторых кинематических следствий теории относитель-
относительности. Пусть в системе отсчета S (рис. 67) тело т движется со
скоростью v относительно координатной системы OXY, неизменно
дает снимок с гигантски
т.
§ 31] ГРАНИЦЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ МЕХАНИКИ 103
связанной с системой отсчета 5. Пусть имеется вторая система
отсчета S'; с этой второй системой отсчета неизменно связана своя
координатная система О'Х'У, оси которой О'Х' и О'У будем счи-
считать параллельными осям ОХ и О У. Предположим, что система S
движется относительно системы S' в направлении положительной
ОСИ ОХ СО СКОРОСТЬЮ Vq.
В системе S* тело т представляется движущимся со скоростью v,
составляющие которой на координатные оси равны vx и vy. В системе S'
скорость тела будет иной, так как система S движется относи-
относительно S' со скоростью у0.
Согласно классическим представлениям, составляющие скорости
тела м по осям О'Х' и О'У в системе S' равны
^ = ¦»* + ¦% v'y = vy A)
Эти формулы выражают собою обычное правило сложения ско-
скоростей.
По теории относительности правило сложения скоростей иное,
а именно:
B)
где с — скорость света. Легко проверить, что когда скорости v№ и
vx малы по сравнению со скоростью света, формулы теории отно-
относительности B) переходят в классические формулы сложения ско-
скоростей A).
Сравним результаты, даваемые формулами A) и B), для неко-
некоторых конкретных случаев.
Предположим, что в кабине аэроплана, летящего над Землей
со скоростью г>0 = 360 км/час =\00 м/сек, делается в направлении
полета аэроплана выстрел, причем скорость пули относительно аэро-
аэроплана г/л=1000 м/сек. Тогда с точки зрения классической меха-
механики скорость пули относительно Земли равна
v'x = vx +¦ г>о = 100 м/сек +¦ 1000 м/сек = 1100 м/сек.
По теории относительности, согласно первой из формул B):
1100 , 1100 .,
..<—_ g м/сек,
-
еа т C-10е)я
или приближенно
г>;=1100A — 1,1- 10-1а) м/сек,
откуда видно, что теория относительности в этом случае дает ре-
результат, отличающийся от классического примерно на 10'1а-ю часть
104 РАБОТА И ЭНЕРГИЯ [ГЛ. III
суммарной скорости. Другими словами, результаты классической тео-
теории и теории относительности здесь практически полностью сов-
совпадают.
Если же каждая из складываемых скоростей щ и vx равна поло-
половине скорости света с, то суммарная скорость по теории относи-
относительности равна
I J.1
вместо с, как это получается по классической формуле A). Здесь
различия между следствиями из обеих теорий заметны. Они еще
больше, если, например, каждую из слагаемых скоростей положить
равной 0,9 с.
По теории относительности скорость никогда не может превы-
превышать скорости света с в вакууме. По формулам B) мы получим
результирующую скорость, не превышающую скорости света даже
в том случае, когда каждая из складываемых скоростей сколь угодно
близка к скорости света.
Существенно еще отметить, что по формулам теории относитель-
относительности B) в системе отсчета S' меняется не только составляющая
скорости vx, направленная в сторону движения системы S, но
и составляющая vy, нормальная к скорости т>0 системы S. По класси-
классическим формулам vy одинаково для обеих систем. Если скорости va
и vx малы по сравнению со скоростью света с, то влияние v0 на
составляющую vy весьма малб.
В самом деле, обозначим — =$ и¦ — = р\ тогда обе величины р
и р' малы по сравнению с единицей, и формулу B) приближенно
можно переписать:
Ух + Уо ^ ^ х
Bа)
таким образом, v'x близко к сумме vx-\-v0, значение же Vy отли-
отличается от vy лишь на член второго порядка малости по отношению
к величинам порядка р. и р\
- Второе важное следствие теории относительности, которое мы
рассмотрим, заключается в том, что в системе отсчета, относительно
которой тело движется со скоростью v, масса этого тела больше,
чем в системе отсчета, относительно которой тело покоится, а именно:
§31]
ГРАНИЦЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ МЕХАНИКИ
105
Таблица I
Зависимость массы
от скорости
где т — масса тела в системе отсчета, относительно которой оно
движется, /и0 — в системе отсчета, относительно которой оно покоится
{покоящаяся масса), величина р = —.
Изменение массы по формуле C) мало, пока скорость v мала по
сравнению со скоростью света, и становится большим, когда ско-
скорость v сравнима со скоростью света. При приближении скорости v
к скорости с величина р~*-1, и масса т по формуле C) бесконечно
возрастает. Отсюда видно, что при непрерывном ускорении тела под
влиянием некоторой силы масса тела возрастает, работа, которую
надо совершать, чтобы далее ускорять тело,
тоже возрастает: для сообщения телу скорости,
равной скорости света, надо совершить беско-
бесконечно большую работу; таким образом, ско-
скорость, равная скорости света, для тел с по-
покоящейся массой, отличной от нуля, не
достижима.
Для оценки влияния скорости на массу,
воспользуемся табл. I, где приведены значения
т/т0 для разных р.
Из табл. I видно, что вначале масса т воз-
возрастает со скоростью весьма медленно и на-
начинает быстро возрастать лишь при скоростях,
близких к скорости света. При C = 0,01, т. е.
при скорости v ^0,01 с = 3000 км/сек, масса
т отличается от покоящейся массы /и„ всего
на 0,005%. При скорости v, равной половине
скорости света с, масса т приблизительно на
15,5% превышает покоящуюся массу тв. При скорости же v = 0,9 с
масса уже более чем вдвое превышает та. Измерения массы быстро
движущихся. электронов (см. т. II) вполне точно подтверждают
формулу C).
Согласно динамике, теории относительности, количество движения
тела
в
г
0,005
0,010
0,10
0,50
0,80
0,90
0,95
0,98
0,99
0,995
0,9995
т
Шо
1,00001
1,00005
1,00504
1,1547
1,6666
2,2941
3,2025
5,0252
7,0888
10,0125
31,6268
При этом сила, по-прежнему, определяется как физическая величина,
равная изменению вектора количества движения в единицу времени.
Закон сохранения количества движения выполняется в точности, если
количество движения выражать формулой D).
Для скоростей v, малых по сравнению со скоростью света с,
величина р мала по сравнению с единицей, и формулу C) можно
приближенно переписать:
m — i
(За)
106 РАБОТА И ЭНЕРГИЯ [ГЛ. III
Помножим и поделим выражение для кинетической энергии тела
?* = ^-у- на с2', тогда оно примет вид:
Е ——
откуда по (За)
В динамике теории относительности показывается, что эта фор-
формула E), выведенная нами как приближенная для v <^ с, на самом
деле в точности справедлива для любых скоростей, сколь угодно
близких к скорости света. Формулу E) можно переписать:
т = /я0 -\~ ^~, Eа)
т. е. масса движущегося тела т больше его покоящейся массы т0
на величину Ek/c2. Это следствие допускает весьма важную интер-
интерпретацию: мы можем считать, что масса тела возросла потому, что.
у него появилась кинетическая энергия, что появление кинетической
энергии Ек сопровождается увеличением массы тела на величину,
равную Ек/с\ Теория относительности обобщает этот вывод, утвер-
утверждая, что изменение всякой энергии на величину Е связано с изме-
изменением массы на величину т, численно равную
т = -о- • F)
с2
Обратно, при изменении массы системы на величину т возникает
количество энергии Е=тск.
Таким образом, каждому одному эргу энергии соответствует
масса т= .„ .П10.2г^ 1,Ы0~а1 г. Как видно, эта масса весьма мала:
установка мощностью в 2 000 000 кет (мощность Куйбышевской элек-
электростанции) вырабатывает в 1 час примерно 7,2-1019 эргов энергии,
которой по формуле F) соответствует масса 7,2-1019-1,1 • 10~91 г =
= 8,0' 10~а г, т. е. около 0,080 г. Отсюда видно, что технически
достижимым количествам энергии соответствуют совершенно
ничтожные массы. Однако при процессах, связанных с превраще-
превращением элементов, изменения массы, обусловленные изменениями
энергии, вполне заметны (см. т. III).
Равенство F) выражает общую взаимосвязь между энергией и
массой. Содержание этого равенства подвергалось многочисленным
идеалистическим извращениям: так, утверждалось, что якобы из него
следует возможность „превращения" массы в энергию и обратно,
или что закон сохранения имеет место лишь для суммы массы и
энергии системы, а что масса, и энергия, взятые в отдельности, не
сохраняются. Все эти выводы совершенно не верны и в конечном
счете ведут к отрыву представления об энергии от представления
о материи, т. е. к идеализму. В действительности физические вели-
§ 31] ГРАНИЦЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ МЕХАНИКИ 107
чины масса и энергия являются одними из наиболее основных харак-
характеристик тех конкретных видов движущейся материи, с которыми
имеет дело физика. Для полностью изолированной системы сохра-
сохраняется как ее масса, так и ее энергия. Равенство F) указывает на
глубокую взаимосвязь между обеими этими величинами, оно указы-
указывает, что невозможно изменение одной из них без одновременного
изменения в пропорциональном количестве другой.
Перейдем теперь к ограничениям представлений классической
механики, обусловленным размерами тел. Как мы отмечали, для
всех макроскопических тел, т. е. тел, состоящих из большого числа
атомов, классическая механика приложима практически вполне точно.
Однако отдельные элементарные частицы, например, отдельные
электроны, проявляют свойства, отличные от тех, которые вообще
могут быть приписаны „частице" в том смысле, как мы употребляем
слово „частица" в механике. Говоря обычно о „частице", мы подрав
зумеваем, что по отношению к частице можно ответить на два
вопроса: 1) где она находится? и 2) с какой скоростью она движется?
Ответы на эти два вопроса, т. е. задание координат частицы х, у, z
и вектора ее скорости v для каждого данного момента времени,
определяют траекторию частицы и характер ее движения по этой
траектории. Опыты же, как мы это впоследствии увидим (см. т. III),
убеждают нас, что пучок электронов проявляет особое свойство
(диффракцию), характерное, с точки зрения обычных представлений,
для распространения волн. По отношению же к волновому процессу
нельзя ставить вопроса о месте, где волна находится, в том смысле,
в каком он ставится по отношению к частице. В самом деле, волны
охватывают все пространство, где они распространяются, например
всю поверхность моря; можно только говорить, где расположены
гребни или впадины волн, причем для волн на поверхности моря
это будут семейства линий, а не точки, определяемые тремя
координатами. Отсюда — опытный факт, указывающий, что электрон
(а также всякая другая элементарная частица) не есть „частица"
в обычном смысле слова, ведет к тому, что и понятия, применимые
к частице, нельзя в точности прилагать к электронам. Анализ данных
опытов, произведенный квантовой механикой, показывает, что одно-
одновременное указание координат электрона х, у, z (ответ на вопрос,
где находится электрон) и его скорости v (ответ на вопрос, с какой
скоростью и в какую сторону движется электрон) может быть дано
лишь с известной степенью приближения. Чем с меньшей неопреде-
неопределенностью Ах определена координата электрона х, тем с большей
неопределенностью Avx одновременно определена составляющая его
скорости vx. Степень возможного приближения определяется кванто-
квантовой механикой, а именно квантовая механика утверждает, что между
«допусками" Ах и Avx существует соотношение
Ax-Avx^-, G)
108 РАБОТА И ЭНЕРГИЯ [ГЛ. III
где т— масса частицы, a h — постоянная, называемая постоянной
Планка и равная
h = 6,624 • Ю7 эрг сек.
Соотношение G), носящее с точки зрения квантовой механики
общий характер, называется соотношением неопределенности.
Физический смысл соотношения неопределенности будет более
полно разобран в т. III. Здесь лишь отметим, что рядом буржуазных
физиков из соотношения неопределенности делаются неправильные
идеалистические выводы о том, что якобы невозможно объективное
пространственно-временное описание свойств электронов. В действи-
действительности же речь идет не о невозможности объективного описания
свойств электронов, а о том, что реальные свойства объективно
существующих электронов отличны от свойств материальных точек
(„частиц") классической механики. Электрон (а также любая другая
элементарная частица) может лишь приближенно трактоваться как
„частица" классической механики. Соотношение неопределенности
указывает границы применимости представлений классической меха-
механики.
Ввиду малости постоянной Планка h неопределенность в коорди-
координатах и скорости сказывается лишь на элементарных частицах. Рас-
Рассмотрим сперва пылинку с массой т= Ю~п г и предположим, что
мы определяем ее координаты х с неопределенностью порядка
Ах= 10~6 см (т. е. 0,01 мк), тогда неопределенность в составляющей
скорости Avx по соотношению G) должна быть порядка:
. h 6,6 • 107 см , п . /
Af~ = 1А ,. ,п . — «=* 10 " см сек,
10~12 • 10"" сек '
т. е. неопределенность в скорости h.vx совершенно ничтожна. Дру-
Другими словами, координату и скорость весьма малой пылинки можно
практически измерять сколь угодно точно; пылинка есть „частица"
в обычном ьмысле слова.
Рассмотрим теперь электрон, траекторию которого мы зафикси-
зафиксировали следующим образом: электрон пролетел через малое отвер-
отверстие d в диафрагме, диаметр которого 0,01 см, и затем, попав на
фосфоресцирующий экран, дал на нем вспышку (быстрые электроны
способны вызвать такого рода вспышки—„сцинтилляции"), положе-
положение которой мы также отметили с точностью до 0,01 см.
Таким образом, в этом случае для электрона Ддг=10~г см,
откуда по G), зная, что масса электрона т == 9 • 108 г, получим
неопределенность в скорости:
a h 6,6 • Ю-27 см _ , п2 ,
Дя.:~'—т— = п ,л ,, 1Л й ^7-102 см сек.
х тАх 9-108-10~2 сек— '
Здесь неопределенность в скорости в абсолютной мере значительна;
однако если мы примем во внимание, что скорость самого электрона
в такого рода опыте будет весьма значительна, а именно, порядка
§ 31] ГРАНИЦЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ МЕХАНИКИ 109
108 см\сек, то мы увидим, что неопределенность, вытекающая из
соотношения G), составляет лишь приблизительно 0,001% от самой
скорости. Другими словами: в указанных условиях электрон еще
вполне может рассматриваться в виде „частицы", положение и ско-
скорость которой можно одновременно определять практически с боль-
большой точностью. Опыты указанного типа и служили первоначально
для выявления свойств электронов, поэтому первоначально об элек-
электроне было составлено представление, как о „частице", к которой
должны быть применимы классические представления.
Рассмотрим, наконец, электрон, движущийся внутри атома. Так
как размеры самого атома представляют собою величины порядка
10~8 см, то, по крайней мере, с такой точностью должно быть зафи-
зафиксировано и положение электрона:
Отсюда по G):
h 66 • 10-" см ,
см сек.
Так как и сама скорость электрона в атоме есть величина порядка
108 см/сек, то полученный нами результат означает, что если зафик-
зафиксировано положение электрона внутри атома, то при этом его ско-
скорость является неопределенной; другими словами: электрон внутри
атома уже ни в коей мере не может рассматриваться как „частица".
И, действительно, попытки рассматривать движение электронов внутри
атомов с точки зрения классической механики приводят к явным про-
противоречиям. То же относится к целому ряду других явлений, где
с классической точки зрения требовалось бы определять положение
электрона с „атомной точностью". Все эти явления описываются
правильно квантовой механикой.
h
mAx
9
Ax
6,6-
• 10-
^10"8
Ю-27
28 . 10-B
CM.
CM
сек
ГЛАВА IV
СИЛЫ ТЯГОТЕНИЯ
§ 32. Силы тяготения. Все тела взаимно притягиваются. Такие
явления, как падение тел на Землю, движение Луны по замкнутой
орбите вокруг Земли, планет — вокруг Солнца и т. д., происходят
под влиянием сил всемирного тяготения. Закон, которому подчиняются
силы тяготения, был впервые сформулирован Ньютоном в 1687 г.
По закону всемирного тяготения Ньютона: всякие два тела при-
притягиваются друг к другу с силой, прямо пропорциональной про-
произведению из их масс и обратно пропорциональной квадрату
расстояния между ними. Обозначая массы тяготеющих тел через mi
и mit расстояние между ними — через г, получим
где k — определенная постоянная, так называемая постоянная тяго-
тяготения; ее численное значение зависит от того, в каких единицах
измеряются сила /, масса т и расстоя-
расстояние г.
Закон Ньютона в указанной форму-
формулировке справедлив лишь в том случае,
если размеры тел весьма малы по сравне-
сравнению с расстоянием г между ними.
В случае, если размеры тел сравнимы
Рис. 68. Элементарные объ- с тем расстоянием, на котором тела
емы тяготеющих тел. находятся друг от друга, каждое Из тел
следует разбить на элементы (рис. 68);
для каждой пары элементов справедлив закон тяготения Ньютона,
так что сила взаимодействия i-ro элемента первого тела и А-го эле-
элемента второго тела будет равна
Полная сила взаимодействия выразится как векторная сумма всех
элементарных сил Дт,^:
i, ft
1 Так как элементы, на которые разбиваются тела, должны быть взяты
бесконечно малыми, то задача на самом деле сводится к интегрированию.
§ 32] СИЛЫ ТЯГОТЕНИЯ 1 11
Результат такого вычисления имеет весьма разнообразный вид для
тел разной формы; он особенно прост для случая тяготения одно-
однородных шаров: два однородных шара взаимно тяготеют друг к другу
с силой /== k w' 'а т", где mi и tn% — массы шаров, а г — расстоя-
расстояние между их центрами. Это выражение, совпадающее с форму-
формулой A), справедливо для любого расстояния между'шарами.
В течение XVIII и XIX столетий многие физики придерживались
неправильного, идеалистического взгляда на тяготение, как на некое
„действие на расстоянии" без всякой роли промежуточного про-
пространства.
В действительности всякое тело вызывает в окружающем про-
пространстве изменения, ведет к образованию поля тяготения, пред-
представляющего собой особый вид материи (ср. со сказанным в т. II об
электромагнитном поле). Взаимное притяжение тел вызывается их
взаимодействием с полями тяготения.
Из закона всемирного тяготения следует, что у поверхности
Земли все тела должны падать с одинаковым ускорением. В самом
деле, ускорение, приобретаемое телом с массой т:
т '
где /— сила, с которой тело притягивается земным шаром. По закону
тяготения Ньютона:
где Мз — масса Земли и /?з — радиус земного шара, отсюда
но так как масса Земли и ее радиус являются величинами постоян-
постоянными, то, следовательно, мы получаем, что все тела у поверхности
Земли, независимо от их массы, падают с одинаковым ускорением
Mr,
ё» = Ьщ- . B)
Здесь речь идет о свободном падении тел при 'отсутствии сил
сопротивления, в том числе сопротивления воздуха. Также не прини-
принимается во внимание зависимость силы тяжести от широты местности
(см. § 23).
Сила, с которой какое-либо тело массы т притягивается к Земле, зави-
зависит от высоты А, на которой тело находится над поверхностью Земли. По
закону тяготения Ньютона тело притягивается к Земле с силой:
f—Ь
7 Л3
112 силы тяготения [гл. iv
где /? — расстояние от центра Земли до тела; так как /? = /?3 + Л, то
f=k-
1Лз т "у
Сила / представляет собою вес тела Pft на высоте Л; обозначая вес тела
у самой поверхности Земли через Ро, имеем
т-М3 Р. УД
так как практически высота h всегда очень мала по сравнению с радиусом
земного шара /?3> т0 приближенно
_i о
Радиус земного шара Л?3 = 6370 км, отсюда для высокой горы, высотой
в 6,4 км, имеем
т. е. вес тела на такой горе будет лишь на 0,2°/0 отличаться от его веса на
уровне моря. Хотя зависимость сил тяготения от расстояния и может быть
замечена по наблюдениям над весом тела у поверхности Земли, но, ввиду
малости этой зависимости, она не пригодна для точной проверки закона
обратной пропорциональности сил тяготения квадрату расстояния между
телами. Ньютон установил обратную пропорциональность сил тяготения
квадрату расстояния между ними, рассматривая движение Луны! Ход рассу-
рассуждений Ньютона следующий: если справедлив закон тяготения в том виде,
в каком его дает формула A), то сила, с которой Земля притягивает Луну,
равна:
Мл ¦ мз
где Мя — масса Луны и R — ее расстояние от Земли. Отсюда ускорение,
испытываемое Луной и направленное к Земле, равно
w —J- = k~
Мл R2
Вводя сюда выражение для ga по B), получим
Это ускорение представляет собою центростремительное ускорение Луны
при движении ее вокруг Земли по круговой орбите. Из астрономических
наблюдений известно, что расстояние от Земли до Луны в 60 раз больше
радиуса Земли, откуда
_!« _J>!L_^L_027 см/сек*
w" - 60а ~ -3600 сек2 ~ ' СМ1 К •
§ 32] . СИЛЫ ТЯГОТЕНИЯ 1 13
С другой стороны, то же самое центростремительное ускорение Луны
может быть вычислено кинематически:
где v — линейная скорость Луны на ее орбите, Т—период ее обращения
вокруг Земли, равный 27 суткам 7 часам 43 минутам, что составляет
2 360 580 сек. Пользуясь этими данными и тем, что Я = 60 • А?з = 60¦ 6370 км,
получим
4кг-60 • 6370 • 10» см
W
W» = B 360580)* ^
Таким образом, оба способа вычисления центростремительного ускорения
Луны дают вполне совпадающие результаты, что и служит подтверждением
правильности формулы A).
. Значение постоянной тяготения k было впервые измерено Кэвен-
дишем в 1798 г. с помощью крутильных весов. Прибор, которым
пользовался Кэвендиш, схематически предста-
представлен на рис. 69. К горизонтальному коромыслу
А на двух стержнях были прикреплены два
свинцовых шара М% и Мь каждый из которых
имел массу 158 кг. Под коромыслом к непо-
неподвижной головке В прикреплена тонкая про-
проволока С, несущая легкий стержень /, к концам
которого подвешены два небольших свинцовых J^>i у ~Щ
шарика Wj и mt; массы этих шариков в опытах
Кэвендиша брались по 730 г. При поворачива-
поворачивании коромысла А большие шары приближались рис. 69. Схема опыта
к маленьким и притягивали их к себе; при- Кэвендиша.
тяжение можно было заметить по повороту
стержня I, несущего шарики /я, и тг. Зная упругие свойства про-
проволоки С, можно было измерить силу притяжения и отсюда опре-
определить значение постоянной тяготения k. Впоследствии опыты Кэвен-
Кэвендиша неоднократно повторялись. В настоящее время для постоян-
постоянной k принимается значение:
k = 6,685-10"8 см%\г сек1;
отсюда следует по формуле A), что два шарика, массой по 1 г каж-
каждый, расположенные так, что расстояние между их центрами равно
1 см, притягиваются с силой 6,685 • 10~8 дин.
Постоянная k не есть просто число, но обладает размерностью;
размерность k определим из соотношения:
mi ¦ т%'
отсюда
откуда следует, что в CQS-системе k измеряется в см3/г сек\
5 С. Э. Фриш в А. В, Тыморева
114 СИЛЫ ТЯГОТЕНИЯ [ГЛ. IV
Указанную размерность постоянной k мы получили, установив единицу
силы и ее размерность с помощью второго закона Ньютона: f=mw. Однако
можно поступить наоборот: положить в законе всемирного тяготения A) по-
постоянную k = 1 и считать ее величиной безразмерной, но зато ввести новую
постоянную к' во второй закон Ньютона, написав его в виде:
f=.k'mw. C)
Тогда, пользуясь CGS-системой, мы примем за единицу силы — силу,
с которой шарик с массой в 1 г притягивает к себе другой шарик с массой
также в 1 г, расположенный от него на расстоянии, отсчитанном между цен-
центрами шариков, в 1 см. Эта единица силы равна 6,685 • 10~8 дин.
Размерность силы выразится при этом следующим образом:
вместо обычной размерности [f] = MLT~*. Постоянная же k' во втором
законе Ньютона (ее можно назвать „динамической постоянной") будет обла-
обладать размерностью:
[R j — [m]:. W MLT-*
ее численное значение окажется равным
Таким образом, исходя из разных законов, мы можем получить различ-
различные CGS-системы единиц. Размерность одних и тех же физических величин
может оказаться в различных системах различной. Обычная CGS-система
может быть названа „динамической", а система CGS-единиц, в которой еди-
единица силы и ее размерность устанавливаются на основании закона тяготе-
тяготения,— „гравитационной". В этих обеих системах размерности скорости, уско-
ускорения и других кинематических величин одинаковы, но размерности силы,
энергии, работы, мощности, момента сил и т. д. — разные. В механике
употребительна лишь одна из систем — „динамическая", в учении же об
электричестве и магнетизме, как мы увидим в т. II, употребляют две различ-
различные CGS-системы — так называемые „электростатическую" и „электромаг-
„электромагнитную" системы.
Знание постоянной k тяготения позволяет определить массу и плотность
Земли, а также массу других небесных тел.
Воспользовавшись формулой B), имеем
откуда, зная численные значения ускорения силы тяжести ga, радиуса
Земли /?3 и постоянной тяготения k, непосредственно определяем массу зем-
земного шара, для которой получается значение: М3 = 5,98 • 10" г.
Среднюю плотность земного шара найдем из соотношения
М3
1^
откуда получается значение d = 5,5 г/см\
§ 33] МАССА ИНЕРЦИОННАЯ И ТЯГОТЕЮЩАЯ. РАБОТА СИЛЫ ТЯЖЕСТИ 115
Масса центрального светила, вокруг которого обращается спутник, может
быть определена следующим образом. Пусть Мс — масса центрального све-
светила, М,—масса спутника, Rt — расстояние между ними. Сила притяжения/
создает центростремительное ускорение спутника
откуда
где Ti—период обращения спутника. Отсюда имеем
Ме~Т"Т\ш
т. е., зная радиус орбиты спутника и период его обращения, мы можем
определить массу центрального светила. Так, по радиусу земной орбиты и
продолжительности года находим массу Солнца Мс=1,98 • 10" г.
Из формулы D) также следует:
Ц ~~ 4я« •
величина, стоящая справа, имеет постоянное значение для всех спутников,
обращающихся вокруг данного центрального светила. Отсюда: квадраты вре-
времен обращения спутников (планет) вокруг центрального светила (Солнца)
относятся как кубы их расстояний от центрального светила (Солнца). Этот
закон по отношению к планетам был установлен Кеплером и носит название
третьего закона Кеплера.
§ 33. Масса инерционная и тяготеющая. Работа силы тяжести.
Физическая величина масса входит в два основных и не зависящих
друг от друга закона — во второй закон Ньютона: /= mw и в за-
кон всемирного тяготения: / = k —-j=-.
Во втором законе Ньютона масса характеризует инерционные
свойства тел. В законе всемирного тяготения масса характеризует
способность тел создавать поля тяготения и испытывать действие
полей тяготения.
Может быть поставлен вопрос: являются ли массы, фигурирую-
фигурирующие в обоих законах, одной и той же физической величиной или
это две разные величины, лишь как-то связанные между собой?
Таким именно образом исторически возникли понятия о массе инер-
инерционной, фигурирующей во втором законе Ньютона, и массе тяго-
тяготеющей, фигурирующей в законе всемирного тяготения. Опыты
убеждают нас, что обе массы, если только вообще имеет смысл
различать их, пропорциональны друг другу.
Прежде всего это вытекает из того факта, что ускорение gu сво-
свободного падения одинаково для всех тел. Точное измерение уско-
ускорения go при действительно свободном падении тел затрудни-
затруднительно, но наблюдения над качанием маятников позволяют измерить
?0 с большой точностью. Еще самим Ньютоном было показано, что
б» -
116 СИЛЫ ТЯГОТЕНИЯ [ГЛ. IV
пропорциональность между инерционной и тяготеющей массами вы-
выполняется с точностью до тллл- Бессель производил опыты над маят-
1UUU
никами из самых разнообразных веществ и пришел к тому же
результату с точностью до ._ „„. Впоследствии было показано, что
та же пропорциональность выполняется и для радиоактивных ве-
веществ.
С весьма большой точностью пропорциональность между мас-
массами тяготеющей и инерционной была показана Этвешем в 1894 г.
с помощью крутильных весов. Идея опытов Этвеша заключается
в следующем: на поверхности земного шара направление силы тя-
тяжести Pf определяется как направление равнодействующей силы
притяжения тела к центру Земли и инерционной центробежной
силы (см. § 23). Первая сила обусловлена тяготеющей массой тела,
вторая — его инерционной массой. Если обе эти массы не пропор-
пропорциональны друг другу, то направление силы тяжести Р? должно
быть несколько различным для разных тел. Этвеш укреплял на
одном конце коромысла крутильных весов определенную платиновую
массу, на другом — испытуемое тело. Прибор ориентировался так,
что коромысло имело определенное направление, например, с во-
востока на запад. Затем прибор поворачивался на 180°.
При поворачивании, в случае если инерционная и тяготеющая
массы не пропорциональны друг другу, должна бы возникнуть пара
сил и коромысло должно было бы несколько повернуться. На самом
деле не наблюдалось отклонений, превышающих 6 • 10~А дуговых
секунды; наблюдаемые весьма малые отклонения носили случайный
характер. Пропорциональность обеих масс соблюдалась с точно-
точностью, достигающей одной двухсотмиллионной доли.
Таким образом, из всех опытов вытекает невозможность разли-
различать массы — тяготеющую и инерционную: опыты убеждают нас,
что мы имеем дело лишь с различными проявлениями одной и
той же физической величины — массы. Теория тяготения Эйнштейна
подтвердила этот взгляд. Таким образом, в настоящее время вопрос
о существовании якобы двух различных физических величин — массы
инерционной и массы тяготеющей — имеет лишь исторический
интерес.
Как было указано в § 32, всякое тело вызывает в окружающем
пространстве поле тяготения. В частности, такое поле создает зем-
земной шар. Так как силы тяготения, вызванные земным шаром, назы-
называются силами тяжести, то поле, окружающее Землю, может быть
также названо полем силы тяжести. Вблизи поверхности Земли
сила тяжести практически постоянна; в этом случае поле силы
тяжести называется однородным.
Как было показано в § 27, работа в поле силы тяжести
не зависит от формы и длины пути, а только от того, на-
§ 33] МАССА ИНЕРЦИОННАЯ И ТЯГОТЕЮЩАЯ. РАБОТА СИЛЫ ТЯЖЕСТИ 1 17
сколько в результате движения тела изменилась высота его
поднятия.
Если мы из точки В пройдем в точку В' сперва по пути s\ a
затем по пути &" (рис. 70), то работы А' и А", совершенные в этих
двух случаях, по сказанному, должны
равняться друг другу: Л'= ¦4"; при
движении из точки В' в точку В по
пути s" будет совершена работа
А'" = — А". Отсюда, если мы совер-
совершим замкнутый путь, пройдя сперва
из точки В в точку В' по пути s', a
затем обратно из точки В' в точку В
по пути s", то в сумме будет совер-
совершена работа:
Авв'в = А' + А'" = А' — А" = 0.
Тот же результат непосредственно
получается из того соображения, что
при возвращении обратно в точку В изменение потенциальной энер-
энергии оказывается равным нулю. Таким образом, при движении в поле
силы тяжести по замкнутому
пути суммарная работа равна
нулю.
Вывод о том, что работа зависит лишь
от положения начальной и конечной точек
пути и не зависит от формы пути, спра-
справедлив и для неоднородного поля сил
тяготения.
При рассмотрении двух тел с масса-
массами ;rti и т2, притягивающихся друг к другу
по закону всемирного тяготения:
, . mim2
Рис. 70. Работа сил тяготения
не зависит от формы путей
s' и s".
8
Рис. 71. • Потенциальная энергия
двух тел, притягивающихся по за-
закону Ньютона, изображается гипер-
гиперболой.
можно показать, что их взаимная потен-
потенциальная энергия равна
A)
Знак минус соответствует тому, что
потенциальная энергия двух бесконечно
удаленных одно от другого тел (г = оо) условно положена равной нулю; при
этом потенциальная энергия имеет наибольшее значение, так как для раздви-
жения тел надо совершать положительную работу внешними силами; при
сближении тел их потенциальная энергия убывает, следовательно, она при-
принимает значения, меньшие нуля, т. е. отрицательные.
Графически потенциальная энергия тяготеющих тел, выражаемая форму-
формулой A), представится кривой, изображенной на рис. 71. Эта кривая — ветвь
гиперболы.
Предположим, что взаимно тяготеют два тела 1 и 2; будем рассматри-
рассматривать движение тела 2 относительно тела 1. Если полная энергия тел равна Е
1 18 СИЛЫ ТЯГОТЕНИЯ [ГЛ. IV
(рис. 71), то это означает, что тело 2, находясь на бесконечно большом рас-
расстоянии оттела 1_ двигалось со скоростью v0, определяемой равенством:
откуда va=y —.
Кинетическая энергия ?А0 изображается отрезком АВ. При уменьшении г
(тело 2 приближается к телу 1) потенциальная энергия начинает убывать и
принимает отрицательное значение; кинетическая энергия возрастает, вместе
с тем возрастает и скорость тела 2. Для некоторого определенного расстоя-
расстояния г, представляемого отрезком ОС, кинетическая энергия изобразится
отрезком DF; этот отрезок направлен снизу вверх, что соответствует поло-
положительному знаку кинетической энергии. Потенциальная энергия предста-
представляется отрезком CD; этот отрезок направлен вниз, что соответствует отри-
отрицательному значению потенциальной энергии.
Сумма кинетической и потенциальной энергии Еь + Ер во все время
движения остается равной полной энергии Е:
B)
p
Считая тело 1 неподвижным, получим, что Eft = —т,—, где г> — ско-
скорость второго тела относительно первого, когда расстояние между ними
равно г. Пользуясь этим выражением для Ek из равенств (/) и B) получим:
откуда
1 /IE . , 2mi
V m~a "r г Г - • r
Если тело 2, находясь на бесконечном расстоянии от тела 1, имело
скорость г1„ = 0, то:
(За)
Рассмотрим случай^тяжелого тела с массой т, падающего из бесконеч-
бесконечности на Землю с начальной скоростью г»0 = 0. Тогда по формуле (За) при
достижении поверхности Земли оно будет иметь скорость
v =
где М3—масса Земли, R3—ее радиус. Подставляя сюда ft=6,685-10"' см/г-сек*,
М3 = 5,98.10" г и ./?3 = 6.37-108 см> получим:
о = 1/ 6,685 • 10- 2Я5Й8-'Г ~- = 11.2 • 10'-^.
Г 6,37-108 сек ' сек
Таким образом, тело падающее на поверхность Земли из бесконечности
под влиянием притяжения Земли достигает скорости 11,2 км/сек. Наоборот,
чтобы тело брошенное с поверхности Земли вертикально вверх не упало
обратно на Землю — (при пренебрежении сопротивлением воздуха), а улетело
в бесконечность, ему надо сообщить скорость 11,2 км/сек. Эта скорость
называется второй космической скоростью.
ГЛАВА V
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 34. Движение твердого тела. Движение твердого тела опре-
определяется приложенными к нему внешними силами. Особенно харак-
характерными видами движения твердого тела являются поступательное
движение и вращение (см. § 12). Можно показать, что к ним сво-
сводится любое сложное движение твердого тела. При поступатель-
поступательном движении все точки твердого тела двигаются с одинаковыми
скоростями v и одинаковыми ускорениями w. Если мысленно раз-
разбить твердое тело на элементы с массами Д/иг, то для каждого из
элементов по второму закону Ньютона имеет место соотношение:
Aml.w = ii + Fi. A)
где fj — внутренняя" сила (т. е. происходящая от других элементов
того же тела), a Ft — внешняя сила, действующая на данный эле-
элемент. По третьему закону Ньютона сумма всех внутренних сил
равна нулю, поэтому, суммируя выражения A) по всем элементам,
получим
Д1у_.?^, или M-w = F, B)
где М = ^ikml — масса всего тела, a F = 2Fi — векторная сумма
всех внешних сил. Вектор F называется главным вектором внеш-
внешних сил.
Уравнение B) позволяет определить ускорение поступательного
движения твердого тела по массе тела М и главному вектору внеш-
внешних сил F. Таким образом, рассмотрение поступательного движе-
движения твердого тела можно заменить рассмотрением движения
одной материальной точки с массой, равной массе тела, и нахо-
находящейся под действием силы, равной главному вектору внешних
сил.
При более сложном непоступательном движении твердого тела
разные его точки обладают разными скоростями \ь и ускорениями w;.
Однако можно мысленно разбить тело на столь малые элементы, что
в пределах каждого из них скорость и ускорение остаются постоян-
постоянными. Тогда для каждого из элементов получим
120 ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. V
Суммируя это равенство по всем элементам тела и замечая, что
снова ?fi = 0, получим
SA«l-w1 = SF,=^F, C)
где F— по-прежнему главный вектор внешних сил. Однако равен-
равенство C) нельзя непосредственно свести к уравнению вида B), так
как теперь ускорения w?- разных элементов разные.
Введем некоторое ускорение we- определяемое равенством
wc = ^ . D)
где М— масса всего тела. Тогда, умножая левую и правую части
равенства D) на М и пользуясь равенством C), получим
M-wc = F. E)
Можно показать (см. мелкий шрифт), что we есть ускорение
некоторой точки С, координаты которой хс. Ус, *с определяются
через координаты отдельных элементов тела хи yit zt соотноше-
соотношениями:
_Sj>|Am,. _
Ус— м , гс—
Точка С называется центром масс тела (или центром инерции).
Центр масс совпадает с центром приложения равнодействующей
сил тяжести. Из уравнения E) следует, что центр масс тела дви-
движется так, как движется материальная точка с массой, равной
массе тела, под влиянием силы, равной главному вектору внешних
сил. Если главный вектор внешних сил равен нулю, то центр
масс тела покоится или движется равномерно и прямолинейно.
Внутренние силы не могут изменить скорости центра масс.
Покажем, что действительно центр масс, координаты которого даются
равенствами F), движется с ускорением, определяемым равенством D). Для
этого воспользуемся тем соотношением, что проекции ускорения на коорди-
координатные оси выражаются вторыми производными по времени от координат
той точки, ускорение которой рассматривается.
Беря вторые производные от хс, ус, гс, получим, что проекции уско-
ускорения центра масс на координатные оси равны:
ar 2j Afflj • wxi
M ~~ M '
м — м
2
A/"
G)
§ 35] ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА. МОМЕНТ СИЛЫ И МОМЕНТ ИНЕРЦИИ 121
где wXi, wyi, wzi—проекции ускорения i-ro элемента на координатные оси.
Так как само ускорение wc есть геометрическая сумма его составляющих
вдоль осей, то из равенств G) следует, что wc совпадает с выражением,
даваемым формулой D).
§ 35. Вращение твердого тела. Момент силы и момент инер-
инерции. При рассмотрении вращения твердого тела с динамической
точки зрения наряду с понятием о силах вводится понятие о мо-
моментах сил и наряду с понятием о массе — понятие о моменте
инерции. Для того чтобы выяснить содержание понятий — момент
сил и момент инерции, рассмотрим сперва
движение одной материальной точки А с
массой т, удерживаемой на окружности ра-
радиуса г с помощью какой-либо связи (рис. 72).
Пусть на точку А действует постоянная по ве-
величине сила f. Тогда точка А приобретает по-
постоянное тангенциальное ускорение wt, опре-
определяемое тангенциальной составляющей ft:
ft=fcosa = mwt. A)
Нормальная составляющая силы f совместно
с реакцией связи создает нормальное уско-
ускорение.
Введем угловое ускорение C = -^-, тогда равенство A) заменится
выражением:
/cos л = тг-ф;
умножим правую и левую части этого выражения на г, получим:
/г cos a = тт1 • C. B)
Произведение г cos а равно длине перпендикуляра, опущенного на
направление силы из точки О (рис. 72). Величина
M=/r cos a, C)
численно равная произведению величины силы f на длину перпен-
перпендикуляра, опущенного на направление силы из точки О (центра
вращения), называется моментом силы относительно точки О.
Величина
1 = тг\ D)
численно равная произведению массы т точки А на квадрат ее
расстояния от точки О (центра вращения), называется моментом
инерции точки А относительно точки О.
Вводя момент силы М и момент инерции /, перепишем равен-
равенство B):
М = 1% E)
Сравнивая равенства A) и E), видим, что угловое ускорение р
таким же образом связано с моментом силы М и моментом инерции
122
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[гл. v
/, каким линейное ускорение wt связано с силой ft и массой т
точки А. При описании вращательного движения с помощью угло-
углового ускорения р роль силы играет момент силы М, роль массы
т — момент инерции /. Под влиянием сил с равными моментами
точка А приобретает равные угловые ускорения р. Таким образом,
различные силы f эквивалентны в смысле вызываемого ими вра-
вращения, если равны их моменты. Разные мате-
материальные точки получают под влиянием равных
моментов сил одинаковые угловые ускорения,
«ели одинаковы их моменты инерции. Таким
образом, материальные точки с разными
массами т эквивалентны в смысле приобре-
приобретаемого ими углового ускорения, если равны
их моменты инерции.
Перейдем теперь к рассмотрению твердого
тела, вращающегося вокруг неподвижной оси
00' (рис. 73).
Рис. 73. Разбивка вра- для характеристики способности силы вы-
щающегося твердого v v
тела на элементарные зывать вращение вокруг данной оси вводится
части. понятие о моменте сил относительно оси.
Очевидно, что сила, действующая вдоль на-
направления, пересекающегося с осью, вокруг этой оси не может
вызвать вращения. Также очевидно, что и сила, параллельная оси,
не вызовет относительно нее вращения. Момент силы относительно
оси создается только той составляющей силы, которая лежит
* в плоскости, перпендикулярной к оси. Поэтому, выделяя в твердом
теле малый элемент с массой Д/га,-, мы будем рассматривать только
ту составляющую действующей на него силы, которая лежит в пло-
плоскости, перпендикулярной к оси вращения 00'. Обозначим эту со-
составляющую через Afj.
Пусть сила At{ образует угол а,- с касательной к траектории
массы Д/га;. Угол аг считаем острым. Тогда для этого элемента
можно написать равенство B):
Aftrt cos at = Д/я/fp,
где р — угловое ускорение элемента.
Такие же равенства мы можем написать для всех прочих элемен-
элементов, а затем просуммировать их:
t=2 Д«Л- р;
угловое ускорение р постоянно для всех элементов, поэтому его
можно вывести из-под знака суммы:
2 Д/irjCOS at =
Д/и/|.
F)
35] ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА. МОМЕНТ" СИЛЫ И МОМЕНТ ИНЕРЦИИ 123
Величина М = 2 ^firi cos ai представляет собою сумму моментов
t
сил, действующих на все элементы твердого тела, т. е. она представ-
представляет собою полный момент М сап, действующих на твердое тело,
относительно оси вращения ОСУ. При этом нужно произведение
Д/^соза, брать со знаком плюс, если точка приложения силы Af^
обходит ось в направлении действия силы Af(l и со знаком минус —
в противном случае. Величина
/ = 2Д«Д G)
равная сумме моментов инерции отдельных элементов, на которые
мы разбили тело, называется моментом инерции тела относи'
тельно данной оса 00'.1 Вводя полный момент сил М и момент
инерции /, перепишем равенство F):
Af = /p, Fa)
т. е. для твердого тела справедливо равенство, совпадающее с ра-
равенством E).
Угловое ускорение C, приобретаемое твердым телом:
т. е. оно прямо пропорционально приложенному моменту сил М и
обратно пропорционально моменту инерции /. Сравнивая соотноше-
соотношение Fа) с равенством A), выражающим второй закон Ньютона,
видим, что для вращения твердого тела вокруг неподвижной оси
имеет место соотношение, вполне аналогичное второму закону Нью-
Ньютона, только роль линейного ускорения играет угловое ускорение,
роль силы — момент силы и роль массы — момент инерции.
Из равенства Fа) следует, что если момент сил, действующих на
тело, равен нулю, то и угловое ускорение Р = 0, т. е. тело вращается
с постоянной угловой скоростью ш, если только его момент инерции /
остается постоянным.9 В частном случае ш = 0, т. е. тело покоится.
1 На самом деле элементы массы должны быть взяты бесконечно малыми,
тогда суммирование заменяется интегрированием, и для момента инерции
тела мы получаем выражение:
Вводя плотность тела р, имеем: dm=pdV, где dV—элемент объема.
Отсюда
/=$PrW; Ga)
интегрирование должно быть распространено на весь объем тела V.
8 Момент инерции твердого тела, вращающегося вокруг неподвижной
оси, может меняться лишь в том случае, если отдельные части твердого
тела связаны друг с другом не жестко. Для зтого случая формула Fа)
124
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. V
а)
6)
Рис. 74. Момент силы f относи-
относительно точки О определяется
вектором М.
Как мы видели (см. § 13), угловая скорость ш и угловое ускорение Р
могут рассматриваться как векторы. Момент силы / относительно точки
может также рассматриваться как вектор, и равенству Fа) может быть при-
придан векторный характер.
Рассмотрим силу f (рис. 74 а), момент которой относительно точки О
мы хотим определить. Очевидно, полную характеристику момента составляют:
1) численное значение момента, равное
/г cos о; 2) плоскость, в которой лежат сила f
и точка О; 3) направление, в котором дей-
действует сила. Все эти три характеристики
могут быть выражены с помощью одного
вектора М, если мы: 1) положим численное
значение вектора М равным/г cos а, 2) про-
проведем его перпендикулярно к плоскости,
в которой лежат сила f и точка О, и 3) на-
направим его так, чтобы это направление
было некоторым однозначным образом свя-
связано с направлением силы. В качестве такой
связи между направлениями выберем опять
„правило буравчика" (ср. § 13 и рис. 28): направление вектора М определится
поступательным движением буравчика, расположенного в точке О, если на-
направление вращения его головки совпадает с направлением действующей
силы. Тогда в случае, представленном на рис. 74а, вектор М будет направлен
вверх, а в случае, представленном на рис. 746—
вниз. Вектор Мявляется вектором момента силы.
Вводя в рассмотрение угол Z г, f между
векторами г и f, получим а= Z. г, f у, от-
откуда для численного значения момента силы f
найдем:
Af=/- r ¦ sin(,/ r, f).
Следовательно, если мы воспользуемся вве-
введенным в § 13 представлением о векторном
произведении, то получим, что момент силы f
выражается векторным произведением:
M = rxf, (За)
где г есть радиус-вектор, проведенный из точки О, относительно которой
берется момент, к точке приложения силы f.
Рассмотрим еще момент так называемой пари сил. Парой сил назы-
называются две равные и направленные в противоположные стороны силы,
не действующие вдоль одной прямой (рис. 75). Будем брать момент пары
относите.льно точки, лежащей в плоскости сил. Момент пары не зависит от
положения тонки О, относительно которой он берется. Возьмем произ-
произвольно расположенную точку О.(рис. 75). Тогда момент силы ft относительно
точки О численно равен /in cos а, и направлен перпендикулярно к плоскости
рисунка вперед. Момент силы U численно равен /2ra cos ог и направлен пер-
перпендикулярно к плоскости рисунка за плоскость рисунка. Таким образом,
моменты /tf-jcoscti и /sra cos os направлены в противоположные стороны и,
следовательно, суммарный момент обеих сил, образующих пару, равен
М =/2Г2 COS аа —/,ri COS о».
Рис. 75. Момент пары не за-
зависит от положения точки О,
относительно которой он
берется.
не применима, так как ее вывод предполагает, что составляющие сил, напра-
направленные по связям, компенсируются реакциями связей, а не вызывают пере-
перемещения одних частей твердого тела относительно других, как это будет
иметь место при нежестких связях.
§ 36]
МОМЕНТЫ ИНЕРЦИИ НЕКОТОРЫХ ТЕЛ
125
M
f
Силы fi и f3 численно равны друг другу; обозначим их общее значение через/,
а разность racosaa—ncosai обозначим через / (/ есть расстояние между
прямыми, вдоль которых действуют силы),
тогда
M=fl; (8)
/ называется плечом пари. Момент пары
М численно равен произведению из числен-
численного значения / одной из сил пары на плечо
пары /. Направление вектора момента пары
связано с направлением действия сил, обра-
образующих пару, правилом буравчика (рис. 76).
Вводя вектор момента сил, можно, как
оказывается, переписать равенство Fа) в
векторной форме:
М = /.р\ (9)
Рис. 76. Момент пары опреде-
ляется вектором М.
При М = 0, т. е. при отсутствии момента сил, действующего на твердое
тело, р = 0, что означает, что вектор угловой скорости ш постоянен, т. е.
твердое тело не только вращается с постоянной по численному значению
угловой скоростью, но что и направление оси вращения
остается постоянным.
§ 36. Моменты инерции некоторых тел.
Рассмотрим моменты инерции некоторых тел отно-
относительно определенных осей. В качестве простей-
простейшего примера рассмотрим момент инерции тонко-
тонкостенного полого цилиндра (кольца) (рис. 77)
с массой т и радиусом R относительно его оси
симметрии ОСУ. Разобьем цилиндр на элементы
в виде полосок, ограниченных образующими ци-
цилиндра (одна такая полоска заштрихована на
рис. 77). Ввиду малой толщины стенок цилиндра
можно считать, что все части такой полоски
лежат на одинаковых расстояниях R от оси ОСУ. Поэтому момент
инерции отдельной полоски равен Д/ = Д/га^2, где Д/га,-— масса
полоски. Момент инерции всего тонкостенного полого цилиндра:
Рис. 77. Определе-
Определение момента инер-
инерции полого ци-
цилиндра.
но
представляет собою массу т всего цилиндра, откуда
A)
Относительно какой-либо другой оси момент инерции того же
цилиндра будет иной.
Моменты инерции некоторых других тел приводим без вы-
вычислений, так как эти вычисления потребовали бы интегриро-
интегрирования.
126
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. V
Момент инерции сплошного цилиндра (диска) относительно оси
цилиндра (рис. 78):
B)
Рис. 79. Момент инерции полого
цилиндра относительно оси 00'
равен -j »"(
Рис. 78. Момент инерции ци-
цилиндра относительно оси 00'
равен -я- т/?".
Момент инерции полого толстостенного цилиндра относительно
его оси (рис. 79):
± C)
I
где /?| и /?, — его внешний и внутренний радиусы.
Момент инерции стержня
О длиной I относительно оси, про-
проходящей через середину стер-
стержня перпендикулярно его длине
б)
о'
(рис. 80а):
1
D)
Рис. 80. Момент инерции стержня Момент инерции стержня
относительно оси 00', проходящей длиной I относительно оси, про-
через его середину, равен 1 тР и ходящей у конца стержня пер-
12 пендикулярно его длине (рис. 80о):
относительно оси, проходящей через
его конец, равен -^-mi'. I=-^ml\ E)
О О
Момент инерции шара относительно оси, проходящей через его
центр:
I=jmR\ F)
Размерность момента инерции определяется из соотношения
откуда
§ 37] МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ 127
Таким образом, в CGS-системе момент инерции измеряется в гсм\
в технической системе — (техн. ед. массы)-л*.
В международной системе единиц (MKS) момент инерции выра-
выражают в кгм*, так как в ней за единицу массы принят килограмм,
а за единицу длины метр.
Приведем пример на определение углового ускорения тела по заданным,
моменту сил и моменту инерции.
Пример. К колесу радиуса /? = 0,5 м с моментом инерции / = 20кгм*
приложен постоянный момент сил М = 5 кГм. Найти: 1) угловое ускорение
и 2) линейную скорость точек на ободе к концу 10-й секунды (начальную
скорость считать равной нулю).
Решение. Угловое ускорение колеса
Будем для расчета пользоваться технической системой единиц, тогда
i 20
= gg- техн. ед., откуда
5-98
Р = сек.~г = 2,45 сек."'.
Угловая скорость через время t после начала движения будет
*> = Р<,
а линейная скорость точек на ободе
» = ш/? = 2,45 • 0,5 • 10 м/сек= 12,25 м/сек.
Если для какого-либо тела известен его момент инерции относительно
оси, проходящей через центр тяжести, то легко может быть найден и момент
инерции относительно любой оси, параллельной первой.
Этот переход от однога момента инерции к другому производится по
следующей теореме: момент инерции относительно любой оси вращения
равен моменту инерции относительно параллельной ей оси, проходящей
через центр тяжести, сложенному с произведением массы тела на
квадрат расстояния центра тяжести тела от оси вращения.
В качестве примера определяем момент инерции шара относительно
одной из его касательных.
Согласно приведенной теореме:
где lt—момент инерции относительно касательной, 1С — момент инерции
относительно оси, проходящей через центр тяжести, т — масса шара и
а—расстояние от касательной до центра шара. Так как для шара a=R
2
и /с = -=- mR', то
It = j mR* + mR1 = j mR*.
§ 37. Момент количества движения. Рассмотрим первоначально
материальную точку с массой т. вращающуюся по окружности ра-
радиуса г (рис. 72). Для такой точки имеет место соотношение:
A)
128 ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. V
где /— сила, действующая на точку, a wt — тангенциальная соста-
составляющая ее ускорения. Предположим, что сила / постоянна по ве-
величине и составляет один и тот же угол а с касательной к окруж-
окружности во всех точках пути.
Тогда wi = Av/M, и равенство A) принимает вид:
/ cos а • Д^ = т Да.
Умножая правую и левую части этого выражения на г, получим
/г cos a • М = гт Дв. B)
Величина /г cos а представляет собой момент М силы / относи-
относительно центра вращения О; кроме того, ввиду постоянства массы т
и радиуса г, выражение гт. Ьт можно переписать в виде Д (rmv).
Тогда равенство B) примет вид:
М М = Д (rmv). C)
Если момент сил М непостоянен, то в выражении C) следует
брать столь малый промежуток времени At, чтобы в течение этого
промежутка времени момент сил М мог считаться постоянным. Для
конечного промежутка времени можно ввести в рассмотрение сред-
среднее значение момента сил М и тогда
М At = A (rmv). (За)
Величина p = rmv называется моментом количества движения
материальной точки, вращающейся по окружности, а М At -— импуль-
импульсом момента сил. Равенство C) утверждает, что изменение мо-
момента количества движения численно равно импульсу приложен-
приложенного момента сил. Оно аналогично равенству D) § 17, выражаю-
выражающему связь между изменением количества движения и импульсом
силы.
Понятие о моменте количества движения р материальной точки мы ввели
для частного случая движения материальной точки по окружности, когда
скорость ее все время перпендикулярна к радиусу г. В общем случае дви-
движения материальной точки под ее моментом количества движения относи-
относительно некоторого центра О подразумевается величина, численно равная
произведению из количества движения точки mv на длину перпендикуляра,
опущенного из центра О на направление скорости точки v (вектор1 v про-
проводится из того места, где в данный момент находится материальная точка).
Момент количества движения является вектором, направление которого
определяется правилом буравчика: вектор р перпендикулярен к плоскости,
в которой лежат вектор скорости v и центр О, и направлен в сторону по-
поступательного движения буравчика при вращении его головки от вектора г
(радиус-вектор точки)'к вектору V. Таким образом, вектор момента количе-
количества движения определяется векторным произведением p = rXmv и равен-
равенство C) в общем случае должно быть также переписано в векторном виде:
где Др — векторная разность моментов количества движения ps — pi.
§ 37] МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ 129
Соотношение C) легко обобщить и на случай твердого тела, вра-
вращающегося вокруг неподвижной оси. Для этого разобьем твердое
тело на отдельные элементы с массами Д/я,-, подобно тому, как это
мы делали в § 35.
Для каждого такого элемента будет выполняться равенство:
Д/i ¦ rt cos а,- At = Г; Д/лг Avt,
или, так как Дг»,- = Дм • rt, то
Д/i • Г; cos a-i At = Д/и,г? ¦ Дш.
Суммируя эти выражения для всех отдельных элементов твер-
твердого тела, получим:
Д] Д/,- • rt cos at At = 2] Д/и»г| • Дш,
или, так как ^jAf^iCos a.i = M— момент сил, действующих на твер-
твердое тело, а Д]Д/я,г| = /—момент инерции тела, то
i
i
Если момент сил М непостоянен, то следует брать его среднее
значение за промежуток времени Д? и тогда
Так как момент инерции твердого тела относительно данной оси
есть величина постоянная, то последнее равенство можно переписать
в виде:
MAt = A(Iu>), D)
где справа стоит изменение величины Ло. Величина М At называется
импульсом момента сил, приложенных к твердому телу, а вели-
величина /<» — моментом количества движения твердого тела, вра-
вращающегося вокруг неподвижной оси. По равенству D), изменение
момента количества движения твердого тела численно равно
импульсу момента приложенных к нему сил.
Равенство D) мы, вывели, положив момент инерции тела постоян-
постоянным, но оно, как оказывается, справедливо и тогда, когда во время
движения момент инерции каким-нибудь образом меняется. И в этом
случае изменение момента количества движения Д (/со) определяется
импульсом момента приложенных сил.
Из формул C) и D) следует, что при отсутствии момента
сил (Л1 = 0) момент количества движения остается постоянным.
Это следствие известно под названием закона сохранения момента
количества движения.
130
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[гл. v
В частном случае движения материальной точки по окружности
имеем из C) при М = 0:
mvr = const. E)
В общем случае движения материальной точки при M=±=Q:
г X mv = const. F)
Для твердого тела из D) при М = 0 следует:
/.<о = const. G)
В случае неизменного момента инерции, при отсутствии внешних
сил, угловая скорость вращающегося тела остается постоянной; этот
fa результат мы уже получали непосредственно
из формулы Fа) § 35.
Если, при отсутствии внешних сил, ме-
меняется момент инерции, то начинает меняться
и угловая скорость <о, так что произведение
/ш остается постоянным: если момент инерции
/ возрастает, то угловая скорость ш убывает,
и наоборот.
Сохранение момента количества движения
может быть продемонстрировано с помощью
человека, стоящего на скамеечке, могущей без
трения вращаться вокруг вертикальной оси
(„скамья Жуковского"). Пусть человек, дер-
держащий в расставленных руках гири (рис. 81),
приведен вместе со скамеечкой во вращение
с угловой скоростью ад. При этом человек
имеет определенный момент количества дви-
движения /ш, который, при равенстве нулю момента внешних сил,
должен сохраняться. Если человек опустит руки, то его момент
инерции уменьшится, в результате этого возрастет угловая ско-
скорость его вращения ш. Если человек снова поднимет руки, то
угловая скорость ш примет прежнее значение.
Момент количества движения Р = /ю есть величина векторная,
имеющая то же направление, что и вектор угловой скорости и.
Отсюда и равенство D) на самом деле носит векторный характер:
где ДР = /<о.2— /ох представляет собою векторную разность
моментов количества движения 1(Л. В таком виде оно совершенно
аналогично равенству D) § 17, выражающему для материальной точки
связь между изменением вектора количества движения и вектором
импульса сил. Равенство (8) применимо не только к случаю враще-
вращения твердого тела около неподвижной оси, но и к случаю произ-
произвольного движения твердого тела, если соответствующим образом
Рис. 81. При опускании
рук с гирями человек
начинает вращаться
скорее.
§ 38]
ГИРОСКОПЫ
131
обобщить понятие момента количества движения. Равенство (8) при-
применимо и к системе тел, только тогда под Р надо подразумевать
вектор суммарного момента количества движения и - ^
под М — вектор суммарного импульса сил.
Закон сохранения момента количества движения для
системы, состоящей из двух тел, можно продемонстриро-
продемонстрировать, дав в руки человеку, стоящему на скамеечке, колесо
с массивным ободом (рис. 82). Если человек со скамеечкой
сперва покоился, а затем, держа ось колеса вертикально,
привел колесо во вращение, то сам он вместе со скамееч-
скамеечкой начнет вращаться в противоположную сторону. Это
произойдет оттого, что силы, которые человек приклады-
прикладывает к колесу, являются внутренними, а потому общий
момент количества движения, сперва равный нулю, таким
и останется. Этот опыт аналогичен опыту с человекам,
бегущим по тележке (§ 18), который демонстрирует сохра-
сохранение количества движения системы.
Из равенства (8) следует, что при отсутствии внешних
сил (М = 0) момент количества движения Р сохраняется
не только по величине, но и по направлению. Последнее
может быть продемонстрировано снова с помощью человека,
стоящего на скамеечке и держащего в руках вращающееся
колесо: всякое изменение направления оси колеса (напри-
(например, ее поворачивание на 90° или на 180°) при постоянстве
числа оборотов колеса ведет к изменению угловой скорости
вращения самого человека на скамеечке.
§ 38. Гироскопы. Свойство вращающегося твердого
тела сохранять направление оси вращения, а также харак-
характер сил, действующих со стороны оси тела на опоры при
внешних воздействиях, используется для различных техни-
технических целей. Применяемые в технике массивные симметричные тела, вращаю-
вращающиеся с большой угловой скоростью, носят название волчков или гироскопов.
Свойство гироскопа сохранять неизмен-
неизменной ось вращения, при равенстве нулю мо-
момента внешних сил, может быть продемон-
продемонстрировано с помощью карданова подвеса.
Карданов подвес (рис. 83) состоит из
двух колец, внешнее из которых свободно
поворачивается вокруг оси, проходящей
через острия АА', а внутреннее — вокруг
оси, перпендикулярной к ней, проходящей
через острия ВВ. Ось СС гироскопа D
опирается на внутреннее кольцо карданова
подвеса, что обеспечивает ей возможность
свободно поворачиваться в пространстве в
любых направлениях. Если привести гиро-
гироскоп в быстрое вращение, то при любом
повороте подставки ось его вращения со-
сохраняет неизменным свое направление.
Если к вращающемуся гироскопу при-
приложить пару сил, стремящуюся повер-
повернуть его около оси, перпендикулярной к оси его вращения, то он ста-
станет поворачиваться около третьей оси, перпендикулярной к первым
двум. Пусть, например, гироскоп D вращается около оси 00' в напра-
направлении, указанном стрелкой на рис. 84. Пусть к гироскопу приложена
пара сил F и F, перпендикулярных к плоскости рисунка и стремящихся
Рис.82. При по-
поворачивании ко-
колеса человек
сам начинает
вращаться в об-
обратную сторону.
Рис. 83. Гироскоп на кардано-
вом подвесе.
132
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[гл. v
повернуть его около оси АА', тогда верхний конец оси гироскопа О' откло-
отклонится направо, а нижний — налево (указано стрелками v' и v), т. е. ги-
гироскоп повернется около оси ВВ', перпендикулярной к плоскости рисунка.
Из рис. 84 видно, что в результате гиро-
гироскопического эффекта гироскоп стремится
расположить ось своего вращения таким обра-
образом, чтобы она образовывала возможно мень-
меньший угол с осью вынужденного вращения АА'
и чтобы оба вращения совершались в одном
и том же направлении.
Парадоксальные на первый взгляд указан-
указанные свойства гироскопа могут быть поняты
на основании следующего рассмотрения.
Пусть имеется гироскоп, вращающийся
в направлении, указанном на рис. 85, и на ко-
который действует пара сил F и F', направленных
так же, как и силы, приложенные к гироскопу,
изображенному на рис. 84. Тогда вектор угловой
скорости ю направлен вниз, а момент М пары
сил F и F' (силы лежат в плоскости, перпен-
перпендикулярной к плоскости рисунка) направлен
вдоль прямой АА' влево. По сказанному на
стр. 125, между моментом пары сил М и угло-
угловым ускорением р", рассматриваемыми как век-
векторы, имеет место соотношение:
Рис. 84. При наличии пары
сил F и F', стремящихся
повернуть гироскоп около
оси АА
р
оси АА , гироскоп поворачи-
поворачивается около перпендику-
перпендикулярной к ней оси ВВ'.
.-¦?-.
где / — момент инерции тела, к которому приложена пара сил с моментом М;
следовательно, ускорение р" направлено в ту же сторону, что и М. Отсюда
получим, что за некоторый малый промежуток времени At изменение угловой
скорости изобразится вектором Д<а, параллельным вектору М, т. е. лежащим
в плоскости чертежа и направленным налево. Это же означает, что ось вра-
вращения гироскопа повернется вокруг оси ВВ'
по часовой стрелке.
Силы, приложенные к связям, удерживаю-
удерживающим ось, равны силам F и F', но направлены
в противоположные стороны; они носят назва-
название гироскопических сил. Например, если ко-
конец О' гироскопа, вращающегося в направле-
направлении, указанном стрелкой на рис. 86, отодви-
отодвигается назад за плоскость чертежа, а конец О —
вперед, то ось оказывает на подшипники да-
давление в направлении стрелок Ft и FJ. Можно
показать, что момент сил Ft и FJ выражается
через векторное произведение момента коли-
количества движения гироскопа /ю на вектор угло-
угловой скорости поворачивания его оси »':
М = /шХм'. A)
Гироскопические силы проявляются при
движении обычного волчка. При наклонном
~>- -л'
Рис. 85. К объяснению ги-
гироскопического эффекта.
положении вращающегося волчка составляющая силы тяжести Ра (рис. 87)
стремится наклонить ось волчка еще больше. Но благодаря гироскопиче-
гироскопическому эффекту, ось 00' отклоняется в перпендикулярном направлении (ука-
(указано стрелкой v) и начинает двигаться („прецессировать") так, что его ось
движется по конической поверхности. В результате прецессии волчок не па-
§ 38]
ГИРОСКОПЫ
133
дает. Действие гироскопических сил может быть также продемонстрировано
с помощью так называемого рычажного гироскопа. Стержень В (рис. 88)
может вращаться относительно стойки А как в вертикаль-
вертикальном, так и в горизонтальном направлениях. На конце
стержня укреплен гироскоп D. Если гироскоп уравнове-
уравновешен грузом Р, то равновесие сохраняется и при вращении
гироскопа. Если же груз Р тяжелее гироскопа, то он вы-
вызывает не наклонение стержня В, а его поворачивание
в горизонтальной плоскости.
Гироскопы находят различные применения в физике и
технике. В 1852 г. Фуко пытался использовать гироскоп
для доказательства вращения Земли. Гироскопический эф-
эффект находит широкое применение в нарезных орудиях.
Винтовые нарезы в стволе орудия сообщают вылетающему
снаряду быстрое вращение вокруг оси и превращают его
в гироскоп с большим собственным моментом количества
движения. Благодаря этому момент сил, возникающий вслед-
вследствие сопротивления воздуха, не ведет к опрокидыванию
снаряда, а лишь вызывает прецессию снаряда вокруг напра-
направления касательной к траектории. Гироскопы используются
также для регулирования движения мин (торпед). Гироскоп
может быть использован и в качестве компаса.
Гироскопический компас представляет собою быстро
вращающийся волчок (до 30000об/мин), плавающий в сосуде
со ртутью. Благодаря суточному вращению Земли, ось
гироскопа стремится расположиться параллельно оси вра-
вращения Земли, т. е. в плоскости меридиана. В настоящее
время гироскопы используются в различных аэронавигационных приборах
(например, „искусственный горизонт"). Большие гироскопы употребляются
для уменьшения качки судов.
Гироскопические эффекты могут также оказывать, при наличии в меха-
механизмах быстро вращающихся массивных частей, вредное влияние. Например,
турбина при поворачивании парохода оказывает,
благодаря возникающим гироскопическим си-
силам, добавочное давление на подшипники.
В
Рис.86. Гироско-
Гироскопические силы
F, и F;, при-
приложенные к свя-
связям, удержива-
удерживающим ось вра-
вращения гиро-
гироскопа.
Рис. 87. Прецессия волчка.
Рис. 88. Рычажный гироскоп.
Вектор угловой скорости разворота парохода <а' в этом случае перпенди-
перпендикулярен к вектору угловой скорости самой турбины ю, откуда численное
значение момента гироскопических сил М' по формуле A) равно
Если расстояние между подшипниками равно /, то М' = /у, где Л —
сила добавочного давления на подшипник. Отсюда
„ /too'
134
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
[ГЛ. V
При большом моменте количества движения турбины A<л—велико) и
быстром развороте парохода (велико ш') силы F± могут достичь значений,
достаточных для разрушения подшипников.
§ 39. Кинетическая энергия вращающегося твердого тела.
Определим теперь работу, совершаемую моментом сил М при пово-
поворачивании тела на определенный угол <р вокруг неподвижной оси
00' (рис. 89). Пусть к твердому телу приложена сила /, касатель-
касательная к траектории точки приложения, момент
которой относительно оси 00' равен М =fr.
При поворачивании тела на угол Д<р точка
приложения силы А переместится на длину
дуги As, откуда работа, совершенная силой
/, будет:
ДЛ =/. ДЯ,
но As = г Дер, где Д<р — угол поворота тела,
следовательно,
ДЛ =fr • Дер
или, так как fr = M есть момент силы /,
ДЛ=М-Д<р; A)
таким образом, работа, совершаемая при пово-
поворачивании тела на угол Д<р, численно равна про-
произведению из момента силы на угол поворота.
В случае, если момент М постоянен, работа, совершаемая при
поворачивании тела на конечный угол <р. будет:
Рис. 89. Работа силы, вы-
вызывающей вращение.
А = М •
B)
При переменном моменте силы М следует по формуле A) опреде-
определить элементарную работу ДЛ, а полную работу Л получить сум-
суммированием элементарных работ.
Рассмотрим теперь тело, вращающееся с данной угловой ско-
скоростью ш вокруг неподвижной оси. Кинетическая энергия его i-ro
элемента будет:
АШ: • О?
где Д/Я; — масса этого элемента и vL — его линейная скорость.
Так как vi = rita, то
Am, • />"
Кинетическая энергия вращения всего тела равна сумме кинети-
кинетических энергий его отдельных элементов:
-2
=^2 miTl
§ 39] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТВЕРДОГО ТЕЛА 135
но по формуле G) § 35 V Апцг1 — I есть момент инерции тела (от-
(относительно оси вращения), откуда
Е> = %. О)
Таким образом, кинетическая энергия вращения твердого тела вокруг
неподвижной оси выражается формулой, совершенно аналогичной
формуле, дающей кинетическую энергию материальной точки, только
роль массы т играет момент инерции /, а роль линейной скорости
— угловая скорость ш.
Мы рассмотрели случай вращения твердого тела около неподвижной
оси 00'. Разберем теперь другой частный случай движения твердого тела,
когда его ось вращения проходит через центр масс и перемещается, оста-
оставаясь параллельной самой себе. Пусть \t—линейная скорость элемента
объема тела с массой Ami и vc—линейная скорость центра масс тела отно-
относительно той же координатной системы. Введем, кроме того, скорость vi
элемента объема тела относительно центра масс, тогда
Кинетическая энергия элемента объема h.Eki равна
Л?*<= ~~2~ — 2
или по D)
Кинетическую энергию всего тела Еь получим, взяв сумму кинетических
энергий всех его элементов:
E)
Первый из членов в правой части этого равенства представляет собою,
как легко видеть, кинетическую энергию массы т, равной массе всего тела,
то}*
движущейся вместе с центром масс: —я--. Для второго члена на основании
рассуждений, аналогичных приведенным в основном тексте, получим, что он
равен кинетической энергии вращения твердого тела относительно оси вра-
вращения, проходящей через центр его масс -^-. Третий член, как можно по-
показать, равен нулю. Действительно, рассмотрим произведение &mpQXv'tx. За-
Заметив, что по D) v'ix = vix — vCx, перепишем его в виде:
F)
Обозначим координаты центра масс через хс, ус, гс и координаты 1-го
элемента тела — через Xi, yi, Zi. Тогда vCx = xc и vix = X{, где точки над
буквами означают первую производную по времени. Воспользовавшись этим
равенством, перепишем выражение F):
136 ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. V
Суммируя G) по всем элементам тела, получим
2 ^mivcxv'ix=*с 2 Лш'--*«—т*ъ
Но по формуле F) § 34 2 Дт(Л,- = тЛс, откуда находим
Такое же равенство найдем и для двух других составляющих скоростей
по осям, откуда следует:
>! Д/П; (Vn V', -4- Vr V'i A-Vr V'- ) = 0.
Z-i t \"Cx ix ' "Cy"iy т Cz ill "•
После этого равенство E) принимает вид:
mv% Л»8
p. L j
* — 2 2'
т. е. полная кинетическая энергия твердого тела равна сумме кинети-
кинетической энергии массы т, равной массе всего тела, движущейся вместе
с центром масс, и кинетической энергии его вращения относительно оси
вращения, проходящей через центр масс.
Разберем несколько примеров на определение кинетической энергии вра-
вращающегося твердого тела.
Пример 1. Маховое колесо, имеющее вместе с валом момент инерции
200 кгм*, вращается, делая 180 об/мин. Через 2 мин. после того, как на ко-
колесо перестал действовать вращающий момент, оно остановилось под влия-
влиянием сил трения в подшипниках. Считая трение в подшипниках постоянным,
определить момент сил трения.
Решение. Работа сил трения в подшипниках совершается за счет
кинетической энергии вращающегося махового колеса:
—тр- = Mf,
z
где шо — начальная угловая скорость махового колеса, / — его момент инер-
инерции, <р—угол, на который повернется маховое колесо до остановки, М—иско-
М—искомый момент сил трения в подшипниках. Считая вращение колеса равномерно-
равномерного .
замедленным, получим (p = -KL t, где t — время, в течение которого маховое
колесо останавливалось, отсюда
Угловая скорость ио = 2тспо, где по = 18О об/мин = 3 об/сек, откуда
м=Нртщ^ кГм =3'2 кГм-
Пример 2. Какую часть от общей кинетической энергии составляет
энергия вращения для катящихся: а) обруча, 6) сплошного цилиндра, в) шара.
Решение. При качении без скольжения скорость на ободе тела равна
его поступательной скорости v. Отсюда для обруча, для которого / = т^?а
и г» = ш/?, получим, что кинетическая энергия его вращения при качении Бар
равна
„ Лл^ ту*
ВР — 2 — 2 *
§ 39] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТВЕРДОГО ТЕЛА 137
Полная кинетическая энергия Е^ складывается из энергии вращения Явр
/яг»2
и кинетической энергии поступательного движения —^— , следовательно:
_ till)* , г, о г, 1 г, /О,
Еь = -7=—г- Еа„ = mv2, откуда свп = -=¦ Еь. (8)
Для сплошного цилиндра:
I = — Wi(?2, откуда ?Ер = -^- = ^|-;
3 1
»р = Т mwa' откУда ?вР = -з?'а. (9)
/ш9 1
откуда Евр == — = —,
?й = ~2—h -5" шг'а == То mv3> 0ТКУда ?вр = у ?*• A°)
Пример 3. С наклонной плоскости высотой h скатываются: а) обруч,
б) сплошной цилиндр, в) шар. Найти поступательные скорости, которые они
будут иметь, скатившись до конца плоскости. Сравнить эти скорости со
скоростью, которую имело бы тело, соскальзывающее по плоскости без трения.
Решение. Полная кинетическая энергия скатывающегося тела:
_ пи»' , /<о8
полная
Для
полная
энергия
„ mv*
шара:
'-4
энергия
Так как кинетическая энергия возникает за счет потенциальной энергии
Ep = mgh, то
~2 \т + ~#г] v=mSh' 0ТКУда v=z
т+7?
или
(П)
Так как скорость тела, соскальзывающего без трения с наклонной плоскости
высотой h, равна
то видим, что для тела, скатывающегося без трения, эта скорость в
1/ 1+jTpa Раз меньше, где /—момент инерции тела, т — его масса и
— его радиус.
Для обруча, для которого /=mR2, имеем
133 ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА [ГЛ. V
т. е. скорость, которую он приобретает, скатываясь по наклонной плоскости,
в ]^2 = 1,41 раза меньше, чем для тела, соскальзывающего без трения.
Для сплошного цилиндра I = -^mR1, откуда
т. е. в 1/ у = 1,23 раза меньше, чем для соскальзывающего тела.
2
Для шара I = -=- тД*, откуда
о
т. е. в Т/ -^- = 1,18 раза меньше, чем для соскальзывающего тела.
ГЛАВА VI
движение жидкости
§ 40. Движение идеальной жидкости. Линии и трубки тока.
До сих пор мы рассматривали движение тел, сводящееся к их пере-
перемещению относительно других тел или, в случае твердого тела, также
к вращению вокруг определенной оси. Однако возможно движение,
которое сводится к перемещению различных частей одного и того же
тела друг относительно друга; при этом, если тело может рассма-
рассматриваться как непрерывное и бесконечно большое, его называют
сплошной средой. Сплошная среда может представлять собою упру-
упругое твердое тело, в этом случае в нем могут возникать сдвиги одних
частей относительно других и колебания (волны); сплошная среда
может представлять собою несжимаемую жидкость, в которой могут
возникать течения; наконец, сплошная среда может быть сжимаемой
жидкостью или газом, в которых возможно возникновение как тече-
течений, так и колебаний. Часть механики, занимающаяся изучением дви-
движения жидкости, называется гидродинамикой.
Рассматривая движение жидкости, в большинстве случаев можно
с достаточной степенью приближения считать жидкость абсолютно
несжимаемой и полагать, что перемещение в ней одних слоев отно-
относительно других не связано с возникновением сил трения (отсут-
(отсутствует внутреннее трение, или вязкость). Такая абсолютно несжи-
несжимаемая и абсолютно невязкая жидкость на-
называется идеальной. „Идеальная жидкость"
служит лишь более или менее хорошим при-
приближением к реальным жидкостям.
Будем определять движение частиц жид-
жидкости относительно некоторой определенной
системы отсчета. Тогда каждой частице соот-
соответствует свой вектор скорости. Вся жидкость
представляет собою, как принято говорить,
поле вектора скорости. В поле вектора ско-
скорости мы можем провести линии, касательные к которым в каждой
точке совпадают с направлением скорости частицы жидкости в этой
точке (рис. 90). Такие линии называются линиями тока. Принято
проводить линии тока так, чтобы густота их была больше там, где
Рис.
90. Линии тока
жидкости.
140 ДВИЖЕНИЕ ЖИДКОСТИ [ГЛ. VI
больше скорость течения жидкости, и меньше — там, где жидкость
течет медленнее. В случае установившегося (стационарного) тече-
течения, скорость жидкости в каждой точке остается постоянной во
времени. В этом случае линии тока также остаются неизменными
и совпадают с траекториями отдельных частиц жидкости. Линии
тока в жидкости можно сделать видимыми, пустив в нее струю
краски или подмешав какие-либо заметные взвешенные частицы.
На рис. 91 а, б, в представлены линии тока, получаемые при обте-
с; б) в)
Рис. 91. Линии тока жидкости.
кании жидкостью круглого цилиндра, пластинки, поставленной пер-
перпендикулярно к потоку, и тела обтекаемого рыбовидного сечения.
Часть жидкости, ограниченную линиями тока, называют трубкой
тока. Все частицы, находящиеся в некотором сечении трубки тока,
при движении продолжают двигаться внутри трубки тока и не вы-
выходят из нее. Также извне никакие частицы не проникают внутрь
трубки тока. Возьмем трубку тока и
выберем два каких-либо нормальных
ее сечения AS! и AS2 (рис. 92). За
v еДиницУ времени через сечение ASi
* протечет объем жидкости, равный
Рис. 92. Трубка тока жидкости. ASi^i- где щ — скорость течения жид-
жидкости в том месте, где произведено
сечение ASt. Через сечение ASa за единицу времени протечет объем
жидкости ASat>a, где v.2 — скорость течения жидкости в месте сече-
сечения ASg- Для несжимаемой жидкости через сечение ASt протечет
такой же объем, какой протек через сечение A5t, откуда
ASi • i>! = Д52 • г»2.
Так как это соотношение справедливо для любых двух сечений
трубки тока, то мы можем вообще написать, что для трубки тока
Д51 • v = const,
т. е. что произведение скорости течения несжимаемой невязкой
жидкости на поперечное сечение трубки тока есть величина постоян-
постоянная для данной трубки тока. Это соотношение известно под назва-
названием теоремы о неразрывности струи.
При стационарном течении несжимаемой невязкой жидкости по
какой-либо действительной трубе объем этой трубы совпадает с труб-
§ 40] ДВИЖЕНИЕ ИДЕАЛЬНОЙ ЖИДКОСТИ. ЛИНИИ И ТРУБКИ ТОКА 141
кой тока. Отсюда, по теореме о неразрывности струи, в тех местах,
где труба шире, жидкость течет медленнее, и в тех местах, где
труба уже, жидкость течет быстрее.
Представим себе трубку тока, сужающуюся по направлению тече-
течения; поступая в более узкую часть трубки тока, жидкость начинает
течь скорее, т. е. она приобретает ускорение. Следовательно, на
жидкость, втекающую в более узкую часть трубки, действует со сто-
стороны жидкости, еще находящейся в широкой части трубки, некото-
некоторая сила. Такая сила, возникающая внутри объема жидкости, может
возникнуть только за счет разности давлений в различных частях
жидкости. Так как сила направлена в сторону узкой части трубки,
то отсюда следует, что давление в широких местах трубки
больше, чем в узких. В местах
сужения трубки тока давление по-
понижено.
Напомним, что под давлением
р подразумевается величина, чи-
численно равная силе /, действующей
нормально на некоторую площадку,
деленной на величину этой пло-
площадки AS.
Выделим из текущей струи не-
некоторую определенную массу Д/я
жидкости, протекающую сперва че-
через сечение трубки тока ASi, a
затем через сечение ASa (рис. 93). Скорость жидкости в месте
сечения ASj обозначим через vt и давление — через pit а скорость
и давление в месте сечения ASa — соответственно через п9 и Pi-
Предположим еще, что трубка тока расположена не горизонтально,
но под некоторым наклоном; обозначим высоту, на которой распо-
расположено сечение ASi, через hit а высоту, на которой лежит сечение
AS3, — через Аа. При протекании массы жидкости Д/я совершается
некоторая работа, так как на эту массу жидкости действует сила,
обусловленная наличием в жидкости давления р.
Пусть Et — полная энергия массы жидкости Д/я в том месте, где
она протекает через сечение ASi, а Ег— полная энергия массы
жидкости Д/я в том месте, где она протекает через сечение AS8.
По закону сохранения энергии изменение энергии ?а—Ех равняется
работе внешних сил, перемещающих массу Д/я от сечения kst к се-
сечению ASa:
Е, — Е1=А. A)
Энергии ?", и ?, складываются из кинетических и потенциальных
энергий массы жидкости Д/я:
Рис. 93. Трубка тока жидкости.
4т • v\
/я •
а == —s-s -4- Д/ге •
142 ДВИЖЕНИЕ ЖИДКОСТИ [ГЛ. VI
Нетрудно убедиться в том, что работа А совпадает с работой,
совершаемой при перемещении всего участка жидкости, заключен-
заключенного между сечениями AS4 и Д52, в течение такого времени At, за
которое через эти сечения будет перенесена масса жидкости Am.
Для перенесения массы Am в месте расположения первого сечения
жидкость должна сдвинуться на отрезок Al1 = viAt, а в месте рас-
расположения второго сечения — на отрезок Д/4 = v^At. Силы, действую-
действующие на оба конца выделенного участка жидкости, соответственно
равны fi=Pi&Si и /j = — p^ASi- Первая сила положительна, так
как она направлена в сторону течения жидкости; вторая отрица-
отрицательна, так как она представляет собой силу, действующую на рас-
рассматриваемый участок со стороны жидкости, находящейся правее
сечения, и, следовательно, направленную в сторону, противоположную
течению жидкости. Окончательно находим
А =ЛД/, +/аД/а=p1ASivlM — p^AS^At
Подставляя найденные значения Е1г Et и А в A), получим
m2'"* + Am • ghi ^± — Am • gkl = p1kS1vlM —ptbSiViM,
или
^i -f Д т ¦ gh, + Pi bS^M = ^i + Am ¦ ght + p^S^M B)
По закону неразрывности струи объем, занимаемый массой жидко-
жидкости Am, остается постоянным:
Деля правую и левую части равенства B) на этот объем AV и эа-
мечая, что AmjAV есть плотность жидкости р, получим
% ^ C)
Это уравнение было впервые выведено выдающимся физиком
и математиком, петербургским академиком Даниилом Бернулли
A700—1782) во время его работы в России. Оно называется уравне-
уравнением Бернулли.
Для трубки тока, расположенной горизонтально (fe1 = Ai), уравне-
уравнение Бернулли дает:
!? + л = Й. + А. (За)
Из формулы (За) и теоремы о неразрывности струи видно, что
при течении жидкости по горизонтальной трубе, имеющей различные
сечения, скорость жидкости больше в местах сужений, давление же
§ 40} ДВИЖЕНИЕ ИДЕАЛЬНОЙ ЖИДКОСТИ. ЛИНИИ И ТРУБКИ ТОКА 143
больше в широких местах. Последнее можно продемонстрировать,
установив вдоль трубы ряд манометрических трубок а, Ъ, с (рис. 94).
Высота уровня жидкости в этих трубках
измерит давление р в трубе. В соответ-
соответствии с законом Бернулли, опыт пока-
показывает, что в манометрической трубке
Ь, прикрепленной к узкой части трубы,
уровень жидкости ниже, чем в маноме-
манометрических трубках, прикрепленных к ши-
широким частям трубы.
Если в поток жидкости поместить неподвижную манометрическую
трубку, загнутую нижним концом против потока („трубка Пито",
рис. 95), то линии тока изменятся вблизи такой
трубки. Скорость жидкости перед отверстием
будет равна нулю. Применяя к этому случаю
формулу (За) и полагая г».2 = 0, получим
Рис. 94. Зависимость давле-
давления от ширины трубки.
Рис.
95. «Трубка
Пито".
воздух
Манометрическая трубка с отверстием, обра-
обращенным навстречу потоку, измерит давление рг,
которое, как видно, больше давления pt на вели-
величину ^*-. (Давление рх измерил бы манометр, движущийся вместе
с потоком.) Зная plt по измерению р% можно найти скорость потока
¦»!• Величину ~?- иногда называют „динамическим
давлением*.
В узких частях трубки при больших скоростях
течения давление р может стать отрицательным.
В этом случае жидкость, протекающая по узким
частям трубки, находится в состоянии всесто-
всестороннего растяжения. Если давление в широкой
части трубки атмосферное, то в узкой части оно
меньше атмосферного. Струя будет тогда оказы-
оказывать засасывающее действие. На этом засасываю-
засасывающем действии суженной струи основана работа
целого ряда приборов, например, пульверизатора
и водоструйного насоса. Схема водоструйного
насоса представлена на рис. 96. Вытекающая с
большой скоростью вода из суженного конца
трубки А засасывает пузырьки воздуха и увле-
увлекает их с собою.
При помощи уравнения Бернулли можно найти скорость истече-
истечения жидкости из отверстия. Если сосуд широкий, а отверстие мало
(рис. 97), то скорости жидкости в сосуде малы и весь поток можно
Рис. 96. Водоструй-
Водоструйный насос.
144 ДВИЖЕНИЕ ЖИДКОСТИ [ГЛ. VI
рассматривать как одну трубку тока. Давление как в верхнем сече-
сечении (у поверхности АВ), так и в нижнем сечении (у отверстия а)
равно атмосферному р0. Поэтому уравнение Бернулли C) прини-
принимает вид:
^ + ^-й2) = §. C6)
Если мы рассмотрим случай вытекания струи при скорости г»! = О
и положим hx — А4 = h (рис. 97), то получим
т. е. скорость, приобретаемая струей при стекании с высоты h,
равна скорости, приобретаемой телом, свободно падающим с той же
высоты.
§ 41. Применение закона сохранения количества движения
к текущей жидкости. К любому объему текущей жидкости, как и
ко всякому другому движущемуся телу, применим закон сохранения
количества движения (§ 20). Если количество движения объема
жидкости изменяется на величину AK = /ra^v, то одновременно у
другого объема жидкости или у твердого тела,
с которым жидкость соприкасается, должно
произойти изменение количества движения
на величину ДК' = —ДК- К движению жид-
жидкости применим также и закон сохранения
момента количества движения (§ 37).
j^ Применение этих законов позволяет ре-
*%?- шать ряд вопросов, например вопрос о реак-
„ ., „ ^ ции текущей жидкости на стенки сосуда.
Рис. 97. Вытекание струи -^ J J
из бокового отверстия. Если СТРУЯ жидкости вытекает из от-
отверстия а в сосуде (рис. 97), то скорость
ее возрастает и она приобретает некоторое количество движения.
Если внешние силы отсутствуют, то общее количество движения
системы сосуд—жидкость должно остаться неизменным. Поэтому
сосуду будет передано количество движения, численно равное
количеству движения, приобретенному струей. Сосуд должен
прийти в движение в направлении, обратном движению жидкости
в струе. Действительно, если сосуд поставить на тележку, чтобы
он мог свободно перемещаться, то при вытекании струи сосуд с те-
тележкой начнет двигаться в направлении, противоположном направле-
направлению вытекания струи.
Реакция вытекающей струи используется в качестве движущей
силы в реактивных снарядах и реактивных двигателях.
На законе сохранения количества движения основано также дей-
действие гребных винтов. Винт парохода вызывает движение воды на-
назад, причем струи отброшенной винтом воды приобретают некото-
некоторое количество движения. По закону сохранения количества движе-
§ 41] ПРИМЕНЕНИЕ ЗАКОНА СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ 145
ния равное количество движения приобретает пароход. На том же
принципе действует пропеллер самолета, отбрасывающий назад струю
воздуха; воздух при этом с механической точки зрения может рас-
рассматриваться как жидкость (сжи-
(сжимаемая).
Количество движения есть вели-
величина векторная, поэтому изменение
количества движения некоторого
объема жидкости имеет место не
только когда скорость жидкости
меняется по численному значению,
но и когда она меняется по наира- ,. л„ ,,, ' ~
г Рис. 98. Жидкость, текущая по изо-
влению. гнутой трубе, действует на трубу
При течении жидкости по изо- с силой реакции F1.
гнутой трубе (рис. 98) с постоян-
постоянной по численному значению скоростью v, количество движения
любого объема жидкости непрерывно меняется за счет загибания
трубок тока жидкости. За время At через некоторое сечение Si
трубы переносится масса жидкости т = pSji/^, где р — плотность
жидкости, а 7», — численное значение ее скорости.
Количество движения этой массы жидкости равно
здесь Vj — вектор скорости жидкости, протекающей через сечение 5,.
У второго сечения трубы S2 количество движения той же массы
жидкости равно
Кз = pSaT/a • v2 At.
Пусть сечение трубы постоянно: Si^S<j = .S, тогда v1 = г»а = г»
и для изменения количества движения получим
ДК = К2 — K1 = pSv(v, — v,)A*. A)
Это изменение количества движения: должно равняться импульсу
сил, действующих на жидкость со стороны стенок трубы. Обозна-
Обозначая суммарную силу, действующую на жидкость, через F; имеем
по A):
F • Дг = ДК = pSv (v, — v,) Д*.
откуда
F = pS*(v, —v,). B)
По третьему закону Йьютона сила F', численно равная F, но на-
направленная в противоположную сторону, будет действовать со сто-
стороны текущей жидкости на стенки трубы.
Таким образом, жидкость, текущая по изогнутой трубе, дей-
действует на трубу с силон реакции F" (рис. 98), направленной в сто-
сторону, противоположную направлению изгиба трубы.
6 С. Э. Фриш и А. В. Тиморева
146 ДВИЖЕНИЕ ЖИДКОСТИ [ГЛ. VI
Реакция текущей жидкости на стенки изогнутой трубы исполь-
используется в водяных и паровых турбинах. Струя жидкости или пара,
протекая по искривленным каналам колеса турбины, создает силы
реакции, момент которых и вызывает вращение колеса турбины.
В других конструкциях поток жидкости или пара вытекает из
неподвижной трубы и попадает на лопатки колеса турбины. Лопатки
отклоняют поток жидкости или пара, в результате чего поток изме-
изменяет свое количество движения. Сила реакции, действующая при
этом на лопатки, вызывает вращение колеса турбины. Момент сил
будет наибольшим, когда поток жидкости или пара сильнее всего
меняет свое количество движения. Поэтому лопаткам колеса турбины
придают такую форму, чтобы поток, протекая около лопаток (без
удара о них), по возможности сильно терял свою скорость.
Реакция вытекающей струи используется в качестве движущей
силы при реактивном движении, например, в ракетах или ракетных
снарядах. В камере ракеты происходит
сгорание взрывчатой смеси. Образующиеся
при этом газы вытекают через специаль-
специальное сопло а в задней части снаряда (рис. 99).
Благодаря большой скорости вытекания,
Рис. 99. Реактивный снаряд, количество движения, приобретаемое га-
газами, велико. Равное количество движе-
движения, направленное в противоположную сторону, приобретает ракета,
что и вызывает ее движение вперед.
Для сообщения скорости ракете не требуется взаимодействия
с другими телами или окружающей средой. Поэтому ракета может
двигаться и в безвоздушном пространстве.
Пионером применения реактивного движения был выдающийся
советский изобретатель К. Э. Циолковский A857—1935), давший не
только основы расчета реактивного движения, но и конструкции ра-
ракет для исследования высоких слоев атмосферы и космических про-
пространств.
Современные искусственные спутники Земли и космические ракеты
выводятся на орбиту с помощью многоступенчатых ракет, так как
в случае одноступенчатой ракеты была бы слишком велика масса,
которой надо сообщить космическую скорость. Принцип многосту-
многоступенчатой ракеты был впервые выдвинут К. Э. Циолковским. Ракета
использует химическое топливо, причем каждая ступень ракеты имеет
свои баки для горючего и окислителя. Рассмотрим схему движения
трехступенчатой ракеты. Сперва происходит сгорание топлива в
двигателе первой ступени, при этом приводится в движение вся ра-
ракета, как целое. Когда топливо первой ступени оказывается исполь-
использованным, она отделяется и дальнейший, полет ракеты продолжается
за счет работы двигателя второй ступени. По окончании работы дви-
двигателя второй ступени она отделяется в свою очередь и полет про-
продолжает одна третья ступень, масса которой значительно меньше,
§ 41] ПРИМЕНЕНИЕ ЗАКОНА СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ 147
чем масса всей ракеты. Вследствие этого ускорение последней сту-
ступени, при той же реактивной силе, значительно больше и она может
достичь большей скорости.
Наряду с указанным ракетным принципом в настоящее время
используется другой принцип реактивного движения, применяемый в
так называемых воздушно-реактивных двигателях. Схема пульсирую-
пульсирующего воздушно-реактивного двигателя представлена на рис. 100.
В головной части двигателя рас-
расположен диффузор А, служащий
для засасывания воздуха. Посту-
Поступающий через диффузор воздух
проходит через систему клапанов D
и попадает в камеру сгорания В. Рис Ю0. Воздушно-реактивный дви-
Топливо вбрызгивается в камеру гатель.
сгорания через форсунки а и Ь;
клапаны при начале сгорания закрываются. Сгорая, топливо нагревает
воздух, и смесь этого воздуха и газов, образовавшихся при сгорании
топлива, вырывается через сопло двигателя С с большой скоростью.
Общее количество движения струй, поступающих в двигатель и вы-
выходящих из него, возрастает. По закону сохранения количества дви-
движения сам двигатель приобретает количество движения, направленное
вперед и равное увеличению количества движения струй.
В современных авиационных реактивных двигателях воздух, под-
поддерживающий сгорание топлива, нагнетается специальными насосами.
Насос приводится в движение турбиной, действующей за счет струи
газа, вытекающего из камеры сгорания. Реактивное действие струи
создает полезную тягу двигателя. Такой двигатель носит название
турбореактивного. Авиационный турбореактивный двигатель отли-
отличается от простого реактивного двигателя, употребляемого на ракете,
тем, что в нем для сгорания топлива используется кислород атмо-
атмосферного воздуха, а не окислитель, который наряду с горючим несет
в своих баках ракета. Благодаря этому общая масса горючего для
турбореактивного двигателя значительно меньше, чем для реактив-
реактивного. Это преимущество турбореактивного двигателя делает его более
пригодным для самолетов, чем простой реактивный двигатель. Однако,
турбореактивный двигатель не может работать на очень больших
высотах, где плотность атмосферы слишком мала. Он не пригоден
для полетов, выходящих за пределы земной атмосферы.
Большое практическое значение для расчета движения ракет имеют
работы И. В. Мещерского A859—1935), впервые разработавшего теорию
движения тел, масса которых меняется со временем в результате присоеди-
присоединения или отделения от тела масс. И. В. Мещерский показал, что для тела
переменной массы т, движущегося поступательно, имеет место следующее
уравнение движения:
d , ~ , dmt dm2 ,~ч
_(fflv) = F + _L.Vl__JL.Vlf C)
6*
148 ДВИЖЕНИЕ ЖИДКОСТИ [ГЛ. VI
где V —скорость тела, F — главный вектор внешних сил, mt—масса, при-
присоединяющаяся к телу, та — масса, отделяющаяся от тела, vr и v2 — скорости
этих масс. В случае если Vi и v2 равны нулю, это уравнение переходит
в следующее:
которое эквивалентно системе уравнений (8а) § 20.
При изучении реактивного движения (когда имеются только отделяю-
отделяющиеся массы) удобно уравнение C) преобразовать к виду:
mw = F + — . (v — v2),
где w—ускорение тела.
Это последнее соотношение показывает, что тело переменной массы
удовлетворяет обычному уравнению движения, если к главному вектору
м
7^'
внешних сил прибавить член -— • (v — Va), равный произведению относитель-
относительной скорости тела и выбрасываемой массы v —v2 на производную от выбра-
выбрасываемой массы по времени.
§ 42. Движение вязкой жидкости. Во всех реальных жидкостях
при перемещении одних слоев относительно других возникают более
или менее значительные силы трения. Со стороны слоя, движущегося
более быстро, на слой, движущийся медленнее, действует ускбряю-
щая сила. Наоборот, со стороны слоя,
движущегося медленнее, на более быстрый
слой действует задерживающая сила. Эти
силы, носящие название сил внутреннего
трения, направлены по касательной к по-
поверхности слоев. Величина силы внутрен-
-и, него трения / тем больше, чем больше
площадка AS поверхности слоя, которую
уУ- ; —X мы рассматриваем, и зависит от того,
„ ,„, п насколько быстро меняется скорость те-
Рис. 101. Возникновение сил v
внутреннего трения. чения жидкости v при переходе от слоя
к слою. Пусть два слоя (рис. 101), от-
отстоящих друг от друга на расстоянии Дг, текут соответственно со
скоростями г/j и в2. Положим г»! — v$ = Av. Направление, в котором
отсчитывается расстояние между слоями Дг, перпендикулярно к ско-
скорости течения слоев. Величина Av/Az, которая показывает, как быстро
меняется скорость при переходе от слоя к слою, носит название
градиента скорости. Сила внутреннего трения / пропорциональна
градиенту скорости, так что
/=¦4^. AS. A)
Величина i\, зависящая от природы жидкости, называется коэф-
коэффициентом внутреннего трения или коэффициентом вязкости
жидкости. Чем больше коэффициент вязкости, тем сильнее жид-
§ 42]
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
149
кость отличается от идеальной, тем ббльшие силы внутреннего
трения в ней возникают.
Размерность коэффициента вязкости, как легко видеть, равна
L~XMT~X. Таким образом, в CGS-системе вязкость измеряется в
см г сек'1. Эта единица вязкости называется пуазом в честь
французского ученого Пуазейля.
Вязкость жидкости весьма сильно зависит от температуры: она
уменьшается с повышением температуры. Так, вязкость воды при 0° С
равна -rjo = 0,01775 см'1 г сек'1, а при 90°С равна т]90 —
= 0,00320 см'1 г сек'1. Особенно сильно зависит от температуры
вязкость масел; например, вязкость касторового масла при повыше-
повышении температуры от 18° до 40° С падает почти в четыре раза. Ниже
приведены значения коэффициентов вязкости для некоторых жид-
жидкостей:
Жидкость
Вода
Ртуть
Эфир
Глицерин
Т-
1,8
1,7
0,29
46
Коэффициент вязкости
= 0°С
• 10"-
¦ 10
Т =
1,1
1,6
0,25
15
15° С
10"°
10
10
у] в пуазах
Г = 99°С
0,29 ¦ 10
1,2 ¦ 10
Течение газов может также рассматриваться как течение жид-
жидкости, однако, во-первых, коэффициент вязкости у газов гораздо меньше и,
во-вторых, нужно учитывать сжимаемость газов. С увеличением тем-
температуры вязкость газов не падает, как у жидкостей, а несколько
возрастает, как это видно из следующей таблицы:
Газ
Водород
Водяной пар
Воздух
Аргон
Коэффициент вязкости у в пуазах
Г = 0°С
86 • 10-»
90 • 10"»
171 • 10-"
210 ¦ 10"в
Г=15°С
89 • Ю-"
97 • 10-»
181 ¦ 10"»
221 • 10-°
Г = 99° С
106 • 10-"
131 • 10-"
220 • 10-°
П. Л. Капицей было открыто, что жидкий гелий при температуре
около —271°С переходит в особое состояние „сверхтекучести",
при котором вязкость его практически равна нулю. Наблюдения над
движением гелия, находящегося в состоянии сверхтекучести, через
тонкие капилляры и щели показали, что, во всяком случае, его вяз-
вязкость меньше 10~и пуаза. Жидкий гелий, перешедший в состояние
сверхтекучести, носит название „гелия II". Переход из обычного ге-
150 ДВИЖЕНИЕ ЖИДКОСТИ [ГЛ. VI
лия („гелия I") в гелий II представляет собой так называемый фазо-
фазовый переход второго рода, когда некоторые свойства (например,
вязкость) меняются скачкообразно, а другие (например, упругость
пара) меняются постепенно. В состояние сверхтекучести переходит
лишь основной изотоп гелия Не4.
Сверхтекучесть ведет к появлению других специфических явле-
явлений: при наличии температурных градиентов в жидком гелии возни-
возникают весьма интенсивные потоки. При температуре в 2,19° К гелий
представляет собой смесь сверхтекучей и нормальной модификаций,
которые могут течь навстречу друг другу.
С явлением сверхтекучести связано существование так называе-
называемого термомеханического эффекта, заключающегося в том, что
возникающее вдоль узкой щели или капилляра падение температуры
вызывает появление дополнительной разности давлений. Так, если
погрузить в гелий 11 капилляр и нагревать его верхний конец, то из
капилляра начнет бить фонтан. Поэтому эффект, вызванный термо-
термомеханическим воздействием, называется также эффектом фонтани-
фонтанирования.
Гидродинамическая теория сверхтекучести наиболее подробно раз-
развита советским физиком Л. Д. Ландау. В этой теории каждому эле-
элементу объема жидкости сопоставляются два вектора скорости: вектор
сверхтекучего и вектор нормального движения. Таким образом, пред-
предполагается, что гелий при очень низких температурах представляет
собой смесь двух жидкостей, могущих двигаться независимо друг от
друга. Одна из этих жидкостей (сверхтекучая) не обладает трением
и может проникать в тончайшие зазоры и протекать через самые
узкие капилляры. Так, П. Л. Капица наблюдал весьма быстрое про-
протекание сверхтекучего гелия между двумя плоско-параллельными
пластинками, зазор между которыми имел толщину в 5 • 10~в см.
Другая составляющая гелия представляет собой нормальную жид-
жидкость, которая обладает заметной вязкостью и не может течь сквозь
узкие капилляры и щели.
Теорией Ландау было предсказано еще одно новое явление — рас-
распространение тепловых волн. Это явление было экспериментально
наблюдено и изучено В. П. Пешковым и получило название второго
звука в гелии II.
Рассмотренное нами течение жидкости носит название ламинар-
ламинарного (по-латыни — слоистого), так как слои жидкости как бы сколь-
скользят друг относительно друга. При движении жидкости по трубе
с увеличением скорости течение теряет ламинарный характер и ста-
становится беспорядочным. Возникают составляющие скорости, перпен-
перпендикулярные к оси трубы. В каждой точке жидкости происходят
беспорядочные отклонения вектора скорости от его среднего значе-
значения. Такое движение носит название турбулентного. Переход от
ламинарного к турбулентному движению в трубах или каналах ведет
к резкому возрастанию сопротивления.
§ 42] ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ 151
При обтекании вязкой жидкостью тел с увеличением скорости
течение меняет свой характер и становится завихренным. Поток
жидкости, отрывающийся от поверхности обте-
обтекаемого тела, распадается на отдельные вихри.
Вихри, образующиеся позади тела (рис. 102),
уносятся потоком и постепенно затухают.
Уравнение Бернулли, строго говоря, непри-
неприменимо к вязким жидкостям, так как часть
энергии внутри трубки тока превращается, "*"" ^
в результате работы сил трения, в тепло. Однако рис Ю2 Образование
практически уравнение Бернулли неприменимо вихрей,
лишь к весьма вязким жидкостям. Для такой
жидкости, как вода, уравнение Бернулли практически выполняется
достаточно точно.
Роль трения характеризуется безразмерной величиной, называемой чис-
числом Рейнольдса R:
где /—линейные размеры, характерные для рассматриваемого течения жид-
жидкости. В случае течения жидкости по трубе / — радиус трубы, v—средняя
скорость. Отношение к]/р называется кинематическим коэффициентом вяз-
вязкости.
Для того чтобы пояснить роль числа Рейнольдса, рассмотрим элемент
объема жидкости с длиной ребра I. Кинетическая энергия этого объема
равна
Ek = L" l\
Сила трения, действующая на элемент объема жидкости, пропорциональна
его поверхности I2, коэффициенту вязкости т\ и градиенту скорости. Полагая,
что скорость падает до нуля на расстоянии, равном по порядку величины /
(в случае течения по трубе —в радиальном направлении), получим, что гра-
градиент скорости равен v/l. Таким образом, сила трения
Работа этой силы на пути / равна:
A =ft = грр.
Роль трения при течении жидкости мала, если работа А мала по сравнению
с кинетической энергией объема жидкости Ek, т. е. если выполняется нера-
неравенство:
Но -— = R есть число Рейнольдса. Таким образом, роль сил трения при
течении жидкости мала при больших числах Рейнольдса.
152
ДВИЖЕНИЕ ЖИДКОСТИ
[гл/vb
При течении жидкости по трубе переход от ламинарного к турбулент-
турбулентному движению происходит при значении числа Рейнольдса, называемом
критическим. Для течения воды по трубе RKpKal200.
Рассмотрим явления, возникающие при движении тела в жидкости.
Вместо того чтобы считать тело движущимся, а жидкость неподвиж-
неподвижной, можно ставить обратную задачу: рассматривать обтекание не-
неподвижного тела равномерным потоком жидкости. Первоначально
будем считать жидкость идеальной,
т. е. лишенной вязкости. Пусть
тело представляет собой бесконеч-
ный круговой цилиндр, ось кото-
рого перпендикулярна к невозму-
щенным линиям тока (рис. 103).
б
(
Линии тока обходят цилиндр сим-
метрично с двух сторон. В точках
А и D скорость жидкости равна
нулю. У точек В и С линии тока
сгущаются и здесь скорость жид-
Рис. 103. Обтекание неподвижного больше, чем в невозмущен-
тела равномерным потоком невязкой *ичи иилошс, с j
жидкости. н°м потоке. Поэтому давление
в точках А и D будет больше
статического давления в жидкости р, а в точках В и С — меньше.
Если v есть скорость в невозмущенном потоке, то по уравнению
Бернулли [формула (За), § 40] давление в точке А равно
так как скорость жидкости у поверхности тела в точке А мы счи-
считаем равной нулю (vA=0). Таким образом, давление в точке А
больше статического давления р. Такое же увеличенное давление
будет и в точке D. На первый взгляд может показаться, что в
точке D давление должно быть меньше р, но это неверно. В самом
деле, вблизи точки А в потоке скорость частиц жидкости умень-
уменьшается, следовательно, на частицы жидкости действует сила, напра-
направленная влево, а на тело, по третьему закону Ньютона, в точке А
действует сила, направленная вправо. Вблизи точки D скорость
частиц жидкости возрастает, следовательно, на них действует сила,
направленная вправо, а на тело в точке D действует сила, направлен-
направленная влево.
Рассмотрим теперь давление на тело в точке В. Для его опре-
определения надо знать скорость жидкости вблизи поверхности тела
в этом месте. Считая, что на расстоянии, равном примерно радиусу
цилиндра, поток остается невозмущенным, получим, что скорость
vB=2v и тогда по уравнению Бернулли:
=p-\-v-ji откуда находим рв — Р ^Г '
JOf Ш] ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ 153
Давление в точке В оказывается меньше статического давления р.
Такое же давление будет в точке С. Как видно, уменьшение давле-
давления в точках В а С больше, чем увеличение давления в точках А
и D. Благодаря симметрии сумма всех сил, действующих на тело со
стороны обтекающей жидкости, будет равна нулю: ?//= О- Отсюда
следует, что при движении тела в невязкой жидкости оно вовсе
не должно испытывать сопротивления.
При движении тела в вязкой среде возникает сопротивление.
Происхождение этого сопротивления двояко. При малых скоростях
и удобообтекаемой форме тела, когда не возникает вихрей, сила со-
сопротивления непосредственно обусловлена вязкостью жидкости. Слой
жидкости, непосредственно прилегающий к твердому телу, прилипает
к его поверхности и увлекается им полностью. Следующий слой
увлекается за телом с меньшей скоростью. Таким образом, между
слоями возникают силы трения.
В этом случае сила сопротивления по закону, установленному
Стоксом, прямо пропорциональна первой степени скорости, коэф-
коэффициенту вязкости и линейным размерам тела.
Для шаров, движущихся в вязкой жидкости, по закону Стокса
сила сопротивления:
/= бщп, B)
где т) — коэффициент вязкости жидкости, г — радиус шара, v — ско-
скорость его движения.
По формуле Стокса B) можно определить скорость установивше-
установившегося падения шара в вязкой жидкости. Тяжелый шар в вязкой жид-
жидкости лишь в самый первый момент начнет падать ускоренно; по
мере же возрастания скорости его падения возрастает и сила тре-
трения /, которая начинает уравновешивать силу тяжести Р, действую-
действующую на шар. Когда такое уравновешивание сил достигнуто, шар
падает равномерно с постоянной скоростью v, определяемой по фор-
формуле B) условием:
C)
Сила Р, действующая на шар, находящийся в жидкости, по за-
закону Архимеда равна Ро — Pv где Ро — действительный вес шара,
а Ръ — вес жидкости в объеме шара, отсюда Р=Р0 — Рг =
= (р— р') g • -=¦ тег3, где р — плотность шара, а р'-—плотность жид-
о
кости. Подставляя это значение Р в C), найдем
Из формулы D) видно, что скорость падения шара в вязкой жид-
жидкости пропорциональна квадрату его радиуса г. Чем меньше шар,
тем медленнее он падает в данной жидкости. Формула Стокса при-
154 движение жидкости [гл. vi
менима не только к падению шаров в жидкости, но и к падению
маленьких шариков в газовой среде, которую в этом случае можно
рассматривать как вязкую жидкость. Так, скорость падения в воздухе
мелких капелек тумана весьма хорошо определяется формулой D).
При характеристике обтекания шара вязкой жидкостью с помощью
числа Рейнольдса под v подразумевается' относительная скорость потока на
бесконечном удалении от шара, а под длиной / — диаметр шара. Закон
Стокса выполняется при малых значениях числа Рейнольдса.
Для динамического подобия обтекания жидкостью разных твердых тел
необходимо равенство чисел Рейнольдса. При моделировании движения ко-
кораблей, самолетов и т. д., при уменьшенных размерах модели (/2 < /i), если
коэффициент вязкости жидкости в модели и в натуре одинаков, скорость
потока в модели должна быть больше: «2>«i. Для того чтобы не перехо-
переходить к слишком большим скоростям на моделях, следует брать жидкость
с меньшим значением кинематического коэффициента вязкости.
Второй механизм сил сопротивления в вязкой жидкости, о кото-
котором было упомянуто, связан с образованием вихрей. Часть работы,
совершаемой при движении тела в жидкости, идет на образование
вихрей. Энергия вихрей, благодаря наличию внутреннего трения
п жидкости, в конечном счете переходит в тепло. При малых ско-
скоростях вихри не образуются, и сопротивление, испытываемое телом,
относительно мало. При увеличении скорости начинают образовы-
иаться вихри, и тогда сила сопротивления резко возрастает. При
постройке судов и самолетов весьма существенно придать им такую
обтекаемую форму, при которой вихри, по возможности, не обра-
образуются. Сила сопротивления, обусловленная образованием вихрей, при
не очень больших скоростях пропорциональна квадрату скорости.
При скоростях, близких к скорости звука в данной среде, она про-
пропорциональна кубу скорости, а при
сверхзвуковых скоростях пропорцио-
пропорциональна квадрату скорости.
В случае обтекания невязкой жид-
жидкостью несимметричного тела, сумма
сил, приложенных к телу со стороны
jжидкости, не будет равна нулю. Рас-
смотрим для простоты тело в виде
бесконечно длинного полуцилиндра
Рис. 104. Обтекание невязкой /рИС 1Q4) в этом случае линии тока
ГаИ^ГаНси™%Т„РлИоЧженных параллельны плоской поверхности С,
к телу со стороны жидкости, и давление на нее равно р. Давление
не равна нулю. в точке В, по сказанному выше, меньше:
рв<^р. Поэтому возникает результи-
результирующая сила F=2/;^0; эта сила перпендикулярна к линиям тока
в невозмущенном потоке. Она не увлекает тело в направлении потока
(для идеальной жидкости), а лишь стремится его сдвинуть в направ-
направлении, неперпендикулярном к потоку.
§¦42]
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
155
При обтекании несимметричного тела вязкой жидкостью резуль-
результирующая сила F, действующая на тело со стороны потока, не пер-
перпендикулярна к линиям тока. В этом
случае ее можно разложить на две
составляющие: Fconp, направленную
вдоль потока, и Fn, направленную
перпендикулярно к потоку.
На наличии таких сил основано
Подземная
сопр
/7о/}ое
со про/mi3-
Рис. 105. Возникновение подъемной
силы крыла самолета.
действие крыла самолета. Сила F,
определяет лобовое сопротивление,
а сила Fn — его подъемную силу
(рис. 105).
Теорию подъемной силы крыла
самолета дал впервые Н. Е. Жу-
Жуковский A847—1921), основатель теоретической, технической и
экспериментальной аэродинамики, „отец русской авиации", как его
назвал В. И. Ленин.
Рассмотрим еще вопрос о ламинарном течении вязкой жидкости по трубе.
В этом случае, благодаря силам внутреннего трения, скорость течения
жидкости наибольшая в центре трубы (рис. 106). У стенок она равна нулю.
Рассмотрим участок трубы радиуса ?; и длиной
/. Пусть жидкость течет слева направо под
влиянием разности давлений pi—р2.
Вырежем в жидкости мысленно цилиндри-
цилиндрический слой (рис. 107) внутреннего радиуса г
и толщиной dr. На этот слой с внутренней
стороны действует сила внутреннего трения
dv „
Рис. 106. Вязкая жидкость
течет по оси трубы снаиболь-
шей скоростью v. ' йг
здесь S—боковая поверхность цилиндрического слоя, равная 2пг/, откуда
С наружной стороны на слой действует сила /, =f-{-df, направленная в
обратную сторону, чем сила/(сила/ускоряет слой, сила/! его задерживает).
Их сумма равна I
—fi+f=-(f+df)+f=-df.
Выражая силу / по E), имеем
Так как скорость жидкости в центре Рис. 107. В цилиндрическом слое
трубы наибольшая, то dv/dr отрицательно радиуса г жидкость течет с оди-
и сила—df положительна. Эта сила при ста- наковыми скоростями,
ционарном течении должна равняться силе,
действующей на слой, благодаря разности давлений р{ —р2; так как эта послед-
последняя сила пропорциональна площади поперечного сечения слоя S' = 2nr dr, то
(г ?_\ =
— р2), откуда d
dv\
'd-гУ
—ps
г dr.
156 движение жидкости [гл
Интегрируя это выражение, получим
vp*
Полагая г = 0 и замечая, что на оси трубы, где скорость v имеет максимум,
dv/dr также равно нулю, получим, что произвольная постоянная С = 0. От-
Отсюда получим дифференциальное уравнение, определяющее скорость течения
жидкости v как функцию расстояния от оси трубы г:
rfo==rdr.
2/1)
Интегрируя это выражение, получим
2/1 J ¦ 4/1 ^
Постоянную С получим, положив г = 7?, тогда г< = 0, откуда
i__Pi —Ра
— 4/Y|
после чего для v получаем
Эта формула дает скорость течения жидкости в зависимости от расстоя-
расстояния до оси трубы.
Теперь определим объем жидкости V, вытекающий из трубы за неко-
некоторое время t. Из цилиндрического слоя радиуса г и толщины dr (рис. 107)
за время t вытечет жидкость объемом
dV=vt ¦ 2кг dr.
Подставляя сюда вместо v его значение по F), получим
dV= -(;"~Ра)' «V - г3) dr.
Интегрируя это выражение в пределах от 0 до R, получим объем V
жидкости, вытекающей через все поперечное сечение трубы:
откуда
Формула G) носит название формулы Пуазейля; она указывает на
весьма сильную зависимость количества протекающей жидкости от радиуса
трубы (пропорционально #4). Для турбулентного движения формула Пуазейля
непригодна.
Пользуясь формулой Пуазейля можно по объему жидкости, протекающей
через трубку заданных радиуса Л и длины /, определить вязкость -ц. При-
Приборы, служащие для определения вязкости, носят название вискозимегЛров.
** ЧАСТЬ ВТОРАЯ
МОЛЕКУЛЯРНАЯ ФИЗИКА
ГЛАВА VII
ГАЗЫ
§ 43. Атомно-молекулярная теория строения вещества. Пред-
Представление о строении вещества из обособленных частиц—атомов
было высказано еще древними греками. Впервые широкое развитие
атомная гипотеза получила в трудах М. В. Ломоносова. Ломоносов
попытался построить всю физику на основе представления о том,
что химически простое вещество состоит из большого числа вполне
одинаковых обособленных частиц — атомов. В химически сложных
веществах роль обособленных частиц играют молекулы. Опираясь
на свой всеобщий закон сохранения материи и движения, Ломоносов
впервые доказал справедливость представления о непрерывном тепло-
тепловом движении атомов и молекул.
Со времен возникновения атомной теории в химии оказалось
возможным установить на основании закона простых и кратных отно-
отношений относительные веса (или, вернее, массы) атомов, т. е. числа,
которые показывают, во сколько раз масса данного атома больше
или меньше массы какого-либо другого атома. В настоящее время
имеются и физические способы (см. т. II) сравнивать массы (веса)
отдельных атомов или молекул. Относительные веса атомов назы-
называют их атомными весами А. За единицу атомного веса принята
1/16 веса атома кислорода. Таким образом, по определению, атом-
атомный вес кислорода равен 16,0000. Атомный вес самого легкого из
атомов, водорода, равен 1,0078, что означает, что атом водорода
16,0000 ч - с-„г,
имеет массу в ¦ — 15,8762 раза меньшую массы атома кисло-
кислорода. Также, например, атомный вес ртути, равный 200,61, указы-
200 61
вает, что масса атома ртути в ,„ ' = 12,538 раза больше массы
атома кислорода и в i пА^о = 199,06 раза больше массы атома водорода.'
1 В настоящее время известно, что почти для всех элементов существует
по нескольку сортов атомов, отличающихся друг от друга массой (атомным
весом). Атомы данного сорта называются изотопами данного элемента
(см. т. 11). Химические методы определения атомных весов дают средний
атомный вес естественной смеси изотопов.
ГАЗЫ [гл
Относительный вес молекулы по отношению к той же
А'
А
равна m'^m—r. Отсюда, обратно, мы заключаем: если брать
еди-
единице, равной 1/16 веса атома кислорода, называется ее молеку-
молекулярным весом (
Возьмем определенную массу, например т граммов водорода.
Атомный вес водорода обозначим через А. В этих т граммах водо-
водорода содержится определенное число атомов водорода, которое мы
обозначим через п. Возьмем другой элемент с атомным весои А'
в таком количестве, чтобы оно также содержало п атомов. Масса п
А'
атомов этого элемента, очевидно, в -г- раз больше массы п атомов
водорода. Следовательно, масса этого количества данного элемента
раз-
личные элементы в таких количествах, чтобы их массы относились
как их атомные веса, то они будут содержать по одинаковому числу
атомов.
Назовем граммапюмом такое количество данного элемента,
масса которого, выраженная в граммах, численно равна его ап'ом-
ному весу. Тогда на основании сказанного имеем: грамматом любого
элемента содержит одно и то же число атомов. Это чксло,
обозначаемое через N, называется числом Авогадро.
Назовем граммолекулой такое количество данного вещества,
масса которого, выраженная в граммах, численно равна его моле-
молекулярному весу. Так как молекулярные веса определяются по отно-
отношению к той же единице A/16 веса атома кислорода), что и атоиные
веса, то граммолекула любого вещества содержит столько моле<ул,
сколько атомов содержит грамматом. Отсюда: граммолекула любого
вещества содержит одно и то же число молекул, равное числу
Авогадро.
Граммолекулу часто называют молем. Моль представляет собой
единицу массы, имеющую особое значение для каждого данного
вещества. Так, для молекулярного водорода моль представляет собой
единицу массы, равную 2 г, а для молекулярного кислорода — рав-
равную 32 г.
В настоящее время существует большое количество споссбов,
позволяющих определить число Авогадро; с некоторыми из них мы
познакомимся ниже (§ 52), сейчас приведем численное значение
числа Авогадро:
Л/= 6,023 • 10м моль~\
Число Авогадро представляет собою число частиц в определенной
массе вещества, а именно, в одном моле, поэтому оно имеет размер-
размерность [N\=M~l и измеряется в единицах, получающих обозначе-
обозначение или моль'1.
моль
Знание, числа Авогадро дает нам представление о масш
микромира, т. е. мира атомов и молекул; оно позволяет
VH
абе
нам
§ 43] АТОМНО-МОЛЁКУЛЯРНАЯ ТЕОРИЯ СТРОЕНИЯ ВЕЩЕСТВА 159
установить, насколько мелка та зернистая структура вещества, которую
устанавливает атомно-молекулярная теория. Зная число Авогадро,
мы можем подсчитать размеры молекул и их абсолютные массы.
Возьмем 1 см3 воды; его масса 1 г, что составляет -^ моля воды;
1о
следовательно, 1 см3 воды содержит .-j-^- • 10аз = 3,34 • 1022 молекул
воды. Таким образом, в жидкой воде на долю одной молекулы
приходится объем 3 34 ^ 1QJ2 см3 ^ 3 • 10~23 см3. Считая, что в жидкости
молекулы расположены плотно друг к другу, находим, что линейные
размеры молекулы воды представляют собою величину порядка
г= |/3 • 10~аз си^З-ГО"8 см. Линейные размеры других атомов
и молекул представляют собою также величины порядка 10~8 см.
Чтобы более конкретно представить себе размеры атомов и молекул,
приведем два следующих примера: 1) если все количество атомов,
входящих в состав 1 смг меди, расположить в одну линию, то обра-
образуется цепочка длиной почти в 14 миллиардов километров, что при-
приблизительно в 90 раз превышает расстояние от Земли до Солнца;
2) электронный микроскоп позволяет наблюдать микро-кристаллы,
линейные размеры которых составляют сотые микрона. Такой микро-
микрокристалл содержит несколько сот тысяч атомов.
Несмотря на столь малые размеры атомов, современная физика
имеет методы непосредственного доказательства прерывности (как
говорят, дискретности) строения вещества и методы непосредствен-
непосредственного наблюдения отдельных атомов; последнее возможно лишь в тех
случаях, когда атомы несут достаточно большое количество энергии,
т. е. движутся с очень большими скоростями.
Массу т одной молекулы (или одного атома) можно найти из
соотношения:
* = ?. О)
где |i — молекулярный вес (для элемента — атомный вес) и N—число
Авогадро.
Из соотношения A) для массы атома водорода получается
тн= 1,675 • 10~24 г. Отсюда же находим, что единица атомного
веса, т. е. 1/16 массы атома кислорода, равна 1,662 • 10~м г. Таким
образом, для абсолютной массы любого атома имеем:
/и =1,662- КГ24- А г, B)
где А — атомный вес данного атома.
Заменив в формуле B) атомный вес А молекулярным весом ц,
получим абсолютную массу данной молекулы.
Ряд наблюдений убеждает нас, что во всяком веществе имеется
непрерывное внутреннее движение. Это внутреннее движение пред-
160 газы . [гл.
ставляет собою движение молекул, из которых состоит* данлов
вещество. Это движение молекул беспорядочно, никогда не прекра-
прекращается и зависит, как мы увидим дальше, лишь от температуры
вещества.
В наличии такого движения нас убеждает, например, следующий
опыт: если в двух сосудах А и В (рис. 108) имеются различные
газы, например, в одном сосуде водород, а в другом
азот, то через некоторое время после того, как кран С
будет открыт, в обоих сосудах окажется совершенно
равномерная смесь обоих газов. Газы сами собою пол-
полностью перемешаются. Такое перемешивание проис-
происходит и в том случае, когда водород находится в верх-
верхнем сосуде А и, следовательно, никакого стекания
водорода, имеющего меньшую плотность,'или вообще
перемешивания обоих газов под влиянием силы тя-
тяжести быть не может.
Еще более непосредственно в существовании хао- п
тического движения молекул убеждает явление, от- крывании край
ют
крывании край
крытое Броуном в 1826 г. Броун заметил, что наблю- с газы, находя-
даемые в микроскоп весьма малые частицы, взвешенные щиеся в сосудах
в жидкости, находятся в состоянии непрерывного бес- А и В, начинаю
порядочного движения; чем меньше частица, тем ^^
интенсивнее она движется. Это движение, носящее
название броуновского движения, никогда не прекращается, не зависит
ни от каких внешних причин и является проявлением внутреннего дви-
движения вещества. Движущиеся молекулы жидкости при столкновении
с каким-либо твердым телом передают ему некоторое количество дви-
движения. Если тело, находящееся в жидкости, велико, то число молекул,
налетающих на него со всех сторон, также чрезвычайно велико, их
удары в каждый данный момент компенсируются, и тело практи-
практически остается неподвижным. Но если тело достаточно мало, тачая
компенсация может оказаться неполной: случайно с одной стороны
о тело ударит заметно большее число молекул, чем с другой, в ре-
результате чего тело придет в движение. Именно такого рода движе-
движение под влиянием беспорядочных ударов молекул и совершают
броуновские частицы. Сами броуновские частицы в миллиарды раз
больше по массе отдельных молекул, их скорости весьма малы по
сравнению со скоростями молекул, но все же их движение таково,
что оно может быть замечено в микроскоп.
На рис. 109 представлены положения отдельных броуновских
частиц, отмеченные при наблюдении в микроскоп через определенные
промежутки времени. Такое же броуновское движение совершают
и частицы, взвешенные в газе.
Таким образом, вещество не только имеет зернистое строение
состоит из отдельных обособленных частиц, но оно состоит из
частиц, находящихся непрерывно в состоянии движения. Отсюда
VII
§ 44]
ЗАКОНЫ БОЙЛЯ — МАРИОТТА И ГЕЙ-ЛЮССАКА
161
теория строения вещества представляет собою молекулярно-кинети-
ческую теорию. Она впервые была развита для объяснения свойств
вещества в различных агрегатных состояниях М. В. Ломоносовым.
В дальнейшем молекулярно-
кинетическая теория при-
применялась преимущественно
для объяснения свойств ве-
вещества в его простейшем
агрегатном состоянии—га-
состоянии—газообразном. Однако раньше
чем перейти к изложению
основ молекулярно-кинети-
ческой теории, рассмотрим
те эмпирические закономер-
закономерности, которым подчиняются
газы.
§ 44. Законы Бойля —
Мариотта и Гей-Люссака.
Определение температуры.
Газы обладают тем свой-
свойством, что они целиком за-
W
А
Г
[На
1/
J
\
\
\
4-
'•&
'р
А~
У
»и
ч
ё
*
\
г*
i
¦
Vr
V
1
№
w 1
S,
If
1
\
1
\
f
\
V
•
/
9
с
4
•
f
А
Г
\
1*. s
-\
{
и
\
¦
-
Рис. 109. Местонахождения трех броуновских
частиц, отмеченные через каждые 30 сек.
полняют весь сосуд, в котором заключены, и оказывают давление
на ограничивающие сосуд стенки. Давление р представляет собою
физическую величину, численно равную силе, действующей нормально
на единицу площади. Таким образом, если сила, действующая нор-
нормально на площадь S, равна /„, то
А.
О
A)
В CGS-системе давление р измеряется в барах — единицах, равных
давлению силы в 1 дину на перпендикулярную к силе площадку в 1 см\
В международной системе единиц за единицу давления при-
принимается давление, вызываемое силой в 1 ньютон на перпендику-
перпендикулярную к ней поверхность площадью в 1 м1. Эта единица обозна-
обозначается «/ла; очевидно, 1 «Дм* =10 бар. Кроме того, для измерения
давления употребляются еще следующие единицы: 1) техническая
атмосфера, равная давлению силы в 1 кГ на 1 см\ 2) физическая
атмосфера (сокращенно am), равная давлению 1,033 кГ/см?; 3) мил-
миллиметр ртутного столба (сокращенно мм Hg), равный давлению,
оказываемому весом ртутного столба высотой в 1 мм. Давление
760 мм Hg равно одной физической атмосфере. Для перевода этих
единиц друг в друга можно пользоваться следующим соотношением:
1 фаз. ат= 1,033 техн. <ш=1033 Г/о^ = 760 мм Hg =
= 1033-981 бар= 1,013 • 106 бар.
Некоторое количество газа характеризуется следующими четырьмя
величинами: 1) его массой т, 2) занимаемым им объемом V, 3) да-
162
ГАЗЫ
[ГЛ. VII
I'const
влением р, 4) температурой t. Все эти величины зависят друг от
друга; при изменении одной из них, вообще говоря, меняются все
остальные. Формула, закономерно связывающая все эти величины,
называется уравнением состояния.
Прежде чем дать выражение для общего уравнения состояния
газа, приведем более простые эмпирические закономерности, относя-
относящиеся к случаю, когда две из указанных четырех величин поддер-
поддерживаются постоянными.
Для данной массы газа при постоянной температуре (т и t
постоянны) давление газа меняется обратно пропорционально
его объему (закон Бойля — Мариотта):
pV= const (при данных т и t). B)
Графически зависимость р от V для данной массы газа т при
постоянной температуре t выражается равнобокой гиперболой
(рис. ПО). Так как кривая, изображающая
закон Бойля — Мариотта, относится к по-
постоянной температуре, то она носит на-
название изотермы.
Закон Бойля—Мариотта является при-
приближенным, как это уже отмечалось в § 2.
Так, все газы при очень больших давлениях
сжимаются меньше, чем это следует из закона
Бойля — Мариотта. Однако большинство га-
газов при температурах, близких к комнатным,
и давлениях, не слишком отличающихся от
атмосферного, подчиняются закону Бойля —
Мариотта с достаточно большой точностью.
Следующие закономерности, о которых будет идти речь, связы-
связывают давление или объем газа с его температурой. Однако прежде
надо установить, каким образом измеряется сама температура. Нагре-
Нагревание или охлаждение тел, т. е. изменение их температуры, влияет
почти на все их физические свойства: меняются линейные размеры
тел, изменяются их упругие свойства, их электропроводность и т. д.
Любое из этих изменений может быть использовано для измерения
температуры. Исторически, как известно, установился метод изме-
измерения температур по изменению объема ртути с помощью так назы-
называемых ртутных термометров. Однако обычно описываемый способ
градуировки ртутного термометра, который сводится к делению
шкалы на равные части, наперед предполагает, что объем ртути
меняется с температурой t линейно. Если мы заполним термометр
другой жидкостью и совместим для него две точки с двумя какими-
либо точками ртутного термометра (например, точку „О", соответ-
соответствующую температуре таяния льда, и точку „100", соответствующую
температуре кипения воды), а затем также разделим шкалу на равные
части, то показания такого термометра для средних температур
¦V
Рис. 110. Изотерма
Бойля — Мариотта.
§ 44] ЗАКОНЫ БОЙЛЯ — МАРИОГГА И ГЁЙ-ЛЮССАКА 163
разойдутся (хотя и незначительно) с показаниями ртутного термометра.
Таким образом, установленная шкала температур окажется зависящей
от того тела („термометрического" тела), по изменению объема кото-
которого мы измеряем температуру. Так как выбор самого тела (факти-
(фактически ртути) случаен, то случайна и сама шкала температур. Не имея
пока никакой теоретической основы для выбора термометрического
тела, мы все же можем считать, что и качестве термометрического
тела следует выбрать такое тело, которое в остальных своих свой-
свойствах подчиняется наиболее простым закономерностям. В качестве
такого тела может быть выбран газ, наиболее хорошо подчиняющийся
закону Бойля — Мариотта. По соглашению Международного комитета
мер и весов в 1877 г. в качестве термометрического тела был выбран
водород, и было решено измерять температуру с помощью водород-
водородного термометра, считая изменение температуры пропорциональ-
пропорциональным изменению давления водорода, объем которого поддерживается
при его нагревании или охлаждении постоянным.
Таким образом, постулируется, что давление водорода меняется
линейно с температурой:
а<). C)
где pt — давление водорода при температуре t, рй — его давление
при температуре нуль и а — постоянный коэффициент. Равенство C),
отнесенное к водороду, служит определением шкалы температур
(так называемой эмпирической шкалы температур). Если положить
температуру таяния льда равной 0°, а температуру кипения воды при
атмосферном давлении 100° (шкала Цельсия), то коэффициент а имеет
численное значение о_ , 6- = 0,0036613 град'1.
ZIо, [о
Установив способ измерения температур, мы можем поставить
вопрос: как для всех газов зависят их давление и объем от температуры?
Эти зависимости даются эмпирическими законами Гей- Лю с сака.
1. Давление данной массы газа при постоянном объеме меняется
линейно с температурой:
2. Объем данной массы газа при постоянном давлении меняется
линейно с температурой:
V,= Ve(l+M). E)
Коэффициент ар называется термическим коэффициентом давления,
о.у-—термическим коэффициентом объемного расширения. Для всех
газов соотношения D) и E) выполняются приближенно [кроме водо-
водорода, для которого соотношение D) выполняется, по определению,
точно], при этом для всех газов приближенно:
a v=«р = а = 27з град'1. F)
164
ГАЗЫ
[ГЛ. VII
В табл. II даны для некоторых реальных газов эмпирические зна-
значения произведения р V при постоянной температуре для различных
давлений р. Газы взяты при 0°С
Таблица 11
Значения произведения pV
для различных р при О °С
Рат
1
100
200
500
1000
pV
н,
1,0000
1,0690
1,1380
1,3565
1,7200
N2
1,0000
0,9941
1,0483
1,3900
2,0685
о2
1,0000
0,9265
0,9140
1,1560
1,7355
воздух
1,0000
0,9730
1,0100
1,3400
1,9920
в количестве 1 л при давлении
в 1 am. Таким образом, для
каждого из газов при/>=1 am
произведение р V равно еди-
единице. По закону Бойля — Ма-
риотта оно должно было бы
сохранять это значение для
любых давлений.
Как видно из табл. II, в ин-
интервале давлений от 1 am до
-100 am отступления от закона
Бойля—Мариотта невелики:
произведение pV сохраняет
значение, близкое к единице.
Все же для водорода оно оказывается несколько больше единицы,
а для N.2, О.2 и воздуха — несколько меньше единицы. Это значит,
что водород сжимается несколько меньше, чем это требует закон
Бойля — Мариотта, а остальные газы — несколько больше.
При давлении в 1000 am все газы дают сильное отступление от
закона Бойля — Мариотта, достигающее для азота двух с лишним
раз: все они сжимаются меньше,
чем следует ожидать по закону
Бойля — Мариотта.
Еще больше отступления при
очень высоких давлениях. При да-
давлении в 15 000 кГ/см* объем азота
более чем в 16 раз превышает тот,
который он должен был бы иметь
по закону Бойля — Мариотта.
Заметны отступления для реаль-
реальных газов и от законов Гей-Люс-
сака.
Как видно из табл. III, значения
dp и ti|/ для одного и того же газа
не совпадают; для углекислоты рас-
расхождение между а.р и av достигает 0,4%. Для разных газов несколько
различны коэффициенты как ар, так ы av.
Наконец, для данного газа значения ар и ау получаются несколько раз-
разные, в зависимости от того, в каком температурном интервале они опреде-
определены.
Согласно формулам D) и E), имеем
' ' р-рл _ У-Уо
Таблица III
Значения коэффициентов ар
и а,, для газов
Газ
На
Не
N2
СО2
Воздух . . .
ар ¦ 10'
36613
36 601
36 744
37 262
36 750
ау ¦ 10'
36 600
36 582
36 732
37 414
36 760
§ 44]
ЗАКОНЫ БОЙЛЯ — МАРИОТТА И ГЕЙ-ЛЮССАКА
165
Таблица IV
Значения ар и av для воздуха при
р = 1 am для разных температурных
интервалов
здесь р0 и Vo — давление и объем при О "С, а р и V—те же величины при
температуре t. Измеряя р и V, например, для t = 50°, мы найдем средние
значения ар и av для интервала температур от 0 до 50°. По закону Гей-
Люссака значения ар и av не
должны были бы зависеть от
того, какая взята температура Л
Как показывает табл. IV,
относящаяся к воздуху, на самом
деле и от этого требования за-
закона Гей-Люссака наблюдаются
небольшие отступления.
Как видно, отступления
очень незначительны; особенно
они малы для ар. Тем не менее,
газовый термометр, наполнен-
наполненный воздухом вместо водорода,
дал бы некоторые отступления
при измерении температур.
Газ, который вполне
точно подчинялся бы зако-
законам Бойля — Мариотта и Гей-Люссака и характеризовался бы зна-
значениями ар==ау==а==-——о =5_- называется идеальным газом. Свой-
Свойства „идеального газа" являются лишь более или менее хорошим
приближением к свойствам реаль-
реальных газов.
Обозначая изменение давления
газа pt — рЛ через Ар, получим из
формулы D):
ар ¦ 10» . .
Температурные интервалы
0—50°
3675
3676
0—100°
3675
3674
0—150°
3674
3673
0—200°
3674
3672
¦?
Ар = puat,
Dа)
также из E) для изменения объема
AV найдем
AV= Vaat.
Eа)
Из формулы Dа) следует: да-
давление идеального газа при повы-
Рис. 111. в) Зависимость давления шении ег0 температуры на 1°С уве-
газа р от температуры изобра- личивается (при постоянном объеме)
жается прямой (изохорой); 6) изо- на 1/273 давления, которое он имел
хоры, отнесенные к любому коли- ПрИ q° q
Также из Eа) имеем: объем
идеального газа при повышении его
температуры на 1°С увеличивается (при постоянном давлении) на
1/273 объема, который он имел при 0°С.
Графически зависимость давления газа от температуры при по-
постоянном объеме выразится прямой, пересекающей ось ординат
в точке, дающей значение /?0 (рис. 111а). Эта линия носит название
изохоры, что означает, что она относится к постоянным объемам.
2 73
честву газа, все пересекают ось
абсцисс в одной точке А.
166
ГАЗЫ
[ГЛ. VII
Для разных масс газа ра будут иметь разные значения, и изохоры
изобразятся семейством прямых, пересекающих ось ординат на раз-
разных высотах (рис. 1116); однако все эти прямые пересекают ось
абсцисс в одной и той же точке А при значении t= = — 273° С,
так как по формуле D) pt = Q при t = для любых значений ра.
Точно так же зависимость объема газа от температуры при по-
постоянном давлении выразится прямой, пересекающей ось ординат
в точке, дающей значение Va (изоба-
(изобарой).
Для разных масс газа мы получим
семейство прямых, пересекающих ось
ординат на разных высотах и пересе-
пересекающихся в одной точке А, лежащей
на оси абсцисс при t = ^ — 273°С
Рис. 112. Прямые, изображаю- (рис. 112).
щие зависимость объема газа Из рис. llltf и 112 явствует, что
V от температуры t, отнесенные выражения для зависимости давления
к любому количеству газа, все ,
пересекают ось абсцисс в одной или объема газа от температуры упро-
точке А. стятся, если перенести начало коорди-
координат в точку А. В самом деле, введем
новую шкалу температур (температуру в этой шкале будем обо-
обозначать Т), где величина градуса та же, что и в шкале Цельсия,
но где нуль располагается при — 273° С, тогда
T=t-\-2730,1 G)
откуда t= Т— 273°= Т— — , и по D)
т. е.
Так же получим, что
Рт=рйо.Т.
VT=
(8)
Введенная шкала температур носит название шкалы Кельвина
(градус в этой шкале обозначается °К). Из (8) имеем, что давление
газа при постоянном объеме прямо пропорционально температуре
в шкале Кельвина. Также по (9) объем газа при постоянном давлении
прямо пропорционален температуре в шкале Кельвина. При 7=0
по (8) и (9) соответственно получаем, что /7 = 0 и У==0; однако на
самом деле объем вещества никогда не может стать равным нулю.
1 Точнее, T = t +273,13°.
§ 45] УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНЫХ ГАЗОВ. ПЛОТНОСТЬ ГАЗОВ 167
Такое нелепое следствие получилось в результате незаконного
экстраполирования законов Гей-Люссака на слишком низкие темпе-
температуры; всякий реальный газ превратится в жидкость и затвердеет
раньше, чем будет достигнута температура t = — 273° С. Тем не
менее шкала Кельвина и значение нуля температуры в этой шкале
имеют определенный физический смысл, как мы это увидим в даль-
дальнейшем. В связи с этим шкалу Кельвина часто называют абсолютной
шкалой, а нуль в шкале Кельвина (лежащий при — 273,13° в шкале
Цельсия) — абсолютным нулем температур.
§ 45. Уравнение состояния идеальных газов. Плотность газов.
Рассмотрим определенную массу газа т, которая занимает объем Vit
имеет давление pt и находится при температуре 7\. Пусть в другом
состоянии та же масса газа характеризуется объемом, давлением и
температурой: V9, />2, Га. Установим на основании законов Бойля —
Мариотта и Гей-Люссака связь между Vlt pt, Т\ и V2, pit T$.
Для этого, исходя из состояния Vj, p\, Ту, сперва нагреем газ
при постоянном давлении р1 до температуры Г2. Тогда он займет
объем V, причем по формуле (9) § 44:
V=Vl%. О)
В результате этого нагревания газ окажется в состоянии, харак-
характеризуемом объемом V, давлением pt и температурой Г2, поэтому
в окончательное состояние У2, /?2, 7"а его можно перевести изотер-
изотермическим изменением объема, для которого по закону Бойля —
Мариотта:
Подставляя сюда значение V из A), получим
или
откуда следует, что при изменениях состояния данной массы газа
pv
величина -•=- остается постоянной:
^ = В. B)
Уравнение B) выведено французским инженером Клапейроном
A834 г.), который долгое время был профессором Петербургского
института путей сообщения. Численное значение постоянной В
в этом уравнении зависит от количества взятого газа и от тех единиц,
в которых измеряются р, V и Т.
По закону, установленному Авогадро, граммолекулы различных
газов занимают при одинаковых давлениях и температурах оди-
одинаковые объемы. При t = 0° С и давлении р = \ am граммолекула
любого газа занимает объем 22,41 л.
168 ГАЗЫ [ГЛ. VII
Отсюда, если соотношение B) относить не к произвольному коли-
количеству газа, а к одному молю, то постоянная В будет иметь
одно и то же значение для всех газов.
Эта общая для всех газов постоянная обозначается буквой R
и носит название газовой постоянной. Вводя в формулу B) вместо
объема V молярный объем Va (т. е. объем одного моля газа),
получим
C)
Молярный объем Vo имеет размерность 1*/моль и измеряется
в л/моль или смг\моль. Формула C) представляет собой уравнение
состояния. В точности ей удовлетворяет лишь идеальный газ, для
реальных газов она так же приближенна, как и законы Бойля —
Мариотта и Гей-Люссака, из которых она вытекает.
Поэтому она является уравнением состояния идеального газа.
Уравнение C), являющееся обобщением уравнения B), было
установлено Д. И. Менделеевым, который впервые доложил о нем
на заседаниях Русского физико-химического общества в 1874 г. и
опубликовал в 1875 г. В связи с этим мы будем называть формулу C)
формулой Менделеева — Клапейрона.
Численное значение R определим из условия, что при t=O°C,
т. е. при Г=273°К и при р=\ am, объем моля 1/0=22,4 л)моль,
откуда
R=1~ = '973' Л ат1гРа<* моль = 0,082 л am/град моль. D)
Значение R в CGS-системе получим, переводя давление р в бары
и молярный объем Vu в см3/моль:
г, 1033 -981 • 22,4 -10» 3/ д "
^== 2ТТ Р см /гРа" моль =
= 8,31 • 107 эрг/град моль. DаI
Наименование единицы измерения газовой постоянной эрг/град моль
вытекает из того, что бар = дин/см\ откуда бар см3 = дин см = эрг.
Формулу C), справедливую лишь для одного моля газа, легко
обобщить и на любую массу. Для этого обозначим через ц моле-
молекулярный вес газа; тогда, если нри некоторых данных давлении и
температуре один моль газа занимает молярный объем V^, то m
граммов газа займут при тех же давлении и температуре объем
1/=— Vo. Отсюда следует, что для m граммов газа, при данных
давлении и температуре, выражение pV/T также будет в /я/[а раз
больше газовой постоянной R, на так как р V/Т остается постоянным
1 Более точно
R = 8,313 • 107 эрг/град моль = 0,08204 л amjzpad моль.
§ 45] УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНЫХ ГАЗОВ. ПЛОТНОСТЬ ГАЗОВ 169
при всех изменениях газа, то, следовательно, вообще для т граммов
газа:
tf=-?*, откуда ,V=-J/?7: (б)
Формула E) представляет собою обобщение формулы Менде-
Менделеева— Клапейрона, справедливое для любой массы т любого газа;
при этом постоянная R одна и та же для всех газов и имеет
численное значение, даваемое выражениями D) или Dа).
Формула E) связывает все четыре величины т, р, V и 7, харак-
характеризующие данное количество газа. Зная три из этих величин,
мы имеем возможность по формуле E) вычислить четвертую.
Из формулы E) непосредственно определяется плотность газа:
P fe F)
Таким образом, плотность газа оказывается прямо пропорциональ-
пропорциональной его молекулярному весу и его давлению и обратно пропорцио-
пропорциональной абсолютной температуре.
Для газов часто рассматривают относительную плотность, под-
подразумевая под ней отношение плотности данного газа р к плот-
плотности р0 некоторого, выбранного за стандартный, газа, взятого при
тех же давлении и температуре, что и рассматриваемый газ. Тогда
имеем
Р~ RT' ™-~"RT'
откуда относительная плотность рг равна
'-¦?¦-?• G)
Относительную плотность принято брать по отношению к водо-
водороду, для которого приближенно ji0 = 2, тогда относительная плот-
плотность:
?«, = ?*• <7а)
Эта формула позволяет устанавливать путем измерения относи-
относительной плотности по отношению к водороду молекулярные веса
газов.
Рассмотрим примеры на пользование формулой Менделеева— Клапейрона
и на определение плотности газов.
Пример 1. Какой объем в литрах занимает 1 г азота (jj. = 28) при
давлении 380 мм Hg и температуре 27° С?
Решение. Из формулы E) имеем
170 ГАЗЫ |ГЛ. VII
Переводим давление р из мм Hg в атмосферы:.
380 п_
р==760ат= ' *
Переводим температуру в шкалу Кельвина:
Г = 2! +273° = 300°,
и пользуемся для газовой постоянной значением
R = 0,082 л am/град моль, тогда V= l '°f2.'300 л=1,75 л.
Пример 2. Чему равна плотность водорода (fi = 2) при 0° С и давле-
давлении в 1 am?
Решение. По формуле (б):
Если все величины, входящие в правую часть этого выражения, брать
в CGS-системе, ¦ т. е. ц—в г/моль, р—в барах, R — в эрг/град моль,
Т—в градусах Кельвина, то р получится в г/см3.
Если же пользоваться следующей смешанной системой: R брать
в л am/град моль, ц — в г/моль, р—в атмосферах, Т—в градусах Кель-
Кельвина, то р получится в г/л, т. е. в такой системе, где за единицу плотности
принята плотность такого тела, масса 1 г которого имеет объем 1 л.
Очевидно, от численного значения плотности в г1л мы перейдем к чи-
численному значению плотности в г/см", поделив первое из них на 1000. Таким
образом, настоящий пример можно решать двояким способом:
1) переводим давление в бары: р = 1 am = 1033 ¦ 981 бар = 1,013 ¦ 10е бар
тогда имеем '
2 • 1 013 • 10°
Р — 8,31 ¦ 10' • 273"г/СМ — '9 Ш г'СМ '
2) пользуемся указанной смешанной системой, тогда
Р= 1/ 89 Ш2 / 89 105 '3
§ 46. Основные представления кинетической теории газов.
Плотность газов при нормальных условиях (т. е. при 0°С и давле-
давлении в 1 am) примерно в 1000 раз меньше плотности жидкостей.
В жидкости молекулы расположены вплотную друг к другу, отсюда
следует^ что в газах молекулы находятся друг от друга на расстоя-
расстояниях примерно в 3(/l000, т. е. в десятки раз больших, чем их соб-
собственные размеры. Таким образом, можно считать, что газ предста-
представляет собою собрание молекул, разделенных достаточно большими
промежутками. Молекулы беспорядочно движутся, свободно пробегая
путь между двумя последовательными столкновениями друг с другом
или со стенками сосуда, в котором заключен газ. Силы взаимодей-
взаимодействия между молекулами, кроме моментов соударения, настолько малы,
что ими можно пренебречь. Соударения молекул друг с другом и
со стенками происходят без потери энергии по законам соударения
упругих шаров. Такая механическая модель газа,' как собрания
§ 46] ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ 171
свободно и беспорядочно движущихся упругих молекул-шариков, яв-
является слишком упрощенной, но она позволяет объяснить основные
свойства газов. Впоследствии мы увидим, каким образом эта модель
должна быть развита, чтобы более точно учесть свойства реальных
газов. Свойства реальных газов не могут быть объяснены, если исхо-
исходить только из механических представлений. Учитывая сказанное
в § 31 о границах применимости классической механики, мы вообще
должны поставить вопрос, насколько возможно в указанной модели
газа пользоваться представлением о молекулах как о частицах, дви-
движущихся по законам классической механики.
В § 31 нами было приведено соотношение, по которому неопре-
неопределенности в координате Ах и в составляющей скорости l\vx должны
удовлетворять неравенству:
Д* ¦ Дх/Л > -- .
Применим это соотношение к молекуле, движущейся в газе, на-
находящемся при нормальных условиях. В качестве газа возьмем азот,
масса молекулы которого т = 4,7 • 10:) г. Как мы увидим дальше,
молекулы при этом проходят в среднем без столкновения с другими
молекулами путь порядка 10~8 см и обладают скоростью порядка
400 м/сек. Таким образом; для того, чтобы говорить о характере
движения молекул, необходимо иметь возможность фиксировать их
положение по крайней мере с точностью Д.г^10~6 см. При этом
по соотношению неопределенности неопределенность в скорости
будет:
. Л 1 6,6 • 107 , ^,, 1П5 ,
Д"*~т * A^ = 4,7-10-»-10-g^ceK=1'4 ' 10 СМ1СеК'
т. е. около 1/3°/о самой скорости.
Таким образом, в пределах требуемой нами точности мы вправе
рассматривать молекулу как частицу в обычном смысле слова. При
очень больших давлениях, когда молекулы находятся значительно
ближе друг к другу (необходимо брать для Дл: меньшее значение),
или при очень низких температурах, когда мала сама скорость моле-
молекул, такое рассмотрение не годится.
Модель газа как собрания свободно движущихся частиц прежде
всего непосредственно позволяет объяснить свойство газов распро-
распространяться на весь предоставленный им объем, а также взаимно
проникать друг в друга (диффундировать). Удары молекул обусла-
обуславливают давление газа на стенки ограничивающего его сосуда.
Объяснение давления газа на стенки, как возникающего в резуль-
результате удара отдельных молекул, было впервые выдвинуто петербург-
петербургским академиком Даниилом Бернулли в 1738 г. В 1744—1748 гг.
М. В. Ломоносов разработал развернутую теорию атомно-молеку-
лярного строения вещества, впервые доказал справедливость моле-
кулярно-кинетической теории теплоты и объяснил с этой точки
1$-.
172
ГАЗЫ
[ГЛ. VII
зрения многие явления. В дальнейшем молекулярно-кинетическая
теория газов была развита лишь во второй половине XIX столетия
рядом физиков, главным образом, Клаузиусом, Больцманом и Мак-
Максвеллом.
Подсчитаем давление, возникающее в результате удара молекул
о стенки сосуда. Представим себе сосуд в виде куба с длиной
ребра А/ (рис. ИЗ), в котором беспорядочно движется п молекул,
собственными размерами которых мы пре-
пренебрегаем. Ввиду полной беспорядочности
движения молекул, результат их удара о
стенки будет таков, как если бы 1/а всех
молекул двигалась прямолинейно между пе-
передней и задней стенками куба, '/а моле-
молекул — между верхней и нижней стенками
и '/з — между правой и левой стенками куба.
Рис. 113. Усреднение дви- Отдельная молекула, летящая перпендику-
перпендикулярно к одной из стенок, например к пе-
передней, со скоростью v, во время удара
отскочит назад, в результате чего ее коли-
количество движения изменится на величину т ¦ v — т (— v) = 2mv, где
т — масса молекулы; это изменение количества движения определит
импульс силь1, действующей со стороны стенки на молекулу во
время удара:
женин молекул в кубиче-
кубическом сосуде.
где Д/— сила удара и Ы — продолжительность удара. По третьему
закону Ньютона сила, численно равная Д/, будет действовать на
стенку. Отскочив от стенки, молекула полетит к противоположной
стенке и, отскочив в свою очередь от нее, снова вернется к пер-
первой стенке через некоторое время At. Средняя сила Д/, действующая
на стенку за все время между двумя последовательными ударами
молекулы, определится из того требования, что ее импульс Af-At
должен численно равняться импульсу силы Д/, действующей во время
удара Ы, откуда
Af-At = 2mv. A)
Величина At представляет собою время, которое потребно для
того, чтобы молекула, отскочив от передней стенки куба, могла
долететь до его задней стенки и вернуться назад, отсюда
At =
2- Д/
Подставляя это значение At в A), получим
§ 46] ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ 173
Это есть среднее по времени значение силы ударов одной моле-
молекулы. Разные молекулы движутся с различными скоростями vv v&
х>з, ..., и суммарная сила ударов молекул о переднюю стенку равна
--_ти\ mr4 mv\ , rmfr
J M ' М ~Т" д/ Г ¦••-Г д/ t
где и' — число молекул, движущихся между передней и задней стен-
стенками. Вынося /я/Д/, как величину постоянную, за скобки, деля и
умножая правую часть на п\ получим
- п' ¦ т v\ -\- vf -\- vl -j- . ¦. + v*n-
Величина
_,
представляет собою среднее значение квадратов скоростей молекул,
или, другими словами, квадрат средней квадратичной скорости.
Отсюда
Число молекул, движущихся между передней и задней стенками,
может быть положено равным, как мы выяснили, 1/3 от общего числа
молекул п, откуда
Поделив правую и левую части этого равенства на Д/2, получим
но Д/2 — площадь стенки куба, следовательно, //Д/3 — давление р на
стенку, а Д/3 — объем куба, отсюда получаем, что л/Д/3 равно числу
молекул щ в единице объема; окончательно равенство B) прини-
принимает вид:
Таким образом, давление р, оказываемое газом на стенки сосуда,
определяется: числом молекул п0 в единице объема, массой моле-
молекул т и средним значением квадрата их скоростей г>. Формуле C)
можно придать иной вид, поделив и помножив ее правую часть на 2,
тогда
2
НО
mv2
174 газы [гл. vir
есть средняя кинетическая энергия поступательного движения одной
молекулы, откуда
nw Da)
т. е. давление газа может быть также выражено через среднюю
кинетическую энергию поступательного движения молекул газа.
Формула C) или эквивалентная ей формула Dа) носит название
основной формулы кинетической теории газов.
Помножим правую и левую части формулы Dа) на объем одного
моля газа Vo, тогда
pV nVw
но «0V0— число молекул в молярном объеме Vo, т. е. число моле-
молекул в одном моле газа; это число равно числу Авогадро: и0 ^о = М
откуда
но р]/й = 1?Т, где Т—температура газа в шкале Кельвина и ./? — га-
газовая постоянная, отсюда
pVt = j№ = RT. E)
Формула E) непосредственно связывает среднюю кинетическую
энергию поступательного движения молекул w с макроскопическими
величинами, характеризующими газ: с его давлением, объемом и
температурой. Из E) имеем
*=f = l.?r, F)
так как R и N представляют собой величины постоянные, то и
величина
k = j? G)
является величиной постоянной; она носит название постоянной
Больцмана.
Численное значение постоянной Больцмана равно
Щ^^ =1,38 . 10"" эрг/град.
Подставляя в формулу F) постоянную Больцмана, получим
w=^kT. Fa)
§ 46] ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ 175
Формулы F) и Fа) показывают, что средняя кинетическая энер-
энергия поступательного движения молекул зависит только от тем-
температуры, при этом она прямо пропорциональна абсолютной
температуре Т.
Таким образом, абсолютная шкала температур (шкала Кельвина)
приобретает непосредственный физический смысл. При абсолютном
нуле температуры поступательное движение молекул, согласно фор-
формуле Fа), прекращается вовсе. Однако и при абсолютном нуле со-
сохраняются некоторые виды движения внутри молекул и атомов, так
что внутреннее движение материи не прекращается в целом и при
абсолютном нуле. В дальнейшем мы увидим, что практически абсо-
абсолютный нуль достигнут быть не может.
Приведенные выводы позволяют нам определить не только сред-
среднюю кинетическую энергию поступательного движения молекул,
но и ряд других величин, характеризующих молекулярно-кинетиче-
скую природу газа.
Из формулы F) получаем для среднего значения квадрата ско-
скорости молекул:
mN
но т — масса одной молекулы, N—число молекул в одном моле,
откуда mN есть молекулярный вес ц, после чего для средней квад-
квадратичной скорости поступательного движения молекул получаем:
(8)
т. е. средняя квадратичная скорость поступательного движения газо-
газовых молекул прямо пропорциональна корню квадратному из абсо-
абсолютной температуры газа и обратно пропорциональна корню ква-
квадратному из его молекулярного веса.
Для числа молекул пй в единице объема из формулы Dа) по-
получаем
подставляя сюда значение Ш по Fа), найдем
n*=w- (9)
Из формулы (9) следует, что все газы содержат при одинако-
одинаковых давлениях и температуре одно и то же число молекул в единице
объема (этот результат также непосредственно вытекает из закона
Авогадро). При нормальных условиях, т. е. при p=l am и
Т= 273° К, в 1 смг любого газа заключается:
«0 = 2,683 • 1013 слС*
молекул; это число носит название числа Лошмита.
176 ГАЗЫ [ГЛ. VII
Для того чтобы освоиться с порядком численных величин, характери-
характеризующих молекулярно-кинетическую теорию газов, приведем несколько числен-
численных примеров.
Пример 1. Сколько молекул газа должно находиться в единице объема,
чтобы при температуре 27°С давление, оказываемое на стенки сосуда, равня-
равнялось одному бару?
Решение. По формуле (9):
"° = if = щ. id-°-зоо см~* = 2>42 ' 1О'а см"<
т. е. в 1 см3 должно находиться 2,42 • 1013 молекул.
Пример 2. Найти среднюю квадратичную скорость молекул азота
(ц = 28) при: a) i=1000°C, б) t = O°C и в) t= —270° С.
Решение. Подставляя в формулу (8) /? = 8,31 - 107 эрг/град моль,
ц = 28 г/моль и Г=1273°К, получим:
= "|/~
3 ' 8'31 '™? ' 127- см/сек = 1,06 ¦ 105 см/сек = 1060 м/сек.
Так же находим для двух остальных случаев: б) ]/гг>2 = 493 м/сек;
в) ]/лгJ = 51 м/сек. Таким образом, при не слишком низких температурах
скорости газовых молекул чрезвычайно велики. При комнатных температурах
они достигают скорости ружейной пули.
Пример 3. Чему равна в эргах средняя кинетическая энергия посту-
поступательного движения молекул газа при: а) (=1000°С, б) t=O°C,
t = — 270° С.
Решение. По формуле Fа) имеем при ?=1000° С, т. е. при
Г=1273°К;
w = 4АГ=4 ''38 " 10~'в " 1273 э/)г =
так же для других случаев находим: б) w = 5,65- 10—4 эрг и
в) да = 6,21 • 10—в эрг. Таким образом, несмотря на большие скорости, сред-
средние кинетические энергии отдельных молекул, даже при температурах в 1000°С,
очень малы. Это происходит от весьма малой массы отдельной молекулы.
§ 47. Парциальные давления в газовых смесях. Согласно основ-
основной формуле кинетической теории газов [формула Dа) § 46], давле-
давление газа
p = ^naw, A)
где л0 — число молекул в единице объема и w — средняя кинети-
кинетическая энергия молекул при данной температуре Т. При этом фор-
формула A) не зависит от сорта молекул, так как все молекулы при
данной температуре Т имеют одну и ту же среднюю кинетическую
энергию ~w.
Предположим, что мы.имеем дело не с однородным газом, но
со смесью различных газов, причем число молекул в единице объема
первого газа равно /%, второго — и02, третьего — и03 и т. д.
Тогда общее число молекул в единице объема я0 равно
«о = #oi -f~ "оз + иоз ~f- ¦••
§ 47] ПАРЦИАЛЬНЫЕ ДАВЛЕНИЯ В ГАЗОВЫХ СМЕСЯХ 177
и по формуле A) давление, оказываемое на стенки сосуда всей
смесью газов, равно
Р = \ "nw +1- naiw -f- ~ nmw + ... B)
но, очевидно,
представляет собой то давление, которое оказывал бы первый газ,
если бы он один присутствовал в данном сосуде в том количестве,
в котором он присутствует в смеси. Также
2
Pi = у
представляет собою то давление, которое оказывал бы второй газ,
если бы он один присутствовал в сосуде в том количестве, в кото-
котором он присутствует в смеси, и т. д.
Давления plt />9, р3 и т. д. называются парциальными давлениями.
Из формулы B) получаем
Р=Р\+Ръ+Ръ-)г -• C)
Формула C) представляет так называемый закон Дальтона: в слу-
случае идеальных газов сумма парциальных давлений равна давле-
давлению всей газовой смеси.
Из закона Дальтона вытекает следующее: если различные идеаль-
идеальные газы, находящиеся при одинаковом давлении р и занимающие
в отдельности объемы Vt, V2, Va..., привести в соприкосновение
друг с другом путем удаления разделяющих их перегородок, то после
того как произойдет полное смешение газов путем диффузии, их
общее давление не изменится; другими словами: при смешении
идеальных газов при постоянном
давлении суммарный объем не
меняется, т. е. объемы газов сла-
слагаются аддитивно.
Это последнее обстоятельство
может быть проверено путем непо-
непосредственного опыта. Измерение
же парциальных давлений в смеси РиС- 114 Схема опыта для опреДеле-
газов непосредственно затрудни- ния парциального давления водорода,
тельно. Это измерение может быть
проведено, если иметь в распоряжении перегородку, проницаемую
для одного газа и непроницаемую для остальных (полупроницаемую
перегородку). Например, пластинка из накаленной платины хорошо
проницаема для водорода и плохо проницаема для других газов.
Проникающий через полупроницаемую перегородку газ выравнивает
свое парциальное давление по обе стороны перегородки.
Представим себе замкнутый сосуд В из платины (рис. 114),
первоначально эвакуированный, а затем раскаленный. Пусть сосуд В
7 С. Э. Фриш и А. В. Тнморева
178 газы [гл. vii
окружен газовой смесью из водорода и какого-либо другого газа,
химически не активного по отношению к водороду (например, аргона).
Тогда водород начнет проникать внутрь раскаленного платинового
сосуда В, пока его давление на стенки сосуда не выравняется
с обеих сторон. Это будет иметь место тогда, когда давление водо-
водорода внутри сосуда В станет равным парциальному давлению водо-
водорода с наружной стороны, где находится смесь газов. Таким образом,
парциальное давление водорода может быть непосредственно изме-
измерено манометром С.
Опыт может быть проведен в несколько ином виде. Заполним
первоначально как сосуд В, так и пространство, его окружающее,
каким-либо определенным газом, например аргоном, при одинаковом
давлении ра. Заменим затем аргон, находящийся снаружи, смесью из
аргона с водородом, причем давление смеси пусть также равно />0.
парциальное же давление водорода в этой смеси пусть будет р\.
Тогда, если раскалить стенки сосуда В, водород начнет проникать
внутрь сосуда В, в то время как аргон не сможет проникать
из него наружу. В результате получится разность давлений между га-
газовой смесью вне сосуда В и внутри сосуда В. Установившееся да-
давление внутри сосуда В окажется равным рй-\-р\, т- е- будет больше
давления рй на величину ри Это „добавочное" давление рх измерит
парциальное давление водорода в смеси.
Для реальных газов и паров наблюдаются некоторые отступления от
закона Дальтона, подробно исследованные в 1890 г. Б. Б. Голицыным.
§ 48. Внутренняя энергия газа. Число степеней свободы. Как
было показано в § 46, молекулярно-кинетическая теория газов при-
приводит к весьма важному следствию: молекулы газа совершают бес-
беспорядочное движение, причем средняя кинетическая энергия посту-
поступательного движения молекулы w при температуре Т равна
где R — газовая постоянная, N—число Авогадро, k = jj — по-
постоянная Больцмана. Таким образом, средняя кинетическая энергия
поступательного движения молекул определяется исключительно тем-
температурой газа 7", поскольку остальные величины, входящие в выра-
выражение A), являются постоянными. При нагревании или охлаждении
газа, т. е. при сообщении ему или отнятии от него некоторого
количества тепла, меняется энергия движения его молекул.
Для идеального газа кинетическая энергия беспорядочного дви-
движения всех его молекул определяет его внутреннюю энергию. Для
реальных газов, как мы увидим ниже, необходимо принять еще
во внимание взаимную потенциальную энергию молекул, так что для
реальных газов внутренняя энергия представляет собою сумму кине-
кинетической энергии движения молекул и их потенциальной энергии.
§ 48] ВНУТРЕННЯЯ ЭНЕРГИЯ ГАЗА. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ 179
Кинетическая энергия движения молекул, вообще говоря, не
исчерпывается кинетической энергией их поступательного дви-
движения: она может также складываться и из кинетических энер-
энергий вращения и колебания молекул.
Для того чтобы подсчитать энергию', идущую на все виды движе-
движения молекул, необходимо ввести понятие о числе степеней свободы.
Под числом степеней свободы тела подразумевается число не-
независимых координат, которые необходимо ввести для определе-
определения положения тела в пространстве. Так, например, материаль-
материальная точка обладает тремя степенями свободы,
так как ее положение в пространстве определяется
тремя координатами, например, координатами х,
у, z прямоугольной прямолинейной системы коор-
координат.
Положение твердого тела (рис. 115) мы опре-
определим, если зададим: 1) положение его центра тя-
тяжести С в пространстве, 2) направление некоторой
определенной оси 00' и 3) угол поворота твердого
тела вокруг этой оси по отношению к некоторому
начальному положению. Для определения положе- Рис. 115. Твер-
ния центра тяжести нужно ввести три координаты дое тело имеет
х, у, z. Для определения направления оси 00' в шесть степеней
пространстве надо задать еще две координаты, на-
например, два угла Ь и <[>, которые она составляет ,-
с двумя из трех координатных осей. Наконец, угол поворота тела У
вокруг оси 00' определится еще одной координатой (угол <р на
рис. 115).
Таким образом, твердое тело обладает шестью степенями свободы. *
Если отдельные части тела могут еще смещаться (колебаться)
друг относительно друга, то для рассмотрения этих движений нужно
ввести еще добавочные степени свободы, сверх указанных. Наоборот,
если твердое тело по каким-либо причинам (например, полной сим-
симметрии) не приходит во вращение относительно одной определенной
оси, то оно будет обладать числом степеней свободы меньше шести,
а именно — пятью.
Сфера, которая не испытывает вращения, а лишь движется
поступательно, может рассматриваться как материальная точка с тремя
степенями свободы.
Каждая молекула газа обладает определенным числом степеней
свободы, три из которых соответствуют ее поступательному движе-
движению в пространстве.
Основной предпосылкой молекулярно-кинетической теории газов
является предположение о полной беспорядочности движения моле-
молекул; эта беспорядочность относится не только к поступательному
движению, но и ко всем остальным видам движений молекул (вра-
(вращению, колебанию). Ни один из типов движения не имеет преиму-
1*
180 ' ГАЗЫ [ГЛ. VII
щества перед другим, отсюда естественно предположить, что на
каждую степень свободы молекулы в среднем приходится одно и
то же количество энергии w. Это положение известно под на-
названием положения о равнораспределении энергии по степеням
свободы. Исходя из этого положения, легко получить среднюю энер-
энергию wb приходящуюся на одну степень свободы. На поступатель-
поступательное движение молекулы., которому соответствуют три степени сво-
свободы, приходится по A) энергия:
w = -| k T,
отсюда на одну степень свободы приходится средняя энергия
тоо = тА7 = т^O-. . B)
Предположим, что газ состоит из одинаковых молекул, каждая из
которых обладает i степенями свободы; тогда на каждую молекулу
(на все виды ее движений) в среднем приходится энергия
Полный запас внутренней энергии газа получим, умножив это
значение w на число молекул, из которых состоит газ. Если мы
отнесем внутреннюю энергию к одному молю газа, то получим ее
значение ?/о> умножив w на число Авогадро Л/, откуда
±RT. D)
Из формулы D) мы видим, что внутренняя энергия газа выра-
выражается через число степеней свободы молекул i и абсолютную тем-
температуру газа Т. Таким образом, внутренняя энергия данного коли-
количества идеального газа зависит только от его температуры Т и не
зависит от его объема, а следовательно, и давления. В случае реаль-
реальных газов, полная внутренняя энергия, которая, как мы отмечали,
складывается из кинетической энергии движения молекул и их по-
потенциальной энергии, зависит от объема, занимаемого газом. При
этом внутренняя энергия реального газа не исчерпывается механи-
механическими видами энергии (см. § 49).
§ 49. Теплоемкость газов. Пользуясь представлением о вну-
внутренней энергии, мы можем найти выражение для теплоемкости газов.
Под удельной теплоемкостью с какого-либо вещества подразу-
подразумевают физическую величину, численно равную количеству тепла,
которое надо сообщить единице массы этого вещества, чтобы под-
поднять ее температуру на 1°.
Наряду с удельной теплоемкостью мы введем в рассмотрение
молярную теплоемкость С. Под молярной теплоемкостью С ка-
какого-либо вещества подразумевается физическая величина, численно
§ 49] ТЕПЛОЕМКОСТЬ ГАЗОВ 181
равная количеству тепла, которое надо сообщить одному молю этого
вещества, чтобы поднять его температуру на 1°. Очевидно, между
молярной теплоемкостью С и удельной теплоемкостью с имеет место
соотношение: ' i
С=М' Ч , ' (О
где fj, — молекулярный вес данного вещества. «
Для газов надо различать, при каких условиях они нагреваются,
например, при постоянном объеме V или при постоянном давле-
давлении р.
Рассмотрим случай нагревания газа при постоянном объеме V.
В этом случае работа внешних сил равна нулю и все сообщае-
сообщаемое газу извне тепло идет целиком на увеличение его внутренней
энергии U. Отсюда молярная теплоемкость газа при постоянном
объеме Су численно равна изменению внутренней энергии одного
моля газа Уо при повышении его температуры на 1°. Так как по
формуле D) § 48 это изменение равно
—уЯ7- = у/?,
то для молярной теплоемкости газа при постоянном объеме имеем
CV = ±R. B)
Для удельной теплоемкости, воспользовавшись соотношением A),
получим
Из формулы B) следует, что молярная теплоемкость газа при
постоянном объеме Cv определяется числом степеней свободы i его
молекул и значением газовой постоянной R.
В § 45 мы приводили численные значения газовой постоянной R
в эрг/град моль и в л am/град моль; если воспользоваться этими
значениями R, то мы и теплоемкость получим, соответственно, в тех
же единицах. Однако обычно, принято выражать теплоемкость через
количество тепла, передаваемого телу. Единицей же количества тепла
служит калория. Калория („малая" или „граммкалория") равна тому
количеству тепла, которое необходимо сообщить 1 г чистой воды,
чтобы повысить ее температуру от 19,5 до 20,5°С.
Так как передача тепла является формой передачи энергии, при-
причем по закону сохранения энергии определенному количеству пере-
переданного тепла эквивалентно определенное количество энергии,' то
в калориях можно измерять не только количество тепла, но и энер-
энергию, а также работу. Отсюда возникает вопрос, в каком численном
1 Подробнее см. гл. VIII „Основы термодинамики'.
182
ГАЗЫ
[ГЛ. VII
отношении находится калория к другим единицам энергии. Наиболее
точные измерения дают:
1 кал = 4,182 дж;
приближенно мы будем считать 1 кал = 4,18 дж. Пользуясь этим
соотношением между калорией и джоулем, легко перевести численное
значение газовой постоянной R из эрг/град моль в кал/град моль,
а именно:
8 313 • 10*
R = 8,313 « 107 эрг/град моль = -гтк^—т™ кал/град моль =
= 1,9858 кал/град моль.
Приближенно можно принять R = 2 кал/град моль. Пользуясь
этим значением газовой постоянной /?, мы получим по формуле B)
теплоемкость газа Су в кал/град моль.
Для вычисления Су остается выяснить, какое число степеней
свободы i следует приписать тем или другим молекулам. Однако
раньше чем остановиться на этом вопросе, мы выведем выражение
для молярной теплоемкости газа Ср при постоянном
давлении.
При нагревании газа при постоянном давлении р
газ расширяется; сообщаемое ему извне тепло идет не
только на увеличение запаса его. внутренней энергии U,
Jho и на совершение работы А против внешних сил.
Л Таким образом, теплоемкость Ср больше теплоемкости
при постоянном объеме Су на ту работу А, которую
совершает один моль газа при расширении, происхо-
происходящем в результате повышения его температуры Т на
1° при постоянном давлении р:
Рис. lib'. Ра-
Работа, совер- Ср = Су -j- A. C)
шаемая га-
газом, равна/Л. Для подсчета этой работы А, представим себе, что
один моль газа, находящегося при температуре Т и
давлении р, заключен в цилиндр с поршнем (рис. 116). Внешняя
сила, удерживающая поршень, f=pS, где S—площадь поршня. При
нагревании газа при постоянном давлении р на 1° он расширится,
и поршень будет поднят на высоту h; газ совершит при этом работу
A=f-h=p -Sh,
но Sh = AVu, где ДУ0— увеличение объема газа, откуда
A=p-AV,. D)
Увеличение объема газа найдем, воспользовавшись уравнением
состояния идеального газа. При температуре Т и давлении р объем
одного моля газа Vu равен
V — - Т
\
f
&
§ 49] ТЕПЛОЕМКОСТЬ ГАЗОВ 183
При температуре (Т-\-1)° и том же давлении р объем V'Q будет:
следовательно, увеличение объема одного моля газа при повышении
его температуры на 1° равно
Подставив это значение ДУ0 в D), найдем работу А, совершен-
совершенную одним молем газа при расширении, происходящем в результате
нагревания газа на 1° при постоянном давлении р:
A = R.
Таким образом, искомая работа А численно равна газовой по-
постоянной R. Подставив это значение А в C), найдем соотношение
между молярными теплоемкостями газа при постоянном давлении С.
и постоянном объеме Cv'-
Cp = Cv + R. E)
Отс ода, воспользовавшись формулой B), находим выражение
для Ср через число степеней свободы молекул газа
Cp = -^R + R==l-^R. F)
Пользуясь соотношением A) между удельными и молярными
теплоемкостями, находим
или
Из формул B) и F) или Bа) и Fа) получаем
Отношение теплоемкостей при постоянном давлении и при по-
постоянном объеме Ср/Су = ср/су обозначим буквой у, это отношение
зависит только от числа степеней свободы молекул, из которых
состоит газ.
Для того чтобы приписать молекуле определенное число степеней
свободы, нгдо исходить из определенной модели молекулы. До сих
пор мы прииим;1ли молекулы за шары; если такую шарообразную
молекулу сштагь неспособной вращаться, то ей надо приписать
184
ГАЗЫ
[гл. vii
число степеней свободы, равное трем, тогда, пользуясь значением
/? = 1,9858 кал/град моль, получим по B), F) и G):
v = i) R = 2,979 кал/град моль^З кал/град моль,
i = 3
Ср = -к R = 4,965 кал/град моль ?Ё 5 кал/град моль,
Как показывают' результаты измерений, приведенные в табл. V,
эти значения теплоемкостей оправдываются для газов гелия и аргона;
Таблица V
Наблюденные значения молярных теплоемкостей газов
Газ
Гелий, Не
Аргон, Аг
Водород, Но
Азот, N2
Кислород, О2 ¦ •
Окись углерода, СО . .
Пары воды, Н2О
Метан, СН^
Хлороформ, СНС13. . . .
Этиловый спирт, С2Н0О
2,98
2,98
4,87
4,96
4,99
5,01
6,65
6,51
15,2
18,9
5,00
5,07
6,87
6,84
6,90
7,01
8,65
8,51
17,2
20,9
1,67
1,65
1,41
1,41
1,40
1,40
1,31
1,30
1,13
Н
эти газы одноатомны, т. е. те частицы, из которых они состоят,
представляют собою отдельные атомы, а не группы атомов, соеди-
соединенных в молекулы. Таким образом
для одноатомных газов вычисленные
по кинетической теории газов и на-
)-— блюденные значения теплоемкостей хо-
хорошо совпадают между собой, если
число степеней свободы принять рав-
равным трем.
Для двуатомных газов, какими яв-
являются водород, кислород, азот, окись
углерода и т. д., можно принять сле-
следующую модель: два атома А и В жестко соединены между собой
так, что их центры находятся на неизменном расстоянии / друг от
друга (рис. 117).
Так как каждый из атомов не приходит во вращение, то нужно
считать, что такая молекула не вращается относительно оси ОО',
Рис. 117. Модель двуатомной
молекулы.
§ 49] ТЕПЛОЕМКОСТЬ ГАЗОВ 185
проходящей через центры обоих атомов. Поэтому двуатомной моле-
молекуле надо приписать пять степеней свободы. Тогда по B), F) и G):
2 = 5
Cv = -k-R = 4,965 кал/град моль ^5 кал/град моль,
Ср = - R = 6,951 кал!град моль = 7 кал/град моль,
7 = ? =1=1.40.
Из табл. V видно, что эти данные хорошо совпадают с наблю-
наблюдаемыми значениями теплоемкостей для водорода, азота, кислорода
и окиси углерода; таким образом, молекулам этих двуатомных
газов действительно приходится приписать пять степеней свободы.
Считая более сложные (трехатомные а многоатомные) моле-
молекулы за несимметричные твердые частицы, мы должны приписать
им шесть степеней свободы.
Тогда для их теплоемкостей получаем:
Cv = Y R = 6 кал/град моль,
о
Ср = -х R ^ 8 кал/град моль.
Из данных табл. V видно, что эти значения близки к экспери-
экспериментальным данным для паров воды и метана; для таких же сложных
молекул, как СНС1з и СаНвО, теплоемкости получаются гораздо
ббльшие.
Молекула в виде твердой частицы не может иметь более шести
степеней свободы, поэтому для сложных молекул, имеющих мо-
молярную теплоемкость Cv больше шести, необходимо, наряду с по-
поступательными и вращательными степенями свободы, принимать во
внимание и колебательные степени свободы.
Развитая теория теплоемкостей, которая целиком основывается
на классических представлениях, учитывающих лишь механические
виды движения молекул, является приближенной. Из нее, например,
следует, что вее двуатомные газы с молекулами с пятью степенями
свободы должны иметь в точности одинаковые теплоемкости Cv при
постоянном объеме. Число степеней свободы может быть только
целым, и изменение числа степеней свободы на одну должно вести
к изменению теплоемкости на -к- R = 0,993 кал/град моль. Из
той же табл. V видно, что двуатомные газы имеют несколько раз-
различные теплоемкости. Эти различия превышают ошибки наблюдений
и, следовательно, являются реальными. С другой стороны, они много
186
ГАЗЫ
[гл. vii
меньше -к- R. Такие различия не могут быть объяснены с точки
зрения приведенной теории. Из рассмотренной теории следует также,
что теплоемкость газов не зависит от температуры; эксперименты
же показывают, что на самом деле теплоемкости зависят от
температуры: теплоемкость всех веществ при низких темпера-
температурах меньше, чем при более высоких. Например, для газообраз-
газообразного водорода мы имеем:
гк
Су
197°
4,38
90°
3,25
40°
2,98
Как видно, при низкой температуре 7"=40°К, т. е. при t = —233°С,
теплоемкость водорода значительно меньше той, которую мы полу-
получили из классической теории, приписывая двуатомной молекуле водо-
рода пять степеней свободы; она близка к -к- R- Наоборот, при очень
высоких температурах теплоемкости окажутся выше вычисленных.
Только для средних температур классическая теория теплоемкости
дает хорошие результаты. Это объясняется неприменимостью клас-
классических представлений к отдель-
отдельным атомам и молекулам. Пра-
Правильная теория теплоемкости
дается квантовой механикой.
По классическим воззрениям
энергия wa, приходящаяся на лю-
,t бую степень свободы, может ме-
)р
няется скачкообразно.
няться непрерывно. По квантовой
™ории энергия вращения моле-
кул, а также энергия их коле-
колебаний могут меняться лишь скач-
скачками; графически изменение энергии вращения или колебания w
со временем t изобразится ступенчатой линией (рис. 118). Для
энергии вращения обычных двуатомных молекул (азот, кислород)
эти ступеньки представляют собой величины порддка 10~18 эрг.
Средняя энергия, приходящаяся на одну степень свободы -^ kT при
7=300°К, равна й)=2,17-10~и эрг; таким образом, ступеньки
энергии вращения молекул при комнатной температуре малы по
сравнению со средней энергией, приходящейся на одну степень
свободы. Благодаря этому теплоемкость может рассчитываться с
классической точки зрения. При низких же температурах, когда
сама энергия щ сравнима с величиной ступеньки энергии, класси-
классические воззрения непригодны.
§ 49]
ТЕПЛОЕМКОСТЬ ГАЗОВ
187
При этом оказывается, что энергия вращения молекул перестает
изменяться с температурой. В результате теплоемкость всех газов
при низкой температуре стремится к значению Cv=-^R.
Кроме того, при низких температурах по квантовой теории иначе,
чем по классической, рассчитывается среднее значение энергии (при-
(приходится принимать во внимание так называемое „вырождение" газа).
Наконец, при очень низкой температуре газ замерзнет и превра-
превратится в твердое тело. Теплоемкость же твердых тел, как мы увидим
в дальнейшем, стремится к нулю при приближении температуры
к абсолютному нулю.
Что касается энергии колебаний, то ее ступеньки гораздо больше:
для не очень сложных молекул они порядка 2-Ю3 эрг, т. е. при-
приблизительно в 10 раз больше сред-
средней энергии w0, приходящейся на ?«
одну степень свободы при комнат- ?/2
ных температурах. Благодаря этому
при комнатных температурах энер-
энергию колебаний мы можем не рас- 5/?
сматривать: она сказывается лишь
при высоких температурах.1 Для ^
сложных молекул ступеньки энер-
энергии колебаний бывают меньше, и
тогда роль энергии колебаний мо-
молекулы сказывается и при средних ?|
температурах.
На рис. 119 представлен ход
теплоемкости двуатомного газа с
температурой. При высокой темпе-
температуре играют роль колебания (на
них приходится две степени свободы, см. § 93) и теплоемкость
Cv=V2R, при средних температурах Су = 5/2/? и при очень
низких Су=3/2/?. Пунктирная часть кривой, стремящаяся к нулю,
указывает ход теплоемкости после затвердевания газа.
При учете зависимости теплоемкости многоатомных газов от тем-
температуры при очень высоких температурах следует еще принимать
во внимание диссоциацию молекул. Например, при диссоциации
двуатомной молекулы возникнут два атома, каждый из которых имеет
три степени свободы. При полной диссоциации двуатомный газ
" низкие средние вьюокие
температуры
Рис. 119. Ход теплоемкости дву-
двуатомного газа с температурой.
1 Квантовая теория молекул показывает, что в молекулах имеется так
называемая нулевая энергия колебаний, которая не исчезает и при темпе-
температуре, равной абсолютному нулю. Однако следующая за этой „нулевой"
ступенька энергии колебаний лежит настолько выше, что ее приходится
принимать во внимание лишь при очень высоких температурах. Таким обра-
образом, хотя при низких и средних температурах колебания в молекулах и не
отсутствуют вовсе, но они не зависят от температуры и, следовательно,
не влияют на теплоемкость.
188 газы [гл. vii
превратится в смесь двух одноатомных газов, сумма молярных тепло-
емкостей которых будет равна 6/2$.
Поэтому ход теплоемкости двухатомного газа при высо-
высоких температурах будет в действительности отличаться от изобра-
изображенного на рис. 119.
§ 50. Закон распределения скоростей Максвелла. В § 46 мы
рассматривали лишь среднее значение квадрата скорости молекул.
Однако на самом деле молекулы движутся с различными скоростями,
при этом при каждой температуре Т существует наиболее вероятная
скорость vB. Молекулы, скорости которых много больше или много
меньше наиболее вероятной, встречаются редко.
Ввиду полной беспорядочности движения молекул, нельзя ставить
вопроса о числе молекул, которые обладают точно заданной скоро-
скоростью v, так как таких молекул в каждый данный момент вообще
может не оказаться. Но можно поставить вопрос о числе молекул,
скорости которых лежат в некотором определенном интервале ско-
скоростей, например, имеют значения, лежащие между некоторыми дан-
данными скоростями Vi и v.2. Закон распределения скоростей был
впервые выведен Максвеллом. Максвелл, пользуясь теорией вероят-
вероятности, подсчитал число молекул Дга, скорости которых лежат в интер-
интервале скоростей от некоторой заданной скорости в до ti-j-Ди.
Закон Максвелла удобнее формулировать, введя относительную
скорость
где v — данная скорость, a va — наиболее вероятная для молекул
данного газа при данной температуре. По закону Максвелла число
молекул Ли, относительные скорости которых лежат в интервале и,
и -(- Дн, где Дм должно быть взято малым по сравнению с и, равно
4 • B)
Дл = 4=ле
у*.
где п — полное число молекул рассматриваемого газа.
Наиболее вероятная скорость ¦»„ по расчетам Максвелла равна
C)
где jj.— молекулярный вес данного газа, Г —его абсолютная темпе-
температура, R — газовая постоянная. Так как R = kN, a p = mN, где
k — постоянная Больцмана, т—масса молекулы данного газа, N—число
Авогадро, то формуле C) можно также придать вид:
(За)
m
Откладывая по оси абсцисс значение относительной скорости
молекул и, а по оси ординат — значение величины —т— (эта
§ 50]
ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ МАКСВЕЛЛА
189
величина называется функцией распределения), получим кривую,
представленную на рис. 120. Кри-
Кривая имеет максимум при и=1, что
соответствует значению скорости v,
равной наиболее вероятной скоро-
скорости vv
Относительное число молекул
Дя/я, скорости которых лежат в дан-
данном интервале к, и ~\- Дм, равно
произведению ординаты кривой на
Дм, т. е. изобразится площадью
столбика, заштрихованного на рис.
121.
Для того чтобы составить более
конкретное представление о законе-
Максвелла, приведем следующие
данные. Наиболее вероятная ско-
скорость молекул азота (р. == 28) при
148° С равна
-.Г 2 ¦ 8,31 ¦ 107 • 421
~ V 28
= 500 м/сек.
см/сек ==
ал
П-Аи
0,8
/
/
/
1
/
\
\
\
ч
*
ч
0.S
ft*
0,2
0,8 1,2 1,6 2.0 и.
Рис. 120, Функция распределения
Максвелла.
Ли.
п-Ли
При этом распределение моле-
молекул азота по областям скоростей будет следующее:
Рис. 121. Площадь заштрихован-
заштрихованного столбика представляет отно-
относительное число молекул, скорости
которых лежат в данном интервале
скоростей Аи.
Область
скоростей
в м/сек
0<а< 100
100 < v < 300
300 < v < 500
500 < v <С 700
700 <о< 1000
1000 < v
Часть (в °/«) общего числа молекул
азота G'=42ГК), имеющих
скорости, заключенные в указанных
пределах
0,6
12
30
29
23
5,4
Как видно, 59% от общего числа молекул имеют скорости,
лежащие в области между 300 м/сек и 700 м/сек, т. е. в области,
на которую приходится и наиболее вероятная скорость vB = 500 м/сек.
Относительное число медленных молекул (г/<^100 м/сек) и очень
190
ГАЗЫ
[гл. vn
быстрых малб. Однако все же число молекул, скорости которых
более чем вдвое превышают наиболее вероятную (•и^ЮОО м/сек),
достигает 5,4%. Наиболее вероятная скорость молекул данного газа
определяется его температурой: она тем больше, чем выше темпе-
температура; однако в газе и при невысоких температурах в некотором
количестве присутствуют молекулы, движущиеся со значительными
скоростями; наличие таких „горячих" молекул, как мы увидим в даль-
дальнейшем, играет весьма существенную роль для протекания многих
процессов.
Кривая распределения скоростей Максвелла позволяет найти сред-
среднюю арифметическую скорость, для которой, как можно показать,
получается значение:
8ДГ
71A
D)
Таким образом, сопоставляя три рассмотренные нами скорости:
. 1) наиболее вероятную
2) среднюю арифметическую
^1,60/Ж
(JL
Рис. 122. Сравнение наиболее
вероятной vB, средней арифме-
арифметической о и средней квадратич-
квадратичной У v* скоростей молекул.
3) среднюю квадратичную
М- '
них яв-
наиболь-
наибольэтими
видим, что наименьшей из
ляется наиболее вероятная, а
шей— средняя квадратичная (рис. 122). Отношение между
скоростями не зависит ни от температуры, ни от рода газа.
Приведем пример пользования формулой Максвелла. Пусть требуется
определить, какая часть молекул водорода (ц = 2) при Г=300°К обладает
скоростями, лежащими в интервале от 1900 до 1905 м/сек.
Для этого прежде всего находим значение наиболее вероятной скорости
молекул водорода при Т—ЗОО'К:
ШТ ЛГ\ • 8,31 • 10' • 300
I/
vB=
ЛГ\ • 8,
= I/ ¦
см/сек = 1,6• 105 см/сек.
Отсюда значение относительяой скорости, соответствующей скорости
молекул водорода «=1900 м/сек при данной температуре, будет:
1,9 • 10"
ц== =-
Значение Ди определим из
соотношения Ди = —;
так как \v =
1905 м/сек —1900 м/сек = ЬЛФсм1сек, то
дв=да=0'0031-
§ 50]
ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ МАКСВЕЛЛА
191
Значение
имеем
Аи
и-Дц
, соответствующее и =1,2, найдем из рис. 120, откуда
An
и • Аи
= 0,78.
Отсюда относительное число молекул, скорости которых лежат в интер-
интервале скоростей от v =1900 м/сек до г» ==1905 м/сек, равно
— =0,78 • 0,0031 =2,5 ¦ 10-а,
т. е. 0,25% всех молекул имеют скорости, заключенные в указанном интер-
интервале.
Для многих конкретных задач весьма важно знать число молекул, ско-
скорости которых больше некоторого заданного значения и. Число этих молекул
изобразится на графике, дающем закон рас-
распределения Максвелла, площадью фигуры,
заштрихованной на рис. 123. Эту площадь
как функцию скорости и можно вычислить
путем интегрирования формулы Максвелла;
результат такого расчета может быть пред-
представлен в виде таблицы или графика.
Обозначим через па число молекул, ско-
скорости которых больше данной и; на
рис. 124 представлена кривая значения njn
в зависимости от а. Значение ординаты
этой кривой 1,0 для ц = 0 означает, что
все молекулы имеют скорости, заключен-
заключенные между 0 и со; ордината 0,57 для
и=1,0 означает, что 57% всех молекул
имеют скорости, превышающие наиболее
и (практически для и 3)
дующей формулой:
Рис. 123. Площадь заштрихован-
заштрихованной фигуры дает относительное
число молекул, скорости кото-
которых больше данного значения и.
вероятную, и т. д, Для ббльших
. 3) величина nujn приближенно представляется сле-
0,8
0.6
?>,*
0.2
п
\
\
у
\
\
ч
ч
•**
-^-=1,128 и- е-"\
п
E)
О ОЛ 0,8 1,2 1,6 2,0 и
Рис. 124. Ординаты кривой
дают относительное число
молекул, скорости которых
больше данного значения и.
Рассмотрим еще несколько конкретных
примеров.
Пример 1. Какая часть молекул газа
имеет скорости, лежащие между 4«vB и 2ив?
Решение. Так как здесь интервал ско-
скоростей Аи велик, то нельзя непосредственно
пользоваться формулой Максвелла B). Поэтому
пользуемся графиком, приведенным на рис. 124.
Для скорости молекул, равной '/а от наиболее
вероятной, относительная скорость ы = 1/2; по
графику рис. 124 этому значению и соответ-
соответствует — = 0,92, что означает, что 92% всех
молекул движется со скоростями, превышаю-
превышающими ll%va. Также имеем, что скорости 2vB со-
ответствует и = 2; этому значению «соответствует по графику — = 0,05, что
означает, что 5% всех молекул имеют скорости, превышающие удвоенную
наиболее вероятную скорость. Из этих данных имеем, что число молекул,
L 2 92% 5% 87%
у р
скорости которых лежат между Lj2vB
от общего числа молекул.
, у,
и 2va, составляет 92% — 5% = 87%
192 газы
Пример 2. Какая часть молекул имеет кинетическую энергию поё
пательного движения, превышающую удвоенную среднюю кинетическую
энергию поступательного движения?
Решение. Средней кинетической энергиещ|бладает молекула, движу-
движущаяся со средней квадратичной скоростью. Поэтому скорость молекулы,
кинетическая энергия которой равна удвоенной средней кинетической энергии,
будет удовлетворять условию:
Относительная скорость и, соответствующая этому значению V, равна
. _ 2RT
У v у р > а vb у
откуда получаем
=/3=1,73.
По графику рис. 124 значению и = 1,73 соответствует —=0,11, откуда сле-
следует, что число молекул, кинетическая энергия которых превышает удвоен-
удвоенную среднюю кинетическую энергию, составляет 11°/о от общего числа
молекул.
Формула Максвелла B) дает число молекул, скорости которых лежат в
данном интервале скоростей До, независимо от направления скоростей.
Однако может быть поставлен и более частный вопрос: каково число моле-
молекул, скорости которых лежат в данном интервале скоростей и имеют неко-
некоторые определенные направления? Для этого введем в рассмотрение вектор
скорости молекул V, составляющие которого обозначим через vx, vy и v2.
Число молекул, составляющие скоростей которых vx лежат в интервале
vxt vx-\~bvx> составляющие vy — в интервале vy, vy^-&vv, составляющие
vz—в интервале vz, vz + kvz, равно
* я • е AvxAu\jAvz. F)
или
• п • е &vx&Vy&vz, Fа)
где
т (vx -\- v\ + vl)
Еь= ¦— ' кинетическая энергия молекулы.
Допуск, сделанный для составляющих скоростей vx, vy, vlt ограничивает
как интервал, в котором лежит численное значение скорости v, так и ее
направление. В самом деле, введем координатную систему, в которой по
§ 50]
РАСПРЕДЕЛЕНИЕ ЧАСТИЦ С ВЫСОТОЙ
193
осям отложим значения vx, vy, vz (рис. 125); вектор скорости v в этой
системе изобразится стрелкой, начало которой лежит в начале координат.
Условие, что составляющие скоростей моле-
молекулы vx, Vy, v2 лежат в интервале vx, vx-\-Avx;
vy, Vy + Avy; vz, vs-\-Avz, означает, что речь
идет о всех тех молекулах, скорости v кото-
которых изображаются на рис. 125 векторами,
концы которых лежат внутри данного объема
До) — AVvAvv&'0*.
Если ограничить вектор скорости молекулы
лишь условием, чтобы его численное значение
лежало в данном интервале екоростей v, v-\-hv,
то на рис. 126 эти скорости изобразятся век-
векторами, имеющими всевозможные направле-
направления, но длина которых такова, что они оканчи-
оканчиваются внутри шарового слоя радиуса v и тол-
толщины Да.1 Число молекул, скорость которых
удовлетворяет такому условию, выразится фор-
формулой F), где ДоЛДо<,Дг>г должно быть заме-
заменено объемом указанного шарового слоя
откуда по F)
Дсо = 4пиа • До,
п • е
mv*
' 2kT
G)
Рис. 125. Скорости, соста-
составляющие которых vx, Vy, vz
ограничены данными интер-
интервалами Avx, Avy, Avz, изобра-
изображаются векторами, концы
которых лежат в объеме
Дш =
Легко видеть, что формула G) переходит в формулу Максвелла B), если
тносительную скорость и'=~. Обе формулы F) и G) дают
распределение м"о^екул по скоростям. Они отли-
отличаются лишь, способом выбора тех групп моле-
молекул, об относительном числе которых идет речь.
Формуле G) можно придать еще один вид,
вводя вместо скоростей кинетическую энер-
энергию ??. Дифференцируя равенство Ек = -^—,
получим
dE/i = mv dv.
Заменяя дифференциалы dEhadv через малые
интервалы энергии и скорости АЕк и Av, найдем
До = — АЕь.
mv R
Подставляя это значение До в G) и замечая
также, чтоо=^/ —^ , получим
Рис. 126. Скорости, числен-
численные значения которых огра-
ограничены данным интервалом,
изображаются векторами,
концы которых лежат внутри
шарового слоя.
V» (kT)
•е- "T-VE;-AEk. (8)
Формула (8) указывает, какое число частиц Дя имеет кинетическую
энергию, приходящуюся на данный интервал энергий.
') Для наглядности на рис. 126 представлено лишь сечение этого шаро-
шарового слоя плоскостью YZ.
194
газы
[гл. vii
Больцман обобщил закон распределения Максвелла F) на случай, когда
молекулы движутся в поле силы тяжести (в общем случае—в любом сило-
силовом поле). При этом кинетическая
энергия Е/г в формуле F) должна быть
заменена полной энергией молекулы
р, где Е
и
АН
л До/
Рис. 127. График, соответствую-
щий закону Больцмана.
Е = Еь + Ер, где Ер — ее потенциаль-
потенциальная энергия. Кроме того, так как по-
потенциальная энергия, вообще говоря,
зависит от координат, приходится го-
говорить о числе молекул, для которых
ограничены не только скорости опре-
определенным интервалом скоростей, но и
координаты которых также ограничены
определенным интервалом. Окончательно,
вместо закона распределения F) полу-
получается:
Дя =
(8а)
Формула (8а) выражает закон распределения Больцмана. Графически зави-
зависимость Ага/иД<л от Е, где Дш = AvxAvyAv2AxAyAz, изображена на рис. 127.
§ 51. Распределение частиц с высотой. Формула распределения
Больцмана позволяет получить закон убывания числа частиц с высотой в поле
силы тяжести. Представим себе вертикальный столб газа, все части которого
находятся при одинаковой температуре Т. Скорости молекул и Их распре-
распределение по скоростям при этом повсюду (и внизу и вверху) одинаковы и
подчиняются закону Максвелла, которым ,мы будем пользоваться в виде,
даваемом формулой F) § 50.
Распределение частиц по энергиям дается формулой Больцмана (8а)
того же параграфа:
_ Л
• п ¦ е kTbvx&vy&.vzAxAyAz. A)
Полная энергия ? = ?ft-|- Ер, где ?ft — кинетическая энергия и Ер—по-
Ер—потенциальная; в данном случае потенциальная энергия есть энергия молекул
в поле силы тяжести, т. е. Ep = mgh, где h — высота, на которой находится
молекула. Отсюда A) принимает вид:
An =
Ek + mgh
kT AvxAvyAvzAxAyAz,
или, переходя к числу частиц, приходящихся на единицу объема,
8 mgA ^
Распределение молекул по скоростям на любой высоте выражается фор-
формулой Максвелла F) §
m
C)
где гад — число частиц в единице объема на высоте Л.
§ 52]
ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
195
Формулы C) и B) можно согласовать, если считать, что число молекул
в единице объема П/, на высоте h выражается соотношением:
m.gh
nh = пйе
D)
где па — число молекул в единице объема на высоте h~0. Эта формула п
дает закон распределения числа молекул в единице объема с высотой: число
молекул в единице объема ил убывает с высотой экспоненциально (рис. 128).
Пользуясь формулой D), легко получить выражение для зависимости
давления газа от высоты.
Давление газа при данной температуре пропорционально числу частиц га
в единице объема [формула D) § 46], откуда закон убывания давления р
с высотой Л будет тот же, что и закон убыва-
убывания числа частиц:
_ mgh
Ph=Po-e kT
•>«
Рис. 128. Закон убывания
числа частиц в единице
объема с высотой h.
о та
Замечая, что — = -^-, где [л— молеку-
молекулярный век газа, a ft — газовая постоянная,
перепишем последнюю формулу:
V-gh
Ph=Pae RT . E)
Формула E) носит название барометриче-
барометрической Формулы; она указывает, что давление
газа убывает с высотой экспоненциально. Кроме
того, из формулы E) видно, что убывание
давления газа с высотой зависит от молеку-
молекулярного веса: чем больше молекулярный вес газа, тем скорее убывает
с высотой его давление. Формулой E) можно приближенно пользоваться для
определения атмосферного давления ph на разных высотах постольку,
поскольку температуру Т можно считать одинаковой на разных высотах, что
на самом деле не выполняется для значительных разностей высот.
§ 52. Определение числа Авогадро. В газе, находящемся в поле
силы тяжести, число молекул в единице объема убывает с высотой.
Если число молекул в единице объема на нулевой высоте равно щ,
то на высоте h оно равно
ing*
kT
О)
где m — масса молекулы, g — ускорение силы тяжести, k — постоян-
постоянная Больцмана, Т — температура в шкале Кельвина [обоснование фор-
формулы A) см. в § 51].
Формула A), дающая распределение числа молекул с высотой,
была применена Перреном для броуновских частиц и использована
для определения числа Авогадро N. Броуновские частицы (см. § 43)
находятся под влиянием ударов молекул в беспорядочном движении.
Исходя из общих соображений о характере беспорядочных ударов,
можно показать, что средняя кинетическая энергия w одной
196 ГАЗЫ [ГЛ. VII
броуновской частицы равна средней кинетической энергии молекул
при данной температуре Т, т. е.
_ 3 3//?
W = kT=\
Таким образом, совокупность броуновских частиц в точности вос-
воспроизводит модель молекулярно-кинетической структуры газа; только
в этой модели „молекулы" так велики, что их можно видеть в микро-
микроскоп, скорости же их движения малы из-за большой по сравнению
с отдельной молекулой массы. Совокупность броуновских частиц под-
подчиняется всем газовым законам, в том числе и закону A), дающему
убывание числа частиц с высотой.
Из формулы B) мы имеем, что число Авогадро N равно
yV=|4.7\ C)
откуда видно, что, зная среднюю кинетическую энергию w броуновской
частицы "при данной температуре Т, можно непосредственно определить
ч^слр Авогадро N. Однако попытки непосредственного определения
средней кинетической энергии броуновской частицы гг> = —~ по
массе броуновской частицы m и среднему значению квадрата ее ско-
скорости г»9 не привели к желательным результатам. Дело в том, что из-за
хаотического движения броуновской частицы невозможно путем измере-
измерения под микроскопом определить среднее значение квадрата ее скорости
т>4. Поэтому Перрен пошел обходным путем, путем определения сред-
средней кинетической энергии w из закона распределения частиц с высотой.
Броуновские частицы, взвешенные в какой-либо жидкости, не опу-
опустятся все со временем на дно сосуда, но распределятся, благодаря
совершаемому ими движению, с плотностью, убывающей по высоте:
у самого дна частиц будет больше всего, на некоторой высоте над
дном — их будет мало. Закон распределения числа броуновских ча-
частиц и в зависимости от высоты h определится формулой A). Это убы-
убывание числа частиц с высотой происходит чрезвычайно быстро (масса от
броуновской частицы очень велика по сравнению с массой одной мо-
молекулы), оно заметно при изменении высоты h на доли миллиметра.
Подставляя в формулу A) вместо температуры Т ее значение
через w по B), получим
_ЗРй
пн = щ-е 2™> D)
здесь Р — вес броуновской частицы; из формулы D) видно, что по за-
закону убывания числа частиц с высотой, зная их массу т, можно опре-
определить среднюю кинетическую энергию Щ знание же w позволяет
найти по C) число Авогадро N.
Перреном была изготовлена из смолы garcinia тогеГя (гуммигут)
путем многократного центрифугирования весьма однородная эмульсия,
§ 52]
ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
197
состоящая из шарообразных частиц одинакового размера, порядка
микрона. Взвешенные в воде, эти частицы обнаруживали при на-
наблюдении в микроскоп интенсивное броуновское
движение. Число частиц в жидкости убывало
с высотой. Это убывание происходило очень
быстро.
Для наблюдения этого убывания применялся
следующий метод: в предметном стекле (рис.129)
делалось цилиндрическое углубление; это углубле-
углубление заполнялось эмульсией и закрывалось сверху
покровным стеклом. Эмульсия рассматривалась в
микроскоп с малой глубиной изображения. Фоку-
Фокусируя микроскоп на определенный слой эмульсии,
можно было видеть броуновские частицы, находя-
находящиеся в этом слое; изображение частиц, расположен
Обгектив
микроскопа
Покровное
стекло
Предметнее
Эндякия стекло
Рис. 129. Метод на-
наблюдения броунов-
броуновских частиц в мик-
микроскоп.
ных выше и ниже, не попадало в фокус. Передвигая объектив микроскопа,
его можно было фокусировать на различные слои эмульсии и таким
образом замечать изменение числа частиц с высотой.
На рис. 130 представлены мгновенные микро-
микрофотограммы с броуновских частиц, произведенные
для различных слоев жидкости: в нижнем слое
частиц много, а в верхнем — мало. Непосредствен-
Непосредственный подсчет числа частиц п'н, видимых в микроскоп
в слоях на различных высотах h, позволяет опре-
определить закон их убывания с высотой. Так как
число частиц и/,, видимых в поле зрения микро-
микроскопа, пропорционально их числу нд в единице
объема на той же высоте, то числа п'/, должны
удовлетворять формуле D).
Пусть число частиц в слое, лежащем на вы-
высоте hb будет n'hp по формуле D) оно равно
аналогично для числа частиц пл2, находящихся
в слое на высоте йа, получим
3 P ,,. . 3 P,. . t
— Ч Пи =¦(*!—As)
3 2 t» , откуда — = e 2 w
Рис. 130. Распреде-
Распределение броуновских
частиц в слоях на
разной высоте. Чем
выше лежит слой,
тем меньше в нем
частиц.
Здесь п/ц и щ
частиц, видимых
Логарифмируя это выражение и решая его отно-
относительно Щ получим
о г» / г. t \
E)
— 3 P(fl2—i
2 определяются путем непосредственного счета числа
под микроскопом, А2 — Aj — сдвигом объектива
198 газы [гл. vn
микроскопа, который необходимо сделать, чтобы перейти от наблю-
наблюдения числа частиц в слое, лежащем на высоте ht, к слою, лежа-
лежащему на.высоте Л3. Этот сдвиг измеряется микрометрическим винтом.
Остается для определения w найти вес броуновской частицы т.
Вес броуновских частиц Перрен измерял, применяя формулу Стокса
(§ 42). Формула Стокса позволяет по скорости падения частицы
в вязкой жидкости определять ее радиус г. Вес сферической частицы Р
^непосредственно выражается через ее радиус г и плотность р ве-
вещества, из которого она состоит:
где р' — плотность воды.
Скорость падения отдельных частиц, наблюдаемых Перреном, опре-
определить нельзя, так как они совершают броуновское движение. Однако
можно поступить следующим образом: если размешать эмульсию,
налитую в высокий узкий сосуд, так, чтобы частицы в ней распре-
распределились по высоте равномерно, а затем оставить ее в покое, то
частицы начнут оседать; верхняя часть жидкости начнет просветляться.
При этом образуется хотя и несколько размытая (из-за броуновского
движения), но все же заметная для невооруженного глаза граница
помутнения. Скорость опускания этой границы помутнения и даст
скорость падения отдельных частиц. Таким образом могут быть найдены
все величины, необходимые для определения средней кинетической
энергии частицы w. Зная же w, определим, как отмечено, по C)
число Авогадро N.
Другой метод определения числа Авогадро N, примененный Пер-
Перреном, основывается на наблюдении смещения броуновских частиц.
Предположим, что мы наблюдаем проекцию смещения броуновской
частицы на произвольным образом проведенную ось ОХ. Пусть за время
наблюдения t проекция смещения на эту ось равна лг. Если произвести
измерения таких х для многих броуновских частиц, то, как показал
Эйнштейн, среднее значение квадрата х удовлетворяет соотношению:
где R — газовая постоянная, Т — температура в шкале Кельвина,
т] — коэффициент вязкости среды, в которую погружены броуновские
частицы, г—радиус броуновской частицы. Так как все величины,
входящие в эту формулу, кроме N, доступны непосредственному
измерению, то эта формула позволяет найти число Авогадро N.
Измерения, произведенные Перреном, показали, что число Аво-
Авогадро есть величина порядка 6-1023 частиц на моль. Более точных
результатов методы Перрена дать не могут. В дальнейшем (см. т. II)
мы приведем другие способы, которые позволяют определить число
Авогадро более точно. Как уже упоминалось, в настоящее время для
числа Авогадро принимается значение А/ = 6,023-10м моль'1.
§ 53]
ДЛИНА СВОБОДНОГО ПУТИ МОЛЕКУЛ
199
§ 53. Длина свободного пути молекул. Молекулы, находясь
в газе в состоянии непрерывного и хаотического движения, сталки-
сталкиваются друг с другом; между столкновениями они проходят сво-
свободно некоторый путь X. Длина этого пути между двумя столкно-
столкновениями различна, но, благодаря большому числу молекул и беспо-
беспорядочности их движения, можно говорить о средней длине свободного
пути молекул. Подсчитаем эту среднюю
длину свободного пути молекул X.
Рассмотрим некоторую определенную
молекулу, которая движется со скоростью
v; молекулу представим себе в виде ша-
шарика радиуса г. После каждого столкно-
столкновения молекула меняет направление ско-
скорости v, однако для простоты предпо-
предположим, что молекула продолжает после
столкновения двигаться в том же напра-
направлении, в каком она двигалась до столкно-
столкновения. Кроме того, для простоты положим,
что все другие молекулы, кроме рассма-
рассматриваемой, неподвижны. Тогда молекула заденет на своем пути все
те молекулы, центры которых лежат на расстоянии, не большем Чт
(рис. 131) от прямой, вдоль которой она движется.
Следовательно, за единицу времени молекула заденет все те z
молекул, центры которых лежат внутри цилиндра радиуса R = 2r
и длины /, численно равной скорости моле-
--—7~чД.?г КУЛЫ v (Рис- 132); число же молекул z, кото-
г-Г~~ А--?- Рые попадают внутрь такого цилиндра, равно
Рис. 131. Молекула задевает
на своем пути все те моле-
молекулы, центры которых лежат
на расстоянии, не большем
2г от прямой, вдоль которой
она движется.
где щ — число молекул в единице объема.
Подставляя сюда R = 2r и подразумевая под
Рис. 132. Молекула заде- v среднюю скорость движения молекул v,
вает все те молекулы, получим выражение для среднего числа
центры которых лежат столкновений молекул в единицу времени
внутри цилиндра радиу- , 0_
са 2г. 2 = 4тсгЧ/л0. A)
Так как на самом деле другие молекулы тоже движутся, то для
числа столкновении z получается несколько большее значение, чем
даваемое формулой A). _
Соответственные выкладки показывают, что г в \/~2 раз больше:
Размеры молекул являются величинами порядка г^10~8 см; число
молекул в единице объема при нормальных условиях ло^З-1О19
и скорость молекул г>^ё5-104 cmjсек, откуда мы получаем, что
200 газы . [гл. vit
число столкновений, испытываемых молекулами газа в единицу
времени, по порядку величины
г^4.]/2-3,14A0-8K-5-104.3-1019 секг1^ 3-109 сек.
Таким образом, молекулы испытывают при нормальных условиях
несколько миллиардов столкновений в секунду.
Среднюю длину свободного пути молекулы X получим, поделив
средний путь, проходимый ею за единицу времени, на число столкнове-
столкновений в единицу времени z. Так как путь, проходимый в единицу времени,
численно равен скорости Ъ, то средняя длина свободного пути молекулы
X = f C)
Подставляя сюда z по B), получим
или, если ввести вместо радиуса молекулы ее диаметр о = 2г, то
Х = —J Dа)
Из формул D) и Dа) видно, что средняя длина свободного пути
молекул X обратно пропорциональна числу молекул в единице объе-
объема и0. Так как, при постоянной температуре, н0 прямо пропорционально
давлению газа, то получаем
^1 2 Р* (*.\
¦^—*;.—*• ()
где Xt и Х2 — соответственно длины свободных путей молекул, отно-
относящиеся к давлениям газа р± и /?а. Из формулы E) имеем: длина
среднего свободного пути молекул X обратно пропорциональна
давлению газа р при постоянной температуре.
Абсолютное значение средней длины свободного пути молекул
зависит от их диаметра о. В дальнейшем мы увидим, что существуют
методы определения численного значения X для разных газов; по этим
численным значениям 1 по формуле Dа) определяются диаметры мо-
молекул о.' Надо иметь в виду, что найденные таким образом диаметры
не представляют собою в точности действительных размеров молекул.
Прежде всего, молекулы не являются правильными шарами; во-вторых,
процесс столкновения молекул не похож на самом деле на соударение
упругих шаров. Молекулы представляют собою сложные системы,
состоящие из атомных ядер и электронов. Силы взаимодействия между
ними, которые сказываются на малых расстояниях, носят сложный
(отчасти электрический) характер. Процесс столкновения сводится
к тому, что на малых расстояниях молекулы отталкиваются друг от
§ 53]
ДЛИНА СВОБОДНОГО ПУТИ МОЛЕКУЛ
201
друга, причем силы отталкивания возрастают по мере уменьшения
расстояния между ними (подробнее см. § 61). В. результате действия
этих сил скорости молекул меняют свое направление.
Таким образом, диаметр молекул а, вычисленный в предположении,
что молекулы являются упругими шариками, дает лишь некоторое
приближенное представление о размерах молекул; величина а является,
как принято говорить, эффективным диаметром молекулы. Вели-
Величина кг1 называется эффективным сечением молекулы.
Приближенный характер расчетов, приводящих к формуле D), сказы-
сказывается в том, что средняя длина свободного пути молекул на самом деле
несколько зависит от температуры, в то время как по формуле D) она но
должна зависеть от температуры при нагревании при постоянном объеме.
С повышением температуры средняя длина свободного пути молекул не-
несколько повышается. Если среднюю длину свободного пути, вычисляемою
по D), обозначить через Х^, то действительная средняя длина свободного
X при температуре Г
Таблица VI
пути
равна
температуре
Т
Средняя длина свободных путей
и эффективные диаметры молекул
и атомов
Газ (пар)
Водород, Н2 . . . .
Азот, N2
Кислород, О2 . . .
Гелий, Не
Аргон, Аг
X • 10s см
1,123
0,599
0,647
1,798
0,666
<s • 10s см
2,3
3,1
2,9
1,9
3,6
1 °°С+Г'
где С—величина, постоянная
для данного газа; она носит на-
название постоянной Сеэерлэнда,
ее значения определяются из
опытных данных.
Для азота, например, С =
= 102,7°, откуда формула Сё-
зерлэнда дает при 7'= 300° К
среднюю длину свободного пути
X на 12°/о больше, чем при
Т = 200° К.
Приведем теперь неко-
некоторые численные данные.
В табл. VI даны средние длины свободных путей X при нормальных
условиях (р=1 am, t = O°C) для некоторых газов и паров и вы-
вычисленные по этим X эффективные диаметры о.
Для воздуха при приближенных подсчетах среднюю длину сво-
свободного пути X при нормальных условиях можно считать равной
X = 7 -10 см.
Тогда для различных давлений воздуха, согласно формуле E),
получаем значения, приведенные в табл. VII.
Таблица VII
Длина свободного пути молекул воздуха при различных давлениях
Давление в мм ртут-
ртутного столба
Средняя длина свобод-
свободного пути 1 в см ....
760
7 • 10-"
1
5 • Ю-3
0,01
5 • 10-'
ю-4
5- 10'
5- 103
202
ГАЗЫ
[ГЛ. VII
Из табл. VII видно, что средняя длина свободного пути X газовых
молекул, составляющая при нормальных условиях примерно стоты-
стотысячную долю сантиметра, в разреженном газе при давлении в 0,01 мм
Hg достигает величины в 5 мм. В очень сильно разреженном газе
(давление порядка 10~6 мм Hg) длина свободного пути молекул
достигает огромной величины в несколько десятков метров.
Эти расчеты позволяют нам выяснить, что представляет собою газ
в состоянии сильного разрежения, т. е. в таком состоянии, в каком
он находится в сосудах, откачанных современными хорошими насо-
насосами. Так, технически не представляет труда откачать из сосуда
воздух до давления р^. 10~4 мм Hg; при этом число молекул в 1 см3
будет еще приблизительно равно 4-Ю12. Средняя же длина их
свободного пути, по данным табл. VII, равна Х = 50 см. Если раз-
размеры самого сосуда порядка 10 см, то это означает, что каждая
данная молекула несколько раз пролетит через весь сосуд и отра-
отразится от его стенок раньше, чем она на своем пути случайно столк-
столкнется с другой молекулой.
Таким образом, насмотря на то, что в каждом 1 см3 сосуда нахо-
находится еще количество мол'екул, выраженное двенадцатизначным числом,
сосуд может считаться в достаточной мере „пустым": молекулы сво-
свободно летают в нем от стенки к стенке.
§ 54. Опыты с молекулярными пучками. Возможность получать
такие разрежения газа, что средняя длина свободного пути молекул
достигает десятков сантиметров или
А Д | даже нескольких метров, позволяет
G\at\a2 \l \ поставить опыты, в достаточной
Г7 Г*~~~у меРе непосредственно подтверждаю-
—¦—1—1 ' ^ щие правильность основных выво-
выводов молекулярно-кинетической тео-
Рис. 133. Образование молекуляр- рии га3ов
ного пучка. г-г ' „•
7 Представим себе сосуд, разде-
разделенный рядом перегородок (рис. 133).
В перегородках имеются малые круглые отверстия ait aa, располо-
расположенные на одной прямой. Из всего сосуда выкачан воздух до такого
давления, что средняя длина свободного пути молекул больше раз-
размеров сосуда. В часть сосуда А помещен легкоплавкий металл (напри-
(например, натрий), и эта часть сосуда подогревается. Тогда металл К,
испаряясь, дает пары, которые заполняют часть сосуда А при доста-
достаточно низком давлении. Те молекулы этого пара, которые имеют
скорость, направленную по прямой, вдоль которой лежат отверстия а,,
аь пролетают через эти отверстия в часть сосуда В. Благодаря весьма
низкому давлению остаточного газа в сосуде, молекулы движутся
в части сосуда В прямолинейно и равномерно. Вся совокупность моле-
молекул пара металла, пролетевших через отверстия аь аь образует в части
сосуда В прямолинейно распространяющийся пучок молекул. Отсюда
описанный опыт носит название опыта с молекулярным (атомным)
§ 54]
ОПЫТЫ С МОЛЕКУЛЯРНЫМИ ПУЧКАМИ
203
С3\
пучком. Достигнув стенки С, атомы металла прилипают к ней,
если только она достаточно холодна. Таким образом, на стенке С
оседает видимый слой металла, который и указывает на то, что моле-
молекулярный пучок долетел до этой стенки. Форма осевшего на стенке С
слоя воспроизводит форму отверстий аи а2; если эти отверстия круглы,
то и осевшее пятнышко металла круглое. Если по
пути пучка поставить какое-либо препятствие, напри-
например натянуть проволочку /, то на пятне осевшего
металла получится „тень" от этой проволочки. Все
эти опыты непосредственно убеждают нас в прямо-
прямолинейном движении молекул в пучке.
Можно осуществить такое видоизменение опыта
с молекулярным пучком, которое позволит оценить
длину свободного пути молекул. При низком давле-
давлении остаточного газа молекулярный пучок, вылетаю-
вылетающий из отверстия а (рис. 134), достигает противо-
противоположной стенки С; на более близких боковых
пластинках Clt C2, С3, ... металл не оседает. Если
в сосуд добавить газ так, чтобы длина свободного
пути уменьшилась, то молекулы, летящие в пучке,
испытают столкновения, не долетев до стенки С.
Столкнувшись с молекулами газа, они отклонятся
в сторону и осядут на соответственной боковой
пластинке С и на более далеких пластинках. Чем
больше давление добавляемого газа, тем меньше
длина свободного пути и тем на более близкие
боковые пластинки попадают молекулы из пучка.
Этот опыт позволяет оценить среднюю длину свободного пути при
различных давлениях, причем получаются значения, совпадающие по
порядку с вычисляемыми на основе молекулярно-кинетической тео-
теории газов.
Если в молекулярном пучке в момент его вылета из отверстия а в еди-
единицу времени пролетало п0 молекул, то на некотором расстоянии х от отвер-
отверстия а их будет меньше, так как часть молекул, претерпев столкновение
вышла из пучка в стороны.
Теоретический расчет показывает, что на расстоянии х от начала пучка
в единицу времени в нем пролетит пх молекул, определяемых формулой:
Рис. 134. Опре-
Определение средней
длины свобод-
свободного пути моле-
молекул с помощью
молекулярного
пучка.
пх = пае ,
где X — средняя длина свободного пути. Таким образом, число молекул
в пучке убывает по экспоненциальному закону. Если положить х = 2\ то
получим
И2х = пое х =я0е~2 = 0,135 п0>
т. е. только 13,5°/0 от всех молекул в пучке пролетит путь, вдвое превы-
превышающий среднюю длину пути,
204 газы [гл. vii
Наконец, отметим опыты с молекулярными пучками, позволяющие
оценить скорость газовых молекул. Эти опыты были впервые произ-
произведены Штерном.
Идея опыта Штерна заключается в следующем: представим себе
цилиндрический сосуд, по оси которого расположена проволока К
. _^^^ (рис. 135). Проволока /f окружена цилиндриче-
цилиндрической загородкой, в которой имеется щелевое
отверстие а. Во всем сосуде получается высокий
вакуум. В опытах Штерна употреблялась пла-
платиновая проволока, покрытая снаружи слоем
р/ серебра. При нагревании платиновой проволоки
током серебро испарялось и давало мол'еку-
лярный пучок, вылетающий из щели а и дости-
достигающий стенки сосуда в точке Ь. Если весь
Рис 135~Сх1ма опыта сосуд в целом ПРивесги во вращение вокруг
Штерна для определе- оси- проходящей через проволоку К, то пучок
ния скоростей молекул, начнет отставать от сосуда и даст след в сме-
смещенной точке by Легко связать это смещение я
между точками b и Ьх со средней скоростью ъ молекул в пучке.
Пусть радиус сосуда R. Тогда среднее время t, в течение которого
молекулы летят от проволоки К до стенки сосуда, равно
v
За это время i каждая точка на стенке сосуда пройдет путь s, равный
где ш — угловая скорость вращения сосуда. Из последнего равенства
имеем
г s
Приравнивая оба выражения для времени t друг другу, получим
Так как молекулы движутся с разными скоростями, то след в точке Ь{
несколько размазан. Но измеряя смещение s до середины следа и
зная радиус сосуда R и угловую ^—^
скорость его вращения ш, опре- ' ' ^
делим среднюю скорость моле-
молекул v. Измерения, сделанные для
серебра, оказались в хорошем со-
согласии со значением скорости, вы- _ ,„. „
. ^ Рис.136. Схема опыта для опреде-
численным по формулам кинетиче- ления скоростей молекул.
ской теории газов.
Опыт Штерна впоследствии повторялся в различных вариантах,
один из которых представлен на рис. 136.
§ 55} ЯВЛЕНИЯ ПЕРЕНОСА В ГАЗАХ. ДИФФУЗИЯ 205
В вакууме с помощью щелей ah a2 выделяется атомный пучок
висмута, испаряемого в печке А. На пути пучка вращается цилиндр В
со щелью а3. Когда щель а3 располагается против щелей at и а3,
в цилиндр влетают атомы. За время, пока эти атомы летят поперек
цилиндра, он успевает повернуться на некоторый угол, поэтому атомы
попадают не в точку Ь, расположенную против щели а3, но в точку,
несколько смещенную относительно Ь. Более быстрые атомы оказы-
оказываются при этом смещенными меньше, а более медленные — больше.
Получается полоска осевшего металла с разной плотностью в разных
местах. Измеряя плотность осевшего металла, можно найти закон
распределения атомов по скоростям.
Закон распределения молекул по скоростям в молекулярном пучке не-
несколько отличается от закона распределения молекул по скоростям в объеме
самого газа. В объеме газа молекулы распределены по скоростям по закону
Максвелла [формула B) § 50]:
42иаДи. (I)
Дп=4=пеиДи.
у %
В молекулярном же пучке больше быстрых молекул, чем в том газе, из
которого он возник. Дело в том, что быстрые молекулы чаще прорываются
через отверстие в диафрагме, чем медленные. Вычисления показывают, что
если в газе относительное число молекул, скорости которых лежат в интер-
интервале скоростей и, и -\- Ди, равно Дя/л, то в пучке относительное число моле-
молекул, имеющих скорости в том же интервале, равно
Дге' Ди 1/jc
— _1 . и
п' ~ п 2 '
где и — относительная скорость молекул. Отсюда закон распределения моле-
молекул по скоростям в пучке выразится не формулой A), а формулой:
Дга1 = 2я'<г"а и3 Ди. B)
§ 55. Явления переноса в газах. Диффузия. Беспорядочное
движение молекул в газе ведет к их непрерывному перемешиванию,
отсюда два разнородных соприкасающихся газа взаимно проникают —
диффундируют. Перенос молекул газа из одних мест в другие обус-
обуславливает также механизм явлений внутреннего трения в газах и
теплопроводности. Все эти явления, связанные с движением молекул,
носят название явлений переноса.
Во время развития кинетической теории газов против нее дела-
делалось возражение такого рода: если скорости движения молекул дей-
действительно порядка нескольких сот метров в секунду, как этого
требует кинетическая теория газов, тогда взаимное проникновение
должно происходить весьма быстро. Если, например, в какой-либо
части комнаты открыть сосуд с пахучим веществом, то запах должен
бы стать сразу заметным во всей комнате, так как молекулам веще-
вещества требуются лишь доли секунды, чтобы пролететь путь, равный
размерам комнаты. На самом же деле известно, что диффузия га-
газов при атмосферном давлении происходит медленно; в частности,
медленно распространяются запахи. Ошибка в этих рассуждениях
206 ГАЗЫ [ГЛ. VII
заключается в неучете того, что молекулы, благодаря малой длине
свободного пути при атмосферном давлении, непрерывно сталкиваются
с другими молекулами, и, таким образом, „толкутся" на одном месте.
Несмотря на большую скорость, молекула за одну секунду уходит
лишь на очень небольшое расстояние от того места, где она находилась,
путь ее представляет весьма сложную и запутанную ломаную линию.
Разберем прежде всего явление диффузии.
Наблюдения показывают, что при диффузии через некоторую пло-
площадку AS переносится тем ббльшая масса газа AM, чем больше
размеры площадки AS, чем за ббльший промежуток времени At наблю-
наблюдается диффузия и чем скорее меняется в направлении, перпендику-
перпендикулярном к AS, парциальная плотность р диффундирующего газа. Про-
Проведем ось ОХ нормально к площадке AS; пусть парциальная плот-
плотность рассматриваемого газа в двух точках, отстоящих друг от друга
на отрезок Ах, отличается на Др, тогда величина Др/Дх характеризует
изменение плотности газа р на единицу длины в направлении оси ОХ;
эта величина называется градиентом плотности. По сказанному,
ДУН пропорционально градиенту плотности Ар/Ах, величине площадки
AS и времени At:
АМ = — D^^j AS At A)
Величина D, зависящая от сорта газа и от условий, при которых
он находится, называется коэффициентом диффузии. Знак минус
означает, что масса переносится в сторону убывания плотности.
Формула A) характеризует явление диффузии с макроскопической
точки зрения.
Рассмотрим теперь явление диффузии с точки зрения молеку-
лярно-кинетической теории газов. Для простоты рассмотрим два раз-
различных, взаимно проникающих газа,
со столь сходными молекулами, что
их массы и эффективные сечения
можно считать равными друг другу.
Такие молекулы будут иметь при
одинаковых условиях одинаковые
длины свободных путей и одинако-
О
вые скорости.
г Подсчитаем число молекул од-
Рис. 137. Перенос молекул через ного из ДВУХ газов- пролетающих
площадку AS. через площадку Д5 (рис. 137),
перпендикулярную оси ОХ, вдоль
которой происходит изменение плотности газа р. Мысленно выделим
справа и слева от площадки на расстояниях от нее, равных среднему
значению длины свободного пути X, кубические объемы А а В.
Тогда можно считать, что молекулы, вылетающие из любого из этих
кубиков, будут без столкновений долетать до площадки AS.
§ 55] ЯВЛЕНИЯ ПЕРЕНОСА В ГАЗАХ 207
Пусть боковые грани кубиков А и В параллельны площадке Д5
и равны ей по величине; длину ребра кубиков обозначим через /;
очевидно, /а = Д5. Обозначим число молекул рассматриваемого газа,
находящихся в кубике А, через яд. Ввиду полной беспорядочности
движения молекул, как было выяснено в § 46, можно считать, что */3
этих молекул движется вдоль оси ОХ, из них половина — в напра-
направлении положительной оси ОХ и половина — в направлении отрица-
отрицательной оси ОХ. Таким образом, из числа молекул Па, находящихся
в кубике А, число молекул, равное ]/б па, летит по направлению
к площадке AS. Так как площадка AS отстоит на X от кубика, то
все эти молекулы долетят до площадки AS без столкновений и про-
пролетят через нее. Время Ы, в течение которого эти '/б па молекул про-
пролетят через площадку AS, равно тому промежутку времени, на кото-
который последние из молекул, вылетающие из кубика А в направлении
площадки AS, пролетят позже первых; отсюда Ы=-^, где v —
средняя арифметическая скорость молекул. Таким образом, число
молекул Дпд, пролетающих через площадку AS за единицу времени
слева направо, равно
1
•Обозначим через п'о число молекул, приходящихся на единицу
объема в том месте, где находится кубик А, тогда ил = /^/3, и выра-
выражение для Апа можно написать в виде:
AnA = \nA^. = \n'ovP = \n'ovAS. B)
Точно так же получим, что число молекул Дяд, пролетающих
через площадку AS за единицу времени справа налево, будет:
An = ^n'v-AS, C)
где п'1 — число молекул в единице объема в том месте, где находится
кубик В. Отсюда разность между числом молекул, пролетающих
через площадку AS слева направо и справа налево за некоторый
произвольный промежуток времени At, равна
Ап = ±Ъ(п'о — n'J)ASAt. D)
Массу AM, переносимую через площадку AS за время Д? слева
направо (в направлении положительной оси О.Х), получим, умножив
число перенесенных молекул An на массу одной молекулы т, откуда
т- Ап = \ът(п\ — n"u)ASAt E)
\
208 газы [гл. vii
Разность п'й — п'о равна скорости изменения числа молекул в еди-
единице объема в направлении ОХ, т. е. величине Апо/Ах, умноженной
на расстояние между кубиками А и В; это расстояние равно 2Х,
откуда
Подставив это значение п"^ — п'а в E), получим
= _lu«.^ASA*, но «** =
3 Д* hx
л W*ff*> д t»lk_Jt»lL-j IIV^ III/ . —— - ~Г .
величина тщ равна массе рассматриваемого газа в единице объема,
т. е. равна плотности р, откуда
Дяо Др
отсюда
F)
Из этой формулы, в согласии с выражением A), получаем, что
переносимая масса AM прямо пропорциональна градиенту плотности
Др/Ддг, площади AS и времени At. Формулы F) и A) совпадают
между собою, если положить
D = jvZ G)
Таким образом, коэффициент диффузии D оказывается связанным
со средней скоростью движения молекул v и средней длиной сво-
свободного пути X. Средняя скорость движения молекул v пропорцио-
пропорциональна 1/ —, а длина свободного пути X не зависит при постоян-
постоянной плотности газа от его температуры. Отсюда следует, что для
данного газа, при нагревании его при постоянном объеме, коэффи-
коэффициент диффузии D>~~> у/ Т. Для разных газов, но состоящих из моле-
молекул одинакового размера, при одинаковых давлениях и температурах
D<~ ^-р=. Средняя длина свободного пути молекул X, как было по-
казано в § 53, обратно пропорциональна давлению газа, поэтому и
коэффициент диффузии обратно пропорционален давлению газа р:
D~—. Здесь р .означает суммарное давление смеси обоих газов.
В разреженных газах диффузия происходит быстрее, чем в газах
при больших давлениях.
§ 56]
ВНУТРЕННЕЕ ТРЕНИЕ И ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
209
Пбдставляя в формулу G) вместо средней длины свободного
пути X его выражение по формуле Dа) § 53, получим
Таким образом, коэффициент диффузии оказывается непосред-
непосредственно связанным с эффективным диаметром молекул о.
В случае взаимной диффузии двух газов, молекулы которых раз-
различаются размерами, под о можно подразумевать средний диаметр
молекул обоих газов: а = -=- (ot -|- а2).
§ бб. Внутреннее трение и теплопроводность газов. В § 42
мы ввели понятие о коэффициенте внутреннего трения (вязкости) ц
для жидкостей. То же определение пригодно и для
газов.
При течении слоев газа с различными скоростями
между слоями возникают силы: более быстрый слой
ускоряет соседний с ним более медленный слой и,
наоборот, более медленный слой задерживает более
быстрый. Возникающие при этом силы внутреннего
трения / касательны к слоям газа.
При обычных условиях внутреннее трение в газах
гораздо меньше, чем в жидкостях, однако оно может
быть обнаружено на ряде опытов. Схема одного из
таких опытов представлена на рис. 138. Пространство
между двумя коаксиальными цилиндрами А и В
заполнено испытуемым газом. Цилиндр А насажен
на ось О и приводится в быстрое вращение; цилиндр
В подвешен на нити С, угол закручивания которой
может измеряться. При вращении цилиндра А он
увлекает ближайшие к нему слои газа; последние,
благодаря наличию внутреннего трения, увлекают за
собою следующие слои и т. д. В результате вращаю-
вращающий момент оказывается приложенным к цилиндру В, который
поворачивается, пока упругая сила закрученной нити С не уравно-
уравновесит момент сил, приложенных к цилиндру В.
Обозначим скорость течения слоев газа через и, в отличие от
скорости молекул, обозначенной буквой v.
Тогда, аналогично тому, как это было сделано в § 42, мы можем
написать для силы внутреннего трения /:
S, A)
скорости,
Рис. 138. Схема
опыта для опре-
определения вну-
внутреннего трения
в газах.
где т] — коэффициент внутреннего трения, -^ — градиент
AS — площадка, к которой приложена сила /.
8 С. Э. Фриш и А. В. Тинорева
210
ГАЗЫ
[ГЛ. VII
С точки зрения молекулярно-кинетической теории газов, в теку-
текущем газе на скорость беспорядочного движения молекул v наложена
переносная скорость и, одинаковая для всех молекул данного слоя
газа (текущего с определенной скоростью) и различная для различных
слоев. Молекулы, перелетая, благодаря хаотическому движению, из
более быстрого слоя в более медленный, приносят с собою большую
составляющую количества движения ти
и тем самым ускоряют более медленный
слой. Обратно: молекулы, попадающие из
более медленного слоя в более быстрый,
имеют слишком малую составляющую
количества движения ти, в результате
чего они задерживают более быстрый слой.
Выделим в газе мысленно площадку
AS (рис. 139), параллельную слоям, теку-
Щим с различными скоростями и. Пусть
слой / лежит под площадкой AS на рас-
расстоянии средней длины свободного пути
молекул \. Тогда молекулы, летящие из слоя / по направлению
к площадке AS, достигнут ее без столкновений. Из § 55 следует,
что число этих молекул Дя1р пролетающих через площадку AS за
время At из слоя 1, будет:
] молекул пере-
переравное
Рис. 139. Перенос количе-
ства движения.
где щ — число молекул в единице объема. Эти
несут через площадку AS количество движения A
Д К
где щ — скорость течения слоя /.
Точно так же из слоя 2, лежащего над площадкой AS на рас-
расстоянии X, через площадку AS за время At будет перенесено коли-
количество движения
ДА"
где щ — скорость течения слоя 2. Для обоих слоев число молекул
в единице объема л0 одно и т0 же, так как в рассматриваемом
случае мы считаем плотность газа повсюду одинаковой.
^результате этих двух переносов количества движения, происхо-
происходящих в противоположных направлениях, через площадку AS будет
перенесено количество движения
Д# Д# ДЛ\
§ 56] ВНУТРЕННЕЕ ТРЕНИЕ И ТЕПЛОПРОВОДНОСТЬ ГАЗОВ 211
Разность тщ — mtiy может быть переписана в виде: т (иа — i^).
Разность скоростей щ — щ равна градиенту скорости Д«/Д,г, умно-
умноженному на расстояние между слоями 2 и 1; так как это расстояние
равно 2Х, то
о.-«, = (?)
откуда
/яиа — milt = т (д— J 2Х
и, следовательно,
замечая, что величина щт есть плотность газа р, получим
откуда сила /, действующая со стороны более медленного слоя на
более быстрый:
Сравнивая выражения B) и A), видим, что они совпадают, если
положить коэффициент внутреннего трения ц равным
1
¦ц = - рг'Х. C)
Таким образом, и коэффициент внутреннего трения -г] молеку-
лярно-кинетическая теория газов позволяет выразить через величины,
характеризующие молекулярную структуру газа: через среднюю
длину свободного пути молекул X, их среднюю скорость v и плот-
плотность газа р.
формула C) позволяет выяснить характер зависимости коэффи-
коэффициента внутреннего трения к) от давления газа р. Из трех величин р,
X и v, входящих в выражение C), скорость молекул v не зависит
от давления, из двух же остальных величин плотность р прямо
пропорциональна давлению газа р, а средняя длина свободного пути
молекул X обратно пропорциональна р. Следовательно, произведение
рХ~ не зависит от давления газа р, а значит, и коэффициент внутрен-
внутреннего трения газа t\ не зависит от давления газа р. Этот, на первый
взгляд парадоксальный, результат обусловлен следующим: при пони-
понижении давления р уменьшается число частиц и0 в единице объема,
а следовательно, уменьшается и число частиц, переносящих количество
движения из одного слоя в другой. Но зато возрастает длина сво-
свободного пути молекул X, благодаря чему молекулы попадают в дан-
данный слой без столкновений из более далекого слоя, движущегося
с отличной скоростью и. В результате этих двух причин, действующих
8*
212
ГАЗЫ
[ГЛ. VII
в противоположных направлениях, количество движения, переносимое
из слоя в слой, остается постоянным.
Вывод о независимости коэффициента внутреннего трения от
давления хорошо подтверждается на опыте. Так, например, для угле-
углекислоты (СОа) измерения дают следующие значения -ц для различных
давлений:
р в мм Hg ....
•>] в г/см сек....
760
14,9 • 10-»
380
14,9 • 10-'
20
14,8. 10"'
' 2
14,7 . 10-»
0,6
13,8 • 10"'
Из этих данных видно, что при изменении давления от 760 мм
до 2 мм Hg, т. е. при уменьшении в 380 раз, коэффициент внутрен-
внутреннего трения ч\ меняется от 14,9 • 10"9 г/см сек до 14,7 • 10~8 г/см сек,
т. е. практически остается постоянным. Лишь при более низких давле-
давлениях начинает сказываться зависимость к] от давления; несколько ниже
мы выясним условия, при которых т)
начинает зависеть от давления р.
Наконец, рассмотрим еще одно
явление переноса, а именно, яв-
явление теплопроводности в газе.
С макроскопической точки зрения
явление теплопроводности заклю-
заключается в переносе некоторого коли-
количества тепла AQ от более горя-
горячего слоя к более холодному. Если
изменение температуры Т происхо-
происходит в направлении оси ОХ, то через
площадку AS, перпендикулярную к оси ОХ (рис. 140), за время At
будет перенесено количество тепла AQ тем ббльшее, чем больше
площадка AS, чем больше тот промежуток времени Д?, за который
наблюдается перенос тепла, и чем быстрее происходит изменение
температуры Т в направлении оси ОХ, т. е. чем больше градиент
температуры А.Т/&Х. Следовательно, мы можем написать:
D)
Рис. 140. Перенос молекулами
энергии.
где к — величина, зависящая от сорта газа и от условий, при которых
он находится; эта величина называется коэффициентом теплопровод-
теплопроводности. Знак минус означает, что количество тепла AQ переносится
в сторону убывания температуры Т.
Явление теплопроводности в газах обычно осложняется перено-
переносом тепла путем конвекции, т. е. переносом тепла струями газа,
§ 56] ВНУТРЕННЕЕ ТРЕНИЕ И ТЕПЛОПРОВОДНОСТЬ ГАЗОВ 213
возникающими благодаря различию в плотностях частей газа, находя-
находящихся при разных температурах. Для наблюдения теплопроводности
в газах в чистом виде следует наблюдать перенос тепла через газ
между двумя плоскими параллельными поверхностями, расположен-
расположенными горизонтально, причем верхняя поверхность должна иметь более
высокую температуру. Тогда более холодные, а следовательно, и
более плотные слои газа расположатся ниже более горячих и менее
плотных, и в газе не возникает конвекционных потоков.
С молекулярно-кинетической точки зрения процесс теплопровод-
теплопроводности заключается в том, что молекулы из более горячего слоя, где
они имеют большую среднюю кинетическую энергию w, проникая
в более холодный слой, передают молекулам этого слоя часть своей
энергии. Наоборот, молекулы из более холодного слоя, попадая
в более горячий, получают от молекул более горячего слоя некото-
некоторое количество кинетической энергии. В результате более горячий
слой охлаждается, а более холодный нагревается. Перенос количества
тепла AQ означает, с молекулярно-кинетической точки зрения, перенос
через площадку AS определенного количества кинетической энергии
беспорядочного движения молекул.
Введем в рассмотрение, как и при разборе явления диффузии,
два кубика А и В (рис. 140), расположенных от площадки AS на
расстояниях, равных средней длине свободного пути X. Число мо-
молекул, пролетевших через площадку AS из кубика А за время Д*.
по сказанному в § 55, равно
Так как молекулы долетают из кубика А до площадки AS без
столкновений, то каждая из них переносит через площадку AS ту
кинетическую энергию wlt которую она имела в том месте, где лежит
кубик А. Энергия w^ складывается из энергии поступательного и
вращательного движений молекулы, поэтому она в среднем равна
^¦kTv где i — число степеней свободы молекулы, k — постоянная
Больцмана, Т\ — абсолютная температура в том месте, где находится
кубик А.
Отсюда находим, что количество тепла AQlt перенесенное всеми
Апа молекулами через площадку AS слева направо, равно
Аналогично получим, что из кубика В за время At справа налево
через площадку AS переносится количество тепла
n;vASAp. ±
214 газы [гл. vii
где Тъ — температура в том месте, где находится кубик В. В резуль-
результате этих двух переносов количества тепла в двух противоположных
направлениях, в одном направлении, а именно слева направо (в сто-
сторону положительной оси ОХ), через площадку Д5 будет перенесено
количество тепла
Подставляя сюда вместо AQt и AQ2 найденные для них значения,
получим
д Q=т" тk (п'^ Ti —п'
Количество частиц в единицах объема и'о и па обратно пропор-
пропорционально температурам 7[ и 7V, скорости же частиц t)j и г>3 про-
пропорциональны >/7\ и ~\fT%. Следовательно, произведения n'av1 и п'^щ
обратно пропорциональны корням квадратным из соответствующих
температур, ,т. е. при малой разности температур Т\ и 72 отличаются
друг от друга очень мало. Поэтому мы будем считать их равными:
n'fi\. = и>9 = nav.
После этого выражение для AQ примет вид:
AQ = 1 щЪ L k G, — 7а) А№. E)
Разность температур Га — Т\ выражаем через градиент темпе-
температуры Д Г/Дд: и расстояние между кубиками Лий, равное '2к '¦
Подставляя это значение Га — Т\ в E), получим
Сравнивая это выражение с D), найдем, что коэффициент тепло-
теплопроводности * равен
* = — И0Ы • -тг k. F)
3 2
Величину -^ k преобразуем следующим образом: постоянная
Больцмана k = jr., где R — газовая постоянная, а А/—число Аво-
гадро; поэтому
где Cv — молярная теплоемкость газа при постоянном объеме.
§ 56] ВНУТРЕННЕЕ ТРЕНИЕ И ТЕПЛОПРОВОДНОСТЬ ГАЗОВ 215
Воспользовавшись этим преобразованием, перепишем выражение F)
в виде:
Последнее выражение может быть еще преобразовано; величина л0
дает число частиц в единице объема, а N — число частиц в одном
моле газа, откуда па относится к N, как масса единицы объема
газа (равная плотности р) к молекулярному весу ц, т. е. -Л = — и,
следовательно:
N v P fi. VCv>
где cv—удельная теплоемкость газа при постоянном1 объеме. Отсюда
окончательно имеем, что коэффициент теплопроводности * равен:
* = -»¦ pxikcy. Fa)
Коэффициент теплопроводности к, как и коэффициент внутреннего
трения 7], не зависит от давления газа. Это вытекает опять из того,
что плотность р прямо пропорциональна, а средняя длина пути X
обратно пропорциональна давлению р; скорость же молекул v и
удельная теплоемкость газа Cv от давления не зависит. Однако при
очень низких давлениях коэффициент теплопроводности % начинает
зависеть от давления р.
В выражения для коэффициента диффузии D, внутреннего трения i\
и теплопроводности * входит значение средней длины свободного
пути молекулы X; таким образом, по численным значениям любого
из этих трех коэффициентов можно определить среднее значение
длины свободного пути молекул X, а отсюда — и эффективный диаметр
молекул о. Однако если вычислить для какого-либо газа эффектив-
эффективные диаметры его молекул а по численным значениям всех трех
коэффициентов D, т; и и, то получатся несколько различные значения.
Эти различия объясняются приближенным характером приведенных
теорий.
Приближенный характер теорий проявляется еще в следующем:
из формул C) и Fа) следует, что отношение коэффициента теплопро-
теплопроводности y. к коэффициенту внутреннего трения i\ должно равняться
удельной теплоемкости газа при постоянном объеме, т. е.
В действительности же отношение ч/ч) равно Key, где К—мно-
К—множитель, зависящий от природы газа. Измерения показывают, что для
всех одноатомных газов ./^=2,50, а для двуатомных — приближенно
А" =1,90. Более подробная теория приводит к указанным значениям
Л'=2,5 — для одноатомных газов и ЛГ—1,9—для двуатомных.
216 ГАЗЫ [ГЛ. VII
Разберем пример на определение сил внутреннего трения в газе.
Пусть пространство между двумя коаксиальными цилиндрами А И В,
изображенными на рис. 138, заполнено водородом при температуре 27"С.
Радиус внутреннего дилиндра А равен г, = 8 см, расстояние между цилинд-
цилиндрами d = 0,2 см. Внутренний цилиндр вращается, совершая 10 об/сек.
Рассматривая приближенно случай как плоский, определить касательную
силу /, действующую на 1 см2 поверхности внешнего цилиндра В. Диаметр
молекул водорода а считать равным 2,3 • 10~s см.
Решение. В результате внутреннего трения между слоями газа дей-
действует сила /, которая по формуле A) равна
Считая, что скорость газа у поверхности твердого тела совпадает со
скоростью самой поверхности, полу.чим, что такая же сила / действует на
поверхность цилиндра В.
На единицу поверхности цилиндра В действует сила f/S. Для определе-
определения этой силы надо знать градиент скорости До/Лл" и значение коэффициента
внутреннего трения ц для водорода. Градиент скорости Ди/Длс в данном
случае равен
Дн и3 — Ui
где ц« — скорость газа у поверхности внутреннего цилиндра, ut — его ско-
скорость у поверхности внешнего цилиндра. Эти скорости приравниваем скоро-
скоростям самих поверхностей цилиндров А и В, тогда
ц, = 2тсГ1л; ui = 0,
где и — число оборотов внутреннего цилиндра в единицу времени, отсюда
^ = 2*3/1.
Подставляя сюда численные данные, приведенные в условии примера,
найдем
^ = 2 • 3,14 - А . ю сек. = 2512 сек..
Коэффициент внутреннего трения по формуле C) равен:
где v — средняя арифметическая скорость молекул, X — средняя длина их
свободного пути и р — плотность газа. Подставляя сюда (см. § 45, 46,50,53)
— ~77s 1— > v = I/ ¦. p — Тут > ° — ~ьт — Wr >
получим
Здесь R — газовая постоянная, равная 8,31 • 10* эрг/град моль, fi—мо-
fi—молекулярный вес водорода, равный 2 г /моль, N— число Авогадро, равное
6 • 102* моль'1. Пользуясь для Т и а значениями, данными в примере, найдем:
4 = 8,6- 1(Г6 г/см сек.
§ 57] ТЕПЛОПРОВОДНОСТЬ Я ВНУТРЕННЕЕ ТРЕНИЕ ПРИ НИЗКОМ ДАВЛЕНИИ 217
Воспользовавшись полученными численными значениями для градиента
скорости д— = 2512 сек. и для коэффициента внутреннего трения
¦ц] = 8,6- 10~в г!см сек, получим для силы, действующей на единицу поверх-
поверхности цилиндра В:
или
2512
Z.^2- Ю-4 Г,см1.
О
тт—
/У
Аг
§ 57. Теплопроводность и внутреннее трение в газах при очень
низком давлении. Разберем теперь причины зависимости коэффи-
коэффициентов теплопроводности и внутреннего трения от
давления при очень низких давлениях. Рассмотрим
сперва явление теплопроводности.
Пусть имеются две параллельные пластины А\ и А%
(рис. 141) на расстоянии d друг от друга, поддер-
поддерживаемые при температурах 7i и 7"8. Между пласти-
пластинами имеется газ, который передает путем теплопро-
теплопроводности тепло от пластины Ах (считаем 7\^> Tt)
к пластине Ла. Пока средняя длина свободного пути
молекул \ мала по сравнению с расстоянием между
пластинами d, действует разобранный механизм тепло-
теплопередачи: молекулы, беспорядочно двигаясь, пере-
переносят из слоя в слой кинетическую энергию. При
давлении настолько низком, что средняя длина сво-
свободного пути молекул X равна или больше рас-
расстояния между пластинами d, механизм теплопередачи
иной: молекула, ударившись о горячую пластину Ах и
приобретя кинетическую энергию wt, соответствую-
соответствующую температуре Т\ этой пластины, без столкновений
достигает пластины At и отдает ей часть своей энер-
энергии wt. Также молекула, отразившаяся от более холодной пластины Ла
и имеющая меньший запас энергии щ, без столкновений достигает
пластины j4i и отнимает от нее часть энергии. При дальнейшем по-
понижении давления число молекул я, осуществляющих перенос энергии
от п/Гастины к пластине, уменьшится, пути же их останутся без
изменения, молекулы по-прежнему свободно пролетают от пластины
к пластине. Таким образом, при дальнейшем уменьшении давления
теплопроводность газа убывает. Окончательно имеем: коэффициент
теплопроводности газа зависит от давления, когда средняя длина
свободного пути молекул одного порядка или больше расстояния d
между теми телами, между которыми осуществляется тепло-
теплопередача через газ. При \^>d коэффициент теплопроводности прямо
пропорционален давлению р.
Рис. 141. Коэф-
Коэффициент тепло-
теплопроводности на-
начинает зависеть
от давления,
когда длина сво-
свободного пути мо-
молекул становит-
становится больше рас-
расстояния d между
пластинами.
218
ГАЗЫ
[ГЛ. VII
Совершенно аналогично объясняется указанная зависимость коэф-
коэффициента внутреннего трения газов к] от давления при очень низких
давлениях. Если расстояние d между теми поверхностями, между
которыми течет газ, обнаруживающий явление внутреннего трения,
одного порядка или меньше средней длины свободного пути моле-
молекул X, то коэффициент внутреннего трения т] начинает зависеть от
давления р, убывая вместе с давлением.
Из сказанного видно, что абсолютное значение давления р, начи-
начиная с которого коэффициенты х и т] зависят от давлений, опреде-
Аляется расстоянием между теми телами, между кото-
которыми осуществляется перенос тепла ¦ или количества
движения. Например, в случае двух очень близко рас-
расположенных друг к другу пластин, теплопроводность
газа, заключенного между ними, начнет зависеть от
давления при не слишком низком давлении р; если
те же пластины раздвинуть на большое расстояние d
друг от друга, то потребуется гораздо более высокое
разрежение газа, чтобы заметить зависимость тепло-
проводности от давления.
Зависимостью теплопроводности от давления при
низких давлениях пользуются при устройстве термосов
(сосудов Дюара). Обыкновенный термос представляет
собою стеклянный сосуде двойными стенками (рис. 142).
Воздух из пространства между стенками откачан
до столь низкого давления, что длина свободного пути молекул
значительно больше расстояния между стенками. При этих условиях
теплопроводность между стенками меньше, чем если бы между
стенками находился воздух при атмосферном давлении.
В качестве примера произведем следующий расчет. Расстояние между
стенками дюаровского сосуда d = 0,8 см. Между стенками находится водород
при температуре 27° С. Считая диаметр молекул водорода а = 2,3-10~8 еж,
определить, ниже какого значения должно быть давление водорода р, чтобы
его теплопроводность была меньше, чем при атмосферном давлении.
Для того чтобы коэффициент теплопроводности водорода оказался меньше,
чем при атмосферном давлении, средняя длина свободного пути молекул во-
водорода X должна быть больше расстояния между стенками сосуда d, т. е.
X > d.
Средняя длина свободного пути молекул X по формуле Dа) § 53 равна
X— }
Рис. 142.
Устройство
дюаровского
сосуда (тер-
(термоса).
где п0 — число молекул'в единице объема. По формуле (9) § 46 число молекул
в единице объема п0 связано с давлением газа р соотношением:
§ 58]
ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ НИЗКИХ ДАВЛЕНИЙ
219
где k—постоянная Больцмана и Т — температура газа. Подставив это зна-
значение п0 в выражение для X, получим
кТ
откуда из условия X > d следует, что давление р должно удовлетворять со-
соотношению:
Подставив сюда приведенные численные значения, получим
р< 1,37 - Ю- - 300 _ бдр = 220
1/2 -3,14- B,3 • 10-8J-0,8
Переводя это давление в миллиметры ртутного столба, найдем
: 0,015 мм Hg.
Таким образом, давление остаточного газа между стенками дюаровского
сосуда должно быть меньше 0,015 мм Hg, чтобы теплопроводность оказалась
пониженной.
§ 58. Получение и измерение низких давлений. Получение низ-
низких давлений (как принято говорить, „вакуума") в настоящее время
играет большую роль как в лабораторных исследованиях, так и
в технике. Применение вакуума для
различных электротехнических и
радиотехнических целей (электро-
(электровакуумных приборов — кенотронов,
радиоламп и т. д.) дало мощный тол-
толчок для развития вакуумной техники.
Различного рода вакуумные насосы
с применением некоторых добавоч-
добавочных приемов позволяют получать
давления в 10~6 мм Hg и ниже. При
таких давлениях длины свободных
путей газовых молекул достигают
десятков метров.
Простейший воздушный порш-
невый насос совпадает по своему
устройству с водяным поршневым
насосом, отличаясь от него лишь
более точной подгонкой частей и их уплотнением. В настоящее
время, однако, поршневые насосы совершенно вытеснены насосами,
в которых неудобное, с механической точки зрения, движение поршня
взад и вперед заменено вращательным движением лопастей. Такого
рода вакуумный насос изображен в разрезе на рис. 143.
В цилиндрической полости внутри массивного металлического
корпуса насоса помещен эксцентрически металлический цилиндр. Две
L
Рис. 143. Вакуумный насос (разрез).
220
ГАЗЫ
[гл. vii
лопасти S и S', вставленные в разрез в цилиндре и раздвигаемые
помещенной между ними пружиной, разделяют на две части простран-
пространство между цилиндром и стенкой полости. Действие насоса ясно из
схематических рис. 144 а, б, в, г, изображающих последовательные
положения лопастей S л S' при поворачивании цилиндра в направлении,
указанном стрелкой. В положении а газ из откачиваемого сосуда,
присоединенного к трубе С, поступает в область /. По мере пово-
Рис. 144. Схема действия вакуумного насоса: лопасти S и S' при
поворачивании засасывают воздух через трубу С и выдавливают
его через клапан D.
рачивания цилиндра лопасть S отходит (положение б), пространство /
увеличивается, и газ засасывается через трубу С. При дальнейшем
поворачивании цилиндра лопасть S' отключает пространство 1 от
трубы С (положение в), после чего лопасть S' (положение г) на-
начинает вытеснять порцию газа, заключенного в пространстве /, через
клапан D наружу. При вращении цилиндра этот процесс засасывания
газа через трубу С и вытеснения его через клапан D непрерывно
повторяется.
Вращение цилиндра осуществляется электромотором. Для избе-
избежания просачивания газа под лопастями и в других местах насоса
производится непрерывная автоматическая смазка всех его частей
маслом. Ввиду этого такого рода насос носит название масляного
насоса. Часто весь насос целиком погружается в масляную баню.
Насосы, построенные на этом принципе, позволяют достигать давле-
давлений 1СГ4 мм Hg.
Обозначим объем откачиваемого сосуда через V и первоначальное да-
давление газа в нем — через р0. При первом отходе лопасти S образуется
область, объемом AV, которая заполняется газом из откачиваемого сосуда.
В результате этого давление в откачиваемом сосуде падает до значения
Pi=Po v+ikV-
После второго образования области W давление упадет до значения
V I V
58]
ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ НИЗКИХ ДАВЛЕНИЙ
221
Продолжая рассуждение, найдем, что после того как образуется п раз
область ДЦ давление в откачиваемом сосуде упадет до значения
Рп
=/>•(¦
V у»
к+диу •
A)
При постоянном числе оборотов лопастей число актов откачивания я
прямо пропорционально времени откачивания, откуда можно положить
я = not,
Подставляя это значение я в выражение A), найдем
у Г_
I—давление, полученное в откачиваемом сосуде через время t. Последнее
выражение можно переписать:
"""Л B)
Отношение po/pt возрастает по мере убывания давления/^ в откачиваемом
сосуде и служит характеристикой работы насоса. Логарифмируя равенство B),
получим
Так как величины я„, V и AV постоянны для данного насоса и данного
откачиваемого сосуда, то, следовательно,
• lg^ = a, C)
где С—постоянная величина. Для характеристики действия насоса удобно
воспользоваться графиком, откладывая по оси абсцисс время откачки t, а по
оси ординат lg —. Зависимость^— от вре-
времени t изобразится на таком графике прямой.
На самом деле, из-за существования вредных
пространств, не идеальной работы клапанов
и т. д.насосы немогутдатьбесконечнобольшого
разрежения. Для каждого насоса существует
некоторое минимальное давление />Ш]П, ниже
которого он не может дать разрежения. По-
Поэтому графическая зависимость lg— от вре-
времени t представляется в виде прямой, лишь
пока достается заметно больше pmin (рис. 145).
При приближении pt к pmin насос начинает
качать все медленнее и медленнее. Поэтому
для реальных насосов зависимость^— от времени изображается кривой, иду-
Pt
щей при больших г параллельно оси абсцисс. Для того чтобы сравнивать действие
различных насосов, следует брать откачиваемые объемы одинаковыми. Тогда
скорость действия данного насоса определится значением постоянной С.
Кривые, приведенные на рис. 145, относятся к двум разным насосам. Из
способа построения этих кривых видно, что кривая 1 относится к насосу,
*—*
Рис. 145. Графическая харак-
характеристика действия насосов.
222
ГАЗЫ
[гл. vii
качающему более быстро, но неспособному создать хороший вакуум. Кривая //
относится к насосу, способному создать значительно лучший вакуум, но качаю-
качающему медленно.
В тех случаях, когда откачиваемый сосуд соединен с насосом трубой,
скорость откачки зависит еще от размеров этой трубы, а именно от ее
длины и диаметра. Узкие и длинные соединительные трубы'могут в высшей
степени понижать скорость откачки. При больших давлениях, когда газ
течет по трубе как вязкая жидкость, объем протекающего газа определяется
формулой Пуазейля (§ 42), по которой протекающий объем прямо пропор-
пропорционален диаметру трубы в четвертой степени и обратно пропорционален ее
длине. При низких давлениях, когда средняя длина свободного пути моле-
молекул X сравнима с диаметром и длиной трубы, формула Пуазейля непригодна.
В этом случае масса газа AM, протекающего за единицу времени по трубе
диаметром d и длиной /, при разности давлений Ар, выражается следующей
формулой:
Ар, D)
где /?—газовая постоянная, (х —молекулярный вес, Т—абсолютная темпе-
температура газа.
Как видно, и в этом случае количество протекающего по трубе газа
очень сильно зависит от диаметра трубы. Таким образом, во всех случаях
следует пользоваться как можно более широкими и короткими соединитель-
соединительными трубами.
Для получения более низких давлений, чем те, которые полу-
получаются с помощью масляных насосов, в настоящее время упо-
употребляются преимущественно диффузион-
диффузионные, или, как их иногда называют, конден-
конденсационные насосы. Эти насосы не способны
откачивать газ из сосудов, начиная с атмо-
атмосферного давления, но способны создавать
добавочную разность давлений. Поэтому их
употребляют совместно с масляными насд-
сами описанного типа. Масляный насос дает
предварительное разрежение (форвакуум),
которое затем улучшается диффузионным
насосом. Простейший тип ртутного диффу-
диффузионного насоса изображен на рис. 146.
Ртуть, налитая в сосуд А, подогревается
электрической печью. Пары ртути, подни-
Рис. 146. Схема простей- маясь по трубе В, вырываются из сопла L,
затем конденсируются на охлаждаемых во-
водяной рубашкой стенках С и стекают по
трубе М обратно "в сосуд А. Струя паров
ртути, вырывающаяся из сопла L, увлекает с собою молекулы газа,
которые поступают из откачиваемого сосуда через трубу D и затем
откачиваются форвакуумным насосом через трубу N.
Указанный принцип увлечения молекул газа струей конденсирую-
конденсирующихся паров ртути используется в настоящее время в различных
Высокий вакуум
D
шего диффузионного на-
насоса.
§ 58]
ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ НИЗКИХ ДАВЛЕНИЙ
223
вариантах; существуют многочисленные конструкции стеклянных и
металлических диффузионных насосов. Весьма часто употребляют
так называемые многоступенчатые насосы, в которых несколько сопел
расположены последовательно друг за другом. Такие многоступен-
многоступенчатые диффузионные насосы дают лучший вакуум и работают при
худшем форвакууме.
В последнее время в диффузионных насосах заменяют ртуть труд-
труднолетучими органическими жидкостями (тяжелыми погонами нефти и
некоторыми другими жидкостями); такого рода насосы носят назва-
название паромасляных.
Диффузионные ртутные насосы имеют тот недостаток, что из
них попадают в откачиваемый сосуд пары ртути. Давление насыщенных
паров ртути при комнатной температуре B0°С) равно 0,00131 мм Hg.
Таким образом, сами по себе диффузионные ртутные насосы не могут
создать давлений ниже 0,0013 мм Hg. Для избежания этого недо-
недостатка между диффузионным ртутным насосом и откачиваемым сосудом
располагают специально
изогнутое колено соеди-
соединительной трубки („ртут-
(„ртутную ловушку"), которую
охлаждают жидким воз-
воздухом. При температуре
кипения жидкого воздуха
( — 184° С) ртуть нахо-
находится в твердом состоя-
состоянии, и упругость ее на-
насыщенных паров исче-
зающе мала.
Весь агрегат предста-
представлен на рис. 147: А —
масляный форвакуумный
насОс, приводимый во вра-
вращение электромотором,
С — диффузионный на-
насос, D — ртутная ловушка, Е — откачиваемый сосуд. В представляет
собою так называемый форвакуумный баллон; он ставится для того,
чтобы избежать непрерывной работы масляного насоса А. После
того как масляный насос А создал в баллоне В достаточный фор-
форвакуум, кран Ъ может быть закрыт, насос А остановлен; диффу-
диффузионный насос откачивает тогда газ из сосуда Е в форвакуумный
баллон В.
Паромасляные насосы могут работать без ловушек, охлаждае-
охлаждаемых жидким воздухом, и даже без водяного охлаждения, так как
используемые в них жидкости имеют при комнатной температуре упру-
упругость насыщающих паров много ниже упругости паров ртути при
той же температуре.
147. Схема соединения форвакуумного
насоса с диффузионным насосом.
224
ГАЗЫ
[ГЛ. VII
Рис. 148. Ртут-
Ртутный манометр.
Второй вопрос, связанный с вакуумной техникой, —> это измере-
измерение низких давлений. Обычно U-образный ртутный манометр (рис. 148)
позволяет измерять давления не ниже нескольких
долей миллиметра ртутного столба.
В лабораторной практике широко применяется
для измерения более низких давлений манометр
Мак-Леода (рис. 149). Конец манометра D соеди-
соединяется с сосудом, в котором измеряется давление.
Пусть это измеряемое давление равно р. Тогда газ
при давлении р заполняет все части манометра,
в том числе и сосуд Е. При поднятии сосуда А,
соединенного с остальной частью манометра рези-
резиновой трубкой, ртуть поднимается и разобщает ре-
резервуар Е и капилляр В с сосудом, давление в кото-
котором измеряется. Затем ртуть поднимается выше, пока не дойдет
в капилляре В до определенного места. Пусть при этом свободный
объем, оставшийся над поверхностью ртути
в капилляре В, равен AV.
Обозначим объем сосуда Е вместе с ка-
капилляром В через V. Тогда газ, бывший при
давлении р, оказывается сжатым до давления С
При достаточно большом отношении V/&V
давление р' много больше исходного давления
р и может быть измерено по разности уровней
ртути в капиллярах В и С. Измерив р' и зная
численное значение отношения \//Д V", найдем
значение измеряемого давления р.
Для • измерения очень низких давлений, а
также для измерения давления легко конден-
конденсирующихся паров, манометр Мак-Леода непри-
непригоден. Для измерения весьма малых давлений
применяются различные другие манометры.
В качестве примера мы укажем на тепловой
манометр, основанный на том принципе, что ¦
теплопроводность газов при очень низких давлениях зависит от давле-
давления и при этом, практически, зависит линейно (см. § 57). Тепловой
манометр представляет собою колбу, в которой помещена металли-
металлическая нить, накаливаемая током. При данной силе тока температура,
до которой нагревается нить, зависит от ее теплоотдачи, последняя
же, в свою очередь, зависит при низких давлениях от давления окру-
окружающего газа. Таким образом, температура, до которой нагревается
нить, может служить для измерения давления окружающего газа.
Температура нити обыкновенно измеряется по ее сопротивлению.
Рис. 149. Манометр
Мак-Леода.
§ 59]
СВОЙСТВА ГАЗОВ ПРИ ОЧЕНЬ НИЗКИХ ДАВЛЕНИЯХ
225
В
§ 59. Свойства газов при очень низких давлениях. При столь низких
давлениях, при которых средняя длина свободного пути молекул X становится
одного порядка с размерами сосуда, в котором за-
заключен газ, свойства газа отличаются от его свойств
при больших давлениях. Такое состояние газа назы-
называется состоянием ультраразрежения. В состоянии
ультраразрежения более непосредственно сказывается
молекулярно-кинетическая природа газа, чем при боль-
больших давлениях.
Рассмотрим два сосуда А и В, соединенных ко-
короткой и прямой трубкой а (рис. 150).
При обычных условиях давления газа в сообщаю*
щихся сосудах одинаковы; это имеет место и тогда,
когда температуры обоих сосудов Ti и Га различны.
В состоянии ультраразрежения, когда длина сво-
свободного пути молекул больше, чем длина трубки а,
молекулы без столкновений пролетают через всю
трубку, что ведет, как мы сейчас покажем, к нера-
неравенству давлений pt и р* в обоих сосудах. Условие
равновесия заключается в том, что число молекул,
пролетающих через трубку а из сосуда А в сосуд В
и в обратном направлении — из сосуда В в сосуд А, должно быть равно друг
другу. При состоянии ультраразрежения число молекул, пролетающих через
трубку, пропорционально числу молекул в единице объема п„ и их средней
скорости Ъ. Отсюда условие равновесия запишется:
где лО1 — число молекул в единице объема сосуда А, по% — число молекул
в единице объема сосуда В и Hi и и8 — средние скорости молекул в сосудах
А и В соответственно. Так как яо = ~, то соотношение A) может быть пере-
переписано:
Рис. 150. При условии
ультраразрежения при
разных температурах
7\ и Га в сосудах АкВ
устанавливаются раз-
различные давления/»! ир8.
наконец, имея в виду, что скорости vt и и* соответственно пропорциональны
V и YTz, окончательно получим условие равновесия в следующем виде:
откуда
B)
Таким образом, при ультраразреженном состоянии газов давления в двух
сообщающихся сосудах при равновесном"''состр.°н.и.14 ""||"'" друг от друга,
если только р^зЛЙ^Ы температуры <0суЛ8в. При больших плотностях газов
давления в соовщающИнн шсудИЯ выравниваются за счет течения газа, как
сплошной среды, из сосуда с ббльшим давлением в сосуд с меньшим давлением.
Рассмотрим еще одно явление, характерное для ультраразреженного газа.
Пусть в сосуде расположены параллельно друг другу две пластины 1 и 2
(рис. 151). Температура пластины 1 пусть равна температуре стенок сосуда Т\,
температуру пластины 2 обозначим через Г3. При условии улыраразрежения
молекулы летают свободно, не сталкиваясь друг с другом.
226
ГАЗЫ
[гл. vii
Г/
Рассмотрим газ, заключенный между пластинами / и 2. Так как молекулы
не сталкиваются, то они и не обмениваются энергиями между собой. Обмен
энергий происходит лишь при столкновения* молекул с пла-
пластинами 1 и 2, температуры которых равны 7"i и 7». Поэтому
можно считать, что газ между пластинами как бы состоит из
двух газов, молекулы одного из которых имеют средние ско-
скорости v, соответствующие температуре Tit а молекулы дру-
другого— средние скорости «", соответствующие температуре Г2.
Обозначим числа молекул в единице объема для этих двух
групп молекул соответственно через п'о и по-
подавление р', оказываемое на пластину 1 со стороны газа,
находящегося между пластинами, сложится из давления, ока-
оказываемого обеими группами молекул:
1 , -« . 1
Рис.151. Схе-
Схема абсолют-
абсолютного мано-
манометра.
p' — -^nomv +-5-1
C)
где т—масса молекулы.
Обозначим число молекул в единице объема в сосуде вне
пластин через Пц' скорость этих молекул равна v, так как тем-
температура стенок сосуда, поверхность которых значительно
больше поверхности пластин, совпадает с температурой первой пластины.
Давление, которое они оказывают на пластину I, равно
Условие равновесия при ультраразрежении заключается в том, что числа
молекул, летящих через какую-либо площадку в одном и другом направлениях,
должны быть равны друг другу.
Поэтому в пространстве между пластинами 1 и 2 должно быть выполнено
условие:
n'ov =n'0'v". E)
Рассмотрим далее боковую поверхность объема, заключенного между
пластинами. Через какую-либо площадку этой поверхности изнутри объема
вылетают молекулы обеих групп, движущиеся со скоростями v, и v ; внутрь
объема попадают лишь молекулы, движущиеся со скоростью V', число кото-
которых в единице объема равно п0. Следовательно, для условия равновесия между
газом, заключенным между пластинами 1 и 2, и газом, находящимся в сосуде
вне пластин:
n'ov -\-n'0'v" = nav'. F)
Из равенств E) и F) находим:
после чего выражение C) для р' может быть переписано:
р' = -тг nomv (v
¦v"), или />' =
1
1 '
р = -7г namv
Используя формулу D) и замечая, что
Ъ"
- получим P=^V + V rj-
Отсюда разность давлений, испытываемых пластиной 1:
§ 60] РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА 227
Формула G) показывает, что пластина 1 испытывает силу, отталкивающую
ее от пластины 2, если Г2 >> Ти и приближающую, если Та < 7\. Численное
значение этой силы пропорционально давлению даза р в сосуде. Основываясь
на этом явлении, можно сконструировать манометр, позволяющий в условиях
ультраразрёжения определять абсолютное значение давления р. В принципе
устройство такого манометра совпадает со схемой, изображенной на рис. 151.
Пластина 1 делается подвижной; действующая на нее сила измеряется по
углу ее отклонения. По этой силе и по температуре 7"i и Га по формуле G)
вычисляется давление р.
§ 60. Реальные газы. Уравнение Ван-дер-Ваальса. Рассмотрен-
Рассмотренная нами в § 46 молекулярно-кинетическая модель газа представляет
газ состоящим из беспорядочно движущихся молекул, уподобляемых
упругим шарам. Силы между молекулами действуют лишь в момент
удара, причем это — упругие силы отталкивания. Размеры молекул
считаются настолько малыми по сравнению со средним расстоянием
между молекулами, что ими можно пренебречь. Эта модель соответ-
соответствует идеальному газу, т. е. такому газу, который в точности под-
подчиняется законам Бойля—Мариотта и Гей-Люссака. Однако реаль-
реальные газы, как мы указывали, подчиняются этим законам лишь при-
приближенно. При больших давлениях нее газы явно отступают от
закона Бойля—Мариотта.
Считая молекулы шарами, мы должны принять для их радиусов
величины порядка 10~8 см. Отсюда объем одной молекулы
В 1 см3 газа при нормальных условиях находится число молекул
Ло = 3-1О19, откуда собственный объем всех молекул, находящихся
в 1 смъ, равен V' = /z0v^l0~4 см3, т. е. при давлении газа в 1 am
и температуре 0° С лишь приблизительно одна десятитысячная объема
газа приходится на собственный объем молекул. При давлении же
в 5000 am по закону Бойля—Мариотта объем, первоначально равный
1 см3, должен уменьшиться до 2-10~4 см3, при этом половина объема,
занимаемого газом, придется на собственный объем молекул. Очевидно,
в этом случае указанная модель газа непригодна, и отступления свойств
действительных газов от закона Бойля—Мариотта понятны. Таким
образом, причины отступления свойств газов от свойств идеального
газа должны быть, во-первых, обусловлены наличием собственных
размеров молекул, во-вторых, тем, что характер сил взаимодействия
между молекулами значительно более сложен, чем для упругих шаров.
Обе эти причины были учтены Ван-дер-Ваальсом. Первая причина —
собственные размеры молекул — сказывается в том, что молекулы
движутся в сосуде, в котором заключен газ, менее свободно, чем
если бы они были точечными. Объем, предоставленный для свобод-
свободного движения молекул, меньше геометрического объема сосуда V
на некоторую величину Ь. Эту величину Ь, связанную с собственным
объемом молекул, можно считать постоянной для данного количества
228 газы [гл. vii
газа; поэтому объем V в уравнении состояния должен быть заменен
величиной V — Ь.
Для одного моля идеального газа имеет место уравнение
. A)
Как было сказано, мы должны, учитывая роль собственных раз-
размеров молекул, заменить объем моля Vo величиной Vo — b:
-b) = RT. B)
Из уравнения A) следует, что при р-*-оо объем газа Vo—«-О,
т. е. при бесконечном сжатии газа объем его стремится к нулю, что
невозможно: сжатие газа происходит за счет уменьшения свободного
пространства между молекулами, отсюда при очень больших давле-
давлениях молекулы расположатся вплотную, после чего сжимаемость газа
должна быть весьма малой. По формуле B) при р —> оо объем газа
Vo — b\ таким образом, величина Ъ представляет собой тот объем,
к которому стремится объем моля Vo при очень больших давлениях;
он равен объему, занимаемому всеми молекулами, входящими в состав
одного моля, при их плотной упаковке.
Вторая причина — наличие сил взаимодействия между молеку-
молекулами — сводится к тому, что молекулы, находясь на некотором рас-
расстоянии друг от друга, взаимно притягиваются. Эти силы притяжения
лишь при очень малых расстояниях между молекулами (в момент
удара) сменяются более интенсивными силами отталкивания. В резуль-
результате сил притяжения между молекулами газ занимает объем V, мень-
меньший, чем это следует из закона Бойля—Мариотта, как если бы он
находился под ббльшим давлением р', чем то внешнее давление р.
которое на него оказывают стенки сосуда. Таким образом, в выра-
выражении B) внешнее давление р должно быть заменено величиной
p'=p-\-Pi, откуда получаем:
b) = RT. C)
Величина pt называется внутренним давлением газа.
Роль указанных сил притяжения между молекулами п.о-разному
сказывается на молекулах, находящихся внутри объема газа и нахо-
находящихся вблизи стенок. Хотя силБ1 притя-
Жения между молекулами и убывают с рас-
стоянием медленнее, чем силы отталки-
вания, все же они проявляются лишь на
небольших расстояниях. Поэтому в газе
на каждую данную молекулу действуют
Рис. 152. Взаимодействие мо силы притяжения лишь со стороны близких
лекул газа между собою. r n
J молекул. Внутри газа каждая молекула со
всех сторон окружена другими молеку-
молекулами и, в среднем, действующие на нее силы притяжения компенси-
компенсируют друг друга. Вблизи же стенки (рис. 152) газовые молекулы
f
I 60] РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА 229
находятся в иных условиях: их притягивают лишь те газовые моле-
молекулы, которые находятся дальше от стенки. Вообще говоря, газовые
молекулы, находящиеся вблизи стенки, должны взаимодействовать
и с молекулами вещества, из которого состоит стенка. Однако при
температурном равновесии и при условии, что не имеет места при-
прилипание молекул к стенке, средняя энергия молекул, отлетающих
от стенки, равна средней энергии молекул, подлетающих к стенке.
Поэтому, в среднем, явление протекает так, как если бы удары мо-
молекул о стенку были вполне упругими. Отсюда следует, что влияние
стенки можно отбросить.
Ввиду достаточно быстрого убывания сил притяжения между моле-
молекулами, можно считать, что на молекулы, находящиеся у стенки,
действуют лишь те молекулы, которые находятся не далее некото-
некоторого расстояния г от них, т. е. те, которые находятся внутри слоя аЬ
(рис. 152). Число молекул внутри этого слоя пропорционально числу
молекул в единице объема я0. Таким образом, действие сил притя-
притяжения, оттягивающих молекулы от стенки, 'пропорционально щ. Кроме
того, и число молекул, ударяющихся о стенку, также пропорцио-
пропорционально я0. В результате сила, действующая на молекулы, находя-
находящиеся у стенки, и направленная внутрь газа, пропорциональна nj.
Эта сила, отнесенная к единице площади, и определяет внутреннее
давление pv
Величина внутреннего давления pt также зависит и от природы
взаимодействующих молекул, откуда следует, что
~ N
где а — постоянная, зависящая от сорта молекул. I ак как щ = р-,
где N— число Авогадро, a Vo ¦— объем моля газа, то выражение
для р; можно переписать:
a'N"
P
или, обозначая aW' через а, получим
Р1 = ш- D)
' о
Подставляя значение внутреннего давления pt по D) в выраже-
выражение C), получим уравнение Ван-дер-Ваальса для одного моля газа:
E)
Попра'вки Ван-дер-Ваальса а и ft со значительной степенью
точности постоянны для данного газа. Для различных газов они
различны; их численные значения определяются из эмпирических
данных. Постоянная ?? в уравнении Ван-дер-Ваальса имеет значение
прежней газовой постоянной.
230
ГАЗЫ
[гл. vit
При очень большом молекулярном объеме Va можно поправкой Ь
пренебречь по сравнению с Va и величиной .-^- пренебречь по сравне-
сравнено
нию с р, тогда уравнение Ван-дер-Ваальса переходит в уравнение A).
Таким образом, сразу выявляется приближенный характер фор-
формулы Менделеева—Клапейрона: она дает хорошее приближение
к действительности лишь при малых давлениях/» (больших объемах Vo);
при больших давлениях р
Таблица VIII
Сравнение эмпирических данных
и данных по формуле Ван-дер-Ваальса
для 1 л азота при 0° С
Давление
р в am
1
100
200
500
1000
pV
в am л
1,0000
0,9941
1,0483
1,3900
2,0685
в am л
1,000
1,000
1,009
1,014
0,893
необходимо принимать во
внимание роль поправок а, Ь,
т. е. пользоваться форму-
формулой Ван-дер-Ваальса E).
Формула Ван-дер-Вааль-
Ван-дер-Ваальса также не абсолютно точна,
но она является гораздо луч-
лучшим приближением к дей-
действительности, чем формула
Менделеева — Клапейрона.
В табл. VIII приведены ре-
результаты сравнения данных
формул Менделеева — Кла-
Клапейрона и Ван-дер-Ваальса
с опытными данными для азота вплоть до давлений в 1000 am.
Если бы азот в точности подчинялся уравнению состояния идеаль-
идеального газа, то произведение его давления р на значение объема
V, получаемого из экспериментальных измерений, должно было
бы оставаться при данной температуре Т постоянным для всех
давлений. На самом деле, как было уже указано в § 44, это произ-
произведение pV не остается постоянным и принимает значения, приве-
приведенные в третьем столбце табл. II (§ 44), которые мы вновь при-
приводим в табл. VIII. При больших давлениях азот менее сжимаем,
чем это следует из закона Бойля—Марнотта. При давлении в 1000 am
действительный объем азота более чем вдвое превышает тот, кото-
который вычисляется по уравнению состояния идеального газа.
В третьем столбце табл. VIII приведены значения
полученные для того же азота при 0°С в результате подстановки
в это выражение эмпирических значений V. Поправки а' и Ъ' отне-
отнесены к данному количеству азота (см. мелкий шрифт). Для них взяты
значения а'= 1,65 • 10~3 am лг и 6' = 1,36 • 10~3 л. При постоян-
постоянной температуре Т это выражение по формуле Ван-дер-Ваальса
должно оставаться постоянным для всех давлений р.
Данные табл. VIII показывают, что формула Ван-дер-Ваальса во
всем интервале давлений от 1 am до 1000 am гораздо лучше передает
§ 61] БОЛЕЕ ТОЧНЫЙ УЧЕТ ХАРАКТЕРА ПОПРАВОК ВАН-ДЕР-ВААЛЬСА 231
эмпирические данные, чем формула Менделеева—Клапейрона. Для
азота отступления от формулы Ван-дер-Ваальса не превышают 2%,
в то время как отступления от уравнения состояния идеального газа
при />= 1000 am больше 100%.
Уравнение Ван-дер-Ваальса, выражаемое формулой E), относится к одному
молю газа. Посмотрим, как его следует изменить, чтобы оно годилось для
любой массы газа т. Согласно введенному обозначению, Vo есть объем газа,
взятого в количестве одного моля. Обозначим через V объем газа массы т,
тогда при данных температуре и давлении:
V=~Va, F)
где р—молекулярный вес газа.
Подставим в уравнение Ван-дер-Ваальса
' 0 I
вместо Va его значение через V по F), тогда
---RT. G)
Выражение G) и представляет собою уравнение Ван-дер-Ваальса, отне-
отнесенное к газу с любой массой т, причем поправки а и Ь имеют то же чис-
численное значение, что и для одного моля газа.
§ 61. Более точный учет характера поправок Ван-дер-Ваальса.
Рассмотрим роль собственных размеров молекул несколько по-
подробнее.
При выводе основных соотношений кинетической теории газов
в § 46 мы считали, что молекулы свободно летают от стенки к стенке.
Время At, через которое данная молекула, ударившись о стенку,
вновь возвращается к ней, мы полагали рав-
равным времени, необходимому для пролета
молекулы поперек сосуда вперед и назад.
Если принять во внимание соударения мо-
молекул, то окажется, что некоторые молекулы,
претерпев соударение с другими молеку-
молекулами, вернутся к стенке раньше, некоторые
же, наоборот, пройдя из-за столкновений /j
ломаный путь, вернутся позже. В среднем Рис- 153- Столкновение
. , X молекулы со стенкой,
время Дг остается таким, как если бы со-
ударений не было. Однако дело обстоит так,
пока мы пренебрегаем собственными размерами молекул. Рассмотрим
некоторую молекулу диаметра а, которая, отскочив от стенки, уда-
ударяется о другую молекулу и снова возвращается к стенке (рис. 153).
При этом ее центр подойдет к стенке во время удара не вплотную,
но будет находиться на расстоянии, равном ее радиусу г = -=-.
На таком же расстоянии г = о/2 будет находиться ее центр
и от другой молекулы во время столкновения. Благодаря этому,
232 газы [гл. vii
свободный путь окажется уменьшенным на величину г -f- г = а. Однако,
если принять во внимание косые соударения, то это уменьшение
будет не столь значительным. Соответственный расчет показывает,
что оно равно а/2.
Таким образом, длина свободного пути "X окажется уменьшенной
на величину о/2, т. е. будет равна Х' = Х — —. Отсюда средняя дли-
длина свободного пути молекул, соударяющихся со стенкой, окажется
уменьшенной в отношении Х/Х', число же столкновений молекул со
стенкой, а следовательно, и давление окажутся увеличенными в от-
отношении Х/Х'.
Отсюда получаем, что произведение pV0, при данном молярном
объеме Va, будет равно не величине RT, как этого требует урав-
уравнение состояния идеального газа, но величине в Х/Х' раз большей.
pV0 = Rrl. A)
Так как
Г'=х_4.
Воспользовавшись для средней длины свободного пути X выра-
выражением Dа) § 53, получим
1 1
-1-JL i_^
где я0 — число молекул в единице объема. Так как мы рассматри-
ваем один моль газа, объем которого равен Ул, то я0 = гг» гДе
N— число
Вводя
получим
Авогадро,
обозначение
откуда
1
~~2l
V'
X
* 1-
1
а
1
Т1
1
4/
к'
B)
§ 61] БОЛЕЕ ТОЧНЫЙ УЧЕТ ХАРАКТЕРА ПОПРАВОК ВАН-ДЕР-ВААЛЬСА 233
Подставив это выражение Х/Х' в A), найдем
Ц- или p(V(i — b)==RT.
Таким образом, мы приходим к формуле B), выведенной нами
в § 60 менее строго. Приведенный вывод связывает значение кон-
константы Ъ с размером молекул а [формула B)]. Замечая, что объем
одной молекулы v равен
4 а 1 1
получим по B)
b = 3 / • vNSe 4v • N. Bа)
Так как vTV представляет собой объем всех молекул, содержа-
содержащихся в одном моле газа, то из Bа) мы имеем: Ван-дер-Ваальсова
поправка на объем молекул b равна приблизительно учетверен-
учетверенному собственному объему молекул.
Соотношение B) позволяет по числовому значению поправки Ван-дер-
Ваальса Ь определить диаметр молекул а. В самом деле, из B) имеем
Например, для кислорода 6 = 31,6 см*jмоль, откуда для диаметра моле-
молекулы кислорода (ее эффективного диаметра) получаем
' 31'6 см — 29 • 10-« см
eM — W ш см>
3,14-6,02-Ш"
что хорошо совпадает со значениями о, полученными другими способами.
Вторая Ван-дер-Ваальсова поправка а связана с характером сил
взаимодействия между молекулами.
Разберем характер этих сил несколько подробнее. Молекулы
представляют собой сложные электрические системы, подчиняющиеся
законам квантовой механики. Силы взаимодействия между ними носят
отчасти характер кулоновых сил (притяжение между разноименными
зарядами и отталкивание между одноименными зарядами), отчасти
иной характер, получающий объяснение лишь в квантовой механике.
Вообще говоря, можно положить, что между молекулами (рассма-
(рассматриваемыми обычно как электрические диполи) одновременно суще-
существуют и силы притяжения /i и силы отталкивания /2.
Обозначим расстояние между двумя молекулами А и В через г.
Обе силы — силу притяжения /i, которую мы считаем отрицатель-
отрицательной, и силу отталкивания /2, которую мы считаем положительной, —
234
ГАЗЫ
[ГЛ. VII
можно считать обратно пропорциональными расстоянию между моле-
молекулами г, взятому в некоторых степенях х, и х2:
/i — — Т7" **~~^~*'
где Ct и С2 — постоянные величины.
Если ха^>хь то сила отталкивания /4 скорее убывает с расстоя-
расстоянием, чем сила притяжения /t. В этом случае суммарная сила
/=/t ~\-fi на больших расстояниях является силой притяжения, а
на малых расстояниях — силой отталкивания.
Силам /у и /2 соответствуют потенциальные энергии EPl и ЕР2,
равные
Г" С"
? ^> ? =_^> C)
где С' и С" — новые постоянные, а показатели степени k{ и А4
равны: ^i^xj — 1; А3=:х2—1. Силе притяжения /t соответствует
Рис. 154. а) Ход потенциальной энергии притяжения между
молекулами Epi и отталкивания EPi\ б) ход суммарной потен-
потенциальной энергии взаимодействия между молекулами.
отрицательная потенциальная энергия (ср. § 33), а силе отталкива-
отталкивания /2 — положительная. Представим потенциальные энергии ?Р1 и ЕР2
графически, в зависимости от расстояния между молекулами г
(рис. 154 а). При k^^ky кривая, изображающая потенциальную
энергию Ер% сил отталкивания, поднимается при малых г вверх
более круто, а кривая, изображающая потенциальную энергию сил
притяжения EPl, опускается при малых г менее круто. Суммарная
кривая, дающая полную взаимную потенциальную энергию двух
С С"
молекул Ер = EPl -{- EPi = -ц- -)—^-, изображена сплошной кривой
на рис. 154 <?. Ниспадающая ветвь этой кривой CD соответствует
§ 61] БОЛЕЕ ТОЧНЫЙ УЧЕТ ХАРАКТЕРА ПОПРАВОК ВАН-ДЕР-ВААЛЬСА 235
тому, что суммарная сила взаимодействия между молекулами /=
=/i-|-/a является при больших расстояниях г силой притяжения.
Восходящая ветвь DA соответствует тому, что при малых г сум-
суммарная сила / есть сила отталкивания. При расстоянии между моле-
молекулами ra = OL обе силы — сила отталкивания /9 и сила притяже-
притяжения /t — численно равны друг другу. В этой точке суммарная сила /
равна нулю. Точке L соответствует самое глубокое место потенци-
потенциальной ямы D. Это место является местом равновесия. Однако рас-
расстояние г0 даст действительно равновесное расположение молекул
А и В друг около друга только в том случае, если полная энергия
молекул Е меньше „глубины" потенциальной ямы D. Так как в пре-
пределах ямы потенциальная энергия Ер отрицательна, то две первона-
первоначально находящиеся на большом расстоянии друг от друга, а затем
сближающиеся молекулы всегда будут иметь запас энергии больший,
чем „глубина" потенциальной ямы D, а потому они не смогут под
влиянием Ван-дер-Ваальсовых сил сцепиться вместе и образовать более
сложную молекулу. Соединение молекул в одну более сложную воз-
возможно лишь при тройном ударе, когда третья молекула унесет избы-
избыток энергии. Но и в этих случаях при не слишком низких темпе-
температурах 7', когда средняя энергия :l/9 k T, приходящаяся на одну
степень свободы, будет больше значения потенциальной энергии^,
в яме, образовавшаяся сложная молекула не удержится Ван-дер-
Ваальсовыми силами и снова распадется.
Обозначим через Ek кинетическую энергию. Пусть полная энер-
энергия E = Ek-\-Ер изображается пунктирной прямой, проведенной на
рис. 154 б". Будем считать молекулу А неподвижной, а движение
молекулы В рассматривать относительно молекулы А. Тогда (ср. спо-
способ рассуждений из § 33) молекула В, начиная с больших г, вплоть
до расстояния г0, движется к молекуле А со все возрастающей ско-
скоростью из-за наличия на этом участке сил притяжения. В точку L,
соответствующую равновесному расстоянию г0 между молекулами,
молекула В придет с запасом кинетической энергии Ek = E — Ер;
благодаря этому запасу кинетической энергии, она пройдет через
положение равновесия L и будет дальше приближаться к моле-
молекуле А против сил отталкивания, пока вся кинетическая энергия ее
не перейдет в потенциальную энергию, изображаемую отрезком NM.
Потеряв при г = а, где a = ON есть абсцисса точки М, всю свою
кинетическую энергию, молекула В под влиянием сил отталкивания
начнет удаляться от молекулы А, проходя все разобранные этапы
движения в обратном порядке. Расстояние ON=a определяет то
наименьшее расстояние, на которое приближаются центры молекул
друг к другу во время столкновения. Отрезок о = ON представляет
эффективный диаметр (сумму „радиусов") молекул. Как видно, зна-
значение о зависит от значения полной энергии Е, т. е. от той ско-
скорости, с которой молекула В летит по направлению к молекуле А,
находясь на большом расстоянии г от нее. Чем больше Е, тем выше
236
ГАЗЫ
[гл. vii
пересекает прямая, изображающая полную энергию Е, кривую, изобра-
изображающую потенциальную энергию Ер, и, следовательно, тем меньше о.
Таким образом, эффективный диаметр молекул а не есть величина
постоянная: она зависит от скорости сталкивающихся молекул. Однако
если на участке вблизи точки М потенциальная кривая поднимается
очень круто, то при увеличении энергии Е отрезок ON=a меняется
мало, т. е. зависимость эффективного диаметра о от скорости сталки-
сталкивающихся молекул в этом случае
невелика.
Разбираемый характер сил пока-
показывает, что процесс столкновения
молекул вовсе не похож на процесс
столкновения упругих шаров. „Столк-
„Столкновение" молекул есть результат
наличия между молекулами сил от-
отталкивания, зависящих от расстоя-
расстояния г между ними и быстро возра-
возрастающих при уменьшении г.
§ 62. Изотермы Ван-дер-Вааль-
Ван-дер-Ваальса. Критическое состояние веще-
вещества. Уравнение Ван-дер-Ваальса
Рис. 155. Изотермы Ван-дер-Ва-
Ван-дер-Ваальса.
= RT A)
есть алгебраическое уравнение тре-
третьей степени относительно Vo.
Поэтому оно дает либо одно, либо три различных значения моле-
молекулярного объема Vo в зависимости от значений р и Т.1 Нанося
графически зависимость р от Vo из уравнения Ван-дер-Ваальса для
различных Т, мы получим ряд изотерм (рис. 155). Каждая из кривых
рис. 155 (изотерм) соответствует определенной температуре Т: чем
выше температура Т, тем правее и выше лежат на рис. 155 изо-
изотермы. Из рисунка видно, что только при больших температурах Т
изотерма возрастает с уменьшением Vo монотонно, напоминая изо-
изотерму, соответствующую закону чБойля — Мариотта. На такой изо-
изотерме каждому значению давления р соответствует одно значение
молярного объема Vo, так же как это имеет место при подчинении
газа формуле Менделеева — Клапейрона. При более низких темпе-
температурах изотермы дают в определенной области давлений и объемов
горбы. В этой области, вообще говоря, каждому давлению р соот-
соответствуют три значения объема Vo.
1 Алгебраическое уравнение третьей степени с вещественными коэффи-
коэффициентами и свободным членом всегда имеет три решения, однако два из них
могут быть комплексными. Так как объем Va представляет собою вели-
величину вещественную, то для Vtt мы имеем либо одно, либо три разных ре-
решения.
§ 62] ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА. КРИТИЧЕСКОЕ СОСТОЯНИЕ ВЕЩЕСТВА 237
Для того чтобы выяснить смысл этой, на первый взгляд весьма
странной, зависимости, надо обратиться к опыту. На рис. 156 пред-
р ставлены экспериментально по-
полученные изотермы для угле-
углекислоты (СОа). При высоких тем-
температурах Т изотермы углекис-
углекислоты напоминают изотермы иде-
идеального газа. При более низких
0,002 0,01
Рис. 156. Экспериментальные изотермы Рис. 157. Экспериментальная изо-
углекислоты (COS). терма.
температурах характер изотерм совсем иной. Схематически изо-
изотерма, относящаяся к такой более низкой температуре, изображена
на рис. 157.
Для ясности наметим схему опыта, на котором определялась для
углекислоты зависимость молярного объема Vo от давления р. Схема
этого опыта (рис. 158) следующая: в толстостенном цилиндре А
под поршнем В заключен один моль углекислоты,
температура которой Т во все время опыта под-
поддерживается постоянной. Объем Vo, занимаемый
углекислотой при различных положениях поршня,
может быть измерен. Давления, соответствующие
этим различным объемам, измеряются манометром С. Л
При больших объемах Vo с опусканием поршня
В давление углекислоты возрастает монотонно;
этой части процесса соответствует ветвь ON изо-
изотермы, изображенной на рис. 157. Рис.158. Схема опы-
Здесь свойства углекислоты аналогичны свой- та по определению
ствам идеального газа, хотя она и обнаруживает изотерм,
несколько большую сжимаемость, чем этого тре-
требует закон Бойля — Мариотта. При достижении же некоторого
определенного давления р0, которому соответствует объем Vq (точка
N изотермы), поведение углекислоты резко меняется: при даль-
дальнейшем опускании поршня давление рй остается постоянным, на-
238 газы [гл. vii
чинается процесс ожижения углекислоты. Чем дальше опускается
поршень, тем большее количество газа (который при этих условиях
принято называть насыщенным паром) переходит в жидкость. Точка
изотермы М, характеризуемая давлением р0 и объемом V"u, соответ-
соответствует полному переходу всего количества углекислоты, бывшей под
поршнем, в жидкое состояние. При этом под поршнем окажется
только жидкость; дальнейшее продвижение поршня потребует весьма
больших усилий, так как жидкость мало сжимаема. Ветвь изотермы ML
соответствует жидкому состоянию углекислоты.
Давление р0, при котором происходит ожижение, носит название
упругости насыщенных паров при данной температуре Т. При
давлении р, равном упругости насыщенных паров ра, данное коли-
количество вещества может иметь любые молярные объемы, заключен-
заключенные между V'o и V"u. В этой области вещество одновременно суще-
существует в виде двух агрегатных состояний (как говорят, в двух
фазах) — жидкого и газообразного. Чем ближе значение объема к
VI, тем большая часть вещества находится в жидком состоянии и
тем меньшая его доля приходится на газ (пар).
Совершенно аналогичные изотермы получаются и для всех про-
прочих веществ в области тех температур, при которых они могут
быть переведены из, газообразного состояния в жидкое путем
сжатия.
Сравнение экспериментальных изотерм с теоретическими изотер-
изотермами Ван-дер-Ваальса показывает, что область горбов на изотермах
Ван-дер-Ваальса относится к переходу вещества из газообразного
состояния в жидкое или обратно. При этом, однако, переход веще-
вещества из газообразного состояния в жидкое и обратно в действитель-
действительности происходит не по кривой с перегибами, а по прямой при по-
постоянном давлении ра (прямая MN на рис. 157).
Таким образом, изотермы Ван-дер-Ваальса не только более точно,
чем изотерма идеального газа, передают поведение газа, но охваты-
охватывают собою и процесс ожижения газов, а также выражают то свой-
свойство жидкости, которое проявляется в ее малой сжимаемости.
По мере повышения температуры область горбов на изотермах
Ван-дер-Ваальса делается уже, т. е. убывает разность объемов V'a
и VI, где V'o — объем, соответствующий тому случаю, когда при
давлении pQ вещество целиком находится в газообразном состоянии
(в виде пара), a V\ — когда оно при том же давлении р0 целиком
переведено в жидкое состояние. На рис. 159 сопоставлены реаль-
реальные изотермы для различных температур. Незаштрихованная область
относится к газообразному состоянию вещества; область, отмеченная
пунктиром, — к состоянию вещества в двух фазах: 'газообразной и
жидкой; заштрихованная область — к жидкому состоянию.
Среди изотерм Ван-дер-Ваальса есть такая изотерма, которая от-
отделяет изотермы с горбами от изотерм, не имеющих горбов. Эта изо-
изотерма называется критической, а соответствующая ей температура —
§ 62] ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА. КРИТИЧЕСКОЕ СОСТОЯНИЕ ВЕЩЕСТВА 239
критической температурой Тк (см. рис. 155 и 159). Крити-
Критическая изотерма вместо горбов имеет лишь точку перегиба К;
в этой точке касательная к ней параллельна оси абсцисс. "Точка К
называется критической точкой, а соответствующие ей объем VK и
давление рк — критическим объемом и критическим давлением.
Для каждого данного вещества его
критические температура, молярный
объем и давление имеют опреде-
определенные значения.
Понятие о критической тем-
температуре было впервые введено
Д. И. Менделеевым в 1861 г.
В своем исследовании Менделеев
назвал критическую температуру
температурой абсолютного кипения
жидкости и рассматривал ее как
ту температуру, при которой ис-
исчезают силы сцепления между мо-
молекулами жидкости и жидкость
превращается в пар независимо от
давления и удельного объема.
Это понятие о критической темпе-
температуре вполне соответствует совре-
современному представлению о переходе
из жидкого состояния в газообразное.
Рис. 159. Ход экспериментальных
изотерм.
Действительно, из рассмотрения рис. 159, на котором раз-
разграничены газообразное и жидкое состояния и область ожижений,
явствует:
1) при температуре выше критической Тк вещество может суще-
существовать только в газообразном состоянии. Газ, температура кото-
которого Т выше критической температуры Тк, не может быть ни-
никаким сжатием переведен в жидкое состояние. При температурах
ниже критической вещество может существовать в зависимости от
давления либо в газообразном, либо в жидком состоянии, либо одно-
одновременно в виде двух фаз: жидкости и насыщенного пара;'
2) упругость насыщенного пара ра не может иметь значения
большего, чем критическое давление данного вещества рк;
3) объем вещества в жидком состоянии не может иметь значе-
значения ббльшего, чем критический объем данного количества этого
вещества.
'Критические температуры большого числа жидкостей и их смесей
были изучены М. П. Авенариусом и его учениками А. И. Надеж-
диным, В. И. Зайончевским и др. В частности, А. И. Надеждин
' Впоследствии мы увидим, что возможно и одновременное существова-
существование трех фаз: газообразной, жидкой и твердой.
240
ГАЗЫ
[ГЛ. VII
впервые в 1885 г. определил критическую температуру воды C74° С).
Знаменитый русский физик А. Г. Столетов также занимался крити-
критическим состоянием вещества. Он разобрал имевшийся эксперимен-
экспериментальный материал и полностью сопоставил его с теоретическими
данными.
Построим график (рис. 160), в котором по оси абсцисс отложим
температуру, а по оси ординат — удельные объемы (т. е. объемы
единицы массы) жидкости и находящегося в равновесии с ней насы-
насыщенного пара. Так как жидкость при нагревании расширяется, то
кривая LU, изображающая удельный объем
жидкости в зависимости от температуры,
поднимается. По мере повышения темпе-
температуры объем жидкости увеличивается
быстрее, ее коэффициент расширения не-
непостоянен, но возрастает с температу-
температурой. Поэтому кривая LL' изогнута вверх.
Удельный объем насыщенного пара в за-
зависимости от температуры изображается
кривой GG'. При повышении температуры
часть жидкости испаряется, и плотность
Рис. 160. LV — кривая зави- паР0В над ней возрастает. Но повышение
симости удельного объема плотности паров означает уменьшение их
жидкости от температуры; удельного объема, поэтому кривая QQ'
GG1 — кривая зависимости загибает вниз. В некоторой точке К обе
удельного объема насыщен- „, г
ных паров от температуры, кривые сливаются. Так как эта точка
Обе кривые сходятся при соответствует максимальному удельному
критической температуре Тк. объему жидкости, то, следовательно, она
является критической точкой, и соответ-
соответствующая ей температура есть критическая температура Тк. Отсюда
мы видим, что в критической точке удельные объемы жидкости и
пара совпадают. В критической точке пропадает всякое различие
между жидкостью и паром. Переход из газообразного состояния
в жидкое в критической точке происходит непрерывно. Теплота паро-
парообразования жидкости при критической температуре равна нулю.
Также при критической температуре равен нулю и коэффициент
поверхностного натяжения жидкости.
Вблизи критической точки во всем объеме газа образуются и
вновь распадаются местные центры сгущения; благодаря этому веще-
вещество вблизи критической точки дает помутнение, известное под на-
названием опалесценции.
Рассмотрим более подробно различие между экспериментальными
изотермами и теоретическими изотермами Ван-дер-Ваальса. На экспе-
экспериментальной изотерме область горбов заменена прямой MN, еще раз
представленной на рис. 161. Однако оказывается, что ряд точек,
попадающих в область горбов, может быть, при известных условиях,
экспериментально осуществлен. Так, в обеспыленном и свободном
§ 63] ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ВЕЛИЧИН 241
от электрических зарядов пространстве можно получить пары при
давлении р, большем упругости насыщенных паров ра при данной
температуре. Такие пары называются пересыщенными. Состояние
пересыщенных паров изображается частью изотермы Na, попадающей
в область горба. В естественных условиях в верхних слоях атмо-
атмосферы часто образуются большие массы пересыщенных паров. По-
Появление в пространстве, где находятся пересыщенные пары, отдель-
отдельных пылинок, капелек или электрически заряженных частиц вызывает
их конденсацию, что ведет к появле-
появлению тумана.
Вещество в жидком состоянии мо-
может быть получено под давлением,
меньшим упругости насыщенных паров
при данной температуре, без того,
чтобы оно переходило в парообразное ро
состояние; этому состоянию соответ-
соответствует часть изотермы Mb. Среди изо-
изотерм Ван-дер-Ваальса существуют та-
такие, часть которых попадает ниже оси
абсцисс, т. е. в область отрицательных Рис# 1б1 Сравнение теоретиче-
давлений (см. рис. 155). Эти состояния ской и экспериментальной изо-
представляют собою растянутую жид- терм,
кость, они могут быть экспериментально
осуществлены. Например, жидкую ртуть можно заставить держаться
в барометрической трубке при высоте более 760 мм, т. е. когда
давление ртути не целиком уравновешивается атмосферным давле-
давлением. Такой ртутный столб растянут силой собственного веса, тем
не менее он не разрывается.
Этот опыт указывает на наличие в реальных жидкостях внутрен-
внутренних сил сцепления.
-Вовсе не могут быть осуществлены ниспадающие участки изо-
изотерм ab (рис. 161); нужно считать, что они соответствуют совершенно
неустойчивому состоянию вещества.
§ 63. Определение критических величин. Уравнение в приведенных
величинах. Рассмотрение уравнения Ван-дер-Ваальса E) (§ 60) позволяет
установить связь между значением критических температуры, молярного
объема и давления Тк, VOk и рк и поправками а и Ь.
Преобразуем уравнение Ван-дер-Ваальса
ЯТ, A)
помножив правую и левую части на V$/p, раскрыв скобки и собрав члены,
содержащие Va в одинаковых степенях; тогда получим
- р • Р ч
9 С. Э. Фриш а А. В. Тиморева
242 газы [гл. vu
Отсюда непосредственно видно, что уравнение Ван-дер-Ваальса пред-
представляет собою уравнение третьей степени относительно Vo-
Уравнение Ван-дер-Ваальса для критической температуры Т= Тк
^ + )t + V<l-? = O D)
Рк / Рк Рк
имеет в критической точке К (рис. 152) перегиб. Поэтому в этой точке оно
имеет один тройной корень V0K и может быть представлено в виде:
или, если выполнить возведение в степень,
V* - ЗУ0кVI + 3V*0K Vo - VJB = 0. E)
Уравнения E) и D) должны совпадать тождественно, что возможно при
равенстве коэффициентов при одинаковых степенях Vo, откуда имеем:
Рк Рк Рк
Решая эти три уравнения относительно трех неизвестных Гк, V0K и рк,
¦ получим
Г ^ 36 Р ^ F)
Таким образом, критические величины Тк, VoK и рк непосредственно вы-
выражаются через Ван-дер-Ваальсовы поправки а и Ъ.
Пользуясь соотношениями F), можно преобразовать уравнение Ван-дер-
Ваальса. Введем в рассмотрение приведенные давленая, объем а темпера-
температуру я, ш и т, подразумевая под ними отношения давления, молярного
объема и температуры вещества к его соответственным критическим вели-
величинам:
Рк V»K 'R
Тогда, пользуясь равенствами F), найдем
Подставив зти значения р, Vo и Т в уравнение Ван-дер-Ваальса A),
получим после соответственных алгебраических преобразований:
»-1) = 8т. ¦ (8)
1 В алгебре доказывается, что всякое уравнение третьей степени с веще-
вещественными коэффициентами си се и вещественным свободным членом с,:
= 0, C)
имеет три корня xit xs, x», из которых либо все три, либо один вещественны.
Пользуясь значениями корней уравнения C) х1у л:2, лг8, можно представить
уравнение C) в виде:
(х — Xi) (х — л:2) (х — х„) = 0. (За)
Оба выражения C) и (За) тождественно совпадают между собой. В част-
частном случае все три корня уравнения C) могут совпадать между собою:
дг1 = ^2 = дг,=л:к (тройной корень), тогда уравнение (За) принимает вид
§ 63] ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ВЕЛИЧИН 243
Уравнение (8) заменяет уравнение Ван-дер-Ваальса, отнесенное к одному
молю; оно называется уравнением в приведенных величинах.
Кроме приведенных давления, объема и температуры я, ш и ?, уравне-
уравнение (8) содержит только числа. Однако такое кажущееся выпадение констант,
характерных для данного газа, обусловлено тем, что в уравнении (8) стоят
приведенные давление, объем и температура, т. е. отношения давления,
объема и температуры к соответственным критическим величинам данного газа.
Воспользовавшись уравнением в приведенных величинах (8), можно более
точно указать критерии, при которых уравнение состояния идеального газа
должно являться хорошим приближением к действительности. Положим, что
молярный объем газа Vo велик по сравнению с его критическим объемом VV,
тогда по определению приведенный объем <о велик по сравнению с единицей,
откуда уравнение (8) приближенно можно переписать
8
Подставляя сюда вместо я, ш и т их значения по G), получим
РП = |^Г, ' (9)
но, пользуясь соотношениями F), легко видеть, что
3 Гк -*•
где R — газовая постоянная, откуда (9) принимает вид
рУ0 = ЯТ,
что представляет собою формулу Менделеева — Клапейрона, отнесенную
к одному молю. Таким образом, уравнение Ван-дер-Ваальса переходит в фор-
формулу Менделеева — Клапейрона для всех тех случаев, когда объем газа велик
по сравнению с его критическим объемом.
Из уравнения в приведенных величинах вытекает так называемая тео-
теорема о соответственных состояниях. Смысл ее заключается в следующем:
если два разных газа взяты в таких состояниях, что отношения двух из трех
величин р, Vo, T к соответственным критическим величинам рк, УЯк, Тк для
них одинаковы, то одинаковы будут и отношения третьих величин к соответ-
соответственным критическим. Например, если два газа взяты в таких состояниях,
что — = — и ^ = J-,iob T7^-==~U~"—- Эта теорема непосредственно
Pki Ркг Jki 'кг ''от '«м
вытекает из уравнения (8), так как, например, при одинаковых лит для
двух газов одинаковы будут для них и <л.
Теорема о соответственных состояниях для химически сходных веществ,
критические температуры которых не очень разнятся между собою^ оправды-
оправдывается с большей точностью, чем та точность, с которой формула Ван-дер-
Ваальса количественно совпадает с опытными данными для каждого из
веществ в отдельности. Это указывает, что отступления от формулы Ван-дер-
Ваальса, обнаруживаемые такими веществами, носят одинаковый характер.
Количественные отступления от формулы Ван-дер-Ваальса, обнаруживае-
обнаруживаемые реальными веществами, делаются особенно заметными вблизи критиче-
критической точки. Из формулы F) леско получить, что между критическими вели-
величинами рю VoK и Гк имеет место соотношение:
o
или
!йН AОа)
244
ГАЗЫ
[гл. vii
Соотношение A0) заменяет вытекающее из уравнения состояния идеаль-
идеального газа соотношение/>kK0k = #7k- Расхождения между данными формулы
Ван-дер-Ваальса и формулы Менделеева — Клапейрона достигают почти
2,7 раза. Однако и данные формулы Ван-дер-Ваальса далеко не точно схо-
сходятся с опытными данными. Отношение ?л=
^
, которое по формуле (Юа)
должно иметь для всех веществ одно и то же значение 8/3, на самом деле
принимает для разных веществ разные значения, заметно отличные от 8/3.
Значения величин Кк (так называемых критических коэффициентов) для
некоторых газов приведены в табл. IX.
Таблица IX
Значения критических
Газ ...
к, ...
Не
3,13
на
3,03
коэффициентов АГ„
Na
3,42
Аг
3,43
для некоторых газов
оа
3,42
СОа
3,486
нао
4,46
Особенно велико отступление для воды, что объясняется ассоциацией
молекул воды вблизи критической точки в более сложные группы.
§ 64. Внутренняя энергия реального газа. Эффект Джоуля —
Томсона. Как было показано в § 48, внутренняя энергия идеального
газа U представляет собою кинетическую энергию движения его
молекул ?* = 2eV» она не зависит для данного количества газа ни
от его объема, ни от давления, а определяется только его темпе-
температурой Г; для одного моля идеального газа U=Ek = CvT, где Cv—
молярная теплоемкость при постоянном объеме (см. § 49).
В реальном же газе, как мы видели, существенную роль играют
силы взаимодействия между молекулами. Поэтому внутренняя энергия
реального газа складывается из кинетической энергии движения его
молекул и их взаимной потенциальной энергии:
U=Ek + Ep. A)
Взаимная потенциальная энергия молекул зависит от их среднего
расстояния друг от друга, поэтому Ер должно зависеть от объема
газа. При изменении объема газа без обмена энергией с окружающими
телами полный запас внутренней энергии U остается постоянным,
и поэтому из равенства A) следует:
Д?„ = —Д?4, B)
р ft *- '
т. е. за счет изменения потенциальной энергии при изменении объема
реального газа должна измениться и кинетическая энергия движения
его молекул. Так как и для реального газа теплоемкость при по-
постоянном объеме Cv определяется лишь кинетической энергией
§ 64] ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА. ЭФФЕКТ ДЖОУЛЯ—ТОМСОНА 245
в
Рис. 162. Опыт
Джоуля.
движения его молекул, то равенство Ek = CvT (для одного моля)
остается в силе, и из выражения B) вытекает:
Отсюда мы получаем:" при изменении объема бтез совершения внешних
работ и без обмена теплом с окружающими телами температура
. реального газа меняется. Явление такого рода
ер впервые пытался обнаружить Джоуль. Он помещал
^—ffi—> два сосуда А и В, соединенных трубкой с краном С
(С ~Д^ (рис. 162), в калориметр с водой. Из сосуда В
г л г\ воздух откачивался, в сосуде А воздух находился
при некотором давлении р. При открытии крана С
воздух устремлялся из сосуда А в сосуд В,
расширяясь без совершения внешней работы. При
этом никакого изменения температуры калори-
калориметра Джоуль не наблюдал. Отсюда он сделал
вывод, что при изменении объема газа его внут-
внутренняя энергия не меняется.
Несколько позже этот опыт был повторен
в другом более чувствительном варианте Джоу-
Джоулем совместно с Томсоном. В соединительную
трубку между сосудами А и В помещалась пробка из пористого
вещества С (рис. 163). Трубка окружалась теплоизолирующим ве-
веществом. В сосудах А и В давления газа
постоянными. Газ протекал по трубке с пе-
перепадом давлений в месте, где расположена
пробка. По обеим сторонам пробки поме-
помещались чувствительные термометры. При
этом была обнаружена незначительная раз-
разность температур, показываемых обоими
термометрами. Для большинства , газов тем-
температура с той стороны пробки, куда газ
расширялся, была несколько ниже. Для водо-
водорода изменение температуры оказалось обрат-
обратным: при расширении водород нагревался.
Этот эффект, заключающийся в изменении
температуры газа при расширении (без
теплообмена и совершения внешней ра-
работы), носит название эффекта Джоуля — Томсона. Он является
следствием отступления свойств реальных газов от свойств идеаль-
идеального газа.
Эффект Джоуля — Томсона, сводящийся к охлаждению газа при
его расширении, принято называть положительным, а сводящийся
к нагреванию — отрицательным. Впоследствии было выяснено, что
знак эффекта Джоуля — Томсона зависит от того, какая из поправок,
а или Ь, уравнения Ван-дер-Ваальса играет большую роль.
и т>а поддерживались
С
в
Рис. 163. Опыт Джоуля —
Томсона.
246
ГАЗЫ
[гл. vii
, Связь между эффектом Джоуля — Томсона и поправками а и b
уравнения Ван-дер-Ваальса
можно установить путем рассмотрения потенциальных кривых, при-
приведенных в § 61.
Для простоты рассмотрим в отдельности два случая: 1) газ, для
которого поправкой а в уравнении Ван-дер-Ваальса можно пренебречь;
2) газ, для которого можно пренебречь поправкой Ь.
Мы видели, что поправка а уравнения Ван-дер-Ваальса связана
с наличием сил притяжения между молекулами. Поэтому в первом
случае следует считать силы притяжения между молекулами исчезающе
малыми и учитывать лишь силы отталкивания. Тогда потенциальная
энергия взаимодействия молекул Еь, как функция расстояния между
ними г, представится кривой, изображенной на рис. 164а.
г,
....
1
1
-/
1
I
1
о-) б)
Рис. 164. Потенциальные энергии взаимодействия молекул:
а) при наличии сил отталкивания; б) при наличии сил при-
притяжения.
Ббльшему давлению газа pt соответствуют меньшие средние рас-
расстояния между молекулами Г\, меньшему давлению рг соответствуют
ббльшие средние расстояния г4. Отсюда, как видно из рис. 164а,
с уменьшением давления внутренняя потенциальная энергия убывает:
Но при Д.Ер<[0 из равенства C) получается: ^
Таким образом, мы приходим к выводу: газ, для которого можно
пренебречь поправкой а уравнения Ван-дер-Ваальса* но для которого
поправка Ъ играет заметную роль, нагревается при расширении.
Второй случай относится к столь малым размерам молекул, что
их можно считать за точечные. Это означает, что между молекулами
на сколько-нибудь значительных расстояниях друг от друга не суще-
существует заметных сил отталкивания. Приходится принимать во внимание
§ 65] ОЖИЖЕНИЕ ГАЗОВ 247
(кроме моментов столкновения) лишь силы притяжения, которым
соответствует зависимость потенциальной энергии Ер от расстояния г,
изображенная на рис. 1646.
Теперь потенциальная энергия отрицательна и с увеличением г
ее численное значение уменьшается, поэтому
Отсюда, на основании C), получаем: ДГ<^0. Газ, для которого
можно пренебречь поправкой Ь уравнения Ван-дер-Ваальса, но для
которого поправка а играет существенную роль, охлаждается при
расширении.
Реальный газ дает отрицательный эффект Джоуля — Томсона,
если для него главную роль играет поправка b на собственные раз-
размеры молекул; реальный газ дает положительный эффект Джоуля —
Томсона, если для него главную роль играет поправка а на силы
притяжения между молекулами.
Для одного и того же газа, в зависимости от его температуры
и давления, может играть ббльшую роль то поправка Ь, то поправка а.
Поэтому один и тот же реальный газ в зависимости от внешних
условий дает то положительный, то отрицательный эффект Джоуля —
Томсона. При очень высоких давлениях
для всякого газа преимущественную роль
играют собственные размеры молекул,
т. е. поправка Ь; отсюда при очень высо-
высоких давлениях все газы обнаруживают
отрицательный эффект Джоуля—Томсона.
При некоторых значениях давления р
и температуры Т роль обеих поправок а
и b одинакова; в таком состоянии реаль- Рис. 165. Кривая инверсии,
ный газ дает нулевой эффект Джоуля —
Томсона, т. е. он. не нагревается, не охлаждается при расширении.
Состояние, в котором эффект Джоуля — Томсона равен нулю, назы-
называется точкой инверсии. Совокупность точек инверсии образует
кривую, изображенную на рис. 165. Для точки, соответствующей
данным значениям р и Т, эффект Джоуля — Томсона имеет тот или
другой знак, в зависимости от того, по какую сторону от кривой
инверсии лежит точка: если она лежит ниже кривой — эффект
Джоуля — Томсона положителен, если выше кривой, то эффект
Джоуля — Томсона отрицателен.
§ 66. Ожижение газов. Разбор уравнения Ван-дер-Ваальса пока-
показал нам, что газ может быть переведен в жидкое состояние путем
сжатия лишь в том случае, когда его температура Т ниже его кри-
критической температуры Тк. Изотермы углекислоты, приведенные на
рис. 156, показывают, что при температуре выше 31° С, которая
является критической температурой углекислоты, вплоть до самых
высоких давлений углекислота остается газообразной. Лишь при
248
ГАЗЫ
[гл. vii
температуре ниже 31° С изотермы дают изломы, соответствующие
конденсации углекислоты в жидкость.
В табл. X приведены значения критических температур Тк и кри-
критических давлений рк для ряда газов.
Из таблицы видно, что такие газы, как азот, кислород (а следо-
следовательно, и их смесь — воздух), водород, гелий имеют весьма низкие
критические температуры
Таблицах
Критические температуры и критические
давления
Вещество
Вода, Н2О ....
Хлор, С13 .....
Аммиак, NH3 • ¦
Углекислота, СО2
Криптон, Кг-. . .
Кислород, О2. . ¦
Аргон, Аг
Азот, N2
Неон, Ne
Водород, Н2 . . •
Гелий, Не
Критиче-
Критическая тем-
температура
Гк в °С
374
144
132
31
- 62,5
—118,8
—122,4
— 147
—228
—240
—267,9
Критиче-
Критическое дав-
давление
/>к в am
217
76
112
73
54
50
48
33,5
26
12,85
2,2
Следовательно, они могут
быть ожижены сжатием
лищь после предваритель-
предварительного сильного охлаждения.
Пикте использовал для
охлаждения газов явление,
заключающееся в том, что
жидкость при интенсивном
испарении охлаждается в ре-
результате расходования внут-
внутренней энергии на паро-
парообразование (теплота паро-
парообразования). Пикте подвер-
подвергал интенсивному испарению
жидкий сернистый ангидрид,
температура которого вслед-
вследствие этого падала. В со-
сосуде, где происходило испа-
испарение жидкого сернистого
ангидрида, находился змеевик, по которому под большим давлением
пропускалась углекислота. Углекислота при этом ожижалась. Жидкая
углекислота затем испарялась в другом сосуде, через который про-
проходила труба, наполненная сжатым кислородом. В результате интен-
интенсивного испарения жидкой углекислоты ее температура падала до
—130° С, т. е. ниже критической температуры кислорода. При этих
условиях кислород путем сильного сжатия мог быть переведен
в жидкое состояние.
В 1884 г. Вроблевский и Ольшевский ожижили водород, сжимая
его до 190 am и одновременно охлаждая кипящим кислородом.
В конце же прошлого столетия Дюаром и Линде было предложено
использовать для охлаждения газов эффект Джоуля — Томсона.
Схема машины Линде, служащей для получения жидкого воздуха,
представлена на рис. 166. Двухцилиндровый компрессор С, приво-
приводимый в движение электромотором, сжимает воздух до давления
порядка 100 am. Сжатый воздух поступает в змеевик О. Этот змеевик
состоит из нескольких труб, вставленных одна в другую. Сжатый
компрессором воздух проходит по самой внутренней трубе и, до-
достигая вентиля а, внезапно расширяется. При этом его температура
(воздух имеет при этих условиях положительный эффект Джоуля —
§ 65]
ОЖИЖЕНИЕ ГАЗОВ
249
Томсона) падает. Получившаяся порция холодного воздуха подни-
поднимается по внешней трубе змеевика и охлаждает встречную порцию
воздуха, идущего по внутренней трубе от компрессора. Эта вторая
порция сжатого воздуха, таким образом, отчасти охлаждается еще
раньше, чем она достигнет вентиля а. Расширяясь при прохождении
Рис. 166. Машина Линде.
через вентиль а, она еще сильнее охлаждается благодаря эффекту
Джоуля — Томсона.
Этот процесс, повторяемый достаточное число раз, ведет к охла-
охлаждению воздуха дЬ температуры ниже его критической температуры
и к его ожижению.
Жидкий воздух собирается в дюаровском сосуде с, в котором он,
благодаря слабому притоку извне тепла, может сохраняться доста-
достаточно долго.
Так как воздух в основном состоит из двух газов — азота и
кислорода, то и жидкий воздух является смесью двух жидкостей.
Но точка кипения этих двух жидкостей различна: при атмосферном
250 газы [гл. VH
давлении жидкий азот кипит при —195,7°'С, а жидкий'кислород
кипит при —183° С. Поэтому жидкий воздух по мере испарения
обогащается кислородом, так как азот выкипает первым.
Если две трети жидкого воздуха испарились, то остаток содержит
53 % кислорода.
Жидкий воздух в настоящее время находит широкое применение
при лабораторных работах и в технике. В лабораториях он упо-
употребляется для получения высокого вакуума (см. § 60) и для разных
других целей. В технике особо широкое применение получают ма-
машины, дающие раздельно жидкий кислород и жидкий азот. Выде-
Выделение обоих газов из воздуха основано на разнице в их температу-
температурах ожижения и кипения.
Вата или древесный уголь, пропитанные жидким кислородом, дают
весьма сильное взрывчатое вещество, употребляемое при горных
работах. Жидкий кислород употребляется также в авиации при вы-
высотных полетах: испаряясь, он дает газообразный кислород, идущий
на поддержание дыхания летчиков.
Метод фракционного испарения используется также для получения
из воздуха редких газов: гелия, неона, аргона, криптона и ксенона.
Метод Дюара — Линде непосредственно применим лишь для ожи-
ожижения газов, которые при комнатных температурах дают положи-
положительный эффект Джоуля —Томсона.
Газы, дающие при комнатной температуре отрицательный эффект
Джоуля — Томсона, необходимо предварительно охладить ниже точки
инверсии. Так, водород должен быть охлажден до — 80° С, чтобы при
уменьшении давления от 100 am до 1 am он давал положительный
эффект Джоуля — Томсона. Гелий имеет для того же интервала дав-
давлений температуру инверсии — 258° С. После охлаждения ниже ука-
указанных температур (что для водорода достигается с помощью жидкого
воздуха, а для гелия — с помощью жидкого водорода) эти газы могут
быть ожижены путем применения к ним метода Дюара — Линде.
В настоящее время все известные газы переведены не только
в жидкое, но и в твердое состояние. Гелий был впервые ожижен
Камерлинг-Оннесом в 1908 г. Испаряя жидкий гелий при очень низком
давлении, Камерлинг-Оннес достиг температуры в 0,9° К- В последние
годы тем же методом достигнута температура в 0,71° К и путем
адиабатического размагничивания намагниченных тел получена темпе-
температура ниже 0,1° К.1
Для ожижения воздуха, кроме способа Дюара — Линде, упо-
употребляется еще способ, основанный на понижении температуры в ре-
результате совершения газом работы против внешних сил.
1 Из общетеоретических рассуждений следует, что достичь температуры,
,в,, точности равной абсолютному нулю, невозможно. Чем ближе мы подходим
к температуре абсолютного нули, тем труднее получить дальнейшее охлаж-
охлаждение.
§ 65] ОЖИЖЕНИЕ ГАЗОВ 251
В простейшем виде этот принцип осуществляется в машинах,
в которых газ, сжатый до высокого давления, поступает в цилиндр
(„детандер") с поршнем. Отодвигая поршень, газ совершает против
внешних сил работу за счет своей внутренней энергии, что ведет
к понижению температуры газа.
В последнее время П. Л. Капица, используя этот метод, скон-
сконструировал машину для получения жидкого воздуха и других ожи-
женных газов, в которой охлаждение газа происходит за счет работы
вращения турбины.
Возможность с помощью ожиженных газов (воздуха, водорода,
гелия) охлаждать тела до очень низких температур играет в совре-
современной физике большую роль. Все свойства тел зависят от темпе-
температуры, причем эта зависимость становится особенно большой при
очень низких температурах. При приближении температуры к абсо-
абсолютному нулю возникает ряд качественно новых явлений. Мы уже
упоминали (§ 42) о сверхтекучести жидкого гелия. В т. II будет
указано на явление сверхпроводимости, заключающееся в том, что
для многих чистых металлов и некоторых сплавов омическое сопро-
сопротивление становится практически равным нулю при температурах
порядка 1—7°К. При низких температурах сильно меняются маг-,
нитные свойства веществ. Теплоемкость тел при приближении тем-
температуры к абсолютному нулю сама тоже стремится к нулю. Область
физики, изучающая все эти явления, носит название физики низких
температур.
ГЛАВА VIII
ОСНОВЫ ТЕРМОДИНАМИКИ
§ 66. Молекулярно-кинетическое и энергетическое описание
процессов. Молекулярно-кинетическая теория вещества ставит своей
задачей' объяснение макроскопических свойств тел путем детального
разбора тех молекулярных процессов, которые лежат в их основе.
При этом макроскопические, физические величины имеют смысл
средних значений тех величин, которые характеризуют соответ-
соответственный молекулярный или атомный процесс. Так, давление газа
на стенки обусловлено ударами отдельных молекул. Постоянство
давления при данных условиях есть результат того, что, измеряя
давление, мы наблюдаем средний эффект ударов очень большого
числа молекул за промежуток времени, весьма большой по сравнению
со временем отдельного удара.
Разбирая явление диффузии газов, мы видели, что оно также
имеет смысл некоторого среднего эффекта, возникающего в результате
беспорядочного движения молекул. То же относится и к явлениям
внутреннего трения в газах и теплопроводности.
Беспорядочность движения молекул ведет в общем к наличию
определенных закономерностей. Формула распределения скоростей
Максвелла показывает, что среди беспорядочно распределенных ско-
скоростей существует наиболее вероятная скорость, т. е. такая скорость,
значительно отличные от которой встречаются редко. Кинетическая
энергия движения отдельных молекул может принимать самые разно-
разнообразные значения при данном равновесном состоянии вещества,
средняя же энергия, приходящаяся на одну степень свободы, имеет
при этом вполне определенное значение. Это среднее значение
энергии определяет температуру тела. Сумма потенциальных и кине-
кинетических энергий беспорядочно движущихся молекул составляет запас
внутренней энергии вещества.
Таким образом, макроскопические величины обладают определен-
определенными значениями лишь потому, что они являются средним значением
очень большого числа отдельных элементарных процессов. При
наблюдении же явлений в малых масштабах, когда число наблюдаемых
молекул невелико, должны встречаться отступления от установлен-
установленных средних значений.
§ 67] ЭКВИВАЛЕНТНОСТЬ КОЛИЧЕСТВА ПЕРЕДАННОГО ТЕПЛА И РАБОТЫ 253
Такие отступления, называемые флуктуациями (см. подробнее
§ 76), действительно наблюдаются: примером может служить броу-
броуновское движение.
Метод, применяемый для объяснения- макроскопических свойств
тел с точки зрения их молекулярного строения, есть по существу
метод статистический. В настоящее время этот метод имеет столь
широкое применение, что весь раздел теоретической физики, приме-
применяющий его, носит название статистической физики.
Однако возможен и другой способ описания явлений. В § 26 мы
отмечали, что возможно описывать поведение тел и без того, чтобы
входить в детальное рассмотрение тех процессов, которые при этом
происходят. Такое описание возможно, благодаря введению понятий
об энергии, ее превращениях и способах передачи и установлению
тех основных законов, которым подчиняются эти превращения энергии
из одних видов в другие.
Раздел физики, рассматривающий процессы с указанной энерге-
энергетической точки зрения, носит название термодинамики. Термоди-
Термодинамика, не входя в микроскопическое рассмотрение процессов,
позволяет делать целый ряд выводов относительно их общего про-
протекания, столь же достоверных, как и те фундаментальные законы,
которые лежат в ее основе.
Термодинамический метод рассуждений, как относящийся к энер-
энергетической стороне процессов, имеет не только исключительно боль-
большое принципиальное, но и практическое значение. Весьма обширный
класс технических проблем, связанный с переводом энергии из одних
форм,в другие, и с получением за счет энергии работы, может быть
разобран с термодинамической точки зрения.
Законы, лежащие в основе термодинамики, носят название начал
термодинамики. Эти начала установлены как обобщение экспери-
экспериментальных данных; Их достоверность подтверждается в дальнейшем
совпадении весьма большого числа выводов из них с результатами
опытов.
§ 67. Эквивалентность количества переданного тепла и работы.
Раньше чем перейти к формулировке первого начала термодинамики,
рассмотрим более подробно передачу энергии от одних тел к другим
путем совершения работ и путем передачи тепла. Понятие о работе
было нами разобрано в § 25. Представлением о передаче некоторого
количества тепла тому или другому телу мы тоже неоднократно
пользовались. Подвергнем все же это понятие о передаче тепла
более подробному анализу.
Первоначальные понятия о тепловом состоянии тел возникли в ре-
результате тех субъективных ощущений, которые нагретые тела "могут
вызывать. Эти ощущения определяются сложным комплексом фактов,
относящихся не только к телу, степень нагретости которого мы
определяем, но и к воспринимающему органу, каковым чаще
всего является кожа рук. Кажется ли нам данное тело теплым или
254 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
холодным, определяется не только его температурой, но и его тепло-
теплопроводностью и состоянием нашей руки. Для того чтобы установить
объективную оценку теплового состояния тел, используют то поло-
положение, что тела, образующие изолированную группу, с которыми
не происходит никаких изменений, кроме тепловых, при достаточно
долгом соприкосновении друг с другом принимают одинаковую тем-
температуру. На этом основано измерение температур: термометр при
достаточно длительном соприкосновении принимает температуру тела.
Для измерения температур, как мы видели, может быть использо-
использована зависимость любой физической величины от температуры. Эмпи-
Эмпирическая шкала (см. § 44) измеряет температуру по изменению
давления водорода при постоянном объеме.
В первой половине XVIII столетия некоторые ученые считали,
что причиной повышения температуры тел является движение мо-
молекул. Это мнение было развито М. В. Ломоносовым. По мнению
Ломоносова, тепловые явления обусловлены вращательным („коло-
(„коловратным") движением молекул. Ломоносов связывал тепловое состоя-
состояние тел именно с вращательным движением молекул, так как считал,
что вращательное движение является единственно общим для всех
агрегатных состояний вещества. Теория Ломоносова, изложенная
в 1744 г. в трактате „Рассуждение о причине теплоты и холода",
несмотря на указанное ограничение, содержала все основные черты
молекулярно-кинетической теории тепла. В качестве основного аргу-
аргумента в пользу молекулярно-кинетической теории тепла Ломоносов
приводил нагревание тел в результате трения. Этот же факт он исполь-
использовал для критики общепризнанной в то время теории теплорода.
Теория теплорода возникла в XVIII столетии и получила широкое
распространение. По теории теплорода теплота представляет
собою некоторое вещество — теплород, не создающееся и не уни-
уничтожающееся. Считалось, что теплород лишь переходит от более
горячих тел к более холодным: горячее тело содержит больше тепло-
теплорода, холодное — меньше. Несмотря на то, что теория теплорода не
согласовалась с нагреванием тел при работе сил трения, она про-
продержалась до середины XIX столетия.
На основе.теории теплорода развился метод калориметрических
измерений и было установлено понятие о количестве передаваемого
тепла Q. Первые калориметрические измерения были выполнены
в 1750—^1751 гг. в Петербурге Г. В. Рихманом. Понятие о коли-
количестве переданного тепла можно ввести, рассматривая, например, сле-
следующий опыт. Берутся два совершенно одинаковых сосуда, содер-
содержащих одинаковые количества воды при одинаковой температуре Тй.
Затем два различных по своему составу тела, например, одно желез-
железное, а другое свинцовое, но одинаковой массы т, нагреваются до
одной и той же температуры Т, более высокой, чем Го. Если одно
из этих тел опустить в один из сосудов с водой, а другое — в другой
и подождать достаточно времени, чтобы температуры между каждым
§ 67] ЭКВИВАЛЕНТНОСТЬ КОЛИЧЕСТВА ПЕРЕДАННОГО ТЕПЛА И РАБОТЫ 255
из тел и водой выравнялись, то окажется, что вода в сосуде, в ко-
который было опущено железо, нагрелась больше, чем в сосуде,
в который был опущен свинец. Этот факт может быть истолкован
в том смысле, что железо передало воде ббльшее количество тепла A.Q,
чем свинец. Так же, экспериментируя с телами одного состава, можно
установить, что воде передается тем больше тепла, чем больше масса
тела и чем до более высокой температуры оно было первоначально
нагрето. На основании этих опытов было принято, что количество
тепла Дф, переданное телу или отнятое от него, пропорционально
изменению температуры тела Д7" и его массе т:
LQ = cm^. A)
Величина с получила название удельной теплоемкости. За единицу
количества переданного тепла (калорию) было принято такое коли-
количество дередаваемого тепла, которое надо сообщить 1 г воды, чтобы
повысить ее температуру на 1° С. При измерении количества пере-
переданного тепла в калориях удельная теплоемкость воды оказывается
равной единице.
На основании сказанного, измерение количества переданного
тепла A.Q можно производить следующим способом: тело приводится
в соприкосновение с водой таким образом, чтобы теплообмен прак-
практически происходил лишь между телом и водой, тогда по A)
ДС = с/яД7=со/яоД7"о, B)
где с0 и т0 — теплоемкость и масса воды, Д Гв — изменение темпе-
температуры воды, получившееся в результате теплообмена с данным
телом. Так как тй и ДГо доступны непосредственному измерению,
то по B) можно измерить и AQ.
В конце XVIII и в начале XIX столетий, по мере накопления
экспериментального материала, все резче выступала уже показанная
Ломоносовым неспособность теории теплорода объяснить нагревание
тел при работе сил трения.
Румфорд наблюдал непрерывное нагревание стружек при сверле-
сверлении металла. Дэви в конце XVIII столетия показал возможность полу-
получить нагревание при трении двух кусков льда. Джоуль в результате
большой серии работ, выполненных в период с 1843 по 1878 г.,"
показал, что необходимо затратить работу в 4,18 - 107 эрг, чтобы
возникло нагревание тел такое же, как при передаче количества тепла
в одну калорию; наоборот, в случае совершения механической работы
в результате взятого от каких-либо тел тепла, за счет одной калории
всегда получается 4,18 • 107 эрг механической работы. Эти опыты,
впоследствии многократно повторенные в разнообразных видах, уста-
установили общую эквивалентность между количеством переданного
тепла и работой.
256 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
§ 68. Первое начало термодинамики. Эквивалентность между
количеством переданного тепла и работы позволяет обобщить закон,
сохранения механической энергии. Как было сказано в § 28, изме-
изменение механической энергии системы пропорционально работе, со-
совершенной силами, приложенными к системе извне, и внутренними
силами трения. При этом мы не рассматривали тепловые воздействия.'
В общем же случае возможно изменение энергии системы не только
за счет совершения работ, но и за счет передачи тепла и за счет
других воздействий (например, за счет поглощения света).
Рассмотрим некоторую систему и будем переводить ее из одного
состояния в другое. Например, определенное количество газа может
сжиматься под действием внешних сил и одновременно нагреваться
в результате передачи ему некоторого количества тепла. Каждое
состояние системы может быть определено с макроскопической точки
зрения заданием определенных величин, характеризующих это со-
состояние. Такие величины называются параметрами. Для ид$ального
газа параметрами, определяющими его состояние, является любая
пара из трех следующих величин: объем V, давление р и темпера-
температура Т, так как для заданного количества идеального газа его со-
состояние однозначно определяется любой парой из этих трех величин
(например, давление р и температура Т).
Переход системы из одного состояния в другое происходит под
влиянием внешних воздействий, к числу которых относится не только
работа внешних сил ДЛ, но и передача некоторого количества
тепла AQ и другие воздействия. Передача тепла и работа, как
мы видели, всегда эквивалентны друг другу. Для всех других воз-
воздействий, как показывают опыты, также удается установить соответ-
соответственные механические эквиваленты. Далее опыты показывают, что
если система переходит под влиянием внешних воздействий из опре-
определенного состояния / в другое определенное состояние //, то при
всех возможных способах переходов сумма механических эквива-
эквивалентов внешних воздействий остается неизменной.
Эта сумма механических эквивалентов внешних воздействий S^^i
и определяет изменение энергии
{/„—?/, = А 2 АЛ„ . (О
i
где Ui и 1)\\ — энергии системы соответственно в состояниях / и //
и k — коэффициент пропорциональности. . i
Из сказанного видно, что физический смысл име^ раз-
разность энергий двух состояний, сама же энергия MojffeT быть
определена, только если энергию какого-либо состояния условно
принять за нуль (или приписать какое-либо определенное значение).
1 Тем самым мы молчаливо предполагаем, что внешние силы не являются
силами трения, так как работа внешних сил трения сопровождается передачей
тепла системе. I
§ 68] ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ 257
Но если мы припишем системе в каком-либо состоянии определенное
значение энергии, например, в состоянии / — значение энергии ?Д,
то энергия Un в состоянии // будет по формуле A) равняться:
?/„=?/, + ? ? ДЛ,,
Так как по сказанному 2 &Aj не зависит от способа перехода
с
из состояния / в состояние //, то тем самым оказывается, что и
в состоянии // энергия будет иметь вполне определенное значе-
значение U\\. Это означает, что энергия является однозначной функцией
состояния, т. е. однозначно определяется теми же параметрами,
которыми определяется состояние. Если в результате каких-либо
воздействий система сперва переходит из состояния / в состояние //,
а затем снова возвращается в состояние /, то ее энергия принимает
прежнее значение. Следовательно, закон -изменения и сохранения
энергии в ^наиболее общем виде формулируется следующим образом:
изменение энергии системы при ее переходе из одного состояния
в другое пропорционально сумме механических эквивалентов всех
внешних воздействий, ведущих к рассматриваемому переходу си-
системы. При круговом процессе, т. е, таком, в результате которого
система возвращается в исходное состояние, сумма механических
эквивалентов всех внешних воздействий равна нулю, и энергия
остается постоянной.
Закон сохранения энергии, выраженный в таком общем виде, и
носит название первого начала термодинамики.
Поскольку фактически передача энергии путем теплопроводности
играет большую роль, мы будем выделять те воздействия, которые
сводятся к передаче количества тепла Д<2, тогда первое начало термо-
термодинамики мы запишем в следующем виде:
b.U=kbA-\-k'AQ, B)
где Д?/—изменение внутренней энергии системы, Дф— количество
тепла, переданного системе, и ДЛ — сумма механических эквивалентов
всех прочих внешних воздействий. Если прочие внешние воздействия
сводятся к механическим, то ДЛ представляет собою работу внешних
сил, приложенных к системе.
Ввиду эквивалентности количества переданного тепла и работы,
количество переданного тепла AQ можно измерять в тех же единицах,
что и работу (в эргах, джоулях, кГм и т. д.); в тех же единицах
измеряется и энергия. Если все входящие в формулу B) величины
измерять в одних и тех же единицах, то оба коэффициента k и k'
станут равны единице, и формула B) примет вид:
LU=bA-\- AQ. Ba)
258 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
Считая изменение внутренней энергии бесконечно малым, пере-
перепишем соотношение Bа) в виде:
dU=dA-\-dQ. . '
Так как энергия U является функцией состояния и при круго-
круговом процессе ее изменение равно нулю, то dU представляет собой
полный дифференциал. Работа же, совершаемая на замкнутом пути,
во всех тех случаях, когда имеет место нагревание, не равна нулю.
Отсюда следует, что dA не представляет собой в этих случаях
полного дифференциала. Но тогда из B6) вытекает, что и количе-
количество переданного тепла dQ не есть полный дифференциал.
Отсюда получаем, что ни работа, ни количество переданного
тепла не тождественны с энергией. Они имеют тот смысл, что их
сумма определяет изменение энергии.
Наряду с работой ДЛ, совершаемой внешними силами, прило-
приложенными к системе, можно рассматривать работу АА', совершаемую
силами, приложенными к внешним телам со стороны системы. В силу
третьего закона Ньютона ДЛ' = — ДА Вводя в формулу Bа) А А',
перепишем ее в виде:
AQ = A(J+bA'. C)
Записанное в таком виде первое начало.термодинамики утверждает:
количество тепла, переданное системе, идет на увеличение ее
внутренней анергии и на работу, совершаемую силами, приложен-
приложенными со стороны системы к внешним телам.
Первое начало термодинамики подтверждается как теми опытами,
на основании которых была установлена эквивалентность между теплом
и работой, так и совпадением весьма большого числа выводов из него
с наблюдаемыми фактами.
Исторически установление закона сохранения энергии (первого
начала) было связано с неудачами осуществления такой машины, ко-
которая совершала бы работу, не затрачивая при этом никакого вида
энергии и не получая извне тепла. В термодинамике такая машина
называется перпетуум мобиле первого рода. По сказанному, при
возвращении системы в исходное состояние ее энергия принимает
прежнее значение. Поэтому для периодически действующей машины
к концу каждого периода Д?/=0, и совершенная ею работа может
быть получена лишь за счет переданного извне количества тепла AQ,
либо за счет каких-либо других дополнительных внешних источников
энергии. Так как передача тепла есть тоже передача энергии, то можно
говорить вообще о переданной энергии и формулировать закон сохра-
сохранения энергии (первое начало термодинамики) в следующем виде;
невозможно построить перпетуум мобиле первого рода, т. е. такой
периодически действующий двигатель, который производил ,бы за
§ 68] ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ 259
один период работу в количестве ббльшем, чем количество погло-
поглощаемой им извне энергии.
Говоря о ааконе сохранения энергии, существенно отметить сле-
следующее: возможны такие переходы системы из некоторого состоя-
состояния / в отличное от него состояние //, когда сумма механических
эквивалентов внешних воздействий оказывается равной нулю. Тогда
по формуле A) энергии обоих состояний / и // должны равняться
друг другу: f/ц = U\. Это означает, что в системе происходит такой
процесс, при котором параметры системы меняются, но энергия ее
остается постоянной. Примером может служить изотермическое
расширение идеального газа: поскольку температура газа не меняется,
постольку не меняется и его энергия. Параметры же, определяющие
состояние газа (объем V и давление р), меняются. При этом совер-
совершается внешняя работа, и газу передается некоторое количество
тепла, но сумма внешней работы и механического эквивалента пере-
переданного тепла равна нулю.
В случае изолированной системы внешние воздействия отсут-
отсутствуют. Но и в этом случае, за счет взаимодействий между отдель-
отдельными частями системы, в ней могут происходить процессы, и отдель-
отдельные виды энергии (кинетическая, потенциальная и т. д.) могут
меняться. Полная же энергия системы будет сохраняться. Рассмот-
Рассмотрим в качестве примера изолированную систему тел, обладающую
некоторым запасом кинетической и потенциальной энергии. Пусть
в результате взаимодействий между телами, образующими систему,
совершается работа против сил трения. В этом случае, как мы
указывали в § 28, механическая i энергия системы, являющаяся сум-
суммой потенциальной и кинетической энергии тел, будет убывать.
Но в результате работы против сил трения тела нагреются и их
внутренняя (тепловая) энергия возрастет. Полная энергия системы
останется неизменной, лишь отдельные виды энергии перейдут из
одного вида в другой.
Принципиальное и теоретическое значение эквивалентности пере-
переданного тепла и работы было выяснено Робертом Майером
A814—1878), В. Томсоном A824—1907), Клаузиусом A822—1888)
и рядом других физиков. '
Закон сохранения энергии предугадывался давно. В 1748 г.
М. В. Ломоносов, формулируя закон сохранения вещества, сформу-
сформулировал и закон сохранения движения в природе. Он писал: „Все
перемены, в Натуре случающиеся, такого суть состояния, что сколько
чего у одного тела отнимается, столько присовокупится к другому...
Сей всеобщий естественный закон простирается и в самые правила
движения: ибо тело, движущее своей силою другое, столько же
оныя у себя теряет, сколько сообщает другому, которое от него
движение получает". Количественная формулировка закона сохране-
сохранения энергии была дана лишь через 100 лет Робертом Майером
A814—1878) и Гельмгольцем A821—1894) после открытия многих
260 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
процессов, связанных с взаимным превращением различных видов
энергии. Майер пришел к открытию закона сохранения энергии
в результате общих рассуждений, основанных на физиологических
наблюдениях. Он подчеркивал превращение качественно различных
видов энергии друг в друга, причем эти превращения всегда осуще-
осуществляются в определенных количественных (эквивалентных) соотно-
соотношениях. Гельмгольц ввел понятие о кинетической и потенциальной
энергиях и, рассматривая систему, в которой действуют центральные
силы притяжения и отталкивания, установил, что сумма кинетиче-
кинетической и потенциальной энергий для данной замкнутой системы
постоянна. Таким образом, в трактовке Гельмгольца закон сохранения
энергии носил ограниченный механистический характер.
Общий характер закона сохранения и превращения энергии и его
исключительное значение для естествознания были раскрыты Энгель-
Энгельсом. Формой существования материи является движение, понимаемое
как изменение вообще. Движение, понимаемое в таком общем смысле,
не может ни исчезнуть, ни создаться из ничего; в природе возможны
лишь изменения формы существования материи, ее превращения,
происходящие в известных количественных соотношениях. Это есть
общая формулировка закона сохранения, несвязанная с ее физической
формулировкой, которая в зависимости от новых открытий может
изменяться. Энгельс писал: „.. .любая форма движения оказалась спо-
способной и вынужденной превращаться в любую другую форму движения.
Дойдя до этой формы, закон достиг своего последнего выражения.
Посредством новых открытий мы можем доставить ему новые под-
подтверждения, дать ему новое, более богатое содержание. Но к самому
закону, как он здесь выражен, мы не можем прибавить больше ничего".'
Закон сохранения и превращения энергии позволяет вместе с тем
более глубоко выяснить природу физической величины, которая
называется работой. Как мы видели, энергия системы может меняться
за счет совершенной работы. Следовательно, работа является мерой
изменения энергии. Такой смысл работы был отмечен Энгельсом,
который писал: ... .работа — это изменение формы движения, рассма-
рассматриваемое с его количественной стороны".2
Работа и „количество переданного тепла", являясь мерой изменения энер-
энергии, вместе с тем не тождественны энергии. Действительно, энергия характе-
характеризует систему, она является однозначной функцией состояния системы
(см. § 26). Система обладает определенным значением энергии и тогда, когда
с ней не происходит никаких изменений. Понятия же о работе и „количестве
переданного тепла" имеют смысл только тогда, когда происходит процесс,
ведущий к изменению состояния системы, в результате которого меняется ее
энергия. Ни работа, ни „количество переданного тепла" не являются функ-
функциями состояния системы.
Несмотря на то, что после установления эквивалентности между количе-
количеством переданного тепла и работой теория теплорода была полностью оставлена,
1 Ф. Энгельс. Диалектика природы. 1950, стр. 178.
* Гам же, стр. 70.
§ 68] ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ 261
до сих пор слова „тепло" и „теплота" часто употребляются в том смысле,
который им придавала теория теплорода. Так, с одной стороны, „тепло"
употребляется в смысле „количества переданного тепла", которое, как мы
выяснили, эквивалентно работе и является мерой изменения энергии. С дру-
другой стороны, под „теплом", содержащимся в теле, подразумевают тепловую
энергию тела, о которой мы скажем дальше. Такое неоднозначное употребле-
употребление слова „тепло" может легко повести к неясностям, усугубляемым еще тем,
нто в соответствии с неверной теорией теплорода иногда подразумевается,
что количество „тепла", содержащегося в теле, определяется „количеством
переданного тепла". Несостоятельность же последнего утверждения с несо-
несомненностью вытекает из того, что для перевода некоторого вещества из опре-
определенного начального состояния /¦ в некоторое вполне определенное состоя-
состояние // приходится сообщать ему самые разнообразные количества тепла
в зависимости от того, каким образом совершается переход. Возьмем, напри-
например, 1 моль идеального газа, который требуется перевести из состояния /,
характеризуемого давлением />, и температурой 7i, в состояние //, характе-
характеризуемое более высоким давлением ра и более высокой температурой 7.
Этот перевод мы можем провести различным образом. Например: 1) нагре-
нагреваем газ при постоянном давлении р! до температуры 7У, для этого сообщаем
газу количество тепла: Дф = Ср(Г2—7\), где Ср — молярная теплоемкость
газа при постоянном давлении; после этого сжимаем газ изотермически до
давления р2; 2) нагреваем газ при постоянном объеме до температуры 7"а,
для чего сообщаем ему количество тепла AQ' = Cv(Ta—Ti), где Cv—моляр-
Cv—молярная теплоемкость газа при постоянном объеме. После этого сжимаем газ
изотермически до давления р2. В обоих случаях газ переведен из состояния /
во вполне определенное состояние //, количества же переданного ему тепла
AQ и Щ' не равны друг другу, так как Cp=?Cv.
При нагревании газа прип постоянном объеме мы имеем дело только
с передачей количества тепла, которое полностью идет на увеличение запаса
внутренней энергии газа. При нагревании же при постоянном давлении про-
процесс носит более сложный характер: одновременно с передачей количества
тепла производится работа. вы.зва,нная пяппипенир^ гам Тплип пипиррирй.
ныи учет работ и количеств переданного тепла позволяет однозначно учесть
изменение внутренней энергии тела.
Отсюда становится ясной невозможность говорить о „запасе тепла" у тела,
определяемом .количеством переданного тепла'.
Степень нагретости тел, характеризуемая температурой, определяется
интенсивностью беспорядочного молекулярного движения.
Как мы видели (§ 48), температура Т тела в шкале Кельвина однозначно
определяется через среднюю энергию wt, приходящуюся на одну степень
2
свободы молекулы:. T=-r-wlt, где k — постоянная Больцмана. Полная энер-
Я
гия беспорядочного движения молекул (поступательного, вращательного,
колебательного) вместе с возможными видами немеханической потенциальной
энергии составляет запас внутренней энергий тела. Сумму энергий всех видов
беспорядочного движения частиц иногда называют тепловой энергией данного
тела. Однако выделение из общей внутренней энергии тела тепловой энергии
возможно лишь в том случае, если имеется достаточно полная молекулярно-
кинетическая теория данного тела, учитывающая все виды возможных беспо-
беспорядочных движений его частиц и зависимость этих движений от температуры.
При этом, как мы указали в § 49, эта теория не может основываться только
на представлениях классической механики, но должна учитывать особый,
квантовый характер движения молекул.
Выделение тепловой энергии можно произвести лишь для простейших
идеализированных случаев. Так, мы видели (см. § 48), что для идеального
газа взаимная потенциальная энергия его частиц равна нулю. Следовательно,
262 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
для такого газа тепловая энергия совпадает с его внутренней энергией.
В качестве другого примера возьмем идеализированный двуатомный газ, все
молекулы которого имеют независимо от температуры пять степеней свободы
и подчиняются закону равнораспределения энергии по степеням свободы. Для
такого газа его тепловая энергия равна -^-kTN, где N—число молекул газа.
Для всех же реальных тел такое выделение тепловой энергии невозможно.'
Поэтому мы ограничимся в дальнейшем рассмотрением лишь полной внут-
внутренней энергии тел, не выясняя, из каких отдельных видов энергии она
состоит.
Эквивалентность количества переданного тепла и работы, а вместе с тем
и их специфические особенности сказываются особенно ясно при разборе
отдельных явлений с молекулярно-кинетической точки зрения. Пусть движу-
движущийся молоток ударяет о пружину и сжимает ее. Здесь кинетическая энергия
упорядоченного движения молотка перешла, в результате совершения работы
упругих сил, в потенциальную энергию сжатой пружины. Возьмем другой
пример: определенное количество газа нагревается на ДГ° путем теплопро-
теплопроводности при соприкосновении с другим количеством газа, находящимся при
более высокой температуре. Этот процесс, сводящийся с макроскопической
точки зрения к передаче некоторого количества тепла от горячего газа более
холодному, с молекулярно-кинетической точки зрения представляет собой
процесс выравнивания средних кинетических энергий беспорядочного движе-
движения молекул обоих газов. На этих особенностях передачи энергии путем совер-
совершения работы (в результате наличия упорядоченного движения) и путем пере-
передачи тепла (в результате наличия беспорядочного молекулярного движения)
мы еще в дальнейшем остановимся.
Существенно отметить, что при измерении количества переданного тепла
по эквивалентным количествам затраченной работы было установлено, что
теплоемкости всех тел, в том числе и воды, не являются вполне постоян-
постоянными величинами, но несколько зависят от температуры. Поэтому „количество
переданного тепла" AQ, определяемое соотношением A)
само по себе еще не может служить мерой изменения энергии системы.
Такой мерой оно может служить лишь после того, как в результате уста-
установления эквивалентных работ для каждого температурного интервала ДГ
определен вид зависимости теплоемкости от температуры Т. „Первичной
мерой" изменения энергии системы всегда является механическая работа.
Это еще раз подтверждает уже приведенное нами раньше (§ 26) высказы-
высказывание Энгельса, что „работа — это изменение формы движения, рассматри-
рассматриваемое с его количественной стороны".1
В связи с тем, что теплоемкость воды, как и всех других тел, зависит
от температуры, необходимо уточнить определение калории. В настоящее
время принимается, что калория есть количество переданного тепла, необхо-
необходимое для повышения темпердтуры 1 г воды ох 19,5° до 20,5° С при постоян-
постоянном давлении.
§ 69. Круговые процессы (циклы). Рассматривая какой-либо
процесс с термодинамической точки зрения, мы можем не интересо-
интересоваться, из каких веществ состоит система, но нам важно знать, каким
числом физических величин и какими именно физическими величинами
состояние системы может быть однозначно определено.
Величины, служащие для определения состояния системы и могу-
могущие изменяться под влиянием внешних причин, как сказано выше,
Ф. Энгельс. Диалектика природы. 1950, стр. 70.
§ 69] КРУГОВЫЕ ПРОЦЕССЫ (ЦИКЛЫ) 263
называются параметрами. Количество параметров, необходимых для
однозначного определения состояния системы, зависит от степени
ее сложности. Для того чтобы установить степень сложности системы,
в термодинамике вводят понятие о фазе. Под фазой подразумевают
всякое физически однородное тело или совокупность тождественных
и физически однородных тел. Например, система, состоящая из воды
и насыщенного водяного пара над ней, представляет собою систему из
двух фаз: одной фазой является вода, другой — насыщенный пар. Также
вода и плавающие в ней куски льда будут представлять собою систему
из двух фаз: одна фаза — это вода, другая — совокупность кусков льда.
Простейшей системой является некоторое определенное количе-
количество идеального газа; это будет однофазная система. Параметрами,
однозначно определяющими состояние этой системы, служат две из
трех следующих величин: объем V, давление р и температура Т
(масса газа /я, как определенно заданная, в этом случае параметром
не является). Величины V, р и Т связаны между собою уравнением
состояния, которым для идеального газа служит формула Менделеева —
Клапейрона.
Весьма существенен вопрос о том, является ли данная система
равновесной или неравновесной. Равновесным состоянием системы
называется такое состояние, при котором характеризующие систему
параметры имеют определенные значения, остающиеся без влияния
извне каких-либо причин неизменными сколь угодно долго. Если
эти условия не выполнены, состояние системы будет неравновесным.
Приведем примеры: система, состоящая из жидкости и насыщенного
пара над ней, заключенных в сосуд данного объема V и находящихся
во всех своих частях при одинаковой температуре Т, находится
в равновесном состоянии; здесь все части системы находятся под
одним и тем же давлением. Таким образом, р и Т имеют для системы
определенные значения, остающиеся, так же как и остальные пара-
параметры (относительные количества жидкости и насыщенных паров),
неизменными со временем. Та же система, в которой температуры
жидкости и пара различны, окажется в неравновесном состоянии:
величина Т для нее вообще не имеет определенного значения, а
относительные количества жидкости и пара будут меняться. В каче-
качестве другого примера неравновесного состояния системы можно при-
привести металлический стержень, концы которогб поддерживаются
извне при разных температурах; здесь осуществляется постоянство
температуры в каждой данной точке стержня (стационарное состоя-
состояние), но, во-первых, это постоянство возможно лишь при наличии
внешней причины, поддерживающей концы стержня при данных тем-
температурах, и, во-вторых, температура в разных частях стержня разная.
Графически состояние системы можно изобразить точкой, отложив
по осям координат значения параметров, характеризующих систему.
Например, если состояние системы характеризуется ее объемом V и
давлением р, то, отложив по оси абсцисс объемы, а по оси ординат —
264
ОСНОВЫ ТЕРМОДИНАМИКИ
[гл. viii
р
давления, получим, что состояние системы, характеризуемое данными
р и V, изобразится точкой А (рис. 167), координаты которой суть
р и V. Только равновесное состояние системы может быть изображено
точкой, так как неравновесному состоянию системы не соответствуют,
как мы выяснили, определенные значения
параметров.
Процесс, происходящий в системе, всегда
связан с рядом неравновесных состояний.
Однако можно представить такое протека-
протекание процесса, что для каждого момента вре-
времени каждый из параметров имеет опреде-
определенное значение, и изменение параметров
со временем происходит настолько мед-
медленно, что в течение любым образом выбран-
выбранного малого промежутка времени М система
Рис. 167. Равновесное со- может считаться равновесной. Такой веско-
стояние изображается точ- . v
кой. Равновесный процесс нечно медленно протекающий процесс назы-
изображается кривой. вается равновесным процессом, его можно
считать состоящим из ряда равновесных.
состояний. Ни один реальный процесс, строго говоря, не может
быть равновесным, но чем медленнее он протекает, тем ближе он
к равновесному. Графически равновесный процесс изобразится не-
непрерывной кривой (кривая ABC рис. 167).
Назовем обратимым такой процесс, котдрый может проте-
протекать в обоих направлениях, причем если процесс протек сперва
в одном направлении, а потом в обратном, то система должна
вернуться в исходное состояние без того, чтобы в окружающих
телах произошли какие-либо изменения. Всякий равновесный процесс
обратим, так как он состоит из не-
непрерывного ряда равновесных состоя-
состояний, которые могли следовать друг за
другом как' в одном, так и в обратном
направлении. Неравновесный процесс
всегда необратим, откуда следует, что
реальные процессы, строго говоря,
всегда необратимы, они могут лишь
приближаться к обратимым процессам,
протекая бесконечно медленно. Ниже
мы подробнее разберем случай обра-
обратимых и необратимых процессов.
Представим себе процесс, сводя-
сводящийся к изменению объема V, давле-
давления р и температуры Т данного количества вещества. Определим
работу, совершаемую при переходе из состояния Q в состояние Са
(рис. 168), считая, что переход происходит бесконечно медленно,
т. е. считая процесс равновесным.
Рис. 168. Работа расширения
изображается площадью фи-
фигуры CidBsBi.
§ 69] КРУГОВЫЕ ПРОЦЕССЫ (ЦИКЛЫ) 265
В § 49 было указано, что при расширении газа при постоянном
давлении р совершается работа
A=p(V,— V0. . A)
где Vj — Vi — изменение объема. Это выражение справедливо не
только при расширении газа, но и при расширении любого вещества,
которое мы будем называть рабочим веществом, если только давле-
давление р остается во время расширения постоянным.
Теперь, однако, мы рассматриваем более общий случай, когда
давление не остается постоянным. Поэтому предварительно введем
в рассмотрение бесконечно малое изменение объема Д V, при кото-
котором давление р можно считать постоянным; тогда элементарная
работа ДА, совершаемая при таком бесконечно малом расширении,
равна
kA=pb.V. B)
Графически элементарная работа ДА изобразится площадью густо
заштрихованного столбика на рис. 168. Давление р численно равно
силе, приложенной со стороны рабочего вещества к единице поверх-
поверхности стенки сосуда. Поэтому работа ДА в формуле B) представляет
собою работу сил, приложенных со стороны системы к внешним телам,
т. е. ту работу, которая в формуле C) § 68 была обозначена ДА'.
Подставляя это значение ДА в формулу C) § 68, получим выраже-
выражение закона сохранения энергии в применении к данному элементар-
элементарному процессу:
\\b. C)
Здесь Дф — количество тепла, переданного рабочему . веществу,
&U—изменение его внутренней энергии. Если вещество расширяется
(Д V^> 0), то работа положительна: ДА ^> 0; эта работа совершается
либо за счет передачи извне рабочему веществу количества тепла
(AQ^>0), либо за счет убывания внутренней энергии вещества U,
либо за счет этих обоих источников вместе. При уменьшении объема
рабочего вещества (Д V<^ 0), что может происходить в результате
сжатия вещества внешними силами, работа LA=p\V отрицательна;
это ведет к передаче от рабочего вещества внешним телам количества
тепла (AQ <^ 0), либо к увеличению запаса внутренней энергии тела U,
либо к обоим этим процессам одновременно.
Полная работа, совершаемая при изменении состояния вещества
от точки С\ до точки С2, равна сумме элементарных работ:
А = 2 ДА =2^; D)
графически она изобразится площадью фигуры С^В^, заштрихо-
заштрихованной на рис. 168.
Представим себе, что рабочее вещество, которое, расширяясь,
перешло из состояния Ct в состояние С2 (рис. 169), затем путем
266
ОСНОВЫ ТЕРМОДИНАМИКИ
[гл. viii
сжатия оказалось снова переведено в состояние Q. Пусть процесс
расширения изображается кривой CiC'Cj. Сжатие может быть осу-
осуществлено вдоль той же самой кривой СгС'С\% проходимой в обрат-
обратном порядке. Но можно провести сжатие иным путем так,' чтобы
оно изобразилось, например, более низкой кривой CsC"Ci, для чего
во время сжатия вещество следует поддерживать при другом темпе-
температурном ходе Тг, чем температурный ход Ти при котором оно
расширялось. Для всех веществ, имеющих положительный коэффи-
коэффициент объемного расширения, 7<^7'i, так как для таких веществ
при одном и том же объеме большие давления достигаются при
больших температурах. В дальнейшем мы будем рассматривать только
такие вещества.
Весь процесс, изображаемый замкнутой кривой СхС'С^СС^, назы-
называется круговым процессом или циклом. Подсчитаем сумму работ,
совершенных при цикле, i
Работа А\, совершаемая веществом при расширении, изобразится
площадью фигуры С^СС^Вф^, эта работа положительна: ^i^>0.
Работа Л8> совершаемая при сжа-
сжатии, изобразится площадью фигуры
fi25i; эта работа отрицательна:
В,
<
Суммарная работа
изобразится разностью площадей фигур
С^С^Вф! и CiC"Ca?ofii, откуда сле-
дует, что она равна заштрихованной на
рис. 169 площади, охватываемой кривой
Рис. 169. Работа, совершав- CiCC8C"d. Эта работа положительна.
Обозначим внутренюю эню е
мая при круговом процессе,
равна площади фигуры, охва-
тываемой замкнутой кривой.
Обозначим внутреннюю энергию веще-
ства в состоянии Ci через U\, а в состоя-
нии q — через ?/„. Количество тепла,
переданного рабочему веществу при рас-
расширении CiC'Cj, обозначим через Q,, а количество тепла, передан-
переданного рабочему веществу при сжатии CaC"d> — через Qa. (При
расширении вещество получает количество тепла Qi^>0, а при
сжатии отдает количество тепла Q9^>0, т. е. получает количество
тепла — Q$). Тогда по первому началу термодинамики имеем
Складывая оба эти равенства почленно, получим, что работа А,
совершенная при цикле веществом против внешних сил, равна
' A = Al^-Ai = Ql — Qi. E)
Эта работа при цикле, изображенном на рис. 169, как мы выяс-
выяснили, положительна. Таким образом, в результате процесса,
§ 69]
КРУГОВЫЕ ПРОЦЕССЫ (ЦИКЛЫ)
267
изображаемого циклом СуССцС'Су, оказалось: веществу извне передано
количество тепла Q,, вещество отдало количество тепла Qit меньшее,
чем Qt; за счет разности значений этих количеств тепла Qt — Q%
вещество совершило работу А против внешних сил. Цикл такого
рода носит название прямого цикла. Так как в результате за счет
переданного количества тепла Q4 — Qt совершена работа А, то про-
процесс, изображаемый прямым циклом, представляет собой тепловую
машину.
Как мы видим, при рассматриваемом круговом процессе не все
количество тепла Qlt переданное веществу во время первой половины
процесса, оказалось превращено в работу: часть тепла Q8 снова
отдана вовне. Так как передача тепла происходит сама собой только
от более горячего тела более холодному, то, следовательно, должны
существовать: более горячее тело, передающее веществу количество
тепла Qi (нагреватель), и более холодное тело, которому вещество
отдает количество тепла Q2 (холодильник).
При получении работы за счет переданного количества тепла,
конечно, выполняется закон сохранения энергии: разность Qt — Q,
между значениями количества тепла, взятого извне и отданного, равна
полученной работе А. С практической точки зрения представляет
интерес, какая часть взятого от нагревателя тепла Qt превращена
в работу А, так как количество тепла в
Qit отданное холодильнику, практи-
практически не представляет интереса; по-
поэтому вводится в рассмотрение коэффи-
коэффициент полезного действия:
A _Ql-Q,
F)
Для определения этого к. п. д.
надо рассмотреть конкретный цикл и
вычислить производимые в нем работы.
Мы сделаем это в § 73.
Сейчас рассмотрим цикл, обратный
по отношению к циклу, изображенному
В, в.
Рис. 170. Обратный цикл.
на рис. 169. При обратном цикле (рис. 170) расширение веще-
вещества происходит по кривой CjC"Ca, при этом совершается поло-
положительная работа Ai, численно равная площади фигуры CiC"C25g??i.
Сжатие вещества происходит по кривой CgCCi; совершаемая при
этом работа Аа отрицательна, численно она равна площади фи-
фигуры CiCCjBjfii. Суммарная работа A' = Ai-f-As отрицательна,
так как по абсолютному значению Аа больше А{, численное зна-
значение суммарной работы А' изобразится площадью, охватываемой
замкнутой кривой С^СС^СС^. Положительна будет работа, совер-
совершаемая силами, приложенными к системе со стороны внешних тел,
268 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
Пусть при расширении тело поглощает извне количество тепла Q4,
а при сжатии отдает количество тепла Qy Весь процесс сводится
к следующему: силы, приложенные к системе со стороны внешних
тел, совершают положительную работу А, система получает извне
количество тепла Q2 и отдает количество тепла Qit ббльшее чем Q2.
Количество отданного тепла Qt равно сумме полученного тепла Qa
и работы, совершенной над системой внешними силами:
Машина, работающая по рассмотренному циклу, может служить
холодильной машиной: так как расширение CiC"C2 происходит при
более низкой температуре, чем сжатие CaC"Ci, то количество тепла Qa
может браться -от более холодного тела, а количество тепла Qi
передаваться более горячему. Холодильная машина работает за счет
внешних сил, она „перетаскивает" некоторое количество тепла Q2
от более холодного тела (тем самым охлаждая его еще сильнее)
к телу более горячему.
§ 70. Адиабатические процессы. Уравнение адиабаты. Адиаба-
Адиабатическим изменением состояния системы называется такое изменение,
которое протекает без обмена теплом между системой и окру-
окружающими телами. При адиабатическом процессе система не полу-
получает извне тепла и не отдает тепла окружающим телам. Для адиаба-
адиабатического протекания процесса система должна быть окружена
совершенно нетеплопроводными стенками. Так как совершенно
нетеплопроводн,ых стенок осуществить нельзя, то всякий реальный
процесс может происходить лишь как более или менее точное при-
приближение к адиабатическому. Практически близкими к адиабатическим
оказываются процессы, протекающие настолько быстро, что обмен
теплом с внешними телами не успевает осуществиться в сколько-
нибудь заметных количествах.
Математически адиабатический характер процесса выразится в том,
что AQ = 0, откуда закон сохранения энергии при адиабатическом
процессе примет вид:
Q. A)
При адиабатическом процессе работа ДЛ может производиться
лишь за счет изменения внутренней энергии системы. Если система
совершает положительную работу (ДЛ ^> 0), то внутренняя энергия
системы убывает; если, наоборот, внешние силы совершают над
системой работу (ДА <^ 0), то внутренняя энергия системы возрастает.
Рассмотрим процесс адиабатического расширения идеального газа.
Работа &А, как всегда, равна
LA=pbV, B)
где р — давление газа, а ДУ—изменение его объема. Внутренняя
энергия идеального газа, как было показано в § 48, есть кинетическая
§ 70] АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ. УРАВНЕНИЕ АДИАБАТЫ 269
энергия движения его молекул; отсюда внутренняя энергия од-
одного моля идеального газа равна
где k — постоянная Больцмана, N—число Авогадро, R. — газовая
постоянная. 'Вводя молярную теплоемкость газа при ' постоянном
объеме Су = -4 R, имеем
U=CV-T,
откуда изменение внутренней энергии идеального газа равно
\U=Cv-bT. C)
Подставив в A) значение ДЛ по B) и значение At/по C), полу-
получим выражение первого начала термодинамики в применении к одному
молю идеального газа:
'CvbT-\-pbVa = 0. D)
Из соотношения D) имеем: при адиабатическом расширении
(ДУ0^>0) — газ охлаждается (ДГ<^0);' при адиабатическом сжатии
(AVo<^0) — газ нагревается (Д7"^>0). Таким образом, при адиа-
адиабатическом изменении объема газа его температура не остается
постоянной. Соответственный расчет (см. мелкий шрифт на стр. 271)
позволяет связать это изменение температуры газа Т с изменением
его объема V. Пусть газ, занимая объем Vb имел температуру 7\,
тогда при адиабатическом изменении объема до значения Vs темпе-
температура примет значение Га, причем будет иметь место следующее
соотношение:
Q
где •t = Tf-, т. е. т есть отношение теплоемкостей газа при постоян-
постоянен
ном давлении и постоянном объеме (см. мелкий шрифт на стр. 271).
Воспользовавшись формулой Менделеева — Клапейрона, справед-
справедливой для каждого данного состояния газа, получим
Vt—Pl'Tt'
подставив это значение Vi/Vs в E), получим
Тш_(Рш
Формула F), тождественная по своему смыслу с формулой E),
связывает изменение температуры, происходящее при адиабатическом
процессе, с изменением давления газа.
270
ОСНОВЫ ТЕРМОДИНАМИКИ
[гл. viii
Сравним теперь изотермическое и адиабатическое изменения со-
состояния газа. Для того чтобы расширение газа могло происходить
изотермически, т. е. при постоянной температуре, газу необходимо
непрерывно передавать извне тепло, чтобы компенсировать то паде-
падение внутренней энергии, которое происходит при совершении газом
положительной работы. Наоборот, для того, чтобы сжатие газа про-
протекало изотермически, от него надо непрерывно отбирать тепло,
чтобы запас его внутренней энергии, а вместе с ним и его темпе-
температура не возросли. Изотермический процесс возможен лишь при
идеально хорошем обмене теплом между- газом и внешними телами.
Практически приблизиться к изотермическому процессу можно,
заставляя его, протекать настолько медленно, чтобы температура
газа все время успевала выравниваться с температурой окружаю-
окружающих тел.
Таким образом, мы имеем:
1) изотермическое изменение объема газа возможно при идеально
хорошем обмене теплом с внешними телами; работа сил, приложен-
приложенных со стороны газа к внешним телам, при расширении происходит
извне тепла; работа внешних сил при сжатии газа
s сопровождается передачей от газа
внешним телам соответственного коли-
количества тепла;
2) адиабатическое изменение объе-
объема газа возможно при идеально хоро-
хорошей тепловой изоляции; работа газа
совершается за счет его внутренней
энергии; при расширении газ охла-
охлаждается, при сжатии — нагревается.
Изотермическое изменение газа под-
подчиняется закону Бойля — Мариотта:
за счет притока
Рис. 171. Адиабата проходит
более круто, чем изотерма.
р V= const
для данного количества газа. Пусть
эта зависимость выражается на рис. 171
изотермой ABC. Если мы, исходя из некоторого состояния В,
начнем газ сжимать адиабатически, то его температура, согласно
сказанному, начнет повышаться; благодаря этому, все значения про-
произведения pV будут по численному значению больше, чем при изо-
изотермическом сжатии; отсюда адиабатическое сжатие изобразится
кривой ВА1у идущей кверху круче, чем ветвь изотермы ВА. Точно
так же, если мы, исходя из точки В, начнем газ адиабатически
расширять, то его температура начнет падать, в результате чего
расширение изобразится кривой ВСЬ идущей вниз круче, чем ветвь
изотермы ВС. Кривая AtBCi носит название адиабаты. Таким обра-
образом, при адиабатическом изменении объема газа газ не подчиняется
закону Бойля — Мариотта. Кривая, изображающая адиабатическое
§ 70] АДИАБАТИЧЕСКИЕ ПРОЦЕССЫ. УРАВНЕНИЕ АДИАБАТЫ 271
расширение газа (адиабата), идет круче, чем кривая, изображающая
изотермическое изменение объема газа (изотерма).
Уравнение адиабаты получим, воспользовавшись выражениями E)
и F); приравнивая друг другу их правые части, получим
т— i
. ' (ЙГЧЙ1-
откуда
. ?-(&)'. <"
т. е. при адиабатическом изменении объема давление газа р меняется
обратно пропорционально объему, взятому в степени -у- Из фор-
формулы G) имеем, что при адиабатическом процессе
pV* = const. Ga)
Формула Gа), заменяющая для адиабатического процесса закон
Бойля — Мариотта, носит название формулы Пуассона.
Практически процессы не носят строго адиабатического или строго
изотермического характера, так как невозможно осуществить ни пол-
полной термической изоляции, ни идеального обмена теплом. Действи-
Действительные процессы носят характер, средний между изотермическим и
адиабатическим. Частным случаем реальных процессов являются про-
процессы политропические, для которых имеют место те же формулы,
что и для адиабатических, только -у имеет значение, промежуточное
между Cp/Cv и единицей. В этом случае -у носит название показа-
показателя политропы.
Чем ближе показатель политропы к значению Cp/Cv, тем ближе
процесс к адиабатическому; чем ближе показатель политропы к еди-
единице, тем ближе процесс к изотермическому.
Выражение E) можно вывести, переписав первое начало термодина-
термодинамики D) в дифференциальном виде:
CvdT + pdVo = 0, откуда pdVo = — СvdT.
Поделив это равенство почленно на равенство, выражающее уравнение
состояния идеального газа,
получим
dV0 __ Cv dT R dV0 dT
T7-~~R-'T' или C~V'1^=~T
Так как RICV — величина постоянная, то последнее равенство можно
переписать в виде:
272 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
Но если дифференциалы двух величин равны друг другу, то сами вели-
величины могут отличаться лишь на произвольную аддитивную постоянную:
¦Д-ln Vo = — In T+ const, откуда ln(U0 l/-7M=Const.
Так как величина, логарифм которой постоянен, тоже постоянна, то
\_R_
(8)
Это выражение преобразуем, воспользовавшись формулой E) § 49, откуда
Подставив это значение R/Cv в (8), найдем
Уо~ ' Т= const,
т. е. при адиабатическом процессе произведение из температуры Т на VI'1
остается постоянным, следовательно, . '
TJf[ ~ ' = T3V] ~ '" откуда ¦=? = (j-J
что совпадает с формулой E).
Для того чтобы получить конкретное представление о различии изотер-
изотермического и адиабатического процессов, рассмотрим несколько конкретных
примеров..
Пример 1. Некоторое количество азота, находящегося при темпера-
температуре 27°С и давлении в 1 am, сжимается адиабатически до объема в 5 раз
меньшего, чем начальный. Чему будут равны после сжатия давление и тем-
температура азота? Сравнить давление с тем, которое получится при изотерми-
изотермическом сжатии.
Решение. По формуле Пуассона G):
p,=W,I ' °™УЯ*Р*=Р*[уш
у
В нашем случае р=\ am, pl = 5, и так как азот двуатомный газ, то
(см. § 49)
Отсюда
ра = 1 • 5bl am = 9,5 am.
В случае изотермического сжатия давление определилось бы по закону
Бойля—Мариотта: с
у. -
pt=Pi -^- = 1 -5 am = 5 am.
Температура 7"», которую газ примет после адиабатического сжатия,
определится соотношением E):
Ь = ^\ откуда 7-,= Г1(^У=
или, переходя к шкале Цельсия, получим: 2 = 298° С. Таким образом, при
рассматриваемом адиабатическом сжатии будет иметь место значительно*
§ 71]
РАБОТА ПРИ ИЗМЕНЕНИЯХ ОБЪЕМА ГАЗА
273
нагревание (от 27 до 298° С), и давление почти вдвое превысит то, которое
имеет место при изотермическом сжатии.
Пример 2. В закрытой колбе со стенками, окруженными нетеплопро-
нетеплопроводным материалом, имеется воздух при повышенном против атмосферного
давлении pt и температуре 7\. Открыв кран (рис. 172), дают давлению
воздуха внутри колбы быстро выравняться с атмосфер-
атмосферным давлением Н, после чего кран С закрывают. После
того как температура воздуха внутри колбы снова приняла
значение 7\, давление внутри колбы оказалось равнвш /»2.
Определить по этим данным отношение 7 теплоем-
костей воздуха при постоянном давлении и постоянном
объеме.
Решение. Обозначим объем колбы V%. Мысленно
выделим ту часть 'воздуха, которая остается в колбе после
открытия крана; она занимала некоторый объем Vi, давле-
давление воздуха было pi и его температура 7V
При открывании крана из колбы вырвалась часть воз-
воздуха; оставшийся воздух занял весь объем колбы Vu и
его давление стало равным атмосферному давлению N.
Процесс расширения можно .считать адиабатическим,
так как он протекал быстро и стенки колбы по условию
плохо теплопроводны, поэтому по формуле Пуассона:
VAi Н
(9)
Рис. 172. Схема
опыта по опре-
определению Cp/Cv
для воздуха.
В результате этого адиабатического расширения воздух
охладился до некоторой температуры 7V После того как
его температура снова возросла до первоначального значения Ть его давле-
давление стало больше атмосферного Н и приняло некоторое значение />2- Объем
воздуха при этом остался равным V\.
Так как при этом окончательном состоянии воздуха его температура
та же, что и в начале, то величины 1/2) Vu pi и р2 связаны между собою
законом Бойля—Мариотта:
jjj=g. (Ю)
Сравнивая выражения (9) и A0), получаем
Pt \Pi,
Логарифмируя это соотношение, найдем
lg// —lgjtn=7(lgpa—lgjfi), откуда 7 = т
Таким образом, измерив давления Н, pi и р3, можно получить значение 7
для воздуха.
Изложенный пример представляет собою схему опыта, применяемого для
определения отношения теплоемкостей Ср и Cv газов.
§ 71. Работа при адиабатическом и изотермическом измене-
изменениях объема газа. Определим работу, совершаемую при адиабати-
адиабатическом расширении газа. Эта работа ДЛ, как мы выяснили, целиком
совершается за счет изменения внутренней энергии газа.
Ю С. Э. Фриш и А. В. Тиморева
274 основы термодинамики [гл. viit
Пользуясь соотношением D) § 49, имеем для моля идеального
газа:
AA=pAV0 = — CVAT.
Так как Су постоянно, то это соотношение справедливо и для
конечного изменения температуры. Пусть первоначальная температура
газа 7"i, а окончательная Ть тогда Д Т= Г2 — Тъ и совершенная
работа А равна
A=—CV(T2— T1) = CVT1{1— jr|J.
Заменив по формуле E) § 70 отношение T^/Ti отношением
=^ч , получим
Эта формула и дает нам работу при адиабатическом изменении
объема одного моля газа от значения Voi до значения Vo%; темпера-
температура Ti соответствует объему У01.
Формуле A) можно придать также несколько иной вид; для этого
воспользуемся соотношением E) § 49:
С* i/
v
откуда
Подставив это выражение для Су в A), найдем
Работа, совершаемая при изотермическом расширении газа, про-
производится за счет тепла, передаваемого газу извне. Поэтому она
не может быть определена таким образом, как мы определяли работу,
совершаемую при адиабатическом расширении. Элементарная работа,
совершаемая газом при увеличении его объема на бесконечно малую
величину Д V, по формуле B) § 69 равна
ДЛ =р Д V.
Полную работу А, совершаемую при изменении объема газа от
значения Ц до значения V2, получим, просуммировав все элементар-
элементарные работы:
A
графически эта работа выразится площадью фигуры, заштрихован-
заштрихованной на рис. 173. Фактически указанное суммирование сводится к
§ 71]
РАБОТА ПРИ ИЗМЕНЕНИЯХ ОБЪЕМА ГАЗА
275
интегрированию, результат которого (см. мелкий шрифт на стр. 275)
дает для одного моля газа:
B)
Так как при изотермическом процессе выполняется закон Бойля —
Мариотта, то
Vp Р
Изотерма
откуда выражение B) может быть также
переписано в виде:
A — RTln —. Bа)
Обобщая формулы Aа) и B) на любую
массу газа т, получим:
1) работа А, совершаемая массойгазат
при адиабатическом изменении ее объема
от У, до V», равна Рис- 17а Работа при изо-
термическом расширении
газа изображается пло-
площадью заштрихованной
фигуры.
здесь A — молекулярный вес газа, 7i —
температура газа при его объеме V{,
2) работа А, совершаемая массой газа т при изотермическом
изменении ее объема от Vt до У.2> равна
B6)
Здесь " Т—та постоянная температура, при которой протекает
данное изотермическое изменение объема газа.
Выражение для работы при изменении объема можно подсчитать сле-
следующим образом. Элементарная работа
dA=pdV.
C)
Полная работа при изменении объема от значения Vi до значения V»
выразится определенным интегралом:
= \ pdV.
D)
Это выражение справедливо независимо от того, протекает ли процесс
изотермически или адиабатически.
Для изотермического процесса для одного моля газа выполняется фор-
формула Менделеева — Клапейрона:
10*
276 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
причем температура Т имеет постоянное значение. Выражая давление р
через Vo и Т, получим ,
Подставляя это значение р в D) и вынося R и Т, как постоянные, за
знак интеграла, найдем:
W
что и дает работу, совершаемую одним молем газа при изотермическом
изменении его объема от значения Voi до значения Vn [ср. с формулой B)
основного текста].
Воспользуемся формулой D), чтобы еще раз вывести выражение для
работы, совершаемой при адиабатическом изменении объема. При адиабати-
адиабатическом процессе имеет место формула Пуассона:
p\fl z=.p \Л
где pi и Voi—начальные давление и объем одного моля газа, отсюда
D) у
чину, за знак интеграла, получим:
Подставляя это значение р в D) и вынося р\\А , как постоянную вели-
вели1
Vol v „ oi oa
вынося в последнем выражении —^ за скобки, найдем
01
< 01
Воспользовавшись уравнением состояния идеального газа, имеем
где 7"(—температура, соответствующая газу, когда он занимал объем Voi и
имел давление plt отсюда
что совпадает с формулой (la).
Приведем численный пример на вычисление работы сжатия газа.
Пример. 10 л азота, находившихся при давлении ру = 1 am, сжи-
сжимаются до давления /?2=100 am. Определим работу сжатия для двух слу-
случаев: 1) сжатие производится изотермически; 2) сжатие производится адиаба-
адиабатически.
Решение. 1) При изотермическом сжатии работа, по формуле B6),
равна
§ 72] ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ 277
Замечая, что —#T=piVi и —? = —, перепишем это выражение:
Решая пример в CGS-системе, переводим давление в бары и объем
в куб. сантиметры, тогда рг = 1 ат= 10е бар; Vi = 10 л = 104 см3, откуда:
А = 10» • 104 In щ эрг^ — 4,6 ¦ 10'° эрг = — 4,6 • 103 дж.
2) При адиабатическом сжатии, по формуле A6):
-у 1 * jj. l i^vv J"
Здесь снова пользуемся соотношением —/?7\ =^plVi', кроме того, за-
замечаем, что по формуле Пуассона:
Tf-l
Vi\t Р% (V^ /Р
,-г = —i откуда гу-М = —
Vi) pi J XVi) \pi
Выполняя эти подстановки, находим
т-1
y — 1L \pJ J-
Как и в первом случае, имеем: pi~ 10е бар, Vi = 104 см3, кроме того,
для азота, как для газа двуатомного, у = 1L, откуда
1.4—1
л = ГТ=Гт[1 — юо 14 ]эрг = — 6,8-1010 эрг = — 6,8-10s дж:.
В обоих случаях работа отрицательна, что соответствует тому, что она
представляет собою работу сжатия, вызванного внешними силами. При адиа-
адиабатическом сжатии работа в данном случае оказывается больше, чем при
изотермическом сжатии.
§ 72. Второе начало термодинамики. Рассматривая в § 69 пря-
прямой круговой процесс, производимый с любым рабочим веществом,
мы видели, что он может быть использован как тепловая машина: за
счет количества тепла Qlt полученного от некоторого источника,
рабочее вещество совершало работу А. Одновременно, как мы видели,
количество тепла Q9 передавалось холодильнику. Таким образом, про-
процесс носил сложный характер: от нагревателя бралось количество
тепла Qt; рабочее вещество совершало работу А, меньшую взятого
количества тепла Qjj количество тепла Qq = Qi — А передавалось
более холодному телу (холодильнику). Так как в большинстве слу-
случаев с практической точки зрения представляет' интерес, какую долю
взятого от нагревателя количества тепла Qt составляет работа А, то,
как мы указывали, отношение
может быть названо к. п. д. тепловой машины.
278 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
Очевидно, машина будет тем выгоднее, чем ближе "»] к единице,
т. е. чем большую долю от количества полученного тепла составляет
работа А.
Тепловой двигатель, который обладал бы к. п. д. т) = 1, был бы
необычайно выгодным. Дело в том, что такой двигатель не требовал
бы наличия двух тел — более горячего (нагревателя) и более холод-
холодного (холодильника), он мог бы работать за счет охлаждения любых
окружающих нас тел, например, земной коры или океанов, до темпе-
температур, более низких, чем наиболее холодные из окружающих тел.
Двигатель такого рода получил название перпетуум мобиле второго
рода. Поскольку перпетуум мобиле второго рода не нарушал бы
закона сохранения энергии (первого начала термодинамики), невозмож-
невозможность его построения не очевидна. Однако все попытки построить
периодически действующую тепловую машину, результатами действия
которой были бы только передача рабочему телу некоторым источ-
источником количества тепла Qt и получение работы A = Qi, неизменно
терпели неудачу.
Первым, поставившим в общем виде вопрос о получении работы
за счет взятого от источника количества тепла, был Сади Карно,
который в 1824 г. опубликовал работу: „Размышления о движущей
силе огня". Карно пришел к выводу, что при круговом процессе,
производимом с идеальным газом и состоящем из адиабатических и
изотермических изменений объемов, нельзя избежать передачи тепла
от нагревателя к холодильнику, если только температура холодиль-
холодильника выше абсолютного нуля.
Впоследствии выводы Карно были обобщены Клаузиусом и
В. Томсоном в принцип невозможности осуществления такого пе-
периодического процесса, единственным результатом которого было
бы получение работы за счет взятого количества тепла от
одного источника.
Этот принцип получил название второго начала термодинамики.
Второе начало термодинамики может быть формулировано также
в виде принципа невозможности построения перпетуум мобиле вто-
второго рода, т. е. периодически действующего двигателя, который
давал бы работу за счет охлаждения одного источника количества
тепла.
Справедливость второго начала термодинамики подтверждается
тем, что огромное число выводов из него в точности совпадает
с результатами опытов.
§ 73. Цикл Карно. Коэффициент полезного действия тепловой
машины. Разберем в настоящем параграфе круговой процесс, введен-
введенный впервые в рассмотрение Карно и получивший название цикла
Карно.
Этот цикл представляет собою обратимый круговой процесс,
состоящий из двух изотерм и двух адиабат. Для осуществления
цикла необходимо иметь нагреватель, сообщающий рабочему веществу
§ 73]
ЦИКЛ КАРНО. К. П. Д. ТЕПЛОВОЙ МАШИНЫ
279
соответственное количество тепла при его изотермическом расши-
расширении, и холодильник, принимающий от рабочего вещества соответст-
соответственное количество тепла при его изотермическом сжатии.
Будем, как и в § 69, обозначать количество тепла, переданного
рабочему веществу нагревателем, через Qit а количество тепла, пере-
переданного рабочему веществу холодильником, через — Q2. (Положи-
(Положительно тепло Q2, отданное рабочим веществом холодильнику.)
Работу во всех случаях будем обозначать через А (без знака).
Работа, совершаемая рабочим веществом при расширении, поло-
положительна: Ai^>0; работа, совершаемая при сжатии, отрицательна:
Л,<0.
Разберем цикл Карно, выбрав в качестве рабочего вещества один
моль идеального газа, который первоначально находится в состоя-,
нии (/), характеризуемом объе- р
мом Vol, давлением рх и темпе-
температурой 7"i (рис. 174). Заставим
газ изотермически расширяться,
пока он не займет объем VM
при давлении /?2 [состояние B)].
При этом изотермическом расши-
расширении газ получит от нагрева-
нагревателя количество тепла Qt и со-
совершит работу Ai = Qi.
Исходя из состояния B), пре-
предоставим газу расширяться адиа-
адиабатически до состояния C), ха- Рис. 174. Цикл Карно.
рактеризуемого объемом Vn3 и
давлением р3. При этом температура газа упадет до некоторого
значения 7~2.
Исходя из состояния C), начнем газ сжимать изотермически (при
постоянной температуре 7~2) до состояния D), характеризуемого объе-
объемом Vo4 и давлением рк. При этом газ отдает холодильнику коли-
количество тепла Qa и совершает работу А =—Q2.
Наконец, исходя из состояния D), сожмем адиабатически газ так,
чтобы он принял исходный объем и давление Vol и рг и нагрелся
до исходной температуры Т\.
Покажем прежде всего, что такого рода процесс, состоящий из
двух изотерм и двух адиабат, действительно может быть выполнен
в виде замкнутого цикла. Для этого воспользуемся формулой E) § 70,
по которой при адиабатическом расширении B)->C) имеет место
соотношение:
Условие замкнутости заключается в том, чтобы газ при адиабати-
адиабатическом сжатии от состояния D) к состоянию (/) повысил свою тем-
280 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
пературу от значения 72 до начального значения Тх, т. е. чтобы
было выполнено соотношение:
Сравнивая выражения A) и B), видим, что должно быть выпол-
выполнено условие:
Так как этому условию всегда можно удовлетворить, то, следо-
следовательно, рассматриваемый процесс можно действительно осуществить
в виде кругового процесса (цикла).
' Определим к. п. д. цикла Карно. К. п. д. i] кругового процесса,
по сказанному в § 69, равен
„ D)
где А — суммарная работа, выполненная в результате протекания
всего цикла; Qj — количество тепла, полученного от нагревателя;
Q9 — количество тепла, отданного холодильнику.
Количество тепла Qlt полученного рабочим веществом, равно
работе А\, совершаемой одним молем газа при изотермическом расши-
расширении (/)->B). По формуле 2 § 71 находим для Q,:
Также количество тепла — ф2, полученного от холодильника, равно
работе Л2, совершаемой газом при изотермическом сжатии C)—*-D):
Qi i i g , In ?i.
Подставив эти значения Qt и — Q.3 в выражение D), найдем
Tl 1п Yj* _ Тч 1п ^»?
11^
„ 1101 1^01_
Г In ^
Но из условия замкнутости C) следует, что
?* = ?*. откуда 1 = ^^. E)
Здесь 7"i — температура газа, при которой протекает изотерми-
изотермическое расширение G)->B); Г2 — температура газа, при которой
протекает изотермическое сжатие C) ->{4). При изотермическом рас-
расширении газ получает от нагревателя количество тепла Qit при изо-
изотермическом сжатии — отдает холодильнику количество тепла Qa.
§ 73]
ЦИКЛ КАРНО. К. П. Я. ТЕПЛОВОЙ МАШИНЫ
281
Нагреватель
Температуру нагревателя мы должны взять равной Tlt а температуру
холодильника — равной Т$, так как при более высокой температуре
нагревателя и более низкой температуре холодильника процесс не
мог бы протекать равновесно.
Рассмотренный прямой цикл Карно представляет собою идеаль-
идеальную тепловую машину. Коэффициент полезного действия такой
идеальной тепловой машины т\ определяется только температу-
температурами Тх нагревателя и Тг холодильника.
При протекании одного цикла газ совершает работу:
А = Qt — Qa = TjQ1( F)
где г] — к. п. д., определяемый формулой E). При этом от нагре-
нагревателя оказывается полученным количество тепла Qx и холодильнику
отдано количество тепла Q2, равное
Qa = Qj — Л = A—¦*]) Qi. G)
Чем выше температура нагревателя Тх и чем ниже температура
холодильника 7а, тем выше к. п. д., тем большая часть тепла Q\,
полученного от нагревателя, превращается
в работу и тем меньшее количество
тепла Q2 отдается холодильнику. К. п. д. -ц
может равняться единице лишь - при
73 = 0, т. е. при температуре холодиль-
холодильника, равной абсолютному нулю.
Схема действия прямого цикла Карно
(идеальной тепловой машины) представ-
представлена на рис. 175.
Обратимость цикла Карно позволяет
провести его в обратном направлении
по отношению к рассмотренному. Такой
обратный цикл Карно явится идеаль-
идеальной холодильной машиной. В самом деле,
при обратном цикле Карно внешние силы
совершат над газом положительную ра-
работу А', равную работе А, совершенной
газом при прямом цикле. При этом от холодильника будет получено
количество тепла Qa, которое по формулам F) и G) может быть
представлено в виде:
Нагревателю будет передано количество тепла
Рабочее тело
Полученная
робота
Холодильник
Рис. 175. Схема действи:!
тепловой машины.
Схема действия обратного цикла Карно (идеальной холодильной
машины) представлена на рис. 176.
282
ОСНОВЫ ТЕРМОДИНАМИКИ
[гл. viii
Все изложенные результаты мы получили, предполагая, что цикл
Карно производился с идеальным газом. Однако, исходя из второго
начала термодинамики, можно показать, что обратимый цикл Карно,
проводимый с любым рабочим веществом, имеет тот же самый
к. п. д., что и цикл карно, проводимый с идеальным газом. Для
доказательства предположим, что обратимый цикл Карно, проводи-
проводимый с некоторым рабочим веществом, имеет к. п. д. г( больший,
чем к. п. д. т] цикла Карно, проводимого с идеальным газом: V^7!-
Осуществим первый из этих циклов в прямом направлении (как
более горячее тело
Затраченная
работа
тепловую машину) п раз между нагрева-
нагревателем температуры Т\ и холодильником
температуры Г2. Тогда мы получим ра-
работу пА, причем от нагревателя будет
получено количество тепла nQlt а холо-
холодильнику отдано количество тепла nQ$.
На основании соотношений F) и G),
применимых не только к циклу Карно
с идеальным газом, но и к произволь-
произвольному циклу (если только под tj подразу-
подразумевать к. п. д. рассматриваемого цикла),
мы можем написать:
долее холодное
тело
пА =
(8)
Рис. 176. Схема действия хо-
холодильной машины.
Осуществим цикл Карно с идеальным
газом в обратном направлении (как хо-
холодильную машину) т раз между теми же нагревателем и холо-
холодильником. Для этого мы должны затратить работу тА'\ от холо-
холодильника будет получено количество тепла mQ'^ и нагревателю отдано
количество тепла mQ[. 'При этом выполняется соотношение:
(9)
Мы можем подобрать числа п и т так, чтобы
A0)
Тогда по (8) и (9), принимая во внимание, что
получим
1А
тА'
т. е. в результате проведения прямого цикла я раз и обратного т
раз полученная работа пА окажется больше, чем затраченная тА'\
при этом по A0) холодильнику передано столько же тепла, сколько
§ 73]
, ЦИКЛ КАРНО. К. П. Д. ТЕПЛОВОЙ МАШИНЫ
283
от него взято. Таким образом, оба цикла, взятые вместе, осуществят
перпетуум мобиле второго рода: работа окажется полученной за счет
тепла, взятого от нагревателя, без того, чтобы холодильнику было
бы передано какое-либо количество тепла. Осуществление же пер-
перпетуум мобиле второго рода невозможно по второму началу термо-
термодинамики. Отсюда следует, что мы должны откинуть предположе-
предположение, что ц'^>ц.
Остается предположение, что if <^_ц. Но в этом случае, проводя
цикл Карно с идеальным газом в прямом направлении, а цикл с дру-
другим рабочим веществом — в обратном, мы точно так же смогли бы
осуществить перпетуум мобиле второго рода.
Таким образом, и это второе предположение должно быть
отброшено. Следовательно, остается единственная возможность:
Рассмотрим теперь необратимый (протекающий неравновесно)
цикл Карно, проводимый в прямом направлении, т. е. действующий
как тепловая машина. Обозначим if' его к. п. д. Осуществляя этот
процесс между данными нагревателем и холодильником и заставляя
между теми же нагревателем и холодильником работать обратимый
цикл Карно как холодильную машину, получим на основании рассу-
рассуждений, тождественных с приведенными, что if^i\, где ц— к. п. д.
обратимого цикла Карно.
Для необратимого цикла Карно нельзя показать, что одновременно
его к. п. д. if не может быть меньше % так как этот процесс на
может быть по условию обратим,
т. е. использован как холодильная
машина. Отсюда мы должны огра-
ограничиться следствием, что к. п. д.
необратимого цикла Карно не мо-
может быть больше к. п. д. обра-
обратимого цикла Карно.
Полученные результаты можно
обобщить на любой замкнутый про-
процесс.
Представим себе произвольный
обратимый замкнутый процесс, изо-
изображаемый графически замкнутой
кривой ABCDA (рис. 177). Этот Рис. 177. Любой замкнутый кру-
* *? говой процесс ABCDA может быть
процесс может быть приближенно разбит на элементарные циклы
разбит на бесконечное множество Карно.
бесконечно узких циклов Карно. При
осуществлении всех этих циклов Карно части каждой из адиабат,
проходимые дважды в противоположных направлениях, выпадут.
Останутся изотермы и краевые участки адиабат, образующие в со-
совокупности замкнутую ломаную линию. В пределе эта линия даст
обход по циклу ABCDA. Каждый из этих циклов Карно протекает
В
Q84 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
между температурами Т'ц и 7д>, разными для различных циклов. По
формуле E) к. п. д. А-го цикла Карно равен
п •
Обозначим максимальную из температур, имеющих место при
протекании всего цикла ABCDA, через 7i, а минимальную — через Т.2,
тогда к. п. д. каждого из отдельных циклов Карно:
Отсюда и к. п. д. всего цикла A BCD А будет удовлетворять
условию:
rf'^h^li. (и)
Таким образом, мы приходим к следствию, что к. п. д. ц'" любого
прямого обратимого кругового процесса (тепловой машины) не
может превышать к. п. д. обратимого цикла Карно (идеальной
тепловой машины), протекающего между температурами 7t и 7"а.
Если рассматриваемый замкнутый процесс необратим, т. е. со-
содержит необратимые участки, которые не могут быть изображены на
рис. 177, то, как можно показать, он разбивается на бесконечное
множество циклов Карно, часть которых будет также необратима.
Так как к. п. д. необратимого цикла Карно tju не может быть
больше к. п. д. if]fe обратимого цикла, то формула A1) тем более
справедлива и для любого прямого необратимого кругового про-
процесса.
Второе начало термодинамики утверждает, что невозможен процесс,
единственным результатом которого было бы получение работы за
счет количества тепла, взятого от некоторого источника. Теперь мы
видим, что процессом, сопровождающим получение работы за счет
взятого количества тепла, может быть передача тепла от горячего
тела к более холодному.
Из формул F) и G) имеем: если рабочее тело, совершающее
обратимый цикл Карно, производит работу A=~nQi и получает от
нагревателя количество тепла Q1; то при этом холодильнику пере-
передается количество тепла
где 7] — к. п. д., определяемый равенством E).
Подставив в это соотношение вместо ¦») его выражение по E),
получим
§ 74] технические циклы 285
где 7j — температура того тела, от которого берется тепло (нагрева-
(нагреватель), Та — температура того тела, которому тепло передается (холо-
(холодильник).
Любой другой процесс, проводимый между теми же нагревателем
и холодильником, имея к. п. д. не ббльший, чем к. п. д. обрати-
обратимого цикла Карно, производит ту же работу А (за счет равного ей
количества тепла, взятого у нагревателя), лишь перенося от нагре-
нагревателя к холодильнику количество тепла, не меньшее чем A2).
Таким образом, рассмотрение обратимого цикла Карно дает
нам количественный критерий, позволяющий установить то коли-
количество тепла Q2, меньше которого не может быть передано от
горячего тела к холодному, чтобы, при любом рабочем процессе,
получить заданное количество работы А за счет равного ему
количества тепла Qt — Qir взятого от горячего тела.
Остановимся еще на одном важном следствии, вытекающем из рассмо-
рассмотрения цикла Карно. В § 44 нами была отмечена произвольность шкалы
температур, так как эмпирическая шкала зависит от выбора термометри-
термометрического тела. Лишь выводы кинетической теории газов позволили установить
связь между температурой и кинетической энергией движения молекул,
общую для всех веществ. Рассмотрение цикла Карно позволяет, как это
впервые отметил Кельвин, Также установить шкалу температур, не зави-
зависящую от выбора термометрического тела. Способ установления этой шкалы,
называемой термодинамической шкалой температур, следующий: из фор-
формулы A2) имеем
0 11
Из этого равенства видно, что отношение двух температур Т\1Т% может
измеряться отношением теплот Qi/Qa, где Qt — теплота, получаемая при
обратимом цикле Карно от нагревателя, a Q3 — передаваемая холодильнику.
Как мы видели, к. п. д. т] обратимого цикла Карно не зависит от рода при-
применяемого рабочего вещества. Отсюда и отношение Qi/Q^ не зависит от
выбора рабочего вещества, а следовательно, оно может служить для уста-
установления шкалы температур, независимой от выбора термометрического
тела.
Термодинамическая шкала температур совпадает с абсолютной шкалой
температур, определяемой по термометру с идеальным газом.
§ 74. Технические циклы. В предыдущем параграфе показано, что
наивысшим возможным к. п. д. i] обладает обратимый цикл Карно, для ко-
которого
где ТЛ—температура нагревателя, а Г2 — температура холодильника.
Однако осуществить практически такой цикл невозможно; приближение
к циклу Карно осуществимо лишь при весьма медленном протекании про-
процессов, что также с технической точки зрения неприемлемо. Применяемые
в технических тепловых машинах циклы необратимы и в действительности
даже незамкнуты, так как в них рабочее вещество (пар, сгоревшая смесь)
по окончании цикла выбрасывается наружу. Однако задачей техники является
создание таких циклов, к. п. д. которых по возможности приблизился бы
к к. п. д. цикла Карно. Рассмотрим некоторые из технически применяемых
циклов.
286
ОСНОВЫ ТЕРМОДИНАМИКИ
[гл. vm
1. Рабочий цикл идеальной поршневой паровой машины. Этот цикл
заключается' в следующем (рис. 178):
а) при начале доступа пара из котла в цилиндр давление пара в цилиндре
поднимается от значения ра (соответствующего давлению пара в холодиль-
холодильнике) до значения pi (соответствую-
(соответствующего давлению пара в котле); весь
этот процесс можно считать про-
происходящим при постоянном объеме Vo
(ветвь ЕА)\
б) при продолжающемся доступе
пара из котла в цилиндр поршень
двигается слева направо, в резуль-
результате чего объем увеличивается при
постоянном давлении pt от значе-
значения Vo до значения Vi (ветвь АВ);
в) при дальнейшем движении
поршня направо доступ пара из котла
в цилиндр прекращается, в резуль-
результате чего происходит адиабатическое
расширение пара от объема V\ до
объема V-, (ветвь ВС);
г) при крайнем правом поло-
положении поршня золотник открывает
выход пару из цилиндра в холодиль-
холодильник. Происходит быстрое спадение
давления пара до значения р0 (прак-
(практически при постоянном объеме Va;
ветвь CD);
д) при обратном движении пор-
поршень выталкивает оставшиеся пары
при постоянном давлении ро, умень-
уменьшая их объем от Vi до Vo-
Определим полную работу, со-
совершаемую паровой машиной за один
цикл. Работа на ветвях ЕА и CD
равна нулю, так что полная работа А складывается из следующих работ:
1) работы Ai при изобарическом расширении АВ
Al=pl(V1-Vo);
2) работы Аз при адиабатическом расширении ВС
Рис. 178. Цикл поршневой паровой
машины.
3) работы А> при изобарическом сжатии DE
А = — Po(Va — Vo),
откуда полная работа
Действительный цикл паровых поршневых машин несколько отличается
от разобранного. Для вычерчивания цикла реальной машины применяется
прибор, называемый индикатором.
Схема этого прибора дана на рис. 179. Смещение штифта, несущего
записывающее перо, пропорционально давлению пара в цилиндре. Лист
§ 74]
ТЕХНИЧЕСКИЕ ЦИКЛЫ
287
бумаги А, на котором вычерчивается кривая, движется вместе с поршнем;
таким образом, его смещение пропорционально объему, заполненному паром.
Кривая, получаемая с помощью этого прибора, носит название индикаторной,
диаграммы. Работа, совершаемая
машиной за одно смещение, изо- *
бражается площадью," охватывае-
охватываемой индикаторной кривой.
На рис. 180 сравнены кри-
кривая, изображающая теоретический
цикл 1, и индикаторная диаграмма
действительной машины 2. Как
видно, индикаторная кривая всеми
своими частями лежит внутри кри-
кривой, изображающей теоретический
цикл. Отсюда работа, производи-
производимая реальной машиной, меньше
теоретической. Кроме того, во
всякой реальной паровой машине
имеется ряд вредных потерь тепла Рис. 179. Индикатор.
в топке и в других частях ма-
машины. В результате всего этого к. п. д. паровых машин невелик. Лучшие
паровые машины потребляют на 1 л. с. в час около 0,5 кг угля с тепло-
творной способностью 7000 ккал на 1 кг. Следовательно, такая машина по-
потребляет на 1 л. с. в час энергии 0,5 • 7000 • 427 кГм, совершает же работу
А = 75 • 60 • 60 кГм, откуда ее к. п. д.
75-60-60
4 ~ 0,5-7000-427 -U'18'
Переводя в проценты, имеем -ц'= 18°/о-
Температура котла такой машины около
200°С, а температура холодильника — около 30°.
Обратимый цикл Карно, осуществляемый ме-
между нагревателем и холодильником с такими
температурами, имел бы к. п. д.
П — Т,
Рис. 180. Сравнение теоре- ц
тического цикла паровой ¦'i 4'3
машины с индикаторной диа- „M> B процентах, i) = 36»/o- Сравнение коэффи-
граммой. циентов ¦>)' и -ц показывает, что в реальных
поршневых паровых машинах энергия, разви-
развиваемая при сгорании топлива, используется лишь, примерно, наполовину по
сравнению с теоретически мыслимым пределом. Такой малый к. п. д. поршне-
поршневой паровой машины отчасти обусловлен тем, что ее рабочий цикл отличается
от идеального обратимого цикла вредными потерями; последние могут быть
уменьшены улучшением конструкции.
В паровых турбинах достигаются к. п. д. в 20% и даже несколько
выше.
2. Рабочий цикл четырехтактного двигателя внутреннего сгорания.
Этот цикл состоит из следующих процессов (рис. 181):.
а) при первом ходе поршня слева направо (первый такт) в цилиндр вса-
всасывается через клапан а горючее (пары бензина в смеси с воздухом). При-
Приближенно можно считать, что это всасывание происходит при постоянном
давлении р0, приблизительно равном атмосферному; объем при этом увели-
увеличивается от Va до Vi (ветвь ЕА);
б) в течение второго хода (второй такт; ветвь АВ) поршень, двигаясь
налево, адиабатически сжимает всосанную смесь, уменьшая ее объем от Vt
до ]/%, повышая ее температуру от Та до 1\ и повышая давление от раяорс,
288
ОСНОВЫ ТЕРМОДИНАМИКИ
[гл. viii
в) при помощи электрической искры, проскакивающей у свечи М, сжа-
сжатая смесь взрывается. Начинается третий такт. Сперва происходит почти
мгновенное (без изменения объема, см. ветвь ВС) возрастание давления до
значения р2 и температуры — до значе-
значения Та за счет тепла, выделяемого при
взрыве. Далее, при движении поршня
слева направо происходит приблизи-
приблизительно адиабатическое расширение газа
до объема Vu сопровождаемое паде-
падением температуры 7 до Та (ветвь CD).
При крайнем правом положении поршня,
соответствующем точке D, открывается
выпускной клапан Ь, причем давление
при постоянном объеме 1Л падает до
значения р0 (ветвь DA); температура
падает до значения То;
г) при последнем, четвертом, такте
поршень двигается "влево и при этом вы-
выталкивает отработавший газ через кла-
клапан b наружу (ветвь АЕ).
Подсчитаем полную работу, совер-
совершаемую при цикле. Работы, совершае-
совершаемые при первом и последнем тактах,
равны друг другу и противоположны по
знаку, что непосредственно вытекает из
того, что оба эти такта изображаются
________^___^^ одной и той же прямой АЕ, проходи-
,., п , мой в противоположных направлениях.
Рис. 181. Рабочий цикл двигателя Работы при изохорических (объемы не
внутреннего сгорания. меняются) процессах ВС и AD равны
нулю. Таким образом, работа, совер-
совершаемая при цикле, складывается из работ на ветвях АВ и CD. При адиаба-
адиабатическом сжатии АВ совершается работа
А(Т0)
где m — масса газа, находящегося в цилиндре, fi — его молекулярный вес.
При адиабатическом расширении CD совершается работа
откуда полная работа
7— ;
R
В реальных двигателях сжатие АВ и расширение CD не протекают
строго адиабатически. В частном случае политропического процесса в выра-
выражении A) под f должно подразумеваться не отношение теплоемкостей CpjCv,
но показатель политропы, который, как было указано в § 70, меньше отно-
отношения С JCV.
Выражение A) может быть преобразовано. По формуле E) § 70 имеем
B)
кроме того,
7-1
§ 74] технические циклы 289
Воспользовавшись этими соотношениями, перепишем A):
откуда на основании отношения
р = ? получим Л = I!LC(i_?W _?•.). C)
ii Jo H-V '2/
Определим к. п. д. цикла. Количество тепла Qlt выделяющееся при сго-
сгорании горючего в цилиндре (ветвь ВС), равно
Qi=*jCv (Тш-П). D)
Из C) и D) находим искомый к. п. д. цикла
, А __Т,-Т,
Следует отметить, что наибольшая температура, достигаемая за цикл,
равна 7, а наименьшая Тй\ цикл Карно, совершаемый между температурами
То и Г2, имел бы к. п. д.
1) = -Ц;—-; так как Го < Г8, то y<ni,
т. е. к. п. д. рассматриваемого двигателя внутреннего сгорания ниже к. п. д.
цикла Карно, что и следовало ожидать на основании рассуждений, приведен-
приведенных в § 73.
Пользуясь соотношением B), можно к. п. д. цикла придать вид:
Величина VijV^ называется „сжатием". Таким образом, к. п. д. цикла
определяется всецело сжатием и показателем политропы f.
Выражение для суммарной работы C), совершаемой при цикле, мы по-
получили, рассматривая работы, совершаемые на отдельных ветвях циклов.
Однако тот же результат можно получить, исходя из закона сохранения
энергии. Работа А равна
где Qi—количество тепла, полученного при взрыве горючей смеси, Qt —
количество отданного тепла.
Количество тепла Q, выражается формулой D). Количество тепла ??2
отдается при изохорическом охлаждении, изображаемом ветвью DA, откуда
<?, = -CvG-,—Г,).
Воспользовавшись этими выражениями для Qi и (р2, найдем
что, как легко убедиться, совпадает с C).
290
ОСНОВЫ ТЕРМОДИНАМИКИ
[гл. vin
Четырехтактные двигатели, работающие по указанному циклу, имеют
весьма широкое применение; бензиновые автомобильные двигатели работают
цо этому циклу. Обычно на один вал работают несколько цилиндров (четыре
и более). Рабочая фаза каждого цилиндра сдвинута относительно рабочей
фазы следующего цилиндра на одну и ту же долю периода, чем достигается
плавность хода.
3. Рабочий цикл четырехтактного двигателя внутреннего сгорания
Дизеля. Двигатель Дизеля работает до известной степени сходно с рассмот-
рассмотренным выше бензиновым двигателем внутреннего сгорания. Главное отли-
отличие заключается в том, что применяется весьма большая степень сжатия
(до 30 — 35 am и более). Так как сжатие это происходит приблизительно
адиабатически, то достигается большое повышение температуры. Этого повы-
повышения температуры достаточно для воспламенения горючей смеси, так что
двигатель Дизеля не требует воспламене-
воспламенения горючей смеси с помощью искры. Горю-
Горючая смесь вбрызгивается в цилиндр по
окончании сжатия, причем вбрызгивается
она постепенно, что обуславливает ее отно-
относительно медленное сгорание при изобари-
изобарическом расширении. Эти особенности дви-
двигателя Дизеля позволяют получить более
высокий к. п. д., чем у четырехтактных
двигателей с воспламенением искрой. Кроме
того, двигатели Дизеля работают на более
тяжелом топливе (нефть).
Рабочий цикл двигателя Дизеля заклю-
заключается в следующем:
а) при первом такте поршень засасы-
засасывает в цилиндр атмосферный воздух. Про-
Процесс протекает изобарически при атмосфер-
атмосферном давлении р0 (ветвь ЕА, рис. 182);
б) при втором такте поршень сжимает
этот воздух адиабатически (ветвь АВ) до
высокого давления pi, в результате чего
То до значительно более высокой температуры 7\;
в) в начале третьего такта в цилиндр вбрызгивается горючее, которое
воспламеняется в горячем воздухе и сгорает, вызывая перемещение поршня
при постоянном давлении р& температура при этом, за счет сгорания, повы-
повышается от Ti до Ti (ветвь ВС). Затем смесь продуктов горения и воздуха
адиабатически расширяется (ветвь CD). В конце третьего такта (точка D)
открывается выпускной клапан, в результате чего давление в цилиндре
падает при постоянном объеме V2 до атмосферного давления р0 (ветвь DA);
г) при последнем, четвертом,также смесь удаляется из цилиндра (ветвь АЕ).
Для определения полной работы А, совершаемой при цикле Дизеля, вос-
воспользуемся законом сохранения энергии:
Рис. 182. Рабочий цикл двига-
двигателя Дизеля.
где Qi — тепло, выделившееся при сгорании смеси, Q8— тепло, отданное
окружающему пространству.
Так как по условию сгорание смеси происходит изобарически, то
Q C(T T<)
Процесс, связанный с отдачей тепла (ветвь DA), происходит изохори-
чески, откуда
Qi = — Су G — 7).
§ 741
ТЕХНИЧЕСКИЕ ЦИКЛЫ
291
Воспользовавшись этими выражениями для Qi и Q2, получим
А = -у Cv ft (Та - Г0 - (Г, - Tt)\.
Коэффициент полезного действия цикла Дизеля равен
А 1 ' Гж—Г.
Пользуясь уравнением адиабат и изобар, можно привести это выражение
к следующему виду:
Рп-
г^-1
где V't — объем, соответствующий точке С (рис. 182). Таким образом, к. п. д.
цикла Дизеля определяется значением двух сжатий, Va/Vi и V'JVt, и пока-
показателем политропы if-
Двигатели Дизеля имеют к. п. д., достигающий 35%.
4. Рабочий цикл пульсирующего воздушно-реактивного двигателя. В §41
нами была дана схема пульсирующего воздушно-реактивного двигателя. Ра-
Работе этого двигателя также можно со-
сопоставить определенный цикл (рис. 183).
Поступающий в диффузор А воздух
(см. рис. 100, § 41) проходит из его
более узкой головной части в расширен-
расширенную, благодаря чему скорость воздуха
понижается. При этом, в силу уравне-
уравнения Бернулли (§ 40), давление воздуха
повышается от первоначального значе-
значения рЛ до некоторого конечного значе-
значения pi. Таким образом, происходит сжа-
сжатие воздуха, изображаемое на рис. 183
адиабатой (точнее, политропой) АВ. В ка-
камере сгорания происходит нагревание
рабочей смеси при постоянном давле-
давлении pi (прямая ВС), при этом смеси
передается количество тепла Qu темпе-
температура смеси повышается от 7*i до Г2,
а ее объем возрастает от V3 до V,. В сопле С происходит дальнейшее
адиабатическое расширение, и рабочая смесь выбрасывается наружу с уве-
увеличенной скоростью, что ведет к появлению реактивной силы. Практически
цикл остается незамкнутым, но на схеме его можно замкнуть, полагая, что
рабочее вещество вновь сжимается до объема Vt при постоянном давле-
давлении р0 (прямая DA), при этом холодильнику отдается количество тепла Q3.
Коэффициент полезного действия цикла
п~ Qx Qi'
Так как сгорание и охлаждение смеси происходит при постоянном давлении,
то
В(Т3)
Рис. 183. Рабочий цикл воздушно-
реактивного двигателя.
п т г /т т\ п m ,
Qi = —Cp(Ti—Tt), va = —'
-7'в), откуда 1=al_
292 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. V11I
Из уравнений адиабат АВ и CD имеем
=
Пользуясь этим соотношением между температурами, преобразовываем выра-
выражение к. п. д. т] к следующему виду:
.
1
То
J 2 J I J 1
Таким образом, промежуточные температуры Т3 и Тг не играют роли,
и к. п. д. определяется лишь значением температур Го и 7V
Отношение температур T0/Ti можно заменить отношением объемов Vt
и Vn, воспользовавшись уравнением адиабаты АВ:
Г,
Последнее выражение показывает, что к. п. д. воздушно-реактивного двига-
двигателя определяется лишь сжатием Vi/Vs и показателем политропы -j- Так как
в воздушно-реактивных двигателях, построенных по указанной схеме, сжа-
сжатие невелико, то их к. п. д. мал.
§ 75. Обратимые и необратимые процессы. Обратимым нами
был назван такой процесс, который может протекать в обоих на-
направлениях, причем, если процесс протек сперва в одном направле-
направлении, а потом в обратном, то система должна вернуться в исходное
состояние без того, чтобы в окру-
окружающих телах произошли какие-
либо изменения.
Приведем пример обратимого про-
процесса. Пусть абсолютно упругий тяже-
тяжелый шар закреплен на наклонной пло-
плоскости в точке А (рис. 184). В конце
Рис. 184. Обратимое скатыва- наклонной плоскости, нормально к ней,
ние абсолютно упругого шара. установлена неподвижная абсолютно
упругая стенка В. Если мы опустим
шар, то он скатится по наклонной плоскости, ударится о стенку В,
упруго отразится от нее и снова вкатится по наклонной плоскости
до точки А. Здесь процесс скатывания шара нацело обернулся, шар
снова попал в точку А без того, чтобы в окружающих телах про-
произошли какие-либо изменения.
Примером такого же обратимого процесса могут служить движе-
движения маятника, качающегося без трения: путь, пройденный маятником
за полпериода от точки А до точки В (рис. 185), проходится им
за вторые полпериода в обратном порядке, в точку А маятник
возвращается без того, чтобы в окружающих телах произошли ка-
какие-либо изменения. Вообще, мы можем сказать, что все чисто
§ 75] ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ 293
механические процессы, протекающие без трения и без участия не-
неупругих ударов, обратимы.
На примере идеального цикла Карно мы видели, что и некото-
некоторое количество тепла Qj — Q2 может быть обратимо превращено
в работу А, хотя это превращение и
является лишь звеном более сложного
процесса: его сопровождает перенос ко-
количества тепла Q2 от нагревателя к хо-
холодильнику. Используя тот же обратимый
цикл Карно для осуществления холо-
холодильной машины, мы можем обратно по-
получить за счет работы А количество тепла
Qi — Q2 и перенести обратно от холо-
холодильника к нагревателю количество а в
тепла Q9. Однако мы подчеркивали, что Рис 185 обратимое качание
это возможно лишь при равновесном, маятника.
т. е. при бесконечно медленном проте-
протекании цикла Карно, что практически не осуществимо. Всякий же
реальный переход работы в теплоту протекает необратимо, так как
переход работы в тепло осуществим сам по себе без сопровожде-
сопровождения его какими-либо другими процессами, переход же тепла в ра-
работу может протекать лишь при сопровождении его еще каким-либо
другим процессом.
Необратимым является такой процесс, обратный которому
может протекать лишь как одно из звеньев более сложного про-
процесса.
Таким образом, для необратимых процессов существенно направ-
направление их протекания.. В одном направлении, которое мы будем
называть „положительным", они протекают „сами собою" т. е. они
могут быть единственным процессом, происходящим в замкнутой
системе. В другом направлении, которое мы будем называть „отри-
цатёльным", они могут протекать лишь в сопровождении какого-
либо другого „положительного" процесса. Так, работа переходит
в тепло „сама собою", повсюду и постоянно. Во всех процессах, при
которых фигурируют силы трения или имеют место неупругие вза-
взаимодействия между телами, за счет совершенной работы возникает
теплота. Переход же теплоты в работу наблюдается только как
часть более сложного процесса. При совершении цикла Карно или
другого сходного с ним цикла, превращение тепла в работу сопро-
сопровождается „положительным" процессом переноса тепла от горячего
тела (нагревателя) к более холодному (холодильнику).
Перенос тепла от горячего тела к холодному (явление теплопро-
теплопроводности) является также необратимым процессом. Этот процесс,
сводящийся к выравниванию температур тел, протекает также „сам
собою", т. е. он может быть единственным процессом, происходя-
происходящим в замкнутой системе. Обратный „отрицательный" процесс —
294
ОСНОВЫ ТЕРМОДИНАМИКИ
[гл. viii
А
'¦'У.':'-'.
с
в
перенос тепла от более холодного тела к более горячему—„сам
собою" не происходит. При действии холодильной машины перенос
тепла от более холодного тела к более горячему осуществляется
лишь параллельно с „положительным" процессом, сводящимся к за-
затрате работы А, которая превращается в количество тепла tjQj,
отдаваемое нагревателю.
В качестве еще одного примера процесса, протекающего необра-
необратимо, можно привести расширение газа в пустоту. Представим себе
сосуд, разделенный перегородкой С на две равные части А и В
(рис. 186). Пусть в части А находится газ, в
части В — пустота. Если убрать перегородку, то
газ немедленно „сам собою" расширится, запол-
заполнит часть В и распределится равномерно по всему
сосуду. Обратно сжать его в часть сосуда А
можно, только совершив с помощью внешних сил
некоторую работу. В результате этой работы газ
Рис 186 Распре- нагреется, т. е. „отрицательный" процесс сжатия
деление газа по газа будет сопровождаться „положительным" про-
двум половинам со- цессом превращения работы в теплоту.
сУда- „Положительный" процесс расширения газа
может явиться тем процессом, который сопрово-
сопровождает превращение тепла в работу. Так, при изотермическом расши-
расширении газа все количество тепла Q, которое передается при этом
газу извне, превращается в работу А; здесь нет никакого переноса
тепла от горячего тела к более холодному, но зато происходит
необратимое („положительное") расширение газа. Таким "образом,
всякий „отрицательный" процесс обязательно компенсируется каким-
либо „положительным" процессом.
§ 76. Статистический смысл второго начала термодинамики.
Теперь поставим вопрос: как необратимость реальных процессов
может быть согласована с молекулярно-кинетической теорией ве-
вещества, по которой все процессы являются следствием механического,
а следовательно, обратимого движения молекул?
Согласно молекулярно-кинетической теории, газ представляет
собою собрание беспорядочно движущихся молекул, испытывающих
упругие столкновения друг с другом и со стенками.
Движение каждой из молекул, взятой в отдельности, обратимо.
Спрашивается: почему же необратимо движение совокупности мо-
молекул?
Ответ на этот вопрос дается на основании представления о ве-
вероятности отдельных явлений и статистического подсчета наиболее
вероятных состояний.
Для того чтобы разобрать представление о вероятности, обра-
обратимся к самому простому примеру бросания игральной кости.
Пусть кость представляет собою правильный однородный куб, на
гранях которого поставлены номера от 1 до 6. Бросание кости
§ 76] СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ 295
представляет собою сложный процесс. Вследствие нерегулярных изме-
изменений условий бросания выпад того или иного номера есть явление
случайное. Однако, если мы будем бросать кость достаточно боль-
большое число раз, то каждый из номеров выпадет приблизительно оди-
одинаковое число раз.
Пусть мы совершили всего N бросаний, притом пусть какой-
либо определенный номер выпал т раз, тогда отношение m/N при
большом числе бросаний N стремится к определенному значению
(в нашем случае 1/6). Предел этого отношения т/N при А/->оэ
определяет вероятность р выпада данного номера:
/ ?. A)
N-ка JV
Мы можем обобщить это определение вероятности на любые
события, считая, что если произведено N испытаний, причем число
случаев, благоприятных появлению данного события, оказалось рав-
равным т, то вероятность этого события р также выражается равен-
равенством A).
Вероятность объективно выражает собою некоторое свойство,
фактически присущее данному явлению; она дает числовую характе-
характеристику степени возможности появления определенного события при
данных условиях испытания, могущих повторяться неограниченное
число раз. Необходимо иметь в виду, что вероятность при конеч-
конечном, хотя бы и большом числе испытаний позволяет предска-
предсказать результат испытаний не точно, а лишь приближенно, при-
причем степень приближения возрастает по мере увеличения числа
событий.
Знание вероятностей позволяет определять средние значения раз-
различных величин при многочисленных испытаниях. Предположим, что,
бросая игральную кость, мы хотим найти среднее значение выпавших
номеров. Если в результате N бросаний, номер пх выпал тх раз,
номер иа выпал т^ раз и т. д., то среднее значение выпавших но-
номеров равно:
k
n=^-
N • -,
где k — число различных номеров на кости (в нашем случае k = 6).
При N-+oo, по определению, m{/N -*Pi, где pt — вероятность
выпадения номера nt. Таким образом, при очень большом числе
бросаний среднее значение номеров стремится к значению:
>= S Pini-
i i
296 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
В разбираемом случае все
Pi— /6 й «оо = g = d,0.
Как видим, такого рода подсчет среднего значения носит стати-
статистический характер.
Как было указано в § 66, макроскопические величины, ха-
характеризующие вещество, носят характер средних значений, полу-
получающихся в результате усреднения беспорядочного действия отдель-
отдельных молекул. Фактически мы не можем определить движение
каждой из молекул, и в этом смысле оно случайно. Однако, благо-
благодаря большому числу молекул, средние величины не будут содер-
содержать элементов случайности, а примут при данных условиях опре-
определенные значения. Предположим, что мы наблюдаем ряд различных
макроскопических состояний газа. Каждое из них возникает в ре-
результате не одного какого-то состояния движения молекул, а многих.
Очевидно, что то макроскопическое состояние, которое возникает
в результате ббльшего числа возможных состояний движений от-
отдельных молекул, осуществляется чаще, оно более вероятно. По-
Поясним это на примере газа, распределенного между двумя поло-
половинами сосуда.
Предположим первоначально, что газ состоит всего из четы-
четырех молекул, которые все находятся в части сосуда А (рис. 186);
часть сосуда В пуста. Уберем перегородку С. Тогда некоторые
из молекул, двигаясь беспорядочно, залетят в часть сосуда В,
что будет означать, что газ расширился. В дальнейшем все че-
четыре молекулы станут летать по всему сосуду, однако при этом
не обязательно будет осуществляться такое распределение, что
в каждой из половин сосуда окажутся по две молекулы. Бла-
Благодаря беспорядочности их движения, возникнут и такие распре-
распределения, когда в одной части окажутся три молекулы, а в дру-
другой — одна. Может произойти, что случайно все четыре моле-
молекулы снова залетят в часть сосуда А; если мы в этот момент,
закроем перегородку С, то газ снова окажется весь сосредоточен-
сосредоточенным только в этой части сосуда. Таким образом, в случае четырех
молекул вполне возможно, что газ, сперва расширившись, затем
сам собою сожмется. Процесс расширения газа оказался обра-
обратимым.
Однако такое состояние, когда все молекулы соберутся бла-
благодаря беспорядочности движения в одной половине сосуда,
менее вероятно, чем когда в обеих частях сосуда находится
по некоторому числу молекул. Обозначим' рассматриваемые че-
четыре молекулы соответственно буквами а, Ь, с, d. Тогда воз-
возможны следующие 16 распределений молекул по обеим половинам
сосуда:
§ 76] СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ 297
Распределение молекул
Половины сосуда
А
0
abed
а
b
с
d
bed
acd
abd
abc
abed
0
bed
acd •
abd
abc
a
b
с
d
Число
состояний
} 2
8
Половины сосуда
A
ab
ас
ad
be
bd
cd
В
cd
bd ,
be
ad
ac
ab
Итого ...
Число
состояний
6
16
Благодаря беспорядочности движения, каждое из этих состояний
встречается одинаково часто. Как мы видим, число случаев, когда
молекулы присутствуют в обеих половинах сосуда, равно 14; число же
случаев, когда одна из половин сосуда пуста, равно всего 2. Рас-
Распределение, при котором все молекулы снова окажутся в части
сосуда А, встречается в 16 раз реже других распределений; его
вероятность равна 1/16. Однако при большой скорости движения
молекул состояния следуют быстро друг за другом и, очевидно,
придется не очень долго ждать, чтобы расширившийся газ „сам
собою" снова сжался. Однако так обстоит дело только при очень
малом числе молекул.
Можно показать, что общее число распределений из п молекул
по1 двум половинам сосуда равно z = 2". Из всего этого числа только
одно распределение соответствует случаю, когда все п молекул
находятся в половине сосуда Л и ни одной не находится в поло-
половине В. Практически мы всегда имеем дело с очень большим числом
молекул п. Если положить, что половина сосуда А имеет объем
в 1 см3 и что газ находился в ней при нормальных условиях, то
я = 3-1019 и, следовательно, число возможных распределений
г = 2зоооооооо<юооооооооо_ Только одно из этих z состояний соответ-
соответствует тому, когда газ снова сам собою соберется в часть сосуда А.
Очевидно, вероятность такого события настолько ничтожна, что практи-
практически оно неосуществимо. Таким образом, мы приходим к важному
следствию: необратимость расширения газа в пустоту носит стати-
статистический характер, т. е. „отрицательный" процесс самопроизволь-
самопроизвольного сжатия газа весьма мало вероятен.
Этот результат может быть обобщен: необратимый процесс есть
такой, обратный которому мало вероятен. Случай, при котором
процесс, обратный „положительному", стал бы протекать в качестве
единственного процесса в замкнутой системе, не является принци-
принципиально невозможным.' Практически он не наблюдается благодаря
его исключительно малой вероятности. Все процессы в замкнутой
298 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
системе протекают в сторону увеличения вероятности состояния
системы.
Все сказанное относится и к случаю передачи телу определен-
определенного количества тепла за счет совершенной работы. Такой процесс
означает переход макроскопического движения тела, происходящего
под влиянием внешних сил, в беспорядочное движение молекул.
Следовательно, этот процесс сводится к переходу упорядоченного
движения в беспорядочное — такой переход вероятен.
Получение работы за счет взятого количества тепла означает
переход беспорядочного движения молекул в упорядоченное дви-
движение макроскопического тела — такой переход мало вероятен.
Таким образом, второе начало термодинамики, указывающее на
необратимость перехода работы в тепло, связано с тем, что переход
тепла в работу означает переход от более вероятного состояния
к состояниям менее вероятным. Молекулярно-кинетическая теория
вещества не только не противоречит понятию о необратимости и
второму началу термодинамики, но она придает им более глубокое
вначение и указывает границы их применимости.
Закономерность, выражаемая вторым началом термодинамики,
носит, как мы видим, статистический характер. Статистическая зако-
закономерность, как ясно из сказанного выше, отличается от механи-
механической (динамической) закономерности классической механики, где
для каждого единичного процесса по значению одних физических
величин можно однозначно и сколь угодно точно определить другие.
Тем не менее статистическая закономерность указывает поведение
всей системы в целом и в этом смысле отражает ее объективные
свойства. Каждое отдельное явление случайно, но весьма большое
скопление случайных явлений приводит к необходимости. Статисти-
Статистическая закономерность служит наглядным примером диалектического
единства случайности и необходимости.
Статистическая закономерность приближенна в том смысле, что
полученные на ее основе выводы тем лучше совпадают с резуль-,
татами наблюдений, чем< по ббльшему числу отдельных событий
произведено усреднение. В малых масштабах от статистической зако-
закономерности возможны отступления.
Отсюда следует, что понятие необратимости процессов имеет
смысл, только пока мы имеем дело с телами макроскопическими,
т. е. состоящими из большого числа молекул. К совокупности не-
небольшого числа молекул понятие о необратимости процессов непри-
неприменимо. На примере „газа", состоящего из четырех молекул, мы
видели возможность самопроизвольного сжатия такого „газа". При
небольшом числе частиц становятся практически возможными неко-
некоторые отступления от наиболее вероятного состояния. С макроско-
макроскопической точки зрения, например, наиболее вероятно состояние
газа, соответствующее одинаковой плотности во всех местах. Однако,
если мы выделим в газе два соседних объема, настолько малых,
§ 76] СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ 299
чтобы в них заключалось по небольшому числу молекул, то в них
будут встречаться отступления от равномерного распределения моле-
молекул. Произведенный подсчет распределения четырех молекул по двум
равным объемам показывает, что в этом случае чаще встречаются
состояния, когда в одном объеме — три молекулы, а в другом —¦
одна, чем когда в обоих объемах — по две молекулы.
Такого рода отступления от средних значений, существующие
в малых масштабах, носят, как указывалось, название флуктуации.
Всякая физическая величина, возникающая как среднее из действия
многих молекул, подвергнута флуктуациям. Флуктуации сказы-
сказываются во многих явлениях. Например, флуктуации плотности газа
обуславливают, как мы увидим в отделе, посвященном оптике (т. III),
голубой цвет неба.
Неравномерность ударов молекул, проявляющаяся в малых масштабах,
вызывает флуктуации давления. Эти флуктуации давления обусловливают
движение броуновских частиц (ср. § 43). Броуновские частицы являются
столь малыми объектами, что они уже не подчиняются второму началу термо-
термодинамики. Отдельная броуновская частица может, например, под влиянием
удара молекул, совершающих тепловое движение, подняться в жидкости
против силы тяжести из более низкого в более высокий слой. Механическая
работа поднятия частицы совершится за счет энергии теплового движения
молекул без сопровождения каким-либо другим процессом. Поднявшаяся
броуновская частица может затем, случайно, снова опуститься и перевести
свою потенциальную энергию в энергию теплового движения окружающих
молекул.
В этих микроскопических масштабах процесс перевода тепла в работу
окажется обратимым, второе начало — нарушенным, однако использовать
это нарушение второго начала в макроскопических размерах невозможно.
Всякий механизм, с помощью которого мы пытались бы собрать энергию
броуновских частиц, сам был бы подвержен флуктуациям и не позволил бы
осуществить такое накопление энергии.
Существенно отметить, что наличие флуктуации устанавливает границу
точности наших измерений. Всякий измеряющий прибор, например электри-
электрический гальванометр, обладает подвижной системой (стрелкой), перемещение
которой служит для измерения данной физической величины. Эта подвижная
система сама подвержена флуктуациям—слабым беспорядочным колебаниям.
Средняя энергия этих колебаний, как можно показать, равна V2 kT, где
k — постоянная Больцмана, а Т—температура окружающей среды. Следова-
Следовательно, измеряемая системой энергия (например, энергия электрического
тока) должна быть больше '/a kT. Более точный расчет показывает, что погреш-
погрешность АЕ измерения энергии Е есть величина порядка nkT. Для комнатной
температуры (Г=290°К) получим: nkT = 1,26 • 1(Г20 дж. Таким образом,
при каждой данной температуре Т существует естественный предел чувстви-
чувствительности измеряющего прибора, не зависящий от совершенства его кон-
конструкции.
В большинстве измерительных приборов этот предел далеко не дости-
достигается, но для некоторых очень точных современных измерительных приборов
(электроизмерительных приборов, приборов, измеряющих поток световой
энергии, и т. д.) он достигнут. При данной температуре окружающей среды Т
дальнейшее повышение точности этих приборов невозможно.
Флуктуационные колебания легкой подвижной системы можно использо-
использовать для опытного определения числа Авогадро N. Такого рода определения
дают правильное по порядку значение N. Для наблюдения флуктуационных
300 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
колебаний применяется система, состоящая из весьма тонкой кварцевой нити
с подвешенным к ней очень маленьким и легким зеркальцем. Под влиянием
ударов молекул окружающего воздуха система совершает беспорядочные
крутильные колебания. Эти колебания непосредетвенно наблюдаются с помощью
отраженного от зеркальца луча, который образует на достаточно далеко рас-
расположенной шкале световой зайчик.
Средняя кинетическая энергия Е^ колебаний зеркальца, по сказанному,
равна 4^kT\ С другой стороны, Ek равна средней потенциальной энергии
колебаний Ер.
Воспользовавшись для Ер формулой A7) § 89, получим
где D — модуль кручения нити и <f3—среднее значение квадрата угла откло-
отклонения.
Эта формула может быть переписана в виде:
Так как непосредственные измерения модуля кручения D представляют
трудности, то можно воспользоваться выражением для собственной частоты
крутильных колебаний (см. § 89, где дано выражение для периода Г= —
где / — момент инерции системы.
Тогда соотношение B) принимает вид:
kT
Г
здесь все величины, кроме постоянной Больцмана k, доступны непосредствен-
непосредственному измерению.
Выполнив эти измерения, можно найти k, а следовательно, и число Аво-
гадро N=-j—.
Другая область ограничения применимости второго начала термо-
термодинамики относится к космическим масштабам. На этом необходимо
остановиться в связи с выдвижением со стороны некоторых физиков
и философов второй половины прошлого столетия гипотезы о так
называемой „тепловой смерти вселенной". Рассматривая вселенную
как замкнутую систему и применяя к ней второе начало термодина-
термодинамики, они пришли к выводу, что со временем все разности темпе-
температур между отдельными небесными телами выравняются, и вселенная
должна будет погрузиться в состояние совершенно равномерного
распределения температур („тепловой смерти").
Гипотеза о „тепловой смерти" ведет и к другому выводу —
о „первом толчке", создавшем в мире когда-то неравномерность
температур, т. е. в конечном счете к прямой поповщине — к при-
признанию сотворения мира,
§ 77] НЕРАВЕНСТВО КЛАУЗИУСА. ЭНТРОПИЯ 301
Реакционная сущность теории „тепловой смерти" была вскрыта
Энгельсом, указавшим на ее научную несостоятельность.
Необоснованность вывода о тепловой смерти лежит в незаконном
экстраполировании второго начала на систему, представляющую собою
весь мир. Второе начало связано с представлением о необратимости
процессов, наблюдаемых в масштабах, пространственных и времен-
временных, весьма малых по сравнению с масштабами, в которых происходит
процесс эволюции не только всей вселенной, но хотя бы боль-
большой совокупности звезд. В эволюции даже отдельной звезды, не-
несомненно, играют исключительно важную роль такие процессы, кото-
которые на земном шаре заметной роли не играют, как, например,
превращение элементов. Законы этих процессов нам пока мало
известны.
Таким образом, в распространении второго начала на всю вселен-
вселенную и на бесконечно большие промежутки времени лежит ошибка,
сводящаяся к приписыванию физическим законам абсолютного значе-
значения и к забвению того, что они являются лишь более или менее
хорошими приближениями к действительности (ср. § 2).
§ 77. Неравенство Клаузиуса. Энтропия. В предыдущих параграфах
мы выяснили, что „отрицательные" процессы могут идти лишь в сопровожде-
сопровождении одного из „положительных" процессов.
Рассмотрение обратимого цикла Карно указывает, какое количество
тепла <Э2 должно быть перенесено от нагревателя температуры 1\ к холо-
холодильнику температуры 7, чтобы количество тепла Qi — Qa могло быть пре-
превращено в работу А. Мы воспользуемся сейчас этим количественным соот-
соотношением в том виде, как оно представлено формулой A2) § 73:
Мы условились (§ 73) количество тепла, переданного рабочему веществу
нагревателем, обозначать через Qit а переданного рабочему веществу холо-
холодильником— через—Q^ Изменим теперь обозначение и будем буквой Q
(без знака) обозначать количество тепла, переданного рабочему веществу
как нагревателем, так и холодильником. Тогда, если <Эа означает количество
тепла, переданного рабочему веществу холодильником, то имеет место нера-
неравенство Q2<0; при таком обозначении соотношение A) надо переписать
в виде:
откуда получим
-^+-^=0. B)
Отношение Q/T называется приведенным количеством тепла. Содер-
Содержание уравнения B) может быть формулировано: при обратимом цикле
Парно сумма приведенных количеств тепла равна нулю.
Для любого цикла Карно, как мы выяснили в § 73, к. п. д. удовлетворяет
неравенству:
302 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
(для обратимого цикла имеет место только знак равенства). Потому для любого
цикла Карно получим:
^- + |l<0, Bа)
т. е. для любого цикла Карно сумма приведенных количеств тепла не
может быть больше куля. Это неравенство носит название неравенства
Клаузиуса.
Неравенство Клаузиуса может быть обобщено на любой круговой процесс.
Как мы уже видели (см. § 73), любой круговой процесс может быть раз-
разбит на весьма большое число элементарных циклов Карно. Каждый из этих
элементарных циклов Карно протекает между нагревателем соответствующей
температуры Ти от которого он получает количество тепла Щь и холодиль-
холодильником соответствующей температуры 7^, которому он отдает количество
тепла AQA.
Для этого элементарного цикла напишем неравенство Клаузиуса:
^ ^ C)
Знак равенства выполняется при обратимом протекании элементарного
процесса. <
Суммируя выражения C), написанные для каждого из элементарных
циклов, получим для всего цикла:
т. е. для всякого кругового процесса сумма приведенных количеств тепла
не может быть больше нуля; для обратимого процесса она равна нулю.
В случае обратимого протекания про-
А цесса можно показать, что сумма D) пре-
Р
образуется в контурный интеграл:
^ =0. Da)
Величина dQ в интеграле выражается
через независимые переменные и их диф-
дифференциалы. В качестве независимых пере-
переменных выбираются параметры, определяю-
определяющие состояние (р, V или Г).
Кружок у знака интеграла показывает,
что интеграл распространяется на весь об-
обратимый круговой процесс.
Рис. 187. Различные пути пере- Для необратимого процесса сумма D)
хода между данными состоя- не может быть заменена контурным инте-
ниями А и В. градом, так как переменные интегрирова-
интегрирования р и Т на необратимых участках про-
процесса не имеют определенных значений.
Покажем, что в случае обратимого процесса сумма приведенных теплот
сообщаемых телу, не зависит от пути, по которому шел процесс.
Пусть некоторое тело из состояния А (рис. 187) переходит обратимым
путем в состояние В по пути, изображаемому кривой ACiB. Дополним путь
ACiB до кругового процесса, наметив обратный путь ВС$А. Обозначим сумму
приведенных теплот на пути ACiB через X, а сумму приведенных теплот на
пути ВСзА — через Y, тогда по условию D):
E)
§ 77]
НЕРАВЕНСТВО КЛАУЗИУСА. ЭНТРОПИЯ
303
Наметим еще один путь из состояния А в состояние В, изображаемый
кривой АСгВ; сумму приведенных теплот на нем обозначим Х\, тогда для
кругового процесса АС^ВС^А имеем
Сравнивая это равенство с равенством E), получим
X=Xit
т. е. суммы приведенных теплот для путей ACiB и АС3В равны друг другу.
То же может быть доказано по отношению к любым другим путям, ведущим
из состояния А в состояние В.
Отсюда интеграл
в
dQ
Т'
\
выражающий сумму приведенных теплот для обратимого изменения состоя-
состояния от А до В, не зависит от пути следования процесса, определяясь исклю-
исключительно начальным и конечным состояниями тела. Из этого, обстоятельства
следует, что существует некоторая величина S, характеризуемая состоянием
тела и имеющая в состоянии А значение SA,
а в состоянии В—значение SB, причем раз- р
ность SB —SA равняется:
Ss —i
F)
т. е. равняется сумме приведенных теплот для
любого обратимого процесса, протекающего
между состояниями А и В.
Разность SB — SA определяет разность
некоторой физической величины S, являющейся
функцией состояния; эта физическая величина
называется энтропией.
Приведенный метод рассуждений не по-
позволяет определить абсолютное значение энтро-
энтропии; можно только установить разность энтро-
энтропии SB—SA двух состояний В ч А.
Пусть некоторая замкнутая система, исходя из состояния А, совершает
обратимый круговой процесс ABA (рис. 188); тогда изменение энтропии при
переходе от состояния А в состояние В равно
Рис. 188. При совершении
кругового обратимого про-
процесса энтропия не меняется.
¦-s'i
Обозначим значение энтропии в состоянии А после возвращения в него
по окончании всего цикла через S'A, тогда
«г- ч $dQ
304
ОСНОВЫ ТЕРМОДИНАМИКИ
[гл. vin
Но по условию Dа) для обратимого процесса
в а
С dQ С dQ
\ ~y~~t \ -у = 0| откуда SB—SA= — (S'A— SB), или S'A—SA = 0,
А В
т. е. при совершении кругового обратимого процесса энтропия системы
не меняется.
Рассмотрим переход из некоторого состояния А в состояние В по необра-
необратимому пути, условно изображаемому кривой ACiB (рис. 189); затем вернем
систему из состояния В в состояние А, выбрав для этого обратимый путь
ВСэА; тогда круговой процесс АСХВС^А в целом будет необратим, так как
необратима одна из его частей, отсюда
ACiB необр ВСцА обр
Но по определению интеграл
так что
откуда
ACiB необр
G)
необр
Необратимый
переход
В случае изолированной системы, система в целом не получает и не
отдает тепла, откуда для нее все AQ = Q к сумма, стоящая в правой части
неравенства G), превращается в нуль. От-
Отсюда: в изолированной системе могут про-
протекать только такие процессы, при ко-
которых энтропия системы не уменьшается.
Если в изолированной системе протек
процесс, при котором энтропия осталась
неизменной, то этот процесс может про-
протечь и в обратном направлении, т. е. он
обратим. Если же при процессе энтропия
возросла, то обратный процесс невозможен,
т. е. рассматриваемый процесс необратим.
Таким образом, при протекании в изоли-
изолированной системе необратимого процесса
энтропия системы возрастает.
Мы видели, что для необратимых про-
процессов два возможных направления их про-
протекания неравноценны: в одном направлении
(названном нами „положительным") процесс
может протекать „сам собою", в другом („отрицательном") он „сам собою"
не протекает. Однако до сих пор мы не имели критерия для решения во-
вопроса, в каком именно направлении данный необратимый процесс будет про-
протекать. Введение понятия об энтропии решает этот вопрос: в замкнутой си-
системе процессы протекают в сторону возрастания энтропии: в частном
Обратимый
переход
Рис. 189. Обратимый и необра-
необратимый переходы между состоя-
состояниями А к В.
§ 77] НЕРАВЕНСТВО КЛАУЗИУСА. ЭНТРОПИЯ^Ц^ 305
случае, когда все процессы, протекающие в системе, обратимы, энтропия
остается неизменной.
В § 75 было указано, что необратимый характер процессов связан с пере-
переходом от состояний менее вероятных к состояниям более вероятным. Отсюда
ясно, что и энтропия, определяющая направление протекания необратимых
процессов, должна быть связана с вероятностью. Больцман показал, что энтро-
энтропия S пропорциональна логарифму вероятности состояния:
S = k\nW,
где W—вероятность данного состояния; коэффициентом пропорциональности
служит постоянная Больцмана k.
В
В
1
Поскольку V -~- дает нам лишь изменение энтропии, сама энтропия дан-
X 1
ного состояния определяется лишь с точностью до аддитивной постоянной:
А
(8)
где I -=^ берется по пути обратимого перехода из некоторого состояния,
выбранного за нулевое, в данное состояние А.
Дифференцируя (8), получим выражение для полного дифференциала
энтропии
dS = -у-. (9)
Пример 1. Найти изменение энтропии при охлаждении 100 г воды от
<! = 10" С до t» = 0° С.
По формуле F) изменение энтропии равно
S S - С dQ
Считая для воды изменение объема при нагревании ничтожно малым,
имеем
dQ = mcdT,
где m — масса воды, а с — ее удельная теплоемкость. Для воды теплоемкость
с может считаться постоянной, откуда
Го
Sa — St = mc \ — = тс In ^. A0)
Подставляя в выражение A0) m=100 г, с = \ кал/г град, Ti = 273° К
и Г1 = 288°К, получим
273
S2 —Si = 100 • 1 • In ijgg кал/град = — 5,1 кал/град.
Пример 2. Найти изменение энтропии 280 г азота при изотермическом
увеличении объема в 5 раз.
По первому началу термодинамики
dQ = dU + dA. A1)
11 С. Э. Фриш и А. В. Тиморева
306 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. VIII
Изменение запаса внутренней энергии dU равно
dU = ~-CvdTt
где A—молекулярный вес и Cv — молярная теплоемкость газа при постоян-
постоянном объеме.
Работа dA равна
dA=pdV.
Это выражение работы преобразуем, считая азот идеальным газом:
откуда
т RT
Воспользовавшись этим значением р, найдем для работы dA:
Подставив найденные выражения для dU и dA в A1), получим для идеаль-
идеального газа:
Воспользовавшись этим выражением dQ, получим следующую формулу
для изменения энтропии:
Гц V,
я (Cr dT bdV\
Полагая, что теплоемкость Cv не зависит от температуры, выполняем
интегрирование:
^( I?^j A2)
По условиям данного примера расширение происходит изотермически,
следовательно, Ti=Ti, и по A2):
S2 — Si = — R In }y ^ =^ • 2 • In 5 кал/град = 32,2 кал/град.
(J. Kl ^0
Приведенные рассуждения позволяли определить лишь изменение энтро-
энтропии [формула F), стр. 303]. Значение самой энтропии могло быть определено
лишь с точностью до аддитивной постоянной [формула (8), стр. 305]. Для
определения абсолютных значений энтропии надо знать ее абсолютное значе-
значение хотя бы для какой-нибудь одной температуры. Такое одно значение энтро-
энтропии ^определяет теорема, высказанная Нернстом и иногда называемая третьим
началом термодинамики. По теореме Нернста энтропия всякого вещества
при температуре абсолютного нуля равна нулю.
§ 77] НЕРАВЕНСТВО КЛАУЗИУСА. ЭНТРОПИЯ 307
Будем нагревать один моль какого-либо вещества, начиная с температуры
абсолютного нуля, при постоянном давлении. Для повышения температуры
этого вещества на dT ему необходимо сообщить количество тепла:
dQ = CpdT,
при этом энтропия вещестна возрастает на
CpdT
Интеграл, взятый при постоянном давлении в пределах от нуля до Т,
даст абсолютное значение энтропии моля данного вещества при температуре Г:
Так как при низких температурах теплоемкость не является величиной
постоянной, но зависит от температуры (§ 93), то указанный интеграл может
быть взят, при условии, что известен ход теплоемкости Ср, с температурой
вплоть до значения Г = 0.
11 •
ГЛАВА IX
МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ
§ 78. Строение жидкости. Молекулярное давление. Жидкое
состояние является промежуточным между газообразным и твердым
и имеет сходство как с тем, так и с другим. Как мы видели в § 62,
уравнение Ван-дер-Ваальса описывает не только газообразное со-
состояние вещества, но передает и некоторые свойства жидкого со-
состояния. При этом уравнение Ван-дер-Ваальса -указывает на возмож-
возможность непрерывного перехода из жидкого в газообразное состояние
через критическую точку. Е5близи критической точки различия между
газом и жидкостью незначительны, и жидкость до некоторой сте-
степени может рассматриваться как плотный газ. Но то же уравнение
Ван-дер-Ваальса показывает, что при температурах, значительно
более низких, чем критическая, разница между жидким и газооб-
газообразным состоянием делается весьма заметной. Плотность насыщаю-
насыщающих паров для мнргих жидкостей, при комнатных температурах,
в тысячу или даже в несколько тысяч раз меньше плотности жидко-
жидкости. Среди изотерм Ван-дер-Ваальса, как мы видели в § 62,
имеются изотермы, частично лежащие в области отрицательных
давлений: они указывают на возможность существования жидкости
в растянутом состоянии. Опыты показывают, что такое растянутое
состояние жидкости действительно возможно и соответствует нали-
наличию у жидкостей некоторой прочности на разрыв. В этом отноше-
отношении жидкость становится сходной с твердым телом; В дальнейшем
мы увидим, что сходства между жидкостью и твердым телом имеются
и в ряде других областей, особенно при условиях, близких к затвер-
затвердеванию (кристаллизации) жидкости.
С молекулярно-кинетической точки зрения газообразное состояние
вещества характеризуется большими средними расстояниями между
молекулами, тепловое движение газовых молекул сводится к свобод-
свободному движению на длине свободного пути, в несколько раз превышаю-
превышающего размеры самих молекул. В газах с заметной скоростью про-
происходит диффузия. В жидкостях же молекулы располагаются значи-
значительно ближе друг к другу, чем в газах. Они проявляют большие силы
взаимодействия. Диффузия в жидкостях происходит гораздо медлен-
медленнее, чем в газах. Но вместе с тем строение жидкостей существенно
отличается от строения твердых тел, где диффузия практически
§ 78] СТРОЕНИЕ ЖИДКОСТИ. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ 309
отсутствует. В твердом теле каждая частица (атом, ион) колеблется
около своего положения равновесия, причем в идеальной решетке
твердого кристалла (§ 87) все возможные „места" для частиц заняты.
Жидкость обладает более „рыхлой" структурой, чем твердое тело,
в ней имеются свободные места — „дырки", благодаря чему моле-
молекулы могут перемещаться, покидая свое место и занимая одну из
соседних свободных „дырок". По теории Я. И. Френкеля, тепловое
движение в жидкостях носит следующий характер: каждая молекула
в течение некоторого промежутка времени колеблется около опре-
определенного места равновесия. Молекула меняет место равновесия, пере-
перемещаясь на отрезок порядка размеров самих молекул. Таким образом,
молекулы медленно перемещаются внутри жидкости, пребывая часть
времени около определенных мест, находясь, по образному выраже-
выражению Я. И. Френкеля, в „оседлом" состоянии. Существуют некоторые
особенности в строении жидкостей, напоминающие строение кристал-
кристаллических твердых тел (см. § 95).
В газе средняя кинетическая энергия теплового движения моле-
молекул достаточна, чтобы преодолеть силы притяжения между моле-
молекулами; это ведет к тому, что газовые молекулы разлетаются во все
стороны, и газ распространяется на весь предоставленный ему объем.
В жидкостях, наоборот, средней кинетической энергии теплового
движения не хватает, чтобы преодолеть силы сцепления. Благодаря
этому жидкость представляет собою тело определенного объема.
Из жидкости вырываются лишь наиболее быстрые молекулы, что
ведет к процессу испарения жидкости.
В § 61 мы видели, что взаимная потенциальная энергия двух
газовых молекул имеет при некотором расстоянии г0 между моле-
молекулами минимум (рис. 154). Однако глубина образующейся потен-
потенциальной ямы невелика и меньше средней кинетической энергии i/ikT,
приходящейся на одну степень свободы. Поэтому газовые молекулы
не удерживаются друг около друга, но, сблизившись, снова разле-
разлетаются. Для молекул жидкости средняя кинетическая энергия тепло-
теплового движения, как мы видели, недостаточна, чтобы преодолеть
силы взаимного притяжения молекул друг к другу. В результате
молекулы располагаются достаточно близко друг к другу, и каждая
молекула окружена другими.
Для простоты рассмотрим несколько молекул, расположенных
вдоль одной прямой. Каждая молекула на такой прямой будет иметь
двух соседок — одну справа, другую слева. Поэтому потенциальная
энергия такой молекулы представится суммой двух кривых, подобных
кривой, изображенной на рис. 154. Эти кривые представлены на
рис. 190а пунктирными линиями. Суммарная кривая (сплошная линия)
дает достаточно глубокую потенциальную яму. Для совокупности
молекул образуется волнообразная потенциальная кривая (рис. 1906).
Глубина отдельных потенциальных ям АЕр больше средней кине-
кинетической энергии, приходящейся на одну степень свободы молекулы
310 МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ [ГЛ. IX
жидкости X/ikT. Поэтому каждая молекула пребывает в потенциаль-
потенциальной яме около своего положения равновесия. Однако для жидкости
средняя энергия \/1kT не на много меньше глубины ямы &Ер,
в результате чего кинетическая энергия отдельной молекулы, благо-
благодаря наличию флуктуации, от времени до времени оказывается до-
достаточной, чтобы молекула выско-
Ер чила из потенциальной ямы и заняла
а) \ , новое место между другой парой
молекул.
Указанный характер движения
молекул в жидкостях объясняет как
медленность диффузии в жидкостях,
так и большую, по сравнению с га-
газами, вязкость жидкостей. В газах
внутреннее трение (вязкость) объяс-
б) няется переносом количества на-
г Т ГЛ Г} Г\ Г\ правленного движения молекул из
Р\ I V У II V / \ . слоя в CJI0tt за счет теплового дви-
т жения молекул (§ 56). В жидко-
Рис. 190. Кривые потенциальной х нарад с м механи3мом
энергии молекулы в жидкости. у J
внутреннего трения, имеет место и
другой, связанный с передачей ко-
количества движения за счет удара молекул друг с другом, аналогично
передаче количества движения вдоль ряда соприкасающихся между
собой упругих шаров. Число соударений молекул обратно пропор-
пропорционально свободному объему между молекулами, следовательно, и
вязкость жидкостей обратно пропорциональна этому свободному
объему. Для одного моля жидкости свободный объем равен Vo — Ъ,
где Va— молярный объем жидкости, а Ь — объем, занимаемый
молекулами при их плотной упаковке (величина, аналогичная по-
поправке Ь в уравнении Ван-дер-Ваальса). На основании этого вязкость
жидкости tj может быть положена равной
где С—константа. Эта формула, впервые предложенная А. И. Ба-
чинским, хорошо приложима для многих вязких жидкостей.
Я. И. Френкель, исходя из изложенного выше характера тепло-
теплового движения молекул в жидкостях, показал, что температурная
зависимость вязкости жидкости должна выражаться формулой:
тг] = Л ¦ efer,
где Д?р — глубина потенциальной ямы, в которой находится каждая
молекула. Эта формула также достаточно хорошо оправдывается
в ряде случаев.
§ 78] СТРОЕНИЕ ЖИДКОСТИ. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ 311
Иным способом свойства жидкости можно представить, рассма-
рассматривая потенциальную энергию молекулы, находящейся внутри жидко-
жидкости, по отношению к потенциальной энергии молекулы вне жидко-
жидкости. Потенциальная энергия молекулы внутри жидкости меньше
потенциальной энергии молекулы вне жидкости. Поверхностный слой
жидкости находится в иных условиях, чем весь объем жидкости.
Для перевода молекулы из жидкости наружу необходимо преодо-
преодолеть определенный потенциальный барьер, т. е. совершить опреде-
определенную работу. Средняя энергия теплового движения молекул недо-
недостаточная, чтобы совершить эту работу, в результате чего жидкость
сохраняет свой объем. .
Как мы видели при разборе свойств реальных газов, молекулы,
расположенные у границы газа, благодаря наличию сил притяжения
находятся в иных условиях, чем молекулы внутри газа. Совершенно
аналогичное явление имеет место в жидкостях.
Если мы мысленно выделим в жидкости
какую-либо молекулу, то должны учесть дей-
действие на нее всех других молекул. Однако
силы взаимодействия между молекулами быстро
убывают с расстоянием, так что практически
достаточно учесть действие лишь молекул,
расположенных достаточно близко.
Пусть г — такое расстояние, что силы
взаимодействия двух молекул, находящихся на Рис- '9'- Радиус мо-
расстоянии, большем, чем г, настолько малы, лекулярного действия,
что ими можно пренебречь. Проведем вокруг
данной молекулы А (рис. 191), как центра, сферу радиуса г. Тогда
нам достаточно учесть действие на данную молекулу только тех
молекул, которые находятся внутри сферы радиуса г.
Расстояние г принято называть радиусом молекулярного дей-
действия, а сферу радиуса г — сферой молекулярного действия.
В жидкости в сферу молекулярного действия, проведенную вокруг
данной молекулы А, попадает большое число других молекул. Силы,
с которыми эти молекулы действуют на молекулу А, направлены
в различные стороны и в среднем компенсируются. Таким образом,
результирующая сила, действующая на молекулу внутри жидкости
со стороны других молекул, в среднем равна нулю. Иначе обстоит
дело с молекулами, находящимися у поверхности жидкости. Рас-
Рассмотрим молекулу В, расположенную от поверхности жидкости на
расстоянии, меньшем радиуса молекулярного действия г. Тогда сфера
молекулярного действия, как видно из рис. 191, лишь частично
окажется внутри жидкости, часть же ее будет лежать вне жидко-
жидкости. Пусть лад поверхностью жидкости находится вещество в
газообразном состоянии, например, пар данной жидкости. Концен-
Концентрация молекул в паре мала, поэтому их действием можно вообще
пренебречь. Мы можем, следовательно, принимать во внимание дей-
312 МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ [ГЛ. IX
ствие на молекулу В лишь молекул, лежащих в той части сферы
действия, которая расположена внутри жидкости. При этом ока-
окажется, что на молекулу В действует с разных сторон неодинаковое
число молекул. Силы, с которыми они действуют на,молекулу В,
в среднем не будут компенсированы, возникнет результирующая
сила /, направленная внутрь жидкости. Таким образом, на каж-
каждую молекулу, лежащую от поверхности жидкости на расстоя-
расстоянии, меньшем радиуса молекулярного действия г, со стороны
других молекул действует сила, направленная внутрь жидкости.
На весь слой, лежащий у поверхности жидкости, действуют силы,
направленные нормально к поверхности внутрь жидкости. Поверх-
Поверхностный слой оказывает на всю жидкость давление, называемое
молекулярным давлением. Под влиянием этого давления молекулы
жидкости оказываются сближенными, что ведет к появлению между
ними сил отталкивания, уравновешивающих силы сжатия, вызванные
поверхностным слоем.
Из приведенного рассуждения" видно, что это давление тожде-
тождественно по своей природе с внутренним давлением р' газов, учиты-
учитываемым поправкой а/VI уравнения Ван-дер-Ваальса:
Количественное уравнение Ван-дер-Ваальса находится не в очень
точном соответствии с действительными свойствами жидкого состоя-
состояния вещества, но все же им можно воспользоваться для ориенти-
ориентировочных подсчетов. Так, например, для воды поправка Ван-дер-
Ваальса а = 5,47 am л*/моль*; для жидкой воды
при 0° С объем одного моля Уо = 18 см3/моль =
= 0,018 л/моль, откуда
Р' = -Щ = Ш?ат= 17000
Так же и для других жидкостей внутренние дав-
давления представляют собою величины порядка де-
Рис 192. Олив- сяти тысяч атмосфер.
новое масло в Силы молекулярного притяжения, существующие
СМС спиртом. ° в поверхностном слое жидкости, направлены внутрь
массы жидкости. Если на жидкость не действуют
никакие другие силы, то равновесным окажется такое положение
поверхности, при котором эти силы нормальны к поверхности. Масса
жидкости, на которую не действуют внешние силы, должна под
влиянием сил молекулярного давления принять сферическую форму.
Малые капли жидкости, для которых роль силы тяжести относи-
относительно мала, действительно принимают вид правильных сфер. Для
больших масс жидкости можно обнаружить их стремление принять
сферическую форму, компенсируя силу тяжести на основании закона
§ 79] ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ 313
Архимеда. Например, можно ввести оливковое масло в смесь воды
со спиртом, подобранную так, что ее плотность равна плотности
масла. Тогда сила тяжести, действующая на масло, компенсирована
гидростатическим давлением, и масло под влиянием собственного
молекулярного давления принимает правильную сферическую форму
(рис. 192).
§ 79. Поверхностное натяжение. Явления, обусловленные нали-
наличием молекулярного давления со стороны поверхностного слоя
жидкости на остальные слои, могут быть разобраны и с иной точки
зрения, чем изложенная в § 78.
Из всех геометрических тел сфера имеет при данном объеме
наименьшую поверхность. Поэтому переход данной массы жидкости
от какой-либо несферической формы к сферической связан с умень-
уменьшением ее поверхности. Следовательно, действие
сил молекулярного давления, под влиянием которых
жидкость принимает сферическую форму, аналогично
действию, которое возникло бы, если поверхность
жидкости представляла бы собою растянутую пленку,
стремящуюся сжаться. Все явления, которые вызваны
существованием молекулярного давления, объясня-
ются путем рассмотрения действия такой растянутой рис jgg Сила
пленки. поверхностного
Для того чтобы растянутую пленку удержать в натяжения,
равновесии, нормально к линии ее границы (рис. 193),
надо приложить силу /, касательную к поверхности жидкости,
называемую силой поверхностного натяжения.
Эта сила, очевидно, тем больше, чем больше длина границы
пленки /:
f=o.l. A)
Коэффициент а, зависящий от природы жидкости, называется
коэффициентом поверхностного натяжения.
Из A) можем получить:
Таким образом, коэффициент поверхностного натяжения а чис-
численно равен силе, приложенной к единице длины края поверхност-
поверхностной пленки жидкости. Измеряется а в CGS-системе в дин/см.
Для данной жидкости коэффициент поверхностного натяжения я
зависит от температуры: с повышением температуры он убывает.
При приближении температуры жидкости к критической темпе-
температуре Тк (см. § 62) коэффициент поверхностного натяжения a
стремится к нулю.
Это обстоятельство становится понятным, если вспомнить, что
в критической точке разница между жидким и газообразным состоя-
состояниями пропадает.
314
МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ
[ГЛ. IX
В табл. XI приведены значения коэффициента поверхностного
натяжения а для некоторых жидкостей в CGS-системе.
Определим работу, которую надо затратить, чтобы увеличить
площадь поверхностной пленки жидкости на некоторую величину AS.
Для этого с помощью силы / пере-
передвинем границу пленки (рис. 194) на
отрезок AS параллельно самой себе.
Тогда совершенная работа АА равна
АА =fAs,
но по-A)/=а/, откуда
AA=alAs.
Произведение I As представляет со-
собою увеличение площади пленки AS,
так что
Таблица XI
Значения коэффициента
поверхностного натяжения а
Жидкость
Вода
Ртуть
Глицерин ....
Эфир
а в дин/см
при 20° С
73
540
65
17
Эта работа идет на увеличение энергии пленки АЕ, откуда
или
ДБ
B)
Ba)
Энергия Е представляет собою ту часть внутренней энергии
пленки, которая может быть превращена в работу при изотермиче-
изотермическом процессе. В термодинамике эту часть энергии
называют свободной энергией.
Из равенства Bа) получаем еще одно определе-
определение коэффициента поверхностного натяжения: коэф-
коэффициент поверхностного натяжения а численно ра-
равен отношению изменения свободной энергии по-
поверхностной пленки к изменению площади этой
пленки.
Поверхностное натяжение объясняет многочис-
многочисленные явления, характерные для жидкого состоя-
состояния вещества, например, образование капель при
вытекании жидкости сквозь малое отверстие, обра-
образование пены и т. д. Представим себе пузырь воз-
воздуха А, который всплывает к поверхности жидкости
(рис. 195). Достигнув поверхности, он приподнимает
над собою куполообразный тонкий слой жидкости. Если пузырь
воздуха достаточно мал, то он не сможет прорвать поверхностный
слой и останется над поверхностью жидкости. Совокупность боль-
большого числа таких пузырей образует пену.
Общеизвестно, что мыльная вода особенно легко дает тонкие
пленки, хотя коэффициент поверхностного натяжения мыльной воды
1
Рис. 194. Опре-
Определение работы
при увеличении
площади по-
поверхностного
слоя жидкости.
§ 79]
ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
315
Рис. 195. Пузырь воздуха
жидкости, заклю- под поверхностью жид-
жидкости.
D5 дин/см) значительно меньше коэффициента поверхностного
натяжения чистой воды, равного 73 дин/см. Это объясняется боль-
большой вязкостью мыльной воды, благодаря
чему она стекает под влиянием силы тяже-
тяжести медленнее, чем чистая вода, и поэтому
легче удерживается между поверхностными
слоями. В тонких пленках, где поверхность
очень велика, а масса
ченной между поверхностями, мала, явле-
явления поверхностного натяжения сказываются
весьма резко. Тонкая мыльная пленка оказывается в значительной
мере сходной с растянутой резиновой пленкой и удобна для демон-
демонстрации явлений поверхностного
натяжения. Например, можно за-
затянуть проволочное кольцо мыль-
мыльной пленкой (рис. 196 а); если на
поверхность этой мыльной пленки
положить нитяную петлю, то она
сохранит ту случайную форму,
которую примет в первый момент.
На каждый участок нитки с обеих
сторон действуют одинаковые
силы, которые уравновешивают
вается в кружок мыльной пленкой. друг друга. Если же проткнуть
часть пленки, находящейся внутри
петли, не нарушая целостности остальной части пленки, то силы
больше не будут уравновешены, и внешняя по отношению к петле
часть пленки растянет ее в кружок (рис. 196<5).
Рассмотрим еще образование капель при медлен-
медленном вытекании жидкости из вертикальной трубки. По-
Поверхностное яатяжение не позволяет жидкости сразу
вылиться из трубки. По мере вытекания жидкости по-
поверхностная пленка капли получает сужение, или шейку
(рис. 197 а). Сужение потом разрывается, и нижняя
часть жидкости дает основную падающую каплю, а из
сужения получается добавочная маленькая капелька
(рис. 197 <5).
При очень малом отверстии и недостаточном давле-
давлении со стороны жидкости капля может вовсе не отор-
оторваться. Так поверхностное натяжение приводит к тому,
что жидкость не протекает сквозь мелкосетчатые по-
поверхности, например, через поверхность зонтика или ткань палатки.
а) 6}
Рис. 196. Нитяная петелька растяги-
О
о
6)
а.)
Рис. 197. Об-
Образование
капли.
Пример. Для оценки баланса энергии при изменении поверхности
жидкости определим, какое количество энергии освобождается при слиянии
мелких водяных капель радиусом г = 2- 10~3 мм в одну большую каплю
радиусом R = 2 мм.
316 МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ [ГЛ. IX
Решение. Обозначим число мелких капель, которые, сливаясь, обра-
образуют одну большую каплю, через п. Тогда общая поверхность S всех п
малых капель равна
S = 4яга • п. C)
Поверхность большой капли So = 4и/?2, откуда количество энергии, выде-
выделяемое за счет уменьшения поверхности при слиянии капель, по формуле B)
равно
-^2)a, D)
где а — коэффициент поверхностного натяжения.
Число малых капель п определим из того соображения, что сумма их
объемов равна объему большой капли:
— тсг'я = — tejR», откуда я = -р.
Подставив это значение п в D), найдем
(у — А а.
Подставив сюда численные значения /? = 2 мм, г = 2 ¦ 10~* мм,
а = 73 дин/см, получим
АЕ = 4 • 3,14 • 4 • Кг ¦ A0» — Г) • 73 эрг ?¦* 3,5 • 104 эрг = 3,5 • 10 дж.
Таким образом, за счет уменьшения поверхности воды при слиянии мел-
мелких капель в одну большую освободится энергия 3,5 • 10~а дж. Эта энергия
пойдет на нагревание капли.
Обратно, при разбивании большой капли на малые происходит увеличе-
увеличение энергии поверхностной пленки, которое влечет за собой некоторое
охлаждение капель.
§ 80. Давление под изогнутой поверхностью жидкости. Как
мы выяснили в предыдущем параграфе, поверхностная пленка жидко-
жидкости по своим свойствам сходна с растянутой упругой пленкой.
Поэтому, если пленка ограничена пло-
плоским контуром, то она и сама стре-
. „,,„„„Ш, мится принять 'форму плоскости. От-
а> g\ сюда выпуклая пленка, стремясь стать
Рис. 198. Действие изогнутой плоской, давит на нижележащие слои
поверхности жидкости. жидкости (рис. 198 а, б), а вогну-
вогнутая — их растягивает. Другими словами:
всякая изогнутая поверхностная пленка оказывает на жидкость
добавочное давление по сравнению с тем, которое испытывает
жидкость с плоской поверхностной пленкой; в случае выпуклой
поверхности это добавочное давление положительно, в случае
вогнутой — отрицательно.
Определим значение этого добавочного давления для случая, когда
поверхность жидкости представляет собою часть сферы радиуса R,
Выделим малый сферический сегмент AS (рис. 199). Силы поверх-
поверхностного натяжения, приложенные к контуру, этого сегмента, повсюду
§ 80]
ДАВЛЕНИЕ ПО ИЗОГНУТОЙ ПОВЕРХНОСТИ ЖИДКОСТИ
317
касательны к сферической поверхности. Рассмотрим силу Д/, прило-
приложенную к элементу контура Д/. Эта сила равна
i Af=a-Al, A)
где а — коэффициент поверхностного натяжения жидкости. Будучи
касательной к сферической поверхности, эта сила составляет неко-
некоторый угол с радиусом ОС. Поэтому имеется отличная от нуля со-
составляющая этой" силы Д/i, направлен-
направленная параллельно радиусу ОС. Если по-
поверхность жидкости выпукла, то центр С
"лежит внутри жидкости, и в этом слу-
случае сила ДД сжимает жидкость, ле-
лежащую под сегментом AS, т. е. обра-
образует положительное давление; если
поверхность вогнута, то центр С ле-
лежит вне жидкости, и в этом случае
сила ДД растягивает жидкость, т. е.
оказывает отрицательное давление. Из
рисунка имеем
Д/i = Д/ sin ф,
откуда по A)
Д/i =
Рис. 199. Определение добавоч-
sln <p. ного давления под сферической
поверхностью жидкости.
Эта сила ДД приложена к элементу
контура А1. Такие же силы приложены
ко всем другим элементам контура. Поэтому ко всему сфериче-
сферическому сегменту Д5 приложена параллельно радиусу ОС сила
/i = 2 A/i = <* sin <р • ?Д/.
' Сумма 2 Ы представляет собою длину контура, ограничивающего
шаровой сегмент AS. Этот контур есть окружность; обозначим его
радиус через г, тогда ?Ы = 2"хг, откуда
Из рис. 199 видим:
= а • 2кг sin
sin Ф = х.
B)
Подставив это значение sin у в B), найдем
, _ а . 2яга
/1 D *
Давление р получим, поделив значение этой силы на площадь
той части плоскости, которая ограничена контуром сегмента, т. е.
318 , МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ [ГЛ. IX
на площадь окружности радиуса г, откуда
а ¦ 2яг2
т. е.
Эта формула дает нам значение добавочного давления р, оказы-
оказываемого на жидкость со стороны сферической поверхности.
Как видно, это давление прямо пропорционально коэффициенту
поверхностного натяжения а и обратно пропорционально радиусу
поверхности R. Чем сильнее искривлена поверхность, тем меньше
ее радиус R и, следовательно, тем больше
добавочное давление р.
Наличие добавочного давления под
изогнутой поверхностью ведет, например,
к тому, что внутри мыльного пузыря воз-
воздух находится под большим давлением,
чем внешний воздух. Разность давлений
Рис. 200. Воздух перетекает воздуха внутри и вне пузыря тем больше,
из меньшего мыльного чем меньше радиус пузыря,
пузыря в больший. Эт0 может быть продемонстрировано,
если на концах стеклянной трубки
(рис. 200) выдуто два мыльных пузыря А и В разных диаметров.
Тогда в меньшем пузыре воздух окажется под ббльшим давлением
и начнет по трубке течь в ббльший пузырь. В результате меньший
пузырь полностью стянется, ббльший же еще больше увеличится
в размерах. ч
Пример. Для оценки величины добавочного давления р определим,
под каким давлением находится воздух внутри пузырька радиусом
/? = 5 • 10~а мм, расположенного под поверхностью воды.
Решение. Давление воздуха в пузырьке сложится из атмосферного
давления Н и добавочного давления р, вызываемого пленкой воды, окружаю-
окружающей пузырек (считаем, что пузырек расположен под самой поверхностью
воды, так что слой воды, находящийся над пузырьком, заметного давления
не оказывает).
По формуле C):
P~R'
Для воды 0 = 73 дин/сМу откуда
9 74
р' = ъгт бар=2-92-105 баР-
Так как 1 ат = 1,013-10" бар, то
/> = 0,29 am.
Отсюда давление воздуха в пузырьке
p = H+p=l,2Q am.
§ 81]
ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
319
§ 81. Давление под изогнутой поверхностью жидкостн любой формы.
Выражение, полученное в § 80 для добавочного давления р для случая сфе-
сферической поверхности, может быть обобщено и на изогнутую поверхность
любой формы. Для этого надо ввести понятие о кривизне произвольной по-
поверхности.
Возьмем некоторую произвольную кривую поверхность и восставим
в точке О нормаль ON к этой поверхности. Проведем через нормаль ON
плоскость Pi. Линия пересечения этой плоско-
плоскости с поверхностью называется нормальным
сечением.
Для сферы любое нормальное сечение пред-
представляет собою большой Kpyr./4ifii (рис. 201),
радиус R которого совпадает с радиусом самой
сферы. Величина С = -5-дает кривизну сферы.
К
Для произвольной кривой поверхности раз-
различные нормальные сечения, проведенные че-
через одну и ту же точку О, окажутся различ-
различными геометрическими кривыми, а следова-
следовательно, дадут разную кривизну. На рис. 201
указаны два различных нормальных сечения,
проведенных через одну и ту же точку О.
Одно из этих сечений дает дугу А±В\ с ра-
радиусом кривизны OCi = Ri, другое—дугуЛ2В»
с радиусом кривизны OCi = R%.
В геометрии доказывается, что если через
точку О любой кривой поверхности провести
два взаимно перпендикулярных нормальных
сечения AiBi и A^Bz, радиусы кривизны кото-
которых равны Ai и Rit то величина
Рис. 201. Нормальные сече-
сечения искривленной поверх-
поверхности.
имеет одно и то же значение для любой
пары таких взаимно перпендикулярных нор-
нормальных сечений. Эта величина С называется
средней кривизной поверхности в точке О.
Выберем теперь на кривой поверхности жидкости, имеющей произволь-
произвольный вид, точку О и проведем через эту точку два взаимно перпендикулярных
нормальных сечения AtBi и A2BS с радиусами кривизны Rt и Rs (рис. 202).
Выделим около точки О малый криволинейный четырехугольник DEFG. Длину
дуги DE=FG обозначим через А1и а длину дуги DG = EF—через Д/а.
Тогда площадь рассматриваемого четырехугольника AS = AlL ¦ Al2.
Дальнейшее рассуждение построим вполне аналогично рассуждению,
приведенному в § 80 для случая сферической поверхности. Сила поверхност-
поверхностного натяжения Д/i, приложенная к краю DE, равна
Д/, = оД/,. A)
Для определения давления, действующего на жидкость со стороны изо-
изогнутой поверхности, надо рассмотреть составляющую этой силы Af'it напра-
направленную параллельно радиусу OCi. Из рис. 202 имеем
Д/1 = Д/i • sin (ft. B)
Но приближенно
320
МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ
[гл. IX
Дуга OAi = -?-, а отрезок OCi представляет собою радиус /?i нормаль-
нормального сечения AiBt, откуда
sin w, ?^ г-=^ .
Подставляя это значение sin 91 в B) и воспользовавшись A), получим
д/; = ад/
Замечая, что A/iA/2 = AS, найдем
д/;==вд/1д/,_-.
На край FG действует равная составляющая A/J. Точно так же мы най-
найдем, что на край DO действует направленная параллельно радиусу OCi
составляющая сила
, I
Такую же составляющую Д/i дает край EF. В сумме от всех четырех
сторон криволинейного четырехугольника DEFG действует параллельно ра-
, диусу OCt сила
в* " . ..
откуда
Величина, стоящая в скобках,
представляет собою среднюю кривизну
поверхности в точке О и не зависит,
как указано, от выбора взаимно пер-
перпендикулярных нормальных сечений
AiBi и АгВа.
Давление р, оказываемое изогну-
изогнутой поверхностью на жидкость, най-
найдем, поделив значение силы Д/1 на
площадь AS, откуда
1 \
C)
Эта формула, носящая название
формулы Лапласа, дает значение до-
добавочного давления р, вызываемого
искривленной поверхностью жидкости
любой формы.
Для сферы /?1 = /?2 = /?, где /? есть радиус сферы, откуда добавочное
давление р под сферической поверхностью по C):
1а.
Рис. 202. Определение добавочного
давления под искривленной поверх-
поверхностью.
P==R'
что совпадает с формулой C) § 80.
§ 82]
ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ И ТВЕРДОГО ТЕЛА
321
Рис. 203. Цилин-
Цилиндрическая поверх-
поверхность.
Разберем еще в качестве частного случая поверхность в виде кругового
цилиндра. Возьмем за одно из нормальных сечений сечение, идущее вдоль
образующей цилиндра (рис. 203); это сечение пред-
представляет собою прямую, для которой #) = оо. Второе,
перпендикулярное к нему сечение представляет собой
окружность, радиус которой /?s есть радиус цилиндра R.
Отсюда добавочное давление под цилиндрической
поверхностью р равно
' *-=?• D)
§ 82. Явления на границе жидкости и твер-
твердого тела. Капиллярность. При соприкоснове-
соприкосновении жидкости с твердым телом надо учитывать
как силы взаимодействия между молекулами жид-
жидкости, так и силы взаимодействия между моле-
молекулами жидкости и твердого тела.
Здесь возможны два случая: 1) силы взаимо-
взаимодействия между молекулами жидкости больше,
чем силы взаимодействия между молекулами жид-
жидкости и твердого тела; 2) силы взаимодействия между молеку-
молекулами жидкости меньше, чем силы взаимодействия между молекулами
жидкости и твердого тела.
В первом случае говорят о несмачивании жидкостью твердого
тела. При несмачивании в слое жидкости, прилегающем к твердому
телу, результирующая сила направлена в сторону жидкости.
В равновесном состоянии поверхность жидкости располагается нор-
нормально к силе, в резуль-
результате чего поверхность
несмачивающей жидкости
у вертикальной твердой
стенки расположится, как
показано на рис. 204а.
Капля несмачивающей
жидкости принимает на
горизонтальной поверх-
поверхности форму приплюсну-
приплюснутой сферы (рис. 204<?).
Угол & между касательными к поверхности жидкости и к поверхности
твердого тела называется краевым углом. В случае несмачивания
краевой угол тупой: Ь ^ ^. При 0 = тс говорят о полном несмачи-
несмачивании.
Во втором случае, когда силы взаимодействия между молекулами
жидкости меньше, чем силы взаимодействия между молекулами
жидкости и твердого тела, говорят о смачивании жидкостью твер-
твердого тела. При смачивании в слое жидкости, прилегающем к твер-
твердому телу, результирующая сила направлена в сторону твердого
Рис. 204. Краевой угол несмачивающей
жидкости.
322
МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ
[ГЛ. IX
I
тела. При этом краевой угол острый, т. е. О^у. Если 9 = 0, то
говорят о полном смачивании.
На рис. 205а представлено расположение поверхности смачива-
смачивающей жидкости у вертикальной твердой стенки, а на рис. 2056—
вид капли смачивающей жидко-
жидкости на горизонтальной поверх-
поверхности.
Капля жидкости, помещенная
на горизонтальную поверхность
твердого тела, которое она пол-
<У Ф ностью смачивает, растекается по
Рис. 205. Краевой угол смачивающей поверхности. Капля несмачиваю-
жидкости. щей жидкости принимает более
или менее сферическую форму
(в зависимости от ее размеров) и легко перемещается по поверх-
поверхности твердого тела.
Одна и та же жидкость смачивает одни и не смачивает другие
твердые тела. Так, вода практически полностью смачивает чистую
поверхность стекла и не смачивает, например,
парафин. Ртуть не смачивает стекло и смачивает
чистую поверхность железа и т. д.
Поверхность смачивающей жидкости, находя-
находящейся в узкой цилиндрической трубке, прини-
принимает вогнутую форму (рис. 206а), а несмачиваю-
щей жидкости — выпуклую (рис. 1066). Такого
рода изогнутые поверхности жидкости носят на-
название менисков.
Рассмотрим случай узкой трубки, погружен-
погруженной одним своим концом в жидкость, налитую
в широкий сосуд. Пусть жидкость смачивает ма-
материал, из которого сделана трубка. Тогда внутри
а)
б)
Рис. 206. Форма
менисков: а) сма-
смачивающей жидко-
трубки мениск вогнутый (рис. 207) и при круг- сти, б) несмачиваю
, / * щей жидкости,
лом сечении трубки приближенно представляет
собою часть сферы.
Под вогнутой поверхностью жидкости, по сказанному в § 80,
появится добавочное отрицательное давление [формула C) § 80]:
Р = -
где R — радиус поверхности жидкости и а — коэффициент поверх-
поверхностного натяжения.
Так как под плоской поверхностью жидкости в широком сосуде
добавочного давления нет, то жидкость поднимется в трубке на та-
такую высоту h, при которой давление столба жидкости уравновесит
давление р. Давление, создаваемое столбом жидкости высотой h,
§ 82]
ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ И ТВЕРДОГО ТЕЛА
323
равно pgh, где р — плотность жидкости, g — ускорение силы тяжести;
отсюда условие равновесия имеет вид:
2а
0)
Обозначив через г радиус трубки и через Ь краевой угол, имеем
из рис. 207
'v ~~ cos 8 *
Подставив это значение R в A), найдем
2а ¦ cos 8
B)
чим
Bа)
откуда высота поднятия жидкости
, 2 COS д • а
Вводя диаметр трубки d = 2r, получим
, 4 cos 8 ¦ а
Рис. 207. Поднятие смачи-
смачивающей жидкости в капил-
капиллярной трубке.
Из формулы B) видно, что высота поднятия тем больше, чем
меньше радиус г, т. е. чем Уже трубка. Поэтому поднятие смачи-
смачивающей жидкости особенно заметно в очень узких трубках.
Такие узкие трубки носят название капиллярных от латинского
слова capillus, что значит волос. Само явление изменения высоты
уровня жидкости в узких трубках назы-
называется капиллярностью.
При данном радиусе г капиллярной
трубки поднятие тем больше, чем больше
коэффициент поверхностного натяжения а,
чем сильнее происходит смачивание (чем
меньше краевой угол &) и чем меньше
плотность жидкости р. При полном сма-
смачивании (& = 0) формула B) принимает
вид:
* = ?• <*»
Рис. 208. Опускание несма-
чивающей жидкости в ка-
капиллярной трубке.
Если жидкость не смачивает материал
трубки, то мениск жидкости в трубке
выпуклый, создаваемое этим мениском
добавочное давление положительно и уровень жидкости в трубке
располагается ниже, чем в широкой части сосуда (рис. 208). Вели-
Величина понижения уровня h несмачивающей жидкости дается той же
формулой B), что и высота поднятия смачивающей жидкости.
324
МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ
[ГЛ. IX
Формула B) может быть использована для определения коэффи-
коэффициента поверхностного натяжения а. Для этого стараются подобрать
такой материал, чтобы смачивание (или несмачивание) носило полный
характер. Тогда можно пользоваться формулой B6). Зная радиус
трубки г, плотность жидкости р и измерив высоту поднятия (или
опускания) h, непосредственно вычисляют по B6) значение а.
Явления капиллярности играют большую роль в природе и в прак-
практической жизни. Проникновение воды в почву и во всякого рода
пористые материалы происходит за счет капиллярности. На капилляр-
капиллярности основано действие фитилей, впитывание воды гигроскопической
ватой и т. д. В технике на явлениях смачивания и несмачивания
основана так называемая флотация. Схематически процесс флотации
заключается в следующем: размельченная смесь руды с горной по-
породой, в которую она заключена, взбалтывается в жидкости. Жид-
Жидкость подбирается так, чтобы она смачивала руду и не смачивала
„пустую" породу. Через жидкость пропускаются пузырьки воздуха.
Эти пузырьки, оседая на крупинках породы, не смачиваемой жид-
жидкостью, увлекают их на поверхность жидкости. Смачиваемые же
жидкостью крупинки руды погружаются на дно. Таким образом до-
достигается отделение руды от „пустой" породы.
Рассмотрим еще случай жидкости, находящейся между параллельными
пластинами, отстоящими друг от друга на расстоянии d (рис. 209).
Поверхность смачивающей жидкости между пластинами принимает ци-
цилиндрический вид. Добавочное отрицательное давление под цилиндрической
вогнутой поверхностью по формуле D) § 81
равно:
Р —
R'
где R — радиус цилиндра. При краевом
угле ft:
d_
n_2_ _ 2а cos »
^ — ^оТ» и р~ Т~-
Это давление уравновешивает давление
столба жидкости высотой Л:
2а cos »
Рис. 209. Поднятие смачиваю-
смачивающей жидкости между парал-
параллельными пластинами.
откуда высота поднятия h равна
. 2 cos 8 • а
п =
C)
Сравнивая формулы Bа) и C), видим,
что высота поднятия смачивающей жидкости
между параллельными пластинами, отстоящими друг от друга на расстоя-
расстояние <4, вдвое меньше, чем в трубке диаметром й.
Приведем еще примеры на вычисление высоты капиллярного поднятия
и опускания жидкостей.
Пример 1. Диаметры колен ^/-образной стеклянной трубки (рис. 210)
равны 1 мм и Змм. Чему равна разность уровней воды в обоих коленах?
§ 82]
ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ И ТВЕРДОГО ТЕЛА
325
Решение. Давление ри вызываемое вогнутой поверхностью воды
в более узком колене трубки, уравновешивается давлением, создаваемым
разностью уровней воды в обоих коленах А (рис. 210), и давлением ра, вызы-
вызываемым вогнутой поверхностью в более широком колене:
pl = hfg -\-p2, D)
где р — плотность воды, g—ускорение силы тяжести. Полагая
краевой угол а = 0, имеем по C) § 80:
_2а _2а
fi ' Га '
где ri и Га — радиусы трубок обоих колен.
Вводя вместо радиусов диаметры di=^2rt
лучим
4а 4а
i = 2ra, ПО- =.•=_¦
Подставляя эти значения pi и ра в D), получим
4а , . 4а
откуда
4аП 1\ _ 4 • 73 ( \ 1Л ^
^
=
Рис.210. Под-
Поднятие воды в
более узком
колене
^/-образной
трубки.
Пример 2. Барометрическая трубка (рис. 211), заполненная ртутью,
погружена нижним концом в широкий сосуд. Диаметр внутреннего сечения
трубки равен 0,4 см. Разность уровней ртути А = 758 мм. Чему равно атмо-
атмосферное давление?
Р е ш е н и е. Атмосферное давление не может быть
непосредственно определено по высоте ртутного столба А,
так как к давлению столба прибавляется еще давление
выпуклого мениска ртути в трубке. Таким образом, атмо-
атмосферное давление Р уравновешивает давление ртутного
столба h и добавочное давление р:
Добавочное давление р равно
_ 4а | cos ft |
р~ d
где d — диаметр трубки, а—краевой угол. Отсюда
Рис. 211. Влия-
Влияние капилляр-
капиллярности на высоту
поднятия ртути
в барометриче-
барометрической трубке.
E)
9 Желая, как обычно, выразить атмосферное давление Р
в миллиметрах ртутного столба, мы должны определить,
давлению какой высоты А' ртутного столба равно давле-
давление р. Из соотношения
4а | cos »| _
=A'P* имеем A' =
здесь взято абсолютное значение | cos ft |, так как А' должно быть положительно.
Обозначим атмосферное давление, измеренное в миллиметрах ртутного
столба, через Н, тогда вместо E) получим:
F)
326
МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ
[ГЛ. IX
Полагая для границы ртуть — стекло угол й = я, получим вместо F):
Для ртути а == 540 дин/см и р = 13,6 г/см', откуда
= 76'2 е»
§ 83. Растекание капли по поверхности жидкости. Мономолекуляр-
Мономолекулярные пленки. Рассмотрим каплю (рис. 212) некоторой жидкости /, располо-
расположенную на поверхности CD другой, более плотной жидкости //. Обозначим
поверхностное натяжение первой жидкости через а{ и второй—через аа.
На границе обеих жидкостей также дей-
действует поверхностное натяжение, отлич-
отличное, однако, от тех, которые имеют
место на свободных поверхностях обеих
жидкостей. Обозначим коэффициент этого
поверхностного натяжения на границе
обеих жидкостей через aiJ. В каждой
точке окружности капли сходятся три
пограничные поверхности. Поэтому на
каждУю единицУ длины °КРУЖ"°«И капли
действуют три силы поверхностного на-
тяжения/,,/, и/1>2, направленные каж-
каждая по соответствующей поверхности.
Силы /i и /j,2 стремятся стянуть каплю; сила /2 растягивает ее. Равновес-
Равновесной будет та форма капли, при которой векторная сумма сил tt и f1J уравно-
уравновесится силой f2. Очевидно, это возможно при условии, что /2 </i +/1,2,
откуда следует, что жидкость / может держаться в виде капли на поверх-
поверхности жидкости //, если
Риг 91? Капля мрнрр плотной
жидкости' /на повепхности более
плотной ГиГоси /7
плотной жидкости //.
°2 < ,
Если же поверхностное натяжение а2 настолько велико, по сравнению
с другими, что
а2 ^> а1 4" а1,2>
то в этих случаях равнодействующая сил fi и fi;2 ни при какой форме капли
не может уравновесить силу f2 и капля растягивается по поверхности жид-
жидкости // в виде тонкой пленки. Так, например, многие органические жидкости
(эфир, скипидар) растекаются по поверхности воды. Для некоторых жидко-
жидкостей (бензол, жирные кислоты) явление растекания наблюдается только для
первых капель, помещенных на поверхности чистой воды; последующие капли
уже не растекаются, а остаются на поверхности воды в виде устойчивых
капель. Это объясняется тем, что первые капли отчаст» растворяютгя в воде
и при этом настолько уменьшают ее поверхностное натяжение, что равнове-
равновесие капель становится возможным.
Ленгмюр изучал поведение очень тонких пленок на поверхности воды
с помощью прибора, показанного на рис. 213. Кювета с плоскими краями
наполнена чистой водой; на поверхности воды могут перемещаться две пара-
парафинированные полоски бумаги А и В. Полоску А можно перемещать сво-
свободно; полоска В связана твердо с плечом коромысла весов CD. Если
поверхность воды чистая, то перемещения полоски А не оказывают никакого
влияния на положение полоски В. Ленгмюр растворял жирную кислоту
(нерастворимую в воде) в бензоле и пускал несколько капель такого рас-
раствора на поверхность воды в кювете. Бензол испарялся, и жирная кислота
покрывала поверхность воды тонкой пленкой.
§ 83]
РАСТЕКАНИЕ КАПЛИ ПО ПОВЕРХНОСТИ ЖИДКОСТИ
327
Если позаботиться, чтобы на часть поверхности воды, расположенную
правее полоски В, жирная кислота не попадала, то пленка этой кислоты
Рис. 213. Прибор для определения давления поверхностной пленки.
будет находиться лишь по одну сторону от полоски В и станет ее отодвигать
с силой /, которую можно измерить с помощью весов CD. Всякий сдвиг
полоски А, т. е. изменение поверхности пленки
жирной кислоты, поведет к изменению силы /. fauH
Зная концентрацию раствора и его количе- *сл/
ство, налитое на воду, можно сосчитать число
молекул жирной кислоты, оказавшихся на поверх-
поверхности воды. Отсюда, измерив площадь поверхно-
поверхности воды, заключенную между полосками А и В,
легко определить площадь ш, приходящуюся на
долю одной молекулы. При передвижении поло- ._
ски А площадь ш меняется.
Ленгмюр измерял силу /0, приходящуюся на
единицу длины полоски В, соответствующую раз-
различным значениям ш. Зависимость /0 от <о пред-
представлена на рис. 214. Для относительно боль-
больших <л (больших 20 • 10~1в смп) получается гипер-
гиперболическая часть кривой QS. Начиная от точки S,
кривая имеет прямолинейный вид и круто идет
кверху до точки Н; далее она проходит почти
горизонтально. Характер этой кривой может быть
истолкован следующим образом: при ш ббльших
чем 20 • 10~1в см" площадь, приходящаяся на одну
молекулу, больше ее собственных размеров. Со-
Совокупность молекул жирной кислоты, располо-
расположенных на поверхности воды, образует как бы
двумерный газ. Этот двумерный газ подчиняется обычным газовым законам.
Зависимость между силой /0, приходящейся на единицу длины полоски
(аналог давления), и площадью ш, занимаемой молекулой (аналог объема),
70
60
50
10
20
Ш-10аШг
Рис. 214. Кривая зависи-
зависимости давления поверх-
поверхностной пленки от пло-
площади.
328 МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ [ГЛ. IX
подчиняется закону
где Т-—абсолютная температура пленки и k—постоянная Больцмана.
Начиная от значений ш, соответствующих точке S, молекулы распола-
располагаются вплотную друг к другу. Теперь совокупность молекул жирной кислоты
на поверхности воды образует как бы двумерное твердое вещество. Моле-
Молекулы в такой твердой пленке расположены в один ряд, откуда пленка носит
название мономолекулярной пленки. Пря-
Мономолекулярныи слои мая $Н выражает сравнительно малую сжи-
„„„ маемость мономолекулярной пленки.
Для точек, лежащих левее Н, имеет
место образование складок пленки, образо-
образование двух и более молекулярных слоев.
Абсцисса точки S определяет площадь
<й0, приходящуюся на одну молекулу при их
плотном расположении на поверхности
Рис. 215. Расположение моле- воды. Опыты Ленгмюра показали, что всем
кул жирных кислот в мономо- жирным кислотам, начиная от пальми-
лекулярном слое на поверхно- тиновой (C,6H8iCOOH) до церотиновой
сти воды. (С2бН61СООН), приходится приписать одну
и ту же площадь шо = 21 • 10~1л см1. Так
как эти молекулы имеют вид длинных цепочек различной длины для разных
кислот, то полученный результат можно объяснить тем, что длинные моле-
молекулы жирных кислот на воде располагаются вертикально, их концы с группой
СООН погружены в воду, а углеводные цепи СНа—(СНа)я торчат над
водой (рис. 215).
§84. Испарение жидкостей. Если жидкость находится в откры-
открытом сосуде, она постепенно испаряется, т. е. переходит в газообраз-
газообразное состояние.
Испарение происходит при всякой температуре, но для каждой
данной жидкости с повышением температуры скорость испарения
увеличивается.
Явление испарения, как было указано, объясняется тем, что
в жидкостях, как и в газах, молекулы обладают различными энер-
энергиями как ббльшими, так и меньшими средней энергии, значение
которой определяется температурой Т. Поэтому при каждой темпе-
температуре Т в жидкости находятся настолько быстрые молекулы, что
они, подходя к поверхности жидкости, могут преодолеть притяжение
соседних молекул ¦ и, прорвавшись сквозь поверхностный слой, выле-
вылететь за пределы жидкости. Чем выше температура жидкости, тем
больше число быстрых молекул и тем, следовательно, быстрее идет
испарение.
Во время испарения из жидкости вылетают более быстрые моле-
молекулы, при этом они тратят часть своей энергии на совершение
работы против удерживающих их внутри жидкости сил молекулярного
притяжения. Отсюда получается, что средняя энергия молекул, остаю-
остающихся в жидкости, убывает, т. е. жидкость охлаждается.
Чтобы поддерживать жидкость при испарении при постоянной тем-
температуре, к ней нужно подводить извне тепло. Это тепло носит
название теплоты испарения; передача этого количества тепля
§ 84] ИСПАРЕНИЕ ЖИДКОСТЕЙ 329
жидкости ведет не к повышению ее температуры, но к совершению
работы, затрачиваемой при испарении. .
Под удельной теплотой испарения X подразумевается коли-
количество тепла, которое нужно сообщить единице массы жидкости,
находящейся при температуре Т, чтобы перевести ее в пар при
той же температуре.
Обычно удельную теплоту относят к одному грамму или к одному
килограмму жидкости.
Теплота испарения зависит от температуры жидкости: при стре-
стремлении температуры к критической температуре Гк теплота испарения
стремится к нулю.
Если к испаряющейся жидкости не подводить извне тепло, то она
охлаждается. На этом факте основан способ понижения температур:
заставляя жидкость, помещенную в сосуд с нетеплопроводными
стенками, усиленно испаряться, можно ее значительно охладить
(ср. § 65).
При конденсации пара в жидкость его молекулы взаимно при-
притягиваются, в результате чего их скорости, а следовательно, и их
кинетическая энергия возрастают. Это ведет к нагреванию образую-
образующейся жидкости: теплота, Затраченная при испарении, отдается
обратно при конденсации пара.
При нагревании жидкости до такой температуры, при которой
упругость ее насыщенных паров становится равной внешнему давле-
давлению, испарение жидкости начинает идти не только с поверхности
жидкости, но и в ее толще, где начинают образовываться пузырьки
пара. Такое более бурное испарение носит название кипения. Таким
образом, температура кипения зависит от того внешнего давления,
под которым жидкость находится. При атмосферном давлении
G60 мм Hg) вода кипит при 100° С; при более низком давлении
она кипит при более низкой Температуре, а при более высоком дав-
давлении — при более высокой температуре.
Пузырьки пара, образующиеся при кипении жидкости, легче всего
возникают на пузырьках воздуха, обычно присутствующих в жидко-
жидкости и обыкновенно прилипающих к стенкам сосуда.
Пузырьки воздуха являются теми центрами, около которых начи-
начинается кипение. Жидкость, лишенную воздуха, можно перегреть,
т. е. нагреть выше температуры кипения без того, чтобы она вски-
вскипела. Если в такую перегретую жидкость ввести какие-либо твер-
твердые частицы, к поверхности которых прилип воздух, то она сейчас же
закипит, при этом температура ее упадет до температуры кипения.
Так как закипание перегретой жидкости происходит бурно, то его
обычно стараются избегать, для чего, например, в сосуд с нагре-
нагреваемой водой вводят капиллярные трубки, внутри которых легко
сохраняются пузырьки воздуха.
Теплота испарения А идет на работу А, совершаемую молекулами
при прохождении сквозь поверхностный слой жидкости, и на ра-
330 МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ [ГЛ. IX
боту А', связанную с увеличением удельного объема Va вещества
при его переходе из жидкого в газообразное состояние:
\ = А-\-А'. A)
Толщина поверхностного слоя, в пределах которого действуют
на молекулу силы притяжения, есть величина порядка радиуса моле-
молекулярного действия г (см. § 78). Обозначая среднюю силу, дей-
действующую на длине этого радиуса молекулярного действия, через /,
получим выражение для работы вырывания одной молекулы:
ДА =/./¦.¦
Работа А, совершаемая всеми молекулами, находящимися в еди-
единице массы жидкости:
А =«'¦ ДЛ = я-/г,
где и— число молекул в единице массы.
Работа А' равнй
где V'a — удельный объем пара, Vo — удельный объем жидкости и
р— то давление, при котором происходит испарение. Подставляя
значения Л и Л' в A), найдем
^—V,). B)
Это соотношение не позволяет непосредственно вычислить значе-
значение теплоты испарения X, поскольку остаются неизвестными far,
но оно показывает, что X зависит от той же величины молекуляр-
молекулярного взаимодействия /, которая обуславливает и наличие поверх-
поверхностного натяжения. При повышении температуры уменьшаются и
сила /. и разность удельных объемов V'u пара и Уо жидкости,
откуда, по B), с увеличением температуры убывает и теплота испа-
испарения X. При приближении температуры к критической Тк величина
молекулярного притяжения / стремится к нулю, и одновременно
пропадает разность в удельных объемах пара V'u и жидкости Уо;
отсюда при Т—> Тк, по B), и теплота испарения X—>-0, что, как
было отмечено, действительно имеет место.
Пользуясь вторым началом термодинамики, можно установить зависимость
между упругостью насыщенных паров, температурой, теплотой испарения
и изменением удельного объема при переходе от жидкого к газообразному
состоянию. Для этого предположим, что в цилиндре под поршнем находится
жидкость и над ней ее насыщенные пары. Проведем с этой смесью обрати-
обратимый цикл Карно (см. § 73), Пусть первоначальная температура равна Т и
упругость насыщенных паров при этой температуре р. Проведем сперва
изотермическое расширение. При этом некоторая масса жидкости m испа-
испарится и перейдет в состояние насыщенных паров при прежнем давлении р.
§ 85] РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ 331
Таким образом, расширение произойдет изобарически; на графике (рис. 216)
оно представится изобарой АВ. Для того чтобы это расширение протекало
действительно изобарически, смеси надо пере-
р ¦ дать теплоту испарения
Qi = ml. C)
Увеличение объема AV равно
где V'o — удельный объем пара, а Ко — удель-
удельный объем жидкости. Работа, совершенная при
этом изобарическом расширении, равна
Ai=p • AV=pm(V'o — Vo). D)
Рис. 216. Цикл Карно, про- Затем произведем бесконечно малое адиа-
водимый со смесью жидко- батическое увеличение объема (ветвь ВС); при
сти и ее насыщенного пара. этом температура упадет на dT, а упругость
насыщенных паров понизится на dp. Затем со-*
жмем смесь снова изобарически на величину ДК. Это сжатие изобразится
прямой CD, оно будет протекать при давлении р— dp и температуре Т — dT,
и при нем совершится работа
Наконец, замкнем цикл, производя адиабатическое сжатие DA. В резуль-
результате цикла от нагревателя взято количество тепла Qi и совершена некото-
некоторая работа А. Пренебрегая бесконечно малыми работами, совершаемыми на
адиабатах ВС и AD, можно считать A = Ai-\rAs. Коэффициент полезного
действия обратимого цикла Карно i]' = q-| по сказанному на стр. 281, не
-г1 "г
зависит от природы рабочего вещества и равен —!-=—-, где 7\—темпера-
7\—температура нагревателя (в нашем случае 7") и 7—температура холодильника
(в нашем случае Т — dT). Таким образом:
_ T—(T — dT) _dT
wi ~~ Т ~~ Т •
Подставляя сюда вместо Qu Ax и Аа их значения по C), D) и E), по-
получим
m(V'o-Vo)dp _dT *_!.__* F)
Ш Т' dT~ Т V'o — Vo " (>
Формула F) носит название формулы Клапейрона—Клаузиуса, она
связывает величину dp/dT, характеризующую зависимость упругости насы-
насыщенных паров от температуры, с теплотой испарения X, изменением удель-
удельного объема V'o—Vo и температурой Т. Вид этой формулы не зависит от
природы жидкости.
§ 85. Растворы. Осмотическое давление. Как известно, твер-
твердые вещества, вообще говоря, растворяются в жидкостях, образуя
с ними вполне однородную среду. Однако раствор не представляет
собой простой смеси, подобной смеси газов, химически не реаги-
реагирующих друг с другом. Д. И. Менделеев в результате обширных
исследований, произведенных в 1865—1887 гг., показал, что объем
332 МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ [ГЛ. IX
раствора отличается от суммы объемов растворителя и растворенного
вещества. Процесс растворения связан с выделением или поглощением
тепла. Менделеев установил наличие особых точек, соответствующих
определенным весовым соотношениям растворителя и растворенного
вещества. Все это указывает на наличие энергетических взаимодей-
взаимодействий между молекулами раствора и растворенного вещества и сбли-
сближает растворы с химическими соединениями. Однако для слабых
растворов указанные эффекты играют небольшую роль. В дальней-
дальнейшем мы ограничимся рассмотрением столь слабых растворов, что одна
молекула растворенного вещества приходится на большое число моле-
молекул растворителя. Тогда молекулы растворенного вещества находятся
далеко друг от друга, слабо взаимодействуют друг с другом, и их
совокупность образует подобие газа. Различие с действительным газом
заключается в том, что здесь движение молекул растворенного
вещества затруднено наличием между ними молекул растворителя,
с которыми они непрерывно сталкиваются. Благодаря этому коэф-
коэффициент диффузии растворенного вещества гораздо меньше коэффи-
коэффициента диффузии газов.
Средняя кинетическая энергия теплового движения молекул как
растворителя, так и растворенного вещества та же, что и в газе при
данной температуре Т. на каждую степень свободы приходится в сред-
среднем энергия
где k — постоянная Больцмана.
Совокупность молекул растворенного вещества, будучи подобна
газу, должна оказывать давление (см. § 46)
п
p = -nuw, A)
где и0 — число молекул растворенного вещества в единице объема
раствора. Это давление р называется осмотическим.
Однако, благодаря наличию у жидкости, являющейся раствори-
растворителем, огромного внутреннего давления, вызванного поверхностной
пленкой, непосредственное наблюдение осмотического давления не-
невозможно.
Осмотическое давление р аналогично парциальному давлению
какого-либо газа, подмешанного в малом количестве к другому газу,
находящемуся при большом давлении р. Отсюда и метод наблюдения
осмотического давления должен быть тот же, что и метод наблюде-
наблюдения парциального давления газа. В § 47 нами был описан опыт,
в котором, благодаря наличию перегородки из раскаленной платины,
проницаемой для молекул водорода и непроницаемой для молекул
аргона, можно было непосредственно измерить парциальное давление
водорода. Аналогично можно обнаружить осмотическое давление,
если подобрать перегородку, пропускающую молекулы растворителя
§ 85]
РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
333
что он
и не пропускающую молекулы растворенного вещества. Такого рода
перегородки называются полупроницаемыми. Например, для случая
раствора сахара животный пузырь является прозрачным для молекул
воды и непрозрачным для молекул сахара, откуда следует,
может быть использован для наблюдения и изме-
измерения осмотического давления раствора сахара.
Схема опыта, служащего для обнаружения осмо-
осмотического давления, представлена на рис. 217.
В сосуд с чистой водой погружен маленький со-
сосудик а, нижний открытый конец которого затянут
полупроницаемым пузырем. К верхней части сосу-
сосудика а прикреплена тонкая длинная трубка Ь. В со-
сосудике находится раствор сахара. Аналогично тому,
как в опыте, изображенном на рис. 114, водород
поступал внутрь платинового сосуда в ббльших
количествах, чем выходил из него, так и в сосу-
сосудик а через полупроницаемую перегородку будет
больше проникать воды извне, чем из сосудика а
наружу. Эта лишняя проникнувшая вода поднимет
уровень раствора в трубке Ъ и будет его повы-
повышать до тех пор, пока гидростатическое давление
поднявшегося столба жидкости не окажется рав-
равным осмотическому (.парциальному") давлению рас-
растворенного сахара.
Из формулы A) вытекает, что осмотическое давление должно
подчиняться соотношению Менделеева—Клапейрона:
Рис. 217. Опре-
Определение осмоти-
осмотического давле-
давления с помощью
полупроницае-
полупроницаемой перего-
перегородки.
V
RT,
B)
где т — масса растворенного вещества, (j, — его молекулярный вес,
V—объем раствора, R — газовая постоянная.
Вводя величину
которая представляет собой концентрацию раствора (концентрация
численно равна массе растворенного вещества, приходящейся на еди-
единицу объема раствора), перепишем формулу B):
p = C-RT. C)
Формула C) в применении к осмотическому давлению носит на-
название формулы Вант-Гоффа. Из формулы Вант-Гоффа следует:
1) для данного растворенного вещества при постоянной температуре
осмотическое давление р, прямо пропорционально концентрации С;
2) для данного растворенного вещества при постоянной концентрации
осмотическое давление р прямо пропорционально абсолютной темпе-
334 МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ [ГЛ. IX
ратуре раствора 7; 3) для различных растворенных веществ, взя-
взятых при одинаковых концентрациях и одинаковых температурах,
осмотическое давление р обратно пропорционально молекулярному
весу.
Для большого числа слабых растворов формула Вант-Гоффа C)
оправдывается весьма хорошо. Однако для ряда растворов, например
для растворов неорганических солей, осмотические давления оказы-
оказываются значительно больше вычисленных по формуле C).
Это объясняется распадом молекул этих веществ при растворении
на несколько частей (диссоциацией), в результате чего возрастает
число частиц щ, приходящихся на единицу объема растворителя, и
по формуле A) возрастает и давление.
Растворы, подчиняющиеся формуле C), оказываются непровод-
непроводниками электрического тока, в то время как растворы, обнаруживаю-
обнаруживающие большие осмотические давления, являются проводниками элек-
электричества (электролитами, см. т. II). Отсюда следует, что молекулы
распадаются при растворении не на нейтральные, но на заряженные
части (ионы).
Явления, связанные с осмотическим давлением, играют большую
роль в природе, а именно, в процессах, происходящих в живых
организмах.
Для оцевки величины осмотических давлений рассмотрим следующие
примеры.
Пример 1. В 1 л воды растворено 34 г тростникового сахара (С^НнОц)
при температуре 27° С. Найти величину осмотического давления.
Решение. По формуле B):
т RT
p
здесь величина R представляет собой газовую постоянную, равную
0,082 л am/град моль. Молекулярный вес ц находим, пользуясь приведен-
приведенной химической формулой тростникового сахара и зная, что атомные веса
водорода (Н), углерода (С) и кислорода (О) соответственно равны 1, 12
и 16, откуда (а = 342. Пользуясь этими численными значениями, имеем:
34 0,082 -300 _,о .,
p~w —i—ат ^ ¦ ат"
Из приведенных расчетов видно, что осмотическое давление может до-
достигать величин порядка нескольких атмосфер.
Пример 2. Определить, в каком отношении возрастает осмотическое
давление в результате диссоциации молекул растворенного вещества, считая,
что х-я часть всех молекул растворенного вещества распадается на i частиц
каждая.
Решение. Обозначим число молекул растворенного вещества, прихо-
приходящихся на единицу объема, в предположении, что диссоциация не проис-
происходит, через п0. Если х-я часть молекул растворенного вещества распадается
на I частиц каждая, то число частиц в единице объема станет равным:
«О = Л0Х1 -\- A — X) Л0 = [1 -\- X ((' — 1)] Пц.
§ 86] ДАВЛЕНИЕ НАСЫЩЕННЫХ ПАРОВ 335
Так как давление пропорционально числу частиц в единице объема, то,
следовательно, в результате диссоциации давление возрастет в отношении:
7 = 5=1+*('-1)- D)
Для очень слабых растворов диссоциация бывает полная, т. е. все моле-
молекулы распадаются, тогда х=1, и формула D) принимает вид:
Если, например, все молекулы диссоциируют на две части, то ( = 2и
р'= 2р, т. е. осмотическое давление в результате диссоциации возрастает
вдвое.
Пример 3. Определить меру диссоциации молекул поваренной соли
NaCl при растворении 2,92 г соли в 1 л воды при температуре 27° С, если
известно, что при этих условиях осмотическое давление оказалось равным
1,75 am. .
Решение. Обозначим фактически наблюдаемое осмотическое давление
раствора поваренной соли через р\ а давление, которое имело бы место при
отсутствии диссоциации, через р. Тогда на основании формулы D), выведен-
выведенной в решении предыдущего примера:
У =Р [1+*<*-1I.
По условию i = 2, откуда
Решая это равенство относительно *, найдем
-f-l. «
По формуле Менделеева — Клапейрона
т RT
Подставив это значение р в E), получим
mRT •
Подставляя сюда приведенные численные данные, найдем
* 9^0,44,
т. е. 0,44 всех молекул поваренной соли диссоциированы.
§ 86. Давление насыщенных паров над1 искривленной поверх-
поверхностью и над раствором. Рассмотрим зависимость давления насы-
насыщенных паров жидкости от кривизны ее поверхности. Пусть
некоторое количество жидкости находится в закрытом сосуде; над
жидкостью — насыщенные пары. Давление насыщенных паров над
поверхностью жидкости имеет при данной температуре Т вполне
336
МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ
[ГЛ. IX
определенное Значение р. С высотой это давление убывает по
барометрической формуле (см. § 51).
Представим себе капиллярную трубку А, опущенную одним кон-
концом в жидкость (рис. 218). Предположим, что материал, из которого
сделана капиллярная трубка, полностью сма-
смачивается жидкостью. Тогда мениск жидкости
представит собою вогнутую поверхность в
виде полусферы радиуса г, совпадающего
с радиусом капиллярной трубки. Жидкость
в трубке поднимается на высоту h, равную
по формуле B6) § 82:
А
т
h
2a
r?g'
A)
Рис. 218. Упругость насы-
насыщенных паров на вы-
высоте h меньше, чем над
уровнем жидкости в со-
сосуде.
где а — коэффициент поверхностного натя-
натяжения жидкости ир — ее плотность.
Допустим, что давление насыщенных па-
паров над вогнутой поверхностью жидкости
в капилляре имеет то же значение р, что
оно имеет над плоской поверхностью в сосуде. Тогда пары, испа-
испаряющиеся с вогнутой поверхности в капилляре, расположенной на
отрезок h выше уровня жидкости в сосуде, окажутся под ббльшим
давлением, чем окружающие их пары, так как последние из-за
убывания давления с высотой будут иметь давление р'<^р. Возник-
Возникшие более плотные пары, расширяясь, могут совершить работу, эта
работа окажется совершенной за счет одного источника тепла
с температурой Т, без наличия холодильника, что невозможно
в силу второго начала термодинамики. Таким образом, мы должны
признать, что давление насыщенных паров над вогнутой поверхностью
жидкости' равно давлению р' окружающих паров, так как только
при этом давлении наступит равновесие между паром и жидкостью
в капилляре.
Значение р1 можно было бы определить, пользуясь барометри-
барометрической формулой, но вследствие малого значения высоты к можно
приближенно положить, что разность р—/>' равна давлению одно-
однородного столба паров высотой h и плотностью р0, где р0 — плотность
насыщенных паров данной жидкости при температуре 7, отсюда
p — p'z=hgPl>.
Подставив сюда знамение h по A), найдем
откуда
B)
§ 86]
ДАВЛЕНИЕ НАСЫЩЕННЫХ ПАРОВ
337
Как видно из формулы B), р'<^р, т. е. давление насыщенных
паров над вогнутой поверхностью меньше, чем над плоской. Чем
меньше радиус кривизны поверхности г, тем сильнее отличается р'
от давления насыщенных паров р над плоской поверхностью.
Рассматривая случай несмачивания жидкостью капилляра трубки,
мы получим в капилляре выпуклый мениск жидкости и более низкое
расположение уройня жидкости, чем в окружающем сосуде. Отсюда
с помощью рассуждений, вполне аналогичных приведенным, мы придем
к выводу, что давление насыщенных паров р" над выпуклой поверх-
поверхностью больше, чем над плоской. Давление р" окажется равным:
Pi
p '
Bа)
Из последнего результата вытекает, что давление насыщенных
паров над сферическими каплями больше, чем над плоской поверх-
поверхностью жидкости, и тем больше, чем меньше радиус капель. Капли
разных радиусов, окруженные паром, не могут быть в равновесии.
Меньшие капли будут испаряться, а на ббльших каплях пары начнут
конденсироваться, пока меньшие капли не исчезнут вовсе.
Сравним теперь давление насыщенных паров над раствором
с давлением паров над чистым растворителем.
Еще в конце прошлого столетия Раулем на основании многочис-
многочисленных измерений, преимущественно с органическими веществами,
было показано, что давление насыщенных паров р' растворителя над
раствором нелетучего вещества ниже, чем давление насыщенных
паров р над чистым растворителем при той же температуре. Например,
давление насыщенных паров воды над
водным раствором сахара ниже, чем
давление насыщенных паров воды над
чистой водой при той же температуре.
Обозначим через •/ число молей веще-
вещества, растворенного в v молях чистого
растворителя; тогда по закону, уста-
установленному Раулем, относительное
понижение давления насыщенных па-
Р — р'
ров -—— равно
¦v —j— v'
C)
Рис. 219. К выводу выражения
Закон Рауля может быть выведен ^^"оГ!^^
путем рассмотрения следующего кру- ром.
гового процесса:
1) испаряем в сосуде А (рис. 219) один моль чистого растворителя
при давлении насыщенных паров р. Объем возникших насыщенных
паров обозначим через Vfl;
12 С. Э. Фриш и А. В. Тиморева
338 МОЛЕКУЛЯРНЫЕ ЯВЛЕНИЯ В ЖИДКОСТЯХ [ГЛ. И
2) расширяем с ломощью насоса С эти пары . до такого
объема V'o, чтобы они приняли давление />', соответствующее давле-
давлению насыщенных паров над раствором;
3) конденсируем в сосуде В один моль паров, находящихся при
давлении р', в раствор.
Все три процесса производим изотермически при одной и той же
температуре Т;
4) переводим с помощью полупроницаемого поршня один моль
растворителя из раствора обратно в чистый растворитель.
Сумма работ, совершенных при этом круговом процессе, должна
равняться нулю; в противном случае снова было бы нарушено вто-
второе начало термодинамики, так как весь процесс осуществляется
с одним резервуаром тепла с температурой Т.
Легко проверить, что работы, совершенные при проведении про-
процессов 1) и 3), равны по величине и обратны по знаку, так что при со-
составлении суммы работ для всего кругового процесса они выпадают.
Работа расширения пара с помощью насоса С равна (см. § 71)
Определим еще работу перевода одного моля растворителя из
раствора в сосуд с чистым растворителем. Для этого надо пере-
передвинуть полупроницаемый поршень D на такой отрезок, чтобы
объем растворителя ДУ прошел сквозь поршень. Так как при этом
поршень будет продвигаться против осмотического давления Р, то
будет совершена работа
Объем ДУ представляет собою объем одного моля чистого раство-
растворителя, откуда Д1/ = —, где jj. — молекулярный вес растворителя,
ар — его плотность, отсюда
Требование А\-\- Ла = 0 дает:
откуда получаем для осмотического давления Р
;,. D)
Последнее выражение можно преобразовать. Перепишем выраже-
выражение In —, следующим образом:
In р-, = ]
Р
§ 86] КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА 339
так как изменение давления р — р' мало, то -—~- много меньше
единицы, откуда приближенно:
Воспользовавшись этим приближенным выражением, перепишем
формулу D):
Эта формула позволяет вычислять значение осмотического давле-
давления по понижению давления насыщенных паров над раствором вместо
того, чтобы его измерять, пользуясь полупроницаемыми перепонками,
как это описано в § 85.
По формуле Менделеева — Клапейрона осмотическое давление Р
равно
D_m'RT
— |i/ V
Здесь т' — масса растворенного вещества, a (i/ — его молекулярный
вес, следовательно, т'/р' равно числу молей растворенного вещества,
т. е. равно v'. Отсюда получаем
С другой стороны, -!- = —р, где т — масса растворителя и jj.—
его молекулярный вес, отсюда
где v — число молей растворителя. Подставив эти значения Р и р/(*
в E), получим:
р — о' ч' о — о'
±_ ±_ -—- птнлгля •_ 1_
^~ = Т, откуда р -v + y,
что и представляет собою закон Рауля C).
12*
ГЛАВА X
ТВЕРДЫЕ ТЕЛА
Рис. 220. Кристалл
кварца.
§ 87. Кристаллические и аморфные тела. Твердые тела разде-
разделяются на два типа, весьма существенно отличающихся друг от друга
по своим физическим свойствам, а именно на тела: 1) кристалли-
кристаллические и 2) аморфные.
Основным признаком кристаллического состояния вещества яв-
является наличие анизотропии, которая заключается в том, что одно-
однородное тело в различных направлениях обла-
обладает различными свойствами. Например, коэф-
коэффициент теплового расширения кристаллического
тела различен в различных направлениях; в раз-
различных направлениях различны механические,
оптические и электрические свойства кристал-
кристаллов. Наиболее характерным внешним признаком
кристалла является его правильная геометриче-
геометрическая форма. Общеизвестны правильные геоме-
геометрические узоры, образуемые кристаллами льда при замерзании
воды на поверхности оконных стекол, и правильные формы отдель-
отдельных снежинок. Кристаллы ограничены плоскими гранями, сходящи-
сходящимися в ребрах и вершинах. Обычно грани распола-
располагаются симметрично относительно друг друга. Кварц,
например, образует кристаллы, представляющие со-
собою шестигранные призмы, заканчивающиеся шести-
шестигранными пирамидами (рис. 220); квасцы кристалли-
кристаллизуются в октаэдры (рис. 221), каменная соль — в
кубы и т. д. Углы между гранями в различных об-
образцах одного и того же кристаллического веще-
вещества являются строго постоянными. Например, в кри-
кристаллах кварца угол между гранями призмы и пира-
пирамиды всегда равен 38°13'.
Аморфные же твердые тела изотропны, т. е. они обладают во
всех направлениях одинаковыми свойствами.
Кристаллы имеют определенным образом ориентированные плос-
плоскости, по которым многие из них особенно легко раскалываются.
Например, кристаллы каменной соли раскалываются по взаимно
Рис. 221. Кри-
Кристалл квасцов.
§ 87]
КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА
341
перпендикулярным плоскостям, так что отдельные кусочки каменной
соли после раскалывания имеют форму параллелепипедов; слюда легко
раскалывается на тонкие пластинки. Аморфные же тела всегда дают
неправильные поверхности излома; кусок стекла при раскалывании
образует отдельные кусочки совершенно неправильной случайной
формы.
Различно поведение кристаллических и аморфных тел при пла-
влении> т. е. при переходе из твердого в жидкое состояние. Каждое
данное кристаллическое тело имеет вполне определенную точку
плавления. На рис. 222 кривая А дает ход изменения температуры
со временем при плавлении кристал-
кристаллического тела при равномерном нагре-
вании. Часть кривой be относится к на-
нагреванию кристалла в твердом состоя-
состоянии. При достижении температуры у
плавления Тпл дальнейшее нагревание пл
тела прекращается, как как вся под-
подводимая теплота идет на переход тела
из твердого состояния в жидкое {те-
{теплота плавления). Точка d относится
к тому моменту, когда тело целиком
перешло в жидкое состояние. Даль-
Дальнейшая восходящая часть кривой отно-
относится к нагреванию жидкости. Пример
такого хода плавления дает лед: тем-
температура льда при таянии остается
неизменно равной 0°С, пока весь лед не превратится в воду. Аморф-
Аморфное тело дает на кривой, изображающей ход температуры со вре-
временем (кривая В рис. 222), лишь перегиб, относящийся к. интервалу
размягчения; тело непрерывно переходит из твердого в жидкое со-
состояние. Это обстоятельство сближает, вообще, аморфное твердое
тело с жидкостью, обладающей очень большой вязкостью.
Образцами аморфных тел могут служить стекло, различные сте-
стеклообразные вещества, смолы, битумы и т. д.
Стеклообразное состояние иногда возникает при охлаждении
предварительно расплавленного кристаллического вещества. При
медленном остывании температура может стать ниже температуры
плавления без того, чтобы выделилась скрытая теплота плавления
и вещество перешло в кристаллическую фазу. При этом, однако,
вязкость настолько возрастает, что вещество перестает быть жидким
в обычном смысле слова и становится стеклообразным. Такое вещество
называется переохлажденной жидкостью. Переохлажденная жид-
жидкость неустойчива: со временем в ней происходит процесс кристал-
кристаллизации;
В последнее время особое внимание к себе привлекают аморфные
вещества, состоящие из органических соединений, образующих так
Ь(время)
Рис. 222. Кривые хода темпе-
температуры со временем при плав-
плавлении кристаллического твер-
твердого тела (А) и аморфного твер-
твердого тела (В).
342 ТВЕРДЫЕ ТЕЛА [ГЛ. X
называемые полимеры. В них молекулы более простого соединения
(мономера) объединены в группы. Например, мономер С2Н4О
(паральдегид) дает полимер (ацетальдегид), каждая молекула кото-
которого состоит из трех молекул паральдегида (СаН4ОK. Возможны
весьма высокие степени полимеризации, когда в одну группу, обычно
нитеобразную, объединяются до нескольких тысяч молекул мономера.
Соответствующее твердое аморфное тело представляет собою клубок
та'ких нитеобразных молекул. Примером могут служить натуральный
и искусственный каучуки и другие пластмассы.
На первый взгляд может показаться, что число кристаллических
твердых тел невелико. Однако на самом деле кристаллической
структурой обладают не только те тела, которые обнаруживают не-
непосредственно наблюдаемую внешнюю симметрию формы и анизо-
анизотропию. "Внешне и непосредственно кристаллическая структура за-
заметна только у одиночных крупных кристаллов, какими являются
природные кристаллы кварца (горного хрусталя), куски каменной
соли и т. д. Такие одиночные кристаллы носят название монокри-
монокристаллов. Большинство же твердых тел обладает мелкокристал-
мелкокристаллической структурой, или, как говорят, поликристаллической
структурой. Порошки солей представляют собой собрание отдельных
микроскопических кристалликов. Из раствора какой-либо соли может
быть искусственно выращен большой монокристалл этой соли.
Все металлы также обладают, поликристаллической струк-
структурой. Отдельные кристаллики металла удерживаются друг около
друга молекулярными силами, так что весь агрегат таких мелких
кристалликов образует кусок металла, представляющийся при непо-
непосредственном рассматривании сплошным. Благодаря беспорядочной
ориентации отдельных кристалликов, кусок металла в целом не об-
обнаруживает анизотропии, хотя отдельные образующие его кристал-
кристаллики анизотропны.
Поликристаллическая структура металлов может быть обнару-
обнаружена при рассматривании полированной поверхности металла; иногда
кристаллы настолько крупны, что могут быть замечены простым
глазом, иногда их можно обнаружить лишь с помощью микроскопа.
В последнее время разработаны методы получения монокристаллов
различных металлов. По большей части монокристаллы получаются
при охлаждении расплавленного вещества. При охлаждении в рас-
расплавленной массе обычно образуется несколько центров кристалли-
кристаллизации (ядер); возникающие в этих центрах кристаллики затем раз-
разрастаются в разных направлениях с разными скоростями и ведут
к образованию поликристаллической структуры. Для получения моно-
монокристалла надо создать такие условия, чтобы разрасталось только
одно ядро. Путем внесения в расплавленное вещество „затравки"
(отдельного кристаллика) и очень медленного охлаждения сосуда
с нижнего конца можно получить металлические монокристаллы значи-
значительных размеров (например, в виде стержней длиной в 20 см и более).
§ 87j
КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА
343
В наиболее общем виде симметрия кристаллов была рассмотрена
Е. С. Федоровым, который показал, что существуют 230 различных
способов расположения частиц в кристаллах. Кроме того, Федоров,
установив связь между симметрией и химическим составом кристаллов,
дал метод кристаллохимического анализа.
Внешняя симметрия кристалла является результатом симметрич-
симметричного расположения частиц, из которых он построен. Эта идея была
высказана еще в конце XVIII в. В настоящее время мы имеем не-
непосредственное доказательство того, что атомы в кристаллах рас-
расположены симметрично друг относительно, друга, образуя простран-
пространственную решетку. Это доказательство основано на возможности
получить от кристаллической решетки диффракцию рентгеновых
лучей (см. т. III).
Каждый атом, образующий твердое тело, находится под влиянием
сил взаимодействия со стороны всех соседних атомов. При распо-
расположении атомов по углам определенной пространственной решетки
силы, действующие на каждый из атомов, компенсируют друг друга,
и атом находится в равновесии. Такому расположению атомов со-
соответствует минимум их взаимной потенциальной энергии, что об-
обуславливает прочность всего кристалла в целом.
Таким образом, кристалл представляет собою сложное архитек-
архитектурное построение, прочность которого обусловлена его внутренней
симметрией.
Силы взаимодействия между атомами,1 образующими кристалл,
носят различный характер. В кристаллах солей атомы несут элек-
электрические заряды, они представляют собою
ионы. Положительные и отрицательные ионы
чередуются так, что кристалл в целом нейтра-
нейтрален. В такой ионной решетке, носящей также
название гетерополярной, силы взаимодействия
между частицами являются в основном электро-
электростатическими.
На рис. 223 представлена кубическая ре-
решетка каменной соли (NaCl); такая решетка
является простейшей и принадлежит к куби-
кубической системе. Атомы натрия изображены
черными кружками, они несут положительный
электрический заряд, т. е. являются положи-
положительными ионами. Атомы хлора изображены белыми кружками,
они несут отрицательный заряд, т. е. являются отрицательными
ионами.
На рис. 224 представлена пространственная решетка цинковой
обманки (ZnS). Черные кружки изображают положительные ионы
Zn, белые кружки — отрицательные ионы S. Решетка цинковой
обманки обладает несколько более сложной структурой, чем решетка
каменной соли.
Рис. 223. Кубическая
решетка каменной
соли.
344
ТВЕРДЫЕ ТЕЛА
[гл.
2/1
OS
Рис. 224. Пространствен-
Пространственная решетка цинковой об-
обманки.
В случае химически простых твердых тел, атомы, образующие
пространственную решетку, все нейтральны. Решетка такого кри-
кристалла носит название атомной или гомео-
полярной.
Природа сил взаимодействия в атомной
решетке может быть полностью объяснена
лишь на основе квантовой механики.
На рис. 225 изображено расположение
атомов в кристаллической решетке алмаза.
Кроме ионных решеток (типа NaCl) и
атомных (типа алмаза), принято рассматри-
рассматривать еще молекулярные решетки и решетки
металлрв; первые относятся, преимуще-
преимущественно, к кристаллам многоатомных хими-
химических соединений, например, РаО5, SO3
и т. д.; вторые характерны для металлов
с их большой электропроводностью и металлическим блеском. Кри-
Кристаллы металлов, грубо говоря, можно представить в виде электрон-
электронного облака, в котором на определенных
расстояниях друг от друга расположены
положительные ионы.
Наличие устойчивого равновесия кри-
кристаллической решетки указывает на то, что
между частицами, образующими кристалл,
при сжатии возникают силы отталкивания,
а при растягивании — силы притяжения. Это
может быть объяснено, если положить, что
между частицами одновременно существуют
силы притяжения и силы отталкивания, по-
разному зависящие от расстояния г между частицами. В положении
равновесия эти силы численно равны друг другу. При уменьшении
расстояния г между соседними частицами начинает превалировать
сила отталкивания, а при возрастании этого расстояния превалирует
сила притяжения.
§ 88. Энергия кристаллической решетки. Потенциальная энергия
кристаллической решетки Ер может быть представлена в виде (§ 61):
?» = — t + V. О)
с
где первый член этой формулы ^- соответствует силам притя-
г
С"
жения, второй -|—^ силам отталкивания. На рис. 226 представлен
ход этих членов в отдельности и ход суммарной кривой, изобра-
изображающей потенциальную энергию Ер в зависимости от.расстояния г
между соседними частицами решетки. При A2^>?t силы отталкива-
отталкивания возрастают при убывании г быстрее, чем силы притяжения, что
Рис. 225. Пространствен-
Пространственная решетка алмаза.
§ 88J
ЭНЕРГИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
345
объясняет противодействие кристалла сжатию. Значению г = Гц
соответствует наиболее глубокое место потенциальной ямы; величина
г0 определяет расстояние между частицами в кристалле, не подвер-
подверженном действию внешних сил. Вблизи
положения равновесия каждая частица
может совершать небольшие колеба-
колебания, не выходя за пределы потен-
потенциальной ямы. К таким колебаниям
частиц около положения равновесия
сводится тепловое движение в кри-
кристаллах.
Теория кристаллических решеток
была развита Борном и рядом других
физиков. Борн показал, что, зная пока-
показатели степени ?, и &, в формуле A),
можно рассчитать упругие свойства
кристаллов, энергию образования кри-
кристалла, его оптические свойства и т. д.
Для получения согласия с опытом
для гетерополярных решеток, надо по-
положить kt = 1 и ?2 = 9; для гомео-
полярных решеток &2 имеет ббльшие
значения.
Расчет энергии простейшей кубической кристаллической решетки
типа NaCl схематически может быть представлен в следующем виде.
Потенциальная энергия двух изолированных ионов с зарядами—е
и -\-е, находящихся на расстоянии г0 друг от друга, равна
еР=—е-. B)
Потенциальная энергия двух соседних ионов внутри решетки
будет больше этой величины по двум причинам: 1) на каждый ион
действует не только его ближайший сосед, но и все другие ионы
решетки; 2) ионы, воздействуя друг на друга, вызывают взаимную
поляризацию, которая обуславливает появление сил отталкивания
[второй член в формуле A)].
Вычисления показывают, что для кристалла типа NaCl формула B)
должна быть заменена следующей:
Рис. 226. Зависимость потен-
потенциальной внергии Ер кристал-
кристаллической ионной решетки от
расстояния г между ионами.
Е'„ = — 0,2582-.
Го
Bа)
Потенциальная энергия, выражаемая формулой Bа), численно
равна работе, которую надо совершить, чтобы, вырвав два соседних
иона из решетки, удалить их в бесконечность, другими словами,
она равна работе разрыва связи между двумя соседними ионами
в решетке. В одном моле вещества решетки находится N пар ионов,
346 ТВЕРДЫЕ ТЕЛА [ГЛ. X
и каждый ион в кубической решетке имеет б соседних ионов;
таким образом, чтобы развести все ионы, входящие в состав одного
моля, на бесконечно большие расстояния друг от друга, надо разо-
разорвать 67V связей.
Отсюда полная потенциальная энергия решетки Ер, отнесенная
к одному молю, равна 6NE'P, т. е.:
?¦„ = — 0,2582 --6N. C)
Расстояние г0 между соседними ионами в кубической решетке
определим следующим образом: если р — плотность рассматриваемого
кристалла, [л — молекулярный вес и 1/0 — объем одного моля, то
Объем жеи = г°<1, приходящийся на одну элементарную кубическую
ячейку, получим, поделив Vo на число ячеек в одном моле, которое
совпадает с числом ионов в одном моле, т. е. на 2N,
=ш=т
Подставив это значение в формулу C) для потенциальной энергии,
найдем
?р = — 0,2582-б-е* j/Ml., E)
Так как е и N представляют собой константы, то последнее
выражение можно представить в виде:
Если р выражать в г/сл3, ц — в граммах на моль и Ер — в ка-
калориях на моль, то К имеет численное значение, равное 545.
Для кристаллических решеток типа CsCl или CaF2 получаются
формулы, аналогичные Eа), лишь с другим численным значением
константы К.
Непосредственная экспериментальная проверка расчетов Борна
затруднительна, так как мы не имеем возможности перевести твердый
кристалл в собрание свободных ионов. Косвенно же правильность
расчетов может быть подтверждена несколькими способами.
Рассмотрим, например, реакцию превращения солей NaCl и KJ
в соли КС1 и NaJ:
NaCl(TB) + KJ(TB) = NaJ(TB) + KC1(TB).
Здесь индексы (тв) означают, что химические символы относятся
к твердой кристаллической фазе соответственных веществ. Очевидно,
§
ЭНЕРГИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
347
энергия превращения Д?/ будет равна
Д и= - [Ер (NaCl) + Ер (KJ)] + [Ер (NaJ) + Ep (KCl)]
и, следовательно, может быть вычислена по формуле Eа) через по-
потенциальные энергии ^(NaCl), Ep(K.J) и т. д. кристаллических
решеток NaCl, KJ и т. д. С другой стороны, в первом приближении,
энергия превращения Д?/ равна разности теплот растворения солей
q при условии, что растворы берутся настолько слабыми, чтобы
диссоциация в них могла считаться полной:
Д U= %q = [q (NaCl) + q (KJ)] - [q (NaJ) + q (KCl)].
В табл. XII сопоставлены для ряда солей вычисленные значения
2> найденные через теплоты растворения.
Таблица XII
Реакция
KCl + LiBr =KBr + LiCl
KCl + LiJ =KJ +LiCl
KCl + NaBr = KBr + NaCl
KCl + NaJ =KJ +NaCl
1-4
-7
-3
-5
H3,6
-7,2
-2,0
h3,4
Если принять во внимание, что 2 Я экспериментально опреде-
определяется с небольшой точностью (малая разность относительно
больших величин), то совпадение между 2*7 и Д?/ надо считать
хорошим.
Второй способ проверки сводится к рассмотрению так называемого кру-
кругового процесса Борна — Габера. Этот процесс для случая NaCl представ-
представляется схемой:
NaCl
Сперва мы представляем себе, что один моль твердого кристаллического
NaCl разъединяется на совокупность свободных ионов Na+ и С1~; на это
тратится работа, численно равная потенциальной энергии решетки Ер. Затем
ионные газы Na+ и С1~ превращаются в нейтральные атомные газы Na,ra3>
и С1(газ>- На это тратятся работы, численно равные работам ионизации ^4y(Na)
и А/(С\), отнесенным к одному молю. Далее, газ Na,ra3l превращается в твер-
твердый металлический натрий [тратится работа, равная теплоте испарения L (Na)]
и атомный газ С1(газ,—в половину моля обыкновенного двуатомного газо-
газообразного хлора С1а [тратится работа, равная теплоте диссоциации — 9(С1)[.
Наконец, из твердого металлического натрия и газообразного хлора путем
химической реакции снова получается один моль твердого кристаллического
NaCl; при этом выделяется теплота образования Q (NaCl). При круговом про-
348
ТВЕРДЫЕ ТЕЛА
[гл. х
цессе сумма всех работ и всех полученных и отданных количеств теплоты
(учтенных здесь эквивалентными работами) равна нулю. Поэтому получаем:
- Ер = Aj (Na) + Aj(C\) + L (Na) + 1 q (Cl) + Q (NaCl).
Если измерить каждую из величин, стоящих в правой части этого ра-
равенства, то можно найти значение Ер. На самом деле, непосредственному
экспериментальному определению доступны все указанные величины, кроме
работы образования отрицательного иона С1~. По косвенным соображениям
можно считать Aj(C\) равной приблизительно — 90 кал/моль. Тогда, восполь-
воспользовавшись эмпирическими значениями /4y(Na) = 117 кал, Z.(Na) = 27 кал,
l/2q(Cl) = 29 кал, ?? (NaCl) = 98 кал, найдем, что энергия решетки NaCl
есть величина порядка—180 кал/моль. Формула Eа), если в нее поставить
массу моля каменной соли ц = 58,5 г/моль и ее плотность р == 2,16 г/см*,
дает Ер = —182 кал/моль.
Следует иметь в виду, что более точная теория кристаллических решеток,
особенно желающая представить их поведение при низких температурах,
должна базироваться на квантовой механике.
§ 89. Деформации твердых тел. Под влиянием внешних сил
всякое твердое тело деформируется, т. е. изменяет свою форму.
Упругой называется деформация, исчезающая с прекращением дей-
действия силы. Так, упруго растянутая пружина принимает свою преж-
прежнюю длину после прекращения действия растягивающей силы. С из-
изменением знака силы меняется и знак упругой деформации, например,
если под влиянием растягивающей силы пружина удлиняется, то
под влиянием сжимающей силы она
укорачивается. По закону, установ-
установленному Гуном, величина дефор-
деформации Ах пропорциональна дей-
действующей силе /:
Ax=Kf, A)
где К— постоянная величина для
данной деформации данного твер-
твердого тела.
Рассмотрим простейшую дефор-
деформацию продольного растяжения
или одностороннего сжатия.1 Пред-
Представим себе однородный стержень
длины L с площадью поперечного
сечения 5, к концам которого при-
приложены силы /„, в результате чего
длина стержня меняется на вели-
величину AL
'
L+&L
I
а)
в)
Рис. 227. Деформация растяже-
растяжения (а) и сжатия (б).
Растягивающие силы считаем 'положительными; в этом случае
(рис. 227 a) &L тоже положительно, т. е. стержень удлиняется.
1 Различают одностороннее сжатие от всестороннего, при котором тело
подвергается сжатию одновременно со всех сторон. В дальнейшем мы будем
рассматривать только одностороннее сжатие.
§ 89] ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 349
Сжимающие силы считаем отрицательными; в этом случае (рис. 227 б)
Д? тоже отрицательно; это означает, что, когда стержень подвер-
подвергается одностороннему сжатию, длина его L уменьшается.
Для характеристики деформации существенно не абсолютное
значение удлинения стержня AL, но относительное удлинение AL/jL
Это следует из того, что очевидным образом не одинаково просто
растянуть, например, на Д/. = 1 см два стержня из одинакового
материала и одинакового поперечного сечения, но один из которых
имеет длину L всего в 2 см, а другой — в 10 м. Для растягивания же
таких стержней на одну и ту же долю их первоначальной длины
(например, на ttwwJ придется приложить одинаковые силы /. Таким
образом, деформацию следует характеризовать относительным
изменением длины &L/L.
Для стержней разного поперечного сечения S под влиянием
одной и той же силы относительная деформация b.L\L тем меньше,
чем толще стержень, т. е. чем больше S. Отсюда для упругой де-
деформации растяжения (сжатия) получаем, что относительное изме-
изменение длины Д/.//. должно быть пропорционально величине /„/S,
т. е. силе, отнесенной к единице поперечного сечения стержня.
Эту величину -^ =рп назовем усилием.
Тогда окончательно имеем
-ц = ь-§, или -j=apn, B)
где коэффициент а, носящий название коэффициента упругости,
зависит уже только от материала, из которого сделан стержень.
Наряду с коэффициентом упругости а принято характеризовать
материал обратной величиной:
В = \, C)
которую называют модулем упругости или модулем Юнга. Под-
Подставляя в B) вместо а модуль Юнга Е, получим
№ 1
Т = ¦?'?«•
Из формул B) и Bа) имеем
Е=_ D)
Рп ' MIL ' (V
откуда следует: коэффициент упругости а численно равен относи-
относительному изменению длины kLjL, происходящему под влиянием
усилия, равного единице; модуль Юнга Е численно равен усилию
рт вызывающему относительное изменение длины, равное единице.
При относительном удлинении, равном единице, Д/.= /., откуда
получаем: модуль Юнга Е численно равен тому усилию рп, которое
350 ТВЕРДЫЕ ТЕЛА [ГЛ. X
растягивает стержень вдвое. На самом деле подавляющее число
материалов рвется раньше, чем они будут растянуты вдвое, поэтому
обычно фактически нельзя приложить к стержню, усилие рп, чис-
численно равное модулю Юнга Е.
Предположим, что к стержню первоначальной длины Lo прило-
приложено усилие рп, тогда новая длина стержня будет:
Так как, по формуле B):
то новая длина стержня L равна
1 = 1,A+ад,). E)
Из этой формулы видно, что в пределах упругой деформации
длина стержня меняется линейно с усилием рп. При растяжении
или сжатии стержня внешние силы совершают работу. По формуле
Bа) мы имеем, что сила, приложенная к стержню в каждый данный
момент, равна
т. е. сила не остается во время деформации постоянной, но меняется
пропорционально изменению длины стержня A.L. В § 25 мы опреде-
определяли работу такой переменной силы. Вычислим ее здесь еще раз
иным способом. Пусть длина стержня меняется от значения L до
L-{-AL, тогда работа А равна
где /„ представляет собою среднее значение силы. Ввиду линей-
линейности возрастания силы /„ с удлинением AZ., это среднее значение
силы равно среднему арифметическому из значений силы /я = О
(при Д? = 0) и /п = -^--Д?(при данном Д1), т. е.
Г 1 ES \т л l ES лга
fn = ---j--bL, откуда Л=2"--Г-ДР.
Эта работа пойдет на создание потенциальной энергии упруго
деформированного стержня:
ЦЩ.АЬ\ F)
Таким образом, потенциальная энергия упруго деформированного
стержня оказывается пропорциональной квадрату деформации Д1А
Деформация продольного растяжения или сжатия сопровождается
изменением поперечных размеров деформируемого стержня.
§ 89]
ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ
351
При продольном растяжении стержень дает поперечное сжатие,
при продольном сжатии — поперечное расширение. Относительное
изменение толщины стержня Ldjd пропорционально действующему
усилию рп:
Коэффициент р называется коэффициентом поперечного сжатии
при продольном растяжении.
Отношение
называется коэффициентом Пуассона. Пользуясь выражением для
коэффициента Пуассона, мы можем переписать формулу G) в виде:
Gа)
??<
Для большинства однородных изотропных тел (и металлов) ко-
коэффициент Пуассона а близок по численному значению к 'Д-
Рассмотрим еще одну простую де-
деформацию, называемую деформацией
сдвига.
Деформация сдвига происходит под
влиянием силы ft, касательной к той
поверхности, на которую она дей-
действует (рис. 228). Под влиянием такой
силы слои тела сдвигаются друг от-
относительно друга, и каждая физиче-
физическая прямая (т. е. линия, связанная
с определенными частицами твердого
к поверхности, к которой приложена
торый угол <jj.
Рис- 2Ж Деформация сдвига.
тела) ab, перпендикулярная
сила, поворачивается на неко-
некоj
При малом значении угла сдвига <|» приближенно имеем
, ЬЪ'
где d = ab есть толщина тела, а ЪЬ' — абсолютная величина сдвига
верхнего слоя относительно нижнего. Отсюда видно, что угол
сдвига ф характеризует относительный сдвиг, поэтому в пределах
выполнимости закона Гука получим соотношение:
i) = nf±, (8)
где я — постоянная величина, зависящая только от материала, из
которого изготовлен брусок, называемая коэффициентом сдвига;
S — площадь поверхности, к которой приложена сила ft.
352
ТВЕРДЫЕ ТЕЛА
[ГЛ. X
Вводя усилие pt =Ц-, перепишем формулу (8):
Величина, обратная я,
= я • Pt-
1
(8а)
N=
называется модулем сдвига. Вводя в формулу (8а) вместо коэф-
коэффициента сдвига я модуль сдвига N, получим
Для большинства однородных изотропных тел модуль сдвига N
по численному значению равен приблизительно 0,4 от численного
значения модуля Юнга Е.
Рассмотрим еще деформацию кручения, которая, как
мы увидим, сводится к деформации сдвига.
Возьмем стержень в виде кругового цилиндра дли-
длиной L и радиуса г (рис. 229). Пусть верхнее сечение
стержня закреплено неподвижно, а к нижнему прило-
приложен момент силы М, закручивающий стержень. Введем
в рассмотрение отрезок ОА = р, отложенный вдоль
одного из радиусов нижнего сечения. Под влиянием за-
закручивающего момента отрезок ОА повернется на угол <р
и займет положение ОА'. Относительной деформацией
будет величина <рД, т. е. угол закручивания, отнесенный
к единице длины стержня. В пределах упругой дефор-
деформации эта величина cp/Z. пропорциональна закручиваю-
закручивающему моменту М:
Рис. 229. Дефор'ма-
ция кручения.
A0)
Величина с постоянна для данного стержня; для раз-
различных стержней она зависит от их радиусов и от
свойств материалов, из которых они сделаны. Для определения с свяжем де-
деформацию кручения с деформацией сдвига.
При закручивании стержня его нижний торец испытывает сдвиг относи-
относительно верхнего; прямая ВА поворачивается, принимая положение ВА\ угол
ф является углом сдвига. По формуле (9) угол сдвига ф равен
* = -^-Л, (И)
где pt — касательное усилие, приложенное к элементу поверхности dS, рас-
расположенному у точки А' (см. рис. 230), а ./V—модуль сдвига.
Из рис. 229 имеем
откуда по A1) Pt = N^ = N -^-p.
A2)
Сила, приложенная к элементу поверхности dS, равна PfdS, а ее момент
<Ш = fp{ dS. Вводя полярные координаты S и р (рис. 230), получим для эле-
элемента поверхности dS = p dp db, откуда
dM=pt
§ 89] J ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ
Подставляя сюда значение pt по A2), найдем
353
Полный момент М, приложенный ко всему нижнему торцу стержня, по-
получим, проинтегрировав выражение dM по всей площади круга радиуса г.
М
2it r
= Т J J
откуда получаем
6 = 0р=0
Сравнивая A3) с формулой A0), найдем
2 1
A3)
Из формулы A3) следует: угол закручивания <р зависит от модуля
сдвига N и обратно пропорционален радиусу стержня, взятому в чет-
четвертой степени.
Переписывая формулу A3) в виде:
M=f.f,, оз.)
имеем, что для закручивания проволоки на данный угол у надо приложить
момент М, прямо пропорциональный г4 и обратно пропорциональный длине
проволоки L.
Следовательно, момент зависит весьма сильно от
радиуса. Толстые короткие стержни трудно подвергнуть
закручиванию; наоборот, тонкие длинные проволоки под
влиянием даже очень малых моментов обнаруживают
заметное закручивание. Этим обстоятельством пользу-
пользуются для создания чувствительных подвесных систем
в измерительных приборах.
Например, если маленькую магнитную стрелку под-
подвесить к длинной и тонкой проволоке, то можно опре-
определить малую пару сил, действующую со стороны внеш-
внешнего магнитного поля, по углу, на который эта пара
сил закрутит проволоку; угол закручивания проволоки
определяется по смещению луча света, отражающегося
от маленького зеркальца, прикрепленного к нити. Най-
Найдем, для примера, момент пары сил, способный закру-
закрутить проволоку длиной 5 см и радиусом 0,02 мм на
угол 10'. Модуль сдвига материала проволоки будем
считать,равным 6000 кГ/мм'2.
Для решения воспользуемся формулой A3а):
Рис. 230. К опре-
определению момента
dM, приложенного
к элементу поверх-
поверхности dS.
4
2,
0-0029 КГ мм =
10- кГ мм.
Переводя полученный ответ в Г см, найдем
М=8,74 • 10-" Г см,
т. е. момент силы, равный приблизительно моменту силы в 10~2 мГ, прило-
приложенной к плечу в 1 см, достаточен, чтобы вызвать закручивание упомянутой
проволоки на 10'.
354
ТВЕРДЫЕ ТЕЛА
[гл. х
Рассмотрим еще случай собственных крутильных колебаний тела аЪ
с моментом инерции /, подвешенного к тонкой нити (рис. 231). Момент инер-
инерции самой нити считаем настолько малым, что им можно пренебречь.
По сказанному в § 35, угловое ускорение тела р равно
Р = у, A4)
где М—момент сил, приложенных к телу. С другой стороны, угловое уско-
ускорение р равно второй производной от угла поворота <р по времени: обозна-
обозначая вторую производную по времени двумя точками, поставленными над
буквой <р, получим: Р = <р. Момент сил М, приложенных
к телу, равен моменту, приложенному к нити, но имеет об-
обратное направление, откуда по формуле A3а):
величина D = ^- • j- может быть . названа модулем кру-
кручения данной нити. Подставляя полученные значения р и М
в A4), найдем
Рис. 231. '
Стержень ab,
подвешенный
к нити L.
Как будет показано в § 97, решение такого дифферен-
дифференциального уравнения представляет колебания с периодом
A5)
Таким образом, период крутильных колебаний тела, подвешенного к нити,
всецело определяется его моментом инерции и модулем кручения нити.
Кинетическая энергия колебаний Ek равна
Она не остается постоянной в течение периода, но достигает максимума, когда
тело проходит через положение равновесия, и становится равной нулю в мо-
моменты наибольшего поворота тела (ср. со сказанным в § 112).
Потенциальную энергию Ер определим, воспользовавшись-формулой B)
§ 39, по которой для поворота тела на угол if надо совершить работу
А = Му. A6)
В случае закручивания нити, момент сил не постоянен, но сам зависит
от угла ср, поэтому в формуле A6) надо подразумевать под М среднее зна-
значение момента М = -^- D<f. Отсюда А = Му = -х- Df2. Потенциальная энер-
энергия Ер численно равна этой работе:
?p = i-Z>fa. A7)
В моменты наибольшего поворота тела, когда его кинетическая энергия ?fe
равна нулю, потенциальная энергия Ер, достигая своего максимума, стано-
становится равной полной энергии Е.
Таким образом:
где <рта![ — наибольший угол поворота тела во время его крутильных коле-
колебаний.
§ 90] ПРЕДЕЛЫ УПРУГОСТИ И ПРОЧНОСТИ. ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ 355
§ 90. Пределы упругости и прочности. Пластические дефор-
деформации. Всякое твердое тело дает деформации, подчиняющиеся закону
Гука лишь до известного предела.
Точнее говоря, зависимость относительной деформации от усилия
не является вообще линейной, но отступления от линейности не-
невелики при малых значениях относительной деформации Ах/х и
становятся заметными при увеличении Ьх/х. Графически зависимость
относительной деформации Ах/х от усилия р представлена на
рис. 232 а. При боль-
больших усилиях деформа-
деформация происходит легче,
чем при малых. То зна-
значение усилия р=р„р,
начиная с которого от-
ступления от линей-
линейности становятся за-
заметными, называется
пределом пропорцио-
пропорциональности. Строго го-
говоря, не существует
определенного значе-
значения предела пропор-
Ре
?
Рис. 232. Ход относительной деформации твердого
тела в зависимости от величины приложенного
усилия.
циональности, так как
возможность обнаружить отступления от линейной зависимости опре-
определяется точностью измерений.
При упругой деформации, после прекращения действия внешней
силы, деформация полностью пропадает, т. е. тело принимает преж-
прежние размеры (прежнюю форму). Однако при значениях усилия, пре-
превышающих так называемый предел упругости ре, наступает иной тип
деформации, носящей название пластической деформации, не про-
пропадающей полностью после прекращения действия сил. Пластическая
деформация происходит легче упругой. Если при достижении неко-
некоторой точки Ъ (рис. 232 б), лежащей в области пластической де-
деформации, начать уменьшать усилие р до нуля, то тело не вернется
в исходное состояние по линии ЬаО; убывание деформации изобра-
изобразится пунктирной линией bd, тело сохранит остаточную деформа-
деформацию Ой. Если мы, например, подвергли тело растяжению, зайдя за
предел упругости и достигнув области пластической деформации, то
по прекращении действия сил тело будет иметь ббльшую длину, чем
оно имело первоначально: оно сохранит остаточную деформацию
растяжения.
При все увеличивающемся усилии можно достичь разрушения
стержня; соответствующее значение усилия называется пределом
прочности. Если предел прочности близок к пределу упругости, то
такое тело дает лишь незначительные остаточные деформации: оно
называется хрупким (например, закаленная сталь). Тела, способные
356
ТВЕРДЫЕ ТЕЛА
[гл. х
давать большие пластические деформации, называются „пластиче-
„пластическими"; так, например, свинцовые или цинковые проволоки обна-
обнаруживают значительные пластические и остаточные деформации.
Для реальных твердых тел ход относительной деформации в за-
зависимости от усилия значительно отличается от изображенного на
рис. 232. Он зависит в большой мере для каждого данного материала
от характера его обработки, а также от длительности действия сил.
Одно и то же тело может при кратковременных силах проявлять
себя как хрупкое, а при длительных, хотя бы и слабых силах, об-
обнаруживать настолько сильные пластиче-
пластические деформации, что оно может быть
названо текучим.
На рис. 233 представлена диаграмма рас-
растяжения железа. Прямолинейная часть Оа со-
соответствует выполнению закона Гука; часть ab,
хотя и относится еще к упругой деформации,
но дает уже отступления от закона Гука: здесь
удлинение возрастает быстрее усилия. За точ-
д кой Ъ удлинение может возрастать и без уве-
— личения нагрузки— это область текучести. При
дальнейшем увеличении усилия стержень вновь
приобретает способность сопротивления растя-
растяжению: кривая загибает вверх. Точка d отве-
отвечает разрыву (предел прочности).
Предел прочности й
Рис. 233. Диаграмма растя-
растяжения железа.
Приведем некоторые численные данные, характеризующие упругие свой-
свойства различных металлов.
В качестве примера рассчитаем, воспользовавшись данными табл. XIII,
величину наибольших возможных упругих растяжений для проволок из при-
приведенных в таблице материалов.
Таблица XIII
Упругие свойства металлов
Металл
Свинец
Олово
Медь (мягкая)
Железо (мягкое)
Углеродистая сталь
Молибденовая сталь ....
' Модуль
Юнга
в кГ/мм?
1800
3 000
10 000
19 000
20 000
22 000
Предел
упругости
в кГ/мм3
0,25
0,34
3
5
33
60
Предел
прочности
в кГ/мм2
2
2
20
35
75
150
Наибольшее возможное упругое растяжение (—г-| определится как
' \ L /max
растяжение, вызванное усилием, равным пределу упругости ре.
Отсюда, по формуле Bа) § 89:
/ДМ _Ре
\ L Jmax ~" Е '
где Е—модуль Юнга.
§ 90] ПРЕДЕЛЫ УПРУГОСТИ И ПРОЧНОСТИ. ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ 357
Подставив сюда вместо ре и Е их численные значения, найдем:
.. /ДМ
Материал -;-
\ L /max
Олово 0,00011
Свинец 0,00014
Медь . . 0,00030
Железо 0,00026
Углеродистая сталь . . . 0,00165
Молибденовая сталь . . . 0,00273
Таким образом, в предела: упругой деформации оловянная проволока
может быть растянута лишь приблизительно на 0,01% от своей первона-
первоначальной длины, проволока же из молибденовой стали может быть растянута
почти на 0,3°/,) от своей первоначальной длины.
Реальные твердые тела обнаруживают в большей или меньшей
мере сложную зависимость деформации от времени, не учитываемую
ни законом Гука, ни теми упрощенными схемами, которые мы рас-
рассматривали. Вообще говоря, после начала действия силы деформация
устанавливается не сразу в полной
мере, после же прекращения действия
силы она пропадает не целиком: часть
ее остается и медленно спадает затем
со временем. Схематически зависи-
мость упругой деформации от времени
представлена на рис. 234. Если в мо-
мент времени tu на твердое тело на-
чинает действовать сила, то весьма
быстро устанавливается начальная to C/ Время
упругая деформация АВ, затем под Рис. 234. Зависимость деформа-
влиянием установившейся постоянной иии от времени действия силы,
силы / деформация продолжает мед-
медленно возрастать со временем по кривой ВС'С. Если в момент
времени tt действие силы прекращается, то деформация сперва бы-
быстро спадает на величину CD, равную АВ, а затем спадает медленно
по кривой DEE!. Таким образом, после прекращения действия силы
сохраняется остаточная деформация A'D, спадающая лишь посте-
постепенно; тело медленно восстанавливает свою форму. Это явление
называется упругим последействием.
Упругое последействие легко наблюдать при растяжении резиновой
трубки. Длинная резиновая трубка подвешивается вертикально. К ниж-
нижнему концу на некоторое время прикрепляется груз Р, который
удлиняет трубку на величину Д/.. Сразу после снятия груза Р ре-
резиновая трубка вновь укорачивается, однако на величину \L' <^Д/..
Остается заметное удлинение Ы = AZ. — Д//, которое затем медленно
(в течение десятка минут) пропадает.
Для многих твердых тел часть деформации ВС'С носит необрати-
необратимый, пластический характер. Такие тела ведут себя по отношению
358
ТВЕРДЫЕ ТЕЛА
[гл. х
к слабым, но длительно действующим силам, как тела жидкие, в то
время как при действии больших кратковременных сил они оказы-
оказываются хрупкими. Например, лед или вар текут под влиянием дли-
длительно действующих сил и легко ломаются при кратковременных,
но более интенсивных воздействиях.
§ 91. Деформации с точки зрения кристаллической структуры
твердых тел. Упругие деформации сжатия и растяжения в монокри-
монокристаллах легко могут быть объяснены с точки зрения существования
кристаллической решетки. Равновесие кристаллической решетки, как
было указано в § 87, определяется взаимной компенсацией сил при-
притяжения и отталкивания, существующих между частицами (ионами
или атомами), образующими решетку. Например, в случае ионной
решетки, при сжатии кристалла расстояние г0 между соседними ионами
уменьшается, силы отталкивания становятся больше сил притяжения,
в результате чего появляется Суммарная сила отталкивания, противо-
противодействующая внешней силе, сжимающей кристалл. Чем больше вы-
выведены ионы из положения равновесия, т. е. чем больше деформация,
тем значительнее сила отталкивания. При прекращении действия
внешней силы ионы возвращаются в свои положения равновесия,
решетка принимает прежний вид, что означает, что деформация
кристалла пропала. Точно так же при растяжении кристалла рас-
расстояние г0 между соседними
Таблица XIV
Вычисленные и наблюденные зна-
значения коэффициентов всесторон-
всестороннего сжатия ?
ионами увеличивается, силы при-
притяжения становятся больше сил
отталкивания, кристалл в целом
сопротивляется внешнему растя-
растягивающему усилию.
Теория кристаллических решеток
позволяет вычислить коэффициенты
всестороннего сжатия для ионных кри-
кристаллов типа NaCI. В табл. XIV при-
приведены наблюденные и вычисленные
значения коэффициентов всесторон-
всестороннего сжатия -J для ряда кристаллов.
Здесь значения f даны в CGS-си-
стеме. Совпадение между вычислен-
вычисленными и наблюденными значениями,
как видно, очень хорошее.
При деформации сдвига проис-
происходит скашивание решетки. В слу-
случае простейшей кубической ионной решетки, каждая элементарная
ячейка решетки из куба превращается в косоугольный параллелепипед,
диагональ ас (рис. 235) оказывается укороченной, диагональ bd —
удлиненной, в результате чего между ионами а и с возникают силы
отталкивания, а между ионами b и d — силы притяжения. Решетка
стремится восстановить спою прежнюю форму, что и обуславливает
возникновение упругой деформации сдвига.
Кристалл
NaCI
NaBr
NaJ
КС1
КВг
KJ
T1CI
TIBr
T1J
Тнабл-Ю12
4,1
5,1
6,9
5,0
6,2
8,6
4,7
5,1
6,7
1выч ш
3,56
4,73
6,30
5,36
6,64
8,68
4,69
5,36
6,76
§ 91] ДЕФОРМАЦИИ С ТОЧКИ ЗРЕНИЯ КРИСТАЛЛИЧЕСКОЙ СТРУКТУРЫ 359
В случае сдвига легко объяснить также появление пластической
и остаточной деформаций. Благодаря геометрически 4 правильному
расположению атомов (или ионов), в пространственной решетке
кристалла существуют пло-
плоскости, вдоль которых мо-
может произойти соскальзыва-
соскальзывание частей решетки друг
относительно друга на-
настолько, что положитель-
положительные ионы снова располо-
расположатся над отрицательными.
с- 235. Скашивание кристаллической ре-
шетки при деформации сдвига.
Тогда взаимное расположе-
ние этих ионов окажется
таким же, как и в перво-
первоначальной решетке, и не будет сил, стремящихся сместить их об-
обратно. Этим объясняется остаточная деформация.
На первый взгляд представляется более трудным объяснить воз-
возможность остаточной деформации в монокристаллах при растяжении.
На самом деле оказывается, что такие деформации сводятся также
к сдвигам, т. е., в конечном счете, снова к соскальзыванию одних
слоев вдоль других.
Представим себе стержень с круговым сечением, вырезанный из
монокристалла так, что плоскости, вдоль которых может происходить
соскальзывание, проходят косо, как ука-
указано на рис. 236а. Такой стержень в из-
известном смысле сходен со стопой монет.
При растягивании стержня в нем проис-
происходят соскальзывания по косо располо-
расположенным плоскостям, в результате чего
стержень в целом делается длиннее
(рис. 2366), т. е. дает остаточную дефор-
деформацию растяжения. При этом, очевидно,
должна изменяться форма стержня: его
а) б) сечение из круглого должно стать эллип-
„ .„. „ тическим. Опыты, произведенные над рас-
Рис. 236. Сдвиг по плоско- v y
стям спайности при растя- тяжением монокристаллических палочек
жении стержня, вырезанного цинка, показали, что при образовании
из монокристалла. остаточной деформации круглое сечение
принимает овальную вытянутую форму.
Поверхность таких цинковых палочек, первоначально гладкая, после
растяжения делается шероховатой.
Все это подтверждает точку зрения, что остаточная деформация
растяжения обусловлена соскальзыванием частей кристалла вдоль
определенных плоскостей.
Теория кристаллических решеток позволяет вычислить прочность
кристаллов. Однако вычисленные значения предела прочности для
360 ТВЕРДЫЕ ТЕЛА [ГЛ. X
монокристаллов оказываются гораздо выше фактически наблюдаемых.
Так, теоретический предел прочности для кристаллов каменной соли
имеет значение, близкое к 200 кГ/мм'1. Это значит, что следовало
бы приложить силу в 200 кГ к стержню из каменной соли с попе-
поперечным сечением в 1 ммг, чтобы его разорвать. На самом деле
стержни, вырезанные из монокристалла каменной соли, разрываются
при нагрузке не более lj9 кГ\мм*\ таким образом, эксперименталь-
экспериментальные данные оказываются в четыреста раз меньше теоретически вы-
вычисленного значения. Это огромное расхождение объясняется, однако,
не неправильностью теории кристаллической- решетки, но тем, что
расчеты относятся к идеальному кристаллу, представляющему собой
совершенно правильную однородную решетку; всякий же реальный
кристалл обладает большим числом дефектов: в нем существуют
места, где нарушается правильная структура решетки; особую роль
играет также поверхность, где условия иные, чем внутри кристалла.
Большую роль должны играть трещины на поверхности кристалла:
достаточно на поверхности появиться микроскопической трещинке,
чтобы на грани трещинки получилось перенапряжение, в результате
которого трещинка начинает идти дальше и ведет к разрыву всего кри-
кристалла. Чтобы исключить роль поверхностных трещинок, А. Ф. Иоффе
брал палочку каменной соли, подвешивал к ней груз, настолько ма-
малый, чтобы не наступал разрыв, и опускал ее в теплую воду, в ко-
которой происходило растворение соли. При растворении поверхно-
поверхностного слоя уничтожались бывшие на нем повреждения, новые же
не успевали образоваться, так как растворение велось непрерывно.
По мере растворения палочка становилась все тоньше и, наконец,
разрывалась под влиянием силы тяжести привешенного к ней груза.
По площади поперечного сечения палочки в момент разрыва и по
величине подвешенного груза определялся предел прочности, кото-
который значительно превосходил обычный предел прочности кристаллов
каменной соли. В некоторых случаях Иоффе наблюдал разрыв лишь
при напряжении в 160 кГ/мм2, т. е. в триста раз большем, чем
обычно, и близком к теоретическому. Возможно, что роль воды
в опытах Иоффе не ограничивается удалением поверхностных тре-
трещинок и носит более сложный характер, но во всяком случае опыты
Иоффе указывают на возможность обнаружить прочности монокри-
монокристаллов, близкие к теоретическим расчетам.
Практическая прочность кристаллов в сотни раз ниже их теоре-
теоретической прочности. Решетка реальных кристаллов отличается от
идеальной. В ней всегда имеются внутренние дефекты: наличие пу-
пустых, незанятых частицами мест и местные нарушения порядка.
Ничтожные дефекты на поверхности и внутри решетки ведут к раз-
разрыву всего кристалла.
Поликристаллические тела практически оказываются прочнее мо-
монокристаллов. Механические свойства поликристаллических тел, како-
каковыми являются обычные металлы, обусловлены формой отдельных
§ 92] ТЕПЛОВОЕ ДВИЖЕНИЕ В ТВЕРДЫХ ТЕЛАХ 361
кристаллов и силами сцепления между ними. Всякое изменение
формы отдельных кристалликов, из которых состоит кристаллическое
тело, а также изменения в их взаимном расположении ведут к суще-
существенным изменениям механических свойств всего твердого тела
в целом.
Изменениями формы и расположения кристалликов объясняется
влияние на прочность и другие механические свойства металлов про-
прокатки, ковки, закалки и иных видов холодной и горячей обработки.
§ 92. Тепловое движение в твердых телах. Расширение твер-
твердых тел. Каждая частица (атом или ион), из которых построена
пространственная решетка кристаллического твердого тела, совершает
колебания около положения равновесия. Энергия этих колебаний и
представляет собою внутреннюю энергию твердого тела. Таким обра-
образом, тепловое движение частиц в твердом теле отличается по своему
характеру от теплового движения частиц в газах и жидкостях. В газах
отдельные молекулы свободно летают, испытывая друг с другом
лишь упругие столкновения; этим объясняется сравнительно большая
скорость диффузии газов. В жидкостях молекулы непрерывно стал-
сталкиваются при своем беспорядочном движении с соседними молеку-
молекулами. Они „толкутся" около одного места и, как было указано
в § 78, лишь постепенно перемещаются. Диффузия в жидкостях су-
существует, хотя и происходит медленнее, чем в газах. В кристалли-
кристаллической решетке твердого тела каждая частица (атом или ион) имеет
определенное положение равновесия, около которого она совершает
колебания. Кроме того, в твердом теле частицы, вообще говоря,
могут переходить с места на место; однако эти переходы достаточно
редки. Диффузия в твердых телах происходит чрезвычайно медленно.
Требуются весьма тонкие наблюдения, чтобы заметить некоторое
проникновение двух соприкасающихся металлов друг в друга, причем
такое проникновение может быть обнаружено лишь после длитель-
длительного соприкосновения тел.
При повышении температуры твердого тела отклонения частиц
от их положений равновесия возрастают. Это ведет к тепловому
расширению твердого тела.
Полагая длину твердого тела при температуре 0° равной Lo, мы
получим, как известно, для удлинения тела Д? при нагревании его
до температуры t:
M = aLot, A)
где а — коэффициент линейного теплового расширения твердого
тела. Отсюда длина тела Lt при температуре t будет равна
Lt = Lu-\-M = L,{\+at), B)
т. е. длина твердого тела возрастает линейно с температурой. На
самом деле это соотношение ввпГолняется не вполне точно, коэффи-
коэффициент теплового расширения а несколько зависит от температуры
362 ТВЕРДЫЕ ТЕЛА [ГЛ. X
(ср. со сказанным в § 44), но для большинства практических целей а
можно считать постоянным. Для твердых тел коэффициенты линей-
линейного расширения малы и представляют собою величины порядка 10~5
и 10 град'1.
В результате линейного расширения возрастает и объем тела.
Представим себе тело в виде куба с длиной ребра 10 и обозначим
его первоначальный объем, равный L30, через Уо. Тогда объем при
температуре t окажется равным
Возводя бином A -j- at) в куб и пренебрегая членами, содержащими а*
и а3, получим
V= V0(l-{-3at).
Обозначим За через Ь, имеем
V=Vu(\+bt). C)
Величина Ь называется коэффициентом объемного теплового
расширения твердого тела. Из приведенного расчета следует, что
приближенно коэффициент Ъ равен утроенному коэффициенту линей-
линейного расширения.
Для анизотропных кристаллов коэффициент линейного расшире-
расширения а различен для различных направлений. Это ведет к тому, что,
расширяясь, кристалл не остается подобен самому себе: он меняет
свою форму. Некоторая физическая прямая (т. е. линия, связанная
с определенными частицами твердого тела) при тепловом расширении
кристалла, вообще говоря, не остается прямой. Однако в каждом
кристалле есть такие направления, вдоль которых физическая прямая
остается прямой и при тепловом расширении. Эти направления назы-
называются кристаллографическими осями. Значения коэффициентов
теплового расширения а вдоль кристаллографических осей называются
главными. В общем случае кристаллы обладают тремя осями и тремя
различными главными коэффициентами линейного теплового расшире-
расширения аи а4 и а3. Для кристаллов некоторых систем эти три напра-
направления взаимно перпендикулярны.
Представим себе параллелепипед, вырезанный из кристалла, со
взаимно перпендикулярными осями, с длиной ребер, при темпера-
температуре 0° равной Z.ol, L02, Lm. Объем этого параллелепипеда Vo=
= Z,Oi • Lm • Lm. При нагревании до температуры t ребра примут
значения:
Новый объем параллелепипеда будет равен
§ 93] ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ 363
Производя перемножения и пренебрегая всеми членами, содержа-
содержащими произведения величин а1г а2, а3, получим приближенно
V=VO[1+(«i + «a +«а)']-
С другой стороны, можно положить
V=V0(l+bt),
где Ъ — коэффициент объемного теплового расширения кристалла.
Из сравнения двух последних формул получим
D)
Таким образом, коэффициент объемного расширения кристалла
приближенно равен сумме его главных коэффициентов линейного
расширения. Для изотропного тела а1 = а2 = аз = а. и мы снова
получаем из D) уже выведенное нами соотношение Ь = Ъа.
В результате нагревания в твердых телах, если они не могут при этом
свободно расширяться, возникают большие механические напряжения. Для
оценки этих напряжений произведем следующий расчет. Пусть стержень
длиной Lo при нагревании от 0° до t° удлинился на величину
Д1 = aLot,
где а — коэффициент линейного расширения материала, из которого сделан
стержень. Для обратного укорочения стержня путем упругой деформации
сжатия на величину LL надо приложить к нему усилие рп, определяемое
формулой Bа) § 89:
LL — ~? L«Pn i
где Е—модуль Юнга материала стержня. Приравнивая друг другу оба
значения Д?, получим
1
-р Lapn = aLot, откуда рп = aEt.
Для железа, например, а= 1 • 10~5 град'1 и ? = 2 • 104 кГ/ммя, откуда при
повышении температуры на <=1°С, к стержню, чтобы компенсировать его
тепловое расширение, надо приложить усилие
рп ЙЁ1 • 10~6 • 2 • 104 кГ/мм* = 0,2 кГ/мм* = 20 кГ/см*.
С возможностью возникновения таких напряжений при нагреваниях при-
приходится считаться в строительной технике. Чтобы избегнуть этих напряже-
напряжений, рельсы железнодорожных путей укладывают со свободными проме-
промежутками на стыках, фермы мостов и других сооружений у концов не закреп-
закрепляют жестко, но укладывают на катки и т. д.
При соединении различных материалов необходимо еще принимать во
внимание напряжения, могущие произойти от разных значений коэффициентов
расширения.
§ 93. Теплоемкость твердых тел. Запас внутренней энергии
твердого тела представляет собою запас энергии колебаний частиц,
из которых оно построено, а также их взаимной потенциальной
энергии. Частицы (атомы или ионы), образующие кристаллическую
решетку, вообще говоря, не являются независимыми, так как между
364 ТВЕРДЫЕ ТЕЛА [ГЛ. X
ними существуют значительные силы взаимодействия. Поэтому коле-
колебания частиц надо рассматривать как связанные; в решетке, как
в целом, возникают колебания различных частот, энергия которых
и должна быть учтена.
Однако при достаточно высоких температурах, когда энергия
колебаний становится большой, частицы можно рассматривать как
независимые. Каждая из частиц совершает около положения равно-
равновесия колебательное движение. Для определения средней энергии
колебаний частицы надо принять во внимание, что она обладает за-
запасом как кинетической, так и потенциальной энергии. На каждый
из этих видов энергии в среднем придется одинаковая энергия. Та-
Таким образом, если обозначить среднюю кинетическую энергию ча-
частицы через wk, то полное значение средней энергии частицы будет
В пространственной кристаллической решетке каждая частица
может колебаться около своего положения равновесия в любом на-
направлении; следовательно, ее ' скорость v должна быть задана как
вектор. Отсюда получаем, что каждая частица обладает тремя сте-
степенями свободы L Поэтому средняя кинетическая энергия ~wk =
= -у kT= — kT, а полное значение средней энергии одной частицы
Полную внутреннюю энергию одного моля твердого тела U по-
получим, умножив среднюю энергию одной частицы на число незави-
независимо колеблющихся частиц, содержащихся в одном моле. Для хими-
химически простых твердых кристаллических тел число независимо колеб-
колеблющихся частиц в одном моле' совпадает с числом Авогадро N,
так что
U=w-N=3NkT=3RT, A)
где R — газовая постоянная.
Для твердых тел, обладающих малым коэффициентом теплового
расширения, теплоемкости при постоянном объеме и постоянном да-
давлении практически не различаются. Поэтому в дальнейшем мы их
не будем различать. Тогда имеем: атомная теплоемкость химически
простого кристаллического твердого тела, численно равная увеличе-
увеличению внутренней энергии U при повышении температуры на 1°, по
формуле A) будет равна
а так как газовая постоянная ^ = 2 кал/град моль, то
С^б кал/град моль, B)
1 Для элементов в твердом виде под словом „моль" следует подразуме-
подразумевать грамматом.
§ 93]
ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
365
Таблица XV
Атомная теплоемкость
элементов в твердом
состоянии
т. е. атомная теплоемкость всех химически простых кристал-
кристаллических твердых тел при достаточно высокой температуре
равна 6 кал/град моль. Это утверждение носит название закона
Дюлонга и Пти.
Без более детального разбора характера колебаний взаимодей-
взаимодействующих между собою частиц, образующих кристалл, нельзя вперед
указать, какая температура должна считаться для данного тела до-
достаточно высокой, чтобы выполнялся за-
закон Дюлонга и Пти. Сами Дюлонг и Пти
установили свой закон на основании эм-
эмпирических данных, полученных для ряда
твердых тел при комнатных температу-
температурах.
Таблица XV дает значения атомных
теплоемкостей некоторых химических про-
простых твердых тел.
Из таблицы видно, что для большин-
большинства из приведенных веществ (Al, Fe, Аи,
Cd и т. д.) атомная теплоемкость близка
к 6 кал/град моль, т. е. для них ком-
комнатная температура достаточно высока,
чтобы атомы колебались практически не-
независимо друг от друга; для этих тел за-
закон Дюлонга и Пти выполняется. Для
алмаза, кремния и бора при комнатной
температуре атомные теплоемкости много
меньше 6 кал/град моль; это означает,
что в кристаллических решетках этих ве-
веществ при комнатных температурах колебания атомов еще нельзя
считать независимыми. При температуре 985° С атомная теплоем-
теплоемкость алмаза становится равной 5,52, г. е. приближается к ожидае-
ожидаемому значению 6.
Многие кристаллы химически сложных веществ носят ионный
характер. В этих кристаллах нельзя выделить отдельные молекулы
данного вещества, как их можно выделить в газообразном состоянии.
В кристаллической решетке лишь правильно чередуются все те
атомы, в виде ионов, которые входили в состав молекул газа дан-
данного вещества. Отсюда число частиц, образующих моль этого веще-
вещества в кристаллическом состоянии, равно числу атомов в моле этого
вещества. Так, один моль газообразного хлористого натрия содержит
в себе число молекул NaCl, равное числу Авогадро N. В кристалле
же каменной соли мы имеем расположенными по узлам решетки
(рис. 223) ионы Na+ и СГ, общее число которых (ионов Na+ и
ионов С1~ вместе) равно 2Л/. Считая по-прежнему, что каждому
из ионов в решетке соответствует средняя энергия w = 2 • у k T,
Вещество
Алюминий, А1.
Алмаз, С
Железо, Fe . . .
Золото, Аи ...
Кадмий, Cd. .
Кремний, Si. .
Медь, Си ....
Олово, Sn . . .
Платина, Pt. .
Серебро, Ag. .
Цинк, Zn . . . .
Бор, В
Атомная
теплоем-
теплоемкость С
6,14
1,35
6,36
6,36
6,11
4,67
5,91
6,63
6,29
6,13
6,10
2,51
366
ТВЕРДЫЕ ТЕЛА
[ГЛ. X
Таблица XVI
Молярная теплоемкость
твердых соединений
получим, что молярная теплоемкость кристаллической каменной соли
должна равняться:
С = 2у k • 27V= %kN= 6R,
или приближенно 12 кал/град моль. То же рассуждение справедливо
и в том случае, когда атомы, оставаясь в решетке нейтральными,
колеблются независимо друг от друга. Отсюда следует, что прибли-
приблизительно 12 кал/град моль должна равняться молярная теплоем-
теплоемкость и всех других двуатомных соединений в твердом состоянии.
Так же получим, что трехатомные соединения должны иметь моляр-
молярную теплоемкость, приблизительно равную 18 кал/град моль, а че-
четырехатомные — равную 24 кал/град моль
Ч т. д.
Этот вывод совпадает с эмпирически
установленным законом Джоуля и Коппа,
по которому молярная теплоемкость
твердых соединений равна сумме атом-
атомных теплоемкостей элементов, входя-
входящих в состав этих соединений.
Закон Джоуля и Коппа может быть
справедлив лишь при таких высоких тем-
температурах, при которых колебания частиц
можно считать независимыми.*
Таблица XVI показывает, что для ряда
твердых соединений при комнатной тем-
температуре закон Джоуля и Коппа выпол-
выполняется достаточно хорошо.
С понижением температуры теплоемкость всех твердых тел па-
падает. Падение теплоемкости с температурой графически представлено
на рис. 237. При стремлении темпе-
температуры к абсолютному нулю теп-
теплоемкость всех твердых тел стре-
стремится к нулю. Ход теплоемкости
твердых тел при очень низких темпе-
температурах может быть объяснен лишь
на основании квантовой механики.
В § 49 мы отмечали, что, согласно кван-
квантовой механике, энергия отдельных частиц
меняется лишь скачкообразно. Это отно-
относится и к энергии колебаний атомов (или
ионов) в кристаллической решетке. Порция
Вещество
CuO
NaCl
СаС12
ВаС12
KNO, ......
Моляр-
Молярная теп-
лоем-
лоемкость С
11,3
12,1
18,2
18,6
24,1
Рис. 237. Ход [еалоемкости
твердых тел с температурой.
энергии, на которую скачкообразно меняется энергия колеблющейся в ре-
решетке частицы, равна hi, где h — постоянная Планка, равная 6,6- 1(Г27 эрг сек,
и v—частота колебаний частицы. При тех температурах, при которых средняя
энергия -к-kT, приходящаяся на одну степень свободы, велика по сравнению
с hi, энергию колебания частицы можно считать меняющейся непрерывно
§ 94] ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ 307
с температурой Т и, следовательно, применять классическую теорию. При
таких низких температурах, при которых средняя энергия -^ кТ одного по-
порядка с порцией энергии hi, расчет должен производиться на основе кванто-
квантовой механики. Частота колебаний частиц в кристаллической решетке есть ве-
величина порядка 1012 сек., откуда из неравенства
получаем, что классический способ расчета пригоден для температур, удовле-
удовлетворяющих условию:
о . fj fj . ю~27 . 1012
^ 1,4 . Ю-" К =100 К.
Таким образом, для комнатных температур G"=300°К) годится класси-
классический способ расчета теплоемкостей, при температурах же порядка—200° С
необходимо рассчитывать теплоемкость по квантовой теории.
Основы квантовой теории теплоемкости твердых тел были даны Эйнштей-
Эйнштейном. Затем Дебай принял во внимание большую роль взаимодействия частиц,
образующих решетку, при низких температурах. Дебай рассматривал не коле-
колебания отдельных частиц, но колебания, устанавливающиеся в решетке, как
в целом. Он показал, что в кристаллической решетке должны установиться
стоячие волны, различник частот, вплЪть до акустических.
Суммируя энергию всех этих колебаний кристаллической решетки и
учитывая их зависимость от температуры, согласно квантовой механике,
Дебай пришел к результатам, очень хорошо согласующимся с опытами. Для
очень низках температур теплоемкость твердых тел меняется пропор-
пропорционально третьей степени абсолютной температуры.
Теория Дебая замечательна тем, что она связывает тепловые колебания
в кристаллах с их акустическими колебаниями.
Советский физик Л. И. Мандельштам указал, то наличие тепловых упругих
волн в кристаллах должно сказаться на характере света, рассеянного от кристал-
кристаллов (см. т. III). Предсказанное Л. И. Мандельштамом явление было наблюдено
советским физиком Е. Ф. Гроссом; тем самым существование упругих тепло-
тепловых колебаний в твердых телах оказалось экспериментально подтвержденным.
§ 94. Плавление и испарение твердых тел. Как указано в § 87,
. кристаллические твердые тела имеют определенную температуру
плавления. Эта температура несколько зависит от внешних условий.
Если плавление вещества сопровождается увеличением объема
(что имеет место для большинства веществ), то при увеличении
давления температура плавления повышается: уже расплавленное
вещество может при увеличении давления вновь затвердеть.
Если плавление вещества сопровождается уменьшением объема
(вода, висмут, сурьма и некоторые другие вещества), то при
увеличении давления температура плавления понижается; уже
затвердевшее вещество может при увеличении давления вновь
сделаться жидким. Лед под давлением тает при температуре ниже
0° С; точка плавления льда понижается на 1° при увеличении давле-
давления приблизительно на 130 am.
При очень высоких давлениях вещества, которые при плавлении
расширяются, можно удержать в твердом состоянии при темпера-
температуре выше критической.
368 ТВЕРДЫЕ ТЕЛА [ГЛ. X
Так, хлористый фосфор может быть в твердом состоянии при
давлении 2050 кГ/см* при *=102°, в то время как его критиче-
критическая точка лежит при р = 75 кГ/см* и ^ = 50°. Также углекислота,
критическая температура которой равна 31°, при давлении р =
= 12 000 кГ/см* остается твердой при tf = 93° С.
При разборе изотерм Ван-дер-Ваальса мы видели, что при тем-
температуре выше критической они идут плавно, что не позволяет при
этом различать две фазы — газообразную и жидкую. Однако твер-
твердое состояние оказывается возможным и при температуре выше кри-
критической.
Процесс перехода из твердого состояния в жидкое связан с за-
затратой энергии; другими словами, для того, чтобы данную массу
твердого тела перевести в жидкое состояние при той же темпера-
температуре, необходимо сообщить телу некоторое количество тепла, назы-
называемого теплотой плавления. При затвердевании жидкости эта
энергия выделяется в виде тепла. Теплота плавления весьма раз-
различна для разных веществ; так, для воды она равна 80 кал/г, а для
ртути — всего 2,75 кал/г. ,*;У^' •' - "
На стр. 331 мы видели, что, рассматривая цикл Карно, проводимый со
смесью жидкости и насыщенного пара над ней в качестве рабочего вещества,
можно установить связь между зависимостью упругости насыщенных паров
от температуры и теплотой парообразования. Однако все приведенные там
рассуждения остаются в силе и тогда, когда в качестве рабочего вещества
берется смесь твердой и жидкой фаз какого-либо тела.
Таким образом, формула [F), стр. 331]:
dT~ T V, — V»
A)
остается справедливой и в том случае, если считать Т за температуру пла-
плавления, \ — за теплоту плавления, V'a и Va— соответственно за удельные объемы
жидкой и твердой фаз и р — за давление, под которым находится смесь.
Формулу A) можно переписать также в
тогда она дает изменение температуры плавления dT при изменении давле-
давления на dp.
Из формулы B) непосредственно вытекают указанные правила: если
удельный объем жидкости больше удельного объема твердой фазы (V'o > Vo),
то при увеличении давления (dp^>0) точка плавления повышается, если
Уо < У<>| то при повышении давления точка плавления понижается. Например,
удельный объем льда при 0° С равен. Va= 1,0908 см'/г, удельный объем воды
при той же температуре V'o= 1,0001 смг, теплота плавления льда Х =
= 79 кал/г = 33 ¦ 108 эрг/г. Отсюда вблизи Г=273°К изменение давления
на dp дает изменение температуры плавления на
dT= 273 °'°907 d
где р выражено в барах.
§ 94] ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ 369
Если р выразить в атмосферах, то
rf 7" = — 0,0076 dp.
Отсюда получаем, что для понижения температуры плавления льда на 1°
надо увеличить давление на nrUY,R am= 130 am, в согласии с данными,
U,UU iO
приведенными в основном тексте.
Температура плавления очень сильно зависит от чистоты данного
вещества. Иногда незначительные примеси могут заметно понизить
температуру плавления. Для сплавов, которые не представляют
собою определенных химических соединений, но могут быть полу-
получены при любых пропорциях сплавляемых
веществ, зависимость температуры плав-
плавления от состава сплава имеет харак-
характерный ход, представленный на рис. 238.
Пусть сплав образован двумя элемен-
элементами А и В. По оси абсцисс отложены
количества веществ А и В в сплаве,
причем направление слева направо соот- ~д
ветствует возрастанию количества веще-
вещества А. По оси ординат отложены темпе- Рис- 238' Зависимость тем-
г „ _ пературы плавления от со-
ратуры плавления сплава. Точка Тв от- става сплава
носится к температуре плавления чистого
вещества В; малые примеси вещества А ведут к понижению темпе-
температуры плавления. В точке С достигается минимум температуры
плавления; состав сплава, отвечающего точке С, называется эвтек-
эвтектическим. Далее температура плавления повышается, достигая
точки Та, которая относится к чистому веществу А. Из хода кри-
кривой видно, что малая добавка второй компоненты (как менее туго-
тугоплавкой к более тугоплавкой, так и, наоборот, более тугоплавкой
к менее тугоплавкой) всегда ведет к понижению температуры
плавления по сравнению с температурой плавления чистого вещества.
Твердые тела, как и жидкости, при всякой температуре испа-
испаряются в большей или меньшей степени, образуя пар данного ве-
вещества.
Будем охлаждать жидкость в закрытом сосуде, причем пусть
над жидкостью имеются лишь насыщенные пары. По мере пониже-
понижения температуры давление паров падает; пусть ход этого давления
с температурой изображается кривой CD на рис. 239.
Точке D соответствует температура затвердевания жидкости
под давлением насыщенных паров. При достижении точки Д при
дальнейшем отнятии тепла, начнется переход жидкости в твердое
состояние, причем температура остается постоянной, пока вся масса
жидкости не перейдет в твердое состояние. За все это время и
давление насыщенных паров остается постоянным и равным орди-
ординате точки. D. Когда вся жидкость перейдет в твердое состояние, над
13 С. Э Фриш и А. В, Тиморева
370 ТВЕРДЫЕ ТЕЛА [ГЛ. X
твердым телом будет по-прежнему насыщенный пар. При дальней-
дальнейшем охлаждении твердого тела начнет падать и давление насыщен-
насыщенных паров, но по новой кривой DQ.
Таким образом, в точке D смыкаются две кривые: кривая QD,
дающая зависимость давления насыщенных паров от температуры
над данным веществом в твердом состоянии, и кривая CD, дающая
зависимость давления насыщенных паров от температуры над тем
же веществом в жидком состоянии. При температурах ниже тем-
температуры, соответствующей абсциссе точки D, пар может быть
в равновесии только с твердым телом, при температурах выше этой
температуры — в равновесии только с жидкостью. В точке D все три
состояния вещества — твердое, жидкое и насыщенный пар над
ними — или, как говорят, все три фазы, находятся в равновесии.
Поэтому точка D называется тройной точкой.
Температура тройной точки есть температура плавления вещества,
находящегося под давлением его насыщенного пара. Если вещество
подвергнуть ббльшим давлениям, то
и температура плавления изменится.
Как было указано, для большинства
тел при повышении давления тем-
температура плавления тоже повы-
повышается.
Можно построить кривую, выра-
выражающую зависимость между темпе-
температурой плавления и давлением.
Эта кривая пройдет через тройную
точку D; на рис. 239 она представ-
Рис. 239. Тройная точка лена ли™ей DL Рисунок 239 от-
;_ тверда, фаза; 2 -жидка, фаза; Н0СИТСЯ К СЛУЧЗЮ' К0ГДЭ темпеРа-
з — газообразная фаза. тура плавления тела возрастает
с повышением давления.
Так как температура плавления зависит от давления очень слабо
(кривая DL идет круто вверх), то при обычных давлениях (порядка
атмосферного) температура плавления совпадает с температурой
тройной точки.
По большей части мы имеем дело с твердыми телами при тем-
температурах много ниже температуры их тройной точки (железо и
другие металлы при комнатной температуре), поэтому давление их
насыщенных паров ничтожно, и испарение этих твердых тел прак-
практически отсутствует. Но вблизи тройной точки давление насыщенных
паров над твердым телом может быть вполне заметным. Так, вода
в тройной точке (при 0,00748й С) имеет давление насыщенных паров
jt70 = 4,58 мм Hg; при—1ЧС над льдом упругость насыщенных
паров равна 4,22 мм Hg и при —10° С еще равна 1,95 мм Hg.
Этими сравнительно большими упругостями насыщенных паров
объясняется легко заметное испарение твердого льда, в частности —
§ 95]
КВАЗИКРИСТАЛЛИЧЕСКОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
371
факт „высыхания" мокрого белья на морозе. Иод имеет в тройной
точке A14° С) давление насыщенных паров 90 мм Hg; это большое
значение давления насыщенных паров позволяет удобно демонстри-
демонстрировать на кристаллах иода процесс испарения („возгонки") твердых
тел.
Ряд веществ имеет и в тройной точке очень низкие давления
насыщенных паров; так, серебро при температуре плавления (962° С)
обладает давлением насыщенных паров всего 2 • 10~3 мм Hg.
§ 95. Квазикристаллическое строение жидкостей. В § 78 мы
уже указывали, что природа жидкостей, особенно вблизи температур
затвердевания, во многом сходна с природой твердых тел. Теперь
мы познакомимся с этим сходством более подробно.
Прежде всего следует отметить, что при плавлении (или, соот-
- ветственно, затвердевании) свойства вещества меняются гораздо
меньше, чем при испарении.
Мы уже указывали, что плавление сопровождается значительно
меньшим изменением удельного объема, чем испарение, если послед-
последнее происходит при температурах более низких, чем критическая.
Теплоты плавления малы по сравнению с теплотами испарения.
Например, натрий и ртуть имеют при температурах кипения
теплоты испарения соответственно равные 25 000 кал/моль и
14 000 кал/моль.
Теплоты плавления тех же элементов соответственно равны
610 кал/моль и 570 кал/моль.
В табл. XVII сравнены молярные теплоемкости для ряда веществ
в твердом и жидком состояниях.
Таблица XVII
Молярные теплоемкости при постоянном давлении
твердых и жидких веществ
Ср (твердое). . .
Ср (жидкое) . . .
Na
7,6
8,0
Hg
6,7
6,7
Pb
7,2
7,7
Zn
7,2
7,9
Al
6,14
6,25
HCl
12,27
14,73
CH4
10,0
13,5
Из таблицы видно, что теплоемкости веществ как простых, так
и химически сложных при переходе из твердого состояния в жид-
жидкое меняются мало. Это непосредственно указывает, что характер
теплового движения частиц в жидком состоянии близок к характеру
теплового движения частиц в твердых телах. На этом выводе и осно-
основывается указанная в § 78 теория Я. И. Френкеля, по которой мо-
молекулы жидкости совершают колебания около временных положений
равновесия. Различие между твердым, и жидким состоянием за-
заключается в следующем: в твердых телах каждая частица (атом или
ион) колеблется около определённого положения равновесия, кото-
которое остается неизменным длительное время; в жидкости каждая
13*
372 ТВЕРДЫЕ ТЕЛА [ГЛ. X
частица также колеблется около определенного положения равно-
равновесия, но в течение гораздо более короткого промежутка времени,
после чего она меняет свое положение равновесия. Называя среднее
время т, в течение которого частица пребывает около определенного
места равновесия, временем „оседлой" жизни, имеем: твердое со-
состояние вещества характеризуется большим временем „оседлой"
жизни, жидкое — сравнительно небольшим временем „оседлой" жизни.
В предыдущих параграфах мы видели, что в твердом кристалли-
кристаллическом состоянии тел частицы расположены с определенной про-
пространственной симметрией по узлам правильной геометрической
решетки. Спрашивается, существует ли в расположении частиц жид-
жидкости (вернее, их временных положений равновесия) также неко-
некоторый порядок? Целый ряд фактов заставляет ответить на этот
вопрос утвердительно: тепловые колебания частиц в жидкости не
независимы, в жидкостях может быть обнаружено наличие таких
же тепловых -упругих волн, какие существуют в твердых телах
(стр. 367); рентгеновы лучи, проходя через жидкость, дают, хотя и
размытую, но все же определенно заметную диффракционную кар-
картину (см. т. III). Но вместе с тем необходимо отметить, что жид-
жидкости (за очень редкими исключениями) не обнаруживают никакой
анизотропии, характерной для кристаллических твердых тел с их
правильным расположением частиц по узлам геометрической решетки.
Эти кажущиеся противоречия устраняются на основании гипотезы,
по которой в жидкостях осуществляется так называемый' ^ближний
порядок" в расположении частиц.
Под „ближним порядком" подразумевается такое расположение
частиц, когда приблизительно правильно расположены частицы, бли-
ближайшие к данной. По мере того, как мы будем отходить от данной
частицы, порядок в расположении остальных частиц по отношению
к данной будет все более и более нарушаться. В пределах значи-
значительного объема частицы практически расположены беспорядочно.
Такое расположение частиц соответствует структуре, отличной от
истинной кристаллической структуры твердых тел, при которой
осуществляется „дальний порядок". При наличии „дальнего порядка"
частицы расположены правильно по узлам геометрической решетки
в пределах значительного объема.
Из сказанного видно, что жидкость имеет до некоторой степени
упорядоченное строение лишь в пределах малых объемов; такая
структура носит название квазикристаллической (кристаллопо-
добной).
При повышении температуры время „оседлой" жизни частиц
в жидкости становится все меньше и меньше, и жидкость по своим
свойствам отходит от свойств твердых тел и приближается к свойствам
плотных газов.
Приведенная теория позволяет также объяснить механические
свойства жидкостей.
§ 96] АБСОРБЦИЯ И АДСОРБЦИЯ ГАЗОВ ТВЕРДЫМИ ТЕЛАМИ 373
Как известно, жидкости текучи. Однако при действии очень
кратковременных сил вязкие жидкости проявляют свойства хрупкости
и способны давать упругие деформации. Еще во второй половине
прошлого столетия Максвелл развил формальную теорию такого
состояния вещества, при котором одновременно могут проявляться
и текучесть, и упругая деформация.
Напряжение в таком веществе спадает не сразу после прекра-
прекращения действия силы, но по закону:
где рл— начальное значение напряжения, pt — напряжение через
время t после прекращения действия силы. Величина т носит на-
название времени релаксации.
По Максвеллу, вещество ведет себя как твердое, если сила
действует в течение промежутка времени, меньшего времени релак-
релаксации т, и как жидкое, если сила действует в течение времени,
ббльшего t. По теории Я. И. Френкеля, вещество должно вести
себя как твердое под влиянием сил настолько кратковременных,
что они действуют в течение промежутка времени, меньшего вре-
времени „оседлой" жизни частиц. Действительно, в течение столь ма-
малого времени частицы остаются около своих положений равновесия,
и вещество обладает структурой, характерной для твердого состоя-
состояния. Если время действия силы больше времени „оседлой" жизни
частиц, то вещество обнаруживает вязкое течение, т. е. ведет себя
как жидкость. Таким образом, в теории Я. И. Френкеля время ре-
релаксации приобретает непосредственный физический смысл: оно
совпадает со временем „оседлой" жизни частиц,
§ 96. Абсорбция и адсорбция газов твердыми телами. Опыты
показывают, что если какое-либо твердое тело, находившееся в со-
соприкосновении с газом, поместить в сосуд, из которого проис-
происходит откачка, то тело выделяет тот газ, с которым оно было
в соприкосновении. Отсюда следует, что твердые тела поглощают
газы.
Это поглощение тем больше, чем больше давление газа и чем
больше поверхность твердого тела. Порошки поглощают значительно
больше, чем сплошные тела того же состава и той же массы. Это
показывает, что поглощение, хотя бы частично, носит характер при-
прилипания газа к поверхности твердого тела.
Более подробное изучение поглощения указывает на существо-
существование двух различных видов поглощения газов твердыми телами,
называемых адсорбцией и абсорбцией. Адсорбция заключается в при-
прилипании газа тонким слоем к поверхности твердого тела. Абсорбция
(или окклюзия) сводится к действительному поглощению газа всей
массой твердого тела, т. е. к процесс]', аналогичному растворению
газов жидкостями.
374
ТВЕРДЫЕ ТЕЛА
[ГЛ. X
Адсорбированный газ может образовать на поверхности твердого
тела мономолекулярную пленку, аналогичную мономолекулярным
слоям, которые могут существовать на поверхности жидкости (§ 83).
Образование мономолекулярного слоя газа на поверхности твер-
твердого тела обусловлено наличием больших сил взаимодействия между
молекулами газа и твердого тела. Надо считать, что эти силы,
носящие характер сил притяжения, действуют лишь на очень малых
расстояниях. Поэтому,, когда на первый слой молекул газа попадают
новые молекулы, то на них действуют силы лишь со стороны мо-
молекул этого первого слоя, а не молекул твердого тела; эти силы
недостаточны, чтобы удержать молекулы газа в виде второго слоя.
В вакууме адсорбированный слой молекул постепенно срывается
и освобождает поверхность твердого тела. Чем выше температура,
тем скорее идет процесс выделения газа с поверхности твердого
тела.
Абсорбция (или окклюзия) идет в основном лишь при высоких
температурах, так как только при этих температурах наблюдается
заметная диффузия газа внутрь твердого тела.
Некоторые твердые тела способны окклюдировать газ в очень
больших количествах, так что объем поглощенного газа (отнесенный
к нормальным условиям) в сотни раз может превышать собственный
объем твердого тела. Раскаленный палладий поглощает водород
в объемах, отнесенных к нормальному давлению, до 1000 раз
превышающих собственный объем палладия. Сильно поглощают во-
водород щелочные металлы, особенно натрий. При нагревании в ва-
вакууме окклюдированные газы выделяются.
Явления адсорбции и абсорбции (окклюзии) играют большую
роль в вакуумной технике. Для обезгаживания всех твердых (осо-
(особенно металлических) частей, вводи-
вводимых внутрь вакуумного прибора, их
необходимо сильно прогревать под
непрерывной откачкой. С другой сто-
стороны, явлениями адсорбции пользуются
и для улучшения вакуума. Для этих
целей пользуются, главным образом,
способностью древесного угля сильно
адсорбировать многие газы, особенно
при низких температурах.
К сосуду А, в котором желательно
улучшить вакуум (рис. 240), присое-
Рис. 240. Улучшение вакуума диняют сосуд В, содержащий предва-
путем поглощения газов охла- рительно обезгаженный уголь. При
ждаемым углем. погружении сосуда В с углем в жид-
жидкий воздух он охлаждается до темпе-
температуры—184° С и при этом поглощает остатки газа в сосуде Л;
таким образом может быть получен вакуум порядка' 10~6 мм Hg.
АБСОРБЦИЯ И АДСОРБЦИЯ ГАЗОВ ТВЕРДЫМИ ТЕЛАМИ
375
Таблица XVIII
Объемы газов, поглощае-
поглощаемых углем при темпера-
температуре жидкого воздуха
В табл. XVIII приведены объемы различных газов (отнесенных
к нормальным условиям), поглощаемых единицей объема угля при
температуре жидкого воздуха.
Из табл. XVIII видно, что меньше всего при температуре жид-
жидкого воздуха поглощается гелий. Этим свойством гелия пользуются
для его очистки от загрязнений: при про-
пропускании загрязненного гелия через сосуд
с охлажденным углем газы, примешанные
к гелию (азот, кислород и т. д.), сильно
поглощаются углем, сам же гелий погло-
поглощается лишь в очень небольших коли-
количествах.
Для того чтобы уголь обладал свой-
свойством сильно адсорбировать газы, он дол-
должен быть получен в пористом виде и сво-
свободным от обычно присутствующих в его
порах углеводородов. Для этого его про-
прогревают в закрытом сосуде при темпера-
температуре 350—400° С, попеременно впуская
и откачивая воздух.
Такая обработка носит название акти-
активизации угля. Активированный уголь на-
находит применение также в оборонной технике: обычные противо-
противогазы содержат в себе активированный уголь.
На поверхности твердого тела могут адсорбироваться не только
газы, но и жидкости. Адсорбированные вещества меняют свойства
поверхности твердого тела. Некоторые твердые тела под влиянием
веществ, адсорбированных на их поверхности, обнаруживают пони-
понижение прочности. При этом, по-видимому, существенную роль играют
микроскопические трещинки и зазоры между отдельными кристал-
кристалликами поликристаллических тел (металлов). Молекулы адсорбиро-
адсорбированной жидкости проникают в микротрещины и расширяют их. Это
явление находит практическое применение: смачивая поверхность
твердого тела соответствующей жидкостью, можно уменьшить работу
резания.
Газ
Гелий ....
Водород . .
Азот
Аргон ....
Кислород . .
Объем газа,
поглощае-
поглощаемого
единицей
объема
угля
15
135
155
175
230
ЧАСТЬ ТРЕТЬЯ
КОЛЕБАНИЯ И ВОЛНЫ
_f
б)
I
+1Г
ГЛАВА XI
ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
§97. Гармоническое колебание. Как было показано в § 89, при
упругих деформациях, удовлетворяющих закону Гука, возникает сила,
направленная к положению равновесия и пропорциональная деформа-
деформации. Рассмотрим характер движения, происходящего под действием
такой силы.
Предположим, что груз А зажат между двумя пружинами. Обе
пружины одинаково растянуты, и груз находится в равновесии в по-
ложении О (рис. 241 а). Выведем груз
из положения равновесия направо (рис.
^* ^ на отРезок ~~\~х (положительными
считаем отрезки, отложенные слева на-
право), тогда правая пружина окажется
сжатой- левая — растянутой, и на груз
будет действовать сила —/, направленная
к положению равновесия О и тем ббль-
шая п0 численному значению, чем больше
смещение х. Под 'влиянием этой силы
j груз А начнет двигаться к положению
8) •vW^/\f\/\/'>S# равновесия с возрастающей скоростью.
^?-тО Когда он снова попадет в положение
~х равновесия (рис. 241 в), сила станет рав-
ной НуЛЮ) но у груза будет запас ско-
Рост—«. благодаря чему он перейдет
через положение равновесия и продол-
продолжит движение налево. При этом левая
пружина сожмется, правая растянется, и на груз начнет действовать
сила_|_у; направленная направо к положению равновесия. Эта сила
будет тормозить груз, пока он не остановится; затем он начнет дви-
двигаться обратно к положению равновесия. Таким образом, устано-
установится колебательное движение груза А около положения равновесия.
Другим примером колебательного движения может служить
движение плоского маятника (рис. 242). Если нить маятника
вертикальна, то сила тяжести Р, приложенная к грузу маятника,
+f
Рис. 241. Колебание около
двумя пружинами.
§ 97] ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ 377
уравновешивается натяжением нити. Однако, если маятник отклонить
из положения равновесия на некоторый угол <р, то только часть силы
тяжести Р уравновесится реакцией нити, именно, составляющая силы
тяжести Рп, параллельная нити. Составляющая Pt, перпендикулярная
к нити, численно равная Psin^ и направленная к положению равно-
равновесия маятника, останется неуравновешенной. Если угол <р мал, то
синус можно заменить самим углом, тогда Pt
приближенно равна Р<р. Здесь смещение груза
маятника из положения равновесия опреде-
определяется углом <р. Сила, возвращающая груз
маятника в положение равновесия, при малом
угле <р пропорциональна углу <р.
Под влиянием этой силы маятник придет
в колебательное движение около положения
равновесия. В этом случае движение опреде-
определяется не упругой силой, а составляющей силы
тяжести Pt, которая направлена к положению
равновесия и пропорциональна (при малых
углах ^р) отклонению маятника из положения рис> 242. Колебания
равновесия. Таким образом, эта сила по своему маятника,
характеру аналогична упругой силе. Колеба-
Колебания, вызываемые этой силой, при малых углах <р совпадают по харак-
характеру движения с колебаниями, вызываемыми упругой силой.
Силы, не упругие по своей природе, но аналогичные им по виду
зависимости от смещения, называются квазиупругими.
Приведенные примеры показывают, что действие упругой или
квазиупругой силы вызывает колебательное движение. Рассмотрим
колебательный процесс более подробно.
Определим положение материальной точки с массой т ее сме-
смещением х из положения равновесия; в положении равновесия х = 0.
Для упругой (или квазиупругой) силы / характерно то, что она
пропорциональна смещению х и направлена к положению равновесия;
следовательно, можно написать:
f= — kx. A)
Знак минус означает, что сила направлена в сторону, противополож-
противоположную смещению х; например, при смещении вверх сила действует
вниз, при смещении вниз сила действует вверх и т. д. Коэффициент k
положителен. По второму закону Ньютона:
/= — kx, B)
где w — ускорение рассматриваемой материальной точки.
Ускорение w равно второй производной смещения по времени,
т. е. w =—у; будем сокращенно обозначать вторую производную
по времени двумя точками, поставленными над той величиной, от
378 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XI
которой берется производная, тогда w=x. Подставляя это выра-
выражение для w в B), получим
C)
или
± (За)
Так как k и т — обе величины положительные, то их отношение
можно приравнять квадрату некоторой величины ш, т. е. мы можем
ввести обозначение
Величина <о по причинам, указанным ниже, называется круговой
(или циклической) частотой колебания.
Тогда уравнение (За) можно переписать в виде:
Jc = — ufx. E)
Наша задача теперь сводится к определению движения точки,
относительно которой известно, что ее ускорение по формуле E)
пропорционально ее отклонению х из положения равновесия и на-
направлено в сторону положения равновесия. Движение точки известно,
если известно ее положение как функция времени; в данном случае
надо определить смещение х как функцию от времени t Следова-
Следовательно, нам надо найти такую связь между х и /, чтобы она удо-
удовлетворяла уравнению E). Легко проверить, что эта связь дается
уравнением:
х= a cos {wt -f- a), F)
где а и а — произвольные постоянные, которые могут быть опреде-
определены из начальных условий. Действительно, взяв вторую производ-
производную от х по времени, мы увидим, что полученное значение Л
обращает уравнение E) в тождество. Множитель а называется ам-
амплитудой, аргумент tat -f- a — фазой, постоянная а — начальной фазой
колебания. С одинаковым правом мы могли бы взять уравнение
в виде:
х = a sin (wt-\-а), G)
при этом при определении постоянной а в каждом частном случае
мы получили бы для а другое значение, чем по уравнению F). При
этом другом значении постоянной а численное значение синуса
в уравнении G) в каждый данный момент времени равнялось бы
численному значению косинуса в уравнении F), т. е. движения,
описываемые уравнениями F) и G), были бы тождественны.
Уравнения F) или G) называются уравнениями гармонического
колебательного движения; перейдем к их исследованию.
§ 97] ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ 379
Основное свойство гармонического колебательного движения —
это его периодичность. Положим, для простоты, начальную фазу
а = 0, тогда
х = a cos at. Fa)
При ? = 0 имеем cosutf = -|-l, откуда х = -\-а. Условимся поло-
положительные значения смещения откладывать направо, а отрицатель-
отрицательные— налево от положения равновесия (рис. 243). Тогда материаль-
материальная точка А, совершающая гар-
гармоническое колебательное дви- f —-— ^
жение, в момент времени t = 0 'Л ° # _j*
смещена из положения равно- * v '
весия направо, на отрезок а. v -^ м : v »
Это — максимальное возмож- ~а +<*
ное смещение точки направо, Рис. 243. Смещение колеблющейся точки
так как cos Ы не может быть из положения равновесия,
больше -f-1. При возрастании
времени t значение cos <ot начнет убывать — точка будет переме-
перемещаться налево, двигаясь к положению равновесия О. В момент
времени, определяемый условием arf = ~, т. е. при ? = -^-, точка
окажется в положении равновесия О. При дальнейшем возрастании
времени косинус примет отрицательные значения, точка А сместится
налево от положения равновесия. В момент времени t = — косинус
примет значение —1, откуда х = — с, т. е. точка достигнет край-
крайнего левого положения. Затем она начнет двигаться направо, вто-
вторично пройдет положение равновесия О и в момент времени t= T=
=— снова достигнет крайнего смещения вправо. После этого все
движение начнет повторяться. Таким образом, точка возвращается
в исходное состояние движения через время
Т=-, (8)
О)
это время Т является периодом колебаний. За время, равное пери-
периоду Г, колеблющееся тело А пройдет каждую точку своего пути
(кроме точек, соответствующих крайним отклонениям х = ±а)
дважды: один раз —двигаясь в одном направлении, и в другой
раз — двигаясь в обратном направлении.
Величина а> = -=- представляет собою число колебаний в 2-к еди-
единиц времени. Величина а, называемая амплитудой, дает наибольшее
возможное смещение колеблющейся точки от положения равновесия.
При а. ф. 0 имеем, что в начальный момент времени t = Q точка А
находится в месте, определяемом значением Ar = acosa. Исходя из
этой точки, можно также проследить весь характер движения за
380
ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
[ГЛ. XI
период Т. Следовательно, начальная фаза а определяет положение
колеблющейся точки в начальный момент времени ^ = 0.
Наряду с циклической частотой (о, можно ввести в рассмотрение
и обычную частоту v = y, дающую число колебаний в единицу вре-
времени. Сопоставляя все три величины ш, v и Т, имеем между ними
связь:
- = 2,cv=?. (9)
Подставляя эти значения <о в F), получим еще два следующих
выражения для гармонического колебательного движения:
х = a cos
v^ -f- a),
х = a cos I y t ~т~а) •
F6)
(бв)
2тс
Пользуясь формулой D) и соотношением Т= —, получаем для
периода величину:
7-=:
A0)
Таким образом, мы видим, что период колебания зависит исклю-
исключительно от динамических характеристик задачи: массы m и коэф-
коэффициента k.
Во многих приложениях, связанных с рассмотрением колебатель-
колебательного процесса, удобен геометрический способ представления колеба-
колебания с помощью вектора ампли-
амплитуды.
Этот способ сводится к сле-
следующему. Возьмем ось, которую
назовем осью X (рис. 244), и вы-
выберем на ней произвольную
точку О. Из этой точки под
углом а, равным начальной фазе
колебания, отложим в некотором
масштабе вектор, численно рав-
равный амплитуде а. Из рисунка
x'acos видно, что проекция вектора а на
Рис. 244. Представление гармониче- ось X даст в том же масштабе
ского колебательного движения как начальное смещение точки х —
проекции вектора а, вращающегося „
с постоянной угловой скоростью. = a cos а. Будем вращать вектор
амплитуды с угловой скоростью со
против часовой стрелки, тогда в некоторый момент времени t он
образует с осью X угол, равный <at-\-o., при этом его проекция на
ось X будет равна
х = a cos (wt -(- а),
§ 98] СКОРОСТЬ И УСКОРЕНИЕ. ПРИМЕРЫ 381
т. е. будет давать смещение колеблющейся точки в момент вре-
времени L Отсюда мы можем сделать заключение: гармоническое ко-
колебательное движение представляется движением проекции на не-
некоторую ось конца вектора, амплитуды, отложенного из произвольной
точки оси под углом, равным начальной фазе, и вращающегося с угловой
скоростью ш вокруг этой точки. Отсюда становится ясным, почему
величина ш называется круговой частотой.
§ 98. Скорость и ускорение при гармоническом колебательном
движении. Примеры. Смещение х материальной точки А, совер-
совершающей гармоническое колебательное движение, по формуле F)
§ 97 равно
х = a cos (wt-\-а), A)
где а — амплитуда колебания, ш —- круговая частота и а — начальная
фаза. Скорость точки v численно равна производной по времени
от смещения л;, т. е. v = jr- Обозначим первую производную по
времени точкой над буквой, выражающей ту величину, от которой
берется производная. Тогда, выполняя дифференцирование, имеем
v = x = — аш sin (oit-\-a). B)
Ускорение точки А получим, беря производную от скорости по
времени:
w==^ = x = — aaJcos((o^ + a). C)
Вводя в формулы B) и C) вместо ш период 7"= —, получим
2я . /2я , , \ ,- .
asinjf + a) Bа)
(За)
Последнее равенство на основании формулы A) может быть еще
переписано:
4тс2
W X
откуда снова получим, что ускорение при гармоническом колеба-
колебательном движении пропорционально смещению х и направлено
к положению равновесия (ср. стр. 377).
Из формул Bа) и (За) видно, что скорость и ускорение точки,
совершающей гармоническое колебательное движение, являются пе-
периодическими функциями от времени с тем же периодом Т, каким
обладает и смещение х. Проследим изменения скорости и ускоре-
ускорения за время одного колебания. Для этого составим табличку зна-
382
ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
[ГЛ. XI
чений v и w для различных моментов времени, сопоставив их со
значениями смещения х для тех же моментов времени. Начальную
фазу а. снова, для простоты,
Т а 6 л и ц а XIX
Значения х, v и w при гармоническом
колебательном движении для разных
моментов времени
полагаем равной нулю.
Из таблицы видно: скорость
достигает максимальных по аб-
абсолютной величине значений
| "о |та* ==уа ПРИ прохожде-
прохождении колеблющейся точкой А
положения равновесия; при
крайних отклонениях х = zt a
скорость равна нулю. Ускоре-
Ускорение, наоборот, равно нулю при
прохождении положения рав-
равновесия (в этот момент сила
равна нулю) и достигает по аб-
абсолютной величине максималь-
максимальных значений \w\m^ = -^2- а при
крайних отклонениях. Ускоре-
Ускорение всегда направлено к по-
положению равновесия.
Амплитуда колебания и начальная фаза, как было сказано выше,
определяются из начальных данных. Предположим, что в начальный
момент времени * = 0 известны скорость v0 частицы и ее смеще-
смещение jc0. При этих условиях, подставляя ( = 0 в выражения A) и B),
имеем
хй = a cos a, v0 = — mo sin а, D)
или
-? = — a sin а. E)
Возводя в квадрат и складывая почленно выражения D) и E),
получаем
•*о+§ = я9, откуда a=l/*2 + i°. F)
t
0
1 ¦
-I1
iT
т
X
+ а
0
— а
0
+ °
V
0
2л
-1°
0
+ 7-
0
w
_^а
0
, 4л2
i- p a
0
Деля выражение E) почленно на хо = а cos а, найдем
G)
Выражения F) я G) дают амплитуду а и начальную фазу а,
определяемые через начальное смещение х0 и начальную скорость v0.
Таким образом, мы видим, что точка данной массы, находясь под
действием одной и той же упругой силы, может совершать колеба-
колебания различной амплитуды и с различными начальными фазами
§ 98] СКОРОСТЬ И УСКОРЕНИЕ. ПРИМЕРЫ 383
в зависимости от начальных условий, в то время как период ее всегда
остается одним и тем же.
Если груз, подвешенный на пружине, вывести из положения
равновесия, то он начнет совершать колебания, амплитуда которых
будет зависеть от того, насколько была вытянута пружина перед
началом движения и какая начальная скорость была сообщена грузу;
период колебания будет независимо от величины амплитуды опреде-
определяться только массой груза т и „жесткостью" пружины k.
Начальная фаза колебания, как видно из приведенного рас-
рассмотрения, зависит от выбора начального момента: можно, например,
взять за начальный момент тот, при котором смещение точки хй =
= -\-а, тогда из соотношения F) следует, что va = 0 и по соотно-
соотношению G) начальная фаза равна нулю: а = 0.
Рассмотрим несколько примеров.
Пример 1. Определить период колебания груза весом Р = 2,5 кГ,
привешенного к пружине, если пружина под действием силы 3 кГ растяги-
растягивается на 9 см. i
Решение. Коэффициент упругости пружины мы получим, если силу
3 кГ поделим на вызываемое этой силой смещение:
3 1
k = -g кГ/см = д- кГ/см,
после чего определим по формуле A0) § 97
| =2. /1=2* /|^сек. = 0,55 се,
Пример 2. Определить период колебаний математического маятника
/длины I.
•' Математическим маятником называется такой маятник, весом нити кото-
которого в условиях задачи можно пренебречь.
Решение. Обозначим через т массу груза маятника. Предположим,
что маятник отклонен на угол <р от вертикали. Силой, движущей груз маят-
маятника по направлению к положению равновесия, является составляющая силы
тяжести Р(, перпендикулярная к нити (рис. 242). По сказанному на стр. 377,
эта составляющая Pt при малом угле отклонения <f приближенно равна по
численному значению P<f и направлена к положению равновесия, откуда
Pi = -P<f = -mg<f, (8)
где g—ускорение силы тяжести; знак минус означает, что сила Pt напра-
направлена в сторону, противоположную той, в которую отсчитываются положи-
положительные углы 9-
Касательное к траектории груза ускорение равно Щ, откуда по второму
закону Ньютона:
ml'j = Р^
или по (8)
тЩ = — mgf, откуда Ц = — у <р.
Обозначим g/l через ш2, получим
384
ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
[ГЛ. XI
Это уравнение относительно углового смещения маятника у вполне ана-
аналогично уравнению E) § 97. Поэтому <р явится периодической во времени
функцией с периодом
(9)
Формула (9) и дает искомый период колебания математического маятника,
который, оказывается, зависит лишь от длины маятника / и ускорения силы
тяжести g в данном месте земного шара.
Пример 3. Определить период колебания около оси О (рис. 245) тела,
весом Р, центр тяжести которого С расположен на расстоянии а от оси вра-
вращения. Углы отклонения <р тела от положения равновесия считать малыми.
Решение. Силу тяжести Р можно считать приложенной к центру тя-
тяжести С. Как и в предыдущем примере, тело будет двигаться к положению
равновесия под влиянием составляющей силы тяже-
тяжести Р^ которая при малых углах <f приближенно равна
pt = Р(р_
Момент этой силы по отношению к оси враще-
вращения О (см. § 35) равен
М=Р1а = — Руа. A0)
Под влиянием этого момента М тело приобре-
3 = ^| = ? (см.§35),рав-
М
тает угловое ускорение
ное
Х>Р/} где /—момент инерции тела относительно оси О.
Подставляя в это последнее выражение вместо М его
значение по A0) и у вместо р, получим ¦
Рис. 245. Колебания
тяжелого тела около
оси О.
Ра
4 = 7—?¦
Это уравнение вполне аналогично уравнению E)
§ 97 или уравнению относительно <р> рассмотренному
в предыдущем примере. Отсюда мы получаем: при малых углах отклонения <р
тело будет совершать около положения равновесия гармоническое колеба-
колебательное движение с периодом
= 2я 1/ —.
V mga
воспользовавшись соотношением p = mg, где т — масса тела, перепишем
выражение для периода
—. (Па)
mga v
Тело, способное указанным образом колебаться около положения равно-
равновесия, называется физическим маятником.
Величину ^i
1 = — A2)
та v '
принято называть приведенной длиной физического маятника.
§ 99] ЭНЕРГИЯ ГАРМОНИЧЕСКОГО КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ 385
Так как в выражение момента инерции У (см. § 35) входит масса, то при-
приведенная длина физического маятника L не зависит от его полной массы,
а зависит только от его геометрической формы и от распределения масс.
Подставляя в A1а) значение приведенной длины маятника, получим
таким образом, формула для периода колебания физического маятника при-
принимает вид, аналогичный формуле для периода колебаний математического
маятника [формула (9) предыдущего примера].
§ 99. Энергия гармонического колебательного движения. Пусть
материальная точка массы т совершает колебания под влиянием
квазиупругой силы
/= — kx,
где х — смещение точки из положения равновесия. Совершая ко-
колебания, материальная точка обладает скоростью, а следовательно,
и кинетической энергией
Ek = ±mv\ A)
Кроме того, колеблющаяся точка будет обладать и потенциаль-
потенциальной энергией. То обстоятельство, что точка имеет различную ско-
скорость в различных положениях, показывает, что кинетическая энер-
энергия точки Ek меняется со временем. Очевидно, что меняется при
этом и потенциальная энергия. Потенциальная энергия измеряется
работой внешних сил, которая совершена для того, чтобы вызвать
определенное смещение х. Как было показано в § 25, работа уп-
упругой силы численно равна /гх*/2. Таким образом, получаем для
потенциальной энергии Ер выражение:
Ep = ±kx\ B)
Подставляя в формулы A) и B) вместо v и х их значения по
выражениям A) и B) § 98, получим:
Ек = ^та*а>> sin9 И + а), Aа)
Ер = -i*a« cos2 (o>t + а). Ba)
Кинетическая энергия Е/, имеет значение нуль там, где потен-
потенциальная достигает максимума, т. е. в положениях крайнего откло-
отклонения; кинетическая энергия достигает максимума при прохождении
через положение равновесия, потенциальная энергия в этой точке
равна нулю.
Полная энергия Е колеблющейся точки выразится суммой энер-
энергий обоих видов, т. е.
Е = Ek + Е„ = \ maW sin9 (шг + а) + \ ka1 cos2 (cor + а).
386 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XI
Так как, согласно принятому обозначению, m<al = k, то это вы-
выражение можно написать в виде:
откуда
?•= 1 Ааа sin2 (id + а) + \ ka* cos9 (arf + а),
E=\ka\ C)
т. е. полная энергия Е пропорциональна квадрату амплитуды
колебания и пропорциональна коэффициенту упругости k.
Воспользовавшись равенством k = та? = т -^-, можно формулу
C) переписать также в виде:
Ц^\ D)
Из формул C) и D) видно, что полная энергия постоянна во
все время колебания, как это и должно быть на основании закона
сохранения энергии.
В положениях крайнего смещения вся энергия переходит в по-
потенциальную, при прохождении через положение равновесия вся
энергия переходит в кинетическую; во всех прочих положениях ко-
колеблющейся точки имеются энергии обоих видов. Графическое изо-
изображение энергии при колебательном движении было рассмотрено
в § 29. .
Из сказанного видно, что во время колебательного движения
энергия все время переходит из потенциальной в кинетическую
и обратно. При этом за один период Т полная энергия Е дважды
целиком переходит в кинетическую энергию Ek (при двух прохож-
прохождениях положения равновесия) и дважды целиком переходит в по-
потенциальную энергию Ер (при обоих крайних положениях). В из-
известном смысле можно при этом говорить о „колебании" энергии,
подразумевая под этим ее переход то в кинетическую, то в потен-
потенциальную. Из сказанного видно, что это „колебание" энергии про-
происходит с периодом Т, вдвое меньшим, чем период самого коле-
колебательного движения Т.
Рассмотрим следующий пример на определение энергии колебания.
Определить энергию колебания груза, подвешенного к пружине, по сле-
следующим данным: груз в начальный момент оттянут на 8 см из положения
равновесия и затем предоставлен самому себе. Относительно пружины из-
известно, что она вытягивается под влиянием силы в 2 кГ на 1 см.
Решение. Так как в начальный момент груз не имеет скорости (w() = 0)>
то амплитуда колебаний a=jeo = 8 см.
Коэффициент упругости k определится следующим образом:
k = j кГ]см = 2 кГ/см = 2 ¦ 980 ¦ 10» дин/см,
§ 100] СЛОЖЕНИЕ КОЛЕБАНИЙ, ПРОИСХОДЯЩИХ ВДОЛЬ ОДНОЙ ПРЯМОЙ 387
а, _^-
U»
откуда полная энергия
Е = -^ ka* = ~ • 2 • 980 • 10» • 64 эрг ^ 6,3 • 10' эрг = 6,3 дж.
Следует обратить внимание, что этот результат не зависит от массы колеблю-
колеблющегося тела.
§ 100. Сложение колебаний, происходящих вдоль одной пря-
прямой. Часто приходится иметь дело с таким движением, при кото-
котором тело участвует одновременно в двух или нескольких колебаниях.
Например, если мы подвесим груз на пружине к потолку рессорного
вагона, то груз будет со-
совершать колебания относи-
относительно точки подвеса, ко-
которая, в свою очередь,
совершает колебания на рес-
рессорах вагона; таким обра-
образом, груз будет совершать
движение, складывающееся
из двух колебаний одного
направления.
Рассмотрим, какое ре-
результирующее движение по-
получается при сложении J
колебаний. _ „.„ о
j. Рис. 246. Сложение векторов, представляю-
пачнем С рассмотрения щих гармонические колебательные движе-
сложения двух колебаний - ния одного периода.
одинакового направления и
одинакового периода, происходящих с некоторою разностью фаз и
имеющих разные амплитуды. Возьмем колебания:
Xi = ax cos (urf -|- a^, х% = aa cos Ш -(- а9). A)
Круговые частоты ш обоих колебаний одинаковы, так как по пред-
предположению равны их периоды.
Смещение х. из положения равновесия, при участии тела одно-
одновременно в обоих колебаниях, выразится алгебраической суммой
смещений х^ и jc4:
cos (wt -\- a2). B)
х =±=
= at cos
Выполним это сложение графически. Представим оба колебания
векторами амплитуд (см. § 97), отложенными от произвольной точки О,
лежащей на оси X (рис. 246). Амплитуда а4 откладывается в на-
начальный Момент под углом а\ к оси X, амплитуда аа — под углом а9.
Обе амплитуды вращаются с одинаковой угловой скоростью о> про-
против часовой стрелки. Следовательно, угол между векторами а2 и at
все время остается равным оса — at. Так как сумма проекций двух
векторов на некоторую ось равна проекции на ту же ось вектора,
388 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XI
являющегося их суммой, то результирующее колебание может быть
изображено вектором амплитуды а, получающимся геометрическим
сложением векторов амплитуд at и а9, т. е.
а = а! + а2. C)
Из рис. 246 имеем
а2 = а' -f- а\ -4- 2ага^ cos (а2 — at). . D)
Вектор результирующей амплитуды а, очевидно, вращается с той
же угловой скоростью, что и векторы амплитуд складываемых ко-
колебаний.
Угол а, который образует вектор результирующей амплитуды
с осью X в начальный момент, как видно из рис. 246, равен
, ВС <Ji sin ац -\- а% sin ая .<-..
° OB at cos a, 4- а3 cos a2 ' ¦ V /
Само результирующее колебание выразится проекцией вектора ампли-
амплитуды а на ось X, т. е. оно будет равно
х = хх -\- дга = a cos ((at -j- a). F)
Таким образом, мы видим, что результирующее движение предста-
представляет собою гармоническое колебание, происходящее вдоль той же
прямой, что и слагаемые, и с периодом, равным периоду^ слагаемых
колебаний. Амплитуда а и начальная фаза а результирующего коле-
колебания определяются соответственно через амплитуды и начальные
фазы слагаемых колебаний по формулам D) и E).
Важно заметить, что, согласно формуле D), амплитуда резуль-
результирующего колебания а зависит от разности фаз оса — «i слагае-
слагаемых колебаний. Так как косинус не может быть больше -f-1 и
меньше — 1, то из формулы D) видно, что результирующая ампли-
амплитуда а не больше суммы и не меньше разности слагаемых ампли-
амплитуд ах и а2, т. е. она'заключена в пределах
Если разность фаз слагаемых колебаний равна 0 или 1Ы, где
k—целое число, то косинус разности фаз равен -J-1, и мы полу-
получаем по формуле D)
аа = а\-\-а\-\-2ахаг, откуда а =^ах-4-аь '
т. е. амплитуда результирующего колебания а равна сумме ам-
амплитуд складываемых колебаний at и а8 при разности фаз
a, —a1 = 2Aic, где k = 0', .1, 2, 3, ...
Если разность фаз слагаемых колебаний равна нечетному числу тс,
то косинус разности фаз равен —1, и для амплитуды а получаем
по D) значение:
а* = а\-4-а\ — 1а^аь откуда а = |аа — а^\.
§ 100] СЛОЖЕНИЕ КОЛЕБАНИЙ, ПРОИСХОДЯЩИХ ВДОЛЬ ОДНОЙ ПРЯМОЙ 389
Мы берем здесь абсолютное значение разности аа — аи так как
амплитуда а по самому смыслу амплитуды может быть лишь вели-
величиной положительной.
Отсюда амплитуда результирующего колебания а равна абсо-
абсолютному значению разности амплитуд складываемых колебаний а2
и п\ при разности фаз <*2 — *i =
= Bk-\-\)n, где k = 0, I, 2, ...
Предположим теперь, что сла-
слагаемые колебания происходят по
одному направлению, но с раз-
разными периодами. Тогда в вектор-
векторной диаграмме колебаний (рис.
247) векторы слагаемых ампли-
амплитуд 3] и а., вращаются с разными
угловыми скоростями, в резуль-
результате чего угол между ними не
остается постоянным, а с тече-
течением времени меняется. Вслед-
Вследствие этого меняется и величина
результирующей амплитуды а.
Предположим, что слагаемые ко-
колебания имеют круговые частоты
Рис. 247. Сложение векторов, пред-
представляющих гармонические колеба-
колебательные движения разных периодов.
лебани ру
о), и оз9. Так как разность фаз слагаемых колебаний переменна, то
можно в качестве начального момента взять такой, при котором на-
начальные фазы обоих колебаний одинаковы, т. е. представить коле-
колебания в виде:
Xl = at cos ((У + а), хг = а2 cos 0V + <*)¦ <7)
где предположим, что ^щ
Разность фаз слагаемых амплитуд будет равна («v— a>\)t. Под-
Подставляя это значение разности фаз в формулу D) вместо сц — а„
получим для квадрата результирующей амплитуды
. (8)
cos (wa —
Таким образом, величина амплитуды а результирующего коле-
колебания меняется со временем с определенным периодом.
Угловая скорость вращения вектора результирующей амплитуды
при этом непостоянна, так что результирующее движение не является
гармоническим колебанием.
Рассмотрим специально результат сложения двух колебаний рав-
равных амплитуд ai = aa, периоды и, следовательно, круговые частоты
которых очень мало отличаются друг от друга.
Полагая в формуле (8) ai = aa. получим
а4 == 2а*
cos
— u)j) t] = \a\ cos*
390 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XI
или
ш2 — oil
a, cos —гг—-
(9)
Мы берем здесь, как и на стр. 388, абсолютное значение величины,
стоащей справа, так как амплитуда есть величина существенно по-
положительная. Период абсолютного значения косинуса равен ie; сле-
следовательно, период т изменения абсолютного значения амплитуды
будет тем промежутком времени, за который аргумент косинуса из-
изменится на it, т. е. -с определится из условия:
Cue ~~ СО»
—о—t = ic,
откуда
*= 2" . (Ю)
(Од tl&i
Частота м изменения амплитуды, т. е. величина, обратная пе-
периоду х, равна
т. е. частота м изменения амплитуды результирующего колеба-
колебания равна разности частот va — Vj слагаемых колебаний. Угол,
который образует результирующая амплитуда с осью X, как видно
из рис. 247, равена>1"^1 -\- а, следовательно, вектор результи-
результирующей амплитуды в этом случае вращается с постоянной угловой
скоростью, равной полусумме круговых частот слагаемых колебаний.
Результирующее движение мы получим, если возьмем проекцию
вектора результирующей амплитуды на ось X, откуда результирую-
результирующее смещение х равно
или по (9)
-4-
(И)
Так как по предположению <оа очень близко к (Oj, то величина ш' =
= (о.3 — cot мала по сравнению с величиной <at -(- <оа, откуда мы
имеем: результирующее колебание A1) можно рассматривать как
гармоническое колебательное движение, происходящее с круговой
частотой *"' +ш» t аМплитуда которого а, однако, сама не остается
постоянной, но медленно меняется периодически со временем, со-
согласно соотношению (9). Период т изменения амплитуды а дается
формулой A0). Графически колебание такого рода представлено
§ 101] СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ 391
на рис 248. Амплитуда этого колебания то увеличивается, то умень-
уменьшается; это явление носит название биения.
Рис. 248. Биение.
§ 101. Сложение взаимно перпендикулярных колебаний. Рас-
Рассмотрим теперь результат сложения двух колебаний, происходящих во
взаимно перпендикулярных направлениях. Предположим сперва, что
материальная точка участвует одновременно в двух взаимно перпен-
перпендикулярных колебаниях с одинаковыми периодами. Пусть за напра-
направления колебаний взяты оси ОХ и OY.
Тогда уравнения колебаний будут:
х = at cos (<at -\- at), у = а9 cos (<ot -|- а9), A)
где й] и ait otj и а9 — соответственно амплитуды и фазы первого и вто-
второго колебаний.
Определим уравнение траектории точки, для чего исключим из
уравнений A) время.
Перепишем уравнения A) в виде:
— = cos (at • cos at — sin tot • sin au B)
,— = cos <ot • cos as — sin <at • sin a2. Ba)
Умножая B) на cos aa и Bа) на cos at и беря их разность, по-
получим
— cos as — — cos at = sin ait • sin (a4 — o^).
Умножая B) на sin a2 и Bа) на sin at и беря их разность, получим
— sin a4 — — sin aj = cos wt • sin (os'— ot).
Возводя в квадрат и складывая почленно последние два уравне-
уравнения, находим уравнение траектории:
%+5 - Шcos (аа - a°=sln2 (- - a°- C)
Это уравнение представляет, вообще говоря, уравнение эллипса,
характеристики которого определяются значением разности фаз <ха—а{.
332
ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
[ГЛ. XI
Разберем частные случаи. Пусть разность фаз а9 — я, слагаемых
колебаний равна нулю, т. е.
oij = а2 = я.
Уравнение траектории C) в этом случае примет вид:
^_2^ = 0 или (?_>ув0, откуда *=**,
т. е. мы получили уравнение прямой, проходящей через начало ко-
координат и образующей с осью ОХ угол, тангенс которого равен ~
(рис. 249а).
У
N
У-
X
0 т Г
б)
Рис. 249. При сложении двух взаимно перпендикулярных колеба-
колебательных движений, происходящих с одинаковыми или противопо-
противоположными фазами, возникает гармоническое колебательное дви-
движение вдоль прямой.
По этой прямой точка совершает гармоническое колебание, так
как положение точки на прямой дается отрезком s, равным
s = /л:2 -\-y* = у a] cos2 (tot -f a) -\- a\ cos8 (arf-fa) =
= У a\-\-a\cos (tat-\-a);
период результирующего колебания равен периоду слагаемых коле-
колебаний, а амплитуда а результирующего колебания равна
Предположим теперь, что разность фаз аа — о^ слагаемых коле-
колебаний равна it, т. ?.
Уравнение траектории C) в этом случае примет вид:
х2 , Vs . 2ху п х
§ 101] СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ
393
Это уравнение представляет собою уравнение прямой, расположен-
расположенной, как показано на рис. 249<Г; по этой прямой точка совершает
гармоническое колебание с той же амплитудой, что и в предыдущем
случае.
Если разность фаз а2 — at слагаемых ¦ колебаний равна я/2 или
Зя/2, то уравнение траектории имеет вид:
Это — уравнение эллипса, отнесенного к осям ОХ и OY (рис. 250).
Если разность фаз as —D = -=-, то точка движется по эллипсу по
часовой стрелке. Это можно показать, если написать уравнения сла-
слагаемых колебаний в следующем виде:
х = at cos (otf -(- a),
у = aq cos (wt -f- a -f- ~) = — a% sin (utf -\-a).
В некоторый момент времени аргумент обоих выражений равен
нулю; при этом колеблющаяся точка находится в точке А (рис. 250); *
в следующий момент вре-
У мени аргумент возрастает,
следовательно, х будет по-
положительным, у— отрица-
отрицательным; точка пойдет вниз
и сдвинется по направлению
часовой стрелки. Если раз-
разность фаз слагаемых коле-
колебаний равна Зтг/2, то анало-
аналогичным рассуждением можно
показать, что точка по
эллипсу движется против
часовой стрелки.
При изменении знака
разности фаз движение по
эллипсу меняет свое на-
Рис.250. Возникновение эллиптического дви-
движения при сложении двух взаимно перпен-
перпендикулярных гармонических колебательных
движений.
правление на обратное, например при аа — ai= —
получаем
движение против часовой стрелки, а при <х2 — ац= — у.— по часо-
часовой стрелке. Очевидно, что при равенстве амплитуд эллипс превра-
превращается в окружность.
Таким образом, два взаимно перпендикулярных гармонических
колебания
х = a cosmt, y = acos Ш -\- ^-) i E)
= a cosmt, y = acos Ш -\- ^-) i
394
ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
[ГЛ. XI
которые можно переписать в виде
х = a cos tat, у = — а sin u>t, Ea)
дают в сумме равномерное движение по окружности радиуса а
с угловой скоростью <о, происходящее по часовой стрелке.
Обратно, равномерное движение, происходящее по окружности
радиуса а по часовой стрелке, с угловой скоростью ш, может быть
разложено на два взаимно перпендикулярных гармонических коле-
колебательных движения, представляемых формулами E) или Eа).
Также два взаимно перпендикулярных гармонических колебания:
x=acosmt
, у = а cos !
-^\ = a sin at
F)
дают в сумме равномерное движение по окружности радиуса а, с угло-
угловой скоростью ш, происходящее против часовой стрелки.
Все прочие значения разности фаз, кроме ± ic/2 и dt3ir/2, дают
эллипсы, не приведенные к'осям ОХ и ОК. Некоторые из возмож-
возможных видов траекторий, возникающих при сложении взаимно перпен-
перпендикулярных гармонических колебательных движений одного периода,
изображены на рис. 251.
Гх
Рис. 251. Различные виды траекторий движений, возникающих
при сложении двух взаимно перпендикулярных гармонических
колебательных движений одного периода.
Из приведенного рассмотрения следует, что движение точки по
эллипсу также может быть разложено на два взаимно перпендику-
перпендикулярных колебания, разность фаз между которыми определяется видом
вллияса и направлением движения точки.
Если взаимно перпендикулярные колебания происходят с различ-
различными периодами, то в результате сложения колебаний получаются
траектории более сложной формы, изображенные для некоторых
частных случаев на рис. 252; эти траектории называются фигурами
Лисажу.
Наконец, рассмотрим возможность разложить прямолинейное коле-
колебание точки на два „круговых колебания'. Чтобы уяснить это, обра-
обратимся к рис, 253. Представим себе, что точка одновременно участвует
§ 102]
8АТУХАЮЩИЕ КОЛЕБАНИЯ
395
в двух смещениях из положения равновесия О. Одно смещение
представлено вектором О А, другое — вектором ОА^, численно рав-
равным О А. Длину каждого из этих век-
векторов обозначим через а. Результирую-
Результирующее смещение выражается геометри-
геометрической суммой обоих смещений; сле-
следовательно, положение точки будет
даваться точкой В рис. 253. Предпо- .
ложим, что векторы смещения вра-
вращаются вокруг точки О в двух про- Рис..252. Различные виды траек-
тивоположных направлениях с одина- торий движений, возникающих
новой угловой скоростью ш, тогда при сложении двух взаимно
результирующее смещение будет от- перпендикулярных гармониче-
р } г* "* „ лп ских колебательных движений
кладываться по прямой ОБ, которую различных периодов,
назовем осью X. Расстояние точки В
от положения равновесия О в некоторый момент времени опреде-
определится величиною х, которая, как видно из рисунка, равна
х = 2а cos (wt -\- a),
т. е. результирующее смещение представляет собою гармоническое
колебание с амплитудой, равной удвоенному радиусу окружности,
по которой вращаются концы век-
векторов О А и OAi. Период колеба-
колебания равен периоду обращения
векторов смещения.
Отсюда вытекает, что смеще-
смещение при прямолинейном гармо-
гармоническом колебаний можно пред-
представить как геометрическую сумму
двух векторов смещения, вращаю-
Рис 253 Сложение двух круговых щихся „противоположных на-
колебаний, представляемых векторами к „
ОА и О Аи вращающимися в проти- правлениях с угловой скоростью,
воположных направлениях. равной круговой частоте ш коле-
колебания. Величина векторов равна
половине амплитуды колебания, и векторы расположены в каждый
данный момент симметрично по отношению к прямой, по которой
происходит колебание.
§ 102. Затухающие колебания. На практике всякое колебание
материальной точки, которое не поддерживается извне, затухает,
амплитуда его колебания с течением времени уменьшается. Причина
затухания обуславливается силами, тормозящими движение, например,
силой трения в месте подвеса при колебании маятника или силой
сопротивления среды. Чтобы исследовать этот вопрос, надо написать
уравнение, выражающее второй закон Ньютона, принимая в расчет
силы сопротивления. Мы ограничимся рассмотрением случая, когда
точка совершает прямолинейное колебание в вязкой среде. Сила
396 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XI
сопротивления среды зависит от скорости движения точки и, как
мы видели (§ 42), в случае малых скоростей ее можно считать про-
пропорциональной скорости; направлена она в сторону, противополож-
противоположную скорости; таким образом, силу сопротивления можно положить
равной — гх, где г — постоянная величина, называемая коэффициен-
коэффициентом сопротивления. Эта сила прибавится к упругой силе — kx, от-
откуда полная сила, действующая на точку, равна /= — kx — гх
и, следовательно, второй закон Ньютона может быть написан в виде:
— kx — гх. A)
Деля правую и левую части этого уравнения на .массу т, полу-
получим
k
г— * г Т *
Введем обозначения
где (оо и р — положительны. Тогда уравнение Aа) примет вид:
!=«* ъ-^
A6)
С помощью подстановки можно уравнение A6) привести к виду,
уже рассмотренному нами в § 97. Для этого введем новую пере-
переменную z, связанную с х соотношением:
х = г-е~&. C)
Проведем замену переменных в уравнении A6), пользуясь равен-
равенствами:
x = e~V -z — pe-P'-z;
Подставляя эти значения х и х в уравнение A6) и сокращая все
члены на множитель е~^, получаем
z — 2р -f р*г = — wbz + 2р2г — 2р?
или
5 = _(<о5 — f)z. D)
Положим, что сопротивление среды настолько мало, что
Тогда <о§ — ра есть величина положительная, и мы можем ввести
обозначение: <о5 — Ра = "Л после чего уравнение D) принимает вид:
2== —ш92. Dа)
1 При большом сопротивлении среды р* > <оЦ; тогда, как можно показать,
движение становится непериодическим. Этот случай мы не будем рассматри-
рассматривать.
§ 102]
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
397
Уравнение Dа) совпадает с уравнением E) § 97, решение кото-
которого нам известно. Поэтому по аналогии мы можем написать реше-
решение уравнения Dа) в виде:
z = а0 cos (u>t -\- а),
E).
где а0 и а — постоянные, которые должны быть определены из
начальных условий. Повторяя все рассуждения, приведенные в § 97,
заключаем, что z меняется периодически, причем период изменения z
равен
_ 2*
1
или, подставляя вместо ш его значение ш2 = (в0 —
2тс
т=-
(в)
Воспользовавшись выражениями B), можно представить период
колебаний Т еще в виде:
Т=
V
km —т г
Fа)
Подставляя в решение E) вместо z его значение, получаем по
формуле C) уравнение движения точки под действием упругой силы
в среде с сопротивлением:
х = о0е- Р' cos (arf -(- я), G)
которое можно также представить в виде
X = a cos {ynt -\- a).
Gа)
Это решение представляет собою колебание с амплитудой а =
= аое~^, уменьшающейся с течением времени. Период колебания
"" "в среде с сопротив-
сопротивлением больше, чем период коле-
точки такой же
бания Та = —
массы m под действием такой же
упругой силы /= — kx в среде
без сопротивления. График зависи-
зависимости х от времени представлен на
рис. 254. Как видно, колебания за- Рис, 254. Затухающие колебания,
тухают со временем.
Логарифм отношения двух последовательных значений амплитуд,
отстоящих друг от друга на время, равное периоду Т, называется
*
398 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XT
логарифмическим декрементом затухания. Обозначив логарифми-
логарифмический декремент буквой X, имеем по определению
%^ т. е. Х = (ЗГ. (8)
Вводя в выражение G) вместо C логарифмический декремент X
по формуле (8) и вместо ш — период Т= — , получим еще сле-
следующее выражение для затухающих колебаний:
-х- i t \
х = айе т cos.f2ity + aj, G6)
где период Т определяется формулой F) или Fа).
Логарифмический декремент X можно определить непосредственно
из наблюдений, измерив значения амплитуд а4 и а2 двух последую-
последующих колебаний, тогда по определению:
Зная X, можно, пользуясь соотношением
г=2$/п = 2 у/и,
определить коэффициент сопротивления г.
По формуле G) колебания прекращаются полностью лишь через
бесконечно большой промежуток времени. На самом деле колебания
прекращаются через конечный промежуток времени, так как при
амплитуде одного порядка величины с атомными размерами колеба-
колебания макроскопической системы, как целого, невозможны. Энергия,
сообщенная системе при выводе ее из положения равновесия, при
наличии затуханий, понемногу тратится на работу против сил трения.
Чтобы поддержать колебания незатухающими, к системе надо не-
непрерывно подводить извне энергию.
Примером системы, колебания которой, несмотря на наличие сил
трения, происходят благодаря подводимой энергии с неизменной
амплитудой, может служить часовой маятник. Храповой механизм
подталкивает маятник в такт с его колебаниями. Энергия, переда-
передаваемая при этом маятнику, берется либо за счет раскручивающейся
пружины, либо за счет опускающегося груза.
Система такого рода, поддерживающая неизменной амплитуду
своих колебаний, носит название автоколебательной системы.
Для того чтобы составить более конкретное представление о затухающих
колебаниях, разберем два следующих примера.
Пример 1. Логарифмический декремент колебаний маятника равен X =
= 0,02. Определить, во сколько раз уменьшится амплитуда колебаний после
100 полных качаний маятника.
§ 103] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 399
Решение. В начальный момент времени t = 0 амплитуда колебаний
t
р/ —л -^
а = п^е = п^е
равна аа.
После 100 колебаний, т. е. в момент времени t = 100 Т, амплитуда коле-
колебаний равна
aioo = aoe~x<100, откуда -^-= г~шг = е*' 10° = еа = 7,4,
вюо е~
т. е. амплитуда колебаний маятника уменьшается после 100 колебаний в 7,4
раза.
Пример 2. Определить логарифмический декремент затухающих коле-
колебаний маятника длиной / = 50 см, если он за 8 мин. качаний теряет 99°/о
своей энергии.
Решение. Обозначим энергию колебаний маятника в начальный момент
через Еа, а энергию его колебаний через время ? = 8мин. = 480 сек.— через
Et, тогда по условию
Fo = T0O*
Так как энергия колебаний прямо пропорциональна квадрату амплитуды, то
аа У 100 10*
Амплитуда в начальный момент <=0 равна а0; амплитуда через время t
_XJ_
равна at = aoe т, где Г—период колебаний маятника, отсюда
\ —- 1 "Т*
—I =е г = тп, а искомый декремент затухания \ равен Х = —In 10.
Ввиду слабости затуханий, можно приближенно выразить период колебаний Г,
пользуясь обычной формулой для периода колебаний маятника:
тогда
1п1П.'= 0,0068.
§ 103. Вынужденные колебания. Рассмотрим теперь колебания,
которые совершает материальная точка, если на нее, кроме упругой
силы и сил сопротивления, действует еще добавочная периодическая
сила. Пример такого случая мы( имеем, если груз, подвешенный на
пружине, добавочно подталкивается, причем толчки происходят через
равные промежутки времени. Мы предположим, что эта добавочная
вынуждающая сила /i меняется со временем по закону синуса или
косинуса, т. е. что она, например, имеет вид:
t. A)
400 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ . [ГЛ. XI
Такое предположение сводится к тому, что сила -меняется во
времени периодически с периодом Т=—; величина И называется
амплитудой силы и представляет наибольшее значение силы.
В этом случае уравнение, выражающее второй закон Ньютона,
напишется в виде:
mx = — kx — rx-\-H cos <ot; B)
справа стоит сумма силы упругости — kx, силы сопротивления
среды — тх и вынуждающей силы Н cos wt. Перепишем это уравне-
уравнение в виде
cos wt, Ba)
где и, и р имеют те же значения, что и в § 102 [формула B)],
a h равно отношению амплитуды силы к массе точки
При отсутствии вынуждающей силы (hcosu>t = 0) и силы тре-
трения точка колеблется с круговой частотой ш0 (собственные колеба-
колебания).
Попытаемся теперь найти решение уравнения Bа), положив х
равным
х = a cos {wt -\- а); D)
другими словами, мы будем искать решение, предполагая, что в ре-
результате действия всех сил получится колебание периода, равного
периоду вынуждающей силы. Подставляя функцию D) в уравнение
Bа), определим величины а и а из требования, чтобы уравнение
обратилось в тождество. Для первой и второй производных от х
по t из выражения D) найдем
х = — aw sin (wt -\-а), х = — аша cos (wt -f- а);
подставляем эти значения х и х в уравнение Bа), получим
— aw* cos (wt + а) = — ш^а cos (a>t -}- a) -j- 2$aa> sin (mt -}- а) -(- h cos u>t,
или, представляя тригонометрические функции от сложного аргумента
в раскрытом виде:
— аи)'2 (cos mt cos a — sin wt sin a) =
= — шоа (cos wt • cos a — sin a>t • sin a) -j-
~\- 2j3auj (sin wt • cos a -\- cos wt • sin a)-\-h cos <at.
Чтобы это уравнение обратилось в тождество, надо, чтобы коэф-
коэффициенты при cos wt в обеих частях равенства были равны и
коэффициенты при sin wt в обеих частях равенства были также равны;
§ ЮЗ]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
401
таким образом, получаем
— аш* cos а = — ашЬ cos а -|- 2фаш sin а ~\- h,
дао'2 sin а = аюо sin а -|~ 2fya<o cos а
или
a (cog — со3) cos a — 2f3a«) .sin a = h,
a (cog — ш3) sin a -\- 2paa> • cos a = 0.
Из второго уравнения E) получаем
E)
F)
Возводя в квадрат и складывая оба уравнения E), имеем
откуда
G)
Выражения F) и G) определяют фазу и амплитуду установившихся
вынужденных колебаний.1
Если тело первоначально покоилось, а затем на него начала дей-
действовать вынуждающая сила /, = #• cos mt, то оно начнет совершать
вынужденные колебания, амплитуда
которых будет возрастать, пока не до-
достигнет значения, определяемого ра-
равенством G). Возрастание со временем
амплитуды вынужденных колебаний
представлено на рис. 255. Когда вы-
вынужденные колебания установились,
дальнейшее возрастание амплитуды
прекращается.
Из формул F) и G) видим, что
амплитуда а и фаза а вынужденных
колебаний зависят от соотношения частоты со вынуждающей силы
и частоты ш0 собственных колебаний точки. Колебание, вообще
говоря, происходит не „в фазе" с силой, т. е. наибольшего сме-
смещения точка достигает не в тот момент, когда сила наибольшая. Из
формулы F) видно, что если сопротивление среды равно нулю, т. е.
р = 0, то в этом случае колебание и сила имеют одинаковые фазы;
во всех прочих случаях фаза а ф- 0. Наиболее интересным пред-
Рис. 255. Возрастание со вре-
временем амплитуды вынужденных
колебаний.
1 В теории дифференциальных уравнений показывается, что для определе-
определения общего решения уравнения Bа) необходимо решение D) сложить с реше-
решением уравнения jf = — <*\x. — 2$?; однако решение этого последнего уравне-
уравнения, как было выяснено в § 102, представляет собою затухающие колебания,
которые с течением времени перестают играть заметную роль. Решение же
D) является незатухающим и имеет место во все время существования вы-
вынуждающей силы Д.
1{АЪ с- Э. Фриш и А. В, Тиморева
402
ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
[гл. хт
ставляется выражение G) для амплитуды вынужденных колебаний.
Амплитуда колебаний пропорциональна амплитуде силы. Если ме-
меняется частота <о вынуждающей силы при постоянной частоте <а0
собственных колебаний, то при этом будет меняться и амплитуда
вынужденных колебаний. Можно показать, что амплитуда вынуж-
вынужденных колебаний имеет максимум при частоте вынуждающей
силы (орез, удовлетворяющей соотношению шрез = а>§ — 2р2.' Появле-
Появление такого максимума представляет собою явление резонанса. На
основании полученного соотношения резонансная частота шрез равна
Vs=/4Zr2^ (8)
При этом по G) максимальная (резонансная) амплитуда дости-
достигает значения
« (9)
Если сопротивление среды равно нулю, т. е. р = 0, то макси-
максимум амплитуды получается при
т. е. когда частота вынуждающей силы ш делается равной частоте ш0
собственных колебаний; в этом случае амплитуда вынужденных ко-
колебаний становится бесконечно
большой. При отличном от нуля
значении р амплитуда никогда не
достигает бесконечности, и ма-
максимум ее получается при зна-
значениях <орез, меньших <о0. Зависи-
Зависимость амплитуды вынужденных
колебаний от частоты вынуждаю-
вынуждающей силы приведена на рис. 256
для разных значений р. Мы ви-
видим, что чем больше коэффициент
затухания р, тем менее остро вы-
выражен максимум амплитуды.
Кривые рис. 256 называются
резонансными кривыми. Резонан-
Резонансные кривые имеют тем более
высокий и острый максимум, чем
меньше затухание р резонирую-
резонирующей системы. Так как на самом
деле р всегда отлично от нуля, то
бесконечно больших амплитуд при резонансе получиться не может.
Рассмотрим еще зависимость фазы вынужденных колебаний а от
частоты [формула F)]. При 0^(о<^(о0 для тангенса получаются
0,2 0,4 0,6 0,8 1,0 t,2 1Л 1,6 1,8 2,0
Рис. 256. Зависимость амплитуды вы-
вынужденных колебаний от частоты
вынуждающей силы для различных
коэффициентов затухания.
1 Чтобы в этом убедиться, надо найти минимум знаменателя выраже-
103]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
403
отрицательные значения, следовательно, для а получим следующие
неравенства: 0^=а^> ^- или it^<x^>-^-. Полагая в первом из
уравнений E) ш = 0, найдем: au)Jcosa = A, а так как амплитуды а
и h положительны, то при (о = 0 получаем, что cos a должен быть
больше нуля. Это условие заставляет выбрать из двух неравенств
одно: 0:=sa^> у. Таким образом, при 0^(о^(в0 разность фаз a
отрицательна, т. е. вынужденные колебания отстают по фазе от
вынуждающей силы. При приближении значения со к резонансной
частоте шреа отставание по фазе возрастает. При условии резонанса,
когда ш = (орез= j/(o* — 2j32, по формуле 0
F) фаза вынужденных колебаний опреде- 0
ляется соотношением:
(DM,
tg a = —
В случае острого резонанса
и для tga приближенно получаем
мало
Так как шо/р велико, то фаза а близка Рис 257. Зависимость фазы
вынужденных колебаний от
частоты вынуждающейсилы,
к — тс/2. Для со = (о0 фаза а= » •
При (о^>ш0 тангенс угла а положителен,
следовательно, <х<^—¦=-, т. е. отставание по фазе еще больше. Для
частот вынуждающей силы, много ббльших частоты собственных
колебаний ш0, фаза а, оставаясь отрицательной, стремится к —тс.
Зависимость а от отношения" (в/ш0 представлена графически на
рис. 257 для двух разных значений |3: кривая / относится к мень-
меньшему значению р (малое затухание), кривая 2— к большему значе-
значению р (большое затухание).
Вблизи резонанса, где а^— -^-, сила положительна во все
время движения от максимального отрицательного смещения до мак-
максимального положительного смещения и отрицательна во время об-
обратного движения, так что она непрерывно увеличивает размах ко-
колебаний. Это увеличение амплитуды колебаний происходит до тех
пор, пока вся работа внешней силы не пойдет на преодоление силы
ния G). Для этого приравниваем нулю производную знаменателя:
— 2 (<og — <ов) • 2ш + 8р2ш = 0.
Так как ю не нуль (ш = 0 соответствует максимуму знаменателя), то знамена-
знаменатель выражения G) достигает минимума при
404 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XI
трения, вызывающей затухание колебаний. При этом достигается
значение амплитуды установившихся вынужденных колебаний.
Работа внешней силы максимальна при разности фаз — тс/2, т. е.
при частоте, близкой к резонансной. При иных сдвигах фаз сила
частично действует ускоряюще, частично же противодействует дви-
движению. При а = 0 или а = — тс сила в течение половины времени
ускоряет движение, в течение же другой половины времени проти-
противодействует ему, т. е. в общем не совершает никакой работы.
Отсюда следует, что вне области резонанса внешняя сила про-
производит лишь незначительную работу, при резонансе же работа воз-
возрастает. Этот эффект выражен особенно сильно при остром резо-
резонансе. В этом случае р мало и, как видно из рис. 257, достаточно
величине со измениться от значений, немного меньших ш0, до зна-
значений, немного ббльших ш0, чтобы а изменилось от значения,
близкого к а = 0, до значения, близкого к а = — ir. В этом смысле
можно говорить об изменении разности фаз между силой и смещением
на противоположную при переходе частоты через значение изо = шРез'
Явления резонанса играют большую роль во многих физических
процессах и в технике. В некоторых случаях в технике явления
резонанса вредны. Рассмотрим, например, мотор с эксцентриком,
укрепленный нЪ подставке, способной совершать упругие колебания.
При вращении мотор создает периодическую силу, сотрясающую
подставку и приводящую ее в состояние вынужденных колеба-
колебаний.
При наступлении резонанса мотор передает подставке значи-
значительную энергию, и амплитуда ее колебаний может достичь разме-
размеров, опасных для ее прочности. При дальнейшем возрастании числа
оборотов мотора изменяется разность фаз между силой сотрясений
и смещениями подставки, работа мотора на раскачивание подставки
уменьшается, и число его оборотов возрастает, что также вредно,
так как может привести к порче мотора.
Особый вид резонанса представляет собой так называемый пара-
параметрический резонанс. Колебания в системе могут возникнуть ^ не
только под влиянием рассмотренных вынуждающих сил, но и под
влиянием периодического изменения одного из ее параметров, кото-
который при свободных колебаниях остается постоянным. Например, в
механической системе колебания могут возникнуть в результате изме-
изменения ее момента инерции, размера, натяжений и т. д. Достижение
максимальной амплитуды колебаний наступает при определенном
отношении между частотой vn изменения параметра и средней часто-
частотой собственных колебаний ~^0, а именно, когда vj~^a = 2/k, где
k — целое число, т. е. когда vn/^o принимает одно из значений: 2, 1,
1/2, 1/3 и т. д.
Условие возникновения параметрического резонанса выполняется
тем легче, чем сильнее изменение параметра и чем меньше потери
энергии системы (трение, сопротивление). Чаще всего параметричес-
§ 104] ПРЕДСТАВЛЕНИЕ НЕГАРМОНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ 406
кий резонанс возникает при ^В- = 1. Простейшим примером параме-
параметрического резонанса служит раскачивание качелей, когда качающиеся
приседают в такт с колебаниями качелей. В результате приседаний
приведенная длина физического маятника, который представляют
собой качели, периодически меняется. Другой пример параметричес-
параметрического резонанса — возбуждение колебаний в струне путем периоди-
периодического изменения ее натяжения. Если частота периодического изме-
изменения натяжения струны близка к удвоенной частоте ее собственных
колебаний, то в струне возникнут сильные поперечные колебания,
хотя внешние силы (натяжение), действуют вдоль струны. Колебания,
возникающие вследствие параметрического резонанса, могут оказаться
вредными, например, в машинах, где имеются вращающиеся части,
они могут привести к разрушению подшипников.
Разберем пример на вынужденные колебания.
Пример. Тело массой 400 г подвешено к пружине. Пружина растяги-
растягивается на 1 см под влиянием силы 40 Г. Логарифмический декремент затуха-
затухания колеблющегося тела Х= 1,57. Определить период колебаний, при котором
наступает резонанс, и резонансную амплитуду, если амплитуда вынуждающей
силы равна /7 = 200 Г.
Решение. При малом затухании ш==а0 и, следовательно, логарифмический
декремент X = — C^ -— р. Подставляя в формулу (8) вместо р его приближен-
приближенное значение через X, получим для резонансной частоты
в нашем случае
¦"¦ / I/I jO' \ fm*^/ л лл
отсюда
1 ,л,
* pea—ПОЛ ° * рез—1»и1 1о*
где Грез — период, при котором происходит резонанс, Го—период собствен-
собственных колебаний тела на пружине. По данным примера:
Таким образом, резонанс имеет место при периоде
Гре9= 1,07-0,63 сек. ^0,67 сек.
Введя в формулу (9) вместо h его значение Н/т и вместо р логарифми-
логарифмический декремент X, получим
т
откуда, пользуясь численными данными, найдем врез = 10 см.
§ 104. Представление негармонических колебательных процес-
процессов при помощи гармонических колебаний. До сих пор мы рас-
14 С. Э. Фриш в А. В. Тиморева
406 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XI
сматривали в основном простое гармоническое колебательное дви-
движение, т. е. движение, при котором смещение х колеблющейся
частицы из положения равновесия имеет вид:
х = a cos (tat -\-a), A)
или, что то же самое (см. стр. 375)
х = a sin (cat-f- a'), (la)
где а — амплитуда колебаний, <о — круговая частота колебаний, а и
а' — начальные фазы. Такое колебание графически изображается
синусоидой.
Однако реальные колебания могут лишь более или менее точно
походить на строго синусоидальные колебания, так как всякие реаль-
реальные колебания сопровождаются затуханием (см. § 102). Кроме того,
весьма часто колебания, вообще, носят более сложный характер.
Тем не менее рассмотрение гармонических колебаний имеет боль-
большое значение, так как сложное колебание можно представить как
сумму гармонических колебаний.
Мы видели (§ 100), что при сложении двух гармонических коле-
колебательных движений xt и хь совершающихся вдоль одной а той же
прямой и имеющих одинаковую частоту щ, результирующее коле-
колебание является также гармоническим колебательным движением. Но
так обстоит дело лишь при сложении колебаний одной частоты. При
сложении двух гармонических колебательных движений разных
частот суммарное колебание носит более сложный характер. На
рис. 258 в верхней строке графически изображено гармоническое
колебательное движение определенной частоты wj и определенной
амплитуды Й1 (по оси ординат отложено смещение xh по оси аб-
абсцисс — время). В средней строке изображено другое гармониче-
гармоническое колебание х%, происходящее с частотой ш2, в 4,5 раза меньшей,
чем частота mj первого движения, и с амплитудой а9 = 2,5 ах. На-
Наконец, в нижней строке пред-
м>лллллллпАлл oil ставлено колебание, являю-
ViV/VVVVVVVViVA/V щееся суммой двух первых;
смещение х точки, совершаю-
совершающей это сложное колебание,
в каждый данный момент равно
Мы могли бы поставить
_j задачу обратно и, имея слож-
Рис. 258. Сложение двух гармонических ное колебание заданным, по-
колебательных движений частоты coi и ша. смотреть, на сумму каких
гармонических колебательных
движений оно разложимо. В случае сложного колебания, изобра-
изображенного на нижней строке рис. 258, оно разложимо на два гармони-
гармонических колебания, изображенных на двух других строках рис. 258.
§ 104J ПРЕДСТАВЛЕНИЕ НЕГАРМОНИЧЕСКИХ КОЛЕВАТЕЛЬНЫХ ПРОЦЕССОВ 407
В § 100 мы рассмотрели явление, известное под названием
биения. Оно сводилось к тому, что два колебания je1 = a1co$(<V-|-a)
и xi = a1cos(wit-\-a), частоты ш1 и о>а которых близки друг
к другу, при сложении дают колебание частоты ш = -^ (<% -f- а>9) с
амплитудой а, меняющейся по закону:
а =
1
t
B)
Обратно, мы можем сказать, что сложное колебание, амплитуда
которого меняется по закону B), может быть разложено на два
чисто гармонических колебательных движения с частотами <oi и (»а.
Аналогично можно себе представить иное сложное колебание,
амплитуда которого медленно (по сравнению с периодом самих ко-
колебаний) меняется по какому-либо другому закону. Такого рода ко-
колебание носит название модулированного колебания. Модулирован-
Модулированное колебание не представляет собою гармонического колебатель-
колебательного движения, но может быть разложено на ряд гармонических
колебательных движений. Возьмем для примера колебание
амплитуда которого меняется по закону:
cos
где aj и аг постоянны, причем считаем а^-^а^ и о)<^ш0. Этот, за-
закон означает, что амплитуда а меняется со временем между значе-
значениями аг-\-ая и «1 — at. Подставив приведенное значение для а
в выражение для х, получим
x =
или
X = в! COS Юв* -J- Ц- COS (%+ш) t-\-~COS (<fl0 — (й) f, C)
т. е. рассматриваемое модулированное колебание может быть раз-
разложено на сумму трех гармонических колебательных движений
с частотами ш0> <о0 -\- ш и <о0 — ш и соответственно с амплитудами
вх, а%12 и аг/2.
Результат сложения двух гармонических колебаний зависит от
их частот, амплитуд и начальных фаз. В зависимости от значения
частот, фаз и амплитуд могут быть получены весьма разнообразные
суммарные колебания. Еще более сложный характер колебаний по-
получится при сложении трех и более гармонических колебательных
движений. Обратно, колебание весьма сложного характера может
быть разложено на достаточное число гармонических колебаний
различных амплитуд и частот.
14*
-ш
b)t со, этот спектр содержит четыре линии
„ пйп - с частотами <в, Зи>, 5со и 7ш; длины
Гебани? СпПрееКдТсРхавлеГг;0 "на" ™* ™й в некотором определен-
рис. 258. ном масштабе равны 10; 1,5; 0,Ь и
0,3 единицам длины.
Изображение сложных колебаний с помощью такого рода спек-
спектров не полно в том смысле, что оно дает лишь частоты и ампли-
амплитуды составляющих гармонических колебаний, не давая их начальные
фазы; однако для многих случаев знания частот и амплитуд вполне
достаточно.
До сих пор мы рассматривали разложение на сумму гармонических коле-
колебаний сложных колебаний, имеющих периодический характер. Движение мо-
может, однако, будучи колебательным, вместе с тем не носить периодического
характера. В качестве примера можно привести затухающее колебание, изо-
изображенное на рис. 254. Здесь амплитуда колебаний непрерывно затухает, так
что некоторое определенное состояние движения, осуществленное один раз,
408 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XI
В теории тригонометрических рядов показывается, что периоди-
периодическую функцию с периодом 2ic
можно представить в виде бесконечного тригонометрического ряда
х = Ай
носящего название ряда Фурье;1 коэффициенты Ал, Alt Ait Аг...
и Bt, Bt, В3... для данного вида F (ш^) вычисляются по определен-
определенным формулам.
Для четной функции, т. е. такой, которая сохраняет свое зна-
значение при изменении знака аргумента на обратный:
все коэффициенты Bit B2, B3t... равны нулю, так что разложение
в ряд принимает вид:
х= Ао-\- AjCOSint-\- Aacos2mt-{- A3cos3ait-f-... (б)
Для нечетной функции, т. е. для такой функции, которая ме-
меняет знак при изменении знака' аргумента:
все коэффициенты Ай, Аь Ait A3,... равны нулю, так что разло-
разложение в ряд принимает вид:
x = B1slnwt-\-Bisin'2<ut-\-BaS{n3wt-{-... F)
Таким образом, видно, что, вообще говоря, любое периодиче-
периодическое колебание может быть математически представлено как сумма
гармонических колебаний кратных частот ш, 2ш, Зсо и т. д.
На рис. 259 внизу представлено колебание, имеющее вид почти
ломаной линии; выше представлены четыре синусоиды, на которые
оно разлагается. Аналитически это разложение имеет вид:
х = 10а sin wt — 1,5а sin 3u>t -f- 0,6а sin 5«rf — 0,3a sin 7wt, G)
в этом разложении Вх= 10а, В3=—1,5а, Вв = 0,6в, 57===—0,3а,
все остальные коэффициенты Bt равны нулю.
1 Более общо показывается, что любая функция y = F(x), удовлетворяю-
удовлетворяющая так называемым условиям Дирихле и заданная в интервале от —/ до-J-/,
может быть представлена в виде ряда:
пх 2кх Зллг
пх 2пх Зкх I <4а)
+ Вх sin -у + Bt sin —у--f ?1» sin -у— -{-...
§ 104] ПРЕДСТАВЛЕНИЕ НЕГАРМОНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ 409
Результат разложения сложного колебания в ряд Фурье можно
представить, записав все те частоты, амплитуды которых отличны от
нуля, и значения соответ-
соответствующих им амплитуд.
Такую запись весьма
удобно делать графиче-
графически, отложив по оси
абсцисс шкалу частот и ^ _ _
проводя в соответствен- ¦ ^\/\/\/\/\/\
ных местах оси абсцисс
вертикальные линии, дли-
>с^Чэ— 0,BslnSwt
¦ o,3sin?u>t
на которых в определен-
определенном масштабе изображает
амплитуду. Такой график
носит название спектра
данного колебания. На
рис. 260' представлен
спектр сложного колеба-
колебания, изображенного на
нижней строке рис. 258.
Так как это колебание
может быть разложено
на две синусоиды с частотами coj и (л^ = -~ и амплитудами а^ и ая =
4,0
=2,5ai, то спектр изобразится двумя линиями, с абсциссами ш1 и
—; длина второй из этих линий в
4,0
2,5 раза превышает длину первой.
На рис. 261 изображен спектр
сложного колебания, представленного
на рис. 259. Согласно разложению G),
этот спектр содержит четыре линии
с частотами со, Зю, 5со и 7ш; длины
этих линий в некотором определен-
определенном масштабе равны 10; 1,5; 0,6 и
0,3 единицам длины.
Рис. 259. Разложение сложного колебательного
движения на ряд гармонических колебатель-
колебательных движений.
А
2,5
Рис. 260. Спектр сложного ко-
колебания, представленного на
рис. 258.
Изображение сложных колебаний с помощью такого рода спек-
спектров не полно в том смысле, что оно дает лишь частоты и ампли-
амплитуды составляющих гармонических колебаний, не давая их начальные
фазы; однако для многих случаев знания частот и амплитуд вполне
достаточно.
До сих пор мы рассматривали разложение на сумму гармонических коле-
колебаний сложных колебаний, имеющих периодический характер. Движение мо-
может, однако, будучи колебательным, вместе с тем не носить периодического
характера. В качестве примера можно привести затухающее колебание, изо-
изображенное на рис. 254. Здесь амплитуда колебаний непрерывно затухает, так
что некоторое определенное состояние движения, осуществленное один раз,
410
ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
|ГЛ. XI
более не осуществляется. Такое непериодическое движение нельзя разложить
в ряд Фурье с прерывным рядом частот ш, 2oi, Зш, ... Оно может быть раз-
разложено на бесконечное множество гармонических колебательных движений,
причем частоты „соседних" колеба-
колебаний будут бесконечно мало отли-
отличаться друг от друга, а амплитуды
АА{ отдельных элементарных колеба-
колебаний будут бесконечно малы'.
Графически такому колебанию
уже не соответствует спектр, состоя-
состоящий из отдельных линий („линейчатый
спектр'): ему соответствует непре-
непрерывный спектр, что означает присут-
присутствие колебаний со „всеми" частсн
тами. Для графического изображения
непрерывного спектра отложим по
А
1В,0
1.5
0.3
I
-OJ
ш Зи> 5iii 7 со
Рис. 261. Спектр сложного колебания,
представленного на рис. 259.
дон-
доноси абсцисс снова частоты <д, а по оси ординат—отношение ДЛ,-/Д<о,-. Тогда
кривая на таком графике даст „распределение амплитуд" по частотам в сплош-
сплошном спектре данного сложного
колебания. На рис. 262 а еще
раз представлено затухающее
колебание, а на рис. 262 б —
„распределение амплитуд" по
частотам в сплошном спектре
этого колебания. Ординаты гра-
графика, умноженные на соответ-
соответственный интервал частот
дают среднюю амплитуду коле-
,о I
|: пЛ/Vvw
г р
г. I а)
Рис. 262. Затухающее колебание (а) и „рас-
„распределение амплитуд" в его спектре (б).
бания в этом интервале частот.
Как видно из рис. 262 б, кри-
кривая имеет максимум, который
оказывается тем острее, чем
слабее затухание.
Для иных непериодических движений получится сплошной спектр с иным
распределением амплитуд по частотам.
Рассмотрим вопрос, каково физическое значение разложения не-
негармонического процесса на гармонические составляющие, т. е. ка-
каким образом можно на опыте выявить эти составляющие (гармо-
(гармоники). Предположим, что зависимость некоторого процесса от вре-
времен^ выражается функцией f(t), которая может быть разложена
в ряд Фурье. Пусть, например, это разложение может быть пред-
представлено в виде:
оо
f(t) = 2 (Ancos wd -\- Bn sin ruat). (8)
Левая и правая стороны этого соотношения математически тожде-
тождественны — совокупность гармоник неотличима от функции f(t).
1 Математически это соответствует представлению функции в виде инте-
интеграла Фурье:
ОЭ +00
F (at) — -i С da \ F (в) cos а (в — Ы) 48.
О —со
§ 105]
ПРЕДСТАВЛЕНИЕ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
411
Для регистрации отдельного члена ряда (8) (отдельной гармоники)
надо подобрать такие условия опыта, при которых эта отдельная
гармоника обнаруживалась бы. Это может быть осуществлено, напри-
например, следующим образом. Предположим, что функция f(t) характе-
характеризует вынуждающую силу, действующую на систему (резонатор),
способную совершать вынужденные колебания (§ 103). Пусть этот
резонатор имеет собственную частоту
колебания (резонансную частоту), совпа-
совпадающую с частотой k<o одной из гармо-
гармоник ряда (8). Если резонансная кривая
резонатора настолько остра, что частоты
соседних гармоник (k± 1)ш лежат в об-
области очень малых амплитуд вынужден-
вынужденных колебаний (рис. 263), то резонатор
будет практически совершать колебания
только частоты Аш с амплитудой, про-
пропорциональней амплитуде гармоники Ы
в разложении (8). Меняя резонансную
частоту резонатора (настройку), можно
последовательно создать условия для регистрации
моник разложения (8).
Явления такого типа имеют место в приборах, выявляющих спек-
спектральный состав какого-либо физического процесса, например свето-
светового или звукового возмущения, или электрического колебания.
§ 105. Представление колебательных процессов с помощью комплекс-
комплексных чисел. Из теории комплексных чисел известно, что комплексное число
? = а • e!f, где any— вещественные числа, е — основание натуральных лога-
логарифмов, l=V—1, может быть представлено в виде a (cos у +' sin у). Та-
Таким образом,
\ = а • elf = а ( cos <р + ' sin у). A)
Отсюда, вещественная часть комплексного числа 5, которую мы обозна-
обозначим | ? |, выразится следующим образом:
пц>
Рис. 263. Амплитуды выну-
вынужденных колебаний.
остальных гар-
151 = a cos <f>.
B)
Так как последнее соотношение носит характер тождества, то, следо-
следовательно, всегда, вместо тригонометрической функции асоэ^.мы можем рас-
рассматривать вещественную часть комплексного числа 5 = а • e'f. Сама по себе
такая замена вполне формальна и ничего нового не дает. Но дело заключается
в следующем: если мы проделаем над рядом комплексных чисел Е определен-
определенные математические действия (сложение, вычитание, умножение, дифференци-
дифференцирование, интегрирование и т. д.), а затем отделим вещественную часть от
мнимой, то получим тот же результат, как если бы проделывали аналогичные
действия над соответственными-тригонометрическими функциями. Это обстоя-
обстоятельство позволяет заменять сравнительно громоздкие тригонометрические
преобразования гораздо более простыми действиями над показательными функ-
функциями. Таким образом, пользование показательными функциями с мнимыми
показателями степени, вместо соответственных тригонометрических функций,
представляет с вычислительной точки зрения большие удобства.
412 ГАРМОНИЧЕСКОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ [ГЛ. XI
Как мы видели, выражение вида
х = a cos (<*t 4- а)
изображает гармоническое колебательное движение с амплитудой а, цикличе-
циклической частотой (о и начальной фазой а; величина t есть время, отсчитанное от
некоторого начального момента.
На основании сказанного ясно, что то же гармоническое колебательное
движение может быть представлено как вещественная часть | 5 | комплекс-
комплексного числа
е = а-е'""' + ». . C)
Мы видели, что при решении многих задач достаточно знать квадрат ам-
амплитуды, т. е. величину а1, так как энергия колебаний пропорциональна а1;
знание начальной фазы а при этом может не представлять интереса. Легко
показать, что для нахождения а1 нет необходимости фактически отделять
в комплексном числе вида C) вещественную часть от мнимой, а достаточно
составить выражение Й*, где ?*— комплексное число, сопряженное с 5. (На-
(Напомним, что сопряженным комплексным числом называется число, получаемое
из данного переменой знаков у всех мнимых единиц t.) В самом деле, комп-
комплексное число, сопряженное с 5, выраженным формулой C), будет:
(За)
Составив выражение ?;*, получим
К* = ае1 «°1 + а) • ае~ Uat +«) = а*, D)
т. е. Й* дает нам непосредственно квадрат амплитуды.
Обобщая выражение C), можно и величину а положить комплексной; в этом
случае она не будет, конечно, непосредственно выражать действительную ам-
амплитуду колебаний, так как действительная амплитуда всегда вещественна.
Выясним, прежде всего, какой физический смысл имеет такая „комплексная
амплитуда". Для этого положим a = aaeiao, где а0 и а0—вещественны, тогда
или 5 = аоег "»< + « + ««'. Dа)
Отделяя вещественную часть от мнимой, получим
| ? | = а0 cos (at + a + «о), E)
откуда видно, что 151 представляет собою гармоническое колебательное дви-
движение с амплитудой а0 и начальной фазой a -f- а0. Таким образом, комплексное
значение амплитуды означает изменение начальной фазы на а0. Легко убе-
убедиться, что и в этом случае 55* дает квадрат вещественной амплитуды: 5;* = в'.
Чтобы выяснить удобство пользования комплексными числами для изо-
изображения гармонических колебательных движений, рассмотрим задачу о сло-
сложении, двух гармонических колебаний xt = at cos (at + а,) н дг» = аа cos (<ot -\- aa)
одинаковой частоты to и происходящих вдоль одной и той же прямой; эта за-
задача была нами рассмотрена методом сложения векторов амплитуд в § 100.
Пользуясь же комплексными числами, получим
Результирующее колебание:
§ 105] ПРЕДСТАВЛЕНИЕ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ 413
Квадрат его амплитуды а4 получим, умножив правую часть на величину, с ней
сопряженную:
а2 = [а^1"»' + V + а2е1 «¦>< + «,'] [а1в-' «о* + V + а%е~1 ш + "а1],
откуда
но по формуле A)
е1 1«, - V _|_ e-i (а3 - «t) _ 2 cos (a, — a,),
откуда
аа = а? + а| + 2а,аа cos '(a, — aL),
что совпадает с формулой D) § 100.
ГЛАВА XII
ВОЛНЫ
§ 106. Распространение волн в упругой среде. Пусть точка,
совершающая колебание, находится в среде, все частицы которой
связаны между собой. Тогда энергия колебания точки может пере-
передаваться окружающим точкам, вызывая их колебание. Явление рас-
распространения колебания в среде называется волной. Пример обра-
образования волн мы получим, если бросим камень на поверхность воды:
область водяной поверхности, которая непосредственно возмущена
падающим камнем, начинает колебаться, причем это колебание рас-
распространяется от этой области к следующим, и мы получаем на
поверхности воды волну. Другой пример образования волны можно
получить, если взять веревку и одному из ее концов придать
ш рукой колебательное движение;
Л
0
в этом случае колебание также
начнет распространяться вдоль
веревки: по веревке побежит
^ __/" волна.
*" *"* Заметим сразу, что при рас-
пространении колебаний колеб-
г ЛЮ1и-иеся частицы не переме-
перемеj щаются с распространяющимся
колебательным процессом, а ко-
,т леблются около своих положений
=— равновесия.
Если частицы колеблются по
тои ж^ прямой, вдоль которой
_ распространяется колебание, то
- мы назовем волну продольной;
если колебания частиц перпенди-
кулярны к направлению распро-
странения колебаний, то волна
называется поперечной.
На рис. 264 представлена схема распространения поперечной
волны. Пять строчек рис. 264 представляют расположение частиц
среды в последовательные моменты времени. Первая строчка дает
Рис. 264. Схема распространения
поперечной волны.
§ 106]
РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ
415
положения частиц в начальный момент времени ^ = 0, когда все
частицы занимают положения равновесия и крайняя частица О лишь
получила ускорение w, направленное кверху. Вторая строчка дает
положение частиц через четверть периода после начала движения:
частица О достигла своего крайнего удаления вверх, частица А при-
приобрела лишь ускорение w, направленное вверх. Третья строчка дает
положение через полпериода после начала движения: частица О про-
проходит положение равновесия, идя вниз, частица А достигла крайнего
удаления вверх, частица В приобрела лишь ускорение w, направлен-
направленное вверх. Четвертая строчка дает положение частиц через три
четверти периода после начала движения: частица О достигла край-
крайнего отклонения вниз, частица А проходит положение равновесия,
идя вниз, частица В достигла крайнего отклонения кверху; частица С
приобретает ускорение w, направленное вверх. Наконец, в пятой
строчке даны положения частиц через период после начала колеба-
колебания: частица О опять проходит положение равновесия, идя вверх;
частица А достигла крайнего отклонения книзу; частица В идет через
положение равновесия вниз; частица С достигла крайнего смещения
кверху; частица D приобрела ускорение w, направленное наверх.
Таким образом можно проследить распространение колебаний дальше.
Рис. 265. Схема распространения продольной волны.
На рис. 265 сделано такое же построение для продольной вол-
волны. Разница только в том, что смещения частиц происходят в
направлении распространения колебаний. Как видно из рис. 265,
при продольной волне мы наблюдаем сближение и удаление частиц
друг от друга, вследствие чего в среде возникают сгущения (области,
обведенные на рисунке) и разрежения; процесс распространения
волны сопровождается перемещением областей сгущения и разре-
разрежения.
Являются ли волны, распространяющиеся в среде, продольными
или поперечными — зависит от упругих свойств среды.
416 волны , [гл. хн
Если при сдвиге одного слоя среды по отношению к другому
слою возникают упругие силы, стремящиеся возвратить сдвинутый
слой в положение равновесия, то в среде могут распространяться
поперечные волны (такой средой, вообще говоря, служит твердое
тело). Если в среде не возникают упругие силы при сдвиге парал-
параллельных слоев друг относительно друга, то поперечные волны не
могут образоваться. Например, жидкость и газ представляют среды,
в которых поперечные волны не распространяются (последнее не
относится к поверхности жидкости, в которой могут распростра-
распространяться и поперечные волны, носящие, однако, более сложный харак-
характер: в них частицы движутся по замкнутым круговым или эллипти-
эллиптическим траекториям). Если в среде возникают силы упругости при
деформации сжатия и растяжения, то в такой среде могут распро-
распространяться продольные волны. Например, жидкость или газ при сжа-
сжатии дают увеличение давления, сила которого, как мы видели,
играет роль силы упругости при деформации сжатия. В жидкости
и в газе распространяются только продольные волны. В твердых
телах продольные волны могут существовать наряду с поперечными.
Скорость распространения продольных волн V, как показывает
теория (см. § 111), обратно пропорциональна корню квадратному
из коэффициента упругости среды
а и ее плотности р:
V =
Приближенно это соотноше-
п „с„ г, ,. ние может быть заменено сле-
Рис. 266. Расстояние между ближай-
ближайшими точками, колеблющимися в оди- дующим:
наковых фазах, определяет длину . .. ~\fE
волны X. v — [/ у>
где Е—модуль Юнга среды.
Скорость распространения поперечных волн зависит от модуля
сдвига Ы: '
Расстояние, на которое определенная фаза колебания распро-
распространяется за один период колебания, называется длиной волны,
длину волны обозначим буквой X.
На рис. 266 сопоставлен ряд точек, отстоящих друг от друга
на X.
Из рисунка ясно, что длина волны представляет собой наи-
наименьшее расстояние между точками, колеблющимися в одинаковых
фазах. Под скоростью распространения волны подразумевается ее
фазовая скорость, т. е. скорость распространения данной фазы
колебания; например, в момент времени ? = 0 точка О на рис. 264
§ 107] ПРИНЦИП ГЮЙГЕНСА 417
имела начальную фазу, т. е. выходила из положения равновесия;
через промежуток времени Т начальную фазу приобрела точка Д
отстоящая от точки О на расстоянии X. Следовательно, начальная
фаза за время, равное периоду Т, распространилась на расстояние,
равное длине волны X. Отсюда для фазовой скорости получаем
определение:
V=y. A)
Представим, что точка, от которой идут колебания (центр ко-
колебания), колеблется в сплошной среде. Колебания распространя-
распространяются от центра во все стороны. Геометрическое место точек, до
которых к некоторому моменту времени дошло колебание, назовем
фронтом волны. Можно также в среде выделить геометрическое место
точек, колеблющихся в одинаковых фазах; эта совокупность точек
образует поверхность одинаковых фаз, или, как говорят, волновую
поверхность. Очевидно, что фронт волны является частным случаем
волновой поверхности. Если среда изотропна, то колебания от центра
колебаний распространяются одинаково во все стороны, в этом слу-
случае и фронт волны и поверхности одинаковых фаз представляют
собою сферы, центр которых лежит в центре колебания. Очевидно,
что радиус фронта волны представляет собою отрезок, на который
колебания с данной фазой распространились за время t, прошедшее
с момента начала колебаний точки, расположенной в центре, откуда
r=Vt,
где V — скорость распространения волн.
Форма фронта волны определяет типы волн, например, плоской
волной называется волна, фронт которой представляет плоскость,
и т. д.
Направления, в которых распространяются колебания, называются
лучами. В изотропной среде лучи нормальны к фронту волны; при
сферическом фронте волны лучи направ-
направлены по радиусам.
§ 107. Принцип Гюйгенса. Весьма
важно для решения различных задач иметь
метод построения фронта волны, относя- »¦
щегося к некоторому моменту времени,
если известен фронт волны в предыду-
предыдущий момент. Такой метод был дан Гюй-
Гюйгенсом в 1690 г.; он носит название
принципа Гюйгенса Рис 26? Малое тие
Гюйгенс дал свой принцип без стро- в nperpafle является новым
гого доказательства; правильность прин- источником волн.
ципа Гюйгенса вытекала только из сравне-
сравнения результатов построений с опытом. Значительно позднее
правильность метода Гюйгенса была доказана на основании общей
418
волны
[гл. хн
в,
теории упругости. Чтобы несколько уяснить себе идею метода Гюй-
Гюйгенса,, рассмотрим следующий опыт. Представим себе, что на по-
поверхности воды распространяется волна произ-
произвольной формы. Поставим на пути этой волны
преграду А с отверстием а, размеры кото-
которого малы по сравнению с длиной волны \
(рис. 267). Волна, дойдя до преграды А, отра-
отразится от нее, а отверстие а в преграде будет
служить источником колебаний, распространяю-
распространяющихся по другую сторону преграды. При этом от
отверстия, независимо от формы распространяв-
распространявшейся волны, пойдут вперед полукольцевые вол-
волны В. Отверстие будет как бы служить новым
центром колебания, от которого колебания рас-
распространяются вперед во всех направлениях. Этот
опыт наводит на мысль, что каждую точку среды,
до которой дошел волновой фронт, можно рас-
рассматривать как новый источник колебаний. От-
Отсюда — сущность принципа Гюйгенса. Предполо-
Предположим, что в некоторый момент известен фронт
волны АВ (рис. 268), пришедшей в направлении,
указанном стрелками. Для построения нового
фронта, относящегося к моменту на промежуток
времени t более позднему, следует каждую точку
старого фронта принять за самостоятельный центр
распространяющихся вперед колебаний. Построим
из каждой точки элементарную волновую поверхность, которая бу-
будет полусферической поверхностью радиуса r= Vt. Огибающая AtBt
всех элементарных волновых поверхно-
поверхностей даст новый фронт волны.
Применим метод Гюйгенса к построе-
построению волновых поверхностей для частных
случаев. Предположим, что в некоторый
момент времени волна имеет форму
сферы радиуса R (рис. 269) и распро-
распространяется из центра колебаний; вокруг
каждой точки фронта опишем элементар-
элементарную волновую полусферическую поверх-
поверхность. Огибающая всех элементарных по-
полусферических поверхностей представит
сферическую поверхность радиуса /?4 =
= i?-|- Vt. Лучи, как было указано, на-
направлены по радиусам от центра. Сфе-
Сферическая волна, распространяясь, имеет
фронт в виде сферы все возрастающего радиуса; для очень боль-
больших радиусов участок фронта волны можно считать плоским. На
Рис. 268. Построе-
Построение нового фронта
волны по Гюйгенсу.
Рис. 269. Построение Гюй-
Гюйгенса для сферической вол-
волны, распространяющейся из
центра С.
§ 108]
УРАВНЕНИЕ ВОЛНЫ
419
рис 270 дан участок плоского фронта волны А В. Принта все точки
этого фронта за самостоятельные колебания и проведя вокруг них
элементарные полусферы, получим огибающую поверх- я
ность в виде плоскости, параллельной плоскости А В.
Лучи, т. е. направления, в которых распространяется
колебание, являются прямыми, перпендикулярными
к плоскости фронта. Отсюда заключаем, что плоская
волна, распространяясь в одной изотропной среде,
остается плоской; лучи представляют собою пучок
параллельных прямых. В однородной изотропной среде
волновой фронт, перемещаясь, всегда остается геоме-
геометрически подобным себе.
Рассмотрим теперь, что будет с плоской волной,
если на пути ее распространения поставлена преграда А
с отверстием а, размеры которого больше длины
волны X (рис. 271). Плоский фронт ВВ, подходя к пре-
преграде А, отразится от нее, а точки отверстия а ста-
станут самостоятельными центрами колебания. Вокруг
каждой точки образуется элементарная полусфериче-
полусферическая волновая поверхность; огибающая этих волновых
поверхностей дает фронт волны за отверстием. Из.
рис. 271 видно, что этот фронт за отверстием пере-
перестает быть плоским, только его средняя часть парал-
параллельна первоначальному фронту; у краев фронт за-
загибается— лучи меняют свое первоначальное направ-
направление. Чтобы полностью учесть такое загибание лучей,
носящее название диффракции, надо сложить колебания, приходя-
приходящие от отдельных точек отверстия, учитывая их фазы. Подробнее
мы рассмотрим диффракцию ниже.
. Чем меньше отверстие, тем силь-
загибание
Рис.270. По-
Построение
Гюйгенса
для плоской
волны.
„I нее выражено
В
Рис. 271. Загибание волны за от-
верстием в преграде (диффракция обоснования
лучей.
Если размер отверстия а меньше
длины волны, то просвет отверстия
послужит единичным центром коле-
колебания, от которого пойдет полусфе-
полусферическая волна, как это имело ме-
место в опыте, послужившем для
принципа Гюйгенса
(рис. 267).
§ 108. Уравнение волны. Выясним, каким образом можно аналити-
аналитически охарактеризовать волновой процесс.
Представим себе первоначально волны, бегущие вдоль некоторой
прямой, например вдоль веревки, один конец которой поддержи-
поддерживается в состоянии колебания. Обозначим через х смещение точки
из положения равновесия. Волновой процесс будет известен, если
энать, какое значение имеет х в каждый момент времени для каж-
420
волны
[гл. хн
Рис. 272. К выводу уравнения
волны.
дой точки прямой, вдоль которой распространяется волна. Другими
словами, надо знать смещение точки х как функцию времени и коор-
координат равновесного положения точек.
Выберем за начало координат Ю
ту точку на прямой (рис. 272), кото-
которая является центром колебаний.
Пусть колебания в точке О происхо-
происходят по закону:
Здесь а — амплитуда колебаний, о» —
круговая частота, t — время, отсчитанное от момента начала колебаний.
Возьмем на прямой произвольную точку А,- лежащую от начала
координат на расстоянии у. Колебания, распространяясь от точки О,
дойдут до точки А через промежуток времени
* — Т' B)
где V — скорость распространения волны. Таким образом, точка А
начнет колебаться на время -с позже точки О. Считая, что волны,
распространяющиеся вдоль рассматриваемой прямой, не затухают,
мы получим, что точка А, когда дойдет до нее, волна, начнет
колебаться с амплитудой а и круговой частотой ш, т. е. ее смеще-
смещение х из положения равновесия выразится:
х = a cos mif, C)
где if— время, отсчитанное от того момента, когда точка А
начала колебаться. Но так как точка А, по выясненному, начала
колебаться на промежуток времени t
позже точки О, то if = t — t; подставляя
это значение f в C), получим
х = а • cos ш (t — т), 0 ^'
или, подставляя сюда вместо -с его зна-
значение по B)
х = а • cos am —^-j.
D)
В
Рис. 273. Плоскость одина-
одинаковых фаз для плоской
" волны.
Это выражение дает смещение х как
функцию времени t и расстояния у точки А
от центра колебаний О; оно представляет собою искомое уравне-
уравнение волны, распространяющейся вдоль прямой О А.
Выражение D) представляет собою уравнение плоской волны,
распространяющейся вдоль направления у. В самом деле, в этом
случае любая плоскость АВ (рис. 273), перпендикулярная к на-
направлению у, представит собою поверхность одинаковых фаз, и,
следовательно, все точки этой плоскости имеют в один и тот же
§ 108] УРАВНЕНИЕ ВОЛНЫ 421
момент времени t одно и то же смещение х, определяемое лишь
расстоянием у, на котором плоскость лежит от начала координат О.
Если мы представим себе плоскую волну, распространяющуюся
в направлении, обратном тому, в котором отсчитывается расстоя-
расстояние у, то в выражении D) у должно быть заменено через —у, тогда
уравнение такой волны примет вид:
x = acoso)U-\-~~). Da)
Выражение D) может быть преобразовано, если мы воспользуемся
соотношением A) § 106, по которому -^¦ = ^ = -?-, где X — длина
волны распространяющихся волн, тогда
х = a cos (<at — 2ic у) >
или, если вместо круговой частоты со ввести обычную частоту
V = 27c"' T0
х = а cos 2ic(v?— ?V E)
Разберем на примере волны, распространяющейся вдоль прямой
(рис. 272), следствия, вытекающие из уравнения D). Волновой
процесс — это процесс двоякопериодический: аргумент косинуса
в формуле D) зависит от двух переменных — времени t и коорди-
координаты у. Таким образом, волна имеет двойную периодичность — в про-
пространстве и во времени. Для данного момента времени t уравнение D)
дает распределение смещения частиц х как функцию их расстояния у
от начала координат; частицы, колеблющиеся под влиянием бегущей
волны в данный момент времени t расположены по косинусоиде.
Данная частица, характеризуемая определенным значением у, совер-
совершает во времени гармоническое колебательное движение:
x = acosu>(t ^ J = a cos (mt — а), где а = ^~- = 2ic -у. F)
Величина а постоянна для данной точки, причем а представляет
собою начальную фазу колебаний в этой точке.
Две точки, характеризуемые расстояниями ух и у^ от начала ко-
координат, имеют разность фаз:
а, — <*! = 2тс * . . G)
Отсюда видно, что две точки, отстоящие друг от друга на рас-
расстоянии, равном длине X, т. е. для которых _уа—^i = X, имеют раз-
разность фаз а4 —a! = 2it; они имеют для каждого данного момента t
одинаковые по величине и направлению смещения х; про такие две
точки говорят, что они колеблются в одинаковой фазе.
422 волны [гл. хи
Для точек, отстоящих друг от друга на расстоянии _у9—yl^=-^-t
т. е. отстоящих на полволны, разность фаз а2 — о^^те; такие точки
колеблются, как говорят, в противоположных фазах — они имеют
для каждого данного момента смещения, одинаковые по абсолютному
значению, но разные по знаку: если одна точка отклонена кверху,
то другая — книзу, и наоборот.
Рассмотренные выше волны, распространяющиеся вдоль одной
прямой, являются частным случаем волн. В упругой среде возможны
волны иного вида, например, сферические волны.
В сферической волне амплитуда убывает обратно пропорционально
расстоянию г от источника колебаний. Зависимость смещения от ко-
координат и времени имеет вид:
X = — COS Ш
('-?)• №
Поверхность равных фаз в некоторый момент времени опреде-
определяется уравнением т = const, т. е. представляет собой сферу радиуса г.
Отсюда и происходит яазвание „сферическая" для такой волны.
§ Ц)9. Интерференция воли. В среде могут распространяться
одновременно колебания, исходящие от разных центров колебаний.
Если две различные системы волн, исходящих из разных источ-
источников, перекрываются в некоторой области, л затем снова расходятся,
то дальше каждая из них распространяется так, как если бы она не
встречала на своем пути другую. Этот принцип независимости распро-
распространения волн известен под названием принципа суперпозиции; он яв-
является весьма характерным для распространения волновых процессов.
Принцип суперпозиции легко проверить, бросив в воду два камня.
После того как кольцевые волны, возникшие около мест падения
камней, проникнув друг через друга, снова разойдутся, они будут
представлять собою по-прежнему правильные круги с центрами в ме-
местах падения камней. Этот факт был замечен еще Леонардо да-Винчи,
который писал: „В обширную и спокойную гладь воды брось одно-
одновременно два камешка на некотором расстоянии один от другого.
Ты увидишь, что вокруг мест, куда упали камни, образуются две
группы круговых волн; разбегаясь, они встречаются между собою —
и тогда круги каждой группы проникают одни сквозь другие".
В области перекрытия волн колебания налагаются друг на друга,
происходит сложение (интерференция) волн, в результате чего коле-
колебания в одних местах получаются более сильные, а в других — более
слабые. В каждой точке среды результирующее колебание будет
суммой всех колебаний, дошедших до данной точки.
Особенный интерес представляет тот случай, когда источники ко-
колебаний колеблются с одинаковой частотой, имеют одинаковые на-
направления колебаний и одинаковые фазы или постоянную разность
фаз. Такие источники называются когерентными. Как мы увидим
§ 109]
ИНТЕРФЕРЕНЦИЯ ВОЛН
423
ниже, в этом случае результирующее колебание в каждой точке среды
имеет постоянную во времени амплитуду, зависящую от расстояний
точки среды от источников колебаний. Такого рода сложение коле-
колебаний называется интерференцией от когерентных источников.
Когерентные источники колебаний можно, например, осуществить
следующим образом: возьмем точечный источник S (рис. 274), от
которого распространяется сфериче-
сферическая волна. На пути волны поставлена
преграда BBi с двумя точечными от-
отверстиями Si и sa, расположенными сим-
симметрично по отношению к источнику S.
Отверстия st и s9 становятся, согласно
принципу Гюйгенса, самостоятельными
источниками колебаний, притом коле-
колеблющимися с одинаковой амплитудой
и в одинаковых фазах, так как их рас*
стояния от источника S одинаковы.
Справа от преграды ВВу будут рас-
распространяться две сферические волны,
и в каждой точке среды колебание
возникнет в результате сложения этих
двух волн. Рассмотрим результат сло-
сложения в некоторой точке А, которая
отстоит от источников st и sa соответ-
соответственно на расстоянии rt и rs. Колебания доходят до точки А с неко-
некоторой разностью фаз, которая зависит от разности расстояний га и г\.
Колебания источников st и ss, имеющие одинаковые фазы, можно
представить в виде:
Ху = я0 cos wt, х% = а0 cos arf.
Тогда колебания, дошедшие до точки А соответственно от ис-
источников St и sa, по формуле (8) § 108 выразятся:
*1 = a, cos 2
Рис. 274. Наложение волн, ис-
исходящих из отверстий Si и s2.
где \ = ?- — частота колебаний. Согласно (8) § 108, —'== —. Одна-
ко если | га — f-il^ri, то приближенно можно считать а^г^а^
Разность фаз слагаемых колебаний в точке А будет
Д« = 2**1^-. A)
Мы видели в § Д00, что амплитуда результирующего колебания
зависит от разности фаз слагаемых колебаний, причем, если разность
фаз равна нулю или кратна 2тс, то амплитуда имеет максимальное
значение, равное сумме амплитуд слагаемых колебаний. Если разяость
фаз равна нечетному числу it, то амплитуда имеет минимальное зна-
424
волны
[гл. xii
чение, равное разности слагаемых амплитуд. Следовательно, в точке А
получится максимум или минимум колебаний в зависимости от того,
с какой разностью фаз Да подходят к точке А оба колебания. Усло-
Условие максимума амплитуды в точке А, по сказанному, имеет вид:
B)
где k — 0, 1, 2, 3,..., откуда максимум колебаний имеет место при
| гй — г, | = а, Bа)
т. е. максимум амплитуды получается в точках, для которых
разность хода лучей равна нулю или целому числу длин волн.
Условие минимума амплитуды в точке А
сводится к требованию:
¦=¦±B*41)*, C)
где опять А = 0, 1, 2, 3 откуда раз-
разность хода лучей должна быть равна
\rt — ri\=Bk-\-lIr, (За)
т. е. минимум амплитуды получается в
точках, для которых разность хода лу-
лучей равна нечетному числу полуволн.
При разностях фаз, имеющих промежу-
промежуточные значения между ± 2Ал и ± BA -j-
-)-1)тс, где А — целое число, имеет место
некоторый средний эффект усиления или
ослабления колебаний.
Таким образом, в результате наложения
двух волн в среде возникают колебания,
амлитуда которых различна в разных точ-
точках среды, при этом в каждой точке среды
получается или максимум амплитуды, или
минимум амплитуды, или ее промежуточное
значение — в зависимости от значения раз-
разности расстояний точки до когерентных
источников.
На рис. 275 представлены две системы интерферирующих волн;
гребни волн изображены сплошными линиями, впадины — пунктирными.
В местах пересечения двух гребней или двух впадин располо-
расположены максимумы колебаний, в местах пересечения гребня и впадины
расположены минимумы. Образование такого рода интерференцион-
интерференционных максимумов и минимумов можно легко наблюдать при распро-
распространении двух систем волн на поверхности воды.
Рис. 275. Интерференция
волн.
§ no]
СТОЯЧИЕ ВОЛНЫ
425
§ 110. Стоячие волны. Особым примером результата интерферен-
интерференции двух волн служат так называемые стоячие волны, образующиеся
в результате наложения двух встречных плоских волн с одинаковыми
амплитудами.
Предположим, что две плоские волны с одинаковыми амплитудами
распространяются — одна по направлению положительной оси у, дру-
другая— по направлению отрицательной оси у. На рис. 276 одна из волн
Рис. 276. Сложение двух волн, распространяющихся
в противоположных направлениях.
изображена тонкой сплошной линией, другая — пунктирной; резуль-
результирующая волна изображена жирной линией. Если начало координат
взять в такой точке, в которой встречные волны имеют одинаковые
фазы, и выбрать отсчет времени так, чтобы начальные фазы оказа-
оказались равными нулю, то уравнения обеих плоских волн можно напи-
написать в следующем виде: для волны, идущей в сторону положитель-
положительной оси у,
JCj = acos2i:(v* — -^V
и для волны, идущей в сторону отрицательной оси у,
хл = a cos 2пЫ 4- у).
Сложение этих двух волн дает
j; = Xi -j- x3 = a cos 2ic Ы — -j- J -j-
a cos
Ы -f- ~- J,
или, раскрывая значение косинусов от сложных аргументов и произ-
производя сокращения,
х=2а cos Bicу) • cos 2ям?. A)
Множитель cos 2тсу? показывает, что в точках среды возникает
колебание с той же частотой v, что и колебания встречных волн.
Множитель 2acosBrcy), не зависящий от времени, выражает
амплитуду А результирующего колебания; точнее — амплитуда, как
426 волны1 [гл. хи
величина существенно положительная, равна абсолютному значению
этого множителя:
А =
B)
Таким образом, амплитуда колебания зависит от координаты у,
определяющей положение точек среды. Возникшее колебание носит
название стоячей волны. В определенных точках амплитуда стоячей
волны равна сумме амплитуд обоих слагаемых колебаний, такие точки
называются пучностями; в других точках результирующая амплитуда
равна нулю, эти точки называются узлами стоячей волны.
Определим координаты точек пучностей и узлов. Амплитуда, опре-
определяемая равенством B), максимальна в точках, для которых
cos B*f)| = l,
в этих точках по B)
А = 2а.
Отсюда положение пучностей определится условием
где k = 0, 1, 2,... Следовательно, координаты пучностей равны
y = ±k^-, C)
где k = 0, 1, 2,...
Расстояние между соседними пучностями мы получим, если возьмем
разность двух значений у, определяемых формулой C) для двух по-
последовательных значений k, откуда
т. е. расстояние между двумя соседними пучностями равно половине
длины тех волн, в результате интерференции которых образуется
данная стоячая волна. Очевидно, в местах пучностей колебания обеих
волн все время совершаются в одной фазе.
В узлах амплитуда результирующего колебания равна нулю, откуда
по формуле B) условие образования узлов:
cos Bя¦¦?)=() или 2«^ = ±B*+1)-|,
следовательно, координаты узлов равны
j, D)
§ по]
СТОЯЧИЕ ВОЛНЫ
427
а значит, расстояние узла от ближайшей пучности равно
4
т. е. узлы и пучности отстоят друг от друга на четверть длины
волны. Узлы образуются в тех местах, где колебания в обоих волнах
вей время совершаются в противоположных фазах.,
Важно заметить, что хотя по формуле A) во всех точках-резуль-
точках-результирующее колебание происходит с фазой, как будто не зависящей
от положения точки (множитель cos 2nvt не зависит от у), однако
на самом деле при переходе через узел фаза колебаний меняется на
противоположную. Это следует из того, что множитель cosBic4-).
определяющий амплитуду, при переходе через нуль в узле меняет
знак; вследствие этого, если по одну сторону узла в некоторый
момент времени смещение х положительно, то по другую сторону
узла оно в тот же момент времени отрицательно.
Так как в данный момент времени множитель cos 2wt имеет для
всех точек одинаковое значение, то все точки между двумя узлами
колеблются в одинаковых фазах, т. е. они одновременно достигают
максимальных отклонений, одновременно проходят через положения
равновесия и т. д. Точки, лежащие по обе стороны одного и того
же узла, колеблются в противоположных фазах, т. е. достигают одно-
одновременно крайних, но противоположных по знаку смещений, прохо-
проходят одновременно положение равновесия, но с противоположно на-
направленными скоростями и т. д. Схема колебаний точек в поперечной
Пучности
а)
/i\ \ /Г
i |
4i/j
4
i
1 /С
к
У t
-У i+|
Узлы
Рис. 277. Схема колебаний в поперечной стоячей волне.
стоячей волне указана на рис. 277 а и б, где нанесены ноложения
колеблющихся точек для двух моментов времени, отстоящих на
полпериода.
В продольной стоячей волне смещения точек параллельны оси у.
На рис. 278 а и б даны расположения точек в продольной стоячей
428
волны
[гл. хн
волне для двух моментов времени, отстоящих на полпериода. Мы
видим из рисунков, что в узлах, где скорости колеблющихся точек
равны нулю, получается наиболее резкое изменение плотности среды:
частицы то приближаются с двух сторон к узлу, то от него удаляются.
Пучности
¦ -Ь— —4 -т— —+ -г—
а) —<^-4>o-feoooyxx>o<fr-o-o—о—&о-^оо-ооу>соо^»о <f ооуооо-у—^— / t
! I ! ! ! ! ! ! ! ! !
Узлы
Рис. 278. Схема колебаний в продольной стоячей волне.
Образование стоячих волн происходит обычно при интерференции
бегущей вперед и отраженной волн. Например, если один конец
веревки укрепить неподвижно, то отраженная в месте закрепления
веревки волна будет интерферировать с бегущей вперед и образовы-
образовывать стоячую волну. Узловые точки, остающиеся при этом неподвиж-
неподвижными, находятся друг от друга на расстоянии, равном половине длины
бегущей волны; в месте закрепления веревки, т. е. на границе, где
происходит отражение волны, получается узел.
Вообще же говоря, на границе- отражения может образоваться
или узел, или пучность; это зависит от соотношения плотностей сред.
Если среда, от которой происходит отражение, более плотная, чем
среда, в которой распространяется волна, то на границе получается
узел. Если среда, от которой происходит отражение, менее плотная,
чем та, в которой распространяется волна, то на границе получается
пучность.
Образование узла на границе отражения от более плотной среды
объясняется тем, что волна, отражаясь от более плотной среды, в
месте отражения меняет свою фазу на прямо противоположную; тогда
у границы складываются колебания противоположных направлений,
что и ведет к образованию узла.
Так как фаза меняется на противоположную на расстоянии поло-
половины длины волны, то этот факт принято называть „потерей полволны".
Отражаясь от менее плотной среды, волна не меняет фазы в месте
отражения, поэтому потери полволны не происходит. Благодаря этому
фазы падающей и отраженной волн у границы одинаковы, и в этом
месте получается пучность в результате сложения колебаний одина-
одинаковых фаз.
§ 111] ДИНАМИКА РАСПРОСТРАНЕНИЯ КОЛЕБАНИЙ В УПРУГОЙ СРЕДВ 425
Изменение фазы при отражении волн от границы более плотной
среды и сохранение фазы при отражении от границы менее плотной
среды доказывается в теории упругости на основании общих погра-
пограничных условий на границе двух упругих сред.
§ 111. Динамика распространения колебаний в упругой среде. Тип
волн, способных распространяться в среде, как было сказано выше, зависит
от упругих свойств среды. Распространяются колебания того типа, которые
обусловлены смещением, вызывающим упругую деформацию среды. В среде,
обнаруживающей лишь деформацию сжатия (жидкость, газ), распростра-
распространяются продольные волны, в среде, обнаруживающей как деформацию сжа-
сжатия, так и деформацию сдвига, могут распространяться и продольные, и
поперечные волны. Будем пока рассматривать лишь продольную волну.
Выберем ряд точек, принадлежащих сплошной среде и лежащих на одной
прямой, вдоль которой распространяется продольная волна.
Смещение некоторой точки, лежащей ^на этой прямой, из положения
равновесия обозначим через х. Расстояния между точками, отсчитанные вдоль
той же прямой, будем обозначать
через у. z х+йх
Рассмотрим две точки, равно- г~^~: • ' 1 _.,
весные положения которых от- ;
стоят на dy друг от друга. Пусть ' ^~jjZ
смещения этих точек из их по- "
ложений равновесия в некоторый Рис- 279. К выводу выражения для ско-
момент времени соответственно рости распространения продольной
равны х и x + dx (рис. 279). волны.
Следовательно, смещение точек
на расстоянии dy меняется на величину dx.
Отношение изменения смещения dx к величине первоначального рас-
расстояния между точками dy, т. е. величину dxjdy, назовем относительной
деформацией и обозначим ее буквой s, тогда
s = — A)
При s = -3->0 расстояние между точками увеличивается, что означает
растяжение среды.
, При s = -j— •< О расстояние между точками уменьшается, т. е. среда
оказывается сжатой.
Принимая во внимание уравнение волны
B)
где «а^-круговая частота, а V—скорость распространения волны, можно уста-
установить связь между относительной деформацией dxjdy и скоростью колеблю-
колеблющихся точек dxjdt; действительно, обозначая скорость точек буквой о, имеем
dx .
v х ^- —— amsm
Относительная деформация s определится
Сравнивая последние два выражения, получаем
dx dx
Ш~~ dy'
430 волны [гл. хп
Отсюда видно, что деформация среды dxjdy имеет по абсолютному значе-
значению наибольшую величину в тех точках, где скорость колеблющихся частиц
dxjdt наибольшая, т. е. в области, где точки проходят через положение рав-
равновесия.
Из уравнения волны B) можно получить еще одно соотношение, кото-
которое нам понадобится дальше. Беря вторые производные от х по перемен-
переменным t и у, получим
„ dtx вша
X== -TT = — T7S- COS ш
откуда следует
/ v \
т. е. вторая производная смещения по времени пропорциональна второй
производной смещения по координате, причем коэффициентом пропорциональ-
пропорциональности служит квадрат скорости распространения волны V.
Уравнение C) мы получили, дифференцируя уравнение волны B). Об-
Обратно можно сказать, что чисто периодическая волна, которой соответствует
косинусоида B), удовлетворяет дифференциальному уравнению C). -
Однако в действительности решением дифференциального уравнения C)
является и ряд других функций. Эти функции описывают распространение
в среде волнового возмущения произвольной формы со скоростью V.
Таким образом, дифференциальное уравнение C) в наиболее общем виде
описывает распространение волнового процесса; оно носит название волнового
уравнения.
Для определения скорости распространения волны в упругой среде вос-
воспользуемся законом Гука.
Закон Гука (см. § 89), установленный для деформации в сплошной среде,
показывает, что упругая сила пропорциональна относительной деформации
среды. Если взять, например, участок сплошной среды длиной dy, попереч-
поперечного сечения S, который растянут или
Atf сжат на величину dx, то по закону
Гука упругая сила равна
v /1 dx Ч
где о — коэффициент упругости.
Рассмотрим, какие силы дейст-
Рис. 280. К выводу выражения для ВуЮТ на участок, мысленно вырезан-
скорости распространения продоль- ныи в сплошной среде, в которой
ной волны. распространяется продольная волна
вдоль оси у. Для этого вырежем мы-
мысленно в среде цилиндрический объем, причем пусть образующая цилиндра
параллельна оси у и имеет длину Д_у> а поперечное сечение цилиндра равно S.
Пусть в рассматриваемый нами момент времени этот участок объема растя-
растянут под влиянием сил ft и /а (рис. 280), приложенных к основаниям ци-
цилиндра. Выберем начало оси у у левого основания цилиндра, тогда сила /i
по закону Гука равна
где индекс 0 указывает, что относительная деформация dx/dy вычисляется
для значения .у = 0, т. е. в точках левого основания цилиндра.
§ 111] ДИНАМИКА РАСПРОСТРАНЕНИЯ КОЛЕБАНИЙ В УПРУГОЙ СРЕДЕ 431
Сила, действующая на правое основание, по тому же закону равна
здесь'dx/dy вычисляется в точках правого основания.
Величину dx/dy, которая представляет собою некоторую функцию F (у),
можно разложить в ряд Маклорена:
Ограничиваясь величинами первого порядка малости по отношению к Ау,
получим
ldx\ (dx\ \d (dx\\
dx\ _(dx\ ,\d_ (dx
Так как силы ft и /а направлены в противоположные стороны, то на эле-
элемент объема действует и разность, равная
1 d*x
AyS
Под действием этой силы элемент объема получает ускорение j,
которое равно по второму закону Ньютона действующей силе, деленной на
массу элемента; масса элемента равна произведению плотности р среды на
объем элемента AyS, следовательно:
d'x _ 1 d*x d'x _ 1 d'x
~~d?~ a?AyS ' W У ИЛ" 'dF~T?dyT- ('
Формула D) дает связь между второй производной смещения по времени
d2x/dts и второй производной смещения по координате d%x\dyl; такая связь
уже была нами выведена в формуле C), причем стоящая там величина V
представляла скорость распространения волны. Сравнивая оба выражения,
мы видим, что скорость распространения продольных волн в среде выра-
выражается через плотность и коэффициент упругости среды следующим соотноше-
соотношением:
V'=— или V—Xf—. E)
ар Г ар
Для отдельно взятого цилиндрического объема коэффициент упругости
о = ^Г)где?—модуль Юнга (см. § 89); эта связь позволяет переписать
формулу E) в виде:
V= y -f, Ea)
то совпадает с формулой, приведенной на стр. 416.
. Однако в неограниченной среде при сжатии или растяжении каждый
элемент объема одновременно испытывает боковое сжатие или растяжение
со стороны соседних элементов объема, что ведет к более сложной связи
между коэффициентом упругости среды а и модулем Юнга, а именно:
_ A+а)A — 2а)
а~ A—о)Е >
432 волны [гл. хн
где в — коэффициент Пуассона (см. § 89). Отсюда скорость распространения
продольных волн в упругой сплошной среде равна
~° К E6)
A+«)(!—2а) р'
Так как коэффициент Пуассона есть величина порядка lU, то множитель
1—^——я-г близок к единице, и для сплошной среды приближенно можно
<1+а)A2о)
пользоваться формулой Eа). Таким образом, оказывается, что скорость рас-
распространения продольных волн в упругой среде прямо пропорциональна
корню квадратному из модуля Юнга и обратно пропорциональна корню
квадратному из плотности среды.
Аналогичным образом можно показать, что скорость распространения
поперечных волн в упругой среде равна
где jV— модуль сдвига. ,
Эта формула совпадает с приведенной на стр. 416.
§ 112. Энергия волны. Представим себе волну, распространяю-
распространяющуюся вдоль оси у и заданную уравнением:
х = а cos (о [t
-*)¦
Энергия участка среды, в которой распространяется эта волна,
складывается из кинетической энергии Ek и потенциальной энер-
энергии Ер. Пусть объем участка среды равен т; обозначим его массу
через т и скорость смещения его частиц — через v, тогда кине-
кинетическая энергия
Еь = у mv\
замечая, что т = рт, где р — плотность среды, и находя выражение
для скорости по A)
dx ¦
перепишем выражение для кинетической энергии Ek в виде:
' B)
Потенциальная энергия твердого тела, подвергнутого относитель-
относительной деформации (AL/I), как было выведено в § 89 [формула F)], равна
^P~2\L
Вводя вместо модуля Юнга Е коэффициент упругости а-.
и деля и умножая правую часть на L, получим
§ 112] энергия волны 433
Произведение LS представляет - собой объем т деформируемого
тела; относительную деформацию AZ./L можно представить в виде
dx/dy, где dx — разность смещений чистиц, отстоящих друг от друга
на dy, тогда
Определяя выражение для dx/dy по A):
перепишем выражение для потенциальной энергии в виде:
Сравнивая выражения B) и C), мы видим, что и кинетическая-
и потенциальная энергия меняются в одной фазе, т. е. одновременно
достигают максимума и минимума. Этим энергия участка волны су-
существенно отличается от - энергии колебания изолированной точки,
где при максимуме кинетической энергии потенциальная энергия
имеет минимум, и наоборот. При колебании отдельной точки пол-
полный запас энергии колебания остается постоянным. При колебании
в среде каждый элемент объема • среды связан с окружающей сре-
средой, и энергия из одного участка среды может переходить в дру-
другие. Поэтому полная энергия участка среды, в которой распростра-
распространяется волна, не остается постоянной.
Подсчитаем полную энергию Е элемента объема среды х; скла-
складывая выражения B) и C), получим
Так как по формуле E) § 111 скорость распространения волн V
в упругой среде _
то выражение для полной энергии Е переписываем в виде:
Таким образом, энергия участка волны пропорциональна квад-
квадрату амплитуды колебания, квадрату частоты и плотности
среды.
Введем в рассмотрение плотность энергии е, которую определим как
отношение энергии, заключенной в элементе объема т, к величине этого объема:
E)
434 волны [гл. xit
Плотность энергии в данной точке, как и сама энергия, величина пере-
переменная. Через половину периода плотность энергии принимает первоначаль-
первоначальное значение. Так как среднее значение квадрата
__»-V синуса за период равно '/»> то по E) среднее значе-
И ^ ние плотности энергии
'' I /Л 1
*---\ е у-К\ е=^-ра8ш8. F)
' V В силу того, что энергия не остается локализо-
ванной в данном участке, а перемещается в среде,
" ^ ' можно ввести в рассмотрение понятие о потоке
р 9„, о энергии. Под потоком энергии через поверхность
гис. ZHb за время, будем подразумевать величину, численно равную ко-
равное /, через пло- личеству энергии, проходящей в единицу времени
щадьЯ протечет энер- через данную поверхность.
гия, заключенная в Предположим, что мы берем поверхность S, пер-
ооъеме столоа VI5. пендикулярную к направлению скорости V волны;
тогда через эту поверхность за время, равное пе-
периоду 7", протечет количество энергии, равное энергии, заключенной в столбе
поперечного сечения S и длиной VT (рис. 281); это количество энергии равно
среднему значению плотности энергии I, взятому за период и умноженному
на объем столба VTS, отсюда
E=s-VTS.
Средний поток энергии Р получим, поделив это выражение на время Т,
в течение которого энергия протекает через поверхность S:
~P=l-VS. G)
Подставив сюда значение е по F), найдем
Таким образом, средний поток энергии через поверхность, перпендику-
перпендикулярную к направлению распространения колебаний, равен произведению
средней плотности энергии на скорость распространения волны и на вели-
величину поверхности.
Количество энергии, протекающее в единицу времени через единицу по-
поверхности, называется плотностью потока U. Так как по этому определению
— Р
i/=-jr, то, пользуясь формулой G), получим
о
Z7 = !-V, (8)
т. е. плотность потока равна произведению из средней плотности энергии и
скорости распространения волны.
Так как скорость V представляет собой вектор, то и плотность потока
энергии можно рассматривать как вектор, направленный в сторону распро-
распространения волны. Такой вектор был впервые введен в рассмотрение профес-
профессором Московского университета Н. А. Умовым A845—1915) и носит назва-
название вектора Умова.
Покажем, что, если мы имеем сферическую волну, распространяющуюся
от точечного источника, то средняя плотность потока энергии обратно про-
пропорциональна квадрату расстояния от источника.
Возьмем точечный источник колебаний и проведем сферу радиуса R с
центром в источнике. Волна и энергия, с ней связанная, будут распростра-
распространяться по радиусам, т. е. перпендикулярно к поверхности сферы. За период Г
§ 112] энергия волны 435
через поверхность сферы протечет энергия, равная РТ, где Р— поток энер-
энергии через сферу. Плотность потока U мы получим, если эту энергию по-
. делим на величину поверхности сферы и на время:
_ р- т р
и=-
4тс/?а *
Так как при отсутствии поглощения колебаний в среде и установившемся
волновом процессе средний поток энергии Р постоянен и не зависит от
того, какого радиуса R проведена сфера, то последнее отношение показывает,
что средняя плотность потока обратно пропорциональна квадрату рассто-
расстояния от точечного источника.
Выведенное соотношение, как указано, справедливо при отсутствии по-
поглощения в среде; другими словами, при нашем рассмотрении предполагалось,
что энергия волнового процесса не переходит в какой-либо другой вид энер-
энергии. Однако в действительности энергия колебательного движения в среде
обычно частью переходит во внутреннюю энергию. Это вызвано наличием во
всякой механической среде внутреннего трения. Полное количество энергии,
которое несет волна, будет зависеть от ее расстояния от источника: чем
дальше от источника находится волновая поверхность, тем меньшей энергией
она обладает. Так как энергия пропорциональна квадрату амплитуды, то, сле-
следовательно, и амплитуда колебания уменьшается по мере распространения
волны. Чтобы выяснить закон уменьшения амплитуды, сделаем предположе-
предположение, что при прохождении слоя толщиной dy относительное уменьшение ампли-
йа .
худы пропорционально ау, т. е. напишем уравнение:
da
dy
где.*—постоянная величина, зависящая от природы среды.
Последнее выражение можно, очевидным образом, переписать:
d (In a) = — а
Если дифференциалы двух величин равны друг другу, то сами величины
отличаются друг от друга на произвольную аддитивную постоянную вели-
величину С, отсюда
1п а = — ху + С;
постоянная С определяется из условия, что при у = 0 величина 1п а, рав-
равная In a0, должна равняться С, таким образом:
1п а = 1п а0 — ху, откуда а = аое~*У. (9)
Это выражение дает убывание амплитуды а по мере того, как волна распро-
распространяется в направлении оси у; а0 представляет значение амплитуды при у = 0.
Уравнение плоской волны в среде с поглощением на основании фор-
формулы (9) будет:
/ ' v \
х = асе~хУ • cos<o[rf—~\, A0)
Определим еще убывание энергии волны_с расстоянием. Обозначим Та —
среднюю плотность энергии при j» = 0, через еу — среднюю плотность энергии
на расстоянии у, тогда по соотношениям F) и (9) получим
«~ —Т 0—&*у /I w
•у "~- е0*- • \ /
436 волны [гл. хн
Обозначив 2х через k, перепишем последнюю формулу в виде:
^=Тов-*Л (Па)
Величина k называется коэффициентом поглощения.
§ 113. Явление Допплера. Разберем вопрос о том, какова связь
между колебаниями, испускаемыми источником, и колебаниями,
воспринимаемыми каким-либо прибором, регистрирующим колебания,
если источник и прибор движутся друг относительно друга. При
этом для того, чтобы колебания могли от источника распространиться
до прибора в виде волн, прибор и источник должны быть погру-
погружены в сплошную упругую среду. Предположим, что источник А
испускает колебания периода Т, так что число колебаний, испускае-
испускаемых в единицу времени, равно v = -=-. Пусть некоторый прибор вос-
воспринимает колебания; число колебаний, воспринимаемых прибором
в единицу времени, обозначим V. Разберем связь между / и v для
различных случаев движений прибора и источника относительно
среды, в которой распространяются колебания. При этом для про-
простоты предположим, что эти движения происходят по прямой, соеди-
соединяющей источник с прибором. * ' '
В формулах, которыми мы будем пользоваться, введем опреде-
определенное правило знаков скоростей источника и прибора. Условимся
скорость и источника относительно среды считать положительной,
если источник приближается к прибору. Если источник удаляется
от прибора, его скорость будем считать отрицательной. Аналогич-
Аналогичное условие введем для знака скорости v прибора относительно
среды: при приближении его к источнику считаем его скорость
положительной, при удалении от источника — отрицательной. Ско-
Скорость распространения колебаний в среде обозначим буквой V.
Рассмотрим первый случай: регистрирующий прибор А и источ-
источник В покоятся относительно среды, т. е. и = 0, v = 0. Если
колебания непрерывно идут мимо прибора, то он воспримет столько
колебаний в единицу времени, сколько волн в единицу времени
пройдет мимо него. Так как в,единицу времени волна проходит
расстояние V, то число воспринятых прибором колебаний равно
' — Z- — Z- — 1 —
v — х — ут т v,
т. е. мы получили очевидный результат: число колебаний, воспри-
воспринимаемых прибором в единицу времени, равно числу колебаний,
испускаемых в единицу времени источником.
Второй случай: регистрирующий прибор движется относи-
относительно среды со скоростью v; источник неподвижен, т. е. й==0.
Сперва положим, что прибор движется по направлению к источ-
источнику, т. е. по установленному правилу скоростей в^>0. В этом'
случае мимо прибора за единицу времени пройдет ббльшее число
§ 113] ЯВЛЕНИЕ ДОППЛЕРА 437
волн, чем в том случае, когда прибор покоится относительно среды,
в которой распространяются волны. В самом деле, так как прибор
движется навстречу волнам, то рассматриваемый случай эквивален-
эквивалентен тому, как если бы волны шли мимо прибора со скоростью,
равной сумме скорости волны V и скорости прибора v. Число волн,
прошедших в единицу времени мимо прибора, равно
У+у_У+у
X ~~ VT '
отсюда, так как -=г = м, то
т. е. число воспринятых прибором колебаний больше числа испу-
испущенных колебаний в fl -}--w) раз.
Если прибор удаляется от источника, то по принятому правилу
анаков его скорость в<^0. В этом случае число колебаний vr, вос-
воспринятых прибором, выразится также формулой A), но так как v/V
будет меньше нуля, то / окажется меньше v, т. е. число колеба-
колебаний, воспринятых прибором, будет меньше числа испущенных коле-
колебаний.
Изменение числа колебаний, регистрируемых прибором, при
движении прибора или источника относительно среды носит назва-
название явления Допплера.
Если скорость v прибора равна скорости волны, то прибор
перемещается вместе с волной, и число воспринимаемых им в еди-
единицу времени колебаний равно нулю. Если скорость прибора больше
скорости волн, то волны отстают от х
прибора, прибор отметит, что волны f* "¦•
идут ему навстречу. i у—j
Рассмотрим теперь третий слу- Bi/JL-B
чай: источник движется относи- т—-—Т \ \ ~7
тельно среды со скоростью и; реги- и^ | 4>-w!s—/
стрирующий прибор неподвижен, т. е. I .#
v 0 ^
Положим сперва, что источник Рис 282. Уменьшение длины
движется к прибору: и">0 волны при движении источника
Так как скорость распространения в С1Орону ^пространения
колебаний зависит лишь от свойств
среды, то за один период колебание распространится вперед на длину
волны X независимо от того, движется ли источник относительно
среды или нет; но за это время источник пройдет в направлении волны
путь иТ (рис. 282), в результате чего длина волны окажется равной
\' = \ — иТ= VT—uT=(V — u) T;
15 С. Э. Фриш в А. В. Твморева
438 волны [гл. хн
отсюда число колебаний, воспринятых прибором в единицу времени,
увеличится вследствие укорочения длины волны и будет равно
V
u)T или
т. е. число колебаний, воспринятых прибором, увеличится в отно-
отношении -Y—JT'
Если бы источник удалялся от прибора (и<^0), то произошло
бы увеличение длины волны на величину ДХ = мГ, в результате
чего прибор воспринял бы уменьшенное число колебаний v'<^v.
В четвертом, самом общем, случае предположим, что регистри-
регистрирующий прибор и источник перемещаются одновременно относи-
относительно среды, в которой распространяются волны (я^Оик^О).
Вследствие движения источника длина испускаемой им волны
изменится и станет равной
Х' = \ — иТ.
Вследствие движения прибора число воспринятых им за единицу
V-\-v
времени колебаний окажется измененным в —^— раз; в результате
этих обеих причин число колебаний, воспринимаемых прибором,
окажется равным
.,_ V+v_V + v I v+v ,-.
Таким образом, v' зависит по-разному от скорости прибора v и
скорости источника и относительно среды.
Если скорости v а и направлены не по прямой, соединяющей
прибор и источник, то следует брать их составляющие на эту
прямую.
Изменение числа колебаний в зависимости от движения источ-
источника или регистрирующего прибора легко заметить при восприятии
звуков. Частота звуковых колебаний определяет тон звука: чем
больше число колебаний в единицу времени, тем выше тон. Когда
свистящий паровоз с большой скоростью приближается к наблюда-
наблюдателю, то ясно слышно, как высота свиста меняется в тот момент,
когда, пройдя мимо, паровоз начинает удаляться.
§ 114. Групповая скорость. До сих пор, говоря о скорости распростра-
распространения волн, мы говорили о фазовой скорости, т. е. о скорости, с которой
распространяется поверхность одинаковых фаз. В уравнении плоской волны
х = a cos <о
(<-?)
величина V есть фазовая скорость, т. е. скорость, с которой перемещается
в среде поверхность, представляющая собой геометрическое место точек,
колеблющихся в одной фазе. В этом можно убедиться на основании следующих
рассуждений.
§ 114] групповая скорость 439
В выражении A) г есть отрезок, отложенный в направлении распростра-
нения плоских волн и определяющий положение данной поверхности одина-
одинаковых" фаз (рис. 273). Требование постоянства фаз во времени сводится
к требованию, чтобы аргумент косинуса в выражении A) был постоянен,
т. е. чтобы
— tf) = const,
или, так как круговая частота <» есть величина постоянная, то — к требованию,
чтобы имело место условие:
t — р- = const.
Обозначим значение этой величины, постоянной для данной поверхности
одинаковых фаз, через т, тогда
Очевидно, т определяется моментом времени, от которого отсчитываем
время t; так как мы полагаем ? = 0 для г = 0, то должны положить и посто-
постоянную х равной нулю, откуда
«-? = 0 и V=L,
т. е. V представляет собой скорость, с которой со временем возрастает
отрезок г, другими словами, — скорость, с которой перемещается плоскость
одинаковых фаз.
Релей впервые показал, что наряду с фазовой скоростью волн имеет
смысл ввести понятие о другой скорости, называемой групповой скоростью.
Групповая скорость относится к случаю распро-
распространения волн сложного не косинусоидального
характера в среде, где фазовая скорость распростра-
распространения косинусоидальных волн зависит от их частоты.
Зависимость фазовой скорости волн от их частоты
называется дисперсией волн. Df,_ 0Qq „
Представим себе на поверхности воды волну в Ри^^*?лона!;
виде единичного горба (рис. 283), распространяйте- единичного горба,
гося в определенном направлении. Согласно сказан-
сказанному в § 104, такое сложное колебание может быть расположено на группу
чисто гармонических колебаний. Если все гармонические колебания распро-
распространяются по поверхности воды с одинаковыми скоростями, то с той же
скоростью будет распространяться и образуемое ими сложное колебание.
Но если скорости отдельных косинусоидальных волн различны, то непрерывно
меняются разности фаз между ними, и горб, возникающий в результате их
сложения, непрерывно меняет свою форму и пере-
не совпадающей с фазо-
из слагаемых волн,
реальная волна отлична от идеальной
Рис 284 Отоезок косинусоиды хотя бы потому, что идеальная коси-
косин'усоипы нусоида не ограничена во времени. Мы видели
n.uinnji.unMoi. на СТр^ 4jQ^ Ч10 всякое затухающее колебание сла-
слагается из бесчисленного множества гармонических
колебаний. Всякий отрезок косинусоиды (рис. 284) тоже может быть по тео-
теореме Фурье разложен на бесчисленное множество неограниченных во времени
идеальных косинусоид. Таким образом, всякая реальная волна представляет
собою наложение — группу — бесконечных косинусоид, и скорость ее распро-
15»
сложения, непрерывно ме
Г\ А А А ГУ мещается со скоростью,
\|\/\/\/ ^~" в0" СКОРОСТЬЮ ни одной
U и U U Всякая реальная вол
440
волны
[гл. xu
странения в диспергирующей среде отлична от фазовой скорости слагаемых
волн. Эта скорость распространения реальных волн в диспергирующей среде
и носит название групповой скорости. Только в среде, лишенной дисперсии,
реальная волна распространяется со скоростью, совпадающей с фазовой ско-
скоростью тех косинусоидальных волн, сложением которых она образована.
Составим аналитическое выражение для групповой скорости. Для простоты
предположим, что группа волн состоит всего из двух волн, мало различающихся
друг от друга по длине: 1) волны — с длиной волны X, распространяющейся
со скоростью V;2) волны —
с длиной волны X' = X -\- d\,
распространяющейся со ско-
скоростью
V = V + ^rfX. B)
а)
с\ / // волна 2'волца
J волна
v
/ 2 волна
Рис. 285. К выводу выражения для групповой
скорости.
Относительное располо-
расположение обеих волн для неко-
некоторого момента времени
представлено на рис. 285а.
Горбы обеих волн сходятся
в точке А; в одном месте
расположен максимум ре-
результирующих колебаний.
Пусть V' i> V, тогда вторая
волна обгоняет первую. Че-
Через некоторый промежуток времени т она обгонит ее на отрезок, равный dk,
в результате чего горбы обеих волн будут уже сходиться не в точке А,
а в точке В (рис. 285 б). Место максимума результирующего сложного коле-
колебания окажется смещенным относительно первой волны назад на отрезок,
равный X. Отсюда скорость распространения максимума результирующих
колебаний относительно среды окажется меньше скорости распространения
первой волны на величину Х/т. Эта скорость распространения максимума
сложного колебания и есть групповая скорость; обозначая ее через U, имеем
U—V——.
¦с
C)
Так как'скорость второй волны относительно первой равна V — V, то
подставляя сюда вместо V его значение по B), получим
d\d\
Подставив это выражение для г в C), найдем для групповой скорости
,, „ , dV
D)
Из формулы D) видно, что групповая скорость U тем больше отличается
от фазовой скорости V, чем больше dV\d\ т. е. чем сильнее выражена зависи-
dV
мость скорости распространения волн от их длины. При -тг > 0 групповая
§ 114]
ГРУППОВАЯ СКОРОСТЬ
441
скорость U<V, а при ^Т
имеем U>-V. Таким образом, группо-
групповая скорость U может быть как меньше, так и больше фазовой скорости V.
Групповая скорость меньше фазовой,
dV n .
когда -7sr is- 0, т. е. когда более длин-
аК
ные волны распространяются скорее бо-
более коротких; этот случай носит назва-
название нормальной дисперсии.
Для среды, лишенной дисперсии,
dV
—т
= 0 и
= V, т. е., в согласии со
сказанным выше, групповая и фазовая
скорости совпадают.
Для определения групповой скоро-
скорости можно воспользоваться следующим
графическим методом. Пусть кривая АВ
(рис.286) выражает зависимость фазовой
скорости распространения волн V от
длины волны X. Проведем в точке С, соответствующей данному значению X,
касательную CD. Тогда для отрезка CF имеем
Рис- 286- Графическое нахождение
групповой скорости.
= X . tgo, но tga =
dV
Ж'
откуда CF=K ¦ -Tj-
d\>
Из рисунка имеем
DO = EO — ED,
но EO =
dV
откуда DO = V — X
dV
ж-
Сравнивая это выражение с формулой D), получаем, что на нашем графике
отрезок DO как раз выражает групповую скорость U.
Из рис. 286 легко еще раз установить приведенные выше соотношения:
если скорость волн V возрастает с X (к этому случаю и относится рисунок),
то точка D попадает ниже точки Е, следовательно, групповая скорость U<:V.
Если скорость V убывает с возрастанием X, то, как легко понять, точка D
окажется выше точки Е, что будет соответствовать соотношению U^>V.
Наконец, если волны всех длин распространятся с одинаковой скоростью,
то зависимость V от X изобразится на графике прямой, параллельной оси X.
Тогда точки Е и D совпадут, а следовательно, будут совпадать групповая
скорость U и фазовая скорость V.
ГЛАВА XIII
АКУСТИЧЕСКИЕ КОЛЕБАНИЯ
§ 115. Звуковые колебания и их распространение. В воздухе,
как и во всяком другом газе, колебания распространяются в виде
продольных волн. Достигнув нашего органа слуха — уха, коле-
колебания, частоты которых лежат в интервале приблизительно от 20
до 20 000 колебаний в 1 сек., вызывают специфическое ощущение
звука.
Принято в качестве единицы частоты брать частоту такого
колебательного процесса, при котором в 1 сек. совершается одно
колебание; эта единица частоты по имени немецкого физика Герца
называется герцем (сокращенно обозначается гц). Например, колеба-
колебательный процесс, при котором в 1 сек. совершается 2 колебания,
обладает частотой в 2 гц, а колебательный процесс, при котором
совершается 10 колебаний в 1 сек., — частотой в 10 гц.
Таким образом, колебания, лежащие в интервале от 20 до 20 000 гц,
обладают свойством вызывать ощущение звука и могут быть выде-
выделены по этому признаку в особую группу звуковых или акустических
колебаний, называемых также сокращенно звуком.
Указанное выделение колебательных процессов, происходящих с
частотами, лежащими в интервале от 20 до 20 000 гц, связано с фи-
физиологическими особенностями человеческого органа слуха восприни-
воспринимать колебания именно этих частот. С физической же точки зрения
колебания, например, в 10 гц или в 30 000 гц ничем специфическим
не отличаются от колебаний в 20 гц или 20 000 гц. Поэтому в физике
обычно под словами „звуковые колебания" подразумевают вообще
упругие колебания, распространяющиеся в виде волнового процесса
в газах, жидкостях и твердых телах или образующие в ограниченных
областях этих тел стоячие волны. Упругие колебания с частотами,
превышающими 20 000 гц, принято называть ультразвуками. Упру-
Упругие колебания с частотами меньше 20 гц называются инфразву-
инфразвуками.
Поскольку основной средой, в которой распространяются звуковые
колебания, является воздух, рассмотрим вопрос о скорости распро-
распространения упругих продольных волн в газах.
§ 115] ЗВУКОВЫЕ КОЛЕБАНИЯ И ИХ РАСПРОСТРАНЕНИЕ 443
В § 106 было приведено следующее выражение для скорости
распространения продольных упругих волн в сплошной среде:
A)
где Е—модуль Юнга среды, р — ее плотность. По определению,
для деформируемого упругого стержня модуль Юнга
р ?п_
где рп — усилие, т. е. величина, численно равная силе, отнесенной
к единице поперечного сечения стержня, a &L/L—относительное
удлинение. Для столба газа рп должно быть заменено через доба-
добавочное давление Д/?, вызывающее сжатие газа. Относительную линей-
линейную деформацию LL\L можно заменить относительной объемной
деформацией AV/V, так как мы полагаем, что столб газа сжимается
лишь вдоль своей длины, не меняя своего поперечного сечения.
Таким образом, имеем
V
Полагая изменения давления и объема бесконечно малыми, обозна-
обозначим их через dp и dV. При этом мы должны иметь в виду, что
увеличению давления (положительное dp) соответствует уменьше-
уменьшение объема, т. е. отрицательное dV. Поэтому формулу B) перепишем
в виде:
Е = -% или E=-V%. Ba)
Звуковые колебания происходят настолько быстро, что сжатия и
разрежения газа можно считать адиабатическими, поэтому изменение
состояния газа удовлетворяет формуле Пуассона:
/7V7 = const,
где -г— отношение теплоемкостей газа при постоянном давлении и
Q
постоянном объеме, •( = -?- (см. § 49).
Дифференцируя формулу Пуассона, получим:
V4p + iVT1pdV = 0, откуда |?=_т?.
Подставляя это значение dp/dV в формулу Bа), найдем
444
АКУСТИЧЕСКИЕ КОЛЕБАНИЯ
[гл. хш
наконец, подставив это значение Е в выражение A) для скорости
звуковых колебаний, получим
C)
Подставив сюда вместо плотности р ее значение через давление р,
температуру газа Т и его молекулярный вес р. (см. § 45)
где R — газовая постоянная, найдем
Таблица XX
Скорости звука v в газах
при 0° С
D)
Таким образом, для данного газа скорость распространения
звуковых волн прямо пропорциональна корню квадратному из
абсолютной температуры Т и не зависит от давления газа р.
Для различных газов, взятых при одинаковых условиях, скорости
звука обратно пропорциональны корню квадратному из их молеку-
молекулярных весов.
В табл. XX приведены значения ско-
скорости звука в некоторых газах при темпе-
температуре 0°С.
Большое значение скорости звука в во-
водороде определяется его малым молеку-
молекулярным весом.
При распространении звуковых волн
в атмосфере большую роль играют не-
неоднородности атмосферы. Скорость звука
зависит от температуры воздуха и сте-
степени его влажности. Ветер также влияет
на скорость распространения звуковых
волн. Наконец, волны отражаются на гра-
границе двух сред, в которых они движутся с различными скоростями.
Можно наблюдать отражение звуков от облаков и от границы тумана.
Всем хорошо известно, что звуки лучше доходят по ветру, чем
против ветра. Это явление обусловлено градиентом скорости ветра,
а не скоростью ветра самой по себе, так как она обычно мала по
сравнению со скоростью звука. Скорость ветра у поверхности Земли
меньше, чем на некоторой высоте. Это ведет к загибанию вверх зву-
звуковых лучей, идущих против ветра. Плохая слышимость против ветра
объясняется тем, что звуковые лучи проходят над головой наблюдателя.
Подобное же явление наступает и вследствие наличия градиента
температуры воздуха. В теплом воздухе звук распространяется быстрее,
чем в холодном. Отсюда следует, что если температура понижается по
мере удаления от поверхности Земли, то скорость звука уменьшается
Газ
Воздух
Кислород....
Водород ....
Углекислота. .
Скорость
звука
в м/сек
331
315
1263
258
§ 116] ИНТЕРФЕРЕНЦИЯ ЗВУКОВЫХ ВОЛН 445
с высотой, и звуковые лучи отклоняются вверх. Этот случай со-
соответствует градиенту температуры, имеющему место в середине
жаркого солнечного дня, когда поверхность Земли сильно нагрета.
При этих условиях слышимость бывает плохой. Вечером же при ясном
небе наступает быстрое охлаждение Земли, ведущее к охлаждению
близлежащих слоев воздуха. Температура воздуха возрастает с высо-
высотой, что ведет к загибанию обратно книзу звуковых лучей, идущих
вверх. Этим объясняется хорошая слышимость вечером.
Наконец, неоднородностью атмосферы объясняется образование
так называемых зон молчания, наблюдаемых при распространении
на большие расстояния сильных звуков, например звуков взрывов.
Взрыв слышен на сравнительно близких, а также на очень далеких
расстояниях (сотни километров), посредине же лежит область, где
звука взрыва не слышно.
В выражение скорости звука D) входит отношение теплоемко-
стей ^ = Cp/Cv, что позволяет находить для газов численное зна-
значение этого отношения по измерениям скорости звука.
Остановимся теперь еще на некоторых характеристиках распро-
распространяющейся в газе звуковой волны. В каждой данной точке
среды, в которой распространяется продольная звуковая волна,
сжатия и разрежения сменяют друг друга. Следовательно, давление
газа то возрастает против начального, то становится ниже его.
Наибольшее отличие давления от нормального называется ампли-
амплитудой звука; эта амплитуда обычно измеряется в барах.
Ввиду того что это добавочное давление в волне все время
колеблется, его среднее значение равно нулю. Однако для очень
сильных волн приходится принимать во внимание эффекты, завися-
зависящие от квадрата и более высоких степеней смещения. Колебания
такого рода описываются нелинейными уравнениями и потому на-
называются нелинейными колебаниями. Для нелинейных колебаний
среднее давление не равно нулю. Такая звуковая волна, отражаясь
от преграды, оказывает на нее давление. Величина этого звукового
давления, как показывает теория, равна
где е' — средняя плотность энергии в стоячей волне, образующейся
около преграды; f имеет прежнее значение отношения теплоемко-
стей CpjCv.
Экспериментальна звуковое давление было изучено в лаборато-
лаборатории знаменитого русского физика П. Н. Лебедева A866—1912),
который поставил в общем виде вопрос о давлении, оказываемом
при поглощении и отражении волн (см. т. III).
§ 116. Интерференция звуковых волн. На звуковых волнах
легко могут быть обнаружены характерные явления интерференции,
описанные в § 109. Простейший опыт по интерференции звука
1Г
446 АКУСТИЧЕСКИЕ КОЛЕБАНИЯ [ГЛ. XIII
осуществляется с помощью трубы, схематически изображенной на
рис. 287. Источник звука устанавливается у воронки А, насаженной
на трубу. Далее труба разветвляется, образуя два колена ABD и
ACD. Колено ACD сделано из труб, вставленных друг в друга;
его можно удлинять или укорачи-
^A / вать. Звуковые колебания доходят
/ л до конца трубы Е двумя путями:
I—== ^ по колену ABD и по колену ACD.
— \Л При неодинаковой длине колен
= ^J между волнами, пришедшими в точ-
шят ^ Ку ? по различным коленам, будет
существовать разность хода г9 — гх.
Если эта разность хода равна
Рис. 287. Труба для наблюдения четному числу полуволн, т. е.
интерференции звука. \
ra — ri = 1k-y-, где k — целое чи-
число, то, по сказанному на стр. 423, звук в точке Е усилится по
сравнению с тем, как если бы он проходил по одному колену.
При разности хода в нечетное число полуволн, т, е, когда
ra — ri = BA>-|-1W, будет наблюдаться ослабление звука.
Указанной трубой можно воспользоваться для измерения длин
волн звука, испускаемого данным источником. Для этого надо из-
измерить то смещение трубки С, которое необходимо произвести,
чтобы перейти от одного ослабления звука до другого. Изменение
длины колена даст длину волны X. Этот метод измерения длин
звуковых волн основан на явлении интерференции, поэтому он но-
носит название интерференционного метода. Труба, изображенная
на рис. 287, является простейшим аналогом интерферометров,
применяемых в оптике для измерения длин световых волн.
Практически такую трубу можно использовать для измерения
длины звуковых волн среднего диапазона, так как крайним звуковым
колебаниям соответствуют слишком длинные или слишком короткие
волны. Действительно, в воздухе, где скорость звука Т/ = 331 м/сек,
наиболее медленным звуковым колебаниям с частотой ч = 20 гц
331
соответствует длина волны Х = -™-.и = 16,5 м, наиболее же бы-
быстрым колебаниям v = 2-104 гц соответствует длина волны Х =
= 1,65 см. Средней частоте ч = 500 гц соответствует Х = 66,2 см.
Если в воронку трубы А направить сложный звук, то при
заданной разностц хода г2 — г^ ослабятся те колебания, для кото-
которых эта разность равна нечетному числу полуволн Х/2, ЗХ/2, 5Х/2
и т, д. В результате из сложного колебания выпадает ряд его гар-
гармонических составляющих, и сложное колебание изменит свой
характер. Таким образом, труба играет роль фильтра по отношению
к колебаниям определенных частот.
I 116] интерференция звуковых волн 447
Частным случаем интерференции является интерференция двух
встречных волн одинаковых частот и амплитуд. В этом случае, как
было указано на стр. 425, образуются стоячие волны. Образование
стоячих волн можно непосредственно обнаружить при отражении
звука от стены. Для этого надо воспользоваться источником, испу-
испускающим волны определенной длины волны, которые при этом
должны быть достаточно короткими, чтобы расстояния между сосед-
соседними пучностями были невелики. Приближая и удаляя голову от
стены, можно слышать усиление звука в местах наиболее резкого
изменения плотности, т. е. в местах расположения узлов.
Кундт предложил весьма наглядный способ наблюдать стоячие
волны. Оба конца стеклянной трубки закрываются наглухо пробками
Л и С (рис. 288). Через отверстие в пробке С пропускается зажа-
4111
Ми,,,... Ш
А ВС
Рис. 288. Опыт Кундта по наблюдению стоячих волн.
тый посредине металлический стержень, на конце которого насажен
пробковый диск В, свободно входящий в трубку. Если возбудить
в стержне продольные колебания, натирая его кожей, посыпанной
канифолью, то в нем установится стоячая волна с узлом в месте
зажима и пучностями на концах. ' Пробковый диск В придет в коле-
колебания и возбудит колебания воздуха в трубке. Волна, идущая по
трубке вперед, будет интерферировать с волной, отразившейся от
конца А и идущей назад. Если трубка такова, что на ее длине
укладывается целое число полуволн, то в ней установятся стоячие
волны, на концах трубки образуются узлы смещений. В трубку
насыпаются пробковые опилки, которые разбрасываются в пучностях
и остаются лежать в узлах, благодаря чему места образования уз-
узлов и пучностей делаются непосредственно видимыми. Измерение рас-
расстояния между двумя соседними узлами (или пучностями) Дает поло-
половину длины звуковой волны, возбужденной в трубке. Таким образом,
трубка Кундта также служит для измерения длин звуковых волн.
Образование узлов и пучностей можно также наблюдать в зву-
звучащих пластинках. Здесь мы будем наблюдать образование узловых
линий. Для наблюдения берется латунная пластинка, укрепленная
в середине, и в ней возбуждаются смычком колебания. На пластинку
насыпают немного песка. Когда пластинка колеблется, песок сбра-
сбрасывается с мест пучностей и собирается по узловым линиям. На
пластинке получаются сложные фигуры, по которым можно судить
о роде колебаний. Эти фигуры для ряда частных случаев изобра-
изображены на рис. 289. Вид колебаний зависит от точки возбуждения
пластинки смычком и, кроме того, меняется в зависимости от точки
448
АКУСТИЧЕСКИЕ КОЛЕБАНИЯ
[ГЛ. ХШ
Рис. 289. Узловые линии.
прикосновения к пластинке. Точка возбуждения будет пучностью,
а узловая линия подходит к краю в точке, где мы касаемся
пластинки пальцем. Остальные линии расположатся на пластинке
симметрично. Если коснуться
пальцем угла пластинки и прове-
провести смычком по середине одной
из сторон, то получается фигура,
изображенная на рис. 289 а.
Здесь узловые линии располо-
расположены по диагоналям. Если мы,
наоборот, коснемся пальцем се-
середины края пластинки, а около
угла проведем смычком, то получим вторую фигуру (рис. 289 б).
Касаясь одновременно угла и одной из сторон пластинки и проводя
смычком по середине одной из сторон, мы получим более сложное
расположение узловых линий (рис. 289 в).
Изучение вида узловых линий имеет практическое значение для
выяснения характера колебаний мембран в телефонах и других аку-
акустических аппаратах.
§ 117. Восприятие звуков. Человек воспринимает звуки с помо-
помощью своего слухового аппарата — уха; строение его схематически
представлено на рис. 290. В височ-
височных костях / черепа находится осо-
особый орган—улитка 2, представляю-
представляющий собой небольшую (объемом
около 0,2 см3) костную полость,
наполненную жидкостью (лимфой).
Внутри улитки расположен кортиев
орган, состоящий из волокон, к ко-
которым подходят окончания слухо-
слухового нерва 3. Волокна имеют раз-
различную длину и натяжение, в ре-
результате им соответствуют различ-
различные резонансные частоты. Звуко-
Звуковые колебания по слуховому каналу 4
доходят до барабанной перепонки 5,
затем через систему слуховых
косточек 6 передаются овальному окну 7, ведущему в полость улитки.
При действии звуков определенной частоты определенные волокна
кортиева органа приходят в резонансное колебание и возбуждают
соответствующие нервные окончания, передающие раздражения в мозг.
При действии сложного звука раздражение испытывает ряд нервных
окончаний, в результате чего человек может воспринимать составля-
составляющие сложного звука раздельно.
Возможность оценивать направление распространения звуковых
волн обусловлена наличием у человека парного слухового органа
Рис. 290. Разрез уха человека.
§ 117] восприятие звуков 449
(банауральный эффект). Ощущение направления звуковых волн
возникает благодаря способности мозговых центров учитывать раз-
разность фаз колебаний, достигающих ушей. При звуках высокой ча-
частоты суждение о направлении звука может возникать вследствие
разницы амплитуд звука в обоих ушах. В субъективном звуковом
восприятии мы различаем три характеристики звука: 1) высоту,
2) тембр, 3) громкость.
Высота звука определяется его частотой: чем больше частота,
тем выше звук.
Тембр звука определяется характером колебаний; лишь в ред-
редких случаях звуковое колебание представляет собою чистое гармо-
гармоническое колебание, чаще оно носит более сложный характер
(см. § 118). Состав этого колебания и определяет тембр звука.
Объективная громкость, или, как говорят, сила звука, опреде-
определяется количеством энергии, переносимой распространяющейся
звуковой волной в единицу времени через единичную площадку,
расположенную перпендикулярно к направлению распространения
ВОЛНЫ.
Количество энергии, переносимой волной в единицу времени
через единичную площадку, пропорционально квадрату амплитуды
волны и квадрату ее частоты. Отсюда следует, что сила звука дан-
данной высоты пропорциональна квадрату амплитуды. Однако такой
объективной оценке силы звука не соответствует субъективная оценка
громкости, основанная на непосредственном ощущении. Дело в том,
что наше ухо не одинаково чувствительно к звукам различной высоты,
т. е. различной частоты.
Количество энергии, переносимой в единицу времени через единичную
площадку, расположенную перпендикулярно к направлению распространения
волны, как мы указывали на стр. 434, определяется вектором Умова №.
где ё — средняя плотность энергии волны, а V—скорость распространения
волны. Таким образом, сила звука определяется вектором Умова. Это позво-
позволяет измерять силу звука в объективной мере, например, в CGS-системе,
в эрг/см3 сек. Для этого можно воспользоваться соотношением между звуко-
звуковым давлением и средней плотностью энергии ё- На стр. 445 нами было ука-
указано, что при достаточной мощности звуковая волна оказывает на преграду
давление р, которое определяется средней плотностью энергии ё' в стоячей
волне, образующейся около преграды. Отсюда следует, что, измеряя давление/»
на преграду, можно измерить и среднюю плотность энергии в стоячей волне ё'.
Средняя плотность энергии в бегущей волне I будет вдвое меньше Г. Однако
непосредственное измерение звукового давления с экспериментальной точки
зрения представляет значительные трудности. Поэтому пользуются несколько
косвенным методом. Релеем было показано, что под влиянием звукового дав-
давления на диск, расположенный в поле звуковой волны, должен действовать
момент сил. Для измерения этого момента очень легкий диск подвешивается
к тонкой нити с зеркальцем, и по отклонению отражения светового луча от
зеркальца вычисляется момент сил, поворачивающих диск. Отсюда вычисляется
средняя плотность энергии в звуковой волне и по вектору Умова — громкость
звука. Но и этот метод связан с достаточно тонкими измерениями и практи-
450
АКУСТИЧЕСКИЕ КОЛЕБАНИЯ
[гл. хш
чески пригоден лишь для измерения звуков большой мощности. Обычно им
пользуются для градуировки электроакустических приборов (микрофонов),
служащих для измерения громкостей.
Для того чтобы звуковая волна создала ощущение звука, необхо-
необходимо, чтобы сила звука превышала некоторую минимальную вели-
величину, называемую порогом слышимости. Звук, сила которого лежит
ниже порога слышимости, ухом не воспринимается: он слишком слаб для
этого. Порог слышимости различен для различных частот. Наиболее
чувствительно человеческое ухо к колебаниям с частотами в области
1000—3000 гц; для этой области порог слышимости достигает вели-
величины порядка 10~8 apzjсм* сек. К более низким и к более высоким
частотам ухо значительно менее чувствительно. Колебания с часто-
частотами менее 20 гц и более 20 000 гц ни при каких силах не воспри-
воспринимаются как звуковые.
Колебания очень большой силы, порядка сотен тысяч эрг/смЧек,
перестают восприниматься как звуковые: они вызывают в ухе
осязательное чувство давления, переходящее дальше в болевое ощу-
ощущение. Максимальная величина силы звука, при превышении которой
возникает упомянутое' осязательное (болевое) ощущение, называется
порогом осязания или по-
порогом болевого ощуще-
ощущения. Порог болевого
Порог осязания
Порог J
слышимости
20
f0
ю12
>°ez
50 Ю0 200 500М032-!035-103&2-ЮЬ
Частота В герлаа
Рис. 291. Область слышимости.
ощущения несколько раз-
различен для различных
частот. Между порогом
слышимости и болевым
порогом лежит область
слышимости, изображен-
изображенная на рис. 291.
Субъективная гром-
громкость звука не поддается
точному количественному
измерению. Однако все
же можно произвести оценку интенсивности ощущения, основываясь
на психофизическом законе Вебера — Фехнера, по которому изме-
изменение интенсивности ощущения пропорционально логарифму отно-
отношения энергий раздражителя, вызывающих сравниваемые ощущения.
На основании этого логарифмического закона устанавливается шкала
уровней силы звука. Естественно принять уровень на пороге слы-
слышимости /0 за,, нулевой. Условно за нулевой уровень принимается
уровень, для которого /0=Ю~9 эрг/см* сек, т. е. несколько меньше
порога слышимости для 1000 гц. Тогда по закону Вебера — Фехнера
громкость некоторого звука L пропорциональна логарифму отношения
его силы / к силе того же звука на пороге слышимости /0:
0)
§ П7]
ВОСПРИЯТИЕ ЗВУКОВ
451
где k — коэффициент пропорциональности. Величину L "обычно на-
зывают уровнем силы звука. Положив А = 1, мы тем самым выберем
определенную единицу измерения уровней звука; эта единица носит
название бела.
Таким образом:
= \gj- белов.
B)
Наряду с белами пользуются единицами в 10 раз меньшими,
получившими название децибелов; по этому определению:
L = 10 • lg j- децибелов.
Таблица XXI, дающая приблизительное значение уровней силы
звука для •обычных звуков, позволяет составить более конкретное
представление о характеристике громкостей. Следует, однако, еще
иметь в виду зависимость чувствительности уха от частоты звука.
Таблица XXI
Уровни различных звуков
Звук
Тихий шопот
Шаги
Громкая речь
Шум оживленной улицы . .
Оркестр фортиссимо . . . .
Шум азропланного мотора
на расстоянии 3 м . . . .
Уровень
в деци-
децибелах
30
40
70
90
100
130
Сила звука
в эрг
см3 сек
1 • 10-'
1 • 10"а
1
1 • 101
1 ¦ 101
Амплитуда
давления
в барах
6,4 •
2 • 10-а
0,4
6,4
2,0 • 10
1- 10»
Из табл. XXI видно, что энергии, соответствующие обычным
звукам, весьма невелики. Для иллюстрации этого можно привести
следующий курьезный пример: если бы 2000 человек вели непре-
непрерывно разговор в течение 1!/а часов, то энергии их голосов хватило бы
лишь на то, чтобы вскипятить один стакан воды.
Для объективной характеристики тембра звука сложное звуковое
колебание надо разложить на его гармонические составляющие —
определить его спектр. Такое разложение можно произвести, используя
явление резонанса. Если взять два камертона с одинаковыми часто-
частотами собственных колебаний, расположенные на некотором расстоя-
расстоянии друг от друга, и возбудить сильные колебания в одном из них,
то окажется, что более слабые колебания возникнут и во втором.
В этом можно убедиться, заставив первый камертон внезапно пре-
452 АКУСТИЧЕСКИЕ КОЛЕБАНИЯ [ГЛ. XIII
кратить колебания, например, зажав его рукой. Тогда будет слышно
слабое звучание второго камертона. Если частота собственных колеба-
колебаний второго камертона отлична от частоты собственных колебаний
первого, то явление будет выражено слабее и тем слабее, чем больше
различие в частотах собственных колебаний. Описанное явление
объясняется тем, что звуковая волна, испускаемая первым камерто-
камертоном, достигнув второго, возбуждает в нем вынужденные колебания.
Наибольшего значения амплитуда вынужденных колебаний достигнет
при резонансе. При малом затухании колебаний второго камертона
резонанс практически имеет место при совпадении частот собствен-
собственных колебаний обоих камертонов, и явление резонанса будет доста-
достаточно острым (см. стр. 403). Основываясь на резонансе, анализ слож-
сложного звукового колебания можно произвести следующим образом:
взять большое число камертонов с различными собственными часто-
частотами колебаний <ог и с малым затуханием. Тогда сложное звуковое
колебание вызовет вынужденные колебания заметной амплитуды
только у тех из этих камертонов, собственные частоты колебаний
которых (о, совпадут с частотами шк колебаний,
присутствующих в составе изучаемого сложного
колебания.
Вместо камертонов для анализа звука можно
использовать любые другие системы с определен-
определенными собственными частотами колебаний и малым
Рис. 292. Резона- затуханием. Гельмгольц, впервые производивший
тор с воздушной анализ звуков, пользовался резонаторами с воз-
полостью, душной полостью. Такие резонаторы представ-
представляли собою тонкостенные металлические сферы
с двумя отверстиями — одним ббльшим а и другим меньшим Ъ (на
рис. 292 дано сечение резонатора). Основное отверстие а служит
для проникновения звуковых колебаний внутрь объема резонатора,
а малое отверстие b — для вкладывания его в ухо и определения
на слух интенсивности вынужденных колебаний.
Собственная частота колебаний резонаторов Гельмгольца и>0 при-
приближенно равна
где d — диаметр отверстия а, а V — объем полости резонатора.
Простой тон, входящий в состав изучаемого сложного звукового
колебания, наиболее сильно возбудит тот резонатор, собственная ча-
частота колебаний которого ю0 ближе всего к его частоте.
Таким образом, спектр сложного звука может быть определен
путем последовательного „прослушивания* через ряд резонаторов
и оценки на слух громкости их вынужденных колебаний.
Современная техника позволяет изучать состав звуков с по-
помощью гораздо более совершенной электроакустической методики,
§ 118] ИСТОЧНИКИ ЗВУКОВ. ПОЛУЧЕНИЕ УЛЬТРАЗВУКОВ 453
основанной, однако, также на принципе наблюдения вынужденных
колебаний.
§ 118. Источники звуков. Получение ультразвуков. Всякое
колеблющееся тело может служить источником упругих волн в среде,
окружающей колеблющееся тело, т. е. служить источником звука.
Изучение источников звука имеет особый интерес в связи с развитием
радио и говорящего кино, в которых употребляются громкоговорители,
а также для теории и техники музыкальных инструментов. Однако
на этих специальных вопросах мы не будем останавливаться и рас-
рассмотрим кратко лишь некоторые простейшие источники звуковых волн.
Рассмотрим струну длины /, закрепленную с обоих концов. При
возбуждении колебаний в такой струне устанавливаются стоячие
волны, причем узлы расположатся
в местах закрепления, т. е. на ^„--— —,_^
концах струны; посредине струны с?— _--~"°
образуется пучность (рис. 293а).
Этому колебанию соответствует „-- ---^ _„-- -
определенная частота колеба* ^ ~^с^
ний (Oj. Однако, наряду с указан- ""—-—" -—»--
ной стоячей волной, в струне мо- ,-—-~^ ~'~~^>. -""¦
жет установиться стоячая волна <?v ^Х^ т*г;
с тремя узлами: два узла на кон- """—" '*~-—-' ^-—--'
цах струны и один посредине Рис. 293. Стоячие волны в струне,
(рис. 2936). Этому колебанию закрепленной с концов,
соответствует частота шь вдвое
ббльшая, чем частота первого колебания щ. Точно так же могут
установиться стоячие волны с четырьмя узлами (рис. 293в) и часто-
частотой ш3 = 3<оь и вообще стоячие волны с А —j- 2 узлами (считая и
узлы на закрепленных концах струны) и с частотой колебаний
(?+)
А (+)
Таким образом, одна и та же струна может испускать звуковые
колебания не только с основной частотой юь но и так называемые
обертоны с частотами шА = (^ —|— 1) шь где k — целое число. Вообще
говоря, при колебаниях струны одновременно устанавливается ряд
стоячих волн и, таким образом, струна одновременно испускает,
наряду с основной частотой, и обертоны, сила которых, однако,
значительно меньше силы колебаний основной частоты. Спектр коле-
колебаний (см. стр. 405) такой группы представится из ряда линий,
соответствующих частотам щ, 2(оь 3<аи ...
На рис. 294 изображен акустический спектр скрипки при основ-
основном тоне 640 гц. На рис. 295 представлен спектр колебаний клар-
кларнета при основном тоне 64 гц, а на рис. 296 — рояля B56 гц); на
этом последнем рисунке видно, что наряду с линейчатым спектром
присутствует и область сплошного спектра.
Шумам соответствует наличие лищь сплошного акустического
спектра.
454
АКУСТИЧЕСКИЕ КОЛЕБАНИЯ
[гл. хш
В качестве примера на рис. 297 представлен спектр шума бун-
зеновской горелки.
ю
1
1 I
гчо3 ч-w3 ечо3 8-ю3 ги
Рис. 294. Акустический спектр скрипки при основном тоне 640 гц.
Л
100
Ю
о
но3
Громкость испускаемого звука определяется амплитудой коле-
колебаний звучащей системы. Однако в некоторых случаях источник
колебаний, даже при значитель-
значительных амплитудах, не дает силь-
сильного звука. Например, если на-
натянуть струну между двумя твер-
твердыми зажимами и ударить ее, то
звук получается лишь очень сла-
слабым. Также, если ударить камер-
камертон и держать его в руке, то
звук почти не слышен. Это объяс-
объясняется тем, что в указанных слу-
случаях колеблющиеся струна или
ножка камертона вызывают лишь
замкнутые вихревые потоки воз-
воздуха по соседству и не образуют
сжатий и разрежений воздуха,
Рис. 295. Акустический спектр клар-
кларнета при основном тоне 64 гц.
А
100
w
/•to3 гчо3
¦ю3ги
Рис. 296. Акустический спектр рояля ведущих к возникновению про-
пропри основном тоне 256 гц. дольной звуковой волны. Связь
колеблющейся системы с окру-
окружающим воздухом недостаточна, и система слабо излучает. Для
увеличения излучения надо создать такие условия, при которых
возникновение вихревых движений за- Л
труднялось бы. В связи с этим камер-
камертоны, для усиления их звучания, уста-
устанавливают на деревянных ящиках, а в
музыкальных инструментах (скрипках,
виолончелях) струны прикрепляют к де-
деревянным поверхностям — декам. Коле-
Колебания струны передаются большой по-
поверхности деки, около которой замкну- ¦=
тые потоки воздуха становятся невоз- Рис-297. Акустический спектр
л л -, шума бунзеновской горелки,
можными. Около деки образуются волны
сжатия и разрежения, создающие сильный звук. Ту же роль
играет крышка рояля.
гц.
ИСТОЧНИКИ ЗВУКОВ. ПОЛУЧЕНИЕ УЛЬТРАЗВУКОВ
455
Увеличением излучения объясняется и возрастание громкости
звуков при резонировании систем. Такой опыт в простейшем виде
может быть проведен следующим образом. Звучащий камертон
(рис. 298) располагается над отверстием высокого узкого сосуда,
в который налито немного воды. Если начать понемногу прибавлять
воду, то в определенный момент сила звука
значительно возрастет. Явление объясняется
следующим образом. При соответственной вы-
высоте столба воздуха в сосуде над водой колеба-
колебания воздуха приходят в резонанс с колебаниями
камертона, и их амплитуда сильно возрастает.
У отверстия сосуда возникают попеременно
сжатия и разрежения, которые срывают вихри,
образующиеся вокруг ножек камертона, в ре-
результате чего излучение звука усиливается.
Наконец, рассмотрим особого рода акусти-
акустическую волну, возникающую около тела, дви-
движущегося в рассматриваемой среде со сверх-
сверхзвуковой скоростью (для воздуха со ско-
скоростью больше 330 м/сек). Движущееся с такой
скоростью тело вызывает в среде волну ударного характера, назы-
называемую баллистической волной. Сжатие среды не может распро-
распространяться впереди движущегося
тела, и образующийся фронт
волны располагается лишь за дви-
движущимся телом. Каждая точка
среды, мимо которой прошло
тело, может рассматриваться как
источник сферических волн, рас-
распространяющихся со скоростью
звука в данной среде. Огибаю-
Огибающая этих сферических волн
(рис. 299) имеет форму конуса.
Пусть тело проходит отрезок А А' за время t; за то же время зву-
звуковая волна распространится около точки А на отрезок AB = Vt,
где V—скорость звука. Отсюда угол при вершине конуса <р опре-
определится отношением:
Рис. 298. Резонирова-
Резонирование столба воздуха
над водой.
Рис. 299. Возникновение баллистиче-
баллистической волны.
* »-#-?
#? <¦)
где v — скорость тела. Таким образом, баллистическая волна имеет
фронт в виде конуса с углом растворения, определяемым равен-
равенством A). Возникающая волна не имеет периодического характера,
но представляет собою одну область сжатия, распространяющуюся
со скоростью звука. Такого рода волны возникают от современных
артиллерийских или реактивных снарядов, а также от самолетов, ле-
летящих со сверхзвуковой скоростью. Они производят ощущение резкого
456 АКУСТИЧЕСКИЕ КОЛЕБАНИЯ [гл. XIII
удара. Кроме того, снаряд возбуждает другие колебания (дающие
визг или шипение), вызванные наличием неровностей у снаряда.
Все эти колебания могут наблюдаться лишь после того, как снаряд
пролетел, так как, двигаясь со сверхзвуковой скоростью, он опере-
опережает их распространение.
Для получения ультразвуков чаще всего используется так назы-
называемый пьезоэлектрический эффект (см. т. II). Пьезоэлектрический
эффект заключается в том, что некоторые кристаллы при внесении
их в электрическое поле испытывают механическую деформацию. Для
получения ультразвуковых колебаний употребляются кристаллы квар-
кварца (пьезокварц). Если к пластинке кварца, вырезанной определен-
определенным образом по отношению к ее кристаллографическим осям, при-
приложить с помощью металлических обкладок переменное электриче-
электрическое напряжение, то пластинка начнет колебаться. Колебания
кварцевой пластинки становятся особенно интенсивными, если частота
приложенного электрического напряжения совпадает с частотой
собственных механических колебаний пластинки (явление резонанса).
Подобрав соответственным образом размеры пластинки, можно
получить ультразвуковые колебания с частотой в сотни тысяч герц.
Ультразвуковые волны, благодаря малой длине волны, более слабо,
чем обычные звуковые волны, обнаруживают явление загибания волн
(диффракцию; стр. 419). Это позволяет получать хорошо направлен-
направленные пучки ультразвуковых волн.
В настоящее время ультразвуки широко используются в технике
и, в частности, для направленной подводной сигнализации, для
обнаружения подводных предметов и определения глубин (эхолот)
Кварцевые пластинки одинаковой толщины, вырезанные определенным
образом из кристаллов, пришлифовываются друг к другу в виде
мозаики и вклеиваются между двумя толстыми стальными плитами.
При подведении к плитам переменного электрического напряжения
вся система служит мощным источником ультразвуков.
Принцип устройства эхолота заключается в следующем: от
источника ультразвуков в воде посылается вертикально вниз звуковой
луч, который, достигнув дна, отражается от него и возвращается
обратно. Зная скорость распространения звука в воде, легко по
времени, проходящему от подачи ультразвукового сигнала до его
возвращения обратно (наблюдения эхо), вычислить глубину.
Прием эхо производится также с помощью пьезокварца. Звуковые
колебания, дойдя до пьезокварца, вызывают в нем упругие колебания,
в результате которых на противоположных поверхностях кварца
возникают электрические заряды, которые могут быть обнаружены
и измерены соответственной электрической аппаратурой.
Ультразвуковые волны пригодны для сигнализации в воде, где они
распространяются без заметного поглощения; в воздухе же они весьма
сильно затухают, а потому не пригодны для сигнализации через
толщи воздуха.
§ 119] ОТРАЖЕНИЕ И ПОГЛОЩЕНИЕ ЗВУКОВЫХ ВОЛН 457
Современное техническое применение ультразвуков весьма разно-
разнообразно. Ультразвуки используются для обнаружения дефектов в метал-
металлических изделиях (ультразвуковая дефектоскопия), для измерения
зазоров, толщин и т. д. Некоторые применения ультразвуков связаны
с механическим воздействием, которое мощные ультразвуки оказывают
на ту среду, в которой они распространяются. Так, с помощью ультра-
ультразвуков можно обрабатывать металлические и другие поверхности,
просверливать отверстия, вести очистку деталей и т. д. Ультразвуки
воздействуют на многие физико-химические процессы и на протекание
химических реакций.
§ 119. Отражение и поглощение звуковых волн. Достигнув
границы двух сред, звуковая волна, вообще говоря, отчасти отражается
от границы, отчасти проникает во вторую среду и продолжает в ней
распространяться. При распространении волны в данной среде она
постепенно ослабляется за счет перехода энергии колебаний в другие
виды энергии.
Явления отражения и поглощения звуковых волн играют особую
роль при распространении звуков в замкнутых помещениях. При
проектировании аудитория, концертных залов, театров существенно
учитывать возможность многократных отражений звуковых волн от
стен, потолка и т. д. Наличием этих отражений обуславливаются
акустические свойства помещения.
В настоящее время развилась особая отрасль техники, получившая
название архитектурной акустики.
В помещениях средних размеров звуковая волна претерпевает
несколько сот последовательных отражений от стен и потолка, пока
ее энергия не упадет до порога слышимости. В больших помещениях
звук может быть слышен в течение нескольких секунд после выклю-
выключения источника за счет существования отраженных волн. Слишком
медленное затухание ухудшает акустические свойства помещения,
вызывает чрезмерную „гулкость"—каждая новая часть связного
контекста (например, каждый новый слог речи) перекрывается еще
не затухшими предыдущими колебаниями. Но и чрезмерно быстрое
затухание отраженных волн с акустической точки зрения также
не выгодно — звуки в помещении получаются слишком слабыми
и „глухими". Существует некоторое оптимальное значение зату-
затухания.
При расчетах акустических свойств помещений принято рассчи-
рассчитывать время, в течение которого энергия звука уменьшается до
одной миллионной доли начального значения (W=\0~6 Wo); это
время называется временем реверберации.
Так как затухание волн различной частоты различно, то принято
определять реверберацию при частоте 512 гц. Оптимальное время
реверберации различно для помещений, предназначенных для разных
целей: например, для концертных залов, для аудиторий и т. д.
оптимальное время реверберации есть величина порядка 1 сек.
458 АКУСТИЧЕСКИЕ КОЛЕБАНИЯ [ГЛ. XIII
Обозначим плотность звуковой энергии в помещении в начальный момент
через Wo. Обозначим через а коэффициент поглощения при отражении; пусть
число отражений в единицу времени равно и. Тогда уменьшение плотности
энергии dW за время dt равно
= — anWdt.
Перепишем это выражение в виде:
что, в свою очередь, может быть переписано в виде:
d (In W) = — d (ant).
Как мы уже не раз указывали (ср. стр. 435), если дифференциалы двух
величин равны друг другу, то сами величины могут отличаться лишь на
аддитивную постоянную:
Так как при t = Q по условию W= Wo, то, следовательно,
после чего равенство A) принимает вид:
откуда
Таким образом, плотность звуковой энергии убывает со временем по
показательному закону.
По теории вероятности можно рассчитать число отражений звуковой
волны в течение 1 сек. в предположении, что волны распространяются во
всевозможных направлениях; расчет дает:
— VJL
где v —скорость звука, S — площадь поверхности помещения, V—его объем.
Подставив это значение п в B), получим
W=W(te~'wi . C)
Отсюда видно, что, кроме геометрических факторов S и V, затухание
определяется еще коэффициентом поглощения о.
Для определения времени реверберации полагаем в C)
AV
тогда f=__inl0-.
Подставляя сюда для v значение скорости звука в воздухе, получим
< = 0,163 Jj^-. D)
В табл. XXII приведены значения коэффициентов поглощения (для ча-
частоты 512 гц) для некоторых материалов.
§ П9]
ОТРАЖЕНИЕ И ПОГЛОЩЕНИЕ ЗУКОВЫХ ВОЛН
459
Таблица XXII
Коэффициенты поглощения звуковых волн при отражении
Материал
Бетон
Оштукатуренная кирпичная стена
Известь на деревянной обрешетке
Ковер
Войлок (толщ. 2,5 см на расстоянии 8 см от стены)...
0,015
0,025
0,034
0,20
0,78
Как видно из табл. XXII, коэффициенты поглощения а весьма различны
для различных материалов. Малое значение а для бетона обуславливает «гул-
«гулкость" помещений с бетонным полом и стенами. Сравнительно большое зна-
значение а для ковров, занавесей и т. д. служит причиной „заглушенности*
звуков в помещениях с занавешенными стенами.
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Абсорбция 373
Авенариус 239
Авогадро закон 167
— число 156, 197, 299
автоколебательная система 398
адиабата 268
адиабатический процесс 268
адиабатическое изменение объема
газа 270
адсорбция 373
акустика архитектурная 457
акустические колебания 442
амплитуда 378
— звука 445
анизотропия 340
Атвуда машина 58
атмосфера техническая 161
— физическая 161
атомная теория 157
атомный вес 157
— пучок 202
Баллистическая волна 455
— кривая 32 .
баллистический маятник 94
бар 161
барометрическая формула 195
бел 451
Беряулли Даниил 171
Бернулли уравнение 142
Бессель 116
биения 391
бинауральный эффект 449
Бойля — Мариотта закон 161
Больцман 162, 305
Больцмана закон распределения 194
— постоянная 174
— соотношение между энтропией и
вероятностью 305
Борн 345
Борна—Габера круговой процесс
347
броуновских частиц смещение 196
броуновское движение 160, 195
Вакуум 219
Ван-дер-Ваальса поправки 227, 229,
231
— уравнение 229, 231
в приведенных величинах 241
Вант-Гоффа формула 333
ватт 82
Вебера—Фехнера закон 450
вектор 27
векторное произведение 42
вероятность 294
вес 54, 55
веса зависимость от высоты 112
— — от широты 71
вискозиметр 156
волн интерференция 422
— упругих распространение 429
волны поперечные 414
— продольные 414
— стоячие 425, 447
волны уравнение 418, 430
волчок 131
внутреннее трение 148, 209
при низких давлениях 217
вязкость 148
Газ идеальный 165
— реальный 227
газовая постоянная 168
Галилей 15, 58
гармонического колебательного дви-
движения уравнения 378
гармоническое колебательное движе-
движение 376
Гейзенберга соотношение неопреде-
неопределенности 108, 171
Гей-Люссака закон 163
Гелий 1 150
Гелий 11 149
Гельмголъц 452
Гельмгольца резонатор 452
гектоватт-час 83
Герц 9, 442
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
461
герц 442
гидродинамика 139
гироскоп 131
гироскопический компас 133
— эффект 132
главный вектор сил 119
Голицын Б. Б. 178
градиент плотности 206
— скорости 148, 209
— температуры 212
грамм массы 12, 56
— силы 55
грамматом 158
граммолекула 158
громкости шкала 450
громкость 449
Гросс Е. Ф. 367
Гука закон 348
Гюйгенса принцип 418
Давление 161
— внутреннее в газах 228
в жидкостях 312
— молекулярное 308
— насыщенных паров 238, 335
— парциальное 177
— под изогнутой поверхностью жид-
жидкости 316
— приведенное 242
Даламбера начало 69
Дальтон 177
двигатель внутреннего сгорания 287
— реактивный 147, 291
движение 16
— вращательное 38
— вязкой жидкости 148
— жидкости 139
— криволинейное 29
— Луны 112
— молекулярное 159
— поступательное 37
— прямолинейное неравномерное 20
равномерное 18
— равнопеременное 22
— твердого тела 119
— тяжелого тела, брошенного под
углом к горизонту 31
движения количество 52
декремент затухания 398
дефектоскопия ультразвуковая 457
деформация 348
— кристаллических тел 358
— кручения 352
— одностороннего сжатия 348
— остаточная 355
— пластическая 355
— продольного растяжения 348
— сдвига 351
деформация твердых тел 348
— упругих тел 348
децибел 451
Джоуль 245, 255
джоуль 83
Джоуля и Коппа закон 366
Джоуля—Томсона эффект 245
дина 54
динамика 44
дисперсия волн 439
диссоциация 334
диффракция 419
диффузии коэффициент 206
диффузия газов 205
длина волны 416, 421
— свободного пути молекул 199
Допплера явление 436
Дюара сосуд 218
Дюлонга и Пти закон 365
Единиц система 14
абсолютная 14
международная MS 12
MKS 14
техническая 14
единица массы техническая 55
единицы измерения 12
Жидкости строение 308, 371
жидкость 308
— вязкая 146
— идеальная 139
— переохлажденная 329
— растянутая 241
Жуковский Н. Е. 155
Зайончевский 239
звук 442
звука высота 449
— громкость 449
— тембр 449
звуков восприятие 448
— источники 453
— отражение 457
— поглощение 457, 459
— звуковые колебания 442
— спектры 453
зона молчания 445
Измерение физических величин 10
изобара 166
изотерма Бойля—Мариотта 162
— Ван-дер-Ваальса 236
— углекислоты 236
изотермическое изменение объема
газа 270
изотропное тело 340
изохора 165
462
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
импульс момента сил 129
— сил 53
инверсии точка 247
индикатор 286
индикаторная диаграмма 287
инерциальная система 45
инерции принцип 45
инерционные силы 67, 69
во вращающейся системе 70
интерференция 422
— звука 445
инфразвуки 442
испарение жидкости 328
— твердых тел 370
испарения скрытая теплота 328
Иоффе А. Ф. 360
Калория 181, 255
Камерлинг-Оннес 250
капель образование 315
капиллярность 321
Капица П. Л. 149, 251
карданов подвес 131
Карно Сада 9, 277
квазиупругая сила 377
квантовая механика 16, 107
— теория теплоемкости 180, 363
Кельвин 167
Кеплер 115
киловатт 83
киловатт-час 83
килограмм массы 14, 54
— силы 54
килограммометр 82
килоджоуль 82
кинематика 17
— твердого тела 37
кинематическая теория газов 170
кинетической теории газов основная
формула 174
кипение 329
Клапейрона — Клаузиуса формула 331
Клаузиус 172, 259
Клаузиуса неравенство 301
когерентность 422
колебаний модулирование 407
— представление с помощью ком-
комплексных чисел 411
— резонанс 402
— сложение 387
взаимно перпендикулярных
391
колебания '376
— вынужденные 399
— затухающие 395
— крутильные 354
— негармонические 405
— собственные 400
количество движения 52
конвекция 212
конденсационный насос 222
коэффициент вязкости 148
— полезного действия двигателя внут-
внутреннего сгорания 289, 291
паровой машины 287
реактивного двигателя 291
— тепловой машины 267, 278,
284
— поперечного сжатия при продоль-
продольном растяжении 351
— расширения 163, 361
— трения 51
— — покоя 51
— упругости 349
краевой угол 321
кривизна линии 33
— поверхностей 319
кристалл 340
кристаллографическая ось 362
критическая температура 239, 248
— точка 240
критический коэффициент 244
— объем 239
критическое давление 239, 248
— состояние вещества 236
круговой процесс 266
Кундта метод 447
Кэвендиш 113
Ламинарное течение жидкости 150
Лапласа формула 320
Лебедев П. Н. 445
Ленин В. Я. 8, 11, 15
Линде машина 249
линия тока жидкости 139
Лисажу фигуры 394
ловушка ртутная 223
Ломоносов М. В. 9, 171, 254
лошадиная сила 83
Лошмита число 175
Майер Роберт 259
макроскопическое тело 15
Максвелл 9, 188
Максвелла закон распределения ско-
скоростей 188, 192
Мандельштам Л. И. 367
манометр Мак-Леода 224
— ртутный 224
— тепловой 224
масса 47
— атома 159
— Земли 114
— Солнца 115
— покоящаяся 105
— тяготеющая 115
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
463
массы зависимость от скорости 105,107
материальная точка 16
маятник 376
— математический 383
— физический 384
Менделеев Д. И. 9, 168, 239
Менделеева—Клапейрона формула
168
мениск жидкости 322
метр 12
миллиметр ртутного столба 161
модуль сдвига 352
— Юнга 349
молекул тепловое движение 160, 170
— число в единице объема 175
— эффективное сечение 201
молекула 157
молекулы диаметр 201, 235
— объем 233
молекулярно-кинетическая теория
157, 170
молекулярный вес 158
— пучок 202
моль 158
момент количества движения 127, 130
— инерции 125, 126
— пары сил 124
— силы 121, 122
монокристалл 342
мономолекулярная пленка 327
мощность 81, 82
Нагреватель 267
Надеждин А. И. 239
насос вакуумный 219, 222
— водоструйный 143
— воздушный 219
— диффузионный 222
— масляный 220
натяжение поверхностное 313
натяжения поверхностного коэффи-
коэффициент 313
необратимый процесс 264, 292
неопределенности соотношение 108,
171
неравновесное состояние 263
неразрывность струи 140 }
Нернста теорема 306
Ньютон 15, 44, 111
. ньютон 54
Ньютона второй закон 46, 52
— закон всемирного тяготения ПО
— первый закон 44
.— третий закон 59
Обратимый процесс 264, 292
объем молекулярный 165
— приведенный 243
ожижение газов 247
ожижение паров 238
окклюзия 373
Ольшевский 248
опалесценция 240
ось вращения 38
относительности общая теория 71
— принцип механический-58
— теория 15, 102
относительность движения 17
осмотическое давление 331
Падение тел 24
пара сил 124
параметр 256, 262
паровая машина 286
пары насыщенные 238, 335
перегретая жидкость 329
переноса явления в газах 205
период 39
— колебаний 379
маятника 384
перпетуум мобиле второго рода 278
первого рода 258
Перрен 195
Пикте 248
плавление твердых тел 341, 367
Планка постоянная 366
плотность 13
— газа 169
—• — относительная 169
— Земли 114
поглощение звуков 457
поглощения коэффициент 436, 458
поле вектора скорости 139
— силы тяжести 116
поликристалл 342
полимер 342
политропический процесс 271
полупроницаемая перегородка 333
Попов А. С. 9
порядок ближний 372
— дальний 372
потеря полуволны 42$
правило буравчика 42
превращение энергии 260
предел прочности 355
— упругости 355
пуаз 149
Пуазейля формула 156
Пуассона коэффициент 361
— формула 271
пульверизатор 143
путь 18, 19
— при неравномерном движении 22
— при равномерном движении 19
— при равнопеременном движении
24
пучность 426
464
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Работа 78, 83
— момента сил 134
— при изменении объема газа 265,
273 .
— силы тяжести 116
— упругих сил 84, 350
равновесие системы 263
равновесное состояние 264
равновесный процесс 264
радиус кривизны 34
— молекулярного действия 311
размерности формулы 99
размерность физических величин 99
распределение частиц с высотой
194
раствор 331
растекание капли 326
расширения линейного коэффициент
361
— объемного коэффициент 362
Рауля закон 337
реверберация 457
резонанс 402, 452
— параметрический 403
релаксации время 373
решетка атомная 344
— гетерополярная 343
— гомеополярная 344
— кристаллическая 343
Румфорд 255
Сверхтекучесть 149
Сёзерлэнда постоянная 201
секунда 13
сила 46
— звука 449
— инерции 69, 70
— нормальная 64
— подъемная 155
— потенциальная 89
— тангенциальная 64
— трения 49
— тяготения 110
— тяжести 116
— центробежная 70, 71
— центростремительная 64
силы взаимодействия между моле-
молекулами 228
— внутренние 63
— гироскопические 132
— Кориолиса 73
— при криволинейном движении 64
система отсчета 17
скаляр 27
скорость 18
— групповая 440
— звуковая 444
— космическая первая 73
скорость космическая вторая 118
— молекул наиболее вероятная 188
квадратичная 173, 175, 190
скорость молекул средняя арифмети-
арифметическая 190
— -— экспериментально определимая
204
— неравномерного движения 21
— при гармоническом колебательном
движении 381
— при криволинейном движении 30
— прямолинейного равномерного дви-
движения 18
— равнопеременного движения 23
— распространения волн 416, 429,
444
— средняя 20
— фазовая 416, 439
случайность 295
слышимости порог 450
смачивание 321
снаряд реактивный 146
соответственные состояния 243
сохранение количества движения 61
— момента количества движения 129
движения жидкости 144
— энергии 92, 257
спектр акустический 453
— колебаний 409
сплошная среда 139
статистическая закономерность 295
— физика 253
статистическое толкование второго
начала термодинамики 299, 305
стен 54
степени свободы 179
Стокса закон 153
Столетов А. Г. 9, 240
столкновение молекул 199
— шаров неупругое 62, 88
упругое 87
суперпозиция волн 422
сфера молекулярного действия 311
Тело абсолютно твердое 37
— аморфное 340
— кристаллическое 340
— мелкокристаллическое 342
— поликристаллическое 342
— твердое 340
температура 163
— приведенная 242
.температуры абсолютный нуль 166
— шкала Кельвина (абсолютная) 166,
285
термодинамическая 285
Цельсия 163
эмпирическая 163
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
465
тепла механическая теория 254
— механический эквивалент 255, 257
— приведенное количество 301
тепловая машина 267
тепловое движение в газах 170
в жидкостях 309, 371
в твердых телах 361
теплоемкости зависимость от темпе-
температуры 186, 365
теплоемкость 255
— газа при низких и высоких темпе-
температурах 186
при постоянном давлении 182
при постоянном объеме 181
— двуатомных газов 184
— жидкостей 371
— многоатомных газов 185
— молярная 180, 364
— одноатомных газов 184
— твердых тел 363, 371
— удельная 180
теплопроводности газов коэффициент
212
теплопроводность газов 212
при низких давлениях 218
теплота 253, 258
— испарения 328
теплоты количество 254
термодинамика 253
термодинамики второе начало 277
— первое начало 256
— третье начало 306
термометрическое тело 163
термос 218
техническая единица массы 55
Томсон 245, 259
тонна массы 13
— силы 55
траектория 29
трение 49
— покоя 49
тройная точка 370
трубка тока жидкости 140
турбулентное течение жидкости 150
тяготение 110
тяготения постоянная ПО, 113
Угловая скорость 38
как вектор 41
угловое ускорение 40
узел 426
узловая линия 447
ультразвуки 442, 456
ультраразреженные газы 225
Умов Н. А. 434
Умова вектор 434, 449
упругое последействие 357
упругости коэффициент 349
упругости модуль 349
упругость насыщенных паров 238
уравнение состояния 167
уровень звука 451
ускорение 23
— касательное (тангенциальное) 36
— нормальное (центростремительное)
35
— при гармоническом колебательном
движении 381
— при криволинейном движении 32
— равнопеременного движения 22
— среднее 25
ускоренная система 67
ухо 448
Фаза 378
— начальная 378, 421
Фарадей М. 9
Федоров Е. С. 343
флотация 324
флуктуация 299
Фок В. А. 71
форвакуум 222
Френкель Я- И. 371
Френкеля теория жидкости 309, 373
фронт волны 417
Фуко 133
функция распределения 189
Фурье ряд 408
Холодильная машина 268
холодильник 267
Центр кривизны 33
— масс 120
центробежная сила 65, 70
центробежный регулятор 66
центростремительная сила 64, 70
центростремительное ускорение 36
цикл 266
— двигателя внутреннего сгорания
287
— Дизеля 290
— Карно 278
— обратный 268
— паровой машины 286
— прямой 267
— реактивного двигателя 291
Циолковский К. Э. 146
Частота колебаний 378
— круговая 378
— циклическая 378
Штерн 204
466
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Эйнштейн 15, 71
эквивалентность количества передан-
переданного тепла и работы 255
— энергии и массы 106
Энгельс Ф. 16, 260, 262
энергии графическое представление
95
— плотность 433
— поток 434
— равнораспределение 180
— сохранение 88, 261
энергия 92
— взаимодействия молекул 180, 244
— внутренняя газа 178, 244
тел 257, 261
— волны 435
— гармонического колебательного
движения 386
энергия звуковая 449, 451
— кинетическая 85, 88
энергия кинетическая вращения 134
молекул 174
— потенциальная 89, 90
— — кристаллической решетки 344
тел, притягивающихся по за-
закону Ньютона 117
упруго деформированного тела
98, 350
— приходящаяся на одну степень
свободы 180
энтропия 303
эрг 82
Этвеш 116
эхолот 456
Юнга модуль 349
\\\рЦЪЬ
Фриш Сергей Эдуардович
и Тиморева Александра Васильевна
Курс общей физики, том I
Л., Физматгиз, 1962, стр. 468, с илл.
Редакторы:
Ю. В. Новожилов и Л. И. Орлова
Техн. редактор А. А. Лукьянов
Корректор Л. А. Любович
Подписано к печати с матриц 15/1 1962 г.
Бумага 60 X 92'/ie. Физ. печ. л. 29,25.
Усл. печ. л. 29,25. Уч.-изд.' л. 29,84.
Допечатка тиража 100 000 экз.
Цена 1 р. 00 к. Заказ № 1265.
Государственное издательство
физико-математической литературы
Москва, В-71, Ленинский проспект, 15,
Ленинградский Совет народного
хозяйства. Управление полиграфической
промышленности. Типография № 1
<Печатный Двор» нм. А. М. Горького.
Ленинград, Гатчинская, 26.
О О
ИСПРАВЛЕНИЕ
НА ТИТУЛЬНОМ ЛИСТЕ
Напечатано: Издание одиннадцатое, стереотипное.
Должно быть: Издание десятое, стереотипное,