Text
QUEUEING SYSTEMS
VOLUME 1: THEORY
Leonard Kleinrock
Professor
Computer Science Department
School of Engineering and Applied Science
University of California, Los Angeles
A Wiley-Interscience Publication
John Wiley & Sons
New York • London Sydney Toronto
Л. Клейнрок
. ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
Перевод с английского
канд. техн, наук И. И. Грушко
Под редакцией
д-ра техн, наук В. И. Неймана
МОСКВА МАШИНОСТРОЕНИЕ • 1979
ББК 22.18
К48
УДК 519.872
Клейнрок Л.
К48 Теория массового обслуживания. Пер.
с англ./Пер. И. И. Грушко; ред. В. И. Нейман.—
М.: Машиностроение, 1979.— 432 с., ил.
В пер. 2 р. 30 к.
Книга посвящена вопросам проектирования систем массового обслуживания и повышению эффективности их работы. В ией рассмотрены теоретические вопросы анализа математических моделей систем ожидания. Материал изложен в порядке возрастающей сложности от элементарной теории до наиболее мощной теории, разрабатываемой в последнее время для систем обслуживания общего типа. Она содержит необходимый справочный материал по теории вероятностей и операционному исчислению.
Книга предназначена для научных работников, а также инженеров, занимающихся вопросами теории массового обслуживания и ее практическим применением.
ИБ 2280
Леонард Клейнрок
ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
Редактор Т. В. Абызова
Художественный редактор С. С. Водчиц Технический редактор Т. И. Андреева Корректор И. М. Бореыша
Переплет художника Е. В. Бекетова
ББК 22.18
6Ф0.1
Сдано в набор 13.04.79. Подписано в печать 30.11.79. Формат 60Х 901/1в Бумага типографская № 1. Гарнитура литературная. Печать высокая.
Усл. печ. л. 27,0. Уч.-изд. л. 28,4.
Тираж 10 000 экз. Заказ 1358.
Цена 2 р. 30 к.
Издательство «Машиностроение», 107885, Москва, ГСП-6, 1-й Басманный пер., 3
Ленинградская типография № 6 Ленинградского производственного объединения «Техническая книга» Союзполиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли.
193144, Ленинград, С-144, ул. Моисеенко, 10
© 1975, by John Wiley & Sons, Inc.
Published simultaneously in Canada. No part of this book may be reproduced by any means, nor transmitted, nor translated into a machine language without the written permission of the publisher.
© Перевод на русский язык, «Машиностроение», 1979 г.
Предисловие к русскому изданию
Предлагаемая книга американского профессора Л. Клейнрока посвящена одному из важных разделов прикладной математики — теории массового обслуживания. В отличие от других книг на рассматриваемую тему данная книга написана инженером для инженеров. Этим определяются ее важные достоинства как, впрочем, и некоторые недостатки.
Несомненным достоинством книги является ясное и исчерпывающее изложение важнейших результатов современной теории массового обслуживания, представляющих интерес для инженерных применений. Автор книги принимал активное участие в создании крупнейшей сети вычислительных центров (сети ARPA), и это позволило ему собрать уникальный материал. Указанный материал в основном составляет содержание второго тома книги (В русском переводе отдельная книга: Л. Клейнрок. Вычислительные системы с очередями. М., Мир, 1979 г.) Первый том, по замыслу автора, должен был содержать изложение теоретических основ, необходимых для чтения второго тома. Успешное осуществление этого замысла позволяет рассматривать первый том как самостоятельное пособие, которое может быть полезно не только специалистам по сетям ЭВМ, но и более широкому кругу читателей, применяющих методы теории массового обслуживания.
Современную теорию массового обслуживания используют во многих областях науки, техники и военного дела. Существенное место
5
среди технических применений теории массового обслуживания, наряду с техникой передачи, распределения и обработки информации, занимают вопросы организации производства в машиностроении, поэтому можно ожидать, что эта книга будет встречена с интересом также традиционными читателями издательства «Машиностроение».
Некоторым недостатком книги является проявляемое иногда автором невнимание к математической строгости, свойственное технической литературе. Редактор не стремился обнаружить все неточности такого рода и прокомментировать их; в конце концов, задача перевода состоит не в том, чтобы дополнять и поправлять автора, а в том, чтобы как можно точнее передать его мысли.
Книга написана живым языком, содержит много наглядных примеров. Достоинства книги позволяют с полным основанием рекомендовать ее советскому читателю.
Пользуюсь приятной возможностью принести благодарность профессору Л. Клейнроку, приславшему большой список опечаток, допущенных в оригинале, что позволило своевременно внести необходимые исправления в переводе.
Д-р техн, наук В. И. НЕЙМАН
Введение
Сколько времени на этой неделе Вы провели в очередях? По-видимому, нам не удается избежать частых задержек, и в этом отношении положение непрерывно ухудшается. В предлагаемой книге изучаются явления простоев, ожиданий и обслуживания, которые составляют предмет теории массового обслуживания.
/' Любую систему, в которой поток требований встречает ограниченные средства их удовлетворения, можно рассматривать как систему массового обслуживания (СМО)| В частности, если моменты поступления требований или продолжительность их обслуживания не регламенти-руются^ то при пользовании системой возникают конфликты, и образуется очередь.| Длина этой очереди зависит от двух характеристик потока требований: во-первых, она зависит от интенсивности поступления требований и, во-вторых, от статистических флуктуаций этой интенсивности. Конечно,/если интенсивность поступления требований превышает пропускную способность системы, то система не справляется с потоком этих требований, и начинает расти очередь неограниченной длины.; Однако, даже если интенсивность поступления требований меньше пропускной способности системы, очередь может образоваться из-за статистических флуктуаций и внезапного накопления требований (которое может случиться); влияние таких колебаний в большой степени увеличивается, если средняя нагрузка приближается к пропускной способности системы (но необязательно достигает ее). Простота таких СМО
7
обманчива, и при их исследованиях приходится прибегать к глубоким аналитическим выкладкам. К счастью, исследование СМО может быть выполнено на основе одного хорошо известного фундаментального закона науки. Это — закон сохранения потока, состоящий в том, что интенсивность роста числа требований в системе определяется разностью интенсивностей входящего и исходящего потоков/Этот факт позволяет сравнительно легко составить основную систему уравнений для СМО достаточно сложной структуры.
Целью настоящей книги является изложение теории массового обслуживания для аспирантов первого года обучения. Предполагается, что читатель знаком с начальным курсом теории вероятностей; однако в приложении II дан краткий обзор основных результатов теории вероятностей, необходимых в дальнейшем. Полезно также (но не необходимо) знакомство читателя с операторным методом, хотя и для этого случая в приложении I приведена достаточно полная сводка результатов. Читателю рекомендуется прочитать оба приложения, прежде чем переходить к основному тексту. Хотя язык книги — это язык математики, мы старались по возможности дать неформальное изложение материала, чтобы установить равновесие между обычно применяемыми в таких исследованиях абстракциями и необходимым для практического использования пониманием. Мы надеемся, что выбранный средний уровень изложения достаточен для того, чтобы не шокировать математиков и не поставить в тупик практиков. В ряде случаев мы отказались от строгих доказательств единственности, существования и сходимости, чтобы не затемнять основное изложение. В такие моменты читатель отсылается к другим книгам. Мы отказались от скучного подхода «теорема — доказательство» и предпочли провести читателя через естественную последовательность рас-суждений, чтобы вместе «открыть» результат.
Читателю может показаться, что принятое изложение материала либо слишком элементарно и ограничено, либо далеко от точного и изящного; такой читатель пренебрегает интересами практики. Мы полагаем, что книга, 8
подобная предлагаемой, в которой стираются внутренние препятствия, является полезной и необходимой. Эта книга написана в течение пятилетнего периода, во время которого она была использована для чтения годового (позже, двухчетвертного) курса лекций по теории массового обслуживания в Калифорнийском Университете в Лос-Анджелесе. Материал был разработан в Отделении вычислительной техники факультета инженерных и прикладных наук и прошел успешную проверку в наиболее критической и бескомпромиссной аудитории, а именно у аспирантов. Книга пригодна не только для отделения вычислительной техники, но и для других технических отделений, отделений исследования операций, математики и многих других, специализирующихся в области естественных наук, народного хозяйства, управления и планирования.
Для изложения содержания книги необходимо сначала привести описание очень удобных сокращенных обозначений, принятых в теории массового обслуживания. В их основе лежит трехбуквенное обозначение вида А/В/ш, где А и В описывают соответственно распределение промежутков времени между последовательными требованиями и распределение времени их обслуживания, ат — число обслуживающих приборов. А и В принимают значения из следующего набора символов, интерпретация которых дается распределениями, указанными в круглых скобках: М (показательное), Ег (распределение Эрланга порядка г), Н/? (гиперпоказательное порядка R), D (детерминированное), G (распределение общего вида). Иногда приходится указывать также емкость накопителя системы (которую обозначим через К) или число источников нагрузки (которое обозначим через М); в этом случае будет использоваться пятибуквенное обозначение: А/В/т/К/М. В случае отсутствия одного из Двух последних индексов предполагается, что его значение сколь угодно велико. Так, например, запись вида D/M/2/20 означает систему с двумя обслуживающими приборами, прстоянным (детерминированным) временем между двумя последовательно поступающими требованиями, показательным распределением
9
времени обслуживания и накопителем емкостью 20 требований.
Данная книга является первым томом двухтомной серии, в которой второй том 1 посвящен применениям этой теории к вычислительным системам. Первый том (состоящий из четырех частей) начинается гл. 1, представляющей собой введение в теорию массового обслуживания: в ней устанавливается место СМО в общей схеме потоков в сетях и обсуждаются методы расчета характеристик СМО. Читатель, знакомый с материалом приложений I и II (или прочитавший эти приложения), может перейти к изучению гл. 2, причем здесь необходима некоторая осторожность. Очень важным и простым является1 параграф 2.1. Однако параграфы 2.2—2.4 могут оказаться довольно трудными для читателя, впервые знакомящегося с теорией массового обслуживания; такому читателю целесообразнее пропустить эти разделы и перейти непосредственно к параграфу 2.5, в котором определяется фундаментальный процесс размножения и гибели и впервые применяются метод производящих функций и преобразование Лапласа. После изложения в первой части этих предварительных сведений переходим во второй части к элементарной теории массового обслуживания. Гл. 3 начинается с вывода общего решения для процесса размножения и гибели в установившемся режиме, и большая ее часть посвящена рассмотрению простых, но важных примеров. В гл. 4 эти результаты обобщаются, и рассматривается метод этапов, а затем дается введение в теории марковских сетей массового обслуживания.
Если вычисления, проводимые во второй части, удается свести к алгебраическим уравнениям и теории операторных преобразований, то в третьей части приходится опять вернуться к теоретико-вероятностным методам. Рассмотрение промежуточной теории массового обслуживания начинается в гл. 5 с важнейшего примера СМО типа M/G/1, затем исследуется двойственная ей система G/M/1 и ее естествен-ное обобщение — система G/M/m (гл. 6). В гл. 7
1 См. Клейнрок Л. Вычислительные системы с очере» дями. Пер. с англ. М-, Мир, 1979 г. — Прим. пер.
19
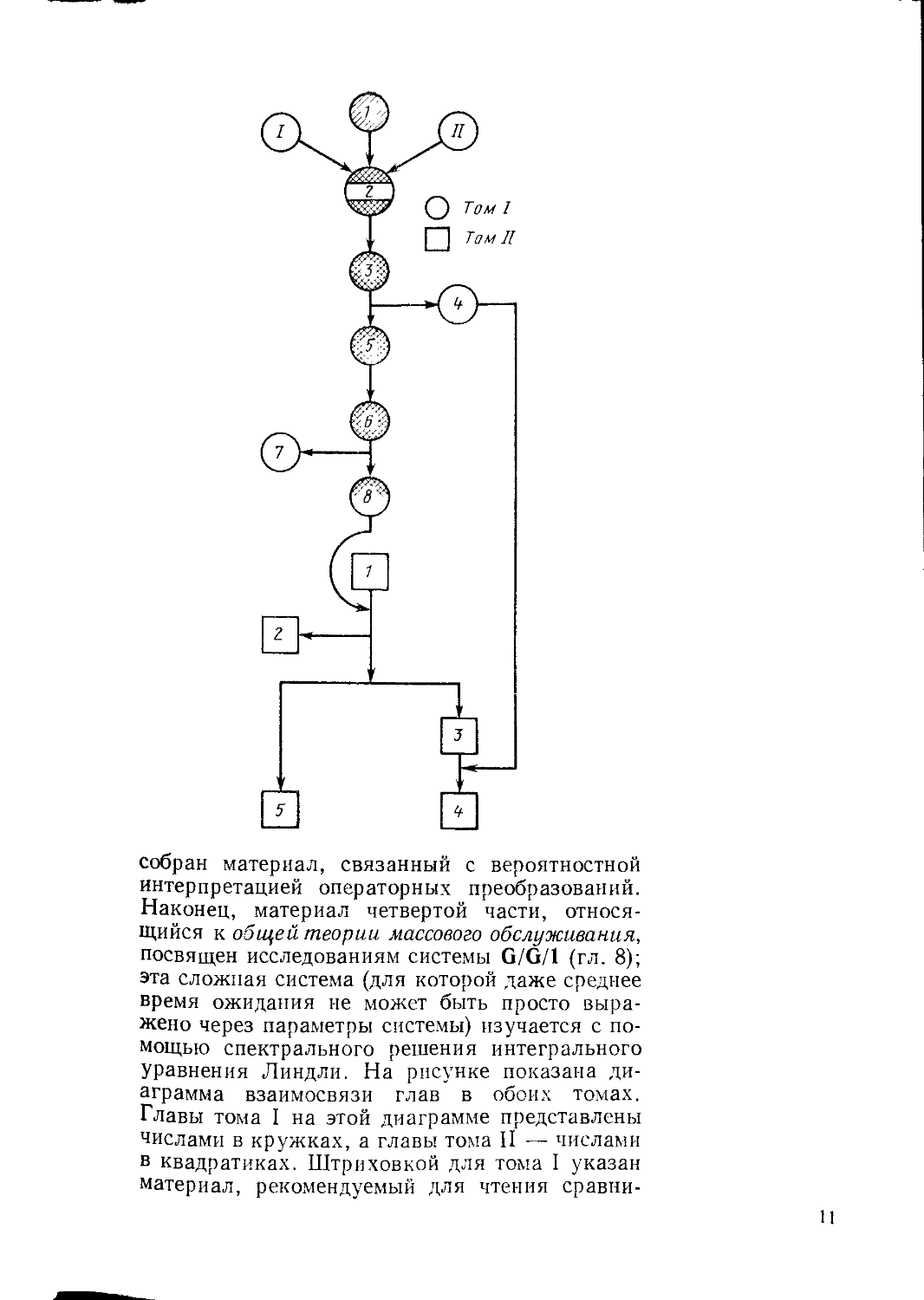
собран материал, связанный с вероятностной интерпретацией операторных преобразований. Наконец, материал четвертой части, относящийся к общей теории массового обслуживания, посвящен исследованиям системы G/G/1 (гл. 8); эта сложная система (для которой даже среднее время ожидания не может быть просто выражено через параметры системы) изучается с помощью спектрального решения интегрального уравнения Линдли. На рисунке показана диаграмма взаимосвязи глав в обоих томах. Главы тома I на этой диаграмме представлены числами в кружках, а главы тома II — числами в квадратиках. Штриховкой для тома I указан материал, рекомендуемый для чтения сравни
11
тельно ненапряженного начального курса по теории массового обслуживания, рассчитанного на один семестр. Штриховка в гл. 2 указывает, что параграфы 2.2—2.4 могут быть при первом чтении опущены; это же относится к параграфам 8.3 и 8.4. Более насыщенный односеместровый курс может включать весь материал первого тома. Том I завершается обзором важнейших результатов, полученных в книге, которые сгруппированы по классам рассматриваемых систем; этот список результатов может быть использован читателем как справочник. Каждый результат сопровождается указанием страницы, на которой он появляется впервые; это упрощает задачу поиска материала.
Каждая 1лава содержит свой список литературы, составленный в алфавитном порядке по авторам и по годам. Все важнейшие формулы отмечены символом ж, и все они включены в итоговый список важнейших формул. Каждая глава содержит также задачи, которые в ряде случаев расширяют материал главы; читателю рекомендуется решить их.
Том II содержит материал, рекомендуемый для второго курса теории массового обслуживания, рассчитан на применение к вычислительным системам. В нем гл. 1 представляет собой обзор основных результатов теории, изложенной в томе I. В гл. 2 изучаются границы, неравенства и приближения, описывающие важнейшие характеристики СМО, включая переходные и нестационарные характеристики; это достигается за счет отказа от попыток получения точных результатов, и при этом удается значительно глубже проникнуть в сущность решения реальных задач. В гл. 3 закладываются основы теории систем с разделением времени, базирующиеся на основных понятиях о СМО с приоритетами. В гл. 4 изучается класс систем, описываемых как СМО с абсолютными приоритетами, но которые больше известны как вычислительные системы с разделением времени. Рассматриваются модели как с одним средством обслуживания, так и со многими средствами, вытекающие непосредственно из результатов гл. 4 тома I. В этой главе также предпринимается попытка использовать диффузионное прибли-12
Жение, развитое в гл. 2. Наконец, в гл. 5 определяется и исследуется очень важный класс сетей связи электронных вычислительных машин, для изучения которых используются вся изложенная теория и еще некоторые дополнительные результаты \ Предлагаемая серия из двух томов начинается с изложения теории массового обслуживания, которая представляет большой интерес и сама по себе. Однако главной целью, подкрепленной личными интересами автора, является применение этой теории к реально существующим системам, в данном случае главным образом к вычислительным системам .
Выбор материала, помещенного в томе I (и особенно в томе II), отражает личные вкусы автора и его интересы в данной области. Например, я предпочел не включать длинные обсуждения методов моделирования или методов численного анализа СМО. Эти вопросы очень важны для исследования реальных СМО, однако они мало подходят в качестве материала для включения в текст учебника; вкратце их возможные применения обсуждаются, но на них не акцентируется внимание.
Может быть, имеет смысл посвятить несколько слов истории и развитию теории массового обслуживания. Нет ничего удивительного в том, что теория массового обслуживания возникла в телефонии в первые два десятилетия нашего столетия благодаря работам А. К. Эрланга, заложившего основы теории намного раньше того времени, когда стала популяризироваться и даже развиваться теория вероятностей. Этот замечательный человек установил многие принципиальные результаты, которые используют в настоящее время. Двадцатые годы нашего столетия были временем плодотворного применения его результатов; это продолжалось вплоть до середины 30-х годов, когда Феллер ввел понятие процесса размножения и гибели 1 2,
1 Фактически автор, вопреки этому обещанию, рассматривает сети связи ЭВМ в двух главах тома II — пятой и шестой. — Прим. ред.
2 В этот же период фундаментальные результаты теории массового обслуживания были опубликованы советскими математиками А. Н. Колмогоровым и А. Я. Хин-чиным. — Прим. ред.
13
н теория массового обслуживания привлекла внимание математиков как объект серьезного исследования. Во время второй мировой войны и в последующие годы эта теория играла важнейшую роль в развитии новой области — исследование операций, — которая казалась весьма многообещающей в первые послевоенные годы. Но из-за сложности реальных систем интерес к теории исследования операций стал уменьшаться, однако математики сразу оценили преимущества теории массового обслуживания. Передовые исследователи продвинулись достаточно далеко в этой сложной и глубокой области математики. Однако вскоре выяснилось, что реально интересующие практику модели не могут быть решены, и поток работ в этой области существенно уменьшился. И только с развитием вычислительной техники работы по теории массового обслуживания опять начали бурно развиваться применительно к широкому классу практических задач, но теперь уже со значительным успехом. В частности, это справедливо и для применений методов теории массового обслуживания к анализу характеристик вычислительных систем, чем и объясняется популярность этой теории среди современных инженеров и ученых. Многие актуальные проблемы формулируются в терминах теории массового обслуживания, и многие методы решения, развиваемые в рамках этой теории, оказываются вполне пригодными для их использования. Более того, применение вычислительных машин для решения уравнений теории массового обслуживания вызвало новый интерес к этой области. Можно надеяться, что предлагаемая книга поможет читателю выработать современное понимание возможностей применения методов теории.
Пользуюсь приятной возможностью завершить введение благодарностями тем лицам и институтам, которые сделали возможным появление этой книги. Прежде всего я хочу выразить благодарность всем тем, кто принимал участие в создании стимулирующей среды в Отделении вычислительной техники Калифорнийского Университета в Лос-Анджелесе, которая ободряла и поощряла мои усилия 14
в этом направлении. Благодарю Агентство перспективных научных исследований Министерства обороны США, которое предоставило мне возможность участвовать в некоторых наиболее перспективных проектах вычислительных систем и сетей, когда-либо разрабатывавшихся. Фонд Джона Симона Гугенхейма предоставил мне в 1971—1972 академическом году стипендию, что обеспечило возможность проведения дальнейшей исследовательской работы в этот период. Сотни аспирантов, прослушавших мой курс по теории массового обслуживания, внесли свой положительный и критический вклад, и я счастлив выразить свою признательность за оказанную мне помощь Арне Нильссону, Джони Вону, Саймону Лэму, Фуаду Тобаги, Фаруку Камуну, Роберту Райсу и Томасу 5 Сайксу. Мои академические и профессиональные коллеги оказывали мне всяческую поддержку в этом начинании. Я признателен всем машинисткам. Большую часть работы выполнила Шарлотта Лярош, и я всегда буду у нее в долгу. Диане Скосайпек и Синтии Эллман я приношу свою глубокую благодарность за быстрое, инициативное и доброжелательное выполнение трудной задачи чтения верстки и исправления опечаток. Кроме того, большой вклад внесли Барбара Уоррен, Джейн Дубинская, Джейн Фуччи и Глория Рой. Я во многом обязан моей семье (и особенно моей жене Стелле), которая оказала мне значительно большую поддержку, чем предусмотрено долгом и брачным контрактом. Наконец, я был бы воистину нерадивым, если бы не поблагодарил мой безотказный диктофон, который все время беседовал со мной.
Март 1974, ЛЕОНАРД КЛЕЙНРОК
ЧАСТЬ I
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
За деревьями трудно увидеть лес (особенно если деревья разбросаны, а не стоят в каком-либо порядке). Аналогичные трудности часто возникают при встрече с набором математических результатов, которыми мы пытаемся овладеть; успех возможен только после того, как будет понята и оценена применимость этих результатов к реально существующим задачам, когда с уверенностью можно сказать, что стала ясной полезность рассматриваемых математических методов.
Две главы, содержащие предварительные сведения, совершенно противоположны по своему характеру. В гл. 1 показаны глобальная картина возникновения систем массового обслуживания и их значение. Здесь для наглядности приведены развлекательные примеры. В гл. 2, посвященной случайным процессам, делается решительный шаг в сторону математических определений (и при этом быстро теряется перспектива). Однако мы призываем читателя не сдаваться перед этой трудностью, так как, возможно, это будет наиболее сложным местом, с которым читатель встретится в данной книге. В частности, гл. 2 начинается с изложения одного полезного графического способа описания динамики потока требований в системах массового обслуживания. Затем вводится понятие вероятностных процессов, которые возникают при исследовании поступления требований, их характеристик и накопления в СМО самого общего вида. Затем читатель подводится с помощью очень простой аргумен-|0
тации к одному из важнейших результатов теории массового обслуживания — результату Литтла. После такого введения в теорию вероятностных процессов предпринимается попытка очень компактного сравнения многих хорошо известных (но не столь хорошо различаемых) процессов в общепринятой терминологии и обозначениях, что приводит в итоге к рис. 2.4, показывающему взаимосвязь между этими процессами; читателю сразу становится ясной центральная роль, которую играет пуассоновский процесс, так как он находится на пересечении всех рассматриваемых в этой главе вероятностных процессов. Затем вводится понятие марковских цепей с дискретным и непрерывным временем; эти параграфы, возможно, представят наибольшую трудность для начинающего, и при первом чтении вполне допустимо этот материал пропустить. В конце параграфа 2.4 мы встречаемся с важными процессами размножения и гибели, и здесь опять приходится вернуться к физическим системам. Фактически читатель мог бы начать изучение с параграфа 2.5, так как рассматриваемый здесь материал почти не связан с остальной частью текста. Только изредка возникает необходимость в более подробном материале из параграфов 2.3 и 2.4. Если читатель осилит материал гл. 2, он будет в состоянии овладеть всем материалом книги.
ГЛАВА 1
Системы массового обслуживания
Занятным предметом этой книги является один из самых безрадостных аспектов нашей жизни, а именно, ожидание в очередях. Резонно спросить: «Какая польза от изучения такого неприятного явления?» Ответ, конечно, состоит в том, что через понимание приходит сочувствие, а именно оно и необходимо, так как с развитием цивилизации люди все больше и больше времени проводят в очередях, и необходимо найти пути преодоления этих неприятностей. Представим себе на минуту, сколько Времени мы проводим ежедневно в очереди того или иного типа:
17
ожидание завтрака; ожидание у светофора; замедление на. улицах и автострадах; задержка при въезде на стоянку автомобиля; очередь у лифта; очередь за утренним кофе; занятость телефона и т. д. Этот список бесконечен так же, как часто бесконечными оказываются и сами очереди.
Упорядоченность очередей в разных странах мира различна. Например, англичане весьма склонны к формированию упорядоченных очередей, в то время как некоторые жители Средиземноморья находят это нелепым (приходилось ли Вам когда-нибудь наблюдать процесс швартования судов в порту Бриндизи?). В армии Соединенных Штатов распространен девиз: «Торопись и жди!» Такова природа явления, которое мы намерены исследовать.
1.1. СИСТЕМЫ ПОТОКОВ
Системы массового обслуживания (СМО) являются примером более широкого класса интересных динамических систем, которые назовем для удобства системами потоков. Система потоков — это система, в которой некоторые предметы текут, движутся или транспортируются по одному или нескольким каналам ограниченной пропускной способности с целью перемещения из одной точки в другую^ Рассмотрим, например, поток автомобильного транспорта по сети автодорог, перевозку грузов по железнодорожной системе, поток воды через плотину, передачу телефонных или телеграфных сообщений, прохождение покупателей через кассу универсама или поток программ в вычислительной системе с разделением времени. В этих примерах предметами являются соответственно автомобили, грузы, вода, телефонные или телеграфные сообщения, покупатели и программы; каналом или каналами являются соответственно сеть автомобильных дорог, железнодорожная сеть, плотина, телефонная или телеграфная сеть, касса универсама, вычислительная система. Ограниченная пропускная способность означает, что канал может удовлетворять требования (предъявляемые к нему предметами) только с конечной скоростью. Очевидно, что анализ таких систем требует специальных аналитических методов, развитых в различных дисциплинах, и, как мы увидим, одной из таких дисциплин является теория массового обслуживания.
(При анализе систем потоков их естественно разбить на два класса: регулярные и нерегулярные потоки. К первому классу относят системы, в которых потоки ведут себя предсказуемым образом. Это значит, что величина потока точно известна и является постоянной на всем интересующем нас интервале; время появления потока в канале и число требований, которые поступают в канал, известны и постоянны. В случае одного канала анализ таких систем тривиален J Например, рассмотрим фабрику по переработке ананасов, на которой пустые жестяные банки транспортируются по 18
Кадавра
Рис. 1.1. Задача о максимальном потоке
конвейерной ленте в пункт, где их заполняют ломтиками ананасов, а затем должны следовать дальше по этой же ленте для последующих операций. Предположим, что при этом жестяные банки поступают с постоянной скоростью по одной банке в секунду и что операция по заполнению одной банки ананасами занимает девять десятых секунды. Это число постоянно тля всех банок и операций по наполнению. Ясно, что такая система будет работать бесперебойно и равномерно, пока будут выполняться указанные выше условия. Можно сказать, что интенсивность R поступления требований в систему равна одной банке в секунду и что максимальная скорость обслуживания (или пропускная способность) С -= 1/0,9 =- 1,1111 .. операций наполнения в секунду. В рассмотренном примере выполняется условие R <Z С. Но известно, что произойдет, если это условие нарушится, т. е. будет R /> С: либо банки, либо ломтики ананасов начнут накапливаться и наводнят всю фабрику! Таким образом, если не допускаются хаотические скопления, то пропускная способность системы должна быть больше, чем интенсивность потока требований. Это справедливо для всех систем потоков. Приведенное простое замечание является почти исчерпывающим для детерминированных потоков с одним каналом. Такие системы не представляют серьезного теоретического интереса.
Более интересным представляется случай регулярного потока, распространяющегося по сети каналов. Для стабильного потока условие R </ С является очевидным требованием для каждого канала. Но здесь возникает серьезная комбинаторная задача. Например, рассмотрим железнодорожную сеть некоторой мифической страны Гатафла, показанную на рис. 1.1. Сценарий сводится к тому, что по этой железнодорожной сети должны перевозить фиги, выращенные в городе Абра, в пункт назначения — город Дадабра. Числа, приписанные на рис. 1.1 каждому каналу (каждой железнодорожной ветке), обозначают максимальное число бушелей фиг, которое может быть пропущено по этому каналу за один день. Теперь мы приходим к следующей задаче о потоке фиг: чему равно максимальное число бушелей фиг, которое может ежедневно направляться из Абры и Кадабру, и каким образом Должен следовать этот поток? Ответ на этот вопрос о максимальной
19
нагрузке потоков в различных сетях хорошо известен в теории потоков в сетях и называется теоремой о максимальном потоке через минимальное сечение. Чтобы сформулировать эту теорему, определим сначала сечение как множество каналов, удаление которых из сети приводит к разрыву всех возможных путей (потоков) от пункта отправления (Абра) в пункт назначения (Кадабра). Пропускную способность такого сечения определим как общий поток фиг, который может пройти через сечение от пункта отправления к пункту назначения. Примером одного такого разреза является набор ветвей из Абры в Зевс, Саксамада в Зевс и Сакса-мада в Ориак; пропускная способность этого разреза равна, очевидно, 23 бушелям фиг в день. Теорема о максимальном потоке через минимальное сечение утверждает, что максимальный поток, который может быть пропущен от начальной точки к конечной, равен минимальной пропускной способности по всем сечениям. В нашем примере можно видеть, что максимальный поток равен 21 бушелю фиг в день (читателю предлагается проверить это). В общем случае надо просмотреть все сечения, разделяющие заданную начальную и конечную точки. Такое вычисление может потребовать огромного времени. К счастью, существует мощный метод, позволяющий определить не только величину максимального потока, но и набор путей, на котором достигается этот максимальный поток. Этот метод известен под названием алгоритма маркировки (он предложен Фордом и Фалкерсоном [1 ]) и является эффективным в том смысле, что объем вычислений растет как небольшая степень от числа узлов; описание этого алгоритма приводится в гл. 5 тома II.
Кроме задачи о максимальном потоке, можно сформулировать многие другие интересные и имеющие смысл задачи о потоках в таких сетях. Например, назначая цену каждому каналу, можно поставить задачу о построении сети минимальной стоимости, обеспечивающей данный поток. Такие же задачи можно ставить и о сетях, в которых имеется не только одна начальная и конечная точка. Усложняя задачу еще больше, можно потребовать, чтобы данная сеть обеспечивала потоки различных типов, например бушелей фиг, ящиков с патронами и бочек с нефтью. Задача о комбинированных (или многопредметных) перевозках является чрезвычайно сложной, и, как правило, для ее решения приходится выполнять вычисления очень большого объема. Эти и многие другие замечательные задачи теории потоков в сетях можно найти в исчерпывающей книге Франка и Фриша [2]; мы встретимся с ними опять в гл. 5 тома II. Теория потоков в сетях использует методы теории графов, комбинаторной математики, теории функций, математического и эвристического программирования.
Вторым классом, который можно выделить в системах потоков, является класс случайных, или вероятностных, потоков. Под этим подразумевается, что время поступления требования на обслуживание (на занятие канала) не определено или непредска-20
зуемо, п что непредсказуемо также число требований, поступающих в систему. Случайность, непредсказуемость и нерегулярность природы таких потоков приводит к существенным трудностям при понимании н решении возникающих здесь задач. Более того, очевидно, что большинство реально возникающих потоков относится именно к этому классу. Простейшим также является случай одного канала (или однолинейной системы); однако если обсуждавшийся выше случай детерминированного или регулярного потока, поступающего в однолинейную систему, был тривиален, то возникающая теперь однолинейная задача имеет определенные трудности, и для ее решения приходится применять многие результаты современной теории массового обслуживания.
Например, рассмотрим вычислительный центр, в котором требования на вычисления обслуживаются группами. Требования на вычисления поступают в систему в непредсказуемые моменты времени, п в момент их поступления вычислительное устройство может быть загружено обслуживанием других требований. Если вычислительное устройство свободно, то, как правило, оно сразу начинает обслуживать вновь поступившее требование, которое пребывает в системе до тех пор, пока его обслуживание не будет полностью завершено. Если же в момент поступления нового требования система загружена, то это требование будет ожидать в очереди до тех пор, пока оно не будет выбрано для обслуживания среди остальных ожидающих требований. До тех пор, пока данное требование не будет выбрано для обслуживания, ни вычислительный центр, ни программист не знают точно, сколько усилий уйдет на обслуживание этого требования в системе; в этом смысле обслуживание требования, действительно, непредсказуемо.
Возникает несколько естественных вопросов, на которые хотелось бы получить разумные и полные ответы. Каково, например, ожидаемое время, которое придется провести требованию в очереди на обслуживание? Сколько требований будет обслужено перед данным? В какое время суток вычислительный центр будет загружен? Каков ожидаемый промежуток времени непрерывной загрузки центра? Эти вопросы требуют ответов в виде вероятностей определенных периодов времени или числа требований, или просто в виде средних значений этих величин. Дополнительные соображения, такие как поломка машины (нередко встречающееся условие), вносят дальнейшие усложнения вопроса; ясно, что в этом случае некоторое приоритетное событие задерживает завершение обслуживания требования. Другие интересные явления могут иметь место, когда требования обслуживаются не в порядке их поступления. Например, в вычислительных системах с разделением времени используются весьма сложные алгоритмы распределения и обслуживания, которые рассматриваются в гл. 4 тома II.
Методы исследования задач с однолинейной системой и случайным потоком являются составной частью теории массового 21
обслуживания, и большая часть материала данной книги посвящена этим методам. При этом предполагается знакомство читателя с основами теории вероятностей, а также с комплексными переменными и некоторыми обычными методами операционного исчисления; обзор этого материала приведен в приложениях I и II.
Как и в случае детерминированного потока, можно сосредоточить внимание на задачах, связанных с сетями каналов, по которым циркулируют случайные потоки. .Примером подобной сети может служить вычислительная сеть. Такая система состоит из ЭВМ, связанны:-; между собой линиями связи, причем пропускная способность каждой линии конечна. Вернемся к фантастической стране Гатафла и предположим, что рассмотренная выше железнодорожная сеть теперь представляет собой вычислительную сеть. Предположим, что клиенты, находящиеся в городе Абра, хотят воспользоваться вычислительным устройством, расположенным в городе Кадабра. Конкретные моменты времен:; возникновения этих требований непредсказуемы, так же как непредсказуемы продолжительности управляющих сигналов или команд, описывающих эти требования. Эти команды должны быть переданы в Кадабру по сети связи как сообщения. Передача сообщения по некоторому пути на сети связи осуществляется после ввода сообщения в сеть в пункте Абра и выбора соответствующего решающего правила (называемого процедурой выбора маршрута). Если часть выбранного пути оказалась занятой, а это возможно, то сообщение должно встать в очередь перед занятым каналом и ждать до тех пор, пока он освободится. Постоянные решения должны приниматься с учетом потока сообщений и процедуры выбора маршрута. Можно надеяться, что сообщение со временем достигнет Кадабры, необходимые вычисления будут выполнены, а результаты опять будут введены в сеть связи для передачи обратно в Абру.
Очевидно, что в описанном примере вычислительной сети возникает много сложных задач теории массового обслуживания, а также теории потоков в сетях и решений. Некоторые из этих вопросов уже были рассмотрены автором раньше [3]. Анализ этих систем откладывается до гл. 5 тома II
Можно надеяться, что введенное понятие1 системы потоков дает читателю представление о том, какое место в общей схеме занимает теория массового обслуживания. Центральными методами этой теории являются методы анализа вероятностных пото-
£ Принятая классификация относит СМО к классу систем потоков. Этот подход подчеркивает применение теории массового обслуживания. Другим подходом было бы отнесение теории массового обслуживания к прикладной теории вероятностных процессов; такой подход подчеркивал бы математический характер теории, а не ее применения! В данном двухтомнике принята первая точка зрения, а именно точка зрения, сйТГТанная с применением теории массового обслуживания как главной задачи, а не с развитием формальных математических результатов. 22
ков. Просмотр периодической литературы ясно показывает бурное развитие и жизнеспособность этой теории и, в частности, расширение важных областей ее применения.
1.2. ХАРАКТЕРИСТИКИ СИСТЕМ МАССОВОГО
ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ
Для полного описания системы массового обслуживания с ожиданием надо указать вероятностные процессы, описывающие входящий поток требований, структуру обслуживающего прибора и дисциплину обслуживания. В общем случае входящий поток требований описывается распределением вероятностей промежутков времени между соседними требованиями, которое обозначается1
A (f) ----- Р [время между последовательными требованиями * (1.1)
В большей части теории v:;|'<-n"nrn пбгтчкгпяпчя Ч'ШДПО-’ЧГЯОТСЩ что промежутки времени между последовательными требованиями являются независимыми, одинаково распределенными случайными величинами (и, следовательно, входящий поток требований образует стационарный процесс восстановления; см. гл. 2). Таким образом, как правило, существенным описанием потока является только функция распределения A (t). Второй статистической величиной, которую надо описать, является время, в течение которого требование пребывает в канале; эта величина обычно называется временем обслуживания, а ее распределение обозначается через В (х) , так что
В (х) =-= Р [время обслуживания < х]. (1.2)
Здесь под временем обслуживания понимается промежуток времени, в течение которого требование находится в обслуживающем приборе.
Для описания структуры обслуживающего прибора и дисциплины обслуживания необходимо ввести в рассмотрение еще некоторые величины. Одной из них является емкость памяти, в которой накапливаются ожидающие требования; обычно ее обозначают через /<, и часто число К предполагается бесконечным. Другой характеристикой является число доступных, обслуживающих приборов. Если это число больше единицы, то функции распределения времени обслуживания для каждого прибора могут быть различными, и этот факт будет отмечаться индексом у функции распределения В (х). Входящий поток требований также может состоять из нескольких классов’, в таком случае каждый из классов требований может быть описан своим распределением А (/) вероятностей промежутков времени между последовательными требо-
1 Запись Р [А ] означает, как обычно, «вероятность события Д».
23
ваниями и распределением В (х) времени обслуживания, что будет отмечаться индексом у этих распределений.
Важнейшей структурной характеристикой системы массового обслуживания является дисциплина обслуживания; она задает порядок выбора требований из очереди для обслуживания. Примерами стационарных дисциплин обслуживания являются обслуживание в порядке поступления (ОПП), обслуживание в обратном порядке (ООП) и случайный выбор требований для обслуживания Е Если поступающие требования различаются по группам и устанавливается некоторый приоритет обслуживания групп, то говорят о приоритетной дисциплине обслуживания.
Характеристики, определяющие доступность обслуживающего прибора, могут быть использованы и в других случаях (например, в задачах, в которых прибор выходит из строя). Кроме того, система массового обслуживания может учитывать такое поведение клиентов, как уход из очереди, переходы из одной очереди в другую, задержку перед входом в очередь, покупку места в очереди, мошенничество в очереди и многие другие интересные и не являющиеся неожиданными поступки, свойственные людям. Мы встретимся с такими явлениями по мере чтения текста (обслуживание в порядке поступления в соответствии с номером страницы).
Указав характеристики системы массового обслуживания, необходимо определить показатели эффективности работы системы, которые будут получены в результате анализа. Интерес в основном представляют время ожидания требованием обслуживания, число требований в системе, длина периода занятости (промежуток времени непрерывной работы обслуживающего устройства), длина свободного периода и текущая задолженность, выраженная в единицах времени. Все эти величины являются случайными, и для их анализа будем искать полное вероятностное описание (т. е. функцию распределения вероятностей). Однако обычно определить функцию распределения — это значит сделать больше, чем требуется, поэтому часто анализ ограничивается вычислением нескольких первых моментов (среднего значения, дисперсии и т. д.).
Дальнейшее изложение материала начинается с рассмотрения простейших соображений и развития непосредственных методов исследования, что позволяет обратить внимание на существенные
1 Соответствующие английские обозначения FCFS (first—соте—first—serve, т. е. первый поступивший первым обслуживается), LCFS (last—соте—first— serve, т. е. последний поступивший первым обслуживается) и RANDOM (случайно). Развитие вычислительной техники и широкое распространение языков программирования, использующих латинский алфавит и некоторые слова английского языка, приводит к тому, что во многих книгах и статьях, издаваемых на русском языке, воспроизводятся английские термины, используемые в языках программирования. Это сдерживает развитие русской научно-технический терминологии, п в работах, непосредственно не связанных с применением ЭВМ, невидимому, должно рассматриваться как явление нежелательное. — Прим. ред. 24
детали~'анализа. Затем будет решено несколько простых задач теории^массового обслуживания, простых по крайней мере по своей формулировке, однако достаточно трудных для решения. Чтобы решить их надлежащим образом, сначала остановимся на некоторых важных случайных процессах, описывающих процесс поступления требований и процесс их обслуживания в СМО.
СПИСОК ЛИТЕРАТУРЫ
1. Форд Л. и Фалкерсон Д. Потоки в сетях. Пер. с англ./Пер. И. А. Вайнштейн. М., Мир, 1966. 276 с.
2. Frank Н. and Frisch I. Т. Communication, Transmission and Transportation Networks, Addison — Wesley (Reading, Mass.), 1971.
3. Клейнрок Л. Коммуникационные сети. Стохастические потоки и задержки сообщений. Пер. с англ./Под ред. А. А. Первозванского. М., Наука, 1970. 255 с.
ГЛАВ А 2
Некоторые важные случайные процессы1
Предполагается, что читатель знаком с основными элементарными понятиями, терминологией и идеями теории вероятностей. Те частные аспекты этой теории, которые необходимы для данной книги, кратко изложены в приложении II с целью облегчить работу тех читателей, которые пожелают быстро восстановить в памяти необходимую информацию; читателю рекомендуется просмотреть этот материал, особенно параграф II.4 о преобразованиях, производящих функциях и характеристических функциях.
В приложение II вошли следующие важнейшие определения, понятия и результаты:
. Пространство элементарных событий, события и вероятность.
. Условная вероятность, статистическая независимость, закон полной вероятности, теорема Байеса.
. Действительная случайная величина, функция распределения вероятностей, плотность распределения и их простейшие свойства.
. События, связанные со случайными величинами, и их вероятности.
. Функции совместного распределения.
1 Читатель при первом чтении может пропустить параграфы 2.2—2.4.
25
. Функции случайных величин и их плотности распределений.
. Математическое ожидание.
. Преобразование Лапласа, производящие функции, характеристические функции, их свойства и взаимосвязь1.
. Неравенства и предельные теоремы.
. Определение вероятностного процесса.
2.1. ОБОЗНАЧЕНИЯ И СТРУКТУРА СИСТЕМ
МАССОВОГО ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ
Прежде чем вплотную заняться изучением теории массового обслуживания от элементарных определений к промежуточной и, наконец, к общей теории, важно понять основную структуру СМО. Попутно читатель увидит направление данного курса.
Задачей настоящего параграфа является определение некоторых символических и графических обозначений и основных вероятностных процессов, которые характерны для систем массового обслуживания. Здесь будут получены простые, но важные для таких систем результаты, связывающие некоторые моменты первого порядка случайных величин. Это даст возможность ввести в рассмотрение величины и процессы, изучению которых посвящены многие страницы книги.
Рассматриваемая система представляет собой систему самого общего вида G/G/m. Вспомним (см. введение), что в такой системе полностью известны распределение вероятностей А (/) промежутков времени между последовательными требованиями и распределение вероятностей В (х) времени обслуживания (все промежутки времени между последовательными требованиями и все продолжительности времени обслуживания предполагаются независимыми друг от друга). Система имеет m обслуживающих приборов, и дисциплина обслуживания произвольна (в частности, она не должна быть обязательно дисциплиной обслуживания в порядке поступления).
^Остановимся на потоке требований, которые поступают на вход системы, проходят через нее и в конце концов покидают эту систему; для этого пронумеруем требования и введем обозначение
Сц — п-е требование, поступающее в систему. (2.1)
Рассматриваемая система можетбытьпредставлена, какпоказано на рис. 2.1: прямоугольник означает собственно систему массового обслуживания, слева изображен поток входящих требований, а справа — выходящий поток. Можно сразу определить некото-
1 Приложение I является памяткой по теории преобразований. Этот материал также важен для полного понимания текста книги.
20
Рис. 2.1. СМО общего вида
рые представляющие интерес случайные процессы. Например, процесс
N (/) А число требований в системе в момент t*. (2.2)
Другим интересным вероятностным процессом является незавершенная работа U (/) в момент t, точное определение которой имеет следующий вид:
(7 (/) А незавершенная работа системы в момент t А
А остаточное время, необходимое для освобождения системы от всех требований, находящихся в пей в момент г. (2.3)
Если U (t) > 0, то говорят, что система занята; система называется свободной (незанятой), если U (/) — 0. Представляют интерес также длительность и локализация периодов занятости и простоя системы. Эти вероятностные процессы можно описать с помощью определенного ниже набора случайных величин или графически путем изображения указанных величин на временной диаграмме, которая будет определена ниже. Начнем с определений. Напомним, что п-е требование обозначено через Сп, и /определим момент хп поступления этого требования:
хп А время поступления требования Сп. (2.4)
Обозначим далее промежуток времени между требованиями C„_i и Сп через tn\
tn А промежуток времени между C„_i и Сп — т„ — xn_i- (2.5)
Так как предполагается, что все промежутки между последовательными требованиями подчиняются распределению А (/), то независимо от п имеем
Р < t\ - A (t). (2.6)
Аналогично введем время обслуживания требования С„ в виде х„ А время обслуживания С,г. (2.7)
Согласно сделанным предложениям, имеем
Р \хп < х] = В(х). (2.8)
Последовательности (tn} и {%„} можно рассматривать как последовательности входных переменных для исследуемой системы, Обра-
* Обозначение а, следует читать «равно по определению».
ботка требовании в системе приводит к образованию очереди, поэтому необходимо определить время ожидания (время, которое требование проводит в очереди) \ Определим его в виде
Щ,г А время ожидания (в очереди) для требования С;1. (2.9)
Полное время, проведенное требованием в системе, складывается из времени ожидания и времени обслуживания и определяется равенством:
sn А время пребывания в системе (очередь плюс обслуживание) для Сп ] - - - хп. (2.10)
Таким образом, для требования Сп определены время его поступления, «его» промежуток времени между последовательными требованиями, его время обслуживания, время ожидания и время пребывания в системе.^
Теперь перейдем к некоторым дальнейшим определениям. Рассмотрим опять промежуток времени tn между двумя последовательными требованиями. Нам понадобится предельная случайная величина, определяемая равенством
/Alim^; (2.11)
П->со
этот предельный переход будем обозначать также следующим образом: tn -> t. (Предполагается, что промежуток времени tn между двумя последовательными требованиями не зависит от номера п, хотя многие представляющие интерес случайные величины не удовлетворяют этому ограничению.) Функцию распределения вероятностей, как правило, будем обозначать через
Р [tn<. t] = An(t), (2.12)
а функцию распределения предельной случайной величины — (2.13)
Этот факт будем также обозначать следующим образом: Ап (/) -> A (t). Для промежутка времени tn между двумя соседними требованиями естественно предположить выполнение равенства Ап (i) — A (t), что приводит к (2.6). Аналогично, плотности распределения случайных величин tn и t будем обозначать через ап (/)
1 В литературе по теории массового обслуживания термины «время ожидания» и «время пребывания в очереди» являются конкурирующими. Иногда первый из этих терминов используют для обозначения полного времени, проведенного требованием в системе; одиако часто эти два определения меняют местами. Попытка устранить это недоразумение состоит в том, что оба термина: «время ожидания» и «время пребывания в очереди» в данной монографии используются для обозначения одной и той же величины, а именно времени, проведенного ожидающим требованием в очереди (но не на обслуживании); более подходящим названием для этой случайной величины было бы, возможно, «потерянное время». Полное время, проведенное требованием в системе, будем называть «временем пребывания в системе» (иногда это время называют также «временем в потоке»), 28
и а (0 соответственно, т. е. а„ (I) -*• a (t). Наконец, преобразования Лапласа (см. приложение II) плотностей распределений соответственно обозначим через Л,‘ (s) и Л* (s), так что в очевидных обозначениях An (s) -> Л* (s). Буквы Л (и а) использованы в этих обозначениях для того, чтобы напомнить читателю о том, что исследуемой случайной величиной является промежуток времени между двумя последовательными требованиями. Естественный интерес представляют моменты распределения этой случайной величины, для которых используется обозначение1
E[tn]/\tn. (2.14)
Согласно принятым обозначениям средний предельный промежуток времени задается2 величиной t в том смысле, что tn t. Величина t, равная среднему промежутку времени между двумя соседними требованиями, очень часто появляется в уравнениях, описывающих СМО, поэтому для нее удобно ввести следующее специальное обозначение:
/Д-^. (2.15)
Таким образом, X соответствует интенсивности поступления требований в систему.
Представляют интерес также моменты более высокого порядка для промежутка времени между соседними требованиями. Произвольный момент k-го порядка определяется равенством
Е [?] A ak, k = 0, 1, 2, ... (2.16)
Это равенство — стандартное определение k-ro момента ак промежутка времени t между сосещщми требованиями; заметим, что непосредственно из этого определения вытекает:
(2.17)
Таким образом, имеются три различных обозначения для среднего промежутка времени между соседними требованиями; в частности, общепринятым является символ а; в тексте книги используются по необходимости все три обозначения.
1 Символ Е [ ] означает математическое ожидание величины, заключенной в квадратные скобки. Другим используемым в книге обозначением для математического ожидания является черта, поставленная над случайной величиной.
2 На самом деле среднюю предельную величину надо было бы обозначить и тильдой, и чертой сверху, но во избежание громоздкости будем писать просто черту; такое обозначение будет использовано в дальнейшем для многих случайных величин.
29
Резюмируя все сказанное о промежутке времени между последовательными требованиями, получаем
tn Л промежуток времени между требованиями Сп и Сп_р,
tn -► t, Ап (t) -> A (f), ап (0 -> а (/), А„ (s) -> Л* (s);
~tn->7= 4- == fli = a, tn~>lk = ak. (2.18)
Л
Аналогичным образом введем следующие обозначения для переменных хп, wn, sn:
хп = время обслуживания требования' Сп,
Хп -> X, В,г (х) -> В (х), Ьп (х) -> b (х), Bn ($) В* (s);
хп~>х= =&1 = 6, х*-->/==(2-19)
к',г - время ожидания для требования С„;
wn -> w, IVп (у) -> W (у), Wn (у) -> w (у), W*n (s) -► IV* (s);
wn -> w = W, w'!t -> wk; (2.20)
sn = время пребывания требования C„ в системе;
sn -> s, Sr! (у) -+S (у), sn (у) -> s (//), S* (s) -> S* (s);
~sn->^==T, sI->Z (2.21)
Все эти обозначения очевидны, за исключением, возможно, специальных символов, участвующих в обозначениях момента первого порядка и иногда моментов более высокого порядка (имеется в виду использование символов X, а, р, b, W и Т). Сошлемся здесь на глоссарий в конце книги, содержащий полный набор обозначений, используемых в'данной книге.
Используя введенные обозначения, опишем теперь временную диаграмму системы массового обслуживания, позволяющую графически проследить динамику системы и выделить детали исследуемых вероятностных процессов. Такая диаграмма для обслуживания в порядке поступления показана на рис. 2.2, однако нетрудно увидеть, как этот рисунок можно преобразовать для произвольной дисциплины обслуживания. На диаграмме нижняя ось времени соответствует очереди, а верхняя — прибору обслуживания. Рассматриваемая диаграмма соответствует случаю одного обслуживающего прибора, хотя легко поддается обобщению. Входящие снизу стрелки (как для осп очереди, так и для оси обслуживания) указывают на поступление требования. Стрелки, выходящие сверху, обозначают уход требования из очереди.
Из рис. 2.2 видно, что требование Cn+i поступило в очередь на обслуживание раньше, чем требование Сп освободило обслуживающий прибор. Так как требование Cn+i может быть обслужено 30
только лишь после того, как требование Сп освободит прибор, то в системе происходят одновременно два события: завершается обслуживание требования С,г, и требование C„+i поступает в прибор обслуживания. Другой пример дает требование С„+2; приходя в систему, требование Сп+2 застает обслуживающий прибор свободным, и обслуживание этого требования начинается немедленно. На диаграмме видно также время ожидания и время пребывания требования Сп в системе (заметим, что wn+2 = 0). Для временного описания системы удобно ввести функции N (/) — число требований в системе и U (t) — незавершенная работа, а также периоды занятости и простоя обслуживающего прибора. Использование временных диаграмм окажется весьма полезным в изложении следующего материала.
В общем случае для системы массового обслуживания естественно ожидать, что с увеличением числа требований растет время ожидания. Одним из проявлений этого правила служит простое соотношение, связывающее среднее число требований в системе, интенсивность потока требовании и среднее время пребывания требования в системе. Наша ближайшая задача — установить это соотношение с целью углубления понимания характеристик таких систем. Возвращаясь к рис. 2.1, рассмотрим вход системы массового обслуживания и подсчитаем число входящих требований как функцию времени. Обозначим эту величине « (0:
а (/) Д число поступающих в промежутке времени (О, f) требований. (2.22)
Перейдем теперь к выходу системы и подсчитаем число требований, выходящих из нее; для этого введем обозначение
6 (/) Д число исходящих в промежутке времени (0, t) требований. (2.2.1)
31
Рис. 2.3. Поступления и уходы
На рис. 2.3 приведены примеры функциональных зависимостей этих двух вероятностных процессов от времени.
Ясно, что число N (/) требований в системе в момент времени t должно удовлетворять равенству
N (t) = a (t) — S (t).
С другой стороны, площадь между двумя рассматриваемыми кривыми, взятая от начальной точки до некоторой фиксированной точки I, представляет собой общее время, проведенное всеми требованиями в системе за время (0, /) (измеренное в единицах «требование — секунда»); обозначим эту накопленную величину у (t). Пусть означает интенсивность (требований в секунду) поступления требований в систему в промежутке времени (0, t), т. е.
Х(^)Д^1. (2.24)
Определим также величину Tt как время, проведенное одним требованием в системе, усредненное по всем требованиям, находящимся в системе в течение времени (0, t). Так как у (/) равно общему времени («требование — секунда») в системе по всем требованиям вплоть до момента t, то ясно, что Tt определяется отношением
Т =_
Наконец, определим величину Nt как среднее число требований в системе в промежутке времени (0, /); эта величина может быть получена как отношение накопленного числа у (t) к длине t промежутка времени наблюдения:
Из последних трех уравнений следует, что
N t = t-
32
Предположим теперь, что рассматриваемая система массового обслуживания такова, что при t —> оо существуют следующие пределы:
X = lim t -> оо
Т= limTV t -> СЮ
Заметим, что для интенсивности поступления требований в систему и среднего времени пребывания требования в системе соответственно используются приведенные выше определения к и Т. Если указанные два предела существуют, то существует также предел для Nt, который обозначим через N. Последний предел соответственно задает среднее число требований в системе:
N = (2.25)
Этот результат, называемый формулойЛиттла, и является именно тем соотношением, которое мы искали. Оно устанавливает, что среднее число требований в системе равно произведению интенсивности поступления требований в систему на среднее время пребывания требования в системе х. Приведенное доказательство не зависит ни от каких-нибудь частных ограничений, накладываемых на вид распределения А (/) входящего потока или на вид распределения В (х) времени обслуживания, ни от числа обслуживающих приборов, ни от конкретного характера дисциплины обслуживания в системе. Этот результат долгое время существовал в виде «фольклорной теоремы»; первым человеком, давшим его строгую формулировку и доказательство, был Дж. Д. К- Литтл [91; некоторые дальнейшие упрощения были даны в работах У. С. Джевелла [7], С. Эйлона [3] и С. Стидхема [13]. Важно подчеркнуть, что на выбор систем массового обслуживания не накладывается никаких точных ограничений. Так, прямоугольник на рис. 2.1 может означать как целую систему, состоящую из очереди и обслуживающего прибора, так и только очередь требований; в последнем случае выведенное соотношение принимает вид
= (2.26)
где Nq — определенное ранее среднее число требований в очереди, a W — среднее время ожидания в очереди.
1 Интуитивное доказательство формулы Литтла сводится к утверждению, что требование, входящее в систему, находит в ней то же самое среднее число требований ,У,_которое остается в системе, когда это требование покидает ее. Эта величина N попросту равна произведению интенсивности К поступления требований в систему на среднее время Т пребывания требования в системе.
2 Л. Клейнрок 33
Третья возможность сводится к тому, что система состоит только из обслуживающего прибора (или приборов); в этом случае равенство (2.25) приводится к виду
Л/, = й, (2.27)
где Ns — среднее число требований в обслуживающем приборе (или приборах), а х — среднее время, проведенное требованием в обслуживающем приборе. Отметим, что в этом случае всегда имеет место равенство
T = x-]-W. (2.28)
Системы массового обслуживания можно различать по частным классам требований, например по приоритетам обслуживания, или по каким-либо другим признакам этих классов; выведенное соотношение применимо к любому из них. Иными словами, как бы мы ни определили систему массового обслуживания, среднее число требований в системе равно произведению интенсивности потока входящих в систему требований на среднее время пребывания требования в системе.
Рассмотрим теперь один из основных параметров р, который называется коэффициентом использования. Этот параметр является фундаментальным в том смысле, что он равен отношению R/C, введенному в гл. 1, т. е. равен отношению интенсивности, с которой работа поступает в систему, к той максимальной интенсивности (пропускной способности), с которой система может выполнять эту работу. Работу, вносимую в систему каждым поступающим требованием, измеряют в секундах \ необходимых для его обслуживания. Таким образом, для однолинейных систем определение параметра р имеет следующий вид:
р Л (интенсивность поступления требований в систему) X
X (среднее время обслуживания) — Кх. (2.29)
Последнее равенство справедливо, так как максимальная интенсивность, с которой однолинейная система может выполнять обслуживание, равна 1 с/с, а каждое поступающее требование вносит работу в количестве х с; поскольку в среднем в систему поступает % требований в секунду, то в среднем каждую секунду все поступающие требования вносят работу, равную Хх с. В случае многолинейной системы (например, когда в системе имеется т обслуживающих приборов) определение коэффициента использования в зависимости от отношения RJC остается тем же самым, причем под пропускной способностью системы теперь понимают
1 Читателя не должно смущать, что работа измеряется в единицах времени, так как здесь предполагается, что эта работа выполняется с постоянной мощностью (сравни: повременная оплата труда). — Прим, ред 34
т с/с; В зависимости от параметров системы это определение можно переписать в виде
-(2.30)
Равенства (2.29) и (2.30) справедливы в случае, когда максимальная интенсивность обслуживания системы не зависит от ее состояния; в противном случае приходится вводить более точное определение. Интенсивность поступления работы в систему иногда называется интенсивностью нагрузки и выражается, как правило, в эрлангах-, в однолинейной системе интенсивность нагрузки равна коэффициенту использования, а в системе с т обслуживающими приборами она равна тр. Параметр р заключен в пределах 0 < < р < 1 и может быть интерпретирован как
р = Е [доля занятых приборов 1. (2-31)
(Для системы с бесконечным числом обслуживающих приборов бессмысленно вводить коэффициент использования р, и вместо него рассматривают число занятых приборов и его среднее.)
Ясно, что для стационарности системы G/G/1 должно выполняться условие R < С, так что 0 < р < 1. Однако случай р = 1 также иногда включают в диапазон стационарности системы (в частности для системы D/D/1). Под стационарностью здесь опять подразумевается тот факт, что существуют предельные распределения для всех представляющих интерес случайных величин и что все требования в конце концов будут обслужены. При этих предположениях можно провести следующие простые рассуждения. Пусть т — сколь-угодно длинный промежуток времени. В этом промежутке ожидаемое число поступающих требований (согласно закону больших чисел) с вероятностью 1 будет примерно равно Хт. Обозначим через р0 вероятность того, что в некоторый случайный момент времени обслуживающее устройство будет свободным. Тогда можно сказать, что в промежутке времени т обслуживающий прибор будет занят (т — тр0) секунд, так что с вероятностью 1 число обслуженных в этом интервале требований очень близко к (т — тр0)/х. Приравнивая число требований в промежутке т к числу обслуженных в этом промежутке требований, для достаточно больших т получаем
X
При т -> оо имеем Хх= 1 —р0. Используя определение (2.29), наконец, приходим к следующему важному выводу для систем
р=1— р0. (2.32)
Интерпретация этого равенства состоит в том, что о в точности Равно доли времени занятости обслуживающего рибора; это 2* 35
согласуется с равенством (2.27) в том, что лх= р равно среднему числу требований в обслуживающем приборе.
Таким образом, мы кратко ознакомились с системой массового обслуживания общего вида, для которой были рассмотрены некоторые основные вероятностные процессы и введены важнейшие определения и обозначения. Кроме того, был установлен результат Литтла, позволяющий по известному среднему значению времени пребывания требования в системе определять среднее число требований в системе (и наоборот). Теперь перейдем к более подробному изучению важнейших вероятностных процессов, встречающихся в системах массового обслуживания.
2.2.* ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ ВЕРОЯТНОСТНЫХ ПРОЦЕССОВ
В конце приложения II дано определение вероятностного процесса, которое по существу устанавливает, что это семейство случайных величин X (/), значения которых индексируются временным параметром I. Например, число зрителей в кинотеатре или атмосферное давление в зале этого кинотеатра как функции времени являются вероятностными процессами (по меньшей мере эти функции можно моделировать вероятностными процессами). Часто вероятностный процесс называют случайным процессом. Случайный процесс можно представить себе как процесс движения частиц в некотором пространстве. В основе классификации случайных процессов лежат три характеристики: пространство состояний, индексирующий параметр (время) и статистические зависимости между случайными значениями процесса X (/), соответствующими разным значениям индексирующего параметра /. Рассмотрим каждую из этих величин для того, чтобы наметить общую основу случайных процессов.
Начнем с пространства состояний. Пространством состояний называют множество возможных значений (состояний) процесса X (t). По аналогии с процессом движения частиц говорят, что процесс характеризуется дискретным множеством состояний, если множество возможных положений частиц в пространстве конечно или счетно; часто такой процесс называют цепью. Пространство состояний цепи обычно задают натуральным рядом чисел: (0, 1, 2, ...}. С другой стороны, если допустимое множество положений частиц в пространстве представляет собой конечный или бесконечный непрерывный интервал (или несколько таких интервалов), говорят, что процесс имеет непрерывное множество состояний.
* Читатель может пропустить параграфы 2.2—2.4 и непосредственно перейти к параграфу 2.5. К пропущенному материалу можно возвратиться, если возникнет в этом необходимость.
36
Рассмотрим теперь индексирующий параметр (время). Если допускаются изменения положения частиц в конечном или счетном числе моментов времени, то говорят о процессе с дискретным (временным) параметром; если же допускаются изменения положений частиц в любой точке конечного или бесконечного промежутка времени (или множества промежутков), то говорят о процессе с непрерывным параметром. В первом случае для обозначения процесса используют символ Хп, тогда как во втором — X (/). Величину Хп часто называют случайной, или вероятностной последовательностью, а величину X (/) — случайным, или вероятностным процессом.
Отличительной особенностью вероятностного процесса является зависимость случайных величин X (t) или Хп от других членов этого же семейства. Согласно определению, данному в приложении II, надо задать полную функцию совместного распределения вероятностей этих случайных величин (их совокупность можно рассматривать как векторную случайную величину, для обозначения которой применяют жирный шрифт) X — [X (/х), X (/.>), 1, а именно функцию
Fx (х; t) А Р [X (F) < хг, . . . X (tn х„)] (2.33)
для всех х = (хх, х2, хп), t = (tlt t.2, ..., tn) и n. Как указано в приложении, такая задача представляет существенную трудность; к счастью, однако , многие представляющие интерес случайные процессы допускают более простое описание. Как бы то ни было, функция Fx (х; t) представляет собой полное описание зависимостей между случайными величинами вероятностного процесса. Ниже описаны некоторые типы обычных вероятностных процессов, характеризуемых различными видами зависимостей между случайными значениями этих процессов. Такая классификация проводится для того, чтобы дать читателю общую картину рассматриваемой области науки и помочь выделить ту ее часть, которая необходима для изучения теории массового обслуживания, а также для выявления ее связи с вероятностными процессами.
Стационарные процессы. Согласно определению, приведенному в конце приложения II, вероятностный процесс Х'([) называется стационарным, если функция Fx (х, t) инвариантна относительно сдвигов во времени для всех значений ее аргументов; иными словами, для произвольно заданной постоянной величины г должно выполняться равенство
Fx (х; t + т) = Fx (х; t), (2.34)
где через t + т обозначен вектор (/х + т, /2 + т, ...,/„ + т).
Процесс X (t) принято называть стационарным в широком смысле, если как первый, так и второй моменты распределения не зависят от выбора точки на временной оси, т. е. если Е [X (/)] не зависит от I, а Е [X (/) X (/) + т) ] зависит только от т и не 37
зависит от t. Заметим, что всякий стационарный процесс является стационарным в широком смысле, но не наоборот. Как и следует ожидать, теория стационарных случайных процессов проще, чем теория нестационарных случайных процессов.
Независимые процессы. Самым тривиальным вероятностным процессом является случайная последовательность, в которой величины {Хп} образуют множество независимых случайных величин, т. е. совместная плотность распределения вероятностей, определенная для рассматриваемого вероятностного процесса в приложении II, разлагается в произведение
/х(х; t)A/v ,.Xn(xv...,xn;
tx)...fXn{x^ tn). (2.35)
Такую последовательность можно назвать случайным процессом лишь очень приблизительно, так как между ее случайными значениями нет связи или зависимости. Такой же независимый случайный процесс может быть определен и для непрерывных вероятностных процессов, и его обычно называют белым шумом (примером такого процесса является производная броуновского движения по времени).
Марковские процессы. В 1907 г. А. А. Марков опубликовал работу ПО], в которой определил и исследовал процессы, известные сейчас под названием марковских. Он рассмотрел простую и очень полезную форму зависимости между случайными величинами, образующими вероятностный процесс, к описанию которой и перейдем.
Марковский процесс с дискретным пространством состояний называется цепью Маркова. Наиболее простая и понятная — это цепь Маркова с дискретным временем. Множество случайных величин {Хп] образует цепь Маркова, если вероятность того, что следующее значение (состояние) равно Хп+1, зависит только от текущего значения (состояния) Хп и не зависит от предыдущих значений процесса. Таким образом, имеется случайная последовательность, в которой зависимость распространяется назад на одну единицу времени. Иными словами, воздействие всей предыстории процесса на его будущее полностью сосредоточено в текущем значении процесса.
Изменения состояний в цепи Маркова с дискретным временем могут происходить только в моменты, предопределяемые натуральным рядом чисел: 0, 1, 2, ..., п, ... . Однако для цепи Маркова с непрерывным временем изменение состояния может произойти в любой момент времени. Таким образом, появляется необходимость ввести в рассмотрение случайную величину, указывающую, как долго процесс остается в текущем (дискретном) состоянии перед тем, как перейдет в другое состояние. Но, поскольку, согласно марковскому свойству, вся предыстория процесса полностью заключена в определении текущего состояния, нельзя ЗЯ
требовать, чтобы описание этого текущего состояния содержало также информацию о том, как долго процесс находится в этом состоянии. Это накладывает существенные ограничения па распределение времени пребывания процесса в данном состоянии. Действительно, как увидим из равенства (2.85), время пребывания в этом состоянии должно быть распределено по показательному закону. Таким образом, показательное распределение является непрерывным распределением без последействия. Это замечание достаточно подробно обсуждается ниже в данной главе. Аналогично в случае цепи Маркова с дискретным временем время пребывания процесса в данном состоянии описывается геометрическим распределением, которое является единственным дискретным распределением без последействия. Требование отсутствия последействия накладывается на все цепи Маркова и является существенным ограничением общности тех процессов, которые будут рассмотрены.
Аналитически марковское свойство может быть записано в виде
? [X (/я+1) = Мг+11 X (t„) = Хп, X (/п1) =
= Х1] = Р [X (tn+1) = хп+11X (1п) = хп], (2.36)
где < t2 < ... < tn < tn+1, a Xt принадлежит некоторому дискретному пространству состояний.
Марковские процессы занимают центральное место в исследованиях систем массового обслуживания с ожиданием и будут неоднократно встречаться в этой книге. Именно поэтому значительная часть данного параграфа посвящена цепям Маркова с дискретным и непрерывным временем.
Процессы размножения и гибели. Один из важнейших частных случаев цепей Маркова известен под названием процесса размножения и гибели.' Этот процесс может быть либо с дискретным, либо с непрерывным временем, а определяющее его условие состоит в том, что допускаются переходы только в соседние состояния. Таким образом, если (без потери общности) в качестве дискретного пространства состояний выбран ряд натуральных чисел, то для процесса размножения и гибели переход из состояния Хп = i возможен только в одно из состояний Xn+1 — i — 1, i или i + 1 и ни в какое другое. Как мы увидим, процессы размножения и гибели играют важную роль в теории массового обслуживания. Однако продолжим общий обзор вероятностных процессов, чтобы увидеть место каждого из них.
Полумарковские процессы. Начнем с обсуждения полумарков-ских процессов с дискретным временем. Дискретная цепь Маркова характеризуется тем, что в каждом единичном промежутке времени процесс переходит из текущего состояния в некоторое другое (а может быть, в то же самое) состояние. Вероятности перехода совершенно произвольны; однако вытекающее из марковского свойства требование, чтобы переход происходил в каждый еди-
39
ничный промежуток времени, приводит к тому, что Время пребывания процесса в данном состоянии подчиняется геометрическому распределению [что будет видно из равенства (2.66)1. Как уже отмечалось, это накладывает существенные ограничения на рассматриваемые процессы. Если же снять это ограничение, т. е. допустить произвольные распределения для времени пребывания процесса в данном состоянии, то это непосредственно приведет к понятию полумарковского процесса с дискретным временем. При этом определяющим будет условие, что разрешаются произвольные распределения вероятностей времени между переходами из одного состояния в другое. Отметим, однако, что сточки зрения моментов изменения состояния процесс ведет себя как обычная цепь Маркова, и фактически можно сказать, что в эти моменты имеет место вложенная цепь Маркова.
Из изложенного непосредственно вытекает определение полумарковского процесса с непрерывным временем. Здесь допускаются переходы из одного состояния в другое в любой произвольный момент времени. Однако в противоположность марковскому процессу, для которого распределение времени пребывания в состоянии является показательным, в данном случае допускается произвольное распределение. Это приводит к процессам значительно более общего вида, которые успешно применяют при исследовании систем массового обслуживания. Относительно моментов времени изменения состояний здесь также появляются вложенные цепи Маркова. Ясно, что класс марковских процессов входит в класс полумарковских процессов.
Случайные блуждания. При исследовании случайных процессов часто встречается процесс, который получил название случайного блуждания. Случайное блуждание можно представить себе как передвижение частицы из одного состояния в другое в некотором (скажем, дискретном) пространстве состояний. Задача состоит в нахождении местоположения частицы в этом пространстве. Отличительная черта случайного блуждания состоит в том, что последующее положение, которое займет процесс, равно предыдущему положению плюс случайное перемещение, величину которого выбирают независимым образом из произвольного распределения; это распределение, однако, является одним и тем же в любом состоянии процесса Е Иначе говоря, последовательность случайных величин {£„) называется случайным блужданием (с начальной точкой в начале координат), если
S„ = Xt + X2+ . . +Х„, n= 1, 2.......... (2.37)
где So = 0, a Xt, Х2, ••• — последовательность независимых одинаково распределенных случайных величин. Индекс п служит только для нумерации переходов процесса из одного состояния в другое; ясно, что если п пробегает дискретное множество, то
1 За исключением, может быть, нескольких граничных состояний.
40
имеет место случайное блуждание с дискретным временем, а если п выбирается из континуума, имеет место случайное блуждание с непрерывным временем. В любом случае предполагается, что распределение промежутков времени между этими переходами произвольно, и, следовательно, случайные блуждания представляют собой частный случай полумарковского процесса Е В случае, когда совместное распределение вероятностей для Х„ дискретно, то говорят о случайном блуждании с дискретным множеством состояний; в этом случае вероятности р^ перехода из /-го состояния в /-е зависят только от разности индексов / — i, что обозначается через qt_j.
Примером случайного блуждания с непрерывным временем является броуновское движение; примером случайного блуждания с дискретным временем является общее число выпадения гербов в последовательности независимых подбрасываний монеты.
Случайное блуждание иногда называют процессом с независимыми приращениями.
Процессы восстановления. Процессы восстановления относятся к случайным блужданиям 1 2. Однако предметом рассмотрения теперь является не последовательность состояний, занимаемых частицей, а число переходов как функция времени. Иначе говоря, рассматривается действительная временная ось, на которую нанесена последовательность точек, соответствующих моментам перехода из одного состояния в другое; распределение длин промежутков времени между соседними точками может быть произвольным', предполагается, что процесс начинается в нулевом состоянии [т. е. что X (0) = 0] и возрастает на единицу при каждом переходе; таким образом X (f) равно числу переходов, которые произошли к моменту времени t. В этом смысле имеет место частный случай случайного блуждания, для которого qx = 1 и д, = = 0 при i 1. Если под случайной величиной Sn понимать момент времени, в который осуществляется n-й переход, равенство (2.37) можно рассматривать как равенство, описывающее процесс восстановления. Как и ранее, {Хп} представляет собой последовательность независимых одинаково распределенных случайных величин, где Хп в данном случае соответствует времени между (п — 1)-м и п-м переходами. Однако при интерпретации равенства (2.37) необходимо соблюдать осторожность, различая рассмотренный только что случай процесса восстановления и описанное
1 Обычно при рассмотрении случайного блуждания в качестве предмета исследования выбирают не распределение интервалов между переходами, а значение (положение) Sn после п переходов. Часто предполагается, что рассматриваемый процесс не имеет последействия, так что случайное блуждание представляет собой частный случай марковского процесса; выбранное здесь определение является более общим, так как допускается произвольный вид распределения вероятностей интервалов между переходами.
2 Эти процессы можно рассматривать как частный случай уже определенных случайных блуждании. Иногда процесс восстановления называют рекуррентным процессом.
41
ранее случайное блуждание. Разница состоит в том, что для процесса восстановления это равенство описывает время п-то восстановления или перехода, тогда как для случайного блуждания оно описывает состояние процесса, а время между переходами является другой случайной величиной.
Важным примером процесса восстановления является поток требований в СМО типа G/G/m. В этом случае время между поступлениями соседних требований обозначают как случайную величину Хп.
Таким образом, предложена классификация некоторых представляющих интерес вероятностных процессов. Для того чтобы помочь читателю в понимании взаимосвязей между марковскими, полумарковскими процессами и их частными случаями, на рис. 2.4 изображена диаграмма, показывающая эти связи для процессов с дискретным пространством состояний. Рисунок выполнен в форме диаграммы Венна. Символ р(/- означает вероятность перехода процесса из текущего состояния i в следующее состояние /. Через fx обозначено распределение вероятностей длин интервалов между переходами. Утверждение, что Д не имеет последействия, для процесса с дискретным временем означает, что Д имеет геометрическое распределение, а для процесса с непрерывным временем — показательное. Кроме того, Д может быть функцией одновременно текущего и следующего состояний процесса.
На рисунке показано, что процессы размножения и гибели образуют подмножество марковских процессов, которые, в свою очередь, являются подмножеством класса полумарковских процессов. Аналогично, процессы восстановления образуют подмножество в множестве процессов случайных блужданий, которое
Рис. 2.4. Взаимосвязь между интересными вероятностными процессами:
ПМП — полумарковский процесс; МП — марковский процесс; СБ — случайное блуждание; ПВ — процесс восстановления; ПРГ -- процесс размножения и гибели; ПП — пуассоновский процесс; ПЧР — процесс чистого размножения
42
Также является подмножеством класса полумарковских процессов. Более того, здесь имеются некоторые процессы восстановления, которые можно классифицировать как процессы размножения и гибели. Аналогично, те марковские процессы, для которых Pi, = qj_t (т. е. для которых вероятности переходов зависят только от разности индексов), перекрывают случайные блуждания без последействия. Случайные блуждания без последействия, для которых = 0 при (/ — г) > 1, пересекаются с классом процессов размножения и гибели. Если дополнительно к предыдущим ограничениям на случайное блуждание наложить требование, чтобы qx == 1, то получим процессы, лежащие в пересечении процессов всех пяти классов, показанных на рисунке. Эгп процессы называют процессами чистого размножения; хотя распределение fx в этом случае должно быть без последействия, для этих процессов может быть распределение, которое зависит от самого текущего состояния. Если fx не зависит от состояния процесса (что приводит к постоянной интенсивности размножения), то, выражаясь буквально и фигурально, получаем вероятностный процесс, лежащий в «центре» исследуемых случайных процессов и обладающий всеми мыслимыми замечательными свойствами! Этот очень частный случай вероятностных процессов, называемый пуассоновским процессом, играет главную роль в теории массового обслуживания. Ниже, в данной главе будут рассмотрены свойства этого процесса.
На этом вопрос о классификации вероятностных процессов завершается. Теперь перейдем к определению и описанию свойств марковских процессов с дискретным пространством состояний. Это приведет нас, естественно, к началам элементарной теории массового обслуживания. Некоторая часть теории марковских процессов с непрерывным пространством состояний будет введена дальше по мере необходимости. Начнем с рассмотрения самого простого случая марковских цепей с дискретным временем и дискретным пространством состояний, а затем перейдем к марковским цепям с дискретным пространством состояний и непрерывным временем.
2.3. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА1
Как уже говорилось, марковский процесс можно использовать Для описания движения частицы в некотором пространстве. Рассмотрим дискретную цепь Маркова, когда частица может занимать в пространстве дискретные позиции, а переход из одной позиции в другую осуществляется в дискретные моменты времени. Для иллюстрации развиваемой теории выберем следующий современный пример.
1 См. сноску на с. 36.
43
Рассмотрим путешественника, переезжающего из города в город на попутных машинах. Обозначим через Хп город, в котором он окажется в полдень n-го дня. Когда путешественник находится в некотором городе i, он предпринимает первую попытку покинуть этот город вечером. Временем передвижения из города в город пренебрегаем. Конечно, поездка может не состояться, и в этом случае путешественник остается в городе i до следующего вечера. Так как движение транспорта между соседними городами непредсказуемо, положение путешественника в некоторые моменты времени в будущем несомненно является случайной величиной. Эту случайную величину, оказывается, можно должным образом описать с помощью цепи Маркова.
Введем следующее определение.
Определение. Последовательность случайных величин Х1г Х2, ..., образует дискретную цепь Маркова, если для всех п (п = 1, 2, ...) и всех возможных значений случайных величин выполняется равенство
P[Xn=j\Xl = i1, X2 = i2, ..., =
= /„.Л = Р [Хп = j | Х^ = . (2.38)
Это условие для нашего примера просто означает, что вероятность попадания путешественника в следующий город зависит только от того, в каком городе он находится в настоящее время, и не зависит от того, какие города он уже посетил. В этом смысле память (последействие) случайного процесса, или цепи Маркова распространяется назад только на непосредственно предшествующее положение. Если Хп = / (в п-й день путешественник находился в городе /), то говорят, что в момент п (или на n-м шаге) система находится в состоянии Е/. Допустим, что путешественник начинает путешествие в нулевой день с некоторым начальным распределением вероятностей Р ]Х0 = Л- Выражение в правой части равенства (2.38) называют вероятностью перехода (за один шаг); оно задает условную вероятность перехода из состояния Eift t на /• — 1-м шаге в состояние £,• на п-м шаге процесса. Ясно, что если известно начальное распределение вероятностей и вероятности переходов, то однозначно можно вычислить вероятность пребывания на ?/-м шаге в любом из возможных состояний |см. приводимые ниже уравнения (2.55) и (2.56)].
Если вероятности переходов не зависят от п, то цепь Маркова называется однородной, и строгое ее определение задается равенством
Pii^P{Xn = j\Xn_l^i\, (2.39)
выражающим вероятность перехода на следующем шаге из текущего состояния Е, в состояние Е,. Нижеследующее относится только к однородным цепям Маркова. Эти цепи таковы, что ве-44
роятностп перехода стационарны во времени1 2; следовательно, если задано текущее состояние, то вероятности различных состояний через т шагов зависят только от этих т шагов и не зависят от текущего времени; целесообразно определить вероятности перехода за т шагов в виде
ДР [Х„+т = №=/]. (2.40)
Используя марковское свойство, выражаемое равенством (2.38), легко вывести следующую формулу для вычисления вероятностей рТ-
р\Т} ^hp^Pkj, т=~-2, 3, ... (2.41)
k
Это равенство означает, что для попадания из состояния £, в состояние Ej за т шагов необходимо сначала попасть из состояния Е, в некоторое состояние Ек за (т — 1) шагов, а затем за один шаг перейти из Ek в Е,. Вероятность этих двух независимых событий (напомним, что мы имеем дело с цепью Маркова) равна произведению вероятностей каждого из них, и, если просуммировать эти произведения по всем возможным промежуточным состояниям Ek, то получится вероятность р^.
Цепь Маркова называют неприводимой а, если каждое ее состояние может быть достигнуто из любого другого состояния; иными словами, для каждой пары состояний £,• и £, существует целое число т0 (которое может зависеть от i и /) такое, что p\fa} > > 0. Пусть далее А — множество всех возможных состояний цепи Маркова. Подмножество состояний называется замкнутым, если нельзя за один шаг перейти из произвольного состояния подмножества Аг в произвольное состояние подмножества А{ (дополнение множества ЛЦ Если Ах состоит из единственного состояния, скажем £,, то оно называется поглощающим; необходимым и достаточным условием того, чтобы состояние £• было поглощающим, является выполнение равенства Рн ~ 1. Если множество А замкнуто и не содержит никакого другого собственного замкнутого подмножества, то получается определенная выше неприводимая цепь Маркова. С другой стороны, если множество А содержит собственные замкнутые подмножества, то цепь называется приводимой. Если замкнутое подмножество состояний приводимой цепи Маркова само не содержит замкнутых собственных подмножеств, то оно называется неприводимой подцепью Маркова; такие подцепи можно исследовать независимо от других состояний.
1 Подчеркнем, что, хотя этот процесс является марковским процессом со стационарными вероятностями переходов, он не обязательно должен быть стационарным случайным процессом.
2 Многие цепи Маркова, встречающиеся в теории массового обслуживания, являются неприводимыми.
45
Может случиться так, что наш путешественник предпочтет не возвращаться в город, в котором он побывал. По правилам его путешествия такое событие может произойти, и нам важно определить его вероятность. Соответственно, пусть
? [первое возвращение в состояние Ej через п шагов после ухода из этого состояния].
Тогда ясно, что вероятность возвращения путешественника когда-либо в город /
I/ = S ^’П) = Р [возвращения в £;].
Вероятности fj позволяют ввести следующую классификацию состояний цепи Маркова. Если f, — 1 для некоторого состояния Ej, то это состояние называют возвратным; если fj <Д, то состояние Ej называют невозвратным. Далее, если единственными возможными шаыми, на которых путешественник может вернуться в состояние £,, являются шаги у, 2у, Зу ,..., (где у > 1 и является наименьшим целым числом, обладающим таким свойством), то состояние Ej называют периодическим с периодом у; если у = 1, то Ej называют апериодическим.
Рассматривая состояния, для которых Д =-= 1, можно определить среднее время возвращения в состояние £,:
М/а£п//п); (2-42)
это среднее время между пребываниями в состоянии Ej. Оно позволяет продолжить классификацию состояний. А именно, назовем состояние £ у возвратным нулевым, если Mj = сю, и возвратным ненулевым, если Mj <оо. Обозначим через л)л) вероятность пребывания системы па п-м шаге в состоянии Е
п<рДР[Хп^Ц- ' (2.43)
Теперь можно сформулировать (без доказательств) две важные теоремы. Первая из них дает описание множества состояний неприводимой цепи Маркова.
Теорема 1. Состояния неприводимой цепи Маркова либо все невозвратные, либо все возвратные ненулевые, либо все возвратные нулевые. В случае периодической цепи все состояния и чеют один и тот же период у.
Предполагая, что путешественник блуждает достаточно долгое время и может побывать в разных городах страны по нескольку раз, естественно поинтересоваться существованием стационарного распределения вероятностей [л;[ того, что он посетит город / в некоторый произвольный момент в будущем. [Распределение вероятностей Рj называется стационарным, если при его выборе в качестве начального распределения вероятностей (т. е. при
4G
Лу = Pj) для всех ii получают равенство л}'0 == Ру.| Нахождение распределения {лу} является основной задачей исследования цепей Маркова. Вторая теорема относится к этому вопросу.
Теорема 2. Для неприводимой и апериодической однородной цепи Маркова всегда существуют предельные вероятности
л/ = lim Лу'!), (2.44)
п -> СО
не зависящие от начального распределения вероятностей. Более того, имеет место одна из следующих двух возможностей:
а) либо все состояния цепи невозвратные или все возвратные нулевые, и тогда itj ~ 0 для всех j, и стационарного распределении не существует;
б) либо все состояния цепи возвратные ненулевые, и тогда Лу . > О для всех j, и в этом случае {л,-} является стационарным распределением вероятностей, причем
В последнем случае величины л, однозначно определяются равенствами
1 -= £ -v. (2.46)
i
= £ МРи- (2.47)
I
Введем теперь понятие эргодичности. Состояние £у называют эргодическим, если оно является апериодичным, возвратным и ненулевым; таким образом, для эргодического состояния выполняются условия fj — 1, Mj <со и у =1. Если все состояния цепи Маркова эргодичны, то сама цепь Маркова называется эргодической. Более того, цепь Маркова называют эргодической, если распределение вероятностей (луп)) как функция от п всегда сходится к некоторому предельному стационарному распределению {лу), которое не зависит от начального распределения вероятностей. Легко показать, что все состояния конечной 1 апериодической неприводимой цепи Маркова эргодичны. Кроме того, используя критерий Фостера [4], можно доказать, что, если система линейных уравнений (2.47) имеет нулевое решение, для которого 2у | Лу | то приводимая и апериодическая цепь Маркова является эргодической. Предельные вероятности {л;} эргодической цепи Маркова часто называют вероятностями состояния равновесия, имея при этом в виду, что влияние начального распределения вероятностей {лу0)} полностью отсутствует.
1 Цепь /Маркова называют конечной, если число ее состояний конечно. Следовательно, неприводимая цепь Маркова типа а из теоремы 2 (т. е. возвратная нулевая или невозвратная) не может быть конечной.
47
Поместим, например, нашего путешественника в фантастическую страну Гатафл.а, показанную на рис. 1.1. Для упрощения примера предположим, что города Нонабель, Кадабра и Ориак уничтожены и сеть оставшихся дорог имеет вид, представленный на рис. 2.5. Стрелки на этом рисунке показывают дозволенные направления передвижения ио дорогам,
(рг/) того, идущую по
а числа что путешественник найдет этой дороге, при условии, что он
задают вероятности попутную машину, пытается выбраться
из города в направлении, соответствующем исходящей стрелке. Заметим, что вероятность того, что он останется в городе Сакса-мад до следующего дня, равна 1/2. Схемы подобного типа называют
диаграммой переходов из одного состояния в другое. Вместо названий городов удобнее пользоваться числами, стоящими в круг-
лых скобках у этих названий.
Для продолжения рассмотрения примера введем общее определение матрицы Р вероятностей переходов, состоящей из элемен-
тов
Р = !/>,/]• -(2.48)
Определяя далее вектор вероятностей
л = [л0, л2, . . .], (2.49)
перепишем систему уравнений (2.47) в форме
л — лР. (2.50)
Для примера, показанного па рис. 2.5, имеем
0 3/4 1/4"
р = 1/4 0 3/4
_1/4 1/4 1/2.
и решение матричного уравнения (2.50) сводится к решению системы трех уравнений:
л0 = 0ло ф- (1/4) лх -j- (1/4) л2;
лг = (3/4) л0 -ф- On, ф- (1/4) л2; (2.51)
л2 = (1/4) л0 + (3/4) лх + (1/2) л2.
Заметим, что коэффициенты первого уравнения в этой системе дополняют до единицы сумму коэффициентов второго и третьего
48
уравнений; это свидетельствует о линейной зависимости между ними. Линейная зависимость между одним из уравнений и другими имеет место всегда, и поэтому для решения системы уравнений нужно ввести дополнительное нормирующее условие, задаваемое равенством (2.46). Соответственно в данном примере потребуем, чтобы
1 = л0 + + я2. (2.52)
Решая систему, состоящую из каких-нибудь двух уравнений из (2.51) и уравнения (2.52), получаем
л0 = 1/5 = 0,20;
ла = 7/25 = 0,28; (2.53)
л2 = 13/25 = 0,52.
Это дает стационарное распределение вероятностей состояний. Ясно, что рассматриваемый пример является примером эргодической цепи Маркова (так как она конечна и неприводима).
Часто представляют интерес переходы системы в произвольный момент времени. Для этого нужно определить вероятности {л;п)} пребывания путешественника в городе / в момент п. Определим вектор вероятностей л(,1> в момент п равенством
л("> = [лГ, л}'г), л^’, . . .]. > (2.54)
Используя теперь определение (2.48) и определение вероятностей переходов, для вектора л(1> находим следующее выражение через матрицу Р и начальное распределение вероятностей состояний л°:
л(1) = Л<0)Р.
Аналогично, для вероятностей состояний на втором шаге имеем
л<2) = л(1)Р = [л<0)Р] Р = л(0)Р2.
Обобщая это рассуждение, приходим к уравнению
л(п> = я^Р, л = 1, 2, . . . , «(2.55)
решение которого может быть получено рекуррентно в виде
л(п) = л<0)Р", п=1, 2, ... я (2.56)
Уравнение (2.55) дает общий метод вычисления вероятностей состояний на п-м шаге процесса при заданной матрице переходов Р и начальном распределении л(0). Согласно данным выше определениям, если существует предел при п -» оо, то вектор стационарного распределения вероятностей задается равенством
л = Нт л(п)
49
(согласно теореме 2 это имеет место для однородной неприводимой апериодической цепи Маркова). Тогда, согласно уравнению (2.55) находим
lim n(,,) lim
и, следовательно, л — лР, что опять да<-г ' равнение (2.50). Заметим, что решение для л не зависит о г начального распределения вероятностей.
Применим эти результаты к рассматриваемому примеру, предполагая что с вероятностью 1 путешественник начинает свой путь в момент 0 из города Абра, при этом
.-г - [1, 0, 0J.
(2.57)
С помощью этого век юра можно вычислить последовательность значений векторов лРезультаты этого вычисления приведены ниже в виде таблицы, в которой указано также предельное значе-
ние вектора л, зал свае: лое решением (2.53):
п ) 1 2 3 4 . . . оо
Л<"! 1 0 0,250 0,178 0,203 0,20
л["> 0 0,75 0,062 0,359 0,254 0,28
л/,") 0 0,25 0,688 0,454 0,543 0,52
Можно предположит! з иначе, а именно, что с вероятностью 1
в момент 0 путешественник начинает свои путь из города Зевс,
что соответствует начальному вектору состояний
л(С’ = [0, 1, 0] (2.58)
и приводит к таблице:
п 0 1 2 3 4 . . оо
л(л) 0 0,25 0,187 0,203 0,199 0,20
л<п) 1 0 0,375 0,250 0,289 0,28
л<п) 0 0,75 0,438 0,547 0,512 0,52
Аналогично, начиная1 с города Саксамад, найдем
л(,1) - [0, 0, 1]; (2.59)
п 0 1 2 3 4 оо
4'° 0 0,25 0,187 0,203 0,199 0,20
л<п> 0 0,25 0,313 0,266 0,285 0,28
1 0,5 0,500 0,531 0,516 0,52
Проделанные вычисления позволяют сделать определенные выводы. Во-первых, уже после четырех шагов величины л(-г1) при фиксированном I мало отличаются друг от друга, независимо 50
от того, с какого города начинался путь. Скорость сходимости этих величин, как будет скоро показано, зависит от собственных значений матрицы Р. Во всех случаях видна быстрая сходимость к предельным величинам и как уже говорилось, независимость от начального положения.
Для того чтобы лучше представить физическую картину про-
исходящего, поучительно проследить за изменением во времени вероятностей состояний цепи Маркова. Для этого введем барицентрическую систему координат, в которой особенно удобно описывать векторы вероятностей. Рассмотрим вектор вероятностей с N координатами (в нашем случае марковский процесс с N состояниями) и (N—1)-мерный тетраэдр. В рассматриваемом примере М -’- 3, поэтому соответствующим двумерным тетраэдром служит правильный плоский треугольник. В общем случае предполагается, что высота этого правильного тетраэдра равна единице. Любой вероятностный вектор л(га) может быть представлен точкой в этом (N—1)-мерном пространстве, если каждую его координату рассматривать как расстояние от соответствующей грани тетраэдра. Иными словами, от грани с номером / отмеряют расстояние, равное /-й координате л/0 вектора вероятностей л(га); если проделать это для всех координат вектора, то в рассматри-
ваемом пространстве определится точка, однозначно соответствующая данному вектору вероятностей.
Таким образом, каждый вектор вероятностей может быть отображен в единственную точку пространства тетраэдра, и для каждой точки нетрудно указать соответствующий вектор вероятностей. В рассматриваемом примере три начальных вектора, задаваемые равенствами (2.57)—(2.59), соответствуют вершинам правильного треугольника (рис. 2.6). Числа, стоящие в скобках при каждой вершине, являются координатами соответствующих векторов вероятностей и представляют собой расстояния этой вершины от соответствующих сторон треугольника. Например,
вектор начального состояния, соответствующего равенству (2.59), должен изображаться верхней вершиной, что и сделано на рисунке.
В предыдущих рассуждениях мы проследили изменение векторов вероятностей состояний системы, начиная с некоторого фиксированного начального вектора состояний. Рассмотрим теперь на рис. 2.6 эти изменения одновременно: точка, соответствующая равенству (2.59)
61
и вектору |0, 0, 1], сдвигается в точку 10,25; 0,25; 0,51; точка, соответствующая вектору 10, 1, 0] — в точку [0,25; 0; 0,75], а точка, соответствующая вектору [1, 0, 0], — в точку [0; 0,75; 0,25]. Теперь ясно, что с какой бы начальной точки внутри равностороннего треугольника ни начиналось движение процесса, эта точка всегда будет отображаться внутрь меньшего треугольника, вершины которого соответствуют указанным новым векторам вероятностей состояний и который задает новую область начальных состояний процесса после первого шага. Из рисунка видно, что этот новый треугольник является уменьшенным вариантом исходного треугольника.
Если теперь продолжить отображение трех точек в соответствии со вторым шагом процесса (необходимые вычисления для которого приведены в трех выписанных выше таблицах), то придем к еще меньшему треугольнику, размещаемому как внутри первого, так и внутри второго треугольников, который задает область начальных состояний процесса после реализации его двух шагов. Такое сжатие будет, очевидно, продолжаться до тех пор, пока не будет достигнута точка сходимости. Точкой сходимости будет предельная точка, задаваемая равенствами (2.53). Это дает полное описание картины движения вектора вероятностей по рассматриваемому пространству.
Если не ограничиваться несколькими первыми членами, то задача вычисления вероятностных векторов л(п) на /i-м шаге по уравнениям (2.55) или (2.56) становится очень трудоемкой. Для нахождения общего решения часто пользуются методом производящих функций. Ниже дано его описание в общем виде, а также приложение этого метода к рассматриваемому примеру о путешественнике. Это дает удобный повод для иллюстрации применения правил действия с производящими функциями, описанными в приложении I *.
Отправной точкой служит уравнение (2.55). Это уравнение является разностным векторным уравнением. Как показано в приложении I, тот факт, что данное уравнение является разностным, позволяет использовать метод производящих функций. В этом случае естественно ввести в рассмотрение следующую векторную производящую функцию (векторный характер рассматриваемых величии не накладывает никаких ограничений, но надо соблюдать осторожность при вычислении обратных величин):
П(2)Л £ л('!)2п. (2.60)
п=0
Эта функция существует в единичном круге, т. е. при |z| с 1. Мы, однако, будем пользоваться ею во всем диапазоне (и =- 1,
s Краткое описание последовательности шагов, необходимых для решения системы разностных уравнений методом производящих функций, дано на с. 92 этой главы.
52
2, ...). Прежде всего умножим уравнение (2.55) на г", а затем просуммируем по п от единицы до бесконечности:
f я<п>гп = f я(л-1)Рг".
П=1 П=1
Таким образом, бесконечное множество разностных уравнений удается свести к одному алгебраическому уравнению. Следуя выбранному методу решения, необходимо вычислить производящую векторную функцию П (г). В левой части этого равенства стоит искомая векторная производящая функция, в которой не хватает первого члена; поэтому имеем
П (г) - л(0) = z ( л'1~1г('г-1И Р.
\п=1 '
В величине, стоящей справа в скобках, нетрудно узнать П (г) (для этого просто надо изменить индекс суммирования). Таким образом, находим, что
II (г) — л(()) = zll (z)P.
В этом векторном уравнении величина г является скаляром, и при необходимости ее можно сдвигать по векторам и матрицам Т Решая это уравнение в матричной форме, сразу приходим к общему решению для рассматриваемого векторного преобразования:
П(г) = л(0)[1 -гРГ1; (2.61)
здесь I — единичная матрица, а символ (—1) обозначает операцию обращения матрицы. Беря обратное преобразование, в силу единственности пары преобразований, получаем вектор распределения переходных вероятностей на n-м шаге; следуя принятым в приложении I обозначениям, имеем
П(г)ф=> л(п) = л(0)Р(,,). (2.62)
Таким образом, опять приходим к равенству (2.56). Сравнивая равенства (2.61) и (2.62), получаем очевидную пару преобразований
[I-гР]’1ффР'1. -(2.63)
Несомненно, что Рп является в точности той же матрицей, которая рассматривалась при нахождении распределения вероятностей состояний на п-м. шаге, так как она прямо определяет вероятности л(п> с помощью равенства (2.56). Поэтому единственное, что надо проделать для определения искомых вероятностей л(га>, — это построить в (2.63) обратную матрицу. Для цепи Маркова
1 Имеются в виду обычные правила внесения или вынесения скалярного Множителя из координат вектора, столбцов и строк матрицы. — Прим. пер.
53
с большим числом состояний эта задача является достаточно сложной. Тем не менее это дает один из формальных способов анализа распределения переходных вероятностей на »-м шаге.
Рассмотрим применение этого метода к примеру с путешественником. Напомним, что матрица вероятностей переходов в этом
случае имеет вид
' 0 3/4
Р 1/4 О
1/4 1/4
1/4
3/4
1/2
Прежде всего образуем матрицу
1 — (3/4)z — (1/4)г
1 — zP =. -(l/4)z 1 - (3/4)г
_-(l/4)z — (l/4)z 1 -(l/2)z_
Далее, для тою
построить ее определитель
чтобы вычнелль матрицу, обратную этой, надо
det(I —zP) — 1 - (1/2) z —(7/16) z2 - (1/16) z3.
Разложение этого многочлена на линейные множители дается равенством
det (1 — гР) = (1 -г)(1 (1/4) z)2.
Легко показать что для неприводимой цепи Маркова число z - - 1 всегда является корнем уравнения, задаваемого определителем (и, как будет показано, именно этот корень приводит к решению, соответствующему установившемуся режиму). Используя стандартные методы вычисления обратной матрицы, для рассматриваемого примера получаем
СП— 2) [1 +(1/4) гр
I 3,3 5 , 1.9,
-X- Z-ГЫ ?" ЧГ --Гс z 3 “ 2 Г Тг Z'
2 16 4 16 4 '16
I I 1 .1 1 I •> О 1 •> О
4~ 16 г~ 4‘г 1 7бг ~162’
Найдя обратную матрицу, можно теперь с помощью обратного преобразования вычислить матрицу Р". Для этого воспользуемся стандартным методом разложения на простые дроби, описанным в приложении I. Тот факт, что мы имеем дело с матрицами, не составляет проблемы; достаточно заметить, что каждый элемент этой матрицы представляет собой рациональную функцию от z и может быть разложен на простые дроби (эта задача упрощается,
54
если записать исходную матрицу в виде суммы трех матриц: постоянной матрицы; постоянной матрицы, умноженной на г, и постоянной матрицы, умноженной на z2). Так как знаменатель рассматриваемых дробно-рациональных функций имеет три корня, то в общем случае эти функции могут быть разложены в сумму трех правильных дробей. Проводя это разложение и группируя члены с одинаковыми степенями z, получаем
Г5 7 131 ГО —8 8 ’
[i_2p]-i = _k|L 5 7 13 , '/5 (1 -|-z/4p 0 2—2
5 / 13 [о 2 — 2
1/25
I + z/4
(2.64)
Легко заметить, что матрица, соответствующая знаменателю I— г, дает то же самое решение для установившегося режима, которое было уже найдено ранее прямым расчетом [см. уравнение (2.53)]. Совпадение всех строк матрицы (2.64) отражает факт независимости решения для установившегося режима от начального состояния. Две другие матрицы, соответствующие корням, не равным единице по абсолютному значению, всегда являются разностными матрицами (сумма элементов каждой строки такой матрицы равна нулю). Выполняя обратное преобразование (с помощью таблиц, приведенных в приложении I), получаем
Это полностью завершает решение, так как уравнение (2.65) сразу дает искомые переходные вероятности л(">. Заметим, что при п = 0 получается единичная матрица, а при п = 1, естественно, должна получиться матрица Р вероятностей переходов. Кроме того, имеются две матрицы, которые в пределе исчезают, сводя правую часть к матрице переходных вероятностей, соответствующих установившемуся режиму. Геометрической интерпретацией этого процесса обращения в пуль является процесс стягивания треугольников на рис. 2.6. Так как скорость сходимости к нулю для этих матриц зависит от характеристических чисел (корней детерминанта), то такую же зависимость естественно ожидать для процесса стягивания треугольников с ростом п па рис. 2.6. Действительно, можно показать, что эги треугольники при уве
55
личении п на единицу каждый раз стягиваются с постоянным коэффициентом пропорциональности. Можно доказать также, что этот коэффициент пропорциональности для произвольного марковского процесса равен абсолютной величине произведения характеристических чисел матрицы вероятностей переходов. В рассматриваемом примере характеристические числа равны 1, 1/4 и 1/4. Следовательно, коэффициент уменьшения площади треугольников с ростом п равен 1/16.
Замечательное изложение метода производящих функций можно найти в двухтомной книге Ховарда [6], в которой рассматриваются такие задачи, а также обсуждаются многие другие методы их решения, в частности метод графов.
До сих пор при анализе дискретных цепей Маркова мы не фиксировали внимания на свойстве отсутствия последействия г, которое состоит в том, что поведение процесса никак не зависит от того, сколько времени провела система в данном состоянии. Ниже будет доказано, что длительность времени пребывания системы в данном состоянии имеет геометрическое распределение; геометрическое распределение является единственным дискретным распределением вероятностей, обладающим свойством отсутствия последействия. Предположим, что система только что перешла в состояние £;. Она останется в этом состоянии на следующем шаге с вероятностью ц,,- и с вероятностью 1—pi; уйдет из этого состояния. Если система действительно останется в этом состоянии, то вероятность того, что на следующем, втором шаге она останется в данном состоянии, по-прежнему равна ра, а вероятность того, что система перейдет в другое состояние, останется равной 1—рп. И так далее. Более того, благодаря марковскому свойству тот факт, что система пребывала в данном состоянии известное число шагов, никак не сказывается на вероятности остаться на следующем шаге в этом же состоянии или перейти в некоторое другое состояние. Так как эти вероятности независимы, то можно записать
Р [система находилась в состоянии точно т шагов и затем сразу перешла в другое состояние] =
= (1-Рн)Ри- (2.66)
Это, конечно, и задает обещанное выше геометрическое распределение. Аналогичная мотивировка будет использована ниже для непрерывных цепей Маркова.
До сих пор мы рассматривали однородные марковские процессы. Напомним, что марковский процесс называют однородным, если его переходные вероятности не зависят от времени. Среди величин, которые мы можем вычислять, имеются вероятности р^
1 Свойство отсутствия последействия более подробно будет рассмотрено позже.
56
Рис. 2.7. Простые траектории вероятностного процесса
переходов из состояния Е, в состояние Е , за т шагов; рекуррентная формула для вычисления этих вероятностей дается равенством (2.41). Перейдем к более общей точке зрения, а именно, допустим, что переходные вероятности зависят от времени. Нашей задачей теперь будет вывод соотношений, являющихся отправной точкой многих дальнейших приложений марковских процессов к задачам теории массового обслуживания. Ближайшие рассмотрения еще некоторое время будут ограничены случаем дискретных цепей Маркова.
Обобщая определение (2.40) переходных вероятностей для однородной цепи, определим вероятность перехода системы из состояния Ei на m-м шаге в состояние Е, на п-м шаге для п т равенством
Рц (т, п) ДР[Х„-= /1 Хт = !]• (2.67)
Как уже отмечалось при рассмотрении однородного случая, если система из состояния Е, на т-м шаге переходит на п-м шаге в состояние Е;, то в некоторый промежуточный момент q она находилась в некотором промежуточном состоянии Ek. Этот процесс изображен на рис. 2.7, где показаны четыре траектории возможного развития вероятностного процесса при переходе из состояния Е, на m-м шаге в состояние Е; на п-м шаге. Состояние процесса отложено по вертикальной оси, а дискретное время — по горизонтальной. На рисунке траектории процесса изображены непрерывной кривой вместо последовательности точек; эта вольность допущена только ради удобства. Заметим, что траектории а и b обе проходят через состояние Ek в момент q в то время, как траектории с и d в момент q проходят через некоторые другие промежуточные состояния. Уверенным можно быть только в том, что траектория в момент q наверняка пройдет через одно промежуточное состояние. Это позволяет выразить вероятность pti (m,
57
и) в виде суммы вероятностей попадания во все внутренние состояния (они взаимно исключают друг друга), а именно
Рц (т, п)^Р {Хп =4, Xq = k\Xm = i) (2.68) к
При in с q < п. Эти уравнения должны выполняться для произвольного вероятностного процесса (необязательно марковского), так как мы учли все возможные и взаимно исключающие друг друга события. Из определения условных вероятностей следует, что эти уравнения можно переписать в виде
Р// (т, п) = 2 Р (X, = k | Хт = k
^i]P[Xn^i\Xm = i, Xq = k], (2.69)
Используя марковское свойство, можно записать
P[Xn^j\Xm = i, Xq = k] = Р [Хп = j\Xq = k\.
Учитывая это в уравнениях (2.69) и используя определение (2.67), при т <: q < п окончательно приходим к уравнениям
Рц ") • S Pik рп, q) pkj (q, п). (2.70)
Уравнения (2.70) называются уравнениями Чепмена.—Колмогорова лля дискретных цепей Маркова. Если цепь Маркова является однородной, то согласно определению (2.40) имеют место равенства pij (т, п) — p(i'^m>, и при п = q + 1 уравнения Чепмена— Колмогорова сводятся к полученным ранее уравнениям (2.41). Уравнения Чепмена—Колмогорова означают, что п—т шагов могут быть произвольным образом разбиты на q—т и п—q шагов, и при этом для вычисления вероятности рч рп, п) надо взять все возможные произведения вероятностей из множества переходных вероятностей за q—т шагов на вероятности из множества переходных вероятностей за остальные п—q шагов, а затем просуммировать эти произведения по всем промежуточным состояниям, возможным в момент q. При этом, естественно, допускаются произвольные разбиения временного интервала, что дает определенные преимущества, которыми мы вскоре воспользуемся.
Сейчас будет удобно записать уравнения Чепмена—Колмогорова в матричной форме. Для однородной цепи Маркова мы обозначили через Р матрицу, элементами которой являются вероятности pt,. Так как теперь эти вероятности зависят от времени, то обозначим через Р (и) матрицу вероятностей переходов за один шаг, т. е.
Р (n) A (n, п---- 1)]. (2.71)
Для однородной цепи Р (п) = Р. В однородном случае была также вычислена матрица Р" вероятностей переходов за п шагов. В случае неоднородной цепи Маркова надо ввести новое определение, 58
и для этого обозначим через Н (/«, п) матрицу вероятностей переходов за несколько шагов:
Н {т, п) Д[рц (т, /г)]. (2.72)
Заметим, что Н (/?, п + 1) = Р (/?) и что в однородном случае Н (л, п + 1) = Р". Используя эти определения, уравнения Чепмена—Колмогорова можно переписать в виде
Н (/«, п) = Н (т, q) Н (q, п) (2.73)
при т < q с 11. Чтобы завершить это определение, потребуем выполнения равенства Н (л, /г) = I, где I — единичная матрица. Все рассматриваемые матрицы являются квадратными, и их размерность равна числу состояний цепи Маркова. Решение уравнения (2.73) сводится к тому, чтобы выразить матрицу Н (т, п) через матрицы Р (/г).
Как уже отмечалось ранее, выбор точки q в интервале между in и п может быть произвольным. Выберем сначала q == п — 1. Тогда уравнение (2.70) перепишется в виде
Ри (т, п) = £ pik (т, п — V)pkj(n— 1, /г), (2.74)
k
или в матричной форме в виде
Н (/и, п) = Н (т, 11 — 1) Р {п — 1). (2.75)
Уравнения (2.74) и (2.75) называются прямыми уравнениями Чепмена—Колмогорова для дискретных цепей Маркова; это название объясняется тем, что данные уравнения выписываются на «переднем» (самом близком к настоящему моменту) конце рассматриваемого промежутка времени. С другой стороны, полагая q = т + 1, получим уравнение
Ри (т, п) = 2 Ptk (т, m+\)pkI (т 4- 1, п), (2.76)
k
матричная форма которого имеет вид
Н (т, п) = Р (m) Н (т 4- 1, л). ° (2.77)
Два последних уравнения называются обратными уравнениями Чепмена—Колмогорова, так как они выписываются на «заднем» (самом отдаленном во времени) конце рассматриваемого промежутка времени. Так как прямые и обратные уравнения описывают одну и ту же цепь Маркова, то естественно ожидать, что решения этих уравнений совпадают. Это действительно имеет место, и общее решение имеет вид
Н {in, п) = Р (m) Р (т -4 1) . . . Р (п — 1), т < п — 1. (2.78) Непосредственной подстановкой легко убедиться в том, что эта матрица является решением уравнений (2.75) и (2.77). Из (2.78) видно также, что в случае однородной цепи Н {т, п)— рп~т,
59
как и утверждалось ранее. Аналогичные рассуждения приводят также к выводу, что обобщенные на случай зависимости от времени вероятности {nyn>} связаны уравнением
л(п+1) = л(п)Р(п), я
решением которого является
= 7t(U)P (0) Р (1) . . . Р(п). п (2.79)
Эти два последние уравнения соответствуют уравнениям (2.55) и (2.56) для однородных цепей Маркова. Уравнения Чепмена— Колмогорова являются средством описания вероятностей, зависящих от времени, и, как мы увидим в следующих главах, позволяют анализировать многие интересные системы массового обслуживания Т
Прежде чем закончить рассмотрение дискретных цепей Маркова, остановимся на частном случае таких цепей — на дискретных процессах размножения и гибели. Процесс размножения и гибели представляет собой марковский процесс, хорошей моделью которого является изменение объема популяции. Следуя этой модели, скажем, что система находится в состоянии Ek, если объем популяции равен k членам. Предположим далее, что объем популяции может изменяться не более чем на единицу, так что рождение приводит к увеличению объема на единицу, а гибель — к его уменьшению на единицу. При исследовании процессов размножения и гибели не допускаются многократные одновременные рождения и гибели; такие процессы классифицируют как случайные блуждания, и они будут рассмотрены ниже. Цепь Маркова рассматривается как однородная в том смысле, что вероятности переходов р,, не зависят от времени; для них допускается, однако, зависимость от состояния системы. Таким образом, для рассматриваемого дискретного процесса размножения и гибели имеем
d,, / = i — 1;
0 в остальных случаях.
Здесь d, — вероятность того, что на следующем шаге произойдет одна гибель, уменьшающая объем популяции до i—1 при условии, что на данном шаге объем популяции равен i. Аналогично bt — вероятность рождения на следующем шаге, приводящего к увеличению объема популяции до i + 1 при условии, что ее текущее
1 Из приведенных рассуждений ясно, что все марковские процессы должны удовлетворять уравнениям Чепмена—Колмогорова. Заметим, однако, что не всякий процесс, удовлетворяющий уравнениям Чепмена—Колмогорова, является марковским; пример можно найти на с. 203 книги [12].
60
значение равно i; 1 — d, — b, представляет собой вероятность того, что ни одно из этих событий не произойдет и на следующем шаге объем популяции не изменится. Допускаются только эти три возможности. Ясно, что d0 — 0, так как гибель не может наступить, если некому погибать.
Однако в противовес интуиции мы допускаем, что Ьо > О, что соответствует возможности рождения, когда в популяции нет ни одного члена. Хотя это можно расценивать как спонтанное рождение или божественное творение, но в теории массового обслуживания такая модель представляет собой вполне осмысленное допущение. А именно, модель такова: популяция представляет собой поток требований, поступающих в систему, гибель означает уход требования из системы, а рождение соответствует поступлению в систему нового требования. Ясно, что в такой модели вполне возможно поступление нового требования (рождения) в свободную систему! Матрица стационарных вероятностей для общего процесса размножения и гибели имеет следующий вид:
1 - Ь1: Ьо 0 0 ... О 0 0 0...’
dx \ — bi -- Ьг 0 ... 0 0 0 0
0 d2 1 - b2 - d., Ь.г . . . 0 0 0 0
Если цепь является конечной, то последняя строка матрицы записывается в виде [0 0 ... 0dN 1 — dv]; это соответствует тому, что не допускаются никакие размножения после того, как популяция достигает максимального объема N.
Матрица Р содержит ненулевые члены только на главной и двух ближайших к ней диагоналях. Из-за такого очень частного вида матрицы Р естественно ожидать, что анализ процесса размножения и гибели не должен вызывать трудностей. Действительно, как было показано, в этом случае легко выписываются в общем виде вероятности состояний на п-м шаге [см. уравнения (2.55) и (2.56)1, а также уравнение (2.50), описывающее предельное поведение системы (при п -> оо). Ранее было также продемонстрировано решение этого уравнения методом производящих функций. Ясно, что для такого простого по структуре процесса, как процесс размножения и гибели, можно ожидать более глубокого анализа полученного решения. Однако это обсуждение откладывается до изложения материала о непрерывных марковских цепях, к исследованию которых мы сейчас и переходим.
61
2.4. НЕПРЕРЫВНЫЕ ЦЕПИ МАРКОВА1
Если движущаяся частица может занимать в пространстве положение из некоторого дискретного множества, но переходы из одного положения в другое разрешаются в любой момент времени, то мы говорим, что это— цепь Маркова с непрерывным временем, или непрерывная цепь Маркова. Для примера с путешественником это означает, что переезды из города в город допускаются в произвольный момент времени дня или ночи. Обозначим через X (/) город, в котором находится путешественник в момент t. Процесс X (/) принимает значения из дискретного множества, в качестве которого выберем упорядоченную последовательность целых чисел, поставив ее во взаимно однозначное соответствие с городами, которые может посетить путешественник.
Определение непрерывной цепи Маркова может быть сформулировано следующим образом.
Определение. Случайный процесс X (0 образует непрерывную цепь Маркова, если для всех целых чисел п и произвольной последовательности /2, ..., /п+1 такой, что /j < t2 < ... < /п+г, выполняется равенство
Р [X (/п+1) = /1X (/J = г\; X (t2) = i2; . .. ; X (tn) =
= г„] = Р [X (tn+1) = j | X (tn) = iJ. (2.81)
Это определение 2 представляет собой непрерывный аналог определения (2.38). Интерпретация этого условия остается прежней: будущие передвижения путешественника зависят от прошлого только через текущее состояние, только от города, в котором он находится в данный момент. Как и следует ожидать, теория непрерывных цепей Маркова аналогична теории дискретных цепей, поэтому можно ограничиться более краткими обозначениями. Кроме того, не будем заострять особого внимания на глубоких вопросах сходимости к пределам, которые возникают при переходе от дискретного времени к непрерывному. Тщательное изложение этих вопросов читатель найдет в работах [4, 12].
Раньше уже говорилось, что течение любого марковского процесса не зависит от того, сколько времени он находится в данном “состоянии; это отсутствие последействия приводит к тому, что для дискретной цепи Маркова время пребывания процесса в данном состоянии является случайной величиной с геометрическим распределением вероятностей [см. доказанное выше равенство (2.66)], а для непрерывной цепи Маркова— случайной величиной с показательным распределением вероятностей. Докажем последнее утверждение. Для этого обозначим время пребы
1 См. сноску на с. 36.
2 Иначе определение марковских процессов с дискретным множеством состояний и непрерывным временем может быть сформулировано в виде
Р [X (0 — /1 X (т) для цст < т2 < t\ = Р IX (0 =--• j I X (т2)].
62
вания процесса в состоянии Е. через т,. Вспомним, что согласно марковскому свойству вся предыстория влияет иа будущее процесса только через текущее состояние. В частности, это означает, что нет необходимости знать, как долго процесс находился в данном состоянии. Отсюда следует, что распределение остаточного времени пребывания в состоянии Е, должно зависеть только от i и не зависеть от того, как долго процесс уже находился в состоянии Е,. Это можно записать в следующем виде:
Р [т; > s + 11 т,- > s] = h (/),
где h (/) — функция, зависящая только от дополнительного времени t (и не зависящая от времени s, уже проведенного процессом в состоянии Е,) *. Эту условную вероятность можно переписать в виде
Р [т(- >> s 4- 11Т; > s] =
_ Р [Т; > S Т; > S] ___ Р [Т/ > S -|- /]
~ р [т, > S] ~ Р [те > S]
Последнее равенство в этой цепочке имеет место потому, что событие т, > s + t влечет за собой событие т,- > s. Используя функцию h (/), еще раз можно записать равенство
Р К- > s + /] = Р [т, >s]h (0- (2.82)
Полагая s = 0 и замечая, что Р [т, > 01 = 1, сразу находим, что Р [т, > /] = h (t). Подставляя это равенство в (2.82), для s, / щ 0 получаем
Е [т; > s -I- /] = Р [rz > s] Р [т; > I]. (2.83)
(Полагая s = t = 0, снова приходим к условию Р К> 0] — 1.) Покажем теперь, что единственной из непрерывных функций распределения, удовлетворяющих условию (2.83), является показательная функция. Полагая g (/) ~ Р [т,- > I] по определению, получаем следующее равенство:
g' (t) = -±-(Р [т,. > /]) = ddt (1 - Р [т, с /]) = (2.84)
где fx. (/) означает плотность распределения случайной величины т,-. Теперь равенство (2.83) устанавливает
g(« + 0 = g(s)g(0-
Вычитая g (/) от обеих частей этого равенства и деля на s, получаем
* Символ s употребляется для обозначения времени только в данном параграфе, и его не следует путать с обозначением формальной переменной преобразований, используемым в остальной части книги.
63
Переходя к пределу при s -> 0 и применяя правило Лопиталя к правой части, находим
О) = g(0g'(0)-
Таким образом, = g' (0), и интегрирование по t дает Ing (/) = g' (OW-j-C.
Так как g (0) = Р [т,- > 0 ] — 1, то С — 0. Итак, g (t) = е®' <°>z, и, поскольку g' (t) = g (/) g’ (0), то
g'(0 = efi' {(l)t g' (0).
Используя равенство (2.84), находим плотность распределения вероятностей случайной величины ту в виде
М=М0)еЛ(0)/, />0. (2.85)
Таким образом, плотность распределения вероятностей времени пребывания процесса в состоянии Е, представляет собой показательное распределение с параметром fx. (0), который, вообще говоря, может зависеть от состояния . О показательном распределении и той важной роли, которую оно играет в марковских процессах, будет говориться еще много.
Для дискретной однородной цепи Маркова были определены вероятности переходов рч — Р [Хп = /|ХП_1 = И, а также вероятности переходов за т шагов pt"l} = Р [Хп+т = j\Xn =Л1; в силу однородности цепи Маркова эти вероятности не зависят от т. Для неоднородных цепей Маркова приходится вводить некоторую дискретизацию временной оси и с ее помощью определять вероятности переходов p(i (т, п) — Р [Х„ = /1 Хт = Л. Совершенно аналогичным образом определим теперь для рассматриваемых непрерывных цепей Маркова следующие, являющиеся функциями времени, вероятности переходов:
Pt, \S, t) A P [X (/) = j | X (s) = i], и (2.86)
где X (/) — положение частицы в момент t > s. Точно так же, как в дискретном случае были рассмотрены три последовательных момента времени т < q < п, для непрерывных цепей Маркова можно рассмотреть три последовательных момента времени s < и t. Вернемся при этом к рис. 2.7 и рассмотрим некоторые реализации процесса, предполагая теперь процесс непрерывным; основное замечание опять сводится к тому, что, попадая из состояния Ei, в котором процесс находится в момент s, в состояние Е, в момент t, процесс должен в некоторый промежуточный момент и пройти через некоторое промежуточное состояние Ek. Поступая дальше точно так же, как и при выводе уравнения (2.70), приходим 64
к следующей системе уравнений Чепмена—Колмогорова для непрерывных цепей Маркова:
Ра (s- 0 = 2 Ptk («. м) Pkj (и, t), (2.87)
k
где i, j— 0, 1, 2, ... Эту систему уравнений! можно записать в виде матричного уравнения, если определить матрицу, состоящую из элементов (s, /), равенством
H(s. /)A[p,;(s. 01- - (2.88)
Тогда система уравнений Чепмена—Колмогорова приводится к виду
Н (s, /) = Н (s, и) Н (u, t), s < и <: /. (2.89)
(Матрица Н (t, t), по определению, равна единичной матрице I.)
В случае однородной дискретной-1 цепи Маркова для ответа на вопрос, является ли данная цепь эргодической, а также для решения других вопросов, необходимо исследовать матричное уравнение л: = лР. Для неоднородного случая вероятности переходов могут быть найдены с помощью уравнения =
= л<°)р (0) Р (1) ... Р (и), которое задает их выражение через вероятности ц,-, (т, п), представляющие собой функции времени. Для непрерывных цепей Маркова вероятности переходов за один шаг заменяются инфинитезимальными интенсивностями, которые будут определены ниже; как увидим, они определяются через производные от функций р^ (s, Z) при t ->-s.
Сейчас перейдем к построению для непрерывного времени аналогов прямого и обратного уравнений. Мы уже вывели уравнение (2.89), представляющее собой аналог уравнения (2.73) для дискретного времени. Теперь нам понадобятся аналоги уравнений (2.74)—(2.77), которые приводят к прямому и обратному уравнениям в обычной и матричной формах. Остановимся, например, на выводе прямого уравнения, исходя из уравнения (2.75), а именно из уравнения Н (т, п) = Н (/и, п — 1) Р (ц — 1), устремляя к нулю длину единичного интервала. Используя это уравнение, запишем следующую разность:
Н (m, п) — Н (т, /г — 1) = Н (m, п — 1) Р (/г — 1) —
— Н (т, — 1) = Н (//г, п — 1) [Р (/г — 1) — I]. (2.90)
Рассмотрим теперь некоторые пределы. По аналогии с тем, как в дискретном случае матрица Р (/г) была определена равенством Р (/г) = Н (/г, п •( 1), в непрерывном случае удобно определить следующую матрицу:
P(Wp,/(O +/И)]. (2.91)
Определим далее матрицу И ($, /) как предел матрицы Н (т, ti) при неограниченном уменьшении единичного временного интервала, а матрицу Р (t) как предел матрицы Р (л). Возвращаясь
3 Л. Клейнрок 65
к равенству (2.90), разделим обе его части па А/ и перейдем к пределу при А/ —► 0. Ясно, что тогда выражение, стоящее в левой части равенства, обращается в производную
аН^’ П- = Н (s, t) Q (0, s < t, в (2.92)
где через Q (/) обозначена следующая предельная матрица
Q(/) = lim (2.93)
Д-~>0
Матрица Q (/) называется инфинитезимальным оператором матричной функции переходов Н (s, f). Другим, более наглядным названием Q (/) является матрица интенсивностей переходов; мы будем пользоваться обоими названиями. Обозначим элементы матрицы Q (/) через qtj (/); они представляют собой упомянутые интенсивности переходов и определяются следующим образом:
7,;(/) = lim ; (2.94)
Д/->9
Яч (/) = lim <z’J-±-Az) , i /. (2.95)
д/->о
Эти пределы имеют следующую интерпретацию. Если в момент t система находилась в состоянии Е,, то вероятность перехода в течение промежутка времени (/, t + AZ) в произвольное (отличное от Д) состояние задается величиной —(/) А/ + о (Nt') *. Таким образом, величину —qtj (t) можно интерпретировать как интенсивность, с которой процесс уходит из состояния Д при условии, что он находился в этом состоянии. Аналогично, условная вероятность перехода процесса в течение времени (/, t + А/) из состояния Ei в состояние Е, при условии, что он находился в состоянии Ei, задается величиной +<?,/ (/) Nt + 0 (Nt). Таким образом, величину д^- (/) можно интерпретировать как интенсивность, с которой процесс переходит из состояния Et в состояние Еj при условии, что Ei — текущее состояние процесса. Так как всегда 2 /Д ($, 0 ~ 1, то из равенств (2.94) и (2.95) следует, / что при всех i
£ Чч (0 = °- (2.96)
* Как обычно, символ о (Д/) («о» малое от Д/) означает произвольную функ-о (Д/)
цию, которая при Д/->0 стремится к нулю быстрее, чем Дг, т. е. lim —т-— =- 0.
В более общем случае говорят, что функция g (f) прдставляет собой о (у (I)) при t -* t., если lim ) 1 0.
lit) |
По поводу определения О () («О» большого) см. с. 301 гл. 8.
66
Таким образом, дана интерпретация для всех членов, входящих в равенство (2.92); оно представляет собой ни что иное, как прямое уравнение Чепмена—Колмогорова для непрерывной цепи Маркова.
Аналогично, исходя из уравнения (2.77), придем к обратному уравнению Чепмена—Колмогорова:
-ЭНЛ’° = — Q (s) Н (s. /), s < t. « (2.97) С/ J
Эти прямое и обратное матричные уравнения могут быть записаны определенным образом в виде систем уравнений для элементов входящих в них матриц. Из прямого матричного уравнения [при дополнительном условии равномерности предельного перехода (2.95) по i при фиксированном71 получаем
+ % qk;(i)pik(s, t). (2.98)
k+i
Пребывание процесса в начальный момент времени s в начальном состоянии £, определяет следующие начальные условия для выбора решения этой системы дифференциальных уравнений:
( 1, если i = /; о,-, (s, s) == { „
' 1 [0, если i А /
Из обратного матричного уравнения получаем
щщзД ф (s> ty (2.99)
k* i
Начальные условия для этой системы записываются в виде
( 1. если i — /;
Ра (t, t) = n ... ' (0, если i /.
Уравнения (2.98) и (2.99) однозначно задают вероятности переходов pi, (s, t) и, конечно, удовлетворяю г уравнению (2.87) и начальным условиям.
Решения прямого и обратного уравнений (2.92) и (2.97), естественно, могут быть записаны и в матричной форме; предполагая, что матрица Q перестановочна с различными значениями t, получим 1
t
Н (s, t) = exp j Q(r)dn . (2.100)
1 Выражение ePZ, где P — квадратная матрица, определяется в виде следующего степенного ряда:
ер-' - I-l-P/юр2-^- + Р3 -Jr+ -
3* 07
Заметим, что эта матрица является также решением уравнения (2.89) и представляет собой непрерывный аналог дискретного решения (2.78).
Теперь о самих вероятностях состояний: по аналогии с определим
л,-(О Л Л [А (О = /], (2.101)
а также вектор этих вероятностей состояний
л(0А[ло(/), П1(Г), л2(/), . . .]. (2.102)
При заданном начальном векторе л (0) распределения состояний вектор л (/) находят как решение уравнения
л (/) л (0) Н (0, t).
(2.103)
общее решение которого, как нетрудно увидеть из (2.100), опре-
деляется равенством
л (/) = л (0) ехр
- t
6
Q (и)du
и (2.104)
Это соответствует дискретному аналогу, задаваемому равенством (2.79). Легко также видеть, что матричное дифференциальное уравнение, соответствующее уравнению (2.103), записывается в виде
^P- = «(/)Q(0-
Это уравнение, подобно уравнению (2.92), может быть записано в виде уравнений для элементов матриц:
dn: (О
= qH (/) Лу (/) ф £ (0 (0- (2.105)
Аналогия между системами уравнений (2.105) и (2.98) не является случайной. Последняя система описывает вероятность того, что в момент t процесс находится в состоянии Е, при условии, что в момент s он находился в состоянии Et. Система (2.98) просто задает вероятность того, что в момент t процесс находится в состоянии £,; информация о начале процесса содержится в векторе л (0) вероятностей начальных состояний. Если лА (0) = 1 при £ = i и я,. (0) = 0 при k 4 i, то можно с уверенностью утверждать, что в момент 0 система находилась в состоянии £,. В этом случае вероятность л, (/) тождественно равна р,;- (0, /). Часто используют обе формы этой вероятности: когда желательно выделить начальное состояние, используют форму р,;- (s, /); если же начальное состояние несущественно, то используют л,- (Z). 68
Остановимся теперь на однородной непрерывной цепи Маркова. В этом случае опустим зависимость от времени и введем следующие обозначения:
/Л, (t) А р,! (s, s R); (2.106)
(0 6 / = 1, 2, . . . ; (2.107)
H(/)AH(s, s + 0-I/MOl; «(2.108)
QAQ(0 = [<?./]. (2.109)
Выпишем основные результаты в соответствующем данному случаю виде. Прежде всего уравнения Чепмена—Колмогорова примут вид
P,;(s-r/)= Е P-*(S)P*;(O ®
k
или в матричной форме 1
H(s + 0 = H(s)H(/).
Прямое и обратное уравнения соответственно будут
-эт— 7;/Рч'(0 + L feP/c (0 (2.110)
и
------------------at---= — Qi.Pii (0 - (2.111) или в матричной форме
«(2.112) и
^1 = QH(/) «(2.113)
с общим начальным условием Н (0) I. Решение этих матричных уравнений имеет вид
H(0-=eQz. «
Сами вероятности состояний цепи связаны системой дифференциальных уравнений d^t f (t)
= S %/Л/ЛО- (2.114)
1 Соответствующий дискретному случаю результат просто имеет вид Р"1+'' _ р»1р'У
69
которые в матричной форме записываются в виде уравнения
at
Можно показать, что для неприводимой однородной цепи Маркова всегда существуют пределы lim р,-7- (/) = не завися-
ОО
щие от начального состояния цепи. Множество {л,} представляет собой предельное распределение вероятностей состояний. Цепь в рассматриваемом случае является эргодической, и, как для всякой эргодической цепи, предельное распределение вероятностей ее состояний не зависит от начального распределения, а именно lim л;- (/) = л,-. Это предельное распределение задается как одно-значное решение следующей системы линейных уравнений:
qti^i + X q^k = 0- (2.115)
В матричной форме эта система записывается уравнением
л0 = 0, (2.116)
где л = [л0, nj, л2, ...]. Это уравнение вместе с нормирующим условием
S л; = 1 (2.117)
/
однозначно определяет предельное распределение вероятностей. Сравним уравнение (2.116) с полученным ранее уравнением для дискретных цепей Маркова, а именно с уравнением л = лР; в последнем уравнении Р — матрица вероятностей переходов; матрица Q, входящая в уравнение (2.116), представляет собой матрицу интенсивностей, переходов.
На этом мы заканчиваем обсуждение цепей Маркова. В таблице на с. 418 дана сводка основных результатов для четырех рассмотренных случаев. Дальнейшие результаты по этому вопросу читатель может найти в работе [11.
Рассмотрев цепи Маркова (с дискретным и непрерывным временем), естественно было бы перейти к марковским процессам с непрерывным пространством состояний. Мы не будем, однако, этого делать, а отложим рассмотрение соответствующего материала до тех пор, пока он понадобится (так, например, в гл. 5 будет рассмотрено интегро-дифференциальное уравнение Такача для системы типа М G/1, а в гл. 2 тома II для построения диффузионной модели С.МО будет введено уравнение Фоккера— Планка). Изучая далее марковские процессы, остановимся на процессах восстановления, случайных блужданиях и, наконец, на полумарковских процессах. При этом предпочтительно также отложить изучение данных вопросов до тех пор, пока они не понадобятся по ходу изложения (например, в гл. 5 будут рассмотрены цепи Маркова, вложенные в полумарковские процессы).
70
Надо признаться, что уравновешенное изложение материала настоящей книги требует введения дополнительного материала по теории вероятностных процессов, и это по мере необходимости будет выполнено. Сейчас остановимся на применении результатов, полученных для непрерывных цепей Маркова, к классу процессов размножения и гибели, которые, как уже говорилось, играют основную роль в анализе СМО. Это непосредственно приведет нас к важным пуассоновским процессам.
2.5. ПРОЦЕССЫ РАЗМНОЖЕНИЯ И ГИБЕЛИ
Раньше в этой главе процессы размножения и гибели были определены как частный случай марковских процессов, для которых допустимы переходы из состояния Ek только в соседние состояния Ek_r, Ek и Это ограничение позволяет во многих случаях значительно углубить решение. Такие процессы оказываются замечательной моделью для всей элементарной теории массового обслуживания, рассматриваемой в гл. 3, и являются отправной точкой для изучения СМО. Дискретный процесс размножения и гибели менее интересен, чем непрерывный, поэтому в дальнейшем он подробно не рассматривается; нет необходимости говорить, что для этого случая проходят почти параллельные выкладки. Далее, переход процесса из состояния Ek обратно в состояние Ek представляет непосредственный интерес только для дискретных цепей Маркова; в непрерывном случае интенсивность, с которой процесс возвращается в текущее состояние, равна бесконечности, и проницательный читатель должен заметить, как аккуратно был исключен этот член в определении (2.94). Таким образом, основное внимание будет сосредоточено на непрерывном процессе размножения и гибели с дискретным пространством состояний, для которого допускаются переходы из состояния Ek только в соседние состояния Д.„х и Ем *.
Раньше процесс размножения и гибели был использован как адекватная модель для описания изменений, происходящих в объеме популяции. Мы говорили, что процесс находится в состоянии Ek, если объем популяции равен я; переход н.з состояния Ек в состояние Ем соответствовал рождению, а переход из Ек в — гибели.
Таким образом, мы рассма 1ривдем изменения в объеме популяции, которые переводят процесс из состояния Е,. только в ближайшие состояния. Обозначим через интенсивность ризмн«-
* Это описание справедливо только в одномерном случае. Позже, в гл. 4, будут рассмотрены многомерные системы, состояния которых описываются дискретными векторами, когда каждое состояние имеет по два соседних в каждом измерении. Например, в двумерно’! случае состояние Ек k задаваемое парой координат (fcp £_>), имеет чеище соседних: л k , Ek , , ,, Е,. и и
71
жения; она описывает скорость, с которой происходит размножение в популяции объема k. Аналогично, через р,>, обозначим интенсивность гибели, задающую скорость с которой происходит гибель в популяции объема k. Заметим, что введенные интенсивности размножения и гибели не зависят от времени, а зависят только от состояния Ек‘, следовательно, получаем непрерывную однородную цепь Маркова типа размножения и гибели. Эти специальные обозначения введены потому, что они непосредственно приводят к обозначениям, принятым в теории массового обслуживания; в зависимости от ранее введен <ых обозначений имеем К ~ и М-* = 4k,k-l-
Требование о допустимости переходов только в ближайшие соседние состояния означает, что qkj = 0 при \k—j\ > I. Более того, так как уже доказано [см. уравнение (2.96) ], что qkj = О, это требование означает, что
(2.И8)
Таким образом, инфинитезимальная производящая матрица для общего однородного процесса размножения и гибели принимает
ВИД Q Pi 0 0 Х-о — (^1 + Pi) 0 0 К (^2 + Г1з1 Рз 0 0 к, (^з + Рз) 0 0 0 . . . Хз
•
Заметим, что за исключением главной и соседних с ней снизу и сверху диагоналей все элементы матрицы равны нулю.
Более точно: некоторый процесс представляет собой процесс размножения и гибели, если он являлся однородной цепью Маркова X (/) с множеством состояний [0, 1, 2, ...], если рождение и гибель являются независимыми событиями (это вытекает непосредственно из марковского свойства) и если выполняются следующие условия:
Вк : Р [точно 1 рождение в промежутке времени (/, t Д/)| объем популяции равен k] = 7.k А/ + о (А/);
Dj : Р [точно 1 гибель в промежутке времени (/, t !- А/) | объем популяции равен k\ = р* А/ + о (А/);
В2 : Р [точно 0 рождений в промежутке времени (/, t Д- А/)| объем популяции равен k] ~ 1 — ~г о (At);
D2 : Р [точно 0 гибелей в промежутке времени (/, t д- А/) | объем популяции равен k \ = 1 — рА AZ 4- о (А/).
Согласно этим предположениям кратные рождения, кратные гибели и одновременные рождения и гибели в течение малого промежутка 72
времени запрещены в том смысле, что вероятность таких кратных событий имеет порядок о (А/).
Будем искать вероятность того, ччо объем популяции в некоторый момент времени t равен k; обозначим эту величину 1
P^t} Л P[X(J) ^/г|. (2.119)
Эту вероятность можно вычислить непосредственно из уравнения (2.114) для вероятностей лу (/) и конкретных значений q^.
Однако, учитывая простоту, с которой для процесса размножения и гибели эти уравнения могут быть составлены непосредственно на основании сформулированных принципов, мы не будем пользоваться развитой в предыдущем параграфе громоздкой техникой, затемняющей простоту основного подхода, а выведем эти уравнения заново. Читателю рекомендуется отметить параллельные этапы и сравнить вывод с описанной ранее общей процедурой. Заметим, что в соответствии с принятыми ранее обозначениями, Рк (/) — лА, (/). Кроме того, пока умолчим о начальных условиях и введем их только тогда, когда они понадобятся.
Начнем с описания динамики Чепмена—Колмогорова, которая в данном случае является чрезвычайно простой. А именно, рассмотрим возможные перемещения частицы, т. е. изменение объема популяции в промежутке времени (/, t + А/). В момент t + А/ процесс будет находиться в состоянии Ek, если произошло одно из следующих трех (взаимно исключающих и исчерпывающих все возможности) событий:
1) в момент t объем популяции был равен k и в течение времени (/, t у- А/) не произошло изменения состояния;
2) в момент t объем популяции был равен k — 1 и в течение времени (/, t + А/) родился один член популяции;
3) в момент I объем популяции был равен k + 1 и в течение времени (/, i 4- А/) погиб один член популяции.
На рис. 2.8 представлены эти три возможности. Вероятность первого события равна вероятности Pk (f) того, что в момент i процесс находился в состоянии Ек, умноженной на вероятность pkk (At) перехода в течение следующих А/ секунд из состояния Ek
1 Использованный здесь символ .¥ (t) для обозначения числа требований в системе в момент времени t выбран для согласования с обозначениями, используемыми в общем случае вероятностного процесса. На самом деле мы должны были, как и раньше писать N (t); вне данной главы везде используется символ v (')•
73
в состояние Е/. (т. е. на вероятность отсутствия на интервале Л/ секунд рождения или гибели); эта возможность описывается первым слагаемым в правой части выписанного ниже равенства (2.120). Второе и третье слагаемые в правой части этого равенства соответствуют остальным двум указанным выше событиям. Переходы в состояние Ек из состояний, не являющихся соседними, не^рассматриваются, так как предполагается, что вероятности таких событий в промежутке времени Л/ имеют порядок о (А/)-Таким образом, можно записать
рк р 'г АО — к (A/) U Pk_x (0/Vl . (АО 4-
(2.120)
Эти три вероятности можно складывать, потому что соответствующие события, очевидно, взаимно исключают друг друга. Ясно, что равенство (2.120) имеет смысл только при k 1, так как популяция не может состоять из —1 члена. Граничное равенство при k — 0 имеет, в частности, следующий вид:
P0(t г АО-Ро 4),Ню (АО 4-Л (О Ло (АО + о (АО, /г-=о. (2.121)
Кроме того, ясно, что в момент / все возможные состояния должны удовлетворять нормирующему условию
= (2.122)
л=о
Теперь воспользуемся предположениями Bv Dlt В2 и О2 для вычисления коэффициентов, входящих в систему уравнений (2.121)—(2.122). Это приведет рассматриваемую систему к виду
Л (t 4- АО = Рк (011 - ^А/ + о (AOJ [ 1 - + о (АО] +
+ Л-i (0 P-ft-i А^ + о (А01 + Л+1 (0 (HmAi +
+ о (А01-Ко (АО, /г^1; (2.123)
Ро () 4- АО = Ро (0 [1 - А0А/ 4- о (АО] +
4-Л(0[И1А( + о(А0]4-о(А0, /г = П. (2,124)
В уравнении (2.124) использовано предположение, что, если объем популяции равен 0, то не может произойти гибели (т. е. Во = 0), по может произойти рождение члена популяции (А,о > 0). Раскрывая скобки в правых частях (2.123) и (2.124), получаем
Рк(1 гА0-Л(0-ЛЛ Щ)А/Л(О +
4- V1A(P^! (0 4- Р-а+1А/Л+1 (0 + 0 (АО, & > 1;
Ро 4 4- А/) .3= Ро (0 - Z0A/P0 (0 + (/) -4 о (АО, k =-- Q.
74
Выделяя теперь Рк (I) из обеих частей в обоих равенствах й деля на AZ, приходим к уравнениям
pk(t + А/) -РкЩ
А/
— — (/./г Ji*) Рк (О Н~ 1-k-iPk-i (0 +
1; (2.125)
Ро + АО Ро ' __ 1 Е> О'.
- Ао/ и[Ч-
-ЬЦ1Р1(0 - А>-= 0. (2.126)
Переходя к пределу при Д/ — сю, видим, что левые части в (2.125) и (2.126) представляют собой производные от Рк (/) по /, а член о (At)/At стремится к нулю. Следовательно, окончательно уравнения записываются в виде
Т + Ы Рк (0 г h-iP^ !Ф) +
т P-k+iPk+i (0> *>1; в (2.127)
-^< = -Vo(/)^MA(0, А = о.
Ясно, что уравнения (2.127) являются искомой системой дифференциально-разностных уравнений, описывающих динамику рассматриваемого вероятностного процесса; в них легко узнать систему уравнений (2.114). Решение этой системы представляет собой характеристику Рк (/). Остается только найти это решение. (Подчеркнем, что при выводе этой системы уравнений в существенной степени использовались уравнения Чепмена—Колмогорова.)
Для решения полученной системы уравнений (2.127) в нестационарном случае, когда вероятности Рк (t) зависят от времени, воспользуемся начальными условиями. Иначе говоря, необходимо задать Рк (0) при k = 0, 1, 2, ... . Кроме того, должно удовлетворяться условие (2.122).
Отвлечемся временно от решения поставленной задачи для того, чтобы описать простой метод непосредственного выписывания приведенных выше дифференциально-разностных уравнений. Начнем с замечания о том, что другим способом описания информации, содержащейся в матрице Q, является диаграмма интенсивностей переходов из одного состояния процесса в другое. На такой диаграмме состояние Ek обозначается овалом, в котором записывается число k. Каждой ненулевой инфинитезимальной интенсивности qij (каждому ненулевому элементу матрицы Q) на диаграмме интенсивностей переходов соответствует направленное от Ес к Ej ребро, которому приписана величина qlS. В диаграмму не включены петли, ведущие из состояния Ek обратно в состояние Ek, так как 1см. равенства (2.96) и (2.118)], члены на главной Диагонали матрицы Q не содержат никакой новой информации.
75
1
А -Аг
Рис. 2.9. Диаграмма интенсивностей переходов для процесса размножения и гибели
На рис. 2.9 показана диаграмма интенсивностей переходов для процесса размножения и гибели общего вида.
Диаграмма позволяет наглядно описать процесс движения некоторой частицы от одного состояния к другому; ребра указывают возможные переходы, а приписанные им числа представляют собой инфинитезимальные интенсивности, с которыми осуществляются эти переходы. Подчеркнем, что числа, приписанные этим направленным ребрам, соответствуют интенсивностям размножения и гибели, а не их вероятностям. Для того чтобы пересчитать эти числа в вероятности, необходимо умножить каждое из них на dt. Тогда получатся вероятности таких переходов в последующий промежуток времени продолжительностью dt. При этом необходимо также вспомнить о петлях, имеющихся в каждом состоянии и определяющих вероятность того, что в последующем промежутке времени продолжительности dt процесс останется в том же состоянии. Подчеркнем еще раз, что диаграмма интенсивностей переходов содержит ту же самую информацию о процессе, что и матрица Q интенсивностей переходов.
Сосредоточив внимание на состоянии Ек, замечаем, что попасть в него можно только из состояний Ек_к или Ем, так же как и, покидая его, можно перейти только в состояния Ек_^ или Ек+1. Именно поэтому подобные процессы принято называть процессами размножения и гибели с переходами в соседние состояния.
Из рассмотренной динамики ясно, что разность между интенсивностью, с которой система попадает в состояние Е,;, и интенсивностью, с которой система покидает состояние должна равняться интенсивности изменения «потока» в это состояние. Это замечание — решающее, оно указывает простой интуитивный способ составления уравнений, определяющих вероятности Рк (/). Фиксируя, в частности, внимание на некотором состоянии Ек, видим, что интенсивность, с которой поток вероятностей направлен в момент t в это состояние, описывается равенством:
Интенсивность потока в состояние Ек ~
= ^k-lP А-1 (0 + Ц/г+1^ А>+1 (0> а интенсивность, с которой поток в момент I покидает это состояние, дается равенством:
Интенсивность потока из состояния Ек = (Х/; fij Р,. (/). Ясно, что разность между этими потоками равна эффективной интенсивности потока вероятностей в состояние Ек.
(/) F Щ+Л+1 (0 -- + Н*) Рк U). -(2.128)
76
Но это уравнение в точности совпадает с уравнением (2.127)! Мы не останавливались подробно на рассмотрении граничного состояния Ео, но легко видеть, что использованная нами аргументация приводит к правильному уравнению для случая k = 0. Заметим, что каждый член уравнения (2.128) имеет вид произведения вероятности пребывания процесса в момент времени t в конкретном состоянии на инфинитезимальную интенсивность ухода из этого состояния. Ясно также, что все наши действия сводились щ к созданию воображаемой границы вокруг состояния Е/, и подсчету интенсивностей; при этом входящему и исходящему потокам приписывались противоположные знаки потоков вероятностей, пересекающих указанную границу; полный баланс определяет производную по времени от интенсивности потока вероятности, входящего в данное состояние.
Фактически совсем необязательно рассматривать уравнения потока для единственного состояния системы. Можно выбрать произвольное множество состояний внутри некоторого контура и выписывать уравнение для всех потоков, пересекающих границу. Единственная опасность, которая появляется при этом, состоит в том, что выписанные уравнения могут оказаться зависимыми', если же рассматривать каждое состояние в отдельности и выписывать уравнение, отражающее закон сохранения для каждого из них, то можно гарантировать, что полученная система содержит независимые уравнения, причем система должна быть дополнена еще одним независимым условием (2.122) *. Таким образом, для составления уравнений, описывающих процесс размножения и гибели, имеется очень простой графический способ. Как станет ясно позднее, этот подход полностью пригоден и для других марковских процессов (включая полумарковские процессы) и часто будет использован в дальнейшем; это замечание подводит нас также к понятиям глобального и локального равновесия (см. гл. 4).
Сейчас важно, чтобы читатель понял и принял тот факт, что описанный процесс размножения и гибели представляет собой основу для обсуждения многочисленных важных задач, представляющих интерес для теории массового обслуживания. Непосредственное решение системы (2.127) в соответствующих частных случаях приводит к описанию переходного режима работы СМО, который для этой книги представляет меньший интерес, чем характеристики системы в установившемся режиме, или в состоянии равновесия Е Однако с целью иллюстрации и дальнейшей детализации этих уравнений, приведем теперь некоторые важные примеры.
* Если число состояний конечно (например, k состояний), то любая система уравнений для k—1 узлов является независимой. Необходимым добавочным уравнением является условие (2.122).
1 Переходные характеристики процесса обсуждаются в другом месте этой книги и более подробно в гл. 2 тома II. Замечательное изложение этого вопроса читатель найдет в работе [2].
77
Рассмотрим простейший процесс чистого размножения, который определяется как процесс, для которого щ = 0 при всех k (заметим, что на рис. 2.4 мы сейчас находимся во втором внутреннем круге!). Кроме того, для еще большего упрощения задачи предположим, что Хь = Л. для всех k = 0, 1,2, ... . (Теперь мы попадаем в самый внутренний круг! Поэтому, естественно ожидать появления некоторых замечательных свойств процесса.) Подставляя эти значения в уравнения (2.127), получаем
,= (0 л. l (/), k > 1; (2.129)
— М>0(/), # = О
Для простоты предположим также, что процесс начинается в нулевой момент времени при нуле членов, т. е.
(1, /<=-=0;
И kpQ. -130>
Отсюда для Ро (I) получаем решение
Подставляя это решение в уравнение (2.129) при k = 1, приходим к уравнению
(/) - l Хе~к .
Решение этого дифференциального уравнения, очевидно, имеет вид
-pi(0 = cte "
Далее по индукции в качестве решения уравнения (2.129) находим
ЬО, z>0. а- (2.131)
Это и есть знаменитое распределение Пуассона. Таким образом, процесс чистого размножения с постоянной интенсивностью Л приводит к последовательности рождений, образующей пуассоновский процесс. Перейдем к более тщательному изучению пуассоновского процесса и найдем его связь с показательным распределением.
Процесс Пуассона занимает центральное место в элементарной и промежуточной теориях массового обслуживания и широко используется. Такое особое положение этого процесса обусловлено двумя причинами. Во-первых, как мы видели, он занимает самую внутреннюю области на рис. 2.4 и, следовательно, обладает многочисленными замечательными и упрощающими аналитическими 78
и вероятностными свойствами; это станет безусловно ясным из дальнейшего обсуждения. Вторая причина состоит в том, что многие реальные физические и естественные процессы можно хорошо моделировать пуассоновскими процессами. Например, одно из первых упоминаний пуассоновского процесса относится к исследованиям Фрая [5], который показал, что пуассоновский процесс хорошо описывает число солдат в армии, убитых копытами своих коней. Другими примерами являются гамма-лучи, излучаемые радиоактивной частицей, и последовательность промежутков времени, в которые возникают вызовы на телефонной сети. Действительно, как показали Пальм [11] и Хинчин [8], во многих случаях сумма большого числа независимых стационарных процессов восстановления (каждый с произвольным распределением времени восстановления) сходится к процессу Пуассона. Этот результат является важной предельной теоремой и объясняет причину, по которой процесс Пуассона столь часто возникает в природе в тех случаях, когда наблюдается совокупный эффект большого числа индивидуумов или частиц.
Поскольку в дальнейших исследованиях СМО будет использован этот аппарат, введем сразу обозначения, применяемые в теории массового обслуживания, а также условимся рассматривать процесс Пуассона как модель потока требований, поступающих в СМО, а не как модель размножения членов популяции. Таким образом, Л. означает интенсивность поступления требований в систему. При начальных условиях (2.130) величина Рк (f) означает вероятность появления k требований в промежутке времени (0, /). Так как интенсивность поступления равна К требований в секунду, то интуитивно ясно, что среднее число требований, поступающих в промежутке длины t, равно М. Проверим это интуитивное утверждение точными вычислениями. Обозначив через К число требований, поступающих в промежутке времени длины t [раньше для обозначения этой величины использовался символ «(£)], получим
Е[К
По определению, е* = 1 ~|- х 4- №/2! + ..., поэтому
Е [Д] = ХД а (2.132)
Таким образом, ожидаемое число поступающих требований в промежутке времени (0, /) равно X/.
ph(t)
Вычислим дисперсию числа поступающих требований. Для этого удобно сначала вычислить следующий момент:
£[Л(/( -1)]=У /ДА - П/’ДО
/г — О
* = 0 k = 2
<- =0
Определяя теперь дисперсию через этот вычисленный момент и среднее значение Е [К], получаем
0-к -= Е Ц\ (Д' - 1)! + Е [/<J - (£ [К\)2 =- (М'у u М - (Му
и, следовательно,
од •— W.
(2.133)
Таким образом, среднее значение и дисперсия для пуассоновского процесса одинаковы и равны М.
На рис. 2.10 показано семейство кривых Pk (t) как функций от k и от М (удобный способ нормирования t).
80
Напомним, что согласно формуле (11.27) приложения II производящая функция для дискретной случайной величины К с распределением вероятностей
& - Р [К = /?] задается равенством
G (г) Е \zk\ = Y zkgk k
при I? | < 1. Применительно к описанному выше процессу Пуассона имеем
£ lz** --S z';Pk{i} S e~w =
и, следовательно,
G(z) /;|гЛ1 <*?/ (2.134)
Производящая функция для распределения Пуассона оказывается очень удобной при решении многих задач. Например, используя специальные свойства производящей функции (см. приложение II), можно очень легко вычислить среднее значение и дисперсию, задаваемые равенствами (2.132) и (2.133), следующим образом
G<i)(l) ^ELe^]^ ^Е[К]
Применяя этот результат к распределению Пуассона, получаем
Е [К] = |г=1 = М
и
ок = G(2) (1)G(1) (1) — [G(1) (I)]2.
Следовательно, для распределения Пуассона
су к = (М)2ем <^1) Ui r U - (V)2 = И.
Это подтверждает предыдущие вычисления.
Пуассоновский процесс был введен как процесс чистого размножения, и было найдено распределение вероятностей Ph (/) поступления k требований в течение заданного промежутка времени I. Найдем теперь совместное распределение вероятностей моментов поступления требований при условии, что в течение рассматриваемого промежутка времени поступило ровно k требований. Разобьем интервал (0, t) на 2 k -j- 1 промежутков, как показано на Рис. 2.11. Обозначим через событие, состоящее в том, что в промежутках )|3,} поступает точно по одному требованию,
1 Необходимо вспомнить сокращенные обозначения, введенные в приложении II [см. (11.25)].
81
Л
о
Рис. 2.11. Разбиение промежутка времени (0, t)
а в промежутках {а,} никаких требований не поступает. Задача состоит в вычислении вероятности события Ak при условии, что на интервале времени (О, /) поступило ровно k требований; согласно определению условной вероятности должно выполняться равенство
Р [Л/; | ровно /г требований в промежутке (0, /)] —
_ Р [Д* и ровно k требований, в промежутке (0, /)] ।
Р [ровно k требований! в промежутке (0, /)] ’ ‘ 1
Для пуассоновского потока требований события на пепересекаю-щихся промежутках являются независимыми, и вероятность совместного события можно вычислить как произведение вероятностей отдельных событий (т. е. пуассоновский процесс является процессом с независимыми приращениями). Согласно (2.131)
Р [одно требование в промежутке р,] =
и
Р [ноль требований в промежутке а,] = е>г/'•
Подставляя эти значения в равенство (2.135), непосредственно получаем
Р[Лд,| ровно k требований в промежутке (0, 01 —
_ (zp, лр2 , , , .^е~Же~Х|3г еХР/г) . е^^1) =
\\Mkik I] “ *
k!
(2.136)
Рассмотрим, с другой стороны, новый процесс, для которого случайной величиной является появление k независимых точек в промежутке (0, t), причем предполагается, что точки равномерно распределены в этом промежутке. Для этого процесса выполним те же вычисления, что и для пуассоновского процесса, а именно,
Р[ЛJровно k требований в промежутке (0, /)] =
= (т-) ргР -ртР- <2-1371
Здесь присутствие члена k\ объясняется тем, что не делается различия между возможными перестановками k точек по k промежуткам. Заметим, что две условные вероятности, задаваемые равенствами (2.136) и (2.137), совпадают, и это позволяет заключить, что, если промежуток (0, t) содержит ровно k точек пуассоновского процесса, то совместное распределение моментов появления этих точек 82
|акое же, как и распределение k равномерно распределенных точек по тому же промежутку.
Кроме того, используя свойства процесса размножения, легко показать, что процесс Пуассона является процессом с независимыми приращениями; иными словами, если определить величину X (s, s ф 0 как число требований, поступающих в промежутке времени (s, s -ф t), то независимо от расположения этого промежутка имеет место равенство
P[X(s, s + = =
Теперь рассмотрим внутреннюю взаимосвязь между пуассоновским процессом и показательным распределением. Это распределение также играет важную роль в теории массового обслуживания. Рассмотрим случайную переменную t, представляющую собой время между соседними требованиями, поступающими в СМО, для которой функцию распределения вероятностей и плотность распределения вероятностей соответственно обозначают А (/) и а (Z). Тогда, по определению, величина а (Z) Л/ ф- о (At) представляет собой вероятность того, что следующее требование поступит не ранее чем через t секунд после последнего пришедшего требования и не позднее чем через (t 4- At) секунд.
Так как согласно определению A (t) является просто вероятностью того, что время между соседними требованиями не превышает t, то, очевидно, эта вероятность дается равенством
A (t) — 1 - Z;Q t\.
Но величина Р [F > t \ является в точности вероятностью того, что в промежутке времени (0, t) не поступит ни одного требования, т. е. вероятностью Р() (t). Следовательно, А (/) = 1 — Ро (t), и для случая пуассоновского процесса из (2.131) получаем следующее выражение для функции распределения:
.lui 1 -е-^, Z > 0. (2.138)
Дифференцируя это равенство, находим плотность распределения
a(t) = Ze~w, t > 0. (2.139)
Приведенные равенства описывают хорошо известное показательное распределение; графики соответствующей функции распределения вероятностей и плотности распределения вероятностей показаны на рис. 2.12.
Равенства (2.138) и (2.139) показывают, что для пуассоновского процесса промежутки времени между соседними требованиями Распределены по показательному закону; обычно говорят, что пуассоновский поток требований характеризуется показательным распределением промежутков между требованиями.
83
7
Рис. 2.12. Показательное распределение;
и -- плотность распределения вероятностей; б — функция распределения вероятна 14 и
Самой замечательной чертой показательного распределения является отсутствие последствия. Это свойство было определено при обсуждении марковских процессов. Как говорит уже само название, прошлая история показательно распределенной случайной величины не играет никакой роли в предсказании ее будущего. Более точно имеется в виду следующее. Допустим, что требование поступило точно в момент 0. Если нужно определить распределение времени до поступления следующего требования, то, очевидно, ответ дается равенством (2.139). Предположим теперь, что прошло некоторое время, скажем to секунд, в течение которого не поступило ни одного требования. В этот момент времени можно опять спросить: «Какова вероятность того, что следующее требование поступит через t секунд, считая с этого момента?». Этот вопрос в точности совпадает с вопросом, который был задан в момент времени 0, но теперь известно, что между последовательными требованиями прошло по меньшей мере t0 секунд. Для ответа на второй вопрос проведем следующие вычисления:
/’|/ Л / ; | ЛН -
_ P\t<t + CJ - Р 1? <
Р \t > U ’ р > М
Согласно равенству (2.138) имеем
и, следовательно,
P[t<i :-C|L>/0] =1-е-?< (2.140)
Этот результат показывает, что распределение времени, оставшегося до поступления следующего требования, при условии, что с момента поступления предыдущего требования прошло уже t0 секунд, тождественно равно безусловному распределению промежутков времени между соседними требованиями. Это дает основа-84
Рис. 2.13. Свойство отсутствия последействия у показательного распределения
ние считать, что время до поступления следующего требования не зависит от того, сколько времени прошло с момента поступления предыдущего требования. Иными словами, будущее показательно распределенной случайной величины не зависит от прошлой истории этой величины, и это распределение остается неизменным во времени. Показательное распределение является единственным непрерывным распределением, обладающим этим свойством. (В случае дискретных случайных величин, как уже говорилось, единственным распределением с таким же свойством является геометрическое распределение.)
Проникнуть глубже в природу свойства отсутствия последействия можно с помощью рис. 2,13. На рисунке дана плотность показательного распределения Ze'7. Для того чтобы по истечении t0 секунд вычислить плотность распределения времени, оставшегося до поступления следующего требования, надо рассмотреть область, лежащую справа от точки t0 (показанную па рисунке штриховкой), так как именно эта область определяет вероятностную характеристику процесса в будущем; участок кривой плотности распределения от 0 до определяется прошлым процесса и уже не содержит никакой неопределенности. Для того чтобы привести заштрихованную область к стандартному для функций плотностей виду, надо ввести такую нормировку, чтобы общая площадь под кривой была равна единице; для этого разделим функцию, представляющую собой «хвост» исходного распределения, на площадь заштрихованной области (которая, очевидно, равна вероятности Р > /01). Эта операция тождественна операции вычисления условного распределения путем деления совместной вероятности события и условия на вероятность условия. При этом заштрихованная область преобразуется во вторую кривую на рис. 2.13. Эта новая функция является точной копией исходной плотности распределения вероятностей, сдвинутой из нулевой точки вправо на t0 секунд. Никакая другая плотность распределе
85
ния не обладает таким свойством, чтобы ее произвольный «хвост» повторял форму исходной функции.
Воспользуемся теперь свойством отсутствия последействия для того, чтобы завершить круг вопросов, описывающий взаимосвязь пуассоновского процесса с показательным распределением. Равенство (2.140) задает функцию распределения вероятностей промежутков между последовательными требованиями при условии, что эти промежутки не меньше f0. Рассмотрим, чему равна вероятность поступления требования в промежутке А/ при условии, что процесс находится в точке Zo. Согласно (2.140) имеем
’Р - Ф 1 е; '-
[1 Д/ф-^^-- . . .] -_?,Д/ф.0(Д/). (2.141)
Равенство (2.141) означает, что, если до момента t0 требование не поступило, то вероятность его появления в следующем промежутке длиной Дг секунд равна A.AZ ф- о (Д/). Но это в точности совпадает с предположением Blt сделанным вначале. Кроме того, вероятность непоступления требования в промежутке (Zo, tn ф-Д/)
Pit -10 г \tz- Z,J - 1 - Р \t < t0 + \t 11 > Zo] =
1 - (1 - e •• = e • 1 • /. AZ -p . . . :
-= 1 — л AZ A- о (AZ).
Это совпадает с предположением В2. Далее,
Р [в промежутке (Zo, Zo ф- AZ) поступают 2 или больше требований] = 1 —Р [0 требований в промежутке (Zo,
Zo -с Д^) ] — Р [1 требование в промежутке (Zo, Zo ф- AZ) ] -= - 1-11- AAZ ф о (AZ) ] — [W ф- о (Ы) I = о (Д/).
Это соответствует предположению относительно кратных событий. Таким образом, приходим к выводу, что предположение о показательном законе распределения промежутков времени между последовательными требованиями (которые независимы одно от другого) влечет за собой утверждение, что процесс является пуассоновским, откуда, в свою очередь, следует, что интенсивность постоянна. Справедливо также и обратное рассуждение. Эта зависимость показана графически на рис. 2.14, где двойная стрелка означает причинно-следственную связь в обоих направлениях.
Так же, как и для пуассоновского процесса, вычислим теперь среднее значение и дисперсию для показательного распределения. Воспользуемся опять двумя методами (прямым и с помощью производящей функции):
СО СО
£ [Z] Л 1 -- j tail] di — j /Ае-Л< di.
0 II
86
Для вычисления этого (простого) интеграла воспользуемся искусственным приемом, основанным на том, что он является частной производной от интеграла, который легко вычислить непосредственно:
оо оо
И'-1''"'40 4 о о
и, следовательно,
142)
Таким образом, среднее значение промежутка времени между последовательными требованиями при показательном распределении равно 1/4 Этот результат интуитивно ясен из равенства (2.141), согласно которому вероятность поступления требования в промежутке времени Л/ равна ЛД/ 4- о (At), т. е. Л должна представлять собой интенсивность поступлений и, следовательно, 1/Х — среднюю длину промежутка времени между поступающими требованиями. Для того чтобы вычислить дисперсию, рассмотрим сначала второй момент для промежутка времени между требованиями:
Е = j Еа (/) dt = f Е dt -
I) и
= ] е-?-' dt = X /1.А = JL .
д/.- J д/.г \ Л. / Л2
о
Таким образом, дисперсия определяется равенством
о~ = Е КО2] - (О2 = 5 - (-у)"
87
и, следовательно,
о~ ~ . (2.143)
t t, '
Обычно эти два момента можно вычислить более просто с помощью преобразования Лапласа плотности распределения вероятностей рассматриваемой случайной величины. Преобразование Лапласа плотности распределения вероятностей промежутка времени между соседними требованиями обозначают через A* (s). Для рассматриваемого случая показательного распределения имеем
со оо
Л* (s) A J e-sfu (/) dt = J e~sthe~Kt dt о о
и, следовательно,
,.p(s) . Д .... (2.144)
Равенство (2.144) дает преобразование Лапласа плотности показательного распределения. Согласно приложению II, среднее значение случайной величины с такой плотностью распределения
7 dA*^ I = 1 I = ± ds (s z.)2 |s_) 7.
Аналогично для второго момента этой случайной величины находим
FI /7121 — d2A* Is) I _ 2А I _______ 2
1141 ds2 |.s=u (sWU' л2’
и, следовательно,
<С7 = £[(//] - Ct)2 .
Отсюда видно, что использование метода преобразований облегчает вычисление моментов.
Заметим также, что коэффициент вариации (см. равенство (11.23) для показательного распределения
СаЛ--Х-=\. (2.145)
В дальнейшем нам понадобится плотность распределения случайной величины X, представляющей собой длину промежутка времени, содержащего k требований пуассоновского процесса. Определим эту случайную величину в зависимости от случайной величины tn, представляющей собой промежуток времени между п-м и (п — 1)-м требованиями (поступление нулевого требования предполагается в пулевой момент времени). Тогда
к
X == tn.
88
Обозначим через /л- (л) плотность распределения этой случайной величины. Из приложения II непосредственно следует, что плотность распределения случайной величины X задается сверткой плотностей распределения всех величин tn, так как эти величины статистически независимы. Но так как вычисление свертки является достаточно трудоемким, воспользуемся дальнейшим результатом приложения II, согласно которому преобразование Лапласа плотности распределения суммы независимых случайных величин равно произведению плотностей распределения слагаемых. В рассматриваемом случае каждая из величин tn распределена по показательному закону, и, следовательно, преобразование Лапласа плотности распределения вероятностей случайной величины X равно £-й степени функции A* (s), определяемой равенством (2.144); таким образом, определяя через
X*
е
преобразование Лапласа плотности распределения вероятностей рассматриваемой суммы, имеем
X* (s) = [Л* (s)]\
так что
1'2.146)
Теперь надо обратить это преобразование. К счастью, эта пара преобразований содержится в 10-й строке табл. 1.4 приложения I. Таким образом, искомая плотность распределения вероятностей, описывающая длину промежутка времени, необходимого для наблюдения k поступающих требований,
/х(л') Ха- *>0. (2.147,
Это семейство плотностей (содержащее для каждого значения k по одной функции) известно под названием семейства распределений Эрланга. Оно нам понадобится позже при обсуждении метода этапов в гл. 4.
Таким образом, пуассоновский процесс и его взаимосвязь с показательным распределением рассмотрены достаточно подробно. Вернемся теперь к уравнениям процесса размножения и гибели и рассмотрим более общий процесс чистого размножения, в котором интенсивности рождений зависят от состояния (вспомним, что для пуассоновского процесса ХЛ, -= X). По-прежнему предположим,
89
(2.148)
что — 0. Тогда (2.127) могут быть приведены к следующей системе уравнений:
° - k>}’
= М /с = о.
Предположим снова, что начальное распределение задается равенством (2.130), согласно которому (с вероятностью единица) популяция начинается в нулевой момент с нуля членов. Решая уравнение относительно Ро (t), получаем
Р0(1) = е-'-‘.
Общее решение 1 для Рк (Z) и явные выражения для первых двух значений k имеют следующий вид:
Pk (f| e
J- P,.(O) , k --=0, 1, 2, . . .
;<0 (e~A°f — е~лД .
4)
(2.149)
Al — Ao
е —е 1 е 2—е °
Л2 — А1 А2 — Ло J
В качестве третьего примера процесса размножения и гибели, для которого решение зависит от времени, рассмотрим процесс чистой, гибели, в котором популяция начинается, например, с N членов и в ней происходит только гибель без какого бы то ни было восполнения. Таким образом, = 0 для всех k и |ЛА = ц > 0 для k — 1, 2, ..., N. Для этого процесса с постоянной интенсивностью гибели имеем
-uPA (Z) + (Z), 0 < k С .V;
dp.. (t)
-JLLL^^P^t), k=N-
= « = °-
Решая эту систему, как и предыдущую, по индукции, получаем 0<k<N; (2.150)
dP(1 (0 = HtpO*'1 е-и< £ = 0.
at (/V—1) ! ’
Отметим аналогичность этого результата распределению Эрланга.
1 Непосредственной подстановкой (2.149) в (2.148) легко убедиться в справед-
ливости этого решения.
90
И, наконец, рассмотрим процесс размножения и гибели, в котором все интенсивности размножения равны X для /г 0, а все интенсивности гибели равны р для k > 1. Этот процесс размножения и гибели с постоянными коэффициентами представляет самостоятельный интерес и является, возможно, простейшей интересной моделью СМО. Он представляет собой замечательную систему типа М/М/1; вспомним, что это обозначение принято для системы с одним обслуживающим прибором, пуассоновским входящим потоком и показательным законом распределения времени обслуживания (из предыдущего обсуждения ясно, что эта система не имеет последействия). Таким образом, можно записать
М|М|1
| (2.151)
11/г ~ р 1 I В (х) == 1 - е ’ix.
Из предыдущего обсуждения связи показательною распределения промежутков времени между поступающими требованиями с пуассоновским потоком ясно, почему функция A (t) является показательной. Аналогично, так как интенсивность гибели является постоянной (р4 = р, k = 1, 2, ...), те же рассуждения приводят к выводу, что промежуток времени между последовательными моментами гибели также распределен по показательному закону (в данном случае с параметром р). Однако в СМО гибель эквивалентна окончанию обслуживания, и, следовательно, распределение В (х) времени обслуживания также должно быть показательным. Интерпретация условия р0 = 0, означающего, что интенсивность гибели в популяции равна нулю, если ее объем равен нулю, в случае СМО сводится к тому, что обслуживание невозможно при отсутствии требований на обслуживание.
Характеристики системы М/М/1 будут рассматриваться в данной книге всегда при введении новых методов и новых характеристик; все сложные методы будут постоянно проверяться на этом примере, так как такая СМО представляет собой один из простейших объектов возможного применения новых методов. Более того, многие характеристики этой системы присущи и более сложным СМО, поэтому тщательное изучение системы М/М/1 поможет читателю проникнуть в суть важнейших явлений, происходящих в СМО.
Перейдем теперь к первому знакомству с характеристиками системы М/М/1. Из общего уравнения (2.127) для вероятностей Pk (О находим, что соответствующие данному случаю дифференциально-разностные уравнения имеют вид
= -(>- + ц) Pk (t) + PPk-л V) + (О, k > 1; (2.152)
•_= -ХР0 (0 + pPi (0, k = 0.
91
Эту систему уравнений можно решить различными методами. Выберем здесь метод производящих функций, описанный в приложении I. Одно из применений этого метода уже обсуждалось ранее в данной главе [когда векторная производящая функция, определенная равенством (2.60), была использована для получения алгебраического решения системы уравнений (2.55)]. Вспомним, что последовательность шагов при решении систем разностных уравнений методом производящих функций может быть описана следующим образом:
1. Умножить k-e уравнение на zk.
2. Просуммировать все уравнения, имеющие один и тот же вид (как правило, для k = К, К + 1, ...)•
3. Попытаться превратить полученное единственное уравнение в производящую функцию неизвестной функции. Если при этом конечного числа членов не хватает, их надо прибавить в производящую функцию, выполнив при этом соответствующее вычитание так, чтобы не нарушилось равенство.
4. Для исключения неопределенности в преобразованном уравнении воспользоваться «граничными» уравнениями (а именно, теми уравнениями для k = 0, 1, ..., К — I, которые были опущены па 2-м шаге).
5. Решить относительно нужного преобразования полученное алгебраическое, матричное или дифференциальное 1 уравнение. Для устранения последней оставшейся неопределенности воспользоваться нормирующим условием (2.122). * *
6. Обратить полученное решение и выписать точную формулу.
7. Если операции, указанные на 6-м шаге, выполнить нельзя, то можно вычислить моменты, дифференцируя полученную функцию по г и полагая z =-= 1.
1 Иногда на этом шаге получаются дифференциальные уравнения, хотя исходные разностные уравнения являются фактически дифференциально-разностными. В этом случае надо возвратиться обратно к 1-му шагу данной процедуры и рассмотреть все функции относительно переменной, по которой ведется дифференцирование (обычно, относительно времени). Всю процедуру, от 1-го шага до 5-го, повторить, используя преобразование Лапласа функций от этой новой переменной; переменной величиной в производящей функции становится e~st', суммы превращаются в интегралы; а все вычисления производятся по правилам, связанным парой преобразований Лапласа (см. приложение I). Аналогичное «возвращение к 1-му шагу» возникает в тех случаях, когда преобразуемая функция зависит более чем от одной переменной; для каждой дискретной переменной мы пользуемся производящей функцией; а для каждой непрерывной переменной — преобразованием Лапласа.
* Если остаются дополнительные неопределенности, то нужно воспользоваться аналитичностью преобразования: функция будет оставаться ограниченной в области ее аналитичности, если каждому полюсу (вырожденности) функции будет соответствовать корень, в котором рассматриваемая функция обращается в нуль. Эти дополнительные условия полностью устраняют все оставшиеся неопределенности. Такую процедуру будем часто использовать н объяснять в нескольких следующих главах.
92
Применим этот метод к решению системы (2.152). Прежде всего определим зависящее от времени преобразование
(2.153)
Умножим затем /г-е дифференциальное уравнение на zk (1-й шаг) и просуммируем по всем допустимым значениям k (k = 1, 2, ...) (2-й шаг) для того, чтобы выписать единственное дифференциальное уравнение относительно производящей функции вероятностей Р/: (t):
dt
zk.
Ar=l fe = l
Свойство 14 из табл. 1.1 приложения I позволяет вынести в последнем равенстве оператор дифференцирования за знак суммы. При этом сумма становится очень похожей на определенную выше функцию Р (z, t)\ не хватает только члена, соответствующего k = 0; это же утверждение справедливо и для первой суммы в правой части того же равенства. В этих двух случаях для получения производящей функции необходимо просто прибавить и вычесть член Ро (Z) г°. Вторая сумма в правой части равенства, очевидно, равна KzP(z, t), так как здесь имеется лишний множитель z и не пропущен ни один из членов производящей функции. В последней сумме правой части равенства не хватает множителя z и двух первых членов производящей функции. Таким образом, завершая 3-й шаг, имеем
[Р (г, 0 - Ро (/)] = - (?- г ц) IP (г, /) - Г\, (/)] -I-
-у KzP (г, t) 1 -Ь [Р (г, 0 - PQ (/) ~ Л (/) г]. (2.154)
Уравнение, соответствующее k = 0, пока еще не было использовано, и мы воспользуемся им на 4-м шаге для трго, чтобы .исключить некоторые члены из уравнения (2.154): 4
4 Р (Z, I) - -КР (z, t) - н [Р (г, i) - Ро (0) -|-
+ azP(z, t)~-^-[P(z, t)-P0(t)].
Перегруппировав члены в этом уравнении, приходим к следующему линейному уравнению в частных производных первого порядка относительно функции Р (г, /):
г|Р(г, 0 = (1-2)[(ц-МР(г, 0-нРо(01. (2.155)
93
Для решения этого дифференциального уравнения требуются дальнейшие преобразования, указанные в первой сноске к 5-му шагу. Определим, соответственно, преобразование Лапласа нашей функции Р (z, it) равенством 1 * * *
Р* (z, s) A [ e~stP (z. t) dt.
(2.156)
Возвращаясь к 1-му шагу, применяя это преобразование к уравнению (2.155) и пользуясь свойством 11, указанным в табл. 1.3 приложения I, получаем
z [sP* (г, s) — Р (z, 0+)] =-- (1 — z) [(р — Az) Р* (z, s) — p.Pj (s)J, (2.157) где через Ро (s) обозначено преобразование Лапласа функции Ро (О, т. е.
Ро (s) A j e~s’Ptl (/) dt.
(2.158)
Таким образом, теперь имеется преобразование дифференциально-разностных уравнений относительно функции Р (z, t) и по дискретной переменной k и по непрерывной переменной t. Это преобразование записывается в виде равенства (2.157), которое представляет собой простое алгебраическое уравнение относительно дважды преобразованной функции Р* (z, s) и которое можно переписать в виде
г.Р (г. 0+) -p(l-z)/* (s) sz — (1 — г) (и. — /.г)
(2.159)
Продолжим эти преобразования несколько дальше. Из определения (2.153) видно, что
Р (г, 0+) = £ Pk (0+) zft.
(2.169)
Несомненно, Рк (0+) представляет собой просто начальное условие; но если раньше предполагалось, что система в нулевой момент времени является пустой (т. е. что Ро (0+) = 1 и Pk (0+) = О для всех k 0), то теперь введем обобщение и предположим, что в нулевой момент времени имеется I требований, т. е.
1 Для удобства в качестве нижнего предела интегрирования выбран 0+
вместо обычно используемого для неотрицательных случайных величии 0". След-
ствием этого явилось включение в уравнение (2.157) начального условия Р (г, 0+).
94
При i ~ о получаем исходное начальное условие. Подставляя (2.161) в равенство (2.160), непосредственно видим, что
Р (2, 0+) = г‘ .
Подставляя это выражение в равенство (2.159), получаем
_ г‘+1 — Р (1—г) (s)
Р* (г, s) =----°? . (9.162)
' sz — (1—г) (р — /.г)
На этом 5-й шаг почти закончен, за исключением того, что в уравнении появилась неизвестная функция Р* (s). Вторая сноска к 5-му шагу подсказывает, как поступить дальше. Здесь анализ становится несколько сложнее, и продолжать вычисления представляется нецелесообразным; предпочтительней вынести эти утомительные подробности в упражнение (см. задачу 2.20). Ограничимся только замечанием, что Р% (s) можно определить через корни знаменателя в правой части равенства (2.162), после чего получается точное выражение для рассматриваемого двойного преобразования. Далее надо перейти к 6-му шагу и попытаться обратить полученное преобразование по обеим переменным; в результате решения этого упражнения читатель получит окончательное выражение для искомых переходных вероятностей, а именно
Pk(t) = е- < р^-О/-/А_,.(^) 4
оо
+ P(ft"'"i)/24+<+I(aO + (l -Р)РЛ ’ Ъ p-P-Ij (at) j—k+i+‘2
и (2.163)
где
(Х/2)^2"1
{k -\-т) ! т ! ’
а =
и
(2.164)
(2.165)
(2.166,
причем lk (х) — модифицированная функция Бесселя первого рода порядка k. Последнее выражение является наиболее обескураживающим. Приходится признаться, что модель простейшей представляющей интерес СМО (рассматриваемая далее в следующей главе) приводит к неудобному выражению зависимости вероятностей состояний системы от времени. Как следствие, можно ожидать только еще больших сложностей и неясностей при попытке найти временные характеристики СМО более общего вида.
Подробнее о результатах, зависящих от времени, будет сказано ниже. Теперь же нашей основной задачей является исследование характеристик СМО в состоянии равновесия, а не их временных
характеристик (которые значительно сложнее). В следующей главе будут исследованы характеристики СМО типа размножения и гибели в установившемся режиме, а в гл. 4 — более общие, марковские СМО в состоянии равновесия. И только когда мы пройдем гл. 5, 8 и затем гл. 2 тома II, мы вернемся опять к переходным характеристикам систем, зависящим от времени. Перейдем к простейшим характеристикам в установившемся режиме.
СПИСОК ЛИТЕРАТУРЫ
1. Bharucha- Reid А. Т. Elements of the Theory of Markov Processes and Their Applications, McGraw-Hill (New York), 1960.
2. Cohen, J. The Single Server Queue, North Holland (Amsterdam), 1969.
3. Eilon S. A Simpler Proof of L = XW. Operations Research, 17, 915—916 (1969).
4. Феллер В. Введение в теорию вероятностей и ее приложения/Пер. с англ. Ю.В. Прохорова. М., Мир, 1967, т. 2. 756 с.
5. Фрай Т. Теория вероятностейинженеров,Пер. с аН1Л. иод ред. А. Я. Хин-чина. М.—Л., ОНТИ Гостехиздат, 1934, 384 с.
6. Howard, R. A. Dynamic Probabilbstic Systems, Vol. I (Markov Models) and Vol. 11 (Semi-Markov and Decision Processes), Wiley (New York), 1971.
7. Jewell, W. S. A Simple Proof of L = XIV'. Operations Research, 15, 1109— 1116 (1967).
8. Хиичин А. Я. Математические методы теории массового обслуживания. — В кн.: Труды математического института им. В. А. Стеклова. М., Изд. АН СССР, т. 49, 1955. 122 с.
9. Little, J. D. С. A Proof of the Queueing Formula L — KW. Operations Research, 9, 383—387 (1961).
10. Марков А. А. Распространение предельных теорем исчисления вероятностей на сумму величин, связанных в цепь. — В кн.: Записки АН по физико-математическому отделению, VIH серия, Санкт-Петербург, 1908, т. 22, № 9.
11. Palm, С. Intensitatsschwankungen im l ernsprechverkehr. Ericsson Technics, 44, 1 —189 (1943).
12. Parzen, E, Stochastic Processes, Holden Pay (San Franicisco), 1962.
13. Stidham, S. Jr. A Last V. ord on L~ 7.H". Operations Research, 22, 417 421 (1974).
ЗАДАЧИ
2.1. Рассмотрим К независимых источников требований, для каждого из которых промежутки времени между соседними требованиями распределены по показательному закону с параметром kk (иными словами, каждый источник является пуассоновским). Рассмотрим теперь входящий поток, образуемый слиянием потоков от каждого из этих источников. Докажите, что этот общий поток также является пуассоновским с параметром X = 4- Х2 + • +
2.2. Рассмотрим объединенный пуассоновский поток из предыдущей задачи и предположим, что теперь его надо разбить на несколько ветвей. Пусть /?, означает вероятность того, что некоторое требование объединенного потока будет отнесено к подпотоку с номером i. Покажите, что, если интенсивность
96
суммарного потока равна Л требованиям в секунду и если вероятности р, выбираются независимо, то каждый из подпотоков образует пуассоновский процесс с интенсивностью Хр,.
2.3. Пусть {Х,} — последовательность Бернулли, т. е. последовательность одинаково распределенных взаимно независимых случайных величин (с Р [X,- = 1 1 = р и Р {Xj = 0] = = 1 — р). Пусть SiV = Хг + ... + X., — сумма случайного числа N случайных величин Xj, причем N предполагается распределенным по закону Пуассона со средним значением %. Докажите, что величина SN распределена по закону Пуассона со средним значением кр. (В общем случае, распределение суммы случайного числа независимых случайных переменных называется сложным распределением.)
2.4. Найдите плотность распределения вероятностей наименьшей из X независимых случайных величин, каждая из которых имеет показательное распределение с параметром X.
2.5. Рассмотрим однородную цепь Маркова, диаграмма состояний которой имеет вид
а) Найдите матрицу Р переходных вероятностей.
б) При каких условиях (если таковые существуют) цепь будет неприводимой и апериодической?
в) Найдите вектор зт стационарного распределения вероятностей.
г) Чему равно среднее время возвращения в состояние 2?
д) При каких значениях аир выполняется равенство = = л2 = л3? (Дайте физическую интерпретацию этого случая.)
2.6. Рассмотрим дискретную цепь Маркова, для которой матрица вероятностей переходов
Р =
' 1/2 1/2
. 3/4 1/4 . ’
4 Л. Клейнрок
97
а) Найдите вектор л стационарного распределения вероятностей.
б) Найдите [I — zP I"1.
в) Найдите общий вид матрицы Рл.
2.7. Рассмотрим цепь Маркова с состояниями Ео, Elt Е2, ... и вероятностями переходов
где р + q = 1 (0 < р < 1).
а) Является ли эта цепь неприводимой? Периодической? Объясните.
б) Найдите стационарную вероятность л; состояния Выразите л, через рч и л;- для всех j = 0, 1,2, ...
в) Используя результат п. б, найдите выражение, связывающее Р (?) и Р [1 + р (г — 1)1, где
Р (г) = У] л,У.
г) Применяя рекуррентно (т. е. повторно) результат п. в к нему самому, покажите, что на n-м шаге получается
Р (г) = г (г-ъ [1 + рп (г _ 1)ь
д) Из результатов п. г найдите Р (г) и укажите затем л,..
2.8. Покажите, что любая точка, лежащая внутри равностороннего треугольника с единичной высотой (см. рис. 2.6) или на нем, соответствует трехкомпонентному вероятностному вектору в том смысле, что сумма расстояний такой произвольной точки до трех сторон треугольника всегда равна единице.
2.9. Рассмотрим процесс чистого размножения с постоянной интенсивностью %. Выберем промежуток длиной Т и разобьем его на tn сегментов, каждый длиной Tim. Обозначим Tim = Et. а) Предполагая А/ малым, найдите вероятность того, что ровно на k сегментах из m поступит по одному требованию и на остальных m — k сегментах требования не поступят.
б) Перейдите к пределу при А/ —> 0, т. е. при m —* оо и фиксированном Т, и вычислите вероятность Pk (Т) поступления ровно k требований в промежутке Т.
2.10. Рассмотрим популяцию бактерий, объем которой в момент t равен W (/), причем N (0) = 1. Развитие этой популяции будем интерпретировать как процесс чистого размножения, предполагая, что при А/ —> 0 каждый член популяции с вероятностью ХА/ -р о (А/) в промежутке времени (/, t 4- А/) делится и дает два члена популяции или с вероятностью 1 —ХА/ -(-о (Д/) остается в этом промежутке неизменным.
98
а) Пусть Pk (f) = P \N (t) = /г]; выпишите систему дифференциально-разностных уравнений, которым должны удовлетворять эти вероятности.
б) Используя п. а, докажите, что производящая функция Р (z, t) для N (t) задается равенством
в) Найдите Е [М (/)].
г) Найдите Рк (t).
д) Найдите Р (z, /), Е [N (t) ] и Pk (t) при начальном условии М (0) = и > 1.
е) Рассмотрите соответствующую детерминированную задачу, в которой каждая бактерия делится каждые 1/Х секунд, и сравните ответ с п. в.
2.11. Рассмотрим процесс размножения и гибели с коэффициентами
1 X, k = 0; ( ц, k = 1;
x*=lo, k=po-, и* = (о, k+1,
соответствующий СМО типа М/М/1, в которой отсутствуют места для ожидания требований.
а) Выпишите дифференциально-разностные уравнения для pk (0 (k = 0,1).
б) Решите эти уравнения и выпишите ответы в виде функции от Ро (0) и Pj (0).
2.12. Рассмотрим СМО, описываемую процессом размножения и гибели, в которой
Xft = X, й > 0;
11/, = k[l, k 5» 0.
а) Для всех k найдите дифференциально-разностные уравнения, описывающие вероятности
Рк (I) = Р Ik требований в системе в момент /].
б) Определив производящую функцию Р (z, t) в виде
P(z, 0 = 2 Pk{t)z\
6=0
найдите дифференциальное уравнение в частных производных, которому должна удовлетворять эта функция.
в) Покажите, что при начальном условии Ро (0) = 1 решение этого уравнения задается равенством
Р (z, t) = exp (1 - е-и<) (г — 1)).
4
99
г) Сравнивая решение, указанное в п. в, с равенством (2.134), выпишите выражения для вероятностей Pk (/).
д) Найдите предельные значения этих вероятностей при t —> сю.
2.13. Рассмотрим систему, в которой с ростом числа k требований в системе интенсивность размножения падает, а интенсивность гибели растет, т. е.
1 (К - k) X, k < К\ 1 йр, U К;
= ( 0 0, k>K.
Выпишите дифференциально-разностные уравнения для вероятностей
Рк (/) = Р [k требований в системе в момент /].
2.14. Рассмотрим линейный процесс размножения и гибели, для которого = k% и ц>. = k[l.
а) Найдите дифференциальное уравнение в частных производных, которому должна удовлетворять производящая функция Р (z, f), определяемая равенством (2.153).
б) Предполагая, что в начальный момент времени объем популяции равен нулю, покажите, что функция, удовлетворяющая выведенному в п. а уравнению, задается равенством
р , .. р- (1 — 9 — (X — f) z
в) Разлагая функцию Р (z, t) в степенной ряд, докажите, что
/Ш = [1 -а(0][1 -РЮНРЮГ1, &= 1, 2, ...;
Ро(0 = «(0, и найдите а (/) и р (/).
г) Найдите среднее значение и дисперсию числа требований в системе в момент t.
д) Найдите предельную при t —» оо вероятность того, что популяция погибнет.
2.15. Рассмотрим линейный процесс размножения и гибели, для которого ХА = k\ + а и = k[i.
а) Найдите дифференциально-разностные уравнения, связывающие вероятности Pk (/).
б) Используя результат п. а, выведите дифференциальное уравнение в частных производных, которому должна удовлетворять зависящая от времени производящая функция
Р(г, /)= S Pk(t^k.
100
в) Чему равна величина Р (1, /)? Дайте словесную интерпретацию равенства
N (t) = \ua-?--P(z, t).
г) Предполагая, что в нулевой момент времени объем популяции равен i членам, найдите обыкновенное дифференциальное уравнение для W (/) и решите его относительно N (t). Рассмотрите отдельно случаи Л = ц и Л р.
д) Найдите предельное значение (при t —* со) величины N (t) для случая, когда X < р.
2.16. Рассмотрим уравнения движения, задаваемые равенствами (2.148), и определим преобразование Лапласа
PZ(s) = J Pk(t)e~stdt.
В качестве начального условия предположим, что Ро (/) = 1 при t = 0. Преобразуйте систему уравнений (2.148) в систему линейных дифференциальных уравнений относительно (H(s)b
а) Докажите, что решение этой системы дается равенством
РИ5) = -г^--------•
П (S + ^/)
IsesQ
б) Используя п. а, найдите вероятности Рк (f) для случая К (I = О, 1, 2, ...).
2.17. Рассмотрим промежуток времени (0, t), в течение которого поступает пуассоновский поток требований с интенсивностью %. Выведите равенство (2.147), рассмотрев следующие два события: в промежутке (0, t — А/) поступает точно k — 1 требование и в промежутке (t — At, t) поступает точно одно требование. Необходимый результат получается сразу, если перейти к пределу при AZ —> 0.
2.18. Парикмахерская начинает работу в момент времени t = 0. Посетители приходят случайно по закону Пуассона; иными словами, плотность распределения промежутков времени между соседними требованиями a (I) — Каждая
стрижка занимает X секунд (где X — некоторая случайная величина). Найдите вероятность того,что посетитель, пришедший вторым, не будет ждать, а также среднее время ожидания W для следующих двух случаев:
101
i) X = с = const;
U) случайная величина X распределена по показательному закону с плотностью распределения вероятностей
b (х) = ре~^.
2.19. В момент t — 0 требование А поступает для обслуживания в СМО типа М/М/ш и находит все т обслуживающих приборов занятыми и п других требований, ожидающих обслуживания. Все требования ожидают обслуживания столько, сколько необходимо; обслуживание требований осуществляется в порядке их поступления, и после момента t — О новые требования не поступают. Промежутки времени обслуживания предполагаются взаимно независимыми и одинаково распределенными по показательному закону со средним значением 1/р.
а) Найдите среднее время ожидания обслуживания для требования А.
б) Найдите среднюю длину промежутка времени между моментом поступления требования А (момент t = 0) и тем моментом, когда система освободится (закончится обслуживание всех требований).
в) Пусть X — порядковый номер требования А на выходе системы после окончания обслуживания, т. е. X = k, если требование А покидает систему k-м после момента времени t = 0. Найдите вероятность Р [X = k ] (k = = 1, 2, ..., tn + п 1).
г) Найдите вероятность того, что обслуживание требования А закончится раньше, чем обслуживание требования, которое ему непосредственно предшествует в очереди.
д) Пусть w означает время ожидания обслуживания для требования А. Найдите вероятность Р lw > х].
2.20. В этой задаче проследуем от равенства (2.162) к решению для переходного процесса (2.163). Так как функция Р*(г, s) должна сходится в области |z| < 1 при Re (s) >0, то в этой области корни знаменателя (2.162) должны быть также и корнями числителя.
а) Найдите два значения переменной г, для которых знаменатель обращается в нуль, и обозначьте их через ах (s) и а2 (s),. где | а2 (s) | < | ах (s) |.
б) Используя теорему Руше (см. приложение I), докажите, что в единичном круге \z\ < 1 знаменатель функции Р* (z, s) имеет единственный корень.
в) Найдите точное выражение для PJ (s), используя предыдущие рассуждения и требуя, чтобы числитель функции Р* (z, s) обращался в нуль при z = а2 ($).
102
г) Выпишите выражение функции Р* (г, s) через ах (s) = ах и а2 (s) = а2. Покажите далее, что это равенство может быть преобразовано к виду
р* . (z‘ + a2z" 1 + • • • + аг) а2+1/( 1 — “г)
Г S) ~ Act! (1 — г/ах) '
д) Используя неравенство | а21 < 1 и равенство ага2 = р/Х, покажите, что обращение преобразования по z приводит к следующему выражению для преобразования Лапласа P*k (s) переходных вероятностей Pk (/):
P'k (s) = 4- «‘Г*’’ + (£) al’*'3 + (-£-)2 a'i’*’5 + • • •
• + (тр-'"+4Г S •
/=fe+f+2
Заметим, что равенство для Р\ (s) справедливо только при k > i. При k < i некоторые члены исчезают, и получается подобное выражение (которое должно быть обращено в п. е).
е) Воспользуемся, далее, свойством 5 из табл. 1.3 и следующей парой преобразований:
kpkPt~4k (at) (=) [S + ^~W ]~*,
где p = Vp и а определяются равенствами (2.164) и (2.165) и Ik (х)— модифицированная функция Бесселя первого рода порядка k, определяемая равенством (2.166). Используя все эти факты и следующие простые соотношения, связывающие функции Бесселя:
~ lk (х) = 4-i W — 4+1W и
4W = b(x),
покажите, что равенство (2.163) представляет собой обратное преобразование для функции, приведенной в пункте д.
2.21. Пусть Хх, Х2, ..., Xi, ... — независимые, одинаково распределенные случайные величины с плотностью распределения вероятностей fx (х) и характеристической функцией Фх (и) = Е [е/’иХ]. Рассмотрим пуассоновский процесс N (/) с параметром %, не зависящий от случайных величин Xt. Рассмотрим, далее, другой случайный процесс вида
А'(О
Х(0= 2 X.
103
Этот второй процесс представляет собой, очевидно, семейство ступенчатых функций, скачки которых происходят в моменты разрывов случайного процесса N (0; амплитуды этих скачков задаются случайными величинами X,. Покажите, что характеристическая функция этого второго процесса имеет вид
2.22. Пассажиры и такси, прибывающие в точку обслуживания, образуют независимые пуассоновские потоки с интенсивностями 1 и ц соответственно. Обозначим qt длину очереди в момент t, причем эта величина является отрицательной для очереди автомобилей и положительной для очереди пассажиров. Докажите, что, начиная с q0 = 0, распределение случайной величины qt задается разностью между независимыми средними значениями Kt и пуассоновских потоков. Используя нормальное приближение для распределения Пуассона, докажите, что, если К = р, то для больших t вероятность того, что —k равна (2k 4- 1)(4лХ^)-1/2.
ЧАСТЬ П
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
Элементарность здесь означает, что все рассматриваемые системы являются чисто марковскими, и, следовательно, принятое нами описание их состояний оказывается удобным и легко поддающимся анализу. В первой части была выведена система уравнений, описывающая процессы размножения и гибели во времени; в гл. 3 этой части рассмотрено стационарное решение для таких систем. Ключевым результатом данной главы является равенство (3.11), и весь материал по существу является простым применением этой формулы. Фактически она является ничем иным, как решением выведенного в гл. 2 уравнения = 0.
Основным используемым здесь методом является часто встречающийся в этой книге метод вычисления интенсивностей потоков, пересекающих границы замкнутой системы. В стационарном случае просто требуется, чтобы интенсивности входящего и исходящего потоков системы были равны. Применение этого основополагающего принципа является не просто упражнением, он здесь позволяет впервые получить некоторые соотношения, важные для использования при проектировании и расчете СМО. Исследуется’классическая система типа М/М/1 и вычисляются некоторые важные характеристики ее работы. В гл. 3 рассмотрены также в стационарном режиме более сложные модели, включающие конечный накопитель, несколько обслуживающих приборов, конечное число источников требований и т. п.
В гл. 4 рассмотрены системы, описываемые процессами размножения и гибели, а также
105
марковские СМО более общего вида, которые также исследуются в стационарном режиме. Можно видеть, что используемые здесь методы аналогичны применявшимся ранее, но они не приводят к общим решениям типа (3.11); каждая СМО представляет собой самостоятельный случай, и для нее приходится решать систему дифференциальных уравнений, что обусловливает использование метода производящих функций. Здесь же приведен остроумный метод этапов, впервые введенный Эрлангом, и обсуждается его общность. В конце главы описываются также марковские сети массового обслуживания (используемые затем во втором томе), для которых сохраняется важное свойство отсутствия последействия. Этим, однако, исчерпываются возможности применения распределения без последействия, и в следующих главах приходится отказаться от этого удобного подхода.
ГЛАВА 3
Системы, описываемые процессами размножения и гибели в стационарном режиме
В предыдущей главе были рассмотрены различные вероятностные процессы. Указывалось, что марковские процессы играют фундаментальную роль в исследованиях СМОу а после изложения основных результатов теории марковских процессов был проанализирован частный случай марковских процессов — процесс размножения и гибели. Было показано также, что процессы размножения и гибели обладают наиболее удобным свойством, а именно: промежутки времени между моментами размножения и промежутки времени между моментами гибели (когда система не является пустой) описываются показательными распределениями \ Затем была выведена система уравнений (2.127), которая представляет собой основные уравнения движения для процесса размножения и гибели общего вида при стационарных интенсивностях размноже-
1 Это вытекает непосредственно из того, что рассматриваемые процессы являю геи марковскими.
I0G
ния и гибели1. Решение системы уравнений (2.127) описывает переходные характеристики процесса, и некоторые важные частные случаи уже обсуждались ранее. В данной главе изучается предельная форма этих уравнений, характеризующих систему, описываемую процессами размножения и гибели в стационарном режиме.
Важность элементарной теории массового обслуживания определяется ее исторической ролью, а также возможностями описать характеристики, которые встречаются в более сложных СМО. Методы анализа, используемые в этой главе, в основном не распространяются на более сложные случаи; однако полученные результаты проливают свет на важнейшие свойства многих более сложных СМО.
Необходимо ясно представить способ описания СМО с помощью процесса размножения и гибели/ В качестве примера рассмотрим приемную врача, состоящую из комнаты для ожидания (в которой, к сожалению, допускается образование очереди) и кабинета врача, в котором осуществляется непосредственный прием. Каждый момент прихода пациента в приемную рассматривается как поступление требования в систему; с другой стороны, такое поступление можно рассматривать как рождение нового члена популяции, где под популяцией понимается совокупность присутствующих пациентов. Аналогично, уход пациента из приемной после посещения врача можно рассматривать как уход из системы, или, в терминах процесса размножения и гибели, как гибель члена популяции.
Как вскоре будет показано, выбор различных коэффициентов размножения и коэффициентов гибели yk обеспечивает значительную свободу при описании различных СМО. Прежде всего найдем общее решение, описывающее систему в состоянии равновесия.
3.1. ОБЩЕЕ РЕШЕНИЕ ДЛЯ СТАЦИОНАРНОГО
РЕЖИМА
Как мы видели в гл. 2, при любом достаточно сложном наборе коэффициентов нестационарное решение для системы, описываемой процессом размножения и гибели, быстро становится необозримым. Кроме того, если даже мы и можем найти Pk (f), неясно, насколько эти функции могут помочь понять поведение рассматриваемых СМО (слишком много информации иногда является бедствием!). Поэтому, естественно, возникает вопрос, устанавливаются ли в конце концов постоянными вероятности Pk(f) с ростом t, т. е. перестают ли они обнаруживать переходные свойства. Этот вопрос аналогичен уже рассмотренному вопросу о существовании предельных величин л,. Для вероятностей л,г (/) при /-> оо, Для нашего исследования САЮ
1 Эту систему уравнений надо дополнить условием нормировки (2.122) и набором начальных условий {Pk (0)).
107
выбор обозначения предельных вероятностей через pk, а не через является просто вопросом удобства. Итак, пусть
p.AlimPHO. (3-1)
где р,, интерпретируются как вероятности того, что в произвольный момент достаточно отдаленного будущего в системе будет находится k требований (или, что то же самое, система будет находится в состоянии Ek). Представляет интерес вопрос о существовании этих предельных вероятностей, но его исследование отложим до того времени, когда будет получено общее решение для установившегося режима, т. е. предельное решение. Важно понять, что, хотя вероятности рк (в предположении, что они существуют) больше не являются функциями времени t, однако мы не утверждаем, что в этом предельном случае процесс не переходит из одного состояния в другое; конечо, число членов популяции изменяется во времени, но вероятность пребывания системы через достаточно большое время в состоянии с k членами описывается величиной рк.
Предполагая, что пределы (3.1) существуют, можно сразу положить, что производные dPk (tydt в прямых уравнениях (движения) Колмогорова для системы, описываемой процессом размножения и гибели [и задаваемой равенствами (2.127)], при t —> сю обращаются в нуль, и непосредственно получить результат:
О = — (^ + щ) р^ + ^k-iPk-i + > 1; (3-2)
О = — Коро ~Ь HiPii k = 0. (3-3)
Частная задача, связанная с отдельным уравнением при k = О, может быть решена, если раз и навсегда принять, что следующие коэффициенты размножения и гибели тождественно равны нулю:
= Z_2 = X_g =••=();
Ио = Н-i ~ Н-2 = • • • — 0.
Более того, так как абсолютно ясно, что число членов в популяции не может быть отрицательным, то в большинстве случаев можно полагать, что р_г = р_2 = р_3 = ... =0. Таким образом, при всех значениях k = ..., —2, —1, 0, 1, 2, ... уравнения (3.2) и (3.3) могут быть переписаны в виде разностных уравнений:
0 — — (Ч + И*) Pk + ^k-vPk-i 4" H-fc+iPft+i- (3-4)
Кроме того, должно удовлетворяться нормирующее условие
1^=1- (3.5)
Вспомним также результат предыдущей главы, заключающийся в том, что пределы (3.1) не зависят от начальных условий.
Ту же идею составления уравнений при помощи диаграммы переходов из одного состояния в другое, которую мы использовали 108
в гл. 2, можно применить и для составления уравнений равновесия [уравнений (3.2) и (3.3)]. В стационарном случае, очевидно, поток должен удовлетворять условию сохранения в том смысле, что в каждом состоянии входящий поток должен быть равен исходящему потоку. Например, если возвратиться к рис. 2.9 и рассмотреть состояние Ек в установившемся режиме, можно отметить, что
Интенсивность потока в Ек = + H*+iP*+i
и
Интенсивность потока из Ек = (ЛА Ц- р-*) pk-
В состоянии равновесия эти два потока должны быть равны, и поэтому непосредственно получаем
^k-iPk-i + Ш+1/4+1 = + И*) Pk* (3-6)
Но это как раз и есть равенство (3.4)! Разностные уравнения для исследуемой системы в установившемся режиме составляются непосредственно с помощью диаграммы переходов. Те же самые рассуждения о сохранении потока, которые были проведены ранее, могут быть применены к потоку через любую замкнутую границу; например, вместо того чтобы выделять каждое состояние и составлять для него уравнение, можно выбрать последовательность контуров, первый из которых охватывает состояние Ео, второй — состояния Ео и Ег, и т. д., включая каждый раз в новую границу очередное состояние. В таком примере для k-ro контура (окружающего состояния Ео, Ег, ..., Ек_г) условие сохранения потока можно записать в следующем простом виде:
^k-iPk-i == PkPk- (3-7)
Для составления последней системы уравнений нужно провести вертикальную линию, разделяющую соседние состояния, и приравнять потоки через образовавшуюся границу; полученная система разностных уравнений эквивалентна выведенной ранее.
Решение рк уравнения (3.4) может быть найдено по меньшей мере двумя способами. Первый способ состоит в том, что сначала решают уравнения при k = 0 относительно рх, а именно,
= (3-8)
г1
Затем, используя (3.8) и рассматривая уравнение (3.4) при k = 1, получаем
О = — (/-1 + Pi) Pi + + РгРг’’
О = — 4 P-i) —- Ро + ^оРо "Ь РгРг'у
г1
О =-----" Ро К>Ро + К>Ро + РгРг,
Pi
109
и, следовательно,
А - 7^- Л- (3.9)
Вид равенств (3.8) и (3.9) подсказывает, что общее решение уравнения (3.4) нужно искать в виде
Р^= ро- (3’10)
• • • М
Проверить это утверждение можно просто методом математической индукции, используя (3.10) для решения уравнения (3.4) относительно рм. Проведение выкладок показывает, что (3.10) действительно является решением, определяющим вероятности состояний для произвольного процесса размножения и гибели в установившемся режиме, т. е. в предельном случае. Таким образом, все вероятности рк для установившегося режима выражаются через единственную неизвестную константу ра:
/i=1
Рл = Ро П —& = 0, 1, 2,... -(3.11)
<==0 м,+1
(Вспомним, что, по определению, произведение по пустому множеству равно единице.) Равенство (3.5) дает дополнительное условие, позволяющее определить р0; тогда, суммируя по всем k, получаем
’+2 1 ‘v-k=l г=о 11/+1
Это так просто полученное решение для рк в виде произведения является основополагающим равенством элементарной теории массового обслуживания и, фактически, представляет собой отправную точку всех дальнейших исследований данной главы.
Второй, более легкий способ решения уравнения (3.4) состоит в том, что это уравнение переписывают в виде
— ИЛ = \pk — Vk+iPk+x- (3.13)
Определяя
Sk = ^kPk — Ш+iPk+i, (3.14)
из уравнения (3.13) сразу находим, что
(3.15)
Очевидно, из (3.15) следует, что
gk == константа по k. (3.16)
110
Однако так как = р0 = О, то равенство (3.14) дает = О, и, следовательно, решением уравнения (3.16) является ноль. Полагая qk равным нулю, из уравнения (3.14) получаем
P^+i
Решая уравнение (3.17), начиная с k = 0, получаем найденное ранее решение, а именно равенства (3.11) и (3.12).
Обратимся теперь к вопросу о существовании стационарных вероятностей pk, задаваемых равенствами (3.11) и (3.12). Для того чтобы эти выражения задавали вероятности, обычно накладывается требование, чтобы р0 > 0. Это, очевидно, налагает ограничение на коэффициенты размножения и гибели в соответствующих уравнениях. По существу мы требуем, чтобы система иногда опустошалась; это условие стабильности представляется весьма резонным, если обратиться к примерам реальной жизни \ Более того, можно ввести классификацию возможностей, определив сначала следующие две суммы:
00 k-1
ос k
52л2П-£-. (3.19)
k=l 1=0 1
Все состояния Ek рассматриваемого процесса размножения и гибели будут эргодическими тогда и только тогда, когда
Эргодичность: Si < сю, 5 2 — СЮ,
С другой стороны, все состояния будут возвратными нулевыми тогда и только тогда, когда
Возвратный нуль: = сю, 32 = сю.
Наконец, все состояния будут невозвратными тогда и только тогда, когда
Невозвратность: Зх = сю,
*S2 сю.
Только эргодический случай приводит к установившимся вероятностям {рк}, и именно этот случай представляет интерес. Заметим, что условия эргодичности выполняются только тогда, когда, начиная с некоторого k, все члены последовательности ограничены единицей, т. е. тогда, когда существует некоторое k0
1 Так как в этом случае легко могут быть построены контрпримеры, то требуется строгая аргументация, которая сейчас н будет приведена.
111
(и некоторое С < 1) такое, что для всех fe > выполняется неравенство
(3.20) Мл+i
Для большинства рассматриваемых СМО это условие выполняется.
Теперь можно перейти к применению полученного общего решения, задаваемого равенствами (3.11) и (3.12), к некоторым очень важным частным случаям. Но прежде, чем начать эту дискуссию, сделаем замечание для тех читателей, которые чувствуют, что условие допустимости переходов только в соседние состояния, накладываемое процессом размножения и гибели, является слишком жестким. Решения, задаваемые равенствами (3.11) и (3.12), действительно справедливы только для процессов размножения и гибели, при которых допускаются переходы только в соседние состояния. Однако в остальном описанные стационарные методы могут быть распространены на системы более общего вида; эти обобщения будут рассмотрены в гл. 4.
3.2. М/М/1: КЛАССИЧЕСКАЯ СМО
Как уже отмечалось в гл. 2, замечательная система М/М/1 является простейшей нетривиальной системой, представляющей интерес. Она может быть описана с помощью процесса размножения и гибели, если выбрать следующие значения для коэффициентов:
= ^ — 0,1,2,...;
pft = р, k = 1, 2, 3,. . •.
Это означает, что все интенсивности размножения полагаются постоянными и равными X, а все интенсивности гибели полагаются постоянными и равными р \ Предположим также, что пространство состояний является бесконечным и что обслуживание требований осуществляется в порядке их поступления (хотя для многих результатов последнееатребование не является’необходимым). На рис. 3.1 приведена диаграмма интенсивностей переходов для этого важного примера.
Рис. 3. КуДиаграмма/'интексивноетей переходов для СМО типа М/М/1
1 В этом случае средняя длина промежутка между соседними требованиями равна t = 1/Х и среднее время обслуживания равно х = 1/р; это следует из того, что обе случайные величины I и х распределены по показательному закону. 112
Подставляя указанные значения параметров в равенство (3.11), получаем k—1
^ = РоП
f=0
или
№ = Ро(^)'е> ^>0. (3.21)
Этот результат получается непосредственно. Условия эргодичности для рассматриваемой системы (и, следовательно, условия существования стационарного решения pk > 0) состоят в том, что < оо и S2 = оо; первое условие в данном случае записывается в виде
Ряды, стоящие в левой части неравенства, сходятся тогда и только тогда, когда Л/р < 1. Второе условие эргодичности принимает вид
Sa = £ X(pUo) = S V (4г) = °°-
Это последнее условие выполняется, если Л/р < 1; таким образом, необходимое и достаточное условие эргодичности системы М/М/1 просто сводится к выполнению неравенства Л < р. Для того чтобы найти р0, воспользуемся равенством (3.12) [или равенством (3.5), если это удобнее читателю] и получим
Так как Л < р, то эта сумма сходится, и, следовательно,
' 1 — Л/р
Таким образом,
р0 = 1 - А . (3.22)
н
Из равенства (2.29) имеем р — Л/р. Следовательно, согласно условиям стационарности, требуется, чтобы Ос о <1; отметим, что это гарантирует выполнение неравенства р0 > 0. Из равенства (3.21) окончательно получаем, что
pf; (1 _ р) <,*, k^O, 1,2,... я(3.23)
113
Рис. 3.2. Стационарные вероятности р^ для СМО типа
М/М/1
Равенство (3.23) и дает решение в установившемся режиме для вероятностей того, что система содержит k требований х. Важно заметить, что вероятности рк зависят от X и р только через их отношение р.
На рис. 3.2 показаны значения вероятностей pk для рассматриваемой системы, задаваемых формулой (3.23), в случае, когда р = 1/2. Очевидно, что это распределение является геометрическим (которое так же, как и показательное распределение, обладает фундаментальным свойством отсутствия последействия). Продолжая исследование характеристик системы М/М/1, мы увидим, что почти все ее важнейшие распределения вероятностей относятся к типу распределений без последействия. Важной характеристикой СМО является среднее число N требований в системе. Эта величина, очевидно, задается равенством
м== Е /% = (! — р) Е V-
*=0 /г=0
Используя рассуждения, аналогичные применявшимся при выводе формулы (2.142), получаем ос
- р)р 2 р^(1" р)р^:
fe=0
^=-7-2—. "(3.24)
1 — р v '
1 Возвращаясь к формуле (2.163) для переходных вероятностей в системе сразу находим член (1 — р) рк; читатель может легко проверить, что при р < 1 переход к пределу в этой формуле согласуется с полученным здесь решением.
114
Рис. 3.3. Среднее число требований Рис. 3.4. Среднее время пребывания в системе типа М/М/1 требования в системе >:ша А1/-'»/1
как функция р
График среднего числа требований в системе показан на рис. 3.3. Аналогичными методами находим, что дисперсия числа требований в системе
оо
o2n = L (А — N)2Pk',
„2 __ Р
(1—Р)2 •
и (3.25)
Применяя теперь формулу Литтла, из (3.25) непосредственно получаем следующие равенства для среднего времени пребывания в системе:
Т = —
7.
Г = «(3.26)
График зависимости среднего времени пребывания в системе от коэффициента использования р приведен на рис. 3.4. Величина Т, соответствующая точке р = 0, равна среднему значению времени обслуживания требования; иными словами, в этом случае требование не ожидает в очереди и обслуживается в среднем 1/р. секунд.
Графики функций (3.24) и (3.26) довольно выразительны. При стремлении р к единице как среднее число требований в си-
115
стеме, так и среднее время пребывания требований в ней неогра-ничено возрастают *. При р = 1 обе эти величины являются простыми полюсами. Такой тип зависимости от р при р, стремящемся к единице, характерен почти для всех СМО. Мы встретимся с ним опять при изучении системы M/G/1 в гл. 5, а также в случае большой нагрузки в системе G/G/1 (и при вычислении границ для характеристик системы G/G/1, рассматриваемой в гл. 2 тома II). Представляет интерес вычислить также другую характеристику, а именно вероятность того, что в системе имеется по меньшей мере k требований:
Р k требований в системе] =2 р, = L (I — р)р‘ = pft. "(3.2/) i—k i=k
Таким образом, вероятность того, что число требований в системе превысит некоторое граничное значение, описывается убывающей геометрической прогрессией, которая зависит от этого граничного числа и быстро,^стремится к нулю.
Заканчивая параграф, следовало бы найти плотность распределения вероятностей времени пребывания в системе. Однако отложим этот вопрос до исследования более общей системы типа M/G/1 в гл. 5 [равенство (5.118)1. Теперь же продолжим рассмотрение других систем, описываемых процессами размножения и гибели в стационарном режиме.
1 Заметим, что при р = 1 характеристики системы становятся неустойчивыми; это неудивительно, если вспомнить, что условием эргодичности является неравенство р < 1. Может показаться удивительным, как при р -> 1 резко ухудшается характеристика среднего числа требований в системе N и среднего времени Т обслуживания. В гл. 1 для регулярных потоков укзывалось, что при R < С (что соответствует условию р < 1) не возникает никаких очередей и поток требований гладко и быстро проходит через систему. Теперь мы видим, что для системы М/М/1 это не так, и за использование системы на грани ее пропускной способности (но не достигая этой грани) приходится платить чрезвычайно дорого. Интуитивное объяснение этого явления состоит в том, что при случайном потоке (которым характеризуется система М/М/1) возникают такие всплески нагрузки, которые временно перегружают обслуживающий прибор; хотя среднее время незанятости прибора равно 1 — р = р0, оно не может быть распределено равномерно на малых промежутках времени, а выдерживается при достаточно продолжительной работе. С другой стороны, в случае регулярного потока (что соответствует системе типа D/D/1) среднее время незанятости прибора распределено очень равномерно в том смысле, что после каждого промежутка обслуживания (длящегося точно 1/(л секунд) наступает промежуток незанятости прибора, равный в точности (1/Л) — (1/р) секунд. Имение этой изменчивостью обеих случайных переменных — промежутков времени между соседними требованиями и продолжительностей обслуживания — объясняется резкий подъем характеристик вблизи точки р — 1; уменьшение изменчивости любой из этих случайных величин приведет к уменьшению среднего времени ожидания, в чем читатель сможет неоднократно убедиться.
116
3.3. ПЕРЕПОЛНЯЮЩИЕ ВХОДЯЩИЕ ПОТОКИ
В качестве следующего примера рассмотрим случай, когда входящий поток переполняет систему, т. е. когда присутствующих требований становится все больше и больше. Один из способов задания такой модели состоит в следующем выборе параметров размножения и гибели:
= * = 1,2,...;
А. 1
рА = р, k = 1, 2, 3,. ..
Это эквивалентно предположению о том, что интенсивность поступления требований характеризуется гармоническим рядом в зависимости от числа присутствующих в системе требований. Диаграмма интенсивностей переходов для этого случая представлена на рис. 3.5. Применяя равенство (3.11), сразу получаем, что
k—i
na/(i + О /о
—; (3.28)
z=0
'’‘“'’•(’тГтт- <3-29»
Разрешая относительно р0 равенство (3.12), получаем
р0 = е-а/в.
Следовательно, из уравнения (3.32) имеем р = 1 —
(3.30)
Заметим, что условие эргодичности в этом случае выражается просто неравенством а/р < сю. Возвращаясь к равенству (3.29), находим окончательное решение в виде
рк = 'У:'' й = 0>1,2,... (3.31)
Таким образом, число требований, находящихся в системе с переполняющим входным потоком, описывается распределением
Рис. 3.5. Диаграмма интенсивностей переходов для случая переполняющего входящей о IIO-! ОКд
117
Пуассона! Согласно равенствам (2.131) и (2.132) среднее число требований в системе
Для вычисления среднего времени Т пребывания требования в системе опять воспользуемся результатом Литтла. Для этого нам потребуется величина %, которую непосредственно можно вычислить из равенства р — Хх — Х/р. Таким образом, из (3.30) имеем
X = рр = р (1 — е~а^).
Используя это равенство 1 * и результат Литтла, получаем
7 ° 7 оз.-./,.,- <3-32>
3.4. СИСТЕМА М/М/сю: НЕМЕДЛЕННОЕ
ОБСЛУЖИВАНИЕ (БЕСКОНЕЧНОЕ ЧИСЛО
ПРИБОРОВ)
Рассмотрим теперь случай, который можно интерпретировать либо как наличие немедленно обслуживающего прибора, интенсивность обслуживания которого растет линейно с ростом числа ожидающих требований, либо как систему, в которой всегда найдется новый обслуживающий прибор, доступный каждому вновь поступающему требованию. В частности, положим
'/.k == X, k = 0, 1, 2,...;
pfe = Ар, k == 1, 2, 3,.. .
Диаграмма интенсивностей переходов для этого случая показана на рис. 3.6. Переходя сразу к равенству (3.11), получаем
Рис. 3.6. Диаграмма интенсивностей переходов для СМО типа М/М/оо с бесконечным числом обслуживающих приборов
1 Заметим, что этот результат можно было бы получить из равенства X =
= S ^kPk- Читателю рекомендуется провести эти вычисления.
к
118
Нужно ли продолжать дальше? венства (3.33) и (3.28). Так как выписать искомые решения для
Читатель должен сравнить ра-они эквивалентны, можно сразу Pk и N:
= k = 0,1,2,.
А = — . р
(3.34)
Условие эргодичности в данном случае также задается простым неравенством %/р < сю. Может показаться поэтому, что система с переполняющим входящим потоком является в точности такой же, как и система с немедленным обслуживанием. Однако формула Литтла приводит к отличному от (3.32) (и более простому) выражению для среднего времени Т пребывания в системе, а именно, Т = 1/р. Этот ответ, конечно, очевиден, если следовать интерпретации, согласно которой каждому поступающему требованию гарантируется собственный обслуживающий прибор; в этом случае время пребывания требования в системе равно его времени обслуживания, которое в среднем составляет 1/р секунд.
3.5. СИСТЕМА М/М/т: СЛУЧАЙ m ОБСЛУЖИВАЮЩИХ ПРИБОРОВ
Рассмотрим опять систему с неограниченным числом мест для ожидания и постоянной интенсивностью поступающих требований. Предположим, что в системе может быть использовано максимум m обслуживающих приборов. Эти условия можно сформулировать с помощью процесса размножения и гибели в виде
%* = %, fe = 0, 1, 2,...;
1 k\k, 0 k < m;
= min [^р, mp] =
Z/t rv.
Из неравенства (3.20) легко увидеть, что условие эргодичности в данном случае имеет вид %/р < 1. Диаграмма интенсивностей переходов для рассматриваемого процесса представлена на рис. 3.7. Переходя к решению для pk в соответствии с равенством (3.11), видим, что это решение должно быть разбито на две части,
Ал Л л л л
Рис. 3.7. Диаграмма интенсивностей переходов для СМО типа М/М/ш
119
так как зависимость ц,,, от k также имеет две части. Соответственно, при k < tn
П / A. \k 1 /О
Ы ' З’й°)
Аналогично, при k > т, т—I k~ 1
pk = Ро 0) (£' + 1)Р Д = Ро (т) т1тк~т • (3,36)
Объединяя результаты (3.35) и (3.36), получаем
(тр)* ,
Ро->
(о)* т’п .
р0 н , к > т,
,и ml ’ ’
(3.37)
где
Л - 1
Р ==-----< 1
(3.38)
Это выражение для р вытекает из равенства (2.30) и согласуется с данным выше определением этого коэффициента через ожидаемую долю занятых приборов. Теперь с помощью (3.12) можно выписать решение для poi
у1 (/пр)* , у (mp)* 1 1 1
Zj kl 1 ml /г—1 k=m
и, следовательно,
r-tn— I л -1
у (/np)* _u / (mp)* \ / 1 \
4.J k I ' \ ml / \ 1 — p /
(3.39)
Вероятность того, что поступающее требование окажется в очереди, задается равенством
Таким образом,
Р [ожидания]
Р [ожидания) = pk = р0 k=m k=m
120
Эту формулу широко используют в телефонии; она определяет вероятность того, что поступающий на пучок т линий вызов (требование) не застанет ни одной свободной линии (обслуживающего прибора); рассматриваемая формула называется С-фор-мулой Эрланга, а соответствующую вероятность часто обозначают 1 С (т, Х/ц).
3.6. СИСТЕМА М/М/1/К: КОНЕЧНЫЙ НАКОПИТЕЛЬ|
Рассмотрим теперь впервые СМО, для которой фиксировано максимальное число ожидающих требований; в частности, предположим, что в системе могут находиться самое большее К. требований (включая и то требование, которое находится на обслуживании) и что любое поступившее сверх этого числа требование получает отказ и немедленно покидает систему без обслуживания. Поступление новых требований происходит по закону Пуассона, но в систему допускаются только те, которые застают в ней строго меньше, чем К, требований. В телефонии требования, получившие отказ, считаются потерянными; систему с К = I (в которой места для ожидания отсутствуют совсем) называют системой с удалением заблокированных вызовов и одним обслуживающим прибором.
Интересно, что для описания этой как будто сложной системы можно приспособить модель процесса размножения и гибели. В частности, для такого описания будем перекрывать входящий пуассоновский поток на время, когда система заполняется, следующим образом;
:-----------------
к,
О,
k<K\ k^K;
yk = у, k = 1, 2,..., К.
Из неравенства (3.20) видно, что эта система эргодична всегда. Диаграмма интенсивностей переходов для рассматриваемой конечной цепи Маркова показана на рис. 3.8. Переходя прямо к равенству (3.11), получаем
Pk = Po
fe-i
П-,
Iх
k<K,
или
= k<K.
(3.41)
1 В Европе принято обозначение £2, т (W).
121
Рнс. 3.8. Диаграмма интенсивностей переходов для системы М/М/1/К с конечным накопителем
Кроме того, имеет место также
Рь = О, /г>К.
(3-42)
Для того чтобы найти р0, подставим (3.41) и (3.42) в (3.12) и по-
лучим
г К п-1
Ч‘ + ,М,>^Г V k=l J
и, следовательно,
Ро =
1 — Л/р
1 - (fyji)K+I ’
Таким образом, окончательно имеем
Pk =
——У, 0</г<7<;
1 — (Л/р)к+1 '
О в остальных случаях.
(3.43)
Для системы с удалением заблокированных вызовов (К = 1) имеем
f А-,-- > k = 0;
I 1 + М1
= i , Aj=1=K; (3.44)
। 1 + Л/ц ’
I 0 в остальных случаях.
3.7. СИСТЕМЫ М/М/ш С т ОБСЛУЖИВАЮЩИМИ ПРИБОРАМИ И ПОТЕРЯМИ
Рассмотрим опять систему с удалением заблокированных вызовов, в которой доступны т обслуживающих приборов. Каждое вновь поступившее требование подается на свой отдельный обслуживающий прибор, однако если требование поступает в момент, когда все приборы заняты, то оно теряется. Как и прежде, опишем 122
Рис. 3.9. Диаграмма интенсивностей переходов для системы М/М/т с гп обслуживающими приборами и потерями
этот случай путем выбора подходящих коэффициентов размножения и гибели:
. (X, k <_ tn\
=
I 0, k > tn\
pift = /epi, k = 1, 2,. .m.
Здесь опять всегда гарантируется эргодичность. На рис. 3.9 приведена диаграмма интенсивностей переходов для рассматриваемой конечной цепи Маркова.
Используя (3.11), получаем
k-l
или
Мт) ТГ’ k<m'
0, k^> т.
(3.45)
Решение для р0 имеет вид
Ро =
г т
|_Л=0
-1
Этот частный случай рассматриваемых систем представляет большой интерес для телефонии [настолько большой, что во многих книгах по телефонии приводятся таблицы и графики функции (3.45)]. В частности, вероятность рт описывает долю времени, когда все т приборов заняты. Эта вероятность
/т!
"т т
У (Хф)*/А!
*=о
(3.46)
Последнее равенство называют формулой потерь Эрланга. Его часто называют также В-формулой Эрланга и обозначают 1 В (т, Х/ц). Формула (3.46) была впервые получена Эрлангом в 1917 г.
1 В Европе используется обозначение Ег, т (Х/р).
123
3.8. СИСТЕМА М/М/1//М *: КОНЕЧНОЕ ЧИСЛО
ИСТОЧНИКОВ НАГРУЗКИ И ОДИН ОБСЛУЖИВАЮЩИЙ ПРИБОР
В этом разделе рассматривается случай, когда входящий поток требований больше не является пуассоновским с бесконечным числом источников нагрузки, а создается конечной группой возможных клиентов. Структура системы такова, что имеется всего М. источников нагрузки; требование находится либо в системе (состоящей из очереди и одного обслуживающего прибора), либо вне системы и является в некотором смысле поступающим («на подходе»). Если требование находится в группе поступающих, то момент времени его поступления в систему является случайной величиной, распределенной по показательному закону со средним значением 1/Х секунд. Предполагается, что все клиенты действуют независимо друг от друга. Отсюда следует, что если в системе находятся k требований (очередь плюс прибор обслуживания), то М — k требований находятся в числе поступающих, и, следовательно, общая интенсивность поступления требований в этом состоянии равна X (М — k).
Ясно, что эта система в строгом смысле является саморегули-руемой. Когда она перегружается, т. е. образуется большая очередь требований, то интенсивность поступления дополнительных требований убывает, что предотвращает дальнейшую перегрузку системы. Подходящей моделью для описания такой системы является процесс размножения и гибели при следующем выборе параметров;
k ~~ ( 0 в остальных случаях;
= &= 1,2,3,...
Система является эргодической. Предполагается, что в системе имеется накопитель, объем которого достаточен для хранения М требований. Диаграмма интенсивностей переходов для рассматриваемой системы показана на рис. 3.10.
Используя равенство (3.11), для pk сразу получаем решение в виде
k—1
Р.-РоП 0</г<А1.
/л I
* Напомним, что пустое место в любой из двух последних необязательных позиций принятого обозначения свидетельствует о том, что соответствующая величина равна оо; следовательно, в данном случае рассматривается система М/М/1/оо/М.
124
Рис. 3.10. Диаграмма интенсивностей переходов для системы М/М/1//М с конечным числом источников нагрузки одним обслуживающим прибором
Таким образом,
Рн =
/ Л \* М!
Ро \ р ) (М — k)!
(3.47)
о,
k>M.
0-</г< м-,
Кроме того, для р0 получаем
г м
S( X \* М I
\ И ! (М - k)!
* (3.48)
3.9. СИСТЕМА М/М/оо//М: КОНЕЧНОЕ ЧИСЛО ИСТОЧНИКОВ НАГРУЗКИ И «БЕСКОНЕЧНОЕ» ЧИСЛО ОБСЛУЖИВАЮЩИХ ПРИБОРОВ
Рассмотрим опять случай конечного числа источников нагрузки, но теперь предположим, что каждое требование обслуживается в системе отдельным прибором. Такая модель задается следующим образом:
[ ЦМ-k), ('xk< М\
( 0 в остальных случаях;
= &Ц, & = 1, 2, 3,...
Ясно, что эта система также является эргодической. Диаграмма интенсивностей переходов для такой системы показана на рис. 3.11. Для вероятностей pk этой системы из (3.11) имеем
=Ро(±у^'), (3.49)
Рис. 3.11. Диаграмма интенсивностей переходов для системы М/М/<»//М с конечным числом источников нагрузки и бесконечным числом обслуживающих приборов
125
где биноминальные коэффициенты определяются обычным образом:
М \ Л41
k )= — •
Определяя р0, получаем
и, следовательно,
Таким образом,
-Ж)
(1 4- Х/Ц)Л1
(3.50)
О в остальных случаях.
О < k с М;
Не составляет труда вычислить среднее число требований в си
стеме:
Используя частную производную так же, как при выводе равенства (3.24), получаем
V — __ “ I +W
3.10. СИСТЕМА М/М/т/К/М: КОНЕЧНОЕ ЧИСЛО ИСТОЧНИКОВ НАГРУЗКИ, т ОБСЛУЖИВАЮЩИХ ПРИБОРОВ И КОНЕЧНЫЙ НАКОПИТЕЛЬ
Эта достаточно общая система является наиболее сложной из всех рассмотренных выше, и при соответствующем выборе ее параметров она может быть сведена к любому предыдущему случаю (за исключением системы с переполняющим входящим потоком). Предполагается, что имеется конечное число М требований, причем интенсивность поступления каждого требования равна А. Кроме того, система содержит т обслуживающих приборов, каждый из которых описывается параметром ц. Наконец, в системе имеется конечное число мест для ожидания, такое, что общее число требований в системе (очередь плюс обслуживаемые требования) не превышает К- Предполагается, что М. > К > пг, 126
МЛ (М-1)Л (М-т)Л (М-К+1)Л
Рис. 3.12. Диаграмма интенсивностей переходов для системы М/М/ш/К/М с т обслуживающими приборами, конечным накопителем и конечным числом источников нагрузки
требования, поступающие в систему тогда, когда в ней уже имеется К требований, теряются и немедленно возвращаются в группу поступающих так, как будто бы они полностью обслужены. Это приводит к следующему множеству параметров процесса размножения и гибели:
JA(M- k), OcfecK-l; Хь = { Л
I 0 в остальных случаях;
( /гр., О с k < т;
ц.1. = ( ,
I mp, k » т.
На рис. 3.12 представлена наиболее сложная из всех рассмотренных конечных диаграмм интенсивностей переходов. Для того чтобы воспользоваться равенством (3.11), надо рассмотреть две области. В области 0 с k с т — 1 имеем
k-i
^ = РоП = Mk )> 1. (3.51)
В области т < k < К имеем
m—1
Pk = Po П
X (М — t) tnu.
X (М —t) (i +1) ц
(3.52)
Формула для р0 получается весьма сложной и здесь не приводится, хотя она может быть получена непосредственными вычислениями. В случае чистых потерь в системе (т. е. при М > К = т) стационарные вероятности определяются в виде
(
Pk=~k ' ---, /г = 0, 1, 2,. .., т. (3.53)
Это распределение называется распределением Энгсета.
Подобные примеры можно было бы продолжать и дальше, но мы пощадим читателя и этим закончим. Дополнительные примеры даны в задачах. Теперь читателю должно быть ясно, что многие интересные структуры СМО могут быть описаны процессами
127
размножения и гибели. В частности такая возможность была продемонстрирована для случая многих обслуживающих приборов, для случая конечного числа источников нагрузки, для случая конечной очереди и для комбинаций этих возможностей. Общим моментом всех проведенных исследований является использование равенств (3.11) и (3.12) для получения стационарных вероятностей \рк]. В этой главе были рассмотрены только такие системы, для которых стационарные вероятности могут быть найдены с помощью указанных равенств. Однако имеется много других марковских систем, для которых непосредственно получаются простые решения для стационарных вероятностей и которые представляют интерес в теории массового обслуживания.
Стационарное решение для марковских систем рассматривается в гл. 4; в гл. 5 этот материал обобщается на полумарковские процессы, для которых допускается произвольное распределение времени обслуживания В (х), а в гл. 6 мы опять возвращаемся к показательному распределению времени обслуживания, но допускаем произвольное распределение А (!) промежутков времени между последовательными требованиями; в обоих этих случаях рассматриваются вложенные цепи Маркова. Только в случае, когда оба распределения В (х) и А (/) не являются показательными, необходимо пользоваться методами общей теории массового обслуживания, обсуждаемой в гл. 8. (Существует, правда, несколько частных случаев непоказательных распределений, которые могут быть описаны с помощью теории марковских процессов, и они также рассмотрены в гл. 4.)
ЗАДАЧИ
3.1. Рассмотрим чистую марковскую систему, для которой р, 0 < k < К;
= ( 2%, К < k;
Рй = [л, k = 1, 2, 3,...
а) Найдите стационарные вероятности pk для числа требований в системе.
б) Какие соотношения должны связывать параметры системы, для того чтобы она была устойчивой и, следовательно, существовало стационарное распределение? Дайте интерпретацию полученного решения с помощью возможного динамического описания системы.
3.2. Рассмотрим марковскую систему, для которой
= k 0, 0<а<1;
Ил “ р, fe > 1 •
а) Найдите стационарные вероятности рк для числа k требований в системе. Выразите ответ через р0.
б) Найдите выражение для р0.
128
3.3. Рассмотрим СМО типа М/М/2 с интенсивностью входящего потока А требований в секунду и средним временем обслуживания 1/р. секунд, причем А < 2р,.
а) Выпишите систему дифференциальных уравнений для вероятностей Рк (t) как функций от времени.
б) Найдите стационарные вероятности
Рк lim Рк (t).
3.4. Рассмотрим систему М/М/1 с параметрами А и ц, в которой все клиенты являются нетерпеливыми. А именно: при поступлении требования оценивается время предстоящего ожидания w и затем это требование с вероятностью е~“® становится в очередь (или покидает систему с вероятностью 1 — е_“ю). В качестве оценки используется величина w = = k/ii, где k — число требований в системе в момент поступления рассматриваемого требования. Предполагается, что а > 0.
а) Найдите стационарные вероятности рк наличия k требований в системе, выраженные через р0. Дайте выражение для вероятности р0 через параметры системы.
б) При каких условиях для а > 0 и р, > О существует стационарное решение?
в) При а оо найдите точные формулы для рк и для среднего числа требований в системе.
3.5. Рассмотрим систему, описываемую процессом размножения п гибели с параметрами
Аа, (А + 2) А, 1,2, ..;
k = 1, 2, 3,. . .
Все остальные параметры равны нулю.
а) Найдите стационарные вероятности рр, ответ выразите в явном виде только через А, /г и р.
б) Найдите среднее число требований в системе.
3.6. Рассмотрим процесс размножения и гибели с параметрами
А/г = ak (А2 — A), k = Ki, Ах {- 1,. .., Л2;
= — /<,), k = К\ - г 1,- - •, А3,
где Kj <. К.2, а те параметры, которые расположены за пределами Ki < k К2, равны нулю. Найдите стационарное распределение рк (предполагая, что в начальном состоянии система содержит К± < k < К2 требований).
3.7. Рассмотрим систему М/М/т, предназначенную для обслуживания суммы двух пуассоновских потоков; интенсивность /-го потока требований равна А,, а время их обслуживания распределено по показательному закону со значением 1/|Л, (/ = 1, 2). Первый поток является ординарным, поэтому каждое поступающее требование занимает точно один из т
5 Л. Клейнрок 129
обслуживающих приборов; если все т приборов заняты, то вновь поступающее требование первого класса теряется. Для обслуживания каждого требования второго класса требуется одновременно т0 приборов (и оно занимает все эти приборы одновременно на одно и то же показательно распределенное время со средним значением 1/р2 секунд); если в момент поступления требования второго класса в системе имеется меньше чем тп свободных приборов, это требование также теряется. Найдите долю потерянных требований первого и второго классов.
3.8. Рассмотрим систему с конечным числом источников нагрузки и одним обслуживающим прибором, которая была рассмотрена в параграфе 3.8; пусть параметры М и А заменены на М и А'. Можно показать, что, если М -> оо и А' -»• 0 так, что существует предел Л4А' = А, то система с конечным числом источников нагрузки превращается в систему с бесконечным числом источников нагрузки и показательным распределением промежутков времени между поступающими требованиями (с интенсивностью А требований в секунду). Рассмотрим теперь систему, описанную в параграфе 3.10; обозначим параметры этой системы через М, К, т, ц, К. Укажите, какие значения должны принимать эти параметры для того, чтобы получались системы, описанные в параграфах 3.2, 3.4—3.9.
3.9. Используя определение функции В (т, А/ц) из параграфа 3.7 и определение функции С (т, А/ц) из параграфа 3.5, докажите для А/р, >0 и всех т = 1, 2, ... следующие соотношения:
3.10. Рассмотрим систему М/М/1 в дискретном времени, предположив, что ось времени разбита на промежутки длиной q секунд каждый. Предполагается, что события происходят только в конечных точках этих промежутков времени. В частности, вероятность поступления одного требования в конце промежутка равна Ащ а вероятность того, что требование в этот момент не поступит, равна 1 — At? (таким образом, возможно поступление не более одного требования). Аналогично, процесс ухода требований из системы
130
таков, что для требования, находящегося в приборе обслуживания, вероятность окончания обслуживания к концу рассматриваемого промежутка времени равна 1 — а, а вероятность продолжения обслуживания в течение, по меньшей мере, еще одного промежутка времени равна о.
а) Выведите формулы для плотности распределения a (t) промежутков времени между соседними требованиями и плотности распределения b (я) времени обслуживания.
б) Предполагая обслуживание в порядке поступления, выпишите систему уравнений статистического равновесия для вероятностей pk = Р [k требований в системе в конце промежутка дискретизации], где k включает как требования, поступившие в конце данного промежутка, так и требования, которые покидают систему в этой точке.
в) Найдите среднее число требований в этих точках.
3.11. Рассмотрим систему М/М/1 с обратной связью; это значит, что после окончания обслуживания требование с вероятностью о возвращается в хвост очереди через некоторое случайное время, распределенное по показательному закону (со средним значением 1/у секунд); с другой стороны, с вероятностью 1 — о после завершения обслуживания требование навсегда покидает систему. Очевидно, требование может возвращаться в хвост очереди несколько раз перед тем, как навсегда покинет систему. Пусть pkj — стационарная вероятность того, что в системе (т. е. в очереди и в обслуживающем приборе) имеется k требований и что / требований находятся в процессе возвращения в систему.
а) Выпишите систему разностных уравнений, определяющих стационарные вероятности phj.
б) Определяя двойную производящую функцию равенством
Р(?\, Z?) = Е X PkjZklZ^ покажите, чю
Г , 1 — о г, 1 ч
Н 1-------------о Р (0, г2).
L J
в) Используя свойства производящей функции моментов, докажите, что среднее число требований в системе (очередь плюс обслуживающий прибор) равно р/(1 — р), а среднее число возвращений в хвост очереди равно рор/у, где р = М(1 — сг) р.
5*
3.12. Рассмотрим циклическую очередь, в которой Л4 требований циркулируют через два обслуживающих прибора так, как это показано иа рисунке.
Оба прибора характеризуются показательным распределением времени обслуживания с интенсивностями и fx2 соответственно. Пусть рк = Р [k требований на первом этапе и /И — k во втором].
а) Нарисуйте диаграмму интенсивностей переходов.
б) Выпишите соотношения между {рк\.
в) Найдите
м P(z) = % pkzk. /г=0
г) Найдите рк.
3.13. Рассмотрим систему М/М/1 с параметрами X и ц. Требование в очереди может повредиться (покинуть систему без обслуживания) с вероятностью аЛ/ -|- о (Л/) в любой промежуток времени длительности Л/.
а) Нарисуйте диаграмму интенсивностей переходов.
б) Выразите рк+1 через рк.
в) Найдите рк (k = 0, 1,2, ...) при а = ц.
3.14. Рассмотрим подробнее систему М/М/1/К из параграфа 3.6. а) Вычислите рк при л = fx.
б) Найдите N для /, Ли и л - ii.
в) Найдите Т, вычислив предварительно интенсивность входящего потока.
ГЛАВА 4
Марковские системы массового обслуживания в установившемся режиме
Предыдущая глава была посвящена изучению решения для стационарных вероятностей состояний процесса размножения и гибели, имеющего форму произведения (3.11). Преимущество этого решения состоит не только в его простоте, но также и в широких возможностях его применения к системам массового обслу-132
живания, которые уже обсуждались. Если перейти от процессов размножения и гибели к более общим марковским процессам, то рассмотренное решение в виде произведения перестает быть справедливым; однако для чисто марковских систем можно искать и часто удается найти некоторые другие формы решения в виде произведения. В данной главе предпринимается попытка исследовать некоторые из этих марковских процессов, представляющих непосредственный интерес для теории массового обслуживания. Многое из того, что будет сказано, относится к случайным блужданиям марковского типа; их можно рассматривать как несколько более общие процессы размножения и гибели, в которых переходы разрешены не только в соседние состояния, однако их структура все же позволяет найти точные решения. Все основные распределения являются, конечно, показательными.
Здесь опять речь идет о результатах, относящихся к состоянию равновесия. Рассмотрение начинается с общего метода составления уравнений равновесия путем перебора. Затем рассматривается частный случай эрланговского распределения Ег, которое применяется к системам М/Ег/1 и Ег/М/1. Легко видеть, что работу системы М/Ег/1 можно интерпретировать как исследуемый дальше в общем виде процесс с пакетным входящим потоком; аналогично, система Е/М/1 может быть интерпретирована как система с пакетным обслуживанием, которая также будет изучена отдельно. Затем рассматривается более общая система Е^/1 и делается шаг в направлении исследования широкого класса систем типа G/G/1, которые получаются из эрланговских систем путем последовательно-параллельных комбинаций. Наконец, рассматриваются сети массового обслуживания, в которых все основные распределения также предполагаются распределениями без последействия. Как увидим, в большинстве из этих случаев решение получается в виде произведения.
4.1. УРАВНЕНИЯ РАВНОВЕСИЯ
Отправной точкой здесь является уравнение (2.116), а именно nQ = 0, выражающее условия равновесия для общего эргодического непрерывного марковского процесса с дискретным множеством состояний; вспомним, что л представляет собой вектор-строку, компонентами которой являются стационарные вероятности состояний, a Q является инфинитезимальным оператором, элементы которого равны инфинитезимальным интенсивностям переходов рассматриваемого марковского процесса. Как уже говорилось в предыдущей главе, предпочтительнее выбрать для вектора л более распространенное в теории массового обслуживания обозначение через вектор-строку р, /г-й компонентой которого является стационарная вероятность рк нахождения системы в состоянии Ек. Таким образом, задача состоит в решении уравнения 133
Л. pQ 0, при дополнительном ограпиче-
| _ нии, налагаемом нормирующим усло-
Л вием (2.117):
$ *7*" я Л I Pk = 1 •
Это векторное уравнение называется Рис. 4.1. пример системы с пе- уравнением равновесия системы. со^оян’йя"6 только “ соседнио В гл. 3 был описан графический метод составления уравнений равновесия, основанный на анализе диаграммы интенсивностей переходов. В основе этого метода лежит замечание о том, что интенсивность потока вероятностей, входящего в данное состояние, равна интенсивности потока вероятностей, исходящего из этого состояния. Очевидно, что замечание о сохранении потока применимо к более общим процессам, чем процесс размножения и гибели; фактически оно применимо к любой цепи Маркова. Таким образом, можно строить системы с допустимыми переходами не только в соседние состояния, и все-таки считать, что метод сохранения потока будет применим к ним; это соответствует действительности.
Итак, предлагаемый подход состоит в описании цепи Маркова с помощью ее диаграммы состояний и последующем применении принципа сохранения потока к каждому состоянию. Для этой цели графическое описание системы часто оказывается более подходящим, чем словесное, математическое или матричное. Составив такое графическое описание, можно путем перебора состояний выписать уравнения, характеризующие динамику системы. В качестве примера рассмотрим очень простую цепь Маркова с тремя состояниями, показанную на рис. 4.1 (эта система, очевидно, не может быть описана процессом размножения и гибели, так как в ней допускается переход Ео -> Ez). Выписывая условие сохранения потока для каждого состояния, получаем систему уравнений
= ц/д; (4.1)
(X р) Pi:— hpo +
7 . ,
(4-2)
(4.3)
где уравнения (4.1), (4.2) и (4.3) соответствуют условиям сохранения потока в состояниях Ео, Ei и соответственно. Заметим также, что последнее уравнение является в точности суммой первых двух; для конечных цепей Маркова всегда получается точно одно избыточное уравнение. Дополнительным уравнением является, как известно, условие /?(, /л . 1.
134
Решение этой системы уравнений имеет вид
А
(4 1)
Вот так! Просто, как яблочный пирог. Фактически, эго гак же «просто», как решение системы линейных уравнений.
Преимущества метода перебора будут использованы в этой главе для определения стационарных распределений ряда цепей Маркова \
Как и в предыдущей главе, будем рассматривать предельные вероятности pk = lim Р IN (t) = k] при /~>со, предполагая, что эти пределы существуют. Эти вероятности можно интерпретировать как долю времени, в течение которого система находится в состоянии Ек. Фактически эти вероятности можно оценить, определяя частоту нахождения в системе k требований.
Другой величиной, представляющей интерес в СМО (возможно, даже больший, чем предыдущая величина), является вероятность того, что вновь поступившее требование застанет систему в состоянии Д/.; иными словами, для эргодической системы рассматривается стационарная вероятность
г,. — Р [поступающее требование находит систему В СОСТОЯНИИ fife].
Основываясь только на интуиции, можно подумать, что во всех случаях pk = гк-, но легко показать, что это в общем случае неверно. Например, рассмотрим (немарковскую) систему D/D/1, в которую требования поступают равномерно, т. е. ровно через каждые t секунд поступает требование; время обслуживания одинаково для всех требований и равно, например, х секунд. В этой однолинейной системе нетрудно узнать систему с регулярным потоком по единственному каналу (вспомним фабрику по переработке ананасов). Для стабильности режима требуется выполнение условия х < t. Тогда ясно, что в устойчивом состоянии ни одно требование не будет ожидать обслуживания, и, следовательно, r0 = 1 и rk = 0 для всех k = 1, 2, ... Более того, ясно, что доля времени, в течение которого система содержит одно требование (в обслуживающем приборе), равна точно р xlt, а остальное время система свободна; следовательно, р0 1 — р, pi = р, Pk = 0 для всех k = 2, 3, ... Таким образом, в этом тривиальном
1 Должно быть ясно также, что метод перебора позволяет непосредственно выписать и нестационарные вероятности Рк (/) подобно тому, как это было сделано для процесса размножения и гибели; уравнения, содержащие зависимость от времени, фактически будут иметь вид (2.114).
1.'Т>
Гфимере Р', - /у. Однако часто случается, что интуиция оказывается правильной: существует большой класс САК), для ш>т<q<ых /У; Г/, при всех k. Таким классом является класс стабильных
систем с пуассоновским входящим потоком.
Фактически можно доказать даже большее, и ниже будет показано, что для любой СМО с пуассоновским входящим потоком должно выполняться равенство Pk (t) — Rk (t), где, как и ранее, Pk (/) — вероятность того, что система находится в состоянии Ek в момент t, a Rk (0 — вероятность того, что поступающее в момент t требование застанет систему в состоянии £,... В частности, для рассматриваемой системы с пуассоновским входящим потоком обозначим через A (t, t + Л/) событие, состоящее в том, что в промежуток времени (t, t ~Н А/) поступит требование; тогда имеем
Rk (t) Л lim Р [А/ (?) = k | A (t, t 4- Л/)], (4.5)
д^о
где N (/) означает число требований в системе в момент I. Используя определение условных вероятностей, перепишем Rk (/) в виде
Rk(t} == lim
Д'->()
Р [N (0 •-= k, A (t, tp-M)] Р[Ар, /Д-Д/)]
--•= lim
д/^е
Р [А р, / 4- Д/) I (/) -= /г] Р [Л; (?) k]
Р [A Р, t +
Далее известно, что для пуассоновского потока (вследствие отсутствия последействия) событие A (t, t &t) должно быть независимым от числа требований в системе в момент t (так же, как и от самого момента /); следовательно, Р [Л (t, t -Р AZ) | N (t) -= k] — P [Л (t, tp A^)], и, таким образом, имеем
Rk (t) -- - lim P [A' (i) = k],
m-hi
или
(4.6)
Это и требовалось доказать, а именно: нестационарная вероятность того, что поступившее в произвольный момент времени требование застанет систему в состоянии £;>, равна вероятности того, что система в этот произвольный момент находится в состоянии £/,. Очевидно, этот вывод справедлив также и для стационарной вероятности rk того, что поступившее требование застанет k требований в системе, и для доли времени /?/., в течение которого в системе находятся k требований. Такая эквивалентность неудивительна, если учесть, что свойство отсутствия последействия для процесса Пуассона, как только что было показано, обусловливает входящий поток требований, которые действительно «бросают случайный взгляд» на систему.
13G
4.2. МЕТОД ЭТАПОВ — ЭРЛАНГОВСКОЕ
РАСПРЕДЕЛЕНИЕ Ег
Метод этапов позволяет исследовать СМО более общего вида, чем системы типа размножения и гибели. Этот остроумный метод представляет собой еще одно свидетельство блестящего ума А. К- Эрланга, разработавшего этот метод в самом начале нашего столетия задолго до того, как были развиты методы современной теории вероятностей. Эрланг распознал чрезвычайную простоту показательного распределения и увидел в нем мощное средство исследования марковских СМО. Он также заметил, что показательное распределение не всегда позволяет адекватно описать истинную картину распределения времени обслуживания (и промежутков времени между поступающими требованиями). Он должен был также заметить, что допущение о более общих законах распределения времени и обслуживания нарушает марковское свойство и требует более сложных методов исследования \ Изящный аппарат цепей Маркова не давал легкого решения. Однако Эрланг заметил, что распределение времени обслуживания 1 2 может быть разложено в набор составляющих показательных распределений.
Основой метода этапов является свойство отсутствия последействия у показательного распределения; повторим еще раз, что отсутствие последействия выражается тем фактом, что распределение остаточного времени для показательно распределенной случайной величины не зависит от достигнутого «возраста» этой случайной величины.
Рассмотрим схему на рис. 4.2. Здесь показан обслуживающий прибор, время обслуживания которого характеризуется показательным распределением с плотностью распределения
b (%) А = Ре"ЦА', х > 0. (4.7)
Овалом на этом рисунке обозначен обслуживающий прибор, а символ р указывает параметр обслуживания, входящий в равенство (4.7). Вспомним, что согласно результатам гл. 2 среднее значение и дисперсия показательного распределения соответственно равны:
где индекс b у дисперсии о* указывает па то, что она относится к распределению времени обслуживания.
1 Как увидим в гл. 5, современный подход к решению этой задачи, а именно метод вложенных цепей Маркова, был недоступен во времена Эрланга.
2 Аналогичное замечание относится к распределению промежутков между последовательными требованиями.
137
Обсид/киВающий прибор
Рис. 4.2. Одноэтапный обслуживающий прибор с показательным распределением времени обслуживания
Рис. 4.3. Дсухэтапный эрланговский обслуживающий прибор Ег
Рассмотрим теперь систему, показанную на рис. 4.3. Большой овал на этом рисунке означает обслуживающий прибор. Внутренняя структура этого прибора содержит цепочку из двух малых овалов. Каждый из этих малых овалов означает один обслуживающий прибор с показательным распределением времени обслуживания, такой как был показан на рис. 4.2; однако на рис. 4.3 в каждом малом овале стоит символ 2р, означающий, что каждый прибор характеризуется плотностью распределения
/г(у) -= 2ре~4и/) (4.8)
Таким образом, среднее значение и дисперсия для плотности h (у) составляют соответственно Е [t/ J 1/2fx и — (Кар)2. Рассматриваемый двухэтапный обслуживающий прибор действует таким образом, что как только обслуженное требование покинет прибор, на его вход слева поступает новое требование. Это новое требование занимает этап 1 и находится в нем некоторое случайное время, описываемое плотностью распределения h (у). После ухода из первого этапа требование немедленно поступает на этап 2 и находится там случайное время, выбираемое снова независимо на основании плотности распределения h (у). После окончания этого второго случайного промежутка времени требование покидает обслуживающий прибор, и только в этот момент в прибор (слева) может поступить новое требование.
Таким образом, в произвольный момент времени в обслуживающем приборе может находиться одно, и только одно требование Т Отсюда следует, что по меньшей мере один из двух этапов
1 В качестве примера обслуживающего прибора с двумя этапами, в котором
в каждый момент времени может быть занят только один этап, рассмотрим судебную контору в маленьком городе. В ожидании суда образуется очередь ответчиков. Судья рассматривает дело (первый этап обслуживания) и накладывает штраф. Второй этап состоит из уплаты штрафа судебному клерку. Однако, поскольку юрод маленький, судья исполняет также и обязанности клерка, и поэтому он переходит к конторке клерка, взымает штраф, освобождает ответчика, возвращается па свое место, а затем приглашает следующего ответчика для «обслуживания».
138
обслуживания всегда должен быть свободным. Исследуем теперь общее время обслуживания. Ясно, что оно представляет собой случайную величину, равную сумме двух независимых и одинаково распределенных случайных величин. Следовательно, как показано в приложении II, нужно взять свертку двух плотностей распределения, соответствующих каждому из слагаемых. Иначе, преобразование Лапласа от плотности распределения времени обслуживания равно произведению преобразований Лапласа от плотностей распределения для каждого из слагаемых. Так как обе случайные величины распределены одинаково, то надо взять произведение функции на эту же функцию. Прежде всего, как обычно, определим преобразование Лапласа:
В* (si A j & -sxb (,r) dx; о
(s) A I C s-"/l (i/) dy.
I)
(4.9)
(4.10)
Из предыдущих результатов имеем
B*(s) = [//*(s)|2.
Но преобразование Лапласа or показательной функции известно [см. равенство (2.144)], поэтому
^(sj
Таким образом,
2р.
s 2ii
(4.U)
Теперь необходимо обратить преобразование (4.11). Однако читатель, наверное, помнит, что мы уже сталкивались с подобной задачей, получая результат (2.147) путем обращения (2.146). Применяя этот результат, получаем
b(x) = 2Fi(2px)e--^j д > 0. (4.12)
Теперь можно вычислить среднее значение и дисперсию для рассматриваемой двухэтапной системы одним из следующих трех-способов: основываясь на структуре системы, показанной на рис. 4.3: используя функцию В* (х) как производящую функции, моментов; непосредственными вычислениями по плотности распределения вероятностей (4.12). Выберем первый из этих способов как наиболее прямой (читателю предлагается самому проверь гь остальные два способа). Так как время, проведенное в системе, является суммой двух независимых случайных переменных, т<>,
139
очевидно, среднее время обслуживания равно сумме средних значений каждой из этих величин. Таким образом, имеем
Е fx] = 2Е \у] = —- .
Г
Аналогично, так как две суммируемые случайные величины независимы, то для определения дисперсии их суммы нужно просуммировать их дисперсии:
о? = о’и + ой = •
Заметим, что полученные выражения для среднего времени обслуживания в одноэтапной системе, изображенной на рис. 4.2, и двухэтапной системе, изображенной на рис. 4.3, совпадают. Это получилось потому, что параметр каждого этапа в двухэтапной системе был выбран вдвое большим. Заметим далее, что дисперсия двухэтапной системы составляет половину от дисперсии одноэтапной системы.
Мы дали описание двухэтапного обслуживающего прибора, но нам предстоит еще обсудить решающий момент этого описания. Рассмотрим, как меняется состояние системы с пуассоновским входящим потоком и двухэтапным обслуживающим прибором, показанной на рис. 4.3.
Как обычно, частью описания состояния системы должно быть число требований, ожидающих обслуживания. Кроме того, необходимо запастись достаточной информацией об обслуживающем приборе, содержащей необходимую предысторию. Учитывая, что показательное распределение обладает свойством отсутствия последействия, достаточно указать, какая из следующих трех возможностей имеет место в обслуживающем приборе: оба этапа свободны (что означает незанятость обслуживающего прибора); первый этап занят, а второй — свободен; первый этап свободен, а второй — занят. Информацию о состоянии обслуживающего прибора можно задавать указанием номера этапа, занятого требованием. Тогда описание состояния системы сведется к двумерному вектору, первая компонента которого указывает число требований в очереди, а вторая — число этапов, через которые уже прошло обслуживаемое требование. Время, уже проведенное требованием на данном этапе обслуживания, никак не сказывается на дальнейшем функционировании системы. Таким образом, опять получается марковский процесс с дискретным (двумерным) пространством состояний!
Рассмотренный метод обобщается и па случай r-этапного обслуживающего прибора, показанного на рис. 4.4. В этой системе новое требование может поступить в обслуживающий прибор только слева и последовательно проходить через все г этапов обслуживания только после того, как обслуженное требование покинет прибор, обозначенный большим овалом. После ухода 140
Одел уж и бающий прибор
Рис. 4.4. r-этапный эрланговский обслуживающий прибор Е
этого требования из r-го этапа возможно поступление следующего требования и т. д. Время обслуживания на t-м этапе определяется плотностью распределения вероятностей
h (у) — гре~г'4Л у > 0.
(4.13)
Полное время, проведенное требованием в приборе обслуживания, равно сумме г независимых одинаково распределенных случайных величин, каждая из которых описывается распределением (4.13). Среднее значение и дисперсия времени обслуживания на каждом этапе соответственно будут
Е [£]=_!_;
г у
Читателю должно быть ясно, что интенсивность обслуживания на каждом этапе выбрана равной гр для того, чтобы среднее время обслуживания требования оставалось постоянным и равным
£1Y1 = rGr) = V-
Аналогично, в силу независимости продолжительностей обслуживания на различных этапах для вычисления дисперсии нужно взять сумму дисперсий слагаемых:
, / 1 V 1
о* = г - == ——
\ Ф / гр2
Заметим также, что коэффициент вариации [см. равенство (11.23)1
С,(4Л4) 1' Г
Найдем опять плотность распределения вероятностей времени обслуживания. Для этого обобщим рассуждения, приведшие к равенству (4.11); в результате получим
141
h(x)
Г-. Z/7
Рис. 4.5. Семейство
распределений Эрланга Ег порядка г
Как и ранее, обращение преобразования (4.15) не составляет труда и дает
b (х) = ; л- > 0. (4.16)
В этом равенстве нетрудно узнать распределение Эрланга, определенное выше формулой (2.147). Параметры специально подобраны таким образом, чтобы среднее значение для этой плотности распределения не зависело от г. Для того чтобы получить представление о поведении этой функции, рассмотрим ее стандартное отклонение, определяемое величиной
О',, = Л .
V г \ Р )
Очевидно, что стандартное отклонение для распределения Эрланга порядка г составляет 1/]/г от стандартного отклонения одноэтапного обслуживающего прибора. Искушенному читателю уже должно быть ясно, что при увеличении г плотность распределения вероятностей, определяемая равенством (4.16), Должна согласно центральной предельной теореме сходиться к плотности нормального, или гауссовского, распределения. Это действительно верно, но равенство (4.16) говорит больше, указывая фактическую последовательность распределении при увеличении г н показывая, каким образом достигается этот предел.
На рис. 4,5 показаны графики семейства распределений Эрланга порядка г (сравните < рис. 2.10). Из этого рисунка видно, 142
что среднее для всех кривых остается постоянным, а стандартное отклонение стягивается с коэффициентом I/]/"г. Ниже будет показано, что этот предел (при г, стремящемся к бесконечности) для рассматриваемой плотности распределения должен быть импульсной функцией (см. приложение I) в точке х — 1/ц; отсюда следует, что с вероятностью единица время обслуживания в эрлан-говском приборе с бесконечным числом этапов стремится к константе (равной, конечно, среднему значению 1/ц). Далее, из рисунка видно, что максимум рассматриваемого семейства функций сдвигается вправо некоторым регулярным образом. Для того чтобы найти точку, в которой достигается максимум, продифференцируем функцию (4.16) и приравняем результат нулю:
db (х) _ (гр)2 (г—1) (rij.x)r~~e~r>lx (гцх)''-1 (гр)2 ,,
dx (4 — ГЙ (г— 1)!
Отсюда (г.— 1) — грх и, следовательно,
/ г-1\ 1
r ) ' - 0.1Щ
Таким образом, ясно, что абсцисса максимума быстро сдвш ается к своему предельному значению, равному 1/р.
Покажем теперь, что предельное распределение действительно является единичной импульсной функцией; для этого рассмотрим предел преобразований Лапласа, определенного равенством (4.15):
lim В* (s) = lim (—Y-—Y = lim (-. . 1 ,—Y;
lim B* (s) = e-s/|1. (4-18)
Г->оо
Обратное преобразование этой предельной функции находим в строке 3 табл. 1.4 приложения I; оно представляет собой импульс, расположенный в точке х — 1/р..
Таким образом, семейство распределений Эрланга изменяется в очень широком диапазоне, поэтому оно является чрезвычайно полезным для аппроксимации эмпирических (и даже теоретических) распределений. Например, если проведены измерения времени обслуживания и полученные данные достаточны только для оценки среднего значения и дисперсии, то можно построить одну из кривых этого двухпараметрического семейства, для которой среднее значение равно 1/р, а дисперсия 1/гр2; эго дает метод аппроксимации функции В (х), позволяющий (как мы увидим ниже) исследовать СМО. Если измеренный коэффициент вариации больше единицы, то, как следует из (4.14), такая процедура является ошибочной, и надо воспользоваться гиперпоказательным распределением, которое будет описано ниже.
Очевидно, что для каждого члена рассматриваемого семейства плотностей распределения состояние обслуживающего прибора 143
можно описать простым указанием числа этапов, уже пройденных обслуживаемым требованием. Распределение Эрланга порядка г будем обозначать символом Ег (не смешивать с обозначением состояния случайного процесса). Так как рассматриваемое множество состояний является дискретным, мы можем исследовать системы1 типа М/ЕЛ/1. Это исследование проводится в следующем параграфе. Кроме того, эта же методика будет использована в параграфе 4.4 для разложения распределения А (I) промежутков времени между поступлениями требований в распределение Эрланга порядка г. Заметим, что в следующих двух параграфах настоятельно требуется, чтобы по меньшей мере одно из рассматриваемых распределении было показательным (это относится также к гл. 5 и 6).
4.3. СИСТЕМА М/Е;/1
Рассмотрим систему, для которой a (t) = , t :> 0;
д.>0.
Поскольку при анализе такой системы, кроме нахождения числа требований (как это было в гл. 3), нужно еще найти число этапов, через которые остается пройти обслуживаемому требованию, приходится каждое требование в очереди описывать числом г этапов, необходимых для завершения обслуживания. Поэтому будем описывать состояние системы в произвольный момент времени общим числом этапов обслуживания, через которое должны пройти все находящиеся в этот момент в системе требования до полного завершения их обслуживания 2. В частности, если рассматривается состояние системы, характеризуемое наличием k требований, причем обслуживаемое требование находится на i-м этапе обслуживания, то число этапов, через которое предстоит пройти всем требованиям в системе,
/ А остающееся число этапов для всей системы = --= (k — 1) г + (г — I + 1).
Таким образом,
j-^rk-i-'г 1. (4.19)
Пусть, как обычно, pk означает стационарную вероятность наличия k требований в системе; определим затем
Pj А Р [/ этапов в системе]. (4.20)
1 Очевидно, такая система является частным случаем системы М/G/l, исследуемой в гл. 5 методом вложенных цепей Маркова.
2 Заметим, что тем самым принятое описание состояния системы с помощью двумерного вектора переводится в одномерное описание.
144
Соотношение между числом требований и числом этапов позволяет записать
kr
Pk^ L Ph /г= 1,2,3,...
,-=(/^1)^+1
Изящество подхода Эрланга состоит в том, что диаграмму интенсивностей переходов для рассматриваемой системы можно представить так, как показано на рис. 4.6. Сосредоточив внимание на состоянии Д-, видим, что переход в него возможен из состояния, находящегося на г позиции левее, и из состояния Ej+l\ первый переход обусловлен возникновением новых г этапов, когда поступает новое требование, а второй — завершением очередного этапа обслуживания требования в обслуживающем приборе с г этапами. Кроме того, состояние £; может быть покинуто с интенсивностью X за счет поступления требования и с интенсивностью гр за счет завершения обслуживания. Естественно, на состояния Ео, Ei, ..., Ег_х накладываются специальные граничные условия. Для того чтобы упростить эти граничные условия, допустим, как и в гл. 3, что вероятности состояний с отрицательными индексами равны нулю. Таким образом, по определению
Pi = 0, / < 0. (4.21)
Теперь, используя закон сохранения потока, можно путем перебора состояний непосредственно выписать уравнения системы. (Заметим, что речь идет о составлении прямых уравнений в состоянии равновесия.) Таким образом, имеем
= (4.22)
(X 4-rp) Ps = KPj_r -Н грР/+;, /.-=1, 2, . . . (4.23)
Для решения этой системы разностных уравнений воспользуемся методом производящих функций. Таким образом, определим
Р И = 1 Р,?1.
Как обычно, умножим /-е уравнение (4.23) на z> и просуммируем по всем возможным Это дает
I (М Г^РГР I 1 фР,+1г;.
/—1 1=1 /=1
145
Перепишем это равенство в виде
(* + ф) £ Р,?1 - Ро
= U £ PKrZ!
J_ IE V P...Z1
/=1
Выделяя Р (г), находим
(X гр) [Р (г) - Ро] --= UP (г) + U- [Р (z) - Ро - Prz].
Первый член правой части последнего равенства получается с учетом условия (4.21). Упростив это выражение, имеем
Р(г) =
Ро R -I- гц - (г|л/г)] — rpPt % + гр — /.г'’ — (гц/г)
Воспользуемся равенством (4.22) для дальнейшего упрощения: р (?) = грРо I1 — ([/г)]
X + гц — 7.zr — (rjr/z)
и окончательно получим
Р (г) _=---ЛНРо (.1 -U---. (4.24)
г и -{- ?.zr+1 — (Л. ni) г
Константу Ро можно вычислить, учитывая, что Р (1) ; 1, и используя правило Лопиталя; таким образом,
Р(1)= 1 = ф7\-,
' ' ф — Лг
что дает (учитывая, что р0 = Ро)
В рассматриваемой системе интенсивность поступления требований равна X, а среднее время обслуживания фиксировано и равно 1/ц независимо от г. Следовательно, коэффициент использования системы
рДХх = • (4.25)
Подставляя это выражение в (4.24), находим
Р (г) =-----Ф(1 7Р) (1 --. (4.26)
rpi -j- Zzr+1 — р. + ср) г
Чтобы получить распределение числа этапов в системе, надо теперь обратить это преобразование.
146
Для случая г ~ 1, очевидно соответствующего системе М/М/1, не возникает никаких трудностей; в этом случае имеем
р М = ‘ц п ~Р) U — г) = Я —р) (' — г> ' |Л + 7. г2 — (X + р) г 1 + pz2 — (1 + р) г ‘
Знаменатель этой дроби разлагается на простые множители в виде (1 — z) (1 — pz); тогда, сокращая общий множитель (1 — z), получаем
р (Z) = .
' 1 — pz
Найдя эту функцию под номером 6 в табл. 1.2 приложения I, непосредственно определяем, что
Р* = (1 -р)р\ k= 0, 1, 2, . . . (4.27)
В случае г ==- 1, очевидно, рк = Рк, и, следовательно, равенство (4.27) дает распределение числа требований в системе М/М/1, что совпадает с полученной ранее формулой (3.23).
При произвольном г дело обстоит несколько сложнее. Стандартный метод обращения преобразования (4.26) состоит в разложении этой дробно-рациональной функции на простые дроби и обращении каждой из этих дробей по табл. 1.2; так и поступим. Прежде, чем провести разложение на простые дроби, надо найти (г 4- 1) корней многочлена, стоящего в знаменателе. Ясно, что одним из корней является единица. Поэтому знаменатель может быть записан в виде (1 — z) [г|т — л (z + z2 + ... + zr) 1, причем остальные г корней (которые мы обозначим через zi, Z2, ..., zr) являются корнями многочлена, стоящего в квадратных скобках. Найдя эти корни 1 (которые определяются однозначно), можно записать знаменатель в виде гр (1 —z) (1 —z/zi)...(l —zlzr). Подставляя это выражение снова в (4.26), находим
Р (z\ -----------Lzl£------------
(1 — z/zt) (1 — z/z2) ... (1 — z/zr)
Теперь искомое разложение на простые дроби дается равенством
"’Х(гЛ;;г- <4-">
i ~ I
где
1 К (трудной) задаче нахождения корней многочленов сводя1ся многие аналитические задачи теории массового обслуживания.
147
Теперь (используя строку 6 табл. 1.2 приложения I) можно обратить преобразование (4.28) и получить окончательную формулу для распределения числа этапов в системе, а именно
Pj = (1 _ Р) £ A, / = 1, 2, . . . R (4.29) i= 1
где, как и ранее, Ро = 1 — р. Таким образом, для системы М/Ег/1 распределение числа этапов обслуживания в системе представляет собой взвешенную сумму геометрических распределений. Распределение времени ожидания для этой системы может быть вычислено методами, которые будут рассмотрены ниже, в гл. 5.
4.4. СИСТЕМА Е/М/1
Рассмотрим теперь систему Ег/М/1, для которой а ** z >0; <4-30)
Ь (х) == ре’цл:, х>0. (4.31)
Здесь время между моментами поступления требований и время обслуживания поменялись ролями по сравнению с системой, рассмотренной в предыдущем параграфе; эти две системы являются во многих отношениях двойственными.
Рассматриваемая система функционирует следующим образом. Предположим, что в данный момент времени только что появилось требование, которое немедленно вводится в эрланговское устройство, подобное показанному на рис. 4.4; разница, однако, состоит в том, что это устройство рассматривается не как обслуживающий прибор, а как «приемное» устройство. После того, как требование введено слева в это устройство, оно должно пройти г этапов, каждый из которых характеризуется показательным распределением времени пребывания с параметром гХ. Очевидно,что плотность распределения вероятностей времени пребывания требования в таком приемном устройстве определяется равенством (4.30). Когда требование выходит с правой стороны приемного устройства, оно поступает в СМО типа Е/М/1. Немедленно после его поступления с левой стороны в приемное устройство вводится новое требование из бесконечного запаса, и процесс повторяется снова. Поступившее требование присоединяется к очереди, ожидает обслуживания и затем обслуживается по закону (4.31).
Очевидно, адекватное описание состояния такой системы должно содержать не только число требований в системе, но также и информацию о том, на каком этапе приемного устройства находится очередное поступающее требование. Будем полагать, что каждое требование, которое уже поступило (но еще не покинуло систему), вносит г этапов поступления; кроме того, будем считать 148
я J
Рис. 4.7. Диаграмма интенсивностей переходов для г-этапной системы Ег/ЛТ/1
число этапов, уже пройденных принимаемым требованием, дополнительным взносом в число этапов поступления системы. Таким образом, описание состояния системы содержит общее число этапов поступления в систему к данному моменту; если в системе имеется k требований и очередное поступающее требование находится на i-м этапе приема (1 < i < г), то общее число этапов поступления в систему / = rk -Т i — 1.
Воспользуемся опять определением (4.20) и обозначим через Ручнело этапов поступления в систему, а через pk, как обычно, обозначим стационарную вероятность наличия k требовании в системе; эти величины, очевидно, связаны равенством г (*+!)-!
Pk = S Pj- z
p=rk Z
Описанная система представляет собой неприводимую эргодическую цепь Маркова, диаграмма интенсивностей переходов которой представлена на рис. 4.7. Заметим, что, уходя из прибора обслуживания, требование удаляет из системы г этапов поступления. Используя метод перебора состояний, можно сразу выписать уравнения равновесия системы в виде
гКР0 — цРр, (4.32)
гУ.Р;^ г XPj-r 4- pPI+r, 1; (4.33)
(A+p)P/ = rZP7_1 + pP;+r, г с/. (4.34)
Определим опять для этой последовательности вероятностей производящую функцию
Р(г) = ^Р^. i=°
Применим теперь для решения этих уравнений равновесия метод производящих функций.. Уравнения (4.33) и (4.34) различаются только тем, что в первом из них опущен член цР7, поэтому будем преобразовывать эти уравнения в диапазоне значения / > 1, прибавляя и вычитая недостающие члены. Таким образом,
оо Г — 1
L (р -\-гК} РjZ! — X yPjZ1 ---= i=l
-= E rXPj^Z1 + 2 pPf+rZ1-
;=1
149
Выделяя в этом уравнении функцию Р (г), получаем
г-1
(и + л!) [Р (г) - Ро] - z рРр> =
/=1
= гХ2Р(2) + 4 Z
Р(2)-£р/
Исключим член Рг, воспользовавшись уравнением (4.23), и разрешим полученное уравнение относительно производящей функции:
Р(г) =
(1—zr) Рр1' _________/=0________ г pzr+1 — (1 + гр) zr + 1 ’
(4.35)
где, как обычно, использовано обозначение р = = л/ц. Теперь
необходимо найти полюса (корни знаменателя) этой функции. Многочлен, стоящий в знаменателе, имеет (г + 1) корней, одним из которых является единица [в разложении знаменателя на простые множители почти всегда имеется множитель (1 —г)]. Для остальных г корней можно показать (см. задачу 4.10), что точно г — 1 из них лежат в круге |г| <Д, а оставшийся, который обозначим через г0, удовлетворяет условию | z01 > 1. Числитель рассматриваемой функции записан в виде суммы, содержащей неизвестные вероятности Ру. Теперь нужно обратиться ко второму примечанию к 5-му шагу процедуры решения систем разностных уравнений методом производящих функций (см. гл. 2, с. 92), использующему тот факт, что производящая функция для распределения вероятностей должна быть аналитической в области |з| <1, и поступить следующим образом.
Так как функция Р (г) должна быть ограничена в области 121 <Т 1 [см. (11.28)1 и так как знаменатель в этой области имеет г — 1 корней, то числитель должен также обращаться в нуль в этих же самых г — 1 точках. Числитель равен произведению двух множителей; первый из них равен (1 —zr), так что модуль всех его корней равен единице; второй множитель имеет вид суммы. Следовательно, компенсирующие нули числителя как раз должны являться нулями этой суммы (рассматриваемая сумма представляет собой многочлен степени г—1, и следовательно, имеет г — 1 корней). Эти замечания позволяю:' приравнять числитель и знаменатель (поело исключения корней z == 1 и z г,,) и записать равенство
> рС+Сi СщЩ- и i /г V о
где К — некоторая константа, которая должна быть определена. Это позволяет переписать (4.35) в виде
р iz\ =__________LLzl/LJ________
К(\ — z)(l — z/z„) ’
Но так как Р (1) — 1, находим, что К = г/(1 — l/z0), вательно,
Р _ 0 г ) (1 — 1/Zo)
W r(l-z)(l-г/г0) •
и, следо-
(4.36)
Теперь известно все необходимое о полюсах и нулях функции Р (z), поэтому можно разложить эту функцию на простые дроби и взять обратное преобразование по z. Однако функция Р (г), определяемая равенством (4.36), не позволяет сразу перейти к разложению на простые дроби, так как степень ее числителя не меньше, чем степень знаменателя; Поэтому воспользуемся строчкой 8 табл. 1.1 приложения I; согласно таблице из F (г) (=) fn вытекает, что zr F (z) (=) fn_r, где двойная стрелка обозначает пару преобразования. Используя это свойство, выполним следующее разложение функции Р (z):
P(z)^(l
I,'/- , — 1//г0 )
1 — г 1 1 — z/z0 J
Если обозначить через f, обратное преобразование величины, заключенной в квадратные скобки, то очевидно, что обратное преобразование функции Р (z) должно удовлетворять равенству
Pj = /'/ -- (4.37)
Очевидно, что
Найдем сначала решение для Р,- в диапазоне значений / > г; из равенств (4.37) и (4.38) имеем
-z/), j^r. (4.39)
Последнее выражение можно упростить, если заметить, что при z ~ z0 знаменатель правой части (4.35) обращается в нуль; из этого следует, что гр (z0 — 1) = 1 — г/, и, следовательно, равенство (4.39) может быть приведено к виду
P,. = p(zo- Ozo^-1, j>r. (4.40)
С другой стороны, так как == 0 при 0 < j < г, то найти Р,-Для этих значений индекса / не составляет труда; комбинируя это решение с равенством (4.40), окончательно получаем следую-15!
щсе распределение числа этапов поступления для рассматриваемой системны:
4(1-гЛ‘). Ос/- 'г;
р(г0 - !>г.
(4 41)
Используя выписанное ранее соотношение между величинами р, и Р,-, находим (читателю предлагается самому проверить эти вычисления), что распределение числа требований в рассматриваемой системе определяется равенством
(1 — р, /г — 0;
Рк "I Рй- 1)<А, /г/.-о.
Заметим, что это распределение числа требований в системе является геометрическим распределением с несколько видоизмененным первым членом. Далее надо было бы вычислить распределение времени ожидания для рассматриваемой системы; однако отложим это до исследования системы G/M/1 в гл. 6.
4.5. СИСТЕМА С НЕОРДИНАРНЫМ ВХОДЯЩИМ
ПОТОКОМ
В параграфе 4.3 была исследована система М/Е,./1, в которой каждое требование, для того чтобы полностью было завершено его обслуживание, должно было пройти через г этапов. Ключевым моментом решения для такой системы был подсчет полного числа остающихся этапов обслуживания в системе, причем каждое поступающее требование добавляет к этому числу г этапов обслуживания. Эту же систему можно рассматривать и с другой точки зрения, предполагая, что поступление одного требования эквивалентно поступлению г требований, и для каждого из этих г требований необходимо только одноэтапное обслуживание (т. е. время обслуживания распределено по показательному закону1). Указанные две точки зрения, очевидно, определяют идентичные системы: первая является системой М/Е/1, а вторая представляет собой систему М/М/1 с групповыми требованиями объема г. Диаграмма интенсивностей переходов для числа требований в системе с неординарным потоком имеет вид диаграммы, представленной на рис. 4.6; эта же диаграмма, естественно, представляет число этапов в системе М/Е/1. Таг<им образом, производящая функция для числа требований в системе с неординарным входящим потоком должна выражаться равенством (4.26), а распределение числа
1 Для полного соответствия параметр этого показательного распределения надо выбрать равным гр. Однако в дальнейшем он принимается равным просто р. К указанному же требованию возвратимся при сравнении системы с неординарным входящим потоком и системы М/Е,/1.
152
Рис. 4.8. Диаграмма интенсивностей переходов для системы с неординарным входящим потоком
требований в системе — равенством (4.29), так как мы приравниваем число этапов в исходной системе к числу требований в рассматриваемой системе.
Поскольку рассматривается система с неординарным потоком требований, не обязательно фиксировать объем группы требований, поступающих в каждый (пуассоновский) момент времени. Такая группа может иметь случайный объем, причем
gi&P [объем группы равен i], (4.43)
(В качестве примера можно представить семьи случайного размера, приходящие для прививки оспы). Как обычно, предположим, что интенсивность входящего потока (групп) равна %. Выбирая в качестве состояния системы число находящихся в ней требований, получаем диаграмму интенсивностей переходов, показанную на рис. 4.8. Для ясности, на этой диаграмме показано подробно только состояние Ek- Из диаграммы видно, что в состояние можно попасть из любого состояния, находящегося левее состояния Ek (так как допускается поступление группы любого объема); аналогично, из состояния Ek можно попасть в любое другое состояние, находящееся на диаграмме справа от Ek, причем интенсивность
со
Ухода из состояния Ek равна ^gi+?.g2+... — Если обо-
1=1
значить, как обычно, через pk стационарные вероятности наличия требований в системе, то, пользуясь диаграммой переходов, можно выписать следующую систему уравнений равновесия:
*-1
(% + ц) pk = ppft+1 + 2 Pi^gk-i, k > 1; (4.44)
1=0
Ъро = РЛ- (4.45)
В уравнении (4.44) приравниваются интенсивность потока, исходящего из состояния Ek (левая часть равенства), и интенсивность потока, входящего в состояние Ek, причем первый член правой части равенства соответствует завершению обслуживания, а второй член (сумма) — всем возможным способам поступления требований, приводящим к состоянию Ek- Уравнение (4.45) является единственным граничным условием в состоянии Ео. Как
153
обычно, будем решать эту систему методом производящих функций; таким образом,
ОО ПО по ~ I
SPkZk="г Sрмг^1 + X XPi Ksk-iZk- (4лб}
й=1 k=i S tS)
Меняя порядок суммирования в двойной сумме, а именно
и перегруппировывая члены, получаем
со k — 1 со со
Zj Z Pi ^gk-iZk = х S ppp S gk-i^1 =--
*=1 1=0 1=0 ft=t + l
co co
= S Pt1 L giZ>. (4.47)
f=0 f=l
Искомая производящая функция
P(z)AL pkzk\
—k—()
как видно из равенства (4.47), надо также ввести в рассмотрение производящую функцию для распределения объема групп входящего потока требований, определяемую равенством1
G(z)ASg/. (4.48)
/;=1
Выделяя эти функции в равенстве (4.46), получаем
(X -I - р) [Р (г) - р0] = [Р (z) - р0 — piz] ф ХР (г) G (г).
Отметим, что произведение Р (г) G (г) является иллюстрацией соотношения из строки 11 табл. 1.1 приложения I, так как в уравнении (4.44) по существу записана свертка последовательностей {pk} и {&*}• Применяя условие (4.45), упростим это выражение и перепишем его в виде
о /м =_______НРо (1 — z)_______
1 17 р. (1 — г) —- Лг [ 1 — G (z)J ’
Для исключения параметра р0 воспользуемся условием Р (1) = 1; прямая подстановка приводит к неопределенности типа 0/0, рас-
1 Если допустить возможность > 0, т. е. возможность поступления групп требований нулевого объема, то в каждом состоянии диаграммы интенсивностей переходов надо добавить замкнутую петлю, соответствующую нулевому поступлению. В этом случае суммирование при определении производящей функции нужно начинать с нуля; все дальнейшие утверждения пригодны также и для этого случая.
154
крытие которой по правилу Лолиталя дает р0 - 1 — р. В резуль-
тате получаем
р М _________М ( 1 - ----- /4 4дх
* ’ |i (1 — z) — az [1 —G (z)] "
Это — окончательное решение для производящей функции числа требований в системе М/М/1 с неординарным входящим потоком. Если последовательность (gy.j задана, то можно дальше решать задачу обращения этого преобразования. Можно также непосредственно по найденному выражению для Р (z) вычислить среднее значение и дисперсию числа требований в системе (см. задачу 4.8). Заметим, что в данном случае надо аккуратно определить коэффициент использования р. Напомним, что р равно произведению интенсивности поступления требований на среднее время обслуживания. В рассматриваемом случае интенсивность поступления требований равна произведению интенсивности поступления групп требований на среднее число требований в группе. Из равенства (11.29) сразу получаем, что оредшж обто:.: группы требований равен G<n (1). Поэтому естественно заключить, что параметр р для рассматриваемой системы определяется равенством
р (4.50)
Поучительно рассмотреть частный случай, когда объемы всех групп требований равны, а именно, когда
1 1, k = r, gk = I 0, k + r^
Очевидно, это условие приводит к простейшей системе с неординарным входящим потоком, описанной в начале этого параграфа; она в точности соответствует системе М/Е,./1 (в которой надо сделать замену ц на гр, уже обсуждавшуюся ранее в сноске). В этом случае сразу находим, что G (z) — zr, и, подставляя это значение функции G (z) в решение (4.49), получаем результат, совпадающий с (4.26), как это и должно быть.
4.6. СИСТЕМА С ГРУППОВЫМ ОБСЛУЖИВАНИЕМ
В параграфе 4.4 исследовалась система Ег/М/1, в которой входящее требование проходит через г этапов поступления. В этом случае оказалось удобным описывать состояние системы числом этапов поступления (где каждое полностью поступившее требование, находящееся в системе, вносит в это число г этапов). Так же, как была установлена аналогия между системой с неординарным входящим потоком и эрланговской системой обслуживания, рассмотренной в параграфе 4.3, устанавливается аналогия между системой с групповым обслуживанием и эрланговской системой на входе, рассмотренной в параграфе 4.4.
155
Итак, рассмотрим систему М/М/1, в которой обслуживание осуществляется группами по г требований. Это означает, что как только обслуживающий прибор освобождается, он принимает из очереди группу, содержащую точно г требований, и начинает их обслуживать одновременно; время обслуживания этой группы выбирается случайным образом в соответствии с показательным распределением с параметром р. Если к моменту освобождения обслуживающего прибора в очереди накопилось меньше чем г требований, то прибор ждет, пока наберется полная группа из г требований, и только тогда начинает групповое обслуживание, и т. д.1. Требования поступают в виде пуассоновского потока с интенсивностью % по одному в каждый момент времени.
Читателю должно быть ясно, что рассматриваемая система с групповым обслуживанием и система Е/М/1 идентичны. Если начертить диаграмму интенсивностей переходов для числа требований в системе с групповым обслуживанием, получится в точности диаграмма, изображенная на рис. 4.7 (с параметром X вместо гл; это изменение параметра необходимо учитывать только при сравнении системы с групповым обслуживанием и системы Е/М/1). В связи с тем, что эти две системы эквивалентны, распределение числа требований в системе с групповым обслуживанием должно определяться равенством (4.42), так как этапы в исходной системе соответствуют требованиям в рассматриваемой системе.
Вынужденное ожидание обслуживающего прибора в случаях, когда в систему с групповым обслуживанием поступило меньше чем г требований, определенно представляется расточительством. Поэтому рассмотрим теперь систему, в которой обслуживающий прибор после освобождения принимает на обслуживание г требований, если они есть, или меньшее число требований — столько сколько имеется в очереди. Состояние системы будет определяться числом находящихся в ней требований, так что диаграмма интенсивностей переходов для рассматриваемой системы имеет вид, показанный на рис. 4.9. Из диаграммы видно, что все состояния, за исключанием состояния Ео, характеризуются одинаково: переход в данное состояние возможен из левого соседнего состояния, когда поступает требование, и из г соседних состояний справа, когда завершается групповое обслуживание, а переход из данного состояния возможен либо при поступлении требования, либо при уходе обслуженной группы; с другой стороны, в состояние Еп переход возможен из любого из г состояний, находящихся непосредственно справа от него, а уход — из состояния Ео только при поступлении требования. Это приводит к следующей системе
1 Например, маршрутное такси обычно не отправляется до тех пор, пока не наберется полный состав пассажиров, которые обслуживаются одновременно.
156
л л л л л
Рис. 4.9. Диаграмма интенсивностей переходов для системы с групповым обслуживанием
уравнений для стационарных вероятностей pk наличия k требований в системе:
(Z + р.) pk — рРй+г + ^Pk-i, k > 1; (4.51)
^Ро = И (Pl + Pi + • • • + Р г)'
Применим теперь метод производящих функций. Как обычно, определим со
р (Z) = Е PkZk.
Умножая на zk, суммируя и выделяя Р (г), обычным способом
получаем "
(% + ц) [Р (г) -/?„] = -£- Р (г) - S pkzk г' L k=o
IzP (Z).
Разрешая это равенство относительно Р (г), имеем
И PkZk — (А- + р) рогг р /г\ =__.
^гГ+1 — (X -|- р.) гг + |г
Из граничного условия (4.51) следует, что отрицательный член в числителе правой части последнего равенства может быть записан в виде
— ? (^Ро+мл) = ~pzr z; pk, 6=0
и, следовательно, получаем
У, Pk (zk — zr)
Р М =______*=2------------, (4.52)
rpzr+l_(l+rp)zr+1 ’
157
где коэффициент использования р л/цг, так как в рассматриваемой системе в течение промежутка времени средней продолжительности 1/ц секунд может быть обслужено одновременно вплоть до г требований.
Заметим сразу, что знаменатель в правой части равенства (4.52) в точности совпадает со знаменателем функции (4.35), рассмотренной при исследовании системы Е/М/1. Таким образом, можно воспользоваться теми же соображениями относительно расположения корней знаменателя; в частности, среди г + 1 корней знаменателя точно один появляется в точке z = 1, точно г — 1 корней расположены внутри круга | z | < 1, и только один, который обозначается через г0, таков, что | z01 > 1. Рассмотрим теперь числитель функции (4.52). Он представляет собой многочлен степени г. Одним корнем, очевидно, является z = 1. Далее, по уже известным соображениям, функция Р (z) должна оставаться ограниченной в области jz| <(1, и, следовательно, остальные г — 1 корней числителя должны точно совпадать с теми корнями знаменателя, для которых | z | <у 1; отсюда следует, что эти два многочлена степени г — 1 должны быть пропорциональны:
К У Pk № — ?r) fe=o _rpzr+ —(1 rp) Zr 4- 1
1—z ~ (1 — z) (1 — z/z0)
Используя это равенство для сокращения общих множителей числителя и знаменателя в (4.52), получаем
Р ® '
Константу К можно вычислить обычным образом, положив Р (1) = = 1; это приводит к следующему простому выражению для рассматриваемой производящей функции
₽И = Т^-- <4М»
Беря для этого преобразования обратное, получаем следующее распределение числа требований в системе с групповым обслуживанием:
'-2- -<4И>
Опять получилось знакомое геометрическое распределение для марковских СМО!
4.7. ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНЫЕ ЭТАПЫ:
ОБОБЩЕНИЯ
Насколько общим является метет этапов, примененный в параграфе 4.3 для исследования системы М/Е/1 и в параграфе 4.4 для исследования системы Ег/М/1? Распределение Эрланга показано 158
на рис. 4.5; вспомним, что можно изменять его сроднее значение, выбирая соответствующим образом параметр р, и можно выбрать диапазон стандартных отклонений, регулируя его параметром г. Однако при этом выбор коэффициента вариации ограничен: его значение не может превысить значение подобного коэффициента для показательного распределения [из равенства (4.14) видно, что
1//7 , и только для г = 1, т. е. для показательного распределения, получается Сй = 1 ]. Таким образом, случайная величина, описываемая эрлаиговским распределением, является в некотором смысле более регулярной, чем случайная величина с показательным распределением. Но, вообще говоря, могут встретиться и другие случаи.
Возможным обобщением могло бы быть снятие требования о том, чтобы одно из двух основных распределений было показательным; это значит, что можно было бы рассмотреть систему ЕГа/ЕГ/)/1, для которой промежутки времени между поступлениями требований подчиняются эрланговскому распределению порядка га, а время обслуживания подчиняется эрланговскому распределению порядка гь *. С другой стороны, можно попытаться построить обобщение путем расширения класса рассматриваемых распределений, не ограничиваясь распределением Эрланга. К этому сейчас и перейдем.
Необходимо найти такую организацию этапов обслуживания, которая привела бы к получению больших значений коэффициента вариации, чем при показательном распределении. Можно попробовать рассмотреть обобщение эрланговского распределения порядка г, в котором на каждом этапе допускается различная интенсивность обслуживания (скажем, интенсивность /-го этапа равна р,). Позволит ли это расширить диапазон Сь в область значений, больших единицы? В таком случае преобразование Лапласа для плотности распределения времени обслуживания будет определяться не равенством (4.15), а равенством
в* й - (ЛтЛ (Лж-) • (ЛФг) <4-55»
Плотность распределения вероятностей b (х) времени обслуживания просто равна свертке г показательных распределений, каждое из которых имеет свой параметр р,. Легко показать, что в этом случае квадрат коэффициента вариации будет [см. (II.26) приложения II ]
Но для действительных неотрицательных чисел а,- всегда выполняется неравенство < (2fl<)2> так как правая часть содержит ---------- i i
* Вскоре этот случай будет рассмотрен.
159
выражение, стоящее в левой части, плюс еще все неотрицательные смешанные члены. Полагая а,- — 1/р,, получаем, что Сь < 1. Таким образом, обобщение в направлении обеспечения больших значений коэффициента вариации таким путем, к сожалению, не получается.
Рис. 4.10. Система Н2 с двумя параллельными РаНбС 6ЫЛО УСТЯНОВ-этапами обслуживания
лено, что прохождение требования через удлиняющуюся цепочку последовательно соединенных этапов с показательным временем обслуживания приводит к уменьшению разброса времени обслуживания; поэтому естественно ожидать, что параллельная организация этапов должна привести к увеличению разброса времени обслуживания. Это, действительно, справедливо. Рассмотрим систему с двумя параллельными этапами обслуживания, показанную на рис. 4.10. Такая схема может быть противопоставлена структуре обслуживающего прибора, показанного на рис. 4.3.
На схеме на рис. 4.10 входящее требование поступает в большой овал (обозначающий обслуживающий прибор) слева. После поступления требования в обслуживающий прибор, оно с вероятностью at попадает на этап обслуживания 1 и с вероятностью а2 — на этап обслуживания 2, причем a., = 1. Время обслуживания
i-м этапе распределено по показательному закону со средним значением 1/р,-секунд. Новое требование может поступить в обслуживающий прибор только после того, как предыдущее закончит обслуживание и покинет прибор. Из этого описания ясно, что плотность распределения вероятностей времени обслуживания определяется равенством
на
Рис. 4.11. Система с R параллельными этапами обслуживания
Ь (х) = aJpi1e-,li’e +
О,
160
и, следовательно,
В* (s) = а.
М-i j йз
s + И1 1 2 s + р-2
Более общий случай прибора с R параллельными этапами представлен на рис. 4.11. (Сравните его с рис. 4.4). В этом случае, как всегда, внутри большого овала, соответствующего обслуживающему прибору, разрешается в каждый момент времени находиться не более чем одному требованию. Предполагается, что
д
Еа,= 1- (1.56)
Очевидно, что
д
b (х) = Е <2;И/е~,Х‘Г- л.'> 0, (4.57)
1=1
R b*(s) = ZX-
Hz
S + щ
Распределение с плотностью (4.57) называют гиперпоказательным и обозначают Нц. Как ожидалось, коэффициент вариации (Сь Д Afft/x) в данном случае больше единицы и, следовательно, соответствует большему диапазону возможных отклонений, чем при показательном распределении. Докажем это. На основании (11.26) непосредственно следует, что
Для квадрата коэффициента
вариации соответственно имеем
(4.58)
Далее может быть записано неравенство Коши — Шварца (11.35) (для действительных величии at и bt) в виде
(Е ^ь^2 ' (Е (Е ь?)
(4.59)
6
Л. Клейирок
161
Рис. 4.12. Диаграмма интенсивностей переходов для системы М/Н2/1
(это соотношение часто называют неравенством Коши). Если в (4.59) положить а,. =}/'«,, Ь, =- |/"а,/и,-, то получим
(?£)’<(?»-) (S3)-
Но так как, согласно (4.56), первый множитель в правой части последнего неравенства равен единице, то равенство (4.58) можно переписать в виде
С^>1, (4.60)
что и требовалось доказать.
Можно ожидать, что метод этапов окажется пригодным для исследования систем М/Н«/1, Н^/М/1, Н/? /Н^г /1, и это, действительно, справедливо. Причина такой возможности кроется в том, что непоказательный характер обслуживающего (или приемного) устройства можно учесть, просто указывая этап обслуживающего (приемного) устройства, на котором находится в данный момент требование. Эта информация вместе с указанием числа требований в системе позволяет построить цепь Маркова, которая затем может быть исследована так, как это уже делалось в данной главе.
Например, диаграмма интенсивностей переходов для системы М/Н.,/1 показана на рис. 4.12. Индекс kt на этой диаграмме означает, что система содержит k требований, и обслуживаемое в данный момент требование находится на t-м этапе (t = 1, 2). Переходы в состояния с большими индексами полностью аналогичны переходам, указанным на рис. 4.12 для состояний 1,- и 2,-.
Теперь нетрудно перейти к дальнейшему обобщению метода этапов; ведь можно произвольно объединять последовательные в параллельные этапы, получая сложные структуры, подобные показанной па рис. 4.13. Здесь представлены R параллельных ветвей, каждая из которых состоит из г, последовательных этапов 162
Рис. 4.13. Система с последовательно-параллельными этапами обслуживания первого типа
(t = 1, 2, R); время обслуживания на каждом этапе j-й вегви
распределено по показательному закону с параметром г,р,. Очевидно, что такая последовательно-параллельная система обладает большой общностью. Внутри такой системы из всего множества составляющих ее этапов в каждый момент времени может быть занят требованием один и только один из этапов, и никакое повое требование не может поступить в большой овал (соответствующий обслуживающему прибору) до тех пор, пока предыдущее требование не покинет его. Однако заметим, что во всех случаях состояние обслуживающего прибора полностью определяется указанием того единственного этапа обслуживания, на котором находится рассматриваемое требование. Очевидно, плотность распределения времени обслуживания в системе вычисляется непосредственно и имеет вид
b (х) = У а,‘ e-W %>0, (4.61)
1 7 Zj 1 (rt — 1) ! ’ v ’
i=i
и ее преобразование Лапласа задается формулой
(4.62)
Возможным путем дальнейшего обобщения метода последовательно-параллельных этапов является снятие ограничения, состоящего в том, что все последовательные этапы одной ветви имеют одну и ту же интенсивность обслуживания если допустить, что /-й этап j-й ветви имеет интенсивность обслуживания ц,;, то
6* 163
ui c/ji/m n 6 aграбар
Рис. 4.14. Система с последовательно-параллельными этапами второго типа
преобразование Лапласа для плотности распределения вероятностей времени обслуживания примет более общий вид
г —I
Такое обобщение приводит к достаточно сложной системе уравнений.
Другим способом построения последовательно-параллельной системы является следующий. Рассмотрим обслуживающий прибор, показанный на рис. 4.14. Этот прибор содержит г этапов обслуживания, из которых только один может быть занят в каждый данный момент времени. Требования поступают слева и покидают прибор справа. Прежде, чем перейти к i-му этапу обслуживания, осуществляется независимый случайный выбор, согласно которому требование либо с вероятностью р, поступает на следующий i-й этап, где время обслуживания распределено по показательному закону, либо с вероятностью а, немедленно покидает систему; очевидно, для всех i = 1, 2, ..., г должно выполняться условие ai + Р< = 1. После завершения обслуживания на r-м этапе требование покидает систему с вероятностью единица. Можно сразу выписать преобразование Лапласа для плотности распределения вероятностей времени обслуживания для рассматриваемой системы в виде.
где аг+1 -- 1.
Можно попытаться рассмотреть переходы между этапами более общего вида, чем показано на рис. 4.14; например, вместо того, чтобы выбирать между немедленным уходом из системы и переходом на следующий этап обслуживания, можно рассмотреть переходы назад и вперед на произвольное число этапов обслуживания. Кокс [3] показал, что по сравнению с рассмотренной системой, показанной на рис. 4.14, это не дает дальнейшего обобщения.
164
Очевидно, что каждая из трех последних функций В* (s) может быть записана как дробно-рациональная функция от s, т. е. как отношение многочлена от s. Необходимое условие, налагаемое на полюсы функции В* (s) (на корни многочлена, стоящего в знаменателе), состоит в том, что все они должны располагаться на отрицательной действительной полуоси комплексной s-плоскосги. Последнее требование выполняется не всегда, когда бы хотелось, так как в произвольном случае полюсы плотности распределения вероятностей времени обслуживания могут располагаться в произвольной точке отрицательной полуплоскости [т. е. при Re (s) < <0]. Эта задача была исследована Коксом [3] в предположении, что параметры показательных законов могут принимать комплексные значения.
Хотя такое предположение не соответствует никакому физически осуществимому этапу с показательным распределением, доводом в его пользу является то, что если предусмотреть пары комплексно-сопряженных полюсов, то полный обслуживающий прибор будет иметь действительную функцию плотности распределения вероятностей, что соответствует осуществимым случаям. Если допустить комплексно-сопряженные пары полюсов, будет достигнута полная общность задачи синтеза прибора с произвольной дробно-рациональной функцией от s как преобразования Лапласа В* (s) распределения времени обслуживания. Кроме того, получается эффективный метод исследования таких систем путем рассмотрения траектории состояний обслуживающего прибора. Более того, аналогичный метод позволяет построить с помощью последовательно-параллельных этапов распределение вероятностей для промежутков времени между поступающими требованиями и, следовательно, пригоден для исследования любой системы G/G/1, для которой распределения имеют преобразования Лапласа, являющиеся рациональными функциями от s. Далее, можно произвольную нерациональную функцию от $ сколь угодно точно аппроксимировать дробно-рациональными функциями R
Таким образом, в принципе, решена очень общая задача. Обсудим полученный метод решения. Очевидно, для описания состояния системы надо указать число требований в ней, этап при-
1 Здесь мы сталкиваемся с задачей аппроксимации: как наилучшим образом описать приближенно заданное распределение вероятностей, чтобы оно имело рациональное^преобразование Лапласа. Для случая, когда плотность распределения вероятностей задается в численной форме, одна из подходящих процедур была предложена Прони [11]. Если же, с другой стороны, плотность распределения задана в аналитической форме, то представляется трудным описать соответствующую процедуру аппроксимации в общем случае. Конечно, естественно было бы выбрать аппроксимацию с возможно меньшим числом этапов. Однако заметим, что для хорошего приближения среднего значения и дисперсии заданного распределения методом этапов число этапов не может быть значительно меньше 1/с$; к сожалению, отсюда следует, что когда распределение стремится к концентрации около фиксированного значения, необходимое число этапов довольно быстро возрастает.
165
емного прибора, на котором находится очередное поступающее требование, и этап обслуживающего прибора, на котором находится обслуживаемое требование. На основании такого описания молено построить (ужасно сложную) диаграмму переходов. Имея такую диаграмму, можно (путем перебора состояний) непосредственно выписать уравнения равновесия; получится большая система уравнений, которая, как правило, имеет много граничных условий. Однако все эти уравнения линейны по своим переменным, и, следовательно, система может быть решена прямым (хотя и очень утомительным) методом. Спрашивается, что еще более естественное можно предложить в качестве задачи для решения на ЭВМ? Конечно, дискретные вычислительные устройства более всего приспособлены для решения больших систем линейных уравнений (такая задача для дискретных вычислительных устройств значительно проще, чем малая система нелинейных уравнений). При решении на ЭВМ рассматриваемой (фактически бесконечной) системы линейных уравнений, ее надо сначала свести к конечной системе; это можно сделать путем приближения, прежде всего выбрав точку, на которой можно оборвать последовательность р0, pi, р2, ... . Тогда можно решать конечную систему уравнений, а возможно и экстраполировать решение на бесконечную систему; все это идет по пути приближений, и следует надеяться, что вычисления могут быть проведены настолько глубоко, что членами, которыми приходится пренебрегать, действительно можно будет пренебречь.
Не надо переоценивать возможности этой процедуры; рассмотренный метод является скорее не автоматическим правилом, а дает принципиальный подход к решению задачи. Другие аналитические методы исследования более сложных СМО обсуждаются в остальной части этой книги.
4.8. МАРКОВСКИЕ СЕТИ МАССОВОГО ОБСЛУЖИВАНИЯ
До сих пор рассматривались марковские системы, в которых каждое требование проходило одну операцию обслуживания. Такие системы можно называть однофазными. В данном параграфе рассматриваются системы с многофазовым обслуживанием, в которых требование получает обслуживание более чем в одном приборе (узле). Таким образом, можно говорить о сети узлов, каждый из которых представляет собой СМО (некоторые узлы могут иметь несколько обслуживающих приборов) с накопителем для формирования очереди. Требования поступают в систему в различных точках, ждут в очередях обслуживания и, покинув один узел, поступают в другой для дальнейшего обслуживания. Здесь описывается последняя категория систем потоков, обсуждавшаяся в гл. 1, а именно вероятностные потоки в сети.
При исследовании сетей возникает много новых аспектов. Например, важной становится топологическая структура сети, 166
так как она определяет возможные переходы между узлами. Требуется также каким-нибудь способом описать пути отдельных требований. Большое значение имеет описание природы вероятностных потоков с помощью основных вероятностных процессов; например, в случае последовательной цепочки СМО, при которой требование, покидающее i-ii узел, сразу поступает на обслуживание в (t + 1)-й узел; очевидно, что промежутки времени между последовательными уходами требований из предыдущего узла равны промежуткам времени между последовательными поступлениями в следующий узел.
Рассмотрим простейшую последовательную систему с двумя узлами, показанную на рис. 4.15. Каждый овал на этом рисунке изображает СМО, состоящую из очереди и обслуживающего прибора; внутри каждого овала указан номер узла. (Важно не путать такие схемы физических сетей с абстрактными диаграммами интенсивностей переходов, которые были использованы ранее.) Предположим, что входящий поток является пуассоновским с интенсивностью Л, причем каждое требование поступает сначала в узел 7; предположим также, что этот узел содержит единственный обслуживающий прибор, время обслуживания которого распределено по показательному закону с интенсивностью р. Таким образом, узел 1 представляет собой в точности СМО типа М/М/1. Предположим, далее, что узел 2 также состоит из единственного обслуживающего прибора с показательным временем обслуживания с интенсивностью р. Основная задача состоит в вычислении распределения промежутков времени между последовательными требованиями, поступающими в узел 2; это, естественно, эквивалентно задаче вычисления распределения промежутков времени между последовательными требованиями, уходящими из узла 1.
Пусть d (7) означает плотность распределения вероятностей промежутков между последовательными требованиями на выходе узла 1 и, как обычно, пусть D* (s) означает ее преобразование Лапласа. Перейдем к вычислению D* (s )в момент, когда требование покидает узел 1. Возможно одно из двух событий: либо в очереди имеется второе требование, готовое немедленно поступить на обслуживание в узел 1, либо требования нет (накопитель пуст). В первом случае промежуток времени, через которое это следующее требование покинет узел 1, распределен точно так же, как и время обслуживания, и в этом случае получаем
7?* (s) | узел 1 не пуст = В (s).
С другой стороны, если при уходе рассматриваемого первого требования узел оказывается пустым, то приходится ожидать в те-
Рис. 4.15. Система с двумя последовательными узлами
167
чение двух промежутков времени: первый промежуток — время до поступления следующего требования и второй — время обслуживания этого требования. Так как эти два промежутка распределены независимо, то плотность распределения вероятностей их суммы равна свертке плотностей распределения суммируемых величин. Соответственно преобразование Лапласа плотности распределения суммы равно произведению преобразований исходных плотностей распределения, и следовательно,
где для преобразования Лапласа плотности распределения промежутков между поступающими требованиями уже известно явное выражение. Так как время обслуживания является показательно распределенной случайной величиной, то можно записать В* (s) — = p/(s + р); кроме того, как будет показано в гл. 5, вероятность того, что требование покинет систему пустой, равна вероятности того, что поступающее требование застанет систему пустой, а именно, равна 1 — р. Это позволяет записать следующее безусловное преобразование Лапласа для плотности распределения промежутков времени между уходящими требованиями:
D (s) = (1 р) D' (х) | узел 1 пуст i pD (S) | узел I не пуст-
Используя проделанные ранее вычисления, получаем
Простые алгебраические преобразования дают
(4.65) и, следовательно, распределение промежутков времени между уходящими требованиями
D (t) = 1 — e~Ki, t 0.
Таким образом приходим к замечательному выводу о том, что промежутки времени между уходящими требованиями, так же как и промежутки времени между поступающими требованиями, распределены по показательному закону с тем же самым параметром. Иначе говоря (в случае стационарной СМО), входящий пуассоновский поток, протекая через обслуживающий прибор с показательным распределением времени обслуживания, порождает выходящий пуассоновский поток. Этот основополагающий результат обычно называют теоремой Бёрке [1 ]; многие другие авторы также исследовали эту задачу (см., например, [91). Фактически теорема Бёрке говорит больше, а именно, что исходящий поток стационарной СМО типа М/М/ш с пуассоновским входящим потоком с параметром X и показательным распределением времени обслу-168
живания с параметром р в каждом из т приборов является пуассоновским потоком с тем же самым параметром А. Бёрке показал также, что выходной процесс не зависит от других процессов в системе. Доказано также, что система М/М'т является единственной системой с обслуживанием в порядке поступления, обладающей таким свойством. Возвращаясь к рис. 4.15, видим, что в узел 2 поступает независимый пуассоновский поток, и, следовательно, этот узел также представляет собой систему М/М/1, что позволяет рассматривать его независимо от узла 1. Тем самым теорема Бёрке говорит о том, что можно соединить последовательно1 несколько узлов, состоящих из многолинейных СМО (с показательным распределением времени обслуживания для каждого прибора), и при этом будет сохраняться описанное свойство разложения на отдельные узлы. -
Этот вопрос для произвольной сети массового обслуживания исследовал Джексон [5]. Он рассматривал сеть, содержащую N узлов, причем каждый t-й узел состоит из /и,- обслуживающих приборов с показательным временем обслуживания с параметром ц,; в каждый t-й узел извне поступает пуассоновский поток требований с интенсивностью у,-. Таким образом, при N = 1 получаем обычную систему М/М/т. Покидая t-й узел, требование с вероятностью г,7 поступает в /-й узел, причем в формулировке задачи допускается, что г;; > 0. С другой стороны, вероятность того, что после обслуживания в t-м узле требование покинет сеть N
(и никогда не вернется обратно), равна 1 — У Гц. Необходимо /=1
вычислить полную интенсивность потока требований в заданный узел. Для этого нужно просуммировать (пуассоновские) потоки, поступающие извне, и потоки требований (не обязательно пуассоновские), поступающие от других узлов сети. Обозначая через %, полную интенсивность потока, входящего в i-й узел, легко показать, что это множество параметров должно удовлетворять следующей системе уравнений:
Л'
К -= 7, + i = 1, 2, .... /V. (4.66)
Для того чтобы все узлы сети описывались эргодическими цепями Маркова, для всех i должно выполняться требование Z, < </ т,р,. Нужно снова предостеречь читателя от путаницы между понятием узла, используемым в данном обсуждении, и понятием состояния системы, которое ранее изображалось узлом графа.
1 При этом не допускаются переходы, ведущие назад, так как это может нарушить пуассоновскую природу потока, выходящего после обратной связи. Последующее обсуждение работ Джексона показывает, что, несмотря на это, даже в сети с обратной связью отдельные узлы ведут себя так, как если бы на их вход поступал чистый пуассоновский поток, хотя на самом деле это не соответствует Действительности.
169
Самое удивительное состоит в том, что Джексон доказал, что каждый узел (скажем, i-й) ведет себя в сети так, как если бы он был независимой системой М/М/m с входящим пуассоновским потоком с параметром X,. В общем случае полный входящий поток не является пуассоновским. Состояние рассматриваемой системы с N узлом описывается вектором (ki, ki, .... &v), где k, означает число требований в t-м узле (включая обслуживаемые требования). Обозначим через р (ki, ..., kN) стационарную вероятность этого состояния. Аналогично, через р,- (&,) обозначим маргинальное распределение вероятностей того, что в состоянии равновесия в t-м узле будет находиться k, требований. Джексону удалось доказать, что совместное распределение по всем узлам разлагается в произведение маргинальных распределений, т. е. что
p(kb k., . . ., М .= рДк^р., (А) . . . pN(kN) и (4.67)
" «то р, <ь\ представляют собой стационарные вероятности дл« классической системы М/М/m [см., например, равенства (3.37)— (3.39) с очевидными изменениями в обозначениях]. Этот последний результат обычно называют теоремой Джексона. Опять для марковских систем в состоянии равновесия получилось решение в виде произведения.
Модификация сети Джексона была исследована Гордоном и Ньюэллом [4]. Исследованная ими модификация представляет собой замкнутую марковскую сеть в том смысле, что в системе рассматривается конечное и фиксированное число К требований, которые задерживаются в сети так, что ни одно из них не может покинуть сеть и ни одно другое требование не может поступить N
в нее; это соответствует схеме Джексона, в которой У] гИ — 1 и у(. — О /=1
для всех Г (Интересный пример систем этого класса, известных под названием циклических, был рассмотрен ранее Кёнигсбергом [8]; в циклической системе узлы последовательно связаны друг с другом, причем последний связан с первым). В общем случае, рассмотренном I ордоном и Ньюэллом, не приходится надеяться на решение в виде произведения, так как между компонентами век-гора состояний (/<и, ki, ..., kN) имеется следующая зависимость:
У
Е ki = У- (4.68)
<=1
Так как рассматриваемая модель является частным случаем модели Джексона, то предполагается, что рассматриваемый марковский процесс с дискретным .множеством состояний неприводим, и, следовательно, существует единственное стационарное распределение вероятностей р (ki, ki, .... A’v)- Однако в этой модели множество состояний систем конечно; в частности, нетрудно видеть, что число различных состоянии системы равно числу способов раз-170
мещенпя К требований по Л' узлам, т. е. равно бпномалыюму коэффициенту
Сь
Стационарное распределение требований в этой замкнутой сети описывается следующей системой уравнений;
p(kv, k.,, . . fcA) а;(/г;)р =-“ i=i ' 1
= - Z. .-1а/ (k: ~Ь D '-1 X' 'Р 1 = 1 7 = 1 !
X (^i, /г2, . . kj — 1, . . /л 1.Ад), (4.69)
где единичная функция, согласно определению, данному в приложен;;;: I,
входит в уравнения равновесия, и таким образом учитывается тот факт, что когда узел пуст, то интенсивность обслуживания должна равняться нулю. Кроме того, величина
просто означает число требований в См узле, находящихся на обслуживании, при условии, что всего в узле имеется /г, требований. Как обычно, левая часть равенства (4.69) описывает вероятностный поток, исходящий из состояния (/?i, kz, ..., &?/), а правая часть — вероятностный поток, входящий в это состояние из соседних состояний. Продолжим решение рассматриваемой системы уравнений. Определим функцию р,- (k,) следующим образом:
Рассмотрим множество чисел {х.}, представляющих собой решения следующей системы линейных уравнений:
у
Р,Л', = PX'Z/o ' == 1, 2. • - v- (4.71) / = > ‘
Заметим, что эта система имеет такой же вид, как и система л -= =- лР, если за вектор л принять векторы (|uxt, .... иЛ.лд), а эле
ментами матрицы Р считать элементы rtj *. Так как матрица вероятностей переходов (элементами которой являются числа /щ) предполагается неприводимой, то, как известно из предыдущих исследований, система (4.71) должна иметь решение, все компоненты которого положительны; это решение, конечно, определяется с точностью до постоянного множителя, так как система содержит только N — 1 независимых уравнений. Используя эти определения, решение системы (4.69) можно записать в виде
N
Р (kt, k.,, . . kN)= П
где нормирующая константа задается равенством
N
Пт^. (4.73)
k(2A 1=1
Здесь суммирование ведется ио всем векторам состояний к А (Ад, ki, kN), принадлежащим множеству А, являющемуся множеством всех векторов состояний, для которых выполняется условие (4.68). Следовательно, это и есть искомое решение для замкнутой конечной сети массового обслуживания, и, как видим, оно опять получается в виде произведения.
Можно несколько глубже пояснить смысл такой формы получающегося решения, если рассмотреть случай, когда Д'->• оо. Оказывается, что критическими в этих вычислениях являются величины xjtrii. Предположим, что среди этих отношений имеется единственное наибольшее, и обозначим его xi/mr, (xi/mi) > > (Xi/nii'), i у- 1. Тогда можно показать, что р (ki, k-i, ..., kN) ->• О для любого состояния, в котором ki < °0- Это означает, что в первом узле накапливается бесконечное число требований, поэтому его часто называют «узким местом» сети. С другой стороны, предельное маргинальное распределение р (k-z, ..., kN) имеет вид
p(k.,y ka, . . ., kN) = p.2(k.3) p3(k3) . . . p,v(M. (4.74)
Таким образом, для этого маргинального распределения опять получается решение в виде произведения, и , конечно, оно аналогично теореме Джексона (4.67); заметим, что в одном случае речь идет о разомкнутой системе, в которой допускается поступление требований извне, а в другом — о замкнутой. Как будет показано в гл. 4 тома II, такая модель находит большое применение при исследовании вычислительных систем с множественным доступом и разделением времени.
* Опять предостережем читателя, что, е одной стороны, мы рассматриваем цепи Маркова, для которых через р,: принято обозначать вероятности возможных переходов из одного состояния системы в другое, а с другой стороны, в данном параграфе рассматривается сеть, состоящая из отдельных СМО, и величины г1у-означают вероятности перехода требования между узлами (СМО) этой сети. 172
Джексон [6 I рассмотрел класс разомкнутых систем даже более общего вида, который включает только что рассмотренную замкнутую систему как частный случай. Новые идеи, предложенные Джексоном, состояли, во-первых, в том, что входящий поток- требований может зависеть от общего числа требований в системе (используя это допущение, легко построить замкнутую сеть), и, во-вторых, в том, что интенсивность обслуживания в любом узле может быть функцией числа требований в этом узле. Таким образом, определив
S(k)AV|-A>, 4. . . .
можно рассматривать общую интенсивность входящего потока как функцию S (к), где вектор к описывает состояние системы.
Аналогично определяется интенсивность р*. показательного распределения времени обслуживания в t-м узле, содержащем kt требований (включая те, которые в данный момент обслуживаются). Как и ранее, через обозначаются вероятности переходов из узла в узел (/,/ = 1,2,..., N) и принимаются следующие дополнительные определения: г0! означает вероятность того, что входящее в сеть извне очередное требование поступит в узел с номером г, Г/,м+1 — вероятность того, что уходящее из z-го узла требование вообще покидает систему; r0, у+1— вероятность того, что следующее поступающее в систему требование не нуждается в обслуживании и покидает систему немедленно после поступления. Таким образом, в данном случае у,- = rczy (S (к)), где у (S (к)) — интенсивность полного внешнего потока в систему [при условии, что в данный момент в системе имеется S (к) требований ], который предполагается пуассоновским. Легко видеть, что вероятность того, что требование поступит в узел it, пройдет через узлы is, is, ..., in и затем покинет сеть, равна '"о;/; ?.// ( ••• rin_linriaN+1-Вместо того, чтобы искать решение уравнений (4.66) для интенсивностей нагрузки, которые являются функциями общего числа требований в системе, предпочтем найти решение следующей эквивалентной системы уравнений:
N
е, би [- V е.г,-,.. (4.75)
[В случае, когда интенсивности входящих потоков нс зависят от числа требований в системе, уравнения (4.66) и (4.75) различаются только множителем, равным интенсивности полного входящего в систему потока. 1 Предполагается, что решение системы (4.75) существует, единственно и таково, что е, > 0 для всех i; это эквивалентно предположению о том, что с вероятностью единица время циркуляции требования в сети конечно. Величина е. фактически представляет собой среднее число посещений t-го узла во время циркуляции требования по сети.
173
Определим зависящие от времени вероятности состояний в виде
Рк (t) -= Р
система в момент t
находится в (векторном) состоянии к
(4.76)
Используя стандартные методы, можно выписать следующую систему разностно-дифференциальных уравнений, связывающих эти
вероятности:
N
T(S(k))-i- Pfr.(I РьШ-1
Л; N
Т L У (S (к) — 1) гыРк (1) + £ ,Ц*.+1Г/, ,v+A (/+) (0 +
i = i i = 1
/V N
L S Цл,.+ 1Г/,-Рк (Щ /) (/), (4.77)
t=i i=\ I
i
где опущены все члены, в которых хотя бы одна компонента векторного аргумента принимает отрицательное значение; к (Г) = - к за исключением r-й компоненты, принимающей значение k,: — 1; k (i+) - к за исключением t-й компоненты, принимающей значение /г, 1; к (г, /) к за исключением t-й компоненты, прини-
мающей значение kt — 1, и /-й компоненты, принимающей значение kj 1, где i j. Сложность этих обозначений окупается простотой их интерпретации читателем. Джексон показал, что предельное распределение (если оно существует) единственно и в принятых ранее обозначениях должно быть lim рк (О А рк А А р (ki, ki, kN) при t —>-сю.
Для того чтобы выписать стационарные вероятности рк, к сожалению, необходимо ввести следующие дополнительные обозначения:
Л'-1
F(/C)A П у (S (к)), /С = 0, 1, 2, . . .; (4.78)
S(kM
/(к)А_ПП-^; (4.79)
,•=1 f.=i
Я (/С) A S Пк); (4.80)
k (Ел
ГЛ £ ^(Л)Я(Л'), и А л=о
если ряд сходится;
в противном случае,
(4.81)
где множество А, входящее в (4.80), представляет собой то же самое лпюжество, что и в равенстве (4.73). В этих обозначениях обобщенная теорема Джексона устанавливает, что, если G < оо, то для сети общего вида с зависимостями от состояний узлов суще
174
ствует единственное стационарное распределение вероятностей, задаваемое формулой
<4-82)
И снова решение получается в виде произведения. Можно также показать, что в случае, когда входящий поток не зависит от числа требований в системе [т. е. когда у Л у (S (к)) ], то даже при наличии зависимости интенсивностей времени обслуживания от состояний узлов справедлива первая теорема Джексона о том, что совместная плотность распределения вероятностей представляется в виде произведения отдельных плотностей распределения, задаваемого формулой (4.67). Фактически оказывается, что вероятности р, (ki) описываются точно тем же распределением вероятностей числа требований в системе с одним узлом, пуассоновским входящим потоком с интенсивностью уе,- и зависящим от состояния временем обслуживания с интенсивностью р*., которое было получено в гл. 3 для общего процесса размножения и гибели.
Таким образом, из второй теоремы Джексона следует, что в случае входящего потока с постоянной интенсивностью стационарные распределения вероятностей числа требований в отдельных узлах не зависят от остальных узлов; кроме того, каждое из этих распределений аналогично хорошо известному распределению для системы обслуживания с единственным узлом и с теми же самыми параметрами х. Замечательный результат!
Эта последняя теорема, пожалуй, самое большее 1 2, что может быть получено для простых марковских сетей, так как она обобщает теорему Бёрке в ее самом широком смысле. Если попытаться «смягчить» марковские предположения о входящем потоке или времени обслуживания, то процесс на выходе сразу сильно усложнится не только из-за маргинальных распределений, но и из-за отсутствия независимости от других состояний.
Такие марковские сети массового обслуживания приводят к безнадежным системам (линейных) уравнений, описывающим громадное (хотя и конечное) число состояний. И действительно замечательно, что такие системы все-таки допускают достаточно пря
1 Эта модель позволяет также описать замкнутую GMO, исследованную Гордоном и Ньюэллом. Для того чтобы обеспечить постоянство полного числа требований в системе, надо просто положить у (k) = 0 для 4>Ки у (/( — 1) = = оо, где К равно как раз тому фиксированному числу требований, которое должно быть в системе. Для того чтобы сделать равными вероятности переходов нз одного узла в другой в разомкнутой и замкнутой системах, обозначим первые через а вторые через г'у и потребуем, чтобы выполнялось равенство г';. = —’’ij-i- (т/.дтц) Фог); эт° делает эквивалентными предельную обобщенную систему Джексона и замкнутую систему Гордона и Ньюэлла.
2 В гл. 4 тома II описываются некоторые последние результаты, которые в действительности представляют собой обобщение описанной модели на случай различных классов входящих потоков и различных дисциплин обслуживания в каждом узле (допускающих в некоторых случаях более общие функции распределения для времени обслуживания).
175
мые методы решения. Ключ к такому решению лежит в том, что эти системы, как четко описал Кингман [7] и недавно Чанди 12 1, могут быть исследованы с помощью марковских процессов популяций. В частности, марковский процесс популяций представляет собой непрерывную цепь Маркова с множеством состояний, задаваемых конечно-мерными векторами k = (ki, ki, ..., kN), для которых допустимы переходы 1 только между следующими парами состояний: кик (i+j (поступление требования извне в узел г); кик (I) (уход требования из узла i с выходом из сети); кик (i, j) (внутренний переход из узла i в узел /). Кингман дает изящное обсуждение интересных классов сетей и свойств возникающих процессов (используя терминологию и результаты обратимых цепей Маркова). Чанди рассматривает некоторые из этих вопросов, замечая, что стационарные вероятности состояний системы удовлетворяют не только уравнениям глобального равновесия, что мы видели до сих пор (и что обычно приводит к решению в виде произведения), но и что эту систему уравнений можно также разбить на подсистемы меньшего объема, каждая из которых решается проще. Такая подсистема называется системой уравнений локального равновесия; перейдем к ее обсуждению.
Понятие локального равновесия является наиболее ценным в применении к сетям массового обслуживания. Однако оно применимо и к марковской СМО с одним узлом; фактически пример применения метода локального равновесия уже рассматривался. Вспомним уравнения глобального равновесия (уравнения сохранения потока) для общего процесса размножения и гибели в виде равенства (3.6). Эти уравнения были выведены с помощью условия сохранения потока в состоянии Ек для схемы, показанной на рис. 2.9. Тогда же говорилось, что можно рассматривать различные границы, относительно которых должен сохраняться поток, и это приводит к системе уравнений (3.7). Последняя система фактически представляет собой систему уравнений локального равновесия, которые обладают чрезвычайно интересным свойством, состоящим в том, что они позволяют установить соответствие между членами левой части уравнения (3.6) и членами его правой части; например, как следует из (3.7), член Kk_xpk_x в левой части (3.6) равен члену ркрк в правой части этого равенства; применив еще раз равенство (3.7), можно увидеть, что должны быть равны и два оставшихся члена равенства (3.6). Это точно описывает метод локального равновесия, который именно в том и состоит, чтобы найти в системе глобального равновесия подмножество членов, между которыми существует равновесие и которые приводят к системе уравнений локального равновесия.
Важно заметить, что если речь идет об эргодическом марковском процессе, то можно с уверенностью сказать, что имеется единственное стационарное распределение вероятностей, которое яв-
1 См. определения, следующие за равенством (4.77).
176
Рис. 4.16. Поимер простой циклической ceiw (// -- 3; К - 2)
ляется решением основного уравнения rtQ = 0. Затем, если для такого процесса систему уравнений глобального равновесия разложить на множество более мелких систем уравнений локального равновесия, содержащих согласованные члены из глобальной системы (и, конечно, учитывающих все члены глобальной системы), то любое решение, удовлетворяющее системам уравнений локального равновесия, должно также удовлетворять системе уравнений глобального равновесия; обратное утверждение в общем случае неверно. Такам образом, любое решение системы уравнений локального равновесия должно приводить к единственному решению, описывающему рассматриваемый марковский процесс.
В интересующем нас случае сети массового обслуживания определим систему уравнений локального равновесия (соответствующую заданному состоянию сети и заданному узлу i) как систему, в которой приравнивается интенсивность потока из данного состояния сети за счет ухода требований из узла i к интенсивности потока в данное состояние сети за счет поступления требований в узел I*. Это понятие для сетей лучше всего проиллюстрировать простым примером, показанным на рис. 4.16. Здесь представлена сеть с тремя узлами; интенсивность обслуживания в i-м узле равна р, и не зависит от числа требований в нем. Предполагается, что по этой замкнутой циклической сети циркулируют точно К = 2 требований. Очевидно, что пз = гзг = Г21 = 1 и rtj = 0 в остальных случаях. Состояния сети описываются тройками (ki, ki, k-з), где kt — число требований в узле I; в рассматриваемом случае ki + ki k-з --= 2. Таким образом, для рассматриваемой сети имеется точно
состояний; интенсивности переходов между этими состояниями показаны на рис. 4.17.
Система уравнений глобального равновесия для этой сети состоит из шести уравнений (одно из которых, как обычно, избыточно;
* Если время обслуживания не является показательным, а определяется Распределением, содержащим этапы, то приравниваются интенсивности входящего и исходящего потоков для данного этапа обслуживания (а не для самого Узла).
177
Рис. 4.17. Диаграмма интенсивностей переходов для примера сети, показанной на рис. 4.16
дополнительное уравнение вытекает из условия нормирования вероятностей); они имеют вид
HiP(2, 0, 0) = ц2р(1, 1, 0); (4.83)
р2р(0, 2, 0) = р3р(0, 1, 1); (4.84)
р3р(О, 0, 2) = pJp(l, 0, 1); (4.85)
м>(1, 1, 0)+-р2р(1, 1, О) = р.2р(О, 2, 0) Ч-Из/7(1, 0, 1); (4.86)
Н2р(0, 1, 1) + р3р(0, 1, 1) = р3р(0, 0, 2) }-щр(1, 1, 0); (4.87)
Ц1Р(1, 0, 1) + ИзР(1, 0, 1)=дЧ>(0, 1, 1) + HiP(2, 0, 0). (4.88)
Каждое из этих уравнений глобального равновесия имеет такую форму, что левая сторона соответствует потоку, исходящему из данного состояния, а правая — потоку, входящему в это состояние. Уравнения (4.83)—(4.85), как увидим, сами по себе образуют систему уравнений локального равновесия; уравнения (4.86)— (4.88) выписаны так, что в каждом из них первый член левой части уравновешивается первым членом правой части; то же самое относится и ко вторым членам. Таким образом, равенство (4.86) приводит к следующей системе уравнений локального равновесия:
Pi/?(1, 1, 0) = р2р(0, 2, 0); (4.89)
р2/?(1, 1, 0) = ц3р(1, о, 1). (4.9о)
Заметим, например, что в уравнении (4.89) интенсивность по тока, исходящего из состояния (1, 1,0) за счет ухода требований из узла 1, приравнивается к интенсивности потока, входящего в это состояние за счет поступления требований в узел 7; аналогично, уравнение (4.90) описывает такое же равенство для узла 2. Это и есть принцип локального равновесия, и, как нетрудно видеть, уравнения (4.83)—(4.85) уже имеют такой вид. 178
Таким образом, получаются девять уравнений локального равновесия 1 (четыре из них, следовательно, должны быть избыточными, если учесть условие нормирования вероятностей), каждое из которых имеет очень простой вид и поэтому позволяет непосредственно найти решение. Если эта система уравнений действительно имеет решение, то определенно гарантируется, что оно удовлетворяет и системе уравнений глобального равновесия, и, таким образом, найдено единственное решение исходной системы уравнений глобального равновесия. Читатель может легко проверить, что решение выражается следующим образом:
/7(1, 0, 1) р(2. О, 0);
Из
Р (1, 1,0) — -^р(2, 0, 0);
/7(0, 1, 1) р(2, о, 0);
1<2р 3
/7(0, 0, 2)^(-^)2/7(2, 0, 0);
д(0, 2, 0) = (2, 0, 0);
р(2, 0, 0)= Г1 4- Ц1 !11-+ ОоЦщ ( I4' Vp- f‘“'VI-1. (4.91)
L ' Рз ' Щ № \ Из / \ Щ 7 J
Если бы были допущены всевозможные переходы требований из одного узла в другой (а не только рассмотренные в примере циклические переходы), то диаграмма интенсивностей переходов содержала бы вместо однонаправленных переходов переходы в обоих направлениях; однако допускаются только переходы в ближайшие соседние состояния (на рассматриваемой двумерной! диаграмме), поэтому диаграмма переходов всегда может быть изображена на плоскости. Например, если допустить, что четыре требования могут перемещаться по сети с тремя узлами, связанными произвольным образом, то диаграмма интенсивностей переходов будет иметь вид, показанный на рис. 4.18. На этой диаграмме возможные переходы между узлами изображены ненаправленными ребрами (каждое из ребер соответствует двум однонаправленным ветвям противоположных направлений). Кроме того, группы ребер собраны с помощью перечеркивающей линии, которая объединяет ребра, дающие члены одного и того же уравнения локального равновесия. Эти диаграммы могут быть обобщены на большее число измерений, если в системе находится более трех узлов. В частности, в случае четырех узлов получается тетраэдр (т. е. трехмерный симплекс). В общем случае для N узлов в сети получится
1 Читатель может выписать их прямо по рис. 4.17.
179
Рис. 4.18. Диаграмма интенсивностей переходов, иллюстрирующая локальное равновесие ( V -- 3, К --- 4)
(N — 1)-л:ерный симплекс с (/( 1) узлами на каждой грани
(где К — число требований в замкнутой системе).
Заметим, что на этих диаграммах для всех узлов, лежащих па одной п той же прямой (параллельной любому основанию симплекса). одна из компонент соответствующего вектора состояний имеет фиксированное значение, а при переходе на параллельное множество узлов это значение убывает или возрастает на единицу. Уравнения локального равновесия приравнивают потоки в таком множестве ребер, которое связывает данный узел на одной из этих линий постоянного значения компоненты со всеми узлами, лежащими на этой постоянной линии и являющимися смежными и параллельными указанному узлу, и которые уменьшают на единицу компоненту, бывшую постоянной. Это дает в итоге тривиальное правило составления систем уравнений локального равновесия, п если удается найти решение для этих систем, то тем самым находится и решение системы уравнений глобального равновесия!
Как видим, большинство марковских сетей подобного тина приводя г к достаточно сложным системам линейных уравнений. Уол лейс п Розенберг [10] предложили эффективный метод численного решения для большого класса таких систем. Они обсуждают программу вычислений, которая позволяет определить стационарное распределение вероятностей состояний для очень больших конечных марковских сетей массового обслуживания. А именно, программа позволяет решать системы уравнений равновесия в виде (2.50) и (2.116), т. е. в форме л -- лР и лЦ — 0. Предложенный метод относится к процедурам степенной итерации, поэтому, если л (/) является i-м шагом итерации, то на (I -|- [)-м шаге вычис-180
ляется л (i -р 1) — л (i) R, где матрица R равна либо матрице аР -р (1 — а) I, либо матрице [3Q + 1 (где а и |3 — скаляры, а I — единичная матрица), в зависимости от того, какое из дву.х указанных выше уравнений должно быть решено. Скаляры а и [3 тщательно подбирают так, чтобы обеспечить быструю сходимость к решению заданной системы. Получается просто замечательная скорость решения, но за дальнейшими подробностями читателю рекомендуется обратиться к работе [101.
На этом заканчивается изучение чисто марковских систем в состоянии равновесия. Объединяющая особенность материала, рассмотренного в гл. 3 и 4, состоит в том, что все полученные решения имели форму произведения; следовательно, при исследовании марковских СМО решение нужно искать в таком виде. В следующих двух главах допускается, что либо распределение A (f), либо В (х) (но пе оба распределения одновременно) является произвольной функцией при условии, что второе распределение остается показательным.
СПИСОК ЛИТЕРАТУРЫ
I. Burke, P.J. The Output of a Queueing System. Operations Research, 4, 699 -704 (1956).
2. Chandy, К. M. The Analysis and Solutions for General Queueing Networks. Proc. Sixth Annual Princeton Conference on Information Sciences and Systems, Princeton University, March, 1972.
3. Cox, D. R. A Use of Complex Probabilities in the Theory of Stochastic Processes. Proceedings Cambridge Philosophical Society, 51, 313—319 (1955).
4. Gordon, W. J. and Newell J. F. Closed Queueing Systems with Exponential Servers. Operations Research, 15, 254—265 (1967).
5. Jackson, J. R. Networks of Waiting Lines. Operation Research, 5, 518—521 (1957).
6. Jackson, J. R. Jobshop—Like Queueing Svstenis. Management Science, 10, 131-142 (1963).
7. Kingman, J. F. C. Markov Population Processes. Journal of Applied Probability, 6, 1—18 (1969).
8. Koenigsberg, E. Cyclic Queues. Operations Research Quarterly, 9, 22- 35 (1958).
9. Saaty, T. L., Stochastic Network Flows: Advances in Networks of Queues. Pioc. Syuip. Comsestion Theory, Univ, of North Carolina Preec, (Chapel Hill), 86—107, (1965)."
10. Wallace, V. I., anb Rosenberg R. S. Markovian Models and Numerical Analysis of Computer System Behavior. Al-IPS Spring Joint Computer Conference Proc., 141- 148, (1966).
11. Whittaker, E. and Robinson G. The Calculus of Observations, 4-th eil., Blackie London, (194 1).
ЗАДАЧИ
4.1. Рассмотрим изображенную ниже марковскую СМО. Указанные па ребрах величины представляют собой интенсивности
181
размножения и гибели,
требований в системе.
а цифры в кружках указывают число
а) Найдите вероятности
б) Найдите среднее число требований в системе.
в) Рхакис значения принимают величины из и. а и б при У- р? Попытайтесь объяснить эти результаты.
г) Выпишите матрицу интенсивностей переходов Q для этой задачи и матвпчиое уравнение, связывающее. Q и верояг-iiUCiil /Ю. ИЗ И. ci.
4.2. Рассмотрим САЮ типа Ек,'Еп/1, в которой не допускаются очереди. Если поступающее требование застало систему занятой, то оно теряется (уходит без обслуживания). Пусть Ец означает состояние системы, в котором поступающее требование находится на t-м этапе, а обслуживаемое требование — на /-м этапе (при этом механизм поступления требований таков, что в каждый момент времени в принимающем приборе всегда имеется требование, а если в обслуживающем приборе требования нет, то полагают / = 0). Пусть 1/ZeA, — среднее время пребывания требования па любом этапе приемного устройства, а 1 /пр — среднее время пребывания требования на произвольном этапе обслуживания.
а) Начертите диаграмму переходов для этой системы с указанием всех интенсивностей.
б) Составьте уравнения равновесия для Eti, где 1 < i <^k и 1 <С / < п.
4.3. Рассмотрим СМО типа М/Ег/1, в которой не допускается образование очередей. Пусть j означает остаточное число этапов обслуживания в системе, а Рj — стационарную вероятность того, что система находится в состоянии Et.
а) Найдите Ph / = 0, 1, ..., г.
б) Найдите вероятность занятости системы.
4.4. Рассмотрим САЮ типа М/Н2/1, в которой не допускается образование очередей. Предположим, что время обслуживания является гиперпоказательным с параметрами p,L — п щ, — 2ц (1 — aj, как показано па рис. 4.10.
а) Найдите вероятности свободного состояния системы в установившемся режиме.
б) Найдите вероятность занятости прибора 1.
в) Найдите вероятность занятости системы.
182
4.5. Рассмотрим СМО типа М/М/1 с параметрами к п ц, в которую в каждый момент поступления прибывают ровно ио два требования.
а) Начертите диаграмму интенсивностей переходов для рассматриваемой системы.
б) Используя диаграмму интенсивностей переходов, выпишите для pk уравнения равновесия (k = 0, 1, 2, ...) в) Пусть р = 2л/р. Выразите Р (г) через г и р.
г) Используя результаты, полученные в параграфе 4.5 для группового входящего потока, найдите функцию Р (г).
д) Используя Р (г), найдите среднее значение и дисперсию числа требований в системе.
е) Повторите вычисления пи. а—д для случая, когда в каждый момент поступления прибывает равно г требований (и р = гХ/р).
4.6. Рассмотрим СМО типа М/М/1 с параметрами X и и. В каждый момент поступления в систему с вероятностью 1/2 поступает одно новое требование и с вероятностью 1/2 одновременно два новых требования.
а) Начертите диаграмму интенсивностей переходов для такой системы.
б) Выпишите уравнения для стационарных вероятностей pk, используя метод систем с переходами не только в ближайшие соседние состояния.
в) Найдите функцию Р (г) и вычислите все входящие в нее константы так, чтобы Р (г) зависела только от Z и р. Если можно, сократите все общие множители в числителе и знаменателе этой функции [это облегчит решение п. г].
г) Используя п. в, найдите среднее число требований в системе.
д) Повторите вычисления п. в, используя непосредственно результаты параграфа 4.5.
4.7. Для системы с групповым входящим потоком, рассмотренной в параграфе 4.5, предположим (при 0 <а < 1), что gi — (1 — а) а1', 1 = 0, 1,2, ... Найдите в этом случае стационарные вероятности рк того, что в системе будет находиться ровно k требований.
4.8. Найдите среднее значение N п дисперсию cr;v числа требований в системе с групповым входящим потоком, описанной в параграфе 4.5. Выразите ответ через моменты распределения числа требований в группе.
4.9. Рассмотрим следующую модификацию системы М/М/1;
как только обслуживающий прибор освобождается, он принимает из очереди на обслуживание два требования одновременно (если таковые имеются). Из этих двух требований обслуживается только одно, и когда обслуживание кончается, оба требования покидают систему (г. е. второе требование проходит вхолостую).
183
Если в момент освобождения обслуживающего прибора в очи редн оказывается только одно требование, то оно и поступает да а обслуживания; но если во время обслуживания этого требования поступает новое требование, то новое требование поступает в прибор и обрабатывается вхолостую.
Во всех случаях время обслуживания предполагается показательным со средним значением 1/|х секунд, а входящий поток требований — пуассоновским с интенсивностью X требований в секунду.
а) Начертите соответствующую диаграмму состояний.
б) Составьте соответствующую систему разностных уравнений для стационарных вероятностей pk наличия в системе k требований.
в) Найдите выражение Р (г) через р0 и
г) Выразите р1 через /?0.
4.10. Рассмотрим многочлен, стоящий в знаменателе дроби (4.35).
а) Одним из (г + 1) корней этого многочлена является z=l. Используя теорему Руше, покажите, что точно (г — 1) корней лежат в единичном круге |г| < 1.
б) Покажите, что корень z = 1 является единственным корнем на окружности единичного радиуса |г| = 1. [Отсюда, на основании результатов пн. а и б, устанавливаем, что точно г— 1 корней лежат в области |г| <Д, а один корень г0 лежит в области |z0| > 1 ].
4.11. Покажите, что решением системы (4.71) является такое множество переменных {х,-}, для которого (4.72) действительно представляет собой решение системы (4.69).
4.12. а) Начертите диаграмму интенсивностей переходов, показывающую локальное равновесие при У = 3 и ft = 5 для следующей сети.
б) Найдите р (&х, й2, &3).
4.13. Рассмотрим марковскую сеть массового обслуживания с двумя узлами (наиболее общего типа, исследованного Джексоном) при N = 2, m-i — т2 -= 1, рк = jx, (интенсивность
184
обслуживания постоянна), для которой вероятности переходов описываются следующей матрицей:
Hi 0 1 2 О • J
0 0 1 0 0
1 0 0 1 — и а
2 0 1 0 0
где 0 <а < I, а узлы Он Дб -f- 1 представляют собой соответственно источник и поглотитель требований. Предположим также, что в начальный момент времени система содержит К требований (где К — некоторое целое число) и
У (S (&1, &2))
/<Д 4-
A’t -Г k-2
к-, К.
а) Найдите величины е, (г = 1, 2) согласно равенству (4.75). б) Так как N = 2, обозначим р (klf kJ = р (klt К — kJ через pkt. Найдите уравнения равновесия для вероятностей pkv
в) Решите эти уравнения в явном виде относительно /?*,. г) Рассматривая долю времени, в течение которого первый узел занят, найдите время между уходами требований из сети (конечно, через узел /).,
ЧАСТЬ III
ПРОМЕЖУТОЧНАЯ ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
Здесь будут рассмотрены некоторые системы массового обслуживания, к которым еще применимы упрощения, обусловленные их марковской природой. Займемся системами, описываемыми с помощью вложенных цепей Маркова, а именно системами типа М/G/l и G/M/m. В гл. 5 будут выведены уравнения равновесия для систем типа М/G/l, дающие известные уравнения Полячека — Хинчина для длины очереди и времени ожидания. Далее будет рассмотрен вопрос о периоде занятости и, наконец, будут изучены несколько более сложные методы исследования систем массового обслуживания. При этом будут отчасти затронуты и решения, зависящие от времени. Точно так же для систем типа G/M/m в гл. 6 будут получены некоторые результаты, характеризующие систему в состоянии равновесия, и показано, что условное распределение времени ожидания всегда показательно, каково бы ни было распределение промежутков времени между поступающими требованиями! Аналогично будет показано, что длина очереди имеет условное геометрическое распределение. Заметим, что в этой части применяются совершенно иные методы решения, чем в части II, но многие важные характеристики системы оказываются похожими. В частности, средняя длина очереди, среднее время ожидания, средняя продолжительность периода занятости, как и ранее, обратно пропорциональны 1 — р. В гл. 7 будет изучена интересная вероятностная интерпретация преобразований.
186
Методы исследования, примененные в гл. 3 [где явное решение уравнения (3.11) имело вид произведения] и в гл. 4 (сохранение потока), в гл. 5 заменяются рассмотрением производящих функций. Однако в гл. 6 мы вновь возвращаемся к сохранению потока, которое присуще решению уравнения л = ..Г'.
ГЛАВА 5
Система массового обслуживания типа M/G/1
Многочисленные приложения элементарной теории массового обслуживания основываются, на простоте описания состояний системы В частности, для подведения итога протекания процесса в прошлом требуется указать лишь число требований 1 2 в системе в рассматриваемый момент времени. Для чисто марковских систем вся остальная информация об истории процесса не влияет на его протекание в будущем. Таким образом, описание состояний не только одномерно, но также счетно (а в некоторых случаях конечно). Это последнее свойство (счетность) упрощает вычисления.
В этой и следующей главах исследуются системы массового обслуживания, в которых протекают немарковские случайные процессы. Вследствие этого возникают новые задачи, для которых надо искать новые методы решения.
Несмотря на немарковскую природу рассматриваемых систем, существует много подходов к их изучению. В этой главе рассмотрим метод вложенных цепей Маркова, принадлежащий Пальму [13] и Кендаллу [9]. Однако фактически будет рассмотрен и второй подход к этому классу задач, а именно метод этапов. Как было показано, этот метод применим, если преобразования Лапласа плотностей распределения промежутков времени между требованиями и времени обслуживания рациональны
1 Обычно описание состояний дается в виде вектора, характеризующего состояние системы в момент t. Вектор v (/) является вектором состояний, если, задавая v (t) и все входы в систему за время (/, К) (где t < Ц), можно определить вектор v (/,). Очевидно, следует выбирать вектор состояний, содержащий такую информацию, которая позволяет вычислить величины, важные для понимания характеристик системы.
2 В гл. 4 мы видели, что иногда вместо числа требований указывается число этапов обслуживания в системе.
187
(см. параграф 4.7). Этот подход невыгоден тем, что он дает только процедуру решения, но не позволяет получить решение в явном виде. Вследствие этого нельзя изучить свойства решения, присущие целому классу систем.
Третий подход, который будет исследован в гл. 8, состоит в решении интегрального уравнения Линдли [12 |. Этот подход пригоден для системы G/G/1 и, следовательно, может быть применен к некоторым более частным системам, рассматриваемым в данной главе. Четвертый подход, называемый методом дополнительных переменных, обсуждается в задачах в конце данной главы. Более подробно остановимся на нем в следующей главе. Обсуждается также анализ периода занятости [6], который приводит к распределению времени ожидания (см. параграф 5.10). Помимо этого, существуют другие подходы к изучению немарковских систем массового обслуживания, среди которых отметим метод случайного блуждания и комбинаторный метод [21 ], а также метод функции Грина [8[.
5.1. СИСТЕМА M/G/1
Система M/G/1 — это однолинейная система с пуассоновским входящим потоком и произвольным распределением времени обслуживания [функция распределения времени обслуживания обозначается В (х), а плотность распределения b (х)]. Функция распределения промежутков времени между последовательными поступлениями требований имеет вид
Л (f) = 1 - е-и, t ж 0
с интенсивностью входящего потока А. требований в секунду, средним промежутком времени между поступлениями 1/Л. секунд и дисперсией Од = 1/Z2. Как было определено в гл. 2, момент /г-го порядка времени обслуживания обозначается
ос
Xk A J ХкЬ (х) dx, о
а иногда эти моменты обозначают через bk d\x'1.
Рассмотрим вопрос о (векторном) описании состояния системы M/G/1. Если в некоторый момент времени I нужно подытожить полностью прошлую историю системы, то, очевидно, необходимо указать N (/) — число требований, присутствующих в системе в момент I. Кроме того, нужно установить время обслуживания Хо (0, которое к данному моменту получило требование, находящееся в приборе обслуживания. Эту величину необходимо знать, так как процесс обслуживания необязательно является процессом без последействия. (Ясно, что в случае, когда процесс поступления требований пуассоновский, т. е. без последействия, время, прошедшее после поступления последнего требования, ни на это не 188
влияет п не должно нас интересовать.) Таким образом, очевидно, что случайный процесс N (/) не является марковским. Однако вектор IN (t), Хо (/) ] представляет собой марковский процесс и годится для описания системы M/G/1, так как он содержит всю предысторию, влияющую на развитие системы в будущем.
Таким образом, от однокомпонентного описания состояния в элементарной теории массового обслуживания мы пришли к возникающему в промежуточной теории двухкомпонептному описанию. Рассмотрим существенное различие между этими двумя описаниями состояний.
В элементарной теории массового обслуживания достаточно задать число N (0 требований в системе в момент t. Следовательно, здесь имеет место марковский процесс с дискретным пространством состояний, причем число самих состояний конечно или счетно. Переходя к системе, для описания состояния которой нужен двумерный вектор, можно видеть, что число требований в системе N (/) по-нрежпему счетно, но теперь необходимо, кроме того, задать непрерывную функцию Хо (/), представляющую собой израсходованную часть времени обслуживания. Таким образом, от дискретного описания состояния, мы переходим к непрерывному описанию, и эта существенная разница усложняет анализ.
Можно исходить из общей теории, основанной на паре величин [А (/), Хо (01 как на векторе состояний. Такой метод называется методом дополнительных переменных. Исследования такого типа читатель найдет у Кокса [3] и Кендалла [10]; Гендер-сон [7 ] также рассматривает этот метод, но выбирает в качестве дополнительной переменной не прошедшее, а остающееся время обслуживания. В данной книге в качестве метода исследования принят метод вложенной цепи Маркова, который обсуждается ниже. Однако, прежде чем перейти к самому методу, очевидно нужно понять некоторые свойства израсходованного времени обслуживания.
5.2. ПАРАДОКС ОСТАТОЧНОГО ВРЕМЕНИ:
НЕМНОГО ТЕОРИИ ВОССТАНОВЛЕНИЯ
Рассмотрим случай, когда поступающее требование застает обслуживающий прибор занятым. Задачи такого рода неоднократно будут возникать при исследованиях, поэтому эту ситуацию необходимо выделить из общего контекста. Начнем с явного парадокса, который иллюстрируется следующим примером. Предположим, что наш путешественник из гл. 2 прибывает в произвольный момент времени в придорожное кафе и начинает там «ловить» попутную машину. Предположим далее, что машины прибывают к этому кафе пуассоновским потоком с интенсивностью А. машин в минуту. Как долго в среднем пассажир должен ожидать прибытия очередной машины?
1ВД
Tj ЧА Tn-1 t_____________________Тг, Ось
« 9 © 1 времени
Появление пассажира Л
Aj Аг Aj An-i An
Рис. 5.1. Срок службы, время наработки и остаточное время
Имеется, по-видимому, два логичных ответа на этот вопрос. Во-первых, можно считать, что, поскольку средний промежуток времени между машинами равен 1/Х мин, а пассажир прибыл в случайный момент времени, то «очевидно», что среднее время ожидания для пассажира равно 1/2Х мин. Во-вторых, поскольку поток машин пуассоновский, время, остающееся до прибытия следующей машины, не зависит от того, сколько времени прошло с момента прибытия предыдущей машины. Следовательно, пассажир будет ждать в среднем 1/Х мин. Тот же довод можно применить, чтобы показать, что среднее время, прошедшее с момента прибытия последней машины до появления пассажира в кафе, тоже равно 1/Х мин. Но тогда средний промежуток времени между прибытием предыдущей и последующей машины равен 2/Х мин. Этот промежуток оказывается вдвое длиннее, чем он должен быть для пуассоновского потока! Тем не менее второе решение правильно, и таким образом мы встречаемся с явным парадоксом.
Рассмотрим решение этой задачи в случае произвольного распределения промежутков времени между поступлениями. Это исследование относится к теории восстановления, и мы будем часто ссылаться на результаты этой теории, основную часть которых можно найти в прекрасной монографии Кокса [4] или в хорошей обзорной статье Смита [17]. Читателю рекомендуется также посмотреть работу Феллера [5]. На рис. 5.1 показана основная схема. Здесь Ak означает k-ю машину, а тЛ. — момент ее прибытия. Предполагается, что промежутки времени т/;+1 — ты представляют собой независимые, одинаково распределенные случайные величины с заданной функцией распределения:
F (х) Д Р [тА+1 — ту < х]. (5.1)
Определим плотность распределения, также одинаковую для всех промежутков:
Их)Д^. (5.2)
Выберем теперь случайным образом момент t появления путешественника в придорожном кафе. На рис. 5.1 Ап— последняя машина, прибывшая до момента t, а А„— первая машина, прибывшая после момента t. Обозначим через X весь промежуток 190
времени т„ — т„_1( a Y — время ожидания ближайшей машины. Очевидно, последовательность моментов времени {тй} образует процесс восстановления. В теории восстановления предполагается мгновенная замена элементов. В этом случае последовательность {т/г| можно рассматривать как последовательность моментов выхода из строя старых элементов и замены их новыми.
На языке теории восстановления X называется сроком службы рассматриваемого элемента, Y — остаточным временем в момент I, Хо = X — Y — временем наработки элемента к моменту t. Будем следовать этой терминологии и найдем распределение времени наработки и остаточного времени выбранного элемента. Предполагается, что процесс восстановления длится произвольно долго, поэтому нас будут интересовать только предельные распределения.
Замечательный результат, который будет получен, состоит в том, что величина X не распределена по закону F (х). Для рассмотренного примера это означает, что промежуток времени между приходим цутешесгвенника к придорожному кафе и прибытием машины не является типичным промежутком. Фактически в этом и заключается разрешение рассмотренного парадокса: длинный промежуток вероятнее «захватит» момент появления путешественника, чем короткий. В случае пуассоновского процесса поступления это обстоятельство, как увидим, приводит к тому, что выделенный промежуток оказывается вдвое длиннее типичного.
Пусть остаточное время описывается функцией распределения
Е(х) А Р [Y < х] (5.3)
с плотностью
? /Ж -
I ( > ' dx • (5.4)
Аналогично пусть выделенный промежуток времени X описывается функцией распределения
ДДх)АР[Х <х] (5.5)
и соответствующей плотностью fx (х).
В задаче 5.2 читателю предлагается строго вывести плотность распределения / (х) остаточного времени. Здесь же предпочтем интуитивный вывод, основанный на физическом описании рассматриваемой задачи. Основное замечание состоит в том, что длинные промежутки времени между моментами восстановления захватывают на оси времени большие участки, чем короткие промежутки, и поэтому более вероятно, что случайно выбранная точка t попадет на длинный промежуток. Если согласиться с этим, то вероятность выбора промежутка времени длины х должна быть пропорциональна этой длине, а также относительной частоте
191
появления таких промежутков [которая равна f(x)dx\. Таким образом, для выделенного интервала можно написать
fx (х) dx — Kxf (х) dx, (5.6)
где левая часть представляет собой Р [х < X < х dx], а правая часть выражает линейную весовую функцию относительно длины промежутка и включает множитель /(, нормирующий плотность.
Интегрируя обе части равенства (5.6), находим, что К. --- i/иц, где
niyX Е [т/г — т/(_г] (5.7)
представляет собой среднее время между восстановлениями (между прибытиями машин). Таким образом, показано, что плотность распределения выделенного промежутка времени связана с плотностью распределения типичных промежутков времени равенством
х/(х) .
hW-r- '
Это первый важный результат. Перейдем к определению плотности распределения остаточного времени /(х). При условии X = х вероятность того, что остаточное время Y не превышает у, определяется равенством
P[Y <r/|X=x]=f
при 0 с у < х. Это верно, поскольку точка, случайно выбранная в промежутке, должна быть равномерно распределена на этом промежутке. Следовательно, можно записать совместную плотность распределения величия X и Y:
Р [У " С У < У 'г dy, х "У X с х dx] =-f dy_\ / xf (х) dx \ _ / (х) dy dx g.
\ x / m1 ) m-i ‘ '
при 0 < у < x. Интегрируя по х, получим функцию f (у), представляющую собой безусловную плотность распределения величины Y:
что непосредственно дает окончательное равенство
1 -1- (!') в (5.16)
«о
f (у) -=
192
Это второй важный результат. Он выражает плотность распределения остаточного времени через функцию распределения длин промежутков и их среднее значение 1.
Выразим последний результат через преобразования. Применяя обычные обозначения для преобразований, имеем следующие соотношения:
И*) (=И*(з);
1W (=) (s).
Очевидно, все рассматриваемые в этом разделе случайные величины неотрицательны, и соотношение (5.10) может быть непосредственно преобразовано с использованием строки 5 табл. 1.4 и строки 13 табл. 1.3; это дает
Теперь можно обычным путем выразить моменты распределения остаточного времени через моменты распределения срока службы. Обозначим n-й момент распределения срока службы тп и п-й момент распределения отстаточного времени гп, т. е.,
/п„Д£[(т*—(5.12) r„A£[P*]. (5.13)
Применяя равенство (II.26), можно продифференцировать (5.11) и получить моменты распределения остаточного времени. При s 0 получаются неопределенности, для раскрытия которых применяют правило Лопиталя. Эти вычисления дают моменты распределения остаточного времени в виде
Эту важную формулу наиболее часто применяют для нахождения среднего остаточного времени гх:
которое может также быть выражено через дисперсию срока службы (обозначаемую ff2 Ат2 — га2):
Последняя формула показывает, что тг/2, т. е. половина среднего промежутка времени между поступлениями машин, будет пра-
1 Можно также показать, что предельная плотность распределения времени наработки (Хо) та же, что н предельная плотность распределения остаточного времени (К), т. е. дается равенством (5.10).
7 Л. Клейнрок 193
вильным решением в задаче с парадоксом только в том случае, когда дисперсия равна нулю (регулярное поступление). Однако для пуассоновского потока иц = 1/k и а2 = 1/V, что дает = = 1/Х = тх и подтверждает прежнее решение парадокса. Заметим, что (тх/2) с гх, и /у неограниченно возрастает при а2 оо. Этот результат несколько неожиданный, но, как увидим, он будет появляться вновь и вновь.
Перед тем как расстаться с теорией восстановления, воспользуемся случаем, чтобы привести еще некоторые полезные результаты. На языке теории восстановления зависящая от времени наработки интенсивность выхода из строя г (х) определяется как мгновенная интенсивность, с которой выходит из строя элемент, достигший времени наработки х, т. е. г (х) dx Д Р [х < срок службы элемента Ц-dx] срок службы >х]. Из основных законов следует, что эта условная плотность имеет вид
где f (х) и F (х) — плотность распределения и функция распределения срока службы элемента.
Функция восстановления Н (х) определяется как
И (х) Д£'[число восстановлений за промежуток времених], (5.18) а плотность восстановления h (х) является просто интенсивностью восстановления в момент х и определяется равенством
й(х)Д-^-. (5.19)
Теория восстановления насыщена предельными теоремами. Один из важных результатов, называемый теоремой восстановления, устанавливает, что
limh(x) = —. (5.20)
Х-Юо т1
Это означает, что в пределе нельзя распознать, когда начался процесс восстановления; и, таким образом, интенсивность восстановления элементов обратна средней продолжительности промежутка времени между восстановлениями (mJ. Заметим, что h (х) не является плотностью распределения: действительно, интеграл от этой функции в типичном случае расходится. Однако эта функция обладает преобразованием Лапласа, которое обозначим через Н* (з). Легко показать, что существует следующее соотношение между этим преобразованием и преобразованием основной плотности для восстановлений:
Я*(*) = Т^%- (5.21)
194
Это соотношение является преобразованием интегрального уравнения теории восстановления, которое может быть записано в виде
X
h(x) = f (х) 4- J h(x — (/) dt. (5.22)
о
Больше теорию восстановления рассматривать не будем. Читателю опять рекомендуется обратиться к указанным выше источникам.
5.3. ВЛОЖЕННАЯ ЦЕПЬ МАРКОВА
Рассмотрим метод вложенной цепи Маркова и применим его к изучению системы М/G/l. Основная идея, заключающаяся в этом методе, состоит в том, чтобы упростить описание состояний, заменив двумерное описание [М (f), Хо (/) 1 одномерным описанием N (/). Для того чтобы успешно вычислять будущие значения случайных величин, вместе с числом требований в системе надо неявно задавать время, уже проведенное требованием в приборе обслуживания. Кроме того (и этот факт особенно важен), можно добиться упрощения, рассматривая не все моменты времени, а лишь специальным образом подобранную последовательность точек на оси времени. Очевидно, эта последовательность должна быть выбрана так, чтобы, задавая число требований в системе в один из таких моментов и обеспечив дальнейшее поступление требований в систему, можно было бы вычислить число требований в системе в следующий принадлежащий последовательности момент. Поэтому необходимо как-нибудь зафиксировать время, уже проведенное требованием в приборе обслуживания.
Как определить последовательность моментов, обладающую этим свойством? Таких последовательностей можно построить сколько угодно. Особенно удобна последовательность моментов ухода обслуженных требований. Очевидно, что, определив число требований в момент, когда обслуженное требование покидает систему, и прибавив число поступивших позже требований, можно найти число требований в системе для любого момента времени в будущем. Здесь считается, что в момент ухода обслуженного требования время, потраченное на обслуживание следующего требования, равно нулю, так как обслуживание в этот момент только начинается (если система не остается пустой) *. (Имеются другие последовательности моментов времени, обладающие этим же свойством; например, последовательность моментов, взятых точно через секунду после начала обслуживания. Если определить число требований в системе в один из таких моментов, можно будет определить число требований в системе в любой такой же момент в будущем. Такая последовательность моментов вре-
Более того, предполагается, что никакое другое требование в очереди не получает обслуживания.
7* 195
мени менее удобна, чем последовательность моментов ухода требований, так как здесь необходимо позаботиться о случаях, при которых обслуживание длится меньше одной секунды).
Читатель, должно быть, узнал в описанном процессе полу-марковский процесс, при котором изменения состояний происходят в момент ухода требования. Для таких моментов определим вложенную цепь Маркова как число требований, имеющихся в системе в момент ухода очередного обслуженного требования. Переходы имеют место только во вложенных точках и образуют дискретное пространство состояний. Распределение времени между переходами равно распределению времени обслуживания В (х) всякий раз, когда после обслуживания остается по крайней мере одно требование, и равно свертке распределения промежутков времени между поступлениями требований (показательного распределения) с b (х) в случае, когда уходящее требование оставляет систему пустой. Во всяком случае, характеристики цепи в этих вложенных точках полностью описываются марковским процессом, н здесь применимы результаты, рассмотренные в гл. 2.
Используемый здесь подход состоит в том, чтобы рассматривать исключительно моменты ухода требований и описывать состояние числом требований, остающихся в эти моменты в системе. Приступим к решению сформулированной задачи. К счастью, решение для вложенных марковских точек обеспечивает решение для всех моментов времени т. В задаче 5.7 читателю предлагается вновь вывести некоторые результаты для системы M/G/1, применяя метод дополнительных переменных. Этот метод годится для всех моментов времени и (как и должно быть) дает те же результаты, что и метод вложенной марковской цепи. Это еще раз доказывает, что наше решение справедливо для всех моментов времени. На ближайших страницах устанавливаются результаты, касающиеся распределения длины очереди, времени ожидания и периода занятости (все в форме преобразований). Результаты, относящиеся ко времени ожидания и периоду занятости, никоим образом не ограничиваются описываемым «вложением». Таким образом, даже если бы нельзя было применить другие методы, эти результаты, полученные с помощью вложенных цепей, остались бы в силе.
1 Это удачное обстоятельство обусловлено тем фактом, что входящий поток является пуассоновским, и поэтому, как показано в параграфе (4.1), вновь поступающее требование создает момент случайного наблюдения системы обслуживания. Кроме того, в задаче 5.6 читатель подводится к доказательству того, что для любой системы, у которой состояния изменяются единичными скачками (положительными или отрицательными), предельное распределение числа требований, остающихся после ухода некоторого требования, является таким же, как и предельное распределение числа требований, имеющихся в наличии при новом поступлении. Этот результат справедлив для произвольного распределения времени обслуживания и произвольного входящего потока. Следовательно, для системы M/G/1 поступления, уходы и случайные наблюдения дают одно и то же распределение числа требований в системе.
196
Для того чтобы окончательно
. {л-7)(А)(л+/)
убедить читателя, теперь предла- Ч—< 2>—
гается интуитивное подтвержде-ние эквивалентности предельных Рис- 5-2- Переходы для систем С еди-„ 1 ничпым изменением состоянии
распределении, рассматриваемых для моментов ухода и моментов поступления требований. Характеризуя состояние системы числом требований в ней, можно наблюдать изменение состояния системы во времени. Если следить за системой непрерывно, можно •заметить, что переходы в системе происходят только в соседние состояния. В частности, если состояние системы, содержащей ,k требований, обозначено через Е:, то возможны только переходы Ek E/,+i и Ек -> Ек х (причем последний переход возможен .лишь при k > 0). Это показано на рис. 5.2. Заметим теперь, что число переходов типа Е,, -> Ek+l отличается не более чем на единицу от числа переходов типа Е/1+1 -> Ek. Первый из этих переходов соответствует поступлению требования и возникает в момент поступления. Второй переход соответствует уходу требования и возникает в момент ухода. После того, как система проработает сколь угодно долго, число переходов вверх должно быть по существу таким же, как число переходов вниз. Так как это движение вверх и вниз относительно Ek происходит по существу с одной и той же частотой, то отсюда можно заключить, что состояния системы, определяемые уходами требований, имеют то же предельное распределение вероятностей гк, что и состояния •системы, определяемые поступлением требований (<Д). Таким образом, обозначив через N (/) число требований в системе в момент t, можно сделать следующие два вывода.
1. Для пуассоновского потока требований всегда справедливо равенство [см. (4.6)1
Р [N (0 = k ] = Р [поступление в момент t застает k требований в системе],
т. е.
PkU) = Rk(t). (5.23)
2. Если в некоторой (возможно, немарковской) системе число требований N (t) может быть изменено только на (плюс или минус) единицу, то из существования одного из приведенных ниже распределений следует существование другого и их равенство (см. задачу 5.6):
rk & lim Р [поступление в момент t застает /? требований в си-стеме];
d* Д lim Р [уход в момент t оставляет k требований в системе); t~> ер
гк --= ак. в (5.24)
197
Таким образом, для системы М/G/l справедливо rk • Pk = dk-
В этой главе прежде всего будет найдено среднее число требований в системе — результат, называемый формулой Полячека — Хинчина для среднего значения г. После этого будет получена производящая функция распределения числа требований в системе, а затем преобразования Лапласа распределений времени ожидания и времени пребывания требования в системе. Последние результаты будем называть формулами Полячека — Хинчина для преобразований. Кроме того, найдем преобразования распределения периода занятости и числа требований, обслуженных за период занятости. Затем покажем, как получить время ожидания из анализа периода занятости. Наконец, выведем интегро-дифференциальное уравнение Такача для незавершенной работы в системе. Начнем с введения некоторых обозначений и установим вероятности переходов, связанные с рассматриваемой вложенной цепью Маркова.
5.4. ВЕРОЯТНОСТИ ПЕРЕХОДА
Использование моментов времени ухода в качестве вложенных точек на временной оси уже обсуждалось. В эти моменты определяется вложенная марковская цепь как число требований, остающихся после ухода. Читателю должно быть ясно, что таким образом получается полное описание состояний, так как наверняка известно, что вновь поступающее в такой момент требование имеет нулевое время обслуживания, а также что время, прошедшее после поступления последнего требования, не влияет на будущее развитие процесса, так как распределение промежутков времени между поступлениями — без последствия.
Ранее, в гл. 2, были введены некоторые символические и графические обозначения. Читателю рекомендуется освежить в памяти рис. 2.2 и вспомнить следующие определения: Сп означает п-е требование, поступающее в систему; т„ — время поступления C.i, tn х,г — т;1 л—промежуток времени между Сп_г и С,:; хп — время обслуживания требования С,г.
Дополнительно введем две важные случайные величины:
7 ,.г — число требований, остающихся в системе в момент ухода требования С,;
о , — число требований, поступающих в систему за время обслуживания требования С,,.
1 В литературе по теории массового обслуживания имеются заметные разногласия по поводу названии формул для среднего значения и преобразования. Некоторые авторы называют формулой Полячека—Хинчина выражение для среднего значения, другие относят это название к преобразованному уравнению. Мы постараемся уменьшить путаницу, прибавляя к этому названию соответствующие прилагательные.
198
Нас интересует распределение вероятностей q,., т. е. Р [qn — = kl, которое фактически зависит от времени. Предельное (при п -* оо) распределение qn совпадает с которое, как мы знаем, равно р,; — основному распределению вероятностей, обсуждавшемуся в гл. 3 и 4. При нахождении распределения вероятностей qn существенную роль будет играть число требований vn, поступивших за время обслуживания одного требования.
Как и в гл. 2, марковская цепь описывается вероятностями перехода; поэтому определим вероятности перехода за один шаг:
Pu&P[qn^^ i\qn =-*]• (5.25)
Поскольку эти переходы наблюдаются только в моменты уходов, ясно, что неравенство qtH1 < qn — 1 невозможно. С другой стороны, неравенство q,l+1 > q t— 1 возможно для всех значений числа поступлений о,г+1. Легко видеть, что матрица переходов Р = tp,f 1 (z, j 0, 1, 2, ...) имеет следующий вид: .
а() а, а3
а1 ^2 аз
«О С4, 0^2
О а0 ах
О 0 а0
(5.26)
где
а*ДР[г-„+1 = /?].
Например, j-й элемент первой строки матрицы представляет собой вероятность того, что предыдущее требование, уходя, оставило систему пустой, а за время обслуживания требования Сп+1 поступает ровно / новых требований (и все они остаются в системе после ухода требования С,1+1). Точно так же в других строках элемент при j > i — 1 представляет собой вероятность поступления точно j — i +1 требований за время обслуживания требования С„+1 в предположении, что требование С(, уходя, оставляет в системе точно i требований (из этих требований одно сразу поступает на обслуживание, что и дает член -|-1 в последнем расчете). Диаграмма вероятностей перехода для рассматриваемой марковской цепи показана на рис. 5.3, где изображены только переходы из состояния £,.
Вычислим теперь а*. Заметим прежде всего, что входящий процесс (пуассоновский поток с интенсивностью А, требований в секунду) не зависит от состояния СМО. Точно так же время хп обслуживания требования С. не зависит от п и имеет функцию распределения В (х). Следовательно, число поступлений за время обслуживания х,, зависит только от продолжительности хн
199
Рис. 5.3. Диаграмма вероятностей перехода для вложенной марковской цепи типа M/G/1
и не зависит от п. Поэтому можно отбросить индексы у величин vn и х,г и заменить их величинами v и х, так что можно будет записать: Р [хг1 < х] = Р [х < х] = В (х) и Р [vn = k] — Р [и = = k ] = ak. Перейдем к вычислению ak. По формуле полной вероятности
ее
гхк = Р {о = k] = j Р [v = k, х < х с х + dx]. о
Применяя условные вероятности, далее получим
ak — j Р [о = k | х = х] b (х) dx, (5,27)
о
где опять b (х) = dB (x)/dx — плотность распределения времени обслуживания. Так как входящий поток является пуассоновским, вероятность, стоящую под знаком интеграла, можно заменить выражением (2.131), что даст
ак = | e~Kxb(x)dx. (5.28)
о
Эта формула полностью определяет матрицу вероятностей перехода Р.
Заметим, что, поскольку > 0 для k > 0, все состояния достижимы друг для друга. Поэтому рассматриваемая марковская цепь неприводима (и непериодична). Введем обычное определение
р = /,х
и подчеркнем, что данная марковская цепь эргодична, если р < 1 (чтобы не усложнять рассмотрения, будем в дальнейшем предполагать это условие выполненным).
Стационарные вероятности могут быть получены из векторного уравнения р = рР, где вектор р = [р0> Рк Рк ••• 1, а его £-й элемент pk ( = dk) является предельной вероятностью того, что уходящее требование оставляет в системе k требований:
Pk = P[q = k], (5.29)
200
В следующем параграфе определяется среднее значение Е [q ], а в параграфе, приводимом после него, находится производящая функция для pk.
5.5. СРЕДНЯЯ ДЛИНА ОЧЕРЕДИ
В этом разделе выводится формула Полячека — Хинчина для среднего значения длины очереди в пределе. В частности, определяется
q = lim qn, (5.30)
П->оо
Этот предел, очевидно, существует в случае, когда рассматриваемая вложенная цепь эргодична.
Сначала выведем уравнения, связывающие случайные величины qn+1 и Рассмотрим два случая. Первый случай показан на рис. 5.4 (в обозначениях временной диаграммы) и имеет место тогда, когда уходящее требование Сп не оставляет систему пустой (т. е. qn > 0). Заметим, что предполагается дисциплина обслуживания в порядке поступления, хотя это предположение касается только времени ожидания, а не длины очереди или периода занятости. Из рис. 5.4 видно, что qn > 0, так как когда требование Сп уходит, требование Сп+1 уже находится в системе. На рисунке умышленно не показан момент поступления требования Сл+2, так как это неважно для рассматриваемой задачи. Теперь необходимо найти выражение для qn+1 — числа требований, остающихся после ухода требования Сп+1. Оно, очевидно, равно qn — 1 (так как требование Сп+1 уходит) плюс число требований, поступающих за время обслуживания Хя+1. Это последнее слагаемое, по определению, равно w,i+1 и на диаграмме показано светлой стрелкой. Таким образом, имеем
7л+1 = Яп — 1 ~Ь wn+i, Яп > 0- (5.31)
Рис. 5.4, Случай > О
201
Рассмотрим теперь второй случай, когда а.. = 0. т. е. уходящее требование оставляет систему пустой. Этот случай проиллюстрирован на рис. 5.5. Здесь qn, очевидно, равно нулю, так как Сп+1 еще не поступило к моменту ухода Сп. Следовательно, число требований qn+1, остающихся в момент ухода требований Сп+1, равно числу поступлений за время его обслуживания. Таким образом,
^+1 = ^+1, 7<г = °- (5-32)
Объединяя (5.31) и (5.32), получаем
( ?„ - 1 + un+i, 7n>0;
7,1+1 U+i, = (5 }
Здесь удобно ввести — сдвинутую ступенчатую дискретную функцию:
11, /г= 1, 2, . . .;
Мо, <5-34)
которая связана с дискретной ступенчатой функцией б*, определенной в (4.70), равенством Л-, = бй_г Применяя это определение к равенству (5.33), можно теперь записать единое определяющее соотношение для qn+1 в виде
qn+i = Qn — А?л + ^+ь (5.35)
Уравнение (5.35) является ключевым уравнением для исследования систем типа М/G/l. Остается получить из него среднее значение 1 величины qn. Как обычно, мы не будем касаться харак-
1 Здесь можно было бы перейти к следующему параграфу, чтобы получить предельное распределение (вернее, его производящую функцию) числа требований в системе и из него найти среднее зачение числа требований. Однако мы вычислим среднее значение числа требований в системе непосредственно из (5.35), следуя методу Кендалла [9]. Мы предпочитав,м проделать эту дополнительную работу, чтобы продемонстрировать читателю простоту вывода.
202
теристик системы, зависящих от времени (эта зависимость заключена в индексе п), а будем искать сразу распределение предельной величины qn, обозначая ее q. Предположим, что в пределе, при п -> оо, существует /-й момент qn:
lim£ [<?£] = Е [71 (5.36)
П->оо
(мы здесь фактически требуем эргодичности).
Будем считать, что в уравнении (5.35) операции усреднения и перехода к пределу перестановочны. Беря среднее значение от обеих частей равенства (5.35), получаем
£[7„+iJ = Е [<?„] - Е [Д,п] + Е [ил+1].
Переходя к пределу при п -> оо, имеем
£[?] = £ [7] —£ [A j +£[w],
что после упрощения дает
£[Л;] = £[Ь]. (5.37)
Какие сведения получаем мы из этого равенства? (Заметим, что поскольку v — число требований, поступающих за время одного обслуживания, которое не зависит от п, индекс у величины vn может быть опущен даже до перехода к пределу). По определению, Е [и] = среднее число требований, поступающих за время одного обслуживания.
Дадим интерпретацию левой части равенства (5.37). По определению можно непосредственно вычислить
£[А-] = £ АйР^==й] = АоР[^ = О] + А1Р^=1] + . . .
4 k^=0
Но, пользуясь равенством (5.34), можно переписать это в виде £[Д-] = 0{Р["? = 0]} + 1 {£[^>0]},
или
£[А~] = Р[?>0]. (5.38)
Так как мы имеем дело с однолинейной системой, равенство (5.38) может быть также записано в виде
Е [Л-] = Р [занятость системы ]. (5.39)
Пользуясь определением коэффициента нагрузки системы, далее находим
Р [занятость системы ] = р, (5.40)
203
как уже было получено 1 в равенстве (2.32)'. Таким образом, на основании равенств (5.37), (5.39) и (5.40) заключаем, что
Е (о) = р. (5.41)
Мы получили хорошо обоснованное заключение о том, что ожидаемое число поступающих требований за время одного обслуживания равно р (= Ах). Для устойчивости системы требуется, чтобы р < 1; таким образом, равенство (5.41) означает, что в среднем требования должны поступать медленнее, чем они могут быть обслужены.
Вернемся теперь к среднему значению величины q. Взяв математические ожидания от обеих частей уравнения (5.35) и переходя к пределу, мы не смогли получить эту величину, хотя и получили другие интересные результаты. Чтобы найти искомое среднее значение, возведем (5.35) сначала в квадрат, а уже затем определим математическое ожидание от обеих частей полученного равенства:
Qn+i — Яп Д- ^qn Д- Vn+i — 2qn А?п Д- 2</nvn+i 2 At/n^n+i- (5.42)
Из определения (5.34) следует, что (А?п)2 = и qn kqn = qn. Учитывая это и вычисляя математические ожидания в (5.42),, получаем
Е [^+]] = Е [q*] Д- Е [bqn] Д- Е [г£+1] -
- 2Е [g„] Д- 2Е [qnvn+1] - 2Е
В этом равенстве в двух последних слагаемых справа имеется произведение двух случайных величин, стоящее под знаком математического ожидания. Однако заметим, что vn+1 [число поступлений за время обслуживания (п Д 1)-го требования] не зависит от qn (числа требований остающихся после ухода требования Сп). Следовательно, в обоих слагаемых математическое ожидание произведения равно произведению математических ожиданий. Переходя к пределу с учетом (5.36), получаем
0 = £ [ А - ] Д £ [?] - 2£ М Д- 2£ [?] £ [Ь] - 2Е [ А - ] £ [и].
Используем теперь (5.37) и (5.41), чтобы получить следующий вспомогательный результат:
£М = р+ £Й1р)[--; (5-43)
здесь неизвестно только £ [о2].
1 Для любой системы типа М/G/1 мы видим, что Р [q = 0] = 1 — Р [<? > > 0] = 1 —р, и, следовательно, Р [новое требование не стоит в очереди] ==
= 1 —р. Это согласуется с полученным ранее результатом для G/G/1.
204
Вычисляя эту величину, попутно укажем метод нахождения моментов любого порядка. Для этого целесообразно ввести производящую функцию случайной величины v:
У (z) A Е [z“] A P [v = k] zk. (5.44)
*=o
Образуя функцию V (z) из (5.28) и (5.44), получим
У (z) = У j е~кхЬ (х) dx zk.
k=0 0
Здесь операции суммирования и интегрирования перестановочны. Меняя порядок операций, получаем
оо / оо £ \ °°
V (Z) = j У b (х) dx = J e~u ete b (x) dx =
0 \ft=O / 0
= Aj(x) A. (5.45)
о
Введем теперь преобразование Лапласа плотности времени обслуживания
В* (s) A J е~“ b (х) dx. и
Заметим, что равенство (5.45) дает выражение такого же вида с заменой комплексной переменной s на — Xz. Получается важный результат
V (г) = В* (X - Xz). (5.46)
Найденное равенство чрезвычайно важно. Оно описывает связь между производящей функцией распределения вероятностей случайной величины v и преобразованием Лапласа плотности распределения случайной величины х, когда это преобразование находится в критической точке к — кг. Вспомним, что и — это число требований, поступающих за промежуток времени х, и что поток поступающих требований является пуассоновским с интенсивностью к требований в секунду. Нам вскоре представится случай использовать равенство (5.46) для получения дальнейших результатов .
Из приложения II заметим, что различные производные производящей функции, вычисленные в точке z = 1, дают возможность вычислить соответствующие моменты рассматриваемой случайной величины. Точно так же для непрерывных случайных величин можно найти моменты, вычисляя в точке s = 0 соответствующие
205
производные преобразования Лапласа плотности рассматриваемой случайной величины. В частности, из приложения видно, что
в*w (0) Д dsk (-l)*E[7j; s=0 (5.47)
У(1) dV (г) v = dz I , = |Z » 1 (5.48)
1/(2)(1)Д^| v ’ = dz2 \z = = E [и2] - - E [у]. (5.49)
Чтобы упростить обозначения, мы не переходим к пределу после дифференцирования, а сразу подставляем предельные значения аргументов. Далее мы обозначаем чертой сверху математическое ожидание случайной величины, стоящей под чертой Е Тогда
равенства (5.47)—(5.49) примут вид
B*(ft,(0) = (—1)*7; (5.50)
Ч(1)(1)=Ъ; (5.51)
К(2)(1)=?-и. (5.52)
Конечно, при этом должно сохраняться свойство вероятностей
В*(0) = V(l)= 1. (5.53)
Применяя теперь равенство (5.46), постараемся из выражений (5.50)—(5.53) получить моменты случайной величины и. Дифференцируя (5.46), получаем
dV (г) = dB* (к —кг) dz dz ' \ >
Производная, стоящая справа, может быть вычислена в виде dB* (к — кг) _ ( dB* (к — кг)\ / d(k — kz) \ , dB* (y) ~
dz \ d(k-kz) ) \ dz ) k dy ’
где у — к — kz. (5.56)
Полагая в (5.54) z = 1, получим yo(l)==_z^M| .
' dy |z = 1
Но из (5.56) следует, что случай z = 1 соответствует случаю у = 0, поэтому
v(1> (1) == — ХВ’(1) (0).
(5.57)
1 Вспомним обозначения (2.19), а именно Е [х*] -* xk = bk, вместо более громоздкого (х)\ которое нужно было бы применить. Такую же вольность допустим к величинам v и q, т. е. (и)к = vk и (q)k = qk.
206
Наконец, из (5.50), (5.51) и (5.57) окончательно получается
v = Кх. (5.58)
Но Хх — это точно р, и мы снова получили тот же результат, что и в равенстве (5.41), а именно v = р (что, конечно, приятно). Можно снова продифференцировать (5.54), чтобы получить
(г) dz2 - "
Применяя полученную ранее первую производную функции В* (у), получим теперь вторую производную следующим образом:
(X — Хг) d Г _ . dB* (у) 1 _ dz" ~ dz |_ dy J
—
или
^Х2^#. (5.60)
агл at/2 х '
Подставляя в (5.59) г = 1 и используя (5.60), получаем И2)(1)=Х2В’(2) (0).
Сравнивая последний с полученными ранее результатами (5.50) и (5.52), находим
у2 — ц = Х2х2, (5.61)
что дает окончательно решение для v2. Таким образом, получена величина, необходимая для подстановки в (5.43). Если бы мы захотели (и имели бы для этого достаточно энергии), можно было бы и дальше, упражняясь в дифференцировании, выражать моменты величины v через моменты величины х. Однако не будем поддаваться этому искушению.
Возвращаясь к равенству (5.43), используем (5.61) и получим
Я Р + 2 (1 _р) •
(5.62)
Это и есть результат, к которому мы стремились! Он выражает среднюю длину очереди в момент ухода обслуженного требования через известные величины, а именно через коэффициент использования (р = Хх), % и х2 (второй момент распределения времени обслуживания). Перепишем этот результат, введя нормированную дисперсию времени обслуживания С'ь = <т|/(х)2:
Я = Р + Р2
(*+с1)
2 (1 —-р)
« (5.63)
207
Это выражение представляет собой очень известную формулу для среднего числа требований в системе типа M/G/1, которую обычно1 называют формулой Полячека — Хинчина для среднего значения. Подчеркнем, что среднее значение зависит только от первых двух моментов распределения времени обслуживания (х и х2). Кроме того, заметим, что q возрастает линейно с ростом дисперсии времени обслуживания (или, если угодно, линейно с квадратом его коэффициента вариации).
Формула Полячека — Хинчина позволяет найти среднее число требований в системе в моменты ухода обслуженного требования. Однако, как уже известно, она позволяет найти и среднее число требований в моменты их поступления и в любые другие моменты времени. В гл. 2 было введено обозначение N для среднего числа требований в системе. Это обозначение было использовано и в других главах, кроме данной и в дальнейшем мы к нему вернемся. Кроме того, было определено Nq — среднее число требований в очереди (не считая обслуживаемого требования). Найдем связь между N и Nq. По определению,
N ^fikPtq (5-64)
/г=0
Длина очереди на единицу меньше числа требований в системе, если система непуста, поэтому со
S (k- V) Р (q = k],
*=i
(Обратите внимание на нижний предел суммирования.) Отсюда получаем со со
Nq = kP [q = ft] - £ P [<? = ft]. fc=0 k=l
Но вторая сумма равна p, и мы приходим к равенству
ЛГд = дГ-р. (5.65)
Эта простая формула и устанавливает искомую связь.
В качестве примера применения формулы Полячека—Хинчина рассмотрим систему типа М/М/1. Так как для показательного распределения коэффициент вариации равен единице [см. (2.145)], то для такой системы
или
4 = ^, М/М/1. (5.66)
1 См. сноску на с. 198.
208
Равенство (5.66) описывает ожидаемое число требований, остающихся при уходе обслуженного требования. Сравним его с выражением (3.24) для среднего числа требований в системе М/М/1. Рассматриваемые формулы идентичны, и это лишний раз подтверждает приводившееся ранее утверждение о том, что метод вложен-
ных цепей Маркова в слу- Рис’ 5-6’ Пример системы М/Нг/1 чае СМО типа М/G/l дает
решение, пригодное для любого момента времени. В качестве второго примера рассмотрим регулярное обслуживание с постоянным временем обслуживания х. Как уже отмечалось, такие системы обозначаются через M/D/1. В этом случае, очевидно, С1 = 0, и получается
?"Р + ра 2'(Т-р). (5-67)
’-А~2-(тЬр "IM-
Таким образом система типа M/D/1 в среднем содержит на р2/2 (1 —р) требований меньше, чем система М/М/1; это иллюстрирует сделанное ранее утверждение о том, что q убывает с убыванием дисперсии времени обслуживания.
Наконец, в качестве третьего примера рассмотрим систему М/Н2/1, в которой
b (х) = -1- te~Kx + A (2Х) в"2Кх, х > 0.
(5.68)
Это значит, что прибор обслуживания состоит из двух параллельных этапов, как показано на рис. 5.6. Заметим также, что, как обычно, X — интенсивность поступления требований. Можно непосредственно вычислить х— 5/(8Х) и ol = 31/(64Z2), что дает Сь = 31/25. Следовательно,
„ „ , р2 (2,24) _ р , 0,12р2
<7 - Р -г 2 (1 - р7 - + 1 -р
Таким образом, наблюдается небольшое увеличение q при небольшом превышении Сь единицы по сравнению с системой М/М/1. Заметим, что в этом примере р = Хх = 5/8, поэтому q = ~ 1,79, в то время, как для системы М/М/1 при этом же значении р получаем q = 1,66. Мы привели здесь пример системы М/Н2/1,
209
так как он будет использован, наряду с примером М/М/1, при рассмотрении систем типа M/G/1.
Главным результатом этого параграфа является формула Полячека—Хинчина для среднего числа требований в системе [формула (5.63)]. Эта формула представляет собой частный случай результатов, которые будут получены в следующем параграфе. Однако непосредственный вывод этой формулы поучителен. Кроме того, при получении этого результата было установлено основное уравнение (5.35) для системы М/G/l. Мы получили также общую связь между V (г) и В* (s), которая выражается формулой (5.46). Из этой формулы, в частности, можно получить моменты распределения числа требований, поступающих за время обслуживания.
До сих пор не было получено ни одного результата, касающегося времени, проведенного требованием в системе. Сейчас это можно сделать. Вспомним результат Литтла: N = XT. Этот результат связывает среднее число требований в системе N с интенсивностью X поступления требований и средним временем Т пребывания требования в системе. Для системы М/G/l получено с равенство (5.63), которое позволяет найти ожидаемое число требований в системе в момент ухода обслуженного требования. Известно, что q описывает также среднее число требований в случайный момент времени, поэтому можно записать <? = АГ К этому среднему значению можно применить результат Литтла и получить среднее время, проведенное требованием в системе (очередь плюс обслуживание). Таким образом,
Решая относительно Т, получаем
Т = х + Pg((} • (5.69)
Последнее равенство легко объяснить. Общее среднее время, проведенное требованием в системе, состоит, очевидно, из среднего времени, проведенного в обслуживающем приборе, и среднего времени пребывания в очереди. Так как первое слагаемое правой части равенства (5.69) есть, очевидно, среднее время обслуживания, то второе слагаемое должно представлять собой среднее время ожидания (которое будем обозначать IT). Следовательно, среднее время пребывания в очереди
(V/ (1 “Ь Св)
~ 2(1 —р) ’
или
7°—, (5.70)
1 — Р
210
1
где Wo Л Хх2/2 — это среднее остаточное время обслуживания для требования (если такое есть), находящегося в обслуживающем приборе в момент поступления нового требования (последняя формула может быть получена из общей формулы для среднего остаточного времени). Теперь появляется особенно изящный нормирующий множитель. Рассмотрим среднее время Т пребывания требования в системе. Естественно сравнить эту величину с величиной х среднего времени обслуживания одного требования. Отношение Tlx, т. е. отношение времени, проведенного в системе, ко времени, приходящемуся в среднем на обслуживание, характеризует коэффициент неудобства системы, обусловленного наличием в ней других требований. Если пронормировать равенства (5.69) и (5.70), получатся формулы, в которых время выражено в единицах среднего времени обслуживания:
-^ = p0±£i) -(5.72)
х 2 (1 — р)
Каждое из этих двух равенств наряду с формулой (5.63), также называют формулой Полячека — Хинчина. Здесь видна линейная форма влияния статистических флюктуаций на задержку входящего потока (т. е. величина 1 + Сь представляет собой сумму квадратов коэффициентов вариации времени обслуживания и промежутков времени между поступающими требованиями). Из этих же формул видно, что зависимость задержки входящего потока от средней нагрузки системы р явно нелинейна.
Сравним среднее нормированное время ожидания для систем 1 М/М/1 и M/D/1. Коэффициенты Сь для указанных систем соответственно равны 1 и 0. Подставляя их в (5.72), получаем
М/М/1; (5.73)
х 1 — Р
M/D/1 • (5-74)
Заметим, что система с регулярным обслуживанием (M/D/1) характеризуется средним временем ожидания вдвое меньшим, чем система с показательным обслуживанием (М/М/1). Это закономерно, так как время пребывания в системе, так же, как и число требований в системе, пропорционально дисперсии времени обслуживания.
Переходим к определению распределения числа требований в системе.
1 Менее интересен сугубо частный пример системы М/Н2/1, для которой получается W/x = 1,12р/(1 — р).
211
5.6. РАСПРЕДЕЛЕНИЕ ЧИСЛА ТРЕБОВАНИЙ В СИСТЕМЕ
В предыдущих параграфах СМО типа М/G/l характеризовалась вложенной цепью Маркова, в результате чего было установлено основное равенство (5.35). Приведем его снова:
<7n+i = Яп - + уп+1- (5-75)
Взяв математические ожидания от обеих частей этого равенства, мы получили результат, касающийся коэффициента использования системы р [см. (5.41) ]. Возводя (5.75) в квадрат, а затем образуя математические ожидания, мы получили формулы Поля-чека—Хинчина, дающие ожидаемое число требований в системе [равенство (5.63) 1 и нормированное ожидаемое время пребывания требования в системе [равенство (5.71)].
Если бы мы задались целью получить второй момент для числа требований в системе, мы должны были бы сначала возвести (5.75) в куб, а затем взять математическое ожидание от обеих частей полученного равенства. При переходе к пределу при и оо член Е [<73] сократился бы, и осталось бы выражение для определения второго момента. Точно так же, возводя (5.75) в соответствующую степень, а затем взяв математические ожидания в полученном равенстве, можно найти моменты высших порядков величины <7*. В этом параграфе, однако, мы предпочтем найти сразу функцию распределения величины qn (в действительности мы рассматриваем предельную величину q) и получим результат, который дает не само распределение, а его производящую функцию. Хотя в принципе эти два понятия полностью эквивалентны, на практике часто при вычислении обратного преобразования возникают большие трудности. Но моменты распределения можно получить предельно просто, не вычисляя обратного преобразования, а пользуясь известными свойствами производящей функции и ее производных.
Приступим теперь к ^вычислению производящей функции вероятности числа требований, остающихся в системе в момент ухода обслуженного требования. Начнем с производящей функции случайной величины qn, которая записывается в виде
оо
Q„(z) AL p[qn^k\zk. (5.76)
k='j
На основании приложения II (и из определения математического ожидания) заключаем, что эта производящая функция (или z-преобразование) может быть также записана в виде
Qn (2) Д Е [гЧ (5.77)
* В частности, k-я степень приводит к выражению для £[ qk ~!], содержащему первые k моментов времени обслуживания.
212
Нас интересует производящая функция предельной случайной величины q:
Q (z) = lim Qn (z) = S P[q = k]z =E(z'/). (5.78)
П->со k~0
Как обычно, в определениях, связанных с преобразованиями, сумма, стоящая справа в (5.76), сходится к (5.77) только в некотором круге на плоскости z, который определяет максимальное значение [z| (наверняка годится |z| < 1).
Система М/G/l характеризуется равенством (5.75). Используем обе части этого равенства в качестве показателя степени:
"п + 1 <’n~^qn + Vn+l
Z = Z
Образуем теперь математическое ожидание от обеих частей полученного равенства •
Е [zM
Сравнивая с (5.77), мы узнаем в левой части последнего равенства Qn+i (z)- Правую часть этого равенства запишем в виде математического ожидания произведения:
Q,!+1(z)==£[z7,!_4z0,!+1]. (5.79)
Заметим, как и прежде, что случайная величина vn+1 (представляющая собой число требований, поступающих за время обслуживания п + 1-го требования) не зависит от случайной величины qn (числа требований, остающихся после ухода требования Сп). Поэтому и множители под знаком математического ожидания в правой части равенства (5.79) как функции от независимых случайных величин независимы. Следовательно, в этом выражении можно записать математическое ожидание произведения как произведение математических ожиданий сомножителей:
Q„+1(z) = £[z?^4]£[z0,,+1]. (5.80)
Второй множитель справа не зависит от индекса, поэтому заменим в нем vn+1 на v. Из (5.44) известно, что второе математическое ожидание в равенстве (5.80)
E[zVm]^E[z'v] = V(z).
Таким образом, получаем
Qn+1(z) = V(0£[/n-A’«]^ (5.81)
213
В последнем равенстве единственной сложной составляющей является математическое ожидание. Изучим этот член отдельно. Из определения получаем
СО « д
fe=0
Сложность суммы состоит в том, что показатель содержит величину ДА., которая в зависимости от k может принимать два разных значения. Чтобы учесть эту специфику, запишем сумму, выделяя отдельно первый член:
Е \гп ~ =- Р [qn = Oj z ~ °+ L Р [qn = k] г* (5.82)
*=1
Рассматривая сумму в этом последнем равенстве, можно заметить, что она имеет почти тот же вид, что и в равенстве (5.76). Разница состоит в том, что степени z на единицу меньше и отсутствует первое слагаемое. Оба эти различия можно устранить следующим образом:
оо со
Р[дп = 1г]гк-1 = -У£ Ptqn = k]zk -~Plqn = O]z('-
(5.83)
Применяя это равенство к (5.82) и заметив, что сумма в правой части (5.83) равна Qn (z), получаем
Е [zn~^\ = Р [qn == 0] + °1.....
Последнее выражение можно подставить в (5.81) и получить
Q„+1 (г) = V (z) (р [qn = 0] + .
Переходя теперь к пределу при п оо, получим выражение, в котором без труда узнаем (5.36). Таким образом, имеем
Q (г) = У (г) (Р [q = 0] + -^-(г) ~ . (5.84)
Подставив Р [q = 0] = 1 — р и решив (5.84) относительно Q (z), найдем
Q (Z) = V (г) (17^У^/Г— • <5-85)
Наконец, чтобы получить известное уравнение для производящей функции числа требований в системе, умножим числитель и знаменатель на (—z) и подставим полученный результат в (5.46):
.(5.86)
214
Будем считать это уравнение одной из форм уравнения Полячека — Хинчина для преобразования Е
Уравнение Полячека — Хинчина для преобразований позволяет легко найти моменты распределения числа требований в системе. Используя свойства преобразований, выраженные равенствами (5.50)—(5.52), получим Q (1) = 1. Если подставить z = 1 в (5.86), получим неопределенность 2, поэтому надо применить правило Лопиталя. Выполнив эту операцию, придем к необходимости вычисления lim dB* (X — \z)ldz при z-+\, которое было осуществлено в предыдущем параграфе и дало величину р. Эти вычисления подтверждают, что Q (1) = 1. В задаче 5.5 читателю предлагается показать, что Q(I)(1) = <7.
Обычно обращение уравнения Полячека — Хинчина для преобразования оказывается сложным, поэтому приходится довольствоваться вычислением моментов. Однако для системы М/М/1 обращение преобразования имеет простой вид. Поэтому в качестве примера рассмотрим эту систему. Имеем:
В* (s) = ij-, М/М/1. (5.87)
Очевидно, областью сходимости для этой формулы будет область Re (s) > —ц. Подставляя (5.87) в (5.86), получаем
п (?) = (___И_____\,
' \ л— Хг-|-р. / [р./(А. — Zz -|- р.)]— г
или, учитывая, что р = Х/ц, находим
q^)=4^7- <5-88)
Это равенство дает решение для производящей функции распределения числа требований в системе. Мы можем получить аналогичный результат для многих других функций В (х). В случае показательного распределения, разлагая в ряд, легко получить обратное преобразование. Непосредственно находим, что
Р [q = ft] = (1 - р) р\ M/M/1. (5.89)
Это известное решение для системы М/М/1. Если читатель вернется к равенству (3.23), то он увидит то же выражение для вероятности наличия ft требований в системе М/М/1. Однако, если равенство (3.23) было получено для произвольного момента времени, то (5.28) дает решение лишь для моментов ухода обслуженных требований. Тот факт, что решения совпадают, не является неожиданным по двум причинам: во-первых, потому, что, как уже 1 2
1 Эта формула была получена в 1932 г. А. Я. ХинчинымЗП 1 ]• Вскоре мы получим два других уравнения, каждое из которых следует из этого уравнения. Эти уравнения мы также будем называть уравнениями Полячека—Хинчина ДЛЯ преобразования. Они были исследованы Полячеком [14] в 1930 г. и Хинчи-ным в 1932 г. См. также сноску на с. 198.
2 Заметим, что знаменатель уравнения Полячека—Хинчина для преобразования должен всегда содержать множитель (1—z), так как В* (0) = 1.
215
говорилось, вложенные марковские точки дают решение, справедливое для любых точек оси времени, а, во-вторых, потому, что, как можно вспомнить, система М/М/1 образует непрерывную во времени цепь Маркова.
В качестве второго примера рассмотрим систему М/Н2/1, для которой плотность распределения времени обслуживания была задана равенством (5.68). По таблице приложения I можно найти В* (s):
В* (S) = ( — —-____I- (— — — _________7ХЯ-|-Ш____ gg
\ 4 / s -|- X ‘ \ 4 / s + 2А. 4 (s -I- X) (s 4- 2Х) ’
где область сходимости определяется в виде Re (s) > —X. Из уравнения Полячека — Хинчина для преобразования получаем
п м = (1-р)(1-2) [8 + 7 (1 -г)]
4 [ ’ 8-|-7(1— г) — 4г (2 — г) (3 — г)’
Преобразуя знаменатель и сокращая на (1 — г), имеем
п м _ (1 — р) [1 — (7/16) г]
[1 _ (2/5) г] [1 — (2/3)z] •
В результате разложения на простые дроби получаем
Q (г) = (1 — Р) (j _ (2/5)z + 1 — (2/3) г ) ‘
Обратное преобразование находим по таблице (см. строку 6 табл. 1.2):
^ = Р]7 = Й] = (1 -р) [±(2/5)ft +-j-(2/3)*] . (5.91)
Наконец, заметим, что величина р, которая была найдена ранее, равна б/8. Поэтому окончательное решение имеет вид
/4 =4- + /г = 0, 1,2, ... (5.92)
Нас не должно удивлять, что в качестве решения получилась сумма членов геометрических прогрессий.
Дальнейшие примеры будут приведены в задачах. На этом заканчивается обсуждение вопроса о том, сколько требований находится в системе, и начинается исследование задачи о том, как долго требование находится в системе.
5.7. РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ ОЖИДАНИЯ
Рассмотрим распределение времени, проведенного требованием в системе и в очереди. Эти величины довольно легко могут быть получены из предыдущих главных результатов, а именно из уравнения Полячека — Хинчина для преобразования и связанных с ним выражений, носящих, как уже говорилось, такое же название. Заметим, что порядок поступления требований на об-216
СЛуживание до сих пор не влиял на полученные результаты. Однако теперь нужно воспользоваться сделанным ранее допущением о дисциплине обслуживания в порядке поступления.
Чтобы пойти наиболее простым путем, исследуем еще раз происхождение следующего равенства:
V(z) = B*(X-Xz). (5.93)
Обслуживающий t т' 1 Си
прибор Очередь Время —*
।
ft
Vn
Рис. 5.7. К выводу равенства V В* (К—Хг)
Рис. 5.7 должен напомнить читателю построение, из которого получено это равенство. Вспомним, что V (г) — это производящая функция числа требований, поступивших за некоторый промежуток времени при входящем пуассоновском потоке с интенсивностью X требований в секунду. Рассматриваемый промежуток времени оказывается временем обслуживания требования Сп. Дгот промежуток имеет функцию распределения В (х) с преобразованием Лапласа В* (s). Связь между функциями V (г) и В* (s) определяется равенством (5.93). Здесь надо сделать одно важное замечание. Дело в том, что это соотношение справедливо между любыми случайными величинами, одну из которых можно отождествить с числом поступающих требований при пуассоновском потоке, а другую — с промежутком времени, в течение которого подсчитывается число поступивших требований. Очевидно, неважно, какой природы этот промежуток времени, важно лишь распределение его длины. В равенстве (5.93) — это время обслуживания.
Обратим теперь внимание на рис. 5.8, который показывает время, проведенное в системе требованием Сп. На этом рисунке прослеживается история требований Сп. Промежуток времени, обозначенный wn, соответствует времени от момента поступления требо
Рис. 5.8. К выводу равенства Q (г) — S* (X — Хг)
217
вания Сп в очередь до момента, когда требование покидает очередь и поступает на обслуживание. Это, очевидно, — время ожидания требования Сп. На этом же рисунке показано время ха обслуживания требования Сп. Таким образом, общее время sn, проведенное требованием Сп в системе,
+ хп. (5.94)
Ранее qn было определено как число требований, остающихся в системе в момент ухода требования Сп. При дисциплине обслуживания в порядке поступления очевидно, что все требования, находившиеся в системе при поступлении требования Сп, должны были покинуть систему до ухода этого требования. Поэтому требования, остающиеся в системе после ухода требования Сп, это в точности те требования, которые поступили в систему за время пребывания в ней требования Сп. Таким образом, обращаясь к рис. 5.8, можно отождествить число требований, поступающих за время s,t, с ранее определенной случайной величиной qn. Сравним теперь рис. 5.7 и 5.8. В обоих случаях имеется входящий пуассоновский поток с интенсивностью А, требований в секунду. На рис. 5.7 мы отмечаем число требований (уп), поступающих за время хп. На рис. 5.8 мы отмечаем число требований qn, поступающих за время sn.
Определим теперь функцию распределения общего времени, проведенного требованием Сп в системе, в виде
Sa(y) Д P[s„ < у]. (5.95)
Поскольку мы предполагали эргодичность, существует распределение при п -► со. Обозначим его через S (у), а предельную случайную величину через s (т. е. Sn (у) ->- S (у) и sn ->- s). Таки.м образом,
S(y) А Р[~$< у]. (5.96)
Определим, наконец, преобразование Лапласа плотности распределения времени пребывания в системе:
СО
S* (s) A J dS (у) = Е [е~“]. (5.97)
о
С этими данными вернемся к сравнению рис. 5.7 и 5.8. Очевидно, поскольку величина ип аналогична qn, то и функция V (г) аналогична Q (г), так как каждая из этих функций является производящей функцией для соответствующей целочисленной случайной величины. Точно так же, поскольку x,t аналогична sn, го В* (s) 218
должна быть аналогична S* ($). Поэтому по прямой аналогии на основании (5.93) имеем 1
Q(z) = S*(X-Xz). (5.98)
Так как явное выражение для Q (z) уже известно из формулы Полячека — Хинчина для преобразования, то, пользуясь равенством (5.98), можно записать явное выражение для S* (s) в виде
S* (X - Xz) = В* (X — Xz) £~_г)г (5.99)
Перепишем последнее уравнение, введя замену переменной s = = X — Az, что дает
Проведя такую замену в (5.99), получим
«•М-В’йттХ'тйНг)- -(S.ioo,
Равенство (5.100) и дает требуемое явное выражение преобразования Лапласа распределения полного времени пребывания требования в системе М/G/l. Оно выражается через известные величины, полученные из начальной постановки задачи (а именно, функцию распределения времени ожидания В (х) и параметры А и х). Это второе из трех уравнений, которые называют уравнениями Полячека — Хинчина для преобразования.
Из уравнения (5.100) легко вывести преобразование Лапласа времени ожидания, которое будем обозначать IF* (s). Обозначим функцию распределения времени ожидания (в очереди) для Сп через IFra (z/), т. е.
\Vn(y)AP[wn^y]. (5.101)
Определим далее предельные (при п ->• оо) величины Wn (у) -> -> W (у) и wtl -> w, так что
IV (z/) A P\w <у]. (5.102)
Соответствующее преобразование Лапласа имеет вид
IF* (s) A J е-ч/ dIF (у) = Е [е~™]. (5.103)
о
Из равенства (5.94) можно получить распределение величины w, выраженное через распределения s и х (мы опускаем здесь индексы, поскольку рассматриваем установившийся режим системы). Так как время обслуживания требования не зависит
1 Читатель, которого не убедили приведенные рассуждения, может непосредственно вывести (5.98) тем же путем, каким были выведены (5.28) и (5.46)
219
от его времени ожидания, время s пребывания требования в системе является суммой двух независимых случайных величин: w (времени ожидания) и х (времени обслуживания). Таким образом, равенство (5.94) имеет предельную форму:
s — w-4-х. (5.104)
Как показано в приложении II, при сложении независимых случайных величин преобразования Лапласа их плотности перемножаются. Следовательно, S* (s) = W* (s) В* (s). Из уравнения (5.100) получается, что
-(5.105)
Это и есть искомое выражение для преобразования Лапласа распределения времени ожидания. Мы получили третье уравнение Полячека — Хинчина для преобразований.
Перепишем уравнение Полячека — Хинчина для преобразования времени ожидания следующим образом:
л'.-C-wi- <51ое>
В члене, стоящем в скобках в знаменателе, нетрудно узнать преобразование Лапласа, связанное с плотностью остаточного времени обслуживания [см. равенство (5.11)]. Пользуясь специальными обозначениями для плотностей остаточного времени и их преобразований, определим
В* (s) A (5.107)
SX
и запишем
W* (S) = —LzaP—. (5.108)
1 — pS* (s)
Этот результат поистине удивителен, поскольку, как известно, задача анализа системы M/G/1 состояла в том, чтобы учесть ожидаемое время обслуживания для требования, находящегося в обслуживающем приборе. Из этого исследования заключаем, что остаточное время обслуживания для требования, находящегося в приборе, имеет плотность распределения b (х), преобразование Лапласа которой определяется равенством (5.107). В известном смысле есть поэтическая справедливость в появлении этого результата в самом конце решения. Следуя Бенешу [1], найдем обратное преобразование, выраженное через плотности остаточного времени обслуживания. Выражение (5.108) можно разложить в следующий степенной ряд:
Г* (s) = (1 - р) £ рЧВ* «• (5.Ю9)
k=-0
220
Из приложения I известно, что /г-й степени преобразования Лапласа соответствует й-кратная свертка обратного преобразования. Как в приложении I, будем применять для операции свертки символ 0, а для обозначения й-кратной свертки функции f (х) используем нижний индекс в скобках:
М)(х) A/(x)0/(^)QfW® - (5.110)
k—кратная свертка
Применив эти обозначения и взяв почленно обратное преобразование равенства (5.109), получим плотность распределения времени ожидания, которую обозначим w (у) Л dW (y)/dy. Она получается в виде
со ^ (//) = £ (1-p)pfe^) (//)• (5.111)
fe=0
Это наиболее интригующий результат! Он устанавливает, что плотность распределения времени ожидания получается в виде взвешенной суммы сверток плотности остаточного времени обслуживания. Интересно отметить, что весовые коэффициенты просто равны (1 — р) pfe, т. е. совпадают с вероятностями наличия k требований в системе типа М/М/1. Сколь ни заманчивой казалась попытка дать физическое объяснение этого простого результата и связать его с системой М/М/1, нам не удалось найти никакого удовлетворительного интуитивного объяснения этого эффектного выражения. Заметим, что в этом ряду вклад плотностей в распределение времени ожидания убывает в геометрической прогрессии. Таким образом, для р, не слишком близкого к единице, члены ряда имеют все меньшее и меньшее значение, и одним из практических применений этого равенства может быть подбор быстро сходящегося приближения плотности распределения времени ожидания.
До сих пор в этом параграфе были установлены два важных результата, а именно уравнения Полячека — Хинчина для преобразований плотностей распределения времени пребывания в системе и времени пребывания в очереди, которые выражаются соответственно равенствами (5.100) и (5.105). В предыдущем параграфе уже были найдены первые моменты этих двух случайных величин [см. равенства (5.69) и (5.70)]. Сейчас приведем рекуррентную формулу для моментов распределения времени ожидания. Обозначим, как обычно, k-й момент времени ожидания Е через wk. Такач [20] показал, что, если х‘+1 конечно, то конечны также w, w2, ..., и/; примем теперь упрощенные обозначения для моментов времени обслуживания, положив Ьг А х£. Рекуррентная формула Такача имеет вид
k
= (k.'\ w^, (5.412)
i — p Zu ' 1 ' 1 +1
221
где w° А 1. С помощью этой формулы можно выписать первую пару моментов распределения времени ожидания (при этом заметим, что первый момент согласуется с формулой Полячека—Хинчина):
ш5 = 2Й8 + (5.114)
Чтобы получить аналогичным образом моменты распределения времени пребывания в системе, т. е. Е [$* ], которые будем обозначать sk, необходимо просто воспользоваться равенством (5.104), из которого найдем
sk = (w-]-x)k. (5.115)
Применяя биномиальное распределение и учитывая независимость между временем ожидания и временем обслуживания данного требования, находим
*
= (5.116)
Таким образом, формула (5.112) для вычисления моментов распределения времени ожидания позволяет также вычислить моменты распределения времени пребывания в системе. В задаче 5.25 выводится соотношение между sk и моментами распределения числа требований в системе. Простейшим результатом здесь является формула Литтла, другие — представляют собой полезные обобщения.
В конце параграфа 3.2 мы обещали читателю вывести плотность распределения времени пребывания требования в системе типа М/М/1. Теперь мы в состоянии выполнить это обещание. В действительности мы найдем как распределение времени пребывания требования в системе, так и распределение времени ожидания требования для системы М/М/1. Используя равенство (5.87), для системы М/М/1 можно вычислить S* (s) из (5.100):
S*(s)=z-L Г--------s , .1 = Г(1угРЦ, М/М/1. (5.117)
v ’ (s-Ьн) L s — k 4- kp/(s 4- p) J s + p(l—p)’ v
Это дает уравнение для преобразования Лапласа плотности распределения времени пребывания требования в системе, которую мы, как обычно, обозначаем s (р) A dS (y)ldy. К счастью (как всегда в системе М/М/1), здесь можно легко найти обратное преобразование. Таким образом, сразу получаем, что
s(y) = р (1 — р) с'11 Ч-р) у, у 0, М/М/1. и (5.118)
222
Соответствующая функция распределения имеет вид
S(y) = 1 — е-и d-р)
у>0, М/М/1. (5.119)
Точно так же из равенства (5.105) можно получить
Рис. 5.9. Распределение времени ожидания для системы М/М/1
(S + |Х) (1 - р) s-Hp — X)
(5.120)
Прежде чем найти обратное преобразование, приведем правую часть равенства в надлежащий вид, выделив из рациональной функции целую часть:
Г*(8) = (1-Р) +
А (1 —р) s+p(l —Р) ’
(5.121)
Это выражение дает преобразование Лапласа плотности распределения времени ожидания, которую мы обозначим, как обычно, w (у) A dW (y)ldy. Из строки 2 табл. 1.4 приложения I находим, что обратным преобразованием для (1 — р) должна быть импульсная функция в начале координат. Таким образом, получаем
«’(F) = U -P)«oG/) + M1 — р) е~и <i-p)//, f/>0, M/M/1. (5.122)
Отсюда находим функцию распределения времени ожидания
№(//) = 1 — ре-и(1-₽) у, г/> 0, М/М/1. (5.123)
Это распределение показано на рис. 5.9.
Заметим, что вероятность отсутствия очереди равна 1 — р. Если сравнить эту вероятность с описываемой равенством (5.89) вероятностью того, что q = 0, станет ясно, что эти вероятности совпадают (7 = 0 тоже означает отсутствие очереди). Это же описывалось равенством (5.40). Вспомним далее, что нормированное среднее время ожидания было дано равенством (5.73). Тот же ответ, очевидно, получится, если вычислить это среднее значение по формуле (5.123). Интересно заметить, что для системы М/М/1 все важные распределения не имеют последействия. Это относится не только к задаваемым распределениям промежутков между требованиями и времени обслуживания, но и к распределениям числа требований в системе, времени пребывания требования в системе и
223
времени ожидания 1, которые описываются соответственно равенствами (5.89), (5.119) и (5.122).
Оказывается, плотность, описываемую равенством (5.118), можно найти более прямыми вычислениями, и мы здесь изложим этот метод, чтобы продемонстрировать его простоту. Исходной точкой служит полученный ранее результат в виде равенства (3.23) для вероятности наличия в системе k требований, а именно
At = (l —P)Pfe- (5.124)
Повторим еще раз, что это же выражение дается равенством (5.89) и что, как теперь известно, этот результат справедлив для всех моментов времени. Мы хотим построить преобразование Лапласа для плотности распределения времени пребывания требования в системе, рассматривая это преобразование в зависимости от числа требований, находящихся в системе, при условии поступления нового требования. Начнем с возможно более общего случая и рассмотрим сначала систему М/G/l. В частности, определим условное распределение
S (y\k) = Р [общее время пребывания требования в системе <z/| в момент его поступления имеется k требований].
Определим преобразование Лапласа этого условного распределения: со
S*(s|&) Д J e-^dS(y\k). (5.125)
о
Очевидно, что, если поступающее требование не застает в системе других требований, то время его пребывания в системе совпадает с временем обслуживания, т. е.
S* (s|0) = B* (s).
С другой стороны, если поступающее требование застает в системе точно одно требование, время его пребывания в системе складывается из времени окончания обслуживания предыдущего требования и его собственного времени обслуживания. Поскольку эти два промежутка времени независимы, преобразование Лапласа суммы равно произведению преобразований Лапласа слагаемых:
S* (s| 1) = В* (s)B* (s),
где В (s) — преобразование Лапласа плотности распределения остаточного времени обслуживания. Аналогично, если поступающее требование застает k требований в системе, то время его
1 Простая показательная форма для «хвоста» распределения времени ожидания (т. е. для вероятностей, связанных с долгим ожиданием) может быть получена также для системы М/G/l. Мы отложим рассмотрение этих асимптотических результатов до гл. 2 тома II, где установим тот же результат и для более общей системы G/G/1.
224
пребывания в системе складывается из его собственного времени обслуживания и времени обслуживания k требований, находящихся в системе. Эти k -f- 1 слагаемых независимы, и k из них имеют одну и ту же функцию распределения В (х). Поэтому получается произведение k-й степени В* (s) на В* (s):
S*(s|£) = [B*(s)]fcB*(s)- (5.126)
Это равенство справедливо для системы М/G/l. Для системы типа М/М/1, как известно, В* (s) p/(s ц) и такой же вид имеет распределение В* (отсутствие последействия). Таким образом, имеем
$*(«1*0 =(-7+ir)fe+I- (5-127)
Чтобы получить S* (s), остается только умножить преобразование S* (sf/г) на вероятность pk наличия в системе k требований в момент поступления рассматриваемого требования и просуммировать по k:
s*(s) = £ s*(sm.
fc=0
Подставляя в последнее выражение (5.127) и (5.124), получаем
s’ и=S ОДД*’1»1 - р) р‘ = ;+мГ-Р) 128>
k=0
Так как получившееся выражение совпадает с (5.117), то это немедленно приводит к (5.118).
Приведенный упрощенный метод вычисления распределения времени пребывания требования в системе демонстрирует следующий факт. При выводе равенства (5.128) мы рассматривали суммы случайных величин, имеющих одно и то же показательное распределение. Число слагаемых в сумме, в свою очередь, было геометрически распределенной случайной величиной. Было найдено, что такая сумма имеет показательное распределение [см. (5.118)]. Этот результат справедлив и в общем случае, и его кратко можно сформулировать так: геометрическая сумма одинаково распределенных показательных случайных величин имеет показательное распределение.
Для примера проведем теперь вычисление для системы М/Н2/1. Подставив выражение В* (s), задаваемое равенством (5.90), в уравнение Полячека—Хинчина для преобразования плотности времени ожидания, получим
W* (s\ =_____4s (I — р) (s -|— Л,) (s -|— 2Л)_
V ’ 4 (s — X) (s -р Л) (s 4- 2Х) + 8k3 + 7Z2s ’
8
Л. Клейнрок
225
Это выражение можно упростить, разлагая знаменатель па множители:
пр* М _ — Р) (s + Ц (s + 2^-)
* [« + (3/2) А] [« + (1/2) А] •
Деля числитель на знаменатель, выделим правильную дробь, которую затем разложим на простые дроби:
W* (s) = (1 - р) +
А (1 — р) [s + (5/4) к] [s + (3/2) A] [s + (1/2) А]
= (1 — р) [1 +
А/4 ЗХ/4 1
s + (3/2) A '« + (1/2)AJ
Находя обратные преобразования слагаемых (и вспомнив, что р = 5/8), получим плотность распределения времени ожидания:
^(y) = 4uo(^ + ^-e-<3/2)^ + _g.e-(i/2)4 ^0. (5129)
Этим завершается рассмотрение времени ожидания и времени пр ri л 1 р чюовал и я в слсгсмс . Введем теперь период занятости — важный случайный процесс в системах массового обслуживания.
5.8. ПЕРИОД ЗАНЯТОСТИ И ЕГО ПРОДОЛЖИТЕЛЬНОСТЬ
Займемся теперь исследованием системы массового обслуживания с другой точки зрения. Заметим, что любая СМО в процессе работы последовательно проходит периоды занятости, чередующиеся с периодами простоя. Цель этого параграфа состоит в нахождении распределений длительностей периода занятости и периода простоя для системы M/G/1.
Как уже было выяснено, наиболее существенными в управлении системой являются две последовательности случайных величин: последовательность моментов поступления требований и последовательность длительностей обслуживания. Как обычно:
Сп — п-е требование;
т„ — время поступления требования С„;
4 = т„ — т,,._1 — промежуток времени между Сп_х и С„; хп — время обслуживания требования Сп.
Вспомним теперь важный случайный процесс U (t), определенный равенством (2.3):
U (/) А незавершенная работа системы к моменту времени (А
А остаточное время, необходимое для освобождения системы от находящихся в ней в момент времени t требований.
Функция U (t) удачно названа незавершенной работой: она представляет собой тот промежуток времени, который требуется, чтобы полностью освободить систему, если после момента времени t в нее не поступают новые требования. Ее называют иногда виртуальным временем ожидания в момент t, так как при обслу-226
живании в порядке поступления она показывает, как долго должно было бы ожидать в очереди (возможное) требование, если бы оно поступило в момент времени t. Однако такая интерпретация времени ожидания годится только для одной дисциплины обслуживания, в то время как интерпретация на основе незавершенной работы пригодна для всех дисциплин. Характеристики этой функции чрезвычайно важны для понимания работы СМО, когда ее изучают с точки зрения периода занятости.
Обратимся к рис. 5.10, а, который показывает, каким образом период занятости чередуется с периодом простоя. Продолжительности периодов занятости обозначены Ylt Y%, Уз, ..., а продолжительности периодов простоя — h, /2, /з, ... . Требование Ci поступает в систему в момент времени п и приносит с собой работу (т. е. время, необходимое на его обслуживание) продолжительностью Xi. Это требование застает систему свободной, поэтому его поступление завершает предыдущий период простоя и начинает новый период занятости. Предполагалось, что до этого поступления система была пустой, поэтому незавершенная работа, очевидно, равнялась нулю.
В момент поступления требования Ci незавершенная работа, или задолженность системы, совершает скачок на величину х1У так как это время пройдет до освобождения системы, если не поступит новое требование. С момента Tj начинается обслуживание
Рис. 5.10. Работа СМО:
а незавершенная работа и период занятости; б — история требований
8* 227
требования С1г и незавершенная работа убывает со скоростью 1 с/с, т. е. функция U (/) убывает с наклоном, равным —1. Через ti секунд, в момент времени т2, поступает требование С2, что приводит к новому скачку незавершенной работы на величину х2, равную времени обслуживания требования С3. Затем функция снова убывает со скоростью 1 с/с, и так до тех пор, пока поступление требования С9 не приведет к новому скачку на величину х3 в точке т3. Функция U (t) продолжает убывать, пока работает обслуживающий прибор, т. е. пока в момент ту + Yi не завершается обслуживание всех поступивших за это время требований и система не остается пустой. В этот момент кончается период занятости и начинается новый период простоя. Период простоя кончается в момент времени т4, когда поступает требование Ci. Второй период занятости характеризуется обслуживанием только одного требования, а затем снова наступает период простоя. За третий период занятости обслуживаются два требования, и т. д.
Для наглядности на рис. 5.10, б дано обычное изображение той же последовательности требований в системе двух осей времени. На одной из этих осей отмечены моменты времени поступлений, а на другой — время обслуживания требований в том же масштабе, что и на рис. 5.10, а, в предположении обслуживания в порядке поступления.
Таким образом, функция U (/) представляет собой ломаную линию с вертикальными скачками в моменты поступления требования (величина каждого скачка равна соответствующему времени обслуживания), убывающую со скорость 1 с/с до тех пор, пока она положительна. Достигнув значения нуль, функция сохраняет его до поступления следующего требования. Этот случайный процесс есть процесс Маркова с непрерывными состояниями, подверженный скачкам. Такой процесс до сих пор не рассматривался.
Как следует из рис. 5.10, а, моменты уходов могут быть получены, если продолжить убывающие куски U (/) до пересечения с горизонтальной осью. В эти моменты обслуженные требования уходят, и начинается новое обслуживание. Снова подчеркнем, что это замечание относится только к дисциплине обслуживания в порядке поступления. Важно, однако, отметить, что сама функция U (/) не зависит от дисциплины обслуживания! Это утверждение будет справедливым, если прибор остается занятым, пока в системе имеются требования, и если ни одно требование не покидает прибор до полного завершения его обслуживания. Такая система называется «сохраняющей работу» (см. гл. 3, том II). Факт указанной независимости очевиден, если принять во внимание определение U (/).
Теперь о распределении периода простоя и периода занятости. Вспомним, что
А (0 = Р \tn < И = 1 - е-«, t >0; (5.130)
В(х) = Р[хп < х],
228
где А (/) и В (х) не зависят от п. Нас интересуют распределения: F (у) А Р [/п < у ] А распределение периода простоя; (5.131) б (у) А Р [Ytl с у] Л распределение периода занятости. (5.132)
Вычисление распределения периода простоя для системы M/G/1 тривиально. Заметим, что когда система выходит из периода занятости, начинается новый период простоя, который длится вплоть до поступления следующего требования. Так как процесс поступления требований не имеет последействия, то время до следующего требования распределено по закону (5.130), и поэтому
F (у) = 1 — e'Zi/, у > 0. (5.133)
Это все, что относится к периоду простоя в системе М/G/l.
Теперь о периоде занятости; это далеко не так просто. Рассмотрим рис. 5.11. На рис. 5.11, а опять рассматривается незавершенная работа’ U (I). Предположим, что система свободна вплоть до момента х1, когда требование С4 начинает период занятости продолжительностью Y. Время обслуживания этого требования равно х4. Очевидно, что это требование покинет систему в момент Tj + х4. За время его обслуживания в систему могут поступить другие требования, которые продлят период занятости. Как видно из рисунка, в рассматриваемом примере за время обслуживания требования С\ поступает три других требования (Са, Сз и С«). Воспользуемся прекрасной схемой, предложенной Такачем [19]. В частности, поменяем порядок обслуживания и введем дисциплину обслуживания в обратном порядке 1 (вспомним, что продолжительность периода занятости не зависит от порядка обслуживания). Мотивы перестановок требований скоро станут очевидны.
При уходе требования Ci на обслуживание поступает последнее требование, в нашем случае С4. Кроме того, так как все последующие требования этого периода занятости должны быть обслужены раньше любого требования (кроме С4), поступившего за время обслуживания С4 (в нашем примере С2 и С3), последние можно рассматривать (временно) как находящиеся вне системы. Тогда, поступая на обслуживание, требование Ci как бы начинает новый период занятости, который назовем подпериодом занятости2. Подпериод занятости, порожденный требованием С4, будет иметь продолжительность Х4, в точности такую же, как время обслуживания этого требования и всех новых требований, которые, поступая в систему, застают ее занятой (при этом требования С2 и С3 не учитываются). Таким образом, на рис. 5.11 показан подпериод занятости, порожденный требованием С4, в течение которого
1 Это лишь одна из многих перестановок, которая «работает». Обслуживание в обратном порядке удобно с методической точки зрения.
2 В оригинале термин sub—busy period, который некоторые специалисты переводят как «период подзанятости» или «период субзанятости». Оба эти названия представляются неудачными, хотя термин «подпериод занятости» может быть понят гораздо шире,-чем здесь имеется в виду. Прим. ред.
229
обслуживаются в указанном порядке требования С4, С6 и С5. В момент Ti + Xi + Xt этот подпериод занятости кончается, и продолжается тот же обратный порядок обслуживания, применяемый теперь к возвращенному в систему требованию Са. Очевидно, его можно рассматривать как порождающее свой собственный подпериод занятости продолжительностью Ха, за который в обратном порядке (а именно С3, С7, Са и С9) обслуживаются все его «потомки». Наконец, когда система снова оказывается пустой, возвращается требование Са и начинается его подпериод занятости (длиной Хя), которым завершается основной период занятости и в течение которого обслуживаются требования С2, С10 и, наконец, Си.
Рис. 5.11, а показывает, что очертание любого подпериода занятости повторяет в точности очертание главного периода 230
занятости над тем же промежутком времени и только сдвинуто на постоянную величину. Этот сдвиг равен суммарному времени обслуживания всех тех требований, которые поступили за время обслуживания требования Ci и которые не образуют собственные подпериоды занятости. Подробности истории каждого требования показаны на рис. 5.11, в, а общее число требований в системе в любой момент времени при рассматриваемой дисциплине обслуживания показано на рис. 5.11, б.
Таким образом, поскольку речь идет о СМО, постольку это — строго система обслуживания в обратном порядке, от начала до конца. Однако анализ упрощается, если сосредоточить внимание на подпериодах занятости и заметить, что каждый из них статистически подобен главному периоду занятости, порожденному требованием Ci. Это очевидно, поскольку все подпериоды занятости так же,- как и главный период занятости, начинаются с появления одного требования; при этом все требования независимы и имеют одно и то же распределение времени обслуживания. Каждый подпериод занятости продолжается до тех пор, пока система не сбрасывает нагрузку в том смысле, что незавершенная работа U (t) падает до нуля. Таким образом, случайные величины {Л*} независимы, одинаково распределены и имеют ту же функцию распределения, что и главный период занятости Y.
На рис. 5.11, в можно подробно проследить историю конкретного требования. Зачерненные области на этом рисунке показывают время пребывания требований в системе, обслуженных за время пребывания данного требования в системе. При каждом уходе требования обслуживающий прибор «поднимается» к верхнему контуру, чтобы принять то требование, которое на данный момент поступило последним. Иногда может случиться, что обслуживающий прибор «опускается» к требованию, расположенному прямо под ним, как в случае ухода требования Се. Обслуживающий прибор должен все время искать самое высокое требование и находиться при нем до его ухода. Но иногда обслуживающий прибор может «проваливаться вниз», чтобы захватить самое последнее требование (например, в момент ухода требования Са). Это такие моменты, когда начинаются новые подпериоды занятости; и только когда обслуживающий прибор опускается до уровня горизонтальной оси, кончается главный период занятости.
Теперь наша точка зрения ясна: продолжительность Y периода занятости является суммой 1 v случайных величин, первая из которых — время обслуживания требования Ci, а остальные описывают подпериоды занятости, каждый из которых распределен так же, как и сам период занятости. Случайная величина v равна числу поступающих требований за время обслуживания требования Ci. Отсюда получается важное соотношение
У = ...
(5.134)
231
Обозначим функцию распределения периода занятости
G(y)XP[Y <у]. (5.135)
Из предыдущего известно, что Xi имеет функцию распределения В(х), a Хк — функцию распределения G (у). Введем преобразование Лапласа для плотности распределения, связанного с Y-.
G* (s)Aje~^ dG(y). (5.136)
о
Снова напомним читателю, что эти преобразования можно выразить как математические ожидания:
G* (s)AE[e~sy|.
Воспользуемся теперь мощной техникой условных распределений, часто применяемой в теории вероятностей. Эта техника позволяет записать вероятность, связанную со сложным событием, через условные вероятности этого события при соответствующих условиях, для которых условная вероятность может быть вычислена. Если эти условия несовместимы и исчерпывающи, то безусловную вероятность находят по формуле полной вероятности как сумму произведений условных вероятностей на вероятности условий. В нашем случае будем рассматривать Y в зависимости от двух условий: длительности обслуживания требования Ci и числа поступающих за время его обслуживания новых требований. Затем вычислим следующие условные преобразования:
Е [e'sy | Х1 = х, v = k] = Е [е’ ; №+х+-^2)] =
= E[e-sVsX^i • • e-s*2].
Поскольку длительности подпериодов занятости взаимно независимы, последнее равенство можно переписать в виде
Е [e-sy | х± = х, v — k] = E [e"sx] Е [] • • Е [е^].
Так как х — заданная постоянная величина, то Е [e’sx] = e~sx, и, кроме того, так как подпериоды занятости распределены одинаково с соответствующим преобразованием G* (s), то
Е [e~sy | а = х, v = k] = е-« [G* (s)]A.
Поскольку v представляет собой число поступающих требований за время х, то эта величина распределена по закону Пуассона со средним значением "кх. Поэтому можно убрать условие, налагаемое на v, следующим образом:
Е [e~sy | = х] = У [e~sy | Х1 = х, v ~ k\ Р [v = k \ х± = х] =
= £ е~« [G* (s)p -—у— = ?~х [s+x~xa‘ <S>J.
а=о '< ‘
232
Точно так же можно убрать условие, налагаемое на х1; интегрируя с интегрирующей функцией В (х), чтобы, в конце концов, получить G* (s) в виде
со
G* (s) = j е * (s)] dB (x).
о
В последнем выражении легко узнать преобразование плотности распределения времени обслуживания, вычисленное для значения, стоящего в скобках в показателе степени, т. е.
G* (s) = В* [s + % - 2.G* (s)]. (5.137)
Этот главный результат дает преобразование распределения периода занятости для системы М/G/l (при любом порядке обслуживания), выраженное функциональным уравнением (которое обычно нельзя обратить). Указанное равенство было получено в результате рассмотрения подпериодов занятости внутри периода занятости, причем эти подпериоды имеют то же распределение, что и сам период занятости.
Позже в этой главе будет дано явное выражение для функции распределения периода занятости G (у), но, к сожалению, оно не получается в конечном виде [см. равенство (5.169) ]. Отметим однако, что можно численно решить уравнение (5.137) относительно G* (s) при любом данном значении s методом итераций, решая уравнение
G*+1(s) = B*[s-bZ-XG*(s)], (5.138)
в котором полагаем 0 < Go (s) < 1. При р = Zx < 1 предел этой итерационной схемы дает G* (s), и надо попытаться, если это нужно, найти обращение этих вычисленных значений.
Ввиду трудностей, связанных с обращением преобразования, найдем, что удастся, прямо из функционального уравнения; в частности, вычислим моменты периода занятости. Определим
&ДЕ[У*] (5.139)
как fe-й момент распределения периода занятости. Мы намерены получить несколько моментов, выраженных через моменты времени обслуживания xk. Как обычно, имеем
(-1)* G* <*> (0);
Xs = (—!)* В" (0).
(5.140)
Из уравнения (5.137) непосредственно получаем
= - С’ <» (0) = В* с1) (0) [s + X - XG* (s)] |s=0 =
= - B*(D (0) [1 - XG* (О (0)]
233
[заметим, что при s =-- 0 также s А, — z.G* (s) = 0], поэтому gi = x(l + Zgi).
Решая относительно gi и учитывая, что р Хх, получаем
-(5.141)
Сравнивая этот результат с равенством (3.26), находим, что средняя длина периода занятости для системы М/G/l равна среднему времени, проводимому требованием в системе М/М/1, и зависит только от к и х.
Вычислим теперь второй момент периода занятости. Исходя из (5.140) и (5.137), получим
g2 = G* (2) (S) « [В: (’) (s + I - XG- (s))] [ 1 — XG* (1) (s)] I s=0 =
= В* <2) (0) [ 1 - \G* <’) (О)]2 + В* (0) [—XG* <2) (0)],
и, таким образом,
g2=P(i + Xgi)2 +Дд2.
Решая относительно g2 и применяя полученный результат для gi, получаем
__?(1+W _ ^[1 +й/(1 — р)]2
1-Хх ~ Г^Р ’
и, окончательно,
g2 = (f_p)3 • (5.142)
Последний результат дает второй момент периода занятости. Интересно отметить куб в знаменателе, который не возникал при вычислении второго момента времени ожидания, где была только вторая степень [см. равенство (5.114)]. Теперь легко дисперсию периода занятости, обозначаемую через <т|,
2 2 х2 (х)2
— g2 — gl — (1 _р)3 ( 1 _ р)2 >
или
2 oj + Р (х)2 (1 —р)» ’
где о/ — дисперсия времени обслуживания.
Поступая, как и раньше, находим, что
х3 ЗА (х2)2 .
S3 — (1 — р)4 + (1 — Р)5 ’ х4 t 10Лх3х3 . 15?? (х2)3
£4 = (1 _ р)5 "Г {1_руГ -Т (1 _ р)7 -234
вычислить в виде
(5.143)
Заметим, что степень множителя (1 — р) в главном члене повышается на две единицы в каждом следующем моменте периода занятости, и это определяет характеристику при р—»1.
Рассмотрим несколько примеров обращения уравнения (5.137).
Начнем с системы М/М/1. Воспользовавшись равенством
В* (s) =
И
из уравнения (5.137) получаем
G * (s) =---------__________
1 ' s + X — М3* (s) + ц ’
или
X [G* (s)]2 — (р X -j- s) G* (s) 4- И = 0.
Решая это уравнение относительно G* (s) и ограничивая решение искомым (стабильным) случаем, для которого | G* (s)| < 1 при Re (s) > 0, получаем
G* (s) = и + Х- +s ~ [(Н +3. + s>2 - 1/2 . (5.144)
Чтобы получить плотность распределения периода занятости, это равенство нужно обратить, применяя таблицы преобразований. Соответственно получаем
g (у) A е <^) уц &у (М1/21, " (5-145)
ау У (р) '
где /1 — модифицированная функция Бесселя первого рода и первого порядка. Рассмотрим предел
lira G*(s)= lim [ е~!!' dG (у). (5.146)
0<s->0 0<s->0 q
Исследуя правую часть равенства, замечаем, что этот предел просто равен вероятности того, что период занятости конечен, а это эквивалентно тому, что период занятости кончается. Если р <4 1, период занятости, очевидно, кончается с вероятностью единица; однако равенство (5.146) дает информацию и при р > 1. Имеем Р [период занятости кончается] = G* (0).
Исследуя это соотношение для системы М/М/1, из (5.144) непосредственно получаем
G* (0) = И + 1(Р + >42 —4ц7]1/2 = ,
т. е. 2?'
G*(0) =±.
235
Таким образом
। 1, р < 1;
Р [период занятости в системе М/М/1 кончается] = > 1 .
I Т’
(5.147)
Плотность распределения периода занятости, описываемая равенством (5.145), оказывается гораздо более сложной, чем нам хотелось бы для простейшей из интересных систем массового обслуживания! Это показывает, что уравнение (5.137) для более сложных распределений времени обслуживания обычно необратимо.
В качестве второго примера посмотрим, что можно сделать с системой М/Н2/1. Используя выражение для В* ($) в нашем функциональном уравнении для периода занятости, получаем
________8^ + 77 [s + X-W* (s)]____
4[s + X_XG* (s) + X] [s + ?. — A.G* (s) + 2Х] ’
что сразу приводит к кубическому уравнению
4 [G* (s)]3 - 4 (2s + 5) [G* (s)]2 +
+ (4s2 ф 20s+ 31) G* (s) -(15+ 7s) = 0.
Последнее решить нелегко, и это затрудняет наши попытки обратить G* (s). Мы вернемся к функциональному уравнению для периода занятости, когда будем изучать СМО с приоритетами в гл. 3 тома II. Это приведет нас к понятию циклов задержки, которое является прямым обобщением проведенного анализа периода занятости и в значительной степени упрощает рассмотрение СМО с приоритетами.
5.9. ЧИСЛО ТРЕБОВАНИЙ, ОБСЛУЖЕННЫХ
ЗА ПЕРИОД ЗАНЯТОСТИ
В этом параграфе обсуждается распределение числа требований, обслуженных за период занятости. Рассуждения подобны проведенным в предыдущем параграфе как по характеру, так и по результатам, которые будут получены.
Пусть Nbp — число требований, обслуженных за период занятости. Нас интересует распределение вероятностей этой величины, которое обозначим через fn:
fn = Р [Nbp —п]. (5.148)
Лучшее, что можно сделать, — это получить функциональное уравнение для производящей функции этой последовательности, определяемой в виде
оо
Р (г) A Е [zNbP] £ О" (5.149)
/1=1
236
Нулевой член в этой сумме опущен, так как за период занятости хотя бы одно требование должно быть обслужено. Вспомним, что случайная величина v представляет собой число поступающих требований за период обслуживания, и ее производящая функция V (г) удовлетворяет выведенному ранее уравнению, а именно
V(z) = B*(X-Xz). (5.150)
Поступая так же, как при исследовании периода занятости, рассмотрим условие v = k, т. е. предположим, что за время обслуживания Сг поступает k требований. Кроме того, как известно, каждое из этих требований порождает подпериод занятости, и число требований, обслуженных за каждый из этих подпериодов, характеризуется распределением вероятностей fn. Пусть случайная величина Л4, означает число требований, обслуженных за i-й подпериод занятости. Можно сразу записать
Е [zNbP v = 6] = £[г1+Л,1+А,2+--+ЛЧ
и, так как М, независимы и одинаково распределены, то
Е [zNpb Ь;=£] = z FlE[z4 i=i
Но каждая величина Л4. распределена в точности, как Nbp, и поэтому
Е [z^p у = k] =-- z [F (z)]fc.
Исключая условие для числа поступлений, получаем
F (2) = 2 Е [zNbp\v = k] Р [v = k] = z Yj P\v = k][F(z)]*. k=0 k=0
На основании равенства (5.44) в этой сумме узнаем функцию V (z) (т. е. производящую функцию, связанную с величиной v), в которой аргументом является F (z). Таким образом,
F (z) = zV[F(z)|. (5.151)
Но в силу равенства (5.150) можно окончательно записать
F (z) = zB* [X - KF (z)]. и (5.152)
Это функциональное уравнение для производящей функции числа требований, обслуженных за период занятости, напоминает полученное ранее уравнение (5.137).
Из этого фундаментального уравнения можно легко получить моменты числа требований, обслуженных за период занятости. Обозначим k-й момент числа требований, обслуженных за период занятости, hk. Тогда, как известно,
/ц = F(D (1) = В* <’> (0) I -XFO (1)] 4- В' (0).
237
Следовательно,
/ix = Zx/ix + 1,
что немедленно дает
1_
1 —р
h
(5.153)
Далее известно, что Д2' (1) = h2 —h±. Выполняя обычным путем эти вычисления, получим второй момент и дисперсию числа требований, обслуженных за период занятости:
2Р (1 — Р) + Д*2 । 1
(1 — Р)3 Г 1 — Р ’
2 р ( 1 — р) + Х2Х2
0/1 = d '
(5.154)
(5.155)
В качестве примера рассмотрим опять простейшую систему М/М/1 и получим F (z) из (5.152):
И
F (г) = z ——,-р . . , v ' Р + Л — ЛГ (г)
ЛЯИ-(н + Х)Т(г) + иг-О.
F<Z>-TFL[1 -('--Лтй'Д <5156)
К счастью, оказывается, что равенство (5.156) обратимо и можно получить в явном виде вероятность того, что за период занятости будет обслужено п требований:
/« = 4(2”712)рп’1(1+р)1'2п- -(5.157)
В качестве второго примера рассмотрим систему M/D/1. Для этой системы имеем b (х) = «0 (х — х) и из третьей строки табл. 1.4 непосредственно находим, что
В* (s) = e~s*.
Подставляя это в функциональное уравнение, получаем
F (г) = ге~рерг <2), (5.158)
где, как обычно, р = Кх. Удобно произвести замену и = гре~р и Н (и) = pF (г), что позволит переписать уравнение (5.158) в виде и = Н (и) е.н
Это уравнение можно решить [16], после чего первоначальная функция получается в виде
°о J
/?(2) = Ё±тг-е’лРг,!-
П=1
238
Из этого степенного ряда получаем искомые вероятности числа требований, обслуженных за период занятости в системе M/D/1:
«(5.159)
Для случая постоянного времени обслуживания известно, что, если за период занятости обслуживается п требований, то его продолжительность должна быть пх, поэтому можно сразу получить решение для распределения продолжительности периода занятости в системе M/D/1 в виде
п_ t
G S (ЯРя! е~ПР ’ -(5.160)
п=1
где [у/х] — целая часть числа ylx.
5.10. ОТ ПЕРИОДА ЗАНЯТОСТИ КО ВРЕМЕНИ ОЖИДАНИЯ
Во вступительных параграфах этой главы говорилось, что время ожидания можно определить на основании анализа периода занятости. Сейчас мы в состоянии это сделать. Как читатель может догадаться (и как будет показано в гл. 3 тома II), в то время как продолжительность периода занятости не зависит от дисциплины обслуживания, время ожидания зависит в очень большой степени от порядка обслуживания. Поэтому в этом параграфе будут рассмотрены исключительно СМО типа M/G/1 с обслуживанием в порядке поступления. Поскольку мы ограничиваемся такой дисциплиной, изменение порядка, примененное в параграфе 5.8, больше не допускается. Вместо этого теперь нужно разложить период занятости на последовательность зависимых промежутков времени следующим образом. Рассмотрим рис. 5.12,
?.зэ
на котором показан один период занятости для системы с обслуживанием в порядке поступления [в виде функции незавершенной работы U (/)]. Из рисунка видно, что с поступлением требования Сг в момент Tj начинается период занятости. Первый промежуток, который мы рассматриваем, — время обслуживания хг этого требования, которое обозначим теперь Хо. За это время поступают другие требования (в рассматриваемом случае С2 и С3). Все требования, поступившие за время Хо, обслуживаются за следующий промежуток времени, равный сумме времени обслуживания этих требований (в данном случае С2 и С3) и обозначаемый ХР По истечении %! образуется новый промежуток времени продолжительностью Х2, за который обслуживаются все требования, поступившие за время Хг, и т. д. Таким образом, Xt — время, необходимое для обслуживания всех требований, поступивших за предыдущий промежуток времени X,_i. Если число требований, поступивших за промежуток времени X,- принять равным и,-, то столько же требований будет обслужено за время Xi+1. Пусть п0 — число требований, поступивших за промежуток Хо (время обслуживания первого требования).
Таким образом, очевидно, что Y (продолжительность полного периода занятости) можно представить в виде суммы
ос r=Sx(, >=0
где допускается возможность бесконечного числа промежутков времени. Ясно, что для тех промежутков, которые лежат вне периода занятости, предполагается X, = 0. При р < 1, как известно, с вероятностью единица существует конечное число 10, для которого X,- (и длительности всех последующих промежутков) равны нулю. Далее известно, что Х/+1 является суммой щ промежутков времени обслуживания [каждый из которых имеет функцию распределения В (х)].
Определим теперь функцию'распределения величины X, :
X,- (у) А Р [X,. « у]
и соответствующее преобразование Лапласа плотности распределения
с©
X* (s) A J e~s"dX; (//) ^=£[e~sXq. О
Мы хотим вывести рекуррентное соотношение между X* (s). Этот вывод во многом подобен проделанному в параграфе 5.8 и приведшему к уравнению (5.137). Рассмотрим в качестве условий длину промежутка времени X,_i и число n,_i поступивших за этот промежуток требований и введем условное математическое ожидание
Е [e~sX‘ | Xf_! = у, = [В* (s)f.
240
L Последнее равенство следует из того, что при сложении независи-I мых случайных величин соответствующие преобразования Лапласа I перемножаются. Здесь имеются п независимых промежутков вре-| мени обслуживания с одной и той же функцией распределения.
Исключим сначала условие, наложенное на п:
' 00
4 Е [e~sX‘ Хг_г = у] = 2-*^1е-Хг/[В*(5)]'г,
- и=9
а затем условие, наложенное на у:
• Е [e~sA/] = J 2 "VF е~?'" <s)1"
< г/=0 п=0
• Очевидно, выражение слева представляет собой X* (s). В результате вычисления суммы, стоящей справа, приходим к равенству
X*(s) = j W^dX
у==о
В этом интеграле нетрудно узнать преобразование Лапласа плотности распределения Х,_1( а именно
X* (s) = X*_i [X - /.В* (s)]. (5.161)
Это был первый шаг.
Проведем теперь расчеты при условии поступления нового («меченого») требования в течение периода занятости и, в частности, во время Его промежутка периода занятости (продолжительностью Xi). Из материала параграфа 4.1 известно, что поступающие требования пуассоновского потока застают систему в данном состоянии с вероятностью, равной стационарной вероятности того, что система находится в этом состоянии. Теперь мы знаем, что если система попадает в период занятости, то часть времени, приходящаяся на промежуток длительности Xt, описывается отношением Е [X, ]/Е [У ] (это можно строго обосновать с помощью теории восстановления). Рассмотрим требование, поступающее в промежуток времени продолжительности X,. Пусть его время ожидания равно w. Очевидно, что это время равно сумме остаточного времени z-ro промежутка и продолжительностей обслуживания всех требований, поступивших в систему на протяжении того Же интервала, но раньше рассматриваемого требования. Нужно вычислить Е [e-Sffi,|z], т. е. преобразование Лапласа плотности Распределения времени ожидания для требования, поступившего в i-м промежутке времени. Опять проведем расчеты, на этот раз При трех условиях: X,, У,- (определяющее остаточное время этого Промежутка) и X, (определяющее число требований, поступающих Эй z-й промежуток времени, но раньше рассматриваемого требова-241
пия, т. е. за время X,- — У,). Используя, как и прежде, свойство свертки, можно записать
Е [е-™ | I, X,- = у, У,- = г/', Хг- = п\ -= е~^' [В* (s)p.
Предположив, что за время у — у' поступает п требований, мы снимем условие Nt следующим образом:
Е [е-™ | i, XL=y, У(-
у'] — ------...j у е~х <~и-у’>
п=0
:< [B*(s)]'!(»). (5.162)
Уже говорилось, что У, — остаточное время промежутка X,. Равенство (5.9) дает совместное распределение остаточного времени У и полного промежутка X. В этом равенстве У и X играют ту же роль, что и У, и Xt в рассматриваемой задаче. Поэтому, заменяя f (х) dx на dXi (г/) в равенстве (5.9) и замечая, что здесь х' и у' нужно заменить х и у, находим, что совместное распределение для Xt и У,- задается величиной dXt (y}dy'!E [XJ при О < у' с у < оо. С помощью этого совместного распределения можно снять условия X,- и У, в равенстве (5.162) и получить
ео у
£[e-s®|i]= j j (у) dy'/Е {Х^
у=о у'=0
7 [е-М/_е-[?.-?.В* (s)]y]
J [—s + X — А.В* (s)] Е [Xf] dXi у=о
В последнем интеграле нетрудно узнать преобразование Лапласа; поэтому
X*(s) —Х*(Х —XB*(s)) р re-s® I л = . 1 -L_-----IX .
Iе I Н [-s + Л, — ZB* (s)] Е [X,-]
Но теперь равенство (5.161) позволяет переписать второе из этих преобразований и получить
X* , (s) - х*. (s) Р re-sw /1 —______1+1______1 v ___
LC I 4 — [s _ X + XB* (s)] E [XJ
Снимем теперь условие поступления требования в i-й промежуток времени. Умножая последнее выражение на ранее полученную вероятность поступления требования в момент, принадлежащий t-му промежутку времени, и суммируя по I, получаем
Е [е-™ | поступление требования в период занятости] =
SF fe-sS I л Е №1________________!_________ х
п 1 14 Е [К] — [s — Л + А.В* (s)]E[K] л
г=0
ОО
X [Xi+1 (s) — x‘(s)].
,:=о
242
Последняя сумма равна 1 — Хо (s), так как X* (s) = 1 для про-межутк°в, лежащих вне периода занятости (вспомним, что = О идя i > 1’о)- Итак, поскольку Хо = хг есть время обслуживания, <Ю Хо (s) = В* (s), и мы приходим к соотношению
Е [e~saJ | поступление требования в период занятости] =
1 — В* (s)
- [s- Л + ZB* (S)] Е [У] ’
Как известно, вероятность поступления требования в период занятости р = Хх (и в этом случае требование наверняка должно ждать). Кроме того, можно вычислить среднее время занятости Е [К] либо из предыдущих расчетов [см. (5.141)], либо из элементарных соображений1, что дает Е [У] = х/(1 —р). Таким образом, снимая условие поступления требования в период занятости, получаем
£[е-^]-(1 -p)E[e-s®| поступление требования в период простоя] -1-
-|- р£ [e~s® | поступление требования в период занятости] =
= о - Р)+р!'-ГЛ’и1, п - ° Л‘-Дв’-й- <5-163> [S — X + ZB* (s)] X S A-fAD
Но это в точности уравнение Полячека—Хинчина для преобразования времени ожидания, а именно W* (s) Л Е [e~s®], полученное в (5.105).
Таким образом мы показали, как перейти от анализа периода занятости к вычислению времени ожидания. Этот метод описан в работе [2]. Нам еще представится случай вернуться к нему в гл. 3 тома II.
5.11. КОМБИНАТОРНЫЕ МЕТОДЫ
Во вступительных замечаниях к этой главе говорилось, что к изучению системы М/G/l применимы методы случайного блуждания и комбинаторные методы. Воспользуемся случаем, чтобы указать некоторые аспекты этих методов. На рис. 5.13 повторяется Функция U (/), изображенная на рис. 5.10, а, и, кроме того, построена функция R (t), описывающая случайное блуждание. Функция R (t) такая же, как и функция U (t), с той лишь разницей, что она не поглощается в нуле, а убывает с той же скоростью 1 с/с
При вычислении Е |У | можно воспользоваться следующими простыми отражениями. В течение длинного промежутка времени (скажем, /) обслуживании прибор занят долю времени р. Каждый период простоя в системе M/G/1 Пш?еДНеМ имеет Длительность 1/Х, поэтому можно ожидать в среднем (1 — р) ериодов простоя. Таким же приблизительно будет число периодов занятости. спрЭТОМУ’ так как среднее время, охватывающее периоды занятости, равно pt, £ Дняя продолжительность каждого периода занятости должна быть pttU X
(1 р)'1 = х/(1 —р), При t -♦ оо этот расчет становится точным.
243
под горизонтальной осью. Конечно, она тоже имеет вертикальные скачки в моменты поступления требований. Рис. 5.13 приведен для того, чтобы определить так называемые лестничные индексы.-. k-ы. (нижним) лестничным индексом называется момент времени, когда случайное блуждание R (t) поднимается из k-ro нового минимума. Высота этого минимума называется лестничной величиной. На рис. 5.13 первые три лестничных индекса отмечены светлыми точками.
Теория флуктуаций занимается изучением распределения таких лестничных индексов, чему уделено много внимания в книгах [5, 15], в которых рассмотрены приложения этой теории к процессам массового обслуживания. Здесь только заметим, что каждый лестничный индекс определяет момент поступления требования, начинающего новый период занятости, и именно этим интересен для теории массового обслуживания. Кроме того, как это видно из рис. 5.13, когда R (£) падает до предыдущей лестничной величины, период занятости кончается. Таким образом, период занятости расположен между лестничным индексом и первым после него моментом, когда R (t) падает до соответствующей лестничной величины. При этом функции R (i) и U (t) имеют одинаковый график, но первый сдвинут по сравнению со вторым на величину, в точности равную общему времени простоя с момента окончания первого периода занятости. Очевидно, оперируя лестничными индексами, можно быстро вникнуть в методы комбинаторной теории.
В том же духе Такач успешно применил комбинаторную теорию к исследованию периода занятости. Он глубоко изучает этот вопрос в своей книге [21 ], посвященной комбинаторным методам и их применению в теории массового обслуживания, и дает в этой книге обобщение классической теоремы о голосовании. Классическая теорема о голосовании посвящена подсчету голосов при двусторон-244
:. ЙИХ выборах с кандидатами А и В. Если предположить, что А f- набирает а голосов, а В набирает b голосов и что а mb, где 1 т — неотрицательное целое число, и если Р означает вероятность 'того, что в процессе подсчета голосов все время сохраняется 'неравенство а (/) mb (i), причем все последовательности подачи голосов равновероятны, то классическая теорема о голосовании утверждает, что
(5.164)
Эта теорема впервые появилась в 1887 г. (об ее истории см. работу [21]). Такач обобщил эту теорему и перефразировал ее, заменив голосование извлечением карт из урны следующим образом. Рассмотрим урну с п картами, где карты отмечены неотрицатель-п
ными целыми числами kly k2, ..., krl и где У' k, = k с п (т. е. i=i
i-я карта отмечена числом k,). Предположим, что все п карт извлекаются без возвращения из урны. Пусть vr (г = 1, 2, ..., п) — номер карты, вынутой при r-м извлечении, и пусть
Nr = v2 + . . . + vr, г = 1, 2, . . ., п.
Таким образом, Nr является суммой номеров всех карт, вынутых при г извлечениях. Обобщение Такача классической теоремы о голосовании утверждает, что
Р [N, <'г для всех г = 1, 2, . . ., п] = . (5.165)
Доказательство этой теоремы не слишком сложно, но мы его здесь приводить не будем. Обратите внимание на простоту теоремы и, в частности, на то, что вероятность не зависит от выбора чисел k,, а зависит только от их суммы k.
Мы можем отождествить vr с числом требований, поступающих в систему за время обслуживания r-го требования в период занятости для системы М/G/l. Тогда (Уг 1) — общее число поступлений за период занятости до окончания обслуживания г-го требования. Таким образом, происходит состязание между Nr ф- 1 и г: если г = Nr -ф 1, то период занятости должен закончиться, так как в этот момент обслужено столько требований, сколько поступило (включая требование, открывшее период занятости). Если теперь обозначить через Nb:> число требований, обслуженных за период занятости, то можно применить (5.165) и получить следующий результат [211:
= = = 1]. (5.166)
Легко вычислить вероятность в правой части, так как входящий и°ток является пуассоновским. Как и прежде, находим вероят-°сть того, что за данный период занятости поступит п требований, 245
умножаем на плотность распределения времени обслуживания п требований и интегрируем по времени. Таким образом,
со 1
Р[Кп = п- 1] = (У)^, (5.167)
о
где Ь(П> (у)— л-кратная свертка b (у) [(см. равенство (5.110)], представляющая собой плотность распределения суммы п независимых случайных величин, каждая из которых имеет плотность распределения b (у). В результате приходим к явному выражению распределения вероятностей числа требований, обслуженных за период занятости:
со
Р [Nbp = п] = J е^Ь(п) (у) dy. - (5.168) и
Мы можем пойти дальше и вычислить функцию распределения периода занятости G (у), интегрируя (5.168) только до у (а не дооо) и суммируя затем по всем п:
У 0°
G (//)== j 2 р п IY = Л'] W dx< 0 /1=1
или у °с _ j
G (*/)=--{ ^e-^^p-&(n)(x)dx. .(5.169)
0 П=1
Таким образом, (5.169) дает явное выражение распределения периода занятости через известные величины. Это выражение можно теперь подставить в уравнение (5.137). Таким образом, получено обещанное ранее выражение, хотя и в виде бесконечной суммы. Тем не менее оно дает возможность численно определить приближенное распределение периода занятости для любой заданной ситуации. Точно так же равенство (5.168) дает явное выражение для числа требований, обслуженных за период занятости.
Читатель возможно заметил, что наше изучение периода занятости в действительности является изучением неустановившихся явлений, и это одна из причин того, что развитие теории натолкнулось на трудности и затормозилось. В следующем параграфе рассмотрим немного дальше некоторые аспекты неустановившихся решений для системы M/G1.
5.12. ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТАКАЧА
В этом параграфе рассмотрим подробнее незавершенную работу и выведем уравнение Колмогорова, описывающее ее характеристики, зависящие от времени. Изучение процесса позволит 246
обнаружить тот факт, что незавершенная работа U (Z) представляет собой непрерывный во времени марковский процесс с непрерывными состояниями и разрывным изменением состояний. Этот процесс — марковский, так как вся прошедшая история его движения суммируется в его текущем значении постольку, поскольку это касается будущего. Это значит, что вертикальные разрывы возникают в моменты поступления требований, которые для системы M/G.'l образуют пуассоновский процесс (поэтому неважно, сколько времени прошло с момента поступления последнего требования), и текущее значение U (t) показывает точно, сколько работы остается в системе в каждый момент времени.
Мы хотим получить функцию распределения для U (Z), если задано ее начальное значение в момент t = 0. Соответственно определим
F (w, t\ w0) Д Р [t/ (t) < w | U (0) = щ0]. (5.170)
Это обозначение несколько громоздко, поэтому опустим начальное значение и применим сокращенное обозначение F (w, t) Л F (w, t\ w0), подразумевая начальное значение щ)0. Необходимо найти связь функции F (w, t -ф AZ) с ее возможным значением в момент t. Заметим, что такое состояние может возникнуть, с одной стороны, если за время (Z, t -ф AZ) не поступало требований [это событие имеет вероятность 1 — /.AZ + о (AZ) 1 и незавершенная работа в момент t была не больше w -ф AZ, а с другой стороны, если за это время появилось одно требование [вероятность этого равна XAZ ф- о (AZ) 1, и работа, оставшаяся в момент Z, плюс работа, внесенная новым требованием, не превышает w. Это замечание приводит к следующему уравнению:
F (w, t + AZ) = (1 - X AZ) F (w -ф AZ, Z) -ф
+ XAZ J В (w - л) dF F dx -ф о (AZ). (5.171)
x~ 0
CrP { X t'}
Очевидно, что ———- dx Д dxF (x, Z) есть вероятность того, что в момент Z выполняется неравенство х < U (Z) < х -ф dx. Применяя формулу Тейлора к первому слагаемому правой части (5.171), получаем
F (ю + AZ, Z) = F (w, t) -ф dF^ ° AZ -к о (AZ).
Подставив это выражение в (5.171), запишем полученное равенство
F(w, t -ф AZ) = F (ю, Z) ф- dF ^w AZ -
- X AZ [F (w, Z) + д/ j +
-ф X AZ | В (w — x) dxF (x, Z)4-o(AZ).
247
Перенеся F (w, i) влево, разделив на Л/ и перейдя к пределу при Л/ — 0, получим, наконец, интегро-дифференциальное уравнение Такача для U (/):
W
dF (w, t) dF (w, t) , r-, л f D / ч . с / л
---Ft---=-----dF~L~XF^W’ + Х J B(w-x)dxF(x, t).
И (5.172)
Такач [18] вывел это уравнение для более общего случая неоднородных пуассоновских процессов, а именно для случая, когда интенсивность входящего потока % (/) зависит от времени. Он показал, что уравнение справедливо почти для всех w 0 и t > О и несправедливо для тех w и t, при которых dF (да, t)ldw имеет накопление вероятности (а именно, импульс). Это получается, в частности, в точке да = 0 и приводит к появлению в выражении dF (да, t)ldw члена F (0, t) и0 (да), в то время как ни один другой член в уравнении не содержит такого импульса.
Мы сможем почерпнуть из интегродифференциального уравнения Такача больше информации, если возьмем его преобразование по да (но не по f). Вводя переменную г, определим
00
W*’(r, t) Д ] e~rwdFw(w, t). (5.173)
о-
Будем пользоваться обозначением (*•) для преобразования по первому (но не по второму) аргументу. Символ W применяется потому, что, как увидим, lim w' (г, Г) = W* (г) при t —> оо, что представляет собой преобразование плотности времени ожидания [см., например, (5.103) ].
Изучим преобразование каждого члена уравнения (5.172) в отдельности. Заметим сначала, что, так как F (да, i) = [ dxF (х, t), то согласно строке 13 табл. 1.3 приложения I (и ее сноске) должно быть
Те-/ п г,., j И7*’ (г, О Ч-/7 (0-, /) F (да, /) e~rw dw =--————*——- ,
О”
и точно так же получаем, что
j В (да) е-™ dw = .
O’-
Однако, так как и незавершенная работа и время ожидания — неотрицательные случайные величины, то всегда должно быть F ((Г, t) = В ((Г) = 0. Мы видим, что последний член в интегро-дифференциальном уравнении Такача представляет собой свертку 248
B(w) и OF (w, t)/dw, поэтому преобразование этой свертки (включая постоянный множитель %) равно (по свойствам 10 и 13 из той же табл. 1.3) KW*' (г, t) х [В* (г) — В (ОД ]/г = X1F*' (г, t) В* (г)/г. Теперь ясно, что преобразование члена dF (w, t)ldw равно W*' (г, t). Но это преобразование включает F (0+, t) — преобразование импульса, расположенного в точке w = 0, и, так как известно, что интегро-дифференциальное уравнение Такача не содержит этого импульса, то его надо вычесть. Таким образом, из уравнения (5.172) получаем равенство
(т) = W*- (л 0 - Р (0+, О - <L -Ь
+ Х (Г) , (5.174)
которое можно переписать в виде
dW*'d(tr’ ° - [г - X + ХВ* (г)] IF*- (г, /) - rF (0+, t). (5.175)
Такач дает решение этого уравнения ([20], с. 51, формула (8)). Теперь можно взять преобразование по второй переменной согласно определенному ранее двойному преобразованию:
F**(r, s) Д J e~s/lF*- (г, t)dt. (5.176)
о
Нам понадобится также определение
Во (s) Л J e"s/B (0+, 0 dt. (5.177)
о
Теперь мы можем преобразовать (5.175), применяя свойства преобразований, приведенные в строке 11 табл. 1.3 (и в сноске к ней), чтобы получить
sF** (г, s) - W*' (г, О') = [г - X + ХВ* (г)] В** (г, s) - rB0* (s).
Отсюда
Неизвестная функция BJ (s) может быть определена, если потребовать аналитичности преобразования В** (г, s) в области Re (s) > > 0, Re (г) > 0. Для этого нули числителя и знаменателя в указанной области должны совпадать. Бенеш [1 ] показал, что знаменатель (5.178) имеет в этой области единственный корень ц = г] (s). Таким образом, W*' (г|, 0“) = г|Во (s), и, записывая 0 вместо 0“, получаем
В** (г, S) =
УУ*’ (г, 0) + (r/п) (Т), 0)
s — г + Л — 'КВ* (г)
(5.179)
249
Вспомним теперь, чго U (0) — да0 с вероятностью единица; тогда из (5.173) получим: W*' (г, 0) = e~rw<>. Таким образом, получаем F** (г, s) в окончательном виде:
«(5.180)
Мы вернемся к этому уравнению в гл. 2 тома II, когда будем изучать диффузионное приближение.
Теперь предстоит исследовать значение этой функции в установившемся режиме. В частности, можно показать, что F (w, t) при t — > оо имеет предел при р <1, не зависящий от начальных условий F (0, да). Обозначим этот предел через F (да) = lim F (да, t) при / - - > оо и из уравнения (5.172) найдем, что он должен удовлетворять следующему уравнению:
Т;.1 - = А/7 (да) — X j B(w — x)dF(x). (5.181)
х—'J
Кроме того, для р < 1 существует предел W* (г) A lim W*’ (г, t) при t —> оо, не зависящий от начальных условий. Переходя в уравнении (5.181) к преобразованию, получим, как и при выводе уравнения (5.174),
R7* (г) - F (0+) = (r) - lB*(r) (г) ,
где F (0+) = lim F (0+, t) при ( - > оо — вероятность того, что незавершенная работа равна нулю. Последнее можно переписать в виде
W* (г} =___.
г — Х + ХВ*(г)
Однако мы требуем, чтобы W* (0) = 1, откуда следует, что неизвестная постоянная F (0+) должна равняться 1 — р. Окончательно получаем
(5-,82)
что в точности, как и предсказывалось, совпадает с уравнением Полячека—Хинчина для преобразования, соответствующего времени ожидания.
Этим пока завершается рассмотрение системы М/G/l. Перейдем к рассмотрению системы G/M/m.
СПИСОК ЛИТЕРАТУРЫ
1. Benes, V. Е. On Queues with Poisson Arrivals. Annals of Mathematical Sta" tistics, 28, 670—677 (1956).
2. Конвей P. В., Максвелл В. Л., Миллер Л. В. Теория расписанин/Пер. с англ. Под ред. Г. П. Башарина. М., Наука, 1975. 300 с.
250
3. Cox, D. R. The Analysis of Non-Markovian Stochastic Processes by the Inclusion of Supplementary Variables. Proc. Camb. Phil. Soc. (Math, and Phys. Sci.), 51, 433—441 (1955).
4. Cox, D. R. Renewal Theory, Methuen (London) 1962./Пер. с англ. Под ред. Ю. К. Беляева. Кокс Д. Теория восстановлений. — В кн.: Кокс Д., Смит В. Теория восстановления. М., Сов. радио, 1967, с. 5—152.
5. Феллер В. Введение в теорию вероятностей и ее приложения/Пер. с англ. Ю. В. Прохорова. М., Мир, 1967, т. 2. 752 с.
6. Caver, D. Р., Jr. Imbedded Markov Chain Analysis of a Waiting-Line Process in Continuous Time. Annals of Mathematical Statistics, 30, 698—720 (1959).
7. Henderson, W. Alternative Approaches to the Analysis of the M/G/1 and G/M/l Queues. Operations Research, 15, 92—101 (1972).
8. Keilson, J. The Role of Green's Functions in Congestion Theory. Proc. Symposium on Congestion Theory, Univ, of North Carolina Press, 43—71 (1965).
9. Kendall, D. G. Some Problems in the Theory of Queues, Journal of the Royal Statistical Society, Ser. B, 13, 151—185 (1951).
10. Kendall, D. G. Stochastic Processes Occurring in the Theory of Queues and their Analysis by the Method of the Imbedded Markov Chain, Annals of Mathematical Statistics, 24, 338—354 (1953).
11. Хинчин А. Я. Математическая теория стационарной очереди. — В кн.: Математический сборник. М., 1932, т. 39, с. 73—84.
12. Lindley, D. V. The Theory of Queues with a Single Server. Proc. Cambridge Philosophical Society, 48, 277—289 (1952).
13. Palm, C. Intensitatsschwankungen im Fernsprechverkehr. Ericsson Technics, 44, 1—189 (1943).
14. Pollaczek, F. Uber eine Aufgabe der Wahrscheinlichkeitstheorie. I—II Math. Zeitschrift., 32, 64—100, 729—750 (1930).
15. Prabhu, N. U. Queues and Inventories, Wiley (New York), 1965.
16. Риордан Дж. Вероятностные системы обслуживания./Пер. с англ. Под ред. А. Д. Харкевича. М., Связь, 1966. 184 с.
17. Smith, W. L., Renewal Theory and its Ramifications. Journal of the Royal Statistical Society, Ser. B, 20, 243—302 (1958).
Смит В. Л. Теория восстановления и смежные вопросы. — В кн.: Кокс Д., Смит В. Теория восстановления/Пер. с англ. Под ред. Ю. К- Беляева. М., Сов. радио, 1967, с. 153—288.
18. Takacs, К. Investigation of Waiting Time Problems by Reduction to Markov Procrsses. Acta Math Acad. Sci. Hung., 6, 101—129 (1955).
19. Takacs, L. Introduction to the Theory of Queues, Oxford University Press (New York), 1962.
20. Takacs, L. A Single—Server Queue with Poisson Input. Operations Research, 10, 388—397 (1962).
21. Takacs, L. Combinatorial Methods in the Theory of Stochastic Processes. Wiley (New York), 1967.
ЗАДАЧИ
5.1. Выведите формулу (5.14) из равенства (5.11).
5.2. Выведите плотность распределения остаточного времени / (х), рассмотренную в параграфе 5.2, используя обозначения рис. 5.1.
а) Учитывая, что событие {Y < у} может появиться тогда и только тогда, когда t <Z т/г </ t + у <Z т/г+1 при некотором k, покажите, что
оо t+y
= 2 I I1 ~F (t + y~x)]dP[xk<X].
fe=i t
251
б) Заметив, что хк < х тогда и только тогда, когда число а (х) «поступлений» в промежутке (0, х), по крайней мере, равно k, т. е. Р [т/( < х] Р [а (х) > k], покажите, что
во ее
Р [т* < х] ~ S kP (а (х) =* й]. J-1 к=1
в) Для больших х среднее значение величины а (х) в п. б равно x/mi. Пусть F (у) = lim Ft (у) при /оо с соответствующей плотностью / (у). Покажите, что f\y) = ——
5.3. Выведем вновь формулу (5.72) Полячека—Хинчина для преобразований.
а) Приняв во внимание, что вновь поступившее требование задерживается на время обслуживания каждого требования, уже стоящего в очереди, и на время окончания обслуживания требования, находящегося в обслуживающем приборе, запишите выражение для W через Nq, р, х и о*.
б) Примените в п. а формулу Литтла для получения равенства (5.72).
5.4. Замените в равенстве (5.85) величину 1 — р неизвестной константой и покажите, что условие Q (1) — V (1) =1 легко приводит к получению для этой константы точного значения, равного 1 — р.
5.5. а) Из уравнения (5.86) получите величину Q(1) (1) и покажите, что она дает выражение для q в равенстве (5.63). Заметьте, что для раскрытия неопределенности в выражении для Q'” (1) придется дважды применять правило Лопиталя. б) Из уравнения (5.105) найдите первые два момента времени ожидания и сравните с равенствами (5.113) и (5.114).
5.6. Докажем, что предельные вероятности гк числа требований, которые застает новое поступающее требование, равны предельным вероятностям dk числа требований, остающихся после ухода требования, в любой системе, в которой состояния меняются только на величину ±1. Пусть, начиная с момента t --= 0, хп — те моменты времени, при которых число N (t) требований в системе возрастает на единицу, а уп — те моменты, при которых N (t) убывает на единицу; п = 1, 2, .... Обозначим N (х~,) через ап, a N (у — через р„. Пусть N (0) = i.
а) Покажите, что, если p„+z с k, то а„+*+1 < k.
б) Покажите, что, если а.г+А,+1 k, то Р„+, < k.
в) Покажите, что п. а и б для любого k должны давать равенство
lim Р [Р„ < k] •= lim'P[an П->со
что устанавливает равенство rk = dk.
252
5.7. В этой задаче исследуем метод дополнительных переменных в применении к системе М/G/l. Как обычно, пусть Рк (t) —
Р IR (0 — k], Кроме того, пусть Рк (t, х0) dx0 — = Р \N (t) — k, х0 < Хо (0 -< х0 4- dx01, где Хо (0 — время обслуживания, полученного требованием к моменту t.
а) Покажите, что
дР0 (О dt
ео
= —ХР0 (0 + j Л (t, Хо) '(Хо) dx0,
О
где Л(х0) = -г2_^-г.
б) Пусть pk = lim Pk (0 и pk (х0) = lim Pk (t, x0) при t—> оо. Из п. а получается результат для установившегося режима:
^Ро = J A(x0)r(x0)dx0. о
Покажите справедливость следующих результатов для установившегося режима [здесь ро(хо)ЛО1:
1) dpk (x0)/dx0 = [—X + г (х0)] pk (х0) 4- Кр^ (х0), k > 1;
©о
2) рк(0) = j р/г+1 (х0) г (х0) dx0, k > 1;
о
3) Pl (0) = j р, (х0) г (х0) dx0 + Хр0. о
в) Четыре равенства в п. б определяют стационарные вероятности в сочетании с соответствующим нормирующим условием. Получите это нормирующее условие, выразив его через Ро и pk (х0), k = 1, 2, ...
г) Пусть R(z, х0)= У) Pk(xo)zk- Покажите, что fe=l
dR (z, х0)/дх0 = [Xz — X — г (х0)] R (z, х0)
и
zR (z, 0) = j г (х0) R (z, х0) dx0 + Xz (z — 1) p0. 0
253
д) Покажите, что решением для 7? (г, х0) в п. г должно быть
о
R (z, х0) = R (г, 0) е
R (г, 0) = Хг<г~1)р°
' ’ 7 г — В* (Л — Хг)
е) Определив R(z)Aj R(z, x^dx^ покажите, что R(z)^R(zt0)l-^_^.
ж) Из нормирующего условия, выведенного в п. в, покажите теперь, что р0 — 1 — р, р = Кх.
з) Согласно равенству (5.78) определим теперь Q (?) — р0 + -i R (z). Покажите, что Q (г), выраженное таким образом, идентично уравнению Полячека—Хинчина для преобразования (5.86). (Дополнительные подробности этого метода см. в [3].)
5.8. Рассмотрим систему M/G/oo, в которой любое требование находит свободный прибор. Следовательно,
s (г/) = Ь (у), Т = х.
Пусть Pk (t) = Р [У (f) = А] и предположим, что Ро (0) --= 1. а) Покажите, что
ео
Pk (0 = У е-^ n=k
at)'1 п!
Т k
[1 — В (х)] dx X
i л n-k
j В (x) dx
0
г *
1 Г
Указание : y- 5 (x) dx есть вероятность того, что обслу-о
живание требования заканчивается в момент t, в предположении, что момент поступления распределен равномерно в промежутке (0, t). См. также (2.137).]
б) Покажите, что pk Д lim Pk (t) при t —» сю имеет вид
Pk =
k\
независимо от вида функции В (х).
5.9. Рассмотрим систему М/Еа/1.
254
а) Найдите выражение для G* ($) в виде многочлена.
б) Найдите S (у) Р [время в системе cyl.
5.10. Рассмотрим систему M/D/1, в которой х = 2 с.
а) Покажите, что остаточное время обслуживания имеет прямоугольную плотность распределения b (х).
б) Для р — 0,25 покажите, что результат (5.111), взятый с четырьмя членами, дает хорошее приближение распределения времени ожидания.
5.11. Рассмотрим систему M/G/1, на вход которой поступает неординарный поток требований с интенсивностью X и вероятностью одновременного поступления гтребований, равной gr. а) Покажите, что производящая функция числа требований, поступающих за время t, равна где
G (2) = Е g/.
б) Покажите, что производящая функция случайной величины, vn, представляющей собой число требований, поступивших за время обслуживания одного требования, равна В* [X — XG(z)L
5.12. Рассмотрим систему М/G/l с тем же потоком требований, что и в предыдущей задаче.
а) Применяя метод вложенных цепей Маркова, найдите среднюю длину очереди в моменты ухода требований [Указание. Покажите, что
v — р = XxG*1) (1)
и
о+мс1+1 - g)&)2’
где Сг — коэффициент вариации размера группы поступающих одновременно требований, a g — среднее значение этой величины. ]
б) Применяя тот же метод, покажите, что производящая функция длины очереди в моменты ухода требований имеет вид
(?(;) — Р) (’— G (г)) В* [^ —XG (г)]
(В* [?. — ?.G (г)] — z)g ’ "
Применяя результат Литтла, найдите отношение W/x среднего времени ожидания к среднему времени обслуживания, в) Применяя тот же метод (вложенных цепей Маркова), найдите среднее число групп в очереди (усредните по моментам ухода). [Указания. Покажите, что D (z) = р* (X — Xz), где D (z) — производящая функция числа групп требований, поступающих за время обслуживания целой группы, и где Р* (s) — преобразование Лапласа плотности распределения
255
времени обслуживания целой группы. Заметьте также, что р* (s) -= G [В* (s) ], а это позволяет доказать, что т2 = = (x)2(g2 — g) + x2g, где т2 — второй момент распределения времени обслуживания группы. ]
г) Применяя результат Литтла, найдите время Wg ожидания группы в очереди (которое измеряется с момента поступления группы до начала обслуживания первого требования этой группы) и покажите, что
1^..
2 (1 - р)
С2
1 + дс, g
д) Покажите, что если поступившие одновременно требования в пределах группы обслуживаются в случайном порядке, то отношение среднего времени ожидания для отдельного требования к среднему времени обслуживания отдельного требования равно величине из п. г, увеличенной на (1/2) g (1 + С'б) - 1/2.
5.13. Рассмотрим систему М/G/l, в которой обслуживание происходит мгновенно, но возможно только в специальные моменты обслуживания, причем промежутки между этими моментами успешного обслуживания независимы и имеют функцию распределения F (х). Максимальное число требований, которое может быть обслужено одновременно, равно т. Заметим, что это система группового обслуживания.
а) Покажите, что если — число требований в системе непосредственно перед п-м моментом обслуживания, то
Qn+i —
Чп+vn — m, qn>-m\ vn, qn < m,
где vn — число поступлений между п-м и (п + 1)-м моментом обслуживания.
б) Докажите, что производящая функция величины ип есть F* (К — Az). Исходя из этого, покажите, что
т-1
У' Pk(zm~ zk)
/И / \ k=0
где pk = р [q = k], k = 0, ..., т — 1.
в) {pk\ может быть определено из того условия, что в единичном круге на комплексной плоскости числитель и знаменатель дробно-рациональной функции Q (z) обращаются в нуль в одних и тех же точках. Исходя из этого, покажите, что, если F (х) = 1 — то
где zm — лежащий вне единичного круга нуль функции zm [1 + (1 — z)/ji 1 — 1.
5.14. Рассмотрим систему М/G/l с групповым обслуживанием. Если обслуживающий прибор свободен, он принимает из очереди одновременно два требования, а если в очереди имеется только одно требование, то принимает это одно требование. В любом случае время обслуживания группы (объема 1 или 2) имеет распределение В (х). Пусть qn — число требований, остающихся после н-го момента обслуживания; vn — число поступлений за время n-го обслуживания. Обозначим В* (s), Q (?) и V (г) соответственно преобразования, связанные с величинами х, q и и. Пусть р = = %х/2.
а) Применяя метод вложенных цепей Маркова, найдите
E(q) = lim E(qn), П-> 00
выразив зависимость от р, о* и Р (q = 0) А р0.
б) Найдите Q (г) как функцию от В* (), р0 и pr А Р (q = 1). в) Выразите рг через р0.
5.15. Рассмотрим систему М/G/l со следующим изменением. Обслуживание не начинается, пока не будут готовы для обслуживания по крайней мере два требования. Эти два требования поступают на обслуживание вместе, но обслуживаются индивидуально, независимо друг от друга, одно после другого. Момент окончания обслуживания второго из этих требований называется критическим, и такие моменты используются в качестве точек вложенной цепи Маркова. Сразу после критического момента на обслуживание принимается следующая пара готовых для обслуживания требований, если таковая имеется, в противном случае обслуживающий прибор ждет, и т. д. Положим, qn — число требований, остающихся в системе непосредственно после n-го критического момента; vn — число требований, поступивших в систему за время обслуживания п-й пары требований.
а) Выведите соотношение между qn+1, qn и щ!+1.
б) Найдите
00
V(z)= S P[vn-=k]zk. Л=»0
в) Найдите выражение для Q (г) = lim Qn (z) в зависи-п-><»
мости от р0 = Р [</ = 0], где
00
Q„(z)== Е P[qn = k]zk.
k=0
9 Л. Клейнрок
257
г) Как можно найти р0?
д) Опишите (на вычисляя) два метода нахождения q.
5.16. Рассмотрим систему М/G/l, в которой обслуживание задается следующим образом. После поступлений требования бросают монету, которая может выпасть лицевой стороной с вероятностью р. Если выпадает лицевая сторона, то время обслуживания равно нулю, если обратная сторона, то время обслуживания имеет следующее показательное распределение:
Р&~рх, х >0.
а) Найдите среднее время обслуживания х.
б) Найдите дисперсию времени обслуживания ст*.
в) Найдите среднее время ожидания W.
г) Найдите IE* (s).
д) Из п. г найдите W.
е) Из п. г найдите W (/) = Р [время ожидания <Р.
5.17. Рассмотрим систему М/G/l. Пусть Е — событие, состоящее в том, что с момента поступления последнего требования прошло Т секунд. Начнем с момента поступления требования и измерим время w до следующего появления события Е. Это измерение может включать подсчет числа поступающих за указанное время требований.
а) Пусть A (t) — распределение таких промежутков времени между поступающими требованиями, в течение которых событие Е не наступает. Найдите А (/).
со
б) Найдите A* (s) = j e~stdA(t).
о
в) Найдите W* (s | п) = J е'5® dW (w | п), где IE (щ | ri) = о
= Р [время до события Е < и>| событие Е наступает до п требований ].
00
г) Найдите IP* (s) = j ersa>dW(w), где W (w) = P [время до о
события Е < w],
д) Найдите среднее время до события Е.
5.18. Рассмотрим систему М/G/l, в которой время разбито па промежутки длиной q секунд каждый. Предположим, что поступления имеют распределение Бернулли, т. е.
Р [1 поступление в любом промежутке] = Kq;
Р [0 поступлений в любом промежутке] = 1 — kq;
Р L> 1 поступления в любом промежутке] =0.
258
Предположим, что время обслуживания х кратно q, так что Р [время обслуживания = nq секунд] = gn, п = 0, 1,2,... а) Найдите Е (число поступлений в одном промежутке), б) Найдите интенсивность поступлений.
в) Выразите Е [х] £±х и Е [х (х — q) ] = х2 — xq в зависимости от моментов распределения gn (т. е. пусть
00
gk й S nkgn п=0
г) Найдите ута — Р [за nq секунд поступает т требований ].
д) Пусть vm — Р [за время обслуживания требования поступают т новых требований ] и пусть
во ео
V (г) = 2j Vmzm и G (г) = £ gmzm. tn~O m=*Q
Выразите V (г) через G (г) и параметры системы X и q.
е) Найдите среднее число поступлений за время обслуживания, определенное в п. д.
5.19. Предположим, что в системе М/G/l стоимость ожидания в очереди определяется из расчета с (/) долларов за t секунд ожидания, где с (t) = ае-₽< Найдите среднюю стоимость ожидания. Определите также условия, при которых средняя стоимость конечна.
5.20. Найдем распределение промежутков времени между уходами обслуженных требований для системы М/G/l. Обозначим искомую плотность распределения через d (t).
а) Найдите преобразование Лапласа D* (s) этой плотности, налагая сначала условие наличия очереди, а затем условие отсутствия очереди в момент ухода требования. Комбинируя эти результаты, найдите преобразование Лапласа D* (s) искомой плотности, а из нее получите плотность распределения.
б) Дайте явное выражение для функции распределения D (/) или плотности распределения d (г1) = dD промежутков времени между уходами при постоянном времени обслуживания, т. е. когда
5.21. Рассмотрим следующий модифицированный порядок обслуживания в системе М/G/l. Вместо обратного порядка обслуживания, который был показан на рис. 5.11, предположим, что после промежутка времени хх появляется подпериод занятости, порожденный требованием С2, затем подпериод занятости, порожденный требованием С3, п т. д., до окончания периода занятости. Пользуясь данными о последо-9* 259
вательности поступлений и времени обслуживания, представленными на верхнем контуре рис. 5.11, а, перечертите графики, указанные на рис. 5.11., а, б, в, в соответствии с вышеуказанным порядком обслуживания.
5.22. Рассмотрим систему М/G/l, в которой уходящее требование может с вероятностью р опять стать в очередь или с вероятностью <?=1 — р уйти навсегда. Обслуживание происходит в порядке поступления, а время обслуживания возвращающегося требования не зависит от его предыдущего времени обслуживания. Пусть В* (s) — преобразование плотности распределения времени обслуживания, а В*т (s) — преобразование плотности распределения общего времени обслуживания требования.
а) Найдите В? (s) в зависимости от В* (s), р и q.
б) Пусть хт — п-й момент общего времени обслуживания. Выразите х'т и х^ через х, х2, р и q.
в) Покажите справедливость следующей формулы:
_ п ___
vn , р / П \ Ykvn-k
Хт = х +—L и ) т • 4=1
г) Пусть Qr (z) = s йгЛ
где pkT = P [число требований в системе = k\. Докажите, что в случае Хх <Z q
п 1,1 - fl _ <7(1 —z) В* [X (1 —z)]
Чг’-1 V q J (q-j-pz) В* [X (1 — г)] — г
д) Найдите среднее число AZ требований в системе.
5.23. Рассмотрим систему М/G/l с обслуживанием в порядке поступления и следующими изменениями. Обслуживание продолжается до тех пор, пока в системе есть требования. Если система освобождается, прибор обслуживания закрывается на некоторое время, которое может быть случайным. По окончании этого времени прибор возобновляет обслуживание. Если при этом в системе требований не оказывается, прибор закрывается опять. Пусть F (г) = Xj fjzl — производящая функция распределения числа требований, ожидающих обслуживания, когда система открывается после перерыва при наличии хотя бы одного ожидающего требования (т. е. fj — вероятность того, что в начале рабочего периода обслуживающего прибора имеется / требований, ожидающих обслуживания).
а) Получите выражение для q,l+1 через qn, vn+1 и / (число требований, поступивших во время перерыва в обслуживании).
260
б) Найдите зависимость при п -+ оо для Q (z), где Q (z) = = lim Е [z^], от р0 (вероятность того, что уходящее требование не оставляет после себя ни одного требования). [Указание. Воспользуйтесь условием, накладываемым на /]. в) Покажите, что р0 = (1 —p)/Fll) (1), где F”’ (1) = = dF (z)/dz|J==i.
г) Предположим теперь, что прибор обслуживания возобновляет работу, как только поступает новое требование. Найдите для этого случая F (г) и покажите, что если подставить это решение в ответ п. б, то получится классическое решение для системы M/G/1.
5.24. Известно, что поступающее требование, застающее k других требований в системе, должно ждать в течение остаточного времени обслуживания требования в приборе плюс полное время обслуживания k—1 требований.
а) Применяя определение и подход задачи 5.7, покажите, что преобразование плотности распределения времени ожи Дания можно выразить в виде
ОО 00
№’(5) = А)+ Г У /’ft(x0)lB*(s)]fc-1X
О ft=l
Р — г (и) du J г (и) du
xje-..r(9+,o)e Ь
О
б) Покажите, что выражение из п. а сводится к W* (s), полученному в (5.106).
5.25. Соотнесем k-й момент s* времени пребывания в системе k-му моменту Nk числа требований в системе.
а) Покажите, что выражение (5.98) непосредственно приводит к формуле Литтла, а именно, что
N = йАХТ.
б) Выведите из равенства (5.98) следующее соотношение между вторыми моментами:
¥г —y =
в) Докажите общее соотношение
У(У- 1)(А/-2)...(У-£ + 1)= V?.
ГЛАВА 6
Система типа G/M(m
До сих пор рассматривались СМО типа М/М/1 и ее модификации (элементарная теория массового обслуживания), а также СМО типа М/G/l (промежуточная теория массового обслуживания). Естественно теперь изучить систему типа G/M/1, в которой распределение А (/) промежутков времени между поступающими требованиями произвольно, а время обслуживания показательное. Но оказывается, что исследование многолинейной системы G/M/m ненамного сложнее исследования однолинейной системы G/M/1; поэтому приступим сразу к рассмотрению многолинейной системы. Это исследование, как и исследование системы типа М/G/l, проводится методами промежуточной теории массового обслуживания и также может основываться на применении метода вложенных цепей Маркова, как это изящно описано у Кендалла [3].
6.1. ВЕРОЯТНОСТИ ПЕРЕХОДА ДЛЯ ВЛОЖЕННОЙ
ЦЕПИ МАРКОВА (СИСТЕМА G/M/m)
Рассматриваемая система содержит т приборов, которые обслуживают требования в порядке их поступления. Требования поступают поодиночке с промежутками времени между поступлениями, распределенными независимо, с одной и той же функцией распределения А (/) и средним значением 1/%. Время обслуживания распределено по показательному закону со средним значением 1/р, одинаково и независимо для всех требований. Будем рассматривать только установившийся режим (см. обсуждение ниже).
Как 11 в случае системы M-'G/1, состояние которой характеризовалось непрерывными величинами, в системе G/M/m тоже имеют место непрерывные характеристики состояний, описывающие время, прошедшее с момента поступления последнего требования; система также характеризуется числом находящихся в ней требований. Эго справедливо, поскольку вероятность поступления требования в любой конкретный промежуток времени зависит от времени, прошедшего с момента поступления последнего требования. Анализ системы можно провести, используя двумерное описание ее состояний, содержащее время, прошедшее от момента поступления последнего требования, и число требований в системе. Такая процедура, как уже говорилось, называется методом дополнительных переменных. Второй подход, очень похожий на тот, которым мы пользовались для исследования системы M/G/1, является методом вложенных цепей Маркова, которым и восполь-262
OSслужиВающий прибор
Очередь
Обслуживание
Vn*i.
Рис. 6.1. Точки вложенной цепи Маркова
зуемся ниже. Третьим был рассмотрен метод этапов (см. гл. 4).
Если мы намерены применить метод вложенной цепи Маркова, то выбранные точки, порождающие эту цепь, должны в косвенном виде содержать информацию о времени, прошедшем с момента поступления последнего требования, по аналогии с рассмотренным израсходованным временем обслуживания в системе М/G/1. Естественно выбрать в качестве такой последовательности точек последовательность моментов поступления требований. Конечно, в такие моменты время, прошедшее после поступления последнего требования, равно нулю. Поэтому определим:
q'n = число требований, находящихся в системе непосредственно перед поступлением требования Сп.
Обозначим эту случайную величину через q'n, для отличия от числа ^„требований, остающихся в системе М/G/l после ухода требования Сп. На рис. 6.1 показана последовательность моментов поступления требований, отождествляемая с последовательностью точек временной оси, порождающей вложенную цепь Маркова. Очевидно, что последовательность {q„} образует цепь Маркова с дискретными состояниями. Определяя
v’n+i — число требований, обслуженных между поступлениями требований Сп и С„+1, сразу же обнаруживаем, что должно иметь место следующее основное соотношение:
q’n+i = + 1 — Vn+i. (6.1)
Вычислим теперь вероятности перехода для состояний цепи. Обозначим
Pii = P[qn+i = j\qn = «]. (6.2)
Очевидно, pij просто равно вероятности того, что за промежуток времени между поступлениями обслужено i + 1 — / требований. Далее ясно, что
ptj = 0 при / > i ф- 1, (6.3)
так как число находящихся в системе требований в промежутке времени между поступлениями требований Сп и Сп+1 самое боль-
263
Рис. 6.2. Диаграмма вероятностен перехода вложенной цепи Маркова для системы G/M/m
шее равно i + 1. Диаграмма вероятностей переходов марковского процесса имеет переходы, показанные на рис. 6.2. Здесь указаны только переходы из состояния
Поскольку речь идет только о результатах, связанных с установившимся режимом, необходимо исследовать условия, при которых рассматриваемая цепь Маркова эргодична. Легко показать, что, как и следовало ожидать, условие эргодичности имеет вид к <//иц, где X — интенсивность входящего потока, а ц— параметр показательного обслуживания (т. е. х = 1/ц). Как определено в гл. 2 и использовано в параграфе 3.5, введем коэффициент нагрузки системы
(6-4)
Он равен интенсивности поступления работы в систему обслуживания (Кх = Х/ц. секунд работы за проходящую секунду), деленной на максимальную интенсивность, с которой система может работать (пг секунд работы за проходящую секунду). Таким образом, условие эргодичности просто имеет вид р </1. В эргодическом случае мы уверены в существовании стационарного распределения вероятностей, описывающего число требований, находящихся в системе в моменты поступления требований. Поэтому определим
rk = limР [q'n =- k] (6.5)
n-> ОО
и будем искать это распределение вероятностей для системы G/M/m. Как известно из гл. 2, прямой метод нахождения стационарного распределения вероятностей состоит в решении системы линейных уравнений
г = гР, (6.6)
где
г = Ко, и, г2,...] (6.7^
и Р — матрица, элементы которой совпадают с вероятностями р(/-перехода за один шаг.
Первая задача состоит в том, чтобы найти эти вероятности перехода за один шаг. Для этого рассмотрим четыре области 264
на плоскости i, j, показанные на рис. 6.3, где изображен случай т = 6. Относительно области 1 из равенства (6.3) известно, что pQ = 0 при i + 1 </. Далее, область 2 определяется неравенствами / < < i + 1 < т, что соответствует тому случаю, когда ни одно требование не ждет, а все присутствующие требования обслуживаются. За время между поступлениями требований, как мы видим, закон-ч тся обслуживание i + + 1 — / требований. Так как время обслуживания показательно, вероятность завершения обслуживания любого заданного требования за t секунд после поступления требования Сп равна 1 — Точно так же вероятность того, что данное требование за время t не покинет систему, равна е_(Х6 Поэтому в этой области
P[i’+ 1 — / уходов за t секунд после поступления требования
С(1|<7,'г= i] - (6.8)
где биноминальные коэффициенты
( X) =(Т)
просто дают число вариантов выбора i + 1 — / уходящих требований из i + 1 возможных, находящихся в системе. Если t„+l — промежуток времени между поступлениями требований Сп и С,1+1, то равенство (6.8) дает вероятность Р [q'n+i = j\q'n = i, tn+1 = N. Снимая условие, накладываемое на tn+1, т. е. интегрируя по промежутку времени между требованиями, получим
Pij ; = j [1 — е-мД1+1,е~^/сМ (j), i + 1 < tn. (6.9)
о
Рассмотрим далее область 3, характеризуемую неравенствами + 1, I > tn*. Она соответствует тому простому случаю, когда все т приборов заняты на протяжении всего проме-
* Точка i = т — 1, j = т может быть отнесена либо к области 2, либо к области 3.
265
жутка времени между поступающими требованиями. При этом предположении, поскольку время обслуживания распределено по показательному закону, число обслуженных за такой период требований распределено по закону Пуассона с параметром тр. (фактически это процесс чистой гибели с параметром тр). Событие, состоящее в том, что tn+1 = I и что на протяжении отрезка времени t все т приборов заняты, будем называть сокращенно <Р, все т заняты». Имеем:
P[k требований обслужено \t, все т заняты] =
-
~ k! с
Как указывалось ранее, чтобы перейти из состояния i в состояние /, необходимо, чтобы за время t было обслужено ровно i + 1—/ требований. Имея это в виду и снимая условие, наложенное на Ki+i> получаем
00
pi,- = j Р [i 4- 1 — / требований обслужено 1t, все т заняты] dA (/), и
или
со
Рч - J dA (<)’ m L (6.10)
0
Заметим, что в этом равенстве индексы i и / появляются только в виде разности i + 1 — /; поэтому целесообразно ввести новую величину, зависящую от одного индекса:
₽1+1_/ &Pij, m<i, (6.11)
где — вероятность обслуживания п. требований за промежуток времени, в течение которого все tn приборов остаются занятыми. Таким образом, полагая п — I + 1 — /, имеем
оо
Рл = Л./+1-л= J и (6.12)
О < п с i 4- 1 — т, т<.1.
Последний случай, который необходимо рассмотреть (область 4), определяется неравенствами / <(т <щ 4~ 1; он описывает ситуацию, когда поступающее требование Сп застает т требований на обслуживании и i — т требований в очереди (к которой оно и присоединяется). При поступлении требования Сп+Х в системе находится ровно / требований, все на обслуживании. Если пред-260
Полагается, что для разгрузки очереди требуется у секунд, то Рц можно вычислить прямым путем (см. задачу 6.1), что дает
00
о
f (тщУ"” ) (i — т)!
(e-ui' — e-»t)n
/ < tn < i 4- 1.
tnydy dA(t),
- (6.13)
Таким образом, равенства (6.3), (6.9), (6.12) и (6.13) дают полное описание вероятностей перехода для системы G/M/m.
Подставив эти вероятности в матрицу перехода, получим
Рао Poi 0 0
Рю Р11 Р12 0
Р-29 Pil Р22 р28
Pni-2,0 Р т-2,1 • • • Рт-2, т-1 0 0 0 ...
Рт-1,0 Рт-1,1 • * • Рт-1,т-1 Ро 0 ...
Рт, 0 Pm, 1 ... P:/l, Р1 Ро 0 ...
Рт+п, 0 Рт+п, 1 ... Pm+rii т-1Pn+iP«- . . Ро О
В этой матрице члены, расположенные над диагональю, равны нулю; члены р„ находят из равенства (6.12). «Граничные» члены, обозначенные в матрице общим символом /?,,, определяют либо по формуле (6.9), либо по (6.13) в зависимости от значений индексов. Наиболее важными являются вероятности перехода р„.
6.2. УСЛОВНОЕ РАСПРЕДЕЛЕНИЕ ДЛИНЫ ОЧЕРЕДИ
Теперь мы в состоянии найти стационарные вероятности rk, удовлетворяющие системе линейных уравнений (6.6). Здесь мы, возможно, могли бы угадать вид rk так, чтобы удовлетворялгтсь эта система уравнений, но мы предпочитаем мотивировать получаемые результаты следующими ниже интуитивными соображениями. Определим
Nk (/) = число моментов поступления требований за время (О, /), когда поступающее требование застает систему в состоянии Ек, при условии, что в момент t = О было 0 требований. (6.14)
Как видно из рис. 6.2, система может переместиться вверх не более
267
чем на одно состояние, но одним переходом вниз система может переместиться на много состояний. Рассмотрим эти премещения и определим (для tn — 1 < k):
<sk = Е [число попаданий в состояние Ем между двумя попаданиями в состояние (6.15)
Вероятность того, что перед возвращением в состояние Ем не будет попадания в состояние Ek, равна 1 — р0 (так как, если система находится в состоянии Ek, она может перейти в состояние Ek+1 только в том случае, если не обслужено ни одно требование, вероятность чего равна р0; вероятность того, что обслужено, по крайней мере, одно требование, равна 1 — р0). Пусть, далее, у = Р [система покидает состояние и через некоторое время возвращается в него, не проходя ни через одно состояние Ej, где k] = Р [система покидает состояние Ek+i и через некоторое время возвращается в него, не проходя состояние Ek ].
Это верно, так как из состояния Е, при j < k можно попасть в состояние Ek+i только через Ek (движение вверх только на одно состояние за один шаг). Заметим, что, если k > т — 1 (все т приборов заняты), то у не зависит от k. Легко вычислить, что
Р [п появлений состояния Ем между двумя появлениями СОСТОЯНИЯ £й[ = Yn-1(l — у) Ро,
т. е. равна произведению безусловной вероятности достижения состояния Ей+1 на вероятность возвращения в Ek+l без предварительного захода в Ek и на вероятность попадания в Ek без предварительного возвращения в Ek+V. Отсюда вычисляем ст/г = 00
= У пуп~1 (1 — у) ро — среднее число попаданий в состояние п— 1
Ek+1 между двумя попаданиями в состояние Ek. Таким образом, Gk = ~ j -при k > tn — 1.
Заметив, что <тй не зависит от k, опустим индекс и получим
РАС- t при /г > /п — 1. (6.16)
Из определения (6.15) следует, что число а должно быть пределом отношения числа пребываний системы в состоянии £&+i к числу пребываний в состоянии Поэтому можно записать
p==lim (6.17)
Но этот предел является просто отношением стационарной вероятности пребывания системы в состоянии Е1;+1 к стационарной вероятности пребывания системы в состоянии Ек. Следовательно, rA+i = ork, k > tn — 1. (6.18)
268
Решение последнего уравнения очевидно:
rk — Kok, (6.19)
где К. — некоторая константа. Это основной результат, который устанавливает, что для случая k т — 1 число требований, находящихся в системе в моменты поступления требований, имеет геометрическое распределение. Остается найти о и К., а также гЛ для k — 1-
Интуитивные соображения (которые можно строго обосновать с помощью результатов теории восстановления) привели нас к основному равенству (6.19). Можно было бы, конечно, этот результат угадать («вытащить из шляпы»), предположив, что решение уравнения (6.6) следует искать в форме вектора
г = [г0, /у, г2,...,гт_2, Квт~\ Кат, Kam+l, .. .]. (6.20)
Эта догадка конечно, верна (как показали вычисления). Если есть сомнение в результате, его легко можно проверить, рассмотрев /г-е уравнение (k > т) в системе (6.6), которое имеет вид
Г1{ Кв11- rtplk = Ц r:pik = £ /C<7‘pt+i_*.
i=0 /=£-1
Сокращая на К и на <т, находим
0=2 о‘'+1-*р,+1_4. i=k-\
Меняя индекс суммирования, окончательно получаем
оо
п = L п=0
Из (6.12) мы можем определить что позволит выполнить следующее вычисление:
° = S 1 —pr~^rntktdA(t') = j <dA(t).
п^О i=0 ’ О
Это уравнение должно удовлетворяться, если наша догадка верна. Однако в последнем интеграле нетрудно узнать преобразование Лапласа плотности распределения промежутков времени между требованиями, вычисленное в определенной точке. Следовательно,
о = А* (тр —- три). и (6.21)
Это функциональное уравнение для <т должно удовлетворяться если предполагаемое решение приемлемо. Можно показать [4], что если р < 1, то имеется единственное действительное решение для о в области О <С о <С 1, которое мы и нашли. Заметим, что всегда имеется решение о = 1, так как А* (0) = 1.
269
Мы имеем теперь определяющее уравнение для о, и остается найти постоянную К, а также rk для k = 0, 1, т — 2. Но прежде чем рассматривать эти вопросы, установим некоторые дополнительные важные результаты для системы G/M/m, используя пока основной результат (6.19). Этот результат устанавливает, что для k т — 1 число требований в системе имеет геометрическое распределение. Исходя из этого, вычислим теперь вероятность ожидания для поступающего требования. Ясно, что
Р [поступающее требование ждет] =
со со
k=m k~m
(6.22)
(Эта операция дозволена, так как согласно сказанному выше О <С 1-) Условная вероятность того, что очередь имеет длину п при условии ожидания поступающего требования,
Р [длина очереди = п | поступающее требование ждет] =
__ ___________г т+п___________,
Р [поступающее требование ждет] 5
Р [длина очереди = п [ поступающее требование ждет] =
Кпт+п
= ——--------= (1 — а) а", п > 0. as (6.23)
/Са"7(1 — а) '
Таким образом, заключаем, что условное распределение длины очереди в системе G/M/m (при условии, что очередь существует) имеет геометрическое распределение.
6.3. УСЛОВНОЕ РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ ОЖИДАНИЯ
Будем теперь искать распределение времени ожидания в предположении, что требование должно ждать. На основании равенства (6.23) ожидающее требование застает в системе т + п требований с вероятностью (1 — <т) оп. При этом условии поступающее требование должно ждать ухода п + 1 требований, пока оно попадает на обслуживание, и этот промежуток времени и составит его время ожидания. Поэтому необходимо найти распределение длины промежутка времени, являющегося суммой п + 1 независимых случайных величин с показательным распределением (каждая с параметром ту). Результирующая свертка наиболее просто выражается через преобразование, т. е. представляет собой обычное произведение преобразований.
Таким образом, обозначая через W* (s) преобразование Лапласа плотности распределения времени ожидания в соответствии 270
с (5.103) (т. е. как Е [e_st“ ]) и определяя
W* (sfn) = Е [e_s® | поступающее требование ждет
и длина очереди = п], (6.24)
имеем
U7* = (s|n) = )"+1. (6.25)
\ о ”j"- /1 V /
Но, очевидно,
ОС
U7* (s| поступающее требование ждет) = Xj W* (sj n) P [длина n=0
очереди = n | поступающее требование ждет];
тогда из равенств (6.25) и (6.23) получаем
W* [s | поступающее требование ждет] =
= У (1 - о) (JL_Yl+1 = (1 - a) J.
' \ S + /пр / s + "Щ —
п—0
К счастью, легко найти обратное преобразование Лапласа, и при этом получается условная плотность распределения времени ожидания:
w (у | поступающее требование ждет) = (1 — о) туе~т'1 <1_а)у, у 5> 0. а (6.26)
Вот так сюрприз! Условная плотность распределения времени ожидания для системы G/M/m описывается показательным законом!
Таким образом, пока получены два главных результата: во-первых, тот факт, что длина очереди имеет, как показывает равенство (6.23), условное геометрическое распределение с параметром о, и, во-вторых, что условное распределение времени ожидания, как показывает равенство (6.26), является показательным с параметром ту (1 — о). Параметр сг находят как единственное в области 0 <а <1 решение функционального уравнения (6.21). Продолжим поиск распределения г/г. Решение этого вопроса было доведено до результата (6.20). Остается найти постоянную К и первые т — 1 членов этого распределения. Прежде чем приступить к этим последним шагам, исследуем важный частный случай.
6.4. СИСТЕМА ТИПА G/M/1
Эта система, двойственная по отношению к системе M/G/1, по-видимому, является наиболее важной. Так как т = 1, то (6.19) дает решение для rk при всех значениях k, т. е. г/г = /(о*, k = 0, 1, 2,. . .
Теперь К легко вычислить, поскольку сумма вероятностей должна равняться единице. Отсюда непосредственно получаем
/;,= (!—o)ak, k = 0, 1, 2,..., га (6.27)
271
где (т — единственное решение уравнения
а = Д*(р,-ца) и (6.28)
в области 0 < 1.
Таким образом, система G/M/1 приводит к геометрическому распределению числа требований в моменты поступления нового требования; это справедливо как безусловное утверждение безотносительно к виду распределения промежутков времени между поступающими требованиями. Такой пример уже был рассмотрен [см. (4.42)] для системы Е/М/1. Заметим, что вероятности состояний pk = Р [k требований в системе ] отличаются от распределения (6.27), тем, что р0 = 1 — р, в то время как г0 = 1 — о, и Pk = Р (1 — п) — Рга-1 при k — 1, 2, ..., (см. равенство (3.24) на с. 209 в работе [1 ]). Для системы М/G/l pk = гк.
Требование вынуждено ждать обслуживания с вероятностью 1—г0=о, и можно применить (6.26), чтобы получить безусловное распределение времени ожидания следующим образом (событие А состоит в том, что поступающее требование ждет, а Ас — противоположное событие):
W (у) = Р [время ожидания < у] = 1 — Р [время ожидания > > у | А ] Р (А) — Р [время ожидания > у | Ас ] Р (Ас).
(6.29)
Очевидно, последний член в этом равенстве равен нулю. Остающаяся условная вероятность может быть получена интегрированием (6.26) от у до со при т — 1. Эго вычисление дает е~н у, и, так как о есть вероятность ожидания, непосредственно из (6.29) получается, что
№(//)= 1у>0. и (6.30)
Мы пришли к заслуживающему внимания заключению о показательном распределении времени ожидания (со скачком в нуле величины 1 —о) для системы G/M/1. Если сравнить этот результат с данными о распределении времени ожидания для системы М/М/1 [см. (5.123) и рис. 5.9], то можно увидеть, что рассматриваемые результаты совпадают при р = о. Таким образом, распределение времени ожидания для систем G/M/1 и М/М/1 имеет одну и ту же форму\
Прямым вычислением можно найти также, что среднее время ожидания в системе G/M/1
W =—а (6.31) JLl(I—<Т)
Пример. Проиллюстрируем теперь этот метод на примере системы М/М/1. Так как А (/) — 1 — е-х'(/ > 0), непосредственно получаем
A* (s) •= . (6.32)
д р /V
272
Применяя (6.28), находим, что о должно удовлетворять уравнению
ц — 1хсг X ’
или
рю2 — (р. 4~ ° 4~ = О,
что дает
(о — 1) (ро — X) == 0.
Из двух решений для о решение ст = 1 не подходит ввиду условия стабильности (0 •< ст< 1); следовательно, единственным подходящим решением является
ct=A = Pi м/М/1,(6.33)
что, в силу (6.27), дает
гА==(1—р)р\ £>0. (6.34)
Это, конечно, обычное решение для системы М/М/1. Далее, полагая в (6.30) о = р, получаем известное решение (5.123).
Пример. В качестве второго (гораздо более интересного) примера рассмотрим систему G/M/1, в которой плотность распределения промежутков времени между поступающими требованиями имеет преобразование Лапласа вида
= (6 35)
Заметим, что это соответствует системе Ег/М/1, в которой два этапа поступления имеют разные интенсивности. Эти интенсивности выбраны кратными интенсивностями обслуживания р.. Как всегда, сначала найдем о из (6.28), в результате чего получим
ст=__________.
(р + ро + ц) (ц — цстД- 2ц)
Это сразу приводит к кубическому уравнению
ст3 — 5о2 бст — 2 = 0.
Наверняка известно, что ст = 1 всегда является решением уравнения (6.28), и это позволяет разложить кубический многочлен на множители
(о - 1) (о - 2 - /2) (о — 2 + /2) = 0.
Из трех корней подходит только корень 2 — |/"2 (так как необходимо соблюдение условия 0 < ст •< 1). Поэтому равенство 273
(6.27) непосредственно дает распределение числа требований в системе (наблюдаемое в моменты поступления требований):
гЛ---(/2-1)(2 —/2)\ 6 = 0, 1, 2, ... (6.36)
Аналогично находим, что
= 1 — (2 — /2)е’м(1<2'1)\ г/>0 (6.37)
для распределения времени ожидания.
Вернемся теперь к более общей системе G/M/m.
6.5. СИСТЕМА ТИПА G/M/m
В конце параграфа 6.3 было отмечено, что для решения системы типа G/M/m в общем случае неизвестными остаются только постоянная К. и т — 1 «граничных» вероятностей г0, п, ..., г„г_2. Решение ищем в виде (6.20). Вынося множитель Астт-1, получаем г = Act"1- 1 [л0, . . ., Rm_2, 1, ст, ст2, ст3, . . . ], я (6.38)
где
= 6 = 0,1, ..., т — 2. (6.39)
Кроме того, для удобства записи обозначим
7 = Act'"-!. (6.40)
Первые т — 1 уравнений, представленных в матричном уравнении (6.6), до сих пор еще не использовались. Теперь они потребуются для вычисления неизвестных членов. Используя вероятности перехода можно записать равенство
Rk = У, 6 = 0,1, ..., m —2,
в котором определение R,., даваемое равенством (6.39), можно распространить на значения, выходящие за пределы 6 = т — 2, и использовать (6.19), т. е. принять Rt = ст‘-"1+’ для i т —1. «Хвост» записанной суммы можно выразить в виде
т—2 оо
Rk- S Riptk-R S Gl+1'mpik-
i=k-\
Решая это уравнение относительно первого члена первой суммы, находим, что
/71—2 со
Rk - RiPtk ~ L °M~mPik
/?/;1 =------------------------------ (6.41)
" Pk-i, k
для 6 = 1, 2, ..., m — 1. Система (6.41) — треугольная система с неизвестными R/:. В частности, можно исходить из того, что 274
Rm-i = 1 [см. (6.38)], и рекуррентно решать уравнение для k = т — 1, m — 2, 0. Наконец, используем для вычисления
постоянной J свойство суммы вероятностей (это вычисление эквивалентно вычислению Д'):
т-2 оо
k=0 k=m-\
ИЛИ
1
m—2
a (6.42)
Таким образом, подготовлено все необходимое для вычисления распределения числа требований в системе. Отметим, что Такач [4 ] дает явное (хотя и сложное) выражение для этих вероятностей.
Определим теперь распределение времени ожидания в системе. [Условное распределение уже было получено, оно задается равенством (6.26). ] Прежде всего вероятность того, что поступающее требование не должно ждать, получается в виде
m-I т-1
w/(0)= ^rk=JlR,
(6.43)
С другой стороны, если поступающее требование застает k > tn других требований в системе, то оно, прежде чем поступить на обслуживание, должно ждать, пока ровно k — т + 1 требований не покинут систему. Так как в это время т приборов непрерывно работают, то время между уходами обслуженных требований распределено по показательному закону с параметром ту, поэтому распределение времени ожидания должно быть распределением Эрланга порядка (k — т + 1), полученным в равенстве (2.147). Таким образом, для этого случая (/г > т) можно записать
Р [w с у [ поступающее требование застает в системе
У
k требований] = j ——е.~т^-х dx.
Если перейти к безусловному распределению, то
W (у) = F(0) + J
Sf (mp) (myxf-"1 ak~m+L
J (/г - т) I
k~m 0
У
X fTm»xdx = F (0) + Jg J туе~т»х G-^dx. (6.44) о
275
Теперь можно воспользоваться выражениями (6.42) и (6.43) для J и W (0), чтобы получить после интегрирования в равенстве (6.44) формулу
W (у) = 1-----------5-^-----е‘тц <1'<” У’ У>0- • (6.45)
1 + (1 - a)
*=о
Это окончательное решение для распределения времени ожидания, и оно показывает, что в общем случае для системы G/M/m все еще получается показательное распределение (с точкой накопления в нуле) времени ожидания!
Среднее время ожидания может быть вычислено либо по (6.45), либо следующим образом. Как известно, если поступающее требование застает k т других требований в системе, оно должно ждать окончания обслуживания k — т + 1 требований. Обслуживание каждого требования длится в среднем 1/тр, секунд. Найдем теперь среднее время ожидания как безусловное математическое ожидание:
со
= У _1_ (£__ m _{_ 1)г&.
k=m
Но в пределах суммирования, как известно, rk = K<Jk и, таким образом,
ft=m
что после простых вычислений дает
W_______Кот __ Jo
— тц (1 — а)2 тц (1 — а)2
6.6. СИСТЕМА ТИПА G/M/2
Посмотрим, насколько далеко удается продвинуться в исследовании системы G/M/2. Из равенства (6.19) получаем непосредственно
k= 1, 2, ...
Так как сумма вероятностей равна единице, то
rk — 1 — ro + K^k-
6=0 k=l
Это приводит к следующему соотношению между К и г0:
К = (i-roHt-gl. (6.46)
276
Теперь наша задача состоит в том, чтобы получить еще одно соотношение между этими величинами. Это можно сделать с помощью равенства (6.41), согласно которому
Ri — У- а1 !Рн
(6.47)
Pol
Но Ri = 1. Знаменатель (6.47) задается равенством (6.9), а именно
о
Нетрудно видеть, что
) [1 — е-^]°е-ц'бМ (t).
Poi = Л*(н).
(6.48)
Рассматривая вероятности лителе, можно видеть, что жен быть вычислен из (6.9), а члены ра для i = 2, 3, 4, ... — из (6.13). -
переходов за один шаг в сумме в чис-они делятся на два типа: член ри дол-
В результате имеем
Здесь
Pn= j( J ) [1 ~ е-Ие-^Д (0-о
опять нетрудно узнать преобразование Лапласа
рц = 2Д*(н) — 2Д*(2р).
(6.49)
Таким
образом, для i = 2, 3, 4, ... имеем г ' г_2
‘ j -!?2Гг(е-ЦУ~е-ц<)2^ dA(t). о
Л, - J
о
е-ni-
(6.50)
Подставим в
(6-47)
найденные величины Ri и poi;
X* (и)
1 — 2 А* (р) +2Д* (2р) — S о1’-1 ра . i=2
(6.51)
Используя равенство (6.50) и проводя суммирование в последнем равенстве под знаком интеграла, получаем
J, а^ра = 2Д*(2рН-----(2Н-2Но)—4оД* (р)
1=2
Но из равенства (6.21) следует, что о = А* (2р— 2ро);
2а — 1
(6.52)
тогда
- 9
S о'Д,, - 2А‘ (2g) + — 2/И (g)).
277
Подставив снова значение суммы в равенство (6.51), находим, чти
/? 2А* W - 1
л° (2а—1)4* (р)'
Однако из (6.39) известно, что Ro = г0/Ко, поэтому можно выра-
зить г0 в виде
Ко [1 — 24* (И)] (1 - 2а) 4* (р)
(6.53)
Таким образом, (6.46) и (6.53) определяют два уравнения с двумя неизвестными К и г0, совместное решение которых дает
(1 —a) [1 — 24*(р)] .
° 1 —а—4*(р)
К = А* (р) (r! ~g) (1^2g\ •
u ' о [1 — а — 4* (р(]
Окончательно распределение числа требований в системе G/M/2 получается в виде
(1-а) [1-24* (р)] п.
1 _ а _ а* (Ц) > « —
А’ (р)(! ~ g) (1 ~ ,2g) k1,2,. . .,
1 — о — Л* (|л) ’ ’ ’ ’
(6.54)
где ст—единственный корень уравнения ст = А*(2р— 2ро), лежащий в единичном круге. Аналогично, распределение времени ожидания в этой системе, полученное в виде (6.45), принимает вид
Г(у)=1------g(1~2?)^*z? р>0. (6.55)
1—а —4*(р) ’ а v '
Пример. В качестве примера рассмотрим систему М/М/2. Из равенств (6.21) и (6.32) имеем следующее выражение для ст:
X ° ~ 2р — 2ра + /. ’ ’
которое приводит к квадратному уравнению 2рст2 — (X 2р) ст — + X = 0. Вспомнив, что, по определению, р = Х/mp, т. е. в данном случае р = Х/2р, находим два корня этого уравнения: ст — 1 и ст = р. Очевидно, допустим только второй из них. Подобным же образом имеем
А*(р) = —А- = т--2?0,. .
р + /. 1 + 2р
Непосредственно из (6.54) получается решение для распределения числа требований в системе
278
и распределение времени ожидания
R7(z/)= 1 —-I^Le-2»‘<1-P>4'> t/>0. (6.57)
Сравнивая (6.56) с результатами и гл. 3 [равенства (3.37) и (3.39) 1, убеждаемся, что при т — 2 они совпадают.
Этим исследование системы G/M/m заканчивается. Некоторые дальнейшие интересные результаты можно найти в работе [2]. В следующей главе преобразования рассматриваются как вероятности, в результате чего достигается значительное сокращение аналитических усилий, необходимых для решения стационарных и нестационарных задач теории массового обслуживания.
СПИСОК ЛИТЕРАТУРЫ
1. Culicii, J. V». Tiie Single Server Queue. Wiiey (New-York), 19b9.
2. De Smit, J. H. A. On the Many Server Queue with Exponential Service Times. Advances in Applied Probability, 5, 170—182 (1973).
3. Kendall, D. G. Some Pboblems in the Theory of Queues. Journal of the Royal Statistical Society, Ser. B., 13, 151 —185 (1951).
4. Takacs, L. Introduction to the Theory of Queues. Oxford University Press (New-York), 1962.
ЗАДАЧИ
6.1. Докажите равенство (6.13) [Указание. Воспользоваться условием, что время между поступающими требованиями равно t, а затем условием, что для разгрузки очереди требуется время (</)].
6.2. Рассмотрим систему Еа/М/1 (с бесконечным числом мест для ожидания).
а) Выразите гк через о.
б) Вычислите о в явном виде.
6.3. Рассмотрим систему М/М/т.
а) Как сравнить рк с г4?
б) Сравните (6.22) и (3.40).
6.4. Докажите равенство (6.31).
6.5. Покажите, что (6.52) следует из (6.50).
6.6. Рассмотрим систему Нг/М/1, где Д = 2, Д = 1, р. = 2 и ai = 5/8.
а) Найдите о.
б) Найдите гк.
в) Найдите w (у).
г) Найдите W7.
6-7. Рассмотрим систему D/M/1 при р = 2 и том же р, что и в предыдущей задаче.
а) Найдите о (с точностью до двух десятичных знаков).
б) Найдите гк.
279
в) Найдите w (у).
г) Найдите W.
6.8. Рассмотрим систему типа G/M/1 с одним местом для ожидания Выразите rK (k — 0, 1,2) через р и A* (s).
6.9. Рассмотрим систему G/M/1, в которой стоимость ожидания в течение у секунд равна с (у) =
а) Найдите среднюю стоимость ожидания требования.
б) При каких условиях средняя стоимость будет конечной?
ГЛАВА 7
Метод коллективных меток
Работа по исследованию случайных процессов, встречающихся в теории массового обслуживания, обычно состоит из двух частей. Первая часть работы, как правило, требует тщательной вероятностной аргументации для того, чтобы получить выражения, содержащие интересующие нас случайные величины х. Вторая часть работы содержит анализ, причем здесь приходится формально манипулировать некоторыми символами либо в оригинальной, либо в преобразованной области. Так как вероятностная аргументация должна проводиться с большим вниманием, она оставляет приятное ощущение понимания физического смысла. С другой стороны, хотя проводимые аналитические выкладки обычно сводятся к достаточно прямым (хотя и трудным) формальным операциям, мы часто остаемся с неприятным ощущением, что эти операции по отношению к исходной задаче не имеют ясной и понятной интерпретации. Этот «нефизический» аспект решаемой задачи, как правило, возникает при переходе в область преобразовании (преобразования Лапласа или производящих функций).
В этой главе будет показано, что можно оперировать с преобразованиями, сохраняя при этом вероятностную трактовку-Для этого имеются две самостоятельные операции: метка требований и наблюдение процесса «катастроф». Вместе эти два метода называют методом коллективных меток. Обе операции не обязательно применяют одновременно, и ниже они исследуются порознь-Этот материал взят главным образом из работы [1 ]. Соответствующие идеи, дающие вероятностную интерпретацию преобразова ниям, были предложены в работе [2].
1 Например, аргументация, приводящая к (5.31) п (6.1).
280
7.1. МЕТКА ТРЕБОВАНИЙ
Предположим, что на входе GMO имеется устройство, которое метит входящие требования с вероятностями
Р [требование мечено] = 1 —г; (7.1)
Р [требование не мечено] = г, (7.2)
где 0-<г< 1. Предположим, что устройство метит требования с этими вероятностями независимо от всех других аспектов обслуживания. Как увидим ниже, этот процесс маркировки позволяет очень естественным путем получить производящие функции.
Будет поучительно проиллюстрировать применение процесса маркировки примерами.
Пример 1. Пуассоновский входящий поток. Прежде всего рассмотрим пуассоновский входящий поток с интенсивностью К требований в секунду. Предположим, что требования маркируются так, как говорилось выше. Рассмотрим вероятность
q (г, tjA Р [ни одно меченое требование за время (0, t) не поступило]. (7.3)
Очевидно, k требований за время (0, f) поступают с вероятностью (M)ke~ulk\. Кроме того, с вероятностью г* ни одно из этих требований не будет мечено. Последнее справедливо, поскольку маркировка разных требований осуществляется независимо. Суммируя по всем k, получим
q (z, t) = zk = ew P-O. (7.4)
*=o
Возвращаясь к равенству (2.134), видим, что выражение (7.4) представляет собой просто производящую функцию для закона Пуассона. Следовательно, эту производящую функцию можно
интерпретировать как вероятность, определенную равенством (7.3). Это не единственный случай, когда'производящей функции можно дать вероятностную интерпретацию.
Пример 2. Система М/М/оо. Рассмотрим СМО с процессом размножения и гибели, имеющую бесконечное число обслуживающих приборов. Предположим, что в момент t = 0 имеется i требований. Параметры системы, как обычно, X и р [т. е. А (/) = = 1 __ е-м и В (х) = 1 — е~^ ].
Представляет интерес величина
„ -Р* (t) = Р [k требований в системе в момент /]. (7.5)
Определим ее производящую функцию формулой (2.153):
р(г, о = (7'б)
6=0
УДем опять метить требования в соответствии с правилами (7.1) ® (7.2). По аналогии с примером 1 равенство (7.6) можно интер-Ретировать как вероятность того, что в системе в момент t не
содержится меченых требований (здесь член zk опять представляет вероятность того, что ни одно из имеющихся в системе требований не отмечено). Отсюда главное замечание: можно вычислить Р (z, t) прямо, находя вероятность того, что в системе в момент t нет меченых требований, вместо того, чтобы находить вероятность Pk (t), а затем вычислять ее производящую функцию!
Приступим к делу следующим образом: чтобы найти вероятность того, что ни одно из требований, присутствующих в момент t, не отмечено, подсчитаем эту вероятность для требований, присутствующих в момент 0, и для тех, которые поступают за время (0, t). Для любого требования, присутствующего в момент О, вероятность того, что оно все еще находится в системе в момент t и является меченым, получается как произведение вероятностей (1 — z) [1 — В (/)], где первый множитель соответствует вероятности того, что требование мечено, а второй — вероятности того, что обслуживание длится больше, чем t. Следовательно,
Р [требование, находящееся в системе в начальный момент, не является меченым и находится в системе в момент И =
— 1 __ (1 — г) е-м-С
Для новых требований, которые поступают в течение промежутка (0, t), имеем, как и раньше, Р [k требований в промежутке (0, t) ] = (ht)ke~M/k\. Если за этот промежуток времени поступают k требований, то моменты их поступления распределены в этом промежутке равномерно [см. (2.136)]. Рассмотрим одно из таких требований и предположим, что оно поступает в момент т < t. Оно не будет меченым требованием, присутствующим в момент t, с вероятностью
Р [новое требование не является меченым требованием, присутствующим в момент t, если оно поступает в момент т«7] =
= 1-(-г)[-В(^-т)]. (7.7)
Однако при Ост<t, Р [момент поступления < г] = x/t,поэтому Р [новое требование в момент t все еще находится в системе] =
= М('-’>4=-'^- <7-8>
о
Снимая условие, накладываемое на время поступления в равенстве (7.7), как показано в (7.8), получаем
Р [новое требование не является меченым требованием, на-]____________________________________________е-щ
ходящимся в системе в момент /1 = 1 — (1 — г)—— -.
[it
Таким образом, можно вычислить вероятность того, что в момент t нет меченых требований, следующим образом:
оо
Р (г, О = У Р Ik требований поступают в промежутке (0, /) 1 X 282
X {Р [повое требование не является меченым требованием, присутствующим в момент N}ft [Р [первоначальное требование является меченым требованием, присутствующим в момент Л}‘.
Применяя полученные равенства, приходим к соотношению
t 00
f Plz, 0 = У 4r~e'W [1-(1-г)1=7Г“] [l-(l-z)e-H',
j feo '
l которое дает известный результат:
I Р 0, о = [1 — (1 — z) е-^Т е-<*/и) (7.9)
г Читателю должно быть ясно, что обычный путь получения этого { результата предельно сложен.
J Пример 3. Система М/G/l. В этом примере мы рассматри-| ваем систему типа М/G/l с обслуживанием в порядке поступления. = Напомним, что случайные величины wn, tn+1, tn+2, хп, xn+i, ...
взаимно независимы. Как обычно, определим преобразование j. Лапласа В* (s) и (s) соответственно плотностей распределения | времени обслуживания b (х) и времени ожидания wn (у) для тре-'. бования Са. Определим событие
(среди требований, поступивших в про-1
• {нет М в wn] А {должение времени ожидания требования 1(7.10) - |с„, нет меченых. J
Найдем вероятность этого события Р [нет М в wn]. Рассматривая <[ условные вероятности при условиях, налагаемых на число поступающих требований и на время ожиданий wn, а затем снимая 4 эти условия, получим
Р [нет М в wn] =-- ^^~-^-KyzkdWn(y)^= dWn(y').
’ о о
В интеграле легко узнать (X — Xz), так что
| Р[нет М в шп]=Ч7*(Х— Xz). (7.11)
С Таким образом, снова получается простая вероятностная интер-। претация для преобразования Лапласа одного из важных распре-Iделений. Аналогичными рассуждениями можно получить
Р [нет М в х„] = В*(Х — Xz). (7.12)
Это последнее соотношение дает другую интерпретацию старого выражения, полученного в гл. 5.
Теперь приходит время сделать потрясающее открытие! Очевидно, что поступление требований за время ожидания требования С,г и поступление требований: за время его обслуживания Должны быть независимы между собой, так как эти промежутки времени не пересекаются, а процесс поступления требований не : 283
имеет последействия. Поэтому события, состоящие в том, что поступающие за эти промежутки времени требования не мечены, тоже независимы, и вероятность их совместного осуществления равна произведению вероятностей этих событий. Следовательно, можно записать
Р [нет М в wn 4- хп] = Р [нет М в wn\ Р [нет М в х„]; (7.13)
Р [нет М в wn + хп] = W* (X— Xz)B*(X— Xz). (7.14)
Этот последний результат приятен по двум причинам. Во-первых, потому, что он утверждает, что вероятность совместного осуществления двух независимых событий равна произведению вероятностей этих событий [равенство (7.13)]; во-вторых, потому, что он утверждает, что преобразование плотности распределения суммы независимых случайных величин равно произведению преобразований плотности распределения слагаемых [равенство (7.14)]. Эти два хорошо известных результата (относящихся к совместному осуществлению событий и к сумме независимых случайных величин) привели к новому, имеющему глубокий смысл, открытию: умножение преобразований соответствует не только сложению двух независимых случайных величин, но также и умножению вероятностей двух независимых событий! Возможность увидеть связь между такими фундаментальными законами представляется не часто.
Продолжим теперь рассуждения. В данный момент соотношение (7.14) нужно, чтобы выразить вероятность того, что за время wn + *п не поступит ни одного меченого требования. Вычислим эту вероятность исходя из других соображений. Очевидно,
Р [нет Л4 в wn -ф хп] = Р [нет Л4 в wn ф- хп и Cn+i мечено] 4--|-Р[нет М в + и С,,1+1 не мечено]. (7.15)
Кроме того,
Р[нет в wn-j-Xn и С„+1 мечено] = 0, если w„+l > О, так как, если требование Сп+1 должно ждать, то оно поступает в промежутке времени wn + хп, и не может быть, чтобы оно было мечено и чтобы одновременно осуществилось событие {нет М в wn 4~ хп}. Следовательно, первый член в (7.15) справа должен быть равен Р [аул+1 = 0] (1 —z), где второй множитель просто равен вероятности того, что требование С„+1 мечено.
Рассмотрим теперь второй член в правой части (7.15). Как видно из рис. 7.1, между требованиями Сп и С„+1 других требований не поступает, поэтому интересующие нас требования (а именно, поступающие после Сп+1, но все еще в промежутке wn + *«) должны относиться к промежутку а»„+1, который КОН-284
On
Обслуживающий прибор
Wn
Время
Очередь
Сп+1
'1 Требования не 11 поступают г*~ Ь/7 C/7+Z
™П->1
ft
Требования, представляющие интерес
Рис. 7.1. Поступление требований в промежутке времени wn ft- хп
чается вместе с промежутком wn + хп, Поэтому второй член справа должен быть
Р [нет М в wn хп и Сп+1 не мечено] =
= Р [нет М в шл+1] Р [Сп+1 не мечено] = Р [нет М в wn^]z.
На основании этих замечаний и с учетом равенства (7.11) можно переписать (7.15) в виде
Р[нет М в wn + xn] = (1—z)P[C„+1 поступает после wn + хп] + г!17*+; (X — Хг).
Если теперь представить себе другой, отдельный процесс маркировки, при котором с вероятностью единица метятся все требования (дополнительной меткой), и рассмотреть случай, когда ни одно из таких меченых требований не поступает за время wn + хп, то это будет означать, что вообще ни одно требование не поступает за этот промежуток времени (т. е. требование С,-г+1 поступает после w„ + хл). Эту вероятность можно рассчитать по формуле (7.14) при г = 0 (так как это гарантирует, что все требования мечены), что даст W* (X) В* (X). Таким образом, Р [нет М в дал + хл] = (1— z)H7*(X)B*(^ + zll7*+I(X — Xz). (7.16)
Теперь имеются два выражения для Р [нет М в wn + х„], которые можно приравнять и получить
Г* (X — Xz) В* (X — Xz) = (1 — z) Г: (X) В* (X) 4- zW*+ j (X — Xz). (7.17)
Интересная часть закончена. Применение метода коллективных меток приводит к равенству (7.17), которое не так легко получить другими методами, но которое фактически подтверждается результатами, полученными другими методами. Вместо того, чтобы останавливаться на технике дальнейшего исследования этого равенства, сошлемся на работу [1 ], где приведены дополнительные подробности для случая решения, зависящего от времени.
285
Теперь для р •< 1 имеем эргодический процесс с №*($) = = lim W* (s) при п-»-оо. Равенство (7.17) сводится при этом к виду
IT* (X — Xz) В* (X — Xz) = (1 — z) Г* (X) В* (X) + z№* (X — Xz). Производя замену переменной s — X — Xz и решая относительно IT* (s), получаем
т sW* (X) В* (X) w — s — X + ХВ* (s)
Так как W* (0) = 1, ходим к выражению
вычисляем W* (X) В* (X) = (1 — р) и при-
F* (8) =
S (1 — р)
s — X + ХВ* (s) ’
(7.18)
которое, очевидно, является уравнением Полячека—Хинчина для преобразования плотности распределения времени ожидания.
Мы рассмотрели три примера, когда маркировка требований позволяет путем чисто вероятностных рассуждений получить выражения, связанные с преобразованиями. Здесь был использован прямой, хотя и утомительный, анализ глубоких, нофизически обоснованных рассуждений. Рассмотрим теперь процесс катастроф.
7.2. ПРОЦЕСС КАТАСТРОФ
Метод коллективных меток можно несколько расширить, если перейти к исследованию процессов «катастроф». Начиная отсчет времени от нуля, рассмотрим некоторое событие, наступающее в момент времени t (t > 0), и обозначим через f (t) плотность распределения, связанную с моментами времени наступления этого события. Кроме того, пусть имеется независимый одновременно протекающий процесс катастроф, который порождает катастрофы 1 по закону Пуассона с интенсивностью у.
Вычислим вероятность того, что событие в момент t наступает перед первой катастрофой (считая от момента времени 0). Записывая условную вероятность при фиксированном t и интегрируя затем по t, получаем
Р [событие наступает перед катастрофой] —
со
= Je-v7(/)^ = F-(?), (7.19)
о
где, как обычно, / (t) фф F* (s) — пара преобразований Лапласа. Таким образом, получается вероятностная интерпретация преоб
1 Катастрофа — просто выразительное название, которое дано этим порождаемым моментам времени в отличие от события, наступающего в момент t.
286
разования Лапласа (вычисленного в точке у) плотности распределения времени наступления события, а именно: это вероятность того, что событие с такой плотностью распределения наступит раньше, чем катастрофа, возникновение которой описывается пуассоновским процессом с интенсивностью у. В качестве второй иллюстрации и применения процессов катастроф рассмотрим последовательность событий (т. е. поток однородных событий) в промежутке времени (0, оо). Начиная отсчет с нулевого момента времени, можно вычислить плотность распределения времени до n-го события, которую обозначим /(л) (f) *, и функцию распределения вероятностей F(ny (0, где. как и прежде, плотность распределения промежутка времени между событиями равна f (f). Таким образом,
^(л) (0 = Р [я-е событие наступает в момент t].
Представляет интерес выражение для функции восстановления Н (t), которая, как известно из параграфа 5.2, равна ожидаемому числу событий (восстановлений) за промежуток времени длины t. Начнем с определения:
Рп (() = Р [за время (0, t) наступает точно п событий]. (7.20) Функция восстановления может быть вычислена как со
H(t)=E [число событий за время (0, ()] — У пРп (t). п=<)
По определению Рп (/) = Fn (t) — />+!) (0> поэтому
со со
н (f) = I п [F(n) (t) — F(ri+^t)] = Е Ем (0- (7.21)
л=0 п=1
Если одновременно имеется пуассоновский процесс катастроф (с интенсивностью у), можно найти математическое ожидание следующей случайной величины:
Nc А число событий, наступающих до первой катастрофы. (7.22) С вероятностью ye~yl dt первая катастрофа происходит в промежутке времени (t, t + df)r и тогда Н (t) представляет собой среднее значение числа событий, наступающих до первой катастрофы: Н (t) = Е HVC| первая катастрофа, происходит в промежутке времени (t, t-pdt)].
Умножая условные математические ожидания на вероятности условий и интегрируя по t, получаем
£[УС]= ^H(t)y^‘dt. о
(7.23)
* Здесь используется нижний индекс п, чтобы напомнить определение (5.110) n-кратной свертки. Очевидно, (t) и есть n-кратная свертка плотности распределения срока службы f (/).
287
В параграфе 5,2 было введено преобразование Лапласа Н* (s) плотности восстановления h (/), определяемой в виде h (/) Д A dH тогда
H'(s) A j h(t)e-stdt. (7.24)
О
Интегрируя последнее равенство по частям, в правой части полу-ео
чаем j sH (t) e.-3tdt\ тогда из (7.23) (произведя замену s = у) найдем о
Е[Мс] = Я*(у). (7.25)
Вычислим теперь Е [A7C] другим способом. Из равенства (7.19) видно, что катастрофа возникает до первого события с вероятностью 1 — F* (у), и в этом случае Nc = 0. С другой стороны, с вероятностью F* (у) по крайней мере одно событие наступит до катастрофы. Пусть Мё — случайная величина Nc — 1 при условии, что произошло по крайней мере одно событие. Тогда Nc = 1 + N'c- Поскольку пуассоновский процесс — процесс без последействия и поскольку наступающее событие порождает вложенный марковский процесс, величина N'c должна иметь то же распределение вероятностей, что и Nc. Поэтому, образуя математическое ожидание величины Nc, можно написать
Е Ш = 0 [1 —F*(у)] + {1 + ЕF* (у).
Это непосредственно дает
(7.26)
Таким образом, имеются два выражения для Е [Мс]. Приравнивая их (и произведя замену s = у), окончательно получаем
= (7.27)
В этом последнем можно узнать выражение преобразования интегрального уравнения теории восстановления [см. уравнение (5.21)]. Его интегральная форма дана в уравнении (5.22).
Метод коллективных меток указывает чрезвычайно изящный путь получения некоторых важных и полезных результатов теории случайных процессов. С другой стороны, этот метод не дал пока никаких результатов, не полученных ранее другими методами. Поэтому его принципиальное значение в настоящее время заключается в том, что он дает возможность иначе увидеть фундаментальные соотношения, глубже проникнуть в вероятностную структуру процессов.
288
На этом заканчивается изучение промежуточной теории массового обслуживания. В последующей части мы рискнем проникнуть в царство систем массового обслуживания типа G/G/1.
СПИСОК ЛИТЕРАТУРЫ
1. Runnenburg, J. Th. On the Use of the Method of Collective Marks in Queueing Theory, Proc. Symposium on Congestion Theory, eds. W. L. Smith and W. E. Wilkinson, University of North Corolina Press (1965).
2. Van Dantzig, D. Sur la methode des fonetions generatrices. Colloques inter-nationaux du CNRS, 13, 29—45 (1948).
ЗАДАЧИ
7.1. Рассмотрим систему типа М/G/l, показанную на рисунке.
Интенсивность поступающего потока требований в системе равна X, а функция распределения времени обслуживания В (х). Требования обслуживаются в порядке поступления из очереди А до тех пор, пока они либо покидают обслуживающий прибор, либо получают а секунд обслуживания и направляются в блок накопления (см. рисунок). К тому моменту, когда очередь А разгрузится и обслуживающий прибор станет свободным, в блоке накопления соберется группа требований. В этот момент блок накопления выбрасывает накопленные требования в виде группового поступления в очередь В. Очередь В получает доступ к прибору обслуживания до нового поступления требования (называемого «стартовым») в очередь А, после чего обслуживающий прибор переключается с очереди В на очередь А, а обслуживавшееся требование возвращается в «голову» очереди В. Блок накопления опять начинает заполняться, и процесс повторяется. Пусть gri = Р [блок накопления поставляет в очередь В группу требований объема nJ;
G (г) -= £ gnz’1. n=>J
10 Л. Клейнрок
289
а) Дайте вероятностную интерпретацию величины G (г), используя метод коллективных меток.
б) Считая, что стартовое требование попадает в блок накопления, и используя метод коллективных меток, найдите [выражая через X, а, В (•) и G (z)] вероятность Рк = Р [за время обслуживания стартового требования в очередь А поступают k требований, и ни одно меченое требование не поступает в блок накопления из k подпериодов занятости, порожденных в очереди А каждым из этих требований I. в) Считая, что стартовое требование не достигает блока накопления, найдите определенную выше вероятность Рк. г) На основании п. бив выпишите уравнение (содержащее интеграл), связывающее к, а, В (•) и G (г).
д) На основании п. г найдите средний размер группы
оо
« = S ngn-
п=0
7.2. Рассмотрим систему типа M/G/oo. Требуется найти вероятность Р (z, t), определенную равенством (7.6). Предположим, что система содержит 1 = 0 требований в момент t = 0. Пусть р (/) — вероятность того, что требование, поступившее за промежуток времени (0, I), все еще присутствует в момент t. Будем действовать, как в примере 2 параграфа 7.1.
а) Выразите р (f) через В (х).
б) Выразите Р (z, t) через %, t, z и р (t).
в) Из п. б найдите Pk (/), определенную равенством (7.5).
г) Из п. в найдите lim Pk (t) Pk при
7.3. Рассмотрим систему типа М/G/l, свободную в момент 0. Пусть р = Р [за время, пока обслуживающий прибор занят требованиями, поступившими в промежутке времени (0, t), не произойдет катастрофа 1 и пусть q = Р [не произойдет катастрофы за время (0, t + U (/)], где U (I) — завершенная в момент tработа. Катастрофы происходят с интенсивностью у. а) Найдите р.
б) Найдите q.
в) Интерпретируйте р—q как вероятность и найдите независимое выражение для нее. Затем используйте п. а и б для установления связи между распределением незавершенной работы и В* (s).
7.4. Рассмотрим систему типа G/M/m. Корень ст, определяемый уравнением (6.21), играет центральную роль в решении. Проверьте уравнение (6.21) с точки зрения метода коллективных меток и дайте вероятностную интерпретацию для <т.
ЧАСТЬ IV
ОБЩАЯ ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
Вступая в предгорье систем типа G/G/1, мы становимся на зыбкую почву. Для этих систем неизвестно даже среднее время ожидания! Тем не менее в гл. 8 будет развит спектральный метод исследования этих систем, который зачастую приводит к полезным результатам. Трудная часть этого метода, как это часто можно было видеть, сводится к определению положения корней функции. Спектральный метод невыгоден из-за отсутствия общих характеристик модели системы. Каждая новая система должна исследоваться сама по себе. Однако в этой главе будет обсуждаться алгебра Кингмана для очередей, которая очень тонко выявляет общие построения всего разнообразия методов, использованных до сих пор, для наступления на систему типа G/G/1. Наконец, будет введено понятие двойственной системы, некоторые основные результаты будут выражены через периоды простой системы и через двойственные системы.
10*
291
ГЛАВА 8
Система массового обслуживания типа G/G/1
До сих пор при изучении систем массового обслуживания типа М/М/1, М/G/l и G/M/m эффективно использовались марковские свойства этих систем. Теперь придется отбросить многие (хотя и не все) упрощения, вытекающие из марковских свойств, и искать новые методы изучения более сложной системы типа G/G/1.
В этой главе будем решать уравнения для системы типа G/G/1 спектральным методом, используя технику преобразований и методы теории функций комплексного переменного. Имеются, однако, и некоторые другие подходы. В параграфе 5.11 были введены лестничные индексы и указан путь, связывающий их с важными характеристиками систем массового обслуживания. Эти идеи могут быть распространены и применены к общей системе типа G/G/1.
Флюктуации сумм случайных величин (т. е. лестничные индексы) изучал Андерсен [1—3], а также Спитцер [13, 15], который упростил и продолжил работу Андерсена. Это привело (среди других результатов) к тождеству Спитцера, значение которого в исследованиях по теории массового обслуживания очень велико. Значительно раньше (в 1930 г.) Полячек рассматривал формальный подход к решению таких систем, и его подход (итог которого относится к 1957 г. [10]) называется сейчас методом Полячека. Позже Кингман [7 ] построил алгебру очередей, которая определила место всех этих методов в общем здании и вскрыла их общность. Он заметил, где и почему решение проблемы наталкивается на трудность, но, к сожалению, показал также, что этот метод неприменим к многолинейным системам массового обслуживания. Кейлсон [6] применил метод функции Грина. Бенеш [4] изучал систему типа G/G/1 с использованием незавершенной работы и других относящихся к ней понятий.
Установим теперь основные уравнения для этой системы.
292
8.1. ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ЛИНДЛИ
В рассматриваемой системе массового обслуживания промежутки времени между поступающими требованиям независимы и имеют произвольную функцию распределения А (4). Продолжительности времени обслуживания также независимы, причем время обслуживания имеет произвольную функцию распределения В (х).
Предполагается, что имеется один обслуживающий прибор и что обслуживание осуществляется в порядке поступления требований. В этом параграфе получено основное соотношение между случайными величинами, характеризующими систему, которое приводит к интегральному уравнению Линдли. Решение этого уравнения дано в следующем параграфе.
Рассмотрим последовательность поступающих требований, пронумерованных индексами, и вспомним принятые ранее обозначения:
Сп — п-е требование, поступающее в систему;
4„ ~ — тп_1 — промежуток времени между поступлениями
требований Сп_г и СД
хп — время обслуживания требования Сп\
wn — время ожидания требования Сп (в очереди).
Предполагается, что случайные величины {4„| и [хл| независимы и задаются соответственно функциями распределения А (4) и В (х), не зависящими от индекса п. Как обычно, для упрощения анализа ищем марковский процесс. Вспомним, что для системы типа М/G/l незавершенная работа U (4) для всех 4 является марковским процессом. Для системы типа G/G/1 должно быть ясно, что хотя процесс U (I) уже не будет марковским, в него вложен марковский процесс, определенный в моменты поступления требований. В эти моменты возрождения вся прошлая история, влияющая на будущие характеристики системы, собрана в текущем значении функции U (t). А именно, для систем с обслуживанием в порядке поступления значение незавершенной работы непосредственно перед поступлением требования Сп в точности равно времени ожидания wtl, и этот марковский процесс и будет в дальнейшем объектом изучения.
На рис. 8.1 и 8.2 использованы обозначения для очередей в виде временных диаграмм (как определено на рис. 2.2). Они иллюстрируют историю требования Сп в двух случаях: рис. 8.1 представляет случай, когда требования Сп+1 поступает до того, как требование С„ покидает обслуживающий прибор, а рис. 8.2 изображает случай, когда Сп+1 поступает в освободившуюся систему. Из рис. 8.1, ясно, что 4,1+1 wn+1 = w„ + хп. Таким образом,
= wn + хп — tn+i, если wnA-xn — 4„+1>0. (8.1)
293
____wn____
ОЬслуживашлии I
vnufinp
Время
Очередь
Рис. 8.1. Случай, когда требование + , поступает в занятую си-
стему
Условия, выраженные соотношением (8.1), гарантируют, что, поступая в систему, требование С,.+1 застает ее занятой. Из рис. 8.2 непосредственно видно, что
®л+1 = 0, если wn Ч-х„ — f„+1< 0, (8.2)
и это условие гарантирует, что поступающее требование застает систему свободной. Для удобства определим новую (основную) случайную величину и„ в виде
unAxn — tn+1. (8.3)
Эта случайная величина представляет собой разность между временем обслуживания требования Сп и промежутком времени между поступлениями требований С„+1 и Сп (для стабильных систем требуется, чтобы математическое ожидание величины ип было отрицательным). Объединяя (8.1)—(8.3), получим следующее фундаментальное и все еще элементарное соотношение, впервые установленное Линдли [8]:
4- и„, если wn 4- и„ 0;
W„+1 = 1 , л (8.4)
[ 0, если wn-\-un^Q. '
Член wn иа представляет собой сумму незавершенной работы (te»„), имеющейся в системе при поступлении требования Сп, и времени обслуживания (хл), которое это требование добавляет к незавершенной работе, без учета промежутка времени (^+1)
294
до поступления следующего требования C„+i. Если эта величина неотрицательна, то она представляет собой ту незавершенную работу, которую застает при своем поступлении требование C,i+1, т. е. время ожидания w.l+1. Однако, если эта величина оказывается отрицательной, это означает, что незавершенная работа, имеющаяся в системе уже после поступления требования Сп, оканчивается до поступления следующего требования, т. е. требование CllVi застает систему пустой.
Уравнение (8.4) можно переписать в виде
inax [0, w„ | z/J. (8.5)
Введя обозначение (х)+Л max [0, х], получим
^л+1 = Иг + »„)+.
е (8.6)
Так как случайные величины {tn] и {xj независимы и между собой и внутри каждой совокупности, то можно заметить, что последовательность случайных величин (uz0, wlt w2, ...} образует марковский процесс со стационарными вероятностями перехода. Это непосредственно видно из равенства (8.4), так как последняя величина а»„+1 зависит от предыдущей последовательности величин Wt (i = 0,1, ..., п) только через последнюю величину wn плюс случайную величину и,„ не зависящую от случайных величин Wi при всех i с п.
Решим последовательно уравнение (8.5), начиная с ш0. Имеем (определяя Со как начальное требование).
= (®о ~г “о)+;
w2 = (uzj 4 и()+ = max [0, wt -|- ut] —
= max [0, Uy 4- max (0, w0 4- »0)l —
= max [0, ult tiy 4- u0 4- w0];
ws = (w2 4- u-iY = max [0, w2 + =
= max [0, и2 4- max (0, ult ut 4- «-0 4~ ay0)l =
= max [0, u2, u2 4~ Uy,u2 4~ Uy 4- u,t 4~ Щ)] —-
wn = (“»«-! 4- «л-1)+ = max [0, un_y] =
= max-[0, un_y, utl_y 4- un_2,. . un_y p------5
4- Mi, un~i Uy -f- Uq ИА)].
(8-7)
Однако, поскольку последовательность случайных величин [и,] состоит из независимых одинаково распределенных величин, то 295
они «взаимозаменяемы», и можно рассматривать новые величины w'n с тем же распределением вероятностей, что и w„, где
w’n A max [0, tii, utt 4
-\-щ -4 и,, ..., //„ f tit -|- tin_2, ии 4 //г 4 - • И ча.2 I- 4„_i г о»0].
(8.8)
Равенство (8.8) получается из (8.7) перенумерацией случайных величин и,. Теперь удобно определить величины Un в виде
п-1
и., --= So«/.
t/o = O. (8.9)
В новых обозначениях равенство (8.8) можно переписать в виде
Wn = max(t/0, (71, (/2, Un-л, Un-^wo]. (8.10)
Из последнего выражения видно, что при w0 = 0 величина w„ может только возрастать с ростом п. Поэтому должна существовать предельная (возможно бесконечная) случайная величина w = = lim w', причем
w — sup (/„. (8.11)
n>0
Вложенная цепь Маркова эргодична, если с вероятностью единица величина w конечна; и если так, то как функция распределения величины wn, так и функция распределения величины w'n сходятся к функции распределения величины w. В этом случае распределение величины w представляет собой распределение времени ожидания. Линдли 18] показал, что при условии 0 < Е [| и„ |] < со система стабильна тогда и только тогда, когда Е [uj < 0. Поэтому в дальнейшем будем предполагать, что
£[«„|<0. (8.12)
Неравенство (8.12) представляет собой обычное условие стабильности, что видно из следующего:
Е [н„] = Е[хп — tn+l\ = Е [х(1] — Е [4+1] = х —1 = i (р — 1), (8.13) где, как обычно, предполагается, что среднее время обслуживания равно х, а средняя длина промежутка_времени между поступающими требованиями равна t (и р = х/(). Из выражений (8.12) и (8.13) видно, что для стабильности системы надо потребовать, чтобы р < 1; это постоянно встречавшееся в предыдущих главах условие представляет собой условие стабильности.
Определим, как всегда, стационарную функцию распределения для w„ (и, следовательно, для w'n) в виде
lim Р [да,, с у\ = lim Р [а'п < у\ --= № (у). (8.14)
Ц-i» оо Ц > Г..
!96
Рис. 8.3. Незавершенная работа U (t) для последовательности поступлений и уходов требований
Этот предел должен существовать при р < 1 [8]. Следовательно, W (у) будет функцией распределения времени, проведенного в очереди. Эта функция предполагается стационарной. Не задерживаясь на доказательстве ее существования, остановимся на методе ее вычисления. Как известно, для таких марковских процессов это предельное распределение не зависит от начального значения щ0.
Прежде чем перейти к формальному выводу, исследуем, каким путем равенство (8.7) фактически позволяет получить время ожидания. Проделаем это на примере. Рассмотрим рис. 8.3, иллюстрирующий незавершенную работу U (t). Для последовательности поступлений и уходов требований, приведенных на этом рисунке, в таблице указаны значения длин промежутков времени между поступлениями £,;+1, времени обслуживания х„, случайных величин ип и значения времени ожидания wn, найденные по рисунку. В последней строке таблицы приведено время ожидания wn, вычисленное по (8.7), как показано ниже.
Таблица значений величин к рис. 8.3
п 0 1 23456789...
61+1 xn Щ1 wn 12 2 1 2 3 12 11—11 0 12 1 0 12 1
5 1 2 7 1 . . .
1 3 1 1 2 3. .
-4 2 -1-0 1 ...
2 0 2 1 0 1..
2 0 2 1 0 1..
. определено по рис. 8.3 . вычислено по уравнению (8.7)
»о-О;
а>1 — max (0, z/„) . max (0, 1) = 1;
w2 ~ max (0, щ, u4 -ф ий + иД п1ах (0, 1, 2)—2;
0*3 = max (0, u2, u2 uL |- ua te>0) — max (0, —1, 0, 1) — 1;
max (0, и2, u2 u2, ф н-i + ":i “b "2 + Щ + ч0 4- вд0) =
= max (0, 1,0, 1, 2) — 2;
297
II |> < > ;i . >, i ,;ч e н и e т а б л н и ы
ws-= max (0, щ, zz4-|-«5, llt 4 uaua, e4T«3 p«2 l-Kj, «)ф«>'|-"з + + «1 + u„ -|- K'o) — max (0, —4, —3, —4, —3, —2) 0;
m6 --max (0, 2, 2, -1, —2, — 1, 0) = 2;
w- = max (0, — 1, 1, —3, —2, —3, —2, —I) 1;
ш8 = max (0, —6, —7, —5, —9, —8, —9, —8, —7) = 0;
ki9 — max (0, 1, —5, —6, —4, —8, -7, —8, —7, —6)^1.
Эти вычисления довольно примечательны. Например, как только будет найдено такое т, при котором w,n = 0, вычисления wn для всех n > m в последующих расчетах по (8.7) не потребуются. Это является следствием того факта, что после окончания периода занятости время обслуживания и промежутки времени между поступающими требованиями в этом периоде не могут влиять на вычисления в следующих периодах занятости. Таким образом, здесь сказывается изолирующий эффект периодов простоя, возникающих между периодами занятости. Кроме того, koi Дс1 — о, последний справа член J сг^даст (с соратпым знаком) общее время простоя системы за время (0, тт).
Приступим теперь к теоретическому вычислению W (у). Обозначим через С„ (и) функцию распределения случайной величины щ, т. е.
(м) А Р К = 4, — tn+1 < м],
(8.15)
и заметим, что возможные значения и,, не ограничены полупрямой. Выразим С„ (и) через А (/) и В (х):
С„ (и) = Р [хп — tn+1 < и] J Р [хп « и з ;л+11 tn+1 = t] dA (t). и
Однако время обслуживания требования С,г не зависит от tn+u поэтому
Сп(и')-= j В (м + t) dA. (/). (8.16)
i=0
Таким образом, как и следовало ожидать, Са (м) не зависит от п, и можно написать
Сп(и)ДС(и) — j В (и LJ)d4(/). (8.17)
(=0
Итак, пусть и означает случайную величину и — х — I. Заметим, что интеграл, стоящий в равенстве (8.17), очень похож на свертку а (0 и В (х). Он не является точной сверткой, так как С (и) представляет собой функцию распределения разности величин хп 298
и а не их суммы. Применяя обозначение свертки Э и определяя с„ (и) A dCn (u)/du, получаем
c„(w) — с (и) = «(—и) 0 h (id. я (8.18)
Удобно (опять) определить функцию распределения времени ожидания требования С„ в виде
1УДу)-= Р [да„ < у[. (8.19)
Для у > 0 из равенства (8.4) получаем
со
W>1+1 (у) = Р [ЗУ„ + < у] = j Р l«n < У — w I wn = w\d.Wп (w).
G-
А теперь снова, поскольку ип не зависит от получаем
со
Wn+1 (у) = j" Cn(y—w)dWn(w) при у>0. (8.20)
и-
Однако, как постулировано равенством (8.14), это распределение имеет предел W7 (у), поэтому получается следующее интегральное уравнение, определяющее предельную функцию распределения времени ожидания для требований в системе типа G/G1:
W=~-J'c(y
и
да) dW (да) при у > 0.
Далее ясно, что
W (у) — 0 для у ' 0.
Объединяя два последних равенства, получим интегральное уравнение Линдли. [81, которое является уравнением типа уравнения Винера—Хопфа [14]:
«7(у) =
j С (у — w)dW(w), о-
У>0;
(8.21)
У < 0.
Уравнение (8.21) может быть переписано ио крайней мере в двух полезных формах, которые будут сейчас получены. Интегрируя по частям, находим (при у 0)
IF (у) С (у - - да) IV7 (да) | : J W .
'' dC (у — да) =• liin С п/ — да) 1У <да) — ( (у) IF (0 ) |
-> -х
J IF (да! УС (у — да).
"99
Очевидно, что lim С (у — w) = 0 при w --> со, так как С (и) при п — > оо является вероятностью того, что промежуток времени между поступающими требованиями стремится к бесконечности. Эта вероятность равна нулю, если промежуток времени имеет конечные моменты распределения. Аналогично, W (0") = 0, поэтому интегральное уравнение Линдли может быть переписано в виде
W(y) =
со
j W (ш) dC {у — о>), у > 0;
о~
(8.22)
Покажем теперь третью форму этого уравнения. После простой замены переменной и = у — w в уравнении (8.22) получаем
^) =
ц
j (У — w) dC (и),
— оо
о,
(8.23)
Все три уравнения, (8.21)—(8.23), описывают основные характеристики системы типа G/G/1. Эти интегральные уравнения, как уже отмечалось, являются уравнениями типа Винера—Хопфа и небезызвестны в теории случайных процессов.
Из этих форм интегрального уравнения можно заметить, что интеграл Линдли почти, но не совсем, имеет вид свертки. Важным отличием является то, что интегральная форма уравнения Линдли имеет место только для неотрицательных значений аргумента. Для отрицательных значений аргумента функция распределения тождественно равна нулю. Так как интеграл получается только для полуоси, то для решения уравнения, к сожалению, приходится пользоваться техникой, заимствованной из теории функций комплексной переменной и контурного интегрирования. С аналогичными трудностями приходится иметь дело в математической теории связи при расчете оптимальных линейных фильтров. Там также оптимальное решение описывается интегральным уравнением Винера—Хопфа, с тем отличием, что в случае линейного фильтра неизвестная функция появляется в виде одного множителя под интегралом, а в теории массового обслуживания неизвестная функция появляется в обеих частях уравнения. Тем не менее техника решения удивительно похожа, и читатель, знакомый с теорией оптимально реализуемых линейных фильтров, легко узнает приводимые доводы.
В следующем параграфе будет дано весьма общее решение интегрального уравнения Линдли с помощью спектральных методов (методов преобразований). В задаче 8.6 решение проверяется на примере, не требующем преобразований. Выбранный пример 300
относится к системе типа D/Е,/1, рассмотренной Линдли. В этом (прямом) подходе”' требуется сделать предположение о форме решения. Сейчас рассмотрим спектральное решение уравнения Линдли, в котором не требуется предположения о форме решения.
8.2. СПЕКТРАЛЬНОЕ РЕШЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ЛИНДЛИ
В этом параграфе будет описан метод решения интегрального уравнения Линдли, основанный на спектральном разложении [12]. Исходным пунктом будет служить уравнение в форме (8.23). Как уже отмечалось, это уравнение можно было решить непосредственно, если бы справа стояла настоящая свертка (в действительности эта свертка только для неотрицательной полуоси переменной у). Чтобы обойти эту трудность, применим следующую простую схему: определим «дополнительное» время ожидания, которое дополняет свертку и которое дает значение интеграла только для отрицательных у, т. е.
№ (г/)Д
у
J Wz (у — и) dC (у), — со
У <0.
(8.24)
Заметим, что левая часть уравнения (8.23) по аналогии могла бы быть обозначена через W+ (у). Сложив (8.23) и (8.24), получим справа интегральное выражение для всех значений аргумента, т. е.
У
W (У) + (У)— J (У — и)с («) du для всех действительных у,
— со
(8.25) где через с (и) [Д dC (u)/du] обозначена плотность распределения величины и.
Для начала предположим, что плотность распределения промежутка времени между поступающими требованиями имеет вид 1 0 (e~fl9 при t •—> оо (где D — некоторая положительная постоянная), т. е.
Ит-^-<оо- (8.26)
е
Условие (8.26) означает, что плотность распределения, связанная с промежутками времени между поступающими требованиями,
1 Обозначение О (g (х)) при х —> х0 относится ко всякой функции, которая (при х -+ х0) стремится к нулю, по крайней мере с той же скоростью, что и g (х), где g (х) > 0, т. е. lim I | К < со.
301
для больших промежутков времени убывают по крайней мере так же быстро, как показательная функция. При этом условии, как видно из равенства (8.17), характер функции С (w) при и —оо зависит от характера промежутков времени между поступающими требованиями. Это справедливо, поскольку при больших отрицательных значениях и аргумент функции распределения времени обслуживания положителен только при больших значениях t, которые являются также значениями аргумента плотности распределения промежутков времени между поступающими требованиями. Следовательно, можно показать, что
1- С (и)
hm —ЕД <.,00.
w->— оо е
Это значит, что С (и) = О (eDu) при и —> — оо. Если использовать этот факт в уравнении (8.24), то легко установить, что также 1F_ (у) = О (eDjz) при у •—» — оо.
Определим теперь некоторые (двусторонние) преобразования.
Для функции W_ (у) определим преобразование Лапласа
оо
Ф_(8)Д J lE_(z/)e-sv< ---------00
(8.27)
В силу условия, установленного при рассмотрении асимптотического свойства W_ (у), ясно, что функция Ф_ (s) аналитична в области Re (s) < D. Аналогично для функции распределения времени ожидания W (у) определим
оо
Ф+(5)Д J W(y)eSIIdy. — со
(8.28)
Заметим, что Ф+ (s) есть преобразование Лапласа функции распределения времени ожидания, в то время как в предыдущих главах было определено преобразование Лапласа W* (s) плотности распределения времени ожидания. Поэтому в соответствии со строкой 11 табл. 1.3 приложения I имеем
зФ+ ($) •= 1Г': (s).
(8.29)
Исключая на основании уравнений (3.23) и (8.2-1) области, в которых функции обращаются в пуль, можно переписать эти преобразования в виде
Ф (,s)j VE (//) е .(у; (8.30)
<!»., (s) ] W (у)е dy.
(1
(8.31)
302
Так как функция W' (у) является функцией распределения (и поэтому она ограничена при у - > оо), то Ф+ (s) аналитична при Re (s) > 0. Как обычно, обозначим через A* (s) и В* (s) соответственно преобразование Лапласа плотности распределения промежутков времени между поступающими требованиями и плотности распределения времени обслуживания. Заметим из условия (8.26), что А* (—s) аналитична в области Re (s) < D, как и функция Ф_ (s).
Как следует из приложения I, преобразование Лапласа свертки равно произведению преобразований Лапласа свертываемых функций. Равенство (8.18) дает почти свертку плотности распределения времени обслуживания и плотности распределения промежутков времени между поступающими требованиями. Единственная трудность состоит в том, что у второй из этих плотностей аргумент отрицателен. Тем не менее отмеченный выше факт умножения преобразований действует и при отрицательном аргументе (в этом состоит задача 8.1). Таким образом, для преобразования Лапласа функции с (и) находим
C*(s) —/1*( -s)B*(.s). (8.32)
Вернемся теперь к уравнению (8.25), выражающему фундаментальное соотношение между величинами, характеризующими рассматриваемую задачу, и функцией IE (у) распределения времени ожидания. Очевидно, время, проведенное в очереди, должно быть неотрицательной случайной величиной, поэтому в правой части (8.25) стоит свертка функции распределения времени ожидания и плотности случайной величины и. Поэтому преобразование Лапласа этой свертки должно быть произведением преобразования Лапласа Ф+ (s) (для функции распределения времени ожидания) и С* (s) (для плотности распределения величины и). Как следует из (8.30) и (8.31), преобразование левой части равно Ф+ (s) + Ф_ (s), следовательно,
Ф+ (s) + Ф_ (s) = Ф+ (s) С* ($).
Таким образом, из равенства (8.32) получается
ф+ (S) + ф_ (S) = Ф+ (s) Л* (—S) В* (s), что дает
Ф_ (S) = Ф+ (s) [Л* (—S) В* (s) - 1]. (8.33)
Мы уже установили, что функции Ф_ (s) и А* (—s) аналитичны в области Re (s) < D. Кроме того, так как Ф+ (s) и В* (s) являются преобразованиями ограниченных функций неотрицательных переменных, обе эти функции аналитичны в области Re (s) > 0.
Перейдем к спектральному разложению. Его цель состоит в том, чтобы для выражения
Л*(---5)В*(в) — I (8.34)
303
найти подходящее представление в виде произведения двух множителей. Задержимся немного, чтобы вспомнить метод этапов, посредством которого Эрланг реализовал простую идею аппроксимации распределения с помощью объединения последовательных и параллельных показательных этапов. Преобразование Лапласа, которое может быть получено таким образом, было в общем виде дано равенствами (4.62) и (4.64). Легко видеть, что они представляют собой рациональную функцию от s (т. е. частное от деления двух многочленов от s). Можно попытаться подобным же образом аппроксимировать каждое из преобразований Лапласа А* (—s) и В* (s). Если это удастся, то выражение (8.34) также будет рациональной функцией s. Выберем для рассмотрения такие системы массового обслуживания, для которых A* (s) и В* (s) можно надлежащим образом аппроксимировать такими рациональными функциями (или которые с самого начала имеют такой вид). В этом случае можно предложить следующее спектральное разложение:
Л*(—s)B*(s) — 1==^-. -(8.35)
Очевидно, ’F+ (s) 'lr_ (s) будет некоторой рациональной функцией от s, и теперь желательно найти для этого выражения разложение на множители. В частности, желательно найти такое разложение, при котором:
Для Re (s) >0 функция ЧД (s) является аналитической без нулей в этой полуплоскости; (8.36)
Для Re (s) < D функция (s) является аналитической без нулей в этой полуплоскости.
Кроме того, эти функции должны обладать следующими дополнительными свойствами:
для Re (s) > 0 lim ^s-- .= 1; |s|->oo S
_ (8.37)
для Re (s) < D lim — — j S
Условия (8.37) удобны и должны иметь в пределе противоположную полярность, так как при s, стремящемся к бесконечности по мнимой оси, обе функции А* (—s) и В* (s) должны стремиться к нулю (если предположить существование конечных моментов распределения и исключить возможность наличия у функций A (t) и В (х) бесконечного числа разрывов). При этом в левой части (8.35) в пределе получается —1, что и достигается при делении надлежащим образом подобранных пределов из условий (8.37). Основная трудность метода состоит в том, чтобы найти функции W+ (s) и ¥_ (s), удовлетворяющие требуемым условиям. Однако, 304
предположив, что такое разложение найдено, равенство (8.33) можно записать в виде
ф_(*) = Ф+(«)^
или
Ф_ (s) Чг (s) = ф._ (s) 'F. (s),
(8.38)
причем общая область аналитичности обеих частей равенства (8.38) характеризуется неравенствами
0^Re(s)<£>. (8.39)
В справедливости последнего можно убедиться следующим образом. Мы уже предполагали, что функция (s) аналитична в области Re (s) > 0. Это же справедливо для функции Ф+ (s), являющейся преобразованием Лапласа функции, тождественно равной нулю для отрицательных значений аргумента. Следовательно, произведение этих двух функций тоже должно быть аналитической функцией в области Re (s) > 0. Аналогично, функция 'F (s) является аналитической в области Re (s) < D, и на основании (8.27) функция Ф_ (s) также аналитична в этой области. Следовательно, произведение двух последних функций также представляет собой функцию, аналитическую в области Re (s) < D, а общая область аналитичности обоих произведений определяется неравенствами (8.39).
Равенство (8.38) устанавливает, что эти две функции равны в общей области аналитичности и представляют собой функцию, которая может быть аналитически продолжена как в область Re (s) < 0, так и в область Re (s) > D. Значит, ее аналитическое продолжение не имеет особенностей во всей конечной s-плоскости. Установив, что функция Ф+ (s) ЧС ($) = Ф_ (5)ЧС (s) аналитична и ограничена во всей s-плоскости, и предположив выполненными условия (8.37), можно применить теорему Лиувилля [17]*, которая устанавливает, что эта функция должна быть постоянной величиной (скажем, А). Таким образом,
ф_ (s) У-(S) = ф+(s) Т+(s) ==/<. (8.40)
Отсюда непосредственно
ф+(>) - <8-41> 1 +
Вспомним, что все проведенные выкладки были нужны для того, чтобы найти выражение функции распределения времени ожидания, преобразование Лапласа которой есть функция Ф+ (s), записанная сейчас в форме (8.41). Остается продемонстрировать метод вычисления постоянной К.
* Теорема Лиувилля устанавливает, что «Если функция f (г) аналитична И ограничена для всех конечных значений г. то / (z) равна константе».
305
Так как s'l>+ (s) -= (s), то
s=P+(s) dW(y).
Рассмотрим предел этого выражения при s - 0. Работая с правой частью, получим
lim f e~s>'dW (у) = j' dW (у) ~ 1. s^o i j
(I- II-
Таким образом, устанавливаем, что
lim зФ+(s) -= 1. (8.42)
s^O
Это ничто иное, как теорема о предельном значении (строка 18, табл. 1.3), и она следует из того, что W (оо) = 1. Из (8.41) и этого последнего результата получаем
lim хФ+ (:;) lim I,
s->i) V-| 's,
так что можно написать
Д' = Нт—---. (8.43)
s->l’ S
Равенство (8.43) дает значение Д’ для подстановки в (8.41). Если разложить функцию ¥+ (s) в ряд Тейлора в окрестности нуля PF+ (s) = Т+ (0) + st;1’ (0) + (s2/2!) ЧТ(0) + •• ] и учесть, что Ф+ (0) = 0 [это следует из (8.35) и (8.36) ], то легко видеть, что
К = lim , (8.44)
и это дает другой путь вычисления постоянной Д. Можно далее определить постоянную К, найдя значение Ф+(s) ЧД. (s) где-нибудь в области Re (s) >0 [см. (8.40) J. Выберем для такой проверки предел при s- >оо, поскольку из (8.37) известно, что T+(s) при s—>со ведет себя, как з.
Следовательно,
ео
К lim Ф+ (s) T+ (s) --- lim Ф+ (s)s- = lim s j e*s''' W' [y] dy. S co S -> co S -> co _
0
Выполнив замену переменной sy = x, получим
d.X.
30(5
При s —> оо можно вынести за знак интеграла постоянный член W (0+) и вычислить оставшийся интеграл, равный единице. Тогда получим
К = Ч7(0+). (8.45)
Это устанавливает, что постоянная К есть вероятность того, что поступающее требование застает систему свободной, т. е. не должно ждать *.
Таким образом, в предположении, что спектральное разложение (8.35) может быть вычислено, можно сразу найти преобразование Лапласа функции распределения времени ожидания по формуле (8.41), где постоянная К определяется одним из трех выражений (8.43), (8.44) или (8.45). Остается найти еще обратное преобразование, но задачи, связанные с такими вычислениями, уже неоднократно были рассмотрены ранее.
Можно решать задачу с помощью функции (s) вместо функции 4*+ (s), и иногда это упрощает вычисления. В таких случаях нужно исходить из равенства (8.35), чтобы получить
4f+(s) = 4l * *'_(s)[A*(—s)B*(s)—1]. (8.46)
Тогда из равенства (8.41) следует, что
ф+ [A* (-S) В* (s) ЛПруДГТ (8-47)
Чтобы вычислить в этом случае постоянную К, нужно продифференцировать равенство (8.46) при s = 0; это дает
YV’ (0) = [А* (0) В* (0) - 1] Ч^1’ (0) +
+ 'К. (0) [Л* (0) В* (1) (0) - А*(1) (0) В* (0)]. (8.48)
В левой части, как видно из (8.44), стоит постоянная К, а вычислив правую часть, можно получить К. = 0+Чг_(0) [—х + /1, что дает
К^¥_(0)(1 -р)7. (8.49)
Таким образом, используя для решения 'F (s), получим преобразование функции распределения времени ожидания в виде (8.47), где постоянну.ю вычисляют по формуле (8.49).
Подводя итог, можно сказать, что, если нужно найти спектральное разложение (8.35), выбирают один из двух возможных методов получения преобразования Лапласа функции распределения времени ожидания. Первый метод дает
ф (.) __J—lim- 11 л («.59)
+ и 'И, (Д .S ЧМА
1 Заметим, что W (0 ) необязательно равно величине 1—р, которая представ-
ляет собой долю времени простоя обслуживающего прибора (раш-щ-ню име-от
место для систем типа M/G/1).
307
Im(s)
s плоскость
а второй приводит к формуле
Ф+(5) =
(0)(1 ~p)F
[Л* (—s) В* (s)—~ 1] T'_ (s)
—X-------о---- --------и---------
-ji -/1+Л Л fiefs)
Рис. 8.4. Нули и полюсы функции для системы М/М/1
(8.51)
Продемонстрируем теперь на некоторых примерах применение полученных результатов.
Пример 1. Система М/М/1. Наш старый друг, система М/М/1, представляет собой самый простой случай и послужит здесь для
того, чтобы с наибольшей ясностью показать смысл спектрального разложения. Так как и промежутки времени между поступающими требованиями, и время обслуживания имеют показательное распределение, то Л* (s) = V(s + X) и В* (s) = p/(s + р), где х = 1/р и t = 1/Z. Чтобы вычислить Ф+ (s) (преобразование функции распределения времени ожидания), нужно сначала получить выражение (8.34), т. е.
л* (—S) В* (s) - 1 = (-- 1 = -А + \(|/ ’ ’ у I — s / \ s |I / (Л —s)(s + p)
Тогда из (8.35) находим
= Л* (-s) В* (S) - 1 = / (8.52)
На рис. 8.4 показано расположение нулей (обозначенных кружками) и полюсов (обозначенных крестиками) на комплексной s-плоскости для функции (8.52). Заметим, что в этом примере корни числителя (нули функции) и корни знаменателя (полюсы функции) уже найдены. В общем же случае нахождение этих корней составляет наиболее трудную часть метода спектрального разложения. Для разложения потребуем выполнения условий (8.36) и (8.37). Учитывая нули и полюсы на рис. 8.4, и вспомнив, что функция ЧД (s) должна быть аналитической и не иметь нулей в области Re (s) > 0, включим в эту функцию множители, дающие два нуля (s = 0 и s = —р + к) и один полюс (s = —р). Точно так же функция V_(s) должна быть аналитической и не иметь нулей в области Re (s) < D при некотором D > 0. Это условие будет удовлетворено, если Чг_ (s) будет содержать оставшийся полюс (s == /•) и будет выбрано D = к. Это показано на рис. 8.5.
Таким образом,
T(s) = A -s. (8.5-1)
308
l'in(S)
S-ПЛОСКОСгпь
5 - плоскость
Re(s)
*-------
A Ri:(s)
^+(s) a)
1/-ф (5)
6)
Рис. 8.5. Разложение на 'Г* (s) и 1 '4f_ (•>) для системы М/М/1
Заметим, что условие (8.37) в пределе при s -- > оо удовлетворяется.
Остается найти К.. Из равенства (8.43) имеем
л = lim —— ' = lim —-------- -= 1 -- о. (8.5,'))
s-M) 5 s->0 5
Поэтому выражение для преобразования Лапласа функции распределения времени ожидания для системы М/М/1 из равенства (8.41) имеет вид
°+(s) -Т7ГГ7ГП5Г • (8.56)
о э j- г-)
Здесь, как правило, надо попытаться получить через обратное преобразование функцию распределения времени ожидания. Однако для системы типа М/М/1 уже было получено обратное преобразование для W* (s) = «Ф+ (s) при переходе от (5.120) к (5.123). Решение получается в виде
ГС//)^ 1//>0. (8.57)
Пример 2. Система G/M/1 *.
В этом случае В* (s) = p/(s + и), но теперь А* ($) совершенно произвольно. При этом
и
Ч\ (s) _ р A" (~s) — s — р о г-
ГП--------’
Для разложения надо найти корни числителя последнего уравнения. Не будем останавливаться на полюсах функции Л* (—$), так как они должны лежать в области Re (s) > 0, т. е. А (/) = 0
* Этот пример требует для нахождения корней использовать теорему Руше. Такой способ часто бывает необходим для решения конкретных задач о системах типа G/G/1 методом спектрального разложения. Конечно, эта система уже Рассматривалась в разделе 6.4, и результаты применения обоих методов будут сравниваться.
309
для t <_ 0, и можно попытаться найти такую функцию (s), которая не содержит этих полюсов. Поэтому исследуем только нули функции, т. е. решим уравнение
s -ф- р — рЛ* (—s) = 0. (8.59)
Очевидно, одним корнем является s == 0. Чтобы получить остальные корни, применим теорему Руше (она приведена в приложении I, однако повторим ее и здесь).
Теорема Руше. Если функции f (s) ng (s) аналитичны внутри замкнутого контура С и если | g (s) | < | f (s) | на С, то внутри C
функции / (s) и f (s) -\-g (s) имеют одно и то же число нулей.
Чтобы найти корни уравнений (8.59), положим
f (s) •-= s + р;
£(s) = — рЛ* (--S).
По определению,
со
л‘(—s) = \estdA(i).
(J-
Выберем в качества контура С полуокружность сколь угодно большого радиуса, лежащую в левой полуплоскости с диаметром на мнимой оси, как показано на рис. 8.6. Такой контур выбирают для того, чтобы включить все нули и полюсы, лежащие в области Re (s) < 0, которые нужно будет ввести в функцию Т+ (s) [вспомним, что V_(s) не должна содержать таких нулей и полюсов]. Теорема Руше дает информацию о числе нулей и полюсов в полуплоскости Re (s) < 0, подлежащих рассмотрению. Как обычно, предположим, что действительная и минимальная части комплексной переменной s обозначены с» и <о соответственно, т. е. что при / = —1 s о + /о). Теперь для Refs) = о с 0 имеем е'“
< 1 (/ > 0); тогда
1(4
В то же время
|f(s)| = |s + p|. (8.61)
Рассматривая кишур С, замечаем, что на основании (8.60) и (8.61) для всех лежащих на нем точек, кроме точки s = 0, имеет место
1/4)| =4"' I Г I - I1 I Л?0) I- (8 62)
Это следует из того, что s + р (для s на контуре (?) является вектором, длина которого равна расстоянию от точки — р до точки контура $. Для того чтобы можно было применить теорему Руше, остается показать, что в окрестности нуля имеет место неравенство |/(s)| > |g(s)|- Для этой цели изменим контур С, обходя нуль по полуокружности малого радиуса, лежащей в левой полуплоскости (см. рис. 8.7). Заметим, что при s = 0 имеем |g (0) | = = |/(0)| =р, что не удовлетворяет условию теоремы Руше. Обход начала координат по полуокружности малого радиуса е, лежащей в левой полуплоскости, устраняет это затруднение следующим образом. Рассматривая па этой полуокружности произвольную точку, радиус-вектор которой образует угол 9 с осью о, можем записать s = ст + /со = — е cos 0 ~Ь /е sin 0; таким образом,
| /'(s) |г — |s + р. | —е cos 0 +- /е sin 0 -у у |2.
Умножая s -J- р на комплексно-сопряженную величину, получаем
| f (s) |2 = (ц — ь- cos О)2 о (е) --= ir— 2pecos0 у о (в). (8.63)
Заметим, что наименьшее значение для | f (s) | получается при 6 = 0. Вычисляя g (s) на том же пути обхода, получаем
|£(ДГ2
е(_Е C.S е si.. w
0“
4
ЗП
Разлагая в степенной ряд функцию под знаком интеграла, имеем
! [1
I g ($) |2 р2
(— Е COS fl у /Е SIH 0) I -\- • • • ] d.A (t)
Интегралы в этом ряду пропорциональны моментам распределения промежутков времени между поступающими требованиями; тогда
| g (s) |2 = р21 1 — st cos 0 — /е? sin 0 о (e) |2.
Чтобы получить (s)|2, умножим g (s) на комплексно-сопряженную величину:
| g (s) |2 — и2 (1 — 2г/ cos 0 о (e)) = p2— -— cos 0 )- о (e), (8.64)
p
где, как обычно, p == x!t = l/ttZ.
Так как 0 принимает значения —л/2 С0< л/2, что дает cos 6>0, то при к —> 0 на полуокружности, обходящей начало координат,
р2— 2pECosfl_'_- р2 — —i-cosO. (8.6 )
Это справедливо, поскольку для стабильной системы р < 1. Левая часть неравенства (8.65) с точностью до величин порядка представляет собой \f (s)|2 из равенства (8.63), а правая часть с той же точностью совпадает с выражением (8.64) для \g (s) |2.
Таким образом, показано, что в окрестности нуля (s) | > > IS (s) I- Факт, установленный теперь для всех точек контура С, позволяет применить теорему Руше, согласно которой f (s) и f (s) 4-+ g (s) имеют одинаковое число нулей внутри контура С. Так как / ($) имеет только один нуль (s = —р), то и f (s) g (s) имеет лишь один нуль в области Re (s) < 0. Пусть этот нуль будет в точке s = — sv Как упоминалось ранее, точка s = 0 также является нулем уравнения (8.59). Поэтому (8.58) можно записать в виде
(S) = Г М* (—s) — S — р 1 Г S (S + S1) ) <8 66х
Ч1-- (s) L s (S Н- S1) J L S + р J ’ V '
где член, стоящий в первых скобках, не имеет ни полюсов, ни нулей в области Re (s)<0 (единственные два нуля s = 0 и s= —«г имеющиеся в полуплоскости, здесь выделены). Расширим теперь область Re (s) < 0 до области Re (s) < D, выбирая D так, чтобы в новой области не появились дополнительные нули или полюсы уравнения (8.59). Выражение, стоящее в первых скобках, примем за [¥_ (s)]"1 и заметим сразу же, что член, стоящий во вторых скобках, можно принять за Т+ (s), поскольку его нули (s == 0-312
s — —s-l) и полюсы (s— —p) лежат в области Re (s)>0. Поэтому можно провести разложение (8.66) в следующем виде:
.И:'’ ; (8-67)
¥ (s) = - —Ь . (8.68)
S + р — (—S) v '
Функции, описываемые последними двумя равенствами, удовлетворяют условиям (8.36) и (8.37). Вычислим постоянную /<:
K = = S1- ^Ц7(0*-). (8.69)
s->0 s s->0 s “Г P P
Из равенства (8.41) получаем
ф /s) — Мр+А + '-1 ps (s + 1) ’
что после разложения на простые дроби дает
Ф+(«) =4~-~TqSr- (8.70)
Находя по таблицам обратные преобразования Лапласа, получаем окончательное решение для системы типа G/M/1:
1Г(у) .= 1 — (1 - ¥)е”5,;/, ?/>0. (8.71)
Настоятельно рекомендуем читателю сравнить этот последний результат с результатом (6.30), который также относится к системе типа G/M/1. Сравнение с очевидностью показывает, что в обоих случаях имеется единственная постоянная, которую надо вычислить. В решении, полученном здесь, эта постоянная является корнем уравнения (8.59) в области Re (s) < 0. В равенстве, приводимом в гл. 6, надо решить уравнение (6.28), которое эквивалентно уравнению (8.59).
Пример 3. Система типа Ег/М/1.
Пример, решенный для системы типа G/М/1, не может быть решен для системы общего типа. Поэтому поучительно рассмотреть частный случай системы типа G/M/1 и довести до конца вычисления. Выбранный здесь пример рассматривался в гл. 6. Речь идет о системе типа Е2/М/1, в которой два этапа поступления требований имеют разные интенсивности гибели и для которой A* (s) задается равенством (6.35). Для этого примера заметим, что полюсы функции А* (—§) имеют место в точках s = р, s = 2р, которые лежат в области Re (s) > 0. В качестве первого шага разложения образуем
М- = A*(-S)B*(S)_ ] = 2g ] - 1 =
. ~s (s — р + р К2 ) (s — р — р /2~) ,с, 79х
(s 4-р) (р — s) (2р — s)
313
Спектральное разложение заметно упрощается, если изобразить полюсы и нули на комплексной плоскости, как это показано на рис. 8.8. Очевидно, что два полюса и один нуль, лежащие в правой полуплоскости, надо связать с ’Jr_ (s). Кроме того, так как полоса 0 < Re (s) < р не содержит ни нулей, ни полюсов, выбираем D = р, и оставшиеся два нуля и полюс, лежащие в области Re (s) < D, относим к функции (s). Обратим внимание на то, что нуль, расположенный в точке s = (l — j/2) р, является единственным корнем выражения рД* (—s) — s — р, расположенным в левой полуплоскости, и поэтому sx -= (1 — |/2) р. Ясно, что нет необходимости в дальнейшем решении задачи, поскольку это решение уже дано в виде равенства (8.71). Однако продолжим построение другой формы решения, чтобы сделать более ясными остающиеся шаги.
Проведя разложение, перепишем равенство (8.72) в виде
V+ (s) _ I — (s — р—-рК2) I I s (s — р р / 2
V- (s) ‘ L (И — Я (2Р — «) J L s р
В этой формуле вторых Т+ (s),
выражение в первых скобках есть 1/4J_ (s), а во т. е.
s (s - р + р /2) _ 3
+ v ’ s + р v '
Из (8.69) вычисляем /С:
K = -S1- = _ 1 (8.7!)
|Л
Это соответствует W (0+), т. е. вероятности того, что вновь поступающее требование не ждет обслуживания. Наконец, подставив это значение в (8.71), находим выражение
W (у) --= 1 — (2 — 1/’2)е-ц(/2 ~1)у, у^О, (8.75) которое, как и следовало ожидать, в точности совпадает с (6.37). 314
Метод спектрального разложения был успешно применен Райсом [111, который рассматривал период занятости для системы типа G/G/1. Среди полученных интересных результатов имеется один, касающийся предельного распределения долговременного ожидания в случае большой нагрузки (этот результат будет рассмотрен в параграфе 2.1 тома II). Райс дает подобное приближение для продолжительности периода занятости в случае большой нагрузки.
8.3. АЛГЕБРА ОЧЕРЕДЕЙ КИНГМАНА
Установим снова фундаментальные соотношения, характеризующие систему типа G/G/1. Для ип = хп — имеется основное соотношение
®,!+г = + ип)+. (8.76)
Кроме того, как было показано, ШаХ [0, 4~ ^п~2у • ‘у Ч
4- • • щ, иа^ + • 4 ии 4 щ0].
Ранее говорилось о том, что {оуД есть марковский процесс со стационарными вероятностями перехода. Его общая стохастическая структура задавалась вероятностью Р [ш,п+н < y[wm = х], которая может быть вычислена как «-кратный интеграл от «-мерной совместной плотности распределения п случайных величин wm+1, ..., wm+n по области, в которой wm+n < у. Это вычисление чрезвычайно сложно, поэтому приходится искать другой путь решения задачи. Полячек [10] использовал спектральный подход и получил решение с помощью комплексных интегралов. Линдли [8] заметил, что wn имеет то же распределение, что и случайная величина w'n, определенная ранее как
wn - шах [6/(|, 7/(, ПГ1|-щ0].
В случае, когда р = xit < 1, что соответствует неравенству Е 1ип] <0, существует устойчивое решение для предельной случайной величины w в виде
® = supt7n (8.77)
nis'J
независимо от w0.
Метод спектрального разложения, изложенный в предыдущем параграфе, представляет собой подход Смита [12] к решению интегрального уравнения Линдли (типа уравнения Винера— Хопфа). Другой подход, использованный Спитцером, приводит к тождеству Спитцера [14]. Имеется много доказательств этого Тождества и, в частности доказательство Вендела [18], в котором используется алгебраическая структура задачи. Кейлсон [6] продемонстрировал приложение функций Грина к изучению си
315
стем типа G/G/1. Бенеш [4] также рассматривал систему G/G/1, исследуя незавершенную работу и ее дисперсию. Эти многочисленные подходы, каждый из которых достаточно сложен, заставляют задуматься над тем, нет ли какого-нибудь существенного описания системы, которое позволило бы указать место каждого из методов решения в общем построении. В 1966 г. Кингман [7 ] сформулировал эту задачу и ввел свою алгебру очередей, выявляющую их общую структуру. Эта алгебра будет вкратце рассмотрена в настоящем параграфе.
Из равенства (8.76), очевидно, можно было бы итерационным путем найти плотность распределения да,|Ь1, начиная с п = О при заданной плотности распределения w0. Вспомним, что распределение величины и„ [с плотностью с (и)] не зависит от п. К итерационной процедуре можно было бы приступить следующим образом. Допустим, что плотность распределения величины wn уже вычислена. Обозначим ее через wtl (у) A dWn (y)ldy, где W„ (у) = Р [ау„ < у]. Чтобы найти w;i+1 (у), будем следовать равенству (8.76) и построим плотность распределения суммы w„ + ип, которая в силу независимости слагаемых равна свертке wtl (у)®с(у). Эта свертка дает плотность распределения, принимающую неотрицательные значения как для положительных, так и для отрицательных значений аргумента. Однако равенство (8.76) требует [в качестве следующего шага в вычислении wn+1 (у) 1 вычисления плотности распределения величины (w,t + и,.)+. Это значит, что нужно собрать всю вероятность, связанную с отрицательными значениями аргумента в уже найденной плотности, т. е. в плотности wn (у)® с (у), и поместить ее в виде импульса в нуле для w,i+1 (у). Величина этого импульса будет равна интегралу от предыдущей плотности по отрицательной полуоси. В этом случае говорят, что вероятность перенесена с отрицательной полуоси в начало координат. Значение, найденное для свертки при положительных значениях аргумента, сохраняется для wn+1 в этой области.
Алгебра, описывающая рассмотренную операцию, и есть введенная Кингманом алгебра для изучения системы G/G/1. Итерационная процедура продолжается при следующем образовании свертки w„+1 (у) и с (у), переносе вероятности с отрицательной полуоси в начало координат для получения w„+2 (у), затем тем же путем образуется а>„+3 (у) и т. д. Элементы этой алгебры — все конечные меры с определенным знаком на действительной оси (например, плотности распределения на действительной оси). Для любых двух таких мер, например 1гг и й2, их сумма h± + h2, а также произведения каждого из них на скаляры принадлежат к этой алгебре. Операция умножения определяется как свертка /li© Л2. Можно показать, что эта алгебра действительна и коммутативна. Существует также единичный элемент е, такой что е® h = h для всякого h из алгебры, и, очевидно, что такой единицей будет единичный импульс в начале координат.
316
Нас интересуют измеримые операторы, отображающие действительные функции в другие действительные функции. В частности, рассмотрим оператор, отображающий х в (х)+, где, как обычно, (х)+Л max [0,%]. Обозначим его л (не путать с вектором установившихся вероятностей, введенным в гл. 2). Таким образом, если А означает некоторое неизмеримое событие и /г(Л) = = Р (и : X (со) Т Л} означает меру этого события, то л определяется равенством
л[/1(Л)] = Р(со:Х+(со)еЛ).
Отметим линейность этого оператора, т. е. л (ah) = ал(й) и л (h± + /i3) = л (/ij + л (/i2). Таким образом, имеется коммутативная алгебра с единицей и линейный оператор л, отображающий эту алгебру в себя.
Так как ((х)+)+ = (х)+, то оператор л отличается важным свойством: л2 = л. Линейный оператор, обладающий таким свойством, называется проекцией. Проекцию, ранг и нулевое пространство которой являются подалгебрами основной алгебры, называют проекцией Вендела. Можно показать, что л обладает этим свойством, что и обеспечивает возможность найти решение для системы типа G/G/1.
Вернемся к изучению системы массового обслуживания G/G/1. Вспомним, что случайная величина ип имеет плотность распределения с (и) и что время ожидания п-го требования шп имеет плотность распределения wn (у). По-прежнему, поскольку ип и wn независимы, wn + ип имеет плотность распределения : с (у) ® wn (у). Кроме того, так как wn+1 = (wn 4- ц„)+, то
wn+i (У) = л (с (у) © wrt (у)), п = 0,1,..., (8.78)
s. и это уравнение позволяет получить по индукции плотность рас-j пределения времени ожидания. Теперь, если р < 1, предельная : плотность w (у) существует и не зависит от да0. Следовательно, w должна иметь ту же плотность распределения, что и (w + й)+ (факт, замеченный Линдли [8]). Это дает основное уравнение, 1 определяющее стационарную плотность распределения времени ожидания в системе типа G/G/1:
да (у) = л (с (у) &W (у)). (8.79)
J Решение этого уравнения играет главную роль при изучении системы типа G/G/1. Оставшаяся часть параграфа посвящена сжа-( тому изложению некоторых изящных результатов, связанных с I этой алгеброй. Мы рекомендуем продолжать чтение только самым г храбрым.
Разные методы, указанные выше, отличаются друг от друга тем, что для них формально по-разному строится алгебра и ре-। шается уравнение (8.79). Чтобы сопоставить различные подходы, ж введем теперь тождество Спитцера. Чтобы установить это тож-К 317
дество, которое включает рекуррентное соотношение (8.78), надо ввести следующую производящую функцию:
Х(г, у)-= S (8.80
П=Л
Сложение и умножение на скаляр для этого степенного ряда могут быть определены как обычно, а операция умножения определяется как свертка. Тогда тождество Спитцера можно записать в виде
X (г, у) = е~я (7>л (wn (у) ея (v>~v), (8.81)
где
у Alog[e-~ zc(y)\. (8.82)
Таким образом, wn (у) может быть найдено, если разложить X (z, у) в ряд по степеням z и взять коэффициент при г11. Нетрудно показать, что
X (г, у) = ц.у (у) -|- гл (с (у) Q X (г, у)). (8.83)
Можно также построить производящую функцию последовательности Е [е”ьги,г] A W* (s), что позволяет найти преобразование предельного времени ожидания. А именно
limlF’(s) = F* (s) AE|e^stS|, П->оо 1 J
если только р < 1. Это приводит к следующему равенству, которое называется тождеством Спитцера и непосредственно применимо к решению рассматриваемой задачи теории массового обслуживания:
Трудно было ожидать, что это выражение окажется простым Т
Если рассматривать W„ (s), то можно ввести другую действительную коммутативную алгебру (в которой произведение определяется обычным умножением, а не сверткой, как можно было ожидать). Алгебраическое решение основного уравнения (8.79)
1 Из этого тождества легко найти что
ОО
= У 4 Е [(Ш
318
может 6i,iTb получено в любой из этих двух алгебр. В случае преобразования нужно оперировать со степенным рядом
X' (z, s) A Г;(з)г'1 (8.85)
вместо ряда, введенного равенством (8.80).
Полячек рассмотрел последний случай и для системы типа G/G/1 получил следующее уравнение, характеризующее работе системы:
X\?,S).-K(s) ; (8.86)
/С— 00
а затем, преодолев значительные трудности, показал, что решение этого уравнения должно иметь вид
X*(z, s)^e-^(s’)n(^(s)e’i(?<s”-:?<s)j, (8.87)
где
Y (s)Alog(l —zC*(s)) и
Когда С* (s) имеет достаточно простой вид, это выражение может быть вычислено с помощью контурных интегралов.
С другой стороны, описанный в предыдущем параграфе метод применения спектрального разложения может быть следующим образом перефразирован в терминах этой алгебры. Если заменить $Ф+ (s) на W* (s) и sU>_ (s) на 1Г7 (s), то основное уравнение даст
IP* (s) + IVL (S) = С* (s) IV* (S).
В соответствии с (8.83), переходя к преобразованиям, получаем л (X* (z, $) — IV() (s) — zC* (s) X* (z, s)) = 0, и спектральное разложение будет иметь вид
1 — zC* ts} - е" (s,)ev (s) (s)). (8.88)
Это спектральное разложение, конечно, наиболее важно.
Несмотря на все свое изящество, унификация систем массового обслуживания с помощью алгебры очередей не дала до сих пор больших возможностей для развития теории. В частности, как указал Кингман, такой подход не дает легкого обобщения на систему типа G/G/m, так как образ этой алгебры представляет
319
собой подалгебру, а ее пулевое пространство подалгеброй не является. Следовательно, здесь проекция Вендела не получается. По-видимому, в приведенном обзоре наибольшая информация содержится в важном уравнении (8.79), дающем основное условие, которому должна удовлетворять плотность распределения времени ожидания. Его рекуррентная форма (8.78) будет использована в гл. 2 тома II.
8.4. ВРЕМЯ ПРОСТОЯ И ДВОЙСТВЕННОСТЬ
Здесь будет получено выражение для IF* (s) через преобразование плотности распределения времени ожидания и будет дана интерпретация этого результата с помощью понятия двойственности в теории массового обслуживания.
Вернемся к основному равенству (8.5), т. е. к
u>„+1 = max [0, wn-^un].
Определим теперь новую случайную величину, которая является как бы «другой половиной» времени ожидания, а именно
Уп = — min [0, wn ип]. (8.89)
Эта случайная величина в некотором смысле соответствует изученной ранее случайной величине, имеющей функцию распределения (у). Из последних двух уравнений замечаем, что когда уп > 0, то w,l¥1 = 0, и в этом случае уп является просто длиной периода простоя, прекращающегося с поступлением требования C,!+i. Кроме того, так как либо w,l+J, либо у,, равно нулю, то wn+]yn = о. (8,90)
Примем соглашение, что период простоя существует, если он имеет ненулевую длину; при этом, если у., и wn+1 одновременно равны нулю, мы говорим, что продолжается период занятости (надоевшая тривиальность).
Из определения очевидно, что во всех случаях
Уи^^п + un- (8-9D
Из этого последнего равенства может быть получен ряд важных результатов. Начнем с нахождения средней длины очереди, как это было сделано в гл. 5, где к системе типа М/G/l был применен метод вложенных цепей Маркова. В частности, возьмем математическое ожидание от обеих частей равенства (8.91):
Е [wn+i] — Е = Е [Щ-J г Е [ип\.
Предположим, что Е [ип ] < 0, и это (за исключением систем D/D/1, для которых годится даже условие Е [«., ] с 0) является необходимым и достаточным условием стационарности (и единственности) распределения времени ожидания независимо от и. 320
Это требование равносильно требованию р = xlt < 1. В этом случае имеем 1 11
lim £ [шл+1] == lim£ [ш„],
П->оо П~>оо
при этом предыдущее равенство дает
Е[у] = -Е[и], (8.92)
где уп —♦ у и ип — > и. (Заметим, что периоды простоя независимы и. одинаково распределены, но продолжительность конкретного периода простоя зависит от продолжительности предыдущего периода занятости). Теперь, поскольку из (8.13) имеет место Е [и] = = 7(р — 1), получаем
£ [z/] = Г(1 —-р). (8.93)
Возведем (8.91) в квадрат и возьмем от обеих частей математическое ожидание:
Шп-pi— 2шп_|-1Уп Уп — wn -|- 2wnun ип.
Применяя (8.90) и учитывая, что моменты предельного распределения wn не зависят от п, получаем
Е Ку)2] = 2£ [шй] 4- Е [(и)2].
Обратимся снова к более простой записи моментов: wk А А Е [ш)&] и т. д. Так как ш„ и ип независимы, то Е [wu] = wu. Пользуясь этим и равенством (8.92), находим
~ д nr/ и3 у2
w A If = ——-— —.
— 2и Чу
(8.94)
Вспомнив, что среднее значение остаточного времени случайной величины х равно х2/2х, находим, что W — просто среднее остаточное время величины и минус среднее остаточное время величины у.
Вычислим теперь второй момент величины и. Так как и = = х — t, то и2 = (х — ?)2, что дает
и2 — о а 4“ О& 4" (t)2 (1 — р)2, (8.95)
1 Требовать выполнения равенства lim Е [»*] = lim Е ,,] надо с осторожностью, так как здесь разные случайные величины. Этот вопрос опустим и отошлем читателя за подробностями к работе [19].
11 Л. Клейнрок 321
где Оа и оь — дисперсии промежутков времени между поступающими требованиями и времени обслуживания. Подставляя это выражение в предыдущую формулу, приведем ее к виду
W = ^+о| + (02£-р);_ _ £_ . %
2/(1-Р) ?-У
Теперь надо вычислить первые два момента распределения величины у (известно, что у = t (1 — р), но желательно найти его иначе, чтобы определить постоянную). Введем условные моменты, связанные с появлением периода простоя, а именно определим r0 = Р [у > 01 ~ Р [поступающее требование застает систему свободной]. (8.97)
Очевидно, что система стабильна, когда г0 > 0. Кроме того, так как период простоя считается наступившим, если он имеет ненулевую длину, то
Р 1У < УI У > 0] = Р [период простоя < у], (8.98)
а это — функция распределения периода простоя, обозначенная ранее через F (у). Обозначим через I время простоя системы. Проведем следующие вычисления:
У = Е [У | ~У = 0] Р [У = 0] + Р [У I У > °] Р 1У > °! =
= 0-[-гоЕ [у | у > 0].
Математическое ожидание в этом выражении представляют собой среднее значение I, поэтому
y=rj. (8.99)
Аналогично находим
? = rjk. (8.100)
Так, в частности, у2!2у = PI2I (г0 сокращается), и, следовательно, можно переписать выражение (8.96) для W в виде
1у7 °а + °Ь + (Q2 (1 ~ Р)2 Z!_. а (8.101)
2/-(1-р) 2/
К сожалению, пойти дальше в определении W для системы типа G/G/1 не удается. Теперь необходимо найти первые два момента распределения периода простоя. В общем случае для системы типа G/G/1 не удается просто вычислить эти моменты, так как период простоя зависит от того, как проходил предыдущий период занятости. Однако в гл. 2 тома II будут наложены ограничения на второй член в этом уравнении, что по волит найти границы среднего времени ожидания 1F.
Как было сделано в гл. 5 при исследовании системы типа М/G/l, вернемся теперь к основному уравнению (8.91), связыва-322
ющему важные случайные величины, и попытаемся найти преобразование плотности распределения времени ожидания W* (s) Л A Е [e~S№ ] для системы типа G/G/1. Можно ожидать, что оно будет включать также распределение времени простоя. Взяв среднее обеих частей равенства (8.91), получим
Однако, так как шп и ип независимы, находим
Е [e-s (а’л+1-^) j = Е j Е [e-s"n ] _ (8 102)
Чтобы вычислить стоящее слева математическое ожидание, используем тот факт, что только одна из двух случайных величин, wn+1 или уп, может быть ненулевой. Соответственно,
Е [e-S _ Е [е-‘ (~^) | Уп > 0] р [уп >0] +
+ B[e~S“''i+1|yn = 0j/’fyn = 0]. (8.103)
Чтобы вычислить правую часть этого последнего выражения, воспользуемся тем, что
£[e-s^1]=£[e-s“’-1|y„ = o] х
X Р [уп = 0] + Е [е“™-! | Уп > о] Р [уп > 0]. (8.104)
Однако, так как хшп+луй — 0, то Е [e~SWfi+i | уп > 0] = 1. Используя определение г0 [см. (8.97) ] и переходя к пределу при п —► оо, из (8.104) получаем следующее выражение преобразования:
Е [e~sw | у = 0] Р [у = 0] = Г* (s) —г0.
Поэтому предельное выражение (8.103) можно записать в виде £[е-5("-й] = Z*(-^/-o+^‘(s)~ro, (8.105)
где I* (s) — преобразование Лапласа плотности распределения (8.98) времени простоя. Таким образом, из этого последнего уравнения и равенства (8.102) получается непосредственно
W* (s) С* (s) = r0I* (—s) + W* (s)—r0,
где, как и прежде, С* (s) — преобразование Лапласа плотности распределения случайной величины и. Это последнее уравнение окончательно дает [9 ] формулу
^(s) = zt^wL’ ™ (8.Ю6)
представляющую собой обобщение уравнения Полячека—Хинчина, приведенного в гл. 5, и примененное теперь к системе типа G/G/1. Очевидно, это уравнение справедливо, по крайней мере
И* 323
вдоль мнимой оси комплексной s-плоскости, так как в этом случае оно дает характеристическую функцию различных заведомо существующих распределений.
Пример 1. Система М/М/1. Для этой системы известно, что период простоя имеет то же распределение, что и промежуток времени между поступающими требованиями, т. е.
F(i/) = P[/<i/] = l —у>0. (8.107)
Поэтому / = 1/1, /2 = 2/12, а также = 1/12 и а*— 1/р2. Подставляя эти значения в (8.101), находим
ГР = 12(1/1а + 1.Ф2)4-(1-Р)2 _ _ 1_
27 (1 — р) л
и, следовательно,
(8.108)
что, очевидно, совпадает с результатом, полученным для системы типа М/М/1 ранее.
Как известно, /* (s) = —и С* (s) = —------^4—;—- Кроме того,
' ' s-f-A ' ' (7— s) (s 4- pi) н
для пуассоновского потока поступающих требований вероятность того, что требование застанет систему свободной, совпадает с долей времени простоя системы, т. е. г0 = 1 — р, поэтому равенство (8.106) дает
__(1 — р) [ 1 —1/(1 —s)]_ — (1 — р)s (s 4~ р) _
' ' — 1 — Хр./(7 —s) (s 4-р.) ~ (/. — >) (s-ф р) — Ар
что совпадает с формулой (5.120).
Пример 2. Система М/G/l. Распределение времени простоя для системы М/G/l то же, что и для системы типа М/М/1, однако дисперсия времени обслуживания неизвестна. В этом случае
12[(1/12) + ^]4-(1-р)2 1 рЦ1+<)
и/ =------------------------ —ТГ-=ДГ ’ (8-11 (}
что представляет собой формулу Полячека—Хинчина. Кроме того, C*(s) = B*(s)l/(1— s) и снова г0 = 1 —р. Тогда равенство (8.106) дает
= (l-p)[l-l/(l-s)] _ S (1 —р)
1 ' 1 — [7/(1 — s)] В* (s) S — 7 4-ZB* (S) ’
(8.111)
что представляет собой уравнение Полячека—Хинчина для преобразования плотности распределения времени ожидания!
Пример 3. Система D/D/1. В этом случае время простоя постоянно и имеет вид I = t — х = t (1 — р). Следовательно. 324
I = /(1 — p), /2 = (/)2, a oi = er* = 0, поэтому равенство (8.101) дает
2?(1—p) 2
тогда
Ii7== 0. (3.112)
Последнее, очевидно, верно, так как в соостоянии равновесия время ожидания в стабильной системе D/D/1 всегда равно нулю.
Так как х, t и I постоянны, то В* (s) = e-SA', Л* (s) =--= e~sZ~ и [* (s) = e-si = e-si (i-p) Кроме того, с вероятностью единица поступающее требование застает систему свободной, т. е. r0 = 1. Тогда равенство (8.106) дает
1 Г1 _ ps~ (1-Р) I
W* (s) = И?——=-! = 1. (8.113)
1 _ es/e”sx
Следовательно, w (у) = и0 (у), т. е. представляет собой импульс в начале координат, что, конечно, равносильно отсутствию ожидания.
Исследование распределения времени простоя естественно проводит к изучению двойственной системы массового обслуживания. Этот материал связан с лестничными индексами, определенными в параграфе 5.11. Рассматриваемое случайное блуждание представляет собой последовательность значений, принимаемых величиной Un [как определено равенствами (8.9)]. Обозначим через Un,t значение, принимаемое величиной U;, при &-м возрастании лестничного индекса (моменты, когда функция впервые опускается ниже своего последнего максимума'). Так как и < 0, то очевидно, что lim Un — —<х> при п —«• оо. Поэтому существует (единственное) целое К, являющееся наибольшим возрастающим лестничным индексом для Un. Теперь из равенства (8.11), повторяемого здесь еще раз, следует, что w = sup Un\
очевидно, что w = UnK. Определим теперь случайную величину /,г (которая, как мы увидим позже, связана с временем простоя) в виде
’и (8.114)
для k < К. Таким образом, Ik — это просто величина, указывающая, насколько новая возрастающая лестничная высота превышает предыдущую лестничную высоту. Поскольку случайные величины ип независимы, случайные величины ?<, при условии, налагаемом на К, независимы и одинаковы распределены.
325
Если теперь положить 1 — а = Р [Un < Unk для всех п > то можно легко вычислить распределение вероятностей величины К в виде
Р[Л = /г] = (1 — a)ok. (8.115)
В задаче 8.16 показано, что (1 — о) = Р [ш = 0]. Кроме того, очевидно, что
Л + Л + • • • + /к = иП1 - ипо + иП2 -
+ • • • + U пк-Un^ — UtiK,
где п0 А 0 и U 0 А 0. Следовательно, w имеет то же распределение, что и Zj + • • + 1%, так что можно записать
Е [e-sw“ ] = Е [i? [e's (?1+ ' " +?к) | к] ] =
= £[(?(s))x], (8.116)
где I* (s) — преобразование Лапласа плотности распределения каждой из величины 1К (каждую из которых будем обозначать просто через /). Теперь можно вычислить математическое ожидание, стоящее в (8.116), используя распределение величины К из равенства (8.115):
№*(S) = —. и (8.117)
1 — а7‘ (s)
Таким образом, это еще одно выражение для W* (s) в системе типа G/G/1.
Дадим теперь интерпретацию случайной величине I, рассматривая «двойственную» систему массового обслуживания (величины, связанные с этой системой, будем отмечать знаком Д). Двойственной для рассмотренной выше системы типа G/G/1 будет такая система массового обслуживания, у которой время обслуживания х,, первоначальной системы становится промежутком времени t,l+i между поступающими требованиями, а промежутки времени 4+1 между поступающими требованиями в первоначальной системе становятся временем обслуживания хп*. Очевидно, что для двойственной системы случайная величина ип = хп — t,i+i =
Очевидно, если первоначальная система стабильна, то двойственная нестабильна, и наоборот, за исключением случая, когда р = 1 и обе системы нестабильны.
326
- tn*x — xn = ~un й, определяя Un = u0 + • • + u„_i для двойственной системы, получим
ип~-ип.
(8.118)
Это соотношение определяет связь между обеими системами. Из обсуждения материала параграфа 5.11 ясно, что верхние и нижние лестничные индексы в двойственных системах меняются местами (то же верно для лестничных высот). Поэтому первый верхний лестничный индекс первоначальной системы соответствует первому лестничному индексу двойственной системы. Однако вспомним, что нижние лестничные индексы соответствуют поступлению требования за период простоя. Обозначим это требование через СП1. Ясно, что длина периода простоя, заканчивающегося этим требованием, в двойственной системе является разностью между накопленными промежутками времени между поступающими требованиями и накопленным временем обслуживания всех требований вплоть до поступления рассматриваемого требования (это обслуживание должно осуществляться в первый период занятости). Иначе говоря, для двойственной системы
Длина первого периода простоя после первого периода занятости
П! — rtj —1 nt — 1
— Xi хп ~ X хп — X in+i — ио Н- ui п=0 п==0
+ • + иП1-1= иП1 = Л,
(8.119)
где на последнем шаге использовано равенство (8.114). Таким об-разом, случайная величина I — это просто продолжительность периода простоя в двойственной системе, и равенство (8.117) связывает преобразование плотности распределения времени ожидания первоначальной системы с преобразованием плотности распределения времени простоя в двойственной системе [в отличие от равенства (8.106), связывающего преобразование плотности распределения времени ожидания с преобразованием плотности распределения времени простоя в одной и той же системе].
Изучение двойственных систем позволяет довольно просто получить ряд важных заключений (подробно они рассмотрены У Феллера [5], в частности в параграфах VI.9 и XI 1.5). Рассмотрим два результата из этой области.
Пример 4. Система GIJAIX. Если имеется стабильная система типа G/M/l (с t = 1/Хи х = 1/р), то двойственной ей будет нестабильная система типа M/G/1 (с? = 1/р, х = Ш), так что I (период простоя в двойственной системе) будет иметь показательное распределение. Следовательно, 7* (s) = p/'(s + р.), и из (8.117) по-
327
лучаем следующий результат для первоначальной системы типа G/М/1:
HZ* (s) = .U —. ' ' s 4“ р- — пр
Взяв обратное преобразование, найдем функцию распределения времени ожидания
W(y) = 1— ае“и(1~ст>^ г/>0, (8.120)
что в точности совпадает с равенством (6.30).
Пример 5. Система М/G/l. В качестве второго примера рассмотрим систему типа М/G/l, двойственная система которой принадлежит к типу G/M/1. Так как а = Р [ш > 0], то для системы типа Ai/G/l должно быть о = р. В двойственной системе, поскольку период занятости заканчивается в случайный момент времени (и так как распределение времени обслуживания в этой системе не имеет последействия), период простоя будет равен остаточному значению промежутка времени между поступающими требованиями. Поэтому из равенства (5.11) следует, что
7*(s) = ^O-). (8.121)
SX
Если эти расчеты применить к (8.117), то получим
W* ($) =--------, (8.122)
1 — р {[1 — В* (s)]/sx)
что представляет собой уравнение Полячека—Хинчина для преобразования плотности распределения времени ожидания [см. (5.106)].
Этим завершается изучение систем типа G/G/1. К сожалению, в этом общем случае мы не в состоянии дать аналитические выражения для распределения времени ожидания в явном виде через известные величины. Фактически, не удается даже определить среднее время ожидания ИИ Тем не менее удалось получить довольно эффективный метод для изучения рационального случая с помощью спектрального разложения. В гл. 2 тома 11 мы вернемся к системам типа G/G/1 и сумеем, применяя границы, неравенства и приближения, найти многие важные свойства этих систем.
СПИСОК ЛИТЕРАТУРЫ
1. Andersen, S. Е. On Sums of Symmetrically Dependent Random Variables Skan. Aktuar., 36, 123—138 (1953).
2. Andersen, S. E. On the Fluctuations of Sums of Random Variables, I, Math. Sea nd., 1, 263—285 (1953).
3. Andersen, S. E. On the Fluctuations of Random Varibles, II. Math. Scand., 2, 195—223 (1954).
4. Benes, V. E. General Stochastic Processes in the Theory of Queues, Addison— Wesley (Reading, Mass.), 1963.
328
5. Феллер В. Введение в теорию вероятностей и ее приложения. Том. 2/Пер. с англ. Ю. В. Прохорова. М., Мир, 1967. 752 с.
6. Keilson, J. The Role of Green’s Functions in Congestion Theory. Proc. Symp. on Congestion Theory (edited by W. L. Smith and W. E. Wilkinson). Univ, of North Carolina Press (Chapel Hill), 43—71 (1965).
7. Kingman, J. F. C. On the Algebra of Queues. Journal of Applied Probability, 3, 285 - 326 (1966).
8. Lindley, D. \r. The Theory of Queues with a Single Server. Proc. Cambridge Philosophical Society, 48, 277—289 (1952).
9. Marshall, К. T. Some Relationships between the Distributions of Waiting Time, Idle Time, and Interoutput Time the GI/G/1 Queue. SIAM Journal Applied Math., 16, 324—327 (1968).
10. Pollaczek, F. Problemes Stochastiques Poses par le Phenomene de Formation d‘une Queue d'Attente a un Guichet et par des Phenomenes Apparentes, Gauthiers Villars (Paris), 1957.
11. Rice, S. O. Single Server Systems, Bell System Technical Journal, 41, Part I: «Relations Between Some Averages», 267—278, and Part II: «Busy Periods», 279—310 (1962).
12. Smith, W, L. On the Distribution of Queueing Times. Proc. Cambridge Philosophical Society, 49, 449—461 (1953).
13. Spitzer, F. A Combinatorial Lemma and its Application to Probability Theory. Transactions of the American Mathematical Society, 82, 323—339 (1956).
14. Spitzer, F. The Wiener-Hopf Equation whose Kernel is a Probability Density. Duke Mathematics Journal, 24, 327—344 (1957).
15. Spitzer, F. A Tauberian Theorem and its Probability Interpretation. Transactions of the American Mathematical Society, 94, 150—160 (I960).
16. Syski, R. Introduction to Congestion Theory in Telephone Systems, Oliver and Boyd (London). 1962. f-1"’
17. Titchmarsh, E. C. Theory of Functions, Oxford Univ. Press (London), 1952.
18. Wendel, F. G. Spitzer's Formula; a Short Proof. Proc. American Mathematical Society, 9, 905—908 (1958).
19. Wolff, K. W. Bounds and Inequalities in Queueing. Unpublished notes, Department of Industrial Engineering and Operations Research, University of California*‘(Berkeley), 1970.
ЗАДАЧИ
8.1. Покажите на основании равенства (8.18), что С* (s) —
= Л* (—s) В* (s).
8.2. Найдите С (и) для системы типа М/М/1.
8.3. Рассмотрите систему типа M/D/1 с фиксированным временем обслуживания х секунд.
а) Найдите функцию С (и) — Р [иг1 < и ] и постройте ее. б) Найдите Е [ип].
8.4. Для данной ниже последовательности случайных величин составьте рисунок, соответствующий рис. 8.3, и заполните следующую таблицу:
п 012 3 456789
Чц измеренное вычисленное
2 1 1 5 722116..
3 4 2 3 342113...
329
8.5. Рассмотрите случай, когда р = 1 — е для 0 < е < I. Представим W (у — и) в уравнении (8.23) в виде
W {у—и} = IP (у) - uW["' (у) + (у) + R (и, у),
где ЦП"> (у) — п-я производная W (у) и R (и, у) такова,
У
что J R (и, y)dC(u) пренебрежимо мал по сравнению с ма-— оо
лым изменением W (у), когда р == 1 — 8. Пусть uk означает А-й момент распределения величины и.
а) При этих условиях приведите интегральное уравнение Линдли к линейному дифференциальному уравнению второго порядка, содержащему и2 и и.
б) Решите найденное в п. а уравнение с граничным условием W (0) = 0 и выразите среднее время ожидания W через первые два момента распределения величин tux.
8.6. Рассмотрим систему типа D/E/1 с постоянным промежутком времени между поступлениями требований (t секунд) и плотностью распределения времени обслуживания, заданной равенством (4.16).
а) Найдите С (и).
б) Покажите, что интегральное уравнение Линдли дает
W (у — t) = 0 для у <Zt и
У
W (у —~t) = | IP {у — w) dB (да) для у > t. о
в) Предположим, что решение для W (у) задается в виде
IP' (у) == 1 -ф £ , у > 0,
i=i
где а,- и а, могут быть комплексными, но где Re (а,) < 0 для i = 1,2 ..., г. Пользуясь этим предположением относительно решения, покажите, что должны удовлетворяться следующие уравнения:
У-------п = 0, / = 0, 1, . .., г—- 1,
где а0 = 1 и а0 = 0. Заметим, что {а,} могут быть найдены из первой последовательности (трансцендентных) уравнений, 330
а вторая последовательность дает {а(|. Можно показать, что az различны (см. работу [16]).
8.7. Рассмотрим следующую систему массового обслуживания, в которой очередь не допускается. Требования, застающие систему занятой, теряются.
а) М/М/1: найдите pk = Р [в системе k требований].
б) М/Н 2/1 (см. рис. 4.10), полагая = а, а2 = 1 —а, =
= 2ра, р2 = 2р. (1 —а):
1) найдите среднее время обслуживания х;
2) найдите р0 (система свободна), ра (требование в блоке 2ра) и (требование в блоке 2р (1 —а)).
в) Н2/М/1: А (/) — гиперпоказательное распределение, как в п. б, но с параметрами рх = 2ла и ц2 = 2а (1 —а). Начертите диаграмму переходов (с маркировкой ветвей) для следующих четырех состояний: Е,;- — состояние с поступающим требованием на этапе i и / требованиями на обслуживании (i = 1,2 и j = 0,1).
г) М/Е/1: найдите Pj = Р [остается пройти j этапов обслуживания ].
д) M/D/1: время обслуживания постоянно и равно х\
1) найдите вероятность того, что система свободна;
2) найдите долю потерянных требований.
е) Ег/М/копределам четыре состояния £\z, где i — число этапов, через которые осталось пройти поступающему требованию; a j — число требований на обслуживании. Начертите диаграмму переходов с маркировкой.
8.8. Рассмотрим систему массового обслуживания с одним обслуживающим прибором, в которой промежуток времени между поступающими требованиями с вероятностью а берется из показательного распределения со средним значением 1/Х и с вероятностью 1 — а из показательного распределения со средним значением 1/р. Обслуживание — показательное с интенсивностью р.
а) Найдите A* (s) и В* (s).
б) Найдите выражение для Т+ (s)/W_ (s) и нарисуйте схему с нулями и полюсами на s-плоскости.
в) Найдите ¥+ (s) и ¥_ (s).
г) Найдите Ф+ (s) и W (у).
8.9. Рассмотрим систему типа G/G/1, в которой
Л* = (s + 1) (s 4-2) ’
а) Найдите выражение для Т+ (s)/¥_ (s) и постройте схему с нулями и полюсами на s-плоскости.
331
б) Примените спектральное разложение для вычисления ЧД (s) и Ч'_ (з).
в) Найдите Ф+ ($).
г) Найдите 17 (у).
д) Найдите среднее время ожидания W.
е) 17 (у) было найдено методом спектрального разложения. Можно ли описать другой путь получения 17 (z/)?
8.10. Рассмотрим систему типа М/G/l. Применяя метод спектрального разложения к интегральному уравнению Ли; дли, найдите: а) ЧД (s) (Указание: Интерпретируйте [1 — В* (s) ]/sx); б) ЧД (s);
в) sO+ (s).
8.11. Рассмотрим систему типа Е?/ЕД1.
а) Покажите, что
4+ (Д = F(s)
ф. (s) 1 — F (s) ’
где В ($) = 1 — (1 — sikqyi (1 -f- s/pr)r.
б) Для р < 1 покажите, что F ($) имеет один нуль в начале координат, нули $ь s2, ..., sr в полуплоскости Re (s) < 0 и нули sr+1, ..., в полуплоскости Re (s) > 0.
в) Выразите ЧД (s) и 4f_ (s) через s;.
г) Выразите 17* ($) через s(- (i = 1,2, ..., г + q— 1).
8.12. Покажите эквивалентность равенств (8.71) и (6.30).
8.13. Рассмотрим систему типа D/D/1 с р < 1. Предположим = 4? (1 — р).
а) Вычислите w,L (у), применяя процедуру, определенную равенством (8.78) для п — 0, 1, 2, ... .
б) Покажите, что известное решение для
W (у) = lim wn (у)
П->оо
удовлетворяет уравнению (8.79).
8.14. Рассмотрим систему типа М/М/1 с р < 1. Предположим, что ю0 = 0.
а) Вычислите (г/), применяя процедуру, определенную уравнением (8.78).
б) Повторите вычисления для w2 (у).
в) Покажите, что известное решение для
w (у) = lim w„ (у)
П-> со
удовлетворяет уравнению (8.79).
г) Сравните w2 (у) с w (z/).
8.15. Возводя (8.91) в куб, а затем образуя математические ожидания, выразите а ~ (дисперсию времени ожидания) через первые три момента распределения величин t, х и I.
332
8.16. Покажите, что из равенства (8.117) вытекает Р = 01 = = 1 — а. Для этого найдите постоянный член в разложении W* (s) в степенной ряд.
8.17. Рассмотрим систему типа G/G/1.
а) Выразите /* (s) через преобразование плотности распределения времени простоя данной системы.
б) Используя п. а, найдите /* (s), когда исходная система принадлежит простейшему типу М/М/1.
в) Используя п.а, покажите, что преобразование плотности распределения времени простоя в системе типа G/G/1 получается в виде
, 1 — A* (s)
st
что подтверждает формулу (8.121).
г) Поскольку либо исходная, либо двойственная ей система должна быть нестабильна (за исключением системы типа D/D/1), рассмотрите вопрос о существовании преобразования плотности распределения времени простоя для нестабильной системы массового обслуживания.
Заключение
Мы посвятили восемь глав (и два приложения!) изучению теории массового обслуживания. Иногда нас приводили в восторг красота и общность результатов, но чаще расстраивало отсутствие реального прогресса в теории. (Нет, мы никогда не обещали Вам цветущего сада!). Однако мы не теряли веру в то, что изучение сможет вооружить вас ценными методами для практического решения многих неотложных на сегодняшний день задач, связанных с перегрузкой систем обслуживания. Мы поддержим эту веру в следующем томе.
В томе II, после краткого обзора содержания тома I, начнется менее строгое, чем это делалось раньше, рассмотрение системы типа G/G/1. В гл. 2 мы войдем в новый мир, оставив в стороне строгость (и муки) точного решения поставленных задач. Здесь нам придется согласиться с рядом житейских фактов, показывающих, что наши модели не наилучшим образом описывают изучаемые системы. Поэтому мы должны будем решать задачи приближенно и налагать на решения некоторые ограничения. Будут найдены верхние и нижние границы для средней задержки в системе типа G/G/1, что по-видимому, относится к наиболее полезным приближениям для систем с большой нагрузкой. Это приближение фактически предсказывает, что время длительного ожидания имеет показательное распределение. Затем будет введен новый класс моделей, в которых дискретные процессы поступления и ухода требований заменяются сначала непрерывным приближением (слу-334
чайные процессы заменяются их математическими ожиданиями, являющимися функциями времени), а затем диффузионным приближением (при котором допускаются отклонения от этих средних). К счастью, оказывается, что эти приближения дают вполне приемлемые результаты для достаточно общих систем массового обслуживания. Фактически они позволяют даже исследовать переходные характеристики не только стабильных, но и насыщенных систем, и это составляет содержание последнего раздела гл. 2, где излагается новый, по-настоящему эффективный метод приближения часа наибольшей нагрузки, предложенный Ньюэллом.
Гл. 3 указывает пути применения некоторых важных результатов, полученных для систем массового обслуживания с приоритетами, в вычислительных системах коллективного пользования с множественным доступом. Здесь изучаются методы и рассматривается их применение к некоторым важным дисциплинам обслуживания. Устанавливается закон сохранения для систем с приоритетами, что предотвращает бесполезные исследования нереализуемых дисциплин обслуживания.
В остальной части тома II рассматриваются приложения, главным образом в области вычислительных систем, так как эти приложения теории массового обслуживания, по-видимому, наиболее современны и успешны. По сути дела для научных работников, занятых в области вычислительных систем, пытающихся осмыслить весь комплекс взаимодействий потребителей, программ, процессов и ресурсов, при изучении распределения ресурсов и потоков заданий в вычислительных системах, вероятно, единственно пригодным аппаратом является теория массового обслуживания. В гл. 4 рассматривается вычислительная система с множественным доступом, которая изолирована от многих других систем и обрабатывает требования большого числа конкурирующих потребителей. Исследуется пропускная способность системы, время реакции, а также использование ресурсов. Основная часть этой главы посвящена особому классу алгоритмов, называемых алгоритмами разделения процессора, так как эти алгоритмы наиболее пригодны для ана
335
лиза очередей и охватывают сущность более трудных и сложных распределительных алгоритмов. Гл. 5 посвящена сетям ЭВМ. Эта область развивается, по-видимому, наиболее интенсивно в молодой отрасли вычислительной техники (тот факт, что большинство ссылок относится к трем последним годам, — сам по себе достаточно показателен). Глава посвящена развитию методов анализа и расчета сетей связи ЭВМ и ставит много важных нерешенных задач. В качестве примера везде рассматривается конкретно существующая сеть ARPA. На этом примере читателю показываются мотивировки и оценки различных технических разработок.
Теперь Вам читатель, остается отточить и использовать полученный Вами новый инструмент. Мир ждет результатов!
ПРИЛОЖЕНИЕ I
Памятка о преобразованиях: производящая функция и преобразование Лапласа
В этом приложении выведены некоторые свойства и выражения для производящей функции (z-преобразования) и преобразования Лапласа в таком виде, в каком их применяют в настоящей книге и в теории массового обслуживания. Обзор начинается с производящей функции, действия с которой более наглядны. Форма и свойства обоих преобразований очень похожи, и их сравнение проводится при обсуждении преобразования Лапласа.
1.1. ЗАЧЕМ НУЖНЫ ПРЕОБРАЗОВАНИЯ?
Продвигаясь вперед в изучении интересующих нас физических систем, мы постоянно сталкиваемся с преобразованиями, возникающими в той или иной форме. Существует большое разнообразие преобразований (например, z-преобразование, преобразование Лапласа, преобразование Фурье, преобразование Меллина, преобразование Ханкеля, преобразование Абеля) и большое разнообразие названий (например, преобразование, характеристическая функция, производящая функция). Чем объясняется столь частое появление преобразований? Ответ состоит из двух частей. Во-первых, преобразования естественно возникают в формулировке и решении задач, имеющихся в СМО. Во-вторых, вводя их в методику решения, мы значительно упрощаем вычисления. Более того, часто аппарат преобразований дает единственно возможный путь решения задачи.
Так как преобразования возникают естественно, следует поинтересоваться тем, что вызывает их возникновение. Ответ можно получить, рассматривая инвариантные во времени линейные системы. Система в том смысле, в каком здесь применяется этот термин, и есть преобразование, или отображение, или зависимость между двумя функциями на входе и на выходе. Представим систему общего вида типа «черный ящик» с функцией f на входе и функцией g на выходе, как показано на рис. 1.1. Таким образом, система оперирует с функцией /, чтобы произвести
337
функцию g. В дальнейшем будем у 0 д- смо г с предполагать, что эти функции зависят от независимого времен-------------------- нбго параметра t. Этот произ-Рис. 1.1. Система общего вида ВОЛЬНЫЙ Выбор Не Ограничивает
общности, но удобен. Остановимся на некоторых обозначениях более подробно. Итак, предположим f = f (/). Чтобы указать на зависимость между / (/) и g (0, применим запись вида
f(0-g(0 (1.1)
для обозначения того факта, что g (/) появляется на выходе системы, если / (/) подается на ее вход.
Система называется линейной, если при (t) —> g± (/) и
/2 (0 ~* ^2 (^) справедливо следующее соотношение:
afi (О + bf2 (0 - > ag± (t) + bg2 (0, (1.2)
где а и b не зависят от переменной I. Далее, система называется инвариантной во времени, если кроме (1.1) справедливо также
f (t + т) - > g (t + т)
(1.3)
при любом т. Если справедливы оба указанных соотношения, то говорят об инвариантной во времени линейной системе.
При исследовании такой системы в решении всегда появляется комплексная показательная функция времени. Как будет показано далее, интересующие нас преобразования просто дают возможность разложения функций времени в суммы (или интегралы) комплексных показательных функций. Таким образом, комплексные показательные функции образуют строительные блоки преобразований, поэтому прежде всего нужно попытаться понять, почему показательные функции в нашем представлении связываются с такими системами.
Поставим основной вопрос, а именно: какие функции времени могут проходить через инвариантные линейные системы, не меняя формы? Иначе говоря, для каких f (i) будет g (t) = Hf (/), где H — некоторый скалярный множитель (по отношению к /)? Найдя такие функции, мы определим так называемые собственные функции или характеристические функции, или инварианты системы. Обозначим эти собственные функции через fe (/). Будет показано, что они должны иметь следующую форму (с точностью до произвольного скалярного множителя):
Д(0 = е5/> d-П
где s — в общем случае комплексная переменная. Таким образом, комплексные показательные функции (1.4) образуют множество собственных функций для всех инвариантных во времени линейных систем. Этот результат настолько важен, что имеет смысл 338
посвятить несколько строк его выводу. Итак, предположим, что на входе системы имеется функция fe (t), и на ее выходе функция ge (0, т. е.
Л (О =es/->ge(/).
Но на основании свойства линейности
es7e(/) = es(^)^eST&(/), где т и, следовательно, eST постоянны. Далее, в силу инвариантности во времени,
7(/ + т) = е8(/+т) -ge(/ + x).
Из этих двух соотношений следует, что eST&(0 = ge(t + t).
Единственным решением этого уравнения является функция вида и это совпадает с ранее высказанной гипотезой о том, что комплексная показательная функция не меняется при прохождении через инвариантную во времени линейную систему, если не считать скалярного множителя Н. Этот множитель не зависит от t, но, возможно, зависит от s, поэтому будем писать Н = Н (s). Таким образом, окончательно приходим к заключению, что
esi^H(s)esi, (1.5)
и этот основной результат выявляет собственные функции рассматриваемой системы.
Таким образом, комплексные показательные функции оказываются основными функциями при изучении инвериантных во времени линейных систем. Кроме того, если на вход такой системы поступает показательная функция, то путем тривиальных выкладок из равенства (1.5) можно получить функцию на выходе, если известна функция Н ($). Естественно задаться целью, если это возможно, представить / (/) в виде суммы (или интеграла) комплексных показательных функций, каждая из которых вносит некоторый вклад в соответствии с формулой (1.5) в общую выходную функцию g (Z). Тогда общая выходная функция может быть получена суммированием (интегрированием) этих компонент на выходе. (Тот факт, что сумма отдельных слагаемых на выходе является такой же суммой, как и сумма отдельных слагаемых на входе, — т. е. разложение в сумму комплексных показательных функций, — следует из линейности системы. Процесс разложения функции на входе в сумму показательных функций, вычисления для каждой из них функции на выходе [по формуле (1.5) ], а затем восстановления выходной функции из сумм показательных функций и называют в анализе методом преобразований.
339
Этот подход, как можно видеть, вполне естественно вытекает из сказанного выше. В этом смысле преобразования возникают совершенно естественным путем. Кроме того, как известно, такие системы описываются линейными дифференциальными уравнениями с постоянными коэффициентами; таким образом, широко распространенное применение преобразований при решении таки?; уравнений не должно быть неожиданным.
Мы пока еще не дали точного определения преобразования. Наберитесь терпения. Сначала мы попытаемся ответить на вопрос: зачем нужны преобразования? Если следовать по пути рассуждений, вытекающих из равенства (1.5), можно очень быстро прийти к преобразованию Лапласа. Однако сейчас нам удобнее рассматривать не функции непрерывного времени, а только функции дискретного времени. Эта ориентация приводит к производящим функциям; к преобразованиям же Лапласа мы вернемся в этом приложении позже. Основанием для такого переключения служит большая наглядность операций на оси дискретного времени по сравнению с операциями на оси непрерывного времени (при этом временно откладывается также введение единичной импульсной функции).
Итак, рассмотрим функцию /, определенную только на дискретном множестве временных точек, которые предположим кратными некоторой основной единице времени Т. Таким образом, f (t) = f (t = nT), где п = ..., —2, —1, 0, 1, 2, ... Чтобы совместить эти обозначения с ранее введенными, обозначим через функцию f (t = пТ). Предположим далее, что рассматриваемые системы тоже дискретны во времени. Следовательно, будем рассматривать линейные инвариантные во времени системы с функцией па входе / и функцией на выходе g (это тоже функция дискретного времени), для которых имеются три соотношения, соответствующие соотношениям (1.1)—(1.3):
/п-’Яп; (1-6)
+ ag„}bgn}‘, (1.7)
fn+m->gn+m, б-8}
где m — некоторое целое число. Здесь соотношение (1.7) выражает линейность, а соотношение (1.8) — инвариантность во времени для дискретной системы. Поставим для дискретных систем тот же фундаментальный вопрос и, конечно, получим по существу тот же ответ, а именно, что собственные функции имеют вид
Опять собственными функциями оказываются показательные комплексные функции. Теперь удобно ввести обозначение
zAe~sr (!Я
340
и записать собственные функции в виде
Так как s — комплексная переменная, то г — тоже комплексная переменная. Делая по существу те же шаги, что и при переходе от (1.4) к (1.5), найдем, что
г~п — Н (z) z~n, (1.10)
где И (z) — функция, не зависящая от п. Это соотношение просто выражает тот факт, что множество функций {г-") для любого значения г образует множество собственных функций для дискретных инвариантных во времени линейных систем. Кроме того, функция (постоянная) Н как в равенстве (1.5), так и в равенстве (1.10) указывает точно, сколько данных комплексных показательных функций выдаст эта линейная система при подаче на ее вход одной такой функции. Следовательно, функция Н фактически описывает влияние системы на эти показательные функции; на этом основании ее обычно называют функцией системы (или передаточной функцией).
Продолжим рассуждения дальше. Как хорошо известно, лучший способ узнать, что находится внутри системы, — взломать ее решительно и быстро. Для рассматриваемых систем это соответствует подаче на вход сигнала только в момент t = 0 и последующему наблюдению за выходом. Это приводит к определению дельта функции Кронекера (известной также под названием единичной функции):
Если подать ип на вход рассматриваемой системы, то реакцией на выходе будет так называемый единичный отклик, обозначаемый hn. Таким образом,
* hn.
Из соотношения (1.8) можно также записать
^m+re * ^п+г.т
Из свойства линейности в соотношении (1.7) следует
m.
Конечно, можно умножить оба выражения на единицу: z~nznzmun+m -^z~nznzmhn+m. (1.12)
Далее, если рассмотреть последовательность входящих функций {fn'1} и для каждой из них обозначить функцию на выходе fn}—>gn\ то по свойству линейности системы получим
I/n’-Sgn’- (1.13)
i i
341
Если последнее замечание применить к соотношению (1.12), то получим
z~n Е un+mzn+m L hn+mZ"+m, т tn
где сумма распространяется на целые значения т. Из определения (1.1.1) ясно, что сумма в левой части соотношения имеет только один ненулевой член, а именно при т = —п, и этот член равен единице. Кроме того, в правой части произведем замену индекса суммирования, что даст
z~n > z~n У, hkz . k
Последнее соотношение имеет теперь тот же вид, что и соотношение (1.10). Поэтому очевидно, что справедливо равенство
H(z)=^hkzk. (1.14)
k
Оно связывает функцию системы Н (г) с единичным откликом hk. Вспомним, что инвариантная во времени линейная система полностью 1 характеризуется заданием функции Н (г), так как в этом случае определяется выходная функция для любых собственных функций. Аналогично этому значение единичного отклика также полностью характеризует работу инвариантной во времени линейной системы. Поэтому не является неожиданностью существование явной связи между этими двумя характеристиками, которая выражена и равенством (1.14).
Наконец, мы в состоянии ответить на вопрос: зачем нужны преобразования? Ключ ответа лежит в равенстве (1.14), которое само по себе является преобразованием (в данном случае производящей функцией), обращающим 2 3 функцию времени hk в функцию комплексной переменной Н (г). Это преобразование возникает естественно при изучении инвариантных во времени линейных систем, а не вводится искусственным путем. Позже мы увидим, что аналогичное соотношение существует и для систем с непрерывным временем, что приводит к преобразованию Лапласа. Вспомним, что системы с непрерывным временем могут быть описаны линейными дифференциальными уравнениями с постоянными коэффициентами, и применение преобразований значительно упрощает решение таких уравнений. Неудивительно, что системы с дискретным временем приводят к системам линейных
1 Полная характеристика понимается в том смысле, что единственной допол-
нительно требуемой информацией является начальное условие системы (т. е. начальные состояния всех элементов, накапливающих энергию). Обычно предполагается, что система находится в состоянии с нулевой энергией, и в этом случае действительно имеется полная характеристика.
3 Преобразования не только меняют форму, в которой представлена информация, описывающая данную функцию, но также представляют эту информацию в упрощенном виде, удобном для математических операций.
342
разностных уравнений с постоянными коэффициентами, решение которых упрощается применением производящих функций. Наконец, функции на входе / и на выходе g легко разлагаются во взвешенные суммы комплексных показательных функций при помощи преобразований, и, конечно, если такое разложение проведено, то такие результаты, как (1.5) или (1.10), непосредственно дают покомпонентные выходные функции для каждой из составляющих на входе. Общая выходная функция получается при этом суммированием выходных составляющих в соответствии с соотношением (1.13).
Тот факт, что эти преобразования естественно возникают при изучении указанного вида систем, в действительности дает лишь частично ответ на основной вопрос, касающийся применения преобразований в анализе. Другим, более прагматическим основанием для применения преобразований является то, что они значительно упрощают анализ. Очень часто фактически анализ можно провести, только применяя преобразования, что приводит к частному решению, из которого получают характеристики системы.
Остальная часть данного приложения посвящена рассмотрению примеров и свойств преобразований двух указанных видов, столь важных в теории массового обслуживания.
1.2. ПРОИЗВОДЯЩИЕ ФУНКЦИИ
Рассмотрим функцию дискретного времени fn, принимающую ненулевые значения только при неотрицательных значениях индекса, т. е. при п — 0, 1, 2, ... (иначе говоря, полагаем для удобства, что fn = 0 при п < 0). Теперь необходимо сжать эту бесконечную последовательность в одну функцию таким образом, чтобы при желании можно было эту сжатую форму снова перевести в начальную последовательность. Для этого нужно «отметить» каждый член последовательности Д. Мы отмечаем fn, умножая его на гп. Так как каждый член последовательности имеет свой индекс п, то и маркировка для каждого члена последовательности своя; z выбираем как некоторую комплексную переменную, допустимые значения которой будут рассмотрены вкратце.
Отметив каждый член, просуммируем их, чтобы образовать сжатую функцию, представляющую собой первоначальную последовательность. Таким образом, образуется производящая функция (называемая также z-преобразсванием [2, 5], или геометрическим преобразованием) для fn:
со
F(z)AL//. (1.15)
п=0
Очевидно, что F (z) является функцией только переменной z, так как по индексу п идет суммирование. В обозначении, прини-343
маемом для производящей функции, используются прописные буквы, соответствующие строчным буквам, описывающим последовательность, как, например, в равенстве (1.15). Точно такую же форму имеет равенство (1.14).
Производящая функция для последовательности существует, если члены последовательности возрастают не быстрее, чем по закону геометрической прогрессии, т. е. если при некотором а > 0 будет выполняться равенство
lim =0.
ап
Каждая такая последовательность имеет единственную производящую функцию.
Если сумма всех членов последовательности конечна, то круг j z ] -< 1 наверняка представляет собой область аналитичности функции F (z) *. В этом случае
оо
Е(1) = £/п. (1.16)
п=0
Рассмотрим теперь некоторые важные примеры производящих функций. Условимся обозначать соотношение между последовательностью и се производящей функцией двойной обоюдоострой стрелкой1. Таким образом, равенство (1.15) может быть записано в виде
Д<=>Е(г). (1.17)
В качестве первого примера рассмотрим единичную функцию, определенную равенством (1.11). Для этой функции в формуле (1.15) только один член в бесконечном ряду отличен от нуля, поэтому немедленно получается пара преобразований
и„<=>1. (1.18;
Второй пример связан с первым и относится к единичной функции, сдвинутой вправо на k единиц, т. е.
( 1, п = k\ “"-''’ДО, n^k.
* Функция комплексной переменной называется аналитической в некоторой области, если она имеет производную в каждой точке этой области. Условие Коши—Римана, необходимое и достаточное для аналитичности такой функции, можно найти в любом учебнике по теории функций комплексной переменной [I] (см. также: Свешников А. Г., Тихонов А. Н. Теория функций комплексного переменного. М., Наука, 1967, 304 с. — Прим. пер.).
1 Двойная линия означает соотношение преобразования, а обоюдоострая стрелка указывает на возможность перехода в обоих направлениях: f => F 11 F~->f.
344
В равенстве (1.15) также только один член в бесконечной сумме отличен от нуля, что дает
“n-k
В качестве третьего примера рассмотрим единичную ступенчатую функцию, определяемую как = 1 для п = 0, 1, 2, ... (вспомним, что все функции равны нулю при п <0). В этом случае получается сумма членов геометрической прогрессии, т. е.
V=>S 1?" = -rLT- (1.19)
Заметим, что в этом случае для существования производящей функции должно выполняться условие |z| <1. Чрезвычайно важным, часто встречающимся примером является геометрическая прогрессия
fn^Aan, п= О, 1, 2, ...
Ее производящая функция может быть вычислена в виде
00 00
F (z) = Е Aanzn = A Z («z)n = ——-. л=0 л=0 1 ~аг
Таким образом,
: ЛаП<=>ь4г7> (1-20)
| и, конечно, областью аналитичности этой функции будет круг | И < 1/|а|. Заметим, что здесь |а| может быть больше или । меньше единицы.
\ Линейные преобразования типа производящих функций обладают рядом важнейших свойств. Многие из них перечислены
; в табл. 1.1. Однако для нас поучительно вывести свойство свертки, наиболее важное для теории массового обслуживания. Рассмот-; рим две функции дискретного времени f,t и gn, принимающие не-, нулевые значения только для неотрицательных индексов. Соот-i ветствующие им производящие функции будут F (г) и G (г). . Пусть 0 означает операцию свертки, которая для и gn опреде-; ляется следующим образом:
? п
I п О ёп Z f П-kSk 6=0
Найдем производящую функцию свертки функций fn и gn-, 00 оо д
fn О Sn <==> S (fn О Sn)Zn=Tl S
• д=Ю n=0 k=Q
у Однако, поскольку
Ж' 00 п « 00
t Z E =Z E,
ak n=o fe==o fc=o n—k
К 345
Таблица 1.1
Некоторые свойства производящих функций
ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОИЗВОДЯЩАЯ ФУНКЦИЯ
1. fn, л = 0, 1,2, ... п*) = S fnzn п = 0
2. afn + bgn 3. anfn 4. fn/k, п = 0, k, 2k,... aF (г) -f- bG (z) Р (аг) Р(г*)
5. fn+i 4^ w-^oi
6. fn+k> k 0 Р V г* i=i '1-1
7. fn-i 8. fn-k> k 0 zF(z) zkF (г)
9. nfn
10. n (n — 1) (n — 2). . . (n — m + I) fn dm zm — F (z) dzm ' '
11- fnQgn 12. fn — fn-i 13. £ fk, n = 0, 1, 2, . . . k=0 d t , 14. fn (a — параметр последо- вательности fn) F (Z) G (г) (1 — z)F(z) F(z) 1 — z 4-P (г) да
15. Свойство суммы ряда CO ^(1)= 2 fn n = 0 00
16. Свойство знакопеременной суммы F (-1) = (-D"fn n = 0
17. Теорема о начальном значении F (0) = f0
18. Теорема о промежуточных значениях 19. Теорема о предельном значении 1 dnF(z) I Ш dzn |г = 0 ln lim (1 — z) F (z) = /<» z-> 1
346
то
СО 00 / ОО \ f 00
fnОgn <-> I g^k E fn-^-k = E g/ E fm*m n=0 n=k \k=Q / \ms=0
= G(z)F (z).
Полученный результат можно сформулировать так: производящая функция свертки двух последовательностей равна произведению производящих функций этих последовательностей.
В табл. 1.1 помещены некоторые важные свойства производящих функций, а в табл. 1.2 приведены некоторые важные известные производящие функции.
Таблица 1.2
Производящие функции некоторых последовательностей
ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОИЗВОДЯЩАЯ ФУНКЦИЯ
1. fn, п= 0, 1,2... р (Z) = El
п=о
(1, п = 0;
2. ип = 1 1
[0, п 0
3. un_k г*
4. в„=1, п=0, 1, 2,. .. 1
1 —г
5. г*
i — г
6. Ло/1 А
1 — аг
7. пап аг
(1 — аг)2
г
(1-г)3
9. п2ал аг (1 + аг) (1 — аг)3 г(1 + г)
10. п2
(1—2)3
11. (П 4-1) а" 1
(1 — аг)2 1
12. (п + 1)
(1-г)2
13. (п + tri) (п + т — 1). . . 1
... х (п. + 1) (l-az)"1-1
14. -1- е-
п !
347
Сделаем некоторые замечания, касающиеся этих таблиц. Во-первых, в табл. 1.1 заметим, что свойство 2 — это свойство линейности, а свойства 3 и 4 относятся к изменению масштаба соответственно в области определения производящей функции и на оси времени. Свойства 5—8 характеризуют смещение во времени и особенно полезны. В частности, заметим, что на основании свойства 7 единичная задержка (задержка на единицу времени) приводит к умножению производящей функции на z, в то время как из свойства 5 следует, что единичное опережение приводит к операции, содержащей деление на z. Свойства 8—10 относятся к умножению последовательностей на множители вида п (п — 1) ... (п — т). Их комбинацию можно применить, например, при нахождении производящей функции для последовательности /г2/^; это может быть сделано с учетом того, что п2 — п (п. — 1) 4- п, и поэтому преобразование n.2fn просто равно
2 d2F (z) dF (г) dz2 ' г dz '
Это показывает, как с помощью простой техники дифференцирования можно получать более сложные производящие функции.
Вероятно, однако, наиболее важным является свойство 11, показывающее, что производящая функция свертки двух последовательностей равна произведению производящих функций этих последовательностей. Свойства 12 и 13 относятся к вычитанию и сложению членов последовательности. Свойство 14 показывает, что если а — независимый параметр последовательности fn, то дифференцирование последовательности по этому параметру эквивалентно дифференцированию производящей функции. Свойство 15 также важно и показывает, что для получения суммы всех членов последовательности можно вычислить производящую функцию в точке z =» 1. Свойство 16 указывает, как вычислить знакопеременную сумму. Теорема о начальном значении, дающая свойство 17, вытекает из определения производящей функции и показывает, как вычислить нулевой член последовательности непосредственно из производящей функции. С другой стороны свойство 18 показывает, как вычислить любой член последовательности прямо из производящей! функции, используя дифференцирование. Это один из методов вычисления последовательности по производящей функции. Из свойства 18 видно, что последовательность fn образует коэффициенты разложения функции F (z) в ряд Тейлора в окрестности нуля. Так как разложение в степенной ряд единственно, то ясно, что обратный процесс тоже единствен. Свойство 19 дает прямой метод для вычисления предела последовательности из ее производящей функции.
Табл. 1.2 содержит некоторые важные производящие функции-Эта таблица может быть значительно расширена, если применить свойства, помещенные в табл. 1.1. В некоторых случаях это 348
I' проделано. Например, строка 5 табл. 1.2 получена из строки 4 | с помощью теоремы о запаздывании, составляющей свойство
8 табл. 1.1. Одно из наиболее важных соотношений содержится в строке 6.
) Таким образом, показан эффект сжатия последовательности f;t й в одну функцию комплексной переменной F (г). Вспомним, что переменная z нумерует члены последовательности fn так, чтобы г их потом можно было получить обратно из сжатой функции. С (Для этого член fn нумеруют множителем г".) Мы видели, как об-j. разуется производящая функция последовательности [с помощью | равенства (1.5)]. Обратная задача состоит в том, чтобы найти по-I следовательность fn по ее производящей функции F (г). Для осуществления такого обратного преобразования имеется три
I основных метода.
? Первый метод — метод степенных рядов, который состоит । в разложении данной производящей функции в ряд по степеням г.
Если это проделано, то fn находят как коэффициенты при соот-4 ветствующих степенях zn. Степенной ряд можно получить двумя путями. Первый из них уже был указан в теореме о промежуточ-> ном значении, сформулированной в виде свойства 18 в табл. 1.1, j а именно
f = 1 dnF (г)
П п[ 2=и0
• (этот метод удобен, если требуется найти несколько первых чле-; нов разложения, но довольно утомителен, если нужно много членов ряда). Второй путь целесообразен, если F (г) может быть выражена как рациональная функция от г (т. е. представляет собой частное от деления многочлена от сна многочлен от г). В этом . случае надо разложить знаменатель на множители, что позволяет ' непосредственно найти главные члены степенного ряда. В любом . случае метод степенных рядов труден, когда требуется найти ; много членов ряда.
Второй, наиболее полезный метод обращения производящей г функции — это метод проверок. Он состоит в том, чтобы выразить . функцию F (z) так, чтобы она состояла из частей, в которых можно узнать известные производящие функции, например, из табл. 1.2. Стандартный подход для представления F (г) в таком виде состоит в разложении на простые дроби х. Обсудим теперь такой . подход.
Разложение на простые дроби — это алгебраический прием I представления рациональной функции в виде суммы простых чле-’ нов, для каждого из которых легко найти обращение. В частности, : попытаемся представить рациональную функцию в виде суммы членов, каждый из которых имеет либо простой, либо кратный л _________
С
1 Эта процедура связана с разложением функции в ряд Лорана в окрестности полюса [4].
349
полюс (см. строки 6 и 13 табл. 1.2). Так как производящая функция суммы равна сумме производящих функций слагаемых, можно, применяя свойство 2 табл. 1.1, найти обращение каждого из простых слагаемых и таким путем получить искомое обращение. Чтобы получить разложение на простые дроби, поступим следующим образом. Предположим, что функция F (z) рациональна, т. е.
где как числитель N (г), так и знаменатель D (z) являются многочленами от z *. Предположим далее, что функция D (z) уже разложена на множители, т. е.
k
D (z) — П(1 — (1.21)
i=i
В этом равенстве символ произведения означает операцию умножения:
к
П . ak.
Из равенства (1.21) следует, что i-й корень z — 1/а,- имеет кратность mt. (В большинстве задач, представляющих интерес, основная трудность решения состоит в нахождении корней а,- произвольного многочлена типа D (z), что позволяет разложить многочлен на множители в соответствии с равенством (1.21). Здесь предполагается, что эта трудная задача уже решена). Если F (z) уже представлена в таком виде, то ее можно выразить следующим образом [4]:
е и = щпйгт+ + " +та +
_ Л21____________. А21Г.2
(1 —a2z)”2'' (1-ааг)'«>-1 ’Г"' Г(1тЗД
J_____dAl_____I_______________L . . . I_. П 9 Ji
,m/, /1 A-1 (1 — а.:,г')'
(1 — одг) (1 — а*г) Л \ >
Это и есть искомая форма разложения, так как каждый член такой суммы имеется в табл. 1.2. В частности, сюда относится строка 13,
* Заметим, что разложение на простые дроби возможно только тогда, когда степень многочлена в знаменателе строго больше степени многочлена в числителе. В противном случае надо делить числитель на знаменатель до получения остатка, степень которого меньше степени знаменателя. Этот остаток, деленный на первоначальный знаменатель, указанным методом может быть разложен на простые дроби. Целая функция, полученная при таком делении, тоже должна быть обращена, для чего надо воспользоваться строкой 3 из табл. 1.2. Другоп путь для понижения степени числителя состоит в том, чтобы, если это возможно-выделить в числителе множитель с достаточно высокой степенью г.
350
а в простейшем случае — строка 6. Таким образом, если удается В осуществить разложение на простые дроби, то методом проверок > можно найти последовательность fn. Остается описать метод У определения коэффициентов Atj. Общее выражение для них имеет | вид
I А —1 (— 1 У-1 Гп — а2\т‘ Л’(г) 1
А“ (/-О-' k «J dzi-' L(1 а,2) £>(г) J г=1/а. • (L23)
j Эта довольно громоздкая процедура на самом деле достаточно I проста, если только функция F (z) не очень сложна.
f Здесь целесообразно привести пример для иллюстрации ме-| тода. Предположим, что функция F (г) задана в виде
f F (z) =---4- (1 — 8г)- ,j
g r W (1 — 4г) (1 — 2г)2 '
J В этом примере числитель и знаменатель имеет одну и ту же степень, поэтому надо привести выражение к нормальному виду ; (чтобы степень числителя стала ниже степени знаменателя). ; В этом случае наша задача проста, так как можно вынести мно-? житель z2 (чтобы степень числителя стала ниже степени знамена-! теля, достаточно вынести множитель z, но, очевидно, в этом примере лучше вынести сразу z2 и этим упростить вычисления).
: Таким образом, получаем
i р 1г\ г1 Г____1(L~..8£)___1
! W [ (1 — 4z) (1 —2z)2 J •
Обозначим член в квадратных скобках через G (z). Заметим, что в этом примере знаменатель имеет три нуля: в точке z = 1/4 и ; двойной нуль в точке г = 1/2. В обозначениях равенства (1.21) г k = 2, = 4, тг = 1, a2 = 2, m2 — 2. Из равенства (1.22)
; получаем
р д 4(1 — 8г)_______________Al । А1 । А32
(1 _4г) (1 „2г)2 (1—4г) (1— 2г)2 ' (1 —2г) ’
Коэффициенты типа А1г (т. е. коэффициенты при простых полюсах) легко получить умножением начальной функции на множители, дающие в знаменателе этот нуль, и вычислением полученного произведения в самой этой точке (т. е. вычислением в точке z, обращающей этот множитель в нуль). В рассматриваемом примере
Дп = (1 - 4z) G (г) Ь=1/4 = = - 16.
1» Коэффициент Л21 может быть подобным же образом вычислен 1’ из формулы (1.23):
3 Л21 = (1 - 2z)2 G (г) |г=!/2 = = 12.
351
Наконец, чтобы вычислить Л23, надо в соответствии с формулой (1.23) применить дифференцирование:
= - Т 4 (0 - 2г>*й W1 !•-'« - - U =
=____L (1-4г) (-32)-4(1-8г) (-4) I _
2 (1 —4г)а |г=1/2 “ °’
В результате окончательно получим
Г( 1 —16 । 12 । 8
° w “ 1 - 4г 1 (1 — 2г)г ' 1 — 2z '
Приведением к общему знаменателю легко проверить, что полученная функция действительно совпадает с первоначально заданной.
Следующим шагом найдем обращение функции G (г) методом проверок. Для этого заметим, что первый и третий члены имеют вид, который показан в паре преобразований 6, а второй член — ьид, что в паре 13 табл. 1.2. Это в сочетании со свойством линей ностп (свойство 2 в табл. 1.1.) непосредственно дает
0(2) <->gn =
( 0, п < 0;
= ( —16(4)"+ 12 (п 4- 1) (2)”-Ь 8 (2)", п = 0,1,2,... (L25)
Теперь надо учесть множитель г2, чтобы получить выражение fn. Как уже указывалось, для этого надо использовать свойство 8 из табл. 1.1, что даст (для /1 = 2, 3, ...)
fn = —16 (4)”*2 ф- 12 (п - 1) (2)"“2 + 8 (2)п~2.
Таким образом,
( 0, п<(2;
fn=~'\ (Зп — 1)2”-4", п = 2, 3, 4, ...
Это завершает решение примера.
Третий метод нахождения последовательности по производящей функции основан на формуле обращения. Этот метод основан на вычислении интеграла
L = d2’ ^-2&)
где / = ]/—1 , и интеграл берется в комплексной z-плоскости по замкнутому контуру С, окружающему 1 все полюсы функции __________ i .'
1 Так как лемма Жордана (см. с. 369) требует, чтобы F (г) -V0 при z)-> оо по любому пути, то будем требовать, чтобы рассматриваемые функции F (г) обладали этим свойством. Следовательно, для рациональной функции переменной г, если степень знаменателя не ниже степени числителя, надо делить числитель на знаменатель, пока степень остатка не станет ниже степени знаменателя. Целая часть, полученная при таком делении, легко обратима методом проверки, как показано ранее, и остается применить формулу обращения только к оставшейся функции.
352
F (г). Этот метод вычисления удобно применять в том случае, • когда выражение не содержит множителей вида zk. Если такие 9 множители имеются, то надо проводить вычисления без них, а у окончательное решение получать затем, пользуясь свойством 9 4 табл. 1.1, как будет проделано ниже. Контурное интегрирование наиболее легко выполнить, пользуясь теоремой Коши о вычетах [4]. Теорема эта может быть сформулирована следующим образом.
Теорема Коши о вычетах. Интеграл от функции g (г) ио замкнутому контуру С, внутри которого функция g (z) имеет только изолированные особые точки, равен сумме вычетов в этих точках, умноженной на 2л/, если функция g (г) аналитическая 1 внутри и на самом замкнутом контуре С.
Изолированной называется особая точка, в некоторой окрестности которой нет других особых точек функции. Классическим ' примером является простой полюс (полюс первого порядка, см. ниже). Если z = а — изолированная особая точка функции g (z) и если у (z) = (z — a)mg (z) аналитична в точке z = а и у (а) у= 0, то говорят, что функция g (z) имеет в точке z = а полюс порядка т, и вычет га в этой точке определяется следующим образом:
I Ж"-1
= (1.27)
Заметим, что вычет, определяемый по этой формуле, имеет почти тот же вид, что и коэффициент Л,7 в равенстве (L23). Разница заключается только в форме записи множителя, определяющего полюс.
: Таким образом, определены все понятия, нужные для примене-
i ния теоремы Коши о вычетах к вычислению интеграла (L26) и, значит, к определению функции времени fn по заданной производящей функции. Для иллюстрации проведем вычисление преды-t дущего примера, заданного равенством (1.24). Используя (1.26), получаем
/ —1 f -1г'1’" (1 - 8z) .
/7 z=- — • CD -------------- П7
ёп ’ 2л/ У (1 — 4г) (1 — 2г)2 ’
где С — окружность достаточно большого радиуса, включающая полосы z =• 1/4 и z = 1/2. Пользуясь теоремой о вычетах и формулой (1.27), находим вычет в точке z = 1/4:
П/4 - (г-4)
4г~1~п(1 — 8z) I _ (1 — 4z) (1 — 2г)2 |г=1/4 —
—(1/4)-1'” [1 -(8/4)] [1 — (2/4)]2
= 16 (4)”,
1 Функция F (г) комплексной переменной г называется аналитической в некоторой области комплексной плоскости, если она однозначна и дифференцируема в любой точке этой области.
12 Л- Клейнрок 353
а затем вычисляем вычет в точке z - 1/2:
d Г/ 1 \2 4г-1-'1 (1-8г) 1
dz |Д 2 ) (1 —4z) (1 — 2г)2 ]
г—1/2
d Г г'1-" (1 —8г) 1 I
dz [ 1—4z J |г=1/2
_(1 — 4z) [(—1 — я) г~2~л (1 -8г) +г~1~п (—8)]—г-1-" (1—8г) (-4) I (1 — 4z)2 |z=l/2
= (-1) [(-1 - п) (-3) + (1/2)-1"1 (-8)] -
- (1/2)'1-" (—3) (—4) = —12 (п + 1)2" + 16 (2)" - 24 (2)",
после чего сумму этих вычетов умножаем на 2nj и для получения выражения (1.26) делим на—2л/ (что дает умножение суммы вычетов на •—1). В результате получаем
gn = —16 (4)" +12 (п +1)2" 4- 8 (2)", п = 0, 1,2, ...
Это последнее выражение в точности совпадает с gn, полученным в формуле (1.25) методом разложения на простые дроби. С этого момента решение продолжается, как в предыдущем методе, что подтверждает согласованность этих двух подходов.
Таким образом, проведен обзор некоторых методов применения и обращения производящих функций, образуемых для функций дискретного времени. Применения этих методов при решении дифференциальных уравнений подробнее описаны ниже, в параграфе 1.4.
1.3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Преобразование Лапласа [7], определяемое ниже, обладает многими свойствами, характерными для производящих функций. Поэтому обсуждения этого параграфа образуют очень близкие параллели с результатами предыдущего параграфа.
Рассмотрим функции непрерывного времени, принимающие ненулевые значения только для неотрицательных значений непрерывной переменной t. [Опять для удобства будем считать, что f (0 — 0 при t < 0. Для более общего случая большинство применяемых методов обсуждается ниже в связи с равенством (1.38)]. Как и для функций дискретного времени, здесь желательно преобразовать функцию непрерывного времени в функцию новой комплексной переменной (скажем, s). В то же время желательно иметь возможность получить обратное преобразование в область переменной t, для чего надо каким-то образом «отметить» f (/) для каждого значения t. На основании рассуждений, проведенных в параграфе 1.1, в качестве такой метки целесообразно применить e-sZ. Комплексную переменную s можно записать в алгебраической форме: s — а 4 /со, где / — ’]/’—1. Умножив f (^ 354
на эту метку и проинтегрировав по всем ненулевым значениям, получаем преобразование, определяемое следующим образом:
ео
F*(s)A j fWe~st dt. (1.28)
—-со
Здесь вновь применено общее для преобразований Лапласа обозначение, при котором прописную букву используют для преобразования функции от времени, обозначенной той же строчной буквой. Такое преобразование называют обычно «двусторонним» преобразованием Лапласа, так как интегрирование проводится как по положительной, так и по отрицательной полуоси. При t < 0 предполагается, что f (t) = 0, и в этом случае нижний предел интегрирования может быть заменен О', что определяется как предел 0 — 8 при 8 —> 0 (е > 0). В дальнейшем этот предел часто обозначается просто 0, под которым понимается 0“ (обычно это не вносит путаницы). Как известно, существует также «одностороннее» преобразование Лапласа, в котором нижний предел интегрирования заменен на 0+, что понимается как предел 0 + е при 8 —> 0 (8 > 0). Это одностороннее преобразование Лапласа имеет приложения при исследовании переходных процессов в линейных системах. Важно, чтобы читатель различал эти два вида преобразований с нулем в нижнем пределе интегрирования, так как в первом случае (двустороннее преобразование) всякое накопление в нуле (как, например, определяемый ниже единичный импульс) будет включаться в преобразование, а во втором случае (одностороннее преобразование) оно будет опускаться.
В рассматриваемом случае, для которого f (0 = 0 при t <0 преобразование можно записать в виде
оо
F*(s) = jf(t)e~s/dt, (1.29)
о
где, повторяем, нижний предел интегрирования понимается как 0". Это преобразование Лапласа наверняка существует, если f (0 возрастает не быстрее показательной функции, т. е. если существует действительная постоянная с, удовлетворяющая условию
lim [ | f(t)\ ect dt < оо.
Наибольшая нижняя граница множества таких с обозначается сги и называется абсциссой абсолютной сходимости. Опять подчеркнем, что преобразование Лапласа F* (s) для данной функции f (0 единственно.
Если интеграл от f (0 конечен, то правая полуплоскость Re (s) > 0 представляет собой область аналитичности функции 355
F* (s). Обозначение Re ( ) читается как «действительная часть стоящей в скобках комплексной функции». В таком случае в соответствии с равенством (1.16) имеем
F*(0) = j о
(1.30)
Из определения (1.9) видно, что свойства производящей функции при z = 1 соответствуют свойствам преобразования Лапласа при s = 0, как, например, в равенствах (1.16) и (1.30).
Рассмотрим некоторые важные примеры преобразований Лапласа. Обозначения, применяемые здесь, совпадают с теми, которые были введены соотношением (1.17) для производящих функций, а именно, для обозначения соотношения между функцией и ее преобразованием применяется двойная обоюдоострая стрелка. Таким образом, равенство (1.29) может быть записано в виде /(/)<=>/=’*(«). (1.31)
Применение двойной стрелки, как и раньше, обусловлено единственностью преобразования.
Как и в случае производящей функции, наиболее удобным методом обращения преобразования, т. е. вычисления f (t) по F* (s), является метод проверок, т. е. поиск обратного преобразования по таблице. Поэтому обратим внимание на вычисление некоторых преобразований Лапласа. Одно из наиболее важных преобразований — преобразование односторонней показательной функции, т. е. функции
/(> I 0, f<0.
Вычислим преобразование этой функции следующим образом:
/(f) <=>(S) = j AeTaie~stdt = А°^ е~(s+a) f dt = .
0 0
Таким образом, получено фундаментальное соотношение
Ле'а'б (/)<=>-А-, (1.32)
v ' s + а ’ v
где для непрерывного времени единичная ступенчатая функция определена как
1 1,
бЧо, £<0. <L33)
Нетрудно видеть, что единичная ступенчатая функция фактически является частным случаем показательной функции с Л = 1 и а = 0, что непосредственно дает еще одну пару:
б (/) <=> 4- (1-34)
356
Заметим, что преобразование (1.32) имеет абсциссу сходимости == —а.
Таким образом, вычислены следующие аналоги производящей функции и преобразования Лапласа: геометрический ряд [соотношение (1.20)] и показательная функция [соотношение (1.32)], а также единичная ступенчатая функция [соотношения (1.19) и (1.34) соответственно]. Остается найти непрерывный аналог единичной функции, определенной равенством (1.11), производящая функция которой задается соотношением (1.18). Это приводит к понятию единичной импульсной функции. Единичная импульсная функция играет важную роль в теории преобразований, теории линейных систем, а также в теории вероятностей и теории массового обслуживания. Поэтому необходимо научиться оперировать этой функцией.
Примем следующее обозначение:
и0 (?) А единичная импульсная функция, возникающая в точке t - 0.
Функция и0 (0 соответствует импульсам единичной площади со столь высокой концентрацией и такой короткой длительности, что их нельзя отличать с помощью существующих измерительных приборов от других, возможно, более коротких импульсов. Поэтому, как и следует ожидать, точная форма импульса неважна, существен только момент его появления и его площадь. Эта функция была изучена, и ее применяли ученые на протяжении многих лет [4], среди них Дирак, поэтому единичную импульсную функцию часто называют дельта-функцией Дирака. Долгое время чистые математики воздерживались от применения функции и0 (/), так как она не подходит под математическое определение функции. Но не так давно теория распределений Шварца [6] подвела под понятие единичной импульсной функции твердую математическую базу. Частично трудность заключается в том факте, что единичная импульсная функция не является функцией в обычном смысле слова, а только обеспечивает возможность символических операций над разрывными выражениями и их производными. В этом обзоре единичный импульс вводится как предел последовательности без обращения к более тонкому понятию обобщенной функции, используемому в более строгих построениях.
Как было замечено ранее, точная форма импульса неважна, поэтому при обсуждении выберем в качестве импульса функцию
fa (0 =
а,
0,
1 .
2а ’
1
2а
Этот импульс представляет собой прямоугольник, высота и ширина которого зависят от параметра а, как показано на рис. 1.2. Однако площадь прямоугольника постоянна и равна единице (от-357
Рис. 1.2. Последовательность функций, дающих в пределе единичную импульсную функцию и0 (О
сюда название единичной импульсной функции). При возрастании а импульс становится выше и уже. Предел этой функции при а —» оо (или предел любой другой из бесконечного множества функций с подобными свойствами, т. е. с возрастающей высотой, убывающей шириной и единичной площадью) и есть то, что понимают под единичной импульсной функцией. Таким образом, приходим к следующему описанию единичной импульсной функции:
[ оо, t = 0;
U°^ = | 0, t + Q,
J «ода=1.
расположенной в точке появления импульса, с числом у конца стрелки, указывающим площадь импульса. Следовательно, взятая А раз единичная импульсная функция, помещенная в точке t = а, обозначается А и,, (t — а) и изображается, как на рис. 1.3.
Рассмотрим теперь интеграл от единичной импульсной функ-и°' а ции. Очевидно, что, если интег-
д рировать от —оо до t, где t < 0,
то интеграл должен равняться нулю, а если t > 0, то в этом интеграле будет заключена вся единичная площадь, поэтому
0 а t ( 1, t > 0;
Рис. 1.3. Графическое изображение J ^0 (^) If) / <-< f)
функции Аи0 (i — а) ; • у —w ’
358
Но, как сразу видно, правая часть представляет собой единичную ступенчатую функцию, определенную равенством (1.33). Таким образом, приходим к выводу, что интеграл от единичной импульсной функции равен единичной ступенчатой функции, и, значит, «производная» единичной ступенчатой функции должна совпадать с^единичной импульсной функцией. Однако надо признать, что производная от разрывной функции (ступенчатой функции) не определена должным образом. Чтобы эта операция опиралась на ^твердый математический фундамент, надо вновь обратиться к ,теории распределений. Поэтому предположим, что эта операция обоснована, и станем применять единичную импульсную функцию как обычную функцию.
Одним из очень важных свойств единичной импульсной функции является ее просеивающее свойство. Оно состоит в том, что для произвольной дифференцируемой функции g (/) имеет место равенство
со
j u0(t-х) g{x) dx = g(t).
Последнее равенство просто утверждает, что интеграл от произведения функции g (х) на импульс, расположенный в точке х = t, «просеивает» функцию g (х), оставляя только ее значение g (t) в точке I. Заметим, что можно также определить производную единичного импульса, которую обозначим через иу (t) ~ = duo (t)/dt. Она известна как единичный дублет и обладает тем свойством, что равняется нулю всюду, кроме окрестности начала координат, где она стремится к оо слева от нуля и к —оо справа от нуля, и, кроме того, ограничивает нулевую площадь. Такие функции соответствуют, например, электростатическим диполям, встречающимся в физике. Действительно, импульсную функцию можно уподобить силе, приложенной к листу бумаги, положенному на острие ножа, когда лист прижимается вниз, а единичный дублет подобен силе, действующей на лист бумаги, когда его разрезают ножницами. Можно также определить производные высших порядков, и в общем случае должно быть ип (t) = = dun_x (t)!dt. В самом деле, как уже известно, можно, идя обратным путем, интегрировать эти функции, как, например, при получении единичной ступенчатой функции в виде интеграла от единичной импульсной функции. Очевидное обозначение для единичной ступенчатой функции должно было бы быть п_1 (Z), поэтому можно написать и0 (/) = du_Y (t)!dt. [Заметим, что для единичной ступенчатой функции используется также обозначение 6 (/), как в равенстве (1.33)]
Таким образом, определена бесконечная последовательность специальных функций, которая начинается с единичного импульса и содержит как производные высших порядков, такие, как дублет 359
и т. д., так и интегралы от единичного импульса, приводящие к единичной ступенчатой функции
Л г (/, I > 0;
НО-_Х-(о, (<0.
параболе
/ А Г /2 4-, / > 0;
М-3 (0 = J М-2 (л-) dx ---= Z
— оо о, t < о
и, в общем случае, к функции
(п-1)! ’
«-П =
(1.35)
Все это семейство называется семейством сингулярных функций, и наиболее важными из него являются единичная ступенчатая и единичная импульсная функции.
Вернемся теперь к главной теме обсуждения и рассмотрим преобразование Лапласа функции м0 (Z). Непосредственно из равенства (1.28) получим
00
«0 (0 <=> j «0 (0 e~s/ Л = 1.
О
(Заметим, что нижний предел интегрирования понимается как О"). Таким образом, единичный импульс своим преобразованием Лапласа имеет постоянное число — единицу.
Рассмотрим теперь некоторые важные свойства преобразований. Как и в случае производящих функций, наиболее важным является свойство свертки, и оно будет теперь выведено для случая непрерывного времени. Итак, рассмотрим две функции непрерывного времени f (Z) и g (0, принимающие ненулевые значения только при t > 0. Обозначим их преобразования Лапласа соответственно через F* (s) и G* (s). Снова определяя ® как оператор свертки, т. е. оо
f(t)Qg(t)~ J f(t-x)g(x)dx, (1.36)
-00
что в данном случае сводится к интегралу
t
f (/) ® g (0 = J / (/ - X) g (х) dx,
О
360
будем искать преобразование свертки. Формально оно получается из равенства (1.28) следующим образом:
оо
m 0 g ю <=> f а (о о g со) ^st dt= о
ОО t
--= [ [ f (t — -v) g (x) dxe~st dt -о ii
eo oo
- f J f(t-x)^^dtg(x)^xdx^ x=<) t~x
— J g (x) e"sxdx J f(v)e""du. x=0 v=0
В результате получаем
iW0gW<=>^ (S)cr(s).
Опять преобразование свертки двух функций равно произведению их преобразований. В табл. 1.3 содержатся некоторые важные свойства преобразований Лапласа, а в табл. 1.4 некоторые важные преобразования. В этих таблицах использованы принятые обозначения:
(1.37)
J ... pw dx = (t).
п раз t
Например, /<-1)(0= J f (х) dx; если же речь идет о функции, равной нулю при t < 0, то f(-1> (0~) = 0. Подчеркнем здесь, что одностороннее преобразование, в котором в качестве нижнего предела интегрирования используется 0+, повсеместно применяется при анализе переходных процессов, но мы предпочитаем 0", чтобы включить импульсы в начале координат.
Табл. 1.3 свойств преобразований Лапласа позволяет вычислять многие преобразования. Свойство 2 устанавливает линейность, а свойство 3 описывает эффект изменения масштаба. Свойство 4 дает эффект сдвига во времени, в то время, как двойственное ему свойство 5 дает эффект смещения в области определения преобразования. Свойства 6 и 7 показывают эффект умножения на I (в некоторой степени), что соответствует дифференцированию в области преобразования. Аналогично свойства8 и 9 соответствуют эффекту деления на I (в некоторой степени), что соответствует интегрированию. Свойство 10, наиболее важное (оно было вы-
361
Таблица 1.3
Некоторые свойства преобразований Лапласа
ФУНКЦИЯ ПРЕОБРАЗОВАНИЕ
1- f(t), 2. af (t) +bg(t) F* (S) = f f (0 e-stdt о- aF* (s) + bG* (s)
aF* (as)
4. f(t-a) 5. e~aif(f) 6. tf(t) e~asF* (s) F* (s 4- a) dF* (s)
ds
7. lnf (0 / dnF* (s) dsn
8. -Ш- J F * (Si)
st = s
9. Ж Is1 co co co j dsj j ds3. . . J dsnF* (sn)
S1=S S^St sn=sn-l
iO. f (i) & g (6 ,, , df(t) dt r* (s) G‘ (s') sF* (s)
,9 dnf(t) s^F* (s)
dtn
13. j F* (s)
s
— co
14. j . . . j f (0 (dt)n — co —co F* (s)
n раз
15. ~ f (0 (a — параметр) 4-F(s) da
16. Свойство интегрирования 17. Теорема о начальном значении F* (0) = j f (t) dt 0- lim sF* (s)= lim HO S-> co t -> 0
362
Продолжение табл. 1.3
ФУНКЦИЯ ПРЕОБРАЗОВАНИЕ
18. Теорема о предельном значении lim sF* (s) = lim f(t), если sF* (s) S->0 t -> oo аналитична для Re (s) >- 0
♦ Для полноты картины покажем, как в случае, когда функция может принимать
выглядят преобразования в строках 11—14 ненулевые значения при t < 0:
dy (=) snF* (s) — sn-'f (О-) — sn-2f^ (О’)---------f'n~» (О'),
dtn
F* (s)
s
п раз
f'~ly (0~)
f(~2)(0~)
f(-n> (O')
s
s
sn
Таблица 1.4
Некоторые пары преобразований Лапласа
ФУНКЦИЯ преобразование
со
1. fit), F*(s)= j f(t)-t-s!dt
о-
2. uQ (1) (единичный нмпульс) 1
3. иа (t — a) e-as
4- ип (/) Д (t) st
5. 'м((|М(0 (единичная функция) J_ s
e-as
6. u.j (t — а) s
fn-1 1
7- i‘-n(t)& sn
A
8. Ле~а/6 (0 s a
9. /е-а/б(О 1 (s + a)2
10. -4 e~aZ6 (t) nl 1 (s + a)n+1
363
ведено ранее), показывает эффект свертки во времени, приводящей к простому умножению в области преобразований. Свойства 11 и 12 описывают эффект дифференцирования во времени. Следует отметить, что это соответствует умножению на s (в степени, равной числу дифференцирований по времени) первоначального преобразования. Таким же образом свойства 13 и 14 показывают эффект интегрирования по времени, приводящий к делению на s в области преобразований. Свойство 15 означает, что дифференцирование f (/) по параметру соответствует той же операции в области преобразований. Свойство 16 (свойство интегрирования) определяет простой путь вычисления интеграла через значение преобразования в нуле. Свойства 17 и 18 (теоремы о начальном и о предельном значениях) показывают, как вычислить f (t) при t = 0 и I — оо прямо из преобразования.
В табл. 1.4 дается довольно краткий перечень важных пар преобразований Лапласа. Существует много более подробных таблиц, которые можно найти в других источниках (см., например, [3]). Конечно, как уже говорилось ранее, указанная таблица может быть значительно расширена с помощью свойств, перечисленных в табл.1.3. Заметим, например, что пара 3 в табл. 1.4 может быть получена из пары 2, если применить свойство 4 из табл. 1.3. Еще раз отметим, что табл. 1.4 ограничена, так как в нее включены только функции, находящие применение в этой книге.
До сих пор при рассмотрении преобразований Лапласа предполагалось, что f (t) — 0 при t < 0. Этого достаточно для большинства случаев, которые здесь рассматриваются. Однако иногда может возникнуть необходимость в рассмотрении преобразований функций, которые могут быть отличны от нуля на всей действительной осп. В таком случае надо опять взять нижний предел интегрирования -- сю, т. е.
Д' dt.
(1.38)
Легко показать, что такое (двустороннее) преобразование Лапласа может быть вычислено через односторонние функции времени и их преобразования следующим образом. Сначала введем оп-
ределения
Д (/)
(Ж с 3.0; (О, t > 0;
f 0, К<0;
/+(/) U(0, ^>0,
из которых немедленно следует, что
/(0 -I-/'ДО-
364
Заметим теперь, что L (—0 принимает ненулевые значения только на положительной полуоси, а функция f+ (/) •— только на неотрицательной полуоси. Поэтому
/+(0<=>г+ (s);
<=>F*_ (s),
где преобразования определены, как в равенстве (1.29). Нужно, однако, получить преобразование для f_ (Z). Легко показать, что оно имеет вид /У (0 4^ F- (—s)- В силу линейности преобразований можно, наконец, записать двустороннее преобразование:
Г(8) = ^(-8) + ^(5).
Как всегда, это преобразование Лапласа имеет абсциссу абсолютной сходимости. Обозначим о+ абсциссу абсолютной сходимости F* (s). Тогда областью сходимости для F* (s) будет полуплоскость Re (s) > о'+. Точно так же, если — абсцисса абсолютной сходимости F* (s), то полуплоскость Re (s) > определяет область сходимости Fl (s). Тогда F* (—$) будет иметь ту же абсциссу сходимости о_, но область сходимости для нее будет Re (s) < а_. В этой ситуации F* (s) сходится в полосе ст < Re (s) < тогда и только тогда, когда о+ < о_. В противном случае определение F* (s) бесполезно. Очевидно, аналогичные рассуждения можно провести для производящих функций в случае, когда функции дискретного времени могут принимать ненулевые значения при отрицательных значениях индекса.
До сих пор рассматривался эффект отметки функции времени f (t) показательной комплексной функцией e“s/ и сжатия (интегрирования) по всем отмеченным функциям с целью получения новой функции, а именно преобразования F* (s). Смысл меток состоит в том, чтобы потом можно было «обратить» преобразование и снова получить из него первоначальную функцию. Известно, что в принципе это возможно, так как преобразование и функция времени соответствуют друг другу взаимно однозначно.
До сих пор изучались переходы в одном направлении: от f (/) к F* (s). Займемся теперь задачей обращения преобразования F* (s) для получения f (t). Имеются два основных метода получения такого обратного преобразования: метод проверок и формальный метод обращения интеграла. Эти два метода во многом схожи.
Рассмотрим первый метод — метод проверок, дающий наиболее полезную схему обращения преобразований. Здесь, как и в случае производящей функции, задача сводится к тому, чтобы представить F* (s) в виде суммы членов, для каждого из которых обратное преобразование может быть найдено по таблицам. Тогда можно, пользуясь свойством линейности, искать обратные преобразования для слагаемых, а затем, сложив их, получить обратное преобразование для суммы. Опять основным методом представле
365
ния F* (s) в виде суммы является метод разложения на простые дроби. Здесь этот метод будет описан сокращенно, так как он достаточно подробно описывался в случае производящих функций. Прежде всего предположим, что F* ($) — рациональная функция аргумента s, а именно
где числитель N (s) и знаменатель D (s) — многочлены от s. Предположим снова, что степень числителя ниже степени знаменателя. Если это не так, нужно разделить числитель на знаменатель до получения остатка, степень которого ниже степени знаменателя. Будем применять разложение на простые дроби только к правильной рациональной функции, а степенные функции, полученные при делении, обращать непосредственно, применяя строку 4 табл. 1.4. Дополнительно предположим, что «трудная» часть задачи решена, т. е. что знаменатель уже разложен на множители:
k
£>(s)= П (* + От' - (1-39)
i=i
Если F* (s) задана в такой форме, то ее можно представить в виде суммы:
Вц t______________В12______L . . . I ^т1 Вл
(s-|-ai)m‘ (s + ai)mi-1 (s + ai) (s-\-a2)m*
В22 , , В-т2 । , Ва
(s + 02)m=-r' r (s + a3) (s + akfk
।Bk2 i . . . i Bkmh
‘ / t 1 ' (s + Clk)
(s + a*) K
(1.40)
Выразив F* (s) в таком виде, можно по табл. 1.4 найти обращение каждого из слагаемых. В частности, пары 8 (для простых полюсов) и 10 (для кратных полюсов) дают на это прямой ответ. Как и прежде, для вычисления коэффициентов В,, имеется общая формула:
1 (/-1)!
(1-41)
Таким образом, получается полное описание обращения преобразования методом проверок в случае, когда функция F* (s) рациональна и D (s) разложена на множители, как в формуле (1.39). Этот метод хорошо работает в тех случаях, когда функция F* (s) не чересчур сложна.
366
Чтобы лучше осветить сформулированные принципы, рассмотрим простой пример. Предположим, что функция F* (s) задана в виде
. 8 (s3 4-3s + 1) ._ .„.
f*(s)—(s + 3)(s + l)3- (1.42)
Здесь знаменатель уже разложен на множители, и можно сразу приступить к разложению функции F (s) на простые дроби в соответствии с формулой (1.40). Заметим, что здесь k = 2, = 3,
т1= 1, а2 = 1, т2 = 3. Так как степень знаменателя (4) выше степени числителя (2), можно сразу записать разложение в виде
р* ____ Вц _|___^21____I___В-22___! В-23
( ’ S + 3 (s + I)3 Т- (S + 1)2 1" (s + 1) •
Вычислим коэффициенты Вц. Коэффициент Вп особенно прост, так как для его вычисления не требуется дифференцирования. Получаем
511 = (s + 3)F*(s)|s=_3 = 8 ^-~У °- = -1 •
Коэффициент В21 вычислить также просто:
В21 = (S + 1)8 к* (S) |s=_! = 8 -(-+|+ о = _ 4.
Для получения B22 надо провести одно дифференцирование, а именно
- - 8
R d г 8(s2 T3s + l) Ч
s + 3 JU—l
(s + 3) (2s + 3) - (s2 -I- 3s + 1) (1)
(s + 3)2 |s=—I '
s2_|_6s+8 । 1-6 + 8
8 ' (s + 3)3 U-l - : 8 (2)2 6-
Наконец, вычисление В23 включает двукратное дифференцирование. Однако первое дифференцирование уже было проведено, и можно воспользоваться производной, полученной при вычислении В22 до постановки значения s = —1. Заметим, что поскольку / =3, то в равенстве (1.41) (/ — 1)! — 2!. Таким образом,
р 1 d2 Го (s2 + 3s+ 1)4 Ьгз~ дг dS* L s + з JU-i"
- 1 4 Г S2 + 6s + 8 11
~~ 2 > ds L (s + 3)2 JU-1
(s + 3)2 (2s + 6) - (s2 + 6s + 8) (2) (s + 3), (s+3)4
, (2)2 (4)-(l - 6 + 8) (2) (2) __
’ (2)4
367
L
Этим завершается вычисление постоянных В^, что дает окончательное разложение на простые дроби:
Т+Т + (s-p I)3 "(s + 'i)2 + (s + 1) ’ I-43^
Эта последняя форма годится, как и было обещано, для обращения методом проверок. В частности, легко видеть, что первое и последнее слагаемые входят в пару 8, а второе и третье слагаемые — в пару 10 табл. 1.4. Таким образом, при t > 0
f (f) = — 2i2e~t 4- ф е‘, (1.44)
и, конечно, f (/) = 0 для t < 0.
В методе проверок имеется два способа, с помощью которых можно проверить, не допущена ли ошибка. Первый способ — полученное разложение на простые дроби можно привести к общему знаменателю и проверить, получится ли при этом первоначальная фунция F* (s). Второй способ — получив окончательно функцию f (0, можно найти для нее преобразование Лапласа и проверить, совпадает ли оно с первоначальным (конечно, при этом получается функция F* (s), разложенная па простые дроби).
Второй, метод нахождения f (/) по F* (s) состоит в применении обратного преобразования:
"c+i™
j ^-(S)es74s (1.45)
ас-/оо
при £ > 0 и <те > crQ. Интегрирование в комплексной плоскости s идет по прямой, параллельной мнимой оси и лежащей справа от абсциссы о.. абсолютной сходимости функции F* ($). Обычный
метод вычисления такого интеграла основан на применении тео-
ремы Коши о вычетах к вычислению интеграла по замкнутому контуру в комплексной области. Замкнутый контур выбирают в виде полуокружности достаточно боль-
Рис. 1.4. Замкнутый контур для обратного интеграла
шого радиуса, как показано на рис. 1.4. Здесь контур интегрирования состоит из прямолинейного отрезка 8д — Sj И полуокружности Sj — -- sa — Если радиус окружности стремится к бесконечности и при этом интеграл по полуокружности стремится к нулю, то предел интеграла по всему замкнутому контуру совпадает с интегралом, стоящим в равенстве (1.45). Чтобы установить, что интеграл по полуокружности стремится к пулю, применим лемму Жордана.
368
Лемма Жордана. Если | F* (s) | —> 0 при R -> оо на полуокружности Sj — s2 — s3, то при t > О
j К* (s) est ds —О
S1“S2“S3
Таким образом, чтобы вычислить интеграл (1.45), надо сначала показать, что функция F* (s') удовлетворяет условиям леммы Жордана. Затем, интеграл по замкнутому контуру можно вычислить с помощью теоремы Коши о вычетах. Это легко проделать, если функция F* (s) рациональна и ее знаменатель разложен на множители. Чтобы применить лемму Жордана, предположим опять, что степень числителя строго меньше степени знаменателя, а если это не так, исключим из рассмотрения целую часть от деления числителя на знаменатель. Это все, что относится к рассматриваемому методу. Применим его к предыдущему примеру, а именно к функции, задаваемой равенством (1.42). Заметим, что к этой функции применима лемма Жордана, поэтому можно сразу воспользоваться теоремой Коши о вычетах. Полюсы функции F* (s) расположены в точках s = —3 и s = —1. Начнем с вычисления вычета относительно точки s = —3, т. е.
Аналогично вычисляют вычет относительно точки s = —1, что требует, однако, дифференцирования, указанного в формуле (1-27):
1 F 8(s2 4-3s+Y)es/ I
2 ds3 (s-1-3) [s=—1
+ I)3/7” (s) es/|s=__i
"(s -I- 3) [8 (2s (- 3) es/ 4- 8 (s2 4- 3s -ф 1) /esZJ—I
1 cl — 8 (s2 4-3s 4- l)esZ
2 ds (s 4 3)2 “
s=— 1
- 4- -(s4~3)*!(s+3)2[8 (2s+3>eS/+8 +3s+tet+
4 (s + 3) 8 [2es< - ф (2s ф- 3) Zes(] ф- (s -ф 3) 8 [(2 s ф 3) test - ф
| (s2 ф- 3s ф-1) t2esl\ - 8 (2s ф- 3) es/ - 8 (s2 ф- 3s -ф 1) tesi \ -- [(s + 3) 8 [(2s 4- 3) esZ -ф (s2 ф- 3s-ф 1) test] -
- 8 (s2 ф- 3s ф- 1) e^] 2 (s ф- 3)} |s=_i = еГ‘ ф-
Складывая эти вычеты, находим
f (t) = —e'3/ + e'1 4- - 2fV, t > 0.
Очевидно, здесь получено решение, совпадающее с решением (1.44), как это и должно быть. Опять при t < 0 функция f (/) 0.
369
В предыдущих рассуждениях о двустороннем преобразовании Лапласа были рассмотрены функции времени /_ (t) и Д (t), определенные соответственно на отрицательной и положительной действительной полуосях. Было также замечено, что преобразования этих функций аналитичны соответственно в левой и правой полуплокостях, считая от соответствующих им абсцисс абсолютной сходимости. Кроме того, в методе обращения [применение равенства (1.45)] было указано, что можно получить результат для t > 0, взяв указанный замкнутый контур и интегрируя против часовой стрелки. Отметим теперь, что замкнув прямолинейный отрезок полуокружностью, лежащей справа от него, можно также получить результат для t < 0 в предположении применимости леммы Жордана. С целью обращения двустороннего преобразования Лапласа получим сначала f (t) для положительных, а затем для отрицательных значений t. Для первой части возьмем вертикальный прямолинейный отрезок внутри полосы сходимости
< Од < Од и замкнем его полуокружностью, лежащей слева от него, а для второй части возьмем тот же прямолинейный отрезок, но замкнем его полуокружностью, лежащей справа от него.
Как можно ожидать, при контурном интегрировании иногда необходимо узнать точно, сколько особых точек функции лежит внутри замкнутого контура. Очень сильная и полезная теорема, помогающая ответить на этот вопрос, формулируется следующим образом.
Теорема Руше. [4]. Если f (s) и g (s) — аналитические функции переменной s внутри и на замкнутом контуре С — и если на этом контуре | g (s) | < |/ (s) |, то функции f (s) и f(s) + + g (s) имеют одно и то же количество нулей внутри контура С.
1.4. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ
РАЗНОСТНЫХ И ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Как уже отмечалось, метод преобразований особенно удобен при решении как разностных, так и дифференциальных уравнений с постоянными коэффициентами. В этом параграфе будет продемонстрирована техника этого метода. Начнем с разностных уравнений с применением производящих функций, а затем перейдем к дифференциальным уравнениям с применением преобразований Лапласа. Это послужит подготовкой к решению более сложных дифференциально-разностных уравнений, встречающихся в тексте, для которых требуется совместное применение обоих методов.
Рассмотрим следующее общее линейное разностное уравнение А-го порядка с постоянными коэффициентами:
aNgn-u + aN_ign.N+i -Н • • • щ aogn ----- еп, (1.46)
370
где at — известные постоянные коэффициенты; £,• — неизвестные искомые функции и — заданная функция п. Дополнительно предположим, что заданы N граничных уравнений (например, начальных условий). Как всегда в таких уравнениях, искомое решение состоит из общего решения однородного и частного решения неоднородного уравнения, а именно
gn = gn} + gn\
в точности, как и в дифференциальных уравнениях. Известно, что однородное решение должно удовлетворять однородному уравнению
t‘Ngn-N -)-••• 4~ Ctogn — 0. (1-47)
Общее решение уравнения (1.47) имеет вид
g{nh} = Aant
где А и а подлежат определению. Если подставить предложенное решение в уравнение (1.47), то получится
aNAan~N 4 aN^iAan"N+l 4 • ' ’ + = 0. (1-48)
Это уравнение tV-го порядка, очевидно, имеет 2V корней аъ а2, ..., ад,, которые первоначально будем считать различными. С каждым таким решением связана произвольная постоянная Ait определяемая из начальных условий (которых должно быть N).
Вынося и отбрасывая общий множитель ДаД-Л' в уравнении (1.48), получим характеристическое уравнение для определения значений ад
Un -Е 4 4- • • • 4- ‘ЕаЛ — 0. (1-49)
Таким образом, задача нахождения однородного решения свелась к решению характеристического уравнения (1.49). Если корни этого уравнения различны, то однородное решение имеет вид
g,?’ = Аа" 4 л2а2 4 • • - 4 .4д,адг.
В случае одинаковых корней дело обстоит иначе. В частности, пусть aj — корень кратности k. Тогда k одинаковых корней внесут в однородное решение вклад вида
(Яц/г 4 A Y>nk 2 4 ’ 4~ "41, 4' A j*) а?;
это имеет место и для других корней.
Что же касается частного решения неоднородного уравнения
, то известно, что его надо искать в форме, зависящей от вида еп.
Проиллюстрируем изложенные принципы на примере. Рассмотрим разностное уравнение второго порядка
6,4 — Sgn-i i -- 6 (4")” > n = 2, 3, ... (Е50)
371
Это уравнение устанавливает соотношение между неизвестными функциями gn для п = 2, 3, 4.... Конечное, надо задать два начальных условия (так как порядок уравнения равен 2), поэтому выберем их так: g0 = 0; gr = 6'5. Чтобы найти однородное решение, необходимо составить уравнение (1.49), которое в рассматриваемом случае получается в виде
6а2 — 5а 4- 1 = 0.
Корни а этого уравнения: а j = 1/2, а2 -= 1/3, и, следовательно, однородное решение имеет вид
Частное решение должно быть подобрано. Ищем его в форме свободного члена, т. е. в виде
Если подставить предполагаемое решение в уравнение (1.50), то получится /3=1, что подтверждает правильность решения. Полное решение получается в виде
„ _ „('о - „(/и __ л / П" , J /_LY! । / 1 у1 Sn Sn И gn — 9 у ] /4а з у \ 5 / ’
Используем начальные условия, чтобы найти Лт и Л2. Это даст Лх = 8 и Л2 = —9. Таким образом, окончательное решение имеет вид
*»(4Г-(1Г+(!)’• -
Этим завершается стандартное решение разностного уравнения.
Опишем теперь применение метода производящих функций для решения разностных уравнений. Предположим опять, что дано уравнение (1.46), справедливое для п = k, k 4 1, ... Сначала определяется следующая производящая функция: 00
G(2) = Lg/. U-5^
/1=0
Из проведенного ранее обсуждения известно, что, зная G (z), можно, пользуясь техникой обращения, найти Следующим шагом умножим п-е уравнение из (1.46) на гп и просуммируем полученные выражения от k до бесконечности, т. е. образуем сумму
СО N Со
Ё S <iign-iz" е„гп-11—k ('=0 11—k
Попытаемся в этом уравнении распознать функцию G (z). Затем решаем относительно G (z) это алгебраическое уравнение, после чего находим обращение функции G (г).
372
Рассмотренный метод нс требует угадывания частного решения и в этом отношении проще предыдущего. Однако, как будет показано ниже, он сохраняет основную трудность — решение характеристического уравнения (1.49), а в общем случае это п есть самая трудная часть решения. Однако, даже если нельзя решить характеристическое уравнение, из функции вида G (г) все же удается получить многие важные свойства решения gn.
Решим предыдущий пример методом производящих функций. Начнем с умножения (1.50) на zn и суммирования от двух до бесконечности, так как уравнение справедливо именно при этих значениях. Получим
ОО ОС' ОО со
S ^z" ~~ S5g"-’2"4 S- S6 (4)"z'1-n=2 n=2 ll=2 ll=2
Вынесем из каждой суммы z в такой степени, чтобы остающиеся ПОЧ чпяклат rvntoT T r'TrVZ2.'! I! С02П2Д2ЛИ С ПЬ’ДСКСиМII Ьро
СО СО ОО СО
о s -* s " S *(*)’'• <1=2 п—2 11=2 п—2
Остановимся на первой сумме. Она равняется функции G (г) без нулевого и первого членов [см. уравнение (1.52)1. Учитывая это замечание для остальных сумм слева и произведя суммирование геометрической прогрессии, стоящей справа, найдем
6 |G (г) — g0 - fiiz] — 5z [G (z) — gol - j- z2G (г) - •
Необходимо обратить внимание на то, как первое слагаемое слева в этом последнем уравнении отражает суммирование без первых двух членов. Решая алгебраическое уравнение относительно G (z), находим
G (г) = 6go + 6g]Z ~ 5gog + (625) г2/Н ~ ОЯ г1 ' ' 6 — 5г -|- г2
Если теперь использовать начальные условия для g0 п git то получим
G(z) = ______________________________
’ \ 5 ) [1 —(1/3)г] [1 - (1,2) г] [ 1 -- (1.,5) г) ’
Разлагая это последнее выражение на простые дроби, будем иметь = __ —9 .8,1
1 1 — (1/3) г ’’ 1 — (1/2)7 ~ "ГПТ/бУТ ’
что обычными методами обращения приводит к решению
»(1Г- »(Я+(1)'. -<-0. !, 2. ...
373
Заметим, что последнее решение в точности то же самое, что и решение (1.51), и этим обеспечивается проверка метода. Здесь нужно отметить, что даже в тех случаях, когда обращение функции найти не удается, можно найти некоторые ее важные характеристики. Например, можно определить непосредственно сумму всех членов в виде G (1), т. е.
Рассмотрим теперь приложение преобразования Лапласа к решению линейных дифференциальных уравнений с постоянными коэффициентами. Рассмотрим уравнение Af-го порядка в следующей форме:
аи -Zn~ 4 + • • • H «I —щ «of (0 = <?(/). (1.5.3)
Здесь коэффициенты a, —заданные постоянные, a e (t) — заданная управляющая функция. Вместе с уравнением должно быть задано N начальных условий для получения единственности решения. Типично в качестве начальных условий задавать первые N производных в некоторый, обычно нулевой, момент времени. Это требуется для нахождения функции f (t).
Как обычно, назовем однородным решением /(/г) (/) решение однородного уравнения [<?(/) = 01 и частным решением (/) — любую функцию, удовлетворяющую неоднородному уравнению. Решение однородного уравнения ищут в виде
/(/!) (0 = Леа/.
Если подставить его в уравнение (1.58), получим
aNAaNeat 4- aN-iAaN'leat -(-••• + UiAaea< поЛе“* = 0.
Это уравнение имеет те же N решений а1; а2, ..., ап, что и характеристическое уравнение
а^а"’ + a^-iaNA + • • 4-«i“ + «о — 0,
эквивалентное уравнению (L.49) с перенумерованными индексами коэффициентов. Если все а, различны, то общее решение однородного уравнения имеет вид
fw (/) = Лщ"*' 4 Л2еК!‘ • • • -4 An^.
Вычисление коэффициентов Л,- основано на использовании начальных условий. В случае кратных корней имеем следующую модификацию. Предположим, что «1 — корень кратности Этот кратный корень внесет в однородное решение следующий вклад:
(Л14* 1 4~ ЛыК "4~ " 4 Aik~\t 4- Лц.) еа,/.
374
Эта же модификация очевидна в случае более чем одного кратного корня. Как обычно, для нахождения частного решения (/) неоднородного уравнения приходится гадать. Общее решение неоднородного уравнения есть сумма общего решения однородного и частного решения неоднородного уравнений, т. е.
/(/) (0 + /(₽) (О-
Применим этот метод в иллюстративных целях к решению следующего дифференциального уравнения:
6 4-9Н0 = 2^ (1.54)
с двумя начальными условиями: f (0“) = 0 и df (O^/dt = 0. Составляя характеристическое уравнение
а3 —6а-|-9 = 0, (1.55)
находим следующие кратные корни: = а2 = 3; такшм образом, однородное решение должно иметь вид
Г’(Л4 !-41г)е?/.
Строя соответствующую догадку для частного решения, проверим решение
Г (О = В1 + В4.
Подставляя это предполагаемое решение в уравнение (1.54), находим Вг = 4/27 и В2 = 2/9. Таким образом,’общее решение неоднородного уравнения имеет вид
f (0 = Ип/ ’И Аа)e"Z + + -у / *
Так как согласно начальным условиям и функция / (/) и ее производная в точке t = 0“ равны нулю, тоЛн = 2/9 и А 12 = 4/27, что дает окончательное полное решение
/«)-4(/-4-)ei'-;-4(s-I 4). 1>0. (1.56)
Преобразование Лапласа дает другой метод решения линейных дифференциальных уравнений с постоянными коэффициентами. Этот метод основан на свойствах И и 12 из табл. 1.3, которые связывают производные функции по времени с ее преобразованием Лапласа. Идея метода состоит в применении преобразования Лапласа к обеим частям уравнения, что приводит к уравнению, содержащему преобразование неизвестной функции f (t), которое, как обычно, будем обозначать через F* (s). Затем это алгебраическое уравнение решают относительно F* (s), и для получения искомой функции f (/) любым доступным методом находят обратное преобразование.
375
Применим эту технику к уже рассмотренному примеру. Начнем с преобразования обеих частей уравнения (1.54), для чего запишем начальные условия в следующем виде:
82Л* (s) - sf (О-) - (О’) - 6sF* (s) + 6f (О") -{- 9F* (S) = 4 •
Проводя эту последнюю операцию, мы использовали пару 7 преобразований Лапласа из табл. 1.4. Так как оба начальных условия нулевые, можно опустить некоторые члены в этом последнем уравнении и сразу вычислить
Т* =--------т/2_____
' ' s2 —6s-1-9 '
Теперь надо разложить знаменатель этой функции на множители, т. е. решить задачу, с которой мы встретились при решении уравнения прямым методом и которая составляет основную трудность как прямого, так и непрямого методов. Проведя это разложение, получим
2 ' ,S- S2(S_3)2-
Теперь можно разложить эту функцию на простые дроби:
2/9 4/27 2/9 —4/27
s2 s >' (s — З)2 ' s—3 ‘
Переходя, как обычно, к обратным преобразованиям, для t > О получаем
,• 2 , 4 ,2,з/ 4 з/
/ (t) — 9 t + *27- ~i~ V te 27“ е ’
что совпадает с решением (1.56), найденным ранее.
При изучении систем массового обслуживания мы часто сталкивались не только с разностными или дифференциальными уравнениями, но также с комбинацией таких уравнений, т. о. с дифференциально-разностными уравнениями. Так, если обратиться к уравнению (1.53) и заменить функции времени, зависящими от индекса, скажем п, а затем выделить последовательность дифференциальных уравнений для различных значений п, то получается бесконечная /последовательность дифференциальноразностных уравнений. Решение такихТуравнений часто требует применения как производящих функций для дискретных индексов п, так и преобразований Лапласа для непрерывного пара-метра'времени t. Примеры анализа такого рода имеются в самом тексте.
376
СПИСОК ЛИТЕРАТУРЫ
1. Ahlfors, L. V. Complex Analysis. 2nd Edition. McGraw—Hill (New York) 1966.
2. Cadzow, J. A. Discrete Time Systems. Prentice-- Hall (Englewood Cliffs N.J.), 1973.
3. Doetsch, G. Guide to the Applications of Laplace Transforms. Van Nostrand (Princeton), 1961.
4. Guillemin, E. A. The Mathematics of Circuit Analysis. Wiley (New York),
5. Jury, E. I, Theory and Application of the z-Transform Method. Wiley (New York), 1964.
6. Schwartz, L. Theorie des Distributions, 2nd printing. Actualities scientifi-ques et industrielles Nos. 1245 and 1122, Hermann et Cie. (Paris), Vol. 1 (1957), Vol. 2 (1959).
7. Widder, D. V. The Laplace Transform Princeton University Press (Princeton), 1946.
1 Рекомендуемые автором пособия могут быть заменены аналогичными учебниками на русском языке (см., например, примечание на с. 344). Прим. ред.
ПРИЛОЖЕНИЕ II
Памятка по теории вероятностей
В этом приложении приводится обзор избранных разделов теории вероятностей, связанных с изучением теории массового обслуживания. Большей частью важные определения и результаты только перечислены и снабжены подходящими примерами. При этом предполагается, что читатель знаком с этим материалом, соответствующим хорошему начальному курсу теории вероятностей. Такой курс, как правило, опирается на одно из пособий, содержащих дополнительные подробности и выводы [1—4].
Теория вероятностей занимается описанием случайных событий. В соответствии со словарным определением, случайным называется событие, лишенное преднамеренности и регулярности. Нет ничего более далекого от истины! В действительности существует четкая регулярность, проявляющаяся при накоплении случайных событий, что и делает теорию вероятностей интересной и полезной. Понятие статистической регулярности занимает центральное место в предлагаемом обзоре. Например, при четырех бросаниях правильной монеты можно в среднем ожидать двух выпадений герба и двух выпадений числа. Конечно, имеется один шанс из шестнадцати, что герб не появится ни разу. Следовательно, если возникнет такая необычная последовательность событий (ни одного герба), это не вызовет ни особого удивления, ни подозрения в фальшивости монеты. С другой стороны, если монету бросать миллион раз, то опять ожидается выпадение приблизительно половины гербов и половины чисел. Но если не появится ни одного герба и в этом случае, то это вызовет не просто удивление, но и возмущение и даст право с полной уверенностью утверждать, что монета фальшивая. Действительно, имеется 10s8 шансов против одного, что появится, по крайней мере, 490 000 гербов.
Под статистической регулярностью понимается именно то, что при большом накоплении случайных событий появляется возможность точных утверждений.
378
II. 1. ПРАВИЛА ИГРЫ
Опишем правила игры для создания математической модели вероятностной ситуации, соответствующей реальному эксперименту. Обычно исследуются три характеристики таких экспериментов: 1) множество возможных исходов эксперимента; 2) группировка этих исходов в классы, называемые результатами-, 3) относительная частота этих классов при многократном независимом повторении эксперимента.
Относительная частота fc класса с равна отношению числа исходов эксперимента, попадающих в этот класс, к числу проведенных экспериментов. С возрастанием числа испытаний в соответствии с понятием статистической регулярности можно ожидать, что fc стремится к определенному пределу.
Создаваемая здесь математическая модель тоже обладает тремя интересными характеристиками, в точности соответствующими трем перечисленным характеристикам реального эксперимента. Это соответственно:
1. Пространство элементарных событий, обозначаемое S; оно соответствует множеству взаимоисключающих друг друга исчерпывающих исходов модели эксперимента. Каждый элемент (т. е. возможный исход) <о множества S называется элементарным событием.
2. Совокупность событий {А, В, С, ...), обозначаемая через <5, в которой каждое событие есть множество элементарных событий {<о}. Событие соответствует классу результатов в реальном эксперименте.
3. Вероятностная мера Р, дающая отображение событий, определенных на S, в множество действительных чисел; Р соответствует относительной частоте в реальной ситуации. Обозначение Р [А ] используется для определения действительнного числа, соответствующего событию А. Эта функция должна удовлетворять следующим условиям (аксиомам):
а) 0 < Р [А ] с 1 для любого события А; (II-1)
б) Р [S] = 1; (II.2)
в) если А и В несовместны, т. е. взаимно исключены [см. ниже (II.4)], то
Р[А U В]-Р[А] +Р[В]. (П.З)
Здесь удобно ввести некоторые теоретические обозначения (например, употребление символа [J в свойстве в). Обычно, событие А описывается следующим образом: А = (со : <о обладает некоторым свойством}. Это читается как: «А — множество элементарных событий ю, удовлетворяющих свойству, определяющему принадлежность к событию А». Определим далее
Ас = [со : со не в А} = дополнение А (событие, противоположное А);
379
A J В = [со : со в А или В или в обоих} = объединение А и В;
A f] В = АВ = {со : со в А|‘и в В} = пересечение А и В-ср = Sc = нулевое событие (не содержащее ни одного элементарного события, в то время как S содержит все элементарные события).
Если АВ = ср, то А и В называются взаимоисключающими (или несовместными). Множество событий, объединение которых образует пространство элементарных событий, называется исчерпывающим. Следовательно, можно дать также определение множества взаимно несовместных исчерпывающих событий ((А 1г А.,, ..., А,}, обладающих следующими свойствами:
AiAj = ср для всех i j; AY (J A.. (J ... J Ап _= S. (11.4» Заметим, что
A (J Ас = S, ААС = ср, AS = A, Acp = cp, A U S = S, AU<p = A, Sc — ф и фс = S.
Отметим также, что операции объединения и пересечения коммутативны, ассоциативны и дистрибутивны.
Тройка (S, S, Р) совместно с аксиомами (II.1)—(II.3) образует вероятностную систему. Трех аксиом достаточно для аксиоматического построения теории вероятностей в случае, когда множество событий, которые могут быть определены на пространстве элементарных событий, конечно. (Когда число таких событий бесконечно, необходимо добавить аксиому, обобщающую аксиому (П.З) на бесконечное объединение несовместных событий. Это приводит к понятию борелевского поля и бесконечной аддитивности вероятностной меры, однако в настоящей памятке дальнейшие подробности не обсуждаются.) Отметим, наконец, что аксиома (II.2) устанавливает нормировку, и выбор в качестве нормировки единицы совершенно произволен (хотя и вполне естествен).
Перейдем к дальнейшим определениям. Первым из них будет определение условной вероятности. Условная вероятность события А, если известно, что наступило событие В (обозначаемая через Р [А | В ]), определяется как
Р)А |Bi AM,
если Р [В ] =р 0. Введение условного события В заставляет рассматривать наряду с первоначальным пространством элементарных событий S пространство элементарных событий, определяемое событием В. Так как это новое пространство должно иметь полную вероятность, равную единице, то вероятности, связанные с этим условием, должны делиться на Р [В ], что и проделано выше.
380
Вторым необходимым дополнительным понятием является статистическая независимость событий. Два события А и В называют статистически независимыми, тогда и только тогда, когда
Р[АВ\ = Р[А]Р\В]. (II.5)
Для трех событий А, В, С требуется, чтобы каждая пара этих событий удовлетворяла (II.5) и, кроме того,
Р [АВС] -= Р [А] Р [В] Р [С].
Это определение распространяется, конечно на п событий, если требовать выполнения соответствующих равенств для п-кратных произведений, всех (п — 1)-кратных и так далее до всех двукратных произведений. Легко видеть, что для двух независимых событий А и В всегда Р [А | В ] = Р [А I; это просто означает, что сведения о наступлении события В ни в коей мере не влияют на вероятность наступления независимого события А.
Теорема о полной вероятности чрезвычайно проста и важна. Она связывает вероятность события В с множеством взаимно несовместных исчерпывающих событий [АД, определенных условиями (II.4). Эта теорема утверждает, что
Р[В] = L В [А,В];
1=1
это означает, что событие В наступает совместно точно с одним из взаимно несовместных исчерпывающих событий А,. Однако из определения условной вероятности можно написать
Р [А;В] = Р [А, В] Р [В] = Р [В|АJ Р [А,].
Это дает вторую важную форму теоремы полной вероятности, а именно
Р [В] = Е Р[ВААР [А,]. <=1
Последнее равенство, по-видимому, одно из наиболее полезных в теории массового обслуживания. Оно позволяет применить при нахождении вероятности некоторого сложного события следующий подход: сначала связать событие В с некоторыми условиями А, таким образом, чтобы вычисление вероятностей при этих условиях было менее сложно, затем умножить эти условные вероятности на вероятности условий для получения совместной вероятности Р [А,В]; если удается это проделать для множества {А,} взаимно несовместных исчерпывающих событий, то можно затем просуммировать полученные вероятности и найти вероятность события В. Можно расширить этот подход, связывая событие В с условиями разного типа, снимая эти условия умножением условных вероятностей на вероятности условий и суммируя полученные вероятности по всем возможным видам условий. Этот подход многократно используется в книге.
381
Переходим к известной теореме Байеса. Снова рассмотрим множество {Д,} взаимно несовместных исчерпывающих событий. Теорема утверждает, что
mW-
/=1
Эта теорема позволяет вычислять вероятности одного события, обусловленного другим, через вероятность второго, обусловленного первым, и другие подобные члены.
Проиллюстрируем эти идеи простым примером. Допустим, что Вы только что вошли в казино в Лас-Вегасе. Вы приближаетесь к банкомету, имеющему брата-близнеца. Близнецы неразличимы. Известно далее, что один из близнецов честный банкомет, а другой плутует в том смысле, что, играя с честным, вы проигрываете с вероятностью 1/2, а играя с нечестным, проигрываете с вероятностью р (если р больше 1/2, он плутует против Вас, а если р меньше 1/2, он плутует в Вашу пользу). Далее, одинаково вероятно, что, войдя в казино, Вы застали одного или другого из близнецов. Допустим, Вы играете с тем банкометом, которого застали, и проигрываете. Вы разочарованы и хотите вычислить вероятность того, что Вы играли с нечестным банкометом, так как если эта вероятность близка к единице, у Вас есть основания для иска против казино. Пусть событие DH состоит в том, что Вы играли с честным банкометом, a Dc — в том, что Вы играли с мошенником. Пусть далее событие L означает Ваш проигрыш. Следовательно, Вы хотите найти Р [£>с| L1. Непосредственно не видно, как провести такое вычисление. Однако применение теоремы Байеса делает это вычисление тривиальным:
р tn I т 1 ______Р[£| £><;]£ [£>с]__
1 с| 1 P[L\Dc]P[Dc] + P[L\Dh]P[Dh] '
В этом применении теоремы Байеса множество взаимно несовместных исчерпывающих событий есть совокупность [DH, Dc], так как одно из этих событий должно наступить, а оба вместе наступить не могут. Задача теперь тривиальна, так как каждый член справа легко вычислить. Это дает
Таким образом, найдена вероятность того, что Вы столкнулись с мошенником, если известно, что Вы '.проиграли одну партию. 382
Эта вероятность может меняться от 0 (р 0) до 2/3 (р = 1). Значит, даже имея дело с абсолютно бесчестным банкометом (р = 1), Вы, проиграв одну партию, можете лишь с вероятностью 2/3 утверждать, что он плутует.
В заключение элементарной части вспомним, что число перестановок из N элементов по К равно
а число сочетаний из N элементов по К, обозначаемое через ,
IN\ = N[ \k) К! (Л/— /Ol-
li^. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
До сих пор описывались вероятностные системы, состоящие из троек (S, <£, Р), т. е. пространства элементарных событий, множества событий и вероятностной функции, определенной на этом множестве. Теперь нужно определить такое важное понятие как случайная величина. Случайная величина — это переменная, значение которой зависит от исхода случайного эксперимента. Так как исходы случайных экспериментов представляются точками со С S, то каждому такому исходу можно сопоставить действительное число X (ю), представляющее собой значение случайной величины, принимаемое ею, когда эксперимент имеет исход со. Следовательно, случайная (действительная) величина X (со) представляет собой функцию, определенную на пространстве элементарных событий, или, если угодно, отображение точек пространства элементарных событий на (действительную) прямую.
В качестве примера рассмотрим случайный эксперимент, состоящий из одной партии игры в «дубинку» в Лас-Вегасе. Пространство элементарных событий состоит из всех возможных пар выигрышей, которые могут быть получены игроком и банкометом. Предположим, что все такие элементарные точки разделены на три группы событий: проигрыш L, ничья D и выигрыш W. Чтобы вероятностная система была полной, сопоставим каждому из этих событий вероятности *: Р [L] = 3/8; Р [D ] = 1/4, Р [F] = 3/8. Таким образом, вероятностная система может быть представлена диаграммой Венна, как на рис. П.1.
Теперь о случайной величине X (со). Допустим, что выигрыш составляет 5 долларов, ничья 0 и проигрыш составляет 5 долларов (т. е. потеря 5 долларов). Пусть выигрыш игрока в «ду-
1 Практически это наиболее трудный шаг — определение подходящих чисел при построении модели реального мира.
383
Рис. IL1. Вероятностная система для примера игры в «дубинку»
бинку» (в одной партии) — случайная величина X (со), . которая может быть определена в виде
-г 5, <о(£ IF;
О, со £- D;
—5, co£L.
Аналогично можно представить эту случайную величину в виде отображения, как показано Йа рис. II.2. .
Областью определения случайной величины X (со) является множество событий ё, а значения, принимаемые ею, образуют ее область значений. Заметим попутно, что вероятность Р можно
саму по себе тоже рассматривать как случайную величину, так
как она удовлетворяет этому определению, однако эта величина имеет еще ограничения, задаваемые аксиомами (II. 1)—(П 3).
Будем главным образом интересоваться вероятностями, с которыми случайная величина X (со) принимает,те или иные значения. Введем следующее сокращенное обозначение для события:
[X — х] = (со : X (со) = xj.
(Н.6)
Рассмотрим вероятность этого события, которую будем обозначать как
Р [X = х] = вероятность того, что X (со) равно х.
Эта вероятность в точности равна сумме вероятностей тех событий со, для которых X (со) = х. В рассматриваемом примере
Р[Х = -5] = 3/8; Р[Х = 0]--1/4; Р [X = 5] = 3/8. (II.7.)
Другой удобной формой выражения вероятностей, связанных со случайной величиной, является функция распределения веро-
384
ятностей. С целью введения этой функции используем обозначение, подобное (II.6), а именно
[X < х] = {и: X (ы) = х].
Тогда функция распределения вероятностей (Или просто функция распределения) определяется как
• ' Fx(x)
что выражает вероятность того, что случайная величина X примет значение, меньшее или равное х.
Важные свойства функций распределения:
Fx(x)>(0; Fx(oo)==l; Fx(-oo) = 0; (П.8)
Fx Ф) — ^(а) == Р [а < X < Ь] для а<Ь; • (II.9)
Дх (Ь) > Fx (а) для а « Ь,
Таким образом, функция распределения Fx (%) — неотрицательная монотонно убывающая функция с пределами соответственно 0 и 1 в' точках — оо и +оо. Кроме того, Fx (х) предполагается непрерывной справа. Для рассмотренного выше примера игры в «дубинку» функция распределения ^выигрыша дана на рис. П.З. Заметим, что в точках разрыва функция распределения принимает большее значение «(как отмечено кружочками), так как функция непрерывна справа. Из свойства (II.9) можно легко вычислить вероятность того, что случайная"величина лежит в заданном интервале. Так, для рассматриваемого примера можно-написать
Р [—2 <( х « 6] = 5/8, Р [1 < х < 4] — 0 и т, д.
При вычислениях часто бывает удобнее пользоваться не самой функцией распределения, а другой функцией, тесно связанной с функцией распределения. Таким образом мы приходим к опре-
13 л. Клейнрок ' 385
делению плотности распределения вероятностей в следующем виде:
' (П.Ю)
Естественно, немедленно возникает вопрос о том, существует ли эта производная, и если да, то на каком интервале. Не вникая пока в этот вопрос, будем полагать, что (х) обладает всюду непрерывной производной (что неверно для рассмотренного примера). Как увидим далее, плотность можно определять и тогда, когда функция распределения имеет скачки. «фбрАтив» равен-’ ство (11.10), получим
X
FxW = J (II.И)
— ео '
Из этого равенства и из (II.8) следует, <jro fx (х) > 0. Так как Fx (оо) = 1, то из равенства (11.11) получаем
оо
J fxWx = 1. — оо
Следовательно, плотность распределения является функцией, интегрирование которой по интервалу дает вероятность попадания случайной величины в этот интервал, а именно, для а < b имеем » ь
Р [а < X с b] = j fx (х) dx. а
При а —♦ Ь, в силу аксиомы (II. 1), из последнего равенства следует также, что fx (х) > 0.
В качестве примера рассмотрим показательно распределенную случайную величину, для которой
ЗД = ( 0 ’ (11.12)
где % > 0.
Соответствующая плотность распределения имеет вид f . . ( Хе'Хх, 0<х; ... .
0. х<0. (1ИЗ)
Для этого примера вероятность того, что случайная величина лежит между а и b (а > 0, b > а), может быть вычислена по любой из двух формул:
Р [а < х с ft] = Fx (Р) - Fx (а) = еКо - е’^;
ь
Р [tz < х < b] = j fx (х) dx = е ''а — e“u.
386
Заметим, что в рассмотренном выше примере функция распределения имеет производную, равную нулю, всюду, кроме трех критических точек (х = —5, 0, +5). Чтобы дополнить определение плотности распределения в случае разрывной функции распределения, надо ввести функцию, интегрирование которой по; окрестности точки разрыва даст величину скачка в точке разрыва. В рассмотренном1 примере плотность распределения шэлжна быть такой, чтобы интегрирование от —5 —е до —5 +е ццтя малого-е) давало бы вероятность 3/8. Такая функция уже изучалась в приложении I. Это — импульсная функция (или дельта-функция Дирака). Вспомним, что эта функция задается равенствами
[ оо, х = 0; “JW = l 0. х + 0, а также, что она является производной единичйой ступенчатой функции, как это можно увидеть из равенства
f / s j ( 0, х < 0;
J» I 1, х > 0.
Применяя графические обозначения, принятые на рис. 1.3, можно должным образом описать плотность распределения вероятностей выигрыша в примере с игрой’в «дубинку», как это сделано на рис. II.4. Заметим сразу же, что это описание дает в точности ту же информацию, которую давали равенства (II.7); поэтому применение импульсный функций не облегчает рассмотрение таких задач. В частности, если определить дискретную случайную величину, принимающую значения из дискретного множества (конечного или счетного), то применение плотностей распределения вероятностей 1 чрезвычайно громоздко и не вызы. вается необходимостью, хотя оно, очевидно, укладывается в об
1 В дискретном случае функцию Р [X = х*] часто называют функцией массы вероятности. Обоб1Д?нне плотности распределения вероятности приводит к понятию функции плотности массы.
13* 387
Рнс. 11.5. Функция распределения вероятностей (а) н плотность распределения вероятностей (б) срока службы автомобиля »•
щее определение. С другой стороны, непрерывного множества возможных значений случайной величины естественно применять плотности распределения также и тогда, когда имеется • ненулевая вероятность некоторого определенного значения (т. е. когда функция распределения имеет скачок). В этом случае применение плотности распределения необходимо, так же как и введение импульсной функции для подсчета вероятностей в точках накопления.
Таким образом, мы приходим к необходимости различать дискретные случайные величины, непрерывные случайные величины (для которых функции распределения непрерывны и всюду дифференцируемы) и смешанные случайные величины, содержащие и непрерывные и дискретные части \ Так, например, рассмотрим случайную величину, описывающую срок службы автомобиля. Предположим, что имеется отличная от нуля вероятность р того, что автомобиль негоден с самого начала, т. е. что срок службы его равен нулю. С другой стороны, если автомобиль в момент его приобретения пригоден к использованию, то будем предполагать, что оставшийся срок службы распределен по показательному закону, который задается формулами (11.12) и (11.13). Следовательно, для срока службы автомобиля получаются функция распределения и плотность распределения, изображенные на рис. II.5. Таким образом, становится ясно, что для описания интересующей нас случайной величины необходима импульсная функция.
Мы рассмотрели понятие вероятностной системы (S, S’, Р) и понятие случайной величины X (со), определенной на пространстве S элементарных событий. Конечно, нет никаких причин, мешающих определить на одном и том же пространстве элементарных событий много случайных величин. Рассмотрим две случайные величины X и Y, определенные для вероятностной си
1 Можно показать, что всякая функция распределения может быть представлена в виде суммы трех слагаемых, а именно функции скачков (содержащей только оазрывные скачки), чисто непрерывной части и сингулярной части (которая редко возникает в функциях, представляющих интерес, « в этом тексте ее больше рассматривать не будем).
388
стемы (S, <S, P). В этом случае естественным является обобщение понятия функции распределения на две случайные величины, а именно
Fxy(x, у)~Р[Х^.х, Y^y];
что представляет собой вероятность того, что X принимает значение, меньшее или равное х, и в то же время Y принимает значение, меньшее или равное у, т. е. это сумма вероятностей, связанных со всеми элементарными точками в пересечении двух событий: {со : X (со) < х}, {со : Y (со) < у].
Функция FXy (х, у) называется совместной функцией распределения вероятностей. Конечно, с этой функцией связана совместная плотность распределения вероятностей, т. е. функция, определенная как
Если дана совместная плотность распределения, то по ней можно «1айти плотность распределения одной из величин, интегрируя по всем возможным значениям второй переменной, т. е.
» fx(x) = j Ixy(x, у) dy. (П.14)
“•ОО
Теперь можно дать определение понятия независимости двух случайных величин. Две случайные величины называются независимыми тогда и только тогда, когда
fxY (X, у) == fx (X) fy (у),
т. е. если совместная плотность распределения есть произведение их одномерных плотностей распределения. Это очень похоже на определение независимости двух событий, данное равенством (II.5). Однако для трех и болбе случайных величин определение по существу остается тем же, что и для двух случайных величин, а имейно: величины Хг, Хг, ..., Хп называются независимыми тогда и только тогда, когда
х2 , ..., хя) = fX1 (xi) [Хг (х|) .. .^fXn (х„).
ЭЛ последнее значительно проще, чем требование независимости нескольких событий.
Для нескольких случайных величин теперь можно следующим образом определить условные распределения плотности. Можно, например, искать функцию’распределения случайной величины X при условии, что случайная величина Y принимает определенное значение. Эту функцию запишем в виде Р [X < х| У = г/].
389
Рис. II.6. Область интегрирования для У = = Xi + Xg < у
Аналогично, условная плотность распределения X при заданном значении V определяется как
/х|у(х|//)^Р[Х^х|Г=г/] = _ fxY (X, у) fy (у)
Заметим опять, что случайная величина определена как отображение пространства элементарных событий для некоторой вероятностной системы на действительную прямую и из этого отображения легко полу
чить функцию распределения.
Однако обычно случайная величина не задается через пространство
элементарных событий и отображение, а задается сразу функцией
распределения или плотностью.
Можно определить случайную величину Y через другую случайную величину X и в этом случае называть Y функцией случайной переменной X. Тогда в наиболее общей форме имеем
y-g(X),
(11.15)
где g (•) — некоторая данная функция своего аргумента. Таким образом, зная значение X, можно вычислить значение Y. Однако значение X зависит от элементарного события со; значит, от него зависит и значение Y, которое, следовательно, можно записать в виде Y = Y (ю) = g (X (со)). Если известна функция распределения случайной величины X и функция g (•), то обычно можно найти функцию распределения величины Y. Общая формула имеет вид
FY (у) = Р [Y « y] = Pl{a>:g(X (а>)) у)].
Как правило, однако, вычисление по этой формуле достаточно сложно.
Случайная величина может быть функцией многих других случайных величин. В частности, нередко возникает сумма нескольких независимых случайных переменных {Х<}, а именно
к = £ х,. 1=1
(11.16)
Рассмотрим функцию распределения суммы двух независимых случайных величин (и — 2). Очевидно, это распределение определяется равенством
Fy (у) — Р [У < у] = Р[Х^Х2 < у].
390
Здесь возникает картина, показанная на рис. II.6. Интегрирование по заштрихованной области дает
“ у—х2
Ру(у) = J j /х,х2 (Л'1, x>)dxidx2.
В силу независимости и Х2, получаем функцию распределе-ния величины Y в виде
=° Г У~Хг
Fv(y) = J j fx,(xi)dxt
fx2 (*2) dx2 =
= j Fx, (y — x2) fx, (x2) dx2. —•00
Наконец, образуя плотность распределения по этой функции распределения, получаем 00
fv (У) = j fx, (У — х2) fx2 (х2) dx2.
s—00
Это последнее равенство является сверткой плотностей распределения величин Х± и Х2, и, как и в равенстве (1.36), оператор свертки (который коммутативен и ассоциативен) обозначим точкой, заключенной в кружок, т. е.
fy(y) = fx, (y)®fx2 (у).
Подобным же образом легко показать, что для произвольного п плотность распределения величины У, определенной равенством (11.16), равна свертке плотностей величин X,, т. е.
fy(y)-fx1(y)efx2(y) © ... &fxn(y). (11.17)
11.3. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
В этом параграфе будут рассмотрены некоторые меры, связанные с функцией распределения и плотностью распределения случайной величины. Эти меры в общем случае называют математическими ожиданиями и получают интегрированием плотности распределения. Как было показано в предыдущем параграфе, определение плотности заключает в себе некоторые затруднения, которые могут быть устранены введением импульсных функций. Однако в большей части литературы по теории вероятностей и почти во всей литературе по теории массового обслуживания использование импульсных функций не принято. В результате приходится вводить специальные понятия, позволяющие обойти задачу дифференцирования разрывных функций. Вследствие этого многие интегралы приходится вычислять как
391
интегралы Стилтьеса вместо обычных знакомых всем интегралов Римана.
Остановимся кратко на определении интеграла Стилтьеса. Интеграл Стилтьеса определяется для неубывающей функции F (х) и непрерывной функции (р (х). Выбирают две последовательности точек {tk} и {£*}, такие, что < tk, и фор-
мируют суммы
S <P(W&) -k
Когда max | tk — tk_r | —>• 0, эти суммы стремятся к пределу, не зависящему от последовательностей [4} и и называемому интегралом Стилтьеса от <р по F. Интеграл Стилтьеса записывают в виде J <р (х) dF (х). Конечно, в качестве F можно взять функцию распределения и dF (х) выразить через плотность распределения (скажем, f (х)):
dF (х) — f (х) dx.
Без применения импульсных функций плотность может не существовать. Однако интеграл Стилтьеса всегда существует, и это позволяет обойти вопрос об импульсах. Но в данной работе импульсные функции введены, и это позволяет свободно оперировать и интегралом Римана, и интегралом Стилтьеса. Когда импульсы учтены в функции f (х), имеет место следующее тождество:
j <Р W dFJx) = j q> (х) / (х) dx.
В этом тексте мы будем пользоваться обоими обозначениями, чтобы ближе познакомить читателя с более употребимым в теории массового обслуживания понятием интеграла Стилтьеса и более легко вычисляемым при использовании импульсных функций интегралом Римана. После всего сказанного можно перейти к определению математического ожидания.
Математическое ожидание действительной случайной величины X (со), обозначаемое через Е [X] или X, определяется следующим равенством:
Е [Х\^Х^ j xdFx(x). (11.18)
— оо
Это выражение дано в форме интеграла Стилтьеса. В форме интеграла Римана:
Е [X] = X = j xfx (х) dx.
392
Математическое ожидание случайной величины X называется также ее средним значением. Можно записать
оо О
Е [X] = j [1 — Ех (х)] dx— j Fx x)dx, О — »
что, как легко видеть при интегрировании по частям, равносильно (11.18), поскольку Е (X) < оо. Для неотрицательных случайных величин эта формула дает
оо
Е[Х] = j[l-Fx(x)]dx, Х>0. о
В общем, математическое ожидание представляет собой сумму (интеграл) произведений возможных значений случайной величины на вероятности этих значений.
Рассмотрим теперь снова случайную величину Y, которая является функцией случайной величины X, а именно, как в равенстве (11.15),
Г = £(Х).
Для этой случайной величины математическое ожидание Еу [К] может быть определено, так же как и для величины X, через ее функцию распределения. Индекс Y при математическом ожидании нужен, чтобы отличать математическое ожидание по отношению к У от математического ожидания по отношению к другой случайной величине (в данном случае X). Таким образом,
оо f yfr,(y)dy.
— оо
Для вычисления последнего равенства требуется найти либо Fy (у), либо fy (у), что, как указывалось в предыдущем параграфе, может быть очень сложно. Однако основная теорема о математических ожиданиях дает более прямой путь вычисления математического ожидания функции через функцию распределения ее аргумента, а именно
<30
Еу [Г] = Ех [g (X)] = j g (х) fx (x) dx.
393
Можно определить математическое ожидание суммы двух случайных величин, обобщая очевидным образом одномерный случай: оо оо
Е[Х-|-У] = j j (* + y)fXy(x, y)dxdy=>
—оо —оо
ОО ОО ОО ОО
= xfXY(x, y)dxdy+ j j yfxY^x, y)dxdy = «—•co — oo —oo — oo
00 00
= j xfxdx+ j yfY(y)dy — E[X]-{-E[Y], (11.19)
Это можно также записать в виде X + Y = X + Y. При переходе от второй строки к третьей использовано равенство (П.14) предыдущего параграфа, выражающее одномерные плотности через совместную плотность двух случайных величин.
Таким образом, получен очень важный результат, состоящий в том, что математическое ожидание суммы двух случайных величин всегда равно сумме математических ожиданий этих величин, и здесь неважно, зависимы или независимы слагаемые. Это очень изящное свойство является следствием линейности оператора математического ожидания. Обобщение этого утверждения на любое число случайных величин, зависимых или нет, формулируется так: математическое ожидание суммы всегда равно сумме математических ожиданий слагаемых, т. е.
£[Х1 + Х2-Ф ... +Хп] = £(Х1]4-£[Х2]+
Аналогично можно поставить вопрос о произведении двух случайных величин, т. е.
00 00
Е [ХУ] = J J xyfxY (х, у) dx dy.
--<30 —. 00
В частности, когда случайные величины X и Y независимы, можно записать их совместную плотность как произведение их индивидуальных плотностей распределения и получить
<30 00
Е[ХУ]= J J xyfx(x)fY(y)dxdy = E[X]E[Y], (11.20)
— ОО — <30
Это последнее равенство (которое можно записать также в виде XY = ХУ) означает, что математическое ожидание произведения равно произведению математических ожиданий, если случайные величины независимы. Результат, аналогичный этому, получается также для функций независимых случайных величин. 394
Иначе говоря, если случайные величины X и Y независимы и-если функции от них обозначить через g (X) и h (Y), то на основании тех же доводов, которые привели к равенству (11.20), можно показать, что
£ [g (X) h (У)] = Е [g(X)] Е \h (У)]. (11.21 >•
Во многих задачах приходится иметь дело с математическими ожиданиями степеней случайных величин. Это встречается так часто, что таким величинам дано специальное название, а именно, математическое ожидание п-к степени случайной величины называется ее /г-м моментом. Таким образом, по определению (в действительности это следует из основной теоремы о математических ожиданиях), /г-й момент величины X задается равенством
Е\Хп]^Хп± J xnfx(x)dx. — оо
Кроме того, определяется п-й центральный момент этой случайной величины
оо
(Х-Х)"^ j (x-X)nfx(x)dx-— оо
/г-й центральный момент может быть выражен через п первых моментов. Чтобы показать это, запишем сначала следующее тождество, основанное на свойстве бинома:
п
(Х — Х)п = Q Xk(—X)n-k.
fe=0
Взяв математическое ожидание от обеих частей этого равенства,, получаем п п
(х^ху = У Q хь(—х)"-А = У Q xk(-х)пЛ
k=O fc=0
(11.22)-
При переходе от первого равенства ко второму здесь использован тот факт, что математическое ожидание суммы равно сумме математических ожиданий слагаемых и что математическое ожидание постоянной величины равно этой величине.
Теперь некоторые замечания. Во-первых, заметим, что нулевой момент случайной величины равен единице. Центральный нулевой момент тоже должен равняться единице. Первый центральный момент равен нулю, так как
(X —X) = X — X = 0.
395-
Второй центральный момент особенно важен и называется дисперсией. Для дисперсии вводится специальное обозначение:
Ox £= (X —X)2 X2 - (X)2.
Во второй части последнего равенства использовано равенство (11.22), позволяющее выразить дисперсию (второй центральный момент) через два первых момента.
Корень квадратный из дисперсии ох называется стандартным отклонением. Отношение стандартного отклонения к среднему значению случайной величины — наиболее важная величина в статистике и в теории массового обслуживания. Это отношение называется коэффициентом вариации и обозначается
Сх=^=-- (11.23)
Л
114. ПРЕОБРАЗОВАНИЯ, ПРОИЗВОДЯЩИЕ ФУНКЦИИ И ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Теория вероятностей оперирует с большим разнообразием функций (в частности, математическими ожиданиями), тесно связанными друг с другом. Сюда относятся характеристическая функция случайной величины, производящая функция ее моментов, преобразование Лапласа плотности распределения и ее производящая функция вероятностей. В данном параграфе будут даны определения этих понятий и указаны различия между ними, а также показано их основное общее свойство.
Характеристическая функция случайной величины X, обозначаемая через Фх (и), определяется в виде
оо
Фх(ы) =£ [е/иХ] = J eiaxfx(x)dx,
— оо
где j = К—1 £и и — действительная переменная. (Заметим, что за исключением знака в показателе степени характеристическая функция совпадает с преобразованием Фурье плотности распределения). Очевидно, что
оо
|Фх(«) |< J И* I 1/xWldx,
-00
я, так как | eiих| = 1, то
оо
Фх(«)|< J fx(x)dx;
«•оо
это показывает, что
|Фх(«)|«: 1.
.396
Разлагая показательную функцию под интегралом в степенной ряд и интегрируя почленно, получим следующее важное свойство характеристической функции:
(«) = j fx W [ 1 + iux + + • • ]dx =
= ...
Из этого выражения видно, что характеристическая функция разлагается в ряд, содержащий все моменты случайной величины X. Положив и = 0, найдем, что (0) = 1. Аналогично, взяв производную дФх (и)/du, а затем положив и = 0. получим jX, Таким образом, получается общая формула
ЛпФх («)
(11.24)
Этот важный результат позволяет находить моменты случайной величины X любых порядков. Так как это свойство часто применяют, удобно ввести следующее упрощенное обозначение [совпадающее с (1.37)] для n-Й производной произвольной функции g (х), вычисленной в фиксированной точке х ~ х0:
dng lx) dxn
(II.25>
х=ха
Следовательно, результат (11.24) можно переписать в виде
(0) = jnxn.
Производящая функция моментов, обозначаемая Мх (v), вводится ниже вместе с удобным дифференциальным соотношением, позволяющим непосредственно вычислить n-й момент случайной, величины X:
Mx(y)AE[evX] = j evxfx(x)dX-,
--ОО
Al<"’(0) = X",
где v — действительная переменная. Из последнего соотношения видно происхождение названия «производящая функция моментов». Вывод этого соотношения такой же, как и для характеристической функции.
Другая важная и полезная функция — преобразование Лапласа плотности распределения случайной величины X. Целесообразно теперь обозначать функции распределения разных случайных величин разными буквами, чтобы не применять индексов. Так, например, если случайная величина X представляет
397
•собой промежуток времени между моментами поступления требований в систему, то ее функцию распределения будем обозначать через А (х):
А (х) = Р [X х]
/здесь А — начальная буква английского слова «Arrival»). Плотность распределения для этого случая будем обозначать а (х). Наконец, соответствующее преобразование Лапласа плотности распределения а (х) обозначим через A* (s):
со
A* (s) = Е [е“®х] — j eTsxa (х) dx,
— ОО
где s — комплексная переменная. Здесь использовано «двустороннее» преобразование Лапласа; однако в параграфе 1.3 отмечалось, что, так как большинство встречающихся в теории массового обслуживания случайных величин неотрицательно, часто пишут
A* (s) = [ eTsxa (х) dx.
6
Опять обратим внимание на то, что нижний предел интегрирования 0 означает О-, т. е. нуль включается в область интегрирования, чтобы получить возможность включать любые импульсные функции в нуле. Аналогично производящим функциям моментов и характеристическим функциям, моменты случайной .величины X могут быть найдены по формуле
A*(fl) (0) = (—1)" (11.26)
Для неотрицательных случайных величин
со
|A*(s)| < j Ie-sx| |a(x)|dx. о
Но комплексная переменная s состоит из действительной части Re (s) = о и мнимой части Im (s) = ®, т. е. s = а + /ю. Тогда
| e-s* | = | e- 5xe’/wx | < | e'“ | | е"/шх | = | e"ax( .
Кроме того, | < 1 при Re (s) > 0, поэтому, учитывая два
оо
последних равенства и соотношение Ja(x)dx=l, можно за-и
.писать
| A* (s) | < 1, Re (s) > 0.
398
Очевидно, что три функции Фх («), Л1Х (и) и A* (s) тесно связаны друг с другом. В частности, справедливо следующее соотношение:
Ox(sj) = Mx(-s) = A* (s).
Поэтому неудивительно, что свойства производящей функции моментов (при дифференцировании) также аналогичны свойствам характеристической функции и преобразования Лапласа. Это центральное свойство, которое используется в теории массового обслуживания. Таким образом, n-й момент случайной величины X может быть вычислен по одной из следующих формул:
(0);
Хп = М(х (0); =(— IfA’0” (0).
По-видимому, целесообразно привести пример для демонстрации этих свойств. Рассмотрим непрерывную случайную величину X, которая представляет собой промежуток времени между требованиями, поступающими в систему, и распределена по показательному закону, т. е.
fx (х) = а (х) =
0,
х>0;
х<0.
Прямой подстановкой в определяющие интегралы получаем
Всегда справедливы равенства
фх(0) = Мх(0) = А*(0) = 1,
и, очевидно, в рассматриваемом примере это тоже так. Используя выражения для первого момента, получаем, исходя из любой из трех функций, что
Любая из трех функций дает также второй момент в виде "у2_____________________________
Л А.2
и все дальнейшие моменты.
В случае дискретной случайной величины, например при ^ = Р[Х = Й],
399
нужно использовать производящую функцию вероятностей, обозначаемую G (г), а именно
G (z) = £ [гх] = 2 ^ёк, (11.27)
k
где г — комплексная переменная. Из обсуждения в приложении I ясно, что G (г) представляет собой ничто иное, как производящую функцию последовательности gk. Как и для непрерывных преобразований, при |г| < 1
|С(г)| < Е И k
таким образом, |G(г)| < 1 при |z|cl. (11.28)
Заметим, что первая производная, вычисленная в точке z = дает первый момент случайной величины X:
G(1) (1)=Х, (11.29)
а вторая производная дает
G(2)(l) = 5?— X
точно так же, как и для непрерывной случайной величины К Заметим, что во всех случаях
G(l)=l.
Применим этот метод для рассмотренного ранее примера игры в «дубинку». Используя либо равенства (II.7), дающие дальнейшие вероятности различных выигрышей, либо импульсные функции, изображенные на рис. II.4, находим производящую функцию вероятностей выигрыша в игре в «дубинку»:
ои-4^+т+тЛ
Заметим здесь, что G (1) = 1, и далее, что средний выигрыш может быть вычислен как
X = G(1)(1) = O.
Рассмотрим теперь сумму п независимых случайных вели-п
чин Xt, а именно У = У, Xt, как это определено равенством (11.16). 1=1
Если образовать характеристическую функцию этой величины,
то
получается
Фг(и)Д£[е',“У] = Е
п
/“2 xi е i=1
= E[e’uXieiuX»- • е1',х'>].
1 Таким образом, имеем: сгх = G(2> (1) + G(l> (1) — [G(1> (I)]2.
400
Но в равенстве (II.21) было показано, что математическое ожидание произведения функций от независимых случайных величин равно произведению математических ожиданий этих функций. Применяя это к предыдущему равенству, получаем
Фу (и) = Е [е/цХ1] Е [е'“хи • • • Е [е/иХ"].
Правая часть этого равенства представляет собой произведений характеристических функций и поэтому
Ф/ («) = Фхх («) Фх2 («)••• Фхп («)• (П.30)
В случае, когда все величины Хг распределены одинаково, все характеристические функции тоже одинаковы, поэтому индексы у величин Xt можно отбросить и записать полученный результат в виде
фу(ц) = [фх(ы)]«. (П.31)
Таким образом, показано, что характеристическая функция суммы п независимых одинаково распределенных случайных. величин равна п-к степени характеристической функции одного слагаемого. Этот важный результат справедлив также для преобразований других видов, а именно для производящей функции моментов, преобразования Лапласа и производящей функции вероятностей. Это определяющее свойство в немалой степени способствовало широкому применению преобразований в теории вероятностей и теории случайных процессов.
Скажем еще несколько слов о суммах независимых случайных величин. Равенство (П.17) показывает, что плотность распределения суммы независимых случайных величин равна свертке плотностей слагаемых. Равенство (11.30) показывает, что в этом же случае преобразование суммы равно произведению преобразований слагаемых. Из равенства (11.19) следует, что (безотносительно к независимости) математическое ожидание суммы равно сумме математических ожиданий, т. е.
У = Хх -f- Х2 + • • • + Хп. (11.32)
Для п = 2 второй момент величины Y
= (Xi + Х2)2 = X? + 22GX2 + (2G)2.
Но в этом случае также
(F)2 = (X, + Х2)2 = (ХО2 + 2ХхХ2 + (Х2)2.
Образуя дисперсию величины V и используя последние два равенства, получаем
а2у = Г5 - (У)2 = Х1 - (Xi)2 + Xl - (Х2)2 +
~Н 2 (Х1Х2 — Х1Л2) = Ох, + + 2 (Х1Х2 — XiX2).
14 Л. Кл ейнрок 401
Если теперь Х± и Х2 независимы, то Х±Х2 — XtXs, и это даег окончательный результат:
of = Сх. + <Л:2.
Таким же путем можно показать, что дисперсия суммы п независимых случайных величин равна сумме их дисперсий, т. е.
Оу = О’х1 + °Х2 + • • • + G~Xn
Продолжая рассматривать независимые случайные величины, предположим, что их число в сумме тоже случайно, т. е. определим
N
Y=%Xh
i=l
где {XJ — последовательность одинаково распределенных независимых случайных величин со средним значением X и дисперсией Ох, аМ — тоже случайная величина со средним значением N и дисперсией о^. Предположим также, что N не зависит от Xt. В этом случае Fy (у) называется сложным распределением. Найдем теперь Y* (s) — преобразование Лапласа плотности распределения величины У. По определению преобразования, пользуясь независимостью всех случайных величин, можно написать
Но поскольку {XJ распределены одинаково, получается равенство
У*(з) = £ [X*(s)]nP [X = /г];
п=0
(11.33)
через X* (s) обозначено преобразование Лапласа каждой из величин X,. Равенство (II.33) есть ничто иное, как производящая функция случайной величины /V, которую мы в соответствии с равенством (11.27) обозначаем через N (г), где г заменено на X* (s). Таким образом, получаем окончательный результат:
y*(s) = X(X*(s)). (11.34)
Следовательно, случайная сумма одинаково распределенных независимых случайных величин имеет преобразование, которое связано указанным выше образом с преобразованиями слагаемых и числа слагаемых. Найдем теперь выражение, аналогичное выражению (II.32). Согласно этому равенству в случае одинаково распределенных слагаемых X,- имеем У = «X, где п 402
данная постоянная. Теперь, однако, число членов в сумме случайно, и надо заново искать Y. Приступим к этому, вооружившись свойством производящей функции моментов (11.26). Дифференцируя (11.34), полагая s = 0 и меняя знак, получаем
У = NX.
что вполне разумно. Аналогично можно получить дисперсию такой случайной суммы, дважды дифференцируя и затем вычитая квадрат математического ожидания; это дает
= г(Х)2<Дл
Интуитивно этот результат, вероятно, не столь очевиден.
II.5. НЕРАВЕНСТВА И ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
В этом параграфе приведем некоторые классические неравенства и предельные теоремы теории вероятностей.
Рассмотрим сначала границу вероятности того, что случайная величина превысит некоторое значение. Если известно только математическое ожидание случайной величины, то для неотрицательной случайной величины может быть установлено следующее неравенство Маркова:
Р[Х^х\<^.
Так как здесь использовано только математическое ожидание, это неравенство довольно слабое.
В неравенстве Чебышева используются и математическое ожидание и дисперсия. Оно утверждает, что для любого х О
Р[\Х — Х\>х]<^.
Другие простые неравенства содержат моменты двух случайных величин. Здесь имеется в виду, во-первых, неравенство Коши—Шварца, согласно которому квадрат математического ожидания произведения не превышает произведения вторых моментов:
(ХУ)2<Х2У2. '(11.35^
Обобщением этого неравенства является неравенство Гельдера, которое для а > 1, (5 > 1, а-1 + (З-1 = 1 и X > О, У > 0 утверждает, что
если указанные математические ожидания существуют. Заметим, что неравенство Коши—Шварца является важным частным случаем, когда а = р = 2. Неравенство треугольника связывает 14* 403
математическое ожидание модуля суммы с суммой математических ожиданий слагаемых модулей, а именно:
Обобщение неравенства треугольника, известное как Сг - неравенство, имеет вид
| Х + Y\' < Сг[| Х|' + |У и,
где
Укажем теперь границу математического ожидания выпуклой функции g произвольной случайной величины X (для которой предполагается существование первого момента X). Выпуклой называется функция g (х), лежащая всюду под своими хордами или на них, г. е. для всех <5 х2 и 0 сас 1 эта функция удовлетворяет неравенству
g (a*i + (1 — «) *2) « ag (*i) + (1 — «) £ (х2).
Для такой выпуклой функции g и случайной величины X справедливо неравенство Енсена в следующем виде:
gW > g(X).
Для сумм случайных величин имеются некоторые очень красивые предельные теоремы. Рассмотрим снова сумму п независимых одинаково распределенных случайных величин X,-, но разделим теперь эту сумму на п:
^--4 £ х‘-
Это среднее арифметическое часто называют выборочным средним. Предположим, что каждая из величин X,- имеет математическое ожидание X и дисперсию фх- Из предыдущего обсуждения, связанного с математическим ожиданием и дисперсией суммы, следует, что
ГЛ = Х;
Если теперь к случайной величине Wn применить неравенство Чебышева и подставить полученные характеристики этой величины, то можно выразить границу через среднее значение и дисперсию самой случайной величины X:
Р[| Wn-х| > х] • (П.36)
404
Этот очень важный результат утверждает, что среднее арифметическое суммы п независимых одинаково распределенных случайных величин приближается к своему математическому ожиданию с возрастанием п. Это следует из того, что-величина о2х/'нх2 убывает с возрастанием п (о2х/х2 остается постоянным). Фактически, это непосредственно приводит к слабому закону больших чисел, который состоит в том, что для любого е > О
limP[|F„ — Х|>е] = 0. И->ео
Усиленный закон больших чисел утверждает, что с вероятностью единица
lim Wn = X. П-> СО
Рассмотрим опять сумму п независимых одинаково распределенных случайных величин, каждая из которых имеет математическое ожидание X и дисперсию Центральная предельная теорема рассматривает нормированные случайные величины Zn, определенные следующим образом:
S Xi-nX
Zn=i=A (П.37)
oxV п
и утверждает, что функция распределения величины Zn стремится к стандартному нормальному распределению при п —> оо. Это значит, что для любого действительного х
lim Р [Zn < х] = Ф (х), П~><х>
где
X
Ф(Х)Д J
— со
Следовательно, надлежащим образом нормированная сумма большого числа независимых случайных величин имеет распределение, близкое к нормальному, называемому иначе гауссовым распределением. Имеется много других форм центральной предельной теоремы, например для случая независимых случайных величин.
Существует довольно сложный прием оценки «хвостов» распределения суммы большого числа независимых слагаемых, который приводит к так называемой границе Чернова. Он дает неравенство, подобное неравенствам Маркова и Чебышева, но в нем полностью используется распределение самой случайной величины (в частности, производящая функция моментов). Рассмотрим
405
сумму п независимых одинаково распределенных случайных величин Х;:
i=i
Из равенства (11.31) известно, что производящая функция MY (v) моментов величины Y связана с производящей функцией Л4Х (и) моментов каждой из величин X,- соотношением
Mr(v) = [Mx(v)]n. (П.38)
Как и в предыдущих неравенствах, будем искать вероятность того, что сумма превышает некоторое определенное значение. Эта вероятность задается формулой
P[Y>y]=^fy(w)dw. (11.39)
у
' Очевидно, что для v 0 единичная ступенчатая функция [см. равенство (1.33)] ограничена сверху следующей показательной функцией:
и-1 (w — у) < е° .
Подставляя это неравенство в (11.39), получаем
«9
Р [У > у] с е-04' J eva>fY (®) dw Для v > 0.
— 00
Но интеграл, стоящий справа, представляет собой производящую функцию моментов для Y; тогда
Р[Г>^]<е-°4'Л1у(р), о>0. (11.40)
Определим теперь «семиинвариантную» производящую функцию: у (и) Д In М (о).
Применяя это определение к (11.38), получаем немедленно, что yr(i>) = nyx(i>),
и применяя это последнее к уравнению (II.40), приходим к неравенству
P[Y>y]<.e~vy+nvx<v\ у>0.
Так как это неравенство имеет место для всех v (>0), можно выбрать v так, чтобы получить наилучшую границу. Это легко достигается дифференцированием показательной функции и приравниванием производной нулю. Таким образом, оптимальное соотношение между v и у получается в виде
у = пу$(р). (11.41)
406
Таким образом, граница Чернова для «хвоста» распределения окончательно получается в виде 1 *
Pt[Y (")], у>0. (11.42)
По-видимому, целесообразно привести пример, демонстрирующий применение этой последней ограничивающей процедуры. С этс^р целью вернемся ко второму параграфу этого приложения, в котором были определены шансы того, что при миллионе бросаний монеты появится, по крайней мере, 490 тыс. гербов. Конечно, это равно вероятности того, что при таком эксперименте появится не более 510 тыс. гербов, если монета нефальшивая. В этом примере случайная величина X может быть выбрана следующим образом:
( 1, герб;
(0, число.
Так как Y — это сумма миллиона таких величин, то п = 106, и мы ищем вероятность того, что Y достигает величины 510 000 или превышает ее, т. е. Р (Y > 510 000). Производящая функция моментов для X
яти=4-+4-еР;
тогда
Тх(Р) = 1п-1-(1 + е’).
Аналогично,
Из равенства (П.41) получаем
П?О) (и) = 106.g = 5ю 000 = у.
1 + е
Следовательно,
— 49
1 51
У = 1ПТ9-
Таким образом, ясно, как можно вычислить и. Подставляя это значение снова в (11.42), заключаем, что
Р [У > 510 000] Се10‘Пп (50/49)-0,51 In (51/49)],
1 Такой же вывод дает границу «нижнего хвоста», если все три неравенства
в (11.42) заменить на обратные (например, v < 0).
407
Вычисления показывают, что вероятность того, что число гербов при миллионе бросаний монеты превысит 510 000 меньше 1СГ88 (именно таким образом было получено это число в начальном параграфе). Другой путь вычисления этой вероятности дает центральная предельная теорема. Проделаем это для того же примера. Для этого требуется вычислить математическое ожидание и дисперсию величины X, что дает X = 1/2 и Ох = 1/4. Тогда из равенства (11.37) получаем
7 __ Г—10» (1/2) (1/2) 103 •
Если требуется, чтобы Y > 510 000, то это равносильно тому, что Zn должно быть больше 20. Если обратиться к таблицам нормальной функции распределения, то найдем
P[Z>20] = 1—Ф (20)~25 -1СГ90.
Снова получается, что такой исход эксперимента практически невозможен. С другой стороны, неравенство Чебышева в виде (11.36) позволяет сделать лишь следующую оценку:
Р [| - Ф | > 0,01 ] < _25 10-‘.
Этот результат вдвое больше того, который должен быть, так как здесь в действительности вычислены оба «хвоста» распределения (а именно, получена вероятность того, что появляется более чем 510 000 или менее чем 490 000 гербов). Поэтому из неравенства Чебышева следует, что вероятность появления более чем 510 000 гербов меньше или равна 12,5-ЮД Заметьте, какой неточный результат дает неравенство Чебышева по сравнению с центральной предельной теоремой, которая в этом случае дает результаты, сравнимые с границей Чернова.
11.6. СЛУЧАЙНЫЕ ПРОЦЕССЫ
Часто говорят, что теория массового обслуживания — это часть теории случайных процессов. Действительно, основная часть этой книги является прямым следствием соответствующих разделов теории случайных процессов. Здесь мы дадим некоторые основные определения и понятия.
Начнем с рассмотрения вероятностной системы (S, &, Р), которая состоит из пространства элементарных событий S, множества событий {Л, В, ...} и вероятностной меры Р. Кроме того, уже введено понятие случайной величины X (со). Случайный процесс может быть определен следующим образом. Для каждого элементарного события со £ S определяется функция времени X (t, со). Это семейство функции образует случайный процесс. Наоборот, можно сказать, что для каждого t, принадлежащего некоторому множеству значений параметра, выбрана случайная 408
величина X (t, со). Эта совокупность случайных величин зависит от t. Таким образом, случайный процесс (или случайная функция) есть функция 1 X (I), значения которой — случайные величины. Примером случайного процесса может служить система закрытых цен для обеспечения безопасности Нью-Йорской фондовой биржи. Другим примером является температура вранной точке земного шара как функция времени.
Мы непосредственно сталкиваемся с задачей дать полную характеристику случайного процесса X (f). С этой целью определим для каждого дозволенного значения t функцию распределения, которую обозначим через Fx (х, t):
Fx(x, t) = P[X(t)^x].
Далее, для любых п дозволенных значений t, \tlt t2, ..., tn], определим совместную функцию распределения:
F хгх2... хп (и, Xl,---,Xn\ t\, h,-. ,tn) А. В [X (Л) < Xl,
X (t2)<.x2,. ..,X(tn) <xn].
Будем пользоваться векторным обозначением Fx (х; t) этой функции.
Случайный процесс называется стационарным, если все Fx (х; t) инварианты по отношению к сдвигу во времени, т. е. если для любой постоянной т справедливо следующее равенство:
Fx(x; t4-T)=Fx(x; t),
где обозначение t + т относится к вектору (й + т, t2 -f- т, ..., tn + т). В теории случайных процессов наиболее интересны стационарные случайные функции.
Чтобы полностью охарактеризовать случайный процесс, надо задать Fx (х; t) для всех возможных множеств {хД и при всех п. Это в общем случае чудовищная задача! К счастью, для многих интересных случайных процессов возможно очень простое описание.
Для этого нужны некоторые определения. Во-первых, определим плотность распределения вероятностей случайного процесса как
с , . a dFx <х; fx (X, t) A dx
Во-вторых, введем в рассмотрение среднее значение случайного процесса, т. е. ее
X (/) = Е [X (/)] = j xfx (х, t) dx.
1 Обычно ее обозначают X (t, и), но для упрощения можно писать X (/).
409
Далее введем автокорреляционную функцию процесса X (/) как Rxxth, /2) = £[Х(/1)Х(/2)] =
•» ее
= [ J xiXifx.x, (xt, х2; ti, tydxidxi.
—•00 —^ое
Так называемая корреляционная теория случайных процессов, получившая широкое развитие, классифицирует и различает процессы только по их средним значениям X (/) и автокорреляционным функциям RXx (Л, ^)- В случае стационарного случайного процесса имеем
Х(7) = Х; (11.43)
#хх(*1Л2) = Яхха1 — У, (П.44)
т. е. Rxx является функцией топью? разности т — — /2.
ь стационарном случае, следовательно, случайный процесс в корреляционной теории характеризуется только постоянной (среднее значение X) и функцией одной переменной RXx (х).
Случайный процесс называется стационарным в широком смысле, если для него выполняются равенства (11.43) и (11.44). Заметим, что все стационарные процессы стационарны в широком смысле, но не наоборот.
СПИСОК ’ЛИТЕРАТУРЫ 1
1. Davenport, W. В. Jr. Probability and Random Processes. McGraw—Hili (New York), 1970.
2. Феллер В. Введение в теорию вероятностей и ее приложения. Том. 1./Пер. с англ. Под ред. Е. Б. Дынкина. М., Мир, 1964 . 498 с.
3. Papoulis, A. Probability, Random Variables, and Stochastic Processes. McGraw— Hill (New York), 1965.
4. Parzen, E. Modern Probability Theory and Its Applications. Wiley (New York), 1960.
1 Рекомендуемые советские учебники: Гнеденко Б. В. Курс теории вероятностей. М., Наука, 1969. 408 с.
Веитцель Е. С. Теория вероятностей. М., Наука, 1969. 576 с. — Прим. ред.
Глоссарий1
(Ниже приведены только те обозначения, которые часто используются в данной книге)
Обозначение 2 Определение Ссылка на типичную страницу
ООП ОПП (/) = A (t) Л’ (s) = Л* (s) a-k (0 = а (/) Вп (х) = В (х) В; (s) = В* (s) bk bn (х) = Ь (х) Сь Сп Сп (и) — С (и) О’(s) = С* (s) с„ (и) = с (и) D dk Е [X] = X Ei Обслуживание в обратном порядке Обслуживание в порядке поступления Преобразование Лапласа функции а (/) Момент fe-ro порядка случайной величины с плотностью распределения вероятностей а (/) dAn (t)/dt = dA (t)ldt P [x„ C x] = P [x < x] Преобразование Лапласа функции b (x) Момент fe-ro порядка случайной величины с плотностью распределения вероятностей b (х) dBn (x)/dx = dB (x)/dx Коэффициент вариации времени обслуживания n-е требование, поступающее в систему Р [ип С и] Преобразование Лапласа функции сп (и) = с (и) dCn (и)/du = dC (u) /du Детерминированное распределение P[9 = fe] Математическое ожидание случайной величины X i-e состояние системы 2ч- 24 28 30 29 30 30 30 30 30 207 26 298 303 298 9 197 392 44
1 В тех случаях, когда одно и то же обозначение используется в нескольких смыслах, неопределенность устраняется в тексте (нлн специальной оговоркой).
2 Обозначение Уп-+ У используется для указания того, что у = Нт уп при п -> <*>, равно как у (/) -> у обозначает, что у = lim у (?) при / со.
411
Продолжение
Обозначение 2 Определение Ссылка на типичную страницу
Ег Распределение Эрланга порядка г 142
Ex W Р [X < х] 385
fx W dFx (x)/dx 386
G Распределение произвольного вида 9
G(y) G* (s) Распределение периода занятости Преобразование Лапласа функции 232
g(y) 232
gk Момент fe-ro порядка периода занято-
сти 233
g(.y) dG (y)/dy 235
Hr Im (s) Гиперпоказательное распределение X-го порядка Мнимая часть комплексной перемен- 161
НОЙ S 311
In-+ I Длительность n-го периода свободного
СОСТОЯНИЯ 322
I* (s) Преобразование Лапласа плотности распределения вероятностей периода свободного состояния 323
Г (s) Преобразование Лапласа плотности распределения вероятностей периода свободного состояния дуальной си-
стемы 326
X Объем конечного накопителя 9
Показательное распределение 9
M. Объем конечной популяции 9
m Число обслуживающих приборов 9
Nq (t) -> Nq Длина очереди требований в момент t 33
N(t)-+N Число требований в системе в момент t 27
0 (%) lim О (х)/х = К х->0 301
o(x) lim о (х)/х •— 0 66
я->0
p Матрица вероятностей перехода 48
P[4j Вероятность события А 379
P [A ] S] Условная вероятность события А при условии события В 380
PkW р [X (0 = *j 73
PH Р [следующее состояние Д;/текущее состояние £(- ] 44
Pij (s. 0 Р [X (0 = i | X (S) = 11 64
Pk <2 (г) Р [k требований в системе ] Производящая функция от Р [q = 108
= k] 212
4il (0 Интенсивность перехода в момент t 66
412
Продолжение
Обозначение 2 Определение Ссылка на типнч ную страницу
qn -> q Число требований в системе, остав-
шихся после ухода требования Сп 19Т
q'n q' Число требований в системе при по-
ступлении требования Сп 263
Re (s) Действительная часть комплексной
переменной s 355
rH Р [следующий узел / | текущий узел 1] 169
rk Р [q' = А] 197
Sn (У) s (n) Р [Sn < у] -+ Р [S < у] 30
s*n (s) 5’ (s) Преобразование Лапласа функции
Sn (У) -> s (у) 30
s Переменная преобразования Лапласа 354
s„ -> s Время пребывания в системе (для 28
требования Сп)
Sn (y) s (y) dSn (y)/dy -> dS (y)/dy 30
sn -> s = T Среднее время пребывания требова-
ния Сп в системе 30
Момент fe-ro порядка случайной ве-
личины с плотностью распределения
вероятностей sn (у) 30
T Среднее время пребывания в системе 30
tn-+~t Промежуток времени между последо-
вательными требованиями (С„_х и
Сп) 27
Tn =7= 1A Средняя длина промежутка между
последовательными требованиями 29
Момент k-ro порядка случайной ве-
личины с плотностью распределения
вероятностей a(t) 29
U (0 Незавершенная работа системы в мо-
мент t 27
«0 (0 Единичная функция (дельта-функция
Дирака) 387
tin и ~ Хп tn+1 и — х *1 294
V(z) Производящая функция от Р [и =
= k} 205
Vn -г V Число требований, поступающих в те-
чение промежутка времени обслужи-
вания требования Сп 199
W Среднее время пребывания в очереди 30
Wo Среднее остаточное время обслужива-
ния 211
W- (У) Дополнительное время ожидания 301
413
П'р о д о л же и и е
^Обозначение 2 Определение Ссылка на типичную страницу
Wn (у) w (у) < (s) -> Г* (s) Wn -> W р [К'п « У] -> р [а< « у] Преобразование Лапласа функции ®п (У) Время ожидания требования Сп в очереди 30 30 30
3 h и ГЪ _ t э 4 -s t * = - L is -$ 1 а dWn (y)/dy dW {y)/dy Среднее время ожидания (для требования С„) Момент fe-ro порядка случайной величины с плотностью распределения вероятностей wn (у) Состояние вероятностного процесса X (1) в момент t 30 23 J ) 30
хп -> ~х ~xk Время обслуживания (требования Сп) Момент fe-ro порядка случайной величины с плотностью распределения вероятностей b (х) 30 30
хп = X — 1/Ц Среднее время обслуживания 30
Y Длительность периода занятости 226
а(0 Yz 6(f) Переменная производящей функции Число требований, поступающих в промежуток времени (0, t) Внешняя интенсивность поступлений требований в узел i Число требований, уходящих в промежуток времени (0, t) 343 31 169 31
А. Средняя интенсивность поступления Интенсивность размножения (поступления) при N = k 29 71
Н В* Средняя интенсивность обслуживания Интенсивность гибели (обслуживания) при N = k 30 71
л W -> л л1п) лк П <н Вектор вероятностей состояний Р [система находится в состоянии Ек] аг а2 . . . (обозначение произ- 48 46
i =! ведения) 350
р Коэффициент использования 34
а Корень для системы G/M/m Дисперсия промежутка времени между соседними требованиями 269 322
414
Продолжение
Обозначение 2 Определение Ссылка на типичную страницу
Дисперсия времени обслуживания 322
Vn Время поступления требования Сп
ф+ (S) Преобразование Лапласа функции
W+ (у) 302
Ф (s) Преобразование Лапласа функции 302
И'- (У)
д Равенство по определению 27
(0, 0 Интервал от 0 до t 32
X = Е [X] Математическое ожидание случайной 392
величины X
(у)+ max [0, у\ 295
(п\ Биномиальный коэффициент, равный
\k) я! k ! (п — fe)! 126
A/B/m/K/M СМО с т обслуживающими приборами, распределениями вероятностей А (!) и В (х), обозначенными соответственно А и В, накопителем емкости К и популяцией требований объема М (отсутствие любого из двух последних символов означает, что соответствующая величина предпо-
лагается сколь угодно большой) 9
F(,1) (а) dnF (y)/dyn\y=ia 397
f(k) w f (X) 0 ... 0 f (х), fe-кратная свертка
f^g Оператор свертки / на входе дает g
на выходе 338
Л{-)В Из утверждения А вытекает утвержде-
ние В, и наоборот 87
f {—} F f и F являются парой преобразований 344
0 Оператор свертки 345
Важнейшие результаты
Ниже в виде сводки формул приведены важнейшие результаты этой книги (отмеченные знаком ж). Справа указан номер страницы, на которой впервые значимо появляется соответствующий результат; это делается для того, чтобы помочь читателю найти в тексте описание и теорию, относящуюся к данному равенству.
СМО общего вида
р = Хх (G/G/1) о Л Kxltn (G/G/m) 34 35
T^x±W 34
N — KT (формула Литтла) 33
Nq = KW 33
Nq = N — p 9 208
dPk (t)jdt = интенсивность потока в Ек—интенсивность из Ek 76 Pk~rk (Для пуассоновского входящего потока) 198
О. cl:i [Л/ (/) делает единичный скачок]. 197
Марковские процессы
Важнейшие результаты для дискретных цепей Маркова приведены в таблице на с. 418—419.
Пуассоновские процессы
РЛ(0=--^е-«, fe>0, is >0 78
79
cN(t) = M 80
E [zN (')J =-- ex< <*-’> 81
416
Системы размножения и гибели
jp,. т
= (Л* "1“ М-а) k (fl "+ ^k-i^k-i (г) + M-A+i^k+i U)> Л > 1 /5
-^- = _%оРо(/) + И1Р1(0, й = 0 75
*-> х.
Pk = Ро П —(стационарное решение) НО
М/М/1
Pk (0 = е- <^+и) t р(*-о/2Л_г (а/) + р(^-<--')/2/,+(.+1 (а/) +
+ (1— Р)Р\ Е. p-W^a/) 95
/=А+«4-2 J
Ра==(1—P)Pfc НЗ
лГ = р/(1—р) 114
а^ = р/(1— р)2 115
Ц7= Р/м_ 2П
1 —р
Т = т1^ 115
1 —р
P[>>k требований в системе] = pft 116
s(^) = p(l — ple-^C-PJJ'.t/>0 222
S (у) = 1 — e-м <’-p) n, z/ > 0 223
HZ/) = (1 — P)«o(j/) + ^(l — р)е~Р<1-Р)г/, у > 0 223
417
Итоговые результаты для цепей Маркова
ДИСКРЕТ1 ЮЕ ВРЕМЯ
ОДНОРОДНАЯ НЕОДНОРОДНАЯ
Вероятность перехода за один шаг .Матрица вероятностей переходов за один шаг Р ' - / 1 Хп = г] Р^[Р171 P/j (n, n-^r 1) A A /> । Л.-.- '] P («) [Plj (« 11 A- 1)]
Вероятности переходов за т шагов Матрица вероятностей переходов за т шагов = / I Хп = t] p<m) д [р<р’] P/у И. «)£ = P [Xn = j | Xm = i] H (m, n) A n)J
У равнение Чэпмена — Колмогорова k p(m) _ p(m — ?)р(<?) Pij (m, ri) = = X Pik (m> 9) PA/ (Q> k H (m, n) = = H (m, q) H (</, n)
НЕПРЕРЫВНОЕ ВРЕМЯ
ОДНОРОДНАЯ | НЕОДНОРОДН \я
ptf£Plx (Мд0 -:= --= / 1 X (!) i] P,-j(P A P [X (I + Д0 = --/IMO -»] p (0 A [pz/ (/, t + Л0]
Рг/(ПАР[Х (s+0 = = i 1X (s) = i] H (0 a [Pif (0] plt (s- 0 = AP[X(0 = /|X(s) = i] H (s, 0 &[Ptj (s, 0]
I
p,j (0 = = X Pi;, (t — 0 pk: (s) k H(0 = H(/ —s)H(s) P4 («, 0 -= = E P>k^’ U^Pk! k H (s, 0 = H (s, P) Я (и, !)
Продолжение
ДИСКРЕТНОЕ ВРЕМЯ
ОДНОРОДНАЯ НЕОДНОРОДНАЯ
Прямое уравнение Обратное уравнение Решение р("0 _ р(т— 1)р р("0 — рр(т~1) р(т) — р»> Н (т, п) = = Н (т, п— 1) Р (п— 1) Н (т, л) = = Р (пт) Н (лг+ 1, л) Н (т, п) = = Р(лг)Р(лг + + 1) • • • Р(п-1)
Матрица интенсивностей переходов — —
Вероятность состояния Матрица вероятностей состояний л(п> Д [л<п>] л)ге)ДР[Х =/] Л<П) А [Л<П>]
Прямое уравнение Решение Стационарное решение = Л(”-л''1’ = л*0’?" л = лР л(ге) =л('г”'1)Р(л— 1) Я(Л) = я(0)р (0)Р (1) . . . ... Р (л — 1)
Пара преобразований [I —гР]-1(=) Р" —
НЕПРЕРЫВНОЕ ВРЕМЯ
ОДНОРОДНАЯ НЕОДНОРОДНАЯ
dH (O/df = H (0Q dH (0/<Я = QH (0 Н (/) = eQZ dH ( = Н ан ( = —с н = ехр ?, t)/dt — (s, t)Q(t) >, t)/ds = i (s) H (s, t) S, t) = • / j Q.(u) du _s
„ , Р — I Q lim Д‘->0 QW=Iim
щ (0 д Р [X (0 = /] я (0 л [Л/ (/)] п/(0й'Р[^(0 = /] Л (/) А [Л/ (/)]
сл (l)/dt = л (7) Q л (0 == л (0) eQf nQ = 0 ал (/)/d п (0 X ехр =- Л (/) Q ( = я (0) X J Q (u) du j; )
[si-Q -i<=>H (0
M/M/m
W{y) = \— ре-м Р-р)у, y^Q 223
p ' промежуток времени ‘ между соседними событиями < t = 1— е-«, i>0 168
g (^) A..- \i/2 e“(Х+ц) * Л [2^ (M1/21 235
У \Р/
1 (2n—2\
fn=T\ n_ J P"-1 u + P)I-2n 238
—‘Гк+И-У, 122
1 — (X/p,)K+1 \ н /
'k = ' (M/M/1/К)
О в остальных случаях
All / Л
Pk = M И - (M/M/1//M) 125
у мл / x \ <
£j (Л4—i)1 к и )
____Ц(1-р)(1-г) H(l-z)-Xz[!-G(z)]
= 0,1,2,...
- (M/M/1 групповое поступление)
(M/M/1 групповое обслуживание)
P* =
(тр)А Р^-РГ’
(p)k тт Ро^г-
Po =
У (mp)k
A kl
L*=o
-1
154
159
120
120
P [ожидания] =
rm-l
— (С-формула Эрланга)
120
P^ =
" m—1
Pk
, k > m
1______
1 — p
1 —P
1_
1 —p
. I т
у^1(м;м/т/т)
KI JmbJ I 1
123
(Л/ц)от I у
Рт ml
I i=s=Q
(M/M/m/m) (Формула потерь Эрланга)
123
420
M/D/1
— р р2 9 1-р 2(!-р) 209
[И Рх 211
2(1-р) [Z//X] ,
G(//)= 2 Т— е~ЛР 239
л=1
г (ftp/1-1 е—"р 1п п\ 239
c
Ег (распределение Эрланга порядка г)
, , . ru, (гцх)г—1 е~ЛЦХ п 142
1 142
Р(г)1/2
М/Ег/1
/’/ = (1-P)S А^Г1’ /=1, 2,...,г 148
i=i
Ег/М/1
( 1 — р, k = 0;
Рк = 1 Р(г£— 0г~г*> &>о 152
Hr (гиперэкспоненциальное распределение порядка г)
R
b (х) = S а^е-^*, х > 0 161
1 162
Марковские сети
N
К — Vi + ^jrji 169
p(klt k2, . . kN) = p^ki) p2(k2) .. . pN(kN) (сеть разомкнута), где
p, (k^ — решение для изолированной системы M/M/mz 170
1 N xki p (klt k2,...,kN)- G (/<) П p (ki) (сеть замкнута) 1 = 1 172
Срок службы и остаточное время
fx(x) = (плотность распределения вероятностей остаточного времени для дискретного времени) 192
421
Ну) — ~(плотность распределения вероятностей остаточно-
го времени) 192
с* i \ 1 — F* (s) i „ -г г (s( = —sinx ’ (преобразование Лапласа плотности распреде-
ления вероятностей остаточного времени) Г 193
п (/2 | mi VHUiuCn 1 п 1и иирлдпа ДЛл! UL1C11U4MU1U ьре.чгни; 1ь*о
G = (среднее значение остаточного времени) 193
г (х) = - И) (интенсивность отказов) 191
M/G/1
rk — Pk = d-k 198
Л , Л — — Л 1 4'i-t-i 'nt- 1 v«+l 202
V = р 204
V- ~-v = Х2х2 = р2 (1 + Сь) 207
V(z)=--5*(^~ М 205
<? = р + ра (формула Полячека—Хинчина) 210
Т (1 ' Св) --- = 1 + Р 2 рТ_р) (формула Полячека—Хинчина) 211
W (14- С2) — = р 2 р (формула Полячека—Хинчина) 211
W = t(формула Полячека—Хинчина) 210
211
Q (z) = В* (X—Xz) д’ n р) (J ~Z) - (уравнение Полячека— D (А А<&) 2 -Хинчина)
214
F* (s) — s (s) (УРавнение Полячека—Хинчина) 220
с*/<а R* (<;} s(l—Р) 219
j W с W s _ х + zb* (S)
Р [/ < у] = 1 — е_Хг/, у > 0 229
G* (s) = B*(s + A—AG*(s)) 233
g Gj} “is е~~кх («1 Ь(,:) dx 246
X Т—р 234
422
X2 OQ/1
42 (1—p)3
. . дв+р(х)2 e (1—p)3 234
_ *3 3Z (x2)2 gs- (l-p)4 1 (1—p)5 234
, lOiUV . 15X2 (Г2)3 934
04 ([_p)5 . (1_р)в > (1_p)7
F(z) = zB*[A — A,F(z)] 237
«
P \Nbp - n\ — J ( y)n[ e ^y) dy 0 246
1 i —p 238
, __ 2p (1 — p) -j-W1 1 (I-P)3 1 1-P 238
_2 _ P (1 — P) + A2^ h (1—P)3 238
dF (w, t) dt
t} +
w
-J-А j B(w— x)dxF(x,t) (интегро-дифференциальное 248 x=o уравнение Такача)
x Р7-П) e-1'1'4’» - e-™» F** (r, s) = \ . r-j 250 v ’ 7 ЛВ* (s) — A + r — s
Q (z) = (1 — p) (1 — z) В* [X — AG (z)] , , o-- _ _z (групповое поступление) 255
M/G/oo r\k pk = e-f 254 /v I T = x 252 s (У) = b (y) 252
G/M/l rA = (l—o)cr\ £ = 0,1,2,... 271 о = Д*(ц — цст) 272 F (z/) = 1 — ae-n f1-0’ у, у 0 272
-123
G/M/m
?M-1 = Я,г + 1 — vn+l 263
o = A* (mp — /про) 269
P [длина очереди = n | очередь на входе] = (1— 0)0”, n>0 270
г = J [/?„, /?т_2, 1, ст, ст2, ст3,... ] 274
т—2 «о Е °i+i~mPik р i=k 1=т—\ 274
- Pfe—l, fe
Pij = 0 for j > i 4- 1 263
7 / i + 1 \ Pij = J ; [1 — dA(t), /< i+ 1 cm 0 \ ! J 265
oo
Рл = Pi, <+1_л = j dA(t), Ocnci+l—m, m<.i 266
о
Pij = j j (i —m)i (e WiZ —e lli)m ! mydy -0 dA (/), 267
/ < m < i + 1
—4=^- 275
1 ° k=0
W = J(1 тц (1 — о)2 276
w (//'очередь на входе) — (1 —о) /пре-"1*1 О-a)> 0 271
W(y) = 1 4^2—е“тИ<1“а)У, // > 0 276
l+(l-a) 2 Rk
&===0
G/G/1
wn+i = (wn + uny 295
c(u) — a (— u) Q b (u) 299
my) J — u)dC(u), y^-0-, . (интегральное уравне- 300
I °- У q ние Линдли)
.4*(-s)B*(s)-l =£# i— p; 301
фм„_1_Ип1
+ u (s) s"0 s v+ (s)
424
Ф (s) _____y-Wd-p)'
+ W [Д* (— s) B* (s) — 1]'1C (s)
o^ + ^ + mi-P)2 p
27(1—p) 2/
U7 = _X—X
2u 2y
w = sup Un
n>0
w(y) = л(с(у) ®w(y))
П7* fcl _ ro t1 —
W 1 — C* (S)
1 — a
W*(s)
308
322
321
296
317
323
326
1 — a/* (s)
УКАЗАТЕЛЬ
Абсцисса абсолютной сходимости 357, 365
Автокорреляция 410
Аксиоматическая теория вероятностей 383
Аксиомы теории вероятностей 379
Алгебра действительная коммутативная 316
— очередей 315—320
Алгоритм маркировки 20
Аналитическая функция 344, 353
— изолированная особая точка 353
Аналитическое продолжение 305
Аналитичность 344
— область 345
Барицентрические координаты 51
Борелевское поле 380
Вероятностная мера 379
— система 380
Вероятностное обоснование 280
Вероятностный процесс 36
— классификация 36—43
— последовательность 36
— стационарный 37
Вероятность перехода 44
— в состоянии равновесия, 47
Вектор состояний 187
Вендел, проекция 317
Взаимозаменяемые случайные гели-чины 296
Виртуальное время ожидания 226—229
(см. также «Незавершенная работа»)
Вложенная цепь Маркова 40, 195—198
Временная диаграмма 30—36
Время в системе 28
— дополнительное 301
— между требованиями 23, 27
— наработки 191
— обслуживания 23, 27
— ожидания 28
426
— простоя 321, 325
Восстановление, процесс 41—43
— интегральное уравнение 195, 288
— теорема 194
— теория 194
— плотность распределения 194
— функция 194, 287
Входные переменные 27
Выпуклая функция 404
Гауссовское распределение 405
Геометрический ряд 345
Геометрическое преобразование 344
— распределение 56
Глоссарий 411—415
Граница Чернова 405
Групповое обслуживание 155—158, 183, 256
— поступление 152—155,183, 255, 289
Двойственная СМО 321—322
Двойственность 320—328
Дельта-функция Дирака 357
— Кронекера 341
Диаграмма интенсивностей переходов
75
Диаграмма переходов 48
Дисциплина обслуживания 24
Дифференцнально-разиостное уравнение 75, 375
Дифференциальное уравнение 374—376
— линейное с постоянными коэффициентами 340; стандартное решение 374—375
— решение методом преобразования Лапласа 375—376
Диффузионное приближение 335
Единичная задержка 397
Единичная импульсная функция 357— 358
— ступенчатая функция 171, 202
— функция 341, 344
Единичное событие 397
Единичный дуплет 357
— отклик 341
Жордана лемма 369
Закон больших чисел усиленный 405
— слабый 405
Замкнутое подмножество 46
Инвариантность по времени 338, 340
Интеграл Римана 392
— Стильтьеса 392
Интегральное уравнение Винера—Хоп-фа 300
— Линдли 299—300, 330
Иитегро-дифференциальное уравнение
Такача 248
Интенсивность нагрузки 35
Инфинитизимальный оператор 66
Канал 18
— пропускная способность 19
Комплексная переменная 341
— s-плоскость 308
Комплекснозначная функция времени
338—339
Контур 310
Корень кратный 374
Коши—Римана условие 344
Коэффициент вариации 88
— использования 34
Критерий Фостера 47
Лапласа преобразование 337, 354—370
— вероятностная интерпретация 283— 286
— двустороннее 354, 364
— одностороннее 354, 364
— таблица пар преобразований 363
— таблица свойств 362
Лестничный вес 224
— индекс 224; верхний 327; нижний
244, 325
Линейная система 338
Линейность 340, 348, 361
Литтла результат 33
— обобщение’261
Маргинальная плотность 389
Марковские сети, сводка основных результатов 421
Марко >ский процесс 38
— размножения 39
Марковское свойство 39
Математическое ожидание 29, 391—396
— основная теорема 393
Матрица интенсивностей переходов 66
Мера 317
— конечная 317
Метка требований 281—286
Метод дополнительных переменных 189
— проверки 76
— производящих функций 91—93
— этапов 137—144
Момент 395
— центральный 395
Незавершенная работа 27, 226—229, 293
— преобразование, зависящее от времени 250
Независимость 389
Независимые процессы 38
Независимые случайные величины, произведение 401
— сумма 401
Немедленное обслуживание 118—119
Неравенство Гельдера 403
— Енсена 404
— Коши—Шварца 161, 403
— Маркова 403
— треугольника, 403
— Чебышева 403
— Сг 404
Несовместимые события 380
Нормальное распределение 405
Нулевое событие 397
Область сходимости 370
Обратные уравнения Колмогорова—
Чепмена 59, 65, 67
Обращение преобразования Лапласа, метод проверки 365—368
— метод вычисления обратного интеграла 368—370
Обращение преобразования Лапласа плотности распределения 398
Объединенный пуассоновский поток 96
Однородная цепь Маркова 44
— неприводимая 45
Отношение вход/выход 338
Остаточное время 27, 191 —192, 240—
241 (см. «Незавершенная работа»)
— моменты 193
— плотность распределения 192, 251 — 252
— сводка основных результатов 421 — 422
— среднее 193, 321
Остаточное время обслуживания 221
Парадокс остаточного времени 189—195
Параллельно-последовательные этапы 158—166
Параллельные этапы 155—158
Переполняющие входящие потоки 117
Переходные вероятности за один шаг 44 — за т шагов 44
427
— В-формулa 123
— С-формула 121
Этапы 137—144
D/D/1 пример 325
D/Er/1 330
Ег (распределение Эрланга порядка г) 421
— спектр разложения 303, 313—314
Е2/М/1 148—152
— сводка основных результатов 421
G/G/1 35, 292—329
— время ожидания 322
— определяющее уравнение 293
— преобразование времени ожидания 323, 425
— сводка основных результатов 424—
425
G/G/m 26
G/M/1 271—274
— время ожидания 272
— двойственная СМО 321—322
— распределение времени ожидания 272
— сводка основных результатов 423
— спектральное разложение 309
G/M/2 276—279
— распределение времени ожидания 278
— распределение числа требований 278
G/M/m 262—280
— вероятности переходов 262—267
— вложенная цепь Маркова 262
— распределение времени ожидания 275—276
— сводка основных результатов 424
— среднее время ожидания 276
— условная плотность распределения времени ожидания 270—271
— условное распределение длины очереди 267—270
— функциональное уравнение 267
Нг (гиперэкспональное распределение
с г этапами) 161, 421
M/D/1 209, 239
— период занятости 239; плотность распределения вероятностей 239
— сводка основных результатов 421
— среднее время ожидания 211
М/Е2/1 254—255
М/Ел/1 144—148
— сводка основных результатов 421
M/G/1 188—261, 289
— вероятностная интерпретация 283— 284
— временные характеристики 283—286
— время в системе 224; преобразование 219
— время ожидания, моменты 221
— дискретное время 258
— дуальная СМО 328
430
— плотность распределения 221
— описание состояний 188
— переходные вероятности 198—201
— период занятости 226—236; моменты 234—235; 238; преобразование 233; распределение вероятностей 246
— пример 324
— распределение вероятностей периода простая 229
— распределение вероятностей промежутков между уходами 259
— сводка основных результатов 422— 423
— СМО с обратной связью 260
— среднее время ожидания 210
— среднее время пребывания в системе 210
— средняя длина очереди 201—211
— число обслуженных требований 238
M<'G/oo252
— временные характеристики 290
— сводка основных результатов 423
М/Н2/1, пример 209, 255
М/М/1 91—96, 113—116, 417, 420
— анализ переходных вероятностей 95, 102—103
— дискретное время 130
— дисперсия числа требований 115
— обратная связь 131
— период занятости 238
— плотность распределения вероятностей пребывания в системе 222— 223
— пример 324
— сводка основных результатов 417, 420
— спектральное разложение 307—308
— среднее время в системе 115
— среднее время ожидания 211
— среднее число требований 114
— число обслуженных требований 238;
плотность распределения 236
М/М/2 129
М/М/т 119—121
— сводка основных результатов 420
М/М/оо 118—119
— временные характеристики 281
М/М/1/К 121 — 122
М/М/1//М 124—125
М/М/ш/М 122—123
М/М/т/К/М 126—128
М/М/оо//М 125—126
г-преобразование 337, 343—354, 400
— метод 92—93
— обращение методом проверки 365;
методом степенных рядов 365; по формуле 352, 365—368
— таблица пар преобразований 347
— таблица свойств 346
ОГЛАВЛЕНИЕ
Введение......................................................... 7
Часть I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ........................ 16
Глава 1. Системы массового обслуживания....................... 17
1.1. Системы потоков.................................. 18
1.2. Характеристики систем массового обслуживания с ожиданием ........................................... 23
Глава 2. Некоторые важные случайные процессы.................. 25
2.1. Обозначения и структура систем массового обслуживания с ожиданием...................................... 26
2.2. Определение и классификация вероятностных процессов ................................................. 36
2.3. Дискретные цепи Маркова......................... 43
2.4. Непрерывные цепи Маркова ....................... 62
2.5. Процессы размножения и гибели.................... 71
Часть II. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ 105
Г л а в а 3. Системы, описываемые процессами размножения и гибели в стационарном режиме.......................................... 106
3.1. Общее решение для стационарного режима......... 107
3.2. М/М/1: классическая СМО ....................... 112
3.3. Переполняющие входящие потоки.................. 117
3.4. Система М/М/оо: немедленное обслуживание (бесконечное число приборов) ................................ 118
3.5. Система М/М/m: случай т обслуживающих приборов 119
3.6. Система М/М/1/К: конечный накопитель............ 121
3.7. Системы М/М/m с иг обслуживающими приборами и потерями ............................................. 122
3.8. Система М/М/1//М: конечное число источников нагрузки и один обслуживающий прибор......................... 124
3.9. Система М/Моо//М: конечное число источников нагрузки и бесконечное число обслуживающих приборов . . . 125
3.10. Система М/М/т/К/М: конечное число источников нагрузки, т обслуживающих приборов и конечный накопитель .............................................. 126
Глава 4. Марковские системы массового обслуживания в установившемся режиме.................................................... 132
4.1. Уравнения равновесия ........................... 133
4.2. Метод этапов—эрланговское распределение ЕГ . . . 137
4.3. Система М/Ег/1.................................. 144
4.4. Система Ет/М/1.................................. 148
4.5. Система с неординарным входящим потоком......... 152
4.6. Система с групповым обслуживанием............... 155
4.7. Последовательно-параллельные этапы: обобщения . . . 158
4.8. Марковские сети массового обслуживания.......... 166
Часть III. ПРОМЕЖУТОЧНАЯ ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ ......................................................... 186
Глава 5. Система массового обслуживания типа M/G/1............. 187
5.1. Система M/G/1 188
5.2. Парадокс остаточного времени: немного теории восстановления ......................................... 189
431
5.3. Вложенная цепь Маркова ............................ 195
5.4. Вероятности перехода............................... 198
5.5. Средняя длина очереди ............................. 201
5.6. Распределение числа требований в системе........... 212
5.7. Распределение времени ожидания .................... 216
5.8. Период занятости и его продолжительность........... 226
5.9. Число требований, обслуженных за период занятости 236
5.10. От периода занятости ко времени ожидания........... 239
5.11. Комбинаторные методы .............................. 243
5.12. Интегро-дифференциальное уравнение Такача .... 246
Глава 6. Система типа G/M/m ........................................ 262
6.1. Вероятности перехода для вложенной цепи Маркова (система G/M/m).......................................... 262
6.2. Условное распределение длины очереди............ 267
6.3. Условное распределение времени ожидания............ 270
6.4. Система типа G/M/1 271
6.5. Система типа G/M/m.................................. 274
6.6. Система типа G/M/2 ................................. 276
Г л а в а 7. Метод коллективных меток .............................. 280
7.1. Метка требований .................................. 281
7.2. Процесс катастроф.................................. 286
Часть IV. ОБЩАЯ ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ .... 291
Глава 8. Система массового обслуживания типа G/G/1................ 292
8.1. Интегральное уравнение Линдли .................... 293
8.2. Спектральное решение интегрального уравнения Линдли 301
8.3. Алгебра очередей Кингмана......................... 315
8.4. Время простоя и двойственность .................. 320
Заключение ....................................................... 334
Приложение I. Памятка о преобразованиях: производящая функция и преобразование Лапласа........................................ 337
1.1. Зачем нужны преобразования? ...................... 337
1.2. Производящие функции.............................. 343
1.3. Преобразование Лапласа............................ 354
1.4. Применение преобразований к решению разностных и дифференциальных уравнений........................... 370
Приложение II. Памятка по теории вероятностей.................. 378
II. 1. Правила игры.................................... 379
II.2. Случайные величины............................... 383
II.3. Математическое ожидание.......................... 391
11.4. Преобразования, производящие функции и характеристические функции . . *....................... 396
11.5. Неравенства и предельные теоремы................. 403
II.6. Случайные процессы............................... 408
Глоссарий ........................................................ 411
Важнейшие результаты.............................................. 416
Указатель......................................................... 426
5.3. Вложенная цепь Маркова ............................ 195
5.4. Вероятности перехода............................... 198
5.5. Средняя длина очереди ............................ 201
5.6. Распределение числа требований в системе........... 212
5.7. Распределение времени ожидания .................... 216
5.8. Период занятости и его продолжительность.......... 226
5.9. Число требований, обслуженных за период занятости 236
5.10. От периода занятости ко времени ожидания.......... 239
5.11. Комбинаторные методы ............................. 243
5.12. Интегро-дифференциальное уравнение Такача .... 246
Г л а в а 6. Система типа G/M/m ................................... 262
6.1. Вероятности перехода для вложенной цепи Маркова (система G/M/m) ........................................ 262
6.2. Условное распределение длины очереди............... 267
6.3. Условное распределение времени ожидания........... 270
6.4. Система типа G/M/1 271
6.5. Система типа G/M/m................................ 274
6.6. Система типа G/M/2 .............................. 276
Глава 7. Метод коллективных меток ................................. 280
7.1. Метка требований .................................. 281
7.2. Процесс катастроф.................................. 286
Часть IV. ОБЩАЯ ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ .... 291
Г л а в а 8. Система массового обслуживания типа G/G/1............. 292
8.1. Интегральное уравнение Лнндли ..................... 293
8.2. Спектральное решение интегрального уравнения Линдли 301
8.3. Алгебра очередей Кингмана.......................... 315
8.4. Время простоя и двойственность ................... 320
Заключение ........................................................ 334
Приложение I. Памятка о преобразованиях: производящая функция и преобразование Лапласа........................................... 337
1.1. Зачем нужны преобразования? ....................... 337
1.2. Производящие функции............................... 343
1.3. Преобразование Лапласа ............................ 354
1.4. Применение преобразований к решению разностных и дифференциальных уравнений............................ 370
Приложение II. Памятка по теории вероятностей.................... 378
П.1. Правила игры...................................... 379
П.2. Случайные величины................................ 383
П.З. Математическое ожидание........................... 391
II.4. Преобразования, производящие функции и характеристические функции .................................... 396
II.5. Неравенства и предельные теоремы.................. 403
II.6. Случайные процессы................................ 408
Глоссарий ......................................................... 411
Важнейшие результаты............................................... 416
Указатель.......................................................... 426